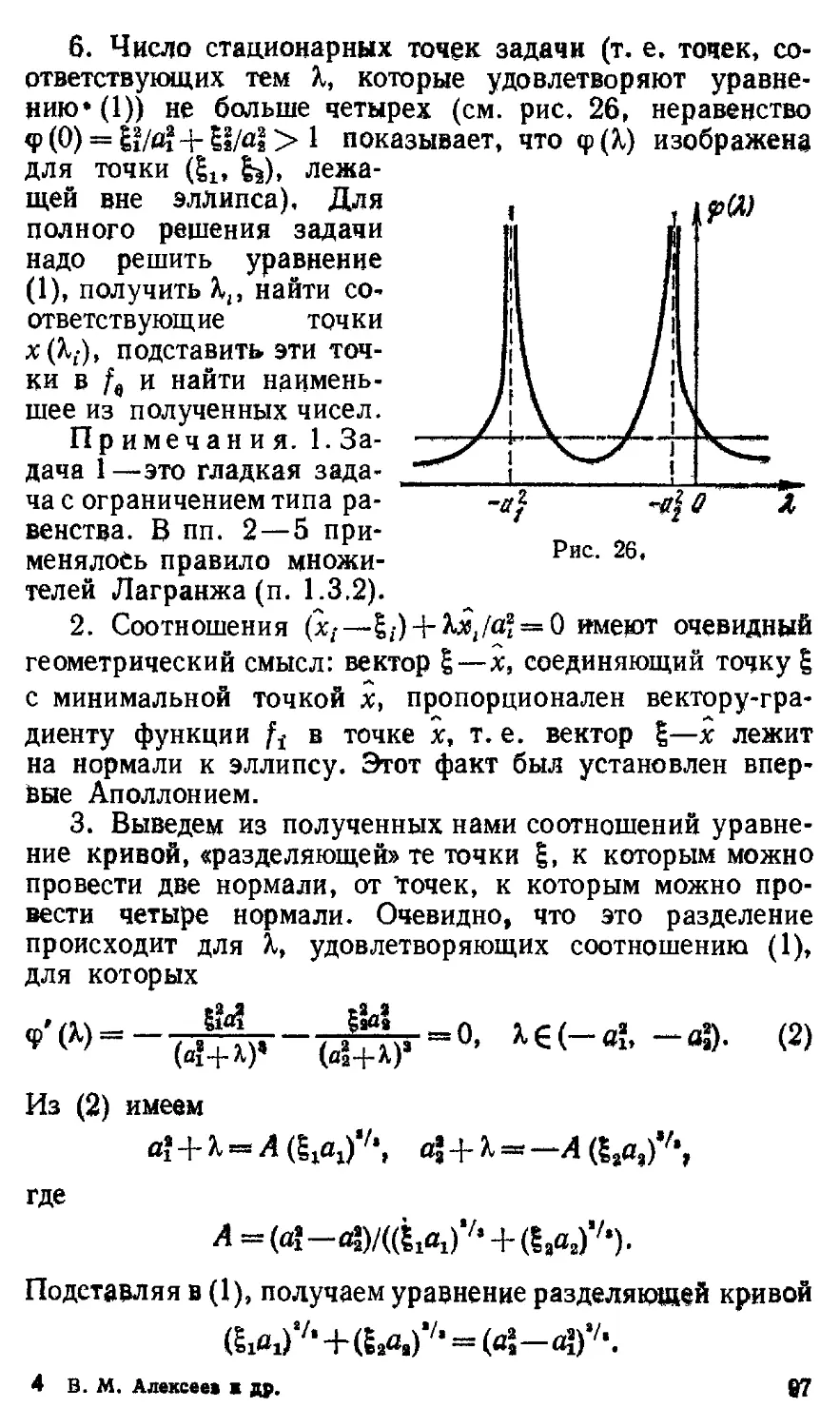
Автор: Фомин С.В. Тихомиров В.М. Алексеев В.М.
Теги: вычислительная математика численный анализ математика
Год: 1979
Текст
В. М. АЛЕКСЕЕВ
В.М. ТИХОМИРОВ
С. В. ФОМИН
ОПТИМАЛЬНОЕ
УПРАВЛЕНИЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов математических специальностей
высших учебных заведений
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 7 9
22.18
A 48
УДК 519.6
Оптимальное управление. Алексеев В. М.;
Тихомиров В. М,, ФоминС. В.—М.: Наука.
Главная редакция физико-математической литера-
туры, 1979.
Книга написана на основе преподавания курса
«Оптимальное управление» на механико-матема-
тическом факультете МГУ. Она состоит из трех
концентров: 1) элементарный вывод основных усло-
вий экстремума и решение конкретных задач;
2) применение теорем дифференциального исчис-
ления В банаховых пространствах к доказательству
необходимых условий экстремума; 3) дополнитель-
ные'вопросы теории экстремальных задач. Особен-
ностью книги является единый подход к различ-
ным задачам иа экстремум.
Книга согласована с учебником А. Н. Кол-
могорова и С. В. Фомина «Элементы теории функ-
ций и функционального анализа».
© Главная редакция
физико-математической
литературы
издательства «Наука», 1979
ОГЛАВЛЕНИЕ
Предисловие................................................. 7
Глава I. Введение.......................................... 11
§ 1.1. Как возникают экстремальные задачи? .............. 11
1.1.1. Классическая изопериметрическая задача. За-
дача Дидоны (12). 1.1.2. Другие старинные экстре-
мальные задачи в геометрии (16). 1.1.3. Вариаци-
онный принцип Ферма и принцип Гюйгенса. Задача
о преломлении света (20). 1.1.4. Задача о брахисто-
хроне. Зарождение вариационного исчисления (24).
1.1.5. Аэродинамическая задача Ньютона (27).
1.1.6. Задача о рационе и транспортная задача (28).
1.1.7. Задача о быстродействии (29).
§ 1.2. Как формализуются экстремальные задачи? .... 29
1.2.1. Основные определения (29). '1.2.2. Простей-
шие примеры формализации экстремальных задач
(31). 1.2.3. Формализация задачи Ньютона (33).
1.2.4. Различные формализации классической изопе-
риметрической задачи и задачи о брахистохроне.
Простейшая задача о быстродействии (35). 1.2.5. Фор-
мализация транспортной задачи и задачи о рацио-
не (38). 1.2.6. Основные классы экстремальных за-
дач (39).
§ 1.3. Правило множителей Лагранжа и теорема Куна—Так-
кера .................................................. 44
1.3.1. Теорема Ферма (44). 1.3.2. Правило множи-
телей Лагранжа (47). 1.3.3. Теорема Куна —Так-
кера (52). 1.3.4. Доказательство конечномерной тео-
ремы отделимости (57).
§ 1,4. Простейшая задача классического вариационного ис-
числения и ее обобщения................................ 58
1.4.1, Уравнение Эйлера (58). 1.4.2. Необходимые
условия в задаче Больца. Условия трансверсаль-
ности (64). 1.4.3. Расширения простейшей зада-
чи (66). 1.4.4. Игольчатые вариации. Условие Вейер-
штрасса (74). 1.4.5. Изопериметрическая задача и
задача со старшими производными (77).
§ 1,5. Задача Лагранжа и основная задача оптимального
управления............................................. 80
1.5.1. Постановки задач (80). 1.5.2. Необходимые
условия в задаче Лагранжа’ (82). 1.5.3. Принцип
3
максимума Понтрягина (84). 1.5.4. Доказательство
принципа максимума в задаче со свободным кон-
цом (87).
§ 1.6. Решение задач.................................... 94
1.6.1. Геометрические экстремальные задачи (95).
1.6.2. Аэродинамическая задача Ньютона (99).
1.6.3. Простейшая задача о быстродействии (103).
1.6.4. Классическая изопериметрическая задача и за-
дача Чаплыгина (107). 1.6.5. Задача о брахисто-
хроне и некоторые задачи геометрии (112).
Глава II. Аппарат теории экстремальных задач ..... 115
§ 2.1. Предварительные сведения из функционального ана-
лиза ................................................. 115
2.1.1. Линейные нормированные и банаховы про-
странства' (115). 2.1.2. Произведение пространств.
Фактор-пространство (117). 2.1.3. Теорейа Хана —
Банаха и ее следствия (120). 2.1.4. Теоремы отде-
лимости (123). 2.1.5. Теорема Банаха об обратном
операторе и лемма о правом обратном отображении
(127). 2.1.6. Лемма о замкнутости образа (129).
2.1.7. Лемма об аниуляторе ядра регулярного опера-
тора (130). 2.1.8. Абсолютно непрерывные функции
(130). 2.1.9. Теорема Рисса об общем виде линей-
ного функционала в пространстве С, Формула Ди-
рихле (134).
§ 2.2. Основы дифференциального исчисления в линейных
нормированных пространствах .......................... 136
2.2.1. Производная по направлению, первая вариация,
производные Гато и Фреше, строгая дифференцируе-
мость (137). 2.2.2. Теорема о суперпозиции диффе-
ренцируемых отображений (144). 2.2.3. Теорема о
среднем и ее следствия (147). 2.2.4. Дифференциро-
вание в произведении пространств. Частные произ-
водные. Теорема о полном дифференциале (151).
2.2.5. Производные высшнх порядков. Формула Тей-
лора (154).
§ 2.3. Теорема о неявной функции ..................... 161
2.3.1. Формулировка теоремы о существовании не-
явной функции (161). 2.3.2. Модифицированный прин-
цип сжимающих отображений (162). 2.3.3. Доказа-
тельство теоремы (163). 2.3.4. Классические теоремы
о неявной функции и обратном отображении (166).
2.3.5. Касательное пространство и теорема Люстер-
ника (171).
§ 2.4. Дифференцируемость некоторых конкретных отобра-
жений ................................................ 174
2.4 1. Оператор Немыцкого и оператор дифференци-
альной связи (174). 2-.4.2. Интегральный функцио-
нал (178).' 2.4.3. Оператор краевых условий (181).
§ 2.5. Необходимые сведения из теории обыкновенных диф-
ференциальных уравнений.............................. 183
2.5.1. Основные предположения (184). 2.5.2. Локаль-
ная теорема существования (186). 2.5.3. Теорема
единственности (189). 2.5.4. Линейные дифференци-
4
альные уравнения (191). 2.5.5. Глобальная теорема
о существовании и непрерывной зависимости реше-
ния от начальных данных и параметров (195),
2.5.6. Теорема о дифференцируемой зависимости ре-
шений от начальных данных (201). 2.5.7. Классиче-
ская теорема о дифференцируемой зависимости реше-
ний от начальных данных (204).
§ 2.6* . Элементы выпуклого анализа................... 208
2.6.1. Основные определения (208). 2 6.2. Выпуклые
множества и функции в линейных топологических
пространствах (216). 2 6.3. Преобразование Лежан-
дра—Юнга —Фенхеля. Теорема Фенхеля—Моро (224),
2.6.4. Субдифференциал. Теорема Моро — Рокафел-
лара. Теорема Дубовицкого—Милютина (229),
Глава III. Принцип Лагранжа для гладких задач с ограни-
чениями ............................................... 238
§ 3.1. Элементарные задачи............................ 238
3J.1. Элементарные задачи без ограничений (238).
3.1.2. Элементарная задача линейного программиро-
вания (243). 3.1.3. Задача Больца (244). 3.1.4. Эле-
ментарная задача оптимального управления (247).
3.1.5. Принцип Лагранжа для задач с равенствами и
неравенствами (248).
§ 3.2. Принцип Лагранжа для гладких задач с ограниче-
ниями типа равенств и"неравенств ..................... 252
3.2.1. Формулировка теоремы (252). 3.2.2. Правило
множителей для гладких задач с равенствами (253).
3.2.3. Редукция задачи (256). 3.2.4. Доказательство
теоремы (257).
§ 3.3* . Принцип Лагранжа и двойственность в задачах вы-
пуклого программирования.............................. 261
3.3.1. Теорема Куна — Таккера (субдифференциаль-
ная форма) (261). 3.3.2. Метод возмущений и тео-
рия двойственности (263). 3.3.3. Линейное програм-
мирование: теорема существования и теорема двой-
ственности (269). 3.3.4. Теорема двойственности для
задачи о кратчайшем расстоянии. Лемма Хоффмана
и лемма о минимаксе (275).
§ 3.4* . Необходимые условия второго порядка и достаточ-
ные условия экстремума в гладких задачах .... 287
3.4.1. Гладкие задачи с равенствами (287). 3.4.2. Глад-
кие задачи с равенствами и неравенствами — необхо-
димые условия второго порядка (289). 3.4.3. Доста-
точные условия экстремума для гладких задач с ра-
венствами и неравенствами (293).
Глава IV. Принцип Лагранжа в задачах классического ва-
риационного исчисления и оптимального управления . . . 297
§ 4.1. Принцип Лагранжа для задачи Лагранжа.......... 297
4.1.1. Постановка задачи и формулировка теоремы
(297). 4.1.2. Редукция задачи Лагранжа к гладкой
задаче (303). 4.1.3. Обобщенная лемма Дюбуа —Рей-
мона (306). 4.1.4. Вывод условий стационарности
S
(308) . 4.1.5. Задача со старшими производными.
Уравнение Эйлера—Пуассона (310).
§ 4.2. Принцип максимума Понтрягина ................... 314
4.2.1. Постановка задачи оптимального управления
(314). 4.2.2. Формулировка принципа максимума.
Принцип Лагранжа в задаче оптимального управле-
ния (319). 4.2.3. Игольчатые вариации (322). 4.2.4.
Редукция к конечномерной задаче (326). 4.2.5. Дока-
зательство принципа максимума (328). 4.2.6. Дока-
зательство леммы о пакете иголок (335). 4.2.7. Дока-
зательстволеммыоб интегральных функционалах (345).
§ 4.3* . Задачи оптимального управления, линейные по фа-
зовым переменным ...................................... 347
4.3.1. Редукция задачи оптимального управления,
линейной по фазовым переменным, к задаче ляпу-
новского типа (347). 4.3.2. Теорема Ляпунова (350).
4.3.3. Принцип Лагранжа для ляпуновских задач
S.. 4.3.4. Теорема двойственности (361). 4.3.5.
нцип максимума для задач оптимального управ-
ления, линейных по фазовым переменным (366).
§ 4.4. Применение общей теории к простейшей задаче клас-
сического вариационного исчисления .................... 370
4.4.1. Уравнение Эйлера. Условие Вейерштрасса.
Условие Лежандра (370). 4.4.2. Условия второго по-
рядка для слабого экстремума. Условия Лежандра
и Якоби (373). 4.4.3..Гамильтоновформализм. Теорема
об интегральном инварианте (377). 4.4.4. Достаточные
условия абсолютного экстремума в простейшей за-
даче (386). 4.4.5. Сопряженные точки. Достаточные
условия сильного и слабого экстремума (391).
4.4.6. Теорема Э. Нётер (402). 4.4.7. Вариационный
принцип и законы сохранения в механике (407).
Комментарии и путеводитель по литературе ................. 411
Литература ............................................... 414
Список основных обозначений............................... 420
Предметный указатель...................................... 425
ПРЕДИСЛОВИЕ
Одной из характерных особенностей современной
эпохи является все возрастающее внимание к проблемам
управления. Как никогда прежде, ощущается потреб-
ность в плодотворном и эффективном использовании при-
родных богатств, огромных людских ресурсов, мате-
риальных. и технических средств. Говоря о наиболее
приметных явлениях научно-технического прогресса в
XX веке, обычно называют расщепление атома, освое-
ние космоса, создание электронной вычислительной тех-
ники. На этом фоне теория управления выглядит пока
менее эффектно, хотя в развитии современной циви-
лизации она уже играет выдающуюся роль, и есть осно-
вание думать, что в будущем эта роль станет еще зна-
чительней.
Всюду, где имеется возможность активного участия
человека, возникает проблема отыскания наилучшего,
или, как говорят, оптимального из возможных управ-
лений. Вызванные к жизни потребностями экономики и
техники, оптимизационные проблемы потребовали в свою
очередь создания новых разделов математики.
В 40-х годах исследование задач экономики породило
новое направление анализа, получившее название ли-
нейного и выпуклого программирования. В те же годы
приобрели актуальность задачи управления летательными
аппаратами и технологическими процессами сложной
структуры. Соответствующая математическая теория была
создана в середине пятидесятых годов и получила на-
звание теории оптимального управления. Выдающуюся
роль сыграл в этом «принцип максимума» Л. С. Понт-
рягина. В теории оптимального управления произошел
синтез идей и методов исследования, с одной стороны
восходящих к классикам вариационного исчисления, а
У
с другой—вполне современных. Ее развитие самым су-
щественным образом связано с именами советских мате-
матиков.
Эта книга задумана как учебное пособие по различ-
ным курсам оптимизации, читаемым в университетах и
вузах ,с повышенной математической подготовкой. Рас-
скажем вкратце об общем замысле и плане книги.
История исследования задач на экстремум, или, как
сейчас обычно говорят, «экстремальных задач» началась
не в наши дни — в той или иной мере такие'задачи
всегда привлекали внимание математиков. Мы хотели
раскрыть перед читателями с самой разной предвари-
тельной подготовкой эту связь времен и неразрывность
научной дороги. Это сделано в первой главе, рассчи-
танной на широкую аудиторию. Хотя используемый здесь
математический аппарат минимален, мы старались вы-
держать стиль точного математического текста, ограни-
чиваясь наиболее выразительными, но элементарными
фрагментами истории изучения экстремальных задач.
Наша цель—связать воедино первоначальные замыслы
И. Кеплера и П. Ферма, задачи, поставленные X. Гюй-
генсом, И. Ньютоном и И. Бернулли, идеи и методы
Ж. Лагранжа, Л. Эйлера, и К- Вейерштрасса с совре-
менным этапом теории, непосредственно продолжающей
исследования великих предшественников. Кроме того,
в первой главе описаны методы решения конкретных
задач и приведены примеры решения на базе единой
идеологии задач, поставленных в разные времена уче-
ными разных направлений.
Остальная часть книги адресована по преимуществу
математикам. Возникновение новой теории стимулировало
развитие и старых и новых разделов математического
анализа. Не все эти разделы должным образом пред-
ставлены в современном математическом образова-
нии.
Нам представляется, что фрагмент классического ана-
лиза, объединенный вокруг темы «неявная функция»,
играет ныне исключительную роль во всех аспектах
конечномерного и бесконечномерного анализа. То же
самое можно сказать и об основах выпуклого анализа.
Наконец, для теории оптимального управления сущест-
венно, что основные факты теории дифференциальных
уравнений остаются верными и для уравнений с раз-
рывными правыми частями.
fi
Названные выше три раздела анализа и геометрии
излагаются во второй главе.
Изложение теории собственно экстремальных задач
представлено в третьей и четвертой главах. Их главную
часть составляет содержание обязательного полугодового
курса, читавшегося авторами на механико-математиче-
ском факультете МГУ. Текст препарирован так, что
доказательства основных теорем занимают не больше
одной лекции. Всюду выдержан принцип полноты из-
ложения. Мы старались везде избежать пропусков, ссы-
лок на очевидность и т. д.
Некоторые стандартные обозначения (из теории мно-
жеств, функционального анализа и т. п.) употребляют-
ся в тексте без пояснений. Поэтому для облегчения ори-'
ентировки читателей в конце книги приведен список ос-
новных обозначений с краткой их расшифровкой.
Параграфы, номера которых отмечены в тексте и в ог-
лавлении звездочкой, призваны подвести читателя к со-
временным методам теории экстремальных задач. Здесь
изложение более соответствует монографическому стилю,
допускаются отдельные, правда минимальные, ссылки
на теоремы, хотя и ставшие классическими, но находя-
щиеся пока за пределами традиционных программ. Эти
параграфы написаны на основе специальных курсов «Вы-
пуклый анализ», «Дополнительные главы теории экстре-
мальных задач» и других, также читавшихся на меха-
нико-математическом факультете МГУ в течение ряда лет.
Более подробно о содержании читатель может узнать
из оглавления, где выделены и названы все важнейшие
результаты и факты, нашедшие отражение в книге.
Из сказанного следует, что мы рассчитываем на раз-
ную читательскую аудиторию: пр'ежде всего—на студен-
тов университетов и вузов с повышенным математическим
курсом, но также и на инженеров, экономистов и мате-
матиков, сталкивающихся с необходимостью решать раз-
личные экстремальные задачи. Для этих читателей напи-
сано введение, а для тех, кто интересуется теорией
экстремальных задач более серьезно, в ионце помещен
путеводитель по литературе — монографической и обзор-
ной.
В постановке и лекционной разработке на механико-
математическом факультете МГУ курса «Оптимальное
управление» очень большая заслуга принадлежит Сергею
Васильевичу Фомину; по его же инициативе создана и
9
настоящая книга. В ней использован первоначальный
конспект лекций, написанный С. В. Фоминым совместно
с В. М. Тихомировым. Безвременная кончина Сергея
Васильевича в расцвете сил и таланта не дала ему воз-
можности увидеть завершение своих замыслов.
Мы выражаем свою искреннюю признательность кол-
лективу кафедры общих проблем управления механико-
математического факультета МГУ, принимавшему активное
участие в обсуждении как методики преподавания курса
«Оптимальное управление», так и характера изложения
отдельных затрагиваемых в книге вопросов.
Мы считаем своим обязательным долгом отметить, что
на формирование математических концепций, положен-
ных в основу этой книги, значительное влияние оказала
творческая деятельность А. А. Милютина.
Мы благодарны А. И Маркушевичу за ценные кон-
сультации, а также А. П. Буслаеву и Г. Г. Магарил-
Ильяеву, внимательно прочитавшим рукопись и сделав-
шим ряд весьма полезных замечаний.
В. М. Алексеев,
В. М. Тихомиров
ГЛАВА I
ВВЕДЕНИЕ
§ 1.1. Как возникают экстремальные задачи?
Людям свойственно стремление к лучшему, и если
им приходится выбирать из нескольких возможностей,
то желание найти среди них оптимальную представ-
ляется вполне естественным.
Слово «оптимальный» происходит от латинского ор-
timus, что значит—наилучший, совершенный. Для того
чтобы найти оптимальную из возможностей, приходится
решать задачи на отыскание максимума или минимума,
т. е. наибольших и наименьших значений каких-то ве-
личин. Оба эти понятия—максимум и минимум—объеди-
няются единым термином «экстремум» (от латинского
extremum, означающего «крайнее»). Поэтому задачи на
отыскание максимума или минимума называют экстре-
мальными задачами.
Методы решения и исследования различного рода
экстремальных задач составляют специальные разделы
математического анализа. Почти тот же смысл вклады-
вается в название «задачи оптимизации»; в последнем
более отчетливо прослеживается связь с практическими
применениями математики.
Цель этой книги познакомить читателя с теорией и
приемами решения экстремальных задач. Но прежде,
чем переходить к формальному, логически последователь-
ному изложению этой ветви математики, мы хотим обра-
титься к прошлому, чтобы лучше понять причины,
побуждающие ставить и решать экстремальные зада-
чи в их прикладном аспекте, т. е. как задачи опти-
мизации.
11
Mercati que solum, facti
de nomine Byrsam
Taurino quantum possent
circumdare tergo
P. Vergilius Maro «Aeneas»1)
1.1.1. Классическая изопериметрическая задача. Задача
Дидоны. Задачи отыскания наибольших и наименьших
величин были поставлены впервые античной наукой. Древ-
нейшей из известных экстремальных задач является, по-
жалуй, классическая изопериметрическая задача. Трудно
сказать, когда впервые была высказана мысль о наи-
большей «вместимости» окружности и сферы среди всех
замкнутых .кривых одной и той же длины, или поверх-
ностей одной и той же площади. Один из последних уче-
ников афинской школы платоников Симплиций (VI в. н. э.),
составивший незадолго до окончательного краха античной
цивйлизации обширный комментарий к трудам Аристо-
теля (IV в. до н. э.), пишет: «Доказано до Аристотеля,
ибо он пользуется этим, как известным, а затем более
полно—Архимедом и Зенодором, что среди изоперимет-
рических фигур наиболее вместимым является круг, а
среди изопифанных — шар». В этих словах обозначена
постановка следующих экстремальных задач: среди плос-
ких замкнутых кривых, имеющих заданную длину, найти
кривую, охватывающую наибольшую площадь, и среди
пространственных замкнутых поверхностей, имеющих за-
данную площадь, найти поверхность, охватывающую наи-
больший объем. Для философа-платоника такая поста-
новка задачи естественна и связана с поисками- идеаль-
ных форм. Недаром круг и шар были в древности сим-
волами геометрического совершенства.
Более прозаическую мотивировку той же изопери-
метрической и ряда близких к ней задач мы находим,
пусть даже в несколько наивной, но достаточно отчет-
ливой форме в легенде о Дидоне. Напомним ее, следуя
«Энеиде» римского поэта Вергилия, две строки которо-
приведены выше в качестве эпиграфа.
Финикийская царевна Дидона и с ней небольшой от-
ряд жителей города Тира, спасаясь от преследований
тирана—брата Дидоны, покинули родной город и в поис-
ках счастья отправились на кораблях на запад вдоль
х) Столько купили земли и дали ей имя Бирса, сколько смогли
окружить бычьей шкурой. (П. Вергилий Марон «Энеида»).
12
берегов Средиземного моря. Выбрав на африканском побе-
режье удобное место (нынешний Тунисский залив), Дидона
и ее спутники решили основать здесь поселение. По-види-
мому, эта идея не вызвала энтузиазма у местных жите-
лей, но все же Дидона удалось 'уговорить их предво-
дителя Ярба, и он неосторожно согласился уступить
Дидоне клочок земли, «который можно окружить бычьей
шкурой». Не сразу понял простодушный Ярб хитрость
и коварство финикиянки. -Разрезав шкуру на тонкие
полоски, Дидона связала их в один длинный ремень и,
окружив им значительную территорию, заложила на
ней город Карфаген1). В память об этой истории кар-
фагенская цитадель получила название Бирса2). Все эти
события легеада относит к 825 (или к 814) г. до н. э.
Анализируя ситуацию, мы обнаруживаем несколько
возможностей поставить здесь задачу оптимизации.
А) Требуется указать оптимальную форму участка
земли, который при заданной длине периметра.! имеет
наибольшую площадь S.
Ясно, что это та же самая классическая изоперимет-
рическая задача3). Ее решением является круг.
Упражнение. Считая бычью шкуру прямоугольником 1X2 м
и приняв ширину ремешка 2 мм, найдите L и максимальное S.
(Авторам не удалось найти точные размеры Бирсы. Располо-
женная на высоком (63 м) холме, она вряд ли была особенно боль-
шой. Для сравнения — длина стен Московского Кремля 2235 м.)
Решение изопериметрической задачи заключено в сле-
дующем утверждении:
Если спрямляемая кривая длины L ограничивает плос-
кую фигуру площади S, то
L*^4nS, (1)
причем равенство имеет место тогда и только тогда,
когда кривая—окружность.
Неравенство (1) называется изопериметрическим; его
доказательство можно найти в [21].
Б) Другие постановки задачи получаются, если, как
1) Финикийское Картадашт—новый город.
2) На языке пунийцев (так римляне называли жителей Карфа-
гена)—шкура. Это название употребляется до сих пор.
3) Еще одна реальная ситуация, приводящая к той же задаче,
описана Л. Н. Толстым в рассказе «Много лн человеку земли нужно».
Разбор этого рассказа с точки зрения геометрии см. Я- И. Перель-
ман «Занимательная геометрия».— М.—Л.: Гостехиздат, 1950, гл. 12.
13
это естественно считать, Дидона хотела сохранить выход
к морю. В отличие от классической изопериметрическон,
мы будем называть эти задачи задачами Дидоны. Для
простоты рассмотрим сначала слу-
чай прямолинейного берега
' Д (рис- О-
/ Ъ 1 Первая задачаДидоны.
—-У------------Z—/ Среди всех дуг длины L, содержа-
\ г щихся в полуплоскости, ограничен-
/ ной прямой I и с концами А,
""----z В£1, найти такую, которая вме-
рис. 1. сте с отрезком [ЛВ] ограничива-
ет фигуру наибольшей площади S.
Решение. Пусть АСВ—произвольная допустимая
дуга скопцами А, В£1, ограничивающая фигуру пло-
щади S (рис. 1). Отразив ее симметрично относительно I,
мы получим замкнутую кривую длины 2L, ограничиваю-
щую фигуру площади 2S. Согласно изопериметрическому
неравенству
(2L)2>4n2S, (2)
откуда
S<L2/(2n). (3)
Следовательно, максимальным значением S может быть
только В2/(2л), и это значение действительно достигается,
если АСВ — полуокружность, опирающаяся на диаметр
[ЛВ]. Задача имеет единственное решение с точностью до
сдвига отрезка вдоль прямой (почему?).
В) В предыдущей задаче положение концов Л и В
искомой дуги можно было выбирать на прямой I произ-
вольно. Что произойдет, если эти р
концы будут заданы? '
Вторая задача Дидоны.
Среди всех дуг длины L, лежащих в I / \
полуплоскости, ограниченной прямой I / U
I, и с заданными концами А, В £1 —V~ g------4-—,
найти такую, которая вместе с от- ” 1
резком [ЛВ] ограничивает фигуру
наибольшей площади. Рис. 2.
Решение. Ясно, что задача име-
ет смысл только при L >^[ АВ | (в противном случае ли-
бо нет ни одной дуги, удовлетворяющей условиям зада-
чи, либо (при АВ |) такая дуга только одна—сам
отрезок [ЛВ]). Естественно ожидать по аналогии с преды-
14
дущим, что решением будет дуга окружности, для кото-
рой [ЛВ] является хордой.Такая дуга АСВ определя-
ется единственным образом. Дополним ее до полной ок-
ружности дугой ADB (рис. 2). Длину дуги ADB обозна-
чим X, а площадь сегмента, ограниченного этой дугой и
отрезком [ЛВ],— о.
Пусть теперь АСВ—произвольная дуга, удовлетворяю-
щая условиям задачи и ограничивающая вместе с [ЛВ]
площадь S. Замкнутая кривая ACBD имеет длину L4-X
и ограничивает площадь S4-O- Согласно (1) 4л(54-о)^
^(L-j-1)2, откуда
1
Как и в (1), равенство, а значит, и максимальная S до-
стигаются тогда и только тогда, когда кривая ACBD
является окружностью, т. е. когда дуги равны: АСВ=АСВ.
Обратим внимание на следующее различие в двух
разобранных задачах. В первой задаче Дидоны запас
конкурирующих кривых больше, поскольку положение
точек Л и В не задано. Впрочем, без ограничения общ-
ности одну из них, скажем Л, можно считать фиксиро-
ванной. Положение точки В тогда определяется допол-
нительным условием: АСВ не просто дуга окружности,
как во второй задаче Дидоны, но это полуокружность.
В эквивалентной форме: в своих концах искомая дуга
подходит к прямой I под углом 90°. Мы увидим потом,
что здесь проявляется общий принцип: предоставляя кон-
цам искомой кривой некоторую свободу, мы должны по-
требовать, чтобы в них выполнялись некоторые условия,
называемые условиями трансверсальности. Форма же ис-
комой «кривой в обеих задачах одинакова, она опреде-
ляется некоторым уравнением (уравнением Эйлера), которое
должно выполняться вдоль кривой. В нашем случае во
всех точках искомая кривая должна иметь одну и ту же
кривизну.
' Г) Рассмотрим теперь, что произойдет, если берег не
является прямой линией^ ограничась случаем фиксиро-
ванных концов, Легко сообразить, что если между точ-
ками А и В берег мало отличается от прямой, то реше-
нием остается та же дуга окружности АСВ, что и раньше.
Предыдущее доказательство применимо полностью,
только буквой а следует обозначать площадь, заштрихо-
15
ванную на рис. 3. Отсюда же видно, что будет в случае,
когда между А и В находится глубокий залив. Пусть,
например, между А и В берег прямой, но из точки D
перпендикулярно АВ прорыт канал DC. Считая, что гра-
ница города должна проходить по суше, мы видим, 'что
решением задачи будет та же дуга АСВ, пока точка D
остается внутри нее (рис. 4, а). Если же канал DC пересек
дугу АСВ, но еще | АС | +1 СВ | < L, решением является-
кривая, составленная из двух дуг окружностей АС и СВ
Рис. 3. Рис. 4.
(рис. 4,6). В предельном случае | АС Ц-| СВ | = L реше-
нием является ломаная АСВ, а при [ ЛСЦ-[СВ| > L
решение не существует.
Рассмотренный вариант можно было бы назвать зада-
чей Дидоны с фазовыми ограничениями.
Д) Наконец, остановимся еще на одном варианте
задачи Дидоны. Пусть по каким-то соображениям (на-
пример, ввиду запрета жре-
цов бога ЭшМуна, храм кото-
Cf Рого впоследствии находился
/ X. в Ди рее) стены города нельзя
г-, X_______________Л.— вести более чем под углом
А в 45° к линии берега, который
Рис. 5. мы снова предполагаем пря-
мым. Такая задача была бы
уже задачей оптимального управления. Ее решение можно
найти при помощи принципа максимума Понтрягина,
с которым мы познакомимся ниже. В типичном случае
решение выглядит, как на рис. 5. Отрезки АС и BE
образуют с линией берега угол 45°, a CDE—дуга окруж-
ности.
1.1.2. Другие старинные экстремальные задачи в гео-
метрии. Уделив изопериметрической задаче достаточно
много места, мы остановимся на некоторых других экст-
16
ремальных задачах с геометрическим содержанием, кото-
рые рассматривались математиками разных веков. Такие
задачи встречаются, в частности, в трудах величайших
математиков античности—Евклида, Архимеда и Аполло-
ния.
В «Началах» Евклида (IV в. до н. э.) мы находим лишь
одну задачу на максимум (книга 6, предложение 27).
В современной редакции она
выглядит так.
Задача Евклида. В
данный треугольник АВС впи-
сать параллелограмм ADEF
(рис. 6) наибольшей площади.
Решение. У искомого па-
раллелограмма 'точки D, Е и
F являются серединами соответ-
ствующих сторон данного тре-
угольника. Доказать это можно
разными способами. Например,
легко показать, что площади
параллелограммов DDGE и FHEF одинаковы. Отсюда
следует, что площадь параллелограмма ADEF меньше
площади параллелограмма ADEF, ибо последняя равна
площади фигуры ADGEHF, содержащей параллелограмм
ADEF.
В дошедших до нас сочинениях Архимеда (III в. до н. э.)
изопериметрическая задача не упоминается. Доныне не-
известно, что было сделано Архимедом в этой области,
и потому приведенные в п. 1.1.1 слова Симплиция оста-
ется пока загадочными. Решение же одной изопифанной
(т. е. относящейся к фигурам равной площади) задачи
имеется в сочинении Архимеда «О шаре и цилиндре». Там
ставится и решается задача о максимальном объеме, кото-
рый могут иметь сегменты шаров одинаковой по площади
боковой поверхности.
Ответом в этой задаче является полушар (подобно
тому, как полукруг является решением второй задачи
Дидоны).
«Коника» или «Конические сечения»—так называется
величайшее творение Аполлония (III—II в. до н. э.).
К нашей теме относится пятая книга «Конических сече-
ний». Вот что пишет Ван дер Варден: Аполлоний ста-
вит «задачу о том, как провести из одной точки О к
17
коническому сечению самый длинный и самый короткий
прямолинейные отрезки. Однако он дает больше, чем
обещает: он определяет все проходящие через О прямые,
которые пересекают коническое сечение под прямым углом
(в настоящее время их называют нормалями), разбирает,
при каком положении О задача имеет два, три или четыре
решения». Перемещая точку О, он «определяет ординаты
граничных точек 6± и G2, где число проходящих через О
нормалей разом переходит с 2 на
h 4 и обратно»1) (рис. 7).
/\ / Вместе с гибелью античной
^-4- цивилизации научная деятельность
в Европе замирает примерно до
{ J р- V A XV века. В XVI в. закладываю-
f --—_Д тся ОСновы алгебры и появляю-
k \ /q f тся первые экстремальные задачи
алгебраического содержания.
\ / Вот, напРимеР> задача, предла-
\ / гавшаяся Н. Тартальей (XVI в.):
у разделить число восемь .на две
части так, чтобы произведение про-
Рис- 7- изведения этих частей на их раз-
ность было максимальным.
До XVII в. не было выработано никаких общих прие-
мов решения экстремальных задач, и каждая из них
решалась специально для нее разработанным приемом.
В 1615 г. вышла книга И. Кеплера «Новая стереометрия
винных бочек»2 *). Кеплер начинает книгу так. «В тот год,
как я женился, урожай,винограда был хороший и вино
дешево, а потому мне, как хорошему хозяину, следовало
запастись вином. Я купил его несколько бочонков. Через
некоторое время пришел продавец—измерить вместимость
бочонков, чтоб назначить цену за вино. Для этого он
опускал в каждый бочонок железный прут, и, не при-
бегая ни к какому вычислению, немедленно объявлял,
сколько в бочке вина». (Этот «метод» мы иллюстрируем на
рис. 8.)
Кеплер очень удивился. Ему показалось странным,
как с помощью одного измерения можно вычислить вме-
^Ван дер Варден Б. Л. Пробуждающаяся наука.—М.:
Физматгиз, 1959.
2) Кеплер И. Новая стереометрия винных бочек.— М.— Л.:
ОНТИ-^-ГТТИ, 1935.
18
стимость бочек разной формы. «Я счел для себя подхо-
дящим,— пишет Кеплер,— взять новый предмет матема-
тических занятий и исследовать геометрические законы
такого удобного измерения, и выяснить его основания».
Для разрешения поставленной задачи Кеплер заклады-
вает основания интегрального и дифференциального ис-
числения и заодно дает первые общие /
правила решения экстремальных задач. /
Он пишет (цитируем по книге Е. А. «Л—
Предтеченского)х) «Кеплер, его жизнь
и научная деятельность»: «Под влияни- /
ем благодатного гения, бывшего, без /
сомнения, хорошим геометром, бочары /
стали придавать бочкам ту форму, ко- _____________
торая при данной длине линии, измерен- рис 8
ной мерщиком, дает возможность судить
о наибольшей вместимости бочки, а так как вблизи
всякого максимума изменения бывают не-
чувствительными, то небольшие случайные откло-
нения не оказывают заметного влияния на емкость».
В выделенных нами словах и заложен тот основной
алгоритм нахождения экстремумов, который впоследствии
был оформлен в точную теорему сначала (для многочле-
нов) Ферма (1629 г.), а затем—Ньютоном и Лейбницем и
получил название теоремы Ферма.
- Отметим еще, что Кеплер решил несколько конкрет-
ных экстремальных задач, в частности задачу о цилиндре
наибольшего объема, вписанном в шар.
В заключение этого пункта приведем еще одну гео-
метрическую задачу, которой в XVII в. интересовались
многие математики (Каральери, Вивиани, Торичелли,
Ферма и др.). В XIX в. ею занимался немецкий геометр
Штейнер, и потому эту задачу часто называют задачей
Штейнера* 2).
Задача Штейнера.' В плоскости треугольника
найти точку, сумма расстояний от которой до вершин
треугольника минимальна.
Решение. Приведем изящное геометрическое реше-
ние этой задачи для остроугольного треугольника. Пусть
2) Предтеченский Е. А. Кеплер, его жизнь и научная де-
ятельность,—Петербург: изд. 3. И. Гржебцна, 1921.
2) Отметим заодно, что впоследствии подобные задачи стали воз-
никать при строительстве дорог, нефтепроводов и городских комму-
никаций,
19
в треугольнике АВС (рис. 9) величина угла С 60°.
Совершим поворот треугольника АВС вокруг точки С на
угол 60°. Получим треугольник А'В'С. Возьмем теперь
любую точку D в треугольнике АВС, а через D' обо-
значим образ D при нашем повороте. Тогда сумма длин
[ AD | + | BD | -|-| CD | равна длине ломаной | |Ц-|£)£)'|-|-
+ О*Л'|, ибо треугольникCDD' равносторонний и |О'Л'| =
= DA |.
Пусть теперь Ь—точка Торичелли, т. е. точка, из ко-
торой все стороны треугольника видны под углом 120°,
и О'—образ D при повороте. Нетрудно понять, что тогда
точки В, D, D' и А' лежат на одной прямой и, значит,
точка Торичелли и является решением задачи. В
Мы познакомили читателя с несколькими экстремаль-
ными задачами геометрического содержания, поставлен-
ными и решенными в разные вре-
мена. Постановку их лишь час-
тично можно оправдать практи-
ческими потребностями — основ-
ным стимулом здесь, пожалуй,
было желание показать красоту
самой геометрии.
1.1.3. Вариационный принцип
С Ферма и принцип Гюйгенса. Зада-
ча о преломлении света. С именем
Пьера Ферма связана формулиров-
ка первого вариационного прин-
ципа для физической проблемы.
Речь идет о вариационном прин-
ципе Ферма в геометрической оп-
тике. Экспериментально закон пре-
ломления света был установлен
Снеллиусом. Вскоре Декарт дал теоретическое объяснение
этого закона. Однако при этом у Декарта получалось,
что в более плотной среде (скажем, в воде) скорость
распространения света больше, чем в менее плотной (на-
пример, в воздухе). Этот факт многим показался сомни-
тельным.
Ферма дал другое объяснение явления. Его основная
идея состояла в том, что луч света «избирает» такую
траекторию, вдоль которой время, затрачиваемое на пре-
одоление пути от одной точки до другой было бы мини-
мальным (в сравнении с любыми другими траекториями,
20
соединяющими те же точки). В однородной среде, в ко-
торой скорость распространения света во всех точках и
во всех направлениях одинакова, время, затрачиваемое
светом на прохождение некоторой траектории, пропор-
ционально ее длине. Поэтому траектория минимального
времени, соединяющая точки А и В—это просто отрезок
[ДВ]: в однородной среде свет распространяется прямо-
линейно.
Вывод закона преломления Снеллиуса из вариацион-
ного принципа Ферма сейчас содержится в школьных
учебниках (см. также п. 1.6.1).
В основу принципа Ферма положено допущение о том,
что свет распространяется по некоторым линиям. X. Гюй-
генсу (1629—1695) принадлежит другое объяснение зако-
нов распространения и преломления света, основанное
на представлении о свете как о волне, фронт которой
движется со временем.
Отвлекаясь от обсуждения физических предпосылок
этой идеи, и, в частности, от вопроса 'о том, что такое
свет—волна или поток частиц, дадим следующее, скорее,
наглядное, чем строгое, определе-
ние. /С \ I 7/\
Волновым фронтом St называе- /Х?\\ //Х\
тСя множество точек, которых до- 5^
стигает за время t свет, распрост- I
раняемый некоторым источником So.
Если, например, источник So— х//1\ у'
это точка, а среда однородна, то
St—это сфера («сферическая волна») Рис. 10.
радиуса vt с центром в So (рис. 10).
С ростом t волновой фронт расширяется равномерно во
все стороны со скоростью V. Линии же распространения
света образуют пучок лучей (радиусов), ортогональных St
в каждый момент t. По мере удаления от источника сфе-
рическая волна становится все более и -более плоской и,
если мы вообразим источник бесконечно удаленным, то в
пределе волновой фронт оказывается плоскостью, равно-
мерно движущейся со скоростью v и остающейся пер-
пендикулярной пучку лучей света, которые теперь па-
раллельны между собой (рис. 11).
Для определения движения волнового фронта в более
сложных ситуациях Гюйгенс пользуется следующим пра-
вилом («принцип Гюйгенса»). Каждая точка волнового
фронта St сама становится вторичным источником, через
21
время Л/ мы получаем семейство волновых фронтов от
всех этих вторичных источников и истинный волновой
фронт St+ы в момент 14-Д/ есть огибающая этого семей-
ства (рис. 12).
Легко видеть, что распространение света от точечного
источника в однородной среде* и предельный случай плос-
кой волны удовлетворяют принципу Гюйгенса. В качестве
примера применения этого принципа в простейшей неод-
нородной среде приведем вывод
закона Снеллиуса «по Г юйгенсу».
Пусть параллельный пу-
чок световых лучей падает на
плоскую границу S раздела двух однородных сред; для
простоты будем представлять себе, что S горизонтальна,
а свет падает сверху (рис. 13). Через и v2 обозначим
скорости распространения света над и под S и через ах
и а2—углы падения и преломления (отсчитываемые от
нормали N к S). Волновой фрон!1 AtA2A движется со ско-
ростью и в некоторый момент t свет, вышедший из
точки А достигает границы 2 в точке В. После этога
22
точка В становится вторичным источником сферических
волн, распространяющихся в нижней среде со скоростью v2.
В ’точку Сх свет придет в момент t[= 14- ' = <+
а в промежуточную точку D £ [ВСХ]—в
момент t2 = t +1BD | . К моменту tt сферическая волна
от вторичного источника В будет иметь радиус г± =«
=ц2 (^—0 = I BCJ-^-sinaj, а волна от D—радиус г2 =
==у2(^х—12) = | DC\ | sin at. Касательные CtC и CtC2 к
этим сферам совпадают, поскольку
sinBCxC = । = ^-sina1 =s рС1| = sinOC1C2.
Точка D была взята на ВС1 произвольно, и, следова-
тельно, вторичные волны в момент имеют огибающей
прямую СС±, образующую с S угол а2 такой, что sina2«
= -^-sina1. А это и есть закон Снеллиуса
Sin «2_ V2
sin Vi '
Принципы Гюйгенса и Ферма тесно связаны между
собой. В самом деле, пусть нам известно положение вол-
нового фронта St в некоторый момент t. Где он будет
находиться через некоторое время АР Возьмем точку
(рис. 14). По определению существует A£S0 и
23
путь ЛС, который свет проходит за время и, в
соответствии с принципом Ферма, любой другой путь из
Д в С требует большего времени. По непрерывности .на
дуге АС найдется точка В такая, что от Я до В свет
проходит за время t, а от В до С—за время АЛ Так
как дуга АС обладает свойством минимальности, то. этим
же свойством должны обладать и дуги АВ и ВС. Дейст-
вительно, если бы существовал, например, путь, по ко-
торому из Д в В свет мог бы добраться меньше чем за
время t, то, дополнив этот путь дугой ВС, мы бы полу-
чили путь из А в С, по которому свет идет меньше чем за
время ^4-А/, а это невозможно. Отсюда следует, во-пер-
вых, что B£St, а во-вторых, что точка С принадлежит
волновому фронту, отвечающему точечному источнику
света, находящемуся в В, и времени At Это вполне со-
гласуется с принципом Гюйгенса: точка В стала вторич-
ным источником и распространяющаяся от иее волна
оказалась через время Ai в точке С. Идея волнового
фронта, принцип Гюйгенса и рассуждение, набросок ко-
торого мы только что привели, явились базой для будущей
теории Гамильтона—Якоби, а в середине нашего века—
для так называемой теории динамического программиро-
вания, которая является важным инструментом решения
прикладных экстремальных задач.
* * *
Вслед за вариационным принципом Ферма было от-
крыто множество других вариационных принципов —
сначала в механике, а затем в физике. Со временем у
большинства ученых созрела уверенность в том, что при-
рода всегда «избирает» движение, как бы решая некоторую
задачу на экстремум. Здесь уместно привести слова Эй-
лера: «В мире не происходит ничего, в чем не был бы
виден смысл какого-нибудь максимума или минимума».
В наши дни Карл Зигель позволил себе такое шутливое
высказывание: «По Лейбницу наш мир является наилуч-
шим из всех возможных миров, а поэтому законы можно
описать экстремальными принципами».
1.1.4. Задача о брахистохроне. Зарождение вариаци-
онного исчисления. В 1696 г. появилась заметка И. Бер-
нулли с интригующим заглавием: «Problema novum, ad
cujus solutionem mathematici invitantur» («Новая задача,
к решению которой приглашаются математики»). В ней
24
была поставлена следующая задача: «В вертикальной пло-
скости даны две точки А и В (рис. 15). Определить путь
АМВ, спускаясь по которому под действием собственной
тяжести тело М, начав двигаться из точки А, дойдет до
точки В в кратчайшее вре-
мя» *).
Решение этой задачи, по
словам Лейбница, «столь пре-
красной и поныне неизвест-
ной», было дано самим И. Бер-
нулли, а также Лейбницем,
Я. Бернулли и еще одним
анонимным автором, в котором знатоки «ех unge leonem»
(по словам И. Бернулли)2) сразу же узнали Ньютона.
Кривая наикратчайшего спуска или брахистохрона ока-
залась циклоидой. Решение Лейбница было основано на
аппроксимации кривых лома-
ными. Развитая впоследствии в
работах Эйлера, эта идея’за-
ложила основы прямых мето-
дов в вариационном исчисле-
нии. Замечательное 'решение
Я .Бернулли использовало прин-
цип Гюйгенса и идею «волново-
го фронта». Однако наиболь-
шую популярность получило
решение самого автора. Его
мы и приведем.
Введем в плоскости систе-
му координат (х, у) так, чтобы
ось х была горизонтальна, а ось у направлена вниз.
В соответствии с законом Галилея скорость тела М в точке
с координатами (х, у (х)) (если тело без трения спускается
по кривой у(-)—см. рис. 16) не зависит от формы кривой
у(>) между точками А и (х, у(х)), а зависит лишь от
ординаты у(х) и равна ]/~2gy(x), где g—ускорение силы
тяжести. При этом требуется найти наименьшее_ время,
которое потребуется на преодоление пути от А к‘В, т. е.
J) Может быть нелишне напомнить, что некоторый отдаленный
намек на постановку задачи о брахистохроне содержится в «Беседах»
Галилея.-Там доказывается, что, двигаясь по хорде, тело придет
в конечную точку позже, чем двигаясь по Окружности, стягиваемой
хордой.
а) По когтям (узнают) льва (лат.).
надо минимизировать интеграл
АВ АВ
ds
V 2gy (X) ’
где ds—дифференциал длины дуги.
Но (в силу принципа Ферма из п. 1.1.3) мы по-
лучим в точности ту же задачу, если будем иссле-
А довать траектории света в не-
V-a2 однородной (двумерной)среде, где скорость в точке (х, у) равна ]^2gy. Далее, И. Бернулли «дро- бит» среду на параллельные
\ 1 слои, где считает скорость посто-
\1 «п 4 0 Рис. 17. янной и равной vt, / = 1,2, ... (рис. 17). В силу закона Снелли- уса получаем = sina^ = _ M=const> Vi v2 Vi ’
где а;—углы падения луча. Переходя к пределу при
измельчении слоев (Бернулли, разумеется, не останавли-
вался ра обосновании законности такой процедуры), по-
лучаем, что
Const
v(x) LUllbL>
где v(x) = ]/r2gy(x), a a (x) — угол между касательной
к кривой //(•) в точке (х, у(х)) и осью Оу, т. е. sina(x)=-
— 1/К1 +(у' (х))2. Итак, уравнение брахистохроны:
V^+(y")iV"y = c^y'^ -i/^Ey^-^j==dx.
Г у ус—у
Интегрируя его ^подстановкой у — С sin2, dx =а
= Csin2yd/), приходим к уравнениям циклоиды:
* = sin/), y = -f-(l— cos/).
Подчеркнем различие между задачей Евклида и Кеп-
лера (о вписанном цилиндре) и, скажем, задачей о брахи-
стохроне. Множество всех вписанных в треугольник па-
26
раллелограммов и множество всех вписанных в шар
цилиндров зависят от одного параметра. Таким образом,
в этих задачах требуется найти экстремум функции одного
переменного. В задаче же о брахистохроне мнол^ство всех
кривых, соединяющих две точки, бесконечномерно. Здесь
требуется найти экстремум функции бесконечного числа
переменных. История математики проделала неожиданный
скачок—от единицы сразу к бесконечности, от теории
экстремумов функций одного переменного—к теории задач
типа задачи о брахистохроне, т. е. к вариационному ис-
числению, как стали называть этот раздел в XVIII в.
Вскоре после работы И. Бернулли было решено много
' задач, подобных задаче о брахистохроне: о кратчайших
линиях на поверхности, о равновесии тяжелой нити и
другие.
Годом же рождения вариационного исчисления при-
нято считать 1696 г.— год брахистохроны. Однако истори-
чески это не совсем верно. Об этом мы расскажем в сле-
дующем пункте.
1.1.5. Аэродинамическая задача Ньютона. В 1687 г.
вышли «Математические начала натуральной философии»
Ньютона. В разделе седьмом, озаглавленном «О движении
жидкостей и сопротивлении брошенных тел», Ньютон
рассматривает задачу о сопротивлении шара и цилиндра
в «редкой» среде1). Затем в «Поучении» Ньютон исследует
вопрос о сопротивлении усеченного конуса, движущегося
в той же «редкой» среде. Ё частности, он обнаруживает,
что среди всех конусов, имеющих данную ширину и вы-
соту, наименьшее сопротивление будет испытывать конус
с углом 135°. Заметив мимоходом, что данный результат
может быть «не бесполезен при построении судов», Ньютон
пишет так: «Quod si figura DNFG ejusmodi sit ut, si ab
ejus puncto quovis V ad axem AB demittatur perpendicu-
lum NM, et dicatur recta GP quae parallela sit rectae
figuram tangenti in N, et axem productam sicet in P,
fuerit MN ad GP ut GPcub ad iBPy.GB4, solidum
quod figurae hujus revolutione circa axem AB describitur
resistetur minime omnium ejusdem longitudinis & latitu-
dinis».
Сказанное Ньютоном можно перевести следующим обра-
зом: «Когда же кривая DNFG будет такова, что если из
х) См. предложение 34, теорема 28 в кн : К р ы л о в А. Н. Со-
брание трудов, т. 7.— М.— Л.: Изд. АН СССР, 1936.
27
любой ее точки N опустить на ось АВ перпендикуляр
и [из заданной точки G] провести прямую GP, парал-
лельную касательной к кривой в точке N, пересекаю-
щую ось в точке Р, то [имеет место пропорция] MN‘.GP=
=GP3:(4B‘PxG-Bi), тогда тело, получающееся вращением
этой кривой около оси АВ, будет испытывать наименьшее
сопротивление в вышеупомянутой редкой среде среди дру-
гих тел той же длины и ширины» (см. рис. 18, принад-
лежащий Ньютону). Ньютон не дал объяснения тому,
как он пришел к своему решению. Впоследствии он пере-
дал своим комментаторам
наброски вывода, но они*
были опубликованы лишь
в 1727—1729 гг., когда
уже завершался первый
этап вариационного исчис-
ления. Подготовительные
материалы Ньютона, опуб-
ликованные лишь в наше
время, показывают, что
он владел элементами мно-
гих конструкций,л впоследствии осуществленных Эйле-
ром и Лагранжей. Как мы увидим далее, задачу Ньютона
следует отнести даже собственно не к вариационному
исчислению, а к оптимальному управлению, теория кото-
рого начала разрабатываться в пятидесятые годы нашего
века.
1.1.6. Задача о рационе и транспортная задача. Пред-
положим, что запасы некоторого продукта распределены
по нескольким, базам и что этот продукт должен быть
доставлен нескольким магазинам. Стоимость перевозки
единицы продукта от каждой базы до каждого магазина
известна, и известно, сколько продукта должно быть до-
ставлено в каждый магазин. Транспортная задача заклю-
чается в составлении оптимального в этой ситуации плана
перевозок, т. е. в указании того, какое количество дан-
ного продукта надо перевезти из каждой базы в каждый
магазин, чтобы суммарная стоимость перевозки была мини-
мальной. Похожая задача о рационе состоит в том, чтобы
при определенном ассортименте продуктов, заданном со-
держании в каждом из них питательных веществ и из-
вестной стоимости единицы каждого продукта составить
рацион, удовлетворяющий необходимым потребностям
с минимальными денежными затратами.
28
Такого рода задачи в огромном количестве возникают
в конкретной экономике. Обе упомянутые выше задачи
относятся к разделу, называемому линейным программи-
рованием. Теория линейного программирования была по-
строена лишь в сравнительно недавнее время—в соро-
ковые-пятидесятые годы нашего века.
1.1.7. Задача о быстродействии. Приведем простейший
пример экстремальной задачи с «техническим» содержа-
нием. Пусть имеется тележка, движущаяся прямолинейно
без трения по горизонтальным рельсам. Тележка управ-
ляется внешней силой, которую можно изменять в задан-
ных пределах. Требуется остановить тележку в опреде-
ленном положении в кратчайшее время. Эту задачу мы
называем далее простейшей задачей о быстродействии.
Особенность постановок экстремальных задач техники
состоит в том, что действующие силы делятся на две
части. Одна из них—это силы природы (скажем, сила
тяготения), другая (скажем, сила тяги) регулируется
человеком. При этом, естественно, возникают ограничения
на управляемые воздействия, связанные с техническими
возможностями.
Теория решения подобных задач была построена еще
позже—в конце пятидесятых годов. Ее называют тео-
рией оптимального управления.
* * *
Итак, откуда берутся экстремальные задачи? Приве-
денными здесь примерами мы постарались показать, что
ответов на этот вопрос много. Экстремальные задачи воз-
никают как из естествознания, из экономики и техники,
так и вызываются потребностями самой математики. По-
этому теория экстремальных задач и ее практический
аспект—теория оптимизации—приобрели в наши дни боль-
шую популярность.
§ 1.2. Как формализуются экстремальные задачи?
1.2.1. Основные определения. Каждая из задач § 1.1
была сформулирована в содержательных терминах три
частной области, где эта задача возникла. Обычно экстре-
мальные задачи ставятся именно такУ и, вообще говоря,
не всякую задачу обязательно надо решать аналитически.
К примеру, задачи Евклида и Штейнера мы решили чисто
геометрическим способом. Однако если мы все-таки желаем
29
воспользоваться преимуществами аналитического подхода,
то первое, что необходимо, это осуществить перевод за-
дачи с «содержательного» языка на формальный язык
анализа. Такой перевод называется формализацией.
Точно поставленная экстремальная задача включает
в себя следующие элементы: функционал1) f: X—»-R,
определенный на некотором множестве X, и ограничение,
т. е. некоторое подмножество CsX, (Через R обозна-
чается «расширенная вещественная прямая», т. е. сово-
купность всех вещественных чисел, пополненная значе-
ниями '—оо и +<».) Множество X называется иногда
классом допустимых элементов, а точки х£С—допусти-
мыми по ограничению. При этом сама задача формули-
руется так: найти экстремум (т. е. нижнюю или верх-
нюю грань) функционала f при условии, что х £ С. Для
той же задачи будет употребляться стандартная запись:
/(х)—* inf (sup); х£С. (1)
Таким образом, для точной постановки надо описать
X, f и С.
Если Х — С, то задача (1) называется задачей без
ограничений. Точку х будем называть решением задачи (1),
минималью (соответственно, максималью) или абсолютным
минимумом (максимумом), если f (х) f (х) (соответственно
f(x)^f (х)) для всех х € С-! Как правило, все задачи будем
записывать как задачи минимизации, заменяя задачу
/(х)—>sup, xgC, задачей f(x) —> inf, х(-С, где f(x) —
= —f(x). В тех случаях, когда хотим’подчеркнуть, что
для нас безразлично, рассматривается ли задача мини-
мизации или максимизации, мы пишем f(x)—>extr.
Далее, множество X у нас обычно бывает наделено
топологией, т. е. в нем имеет смысл понятие близости
элементов. Это можно сделать, например, задав в X набор
окрестностей (как это стандартно делается в R” или в нор-
мированном пространстве). Если X—топологическое про-
странство, то х называется локальным минимумом, если
существует такая окрестность U точки х, что х — решение
задачи /(х)—> inf, xgCntA Аналогично определяется
локальный максимум.
*) В теории экстремальных задач числовые функции часто на-
зывают функционалами.
30
1.2.2. Простейшие примеры формализации экстремаль-
ных задач. Приведем формализацию некоторых задач § 1.1.
Начнем с задачи Евклида (см. п. 1.1.2, рис. 6).
Из подобия треугольников DBE и АВС получаем: h(x')/H=
— x/b. Здесь х—сторона |AF| параллелограмма ADEF,
Н—высота ДДВС, /i(x)—высота /\BDE, b = | АС | —
длина стороны АС. Площадь параллелограмма ADEF
равна (Н—1г(хУ)х=Н(Ь—х)х/Ь. Теперь получаем сле-
дующую формализацию задачи Евклида:
# , х-х —»sup, O^x^b, ффх(х—Ь)—х б [О, Ь]. (1)
Три элемента, из которых состоит всякая формализация,
здесь суть:
X = R, f = H(b— x)x/b, С = [0, Ь].
Формализуем задачу Архимеда об изопифанных
сегментах шаров ^см.,п- 1.1.2). Пусть h—высота шаро-
вого сегмента, R—радиус шара. Объем шарового сег-
мента, как известно из геометрии, равен лЯ2(7?—/i/З),
а площа'дь поверхности 2лRh. Отсюда видно, что задачу
Архимеда можно формализовать двояко:
л/г2 —I") —*SUP, 2л/?/г = а, 2/?^/г^0, (2)
или, исключая R из функционала в (2),
ha nh? п , / а
Т—T-sup, -
(2')
(последнее неравенство проистекает из-за того, что
/ггС2/?=>гг^л/г2). В первом случае X = R2, f=nh2(R—h/3),
C = {(R, /г)| 2л7?/г = ц, 2R'^h\’, во втором, полагая
X = [0, ]/а/л], имеем задачу без ограничений с функцио-
налом f = ha/2 — лН3/3.
Задача Кеплера о максимальном по объему ци-
линдре, вписанном в шар (см. п. 1.1.2), допускает такую
очевидную формализацию:
2лх(1 —х2)—>sup; 0<х^1 (X = R, С=[0, 1]). (3)
31
Здесь шар имеет единичный радиус, а х—длина поло-
вины высоты цилиндра.
Вопрос о преломлении света на границе двух
однородных сред, решаемый с помощью вариационного
время
Рис 19.
ния луча. Тогда
В равно
принципа Ферма (см. п. 1.1.3
рис. 19), сводится к такой за-
даче. Пусть две однородные
среды разделены плоскостью
г = 0, причем скорость распро-
странения света в верхнем полу-
пространстве равна vu а в ниж-
нем v2. Мы ищем траекторию лу-
ча, идущего из точки А =>
— (0, 0, а), а > 0, в точку
В = (|, 0, —Р), Р > 0. По сооб-
ражениям симметрии луч будет
дежать в плоскости z/=0. Пусть
С=(х, 0, 0)—точка преломле-
распространения луча из Л в
В соответствии с принципом Ферма координата иско-
мой точки х, где происходит преломление, находится из
решения задачи
(X = C=R). (4)
Заметим, что получилась задача без ограничений.
Аналогично следующая задача без ограничений
|х—Bi I+ II —inf,
(5)
где Х = С—R2, Si. |8— три заданные точки плоско-
сти R*, [ х | = Vxl + является формализацией задачи
Штейнера (см. п. 1.1.2). Отметим важную особенность
функционала задачи (5) — ои является выпуклой, но не
всюду дифференцируемой функцией.
Задача Аполлония о кратчайшем расстоянии от
точки |== (11, I,) до эллипса, задаваемого уравнением
32
Xi/<4 + xl/al=l, допускает, очевидна, такую формализацию:
£ 2
4+4“ i (6)
Й1 Й2
(/ 2 2 \ \
x=r, c=L 4+4 = 11).
I Я1 Й2 ' '
л с=h 4+4
Итак, мы познакомились с ‘формализацией простейших
задач. Формализация более сложных задач, возникаю-
щих в естествознании, технике или экономике, обычно
составляет специальную и не слишком тривиальную про-
блему. Там сама формализация зависит от физических
или иных гипотез. В следующем
пункте мы покажем это на приме-
ре задачи Ньютона.
1.2.3, Формализация задачи
Ньютона, Формализация этой за- Г . 1
дачи зависит, естественно, от за- Vs --------
конов сопротивления среды. Нью- j
тон представлял себе среду (он *7
называл ее «редкой») состоящей
из неподвижных частиц фиксиро- Л
ванной массы т, являющихся аб- / tte
солютно упругими шарами. При-
мем и мы эту гипотезу.
Пусть тело вращения вокруг Рис. 20.
оси х (рис. 20) движется в на-
правлении, обратном оси х («вниз») в описанной иами
«редкой» среде Ньютона со скоростью о. Элемент dr на
оси г при вращении вокруг оси х описывает кольцо
площади d&=*2nr dr, и этому кольцу соответствует
пояс dS на самом теле вращения. За время dt этот
пояс «вытеснит» объем dV = 2nr drvdt. Пусть р—плот-
ности среды. Тогда число частиц, ударившихся о слой,
равно A?=-+-dV где т—масса частицы.
Подсчитаем силу dF, действующую на слой dS за время dt.
Пусть участок ds наклонен к оси г под углом <р. Отра-
жаясь от d2, одна частица получает приращение импульса,
равное m(v2—v2) = — 2mt!cos<p-n, где v = |v1| = jv4|,
п—единичный вектор нормали к dS, a <p = arctg^ —
угол ds с горизонталью.' В силу третьего закона Ньютона
тело получает противоположное приращение импульса
m2ucos<p-n, а за время dt таких приращений будет N,
2 В. М. Алексее» и др. 33
причем в силу симметрии компоненты импульса, ортого-
нальные оси вращения, всумме дают нуль, а осевая ком-
понента суммарного приращения импульса равна
Ntn 2v cos ф cos ф = v — m2v cos2 ф =
= 4piw2r dr dt cos2 ф.
В силу второго закона Ньютона это выражение равно
dFdt, откуда dF = kr dr cos2 ф, £ = 4pnv2, а общая сила
сопротивления равна
R
о
г dr
\+(dx/dr)* 4
(1)
Таким образом, заменив г на t и R на Т, мы при-
ходим к экстремальной задаче-
т
'f-ГГТ —inf’ ^(0) = 0, х{Т) = 1.
4 1 + х
(2)
Легко сообразить, не решая задачи (2) (впервые это
отметил Лежандр в 1788 г.), что нижняя грань в задаче
равна нулю. Действительно, если
выбрать ломаную х(-) с очень
большой по модулю производной
(рис. 21), то интеграл (2) будет
очень мал. С другой стороны,
для любой функции х(-) интеграл
в (2) неотрицателен. Таким обра-
зом, нижняя грань значений ин-
теграла равна нулю.
Рис. 21. Отмеченное только что обстоя-
тельство неоднократно вызывало
критику, иногда и злорадную. Один из последних при-
меров — в книге Янга1) говорится: «Ньютон сфор-
мулировал вариационную задачу о теле вращения, испы-
тывающем наименьшее сопротивление при движении в газе.
Принятый им закон сопротивления физически абсурден,
в результате чего поставленная им задача не имеет реше-
ния (чем более зазубрен профиль, тем меньше сопротив-
ление). .. Если выводы Ньютона хотя бы приблизительно
*) Я н г Л. Лекции по вариационному исчислению и теории оп-
тимального управления.— М.: Мир, 1974.
34
были верны, то мы не нуждались бы сегодня в дорого-
стоящих экспериментах в аэродинамических трубах».
Задорно сказано! Многих людей утешает мысль, что
и великие грубо ошибаются. Но так ли обстоит дело
в данном случае? Прежде всего, заметим, что сам Ньютон
не формализовал свою задачу—это за него сделали (и не
вполне удачно) другие. Для правильной формализации
надо учесть неявно подразумевавшуюся монотонность про-
филя (при зазубренном профиле частицы испытывают
многократные отражения, что искажает всю картину).
Требование монотонности делает задачу физически осмыс-
ленной. С учетом этого обстоятельства решение самого
Ньютона не только «приблизительно» верно, но порази-
тельно верно в деталях, о чем речь пойдет впереди.
Более того, физические гипотезы, выдвинутые Ньютоном,
и само его решение аэродинамической задачи оказались
весьма актуальными в современной сверхзвуковой аэро-
динамике, когда на очередь дня встало построение сверх-
скоростных и высотные летательных аппаратов.
Допущение о монотонности приводит к следующей
правильной формализации задачи Ньютона:
т
— х(0) = 0, x(T) = g, X€R + . (3)
J 1 + х*
1.2.4. Различные формализации классической изопери-
метрической задачи и задачи о брахистохроне. Простей-
шая задача о быстродействии. Первые две из упомяну-
тых в заглавии задач принадлежат к числу известней-
ших, но оказываются едва ли не самыми трудными для
полного исследования. Мы дважды формализуем каждую
из них — один раз традиционным, общеизвестным спосо-
бом, другой—менее известным. Этим хотелось бы под-
черкнуть принципиальную -неединственность процедуры
формализации. На самом деле, выбор удачной формали-
зации составляет самостоятельную проблему и во многом
успех при решении задачи зависит от искусства, которое
здесь будет проявлено.
Начнем с классической изоперйметрической задачи.
Пусть длина кривой равна L, а сама кривая задана пара-
метрически функциями х(-), </(•)> причем в качестве
параметра взята длина дуги s, отсчитываемая вдоль кри-
вой от некоторой ее точки. Тогда в любой точке выпол-
2* 35
нено соотношение x2(s)4-y2 (s)= 1, и, кроме того, х (0)=х (L),
у (0) = у (L), так как кривая замкнута.
Для большей определенности в расположении иско-
мой кривой можно потребовать также, чтобы ее центр
тяжести попал в начало координат, т. е. чтобы имели
L L
место равенства J х (s) ds = J у (s) ds = 0. Площадь S кри-
o о
L
вой (х(«), {/(•)) равна § хуds. Отсюда получаетсяследую-
о
щая формализация:
L
S— J xyds—>sup; x2(s)+y2(s)= 1,
Ь L ° (1)
( x(s)ds«e J y(s)ds —0, $(0) = x(L), y(O) = y(L).
о о
Однако ту же задачу можно формализовать и по-дру-
гому. Представим себе самолет, пилот которого получил
задачу облететь за заданное время возможно большую
площадь и вернуться на свой аэродром. Если максималь-
ная скорость самолета не зависит от направления полета,
то данная задача приобретает следующую естественную
формализацию.
т
Площадь должна быть максимальна & j (х (t) о (t) —
о
— y(t)u(t))di—+supt где x(Z) = u(Z), У(0 = у(0-
Максимальная скорость самолета равнаУФФи2Ц-ц2^У2.
Самолет возвращается иа свой аэродром фф х (0) = х (Г),
у(0) = у(Т).
Возможна и более общая постановка, когда макси-
мальная скорость зависит от направления (например, при
наличии ветра). Тогда мы получаем более общую задачу:
т
•^(хи—yu)dt—>sup, x = u, y=v,
о
x(0) = x(T), у(0) — у(Т), (и, о)€А, (2)
где А—множество всех допустимых скоростей самолета.
Если А—круг, то мы, очевидно, приходим к клас-
сической изопериметрической задаче, если Д—.«сдвину-
36
Йряй» круг (что соответствует постоянному ветру), то
ролучается известная задачу Чаплыгина.
* Приведем теперь самую традиционную формализацию
4-ада-чи о брахистохроне. Введем, как и в п. 1.1.4
8(рис. 16), в плоскости систему координат (х, у) так,
чтобы ось х была горизонтальна, а ось у направлена
вниз. Не ограничивая себя в общности, можно считать,
что точка А совпадает с началом координат. Пусть коор-
динаты точки В~(хр у^, хг>0, «/г > 0 (см. рис. 16)
и У(’)—функция, задающая уравнение кривой, соеди-
няющей точки А и В. Напомним, что в соответствии
с законом Галилея скорость тела М в точке (х, у(х))
зависит не от формы кривой у(-) в интервале (0, х),
а лишь от самой ординаты у(х), причем эта скорость
равна j/2gy (х), где g—ускорение силы тяжести. Следо-
вательно, время Т, требуемое для преодоления участка
Кривой длины, ds = ]/dx3‘+dy2 на участке от (х, у(х)) до
(x+dx, y(x)+dy), равно ds'V^gy (х). Отсюда получается
следующая формализация задачи о брахистохроне:
xt _____
3 (#()) = § ^t^)2dx->mf, у(0) = 0, у(х1) = у1. (3)
Приведем другую формализацию задачи о брахисто-
хроне, идейно близкую ко второй формализации клас-
сической изопериметрической задачи, следуя упоминав-
шейся статье И. Бернулли 1696 г., в которой он отталки-
вался от вариационного принципа Ферма.
Представим себе неоднородную среду, в которой ско-
рость распространения света зависит лишь от «глубины»
у по закону v2 = 2gy. Тогда луч света в соответствии
с вариационным принципом Ферма будет проходить путь
от Л до В в кратчайшее время. Так получается форма-
лизация задачи о брахистохроне в виде задачи о быстро-
действии:
«Т—>inf, x=Vyu, y = Vyv, u2 + v2 = 2g,
х(0) = у(0) = 0, х(Т) = хх, у (Т) = У1.
Аналогично выглядит и формализация простейшей
задачи о быстродействии (п. 1.1.7). Пусть масса
тележки пг, ее начальная координата х0, а начальная
скорость v0. Внешнюю силу (силу тяги) обозначим через и,
37
а текущую координату тележки—через x(t). Тогда по
закону Ньютона тх = и. Ограничение на тягу зададим
в таком виде: и2]. Отсюда
Т—* inf, тх = и, «€[“! “а]» (5)
х(0) = хо, i(0) = vo, х(Т) = х(Т) = 0.
Получилась постановка, весьма похожая на (2) и (4),
Отметим одно важное обстоятельство. На самом деле
мы «недоформализоВали» еще наши задачи. Например,
в формализации (3) не указана точно область определе-
ния функционала 3 и, следовательно, пока неизвестно,
на каком классе кривых рассматривалась задача (т. е.
не определено множество X п. 1.2.1), То же относится
и к остальным формализациям этого пункта. Впрочем,
«классики» зачастую вообще не обращали внимания на
аккуратную формализацию задач, а просто решали их
«недоформализованными». Но мы хотим в дальнейшем,
быть педантичными и точными до конца, а потому при-
дется заниматься этим несколько скучным делом—ука-
зывать всякий раз, в каком классе объектов ищется (или
было найдено) решение.
1.2.5. Формализация транспортной задачи и задачи
о рационе. Начнем с транспортной задачи. Введем такие
обозначения:
а}—количество единиц продукта, находящегося на i-й
базе, 1 i ^.т,
—потребность (в тех же единицах) в j-м магазине,
1 п,
Cij —стоимость перевозки единицы продукта из i-й базы
в /-й магазин,
х^—планируемое количество единиц продукта для
перевозки из i-й базы в /-й магазин.
• т п
Тогда стоимость перевозки равна 2 2 и ее
i= 1 / = 1
нужно минимизировать. Ограничения при этом следующие:
a) x(y£R+ (очевидное ограничение на величину пере-
возки);
п
б) (нельзя вывезти больше того, что есть);
Ж
в) = (нужно перевезти ровно столько, сколько
необходимо).
38
В итоге получается следующая формализация:
п пт
2 2cj7x,7->inf, s 2хч=ь}, xzyeR+. (i)
£=i/=i I =i i=i
Задача о р а ци о не формализуется так же просто.
Пусть имеется п продуктов (зерно, молоко и т. п.) и т
Веществ (жиры, белки, углеводы и пр.)'. Допустим, что
для полноценного питания необходимо bj единиц /-го ве-
щества. При этом а17 есть содержание /-го вещества в еди-
нице i-го продукта, а с,— цена единицы i-ro продукта.
Обозначив через xz потребление i-ro продукта,-полу-
чаем задачу
п п
£ c;xf->inf, х(-^0. (2)
i=i i=i-
1.2.6. Основные классы экстремальных задач. Мы
кратко упомянули уже в § 1.1, что в теории экстремаль-
ных задач выделилось несколько достаточно ясно очер-
ченных- классов задач. Прежде чем их описывать, про-
ведем беглый обзор тех способов, какими задавались
ограничения в задачах, формализованных выше.
- Во-первых, нам встретились формализации, где огра-
«ичения отсутствовалй вовсе (скажем, в задаче о прелом-
лении света или задаче Штейнера). Во-вторых, случалось,
что ограничения были заданы системой равенств (напри-
мер, в задаче Аполлония, в задаче о брахистохроне
В формализации (3) п. 1.2.4, где равенствами заданы
краевые условия). В третьих, ограничения задавались
неравенствами (например, в транспортной задаче). Нако-
нец, в четвертых, некоторые ограничения записывались
в виде включений (например, ограничение xg R+ в задаче
Ньютона, ограничение ^, v) £ А, где А = {(u, v); u24-v2^ 1},
в классической изопериметрической задаче в формализа-
ции-(2) п. 1.2.4).
Подчеркнем некоторую условность такого разделения.
Скажем, ограничение x£R+ в задаче Ньютона можно
было бы записать в виде неравенства х^О, а ограни-
чение (и, v) С А в классической изопериметрической задаче
можно было бы записать в виде неравенства и2 + и2^1.
Наоборот, всякое неравенство /(х)^0 можно заменить
на равенство /(х) + « = 0 и включение u^R+ и т. д.
Тем не менее с точки зрения, принятой в этой книге,
разделение ограничений на равенства и неравенства,
39
с одной стороны, н включения—-с другой, имеет свой
смысл. В курсах анализа приводится (а в § 1.3 об этом
будет сказано подробно) правило множителей Лагранжа
для решения задач на «условный экстремум». Как известно,
применение этого правила начинается с составления «функ-
ции Лагранжа», в4 которую входят как исследуемый функ-
ционал, так и функции, задающие ограничения. Может
оказаться, что по разным причинам некоторые ограничения
выгодно не включать в функцию Лагранжа. Так вот,
в виде включений мы и выделяем именно те ограничения,
которые при решении соответствующей задачи в функцию
Лагранжа не войдут. При этом, как и при формализации
задачи (где бывает много способов и выб!р удачного за-
висит от искусства исследователя), в вопросе о разбиении
ограничений нет однозначности. Перейдем к описанию
основных классов экстремальных задач.
В Дальнейшем с достаточно общих позиций будут
рассмотрены следующие четыре класса.
1. Гладкие задачи с ограничениями типа
равенств и неравенств. Здесь класс допустимых
элементов X будет обычно нормированным пространствомJ),
и ограничение С задается равенством Г(х) = 0, где F—
отображение X в другое нормированное пространство Yf
и конечным числом неравенств /(-(х)^0, i = 1, .... т.
В итоге получается класс задач
(х) —»• inf, F(x) = 0, i— 1, (1)
При этом предполагается, что функции i = 1, 2, ..., т,
и отображение F обладают некоторыми свойствами глад-
кости. Гладкую задачу fB(x) —> inf будем называть эле-
ментарной гладкой задачей * 2).
II. Классическое вариационное исчисле-
ние. Здесь традиционным классом допустимых элементов
является банахово пространство X —Cl([Z0, fj, Rh) не-
прерывно дифференцируемых n-мерных вектор-функций
x(') = (Xi(-), ...» х„(-))» в котором норма задается
х) Термины «нормированное пространство» и «банахово про-
странство» используются здесь и ниже только для корректности
постановки задачи. Точные определения читатель найдет в it. 2.1.1.
В задаче (1) можно для простоты считать, что x=(xlf ..., хи)—век-
тор в л-мерном арифметическом пространстве R".
2) Задачи на максимум или с неравенствами другого знака (^)
легко приводятся к виду (I), см. § 3.2.
40
формулами
|!х(-)|]г = тах(||х(-)1!0. k('-)llo).
Цх(-)[[0 = max ( max |xz(Z)|\.
I < »< n \t e[/0, M /
Функционалы в задачах классического вариационного
исчисления бывают обычно следующих типов:
— интегральные, т. е._ функционалы вида
- ц
3 (х (•)) — $ L (t, х, х) dt =
Л)
...» x„(f), Xf(O. (2)
tp
— терминальные, т. e. функционалы вида
^(x(.)) = Z(x(ie), x(Zx))= '
— Z(Xi(f0), xn(Ze), Xi(Zi), • xn(it)); (3)
— смешанные функционалы вида
^(x(.)) = 5,(x(-))+<F(x(.)). ' (4)
(В дальнейшем функционалы (4) мы называем также функ-
ционалами Больца.)
Ограничения в задачах классического вариационного
исчисления обычно распадаются на две части:
— дифференциальные связи вида
M(t, x(t), х (t)) — 0 & М; (i, x1(t), ..x„(t), xy(fl, ...
.... x„(Z)) = O, Z==l, 2, .... p; (5)
— граничные условия вида
ф(х(/0), x(G)) =
= 0ФФф/(Xj(Zo), x„(Z0), x1(Zl), .... Xp(Zj)). (6)
j = 1, 2, .... s.
В (2) и (5) L, Mi и в (3) и (6), l, ф,- —гладкие функ-
ции 2п +1 и 2п переменных соответственно. Задача
5(х(•))-*inf, M(f, x,i) = 0, Ф(х(/0), х(О)==0 (7)
называется задачей Лагранжа. Задача
^(х (•))—> inf, M(t, х, х) — 0, ф(х(/в), x(Zx)) = O
называется задачей Больца.
41
Задача
<^(х ()—» inf, M(t, х, х) = 0, ф(х(/0), х(^)) = 0
называется задачей Майера.
Задачу без ограничений
&(x(.')) = $L(f, х(0. x(t))dt + l(x(t0), xO->inf (8)
будем называть элементарной задачей Больца.
Задача
t,
3 (х(-)) = ^ L(t, x(t), x(t))dt —»-inf, x(f0) — x0, x(ti) = xi
^0
• (9)
называется простейшей векторной задачей классического
вариационного исчисления, а в случае, если п=1, то —
простейшей задачей классического вариационного исчисле-
ния. Для простоты здесь мы ограничились задачами
с фиксированным временем.
Более общую постановку, в которой функционал и
ограничения зависят также от переменных t0 и tit
читатель найдет в гл. IV.
III. Задачи выпуклого программирова-
ния. Здесь класс допустимых элементов X является
линейным пространством, а ограничение С задается си-
стемой равенств F(x) = 0, (где F: X—+ Y, Y—другое
линейное пространство), неравенств /(-(х)^0, i = l,
2, ..., т, и включений х£Л. В итоге получается класс
задач
fo(x)-^inf, F(x) = 0, f,-(x)<0, i = l, ».., m, x£A. (10)
При этом предполагается, что функции fh i — Q,
1, ..., т, выпуклы, отображение F аффинно (т. е. F (х) =
— Лх4-т|, где т]—фиксированный вектор, а Л—линейный
оператор из X в У), а А — выпуклое множество. Если
в (10) все функции ft линейны, а А — некоторый стан-
дартный конус, то задачу (10) называют задачей линей-
ного программирования. Если в (10) ограничения отсут-
ствуют, то задачу f0 (х) —> inf с выпуклой функцией [0 мы
называем элементарной выпуклой задачей без ограничений.
IV. Задачи оптимального управления.
В этой книге будет рассмотрен следующий класс задач
42
оптимального управления, где х € R", и € Rr:
f{x{-), и(-), t0, G) =
ii
*= $ f(t, x(t), и (0)dt + g(t0, x(t0), it, x(/1))->inf, (11)
^0 '
x = cp(t, x, u), ф(£0, x(£0), G, x(^)) = 0, u£U.
При этом в (11) моменты t0 и tt, вообще говоря,
не фиксированы, все функции /: RxRnxRr —* R,
<р: Rx R"x Rr —> R”, ф: RxR’xRxR" —* R*,
g=iRx R”X R X Rn—* R предполагаем непрерывными по
совокупности переменных и непрерывно дифференцируе-
мыми по переменным t и х; множество U—некоторое,
вообще гбворя, произвольное подмножество Rr.
Для полного описания задачи осталось лишь объяс-
нить,. что же составляет здесь класс допустимых элемен-
тов. На первых порах будем рассматривать совокупность
вектор-функций (х(-), «(•)), где «(•) определена и ку-
сочно-непрерывна на |70, причем для всех t выполнено
включение и (?) gU, а х(-) непрерывна на [£0, /г] и диф-
ференцируема во всех точках, кроме тех, где «(•) терпит
разрыв; при этом во всех точках дифференцируемости
х(-) выполнено равенство х(0 = ф(^, x(t),
' Задачи, в которых функционалом является tlt назы-
ваются задачами о быстродействии.
* * *
Теперь можно посмотреть, в какие классы попадают
задачи пп. 1.2.1—1.2.5.
Задачу Евклида (см. (1) п. 1.2.2) можно отнести
и к гладким задачам и к задачам выпуклого програм-
мирования. Задача Архимеда в формализациях (2)
•и (2') п. 1.2.2 и задача Кеплера (3) п. 1.2.2 отно-
сятся к числу гладких задач. Задача о преломле-
нии света (см. (4) п. 1.2.2)—это и элементарная глад-
кая задача, и элементарная выпуклая задача. Задача
Штейнер-а (см, (5) п. 1.2.2)—элементарная выпуклая
задача. Задача Аполлония (см. (6) п. 1.2.2) — глад-
кая задача с ограничениями типа равенств. Задача
Ньютона (см. (3) п. 1.2.3)—задача оптимального управ-
ления. Классическая изопериметрическая
задача в формализации (1) п. 1.2.4 относится к клас-
43
сическому вариационному исчислению, а в формализа-
ции (2) — к оптимальному управлению. Задача о бра-
хистохроне (см. (3) п. 1.2.4) — простейшая задача
классического вариационного исчисления; эта же задача
в формализации (4) п. 1.2.4—задача о быстродействии
оптимального управления. Транспортная задача
и задача о рационе (см. (1) и (2) и. 1.2.5) — задачи
линейного программирования; простейшая задача
о быстродействии—задача оптимального управ-
ления.
Итак, задачи формализованы и классифицированы..
Посмотрим теперь, что может дать для их решения* ап-
парат анализа.
§ 1.3. Правило множителей Лагранжа
и теорема Куна—Таккера
1.3.1. Теорема Ферма. Первый общий аналитический
прием решения экстремальных задач был разработан
Пьером Ферма. Открыт он был, по-видимому, в 1629 г.,
но впервые достаточно полно изложен в письме к Робер-
валю в 1638 г. Можно посоветовать читателю обратиться
к книге Декарта1), где приведено это письмо, и самому
вникнуть в первоначальную мысль Ферма. На современ-
ном языке (правда, у Ферма лишь для полиномов) прием
Ферма сводится к тому, что в точке экстремума х в задаче
без ограничений /(х)—>extr должно иметь место равен-
ство f (х) = 0. Как мы помним, первый намек на этот
результат содержится в словах Кеплера из «Стереометрии
винных бочек».
Точный смысл рассуждения Ферма приобрели через
46 лет, когда в 1684 г. появилась работа Лейбница,
в которой закладывались основы математического анализа.
Уже само заглавие этой работы, которое начинается так:
«Nova methodus pro maximis et minimis...» («Новый
метод нахождения наибольших и наименьших значе-
ний. ..»), показывает, И&кую важную роль сыграла задача
о нахождении экстремумов в становлении современной
математики. В своей статье Лейбниц не только получает
в качестве необходимого условия соотношение f (х) = 0
*) Р. Декарт. Геометрия./ С приложением избранных работ
П. Ферма и переписки Декарта.— М. — Л.: ГОНТИ, 1938, с. 154.
44
(сейчас этот результат называют теоремой Ферма), но и
употребляет второй дифференциал для различения мак-
симума и минимума. Следует, конечно, напомнить, что
большинство излагаемых Лейблицем фактов было к тому
времени известно также и Ньютону. Но его работа «Ме-
тод флюксий», завершенная в основном к 1671 г., была
опубликована лишь в 1736 г.
Перейдем теперь к самой теореме Ферма, напомнцв
предварительно некоторые факты из анализа. Начнем
с одномерного случая, когда функции определены на ве-
щественной прямой R. Функция fi R —>-R одного пере-
менного называется дифференцируемой в точке х, если
найдется такое число а, что
f(x+X)=f(i)+aX + r(X),
где /'(^) = о(|Х|), т. е. для'любого е >0 найдется 5"> 0
такое, что из [ X | 6 следует | г (X) | е | X |. Число а на-
зывается производной f в точке х и обозначается f' (х).
Таким образом, f'(x) = lim (/(х4-Х) —f (x))/X.
л -> о
Теорема Ферма. Пусть f—функция одного пере-
меннога, дифференцируемая в точке х. Если х—точка ло-
кального экстремума, то
f'(x) = O. (1)
Точки х, в которых выполнено соотношение (1), на-
зываются стационарными.
В соответствии с общими определениями п. 1.2.1
точка х доставляет функции f локальный минимум (мак-
симум), если найдется такое е > 0, что из неравенства
|х—х|<е следует неравенство f(x)^f(x) (^f(x)). Со-
гласно теореме Ферма точки локального экстремума (мак-
симума или минимума) являются стационарными. Обрат-
ное, разумеется, неверно: например, f(x) = xa, х~0.
Доказательство. Допустим, что х—локальный
минимум функции /, но f (х) 0. Пусть для опреде-
ленности a < 0. Задав е = |а|/2, найдем из определения
производной такое S > 0, что из | X | < 6 следует ) г (X) | <
< )а]| Х|/2. Тогда для 0<Х<6 получаем
/ (х 4- X) == f (х) 4- ой + г (X) <
f (х) 4-ой 4-Ml tx) -ML < f (2),
46
т'. е. х не является точкой локального минимума f. Про-
тиворечие доказывает теорему. В
Для многих переменных (а тем более для «бесконеч-
ного числа переменных») имеется несколько разных опре-
делений производных. Более подробно говорится об этом
в гл. II (см. п. 2.2.1). Здесь мы напомним лишь основ-
ное определение (в бесконечномерном случае принадле-
жащее Фреше).
Функция f: R" —•► R п переменных называется дифферен-
цируемой в точке х, если найдутся числа (04, ..., а„)
(кратко обозначим их через а) такие, что
п
f (x + h) = f (х) + 2 aihi + г (/i),
i = 1
где-'| г (h) | = о (| h |), т. e. для любого e > 0 найдется S > О
такое, что из | h | = У Л? + ... + ЛД < 6 следует | г (h) (С
^е|й|. Набор « = («!, ..., ап) называется производной f
в точке х и обозначается также f (х). Подчеркнем, что
f’ (х)—это набор из п чисел. При этом число а,-=
= lim [f (х + Хе,-) —f (х)]/Х, где е,- = (О, ..., 1, ..., 0) (еди-
о
ница стоит на i-м месте), называется i-й частной произ-
водной f и обозначается fx. (х) или ^-(х). Таким обра-
зом, f' (х) = (fXl (х), ..., fXn (х)). Соотношение f (х) = 0
означает, что fXi (х) = ... — fx„ (х) — 0.
Из «одномерной» теоремы Ферма вытекает очевидное
следствие:
Следствие (теорема Ферма для функций п
переменных). Пусть f—функция п переменных, диф-
ференцируемая в точке х. Если 'х-г-точка локального ми-
нимума функции f, то
f (x) = 0&fx.(x) = 0, 1=1, .... п. (2)
Точки x^R", в которых имеют место равенства (2),
также называются стационарными.
Доказательство следствия. Если х достав-
ляет экстремум функции f, то точка нуль должна быть
экстремумом функции <р,- (X) = f (х + Хе,). По теореме Ферма
def
ф}(0) = 0. Но (pi(O) = fx,(x).
46
1.3.2. Правило множителей Лагранжа. Этот пункт по-
священ гладким конечномерным задачам. Еще раз напом-
ним о причудливости исторического развития нашей темы.
Вслед за методом решения одномерных экстремальных
задач наступила эра классического вариационного исчис-
ления. Для задач вариационного исчисления с ограниче-
ниями, т. е. в бесконечномерной ситуации, Лагранж
сформулировал в «Аналитической механике» (1788 г.)1)
свое знаменитое правило множителей, и только спустя
примерно десятилетие в «Теории аналитических функ-
ций» в 1797 г. он применил его к конечномерным задачам.
Конечномерной гладкой экстремальной
задачей с ограничениями т и ц а равенств (или
задачей об условном экстремуме) называется
задача
/0(х)—>extr, /i(x)=.’. • = fm(x)-O. (L)
Функции fk: Rn—+R, £ = 0, 1, ..., m, должны здесь
обладать некоторыми свойствами гладкости (т. е. диф-
ференцируемости). В этом пункте будем предполагать,
что в некоторой окрестности U пространства R" все функ-
ции fk непрерывно дифференцируемы (в том смысле, что
все частные производные dfkldxi существуют и непрерывны
в U).
Точка /й(х) = 0, £=1, 2, ..., т, доставляет
локальный минимум (максимум) в задаче (1) в том
случае, когда найдется такое в > 0, что если точка х б U
удовлетворяет всем ограничениям (f{ (х) = 0, i = 1, ..., т)
и |х—х|<8, то (соответственно fa(x)^
C/oU))-
Функцию
т
^ = ^{х, К, \)=2W*(x). (2)
fe=0
где X~()ч, ...» Хт), называют функцией Лагранжа за-
дачи (1), числа Хо, Хг, ..., Хж—множителями Лагранжа.
Правило множителей Лагранжа. 1. Пусть
в задаче (1) все функции fa, flt непрерывно диф-
ференцируемы в окрестности точки х. Если х—точка
локального экстремума в задаче (1), то найдутся мно-
г) Лагранж Ж- Аналитическая механика.— М.—Л.: Гостех-
издат, -1950.
47
жители Лагранжа У. (X, ..., 1т) и л0, не равные одно-
временно нулю и такие, что выполняются условия ста-
ционарности функции Лагранжа по х
ЬЛ) = 0фф.2\.(£А. ...,k,\) = 0, (3)
i = l, 2....п. ’
2. Для того чтобы Ло=4О, достаточно, чтобы векторы
Д(х), были линейно независимы.
Таким образом, для определения х, X и Ло получа-
ется п-rm уравнений:
(Пк \
(*)у ““ i 1, ...» я, fi (х) я= ... =» fm (х) = О
(4)
с п-J-m+l неизвестными. Следует учесть, что множители
Лагранжа определены при этом с точностью до пропор-
циональности. Если известно, что \У=0 (а это—важ-
нейший случай, ибо если \ = 0, то соотношения (3) от-
ражают лишь вырожденность ограничений и не связаны
с функционалом), то можно, умножив все на константу,
добиться равенства Хо=1. Тогда число уравнений срав-
няется с числом неизвестных.
В более симметричной форме уравнения (4) записы-
ваются так:
^ = 0, J2\ = 0. (4')
Их решения называются стационарными точками за-
дачи (1).
Со времен Лагранжа (слова Лагранжа приводятся
чуть ниже) почти на протяжении целого века правило
множителей формулировалось с Хв=1, хотя без допол-
нительных предположений, например линейной независи-
мости, в таком виде оно неверно. Для подтверждения
сказанного рассмотрим задачу
Xi~*inf, x|4~xi = 0.
Очевидным и единственным ее решением является
х = (0, 0), ибо это—единственная допустимая точка. По-
пробуем теперь составить функцию Лагранжа с Хо = 1
и применить далее алгоритм (3). Имеем 2 — (Xi-j-xl)»
48
откуда
^ = 0^2К+1=0, 4^ = 0=ф2Хх, = 0
oxi 1 ахг 2
и первое из этих уравнений несовместно с уравнением
х?4~х! = 0.
В качестве условия регулярности, гарантирующего,
что Хот^О, обычно используют линейную независимость
производных fi (х), .... fm(x) (см. выше утверждение 2
теоремы). Однако проверка этого условия обычно слож-
нее, чем проверка непосредственно из уравнений (3) того,
что 10 не может равняться нулю (см. решения задач
в § 1.6). Поэтому приведенная выше формулировка тео-
ремы, не содержащая никаких дополнительных предпо-
ложений, кроме гладкости, очень удобна.
Доказательство теоремы опирается на одну из важ-
нейших теорем конечномерного дифференциального исчис-
ления—теорему об обратной функции [14, т. 1, с. 455],
[9, т. 1, с. 259].
Теорема об обратной функции.' Пусть
^(Хц ...,х^), ..., ф,(х1, ...,xs)—s функций s пере-
менных непрерывно дифференцируемых в некоторой окрест-
ности точки х. Пусть при этом якобиан
\ ОХ/ /
отличен от нуля. Тогда существуют такие е0 > 0 и So > О,
что для любого т] = (Л1> I ЛI6о найдется £,
|£| ^60, такое, что ф(х4-|) = 'ф(х)4-тъ и приэтомЪ,—*®,
когда ц —*0.
Более общие варианты этой теоремы будут доказаны
в § 2.3.
Доказательство правил а, множителейЛаг-
ранжа. Пусть точка х доставляет локальный минимум
в задаче (1). Возможно одно из двух: или векторы
/»(х), ..., f'm(x) линейно зависимы, или эти векторы
линейно независимы.
А) Пусть векторы линейно зависимы. Тогда ненуле-
вые Kk, k = 0, 1, ..., т, для которых имеют место усло-
вия (3), можно подобрать по определению.
Б) Пусть векторы линейно независимы. Приведем это
к противоречию с тем, что х—локальный минимум в за-
даче (1).
49
Рассмотрим отображение Ф (х) = (/0 (х)—f0 (х), ft(x),...
.. .,fm (х)). По условию векторы f'o (х), ..., f'm (х) линейно
независимы, т. е. ранг матрицы
(df0 (х) df0 (х)
дхх ’ ’' ’ ’ дхп
• ................. •
dfm (х) . . dfm (х)
дхх ’ '* ’ ’ дхп
равен /п+1. Допустим для определенности, что первые
m-f-1 столбцов матрицы А линейно независимы, т. е.
(df0 (х) df0 (х) \
Зхх ’ dxm + i \
. .............Ь#0.
dfm (X) dfm (X) У
дхг ’ dXm-i-1/
Следовательно, функции
Ф1(хп хт+1)= Л Л
— fa (xv • • • > хт + 1< хт + г< • • • , xn)~fо (х1> • • • »хп)г
Ф2 • • • > хт + 1) = fl (х1> ’ • • > хт + 1’ хт + 2> • • • > хп)’ • • • >
Фи + 1 (х1< • • • > хт + 1) = fm (х1> • • • > Л'т + 1> хт + 2> • • •, хп)
удовлетворяют условиям теоремы об обратной функции.
По этой теореме для любого е, 0 < е < е0, найдутся
х1(е), .. .um+i(e), такие, что
ft (Х1 (6)’ • • • > хт + 1 (6)> Л'т + 2> • • • > хп) fО W ~ 6’
fi (*х (е)..хт+1 (е), хт+г, ... , х„) = 0, (5)
fm(xi(e)> •:-.^+1(е)Лт+г, ...,х„) = 0,
причем х,(б)—>-хгприб—>-0, i=l,2, ..., т + 1. Но из (5)
прямо следует, что точка х не является точкой локаль-
ного минимума. Искомое противоречие получено. Утвер-
ждение 2 теоремы очевидно. |
Обобщение^ правила множителей Лагранжа на беско-
нечномерные задачи с равенствами и неравенствами будет
дано в гл. III.
А теперь—еще несколько слов об истории. Первое
упоминание о правиле множителей содержится в работах
50
Эйлера по изопериметрическим задачам (1744 г.)- Затем
оно было выдвинуто Лагранжем в его «Аналитической
механике» (1788 г.) для широкого класса задач вариацион-
ного исчисления (так называемых задач Лагранжа, о чем
будет еще сказано). В 1797 г. в книге «Теория аналити-
ческих функций» Лагранж затрагивает вопрос и о конеч-
номерных задачах1).
Он пишет: «Оп pent les reduire а се principe generale.
Lors qu’une fonction de plusieurs variables doit etre un
maximum ou minimum, et qu’il у a entre ces variables
une ou plusieurs equations, il suffira d’ajouter .a la fonc-
tion proposee les fonctions qui doivent Иге nulles, mul-
tlpliees chacune par une quantite indeterminee, et la cher-
cher ensuite le maximum ou minimum comme si les.va-
riables etaient independantes; les equations qu’on trouvees,
serviront a determiner toutes les inconnues».
«Можно высказать следующий общий принцип.
Если ищется максимум или минимум некоторой функ-
ции многих переменных при условии, что между этими
переменными имеется связь, задаваемая одним или не-
сколькими уравнениями, нужно прибавить к минимизи-
руемой функции функции, задающие уравнения связи,
умноженные на неопределенные множители, и искать за-
тем максимум или минимум построенной суммы,’ как если
бы переменные были независимы. Полученные уравнения,
присоединенные к уравнениям связи, послужат для опре-
деления всех неизвестных».
Не будет преувеличением сказать, что основная часть
этой книги посвящена раскрытию замысла Лагранжа
в применении к задачам разной природы. Изложим здесь
еще'раз основную мысль Лагранжа. Пусть требуется
найти экстремум в задаче (1). Тогда следует составить
функцию Лагранжа (2) и рассмотреть задачу S (х, X, Хо) —>
—>extr без ограничений. Необходимое условие в этой
задаче без ограничений в соответствии с теоремой Ферма
для функций п переменных дает нужные уравнения J?x=0.
Итак, в соответствии с принципом Лагранжа уравнения
для экстремума в задаче с ограничениями совпадают
с уравнениями для задачи 2? (х, X, Хо)—>extr без ограни-
чений при надлежащем выборе множителей Лагранжа X, Хо.
*) Lagrange J. L. ТЬёопе des fonctions analytiques, Paris,' 1813.
51
Мы увидим далее, что для очень большого числа за-
дач общий замысел Лагранжа оказывается правильным.
1.3.3. Теорема Куна —Тдккера. В этом пункте мы рас-
смотрим задачи выпуклого программирования, для кото-
рых идея Лагранжа приобретает наиболее завершенную
форму. Этот класс задач стали изучать сравнительно не-
давно. Основы теории линейного (а это частный случай
выпуклого) программирования были заложены в работе
Л. В. Канторовича в 1939 г. Теорема Куна—Таккера —
основной результат этого параграфа—была доказана
в 1951 г.
Рассмотрим следующую экстремальную задачу {задачу
выпуклого программирования):
f0(x)—* inf, f(-(x)^0, i = 1, .. .,m, x£A, (1)
где X — линейное пространство (не обязательно конечно-
мерное), fi~выпуклые функции на X, А — выпуклое под-
множество X. Отметим, и это существенно, что (1) — это
задача минимизации,-а не максимизации.
Напомним, что множество С, лежащее в линейном
пространстве называется выпуклым, если вместе с любыми
двумя своими точками х и у оно содержит также и весь
отрезок [х, у] = {г | г = ах 4- (1 —а) у, 0 а 1}. Функция
f: X —+ R называется выпуклой, если для любых х и у € X
выполнено неравенство Иенссена
f(ax + (l— a)z/)<af (x)-j-(l— a)f{y), Va, 0<a<l,.
или, что то же самое, если «надграфик» f, т. е. множество
epi f = {(a, х) € R X X | a > / (х)}
является выпуклым множеством в произведении RxX.
Функцию
т
^=^(х,х,х0)=» 2х^(х), (2)
А = 0
где X =₽ (Xv ..., Хй) называют функцией Лагранжа зада-
чи (1), чисда Хо, ..., Х/л—множителями Лагранжа. При
этом в выражении (2) не нашло места ограничение х € А.
Теорема Куна—Таккера. 1. Пусть X—линей-
ное пространство, X—► R, i = 0, 1, ..., т,—выпуклые
функции на X, А—выпуклое подмножество X.
52
Если х является решением задачи (1), то найдутся
множители Лагранжа X, не равные одновременному лю
и такие, что:
a) minJ?(x, X, Х0) = ^’(х, X, Хо) (принцип минимума)-,
хе А
б) X;^s 0, i = О, 1, ..., т (условие неотрицательности);
в) /(х) = 0, i — 1, 2, ..., т (условие дополняющей не-
жесткости).
2. £слиХо=£О, то условия а) —В) достаточны для
того, чтобы допустимая точка х была решением задачи (1).
3. Для того, чтобы Хо=#О, достаточно, чтобы наш-
лась точка х£А, для которой справедливо условие Слей-
тера fi (х) < 0, i = 1, ..., т.
Таким образом, если выполнено условие Слейтера, то
можно считать Хо = 1.
Соотношение а) отражает мысль Лагранжа в наиболее
'завершенной форме: если х доставляет минимум в задаче
с ограничениями (типа неравенств), то эта же точка до-
ставляет минимум функции Лагранжа (в задаче без тех
ограничений, которые включены в функцию Лагранжа).
Соотношения б) и в) характерны для задач с неравенст-
вами (подробнее см. § 3.2).
Доказательство теоремы Куна—Таккера опирается на
одну из важнейших теорем выпуклого анализа—теорему
отделимости. Правда, здесь нам достаточно ее простей-
шего конечномерного варианта, который мы сейчас сфор-
мулируем, а докажем в следующем пункте.
Конечномерная теорема отделимости.
Пусть С—выпуклое подмножество в R^, не содержа-
щее точки 0. Тогда найдутся такие числа аи ..., aN, что
для любого х = (хх, х#)£С выполняется неравенство
N
2 > о (3)
N
(другими словами, гиперплоскость azx, =0, проходя-
щая через 0, делит R v на две части, в одной из кото-
рых целиком лежит С).
Доказательство теоремы Куна — Таккера.
Пусть х—решение задачи. Не ограничивая себя в общно-
сти, можно считать, что /в (х) = 0, —иначе введем новую
53
функцию f^^ = f0(x)—f0(x). Положим
с = {р> € R“+1, и = (|Ло» • < • | Эх е Л: /0 (х) < ц0,
*>!}• (4)
Дальнейшую часть доказательства разбиваем на несколько
этапов.
А) Множество С непусто и выпукло. Действительно,
любой вектор р € Rm+1 с положительными компонентами
принадлежит С, ибо в (4) можно положить х — х. Сле-
довательно, множество С непусто. Докажем его выпук-
лость. Пусть р = (р.о, ...,gm) и и' = (р;, .... i4) € С,
O^a^l, х и х—такие элементы из А, что (в соот-
ветствии с (4)) Д, (х) < р0, f0 (х') < p-i, fi UKgz. ft (x')<pt:,
i>l. Положим xa = ax + (l—a)x'. Тогда xaG^4. по-
скольку А выпукло, а ввиду выпуклости функций f(
fi (xa) = ft (ax + (1 — a) x') <
, ,, . ,J <ap0 + (l—a)pj, i = 0,
т. e. точка a|x + (l—a)p/£C.
Б) Точка 0£R'B+1 не принадлежит С. Действительно,
если бы точка 0 принадлежал^ С, то ввиду определения (4)
отсюда следовало бы, что имеется элемент х£ Л, для ко-
торого выполняются неравенства: fo(x)<0, Д(х)^0,
Но из этих неравенств следует, что х не есть решение
задачи. Значит, 0(£С.
Поскольку С выпуклой 0(£С, можно применить тео-
рему отделимости, согласно которой найдутся такие
Лв,..., что
т
2^>0 (5)
г=о
для любого р’^С.
BJ Множители i 0 в (5) неотрицательны. Дей-
ствительно, в п. А) мы говорили уже, что любой вектор
с положительными компонентами принадлежит С, в част-
ности, С принадлежит вектор (е, ..., 8, 1, е, ..., е), где
8 > 0 и 1 стоит на i0-M месте, i0^ 0. Подставив эту точку
в (5), получаем, что \ —е 2 откуда в силу про-
° 1 *5
извольности 8 > 0 следует, что XJo 0.
54
Г). Множители Xlt 1, удовлетворяют условиям до-
полняющей нежесткости. Действительно, если //о(х) = 0,
/в>1, то равенство Х/о//о (х)=0тривиально.Пусть//о(х)<0.
Тогда точка (6, 0, .,., 0, f/g (х), 0, ..., 0), где число //о (х)
стоит на /0-м месте, а 6 > 0°, принадлежит С—достаточно
взять точку х-в качестве точки х в (4).
Подставив эту точку в (5), получим, что Хд/уо(х)^
— Хо6, откуда из-за произвольности 6 > 0 получается
неравенство Х/о^0. Но было доказано в п. В), что
Х/о>0, значит, Хд = 0 и Х/(/Л(х)=0.
Д) В точке х выполнен принцип минимума. Действи-
тельно, пустьх А. Тогда точка (f0 (х) -J-6, (х), ..., fm (х))
принадлежит С для любого S > 0 (см. определение (4)).
Поэтому с учетом (5) Wo (х)-J-2 Х(Д (х)> — Хо6,
1 = I
а отсюда (в. силу произвольности 6 > 0) следует неравен-
ство 2 (х, X, Хо) 0.
Теперь же, если учесть равенство /0(х) = 0 и условия
дополняющей нежесткости, получаем для любого х£А
т
(х, X, Хо) > 0 - 2 (X) = Я (х, X, Хо).
i=0
Утверждение 1 теоремы доказано.
Е) Докажем утверждение 2. Если допустить, что
Хо=#О, то можно считать Хо=1 (ибо множители Лагран-
жа, удовлетворяющие соотношениям а)—в) теоремы, со-
храняют свои свойства при умножении на любой поло-
жительный множитель). Но тогда для любого допустимого
х(хЕЛ, /((х)^0, i^sl) получаем
б) а)
/о W > /о И + 2 Kfi (X) = 2 (х, X, 1) >^(Х, X, 1) =
1 = 1
л m в)
= fo(x) + 2 V/ (х) =f0(x\,
1=1
т. е. х является решением задачи.
Ж) Докажем утверждение 3. Пусть выполнено усло-
вие Слейтера, (т. е. для некоторого х£А имеют место
неравенства (х) < 0, i 1), но при этрм в утверждении 1
55
£, = 0. Тогда сразу же получается противоречие (в вы-
кладке используется, что не все Х(.==0, i^l):
- Я (х, X, 0) = 2 (х) < 0 = 2 (х, X, 0),
/=0
в то время как вследствие а) 2? (х, X, 2? (х, X, 0). Ц
Приведем еще один вариант теоремы Куна—Таккера.
При выполнении условия Слейтера Хо > 0 и поскольку
множители Лагранжа определены с точностью до поло-
жительного множителя, можно считать, что Хо= 1. Теперь
функция Лагранжа
^(х, К l) = f0(x)+ 2 ^.(х)
4=1
определена на множестве
XxR+='{(х, Х)"|х = (хр ...,хя)£ЛХ=*
*=(Xf......хв)А>0}
и соотношения а)—в) равносильны тому, что (х, X) яв-
ляется ее седловой, точкой, т. е.
minJ?7 (х, X, 1) — 2{х, X, 1)= max J? (х, X, 1). (6)
Действительно, левое равенство (6) совпадает с а), а
правое является следствием в) и б):
т
2 Cx,kl)^f о (х) + X л (X) = fB (X) >
т
+ ь, 1). В
В §§ 2.6, 3.1, 3.3, 4.3 мы расскажем о других теоре-
мах выпуклого анализа и выпуклого программирования.
Замечание. В «выпуклом анализе» оказывается
удобным рассматривать функции со значениями в расши-
ренной числовой прямой R = R и {— °°, +°°}, т. е. удоб-
но разрешить функциям принимать бесконечные значения
— оо, +°°- На расширенную числовую прямую распро-
страняются с некоторыми ограничениями правила ариф-
метики (об этом подробнее сказано в примечании вп. 2.6.1).
Легко убедиться в том, что приведенное доказательство
теоремы Куна—Таккера остается применимым без изме-
нений и к таким функциям.
1.3.4. Доказательство конечномерной теоремы отделимости.
Формулировка теоремы была приведена выше. Напомним, что С —
выпуклое множество в R^ и 0(£с.
А) Пусть lin С— линейная оболочка множества С, т. е. наимень-
шее линейное подпространство, содержащее С. Возможно одно из
двух: либо lint? Ф R-^, либо linC = RAr. В первом случае lin С —
собственное подпространство в R^, и потому существует содержащая
его гиперплоскость 2 а/х<=0, проходящая через нуль. Оиа и яв-
i=i
ляется искомой.
Б) Если lin С = RW, то из векторов, принадлежащих С, мы можем
выбрать N линейно'независимых и потому образующих базис В R^.
Обозначим их ех.....е^-.е^С, i=l,...,V,
Рассмотрим в- два выпуклых конуса: «отрицательный ортант»
( N S
= < X^R^ Х = 2 р1е1> ₽г < 0, i— 1, .... N > и коническую обо-
it*! J
лочку множества С:
\ I /ж 1
s, S любое
Эти конусы не пересекаются. Действительно, если бы вектор
*=“**• 2 Yze/. У; > 0, принадлежал то нашлись бы такие s£N,
“1
' s-
ctf 0 н t/CC, Что х = «Л[. Но тогда точка 0 оказалась бы при-
надлежащей С, ибо эта точка могла бы быть представлена в виде
выпуклой комбинации
s
о=2
«=1
S N
2 “t‘Ii+2 w
точек из С.
В) Поскольку открыто, из доказанного в Б) следует, что ин
одна из точек ие может принадлежать замыканию множества
«Ж’а- (Отметим, что SKг замкнуто и выпукло. . Почему?) Возьмем
w
Произвольную точку из например х0 = — 2 ~ei, и найдем бли-
_ t=i
жайшую к ней точку Такая точка существует, а имение,
зТо та из точек компактного множества Й?2Г)В(х0, | х0|), в которой
непрерывная функция / (ж) = | х--х01 достигает своего минимума.
S7
Г) Проведем через £в гиперплоскость Я, перпендикулярную
хб—н покажем, что она искомая, т е. что 0£Я и множество С
целиком лежит в одном из двух замкнутых полупространств, огра-
ниченных этой гиперплоскостью-. Мы докажем даже больше, а именно,
если Я—внутренность того из полупространств, которое содержит
точку х0, то H[\SK2 = !3. Поскольку множество С С ойо целиком
содержится в замкнутом .полупространстве, дополнительном к Я.
Предположим противное, и_пусть ^г^ЯП^а- Тогда угол
острый. Кроме того, [§0, поскольку Ж.г выпукло. Опустим
из х0 на прямую (£в, перпендикуляр (х0, £2),_|гё(£оЛ1) и пока-
жем, что £0 ие является ближайшей к х0 точкой «¥2. Действительно,
точки |0, и £2 лежат на одной прямой н §2£Я (почему?). Если
5а€[?о> 511,то g2£^2 и |яв—£2| < | х0— §01 (перпендикуляр меньше
наклонной). Если же лежит между |в и |2, то | х0—[ < | х0—10| (из
двух наклонных та меньше, основание которой лежит ближе к осно-
ванию перпендикуляра)
С другой стороны, Я проходит через точку 0, ибо иначе луч,
исходящий из 0 в направлении точки £0 и целиком лежащий в
(почему?), обязательно имел бы общие точки с Я.
§ 1.4. Простейшая задача классического
вариационного исчисления и ее обобщения
1.4.1. Уравнение Эйлера. Вскоре после работы И. Бер-
нулли о брахистохроне стали появляться (и решаться)
многие задачи того же типа. И. Бернулли поставил перед
своим учеником Л. Эйлером проблему найти общий путь
их решения.
В 1744 г. вышел труд Эйлера «Methodus inveniendi
lineas curvas maximi minimive proprietate gaudentes sive
solutio problematis isoperimetrici latissimo sensu accepti»,
«Метод нахождения кривых линий, обладающих свойст-
вами максимума или минимума, или решение изопери-
метрической задачи, взятой в самом широком смысле»,
в котором.были заложены теоретические основы нового
раздела математического анализа. В частности, аппрок-
симируя кривые ломаными, Эйлер вывел дифференциаль-
ное уравнение второго порядка, которому должны были
удовлетворять экстремали. Впоследствии Лагранж назвал
его уравнением Эйлера. В 1759 г. появляется первая ра-
бота Лагранжа и с ней новые методы исследования.
Лагранж «.варьирует кривую, подозреваемую на экстре-
мум, выделяет из приращений функционалов главные ли-
нейные части, которые называет вариациями, и пользуется
тем, что в точке экстремума вариация должна обращаться
58
в нуль. Метод Лагранжа становится впоследствии обще-
принятым. Этим методом и мы выведем далее уравнение
Эйлера. Отметим еще, .что носле работ Лагранжа по
предложению Эйлера весь раздел математики, к которому
применялся метод Лагранжа, стали называть вариацион-
ным исчислением.
Перейдем к выводу уравнения Эйлера для простейшей
задачи классического вариационного исчисления. В п. 1.2.6
этим именем была названа экстремальная задача
л
J(х(•)) = $ Ш x,x)^ — extr, х(/0) = х0, х(/х)=хй (1)
^0
рассматриваемая в пространстве непрерывно дифферен-
цируемых функций (T-ftt,,, ZJ), —оо < t0 < < оо. Про-
странство С1^, ^]) является банаховым; т. е. полным
нормированным, относительно нормы:
II х (•) IL — max ( max | х (t) |, max ]х(/)|).
Будем предполагать, что функция L (ее называют
интегрантом или лагранжианом задачи) непрерывна по
совокупности переменных вместе со своими частными
производными Lx и Li.
Теорема. (Необходимое условие экстре-
мума в простейшей задаче классического
вариационного исчисления.) Пусть функция
х (•) € С1 ([70, Ц) доставляет локальный экстремум в зада-
че (1). Тогда она удовлетворяет уравнению
—~-Li(t,x(t), x(t))+Lx(t,x(t),x(t)) = O. (2)
Уравнение (2) называется уравнением Эйлера. Допу-
стимая функция х(-), для которой оно выполнено, на-
зывается стационарной .точкой задачи (1) или экстре-
малью. Таким образом, локальные экстремумы задачи
являются экстремалями; обратное, вообще говоря/неверно.
Локальный экстремум в пространстве С1 (]70, fj) в ва-
риационном исчислении называют слабым. В соответствии
с общими определениями функция х(-) доставляет ло-
кальный минимум (максимум) в задаче (1) в пространстве
Сх([70, G]), если .найдется такое е > 0, что для всякой
функции х(-)€С*([£0, fj), для которой х(/0) = х(^) = О
и IIх(Olliвыполняется неравенство
5(х(-) + х(-))>5(х(.)) (<^(х(.))).
Доказательство теоремы проведем дважды. Сначала
Воспользуемся рассуждением Лагранжа. Правда, при этом
придется дополнительно предположить, что функция
непрерывно дифференцируема. Затем
докажем важную лемму Дюбуа-Реймона, из которой наша
теорема вытекает и без дополнительного допущения. Обоб-
щение конструкции Дюбуа-Реймона окажется существен-
ным в гл. IV.
Доказательство теоремы складывается из трех
этапов.
А) Определение первой вариации по Ла-
гранжу, Пусть х (•) £ С1 ([Zo, t J). Рассмотрим функцию
Х>—>ф(Х) = 3 (х(-) + Хх(>)). Имеем
Ф(Х) = J F (t, tydt = J L (t, x(i) + Kx(i), x (i) + Kx(t))dl.
^0 ^0
Допущения, наложенные на L, позволяют дифферен-
цировать функцию F под знаком интеграла (для этого
достаточно, чтобы функции (/, X)—>Г(/,Х) и (/, X)—♦
—X) были непрерывными [14, т. 2, с. 661], [9, т. 2,
с. 107]). Дифференцируя и подставляя Х = 0, получаем
<№) = $(q(t)x(i) + p(t)x(t))dt, (3)
/о
где
р (0 = Li (t, X (0, X (/)), q (t) — Lx(t,x (0, X (0).
Итак, lim (3 (x(-) + Xx (•))— 3 (x(-))/X) существует
i.4-0
для любого ([ta, /J). Обозначим этот предел
§5(х(*), х(-)). Функция х(-)|—(х(-), х(-)) называет-
ся первой вариацией по Лагранжу функционала 3.
Б) Преобразование первой вариации с по-
мощью интегрирования по частям. Пусть
x(te) = x(ti) — Q и функция р(-) непрерывно дифферен-
60
цируема. Следуя Лагранжу, имеем
tt
S3 (х (•), х (•)) = $ («у (0 х (О + р (О х (t}) dt =«
t,
t,
= 5 a(t)x(t)dt, (4)
*0
где a (/) = — p (0 + q (0 (произведение p (t) x (t) обращается
в нуль на концах промежутка интегрирования).
Нам известно, что х (•) доставляет локальный экстре-
мум, для определенности пусть это будет минимум, в за-
даче (1). Отсюда следует, что функция >ф(Х) имеет
локальный минимум в нуле. Вследствие теоремы Ферма
(см. п. 1.3.1) ф' (0) = 83 (х(-), х(-)) = 0. Сопоставляя это
с (4) мы получаем, что для произвольной функции %(•)€
С С1 ([/0, fj) такой, что x(fo) = x(i1) = O, имеет место ра-
венство а (!) х (t) dt = 0.
t0
В) Основная лемма классического вариа-
ционного исчисления. (Лемма Лагранжа.)
Пусть непрерывная функция tt->a(t), t £ [t0, /х] обладает
тем свойством, что a (t)x(t)dt = O для любой непрерывно
to
дифференцируемой функции х(-),у которой х (t0)—x (У^О.
Тогда a(t)z=0.
Доказательство. Допустим, что, а(т)^=0 в не-
которой точке т£[/0, /J. Тогда вследствие непрерывности
а(-) найдется отрезок Д = [т1, т2]с (/„, /х), на которома(-)
не обращается в нуль. Пусть для определенности a(t)^
/п > 0, t € Д. Построим функцию
Х<'Н о, ($д.
Нетрудно проверить, что x(-)€Cl([i0, /J); кроме того,
х(/0) = x(/i) = 0. По условию леммы a(t) x(t)dt = 0.
С другой стороны, по теореме о среднем [14, т. 2, с, 115],
61
to to
[9, т. 1, c. 344] J a(t) x(t)dt = a(B) J x(f)dt > 0, и это
противоречие доказывает лемму. Щ
Сопоставляя полученное в А) и В), убеждаемся, что
— а это и требовалось доказать.
Г) Лемма Д юб у а-Р ей м он а. Пусть на [A, Al Функции
of-) и Ь (•) непрерывны, и пусть
*
j (a (t) х (t)-\-b (t) х (t)) dt =0 (5)
io
для любой х(-)€С1([/0, /1]) такой, что х (t0) = х (А) = 0. Тогда функ-
ция а(-) непрерывно дифференцируема и da(t)/dt = b (t).
Доказательство. Интегрируя в (5) второе слагаемое в по-
дынтегральном выражении по частям, 'получаем
t, t t
0 = f (a (t)—r С b (s) ds) x (t) dt-{- f b (s) ds x (t) И* =
J J J 1*0
t*
= J (a (t) — * (s) ds) x (t) dt. (6)
to to
t
Докажем, что ф (/) = a (/)— J b (s) ds = const. Если это не так,
to r
то навдутся*такиеTi ит2, что ф (тх) =£ ф (т2). Без ограничения общно-
сти можно считать, что тх и t2—внутренние точки отрезка [£0> М и
ф (тх) > ф (т2). Выберем б > 0 так, чтобы [т,—б, т<4- 6]С (А> АЬ
1 = 1, 2, и чтобы ф (sH-t,)—-ф (s4-T2)3sa > 0 при | s |^б.
Теперь возьмем функцию х (•), производная которой имеет спе-
циальный вид
( ri + 6)(t-Tb-6), tGhx-б, Тх+б],
ж(0 = ] +(i~T2 + 6)(t—т2—б), /0т2-6, т2+б], (7)
\ 0 для остальных t.
h
Если положить х(А)=0, то в силу (7) х{А)= J х (i) dt = O, так что
t о
для такой х(-) должно иметь место (6), но
6Г А "1 т,+6 г2+в
J a(t) — ^b(s)ds x(t)dt= tf (t) х (t) dt-ф- (f (t) x (t) dt
io io * Ti—в Xo—в
6 6
= (ф (Tx + s) — ф(тг-|-5)) (6—s)(s + 6)ds5sa J (6—s) (s 4-6) ds > 0.
-6 -6
62
t
Противоречие показывает, что q>(t)=o(t)—6 (s) ds=const, а тогда
^0
а(-) дифференцируема и da!dt = b. В
Применив лемму Дюбуа-Реймона к первой вариации (3), полу-
чаем, что p(-)£Ci([f0, /13) и p’(t)=<?(0-
В только что проведенных рассуждениях заключен
зародыш так называемого метода вариаций, с помощью
которого выводятся различные необходимые условия эк-
стремума. Суть его состоит в следующем. Пусть х—точка,
подозреваемая на минимум в задаче f(x)—>inf, х£С.
Тогда можно попытаться построить непрерывное отобра-
жение Х>-»х(Х), XgR+ так, чтобы х(О) = х и х(Х)£С,
О^Х^Х0. Эту кривую естественно назвать вариацией
аргумента. Положим <р (Х) = /(х(Х)). Допустим, что функ-
ция ф оказывается дифференцируемой справа по X. Если
х—действительно точка минимума, то должно выпол-
няться неравенство <р' (4-0) = lim (<p (X)—<р(О))/Х^О, по-
скольку, очевидно, <р(Х)^ф(О)=/(х). Если удается по-
строить достаточно массивное множество вариаций аргу-
мента, то полученный набор неравенств q/(4-0)^0,
относящихся ко всем вариациям, образует некоторое
необходимое условие минимума. При выводе уравнения
Эйлера использовались «вариации по направлениям»:
х(Х)=.х4~Хх. При выводе необходимого условия Вейер-
штрасса и принципа максимума будут использоваться
вариации другого вида—так называемые «игольчатые»
(см. пп. 1.4.4 и 1.5.4).
В заключение отметим следующие два первых интег-
рала уравнения Эйлера:
1) Если лагранжиан L не зависит от х, То уравнение
Эйлера имеет очевидный интеграл
= x(t)) = const.
Этот интеграл называют интегралом импульса.
2) Если лагранжиан L не зависит от t, то уравнение
Эйлера имеет первый интеграл
Я(0 = Ь; (х(0, x(t))x(t) — L(x(f), x(t)) — const.
Он называется интегралом энергии (оба названия восхо-
дят к классической механике; мы еще будем иметь воз-
63
можность к этому вернуться; см. п.п. 4.4.6 и 4.4.7). Для
доказательства вычислим производную:
+ x(0)x(0—
-Ц£(0. х(0)х(0-ЬД^(0, х(0)х(0 =
*(-^-^(x(0, x(t)) — Lx(x(t), х(0))х(0«0
в силу уравнений Эйлера. Следовательно, //(/) = const.
Замечание. По ходу дела мы использовали допол-
нительное предположение о существовании второй произ-
водной x(t). Это предположение можно ослабить, но совсем
без него обойтись нельзя.
Отметим еще, что уравнение Эйлера—это дифферен-
циальное уравнение второго порядка. Его общйй интег-
рал зависит (вообще говоря) от двух произвольных пос-
' тоянных. Их значения мы находим из граничных условий.
1.4.2. Необходимые условия в задаче Больца. Условия
трансверсальности. Простейшая задача, рассмотренная
в предыдущем пункте,—это задача с ограничениями: гра-
ничные условия х(У = х'о, x(ij) = Xi образуют два огра-
ничения типа равенств. Следующая задача—так назы-
ваемая задача Больца—является задачей без ограниче-
ний. Пусть L удовлетворяет тем же условиям, что и в
п. 1.4.1; 1 = 1(х9, хг)—непрерывно дифференцируемая
функция двух переменных. Рассмотрим Задачу на экст-
ремум в пространстве С1 ([/0, ^]):
t,
£(х()) — $L(t, х, x)xtx-j-l(x(te), х^))—* extr. (1)
Ее и называют задачей Больца.
Теорема (необходимое условие экстрему-
мы а в задаче Больца). Пусть функция х (•) ё С1 ([7в/ /,])
и доставляет локальный минимум в задаче (1). Тогда вы-
полняется уравнение Эйлера
—m i(o)*o (2)
64
и условия трансверсальности:
LiUi’ *(O> x(Q = -^^^. (3)
Доказательство. Действуя в точности так, как
на первом этапе доказательства теоремы предыдущего
пункта, получим такое выражение для первой вариацйи
функционала 53:
6S(x(-), *(•)) =
л
= J (<7 (/) х(^) + р (/) X (/))rf^4-«xox(/o) (^1). (4)
где р(-) и q(-) определены соотношениями (3) предыду-
щего пункта, а а(. — , i = 0, 1. Так как
х'(.)—точка локального минимума, 8Я(х(-), х(-)) = 0
для любой точки х(-) € С1 ([70, fj). В частности,
65?(х(‘-), %(•)) = 0 для любой x(-)GC1([Z0, /,]), у кото-
рой х (t0) ~ х (tj) = 0. По лемме Дюбуа — Реймона функ-
ция р(-) непрерывно дифференцируема и при этом
^&=q(t)- Интегрируя (4) по частям и используя то,
что p(t) = q(t), приходим к следующему выражению для
первой вариации ио Лагранжу функционала Больца:
0=8Я(х(-), х(-))^
= 5 (? (О—Р Ю) X (О dt + (а0—р (/„)) х (Q +
*0
+ (“i + Р (QMQ = («о—Р (QMQ + (а,+р О х (tj. (5)
Положив, в (5) последовательно х (/) = (/—10), а затем
t—tlt получаем, что a0 = p(Q, —<Xi — p{t^-
Итак, мы снова получили уравнение второго порядка
и два краевых условия—условия трансверсальности.
Выше была рассмотрена «одномерная» задача Больца.
Совершенно аналогично ставится векторная задача:
t,
#(х(-))== $L(f, хх, .... х„, хп .... x„)d/ +
rl-/(Xi(U> xn(t.), х^О, .... extr, (1')
3 в. М. Алексеев и др.
65
где
L-. RxR'xR' R, /: R”xR'’ —* R.
Необходимые условия экстремума здесь также имеют
вид (2)Л (3), только соответствующие уравнения надо
понимать векторно:
Л (о.....х„(о)+
+LXj(t, .... ;п(о, А(о...........х„(О)=о, (2')
Лх, (^’ ^1(^1)' Хп (Q, Х1(О> •••> хп(^1))~
__ ( (*1 (<»).. %П (^р)т *1 (^1),1 %п (Л)) (3*)
t=0,l; / = 1, . .., п.
1.4.3. Расширения простейшей задачи. Простейшую
задачу классического вариационного исчисления в п. 1.4.1
мы рассматривали в пространстве С1 ([i0, fj). В этом —
определенная дань традиции. Пространство С1 ([/„, ZJ),
конечно, удобно, но далеко не для каждой задачи оно
является естественным. В частности, при тех предполо-
жениях относительно интегранта (непрерывность L, Lx,
L- по совокупности переменных (t, х, х)), существование
решения в пространстве С1 ([/„, ft]) не всегда можно га-
рантировать. Приведем один из простейших примеров.
Пример Гильберта. Рассмотрим задачу
1
3 (х(•)) = J f/ax2di —»inf, х(0) = 0, х(1) = 1.
о
Здесь уравнение Эйлера имеет интеграл импульса
(см. п. 1 4.1) Г/ах = С, откуда следует, что единственной
допустимой экстремалью является x(t) = t'^. Эта экстре-
маль не принадлежит пространству Сх([/и, ij) (почему?).
Вместе с тем она доставляет абсолютный минимум в за-
даче. Действительно, пусть х(-)—любая абсолютно-не-
прерывная функция1), для которой интеграл 3(х (•)) конечен
*) Об абсолютно непрерывных функциях говорится в п. 2.1.8.
Читатели, не знакомые с этим понятием, могут считать, что х( )
непрерывно дифференцируема в полуинтервале (0, 1], интегрируема
в несобственном смысле на отрезке [0, 1], имеет конечный интеграл
3(х( )) и х(0) = х (1) =0.
66
и х(0) = х(1) = 0. Тогда
I
?(х(-)+х(-))=5 i!/»(?(o+^(oi(o+i2(o)^=
о
1
= Я(х(.)) + |р(0^ + *(х(-)) =
о
= 5Г(х(.))4-3'(х(.))>5'(х(-)).
Итак, решение задачи существует, но не принадлежит
пространству Сх([/0, fj).
Среди знаменитых «проблем Гильберта» некоторые по-
священы вариационному исчислению. В частности, в двад-
цатой проблеме речь идет о существовании решения.
Гильберт*) пишет так: «Я убежден, что эти-доказатель-
ства существования можно будет провести с помощью неко-
торого общего основного положения, на которое указы-
вает принцип Дирихле и который,_ вероятно, приблизит
нас к вопросу о том, не допускает ли решение каждая
регулярная вариационная задача..., если в случае необ-
ходимости самому понятию решения придать расширен-
ное толкование». Оптимизм Гильберта подкрепляется ог-
ромным опытом классического анализа. Здесь мы вкратце
обсудим проблему «расширенного толкования» решения
на примере простейшей вариационной задачи.
Одна из конструкций расширения состоит в том, что
к первоначальному классу допустимых элементов добав-
ляются новые и функционал при этом доопределяется на
этих новых элементах. В этом направлении мы сделаем
скромный шаг — осуществим расширение простейшей за-
дачи на класс кусочно-гладких функций.
Напомним, что кусочно-гладкой функцией на [/0, /,]
называется функция х(-)^ обладающая тем свойством,
что сама она непрерывна, а ее производная кусочно-
непрерывна, т. е. непрерывна всюду на [Zo, /J, за ис-
ключением конечного числа точек ta < <... < тт < tlt
и при этом в точках т, производная х(-) имеет разрывы
первого рода. Например, функция
(О, —
х^~ fisiny, 0 < t,
*) Проблемы Гильберта/Под ред. П. С. Александрова.—М.: Нау-
ка, 1969, с. 55.
3* 67
имеет производную, которая не является кусочно-непре-
рывной-. Совокупность всех кусочно-гладких функций на
[i0, fx] обозначим /СС1^,
Интегральный функционал
3 (х(•))=$£(/, х(0., x(t))dt (1)
^0
(ср. п. 1.4.1) естественно продолжается на элементы
х (•) С КС1 ([^в, fj), поскольку для таких х(-) подынтег-
ральная функция кусочно-непрерывна и интеграл суще-
ствует.
Рассмотрим теперь простейшую задачу
3 (х(-))—*extr, х(\) = х0, x(Q = xt (2>
в-пространстве /(С1([^о, /х]). В конце этого пункта будет
приведен пример функции L, удовлетворяющей стандарт-
ным условиям, для кЪторой задача вида (2) в простран-
стве С1 ([i0, /J) решения не имеет, а в 7<С1([/0, /х]) —
имеет, так что проведенное расширение задачи оказыва-
ется разумным (хотя в примере Гильберта минимум не
достигается и в КС1).
Несколько аккуратней надо быть с понятием локаль-
ного решения. Если’ в окрестность элемента х(-)£
€ КС1 ([<„, fx]) мы будем по-прежнему зачислять такие
х(-), что малы как сами разности x(i)—x(t), так и их
производные (ср. определение слабого экстремума в
п. 1.4.1), то вновь добавленные элементы будут распо-
лагаться далеко j?t старых. Действительно, если..произ-
водная х(-) имеет в некоторой точке скачок величины 6,
то ни одна из функций х(-) £ С1 (р0, /J) не может удов-
летворять неравенству |х(А)—х(^)| < 6/2 для всех t (для
которых х(0 существует). Это, вообще говоря, неудоб-
но: обычно хотят, чтобы старое пространство лежало
в расширенном всюду плотно. Поэтому близость в
КС1^, Ц) мы будем определять, сравнивай только
сами функции, но не их производные. Это приводит
к замене понятия слабого экстремума (п. 1.4.1) понятием
сильного экстремума.
Определение. Функция х(-)€КС1 ([£„, Ц) достав-
ляет сильный минимум (максимум) в задаче (2), если су-
ществует такое е > 0, что для любой x(-)£KC1([t0, /х]),
68
для которой x(t9) = xB, x(Q==xf и
h(-)“*(')llo = sup l*(0—x(O|<e, (3)
*е[4.М
выполняется неравенство 3 (х (•)) > 3 (х (•)) 3 (х (•))).
Лемма о скруглении углов. 1) Если функция
L — L(t, х, х) непрерывна по совокупности аргументов,
цло
inf 3(x(-)) = inf J(x(-)). (4)
x(-)sKC‘ ((?„ f,J) *(•)«=<?• ([?,. М)
л-(6) = ^0. * (*i) = *i X (ia)=xa. X (fO~x\
2) Равенство (4) сохранится, если брать только те
х(-)€-КС1([^о, М)> которые удовлетворяют неравенствам
(3) дл$ заданных х(-) и е > 0.
3) Утверждение остается верным и при замене inf
ца sup.
Доказательство. Поскольку КС1^, /х])гз
эС1^, £х]), левая часть в (4) не больше правой и нужно
лишь доказать обратное неравенство. Предположим про-
тивное. Если inf 3 (х (•))< inf 3 (х(-)), то найДутся такая
кс« с>
кусочно-гладкая х(-) и такое т] > 0, что J(x(-))<
<inf3,(x(-))—л., Пусть Th i = l,2, . ... т, — точки раз-
с,
рыва производной х и Д^х^ + О)—х(т(-—0) — ее скач- -
ки в этих точках.
На замкнутом ограниченном множестве
ЗС= {(t, х, х) 1tB t tlt |х — х(/)|^
<шах| Д,-|60/4, |х—x(t) |<тах|Д;|/2}
Непрерывная функция L ограничена: \L (t, х, х)|^М.
Функция
непрерывна, а ее производная при £ = 0 имеет скачок ве-
—график которой
получается из графика а(-) подобным преобразованием
и сдвигом (рйс. 22) также непрерывна, и ее производная
непрерывна, кроме точки т(., где она по-прежнему имеет
скачок — 1.
Теперь нетрудно проверить, что функция
т
х6 (0 = х(0+ S AzSa (Цр)
непрерывна вместе со своей производной на [/0, fj, причем
' х6 (t) sax (/) вне отрезков
‘«/Ч-вЬ В частно-
T'f ~==a"T*/7 сти,для достаточно малых
* 1 ‘6 эти отрезки не пере-
Рис‘ 22, крываются, xa(/z) =
— x(ti)^xit t = 0,l, и |хй(/) — x(/)|Cmax| AJS/4,
|хв(0 —£(0 |Cma‘x|AJ/2, ибо согласно (5) ]а(/)|С 1/4»
|а (7)|^1 /2. Поэтому при S < So
3 (хе())-? (*(•)) =
г,
— хе(0, x6(t))dt—^L(t, x(t), x(t))dt =
to
m V
= 2 J (L(t, x6(t), X& (/))—£(/, ?(/), x(t)))dt
£=1 rz-e
и, следовательно,
3 (x6 (•)) C 3 (x (•)) + 4/nS M <
< inf 3 (%(•)) — T] + 4m6M < inf 3 (x(-)),
, c* c«
если 6 достаточно мало. Так как xe(-)gC1([ie, /J), мы
пришли к противоречию. При малых S функция хв(-)
будет удовлетворять неравенствам (3), если х(.) им
удовлетворяет. Отсюда следует второе утверждение лем-
мы. Третье утверждение очевидно. В
Следствие. Если функция x(-)€C1(j/0, /J) достав-
ляет в задаче (2) абсолютный или сильный минимум (мак-
симум) в пространстве С1 ([/„, /J), то она обладает тем
же свойством и в пространстве КС1 ([f0, /J).
Проведенное нами расширение на самом деле не всегда
оказывается достаточным. Кроме того, пространство
КС* ([/0, ^]) не является полным (относительно метрики,
определяемой левой частью (3)). Более естественным
было бы расширение задачи на класс VTt (Г/о, /J) функ-
ций, удовлетворяющих условию Липшица *). Но это по-
1) Отметим, однако, что и при этом расширении мы ие получим
существования в примере Гильберта: функция fi—► /'/» условию Лип-
шица не удовлетворяет.
70
требовало бы некоторых сведений из теории функций.
Есть и еще одна важная конструкция расширения
простейшей задачи, которую мы здесь обсудим на примере.
Пример Еольца. Рассмотрим задачу
1
5(%-(.))=$((1—?)a + x2)d/-^inf, х(0) = 0, х(1) = £.
о
Допустим, что В = 0.
Тогда ясно, что решение
задачи не существует. Дей-
ствительно, нижняя грань
функционала равна здесь
нулю. Для того чтобы по-
нять это, достаточно рас-
смотреть минимизирую-
щую последовательность
функций из КС1 ([0, 1]):
Рис. 23.
t
хп (t)— J sign sin 2лпт(£г, п — 1,2, ... (рис. 23).
о
Функции хп(-) равномерно стремятся к нулю и
за исключением конечного числа точек, т. е. 3 (хп ('))==
1
₽ J >-0. С другой стороны, если хо(‘) = О, то
о
1
3(х0(-))~ 1, а если х(-)^0, то 3 (х(-))^ $ x'2dt> 0.
о
непрерывное снизу» расширен,
нал 3 заменяется функционал
Дело в том, что функ-
ционал 3 не полунепре-
рывен снизу—мы устано-
вили, что в любой близо-
сти от функции Хо(.)==О,
где функционал принима-
ет значение единица, есть
функции, где значение
функционала значительно
меньше (3 (хп (•) —+ 0). Так
вот, возможно «полу-
(е задачи, когда функцио-
Нт ?(%(•)),
у <•) -*х <)
71
а сам запас первоначальных функций (скажем, С*(р0, У)
или Ц)) остается прежним. Предельный пере-
ход у (•) —* х (•) понимается здесь в пространстве С ([/0, Ц)
(т. е. в смысле равномерной сходимости). Оказывается,
что функционал допускает простое описание. В при-
мере Больца
1
о
где
(?-1)+
О,
?— 1,
В общем случае, когда
3 (х(-)) — ^ L(i, х, x)dt,
6
ft
ф (x(-))=*^L(t, х, x)dt,
^0
где L—«овыпукление» L по x, т. e. функция x—*L(t, x, x)
есть наибольшая выпуклая .функция, не превосходящая
функции х—*L(t, х, х). Это утверждение называете^
теоремой Боголюбова
Этот же пример Больца можно использовать для по-
строения задачи (2),ja которой минимум достигается на
кривой с изломом. Однако по чисто техническим сообра-
жениям мы рассмотрим 'несколько иную задачу:
3 (х(')) = ^(f(x) + x2)dt-^ ini, x(t0) — x0, х^) = х1Г (6)
где функция
/(ц) = ((|ц|-1)+Г =
(и — I)2, 1,
О, |и|С1.
(u-4-l)2, — 1
непрерывно дифференцируема и выпукла (рис. 24).
В частности, график /(и) лежит не ниже любой своей
касательной, т. е. всегда
f (у) >/(«) + Г (») (У—и).
га
Поэтому для любых двух функций X ( ), X (•) £ КС1 ([i0, / J),
удовлетворяющих заданным граничным условиям x(tt) =
= x(tl) = xt, i — b, 1, имеем
J(x<-))-3f(^(-)) =
= $ (И* (0)-f (*(0)+X’ (0-*a (/))di >
to
>5(f(i(o)(x(o-x(o)+
^9
+ 2x (f) (x (/)—x (0) + (x (0—x (0)2) dt >
tt
> $ (f (x (0) (X (0-i (0) + 2* (0 (*(0~x (0))dt-
fo
Предположим теперь, что x(-) во всех точках диффен-
цируемости удовлетворяет уравнению Эйлера
4Г(*(0)’=2х(0.
(7)
Интегрируя по частям на каждом отрезке непрерывности
х(-), получаем
ЗГ(х(.))-^(х(.))>
> J (- 4 f(х (о (0) dt+
+ S [f' U (L + 0) — f' (X (т,—0» (x (т,)—X (тг)) = 0,
если в дополнение к (7) функция р (/)=/' (х(0) (импульс)
непрерывна. Таким образом, функция х(-), удовлетво-
ряющая уравнению Эйлера, условию непрерывности р(>)
й краевым- условиям, является решением задачи (6).
Например, x(^) = elfl с изломом в точке t — О является
решением этой задачи для t0 = ~-1, ^=1, х0=хг = е.
Действительно,
I ef, t^0,
х^) = 1е-<, /<0,
73
откуда и, значит,
л ( 2(ef —1), 1^0,
Р(0 = Г(х(0) = | 2(_е-<+1), t<0,
скачка в точке i = 0 не имеет: р (4-0) = р (— 0) = 0. Кроме
того, — р (!) = 24 Н = 2х (/), так что уравнение Эйлера
удовлетворяется.
1.4.4. Игольчатые вариации. Условие Вейерштрасса;
Понятна сильного экстремума ввел в вариационное ис-
числение Вейерштрасс. Для доказательства необходимого
Рис. 25.
условия сильного минимума Вейерштрасс .употребил
специальные вариации такого вида (рис. 25, а)
Г £Х4-(£—т)£, ^€[т—X, т],
Л1(0^Лх(^;т, g) = | gx—(/—T)g/X, /€[т, Т4-/М,
(1)
хНО =* (0+М0-
Производная вариации hK(-) имеет вид, изображен-
ный на рис. 25, б. Эта производная несколько напоми-
нает иголку, в связи с чем подобные вариации называют
«игольчатыми». Игольчатые вариации приспособлены
к исследованию задач на сильный экстремум.
74
Перейдем к выводу необходимого условия Вейер-
штрасса. Рассмотрим простейшую задачу классического
вариационного исчисления
х> x)dt—>inf, x(f0)=»xe, л(^) = х1 (2)
на классе /<CJ([/OI (J) кусочнр-гладких функций. Пусть
%(•) — экстремаль, подозреваемая на сильный минимум;’
-для простоты будем считать ее'гладкой.
Следуя общему замыслу метода вариаций, рассмот-
рим функцию
q>W==J(xi(-)M(x(-HM’)). (3)'
где hx определено формулами (1), т—внутренняя точка
Во. #i]» £—произвольное число.
Для достаточно малых функция %*,(•) допустима
в задаче (2), т. е. Х1(^) = х(/г) + Ах(/() =х(, i = 0, Г.
Функция <р( ) определена при неотрицательных К. Докажем,
что она дифференцируема справа в точке нуль Из определения (1)
сразу видно, что
а) |А1(.)|в= шах Щ(0|=О(Л),
\ (4)
б) |Ах(01 =g/X=O(/X), <€(т, т+УТ).
Отсюда
ф(к)-ф(0)~ J i(O+S)-L (t, x(f), x (t)))dt+
x-k
x+Vk
+ J (L(t,xK(t), xK(t))-L(t,x(t),x(t)))dt^1+^2. (5)
T
Интеграл в (5) можно оценить так:
^1=Л(£(т, х(т), х(т)-Н) — £(т, х(т), х (т))) + о(Л) (6)
(надо воспользоваться теоремой о среднем нз дифференциального
исчисления, см, п. 2.2.3, и оценкой (4а)).
Для оценки второго интеграла представим разность
Д=£(£ x(t)+hk(t), x^+hxd^-Hf, x(t), x(t))
в виде
A=£jf(/, х(<), x(t))h^(t)-\-L.*(t, x(fy, x (/)) (/)-}-о
75
(опять-таки надо применить теорему о среднем и оценку (46)), про-
интегрируем второй член по частям и воспользуемся тем, что
+£ЖК =0
dt х 1 х | х
(ибо х( )—экстремаль). В итоге получаем
x+'V~
5М,;.(т, х(т), х(т)) + о(УТ)^ =
- = — ^L-x(x, x(i), х(т))4-о(Х). (7)
Сопоставляя (6) и (7), находим
<р(Л)—ф(0) = Л(£(т, х(т), х(т)-Н) —
— £(т, х(т), х(т))—££. (т, х(т), x(t))) + oj(X). (8)
Таким образом, функция <р( ) имеет в точке /.«0 правую
производную
ф'(+0)= lira
Mo л
= £(т, х(т), х(т)+£) — £(т, х(т), х (т)) —^(т, х(т), х(т)).
Но если х (•) доставляет сильный минимум, то 3 (хЛ (•))
>?(х(-)) и, значит,
ф' (+0) = Нт (ф (X)— (0))/Х > О,
т. е. выполнено соотношение
<£(т, х(т), х(т), х(х) + 1) =
= L(x, х(т), х(т)+£)—L(t, х(т), х(т)) —
-IL- (т,х(т),х(т))>0 (9)
для любого IER- Функция
х, у, z) = L(t, х, z)—L(t, х, y)—(z—y)Lu(i, х, у)
называется функцией Вейерштрасса.
Таким образом, доказана следующая
Теорема (необходимое условие Вейершт-
расса для сильного минимума).
Для того чтобы экстремаль х (•) € С1 ([70, (J) простей-
шей задачи классического вариационного исчисления (2)
доставляла сильный минимум, необходимо, чтобы для
76
любого т£[/0, £г] и любого В £ R было выполнено нера-
венство
£ (т, х (т), х(т), х(т) + В) = Ь(т, х(т), х(т)-Н)~
— L (т, х(т), х (т)) — ZL;. (т, х (т), х (т)) > 0.
1.4.5. Изопериметрическая задача и задача со стар-
шими производными. Изопериметрической задачей (с за-
крепленными концами) в вариационном исчислении назы-
вают обычно такую задачу:
t,
(*(•)) = $ ft х> x)dt—+ extr,
3t(x(-)) = § hit, x> ~ai’ i = 1> - • - ,m,
^0
X(^o)~XO> x(/1) = xi.
v Предполагается, что функции удовлетворяют тем
же условиям, что и L в п. 1.4 1 они сами и их част-
ные производные по х и х непрерывны по совокупности
переменных. Для простоты ограничимся случаем т = \.
Теорема (необходимое условие экстре-
мума в изопериметрической задаче) Пусть
функция х(-) доставляет локальный (относительно про-
странства Cl([ZQ, fx])) экстремум в задаче
t,
3f0(x(-)) = J Ш х> x)dt—>extr,
^i(x(-)) = J x< x)dt — ait x(Q = xp i = 0, 1 (Г)
/о
и при этом функции t н- fox(t, x(t), х(1)) и х (/),
x(t)) принадлежат С1([/о, fj). Тогда найдутся числа
Хо, не равные нулю одновременно и такие, что для
интегранта L=\f0 + ^1f1 выполнено уравнение Эйлера
- L- (t, х (t), х (t))+Lx (t, x (0, x (0) = 0. (2)
Доказательство. А) Аналогично тому, как это
было проделано в начале доказательства теоремы п. 1.4.1,
77
вычисляем первые вариации функционалов 36 и ?! по
Лагранжу:
6?,-(£(•), х(•)) = $ (Pi (0* (0 + Pi (О х (0)dt, i = о, 1, (3)
где
= x(0,x(0)> Qi(t) = fiX(t> x(t), х(0).
Возможно одно из двух: или 6?г = 0, Ух(-)£
ССЦро, У), х(/о) = х(^) = О или 65\=ЙО. В, первом
случае по теореме п. 1.4.1 *
- w fli * (0. X (0) + flx (t, X (t), xt) = (0)
и, положив lo = O, Xj= 1, немедленно получаем (2).
Б) Пусть 6?j^fe0 и, значит, существует функция
У (•) € С1 ([£0, М). y(ta) = y(t1) = O, для которой вариация
6?х(х(-), у(-))^0. Рассмотрим функции двух переменных
Ф/(а,Р) = ?,- (х(.)+ах(.) +₽!/(•)), i = 0, 1,
предоставив читателю проверить, что они непрерывно
дифференцируемы в окрестности нуля, причем
д-Ч1Ш=83;(х(-), Х(-)), ^^ = б?/(х(-), !/(•)).
Лемма. Для
х (t0) — х (tt) = О
д (фО, ф1) (Q Q) _
д<Ро
др
d<pi
др
а.(а, Р)
дфо
_ да ’
(0. 0)
любой х (•) £ С1 (|7e, fj) такой, что
S20(x(.), х(-)), 6?0(^(.), !/(•))
6?1(^(-), х(-)), 6?!(;(-), ?(•))
= 0.
(4)
Доказательство. Если определитель (4)#= 0, то
отображение (а, Р) и» (<р0 (а, Р), «рДа, р)) переводит неко-
торую окрестность точки (0,0) на некоторую окрест-
ность точки (ср0 (0, 0), ср! (0, 0)) (соответствующую теорему
об обратном отображении мы уже использовали §п. 1.3.2).
В частности, найдутся такие а и р, а, следовательно, и
допустимая функция x(-)4-ax(-) + pz/(-), что <р0(а, Р)=
=?0(х(-)+ах(->+р^(-)) = ?0Хх(.))—е, где е > 0, а
78
cpja, ₽) = <₽! (О, 0) = 51(x (•))=«!• Это противоречит тому,
что х(-) доставляет локальный минимум в задаче (1).Ц
В) Из равенства (4) имеем
oSi (х(-), {?())
(знаменатель здесь по предположению отличен от нуля).
Полагая Х„= 1, — 830(х(-), у(-)) /83г (х(-), у(-У),
убеждаемся, что
Ка83а (х (•), х (•)) + к1831 (х ("), х(•)) = О (5)
для любой х/-') б С1 ([/„, /J), у которой х(/о) = х(/х) = О.
Легко видеть' что левая часть (5) имеет вид
$ ((^оРо(0+\Р1 (0) * (0 + (Мо (0 + (0) * (0) dt.
Применяя основную лемму вариационного исчисления,
получаем уравнение
- 4 (КРо (0 -ЬXxpx (0) + (Куа (0+х141 (0) = о,
совпадающее с (2). |
Задачу (Г) впервые рассмотрел Эйлер в своей зна-
менитой работе 1744 г. Там же методом ломаных было
получено соотношение (2). Собственно говоря, это и со-
ставляло основное содержание работы. Несомненно, в ней
уже содержатся начала метода множителей Лагранжа.
В заключение бегло рассмотрим задачу со старшими
производными:
ti
Я (х (•)) = $ f (t, х, х, х, ..., х^) dt —>extr,
^0
х^)(//) = х{, i = 0, 1, J = 0, ..., п — 1.
За подробностями отошлем читателя к [2J или [3]. Эту
задачу будем исследовать в пространстве Сп([/0, /,])
функций, непрерывных вместе с производными до порядка
п на отрезке \ta, ij. Функцию f и ее производные по
х, х, ..., х(п) будем предполагать непрерывными по со-
вокупности переменных. Пусть х(-)—функция, подо-
зреваемая на экстремум. Вычислим первую вариацию
79
функционала по Лагранжу:
33(х(-), *(•)) = $ ]dt, (7)
«Л'=° /
где р (/) = А-(/, x(t)....х(п>(0).
OX'J>
Из условия локальной экстремальности вытекает, что
дЗ(х( ), х (-)) = 0, если только (/,-) = 0, i = 0, 1,
/ = 0, 1, ...,п—1. Интегрируя (7) по частям (предоста-
вив читателю сформулировать нужные требования иа
гладкость pj ( )), преобразуем первую вариацию к виду
/ п X
б^(х(.),х( )) = Ч 2-(-1УрГ(О )x^dt
(0\>=° - /
и, применив обобщение основной леммы.^ классического
вариационного исчисления на случай функций из Сп ([£„, /J)
с условиями x(J}(ti) = O, i = 0, 1, j = 0, 1, ...,п — 1 (это
обобщение также предоставляем продумать читателю),
получим, что необходимым условием экстремальности
х ( ) является выполнение следующего уравнения, назы-
ваемого уравнением Эйлера—Пуассона'.
п
х(о, ...,>>(о)=о. '
§ 1.5. Задача Лагранжа и основная задача
оптимального управления
1.5.1. Постановки задач. Важным этапом в историй
естествознания явилось сочинение Жозефа Луи Лагранжа
«Аналитическая механика», опубликованное в 1788 г.
В частности, трактат Лагранжа сыграл исключительную
роль и в развитии вариационного исчисления. Именно
там была поставлена следующая задача на условный
экстремум:
t,
2 (х(-)) = $ f x(t), x(t)) dt—>extr, (1)
Ф (t, x (t), x{t)) = О ФФ Ф7 (t, x (t), x (0) “0.
/ = 1, ..., tn, (2)
X (^o) = Л'о> ^(^i) —Xj.
80
Здесь х(-): fo. Ц—*Rn, f: RxR"xR"—*R,
Ф: RxR”x.Rn —>R“. Задачу (1) и различные ее моди-
фикации, связанные с дополнительными ограничениями
(другими граничными условиями, дополнительными ин-
тегральными соотношениями и т.п.; см. также 1.2.6),
стали называть впоследствии задачей Лагранжа. Для
решения задачи (1) Лагранж использовал тот основной
Прием, о котором говорилось в п. 1.3.2,—правило мно-
жителей. Впрочем, оно не было им аккуратно обосно-
вано, и потребовалось более ста лет для того, чтобы
Придать рассуждениям Лагранжа вид строго доказанной
теоремы.
Отметим два наиболее важных частных типа ограни-
чений, охватываемых общим выражением (2). Ограни-
чение Ф(/, х) = 0, когда функция в (2) не зависит от х,
называется в вариационном исчислении фазовым. В меха-
нике фазовые ограничения называют также голономными
связями.
Другой случйй—когда соотношения (2) можно раз-
решить относительно производных х. Тогда это ограни-
чение записывается в форме уравнений х = ф(£, х, и),
*(•): К. M-*Rn,«(-): M->Rr,<p: Rx R‘х Rr—*Rn.
Переменные x(-) здесь называют фазовыми, переменные
“(•)—управлениями. Этому важнейшему случаю мы и
уделим основное внимание. Точнее говоря, будем рас-
сматривать далее задачу
^(х(-), «(-)) =
= x(Z), w(f))d/+^0(x(Q,x(/i))-*extr, (Г)
to
x—ср(Л x, u) = 0, ф(х(/0), х(^)) =
= 0(«фДх(^, x(/i))==0, /=1, .. ,,s).- (2')
При этом в (Г), (2') f V—>R, ср- V—>Rn, ф: W —>RS,
где V и W—открытые множества в пространствах Rx
xR"xRr и RnxRn соответственно. Моменты времени
и t± будем считать здесь фиксированными.
Ограничение х—ф(£, х, и) = 0 называется дифферен-
циальной связью, ограничения ф(х(/0), х(^)) = 0 назы-
ваются граничными или краевыми условиями. Задачу
(Г), (2') будем называть задачей Лагранжа в понтря-
гинской форме.
81
Все функции f, ф и ф предположим непрерывно диф-
ференцируемыми.
Далее в гл. IV будет рассмотрен еще более общий
случай, когда ta и tr также могут меняться, допуска-
ются изопериметрические ограничения типа равенств,
неравенств и т. п.
Задачу (Г), (2') будем рассматривать в банаховом
пространстве Z = C’x([f0, Rn)xC([70, Rr) Иначе
говоря, будем рассматривать пары (х(-), «()), гдех(-)—
непрерывно дифференцируемая n-мерная вектор-функция,
а «(•)—непрерывная r-мерная вектор-функция. Пару
(х(-), и(-)) будем иногда сокращенно обозначать через г.
Элемент г=(х(-), «(•)) £Z будем называть управляемым
процессом в задаче (Г), (2'),*если х (£) = ср (t, x(t), u(t)),
7], и допустимым управляемым процессом, если,
кроме того, удовлетворяются краевые условия. Допусти-
мый элемент z = (%(), «(•)) будет называться оптималь-
ным в слабом смысле процессом или слабым минимумом
в задаче (1'), (2'), если он доставляет локальный мини-
мум в задаче, т. е. если найдется такое е > О, что коль
скоро- ||х—Mi<e и IIй — и||0<е, то 3(z)^3(z). •
1.5.2. Необходимые условия в задаче Лагранжа.
Попробуем применить к задаче (17, (2') предыдущего
пункта общий прием Лагранжа, о котором шла речь
в п. 1 3.2. По аналогии с конечномерным случаем функ-
цию Лагранжа следует записать так:
^(х(-).и(-); X0)=Jl^ + /, (1)
*0
где
L (t, х, х, и) = р (t) (х—ф (t, х, и)) + kaf (t, х, и), (2)
3
I (Хо, Х±) = 2 Р/Ф/ С^о, л'1), ^Р-о- (3)
] =0
То, что «терминальная часть» или терминант функции,
Лагранжа I имеет вид (3), не вызывает сомнения—здесь
имеется полное подобие с конечномерным случаем. Что
же касается ограничения х = ф (t, х, и), то оно должно
выполняться для всех t £ [£0, ix], и соответствующий «мно-
житель Лагранжа» р (•) по аналогии должен быть функ-
цией t, а его вклад в функцию Лагранжа имеет вид
интеграла, а не суммы.
82
Итак, функция Лагранжа составлена. Следуя рецепту
Лагранжа, нужно теперь искать условия экстремума
полученного выражения, «как если бы переменные были
Независимы». Иначе говоря, следует рассмотреть задачу
«(•); Р(-). Ц, 4)->extr, (4)
считая множители Лагранжа фиксированными. Задача (4)—
это задача Больца, рассмотренная в п. 1.4.2. Выписан-
ные там условия экстремума в применении к задаче (4)
приведут к правильным уравнениям, называемым урав-
нениям Эйлера—Лагранжа. Точнее, имеет место следую-
щая теорема.
Теорема Эйлера—Лагранжа. Если г=
= (х(-), «(•))—оптимальный в слабом смысле процесс для
задачи (Г), (2') п. 1.5.1, то найдутся множители Лаг-
ранжа Хо = р.о0 в задаче на минимум и ^0 в задаче
на максимум, р (•) € С1 (1Л, R"). р = (р1, •••> £,), не
равные одновременно нулю1) и такие, что будут выпол-
нены уравнения Эйлера
x(t), h(t)) + Lx(t,x(t),x (t), u(t))=O,
(5)
Lu(t,x(t), x(t), u(t)) = O, (6)
и условия трансверсальности
Lx(tk, x(tk), x(tk), «O = (-l)*^(x(Q, х(Ш
A = 0,l. (7)
Вследствие того, что L не зависит от и, а I от и,
уравнение Эйлера по «имеет вырожденный вид (6), а
условий трансверсальности «по и» нет вовсе.
Эту теорему (и даже в несколько более общем виде)
мы докажем в § 4.1 как прямое следствие общей теоремы,
х) Математик-пурист отметит вопиющую неточность в этой фразе:
Ло и ц, это числа, а р( )—элемент функционального пространства,
так что они и не могли бы равняться одному и тому же нулю
одновременна. Каждое из них может равняться или не равняться
своему нулю в своем пространстве. Однако все мы так привыкли
отождествлять нули всех пространств, что эта фраза уже не режет
глаз.
83
касающейся правила множителей Лагранжа для гладких
бесконечномерных задач.
Отметим, что из этой теоремы следует необходимое
условие экстремума в изопериметрической задаче (с про-
извольным числом изопериметрических условий) и урав-
нение Эйлера—Пуассона для задач со старшими произ-
водными. Изопериметрические ограничения
tt
St(x(-))=s\ft(t, х, x)dt = at, i=l, ...,m;
to
можно учесть, введя новые фазовые переменные, связан-
ные со старыми дифференциальной связью' xn+l(t) =
“ fit хг (0, • •., х„( /), хг (t), х„ (0) и удовлетворяю-
щие краевым условиям
х„+А*1)~*п+1(*о) = “и т.
Если теперь применить теорему Эйлера—Лагранжа, то
получатся нужные необходимые условия в изоперимет-
рической задаче. При исследовании задачи со старшими
производными ее можно свести к виду (Г), (2')-, полагая
х = х±, х1 = х2, ..., хп = и и применяя далее теоре'му
Эйлер а—Л агр анжа.
1.5.3. Принцип максимума Понтрягина. В пятидесятых
годах многочисленные потребности прикладных дис-
циплин (техники, экономики и др.) стимулировали поста-
новку и рассмотрение нового класса экстремальных задач,
получивших название задач оптимального управления.
Необходимое условие экстремума для задач этого класса_—
«принцип максимума»,—сформулированное Л. С. .Понт-
рягиным в 1953 г., было доказано ц развито впоследст-
вии им, его учениками и сотрудниками (см. [12]). Важно
отметить, что это условие имеет существенно иную форму
в сравнении с классическими уравнениями Эйлера и Лаг-
ранжа: в качестве обязательного условия в решениегзадачи
оптимального управления входит решение вспомогатель-
ной задачи на максимум (отсюда название—«принцип
максимума»).
Здесь мы будем рассматривать частный случай общей
постановки задачи оптимального управления, когда ЕГза-
даче Лагранжа в понтрягинской форме (см. (1')’и (2')
п. 1 5.1) появляется еще одно дополнительное условие
иа управление: ugU. Точнее говоря, будет рассматри-
«4
ваться такая задача:
«(•)) =
=*$ f(t, x(i), u(t))dt+y0(x(tt), xO-Hnf, (1)
to
x(t)—<f(t, x(f), u(t))-0, фу(х(/0), x(^))=0,
/ = 1, ...,s, (2)
u£ll. (3)
Функции f, ф, фу—такие же, как в (Г), (2') п. 1.5.1,
а 11—фиксированное множество в Rr. Более общая задача
будет рассмотрена в гл. IV.
Задачу Лагранжа мы рассматривали в некотором ба-
наховом пространстве. Здесь же, желая применять самые
простые средства, изберем иной путь описания допусти-
мых элементов, сходный с тем, о котором шла речь в
п. 1.4.3, где простейшая задача классического вариацион-
ного исчисления была расширена до задачи в простран-
стве КСЦЦо, ZJ) кусочно-дифференцируемых функций.
Пару (х(-), «(•)) будем называть управляемым про-
цессом в задаче (1) — (3), если управление u(-): [i0,y—►
—>11—кусочно-непрерывная функция, фазовая траекто-
рия х(-) кусочно-непрерывно дифференцируема и при этом
всюду, кроме точек разрыва управления «(•), функция
х (•) удовлетворяет дифференциальному уравнению х (f) =»
= ф(/, х(0> «(0)- Управляемый процесс называется до-
пустимым, если, кроме того, удовлетворяются краевые
условия.
Допустимый процесс (х (•), ы(•)) называется оптималь-
ным, если найдется такое е > 0, что для всякого допу1
стимого управляемого процесса (х(-), «(•)) такого, что
|х(0—х (£) | < е, у выполняется неравенство
5(х(.), «(.))>5(х(.), «(.)).
Попробуем снова применить к задаче (1)—(3) общий
прием Лагранжа, о котором речь шла в п. 1.3.2. Функ-
ция Лагранжа задачи (1) — (3) будет иметь тот же вид,
что и в задаче Лагранжа — ограничения типа принадлеж-
ности («611) в функцию Лагранжа не включаются. Итак,
-2’(*(•). «(•);?(•)> M = *(4)
t»
85
где
L(t, х, х, и) = р(О(х—<р(0 x, u)) + k9f(t, x, и),
8
i (xe, xt) = 2 м>> xi)* и»=к
• /=0
(5)
(6)
Далее, как всегда, нужно рассмотреть задачу
u(-);p(-)> р, \) —>inf (7)
(считая множители Лагранжа фиксированными) «как если
бы переменные были независимы». Задача (7) естествен-
ным путем распадается на две: ,
«(); Р(-)> И. X0)->inf (пох(-)), (8)
-S7 (£(•). u(-); р(-), р, М—>inf (пои(-)€^),(9)
где через 41 мы обозначили множество кусочно-непрерыв-
ных функций со значениями в 11. Задача (8)—это снова
задача Больца; задача же (9) имеет, как легко понять,
следующий простой вид:
u(-ye4L, (10)
^0
где v(t, u)=\f(t, x(t), u)—p(t)q(t, x(i), u). .
Необходимое (и достаточное) условие экстремума
в задаче (10) совершенно очевидно: «(•JC'M доставляет
минимум в задаче (10) тогда и только тогда, когда всюду,
кроме точек разрыва «(•) выполнено соотношение
min%(t u) = x(f,
HSU
<=>minZ,(Z, x(t),x(t), u) = L (t, x (t), x(t),
us it
ФФтах[р(0ф(^> x(t), x(t), u)] =
И611
= p(O<p(t x(t), 2(0, «(0). (11)
Необходимые условия экстремума в задаче (8), соеди-
ненные с( 11),приводят к необходимым условиям экстремума
в задаче (1)—(3), получившим название принципа
максимума Понтрягина (из^а специфического вида
условия (11)). Точнее, имеет место следующая теорема.
86
Теорема (принцип максимума Понтря-
гина). Если (х(-), и(-)).есть оптимальный процесс для
задачи (1)—(3), то найдутся множители Лагранжа
£о = Ро>О, p(-)^KCr([ta, fj, R”*), [л= (цх, цДне
равные нулю одновременно и такие, что выполнено урав-
нение Эйлера
x(t), x(t), u(t)) — Lx(t, x(t), x(t), u(t)),
' X (12)
принцип максимума (ll)'u условие трансверсальности
Lx(t, x(t), x(t), H(0)|f=/ft = (-l)^(i(/o),
k=0,l. (13)
1.5.4. Доказательство принципа максимума в задаче со
свободным концом. Здесь принцип максимума Понтря-
гина будет доказан в простейшей ситуации, когда тер-
минальная часть функционала отсутствует, один из кон-
цов закреплен, а второй свободен, т. е. в (1) п. 1.5.3
фо = О, а в (2) фу(х0, х1) = хв/—хвр /=1, ..., п.
Таким образом, мы имеем задачу
t,
3(х(-), и (•)) = f(i, х (t), и (t)) dt —► inf, (1)
x(t)—ф(/, x(t), u(i)) = o, x(tt) = xB, (2)
и € П. (3)
Функции f, fx, <p, фд. предполагаются (как и в преды-
дущем пункте) непрерывными по совокупности пере-
менных.
Посмотрим, как выглядит в этом случае принцип мак-
симума Понтрягина. Поскольку у нас функция I (ха, хг) =
т
— (%о<—хы) не зависит от хх, из условий трансвер»
i=i
сальности (13) п. 1.5.3. получаем
(^i. х (/х), х (/х), и (fx)) = р (/х) = 0. (4)
Далее, уравнение (12) п. 1.5.3 приобретает вид
Li + Lx = 0 е>-р (0 = р (0 (0- V, (0» (5)
87
где мы ввели сокращенные обозначения: fx (t) — fx (t, x (t),
«(/)), Ф*(0 = Ф*(^ x(0> «(0)- Если допустить, что Xo = O,
то вследствие единственности решения задачи Коши для
однородного уравнения (5) должно быть р (•) = 0, а значит,
ж, силу условия трансверсальности на левом конце (см.
(13) п. 1.5.3) и [л = 0. Но это противоречит условию тео-
ремы, согласно которому не все множители Лагранжа
могут быть одновременно нулями. Значит, Хо=/= 0 и можно
считать Хо=1. Но тогда р(-) однозначно (в силу един-
ственности решения задачи Коши для линейной Неодно-
родной системы) определяется уравнением (5) и краевым
условием (4). Суммируя сказанное, можно сформулиро-
вать принцип максимума так:
Теорема (принцип максимума Понтря-
гина- для задачи со свободным концом).
Если процесс (х(-), «(•)) является оптимальным в задаче
(1)—(3), то для решения р(-) системы
-p(t) = p(t)^x(t)-fx(t) (6)
с краевым условием
P(*i)===0 (7)
в точках непрерывности управления «(•) выполнен прин-
цип максимума
тах(р(0ф(<» х(0> u)~f(t,x(t), и)) —
и«П
• = р (0 ф (t, X (/), и (t, X (t), и (/)).
Для доказательства этой теоремы, как и в предыду-
щих случаях, воспользуемся методом вариаций. Начнем
с определения элементарной—вейерштрассовской—иголь-
чатой вариации, аналогичной той, что была применена
в п. 1.4.4. Обозначим через То множество тех точек из
(t0, tj), в которых функция «(•) непрерывна. Зафикси-
руем точку т^Т0, элементе» £11 и число X > 0 настолько
малое, что [т—X, т]с[/0, fj.
Управление
... .. . f'u(t), если ^[т—X, т), ,о.
” есЛи (8)
88
,назовем элементарной игольчатой вариацией управления
«(•). Пусть xK(t) = Xt,(t\ т, и) —решение уравнения х =
==<р(/, х, и%(0) с начальным условием х%(£0) = х(£0)==хв.
Назовем х^(0 элементарной игольчатой вариацией траек-
тории, а пару (x^(Z), uK(t))—элементарной вариацией
процесса (х(-), «(•))• Пару (т, v), определяющую эту
вариацию, будем называть элементарной иголкой.
Доказательство теоремы как обычно разбиваем
на этапы. Первые два этапа целиком относятся к теории
обыкновенных дифференциальных уравнений.
А) Лемма о свойствах элементарной вари-
ации. 1. Пусть элементарная иголка (т, о) фиксирова-
на. Тогда существует такое Хв>0, что при
1) траектория х%(-) определена на всем отрезке [iB, / J
и при Х|0 Хл(0~*х(/) равномерно на [/в, т];
2) при t^x, существует и непрерывна по
X производная
^xK(t-, т, v) = zA(i; т, о),
которая при Х = 0 определяется как производная справа’,
3) функция t>->y(tf=z0(t, т, v) на отрезке [т,
удовлетворяет дифференциальному уравнению
У=Чх(*)у (9)
и начальному условию
у(т) = ф(т, х(т), и) — ф(Т, х(т), и(т)). (10)
Доказательство леммы основано на двух извест-
ных фактах теории обыкновенных дифференциальных
уравнений: локальной теореме существования и единст-
венности и теореме о непрерывно дифференцируемой за-
висимости решения от начальных данных. Эти теоремы
в нужной для нас форме'содержатся в стандартных учеб-
никах по обыкновенным дифференциальным уравнениям
[10, 11, 15]. Кроме того, читатель может обратиться к
тексту § 2.5.
Докажем лемму сначала для случая, когда функция и( ) непре-
рывна.
Рассмотрим дифференциальные уравнения
’х =<p((, х, u4(t)). (11)
х =<v(t, х, u(t)). (12)
89
Согласно (8) Правые части этих уравнений совпадают при t < т—А,
а так как х^(<о) = *о=*(^о)> то п0 теореме единственности решения
задачи Коши х?Д/) = х(1) при t < т —А и по непрерывности
g(A) = xA(T-A) = £(r-A). (13)
В частности, g (X) непрерывно дифференцируема по А, и
g(0)=x(T), (0)= — х(т)= —ф(т, х(т), и (т)). (14)
Обозначим через Е (t, s, g) решение задачи Коши для дифферен-
циального уравнения с фиксированным управлением v:
х =<₽(*. х, v), x(s)=g. (15)
В соответствии с локальной теоремой существования и единствен-
ности можно подобрать такие > 0 и > 0, что Е (t, s, I) опре-
делено при
р—т| < 61, |s—т| < 61; |g — х(т)| < еь
а в силу теоремы о зависимости решения от начальных данных Е —
непрерывно дифференцируемая функция.
Согласно (8) и (13) для определения x^(t) на отрезке [т—X, т]
мы должны в (15) положить g = g(A) = x(r — А) и если Аг < 6 выбрано
так, что |g (А) —х (т) | < ег при 0 < А Аг, то
xK(t) = S,(t, т —A, g (А)), т—А</^т.
В частности,
т](А) = хЛ(т) = Е (т, т —A, g(А)), (16)
будучи суперпозицией непрерывно дифференцируемых функций, сама
непрерывно дифференцируема по А и
т] (0) = х (т), т]' (0) = - Es (т, т, g (0)) + Е g(т, т, g (0)) g' (0) =
= — S«(t, т, g(0))-S5(x, т, I (0)) ф (т, х (т), и(т» (17)
в силу (14). Решение Е (t, s, £) задачи Коши (15) удовлетворяет
эквивалентному интегральному уравнению
t
B(f, s, g) = £+$<₽(<?. Н (a, s, g), v)da. (18)
s
Дифференцируя его по s, имеем
аде, s, g)=
t
= —<p(s, S (s, s, g), г)+^фж(а, S(O, s, g),t») Bs(o, s, g) da
s
и, полагая t = s — x, g = x(T), получаем (с учетом очевидного тож-
дества E (t, i, g) = g)
ЕДт, t, x(x)) = —ф(т, х(т), v). (19)
90
Аналогично, дифференцируя (18) по £ и подставляя те же значения
аргументов, получаем
Sj(t, т, х(т)) = Е (20)
(здесь £ = (Э§(7Э§*) = (6д) —единичная матрица). Подставляя (19) и
(20) в (17), имеем
ц(0) = £(т), т)' (0) = <р(т, х (т), V)— ф(т, х (т), и(т)). (21)
Далее, функция S непрерывна в точке (т, т, х(т)), причем
3 (т, т, х(т)) = х(т), а £(•) непрерывна в точке т. Поэтому для лю-
бого е > б существует такое б > 0, что при
|/—т|<6, | s—т|<6, |£—£(т)|<6
выполняются иеравенства
| S (/, s, §)—х (т)| < е/2, |J(0-J(t)|<b/2. (22)
Возьмем положительное ^<6 столь малым, чтобы при 0<К<%х
выполнялось неравенство | g(А,)—х(т)| < 6. Тогда для т—
s = t—Л и £ = |(А) будут иметь место неравенства (22), откуда
xfc(0-£(0l=|a(*,T-b. 6(*))-£(01<
<|Э(С т—Л, g(X))— х(т)Ц-|х(т) — х(<)| < е/2+е/2 = е.
ПОСКОЛЬКУ X^(t)sa X (t) при — X,
0<k<l1>=£|xx(/) — x(<)| < e, 4«SU<T,
чем доказано первое утверждение леммы.
Теперь обозначим через X ( , т]) решение задачи Коши для урав-
нения (12) с начальным условием х(т) = т}. По теореме о зависимости
решений от начальных данных существует такое в2, что X (f, г])
определено при | q-— х (т)| < е»,, т< t < и является непрерывно
дифференцируемой функцией. Согласно (8) и (16), а также в силу
теоремы единственности x^(t} = X (t, г] (?«)). Снова, как суперпозиция
непрерывно дифференцируемых функций, xfe(0 непрерывно дифферен-
цируема по (t, А) пфи T<i</x и 0<Х<Х2, где Х2 выбрано так,
чтобы при 0<-к<ка выполнялось неравенство | г](X)—х (т)| < е2.
Полагая k0 = min (Х.п Х.2), мы видим, что верно второе утверждение
леммы.
Переходя от уравнения (12) к эквивалентному интегральному
уравнению, имеем с учетом (16)
t
Ь. (0 = П (М + $ Ф(<т> (а), и (а)) da.
т
Дифференцируя это уравнение по Л и полагая затем Х = 0 и обо-
значая, как и в условии леммы, y(t)=-£rxK(t) I , находим
С*Л I о
i
У (0 = п' (0) + J Фл (°, х (а), и (а)) у (а) da.
т
91
Это интегральное уравнение эквивалентно’ уравнению (9) с началь-
ным условием у(т) = т]'(0), совпадающим с (10) ввиду (21).
Если управление и (•) — кусочно-непрерывная функция, то посту-
паем следующим образом. Для простоты пусть точек разрыва две,
скажем, и ctj, и т (в которой «(•) должно быть непрерывным)
расположена между ними: /0 < < т < а2 < t±. В полосе
системы (11) и (12) (в кот^ых при / = at нужно считать управление
равным его предельному значению u(cii—0)= Uni и (/)) совпадают
Л - о
и по теореме единственности х^(1) х(i).
Теперь переходим в. полосу а!</<а2 (снова полагая на ее
границах управление равным предельным значениям u(cti-|-O) при
/ = 061 и «(а2—0) при / = а2). Здесь мы решаем уравнения (11) и (12)
с начальным условием х=х(ат). Наши предыдущие утверждения
применимы, и мы убеждаемся в непрерывной дифференцируемости
Хд.(О по Л.
Наконец, в полосе а2</</х (с тем же соглашением о значе-
нии управления при / = а2) решаем наши дифференциальные урав-
нения с начальными условиями х^(а,^ и х(а2). Еще раз ссылаясь
на теорему о зависимости решения от начальных данных, доказы-
ваем непрерывную дифференцируемость хк(/) по Л приа2</</1
d I
и вычисляем р(/)=^х^(/)| 0 тем же способом, что и раньше. Н
В) Лемма о приращении функционала.
Положим = (а(-), «л(-)) и докажем, что эта функ-
ция дифференцируема справа в точке Х = 0.
Пусть р(-)—решение системы (6) с краевым условием
(7). Тогда
%'(+0) = |;Зг(^(-). “x(-)L.0 = a(^ о)»
ИЛ |Л=г т U
где
а(х, 0—/(т, х(т), й(т))—
—р(т)[ср(т, х(т), о)—ф(т, х(т), и(т))]. (23)
Доказательство. Поскольку
(1 it
ХМ-Х(О) = $/(^^(О. «г(0)Л-р(«. *(0- u(t))di=
io in
it
= 5 [/(*> >.«(/))—/(Л <(0> «(0)]Л+
t
T
+ $ 1У (** x(t), «(/)]*»
x-k
9i
имеем
Х'(О)»Ит xWvX(0)=^p (t, 4(t), 2(О)л|к=+о+
T
+шТ S t/(Z’ Хк®’
+ T-X
«(/)] dt.
Поскольку по лемме n.-A) x^(t) непрерывно дифференцируема по X,
В первом члене применимо обычное правило дифференцирования Под
Виаком интеграла, а во втором воспользуемся теоремой о среднем,
после чего
h
т
+ Пт [/ (с,
хл(с)> v)—f(c> х(с), «(с)] —
— x(t), u(i)) y(t)dt+f(x, х(т), v)—f(T,' ?(т), u(r))
т
(24)
(вдесь мы воспользовались тем, что т—Х<е<т и потому с—*т;
х?а(с) -у»- х(т) в силу первого утверждения леммы п. А); у (^ обозна-
чает то же, что и в этой лемме.
Далее, р(-) удовлетворяет системе (6), а у( ) удовлетворяет си-'
стеме (9). Поэтому
=—р (О Ф* (0 у (0+Гх (О у (0(О ф х (0 у (0 у (О-
Интегрируя это равенство в пределах от г до ft и учитывая
краевое условие (7) для р(-) и условие (10) для у(-), получаем
t, it
J. fx (0 У (0 dt = J [p (/) у (01 dt = p(t}y (0 £ “
=.—р(т)[ф(т, £(т), v)~<p(t, x(t),'h(t))]. (25)
Сопоставив (24), (25) и (23), получаем, что %'(-НД = а (т, и). Ц
В) Завершение доказательства. Если правый
конец свободен, то в силу леммы п. А) всякая элемен-
тарная вариация допустима (при достаточно малом X).
Значит, если (х(-), «())—оптимальный процесс, то при
малых X
5Ы-)» и(-))т(*)>х(о)=»х'(+о)>о.
93
Применив лемму п. Б) получим, что условие а(т, ц)^0
необходимо для оптимальности (х(-), «(•)). Но и
были произвольны. Мы доказали, следовательно, что
для любого t, принадлежащего множеству точек непре-
рывности управления «(•), и для любого выполнено
неравенство
p(t)<p(t, x(t), x(t), u)^.
<p(O<p(*, x(t), x(t), £(/)),
равносильное неравенству я(/, м)>0и (11). Теорема пол-
ностью доказана.
§ 1.6. Решение задач
Задачи, о которых говорилось в начале главы,— за-
дачи, поставленные с разными целями и в разные вре-
мена,— здесь будут рассмотрены единообразно, по одной
стандартной схеме, диктуемой принципом Лагранжа.
Эта схема состоит из шести этапов:
1. Запись формализованной задачи и обсуждение про-
блемы существования и единственности решения.
2. Составление функции Лагранжа.
3. Применение принципа Лагранжа.
4. Исследование возможности £о = О.
5. Нахождение стационарных точек, т. е. решение урав-
нений, вытекающих из принципа Лагранжа.
6. Исследование стационарных точек, выбор решения
и запись ответа.
Во всех задачах, о которых пойдет речь, принцип
Лагранжа является строго обоснованной теоремой либо
уже доказанной, либо доказываемой в последующих гла-
вах. Применимость единой схемы к задачам столь раз-
ного содержания подчеркивает универсальность этого
принципа. Разумеется, рассматривая другие задачи, ис-
следователи могут столкнуться с ситуациями, которые не
подходят ни под одну из известных конкретных схем
(классическое вариационное исчисление, оптимальное
управление, линейное программирование и т. п.). Тем
не менее и здесь принцип Лагранжа в том или ином его
понимании может оказаться верным или, по крайней
мере, может быть полезным ориентиром. Понимание общих
идей и ситуаций, в которых он применим,— о них речь
94
пойдет в гл. III и IV—может помочь-найти необходимые
условия экстремума и в измененной обстановке. Впрочем,
не Менее важно отдавать себе отчет и в том, что прин-
цип Лагранжа верен не всегда, и потому опасно при-
менять его бездумно.
1. 6.1. Геометрические экстремальные задачи. Здесь
решены все задачи, поставленные в п. 1.1.2 и форма-
лизованные в п. 1.2.2. Первый этап предложенной схемы
предполагает обсуждение вопроса о существовании реше-
ния. Геометрические задачи этого пункта конечномерны,
и существование решения в них обеспечивает следующая
теорема.
Теорема Вейерштрасса. Пувть функция
f: R‘v—>R непрерывна и для некоторого а множество
S?af ~ {x\f (х)^а} непусто и ограничено. Тогда решение
задачи f (х) —> inf существует.
Доказательство этой теоремы очевидным образом
следует из классической теоремы Вейерштрасса о сущест-
вовании^ минимума непрерывной функции на ограничен-
ном и замкнутом подмножестве в Rv [14, т. 1, с. 176,
370], [9, т. 1; с. 234], ибо множество очевидно,
замкнуто.
Переходим к решению задач.
Задача Евклида о вписанном параллелограмме.
Эта задача была формализована так (см. (1) п. 1.2.2):
1. Fo(х) = х(х—b)—*inf, О^х^б.
Мы опустили несущественный множитель Н/b и свели
задачу к задаче минимизации. Функция fa непрерывна,
отрезок [0, 6] ограничен и замкнут. По теореме Вейер-
штрасса решение задачи существует. Пусть это реше-
ние х. Ясно, что х=/=0 и х^=Ь, ибо (0) = /0(Ь) = 0, а
функция принимает и отрицательные значения. Значит,
х£(0, 6). Функция f0—гладкая. Поэтому надо искать
стационарные точки в задаче /0(х)—*inf.
2 — 5. /о(х) = О=>х = &/2.
6. В силу единственности стационарной точки х =
=6/2 Е [0, 6] есть решение задачи, т-. е. искомый парал-
лелограмм ADEF характеризуется тем, что | AF |=| АС |/2,
т. е. F есть середина отрезка [Д, С]. Этот факт и был
установлен в п. 1.1.2 геометрическим путем.
Примечание. Наша задача оказалась элементар-
ной гладкой задачей. Поэтому функция Лагранжа не
95
выписывалась и пп. 2—5 «слились». Была использована
теорема Ферма (п. 1 3.1).
Задача Архимеда об изопифанных сегментах
шаров (п. 1.2.1). Решение здесь совершенно аналогично
задаче Евклида и поэтому приводится без комментариев.
1. f9(h)~ha!2— л/Р/З-—*sup;
2—5. Д(^) = 0=>/1==]Аг/2л.
6. Значение fe в нуле равно нулю, а в точке Уа/п
меньше, чем значение в стационарной точке Уа/2п. Зна-
чит, h~]/а/2я есть решение задачи. Вспомнив, что а=
получаем h. = т. е. искомый шаровой сегмент
является полушаром (высота равна радиусу).
Задача Аполлония о кратчайшем расстоянии от
точки до эллипса. Она была формализована так (см. (6)
п. 1.2.2):
1- *2) = (*x—£1)2+(*2—£s)a-+inf;
=(Xi/fli)a + (x2/fl2)2 = 1. Эллипс—ограниченное и замкну-
тое множество, функция /0 непрерывна, значит, решение
x = (xlt х2) по теореме Вейерштрасса существует. Функ-
ции fe и гладкие.
2. ^=Х0((х1-|1)2+(х2-^)а)+\((х1/й1)2+(хг/аа)а-1).
3.
-£\-а = О =ф (х2—У + Ххх2М = 0.
4. Пусть Хв = 0. Тогда £^^0 (множители Лагранжа
не равны нулю одновременно!). Значит, из 3-го этапа
следует, что xt = х2 = 0 (О, 0) = /1(х1, х2)=*0=#1.
Итак, Хо ф 0, и можно положить = 1. Обозначим при
этом Х1 = Х.
5. (Для простоты ограничиваемся случаем, когда
615*^0).
(x-51) + ^z/a? = 0, i = < — 1,2.
Подставляя в уравнения эллипса, получаем
ЬМ , ... ,п
*^*(а’+х)* + (а*+х)* L W
96
6. Число стационарных точек задачи (т. е. точек, со-
ответствующих тем X, которые удовлетворяют уравне-
нию* (1)) не больше четырех (см. рис. 26, неравенство
<p(0) = Bi/Oi + Ba/Oa> 1 показывает, что <р(Х) изображена
для точки (£lt £з), лежа-
щей вне эллипса). Для
полного решения задачи
надо решить уравнение
(1), получить X,, найти со-
ответствующие точки
x(Xf), подставить эти точ-
ки в и найти наимень-
шее из полученных чисел.
Примечания. 1. За-
дача 1 —это гладкая зада-
ча с ограничением типа ра- -uj 2
венства. В пп. 2—5 при-
менялось правило множи- Рис' 261
телей Лагранжа (п. 1.3.2).
2. Соотношения (х;—gJ + X^/a? —О имеют очевидный
геометрический смысл: вектор £—х, соединяющий точку £
с минимальной точкой х, пропорционален вектору-гра-
диенту функции в точке х, т. е. вектор 5—х лежит
на нормали к эллипсу. Этот факт был установлен впер-
вые Аполлонием.
3. Выведем из полученных нами соотношений уравне-
ние кривой, «разделяющей» те точки £, к которым можно
провести две нормали, от ’точек, к которым можно про-
вести четыре нормали. Очевидно, что это разделение
происходит для X, удовлетворяющих соотношению (1),
для которых
Х£(-а!' ““»• <2)
(01 *ТЛ/
Из (2) имеем
а? + X = А o’+X » -Л (^а,)’4,
где
Л=(<й-^)/((51а1)*/‘ + (5,аг),/*).
Подставляя в (1), получаем уравнение разделяющей кривой
(ё101)!/*+(ё 2оа) ‘/г = (al—о?)’7*.
4 В. М. Алексее» др. g7
Это — уравнение астроиды (см. рис. 7 в-§ 1.1). Вне астроиды
каждая точка имеет две нормали, внутри нее—четыре,
на самой астроиде—три (за исключением вершин’, где
имеется две нормали). Описанный здесь результат также
был получен Аполлонием в его «Конике».
Задача Кеплера о вписанном цилиндре (см. (3)
в п. 1.2.2). Решение этой задачи подобно решению за-
дачи Евклида, и мы его не комментируем.
1- 1о(х) — х(х*—1)—> inf, O^x^l.
2—5. ^(х) = 0=фЗ? = 1=>х==/3/3.
6. В силу единственности стационарной точки в (0, 1),
х = ]/3/3 есть решение задачи: искомый цилиндр харак-
теризуется тем, что отношение его высоты 2х к радиусу
V1 —? равно У 2.
Задача о преломлении света. Эта задача
была поставлена и решена методом Гюйгенса в п. 1.1.3.
Здесь мы даем стандартное решение ее, восходящее к
Лейбницу (см. (4) в п. 1.2.2).
1. /0 (х) = /а2 + x*/V1 + V р2 + (| -х)2/у2 — inf.
Все лебеговы множества непрерывной функции /0
компактны, и, значит, по теореме Вейерштрасса решение
задачи существует.
2-5. f'(x)^o=>—
VrV а2-f-х2
</₽’+(М!
sin epi sin (р2
v? —-— =--
(см. рис. 19 в п. 1.2.2)-.
6. Точка х, удовлетворяющая последнему уравнению,
единственна (проверьте!), значит, она и является реше-
нием задачи. Итак, точка преломления луча света на
границе двух сред характеризуется тем, что отношение
синуса угла падения к синусу угла преломления равно
отношению скоростей распространения света в соответ-
ствующих средах. Это и есть закон Снеллиуса.
Задача Штейнера. Она была формализована так
(ей. (5) в п. 1.2.2):
1. fo(x) = |x—^l + lx—|2| + |х—В3| —>-inf, x£R2,
B.-6R2, i = 1,2,3, |х| = Кх? + х2.
98
Решение задачи существует по теореме Вейерштрасса
(проверьте!). Возможно одно из двух: либо решение
совпадает с одной из точек t = 1, 2, 3, либо не сов-
падает ни с одной. Будем решать задачу в последнем
случае. Тогда функция будет гладкой в окрестности точки х
(проверьте!).
2-5.
Мх) = о=>
li—х
I*—lil
li—x . |3 —— х
|х—I2I lx—13|
(3)
6. Уравнение (3) означает, что три единичных вектора,
смотрящие из х в сторону g2, Jj3 соответственно, в
сумме равны нулю. Значит, эти векторы параллельны
сторонам равностороннего треугольника, и, следовательно,
величины углов £]Х£а, £ax£s, В3хВх, под которыми из точки х
видны стороны треугольника, равны 120°. Таким образом,
точка х является точкой Торичелли. Она может быть
найдена как точка пересечения двух дуг окружностей,
стягиваемых хордами [?п |а] и [|1( £3] и вмещающих
углы 120°. Это построение возможно, если только ни один
из углов треугольника не больше 120°. В противном слу-
чае дуги не пересекаются, и, значит, невозможно, чтобы
точка х не совпадала ни с одной из точек i=l, 2, 3.
Но тогда она должна, очевидно, совпадать с вершиной
тупого угла, ибо против тупого угла лежит самая боль-
шая сторона треугольника.
Ответ: Искомая точка есть точка Торичелли, если
все величины углов треугольника меньше 120° и есть вер-
шина тупого угла в остальных случаях.
Итак, все геометрические задачи, о которых говори-
лось в п. 1.1.2, а также задача о преломлении света из
п. 1.1.3 решены. Заодно решим и задачу Тарта льи:
fo(x)~x(8—х)(8—2х)—>sup, 0=0^4.
2—5. f'o (х) = О =Ф Зх2—24х + 32 = 0 => х = 4—4/]/"3.
6. Ответ: Одно число равно 4—4/]/"3, другое 4+ 4/^3.
1.6.2. Аэродинамическая задача Ньютона. Эта задача
была поставлена в п. 1.1.5 и формализована в п. 1.2.3.
tdt
14-и2
inf, х = и,
х(0) = 0, х(Т) = £, uGR +
4*
99
Для такого рода задач доказать непосредственно тео-
рему существования не совсем просто. Главная беда —
невыпуклость интегранта 0(1 +us) по и при и^О. Но
тем не менее эту задачу мы решим до конца. Наш даль-
нейший план таков. Предположив, что решение задачи
существует, мы' применим к гипотетическому решению
принцип Лагранжа. Выяснив, что существует единствен-
ная допустимая в задаче стационарная кривая (т. е. до-
пустимая кривая, для которой выполняются Все условия,
диктуемые принципом Лагранжа), непосредственной вы-
кладкой убедимся, что именно она доставляет абсолют-
ный минимум. В заключение вспомним слова Ньютона и
убедимся, что.найденное решение в точности то, которое
было Им описано в 1687 г.
т
2. & + +
Z.==T^?- + p(x-w).
3. Уравнение Эйлера:
—^; + Z.x = o=^p(O = c°nst = po. (1)
Условие трансверсальности:
Р0 = Р0 = —Рт- (2)
Условие минимальности по w:
роы>—-------pou(0, V«>0. (3)
1 + u2 l + «*(0 v
4. Если допустить, что Хо = 0, то необходимо, чтобы
р0 0 (ибо иначе из (2) вытекали бы равенства Хо = ра =
= р0 = Pi = 0, но все множители Лагранжа не могут
обратиться в нуль одновременно). Если же Хо = О иро+=0,
то из (3) следует, что й (0=0, а значит, х(0= $ и (0 dt @ 0.
о
Но тогда искомое тело не имеет «длины»—оно явля-
ется плоской пластиной. Если же | > 0, то^^О и
можно считать, что Хо = 1. Отметим еще, что случай
ро^О также невозможен, ибо при этом функция
100
,// (J 4- и») — pou монотонно убывает и (3) не выпол-
няется при и > и (Z).
5. Из (3) (с Ло=1) следует, что до некоторого мо-
мента оптимальное управление равно нулю (проверьте,
что при р0<0 и малых t функция «^->(//(1 4-u»))—рои
достигает минимума при и = 0). Затем оптимальное управ-
ление й(-) должно быть найдено из уравнения
2м/
^-(1+м2)2 ’
(4)
нолучающегося из уравнения £а = 0. Момент излома т
определяется тем, что функция и —+ (т/(1 + и2)) —раи имеет
два равных минимума — в нуле и в точке, определяемой
из (4) при t — х. Иначе говоря, в момент излома должны
удовлетворяться соотношения (далее через и (т) обозна-
чено и (г 4-0) =/=0):
2и(т)т т
—Ро —-----------, -—s------р.и(т) = т. (5)
(14-и» (т))2 14-м» (т) й v '
Из второго уравнения получаем: — и2(т)т/(1 4-ы»(т))=
==рв«(т), откуда рв = —ти(т)/(14-и2(т)). Подставив
это соотношение в первое уравнение (5), находим, что
tt* (т) = 1 =Ф и (т) = 1 (ибо й > 0) и 'тогда снова нз пер-’
вого уравнения (5) получаем равенство т = —2р0.
После излома оптимальное решение удовлетворяет
соотношению (4), из которого следует, что
С6)
Но
dx dx dt dt pa f 1 , o , „
- = u=> — = —- — =tu — = — -----k 2u 4- 3u31 .
dt du dt du du 2 \ и ~ ~ J
Интегрируя это соотношение с учетом равенства х (т) — 0,
ы(т) = 1, получаем параметрические уравнения искомой
оптимальной-кривой
t----7(4+2“ + “’)’ р,<°-
101
Рис, 27.
6. Кривую (7) называют кривой Ньютона. При этом
в (7) и£[1, со). Нетрудно понять, что пересечение пря-
мой х = аЛ с кривой Ньютона, соответствующей пара-
метру р0 = —1, единственно. Действительно, х(-,—1)
непрерывна и выпукла, ибо
d2x _ du _ 1 „
dt2 ~ dt —’'dt/du""
Но, с другой стороны, из формул (7) видно, что кривая
Ньютона х(-, ра) получается из,кривой х(-, ^1) гомо-
тетией с центром в (0, 0) и коэф-
фициентом | рв | (рис. 27). Значит,
для того чтобы провести кривую
семейства (7) через заданную точ-
ку (£, Т), нужна найти точку пе-
ресечения прямой х=ЩТ с кри-
вой х (•, —1) и затем сделать
соответствующую гомотетию кри-
вой £(•, —1). Получим допусти-
мую кривую х(-). Убедимся, что
она дает абсолютный минимум
в задаче. Для этого вернемся
к соотношению (3) с Хо= 1. Пусть х(-)—любая допусти-
мая кривая (т. е. х (•) € КС1 ([0, Т]), х(0) = 0, х(Т) = 1).
Тогда в силу (3)
—z-------рох (t) —х----------pau(t).
1 + х2(/) \ + u(t)2 ™ k '
Проинтегрировав это соотношение и учитывая, что
_ т т
u(t)==x(t) и J x(t)dt = J х (t)dt = Jj, получаем
о о
т т
с tdt г t'dt
J 14-х2 1 + х2’
о о
Задача полностью решена.
Примечания. 1. В п. 2—5 применялся принцип
Лагранжа для задачи оптимального уравнения, сводя-
щийся к принципу максимума Понтрягина (п. 1.5.3).
2. Сопоставим теперь полученное решение с реше-
нием, описанным самим Ньютоном. Вспомним слова
Ньютона, приведенные в п. 1.1.5 и посмотрим еще раз
на его чертеж (рис. 18). При этом наряду с буквами,
'расставленными самим Ньютоном, используем еще и
некоторые наши обозначения. Имеем:) MN j = t, \ ВМ |=х,
)BG | — т, угол BGP — q, и тогда из построения Ньютона
получаем, что
tgcp=x(i), | BP |/| BG | = tg ср =Ф | ВР | = тх,
|GP j2 = | BG |2 4-1 BP j2 = (x2 + 1)t2.
Теперь из пропорции Ньютона
|Aftf }:| GP’| = | GP |8:4 ] BP |X j GB |\
подставляя наши обозначения, получаем
t _ т8(х2+ 1),/г Xi = т_ ,g.
4тэт2 ^(?+1)2 4' ( >
Но это—не что иное, как соотношение (4), в которое
Подставлено значение рв = — т/2. Из (8), рассуждая так
же, как и раньше, мы находим интегрированием выраже-
ние (7) для кривой Ньютона. Отметим еще, что «затуплен-
ность» кривой и условие на с качок в точке Got (угол там
равен 135°) были по существу предусмотрены Ньютоном в
его «Поучении» об усеченном конусе.
Таким образом, задача Ньютона была им решена
полностью, но смысл егог решения оказался недоступным
ни для его современников, ни для многих его последо-
вателей—вплоть до нашего времени.
- 1.6.3. Простейшая задача о быстродействии. Постав-
ленная в п. 1.1.7, эта задала была формализована сле-
дующим образом:
Т—>inf, tnx = u, uCfw,, u,l,
L r. 2J (1)
x(0) — x0, x(O) = vo, x(T) = x(T) = 0
(cm. (5) в n. 1.2.4). Случай u1 = u2 интереса не предста-
вляет, поскольку при этом не для всякой пары (х0, v6)
существует функция х(-), удовлетворяющая всем огра-
ничениям (1), а если такая функция существует и отлична
от тождественного нуля, то значение Т определяется
однозначно, так что задачи минимизации в сущности и нет.
При и1 < и2 мы можем уменьшить число параметров
задачи при помощи замены x(t) = B(t—Т)2,
В терминах функции £(•) общий вид задачи (1) не ме-
няется, но параметры х0, t»0, ut, иг приобретают другие
юз
значения. В частности, если положить
Л = (Uj—«2)/2щ, В = («! 4- «2)/4/п,
то £€[—1, 1]. Имея это в виду, будем считать далее
в (1) т—1, и± = —1, «2=+1. Кроме того, обезначим
Х = ХП х = ха.
Теперь приступаем к реализации нашей стандартной
схемы:
т
1. Т — \ 1 'dt—* inf, хх=*х2, х2=«, «€[—1,1],
3 (2)
x1(0) = xo, x2(0) = ott, х1(7') = х2(Т) = 0.
С существованием решения мы поступим точно так же,
как и в предыдущем пункте: найдя нз принципа Ла- -
гранжа функцию х(-), «подозреваемую» на оптималь-
ность, непосредственной проверкой убедимся в том, что
оиа дает нам решение задачи.
т
2. J Ld/4-pl(xl(0)—xo) + p,2(x.2(0)-— р0)4-
о
+v1x1(T')4-vax2(T), (3)
где L«=Xa4-p1(x1-~x2)4-p2(x2—«).
3, Уравнения Эйлера—Лагранжа:
-лЧ+£'.=0’ тг-W
.Условия трансверсальности:
Л(°) = Н1» Р8(°) = Н». = —*!, Р2(Т)=—v2. (5)
При-нцип максимума: опустив не зависящие
от и слагаемые, можно записать это условие в виде
F» (0 и (0 = max Jp2 (0 «} = | р2 (01,
-1 <и< 1
или
/ signp2(0, если р2(0#=0,
U ' Д любое из [—1, 1], если p?(Z)=?O.
Кроме того, в рассматриваемой задаче переменным
является также конечный момент времени Т (ьець именно
его МЫ и минимизируем), так что формально эта задача
104
е укладывается в рамки и. 1.5.3. Можно показать, и
pro будет сделано в гл. IV, что в такой ситуации к урав-
нениям (4)—(6) следует добавить еще и условие = О
(стационарность функции Лагранжа по Т), вполне согла-
сующееся с общей идеологией принципа Лагранжа. Диф-
ференцируя (3) по Т и учитывая равенства х2 (Т) = и (Т),
it(T) = x2(T)==0, получаем
^r= 4 + v2rI(T)«0. (7)
4. Обращается ли Хо в нуль или нет—специальной
роли в данной задаче не играет, поскольку 10 не входит
В (4)-(6).
5. Из уравнений (4) заключаем, что p2(f)s const, а
р2(-)— произвольная линейная функция. При этом
р2(/)^0, ибо
(4) (5) л (7) ~
Рг (О = 0 Pi 0 =>> Pi = Из= — ^2= 0 Х.0 = О
и все множители Лагранжа оказываются нулями.
.Линейная функция, отличная от тождественного нуля,
обращается в нуль на отрезке [О, Г] не более одного
раза. Поэтому из (6) получаем следующие возможности
для оптимального управления:
а) и(*)^1;
б) ц(0^-1
(р2(-) не обращается в нуль на [О, Г]),
( 1, 0</<т,
в) = | _ 1, т< t^T,
„ ( — 1, 0 t < т,
г) = 1, т <
(р2(-) обращается в нуль в точке i = r, значение управ-
ления в точке т несущественно, так как изменение его
в- одной точке не оказывает влияния на функцию х (•)
(почему?); по той же причине можно опустить случай
т = Т и т = 0.)
Дальнейшие рассмотрения удобно вести на фазовой
плоскости (х1, х2) ^рис. 28). Решая задачу Коши
х2 = u(f), Xi(T) — xt(T) = Q (8)
105
для одного из управлений а) — г), получаем единственное
решение, а с ним и единственную начальную точку
(х0, ио) — (*1 (0)> ^(0))» которая этому решению соответ-
ствует. Нетрудно проверить, что при всевозможных т
и Т эти начальные точки однозначно покрывают всю
плоскость. Прежде всего,
х1 = х2, х2 = 1 = х|/2+CV (9)
хг = хг, х2 = —1 =»%! = —х^/2 + С3, (10)
и, таким образом, фазовые траектории на участках посто-
янства управления лежат на параболах одного из се-
мейств (9) или (10).
Управлению а) соответствуют начальные точки, лежа-
щие на дуге OF А (рис. 28): х0 = v20/2, va < 0; управлению б)—
точки на дуге ODB: ха =— v2a/2, по>0.
Начальные точки С, лежащие слева от разделительной
линии BDOFA (х0 =— и0|и0|/2) отвечают управлениям в):
на дуге CD семейства (9) и(()з1, в момент / = т по-
падаем в точку D, происходит переключение управления,
и далее движемся по дуге DO с и(1) =—1. Аналогично
начальным точкам Е справа от разделительной кривой
соответствуют управления г).
6. Остается показать, что найденное единственное реше-
ние x(t) = Xx(/), отвечающее заданной начальной точке
(хв, п0), действительно доставляет решение задаче (2).
Предположим, что некоторая функция х (•) определена
на отрезке [0, Г], имеет кусочно-непрерывную вторую
производную и х(0) = х0, х(0) = цо, х(Т) — х(Т) = 0, при-
чем Т^Т. При Т <Т мы доопределим х(-), положив
x(Z) = O, t£\T, Т]. После этого обе функции х (•) и х ()
106
будут определены на одном и том же отрезке [О, Т] и
будут иметь одинаковые граничные значения
х(0) = х(0) = х„, х(0) =£(0) = v„,
х (Т) = х (Г) == х (Т) = х (Т) = 0.
Покажем, что если | х | 1, то %(•) = х(-)н, в частности,
неравенство Т <Т невозможно. Тем самым будет дока-
зана оптимальность функции х(-). Ввиду симметрии за-
дачи ограничимся управлением в) (или его предельным
случаем а)). Если | х| 1, то, интегрируя дважды нера-
венство x(t) 1 и учитывая (11), получаем
т t
х(т)—-х(т) = J J (1—-x(s))dsd/^O, (12)
о о
причем равенство здесь возможно, только если во всех
точках 'непрерывности x(s)= 1, а тогда х (Z)ee=x(/),
€[0, т].
Аналогично, интегрируя дважды неравенство х —1,
получаем
т т
х(т)—х(т) = J $ (—1—x(s))dsd/<0, (13)
т t
причем и здесь равенство возможно лишь, если x(s)= — 1
и x(t) = x(t), f£[T, Г].
Сравнивая (12) и (13), находим, однако, что х(х) —
= х(т), а тогда, как уже было сказано, 'x(t) = x(t'),
^[0, Л-
Примечание. Из соотношений (5) — (7) следует
равенство 4 = | р2 (Т) |, и, таким образом, равенство 4 = 0
в этой задаче оказывается возможным, когда р2(-) обра-
щается в нуль при t = T. Тогда функция р2 (•) й 0 (ибо
иначе все множители Лагранжа были бы нулями) и вслед-
ствие равенства р2 (Т) = 0, р2 (•) не меняет знака и, значит,
переключений управления нет вовсе. Следовательно,
случай 4 = 0 соответствует движению по линиям пере-
ключения А ВО и BDO.
1.6.4. Классич*еская изопериметрическая задача и
задача Чаплыгина. Стариннейшая экстремальная задача —
первая из двух названных в заголовке—-была поставлена
107
в п. 1.1.1 и формализована разными способами в п. 1 .,2.4.
В частности, формализация (2) п. 1.2.4 сводит ее к более
общей задаче, охватывающей также и задачу Чаплыгина.
Исходя из этой формализации, приведем сейчас решение
обеих з'адач, следуя нашей стандартной схеме. Итак:
т
1. S = yu)dt —>sup;
y — v, (и, v)£A, x(0) = x(T), y(0) — y(T).
Множество допустимых скоростей А будем считать
замкнутым выпуклым ограниченным множеством в R*.
Упражнение. Покажите, что для разрешимости поставлен-
ной задачи необходимо, чтобы 0£А. Указание: можно восполь-
зоваться результатом упражнения 2 в п. 2.2.3.
2. ^^^Ldt + ^(x(Q)-x(T)) + v(y(O)-y(T)), (2)
о '
где
L = — -°(XV—уи) + р (х—и) + q (у—у).
3. Уравнения Эй лера—Лагранжа:
—+ —0=Ф—р—-^-v= О,
Условия трансверсальности:
р(0) = р(Т) = р, q~(O) = q(T) = J.
Принцип максимума:
(ЯО-^Ио)«(О + ($(О+^(о)у(О =
« Шах. ((p(t)—h-y(t)} « + (<7(0 W
4. Если допустить, что 4 = 0, то из уравнений Эй-
лера-Лагранжа p(t) = const, q (t) = const, причем
P2 + <72 > 0, ибо иначе ввйду условий трансверсальности
все множители Лагранжа оказались бы нулями. Теперь
108
принцип максимума приобретает вид
pu(t) + qv(t)= max (pu + qv),
(и, »)бЛ
откуда видно, что (u(f), v(f)) все время принадлежит од-
ной и той же прямой, а именно одной из двух опорных
к множеству А прямых,-перпендикулярных вектору (р, q)
(рис. 29). Поэтому
х(0 = и (0 = и (0)-—a (Z) q,
y(t) = v(t)=v(O) + a(t)p,
откуда, интегрируя, получаем
t
х (t) = х (0) -г U (0) t— 5 a (/) dt • q,
°t , (5)
y(t)=y(O) + v(O)t +ja(t) dt-p.
Полагая в (5) t = T и используя краевые условия
х(0) = х(Т), у(0) = у(Т), убеждаемся, что вектор (q,—р)
пропорционален (ц(0), о(0)),
После чего из (5) видно, что
(x(t), y(t)) все время лежит
на прямой, проходящей через
(х(0), р(0)) параллельно вектору
(q, —р). Следовательно, замкну-
тая кривая {(х(0> У
вырождается (лежит на прямой)
и ограничиваемая ею площадь
равна нулю (покажите это аналити-
чески, исходя из указанного вы-
ше выражения для S!). Следовательно, эта кривая не
может быть оптимальной.
5. Из этапа 4 следует, что можно положить \==1.
Тогда из (3)
р + тг =0=»p(/)-bMp- = fc = const,
q— J = 0 =ф 9 (/) — а=: const.
109
Подставляя эти выражения в (4), получаем
(х (0—a) v (О — (У (О — b) u(t) =
= max {(х(0—a)v—(y(t)—b)u}. (6)
(и, v) gA
Оставляя теперь в стороне общий случай, ограни-
чимся двумя частными вариантами.
а) Классическая изопериметрическая за-
дача. Здесь
А —{(и, v) | iz2-j-v2^ 1}
и из (6) находим
х(0 = «(0 = -^^, у(0=?(0=^^, (7)
где
^ = ((i(Z)-a)2+(y(0-6)2)V2
(скалярное произведение векторов (х—а, у—b)n(v,—и)
будет наибольшим, когда они одинаково направлены и
второй имеет максимально возможную длину, т. е. 1).
Из (7) имеем
г (»)=°.
т. е. на оптимальной траектории
^(x(t),y(t))^((x(t)-ay + Cy(t)-by)'/^
= max ((х(0 — a)v—-(yit)—b)iz) = 7? = const. (8)
(u, v) g A
Отсюда заключаем, что оптимальная траектория яв-
ляется окружностью с центром в точке (а, Ь) и радиу-
сом R Поскольку угловая скорость движения по этой
окружности равна
$ = ^((х-а)у—(у—Ь)х)^±,
и через время Т мы должны возвратиться в ту же точку
7*
(быть может, совершив несколько оборотов), 2пп=— и
Т *
#=2лп‘ Площадь-, ограниченная найденной кривой,
110
будет при этом равна
т т т
S = ^'\(xv—yu)dt=~ {(xy—yx)dt = -^ ^((x—ajy —
Следовательно, п=1 (окружность обходится только один
раз) и S = T2/in,. Заметим, что здесь Т — это длина кривой.
б) Задача Чаплыгина. Здесь
Л ={(«, v)|(«—и0)2 + у2СУ2},
(иа, 0)—вектор скорости ветра, V | и01 — максимальная
скорость самолета. Для решения вспомогательной экст-
ремальной задачи
(x(t) —cftv—(y(t)-—b) и—>sup,
(и —«0)2J-t^V2,
можно, например, сделать подстановку « = «0 + £, у = г|
и воспользоваться тем же геометрическим соображением,
что и в предыдущем случае. Это дает уравнения
где теперь уже величина
7?(0 = ((х(0-а)2 + (у(0-Ь)2)‘/а
не будет постоянной. Однако
^=лЬг((^(О-«)^(О+(НО-ь)у(О)=
_x(t)—a __uady{t)
R[t) U°~V dt ’
так-что
(X (0, У (0) = R (*)~ $ У (0 = ((* (0—а)2 + (у (tnbYi1*-
max {(*(0—a)v—(y(t)—b)4 = const. (9)
v (u, v)eA
Следовательно, оптимальная кривая—это эллипс с урав-
нением,
((x—ay + (y—b)2)l/i—^y = const. (Ю)
111
Как и в предыдущем случае, можно показать, что он
обходится траекторией у (0) ровно один раз. Заме-
тим, что если бы скорость самолета была меньше ско-
рости ветра (V < | иа |), он не мог бы вернуться в-исход-
ную точку (докажите это и сравните с упражнением в
начале этого пункта), а кривая (10) была бы гипербо-
лой, т. е. незамкнутой.
Примечание. Вопреки принятой схеме, мы обошли
молчанием вопрос о существовании решения. Это не слу-
чайно: простой ссылкой на теорему Вейерштрасса здесь
не обойдешься. Наметим вкратце возможный путь рас-
суждений.
Прежде всего без ограничения общности можно счи-
тать, что х(0)= 1/(0) = 0.
Используя теорему Арцела [КФ, с. 110—111], можно
установить, что множество пар функций {(%(•), у (•))},
удовлетворяющих на отрезке [0, Г] обобщенному усло-
вию Липшица
$A,t^ t„ 0< tit < Т (И)
\ *1 *2 »1 —"*2 / 4
и краевым условиям
x(0) = x(T) = 0, //(0) = i/(T) = 0
компактно в пространстве С([0, T])xC([0, TJ).
Далее, на этом множестве функционал «площадь» оп-
ределен и является полунепрерывной снизу функцией.
Применяя соответствующее обобщение теоремы Вейер-
штрасса, убеждаемся в существовании решения(х(-), у(-)).
Наконец, функции, удовлетворяющие условию (11),
дифференцируемы почти всюду, причем (x(t), у(£))£ А.
На эту ситуацию оказывается возможным распространить
принцип максимума, и, следовательно, к решению (х(-),
у(-)) применимы приведенные выше рассуждения.
1.6.5. Задача о брахистохроне и некоторые задачи
геометрии. Рассмотрим следующую серию простейших
задач классического Вариационного исчисления:
1.
Х1 ________
3 (у (•)) = $ У*У\+у'г(1х-+ inf; у(хл) = уа, у(х^ = уг.
*0
(1)
112
эи а = — 1—задача о кратчайших линиях на плоскости
В нее попадает несколько интересных задач: при а=0
получается задача о кратчайших линиях на плоскости,
при а = —1/2 — задача о брахистохроне (см. п. 1.2.4),
при ос= 1 —задача о минимальной поверхности вращения;
п
Лобачевского в интерпретация Пуанкаре (полуплоскость
Пуанкаре [13, с. 131 — 132]).
Интегрант fa^y^ 1 4- у'г в задачах (1) не зависит от х.
Поэтому уравнение Эйлера (п. 1.4.1) имеет интеграл
Энергии,
жащие в
2—4.
из которого мы и находим все экстремали, ле-
верхней полуплоскости.
ifldy
y’fay‘—f = const (1 + g'*) = Da. (2)
5. Сначала разберем случай отрицательных а: а»— р,
р > 0. Тогда
y&dy . „
-д=ах => х
У Di—yW
замену
Г) VP
gap =D3sina t => y=D1^ sin1/? t =>dg = —5—sin^P-^cos/d/.
(3)
Подставляя полученные выражения в (3), приходим к
следующим соотношениям (D1/? = C):
t
g = Csin1/?/, x = Ci + y J sin1/? s ds.
В частности, если p= 1/2 (брахистохрона), получается
семейство циклоид, заданных в параметрической форме
(т = 2£):
У(т, С, С1)=-~- U—cost), х(т, C,.C1) = C1 + y(t—sinr).
Если р—1 (полуплоскость Пуанкаре), получаем семейство
полуокружностей
y(t, С, С^ = С sin t, x(t, С, С1) — С1—С cost
^(х-С^ + у^СК
Из серии а > 0 решим лишь пример о минимальной по-
верхности вращения. Из (2) имеем
.. =dx.
У D2y2— 1
113
С помощью подстановки
Dy = ch t D dy = sht dt, ]/D2y2—l==sh£
находим двупараметрическое семейство цепных Линий:
У = i chJOx + ДО-
ПОЛУЧИВ во всех случаях двупараметрическое семейство
экстремалей (решений уравнений Эйлера), нужно теперь
подобрать постоянные интегрирования так, чтобы удов-
летворялись краевые условия 2/(xJ = г/;, и перейти к
этапу 6 — исследованию найденных решений и записи
ответа.
Это, однако, здесь сделано не будет. Вспомнив, что
вдобавок мы снова уклонились от обсуждения вопроса
о существовании решения, читатель с еще
. . । . большим основанием, чем в предыдущем
\ I / пункте, вправе заявить: «Неладно что-то
М в оптимальном королевстве!» И действи-
VI У/ тельно:
При а>0 задача (1) может не иметь
\ К обычного решения. Например, если в за-
\ / даче о минимальной поверхности враще-
\ / ния (а = 1) граничные условия симмет-
ричны (г/(—Хд) — у(хв)), то надлежит ис-
у кать симметричную экстремаль, т. е.
y = chDx/D. Все экстремали этого вида
Рис. 30. получаются из экстремали z/ = chx гомо-
тетией, и в совокупности они заполняют
только угол, а не всю полуплоскость (рис. 30)-. Поэто-
му при достаточно большом хв задача, скажем, с усло-
виями у(—ха) = у (х0) = 1, неразрешима.
При а<0 интегрант в задаче (1) стремится к беско-
нечности при г/—>0. Поэтому, например, задача о бра-
хистохроне а — —1/2 с обычными краевыми условиями
г/(хо) = О, у(х1)>0 (п. 1.1.4) вообще не укладывается в
стандартные рамки.
Для того чтобы получить полное решение задач се-
рии (1), нужна дополнительная работа.
ГЛАВА II
АППАРАТ ТЕОРИИ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
Читатель познакомился с различными постановками
экстремальных задач, с основными понятиями и общими
идеями, а также получил представление о некоторых
приемах решения этих задач. Теперь мы переходим к
последовательному и достаточно формальному изложению
соответствующей математической теории.
Общность развиваемой теории и ее сравнительная
простота оказались возможными за счет свободного ис-
пользования фактов и понятий, относящихся к смежным
разделам математики, в первую очередь функциональ-
ного анализа. Здесь они изложены в нужной нам форме.
Значительную часть главы составляет то, что можно
было бы назвать «Элементами дифференциального исчис-
ления».
§ 2.1. Предварительные сведения
из функционального анализа
В этом параграфе рассказывается о тех фактах функ-
ционального анализа, на которые мы далее опираемся
при иостроении теории экстремальных задач. Доказа-
тельства, которые можно прочесть в учебнике А. Н. Кол-
могорова и С. В. Фомина [КФ], мы, как правило, опус-
каем.
2.1.1. Линейные нормированные и банаховы прост-
ранства. Напомним, что линейное пространство X назы-
вается нормированным, если на X определен функционал
Ц-Ц: X—>R, называемый нормой и удовлетворяющий трем
115
условиям:
а)
||х||>0, Vx£X и ||х|| = 0 &х = 6,
б)
||ах|| = |а|||х||, Vx$X, Va£R, (1)
в)
ki+^Kkill+hji, vxx, хаех>
Иногда, чтобы подчеркнуть, что норма задана именно
в X, мы пишем
Всякое нормированное пространство становится мет-
рическим, если ввести в ием расстояние
Р(%1, х2)=||х1 —х2||.
Полное (относительно введенного расстояния) линей-
ное нормированное пространство называется банаховым
пространством.
Упражнения. Пусть X = R2. Какие функции из перечислен-
ных ниже и при каких зиачениях параметров задают норму в X?
1. Л/(х) = (|х1|^+|х2|/')1/^, 0<р<оо;
2. А/ (х) = | ацХ1 + а12хг 1 + | аа1х1 + а22х21;
3. N (х) = ГПЗХ {| I» I ^21^1 "F ^22^2 I}*
4. Описать все нормы в R2..
5. Доказать, что все нормы в R2 эквивалентны. (Нормы и
У2 называются эквивалентными, если существуют такие с > 0 и
С > 0, что cN1(x)^NS!(xXCN1 (х), vxgX.)
Совокупность X* всех линейных непрерывных функ-
ционалов на X (сопряженное к X пространство) явля-
ется банаховым пространством, если задать в X* норму
||х*||х*= sup <х*,х>,
IIX НЛ < 1
где <х*, х> означает результат применения к х функцио-
нала х*.
Подробнее об этом см. [КФ, гл. IV, § 2].
Упражнение 6. Найти нормы в пространствах, сопряженных
к описанным в упражнении 1—4.
Для нас важнейшую роль будут играть следующие
банаховы пространства.
Пример 1. Пространство С (К, R") непрерывных
вектор-функций х(-): К—*R", заданных на компакте К
116
с нормой
||x(-)||o = max|x(O|.
t Е К.
Пространство С (К, R) мы обозначаем просто С (Л).
Пример 2. Пространство Cr([Z0, R”) г раз не>
прерывно дифференцируемых вектор-функций х (•):
[/0, М-*R”> заданны^ на конечном отрезке [/0,/JcR,
с нормой
||x(-)[|r = max(||x(-)||0, •k(r> (-)llo)-
Пространство С ([70, R) мы обозначаем С([/0, ZJ).
Упражнения.
Т. Доказать, что всякое конечномерное нормированное простран-
ство является банаховым.
8. Доказать, что единичный шар конечномерного нормирован-
ного пространства является выпуклым, замкнутым, ограниченным
центрально-симметричным множеством, для которого начало коор-
динат является внутренней точкой, и наоборот, для любого выпук-
лого замкнутого ограниченного центрально-симметричного множества,
для которого начало координат является внутренней точкой, суще-
ствует такая норма, в которой это множество является единичным
шаром.
9. Привести пример нормированного, но не банахова пространства.
2.1.2. Произведение пространств. Фактор-простран-
ство. Пусть X и Y—линеййые пространства. Их произ-
ведение ХхК, т. е. множество всех пар (х, у), х£Х,
y£Y, превращается в линейное пространство, если опе-
рации сложения и умножения на число определить по-
координатно:
(*i> У1) + (ха, уг) = (хх + х2, уа + yj, а (х, у) = (ах, ау).
Если X и У—нормированные пространства, то ив про-
изведении XxY можно ввести норму, например, так:
||(х, i/)||xxy = max{||х|]х, »}• (П
« -
Упражнение. Проверьте, что || х ||д+1| у ||у и К || *]& +11
Также некоторые нормы в ЛХУ, эквивалентные норме (1).
Имеют место следующие очевидные леммы.
Лемма 1. Если X и Y—банаховы пространства, то
и XxY банахово.
Доказательство предоставляется читателю.
117
Лемма 2. Всякий линейный функционал Л £ (X х К)*
однозначно представим в виде
<Л, (х, = <х*, х> + <у*, у>, (2)
где х*£Х* и у* £Y*.
Доказательство. Положим <х*, х> = <Л, (х, 0)>,
<#•, г/> = <Л, (0, г/)>. Линейность этих функционалов оче-
видна, а непрерывность ограниченность) вытекает из
оценок:
|<х\ х>|<||Л||||(х,0)||==||Л||||х||,
1<У*. г/>|^|(Л||||(О, г/)||==||Л||||г/||.
Однозначность представления (2) также не вызывает
сомнений. |
Поскольку при любых х*£Х* и y*£Y* формула (2)
определяет некоторый функционал Л g (X х У)*, то мы по-
лучили полное описание пространства (ХхК)*. Кратко
оно дается следующей формулой: (ХхК)* = Х*фУ'*.
Пусть теперь X—линейное пространство, L—неко-
торое его подпространство Положим хоэх', еслих—х' £L.
Введенное отношение будет отношением эквивалентности
(ибо ОЧеВИДНО, ЧТО X <Х> X, Хг ОО Х2 => Х2 ОО Х± И Хх оо х2,
х2<х>х3=>х1<х>х3), а значит [КФ, гл. I, § 2] опреде-
лено разбиение X на классы. Класс эквивалентных эле-
ментов по введенному выше отношению называется клас-
сом смежности по подпространству L. В совокупности
классов смежности естественным образом вводятся опе-
рации сложения и умножения на число (КФ, гл. III,
§ 1, п. 4); при этом выполняются аксиомы линейного
пространства. Таким образом, совокупность классов смеж-
ности превращается в линейное пространство, называе-
мое факта р-пространством X по L и обозначаемое X/L.
Классом смежности л(х), которому принадлежит эле-
мент х£Х, является класс х-\-Ь. Отображение л: X—+XIL
является линейным (докажите!). Его называют канони-
ческим отображением X на Х/L. (Отображение л являет-
ся, разумеется, эпиморфизмом1).) Очевидно, чтоЛ = Кег л.
Пусть теперь X — нормированное пространство и L—
его подпространство. Положим
RiIx/l= inf IIX к,
«в
1) То есть отображает X на все X/L.
(3)
или
||?||x/L= inf ]]x|]x= inf ||x0 4-/J. (3')
x’eL
Из определений (3), (3') сразу следует, что оператор
л непрерывен (|| лхЦ^ЦхЦ) и для любого £ € Х/L найдется
х£Х, для которого
ЯХ = 1, hK2^||x/L. (4)
Теорема о фа ктор-п ростр а нстве. Пусть X —
нормированное пространство и L—его замкнутое подпро-
странство. Тогда функция Ц-Цх/l, задаваемая соотноше-
нием (3), является нормой на Х/L. Если пространство
X является банаховым, то фактор-пространство Х/L с
нормой Ц-Цх/z. также является банаховым.
Доказательство. Необходимо доказать, во-пер-
вых, что функционал ||-||х/ь удовлетворяет аксиомам нор-
мы и, во-вторых, что полнота X влечет за собой полно-
ту Х/L. Докажем первое утверждение теоремй, т. е.
проверим выполнение аксиом (1) п. 2.1.1.
Аксиома a): ||?||x/l^0 (Vg) вследствие неотрица-
тельности нормы в X. Если £ = 0, то в качестве х£%
можно взять х = 0, и потому ||0||х/ь = 0. Пусть ||£||х/ь—0.
Тогда из (3) следует, что существует последовательность
xn£t такая, что ||х„|| —>0, т. е. хп—>0. Вследст-
вие замкнутости 0 С т е. J; есть нулевой элемент в X/L.
Аксиома б): Пусть a£R. Тогда, если лх = £, то
||а?||х/ь= inf inf 11ал:11 —lal mf h|| = |a]||g||.
n(/=aB iw=g лх=|
Аксиома в):
+ inf l|xx 4-x2 4-x' || = inf ||x14-xl4-xa4-x;||<
xJeL
< inf hi 4- < II4- inf h24-x;||=h1||x/L4-H2||x/L.
Докажем второе утверждение теоремы, т. е. полноту
Х/L. Пусть —фундаментальная последовательность
в Х/L, т. е.
Ve>0 3A(e). п > N (в) =>||?и+ет—Цх/z. < в, V/n>l.
Выберем вЛ — 2“* и номера nh такие, что ||||^2~ft,
119
Л>1. Тогда ЦЕПэ—6П1ЦС1/2, и вследствие (4) сущест-
вуют представители xt £ gnj такие, что ||хг—xjl^l. Ана-
логичным путем построим элементы {xn}nS;3 так, что
||хй —xft_1|K2-(A-1), 6 = 3, 4, ... Последователь-
ность {хА}*=1 фундаментальна в X (проверьте), а X—пол-
но но условию. Значит, существует предел x#==limxx.
Рассмотрим класс |0 = лх0. Тогда
||ВП. ||х/£ — Inf || xk Х0 х ||хС||*й Хв ||х ► 0 .
в x'eL ~
„Итак, ►Во» а тогда и В„—+В« в силу фундаменталь*
ности {£„} Значит, X/L—полное.
Упражнения.
1. Пусть Х — С ([0,1]), ОСП < т3 < ... < тя< 1, подпростран-
ство L состоит из функций х (-)£С ([0,1]) таких, что x(t,) = 0,
{*1, ..., т. Найти фактор-пространство Х/L и определить |j-||x7£-
2 . Обобщить результат упражнения 1 и доказать, что если F —
замкнутое подмножество отрезка [0, 1J и
Lf = {x( )£C(10, l])|x(t)=0, W,
то пространство С ([0, !])/£/? изометрически изоморфно пространству
C(f).
2 .1.3^ Теорема Хана—Банаха и ее следствия. В тео-
рии экстремальных задач важную роль играют теоремы
отделимости и некоторые другие факты выпуклого ана-
лиза. .Большинство из нйх является следствием теоремы
Хана—Банаха, которую часто называют первым основ-
ным принципом линейного анализа. Учитывая, что эта
теорема входит во все стандартные курсы функциональ-
ного анализа, ограничимся здесь лишь ее формулиров-
кой и некоторыми важнейшими следствиями.
В этом пункте X—линейное пространство, R — рас-
ширенная числовая прямая, т. е. R=±R(j{—°°, 4-оо}.
Определение 1. Функция р: X—>R" называется
выпуклой и однородной, если
Р (х 4- у) С р (х) + Р (у) для. любых х, у£Х, ) (1)
р (ах) = ар (х) для любых х£Х и а > 0. (2)
Примеры. 1) X нормированное пространство,
р(х) = 1|х||.
2) X—линейное пространство, L—линейное подпро-
странство в X,
I 0, x£L,
'<*>=( +».
120
3) X—линейное пространство, llt lm—набор ли-
нейных функционалов на X; р(х) = max(<Zn х>, ...
х».
- Важный пример доставляет следующее
Определение 2. Пусть Д—выпуклое подмноже-
ство линейного пространства X, содержащее 0. Его функ-
ция Минковского рД(>) определяется равенством
рД (х) = inf {t > 0|x/f Д} (3)
(если таких t > 0, что x/t^A, нет вовсе, то р Д (х) =
= + оо).
Предложение 1. Функция Минковского неотри-
цательна, выпукла и однородна',
{х|рД (х) < 1}е ДЕ{х|рД(х)<1}. (4)
Если X—линейное топологическое пространство1), то
р А (•) непрерывна в точке 0 тогда и только тогда, когда
0 g int А.
Доказательство. Если рА(х) или pA(i/) равно
4-оо, то (1) верно. Поэтому пусть рД (х) < 4- °° и
рД (у) < 4- оо. По определению для любого е>0 най-
дутся такие t и s, что
р < t < рД (х)4-е/2 и x/t£A,
О < s < рА (у)4-е/2 и у/з^А.
Но тогда
х-bi/ _ х t , у s я
7+Т "" ~ Гй + T7+s *
поскольку А выпукло, и следовательно,
рД (х4-«/Х^4’5<рД (х)4-рД («/) 4-е.
Ввиду произвольности е верно (1). Далее, для а>0
рД (ах) = inf {/ > О, ах// g Д) = inf {os > 0, x/s g Д} =
= ainf{s>0; x/s g А} = apA (x),
тдк что верно (2).
Неотрицательность рД (х) и второе включение в (4) сле-
дуют непосредственно из определения. Если рД(х)<1,
то существует t g (О, 1), для которого x/t g А, а поскольку
4 О линейных топологических пространствах см, [КФ, гл, III,
$ б].
121
0£Д и А выпукло,
х = 0-(1 — t)+~t€A,
так что первое включение в (4) верно.
Пусть теперь X—линейное топологическое простран-
ство. Тогда имеет место следующая цепочка эквивалент-
ностей: рД(-) непрерывна в0«
Ve > 0, 3£7е Э 0, Vx£f/e, рД(х)<е<^
ЭС/хЭО, VxCl/ц рД (х) < 1
ЗД^О, t/jcA^OCintA
(здесь Ue и Ut—окрестности точки 0; вторая эквива-
лентность .верна ввиду однородности рД () и возможности
положить Ug — sUj). | *
Предложение 2. Для того чтобы линейный функ-
ционал х* на линейном топологическом'пространстве' X
был непрерывен, необходимо и достаточно, чтобы для
некоторой выпуклой однородной непрерывной в точке fl
функции р(-) для всех х^Х выполнялось неравенство
<х*, х><р(х). (5)
Доказательство. Необходимость устанавливаем
сразу, полаг.ая р(х)=?|<х*, х>|.
Предположим теперь, что верно (5) и р (х) непрерывна
в точке 0. Тогда для любого е>0 найдется окрестность
С/ЭО такая, что р(х)<8 для всех x£U. Поскольку
0 U и 0=(—0) € (—£/)> существует окрестность W та-
кая, что 0 £ W с U Л (— U}- Если х € Ц7, то х их— х € U
и в силу (5)
<х*, х> <1 р (х) < е,
<х*—х> < р (— х) < е.
Следовательно, |<х*, х>| < е для всех x£W, т. е. х* не-
прерывен в 0. Остается заметить, что линейный функ-
ционал, непрерывный в одной точке, непрерывен на X
[КФ, стр. 174].
.Теорема Ха_на— Банаха [КФ, стр. 134—137].
Пусть р\Х—>R—выпуклая однородная функция на
линейном пространстве X, и пусты-1: L—>R—линейный
функционал на подпространстве L пространства X та-
кой, что
<1, х>^р(х) для всех x£L. (6)
122
Тогда существует линейный функционал Л, определенный
на всем X, являющийся продолжением I, т. е.
<Л, %>==</, x>, x£L, (7)
и удовлетворяющий неравенству
<Л, х>^р(х) для всех х£Х. (8)
Следствие 1. Пусть X—нормированное простран-
ство и ха£Х, хо=#0. Тогда найдется элемент А£Х*
такой, что ||Л|| = 1 й <Л, х0> = ||х01|.
/Доказательство. На подпространстве
L = {х | х = аха, a g R}
зададим линейный функционал I, полагая
</, ах0> = а||х0||. (9)
Функция р (х) = || х ||—выпуклая однородная и </, ах0> —
= а [I ха || | а 11| ха || = || аха || = р (ах0), так что имеет место
неравенство (6). По теореме Хана — Банаха I продол-
жается до линейного функционала Л на всем X, причем
выполняются соотношения (7) и (8). Вспоминая опреде-
ление нормы функционала (п- 2.1.1), имеем из (8)
||Л||= sup <Л, х>^ sup р(х) = 1,
11*11=1 11*11=1
так что, в частности, Л£Х*.
С другой стороны, и^ (7) и (9)
(А, х0> = <;/, хаУ = || ха |,
так что верно второе утверждение доказываемого след-
ствия и, кроме того,
'Л|’Ж<Л’Х>>(Л’ таг)=>’
а потому ||Л||= 1. |
Из следствия 1 немедленно вытекает
Следствие 2. Если нормированное пространство X
нетривиально (т. е. Х=#{0}), то и сопряженное к нему
пространство X* нетривиально.
2.1.4. Теоремы отделимости. В этом пункте X—ли-
нейное топологическое пространство, X*—сопряженное
к нему пространство, состоящее из всех линейных не-
прерывных функционалов на X.
123
Определение 1. Функционал х*€X* разделяет
множества АсХ и ВсХ, если
sup<x*, х><1 inf <х*, х>, (1)
хёА хеВ
и строго разделяет А и В, если
sup <х*. х> < inf <х*, х>. (2)
хёА хёВ
Геометрически неравенство (1) означает, что гипер-
плоскость
Н (х*, с) = {х|<х*, х> = с},
где sup<x*, inf <х*. х> отделяет множества. А
хёА хеВ
н ~В друг от друга в том смысле, что А лежит в одном
полупространстве (Я+(х*, с) — {х\<.х*, х>^с}), порож-
денном Н (х*, с), а В — в другом (//_ (х*, с) = {х| <х*,х>^с})
(рис. 31), неравенство (2) означает, что при этом с можно
Рис. 31.
Рис. 32.
выбрать так, чтобы А и В лежали внутри соответству-
ющих полупространств и не имели общих точен с Н (х*, с)
(рис. 32).
Первая' теорема отделимости. Если множе-
ства АсХ и ВсХ выпуклы, непусты и не пересекаются
между собой, причем А открыто, то существует нену-
левой линейный непрерывный функционал, разделяющий
А и В.
Доказательство. А) Поскольку Л и В не пусты,
существуют точки аа£А, Ъй£В. Множество
С —(А — ав) — (В—&0) = {х|х = а—а0—b + bB, agA, Ъ £ В},
очевидно, выпукло (см. также предложение 1 и упраж-
нение 2 в п. 2.6.1), содержит 0 и открыто (действительно,
124
если х = а—аа—&4-Ь0 и а € А, то существует окрестность U,
a^U с А, а тогда x^U—а0—Ь-\-ЬасС. Кроме того,
с = Ьа—а0^С, так как в противном случае Ьо—а0 = а —
— a0—b+b0 для некоторых а$А и fig В, откуда а — b£
£ А п В, т. е. эти множества пересекаются, вопреки ус-
ловию.
Б) Обозначим через р(х) функцию Минковского мно-
жества С. Согласно предложению 1 п. 2.1.3 р(х)—неот-
рицательная выпуклая однородная и непрерывная
в точке 0. Кроме того, р(х)^А для всех х$С.
В) На подпространстве
Л = {х|х = ас = а(Ьо—а0), a£R}
определим линейный функционал I, полагая </, ас> =
= ар(с). Тогда для а>0 имеем </, ас> = ар(с) = р(ас),
а для а^О </, ас> = ар (с) 0 (ас), поскольку
р(-) неотрицательна. Следовательно, для всех x£L вы-
полняется неравенство </, х> р (х) и по теореме Хана —
Банаха I можно продолжить до линейного функционала Л
такого, что
<Л, ас> = </, ас> = ар(с), a£R (3)
и
<Л, хХр(х), х£Х. (4)
Поскольку р(-) непрерывна в 0, из (4) следует непре-
рывность функционала Л (предложение 2 п. 2.1.3).
Г) Для любых а$А и Ь£В имеем
<Л, а—&> = <Л, а—-а0—& + &„> +<Л, а0—АХ
< р (а—а0—Ь + &0) + </, (—1) (Ьа —а0)> < 1— р (Ьа—аа),
поскольку а—ай—b + ba£C, а на С функция р(х)^1;
кроме того, мы использовали (4). Но при Q < t 1 точка
А—a9)lt — c/t не может принадлежать множеству С, ибо
Q выпукло и содержит 0, а на [0, с//] лежит'точка с ~
— Ьй—ай^С. Поэтому
p(&e-aj = inf{f>o|^pec}>l. (5)
Следовательно, <Л, a—b>^ 1—-рА~А)<0 для любых
а£А и Ь£В. В неравенстве <Л, а> <Л, Ь> а € А
и Ь£В можно выбирать независимо, поэтому
sup <Л, а> inf (Л, Ь).
аеЛ Ьев
125
Кроме того, согласно (3) и (5) <Л, b0—а„> = р (btt—a0) 1,
так что Л^=0. Значит, Л разделяет Л и В. |
Замечание. В п. 1.3.3 мы уже доказали теорему
отделимости в случае конечномерного пространства X.
Сравнивая ее условия с условиями только что доказан-
ной теоремы, мы видим, что в конечномерном случае
можно опустить условие открытости А (то, что в п. 1.3.3
одно из множеств было точкой, — не существенно). Ус-
ловия первой теоремы отделимости можно ослабить
и требовать, чтобы int/l^=0 и (int Л)Г)В — 0- Однако
совсем обойтись без существования внутренних точек
хотя бы у одного из множеств нельзя.
У пр аж н е н ия.
1. Пусть А — выпуклое множество в линейном топологическом
пространстве X, int А 0 и х* g X*. Докажите, что
sup<x*, х> = sup <х*, х> (6)
х € А х € ни А
2 Выведите из (6) теорему отделимости для случая выпуклых
А и'В, таких, что int А Ф 0, В 0, Bfjint А = 0.
3. Докажите, что в пространстве Х = 1-2 компактный эллипсоид
А — \ х — [х^1 £ /2
2 k2xk < 1
*=1
и луч
B = {x=[xk]\xk = t/k, t > 0}
нельзя разделить никаким непрерывным линейным функционалом.
Вторая теорема отделимости. Пусть X—ло-
кально выпуклое линейное топологическое пространство
'[КФ, стр. 169], А—непустое, замкнутое выпуклое под-
множество в X и х£Х—точка, не принадлежащая А.
Тогда найдется ненулевой линейный непрерывный функ-
ционал, строго разделяющий А и х.
Доказательство. Поскольку х^АиА замкнуто,
существует окрестность V Э х такая, что А П V = 0. Ввиду
локальной выпуклости X существует выпуклая окрест-
ность В eV точки х. Ясно, что В П А = 0 и по первой
теореме отдел.имости существует ненулевой функционал х*,
разделяющий А и В:
sup <х*, х> inf <х*, х>.
" хеЛ хеВ
Остается заметить, что
inf <х*, х> < <х*, х>,
хев
126
ибо нижняя грань ненулевого линейного функционала х*
не может достигаться во внутренней точке х множе-
ства В. |
Определение 2. Аннулятором А1- подмножества X
линейного пространства X называется множество тех ли-
нейных функционалов I на X, для которых </, х> = 0
для всех х£ А.
Заметим, что А± всегда содержит OgX*.
Лемма о н е тр и в и а л ь н ост и аннулятора.
Пусть L—замкнутое подпространство локально выпук-
лого линейного топологического пространства X, причем
Ь^=Х. Тогда аннулятор IA- содержит ненулевой элемент
х*$Х*.
Доказательство. Возьмем любую точку, xf^L.
По второй теореме отделимости существует ненулевой
функционал х* С X*, строго разделяющий х и L (L—под-
пространство линейного пространства и, следовательно,
выпукло):
sup <х*, х> < <х*, х>. (7)
xeL
Если бы существовало ха £ L, для которого <х*, xo>s#O
то, поскольку ах0££ для любого agR, было бы
sup <х*, х> sup <х*, ах0> = + оо,
xkL аб R
вопреки (7). Следовательно, <х*, х> = 0 на L, и потому
х*£1А-.
2.1.5. Теорема Банаха об обратном операторе и лемма
о правом обратном отображении. Вторым принципом ли-
нейного анализа является следующая теорема:
Теорема Банаха об обратном операторе.
Пусть X и Y—банаховы пространства, A: X——не-
прерывный линейный оператор. Если А является моно-
морфизмом, т. е.
Кег А = {х | Ах = 0} = {0},
и эпиморфизмом, т. е.
Im А = { е/| у = Ах, х€Х} = К,
то А — изоморфизм между X и Y, т. е. существует ли-
нейный непрерывный оператор М = A-1: Y -^Х такой, что
МХ = 1х, АМ — 1у.
127
Доказательство [КФ, стр. 225]. В нашем курсе
будет многократно использовано такое следствие теоремы
Банаха:
Лемма о правом обратном отображении.
Пусть X и Y—банаховы пространства, Л—непрерывный
линейный оператор из X в Y, являющийся эпиморфизмом.
Тогда существует отображение M:Y-^X (вообще говоря,
разрывное и нелинейное), удовлетворяющее условиям.
Л о М~=1У,
| М (у) |К С || у || для некоторого С > 0.
Отметим, нто в силу второго условия М—непрерыв-
ное в нуле отображение.
Доказательство. Оператор Л непрерывен, сле-
довательно, его ядро КегЛ, являющееся прообразом
точки нуль, будет замкнутым подпространством. По тео-
реме о фактор-пространстве (п. 2.1.2) пространство Х/Ker Л
банахово. Определим оператор Л: Х/КегЛ-^У, положив
Л£ = Лх на классе смежности | = Это определение
корректно: xlt x2^t=^>nx1 — лх2 = 1=^х1—х2€КегЛ=з>
=>AXj = Лх2. Оператор Л линеен: если nx£ = g£, i = 1, 2, то
Л (а^ 4-а3|2)= Л («Л 4-а2х2) =
= ctjAxj 4- а2Лх2 = o^Alj 4- ааЛ§2.
Оператор Л непрерывен: для любого *€$
11Л?||=||Лхк11Л1к11.
откуда
улиС||Л||1П1||хМЛ||Шх/Кегл.
хе J
Наконец, оператор Л биективен (взаимно однозначен).
Действительно, Л—эпиморфизм вместе с Л: Уг/£У Зх^Х,
Лх = у=Ф для £ = л(х), А£ = у. С другой стороны,
КегЛ —0: Л£ = 0, ях = ?=ФЛх = 0=Фх€КегЛ=^^ = 0.
Итак, доказано, что оператор Л есть непрерывный
линейный биективный оператор из X/КегЛ в У. По тео-
реме Банаха об обратном операторе существует непре-
рывный обратный к Л оператор М — A~l, М: У —►Х/КегД.
Для элемента Ъ,£М.у найдем в соответствии с (4) п. 2.1.2
такой элемент х=вх(£), что х€? и ||^IK2||£||x/kwA.
128
Положим Л4(#) = х(|). В итоге
(Л о М) (у) = Ax (g) = Л£ = ЛЛ4г/ = у,
IIW) ЙМ&Ж 2 III Цх/Ker Л = 2 II Му llx/Ker Л
<2||M||||y||.
2.1.6. Лемма о замкнутости образа. Пусть X, Уи2 —
банаховы пространства, A: X-->-Y и В: X —*2—линей-
ные непрерывные операторы. Равенство
Сх=(Ах, Вх)
определяет линейный непрерывный оператор С: X —* YxZ.
У п ражиеиие. Докажите, что если норма в Y XZ определяется
равенством (1) п. 2.1.2, то ||С||=тах{||4||, ||В||}.
Лемма о замкнутости образа. Если подпро-
странство Im А замкнуто в Y и подпространство В Кег А х)
замкнуто в %, то подпространство Im С замкнуто eYxZ.
Доказательство. Замкнутое подпространство Y=
' = Im А банахова пространства Y само является банахо-
вым пространством и А: X—►К—эпиморфизм. По лемме
из п. 2.1.5 существует правое обратное к А отображе-
ние ^М\ Y—>Х. Пусть (у, г) принадлежит замыканию
образа оператора С. Это означает, что найдется после-
довательность {х„|п>1} такая, что у = lim Ахп, г**
п -► ®
= Пт Вх„. Положим
£„ = М(Ах„—у)
(ygY как предел элементов AxngY). Учитывая свойства
М, получаем
А (хп—1„) = Ахп — (4 о М) (Лх„ — у) = у,
|| || = || М (А хп - у) || < С|| А хп - у || -> 0.
Поэтому В1п—*0 и lim В(хп—!„) = lim Bxn~z, т. е. г
принадлежит замыканию множества
2 = {£ = Вх| Ах = у\.
Это множество является сдвигом подпространства В Кег А:
Си £2 € 2 =$ £; = ВХ{, Ах( = у, i — 1, 2
=> -“£1 = В (х2 — Хх), А (Х2 — Хх) = 0 =Ф = £1 +
£2—SiCBKerA.
х) То есть образ-ядра оператора А при отображении В,
5 В М. Алексеев и др. 129
Но В Ker Л замкнуто по условию, значит, замкнуто
и множество S. Следовательно, г, принадлежащий за-
мыканию S, принадлежит и самому S, что означает су-
ществование элемента х, для которого Ах = у, Вх = г.
Итак, (у, z)GImC. |
2.1.7. Лемма об аннуляторе ядра регулярного опера-
тора. Пусть X, Y—банаховы пространства, А: X —>У —
линейный непрерывный эпиморфизм. Тогда (Кег Л)1--Im А*.
Доказательство. А) Пусть х* € Im Л* & х* = А*у”.
Тогда, если х С Кег Л, то <х*, х> = <А*у*, х> = <у*, Лх> = О,
т. е. Im Л* с: (Кег Л)-1-.
Б) Пусть х* С (Кег Л)-1-, т. е. Лх = 0=?><х*, х> = 0.
Рассмотрим отображение С: X —> R х Y, Сх = (<х*, х>, Ах).
Образ ядра Л при отображении х* есть нуль, т. е. замк-
нутое множество, и по лемме о замкнутости образа (п. 2.1.6)
Im С—замкнутое подпространство в RxK. Оно не совпа-
дает с R х К, поскольку, например, (1,0) 0m С (дейст-
вительно, ерли (а, 0) = «х*, х>, Ах), то Ах — 0=»а =
= (х*, х) = 0).
По лемме о нетривиальное™ аннулятора замкнутого
собственного подпространства (п. 2.1.4) существует не-
нулевой линейный непрерывный функционал А С (Im С)1 с
cz (RxK)* и, вспоминая лемму об общем виде линейного
функционала на произведении пространств (п. 2.1.2),
находим число Хо g R* = R и элемент у* g Y* такие, что
<Хох* -{- А*у*, х> = Хо <х*, х> 4- <у*, Лх> =
= <A, Cx> = 0, Ух.
Случай Хо = О невозможен, ибо 1тЛ=У и, значит,
(у*, Лх> = 0 =Ф у* = 0 =$• А = 0.
Следовательно, х*=Л*(—г/*Д0), т. е. х* С Im Л* и (Кег Л)хс:
с Im А*.
2.1.8. Абсолютно непрерывные функции. В теории
оптимального управления постоянно приходится иметь
дело с дифференциальными уравнениями вида
x = q(t, X, u(f)), (1)
где «(•)— заданная функция, называемая управлением.
При этом, хотя функция <р(£, х, и) достаточно хорошая
(непрерывная или даже гладкая), управление «(•) тако-
вым, вообще говоря, не является. Оно может быть ку-
130
сочно-непрерывным, а иногда даже удобно считать «(•)
всего лишь измеримой функцией. Поэтому правая часть
уравнения (1) может оказаться разрывной, и следует
уточнить, что понимается под его решением.
Замечание. В этом пункте «измеримость», «инте-
грируемость», «почти всюду» и т. д. понимаются в обыч-
ном лебеговом смысле [КФ, гл. V, §§ 4, 5]. То же правило
сохраняется и в остальной части книги, за редкими ис-
ключениями, оговариваемыми особо: например, в форму-
лах следующего пункта интеграл понимается в смысле
Стилтьеса или Лебега — Стилтьеса [КФ, гл. VI, § 6].
Если речь идет о векторнозначных или матричных функ-
циях, то соответствующими свойствами должна обладать
каждая их компонента. Например, функция %(•) =
==(xt(-), ..., *„()): [а, |3]—>Rn измерима и интегри-
руема, если каждая из? числовых функций х1 (•): [а, |3] —> R
обладает тем же свойством, и по определению
В /3 ₽ \
J x(l)dt ==($ x1(t)dt, ..., \xn(t)dt'i. (2)
а \а а /
Наиболее естественно считать (мы так и поступим),
что дифференциальное уравнение (1) вместе с начальным
условием x(ta)=x0 эквивалентны интегральному урав-
нению
t
х (t) = х0 4- J ф (s, х (s), и (s)) ds.
^0
(3)
Для тогб чтобы это было справедливо, х(-) должна
быть неопределенным интегралом своей производной, т. е.
необходимо, чтобы имела место формула Ньютона—Лейб-
ница
t
x(t) — x(x') = x(s)ds.
т
(4)
Функции х(-), Для которых выполняется (4), в лебегов-
ской теории интегрирования называются абсолютно не-
прерывными [КФ, гл. VI, § 4]. Важно, что этим функ-
циям можно дать другое, эквивалентное и эффективно
проверяемое определение.
5* 131
Определение. Пусть X—-линейное нормированное
пространство, А ~ [а, [3]—отрезок числовой прямой. Функ-
ция х(-): А—»-Х называется абсолютно непрерывной, если
для всякого е > 0 найдется такое 6 > 0, что для любой
конечной системы попарно непересекающихся интервалов
(аж, pk) с [a, §], 6=1, 2, сумма длин которых
S (₽*—а*) < в»
fess 1
выполняется неравенство
N
2 II •*(₽*)—х(а*)||<е.
few 1
(5)
(6)
Пример. Функция х(-): &~+Х, удовлетворяющая
условию Липшица
kw-xWliaK-'U ilt t3$&,
абсолютно непрерывна. Действительно, здесь 6 = е/Х.
Непосредственно из определения видно, что абсолютно
непрерывная функция равномерно непрерывна на А (берем
Предложение 1. Пусть X и Y—линейные норми-
рованные пространства, отрезок числовой прямой.
Если функции Xi(-Y А—*Х, 1 = 1, 2, абсолютно не-
прерывны и 0^^.,'то и функция с1х1(-) + с2х2(-) абсо-
лютно непрерывна.
Если функции х(-): А—*Х и А(-): А—►=2’(Х, Y)
абсолютно непрерывны, то и функция А(-)х(-): А—>Y
абсолютно непрерывна.
Если функция Ф(-): G—удовлетворяет условию
Липшица на множестве %?cG, а функция х(-): A—
абсолютно непрерывной im х(-) = {у\у — x(t), ££А}сЗ£,
то функция Ф (%(•)): А —> Y абсолютно непрерывна.
Доказательство. Первое утверждение непосред-
ственно следует из определения (см. также [КФ, стр. 343]).
Для доказательства второго заметим, что х(-) и Д(-),
будучи непрерывными, ограничены, так что
\\х(Ы^'Мх, ||Д(О||<МЛ, /€Д.
132
Теперь для любой системы иепересекающихся интервалов
(а*, РА)с:Д, fc==l, N, имеем
N
2 IIА (Ра) х (Ра) — А (“а) х (*а) К
£ее 1
<2 И(0*)х(РЛ)-Л(М*(аЛ)|| +
k= 1
+ 2 И (Ра) х (а*)—А (а*) х (аА) ||
k— 1 *
ЛГ
С 2 IIА (Ра) IIIIх (Ра) (“а) II + 2 || л (₽А) - A (a J || || х (aA)||<
А=1 А=1
<мл 2 h(Ра)-x(«a)II + Mx 2 М(₽А)-Л (аА)||.
А=1 А=1
Выберем 6 > 0 так, чтобы из (5) следовали неравенства
N N
S ||х (₽А)-х (аА) || < ^ , £ || А (₽А)-А (аА)[| < .
Тогда
£ [| А (₽А) х (рА) - А (аА) х (aA)|| < МА + ~ Мх - в,
Так что Л(-)х(«) абсолютно непрерывна.
Аналогично, если
||Ф(Х1)—Ф(х2)||<К||л:1—х2||, ’v*i. х2£№,
ТО
N N
2 ||Ф(*(Ра))—Ф(*(«а)Ж 2 И (Ра)—Х(схл)[( < 8,
Ass 1 k= 1
если б > 0 выбрано так, чтобы из (5) следовало (6) с за*
Меной е на e/k. |
Основную теорему этого пункта мы сформулируем
только для конечномерного X, чтобы не определять опе-
рацию интегрирования в произвольном нормированном
Пространстве (для X = R" достаточно иметь в виду (2)).
Только этот случай нам в дальнейшем и понадобится.
Теорема Лебега [КФ, стр 345] Если функция
х(-): A->R" абсолютно непрерывна, то она диффереи-
133
цируема почти всюду, ее производная х(-) интегрируема
на А и для всех t, т£Д имеет место равенство (4).
Если функция £(): интегрируема на А и
t
т£Д, то функция х(/) = J £(s)cfs абсолютно непрерывна
т *
и х (/) = £ (t) почти всюду.
В соответствии с этой теоремой мы будем в дальней-
шем функцию х(-) называть решением дифференциального
уравнения (1), если она абсолютно непрерывна и удов-
летворяет (1) почти всюду. Действительно, по теореме
Лебега этого достаточно, чтобы из (1) следовало (3).
Обратно, если х(-) удовлетворяет (3) (т. е., в частности,
Z—x(t), u(t))—интегрируемая функция), то по
теореме Лебега х(-) абсолютно непрерывна и почти всюду
имеет место (1).
В заключение этого пункта приведем еще одно утвер-
ждение, числовой аналог которого хорошо известен в ле-
беГовской теории интегрирования, и доказательство кото-
рого предоставляется читателю в качестве упражнения.
Предложение 2. Измеримая функция х(-): Д—>Rn
интегрируема тогда и только тогда, когда | х (•) | интег-
рируема. При этом
x{t)dt
А
J |x(/)|dL
А
(7)
2.1.9. Теорема Рисса об общем виде линейного функ-
ционала в пространстве С. Формула Дирихле. Опреде-
ления функции ограниченной вариации и интеграла
Стилтьеса мы будем предполагать известными [КФ,
гл. VI §§ 2 и 6]. Функцию ограниченной вариации
о(-): [а, р]—>- R будем называть канонической, если она не-
прерывна справа во всех точках интервала (а, р) и
о(а) = 0.
Теорема Ф. Рисса [КФ. стр. 369]. Каждому не-
прерывному линейному функционалу х*£С([а, р])* соот-
ветствует каноническая функция ограниченной вариации
о(-): [а, р]—>R такая, что для всех х(-) £ С ([а, р])
₽
<х*, х (•)>=;$ x(t)dv(t), (1)
сс
134
и такое представление единственно: если для всех %(•)€
£С([а, И) и для канонической и(-)
Р
J x(t)dv(t) = Q,
a
то u(f) = O.
Эта теорема легко обобщается на векторный случай.
Пусть е1 = (1, 0, .... 0), е2 = (0, 1, ..., 0), ... —единич-
ные векторы стандартного базиса в R". Произвольный
элемент х(-) = (х1(-), ...,%„()) £ С ([a, fj], R") представ-
ляется в виде
п
Х(-)= S
k= 1
Если теперь x*gC([a, |J], R")*, то
<х*? %(•)>= S <х*> Xk(-)ek> = 2 <4. «*(•)>»
fe= I k—I
где функционалы x*k£C ([a, [3])* определяются равенствами
<х£, £(-)> = <х*, g(-)eft>. Применяя к хк теорему Рисса,
получаем представление
п г
<х>, х()>=% \xk(t)dvk(t). (2)
k=l а
Набор функций ограниченной вариации о(-^ = (о1(-), •••
..., vn (•)) естественно назвать векторнозначной функцией
ограниченной вариации (значения — вектор-строчки)
«(•): [а, [3]—>-Rn*. Тогда формула (2) может быть пере-
писана в виде
Р
<х*, х (•)> = § dv (t) х (t), (3)
a
Совпадающем с (1) с точностью до порядка сомножителей.
Как и в теореме Рисса, соответствие между х* и о(.)
будет взаимнооднозначным при соблюдении условия «ка-
ноничности» функции о(-).
Каждая функция ограниченной вариации о(-):
a, p]->R определяет обобщенную меру (или «заряд»
КФ , гл. VI § 5]). Интеграл Стилтьеса (1) и есть интеграл
по этой мере. Аналогично векторнозначная функция
Ограниченной вариации t^*): [a, |3]—>Rn* определяет на
135
[a, 0] меру с векторными значениями, интегралом по
которой является (3). Меру, соответствующую функции
ограниченной вариации v(t), принято обозначать dv(t).
Если уД-) и и2(-)—две функции ограниченной ва-
риации на отрезке [а, 0], то на квадрате [a, 0]х[а, 0]
определено произведение мер dwj-jxd^ (•) и справедлива
теорема Фубини [КФ, стр. 317]. В частности, имеет место
известная формула для перестановки пределов интегри-
рования («формула Дирихле»):
s)di\(s)}<to2(O = J s)dD2(0pV!(s). (4)
a la ' a Is >
При обобщении формулы (4) на векторнозначные функ-
ции (а это нам далее понадобится) следует быть внима-
тельным к порядку сомножителей. Например, если
/(•>•): [a, р]х[а, 0](R", R"),
М'): [а, 0]-> R”, у2(-): [а, 0]R”*,
то (4) следует писать так:
0 z t 1 ₽ ( р 1
s)dv1(s)>=U\dvi(t)f(t, sJMyJs). (5)
a \a / a vs '
§ 2.2. Основы дифференциального исчисления
в линейных нормированных пространствах
Дифференциальное исчисление—это тот раздел мате-
матического анализа, в котором изучаются локальные
свойства гладких отображений. На интуитивном уровне
гладкость отображения означает возможность локально
аппроксимировать его подходящим аффинным отображе-
нием—дифференциалом, или, более общо, полиномиаль-
ным отображением, и получить отсюда информацию
о свойствах изучаемого отображения. Наряду с выпуклым,
анализом дифференциальное исчисление является основ-*
ным аппаратом теории экстремальных задач.
Основы дифференциального исчисления скалярных
функций на прямой были заложены Ньютоном и Лейб-
ницем. Задачи вариационного исчисления потребовали
распространить понятие производной и дифференциала
на отображения многомерных и бесконечномерных про-
странств. Это было сделано Лагранжем в XVIII в. и
136
в наше время более полно Фреше, Гато, Леви и другими
математиками.
2.2.1. Производная по направлению, первая вариация,
производные Гато и фреше, строгая дифференцируемость.
Хорошо известно, что для вещественных функций одного
"вещественного переменного два определения—существо-
вание' конечного предела
lim.Ffi+Zi)_F(;)
h V’
и возможность асимптотического разложения при /г—* О
F(x+h)~F(x) + F'(x)h + o(h) (2)
— приводят к одному и тому же понятию дифферен-
цируемости. Для функций нескольких переменных, а тем
более для функций с бесконечномерной областью опре-
деления дело обстоит не так просто. Определение (1) и
обобщающее его определение частной производной при-
водят к понятиям производной по направлению, первой
вариации и производной Гато. В то же время обобщение
определения (2) приводит к производной Фреше и строгой
дифференцируемости.
Пусть X и У—линейные нормированные простран-
ства, t7 — окрестность точки х в X, F—отображение
из U в Y.
Определение 1. Предел
(3)
Х|0 А
в предположении, что он существует, называется произ-
водной F в точке ~х по направлению h и обозначается
F'(x ; h) (а также у других авторов (V*F)(x), DhF (х),
f>hF(x)). Для вещественных функций (Y = R) мы будем
понимать (1) несколько расширенно, допуская в качестве
предела —оо и 4-°°-
Определение 2. Пусть для любого h£X суще-
ствует производная по направлению F' (х; h). Отображе-
ние 6+F(x; -):Х —определяемое формулой 6+f (х;/г) —
~ F' (х; h), называется первой вариацией отображения
F в точке х (про функцию F мы говорим в этом случае,
что она имеет в точке х первую вариацию).
137
Если 6+ (х, —h) = — 6+ (х, h) при всех h, иначе го-
воря, если для любого h £ X существует предел
6F (х, h) = lim ,
%->-о А
то отображение h i—> 6F (х; h) называют первой вариацией
по Лагранжу отображения F в точке х (см. п. 1.4.1).
Определение 3. Пусть F имеет в точке х первую
вариацию и при этом существует линейный непрерыв-
ный оператор X£.S?(X, Y) такой, что 6+F(x; h)^Xh.
Тогда оператор Л называется производной Гато ото-
бражения F в точке х и обозначается F'r(x).
Таким образом, F[-(x)—это такой элемент из Г?(Х, Y),
что для любого h £Х при Х|0 выполняется соотношение
F (х+ ‘kh) = F (х) +о (^). (4)
Несмотря на внешнее сходство соотношений (2) и (4),
между ними есть глубокое различие. Как мы увидим
ниже, уже для X = R2 функция, дифференцируемая по
Гато, может не быть непрерывной. Дело в том, что
в разложении (4) о (7.) не обязана быть равномерной по А.
Определение 4. Пусть в окрестности точки х
отображение F можно представить в виде
F(x+Z0 = F(x)+A(f0+aVi)||M, (5)
где Л€Г?(Х, Y) и
lim ||а(Л)|| = ||а(0)|| = 0. (6)
[1М->о
Тогда отображение £(•) называют дифференцируемым
по Фреше в точке х и пишут F^D1(x). Оператор Л на-
зывается производной Фреше (или просто производной)
отображения F в точке х и обозначается F' (х).
Соотношения (5) и (6) можно записать еще и так:
F(x + ^) = F(x) + F'(x)[/i] + 0(H||). (7)
Отсюда легко следует, что производная Фреше определена
однозначно (для производной Гато это очевидно, по-
скольку однозначно определение производных по направ-
лению), ибо равенство ЦЛ^—Л2Л || = о (|| И ||) для операто-
ров Л;£J?(X, У), t = l, 2, возможно лишь npHAj = Aa.
138
Наконец, на языке е—б (5) и (6) формулируются так:
для любого е > 0 найдется б > О, при котором для всех h
таких, что ЦАЦ <б, выполняется неравенство
\\F(x+h)-F(x)-Ah\\^e\\h\\. (8)
Это делает естественным дальнейшее усиление.
Определение 5. Отображение F называют строго
дифференцируемым в точке х (и пишут F £SDr (х)), если
существует такой оператор X^JF(X, У), при котором
для всякого е->0 найдется такое б > 0, что для всех
хх и х2, удовлетворяющих неравенствам ||хх—х||<б,
Цх2—х|| < б, выполняется неравенство
ll^7 (xi) F (**) Л. (хх —х2)||^ е||хх х21|. (9)
Полагая в (9) х2 = х й Xj^ — x-Fh, получаем (8), так
что строго дифференцируемая функция дифференцируема
также и по Фреше и Л = 77'(х).
Производная F' (х) (Гато, Фреше или строгая) по
определению является линейным отображением из X в Y.
Значение этого отображения на векторе h£X мы будем
часто обозначать F' (х) [/г]. Для числовых функций одного
переменного (когда X = K=R) пространство J? (X, У)=
=J?’(R, R) линейных непрерывных отображений из R в R
естественно отождествляется с R (линейной функции y=kx
сопоставляется ее угловой коэффициент k). Именно в этом
смысле в элементарном анализе производная в точке—это
число (угловой коэффициент касательной), а соответствую-
щее линейное отображение-из R bR—это дифференциал
dy = F'(x)dx (здесь dx и dy—элементы одномерного век-
торного пространства R).
Хорошо известно также, что для функций одного
переменного определение 3 (или совпадающее с ним в этом
случае определение первой вариации по Лагранжу) и
определение 4 эквивалентны (функция имеет производную
в точке тогда и только тогда, когда в этой точке она
имеет дифференциал) и приводят к одному и тому же
понятию производной, введенному по сути дела Ньютоном
и Лейбницем. Определение 2 применимо здесь к функ-
циям, имеющим в точке х обе односторонние производ-
ные, не обязательно совпадающие. Для функций несколь-
ких переменных (1 < dim X < оо) в элементарном анализе
употребляются определение 1 (если h—единичный вектор,
139
то (З)-гЭто обычное определение производной по направ-
лению; если h—базисный вектор оси ОХк, то заменив
в (3) МО на %—>0, получим определение частной про-
изводной dF;dxk) и определение 4 (существование полного
дифференциала).
Обобщение понятия производной на бесконечномер-
ные пространства было стимулировано задачами вариа-
ционного исчисления. Определение первой вариации
(х; h), ее обозначение и название дал Лагранж. На
языке-функционального анализа это же определение было
дано Гато, а потому первую вариацию по Лагранжу
иногда называют дифференциалом Гато. Требование ли-
нейности в определении производной Гато стало обще-
принятым после работ П. Леви. Наиболее употребительно
в анализе (как конечномерном, так и бесконечномерном)
определение производной Фреше, однако для многих
целей (в частности, и для наших дальнейших) существо-
вания производной Фреше в точке не хватает, надо чуть
больше. Это и привело к понятию строгой дифферен-
цируемости.
Предложение 1. Между определениями 1—5 и
непрерывностью функции имеют место следующие импли-
кации:
4
непрерывность
£ те we а
Я
непрерывность
£ окрестности
mown а
ни одна из которых не может быть обращена.
Доказательство. Положительная часть доказа-
тельства (т. е. существование импликаций) немедленно
следует из определений, а отрицательная (невозможность
обращений) подтверждается набором контрпримеров,
подробный разбор которых предоставляется читателю
в качестве упражнения.
1) 2 не влечет 3: R—>R, fi(x) = |x|.
В точке х = 0 вариация нелинейна. Тот же пример по-
казывает, что из непрерывности в точке не следует диф-
ференцируемости по Фреше или Гато.
140
2) 3 не влечет 4: /2: R2—*R,
( 1, х, = xl, х, > О,
f (х X ) = <
/г\ и 2/ I о в остальных точках.
Этот пример показывает, что функция может быть диф-
ференцируемой но Гато (в точке (0, 0)), не будучи не-
прерывной.
3) 4 не влечет 5: /3: R —>-R,
( х2, х рационально,
(х) — \ п
13' ' I 0, х иррационально.
В точке y-О эта функция дифференцируема (по Фреше),
но не строго дифференцируема. ||
Упражнения.
1. Покажите, что функция R2—► R, определяемая в поляр-
ных координатах на R2 равенством
/4 (х) = г cos 3<р (х = (хх, x2) = (rcos<p, г sin <р)),
имеет в точке (0, 0) первую вариацию по Лагранжу, но не диф-
ференцируема по Гато.
2. Если функция FgSZ?1^, то в некоторой окрестности точки х
она удовлетворяет условию Липшица.
3. Если числовая (X=F=^R) функция F£SDl(x), то F' (х)
существует почти во всех точках некоторой окрестности точки х.
Предложение 2. Если отображения F(. U—+Y,
1=1, 2, и A: U-^.S’IY, Z), где Z—нормированное ли-
нейное пространство, дифференцируемы в смысле одного
из определений 1—5 (одного и того же для всех трех ото-
бражений), то: для любых ос,- £ R, 1 — 1, 2, отображение
F = axFt + a2F2 в точке х дифференцируемо в том же
смысле, причем
F’ (х) = axF; (x)+a2F'2(x),
или
F'(x; h)^axF{(x; h)+a2F2(x; h);
отображение
Ф = ДГ,.
в точке х дифференцируемо в том же смысле, причем
ф'(х; й) = А'(х; h) F'{ (х) + 4 (х) F'( (х; h).
Доказательство непосредственно получается из
определений. |
141
В частном случае, когда X=R и A: U —»- S? (К, R)—Y*,
Ф(х) = <Л(х), F, (х)>—числовая функция, и последнюю
формулу можно переписать так:
<Л(х), Л (х)>'= <Л' (х), Z7, (х)> + <Л (х), F't(x)y,
что вполне соответствует обычной формуле дифференци-
рования.
Приведем два простейших примера вычисления про-
изводных.
1) Аффинное отображение. Отображение
А: X—>-Y одного линейного пространства в другое на-
зывается аффинным, если существует линейное отобра-
жение Л: X—>Y и константа a£Y такие, что
Л (х) — Ах + #•
Если X и Y—нормированные пространства, а Л g ^(Х, Y),
то отображение А строго дифференцируемо в любой
точке х и при этом
Л' (х) = Л.
Это утверждение проверяется непосредственно. В част-
ности, если Л линейно (а = 0), то А' (х) J/iJ = A (h), а
производная постоянного отображения (Л = 0) равна нулю.
Упражнение 1. Докажите обратное, если производная (до-
статочно в смысле Гато) отображения А" X—>-К существует в каж-
дой точке х£Х и для всех х одна и та же, то А — аффинное ото-
бражение.
2) Полилинейное отображение. Пусть X и
Y—линейные топологические пространства, а £?П(Х, К)—
линейное пространство непрерывных полилинейных ото-
бражений декартова произведения Хп — Хх ... хХ в У.
п раз
Напомним, что отображение П (х1( ..., х„) называется
полилинейным, если при каждом i отображение
х,^П(хх, ..., х(_Х) х„ х, + 1...х„)
линейно. Если X и У нормированы, то непрерывность П
равносильна ограниченности, т. е. конечности числа
||П|| = sup ||П(хх, ..., х„)||. (10)
lIvnlKl.
В этом случае Sn (X, У) является нормированным
линейным пространством с нормой (10) и выполняется
142
неравенство
]|Пбхх....хпЖ||П||Ы| • • • КЧ- (И)
Функция Qn (х) = П (х, ..., х) называется формой сте-
пени п (при п = Ч квадратичной, прип = 3—тернарной),
отвечающей полилинейному отображению П. Из опреде-
лений вытекает, что
'Q„(x4-ft) = Q„(x)-f-S п(*....h> *) + о(||/г||2), (12)
г= 1
а потому Q„(-) дифференцируема по Фреше в каждой
точке х и
п
Q™WN=2n(i............h,...,x) (13)
1=1
(в обеих формулах (12) и (13) в t-м члене суммы аргу-
мент h стоит на t-м месте, а остальные аргументы
равны х). Если отображение П симметрично, т. е.
И (хх, ..., х„) не меняется при любой перестановке аргу-
ментов xt, то (13) превращается в
Q„ (х) [/i] = nil (h, х, .... х).
В частности, если X— вещественное гильбертово про-
странство со скалярным произведением (-]-), А б ^(Х, X)
и П(х1, х2) = (Лх! 1х2), то Q2 (х) = (Лх | х)—квадратичная
форма оператора А—дифференцируема и
Qa (г) [/г] --- (Лх | /г) ф- (Ah | х) = (Ах 4- А*х | h),
так что Q2 (х) естественно отождествляется с вектором
Лх-)-Л*х. Например, для Qa (х) = х/2 (х | х) = х/а ||д: |]а про-
изводная Q' (х) = х.
Упражнение 2 Докажите, что Qn(x)=II(x, ..., х), где
n^Jfn(X, У) строго дифференцируема при всех х
Более сложный пример доставляет
Предложение 3. Пусть U a. S?(X, Y)—множе-
ство непрерывных линейных операторов А: X—>-У, для
которых существует обратный оператор Л-1^=2’(У, X).
Если хотя бы одно из пространств X или Y банахово,
то U открыто и функция Ф (Л) = Л-1 дифференцируема по
Фрешевлюбой точке А С U, причем®'(А) [Н] =—4~*ЯЛ-1.
143
Доказательство. Если пространство X банахово,
со
то ряд 2 (—А"1//)* сходится в .2' (X, X) при ||Я||<
*=°
<||4-1||"1 и, как нетрудно проверить непосредственно,
(А+Н)
00
2 (—Л ~v/)fe а-*
fe=0
г>
2 (—
k=0
(А + Н) х» /у.
Следовательно,
(Л+Я)-1= 2 (—A-WfA-t
ft = 0
(14)
при ||Я|[< || Л-1||-1, 'так что В (А, || А"1 ||-1)с U и U от-
крыто.
Если пространство Y банахово, то (14) следует заме-
нить на
(Л+#)-!== Z-i 2 (—ЯА-1)*.
*=о
Далее, из (14) имеем
||(А+Я)-* — А"-1 + А~-М/А -11| =
я л-* ця|)«||/-|| =
при Н—+0, а следовательно, функция Ф(А) = Л-1 диф-
ференцируема и ее производная Фреше Ф' (4) [ • ] =
= —Л"^-)/"1.
Упражнение J!. Докажите, что Ф (А) строго дифференци-
руема в любой точке A£U.
2.2.2. Теорема о суперпозиции дифференцируемых ото-
бражений.
Теорема о суперпозиции. Пусть X, Y, Z —
нормированные пространства; U—окрестность точки х
в X, V—окрестность точки у в Y; <р: U—>1/, <р(х) = р;
ф: V —* Z; f = ф о q>: U —>Z—суперпозиция отображений
Ф и ф.
144
Если ф дифференцируема по Фреше в точке у, а ф
в точке х дифференцируема по Фреше (дифференцируема
по Гато, имеет первую вариацию или имеет производную
по направлению h), то f обладает в точке х тем же
свойством, что и у, и р.ри этом
Г (*) = Ф' (У) оф' (х) (1)
или
f' (х-, h) = ф' (у) [ф' (х; Л)]. (2)
Если ф строго дифференцируема в у, а ф строго диф-
ференцируема в х, то f строго дифференцируема в х.
Доказательство. Рассмотрим подробно два край-
них случая—производную по направлению и строгую
дифференцируемость.
А) По определению производной Фреше
(у) = Ф (У) + Ф' (У) [У —у] +а (УМ У —У II» ’
где
lim а(у) = а(у) =0.
Если существует
ф'(х; h} = Ит Ф(*+ ~Ф (X), = Ит Ф-(х±М)-у.. t
Х|0 А МО А
то
lim fCx+W—fC*) _ цт Ф(ф’(х4-у))—ф(у) __
х । о А х; о "
_ Пт Ф' Су) [ф (X + Л.Л)—у]+tx (ф (л-b Щ) II ф (х 4-U)—у II
МО
1
= ф'(у) ГИт Ф +
Х|о А J
+ Пта(ф(х4-Х.й)) lira У II д
МО хи А И
= Ф'(у)[ф'(£ Л)] +<х(у)|| ф' (х-, h) || =
= ф'(у)[ф'(х; Л)],
что‘и доказывает (2).
Б) Обозначим для краткости 4! = ф'(х), Л2 = ф'(^).
По определению строгой дифференцируемости для любых
145
er > 0, e2>0 найдутся такие бх > 0, б2 > О, что
II «i—ill <&i, II х2— х|| < =»|| Ф (хх) — ч> (х2)—А, (хх — х2) || С
=O1||x1—x2||, (3)
|| У1—УII < б2» IIУ2 —У II < 82 =^11Ф (44)—Ф (Уа)—А (Уг—у3)|| С
<е2||//х —1/2||. (4)
Для любого е > О подберем > 0 и е2 > 0 так, чтобы
выполнялось неравенство
ei|| Ля|Ц-е2|| Л1|Ц-е1е2 < е;
по этим е1, 82 найдем 61>0, б2 > 0 так, чтобы имели
место соотношения (3) и (4), и наконец положим
Если теперь ||хг—х)| <6 и ||х2—х|| < б, то в силу (3)
k(xt)—ф(х2)||<
< IIФ (*i)—Ф (х2)—Л1 (х± — х2) II +1| Л! (хг—х2) II с
< Si II *1—Хг 11 + IIА1IIII Xi—х2 II = (И А! II + ех) || xt—х21|. (5)
Полагая в этом неравенстве поочередно xt = x и х2=х,
получаем
IIФ (Xi)—ф (х) II = II ф (х{) — у II < (IIAi II + Ei) б < б2,
так что для г/,- = ф(х;) справедливо (4). Используя теперь
(4), (3) и (5), получаем
II f (х^) f (х2) Л2ЛХ (xr х2) ||
< IIФ (ф (*1)) —Ф (Ф (*а)) ~ А (ф (Xj) —ф (х2)) || +
+11А (ф (xj — ф (х2))—Л2ЛХ (хх—х2)|| <
О2II ф (Хг)—Ф (х2) II +11Л2IHI ф (хх)—ф (х2) — A (xr —х2) II
е2 (II АII + е1) II Хг —х21| +|| А 21| ег || хх — х21| =
= (б2 II Л! || + EjE2 +|| Л2 || Ех) || Xj Х2 || Е || Хг Х2 ||,
что и означает строгую дифференцируемость f в точке х.
Полагая в этих рассуждениях х2 — х, xr = x + /i, мы
получим доказательство теоремы для случая дифферен-
цируемости ф по Фреше. Остальные утверждения полу-
чаются анализом уже доказанного равенства (2). |
Следующий контрпример показывает, что теорема о
суперпозиции не имеет, вообще говоря, места, если ф
дифференцируема лишь по Гато.
146
Пример. Пусть X = K = R2, Z=R;
Ф(х) = (ф1(х1, х2), фг(хп х2)) = (х?, *2);
( 1 при у, = yl, у2 > О,
ф (У) ~ Ф (Уи #г) = { л
4 2 ( О в остальных случаях
(ср. с контрпримером в доказательстве предложения 1
п. 2.1.1). Здесь q> дифференцируема по Фреше в точке
(О, 0) и даже строго (проверьте!), ф дифференцируема
по Гато в (0, 0), однако функция
( 1 при х, = I х, I >0,
/ (х) = (ф О ф) (х) = ф (Xi, х2) = \ л
I \ \ ( 0 в остальных случаях
не дифференцируема по Гато в (0, 0) (и даже не имеет
в этой точке производных по направлениям h = (1,1)
и h — (—1,1).
Следствие. Пусть X и Y—нормированные про-
странства. U—окрестность точки у в Y,‘f: {/-—>- R диф-
ференцируема по Фреше в точке у и Ag=g’(X, Y). Тогда
f о Л: Л-1 ({/) R дифференцируема по Фреше в точке
х=А~1(у) и
(/о Л)'(х) = Л* (/'о Л) (х). (6)
Доказательство. В соответствии с определениями
(/' о Л)(х) =/' (Л^)=/' Су) (Л r) = k*
и
(/ о л)' (х)=f' (л2) о л=f Су) о л е я? (X, R) = х*.
Теперь имеем для любого h £ X
<л* (Г о Л) (х), h> = <(/' о Л) (х), лл>=Г Су) [Aft] =
= (f (ft)o A)ft = </'(ft)° А- ft> = <(/О Л)'(х), ft>,
чем доказано (6).
2.2.3. Теорема о среднем и ее следствия. Хорошо из-
вестно, что для числовых функций одного переменного
справедлива теорема Лагранжа, называемая также тео-
ремой о среднем значении илиформулой ко-
нечных приращений: если функция f: [a, ft] —> R
непрерывна на отрезке [a, ft] и дифференцируема в ин-
тервале (а, Ь), то существует точка с € (а, ft) такая, что
f(b)—f(a) = f(c)(b—a). (1)
147
Нетрудно убедиться также в том, что формула (1) остается
справедливой и для числовых функций /(х), аргумент
которых принадлежит произвольному линейному тополо-
гическому пространству.
В этом случае
[a, Ь] = {х[х = а + ЦЬ—a),
аналогично определяется интервал (а, Ь), а дифференци-
руемость можно понимать в смысле Гато. Полагая
Ф(/) = /(а+ /(&-<*)),
мы сводим доказательство к случаю одного вещественного
переменного.
Совсем не так обстоит дело для векторнозначных функ-
ций.
Пример. Пусть отображение /: R —>- R2 определяется
равенством f (t) — (sin t,—cos /). Тогда для каждого t суще-
ствует (строгая) производная Фреше f (/) (докажите!):
f (t) [а] = (cos t, sin t) а = (a cos t, a sin/).
В то же время для любого с
f (2л)—f(O) = O#=f (с)[2л—0] = (2л cosc, 2л sine),
так что формула (1) не имеет места.
Можно заметить, однако, что сама формула (1) ис-
пользуется в анализе много реже, чем вытекающая из
нее оценка |/(Ь)—/(а) | «С М. | b—а|, где М = sup | f (х) |.
Мы покажем сейчас, что в этом более слабом виде утвер-
ждение распространяется уже на случай произвольных
нормированных пространств. По традиции оно сохраняет
название «теорема о среднем», хотя, конечно, должно
было бы именоваться «Теоремой об оценке конечного при-
ращения».
Теорема о среднем. Пусть X и У—нормирован-
ные линейные пространства и открытое множество U s X
содержит отрезок [а, Ь].
Если функция f: U —► У дифференцируема по Гато
в каждой точке х£[а, />], то
||f(b)-Ha)K sup ||f (C)||||b-a||. (2)
с 6[а,6]
Доказательство. Возьмем произвольно у*£¥* .
и рассмотрим функцию
ф (О = <У*> f(a + t(b—a))>.
148
В каждой точке отрезка [0,1] эта функция имеет Лево-
и правостороннюю производные:
а|0 ~а
= Нт (и* Ma + (t—a)(b--a)) — f(a+t(b—a)) \ _
а|0 ’ ~а '
— — (и* lim ^a+t (й—_
** ’ а|0 а '
=» — <У*, f'(a + t(b'— а))[— (&—а)]> =
«<«/*, f'(a + i(b —а))[&— а]>,
и аналогично
ф; (/) = пт ф (.'+«) ф^..д<у*, /' (fl + / (b-a)) [Ь-а]>.
а 0 а
Так как эти производные.совпадают, то Ф(/) дифферен-
цируема (в обычном смысле) на [0, 1], а потому и не-
прерывна на том же отрезке. По формуле Лагранжа су-
ществует такое 0 € (0, 1), что
<У*, /(&)-/(а)>=Ф(1)-Ф(О) = Ф'(0) =
— <У*, f (а + 0(Ь— а)) [6—а]>.
Воспользуемся теперь следствием 1 из теоремы Хана —
Банаха (п. 2.1.3), согласно которому для любого эле-
мента у Е У найдется линейный функционал у* € У* такой,
что ||у*||=1 и (.у*, y> —||g||. Выбрав именно так функ-
ционал у* для элемента у = f (b)—[(а), получаем
||f(b)-f(a)|| = <//*, f(b)-f(a)>~
=*<у*, f'(a+9(b—a))[d—oj>^
<||У‘|1И'(а4-0(&-а))||||&-а||< sup (c)IIP~a||,
ce[a, f>]
что и требовалось доказать. |
Приведем несколько следствий из теоремы о среднем.
Следствие 1. Пусть выполнены все условия теоремы
о среднем и ЛС-2’(Х, К). Тогда
||f(b)-f(a)-A(b-a)||< sup Г (С)-Л||||Ь-< (3)
с 6 [а, 6]
Доказательство. Применим теорему о среднем
к отображению g(x) = [ (х) — Хх. |
Следствие 2. Пусть X и У—нормированные про-
странства, U — окрестность точки х в X и отображение
149
f: U —»- Y дифференцируемо no Гато в каждой точке x£U.
Если отображение xt—^f'r(x) непрерывно (в равномерной
операторной топологии пространства S? (X, К)) в точке х,
то отображение / строго дифференцируемо в х (а следо-
вательно, и дифференцируемо по Фреше в той же точке).
Доказательство. По заданному е>0 йайдем
5 > 0 так, чтобы выполнялось соотношение
II х—i|| <6=?>||/r(x) — /г(х)||<е. (4)
Если 11%! — х|| <6 и ||х2—х[| < 8, то для любого х = х1+
4- Z(x2—xjefXi, x2j,0C^Cl, И -
||х х|| = (|X1 + Z(X2 Хх) Л'|| =
= || t (X, — X) + (1 — t) (Xi — X) |[s^
<f||x2—х||4-(1 —OHi—х|1 < /8-f-(l —/)6™8,
так что в силу (4) || fr (х) — /'(х)||<е.
Применяя следствие 1 для Л = Д-(х), получаем
||/(Х1) —/(х2) — /г (х) (Xj-х2)|| <
< sup II/г w—frWIIhi—*2II <8II Xi—х2||,
хе |Х1, лг2]
что и означает строгую дифференцируемость / в х.
Определение. Пусть Хи К—нормированные про-
странства. Отображение F: U—>-К, определенное на не-
котором открытом подмножестве UcX, принадлежит
классу Сх({/), если в каждой точке x£U оно имеет про-
изводную и отображение xh->F'(x) непрерывно (в равно-
мерной операторной топологии).
Следствие 2 показывает нам, что здесь можно не ого-
варивать, какая производная имеется в виду. Этим заме-
чанием постоянно пользуются при проверке дифферен-
цируемости конкретных функционалов: доказывается су-
ществование производной Гато и проверяется ее непре-
рывность, а это уже гарантирует строгую дифференци-
руемость (и, значит, существование производной Фреше).
Упражнения. Пусть в условиях теоремы о среднем Y = R”
н отображение х—>- /г (х) непрерывно в UcX. Тогда
1
1) f(b)-f(a)=^ fr (a+t(b-a))dt[b~a]. (5)-
О
150
2) Существует оператор (X, Y), принадлежащий замкну-
той выпуклой оболочке (см. п. 2.6.2) множества (/г(х), ^1}
и такой, что
f(b)—f(a)=A(b—a).
3) Обобщите 1) и 2) на случай произвольного банахова про-
странства Y, определив подходящим образом интеграл в (5).
2.2.4. Дифференцирование в произведении пространств.
Частные производные. Теорема о полном дифференциале.
В этом пункте X, Y, Z—нормированные пространства.
Рассмотрим сначала случай отображения, значения кото-
рого лежат в произведении YxZ, F: U ^YxZ, UcX.
Поскольку точкой YxZ является пара (у, г), отображе-
ние F также состоит из двух компонент: F (x)=(G (х), Н (х)),
где G: U—► К, Н: U —*Z. Непосредственно из определе-
ний выводится следующее
Предложение 1. Пусть X, Y, Z—нормированные
пространства, U—окрестность точки х в X, G: U -* Y,
Н: U-+Z.
Для того чтобы отображение F — (G, Н): U —> YxZ
было дифференцируемо в точке х в смысле одного из опре-
делений 1—5 п. 2.2.1, необходимо и достаточно, чтобы
этим же свойством обладали G и Н. При этом
F'(х) = (G'(х), Н'(х)),
или
F' (х, h) = (G'(x, h), Н' (х, h)).
Перейдем теперь к случаю, когда область определе-
ния отображения F: U -+Z лежит в произведении про-
странств UcXxY.
Определение. Пусть X, Y, Z—нормированные
пространства, U — окрестность точки (х, у) в ХхУ,
F: U-^Z.
Если отображение xh->F(x, у) дифференцируемо в
точке х (по Гато, по Фреше или строго), то его произ-
водная называется частной производной по х отображе-
~ ~ - dF - -
ния F в точке (х, у) и обозначается Fx (х, у) или (х, у)..
Аналогично определяется частная производная по у
У) = ^Г& У)-
Теорема о полном дифференциале. Пусть
X, Y и Z—нормированные пространства, U—окрест-
151
ность в XxY, F: U —* Z— отображение, имеющее в каж-
дой точке (х, у) € W частные производные Fx (х, у) и Рг (х, у}
в смысле Гато.
Если отображения (х, у) н-> Fx (х, у) и (х, y)t->Fy (х, у)
непрерывны в точке (х, y)GU в равномерной оператор-
ной топологии, то F строго дифференцируема в той же
точке и при этом
F (х, y)U, П] = Fx(x, y)l-\-Fv(x, у)ц.
Доказательство. Задавшись произвольным 8 > О,
выберем 6 > 0 столь малым, чтобы «прямоугольная»
окрестность
V = S(x, 8)хВ(у, 6) = {(х, *li<6> РУ—Й<6}
точки (х, у) содержалась в U, и ’в ней выполнялись не-
равенства
\\FAx, У)-Гх(х, уЦ<г, \\Fy(x,^y)-—Fy(x, у)\\< е. (1)
Теперь имеем
Д =
—F (х1,у1) F (x1,y2)—Fx(x, у) (Xj х2) Fy (х, у) (,У1—уг)^
=[/7(л:1, yj—F(xa, у^ — Fx(x, у}^— х2)] +
+1? (х2, yJ—Ffa, y2)—Fy(x, у)(Ух—у2)].
Легко видеть, что если точки (хп г/х), (х2, у2) лежат в V,
то и (х2, г/j) G V и, более того, оба отрезка [(хх, уг), (х2, ух)]
И [(х2, У1)> (Х2, z/a)J содержатся в Vet/. Поэтому функ-
ции xt->F(x, yj и 'y>-+F(x2, у) дифференцируемы по
Гато: первая имеет производную Fx на [х1( х2J, вторая Fy
на [Ух> у2]- Применяя теорему о среднем к этим функ-
циям (в форме неравенства (3) п. 2.2.3 с соответствую-
щими Л), получаем в силу (1)
(*!, У1)€^. (х2, у2)еУ=^
=^i|A||<eSUp^{||Fx(S> У1) — Fx(x, УШ*!—
+ SUP Vi)—Fy(x, у)||||У1—У2||}^
<ehi—х2[| + е|]У1—у2||.
Следствие. Для того чтобы FgC1 (t/), необходимо
и достаточно, чтобы в U частные производные Fx и Fy
были непрерывны.
152
Как предложение 1, так и теорема о полном диффе-
ренциале без труда обобщаются на случай произведения
любого конечного числа пространств.
' Остановимся еще на конечномерном случае. Пусть
F' U—*Rm определена на открытом множестве (7cRn.
Поскольку естественным образом
Rm = Rx ... xR,
R'I-Rx...)<R,
tn раз
n раз
можно воспользоваться как предложением 1, так и тео-
ремой о полном дифференциале. Если
Матрица порядка тхп
называется матрицей Якоби отображения F в точке х.
Легко видеть, что это есть не что иное, как матрица
линейного оператора F' (х)\ Rn—*Rm, отвечающая стан-
дартным базисам в R” и Rffl.
153
В классическом анализе обычно обозначают
/dXj \
h = dx =
и формула (2) имеет вид
VI и* S' \ j
(х) = Е
>=1 •
Доказанное в этом пункте утверждение является обоб-
щением хорошо известной теоремы о том, что существо-
вание непрерывных частных производных является доста-
точным условием дифференцируемости функции несколь-
ких переменных.
2.2.5. Производные высших порядков. Формула Тей-
лора. В этом пункте X и Y — нормированные простран-
ства, U—открытое подмножество в X. Дифференцируе-
мость всюду понимается в смысле Фреше.
Если отображение f: U —>У дифференцируемо в каж-
дой точке x^U, то определено отображение f (х): U—*
—>^(Х, Y). Поскольку J? (X, Y) также является нор-
мированным пространством, можно ставить вопрос о суще-
ствовании второй производной
Г(х) = (П'^е^(х, ^(х, у)).
По индукции определяются производные высших поряд-
ков: если в U уже определена (х), то
(х) = (х)€^(Х, ..., &(Х, У) ...).
п раз
Определение 1. Пусть f: U—>У. Будем гово-
рить, что /<п> существует в точке x£U, если в некото-
рой окрестности этой точки существуют f' (х), ^"(х), ...
..., и существует /(п)(х).
Если /(п) (х) существует в каждой точке х € U и ото-
бражение Xi—»/*"’ (х) непрерывно в равномерной (порожден-
ной нормой) топологии пространства2?(Л, ...,3?(Х, У). ..),
то f называется отображением класса 0(1/).
В дальнейшем нам понадобятся некоторые свойства
полилинейных непрерывных отображений (см. пример 2
в п. 2.2.1).
154
Предложение 1. Нормированные пространства
S?n (X, Ут (X, У)) и ^п+т (X, У) изометрично изоморфны.
Доказательство. Если л£,2'п(Х, ^’т(Х, У)),
то л (хх, ..., хп)£ £т {X, У) и равенство
П (хх, хп, хп+1, хп+т) =
= л (х±, хп)[хп+1, хп+т] (1)
определяет полилинейное отображение П пространства
Хп+т = Хх ... хХ в У. Обратно, всякое такое отобра-
п+т раз
жение П определяет при помощи равенства (1) полили-
нейное отображение л пространства Хп==Хх...хХ
в пространство полилинейных отображений Хт в У
Остается заметить, что
ЦП||= sup ||П(х1, ..., х„+и)[|=
II xt || < 1
I! хп + т 11 < 1 • *
= sup sup л(хх............x„)fxn+1, ..., xn+/n] =
И. IK 1 Ilxn+1IK 1
11 xn II < 1 ||Хи+я!К^
= sup ||л(хх, ..., х„) [| = || л
IIX. IK 1
II Хп II < 1
Следствие 1. (X, 2? (X, 2\Х, У) ...)) изо-
. s п раз
метрично изоморфно 2п(Х, У).
Таким образом, можно считать, что f<n) (х) £ 2п (X, У). '
Значение этого полилинейного отображения на векторах
(£i> U будем обозначать /(п>(х)[£-х, Ц. В соот-
ветствии с индуктивным определением
r»>(x0)|U .... м =
мо « • /
Для произвольного П£^п(Х, У) и произвольного
набора различных индексов (i1( ..., ift), каждый из ко-
торых принимает одно из значений 1, 2, ..., п, обо-
значим
Пч ..(х;Лх, •.., йА) = П(х1, • •., x„)Ui;=ft;, i=i, 2.k,
I Л-=х, ....>k.
155
Предложение 2. Если П^^п(Х, Y) и Q (х)=
= П (х, ..., х), то
»
Q.' (*)[M= S n,-(^ М.
1 = I
п п
<?"(*) Рч, ftj= S S П,.,(х; Л1( Я2),
<=1 i=i
(3)
<2(n,W[*i.......М=' S П(Л/(......м.
Q <*’(х)== 0 при й>п
(в формуле для Q(m суммирование производится по всем
перестановкам индексов).
Доказательство этих формул получается непосредст-
венной выкладкой (ср. также пример в п. 2.2.1). Заме-
тим, что из (3) видно, что каждая производная Qu’
является симметрической функцией от (hlt .. Ниже
мы увидим, что это не случайно.
Предложение 3. Если отображение П g (X, У)
симметрично и Q (х) = П (х, ..., х) == О, то П = 0.
Доказательство. Положим —
Ф Pi....О = Q (fiXi + • • + t„xn) =
= 2b Л, • ^пП(х^... х/„)==
ц.....м
= S ^...«Д1(х,-............xin)~
О < < п
2b G* • • • tnnN№l,. ,а„п (Хг ,. . . , Xj, ., Хп, . . ., хп),
О < а.- < п > »» । ’- ..
2а/=п «1 раз otn раз
— где . в собраны члены, у которых среди индексов
t\, ..., in равны единице а2 штук, ..., равны п—ам
штук, a Nai...an—число членов в этой сумме (в послед-
нем переходе мы воспользовались симметрией П).
По условию <р(^, .... tn) = 0, поэтому равны нулю
все коэффициенты этого многочлена. В частности, равен
нулю и коэффициент nin^, ..х„) при Ц
Теорема о смешанных производных. Если
для функции f: U —> Y существует .вторая производная
/" (х), то для всех £, т]ёЛ_
Г T]]=rw[n. I].
156
- Доказательство. По определению второй про-
изводной
Г (*)—f (*) = (Г)' (*) [х—*] + а(х) IIX—х II,
где а(х)€^(Х, У) и
lim а (х) =а (х) = 0. (4)'
Х-9-Х
При достаточно малых ц и х, близких к х, функция
<р(х) = /(х + т])— f(x)
определена и
ф'(Х) = /' (х + Т]) —(х) = /'(х + л) — /'(х) — (/' (х) — f'(xj)= •
= (Г)' (х) [х + Т] — х] + а (х + Т]) h + Л—*11—
—(/')' (х) [х—х]—а (х) II х—х|| =ч
= (/-)' (*) Ы + «(х + ц) II х—х + Т) II—а (х) ||х—х||.
В частности,
ф' (*) = (/')' (х) [т]]+а (х +1]) h ||, (5)
и потому
ф'(х) — ф'(х) =
= а(х + т])[|х—х + г|[|— df(x)||x—Х|| — «(x4-ri)||r][(. (6)
В силу (4) для любого е > 0 найдется такое 6 > 0, что
||х—х|| < 6=Ф||а(х)|| < 8, (7)
откуда ввиду (6)
||х—х|[<6/2,
|| т] || < 6/2 =» || q>' (х)—ф' (х) || < 28 (1| х—х || + h Ц). (8)
При достаточно малых £ и ц вторая разность
Д(Т|, 5) = /(хЧ| + т1)-/(хЧ|)-/(£+т1)+/(;) (9)
имеет смысл и, Используя (5), (7) и (8), мы получаем при
III II <6/2, h II <6/2
||Д(n, I)-Г(*)[л, 1]||= ~
= IIФ (* +1)—Ф (*) — ((/')' (х) [П]) [I] В =
= ||ф(х + 1)—ф(х)—ф'(х) [l]+a(x + n)[l]hlllK
< sup ||ф'(х)—ф'(x)||||l|H-||a(x+Ti)lllll|lh|K
хе <28dllB+IW)BIIH-8||l||hB<38(|iq+h|i)BE||.
157
Заменяя | и т] на fg, /т], где теперь | и т] могут
быть любыми фиксированными, a ZgR должно быть
мало, мы получаем неравенство
||Д(^т], ф-l]K3ei2(||B|| + hll)HII- (Ю)
Меняя местами в проведенных выше рассуждениях £
и т], мы получаем наряду с (10) неравенство
||A(/L hi)_^(£)[g, п]КЗетЖИМ< (11)
Но Д (£т]> ^) = Д(/|, /т]), поскольку вторая разность (9)
симметрична относительно £ и т] и из (10) и (11) выте-
кает по сокращении на t2 неравенство
\\f" (i)h, 1]-Г(*Ж л] Ж Зе (Н11+HI)2.
Ввиду произвольности е это приводит к (3). |
Название, которое мы дали этой теореме, связано
с тем, что в классическом анализе ей соответствует тео-
рема о независимости смешанной производной от по-
d2f d2f
рядка дифференцирования: 57^ = ^ (почему?).
Следствие 2. Производная /(rt)(x) (если сущест-
вует) является симметрической полилинейной функцией.
Доказательство. При п = 2 это утверждение
только что доказанной теоремы. Далее рассуждаем по
индукции, используя равенства
((f(n-1,)(x)[g])hi, ViH'+xHL
= ((/<»-2>)"(х)[|, тц1)И, П„-х].
Воспользовавшись индукционной гипотезой, получаем из
левого равенства инвариантность /1"’(J0[5, Лл,
относительно перестановки аргументов т](, а из тео-
ремы 1 и правого равенства следует инвариантность
относительно транспозиции £ и t]r Для доказательства
симметричности /<п) (х) этого достаточно.
Переходя от симметрической полилинейной функции
к соответствующей ей форме (см. пример в 2.2.1), мы
получаем из производной дифференциал.
Определен ие 2.
dnf(xa; h) = fn(xa)[h, ..., /г].
Пример. Если Q (х) = П (х, ..., х), где П g S?n (X, Y),
то, согласно предложению 2,
dkQ (0; h) = 0 при k += п
158
и
dnQ (6; h) = k!Q(h).
Лемма. Если ftn)(x) существует и f(x) = O, f'(x)=‘
= О...../(п) (х) = О, то
lim
л—о
||ДаГ+М
ЦЛГ
О.
Доказательство. При п—1 утверждение верно
по определению производной. Далее рассуждаем по
индукции. Пусть п>1. Положим g(x) = f'(x). Тогда
g(x) = 0, ...» £("-1) (х) — 0, и по индукционной гипотезе
для всякого е > 0 найдется такое 6 > 0, что
U(х + МII <еIIhiIIя-1 ПРИ kill <8-
Теперь по теореме о среднем при ||/i|]<6 имеем
\\f (x + h)[\ = {[f(x + h)^f(x) —f' (x^/iJK
sup ||f (x + M—/'(x)ИЦ/i|| =
e[0. ft]
= sup U(x + /i1)||||/iK SUP
ft, e [0. ft] ft, e [o. ft]
Теорема о формуле Тейлора. Если fn(x) су-
ществует, то
f (x + h) = f (x)+df (x; h)+ ... 4-ld«f(x; h)+an(h)\\h\\n,
где
lima(/i) — a„ (0) = 0.
n->o
Доказательство. Рассмотрим функцию
g (?) = f (X + g)-/ (x)-df (£; g)-... -1 d"f (x; I).
Воспользовавшись приведенным выше примером и ра-
венством dkf(x; £) =/lA) (х) [1, ..., 1], /1А)(х) ^^k(X, Y),
получаем dkg(Q\ h)=dkf(x, h) — ^(kldkf(x-, h)) — Q.
Применяя следствие 1, согласно которому g'** (0) —
симметрическая функция из J?k(X, Y), и предложение 3,
согласно которому симметрическая функция обращается
в нуль, коль скоро обращается в нуль соответствующая
ей форма, мы заключаем, что g'(0) = 0, ..., g(n)(0) = 0.
159
По лемме ||g(|)[[ = o([| £[["), и утверждение теоремы дока*
зано, причем ап(Л)=£^ при Л^=0. |
Упражнение. Если (х) существует в звездной окрест-
ности точки X, то
1) |/(*+A)-/(S)-d/(x, *)|<
< sup || /<») (С) || Itf ;
ле[х, х+Л}
2) |/(*-М)—/(х) — df (Г, Л)—- .--~dnf(x, Л)|<
С sup || /<») (с) — /<») (х) || ,
се[х, х+Л] п>
Указание. Один из возможных путей решения- при п > 1
производная /' (х) непрерывна в окрестности точки х, и можно вос-
пользоваться равенством
1
f(x + h)-f(x)=^f (xa+th)dt[hl
о
(см. упражнение в п. 2.2.3).
Неравенства этой задачи являются обобщениями
классической формулы Тейлора с остаточным членом в
форме Лагранжа, в то время как теорема дает нам
ту же формулу с остаточным членом в форме Пеано.
Доказательство существования старших производных
в смысле Фреше у конкретных отображений зачастую
сопряжено с громоздкими выкладками. В то же время
вычисление производных, а точнее, дифференциалов,
т. е. соответствующих однородных форм, обычно можно
произвести сравнительно легко. Чаще всего это делается
с помощью понятия вариации по Лагранжу.
Определение 3. Функция / = U —+ Y в некоторой
точке x^U имеет п-ю вариацию по Лагранжу, если для
любого h$X функция q(a) = f(x + ah) дифференцируе-
ма в точке а = 0 до порядка п включительно. При этом
n-й вариацией f в точке называется отображение
(х; h), определяемое равенством
/г) = <р‘п>(О)=^/(х + аЛ)|а=о. (12)
160
Следствие 3. Если существует (х), то f имеет
п-ю вариацию по Лагранжу в точке х, причем
bnf(x-, h)=dnf(x', h)=fw-(x)[h.h]. (13)
Доказательство легко получается по индукции
из формулы Тейлора, так как, согласно последней,
f(x+ah)=^f(x)+^df(x-, Л)+ • • • + ~drf(x; Л) + о(ап).
Таким образом, если мы заранее уверены в сущест-
вовании производной /(rtl (х), то вычислить dnf(x',h) МОЖНО,
пользуясь формулами (12) и (13) на основе дифферен-
циального исчисления для функций" скалярного аргу-
мента, что, конечно, много проще. Согласно предложе-
нию 3 Дифференциалом dnf(x', А) производная f "’(х) (т. е.
полилинейная функция) однозначно определяется.
Обратное, конечно, неверно: функция может иметь
п-ю вариацию, не имея производной Фреше
Читателю предоставляется самостоятельно вйяснить,
какими "дополнительными свойствами должна обладать
п-я вариация, чтобы был верен аналог достаточного
условия дифференцируемости (следствие 2 п. 2.2.3).
§ 2,3, Теорема о неявной функции
Доказываемое в этом параграфе обобщение классиче-
ской теоремы о неявной функции может быть с успехом
применено в различных разделах анализа. В дальней- ,
шем мы будем иметь возможность в этом убедиться.
2.3.1. Формулировка теоремы о существовании не-
явной' функции. Пусть X—топологическое пространство,
У и Z—банаховы пространства, IF—окрестность точки
(х0, Уа) в XxY, Т—отображение из W в Z, (ха,у0) — г0.
Если:
1) отображение xt—*¥(х, р0) непрерывно в точке х0;
2) существует линейный непрерывный оператор
Л:-У—>Z такой, что для любого е>0 найдутся число
8 >0 и окрестность S точка х0, обладающие тем свой-
ством, что из условия х£В и неравенств \\у'—pe(|<6j
|jp"—Poll <6 следует неравенство
’ У')—р") —Л(р'—p")||<8jp'—р"||;
3) ЛУ = 2,
6 В М. Алексеев и др.
161
то найдутся число /С > 0, окрестность 41 точки (х0, г0)
в XxZ и отображение ср. —»¥ такие, что:
а) ¥ (х, ср (х, г)) = г;
б) ||<р(х, г)—^||<Л||Т(х, уа)—г||.
2.3.2. Модифицированный принцип сжимающих ото-
бражений.
Лемма. Пусть Т—топологическое пространство,
F—банахово пространство, V—окрестность точки
(f0, 5/о) в ТхУ.Ф—отображение из V в Y. Тогда, если
существует окрестность U точки ia в Т, число 0 > 0 и
число 0, О<0< 1, такие, что из t£U, ||у—уо||<0
следует:
а) (/, O)(f, z/))€V;
б) [|Ф(*, Ф(/, у))-Ф(*, уЖ0|(Ф(^ y}—yf,
в) II Ф(*. УьУ-Уь || < 0(1-9),
тс последовательность {*/„(01 ft 5*0}, рекуррентно опре-
деляема#. равенствами
Уа(Г) = Уа> yn(i)^(t, i/n-f(0),
при любом t £U содержится в шаре В (г/0, 0) =
— {у HI у—t/o||<0} и равномерно по t£U сходится к
отображению /н-><р(7), причем
Доказательство. Доказываем лемму по индук-
ции. Пусть t — некоторый элемент из U. Обозначим через
Г„ утверждение: «элемент yk(t) определен дляО^/г^п
и принадлежит В(уп, 0)». Вследствие того, что i/0(/) =
— уа€.В(уп, 0), утверждение Го верно. Пусть Гп верно.
Тогда для l^k^n имеем
Ь^(0~уИ0!Н|Ф(*. ^(О)-Ф(^, ^-1(0)11 =
=||Ф(/, Ф(0 Ф(0 ^_i(0)ll<
<0||Ф(^ yk-i(i))-ук-лт^\\ук^~Уь-лт-
Отсюда, продолжая проведенное рассуждение, получим
||^+i (0—Уь (t) (0—Уь-i (О К
^у.-Л^-у^Ш^-^туЛ^-у^
=еА1|ф(*> у,)-уЛ-
162
Пусть теперь 6 > 1, £ + Z n -f- 1; тогда вследствие
неравенства треугольника
1Уй+i (О Уь (011“
=||Уй+г(0—Ул+г-АО + Уй+г-ИО —•••+Уй+1(0—УИОК
<(0^-1+...+0*)йФ(^ z/J-z/JK
<(S 9s)||Ф(0 Уо)-УоН^Р(0 Уо)—Уо11<®*₽ (О
В частности, полагая в(1)^ + / = и + 1, k = \, и исполь-
зуя условие в), получаем
|y«+i(0—Уо11=11уй+1(0—У1 (0+У1(0—у»1К
<Цуп+1(0-УЛОЖМО-Уо11<9₽+₽(1- 0)=₽-
Значит, Гп+1 верно, откуда по индукции утверждение
верно для всех п. Но тогда из (1) получаем
||yr+z(0-yU0KT^0ll°(Z’ Уо)-У->»> VZ> Ж1- (2)
Из (2) следует^ что последовательность
фундаментальна и вследствие полноты Y сходится к не-
которому элементу, который мы обозначим <p(i). Пере-
ходя в (2) к пределу при I—»-оо, получаем,, что
да
Иф(О-Ул(0КгЬР(0 Уо)—Уо11 <0feP- (3)
I
Из (3) следует, что отображение tt—t£U, равно-
мерно сходится к отображению Наконец, по-
ложив в (3) k=\, получим
Вф(О—Уо8=|1ф(О—У1(0+У1(О—УрК
<Д||Ф(0 Уо)-УоН1|Ф(0 Уо)-У, 11 = .
2.3.3. ‘Доказательство теоремы. Доказательство сфор-
мулированной. в п. 2 3 1 теоремы разбиваем на несколько
пунктов.
А) По условию теоремы Л есть эпиморфизм из Y в Z.
Значит, по лемме о правом обратном отображении
(п. 2.1.5) существует отображение M:Z—такое, что
(ЛоМ)(г) = г, (1)
11М(г)||<СИ (2)
ь*
163
для некоторого ОО. Положим Т — XxZ и проверим
применимость леммы п. 2.3.2 для отображения •
Ф(Л у) = Ф(х, г, y) = y + M(z—W(x, у)).
Б) Задав 0, О<.0<1 и е = 0/С, где С—константа
из (2), найдем окрестность 8t точки хв и число ро > О
так, чтобы из неравенств ||у' —у0|| < Ро, Цу"-~У0|1 < в»
следовало (в соответствии с условием 2) теоремы) не-
равенство (при х€Зх)
||Т(х, y')—W(x, /)-Л(/-У)К<Ф'-П (3)
Обозначим V = EjXZx В (у0, ро).
В) Пусть р = ро/(С (| Л|| + 2). Используя непрерывность
функции (х, z)i—> + (х, у0)—г в точке (х0, г0) (см. усло-
вие 1) теоремы), выберем окрестность EjCrBi точки х0
и у > 0 так, чтобы из (х, г) G/U = Е2 хВ (г0, у) следовало не-
равенство
F(x, у„)-г|| <Р(1—0)/С. (4)
Г) Если (х, г)^^ и уЕВ(у0> Р)> т0
def (S)
||ф(х, г, у)—yJMy—У„ + М(г—Т(х’, у))||<
ск—Увй+Ск—^(^ у)1КИу—y«li+
+ С{||г—Т(х, у0)—^(х, у) + ¥(х, уи) + Л(у—у0) —
- Л (у—у0) ||} +1| у-ув || + С {|| г- Т (х, ув) || +
(3)
+ ||4f(x, у)—¥(х, у0)-*Л(у—у0)|| + ||Л(у—у0)||}<
<||У—Ув|| + С {||г—¥(х, у0)|| + е|1у—Уо11 + ||Л||||у— у0||} <
<(4 +0 + С||Л||)||у-у0|| + С||г-у(х, у„)|| (5)
(ибо еС = 0!).
Из (5) в силу (4) получаем, во-первых, что
Цф(х, г, у)~у0|| <
<(1+0 + С||Л||)р + Се1^ = (2 + С|(Л||)р^рв. (5')
Значит, выполнено условие а) леммы п 2.3.2: (х, г,
Ф(х, г, у))€У Во-вторых, при у = у0 получаем
1|ф(*,2о.Уо)-Уо11сО-^(х, Уо)!|<сЦ+^=р(1--е).
(5")
Значит, выполнено условие в) леммы п. 2.3.2.
164
JX) Если снова (х, г) £ % уе&(ув, ₽), то
def
|>(х, г, Ф(х, г, у)) — Ф(х, г, у) =
= Ф(х, г, у) 4-М (г —Т(х, Ф(х, г, у))) — Ф(х, г, у) =
= М(г-Т(х, Ф(х, г, у))). (6)
При этом вследствие (1)
ЛФ(х, г, у) = Л// + ЛМ(г—(х, у)) =Лу + г—Т (х, у),
откуда”
г = Т(х, у)4-Л(Ф(х, г, у)—у). (7)
Цодставляя (7) в (6) и учитывая, что в силу (5')
^(х, г, у)£В(уй, р0), получаем
(6)
|Ф(х, г, Ф(х, г, г/)) —Ф(х, г, г/)|| =
(2) * (7)
= ||М(2-Т(х, Ф(Х, 2, y)))KCh-T(X, Ф(Х, 2, 1/))|| =
(3)
= С||Т(х, Ф(х, 2, //))-Т(х, г/)—Л(Ф(х, 2, у)-у)\\^
<Се[|у—Ф(х, г, у)|| =5=01|г/—Ф(х, г, у){\. (8)
Таким образом, выполнено условие б) леммы н. 2.3.2.
Е) Еще раз сравним лемму п. 2.3.2 и наши построе-
ния. Топологическому пространству Т в лемме соответ-
ствует у нас произведение XxZ, точке t0—точка (х0, г0),
окрестности U точки ta— окрестность ‘Й точки (х0, г0),
окрестности V в лемме соответствует окрестность V,
построенная в Б), отображению (/, у)н-*Ф(/, г/) соответ-
ствует у нас отображение (х, г, г/)н-*.ф(х, г, у), числур
в лемме соответствует число р, построенное в В).
Тогда соотношение (5') означает, что выполнено усло-
вие а) леммы, соотношение (5")—что выполнено усло-
вие в), наконец, соотношение (8) означает, что выполнено
условие б). Значит, можно применять лемму.
Ж) По лемме, последовательность {уп(х, г)|п>0},
(х, 2)^41, определяемая рекуррентно равенствами
уа(х, г) = р0> уп+1(х, г)=Ф(х, г, уп(х, г)),
содержится при всех в шаре В(уа, р) и равно-
мерно сходится к функции ф(х, г), причем
def
||<р(х, г) —г/0||^||Ф(х, 2, уа) — г/011/(1— 0) =
(2) с
= 1|М(2-Т(х,Уо))Ц/(1-0)<т^М-^(х, Ув)Ц,
1Б5
так что выполняется утверждение б) теоремы с
= С/(1—9).
3) ||¥(х, ф(х, z))-2||<
(1)
ф(х, 2))—¥(х, (X, (X, г)) — г
<11 ¥ (к, ф (х, г)) —Т (х, уп (х, г)) —Л (ф (х, г) — уп (х, г)) ||+
(3), (2)
+ ||Л(ф(х, г)— уп(х, г))|| + ||ЛМ (г—^(х, уп(х, г)))|| <
<е||ф(х, г) — уп(х, г)|| + ||Л||||ф(х, г)—уп(х, г)|| +
- +ЦЛ1111 yn+i (х, 2)—уп(х, z)||—>0
при п—>-оо. Поэтому ^(х, ф(х, г)) = г. И
2.3.4. Классические теоремы о неявной функции и
об обратном отображении. Из доказанной выше общей
теоремы легко выводятся две классические теоремы, по-
стоянно используёмые в различных прикладных для
анализа областях, например в дифференциальной гео-
метрии. По сравнению с п. 2.3.1 мы усилим в двух на-
правлениях требования, предъявляемые к функции +.
Во-первых, теперь она будет предполагаться непрерывно
дифференцируемой, а во-вторых,—и это наиболее су-
щественно— оператор Л, входящий в формулировку
теоремы п. 2.3.1, будет предполагаться обратимым. Все
это обеспечивает гладкость и единственность неявной
функции.
А) Классическая теорема о неявной
функции. Пусть X, Y, Z—банаховы пространства,
W—окрестность в ХхУ, W:W—+Z—отображение из
класса С1 (1У). Если:
1) + (х0, уо) = 0; (1)
2) существует обратный оператор [Ту(х0, г/0)]“г€
g3?(Z, Y), то существуют такие е > 0 и S>0 и та-
кое отображение ф: В (х0, б) —У класса С1 (В (х0, б)), что:
а) ф (х0) = у„; (2)
б) ||х —-х01| < б =?>||ф (х)— у0||<е и Т(х, ф(х))э0;
в) в «прямоугольнике» В (х0, б) х В (у0, е) равенство
Т (х, у) = 0 возможно только при у — (р(х)',
г) ф' (х) = -[Т„ (х, ф (х))]-1 (х, ф (х)). (3)
Доказательство. Из непрерывной дифференци-
руемости + в W следует выполнение условий 1) и 2)
166
теоремы существования неявной функции из п. 2*3.1
(для проверки 2) надо положить Л = ^(х0, уа) и вос-
пользоваться теоремой о среднем). Условие 3) выпол-
нено, поскольку существует Чг~1(х0, уй). Значит, по этой
теореме найдутся число К > 0, окрестность U Эх0 и ото-
бражение ф: U —► Y такие, что
Т (х, ф (х)) =г 0, (4)
ЙФ(х)—1|КН(х, уа)\\. (5)
Полагая в (5) х — ха и используй (1), получаем (2), а
(4) дает вторую половийу утверждения б).
Б) Отображение 4FgC1:(iy) и потому строго диффе-
ренцируемо в точке (х0, у0) (следствие 2 п. 2.2.3). Сле-
довательно, для всякого х > 0 найдется такое е. (и) > 07
что
hr—л;0||<8(х), \\у{—yj|<e(x), i = 1, 2,
II УР" (xit К/х) У2) Ьо» Уо) hl ^2)
—^»ho, Уо)(У1—&Ж к max {|| хг—х2||, \\У1—#2[|}. (6)
Сначала .положим х0 = 72 ll^1 ho> Уо) II-1 и найдем
соответствующее в = е(х0). Поскольку Чг(х, у) непрерывна
и 4f(x0, уа) = 0, найдется такое б, 0 < б < е, 'что
В(ха, б) = {х|||х—х0||<6} с U
и '
р (5)
||х—х0 II < б =5> [[ ^ (х, ^0)||<у=4>||ф(х) — #oll<8» (7)
а следовательно, выполняется первая половина утвержде-
ния б).
Предположим теперь, что Ч’’ (х, у) = 0 в точке (х, у) £
£В(Хо, б)хВ(у0, е). Применяя (6) с указанным выше х0
(х1 = х2=х, Уг^у, г/2 = ф(х)), имеем
й—фЬ) 11=11 Vho> Уо) ^ho, Уо) (у—<ph))llc
Cll^ho» Уо) 1111 ¥(х, у)—Т(х, ф(*))—^(х0, уа)(у—ф(х))||2
^Cll^gho» Уо) 111ко11у фh)II — IIу—Th)ll>
что возможно лишь при у = ф(х), т. е. верно утвержде-
ние в).
167
В) При тех же хл, в, 6 положим в (6) Xi = x, х2 = ха,
У1 = Уг = Уа- Тогда
J*—х-0||<6^>)|Т(х,^0)—V(xa, //„)—(х0, уа) (х—ха)||<
(5)
<хаЦх—Хд||=ф||Т(х, j/oHKdl'FxCXo, Ml + Zo)k~-Xi=>
=Мф(х)— «/oIKO^Xo. i/o)|| + xo)||x—*»![ (8)
Теперь зададим произвольно хх > 0 и применим (6) к
Х^ —X, Х2 = Ха, ^/з = ^/о*
Для
6, = mгп <[е (х.), . -л 8 ;.. ,—Д
1 р х'’ М|Ф*(*о. г/оН+ко) J
имеем
h—Хо II <6X=?> II (x0, г/д)Чгх(ха, ^о)(х—х0)+ф(х)—г/0!Н
= 11^ Хо> 0O)X—*a)+^(x<» t/a) (ф(х)—уа)}||^
Уо)ин(х, Ф(х))-ччхд,уд)-
' (6)
—(Хд, уа)(х—Хд)—(Хд, г/д) (ф (х)—0д)]|<
(8)
< II(Хо, у9) II%! max {[х—Хд ||, II ф (х) — г/д ||} < Схг || х—ха||,
где
C = ||¥j1(xe, г/д)||шах{1, К (||ТХ (ха, г/а)|| + ОЬ
Поскольку хх можно выбирать произвольно, доказанное
неравенство означает, что при х-^ха
^(Хо, Уа)^х(ха, г/0)(х—Хд) + ф(х) —г/0 = о(х—х„)
или
ф(х) = «/о+[—Т^Ч^д. Уо)Чх(ха, г/о)](*~*0)+о(х—х0),
а следовательно, существует производная Фреше ф'^о)»
и равенство (3) имеет место при х = х9.
Чтобы доказать дифференцируемость ф при осталь-
ных х, напомним, что множество операторов Л, для
которых-существует обратный, открыто в 2 (X, Y) (пред-
ложение 3 в п. 2.2.Г). Поэтому, уменьшив, если нужно,
6, мы можем считать, что Т/(х, ф(х)) существует при
IX—х9 II <6.
Теперь можно повторить все доказательство, заменив
точку (х0, г/д) точкой (х, ф(х)), где ||х—х„||<6. В силу
доказанной выше единственности мы получим ту же
168
самую функцию ф(х) (по крайней мере, если ||х—х|| до-
статочно мало} и для нее формула (3) будет верна при
х = х. Так как х было произвольно, то утверждение г)
имеет место при всех х€В(х0, 8).
Наконец, производная <р' (х) непрерывна, так как,
согласно (3), она представляется в виде суперпозиции
непрерывных отображений хь->(х, ф(х)), (х, у)и-» ТДх, у),
(х, (х, I/) и Лн->Л-1 (последнее непрерывно, по-
скольку оно дифференцируемо по Фреше согласно пред-
ложению 3 п. 2.2.1). В
Замечание. Если в дополнение к условиям теоремы
г>2/ то ф€<?(В(х0, 8)).
Действительно, ~из формулы (3) и теоремы о супер-
позиции можно вывести, что
ф" (х) = — (X, ф (х))-1 О (х, ф (х))}’
существует и непрерывна. Далее рассуждаем по индукции.
Теорема об обратном отображении. Пусть
Y и Z—банаховы пространства, W—окрестность точки
ув в Y, Y: U7 —>Z—отображение класса С1 (W), г9 = Щув).
Если существует обратный оператор Т'^/о)-1 € «^(Z, Y)t
то:
а) существует такое е > 0, что В (уй, е) с W а
V={z|z = ’F(i/), \\у—у„\\ <e} = W(B(ya, (^—окрест-
ность z0 в Z;
б) существует отображение Ф: V—класса С*(У),
обратное к W [ В (ув, е), т. е. такое, что
у = Ф(г)^г = Т(У). (у,2)£ B(ya,e)xV-, (9)
в) Ф'(г) = рР'(Ф(г))]-1. (10)
Доказательство. А). Отображение ¥€С1(^')
строго дифференцируемо в каждой точке W, в частности
и в уй. Поэтому для всякого х>0 найдется е(х)>0
такое, что
Poll <е(и), i = l, 2, =Ф
^||У(у1)’-^(рг)-ТЧу0)(!/1-ргЖхк1-ря||. (11)
Выберем е > 0 так, чтобы для всех у^.В(ув, е) суще-
ствовал обратный оператор Т' (р)~х (см. предложение 3
п. 2 2 1) и чтобы было е < е(х0), где хв = ||(^0)-11|-1.
169
Последнее обеспечивает инъективность отображения Ф
на В(у0, в):
У1> Ул£В(у0, в), ^(у1) = Т(уа)=Ф
=» hi—у 2II=II ф' (у0) ~1 ф' (у0) (У1—у8)1К
< IIЧ" (Уо)-11111 Ф (Ух) -Ф (Уз) -Ф' (Уо) (Ух—Ух)|| С
^ЦФ (Уо) 1 hjl1| hx Уа 11 = у II Ух УаИ^ У1~ У г-
Далее мы докажем, что шар В(у0, в) — тот самый,
о котором говорится в п. а) теоремы, а пока положим
V = y¥(B(ya, в)). Ввиду инъективности отображения
Ф | В (уа, в) оно обратимо, так что существует Ф: V —►
—>В(г/в,в), обладающее свойством (9).
Б) Для любой точки у£В(у0, в) применим теорему
п. 2.3.1 к отображению Ф1 (у) (не зависящему от х, так
что пространство X может быть любым) в окрестности
точки у. Условие 1) этой теоремы здесь тривиально;
условие 2) превращается в условие строгой дифференци-
руемости в точке у и, как было отмечено, выполнено,
Причем А = Ф' (у); условие 3) выполнено, поскольку
у€В(у0, б) н в соответствии с выбором в существует
ф'(у)-1-
По теореме п. 2.3.1 существует окрестность U точки
г = Ф(г/) и отображение q>: U —такие, что
Т(ф(г))зг, (12)
1|ф(2)—у|КК||г—г|| (13)
для некоторого К > 0. Возьмем б > 0 столь малым, чтобы
B(z, б) az U и чтобы было б < (в—ho—у||)/^- Тогда
Ц 2 -2 || < б‘2 || ф (2) -У |[ <
=> II ф(2) - Уо || < 6 => z = Ф (Ф (z)) € Ф (В (ул, в)) =
= V => В (£, б) с V.
Таким образом, каждая точка zgV имеет окрестность
В (г, б) с V, ‘ так что V открыто. Кроме того, для
г € В (z0, б)
(12)
ЧГ(ф(г)) = г=Чг(Ф(г))=Фф(г) = Ф(г) (14)
в силу инъективности Ф1.
170
В) Докажем теперь дифференцируемость отображе-
ния Ф и формулу (10). В силу строгой дифференци-
руемости Т в точке у — Ф (г) имеет место аналог (11): для
всякого х>0 найдется е(х)>0 такое, что
\\Уг~ У||<Б(Х)- *=1,2,=»
=$> II (Ух)-^ (У2)-^' (У) (У1-У2) II IIУ1 -у* II- <15)
Полагая здесь г/1 = Ф(?), У2 = У = Ф(2), имеем
Р МА (‘ЗИП) (15)
||Z — г||<4р ===^ 11ф(г)—у\\ <е(х)=»
=»||¥(Ф (г))-¥(Ф (£)) (У) (ф (г)-ф (г) || <
„ (13) Л (12)
<х|]Ф(г) — #||<xK||z--z||=»
=»||г-г~-Т' (^(Ф(г)-Ф(г)ЖхК||г-г,|=»
=»||Ф(г)—Ф(г)—Т (уГЧг-ЮЬ
= IIЧ'СуГ1 (г-г-W' (у) (Ф(г)-Ф (£)))||<
<|| Т' (у)’11||| z-z II-
и потому
Ф(г)—Ф(г)—1Jf' (г/)-1(г—г) =о (г — г)
при г—►г, так как к произвольно. Поэтому существует
производная Фреше Ф' (г) = 1¥'(у)’1, так что (Ю) Д°ка’
зано. Производная Ф' (г) непрерывна на V, так как,
согласно (10), она представляется в виде суперпозиции
непрерывных отображений г-—>Ф(г), у*-»4f,(y) и Л-—»Л-1
(последнее непрерывно в силу предложения 3 п. 2.2.1).
2.3.5. Касательное пространство и теорема Люстер-
ника. В этом пункте X—нормированное пространство,
М — некоторое его подмножество.
Определение. Элемент h С X называется касатель-
ным вектором к М в точке ха£М, если существуют
такие е>0 и отображение г: [—‘е., е]—>Х, что:
a) xa + ah-\-r (а)£М,
б) г(а) = о(а) при а—>0.
Элемент h С X называется односторонним касательным
вектором к М в точке ха € М, если существуют е > 0 и
отображение г: (0, е)—*Х такие, что выполнено а), и
б) имеет место при a JO.
Множество всех касательных векторов к М в точке х0
обозначается Т^М, множество односторонних касатель-
171
ных ректоров— Т^М. Очевидно, что ТХ„М с ТХ,М и чТо
TXaM — TXoMri (— ТХ„М). Если множество ТХоМ является
подпространством в X, та оно называется касательным
пространством к М. в точке х0.
Рис. 33 Рис. 34.
Замечание. В геометрии обычно касательной пря-
мой, плоскостью и-т д. называют не TXtMt а аффинное
многообразие x0 + TXllM (рис. 33)..
Примеры (подробные доказательства предостав-
ляются читателю).
1) X = R‘, Л4 = {(х, ^)|х>0} (рис. 34); Т+0.в)Л4 = М,
= {(0, &) I b € R}, Т(1. 0,М = Ttt, OiM = R2.
2) X=R2, М = ((х, ^)|х>0, y>0} = R2 (рис. 35);
T(1.e)M=={(a, 0)|agR}, 7<(), о)М=(О}, T<Gll>^={(0,6)^eRb
П1(0)Л4 = {(а, Ь)| a€R, &>0}, в)Л4 = М, Т^1}М
= {(а, b)(a>0, 6£R}.
172'
3) X = FxR, где Y—нормированное 'пространств©,
Д1 = {((/, z) | 2 —конус (рис. 36).
Ло. 0)М = {0}, ТГ0,0)М = М.
Упражйения.
1 Предполагая, что У—гильбертово пространство (например,
F = R2), найдите Т|(д(I)Af и T^iyV)M в примере 3) при у £ 0
(рис. 36).
2 . Найдите ТаМ. и ТдМ, где:
а) М = {2-»|Л=1, 2, . .} (J {0}с R, «^0;
б) Л1={-1|л=±1, 2, ...| U {OJCR, а=^У,
в) Л4 = {(х, 0|х2 = р«} с R2, а = (0, 0) и а = (1, 1);
г) Л1 = {(х, 0| х2<;0} с R2, a==J0, 0) и в=(1, 1);
д) М = {(х, у) | х22а0} с R2, а=(0, 0) и а=(1, 1);
е) Л4 = {(х, у, z) I г— 1, если х и у рациональны, z = 0 в осталь-
ных случаях}, а = (0, 0, 1)
Во многих случаях, в том числе й представляющих
интерес для теории экстремальных задач, множество
касательных векторов может быть найдено при помощи
следующей общей теоремы.
Теорема Люстернйка. Пусть X, Z—банаховы
пространства,- U—окрестность точки хй в X, F-. U —+Z,
Р(хй) = $.
Если F строго дифференцируемо в точке ха и F' (х0)
является эпиморфизмом, то множество М = {х| 77(х) = 0}
имеет в точке х„ касательное пространство
Tx,M = TtM = ^F' (х0).
Доказательство. А) Пусть h£TXaM. Тогда, если
/•(•)— отображение из определения одностороннего каса-
тельного вектора, то в силу строгой дифференцируемости
0 = F (х0 ah + г (а)) = F (х0) Н-аТ7’ (х0) h + о (а) =
— aF’ (х0) h + о (а).
Значит, F' (х0) /i = 0 и ТХаМ с Ker F' (х0).
Б) Применим теорему П. 2.3.1 к отображению
¥ (х, у) = F (х у). Вследствие строгой дифференцируе-
мости F отображение хн-> ¥ (х, 0) непрерывно в тоЧкё хв и
F (х, /)-¥(х, y")-Fr (ха)(у'~у")\\^е\\уг^у"1 .
если ||х—х0|| < 8, \\у'\\ <8, Ц/|| < 8. Условие 3) теоремы
п. 2.3.1 также выполняется, ибо F' (х0) отображает X
173
на Z. В соответствии с этой теоремой существует отобра-
жение <р: U —»- X окрестности U с: X точки х„ такое,
что
Т(х, ф (х)) == 0 о F (х + ф (х)) =s О,
||ф(х)КК||Т(х, 0)||=КИ(х)й.
Остается лишь положить г (а) = ф(х0 + а/г). Тогда,
F (х0 + а/г + г (а)) = F (х0 + ah -рф (х0 + аЛ)) = О,
IIг (а)|| = || Ф (х0 + ah) ||СКИ(х0+оЛ)[| =
= К [| F (х, + ah) - F (х0) || = К || F' (х0) ah + о (||аЛ ||) || = '
= К||аГ (х„) Л4-о (а)||,
и если Л€КегГ'(х0), то ||г (а)|| = о(а). Следовательно,
КегГ(х0)сТ^Л1сТ*Л4.
На уровне геометрической интуиции теорема Люстер-
ника выглядит весьма прозрачно. Пренебрегая стро-
гостью, можно определить касательное пространство L
к множеству М в точке х0 тем, что «с точностью до
бесконечно малых высшего порядка» М аппроксимируется
аффинным многообразием xa+L. Но «в бесконечно малой
окрестности» точки х0 функция F аппроксимируется своей
линейной частью:
F (х)« F (х0) + F' (х0) (х — х0) = F' (х0) (х — х0) (1)
(точка ха£М, и потому F(xa) = Q), а множество М =а
= {x|F(x) = O} аппроксимируется множеством
М = {х | F' (х0) (х—х0}= 0} = Ker F' (х0) + ха.
Таким образом, «с точностью до бесконечно малых
высшего порядка» М совпадает с аффинным многообра-
зием УЙ = х0 + КегР'(х0), и, следовательно, KerF'(x0) —
касательное пространство.
§ 2,4, Дифференцируемость некоторых конкретных
отображений
2.4.1. Оператор Немыцкого и оператор дифференци-
альной связи. Пусть U—открытое множество в RxRn,
и пусть функция f(t, х): Uи ее частная произ-
водная fx(t, х) непрерывны в U. Зададим равенством
<№(x(-))(t)^f(t,x(t)), (1)
174
отображение Jf: ЭД—*С([/0, Rm), определенное на
множестве
Эд = {X (•) ёс ([М м, R") | (t, X (/)) eu, < t < (2)
Это отображение- мы будем называть оператором Не-
мыцкого.
Упражнение 1. Проверьте, что множество (2) открыто
в C([ta, (J, R«).
Предложение 1. Оператор Немецкого, заданный
соотношением (1), непрерывно дифференцируем на мно-
жестве (2) и при этом
= (3)
где
— матрица Якоби.
Доказательство. Вычислим сначала первую ва-
риацию по Лагранжу отображения <Jf. По определению
6<Г(х(-); й(-)) = Нт <х< ».
а -> 0 а
Слева и справа здесь стоят элементы пространства
С ([/„, т. е. некоторые функции от t £ [Zo, ZJ.
При фиксированном t имеем
lim ^^()+^(-))(О-оУ(^( ))(О
а -> о а
= lim x(Q)
а-> 0 ' а
-fx^x(t))b(t) = fxd)h(i). (5)
Чтобы убедиться в том, что сходимость здесь имеет место
также в смысле пространства С ([/0, Zx], R“), т. е. что
она равномерна, заметим, что для некоторого а > 0
компакт
= х)||х—x(Z)|^a, ta t с U
и на этом компакте fx равномерно непрерывна. Это
значит, что
Ve>0,36>0, |f —f|<6, |х' —х"|<б=Ф
=^>11/х(^,^)-/ДПх")||<8.
175
Если |«| < 6/ЦЛ (-)||с, то по теореме о среднем (п. 2.2.3)
| («(» (() h (()(1 _
_ пи 1^-
*= ШЛА I ————. — ———
ig[i0, ЦП а II
< ’max max |[fx(Z, X(t) + Qa,h(t))—fx(t, x(/))|||/i(0K
GI бе[О, 11
Ce||Mc- (6)
Поэтому сходимость • (5) действительно равномерна и
доказано существование первой вариации по Лагранжу
Поскольку первая вариация задается линейным опера-
тором
<Гг(*(•)): С(Ро, Rn)->C([/0, Ц, R-),
а именно о№г (.*(•))—это оператор умножения на матрич-
ную функцию fx (/) и этот оператор, ограничен:
Иг(*Н)К max (7)
i € Не, G)
то о№ (%(•)) дифференцируем по Гато. Чтобы доказать
непрерывность производной Гато, оценим норму разности
Иг (*(-))-<Лг(£ (•))!!= .
= (ift(Sup<iHr(^(-))[ft(-)]-ofrr(x(-))[fe(-)]b
-= sup max ||fx(f, x(0)/i(0—fx(t, *(0)M0ll<
11» ( Mlc< tt]
< max \\fx(t, x(t))—fx(t, x(t))\\.
Ц]
Снова с помощью компакта й? и равномерной непре-
рывности fx, убеждаемся в непрерывности clfj- (%(•)) от-
носительно Применяя теперь следствие 2 из
п. 2.2.3, мы убеждаемся, что (%(•)) имеет в каждой
точке множества 41 производную Фреше и строго диффе-
ренцируемо. Ввиду равенства — производная
фреше непрерывна в 41. |
Упражнение^. Докажите, что в (7) имеет место равенство.
Пусть теперь U — открытое множество в RxRnxRr,
и пусть функция f (t, х, и): U —» R" и ее частные про-
176
изводные fx, ftt непрерывный U. Отображение off: ад —
—*C([Z0, ZJ, Rm), определенное на множестве
M4), «(-))|(Лх(0,«(0)€(Л
^СЦ[10, /J, R«)xC([Z0, G], RO (8)
равенством
#(*(•), u(.))(t)^f(t,x(t),u(t)), (9)
мы также будем называть оператором Немыцкого.
Предложение 2. Оператор Немыцкого, заданный
соотношением (8) непрерывно дифференцируем на множе-
стве (9) и при этом
<Г (£(•), «(•))₽»(•), ^)](W^0MW«<^(*)> (10)
-где
, U1........ (11)
“(0)’ ‘ = 1’ (12)
Доказательство. Как и в предыдущем случае,
у отображения <№ существуют частные производные
о№х(£(.),
«(-))[v(-)](0=/»(*W)»
и отображения
о№х: ад—^(С1 ([*<>. OL R°)> <Ж, 0L R01)),
o№Bt ад — ^(СЧРо. м. R'), С(Ро. Rm))
непрерывны в ад. Остается сослаться на теорему о пол-
ном дифференциале из п. 2.2.4. Ц
Пусть далее U и ад—те же, что и в предыдущем при-
мере, функция <p(t, х, и): U—> R" и ее частные произ-
водные фх, <рк непрерывны в U. Отображение Ф: ад—*
—-С(р0, ZJ, R"), определенное равенством
Ф(х(-), u(-))(0 = i(0-T(0 х(0, ц(0), (13)
'будем называть оператором дифференциальной связи.
Предложение 3. Оператор дифференциальной,связи,
заданный соотношением (13), непрерывно дифференцируем
17?
на множестве (8) и при этом
ф'(х(-), и(.))[Л(.)> *(•)](*) =
= Ь(/)-фх(ОН(О-фв(О^(О. (14)
где
(°\ h / = 1...»). (15)
»‘ = 1..п, k = l, ...,г). (16)
Доказательство. Отображение Ф есть разность
линейного непрерывного оператора (х(-), u(-))f—>х(-) и
оператора Немыцкого е№(х(-), и(-)) (t) = <p(t, x(t), u(t)).
Поэтому доказываемое утверждение следует ^з общих
свойств производных (п. 2.2.1) и предложения 2. |
2.4.2. Интегральный функционал. Пусть U—открытое
множество в Rx R“X R", и пусть функция f (i,x,x): IJ—>R“
и ее частные производные fx, непрерывны в U. Отобра-
жение 3: ►R'” зададим на множестве
Г = U(-) (1А> М, R”) I (*. x(t), х(0) € и, t^t^} (1)
равенством
tt
3 (х(-))=\f(i, x(t), x(t))dt. (2)
^0
Предложение 1. Интегральное отображение (2)
непрерывно дифференцируемо на множестве (1) и при
этом
(3)
А)
где
= /=1......и), (4)
h (t)&(^(t,xtf),x(t)), i=\,...,m, j = l,...tn\ (5)
\ ^х/ I
Доказательство. Представим отображение (2)
в виде суперпозиции
3 = 1 ооГоР,
где
D: C([t0, ZJ.R^-^R»
178
— линейный непрерывный оператор, определяемый ра-
венством
о№: ^->C([Z0, у, R“)
—оператор Немыцкого, определяемый равенством (9)
п. 2.4.1 (при г = п), и
/: C([/G, G], Rm)-+R®
— операто'р интегрирования
ti
I (%(•)) — J x(t)dt
^0
также линейный и непрерывный. Все эти операторы диф-
ференцируемы (см. п. 2.2.1 и предложение 2 п. 2.4.1),
причем производная линейного оператора совпадает с ним
самим, а производная оператора Немыцкого дается фор-
мулой (10) п. 2.4.1. По теореме о суперпозиции
3'(x(-)) = Ix>^'(Dx(-))oD, (6)
т. е.
5,'(S(-))[^(-)] = Z{o№z (Z?x(.))[Z?ft(.)]} =
= /{<Г (£(•),
~I{UWt) + h(W)} =
^0
Этим доказана формула (3). Непрерывность 3' (%(•)) сле-
дует из непрерывности производной оператора Немыц-
кого и равенства (6). |
Упражнение. Найдите нормы операторов D и /.
В задачах классического вариационного исчисления и
оптимального управления рассматриваются также интег-
ральные функционалы вида (2) с переменными пределами
интегрирования ta и Чтобы включить их в общую
схему, поступим следующим образом.
Пусть предположения относительно х, х) те же,
что и раньше, AsR— цекоторый отрезок,
= ta, ^\х(-)£СЦЬ, R»), (/, х(0, x(t))£U,
*£А, ta, int А). (7)
179
Определим отображение 3-. CIL—+Wa равенством
3(х(-), ttt, f(t, x(t), x(t))dt.
(8)
Предложение 2. Интегральное отображение (8)
непрерывно дифференцируемо на множестве (7) и. при этом
З'(х(-), t0, О[Л(-), Ь.
= $ (fx (0 h (0 + f- (t) h (0) dt+f (/*)
где fx(t) и f^ft) даются формулами (4) и (5), a
= ~x(t), 2(0)-
(10)
Доказательство. Воспользуемся теоремой о пол-
ном дифференциале из п. 2.2.4. Частные производные
существуют в соответствии с предложением 1 и класси-
ческой теоремой о производной интеграла по верхнему
и нижнему пределам интегрирования:
?<((4). h, ?Ж]=-Ж)%.
^ (*(•). О О [4.]=f(Оч-
Приступаем к проверке непрерывности частных про-
изводных.
A) pfo(x(-), ta, t^3ta{x{-}, К ОН
=, sup ||Ж,*(О.*(О)Т0—Ж. Ж).
II То || 1
Cino z(o, f(o)-/(o ж»), j(O)|.
(И)
Кроме того,
|х(ОЖ(?0)|<|х(О—х(ОЖЖ)—Ж)|<
<k(-)-x(.)H-|x(Q-x(f.)|, (12)
I X (ta) X (t0) | < \x (tg) X (tg) | -|-| X (tg) X (tg) | <
<l|f(-)-x(-)k+|x(O-x (f0)|. (13)
180
Поэтому, если и х(-)—*х(-) в СХ(Д, R"), то
x(t0) —>x(Q, x(t0) —+ x(Q и, значит, правая часть нера-
венства (11) стремится к нулю. Следовательно,
5f0(x(-), ^о> ^i) непрерывно зависит от (х(-), t0, /х) (от
tx эта производная не зависит вовсе). Непрерывность
(х(-)„ t0, t±) проверяется аналогично.
Б) Выберем число а > 0 так, чтобы компакт
{(/, х, w)||x—'х(0[Са> |«—х(/)|^а, t£k}e.U.
На этом компакте производные fx(t, х, х) и х, х)
равномерно непрерывны и ограничены. Теперь при
||х(-)—х(•)Ис1 =Са имеем:
к ци=
= sup |Jo+/-4)^-j‘o + ^A)^|c
IIЛ ( ) < I ta "
s<^1uW+/;M+iUft+^>‘i'i+
+|j W«-/«)'+(/;-Fj'M) <
<тах{||/х(/, x, »)|| + ||^(*, x, ы)||}(|^ —M + Po~ G>l) +
+ тах{||/я(/, x(t), x(t))—fx(t, x(t), x(i))|| +
Ре» G]
+IIZ; (t, x(t), x(t), x(O)||b
Первый член стремится к нулю при и
Второй оценивается с использованием равномерной не-
прерывности так же, как в доказательстве предложения 1
п. 2.4.1, и тем самым стремится к нулю, когда х (•) —► х (•)
в пространстве С1 (A, R").
Применяя теорему о полном дифференциале, полу*
чаем (9). |
2.4.3. Оператор краевых условий. Пусть функция
Ф(^о> *i): W'—»-R* непрерывно дифференцируема
181
на открытом множестве IFcRxR"xRxRn, и пусть
Г = {(х(.), ta, ^(.НСЧД, R”), '
^intA, (fG, х(О, (1)-
Отображение Ч": *RJ, определяемое равенством
¥(х(.), ia, О = ф(*в> x(ta), tlt x(fj), (2)
называется оператором краевых условий.
Предложение. Оператор краевых ‘условий (2) не-
прерывно дифференцируем на множестве (1) и при этом
¥'(*(•). А>. т0, ч]=
=ад+КV1 (*»)+* (*о) [h UM*(Мb], (3)
где
*(О. *1’ 1=0, 1» (4)
tlt x(fi))> t =0, 1. (5)
Доказательство. А) Рассмотрим сначала прос-
тейшее отображение ev: С1 (A, R”)xintА —>R”, опреде-
ляемое равенством
ev(x(-), ta) = x(ta)
(отображение значений). По х(-) это отображение ли-
нейно, и потому
evX(.)(x(-), Г0)[М-)] = Ц?0).
Частная производная по ta—это обычная производная
evfo(x(-), ?0)[r0] = x(f0)T0.
Проверяем непрерывность:
||evx(.)(x(-), Q—evx(.)(x(-), fG)|| =
= sup [\h (/„)— h (4)11^
c sup sup [[4(9)111 /й—2tt| 1 — 0
II* (-)llci< i e6[/„,7„]
при Zo—> ta. Далее
||ev<0(x(->, /„)—evi„(x(.), /0)|| =
= sup I|x(/„)'ee—x(f0)T0|l=||x(Q—X(fo)||—0, .
I | < 1
182
когда ta—+ и %(•) —►x(-) в пространстве С1 (A, R"),
как эЛ было показано при доказательстве предложения 2
п. 2.4.2 ^неравенства (12) и (13)). В силу теоремы о пол-
ном дифференциале (п. 2.2.4)
ev(x(-), f0)'[/i(-), то] = /1(?о)4-х(Отв.
Аналогично убеждаемся в непрерывной дифференцируе-
мости отображения (*(), Zi)-->x(/1).
Б) Воспользовавшись теоремой о суперпозиции, убеж-
даемся в дифференцируемости отображения (2) и спра-
ведливости равенства (3). |
Упражнение 1. Пусть отображение ev: С1 ([0, 1 ]) Х(0, 1) R
определено формулой ev(x(-), ta) = x(tB) (ср. п. 2.4.3). Докажите,
что:
а) для существования второй вариации б2 ev (*(•), tB) необхо-
димо и достаточно, чтобы существовала х (tаУ и при этом
6* ev (*(), ta) [fl (), т] = 2Л(^0)т4 х(/0)т2;
б) отображение ev не имеет второй производной Фреше, хотя
его первая производная Фреше дифференцируема по Гато.
Указание, h {tB-[-x)~h (tB) 5й о (|) Л ||2 +т2).
§ 2.5, Необходимые сведения из теории
обыкновенных дифференциальных уравнений
Как уже отмечалось в п. 2.1.8, дифференциальные
уравнения х = ф(/, х, u(t)), рассматриваемые в задачах
оптимального управления, имеют свою специфику. По-
скольку мы допускаем разрывные управления «(•), их
правая часть не обязана удовлетворять условиям стан-
дартных теорем из курса дифференциальных уравнений.
К тому же нужные сведения о решениях не всегда из-
лагаются в этих курсах в удобной для нас форме. Поэ-
тому для полноты изложения, а также чтобы проиллюст-
рировать возможность применения здесь общих теорем
§§ 2.3 и 2.4, мы приводим в этом параграфе доказатель-
ства основных теорем: существования, единственности и
дифференцируемости решений, а также некоторые спе-
циальные утверждения, относящиеся к линейным систе-
мам. Часть формулировок дана в несколько более общей
форме, чем это обычно необходимо. Чаще всего мы имеем
дело только с кусочно-непрерывными управлениями «(•),
но и в этом случае удобно говорить об «измеримости»,
«интегрируемости» и т. п.
183
Функция х(-) называется решением дифференциального
уравнения
x = F(t, х),
если она абсолютно непрерывна (см. п. 2.1.8) и удов-
летворяет уравнению почти всюду.
В эквивалентной форме х(-) должно быть решением
интегрального уравнения
t
x(f) = *O0) + $-F(s, x(s))tfe.
^0
2.5.1. Основные предположения. Здесь -й далее будем
предполагать, что G— открытое множество в RxR" и
что функция Г: G—»-Rn удовлетворяет следующим трем
условиям:
А) Для любого х функция t^-F(t, х), определенная
на сечении Gx-={/|(Z, x)£G}, измеримая интегрируема
на любом конечном отрезке, содержащемся в Gx.
Б) Для любого't функция x^F(t, х), определенная
на сечении Gt = (x|(/, x)£G}, дифференцируема (хотя бы
в смысле Гато).
В) Для любого компакта существует такая ло-
кально интегрируемая функция fe(-), что
{\Fx(t, x)\\^k(t), V(t, x)£W. (1)
(Функция называется локально интегрируемой, если она
интегрируема на любом конечном отрезке.)
Типичный пример доставляет функция F (t,~ х) =
х, где <р(/, х, и) и q>x(i, х, и) непрерывны
на a u: R—кусочно-непрерывна. Условия А)
и Б) здесь очевидны, a k(t) можно положить равной
максимуму х)|| на Ж1. Другой пример—F(t, х).=
— A(f)x, где А(-) измеримая локально интегрируемая
матричная функция,
A: R —^(R«, R»).
Замечание. Условия А)—В) более ограничитель-
ны, чем известные условия Каратеодори [6], но они лучше
приспособлены, с одной стороны, к нашим потребностям
(рассмотрение уравнений x = <p(i, х, u(t)) с разрывными
управлениями «(•), но с существованием производной ср*),
и к нашим возможностям (аппарат дифференциального
исчисления § 2.2), с другой.
184
Лемма 1. Для любого компакта 3CcG существует
локально интегрируемая функция х(-) такая, что
\F(t, x)|^x(Z), V(f, х)£ЗГ. (2)
Доказательство. Поскольку 3^—компакт, суще-
ствуют такие6 > 0 и е > О, что для любой точки (Zo, x0) £3?
«цилиндр»
ctoxo = {(z. lx—x0|^e)cG.
Для этого цилиндра, согласно В), найдем локально ин-
тегрируемую функцию ktaX(j(t).
Снова используя компактность, покроем конечным
числом цилиндров: З^сг U Cftxi-
Функция
х(0= S[l/7(^> х^ [ + khx.(t)-e] ti+6i(i)
— искомая (Х[а, Р] () — характеристическая функция от-
резка [а, р]; |?(£, х,)| интегрируема на [t,-—6, /,+6]
в силу А)). Действительно,
(t, x)€3£=>3i, (t, x)£CtiXi=>
=>1Ш x)|<|F(Z, xf)| + |F(^ x)—F(t,
<\F(t, x)|+ sup \\Fx(t, c)||e^x(f)
C6 (x, ж(}
(отрезок [(/, x), (t, Xi)\cCt.x. и применима теорема о
среднем п. 2.2.3)).
Лемма 2. Если функция х: A—*R" непрерывна на
отрезке А и ее график {(Z, x(t))\t£&} лежит в откры-
том множестве GcRxR", а функция F: G—>Rn удов-
летворяет условиям А)—В), то функция Zt—>/(Z)=s
=-F(t, хЩ) измерима и интегрируема на А.
. Доказательство. При достаточно малом 8>0
— х) 11 х—ZgA}cG,
и пусть k(-)—функция, отвечающая этому компакту
в силу условия В). Непрерывная функция х(-) является
равномерным пределом кусочно-постоянных функций х„ (•)
и без ограничения общности графики хп (•) лежат в 3£.
На каждом интервале постоянства х„(-) функция
Zt->/n(Z)=j;'(Z, xn(t)) измерима и интегрируема по ус-
ловию А),, а потому /„(•) измерима и интегрируема на А.
185
Используя теорему о среднем (п. 2.2.3) и (1), имеем
\fn(t)-f(t)\ = \F(t, xn(t))—F(t, x(t))\^
откуда f(t) при всех а значит, /(•) изме-
рима как предел измеримых функций [КФ, стр. 284].
Накойец,
x(t)\
и, следовательно, [(f) интегрируема.
2,5.2. Локальная теорема существования. Пусть на
открытом множестве GcRxR" функция F: G—>Rn
удовлетворяет условиям А.) — В), и пусть компакт %?cG.
Тогда существуют такие б > 0 и е > 0, что для лю-
бой точки (t, х)^ЭС и для (ta, х0), удовлетворяющих не-
равенствам
Ио— ^|<8, |х0—х|<е, (1).
решение X (Z, tB, х0) задачи Коши
f x = F(t, х),
I = V
определено на отрезке [?—б, 'f-|-6] и является непрерыв-
ной функцией по совокупности аргументов.
Доказательство. Применим к рассматриваемой
ситуации принцип сжимающих отображений в формули-
ровке п. 2.3.2. Задача Коши (2) эквивалентна интеграль-
ному уравнению
t
x(/) = x0-|-jj F(s, x(s))ds, (3)
^0
и мы применим лемму п. 2.3.2 к отображению
(•)
(ta, х„, х(.))н-»Ф(/0, ())=%„ + J F(s, x(s))ds. (4)
По-
выберем у и р так, чтобы
Я\ = {(/, х)|И—|х—х|^р, (Г, x)€W}<=G,
и пусть k(-) и х(-) — интегрируемые функции, отвечаю-
щие в силу В) и леммы 1 п. 2.5.1 этому компакту. Зай-
мемся проверкой условий леммы п. 2.3.2. Топологическим
186
пространством Т здесь будет множество (1), U = T,
У = С([?—б, M-SJ, R"), где 6, 0<б^у, мы подберем
позже; y0(s)z^x,
V = {(/0, х0, х(-))|]/0—?|<8, |х0—х|<е,
.(5)
Константы е и 0 таковы, что 0 < 0 < 1 и 0 < е < 0(1 —0).
Условие в) п. 2.3.2 выполняется, если для /£[/—б,
f-|-6]
t
|xe+jF(s, x)ds—xl <0(1—0).
^0
(6)
По лемме 1 п. 2.5.1
точно малым, будем
| F(s, х) | (s), и, выбрав б доста-
иметь
7+6
7-6
| F (s, х) | ds
7+6
$ x(s)ds<0(l—0)—е,
7-6
(7)
откуда следует (6), поскольку
t t
[x0+$/7(s, x)ds—x|^|x0—x | +1 J F(^, x)ds|<
*0 fo
?+6
^e-|- |F(s, x) |ds <0(1—0).
7-6
Условие a) n. 2.3.2 означает, что отображение
(tB, xa, х(-))н->(/0, х0, Ф(/о, х0, х(•))) переводит У в себя.
Оно выполняется, если
t
] х0 4- § Т7 (s, x(s))ds—х| < 0
для (t0, Хд, х(-))€У и /£[?—6, ?+б]. Оценим здесь
левую часть, используя (6), теорему о среднем и (1)
187
п. 2.5.1!
t '
x0+Jf(s, x(s))ds—x
^0
x(s)) — F(s,'x)}ds <
?+6
<0(1 — 0)4- J fe(s)|x(s)—xjds<
?-6
•’ t+6
<0(1— 04- 5 £(s)ds)<0,
t-6
если выполняется неравенство
t+&
J k (s) ds < 0,
t-6
(8)
чего мы можем добиться, уменьшив, если нужно, 6.
Наконец, поскольку уже проверено условие а), усло-
вие б) п. 2.3.2 выполняется, если
ЦФ(^ ха, х(.))-<Ж, х0, //(•))||<0М-)-И-)|1
для любых (ta, x0, %(•))€^ и (t0, xa, z/(-))gV. Ho
||Ф(^о. xa,
t
e=max \ {F(s, x(s)) — F(s, y(s))}ds <
* t0
ft-6
< J £(s)ds|]x(.)—
t-6
в силу (8).
Таким образом, лемма п. 2.3.2 применима, и потому
Ьоследовательность Х„(- , t0, х0), определяемая равен-
ствами Ха (• , ia, х0) = х и
()
^в+1(- » *o) = *o + J F(s,Xn(st tB, x0))ds, (9)
188
равномерно по (tB, ха) из (1) сходится в пространстве
С[(?—6, F+6], R"), т. е. равномерно по t £ [/—6, ? + 6].
Переходя к пределу в (9), получаем, что X (t, ta, ха) —
= limAn(i, ta, х0) удовлетворяет интегральному урав-
нению (3) и, следовательно, является решением задачи
Коши (2). По индукции легко проверяется, что X (t, ta, ха)
непрерывны, а поскольку сходимость равномерна, то и
X (Л ^о> хо) непрерывна по совокупности аргументов. |
2.5.3. Теорема единственности.
Лемма (неравенство Гронуолла). Пусть не-
отрицательные функции а(*) и «>(•) измеримы на от-
резке А, причем а ()<£>() на А интегрируема. Если для
некоторых Ь>0 и т £ А и для всех t£ А выполняется
неравенство
то для всех /£А
- <о (t) be
(2)
Доказательство. Пусть сначала t т. По
условию
N = J a(s)(o(s)ds < оо
д
и, согласно (1),
По индукции находим, чт,о из (1) вытекают неравенства
от!
y«(s)ds . (3)
,т
Действительно, при /п = 0 (3) верно, а если (3) верно
при некотором т, то, подставив эту оценку в (1) и вос-
189
пользовавшись равенством
4+1
А4-1
Г t
а (ст) da
т
убеждаемся, что (3) верно для /и+1. Переходя в (3)
к пределу при т—>оо, получаем (1).
При рассуждаем аналогично, надо лишь везде
поменять местами пределы интегрирования. (Заметим,
что функция а(-) не обязательно интегрируема, так что
правая часть в (2) может оказаться бесконечной.) Ц
Теорема единственности. Пусть функция
F: G—*R" удовлетворяет условиям А)—В) п. 2.5.1 в от-
крытом множестве G cR х Rn; Af, i = 1,2, — интервалы в R
и Xi(): — два решения задачи Коши (2) п. 2.-5.2,
графики которых содержатся в G. Тогда %,(/)== x2(t)
для всех t € Ах П Да.
Доказательство. Множество A = {Z|x1(Z) = x2(Z)},
очевидно, замкнуто в Дх П Д2 и непусто, поскольку ta g А.
Остается проверить, что оно открыто, и тогда утвержде-
ние теоремы будет следствием связности интервала Дх п Д2.
Пусть ZgA, так что x1(t) = x2(Z) — х. Выберем такие
у >0 и ₽>0, чтобы 3£ = {(Z; х)| | Z—Z^y, |х—x|^[3}<=G
и чтобы (Z, X;(Z))£9£ при IZ—Z|^y; функция k(t) от-
вечает ЭС в силу условия В) п. 2.5.1.
Применяя теорему о среднем (п. 2.2.3) и неравен-
ство (1) п. 2.5.1, находим, что
|^(Z)-xa(Z)|<
t
$ [F (s, xjs)) —F(s, x2(sj)]ds
t
5 k (s) I Xi (s)—x2 (s)| ds
t
Если теперь к функции w (Z) = |xx (Z)—x2 (Z)| применить
190
на [/—у, ? + у] только что доказанную лемму (a(t) — k (t),
b — О), то, согласно (2), хДО^хД/).
Следовательно, (t—у, / + у)сД,и Д открыто. |
2.5.4. Линейные дифференциальные уравнения. В этом
пункте Д—отрезок числовой прямой,
A: A->^(R", R"), b: Д —R« и с: A->*R"‘
— интегрируемые матричная функция и две вектор-функ-
ции; х = (хх....x„)€R", P = (Pi.....P»)CR"*- Мы
будем рассматривать линейные системы дифференциаль-
ных уравнений
х = А(()х + &(0 (1)
и
р = — pA(t)+c(t) (2)
(иногда систему (2) называют сопряженной сис-
теме (1)). Хорошо известно, что для линейных систем
существование решений удается доказать нелокально,
в нашем случае—на всем отрезке Д.
Лемма. Если функции A: A->-^(Rn, R"), b: Д—>R”
и с: Д—>-Rn* измеримы и интегрируемы на отрезке Д, то.
любая задача Коши для уравнений (1) и (2), поставленная
в момент /0£Д, имеет единственное решение, и это ре-
шение продолжается на весь отрезок Д.
Доказательство. Поскольку все рассуждения
аналогичны, ограничимся уравнением (1). Для удобства
продолжим функции А(-), &(•) и с(-) на все R, поло-
жив их равными нулю вне Д. Тогда функция
F(t, x) = A(t)x + b(t)
будет удовлетворять условиям А)—В) п. 2.5.1 в области
G = R X R", и потому к дифференциальному уравнению (1)
применима теорема единственности п. 2.5.3 и локальная
теорема существования п. 2.5.2 в каждой точке (?, х), так
что решение уравнения (1), у которого х (f) = х, заведомо
единственно и определено на некотором отрезке [?—5,
v t +8].
Заметим теперь, что если |х|^Л4, то
|F(Z, х)|<||'Д +
IM- «)|=М (011-
1»
Вернувшись к доказательству теоремы и. 2.5.2, мы мо-
жем выбрать достаточно произвольно константы у, [3, 0
и 8, например, положив 0=1/2, р = 4, в = у = 1, и тогда
неравенства (7) й (8) п. 2.5.2, определяющие S, Приобре-
тут вид
f+б Г+6
М J || A (s)||ds 4- J | b (s)| ds < 1,
Г-б t-e
t +6 • (3)
$ IIЛ (s)||ds< 1/2.
f-e
Поскольку |] Л(-)|| и I £>(•)] интегрируемы, то мы можем
выбрать 8>0 столь малым (и не превосходящим у = 1),
чтобы неравенства (3) выполнялись при всех ? [КФ,
стр. ’801]. Следовательно, решение уравнения (1), у ко-
торого x(i) = x, определено на отрезке [?—8, ?J-6] с га-
рантированным 6, одним и тем же для любого t и лю-
бого-х, такого, что |х|^.М.
Пусть теперь заданы g Д и х0 и ищется решение
уравнения (1), у которого
х(/0)=~х0. (4)
Положим
Задача Коши (1), (4) эквивалентна интегральному урав-
нению
t t
+ $ A (s) х (s) ds + b (s) ds,
to ta
откуда
[x(/)|<|x0| + J>l(s)x(s)ds + Jb(s)rfs
t
< (koi + $ Ib(s)|ds) + $|]Л (s)|||x(s)|ds|. (6)
'A / t,
, »
Решение x(-) задачи (1), (4) заведомо определено на от-
резке Дх = [/0—б» ^+6]. Применяя на этом отрезке
лемму п. 2.5.3 к функций ш (/) —) х (/)|, ^а(/) = ||Л (/)||,
Ь »= |хв | | b (s)| ds} , получаем неравенство
|х(О|^(|*о| +$16(8)1^6
\ д , /
t
J M(s)||ds
/о
(7)
и, в частности, |х(/0 ±5)|<JM согласно (5). Поэтому
в точках (/0±5, х(^0±6)) снова можно воспользоваться
локальной теоремой существования и продолжить ре-
шение х(-) на отрезок Д2 = р0 —25, /04-25].
Дальше процедура повторяется. Неравенство (6) спра-
ведливо на Д2, а значит, на Да верно'(7) и | х (/e ± 25)| М
и т. д. За конечное число шагов мы продолжим реше-
ние задачи Коши (1), (4) на весь отрезок Д. |
Явные формулы для решений систем (1) и (2) выра-
жаются через фундаментальную матрицу решений одно-
родной системы
x—A(t)x. (8)
Определение. Фундаментальной матрицей Q (f, т)
рецГений системы (8) называется матричная функция
£2: ДхД—Rn), являющаяся решением задачи Коши
= т), (9)
й(т, т) — Е. (10)
Другими словами, каждый столбец матрицы Q(/, т)
является решением системы (8), а при / = т эти п столб-
цов обращаются в набор единичных векторов стандартного
базиса в R" 6i = (l, 0, ..., 0), е2=«=(0, 1, ..., 0), ...
.... е„ = (0, б, .... 1).
Теорема. Если матричная функция Л(-) интегри-
руема на отрезке Д, то фундаментальная матрица т)
системы (8) существует и непрерывна на квадрате ДхД,
причем:
1) Q(Z, s)Q(s, t) = Q(Z, т) для всех t, s, т^Д; (11)
2) й(/, т) при каждом t является решением диффе-
ренциального уравнения
----й(/, т)Л(т). (12)
7 В. М. Алексеев др.
193
Кроме того:
3) Если функция Ь: Д—>R" интегрируема на отрезке А
и %(•)— решение системы (1), то для любых t, т£Д
t
x(t) = Q(t, т)х(т)4-Q(/, s)b(s)ds. (13)
т
4) Если функция с: Д —► R"* интегрируема на отрезке Д
и Р(') — решение системы (2), то для любых t, т£Д
р (^) = р (?) Q (т, t)—^c(s)Q(s, t)ds. (14)
t
Доказательство. Непосредственной подстановкой
с использованием (9) проверяется, что для любого £ € R"
функции
хх(0 = Й(/, s)Q(s, т)^ и x2(/) = Q(/, т)£
являются решениями системы (8), а так как в силу (10)
x1(s) = Q(s, s)Q(s, t)£ = Q(s, t)^ = x2(s),
то по теореме единственности
Q{t, s)Q(s, т)^ = х1(0 = ^(0 = ^(^ ’’OS-
Поскольку £ любое, должно выполняться (11). Фикси-
руя в (11) s, мы представляем функцию пары перемен-
ных Q(^, т) в виде произведения двух функций одной
переменной, а так как обе они непрерывны, то Q непре-
рывна по (/, т) на ДхД. В частности, она ограничена.
Полагая в (11) t = x, получаем П(/, sJQ^s, t) = E, откуда
Q(/, s)==[Q(s, О]-1.
Согласно предложению 3 п. 2.2.1 матричная функция
/(Л) = Л-1 непрерывно дифференцируема на множестве
обратимых матриц и
f (Л)[Н] = -Д-1ЯЛ-1. (15)
Множество = (Л | Л = Q(s, /)> s> t^A} является обра-
зом компакта ДхД при непрерывном отображении
Q: ДхД—>o2’(Rn, R"), а потому это компакт и на нем
функция f ограничена: ||f (Л)||^Л4 —и удовлетворяет
условию Липшица, так как
Д/(Л)-/(В))|=||В-1-Л-Ч|=||-В-1(В-Л)Л-Ч|<Л42р7-ЛИ-
194
Согласно предложению 1 п. 2.1.8 функция
<p(s) = Q(£, s)=Q(1?, = f (Q(s, t))
абсолютно непрерывна, и в силу (15) и теоремы о супер-
позиции п. 2.2.2 почти всюду
J^L=-[Q(S, ;)]-i^LA[Q(S, /)]-! =
= — [Q(s, ^)]-х Л (s) Q (s, /)[Q(s, 0]~1 = —sM(s),
чем доказано (12).
Представив правую часть (13) в виде
т)
t
х(т)4-$Й(т, s)b(s)ds
Т
(16)
мы убеждаемся в ее абсолютной непрерывности. Дейст-
вительно, Q(t, s)b(s) интегрируемо (как функция s) на Д,
а интеграл от интегрируемой функции абсолютно непре-
рывен (п. 2.1.8). Следовательно, квадратная скобка в (16)
абсолютно непрерывна по t. Остается заметить, что про-
изведение двух абсолютно непрерывных функций также
абсолютно непрерывно (предложение 1 п. 2.1.8).
Равенство (14)- доказывается аналогично. |
2.5.5. Глобальная теорема о существовании и непре-
рывной зависимости решения от начальных данных и
параметров. Вернемся к рассмотрению задачи Коши:
x = F(t, х), (1)
x(Z0) = x0 (2)
для дифференциальных уравнений, правая часть которых
удовлетворяет условиям А)—В) п. 2.5.1. Используя ло-
кальную теорему существования и теорему единствен-
ности, мы можем, как это и делается ц курсах диффе-
ренциальных уравнений, продолжить решение Х(>, ta, ха)
задачи Коши (1), (2) на максимальный интервал его
существования (а, Ь). При этом из теоремы п. 2.5.2 сле-
дует, что при t\a и при t\b это решение должно поки-
дать любой компакт 3£cG, ибо, пока (t, х(/))£3£, ре-
шение гарантировано продолжается на интервал (Z—6,
^ + 8), откуда а-{-8</<Ь—8 ввиду максимальности
интервала (а, Ь). Следующая теорема показывает, в ка-
ком смысле Х(- , ta, ха) непрерывно зависит от (ta, х0).
Теорема 1. Пусть на открытом множестве GcRх
XR" функция F: G—►R" удовлетворяет условиям А)—В)
7* 195
п. 2.5.1, и пусть х: [?0, fj—>R"—решение уравнения (I),
график которого Г ?={(£, х (/))р0 t ^ZjcG.
Тогда существуют б >0 и окрестность Go Г такие,
что для любых (ta; xa)£G решение Х(- , ia, ха) задачи
Коши (1) — (2) определено на отрезке Д = [?о—5, fj+б] и
функция (t, ta, х0)ь—*Х(/, tB, ха) является непрерывной
функцией по совокупности аргументов на & xG. В част-
ности, при ia—>-т, ха—>-х(т) решение X(t, ta, х0)—>-х(/)
равномерно по ££Д.
Доказательство. А) Применив локальную теорему
существования в точках (/0, x(F0)) и (/$, xit-^), продол-
жим решение х(-) на некоторый отрезок Д = [£о—б,
^+6] так, чтобы график х(-) по-прежнему содержался
в G. После этого выберем е так, чтобы компакт •
9£ = {(/, х)| |х—x(t)\ ^е, ^Д}сб.
Применив к теорему п. 2.5.2, найдем такое 6 > 0,
чтобы при (ta, х0)£3£ решение Х(- , ta, х0) было опре-
делено на [/0—б, ^0 + б]. Наконец, пусть k(t) и х(>) —
локально интегрируемые функции, соответствующие X
согласно условию В) и лемме 1 п. 2.5Л.
Обозначим теперь
G = {(t х)р€(Л-б, ?X + S), |х—х(£)|<е}
и покажем, что при достаточно малом е > 0 эта область
обладает свойствами, указанными в формулировке теоремы.
Б) Пусть два решения х((-), t = l, 2, уравнения (1)
определены на отрезке [0, у]сД, причем (t, х( (/))£&?,
0 t у, и пусть т€[0, у]. Применяя теорему о сред-
нем (п. 2.2.3) и* неравенство (1) п. 2.5.1, получаем
t t
= хх (т) + $ F (s, x1 ($)) ds—x2 (t) — J F (s, x3 (s)) ds <
T t *
t
<|xi(t) — ха(т)|Ц- J [F(s, x1(s)) —F(s, x8(s))]ds <
x
i
<|Хх(т) — хг(т)|+ J jfe(s)|x1(s)—x2(s)|ds . (3)
Л X
196
По лемме п. 2.5.3 (a(s) = k(s), oj(s) = |x1(s)—х2 (s)|,
b — [Xifc)—хг (т)[) имеем
J k (s) ds
1*1(0— *а(01<1*1(т)—*2(T)le Т - (4)
В) Выберем теперь е > 0 так, чтобы
(s)ds
еед =Ce,
(5)
и пусть (ta, x0)£G. Поскольку GсX, решение х(-) =
=Х(-, ta, ха) определено на [0, у] = [^—б, /0 + б]Г|Д.
Покажем, что оно останется на этом отрезке в 3$?. Дей-
ствительно, пусть
Т = $ир{/ро</<тт{/о + 6, 0 + §};
(s, x(s))£ftr, VsG[0. *]}• (6)
На отрезке [/0, Т] к решениям х(-) и х(-) применимы
рассуждения п. Б) доказательства и в силу (4)
т
§ k (s) ds £ k(s)ds
|x(T)—-x(T)K|x0— *(М1^ <еед <8.
Но тогда (Т, х (Т')УЕ int и точка (t, x(t)) остается в X
и прй* t > Т, близких к Т, что противоречит определе-
нию (6). Аналогично рассуждаем и для t^.ta.
Поскольку (Р, x(p))€3T и (у, x(y))€9T решение х(-)
определено на отрезке [70—28, ^0-|--2б]П Д. К этому от-
резку снова применяем те же рассуждения и убеждаемся,
что (t, х(0) остается в X. Продолжая эту процедуру,
убеждаемся, что %(•) определено на Д.
Г) По доказанному любое решение Х(-, ta, ха) ос-
тается в X, если (t0, xa)£G. Вспоминая о функции х(-),
получаем неравенство
IX (tlt ta, ха) — X(t, t0, х0)|— v
s= F (s, X(s, i0, xa))ds J x(s)ds . (7)
197
Возьмем теперь два решения, у которых (ta, xa)£G и
xa)^G. Тогда ввиду (4) и (7)
|Х(/, Го, x0)—X(t, ta, xG)|<
^|X(F, ia, xa)—X(t, ta, x0)|4-|X(^, ta, xa)—X(i, Zo, x0)[<
t
x (s) ds
t
+ |Л—X(ta, t0, x0)|e
t
J* k(s)ds
J\(s)ds
ед (8)
что, очевидно, стремится к нулю при t—* t, ta—* ta, ха-»-ха,
доказывая непрерывность X(t, ta, х0). Полагая в (8)
t = t, ta = x, х0 = х(т) и вспоминая, что по теореме един-
ственности X (t, т, х(т)) = x(t), имеем
f ~ el
[x(t)—X(t, ta, x0)|< ||х(т) — x0| + J x(s)ds|eA
\ to у
откуда X(i, ta, x0)—>-x(t) равномерно при x0 —*х(т),
V—т.
Перейдем теперь к непрерывной зависимости решений
от параметра. Предположим, что нам дано семейство
дифференциальных уравнений
x = Fa(t, х), (9)
зависящих от параметра а£?1, где 31—некоторое топо-
логическое пространство.
Теорема2. Пусть на открытом множестве G с R х R"
функции семейства {Fa: G—> R" | ос С 91} удовлетворяют
при каждом ag3( условиям А) и Б) п. 2.5.1; х: [f0, t^\—>-
—>-R"—решение уравнения (6) при а==а и график Г —
={(/, x(Z))j £osC fjcG, и пусть еще выполняются ус-
ловия
В') Для любого компакта %?czG существуют такие
локально интегрируемые функции х(-) и k(-), что для
198.
любых (i, х)^Уъ, ag?l имеют место неравенства
*)|О(0> Иах(*. *)|1<*(0- ЦО)
?i
Г) lim 5 |Fa(s, x(s)) —F~(s, x(s))\ds = 0. (11)
a->a 7
* 0 '
Тогда существуют § > 0, окрестность Go Г в G, и
окрестность U$a в 21 такие, что для (ta, x0)£G, a£U
решение xa(t, t0, x0) задачи Коши (9), (2) [определено на
отрезке &=[ta—8, и при ta—>Tg[f0, ^], xa—>-x(t),
a—>a
Xa(t, ta, x0)—-x(0
равномерно no /€[?0, ^J.
Доказательство этой теоремы проводится по той
же схеме, что и доказательство теоремы 1 с небольшими
изменениями. В пункте А) мы учитываем, что число б
в локальной теореме существования определяется нера-
венствами (7) и (8) п. 2.5,2 и в силу условия В') может
быть выбрано одним и тем же для всех ag2(.
В пункте‘Б) заменяем хД-) решением ха(-) уравне-
ния (9), а х2(-) — решением х(-). В оценке следует учесть,
что теперь правые части уравнений разные, в связи с чем
|Ха(0 — *(0|<
<|Xa (Т)—Х(Т)|4
k(s)[xa(s)—x(s)[ds
и (4) заменяется неравенством
1Ха(0~ *(0К( 1МТ) — *(т)| +
(4')
В неравенстве (5) надо заменить е на 2s, а & и U
следует с учетом условий В') и Г) выбрать так, чтобы
199
выполнялисо неравенства
^{Fa(s, x(s)) — F~(s, x(s))}ds <
< J |Fa(s, x(s) — F~(s, x(s))|ds<
*0-6
х (s) ds j 4?
ti
+ $l^a(s, x(s))—F^(s, £(s))|ds<e. (12)
10
Тогда рассуждения пункта В) (с заменой (4) на (4') ос-
таются в силу одновременно для всех a£U.
В пункте Г) следует в неравенство (8) внести уточ-
нение, вытекающее из замены (4) на (4'), после чего мы
получаем
1Х«(^
► Т
—х(т)|+ J x{s)ds -|-
^0
4-$ |Fa(s, x(s))-—Fg(s, x(s))|ds
J k(s)di
g?0
и остальное очевидно. |
Следствие. Если выполнены все условия теоремы 2,
причем условие Г) в усиленной форме:
Г') для любой функции х: [^0, /J—►R", график кото-
рой лежит в G и любого а.
Ит 5 |^a(s, x(s)) — F-(s, X(s))|ds = O,
то решение xa(t, h, x0) задачи Коши (9), (2) является
на KxGxU непрерывной функцией от (t, t0, х0, а).
Доказательство. При любых (70, x0)£G и a,^U
график решения х(-) = %-(•, ta, х0): Д—>Rn лежит в G.
200
Теперь мы можем применить теорему 2, заменив в ее
условиях х(-) на х(-)- В
Аналогом основного свойства фундаментальной ма-
трицы линейной системы (формула (11) предыдущего
пункта) является следующее тождество:
Х(Л т, X (т, /0, х0))^Х(Л tB, х0). (13)
Оно автоматически вытекает из теоремы единственности,
поскольку каждая из частей является решением уравне-
ния (1) и при / = т обе они совпадают. Читателям ре-
комендуется продумать связь между этим тождеством и
принципом Гюйгенса п. 1.1.3.
2.5.6. Теорема о дифференцируемой зависимости ре-
шений от начальных данных. До сих пор наше изложе-
ние было основано на сравнительно слабых предположе-
ниях А) — В) п. 2.5.1. Чтобы продвинуться далее и
установить дифференцируемость решения задачи Коши
X (t, t0, х0) по начальному значению хв, эти предполо-
жения придется несколько усилить. При этом открывается
возможность применения классической теоремы о неявной
функции. В доказательстве теоремы этого пункта мы не
будем останавливаться на существовании решения X (t,
Ц, х0) для (Zo, x0)€G и его продолжимости на все t^k.,
поскольку и то и другое следует из теоремы 1 п. 2.5.5.
Тем не менее читателю полезно убедиться в том, что оба
эти факта также вытекают из теоремы о неявной функции
и при желании можно было бы обойтись без ссылки на
предыдущий пункт. (Аналогичное рассуждение будет
полностью проведено в п. 2.5.7, где при еще более силь-
ных предположениях доказывается дифференцируемость
по t0 и теорема о неявной функции применяется в не-
сколько ином варианте, чем здесь.)
Теорема. Пусть на открытом множестве G с R х R"
функцияF:G—+Rnудовлетворяет условиям А) и В) п. 2.5.1
и условию:
Б') для любого t функция х>—> F (t, х) непрерывно диф-
ференцируема на сечении Gt = {x|(f, x)£G}. Пусть
х: [£0Л] — R" —решение уравнения (1) п. 2 5.5, график
Г = {(£, х(0)1 4} которого содержится в G, ипусть
б, е u G—те же, что в теореме 1 п. 2.5.5; Д = [?о—8,
G + 6].
Тогда для любого фиксированного ta£h. отображение
xoi-*X(«, t0, х0) из В(х(10), е) в С (Л, R") непрерывно
201
дифференцируемо по Фреше, причем
dX(t’d*°o’Xo) = ^ и. (1)
где Q—фундаментальная матрица решений уравнения в
вариациях
z = Fx(t, X (t, t0, х0))г. (2)
Доказательство. Пусть компакт 9? и функция
k(t)—те же, что и в теореме 1 п. 2.5.5. Множество
. 8 = {х(.)ЕС(Д, R")|(i, x(Z))cG, teb},
очевидно, открыто в С (A, R"). Равенством
t
& (х0> х (•)) (О = *0 + 5 F (s> х GO) ds—x(t) (3)
определим отображение $F: R"X$—>С(А, R"). Очевидно,
что
Г(х0,х(.)) = 0«х(О^Х(М0,х0). (4)
✓
• Пусть х0 С 6 (x(f0), е) фиксировано и х(/) =Х (£, t0, х0).
Проверим, что в окрестности точки (х0, х(•)) применима
классическая теорема о неявной функции п. 2.3.4. Дей-
ствительно, сГхДХо, х(-))[Е0] = Е0, очевидно, непрерывна.
Теперь вычислим производную Гато:
X(-))[U’W) =
= lim <F(xp, x(-) + «g(-))—(ХО, х(-)) =
а|0 а Л
= lim С f(5,x(s) + aUs))-r(s,x(s)) ds _ (
0 J “
t
= ^Fx(s, x(s))l(s)ds-l(t). (5)
^0
Чтобы убедиться в существовании предела, равномерного
по t, заметим, что по теореме о среднем (п. 2.2.3)
t
С f (s, x(s)) + ag(s))— F(s, x(s))
J a
t
—-^Fx(s, x(s))l(s)ds ^ra(s)ds,
fo Д
202
где
ra(s)= max ||ГЖ(8, c)-Fx(s, x(s))|||g(s)|.
ce[x(s), x(s)+a£(s)]
Ввиду условия Б') ra(s)—*0 при каждом s и а|0». а
в силу (1) п. 2.5.1 | ra(s)| г^2& (s)||g||. По теореме Лебега
об ограниченной сходимости [КФ, стр. 302] убеждаемся
в существовании предела (5).
Оператор
t
^(.)(х0, х(-)) [£(•)](/)=$ Fx(s, x(s))£(s)ds
^0
ограничен:
=S^max
t
t
$Их(8. X(S))|[lg(S)[dS
Д
и непрерывно зависит от х(-), так как
х(-))—^(-)(х0, х(•))|| =
t t
= sup sup \ Fx (s, x (s)) £ (s) ds — \ Fx(s, x(s))g (s)ds
1
< J||Fx(s, x(s)) —Fx(s, x(s))||ds.
Д
При ||x(-)— x(•)|| —>0 имеем в силу Б')
HF^s.x^-RJs, x(s))||->0, Vs€A,
и снова в силу (1) п. 2.5.1 ||Fx (s, x(s))— Fx (s, x(s))||
^2&(s), так что применима теорема Лебега. Сославшись
на следствие 2 п. 2.2.3, устанавливаем, что существует
непрерывная производная Фреше <FX<.).
Пусть iq(-)gC(A, R") произвольна. Согласно (5)
^(•) (х0, х (•)) [£ (•)] = 1] (•) о
i
&$Fx(s, x(s))g(s)ds—g(O = n(O (6)
ta
и для применимости теоремы о неявной функции
нужно убедиться в однозначной разрешимости этого урав-
нения. Подстановкой 5 (0 + 1! (0 = ^(0 приведем его к
203
интегральному уравнению
t
£ (0 = $ Рх (s. х (s)) К (s)—i] (s)] ds, ,
^0
которое в свою очередь эквивалентно линейному диффе-
ренциальному уравнению
Остается сослаться на лемму п. 2.5.4. По теореме Банаха
(п. 2.1.5) ограничен.
По теореме о неявной функции существует непрерывно
дифференцируемое в некоторой окрестности U Э ха ото-
бражение <р: U —>С(Д, R") такое, что (х0, <р(хо)) = О.
Согласно (4) <р (х0) (t) = X (t, te, х0), так что отображение
x0>->X (t, t0, х0) действительно дифференцируемо по Фре-
ше в точке х0. По той же теореме о неявной функции
dX(i^’Xo) t = ф' (*о) Ко] (0 = - (^> о >ТХа KJ) (I) = I (t)
и, как уже было найдено, g(t) —решение интегрального
уравнения (6), принимающего вид
J Fx (s, х (s)) g (s) ds—В (t) = — ge.
to
Следовательно,
t = ^(s,x(s))g, =
и по теореме n. 2.5.4 g(t) = Q(t, t0) g0. Отсюда
t0,x0) = Q(t, Q.
2.5.7. Классическая теорема о дифференцируемой за-
висимости решений от начальных данных. В этом пункте
мы снова будем рассматривать задачу Коши
х = F(t, х), (1)
x(t0) = x0, (2)
но уже в классической ситуации, когда F (I, х) и ее ча-
стная производная Fx(t, х) непрерывны в G. Для удоб-
ства читателей, доказательство формулируемой ниже тео-
ремы будет проведено независимо от доказательств теорем
204
пп. 2.5.5 и 2.5.6. Ссылки на'локальную теорему сущест-
вования (п. 2.5.2) и теорему^ единственности (п. 2.5.3)
можно заменить ссылками на любой учебник по диффе-
ренциальным уравнениям.
Теорема. Пусть на открытом множестве Gc R х R"
функция F: G—<-R" и ее частная производная Fx непре-
рывны, и пусть х: [?0» ?i]—» R"—решение уравнения (1),
график которого Г = {(£, х (£)) I t0 t содержится в G.
Тогда существует такое 6 > 0 и такая окрестность
G =эГ, что для любых (t0, xa)£G решение X(t, f0, х0) за-
дачи Коши (1), (2) определено на А = [?0—6, +§], яв-
ляется непрерывно дифференцируемой функцией по совокуп-
ности аргументов в области (i0 — 6, ^ + S)xG и при этом
X (t, т, х(т)) — х(г), (3)
^-(^, т,х (%)) = £(/, х(/)), (4)
^(^^х(т))1 = -Й(/,т)Г(т,х(т)), (5)
и*>0
1-*О —
где Q(t, т)—фундаментальная матрица решений системы
уравнений в вариациях
z = Fx(t;x(t))z.
Доказательство. А) Применив локальную теорему
существования в точках (F0,x(?0)) и(Г1,х(?1)), продол-
жим х(-) на отрезок А = [?0—6, +6] так, чтобы гра-
фик {(t, х(/)) 11 С А} по-прежнему содержался в G. После
этого выберем е > 0 так, чтобы
= {(^, х) р € А, |х—x(f)|^e}cG.
На компакте 9? функции F(t, х) и Fx(t, х) равномерно
непрерывны.
Б) Теперь в области
S = {(x(.), t0, хо)Цх(О—х(0|<
< е, V/ €А; f0€int А, х0€ Rn}c С* (A, Kn)xRxR“
определим функцию <$Г: >-С(А, RB)xRn равенством
/ dx (0 р ц X(t))\
0(0 = dt ( ()) • (7)
\ x(t0)—xa J
305
Очевидно, что равенство (х(-), ^о> х0)== 0 эквивалентно
задаче Коши (1), (2). В частности, по условию теоремы
F (х(-),' т, х(т)) = 0.
Функция непрерывно дифференцируема в области
Действительно, в (7) входят линейные отображения
x(-)>-^-dx(-)/d/, х01-э-—х0, оператор краевых условий
(х(-), £0)н->х(/0) и оператор Немыцкого {х (/)}>—>{F(£,
х(0)}, ’ которые непрерывно дифференцируемы согласно
пп. 2.4.1, 2.4.3. При этом
^(.)(х(-), f0, х0Ш(.)]=(^~^(Лх(ЬК\ (8)
V 5 (/о) /
/ о \
(х(’)> ^о> хо) [о] = \'х (/0)а/ ’ (9)
(Х( )> ^0» Хо)[^о] = —g0) ' (Ю)
В) Пусть х=х(?), так что (t, х)£Г. Проверим обра-
тимость оператора F* (> (х (•),?, х). Равенство
^о(х(-), ?, i)[U-)]=(^))eC(A, R")xRn
эквивалентно задаче Коши
|-Л(^,х(0)^ = и0. (11)
которая по теореме п. 2.5.4 имёет решение
Е(0 =Й(/,?)у + J Й(/, s)£(s)ds.
?
Таким образом, F\( ( отображает банахово пространство
С1 (A, R") на все банахово пространство С (A, R")x R".
Поскольку при £(•) = () и у = 0, задача (11) имеет только
нулевое решение, вТЛ(, взаимно однозначен. По теореме
Банаха (п. 2.1.5) оператор F^1, существует и ограничен.
Г) По классической теореме о неявной функции
(п 2.3.4) существует такое 6 > 0 и такое непрерывно
дифференцируемое отображение
Ф:* {(Ч, хо) I Ро -11 < б, | х0 - х | < 6} -> С1 (A, R"),
что
(ФРо> хо)> ^о> Хо)^0.
206
Обозначим
X(f, t0, x0) = O(f0,x0)(0.
Тогда X(t, ta, x0)— решение задачи Коши (1), (2) и при
этом
дХ dt = F(t,X(t, f0,X0)), (12)
дХ dt0 ЗФ ,, .... dt0 0’ Хо) (0» (13)
дХ дхл дф ., . ... дх0 (14)
Если (70, х„)—*(/0, х0),тоФ(70,х0) —Ф(го, х0)в(?(А, R”),
т. е. Х(/, 70,х0)^Х(/, /0, х0) равномерно на А. Отсюда
вытекает непрерывность X (t, t0, х0) по совокупности аргу-
ментов. То же рассуждение вместе с формулами (12) — (14)
показывает, что и производные функции X (t, t0, х0) не-
прерывны.
Д) Предыдущие рассуждения были применимы к на-
чальным условиям (t0, х„), находящимся в б-окрестности
точки (?, х) С Г. Эта точка выбиралась произвольно, и
можно покрыть весь график Г такими окрестностями.
Если Х(1) (/, t0, х0) и Х(2)(/, /0, х0) определены в двух из
этих окрестностей, которые имеют общую точку х0),
то
Х(1>(*о, x0) = x0 = X<s>(^, f0,x0)
и по теореме единственности п. 2.5.3
(t, ta,x0) = Xm(t, t0, х0), V/€A.
Следовательно, X (t, t0, x0) корректно определено для
(t0, х0), принадлежащих некоторой окрестности-Г и, оче-
видно, непрерывно дифференцируемо в этой окрестности.
Е) Остается получить формулы (3)—(6). Равенство (3)
имеет место по теореме единственности, а тогда (4) яв-
ляется следствием (12). По теорёме о неявной функции
' <ЭФ ,, . д-
dt0 И»’ х»'---х( > 0 t0>
а потому из (13) и (9) имеем
#(Л х,х(т))[а] = —^,(х(-), т, х(х))(0 V
\х(т)а/
207
Поэтому (t, т, х (т)) является (по t) решением задачи
Коши (11) с С = 0 и у = — х(т)= — F (т, х'(т)), и потому
имеет место (5).
Аналогично
х0)« —F^.)oFXe,
а потому из (14) и (10) имеем
т, х(т))[у] = — (*(•), т, х(т))
дХ
Следовательно, -^-(f, *, х(т)) является (по t) решением
задачи Коши (11) с £ = 0, откуда
-|^(?, т, х(т))[у] = Й(*, т)у,
а это равносильно (6). В
§ 2.6*. Элементы выпуклого анализа
Выпуклый анализ—это раздел математики, где изу-
чают выпуклые множества и функции. Роль этих поня-
тий была уже продемонстрирована в п. 1.3.3 (теорема
Куна—Таккера) и, учитывая, что в большинстве совре-
менных работ по экстремальным задачам выпуклость за-
нимает важное место, мы, кроме элементарных сведений,
даем здесь набросок теории двойственности (теорема
Фенхеля—Моро) и рассказываем о простейших свойствах
субдифференциала—понятия, обобщающего на случай
выпуклых функций понятие дифференциала. В §§ 3.3,
3.4, 4.3 будет показано, как применяются эти понятия.
Изложение этого параграфа опирается по преимуществу
на пп. 2.1.3 и 2.1.4.
2.6.1. Основные определения. Пусть X—линейное ве-
щественное пространство.
Определение 1. а) Множество С с X называется
выпуклым, если вместе с любыми двумя своими точками xt
и х2 оно содержит весь отрезок
[xj, х2] = {х| х = ах! + (1 —а) х2, 0 1).
б) Множество Ac X называется аффинным многообра-
зием, если вместе с любыми двумя своими точками хх и
208
х, оно содержит всю прямую
{х|,х = ах1+(1—а)х2, a^R}-
в) Множество /(с X называется конусом (с вершиной
в начале), если вместе с любой своей точкой х0 оно со-
держит весь луч
{axo|a>0}.
Пустое множество по определению считается выпук-
лым, аффинным многообразием и конусом. Совокупность
всех выпуклых множеств из X обозначается ЗЦХ).
Непосредственно из определения 1 вытекает
Предложение 1. а) Пересечение любого числа вы-
пуклых множеств (соответственно аффинных многообра-
зий или конусов) само является выпуклым множеством
(соответственно аффинным многообразием или конусом).
б) Образ f(A) и полный прообраз f~l(B) выпуклых
множеств (аффинных многообразий, конусов) AcX,BcY
при линейном отображении f: X —> Y является выпуклым
множеством (аффинным многообразием, конусом).
в) Сдвиг С + § выпуклого множества С (аффинного
многообразия) является выпуклым множеством (аффинным
многообразием).
г) Конус К является выпуклым множеством тогда и
только тогда, когда
Хц £ К fal “Ь ^z) С К*
д) Аффинное многообразие А явл_яется линейным под-
пространством в X тогда и только тогда, когда О^А.
Упражнение 1. Докажите, что аффинное многообразие яв-
ляется сдвигом некоторого линейного подпространства.
Определение 2. а) Пересечение всех выпуклых
множеств С, содержащих данное-множество М, называется
выпуклой оболочкой множества М и обозначается conv Л1;
convAf = А С, С£$$(М). (1)
CD м '
б) Если в (1) вместо выпуклых множеств берутся все-
возможные выпуклые конусы ХэМ (аффинные многооб-
разия A z>M, линейные подпространства L z>M), то пе-
ресечение называется конической (соответственно аффинной
или линейной) оболочкой М и обозначается cone М (aff М,
lin М).
209
Определение 3. Пусть хх.....хп—элементы из X.
Элемент
п
х=^Х.*# (2)
называется линейной, аффинной, конической или выпуклой
комбинацией х1; ..., хп, если в (2) соответственно:
для линейной—любые,
п
для аффинной—У Ь
i=i
для конической—\-^0,
п
ДЛЯ выпуклой—2^1=1’ А,;. ^0.
1=1
По индукции доказывается, что если хг, .хп при-
надлежат выпуклому множеству С, выпуклому конусу К,
аффинному многообразию А или линейному подпростран-
ству L, то соответственно их выпуклая, коническая, ли-
нейная или аффинная комбинация принадлежит С, К, А
или L.
Предложение 2. а) Выпуклая (коническая, аффин-
ная или линейная) оболочка множества М состоит из
всех выпуклых (конических, аффинных или линейных) ком-
бинаций элементов из М.
б) Множество М~выпукло (является выпуклым конусом,
аффинным многообразием или линейным подпространством)
тогда и только тогда, когда оно совпадает со своей вы-
пуклой (конической, аффинной или линейной) оболочкой.
Доказательство проведем для выпуклого мно-
жества М—в остальных случаях оно аналогично. Обозна-
чим через iVf множество всех выпуклых комбинаций то-
чек из М. Множество М zoM и выпукло, ибо если •
*1 = 2 ^tiXii, Х2 = 2 0»
1=1 1=1
"*/
2«./=1. 7=1,2,
i=i
то для а£[0, 1]
aXj+O— а)х2== 2 ““п*п + S (1—“)“12*12*
i=i i=i
а эта последняя сумма является выпуклой комбинацией
210
точек xu, ..., xmil, x12, ..., xma2. Значит, conv M c M (ибо
conv Л1 есть пересечение всех выпуклых множеств, со-
держащих М). С другой стороны, как было замечено
выше, каждая точка из М содержится в любом выпук-
лом множестве, содержащем М, и потому MaconvAf.
Если М выпукло, то в (1) можно взять С — М, и
тогда, очевидно, conv М = М. Обратно, если conv М = М,
то М выпукло по определению выпуклой оболочки и
предложению 1 а). Ц
Упражнение 2. Докажите, что алгебраическая сумма
( п 1
+ • . + Л4л = < х | х= 2 ХО xi£M, i = 1, •, п >
I i=l J
конечного числа выпуклых множеств (конусов, аффинных многооб-
разий, линейных подпространств) обладает тем же свойством.
Пр и меры. 1) Выпуклые непустые множества на
прямой — это одноточечные множества и промежутки всех
видов (отрезки, интервалы, полуинтервалы, . лучи замк-
нутые и открытые и вся прямая).
2) Всякое линейное подпространство или аффинное.
многообразие—выпуклое множество.
У п р'а ж н е н и е 3. Докажите эти утверждения.
.3) Выпуклым многогранником Называется выпуклая
оболочка конечного множества точек. Важный частный
случай—п-мерный симплекс, т. е. выпуклая оболочка
п+1 аффинно независимых точек (никакая из них не
является аффинной комбинацией остальных).
Упражнение 4. Докажите, что выпуклая оболочка трех точек
в R* не лежащих одной прямой (двумерный симплекс), является
треугольником с вершинами в этих точках. Что будет, если точки
лежат на одной прямой?
В конечномерном пространстве предложение 2 можно
усилить. Соответствующее утверждение мы называем тео-
ремой Каратеодори, хотя, строго говоря, это название
относится лишь к той его части, в которой идет речь
о выпуклой оболочке.
Теорема Каратеодори. Пусть dim (lin А) < со.
Каждая точка, принадлежащая выпуклой (конической, аф-
финной или линейной) оболочке множества А, является
выпуклой (конической, аффинной или линейной) комбина-
цией не более чем s точек ....xs из А.
211
Для выпуклой и аффинной, оболочек s = n + l и точки
Хр ..., xs можно считать аффинно независимыми.
Для конической и линейной оболочек s — n и точки
хг можно считать линейно независимыми. -
Доказательство. А) Ограничимся наиболее слож-
ным случаем выпуклой оболочки, указав затем, какие
изменения следует внести в доказательство в остальных
трех случаях.
Согласно предложению 2 а) каждое х € conv А может
быть представлено в виде
х = А,1х1 + ... > О,
k
2*/ = 1. XitA (3)
;=i
(в определении выпуклой комбинации Х;>0, но ясно,
что Z; = 0 можно опустить).
Покажем, что если-хр ..., хк аффинно зависимы, то
число точек в этом наборе можно уменьшить, сохранив
представление вида (3). Действительно, если точки
Хр ..., хк рффинно зависимы, то одна из них есть аф-
финная комбинация остальных; без ограничения общности
х* = Р1Х1+... 4-pft_1x)e_1, 2 1- Положив еще
Х=1
k k
ж — 1, имеем р {х{ — 0, Н i = 0. Пусть теперь
( %* I 1
a —min <----! ц, < 0>.
I RI 1 J
Тогда
k ь k k
x = 2 Kxi + « S IMf = S (bf + «Hz) X. = S К X{,
i=l i=l f=l
причем все в силу выбора а и по крайней мере
одно из них равно нулю. Удалив из набора {xv ..., хй}
те Хр /для которых X/ — 0, мы получаем представление
/ k k
вида (3) с меньшим числом точек ( хй +
\1==1 /=1
я \
Обозначим через s(x) наименьшую мощность набора
{Хр ..., хА}, для которого представление (3) возможно
(в каждом непустом' множестве натуральных чисел есть
212
наименьшее). Только что проведенное рассуждение пока-
зывает, что в наборе {xlt . ..,xJ(x)} точки должны быть
аффинно независимы. Остается заметить, что в п-мерном
пространстве любые п + 2 точки {хх........xn+i} аффинно
зависимы. Действительно, точки xz —x„+2,i=l, ..., n+1,
должны быть линейно зависимыми, и если, например,
л / п \
%п+1 ^п+а = 2 (^i •'"и + а)» ТО Хп + 1=1 1 2 )&п+2~Ь
i = l \ 1=1 /
п п п
4- 2 ^;Х1. Так как 1 — 2 + S 1 > то х„+1 является
1 • i'=l
аффинной комбинацией остальных.
Б) Для случая аффинной оболочки в приведенном
рассуждении опускается все, связанное с неравенствами
X,- > О, и можно положить а = — Zz/p(- для любого
i с рг#=0. .
В остальных двух случаях аффинные комбинации за-
меняются линейными и число линейно независимых то-
чек не может быть больше п. Для конической оболочки
сохраняются рассуждения с неравенствами; для линейной
оболочки и их можно опустить. В
Переходим к описанию выпуклых функций. Здесь,
как и далее в этом параграфе, будем называть функцией
отображение f: X—>R, где R = RU{—оо, Ч-оо) — рас-
ширенная числовая прямаяJ). С каждой функцией можно
связать два множества:
dom f = {х € X | f (х) < + оо},
epi j(x, a)€XxR|a>f(x), x€domf},
называемые соответственно эффективным множеством и
надграфиком функции f.
!) Арифметические операции и неравенства, в которых участвуют
несобственные числа + оо и — оо, определяются так (далее a £ R
любое, р > 0):
(4* 00 )4 ( 4 °°) — 4 » (4“ ) (i оо) — ± оо, 4* оо > о,
+ оо4я = ± оо, (— оо) (± оо)= 4 оо, — оо < а,
’(—oo)-j“(— оо) = —00, (±0®) Р=±°®, + 00 >—оо,
— (4-оо) =—оо, (4 оо)'0 = 0,
— (—оо) оо, '(± оо) (— р) = -F °о;
выражения (-]-оо)—(-]-оо), (4оо)4(—оо) и (—ао)—,(—оо) объяв- '
ляются лишенными смысла; ие определяются и операции деления с
несобственными числами.
213
Упражнение 5. Докажите, что множество С с X X R
является иадграфиком некоторой функции /: X —>- R тогда и только
тогда, когда (х, а)£С, >(х, р) £ С.
Определение 4. Функция/, у которой dom/^ 0
и всюду f (х) > — оо, называется собственной, остальные
функции называются несобственными. Функция /: X —»- R
на линейном пространстве X называется выпуклой, если
epi f — выпуклое множество в XxR. Совокупность всех
выпуклых функций на X обозначим (X).
Прямо из этого определения вытекает
Предл ожение 3. а) Для выпуклости собственной
функции f необходимо и достаточно, чтобы для любых
точек X; £ dom / и любых а( 0, i — 1, ..., п, таких, что,
п
2 а,- = 1, выполнялось неравенство Иенссена:
i=i
/(х) ={
п
б) Сумма 2 fi (х) конечного числа и верхняя грань
I = 1
Vafa (х) = SUP {fa (х)} любого семейства выпуклых функций
а
выпукла.
Примеры. 1) Выпуклые функции на пря-
мой. Пусть /0(х): (а, |3)-->R, причем на интервале
(а, ₽) <= R существует производная /Дх), которая не
убывает. Положим
/0(х),^х€(а, Р),
4- оо''' х(£ (а, Р).
Для этой функции dom f — (а, Р). Проверим, что она
выпукла. Произвольная точка отрезка, соединяющего
точки (хг, г() С epi f, i=l,2, имеет вид + Д—а)х2,
aZj-f-U—а£[0, 1]. Применим формулу Лагранжа:
агх + (1 — а) z2—f (ах1 + (1 — а) х2) >
> af (*i) + (1 — а) f (Xj—f (ахх + (1 —а) х2) =
= (сх) (хх — (ахх + (1 —а) х2)) +
+ (1 — а) f (с2) (*2 — (ахх + (1 — «) *2)) =
= а (1 —а) (f' (сх) —/' (с2)) (хх—х2) > О,
так как х1^с1^ах1 + (1—а)х2^с2^х2 и производная
по условию не убывает. Следовательно, (ахх4-(1—ос)х2,
azx + (l—a}z2)Gepif и f выпукла. Ц
214
Упражнение 6. Пусть выпуклая функция ft R —► R конечна
на интервале 7 = (а, р). Докажите, что f непрерывна на 7 и имеет
в каждой точке х£/ левую и правую аронзводные f'-(x), f'+ (х),
которые на I не убывают и совпадают всюду, кроме не более Чем
счетного множества точек.
2) Пусть на выпуклом открытом множестве U нор-
мированного пространства X функция принадлежит
классу С2 (п. 2.2.5) и ее второй дифференциал d2f0 =
=Д (х) Г£> неотрицателен. Как и в'предыдущем при-
мере, положим
... I fо (*), х £ U,
+оо, x^U.
Ограничение этой функции на любую прямую в X обла-
дает свойствами функции, рассмотренной в предыдущем
примере (докажите!). Поэтому f выпукла (для проверки
выпуклости epi / достаточно ограничиться всевозможными
сечениями этого множества двумерными вертикальными
плоскостями в XxR).
Эти примеры дают нам большой запас конкретных
выпуклых функций. Таковыми будут на R функции ех,
ах2 + Ьх-^-с при а^О, —1пх (дополненный значением
4-оо при х^О) и т. д. В евклидовом пространстве вы-
пуклой является квадратичная функция f(x) = (Ax|x)4~
4-(Ь | х) + с, где А—положительно определенный симмет-
ричный оператор.
3) Индикаторная функция. Так называется функция
( ф-оо, х(М,
о, Ла.
Ясно, что 6Д (х) £ (X) тогда и только тогда, когда
Д€$(Х).
4) Функция Минковского (см. п. 2.1.3). Неравенство
Йенсена (4) является источником многих важных не-
равенств, используемых 6 разных разделах математики.
В частности, применив его (с а,= 1//г) к функциям
fi (*)
f2 (х) = |
— 1п х, х > О,
4~ оо,
xln х,
О,
Ч-оо,
х^ О,
х > О,
х = 0,
х < О,
215
ма получаем в первом случае известное неравенство
Коши между средним арифметическим и средним геомет-
рическим, а во втором—важное в теории вероятностей
неравенство для энтропии распределения (pv ...,р„),
п
где р^х^^, xz>0,
п
Н (р) = — 2 Pi In Pi С In п-
i = I
2.6.2. Выпуклые множества и функции в линейных
топологических пространствах. Предположим теперь, что
Х^~локально выпуклое линейное топологическое прост-
ранство [КФ, гл. III, § 5]. Как известно, в этом случае
сопряженное пространство X*, состоящее из всех линей-
ных непрерывных функционалов, является достаточно
богатым (см. там же, гл. IV, §§ 1—2), и это нам до-
ставляет большой запас выпуклых множеств и функций.
Простейшими выпуклыми множествами в X являются
гиперплоскости и полупространства (здесь х* g X*)
Н (х*, а) = { х | <х*, х> = а}—гиперплоскость,
Н± (х*, а) = {х | <х*, х> 1—замкнутые полу-
Н_ (х*, а} = (х | <х*, х> > а} j пространства,
fL(x», а) = ]х]<х*, х>< а} 1 — открытые
Й. (Х-, а) = {хI <Л х> > а) 1
Упражнение 1. Проверьте, что эти множества .выпуклы.
Далее, назовем выпуклым полиэдром пересечение конеч-
ного числа замкнутых полупространств (подчеркнем, что
это пересечение не обязано быть ограниченным множе-
ством).
Упражнение 2. Докажите, что в R" всякий выпуклый много-
гранник (п. 2.6.1) является выпуклым полиэдром и что всякий
ограниченный выпуклый полиэдр является выпуклым многогран-
ником.
Приведем сводку нужных в дальнейшем топологиче-
ских свойств выпуклых множеств (по поводу встречаю-
щихся топологических терминов см. [КФ])-
Предл о ж е н и е 1. Пусть А —выпуклое множество.
Тогда:
а) все точки полуинтервала [х15 х2), где jq^intA,
х2€А, принадлежат intA;
216
б) внутренность int А и замыкание А множества А
выпуклы-, если int Л =/= 0, то ,4 = intA.
Доказательство, а) Пусть V с А—выпуклая
окрестность точки хг. Произвольная точка х€[хд, х2)
имеет вид х = ах1 + (1 —а) х2, 0 < а 1 и аУ + (1 —а) х2—
ее окрестность, содержащаяся в А, т. е. х£ int Л.
Из утверждения а) следует, что Л с int Л, если
intA=£0, откуда Л cz int Л. Обратное включение оче-
видно.
б) Если х, £пйЛ, 1 — 1, 2, то, согласно ajjx^ х2]€
€ int Л, т. е. mt Л выпукла. Пусть тедерь х, £ Л, i = l, 2.
Возьмем любую выпуклую окрестность нуля V. По опре-
делению замыкания существуют х' g (х, 4-V) А Л, i=l,2.
Для произвольной точки х — осх,,+(! —а) х.2 € [хп х2] по-
ложим х' = ах',. + (1 — а) х2. Тогда х' С Л, и х' € ос (хг + V)+
+(1—а) (х2 + V) = х + V, т. е. каждая окрестность точки х
пересекается с Л, откуда х^Л и Л выпукло. Ц
Определение 1. Пересечение всех замкнутых
выпуклых множеств, содержащих множество Л, назы-
вается выпуклым замыканием множества Л и обозначается
conv Л.
Ясно, что conv Л выпукло и замкнуто.
Предложение 2. a) conv Л = Л <=> множество А
выпукло и замкн у то-,
б) conv Л совпадает с пересечением всех замкнутых
полупространств, содержащих А;
в) conv Л = conv Л;
Доказательство. Первое утверждение непосред-
ственно следует из определения. Включение conv Л с
с conv Л также очевидно (не всякое выпуклое множе-
ство, содержащее Л, еще и замкнуто), а потому conv Л с
с conv Л. С другой стороны, conv Л, будучи выпуклым
-(предложение 16)), замкнутым и содержащим Л, должно
по определению содержать также и conv Л, откуда
conv Л = conv Л.
Далее, обозначим через В пересечение всех замкну-
тых полупространств, содержащих Л. Тогда conv Л с В
(не всякое замкнутое выпуклое множество, содержащее А,
является еще и полупространством). Пусть точка' х0(£
(£conv Л. По второй теореме отделимости (п. 2.1.4) суще-
217
ствует линейный функционал х* g X*, строго разделяю-
щий' х0 и conv А
<х*, х0> > sup <х», х> = а.
хеconv А
Отсюда х0 Н+ (х*, a) z> conv A z> А, и потому х0(£й.
Следовательно, conv А = В. Ц
Упражнение 3, В гильбертовом пространстве 12 рассмотрим
бесконечномерный эллипсоид В=< х = (х1; х2, ...) У](х„/ап)2<1 }>
п= 1
С полуосями ап.
а) Докажите, что множество В выпукло и замкнуто,
б) Найдите условия на ап, при которых int В S3.
в) Пусть int В Ф S3 и точка = у2, •) лежит на границе
эллипсоида, т. е. 2 (Уп1ап)2='- Докажите, что через у можно
п= 1
провести гиперплоскость так, что В будет лежать по одну ее сторону,
г) Всегда ли верно предыдущее утверждение, если int В = 0?
Подобно тому как простейшими выпуклыми множест-
вами являются полупространства, простейшими выпук-
лыми функциями будут аффинные функции
а(х) = <х*, х>—b, х*£Х,
Упражнение 4. Докажите, что а (-) выпукла; найдите epi а.
Предложения 1 и 2 имеют свои аналоги. К их фор-
мулировке мы и перейдем.
Определение 2. Пусть /: X—*R. Функция f,
определяемая условием epi/ = epi/, называется замыка-
нием функции /; если / = /, то функция называется
замкнутой. Функция conv /, определяемая условием
epi (conv /) = conv (epi /), называется выпуклым замыка-
нием f.
Упражнение 5. Проверьте, что epi / -и conv f суть надгра-
фики некоторых функций (см. упражнение 5 п. 2.6.1).
Ясно, что сопу/ = /ф»/ выпукла и замкнута.
Напомним.также, что функция /: X—► R называется
полунепрерывной снизу в точке х0, если lim / (х) /(х0),
х~?ха
и просто полунепрерывной снизу, если то же самое верно
для любого х0.
218
Упражнение 6. Докажите, что f: X —>- R полунепрерывна
снизу тогда и только тогда, когда для любого с £ R множество
= {х | / (х) < с} замкнуто в X.
Предложение 3. а) Для того чтобы собственная
функция была замкнутой, необходимо и достаточно,
чтобы она была полунепрерывна снизу.
б) Для того чтобы выпуклая функция f была непре-
рывной на int dom f достаточно, чтобы f была ограни-
чена в окрестности U некоторой точки х и конечна
в точке х.
При этом, f собственная, rint domf^=0,
int ерг/ = {.(х, a) g X х R | х £ int dom f, а > f (х)} 0
и
f (х) = (convf) (х), Vxgintdomf.
В соответствии с упражнением 6 будем проверять
замкнутость множеств ДД.
Доказательство. А) Пусть f замкнутая функция.
Тогда epi/—замкнутое множество в XxR. Гиперпло-
скость Н = {(х, а|а = с} также замкнута. Значит, замк-
нуто и множество Д?с f={x\f (х) с}, ибо epi f П Н={(х, с) |
и отображение xi—>(х, с) является гомеомор-
физмом.
Пусть наоборот, все £?ef замкнуты и (х0, а0)(£ерЦ.
Тогда f (х0) >а0, а следовательно, f (х0)>а04-е для
некоторого е > 0 и х0 ^а„+ еЛ Ввиду замкнутости ^ао+6 f
существует- окрестность УЭ х0 такая, что V П S’ao+e.f=0,
т. е. f (х) > а0+е, х £ V. Открытое множество {(х, а) | х € V,
а<а0 + е} содержит (х0, а0) и не пересекается с epif.
Следовательно, дополнение к epi f открыто, а сам epi f
замкнут.
Б) Лемма. Пусть X—локально выпуклое простран-
ство, V—выпуклая окрестность точки х в X, f—выпук-
лая, функция jia X, принимающая в точке x£V конечное
значение (| f (х) | < оо) и ограниченная в V сверху. Тогда
f непрерывна в- точке х.
Доказательство леммы. Произведя сдвиг
х>—>х + х и вычитая из f константу f(x), сведем дело
к случаю, когда х = 0, 0 £ V, f(0) = 0, supf(x)^C. При
хе V
этом V можно считать симметричной окрестностью нуля
219
(иначе мы рассмотрели бы U7 = V П (— V))- Пусть 0 < а < 1
и x^aV. Тогда x/agV и из-за выпуклости f мы имеем
f (х) = / ((1 — а) 0 4-ах/а) ^ (1 — а) / (0) + а/ (х/а) <аС.
С другой стороны, —x/agV ввиду симметрии V и, ис-
пользуя равенство 0 = х/(1 +а)+а/(1 4-а) (— х/а) и вы-
пуклость f, получаем
0 = / (0) = /(х/(1 +а)+а/(1 +а) (—х/а))<
< 1/(1 +а)/(х)4-а/(1 +а)/(—х/а),
а, значит, /(х)^— ос/(—х/а)^ — аС.
Итак, если х£аУ, то |/(х)|^аС, т. е. / непрерывна
в нуле. |
Следствие. В условиях леммы int dom/^=0.
В) Возвращаемся к доказательству пункта б) предло-
жения 3. По лемме и следствию из нее / непрерывна
в х и int dom 0.
Предположим, что f(y) = —°° для некоторого у, т. е.
для любого a£R точка (у, a) С epi f. Поскольку epi f
выпукло,
((1— X) x-J-Xy, (1 — Z)/(x) + ?.a)€epi/,
для любого agR, откуда /((1— X.) х-J-Zr/) =—оо, что
при противоречит непрерывности f в х. Таким об-
разом, /(у)>—оо всюду, т. е. f является собственной.
Пусть теперь у £ int dom f. Найдем р > 1 такое, что
z = x + p (у—х) £ int dom / (это можно сделать, ибо пере-
сечение открытого множества int dom f с прямой, прохо-
дящей через х и у, есть открытый интервал этой прямой).
Гомотетия G с центром в г и коэффициентом (р — 1 )/р
переводит х в у и окрестность V в окрестность V
точки у. При' этом, если £€С(У) = У', то £==
(р —l)/px + z/p, x£V н
?5ледовательно, f непрерывна в точке у по лемме, т. е. f
непрерывна на int dom f.
Если (х0, а0) £ int epi f, то по определение найдутся
окрестность U7 точки х0 и е > 0 такие, что
{(х, ot) | х € №, | а—а01 < е} с epi f,
220
откуда x0£intdomf и a0>f(x(l). Обратное включение:
{(х, а) | х int dom f, а > f (х)} а int epi f
очевидно; в частности, intepif^=0.
Поскольку f выпукла, conv (epi f) = epi f. Вспоминая
определение 2 и предложение 2в), имеем
epi (conv f) = conv (epi /) = conv (epi f) = epi (f) z> epi (J).
» _____________________
Следовательно, всегда (conv /) (x) f (x). Если же f непре-
рывна в точке х (или хотя бы полунепрерывна снизу)
и f (х) > а, то это же неравенство сохранится и в целой
окрестности точки х, а потому (х, а) (£ epi / = epi (convf)
и (conv f) (x) > а. Поэтому (conv f) (x) = f (x). В частности,
в условиях пункта б) доказываемого утверждения это
равенство верно для х^ int (dom f). Ц
Упражнение 7. Пусть f выпукла на X и f (х) = — оо
в некоторой точке х£ int dom). Тогда /(х)»—сс, Vx £ int dom f.
Определение' 3. Аффинная функция а(х) —
=<х*, х>—b называется опорной для функции f, если:
а) а (х) f (х) для всех х;
б) для всякого е > 0 найдется такое х, что а (х) >
>f(x)—е. Другими словами,
b = sup{<x*, х>—f(x)}. (1)
X
Теорема Минковского. Собственная функция f
выпукла и замкнута тогда и только тогда, когда она
является верхней гранью множества всех своих опорных
аффинных функций.
Доказательство. 1) «Тогда». Аффинная функция
выпукла и замкнута, так как ее надграфик—замкнутое
полупространство. Далее, для любого семейства функ-
ций имеем*
epi {sup fa\ = / (х, z) | z > sup fa (х)} =
= П {(х, z)|z>/a(x)}= П epifa, (2)
a a
и если все fa выпуклы и замкнуты, то epi fa—выпуклые
замкнутые множества и их пересечение обладает тем же
свойством.
2) «Только тогда». По условию B = epif—замк-
нутое выпуклое непустое множество в X х R. Согласно
221
предложению 2 В является пересечением всех содержа-
щих его замкнутых полупространств. Так как всякий
линейный непрерывный функционал на X х R имеет вид
<х», x>+Zz, х*£Х*, (см. п. 2.1.2), замкнутое полу-
пространство определяется неравенством
<х*, х> + ^г^Ь- (3)
Поскольку B — epif непусто и вместе со всякой своей
точкой (х0, г0) содержит все точки (х0, г), г > za, В может
содержаться в полупространстве (3), только если А.^0.
При Z = 0 полупространство (3) будем называть верти-
кальным. Очевидно, что
epi/== {(х, г)|/(х)^г} с {(х, г)|<х*, х>^Ь}<&
dom / с {х | <х*, х> «С Ь} = Н+ (х*, Ь) =>
=> epi f с Н+ (х*, Ь) х R.
При X < 0 все члены неравенства (3) можно разде-
лить на |Х|, так что можно считать Х =— 1 и полупро-
странство (3) совпадает с надграфиком аффинной функ-
ции а(х) = <х*, х>—Ь. Но
В = epi f с epi a а (х), Ух.
Поэтому
epi/== A epi a A П [Н+ (х*, b) х RJ. (4)
dom f С Н +
Теперь заметим, что хотя бы одна аффинная
существует (в противном случае epi / вместе с точкой
(х0, г„) содержало бы все точки (х0, г), г g R, откуда
/(х0) =—оо, вопреки тому, что f—собственная). Но
epia0D//+ (**, b)x R = {(x, г) | ай (х) г^г, Q*. x>^fe} =
= А {(х, г)|ав(х)4-Х.«х», £>— b)^z} =
= A epi (х) + X «х*, х>— Ь)},
о
и если аа (х) f (х) и dom/ с Н+ (х*, Ь), то
/ (х) < + °? => <х*, х>—bt;ZO=>ao (x)-f-A. «х*, х>—b)^f(x).
Следовательно, epi ай А [Н+ (X*, Ь) х R]c: A epi а, так
a<f
что в (4) мы можем избавиться от всех вертикальных
222
полупространств Н¥(х*,Ь). Итак,
epi / = A epi а
a<f
и, согласно (2),
/(х) — sup {о(х) | а (х) аффинная и <Г/(х)}. (5)
Остается заметить, что в (5) можно брать только опор-
ные к f функции, поскольку верхняя грань не изме-
нится, если из всех функций а(х) = <х*, х>—b^f(x)
с одним и тем же х* мы оставим ту, у которой b опре-
деляется равенством (1), т. е. опорную. Ц
Упражнение 8. §рли f: X —> R выпукла и замкнута и
f (х) = — оо, то / (х) = — оо, Vx £ dom f.
Для гладких функций мы можем воспользоваться
следующим утверждением.
Предл ожение 4. Если функция f выпукла и диф-
ференцируема по Гато в точке х0, то функция а(х)=
= </г(хо)> х—хо> + /(хо) является для нее опорной.
Доказательство. Условие б) определения 3 сле-
дует из равенства а(х0) = /(х0). Предположим, что
f(x1)<Ca(x1) для некоторого Хр Тогда f (хД < a (хД—е
для некоторого е > 0, и потому при 0 < а < 1
/(х0+а(х1—х0)) = /((1—а) х0 + ахД<
^(1— a)f(x0)+a/(x1) < (1— а)/(х0)+а(а (хД—е) =
^(1—a)f(x0) + a(f(x0) + <ft-(x0), Xi—х0> — е) =
= Нхо)+«</г(хо)> Xi—х0>—осе.
Следовательно,
<fr (хД, х,-х0> = 1 im•/(Хо)
а|0 а
<</г(хо). *о>—е,
что противоречиво. Тем самым выполнено и условие а). Ц
Пусть теперь функция f: X —> R дифференцируема
по Гато в каждой точке х0£Х. Составим для нее функ-
цию Вейерштрасса (ср. п. 1.4.4):
<£(х> х0) = /(х) — f(x0) — <fr(xa), х—х0>.
Предл ожение 5. Для того чтобы f была выпуклой,
необходимо и достаточно, чтобы выполнялось неравенство
<§(х, хД>0, Vx, х0.
Доказательство, а) Если f выпукла, то <§ (х, х0)
^0, Vx, х0 в силу только что доказанного предложения 4.
223
б) Пусть х^ах^Ц—et)x2, O^a^l. Неравенства
£ (*i, *0) О, в? (x2, x0) О означают, что точки (х1( f (xj),
(x2, f(x2)) лежат в полупространстве {(x, z)|z>f(x0) +
+ <fr(x0), x—x0>}. Следовательно, и отрезок, их соеди-
няющий, лежит в том же полупространстве, а потому
af(*i) + (l—a)f(*2)>
>f(x0) + <f'(x0), axx + (l — a)x2 —x0> = f(x0).
Таким образом, выполнение условия Вейерштрасса
из п. 1.4.4 для всех точек (t, х, х) эквивалентно выпукло-
сти лагранжиана L(t, х, х) по х.
2.6.3. Преобразование Лежандра — Юнга — Фенхеля,
Теорема Фенхеля — Моро. По-прежнему пусть X — ло-
кально выпуклое линейное топологическое пространство,
а X*—его сопряженное. Зададимся теперь произвольной
функцией f: X —>• R и исследуем подробнее множество
ее опорных функций. Естественно считать при этом функ-
цию собственной, так как в соответствии с определением
/ (х) а (х) > — оо всюду, если f имеет хотя бы одну
опорную, а случай f(x) = 4-oo тривиален: любая аф-
финная функция является опорной.
Определение. Функция на X*, определяемая ра-
венством
f*(p) = sup{<p, х>—f(x)} . (1)
хеХ
называется сопряженной к f функцией или ее преобразо-
ванием Юнга — Фенхеля (иногда преобразованием Ле-
жандра), а функция х
f**(x) = sug (<р, х> — f*(p)} (2)
—второй сопряженной к f функцией.
Из равенства (1) п. 2.6.2 видно, что множество опор-
ных для f функций находится во взаимно однозначном
соответствии с множеством тех р£Х*, для которых f*(p)
конечно:
(Р. Г (р)¥=±«>) ^ар (х) = <р, х>—f*(p). (3)
Замечание. Несмотря на кажущуюся симметрию
формул (1) и (2), f**^(f*)*. Дело в том, что (/*)* по
определению следует рассматривать на (X*)*, а не на X.
Только для рефлексивных пространств (/*)* и /** естест-
венно отождествляются.
224
Предложение L 1) Функции f* и f** выпуклы
и замкнуты.
2) Для любых х$Х и р$Х* выполняется неравенство
Юнга:
f(x)+f*\p)><p, х>. (4)
3) /**(х)=^/(х), Ух.
4) Если f(x)^g(x),mof* (p)^g* (p)uf** (х)С<** (х).
Доказательство. 1) Из (1) и (2) видно, что обе
функции получаются как верхняя грань некоторого мно-
жества аффинных функций, а потому их надграфики
являются (по формуле (2) п. 2.6.2) пересечением замкну-
тых полупространств и, значит, выпуклы и замкнуты.
2) Из (1) вытекает, что при ^любых х£Х ир£Х*
должно быть f*(p)^<p, х>— f(x), что равносильно (4).
3) По уже доказанному /(х)></>, х>—f* (р), откуда
f(x)>sup{<p, х>—/*(?)} = f**(x). _
*
Й Очевидное следствие определений. В
римеры. 1) Пусть f(x) = <xj, х>—Ь—аффинная
функция. Такая функция имеет только одну опорную —
себя самое, Поэтому
{4-СО, Р^Ха,
ь, р~ х0-,
и
/** (х) =? sup {<р, х>—f*(р)}**<xj, х>— (6)
р
2) Пусть, как и в примере 1 п. 2.6.1,
.. . J fo(x), а<х<р,
'(Х)=(+<»» х£(а, р),
причем f’0(x) на (а, Р) непрерывна и монотонно возра-
стает. Обозначим • -
Д= lim f’0(x), В = lim f'0(x).
x-t-a + О - О
Для любого р€(Л, В) равенство р = fо (х0) выполняется
при некотором xog(a, Р). Так как f (х)—выпуклая функ-
ция, то (предложение 4 п. 2.6.2)
а (х)== f (х0) + f (х0) (х—х0) =.рх—(px0~f (х0))
8 в. М. Алексеев в др.
— опорная функция, и, значит, равенства
f*(p-) = PX0—P~f’t>(xo) (7)
задают f* (р) параметрически в (Л, В) (функция /*, опре-
деляемая равенствами (7), называется в классическом
анализе преобРазованием ЛежандРа f0).
Упражнения.
1. Что можно сказать в этом примере о f* (р) при р^(А, В)?
2. Для следующих функций f на R указать dom /, epi f, прове-
рить выпуклость и замкнутость и вычислить f* и /**:
а) ах2+&х4-с, а 5г О,
в) 11 х | -1 |,
/ - /Т+Л | х |к 1,
I + а>, I х | > 1,
ж) ех,
<х In х, х > О,
и) ( 0, х = О,
1+ оо, х < О,
{уй
— , xSsO, . ...
а
+ оо, х < О
н) \х\а!а (а^1).
б) | х|+| х—а|,
( 0, а<х<В,
’>81“'Р1 (')“{», щ.
. |х| < 1,
I + °°> | х I 1,
( —In х, х > О,
3Но, х<0,
X 1п X,
—|— 00 ,
х > О,
х<0,
м) / а ’
1о,
ХЭгО,
х < О
(а2а1),
3) Следующий пример мы используем далее в § 3.3.
Предложение 2. Пусть функция f: R3 * 5-—>R опре-
делена Равенством f (x) — f (xlf ..xs) = max^, ..., x,}.
Тогда
f*(P) = f*(Pv •••> Рз) = '
s
О, если Pi^O, SPi—Ь
z = i
+ оо в остальных случаях.
Доказательство. Поскольку f является макси-
мумом конечного числа линейных (а значит, выпуклых
и непрерывных) функций, ее выпуклость и непрерыв-
ность очевидны.
S
Если р,>0, 2S рх• = 1, то <р, х>^тах{х1, . ..,х,},
i = 1
и потому
f* (р) = sup {<р, х>—тах{х!, .... х5}} = 0.
X
226
С другой стороны, если f*(p)< + °o, то обязательно
f*(p) = O (в силу однородности функций хн-><р, х> и
хн->тах{х, ..xf}), т. е. для таких р выполняется
неравенство
S
2 Р;Х(—max {%!,..., х,}^0, Ух.
i = i
Подставляя в это неравенство Xj — Q, j^=i, %,- = £, полу-
чаем рД^тах{^, 0}, откуда р;>0. Положив в том же
неравенстве х{ — а, 1 = 1, .s, получаем
S , s
а 2 Pi Vag R 2j Pi~ !• M
i=l Z=1
4) Сопряженная функция к 'норме в нор-
мированном пространстве.
Предложение 3. Пусть X — нормированное про-
странство, М(х) = ||х||- Тогда N* совпадает с индика-
торной функцией 6В* 'единичного шара сопряженного
пространства X*, a, N** (х) = У (х).
Доказательство. Если ||р|| > 1, то <р, х0> >||х0||
для некоторого х0, и тогда
f* (p) = sup{<p, х>—||x||}>sup{<p, ах0>—а||х0[|} = +оо.
х а>0
Если же ||р||^1, то <р, х>^||х|| и
f*(p) = sup«p, х>—|]х|[) = 0.
X
Далее,
Г* О) = sup {<р, х>—/* (p)} = sup{<p, х>}=|[х||=у (х).
р iIpiki
5) Пусть X = R, f(x)= 1/(1 +х2). Тогда, как легко
понять,
(0, р = 0,
/•(₽)=[+оо,
и, таким образом, равенство /** (x) = f(x), которое мы
наблюдали в примерах 1) и 4), здесь не выполняется.
Следующая теорема, которая принадлежит к числу
важнейших в выпуклом анализе, показывает, что совпа-
дение f и f** отнюдь не является случайным.
Теорема Фенхеля—Моро. Пусть X—локально
выпуклое топологическое линейное пространство, f: Х—>
—> R—функция, всюду большая —оо. Тогда
8*
227
a) f** (x) sb f (x) тогда и только тогда, когда f выпукла
и замкнута.
б) f** (х) = sup {а (х)| а(х) —аффинная и t^f(x)}.
в) Если существует хотя бы одна аффинная функ-
ция a(x)^f (х) (эквивалентные условия: f* (р)^ + еа или
f**(x)> — оо всюду), то f** (х)—наибольшая из замкну-
тых выпуклых функций, не превосходящих f(x), т. е.
f** = convf.
г) (/**)•=/*.
Доказательство. А) «Только тогда» следует из 1)
предложения 1. Предположим теперь, что a(x)^f(x) —
аффинная функция. В примере 1) мы установили, что
а**(х) = а(х). Воспользовавшись снова предложением 1,
имеем
а (х) = а** (х) < f** (х)< f (х),
а потому
sup {й (х) | а (х)—аффинная и f (х)} /** (х) f (х). (8)
Отсюда прежде всего следует «тогда» в а), ибо когда f
выпукла и замкнута, левая и правая части в (8) совпа-
дают (для собственной f по теореме Минковского, а если
/==s-|-oo, то и левая часть равна +<»). Тем самым а)
доказано. _
Б) Для произвольной f возможны три случая. Если
аффинной функции а(х)^/(х) не существует, то /* (р) —
= sup {<р, х>—f (х)} = + оо при всех р и, значит, /*• (х) =
X
= — оо. Но в этом случае и левая часть в (8) равна
— оо (sup 0 = -а> по определению), т. е. б) имеет место.
Если же существует аффинная а(х)^/(х), то из (8)
вытекает, что /**(х)>— оо всюду. Остаются две воз-
можности. Если /** (х) = + оо, то' f(x)^ + oo и обе
функции равны левой части в (8), так как аффинная
функция здесь может быть любой. Если же /**—собст-
венная, то по теореме Минковского
/**(x) = sup{fl(x)|a(x) опорная для f** (х)}.
Сопоставляя с (8), находим sup {а (х) | а (х) аффинна и
f (*)} f * * (х) — sup {а (х) Iа (х) опорная для /* * (х)}
sup \а (х) | а (х) аффинная иf(x)}. Таким образом,
н в этих случаях б) имеет место.
В) Пусть далее существует аффинная функция а (х)
^/(х) и £(х) =С/(х)—произвольная замкнутая выпуклая
228
функция. Положим
ft(x) = sup{g(x), f**(x)}.
Эта функция замкнута, выпукла и всюду /(x)^ft(x)>
> — оо. Следовательно, *
ft (х) = ft* * (х) f * * (х) ft (х),
а потому ft(x) = f**(x) и g(x)^f**(x), чем доказано в).
Г) Поскольку /•* (x)^Zf (х), то (f**)*(p) С дру-
гой стороны, в силу неравенства Юнга f (х) :> а (х) —
« <р, х>—f*(p), откуда при конечном [*(р)в силу (8)
/••(х)>а(х) и (f**)*(p) =
= sup«p, х>—f(x))<sup(<p, х>—а («)) = /• (р).
X X
Случай f»(p) = 4-oo тривиален, а при = —<х>
получаем
f (х) = f** (х) ss 4- оо и (/••)• (р) = — оо = f* (р). Ц
Упражнение 3. Пусть f выпукла и ограничена сверху в
окрестности некоторой точки. Тогда f** (х) = /(х), Vxgint dom f.
2.6.4. Субдифференциал. Теорема Моро — Рокафеллара.
Теорема Дубовицкого — Милютина. Пусть X—локально-
выпуклое линейное топологическое пространство, / —
функция на X,” f: X—
Определение. Субдифференциалом f в точке х0
называется подмножество X*, состоящее из таких эле-
ментов х*£Х*, для которых выполнено неравенство
f(x)—f(x0)><x% х—х0>, Yx£X. (1)
Субдифференциал функции f в точке х0 обозначается df (х0).
Таким образом, df(xQ)—это множество «угловых ко-
эффициентов» аффинных функций а(х) = <х*, х>— Ь,
опорных к f в точке х0, т. е. таких, что в формуле (1)
п. 2.6.2 верхняя грань достигается в х0:
й = <х*, х0>—f(x0). (2)
Предложение 1. Субдифференциал df(x0) явля-
ется выпуклым (возможно пустым') множеством в X*.
Доказательство. Пусть xf* € df (х0), t = 12. Тогда
по определению /(х)— f(xo)><xj, х—х0>, /(х) —f(x0)>
<xj, х—х0>. Умножив первое неравенство на а, вто-
рое—на (1—а), где а£[0, 1], и складывая, получаем
Дх)—Дх0)><ах1’4-(1— a)xL х—х0>, ¥х.
229
Примеры. 1) Субдифференциа лы некото-
рых функций на прямой и плоскости. Пре-
доставим читателю проверить, что:
([—1, 1], х = 0,
a) fi(x) = |x|, (x€R)=5>af1Qf)=|signx> х¥=0.
б) f2(x) = K^+^, (X€R2)=»
Г {УIV г/i2 + I/!С 1}, х = 0,
=> df2 (х) = < JL = /_Д____х2 \
I |х| I 2 , 2’ 1/ 2 . 2 Ь
' V \~Ь ^2 V Л-1 “Ь ^2 J
в) f8(x) = max(|x1|, |х2|), (x£R2)=»
+ х=0,
• \ _J (signxi’ °)’ Ы >Ы.
=^>ЩДх) | (0, signx2), |х2|>|х1[,
I conv((signxltO), (0,signx2)), IxJ^x^z, z=/=0.
2) Субдифференциал нормы в нормиро-
ванном цр остр а нстве.
Предложение 2. Пусть X—нормированное про-
странство, Х*—его сопряженное, N (х) = ||х||. Тогда
dN (х) =
г В*, где В*—единичный шар сопряженного про-
• странства, если х = 0,
, {х*£Х*|||х*[|= 1, <х*, х> = ||х||}, если х^=0.
Доказательство. Как было отмечено выше (со-
отношение (3) п. 2.6.3), множество опорных функций
к f находится во взаимно однозначном соответствии
с множеством (х*£Х*, f*(x*)^= ± оо}, причем
Цх‘(х) = <Х*, Х>— /*(х*).
Согласно предложению 2 п. 2.6.3
(О, 1|х*||<1,
так что опорными к N являются функции <х*, х>, ||х*||^ 1.
Равенство (2) превращается в
0 = <х*, х0>—||х„|1, (3)
так что любая функция х—*<х*, х>, |jx*j|^l является
опорной к N в точке х0 = 0 и dN (0) = В*. Если же х0 =/= 0,
230
то множество х*£В*, для которых имеет место (3), совпа-
дает с указанным в формулировке. Ц
В приведенных выше примерах субдифференциал су-
ществовал в каждой точке. Разумеется, для невыпуклых
функций (например, для —] х |) его может не быть ни
в одной точке. Однако и выпуклые функции могут не
иметь субдифференциалов даже в точках из эффективной
области.
Вот простейший пример:
—V1 —х2,
-|- оо
|х|С1,
|х.|>1.
В точках Хх = + 1 и х2 =—1 субдифференциал пуст.
Достаточное условие существования субдифференциала
будет получено далее (см. следствие из теоремы Моро —
Рокафедлара).
Следующая теорема является аналогом в выпуклом
анализе теоремы о линейном свойстве дифференциала.
Теорема Моро—Рокафеллара. Пусть f{, i =
== 1, ..., п,—выпуклые собственные функции на X. Тогда
/ п \ п
д[ S Л (x) = Saf,.(x). (4)
V = 1 / i— 1
Если же в некоторой точке х все функции, кроме,
быть может, одной, непрерывны, а эта последняя в ~х
конечна, то в любой точке х имеет место равенство
/ п \ п
(5)
Доказательство. Ограничимся случаем п=^2;
большее число слагаемых рассматривается по индукции.
Включение д]г (х) + 5/2 (х) с д + Д.) (х) сразу следует из
определения субдифференциала.
Пусть Хо £d(fi + /2) (х0). Без ограничения общности
можно считать, что хо = О, х2 = 0, /Д0) = 0, /=1, 2.
Действительно, если эти соотношения не выполнены, то
вместо и f2 можно рассмотреть функции
(х) =/х (х0х) /1 (х0) <х0, х>,
g2(x) = f2 (хв + х) —f2(x0).
Итак, пусть + Согласно (1) это означает,
231
что
min (А (х) + /8 (х)) = Л (0) + f2 (0)«0.
X
Пусть X—та точка, где ft непрерывна, а /8 конечна.
Рассмотрим два выпуклых множества
Ct = |(х, а) ] а > Д (х), х € int dom f J «int epi fn
Ca = {(x, а) I—a>/a(x)}.
Ясно, что множества Ct и Са выпуклы, • непусты
((х, — fa (х)) € Са), С\ открыто и 0ъ силу предложения 3
б) п. 2.6.2: непрерывная в точке х функция ограни-
чена в ее окрестности) и С1Г)С2 = 0. Действительно,
если (aa, xJ^CjnCj, то <сс< —т. е.
0 = min (f j (х) + fa (x)) C fi (*i) + L (*i) < 0»
X
-чего не может быть. По первой теореме отделимости (см.
и. 2.1.4) Сг отделяется от С2 ненулевым линейным функ-
ционалом (xj, р):
inf «хГ, х> + ра)> sup (<xj, х> + ₽а). (6)
(х, а) е С, (х, а) е С,
Ясно, что р^О, ибо иначе верхняя грань равнялась бы
-f-oo. Если допустить, 4TQ 0 = 0, то
sup <xj, х>С inf <xj, х>.
хе int dom h xedgm fa
Но максимум линейной функции не может достигаться
во внутренней точке, а потому
<Xi, х> < sup <xj, х>^ inf <xj, х>^<л£, х>.
хе int dom ft хе dom fa
Противоречие показывает, что ₽^=0. Следовательно,
можно в (6)^ поделить все члецы на |р|, и тогда, если
обозначить Xi = |р |-1xJ и воспользоваться тем, что epi
Sint epi f1~C1 (предложение 1 п. 2.6.2), мы получим
sup{<x*, х>—/\(х)} = sup {<x1‘, x>—a}=w
x /же dom/,
1 a>/, (X)
— sup {<xf, x>—a}< inf {<x;, X>—a} =
(x, a) 6 C, (x, a) € Cs
= inf {<x;, X> + /a(X)}.
Jt
»2
При х=0 значения функций и фигурных скобках сов-
падают и равны нулю (Л (0) = f2 (0) = 0). Значит,
К (x)~fi (0) > <%> х>, f2 (х) —Ъ (0) > <— %, х>,
т. е.
^*€<?А(0), -«€д/.(Ь)
и
0€^(0)4-^(0). в
Следствие 1. Пусть f—выпуклая функция, непре-
рывная в точке хв. Тогда д/(хв)#= 0.
Доказательство. Рассмотрим функцию
f+‘W-l f(^>’
ОО * Л "7^
Функции f и 6 {х0} удовлетворяют условиям теоремы
Моро—Рокафеллара. Равенство
х* = д (f + б{х0}) (х0) = df (х0) + ав {х0} (х0) = df (хе) + X*
означает, что df(xo)y=0. Ц
На самом деле, субдифференциал df(x^) выпуклой
функции, непрерывной в точке х0, является выпуклым
компактом в «--слабой топологии.
Пусть К—конус (п. 2.6.1). Конус X*, состоящий из
тех элементов х*, для которых <%•, х> 0, Ух € X, на-
зывается конусом, сопряженным с К- Если 0 £ X, то из
определения (1) вытекает сразу равенство Э6Х (0) = — X*-
Следствие 2. Пусть Kit ..., Кп—выпуклые от-
крытые конусы, имеющие непустое пересечение. Тогда
/ п У "
п х, = 2хь
1 / 1=1
Действительно, добавим к X/ начало координат и
рассмотрим функции 6Х(. Применив к ним теорему Моро—
Рокафеллара {в точке х € Л X,, отличной от нуля, все
<=1
6Х, непрерывны), получим, что
(Д ~ 58 (Д *1) (0) = - д ( SX,) (0) =
=-|ж((0)=^ХГ
233
Следствие 3. Теорема Дубовицкого—Ми-
лютина о пересечении конусов. Для того чтобы
выпуклые конусы Кх, ..., Кп, Кп+1, из которых первые п
открыты, не пересекались, необходимо и достаточно,
чтобы нашлись функционалы x*i С К], i = 1, .... n.-f- 1, не
равные одновременно нулю и такие, что 2 xj = 0.
Доказательство. «Необходимо». Не ограничивая
себя в общности, можно считать, что К= ПК(=#0.
Тогда К—открытый конус, не пересекающийся по усло-
вию с Кп+Х. По первой теореме отделимости можно отде-
лить К от /С„+1 ненулевым линейным функционалом
уех*-.
inf <г/*, х>> sup <г/*, х>.
хек xeKn+i
Последнее соотношение означает, что у* С К1*, а
(—1) у* С Хп+1 (точка х = 0— предельная как для К, так
и для К„+х). По следствию 2 разложим у* в сумму у* =*
= 2xt> x*i€Ki, l^i^n-, обозначив (— I)у* через x„+i,
.___1 "
получим требуемое.
«Достаточно». Пусть не равны одновременно нулю
x*c£Ki и 2 # = Пусть xg fl К[, х=4=0, и х* =7^0,
z=i i=i 0
Тогда х£ int/Qo=£ <Xfo, х> > 0 и, значит,
0 — <2хь х> > 0. Противоречие доказывает теорему. Ц
Теорема Дубовицкого—Милютина о суб-
дифференциале максимума. Пусть fx, ..., fn —
выпуклые функции на локально выпуклом топологическом
пространстве X, непрерывные в* точке х0; f(x) —
= шах {/\ (х), ..., fn(x)}; I = {ix, —набор индек-
сов такой, что
Тогда
J =/(х0) при i£l,
\ <f (хо) яри i (£ I.
df (х0) = conv {dfit (х0) и • • • U dfis (х0)} =
( i S
= < х* | х* = 2 Мь x*k С dfi (х0), Хд, > 0,
I k=\ я
24=1}.
Л=1 I
234
Доказательство. А) Если 1£1 и х* £df; (х0), то
f (х)~ f (*о) = f (х0) > h (х0) >
> <х*, х—х0> =Ф х* € df (х>0) =» df (х0) z> U' dft (хв) =»
=Ф df (х0)э conv { (х0)|,
причем последняя импликация является следствием вы-
пуклости df(x0) (предложение 1).
Обратное включение будет доказано индукцией по
числу функций. При п=1 утверждение очевидно. В даль-
нейшем будем предполагать, что для (п — 1) функции
оно верно.
Б) Лемма. Если функция f(x) выпукла и неравенство
ф(х) = /(х)—f (х0) —<х», х—х0>>0 (7)
выполняется в некотором открытом выпуклом множе-
стве V, причем ф (х) — 0 для некоторого х б V, то х* € df(x0).
Доказательство. Покажем, что неравенство (7)
имеет место при всех' х; утверждение леммы следует
отсюда по определению субдифференциала.
Пусть х произвольно. Функция ф выпукла вместе с f,
и если ф(х)<0, то для любого а£(0, 1)
Ф ((1 —а) х + ах)^(1 —а) ф (х) + аф.(х) = аф (х) < 0.
При достаточно малом а точка (1—a)x4-ax£V, и мы
пришли к противоречию. Следовательно, ф(х)^0 при
всех х. |
В) Пусть х* € df (х0). Покажем, что тогда либо х0
является решением следующей задачи выпуклого про-
граммирования:
Фо {*) = /<, W—f(x0)—<x*, х—хл>—>inf, (8)
,(Pi(x) = fi(.x)— f(x0) — <х», х—хо><0, (9)
либо утверждение теоремы верно. Действительно, если
первое не имеет места, то для некоторого х
Фо(х) < О = фо(хо), Ф, (х)<0, iVij. (10)
По непрерывности неравенство ф0 (х) < 0 сохраняется
в некоторой выпуклой окрестности V Э х, т. е.
fh (х)~ f(xa) < <х*, х—xQ>, x£V. (11)
235
Теперь вспомним, что x*€df(x0), а следовательно,
должно выполняться неравенство
maxtfjx), ...» f„(x)}—f(xe)><x*, х—х0>.
Сопоставив его с неравенством (11), заключаем, что при
x£V имеет место неравенство
Ф (х) = max {f; (х) 11V4}— f(xe) — <х\ х—х0>>0. (12)
В то же время, согласно (10),
Ф(х)~=тах{/,(х) | iVt'J—f(xa)—<х*, х—х0>^0,
так что ф(х) —0 и по лемме х*€й/(х0), где
f(x) = max {f,(x) |
Поскольку f образовано (n—1) функцией, то в силу
индукционной гипотезы • .
х* € conv ^U2 dflk (х0)| cconv dftk (x0)| .
Г) Зная, что х0—решение задачи (8)—(9), мы можем
воспользоваться теоремой Куна — Таккера (п. 1.3.3); сле-
дует обратить внимание на замечание, сделанное после
доказательства этой теоремы: хотя в силу предложения 3
п. 2.6.2 наши функции непрерывны на int dom, вне него
они могут обращаться в 4- оо.
По теореме Куна—Таккера существуют не равные
нулю одновременно множители Лагранжа Хо, Х(-^0,
для которых х0—точка минимума функции Лагранжа
^(х; 1) = 10ф0(х)+ S
< ¥= I, -
Кроме того, должны выполняться условия дополняющей
нежесткости, согласно которым Х( = 0, если Ф/(х0) =
= fi(xa)—f(xo)y=O, т. е. при Перенумеровав Хо
в Xf, и ф0 в ф/,, имеем J?(x, Х) = 2^/Ф/(х)» а так как.
is i *
множители Лагранжа определены с точностью до поло-
жительного множителя, можно считать, что
i6i
Теперь имеем
^(х, Х)>^(хв, Х)Ф> £ Х(ф(х)>0«
iel
« 2W.(*) — ( SXzV(x0)~f 2хЛ <х», х—х0>>0«
lei \ie/ } \1б/ ]
е^(2у;(-)Ш
\,ZG I )
236
Применяя теорему Моро—Рокафеллара и учитывая, что-
из определения субдифференциала вытекает очевидное
равенство
d(z/)(x0)=xa/(x0),
справедливое при А, > О, мы убеждаемся в том’, что
Х/^0, S А,, =» 1,
т
Г ЛАВ A HI
ПРИНЦИП ЛАГРАНЖА ДЛЯ ГЛАДКИХ ЗАДАЧ
С ОГРАНИЧЕНИЯМИ
Основная цель этой главы—обоснование принципа
Лагранжа для гладких задач с ограничениями типа ра-
венств и неравенств, а также вывод достаточных усло-
вий экстремума для таких задач. Общие результаты этой
главы применяются затем в гл. 4 к задачам классиче-
ского вариационного исчисления и оптимального управ-
ления. Поскольку на элементарном уровне часть материала
излагалась уже в гл. 1, читателю рекомендуется парал-
лельно просматривать соответствующие места в §§ 1.3—1.4.
§ 3.1. Элементарные задачи
3.1.1. Элементарные задачи без ограничений. Пусть
X—топологическое пространство, U—окрестность в X,
f: U—>R. Задача
f (х) extr (3)
называется элементарной задачей без ограничений (эк-
стремальной—здесь и далее подразумевается).zB случае,
если X—линейное нормированное пространство и f обла-
дает гладкостью в каком-либо смысле, то задачу (з)
называют элементарной гладкой задачей-, если X—линей-
ное топологическое пространство и f—выпуклая функция,
то задачу (§) на минимум называют элементарной выпук-
лой задачей. -
Определение локального экстремума для задачи (з)
см. в п. 1.2.1. Если х доставляет локальный минимум
(максимум, экстремум), в задаче (3), мы пишем кратко
х£ locmin3 (х£ locmax 3, x£locextr3). Определения раз-
238
личных терминов, связанных с понятием гладкости см.
в § 2.2.
Начнем с простейшего—одномерного случая, когда
X = R.
Лемма. Пусть функция f: U—> R определена на
некотором интервале U = R, содержащем точку х.
а) -Если f имеет в точке х производные справа и слева
и xClocminj (locmaxj), то
f (х + 0)>0, f’ (х—0Г<0 (Г(;+0)<0, f (х—0)>0).
(1)
Если же в (1) выполнены строгие неравенства, то х£
glocminj (locmaxj).
Пусть далее функция f дифференцируема k раз в точке х.
б) Если х € locmin з (locmax 3), то либо fw(x) = O,
либо существует такое s, 1 s^pfe/2], что
= f<“)(x)>0 (f™(x)<0).
(2)
в) Если существует такое s, 1 s [&/2J, что вы-
полнены соотношения (2), то xglocminj (locmax 3).
Утверждение б) при k— 1 (xg locextr 3=Ф/' (х) = 0)
известно в анализе как теорема Ферма. Эту теорему мы
доказали в п. 1.4.1.
Доказательство. Утверждения а) сразу следуют
из определений односторонних производных и локаль-
ного экстремума. Утверждение б) при k = 1 (теорема
Ферма) вытекает из а), если учесть, что существование
производной влечет за собой равенства f (х) = f (х + 0) =
= f' (х—0). Пусть далее k > 1 и для определенности
речь идет о минимуме. По формуле Тейлора
ft
f(x+ft) = £,-^^/i* + o(/ift). (3)
у = 0 ‘‘
Пусть f (х)= ... (х) — 0, f(m) (х) #= 0.
Возможно одно из двух: т — нечетно и т—четно. В пер-
вом случае пусть <p (£) = f (x-J-j/I), £ € R. Из (3) следует
тогда, что <р € D1 (0) и ср' (0) = f(B” (х)/т! =И= 0, а по теореме
Ферма должно быть <р'(0) —0. Противоречие показывает,
239
что т должно быть четным. Но тогда, полагая
ф(£)=7 .получаем нз (1) ф'(+0) =
= f<m) (х)//я! > 0, доказывающее утверждение б). Утверж-
дение в) сразу вытекает из формулы Тейлора f(x+h) —
— f(x) + fiw[x)hs/(^)\+o(h2s), из которой видно, что
если f,w) (х) >0, то х £ locmin 3, если же ftu> (х) < 0, то
xglocmaxj. В
Следующие утверждения являются почти непосред-
ственными следствиями определений.
Теорема 1 (необходимое условие экстре-
мума первого порядка). Пусть 8 (3) X—нормиро-
ванное линейное пространство и функция f имеет в точке
x£U производную по направлению h.
Если xglocminj (xglocmaxj), то ,
Г(х;Л)>0- (f(x;/i)<0). (4)
Следствие 1. Пусть f имеет первую вариацию
(первую вариацию по Лагранжу) в точке х. Если х £ locmin 3
(xCbcmaxj), то
6+f(x,h)^Q, УН$Х (6+/(х, ft)<0, VA6X) (5)
(в/(х, ft)=o, vftgx).
Следствие 2. Пусть f имеет производную в смысле
Фреше (Гато) в точке х. Тогда, если 2 € locextr 3, то
(fr(x) = O). (6)
Утверждение следствия 2 также называют теоремой
Ферма. Точки х, я которых выполнено равенство (6),
называют стационарными точками задачи (3).
Теорема 2 (необходимое условие экстре-
мумаг второго порядка). Пусть в (3) X—нормиро-
ванное линейное пространство и f имеет вторую вариа-
цию по Лагранжу в точке x£U. Тогда, если х£ loaning
(xglocmaxg), то выполнены следующие соотношения'.
df(x, h) — 0, УН^Х, (7)
67(Х, Л)>О, УН^Х («*/(£, Л)^0, УН$Х). (8)
Док азательство. Равенство (7) содержится
в следствии 1. Неравенства (8) немедленно вытекают из
240
определения второй вариации по Лагранжу и утвержде-
ния б) леммы. В
Следствие 3. Пусть f имеет вторую производную
в смысле Фреше в точке х. Тогда, если xglocminj (х£
€ locmax 8), то выполнены такие соотношения-.
Г(х) = 0, . (9)
Г(^)>0 (Г(х)^О). (10)
(Эти неравенства означают, что квадратичная* форма
*=[" (х) [h, h\ неотрицательна (неположительна).)
Доказательство. Воспользовавшись формулой
Тейлора (см. п. 2.2.5), имеем
<р (а) = f (х+ah)«f (х) 4-af (х) [ft] + f'Tx) [ft, ft]+о (a»),
откуда
8f(x, A) = g>' (0)=f (x)[A],
&f(x, A) = <p"(0) = /"(x)[A, A],
и остается сослаться на (7) и (8). Ц
Следствие 2 утверждает, что локальные экстремумы
являются стационарными точками. Мы упоминали уже
в п. 1.4.1, что обратное неверно. Чтобы получить до-
статочные условия, приходится привлекать к рассмотре-
нию производные более высоких порядков, как это мы
уже делали в лемме.
Теорема 3 (достаточное условие экстре-
мума второго порядка). Пусть в (3) X—норми-
рованное пространство и f имеет вторую производную
в смысле Фреше. Тогда, есци выполнены соотношения
f'(x)~Q, (П)
f" (х) [А, А] > a || A IIs, YA G х (/" (х) [А, А]а||А|[», YA € X)
(12)
для некоторого а>0, то x^lgcminj (х£locmax3).
Доказательство. Если выполнено первое из не-
равенств (12), то, снова обратившись к формуле Тей-
лора, имеем
/ (к+А) = f (х) + Г (х) [А] 4-ф- [А, А] + о (|| А ||2) >
>f(x) +-J-1|А||24-01|А||2) >/(х),
241
если h^O и ||h||достаточно мала. Следовательно,
xglocming. Случай максимума рассматривается анало-
гично. В
Условие (12) называют условием строгой положитель-
ности (отрицательности) второго дифференциала f.
Замечания. 1. В конечномерном случае, когда
X — R", утверждения теорем 1—3 хорошо известны из
курса математического анализа (см. об этом также
в п. 1.4.1). Теорема Ферма означает следующее:
f (х) = 0 df (х)/дх1 = ... = df (х)/дхп = 0. (13)
Из необходимого условия второго порядка вытекает, что
в конечномерной задаче на экстремум утверждение
xglocming влечет (помимо (13)) неотрицательную опре-
/ d2f (х) \
деленность матрицы ( Ч-- ):
\ OXj f
П
(14)
Условие положительной определенности матрицы
/ d2f(x) \
( -gx. ) гарантирует, как нетрудно убедиться, строгую
положительность второго дифференциала (и, значит,
является достаточным условием минимума в стационар-
ной точке). В бесконечномерных пространствах это не так.
00
Пример. Пусть X = /2, f (х) = 2 ((х)/и3) —х)). Тогда
• / =1
точка х = 0 является стационарной, f' (0) — 0, а второй
дифференциал f в нуле—положительно определенным
f"(O)[h, Л]= 2^/и3.
/=1
Но вместе с тем 0 (£ loaning, ибо на последовательности
{е„/п}"=1 (е; — i-й базисный вектор пространства/2) функ-
ционал f принимает отрицательные значения: f (еп/п) =
= (1/п-) — (1/и4) < 0, а сама последовательность стремится
к нулю.
2. В одномерном случае лемма, с которой начинается
этот пункт, дает в некотором отношении исчерпывающий
ответ на вопрос о том, является ли заданная точка точ-
кой локального минимума бесконечно дифференцируемой
функции f или нет: за исключением тривиального случая,
242
когда все производные в данной точке равны нулю, лемма
дает ответ на поставленный вопрос. Даже для функций
двух переменных такого рода исчерпывающей процедур'ы
по-видимому нет.
3. Неравенства (12) накладывают серьезные ограни-
чения на структуру нормированного пространства X.
Если выполнено первое из них, то симметричная били-
нейная функция (£ | т]) = f" (х)[£, т]] задает в X скалярное
произведение, а неравенства
показывают, что норма, порожденная этим скалярным
произведением, эквивалентна исходной. Следовательно,
X линейно гомеоморфно евклидову (предгильбертову)
пространству. В частности, неравенства (12) не могут
иметь места в пространствах С и С1.
3.1.2. Элементарная задача линейного программиро-
вания. В п. 1.2.6 мы в общих чертах описали класс
задач линейного программирования. Здесь будет рас-
смотрена самая простая из задач этого класса. Для нас
она интересна тем, что при ее рассмотрении мы позна-
комимся с важными условиями экстремума — условиями
соответствия и согласования знаков 'и условием допол-
няющей нежесткости.
Пусть X = R", agR"*—элемент сопряженного про-
странства, а = (а1, ...,ап). Рассмотрим задачу
ах —+ inf (sup); Ф» 2 а;х,-—+ inf (sup); (g)
х,^0. -
Символ здесь означает, что в соответствующем огра-
ничении может стоять один из знаков или —.
Задачу (g) будем называть элементарной задачей линей-
ного программирования.
Будем говорить, что для вектора а выполнено условие
соответствия знаков (с ограничениями х;^0), если
а(-^0 при ограничении x;^0,af^0 при ограничении
х,-^0 и а; может иметь любой знак, если ограничение
имеет вид равенства хг- = 0. В случае, если неравенства
«оборачиваются», т. е. если а{ 0 при ограничении
х(-^0, а^О при ограничении хг^0 (и снова at—лю-
бого знака при х,- = 0), то будем говорить, что выполнено
243
условие согласования знаков. В первом случае мы пишем
а;3*0, во втором а(-^0.
Теорема (необходимое н достаточное
условие экстремума в элементарной задаче
лн-нейиого программирования). Для того,
чтобы точка х £ R" доставляла абсолютный минимум
(максимум) задаче (5) необходимо и достаточно, чтобы
были выполнены:
а) условия соответствия (согласования) знаков
«/^0 (о,^0), (1)
б) условия дополняющей 'нежесткости
арс, = О, i = 1, ..п. (2)
Доказательство. Допустим, что (j)—задача мн-ч
нимизации и i0-e ограничение имеет вид хч>0. Если'
допустить, что а(-о < 0, то нижняя грань в задаче (з)
равна — оо, ибо х1г> может принимать сколь угодно боль-
шие положительные значения. Поэтому условие ^0
необходимо для того, чтобы значение задачи (искомый inf)
было конечно. Если допустить теперь, что altxt то
вследствие условия Х/о^>0 и доказанного неравенства
а(-о^>0 на самом деле а, Х/о > 0. Hq тогда точка х не
будет минималью задачи, ибо на допустимом векторе
х = (хх, ..., О, х/о+1, ..., хп) имеем ах < ах. Доста-
точность условий (1), (2) очевидна: если для определен-
ности (4) — по-прежнему задача минимизации и выполнены
условия соответствия знаков и дополняющей нежесткости^,
то для любого допустимого вектора х £ R” получаем
ax^Q, в то время, как для х в силу (2) ах=0. Ц
Упражнение. Вывести доказанную теорему из теоремы
Куна—Таккера.
3.1.3. Задача Больца. Пусть Д—конечный замкнутый
отрезок вещественной прямой. Рассмотрим банахово
пространство
3 = С!(Д, R")xRxR,
состоящее из элементов £х=(х(-), t^, tt). В этом про-
странстве рассмотрим задачу
®(1) = @(х(-), tt, Q =
ц
— $L(t, x(t), x(t))dt + l(t^, x(t0), tlf x(^))-H.extr. (j)
244
При этом в (j) функции (t, х, x)i-+L(t, х, х) и (£0, х0, xj—*
—->-Z(f0, х0, tx, хл) определены в открытых подмножествах
V и W пространств RxR"xR" и Rx R"X Rx R" соответ-
ственно и t0, Обе функции будем предполагать
по меньшей мере непрерывными. Задача (j) называется
задачей Больца с незакрепленным временем, а функционал
в (5)—функционалом Больца. В п. 1.4.2 был рассмотрен
ее частный вариант, когда и = 1 (о случае п > 1 было
лишь кратко упомянуто) и моменты времени te и были
закрепленными.
Лемма. Пусть функции L и I и их частные произ-
водные Lx, L*, ltt и lx, 1 = 0,1, непрерывны в областях
V и W соответственно. Тогда функционал 33 является
непрерывно дифференцируемым (по Фреше) на следующем
открытом подмножестве пространства В:
^{^(х'С), tt, ^)|х(-)€С1(Д, R");
(t, x(t), x(t))eV‘, (t„, x(ta), tlt t», ^CintA},
и при этом
3B'(x(-), t9, tx)\h(-), т0, T1] = $(4(?)/i(0 +
- ^0
+ LX (i) h (t))dt +L (?j) ь— L (t0) tQ+ltxQ +?t ji + •
+ lXa (h(U4-x (Q *») + u(h(?j) 4-x (f0)Tj, (1)
где
L(t)~L(t, x(t), x(t)), lx(t)~Lx(t, x(t), x(t)),
L-(t) = L-(t, x(t),x (0), It. = It. (4, x (f0), tv x O,
= lx. (t0, X (f0), tv X (£)), J = 0, 1.
Доказательство. Функционал 33 является суммой
интегрального и терминального функционалов. Их не-
прерывная дифференцируемость была доказана в пп. 2.4.2
и 2.4.3. (Терминальный функционал +/(?0, x(t0), tx,
x(tj) является частным случаем оператора краевых
условий.) Чтобы получить (1), остается Воспользоваться
формулами (9) п. 2.4.2 и (3) п. 2.4.3. |
В соответствии с этой леммой» (з) является элементар-
ной гладкой задачей без ограничений. Поэтому мы можем
применять к ней необходимые н достаточные условия
245
экстремума п. 3.1.1. Расшифровка утверждения теоремы
Ферма приведет нас к следующей теореме.
Теорема 1 (необходимое условие экстре-
мума первого порядка в задаче Больца).
Пусть выполнены условия леммы. Если элемент | =
= (х(-), /0, £) € S принадлежит множеству QZ и достав-
ляет локальный минимум задаче (3), то
1) выполнены условия стационарности по %(•):
а) уравнение Эйлера
—^4 (0+4(0 = °, (2)
б) условия трансверсальности по х
i = 0, 1; (3)
2) выполнены условия трансверсальности по t:
М) = (-1)‘ + 14 / = 0’ (4)
где
Соотношения (2) и (3) уже встретились нам в п. 1.4.2.
Условия трансверсальности по t встречаются здесь впер-
вые, но впоследствии в гл. 4 мы постоянно будем иметь
Сними дело.
Доказательство. Было сказано уже, что зада-
ча (3) является гладкой элементарной задачей, и к ней
применима, следовательно, теорема Ферма (следствие 2
п. 3.1.1), согласно которой
f С locextr 3 =$> Si' (f) = 04^®' (f) [ц] = 0,
Vn = (ft(-), ТО, tx)€E. (5)
Вспоминая (1), получаем из (5)
о=®' (f)W =
= J (4 (0 h (0 +4 (0 h (0) dt +aoh (t0) +
+ aik(t1)+P0T0+P1T1, (6)
где для краткости введены такие обозначения:
а,- = Ц’ = 4 + + + i = 0’L (7)
246
Соотношение ^'(f)[t]] = O имеет место для любого эле-
мента т] = (/i(-), т0, tJ. Рассмотрим сначала элементы
вида т] = (А(-)> 0> 0). ЙССЦД, R”), Л(^-) = 0, i=l, 2.
Тогда из {6)
7,
J(£,(0ft (0+^(0 А (0)^ = 0 (8)
*0
для любой вектбр-фуикции h (•) €С*(f?0, ?i)> R") такой,
что /Г(/о) =/i (?i) = 0. Но с такой ситуацией нам при-
шлось уже встречаться в п. 1.4.1. Из леммы Дюбуа-
Реймона, доказанной там^мы сразу получаем соотношение
(2) (в п. 1.4.2 лемма Дюбуа-Реймона была доказана для
скалярных функций, и здесь ее следует применять по-
очередно к каждой компоненте вектор-функции /i(-);
полагая М«) = ... = Л,._1(.) =Л/+1(.) = ••• =Л„(-) = 0,
мы сводим (8) к аналогичному скалярному соотношению
с одной компонентой ЙД-) и получаем i-e уравнение
системы (2)). При этом заодно доказывается непрерывная
дифференцируемость Но тогда в выражении (6)
можно произвести интегрирование по частям, что (с уче-
том (2)) дает
0 = (|) Гн] = (a0-ii О h (it) +
; +(a1+£i(?1))/i(^)+₽0Te+p1T1 (9)
для произвольных векторов h(t0), h(ti) и чисел т0 и тх.
Отсюда и из (7) немедленно следуют соотношения (3)
и (4).
Как мы видим, доказательство теоремы, в сущности,
такое же, как и в гл. I. Только там нам пришлось вы-
числять производные кустарно, а здесь мы воспользо-
вались общими теоремами дифференциального исчисления
§§ 2.2 и 2.4.
3.1.4. Элементарная задача оптимального управления.
Пусть 11—топологическое пространство и ф:Д01 1Дх
Х11—>R. Рассмотрим задачу
it
f(u(-))= u(l))d/—*inf (j)
А)
в пространстве КС ([£0, U) кусочно непрерывных
функций и (• ):[^, ?i]—*11 со значениями в 11. Функцию <р
247
будем предполагать непрерывной в pe, ZjxU. Задачу (j)
назовем элементарной задачей оптимального управления.
Теорема (необходимое и достаточное
условие минимума в элементарной задаче
оптимального у п р а ъл ен я я). Пустьфункцияи(-) £
$КС (ff0, fj, U) и доставляет абсолютный минимум
в задаче (з).- Тогда для любой точки непрерывности
функции «(•) выполнено соотношение
min/(t м) = /(Л u(t)). (1)
и е а
Доказательство. Допустим, что соотношение (1)
не выполнено и существуют точка т (где «(•) непре-
рывна) и элемент ogli такие, что f (т, ,р) < f (т, и(т)).
Вследствие непрерывности функций и
t—*f(t, u(t)) в окрестности точки т найдется такой ин-
тервал А = [т—б, т-4-6], что f (t, и)< f (t, u(t)) при
t € А. Положим и (t) = u (t) при / Л и u (?) — о при / g A.
Тогда /(«(•))</(«()) вопреки минимальности и(-).
3.1.5. Принцип Лагранжа для задач с равенствами и
неравенствами. В гл. 1 уже несколько раз обсуждался
принцип, которому соответствуют необходимые условия
для задач с ограничениями. Здесь, после того как нами
выделены некоторые «элементарные»'задачи, можно под-
вести кое-какие итоги.
Рассматривавшиеся экстремальные задачи были фор-
мализованы так, что ограничения делились на две группы,
первая из которых имела вид равенств. По ограничениям
этой группы составлялась функция Лагранжа. Далее
мысленно ставилась задача о соответствующем экстре-
муме функции Лагранжа по второй группе ограниче-"
ний — по той группе, которая не участвовала в форми-
ровании функции Лагранжа. При этом оказывалось, что
полученная экстремальная задача либо сама оказывалась
элементарной, либо элементарными оказывались «частич-
ные» задачи, получаемые фиксированием всех неизвест-
ных, кроме одного. Необходимые условия для полученных
элементарных задач в своей совокупности и составляли
искомый набор необходимых условий экстремума. Пре-
доставим читателю убедиться, что все необходимые усло-
вия, о которых речь шла в гл. 1, и все необходимые
условия, о которых речь пойдет далее в гл. 4, соответ-
ствуют описанной процедуре. Исключение составляют
248
задачи с неравенствами, в которых появляются допол-
нительные условия. Этими задачами мы займемся в сле-
дующем параграфе, а здесь покажем, что и они также
могут быть включены в рамки описанного «принципа
Лагранжа».
Пусть (для определенности) у нас имеется задача ми-
нимизации
/0(х)—+inf; F(x)=~0, /=1, (j)
где наряду с равенствами встречаются и неравенства
(X и Y в (j)—-линейные топологические пространства,
•fi'. X—>R, F: X —>У). Введением новых переменных и,-
приведем задачу (з) к виду
/о(х)~*infJ ^(х) = 0, Д(х)4-«/*=О,
«,^0, i = ,т, (J)
и разобьем ограничения на две группы, первая из ко-
торых состоит из равенств (F(x) = 0, ft (x) + u(- = 0), а
вторая группа—из ограничений вида «/ЗЙО. Для за-
дачи (з) составим функцию Лагранжа, игнорируя_ огра-
ничения второй группы:
(х, и, y*t A, A,e) == Xefe (х) 4-
+ 5 Ь if. (*)+Ui) + <//*, F (х)>, X = (Xn ..., Хя), k
i=i
условившись о знаке множителя 10 (в задаче на мини-
мум А.0>0, на максимум Хо^О).
В задаче о минимизации функций Лагранжа (при
фиксированных миожителях)
^(х, и, у*, X, Хо) --* tnf
имеется две группы переменных х и и. Если закрепить
переменные и=ц, то получается элементарная задача
без ограничений <гладкая, выпуклая и т. п.), и здесь,
можно написать нужное необходимое условие экстремума,
причем, как легко видеть,' и{ в это условие не войдут.
Если же фиксировать переменные х = х, то получится
элементарная задача линейного программирования. Усло-
вия экстремума, написанные в соответствии с п. 3.1.2,
дают нам условия соответствия знаков множителей
249
Лагранжа л
(1)
и условия дополняющей нежесткости
Kiui = Q^lifi(x) = 0. (2)
Далее мы будем каждый раз пользоваться этой про-
цедурой, но, если у нас имеются ограничения типа не-
равенств, составляя функцию Лагранжа, сразу будем
т
писать ее укороченной: S? (х, у*, X, Zo) = 2 Kfi (х) +
<=о
+<«/*, F(x)>— и именно такую функцию будем называть
функцией Лагранжа .задачи (j). Нужно помнить только,
что к условиям ее экстремума по х следует присоединить
соотношения, вытекающие из (1), (2), а именно, условия
согласования знаков
(Г)
г-
и дополняющей нежесткости
Заметим теперь, что принций Лагранжа (как, напри-,
мер, и теорема Ферма для гладкой экстремальной за-
дачи) дает только необходимые условия экстремума, т. е.
выделяет множество «подозреваемых» объектов, но не
доказывает их «виновности». Поэтому для полного реше-
ния задачи мы должны либо иметь в распоряжении набор
достаточных условий экстремума, либо иметь уверен-
ность в существовании решения.
Первое позволит «провести экспертизу»: каждый из
выделенных необходимыми условиями объектов мы под-
вергаем проверке на достаточность. Найдя среди них
тот, который удовлетворяет достаточным условиям, мы
считаем задачу решенной.
Во втором случае искомое решение (существование
которого заранее известно или доказано) обязано попасть
в число подозреваемых объектов, удовлетворяющих необ-
ходимым условиям экстремума. Вычисляя для каждого
из них значение функционала, мы объявляем решением
тот, где это значение экстремально.
Разумеется, ни тому, ни другому приему нельзя от-
дать предпочтения. Достаточные условия обычно не сов-
падают с необходимыми, и потому могут оставаться
250
«подозреваемые», «вину» которых установить не удается
(например, теоремы п. 3.1.1 не дают ответа о существо-
вании экстремума в точке х для «плоской» функции f(x),
у которой /(*’(х) = 0 при всех k). С другой стороны,
даже зная, что решение существует, мы можем оказаться
в затруднении, если необходимыми условиями выделяется
бесконечное (или просто очень большое) множество по-
дозреваемых объектов.
В большинстве вопросов существования решения
оказывается возможным обойтись усовершенствованным
вариантом классической теоремы Вейерштрасса, которую
мы уже упоминали в п. 1.6.1: существование является
следствием компактности множества допустимых элемен-
тов и полунепрерывности функционала.
Определение. Функция f; Х-~>R, определенная
на Топологическом пространстве X, называется полуне-
прерывной' снизу в точке х0, если lim f (х)^ f (х0), и про-
сто полунепрерывной снизу, если она полунепрерывна
снизу в каждой точке (ср. п. 2.6.2).
Теорема Вейерштрасса. Полунепрерывная снизу
функция f: X —> R достигает минимума на всяком счет-
но-компактном подмножестве топологического простран-
ства X.
Доказательство. Пусть АсХ—счетно-компакт-
ное подмножество и S—значение задачи
f (х) —>inf, х^Л, (3)
т. е.
S = inf f (х).
хе А
По определению нижней грани мы можем выбрать
минимизирующую последовательность задачи (3), т. е.
такую последовательность точек х„^Л, что /(x„)—*S.
По определению счетной компактности из х„ можно
выбрать подпоследовательность х„А, сходящуюся к не-
которой точке х£А. Ввиду полу непрерывности
f(x)< lim f(Xnk)= lim f(x„) = S
и так как, с другой стороны, f (х) не может быть меньше
значения задачи (3), f(x) = S, т. е. х—точка минимума. Ц
Следствие. Пусть f полунепрерывна снизу на то-
пологическом пространстве X. Если некоторое лебеговское
251
множество ^af — {x\f(x)^.a} функции f неНусто и
счетно компактно, то f достигает на X своего ми-
нимума.
§ 3.2. Принцип Лагранжа для гладких задач
с ограничениями типа равенств и неравенств
3.2.1. .Формулировка теоремы. Рассмотрим экстремаль-
ную задачу: -
f0 (х) —+ extr; F(x) — Q, Д(х)^0, i = l,. ..,т. (1)
Символ fi (х) 0 означает, что i-e ограничение имеет
вид либо f; (х) — 0, либо fi (х) 0, либо f, (х) 0.
Задачи типа (1), где X и Y—нормированные про-
странства, fi—гладкие функции на X, a F—гладкое
отображение из X в У, называются гладкими экстре-
мальными задачами с ограничениями типа равенств и
неравенств.
Функцией Лагранжа задачи (1) называется функция
т
3{х, у*, К, X/, (х) + <г/\‘/’(х)>, (2)
4 z=o
где в (2) ^ = (Х!, ..., k0£R, у* ^Y*—множи-
тели Лагранжа.
Теорема (правило множителей Лагранжа
для гладких задач с равенствами и неравен-
ствами). Пусть X и Y—банаховы пространства, U —
открытое множество в X, функции f{: U—>R, i ==
=0, 1, ...,т, и отображение F; U—+Y строго диффе-
ренцируемы в точке х.
Если х доставляет локальный экстремум, задаче (1) и
если
образ Im F' (х) есть замкнутое подпространство в Y, (3)
то найдутся такие множители Лагранжа у*, X, £0, для
которых выполняются-.
а) условие стационарности функции Лагранжа по х
^Х(х, у*, X, £о) = О. (4)
б) условие согласования знаков: Хо 0, если задача на
минимум, £оСО, если задача на максимум,
1^0, i=l,...,m, (5)
252
в) условия дополняющей нежесткости
^if, (х) = О, i = 1 > • • •» т. (6)
Напомним еще, что запись означает следую-
щее: если в формуле (1) ft (х) > 0, то X, СО, если f{ (х)С0,
то 0, наконец, если f{ (х)'= 0, то может иметь
любой знак.
Утверждение о существовании множителей Лагранжа,
удовлетворяющих совокупности условий а)—в), нахо-
дится в точном соответствии с общим приемом снятия
ограничений—об этом как раз и говорилось в последнем
пункте предыдущего параграфа. Поэтому сформулиро-
ванный результат мы называем еще принципом Лагранжа
для гладких задач с равенствами и неравенствами.
Доказательство общей теоремы базируется, с одной
стороны, на теореме' о неявной функции из § 2.3, а с
другой—на теореме Куна—Таккера, т. е. в конечном
счете—на конечномерной теореме отделимости. Теорема
Куна—Таккера была доказана нами в § 1.3, и ссылка
на нее—единственная по существу содержательная ссылка
на первую главу в этой части книги. Привлечение тео-
ремы Куна—Таккера связано с наличием в (1) нера-
венств, и оно несколько осложняет доказательство. Слу-
чай же, когда неравенства отсутствуют, совсем прост,
но вместе с тем и содержателен и поучителен. Поэтому
мы разберем его отдельно, хотя, конечно, этот случай
является автоматическим следствием общего результата.
При чтении следующего пункта мы рекомендуем срав-
нивать параллельно бесконечномерный вариант доказа-
тельства с конечномерным, разобранным в п. 1.3.2.
3.2.2. Правило множителей для гладких задач с равен-
ствами.
Теорема (принцип Лагранжа для гладких
задач с равенствами).
а) Пусть X- и Y—банаховы пространства, U—от-
крытое множество в X, f: U—►R, F: U —^Y—функция
и отображение, строго дифференцируемые в точке х.
Если точка х является точкой локального экстремума
в задаче
# f (х)—>-extr, F(x) = 0 |1)
и если образ ImF'(x)—замкнутое подпространство в Y,
то найдутся такие множители Лагранжа Хв £ R и £ V*,
253
для которых выполнено условие стационарности функции
Лагранжа:
Ях(х, у*, Хо)=Офф<Х/(х), х> + <у*, F' (x)[x]>=Q,Vx. (2)
б) Если выполнено условие регулярности отображения F,
т. е. если Im F' (х) совпадает со всем пространством Y,
то множитель Хо отличен от нуля.
Дока за те ль ств о проведем для задачи на мини-
мум. Определим отображение
F(x) = (f(x)—f(x), F(x)), {/->RxK.
Отображение $F, очевидно, строго дифференцируемо в х
иГЙ=(Г(ДГ«).
Возможно одно из двух: образ ImF'(x) может сов-
падать или не совпадать с пространством R х Y.
А) Разберем сначала случай ImF'(х)=/= R хУ. К ото-
бражению вЕ' (х) применим лемму о замкнутости образа
(п.~2.1.6). Образ Im F' (х) замкнут по условию, образ
f (х) (Кег F' (х)) есть либо {0}, либЪ R, т. е. замкнутое
подмножество R. Значит, по цитированной лемме образ
ImF'(x) замкнут в RxV. Так как он не совпадает с
R х Y, Im F' (х)—собственное замкнутое подпространство.
Но по лемме о нетривиальности аннулятора (п. 2.1.4)
найдутся Число \ и элемент у* (см. п. 2.1.2, где гово-
рится об общем виде линейного функционала в произ-
ведении пространств), не раЬные нулю одновременно
(|\| + ||i/*||=/=0) и такие, что
<W' (х), х> + <у*, F' (х) [х]> =? 0, Vx.
Но это соотношение совпадает с (2).
Б) Пусть теперь Im F' (х) = R х Y. Тогда мы можем
применить теорему о существовании неявной функции
(см. пп. 2.3.1—2.3.3).
Согласно этой теореме1) существуют константа К > 0,
окрестность 41 точки (0, 0) в пространстве R х Y и
х) Приведем сопоставление обозначений теоремы п. 2.3.1 с обо-
значениями этого пункта. X —топологическое пространство в теореме
о неявной функции (н ф) здесь состоит из одной точки {х0},
У (н.ф) ффХ, 2(н.ф Ч'(х, у)=Чт (х0> у) (н ф )^F W, А (н ф.)ф>
4=^F'(х), у0(н.ф.) ФФ х, г0 (н.ф ) O^RxZ. Условие 1) теоремы
254
отображение <р: “И—>-Х такие, что
&(ф(«. !/)) = («> У) и Цф(оь, у)—хЦС/СЦГ^)—(a, i/)||.
(3)
Положим x(s) —<р(—е, 0) = <р (г (е)). Тогда из (3) имеем
Г(х(в)) = г(8)^ (х(в))—f(x) = —в, Г(х(в)) = 0, (4)
II X (8) — х|| = II ф (г (8)) — х||< Д'II (0, 0) — (—8, 0) || = Д' I 8 |. (5)
Из (4), (5) следует, что x(s)—допустимый элемент в
задаче (1), сколь угодно близкий к х и вместе с тем
f(x(e)) < f (х), т. е. x^locmin (1). Противоречие доказы-
вает, что равенство Im<F' (х) = R х Y невозможно. Тем
самым верно утверждение а) теоремы.
В) Пусть F—регулярно в" точке х и \ = 0. Тогда
^*^0 и соотношение (2) приобретает вид: <i/*, F' (х) [х]>=0,
ух. Выберем элемент у такой, что <i/*, у>=£0 (это воз-
можно, ибо г/*^=0), и найдем элемент х такой, что
F' (х) [х] = у (он существует ввиду равенства F' (х) X = Y).
Тогда 0^=<г/*, г/> = <£/*, Д'(х)[х]> = 0. Этим противоре-
чием доказано второе утверждение. Ц
Замечание. Мы построили доказательство по той же схеме,
что и доказательство конечномерного правила множителей Лагран-
жа (п. 1.3.2), и оно оказалось столь же простым и кратким. Прав-
да, это потребовало некоторой подготовки: были использованы три фак-
та из функционального анализа: теорема о нетривиальное™ аннулято-
ра (т. е. в конечном счете ---теорема Хаиа — Банаха), лемма о замкну-
тости образа и теорема о неявной функции. Для завершения общей
теоремы—доказательства правила множителей для задач с неравен-
ствами— нам, помимо этих трех фактов, понадобится еще лишь тео-
рема Куна—Таккера, являющаяся прямым следствием конечномерной
теоремы отделимости (см. п. Е) доказательства теоремы в п. 3.2.4).
Удивительно, что столь малыми средствами, относящимися к общим
математическим структурам, получается результат, в качестве пря-
мого следствия из которого с помощью незначительных вспомога-
тельных средств также общего плана (теорема Рисса о линейных
функционалах в пространстве С и стандартные теоремы о дифферен-
циальных уравнениях) в следующей главе будут выведены содержа-
тельные конкретные результаты: необходимые условия экстремума
в задачах классического вариационного исчисления и оптимального
управления.
удовлетворяется тривиально, условие 2) выполнено вследствие
строгой дифференцируемости |Г, ибо
Ч (ха, у')-Ч (х0, у”)-Л(у'-у") & <F(x')-<F(*")-<F'(x)lx'-*''l,
и, наконец, условие 3) выполнено, поскольку Im^' (x) = RxK.
255
3.2.3, Редукция задачи. Перед тем, как приступить к
доказательству теоремы, сформулированной в п. 3.2.1,
произведем некоторое преобразование ее условий. Сна-
чала, заменив, если нужно, f0 на (—Г)?й, сведем задачу
к задаче на минимум. Если среди ограничений вида
fi(x)^O или /\-(х)^0 есть такие, что f;(x)<0 или со-
ответственно f; (х) > 0, то мы* их отбросим, поскольку с
локальной точки зрения они несущественны, ибо выпол-
няются во всех точках некоторой окрестности точки х.
Далее, если в (1) п. 3.2.1 имеются неравенства f;(x)^O,
/.(£) = О, мы заменим их на неравенства (—l)ft(x)^O.
Равенства же Д- (х) = 0 присоединим к равенству F{x) — 0.
Перенумеровав теперь заново все неравенства, задающие
ограничения, получим следующую задачу, эквивалент-
ную (1):
Д(х) —inf; F(x) = 0, Д(х)<0,
где #(х) = (/(х), .....Ь(х))
0 j р, существует такое е;- = -|-1
/ = т, (Г)
и для каждого /,
или —1, что
f/(x)as8yfy(x). (2')
В задаче (Г) х доставляет 'локальный минимум и при
этом ff (х) — 0, / = 1, ..., in.
Покажем теперь, что для задачи (Г) выполнены все
условия теоремы. Действительно, X и Ух ’бана-
ховы- пространства. Функции Д и отображение F стро-
го дифференцируемы в точке х (в силу того, что F и fj
были таковыми). Осталось показать лишь, что L = Im /'(х)
замкнуто в Y’xR,i-'n. Имеем F' (х) = (F' (х), Ф'(х)), где
Ф' (х) И = «/“+1 (х), х>, ..., <f; (Xs, х)>, Ф' (х):
Образ Im/7'(х) замкнут по условию, а подпространство
Ф' (x)[Ker F' замкнуто, как и любое подпро-
странство конечномерного пространства. Значит, по лемме
о замкнутости образа (п. 2.1.6) ImF' (х) замкнут b/xR*"'".
Предположим теперь, что для задачи (Г) доказывае-
мая теорема верна и, следовательно, существуют мно-
жители Лагранжа у* = (у*, Хд+1, .... ХД Ху, /=0,1,..., in,
для которых верны а) и б) п. 3.2.1 (условия в) выпол-
няются автоматически, ибо f/(x) = O, ...,in).
256
В силу б) Ay > 0, / = О, 1, ..., /й, а в силу а)
•S?х (*» У*1 ^1» - • •» А,в) ==
т
~ 2 W*)+(iM)r(*)-o» (3')
/= О
где = 2 V/W+(?°^)W-
/ =0
Теперь остается положить Х0 = А0, — /~1, ...
..., т, = Ау; }=т4-1, ..., р и А,- = О, если // (х) #= 0.
Полученный набор будет удовлетворять, очевидно, усло-
виям дополняющей нежесткости и условию-согласования
знаков (ибо в (2') е, = +1, когда ограничение имеет вид
fZ/(x)^O и бу =—1 при Кроме того, поскольку
J’ (X, у*, Alt . . ., Xji, X,) = FZ (х, у*, £х-, ..., кт, X)
условие стационарности функции'Лагранжа выполняется
или не выполняется для обеих функций одновременно.
Итак, в дальнейшем можно ограничиться лишь рас-
смотрением задачи (Г). Однако для простоты мы больше
не будем ставить тильду (~) над F, и т.
3.2.4. Доказательство теоремы. Итак, пусть нам дана
задача:
/0(х)—>inf; F(x) = 0, /у(х)<0, / = 1.../и, (1)
причем выполнены все условия теоремы п. 3.2.1 и
fj (х)—О, / = 1, ..., т. Без ограничения общности мо"Жно счи-
тать также, что и /в(х) = 0.
Разобьем доказательство на несколько этапов.
А) Линейный случай. Рассмотрим сначала прос-
тейшую ситуацию, когда /# = х*—линейный функционал,
ft — O, i = l, ..., т, a F—A—линейный непрерывный
сюръективный, оператор. Точка х = 0 решение задачи
<х*, х> —► inf; Лх=0 (Ле^Х, F), Л(Х) = Г) (2)
тогда и только тогда, когда х*€(КегЛ)-!-. По лемме об
аннуляторе ядра (п. 2.1.7) существует элемент y*£Y*
такой, что х*4-Л*у* = 0. Но это соотношение в точности
есть принцип Лагранжа для задачи (2):
х* + Л*у* = О(0, у*, 1)»0,
9 в. М. Алексеев и др. 257
где ^(х, у*, А0) = А0<х*, х>->г<у*,Лх> = <Кох*+Л,*у*, х>—
функция Лагранжа задачи (2). Таким образом, в этой
ситуации принцип Лагранжа верен.
Б) Вырожденный случай. Im F’ (х) есть собст-
венное подпространство Y. Вследствие леммы о нетри-
виальное™ аннулятора (п. 2.1.4) найдется элемент
у* С (Im F’ (х))-1- (г/* о F') (х)=0.Остается положить А,-=О,
i = 0, ..., т, и убедиться в том, что принцип верен и
ъ рассматриваемом вырожденном случае.
Далее считаем, что F—регулярный оператор в точ-
ке х, т. е. Im-F' (х) = У.
Положим для 0 k т
ДА = {х| (х), х> < 0, i — k, А + 1, ..., т,, F' (х) [х] = 0}.
В) Лемма 1 (основная). Если х есть локальное
решение в задаче (1), то множество До пусто. Иначе
говоря,
max (х), х> 0, Vx С Ker F’ (х).
Доказательство. Предположим, что До непусто,
т. е. существует элемент £ такой, что F' (х) [£] = 0, (х),
£> = P,,p,<0, O^i^m. Тогда по теореме Люстерника
(п. 2.3.5) существует отображение г: [—а, а]—>-Х, а>0,
такое, что
(х + А£ + г (А)) = 0, Agf—а, а], г (А) = о (А). (3)
При малых А > 0 имеем для i = 0, 1, ..., т неравенства
Д (х + Ц + г (А)) = Л- (х) + А <л (X), I> + 0 (А) = Ар,. + о(А) <0.
(4,)
Соотношения (3) и (4,) /= 1, ...,т, означают, что
для малых А>0 элемент х + А^ + г (А) является допусти-
мым в задаче (1). Но при этом неравенство (40) проти-
воречит локальной минимальности х. Ц
Г) Лемма 2. Если Ат есть пустое множество, то
для задачи (1) верен принцип Лагранжа.
Доказательство. Пустота Ат означает, что х = 0
является решением задачи
х>—>inf, F'(x)[x] = 0.
В си^у п. А) для этой задачи справедлив принцип Лаг-
258
ранжа, а значит, он справедлив и для задачи (1) (надо
только положить \ = ... =ХЯ1_1 = 0).
Таким образом, из пп. В) и Г) вытекает, что либо
принцип Лагранжа уже обоснован (Ат = 0), либо суще-
ствует такое k, что
Лй = 0, Aft+1^=0. (5)
Д)-Лемма 3, Если выполнены соотношения (5), то
нуль является решением следующей задачи линейного про-
граммирования:
</*(£), х>—► inf; х>^0,
i — k + l, ..., т, F' (x)[x] = 0. (6)
Д о к а з а те л ь ств-о. Предположим, что т]—такой
допустимый в задаче (6) элемент (т. е. <f^(x), т]>^0,
i k +1, F' (х) [т]] = 0), что <% (х), т]> < 0. Пусть £—эле-
мент, принадлежащий Ak+i, т. е. (х), £> < 0,
F' (х) [?] = 0. Тогда при малом е>0 элемент т]4-е£ при-
надлежит Ак в противоречии с (5). Ц
Е) Завершение доказательства. Применяем
к задаче (6) теорему Куна—Таккера (п. 1.3,3), учтя при
этом, что условие Слейтера для этой Задачи выполнено
(из-за непустоты Aft+I). По этой теореме найдутся такие
неотрицательные числа ..., £/л, что точка нуль яв-
ляется решением задачи
<Щх), х>+ 2 (х), х>—»-inf,v F' (х)[х] = 0. (7)
i=A+l . ~
(Это последнее утверждение есть не что иное, как прин-
цип минимума для задачи (6), причем множитель Лаг-
ранжа при функционале взят равным 1 вследствие вы-
полнимости условия Слейтера.) Но задача (7) есть опять-
таки задача, о которой говорилось в п. А). Для нее
верен принцип Лагранжа или, что в данной ситуации
одно и то же, применима лемма об аннуляторе ядра опе-
ратора F' (х). Иначе говоря, существует элемент у*, для
которого
т
fk(x)+ 2 Kift(x) + (y* с F') (х) = 0.
i=k + l
Но это и есть условие стационарности функции Лаг-
ранжа, если положить = ... = £ft_j = 0, = 1. Ц
’*5 259
По ходу доказательства при оказалось, что
Ло= 1. Покажем, что если F регулярно (т. е. Im F' (x)=Y),
то в этом случае вообще никакой набор множителей
Лагранжа, для которого выполнено условие стационар-
ности функции Лагранжа, не может содержать множи-
тель \=0. Действительно, при А1=^0 существует эле-
мент h такой, что F' (x)]7i] = 0, (х), hy < 0, i—1, ..in.
Допустим теперь, что нашлись множители Лагранжа
Х = (Xj..., £m), у*, не равные нулю одновременно и такие,
что еЗ’Дх, у*, £, 0)=0. Тогда ввиду неравенств (х), й>^0
имеем
т
0=^х(х, у*, Z, 0)[/i]= 2Л,<Л'(х), h> + <y*, Р'(х)[Ц>~
i = i
= <f't (x\.h> . = ч, — 0 => y* =?feO,
t =1'
и теперь
0 = J?x(x, у*, X, O)[x] = <z/*, F'(x)[x]>, Vx=> Im F'(x)^=F
вопреки предположению.
Выделим сказанное в отдельное предложение.
Предложение. Для того чтобы в теореме п. 3.2.1
£0 #= 0, достаточно добавить к ее условиям, что Im F’ (x)=Y
и существует элемент h £ Ker F' (х), для которого (х),
hy <0, i=l, ..т.
Дополнительные допущения, о которых здесь гово-
рится, будем называть условиями усиленной регулярности
задачи (1).
В формулировке доказанного нами принципа Лаг-
ранжа участвует важное (и вдобавок единственное, помимо
требований гладкости и банаховости) условие замкну-
тости образа Im F' (х). Необходимо отметить, что без
условий такого типа принцип Лагранжа может оказаться
неверным.
Прежде всего при отказе от требований сюръектив-
ности оператора Ag=2’(X, Y) (X и Y—банаховы прост-
ранства) формула (Кег Л)-1-= Im Л* может оказаться не--
верной, точнее, может оказаться, что Im Л* есть собст-
венное подпространство (КегЛ)-1-. Например, если X=Y—
' ^2, к г (х2, . • •, хп, .. •) /2, Хх — (х2, х2/2, ..., х„/и, ...),
то КегЛ = {0} и, значит, (KerX)1 = Z2, в то время как
ImX = ImX*^=/2 (скажем, элемент у=(1, 1/2,.... 1/п,...)
260
принадлежит lit но решения уравнения Лх = у, очевидно,
не существует).-Теперь мы можем уже привести пример
задачи, для которой принцип Лагранжа неверен.
Пример. Пусть X и Y—банаховы пространства и
оператор Л £ S (X, У) таков, что Кет Л* = {0}, a Im Л* есть
собственное подпространство (КегЛ)1. Выбрав
х* g (Ker A)-L\Im Л*, рассмотрим задачу
<х*, х> —>inf; Лх = 0.
I
Для этой задачи принцип Лагранжа неверен. Дейст-
вительна, х = 0 является точкой минимума, и если бы
нашлись Хо и у* € У* такие, что
-2”х(0, у*, £0) [Л] = 0, V/i g X <=> <х*, + ЛЛ>=0,
Vh € X,
то Х0 = 0(ибо иначе х* g Im Л*), а значит, A*y* — Q=^y*=Q.
Упражнение1). Пусть Z=Y=l2, г = (гх...... г„, . )£/2,
Az = (zt, z2/2, ..., z„/n,^...), p^ImA, X = RXZ, f(x)=f (a, z)=a,
F(x) = /:'(a, z)=Az-]-a2y. Покажите, что для задачи f(x)—Mnf;
f (x) = 0 принцип Лагранжа .неверен.
§ 3.3*, Принцип Лагранжа и двойственность
в задачах выпуклого программирования
3.3.1* Теорема Куна — Таккера (субдифференциальная
форма). Принцип Лагранжа для задач выпуклого про-
граммирования (теорема Куна—Таккера) был уже дока-
зан в п. 1.3.3. В этом пункте дается «субдифференциаль-
ная форма» этой теоремы и проясняются связи с другими
понятиями выпуклого анализа.
Пусть X и У—банаховы пространства, Л: X—>-У — ли-
нейный непрерывный оператор, X —>R, г=0, 1,..., т—
выпуклые функции, a = (ait affi)gRffl, b£Y, Л —вы-
пуклое множество в X. Рассмотрим следующую задачу
выпуклого программирования:
f,(x)—>inf; i = l, ..., m, Ax = b, x$A. (3)
Множество (x|Ax — b} обозначим через В. Функцией
Лагранжа задачи (3) является функция
£\х, у*. X, Хо) =
m
= (X) + S (ft (х)—а) + <y, Ax—by.
______________ 2 = 1
l) Предложено студентом 4 курса В. В. Успенским.
261
Предложение. Пусть х—точка абсолютного ми-
нимума в задаче (3). Тогда х—точка абсолютного мини-
мума в элементарной задаче
f(x) = max(f0(x)—f0(x), f^xj — a,,.fm(x) — am) +
4-6(Л AB)(x)->inf, (3')
где 6 (Af] В)—индикаторная функция множества А П В.
Действительно, если существует элемент х, для кото-
рого /(х)<0, то это означает, во-первых, что х£А,
х£В(Ф^Лх = Ь) во-вторых, что fa (х) < at; i=l, ..., т
(т. е. что х—допустимый элемент в задаче), и, в-третьих,
что fa (х) < Л (х) вопреки условию. |
Теорема (субдифференциальная форма
теоремы К у н а—Т а к ке р а). Пусть в (3) функции
fi, i — 0, 1, ..., т, непрерывны в точке х^АПВ, достав-
ляющей абсолютный минимум в задаче. Тогда найдутся
т
числа %,-^0 такие, что 2 = 1» W/(x) = 0, i^l, и
1 = 0
элемент х* £ 36 (А Г) В) (х), для которых
т
.0€ 2 МЛ(*)+£*•• (1)
1 = 0
Доказательство. Согласно предложению х до-
ставляет абсолютный минимум в элементарной задаче (3').
По теореме 1 п. 3.1.1 0£3f(x). Функция g(x) =
= max(f0(x)—/0(х), А(х)—ап ..., fm(x)—ат} выпукла
и непрерывна в точке х£А А В (т. е. принадлежащей
dom 6 (Л А В)'и, значит, по теореме Моро—Рокафеллара
(п. 2.6.4) df(x)= dg(x)-fadd (А ПВ)(х). Наконец, по тео-
реме Дубовицкого — Милютина (п. 2.6.4) dg (х) =
= conv (dft, (х) (J ... Udf^(x)), где fa— те и только те ин-
дексы, для которых fa(x) = g(x). Таким образом, сущест-
вуют два элемента l*£dg(x) и х*£36(Л А В)(х), для
которых
|* + х* = 0, С conv (dfh (х) U ••• U dfis (х)) <=} =
= 2 Ч-Ч’ Че (Ч S4 = А Ч>°-
Осталось положить А,( = 0, fa}- Ц
262
Упражнение. Пусть В = (х|Лх = 6). Докажите, что если
х0 С то дб (В) (х0) = (Кег Л)1.
Следствие 1 (принцип Лагранжа для за-
дачи выпуклого программирования чс огра-
ничениями типа равенств и неравенств).
Пусть в условиях теоремы А = Х и образ X при отобра-
жении Л замкнут в Y. Тогда найдутся такие множители
Лагранжа A0CR, ACR"1*» y*€.Y*, что
Az 0, i 0, %ifi (х) = 0, i 1,
minJ?(x, у\ А, А0) = а2’(х, у*, А, (2)
X
Действительно, если 1mA есть собственное подпро-
странство в Y, то можно положить А(- = Ао = 0, у* £ (Im Л)-1.
Если жеЛ—сюръективный оператор, то ддВ (x)=(KerA)-L=
= 1шЛ*. Тогда, согласно (1), д^дх^{х, у*, A, A0)=s
tn
— 2 dfi (x) + Im А*, и, значит, по определению суб-
1=0
дифференциала
^(x, у*, A, Ao)—J?(x, y*, A, Ao)—<0, x—x>>0«^
&J?(x, y*, A, k0)^^(x, y*, A, Ao), Vx. Ц
3.3.2. Метод возмущений и теорема двойственности,
В предыдущем пункте задачу выпуклого программирова-
ния (g) мы рассматривали как одну индивидуальную за-
дачу. Со многих точек зрения оказывается естественным
и плодотворным рассмотрение целых семейств задач по-
добного рода. Фиксировав f{, Л, а,-, А и Ь, включим
задачу (g) в семейство
f0(x) ->inf; f,-(x) + a; /=1, ..., m,
Ax + t] = d, xCA. (g (a, i])).
(Разумеется, можно было бы просто объявить а{ и Ъ
переменными параметрами семейства, но, введя параметры
а;, т] так, как указано выше, мы получаем более кра-
сивые формулы.) Совокупность задач {(g (a, т|))} назовем
возмущением задачи (g) — (g (0, 0)).
Мы уже видели в п., 3.3.1, что задача (g) сводится
к элементарной. Сейчас мы проделаем то же самое для
семейства g (а, т]), однако несколько по-другому. А именно,
263
обозначим
( fo(x)> если fi(x) + a,i ^ait Лх+ц=Ь, x€ A,
l(x, a, t])—| _|_oo, в остальных случаях.
(1)
Тогда семейство (j (а, т})) можно записать в виде элемен-
тарной задачи
f(x; а, т])—> inf (по х^Х). (2)
В дальнейшем, говоря о задаче (j (а, т])), мы не будем
различать ее исходную формулировку от (2). Значение
этой задали, т. е. inf f0, при указанных ограничениях
Является функцией от а — (а,, •.., а,л) и ц, которую мы
обозначим через S, S: RmxF —>R и иногда будем назы-
вать S-функцией:
S(a, т]) = inf f (х; а, т]) = inf (3)
х хбА, ft (х) +а(. < о(-, Лх + П=&
Лемма. Пусть F (х, z)—выпуклая функция на про-
изведении линейных пространств X и Z. Тогда функция
S (z) = inf F (х, z)
X
выпукла на Z.
Доказательство. Пусть (z(-, Q£epiS, I = 1, 2
и 1 € [О» И- Тогда S (zz) < t{, i = 1, 2, и для любого s > О
существуют (х(, zz) такие, что F (х(-^ г,) < /, + е, i « 1, 2.
Отсюда в силу выпуклости F
F (Ах*-f-(1—А) х2, Аг1 + (1—X)za)^
^AF (xit zJ-Hl—A)F(x2, г2)<Х(?1+е)+(1— A)(fg4-e)=*
, — A^a (1 —• A) -J-8.
Ввиду произвольности 8 > О
F(Ax$-|-(l—A) x2, Azf -f-(l — A) z2)
Mt + (1 — A) t2 =» S (Azx + (1 -A) г2) sC
<Af1+( 1-A> f2=«>(Az1+(l-A) z2, A/1+(l-A) t2)eepi S.
Предложение 1. Пусть X и Y—линейные прост-
ранства^ АсХ—выпуклое множество, Л: X —► Y—линей-
ное отображение. _
Если функции fi’. X —>R, i = 0, 1, ..., т, выпуклы,
то функция f (x; а, т)), определяемая равенством (1), вы-
пукла на XxRmxK.
264
Доказательство. Множества
= {(х, а, п, OK*. O^epifJ,
М,- = {(х, а, п, О К,- (х)+.а,’^ъ},
МА = {(х, а, ть О|х€А},
Мд = {(х, а, т], f) | Ах + т] = Ь\
выпуклы BXxRraxVxR. Действительно (нарушая иногда
для удобства порядок сомножителей): Мо = epi fnX RraX Y,
MA — 4xR”xyxR, MA=A“1(b)xR'BxR, где Л: (x, г/)»-*
►—>Ax+y—линейное отображение из ХхУ в У и Л4,=
«=oepi{fz — aJxR'^xKxR, где о: (х, ?)>->(х, —t)
симметрия в XxR. Отсюда видно, что все эти множе-
ства выпуклы, и остается заметить, что
epi f== П М/ЛМдОМд. |
1 = 0
Следствие 1. S-функция задачи (}(а, т})) выпукла
на R“xV.
В § 2.6 мы уже видели, что выпуклость позволяет
сопоставлять различным объектам (функциям, множест-
вам) двойственные объекты в сопряженном пространстве.
То же самое справедливо и для задач выпуклого про-
граммирования. Далее мы будем предполагать, что X
и У—локально выпуклые пространства, Х^ и У*—их
сопряженные, А = (А1; ..., Ага) £ R“*.
Определение 1. Семейство экстремальных задач
g(x*; А, т)»)—>-sup(no А€ R"*, К*), (З‘(х*))
где (—l)g(x*; А, т]*) = f (х*; А, т]*)—sпреобразование
Юнга — Фенхеля (п. 2.6.3) функции (х, а, т])|-~>/(х, а, т)),
определяемой равенством (1), называется двойственным
к семейству §(а, р)^(2).
Задача з* = з* (0) называется двойственной к задаче
3 = 3(0, 0) (относительно семейства возмущений § (а, т])).
Значение задачи 3*(х*) обозначим
S(x*)— sup g(x*; А, if).
(X п’)
(4)
Поскольку функция f* выпукла, противоположная ей
функция g вогнута. Двойственные задачи можно было бы
называть задачами вогнутого программирования, но мы
предпочитаем обойтись без нового термина.
265
О пределение 2. Функцией Лагранжа пары се-
мейств j(a, р) и 3*(х*) или расширенной функцией Лаг-
ранжа задачи (j) называется функция .24 X х R"* X Y* —• R,
определяемая соотношениями
oS?(x; А,,
Л*) =
/ т
I /о (*) + 2! ЫЬ (*) — ^)4-<Л% Ах— by,
хе A, AgR™,
— ОО, х£А, A.£R?‘,
4-оо, х(£А.
(5)
При фиксированных (А, ц*) эта функция выпукла по х,
а при фиксированном х выпукла по (А, я*) противопо-
ложная функция .
Заметим, что
J^x; А,- т)*) = & (х, т]*, А, 1), хе A, A^R?’, (6)
где 3—функция Лагранжа задачи (з), определенная
в п. 3.3.1.
Предложение2. Пара двойственных семейств j (а, ц)
и g* (х*) однозначно определяется их функцией Лагранжа,
поскольку
f(x\a, т]) = (—^)*(2’> g(X*’ Л*) =— <^'*(1>, (7)
где *(1) и * (2) обозначают преобразования Юнга—Фен-
хеля по аргументам х и (А, т]*) соответственно.
Доказательство. Поопределению преобразования
Юнга—Фенхеля
— g(x*; А, л*) ==/*(**; А, т]*) =
= sup {<х*, х>4-Аа4~<Л*< т]>—f(x; А, т])} =
(X, а, Т1)
= sup {<х*. х> + Аа + <п*, Л>—fo(x)} ~ ’
хеА, Ах + т)=Ь
f( (X) +а;< of
I sup< <х*. х>— f„ (х)— 5(fi («)—«,)—<n% Ах—Ь> ?,
J х g А ( i =4 J
“UgRr
t+oo, Z^R“*
= J?*(1>(x*; А,, л*),
чем доказано второе из равенств (7). Попутно мы полу-
266
чили полезное соотношение
g(x*-, A., rf) =
inf(^(x; А,, т]*)—<х*, х>), A,gR7*,
хе А
— оо, A^R"*’-
(8)
С другой стороны1),
(— J7)*(2)= sup (Zcc + <r]*, t]> + J?(x; %, т|*)) =я
(^. л")
4-оо, х(£ А,
sup (Zcc + <T]*, т]> + f0 (x) 4-
— • X>0, л* =
I + а,-)4-<П’.Лх—b>)
x « i = 1
' 4-00, если x(£ А или Ax — b=/=— г] или f{ (x) — a(> —at
= для некоторого i, —
f0 (x) в остальных случаях
= f(x; a, tj).
Следствие 2. Сопряженная функция к S-функции
задачи g (а, т]) имеет вид-~
г — inf ^(x.n’A, 1)A€R7\
S*(A,, n») = —g(0; A., n*) = < xeA
I 4-00, A^R™.
(9)
Доказательство. По определению
S*(A,, т]*) = sup (Ха4-<Л*> т1>— inf /(х; а, г])) —
(а, Л) X
= sup (Xa4-<Tf, Т]>—f(x; а, т])) = —g(0; A,, if),
(а, л. х)
после чего (9) следует из (6) и (8).
Таким образом, двойственная к задаче g—g(О, 0)
задача g* = g* (0) может быть сформулирована также и так:
— S*(A,, т|») = inf 3 (х, т]*, А,, 1) —sup; . .
A-SR?*, k ’
Замечание. Определение двойственной задачи
зависит, вообще говоря, от того, в какое семейство
х) Как и в п. 2.6.3, вычисляя сопряженную к функции, опре-
деленной на сопряженном пространстве (в нашем случае на К/я*хК*),
мы считаем результат функцией на исходном пространстве, а не на
втором сопряженном.
267
'возмущений мы включим исходную задачу (3). Равенства
(5) и (6), определяющие расширенную функцию Лагранжа
и равенства (7), показывают тем не менее, что семейства
{(3(а, т]))} и {(3* (х*))} в некотором смысле естественно соот-
ветствуют задаче (3) и, таким образом, задача (3*), экви-
валентная (10), в том же смысле является ее естествен-
ной двойственной.
Упражнение. Покажите, что если функции f; и множество А
выпуклы и замкнуты и если f0(x) не обращается в —оо на множе-
стве допустимых х задачи (3), то двойственное (с учетом сноски к до-
казательству предложения 2) к семейству {(3*(х*))} семейство совпа-
дает с {(3 (а, г]))}, и, таким образом, задачи (3) и (3*) образуют пару
двойственных Друг другу задач.
Теорема двойственности для задач вы-
пуклого программирования. Предположим, что
S-функция семейства {(3 (а, т)))} непрерывна в точке (0, 0).
Тогда: для любых (а, ц) € int (dom S)
S (qc, т])= sup (Zcc + <Tf, t|> -f-inf J? (x, Tf, A, 1)). (11)-
X>0.ri*6T* xeA
Значения задачи (3) и двойственной ей задачи (3*) равны
между собой
inf ' ’ fo(x)=S(O, 0) = S(0) =
хе А
Лх~Ь
f 1 (х) < ар 1=1 т
= sup +а») + <П% Ал—Ь>}|.
?.>о Iх6А 1 <=1 ))
П*<=у*
(12)
Доказательство. По следствию 1 функция S вы-
пукла, а из непрерывности ее в одной точке вытекает
(предложение 3 п. 2.6.2) непрерывность и равенство
S(a, n) = (convS) (а, т]) Для всех (а, J)) € int (dom S). -
По теореме Фенхеля—Моро (п. 2.6.3) и следствию 2
S (а, = т]) = sup (Аа-|-<т]*, т]>—S* (%, т]*)) =
(X, if)
;= sup (Асе + <?]•, 1]> + inf 3 (х, if, М 1))»
. х > о хе а
У*
чем доказано (11). Подставляя а = 0, т] = 0, получаем
(12).
268
Следствие 3 (теорема о минимаксе). В усло-
виях теоремы двойственности справедливо соотношение
sup inf 3 (х, т|*, 1) = inf sup (х, q*, X, 1), (13)
Доказательство. Левая часть (13) равна 2(0)
и в силу (12) совпадает с S(0, 0). Что же касается пра-
вой части, то
inf sup ^(х, Tf, X, l)=inf sup (x; X, ц*) =
хеЛ ?.> о хеА <?., п*)
Я’е г*
= inf ((—^)*<2'(х; 0, 0))= inf /(х; 0, 0)
хеЛ * х^А
согласно (7) и также совпадает с S(0, 0).
3.3.3, Линейное программирование: теорема существо-
вания и теорема двойственности. Пусть X— линейное
пространство, X'—алгебраически сопряженное с ним
(т. е. совокупность всех линейных функционалов на X),
Д’—некоторый полиэдральный конус (т. е. пересечение
конечного числа полупространств Я/={<Х/,'х>^0, х)€Х',
/=1, .... s} —иногда, впрочем, от условия полиэдраль-
ности отказываются).
Экстремальные задачи вида
<Хо, х>—>-inf; fi(x) = <х', x>^bit i = 1.т,х£К, (1)
составляют отдельный класс задач линейного программи-
рования.
В этом пункте будет рассмотрен конечномерный слу-
чай, когда X = R", X'=R"*, K = R£. В этом случае за-
дачу (1) можно переписать так1):
сх-~>-inf; Ax^b, х^0, . (2)
где cgR"*, А==(а,у), j — 1, .... п, i—l, .... т,— мат-
рица, задающая линейный оператор из R" в R?1, b £ Rm.
Символ z'~>z для конечномерных векторов г' и г озна-
чает, что все координаты вектора не превосходят соот-
ветствующих. координат вектора г'- Задачу (2) назовем
конечномерной_ задачей линейного программирования. Эта
1) Напомним, что для конечномерных пространств мы Имеем два
обозначенная:
* в
<с, х>=сх = ^С1Х1, c£R«*, x^R".
1 = 1
269
задача—частный случай общей задачи выпуклого про-
граммирования. Однако в ней имеется еще более специ-
альная структура: все функции здесь линейны и конус
полиэдрален. Как и обычно, условимся, что если зада-
ча (2) несовместна, т. е. не имеет допустимых элементов,
то ее значение считается равным -фоо.
Теорема существования. Если множество до-
пустимых значений конечномерной задачи линейного про-
граммирования (2) непуар.0 и ее значение конечно, то за-
дача имеет решение.
Доказательство теоремы 1 опирается на один
простой факт конечномерной геометрии. Напомним, что
коническая оболочка cone С некоторого множества С с X
определяется равенством
S
и является выпуклым множеством (и. 2.6.1).
Мы будем говорить, что конус cone С порожден мно-
жеством С.
А) Лемма о замкнутости ко нечно порож-
денного конуса в конечномерном простран-
стве. Всякий конус в конечномерном пространстве, по-
рожденный конечным множеством точек, замкнут.
Доказательство. Пусть X = coneCcR-v, С =
= {гп ..., zft}, ZjCR77' Доказательство проведем по ин-
дукции.
1)й=1. Тогда /< = cone{z1} = {x|x = Z1z1, —
полупрямая, т. е. замкнутое множество.
2) Допустим теперь, что лемма верна для k = s — 1.
Докажем ее для k = s. Возможны два случая:
а) конус К содержит векторы —гп ..., —zs. Тогда К
есть подпространство конечномерного пространства и, сле-
довательно, замкнутое подмножество;
б) хотя бы один из векторов (—z,), i = 1, ..., s, на-
пример (— zs) не принадлежит конусу %. Обозначим через
f(i = cone {гп ..., zs_ J. По индуктивному предположению
конус Ki замкнут. Пусть вектор г принадлежит замы-
канию конуса К, т. е. z = limg„; п^1. По опре-
п
делению
СОПе {Zj, . . ., Zs} — 2 — £>п ’^T^'sn^s*
где и
270
Если допустить, что ksn—► оо при п—>ОО, то
— , = Пт = Пт ?«_ е
hsn П-+а> Nsn
(напомним, что £„—►?, и потому а
вместе с £„), т. е.—z^g/C, вследствие-замкнутости /Сп
что противоречит допущению. Значит, Z,in не стремится
к бесконечности и можно выбрать подпоследователь-
ность Xsn , сходящуюся к некоторому числу A,i0 0. В этом
случае
7 —>2 — ~ г-
В силу замкнутости Ki вектор гС/Сх и, следовательно,
2 = 2 + ^sozsC^C- И
Б) Докажем теперь теорему существования.
Рассмотрим в пространстве Rm+1 множество /С, обра-
зованное такими векторами (а, г), а£ R, г € Rm, для каж-
дого из которых найдется хотя бы один вектор x£R"
такой, что сх^ос, Лх^г.
Множество К—это конус, ибо если (а, z)£/C, то для
некоторого x^R+, сх^а, Лх^г. Но тогда для любого
f^O, ZxgR", c(tx)^.ta, A(tx)^tz, т. e. t(a, z)£K-
Покажем, что конус К порожден конечным множест-
вом векторов в R“+1:
£1 = (Cv i ат1)> Ss=(C2» а12» •••» ams:}> •••> Си —
(рп’ ®1л» • •» &тп)>
£л+1 = (1> о...0), С„+2=(0,-1,0, ....,0), ...,^i+ffl+1=
= (0,..., О, -1).
Прежде всего ^€К, так что cone {^, ..., £„+m+1} <z Д'.
Действительно, если 1 надо взять в качестве х
стандартный базисный вектор е,; для остальных i надо взять
х=0. Пусть теперь вектор £ = (а, г) = (ос, гх.zm)g/f.
Тогда для некоторого х£ R", x = (xt, ..., х„) такого, что
X! > 0, ..., х„ > 0 ц некоторых р0 >0, > 0, выпол-
няются соотношения
п п
/=1 j=i
271
Но это как раз и означает, что
?=(“> Z)= 2 */£/+₽o£n+i+ 2]₽Лл+/+1>
xz>0, ₽о>О, ₽,>"(),
т. е.
SCcone^........£„+м+1}.
По лемме из предыдущего пункта конус К замкнут.
По условию теоремы задача (2) имеет допустимый эле-
мент х и значение задачи а> —оо. Из определения К
следует, что точка (а, Ь), где а = сх, принадлежит /С.
При этом, очевидно, что а^а. Следовательно, множество
21 — {a€R|(a, Ь)£К} непусто и a = inf {a|ag8l}, т. е.
(а, Ь) принадлежит замыканию конуса К, а значит, и
самому К. Следовательно, существует элемент х^О, для
которого Ах~^Ь и сх^а, т. е. х—решение задачи. Ц
Переходим к рассмотрению двойственной задачи.
Теорема двойственности приобретает здесь более закон-
ченный вид, чем в предыдущем пункте, поскольку ввиду
специальной структуры S-функция задачи оказывается
замкнутой.
В соответствии с формулами (5) и (6) п. 3.3.2 рас-
ширенная функция Лагранжа имеет вид
J? (х; V) = -
' сх + %(Ь—Лх), x£R",
— оо,
+ 00,
x€R2,
x(£R".
W,
Чвг»
Отсюда мы находим семейство возмущений задачи (2) и
двойственное семейство. Согласно (7) п. 3.3.2
f (х; a) = (— J’)*(S) = sup (Ха+S (х, К)) =
( +оо, x£R",
= 1 sup(1а4-сх + А,(b—Ах), xgR'' —
f ex, х^О, Ax^fb+et,
( + оо в остальных случаях.
Обозначая z — b+a, получаем возмущение задачи (2)
ex—i-inf, х^О, Ax^z. (3)
Аналогично для определения двойственной задачи мы
272
должны вычислить
g (О, X) - (- ^*а’) (О, Л) = - sup (- S (*, Х))=1
( — sup (— сх— к(Ь—Лх)),
— J О оа
(—00, ЦК?,
( М>, %>0, М ^с,
\ — оо в остальных случаях.
Это дает задачу
—>sup; ХЛ^с, (4)
двойственную задаче (2). Она имеет такое же строение,
как задача (2), и легко понять, что если, отправляясь
от задачи (4), построить двойственную задачу по тому
же правилу, по которому из задачи (2) получилась за-
дача (4), то мы вернемся к задаче (2). Поэтому имеет
смысл говорить о паре двойственных задач линейного
программирования.
Теорема двойственности. Для пары двойст-
венных задач линейного программирования справедлива
следующая альтернатива: либо значения задач конечны и
равны и в обеих задачах существует решение, либо в од-
ной из задач множество допустимых элементов пусто. -
В первом случае х £ R" и X £ R"*, в том и только
в том случае, будут решениями задач (2) и (4) соответ-
ственно, когда они допустимы в этих задачах и удов-
летворяют одному из двух соотношений
сх ~ lb, (5)
Х(Лх—6) = (1Л—<?)£. (6)
Во втором случае одна из задач несовместна, а другая
либо несовместна (т. е. ее множество допустимых эле-
ментов пусто), либо имеет бесконечное значение.
Доказательство. А) Построение S-функ-
ции. Снова рассмотрим тот же конус К, что и в теореме
существования. Если (а, г)(-К и то Ф. г)€К.
а потому К является надграфиком функции
S(z) = inf {а|(а, z)eK}. . (7)
Из доказательства теоремы существования следует, что
inf достигается и S(z) есть значение задачи (3) и, сле-
довательно, формула (7) онределяет S-функцию задачи (2).
273
Поскольку /С—выпуклый и замкнутый конус, S-функция
задачи (2) замкнута и выпукла.
Б) Вычислим функцию S*, сопряженнук? с функцией S,
По определению,
$•(*) =
= sup (Xz—S (г)) = sup {А,г—inf {сх| х £ RJ, Ах г}} =
г I г х
= sup {кг—cx|x£RJ, z£Rm, г^Лх}.
(г, х)
Очевидно, что sup{Zz | г £ R“, г<:Лх} = ЛЛх< оо в том
и только в том случае,' когда Z^O.
Таким образом,
( sup(M—с)х, если A,£R+*,
$*(П = {*>о =
( 4~°°> если Z^R+*
, ( 0, если кА ^с, к^О,
— \ 4-оо в остальных случаях.
Поэтому
S**(z) = sup{Zz|M<c, Z>0}. (8)
В частности, отсюда видно, что S**(b)—значение
двойственной задачи (4).
В) Завершение доказательства. Функция S
не может равняться тождественно 4-°°. ибо S (0)^0,
так как нуль—допустимый элемент в задаче сх—► inf,
Лх^О, х^О; следовательно, domS^=0.
Возможно одно из двух:
1) S(z)>— оо, Vz или
2) существует г, для которого S(z) =—оо.
Случай 1) в свою очередь распадается на два:
la) Z?g<iomS и 16) b^domS. В случае la) S—собствен-
ная функция и значение задачи конечно. Вследствие
замкнутости S по теореме Фенхеля — Моро (п. 2.6.3)
S« (b) — S(b) и теперь из (8) видно, что двойственная
задача (4) имеет то же значение, что и прямая (2) и,
в частности, совместна. В силу теоремы существования
решение существует в обеих задачах. В случае 16)
S(Z?) = 4-°°, т. е. задача (2) не совместна. Снова из
теоремы Фенхеля—Моро получаем, что S**(b) = S(b) и,
значит, задача (4) совместна, но ее значение бесконечно.
В случае 2) S (г) = — оо для всех г £ dom S (см. уп-
ражнение 8 п. 2.6.2). По определению S*(Z)==4-oo и
274
S**(z)^=—оо. В частности, S**(b) = — оо, т. е. задача (4)
несовместна.
Если b С dom S, то задача (2) совместна и ее значение
бесконечно: S (Ь) = — оо. Если же dom S, то S(b)=4-oo
задача (2) несовместна. Альтернатива полностью обос-
нована.
Вернемся теперь к случаю 1а). Там, как было дока-
зано, существуют решения задач (2) и (4). Обозначим
их х и X соответственно. Доказано, что значения задач
равны: cx = Xb, т. е. выполнено (5) и, значит,
Х(Ах—Ь) = ХАх—Xb = ХАх—сх = (ХА—с) х,
т. е. выполнено (6). Далее, если х и X—допустимые
элементы (т. е. х^О, А.^0, М ^с, Ах^Ь), то
сх^кАх^ 'кЬ.
Поэтому, если cx = Xb, то х и X—решения задач. Далее,
если Х(Дх—Ь) = (ХД—с)х, то cx — kb, т. е. х и X—ре-
шения задачи.
Таким образом, если х и X—решения, то выпол-
нены и (5) и (6); если х и X допустимы и выполнено
либо (5), либо (6), то х и X—решения задач. Теорема
полностью доказана. Ц
Упражнение. Во что превращается в рассматриваемой
ситуации теорема о минимаксе (следствие 3 п. 3.3.2)?
3.3.4. Теорема двойственности для задачи о кратчай-
шем расстоянии. Лемма Хоффмана и лемма о минимаксе.
Пусть Y—нормированное пространство, BcY—непу-
стое подмножество Y. Величина
5В(П) = Р(П- В)= infh—ПИ (О
уе.В
называется расстоянием от точки т] до множества В.
Исследование функции SB (т]) является одной из основных
в теории приближений (см. [84]). Если В—выпуклое
множество, мы получаем задачу выпуклого программи-
рования. Доказываемая ниже теорема двойственности
имеет в анализе многочисленные приложения.
Итак, пусть В—выпуклое множество. (Далее оно
фиксировано, и мы опускаем индекс В в обозначе-
нии функции S.) Тогда функция т]к-т>5(т]) является
275
S-функцией такой задачи:
||г||—>-inf; у—г-ц, у^В. <2)
Приведем (2) к стандартному виду задачи выпуклого
программирования (см. (j) в п. 3.3.1). Для этого поло-
жим X = YxY, х = (у, г), Л>(х) = || г ||,Хх = г—у, Л: X—+Y,
А=={х = (у, г)| г/€В} и тогда задача (2) примет вид
f0(x)—>inf; Ax4-Tj = 0, х£А. (3)
Из сказанного вытекает выпуклость функции S (след-
ствие 1 п.'> 3.3.2).
В дальнейшем нам понадобится следующее важное
геометрическое понятие.
Определение. Опорной функцией множества BcY
называется функция sB: Y*—>R, определяемая равен-
ством
sB (у*) = sup <у*, уу.
уев
Теорема двойственности для задачи о
кратчайшем расстоянии. Величина S(т]) допус-
кает следующее двойственное представление:
s(n) = P(n. B) = sup{<«/*, уу —sB($/*)[||i/*||Cl}. (4)
Доказательство. Очевидно,- что S(т])0, Утр
С другой стороны, 5(т})^||г/в — т]||, где у9—любая точка
из В. Значит, S—ограничена сверху и снизу и, следо-
вательно, непрерывна всюду на Y (предложение 3 п. 2.6.2).
Теперь можно применить теорему двойственности из
п. 3.3.2. Поскольку в (2) неравенства ,отсутствуют,
функция Лагранжа имеет вид
-^(х, £/•, 1) = || г Ц + <£/*, г—уУ.
Из формулы (11) п. 3.3.2 получаем
•* sup q>—supcy*, «/>) — sup(<— у*, z>—||z||)|=s
= sup T]>—sB («/•)—A* (—«/•)},
y*-
где AT(z) = ||z||, а ЛГ*(г) = О при ||г*||^1 и -}-оо при
|| г*|| > 1. (Предложение 3 п. 2.6.3.) Отсюда следует (4). Ц
В дальнейшем понадобится следующее обобщение
следствия 2 п. 2.6.4.
276
Лемма о сопряженном конусе. Пусть X
и Y—банаховы пространства, A: X —* Y—линейный сюръ-
ективный оператор из X в Y, х$, х*—элементы
сопряженного пространства X*, и пусть
К = {х | <xz*, х> <0, i = 1, ..., s, Ах = 0}
— конус в X.
Тогда всякий элемент xj из сопряженного конуса
К* = {х* | <х*> х> ^0, х £ /С}
допускает представление в виде
-х‘в= 2 М‘+лу
i=l
для некоторых и
S
Доказательство. А) Обозначим L— п Кегх*,
1=0
Z = КегЛ/L, и пусть л: КегЛ—>Z—естественная проек-
ция, отображающая х^КегЛ в класс n(x)gZ, его
содержащий. Покажем, что dimZ 1. Действительно,
пусть г0, ..., г4+1—произвольные элементы из Z,
г, = л(хГ). Однородная линейная система s-|-l уравнений
2 <xj, xz> А,, = ( х*, 2 ^/х/ ) = 0» i = 0, 1, ..., s,
i“о 1 1 /То у 7 ' -
с (s-4-2) неизвестным имеет ненулевое решение Хо, ..., Xf+I.
Тогда
S + 1
х = 2 ^jxj € Кег х*, i » 0, ..., s, =?> х € L =»> 0 = л (х) ж
* S+1 „ , + 1
= 2 (х/)— £
/=0 /=0
Следовательно, любые s + 2 элементов из Z линейно за-
висимы и d = dimZ^s + l.
Б) Выбрав в Z некоторый базис flt .fd, устано-
вим стандартный изоморфизм между Z и R* й между
Z* и Rd*
d
' Z=2^i-h*(£1........W,
d
<Л «> « 2 <z*> fi> £<• =»
i = 1
&) — , f.....
277
Далее, определим функционалы z*£Z*, t = О, 1, s,
равенствами
<zj, л(х)> = <х?, х>
и рассмотрим в Z* выпуклый конус
К — cone {zj, г*} = \г*
2 м, xf>o
Поскольку Z* конечномерно, а конус конечно порож-
ден, то по лемме из п. 3.3.3 он и замкнут.
Предположим, что —z*0£i(. Тогда по второй теореме
отделимости (й. 2.1.4) существует линейный функционал
lg(Z*)*, строго разделяющий {—г;} и К:
<1, — z0*>>sup{</, г‘>|г‘€Д}=зир|д г(*>|
Но тогда обязательно <Z, zJ>^0 (иначе sup = 4-oo),
0 = sup{</, г*>|г*£Л} и </, г0‘> < 0.
Теперь заметим, что I, как и всякий линейный функ-
ционал на конечномерном пространстве Z*, задается
линейной формой
d d d
<1, г*> = 2 2 Ъ<г», 2 alfi)=<z*, а>.
1 = 1' 1=1 1 = 1
d
Выбрав в классе а= 2 atfi €Z= KerA/L представителя
х0£КегЛ, а = л(х0) имеем, с одной стороны,
<x*t, х0> = <zf, л (х0)> = <z?, а> = <1, г‘><0
и, следовательно,
х0€КегЛП П {х| <х?, х><0} = К.
t = 1
С другой стороны,
<(Xq, Xq^> — Л (^о)> = = “'J't %оУ < 0
и, следовательно, х„(£Л? вопреки условию леммы.
Таким образом, предположение —приводит
S
к противоречию, и потому —г„= 2 ^izi Для некоторых
i S 1
278
В) Для любого х £ Ker Л
( X* 4- 2 ^ixt > х ) — ( го + 2 » 11 (*) ) — 0»
«=1 z=i
Поэтому х!+2 А,/Х*€(КегЛ)-*-, и по лемме об ядре ре-
1 = 1
S
гулярного оператора (п. 2.1.7) Хо + 2 КХ1 — Л* (— у*)
для некоторого y*£Y*. Ц
Лемма Хоффмана. Пусть выполнены те же
условия, что и в лемме о сопряженном конусе.
Тогда для функции расстояния от точки х до К.
справедливо неравенство
р(х, 2 <$, х>+4-||Лх|||, (5)
где <_х*, х>+ равно <xf, х>, если <х*, х>>0, и нулю в ос-
тальных случаях, а константа С не зависит от х.
Доказательство. Множество /С. являющееся
пересечением конечного числа полупространств и под-
пространства,— выпуклый конус в X. Вычислим его
опорную функцию s/f. Пусть х*£Х*. Возможно одно из
двух: либо найдется такой элемент х0 £ X, что <х*, х0> > 0,
либо <х*, х>^0, Ух^К. В первом случае s/C(x*);>
>f<x*, х0> VfgR+ и, значит, sK(x*)= 4- оо.
Во втором случае (—1)х* принадлежит сопряженному
конусу конуса /С и, значит, по предыдущей лемме
х*= 2 ^iXi+A*y*, y*£Y*. Итак,
i=I
s/C(x*) = -
0,
если ЗХ;£0, y*£Y*: х*= 2 ^ix* + Х*у,
в остальных случаях.
Применив теперь формулу (4) (теорему двойственно-
сти) к нашей задаче, получаем
р (х, К) =
= sup{<x», х>|х» = 2 h(-x;4-AV, ||х»||^1}. (6)
i=i
Подпространство L= 1ш {х?, ..., xs*} + Im А* является
суммой замкнутого подпространства L^ImA* (ибо
279
1тЛ* = (КегЛ)-Ц а аннулятор всегда замкнут) и конеч-
номерного подпространства L2 = {xJ.....xj}. Поэтому L
замкнуто в X (докажите!) и, следовательно, банахово.
Оператор Af: RxxF* —Ai(%, y)~%k{x* + A.*y* ли-
неен, непрерывен и отображает RJxF* на банахово про-
странство L. По лемме о правом обратном отображении
(п. 2.1.5) существует отображение М^. L-^R-sxY* такое,
что AfoAfj —/д, || МХх*[| С || х* ||. Тогда, если ||x*||CL
S
то || М.Хх* |]<*ху* = 2 IМ +11 У* II Таким образом, в вы-
ражении (6) можно считать, что ]|г/*|]^С,
откуда и получаем
S(x)==p(x, А)
< sup 2 Х(х,* + Л*1/*, х)|о<Х.;<С, ||г/*||<с|^
( S \
2 <x*t, ++ +|| Ах|| /• |
V» 1 J
Заметим, что если конус К задается лишь равенствами
K = {x]<xJ, х> = 0, Лх = 0}
(т. е. является подпространством), то он допускает опре-
деление и через неравенства
/С = {х|<х‘, х>^0, <(—1)х*о х>С0, Лх = 0}.
Применив лемму Хоффмана, получаем и в этом случае,
что
{S
21<*’> х> | + || Ах || ?. (5')
Лемма о минимаксе. Пусть X и Y—банаховы
пространства, Л: X—-Y—сюръективный оператор,
х* € X*, i — 1, .. . ,_s, а = (ах, ..., as). Определим функ-
цию S: RfxV —>R равенством
S(a, у) — inf max (a1 + <xf, x>). (7)
Лх+у=0 1 < s
289
Если max <х’, х> > О для любого х € Кег Л, то имеет
1 < I < S .
место следующая формула двойственности'.
( 5
S(a, f/) = sup< + г/>1«/>0,
\ 1
—1> лу+ 2<мГ=оУ (8)
i=i «=i j
При этом inf в (7) достигается на некотором (быть
может, не единственном') х = х (а, у), и существуют такие
С > О, С > О, не зависящие от а, у, что при подходящем
выборе х(а, у)
[]£(«, у)||<С(|$(а, «/)Ж«1Ш||}<С(|а|+Ы)- (9)
Доказательство. Существование минимума в (7),
выпуклость S и формулу (8) мы докажем редукцией
к Двум стандартным задачам, рассмотренным выше.
А) Вспомогательные отображения. Нам
придется дважды воспользоваться леммой о правом об-
Йатном отображении (п. 2.1.5). Во-первых, существует
[: Y—*Х такое, что ЛоМ = /, ||М(у)||CQ||г/||. Во-вто-
рых, пусть <р: X—>R,f определяется равенством <р(х) =
=«xj, х>, .... <х‘, х». Обозначим £ = <р(КегЛ). По
той же лемме существует отображение р: L—+КегЛ
такое, что
<рор = /, JpQ)||^C2|||.
Далее, как и всякое подпространство в R\ L может
быть задано некоторой системой линейных уравнений
S
S^A = 0, 1 — 1, ..., р, или при помощи отображения
/=1
Р: RJ~>R/’, ₽£=( J условием p£ = 0.
\/=i /
Б) Ограниченность S(a, у). Поскольку
Лх-j-y = 0«£x = M(—г/) + х0, х0 £ Кег Л=> а{ + <х*, х> =*
= а, + <х;, М(—у)> + <х*, х0>, (10)
то, полагая, хо=О, мы получаем, с одной стороны, не-
равенство
inf max (az + <x', х»
Ax+g“0 1 < i < г
def
< max 1 + Сх||хГйЬ11}-^ (H)
i «
281
а, с другой стороны, при Лх-(-г/ = 0, согласно (10),
max (az+<x;, х»> min (а,—C1||x;||||г/||)> — К, (12)
1 < i < s ' 1 < i < s
так как по условию max (<х*, х0>)^0 (х0€КегЛ). Из
1 d<s
(11) и (12) следует оценка
|S(a, у)\^К — max {| az |+С1К1ПЫ1}- (13)
1< i < s
В) Существование минимума. Обозначив а,=
=а; + <х’, М(—у)>-}-и вспоминая, что
х0€КегЛ<^«х1, х0>, ..., <x*s, х0» =
= Ф (х0) € L — (Кег Л) = Кег 0,
мы видим H3z(10) и (7), что S(a, у) + К. является значе-
нием задачи
max (а{ + £,)—> inf; —* inf; <c,0g = O. (14)
В силу (13) S(a, у) 4- 7(^0, и потому к (14) можно без-
болезненно присоедините условие с^О.
Задачу (14) можно привести к стандартному виду
задачи линейного программирования (2) п. 3.3.3) в Rr+l.
Для этого обозначим г0 =с, zt = c—— ah г = (гх, ..., zj,
0 = (1, ..., 1), a = (alt ...,as), г = (г0, г). Условие 0^ = 0
записывается в виде
0£ = О<=>0(с0—г —а) = с00—0г—0а = О^Вг'>Ь,
где
g__f 09 —0А £_____/ 0° А
\-00 0/ \-0а/
— матрица порядка 2px(s-j- 1) и 2р-мерный вектор (фак-
тически мы заменили равенство 0g = 0 двумя неравенст-
вами 0g ^0 и 0g ^0).
Поэтому задача (14) эквивалентна задаче
z0 —>inf, Bz^b, г^О, (15)
имеющей стандартный вид. Эта задача совместна (напри-
мер, вектОр (2К, 2/(—а1г ..., 2К.—af) допустимый;
соответствующее % = и ее значение S(a, у) + К
конечно (и даже неотрицательно). По теореме существо-
вания из п. 3.3.3 она имеет решение г. Следовательно,
282
задача (14) имеет решение |=(S(a, у) + К)$—г—а, и
тогда
S(a, у) + К= max {az+ (,.} =
= max {az + <x*, M (—«/)> + £,•} +K.
i < i < s
и
S(a, y) = max {az4-<xz, x>},
1 i s
где, согласно (10) и определению отображения ц: L—>КегЛ,
х = М(—у) + ц£. (16)
Г) Выпуклость S и теорема двойственно-
сти. Функция (a, г/)>—*S(a, у) является S-функцией сле-
дующей задачи выпуклого программирования:
max(Th, .... r)J—*-mf, — т)/ + <хо x>4-az = 0,
Ax + z/ = 0. (17)
Полагая Z=RJxX, Y — R^XV, z = (r), x),
(?) = max (th, .... th),
Az = «x’i, x> — Th, <x*s, x> —Th, Ax),
приведем (17) к стандартному виду ((з) в п. 3.3.2):
А, (г) —► inf, Лг + (а, i/) = 0. (18)
Следовательно, функция (a, у)>—*S(a, у) выпукла (след-
ствие 1 п. 3.3.2). Согласно (13) она ограничена, а потому
и непрерывна на всем пространстве Y (предложение 3
п. 2.6.2). По теореме двойственности из п. 3.3.2 (напом-
ним, что неравенства в задаче (18) отсутствуют)
S(a, у) =
=sup{<?*, (a, i/)>4-inf[<?», Лг> + шах(т)1, ..., 1%)]}- (19)
г* г
Но z*g(RJxlz)* = Ri,Xlz*, т. е. г* представим в виде
(а, у*), a = (aj, ..., а4) £ R**, y*£Y*t так что
<г», (а, у)> = ао+ <{/•, у>,
S
<г*, Az>= 2 а«(<х«*> х> —П,-) + <г/‘. Лх>.
»=1
(20)
283
Согласно- предложению 2 п. 2.6.3 преобразование Юн-
га— Фенхеля функции f (т]) = max (тн, ..., 1%) имеет вид
' S
f* (a) = sup(aTi—f(n)) = . °’ если а,-> 0, = 1,
ч ,= 1
4-оо в остальных случаях.
(21)
Теперь из (20) и (21) имеем
inf (max (т^, .... nJ + <z*, Az»=
z
{S ’I
ar] — max(rh.nJ—( S +
'i=i J
r s s
= 0,еслиа,->0, Jja/=1, A*y*4- 2^=0,
— оо в остальных случаях.
Подставляя это в (19), получаем (8).
Д) Геометрическая лемма. -Пусть L—подпро-
странство, а К.—конечно порожденный конус в R*. Тогда -
существует такое N > 0, что для любого а £ Rf
р(0, (L 4-а) п К) С Ар (0> L+a)^.N\a\ (23)
(формула остается справедливой и в случае (L 4- а) Л К = 0,
если мы условимся считать, что р(0, 0) = — оо).
Доказательство, а) Пусть К — сопе^,
Разложим каждый вектор на две компоненты—содержа-
щуюся в подпространстве L и ортогональную к нему:
a = b + c, Xi — yi + z;, i = l, т, b, у,£Ь, с, z^IA.
Тогда
р(0, (L4-a) nK) = inf {| g € К, (g—а)£Л} =
S (У: + zi)
i=i
Г т
<inf) 2Ч' max {|у( |}4-1с]
V i= 1 1 < I < т
т Л
Х,->0, 2и=с . (24)
<=i J
С другой стороны,
р(0, L4-a) = inf{|п + аПпёМ =
- Ш1{ 1 П 4- d | п' € L} = | сV[Wk? = к I-
284
Поскольку
in
A.z>0, 2^2.= с^с€сопе{21, ...,zM},
1
мы видим, что (23) будет следовать из (24), если для
некоторого Ni > О
eg cone {zf, ...» zM}=>3X,->0, . •
= (25)
(при этом в (23) мы будем иметь N — Nt max {|#Z|} + D-
1 < i < т
б) Пусть L1 = lin{zi, zm}, dimij^n. Выделим
всевозможные наборы индексов I — .... in}, для ко-
торых {zti, ..Zf„}—базис в Lj. Каждому такому набору
отвечает линейное отображение Л;: R',—*L1, определяемое
л ,
формулой Л/№ 2 x*zfjk. Поскольку {zit, .... zi„}—ба-
зис в Lj, существует обратное отображение.
По теореме Каратеодори (п. 2.6.1) каждый вектор
eg cone {zf, ..., zm} является конической комбинацией
не более чем п линейно независимых векторов г,-
с = XZizZi> О, s^n.
Дополнив, если нужно, набор {zfi, ..., zis\ до базиса
в Lt некоторыми векторами г,- ,* .. •, zin и положив
Lis+i— ... 5=Z,f„ = O, мы видим, что
с = ЛД, A, = (XZi, ..., А,,„), A,IJk^0, I = ..., in).
Поэтому
Л
S п'\ Ь К п II Л/1 li | С К п max {ЦЛ?11|} | с |.
kst I I
Этим доказано (25) для = п max {||Л/1||}.
Е) Завершение доказательства леммы о ми-
нимаксе. Последнее, что осталось нам сделать,—полу-
чить оценку (9). Для этого вернемся к левой из задач
(14). Элемент g = (tz, ..., f,) является ее решением тогда
и ‘только тогда, когда ,
l,-+a,-<S(a, у) + К, i=l, ..., s, IgL (26)
285
(поскольку S(a, у) + К—значение задачи, по крайней
мере для одного индекса здесь будет иметь место равен-
ство). Вспоминая определение а(- в п. В) и обозначая
а = (а1( ..., as), где
а; = а/—S(a, у)—К = а; + <,х*, М(—у)>—S (а, у), (27)
переписываем (26) в виде
Таким образом! — решение (1 4)фф| -\-а € (L+а) А (—R®.).
Поэтому
inf {| |+а 11 £ решение (14)} = р (0, (L+&) Г) (—R+)). '
Поскольку —R$. = cone{—ej, —е,}— конечно по-
рожденный конус, правая часть по геометрической лемме
п. Д) не превосходит ЛГр (О, L 4-а) N | а |. Следовательно,
inf {| f + a| | f решение (14)} ^Л7|а|,
и так как |!|<|f+a|4-|a|,
inf{||||£ решение (14)} <(У-{- 1)|Д|.
Если а=/=0, то (Л71)|а| < (ЛЛ4-2)|а|, и среди ре-
шений задачи (14) мы можем выбрать такое, обозначим
его |, у которого
(f 1 ^(A74-2)|5|. (28)
Если а = 0, то t —0 решение и (28) снова верно.
Воспользовавшись формулой (16), находим по ( эле-
мент х — х(а, у). При его оценке учитываем неравенства
IIM^KCJlyll, ||И(1жс2|11 (29)
(ср. определение правых обратных отображений Мир
в пункте А)) и
/ VI - г— - <г7)
|а| = ( ^VsmaxdaJ..................
v=1 /
</s[ max + y)|]<
1 < £<s
sCyTflal + Cj max ||хИ||!/|| + |S(a, y) |], (30)
1 < s
286
а также оценку (13):
„ (18). (29) (28) л (30)
||х(а, z/)]| C>|| + C2|i|<C>|| + C2(AZ + 2)|a|<
^(l+CaCA^/s max ||хП)||{/|| +
1 < i < s
(13)
+ Q(AZ + 2)/s (И + |5(а, !/)|)C
<Cx(l+/s max ||x;||2C2(AZ+ 2))||t/|| +
1< i < s
+ 2C2 (N + 2) V~s | a |.
Поэтому верно (9) с константами t
С = max {Cj (1 4-C2*(AZ + 2)J/’ s max ||x‘[[, C2 (AZ + 2) К s},
1 < i <<s
C = max{C1(l +Vs max ||x*||2C2(N + 2)),
1 < i < s
2Cg(AZ + 2)/7}.
, § 3.4*. Необходимые условия второго порядка
и достаточные условия экстремума в гладких задачах
Снова разберем сначала случай, когда неравенства
отсутствуют.
3.4.1. Гладкие задачи с равенствами. Рассмотрим за-
дачу
/(х)—>-extr; F(x) = 0. (1)
Теорема 1 (необходимые условия второго
порядка). Пусть X uY—банаховы пространства, U —
открытое множестве в X, функция f'. U —► R и отобра-
жение F: U —строго дифференцируемы в точке x£U
и имеют в этой точке х вторую производную Фреше.
-Если х доставляет локальный минимум (максимум)
в задаче (1) и если F регулярно в точке х (т. е. Im F' (х) = У),.
то существует множитель Лагранжа у* £ Y* такой, что
^Х(х, У*, 1) = 0, (2)
&хх(х, у*, 1)[Л, /т]>0(^0), VfteKerF(x), (3)
где Л? (х, у*, l) = f(x) + <у*, F(x)>.
Док азател ьств о. • Равенство (2) было доказано
в п. 3.2.2. Далее разбираем случай xglocmin (1). Пусть
/igKerF'(x). Согласно теореме Люстерника (п. 2.3.5)
287
h^Tx^, где {x |F(x) = 0), т. e. существует отобра-
жение r(-): [—e, e]—такое, что
F(x + th+r(t)) = 0, r(t) = o(t), /€[-е, e]. (4)
В силу (4) x + th + r(t)—допустимый элемент в задаче
при £€[—8, в] и, следовательно, f(x)<f (х + th + г (/)),
ибо х€ locmin (1). Поэтому
/(x)<f(x + ^ + r(0)=^(x + ^ + r(0, у*, 1)^
= ^(Х, У*, 1)+^х(Х, у*, l)[fft + r (0] +
у*, l)[th + r(t), th + r(t)-]+o(t*)~
= f(x)+^^xx(x, У*> l)[ft, h] + o(t*).
Отсюда немедленно следует <3). (|
Теорема 2 (достаточное условие мини-
мума). Пусть выполнены условия предыдущей теоремы
и, кроме того, для некоторого а > 0 выполнено неравенство
&хх(х, у*, l)[ft, h] > 2а || h ||\ уЛ€КегГ(х). (5)
Тогда х есть точка локального минимума в задаче (1).
Доказательство. Без ограничения общности
можно считать, что f(x) = O. Обозначим через В (hlt h2)
билинейную форму ^^Хх(х, у*, 1)[ЛХ, /г2]. По теореме
о смешанных производных (п. 2.2.5) В —непрерывная
симметричная билинейная форма. Выберем 8 > 0 так,
чтобы
ф(в) = а(1—в)’—2||В||(1-|-8)8—||B||8s-~ >0 (6)
^поскольку ф (0) = а/2 > 0, это сделать можно).
Функции F и 3 (•, у*, 1) по условию имеют в точке х
вторые производные Фреше по х. Воспользовавшись фор-
мулой Тейлора (теорема 2 п. 2.2.5) и учтя, что F(x) = 0,
^(х, у*, 1) = 0, ^Х(х, у*, 1) = 0, йайдем такое бх > 0,
чтобы при ||Л|| <.6Х выполнялись неравенства
|] F (x-\-h)—F' (х) h ||=|| F (x-\-h)-F (x)—F' (xjh^C^hf,
|^(х+Л, ?, 1)-B(ft, ft)|<f||ft|j» (7)
M8
Применяя лемму из п. 2.1.5, построим правое обратное
к F' (х) отображение М: Y—>Х, F'(x)oM = /, ||M(i/)||^
С || у ||. По выбранному ранее е > 0 подберем б, 0 < б < 6t
так, чтобы
дСС1 <е. (8)
Пусть теперь ||Л||<6 и x,+ /i—допустимый элемент
в задаче, т. е. F(x-\-h) = 0 Положим h2 = М (F' (х) /г)
и обозначим через h± разность h—h2. Тогда из оценки
для М(у), (7) и (8) имеем
~ |)М<СР' Cx)h\\^CCM < е||й||, ~ (9)
Г' (х)^! = F' (х) (Л—/i2) = F' (x)h—F' (х) М (F' (x)/i)) = 0.
Таким образом, hr g KerF' (х). Из (9) вытекает, что
(1—e)||/i||^||/i1|| (1+e)j/i[|. В итоге получаем, учиты-
вая (6), (5) и (7):
f(x + h) = ^^ + h, у*, h) —y||/i||a =
= В(/ч + Ь2, +
>В(ЛХ, /ll)_2||B||||<||||^|j-||B||||/iar-|Hir>
> (а(1-б)2_2||В||(1 +б)8_||В||6а-ИМ2 > 0,
т. е. x€locmin(l). Ц
3.4.2. Гладкие задачи с равенствами и неравенст-
вами— необходимые условия второго порядка. Рассмот-
рим задачу:
f0(x)—>inf, F(x)=0, f((x)^O, i = l, ...,m. (з)
Меняя если нужно, знаки функций мы можем свести
к (з) любую задачу из § 3.2. Функция Лагранжа задачи (3)
имеет вид
^(х, у*, К Ч)= 2 Ч,-(*) + <*/*, w>.
1 = 0
Теорема. Пусть X, Y—банаховы пространства,
U —открытое множество в X,x£U, функции ft: U—>R,
i = 0, 1, ..., т и отображение F: U —* У строго диф-
ференцируемы в точке х, имеют в этой точке вторую
производную Фреше и, кроме того, f, (х) = 0, i — 1, ..., т.
10 В. М. Алексеев и др. 289
Если х доставляет локальный минимум в задаче (3),
и если F регулярно в точке х (т. е. Im F' (х) =- Y), то:
а) множество D множителей Лагранжа (у*, к, Zo),
y*£.Y*, ZgR"1*, А,о таких, что
т
2^0, 2^=1, ...
<=о (1)
.S’xlx, у*, X, Хо) = О
является непустым выпуклым компактом в y*xRm*xR;
б) для любого hQ, лежащего в подпространстве
L — {h\<.fi(x), h'> = 0, i^tO, F'(x)h — 0}, (2)
найдутся такие множители Лагранжа (у* (h0), A,(/i0),
что
^хх(х, y*(h0), MU MW* (3)
Доказательство. Обозначим для краткости
Г(х) = Л, ft(x)-xh
А.) Рассмотрим отображение <р: симплекса
/ т 1
2UM, определяемое равенством
I 1 = 0 J
<p(Z, Zo) = 2U*- Тогда
i = 0
(jf, X, 2/Л? + г/*оЛ =
= <p(Z, у+лу = о=>ф(х, X0)G
g ImA*=^>(Z,, Zo) £<?! = <p-1 (ImA*).
По условию ImA = K, а следовательно (n. 2.1.7), ImA‘ =
= (Ker Л)-1- и потому замкнут. Значит, Qj—замкнутое
подмножество компакта и само компакт.
Заметим теперь, что КегЛ* = {0}. Действительно:
h* £ Кег Л* =$> <Л*Л*, х> = 0, Ух <Л*, Лх> =
= 0 , Vx=^>/i* ^(IniA)-1-:^/!* — 0.
Так как замкнутое подпространство 1mA* банахова
пространства само есть банахово пространство, по тео-
реме Банаха существует обратное-к Л* отображение
290
Г: Im Л*—>Y*. Теперь
(У*, М X0)€D^(X, Х^С^,
ф(Х, Ю + Л*у* = 0^(Х, Х0)€<то
У* — — Гф(Х, Хо).
Следовательно, D есть образ компакта при непрерыв-
ном отображении (X, Х„)>—>(—Гф(Х, Хо), Хп Хо) и, зна-
чит, является компактом.
Непустота D следует из принципа Лагранжа, дока-
занного в § 3.2. Выпуклость D является очевидным след-
ствием условий (1). Впрочем, ее можно вывести из
выпуклости а и Im Л*, заметив, что рассмотренные выше
отображения были линейными. Этим закончено доказа-
тельство утверждения а).
Б) Как и в п. 3.3.1, заменим задачу с неравенствами
задачей с равенствами
f(x)=max{f0(x)—f0(x), fx(x)..f„(x)}^inf; F(x)=0. (3')
Если x^locminj, то х£ locminj'. Действительно,
x(£locmin3'=j> Ye > 0, ЗхЕ: ||хЕ— х|| < е,
^(хв) = 0, j(xe) < O=j>fo(xE) < fe(x), f,(xE)<0,
' £= 1, ...,m, F (xE) = 0==> xfr locmin 3.
Далее исследуем задачу (3').
В) Пусть h0£L. Ввиду компактности D найдутся та-
кие (у*, X, Хо), что •
^(h0) = ^xxCx, у*, X, X0)[ft0, Ло] =
= max &хх(х, у*, X, Хо)[Ло, Ло]-
(У*, Л, ?.„)gD
е=тах\ 2 X/;(x)[/i0, Ло]+ <*/*, F” (х) [Ло, /i0]>|X;>0,
v=o
2х,.= 1, 2м:+лу=ок
1 = 0 f=0 J
Утверждение б) эквивалентно неравенству Т (/i0) 0.
Предположим, что Т (Ло) < 0. Обозначив
ai (^) = 1- Л W [Ло> Ло]. 1 = 0.т,
y(^ = ^F"Cx)[hat М, (4)
10*
291
рассмотрим задачу
max (а1-(А)4-<х*, х» —► inf; Ах 4-У (А) = 0. (5)
О < i -С т
Проверим, что к этой задаче применима лемма о ми-
нимаксе из п. 3.3.4. Действительно,
max <х’, х>^0, Ух С Кег Л
О < i < т
— необходимое условие минимальности х в задаче (3)
(лемма 1 п. 3.2.4). Кроме того, по условию оператор Л
сюръективен.
По лемме о минимаксе найдется элемент х0(А), обла-
дающий свойствами:
max (а,(Х) + <х’, х0 (А)» = S (а (А), г/(А)), (6)
О < i < т
где S(a(A), у (А))—значение задачи (5);
II (А) || {max | а,. (А) | + h (А) ||} < СА’. (7)
При этом согласно (8) п. 3.3.4
S(a(A), у(А)) =
12 I
= у max< h0] + <y*, F" (х) [Ло, Ло]> А,>0,
4 U=o
"I m 1 12
2 А,- = I, Sa,.x;-+av = o Цш (8)
i=0 1 = 0 I
Но тогда из (7) вытекает, что ||АЛ04-х0(А)|| = О(А).
По формуле Тейлора (п. 2.2.5)
F (хЧ-х0 (А) 4-АЛ0) = F (х) 4- F'.(x) х0 (А) 4-
4-у F" (х) [A/i0 4-х0 (A), A/i0 4-х0 (А)] 4-о (А2) ==
= Д"(х)[АЙ0, х0(А)]4-уГ(*)кМ. ММ1+
4- о (А2) = о (А2)
(напомним, что
й0 С L с Ker F' (х)
и
Г(;)х0(А)4-(А2/2)Д"(х)[/10, Ло] = О.)
При доказательстве теоремы Люстерника в ц. 2.3.5
было построено отображение <р: U —>- X окрестности U Э х
292
такое, что
Г(х + <р(х))^0 и ||<р(х)||<КHWII-
Полагая г (Х) = <р(х4-х0 (X)4-Xh0), имеем
F (х + х0 (X) + Khe + г (X)) == О,
II г (X) || </СИ F (х + х0 (К) + ХЛ0) || = о (V).
Но тогда, применяя формулу Тейлора к Д- и исполь-
зуя (6) и (8), получим
f (X + х0 (X) + Мг0 + Г (А)) =
= max (f0 (х + х0 (А) + Mia + г (К))—fa (х),
(х-4-х0 (X)-4-X/i0г (X)), i=l, ...,wi) =
= max (<х*, х0(А)> + у/7(х)[Л0, +о (X2)) С
max (<х^ x0(X)>+yft(x)Pi0, ft0h+o(Xs)==
= у?(Л,)+о(Х‘)<0
при малых А2. Итак, Т (Zi0) < 0 =s> x^locmin =з>
x^lbcminj. Противоречие доказывает теорему. Ц
3.4.3. Достаточные условия .экстремума для гладких
задач с равенствами и неравенствами. Как и в предыду-
щем пункте, исследуем задачу
fa (х) -> inf; Г(х) = 0, /Дх)^0. (з)
Теорема. Пусть X, Y—банаховы пространства,
U—открытое множество в X, х £ U, функции U —> R,
i = 0, 1, ...,т, и отображение F: U —+Y—строго диф-
ференцируемы в точке х (допустимой в (^)) и имеют
в этой точке вторую производную Фреше, причем f; (х) = О,
i— 1, ..., т.
Предположим, что существуют множители Лагранжа
X. С R™*. y*^.Y* и число а > 0 такие, что > О
^Х(х, у*, X, 1) = /Их)+ ^tf'iCxj + F'* (х)у*==0 (1)
1 = 1
и
^хх(х, у\ X, 1)[/г, /1]>2а||/1||2 (2)
293
для любого h, лежащего в подпространстве
L={ft|</y'(x), й> = 0, i>l, F'(x)h = O}. (3)
Тогда х доставляет локальный минимум в задаче (3).
Доказательство. А) Пусть x + h—допустимый
элемент, т. е.
+ i>l, F(x+ft) = 0. (4)
Проведем двумя способами оценку величины f0(x+/i).
Имеем
fо.(х + h) = /0 (х+h) + 2 V/ Сх + h) +
i= 1
+ <*/*> ^(х+Л)>—2 %-ifi (x+h)=a
i= 1
= ^(x+h, у*, К, Vf—^KifiCc+h). (5)
1 = 1
Первый способ оценки основан на прямом разложении:
f0(x + h) = ^ (x + h, У*’ 1)“ 2рЛ(х + ^) =
= (х, у*, К, 1) + <2>х(х, у*, К, 1)[й] —
- 2 4i (х)— 2 <W (х), h> + r, (h)=>
1=1 t=i
=foW-2<V:(x), h>+ri(hy, (6)
z=i
где остаточный член есть О (ИИ)2.
Второй способ основан на том, что вследствие не-
» т
равенств Х,х- > 0, (x+h) ^ 0 сумма 2 ’Cft (х+й) ^0
и, следовательно,
f0(x + h)^^ (x + h, у*, К, 1) =
— (х, у*, £, 1) + "2?х(х, у*, 1)И1 +
+ 4“^«(х> У*> !) А] + г2(Л) =
= f0(x) + B(h, h) + ri(h), (7)
294
где через В (h, h) обозначена квадратичная форма
у £'хх(х, у*, К 1)[Я, Я], а остаточный член г2 (Я)-=о(||Я||2).
Б) Обозначим через К. конус, состоящий из тех Л,
для которых <f;(x), Я>^0, i‘2>l, F' (x)h=0.
В силу леммы Хоффмана произвольное h можно раз-
ложить в сумму hx+h2, где hx £К, a h2 допускает оценку:
Г т Л
||М<СЛ 2</Ж h>++\\F'(x)h\\}. (8)
u=i J
Воспользовавшись далее замечанием, сделанным
в п. 3.3.4 после леммы Хоффмана, и формулой (5') п. 3.3.4
hx можно также разложить в сумму hx = h'x'A-hx, гдеЯ(
а Кх допускает оценку
IRI ^{2 <К(Х)’ hx> } = С2|-^<Л-(х), fi;>|. (9)
Мы использовали то, что F’ (х) hx = 0 (ибо hx £ /С) и то, что
I <fi (х), hx> I = I <fi (x), h[ +/ii> I = I <fi (x), hx> I =
= — hx> (ибо <Л(х), Я(> = 0, a <Л(Х), V^O).
В) Из (4) получаем
0=Г(х4-Я)—Г(х)=Г(х)Я4-г0(Я), -
0>/«(x4-fi) = <f£(x),fi> + p,-(fi)> i=l, ...,m,
где II ro (MII и IР / (Л) |—величины порядка 0 (|| Я||2). Исполь- •
зуя эти оценки в (8),. находим, что если хЦ-Я —допу-
стимый элемент, то
ILM<Ci{ 2 |рг(й)|+Цг0(Я)||}. (И)
Фиксировав 6j £ (0, 1], о величине которого мы’по-
заботимся далее, выберем б£(0, ||В||-1) так, чтобы из
неравенства ||Я||^6 следовали бы неравенства
21Р; W1 + 2 к/ (fl) II < ЧIIfl II. II г2 (Я) II 11| я||2. (12)
1=1 /=о
Далее выберем число А > 0 так, чтобы
ЛС2-1(тш\.)— Ci max (Xz [| (х)|() — 1 >0, (13)
295
И, наконец, выберем величину et так, чтобы для е =я
= (С14-Д)«1 выполнялись бы неравенства
е< 1, а(1—е)2 —2||В||е(1 4-е)—||В||е2—а/2|>0. (14)
Г) Завершение доказательства. Пусть х4*
4-й—допустимый элемент. Представим h, как и в Б),
в виде суммы h = h'l-\-h"l-\-h2. Возможны два случая:
а) ||ft;|| > ЛеЛйЦ и б) || hl ||^ AeJ h || В случае а) имеем
из (9) при || h Ц б
ле1[|Л1|<Ill'll<с/- 2 </;(£), л;>). (15)
\ 1 = 1 /
Тогда вследствие (6), (15), (11), (12) и (13) получаем
(6)
f0 (x4-ft) =
™ ~ . <J5), (П), (12)
= fo(x)-2 K + h^+r^h) >
1= 1
(х)4-ДС2х (min^eJftH—
—max (X, || fr(x) ||) Са IIM—ei IIM = ft (x) +
(13)
+ ex ||h [I (ЛСг1 ('min Л,) — max (A, || (x) ||) — 1) > ft (x).
Пусть теперь имеет место случай б). Тогда ||fti||^
Де11| h ||, значит, в силу (11) и (12), если обозначить
h'^hiA-K, то ||/i;|| = H'; + ^2||<(X + С1)е1||Л||’ = е||Л||.
Тогда ft = ft;4-ft;, где (1 —e)||ft||^||ft;||^(l 4-e)||ft||. Теперь
применим эти неравенства, а также (7), (2), (12) и-по-
лучаем
(7)
/о (х 4-ft) > (х) 4-в (ft, ft)4-''2(ft) =
= Л (•*)-И В (fti 4-ft2» ^i4-ft2)4-/'2(ft) =
(2), (12)
“ fo (x) + В (fti, ft1)4-2B(ft1, ft2) 4- В (ft2, ft2)4-r2(ft) 4^
>f0 (x) 4-(a(1-e)2-21|e (1 4-e)-||В||e2—J) ||ft j|2>
^fo<X)-
Теорема доказана.
ГЛАВА IV
ПРИНЦИП ЛАГРАНЖА В ЗАДАЧАХ
КЛАССИЧЕСКОГО ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
И ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Предмет этой главы ясен из ее заглавия. Особое вни-
мание мы уделяем, с одной стороны, выявлению сходства
двух разновидностей теории, подчеркивая это едиными
обозначениями, а с другой—выяснению различий в клас-
сической и современной постановках задач. Сначала мы
рассмотрим необходимые условия в так называемой за-
даче Лагранжа. К этой задаче могут быть сведены многие
остальные задачи классического вариационного исчис-
ления. Затем будет выведен принцип максимума Понт-
рягина, являющийся одним из наиболее важных средств
в современных задачах оптимального управления. Осталь-
ная часть главы посвящена более специальным классам
задач и выводу следствий из общей теории. Менее по-
дробно мы останавливаемся на рассмотрении достаточных
условий экстремума, ограничиваясь только частными си-
туациями.
§ 4.1. Принцип Лагранжа для задачи Лагранжа
4.1.1. Постановка задачи и формулировка теоремы.
Зафиксируем замкнутый отрезок А = [а, fJJcR и рас-
смотрим банахово пространство
S = C4A, R”)xC(A, R')xRxR,
состоящее из элементов £ = (%(•), и(-), £0, fx).
297
В этом пространстве рассмотрим задачу:
«(•). t0, О =
= $ fo(t, X(t), U(t))dt + ^>o(to, x(Q, ilt x(Q)->extr, (1)
^0
x = <p(t, x(f), u(i))> (2)
«(О» t0, *!> =
^2
= \fi(t, x(f), u(t))dt + ^(to, x(f0), XOSSO. (3)
*0
При этом в (1)—(3) fi'. V —► R, ф,-: W —► R, i = 0, 1, ...
m; <p: V—>R", где V и W— открытые множества
в пространствах RxR"xRr и RxR"xRxR" соответст-
венно. Все перечисленные функции предполагаются по
крайней мере непрерывными. Знак gs имеет тот же смысл,
что и в § 3.2.
Задачу (1)—(3) мы называем задачей Лагранжа в понт-
рягинской форме. Частные случаи этой задачи обсужда-
лись в §§ 1.4, 1.5 и в § 3.1. Функционалы того же
типа, что и 33(, содержащие как интегральную, так и
терминальную части, были ранее названы функциона-
лами Больца (см. па. 1.4.2 и 3.1.3). Если в ограниче-
нии терминальная часть является константой,
т. е. оно принимает вид ^fi(t, х, u)dt^ac, то вслед
<0
за Эйлером мы называем такое ограничение изоперимет-
рическим. Если, наоборот, отсутствует интегральный член,
то ограничение ф,- (£0, х(£0), tlt х(^))^0 называется
граничным, или краевым условием.
Ограничение (2) называется дифференциальной связью.
Такой вид дифференциальной связи — разрешенный отно-
сительно х—является характерным признаком понтря-
гинской формы задачи. Лагранж задает дифференциаль-
ную связь уравнением ф(£, х, х) = 0 (вкратце об этом
говорилось в п. 1.5.1).
Наконец, в отличие от гл. I, отрезок времени [ta,
в задаче (1)—(3) не предполагается фиксированным.
Четверку g = (x(-), u(-), t0, tJ^B будем называть
управляемым процессом в задаче (1)—(3), если t0, g int A,
(t, x(t), u(t))€V для и всюду на [70, удовлет-
воряется дифференциальная связь, т. е. — x(f),
298
u(t)), и допустимым управляемым процессом, если эта
четверка является управляемым процессом и, кроме того,
выполнены условия (3).
Четверка | = (х(-), u(-), f0', называется оптималь-
ным в слабом .смысле процессом, или слабым экстремумом
в задаче (1)—(3), если она является локальным экстре-
мумом в пространстве S, т. е. если найдется такое е > О,
что для любого допустимого управляемого процесса
удовлетворяющего условию ||£—f||s<e, выполняется одно
из неравенств: (|) в случае минимума и 53 0 (£)С
в случае максимума.
Функцией Лагранжа этой задачи называется функция
t,
^(х(-). «(•), ta, р(-), К, %0) = \Ldt + l, (4)
^0
.где
MR. р(-)£О(Л, Rn*), Z=(Z1, .... MGR””
— множители Лагранжа,
• т
L(t, х, х, и) = 2 х, u) + p(t)(x—(f>(t, х, «)) (5)
z=o
— лагранжиан, или интегрант, и
т
I (Jot Хо, tlt Xj) = (^о’ ^о> ^1» -Ч) (®)
i = 0
— терминант.
Далее мы в этом и следующем параграфах пользуемся,
как и ранее, следующими сокращениями:
x(t), x(t), u(t)),
Lx(t) = Lx(t, x(t), x(f), «(f)),
Ltt(f) = La(t, x(t), x(t),u(t)),
= x(tay, fx, x(fx)),
^ = £\(х(-), U(-), tQ, fx; p (-), X, Xo) и T. n.
Теорема Эйлера—Лагранжа. Пусть функции
fi‘. V—>R, i = 0, 1, ..., m, <p: V—> R" и их частные
производные по хи и непрерывны в открытом множестве V
пространства RxR"xRr, а функции ф,-: W—>R, i =
299
= О, 1, т, непрерывно дифференцируемы в откры-
том множестве W пространства R х R"-X R X R", и пусть
x(-)gCx(A, R"), u(-)£C(A, Rr), ia, tl £ int А таковы,
что
(t, x(t), u(t))£V, (t0, x(ta), tlt х(О)£Г.
Если £ = (x(-), u(-), t0, является оптимальным •
в слабом смысле процессом для задачи (1)—(3), то най-
дутся множители Лагранжа Хо 0 в случае задачи на
минимум и ^0 в задаче на максимум, р ()£&(&, R"*),
Х = (Х1( ..., lm), не равные одновременно нулю и та-
кие, что:
а) выполнены условия стационарности функции Лаг-
ранжа:
по х(-) (£’х(.)= О):
_А£.(0+^(0 = 0> (7)
^(^) = (-1)йЦ. Л = 1; (8)
по и () (^и(.) = О):
ММ; (9)
no tk
= Л = 0, 1; (10)
б) выполнено условие согласования знаков:
Х,^0, 1 = 1, ...,т; (11)
в) выполнены условия дополняющей нежесткости:
(|) = 0, i = l, .... т. (12)
Как и в §§ 3.1, 3.2, неравенства (11) означают, что
£(>0, если в условии (3) S,-(£M0, \-^0, если в (3)
•®i (Ю 0 и £(- может иметь любой знак, если 59,- (£) = 0.
Утверждение о существовании множителей Лагранжа,
удовлетворяющих совокупности условий а) — в), кратко
называется нами принципом Лагранжа для задачи Лаг-
ранжа (1)—(3).
Покажем, что утверждение теоремы находится в пол-
ном соответствии с общим принципом Лагранжа, о ко-
тором говорилось в гл. 1 и в п. 3.1.5. Действительно,
300
функция Лагранжа 3? является функцией трех аргу-
ментов: х(-), «(•) и (/„, /х). Таким образом, согласно
общему принципу Лагранжа, надлежит рассмотреть три
задачи:
(а) ^ (%(•), «(), ?0, 4; р(-), К А,о)—»extr,
(₽) ^(х(-), «(.), ?0, ?г; р(-), 1, extr,
(у) ^(х(-), «(•), /0, р(-), X, Хо)->extr.
Задача (а) является элементарной задачей Больца,
и условия стационарности (7) и (8) написаны в полном
соответствии с п. 1.4.2 и теоремой п. 3.1.3. Задача (Р)
также является задачей Больца, но вырожденной, по-
скольку и не входит в лагранжиан, a w(/0) и м(/х)—
в терминант. Уравнение Эйлера—Лагранжа поэтому пре-
вращается в (9), а условия трансверсальности становятся
бессодержательными: 0 = 0. Наконец, (у) является эле-
ментарной задачей и (10) есть просто теорема Ферма
(см. пп. 1.3.1 и 3.1.1).
Условия дополняющей нежесткости и условия^ согла-
сования знаков также, как мы знаем, написаны в соот-
ветствии с общим принципом Лагранжа, примененным
к ограничениям типа неравенств (п. 3.1.5)
Таким образом, основную теорему этого параграфа
можно сформулировать так: если, функции, входящие в по-
становку задачи, обладают достаточной гладкостью, то
для локального экстремума выполнен принцип Лагранжа.
Условия стационарности можно переписать в более
развернутом виде. В соответствии с (5) получаем:
~ из (7)
и» Ш
= -р (0 (0 + £ Q!x (0 (7а)
1 = 0
(иногда (7а) называют сопряженным уравнением);
из (9)
0 = - Р (0 + Д ^fia (0; (9а)
из (8)
p(ik) = (-\)klXk, k = 0, 1; (8а)
301
и, наконец, из (10)
0 = (- I)*” L (ik) + + 4%
==(-1)*-11 S МН^ЙМ^)) +
Li=o
+ltk+(-l)kQQX(in)=
=(-i)^ sv,-&)-№)№) +z;
L> = o
tn
или
т
р (tk) ^(tk)~ 2 Qi (tk)=(-i)*A-
1 = 0 R
Функцию
H (t, х, р, u')=Lxx—L=*
= pq>(t, x, и)—j^Qilt, x, и) (13)
i=0
(10a)
мы будем называть функцией Понтрягина рассматривае-
мой задачи. С ее помощью уравнения (7а) — (10а) и урав-
нение (2) можно записать "еще и так:
#=-"«• Й-=° 00
и
№) = (-l)*Lft, #&) = (-1)*"ЧЙ. 6 = 0, 1. (15)
Замечание. Иногда функцию (13) называют функ-
цией Гамильтона. Мы вкладываем в термин «функция
Гамильтона» или «гамильтониан» другой смысл, более
естественный с точки зрения классической механики, и
называем так функцию
3V(t, х, p) = H(t, х, р, и(1, х, р)), (16)
где u(t, х, р)—неявная функция, определяемая из урав-
нения Ha(t, х, р, п) = 0. При выполнении стандартных
условий применимости теоремы о неявной функции урав-
нения (14) принимают обычный вид канонической га-
мильтоновой системы
f = < = (17)
302
Полезно заметить, что набор условий, который до-
ставляет сформулированная теорема, в некотором смысле
является полным. Действительно, для определения неиз-
вестных функций (х(-), р(-), «()) мы имеем систему
из дифференциальных уравнений (2) и (7а) и конечного
уравнения (9а). Выражая из последнего (разумеется,
когда это можно сделать, например, если выполнены
условия теоремы о неявной функции) «(•) через х(-)
и /?(•), мы получаем систему из 2п скалярных диффе-
ренциальных уравнений (эквивалентную системе (17)).
Ее общее решение зависит от 2п произвольных постоян-
ных и еще от множителей Лагранжа %,-, среди которых
т независимых. Добавляя сюда еще t0 и tlt мы получаем
всего 2п+т+2 неизвестных. Для их определения мы
имеем 2п + 2 условия трансверсальности (15) и т усло-
вий дополняющей нежесткости (12).
Таким образом, число неизвестных совпадает с чис-
лом уравнений. Именно это и имелось в виду,, когда
выше было сказано о «полноте» набора условий. Разу-
меется, разрешимости полученной системы уравнений ука-
занное обстоятельство никак не гарантирует.
- 4.1.2. Редукция задачи Лагранжа к гладкой задаче.
Обозначим через Y пространство С (A, R") и запишем
задачу (1)—(3) п. 4.1.1 в виде
.®0 (S) —> extr; Ф(£) = 0, ^г(1)^0, i = l, ...,m, (1)
где
Ф(^)(0=х(0-Ф(Л х(0, «(0)- - (2)
Отображение Ф и функционалы 33 i определены в области
= {(*(•), «(•), h, О1(*. х(о, «(0)ек
t0, ^eintA, (t0> x(t0), t^x^ew}
пространства 3.
Задача (i) имеет тот же вид, что задача п. 3.2.1 пре-
дыдущей главы, для которой принцип Лагранжа был
уже доказан. Предположения соответствующей теоремы
распадались на три группы: банаховость основных про-
странств, гладкость отображений и замкнутость образа
бесконечномерного отображения. Проверим, что в за-
даче (1) все эти требования выполняются.
Банаховость пространств В и К очевидна—про-
странства С1 и С являются основными для нас приме-
рами банаховых пространств (см. пп. 2.1.1 и 2.1.2).
303
Гладкость (а именно непрерывная дифференцируе-
мость по Фреше) функционалов i = 0, 1, ...» т,
следует из результатов § 2.4.
Действительно, с интегральной частью мы можем по-
ступать точно так же, как и в предложении 2 п. 2.4.2,
заменив всюду %(•) на м(-), а дифференцируемость тер-
минальной части доказана в п. 2.4.3 (это оператор крае-
вых условий). При этом, согласно формулам (9) п. 2.4.2
и (3) п. 2.4.3, имеем для ( = (%(•), «(•), ?0, £~), т|==
^(Л(-), о(-), т0, тх)
(f) Ы = $ (Лх (О Л'(О +hu (О ° (0) dt+
^0
+ fi (tl) ri — fi во)то + li'To + ti^i + T'xjl (To) +
+ tfi (K) + M (Ш) +k% ( h) (3)
(ср. лемму n. 3.1.3).
Отображение (2) также непрерывно дифференцируемо
по Фреше (см. предложение 3 п. 2.4.1). Его производ-
ная, согласно (14) п. 2.4.1, имеет вид
o'(l)N(0^A(0-q)x(0A(0-<pe(0v(0- (4)
Из непрерывной дифференцируемости по Фреше функ-
ционалов и отображения Ф следует их строгая диф-
ференцируемость, требуемая в теореме о принципе Лаг-
ранжа.
Замкнутость образа отображения Ф имеет
место в силу его регулярности: образ Ф'(|)Н совпа-
дает с Y. Действительно, взяв произвольное y(-)£Y =
— С (Д, R"), положим у(.) = 0, то = тх = 0. Уравнение
Ф'4)[/1(.), о, о, o](.)=i/(.)
эквивалентно линейному дифференциальному уравнению
h(t)—ix(t)h(t) = y(t) с непрерывными коэффициентами,
которое имеет решение h (•) g С1 (Д, R") в силу теоремы
существования для линейных систем (п. 2.5.4). Таким
образом, выполнены все условия теоремы п. 3.2.1.
Для определенности будем считать, что (1)—задача
на минимум. Согласно принципу Лагранжа, если f =
= (%(•), w(-), t0, ij) — локальная минималь (1), то най-
дутся множители Лагранжа X £ ROT* и элемент у* £
304
£Y* ==(С(Д, R"))* такие, что для функции Лагранжа
у*, к, Х0) = ^(х(-), «(•), ta, у*, К %0) =
ti / tn \ т
= х, u))dt +Емг-(^о. х(МЛ>* О+ '
ta \1 = о ' / 1 = 0
+ у*оф (5)
выполнены условия согласования знаков, дополняющей
нежесткости и стационарности
Д = 0<=> A(.) = 0, ^и(-) = 0, ЛА = 0, 6 = 0, Ь
Три соотношения, из которых складывается правая
часть, мы называем далее стационарностью по %(•),
w(-) и по tk соответственно.
Однако мы замечаем, что функция (5) не тождест-
венна функции Лагранжа (4) п. 4.1.1. Воспользовавшись
теоремой Рисса об общем виде непрерывного линейного
функционала на пространстве С (Д, R") (п. 2.1.9), мы
можем утверждать лишь, что
<«/*> т](-)> =pv(/)r|(0,
д
где v (/) = (vj(/).vn(/))—вектор-строчка из канони-
ческих функций ограниченной вариации. Подставляя это
в (5) и учитывая обозначение (6) из п. 4.1.1, получаем
.£’=$(£ мд x(t), u(t))\dt+
ta \i=0 /
+ jdv(O{x(O—<P(^ x(0> w(0)} +
+ l(to, X{to), tlt %(/,)). (6)
Сравнивая эту формулу с (4) — (6) из п. 4.1.1, мы
видим, что функция Лагранжа 3? получается из 3?, если
функция v(•) абсолютно непрерывна, а ее производная
равна нулю вне [/0, t±] и совпадает с/?(•) в этом отрезке.
Ситуация напоминает здесь п. 1.4.1. Подобно тому как
лемма Дюбуа-Реймона позволила нам там вывести урав-
нение Эйлера без дополнительного предположения о
дифференцируемости функции t —> р (t) =Li (t), подходя-
щее обобщение этой леммы позволит нам сейчас доказать
абсолютную непрерывность функции v(-).
305
4.1.3. Обобщенная лемма Дюбуа-Реймона. Пусть на
отрезке [а, р] векторная функция а(-): [а, р]—> R"*
интегрируема по Лебегу, матричная функция Ь(-):
[а, р]—+^(Rn, R") непрерывна, v(-): [а, pJ-^R"*—ка-
ноническая векторная функция ограниченной вариации;
tk—различные точки интервала (а, р), cft£R“*, k = 0,
1.....Р-
Если для всех h(-)£C1 ([а, р], R") имеет место ра-
венство
Р ₽ р
$ a (i) h (i)dt + $ dv (t) {h (t)-b (t) h (0} +E c*h Уь) = °’
а a fe=0
(1)
то функция v(-) абсолютно непрерывна; ее производная
/?(•) непрерывна на [а, р], кроме, быть может, точек tk,
в которых она имеет пределы слева и справа, абсолютно
непрерывна в любом интервале, не содержащем точек tk,
и при этом
p(t) — a (t) — р (t) b (0 почти всюду, (2)
р(а) = р(р) = О, (3)
Р(^Н-О)—0)=сд. (4)
t
Доказательство. Положив h (t) = у -J- J Г) (s) ds,
• а
мы получаем из (1)
/₽ ₽ Р \ Р i
К a(t) dt — J dv (t) b (/) + У*. ck} y-f- J a(t) J i] (s) dsdt +
\a a fe=0 ) a a
₽ P i P tk
+ \dv(t) ц(Е) — $ dv(t)b(t) $ + n(s)ds = O.
a a a /?=0 a
Так как y£Rn и г] (•)€€([«, p], R") можно выбирать
произвольно и независимо друг от друга, то, во-первых,
₽ 0 р
^a(t)dt — J dv (t) b (/) -j- У1, ck == 0 (5)
a a fe= 0
(ибо можно положить т] () = (), у—любое), а во-вторых,
306
для любого г] (•) g С ([а, р], R") имеет место равенство
Р t 0
$ а (0 $ П (s) ds dt -|- J dv{t) r] (t) —
а а a
0 t P fk
— dv(t) b (t) ^r] (s) ds 4- 52 ck $ Л (s) ds = 0. (6)
a a fe=O а
Меняя в первом и третьем члене порядок интегриро-
вания в соответствии с формулой Дирихле ((5) п. 2.1.9),
обозначая буквой s переменную интегрирования во вто-
ром члене, полагая
f 1, a^Cs^S/,
(S) = | 0( f<S^p (7)
и используя равенство
0 0
a a
(8)
справедливое для абсолютно непрерывных функций [КФ,
стр. 359], преобразуем (6) к виду
0/0 \ 0 0/0 \
J \ \a(t)dtjx\ (s) ds 4“ $dv (s) r| (s) — П ^dv(t)b (/) Jr] (s)ds-^
a \s / a a >s /
& P & &
+ S £ Ck%l^k}(s)*\(s)ds=^ dA(s)q(s)4-$ dv (s)T](s)=O,
a 4=0 a a
(9)
где
s /0 0 p \
A(s) = J a(t)dt—^ dv(f)b (0 + Ц c*X[aufcl (a) f do.
a (.0 О fe=0 )
Функция A(-) абсолютно непрерывна на [a, p] и
A(a) = 0, следовательно, это каноническая функция, а
так как v(-)—также каноническая функция ограничен-
ной вариации, то из (9) и свойства единственности
в теореме Рисса (п. 2.1.9) A(s)4-v(s) = 0. Следовательно,
v (•) абсолютно непрерывна, а ее производная р ($) ~
= v' (s) при s^=tk равна (снова используем (8))
р (s) = v' (s) = — A' (s) =
00 р
= —J a(t)dt +^p(t)b(t)dt—J2 сд[а, tft](s).
s s A=s 0
307
Из этой формулы видно, в свою очередь, что р(«) не-
прерывна всюду, кроме точек tk, где справедливо (4), и
что имеет место (2). Равенство р (Р) = 0 очевидно,
а р(а) = 0 эквивалентно (5), так что доказано и (3). |
4.1.4. Вывод условий стационарности. Итак, мы по-
казали, что если | доставляет локальный минимум в
задаче (1)—(3) п. 4.1.1, то найдутся такие множители
Лагранжа Хо^О, и у*£С(&, R")*, что выпол-
нены условия согласования знаков и дополняющей не-
жесткости для X и условия стационарности
a)Jx() = 0, б)Д() = 0, в) Лй = 0, 6 = 0,1, (1)
где 2 определяется равенством (6) п. 4.1 2, а 2Х{),
2ио и 2tk получаются из 2Х{ >, ), 2tk подстанов-
кой %(•) —х(-), «(.) = «(.), tk = tk, 6 = 0, 1.
Переходим к расшифровке условий (1). При диффе-
ренцировании функции 2 мы будем иметь в виду, что
первый и третий члены формулы (6) п. 4.1.2 образуют
функционал Больца, производная которого дается фор-
мулой (3) того же пункта, а второй член является су-
перпозицией оператора дифференциальной связи и линей-
ного отображения г] () —> J dv (t) г) (t), и его производная
д
получается поэтому интегрированием формулы (4) п. 4.1.2
по dv(t).
А) Стационарность по х (•). Дифференцируя 2
по %(•)> получаем в соответствии с (1а), что при всех
h (•) £ CJ (A, Rn) имеет место равенство
т
0 = Л(, [А (.)] = $ S \fix (0 h (t)dt +
Г =0
*0
+ $ dv (0 {h (0-фх (о h (t)} + lxJi (Fo) +/> (?!>• (2)
д
Рассмотрим сначала случай ?!>?„. Согласно обобщенной
лемме Дюбуа-Реймона из (2) следует, что функция v (•)
абсолютно непрерывна на А, а ее производная р(-)=
=v'(•) непрерывна на А всюду, кроме, быть может,
точек и где она имеет пределы слева и справа, и
выполняются соотношения (2)—(4) п. 4.1.3, которые
308
применительно к нашей ситуации означают, что
т
= —р(0фх(0+х[?о ?1](0 (3)
при ?#=/(), 4» р(®) — р(3) = 0, где а и 0—концы Д,
и что
p(tg-\-O)—p(tg—O) = lx,, p(i1+O)-p(f1-O) = L, (4)
.(здесь — характеристическая функция, равная 1 на
[f0, и 0 вне этого отрезка). Из уравнения (3) видно,
что /?(•) удовлетворяет однородному линейному диффе-
ренциальному уравнению на полуинтервалах [а, ?0) и
(?1( 0]. Поскольку она обращается в нуль в концах а и
0 этих полуинтервалов, по теореме единственности
п. 2.5 3 на Д\[?о, и p(t0 — 0) = р(?1 + 0) = 0.
Обозначим теперь через р(-) решение уравнения (7а)
п. 4.1.1, совпадающее на интервале (ta, с р (•) (в этом
интервале уравнения (7а) п. 4.1.1 и (3) тождественны).
Поскольку (7а) линейно, решение р(-) определено на
всем Д и принадлежит С?(Д, R"*) (п. 2.5 4). Для этого
решения p(t0) — p (?о + 0) и p(,t.l) = p(i1—0), а так как
р(1а—0) = 0 и р(?!-4-0) = 0, то (4) превращается в усло-
вие (8а) п. 4.1.1. Таким образом, для р(-) условия ста-
ционарности (7) и (8) (или (7а) и (8а)) из п. 4.1.1 спра-
ведливы.
При ?! < t0 мы вместо (3) получим уравнение
т
dpldi = — р (0 фДО-Х^, ?,] (0 2 У!х (0.
решение /?(•) которого равно нулю на [a, 4) и (?0, 0].
В этом случае надо обозначить через /?(•) то решение
уравнения (7а) п. 4.1.1, которое совпадает с (— 1)р(-)
на (?!, t0), после чего условия (7), (8) п. 4.1.1 будут
выполнены.
Наконец, при ^ — tg мы снова можем воспользо-
ваться обобщенной леммой Дюбуа-Реймона, "йо теперь
уже v (t)=p(f) = 0 всюду на Д, кроме, быть может,
точки ta — tlf где должно еще выполняться условие
Р (?i Н~0) p(Ji 0) = 1Ха -р?*! = 0. Отсюда 7Хо -\-lXl — 0. Беря
309
в качестве />(•) то решение уравнения (7а) п. 4.1.1, для
которого р(?о) = /хо, мы снова (убеждаемся в том, что
условия (7), (8) п. 4.1.1 выполнены. ,
Б) Стационарность по «(•). Дифференцируя 3?
по и(-) и учитывая, что v(-) абсолютно непрерывна, а
ее производная p(-) = v' (•) отлична от нуля лишь
в интервале (?0, ^), а в этом интервале совпадает ср(-),
имеем
?i ( т. \
о=за [о (• )j=Н Е Kfia м-р (о ф„(/) к (о dt.
V=o )
Так как это равенство имеет место при всех и(-)£
gC(A, R"), то, снова сославшись на единственность в
теореме Рисса (п. 2.1.9), мы получаем
т
SVia(0-p(0<p»(0=o,
г=о '
что совпадает с уравнением (9а), а следовательно, и с
условием (9) п.4.1.1.
В) Стационарность по tk. Поскольку
3(х(-), «(•), te, t±; ...)—J?(*(•)> «(•). *<» ti> •••)=*
= ^dv(t){x(t)—q>(t, x(t), u(t))} —
Д
— ^p(t){x(t)— <p (£, x(t), u(t))}dt=O,
^0
то производные этих двух функций по tk в точке
f = (%(), «(•), ta, tj) совпадают, а так как имеет место
равенство J^(A = 0, то выполняется и условие (10)
п. 4.1.1.
4.1.5. Задача со старшими производными. Уравнение
Эйлера — Пуассона. Снова зафиксируем замкнутый отре-
зок AcR и будем рассматривать пространство
В, = б?(Д, R")xRxR,
элементами которого являются тройки g = (%(•), tB, fx),
где функция х(-):А—>R" непрерывно дифференцируема '
до порядка s включительно; t0, ^CintA. Говоря о за-
даче со старшими производными (в классическом вариа-
ционном исчислении), будем иметь в виду экстремальную
310
задачу
Л (D —extr; i=l........tn, (1)
где
5s, (?)=$/, (Л x(Z), - , х“’(/))<Д +
•• ,x“-"(t0), t1,x(t1), , x(*-l’O (2)
в пространстве Н5. При этом в (1), (2) ft: V—R, ip,:
W—'R, i — 0, 1, . , m, V и W — открытые множества
в пространствах Rx(R")i+i и R x(R"),sX R X(R");! соот-
ветственно, ft и ф,- по крайней мере непрерывны. Тройка
g = (%(.), ta, является допустимой в задаче (1),
(2), если (t, x(t), .. , xli)(0)€V, и
(to, x(t$)....x^-"(t0), t„ xtfj, ...,
Допустимую тройку f = (x(-), ta, t,) мы называем
(локальным) решением задачи (1), (2), если она достав-
ляет функционалу 3*0 локальный экстремум в простран-
стве Е5, т. е. если существует такое е > 0, что для всех
допустимых £ = (х(-), t0, /J, для которых
111-f Ца,< К-ffe| < в, k = 0, 1;
||х—х(’)||с»(д, дп) < е,
выполняется одно из неравенств: 5?0 (£) (g) в слу-
чае минимума и (?) в случае максимума.
Покажем, что задача со старшими производными (1),
(2) сводится к # задаче Лагранжа. С этой целью обо-
значим
х = (хп ..., xjC(R"^,
х(-) = (х(-), х(-), ...,х^’(.)),
U(.)==xw>(.)i p(-) = (/’i(-)> •••>/’.(•))•
Тогда задача (1), (2) приобретает следующий стандарт-
ный вид задачи п. 4.1.1:
$ fo(t>x(t')’ u(t))dt+^o(to, X(to), tu x (/J)—>extr, (Г)
*0
ti
$ ft (t, X(t), u(t))dt+^>l (to, x(to), ty, X^^^O, ,
1 = 1, ..., m, (2')
Xj = Xj + 1, /=1, .... s— 1, xs = u (3).
311
с функцией Лагранжа
^(ж(-), «(•), t9, p(-),K,b9) = \Ldt+l, (4)
^0
где
Lit, х, х, и)=^ ^ifi(t, x, w) +
1= о
s— 1
+ S Pj (0(*/—X/+1) +ps (t) (Xs — u) (5)
и ,~1
l(te, *o> *o> •••’ xo~”> xl> xi.....4’-1)) =
= S Mi (*o> xo> Xot . . xg”1’, tr, Xu Xv ...» X}5-1’). (6)
i=0
Перефразируя на этот случай теорему п. 4.1.2, по-
лучаем необходимое условие экстремума.
Теорема. Пусть функции [р V—>-R, г = 0,
1, ..., т, и их частные производные по х, ..., x<J) не-
прерывны в открытом множестве t/cR X(R'f)i+1, а
функции ф;: W—>R, i = 0, 1, ..., т, непрерывно диф-
ференцируемы в открытом множестве W с R х (Rn)i х
xRx(Rn)i, и пусть х(-)£С*(Д, R"), t0, tt € int Д та-
ковы, что
(t, x(t)....x^(t))eV, t£\-,
(t0, x(Q, x^-^(ta), ilt xd), .... ^-»(fy)ew.
Если £, — (x(-), ta, tx) является локальным решением за-
дачи (1), (2), то найдутся множители Лагранжа-. Хо^О
. в задаче на минимум и ^0 в задаче на максимум,
р(-)=(31(-).......РЛ-песчд, (R«)-),x=(x...........х„),
не равные нулю одновременно и такие, что-.
а) выполнены условия стационарности функции Лаг-
ранжа'.
по х(-) (^Х(.) = 0, ^Н(’.)=0)
р.(t) = fxit, xw>(0),
xit), ..., X^(t).)— Pj-^t),
i=2;..., s, {'
G = xit), ..., x^it))-ps(t),
k = o, 1; (8)
312
no tk
M) = (-1)*+1V k = 0, 1; (9)
б) выполнено условие согласования знаков
Х;^0, г = 1, ...» m; (10)
в) выполнены условия дополняющей нежесткости
V((B)=0> » = 1......т. (И)
Здесь
f (/, х, х, ...» х^) = S Kfi (U, • • •, х<*>), (12)
1=0
H(t)= tpjWx^-Ht, i(0, xw(0) (13)
/=1
и, как обычно,-
*(*»)• • • •’ ^_I)• • •>
и т. п., а неравенства (10) означают, что Л(-^0, если в
задаче (1)' ^,(5)<0, ХгС°, если в (1) ^Д?)>0 и
может иметь любой знак, если в (1) 5\(£) = 0.
Подробные выкладки, приводящие условия (7)—(12)
п. 4.1.1 к аналогичным условиям этой теоремы, предо-
ставляются читателям в качестве упражнения.
Для частного случая задачи со старшими производ-
ными, в котором терминальные члены в (Г) и (2') суть
константы и концы закреплены, утверждение теоремы
можно представить в более простой форме. Условия
трансверсальности (8) и (9) здесь опускаются, а си-
стему (7) можно записать в виде одного уравнения
— =0. (14)
Наконец, если предположить существование нужных
производных, уравнение (13) можно записать в виде
уравнения Эйлера —Пуассона
+ Sh (0- • • • -(-Df (0 =0. (15)
Общее решение этого уравнения порядка 2s содер-
жит 2s проиэвольных'постоянных и зависит еще от чисел
\.......... одно из которых можно выбирать произ-
вольно. Всего в нашем распоряжении оказывается
313
2s-[-т неизвестных. Для их определения мы используем
2s краевых условий (для закрепленных концов) и еще
т условий получаем из условий дополняющей нажест-
кости и неравенств (1) и (10) (проверьте', что всего из
них можно извлечь ровно т равенств). Аналогично
можно проверить, что и в общем случае число уравне-
ний, которые дает теорема, совпадает с числом не-
известных.
§ 4.2. Принцип максимума Понтрягина
4.2.1. Постановка задачи оптимального управления.
Экстремальная задача, которой посвящен этот параграф,
по форме почти совпадает с задачей Лагранжа (1)—(3)
п. 4.1.1. Здесь мы встретимся с тем же функционалом,
той же дифференциальной связью и с теми же ограни-
чениями типа неравенств, что и раньше. Отличие новой
задачи состоит в том, что в ее формулировке явно вы-
делено ограничение на управление вида и (t) € U, где
U—некоторое топологическое пространство.
На первый взгляд это не прибавляет ничего нового
и даже выглядит менее общим. Действительно, в задаче
Лагранжа мы имели дело с условием (/, x(t),
которому должны были удовлетворять допустимые про-
цессы. В частном случае, беря V = GxU, мы расщепляем
это условие на два: (t, x(t))£G и w(/)£U.
Однако разделение переменных на фазовые и управ-
ление, и выделение ограничений на управление оказа-
лось весьма знаменательным. Вместе с ним выделилась
и новая ветвь в теории экстремальных задач, быстро
завоевавшая популярность среди прикладников своими
возможностями применительно к практическим задачам
и позволившая по-новому взглянуть и на классическую
теорию.
Чем же все это было вызвано? В первую очередь не-
обходимостью исследования задач технического содер-
жания. Разделение фазовых переменных и управления и
их связь при помощи дифференциального уравнения—
обычная модель для процесса, развивающегося по зако-
нам природы (дифференциальное уравнение!), но испы-
тывающего воздействие человека, управляющего этим .
процессом в соответствии со своими целями и стремяще-
гося сделать eft) в каком-то смысле оптимальным. Теперь
ясно, что ограничения на управления вида и (/) £ U свя-
зи
заны с ограниченными возможностями воздействовать на
процесс (скажем, с ограниченностью диапазона поворота
рулей управляемого аппарата).
Если принять за U открытое множество в Rr, то ни-
чего нового мы действительно не получим. Однако в тех-
нических и иных прикладных задачах множество U не
обязано быть открытым. Зачастую управление может
быть даже просто дискретным (включено—выключено).
Естественно возникают ограничения, при которых U ока-
зывается замкнутым множеством: насколько это суще-
ственно, мы видели, решая задачу Ньютона (п. 1.6.2).
Уже в простейших задачах оптимального управления
встречаются ограничения вида |w(^)]^C 1 (см. задачу о
быстродействии в п. 1.6.3). В этом последнем случае
множеством допустимых управлений оказывается замк-
нутый шар в сложно устроенном пространстве Л® (Л), и
в типичных случаях оптимальное управление лежит на
границе этого шара (из сказанного в п. 1.6.3 видно,
что при ограничении | и (t) | < 1 задача не имела бы ре-
шения: минимальное время достигается при управлении,
где почти всюду | и (/)| = 1), а эта последняя чрезвычайно
негладкая и «многогранная», а точнее, «бесконечногран-
ная». Все это затрудняет применение обычных методов
дифференциального исчисления, и условия гладкости по
управлению оказываются довольно часто неестественными.
В связи с этим мы не будем больше требовать сущест-
вования производных fia, фа и т. п. и даже само мно-
жество U возможных значений управления будем считать
произвольным топологическим пространством, не обла-
дающим, вообще говоря, линейной структурой. Отсут-
ствие производных по и — второе отличие новой задачи
от старой. Желая оттенить это обстоятельство, функцио-
налы, входящие в формулировку задачи, мы обозначаем
новой буквой, хотя по виду они совпадают с функцио-
налами Больца.
Наконец, последнее отличие — это отказ от непрерыв-
ности управления. В основном это связано с тем, что в
классе непрерывных управлений задача часто не имеет
решения (например, в большинстве задач, где U дис-
кретно или в задаче о быстродействии п. 1.6.3). Следует,
впрочем, отметить, что переход к рассмотрению «ломаных
экстремалей» (что соответствует кусочно-непрерывным
управлениям) делается и в классическом вариационном
исчислении (см. п. 1.4.3). Сама же возможность свобод-
315
кого выбора управления внутри множества 11 (а ею мы
уже воспользовались, «выпуская» игольчатые вариации
при выводе условия Вейерштрасса в п. 1.4.4 л при до-
казательстве принципа максимума в простейшей ситуации
(п. 1.5.4)), порождает скрытую выпуклость по управле-
ниям, с чем связана форма основного условия — прин-
ципа максимума (см. (10), (11) в п. 4.2.2), напоминающая
соответствующее условие в задачах выпуклого програм-
мирования. Здесь эта связь не будет вскрыта в полном
объеме. Мы сделаем это в следующем параграфе, правда
в частном варианте общей задачи.
Итак, рассмотрим экстремальную задачу
^(х(-), «(), 0 =
it
= U(t))dt + ^>a(ta, x(t0), x(^))-*inf, (1)
J'o
x = x(t), u(/)£U, (2)
t,
“(•). x(t), u(t))dt +
• t,
+ $;•(/(), x(t0), tit 1 = 1, 2....tn. (3)
Здесь Gxtt —>R, ф,- .W —► R, i = 0, 1, ..., tn,
<p: Gx.U—*R“, где G и W—открытые множества в про-
странствах RxR" и RxR"xRxRn соответственно, U—
произвольное топологическое пространство. Знак gs имеет
тот же смысл, что в §§ 3.2 и 4.1. Все функции ft, фу, ср
предполагается по крайней мере непрерывными.
Четверку (%(•), и(-), t0, tj) будем называть управля-
емым процессом в задаче (1) — (3), если:
а) управление [tg, /J——кусочно--непрерыв-
ная функция. Ее значения в точках разрыва существен-
ной роли не играют; для определенности будем считать,
что «(•) непрерывна справа для t0^.t<_t1 и слева в
точке
б) фазовая траектория х(-): [/„, >-R" непрерывна
и ее график лежит в G
Г = {(/, x(O)Po<^<M<=G.
в) для всех t € [/<>. кроме, быть может, точек раз-
рыва управления п(-), функция х(-) удовлетворяет диф-
ференциальному уравнению
х(0 = Ф х (0> 11 (0)
316
(в этом случае мы говорим, что х(-) соответствует уп-
равлению «(•); легко видеть, что в точках разрыва уп-
равления х(-) имеет производные слева и справа).
Управляемый процесс называется допустимым, если
удовлетворяются условия (3).
Допустимый управляемый процесс (£(•), u(-), 70,
называется (локально) оптимальным, если найдется такое
е > 0, что для всякого допустимого управляемого про-
цесса (%()> «(•)> ^о> О такого, что
Pit—^[<Б> й = 1 и |х(0—х(01<в
для всех МП[?0, G] (4)
выполняется неравенство
3,о(Л'(')> и(')> ^о> G) З'о (х (’)> и(’)> ^о> ?i)- (5)
Заметим, что и здесь произошло изменение по срав-
нению с задачей Лагранжа: мы не требуем больше бли-
зости’ производных x(t) и x(t). В классическом вариа-
ционном исчислении это соответствует переходу от сла-
бого экстремума к сильному (см. п. 1.4.3).
Поучительно сравнить задачу Лагранжа и задачу оп-
тимального управления в том случае, когда U=Rr ив
п. 4.1.1 V = GxRr. При этом предположении:
Каждый допустимый управляемый процесс (%(•), и(-),
t0, ft) задачи Лагранжа является таковым и для задачи,
оптимального управления (точнее, превращается в тако-
вой при ограничении «(•) на [/0, /J).
* Это означает, что произошло расширение задачи (ср.
п. 1.4.3). Следовательно, значение задачи оптимального
управления не больше значения задачи Лагранжа
(inf '30 inf й?0). Впрочем, при достаточно естественных
предположениях относительно функций Д-, и <р обе
эти величины совпадают (в тривиальном случае, когда
х — и, мы доказали это в лемме «о скруглении углов» в
п. 1.4.3).
Если inf 30 < inf ^0, то, как легко видеть, решения
обеих задач могут существовать или нет независимо друг
от друга. Если же значения задач равны, то возможно
одно из трех:
а) Задача Лагранжа имеет решение: inf ®0 = ®0 (£(•),
£/(•), ^о> М- Тогда та же четверка является и решением
317
задачи оптимального управления, поскольку
З'о(х(-)- «(•). *1)>Ж*(’). «(•)- ?1) =
= inf 33 0 - inf За.
б) Задача Лагранжа не имеет решения, а задача оп-
тимального управления имеет: inf 30 достигается на ку-
сочно-гладкой кривой х(-). Такую ситуацию мы наблю-
дали в примере (6) п. 1.4.3 (при х = и цереход от класса
С1 к классу КС1 как раз и соответствует переходу к за-
даче оптимального управления).
в) Обе задачи не имеют решения: нижняя грань
функционала не достигается и при расширении области
его определения. Так обстоит дело в примере Больца
(п. 1.4.3).
В предыдущих рассуждениях молчаливо предполага-
лось, что речь идет о минимизации по всему классу до-
пустимых управляемых процессов. Однако обычно при
рассмотрении экстремальных задач мы придерживаемся
локальной точки зрения, что, кстати сказать, отражено
и в наших определениях. В п. 4.1.1 допустимый управ-
ляемый процесс (%(•), «(), ta, был назван оптималь-
ным (в слабом смысле), если он доставляет минимум
функционалу Д в некоторой ^-окрестности nd х(-) и
С-окрестности по «(•). Теперь же определение оптималь-
ности предполагает, что минимум За имеет место в более
широкой окрестности, описываемой неравенствами (4).
Фактически это С-окрестность по х(-), а ограничения
на управления не накладываются вовсе. Как уже было
сказано, в классической ситуации это был бы сильный
минимум. Поэтому локальное решение задачи Лагранжа
может не быть оптимальным процессом для задачи опти-
мального управления. Если же в оптимальном процессе
(х(-), «(•), ^о> ^х) управление «(•) непрерывно, то при
наших обычных предположениях относительно функций,
входящих в задачу, этот процесс будет и локальным ре-
шением задачи Лагранжа.
Ограничения (3) не являются самыми общими, кото-
рые приходится рассматривать в задачах оптимального
управления. Мы, например, совсем оставляем в стороне
так называемые фазовые ограничения вида
(t, %(/))(=£>, (6)
318
где D — некоторое подмножество в RxR". Конечно, если
D открыто, то, заменив в определении управляемого
процесса G на G(~\D и уменьшив, если нужно, е в (4),
мы автоматически учтем ограничения (6). Поэтому основ-
ной интерес представляет .случай, когда D не является
открытым множеством и оптимальная фазовая траектория
x(t) выходит для некоторых t на границу D (см. рис. 37;
минимизируется длина кривой, заштрихованная часть
плоскости не принадлежит D). Это приводит к сущест-
венно новым эффектам, в частности, к необходимости
Рис. 37.
ввести в уравнение Эйлера—Лагранжа обобщенную
функцию—производную не абсолютно непрерывной меры
(или заменить это дифференциальное уравнение интег-
ральным с интегралом Стйлтьеса по этой мере).
4.2.2. Формулировка принципа максимум^. Принцип
Лагранжа в задаче оптимального управления. Рассмотрим
снова задачу
к
«(•)- U(t))dt +
^0
+ Фо(^о> tlt х(^))—► inf, (1)
x = q(t, x(t), (2)
«(•). ^o- x(t), u(t))dt +
^0
+ iM*o, h, xOSSO, 1 = 1, 2................m. (3)
Как и в п. 4.1.1, функцией Лагранжа этой задачи
называется функция
к
•2?(х(-), «(•), ^о> ^1", р(’)> \) — \Ldt-{-lt (4)
А»
319
где
4€R, A. = (Xi.....%„)GR“*,
L(t, x, x, u) = S ^tfi (t, x, u) + p(t)(x—y(t,x, w)), (5)
1=0
^(^o> ^o» ^i) = 2 ^/$1 (^o> ^0’ ^1» ^1)* (6)
i = o
Функция p(-): [ta, ^] —► Rn* предполагается непре-
рывной. Там, где этб будет нужно, мы будем считать,
что р(-) определена на более широком промежутке, чем
[£0, ^i], продолжая ее за пределы этого отрезка произ-
вольно, но с сохранением непрерывности. Функция р(-)
и числа %,-, называются множителями Лагранжа задачи
(1)—(3), функция (5)—лагранжианом, (6)—терминантощ.
Наконец, функцию
т
Н (/, х, и, p) = L* х—L = p(p (t, х, и)— 2 ^ifi (t, x, и) (7)
i = 0
мы будем называть функцией Понтрягина. Как и обычно,
будут использоваться обозначения
Lx(t) = Lx(t, x(t), x(t),u(t)), ф(/) = ф(/, x(t), u(t)),
lXk = lXk(ta, £(fo), 4. MO)
и т. Д.
Теорема (принцип максимума Понтряги-
на). Пусть G—открытое множество в пространстве
R X R", W—открытое множество в пространстве R х R" X
xRxR", IX—произвольное топологическое пространство-,
функции fi'. GxU—> R, J = О, 1, ..., т, г/ ф: Gxll^ R"
и их частные производные по х непрерывны в Gxll, а
функции ф,-: W—>-R, i = l, ..., т, непрерывно диффе-
ренцируемы в W.
Если (х(-), w(-), ?0, Q— оптимальный процесс для
- задачи (1)—(3), то найдутся множители Лагранжа
Х0>о, р(-), Х=(Хи ..., л„),
не равные одновременно нулю и такие, что:
а) выполнены условия стационарности и принцип ми-
нимума для функции Лагранжа:
320
no x(-) условие стационарности (J?x(.)=0)
+ (8)
ШН-1)^. £ = o,i; (9)
no u(-) принцип минимума в лагранжевой форме
L(t)=iL(t, x(f), x(t), 'u(t'))^
= minL(t, x(t), x(t),v), (10)
0 g ll
или в гамильтоновой (понтрягинской) форме в виде прин-
ципа максимума
= x(t), u(t), p(t))^
= maxH(t, x(t), v, p (11)
sell
при этом функция H (t) непрерывна на отрезке [?0, fx];
по tk условия стационарности
&k = 0, £ = 0, 1; (12)
б) выполнено условие согласования знаков
^SgO; (13)
в) выполнены условия дополняющей нежесткости
(х (•), и (•)> to> ?i) = 0, i = l,2, ..., т (14)
(как и в предыдущем параграфе неравенства (13) озна-
чают, что X£^sO, если в условии (3) Х£^0, если
в (3) 3^0 и Х£ может иметь любой знак, если 5f = 0).
Утверждение о существовании множителей Лагранжа,
удовлетворяющих совокупности условий а) — в), кратко
называется нами принципом Лагранжа для задачи опти-
мального управления (1)—(3) или принципом максимума
Понтрягина. Как и раньше, это утверждение находится
в полном соответствии с общим принципом Лагранжа
из п. 3.1.5. Поскольку функция Лагранжа $ являет-
ся функцией трех аргументов: х(-), и(-) и (/0,
В. М. Алексеев и др. 321
надлежит рассмотреть три задачи:
(а) ^(х(-), «(•), t0, К', Р(-). — inf,
ф) &(х(-), «(•), ?о, k, р(-),
(?) &(х(-), «(•), ta, ti, Р(-), К inf.
Задачи (а) и (у) здесь те же самые, что и в п. 4.1.1.
Поэтому' и соответствующие условия стационарности по
х(-) и по tk должны выглядеть здесь так же, как и в
задаче Лагранжа и это действительно так. Что же ка-
сается задачи (Р), то это элементарная задача оптималь-
ного управления из п. 3.1.4, и принцип минимума (10)
вполне соответствует условию (1) этого пункта. Таким
образом, приведенная выше формулировка теоремы дей-
ствительно согласуется с общим принципом Лагранжа.
Обычно условия стационарности (8), (9) и (12) запи-
сываются в другой форме: (8) — как уравнение Эйлера —
Лагранжа (называемое также сопряженным уравнением)
т
dp (t)/dt = — р (t)q>x (t) + S Qix (t); (8a)
i = 0
(9) и (12) — как условия трансверсальности
Р (4) + U = 0, -р (?0) + 1Х, = 0 (9а)
и
-Л (^ + 4 = 0, Л(?о) + ^ = О. (12а)
Соответствующие преобразования проделываются так же,
как в п. 4.1.1, и нет нужды их повторять. В точках
разрыва управления в- уравнении (8а) надо брать правую
производную /?+(•) (левая тоже существует). Непрерыв-
ность /?(•) и Н(•) в точках разрыва управления (т.е.
в точках излома х(-)) носит название условия Вейер-
штрасса —Эрдмана.
Можно проделать и здесь анализ «на полноту» набора
необходимых условий, даваемых сформулированной тео-
ремой. В сущности он не будет отличаться от того, что
было сделано для задачи Лагранжа. Вместо того, чтобы
определять «(•) как функцию х(-) и /?(•) из условия
£а = 0, теперь это нужно сделать, исходя из соотноше-
ния (10).
4.2.3. Игольчатые вариации. Как и в простейшей си-
туации, разобранной нами в п. 1.5.4, основной прием в
322
доказательстве принципа максимума, которое будет из<
ложено далее, состоит в замене рассматриваемой нами
задачи"оптимального управления некоторой конечномер-
ной экстремальной задачей или, точнее говоря, целым
набором таких задач. Для этого мы включим оптималь-
ный процесс (х(-), w(-), ta, ?t) в некоторое специальное
семейство управляемых процессов—«пакет» игольчатых
вариаций—и рассмотрим ограничение задачи (1)—(3)
п. 4.2.2 на это семейство.
Нужное нам семейство процессов зависит от. следую-
щих параметров:
начальные данные (t0, х0), конечный момент времени
набор а — (alt ..., а#), где все а(- g R достаточно ма-
лы; для краткости обозначим а = 2сч;
набор т = (ти ..., тдг), где te < т;. <тл?<Г1,
причем среди т,- содержатся все точки разрыва оптималь-
ного управления «();
набор u=(un ..., vn), где
В дальнейшем тип фиксированы, a (tlt t0, х0, а) ме-
няются, и по ним мы будем дифференцировать различные
функции.
Пусть сначала Af=l. Элементарная игольчатая вари-
ация управления и (I), или просто «элементарная иголка»,
отвечающая паре (т, и), определяется равенствами
х fи (0> Гт> т+а)»
u(t; а, т, и) = < ' ” ; (’ (1)
I н, /£[т, т-4-а). v '
Соответственно игольчатая вариация x(t; а, т, и) фазо-
вой траектории х (/) определяется как решение задачи
Коши
х = ф(£, х, u(t; а, т, и)),
х (т) х (т). (
С точностью до несущественного различия (вместо
[т, т-фа) был взят полуинтервал [т—X, т)) мы рассмат-
ривали подобную вариацию в п. 1.5.4. Было обнаружено,
что функция x(t\ а, т, а) дифференцируема по а и при
ее производная г/(/) = ха(Л 0, т, и) является реше-
нием уравнения в вариациях
У — Ч>х(!)У (3)
323
11*
с начальным условием
у(т) = ф(т, х(т), V)—ф(т, х(т), «(т)). (4)
„Следуя п: 2.5.4, мы будем здесь и в остальной части
параграфа обозначать через £2(£, т) фундаментальную
матрицу р'ешений уравнения (3). Кроме того, для сокра-
щения записи введем специальное обозначение для пра-
вой части- равенства (4):
Дф(т, ц) = ф(т, х(т), I»)—ср (т, х(т), w(r)). (5)
В этих обозначениях
y(t) = xa(t; 0, т, v) = Q(t, т)Дф(т, v). (6)
В п. 1.5.4 мы смогли обойтись рассмотрением одной
«иголки». Теперь нам понадобится целый их «пакет», по-
скольку задача стала сложнее, и нам нужно иметь в
распоряжении больше свободных параметров. В пакете
объединяется любое конечное число иголок с парамет-
рами (Т;, vt, а;), i= 1, .... N. При этом существенно,
что некоторые из этих иголок могут различаться только
значениями управления ц,- при одних и тех же rz. По-
этому задавать иголки формулами,вида (1) теперь нельзя:
при одинаковых т( разные иголки будут накладываться
друг на друга. Чтобы избежать этого, мы сдвинем полу-
интервал действия i-й иголки на величину ia = i 2 а/>
так что теперь это будет Дг — [тг + ta, 'Tz + ia + a;] (оче-
видно, что если aj > 0 и достаточно малы, то Д, не пе-
рекрываются).
Согласно сделанным в п. 4.2.1 предположениям опти-
мальное управление «(•) непрерывно слева в точке и
справа — в точке tg. Продолжим «(-)вне отрезка [70, ?г]
с сохранением непрерывности (например, положив u(t) =
= w(?0) при t < ta и и^)==и({г) при t > tr) и впредь
не будем этого оговаривать.
Пусть все az > 0. Определим игольчатую вариацию
управления «(•) формулами
( w (0> С Go— б, U Д;>
~ J J — 1
и (t; а, т, ц) = < г n n \
Vi, t е Дг= T,+i 2 a,, T;+i 2 «/+&, )•
\ L t=i /=i /
(7)
324
Соответствующее семейство фазовых траекторий x(f;
/0, х0, а, т, о) определим как решение задачи Коши
х = ср(^, х, и (t\ а, т, и)), х(^) = х0. (8)
Для краткости далее х0=х(?0).
Лемма о пакете иголок. 1) При достаточно
малых е0 > 0, 6 > О решение задачи Коши (8) такое, что
1^0 ^0 1 < е0’ 1^0 ^0 I < ®0> 0 < < ®о> (0)
определено для t0—6 + 6.
2) Если t0—► t0, х0—>-х0 и аД 0, то x(t; t0, х0, а, т,
о)—>x(t) равномерно на отрезке [f0, ij.
3) Отображение (tu tg, х0, a)t-*x(^; tB, xB, a, v, v)
может быть продолжено до отображения, определенного
и непрерывно дифференцируемого в некоторой окрестности
точки (tv tg, Xg, б), и при этом
dx/dt1 = x{l(t1; tg, Xg, 0, т, и) =
= <P(Ji,/(O> «(О) = Ф(М. (10)
dx/dtg = xt,(t1; tg, Xg, 0, x, y) =
= —□(?!, f0)<p(f0, Xg, w(Q) = — Й(£г, i0)q>(?0), (11)
dx/dXg = xx, (t^, tg, Xg, 0, T, y) = Q(?1, tg), (12)
8x/daft= Xak (t^, tg, Xg, 0, r, y) =
tg)Ki(xk, Vk), (13)
где Q(t, r)—фундаментальная матрица решений системы
уравнений в вариациях (3)-и Д<р(т, у) определено фор-
мулой (5).
Доказательство этой леммы будет приведено в п. 4.2.6.
Ясно, что она обеспечивает нам дифференцируемость тер-
минальных членов, входящих в. условия задачи п. 4.2.2.
Что же касается интегральных членов, то, как и в п. 1.5.4,
мы,посвятим им отдельную лемму.
Лемма об интегральных функционалах.
Пусть функции fi(t, х, и) удовлетворяют тем же усло-
виям, что и в формулировке теоремы п. 4.2.2.
Если u(t, а, т, у) определено при а{ > 0 форму-
лами (7), a x(t-, tg, Xg, а, т, у)—решение задачи Коши (8),
325
то функции
^i(^l’ А>> а)
t,
— J x(t', t0, х0, а, т, v), u(i; а, г, v)) di,
to
i = 0,1, ..., т,
могут -быть продолжены до непрерывно дифференцируемых
в некоторой окрестности точки (fx, t0, х0, 0) функций
и при этом
dF{/dtt= t0, х0, 0) xfy, u(t1)) = fi(t1),
(14)
dFi/dtQ= te, xa, 0) =
= Л‘(^о> -'“О, « (^o)) "b Pol(if)) (p (it)’ •'“О! M Go)) =
= —fi(K) + pat(i'0')i(t0), (15)
dFi/dx^Fix^t^tg, xa, Q) = —poc(ta), (16)
dFi/da^F^iL, f0, x0, О) = Д/Дтй, vk)~
—Poc(tk) Дф(тл, vk), (17)
где poi(~t)—решение задачи Коши
dpoi (x)/dx = —p0l (r) <px (r, x (r), u (t)) +
+ fix^’ x(x), u(-r)), (18)
pot (fi) = 0
для неоднородной линейной системы, сопряженной к си-
стеме уравнений в вариациях (3), а Д/(.(т, v) определяется
формулой, аналогичной (5). Доказательство этой леммы
приведено в п. 4.2.7.
4.2.4. Редукция к конечномерной задаче. График оп-
тимальной фазовой траектории x(t) лежит в области G
и в силу второго утверждения леммы п. 4.2.3. (о па-
кете иголок) график решения x(t\ tn, х0, а, т, и) задачи
Коши (8) того же пункта также лежит в этой области
при t£[t0, /J, если выполнены неравенства (9) п. 4.2.3
с достаточно малым е0. Значит, четверка (х(- ; tg, х0,
а, х, v), и ( ; а, т, и), tg, ^) является управляемым
процессом для задачи (1)—(3) п. 4.2.2.
326
Положим
-^о» 00—’ФХ^О» ^0’ #(^1» ^о» ^0* ОС, Т, и)), (1)
ft
%0, a)=J fi(t, x(t\ tQt x0, a, r, v), и (/; a, r, v)')dtf
fo
z = 0, 1, ..., tn;
(2)
В силу третьего утверждения леммы о пакете иголок
и по теореме о суперпозиции, функции (1) непрерывно
дифференцируемы в некоторой окрестности точки (A, ta,
х0, ОУ- Для функций (2) то же самое следует из леммы
об интегральных функционалах и. 4.2.3.
Теперь мы можем рассмотреть конечномерную экстре-
мальную задачу—сужение задачи (1)—(3) п. 4.2.2 на
построенное семейство управляемых процессов^
А(А> А> ^о> а) = (А» А> хо’ а) _I- (А > А» a) (3)
/<-(А. А- хе, a)=-F((tu А> х0, а)+Т,(А> А. х0, а)^0, (4)
t = 1, 2, ..., т,
aft>0, k = \, 2, ..., N. (5)
Для этой задачи точка (А> А> хо> 0) является локальным
решением. Действительно, если выполнены ограниче-
ния (4), то четверка (х(- ; А’ хо> a> т> у)> и(- 1 “» т> v),
t0, является допустимым управляемым процессом за-
дачи (1)—(3) п. 4.2.2. Если 80 в неравенствах (9) п. 4.2.3
достаточно мало, то в силу второго утверждения леммы
о пакете- иголок выполняются неравенства (4) п. 4.2.1.
Следовательно, верно неравенство (5) п. 4.2.1, откуда
А, (А. А> -^о» а)
= 5,0(х(-; А> х0, т> у)> и (• > «, т, у), А> А)>
>з'0(х(-), «(•), А, А) = ^о(А. А> *0, 0),
f
а это и означает, что (А, А, х0, 0) — локальное решение
задачи (3)—(5).
Применяя к задаче (3)—(5) правило множителей Лаг-
ранжа из § 3.2, получаем следующее утверждение.
Лемма (правило множителей Лагранжа
для вспомогательной конечномерной за-
327
дачи). Существуют такие множители Лагранжа
К>о, %=(\, ...Д„т M’ = (P'i> .... Ы. (6)
не равные нулю одновременно, что для функции Лагранжа
т N
А(^, te, х0, а; К, ц, М = ЕЛ (^ + ^-) +S (7)
1=0 4=1
выполняются-.
1) условия стационарности
т т
A/,=S Мч+1Ж = 0- (8)
1=0 t=0
т т
Л/о=£ £Л»+Е (9)
t=0 г=0
т т
Лх. = X + Е = 0, (10)
1=0 1=0
tn т
+ Х Мч+н4=°, on
[=0 1 = 0
где обозначено = Ла (?х, f0, х0, 0; X, ц, £0) и т. п.-,
2) условия согласования знаков
Ь^О, i—l, 2, ..., т; k=i, 2, (12)
3) условия дополняющей нежеспгкости
МЛй. К К oj + TJ?!, ta, х0, 0)] = 0, (13)
i = l,2, ..., т.
4.2.5. Доказательство принципа максимума. За исклю-
чением одного не совсем тривиального места, остальная
часть доказательства будет посвящена расшифровке усло-
вий (8)—(13) п. 4.2.4. Собственно принцип максимума
(или в лагранжевой форме—принцип минимума), т. е.
соотнбшения (11) (или (10)) п. 4.2.2, получается при этом
из равенств (11) п. 4.2.4, т. е. условий Attft = 0. Каждое
такое условие соответствует одной из иголок, входящих
в «пакет», и если эта иголка определялась парой (тй, vk),
то мы получаем из него неравенство Н(rk, x(rft), vk, -)^
х(тА), ц(тА), •). Таким образом, чтобы получить
принцип максимума, ,мы должны перебрать иголки, отве-
328
чающие всем возможным парам (т, и), тогда как наш
«пакет» содержит любое, но конечное их число. Положе-
ние спасают простые топологические соображения, осно-
ванные на компактности. Применяя «лемму о центриро-
ванной системе», мы можем выбрать «универсальные» мно-
жители Лагранжа, пригодные для всего множества иголок.
А) Существование «универсальных» мно-
жителей Лагранжа. Изучим подробнее условия
(8)—(13) п. 4 2.4, внеся в них значения производных функ-
ций Ft и Т,, вычисленные при помощи двух лемм п. 4.2.3,
и уделяя особое внимание членам, в которые входят па-
раметры иголок (rft, vk).
Производные функций F: даны прямо в лемме об ин-
тегральных функционалах и, обозначив
ЛДт, u) = ff(T, х(т), у) —/,(т, х(т), н(т)) —
—Ро. (т)[ф(т, х(т), у) — ф(т, х(т), «(т)] =
= Af(T, У) — pOt(T) Дф(Т, У), (1)
мы видим, что
= yft),
а ни в одну из остальных производных параметры иго-
лок не входят, так что эти производные имеют одно и
то же значение для любого «пакета иголок» п. 4.2.3.
Аналогично производные функций
(/г, t0, х0, а) = ф, (/„, х0, tlt xf^; ta, х„, а, т, у))
вычисляются по теореме о суперпозиции и лемме о
пакете иголок, причем от параметров иголок зависят
лишь Tiaft. Если обозначить
= x(t0), fp т)[ф(т, х(т), у) —
—ф(т, х(т), и(т))] = ф1Л1П(?1, т)Дф(т, у), (2)
то
= Bt (ts, yfc),
а значения производных Ф(/1, одни и те же для
любого «пакета иголок».
329
Теперь имеем
т т
~ 2 + 2 Th =
B 1-0 B i=0 B
m
= 5 иА))+нл-
t=0
Поскольку, согласно условиям (12) и (11) п. 4.2.4, pft^0
и Aaft = 0, должны выполняться неравенства
2 uft) + B,(Tft, uft)]>0.
£ = 0
(3)
Рассмотрим теперь в пространстве R<“+I>* следующие
множества:
т
$={(*. 4)1 2/>1}.
т
К (т, ц) = {(%, м 2МЛ(т. + v))>0},
t=Q
tn
Tt=Ж 4) 12 К {Fltl + ^z) = 0}, I = о, i,
1=0 1 i
tn 4
X={(%, M 2 x,(A,o+^o)=0},
i =0
и, наконец, множество Z, состоящее из тех (К, Хо), для
которых А,о:>0, а i=l, ..., т, удовлетворяют усло-
виям согласования знаков и дополняющей нежесткости
(12) и (13) п. 4.2.4, тождественных условиям (13) и (14)
п. 4.2.2.
Все эти множества замкнуты, а сфера S еще и ком-
пактна, как замкнутое ограниченное подмножество ко-
нечномерного пространства
Условия стационарности (8)—(10) п. 4.2.4 соответст-
вуют включениям (к, Хо) € 7\, Тв, X, условия согласования
знаков и дополняющей нежесткости — включению (к, Хо) € Z
(все эти условия одинаковы для всех пакетов иголок).
Зависящие от иголок условия (11) п. 4.2.4 выполняются,
когда (к, ka)^X(T:k, vk), k=\, N. Наконец, по-
330
скольку множители Лагранжа определены с точностью
до пропорциональности и не могут одновременно обра-
щаться в нуль, их можно пронормировать так, чтобы
было (X, Х0)^5. Поэтому утверждение леммы предыду-
щего пункта означает, что
5ПТОПЛПХП2П П К(тй, уй)=А0. (4)
6=1
Рассмотрим систему замкнутых подмножеств
К(т, u) = SnTonrinXnZnK(T, v),
т€[?0, G]> «бП, (5)
компактного множества S.
Лемма о центрированной системе. Система
множеств К (т, v) имеет непустое пересечение.
Доказательство. Согласно (4) любое конечное
число множеств К и) имеет непустое пересечение. Такая
система множеств называется центрированной. По изве-
стной теореме [КФ, стр. 99] пересечение центрированной
системы подмножеств компакта непусто. В
Таким образом, существуют
(1, Х0)С /С(т, у)==
те ft, Fi],
pgU
= ХЛТ0ПЛПХП2П П К(т, у). (6)
Т е ft, 711
vs и
Это и есть искомые «универсальные» множители Лагранжа.
Действительно, 1,- не равны нулю одновременно ((X, Хс) С S),
удовлетворяют условиям согласования знаков и допол-
няющей нежесткости ((X, X0)£Z), удовлетворяют усло-
виям Л^= О, 1 = 0, 1, иЛХл=0 ((1, 10)£Т0ПЛПХ) и,
наконец,
tn
S \[Л,(т, У) + В,(т, у)]>0 (7)
j = 0
для всех т C[f0, Zj, v £ П.
331
Б) Вывод принципа максимума. Подставив
(1) и (2) в неравенство (7), преобразуем его к виду
МДГ.(Т> 0 — pthfOAqJfr, v)] +
/П Z-.
тЯдф(T> v)ls
= f(r, x(t), u)— f(x, x(r), h(t))—
—р(т)[ф(T> *(T)> y)~ф(т, X(T)’ “(T))] =
= — /7(т, x(t), V, p{x))+H(r, x(t), w(t), p(x)), (8)
где
f(x, x, «) = £ *, «), (9)
i=0
m m
XiZMO-E T) 0°)
1=0 i=o 1
— решение уравнения Эйлера—Лагранжа (8а) п. 4.2.2,
как мы увидим далее, и
Н (т, х, и, р) = рф(т, х, и)—f(x, х, и) (11)
— функция Понтрягина (ср. (7) в п. 4 2 2).
Неравенство (8), справедливое при всех т£|70, и
у £11, равносильно принципу максимума (11) ns-4.2.2
Н (т, х(т), н(т), р (т)) — max Н (т, х(т), и, р(т)). (12)
В) Вывод условий стационарности по
х(-). Дифференцируя (10) и учитывая, что pot (т) удовлет-
воряют уравнениям (18) п. 4.2.3, а
^^ = -Q(^, т)^(т),
(см. теорему п. 2.5.4), имеем
т
dp(T)/dz= £ XJ—р01(т)^(т) + ^(т)}—
t = 0
т л т
— S т) (Рх ('Г) = —Р (т) Фх (г) + X =
1=0 1 1=0
= —
332
т. е р(-) является решением уравнения Эйлера—Лаг-
ранжа (8а) п. 4.2.2.
Далее, прямо из (10)
г? т л
i=0 i=0 ' 1
/М гх
= — У Ч#- = —(13)
' дхх ')х1 ’ ' '
поскольку р01(1г) = 0 в силу (18) п 4.2.3, a Q(f, t) = E.
Здесь, как и в (6) п. 4.2.2,
т
(^0> -'‘•о» ^1> ^1) ~ 2 ^’11Р1 (^0’ ^0> ^1’ ^1) (14)
__ 1 = 0
— терминант, а полученное равенство (13) равносильно
первому равенству (9а) из п. 4.2.2 .
Наконец, условие АХо = 0, т. е. (10) п. 4.2.4, дает
после подстановки значений производных (12) и (16)
п. 4.2.3
0 = AXo=^j 2 —
i=0 1=0
mm
— S ^iPOi &) +£. "W<*i ~d7~') ~
1 = 0 i = o x 0'
— — 2 ^-iPoi(?0)+ S + 2 q (ix, ta)=.
i=0 1=0 i = 0
= p(U + k0>
так что верно и второе условие трансверсальности (9а)
п. 4 2.2.
Г) Вывод условий стационарности по t{.
После подстановки значений производных (10), (11), (14),
(15) п. 4.2.3 в условия А^^А^^О (8) и (9) п. 4.2.4
получаем с учетом обозначений (9) — (11) и уже дока-
занного равенства (13)
o=Afl= 2 V.G+S
f=0 1=0
т т л
= S ^Ji(^i)+S + 4>ix1-s-l ~
[ = 0 1-0 *“ 1
=f (У+к+/;,ф (Fj=М) -р (У Ф (G)+k = -н (^)+Itl
333
и
т т
о=Аго= S.M4+2
i=0 1=0
т т
= Zj ^'1—А(М + рО/(?о)ф(^о)] + ^2 + Ф<*> д7~]
1 = 0 ' i = o L °.J
*=-f (Q + Д Ъры(?о) Ф(U + f), + lX1 [-Q (tlt f0) <? (?0)] =
=?-нм+ра0)Ф(м+^=я(и+ito.
Этим доказаны обе формулы (12а) п. 4.2.2.
Д) Непрерывность функции /?(•). Вместе
с управлением u(t) функция-
= x(t), u(t), p(t)) =
x(t), + x(t), u(t)) =
' m
=—2 Mz(^> *(0> «(0)+/Ф)ф(^ *(0» «(0)
( = 0
непрерывна справа. Кроме того, каждая из функций
H(t, x(t), v, p(t)) непрерывна по t и, переходя к пре-
делу в неравенстве
H(t, x(t), v, р(х))^.Н (i, x(t), u(t), p (t)) — H (t), (15)
мы получаем
H(x, x(r), v, p(r))^lim — —0),
откуда
H (т) = sup/f (т, x(t), v, р (т)) ^ZZ(t—0). (16)
v gli
С другой стороны,
Н(х—0) = lim H(t,x(t), u(t),p(t)) —
/->1-0
= Н(т, х(г), и (х—0), р(х))= lim Н(х, х(х), v, р(т))^
(х, x(t), и (т), р(х)) = Н (т)
в силу того же неравенства (15). Вместе с (16) это оз-
начает, что Н (х—0)=Я(т), т. е. Н (/) непрерывна и
слева. |
334
4.2.6. Доказательство леммы о пакете иголок. Напом-
ним, что игольчатая вариация x(t\ ta, х0,<х, т, ^оптималь-
ной фазовой траектории х(-)—это решение задачи Коши
х— q>(7, %, и (tf; а, т, у)), (1)
(2)
где в свою очередь вариация w(Z; а, т, у) оптимального
управления и (t) определяется при Иу > 0 формулами
u(t-, а, т, у) = <
(vi’
t € Аг = + ia, +ia + «,),
UAy, a= “у
* i = i
(3)
Доказательство леммы о пакете иголок (лемма п. 4.2.3)
удобно разбить на две части. В первой из них, выделен-
ной в отдельное утверждение, мы доказываем равномер-
ную сходимость проварьированных фазовых траекторий
к х(-). Существенную роль здесь играет не столько ку-
сочная непрерывность управлений, сколько интеграль-
ная сходимость соответствующих правые частей диффе-
ренциальной связи (см. ниже формулу (5)). Чтобы отте-
нить это, мы распространяем утверждение также и на
случай измеримых управлений (определив сначала под-
ходящим образом понятие измеримости в случае, когда
управления принимает значения в произвольном топо-
логическом пространстве). Вторая часть доказательства
леммы о пакете иголок непосредственно связана с кусоч-
ной непрерывностью и- опирается на классическую тео-
рему о гладкой зависимости решений от начальных
условий.
Определение. Пусть U—произвольное топологи-
ческое пространство и /—отрезок числовой прямой.
Отображение и: / —> П называется измеримым (в смысле
Лебега), если существует конечная или счетная после-
довательность непересекающихся измеримых подмножеств
А„ такая, что:
а) ограничение и | Ап продолжается до функции, не-
прерывной на замыкании Ап\
б) /\ U Ап имеет лебегову меру нуль,
п
Ясно, что всякое кусочно-непрерывное отображение
измеримо в смысле этого определения (в качестве А„
берем интервалы непрерывности). Почти также очевидно,
335
что в случае, когда Hc:Rr функция, измеримая в смысле
этого определения, измерима и в обычном смысле [КФ,
гл. V, § 4].
Действительно, пусть «„(•)—функция, непрерывная
на А„, и совпадающая с «(•) на Ап. Полагая w„(7) = 0
вне Ап, мы получаем измеримую функцию на R. Харак-
теристическая функция %л„(-) множества А„ также из-
мерима, а поскольку и (t) = 2 %ав (0 ип (0 почти всюду
п
на /, измерима и u(t).
Упражнение. Докажите, что если UcRr и функция и:
I —> U измерима в стандартном лебеговом смысле, то она измерима
и в смысле приведенного выше определения. Указание: восполь-
зуйтесь С-свойством Лузина [КФ, стр. 291].
В формулировке следующей леммы 31—некоторое ха-
усдорфово топологическое пространство [КФ, стр. 95].
Л ё мм а 1. Пусть функции <р и фх непрерывны в Gх II
х: [4/M—R” —решение дифференциального уравнения
Х = у (f, х, и (/)) (4)
и его график Г = {(7, х (/)) [ tg ts^tJcG.
Пусть далее б0 > 0 и иа: (f0 —б0, + б0) —► П —се-
мейство измеримых управлений такое, что для всех t и
всех а£51 значения ua(t) содержатся в некотором ком-
пакте сП
Пусть, наконец, u(t) = u% (t) для некоторого а £31 и
G+60 •
lim |<р(£, x(t), ua(t)) — q>(t, x(t), u(Z))|cf£ = 0. (5)
а-> а я
/о-Оо
Тогда решения Xa(t, tg, х0) задачи Коши
X = ff>(t, X, ua(t)), x(tg) = xg
при некотором б > 0 определены на отрезке [?0—б, —б]
для всех (tg, х0, а) из некоторой окрестности точки (ta,
x(tg), а) в RxR”xSl и при ta—+ta, xg —> х (f0), а—>а
(/, tg, х0) >х(/)
равномерно по t^.[tg,
336
Доказательство. Применим к рассматриваемому
случаю теорему 2 п. 2.6.5, положив
Fa(t, X) —<р(/, X,
(6)
А) Если Ап—те множества, о которых говорится в
определении измеримости, примененном к иа(-), то при
фиксированном х функции / н-> ср (/, х, wa (/)) непрерывны
на Ап, а следовательйо, х)—измеримые функ-
ции и выполнено предположение А) п. 2.5.1. При фик-
сированном t функции Fa вместе с ср дифференцируемы
по х, так что выполнено и предположение Б) п. 2.5.1.
Б) Для любого компакта функции ср и срх не-
прерывны на компакте а следовательно, и огра-
ничены. Обозначив
М = max | ср (t, х, и) |, Мх = max |1 ср* (t, х, и) ||,
мы видим,” что выполняется условие В') теоремы 2
п. 2 5.5 с = и k(t) = Mx поскольку по условию
иа (О Условие Г) той же теоремы, совпадает сч(5).
Таким образом, к рассматриваемой ситуации приме-
нима теорема 2 п. 2.5 5, из которой и вытекает доказы-
ваемое утверждение. Ц
Доказательство леммы о пакете иголок.
А) Проверим выполнение условий предыдущей леммы.
Часть из них, относящаяся к ср и х(-), входит в усло-
вия теоремы о принципе максимума.
Выше мы уже предположили, что управление и(>)
продолжено вне отрезка |70, Fj, так что при /^С/Оипри
/^^это непрерывная функция. Поэтому мы будем счи-
тать далее, чтоп(-) определена на отрезке Д = [?о—60,
Ч + 80], 80 > 0, а ее точки разрыва лежат в интервале
(?0. Q
Пусть /(1) < tm < . . < tls>—эти точки, tm = tQ—60,
/(S + 1) — функция
,, ( u(t), t < t<x>,
и, (0 = < ~
| —0), t=t^,
непрерывна на отрезке/, /(')] и образ этого от-
резка при непрерывном отображении /—>П компак-
тен в U, поскольку /, — компакт. В соответствии с фор-
337
мулами (3) значения управлений и (t\ а, т, v) лежат в
компакте
3^о= U U {t>!.......М-
1 = 1
Остается проверить условие интегральной сходимос-
ти (5). На компакте
г={(/, х(0, «)| ие^0} = гхгг0
непрерывная функция ср ограничена: |ф|^Л4. При столь
малых «у > 0, что полуинтервалы А, не пересекаются,
из формул (3) имеем
?1+60 ~ ______
] ф (/, x(t), и (t-, а, т, у))—ф (t, x(t), й (t)) | dt —
/-
JV Л N
= S\ |ф(*. x(t),v.)— <f(t, x(t), u(t))\dt ,=
/=1Д/ /=i
= 2Ма->0
при а, 10, так что условие (5) выполнено.
Применяя лемму 1, убеждаемся в справедливости
первых двух утверждений леммы о пакете иголок п. 4.2.3:
для достаточно малого е0 > 0 решение x(t', t0, х0, а, т, у)
задачи Коши (1), (2) при (ta, х0, а), удовлетворяющих
неравенствам (9) п. 4.2.3, определено на A = [f0— 8,
fx + 6] (первое утверждение), и при t0 —> tg, х0 —>х0, а,|0
х(£; ta, х0, а, т, у)—>x(t)
равномерно по t € J70, (второе утверждение).
Б) Перейдем к рассмотрению отображения (fu tg, хд,
а)—*-х(^; tg, а, т, у). Обозначим, как обычно, через
X (/, tg, х0) решение задачи Коши
X — ф (t, х, и (t)), x(ta) = x0. (7)
По теореме 1 п. 2.5.5 функция Х(-, •, •) определена и
непрерывна в области (t„—60, /1 + 5())хС, где G — неко-
торая окрестность графика Г решения х(-). Если же
мы сузим область определения так, чтобы ta и t не пе-
реходили через точки разрыва управления «(•), то
дифференциальное уравнение в (7) удовлетворяет усло-
338
виям классической теоремы о дифференцируемой зависи-
мости решения от начальных данных (п. 2.5.7), так
что X (t, t0, х0) будет непрерывно дифференцируемо по со-
вокупности аргументов. В частности, X непрерывно диффе-
ренцируемо в некоторых окрестностях точек (tk, tk, x(tk))f
поскольку в некоторых окрестностях точек tk управле-
ние «(•) по нашим предположениям непрерывно.
Далее, обозначим через В (£, а, т, у) значение при
1 — решения задачи Коши для уравнения (1) с началь=
ным условием х(?0) = £, т. е.
В (I, а, т, у) =x(ilt t0, 1, а, 7, у). (8)
В соответствии с формулой (13)_п._2.5.5 и формулами
(3), задающими управление u(t, а, т, у), имеем
х (^i> ^о> -^о> т, у) — X (Zj, ?), u (X (^0, tB, х0), и, т, у)) (9)
(от tB до tB мы решаем уравнение х = ср (t, х, и) с управ-
лением u = u(t), а затем от tB до —с управлением
u = u(t;a, т, а) и, наконец, от до —снова с управ-
лением u = u(t). Важно отметить, что, как и формула
(13) п. 2.5.5 формула (9) верна при любом расположе-
нии точек относительно ?г
Если мы теперь сможем продолжить отображение
(5, а)ь->В(£, а, т, у) до отображения класса С1, опреде-
ленного в некоторой окрестности точки (x(tB), 0) (т. е.
сможем продолжить его на отрицательные а,- с сохране-
нием непрерывной дифференцируемости), то в соответст-
вии с формулой (9) и отображение (tiy tB, хв, a)t-*x(^;
/0, х0, “> Ti у) будет продолжено на некоторую окрест-
ность точки (?х, tB, хо,О), а по теореме п. 2.2.2 оно будет
непрерывно дифференцируемым как суперпозиция трех
непрерывно дифференцируемых отображений: (tB, x0)i—>
>->X(tB, tB,xB), (^,7)н^В(?, 7,т, 7), (^, ^-Ло)-
В) Пусть т£(Г0, и ygU фиксированы. Обозначим
через Yv(t, tB, ув) решение задачи Коши
.y=(f(t, у, у), y(tB)=yB. (10)
В силу локальной теоремы существования (п. 2.5.2) и
классической теоремы о дифференцируемости решения по
339
начальным данным (п. 2.5.7) Yv(t, ta, уа) определено и
непрерывно дифференцируемо в некоторой окрестности
точки (т, т, х(т)).
Если т—точка разрыва управления и (•), т. е. и (т—0)=#=
^н(т), то наряду с «(•) рассмотрим управление
\ и (т), t < т.
Поскольку «(•_) непрерывно в некоторой окрестности точ-
ки т, решение X (t, t0, х0) задачи Коши
х = <р (t, х, и (t)), %(^) = х0, (11)
также определено и непрерывно дифференцируемо в не-
которой окрестности точки (т, т, х(т)). Если же т—точка
непрерывности «(•), то самоХ(£, tg, хе) обладает тем же
свойством, и в следующих далее формулах можно счи-
тать Х = X.
Дополним набор т = (т1, точками т0=^/0 и
Тл?+1=^> так что ?0 = т0<т1^...<тл?<тл?+1 = Г1, и
рассмотрим суперпозицию отображений
Е (£, а, т, v)—P о Хд? о Zn °- • -°Xk о о ХА_х о.. .о Z± о Хо,
(12)
где Р(1, а)=ё
хй(5> «) = (^(^+1, g),a) (13)
и
Z*(£, а) = (Х(тА, тА + йа + ай, УОА(т4 + 6а + ал, тА + £а,
Х(тА + /га, тА, 1))), а). (14)
Поскольку Xk и Zk непрерывно дифференцируемы в ок-
рестности точки pft = (x(Tft), 0), причем Xft (pft) = pft+1,
^а(Р*) = Pk> а ? линейно, суперпозиция (12) определена
и-непрерывно дифференцируема в некоторой окрестности
точки р0 = (х(?0), 0)=(х„ 0).
Лемма 2. Если все аА > 0 w достаточно малы, то
Е (1, а, т, v) = S (Е, а, т, v) = x(t1, t0, 1, а, т, ц). (15)
Доказательство. Обозначим для краткости x(t)=
— x(t, ta, g, a, т, v). Если все aA > 0 и достаточно малы,
340
то полуинтервалы Д,, входящие в определение (3), по-
парно не пересекаются и расположены между t0 и tr в
порядке возрастания номеров.
N
Пусть s( =т(-На = т(+t 2 “у—левый конец полуин-
тервала Д,, s0 = r0 —10, sN+1=-xN+1 = t1. Докажем по ин-
дукции, что
x(sk) — X(,sk, хк, gft), (16)
где £ и
gft = PoXft_1oZA._1oXft_2o...oZ1oX0(l, «). ^>1; (17)
в частности, —Р о Xa(g, а) = X (т^, т0, £). Поскольку
при t0 = xg^.t < sx дифференциальные уравнения в (7) и
(1) совпадают и x(r0) = g = X(r0, т0,10), то в этом полу-
интервале x(t) = X(t, т0, £0), и, переходя к пределу при
t—+sx и учитывая тождество X (s1( т0, £„’) = X (sx, тх, X (тх,
т0, £„)), получаем (16) при k=l.
Предположим, что (16) верно для некоторого k. Чтобы
перейти по решению х(-) от sk до sft+.x, надо в силу (3)
проделать следующее. От sk до sA4-aft решаем'уравнение (10)
с начальным, условием z/e = х (sft), в результате чего полу-
чаем x(sft+aft) = KaA (sft + aft, sft, x(sft)). Далее от sA+aft,
т. е. от конца ДА, до sft+1—начала Дй+1, решаем урав-
нение (7) с начальным условием x0==x(sAi + aft) и получаем
равенство
X (s*+i) = X (sk+1, sft+a*, x(sft4-aft)) =
=X(sft+1, sft+aft, Ytk (sft4-aft, sft, x(sA)).
Согласно (13) n. 2.5 5 справедливо тождество
X (t, Т, X (T, tg,'Xg)) == X (t, tg, Xg).
Воспользовавшись им и равенством (16), верным по
индукционной гипотезе, получаем последовательно
x(sk+1)=X (sft+1, rft+1, X (rft+1, хк, X(rft, sk+a.k, x (sk+a.k))))=
~X(sk+1, т*+1, Х(тА+1, xft, X(rA, sk-\-ak,
YVk(sk + ak, sk,X(sk,xk,lk))))). (18)
Теперь заметим, что если все aA > 0, то xk < sk < sk-\-ak,
а так как при t^xk уравнения (7) и (11) совпадают,
то Х(хк, sft + aft, ?) = Х(т*, s* + aA, I) и X(sk, xk, gft) =
₽= X (sk, xk, |ft). Следовательно, используя сначала опре- ,
341
деления (13) и (14), а затем'(17), мы получаем
* + Yvk (sh + ak, sk, X (sk, тАЛО))) =
= P Q Xk ° Zk(^,k,a) = P о Xko Zko X^^o.. .oX0 (£, a) =
Поэтому (18) совпадает с (16), в котором k заменено на
k +1, и, таким образом, (16), верно при всех k~^A.
Остается заметить, что при k=N + \ (16) превращается
в равенство
x(?1) = X(7l, tv b + i) = b+I =
= Р о XN о Zno ... О Хо (I, а) = 3 (5, а, т, v)
(последнее согласно (12)) и, так как по определению
x(fI) = B(g, а, т, у), (15) доказано. Ц
Как уже было сказано, суперпозиция (12) непрерывно
дифференцируема в некоторой окрестности точки (х0, 0).
Следовательно, 3 (£, а, т, у) (которая раньше была
определена только при а, > 0) допускает непрерывно
дифференцируемое продолжение на эту окрестность.
Согласно п. Б) отсюда вытекает,_ что х(^, t0, х0, а, т, у)
допускает (при фиксированных т, у) непрерывно дифферент
цируемое продолжение на окрестность точки-(?v ta, х0, б).
Остается доказать лишь формулы (10) — (13) п. 4.2.3
для частных производных этой функции в точке (tlt t0, х0, б).
Г) Прежде всего заметим, что
, x(t, ta, х0, 0, т, v) = X(t, t0, ха), (19)
x(f, t0, x(t0), 0, т, у) = Х (t, t0, х(/0))=х(/), (20)
x(fl( te, х0, а, т, у) = В (х0, а, т, у). (21)
Согласно (19) и (21) частную производную по х0 мы мо-
жем найти, применяя теорему п. 2.5.6
? Y й 7 7а . ds (хо- £ т> 0 I
х<” и’ т’ v> Ха=х(7о)- дх0 k=J(?o)
= дХ(^’ - L > = Q ?о>’ (22)
где Й(С т)—фундаментальная матрица решений уравне-
ния в вариациях
г = ср* (t, x(t), и (£)) г
(в формуле (2) п. 2.5.6 надо положить F(t, x) — (p(t, х,
и учесть (20)). Этим доказано (12) п. 4.2.3.
342
Теперь воспользуемся формулой (9), заметив, что, как
было сказано в п. Б), в окрестности точек (tk, ik, х(1кУ),
k — 0, 1, производные функции X(t, t0, х0) можно вычис-
лять, применяя классическую теорему о дифференцируе-
мости по начальным данным (формулы (1)—(4) п. 2.5.7,
где снова F(t, x) = q>(t, х, Дифференцируя (9) и
учитывая уже найденную формулу (22), а также, что,
согласно (20) и (21),
Е (X (?0, t0, х (?„)), 0, т, у) = Е (х (?„), 0, т, 0==_ _
= x(t1, ta, х(?0), 0, т, vj^xfy,
имеем
Зх/5/1=ЗХ(?1, tlt =ф(?х, x(?i), и (?!)),
dx/dt0=зз (g, о, х, Бм к=ад>> дХ (f0, t0, х (QM |Zo=?0 =
- Q U [—Ф 6>, х (?0), w (f0))].
Этим доказаны (10) и (И) п. 4.2.3.
Пусть теперь а( =0, i=£k и aft > 0. Обозначим для
краткости
х (t, ак) = х (t, ta, х (/„), (0, ..., 0, ак, ..., 0), т, и).
При таком выборе а, согласно (3), в полуинтервале
4-дифференциальные уравнения (1) и (7)
совпадают и х (t0, <xk)=x (Zo), а потому в этом полуинтервале
х(/, ай) ==%(/) и, переходя к пределу, получаем
x(rft+feaft, ak) = x(xk + kak}. (23)
Далее, при хк + kak t < xk +feaA4-aft мы решаем диф-
ференциальное уравнение (10) с начальным условием (23)
и с v = vk, откуда
x(rA + feaft+aft) =
= ^А(Ъ+^й+аА. xk + kak,x(xk-[-ka.k)). (24)
В оставшемся промежутке xk-j-(k + 1)а* t tr мы снова
возвращаемся к уравнению (7), теперь уже с начальным
условием (24). Этот промежуток мы разобьем на два,
фиксировав s так, что в интервале (rft, s) не было то-
чек разрыва «(•). Величину ак > 0 будем считать столь
343
малой, чтобы было тк < хА + (fe 4- < s. Имеем
x(?i,aft)-=X(?i, s, x(s, aft)) =
= X(tlt s,X(s, -rft + (& + l)aft, x(xft + (&4-l)aft, aft)))=«
= Х(?П s, X (s, Tft+(£ + l)ccft, YVk (rft + (&+ тй +
A-kak, x(xk+kak))).
При дифференцировании этой формулы мы должны учесть
следующие равенства:
4^- (?,, s, х0) I Л = Q(F1, s)
дха ' 1 I Ха-Х (S, 0)=л: (s) ' 1 '
((1) п. 2.5.6; i± и s фиксированы);.
t0, х(хк, 0))|,o=Xfc = — Q(s, ь)ф(тА, x(xft),u(xft)),
^7-(S’ T*’ X°) I *»= * (rft, о)=2(тр =£2(s> Tft)
((5) и (6) n. 2.5.7; классическая теорема применима,
поскольку на отрезке [xft, s] управление «() непрерывно
и + (^ + 1)ай < s)’
дУ. Л .
~дГ(^ ^,x(xA))|r=Tft = <p(xft, x(xft),uft),
дУв I „ ‘
~gT *<” X I h = Tk = — Ф X (Tft)’ Vk)>
° dK0
-g^(Xk, Уа) = ^
(формулы (4) —(6) n. 2.5.7, где следует положить F(t, x)=s
= cp (/, x, vk) и -учесть, что всегда Q(/, t) = E)\ и, наконец,
х(тй) = ф(Ъ, x(tft), u(tJ) из (7).
Таким образом,
“й=°
Эа* ба*
дХ п ,
~377^1’ s’
, дХ
дХ (s, т^, х (Tfe))
,= ?(s)l dt0
^(s, Tft, x(Tk)) xk,x(xk))(k + l) +
-r-^(Tfe> xk’X(.xk))k + ^-(xk, xfc, х(тЛ))х(тй)^|==
= Q s) {— Q (s, t*) cp (xft, x (xft), w (xfe)) (fe +1) +
+ Q(s, тЛ)[ф(тЛ, x(xk),vk)(k + \)—ф(тй,х(тй), vk)k +
+4>(xk, x(xfc), u(xt) fe]} =
. =Q(flt Tft)[q>(TA, x(xk), vk)—<p(Tk, x(xfc), и (xft))J,
344
чем доказано (13) п. 4.2.3 (равенство £2(4, s)£2(s, xk)=
—£2 (4, Tk) имеет место по основному свойству фунда-
ментальной матрицы (11) п. 2.5.4). -
4.2.7. Доказательство леммы об интегральных функ-
ционалах. Пусть Ej = (g0, 'Sj, .--Лт), f = fl- ’>[«).
F = (FB, Ft, ..., Frn) (функции^,- определены в формули-
ровке леммы в п. 4.2.3), u(t, а, т, п) и x(t; t0, х0, а, т, и)
имеют тот же смысл, что и в пп. 4.2.3 и 4.2.6.
Рассмотрим при ak > 0 задачу Коши для системы
(п+/п + 1)-го порядка
a. f х\ ~ - - - ( <р (t, х, и U, а, т, v)) \
Х=( , )= m (t, х, |, и (t, а, т, v)) = ( ------,
\| / \ f (t, х, и (t, а, т, v)) /
(!)
x(ta)~x0, =
Уравнения для х здесь не содержат £ и совпадают с
(1), (2) п. 4.2.6. Поэтому их решением является
х(/; t0, ха, а, т, и), а тогда, как легко видеть,
F (tlt te, ха, а) === g (М tt, х„ а, т, и).
Следовательно, возможность продолжения этой функции
на неположительные ak и непрерывная дифференцируе-
мость в некоторой окрестности (4, 4- *о- 0) вытекают из
леммы о пакете иголок, примененной к системе (1), а
значения производных находятся по формулам, анало-
гичным (10)—(13) п. 4.2.3:
Ц=ф(4). ^=-£2(4-4)ф(4)«
° (2)
^ = £2(4,4), Д = Й(4, тА)Дф(т*, vk),
где
— фундаментальная матрица решений системы уравнений
в вариациях
гМеН; (()О
(3)
345
(Q,y — прямоугольные блоки в матрицей размерами пхп,
п х т, тхп и пгхт соответственно). Учитывая, что <р
не зависит от мы получаем из (3), что Q является
решением задачи Коши для матричного дифференциаль-
ного уравнения
( йц ^12 \ f фх (0 о\ / Йц Й^2\
dt \ Q21 Й22 / (/) О/ \Й21 Й22/
(4)
(ЙцС*, -т) Й12 (т, т)\_ fEn 0 \
\Й21(т, т) Й22(т, t)J \0 Ет) ’
Решая поочередно четыре- матричных ’ уравнения, со-
ставляющие (4), имеем
dQu (t, x)!dt = (О Qu (t, т), Qn (т, т) = Еп,
откуда й„(/, т) = й(£, т)—фундаментальная матрица си-
стемы (3) п. 4.2.3. Уравнениям
dQI2 (t, x)/dt = (О Й12 (Л т), Й12 (т, т) = О,
удовлетворяет й12 (4, т) =s 0, и по теореме единственности
другого решения не может быть. Далее
dQ21 (t, x)/dt = fx (0 Qn = ]к (/) Q (/, т), (t, т) = О,
откуда
t
Й21(/, т)= S fx(s)^(s> x)ds.
т
В частности,
—Й21 (?п т) = р„ (т) = (р00 (т), ..., рат (т))
является решением задачи Коши (18) п. 4.2.3 (см. (14)
в п. 2.5.4; можно убедиться в этом также и непосред-
ственно, дифференцируя по т и учитывая свойства фун-
даментальной матрицы, описанные в той же теореме
п. 2.5.4). Наконец,
dQ23(t, x)/dt = fx(f)Q12(t, t) = 0, Q22(t, t) = Em,
откуда й22(/, т) = Ет. Таким образом,
й(?п ° ).
v 1 ’ \-Ро(т) EmJ
Подставляя в (2) и отделяя то, что относится к
346
§ (if, tB, x0, a, r, v) = F(t1, tB, x0, a), мы получаем
df/dt. = dt/dtB = - Q21 (?x, t.) <? (?0) -Й82 (K h) f(t0) =
л =мш(и-?(и>
dF/dxB = df/dx. = Q21 (fn f0) = — pB (iB),
dF/dak = d&dak = Q2I (tv xk) Дф (xk, vk) +
+ Q88(?1, r*)Af(rft, vk) = — р0(тй)Дф(тй, vk) + kf(xk, vk),
что совпадает с (14) — (17) п. 4.2.3. В
§ 4.3* . Задачи оптимального управления,
линейные по фазовым переменным
Этот параграф посвящен одному специальному классу
задач оптимального управления. Этот класс достаточно
важен и с прикладной точки зрения, но для нас он.
интересен не только этим. На примере задач с линейной ,
структурой по фазовым переменным можно наиболее
отчетливо продемонстрировать одну из самых принци-
пиальных идей всей теории. Речь идет о «скрытой вы-
пуклости», всегда присутствующей в задачах оптималь-
ного управления. Именно она в конечном счете дает
возможность записать необходимое условие в виде «прин-
ципа максимума», т. е. в форме, характерной для задач
выпуклого программирования. И если в предыдущем
параграфе мы старались подчеркнуть связь задач опти-
мального управления с общей теорией гладких экстре-
мальных задач, то здесь на первый план выдвигается
их связь с выпуклым анализом.
Отметим еще, что (как это и характерно для задач
выпуклого программирования) необходимые условия
экстремума почти смыкаются здесь с достаточными.
Наконец, и это тоже важно с точки зрения выявления
скрытой выпуклости, мы будем в этом параграфе рас-
сматривать измеримые управления, а не только кусочно-
непрерывные.
4.3.1. Редукция задачи оптимального управления,
линейной по фазовым переменным, к задаче ляпунов-
ского типа. Пусть Д = ]70, Ц—фиксированный отрезок
числовой прямой, af. Д —► R"’, i = 0, 1, ...,m, и А: Д—>
-^^(R", R")—интегрируемые векторные и матричная
функции; И—топологическое пространство, /у. AxU—>R,
34Z .
i — 0, 1, .... m, mF (•, •): Axil—> Rn—непрерывные
функции; yOi-, y1Z, i = 0, 1, — элементы Rn*, cif
i=l,2, ..., tn,— числа.
Экстремальная задача
Л>(*(-)> «(•))=$ (а0 VMO + MV w(0))^ +
д
+ Too* Vo) + W (Q -* inf,
x = A (t)x + F(t, u(t)), u(t)^U, (1)
Ji(x(-), «(•))=$ (a{(f)x(f) + fi(t, u(t)))dt +
д
H- Yoix Vo) H- Yitx (V)
в которую величины, связанные с фазовой траекторией
х, входят линейно, называется задачей оптимального
управления, линейной по фазовым переменным. Она, разу-
меется, является частным случаем общей задачи опти-
мального управления из § 4.2. Однако здесь мы не-
сколько расширим совокупность допустимых процессов.
Обозначим через множество измеримых (в смысле
определения п. 4.2.6) отображений и: А—>-11 таких, что
функции t t->fi (t, u(t)) и t£+F(t, u(t)) интегрируемы.
Пара (x(>), «()) называется допустимым процессом,
если х('): А —> R" абсолютно непрерывная вектор-функ-
ция (см. п. 2.1.8), «(•)€%
х (t)‘= А (/) х (0 + F (t, и (t))
почти всюду и выполняются неравенства J ( (х (•), и (• ))5sq.
Допустимый процесс (х(-), «(•)) называется оптималь-
ным, если существует такое е > 0, что для любого до-
пустимого процесса (х(-), «(•)), удовлетворяющего усло-
вию ||х(-)—х(')||с(д, r«) < е .выполнено неравенство
• Л(*(-), «(-)>^Л(^(-). «(•)).
Мы покажем сейчас, что линейная структура- позво-
ляет преобразовать задачу (1) к такому виду, где х(-)
и «(•) в некотором смысле. разделены (и, в частности,
отсутствует дифференциальная связь).
Пусть Q(-, •)—фундаментальная матрица (п. 2.5.4)
решений однородной линейной системы
х=Д(?)х. (2)
348
, В соответствии с формулой (13) и. 2.5.4
t
x(t) = Q(t, io)x(to) + \ Q(t, x)F(x, u(x))dx. (3)
to
Подставляя (3), преобразуем функционалы задачи (1):
7i(x(-), »(•)) =
Ц г Г * Ъ
= Па,-(^) Q(t, t0) x(t0) + §Q(t,x)F (x,u(x)) dx /Л +
to I L to J)
' +S ft(t, «(t))dt + yoix (/„) +
to
t.
t,
tl t
= a{ (Z)'Q (/, t) F(t, u
?0 to
(*1
+ <$ a,(f)^(G Q^+Vof + Vu-^^i, Q}x(Q +
tl
+ Vu j Й Gv T) F (T> » (T)) dx=
to
ti । G
== J -j J a; (t) £2 (t, r) dt F (т, u (t)) 4-
to
+ ^-(т, и(т)) + уп-£2(/1( x)F(x, u(t))Lt +
$ G/G, u(x))dx 4-pzx(f0),
где
G/(t, «) = р, (т)Г(т, «)—fi(r, u),
Pi = Yoi Pi Go),
tl
Pi№ = — Vu^(^, T:)-^\ai(t)Q(t, x)dt,
T
i = 0, 1, ..., tn.
(4)
(5)
(6)
(7)
349
Теперь задача (1) приобретает вид
J9(x(-), «()) = —$ Go(*> w(O)^+Pox(^)->inf,
A
(8)
h{x (.),«(.)) = -$ G; (t, и (/)) dt + p,-x (t0) ct.
A
Такую задачу мы будем называть задачей ляпуновского
типа или просто ляпуновской задачей.
4.3.2. Теорема Ляпунова. В установлении связи между
задачами оптимального управления и выпуклого про-
граммирования теорема Ляпунова играет ключевую роль.
Она будет сформулирована здесь для случая векторной
функции р: R—>R" и меры Лебега т на прямой R.
Незначительное усовершенствование доказательств позво-
ляет распространить эту теорему на случай произвольного
пространства с заданной в нем о-алгеброй © и произволь-
ной непрерывной (иеатомической) конечной векторной
мерой р: > R". В приведенной ниже формулировке
©—это о-алгебра измеримых по Лебегу подмножеств
в R, а р (А) = Р
А
В отличие от Других мест нашей книги, здесь и
в следующем пункте нам придется использовать некото-
рые факты из функционального анализа и теории меры,
которые, несмотря на их большое принципиальное зна-
чение, обычно не входят в основные университетские
курсы. Начнем с определений. Термины «измеримость»,
«интегрируемость», «почти всюду» и т. п. далее понима-
ются в смысле Лебега (для измеримости удобно пользо-
ваться определением, приведенным в п. 4.2.6). Две функ-
ции называются эквивалентными, если они совпадают
почтц, всюду.
Определение 1. Пусть А—произвольный проме-
жуток числовой прямой. Пространствами (А) и (А)
называются нормированные пространства, элементами
которых являются классы эквивалентных между собой
функций х: А—>R, обладающих конечной нормой, кото-
рая задается равенствами:
в пространстве АДА):
||х ()!!=. (1)
А
350
в пространстве (А):
||x(-)]|=sup vrai|x(OI = inf sup |x(0|- (2)
Д N.m (Л') = 0 t e
Предложение 1. Пространства Li(&) и Lm (A)
банаховы, причем Lx (А) сепарабельно. Пространство (A)
изометрически изоморфно сопряженному пространству
Li (А)*, так что замкнутые шары в нем *-слабо компактны.
Доказательство .этих утверждений мы заменим следую-
щими ссылками: полнота и сепарабельность пространства
LX(A)—[КФ, гл. VII, § 1] (существование счетного базиса
у меры Лебега на бесконечном промежутке сразу следует
из его существования на конечных отрезках, поскольку
‘каждый такой промежуток представим в виде объедине-
ния счетного числа отрезков); компактность в «-слабой
топологии замкнутых шаров в пространстве, сопряжен-
ном к сепарабельному [КФ’, стр. 202J, изометрический
изоморфизм между Li(K)* и (А) (а, значит, и полнота
последнего) [4, стр. 314].
Определение 2. Пусть X—линейное простран-
ство, А с X. Точка х множества А называется его край-
ней точкой, если
х=ахх + (1—а)х2, 0<а<1, х2 £ А хх = х2.
Упражнение 1. Докажите, что по крайней-мере одна из
точек Xi, .. ., хп является крайней для их выпуклой оболочки
conv {%1, ... 7
Теорема Крейна—Мильмана. Компактное вы-
пуклое подмножество локально выпуклого линейного топо-
логического пространства X содержит по крайней мере
одну крайнюю точку и совпадает с выпуклой замкнутой
оболочкой своих крайних точек.
Доказательство этой теоремы см. [4, стр. 477].
Перейдем теперь к основной теореме этого пункта.'
Теорема А. А. Ляпуно'ва. Если р:‘Д—>Rn,
р (•) = (рх (•), . .., рп (•)) — интегрируемая векторная функ-
ция, то множество
М = Jx С R" I х= J р (t) dt, А € @ I
I А )
Является выпуклым компактом в R". (Напомним, что ® —
это о-алгебра множеств, измеримых по Лебегу Л
351
Доказательство А) Рассмотрим отображение
Л: (А)—► R", определяемое равенством
Л(ф(-)) =
д 'Д'
Оно линейно, и, кроме того, оно непрерывно относи-
тельно «-слабой топологии в LriQ (Л) (по определению эта
топология слабейшая из тех, в которых все отображения
ф(«)*-*<ф(.), р(-)>, p(-)€At(A) непрерывны).
Множество
является замкнутым шаром в £„ (А) (радиуса 1/2 и
с центром в точке ф(-), ф(0 ==1/2). Следовательно, оно
выпукло и, согласно предложению 1, компактно в «-сла-
бой топологии. Поэтому его линейный и .непрерывный
образ ЛЦ7 также является выпуклым и компактным.
Характеристическая функция
J 1,
о, Ц А
любого множества А С S, очевидно, принадлежит W,
а потому
$р(0^=$Х4(0р(0^ = Л(Хл(-))€Л1Г,
А Д
и, следовательно, AfaAW7. Остается доказать, что
Л1==Л1Г.
Б) Пусть точка g^AlF. Ее прообраз W$—W ПЛ'1^)
является пересечением выпуклого и компактного в «-сла-
бой топологии множества 1Г и замкнутого в той же то-
пологии (поскольку Л относительно нее непрерывно)
выпуклого множества (аффинного многообразия) A~x(g).
Следовательно, выпукло и компактно и по теореме
Крейна—Мильмана имеет крайнюю точку х(-)€^.
Если мы Докажем, что х(-) является характеристи-
ческой функцией некоторого множества то тогда
g = х (t) р (t) dt — J р (t) dt^M
Д A
и теорема будет доказана.
Й52
В) Если 0<x(i)Cl и %(•) не является характе-
ристической функцией, то для некоторого е > 0 множе-
ство В8= {/18 О(/) ^ 1 —е} имеет положительную меру.
Функция at—*/п{а) = /п[(/0, а)пВ8] непрерывна и изме-
няется от O = m(to) до т(Ва) — m(tt) (т(В)— мера Лебега
множества В). Задав произвольно А/, выберем ak, k=
= 1.....N — 1 так, чтобы tn(ak) = klNBa. Этим опреде-
ляется разбиение Ве = Br и • • • U BN множества Ве на N
попарно непересекающихся подмножеств
В1 = (—оо, ajn В8, ...» Вк = («*-!, аА]ПВе, ...
• • •> 5№(“дг-1> °о)ПВ8
положительной меры.
Положим теперь
При N > п однородная линейная система
= $ Pi(t)dt = Q
д * вк
имеет ненулевое решение (уг, ..., yN). Соответствующую
функцию (3) обозначим у(•), Если 0 < А, < е max
то
I < е, t £ Ве,
и потому х(-) ± •) с W. При этом
А(х(.)±^(.)) = Л(х(.))±ХЛу(.) =
д
Следовательно, х (•) ± Ад/(-)€ и так как А.=?£=0, то
*(•)—не крайняя точка.
Таким образом, %(•) — характеристическая функция
и теорема доказана. |
4.3.3. Принцип Лагранжа для ляпуновских задач.
В этом пункте А—фиксированный промежуток числовой
прямой (конечный или бесконечный), U — некоторое топо-
логическое пространство.
Лемма о суперпозиционной измеримости.
Если функция f: AxU —»-R непрерывна, а и'. A—+U
12 В. М, Алексеев а др. 353
измерима (в смысле определения п. 4.2.6), то и функция
u(t)) измерима.
Доказательство. Пусть Ап q Д выбраны так, что
т (Д\ и Л„) = 0 (т—мера Лебега) и ограничения м( •) |л„
могут быть продолжены до непрерывных функций на Ап.
Тогда и функции u(t)), t £ Ап, могут быть про-
должены до непрерывных на Л„. |
Пусть теперь заданы непрерывные функции Дх
xU—>-R. Обозначим через ‘U совокупность измеримых
отображений и: Д—>-11, для которых суперпозиции
u(t)) не только измеримы, но и интегрируемы
на Д, так что на QZ определены функции «(•)—►
д
С другой стороны,.пусть X—линейное пространство,
функции gi'. X—» R — выпуклые для i = 0, 1, ..., т' и
аффинные с конечными значениями для i — т' + 1, ..., т,
Л с X — выпуклое подмножество.
Экстремальную задачу
Fo (и (•)) +g0 (х) = $ ft (t, и (/)) di+go (х) -* inf,
д
F, («(•))+£,(*)“ ...
P I 0 Z —• 1 /22Z ' 1J
u(t))dt+gi(x) ’
д . | = o, i = m + 1, ..., tn,
x^A, w(-)gQZ
мы будем называть ляпуновской задачей. В качестве част-
ного случая ляпуновская задача включает в себя стан-
дартную задачу выпуклого программирования, изученную
нами в й. 1.3.3 (надо положить т' = т и ^ = 0), и мы
увидим далее, что теорема Ляпунова позволяет распро-
странить на рассматриваемую здесь более общую ситуа-
цию рассуждения, при помощи которых была доказана
теорема Куна—Таккера.
Функция
п
J(«(.),x,l,l,) = 2 («(•))+£<(*)) (2)
i=0
называется ^функцией Лагранжа задачи (1).
Теорема (принцип Лагранжа для ляду-
новской задачи). Пусть функции Дх% —► R‘
354
непрерывны, gp X—>R выпуклые для i~Q, 1, .... т' и
аффинные конечные для i — tn' + X, ..., т, А с X выпукло.
1. Если пара («(•)» х) является решением задачи (1),
то найдутся вектор Х = (К1, ..., £m)€RCT* и число Хо,
не равные одновременно нулю и такие, что:
гц т
a) min 2 и)= S Хг- (t, «(0) почти всюду, (3)
и б U i = 0 i в О
min 2 Ifgi (x)=S Kgttf) . (4)
xtAi=0 i«0
(принцип минимума)’,
б) \'^0, i = 0, 1, (5)
(условие согласования знаков)’,
в) («(•))+£/(*)}== О, /=1............т (6)
(условия дополняющей нежесткости).
2. Если («(•), x)^.eUx А и существуют такие XgR"’*
и Хо > 0, что выполняются условия (3)—(6), то (и (•), х) —
решение задачи (1).
Доказательство. А) Лемма о выпуклости
образа.
Образ
imF={i=(i0........(«(•)),
отображения и ((и (•)) = (Fo (и (•),..., 3 т («(•))
является выпуклым множеством в Rm+1.
Доказательство. Пусть
= (-)). Л= 1, 2.
Функция р(’) = (рв(’), •••• Рт (•))• R-*-R“+1, опреде-
ляемая равенствами
J fdt, u^W-fitf, uw(t)),
'’'«Mo, 1(1 •
интегрируема, поскольку По теореме Ляпу-
нова множество
Mz=h\?, = \p(t)dt,
выпукло, и так как этому множеству принадлежат точки
0 (А — 0) и fc1 —£а (А = Д), то для любого а€[0, I]
12* _ 355
существуют такие Аа £ ® (т. е. измеримые по Лебегу),
что
а (£}-£!)-
откуда
J fi{t,u^{t)}dt+ $ fi(t, uw(t))dt =
4аПд д\^а
= о& + (1-а)й. 1 = 0, 1, .... т. (7)
Положим теперь
„ wO>W’ ^Л«ПД,
Uay)~\u^(t), t£A\Aa.
Тогда в силу (7)
F/(ua (•)) = <+( 1-<№
так что (wa(-)) = ag1 + (l—а)12. |
Б) С у ще с тв о в а н и е множителей Лагранжа.
Как уже было сказано, наши рассуждения будут парал-
лельны доказательству теоремы Куна—Таккера из
п 1.3.3.
По условию пара (й(-), х)—решение задачи (1). Не
ограничивая общности, можно считать, что Fo («()) +
+ go (*) т= 0 (в противном случае можно вычесть из аГ0+g0
эту константу). Докажем, что множество
C = -ja=(a0, ..., а„)_|Э(й(-), х)СИхА,
^о(и(-)) +ge_(x) < а0, F, (й(-)) +g< (х)
i=l, ..., иг', Fz(w(»)) + gz(x) = az, i — m' + l, ..., т\
(8)
выпукло. Действительно, пусть а*=(а„, .... «*)£(?,
k= 1, 2, 0 < 0 < 1, (w<A) (•), x(ft))—такие элементы из
<?/хД, что
F0(W'w(-)) + gr0(x^)<^,
Fz(M<ft,(-))+g/(x(ft’)l <av т''
1 ’ ( = а?, 1 = т +1.....т.
35в
По лемме о выпуклости образа существует функция
такая, что
F, (и9 (•)) - 0F, (««’ (.)) + (1 -0) F, («<а> (•)),
i = О, 1, .... т.
Кроме того, хе = 0ха) + (1—0)х(а)€А ввиду выпуклости
А и
St (хе) = Si (0х(1) 4- (1 -0) х<а >) = 0g, (х'1’) + (1 -0) g{ (х'а>)
для i = m' + 1, •••, т, поскольку эти функции аффин-
ные. Следовательно,
&i (ме (•)) +£/ (х9)==
=0 [F, («“> (.))+£, (х'1’)] + (1 -0) [F, («<а>(-)) +gz (Х’а’)]=
= 0а,-|-(1—0)аа, i = .....т.
Далее, g0 — выпуклая функция, и потому
& o(Me(-))+fifo(xe) =
= 6F0(W(1> (•)) + ( 1 -0) F0(«<a>( •)) +& (0ха> + (1 -О) х<а’)<
<6 (Fo (м(1)(•)) +& (ха))) + (1 -0) (Fo («(а>(•))+&> (х|а,))<
< 0с4 + (1 —0)0^.
Аналогично доказывается, что
^'/(ме(-))+^(хеХ0а} + (1—0)а/, /= 1, .... т'.
Но тогда из определения множества С видно, что 0а*+
4-(1—0)аа€С, т. е. С выпукло.
Полагая в (8) («(•), х) = («(•), х), получаем включение
С о {а=(а0.....«от)|«о >0. i-l> • • •» т',
az = 0, / = т'4-1, ..., т}. (9)
В частности, С непусто. Кроме того, 0(£С, так как
в противном случае, согласно (8),
^0(й(-))+^(х) <0, Г((й(.))+й((х)<0,
i=l....................т',
^rz(M(,)) + ^(x) = O, i = tn' + 1, • • •, т,
для некоторой пары («(•), х) н, следовательно, (и(-), х)
не является решением задачи (1).
Применяя конечномерную теорему отделимости
(п. 1.3.3), находим такие i = 0, 1....... не равные
357
одновременно нулю, чтЪ для всех d£C выполняется
пт
неравенство 2 0.
г = о
Поскольку (е, 0, ..., X), а, = 1, 0, .... 0) € С, где
1^/<т и а/ = 0 для 1=5^0, /, то выполняется нера-
венство Е^о + Ху^О. Переходя к пределу при е 10, по-
лучаем Ху^О. Точно так же
(е, 0, ..., 0) £ С =з> Хо^ 0,
и таким образом, верно (5).
При любом в > 0
(8, 0...0, ay = F/(u(-))+gy(x), 0, .... 0)6
6 С =^> X0s4-Xy [IFу (u (•)) +£у-(х)] +
>0=^y[Fy(M-))+g/(i)]>0. (10)
Поскольку (й (•),%)—допустимая пара,
^/(«(•))+87 (*){
1 /^/п',
/ = /п' + 1,
т.-
(11)
Вместе с (10) и уже доказанными неравенствами Ху^О,
1^/^/п', это дает (6).
Далее, для любых 8_> 0, («(•), х) 6 ‘ИхЛ, соглас-
но (8),
<^о.(«(-)) +
+&(х)+8» (*(•)) +87 (*)» •••> F„ (и (•))+&,(*))€
€ С »4> 2 i (м (’)) +87 W) + sX0 =
i в О
= ^(u(-), х, X, Хо) + еХ0>0=»^ («(•), х, X, Хо)>0.
Но, согласно (6), (И), j^tn' + i и сделанному выше
предположению о F0 + g0» +’(«(•)> X, X, Х„)=0. Поэтому
для функции Лагранжа (2) выполнен принцип минимума
min -^ («(•), х, W)=^ (й(-), х, X, Хо). (12)
WXA
358
Если же Хв > 0, имеет место (12) и выполняются условия
(5) и (6), то для всякой допустимой пары («(•), х)
(5) т' „
п (« (- )) +go (*)) 2 ^1 №/(«(•))+& (*)) =
г=о
« Л . (12)
= 2 ^(^(“(•))+gzW)=^’(«(•)» X, X, Хо)>
1 = 0
_ ™ „ (6). (И)
> ^(и(-), х, К, Ьо) = 2 (“(•))+£((*)). =
( = 0
= Хо (<^0 (й (•)) +£0 (х)) =$> Г,(«( )) 4-£<Дх)) >
>F0(u(-)4-^0(x)),
так что («(•), х)— решение задачи (1).
В) Редукция к элементарной задаче. Легко
видеть, что соотношение (12) эквивалентно одновремен-
ному выполнению соотношений (4) и
m ч
min У X,#i (и( • )) =
uM « U I =0
= min $ 2 ^ifi (t, u(t))dt— $ 2 (^> «
и (•) e w д f = o д i =o
2 («(•)). (13)
(=0
Действительно, если выполняются (4) и (13), то
&(и(-), х, X, \)=2 (•))+ ^i8i (х)
1=0 - 1=0 <
> 2 (“(•))+ 2 \gi(x) = (и(-), X, X, £0)
для всех и х^А, т. е. имеет место (12). Если
т т
же, например, ^iSi (х) < 2 ^igt^x), для некоторого
_ 1=0 i=0
х£ А, то
т
S (и (•), х, £, £0) = 2 t(u (')) 4*
i = 0
mm m
+ i S z(^(*))+ S ^igi(x),
1=0 " 1=0 i=0
так что (12) не может иметь места.
350
Чтобы перейти теперь от (4) и (13) к принципу мини-
мума, т. е. к (3) и (4), нам нужно показать, что в (13)
можно «внести min под знак интеграла», т. е. показать
что функция н(-) тогда и только тогда является реше-
нием вспомогательной задачи оптимального управления
$ S м(-))<Д—>-inf, «(•)£% (14)
д t=o *
когда имеет место соотношение (3).
Подобное утверждение уже было доказано нами в
п. 3.1.4. Однако там предполагалось, что функция «(•)
кусочно-непрерывна, а здесь она только измерима, так
что нам придется воспользоваться более тонкими рас-
суждениями.
Г) Элементарная' задача с измеримыми
управлениями.
Лемма об условиях минимума в элемен-
тарной задаче оптимального управления.
Пусть \ — промежуток в R, U—топологическое прост-
ранство, функция f: AxU—► R непрерывна и 41—сово-
купность измеримых отображений и: А—>-П таких, что
функции t н-* / (t, и (/)) интегрируемы на А.
Для того чтобы и(-)^41 было решением задачи
J f(t, u(t))dt—»-inf, u(-)^4L, (15)
д
необходимо и достаточно, чтобы равенство
f(t, u(t)) = min f(t, u) (16)
u«U
было верно почти всюду в А.
Доказательство. «Достаточно». Согласно (16)
f (i, и (t)) (t, u(t)) почти всюду для любой и(-)£41,
откуда <F («(•)) (и (•)).
«Необходимо». Пусть «(•) — решение задачи (15).
Поскольку w(-) измеримо, существуют (п, 4.2.6.) изме-
римые множества Ап с А такие, что m(A\lMn) = 0
и и\дп продолжается до непрерывной на Ап функции.
Назовем точку Ап существенной, если т((т—8, т-}-8) П
П Лп) > 0 для любого 8 > 0, и покажем, что равенство
(16) имеет место во всех таких точках.
360
В самом деле, если бы для некоторой существенной
т £ Ап и некоторого v € U выполнялось неравенство
f (т, v) < f (т, и(т)), то ввиду непрерывности функций
«(•)|лп и такое же неравенство сохранилось
бы и в некоторой 6-окрестности точки т в множестве
т. е.
Vi€(T-6, Т + 6)ПА„.
Функция
“(О- ^(Т—6, т + 6)П лп,
/е(т-6,т + 6)п4„,
очевидно, принадлежит ЭД и
^ («(•))-£•(«(.)) = $ [f(t,v)-f(t,u(t))]dt<0,
(х-а, т+в) п Ап
поскольку f(t, u(t)) и т((т—6, т-(-6) П А„) > 0.
Остается доказать, что’ множество несущественных
точек имеет меру нуль. Если т£Д„ несущественна, то
по определению найдется такое 6Х, что т((г—6Х,
т 4-6т) Г) Л„) = 0. Сузив интервал, найдем 1акие рацио-
нальные (ах, рх), что zn((ax, рх) П Л„) = 0. Множество всех
интервалов с рациональными концами счетно, поэтому
не более чем счетно и множество тех из них, которые
имеют вид (ах, рх) для некоторой несущественной точки
тСД„. Пусть это интервалы /2, ... Тогда и/*
k
содержит все несущественные точки Ап и т п U <
<2>(A„n/ft) = o.
*
Поскольку множеств Ап не более чем счетное число,
то объединение множеств несущественных точек каждого
из них также имеет меру нуль. По доказанному (16)
может нарушаться лишь на Д\ U Ап и в несуществен-
п
ных точках, т. е. оно верно почти всюду.
Д) Завершение доказательства. Согласно
В) и Г) для выполнения условия (12) необходимо и до-
статочно, чтобы одновременно имели место (3) и (4).
Заменив в последнем абзаце пункта Б) (12) на (3), (4),
получаем все утверждения доказываемой теоремы. Ц
4.3.4. Теорема двойственности. Обозначения в этом
пункте те же, что и в предыдущем. Напомним, что по-
361
нятие двойственности для задач выпуклого программи-
рования было введено в п. 3.3.2. Оно было связано с
методом возмущений, т. е. с включением индивидуальной
экстремальной задачи в семейство задач того же типа.
Здесь мы поступим точно так же, ограничившись для
простоты одними интегральными функционалами. Кроме
того, мы предположим (и это будет существенно исполь-
зовано в доказательстве), что А—это отрезок числовой
прямой и топологическое пространство U, в котором
принимают значениягразличные управления «(•), сепа-
рабельно, т. е. содержит счетное всюду плотное подмно-
жество Например, в качестве П можно взять любое
подмножество в Rz, С (A, Rn), С1 (A, R"), /.ДА), но про-
странство L„ (А) (см. п 4.3.2) уже несепарабельно.
Упражнение 1. Докажите эти утверждения.
Итак, рассмотрим ляпуновскую задачу
(«(•))==$ f0(t, 11 (t))dt—+ inf,
С ' (8)
ГДп(-))=^Д, u(ty)dt^O, u(t)£lX,
д
i = 1, 2, ..., иг.
Фиксировав fi, включим ее в семейство
Fo («(•))— inf, ГДп(-)) + а(-^0. (з(а))
Как и в п. 3.3.2, S-функция семейства з(а) определяется
равенством
S(a) =
= inf {F0(u(-))[rf(w(-)) + a^Q, u(-)e^} a£R" (1)
Аналогия между ляпуновскими задачами и задачами вы-
пуклого программирования сохраняется и здесь и, хотя
функции tf'i не являются выпуклыми, справедлива
Лемма 1. Функция ал-*S (а) выпукла.
Доказательство. Согласно лемме из п. 4.3.3 мно-
жество
= .......^)|?(. = Г,.(«0))-
выпукло в Rm+*. Переписав (1) в виде
S(a) = inf ^oll/4-a/^O,
и, полагай (£) = £,•(£(,, . ..,Ет)=Д(, мы обнаружи-
ваем, что S (а) является значением задачи выпуклого
362
программирования
g0(l)^inf, gdD + a^O, £€imF.
Эта последняя является частным случаем задачи, рас-
смотренной в п. 3.3.2 (отсутствуют ограничения типа
равенства, в связи с чем У, Л и т, п. следует опустить),
так что выпуклость S обеспечивается следствием 1 п 3.3.2.
Теорема двойственности для Ляпунов-
ских задач. Пусть Л—промежуток в R, U—сепара-
бельное топологическое пространство, функции fp Д х U —*
—>-R, i = 0, 1, ..., т, непрерывны, dl—совокупность из-
меримых отображений и: Д —>- U таких, что функции
tt-fftlt, u(t)) интегрируемы на Д.
Если S-функция семейства j(a) непрерывна в точке
а=0, то для любого a g int (dom S)
S (a) = sup ( Aa + ( Ф (t, A) dt \ , (2)
x>o \ X /
где
Ф (t, A) = inf ( fB (t, u) + 2 Mi (t, u)). (3)>
u eu\ 1 = 1 _ /
Доказательство. А) По лемме функция ai->S(a)
выпукла, а из непрерывности ее в одной точке вытекает
(предложение Зп. 2.6.2) непрерывность и равенство S(a) =
= (convS)(a) для всех a С int (dom S). По теореме Фен-
_хеля—Моро (п. 2.6.3) convS = S**, так что для тех же a
S(a) = S**(a)= sup (Aa—S*(A)f. (4)
Теперь вычислим S*(k). По определению
S* (X) = sup (Aa—S (a)) =
a
= sup JAa—inf J fB(t, и (t)) dt\^ ff (t, и (/)) dt + <0,
a l а а
«(-)e^
а
sup sup
“(•)«» az<-J fpt, U(t)) dt
а
'+co, A(jtR™
m
fB(t, U(t))dt+^ u(t)) dt.
inf \
«(•)ew д .
363
Подставляя найденное выражение в (4), мы видим,
что равенство (2), а с ним' и вся теорема, будут дока-
заны, если мы проверим, что
г т
inf \ (t, и (i)) + У Kifi (t, и (t)) dt = \ Ф(^, K)dt, (б)
L /=1 J д
где Ф(<, к) определено равенством (3).
Б) Лемма 2. Пусть \ — промежуток в R, П—ceria-*
рабельное топологическое пространство, функция f: Дх
xU—► R непрерывна, 41—совокупность измеримых отоб-
ражений и: А—-И таких, что функция ti-»f(t, u(t))
интегрируема на Д.
Тогда функция
4>(t) = mi{f(t, ц)) (6)
celt
измерима на Д, интеграл ^(p(t)dt (конечный или рав-
д
ный —оо) существует и
<р (i) di inf f (t, u)dt= inf $f(i, u(f))dt. (7)
Д Д 11 «ИеЭДД
Доказательство. Пусть 1}—счетное всюду
плотное подмножество в U. Ввиду непрерывности f функ-
ции
ф„(0== min f(t, vk) (8)
1 < n
непрерывны и при n—>оо
Фп(01 lim inf fit y*) = inff(i, rft) =
= \nif(t, v) = q>(f). (9)
sen
Кроме того, существуют функции и„ (•) С ЭД такие, что
<р„(f) = f(t, un(t)). Действительно, при п=1 это верно,
и если <p„_1(O = f(t wn-i(0)> то
фп(0е= min [f(i, vft)]= min^.Ji), f(t, u„)] =
1 k n
= min[f(i, «„.Ji)), /(i, u„)]=f(i, ^„(i)),
где функция
если и„),
W* ( »п, если <p„_1(i) >f(t, vn),
364
принадлежит 'll (ввиду непрерывности функций нера-
венство <p„-i(0 > f (*» vn) выполняется на открытом мно-
жестве, и потому «„(•) измерима; интегрируемость функ-
ции (t, un(t)) = qn(t) следует из непрерывности <рп(0)-
Будучи в силу (9) поточечным пределом непрерывных
(а значит, и измеримых) функций, функция <р(-) изме-
рима [КФ, стр. 284J. Представив ее в виде разности
ф(0 = № 0—[фЮ—f(t, о)]
непрерывной и неотрицательной функций, мы убеждаемся,
что интеграл J <р (/) dt существует, конечный или равный
д
(—оо) (непрерывная на отрезке А функция f(t, v) имеет
конечный интеграл, а интеграл неотрицательной изме-
римой функции <р(/) — f(t, v) существует, поможет рав-
няться -|-оо).
Поскольку f (t, а(/))>ф(0 для любой «(•)£% не-
равенство
inf (t, $ (p(t)dt (10)
и(-)б£мд д
очевидно. Если левая часть равна —оо, то равенство (7)
верно. Если же она конечна, то ввиду неравенств
J <fi(t)dt^ <pn(t)dt —
д д
= 5 f(t, un(t))dt^ inf §f(f, u(t))dt
д «(оеЭДД
последовательность интегралов J <pn(t)dt ограничена. При-
д
меняя теорему Б. Леви [КФ, стр. 303] к неубывающей
последовательности —ф„(*)» мы находим, что функция
ф(-) интегрируема и
§ Ф(0<^ = Нт ф„ (^)df ^inf J q>n(t)dt =
д « -* “ д П д
= inf ^f(t, un(t))dt^ inf ^f(t, u(t))dt.
" л новадд
Вместе с (10) это дает (7). |
По лемме 2 верно (5), что, как мы видели, доказы-
вает теорему.
Упражнение 2. Сформулируйте и докажите теорему двойст-
венности для ляпуновской задачи общего вида (см. (1) в п. 4.3 3).
365
4.3.5. Принцип максимума для задач оптимального
управления, линейных по фазовым переменным. Вернемся
к поставленной в п. 4.3.1 задаче
JAx(-), «(•))==$ [М0*(0 + № u(t))]dt +
д
+ Too^(U + Ti1)^(0-*inf, (1)
x—A(t)x + F(t, u(t)), u(t)^U, (2)
лис-), u(t))]dt+
Д
+ yOiX(to) + yllx(t1)^clx i=\,2,...,m. (3)
Теорема (принцип максимума для задач,
линейных по фазовым переменным). Пусть
функции ар. Д —+ Rn*, i = 0, 1, .... /и, и А: Д —J? (Rn, Rn)
интегрируемы на отрезке Д=[/о, iJcR; U—топологиче-
ское пространство-, fp. ДхИ—>-R, i = 0, 1, ..., т, F: Дх
xU—* Rn—непрерывные функции, ‘Н—совокупность из-
меримых отображений и: Д—>-П таких, что функции
u(t)) и tb-*F(t, u(t)) интегрируемы.
1. Если (х(-), «(•))—оптимальный процесс для за-
дачи (1)—(3), то найдутся такие не равные одновременно
нулю число Х0>0,,вектор ..., Xm)gRm* и абсо-
лютно непрерывная функция р: Д—>-Rm*, что выпол-
няются:
а) уравнение Эйлера—Лагранжа (сопряженное урав-
нение)
p(t) = — p(t)A(t) + '^i!k!a((t)-, (4)
1=й
б) условия трансверсальности
Ж) = (-1)А 2 I (5)
t =0
в) принцип максимума
mzxG(t, v) = G(t, u(t)) (6)
с е u
почти всюду, где
т
G (t, v)= р (t) F (t, v) - 2 Ut (i, v); (7)
i = 0
366
г) условие согласования знаков
51/^0, i= 1, ..., т; (8)
д) условия дополняющей нежесткости
«(.))—cf] = 0, i=l......щ. (9)
2. Если для допустимого процесса (*(•), «(•)) су-
ществуют такие Хо > 0, X£Rm* и абсолютно непрерыв-
ная —► R"1*, что выполняются условия (4)—(9), то
(%(•), «(•))—оптимальный процесс для задачи (1)—(3).
Формально, условия (4) —(9) здесь те же, что и соот-
ветствующие условия в п. 4.2.2 (читатель легко прове-
дет необходимые преобразования от одних условий к
другим), но напомним, что содержание их несколько
иное. Управление «(•) предполагается здесь всего лишь
измеримым, а следовательно, необходимые условия (4) —
(9) из результатов § 4.2 не вытекают.
Кроме того, вторая часть теоремы дает нам доста-
- точные условия оптимальности, чего не было в § 4.2.
Доказательство. А) Редукция к ляпунов-
ской задаче. В п. 4.3.1 задача (1)—(3) уже была
сведена к экстремальной задаче ляпуновского типа (см. (8)
в п. 4.3.1), которая. отличается от задач п. 4.3.3 воз-
можностью присутствия в ограничениях неравенств
Это, однако, не страшно, поскольку терминальные члены
в (8) п. 4.3.1 линейны и, поменяв знаки там, где нужно,
мы снова получим выпуклые функции.
Перенумеруем индексы так, чтобы в (3) ограничения
типа равенства стояли в конце, а затем, как и в § 3.2,
положим = 1 для i=0 и тех i, для которых в (3) стоят
знаки и ==, и е; =— 1 для тех i, для которых в (3)
стоит знак Далее положим g„(x( )) = frox(to) и §Дх(- )) =
='ё/(р/х(/0)—a), t>l.
Теперь задача (8) п. 4.3.1 приобретает стандартный
ляпуЦОвский вид
Л(х(-)> «(•)) = — e0$G0(/, и (t))dt+ga(x ())-* inf.
д
Jz(x(-), «(•))== — е,- J Gi(t, U(t))dt +
д
f sC 0, i=l, ..., m',
+<'<(*<)){ =0. i = m'+l......m, <I0>
где G{ определены формулами (5) п. 4.3.1.
367
Б) «Необходимо». Если (£(•), «(•))—оптимальный
процесс, то по теореме п. 4.3.3 существуют Xz, неотри-
цательные при не равные одновременно нулю
и такие, что
— 2 еД/G, (t, й (/)) = min( — 2 еД/О, (/, ц)) (11)
/в О D \ fss О J
почти всюду,
т т
2 kgi (*(•)) = min 2 (12)
1= 0 *(•) <=o
и
u(;))==o, (13)
Легко видеть, что, полагая lz = elz, мы удовлетворим
условию (8), а из (13) следует (9).
Далее, положим
т
(14)
• 1=0
где р{(‘) определены формулами (7) п. 4.3.1, откуда и
из (6) п. 4.3.1
— = (15)
Непосредственным дифференцированием (или используя
формулу (14) п. 2.5.4) проверяем, чтЬ р(-) является ре-
шением уравнения (4) и (5) верно при k— 1.
Из (7), (14) и из (5) п. 4.3.1 получаем
т
Q(i, v} = p(t)F(t, u) =
м
tn m
= 2 V)— fi(tt ц)]= 2 v),
i = 0 1 = 0
после чего (11) превращается в (6).
Наконец, подставляя в (12) определения glt получаем
2 )х^0)==пйп(2еДД)х.
i =0 / х
т
Такое равенство возможно, только если 2
»=о
зы
m
— 2 eiMi = O, после чего ((5), fe==0) следует из (14)
i' = 0
И (15).
В) «Достаточно». Пусть для допустимого процесса
(%(•), «(•)) нашлись такие \ > О, р(-), что выпол-
няются условия (4)—(9). Пусть, далее, ef—те же, что и
раньше, Л^еД, и /?,(•) по-прежнему определены ра-
венствами (7) п. 4.3.1, так что имеет место (15). Фуйй-
т
цни р(-)= 2 Мг(-) и р(-) удовлетворяют уравнению
i =0
(4) и, согласно ((5), й=1), совпадают при t= tv. По тео-
реме единственности р(/) = р(/) и, следовательно,
(7) т
G(t, v)=p(t)f(t, о)-2Ш-
1 = 0
т т
= 2[Mpdtmt, -«)] = 2 вДД(<, 0 (16)
I =0 {fcO
н
~ (15) -
2М, = 2 Mv0/-M4)>
Г=Г0 t*=0
т т (5)
= 2 Moi—2 Mi(U=p(U-PW«o. (i?)
i = 0 fSO
Из (16) и (6) следует (11), из (9) следует (13), & (8)
с учетом равенств К, = еД, означает, что 0, i =* 1, ...
..., т. Кроме того, из (17) и из определения gt(-) вы-
'Текает, что
т tn т
2 ^i£i(x (•))== 2 MPi*(U— 2 Ma
1*0 $*0 f = i
/ tn \ m m
Ц 2 Mi 2 ktCi**-’ 2
\i=0 ' / 1=1 i=l
И потому (12) также имеет место. По теореме п. 4.3.3
условия (11)—(13) вместе с неравенствами Хо > 0, %в^0
достаточны для оптимальности (х (•), «(•))• И
13 в. М, Алексеев и др, - 369
§ 4.4. Применение общей теории
к простейшей задаче классического
вариационного исчисления
Общую теорию мы применяем здесь к простейшей
задаче классического вариационного исчисления, кото-
рой уделено такое большое место в учебной литературе.
Подобным же образом можно получить необходимые и
достаточные условия слабого экстремума и необходи-
мые условия сильного экстремума и в общей задаче
Лагранжа. Это, однако, заняло бы слишком много
места, не внеся почти ничего принципиально нового.
Поэтому мы ограничились частным случаем, в котором
можно довести исследование до конца и продемонстри-
ровать взаимосвязь старой и новой теории.
4.4.1. Уравнение Эйлера. Условие Вейерштрасса. Усло-
вие Лежандра. Простейшей (векторной) задачей класси-
ческого вариационного исчисления мы называем (ср. п. 1.2.6)
следующую экстремальную задачу:
ft
3 (х(-)) = L (t, x(t), х (0) dt —> extr, (1)
^0
x(t() = x^. (2)
Здесь функция Lx. V—*R по крайней мере непрерывна
в открытом множестве VcRxR"xRn; х0, xlt tg и
фиксированы.
Задача (1), (2) исследуется в двух вариантах. В пер-
вом из них х(-) принадлежит пространству С1 ([/„, Zr], R")
и локальный экстремум в этом случае называется сла-
бым (ср. п. 1.4.1). Во втором х(-) принадлежит про-
странству /СС1([^, ^], Rn) функций с кусочно-непрерыв-
ной производной, наделенному нормой ||х(-)||= sup |х(/)|,
и локальный экстремум в этом случае называется силь-
ным.
Упражнение 1. Проверьте, что пространство КС1 ([/0, , Rn)
нормирование, но не банахово (т. е. не является полным).
В обоих вариантах х(-) называется допустимой, если
ее расширенный график ((/, x(t), x(O)Uo^
и удовлетворяются краевые условия (2). Множество допус-
тимых функций х(-) будем обозначать Вводимые
здесь и далее обозначения и терминология сохраняются
на протяжении' всего этого параграфа. Для краткости
370
задачу (1), (2) мы будем называть простейшей задачей,
опуская остальные подробности.
Упражнение 2. Докажите, что
inf 3(х(-))= inf Я(х()).
TJnC1 (Ко. /.], Я») (Ко. /1]. R")
Указание. Воспользуйтесь леммой о скруглении углов
(п. 1.4.3).
Если х(-) доставляет сильный экстремум в задаче (1)
и при этом х(-) непрерывна, то, очевидно, х(-) достав-
ляет и слабый экстремум.. Поэтому необходимые усло-
вия слабого экстремума являются (в случае непрерыв-
ности х(-)) необходимыми и для сильного экстремума.
Некоторые из необходимых условий мы уже знаем. В § 1.4
элементарными средствами были выведены: уравнение
Эйлера—необходимое условие слабого экстремума и
(для п=1) условие Вейерштрасса—необходимое
условие сильного минимума. Посмотрим теперь на про-
стейшую-задачу с общих позиций. С одной стороны, (1),
(2) сводится к такой задаче Лагранжа;
t,
У(х(.), «(•))=$£(/, x(t), —>-extr, (3)
^0
х = и, х(/0) = х0, х(/1) = х1.
Если предположить, что не только L, но и ее про4
изводные- по х, и непрерывны в V, то к (3) можно при-
менить теорему Эйлера—Лагранжа § 4.1. При этом сла-
бая оптимальность процесса (х(-), и (•)) в задаче (3)
означает в точности то же самое, что слабая экстре-
мальность х(-) в задаче (1), (2).
Если х(-) доставляет слабый экстремум в задаче
(1), (2), то по теореме Эйлера—Лагранжа существуют
такие Хо и функция р(-)€Сх([7о, Ц, R”*), что
p(0=V*(^(0. *(0). p(f) — K0Li(t, x(f), х(0)>
Если Хо = О, то все множители Лагранжа оказываются
нулями; поэтому можно положить\= 1. Исключая р(-),
получаем систему уравнений Эйлера
^-£/(0 = 4(0 (4)
(как всегда, здесь,!; (/) = А; G> х(0> *(0) и т. д.).
13* 37Г
С другой стороны, задачу (3) (предполагая для опре-
деленности, что это задача на минимум; в задаче на
максимум следует заменить L на —L) можно рассматри-
вать как задачу оптимального управления с U=R".
Если предположить, что L и Lx непрерывны по совокуп-
ности переменных, то можно применить к (1), (2) прин-
цип максимума из § 4.2. При этом оптимальность про-
цесса (£(•), и(-)) означает, что
х(.)€КСЧРо. *1]. R”)
доставляет в задаче (1), (2) сильный минимум.
Из принципа максимума следует, что существуют
и кусочно-дифференцируемая функция р (•):
[/0, такие> что
p(0=V.(0> (5)
min {Хо£(/, x(i), и) — р (t) и} =*
= X0L(f, x(Q, х(0)—Р(/Тх(/). (6)
Равенство Х,о = О здесь невозможно, так как из (5) =
=0=^р (/) = const, причем р (0=^=0 (иначе все множители
Лагранжа равны нулю). Но если 10 = 0и р#=0, то (6)
не может выполняться (нетривиальная линейная функция
не имеет минимума на R"). Таким образом, Хо^О'и
можно считать, что = 1.
Условие (6) можно Переписать в субдифференциальной
форме
р(0€(^)(/,л(0, х(())- (7)
Если L дифференцируема также и по х, то из (6) сле-
дует равенство p(t) = L^ (t), и мы, с одной стороны, снова
приходим к уравнению Эйлера (4), а с другой—из (6)
получаем необходимое условие Вейерштрасса
L(t, x(t), и)—Lit, x(t), x(t)) —
— Lx (t, x (f), x (0) (m —x (0) > 0, (8)
V«€R", M-
3T2
Введем в рассмотрение (ср. п. 1.4.4) £—функцию
Вейерштрасса (латинское excessus — излишек)
^(Л х, £, w) = L(/, х, u)—L(t, х, £) —
-L-X(t, х, £)(«-£). (9)
Тогда условие Вейерштрасса (8) можно записать в виде
^(Л x(t), x(t), w)^0, VwgR", V/g[7o, fj, (10)
Если допустить, что не только L и L-x, но и Lxx не-
прерывна в V, то из (8) вытекает неравенство
К^(0>0, (II)
Условие (II) называется условием, Лежандра.
Итак, уравнение Эйлера является необходимым усло-
вием как слабого, так и сильного экстремума. Кроме
того, из принципа максимума мы вывели еще два необ-
ходимых условия сильного минимума—условие Вейер-
штрасса и условие Лежандра (в следующем пункте мы
увидим, что последнее должно выполняться и для сла-
бого минимума).
4.4.2. Условия второго порядка для слабого экстре-
мума. Условия Лежандра и Якоби.
Лемма. Пусть функция L непрерывна в V, а, кроме
того, в V существуют и непрерывны ее производные LXi,
X X . ^~*Х X *
xl ‘ 1 xlxj Х1х]
Если х^СЩ^, Ц, R") удовлетворяет уравнению
Эйлера, то при ||й'( ) ||с» —> 0 справедлива следующая асимп-
тотическая формула:
t,
SCx^)+h(-))^3(x(.))^^{h(tyLxx(i)h(t) +
^0
+ 2hx (/) Lxx (0 h (0 + h (0TL- (0h (0}dt +
/Ц ч
+ о^Г|А(0Р + |А(01’]^> (1)
W •) £ C1 ([*„, fj, R"), h (te) = h (Q = 0.
Доказательство. Как и в п. 2.4.2, окружив
график х(-) компактом, целиком содержащимся в V, и
воспользовавшись затем равномерной непрерывностью
вторых производных функции L на нем для оценки оста-
373
точного члена в формуле Тейлора, получаем разложение
L(t, x(f)+h(f), x(t)+h(f)) —
+1 {Лт (0 Lxx + 2ЛТ (0 Lx- (t) +
. +O)4;(0/i(0}-he(^ Л(-))[|А(О1а+|й(О|а]. (2)
где s(/; Л(-)) —>0 равномерно на А при ||Л(-)||&» —>0.
Интегрируя это соотношение от t9 до tlt а затем еще,
как всегда, интегрируя по частям линейный член q h(t)
и учитыва^ уравнение Эйлера, получаем (1). |
Если £(•) доставляет слабый минимум в задаче (1),
(2) п. 4.4.1, то, заменяя в (1) й(-) на ah(•) и вычисляя
при aj.0 предел lim[3'-(x(-)+a/i(.))— .7 (х ( ))j/a2, мы
получаем, что квадратичный функционал
tt
Q (h (•)) = $ {h- (0 txx (0 h (/),+ 2ftT (t) Lx^t) h(t) +
(3)
R")» Л(^)=Л(4)==0.
Это означает, что функция ft(-)s=0 доставляет слабый
минимум во вторичной экстремальной задаче
Q(/i(-))—+ inf, ftRo)=M*i) = O. (4)
По лемме о скруглении углов (п. 1.4.3) нижние грани
функционала Q в множествах допустимых функций из
пространств С1 ([t0, fj, R") и КС1^, fj, Rn) совпадают.
Поэтому h(-) = 0 доставляет также и сильный минимум
в задаче (4). (Заметим, что ввиду однородности Q ло-
кальные минимумы оказываются и глобальными и раз-
личие между слабым и сильным минимумами сводится
к изменению запаса допустимых функций.)
По доказанному в п. 4.4.1 для задачи (4) Должно
выполняться условие Лежандра, которое, очевидно, имеет
тот же самый вид
V^R0, М, (5)
что и для (1), (2). Таким образом, условие Лежандра
оказалось необходимый не только для сильного минимума,
как в н. 4.4.1, но и для слабого.
374
Уравнение Эйлера для вторичной задачи (4)
% [£« (t) h (t)+tix (t) h (t)]=Lxi(/) h (t)+lxx (t) h (t), (6)
называется уравнением Якоби исходной задачи (1), (2)
п. 4.4.1.
Определение. Точка т называется сопряженной
к точке t0 (относительно функционала Q), если уравне-
ние Якоби (6) имеет решение Л(-), для которого h (/„)=;
==Л(т) = 0, но1)
£..(т)/Г(т)#=0. (7)
Теорема 1 (необходимые условия сла-
бого экстремума в простейшей задаче).
Пусть функция L удовлетворяет условиям леммы.
Если х(-) доставляет слабый минимум в задаче (1),
(2) п. 4.4.1, то
1) х(-) удовлетворяет уравнению Эйлера ((4) п. 4.4.1);
2) выполнено условие Лежандра (5);
3) выполнено условие Якоби: в интервале (£0, ^) нет
точек, сопряженных с t0;
4) выполняется неравенство (3).
В случае, когда х(-) доставляет слабый максимум,
в (3) и (5) следует заменить знак на •
Доказательство. Утверждения 1), 2) и 4) мы
уже доказали (1)—в предыдущем пункте). Поэтому нуж-
но доказать лишь 3). Предположим противное, л пусть
точка тб(^0, ^i)—сопряженная к t0, а /г(.)—соответ-
ствующее решение уравнения Якоби: Л(/о) —/i(t) = 0 и
имеет место (7). Положим
м)={ою' <8)
V у v ь । <
I) Обычно в учебниках по вариационному исчислению сопряжен-
ные точки определяют в рредположении, что выполняется усиленное
условие Лежандра £.^(/)>0. При этом предположении
£^(т)Л(т)=0=^/1(т)=0, и так как Л(т) =0, то цо теореме един-
ственности й(-) = 0. Поэтому условие (7) эквивалентно нетривиаль-
ное™ h (•) и обычно заменяется этим предположением.
375
Тогда
Q(A(-)) =
- $ {h(Mx* (t)h (/) + 2h (0T 4• (t)h (0 +
to
4-£(0T4;(0£(0}^=
* $ A (0T [txx (0 h (/) + Lxi(t) h (/)]dt +
+ S^(0Tl4;(0^(0+4x
(здесь использовано, что h. (t)1 Ъхх (/) h (t)=h (t)TLix (t) h (0).
Вспоминая, что й(-) удовлетворяет^ уравнению (6), про-
интегрируем (с учетом равенств /г (/0) = /г (т)==0) по частям
в первом интеграле, после чего интегралы сократятся.
Таким образом, Q(h(-)) = Q, а это означает, что-Л(-)
доставляет (наряду с функцией Л(-)^0) сильный ми-
нимум в задаче (4). Снова применяем принцип макси-
мума из § 4.2. В соответствии с ним найдутся Хо^О и
такая кусочно-дифференцируемая функция р(-): {70, /х] —
-ч-ft”*, что
Р (0=244; (0^(04- 2^хх (0 h (t),
min (4«т4; №~и4-24а (0т4; (0и~р (0°”
= 4hT (f) £ц (0А (04- 24Й (0т4; (0 Л (0-р (0 а (/). (9)
Тем же рассуждением, что и выше, доказывается, что
4#= 0, и мы можем считать, что 4 = 1/2.
'Из соотношений (9) следует, что
Й0=4;(^й(04-4х(0^С0. (10)
Но для функция h(•)==(), так что из (10) Вытекает,
что р(т + 0) = 0. С другой стороны, р(т—0) =
= £-(т)й(т—0)=4;(т)^(т)#:0 в силу (7). Поэтому
р—разрывна, но она в силу принципа максимума должна
376
быть непрерывной. Противоречие доказывает выполнение
условия Якоби. В
- Итак, мы установили, что все необходимые условия
экстремума в простейшей задаче, которые обычно рас-
сматриваются в курсах вариационного исчисления:
Эйлера, Лежандра, Якоби и Вейерштрасса—являются
следствиями принципа максимума. Перейдем теперь к
достаточным условиям слабого экстремума.
Теорема 2 (достаточные условия сла-
бого экстремума в простейшей задаче).
Пусть функция L удовлетворяет условиям леммы, функ-
ция х(-)^С1([^0, fj], R") и ее расширенный график
{t, х (0, х (/)) | t < t J eV.
Если:
1) функция х(-) удовлетворяет уравнению Эйлера
((4) п. 4.4.1);
2) удовлетворяются краевые условия х (i0) = х0, х (t1)=Xt',
3) выполнено усиленное условие Лежандра
L--{t,x(t), 5(0) >0, М; (11)
4) выполнено усиленное условие Якоби: в полуинтер-
вале (1а, 0] нет точек, сопряженных с t0, то х(-) до-
ставляет строгий слабый минимум '(при замене в (11)
знака > на < — максимум) в простейшей задаче (1), (2)
п. 4.4.1.
Доказательство этой теоремы будет дано в п. 4.4.5.
4.4.3< Гамильтонов формализ^. Теорема об интеграль-
ном инварианте. В п. 4.1.1 мы уже упомянули, что
уравнения Эйлера — Лагранжа вместе с уравнениями
дифференциальной связи можно привести к гамильтоновой
(или канонической) системе вида
x — $Vp(t, х, р), р~ — ЗСx(t, х, р), (1)-
где функция SK называется гамильтонианом (или функ-
цией Гамильтона) исходной задачи. Здесь мы рассмотрим
это преобразование более подробно, оставаясь в рамках
простейшей задачи (1), (2) п. 4.4.1. Переход от уравне-
ния Эйлера этой задачи ((4) п. 4.4.1) к канонической
системе (1) осуществляется при помощи преобразования
Лежандра. Им мы сейчас и займемся.
Определение 1. Пусть функция I: v—>R принад-
лежит классу Cl(v) в открытом множестве v нормиро-
377
ванного пространства X и ее производная взаимно одно*
значно отображает v на d = {р | р = 1' (g),
S: d—>v—обратное к V отображение. Функция h: d—>R,
определяемая равенством
h(p) = <p, Н (/?)> — /(Н (р)),
(2)
называется классическим преобразованием Лежандра
функции Г.
Предложение 1. Пусть функция I: u-^R при-
надлежит классу С2 (и) в открытом выпуклом множестве v
нормированного пространства X. Если Г-. положительно
определена, т. е.
йМ)=/Ш»|]>о, vgeu, vnex, п¥=о, (З)
то преобразование Лежандра h(-) функции /(•) опреде-
лено и совпадает в d с преобразованием Юнга—Фенхеля
(п. 2.6.3) функции
которая выпукла.
Доказательство. Выпуклость I доказана
в п. 2.6.1 (пример 2), взаимная однозначность отобра-
жения gi—*/'(g) доказывается аналогично пункту Б) до-
казательства предложения 2 ниже.
По определению сопряженной функции (п. 2.6.3)
I* (р) = sup {<р, g> —/(g)} = —inf {7(g) —<р, g>}.
%
Если p£d, то р = Г (g) = I' (1) для некоторого
Следовательно, 0 = (? (g)—р) С3[/ (•) —<р, •>](!), откуда
g—точка минимума функции Г(-) — <р, •> и
~1» (р) = - (/"(£) - <р ,1» = <р, g>-/"(g).
Поскольку р = Г(1), то g = 3(p) и по определению
/"•(p) = /i(p).
Вспоминая неравенство Юнга (п. 2.6.3), получаем
Следствие 1. В условиях предложения 1
l® + h(p)^<p,l>, Vp£d, vgeu.
(5)
Чтобы получить из лагранжиана L(t, х, х) простей-
шей задачи ее гамильтониан ^f(t, х, р), нужно произ-
378
вести преобразование Лежандра по аргументу х. Таким
образом,
$%(t, х, р) — рх—L(t, х, х), (6)
гдех нужно исключить, используя соотношение
p~L-x(t, х, х), (7)
так что формулой (6) SK определено корректно, если ото-
бражение x*-*-L-x(t, х, х) взаимно однозначно. (В форму-
лах (6) и (7) х выступает как самостоятельный аргумент;
чтобы не путать его с dx/dt, мы будем далее обозначать
х — %, хотя для соответствующих производных L сохраним
обозначения Lx ,дк/дхг и т. д.).
Предложение 2. Пусть функция (t, х, £) i—> Z. (£, х, 5)
принадлежит классу Cr (V), г ^2 в открытом множестве
VcRxR"xR".
1) Если-.
й) вторая производная Lxx в V не вырождается, т. а
detf-^G, х, g)>#=0, V(^,x, g)eV;
\OXipXf /
б) отображение Р, определяемое равенством P(t, х, В)=
= {t, х, Lx (i, х, £)) взаимно однозначно отображает V на
DcR х R"X R"*, то D открыто, Р"1 £ Сг~х (£>) и функ-
ция SK'. D—> R, определяемая равенствами (6) и (7), при-
надлежит классу Cr(D).
2) Если при любых (t, х) сечение Vti х = •{£](/, х,
выпукло и при любых (t, х, 5) ё V матрица L- (t, х, %)
положительно определена, то условия а) и б) выполня-
ются и заключение п. 1) справедливо.
- Доказательство. А) Обратное к Р отображение,
существующее согласно б), очевидно, имеет вид (t, х, р)*—*
I—>(/, х, E(t, х, р)), так что _
p = L-(t, х, |)»| = S(f, х, р). (8)
Поскольку L£Cr(y), г~^2 отображение Р £Сг~1(у) с
еСЦУ). £го матрица Якоби имеет вид
379
н ее определитель, равный det L - , отличен от нуля со-
гласно а).
Пусть (t0, ха, p0) = P(t0, х0, £0)—любая точка из D.
По теореме об обратном отображении существует окрест-
ность хо> So)» образ которой P(U)g:D является
окрестностью (£0,- х0, ра). Следовательно, D открыто.
По той же теореме Р~1 (которое определено однозначно)
совпадает на P(U) с отображением класса G1. Поскольку
точка (ta, ха, pa)£D—любая, Р~г ££?(/>) Далее, изД8)
видно, что, как неявная функция, S (t, х, р) определяется
уравнением F(t, х, р, %) — р—Л; (/, х, В) = 0, и так как
оно образовано функциями класса Сг-1, то Е, а вместе
с ней и Р~1 принадлежит классу Сг~1 (£>) (см. в п. 2.3.4
замечание после теоремы о неявной функции).
Из (6), (7) и (8) выводим тождество
SK (t, х, р) = рЕ (t, х, p)~L(t, х, Е (t, х, р)). (9)
Дифференцируя его, получаем
“= p&t — —L'x = [p—L-X(t, x, £i)] Lt =
= — Lt(t, x, g(t, x, p)), (10)
&Cx ~P&x ^x Lx == Lx (t, x, a (t, x, p)), (И)
^=8 + pS,-£.S?=S(U, p). (12)
Из формул (10)—(12) видно, что первые производные
функции SK являются суперпозициями функций класса
сг~1, следовательно, сами принадлежат этому классу.
Поэтому $%£СГ(Р).
Б) Если матрица положительно определена, то по
критерию Сильвестра (см. [7], стр. 181—182) detL- > 0,
так что верно а). Пусть сечения VtiX выпуклы. Тогда
для любой пары точек (t, х, 2, точки
(t, х, «^-(-(l— а)§2) С V, a С [0, 1]. Обозначивр*=£^ (t, х, £А),
имеем
Pi—Pi = L-x(t, х, lx} — L-x(t, х, g2)==
I
x’ “11+ U— a)SJda =
о
i
= $£•• (t, x, +
о
880
Если НО P(t, X, gj) = (t, X, pi)^(f, X, pa)=s
= P(i, x, |t), TO px = p2 и
n
Q <Pi Pt’ Si ~ (Pit ~Pii) (Bi; Si») **
i=i
С Д d2L ,, t ,
=-i X г5г(/) x’ a^+
о J'7^1 °xi°xJ
+ (1 -a) L) (Ilf-(11/~Ч2/) dtk > 0,
так как по условию подынтегральная функция положи-
тельна (L- положительно определена). Противоречие
показывает, что рг — pt =$> |j = |2, т. е. верно б). В
Вспоминая следствие 1, получаем
Следствие 2. В условиях второй части предложен
ния 2 для любых (/, х, |)£V, (£-, х, p)£D выполняется
неравенство
W(t, х, p}-\-L(t, х, |)><р, |>.
Перейдем теперь к связи между уравнением Эйлера
-^L- (t, х, x)=Lx(t, х, х) * (IS)
и системой Гамильтона (1). Называя далее х: А—>-Rn ре-
шением уравнения (13) (или пару (xt р): A—>RnxRn*—
решением системы (1)), мы подразумеваем, не оговаривая
этого особо, что (/, х(/), х(/))€Г при всех / (соот-
ветственно (t, x(t), p(t))£D). Для краткости решение
х: A—► R" уравнения Эйлера (13), а также его график
{(/, х (0)1^ С А} мы будем называть экстремалью, а реше-
ние (х, р): A—<-R'’xRn* системы Гамильтона (1) и его
график {(/, x(t), p(t))\t£S}—канонической экстремалью
(из контекста всегда ясно, идет ли речь о функциях или
об их графиках).
Предложение 3. Пу$ть функция Ь£С*(У) удов-
летворяет условиям а) и б) предложения 2.
Пара (х(-), р(-)) тогда и только тогда является ка-
нонической экстремалью, когда х(-)—экстремаль и
p(t)^Lk(t, x{t), x(t)). (14)
Доказательство. А) Пусть х(-)—экстремаль.
Если р(-) определено раренством (14), то, согласно (8),
х(?) = 3(/, х(/), р(0)’ Теперь первое из уравнений (1)
следует из (12), а второе—из (11) и (13).
Ml
Б)Пусть(х(-), />(•))— каноническая экстремаль. Тогда
из (12), (8) и первого из уравнений (1) следует (14), а
тогда второе из уравнений (1) превращается в (13) со-
гласно (11). в
Замечание. Предположение L^C2(V) является
здесь более сильным, чем это действительно необходимо:
как и в п. 4.4,2, достаточно было бы требовать суще-
ствование и непрерывность первых и вторых производ-
ных только по х( и Xj. В справедливости этого замеча-
ния читатель может убедиться сам, внеся необходимые
изменения в формулировки теорем о неявной функции
и об обратной функции из п. 2.3.4. '
Гамильтоновы системы (1) обладают многими замеча-
тельными свойствами (см., например, [1J). Мы ограни-
чимся только одним из них, имеющим отношение к вы-
воду достаточных условий экстремума.
Теорема об интегральном инварианте.
Пусть функция SK принадлежит классу Са в открытом
множестве DcRxRnxRn*, дифференциальная форма со
определяется в D равенством
п
a — pdx—ItjpidXi—SK(t, x, p)dt, (15)
i=i
ГА = {(^(а), xft(a), pk (a)) [a k = 0, 1— два
кусочно-гладких замкнутых контура в D (так что tk (a) =
= xk(a) — xk(b), pk(a) = pM.
Если получается из Га сдвигом по каноническим
экстремалям, -т. е. если для каждого а точки 3\ (а) =
= Go(«), хо(а)> Ро(а)) и ^i(a) = (^i(a). xja), рх(а)) ле-
жат на одной канонической экстремали, то
= (16)
Го Г,
Доказательство. А) Согласно классической тео-
реме о дифференцируемости решений по начальным усло-
виям (п. 2.5.7) и теореме о суперпозиции (п. 2.2.2) решение
задачи Коши для системы (1) с начальными условиями
(?0(a), х0(а), ра (а))—обозначим это решение (x(t, a),
p(t, a)) — будет кусочно-непрерывно дифференцируемо
по а и нецрерывно дифференцируемо по t. Отображение
а: {(/, a)|a<a^&, t £ [/0 (a), ^(a)]}—>£) (при ^(a) <
< Z0(a) надо здесь написать [^(a), Z0(a)]), определяемое
равенством o(t, a) = (^, x(t, a), p(t, a)), задает в D дву-
382
мерную поверхность S (рис. 38). Ориентировав S надле-
жащим образом, будем иметь д2 = 1\—Го (две дуги,
отвечающие а —а и а = Ь, геометрически совпадают, но
имеют противоположную ориентацию, так что интегралы
по этим дугам сокращаются). Согласно формуле Стокса
Ь (ос)
и—<|)(о = dco = J dio[ot, Candida
Г, Г„ 3S 2 а t0 (а)
и равенство (16) будет доказано, если мы проверим, что
dco[ot, о«] = 0.
Б) Дифференцируя форму (15), получаем
п
п
d(s> — 'Ejdpi/x.dXi— fflidt + У (^x.dXi + S^p.dpi) Ad/=
i=i L i=i ‘ ‘J
n
= '^i^dpif\dxi—^x.dxif\dt—5^pidpif\dt] (17)
(напомним, что при внешнем умножении dt/\dt — 0)»
Если g=(gf, 1р) и г) = (n/, г|х, т]^)—два касатель-
ных вектора, то из (17) получим;
dco[g, т)1 ==S)
t=i 1
Ч-
14
nt
nt
pi чр. ш
gp<
4
4
Ч
1
Ч
383
Поэтому
п
°al = —
i = l
1
1
О
4i(U) Pit (Л а)
Х1О. (*> а> “)
О,
поскольку a(t, a) = (x(t, а), р(/, а)) по аргументу I
является решением системы (1), а значит, первая и вто-
рая строки определителя совпадают, Ц
В связи с равенством (16) дифференциальную форму (15)
называют интегральным, инвариантом Пуанкаре —
Картана.
Определение 2. Множество ЛсгР называется ле-
жандровым, если
ф 40 = 0
V
(18)
для любого кусочно-гладкого замкнутого контура'усЛ.
Другими словами, ограничение а> | А—замкнутая форма.
(Понятие кусочной гладкости нуждается здесь в уточ-
нении. Мы будем предполагать, что А является образом
открытого множества GcR* при отображении <p: G—>О-
класса CX(G), и у есть образ при этом отображении
обычного кусочно-гладкого замкнутого контура в G.)
Следующие три примера лежандровых множеств играют
далее существенную рдль.
1) Фиксируем некоторую точку (/0, х0, р0)€£> и рас-
смотрим семейство канонических экстремалей {(х(/, 1),
p(t, X)) | а < t < 0} с начальными условиями
х(/0, Х) = х0, p(f0, %) = %. (19)
Множество
х, р) | x—x(i, ty, P~p{t, ^), |рв—< в,
а < t < ₽}
—• искомое; е > 0 и интервал (а, |3) Э подбираются так,
чтобы ScD.
Действительно, как было сказано выше, замкнутый
кусочно-гладкий контур у с 2—это образ кусочно-глад-
кого контура
Г = {(/(з), %(s))|a^s^Z>, t(a) — t(b), h(a) = h(b)}c
с(а, Р)х(ро—е, р0 + е)
384
при отображении (t, X)i-*(t x(t, X), p(t, X)). Спроекти-
ровав Г на плоскость t = te, получим контур Го = {(£а,
X(s))|a^s^ft, X(a)±=A(ft)}, образ которого
?.«{(*«» x(t9, X(s)), p(tt, К (s)) ] a < s <ft} =
= {(ifо, xa, X(s))\a^s^b} (20)
В силу (19). Поскольку y0 получается из у сдвигом по
каноническим экстремалям, то по теореме об интеграль-
ном инварианте
^6) = = pdx—dt = O,
V Vo Vo
ибо на y0 в силу (20) dx — 0, dt = O- Поскольку (IS) верно
для любого ycS, это множество лежандрово.
2) Пусть в задаче (1), (2) %(•)—числовая функция,,
и пусть задано семейство экстремалей %(•, A): (a, 0)»-*R,
Х€(ап Pi)» причем х(., -уеС'Ца, ₽)*(«!, &)).
Множество
£=Н(Л х, р) | x = x(t, X), p^p(t, X) —
= 4i(^> x(t, X), x(t, X)), t£(a, ₽), Xe(alt 0,)}
— искомое. Действительно, пусть у, у„, Г и Г, опреде-
лены, как выше.
Тогда
dx =
V Vo Vo
Ь
Г* fly
(21)
a
Обозначив через Ф(А) первообразную функции Xi-*
*-*р((9, Х)хх(/0, X), продолжаем равенства (21):
ь
§ \ Ф' (X (s)) Xz (s)ds Ф(X(s)) 0,
7 a
так как X(a) = X(ft) (контур замкнут).
3) Предложение 4. Пусть в открытом множестве
GczRxR" задана функция р: G—+R'1*, р = (р1,\.., рп),
график которой I- = {(t, х, р (t, x))\(t, x)^G}cD. Для
того чтобы S было лежандровым множеством:
а) предполагая, что р непрерывна, необходимо и до-
статочно, чтобы существовала функция S^Cl(G) такая,
385
что
(22)
<23>
б) предполагая, что p£Cl (G), необходимо, а в одно-
связной области G и достаточно, чтобы в каждой точке
(i, х) £ G выполнялись соотношения
dPi .. _ V dPk ; ул „
dt ~ дх‘ dpk dXl> ’ ’
Доказательство. Подставляя p = p(t, х) в (15),
получаем форму
a = p(t, x)dx—х, p(t, x))dt.
Лежандровость множества 2 означает, что ^>со — О
г
для любого TeG. Согласно классической теореме из
анализа это равносильно точности со, т. е. существова-
нию такой S, что (p = dS. Отсюда вытекает а).
Если p^.C1(G), то a^.C1(G) и da> = d (dS) = 0, что эк-
вивалентно (24). Достаточность этого условия при одно-
связности G следует из той же классической теоремы,
что и а). |
Уравнение (23) называется уравнением Гамильтона —
Якоби. Если нам известно некоторое его решение в обла-
сти G, то (22) определяет функцию с лежандровым гра-
фиком.
4.4.4. Достаточные условия абсолютного экстремума
в простейшей задаче. Рассмотрим снова простейшую
задачу классического вариационного исчисления
t,
3 (х^У) — ^ L(t, х, x)dt^-extr, (1)
^0
х(/о) = ^о> x{t1) — x1. (2)
Будет предполагаться, что лагранжиан L принадлежит
классу С1 в открытом множестве VcRxR"xR". Допу-
стимыми для задачи (1), (2) будем считать функции
386
^], R") с кусочно-непрерывной производ-
ной, расширенный график которых {(^, x(i),
/JcV. Для определенности все рассуждения будут
проведены для случая минимума; необходимые изменения
в формулировках в случае максимума читатель легко
произведет, заменив L на —L.
В пп. 4.4.1 и 4.4.2 мы уже видели, что выполнение
условия' Лежандра Lx'x(t) = La (t, x(t), x(t))^O необ-
ходимо для того, чтобы допустимая функция х(-) достав-
ляла минимум в задаче (1), (2). С другой стороны, уси-
ленное условие Лежандра La (t) > 0 является составной
частью достаточных условий минимума. Из него следует,
в свою очередь, выпуклость функции x>-*L (t, х, х) вблизи
точек (t, x(t), x(t)), и это наводит на мысль, что выпук-
лость лагранжиана L по х во всей области определения
должна входить в достаточные условия абсолютного ми-
нимума. Теорема Боголюбова (см. п. 1.4.3) подтверждает
это соображение. Поэтому мы предположим, что
%, g)>o, (3)
и что для любых (/, х) сечение
V*. ж = I (L х, выпукло. (4)
Из предложения 1 п. 4.4.3 вытекает тогда, что функция
Tit х t\_J х’ £)» х> /кч
х, +оо> (t,x,l-)(£V (5)
выпукла по £.
В соответствии с предложением 2 п. 4.4.3 условия (3)
и (4) обеспечивают корректное определение гамильто-
ниана соотношениями
&t(t,x, р) = px—L(t, х, х),
p = L-(t, х, х), (6)
из которых надо исключить х. По следствию 2 того же
пункта
Lit, х, £)+W, х, p)^pl,
V(Z, x, V(/, x, p)£D.
(7)
387
Наконец, мы снова будем иметь дело с дифференциаль-
ной формой Пуанкаре—Картана
ы — pdx—ffl(t,x,p)dt. (8)
Теорема 1 (достаточные условия мини-
мума). Пусть L принадлежит, классу С2 в открытом
множестве VcRx R"X R" и выполняются условия (3) и (4).
Пусть, далее, £> определено так же, как в предложении 2
п. 4.4.3, и G—открытое подмножество в RxR".
Если:
1) х(’): [f0, /J—*Rn—допустима# экстремаль задачи
(1). (2) и ее график
£={(*,
2) существует функция р: G—+ R“* класса С1 (G), гра-
фик которой
S = {(£, х, p(t, х)) | (tr x)£G}a:D
и является лежандровым множеством;
„ def „
3) p(t) = p(t, x(t))^Li(t, x(t), x(t));
mo
z*
L(t, x(i), x(t)dt > J L(t, x(t), x{t))di (9)
^0
для любой допустимой x(-): |7e, /J—>R", удовлетворяю-
щей граничным условиям (2) и такой, что ее график
x(O)|/o^<MeG.
За мечание. Из предложения 3 п. 4.4.3 вытекает,
что производная x(t) — x(t), p(t)) непрерывна вме-
сте с x(t) и рУ) — р(1, x(t)). Поэтому х(-) непрерывно
дифференцируема, хотя допустимыми мы считаем все
кусочно-дифференцируемые кривые. Это обстоятельство
не ограничивает применимости теоремы. Действительно,
В п. 4.4.1 было показано, что существование непрерыв-
ной (и даже кусочно-дифференцируемой) функции р(-)
такой, что р(/) = ДД/, x(t), x(t)) является необходимым
условием (сильного) минимума, вытекающим из принципа
максимума. При условиях (3) и (4) это, как мы видим,
Означает, что х(>) должна быть непрерывной.
Ж
Доказательство. Обозначим p(t) = p(t, x(t)) и.
рассмотрим кривые
Н(*> х(0, р(0) I
Y =={(*> x(t), р(0)РоС^М<=2.
Поскольку х(^-) = х(^), i = 0, 1, и, следовательно, p(t;)—
= p(t,, x(t;)) = p(ti, х(^)) = р(^), концы этих кривых
совпадают и можно рассмотреть замкнутый контур у —
— ycS, который получается, если сначала пройти от
(t<>, x(tB), р (to)) до (tlt х (tj), р (tj) вдоль у, а затем обратно
вдоль у. Ввиду лежандровости S
0= ф со = со—J со. (10)
v-v 7 v
Используя неравенство (7), получаем
\®^\pdx—Wdt^\{p(t)x(t)—9t(t, x(t), p(t))}dt^
V V
*^L(t, x(f), x(t))dt~3 (x(-))t (11)
^0
причем равенство здесь Возможно, только если
p(t)x(t)S^(t, х (t), p(t))**L(t, x(t), x(t)),
т. e. (снова используя (7)) если
p(t)x(t)—W(t,x(t),p(f))=
- max {px(t)~-$?(t, x(f), p)k
{p | (i, x (il, p) ё D}
По теореме Ферма
x(t) = Mp(t, x(t), p(t)). (12)
Поскольку график p лежандров, должны выполняться
равенства (24) п. 4.4.3, откуда с учетом (12)
^=4р<«.*(0)=
, У’^1^_____(д^ I 'Vd^ aPk\ .
di « dxft dt dx'i дръ dxt /
+ *(t)> Pit)). (13)
звэ
Согласно (12) и (13) (%(•)» р(-))— каноническая экстре-
маль. Но (x(ta), p(ta)) = (x(ta), p(t0)), и так как (х(-),
р(-)) тоже является канонической экстремалью (предло-
жение 3 п. 4.4.3), то по теореме единственности %(/) =
= x(f), p(t) = p(f).
Итак из (-11)
J ю = L(t, x(t), х (t)) dt = 3 (х (•)),
у
а для остальных допустимых х(-), графики которых
лежат в G и которые удовлетворяют условиям (2)
$со<5'(х(-)).
V
Ввиду (10) получаем 3(х(-)) > 3(х(-)). |
Следствие. Если в условиях теоремы G совпадает
с проекцией D на RxR" = {(Z, х)}, то х(-) доставляет
строгий абсолютный минимум в задаче (1), (2).
Часть условий только что доказанной теоремы в кур-
сах вариационного исчисления обычно представляют
в несколько иной форме, связанной с понятием поля
экстремалей.
Определение. Пусть Л и G—открытые множества
в R” и Rx R" соответственно. Семейство функций {х (•, X);
[МЧ, (А.)] —R" ( Л. С А} образует поле экстремалей,
покрывающее G, если:
1) х(-, X) является экстремалью (решением уравнения
Эйлера) задачи (1), (2) для любого
2) отображение (f, X)i->(/, x(t, X)) взаимно однозначно
и его образ
{(^, x)|x = x(f, X), ta(E)^t ^^(Х), AgA}=>G.
3) функция р: G—> R"*, определяемая равенствами
p(t, x) = L^(t, x(t, %), left, %)),
' (U)=(U(U))t 1 }
принадлежит классу С1 (G) и имеет лежандров график.
Функция и: G^>Rn, определяемая равенствами
u(t, x) = x(t, К), (t, x) = (t, x(t, К)), (15)
390
называется функцией наклона поля. Экстремаль х(-):
Ро> М— К" включается в поле %(-, •), если ее график
содержится в G и x(t) = x(t, 1) для некоторого Х^Л.
Подставляя (14) и (15) в (8) и, вспоминая определе-
ние лежандрова множества (п. 4.4.3), мы можем усло-
вие 3) переформулировать еще и так:
3') В области G интеграл
(6. Xi)
J {Lx(t, х, u(t, x))dx—
— [L^t, x, u(t, x))u(t, x)—L(t, x, u(t, *))]}<# (16)
не зависит от пути интегрирования между точками (ta, ха)
и (^, л\) (согласно теореме классического анализа по-
следнее равносильно тому, что интеграл по замкнутому
контуру равен нулю). Интеграл (16) называется инвари-
антным интегралом Гильберта.
Теорема Г. Пусть функция L удовлетворяет тем
же условиям, что и в теореме 1, и пусть х(-): [£0, М—►
—>Rn—допустимая экстремаль, график которой содер-
жится в G.
Если х(-) может быть включена в поле экстремалей,
покрывающее G, то %(•) доставляет функционалу (1) ми-
нимум в классе допустимых функций, удовлетворяющих
условиям (2) и таких, что их графики содержатся в G.
Читатели легко убедятся, что это всего лишь пере-
формулировка теоремы 1. Особенно удобна она при п= 1,
так как в этом случае условие 3) приведенного выше
определения следует из 1) и 2) (см» второй из примеров
лежандровых множеств в п. 4.4.3). Этим замечанием можно
пользоваться при решении многих задач.
4.4.5. Сопряженные точки. Достаточные условия силь-
ного и слабого экстремума. В этом пункте мы по-преж-
нему будем предполагать, что L £ С2 (V); х (•) G С1 (|70, Ц,
R") —допустимая экстремаль задачи (1), (2) п. 4.4.4, вдоль
которой выполняется усиленное'условие Лежандра
x(t), х(0)>0, М- (1)
По непрерывности матрица L-x остается положительно
определенной в некоторой окрестности V расширенного
графика {(t, x(t),x(t))\ta^t ^tt}. Окрестность V вы-
391
берем так, чтобы ее сечения | (/, х, |)gV} были
выпуклы. Тогда выполняются условия предложения 2
П, 4,4.3 и соответственно мы можем определить область
DaRxR"xR"* и гамильтониан Ь—*И. класса С2.
Правые части канонической системы
х = (t, х, р), р~ — $Vx(t, X, р) (2)
непрерывно дифференцируемы в D. Каноническую экстре-
маль (*(•), р(-))> отвечающую экстремали £(•), а сле-
довательно, и самое х(-) можно продолжить на некото-
рый интервал, содержащий отрезок [/„, 7Х]. После этого,
сузив, если нужно, V, мы можем считать, что V имеет вид
х, |)||х—£(/)|<е, II—х(01<е, /0 —е< t< ^+е}.
Пусть (t0, х0, po) = (fo, x(fj), Lx (tq, x(^0), x(/0))). По-
строим семейство канонических экстремалей {(х(-, L),
р(>, Х))| X—р9|<6}, определяемых начальными усло-
виями
х(^9, р (/9, X) = X (3)
(ср. первый пример лежандрова множества в п. 4.4.3).
При достаточно малом 6 экстремали этого семейства
вместе с (х(-), р (•)) = (*(•> Ро)> Р(-» Ро)) содержатся
в D при ff]; функции х(-, •), р(-, •), очевидно,
непрерывно дифференцируемы (п. 2.5.7).
Предложение 1, Для того чтобы точка
была сопряженной к ta, необходимо и достаточно, чтобы
drtRnL.J=°- w
Доказательство. А) По теореме п. 2,5.7 сово-
купность производных решений системы (2) по начальным
данным при Х==р9 образует фундаментальную матрицу
решений соответствующей системы уравнений в вариациях
Интересующие нас производные дх/дЪ^, др/д\;, располо-
женные в столбец, составляют половину (п из 2п) столбцов
Ж
этой матрицы и в соответствии с условиями (3)
Vclp/axj Ifaf, . \ei) • I '
Равенство (4) эквивалентно существованию такого нену-
левого вектора с С R", что
|<т'Р.)с=Х|(Т) Р)с^й.
i
Обозначим
Т(о\
,л(0/
ГЛ дх
f±=l ’
п а
L4«’pa)Ci-
Будучи линейной комбинацией столбцов фундаментальной
матрицы, это тоже решение системы (5), причем в силу (6)
F(^) = 0, г|(/о) = с^=О. Кроме того, |(т) = 0.
Итак, равенство (4) эквивалентно существованию Не-
тривиального решения системы (5), у которого g (ta) =s
4(t) = 0.
Б) Лемма. Пара {!(*)> Л(')} является решением Си-
стемы (5), тогдй и только тогда, когда £(•) решение
уравнения Якоби.
+4Л1 (7)
и
($)
Доказательство. По определению (см. п. 4.4.2)
уравнение (7) есть уравнение Эйлера для вторичной экст-
ремальной задачи с лагранжианом
2 = + 2^t (9)
Соответствующий гамильтониан <!р получается преобразо-
ванием Лежандра по g
2. (10)
T} =*=
зэз
Чтобы получить второе из этих равенств, заметим, что
дХ>
откуда
^(^.g) = y^_5 (£U)
о§/ oxj dxi dxtdxj
Аналогично
d%i dh I дх{ dxk ~' J
= Етф- ** +Ет^т- t = (2^4)z.
bxv дх^ ~ dxj dxi
Исключая из (10) (, получаем.
£ =4 {nT^7 n-2r£« b£x\ +
+ ^[1^--1£;х-£^7^1]5}. (11)
Теперь воспользуемся формулами (11), (12) и (8) п. 4.4.3:
$Vx(t, х, p) = — Lx(t, х, S(t, х, р)),
9tp(t, х, p) = H(t, x, p),
p^Li (t, x, 3 (t, x, p)).
Дифференцируя по x и p, получаем:
XX~ ^XX Lgi&x ~ %*xx ^xx^pxt
^xp~ ^xx^p— Lxx&tpp,
Е^^=ЦхЗр=1ц^рр,
0 = = Lxic -\~^xi'^‘x~ ^XX Л~ЕХх^px‘
Отсюда
pp ~ Exx > xp ~ LxxExx » (12)
px= L'xi Lxxt xx^ Exx-\-LxxL'xx^-'xx •
394
Следовательно, (11) можно переписать так:
§ = 1 + 2^хрЧ + ?ЯХХ1}.
Согласно предложению 3 п. 4.4.3 пара {?(), г|(-)}
тогда и только тогда является решением канонической
системы
t = П = (13)
когда ?(•) является решением (7) и выполняется второе
из соотношений (10), совпадающее с (8). Остается заме-
тить, что система (^^тождественна (5). |
В) Завершение доказательства. В первой
части доказательства было показано, что (4) эквивалентно
существованию нетривиального решения {£(•), Т) (•)} си-
стемы (5), у которого £Go) = £(T) —0- По лемме £(•) яв-
ляется решением уравнения Якоби и имеет место (8),
откуда TJ (т) = (т) £ (т). Равенство т] (т) = 0 противоре-
чит (по теореме единственности) нетривиальности реше-
ния, поэтому г] (т) =/=0. Вспоминая определение из п. 4.4.2,
мы видим, что (4) эквивалентно сопряженности точки т
точке t0.
Доказанное утверждение позволяет дать следующее
геометрическое истолкование понятия сопряженной точки.
Пусть снова (%(•), р(-))— каноническая экстремаль, от-
вечающая рассматриваемой экстремали %(•). При доста-
точно малом , 6 канонические экстремали, определяемые
условиями (3), образуют полоску вдоль графика
(рис. 39). При t=ta край этой полоски «вертикален»
395
и проектируется в точку Ло *=(/„, х0). Условие (4), экви-
валентное, как мы видели, равенству ^j-c = O, означает,
что при t = т в точке Вх = (т, х (т), р (т)) полоска касается
некоторого «вертикального» направления (т. е. направ-
ления, параллельного плоскостям t = const, х —const).
Если мы спроектируем полоску в пространство (t, х),
то мы получим пучок экстремалей, выходящий из точки Ао
(рис. 39). Около точки Лт = (т, х(т)) отображение (t, X) —►
—*(/, x(t, X)) перестает быть взаимно однозначным («экст-
ремали, бесконечно близкие к х(-) и имеющие с ней
общее начало, пересекаются в Лт»). Точка Ах также на-
зывается сопряженной с Ло,
Упражнение. На сфере 52 = {(х, у, z) | x2 + i/2-j-za = Z?2} дуги
болящего круга суть экстремали функционала длины Проведем через
ТОЧКУ А» £ S* некоторый большой круг, Найдите иа ием точку, со-
пряженную о Дв.
Предложение 2. Если на экстремали х(-):
выполнено усиленное условие Лежандра (1)
и усиленное условие Якоби (полуинтервал (£0, не со-
держит точек, сопряженных с ia), то эту экстремаль
можно включить в поле экстремалей, покрывающее неко-
торую окрестность G ее графика {(/, x(t)) |t
Доказательство. А) Докажем сначала, что для
достаточно малого 6 > 0 ни одна из точек отрезка [7а,
не будет сопряженной ни к одной точке ^£(/0—6, ta).
В противном случае существуют такие +/0, t^y £[t0, /J
и такие решения £<п)(•) уравнения Якоби (7), что
(/<»>) = (/<«>) = 0,1цт (tf”)^ 0. Ввиду однород-
ности уравнения можно положить |£(п>(#п))| = 1. Перехо-
дя, если нужно, к подпоследовательности, мЫ можем
считать, что £ln> —> /l£[f0, //],
i<r” (/(n>) —> т], | T| | = 1.
При выполнении условия (1) уравнение Якоби сво-
дится к линейной системе (5), коэффициенты которой
непрерывны на отрезке A дз pe, ij, и задача Коши с на-
чальными условиями
Л (^i)=Ец(tj) £ + £^(/1)'^ (ti) = Lxx(ti) т|
396
имеет -для нее решение (§(/), Л(0)- определенное на Л
(п. 2.5.4). По теореме о непрерывной зависимости реше-
ния от начальных данных (п. 2.5.5) g'”’ (/)—*•£ (О и
п(п’ (о=u(o m+W) (о—я (О
равномерно на Л. Но тогда и lw(t) —>-t(t) равномерно
на А.
Далее, 5(^) = 1im5(ftB)) = limg(n)(/r’) = O. При этом
п п
точки t9 = lim 4П) и t't = lim не могут совпадать, по-
rt п
скольку в противном случае t) == |(^) = 0,-ибо
4В>
11 т i = Л I <
а — J I
< lit"” -g Ис+max 11 (?) -1 (® I - 0-
I*;, я
Так как g(/„) = g(Q = 0 и La(ti) g (t'J^O, точка ti € (/e,
сопряжена t0 вопреки условию.
Б) Выберем t'o < t0 так, чтобы на ]70, Ц не было
точек, сопряженных с t'o. Построим семейство канониче»
ских экстремалей (х(-, X), р(-, X)), заменив в (3) tg на t'o.
дх
В силу предложения 1 detро)^=О, Vt£[70, ij.
Определим отображение <р: С$ —> R х R” цилиндра C6=t
=вфв—б, /i+6JxB(/?e, б) равенством ф(/, Х) = (/,x(t, X)).
В точках (т, р0), тё[/0, его якобиан
det ф' = det ( 1 ° 'j = det хк О,
\*t
и мы можем выбрать б так, чтобы это неравенстве/ со-
хранилось во всех точках С$. Кроме того, по теореме
об обратном отображении (п. 2.3.4) у каждой точки (т, р0)
найдется окрестность Ux, которую ф взаимно однозначно
отображает на 1Гт = ф((/т) и ф-^С1^).
Покажем, что при достаточно малом б отображение ф
взаимно однозначно на всем Се- Если это не так, то
существуют две последовательности (/', X’), (/”, X*) такие,
ЧТО Х„ —* Рд, Кц + рд и (tn, X (tn, Х„))=яф (tn, Х„) = ф (tn, Xn) =S
— (in, X(f’n, x;)). Отсюда Гп = Гп.
Переходя к подпоследовательности, мы можем считать,
что *т. При достаточно больших п точки (t'n, X;)
392
И (t”n> и равенство А,А) = ф(С Ki) противо-
речит определению Ux.
Теперь покажем, что G = <р (int Св) является окрест-
ностью графика Г = {(/, х(0) I Поскольку
Г = <р ({(t, р0) 1t0 sC t G, _нужно доказать откры-
тость G. Но если (t, х) = <р(/, A,)£G, (t, то
det q>' (t, Х)=^=0, и по той же теореме п. 2.3.4 некоторая
окрестность точки (/, X) отображается на окрестность
точки (Л х). Поэтому (t, х)— внутренняя точка G и G
открыто.
Таким образом, семейство экстремалей {х(-, X)} вза-
имно однозначно покрывает G. То, что это семейство
образует поле, было показано в первом примере лежанд-
рова множества в п. 4.4.3.
Построенное поле состоит из экстремалей, проходящих
через одну и ту же точку (^, х0) и называется цен-
тральным.
Теперь мы возвратимся к достаточным условиям ми-
нимума. Прежде всего покажем, как из общей теоремы
п. 4.4.4 получаются достаточные условия слабого мини-
мума. Соответствующая теорема была уже сформулирована
в п. 4.4.2.
Доказательство теоремы Якоби (теорема 2
п. 4.4.2). Если на допустимой экстремали х(-) задачи (1),
(2) п. 4.4.4 выполняются усиленные условия Лежандра
и Якоби, то, согласно предложению 2, ее можно вклю-
чить в поле экстремалей, покрывающее некоторую окрест-
ность G графика *(•_). По теореме 1 (или Г) п. 4.4.4
неравенство
fi
3 (х(‘))=^ L(t, x(f), i(0)^>5(%0))
^0
выполняется для всех ([te> /J, Rn), удовлетво-
ряющих краевым условиям х(/0) = х(^0), х (г\) = х (^)
и таких, что график %(•) содержится в G, а расширен-
ный график—в V. Если ||х(-)—х(*)11с‘ достаточно мала,
то последние два условия удовлетворяются. Следовательно,
х(.) доставляет в задаче (1), (2) п. 4.4.4 С^локальный,
т. е. слабый, минимум. |
Перейдем к достаточным условиям сильного минимума.
В этом случае сами функции х(-) и х(-) по-прежнему
398
можно считать столь близкими, что график х(>) содер-
жится в G, но х(-) может быть любым и расширенный
график х(-) не обязан помещаться в V. Вне V условие (1)
не гарантирует выпуклости функции £>-*Z,(tf, х, £), и не-
равенство Юнга, использованное в доказательстве тео-
ремы 1 п. 4.4.4 (см. там формулу (7)), не обязано вы-
полняться. Поэтому в формулировку теоремы придется
ввести дополнительное предположение (условие Вейер-
штрасса) о неотрицательности функции
£(t, х, и, %) = L(t, х, х, и)—Lx (t, х, и) (g—।и).
Теорема Вейерштрасса о достаточных ус-
ловиях сильного минимума. Пусть функция L
принадлежит классу С8 в открытом множестве V с Rx
xR"xR", функция x(-)CCl(|70> М> R")1) м ее росши’
ренный график
Y = {(tt х((),
Если:
1) /(•) удовлетворяет-уравнению Эйлера
-^Lx(t)=h (0;
2) х(-) удовлетворяет краевым условиям
x(.^o)~Xot x(<t1) = X1,
3) $доль х(-) выполнено усиленное условие Лежандра (1);
4) вдоль х(-) выполнено усиленное условие Дкоби: в по-
луинтервале (ta, нет точек, сопряженных с t0;
5) существует окрестность V э Г, для которой выпол-
няется условие Вейерштрасса
£(t, х, и, 5)^0
для всех (1, х, и, £) таких, что (t, х, u)£V, (t, х, s)€V,
то х(-) доставляет сильный минимум в простейшей за-
даче (1), (2) п. 4.4.4 (строгий, если в условии Вейер-
штрасса <£ > 0 при %=£и).
1) Напомним, что х( ), доставляющее сильный минимум, при
выполнении условия (1) должно иметь непрерывную производную,
хотя сейчас задача рассматривается в КС1 ([70, /х], R") (см. заме-
чание после формулировки теоремы 1 п. 4.4.4).
399
Доказательство. Определим окрестность УэГ
так же, как и в начале этого пункта, и построим окрест-
ность G з Г = {(Л х (f)) [ t9 t < f J и поле экстремалей,
покрывающее G; без ограничения общности V**V. Обо*
значим через и (i, х) наклон поля в точке (t, х) **
x(t, X))£G:
u(t, x) = x(f, %) При x=*x{t, X),
и пусть
p(t, x)=Li(t, х, u(t, x)).
Согласно предложению 2 и примеру из п. 4.4.3 функция
р: О —* Кя* имеет лежандров график
х, p(t, х))|(t, x)$G}czb.
Теперь для допустимой х(-), график которой содер-
жится в G,
G
S(x(-))— L(t, х(0, x(t))dt—•
ti ’ г° ;
— ${р(Л x(t))x(t) — $%(t, х(0> Pkt, x{t)))}dt=a
= x(0. x(t), u(t, x(/))x (;!)->
*0
+Ц (t, x (t), и (t, x (0)«(6 x x (t), u(t,x (0))}^=»
t,
s=sj^(£, x{t), u(t, x(t))dt.
Поскольку экстремаль x(-) содержится в поле, x(t)«
Bau(t, x(/)), а потому
it
З(х<г)) — *(0, “(Л x{t))dtmQ. (14)
Следовательно,
it
3(x(-))—5'(x(-))=$^(f, x(0, u(t, x(0), x(t))dt (15)
i,
fкак и В теореме 1 П. 4.4.4
\ » v J
409
По построению (см. доказательство предложения 2
п. 4.4.5) точки (t, x(t, X), x(t, X)) = (f, x, u(t, x))£V = V
при (i, x) = (t, x(t, K))£G и (/, x(t), x(f))£V, поскольку
x(«)—допустимая функция. Следовательно, применимо
условие Вейерштрасса и из (15) 3 (х(;))— 3 (х(-)))>0.
Таким образом, если х(>)€КСх([70, R") допустима,
удовлетворяет краевым условиям и ||х()—х(-)||с столь
мала, что график х(-) лежит в G, то 3 (х(-)) 3(х(-)).
Значит, х(<) доставляет сильный минимум в задаче (1)—(4)
п. 4.4.4.
Равенство 3 (х (•)) = 3 [х ()) возможно при этом только
в случае, когда x(t), u(t, x(t)), x(t)) = Q для всех t,
кроме, быть может, точек разрыва х(-). Если н=?*Ц=з>
!=Ф<Й’>0, то x(f) = tz(f, х(0) И, в частности, х(-) ока-
зывается непрерывной. Далее, согласно соотношениям
(8) и (12) п. 4.4.3,
p(t, x)==Li(t, х, u(t, x) =
o=2(i, x, p(t, x))&u(t, x) — ^p{t, x, p{t, х))яФх(^)«
= t%p(t, x, p(t, x)).
Полученная формула совпадает с (12) п. 4.4.4 и, рас-
суждая, как и там, мы устанавливаем, что x(t)^x(t). Ц
Замечание. Соотношение (15) позволяет показать,
что квадратичный функционал
£(&(•))= I, i)dt
с лагранжианом (9) можно привести к «полному квадра-
ту». Вычисляя функцию Вейерштрасса (и полагая | (0=0)
получаем
Q (В (•)) - УIР (0 (+Р (О-1 [U (0 -п (f) Е-ф)] ВIW, (15)
где Р (t)2 — Lxx (1), а Е(-) и П(-)—решения матричной
системы
Е(0 = ^(03+^(0П,
П(0=-^(0 3-^(0 п
14 В. М. Алексеев в др.
(17)
401
с начальными условиями
S(Q = 0, П (Q = £.
(18)
4.4.6. Теорема Э. Нетер. В п. 1.4.1 мы уже познако-
мились с некоторыми ситуациями, в которых уравнение
Эйлера имеет первый интеграл. Например, если лагран-
жиан не зависит явно от t, т. е. имеет вид L (х, х), то
H = LxX—L = const (интеграл энергии). В этом пункте
мы познакомимся с общим приемом конструирования
первых интегралов для систем дифференциальных урав-
нений, являющихся уравнениями Эйлера некоторых ва-
риационных задач. Этот прием основан на простой
и вместе с тем глубокой теореме, доказанной замечатель-
ной женщиной-математиком нашего века Эмми Нётер.
Универсальный принцип, выражаемый теоремой Нётер,
часто формулируют так:'«Всякая симметрия в мире по-
рождает закон сохранения», или еще: «Инвариантность
системы относительно некоторой группы преобразований
имеет следствием существование в системе первого ин-
теграла». Так, например, инвариантность системы отно-
сительно сдвига по времени, проявляющаяся в том, что
время t не входит в лагранжиан, дает нам интеграл
энергии.
Перейдем к точным определениям. Пусть дано семей-
ство отображений
5а: RxRn —>RxRn, |а|<е0,
$a(t, x) — (j^(t, x, а), Х(/, х, а)).
Относительно него мы будем предполагать, что:
1) функции J и £ принадлежат классу С2;
2) при а—>0
.£(/, х, а) = i-{-aT (t, х)Ц-о(а), ..
- 3i(t, х, а) = х + аХ(/, x)-f-o(a).
Векторное поле (Т (/, х), X (t, х)) будем называть
касательным векторным полем семейства {Sa}. Под дейст-
вием преобразований Sa точка P = (t, х) описывает не-
которую кривую в RxR" и {Т (t, х), X (I, х)}—касатель-
ный вектор к этой кривой в точке Р (т. е. при а = 0;
рис. 40).
Лемма. Пусть х(-)€С2(]70, fj, R"). Тогда сущест-
вуют такие б > 0, е > 0, х(-, )€Са((^0—б, +&)>(,
Х(—в, е), R"), fft(-)€C2((—8, е)), k = Q, 1, что при
402
а£(—8, в) образ графика функции х(-) является графи-
ком функции x(-s а): [70(а,) (а)]—При этом
x(t, O)s=x(O, xa(t, O) = X(t, (2)
^(0) = f(th x(t()). (3)
Доказательство. Образ графика x(-) при отоб-
ражении Sa задается параметрическими формулами
/=т(з, a) = £(s, x(s), а),
x — y,(S, oc) = X(s, x(s), a), |a|^80. ' '
Обе функции т и % как суперпозиции функций класса С2
сами принадлежат этому классу.
Согласно (1)
^(t, х, 0) = 1, -^П,х,0) = 0,
и потому
дт . п. дХ dt , дХ . . ,
-a-(s, 0) =-^7-+-5—л: (s) 1.
ds v ' dt ds 1 дх v >
Используя компактность отрезка /0 < s и непрерыв-
ность бх[дз; находим такие > 0 и 8j > 0, что при
ja^Bj, и /0—бх < s < ^i+6f выполняется неравенство
a) > 1/2. Тогда при фиксированном а£(—в, в)
функция sh»t(s, а) монотонно возрастает и отображает1
По. М на
По (а), /1(а)] = [т(/в, а), т(/о а)] =
= x(t0), а), % (Ji, хИО, а)]. (5)
14* 403
Из этих равенств видно, что ^(а), 1=^0, 1,—функ-
ции класса С2, причем из (1) следует (3).
В силу той же монотонности отображение А, опре-
деленное равенством A (s, а)-= (т (s, а), а), Взаимно одно-
значно отображает прямоугольник П = (/о—fj+SJx
х(—6,, ej на его образ № = Л(П). Поскольку яко-
биан А
... fdt/ds дт/да\ дт . I
det\ о 1 /==’аГ>-2’
то, рассуждай так же, как в доказательстве предложе-
ния 2 п. 4.4.5, устанавливаем, что IF открыто и что
обратное отображение Л-1: W—>П, которое, очевидно,
имеет вид (t, a)h»(o(L a), а), непрерывно дифферен-
цируемо и ст € С* (IF).
Из (4) и (1) имеем t(s, 0) = £(s, x(s), 0)ss. Поэтому
А оставляет на месте точки (s, 0) и то же делает Л-1,
откуда o(t, 0)=s£.
Далее, как неявная функция, сг (•, •) находится из
уравнения F(o, а)==т(ст, а) — Z = 0.- Отсюда, во-первых,
согласно (4) и (1),
<ra(*. = 0), 0)~l-ra (ст (f, 0), ОН
= — x(t), 0)+$х(/, x(t), O)x(t)]~l^(t, x(t), 0) =
= -T(t, x(/)), (6)
а, во-вторых, поскольку F класса С2, то по сделанному
в п. 2.3.4 замечанию .ст £ С2 (IF).
Далее, А отображает отрезок {(s, 0) | s С в себя
и этот отрезок содержится в IF. Следовательно, IF со-
держит прямоугольник (t0—6, fj + 6)x(—в, в), если
6 >0 и в >0 достаточны малы, и на этом прямоуголь-
нике
x(t, ос) = .36 (ст (/, a), x(a(t, a)), a)- (7)
• функция класса С2. При этом в мы выберем так, чтобы
при |а| <8 выполнялись неравенства |f(-(a)— /(-|<6.
Тогда, вспоминая определения функций ст(-, «) и /,(•),
мы видим -из (4) и (7), что образ графика х(-) при
отображении Sa есть график функции х(-, a): [f0(a),
/i(a)J—*R"»
404
Наконец, дифференцируя (7) с учетом (1), (6) и ра-
венства o(t, 0) — t, находим
0) = [Xt(/, х(0> O) + Xx(t, x(t), 0)x(0]aa(f, 0)4-
4-#Ж x(t), 0) = x(t)[—T (t, x(t))] + X(t, x(0);
t. e. верно (2). Ц
Определение. Пусть функция L: V—>R по край-
ней мере непрерывна в открытом множестве KcRx
xR^xR". Интегральный функционал
ti
3(х(-), t0, x(t), x(t))dt (8)
называется инвариантным относительно семейства отоб-
ражений если для любой функции х (•) € С2 ([/e,
R") такой, что {(^, x(t), x(t)')\t0^:t^:t1}cV
3(х(-, а), М“)« M“))^(x(-), t0, (9)
для всех достаточно малых а.
(Здесь х(-, а), /0(а), /Да) построены по х(-), как
в лемме, и интервал, в котором имеет место (9), может
зависеть от х(-).)
Теорема Э. Нетер. Пусть функции L, Lx, Lx не-
прерывны в открытом множестве V'cRxR"xR'i и ин-
тегральный функционал (8) инвариантен относительно
семейства преобразований класса С2, удовлетворяющих
условию (1).~ Тогда функция
<р (£, х, x) = Lb(t, х, x)X(t, х) —
—[Li(t, х, x)x—L(t, х, x)]T(t, x) (10)
постоянна на каждом решении х(-) уравнения Эйлера
(t, x(f), х(/)) = £Л(/, х(0, x(t)) (Н)
таком, что х(-) €С2([/0, fj, R"), {(Л x(t), х(ОШо^
и т-, х(-), х(.))€<?([/„, Q, %п*)-
Доказательство. А) Пусть х(-): |70, G]-—
то решение уравнения (11), о котором говорится в усло-
вии теоремы. Воспользовавшись леммой, построим се-
мейство (х(-, a), f0(a), Ма))> гДе х(’> •)—ФУНКЦИЯ
класса С2 на (t0—б, ^4-б)Х(—е, е). Фиксируем отре-
зок А = [р, у] так, чтобы выполнялись неравенства
/0—б < р < /0 < < у < t14- б, и уменьшим, если нужно,
405
, 0)—axa(f, 0)
a
в так, чтобы при |а|<8 выполнялись неравенства р<
- < t9 (а) < t, (а) < V-
Покажем, что отображение Ф: (—е, е)—^(^(Л, R")x
XR2, при котором a), Z0(a), ^(a)} дифферен-
цируемо по Фреше в точке а=0. Ясно, что достаточно
проверить это для первой компоненты ан»х(., а). Фикси-
ровав е £ (0, е) и применяя теорему о среднем (к диф-
ференцируемым отображениям a—>х(/, a), t—фиксиро-
вано), имеем при | а | е
I x(t, а)—х(/
sup ——— 5-
/ед I
^sup sup I Xa (t, c) — Xa(t, 0)1—+0,
/ед ce[0, a]
I xt(i, a)—xt(t, 0)-axtq (t, 0) I
f I • « I
^silp sup |x/a(f, c) — Xia(t, 0)1—>0,
/еД се[0за]
при a—>0, поскольку xa и x/a равномерно непрерывны
на компакте Ах[—в, е]. Следовательно, в пространстве
С1 (A, R")
х( -, a) = x(-, 0) + axa(., 0) + о(|а|), (J2)
что и означает дифференцируемость по Фреше. Кроме
того, из (12) вытекает, что
Ф'(0) = {*«(•» 0), t'0(O), ЗД}. (13)
Б) Положим 3(a) —(3 оФ)(а) = 3(х(-, a), t0(a),
t1(a)). Согласно (9) 3(a) = 3(0) и, значит, 3’ (0) =
-З'(х(-), t0, ^)[Ф' (0)] = 0. Воспользовавшись форму-
лой (9) из п. 2.4.2 для производной интегрального
отображения, получаем из (13)
Q = 3’(x(-),’t0, О[Ф'(0)] =
tl
= \{Lx(t, x(t), x(t))xa(t, 0) +
+ Li(t, x(f), x(t))xat(t, 0)}dt +
+ L(th x(f,.), ^))ЗДК- (i4)
По предположению, (t, x(t), x(t)) непрерывно диф-
ференцируема. Интегрируя в (14) по частям (как вп. 1.4.1)
406
и учитывая (11), (2), (3) и (10), имеем
0 = [Li (Zz, x((z), х О xa(it, 0) +
+L(t{, x(tz), хОГг(0)]й=
^[L-X(th x(t{), x(t'))X(th хО+ (£(/,-, x(f;), x(Q)-
-L-x (/,-, x(/z), i(fz))x(Q)T(fz, x(f,.))]£,= .
"ф(^1> (^i)) Ф (^o> ^(^o)> *(Q)«
Итак,
Ф(^, х(/х), х£(/1)) = ф(^, x(fe), x(Q).
Повторяя те же рассуждения для произвольного отрезка
j70, Z]c[70, /Д, получаем равенство
ф(Л x(t), х (/))== ср (f0, х(^), x(f0))ss const.
Следствие. Если в условиях теоремы Нётер выпол-
няются предположения а) и б) предложения 2 п. 4.4.3,
тофункция
i|?(f, х, p) = pX(t, x)—W(t, х, p)T(t, x) (15)
постоянна на каждом решении (x(f), p(t)) системы Га-
мильтона (1) п. 4.4.3. (
Доказательство предоставляется читателю. Из
формулы (15) видно, что доставляемый теоремой Нётер
первый интеграл есть значение дифференциальной формы
Пуанкаре — Картана (>) = p.dx—SK dt на касательном век-
торном поле семейства {Sa}.
В качестве примера покажем, как из теоремы Нётер по-
лучаются интегралы энергии и импульса (п. 1.4.1). Если L
не зависит от t, то функционал (8) инвариантен относи-
тельно преобразований (t, x)h»(^+a, х) (проверьте!).
Здесь Т—\, Х = 0, и потому <p = L—Ljc =— SK по-
стоянна. Если же L не зависит от одной из компонент
вектора х, скажем от xk, то функционал (8) инвариан-
тен относительно преобразований (t, х)н»(/, x + a£ft) (про-
верьте!). Здесь 7 = 0, X = ek, и потому Ф = Ь;вй = £; ,
Другие примеры применения теоремы Нётер будут
приведены в следующем пункте.
4.4.7. Вариационный принцип и законы сохранения
в механике. Рассмотрим систему из п материальных то-
чек («частиц») с массами mit ..., тп, r( — (Xi, У{, г() —
407
радиус-вектор i-й точки. Для краткости полагаем
. . , д ( д д \
г=(гп .... r„)€R3", 17-(
Э / Э 9 э-\
дг[ ~Д dxi * dtfi ’ dzi J ‘
Будем предполагать, что взаимодействие частиц между
собой и с внешней средой описывается потенциальной
энергией U (t, г), так что уравнения движения имеют вид
F{^ — dU/dr{. (1)
Кинетическая энергия системы определяется равенством
п
K=^mi(ri\rt). (2)
I = 1
Теорема (вариационный принцип Лаг-
ранжа). Уравнения движения механической системы
суть уравнения Эйлера вариационной задачи
JL(t, г, r)df—>extr, .„
to V5)
r(Q = r°, г(М = Л L =
Доказательство. Из (1) и (2) имеем
„ •• d . ч d дк d r г ди
mtri - dt ~ dt drj ~ & L'i~Lr~ drt' И
Значение этой теоремы выходит далеко за рамки той
простейшей ситуации, которой мы ограничимся. Физики
и механики очень часто описывают свойства системы,
задавая непосредственно ее лагранжиан L. При этом
К, U и L = К—U могут быть выражены не в декарто-
вых, а в каких-то других координатах, в лагранжиан
могут быть введены члены, описывающие магнитные или
гироскопические (не потенциальные) силы и т. д. Как
только лагранжиан задан, уравнения Эйлера вариацион-
ной задачи (3) определяют закон движения рассматри-
ваемой системы.
Вариационный подход удобен, в частности,- возмож-
ностью получения первых интегралов («законов сохра-
нения») при помощи теоремы Нетер. Мы проиллюстри-
руем эту возможность на примере так называемых клас-
сических интегралов: энергии, импульса и момента.
408
а) Консервативная система: U не зависит
от t. Группа преобразований: (t, г)н»(/+а, г). Функ-
ция г(-): |70, >R3n переходит при этом в функцию
Га(-): Е*о4-а, + «]—> R3n, ra(f) = r(f—а). Функцио-
нал (3) инвариантен:
<i + a 6+а
J L(ra(0> ra(i))dt= J L(r(t—a), r(t—a))dt=*
Zo+a f0+a
?,
= $£(r(0, r(t))dt.
to
Касательное векторное поле: T=l, Ц — 0. Первый ин-
теграл:
п Г п 1
t=i г» L*=i 1 J
=- 2Imz(r,|r/)-+K-l/ = -K-a.
i = 1
Следовательно, в консервативной системе полная энергия
является первым интегралом («закон сохранения энер-
гии»),
б) Свободная частица: U не зависит от ра-
диуса-вектора гк одной из частиц. Группа преобразо-
ваний:
(*> >л.....гк, ..., г„)|-*(/, г1У .... гк+а1........гп),
где I € R3 произвольно. Инвариантность функционала (3)
очевидна. Касательное векторное поле:
Тж=0, 7? = ^, ..., J?ft, .... J?n) = (0......I, ...» О).
Первый интеграл:
п
i = l 1 дгк
Так как I произвольно, то Рк = т^к должно быть
постоянно. Таким образом, если k-я частица не взаимо-
действует с остальной частью системы (не вносит вклада
в потенциальную энергию), то ее импульс рк = ткгк со-
храняется.
409
в) Внешние силы отсутствуют. Это означает,
что U зависит только от разностей — 17 и L не ме-
няется, если систему как единое твердое тело передви-
нуть в пространстве, т. е. сделать преобразование (t,
t\, •••. /\-f-a/, .... r„ + a/), где /—произ-
вольный вектор. Здесь Т — 0, /? = (/, /) и сохра-
няется У, И • Так как/произвольно,
то
п
Р— 2 miri = const.
t = 1
Итак, если силы только внутренние, то имеет место
«закон сохранения полного импульса системы».
г) Вращательная симметрия:// зависит только
от попарных расстояний |rf—г}\ между точками. Ла-
гранжиан не меняется, если подвергнуть систему орто-
гональному преобразованию Q, так как
L(6rh 6ri)^K—U =
п .
=4 22 mi 16n)—и (I Qri—®rj I) ==
[ = 1
n
*= 7 22 (pi I ft) — (I ri —ty 1)
t— 1
(ортогональное преобразование не'меняет скалярных про-
изведений и длин). Фиксируем вектор со и рассмотрим
группу преобразований, соответствующую равномерному
вращению системы около начала координат с угловой
скоростью со. Касательное векторное поле: Т = 0, R —
=(сохгп сохг„). Первый интеграл
п п п
ф= 22 Ri = 22 mi (Й \^xrl)^^mi (г,-x Г; I со).
t = l ori i=l i=l
Ввиду произвольности co должен сохраняться вектор мо-
мента количества движения
п
М = 2 /И/Г/Хг,-.
t= 1
КОММЕНТАРИИ И ПУТЕВОДИТЕЛЬ ПО ЛИТЕРАТУРЕ
Литература по теории экстремальных задач огромна. Не пре*
тендуя на полноту, мы ограничились здесь упоминанием лишь не-
которых изначальных работ, основных монографий, учебников и
обзорных статей.
К главе I. § 1.1. История возникновения первых задач на мак-
симум и минимум (помимо цитировавшейся книги Ван дер Вардена)
изложена в [86]; о раннем этапе классического вариационного ис-
числения можно прочитать в [83] и [87]. Экстремальным свойствам
круга и шара посвящена монография [21]. Транспортная задача ис-
следовалась уже в работе Л. В. Канторовича [55]—первой работе
по линейному программированию. Простейшие задачи автоматичес-
кого регулирования были впервые исследованы Бушау [96]. Задача
о быстродействии и ряд других подробно рассмотрены в основопо-
лагающей монографии Л. С. Понтрягина, В. Г. Болтянского,
Р. В. Гамкрелидзе и Е. Ф. Мищенко [12] и во многих других кни-
гах по оптимальному управлению ([23], [27] и др.).
§§ 1.2 —1.5. История принципа Лагранжа рассказана в статье
[45]. Этой же теме, но в рамках классического вариационного ис-
числения, посвящены работы [43], [44].
Укажем еще несколько книг и статей, посвященных затронутым
в этих параграфах темам, и рассчитанных на широкого читателя:
[71], [74], [76], [77], [115]. Основы классического вариационного
исчисления изложены в учебниках [2], [3], [8].
К главе II. § 2.1. Помимо упоминавшихся уже учебников по
функциональному анализу, укажем на книги [92], [107] специально
ориентированные на «обслуживание» теории экстремальных задач.
§ 2.2. Дифференциальное исчисление в линейных нормирован-
ных пространствах (помимо [КФ]) изложено в учебниках [5], [56],
[69] и монографиях [28], [54], [59].
§ 2.3. Бесконечномерные варианты теоремы о неявной функции
изложены в учебниках [5], [56], [69].
Теорема п. 2.3.1 достаточно удобна для построения общей тео-
рии, ибо она содержит классическую теорему о неявной функции и
теорему Люстерника о касательном пространстве и дает оценку
отклонения от ядра отображения. Конструкции, использованные в
доказательстве, фактически содержались в первоначальной работе
[68] (см. также [69]). Другие доказательства и модификации см.
в [54], [65].
§ 2.4. О дифференцируемости других важных конкретных функ-
ционалов см. в [28], [59].
411
§ 2.6. Основы конечномерного выпуклого анализа были зало-
жены Минковским [113], [114] и Фенхелем [101], [102]. Выпуклый
анализ в бесконечномерных^ пространствах был построен в шестиде-
сятые годы в работах Бронстеда [95], А. Я. Дубовицкого и
А. А.’Милютина [46], Моро, Рокафеллара и др. Наиболее полный
обзор конечномерной теории содержится в монографии Рокафеллара
[81], а также (в части, касающейся лишь выпуклых множеств) в мо-
нографии Боннезена и Фенхеля [94]. Бесконечномерная теория
изложена в [16], [52], [54], [62], [79], [84].
В самое последнее время делаются попытки создать синтетичес-
кое, «гладко-выпуклое» исчисление—см. [70], [99], [118].
К главе III. § 3.2. Трудно сказать, кем впервые было доказано
правило миожителей Лагранжа для гладких конечномерных задач
с равенствами и неравенствами. В некоторых американских работах
дается ссылка на работу Валентайна [120] и диссертацию Каруша
[109]. Правило множителей для случая бесконечного числа нера-
венств было доказано Джоном [108]. Очень большую роль в этой
тематике сыграла работа Куна и Таккера [111]. Бесконечномерные
варианты правила множителей изложены в [37], [39], [46], [54],
1ТО], [84].
§ 3.3. .Линейное и выпуклое программирование очень широко
представлено учебной и монографической литературой на русском
языке: [38], [40], [41], [50], [57], [58], [67], [75], [76], [81], [89],
[90].
§ 3.4. Одной из первых работ, посвященных необходимым усло-
виям для задач с ограничениями типа неравенств, была [100]. Ко-
нечномерная теория прекрасно изложена в учебнике Хестенеса [106],
см. также [51], [85]. В недавнее время Е. С. Левитиным, А. А. Ми-
лютиным и Н. П. Осмоловским была, разработана полная теория
условий второго порядка для задач с ограничениями [64], [65].
В последней из названных работ имеется подробная библиография.
В нашем изложении использовались некоторые конструкции этой
работы. См. также [105], [117].
К главе IV. §§ 4.1 и 4.4. Классическому вариационному исчис-
лению посвящено много учебников и монографий. Кроме упомяну-
тых выше см. [20], [63], [91], [93], [97], [103]. Наиболее полно
теория необходимых и. достаточных условий экстремума в задаче
Лагранжа разработана в монография Блисса [20]. Там же изложена
история вопроса. О связях вариационного исчисления и классичес-
кой механики см. [1].
§ 4.2. Первоначальный набросок теории оптимального управле-
ния был изложен в [26] и в обзорной статье Л. С. Понтрягина [78],
затем теория оптимального управления составила содержание моно-
графии Л. С. Понтрягина, В. Г. Болтянского, Р. В. Гамкрелндзе и
Е. Ф, Мищенко [12], давшей толчок бурному развитию всего на-
бавления исследований, связанных с экстремальными задачами.
Доказательство принципа максимума, изложенное в § 4.2, является
обработкой первоначального доказательства В. Г. Болтянского, хотя
в нем не используются никакие иные средства, кроме классического
анализа. Метод центрированных систем использовался в работах
А. Я. Дубовицкого и А. А. Милютина. Сейчас имеется много дока-
зательств принципа максимума, см., например, [24], [31], [46]—[49],
[54], [104], [112].
Теории оптимального управления посвящены учебники [23],
[31], [35], а также монографии [25], [27], [32], [61], [66], [73] я
412
ряд других. В названных монографиях много места уделено реше-
нию разнообразных конкретных прикладных задач.
§ 4.3. Принцип максимума для линейных систем был впервые
доказан Р. В. Гамкрелидзе [36]. Завершенная теория линейных
систем была разработана Н. Н. Красовским [60]. Обзору проблема-
тики, связанной с ляпуновскими задачами, посвящена статья [17],
где содержатся обобщения результатов этого параграфа и имеется
подробная библиография.
Развитие теории ляпуиовских задач привело к изучению вы-
пуклых интегральных функционалов в работах [54], [98], [119]
и Др.
В заключение отметим несколько монографий, в которых чита-
тель сможет ознакомиться с некоторыми принципиальными вопро-
сами теории экстремальных задач, не затронутыми в книге.
Многомерное вариационное исчисление: [ПО], [116].
Теоремы существования: [35], [54], [116].
Достаточные условия в задачах оптимального управления: [22],
[23], [61].
Расширения экстремальных задач: [53], [88].
Двойственные методы в теории экстремальных задач: [52], [88].
Численице методы: [29], [42], [72], [80], [82].
Скользящие режимы: [34].
Динамическое программирование: [18], [19].
Фазовые и смешанные ограничения: [33], [47], [48].
См. также обзор [30].
ЛИТЕРАТУРА
Учебники и учебные пособия, цитируемые
в основном тексте
КФ. Колмогоров А. Н., Фомин С. В. Элементы теории
функций н функционального анализа.—М.: Наука, 1976.
1. Арнольд В. И. Математические методы классической меха-
ники.— М.: Наука, 1974. «
2. Ахиезер Н. И. Лекции по вариационному исчислению.—М.:.
Гостехиздат, 1955.
3. Гельфанд И. М., Фомин С. В. Вариационное исчисление.—
М.: Физматгиз, 1961.
4. Данфорд Н., Шварц Дж. Линейные операторы. / Общая
теория.—М.: ИЛ, 1962.
5. К а р т а н А. Дифференциальное исчисление. Дифференциальные
формы.—М.: ИЛ, 1971.
6. Коддингтон Э. А., Левинсон Н. Теория обыкновенных
дифференциальных уравнений.—М.: ИЛ, 1958.
7. К У P о-ш А. Г. Курс высшей алгебры.—М.: Наука, 1971.
8. Лаврентьев М. А., ЛюстерникЛ. А. Курс вариацион-
ного исчисления.—М.-Л.: Гостехиздат, 1950.
9. Никольский С. М. Курс математического анализа, тт. 1, 2.—
М.: Наука, 1975.
10. Петровский И. Г. Лекции по теории обыкнове1*иых диффе-
ренциальных уравнений.—М.-Л.: Гостехиздат, 1952.
11. Понтрягин Л. С. Обыкновенные дифференциальные уравне-
ния.—М-: Наука, 1965.
12. Понтрягин Л. С., Болтянский В. Г., Гамкрелид-
зе Р. В., Мищенко Е. Ф. Математическая теория оптималь-
ных процессов.—М.: Физматгиз, 1961.
13. Привалов И. И. Введение в теорию функций комплексного
переменного.—М.: Наука, 1977.
14. Ф и хтен г о л ь ц Г. М. Курс дифференциального и интеграль-
ного исчисления, тт. 1, 2,—М.: Наука, 1969.
15. X •Иман Ф. Обыкновенные дифференциальные уравнения. —
М.: ИЛ, 1970,
414
Дополнительная литература
16. Акилов Г. П., Кутателадзе С. С. Упорядоченные вектор-
ные пространства. — Новосибирск: Наука, 1978.
17. Аркин В. И., Левин В. Л. Выпуклость значений вектор-
ных интегралов, теоремы измеримого выбора и вариационные
задачи,—УМН 27, вып. 3, 1972, с. 21—77.
18. Веллман Р. Динамическое программирование.—М.: ИЛ, 1960.
19. Веллман Р., Кал аба Р. Динамическое программирование
и современная теория управления.—М.: Наука, 1969.
20. Блисс Дж. Лекции по вариационному исчислению.—М.: ИЛ,
1950.
21. Бляшке В. Круг и шар.—М.: Наука, 1967.
22. Б о л т я н ск и й В. Г. Достаточные условия оптимальности и
обоснование метода динамического программирования.— Изв.
АН СССР, сер. матем. 28, № 3, 1964, с. 481—514.
23. Болтянский В. Г. Математические методы оптимального
управления.—М.: Наука, 1969.
24. Б о л т я н с к и й В. Г. Метод шатров в теории экстремальных
задач.— Успехи матем. наук 30, вып. 3, 1975, с. 3—55.
25. Б о л т я н с к и й В. Г. Оптимальное управление дискретными
системами.—М.: Наука, 1973.
26. Болтянский В. Г., Гамкрелидзе Р. В., Понтря-
гин Л, С. К теории оптимальных процессов.—ДАН СССР 110,
№ 1, 1956, с. 7—10.
27. Брайсон А., Хо Ю-ши. Прикладная теория оптимального
управления. — М.: Мир, 1972.
28. Вайнберг М. М. Вариационный метод и метод монотонных
операторов в теории нелинейных уравнений.—М.: Наука, 1972.
29. Васильев Ф. П. Лекции по методам решения экстремальных
задач.—М.: Изд. МГУ, 1974.
30. Габасов Р., Кириллова Ф. М. Методы оптимального управ-
ления.— Итоги науки и техники. Современные проблемы мате-
матики. Т. 6.—М.: 1976, с. 133—206.
31. Габасов Р., Кириллова Ф. М. Методы оптимизации.—
Минск: Изд-во БГУ, 197.5.
32. Габасов Р., Кириллова Ф. М. Особые оптимальные управ-
ления.—М.: Наука, 1973.
33. Г а м к р е л и д з е Р. В. Оптимальные процессы управления при
ограниченных фазовых координатах.—Изв. АН СССР, сер. матем.
24, № 3, I960, с. 315—356.
34. Гамкрелидзе Р. В. О скользящих оптимальных режимах,—<
ДАН СССР 143, № 6, 1962, с-. 1243—1245.
35. Гамкрелидзе Р. В. Основы оптимального управления.—
Тбйлиси: Изд. ТГУ, 1977.
36. Г а м к р е л и дз е Р. В. Теория оптимальных по быстродействию
процессов в линейных системах.—Изв. АН СССР, сер. матем. 22,
№ 4, 1958, с. 449—474
37. Гамкрелидзе Р. В., Харатишвили Г. Л. Необходимые
условия первого порядка в экстремальных задачах. / В кн.:
Международный конгресс математиков в Ницце.—М.: Наука,
1972.
38. Гасс С. Линейное программирование.—М : Физматгиз, 1961.
39. Гирсанов И. В. Лекции по математической теории экстре-
мальных задач. —М.: Изд-во МГУ, 1970.
415
40. Гольштейн Е. Г. Теория двойственности в математическом
программировании. — М.: Наука, 1971.
41. Данциг Д. Линейное программирование, его обобщения и при-
менения.—М.: Прогресс, 1966.
42. Демьянов В. Ф., Рубинов А. М. Приближенные методы
решения экстремальных задач. —Л.: Изд-во ЛГУ, 1968.
43. Дорофеева А. В. Вариационное Исчисление во второй по-
ловине XIX в.—Историко-математические исследования XV,
1963, с. 99—128.
^4. Дорофеева А. В.* Развитие вариационного исчисления, как
исчисления вариаций.— Историко-математические исследова-
ния XIV, 1961, с. 101—180.
45. Дорофеева А. В., Тихомиров В. М. От правила множи-
телей Лагранжа до принципа Максимума Понтрягина.—Историко-
математические исследования XXV, 1979.—(в печати).
46. Дубовицкий А. Я., Милютнн А.А. Задачи на экстремум
при наличии ограничений. —ЖВМ и МФ 5, №3, 1965, с. 395—
453.
47. Дубовицкий А. Я., Милютин А. А. Необходимые усло-
вия слабого Экстремума в общей задаче оптимального управ-
ления.—М.: Наука, 1971.
48. Дубовицкий А. Я., Милютии А. А. Необходимые условия
экстремума в задачах оптимального управления со смешанными
ограничениями типа неравенств.—ЖВМ и МФ 8, •№ 4, 1968,
с. 725-770.
49. Дубовицкий А. Я., Милютин А. А. Трансляция уравне-
ний Эйлера.—ЖВМ и МФ 9, № 6, 1969, с. 1263—1284.
50. Еремин И. И., Астафьев Н. Н. Введение в теорию линей-
ного и выпуклого программирования. —М.: Наука, 1976.
51. Зан ГВ ил л У. И. Нелинейное программирование.—М.: Сов.
радио, 1973.
52. Иоффе А. Д., Т ихомиров В. М. Двойственность выпуклых
функций и экстремальные задачи. — УМН 23, вып. 6, 1968,
с. 51—116.
53. Иоффе А. Д., Тихомиров В. М. Расширение вариационных
задач. — Труды ММО 18, 1968, с. 187—246.
54. Иоффе А. Д., Тихомиров В. М. Теория экстремальных
задач.—М.: Наука, 1974.
55. Канторович Л. В. Математические методы организации и
планирования производства.—Л.: Изд-во ЛГУ, 1939.
56. Канторович Л. В., Акилов Г. П. Функциональный ана-
лиз.—М.: Наука, 1977.
57. Карлин С. Математические методы в теорки нгр, программи-
ровании и экономике,—М.: ИЛ, 1964.
58. Карманов В. Г. Математическое программирование. — М.:
Наука, 1975.
59. Красносельский М. А., Эабре-йкоП. П., Пустыл fa-
ник Е. И., Соболевский П. Ё. Интегральные операторы
в пространствах суммируемых функций.—М.: Наука, 1966.
60. Красовский Н. Н. Теория управления движением. Линей-
ные системы,—М.: Наука, 1968.
61. Кротов В. Ф., Гурман В. И. Методы и задачи оптималь-
ного управления.—М: Наука, 1973.
62. Кутателадзе С. С., Рубинов А. М. Двойственность Мин-
ковского и ее приложения. — Новосибирск: Наука, 1976.
4J6
63. Лаврентьев М. А., Люстерннк Л. А. Основы вариаци-
онного исчисления.—М.-Л.: ОНТИ, 1935.—ТТ. I, II.
64. Левитин Е. С., Мялютин А. А., Осмоловский Н. П.
Об условиях локального минимума в задачах с ограничениями./
В кн. Математическая экономика и функциональный анализ.—
М.: Наука, 1974, с. 139—202.
65. Левитин Е. С., Милвэтки А. А., Осмоловский Н. П.
Условия высших порядков локального минимума в задачах с огра-
ничениями.—УМН 33, вып. 6, 1978, с. 85—148.
66. Л и Э. Б., Маркус Л. Основы теории оптимального управ-
ления.— М.: Наука, 1972.
67. Линейные неравенства и смежные вопросы./Под ред. Г, Куна
и А. Таккера.—М.: ИЛ, 1959.
68. Люстерннк Л. А. Об условных экстремумах функциона-
лов,—Матем. сб. 41, № 3, 1934, с, 390—401.
69. Л госте ринк Л. А., Соболев В" И. Элементы функцио1-
нального анализа.— М.: Наука, 1965.
70. М а г а р и л-И л ь я е в Г. Г. Теорема о неявной функции для
липшицевых отображений. — УМН 33, вып. 1, 1978, с. 221—222.
71. Математика на службу инженера./Под ред. Н. X. Розова.—М.:
Знание, 1973.
72. Моисеев Н. Н. Численные методы в теории оптимальных
систем, -г-М.: Наука, 1971.
73. Моисеев Н. Н. Элементы теории оптимальных систем. —М.:
Наука, 1975.
74. Ммшкис А. Д. Математика: Специальные курсы для вту-
збв. — М.: Наука, 1971.
75. Ник ай до X. Выпуклые структуры и математическая эконо-
мика.—М.: Мир, 1972.
76. Нит И. В. Линейное программирование (с обсуждением неко- .
торых нелинейных задач). —М.: Изд-во МГУ, 1978.
77. Оптимальное управление. —М..* Знание, 1978.
78. П о н т р я г и н Л. С. Оптимальные процессы регулирования.—»
УМН 14, вып. 1, 1959, с. 3—20.
79. Пшв?й ич вый Б. Н. Необходимые условия экстремума. —М.:
Наука, 1969.
80. Пшеничный Б. Н., Данилин Ю. М. Численные методы
в экстремальных задачах,—М.: Наука, 1975.
81. РокафелЛар Р. Выпуклый анализ,—М.: Мир, 1973.
82. Р ом а н ов с к и й И. В. Алгоритмы решения экстремальных
задач, —М.: Наука, 1977.
83. Рыбников К. А. Первые этапы вариационного исчисления./
В кн.: Историко-математические исследования, вып. 2.—М.-Л.:
ГИТТЛ, 1949.
84. Тихомиров В. М. Некоторые вопросы теории приближе-
ний,—М.: Изд-во МГУ, 1976.
85. Фиакко А., Мак-Корм ик Г. Нелинейное программирова-
ние. Методы последовательной безусловной минимизации.—М.:
Мир, 1972.
86. Цейтен Г. Г. История математики в древности и в средние
века.-М.-Л.: ОНТИ, 1938. к
87. Цейтеи.Г. Г. История математики В 16 и 17 столетиях. —
М.-Л.: ОНТИ, 1938.
88 Экланд И., Темам Р. Выпуклый анализ и вариационные
проблемы.—М.: Мир, 1979.
417
89. Эрроу К. Дж., Гурвиц Л., Удзава X. Исследования
по линейному и нелинейному программированию.—М.: ИЛ, 1962.
90. Юдин Д. Б., Гольштейн Е. Г. Линейное программиро-
вание (теория, методы, приложения). —М.: Наука, 1969.
91. Янг Л. Лекции по вариационному исчислению и теории опти-
мального управления.—М.: Мир, 1974.
92. В а 1 а к г i s h n a.n A. V. Applied Functional Analysis. N. Y.:
Springer, 1976.
93. Bolz a O. Vorlesungen fiber Variationsrechnung. — Leipzig: 1949.
94. Bonn esen T., Fenchel W. Theorie der Konvexen Kor-
per. — B.: Springer, -1934.
95. В г 0 n d s t e d A. Conjugate convex functions in topological vector
spaces.—Mat. Fys. Medd. Dansk. Vid. Selsk. 34, 2, 1964, p. 1—26.
96. Bushaw D. W. Differential equations with a discontinuous
forcing term. —Princeton: Dept, of Math. Princeton Univ., 1952.
97. Caratheodory C. Variationsrechnung und partielle Diffe-
rentia I gleichungen erster Ordnung. — Leipzig—Berlin: Teubner,
1935.
98. Castaing C.,ValadierM. Convex analysis and measurable
multifunctions. Lecture Notes in Mathematics, № 580. —B.:
Springer, 1977.
99. Clarke F. H. Generalized gradients and applications. — Trans.
Amer. Math. Soc. 205, 1975, p. 247—262. »
100. Cox M. J. On necessary conditions for relative minima.—Amer.
J. Math. 66, № 2, 1944, p. 170—198. .
101. Fenchel W. Convex Cones, Sets and Functions. — Princeton:
Princeton Univ., 1951.
102. Fenchel W. Un conjugate convex functions.—Canadian
J. Math. 1, 1949, p. 73—77.
103. Hadamard J. Calcul des variations.—Paris: Hermann, 1910.
104. H a 1 к i n H. On necessary conditions for optimal control of non-
linear systems.— J. Analyse Math. 12, 1964, p. 1—82.
105. HestenesM. R. Calculus of Variations and Optimal Control
Theory.—N. Y.: Wiley, 1966.
106. HestenesM. R. Optimization theory. The finite dimensional
case. — N. Y.: Wiley, 1975.
107. Holmes R. B. Geometric functional analysis and its appli-
cations.— N. Y.: Springer, 1975.
108. John F. Extremum problems with inequalities as subsidiary
condi tions./ln: Studies and Essays. Courant Anniversary Volume.—
N. Y.: Interscience, 1948, p. 187 — 204.
109. К a rush W. E. Minima of functions of several variables with
inequalities as side conditions.—Chicago: Univ, of Chicago, 1939.
110. Klotzler R. Mehrdimensionale Variationsrechnung. — B.: VEB
Deutscher Verlag, 1971.
111. Kuhn H. W., Tucker A. W. Nonlinear programming./In:
Proc, uf Second Berkeley Symp. — Berkeley: Univ, of California
Press, 1951, p. 481—492.
112. Michel P. Une demonstration elementaire du principe du maxi-
mum de Pontriaguine. — Bull. Math, economiques. 14, 1977.
113. Minkowski H. Geometrie der Zahlen. — Leipzig: Teubner, 1910.
114. Minkowski H. Theorie der Konvexen Korper./In: Gesammelte
Abhandlungen, Bd. II. —Leipzig-Berlin: Teubner, 1911.
115. Moisseyev N. N., Tihomirov V. M. Optimisation./In:
Mathematics Applied to Physics. — N. Y.: Springer, 1970.
418
116. Morrey Ch. В. Multiple integrals in the calculus of variati-
ons.— N. Y.: Springer, *1966.
117. Neustadt L. W. Optimization. A theory of necessary condi-
tions.—Princeton: Princeton Univ. Press, 1976.
118. R ос к a f e 1 1 a r R. T. The theory of subgradients and its appli-
cations to problems of optimization. — Lecture Notes Uni ver. of
Montreal., 1978.
119. R ос к a f e 1 1 a r R. T. Convex—Integral functuonals and dua-
lity./In: Contributions to Nonlinear Functional Analysis. — N. Y.:
Acad. Press, 1971, p. 215 —236.
120. Valentine F. A. The problem of Lagrange with differential
inequalities as added side conditions./In: Contributions to Cal-
culus of Variations.—Chicago: Univ, of Chicago Press, 1933—1937.
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
V—квантор общности: «для всех»
Н—квантор существования: «существует»
=Ф — знак импликации: «из ... следует ...»
знак эквивалентности
def
— —равно по определению
G)
= —равно в силу (4)
х £ А— элемент х принадлежит множеству А
х£ А—элемент х не принадлежит множеству А
0 — пустое множество
A (J В — объединение множеств А и В
А П В — пересечение множеств А и В
А\В — разность множеств А и В
Ас В—множество А содержится в множестве В
А/, В— декартово произведение множеств А и В
Д + В — арифметическая сумма множеств Д и В
{х | Р (х)} — множество элементов х, обладающих свойством Р (•)
{Xj, . ,.,хп, ...} — множество, состоящее из элементов хх, ...
• ••» .
F: X —► Y—отображение F множества X в множество К; функ-
ция F с областью определения 'X, принимающая значения во мно-
жестве У
х>—>F(x)— отображение (функция) F сопоставляет элементу х
элемент F (х); обозначение для отображения (функции) F в случае,
когда желательно указать обозначение его (ее) аргумента
F () — обозначение, которым подчеркивается, что F является
отображением (функцией)
F (А) — образ множества А при отображении F
im Г= {у | y=F (х), х^Х} —образ отображения F: X—► /
Г-1(Д)— прообраз множества Д при отображении F
F | А — ограничение отображения F на множество А
420
Fo б—с^емш.зиция отображений G и F: (Fо G) (x)«= F (G (x))
R—множество всех действительных чисел; чиеловая прямая
R = R(j{—оо, + «} — расширенная числовая прямая
inf A (sup Я) — нижняя (верхняя) грань чисел, входящих в мно-
жество А с R
R" — арифметическое n-мерное пространство, наделенное стан-
дартной евклидовой структурой, элементы Rn следует представлять
себе в виде вектор-столбцов, даже если они по типографским сообра-
жениям набраны в строчку
R+ = {x = (xj...х„) R" |х(->0} — неотрицательный ортант в R”
elt ...,еп—векторы стандартного ортонормированного базиса
в R": ei = (l, 0..0), ..., е„ = (0, Г.., 1)
Rn*—арифметическое n-мерное пространство, сопряженное к R";
элементы R"* следует представлять себе как вектор-строчки
п
рх= <р, х> — ^piXi для любых х R" и р g R"*
i =1
Xе—вектор строчка, транспонированная к вектор-столбцу х
|х|—евклидова норма в R"
| х|2=(х| х) = хтх
п
(х | у) = скалярное произведение в R"
i = Г
|| х[| — норма элемента х в нормированном пространстве
р (х, у) — расстояние от элемента х до элемента у
р (х, Я) = 1пГ {р (х, у) | у £ Я} — расстояние от элемента х до
множества Я
В (х, г) — {у | р (у, х) «5 г} —замкнутый шар с центром х радиуса г
Ь(х, г) = {у | р(р, х) < г}—открытый шар с центром х радиуса г
Я—замыкание множества Я
int Я — внутренность множества Я
ТХМ (ТХМ) — множество касательных векторов (односторонних
касательных векторов) к множеству Я в точке х
={х | / (х) «й а} — лебеговское множество функции f на
уровне а
X*—пространство, сопряженное с X
х*—элемент сопряженного пространства X*
<х*, х>—значение линейного функционала х* £ X* на элементе
х£ X
(х | у)—скалярное произведение элементов х и у гильбертова
пространства
Я-*- = {х* | <х*. х> = 0, х £ Я}— аннулятор множества Я
dimL— размерность пространства L
421
X/L—фактор-пространство «пространства X пс подпростран-
ству L
X(X,Y)— пространство непрерывных линейных отображений
пространства X в пространство У; отображения из пространства
X (Rk, R"1) могут отождествляться с их матрицами относительно
стандартных базисов в R1* и Rm
Хп (X, У)—пространство непрерывных полилинейных отображе-
ний пространства ХХ...ХХ в пространство У
J—единичный оператор; Е или Еп—матрица единичного опе-
ратора из X (Rn, R"), т. е. единичная матрица п-го порядка
Л*—оператор, сопряженный с оператором Л; х> = <р*, Лх>
КегЛ = {х[Лх = 0}— ядро линейного оператора
1тЛ = {//[р = Лх}—образ линейного оператора
хтАх (угАх)—обозначение для квадратичной (билинейной) формы
п
с матрицей А: утАх= 2
i, /=1
А > 0—матрица А положительно определена
А 0—матрица А неотрицательно определена
С (К, К) — пространство непрерывных отображений из К в У;
если У нормировано, то для х (•) £ С (К, И)
l]x(-)ll = l|x(-)llo = sup||x(i)||
ieK
С (/<) = С {К, У), если ясно, о каком У идет речь, или если
.F=R
С ([io, ij])—пространство непрерывных функций на отрезке [i0, ZJ
Cr (U)—множество отображений, имеющих в U непрерывные про-
изводные до порядка г включительно; обычно употребляется в выра-
жениях: «функция f принадлежит классу Сг ((?)» или «отображение
F €
СГ(Д, У) — пространство отображений отрезка AcR в простран-
ство У (обычно y = Rn или R"*), имеющих непрерывные производные
до порядка г включительно; для х(-) £ С (Д, У)
Цх(-)1)=11х (-)|1г = тах {Цх(.)Ц0, || 'х (•) ||0.|| х^ (.) Ц
КС1 (Д, У) — пространство отображений отрезка Д с R в простран-
ство У (обычно У = R" или R"*), имеющих кусочно-непрерывную
производную. Снабжено нормой как подпространство пространства
С (Д, У)
jrL (Д, У)—пространство отображений отрезка Д с R в простран-
ство У (обычно У = R" или Rtt*), каждое из которых удовлетворяет
условию Липшица с некоторой константой Снабжено нормой как
подпространство пространства С (Д, У)
F' (х; h) — производная функции F в точке х по направлению
вектора й
422
b+F (x; •) — первая вариация отображения F в точке х>
6Г(х; •)—первая вариация по Лагранжу отображения F в точ-
ке х
&nF (х; •)—n-я вариация по Лагранжу отображения F в точке х
р'т (х) — производная отображения F в точке х по Гато
F1 (х) — производная отображения F в точке х по Фреше
F' (х) [ft] или F'(х) ft—значение производной отображения F
в точке х на векторе h
F £ D1 (х)—отображение F дифференцируемо по Фреше в ^очке х
F £ SD1(x)—отображение F строго дифференцируемо в точке х
F" (х)—вторая производная отображения F в точке х по Фреше
F" (х) [fti, ft2]~значение второй производной (как билинейной
функции) на паре векторов fti и ft2
cPF (х\ h)'=F" (x)[h, ft]—второй дифференциал 'отображе-
ния F в точке х
FXl (xi, х2) (FXl (xi, x2))—частная производная no Xj (по х2) ото-
бражения F, т. е. производная отображения x]t-i-F(xl, х2) (хан->
(xi, х2))
[xi, х4] = {х | х=ах1-[-(1—а) х2, 0<а< 1} — отрезок, соеди-
няющий точки X], х2
dom f = {х g X [ f (х) < + оо } —эффективное множество функции
f: X —>-R
epif={(x, а) g X XR | f(x)<a, x£ dom/}—надграфик функ-
ции f: X —> R
£>A — индикаторная функция множества A
sA — опорная функция множества А
р.А —функция Минковского множества А
Im А—линейная оболочка множества А
aff А — аффинная оболочка множества А
cone А —коническая оболочка множества А
conv А—выпуклая оболочка множества А
conv А—выпуклое замыкание, т. е замыкание выпуклой обо-
лочки множества А
df (х) —суб дифференциал функции f в точке х
f*( )—функция, сопряженная с функцией f( ), преобразование
Юнга —Фенхеля функции f
f (х) —> inf (sup, extr), x £ С — обозначение экстремальной задачи
х—решение экстремальной задачи
absmin (absmax, absextr)—абсолютный минимум (максимум, эк-
стремум)
х g absmin (3) (absmax (3), absextr (J)) — x доставляет абсолютный
минимум (максимум, экстремум) в задаче J
423
locmin (1 остах, locexir)—локальный минимум (максимум, экстре-
мум)
locmin (3), (locmax (3), locextr(3))—х 'доставляет минимум
(максимум, экстремум) в-задаче 3
3, с®, ^—функционалы в задачах вариационного исчис-
ления и оптимального управления
$—квадратичный функционал вторичной Задачи вариационного
нсчислеиия
х, х) или L=*=L(i, х, х, и)—лагранжиан
—функция Лагранжа
гамильтониан
Я—функция Поигрягина
£—функция Вейерштрасса
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вектор, касательный в точке 171
Возмущение задачи 263
Выпуклое замыкание множества
217
----- функции 218
— программирование 52, 261
Выпуклый полиэдр 216
Гамильтониан 302, 377
Гамильтонова система 302, 377
Гиперплоскость 124, 216
График расширенный 370
Двойственная задача 265
Двойственное семейство 265
Дифференциал 139, 154, 158
Дифференцируемость, достаточ-
ные условия 149
Зависимость решений дифферен-
циальных уравнений от пара-
метра 198
Задача Аполлония 17, 32, 43, 96
— Архимеда 17, 31, 43, 96
— Больца 42, 64
-----, необходимое условие эк-
стремума 246
-----с незакрепленным време-
нем 245
— двойственная 265
— Дидоны 14, 15, 16
— Евклида 17, 31, 43, 95
— изопериметрическая 77, 84
-----классическая 12, 35, 43,
107, 110
— изопифанная 12, 17
— Кеплера 19, 31, 43, 98
— классического вариационного
исчисления простейшая 42, 59,
370
Задача классического вариацион-
ного исчисления, со старшими
производными 79, 84, 310
— Коши 186, 190, 195, 204
— о брахистохроне 24, 37, 44, ИЗ
— об условном экстремуме 47
— о быстродействии 29, 37, 43,
44, 103
----минимальной поверхности
вращения 113
------ преломлении света 22, 43, 98
— оптимального управления 42,
84, 316, 319
--------, линейная по фазовым
переменным 348
--------элементарная 247, 360
--------условие минимума
248, 360
— оптимизации 11
— о рационе 28, 39, 44
— программирования выпуклого
42, 52, 261
----линейного 42, 269
— Лагранжа 41, 81, 317
----в понтрятинской форме 81,
298
— линейного программирования
269
--------двойственная 273
--------конечномерная 269, 270
--------элементарная 243
— ляпуновская 350, 354
— Майера 42
— Ньютона аэродинамическая 27,
33, 43, 99
— Тартальи 18, 99
— транспортная 28, 38, 44
— Чаплыгина 37, 107, 111
— Штейнера 19, 32, 43, 98
— экстремальная 11, 18, 30, 39
428
Задача Экстремальная без ограни-
чений 30
-----геометрическая 95
----- гладкая с ограничениями
типа равенства 253, 287, 288
-------------------и нера-
венств 40, 252, 289, 293
-------------------, конечно-
мерная 47
-----элементарная 40, 238
-----элементарная выпуклая 42,
238
-------- гладкая 40, 238
--------линейного программи-
рования 243
--------оптимального управле-
ния 247, 360
Закон Снеллиуса 23, 98
— сохранения 402 '
-----импульса 410
-----момента количества дви-
жения 410
----- энергии 409
Иголка элементарная 89, 323
Игольчатая вариация траектории,
управления 89, 323, 324
Изопериметрическая задача 77, 84
-----классическая 12, 35, 43, 107,
ПО
Инвариантный интеграл Гильбер-
та 391
Интеграл импульса 63
— энергии 63
Интегральный инвариант Пуан-
каре — Картана 384
— функционал, инвариантный от-
носительно семейства отобра-
жений 405
Интегрант 59, 299
Класс допустимых элементов 30
— смежности 118
Классы экстремальных задач 39
Комбинация аффинная, выпуклая,
линейная, коническая 210
Конус сопряженный 233
Кривая Ньютона 102
Лагранжиан 59 , 299, 320
Лемма Дюбуа-Реймона 62
--------обобщенная 306
— Лагранжа 61
— об аннуляторе ядра регуляр-
ного оператора 130
426
Лемма об интегральных функцио-
налах 325, 345
----- о скруглении углов 69
-----условиях минимума в эле-
ментарной задаче оптимального
управления 360
•— о выпуклости образа 355
-----замкнутости конечнопорож-
денного конуса в конечномер-
ном пространстве 270
------- образа 129
-----минимаксе 280
-----нетривиальности аннуля-
тора 127
----- пакете иголок 325, 335
----- правом обратном отобра-
жении 128
— — приращении функционала
92
-----свойствах элементарной ва-
риации 89
-----сопряженном конусе 277
----- суперпозиционной измери-
мости 353
— Хоффмана 279
Линейное программирование 29,
42, 243, 269
— дифференциальное уравнение
191
Максимум 11
— абсолютный 30, 70
— локальный 30
— сильный 68, 70
— слабый 59, 375, 377
Матрица Якоби 153
Метод вариаций 63
— возмущений 263
Минимум 11
— абсол!отный 30, 70, 390
— локальный 30
— сильный 68, 70, 76, 373, 399
— слабый 59, 82, 375, 377
Многогранник выпуклый 211
Множество выпуклое 52, 208
----- на прямой 211
— лежандрово 384
— эффективное 213
Множители-Лагранжа 47, 52, 252,
299, 320
Надграфик функции 213
Неравенство Гронуолла 189
— для энтропии 216
— Иенссена 52, 214
— изопериметрическое 13
Неравенство Коши 216
— Юнга 225
Несобственные числа 213
Норма 115
— эквивалентная 116
Оболочка аффинная выпуклая,
коническая, линейная 209
Ограничения 30
— изопериметрические 298
— фазовые 81, 318
Оператор дифференциальной
связи 177
— краевых условий 182
— Немыцкого 175, 177
Опорная функция множества 276
Основная лемма классического
вариационного исчисления 61
Отображение аффинное 142
—, дифференцируемое по Фреше
в точке 138
— значений 182
— измеримое 335
— интегральное 178, 180
— обратное 128, 169
— полилинейное 142
— сжимающее 162
— строго дифференцируемое 139
Пакет иголок 324
Поле векторное 402
-1- экстремалей 390
--- центральное 398
Полиэдр выпуклый 216
Полупространство замкнутое, от-
крытое 124, 216
Правило множителей Лагранжа 47
------- для гладких задач с
равенствами и неравенствами
'252
Преобразование Лежандра 224
--- классическое 226, 378
— Юнга — Фенхеля 224
Пример Больца 71
— Гильберта 66
Принцип Гюйгенса 21
— Лагранжа 51, 94, 248
---для гладких задач 252 , 253
-------задачи выпуклого про-
граммирования 263
,----------Лагранжа 300
-------•---оптимального управ-
ления 321
----------------, линейной по
фазовым переменным 366
Принцип Лагранжа для ляпунов-
ской задачи 354
— максимума Понтрягина 87, 320
—-------для задачи со свободным
концом 88
— сжимающих отображений мо-
дифицированный 162
— Ферма вариационный 20
Программирование выпуклое 52,
261
— линейное 29 , 42 , 243, 269
Произведение пространств 117
Производная в точке 45, 46
-------- по направлению 137
— высших порядков 154
— Гато 138
— Фреше 138
----, существование 149, 150
— частная 46, 151
Простейшая задача классического
вариационного исчисления 42,
59, 370
----, расширения 66
Пространство банахово 116
— , касательное в точке 172
— нормированное 115
— сопряженное 116
Процесс допустимый 348
— оптимальный 85, 317, 348
----в слабом смысле 82, 299
---- локально 317
— управляемый 82 , 85, 298 , 316
----допустимый 82, 85, 299, 317
Прямая вещественная расширен-
ная 30
Расстояние от точки до множества
275
Решение дифференциального урав-
нения 184
— экстремальной j задачи 30
Связь голономная 81
— дифференциальная 41, 81, 298
Седловая точка 56
Семейство экстремальных задач
двойственное 265
Симплекс п-мерный 211
Сопряженная система 191
Сопряженное уравнение 301, 322
Субдифференциал 229
— нормы 230
Теорема Банаха об обратном опе«
раторе 127
— Боголюбова 72
427
Теорема Вейерштрасса о доста-
точных условиях сильного ми-
нимума 399
----о существовании минимума
95, 251
— двойственности для задач вы-
пуклого программнроваиня 268
----------линейного програм-
мирования 273
----------о кратчайшем рассто-
янии 276
------ — ляпуновскнх задач 363
— Дубовицкого — Милютина о
пересечении конусов 234
---------- субдифференциале
максимума 234
— единственности 190
— Каратеодори 211
— • Крейна — Мильмана 351
— Куиа — Таккера 52
— , субдифференцнальная
форма 262
— Лагранжа о среднем значении
147
— Лебега 133
— Люстернвка 173
— Ляпунова А. А. 351
— Минковского 221
— Моро Рокафеллара 231
— Нётер Э. 405
— об интегральном инварианте
382
----обратной’ функции 49
----обратном отображении 169
— — оценке конечного прираще-
ния 148
— о Дифференцируемой зависи-
мости решений от начальных
данных 201, 204
----мнннмаксе 268
----непрерывной зависимости
решений от параметра 198
---- неявной функции 161
----------классическая 166
----полном дифференциале 151
----смешанных производных
156
---- среднем 148
----существовании решений
глобальная 195
----------локальная 186
— отделимости вторая 126
----конечномерная 53, 57
---- первая 124
— о фактор-пространстве 119
428
Теорема о формуле Тейлора
159
— Рисса 134
— существования в задаче линей-
ного программирования 270
— Феихеля — Моро 227
— Ферма 19, 45, 239
----для функций п переменных
46
— Хана—Банаха 122
— Эйлера — Лагранжа 83,
— Яиобн о достаточных условиях
слабого минимума 377, 398
Термннант 299, 320
Точка, допустимая по ограниче-
нию 30
— крайняя 351
— седловая 56
— сопряженная 375
— стационарная 45, 46, 48, 59,
240
— Торичелли 20, 99
Траектория фазовая 316
Управление 81, 130,-316
Управляемый процесс 298, 316
----допустимый 317
Уравнения в вариациях 202, 205
— Гамильтона — Якобн 386
— линейные дифференциальные
— Эйлера 15, 59, 64, 371
----Лагранжа 83
----Пуассона 80, 313
— Якобн 375
Условия Вейерштрасса 76, 224, 372
----Эдмана 322
— граничные 41, 81, 298
— Дополняющей иежесткостн 53,
244, 250
— краевые 81, 298
— Лежавдра 373, 374
---- усиленные 377
— Липшица 132
— Слейтера 53
— согласования знаков 244, 250
— соответствия знаков 243, 249
— трансверсальности 15, 65
—• экстремума в задаче линейно-
го программирования 244, 273
----достаточные в гладкой за-
даче 241, 288, 293
----------простейшей зада-
че вариационного исчисления
388, 390, 391, 399
Условия экстремума достаточные
в задаче оптимального управле-
ния, линейной по фазовым пе-
ременным 367
------- — — — — элементар-
ной 248, 360
----, необходимые в гладкой за-
даче 240, 287, 289
---------- изопериметрнческой
задаче 77
--------- — задаче Больца 64, 246
-------------выпуклого про-
граммирования 52, 262
-------------Лагранжа 83, 299
—,-----------оптимального уп-
равления 87, 320
--------------- —, линейной
по фазовым переменным 366
------------ — — — элементар-
ной 248, 360
—. — — — простейшей задаче
вариационного исчисления 59,
371—373, 375
— Якоби 375
----усиленные 377
Условный экстремум 40, 47
Фазовые ограничения 318
— переменные 81
фактор-пространство 118
Форма квадратичная, тернарная
степени п 143
Формализация 30
Формула Дирихле 136
— конечных приращений 147
— Ньютона — Лейбница 131
Фундаментальная матрица реше-
ний однородной системы 193,
205
Функционал 30
— Больца 41, 65, 245, 298
— интегральный 41, 178 , 325
----, инвариантный относитель-
но семейства отображений 405
— смешанный 41
— терминальный 41
Функция абсолютно непрерывная
132
— аффинная 218
Функция Вейерштрасса 76, 223
'373 . •
— выпуклая 52, 214
-----на прямой 214
----- однородная 120
— Гамильтона 302, 377
— , дифференцируемая в точке 45,
46
— допустимая 370
— замкнутая 218
— измеримая 131, 335
— индикаторная 215
-г интегрируемая 131
— Лагранжа 47, 52, 82, 85, 249,
250, 252, 261, 299, 319, 354
-----расширенная 266
— локально интегрируемая 184
— Минковского 121, 215
— наклона поля 391
— несобственная 214
— ограниченной вариации кано-
ническая 134
— опорная 221
— полунепрерывная снизу 218,-
251
— Понтрягина 302, 320
— собственная 214
— сопряженная 224
—, — к норме 227
S-фунКция 264
Экстремаль 59, 381
— каноническая 381
Экстремальная задача, см, За*
дача экстремальна^
Экстремум 11, 30
— локальный 30
— сильный 68, 370
— слабый 59, 299, 370
— условный 40
Экстремума условия, см. Условия
экстремума
Элементарная вариация процесса
89
— игольчатая вариация траекто-
рии, управления 89, 323
— экстремальная задача 40, 42,
238, 243
Алексеев Владимир Михайлович,
Тихомиров Владимир Михайлович,
Фомин Сергей Васильевич
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
М-, 1979 г., 432 стр. с илл.
Редактор Н. Н. Васина
Техн, редактор И. Ш. Аксельрод
Корректор О. ЛТ. Кривенко
ИБ № 2344 '
Сдано в набор 20 06.79. Подписано к печати
25.10 79. Т-17355. Бумага 84хЮ81/82 Тип №2.
Высокая печать. Литературная гарнитура. Условн.
печ л. 22,68. Уч.-нзд л 24,64. Тираж 24 000 экз.
Заказ № 314. Цена книги 1 р 10 к.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и
ордена Трудового Красного Знамени
Первая Образцовая типография
имени А. А. Жданова Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и
книжной торговли.
Москва, М-54, Валовая, 28