Author: Боярчук А.К.
Tags: математический анализ высшая математика дифференциальные уравнения
ISBN: 5-354-00020-3
Year: 2001
Text
А.К.Боярчук
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО: ТЕОРИЯ И ПРАКТИКА
Справочное пособие по высшей математике. Т. 4
М.: Едиториал УРСС, 2001. — 352 с.
«Справочное пособие по высшей математике» выходит в пяти томах и
представляет собой новое, исправленное и существенно дополненное издание
«Справочного пособия по математическому анализу» тех же авторов. В новом
издании пособие охватывает три крупных раздела курса высшей математики —
математический анализ, теорию дифференциальных уравнений, теорию функций
комплексной переменной.
Том 4 является логическим продолжением трех предыдущих ориентированных
на практику томов и содержит более четырехсот подробно решенных задач, но
при этом отличается более детальным изложением теоретических вопросов и
может служить самостоятельным замкнутым курсом теории функций
комплексного переменного. Помимо вопросов, обычно включаемых в курсы
такого рода, в книге излагается ряд нестандартных — таких, как интеграл
Ньютона—Лейбница и производная Ферма—Лагранжа.
Пособие предназначено для студентов, преподавателей и работников физико-
математических, экономических и инженерно-технических специальностей,
специалистов по прикладной математике, а также лиц, самостоятельно
изучающих высшую математику.
Оглавление
Предисловие 3
Глава 1. Основные структуры математического анализа 4
§ 1. Элементы теории множеств и отображений 4
Некоторые логические символы (4) Обозначения, используемые в
теории множеств (5) Натуральные числа. Метод математической
индукции (5) Простейшие операции над множествами (6)
Упорядоченная пара и декартово произведение множеств (7) Бинарные
отношения. Проекции и сечения бинарного отношения. Обратное
бинарное отношение (7) Функциональное бинарное отношение.
Функция и простейшие понятия, связанные с нею (8) Обратная
функция. Композиция отображений (9) Параметрическое и неявное
отображения (9) Изоморфизм (10)
§ 2. Математические структуры 10
Группа (10) Кольцо (10) Тело (10) Поле (11) Векторное пространство
над полем К. Нормированное пространство (11)
§ 3. Метрические пространства 12
Аксиомы метрики. Предел последовательности точек метрического
пространства (12) Шары, сферы, диаметр множества (13) Открытые
множества (14) Внутренность множества (15) Замкнутые множества,
точки прикосновения, замыкание множества (16)
§ 4. Компактные множества 18
§ 5. Связные пространства и связные множества 70
§ 6. Предел и непрерывность отображения из одного метрического 20
пространства в другое
Предел и непрерывность отображения (20) Непрерывность
композиции отображений (21) Непрерывность обратного отображения
(22) Предел и непрерывность отображения в смысле Коши. Некоторые
свойства непрерывных отображений (22) Равномерно непрерывные
отображения (24) Гомеоморфизмы. Эквивалентные расстояния (25)
Глава 2. Комплексные числа и функции комплексного переменного 26
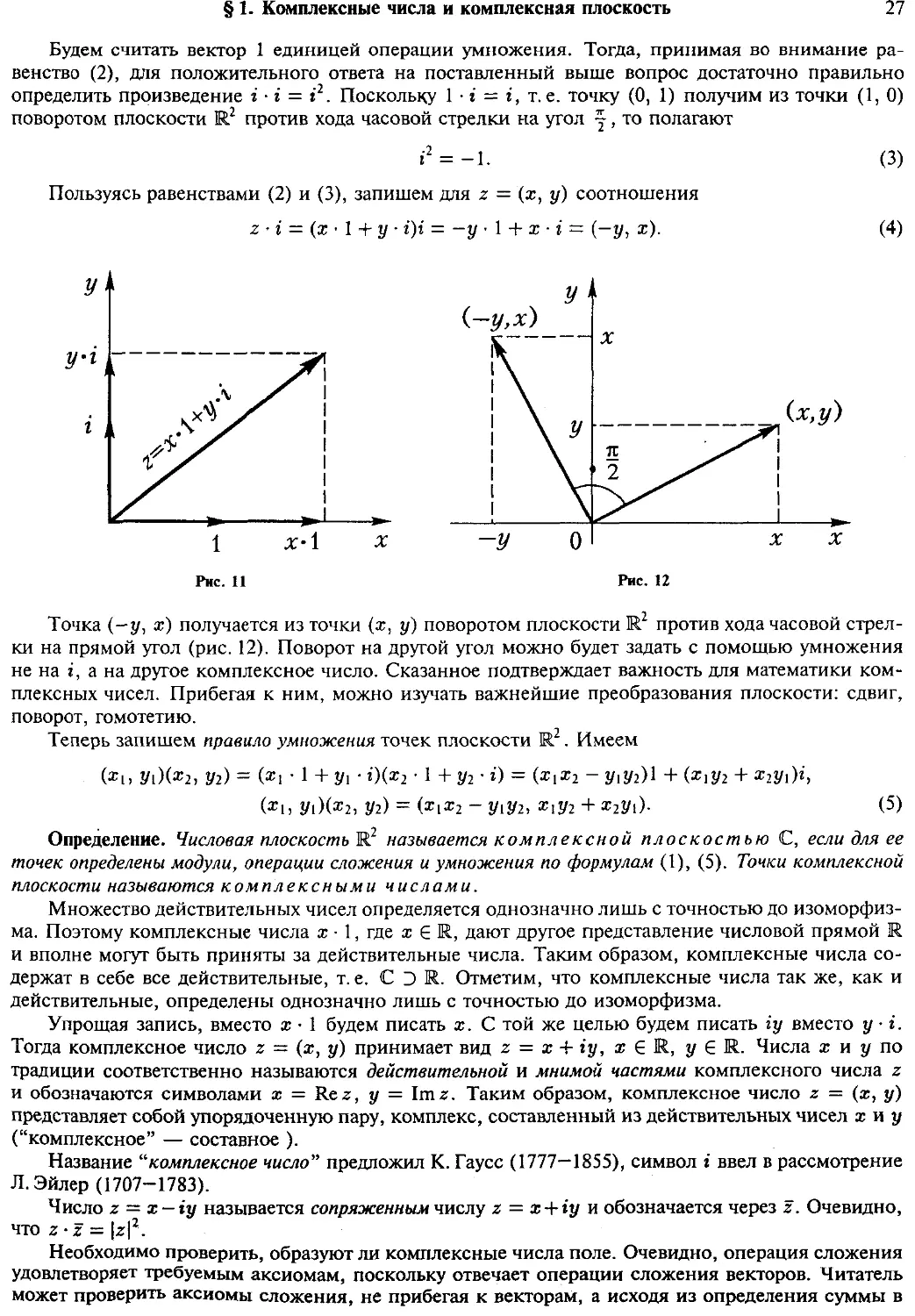
§ 1. Комплексные числа и комплексная плоскость 76
Определение комплексного числа (26) Аргумент комплексного числа.
Тригонометрическая и показательная формы его записи. Умножение и
деление комплексных чисел. Операция извлечения корня из
комплексного числа (28) Стереографическая проекция и ее свойства
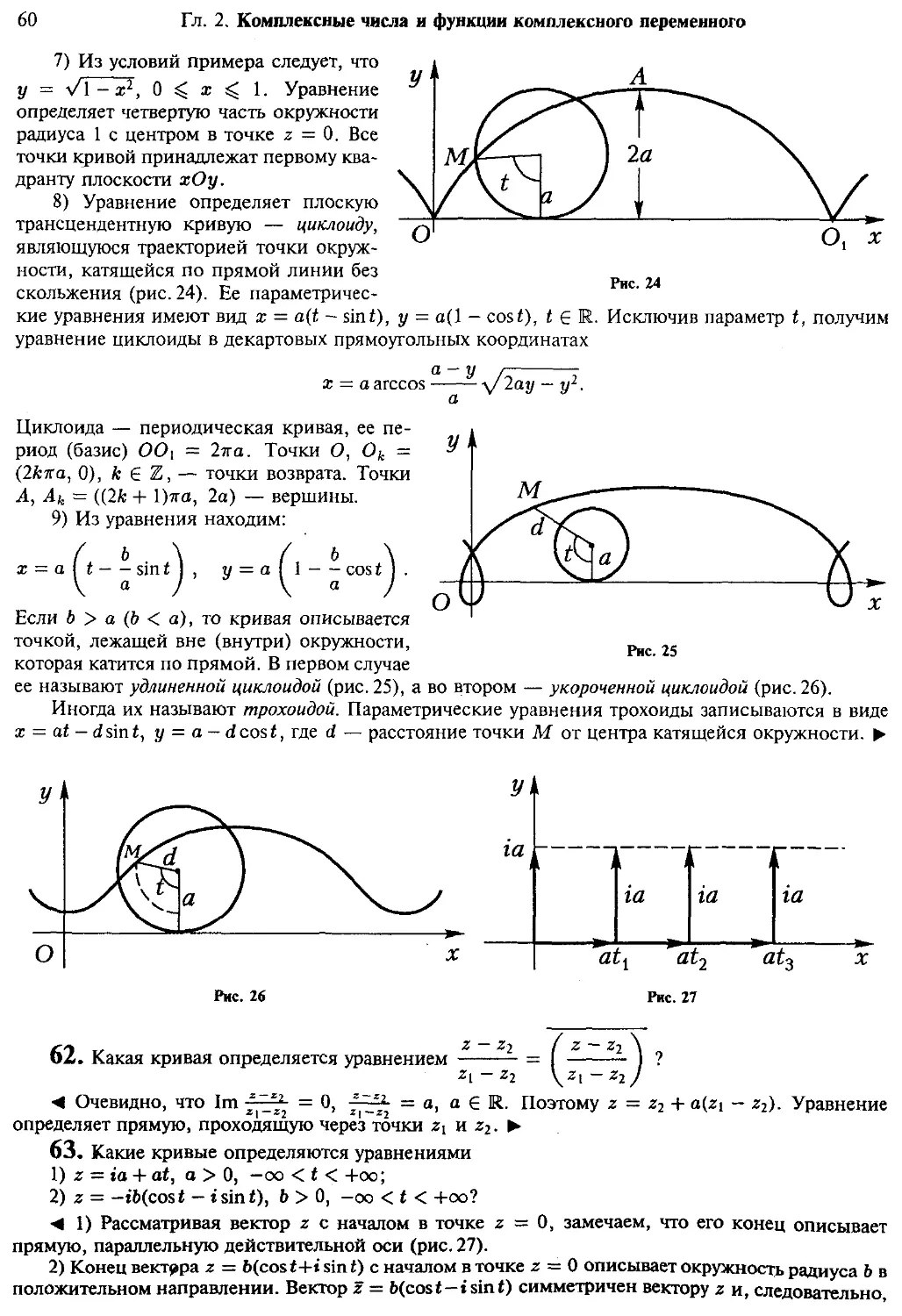
(29) Примеры (31)
§ 2. Топология комплексной плоскости. Последовательности комплексных 43
чисел. Свойства функций, непрерывных на компакте
Топология комплексной плоскости (43) Замкнутые множества, отрезок
и ломаная. Связные множества (45) Последовательность комплексных
чисел и ее предел (45) Свойства компакта К с С (47) Предел и
непрерывность функции комплексного переменного (48)
Арифметические операции над пределами и непрерывными
функциями (49) Предел и непрерывность композиции функций (49)
Свойства функций, непрерывных на компакте (50)
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области 50
Примеры (53)
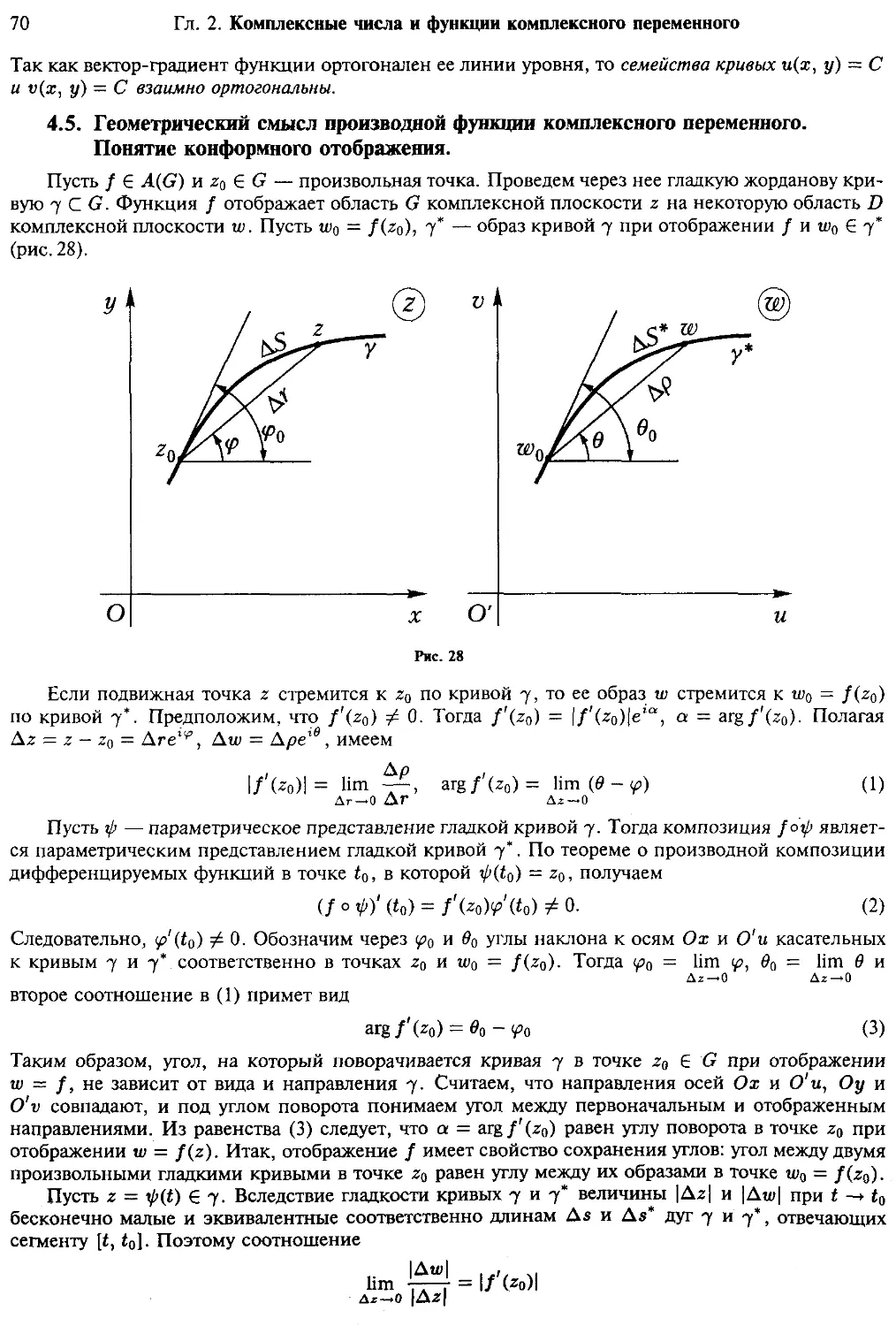
§ 4. Дифференцируемые функции комплексного переменного. Связь между 63
С-дифференцируемостью и R2 -дифференцируемостью.
Аналитические функции
Определение дифференцируемой функции. Правила
дифференцирования (63) Дифференциал функции (66) Критерий
дифференцируемости функции комплексного переменного (67)
Аналитические функции (68) Геометрический смысл производной
функции комплексного переменного. Понятие конформного
отображения (70) Плоские физические поля и их связь с
аналитическими функциями (71) Неравенство Лагранжа (73) Примеры
(73)
Упражнения для самостоятельной работы 79
Глава 3. Элементарные функции в комплексной плоскости 83
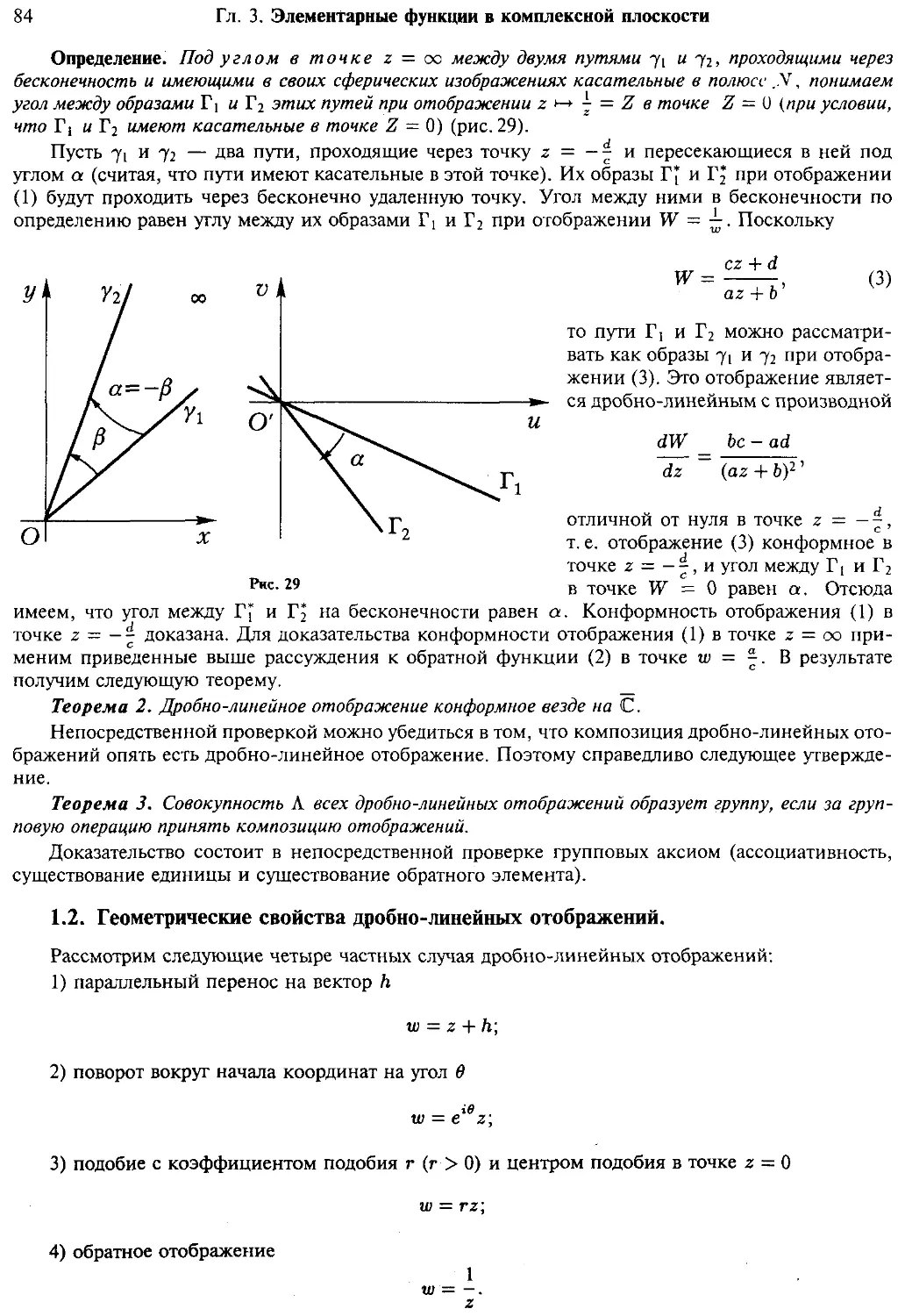
§ 1. Дробно-линейные функции и их свойства 83
Определение дробно-линейной функции. Конформность отображения
(83) Геометрические свойства дробно-линейных отображений (84)
Дробно-линейные изоморфизмы и автоморфизмы (86) Примеры (88)
§2. Степенная функция w = zn (n&N,n>T). Многозначная функция w — y/z
и ее поверхность Римана
Степенная функция (91) Многозначная функция w - y[z и ее
поверхность Римана (92) Примеры (93)
§ 3. Показательная функция w= ez и многозначная функция z=Ln w
Показательная функция w = ez (94) Многозначная функция z=Ln w (96)
Примеры (96)
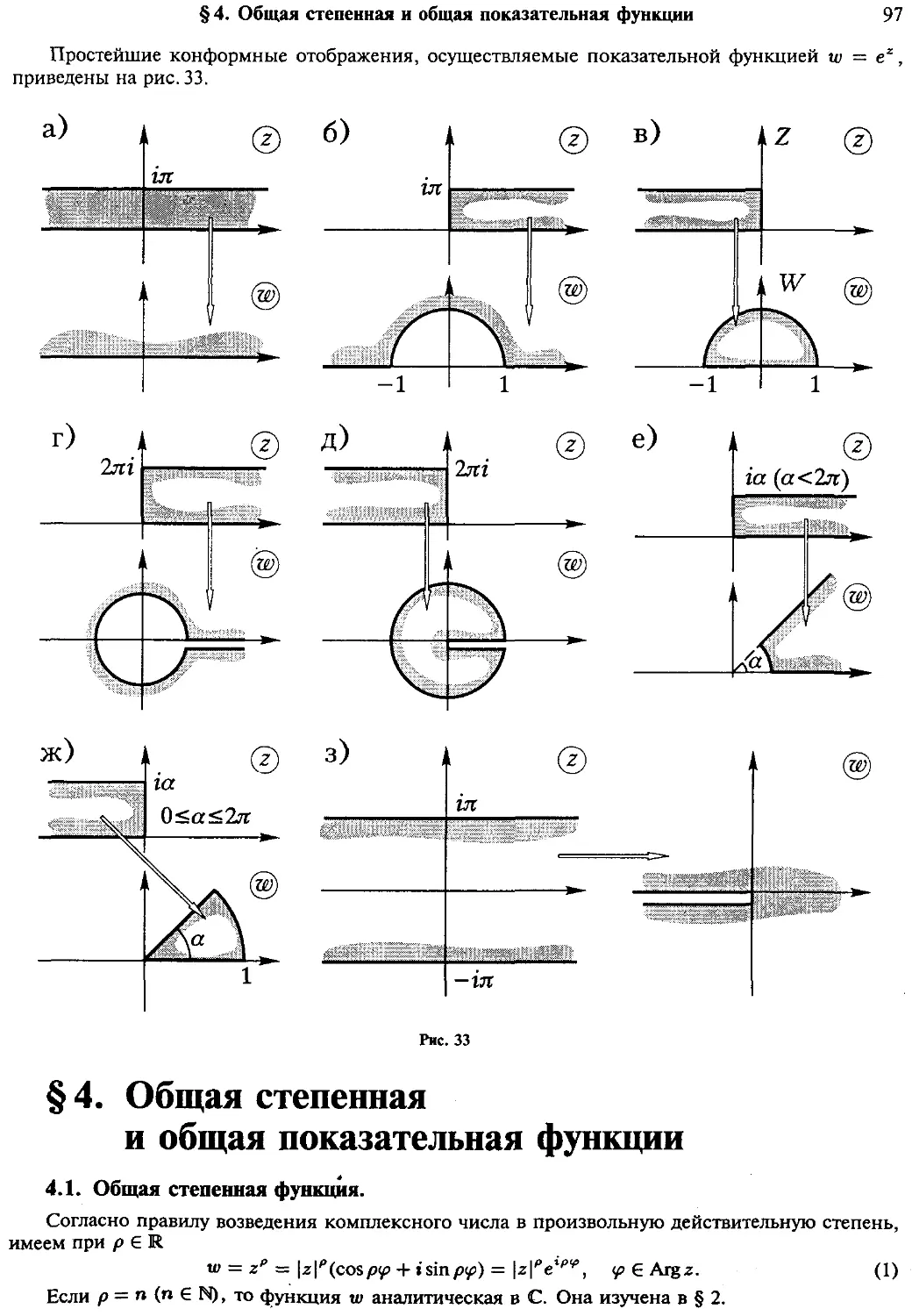
§ 4. Общая степенная и общая показательная функции
Общая степенная функция (97) Общая показательная функция (98)
§ 5. Функция Жуковского
Определение функции Жуковского. Конформность (99) Примеры (100)
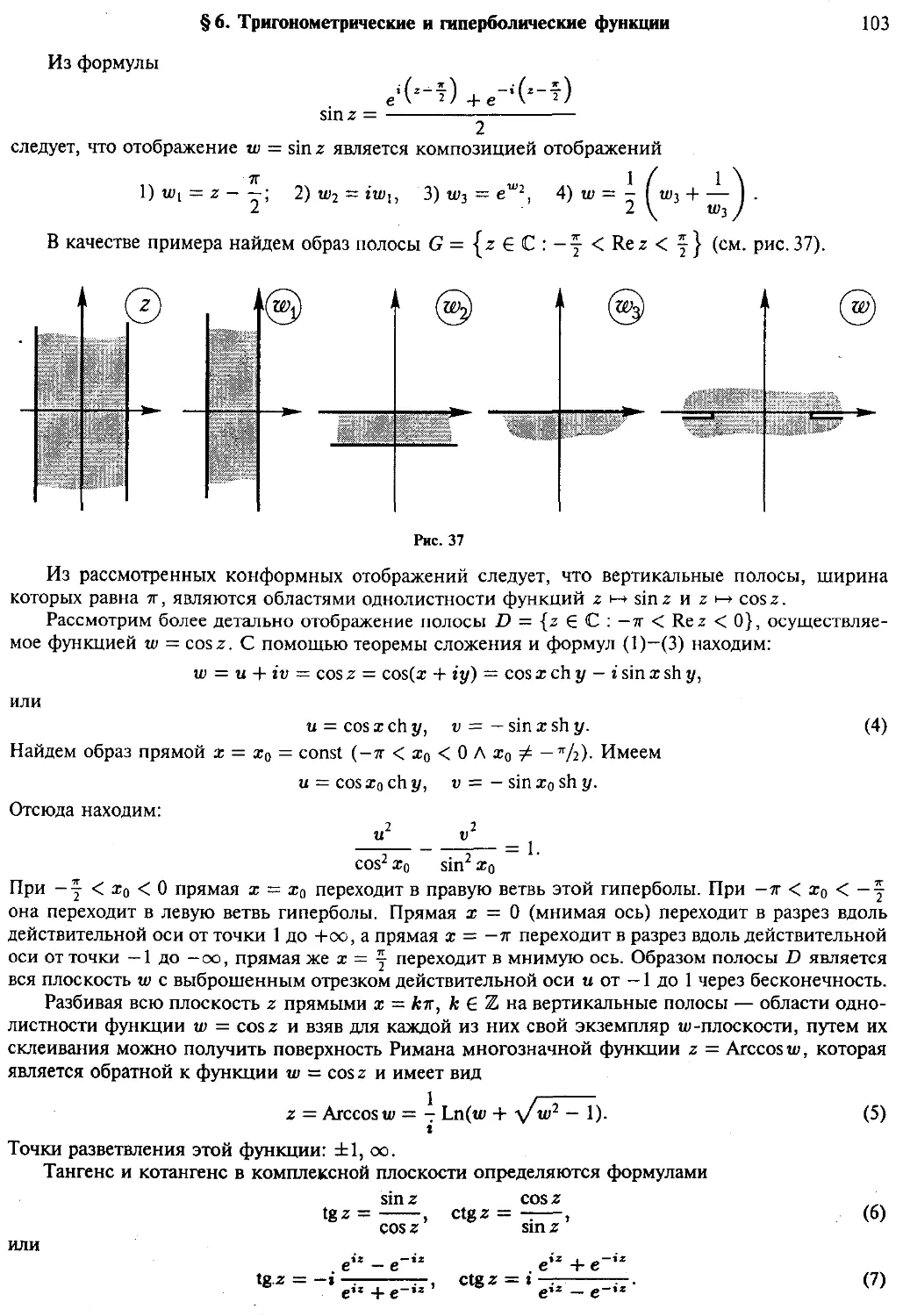
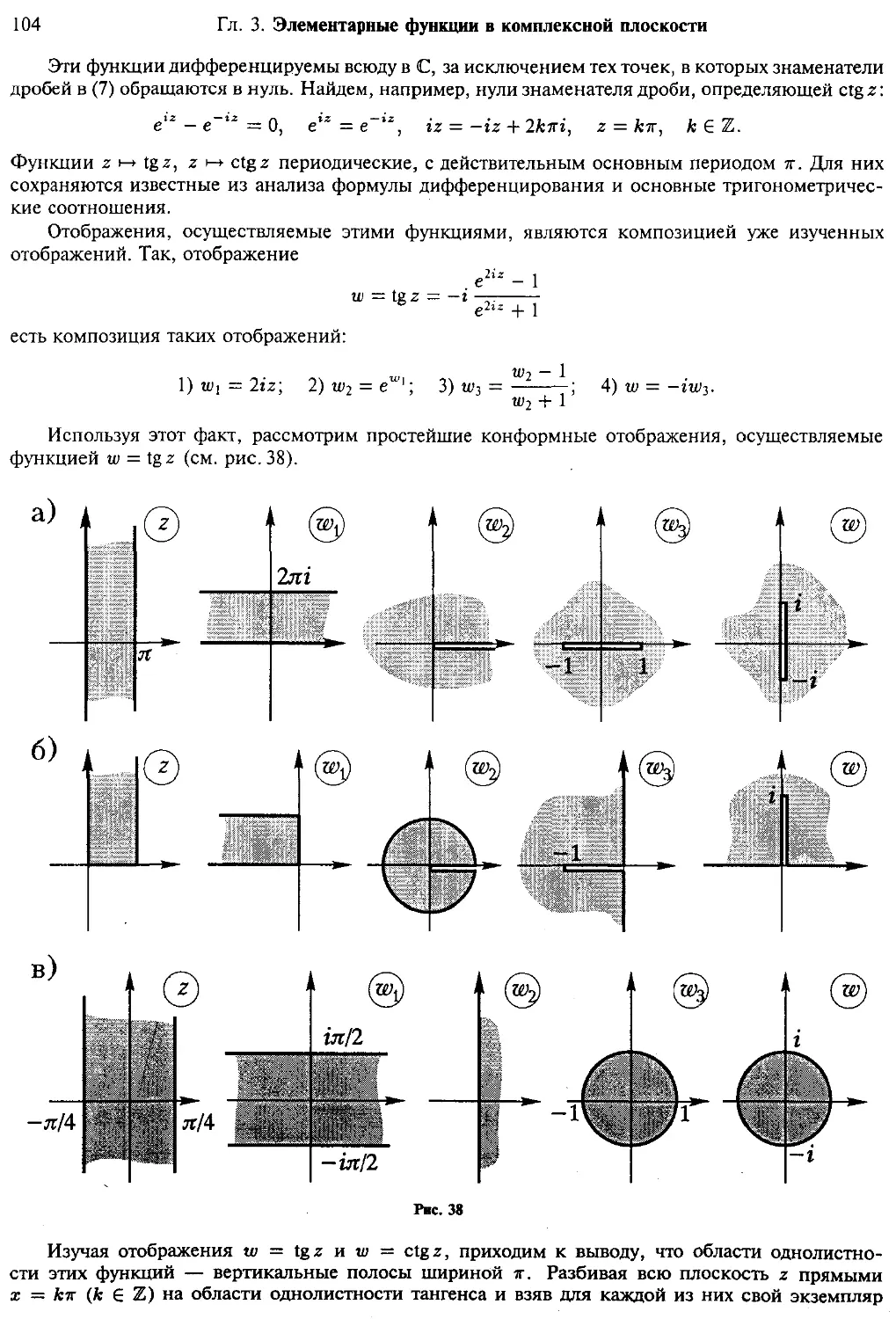
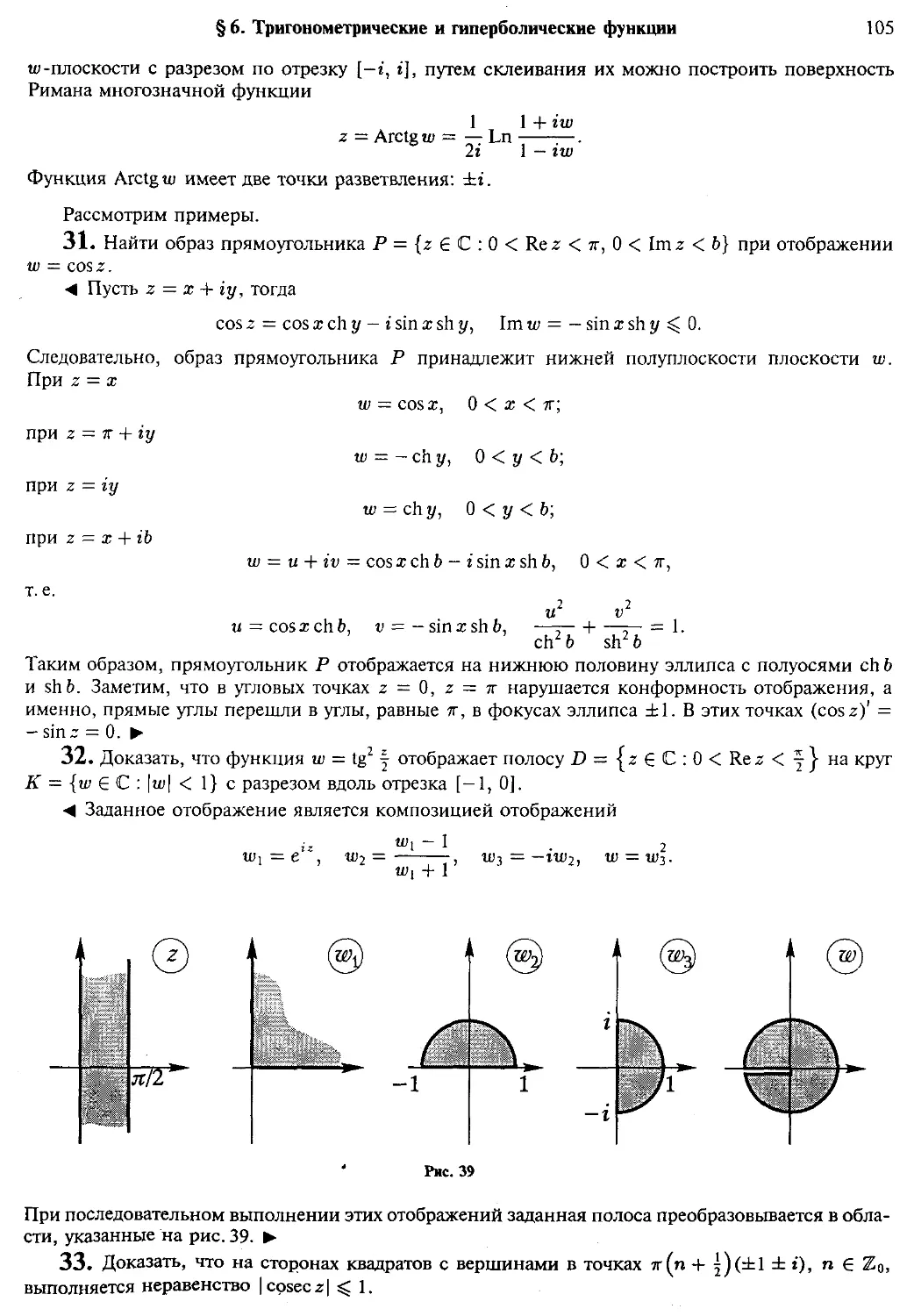
§ 6. Тригонометрические и гиперболические функции
Примеры (105)
Упражнения для самостоятельной работы
Глава 4. Интегрирование в комплексной плоскости. Интегралы
Ньютона — Лейбница и Коши
§ 1. Интеграл Ньютона — Лейбница
Первообразная (149) Интеграл Ньютона — Лейбница (150) Линейность
интеграла. Замена переменных и формула интегрирования по частям
(757)
§ 2. Производные и интегралы Ньютона — Лейбница любых порядков
Определение «-производной и «-интеграла (153) Формула Ньютона —
Лейбница. Производные по пределам интегрирования (154) Формула
Тейлора(156)
§ 3. Производная Ферма — Лагранжа. Формула Тейлора — Пеано
Производная Ферма — Лагранжа (156) Теорема Тейлора — Пеано и ее
обращение (157)
§ 4. Криволинейные интегралы
Интегрирование функций по ориентированной гладкой кривой (759)
Гомотопия двух кривых (путей) (161)
§ 5. Теорема и интеграл Коши
Существование локальной первообразной аналитической функции
(162) Первообразная вдоль кривой (вдоль пути) (165) Теорема Коши
(166) Интегральная формула Коши (172) Примеры (173)
§ 6. Интеграл типа Коши
Определение и основное свойство интеграла типа Коши (775)
Гармоничность действительной и мнимой частей аналитической
функции. Восстановление аналитической функции по ее
действительной (мнимой) части (177) Теоремы Лиувилля и Морера
(178) Главное значение и предельные значения интеграла типа Коши
(179) Формулы Шварца и Пуассона (181) Примеры (184)
Упражнения для самостоятельной работы
41
94
97
99
101
145
149
149
153
156
159
162
175
195
Глава 5. Ряды аналитических функций. Изолированные особые точки 197
§ 1. Ряд Тейлора 197
Общие сведения о рядах (197) Последовательность функций и
функциональный ряд. Поточечная сходимость (198) Равномерная
норма функции. Равномерная сходимость последовательности
функций и функционального ряда (199) Нормальная сходимость
функционального ряда. Признаки Вейерпгграсса, Абеля и Дирихле
равномерной сходимости функциональных рядов (201)
Функциональные свойства равномерной суммы функционального ряда
(203) Степенные ряды (206) Теорема Тейлора (208) Теорема
единственности (210) Примеры (212)
§ 2. Ряд Лорана и изолированные особые точки аналитических функций 219
Теорема Лорана (219) Классификация изолированных особых точек в
С (227) Поведение аналитической функции при подходе к
изолированной особой точке (222) Бесконечная изолированная особая
точка (224) Примеры (225)
Упражнения для самостоятельной работы 229
Глава 6. Аналитическое продолжение 231
§ 1. Основные понятия. Аналитическое продолжение вдоль пути 232
Свойство единственности аналитической функции. Определение
аналитического продолжения (232) Аналитическое продолжение вдоль
пути (234) Инвариантность аналитического продолжения вдоль пути
относительно гомотопных деформаций этого пути (235)
§ 2. Полные аналитические функции 237
Понятие полной аналитической функции (237) Примеры полных
аналитических функций (238) Особые точки полной аналитической
функции (239) Существование особой точки на границе круга
сходимости степенного ряда (240)
§ 3. Принципы аналитического продолжения 240
Примеры (241)
Упражнения для самостоятельной работы 243
Глава 7. Вычеты и их применения 245
§ 1. Определение вычета. Основная теорема 245
Вычет относительно изолированной конечной точки (245) Вычет
относительно бесконечности (246) Теорема о вычетах (247) Примеры
(248)
§ 2. Целые и мероморфные функции 257
Целые функции (257) Мероморфные функции. Теорема Миттаг-
Леффлера (257) Разложение мероморфных функций на простейшие
дроби (259) Примеры (262)
§ 3. Бесконечные произведения 264
Числовые бесконечные произведения (265) Равномерно сходящиеся
бесконечные произведения (267) Представление целой функции в виде
бесконечного произведения (267) Разложение sin? в бесконечное
произведение (26Р) Род и порядок целой функции (270) Мероморфная
функция как отношение двух целых функций (270) Примеры (271)
§ 4. Применение вычетов для вычисления интегралов и сумм рядов 274
Применение вычетов для вычисления определенных интегралов (274)
Применение вычетов к вычислению сумм рядов (278) Примеры (279)
Упражнения для самостоятельной работы 291
Глава 8. Некоторые общие вопросы геометрической теории 295
аналитических функций
§ 1. Принцип аргумента. Теорема Руше 295
Вычисление интеграла —Г ^dz (295) Теорема о
логарифмическом вычете (296) Принцип аргумента (296) Теорема
Руше (297) Примеры (298)
§ 2. Сохранение области и локальное обращение аналитической функции 300
Принцип сохранения области (300) Локальное обращение
аналитических функций (301) Примеры (303)
§ 3. Экстремальные свойства модуля аналитической функции 304
Принцип максимума модуля аналитической функции (304) Лемма
Шварца (305) Примеры (305)
§ 4. Принцип компактности. Функционалы на семействе аналитических 308
функций
Равномерно ограниченные и равностепенно непрерывные семейства
функций (308) Принцип компактности (309) Функционалы,
определенные на множествах функций (310) Теорема Гурвица (311)
§ 5. Существование и единственность конформного отображения 312
Конформные изоморфизмы и автоморфизмы (312) Примеры
автоморфизмов (312) Существование и единственность изоморфизмов
областей, изоморфных единичному кругу (313) Теорема
существования (314)
§ 6. Соответствие границ и принцип симметрии при конформном 315
отображении
Теорема о соответствии границ (315) Принцип симметрии (316)
Примеры (317)
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля — 318
Шварца
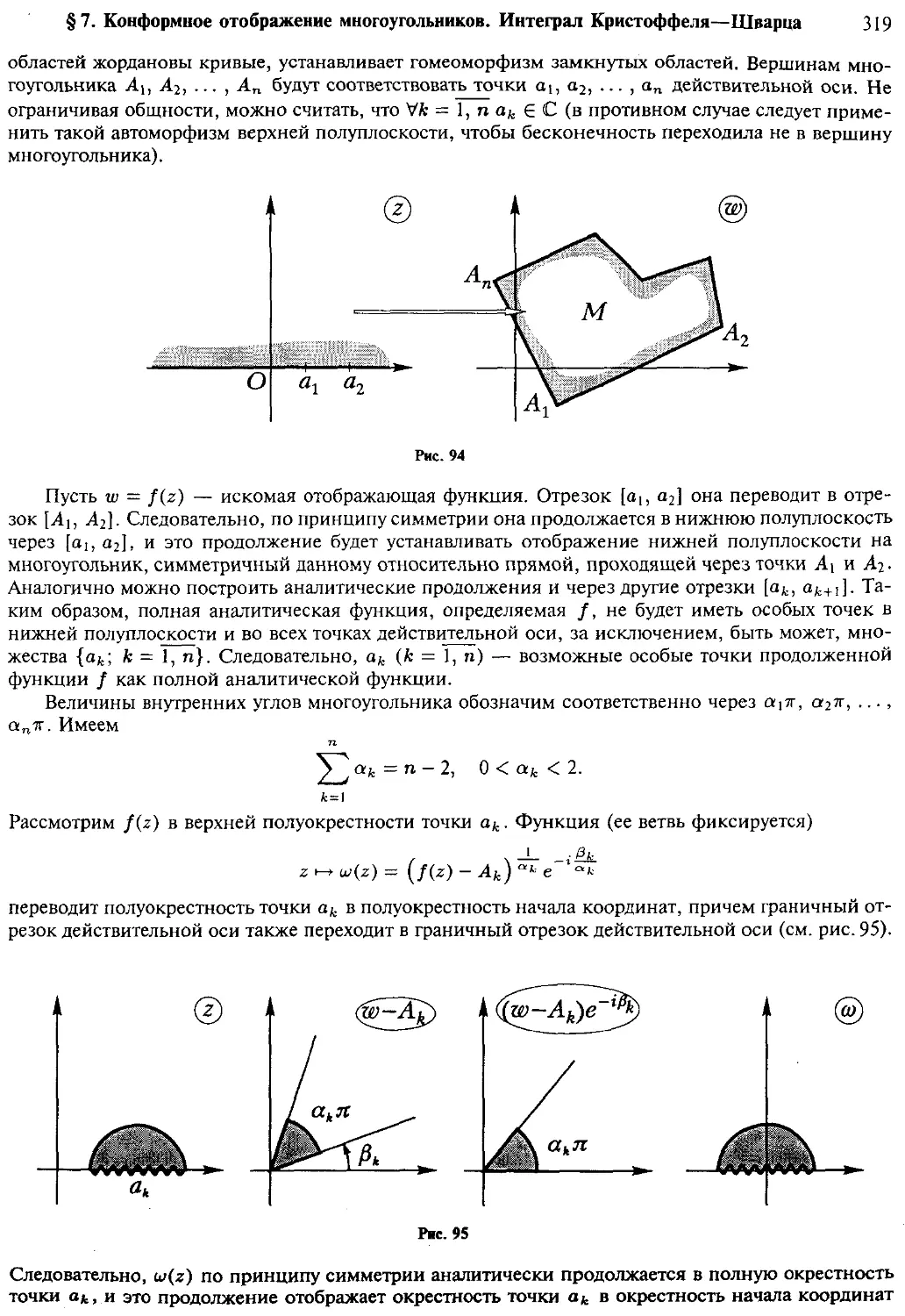
Отображение верхней полуплоскости на многоугольник (318) Случай
многоугольника, имеющего вершины в бесконечности (322)
Отображение верхней полуплоскости на внешность многоугольника
(322) Отображение верхней полуплоскости на прямоугольник (323)
Эллиптический синус и его двоякая периодичность (324) Отображение
единичного круга на многоугольник (326) Примеры (328)
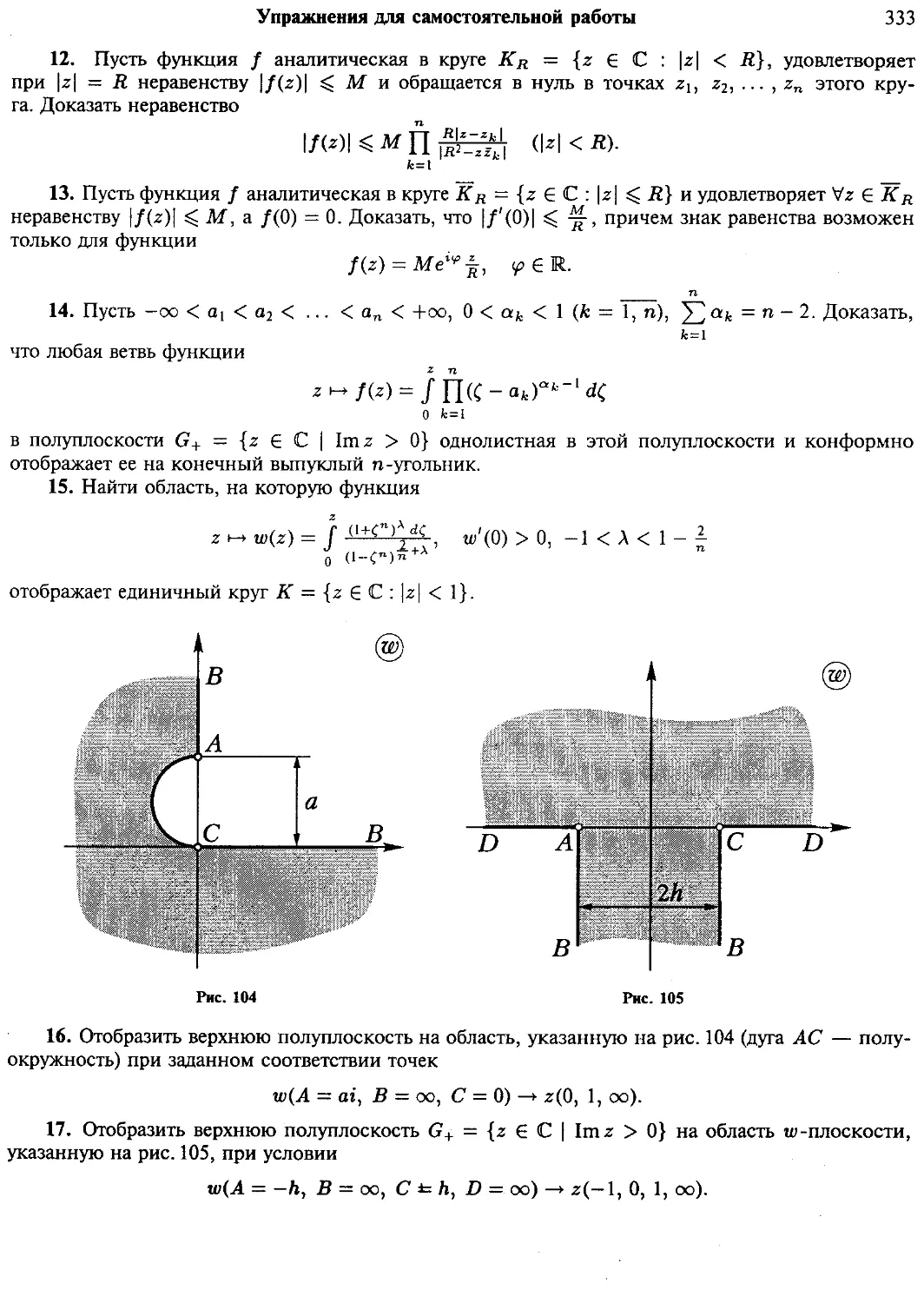
Упражнения для самостоятельной работы 332
Ответы 334
Литература 338
Предметный указатель 339
Предметный указатель
Настоящий предметный указатель призван облегчить поиск терминов по алфавитному
признаку. Для поиска терминов по тематическому признаку пользуйтесь подробно составленным
оглавлением.
В настоящем предметном указателе, как правило, приводятся ссылки на страницу, где термин
определяется. Составитель указателя не ставил своей целью отследить все упоминания
приведенных терминов в книге. Исключение составляют термины, описывающие методы, приемы,
практические результаты: для них в некоторых случаях указаны также задачи, в которых они
используются. Номера задач указаны курсивом по схеме "число:число", где первое число — номер
главы, второе — порядковый номер задачи.
А
Абеля
— теорема, 202
-----вторая, 207-208
-----первая, 207
— тождество, 202
абсолютное значение
— в поле, 11
— в теле, 11
автоморфизм конформный, 312
аддитивность
— интеграла относительно пределов
интегрирования, 151
— криволинейного интеграла, 159
аксиома индукции, 5
аксиомы
— абсолютного значения, 11
— векторного пространства, 11
— длины,11
— метрики, 12
— модуля, 11
— нормы, 11
Аполлония окружность, 41
аргумент комплексного числа, 28
— , главное значение, 28
Архимеда спираль, 40
Б
Бернулли
— лемниската, 59
— числа, 215
Бесселя функция, 226
бета-функция Эйлера, 328
Больцано—Вейерштрасса теорема, 47
Бореля—Лебега теорема, 48 2:60
В
Вейерштрасса
— беконечное произведение, 268
— мажорантный признак равномерной
сходимости функционального ряда,
201
— теорема, 50, 204-205
-----о представлении целой функции
в виде бесконечного
произведения, 269
вектор-функция, 50
векторное пространство над полем, 11
векторы, 11
ветви многозначной функции
однозначные, 92
ветвь многозначной функции Ln w
главная, 96
Виета теорема, 2:21, 2:40, 2:41
внешность простой замкнутой кривой,
52
внутренность
— множества, 15
— простой замкнутой кривой, 52
вычет
— аналитической функции
относительно её изолированной
особой точки, 245
— функции
-----логарифмический, 296
-----относительно бесконечности, 246
Г
Гаусса утверждение, 37
Гейне определение
— непрерывности отображения в
точке, 21
— предела отображения, 21
Гельдера условие, 179
главное значение
— аргумента комплексного числа, 28
— интеграла типа Коши в точке, 179
гомеоморфизм, 25
гомотопия
— замкнутой кривой в замкнутую
кривую, 161
— кривой в кривую, 161
— с фиксированным началом и
концом, 161
граница множества, 17, 45
график отображения, 8, 9
группа, 10
— абелева, 10
— автоморфизмов области, 312
— аддитивная, 10
— коммутативная, 10
— мультипликативная, 10
Гурвица теорема, 311
д
Д'Аламбера признак, 2:51
действительная часть
— комплексного числа, 27
— функции, 48
деформация одной кривой в другую,
161
диаметр множества, 14
Дирихле
— теорема, 155, 203
— признак, 5:8, 5:11
дифференциал функции в точке, 66
дифференцируемость вектор-функции
на сегменте, 51
длина в векторном пространстве, 11
долгота, 31
дополнение одного множества в
другом, 6
Ж
Жордана
— лемма, 275, 7:59
— теорема, 52
Жуковского функция, 99, 318, 3:28,
3:72, 3:74, 3:87-93, 3:95, 3:97,
3:99,3:100,3:101
3
замыкание множества, 16, 45
знаки
— включения, 5
— принадлежности, 5
значение
— аргумента комплексного числа
главное, 28
— бесконечного произведения, 265
— интеграла типа Коши в точке
-----главное, 179
-----предельное слева от кривой, 180
-----предельное справа от кривой, 180
— отображения, 9
И
изоморфизм
— дробно-линейный, 87
— конформный, 312
— множества на множество, 10
интеграл
— Ньютона—Лейбница
-----определенный, 150
-----с фиксированным нижним
пределом и переменным верхним
пределом интегрирования, 150
— в смысле главного значения по
Коши, 179
— Коши, 173
— криволинейный функции по кривой,
159
-----второго рода, 159
-----первого рода, 159
— Кристоффеля—Шварца, 320
-----второго рода, 321
-----первого рода, 321
— типа Коши, 175
-----, значение в точке
-----главное, 179
----- предельное
----------слева от кривой, 180
----------справа от кривой, 180
— Шварца, 181
— Эйлера—Пуассона, 191
— эллиптический первого рода, 323
-----полный, 324
1-интеграл, 153
«-интеграл, 154
К
Кантора теорема, 18, 25
Каратеодори теорема, 315
Кардана формулы, 2:41
квантор
— общности, 4
— существования, 4
кольцо, 10
— коммутативное, 10
— унитарное, 10
компакт, 18, 47
комплексная плоскость, 27
комплексные числа, 27
комплексный потенциал, 72, 2:83
композиция отображений, 9
компонента упорядоченной пары
— вторая, 7
— первая, 7
компоненты связные, 52
континуум,52
— линейный, 52
контур, 160
координата упорядоченной пары
— вторая, 7
— первая, 7
Коши
— интеграл, 173
— критерий, 46, 198, 200
-----для функционального ряда, 201
— определение
-----непрерывности отображения, 22
-----предела отображения, 22
— теорема
-----интегральная, 166-167
-------, обобщение на случай
функции, не являющейся
аналитической на контуре
интегрирования, 168-170
-----о вычетах, 247, 7:42, 7:47
-----, обобщение на случай
неодносвязной области, 171-172
— формула интегральная, 172—173
— ядро, 179
Коши—Лдамара
— теорема, 207
— формула, 5:10, 5:11, 8:6
Коши—Римана условия, 67, 2:72, 2:73,
2:75, 2:77-80
кривая
— гладкая
-----, ориентация, 51
-----ориентированная, 51
-----, параметрическое представление,
51
-----простая, 51
— жорданова, 51
-----замкнутая, 51
— замкнутая, 51
— канторова, 52
— кусочно-гладкая, 52
— непрерывная, 51
— ориентированная
-----противоположно по отношению
к данной, 51
—, параметрическое представление, 51
— простая, 51
-----замкнутая
-------, внешность, 52
-----, внутренность, 52
Кристоффеля—Шварца
— интеграл, 320
-----второго рода, 321
-----первого рода, 321
— формула, 320, 8:22, 8:25
критерий
— дифференцируемости функции f. С -
> С 67, 2:79
— компактности в себе, 47—48
— Коши, 46, 198, 200
-----для функционального ряда, 201
круг сходимости аналитического
элемента, 233
круговое свойство дробно-линейных
отображений, 85
Л
Лагранжа
— ряд, 302
— теорема, 73
Ландау символы, 11
Лапласа оператор, 178
лемма
— Жордана, 275, 7:59
— Шварца, 305, 8:15-17
леммы
— Паскаля, 5
лемниската Бернулли, 59
Линдедёфа результат, 316
линейное пространство над полем, 11
линейность криволинейного интеграла,
159
Лиувшля теорема, 178-179, 4:25
Лопиталя правило, 7:8
Лорана теорема, 219-220
М
мера жорданова множества, 79
метод
— математической индукции, 5-6, 2:53
— от противного, 4
метрика, 12
— сферическая, 43
Миттаг-Леффлера теорема, 258-259,
7:25, 7:27
мнимая часть
— комплексного числа, 27
— функции, 48
многочлен Тейлора, 156
множества
— изоморфные, 10
— непересекающиеся, 6
— равные, 5
множество
— внешних точек данного множества,
15
—, внутренность, 15
— вполне ограниченное в метрическом
пространстве, 18
—, граница, 17, 45
—, диаметр, 14
— жорданово
-----, мера, 79
-----, площадь, 79
— замкнутое, 16, 45
-----связное, 45
—, замыкание, 16, 45
— значений отображения, 9
— компактное, 20
-----в метрическом пространстве, 18
-----в себе, 18, 47
-----относительно метрического
пространства, 18
— линейно-связное, 149
—, образ при отображении, 9
— ограниченное, 14, 44
— определения отображения, 9
— открытое, 14, 45
-----связное, 45
—, покрытие, 18
—, прообраз при отображении, 9
— пустое, 5
— связное в метрическом
пространстве, 20
— точек кусочно-гладкой кривой, 52
— функций
-----компактное
--------в данной области, 309
--------в себе, 311
-----равномерно ограниченное внутри
данной области, 309
-----равностепенно непрерывное, 309
-----внутри данной области, 309
модуль
— в поле, 11
— в теле, 11
— комплексного числа, 26
Монтеля признак компактности, 309—
310
Морера теорема, 179
Муавра формула, 29, 2:17
н
направление обхода границы области
положительное, 162
непрерывность
— отображений взаимная, 25
— отображения, 21, 23
-----в точке, 23
-------в смысле Гейне, 21
-------в смысле Каши, 22
-----равномерная, 24
— функции в точке, 48
неравенство треугольника
— для абсолютного значения, 11
— для метрики, 12
— для модуля, 11
— для нормы (длины) в векторном
пространстве, 11
норма
— в векторном пространстве, 11
— вектора, 11
— функции равномерная, 199
-----, свойства, 199
нуль функции, 212
— кратности п, 212
Ньютона—Лейбница формула, 150
— для «-интеграла, 154—155
О
области
— дробно-линейно изоморфные, 87
— конформно-изоморфные, 312
область, 20, 45
— бесконечносвязная, 53
— замкнутая, 20, 45
— значений отображения, 9
— компактная, 53
— многосвязная, 52
— неодносвязная, 53
— односвязная, 53, 162
-----относительно комплексной
плоскости, 52
-----относительно расширенной
комплексной плоскости, 52
— определения
-----отображения, 9
-----полной аналитической функции
естественная, 237
— отправления отображения, 8
— прибытия отображения, 8
— существования полной
аналитической функции, 237
образ множества при отображении, 9
обращение отношения, 8
объединение множеств, 6
окрестность
— множества, 15
-----открытая, 15
— точки в множестве, 53
5-окрестность точки, 13
£-окрестность бесконечно удаленной
точки, 44
£ -окрестность точки, 44
окружность Аполлония, 41
оператор Лапласа, 178
операции над множествами, 6-7
операция
— обращения отношения, 8
— сложения комплексных чисел, 26
— транспонирования отношения, 8
— умножения комплексных чисел, 27
ориентация
— гладкой кривой, 51
-----противоположная, 51
«-остаток ряда, 203
отношение
— бинарное
-----между элементами множеств, 7
-----обратное, 8
-----, проекция
-------вторая, 8
-------первая, 7
-----функциональное, 8
—, обращение, 8
—, транспонирование, 8
— отображение
— биективное, 9
— взаимно однозначное, 9
— гиперболическое, 125
—, график, 8, 9
— дробно-линейное
-----, нормальная форма, 125
— заданное параметрически, 9
—, значение, 9
— из множества в множество, 8
— конформное
-----в области, 71
-----в точке, 71
— локсодромическое, 125
— множества в множество, 9
— множества на множество, 9
—, множество значений, 9
—, множество определения, 9
— непрерывное, 21, 23
-----в точке, 23
-------в смысле Гейне, 21
-------в смысле Каши, 22
—, область значений, 9
—, область определения, 9
—, область отправления, 8
—, область прибытия, 8
— обратимое, 9
— обратное, 9
— открытое, 301
-----внутреннее, 301
— равномерно непрерывное на
множестве, 24
— разрывное в точке, 21
— эллиптическое, 125
отображения
— взаимно непрерывные, 25
—, композиция, 9
отрезок
— на комплексной плоскости, 45
—, параметрическое представление, 45
П
пара упорядоченная, 7
—, вторая компонента (вторая
координата), 7
—, первая компонента (первая
координата), 7
параллель, 31
параметр, 9
Паскаля леммы, 5
первообразная функции, 149
— вдоль кривой, 165
— вдоль пути, 165
пересечение множеств, 6
петля, 160
Пикара теорема, 224
плоскость
— комплексная, 27
-----расширенная, 29
— экваториальная, 30
плотность, 179
площадь жорданова множества, 79
подмножество, 5
— максимально связное, 52
подпространство метрического
пространства, 17
показательная форма записи
комплексного числа, 28
покрытие множества, 18
поле, 11
— нормированное, 11
полином Чебышева, 229
положительное направление обхода
границы области, 162
полумеридиан, 31
полюс
— северный, 31
— функции, 221
-----простой, 221
— южный, 31
порядок
— полюса, 221
— связности, 53
— А -точки, 211
— целой функции, 270
последовательность
— векторов
-----фундаментальная, 12
— комплексных чисел
-----бимонотонная, 202
— сходящаяся, 46
— точек метрического пространства
-----сходящаяся, 13
-----фундаментальная, 13
-----(С, р), 45
— функциональная, 198
-----поточечно сходящаяся к данной
функции, 198
-----равномерно сходящаяся к данной
функции на данном множестве,
199
-----равномерно фундаментальная,
200
— числовая, 9
— элементов множества, 9
потенциал комплексный, 72, 2:83
правила дифференцирования интеграла
— по верхнему переменному пределу
интегрирования, 151
-----по нижнему переменному
пределу интегрирования, 151
правило
— дифференцирования произведения
функций, 65
— Лопиталя, 7:8
— перестановки пределов
интегрирования, 151
предел
— отображения, 21
-----в смысле Гейне, 21
-----в точке в смысле Коши, 22
-----частичный, 21
— последовательности, 45
-----векторов в нормированном
пространстве, 11
-----точек в метрическом
пространстве, 13
-----частичный, 47
— функции в точке, 48
-----частичный, 48
— функциональной
последовательности
равномерный, 200
представление параметрическое
— гладкой кривой, 51
— естественное, 51
— кривой,51
— натуральное, 51
— нормальное, 51
— обобщенной непрерывной кривой,
52
— отрезка, 45
представления параметрические
экивалентные
— гладкой кривой, 51
— непрерывной кривой, 51
признак
— Вейерштрасса равномерной
сходимости
функционального ряда мажорантный,
201
— Д'Аламбера, 2:51
— Дирихле, 5:8, 5:11
— компактности Монтеля, 309-310
— сходимости ряда необходимый, 198
Прингсхейма теорема, 242
принцип
— аргумента, 297
— двойственности, 7
— исключенного третьего, 4
— максимума модуля, 8:8—10, 8:14
-----вторая формулировка, 305
-----первая формулировка, 304
— непрерывности, 240—241
— однолистности, 303
— симметрии, 317, 8:18, 8:19
-----Романа—Шварца, 137, 241, 3:95
— сохранения области, 300—301
продолжение функции, 9
— аналитическое, 232
проекция
— бинарного отношения
-----вторая, 8
-----первая, 7
— стереографическая, 30
произведение
— бесконечное
-----Вейерштрасса, 268
-----, значение, 265
-----сходящееся, 265
-------абсолютно, 266
-------равномерно в области, 267
— многочленов, 208
— множеств
-----декартово, 7
-----прямое, 7
— степенных рядов, 208
1-производная, 153
«-производная Ферма—Лагранжа
функции в точке, 156
п+ 1-производная, 153
производная вектор-функции, 50
прообраз множества при отображении,
9
пространства метрические
гомеоморфные, 25
пространство
— банахово, 12
— векторное
-----над полем, 11
-----нормированное, 11
— линейное над полем, 11
— метрическое, 12
-----полное, 13
-----связное, 20
— нормированное полное, 12
— топологическое, 45
-----, свойства, 45
Пуанкаре теорема, 270
Пуанкаре—Вольтсрра теорема, 237
Пуассона формула, 182, 4:8
Р
равенство
— множеств, 5
— упорядоченных пар, 7
радиус сходимости степенного ряда,
206
р -раздутие множества, 309
разность множеств, 6
расстояние
— индуцированное, 17
— между точками метрического
пространства, 14
— хордальное, 44
расстояния
— топологически эквивалентные, 25
— эквивалентные, 25
расширенная комплексная плоскость,
29
результат
— Линделёфа, 316
— Шварца, 316
Римана
— сфера, 30, 2:43-47
— теорема, 314—315
Римана—Шварца принцип симметрии,
137, 241, 3:95, 3:97, 3:100, 3:102
род бесконечного произведения, 270
Руше теорема, 297-298, 8:1, 8:3
ряд
— Тейлора, 209
— Лагранжа, 302
— Лорана функции в кольце, 220
— мероморфных функций сходящийся,
258
-----равномерно, 258
— функциональный, 197, 198
-----степенной, 206
-----сходящийся нормально, 201
-----сходящийся поточечно, 199
-----сходящийся равномерно, 200
-----удовлетворяющий равномерному
условию Коши, 201
— Фурье, 7:30
— числовой, 197
-----расходящийся, 197
-----сходящийся, 197
С
свойства
— аналитической функции, 69—70
— векторного пространства, 11
— нормы функции равномерной, 199
— показательной функции, 28
— стереографической проекции, 30
— топологического пространства, 45
северный полюс, 31
s-сеть множества, 18
сечение
— второе, 8
— первое, 8
символ
— дизъюнкции, 4
— импликации, 4
— конъюнкции, 4
— отрицания, 4
— эквивалентности, 4
символы Ландау, 11
синус эллиптический, 324
след кусочно-гладкой кривой, 52
сопряженное число, 27
Сохоцкого
— теорема, 223—224
— формулы, 181
спираль Архимеда, 40
стереографическая проекция, 30
—, свойства, 30
структура математическая, 10
сужение функции, 9
— на множество, 9
сумма ряда, 197
— функционального
-----поточечная на данном
множестве, 199
-----равномерная, 200
-----частичная, 198
— частичная, 197
сфера, 13
— Римана, 30, 2:43-47
Т
Тейлора
— многочлен, 156
— теорема, 209
— формула с остаточным членом,
записанным посредством п-
интеграла, 156
Тейлора—Пеано формула, 157-158
тело, 10
— нормированное, 11
теорема
— Абеля, 202
-----вторая, 207-208
-----первая, 207
— алгебры основная, 298
— Больцано—Вейерштрасса, 47
— Бореля—Лебега, 48, 2:60
— Вейерштрасса, 50, 204-205
-----о представлении целой функции
в виде бесконечного
произведения, 269
— Виета, 2:21, 2:40, 2:41
— Гурвица, 311
— Дирихле, 155, 203
— Жордана, 52
— Кантора, 18, 25
— Каратеодори, 315
— Коши
-----интегральная, 166-167
-------обобщение на случай
функции, не являющейся
аналитической на контуре
интегрирования, 168-170
-----о вычетах, 247, 7:42, 7:47
-----, обобщение на случай
неодносвязной области, 171-172
— Коши—Адамара, 207
— Лагранжа, 73
— Лиувилля, 178-179,4:25
— Лорана, 219-220
— Миттаг-Леффлера, 258-259, 7:25,
7:27
— Морера, 179
— о биективных и непрерывных
отображениях, 52
— о вычетах основная, 247, 7:42,7:47
— о дифференцируемости
произведения бесконечно малой
дифференцируемой функции и
непрерывной функции, 64
— о достаточных условиях
-----равномерной сходимости
бесконечного произведения, 267
-----существования первообразной в
круге, 162—163
— о замене переменной
интегрирования, 152
— о линейности
-----интеграла, 151-152
-----операции дифференцирования,
64
-----равномерного предела, 200
— о логарифмическом вычете, 296
— о монодромии, 236
— о непрерывном образе компакта, 21,
50
— о непрерывности
-----дифференцируемой функции, 64
-----композиции
-------отображений, 21
-------функций, 49
-----нормы, 11
-----обратного отображения, 22
-----сужения отображения, 23
— о почленном интегрировании
равномерно сходящегося
функционального ряда, 204
— о пределе композиции функций, 49
— о производной
-----«-интеграла по пределам
интегрирования, 155
-----композиции, 63-64
-----обратной функции, 65
-----частного, 65
— о равномерной равносходимости
функциональных рядов,
связанных преобразованием
Абеля, 202
— о равносходимости бесконечного
произведения и числового ряда,
265
— о среднем, 173
— о существовании первообразной
аналитической
функции, заданной в односвязной
области, 170—171
— об инвариантности
-----интеграла при гомотопиях пути
интегрирования, 166-167
-----симметричных точек при дробно-
линейном отображении, 86
— об интегрировании по частям, 152
— об обращении формулы Тейлора—
Леано, 158
— об ограниченности компакта, 47
— Пикара, 224
— Прингсхейма, 242
— Пуанкаре, 270
— Пуанкаре—Вольтсрра, 237
— Романа, 314-315
— Руше, 297-298, 8:1-3
— Сохоцкого, 223-224
— Тейлора, 209
— Фреше, 19
— Хаусдорфа, 19
— Штольца, 2:50
тождество Абеля, 202
топология, 44
— метрического пространства, 25
— относительная, 53
точка
— бесконечно удаленная, 29
— кривой
-----конечная, 51
-----кратная, 51
-----начальная, 51
— множества
-----внешняя, 15
-----внутренняя, 15, 45
-----граничная, 17, 45
-----изолированная, 17
— предельная, 17, 45
— особая
-----аналитической функции, 239
-----изолированная, 221
-----многозначного характера, 239
-----однозначного характера, 239
-----устранимая, 221
— последовательности предельная, 47
— прикосновения, 16, 45
— разветвления, 93, 239, 240
-----(п - 1)-го порядка, 93, 240
-----алгебраическая, 93
-------(п - 1)-го порядка, 93
-----бесконечного порядка, 93, 240
-----логарифмическая, 240
— существенно особая, 221
— устранимого разрыва, 21
A-точка функции, 211
— кратная, 211
—, кратность, 211
—, порядок, 211
— простая, 211
точки
— метрического пространства, 12
— симметричные
-----относительно окружности, 85, 86
-----относительно прямой, 85
траектория
— гладкая
-----простая, 51
— непрерывная, 51
транспонирование отношения, 8
тригонометрическая форма записи
комплексного числа, 28
трохоида, 60
У
угол между путями в точке, 84
упорядоченная пара, 7
уравнение деления круга, 35
условие Гельдера, 179
условия Коши—Римана, 67, 2:72, 2:73,
2:75, 2:77-80
утверждение Гаусса, 37
Ф
форма
— Дробно-линейного отображения
нормальная, 125
— записи комплексного числа
-----показательная, 28
-----тригонометрическая, 28
формула
— Коши интегральная, 172—173
— Коши—Адамара, S:10, 5:11, 8:6
— Кристоффеля—Шварца, 320, 8:22,
8:25
— Муавра, 29, 2:17
— Ньютона—Лейбница, 150
-----для п-интеграла, 154—155
— Пуассона, 182, 4:8
— Тейлора с остаточным членом,
записанным посредством п-
интеграла, 156
— Тейлора— Пеано, 157—158
— Шварца, 181
формулы
— Кардано, 2:41
— Сохоцкого, 181
— стереографической проекции
основные, 30, 2:43—47
— Эйлера, 101, 7:23, 7:24
Фреше теорема, 19
функции
— аналитические равные, 237
— гиперболические, 101
— тригонометрические, 101
функционал, 310
— непрерывный на данном элементе,
310
функция
— авторморфная, 325
— аналитическая
-----в бесконечно удаленной точке,
219
-----в замкнутой области, 69
-----в области, 68
-----в точке, 68
-----на бесконечности, 69
-----на кривой, 68
-----на открытом множестве, 68
-----на произвольном множестве, 68
-----полная, 237
-----, свойства, 69—70
— Бесселя, 226
— гармоническая в области, 177
— гармонически сопряженная с
данной, 178
— голоморфная, 68
— С-дифференцируемая, 67
— R -дифференцируемая, 67
— 1-дифференцируемая, 153
— п -дифференцируемая в точке в
смысле Ферма—Лагранжа, 156
— п+ 1-дифференцируемая, 153
— дифференцируемая в точке, 63
— дробно-линейная, 83
— Жуковского, 99, 3:28, 3:72, 3:74,
3:87-93, 3:95, 3:97, 3:99-101, 8:18
— 1-интегрируемая, 153
— интегрируемая в смысле Ньютона—
Лейбница, 150
— кусочно-линейная, 45
— линейная, 66
— ломаная, 45
— мероморфная, 257, 271
-----в области, 259
— моногенная, 65
— непрерывная в точке, 48
— неявная, 10
— обобщенно-непрерывная, 50
— ограниченная на множестве, 50
— однолистная, 48
— показательная, 28, 94
-----общая, 98
-----, свойства, 28
—, продолжение, 9
-----аналитическое, 232
— степенная, 91
-----общая, 97-98
—, сужение
-----на множество, 9
-----с множества на множество, 9
— тока, 72
— целая, 257
-----бесконечного рода, 270
-----конечного рода, 270
-----трансцендентная, 257
— эллиптическая, 325
Фурье ряд, 7:30
X
Хаусдорфа теорема, 19
Ц
циклоида, 60
— удлиненная, 60
— укороченная, 60
Ч
часть ряда Лорана
— главная, 220
— правильная, 220
Чебышева полином, 229
числа
— Бернулли, 215
— комплексные, 27
число комплексное сопряженное
данному, 27
член
— ряда общий, 197
— функционального ряда, 198
— функциональной
последовательности, 198
Ш
шар
— замкнутый, 13
— открытый, 13
Шварца
— интеграл, 181
— лемма, 305, 8:15-17
— результат, 316
— формула, 181
широта, 31
Штольца теорема, 2:50
Э
Эйлера
— бета-функция, 328
— формулы, 101, 7:2?, 7:24
Эйлера—Пуассона интеграл, 191
элемент
— аналитический, 232
— группы
-----единичный, 10
-----нейтральный, 10
-----нулевой, 10
-----обратный данному, 10
— канонический с центром в данной
точке, 233
Ю
южный полюс, 31
Я
ядро
— Дирихле, 35
— Хеши, 179
Предисловие
В учебной литературе, рекомендованной для изучения теории функций комплексного переменно-
го, имеется много содержательных учебников и учебных пособий, авторами которых являются из-
вестные ученые М. А. Лаврентьев, Б. В. Шабат, И. И. Привалов, А. И. Маркушевич, А, В. Бицадзе,
М. А. Евграфов, А. Гурвиц, Р. Курант и другие. К сожалению, большинство из них не приспо-
соблено как по объему, так и по выбору и распределению материала к учебным программам
по теории функций комплексного переменного для физико-математических факультетов уни-
верситетов России и других стран СНГ. Ничтожно мало написано пособий по решению задач.
Начинающему преподавателю, а тем более студенту и аспиранту, нелегко выделить из объеми-
стой книги основной материал так, чтобы образовался целостный, логически завершенный курс,
отвечающий учебной программе.
Указанные выше обстоятельства натолкнули автора на мысль о необходимости написания
на современном уровне требований книги, которая соответствовала бы учебным университет-
ским программам по данному предмету, не была перегружена частностями и содержала большое
количество решенных задач. В книгу включено порядка четырехсот решенных задач средней и
повышенной трудности.
Характерной чертой многих книг по теории функций комплексного переменного является
разнобой и нечеткость основной терминологии. Например, основное понятие аналитической
функции в разных местах одной и той же книги может иметь разный смысл. Это обстоятель-
ство принято во внимание автором, и все рассматриваемые понятия имеют вполне определенный
смысл.
В первой главе книги дано строгое определение функции (а не описание ее, как это при-
нято в большинстве учебников), рассмотрены операции над множествами и основные вопросы
теории метрических пространств. Без включения этого материала в книгу изложение основных
вопросов на современном математическом уровне оказалось бы невозможным. Поэтому читателю
будет полезно хотя бы бегло прочитать эту небольшую по объему главу для понимания осталь-
ных глав, включающих традиционные вопросы, относящиеся к теории аналитических функций,
которая была создана в XIX столетии в первую очередь благодаря работам О. Коши, Г. Римана,
К. Вейерштрасса.
В книге уделено большое внимание практическим вопросам конформных отображений. Но-
выми для читателя окажутся понятия интеграла Ньютона—Лейбница и производной Ферма—
Лагранжа.
Книга рассчитана на широкий круг читателей, владеющих знаниями в объеме стандартных
программ по математическому анализу для студентов физико-математических специальностей
университетов.
Автор
Глава 1
Основные структуры
математического анализа
В этой главе содержатся основные сведения, относящиеся к теории множеств и отображений,
используемые в дальнейшем при изложении основного материала книги. Достаточно полно от-
ражена теория метрических пространств. Рассматриваются понятия и употребляется символика,
принятые в курсах современного математического анализа.
§ 1. Элементы теории множеств и отображений
1.1. Некоторые логические символы.
В математике часто вместо словесных выражений употребляют символику, заимствованную
из логики. Так, вместо выражений “для всех”, “для каждого”, “для любого” употребляют знак V,
а вместо слов “существует”, “найдется” — знак 3. Их называют соответственно квантором общ-
ности и квантором существования. Предложения “для всех... ” и “существует... ” часто сопрово-
ждается некоторыми ограничениями. Обычно эти ограничения записывают в круглых скобках.
Вместо слов “такой, что” употребляют двоеточие или вертикальную черточку.
В формулировке каждой теоремы содержится некоторое свойство А (условие) и свойство В
(заключение), выводимое из А. Коротко выражение “А влечет В” записывается в виде “А => В”
(=> — символ импликации). Обратная теорема, если она справедлива, запишется в виде В => А.
Если данная теорема и обратная ей — справедливы, то свойства А и В эквивалентны, и тогда
записывают А «-> В («-+ — символ эквивалентности), что выражается в форме: “Для того чтобы А,
необходимо и достаточно, чтобы В”, или “А тогда и только тогда, когда В".
Если некоторый объект обладает свойством А или свойством В, то пишут А V В, а также
“А или В” (V — символ дизъюнкции). Запись AV В означает, что справедливо хотя бы одно из
свойств А или В.
Если оба свойства А и В справедливы одновременно, то это записывается в виде А А В, или
“А и В” (Л — символ конъюнкции).
Запись ’’А обозначает “не А”, “не верно, что А” — символ отрицания).
Вместо выражения “существует единственный” употребляют знак ! , а вместо выражения
« >> (iet
равно по определению — знак = .
Утверждение может быть записано с помощью одних лишь логических символов. В этом слу-
чае отрицание свойства, содержащего некоторое количество кванторов V, 3 и свойство Р, должно
получаться заменой каждого квантора V на 3, 3 на V и свойства Р — на его отрицание. Напри-
мер, свойство непрерывности числовой функции в любой точке числовой прямой записывается
одной строкой:
(Va € R) (Ve > 0) (35 > 0) (Vz 6 R, \x - a| < 6) : |/(z) - /(a)| < e.
Свойство числовой функции действительной переменной не быть всюду непрерывной, т. е.
иметь разрыв хотя бы в одной точке, запишется в виде:
(3a е R) (Зе > 0) (V5 > 0) (Эх 6 R, |х - а| < 6) : |/(х) - /(а)| > е.
Некоторые теоремы будем доказывать методом от противного. При этом также используется
принцип исключенного третьего, вследствие чего высказывание А V (А или не А) считается
§ 1. Элементы теории множеств и отображений
5
истинным независимо от конкретного содержания высказывания А. Одновременно считается,
что ~ТА) А, т. е. повторное отрицание равносильно начальному высказыванию.
1.2. Обозначения, используемые в теории множеств.
Понятие множества считаем первичным, и потому ограничимся лишь указанием терминоло-
гии и необходимых в дальнейшем обозначений.
Множество обозначают какой-нибудь буквой, например, М. Запись а € М читается так: “а
есть элемент множества М” или “а из множества М”. Запись М Э х читается так: “множество М
содержит элемент х”. Если элемент х не принадлежит множеству М, то записываем х £ М или
М jfx. Запись М = {а, Ь, с, ...} читается так: “М есть множество, состоящее из элементов а,
Ь, с и т.д.” Множество может содержать лишь один элемент, например, М — {а}. Если Р —
свойство, которым обладают или не обладают элементы множества М, то запись
Му = {а Е М \ а обладает свойством Р}
читается: "Му есть множество всех тех элементов множества М, которые обладают свойством Р”.
Например, запись Му = {а: € R. | х 0} обозначает множество всех неотрицательных действи-
тельных чисел. Символы Е и Э называют знаками принадлежности.
Задавая множество посредством некоторого свойства, часто заранее не знают, существуют ли
вообще элементы, обладающие этим свойством. Поэтому целесообразно ввести в рассмотрение
множество, не содержащее ни одного элемента. Оно называется пустым и обозначается знаком 0.
Пусть Му и М2 — множества. Если каждый элемент множества Му принадлежит множе-
ству М2, то множество Му называется подмножеством множества М2 (рис. 1). В этом случае
записываем Му С М2 или М2 D Му и читаем: “множество М2 содержит множество Му”. Сим-
волы С и D называются знаками включения.
Множества, состоящие из одних и тех же элементов, считаются равными. Очевидно, что
Му = М2 ♦-+ Му С М2 Л М2 С Му.
Если в множестве Му есть элементы, которые не входят в множество М2, то Му не содержится
в множестве М2, что записывается Му <£. М2 или М2 Т> Му.
Отметим, что любое множество М содержит пустое множество в качестве своего подмноже-
ства. Действительно, в противном случае пустое множество содержало бы по крайней мере один
элемент, не принадлежащий множеству М. Но оно вообще не имеет элементов.
Будем пользоваться обозначениями:
0 — пустое множество;
exp М — множество всех подмножеств множества М;
N — множество всех натуральных чисел;
Z(l — множество всех неотрицательных целых чисел;
Z — множество всех целых чисел;
Q — множество всех рациональных чисел;
R — множество всех действительных чисел;
С — множество всех комплексных чисел.
1.3. Натуральные числа. Метод математической индукции.
Важнейшим в математике является множество N всех натуральных чисел. В нем определена
операция сложения и выполняются свойства: 1) если п € N, то (n + 1) 6 N; 2) если некоторое
множество М содержит 1 и из п 6 ЛЕ всегда следует, что (п + 1) £ М, то М D N. Свойство 2)
называется аксиомой индукции. Блез Паскаль (1623—1662) впервые предложил метод доказатель-
ства, основанный на аксиоме индукции, называемый методом математической индукции. Суть
его состоит в следующем.
Пусть даны утверждения Ль А2, А2, ... и доказаны две леммы Паскаля.
Лемма 1. Утверждение Л, справедливо.
Лемма 2. При любом п Е N из справедливости Ап следует справедливость утверждения Ап+1.
Тогда все утверждения Лн Л21 ... справедливы.
Метод математической индукции сводится к аксиоме индукции. Действительно, пусть М =
{n Е N | Ап справедливо}. Согласно лемме 1, 1 € М. По лемме 2 n Е М (n+1) g М. По
аксиоме индукции (Vn Е N) : ng М, т. е. все утверждения Л|, Л2, ... справедливы.
6
Гл. 1. Основные структуры математического анализа
Докажем, например, что Vn G N выполняется равенство
п(п + l)(2n + I)
(1)
6
fe=i
Непосредственной проверкой убеждаемся в справедливости леммы 1. Допуская выполнение
равенства (1) для п € N, имеем
п(п+1)(2п+1) , (п + 1)(2п2 + 7п Ч-6) (п + 1)(п + 2)(2п + 3)
+ (п + 1) = -
6
6
6
fe=i
т. е. лемма 2 также выполняется. Методом математической индукции формула (1) доказана.
Рис. 3
1.4. Простейшие операции над множествами.
Пусть Мх 6 ехрМ, М2 G ехрМ.
Определение 1. Пересечением множеств Мх и
М2 называется множество Мх Г) М2 = {а | а 6 М, Л
а Е М2}.
Пересечение множеств Мх и М2 состоит из всех
тех и только тех элементов, которые принадлежат
множествам Мх и М2 одновременно (рис. 2).
Если таких элементов нет, то говорят, что множе-
ства М[ и М2 не пересекаются, и пишут Мх П М2 =0
(рис. 3).
Определение 2. Объединением множеств Мх и
М2 называется множество Мх U М2 = {а | а € Мх V
а е М2}.
Объединение множеств Мх и М2 состоит изо всех тех и только тех
элементов, которые принадлежат хотя бы одному из множеств Мх, М2
(рис. 4).
Определение 3. Разностью множеств Мх и М2 называется мно-
жество МХ\М2 = {а | а € Мх Л а £ М2}.
Разность множеств Мх и М2 состоит из всех тех и только тех эле-
ментов множества Мх, которые не входят в множество М2 (рис. 5).
Если М1 Э М2, то разность МХ\М2 называется также дополнением
М2 в Л?! и обозначается символом См.М2 (или СМ2, когда это не
может привести к недоразумениям).
Пусть Мх G ехрМ, М2 € ехрМ. Тогда справедливы равенства
С(М, U М2) = СМХ П СМ2, С(М, П М2) = СМ, и СМ2. (1)
§ 1. Элементы теории множеств и отображений
7
Свойства, записанные этими равенствами, называют принципом двойственности. Докажем
первое из них. Пусть х g C(Mt и М2). Имеем
х 6 С(М| U М2) => х £ М\ U М2 => х £ Mi M2 =>
=> x E CMt Л x g CM2 => x € CM| П CM2 => C(M, U M2) C CMi И CM2.
Если у € CM] П CM2, то получим:
у g CM, Г) CM2 => у g CMt ЛуЕ CM2 => у £ Mi \yt M2 =>
=> у g Mi U M2 => у € C(Mi U M2) => CMi П CM2 С C(MX U M2).
Из последних включений следует доказываемое равенство. Второе равенство в (1) доказыва-
ется аналогично.
Принцип двойственности без труда переносится на произвольное семейство подмножеств
множества М:
c|Jmv = Г|слд: сПм^ислд.
(2)
Из формулы (2) видно, что символ дополнения С можно менять местами со знаками и и П,
причем один из этих знаков переходит в другой.
1.5. Упорядоченная пара и декартово произведение множеств.
Важным для математики является понятие упорядо- у
ченной пары (х, у), составленной из элементов одного и
того же множества или из элементов разных множеств
X и Y. Основное свойство упорядоченной пары со- __________________________М(х,у)
стоит в следующем: две упорядоченные пары (ян, yi) и У i
(х2, у2) считаются равными тогда и только тогда, когда ।
= х2 и yi = у2. Элемент х называется первой компо- !
нентой (координатой) пары (х, у), а элемент у — вто- ।
рой компонентой (координатой) той же пары. Понятие ____ t
упорядоченной пары так же, как и понятие множества, х X
можно считать первичным.
С помощью понятия упорядоченной пары вводится 6
еще одна операция над множествами — операция пря-
мого или декартова умножения.
Определение. Декартовым произведением множеств X uY называется множество
X х Y = {(х, у) | х € Х,у € У}.
Декартово произведение двух пересекающихся различных прямых можно отождествить с
плоскостью, проходящей через эти прямые, по правилу “М = (х, у)” (рис. 6). Это свойство лежит
в основе метода координат, предложенного знаменитым математиком Рене Декартом (1596—1650)
для решения геометрических задач, и объясняет название умножения.
Посредством метода математической индукции определяется упорядоченный набор n+ 1 эле-
ментов
(хь х2,..., xn+i) = ((Х|, х2,..., хп), х„+1) , п 2,
и декартово произведение множеств
Xi х Х2 х ... х A’n+i = (X, х Х2 х ... х Хп) х Хп+1.
1.6. Бинарные отношения. Проекции и сечения бинарного отношения.
Обратное бинарное отношение.
Определение. Множество Г называется бинарным отношением между элементами мно-
жеств X и Y, если Г С X х У.
Над бинарными отношениями можно проводить не только обычные для множеств операции
(пересечения и объединения), но и специальные — проектирования и обращения.
Первой проекцией бинарного отношения Г С X х У называется множество
Г! = пр[Г = {х 6 X | Эу € У : (х, у) 6 Г}
8
Гл. 1. Основные структуры математического анализа
Первая проекция бинарного отношения Г состоит из всех первых координат упорядоченных
пар, принадлежащих множеству Г (рис. 7).
Множество Г](х) = {у€У|(х, у)€Г} называется первым сечением Г посредством х
(см. рис.7). Оно состоит из вторых координат всех тех точек из Г, у которых первая коорди-
ната равна х. Первое сечение является пустым множеством Vx % Г|.
Второй проекцией бинарного отношения Г называется множество
Г2 = пр2Г = {у 6 Y | Эх £ X : (х, у) € Г}
Вторая проекция бинарного отношения Г — это множе-
ство всех вторых координат тех упорядоченных пар, которые
принадлежат множеству Г (рис. 8).
Множество Г2(у) = {х € X | (х, у) € Г} называется вто-
рым сечением Г посредством у (см. рис. 8). Оно состоит из
первых координат всех тех точек из Г, у которых вторая ко-
ордината равна у. Второе сечение является пустым множе-
ством Vy £ Г2.
Каждому бинарному отношению Г можно поставить в со-
ответствие обратное бинарное отношение Г-1 по правилу
Г ' = {(у, х) | (х, у) G Г}
(рис. 9). Иногда операцию обращения Г называют операцией транспонирования отношения Г.
1.7. Функциональное бинарное отношение.
Функция и простейшие понятия, связанные с нею.
Бинарное отношение Г называется функциональным, если оно не содержит различных упоря-
доченных пар с одинаковыми первыми координатами.
Сформулируем основное определение отображения из множества X в множество Y.
Определение 1. Упорядоченная тройка множеств (X, Y, Г) называется отображением из
множества X в множество Y, если Г есть функциональное бинарное отношение между эле-
ментами множеств X и Y.
Множество X называется областью отправления отображения, множество Y — областью
прибытия отображения, множество Г — графиком отображения.
Обычно отображение обозначают какой-нибудь строчной латинской буквой, например, f.
При этом вместо f = (X, Y, Г) пишут: f : X —► У. Если X и У известны, то, согласно опреде-
лению, задание отображения / равносильно заданию графика Г.
§ 1. Элементы теории множеств и отображений 9
Первая проекция графика отображения f называется областью (множеством) определения
отображения f и обозначается Df или D(f). Вторая проекция графика отображения f называ-
ется областью (множеством) значений отображения f и обозначается Ef или E(f). Если х 6 Df
и пара (х, у) принадлежит графику отображения f, то элемент у называется значением отобра-
жения f на элементе х и обозначается f(x).
Если известны область определения Df и значения f(x)Vx £ Df, то график Г(/) отображе-
ния f строится по правилу
Г(Л = {(X, f(x)) | х е Df}.
Если Df = X, то отображение / : X —» Y называется отображением множества X в множе-
ство Y и обозначается
X^Y.
Если Df = X,Ef = Y, то отображение f : X —> Y называется отображением множества X
на множество Y и обозначается
X Y.
на
Функция fi = (X, Y, ГО называется сужением функции f = (X, У, Г), если Г, С Г. В этом
случае функция / называется продолжением функции fi с множества Df, = np^ на множество
Df = пр, Г. Если А — множество и А С ПР1Г, то существует такое сужение функции f,
которое имеет свойство А = Dft. Функция ft называется сужением функции f на множество А
и обозначается /|л. Существование сужения функции f на множество А вытекает из того, что
г(/1) = {(х, у) I х е А л (х, у) е г}.
Определение 2. Пусть f : X —» У. Для любого подмножества А С Df подмножество множе-
ства Ef, определяемое свойством “существует такой элемент х € А, что у = f(x)”, называется
образом множества А при отображении f и обозначается через f(A).
Для любого подмножества А' С Ef подмножество множества Df, определяемое свойством
f(x) € А', называется прообразом А' при отображении f и обозначается f~'(A').
Задавая отображение, часто пользуются записью х >-» f(x).
Пусть X — множество. Отображение N X называется последовательностью элементов
множества X и обозначается (хп). Если X — R, то последовательность (г„) называется числовой.
1.8. Обратная функция. Композиция отображений.
Отображение / = (X, У, Г) называется обратимым, если бинарное отношение Г-1 является
функциональным отношением между элементами множеств У и X. В этом случае отображение
(У, X, Г-1) называется обратным отображению f и обозначается /*'. Обратимое отображение /
множества X на множество У называется взаимно однозначным или биективным отображением и
обозначается
лЛк
Тогда Vy 6 У 3! х g X: f(x) = у и полагаем f~\y) = х.
Важным в математике является понятие композиции отображений.
Пусть даны отображения /: X —> У п <р: Т —> X. Композиция отображений р и f обознача-
ется f о ip. Ее область определения состоит из всех тех значений t € Dv, для которых <p(t) 6 Df.
Значение композиции вычисляется по формуле
(f ° ¥>)(t) = f(<e(t)), tZDf^.
1.9. Параметрическое и неявное отображения.
Если заданы отображения
Т~Х, T-^Y,
то определено отображение X у. Его называют заданным параметрически посредством
Отображений <р и ф. При этом переменная t называется параметром.
10
Гл. 1. Основные структуры математического анализа
Рассмотрим отображение X х Y —»G, а также уравнение F(х, у) = с, где с € G — неко-
торый элемент. Если существуют такие множества Р С X, Q С Y, что при каждом фиксиро-
ванном х £ Р уравнение F(x, у) = с имеет единственное решение у € Q, то на множестве Р
определена функция f, для которой Ef = Q. При этом f называется неявной функцией, заданной
уравнением F(x, у) = с.
1.10. Изоморфизм.
Пусть множество Е обладает внутренней бинарной операцией Т, а множество F — внутрен-
ней бинарной операцией ±. Изоморфизмом множества Е на F называется такая биекция
E-^-F,
что V(a € Е, b € Е) f(a Т b) = f(a) _L f(b). При этом множества Е и F называются изоморфными
относительно операций Т и 1.
Пусть, например, Е = N, операция Т — сложение, F = {2П}, операция X — умножение.
Отображение Е F — изоморфизм, поскольку V(n £ N, m £ N) n + m н 2n+r" = 2n • 2m, т. e.
/(n + m) = /(n)/(m).
§2. Математические структуры
Математической структурой называется множество объектов или несколько множеств объ-
ектов различной природы, обладающих системой бинарных отношений и бинарных операций,
подчиненных определенным аксиомам.
2.1. Группа.
Группой называется непустое множество Е вместе с правилом, ставящим каждым двум эле-
ментам а £ Е, b £ Е в соответствие некоторый вполне определенный третий элемент а о Ь £ Е
так, что выполнены следующие условия:
1) операция о ассоциативна: V(a £ Е, b £ Е, с £ Е) а о Ь о с — (а о Ь) о с;
2) в Е существует нейтральный элемент, т. е. такой элемент п, что Va £ Е а о п = а;
3) Va £ Е За' £ Е: а о а' = п (а называется элементом, обратным элементу а).
Если, кроме того,
4) V(a £ Е, b £ Е) ао b = b о а,
то группа Е называется абелевой или коммутативной.
Если в группе Е операция о имеет аддитивное (мультипликативное) обозначение “+” (“•”),
то группу называют аддитивной (мультипликативной), а нейтральный элемент нулевым (единич-
ным) и обозначают соответственно 0 (1). Например, множество Z вместе с операцией сложения
образует коммутативную группу. Множество Q\{0} вместе с операцией умножения также обра-
зует коммутативную группу.
2.2. Кольцо.
Кольцом называется множество R, в котором заданы две бинарные алгебраические операции:
сложение и умножение, причем по сложению это множество — абелева группа (аддитивная группа
кольца R), а умножение связано со сложением законами дистрибутивности:
V(a £ R, b £ R, с £ R) а(Ь + с) = ab + ас, (Ь + с)а = Ьа + са.
Если операция умножения коммутативна, то кольцо называется коммутативным. Если R Э 1,
то кольцо называется унитарным.
Например, множество Q рациональных чисел вместе с операциями сложения и умножения
образует унитарное кольцо.
2.3. Тело.
Если кольцо, лишенное нейтрального элемента относительно операции сложения, образует
группу относительно операции умножения, то оно называется телом.
§2. Математические структуры
11
2.4. Поле.
Тело, в котором операция умножения коммутативна, называется полем.
Например, упорядоченные тройки (Q, +, •), (R, +, •) являются соответственно полями ра-
циональных и действительных чисел.
Определение. Пусть К — тело (поле). Отображение | • | : К —» R+, где R+ = {г € R |
х 0}, называется абсолютным значением (модулем) в теле (поле) К, если V(a g К, /3 € К)
выполняются следующие условия (аксиомы)'.
1) |а| = 0 => а = 0;
2) |а-/3| = |а| • |/3|;
3) |а + /3| |а| + |/3| (неравенство треугольника).
Тело (поле), в котором определено абсолютное значение, называется нормированным.
2.5. Векторное пространство над полем К. Нормированное пространство.
Векторным (линейным) пространством над полем К называется упорядоченная тройка (Е, +, ),
состоящая из множества Е, элементы которого называются векторами, операции сложения и
операции умножения на элементы поля К.
Указанные операции должны иметь следующие свойства, называемые аксиомами векторного
пространства: У(г ЕЕ, у £ Е, z Е Е, А С К, ц 6 К)
1) х + у = у + х;
2) (х + у) + z = х + (у + z);
3) 30 € Е : х + 0 = х;
4) 3(-х) Е Е : х + (-х) = 0;
5) Х(х + у) = Хх + Ху, (X 4- р)х — Хх + рх;
6) (Хр)х = Х(рх);
7) 1 • х = х.
Имея в виду упрощение записей, вместо тройки (Е, +, •) пользуются векторным простран-
ством Е.
В произвольном векторном пространстве Е выполняются следующие свойства:
1) АО = 0;
2) 0-® = 0;
3) (- 1)х = —х.
Пусть Е — векторное пространство над нормированным полем К. Отображение || • || : Е —♦ R
называется нормой (длиной) в пространстве Е, если V(x 6 Е, у € Е, А € К) выполняются условия
(аксиомы):
1) ||z|| = 0 => х = 0;
2) ||Ai|| = |А| • |И|;
3) II® + J/II ||®|| + 111/11 (неравенство треугольника).
Значение нормы на векторе х Е Е называется нормой этого вектора.
Упорядоченный набор (Е, +, •, || • ||) называется нормированным векторным пространством.
С целью сокращения записи обычно пишут Е вместо набора (Е, +, •, || • ||).
Из аксиом 2), 3) следует, что ||0|| = 0, ||ж|| > 0 Ух Е Е. Первое свойство получаем из
аксиомы 2) при А = 0, второе — из аксиомы 3) при у = —х.
Вектор х Е Е называется пределом последовательности векторов (хп) нормированного про-
странства Е, если ||®„ - х|| = о(1). Запись: lim хп = х. Символом Ландау о(1) обозначают
п—*со
бесконечно малые числовые последовательности, т. е. такие, что lim ап — 0. Еще один символ
п—»ос
Ландау 0(1) употребляют для обозначения ограниченных числовых последовательностей.
• Теорема (о непрерывности нормы). Если последовательность (хп) векторов нормирован-
ного пространства Е сходится к вектору х, то ||zn|| -+ ||х||.
◄ Справедливость утверждения следует из неравенств
-IK -я|1ММ- 1И1^ Н®„ -®Н vn€N,
являющихся следствием из неравенства треугольника. ►
В нормированном поле К модуль также является непрерывной функцией.
12
Гл. 1. Основные структуры математического анализа
В векторном пространстве R"* каждое из отображений || ||: Rm —> R, где
пг
||я?|| = У 'xj (евклидова норма), (1)
N i=i
т
||х|) = У , |я;| (октаэдрическая норма), (2)
;=i
||х|| = max |а:;| (кубическая норма), (3)
1<Сг<Стп
удовлетворяет аксиомам нормы.
Последовательность (хп) векторов нормированного пространства Е называется фундамен-
тальной, если
(Ve > 0)(3ne € N)(V(n > пс, р е N)) : ||т„+р - ®„|| < е-
Нормированное пространство Е называется полным, если каждая фундаментальная последова-
тельность (хп) его векторов имеет предел в Е. Каждое полное нормированное пространство
называется банаховым.
Теорема. Каждая сходящаяся последовательность (хп) векторов произвольного нормированного
пространства Е фундаментальна.
◄ Пусть е > 0 и хп —» х. Выберем такое n£ € N, чтобы Уп пе ||жп - аг|| < Тогда
V(n п,, р € N) имеем
||®п+р хп II ||®п+р ~ ®|| Т ||® — ®«|| < ►
Нормированные пространства R и Rm являются полными.
§ 3. Метрические пространства
Метрические пространства являются одной из разновидностей топологических пространств.
Впервые их выделил в 1906 г. М. Фреше (1878-1973) в связи с изучением функциональных про-
странств.
Одной из фундаментальных характеристик взаимного расположения точек множества явля-
ется расстояние между ними. Внедрение метрики (расстояния) позволяет выразить в простой и
доступной форме, на языке геометрии, результаты математического анализа. Наиболее важными
понятиями в теории метрических пространств являются полнота, компактность и связность.
3.1. Аксиомы метрики.
Предел последовательности точек метрического пространства.
Определение 1. Пусть X — произвольное множество. Отображение Хг R называется
метрикой, если V(x g X, у € X, z € X) выполняются следующие условия (аксиомы):
1) р(х, У) = 0 => х = у,
2) р(х, у) = р(у, х) (аксиома симметрии);
3) р(х, у) С р(х, z) + p(z, у) (неравенство треугольника).
Упорядоченная пара (X, р) называется метрическим пространством, а элементы множества X
называются точками метрического пространства.
Каждое нормированное векторное пространство Е превращается в метрическое, если в нем
У(ж С Е, у С Е) метрику определить формулой
Р(х, у) = ||® - у\\. (1)
Проверка выполнения аксиом 1)—3) не представляет затруднений.
Из аксиомы 3) по индукции следует, что V(Xj 6 X, j = 1, п, п 2) выполняется неравенство
Р(®1, ®п) Р(®1, ®г) + Р(®2, ®з) + ...+р(®„-1, ®„). (2)
Если р — расстояние в X, то У(г € X, у € X, z € X) выполняется оценка
1р(х, z) - р(у, z)] р(х, у). (3)
§ 3. Метрические пространства
13
Действительно, из аксиом 2) и 3) имеем р(х, z) р(у, z) + р(х, у) и р(у, z) р(у, х) 4- р(х, z) =
р(х, у) 4- р(х, z), откуда —р(х, у) р(х, z) — р(у, z) р(х, у). Из неравенства (3) следует, что
V(x € X, у € X) р(х, у) 0.
Пример 1. Функция р(х, у) = \х - у\ V(x, у) £ R2 есть расстояние в множестве R, а метриче-
ское пространство (R, р) называется действительной прямой.
Пример 2. Пусть (Rm, 4-, || • ||) — нормированное пространство (см. п.2.5). Отображение
R2m R, где р(х, у) = ||х — т/||, V(x, у) £ R2"1, удовлетворяет аксиомам метрики.
Пример 3. Пусть X — произвольное множество, Е — множество ограниченных отображений
X -^'R. Тогда V(/ € Е, g 6 Е) имеем (/ — <?) € Е и определено число p(f, g) — sup |/(х) — </(х)|.
хёХ
Отображение (/, д) н-» д) является расстоянием в множестве Е. Выполнение аксиом 1)—3)
очевидно.
Определение 2. Пусть (X, р) — метрическое пространство, х € X, хп £ X Vn g N. Точка х
называется пределом последовательности (х„), если р(хп, х) = о(1). В этом случае пишем
х = lim хп. Последовательность точек метрического пространства, имеющая предел, называется
п—>ос
сходящейся.
Теорема 1. Сходящаяся последовательность (хп) точек метрического пространства (X, р)
имеет единственный предел.
•4 Предположим, что lim хп = х0, lim х„ = у0, х0 # у0. Обозначим £0 = р(х0, уо).
П —»'ЗФ п—»ос
По определению предела существуют номера п^ € N, п*.2) € N Vn п*1^ р(хп, х0) < и
Vn > п™ р(хп, у0) < а. Тогда Vn neo = max-fn^’, п<2>} р(хп х0) 4- р(хп, у0) < е0. По нера-
венству треугольника р(х0, у0) = г0 р(хп, ®о) + р(хп, Уо) < £о, если только п nSg. Получили
противоречивое неравенство е0 > е<>, источник которого в предположении, что сходящаяся по-
следовательность имеет два предела. ►
Определение 3. Последовательность (хп) точек метрического пространства (X, р) называется
фундаментальной, если
> 0)(3ne € N)(V(n > п,,р £ N)) : р(хп+р, х„) < е. (4)
Теорема 2. Если последовательность (хп) точек метрического пространства (X, р) сходится,
то она фундаментальная.
Ч Пусть х = lim хп, х £ X. Тогда Ve > 0 3n, £ N : Vn п, р(хп, х) < |. Следовательно,
п—*ос
V(n пс, р £ N) выполняется неравенство р(хп+р, х) < | и из аксиом 2), 3) получаем оценку
Р(х„+р, Хп) р(х„+р, х) + р(х, Хп) = р(хп+р, х) + р(хп, X) < £. ►
Определение 4. Метрическое пространство (X, р) называется полным, если каждая фунда-
ментальная последовательность его точек сходится в нем.
Действительная прямая (см. пример 1) является полным метрическим пространством.
Пусть V(x £ Q, у £ Q) р(х, у) = |х - у\. Метрическое пространство (Q, р) не является
полным, поскольку фундаментальная последовательность рациональных чисел хп = 24- +...4-
сходится к иррациональному числу е £ Q.
3.2. Шары, сферы, диаметр множества.
В теории метрических пространств используется язык классической геометрии.
Пусть (X, р) — метрическое пространство, ха £ X, 6 > 0.
Определение 1. Множество Ов(хо) = {х € X | р(х0, х) < <5} называется открытым шаром
радиуса 6 с центром в точке х0, а также б-окрестностью точки ха.
Определение 2. Множество О((х0) = {х € X | р(х0, х) <5} называется замкнутым шаром
радиуса 6 с центром в точке х0.
Определение 3. Множество S(x0, 6) = {х £ X | р(х0, х) = <5} называется сферой радиуса б
с центром в точке хц.
На действительной прямой открытый (соответственно замкнутый) шар радиуса б с центром
в точке хо £ R есть интервал (х0 — б, х0 4- б) (соответственно сегмент [хо — 5, х0 4- <5]), а сфера
того же радиуса состоит из двух точек {х0 — б, х0 4- <5}.
14
Гл. 1. Основные структуры математического анализа
Определение 4. Пусть (X, р) — метрическое пространство, А и В — два непустых подмно-
жества множества X. Неотрицательное число
р(А, В) = inf р(х, у) (1)
у&В
называется расстоянием от А до В.
Если множество А одноточечное, то вместо р(А, В) записывают р(х, В). Равенство (1) можно
также записать в виде
р(А, В) = inf р(х, В) (2)
х Е А
Если А П В ^0, то р(А, В) = 0, однако р(А, В) = 0 Ап В ^0. Пусть например, А = N,
В = (хп ё Q\xn = п - ±;п Е N\{1}} . Тогда
1
А А В =0, р(А, В) = inf — = 0.
п TL
Определение 5. Пусть (X, р) — метрическое пространство, А С X — непустое множество.
Диаметром множества А называется число
d(A) = sup р(х, у). (3)
хбЛ,у&А
Из определения следует, что диаметр непустого множества может быть неотрицательным дей-
ствительным числом или +оо. Если А С В, то d(A) d(B). Равенство d(A') = 0 выполняется
тогда и только тогда, когда А — одноточечное множество.
Если диаметр множества А конечный, то оно называется ограниченным.
Теорема. Объединение двух ограниченных множеств А и В является ограниченным множеством.
•4 Если а ё A, b Е В ч х, у — любые точки множества A U В, то либо жЕААуЕЛи тогда
р(х, у) d(A), либо х Е В, у Е В ч тогда р(х, у) d(B), либо, например, х Е А, у Е В и тогда
вследствие неравенства треугольника получаем неравенство р(х, у) sj р(х. а) + р(а, 6) + р(Ъ, у),
поэтому
d(A U В) sC р(а, b) + d(A) + d(B). (4)
Пусть е > 0. По свойству точной нижней грани найдется такая пара точек а1 Е А, Ь' Е В, что
р(А, В) р(а, Ъ') < р(А, В) + с.
Поскольку а и Ь — произвольные точки, то, полагая в неравенстве (4) а = а', Ь = Ь', получим
оценку
d(A U В) < р(А, В) + d(A) + d(B) + е.
В силу произвольности выбора е > 0 имеем
d(A U В) $ р(А, В) + d(A) + d(B). ►
Следствие. Если множество А ограниченное, то Vx0 ё X множество А содержится в замкну-
том шаре с центром в точке xq и радиусом г = p(x<h А) + d(A).
3.3. Открытые множества.
Определение 1. Открытым множеством в метрическом пространстве (X, р) на-
зывается подмножество G С X, имеющее свойство:
(Vx Е G) (3d > 0) : ОДх) С G.
Из определения следует, что пустое множество открытое. Все множество X также открытое.
Теорема 1. Каждый открытый шар является открытым множеством.
◄ Пусть (X, р) — метрическое пространство. Если х Е О«(жо) С АГ, то р(х0, х) < 6 и
<5| = б - р(х0, х) > 0. Тогда р(х, у) < <5(, если у Е О6,(х). Оценим расстояние р(х0, у). Согласно
неравенству треугольника имеем
р(.х0, у) < р(хй, х) + р(х, у) < р(х0, х) + <5\ = б.
Таким образом, выполняется включение OSl (х) С Os(xG), т. е. точка х входит в множество О«(х0)
с некоторой окрестностью. ►
§3. Метрические пространства
15
Теорема 2. Объединение любого семейства открытых множеств есть открытое мно-
жество.
Ч Если х G Gx для некоторого А € А, то существует такое б > 0, что
ОДх) CGxC U ►
мел
На действительной прямой любой интервал (а, +оо) открыт как объединение открытых мно-
жеств (а, х) для всех х > а.
Теорема 3. Пересечение конечного семейства открытых множеств есть открытое множество.
-« Достаточно рассмотреть случай двух открытых множеств G\ и G2, а затем провести ин-
дукцию.
Если х g G{ n G2, to существуют такие <5, > 0 и б2 > 0, что С Gt, Og2(x) С G2 и
Os(x) С G, Л G2, где 6 = min{5(, б2}. ►
Пересечение бесконечного семейства открытых множеств, вообще говоря, не является от-
крытым множеством. Например, пересечение интервалов ^), п € N на действительной
прямой есть одноточечное множество {0}, которое считается замкнутым.
3.4. Внутренность множества.
Пусть (X, р) — метрическое пространство.
Определение 1. Открытой окрестностью множества AC X называется любое открытое
множество, которое содержит А. Окрестностью множества А называется любое множество,
содержащее открытую окрестность А.
В случае, когда А = {ж}, ведут речь об окрестности точки х (а не множества {ж}).
Определение 2. Точка х С X называется внутренней точкой множества А С X, если
А является ее окрестностью. Множество всех внутренних точек множества А называется его
внутренностью и обозначается символом intA °.
Внутренность любого промежутка с началом а и концом Ь (а <Ь) на действительной прямой
есть интервал (а, 6), так как точки а и Ь не могут быть внутренними точками промежутков [а, Ь],
[а, Ь), (а, Ь].
Теорема 1. Для любого множества А С X внутренностью int А является наибольшее открытое
множество, содержащееся в А.
◄ Если х € int А, то существует открытое множество G:, С А. содержащее точку х. Для
любой точки у 6 G,. множество А по определению 1 является ее окрестностью, поэтому у 6 int А.
Итак, Gx С intA, intA = |J {ж} С (J Gx С intA. По теореме 2, п.3.3, множество intA
xgint А ж € int А
открытое. Если В С А — открытое множество, то из определения 2 следует, что В С intA. Таким
образом, открытые множества характеризуются условием А = int А. ►
Следствие. Если А С В, то int А С int В.
Теорема 2. Для любой пары множеств А и В выполняется равенство
int(A П В) = int А Л int В.
Включение int(A Л В) С intA Л intB получаем из следствия. Согласно теореме 3, п.3.3,
пересечение intA Л int В является открытым множеством и содержится в пересечении А Л В. По
теореме 1, выполняется включение intA Л intB С int(A Л В). Из полученных включений следует
справедливость утверждения. ►
Внутренность непустого множества может быть пустым множеством, например, для одното-
чечного множества {х} на действительной прямой int{x} =0.
Определение 3. Внутренняя точка множества Х\А называется внешней точкой для А, а
внутренность множества Х\А —множеством внешних точек множества А.
Теорема 3. Для того чтобы точка х € X была внешней для А, необходимо и достаточно, чтобы
выполнялось условие р(х, А) > 0.
◄ Необходимость. Если х G X —внешняя точка для А, то существует шар Os(x) С Х\А
(<5 > 0). Для любой точки у 6 А имеем р(х, у) > 6, следовательно, р(х, А) = inf р(х, у) б > 0.
уЕА
б От французского слова interieur — внутренний.
16
Гл. 1. Основные структуры математического анализа
Достаточность. Пусть х £ X. Обозначим = р(х, А). Из условия 8t > 0 следует
включение О^(х) С Х\Л, вследствие чего х является внутренней точкой множества Х\А. ►
3.5. Замкнутые множества, точки прикосновения, замыкание множества.
Пусть (X, р) — метрическое пространство.
Определение 1. Множество F С X называется замкнутым, если его дополнение CF является
открытым множеством.
Пустое множество, а также множество X замкнуты. Промежутки [а, +оо), (—оо, а] и мно-
жество Z — замкнутые множества на числовой прямой. Промежутки [а, Ь) и (а, Ь] не являются
ни открытыми, ни замкнутыми множествами.
Теорема 1. Замкнутый шар Og С Х(ж0) и сфера S(x0, б) С X являются замкнутыми множе-
ствами.
◄ Если х £ О6(х0), то р(х, О6(х0)) р(х.:1, х) - 6 > 0, в силу чего открытый шар с центром в
точке х и радиусом б1 = р(х0, х) - 8 содержится в дополнении шара ОДжо). Следовательно, это
дополнение — открытое множество. Дополнение сферы S(xa, 6) является объединением откры-
того шара ОДх0) и дополнения шара ОДх0). По теореме 2, п. 3.3, это объединение есть открытое
множество. ►
Теорема 2. Пересечение любого семейства замкнутых множеств замкнуто. Объединение конеч-
ного семейства замкнутых множеств замкнуто.
◄ Если Va £ А множества Fa замкнуты, то множества CFa открыты. Согласно второй
формуле в (2), п. 1.4, имеем
С П = U CFa. (1)
По теореме 2, п. 3.3, множество CFa открыто, в силу чего и множество С р| Fa является
а£А
открытым. Тогда по определению множество Q Fa замкнуто.
<»ел
Докажем вторую часть теоремы. Пусть F{ (i — 1, п) — замкнутые множества. Перейдя к
дополнениям по первой формуле в (2), п. 1.4, получим
CU^ = nCFi (2)
г=1 г=1
п
Так как множества CFi открыты, то, согласно теореме 3, п. 3.3, множество Q СРг является от-
i=i
п п
крытым, а вместе с ним и множество С [J F,. Следовательно, множество (J F, замкнуто. ►
»=i i=i
В частности, одноточечное множество замкнуто.
Определение 2. Точка х0 6 X называется точкой прикосновения множества А С X, если
любая окрестность О6(х0) имеет с А непустое пересечение. Множество всех точек прикосновения
множества А называется его замыканием и обозначается символом А.
Если х 6 X — не точка прикосновения множества А С X, то х является внутренней точкой
дополнения СА. Поэтому замыкание множества А есть дополнение множества его внутренних
точек: А = CintCA. Например, замыкание открытого шара Ое(х0) содержится в замкнутом шаре
0«(®о), но может не совпадать с ним. _
Поскольку int С А есть наибольшее открытое множество, содержащееся в СА, то А_есть наи-
меньшее замкнутое множество, содержащее А. В частности, если А замкнуто, то А = А.
Теорема 3. Для того чтобы точка Xg G X была точкой прикосновения множества А С X,
необходимо и достаточно, чтобы р(х0, А) = 0.
4 Необходимость. Пусть х0 6 X — точка прикосновения множества А С X. Тогда
ж0 £ intCA и, согласно теореме 3, п. 3.4, р(ха, А) = 0.
Достаточность. Если р(ха, А) = 0, то любая окрестность ОДх0) имеет с множеством А
непустое пересечение. ►
§ 3. Метрические пространства
17
Теорема 4. Если ха g X — точка прикосновения множества А С X и х0 £ А, то V6 > О
множество Об(х0) П А бесконечное.
◄ Допустим, что это не так и для некоторого <50 > 0 О^0(х0) П А = {j/i, . •. , По
предположению rk = р(х0, у к) > 0 (k = 1, п). Выберем г > 0 так, чтобы ОТ(х0) С 0So(x0)
и г < min{rH г2, ... , г„}. Тогда Ог(х0) П А =0 вопреки предположению, что а:0 — точка
прикосновения множества А. ►
Определение 3. Точка х0 g X называется предельной точкой множества А С X, если она
является точкой прикосновения множества Л\{го}-
Из теоремы 4 следует, что любая б -окрестность предельной точки множества А С X содержит
бесконечное множество точек из А.
Пусть х0 g X — предельная точка множества А С X. Рассмотрим последовательность
(Обп(х0)) окрестностей точки х0, где 6п = о(1). Тогда Vn g N множество Хп = Oin(z0) П А
бесконечное. В множестве Xt выберем любую точку as,. В множестве Х2 выберем точку х2 # ж,
(это возможно, поскольку множества Xi и Х2 бесконечные). Пусть выбраны различные точки
Х1, х2, ... , хп, Xj g Xj (j = 1, n). В множестве Xn+i выберем точку a:n+I / Xj (j ~ 1, n). По
индукции выбрали последовательность (хп) различных точек хп g А. Из условий р(х„, х0) < 6п
и <5П = о(1) следует, что ха = lim х„. Итак, если х0 — предельная точка множества А С X, то
п—*00
из него можно выделить последовательность различных точек, сходящуюся к х0-
Наоборот, если известно, что из множества А С X можно извлечь последовательность раз-
личных точек, сходящуюся к точке г0 € X, то х0 — предельная точка этого множества, так как
любая 6-окрестность Os(xq) содержит бесконечное множество точек из А.
Можем теперь сформулировать еще одно определение предельной точки множества А С X,
эквивалентное определению 3.
Определение 4. Точка х0 £ X называется предельной точкой множества А С X, если
из него можно выделить последовательность различных точек (хп), сходящуюся к по метрике
пространства (X, р).
Предельная точка множества может принадлежать ему или не принадлежать. Выше было
показано, что если множество А замкнуто, то А = А, т. е. замкнутому множеству принадлежат
все его точки прикосновения, а значит и все его предельные точки, которые, очевидно, являются
точками прикосновения А.
Определение 5. Точка g X называется граничной точкой множества А С X, если она
является точкой прикосновения как А, так и СА. Множество дА всех граничных точек множества
А называется его границей. _ _____
Из определения следует, что дА = А П СА = д(СА). В силу теоремы 2 множество дА
замкнутое и может быть пусто.
Определение 6. Точка х0 ё А называется изолированной точкой множества AC X, если
Э<5 > 0: Oi(xo) П 4\{х0} =0, т.е. ха — точка прикосновения множества А, не являющаяся его
предельной точкой.
Определение 7. Пусть Е — непустое подмножество множества X. Сужение р\Ег называется
расстоянием, индуцированным в Е расстоянием X2 R. Метрическое пространство
(Е, р), определенное этим индуцированным расстоянием, называется подпространством метри-
ческого пространства (X, р).
Теорема 5. Пусть (Е, р) — подпространство полного метрического пространства (X, р). Оно
является полным метрическим пространством тогда и только тогда, когда Е — замкнутое под-
множество множества X.
◄ Необходимость. Пусть (Е, р) — полное метрическое пространство. Предположим, что
Е не является замкнутым подмножеством множества X. Тогда существует последовательность
(х„) точек множества Е, сходящаяся к некоторой точке х g Х\Е. Поскольку последователь-
ность (жп) фундаментальная (метрика в (Е, р) заимствована из (X, р)), то вследствие полноты
пространства (Е, р) существует lim хп = х1, х' g Е. Получили последовательность точек про-
п—*оо
странства (Е, р), имеющую два различных предела — один в Е, другой — вне Е, что невозможно
вследствие единственности предела. Источник противоречия — в предположении, что множество
Е не замкнуто.
18
Гл. 1. Основные структуры математического анализа
Достаточность. Пусть Е — замкнутое подмножество множества X. Каждая фундамен-
тальная последовательность (уп) точек метрического пространства (Е, р) сходится в (X, р) вслед-
ствие полноты последнего, и ее предел принадлежит множеству Е в силу предположенной его
замкнутости. Поэтому множеству Е принадлежат все его предельные точки, т. е. метрическое
пространство (Е, р) полное. ►
§ 4. Компактные множества
Определение 1. Множество К С X называется компактным в метрическом простран-
стве (.X, р), если всякая последовательность (хп) элементов из К содержит сходящуюся подпосле-
довательность. Если их пределы принадлежат множеству К, то оно называется компактным в
себе, или компактом. Если же эти пределы принадлежат множеству X, не принадлежа, может
быть, множеству К, то К называется компактным в пространстве (X, р), или относи-
тельно этого пространства.
Очевидно, что множество К компактно в себе тогда и только тогда, когда оно компактно в
пространстве (X, р) и замкнуто.
Пример 1. Пусть X = [0, 1] и V(x € X, у 6 X) р(х, у) = |х — у\. Метрическое простран-
ство (X, р) компактное в силу классической теоремы Больцано—Вейерштрасса.
Пример 2. Метрическое пространство (R, р), р(х, у) = |ж — V(x € R, у € R) некомпактно,
поскольку подмножество его точек N С R не содержит никакой сходящейся последовательности.
Однако, всякое ограниченное множество X С R компактно по теореме Больцано—Вейерштрасса.
Для компактных множеств точек метрического пространства (X, р) докажем аналог теоремы
о вложенных шарах полного метрического пространства без предположения полноты.
Теорема 1 (Кантора). Пусть дана убывающая последовательность
К'ЭК2Э ... дКпд ....
непустых замкнутых компактных множеств метрического пространства (X, р). Тогда пересечение
К = П Kj не пусто.
◄ В каждом множестве Kj выберем произвольно по точке х,. Получим последователь-
ность (xj), причем {х_,; j t '<} С Kt. Так как множество JT, компактное, то из последова-
тельности (х}) можно извлечь сходящуюся подпоследовательность (Xjk). Пусть х0 = lim xjk.
Так как Vn0 G N начиная с номера jk > п0 все члены этой последовательности принадлежат
множеству Кпо и К„.. замкнуто, то х0 € КПо. Но тогда х0 € Q Kj. ►
j=i
Определение 2. Пусть (X, р) — метрическое пространство и е > 0. Множество Х\ С X
называется е-сетью множества Х2С X, если Тх € Х2 существует такой элемент хс Е Х\, что
р(х, х,) < е.
В частности, множество Х2 может совпадать с множеством X.
Определение 3. Множество Е С X называется вполне ограниченным в метрическом
пространстве (X, р), если Уе > 0 для него имеется в X конечная е-сеть.
Последнее условие эквивалентно следующему: Уе > 0 существует такое конечное множество
F С X, что Ух € Е р(х, F) < е.
Заметим, что из ограниченности множества точек метрического пространства не следует его
вполне ограниченность.
Определение 4. Пусть М — произвольное множество. Покрытием множества Е С М
называется такое семейство (В^)леА подмножеств множества М, что Е С U By.
хел
Связь между компактностью и вполне ограниченностью множества точек метрического про-
странства устанавливает следующая теорема.
§ 4. Компактные множества
19
Теорема 2 (Хаусдорфа). Всякое компактное множество К С X вполне ограничено в метри-
ческом пространстве (X, р).
◄ Предположим, что К компактно, однако для некоторого > 0 не имеет конечной е0-
сети. Возьмем произвольное ж, € К. По предположению множество {х,} не образует г0-сети
для множества К, т. е. р(х\, К) еа. Выберем любую точку х2 g К, удовлетворяющую усло-
вию р(х}, х2) £о- Поскольку множество {хн х2} не является е0-сетью для множества К, то
найдется такая точка х3 £ К, что р(х;, х2) e0(i = 1, 2). Пусть выбраны точки хь х2, , х„,
удовлетворяющие условию р(х,, Xj) ea (i j Л i, j Ss п). Найдем такое х„+1 € К, что
р(х,, хп+[) е0 (г = 1, п). Индукцией по п € N построена последовательность (хп) точек мно-
жества К, члены которой удовлетворяют условию р(х,, х7) е0 (* / j). Из последовательно-
сти (хп) нельзя выбрать сходящуюся подпоследовательность, что противоречит предположению
о компактности множества К. Источник противоречия — в предположении, что К не является
вполне ограниченным. ►
Теорема 3 (Фреше). Если метрическое пространство {X, р) полное, то каждое вполне огра-
ниченное в нем множество Е С X компактно.
◄ Если Е С X вполне ограничено, то Уе > 0 в множестве X существует конечная г-сеть
для множества Е. Пусть (хп) — произвольная последовательность элементов из Е. Поскольку
существует конечное покрытие множества Е открытыми шарами с радиусами, меньшими е, то
по крайней мере один такой шар содержит подпоследовательность (хпь). Таким образом, Уе > О
из любой последовательности элементов множества Е можно выделить подпоследовательность,
расстояние между элементами которой меньше е.
Пусть VngN = ^. Выберем из последовательности (хп) подпоследовательность (а^?)
с расстояниями между элементами меньше 1. Из этой подпоследовательности выделим новую
(х®) с расстояниями, меньше |. Пусть выбраны подпоследовательности (x!;'j j = 1, к. Выде-
лим из (х*^) подпоследовательность (х^+|)) с расстояниями, меньшими Получили после-
довательность подпоследовательностей Образуем новую последовательность (xjf’),
составленную из диагональных членов указанных подпоследовательностей. Члены этой после-
довательности, начиная с номера k € N, принадлежат fc-й подпоследовательности, в силу чего
У(п > к, т > к) р (х^\ х<^>) < |. Следовательно, последовательность (х^1) фундаментальная.
Поскольку пространство (X, р) полное, то lim x(nn) = х, х € X. По определению множество Е
компактное в пространстве (X, р). ►
Из теорем 2 и 3 получаем следующее утверждение.
Теорема 4. Для того чтобы множество Е С X было компактным в пространстве (X, р), необ-
ходимо, а если (X, р) — полное пространство, то и достаточно, чтобы Е было вполне ограниченным
в нем.
Теорема 5. Компактное подмножество К С X полного метрического пространства (X, р)
является компактом тогда и только тогда, когда оно замкнуто в (X, р).
4 Необходимость. Пусть К С X — компакт, т.е. компактное множество. Согласно
теореме 5, п. 3.5, пространство (К, р) является полным, в силу чего множество К замкнутое.
Достаточность. Если множество К С X замкнуто в (X, р), то согласно теореме 5, п.3.5,
пространство (К, р) полное, т. е. К — компакт. ►
Следующее утверждение позволяет дать новое определение компактного в себе множества,
эквивалентное определению 1.
Теорема 6. Пусть F С X — замкнутое множество в метрическом пространстве (X, р). Для
того чтобы F было компактным в себе, необходимо и достаточно, чтобы из любого покрытия этого
множества можно было выделить конечное покрытие.
◄ Необходимость. Пусть F С X — компакт, (Ga)aiA — семейство открытых мно-
жеств, покрывающих F, (еп) — бесконечно малая последовательность положительных чисел,
ь __
xj’’, х^, ... , — конечная е, -сеть для множества F. Тогда F = |J Ft, где = Ое| (х^0) n F.
1=1
Множества F — компактные в себе, причем d(FJ 2е1; где d(F;) — диаметр множества F{.
Предположим, что не существует конечного покрытия множества F. Тогда этим свойством обла-
20
Гл. 1. Основные структуры математического анализа
дает хотя бы одно из множеств F,, которое обозначим через Fit. Рассуждая аналогично, выделим
из F,. компактную в себе часть Fi|i2 диаметром д(Е^2) < 2е2, которую нельзя покрыть никаким
конечным семейством, выделенным из семейства (Go')aZA. Продолжая этот процесс выделения
компактных в себе частей, получим последовательность вложенных друг в друга замкнутых мно-
жеств
Э...,
диаметры которых стремятся к нулю (поскольку 2еп и £„ = о(1)). По теореме 1
существует точка х0 Q F, принадлежащая всем этим множествам. Поскольку семейство (Ga)a€A
покрывает множество F, то существует такое множество G,t() из этого семейства, что хп € GQ||.
Так как Gao — открытое множество, то существует с-окрестность Ое(^о) С Ga,,. Выберем п € N
из условия d(Fili2... in) < е. Тогда справедливо включение Fili2.„in С О£(г0), противореча-
щее предположению о том, что никакое конечное семейство из (Ga)аеА не покрывает множе-
ство . Источник противоречия — в первоначальном предположении, что не существует
конечного покрытия множества F.
Достаточность. Предположим, что из всякого покрытия (GcJ„e,4 множества F можно
выделить конечное покрытие. Пусть М С F - подмножество, не имеющее предельных точек.
Тогда Va; € F существует окрестность О, Дг), не содержащая точек множества М, кроме, быть
может, точки х. Эти окрестности покрывают множество F. Выделим из семейства (О^)х^р
п
конечное покрытие (OCj. (х_,))_|-^. Так как М С |J OCj(Xj) и в каждой окрестности Oej(xj)
;=1
может содержаться не более одной точки из М, то множество М конечное. Следовательно, всякое
бесконечное подмножество М С F должно иметь предельные точки, т. е. F — компактное в себе
множество. ►
Определение 5. Множество К С X точек метрического пространства (X, р) называется
компактным, если из любого покрытия (Ga)a^A множества К можно выделить конечное его
покрытие.
§ 5. Связные пространства и связные множества
Определение 1. Метрическое пространство (X, р) называется связным, если не существует
двух таких открытых непустых подмножеств А С X и В С X, что A U В = X и А П В =0.
Эквивалентная формулировка: метрическое пространство (X, р) связно, если из всех подмно-
жеств множества X только пустое множество и само X одновременно открыты и замкнуты.
Определение 2. Множество Е С X в метрическом пространстве (X, р) связно, если связно
подпространство (Е, р).
Определение 3. Открытое связное множество называется областью.
Определение 4. Область вместе со своей границей называется замкнутой областью.
Действительная прямая является связным пространством. Для того чтобы множество А С К
было связно, необходимо и достаточно, чтобы А было промежутком (ограниченным или нет).
§ 6. Предел и непрерывность отображения
из одного метрического пространства
в другое
6.1. Предел и непрерывность отображения.
Пусть (X, рх) и (У, ру) — метрические пространства, f . X —> К, а:0 € X — предельная
точка множества D f.
§ 6. Предел и непрерывность отображения из одного метрического пространства в другое 21
Определение 1. Точка a g Y называется частичным пределом отображения f в точ-
ке х0, если существует такая последовательность (хп) точек множества Df, что
(хп -> х0) Л (Vn е N хп # х0) Л ( lim f(xn) = а ). (1)
Условия (1) можно записать в виде:
(рх&о, хп) = о(1)) Л (Уп е N Рх(%о, хп) > 0) Л (ру(а, f(xn)) = о(1)).
Множество всех частичных пределов отображения f в точке х0 обозначим символом Ef(x0).
Определение 2. Если множество Ef(xB) состоит из одной точки а, то она называется пре-
делом отображения f в точке х0 и обозначается символом lim /(х).
х—>х0
Смысл определения 2 состоит в том, что для любой последовательности (х„) точек множе-
ства Df, члены которой отличны от х0, сходящейся к х0, последовательность (f(xn)) сходится
к а.
Предел отображения в точке на языке последовательностей принято называть пределом в смы-
сле Гейне (1821—1881).
Определение 3 (Гейне). Отображение f называется непрерывным в точке х0 g Df, если
lim /(а) = /(х0) всякий раз, как только хп —» х0 и Уп € N xn € Df.
* —“О
Если отображение f непрерывное Ух € Df, то будем его называть непрерывным.
Если хо £ Df и является предельной точкой множества Df, то отображение f непрерыв-
но в точке х0 тогда и только тогда, когда lim /(х) = /(х0). В изолированной точке каждое
отображение непрерывное.
Отображение, не являющееся непрерывным в точке х0 € Df, называется разрывным в ней.
Пусть х0 — предельная точка множества Df и х0 6 Df. Она называется точкой устранимого
разрыва для отображения f, если существует lim /(х) Е У. В этом случае отображение /*,
х->ха
определенное формулой
{/(х), если х EDf\{x0},
lim /(х) при х = Хо,
г—х0
является непрерывным в точке х0.
Теорема (о непрерывном образе компакта). Пусть f : X - Y — непрерывное отобра-
жение и Df — компакт. Тогда множество Ef компактное в себе, т. е. непрерывный образ компакта
есть компакт.
Ч Рассмотрим произвольную последовательность точек (уп) из множества Ef = f(Df). Тогда
существует такая последовательность (хп), что Vn € N хп € Df Л уп = f(x„). Согласно опреде-
лению компакта, существуют х0 € Df и подпоследовательность (xnt) такие, что хП|ь —> хо при
k —> оо. По определению непрерывного отображения имеем ynk = /(xnfc) -+ /(х0) = уо € Ef,
что означает компактность в себе множества Ef. ►
6.2. Непрерывность композиции отображений.
Пусть (X, рх), (Y, ру), (Z, pz) — метрические пространства, f : X Y, g : Y —» Z,
EfCDg.
Теорема 1 (о непрерывности композиции отображений). Пусть отображение f
непрерывно в точке х0 € Df, а отображение g непрерывно в точке /(xq) € Dg. Тогда композиция
g ° f непрерывна в точке х0.
◄ Пусть х„ —► х0 и Уп 6 N хп g Dg,,f. Тогда уп = /(х„)/-> /(х0) Л уп € Dg. Поэтому
»(Уп) -+ s(/(®o)) ПРИ »» -* оо. Следовательно, (д о f)(x„) = р(у„) -» у(/(х0)) = (д ° /)(*<>)• ►
22 Гл. 1. Основные структуры математического анализа
Теорема 2. Пусть хп — предельная точка множества Dgaf . Если lim f(x) = у0 и отображе-
ние g : Y -» Z непрерывно в точке у0, то lim g(f(x}) = g(yo).
X—
◄ Полагаем
_ f f(x\ если х € Df\{x0}
' W [ Уо при х = х0.
Отображение f* непрерывно в точке хп. По теореме 1 композиция д о /* непрерывна в этой
точке. Поэтому
lim (д ° f)(x) = lim (д о /*)(г) = (д ° f) (х0) = д(у0). ►
X—»XQ X—’Xq
6.3. Непрерывность обратного отображения.
Теорема (о непрерывности обратного отображения). Пусть (X, рх), (Y, ру) —
метрические пространства, f : X — Y и Df — компакт. Если отображение f непрерывно и
обратимо, то f~l непрерывное.
◄ Пусть (у„) — последовательность точек множества Ef, сходящаяся к у0 £ Ef, и а —
частичный предел последовательности (/-1(уп))- Поскольку Df — компакт, то а € Df. Из
непрерывности отображения f следует, что /(а) является частичным пределом последовательно-
сти (уп), в силу чего /(а) = у0 и а = f~'(y0). Таким образом, все частичные пределы последо-
вательности (/ ‘(у„)) равны / 1(уо), т.е. lim f ‘(yn) = _Г‘(Уо), что означает непрерывность
п—‘ОС
отображения f~l в точке у0. Так как уо — произвольная точка множества Ef, то — непре-
рывное отображение. ►
6.4. Предел и непрерывность отображения в смысле Коши.
Некоторые свойства непрерывных отображений.
Пусть (X, рх), (Y, ру} — метрические пространства, / : X -+ У.
Определение 1. Пусть х0 — предельная точка множества Dj и а € У. Точка а называется
пределом отображения f в точке х0 в смысле Коши, если
(Ve > 0) (35 > 0)(Vx G Df, 0 < рх(ю, ж) < 5) : Ру(а, f(x}) < е. (1)
Теорема 1. Определения предела отображения в точке по Гейне и по Коши эквивалентны.
•4 Пусть lim /(г) = а в смысле Коши, хп —» х0 и Vn € N хп / х0. Тогда для указанного
т ’Xq
в условиях (1) 5 > 0 существует ns € N : Vn ns 0 < рх(х0, хп) < 6. Согласно определе-
нию 1, Vn Э ру(а, f(xn)) < е, т.е. У(г„) -+ а. Получили, что точка а является пределом
отображения f в точке х0 в смысле Гейне.
Предположим, что а = lim J(x) в смысле Гейне, и покажем, что а является пределом
X—
отображения f в точке х0 в смысле Коши.
Допустим, что это не так, т. е. для некоторого е0 > 0 нельзя указать соответствующего 5 > 0
в условиях (1): V5 > 0 Эх 6 Df такое, что 0 < рх(хо, х) < д, однако ру(а, f(x)) е0. Пусть
(5П) — бесконечно малая последовательность положительных чисел. По предположению
(Vn G N)(3xn G £>/)(Vn 6 Nxn # х0 Л 0 < рх(ж0, хп) < 6п) : pY(a, f(xn)) е0.
Поскольку 5„ = о(1), то lim хп = х0, откуда должно следовать предельное соотношение
п—*оо
lim ру(a, f(xn}) = 0,
п—*<х
противоречащее тому, что Vn G N pY(a, f(x„)) е0. Источник противоречия — в предположе-
нии, что а не является пределом отображения f в точке х0 в смысле Коши. ►
Определение 2. Отображение f : X —> Y называется непрерывным в точке х0 G Df в
смысле Коши, если
(Ve > 0)(Э5 > 0)(Vx 6 рх(ж0, ж) < 5) : Рг(/(жо),/(ж)) < е- (2)
Очевидно, что определения Гейне и Коши непрерывности отображения в точке равносильны.
§ 6. Предел и непрерывность отображения из одного метрического пространства в другое 23
Понятие непрерывности отображения в точке носит локальный характер. На это указывают
следующие утверждения.
Теорема 2 (о непрерывности сужения отображения). Пусть отображение f : X —>У
непрерывно в точке х0 € Df, А С Df и х0 € А. Тогда сужение /|л — непрерывное в точке х0
отображение.
◄ Пусть х„ -> х0 и Уп 6 N хп € А. Тогда /|д(х„) = f(xn) -» f(x0) = f\A(x0). ►
Напомним, что множество V С X называется окрестностью точки х0 € X (см. п. 3.4), если
существует такое открытое множество G С X, что х0 g G С V. Если х0 £ А С X, то пересече-
ние А И V называется окрестностью точки х0 в А.
Теорема 3. Пусть существует такая окрестность W точки х0 в Df, что отображение f\w
непрерывно в точке хп. Тогда отображение f : X -+ Y непрерывно в точке хй.
◄ Пусть хп -+ и Vn € N хп € Df. Существует такой номер п0 € N, что Уп п0 хп g W.
Поскольку
/(х„о+„) = /|w(a;no+n) f\w(x0) = f(xa),
то f(xn) —» f(x0) при n -+ oo. По определению отображение / непрерывно в точке х0. ►
Смысл теорем 2 и 3 состоит в том, что свойство непрерывности отображения в точке зависит
только от тех значений, которые оно принимает в некоторой ее окрестности.
Сформулируем понятие непрерывного отображения на языке окрестностей.
Определение 3. Пусть (X, рх) и (У, pY) —метрические пространства. Отображение f: X —»У
называется непрерывным в точке х0 € Df, если для каждой окрестности V' точки /(х0) в
множестве Ef существует такая окрестность V точки х0 в множестве Df, что /(У) С V.
Отображение f называется непрерывным, если оно непрерывно Ух g Df.
Поскольку множества Ое(/(х0)) С Ef, О{(х0) С Df являются окрестностями точек /(х0)
и х0, то понятие непрерывности отображения / в точке хг, можно сформулировать на языке е-
и fi-окрестностей: отображение f : X —» У называется непрерывным в точке х0 g Df,
если для каждой окрестности Or(f(xt.)) С Ef существует такая окрестность Os(x$) С Df, что
f(Os(x0)) С О£(/(г0)).
Теорема 4. Для того чтобы отображение f : X —> У было непрерывным в точке xQ g Df,
необходимо и достаточно, чтобы прообраз /-|(У') каждой окрестности точки f(x0) в Ef был
окрестностью точки х0 в Df.
◄ Необходимость. Если отображение / непрерывно в точке х0 g Df, то из определения 3
следует, что х0 g V С следовательно, прообраз /-1(У') является окрестностью точки х0
в Df.
Достаточность. Если W = /-|(У') — окрестность точки г0 в Df, то существует такое
открытое множество G, что г0 € G С W, в силу чего V' D f(G). ►
Следующие две теоремы носят вспомогательный характер.
Теорема 5. Пусть f : X —* У и хо € Df — точка прикосновения множества А С Df. Если
отображение f непрерывно в точке х0, то /(х0) — точка прикосновения множества f(A).
◄ Если V' — окрестность точки /(х0) в Ef, то по теореме 4 /-1(У') — окрестность точки
в Df. Так как х0 — точка прикосновения множества А, то А П /-|(У') #0. Следовательно,
существует точка х g А Л /-1(У'), в силу чего /(х) 6 /(А) П У', т.е. множество f(A) П У' не-
пустое. Поскольку У' — окрестность точки /(х0), то последняя является точкой прикосновения
множества /(А). ►
Теорема 6. Пусть f : X —> У, А' С Ef, В' С Еf и A1 D В'. Тогда
Г\а!\в') = г\а!)\г\в').
◄ Пусть х g /-1(А'\В'). Тогда
/(х) 6 А'\В' => /(х) 6 А' Л f(x) <£В' => х g Г'(А')Лх £ f'(B') =>
=> z g /-1(А')\/-1(В') => Г1(А'\В') С /-'(А')\/-'(В').
24
Гл. 1. Основные структуры математического анализа
Если у g f l(A')\f 1(В'), то
у g Г'(А') Л у $ f~l(B') => f(y) € А' Л f(y) £В' => /(у) £ А'\В' =>
=*> У 6 ГЧЛ'\В’) => Г1(А’)\Г1(В’) С Г'(А’\В').
Из полученных в конце цепочек импликаций включений следует доказываемое равенство. ►
Следующее утверждение носит глобальный характер.
Теорема 7. Пусть f : X —► Y. Следующие свойства эквивалентны-.
1) / — непрерывное отображение -,
2) прообраз f~l(G) каждого множества, открытого в Ef, открыт в Df-,
3) прообраз f~l(F) каждого множества F, замкнутого в Ef, замкнут в Df-,
4) для каждого множества А С Df справедливо включение f(A) С /(А).
Ч Докажем, что выполняется цепочка импликаций 1) => 4)_=> 3) => 2) => 1). Пусть ото-
бражение f непрерывно и А С Df — произвольное множество, А — его замыкание, состоящее
по определению из всех точек прикосновения множества А. Если х g Df — точка прикосно-
вения множества А, то по теореме 5 f(x) — точка прикосновения множества /(А). Поэтому
f(A) С ДА) И 1) => 4).
Если выполнено условие 4) и F С Ef — замкнутое множество в Еf, А = f '(F), то /(А) С
F = F. Следовательно, А С f~l(F) = А и так как А С А, то А замкнуто. Таким образом,
4) => 3).
Пусть выполнено условие 3). Согласно теореме 6 имеем
/"'(int F) = f~\F\dF) = f~l(F)\f~\dF) = int/~‘(F).
Следовательно, 3) => 2). Осталось установить, что 2) => 1). Пусть выполнено условие 2). Если
V' — окрестность точки f(x) в Ef, то существует открытая окрестность W' С V этой же точки.
Прообраз f~'(W') является открытым множеством в Df, содержащим точку х и содержащимся
в f~'(V'). По теореме 4 отображение / непрерывно в точке х € Df. Поскольку х — произволь-
ная точка, то f — непрерывное отображение и 2) => 1). ►
Заметим, что образ открытого (соответственно замкнутого) множества при непрерывном ото-
бражении, вообще говоря, не будет открытым (соответственно замкнутым). Например, отобра-
жение х w х4, х € R, непрерывное в R, однако образ [0, 1) открытого множества (—1, 1) не
является открытым.
6.5. Равномерно непрерывные отображения.
Пусть (X, рх), (Y, ру) — метрические пространства, f : X —» Y.
Определение. Отображение f называетсяравномерно непрерывным на множестве Df,
если
(Ve > 0) (Эй > 0)(V(a?i G Df, х2 g Df), px(xY, х2) < й) : py(/(a:i), f(x2)) < е. (1)
Очевидно, что равномерно непрерывное отображение непрерывное. Обратное утверждение,
вообще говоря, несправедливо. Например, непрерывная функция х х2, х g R, не является
равномерно непрерывной, так как для данного h > 0 разность (х 4- h)2 - х2 = h(2x + h) может
принимать сколь угодно большие значения.
Теорема 1. Пусть (X, рх), (X, Py), (X, Pz) — метрические пространства, f : X —* Y,
g : Y —> Z. Если fug — равномерно непрерывные отображения на множествах Df и Dg, то
композиция h — gof: X—tZ равномерно непрерывна на множестве Dg°f.
◄ Согласно определению равномерно непрерывного отображения
(Ve > 0)(Нт? > 0)(V(y, g Dg, у2 g Dg), pY(yi, У1) < »?) ' Pz(g(.yi), д(.У1» < e. (2)
Поскольку отображение f равномерно непрерывное, то для указанного у > 0 существует такое
6 > 0, что
V(®t g Df, х2 g P/)(px(a:i, x2) < 6) => pytftxr), f(x2)) < g. (3)
Из (2) и (3) получаем, что Ve > 0 36 > 0:
V(zi g Dgof, x2 g Dgef)(px(xi, x2) < <5) => pz{h(xi), h(x2)) < e,
§ 6. Предел и непрерывность отображения из одного метрического пространства в другое 25
т. е. отображение h = д о f равномерно непрерывное. ►
Теорема 2 (Кантор). Всякое непрерывное на компакте отображение f : X -*Y равномерно
непрерывное.
◄ Пусть Df — компакт, / — непрерывное отображение. Предположим, что / не является
равномерно непрерывным. Тогда существует такое е0 > 0 и две последовательности (хп), («/„)
точек множества Df, что рх(хп, Уп) < ~, однако ру(/(х„), /(у„)) £о- Найдется подпоследо-
вательность (хПк), сходящаяся к некоторой точке х0 6 Df (поскольку Df — компакт). Так как
px(Xnfc, Упь) < и Рх(®о, уПк) < Рх(®о, хпк) + Рх(хПк, у„к), то уп -* Хо при к -> 00. Из
непрерывности отображения f в точке х0 € Df следует, что для указанного е0 существует 6 > 0:
рх(.хо, х) < <5 => ру(/(х0), /(х)) < у. Возьмем номер к € N, при котором рх(.хо, хпк) < 5
и Рх(х0, уПк) < <5. Тогда py(/(xnJ, f(ynk)) Py(/(®„fc), /(®о)) + Ру(/(®о), /(j/nfc)) < £о, что
противоречит определению последовательностей (х„) и (уп). ►
6.6. Гомеоморфизмы. Эквивалентные расстояния.
Пусть (X, рх) и (У, ру) — метрические пространства.
Определение 1. Биективное отображение X Y называется гомеоморфизмом, если f
и непрерывны.
Такие отображения называются взаимно непрерывными. В этом случае обратное отображе-
ние является гомеоморфизмом У на X.
Теорема 1. Пусть (X. рх), (У, Py), (Z, pz) — метрические пространства, X у,
У Z — гомеоморфизмы. Тогда композиция h = д о f является гомеоморфизмом X на Z.
◄ По теореме 1, п. 6.2, биективное отображение X Z непрерывное. Пусть х0 € X.
Согласно теореме 4, п. 6.4, прообраз h~](V") каждой окрестности V" точки Л(х0) = (д ° /)(хо) в
множестве Z является окрестностью точки х0 в X. В силу этого и биекция Z £—>X непрерывна
в точке й(х0). Поскольку ха — произвольная точка, то h~' — непрерывное отображение. ►
Гомеоморфизм может не быть равномерно непрерывным, например, R<—>R, где /(х) = х3.
Определение 2. Метрические пространства (X, рх) и (У, ру) называются гомеоморфными,
если существует гомеоморфизм X У.
Теорема 2. Два метрических пространства, гомеоморфные третьему, гомеоморфны друг другу.
Ч Если пространства {X, рх), и (У; Ру) гомеоморфны пространству (Z, pz), то существуют
гомеоморфные отображения X Z и У Z. Отображение Z £—► У гомеоморфное. По
теореме 1 композиция д1 ° f является гомеоморфизмом X на У. ►
Пусть (X, pt) и (X, р2) — метрические пространства. Если тождественное отображение
х х является гомеоморфизмом, то pt и р2 называются эквивалентными или топологически экви-
валентными расстояниями в X. Из теоремы 7, п. 6.4, видно, что в этом случае в (X, рТ) и (X, р2)
совпадают семейства открытых множеств. Топологией метрического пространства (X, рх) на-
зывают семейство открытых множеств в нем. Эквивалентные расстояния порождают одну и ту
же топологию. Окрестности, замкнутые множества, точки прикосновения, замыкания, внутрен-
ность множества, множества внешних точек, плотные множества, границы, непрерывные функ-
ции являются топологическими понятиями. Топологические свойства метрического пространства
инвариантны при гомеоморфизмах. Понятия шаров, сфер, диаметра, ограниченного множества,
равномерно непрерывной функции не являются топологическими.
Глава 2
Комплексные числа
и функции
комплексного переменного
§ 1. Комплексные числа
и комплексная плоскость
В элементарном курсе алгебры возникновение понятия комплексного числа по большей части
связывают с уравнением х2 + 1 = 0. Прежде всего выясняется, что не существует действитель-
ных чисел, которые удовлетворяли бы этому уравнению. Тогда вводится в рассмотрение новое
“мнимое” число i = и указанное уравнение уже имеет корни ±г. Затем рассматрива-
ются “комплексные числа” х + iy как суммы действительных чисел х и “мнимых” чисел iy.
Правила действий с этими новыми числами позволяют проводить над ними операции, как над
действительными числами, заменяя в конечных результатах г2 на —1. После введения новых чи-
сел оказывается, что все квадратные уравнения вида х2 + рх + q = 0 и, вообще, все уравнения
вида хп + pixn~l + ... +рп_{х + рп = 0 с произвольными коэффициентами имеют решения.
Описанный способ введения комплексных чисел не может нас удовлетворить, поскольку по-
рождает взгляд на них как на объекты, не существующие реально, в буквальном смысле слова
“мнимые”.
Мы пойдем иным путем, а именно, придав схеме введения комплексных чисел геометричес-
кий оттенок.
1.1. Определение комплексного числа.
Рассмотрим плоскость R2 и каждую ее точку z = (х, у),
где х G R, у € R будем считать вектором. В соответ-
ствии с этим определим модуль z, а также операцию сложения
zt = (х,, г/]) и z2 = (х2, у2) по известным правилам для век-
торов (рис. 10)
|г| = у/х2 + У2, Z = Zj + Z2 X = xt + x2 Л у = y{ + y2. (1)
По тем же правилам Va € R полагаем az = (ax, ay).
Согласно теории векторов на плоскости, z можно раз-
ложить по векторам 1 = (1, 0) и i = (0, 1) (рис. 11):
z = х 1 + у • i.
(2)
Возникает вопрос, можно ли, сохранив равенства (1)
и (2), определяющие операции над векторами, ввести one- Рис. ю
рацию умножения точек плоскости R2, превратив их в числа, называемые далее комплексными?
Требование сохранения равенств (1) и (2) является существенным. Без них мы могли бы взять
обратимое отображение R на R2 и принять его за изоморфизм упорядоченных полей, превра-
тив R2 в мало полезное для приложений представление упорядоченного поля действительных
чисел.
§ 1. Комплексные числа и комплексная плоскость
27
Будем считать вектор 1 единицей операции умножения. Тогда, принимая во внимание ра-
венство (2), для положительного ответа на поставленный выше вопрос достаточно правильно
определить произведение i i = i2. Поскольку 1 • i = i, т. e. точку (0, 1) получим из точки (1, 0)
поворотом плоскости R2 против хода часовой стрелки на угол у, то полагают
«2 = -1. (3)
Пользуясь равенствами (2) и (3), запишем для z = (х, у) соотношения
z i = (х • 1 + у • i)i = -у • 1 + х • i — (-у, х). (4)
Точка (-у, х) получается из точки (х, у) поворотом плоскости R2 против хода часовой стрел-
ки на прямой угол (рис. 12). Поворот на другой угол можно будет задать с помощью умножения
не на г, а на другое комплексное число. Сказанное подтверждает важность для математики ком-
плексных чисел. Прибегая к ним, можно изучать важнейшие преобразования плоскости: сдвиг,
поворот, гомотетию.
Теперь запишем правило умножения точек плоскости R2. Имеем
(®i, 2Л)Се2, уТ) = (х, 1 + ух 0(z2 • 1 + У1 О = (ат^г - У\J/2>1 + (*1 У1 + x2J/i)i,
(®1, У1)(®2, г/г) = (Х|Х2 - J/1J/2, Х\У1 + x2Z/i). (5)
Определение. Числовая плоскость R2 называется комплексной плоскостью С, если для ее
точек определены модули, операции сложения и умножения по формулам (1), (5). Точки комплексной
плоскости называются комплексными числами.
Множество действительных чисел определяется однозначно лишь с точностью до изоморфиз-
ма. Поэтому комплексные числа х • 1, где х g R, дают другое представление числовой прямой R
и вполне могут быть приняты за действительные числа. Таким образом, комплексные числа со-
держат в себе все действительные, т. е. С 3 R. Отметим, что комплексные числа так же, как и
действительные, определены однозначно лишь с точностью до изоморфизма.
Упрощая запись, вместо х 1 будем писать х. С той же целью будем писать iy вместо у • i.
Тогда комплексное число z = (х, у) принимает вид z = х + iy, х € R, у € R. Числа х и у по
традиции соответственно называются действительной и мнимой частями комплексного числа z
и обозначаются символами х = Rez, у = Imz. Таким образом, комплексное число z = (х, у)
представляет собой упорядоченную пару, комплекс, составленный из действительных чисел х и у
(“комплексное” — составное ).
Название “комплексное число” предложил К. Гаусс (1777—1855), символ i ввел в рассмотрение
Л. Эйлер (1707-1783).
Число z = х — iy называется сопряженным числу z = x + iy и обозначается через z. Очевидно,
что z -z = |z|2.
Необходимо проверить, образуют ли комплексные числа поле. Очевидно, операция сложения
удовлетворяет требуемым аксиомам, поскольку отвечает операции сложения векторов. Читатель
может проверить аксиомы сложения, не прибегая к векторам, а исходя из определения суммы в
28
Гл. 2. Комплексные числа и функции комплексного переменного
условиях (1). Непосредственная проверка аксиом умножения и аксиом, связывающих сложение
с умножением, приведет к громоздким выкладкам. Этого можно избежать, если ввести другие
характеристики комплексного числа.
1.2. Аргумент комплексного числа.
Тригонометрическая и показательная формы его записи.
Умножение и деление комплексных чисел.
Операция извлечения корня из комплексного числа.
Определение. Пусть z € С и z / 0. Угол ip между радиусом-вектором точки z и ортом
действительной оси называется аргументом числа z (рис. 13).
Аргумент числа z € С, z # 0, определяется неоднозначно, а с точностью до кратного 2тг.
Множество всех значений аргумента z обозначим через Arg z. Если ip € Arg z, то Arg z = {у>+2птг |
n E Z}. За ArgO примем все множество действительных чисел. Иногда ArgO не определяют. В
множестве Argz, z / 0, существует одно и только одно
У 11 значение <р € (-тг, тг], которое называется главным и
\ обозначается argz.
2 X. . Принимая во внимание связь между декартовыми
X. г м и полярными координатами точки (т, у) плоскости R2,
\ имеем
X. x = rc<xp, y — rsinp, (1)
где х = Rez, у = Imz, г = |z|, <р € Argz. Из pa-
--------------S------------J----------->.-► венств (1) получаем тригонометрическую форму записи
0---------------------------------1 X комплексного числа
z = r(cos р + i sin <p), у? £ Argz, r = |z|, (2)
Рис. 13
которая оказывается очень удобной при умножении и делении комплексных чисел. Л. Эйлер ввел
в рассмотрение показательную функцию
ip t-t е"/> = cosy; + i sin у, <р € R. (3)
Запись комплексного числа в показательной форме принимает вид
z = re'v, г = |z|, <р 6 Argz. (4)
Следующее утверждение устанавливает основные свойства показательной функции, опреде-
ленной формулой (3).
Теорема. Пусть у> 6 R , гр € R, k £ Z. Тогда справедливы равенства:
1) е’° = 1;
2) =е<<*’+*);
3) .
5)|е’”| = 1.
◄ Указанные равенства непосредственно следуют из формулы (3) и свойств тригонометри-
ческих функций. Докажем равенство 2). По определению имеем
e've** = (cos ip + i sin y;)(cos гр + г sin гр) =
= (cos<p cos гр — siny;sin t/i) + i(sinycosi/> + cosy; sin ib) = cos(y; + гр) -I- isin(y 4- гр) — >.
Показательная форма записи комплексного числа позволяет значительно упростить операции
умножения и деления комплексных чисел. Если
z5 = Г; = |г.,|, у,-€ Argz.,- (j ~ 1, 2), (5)
ТО
*122 = (г1г2)е<(’₽'+*’2>, - = (6)
22 1*2
Таким образом, для вычисления произведения комплексных чисел нужно перемножить их
модули и сложить аргументы, а при их делении модули делятся и аргументы отнимаются.
§ 1. Комплексные числа и комплексная плоскость
29
Полезна формула Муавра (1667—1754), которая является следствием формулы (3), или может
быть установлена с помощью метода математической индукции: если z = (г cos 93, г sin р), то
Уп 6 N
zn = (г cosip, г sin уз)" = (rn cosnip, rn sin пуз). (7)
Формула Муавра позволяет извлекать корни произвольной целой степени из комплексного
числа. Пусть z = (г cos р, г sin р) и требуется найти такое комплексное число
(8)
(9)
y?-4-2fc тт
(10)
zi = (rj cos^i, г1 sin pi),
чтобы Zi — z. Тогда, в соответствии с формулой (7),
(г" cosny?|, г" sinny^) = (г cos уз, r sin уз).
Приравнивая друг другу модули и аргументы, имеем
гр = г, npi = р + 2kv, к 6 Z.
. При к = 0, п - 1 получаем п разных значений:
nr- (пГ p + 2kir . р + 2кя\
z — I vrcos----------, yr sin-------- ) .
у n n /
Они делят окружность радиуса у/r на п дуг одинаковой длины.
Поле С не является упорядоченным. В упорядоченном поле Р V(a 6 Р, Ь € Р) а2 + Ь2 =
а = 0лб = 0.В поле С это условие не выполняется, например, i2 + I2 = 0, однако i / 0, 1^0.
Отметим, что модуль комплексного числа [z| = у/ х2 + у2 удовлетворяет аксиомам нормы
(см. п. 2.5, гл. 1). Выполнение аксиом 1) и 2) очевидно. Рассмотрим на рис. 10 треугольник с
вершинами в точках 0, z2, zi + z2. Длины его сторон равны: \z2\ (от 0 до z2), |zj (от z2 до z, + z2),
\zt + z2| (от zi + z2 до 0). Поскольку длина стороны треугольника не больше суммы длин двух
других сторон и не меньше абсолютной величины их разности, то
||г11 - lz2l| «J lzt +Z2\ SC |Z,| + |Z2|.
Следовательно, модуль удовлетворяет и неравенству треугольника. Таким образом, упорядочен-
ная четверка Е = (С, +, •, 11) является нормированным векторным пространством над полем R.
Оно превратится в метрическое пространство, если в нем V(Z| £ С, :2 6 С) метрику определить
равенством
й(?1, Z2) = |Z| - z2| (И)
(см. п. 3.1, гл. 1).
Множества натуральных, целых, рациональных, действительных и комплексных чисел, не-
смотря на их существенные различия, имеют много общих признаков, таких как коммутативность
и ассоциативность операций сложения и умножения, дистрибутивность умножения относительно
сложения, существование единичного элемента относительно операции умножения. Возникает
вопрос: можно ли достичь новых результатов, расширяя понятие числа, чтобы упомянутые общие
признаки сохранились?
Ответ на поставленный вопрос дает теорема Ф. Фробениуса (1849—1917), из которой следует,
что поле С комплексных чисел является максимальным числовым полем и дальнейшее расши-
рение понятия числа невозможно.
1.3. Стереографическая проекция и ее свойства.
Для нужд теории аналитических функций комплексную плоскость С дополняют бесконечно
удаленной точкой, соответствующей условному комплексному числу оо. Множество С = С U {оо}
называют расширенной комплексной плоскостью. Для наглядного изображения расширенной ком-
плексной плоскости проведем специальное геометрическое построение.
Введем в пространстве R3 систему координат О£у£ так, чтобы плоскость С совпала с плос-
костью R2 и чтобы оси О£ и Оу совпали с осями Ох и Оу комплексной плоскости z. Построим
сферу 5 радиуса | с центром в точке (о, 0, , которая касается комплексной плоскости в начале
координат (рис. 14). Точки (£, у, 0 Е S удовлетворяют уравнению
£2 + »72 = С(1-С)- (1)
30
Гл. 2. Комплексные числа и функции комплексного переменного
Точку (0,0,1) обозначим через и будем соединять ее с различными точками сферы z'(£,
прямолинейными лучами с началом в N и отмечать на каждом луче точку z = х + iy встречи
его с плоскостью С. Тогда все точки сферы, за исключением точки IV, спроектируются на плос-
кость С. Этим установлено взаимно-однозначное соответствие z w z' между множествами С
и 5\{ЛГ}. Если условимся, что z = оо «-+ ЛГ, то получим взаимно однозначное соответствие меж-
ду множествами С и S. Это соответствие называется стереографической проекцией. Сферу S при
этом называют сферой Римана.
Установим связь между координатами точек z и z . Координаты точки z' удовлетворяют
уравнению сферы (1), а условие, что точки г, z и N лежат на одной прямой, имеет вид
е-о _Т/-0 _ С- 1
х — 0 у — 0 0—1
Следовательно,
£ Л
1-С у i-<
Принимая во внимание (1) и (2), имеем
(2)
откуда
|z|2 1
С = ———, 1 - С = --------------.
Ц l + |z|2 Ц l + |z|2
Получаем обращение формул (2):
х у ]z]2
1 + М2’ '? = 1 4- |г|2 ’ = l + |z|2
Соотношения (1), (2), (3) называются основными формулами стереографической проекции.
Стереографическая проекция имеет два важных свойства:
1) при стереографической проекции окружности всегда переходят в окружности (при этом пря-
мая на плоскости С считается окружностью бесконечного радиуса)',
2) если две кривые на сфере S пересекаются в точке М, а касательные к этим кривым в точке
М образуют угол а, то и угол между касательными к стереографической проекции этих кривых
в точке М' их пересечения также равен а, т.е. величины углов при стереографической проекции
сохраняются.
Для большей наглядности изложенного выше воспользуемся географической терминологией.
Плоскость, проходящая через центр сферы параллельно плоскости £ = 0, называется экватори-
альной. Согласно принятой терминологии, точка А € S лежит на параллели с широтой <р, если
§ 1. Комплексные числа и комплексная плоскость
31
радиус-вектор О'А с началом в центре сферы S образует угол р с экваториальной плоскостью,
причем в верхней по отношению к этой плоскости части сферы у изменяется от 0 до |, а в
нижней части сферы — от — у до 0. Точки сферы, имеющие одну и ту же широту у>, образуют
параллель данной широты. Долготой точки А(£, г/, Q 6 S называют argC^+гц). Совокупность точек
данной долготы Л образует полумеридиан этой долготы. Точка N называется северным полюсом, а
начало координат 0 — южным полюсом.
Рассмотрим примеры.
1. Представить в виде а + ib (а € R, b € R) следующие комплексные числа:
1 - г 2
zi —---------; z2 =--------------;
1 + г 2 1 - Зг
z3 = (l + i73)6;
◄ Воспользуемся правилами действий над комплексными числами и равенством zz = |z|2.
Получим:
2. Найти модули г и аргументы <р комплексных чисел а + Ы (а и b — действительные числа):
z, = Зг; z2 = —2; z3 = 1 + г; z4 = 1 - г'; z5 = 2 + 5г';
z6 = 2 — 5г; z7 = — 2 + 5г; z8 = — 2 — 5г'; z9 = bi (Ь ф 0); zI0 = a + bi.
◄ Под р понимаем главное значение: -тг < argz тг, arctgу — главная ветвь от - у до у.
Определять у легче, если изображать точку z на комплексной плоскости. Имеем
П = kil = 3, у>1 = у; r2 = |z2| = 2, у2 = тг; r3 = |z3| = 72, у3 = f; г4 = |z4| = 72, у4 =
r$ - |zs| - 729, ys - arctg |; r6 = |z6| - 729, y6 = - arctg
r7 - = 729, y7 — тг - arctg I;
r8 = |z8| = 729, y8 = arctg | - тг; r9 = |z9| = |6|, y, = f f sgn6;
По = |Ио| = va2 + b2, <pio = <
arctg |,
тг + arctg
arctg - - тг,
a > 0,
a < 0, 6^0,
a < 0, b < 0. ►
3. Доказать, что 7i имеет следующие четыре значения:
±| (л/з + Тг + гТЗ-Тг) ,
±
◄ Пусть z = i, тогда |z| = 1, argz = у =
Получаем четыре различных значения корня:
тг тг
Zq = cos — + i sin —,
8 8
9ж . . 9тг тг тг
z2 = cos — + г sin — = — cos — — i sin —,
y, tyz = cos a +^k~ + г sin -2-y^-, к = 0, 1, 2, 3.
5ir 5тг Згг Зтг
Zi = cos-----f- г sin — = — cos-----F i sin —,
1 8 8 8 8 ’
13тг 13тг Зтг Зтг
z3 = cos —-—I- i sin —— = cos —------i sin —.
8 8 8 8
32
Гл. 2. Комплексные числа и функции комплексного переменного
Поскольку | созг| = > | sin г| = с°-2х , то
4. Определить комплексные числа z, удовлетворяющие следующим двум условиям:
z - 12 _ 5 z-4
z — 8г 3 ’ z — 8
4 Так как |^|2 = = у, |fr||2 = = 1. то задача сводится к решению
системы уравнений
2г2 + 2у2 + 27г - 50г/ -4-38 = 0,
8г = 48.
Ее решения — z( = (6,17), z2 = (6, 8), т. е. z( = 6 4- 17г, z2 = 6 4- 8г. ►
5. Доказать тождество |а 4- 6|2 4- |а - 6|2 = 4|а|2, если )а| = |Ь|.
◄ Воспользуемся очевидным свойством z, ± z2 = z, ± z2 и тем, что zz = |z|2. Имеем:
|а + 6|2 4- |а - 6|2 = (а 4- Ь)(а 4- 6) 4- (а - 6)(а - Ь) = (а 4- Ь)(а 4- 6) 4- (а — 6)(а - Ь) =
= аа + ab 4- ba + ЬЬ 4- аа - ab - Ьа + ЬЬ = 2(аа + 66) = 2(|а|2 + |6|2) = 4|а|2. ►
6. Доказать тождество |1 — а6|2 - |а - 6|2 = (14- |а6|)2 - (|а| 4- |6|)2 (а € С, 6 € С).
4 Аналогично проделанному выше получим:
|1 — 36|2 — |а — 6|2 = (1 — а6)(1 — ab) — (а — 6)(а — 6) =
= (1 - а6)(1 — аб) — (а — Ь)(а — 6) = 1 - ab — ab 4- aabb — аа 4- ab + Ъа - 66 =
= 1 + |а|216|2 - (|а|2 + |6|2) = 1 + |а6|2 - (|а| + |6|)2 + 2|а6| = (1 + |а6|)2 - (|а| + |6|)2. ►
_ Iе + 6|
7. Доказать тождество -----= = о (а >0; 6 g С Л 6 -а).
|1 + 1|
4 Так как а > 0, то
|а + 6| _
а
а + 6
а
Ъ
а
6
а
6
а
8. Пусть |а| =
или |6| = 1
(а # 6). Доказать, что
а — 6
1-аЪ
= 1.
1
ТО
4 Поскольку
|а - 6|2 = (а - 6)(а - 6) = |а|2 - ab - Ьа + |6|2,
|1 - а6|2 = (1 - а6)(1 - ab) = 1 - аЬ - аЬ + |а6|2.
Если |а| = 1, то
|а - Ь|2 = 1 - ab - Ьа + |6|2, |1 - а6|2 = 1 - ab - ab + |Ь|2,
т. е. |а — Ь| = 11 - аЬ| и | | = 1. Аналогично, если |6| = 1, то | | — i
§ 1. Комплексные числа и комплексная плоскость 33
9. Модули комплексных чисел z,, z2, z3, z4 образуют геометрическую прогрессию, а их ар-
гументы — арифметическую прогрессию. Найти z2 и z3, если zt — \/2, z4 = 4г.
◄ Пусть q — знаменатель геометрической прогрессии, d — разность арифметической про-
грессии. Тогда \z2\ = |z[|g = V2q, |z3| = \zt\q2 = V2q2, |z4| = 4 = т/2д3, откуда q = \/2.
Пусть ipi = argZ; (г = ], 4). Поскольку — 0, to <p2 = d, <f>3 = 2d, <p4 = 3d. Так как
z4 = 4i = (cos 3d -I- г sin 3d), to cos 3d = 0 Л sin 3d = 1. Следовательно 3d = у + 2kir, d —
(A: £ Z). Поскольку d = q>2 = argz2, то -тг < тг. Получаем три значения d: dI =
d2 = | jf, d3 = -у и, соответственно, по три решения для z2 и z3:
z21J = 2e*^, z<2’ = 2e’T, z<3) = 2e-1f,
z^ = 2V2e^, z^ = 2V2ei5-f, z<3> = 2^2е~;’. ►
10. Решить уравнение az + bz = с (a £ С, b € С, c € C).
◄ Если z — решение данного уравнения, то z будет решением уравнения bz + az = с. Решая
систему уравнений
( az + bz = с,
1 bz + az = с,
получим, при условии что |а|2 /- |Ь|2: z =
Если |а|2 = |Ь|2, то система несовместна, за исключением случая, когда f = “ = “ При
выполнении этих условий система сводится к уравнению c&z + cbz = сс, т.е. к Z + Z — |с|2, где
Z = cdz. Последнее уравнение имеет решение Z = j |с|2 + it, —оо < t < +оо. Возвращаясь к z,
получим: z = | £ + i (i £ R). ►
11. Решить относительно z уравнение azz + bz 4- cz + d = 0 (a £ C, b £ С, c € C, d £ C).
Ч Как и в предыдущем примере, данное уравнение равносильно системе
a|z|2 + bz + cz + d = 0,
d|z|2 + bz + cz + d = 0.
Умножим обе части первого уравнения на а, второго — на а и вычтем полученное одно из
другого. Находим: (ас — ab)z — (ас - ab)z + ad — ad = 0. Обозначим (ас - ab)z = Z, тогда
последнее уравнение примет вид
Z — Z = —(ad — ad), т. е. 2г Im Z = —2i Im(ad).
Отсюда получаем
t — i Im(ad) „
Z = t — i Im(ad), t. e. z =---— -----, t € R. ►
ac — ab
12. Установить, когда выполняется равенство Re(ztz2) = (Rezi)(Rez2).
Ч Пусть Z| = г1е**’1, z2 = r2e"f‘~1, <pt £ Argz,, q>2 € Argz2. Тогда получим:
Re(z(z2) = Re(r|r2e‘<*>l+*’2)) = r^^cos^i cosy>2 - sin 7^ sin^2), (ReZ[)(Rez2) = r^cosy’i cos^2.
Указанное в условии равенство выполняется, если sin у, sin^2 = 0, т. е. когда z\ £ R или
z2 £ R. ►
Iz — a I
-—— 1 эквивалентны й
1 — az I
что равенство в обоих случаях достигается при одном и том же z.
◄ Пусть |z| 1. Рассмотрим разность
|z — a|2 — |1 — az\2 = (z - a)(z — а) - (1 — az)(l - az) =
= |z|2 — az — az -I- |a|2 — 1 + az + az — |a|2|z|2 = (|a|2 — 1)(1 — |z|2) 0.
Следовательно, |z| 1 => 1- Пусть < 1, тогда (|a|2 - 1)(1 — |z|2) 0 => |z| 1,
так как по условию |a| < 1.
34
Гл. 2. Комплексные числа и функции комплексного переменного
-g л 1 А
14. Пусть z = х 4- iy # 0. Найти — 4 —.
Z2 Z2
Ч Имеем
1 1 _ z2 4- z2 _ (х - iy)2 4- (х + iy)2 __ 1(х2 — у2)
Z2 Z2 (zz)2 (х2 4 у2)2 (х2 + У2)2 ►
15. Найти главное значение аргумента чисел zx = -2 4 Зг, zi — а 4 ib (а < 0, Ь < 0).
Ч Точка Zi лежит во втором квадранте z-плоскости, поэтому argz! = arctg (~|) 4 тг =
тг - arctg |. Точка z2 находится в третьем квадранте, поэтому argz2 = arctg - - тг. ►
16. Изобразить в тригонометрической форме числа z1 = 1 + г'л/3 и z2 = 1 — cos а + г sin а.
Ч Для z, имеем:
| = У12 + (7з)2 = 2, arg zx = arctg 7з = у.
Для z2:
|z2| = \/(1 - cos а)2 + sin2 а = 2 sin
Считая, что 0 < а < 2тг и замечая, что | argz2| < получаем
sin а а / тг а \ тг — а
sm(argz2) = ——— = cos — = sin (--- , argz2=——.
2 sin у 2 \2 2 / 2
Таким образом,
{ тг тг \ а/ тг — а тг — а \
г. = 2 cos —F i sin — ) , z2 = 2 sin — I cos —---1- i sin-- . ►
\ 3 3/ 2 \ 2 2 /
17. Выразить cos 5a: и sin 5a: через cos а: и sin a:.
Ч Согласно формуле Муавра cos 5x 4 i sin 5x = (cos x 4- i sin x)5. По формуле бинома Ньютона
имеем
(cos х 4- i sin x)5 = cos5 x 4- 5г cos4 x sin x - 10 cos3 x sin2 x - 10г cos2 x sin3 x 4- 5 cos x sin4 x 4- i sin5 x.
Отсюда
cos5x = cos5 x — 10 cos3 a: sin2 x 4- 5 cos a: sin4 x, sin 5a: = 5 cos4 x sin x - 10 cos2 a: sin3 x 4- sin5 x.
Вычислим, например, cos и sin . Имеем:
4 2?r 2 2тг 2 2тг 4 2тГ / 22тг\2 ( 2 2тг\ 2 2тг 4 2тг
0 = 5cos — -10cos — sin — 4-sin — = 5 I 1 - sin — I -10(1 — sin — I sin —4-sin —.
Обозначив sin2 у- = у, получаем квадратное уравнение 16г/2 — 20г/ 4-5 = 0, откуда
2 2тт 10 4- 275 2тг -/10 4 275
y = sin Т = -^6~’ sinT =--------------4-----•
Тогда ____________ ____________
2тг / 10 4 275 \/б — 275 75 - 1
5 V 16 4 4
18. Представить sin4 х в виде многочлена первой степени от тригонометрических углов,
кратных х.
Ч Записывая z = cos х 4- i sin х, z = cos x — i sin x, z — z = 2i sin x, получаем:
sin4 x = 2'^) = — = ~ 4zz(z2 4- z1) 4- 6z2z2 4- z4) = у cos4x - ~ cos2a: 4-
так как zk 4- zk = 2cosfcx, zz = 1, z2z2 = (zz)2 = 1. ►
§ 1. Комплексные числа и комплексная плоскость
35
1 /1 \
JL>. Найти Dn(x) = — - + cosх + cos2x + ... + cosnz I.
2тг у 2 у
п п
◄ Пусть St = cos кх, S2 = У? sin кх, z — cos х 4- i sin x. Тогда
k=0
fc=0
x2- k г"+1-1
S\ + iS2 — / z ~~ ------i—
z — 1
k=o
zn+l - 1
5i = Re--------—
z - 1
cos(n 4- 1)ж 4- г sin(n 4- l)a; - 1
Re-------------------------------
(cos ж — 1) + i sin x
cos nr - cos(n + 1)ж - cos a: 4- 1
2 — 2 cos a:
1 / 1
D„(x) = —- -- 4-51
2тг \ 2
1 sin^-z
2тг 2 sin |
В теории рядов Фурье функцию Dn называют ядром Дирихле. ►
20. Пусть Z| и z2 — смежные вершины парал-
лелограмма, z3 — точка пересечения его диагоналей.
Найти две другие вершины параллелограмма.
◄ Данные и искомые вершины выгодно рассма-
тривать в качестве свободных векторов (рис. 15). На-
чало вектора z} — z2 находится в точке г2, его ко-
нец — в точке z3. Поскольку вектор свободный, то,
помещая его начало в точку z3, получим z4 = z3 4-
(z3 — z2) = 2z3 — z2. Аналогично, z5 — z2 4- (z4 — zi) =
2z3 - z,. ►
21. Пусть |zi| = |z2| = |z3| = 1. Доказать,
что точки Zi, z2, z3 являются вершинами равно-
стороннего треугольника тогда и только тогда, когда
Рис. 15
Z| 4- z2 4- z3 — 0.
Ч Необходимость. Пусть z,, z2, z3 — вер-
шины равностороннего треугольника. Они лежат на единичной окружности с центром в начале
координат и являются корнями уравнения z3 - (cos р 4- isin^) = 0. Таким образом,
(z — zj(z — z2)(z — z3) = z3 — (zx + z2 + z3)z2 4- (zxz2 4- z2z3 4- z3zjz — Z]Z2Z3 = z3 — (cos p 4- i siny?).
Согласно известной теореме Виета Z\ 4- z2 4- z3 = 0.
Достаточность. Пусть z} 4- z2 4- z3 = 0. Обозначим q — zxz2 4- z2z3 4- z3z,. Так как
z3z3 = Z|Zj — z2z2 — 1, to q = ziz2z3(z3 4- zx + z2) = 0 и числа zx, z2, z3 удовлетворяют уравнению
z3 — ziz2z3 = 0. Его корни лежат на единичной окружности. ►
22. Решить уравнение хп '+z“ 2 4- ... 4-ж + 1 = 0 (так называемое уравнение деления круга).
◄ Достаточно решить уравнение zn - 1 = 0, поскольку
zn - 1 = (z - l)(zn-1 4- z-2 4- ... 4- z 4- 1).
n /— Hktr - .
Корни этого уравнения zk = vl = e n (fc = 0, n — 1) можно записать в виде 1, шп, Д, ...,
, где = Z[. В частности,
— 1 4- гх/З Д* 2тг 2тг 1 / г- / ~р\
ш2 = —1, ш3 =-----------, = г, и>5 — е з = cos — 4- г sin — = - ^v5 — 1 4- iV 10 4- 2v5J
(см. пример 17).
Задача представления шп в форме, содержащей лишь квадратные корни, является аналогом
задачи о построении с помощью линейки и циркуля правильного n-угольника, вписанного в
окружность единичного радиуса. ►
23. Решить уравнение 32z5 = (z 4- I)3.
4 Все корни этого уравнения удовлетворяют условию |2z| = |z 4- 1|. Если воспользуемся^,
равенствами х = у — где z = я: 4- iy, то получим равенство (х — 4- у2 = т. е.
Гл. 2. Комплексные числа и функции комплексного переменного
устанавливаем, что корни zk = rfc(cosy>fc H-isin^*,) (к = 0, 4) принадлежат окружности радиуса j
с центром в точке z — |. Полагая z = r(cos 92 + i sin <p), z + 1 = p(cos + i sin гр) (рис. 16), получаем
(2r)s (cos 5<fi + i sin 5<p) = ps (cos Sip + i sin 5ip).
Отсюда p = 2r, <p = ip + ~, к = 0, 4. По теореме
косинусов для треугольника с вершинами в точках 0, z,
г + 1 имеем 1 = 5г2 — 4г2 cos в, 9 = р — ip, а по теореме
_ 1
синусов sin ip — (5 — 4 cos б) 2 sin#. Следовательно,
1 2%fc
1*6 /- ; 3 j
^/5-4cos0fe 5
(sin 9k \
-7= +^,
•>/5 - 4 cos 9k J
к = 0, 4. ►
, Рис. 16
„2m 2m m * k__
и* л x а и r 2 /с 7Г 2
Z4. Доказать, что —------------— = I I (x - 2axcos------------la ), a > 0.
ar — a2 -L-L m
fe=i
◄ Зная один корень x = а уравнения x2m - a2”1 242ce остальные корни получим в виде
аа/2т (к = 1, 2т - 1) (см. пример 22). Поэтому
2т 2т , \/ \ / m \ / 2тп—1\ т „ .
х -а = (х - а)(х - аш2т) ... (х - аш2т) ... (х ~ аш2т ), х - <ш2т = х + а.
Поскольку ш2т = cos ^- + г sin ~ , то
к , 2т— к « r> k fc 2m —fc к fc 1
+ &2m = 2 Rea>2m, ^2m ' &2m = = 1
И
(x — aw2m)(x — aw2™~fc) = x2 - 2axcos-la2 (fc = 1, m - 1). ►
m
25. Пусть zk — произвольные точки, mk > 0 — произвольные числа (fc = 1, n), причем
n n
= 1- Доказать, что всякая прямая, проходящая через точку zQ = У ^mkzk, разделяет
h=l *=!
точки zk, если только не все они размещены на одной прямой.
-< Допустим противное: все точки zk размещены по одну сторону от прямой 7, проходящей
через точку z0. Выберем систему координат, в которой прямая 7 совместится с мнимой осью, а
точка za будет началом координат w-плоскости. Тогда точки zk будут точками wk w-плоскости,
wk = («fc - zo)e,e, где 9 — угол между прямой 7 и мнимой осью z-плоскости. Поскольку, по
п
предположению, Rew*. >0 (< 0) Vk = 1, п, то > 0 (< 0). Однако
fc=i
п п
mkwk = ^(mkZk - mkz0)e'e = 0,
fc=l Jb=l
так как
n n n n
]>2(mfcZfe ~ mkz0) = mkzk - z0 mk = mkzk - z0 = 0.
k=l fc=l fc=l fc=l
Получили противоречие, источник которого в предположении, что все точки zk размещены по
одну сторону от прямой 7.
Рассмотренная задача может быть интерпретирована следующим образом: точки zk с поме-
щенными в них массами тк не могут лежать по одну сторону от прямой 7, проходящей через
центр инерции этой системы материальных точек. ►
§ 1. Комплексные числа и комплексная плоскость
37
26. Доказать утверждение К. Гаусса: нули многочлена
Pn(z) = nanzn~' + (n - l)a„_lzn~2 + ... + 2a2z + ab ak € C, an / 0,
не могут быть размещены вне наименьшего выпуклого многоугольника, содержащего все нули
zt, z2, ... , zn многочлена Рп (рис. 17) (Д', — производная многочлена Р„).
◄ Поскольку P„(z) = а„ [|(г _ гь)> то
t=i
Рп(г) = an(z - Z])(z -z2) ... (z- zn_i) + an(z - zt)(z - z2) ... (z - zn_2)(z - z„)+...+
+ an(z - z,)(z - zri) ... (z -zn) + an(z - z2)(z - z3) ... (z - zn).
Если P'n(z*) = 0, z* zk (k = 1, n), to
P4(z*) =________________1_____________
Рп(г’) an(z* - zi)(z* - z2) ... (z* - zn) X
x (an(z*-zi)... (z*-zn_!)+an(z‘-zi)... (z’-zn_2)(z*-zn)+.. .+an(z*-z2)(z*-z3)... (z*-z„)) =
Тогда и
1 1 1
+ — + ... +.....= 0,
Z’ - Zn Z* - Zn_, Z*-Z!
откуда следует, что
Z* - Z„ Z* — Zn_, Z* - Zi
------— +---------—— + ... + — = 0.
|z’-z„|2 |z‘-zn_1|2 Iz’-zJ2
Из последнего равенства находим:
п п п
z* 5? k* - ziг2 = У7zk\z* - zbi~2’ z*= У?пч?к,
i=i k=i к=1
Рис. 17
где тк =
fe=i
Рис. 18
Таким образом, каждая прямая, проходящая через точку z*, разделяет точки zb z2, ... zn (см.
пример 25). ►
27. Доказать, что оба значения Vz2 - 1 лежат на
прямой, проходящей через начало координат и парал-
лельной биссектрисе внутреннего угла треугольника с
вершинами в точках — 1, 1, z, проведенной из верши-
ны z.
◄ На рис. 18 arg(z + 1) = а1; arg(z - 1) = а2. Тогда
arg(z2 - 1) = + а2,
Vz2 - 1 = |z2 - 1|5е* 2 (fc = 0, 1).
Значения Vz2 — 1 имеют аргументы и £цу22-+тг.
Поскольку а2 = ац + Д, то значения Vz2 - 1 имеют
аргументы О| + f и at + +чг. Угол у наклона биссек-
трисы к оси Ох равен at + ^. Следовательно, оба значения >/z2 - 1 лежат на прямой, проходящей
через начало координат, параллельной биссектрисе внутреннего угла треугольника с вершиной в
точке z. ►
38
Гл. 2. Комплексные числа и функции комплексного переменного
28. Исходя из геометрических рассмотрений, доказать неравенства:
z
И
1)
Iargzj;
2) \z - 1| < ||z| - 1| + |z| |argz|.
◄ 1) Рассмотрим рис. 19. На нем видно, что длина хорды, стягивающей дугу окружности
единичного радиуса, центральный угол которой равен | argz\, не превосходит длины этой дуги.
Знак равенства возможен лишь в случае, когда argz = 0, т.е. z g R, z > 0.
2) На рис. 20 видно, что в криволинейном треугольнике длина стороны, равная |z — 1|, не
превышает суммы длин двух других сторон, одна из которых есть дуга окружности радиуса |z|,
центральный угол которой равен | arg z |, а длина другой равна 11z | — 11. Знак равенства возможен
лишь в случае, когда argz = 0. ►
Рис. 19
Рис. 20
29. Доказать тождество |z1+z2|2 + |z|-
z2|2 = 2<|z, |2 + |z2|2) и выяснить его геометрический
смысл.
Ч Пусть zi = xt + iyx, z2 = х2 + iy2. Тогда
z{ + z2 = Xi + x2 + i(j/i + t/2),
zx - z2 = a:, - x2 + i(yx - y2),
ki + z2|2 = (Xi + x2)2 + (yt + y2)\
|z, - Z2|2 = (x, - X2)2 + (j/! - y2)2,
|zi + z2\2 + |z[ — z2|2 = 2(x2 + x2) + 2(j/J + y2) =
= 2((x? + y2) + (x22 + y22)) = 2(\zx\2 + |z2|2).
В каждом параллелограмме сумма квадратов длин
диагоналей равна сумме квадратов длин его сто-
рон. ►
30. Доказать, что если |zj = |z2| = |z3|, то
z2 — z2 1 z2
arg------= - arg —.
Z3 - Z! 2 Z1
Ч Точки zlt z2, Zi лежат на некоторой окруж- 21
ности с центром в начале координат. Рассмотрим
векторы — z2, Zi — zx, Z[, z2 (рис. 21). Угол arg = arg(z3 — z2) — arg(z3 — zx) опирается на
дугу окружности, соединяющей точки zx и z2. Центральный угол arg = argz2 — argz, опирается
на ту же самую дугу. По известной теореме из элементарной геометрии arg = 1 arg . ►
§ 1. Комплексные числа и комплексная плоскость
39
31. Доказать, что если z1 + z2 + z3 + z^ = 0 и |zj = |z2| = |z3| = |zr4|, то точки z,, z2, z3, z4
либо являются вершинами прямоугольника, либо попарно совпадают.
4 Все четыре точки лежат на окружности с центром в начале координат и при этом zx + z2 =
-(z3 + z4). Векторы zx+z2 и -(z3 + z4) совпадают по модулю
и по направлению лишь в случае, когда, например, z3 = z\,
z4 = z2 или Zi = z2, z3 = z4. В первом случае точки z(, z2,
z3, z4 — вершины прямоугольника. ►
32. Найти вершины правильного п-угольника, если его
центр находится в начале координат, а одна из вершин zx
известна.
Ч Известно, что значения '{fz лежат на окружности ра-
диуса |z| и являются вершинами правильного п-угольника.
Поэтому
= 8 '+ " ’ =[z1|e*arE^e1— =zie’—,
Рис. 22
к = 0, п — 1. ►
33. Точки z1 и z2 — смежные вершины правильного n-угольника. Найти вершину z3,
смежную с z2 (z3 # zj.
• ZZL i 2тг
-4 На рис. 22 видно, что z3 - z2 = (z2 - zt)e* „ . Следовательно, z3 = z2 + (z2 - гДе’ » . Если
_ • Zi
вершины занумерованы в обратном порядке, то z3 = z2 + (z2 — гДе ’ « . ►
34. Даны три вершины параллелограмма zb z2, z3. Найти
четвертую вершину z4, противоположную вершине z2.
Ч Рассмотрим рис. 23. Поскольку векторы z4 - zx и z3 — z2
коллинеарны, и их модули равны, то z4 — zx = z3 — z2, z4 =
Z\ + z3 — z2. ►
35. При каком условии три попарно не совпадающие точ-
ки z\, z2, z3 лежат на одной прямой?
◄ Если эти точки лежат на одной прямой, то аргументы
чисел z3 - Zf и z2 — zx либо равны, либо отличаются на it.
Поэтому отношение является действительным числом.
Полученное условие является необходимым. Докажем его до-
статочность. Пусть ^2^ = а, а С R. Тогда Im = О, что
равносильно соотношению У?~У| = Уравнение прямой,
r V2~V\ х2~х\
Рис. 23
проходящей через точки (arb ух) и (а;2, у2), имеет вид у У| = Точка (г3, г/3) лежит на этой
прямой. ►
36. Выяснить геометрический смысл указанных соотношений
a) |z - 2| + |z + 2| = 5; б) |z - 2| - |z + 2| > 3; в) Rez с; г) Imz < с.
Ч а) Равенство определяет геометрическое место точек плоскости, сумма расстояний от ко-
торых до двух данных точек F = -2 и F2 = 2 есть постоянное число 5. Из аналитической
геометрии известно, что это по определению эллипс, большая полуось которого равна |. Фокусы
эллипса — точки —2 и 2.
б) Геометрическое место точек на плоскости С, удовлетворяющих условию ||z—2| — |z+2|| = 3,
является гиперболой, первая полуось которой равна |. Равенство \z — 2| — [z + 2| = 3 определяет
левую ветвь гиперболы, а неравенство |z — 2| - |z + 2] > 3 — ее внутренность.
в) Неравенство имеет вид х с. Это множество точек, в которое входят прямая х = с и
полуплоскость, расположенная справа от нее.
г) Поскольку Imz = у, то, записав данное неравенство в виде у < с, приходим к выводу, что
ему удовлетворяют все точки полуплоскости, расположенной снизу от прямой у = с. ►
40
Гл. 2. Комплексные числа и функции комплексного переменного
37. Выяснить геометрический смысл неравенств
а) а < argz < /3; б) а < arg(z - z0) < /3 (—л < а < (3 л).
◄ а) Уравнение argz = а задает луч, наклоненный к действительной оси под углом а. Не-
равенства а < argz < 0 задают бесконечный сектор, заключенный между лучами argz = а и
argz = 0, причем сами лучи исключаются.
б) Перенесем начало координат в точку z0, полагая z - z0 = w. Неравенства а < argw < /3
задают внутренность такого же сектора с вершиной в точке z0. ►
38. Выяснить геометрический смысл следующих соотношений.
a) |z| = Rez + 1;
Z — Zi Z — Zi
в) Im--------- = 0, Re---------= 0;
Z — Z2 Z — Zi
я) \z\ < p, p E Argz, 0 $ p < 2л;
6) Re z + Im z < 1;
r) |z - 1| 2|z - i|;
e) |z| < p, p e Argz, 0 < p 2tf.
◄ а) Пусть z = x 4- iy, тогда |z| = y/x2 + y2, Rez 4- 1 = x 4- 1 и исследуемое равенство
принимает вид -^/х2 4-1/2 = х 4-1. После возведения в квадрат обеих частей последнего равенства
получим у2 = 2х 4- 1. Это уравнение параболы с вершиной в точке 0), для которой луч
7 = {(х, у) G R2 |х у = 0 } является осью симметрии.
б) Неравенство запишем в виде х 4- у < 1. Множество точек плоскости С, удовлетворяющих
этому неравенству — полуплоскость, ограниченная прямой, уравнение которой х + у = 1. Начало
координат принадлежит этой полуплоскости.
в) Поскольку (cos<£> 4- i sin^), р G Arg p = Vl - p2, pt G Arg(z - Z|),
p2 € Arg(z - z2), то в первом случае имеем sinр = 0, pt — р2 = ктг, а во втором — cos92 = 0,
Pi - Pi = 7 + 2£л. В первом случае векторы z - zt и z — z2 лежат на прямой, проходящей через
точки Z| и z2 (исключая последнюю), во втором случае угол между этими векторами с точностью
до кратного 2л равен . Поэтому множество Re = 0 является окружностью, диаметром
которой служит отрезок, соединяющий точки z\ и z2 (при этом из окружности удалена точка z2).
г) Пусть z = x + iy. Тогда |х- 1 4-iy| 2|x4-i(y- 1)|, т. е. \/ (х — I)2 4- у2 2-^/х2 + (j/ — I)2.
Возведя обе части полученного неравенства в квадрат, после несложных преобразований находим:
Множество точек плоскости С, определяемое этим неравенством, есть замкнутый круг радиуса
с центром в точке z0 = — | 4-»1.
д) Пусть |z| = г. Кривая, уравнение которой г = р, называется спиралью Архимеда. Поскольку
0 < р < 2л, то речь идет об одном витке этой спирали. Данному неравенству г < р удовлетворяет
множество внутренних точек плоскости С, ограниченное сегментом 0 5С х 2л действительной
оси и одним витком спирали Архимеда.
е) Неравенство определяет множество из предыдущего примера, дополненное интервалом
(0, 2л) действительной оси. ►
39. Определить семейства линий в плоскости С, заданных уравнениями:
a) Re - = с, Im - = с (—оо < с < 4-оо);
в)
Z — Z[
z — z2
= А (А > 0);
б) Re z2 = с, Im z1 = с (—оо < с < 4-оо);
ч 2 -21 / X
г) arg-------= а (—л < а л).
Z - z2
« а) 7 = 7П? = 5^ = { = Re| - ilm Равенство = с определяет
семейство окружностей (х — ^-) 4- уг = где ct = j, с # 0, касающихся в начале координат
§ 1. Комплексные числа и комплексная плоскость 41
мнимой оси. Если с = 0, то х = 0, т. е. семейство включает в себя и мнимую ось. Равен-
ство - -2'+у'2 = с определяет семейство окружностей х2 4- (у + ^-) = где С) = с О,
касающихся действительной оси в начале координат, и включает в себя также действительную
ось, поскольку при с = 0 у = 0.
б) Пусть z = х + iy, тогда z2 = х2 — у2 + i2xy, Rez2 = х2 — у2, Imz2 = 2ху. Если с / 0,
то уравнения х2 — у2 = с и 2ху = с определяют семейства гипербол. Если с = 0, то уравнение
х2 - у2 = 0 определяет пару прямых у = х и у = -х, а. уравнение ху = 0 — пару прямых х = 0
и у = 0.
в) Пусть z = х + iy, z, = хх + iyi, z2 = х2 + iy2. Тогда равенство [jEjf | = А (А > 0)
равносильно такому: (х - хх)г + (у - ух)2 = А2 ((я - х2)2 + (у - у2)2) • Каждая кривая — окруж-
ность, являющаяся геометрическим местом точек, отношение расстояний которых от точек zx и
z2 постоянно (окружность Аполлония относительно точек Z] и z2).
г) Поскольку arg = arg(z — zA- arg(z - z2) = a, —к < a тг, то это равенство определяет
z Z2
семейство дуг окружностей с концами в точках z, и z2 (угол между векторами z - z, и z — z2
равен а). В это семейство входит конечный отрезок с концами в точках z, и z2 (при a = ±тг) и
бесконечный отрезок, содержащий бесконечно удаленную точку (при a = 0). ►
40. Какие необходимые и достаточные условия того, чтобы уравнение z2 + 2az + b = 0 с
комплексными коэффициентами а и 6 имело: 1) действительные корни; 2) чисто мнимые корни;
3) комплекснозначные корни.
◄ 1) Необходимость. Пусть z1 и z2 — действительные корни. Тогда по теореме Виета
t Z[ + z2 = -2a, Zjz2 = b, a £ R, b £ R,
4a2 = z2 + z$ + 2b 2y/(Z[Z2)2 + 2b 4b, a2 b.
Достаточность. Пусть a g R, b £ R и a2 b. Тогда из формулы для нахождения корней
Z| 2 = —a ± Va2 — Ь следует, что Zj и z2 — действительные числа.
2) Необходимость. Пусть z1 и z2 — чисто мнимые. Тогда из формул Виета следует, что
a — чисто мнимое, b — действительное. Поэтому 4a2 = z2 + z2 + 2b Sj — 2|6| + 26 46, откуда
6 a2.
Достаточность. Если 6 a2 и a — чисто мнимое число, то из формулы для нахождения
корней уравнения следует, что оба они чисто мнимые.
3) Уравнение второго порядка всегда имеет два комплексных корня. ►
41. При каких значениях а корни уравнения z3 + 12 (1 4- гУз) z + a = 0 лежат на одной
прямой?
Ч Пусть корни этого уравнения z,, z2, z3 лежат на одной прямой. Тогда zt—z3 = k(z2 — z3),
к = const, к £ R. По теореме Виета zx 4- z2 + z3 = 0, откуда zx = —z2 - z3. Подставив z1 в
равенство z, - z3 = fc(z2 - z3), получим = kx, kx £ R. Следовательно, Im = 0, откуда
x3y2 - x2y3 = 0, Уз = — х3. Взяв вместо точки (х3, у3) любую точку (х, у) на прямой, получим
х2
прямую у = ax, а = щ, проходящую через начало координат. Поэтому имеем
х2
id ie ie
Z\ ~~ X[€ , <2'2 — X^G у Z3 — X^G )
где Xj 0 (j = 1, 2, 3). По формулам Виета получаем р = 0, qel2e = 24е*з”, ге'зе = а, где
р = —(х| + х2 4- х3), q = х1х2 + х1х3 + х2х3, г = —ххх2х3. Поскольку Xj — действительные числа,
то уравнение
х3 + рх2 + qx + r = x3 + qx + r = 0
имеет три действительных корня. Из формул Кардано следует, что коэффициенты q и г должны
удовлетворять условию
Отсюда заключаем, что q 0. Из второй формулы Виета имеем q — -24, el2e = — е з . Поскольку
0 е (“Ь 1]’ то е‘2в = = е~^, 30 = -тг.
42
Гл. 2. Комплексные числа я функции комплексного переменного
Согласно третьей формуле Виета г = -а, а 6 R. Из неравенства (1) при q = -24, г = -а
получаем, что а2 211, т. е. |а| 32х/2. ►
42. Найти все корни уравнения (z+a)n = zn (п 6 N). Доказать, что если а — действительное
число, то все корни zk лежат на прямой, параллельной мнимой оси.
◄ Уравнение эквивалентно при z # 0 уравнению tn = 1, где t = Следовательно,
. 2Ьтг --------
tk = е1 п (к = 0, п — 1). При к = 0 — 1» что невозможно, поскольку z + a # z, если a # 0.
Переходя от t к z, получим
1 1 1 - (cos^ -isin—) a (1 — cos — + i sin
= -°-----ТГТ = ~a
zl = —а-------
1-tfc
2п ~ 2/С7Г
- 2 cos —
a sin2 — + г sin — cos — а{ ктг\ ______________
= -т--------------------2- = -т(1 + гс1ё— (fc=l,n-l)
2 sin2 — 2 \ nJ
Если а € R, то Re zh = — |, т. е. все корни лежат на прямой, параллельной мнимой оси. ►
A't 1 ~ i
4э. Каковы на сфере Римана образы точек: 1) z = 1; 2) z = — 1; 3) z = i; 4) z = .
В примере речь
. Обозначив образы
1
2
(V2 V2 1
^4 — I ~7~i Д
\ 4 4 2
Ч Воспользуемся формулами (3), п. 1.3: $ = 1+^2, 7 = 1+^2, С =
идет об образах точек z{ — (1, 0), z2 = (-1, 0), z3 = (0, 1),
точек Zi соответственно через Z, (г = 1, 4), получим:
/1 1\ Д 1 1\ / 1
Д, — | 7: Д ~ I , ^2 — I — 0, — ] , Z. — I 0, Д,
\2 ’ 2/ ’ у 2 2 у \ 2
Все четыре точки лежат на экваторе, долготы их соответственно равны 0, тг, у, - 4. »-
44. Найти на сфере Римана образы: а) лучей argz = а; б) окружностей 7 = {z £ С : |z| — г}.
◄ а) Если точка z ЕС принадлежит лучу argz = а, то соответствующая ей точка Z — (£, г/, ()
имеет свойство: главным значением arg(£ + 117) является а. Поэтому точка Z принадлежит полу-
меридиану, отвечающему углу а. Справедливо и обратное. Следовательно, образом луча arg z = а
при стереографической проекции является полумеридиан, отвечающий углу а, исключая север-
ный и южный полюсы.
б) Пусть z € С и \z\ = т. Тогда для соответствующей точки Z € S, Z = (£, т/, (), по форму-
лам (3), п. 1.3, получаем, что С = . Поэтому все точки Z лежат на окружности, вырезаемой
из сферы S плоскостью, уравнение которой ( = ууд. Справедливо и обратное утверждение: из
тех же формул (3) следует, что если ( = —у, то для соответствующего z имеем |z| = г. Следова-
тельно, образом окружности 7 при стереографической проекции является окружность сферы S,
лежащая в плоскости £ = Дут. ►
45. Найти на плоскости С образ параллели с широтой tp (— ’Д Д < ’Д) при стереографи-
ческой проекции. Чему соответствуют южный и северный полюсы?
◄ Пусть точки (£, т], О Е S имеют широту <р. Тогда С = | + Поэтому из формул (3),
п. 1.3, находим
= = w = 1E(S + n
1 — £ 1 - sin у \ 2 4/
Каждой точке параллели широты ip соответствует точка плоскости С, находящаяся на окружности
7 = {z € С : |z| = tg + j) } . Обратное утверждение также справедливо. Южный полюс, т. е.
точка широты ip = соответствует точке |z| = 0. Точки, отвечающей северному полюсу, в
плоскости С нет. ►
46. Что соответствует на сфере Римана семейству параллельных прямых на плоскости С при
стереографической проекции?
◄ Рассмотрим семейство параллельных прямых плоскости С, пересекающих ось Оу. Пусть
прямая этого семейства проходит через начало координат и наклонена к оси Ох под углом а.
§ 2. Топология комплексной плоскости 43
Тогда из задачи 44 следует, что ей соответствует меридиан (за исключением северного полюса) с
долготой а.
Пусть у = кх + Ь, к = tga — любая другая прямая этого семейства. Тогда, если точка
Z = (£, у, 0 € S соответствует точке z = х + iy, по формулам (3), п. 1.3, получаем
х kx + b \z\2
= 1 + И2’ 7?= 1 + |z|2 ’ = 1 + И2’
Отсюда у = к£ + = к£ + Ь(1 - (). Поэтому координаты 0 у, С точки Z удовлетворяют
уравнениям
2 2 / iV 1
k£-y-bC = -b и £ + т? =-
Следовательно, точка Z принадлежит окружности, определяемой двумя последними уравне-
ниями. Так как точка (0, 0, 1) удовлетворяет этим уравнениям, то все такие окружности проходят
через северный полюс.
Таким образом, всякому семейству параллельных прямых на плоскости С отвечает на S се-
мейство окружностей, каждая из которых проходит через северный полюс. ►
47. Доказать, что при стереографической проекции окружности, расположенные на сфере,
проектируются в окружности или в прямые на плоскости. Какие окружности на сфере соответ-
ствуют прямым на плоскости?
◄ Рассмотрим на сфере Римана окружность
Г Л£ + Ву + СС, + D = О,
( £2W + (<-D2 = b
где А, В, С, D — некоторые действительные числа. Найдем образ этой окружности при стерео-
графической проекции сферы S на плоскость С.
Пусть точка (0, 0, 1) принадлежит данной окружности. Тогда D + С = 0 и уравнение плос-
кости, в которой лежит заданная окружность, примет вид А£ + Ву = С(1 — £). Принимая во
внимание формулы (2) и (3), п. 1.3, получаем в плоскости С прямую Ах + Ву = С, которая и
есть образ данной окружности.
Из формул (3), п. 1.3, получаем, что £ = (1 — 0х, у = (1 — 0у. Поэтому из уравнения
плоскости Л£ + Ву + СС, + D = 0 следует, что £ = 1 + Ax^gy_c Тогда, подставляя выражения £,
у, С через х и у в уравнение сферы, получаем уравнение кривой в плоскости С:
(D + С)(х2 + у2) + Ах + By = —D.
Если С + D # 0 (т. е. заданная на сфере Римана окружность не проходит через северный
полюс), то эта кривая является окружностью на плоскости С, а если С + D = 0 (т. е. окружность
на сфере проходит через северный полюс), то она переходит в прямую на плоскости С. ►
§ 2. Топология комплексной плоскости.
Последовательности комплексных чисел.
Свойства функций,
непрерывных на компакте
2.1. Топология комплексной плоскости.
В пункте 1.2 показано, что упорядоченная четверка Е = (С, +, •, | |) является норми-
рованным векторным пространством над полем R. Поэтому упорядоченная пара (С, р), где
V(zj G С, z2 € С) p(zx, гг) = |z2 - z,| = y/(x2 - Zi)2 4- (y2 - yO2, есть метрическое простран-
ство. В множестве С введем в рассмотрение так называемую сферическую метрику р.
44
Гл. 2. Комплексные числа и функции комплексного переменного
Пусть t]i, £|), Z2(£2, t?2,£2) — сферические изображения точек zt 6 С, z, 6 С. Хор-
дальным расстоянием fc(Z,, Z2) между точками Z\ и Z2 называется евклидова норма вектора
(6 - 6, 'll - Hi, <2 - <1)> т.е. k(Zi, Z2) = - fi)2 + ('ll - ’h)2 + «2 - Ci)2 - Полагаем
V(Z| € C, z2 € C) p(z|, z2) = k(Z\, Z2). (1)
Согласно основным формулам стереографической проекции имеем
f = ж‘ f = Х1 = У1 = Уг Г = l^il2 , _ Ы2
41 l + |z,|2’ ^2— l + |z2|2’ Ш~1 + Ы2’ 772 l + |z2|2’ 1 + |Z1|2’ С2 l + |Z2p-
Следовательно, если 6 С, z2 6 С, то
2
-2, . / Х1 *1 X
Р (zb zz) = ГТr~f2 ~ Т~, |~12
V + N2 i + lzil27
lzil2
i + hl2
У1_____________Vi V ( |г2|2
ч I + Ы2 i + lzil2J V + N2
|г2|2 2(х:х2 + y1y2 + |z1|2|z2|2)
+ 1 + Ы2
hl2 \
i + l^l27
lz2 ~ 2l|2
(1 + |z,|2) (1 + |z2|2)
|z2 - Zl|
(1 + |z,|2)(l + |z2|2)’
p(zi, z2) = . г-------- ..
V77 + lZl|2 \/7 + 1гз|2
Если z £ С, то p(z, оо) =f -/.1= |2. Таким образом,
—- .-= .=—------- , если zi € C, z2 6 С,
v 1+ IZ1I v 1 + l^l2
—. если Zi EC. z2 = oo.
л/1 + lzil
Упорядоченная пара (С, p) является метрическим пространством.
Заметим, что в множестве С можно пользоваться сферической метрикой. Пусть А С С —
ограниченное множество (напомним, что согласно определению 5, п.3.2, гл.], применительно
к метрическому пространству (С, р), множество А называется ограниченным, если его диаметр
с/(Л) = sup p(zi, z2) = sup |z2 - zi| конечный). Пусть 0 < R < +oo и Vz £ Л |z| R.
Z]EA, zjGA 216Д, z2EA
Тогда V(Z| E A, z2 € А) имеем
Xzb zz)
1 +R2
P<zi, z?) =
lz2 -zll
•\/1 + lzl|2 a/1 + lz2p
P(2!, Z2).
(2)
В рассмотренном случае метрики р и р эквивалентны.
Топологией в метрическом пространстве (ТС, р) называется семейство открытых множеств в
нем (см. п. 6.6, гл. 1). Топология в пространствах (С, р) и (С, р) осуществляется путем введения
в рассмотренные семейства окрестностей.
Пусть е > 0 и z0 € С. Согласно определению 1, п. 3.2, гл. 1, множество
Oe(z0) = {z € С : \z - z0| < е}
называется е-окрестностью точки z0 в метрическом пространстве (С, р). В метрическом про-
странстве (С, р) е-окрестностью точки z — оо является множество
Ог(оо) = {z 6 С : p(z, оо) < е} = < z € С :
z е С : |z| >
т. е. множество всех точек комплексной плоскости С, лежащих вне окружности радиуса
=
1
е--1'
§ 2. Топология комплексной плоскости 45
Согласно определению 2, п. 3.4, гл. 1, точка z£AGC(z£AcC) называется внутренней,
если существует ее е-окрестность О Az) С А. По определению 1, п.З.З^гл. 1, множество G С С
(G С С) называется открытым в метрическом пространстве (С, р) ((С, р)), если оно состоит
лишь из внутренних точек. Согласно теореме 1, п. 3.3, гл. 1, каждая е-окрестность в метрическом
пространстве (С, р) ((С, р)) является открытым множеством.
Определение 1. Совокупность всех открытых множеств в комплексной плоскости С (С) назы-
вается топологией т этой плоскости, а упорядоченная пара (С, т) ((С,г)) — топологическим
пространством. _
Топологическое пространство (С, т) (\С,т)) обладает свойствами:
1) объединение любого семейства (6'м);1£/1 открытых множеств GM С С (GM С С) и пересечение
конечного семейства их являются открытыми множествами (см. теорему 2, п. 3.3, гл. 1);
2) пустое множество 0 и множество С (С) являются открытыми множествами.
Согласно определению 3, п. 3.5, гл. 1, точка z0 £ С (z0 € С) называется точкой прикосновения
множества А С С (Л_С С), если любая ее <5-окрестность Ог(г0) имеет с А непустое пересечение.
Точка z0 € С (z0 £ С) называется предельной для множества А С С (А С С), если она является
точкой прикосновения множества Л\{г0}. Изопределения предельной точки множества А следу-
ет, что любая ее 6-окрестность содержит бесконечное множество точек из А (см. теорему 4, п. 3.5,
гл. 1). Из неравенств (2) следует, что если z оо — предельная точка множества А в топологи-
ческом пространстве (С, т), то она имеет такое же свойство в пространстве (С, т) и наоборот.
Поэтому при определении конечных предельных точек можно пользоваться как евклидовой, так
и сферической метрикой. В этом смысле метрики р и р эквивалентные.
Очевидно, что конечное множество А С С не имеет предельных точек.
2.2. Замкнутые множества, отрезок и ломаная. Связные множества.
Согласно определению 1, п. 3.5, гл. 1, множество F С С (F С С) называется замкнутым,
если его дополнение CF является открытым множеством. Замкнутое множество F содержит все
свои точки прикосновения. Множество всех точек прикосновения множества А С С (А С С)
называется его замыканием и обозначается А (см. определение 2, п. 3.5, гл. 1). По определению 5,
п. 3.5, гл. 1, точка z Е С (z Е С) называется граничной точкой множества А С С (А С С), если
она является точкой прикосновения как А, так и СА. Множество дА всех граничных точек
множества А называется его границей. Оно замкнуто и может быть пустым.
Пусть Z[ £ С, z2 £ С. Множество {z £ С : z = tzi + (1 — t)z2, t £ [0, 1]} называется отрезком
на плоскости С, соединяющим точки z\, z2, и обозначается [zt, z2], Точки z, и z2 называются
его концами. Отображение t i-> z(t), где z(t) = tz{ + (1 — i)z2 Vi £ [0, 1], называется параме-
трическим представлением отрезка [гь z2]. Непрерывная функция [а, Ь] Л R называется ломаной
(кусочно-линейной), если ее график на плоскости R2, отождествленной с плоскостью С, состоит
из конечного числа отрезков. _
Определение 1.Открытое множество G С С (G С С) называется связным, если любые две
его точки можно соединить ломаной, все точки которой принадлежат этому множеству.
Определение 2. Замкнутое множество F С С называется связным, если его нельзя разбить
на две части, расстояние между которыми положительно.
Понятия связности открытых и замкнутых множеств существенно отличаются.
Определение 3. Связное открытое множество называется областью.
Определение 4. Замыкание области называется замкнутой областью.
2.3. Последовательность комплексных чисел и ее предел.
Последовательностью (zn) точек метрического пространства (С, р) называется отображение
N -4 С (см. общее определение последовательности точек в п. 1.8, гл. 1).
Рассмотрим некоторые вопросы теории последовательностей точек метрического простран-
ства, изложенные в § 3, гл. 1, применительно к последовательностям комплексных чисел.
Определение 1. Точка z £ С называется пределом последовательности (zn) (при этом
записываем z = lim zn или zn —► z), если
п—»оо
(Ve>0)(3ne £N)(Vn ^ne):p(z„1z) = |z„-z|<c. (1)
46 Гл. 2. Комплексные числа и функции комплексного переменного
В этом случае последовательность называется сходящейся. Из определения следует, что начи-
ная с некоторого номера n£ £ N все члены последовательности (zn) содержатся в е-окрестности
точки z £ С. Вне окрестности Os(z) могут находиться лишь точки zb z2, ... , zne _!, множество Z
которых ограниченное. Согласно теореме п. 3.2, гл. 1, объединение O£(z) и Z двух ограниченных
множеств является ограниченным множеством. Следовательно, сходящаяся последовательность
ограниченная (ЗМ £ R : Уп € N |z„| М). Для обозначения ограниченных последовательно-
стей (zn) комплексных чисел будем пользоваться символом Ландау z„ — 0(1).
Определение 2. Последовательность (zn) имеет пределом оо (при этом записываем
lim zn = оо или zn —» ос), если
п—
(Уе > 0)(3ns £ N)(Vn пс) : p(zn, со) < е. (2)
Из определения 2 следует, что, начиная с некоторого номера ne £ N, все члены последова-
тельности (zn) удовлетворяют неравенству |zn| > - 1| (см. п.2.1), т.е. находятся вне круга
радиуса Ry — \ 1^ - 11. Условие lim zn = оо равносильно тому, что lim |z„| = +оо.
е V п—*ос п—
Для несобственного комплексного числа оо понятия действительной и мнимой частей, а
также аргумента не вводятся.
Согласно теореме 1, п. 3.1, гл. 1, сходящаяся в метрическом пространстве (С, р) последова-
тельность (z„) имеет единственный предел.
Теорема 1. (zn ~ z) (Rezn —> Rez) Л (Imzn —> Imz).
•4 Необходимость. Пусть zn -* z, тогда p(zn, z) = \zn — z\ —> 0, и из неравенств
| Rezn - Rez| |zn - z|, | Imzn - Imz| |zn - z|,
выполняющихся Vn € N, следуют требуемые свойства
Rezn —>Rez, Imz„-+Imz.
Достаточность. Пусть Rezn —» Rez, Imzn —> Imz. Тогда \z„ — z\2 = (Rez„ - Rez)2 +
(Im zn - Imz)2 —► 0 при n —► оо, t. e. z„ —> z. ►
Таким образом, сходимость последовательности (zn) комплексных чисел равносильна схо-
димости двух последовательностей действительных чисел (Rezn) и (Imz„). Это позволяет пе-
ренести всю теорию пределов последовательностей действительных чисел на последовательности
комплексных чисел. В частности, из ограниченности последовательностей (Rezn) и (Imz„) не-
медленно следует ограниченность последовательности (zn). Сформулируем теоремы для последо-
вательностей комплексных чисел, которые следуют из теорем для последовательностей действи-
тельных чисел.
Теорема 2. Пусть (zn) и (О — сходящиеся последовательности комплексных чисел. Тогда их
сумма (z„ +(„), произведение (zn, (п) и частное (т^-) (приусловии, что Vn £ И # О Л lim #
п—>ос
0) также являются сходящимися последовательностями и при этом
z lim z„
lim (zn +<„) = lim zn + lim <n, lim (zn<n) = lim zn lim <n, lim ~ -.
n—►oo n—>oo n—► ©© n—*oo n—>oo n—»oo n—*cx> in lim in
n—»oo
Теорема 3 (критерий Коши). Последовательность (z„) сходится тогда и только тогда,
когда она фундаментальная, т. е.
(Те > 0) (3ne £ N)(V(n пе, р 6 N)) : p(zn+p, z„) = |z„+p - zn| < е (3)
(см. определение фундаментальной последовательности в п. 3.1, гл. 1).
Поскольку метрическое пространство (R, р), где р(х, у) = |х — у\ Т(х € R, у £ R), полное,
то в силу теоремы 1 полным является и метрическое пространство (С, р), где p(zb z2) = |z2 — zj
V(zt € C, z2 £ C).
Теорема 4. Пусть последовательность (zn) сходится и z = lim z„. Тогда любая ее подпосле-
п—»оо
дователыюсть (z„k) также сходится и lim znk = z.
§ 2. Топология комплексной плоскости
47
Теорема 5 (Больцано — Вейерштрасса). Всякое бесконечное ограниченное множество
Z С С имеет хотя бы одну предельную точку в С.
◄ Пусть (zn) — произвольная последовательность точек множества Z. Она ограничена,
поскольку множество Z ограниченное. Тогда и последовательности (Rezn), (Imzn) ограничены.
Согласно теореме Больцано—Вейерштрасса для последовательностей действительных чисел, из
последовательности (Rezn) можно выделить сходящуюся подпоследовательность (Reznj.). Пусть
lim Reznjt = х, х € R. Рассмотрим подпоследовательность (lmznfc). Она ограничена, поэтому
fc—»ое
из нее можно выделить сходящуюся подпоследовательность (lmz„, ). Пусть lim Imzn, = у,
\ Л-’ТП / **
т—*'Х>
у £ R. В силу теоремы 4 Rezni> х при т —» оо. Рассмотрим подпоследовательность (znk )
последовательности (zn). По теореме 1 lim znk = z = х + iy, z 6 С. Согласно определению 4,
п. 3.5, гл. 1, z является предельной точкой множества Z. ►
Определение 3. Точка z £ С (z £ С) называется частичным пределом последователь-
ности (zn) или ее предельной точкой, если из нее можно выделить подпоследовательность
(z„k), предел которой равен z.
Из теоремы 4 получаем следствие: если последовательность (zn) сходится и точка z £ С —
ее частичный предел, то lim zn = z.
n—»oc
Следует различать предельные точки множеств и последовательностей. Например, последо-
вательность (zrt), где zn = (—1)п имеет две предельные точки: z( = — 1 и z2 = 1, а конечное
множество {—1,1} предельных точек не имеет.
2.4. Свойства компакта К С С.
Все необходимые определения и результаты, относящиеся к свойствам компактных множеств
в метрических пространствах, изложены в § 4, гл. 1. Рассмотрим свойства компакта в метрическом
пространстве (С, р).
Определение 1. Пусть К С С. Множество К называется компактным в себе или ком-
пактом, если из любой последовательности (zn) точек z„ € К можно выбрать подпоследователь-
ность (znk), сходящуюся к некоторой точке z0 € К (см. определение 1, § 4, гл. 1).
Теорема 1 (об ограниченности компакта). Каждый компакт К С С является ограни-
ченным множеством.
◄ Пусть, вопреки утверждению, компакт К не ограничен. Тогда существует такая после-
довательность (zn), что |z„| > п и Vn £ N zn £ К. Из (z„) нельзя выбрать ограниченную
подпоследовательность и, тем более, сходящуюся. Получили противоречие, источник которого в
предположении, что компакт К не ограничен. ►
Заметим, что согласно теореме Хаусдорфа компакт К С С вполне ограничен в метрическом
пространстве (С, р), т. е. Ve > 0 для него имеется в С конечная е-сеть. Поскольку метрическое
пространство (С, р) полное, то по теореме Фреше каждое вполне ограниченное в нем множество
компактно.
Следует также отметить, что не всякое ограниченное множество Z С С является компактом.
Например, множество Z = {z 6 С : |z| < 1} ограниченное, но не компактное в себе, поскольку
любая подпоследовательность последовательности (zn = ^7) его точек сходится к 1 £ Z. Ана-
логично, если множество Z С С имеет предельную точку z0 £ Z, то оно не является компактом.
Теорема 2 (критерий компактности в себе). Множество Z С С является компактом
тогда и только тогда, когда оно одновременно замкнуто и ограничено.
Необходимость. Пусть Z — компакт. Согласно теореме 1 множество Z ограничено.
Допустим, что оно не замкнуто. Тогда существуют такая точка z0 £ Z и такая последователь-
ность (zn), что Vn £ N zn £ Z Л lim zn = z0. Любая подпоследовательность (zn ) сходится к
п—»оо
z0 £ Z, что противоречит определению компакта. Источник противоречия — в предположении,
что множество Z не замкнуто. Следовательно, Z — замкнутое множество.
Достаточность. Пусть множество Z С С замкнутое и ограниченное. В силу замкнутости
оно содержит все свои точки прикосновения (см. п. 3.5, гл. 1). Рассмотрим любую последователь-
ность (zn) его точек. Поскольку она ограничена, то, согласно теореме Больцано—Вейерштрасса
48 Гл. 2. Комплексные числа и функции комплексного переменного
(см. теорему 5, п. 2.3), существует подпоследовательность (z„t), сходящаяся к некоторой точ-
ке z е С. Так как множество Z замкнутое и Vn € N zn £ Z, то z € Z. Согласно определению 1,
множество Z компактное в себе. ►
Теорема 3 (Бореля — Лебега). Из любого покрытия компакта К С С бесконечным семей-
ством (G„')aeA открытых подмножеств Ga С С можно выделить конечное покрытие.
Ч Утверждение является частным случаем теоремы 6, § 4, гл. 1. ►
2.5. Предел и непрерывность функции комплексного переменного.
Понятие отображения из одного множества в другое дано в п. 1.8, гл. 1. Предел, непрерыв-
ность, а также свойства непрерывных отображений из одного метрического пространства в другое
рассмотрены в § 6, гл. 1. Будем изучать отображения f : С -+ С и f : R —> С. При этом результаты,
изложенные в § 6, автоматически имеют силу в рассматриваемых случаях.
Задание комплексной функции комплексного переменного w = /(z), z Е Df, равносильно
заданию двух функций u : R2 —> R и « : R2 R с областью определения Df С R2. При этом
функция и называется действительной частью функции /, а функция v — ее мнимой частью,
т.е. и = Re/, v = Im/, /(z) = u(x, у) + iv(x, у). Таким образом, изучение функций / : С —> С
сводится к рассмотрению свойств двух числовых функций и н v двух независимых переменных
хну.
В теории функций комплексного переменного биективное отображение области G С С на
область D С С
g--d
принято называть однолистной функцией. Это означает, что
(zi £ G, z2 Е G N zx z2) => f(zt) # /(z2).
Определение 1. Пусть f : С —> С и za — предельная точка множества Df. Число а £ С
называется частичным пределом функции f в точке z0, если существует такая последова-
тельность (zn) точек множества Df, что
(zn z0) A (Vn £ N zn / z0) A ( lim f(zn) = a). (1)
Множество всех частичных пределов функции / в точке zn обозначим через Ef(z<>).
Определение 2. Если множество Ef(z0) содержит лишь число а, то оно называется пределом
функции f в точке z0 и обозначается символом lim f(z).
z->z0
Определение 3. Функция f называется непрерывной в точке z0 € Df, если lim f(z„) =
2—z0
f(zg) всякий раз, как только zn —> z0 A Vn £ N zn £ Df.
Если z0 £ Df и является предельной точкой множества Df, то / непрерывна в точке z0 тогда
и только тогда, когда lim f(z) = f(z0).
2 —Z0
В изолированной точке z0 £ Df каждая функция / непрерывна.
Функция /, не являющаяся непрерывной в точке z0 £ Df , называется разрывной в ней.
Пусть zg £ Df — предельная точка множества Df. Она называется точкой устранимого
разрыва для функции /, если существует lim /(z) = а, ст £ С и a # /(zo)- В этом случае
20
функция <р, определенная условиями
(z} = Г Л2), если z £ Df\{zg},
’ la при Z = Zg,
непрерывна в точке z0.
Иногда говорят: “функция / называется непрерывной в точке z0 € Df, если ее приращение
в этой точке бесконечно мало всякий раз, как только бесконечно мало приращение аргумента”. В
этой формулировке под бесконечно малым приращением аргумента понимают бесконечно малую
последовательность (Azn) = (zn - z0), z0 £ Df, z„ £ Df 4n £ N, а под приращением функции /
подразумевают последовательность
(A/(z0, Дг„)) = (/(zo + Az„) - /(z0)) = (Ж) - /(z0)).
§ 2. Топология комплексной плоскости
49
2.6. Арифметические операции над пределами и непрерывными функциями.
Теорема 1. Пусть функции fug непрерывны в точке Zq 6 Df и Dg = Df. Тогда непрерывны
в этой точке функции f + g, f — g, fg. Если дополнительно g(z0) # 0, то функция £ непрерывна в
точке z0.
◄ Пусть zn -> Zq и Vn е N zn e Df = Dg. Тогда /(z„) -► /(z0), g(zn) -► g(z0) и, согласно
теоремам о пределах последовательностей, имеем
lim (/(zn)±p(z„)) = f(z0)±g(z0), lim f(zn)g(zn) = f(zQ)g(z0), lim
7 „-»oo g(zn) g(z0)
Согласно определению 3, п.2.5, функции f ±g, fg, £ непрерывны в точке z0. ►
Теорема 2. Пусть za — предельная точка множества Df 'iDr Если
lim /(z) = a, lim g(z) = [3,
Z^ZO z-
mo
lim (/ ± g) (z) = a ± (3, lim {fg) (z) = afi.
z—>zo z->zo
Если /3 /0, mo
(f\ a
lim I - (z) = -.
Z —Z|) / p
Ч Пусть (z„) — такая произвольная последовательность комплексных чисел, что z„ —> z0 Л
z„ € Df П T>3\{z0}. Тогда, согласно теоремам о пределах последовательностей, имеем
lim (f(zn) ± t?(zn)) = а ± 0, \im (fg)(zn) = а0, lim (-)(z„)=-.
п,—*ос n—>CC n—►ОС \ Q J P
Согласно определению 2, п. 2.5, указанные свойства равносильны утверждению, содержащемуся
в теореме. ►
2.7. Предел и непрерывность композиции функций.
Теорема 1 (о непрерывности композиции функций). Пусть функция f непрерывна
в точке z0 Е Df, а функция р непрерывна в точке (0 С Dv. Если р(£о) = z0, то композиция f ° р
непрерывна в точке (q.
◄ Утверждение является частным случаем теоремы 1, п. 6.1, гл. 1. ►
Справедливо ли аналогичное утверждение для композиции функций f ° р, имеющих пре-
делы в точках zQ и (о? Приводимый ниже пример дает отрицательный ответ на этот вопрос.
Теоремы о пределе композиции, которые будут доказаны, требуют дополнительных ограничений,
накладываемых на функции f и р.
Пример. Пусть / : С —► С, р : С —► С, где
f 1, если z = 0, f еСЛИ C = T<neN)’
J 2 ~ | 0, если z € С\{0}, если
Г 0, если С = (n € N);
Тогда lim f(z) = 0. lim р(() = 0. Вместе с тем (/ о р)(() = < г . , . и
г—о С->о 1, если £ £ \ ~ |n С Nj >
EfQV>(0) = {0, 1}, т. е. lim(/ о р) (0 не существует.
С^о
Теорема 2 (о пределе композиции функций). Пусть Со — предельная точка множе-
ства DfQI/>. Если lim f(z) = a, lim p(Cf) =*z0 и существует такая окрестность Oio точки Со,
что VC 6 (О(о П £>/о^)\{Со} Р(С) + zo, то lim (/ о <p)(Q = а.
С—
- 4 Пусть (£„) — такая последовательность, что —► Со и Vn € N \{С0}. Тогда
гп = Т’К") го Л z„ е £>/\{z0}. Поэтому f(z„) = (f о р)(Сп) —► а при п —► оо. Согласно
определению, lim (/ °р)(£) = а. ►
50
Гл. 2. Комплексные числа и функции комплексного переменного
Теорема 3. Пусть £о — предельная точка множества Dfov. Если lim <р(£) = z0 и функция f
С~*Со
непрерывна в точке zq , то lim (/оу>)(0 =/(z0).
С—'Со
◄ Полагаем
¥>(0, если- ( € ДД{Со},
V (Q> ~ ( 20 ПРИ < = (о.
Функция <р* непрерывна в точке Со • Согласно теореме 1, функция f ° <р* непрерывная в этой
точке. Поэтому
lim (J оу) (О = lim (J о <р*) (С) = (/ о у>*)«0) = /(z0). ►
С—*Со С-*Со
2.8. Свойства функций, непрерывных на компакте.
Теорема 1 (о непрерывном образе компакта). Пусть / : С —» С — непрерывная функ-
ция и Dj— компакт. Тогда множество Ef компактное в себе, т. е. непрерывный образ компакта
есть компакт.
◄ Утверждение является частным случаем теоремы п. 6.1, гл. 1. ►
Определение. Функция / : С -» С называется ограниченной на множестве Df, если
существует такое число ЛГ € R, что Vz g Df \f(z)\ M.
Теорема 2 (Вейерштрасса). Пусть f : С -» С — непрерывная функция и Df — компакт.
Тогда функция f ограниченная, а ее модуль достигает на множестве Df своих наибольшего и наи-
меньшего значений.
М Согласно теореме 1, множество Ef является компактом, т. е. замкнутым ограниченным
множеством. По определению 5 (см. п. 3.2, гл. 1) его диаметр
d(Ef) = sup p(W|, w2)
wj €Ef, wiEEf
есть конечное число,,т. е. d(Ef) € R. Согласно следствию из теоремы п. 3.2, гл. 1, Vw0 € С множе-
ство Ef содержится в замкнутом шаре Ог(шо), где г = inf p(w0, w) + d(Ef). Взяв wa = 0, полу-
чим, что множество Ef содержится в некотором замкнутом шаре конечного радиуса R с центром
в начале координат. Поэтому Vz 6 Df |w| = |/(z)| R, т. e. функция f ограничена. Отожде-
ствим комплексную плоскость С с плоскостью R2. Тогда непрерывная ограниченная функция |/|
принимает на замкнутом ограниченном множестве Df С R2 свои наибольшее и наименьшее зна-
чения, согласно теореме Вейерштрасса для непрерывной функции <р : R2 —» R. Следовательно,
существуют такие точки Z| 6 Df, z2 g Df, что |/(zj)| = inf |/(z)|, |/(z2)| = sup |/(z)| и
z^Df z&Df
& Df выполняются неравенства |/(z()| |/(z)| |/(z2)|. ►
Замечание. При определении непрерывной функции / в точке zq предполагали, что /(zq) £ оо. При
изучении отображений множеств с помощью аналитических функций целесообразно отказаться от этого
ограничения и считать функцию / непрерывной в точке zq, где f(zo) = оо, если lim /(z) = оо. В этом
случае функцию f называют обобщенно-непрерывной. Например, функция С С, где
{|, если z g С\{0, оо},
О при z = оо,
оо при z = О,
обобщенно-непрерывная в плоскости С. Для нее lim /(z) = 0 = f(oo), lim /(z) = оо = /(0).
z —*oo z —*0
§ 3. Непрерывные и гладкие кривые.
Односвязные и многосвязные области
В курсе математического анализа рассматривается понятие производной вектрр-функции f :
R -+ Rm, Df = [а, Ь], где f — (ft, h, , — упорядоченный набор функций fj (j = 1, m).
§3. Непрерывные и гладкие кривые. Односвязные и многосвязные области 51
Вектор-функция f дифференцируема на сегменте [а, Ь] тогда и только тогда, когда на нем диф-
ференцируемы функции fj, и при этом Vt € [a, b] f'(t) = (/[(t), /г(0> • , /™(t)) (в точках а и 6
речь идет об односторонних производных). Отображение [а, Ь] *’ с можно рассматривать
как вектор-функцию р = (y>i, V2) С R2. Тогда, если функции и р2 дифференцируемы на сег-
менте [а, Ь], функция р также дифференцируема и Vt € [а, Ь] ^'(t) = p\(t)+ip2(t) = ^(t)).
Определение 1. Множество 7 С С (или 7 С R2) называется непрерывной кривой (тра-
екторией), если существует непрерывное отображение [а, Ь] 7. При этом отображение р
называется параметрическим представлением кривой у.
Из курса математического анализа известно, что отображение р = (pt, р2) непрерывно то-
гда и только тогда, когда функции pt и р2 непрерывны. Для каждой непрерывной кривой 7
фиксируется одно из двух взаимно противоположных направлений движения подвижной точ-
ки t € [а, Ь], соответствующее возрастанию или убыванию параметра. В первом случае р(а) есть
начало, р(Ъ) — конец кривой, а во втором случае эти точки меняются местами. Кривая, началь-
ная и конечная точки которой совпадают, называется замкнутой. Если 7 С Z С С (7 С Z С С),
то говорят, что кривая 7 лежит в множестве Z или содержится в нем.
Если одна и та же точка кривой 7 соответствует двум или более различным значениям пара-
метра, из которых по крайней мере одно отлично от а и от Ъ, то такая точка называется кратной.
Непрерывная кривая, не имеющая кратных точек, называется жордановой или простой. Другими
словами, кривая 7 С С называется жордановой, если ее параметрическое представление р явля-
ется биективным отображением. Если р(а) = р(Ь), то жорданова кривая называется замкнутой.
Пусть р и ф — параметрические представления непрерывной кривой 7, D.? = [а, Ь],
Dv = [аь bi]. Они называются эквивалентными, если существует такая непрерывная возрастаю-
щая функция [а, Ь] —[я|, Ь|], что р = ф о г]. В этом случае записываем р ~ ф.
Определение 2. Множество 7 С С (или 7 С R2) называется простой гладкой кривой
(траекторией), если существует непрерывно дифференцируемое отображение [а, 6] 7 с от-
личной от нуля производной. При этом отображение р называется параметрическим пред-
ставлением гладкой кривой 7.
Если ф — другое параметрическое представление гладкой кривой 7, П.Ф = [аь &,], и суще-
ствует такая непрерывно дифференцируемая функция [а, 6] [аь bj, что Vt € [а, 6] r)'(t) > О
и ф о ц = р, то параметрические представления риф называются эквивалентными.
Определение 3. Множество 7ор всех эквивалентных параметрических представлений простой
гладкой кривой 7 называется ее ориентацией. Упорядоченная пара Г = (7, 7ор) называется ори-
ентированной гладкой кривой Г.
Очевидно, что ориентация простой гладкой кривой однозначно определяется указанием ее
начальной точки. Ориентацию простой гладкой кривой 7 с параметрическим представлением
р определяют также выбором одного из двух возможных направлений единичного касательного
вектора т(М) = где М = p(t) € 7.
Все параметрические представления р £ 7ор эквивалентны между собой. Их совокупность
называется противоположной ориентацией 7^. Ориентированную кривую Г- = (7, 7^) назовем
противоположно ориентированной по отношению к Г(7, 7ор).
Среди всех параметрических представлений р ориентированной гладкой кривой Г = (7, 7ор)
существует такое, что
р € 70р, Df = [О, Z] и Vt € [а, Ь] |/(i)| = 1,
ь
где I = J — длина кривой 7. Это представление единственное. Оно называется нормаль-
ным {естественным, натуральным). Нормальное параметрическое представление р получаем в
i
виде композиции фог^ где ф 6 7ор, = [а, 6], [0, t] [а, Ь] и Vt € [а, Ь] r)~'(t) = f |^'(т)| dr.
52
Гл. 2. Комплексные числа и функции комплексного переменного
Известен следующий результат.
Теорема 1 (Жордана). Простая замкнутая кривая 7 разбивает всю плоскость С на две
различные области G\ и Gi, общей границей которых она является. При этом одна из областей,
называемая внутренностью 7, ограничена, а другая, называемая внешностью 7 и содержащая
бесконечно удаленную точку, не ограничена.
Например, множества G, = {z £ С | p(z0, z) < г} и Gi = {z £ С | p(z0, z) > г} являются
соответственно внутренностью и внешностью окружности 7 = {z £ С : р(г0, z) = г}.
Определение 4. Пусть G С С — произвольная область. Если для любой замкнутой жордановой
кривой у, принадлежащей G, внутренность 7 также принадлежит G, то область G называется
односвязной (относительно плоскости С).
Примером односвязной области является внутренность окружности.
Внешность окружности, а также круговое кольцо — не односвязны относительно плоско-
сти С, так как для каждой из этих областей можно указать такую окружность, принадлежащую
области, внутренность которой не вся принадлежит области. Для нужд теории конформных ото-
бражений понятие односвязной области обобщается.
Определение 5. Область G С С называется односвязной относительно расширенной ком-
плексной плоскости, если для любой замкнутой жордановой кривой 7, принадлежащей G, внутрен-
ность 7 или внешность 7 также принадлежат G.
Области, не являющиеся односвязными, называются многосвязными. Например, внешность
окружности, которой в расширенной плоскости С принадлежит также и бесконечно удаленная
точка, является односвязной относительно плоскости С, хотя она не односвязна относительно
плоскости С. Круговое кольцо не односвязно как относительно плоскости С, так и относительно
плоскости С.
Если 7 — непрерывная кривая, то она является замкнутым ограниченным множеством. Дей-
ствительно, поскольку параметрическое представление <р кривой 7 — непрерывная функция,
заданная на компакте [а, Ь], то по теореме 1, п. 2.8, множество Ef = 7 является компактным в
себе, т. е. замкнутым и ограниченным.
Определение 6. Упорядоченный набор Г = (Г(, Г2, ... , Г„) гладких ориентированных кривых
Г*. = (7<fc), 7орЬ (к = 1> п) называется кусочно-гладкой кривой, если ‘ч'к ~ 1, п — 1 конечная
точка гладкой ориентированной кривой Г*, совпадает с начальной точкой аналогичной кривой Г^+,.
п
Множество 7 = (J 7<<:) называется следом кусочно-гладкой кривой Г или множеством ее
ь=1
точек.
Следующее утверждение имеет важное значение в приложениях. _
Теорема (о биективных и непрерывных отображениях). Пусть G С С — область
и G D — обобщенно-непрерывная функция. Тогда множество D также является областью и
функция f~' обобщенно-непрерывна в D. Если, сверх того, функция f определена на границе QG, при-
чем является обобщенно-непрерывной на замыкании G, то f отображает 9G на 9D, т.е. граница
образа области G совпадает с образом границы той же области.
Обобщим понятие непрерывной кривой.
Пусть [а, Ь] —I- С — обобщенно-непрерывная функция, причем сегмент [а, Ь] может быть
бесконечным в одну или в обе стороны. Функция р называется параметрическим представле-
нием обобщенной непрерывной кривой 7 в расширенной комплексной плоскости. Если VZ £ [а, Ь]
tp(t) # ос, то обобщенная кривая не проходит через бесконечно удаленную точку. Понятия на-
чальной и конечной точек кривой, замкнутой кривой, кратной точки, жордановой кривой рас-
пространяются на случай обобщенной непрерывной кривой.
Замкнутое связное множество называется континуумом. Континуум, не имеющий внутренних
точек, называется линейным, или канторовой кривой, например, отрезок, окружность. Это другой
подход к понятию кривой на плоскости. Существует и другой подход к понятию односвязной
области.
Пусть М — несвязное множество, А — его связное подмножество. Назовем А максимально
связным, если не существует никакого другого связного подмножества В С М такого, что А С В.
Максимально связные подмножества М называются его связными компонентами. В теории
множеств доказано, что любое множество есть объединение его связных компонент в конечном
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области
53
или бесконечном .количестве.
Область G С С называется односвязной, если ее граница 9G является связным множеством.
Поскольку 9G — замкнутое множество, не имеющее внутренних точек, то граница односвязной
области есть линейный континуум.
Область, граница которой не является связным множеством, называется неодносвязной. При
этом, если число связных компонент границы 9G конечное, то оно называется порядком связности
области G. Если же множество таких компонент бесконечное, то G называется бесконечносвязной
областью.
Область G назовем компактной и обозначим G @ С, если существует круг Кц = {г € С :
\z\ < R < +00}, содержащий в себе G.
Считаем^ что множество Е компактно принадлежит области G и записываем Е <s G, если
замыкание Е принадлежит G, т. е. _
Е <s G О Е С G.
Пусть т — топология расширенной комплексной плоскости С, М С С — связное подмно-
жество, z € М, Oz — окрестность точки z в топологическом пространстве (С, т).
Определение 7. Окрестностью точки z в множестве М называется множество O’z =
Oz П М.
Совокупность всех окрестностей O'z Vz G М будем называть относительной топологией т'
множества М.
В дальнейшем окажется полезным следующее утверждение.
Теорема. Пусть М С С — связное множество и А — его непустое подмножество. Если А
одновременно замкнуто и открыто в топологии т', то М = А.
Применим метод доказательства от противного. Пусть 4' = М\А #0.-Рассмотрим замы-
кание А в топологии т. Очевидно, что оно состоит из точек его замыкания Аг/ в топологии г'
и некоторого множества, не принадлежащего М. Поэтому
А П А! = Ат, Г) 4'.
Поскольку множество 4 замкнуто в топологии т', то 4Т< = 4. Итак,
4 П 4' = 4 П 4' =0 .
Если 4 — открытое множество в топологии т', то его дополнение А' — замкнутое в той же
топологии (предельные точки множества А' не могут принадлежать 4 вследствие его открытости,
следовательно, они принадлежат 4'). Поэтому к пересечению 4' П 4 можно применить те же
рассуждения, что и к 4 П А', в силу чего 4' П 4 =0. Соотношения
M = 4U4', 4П4'=0, А7ПА=0, 4 #0, 4'/0
противоречат связности множества М. Источник противоречия — в предположении, что
4. ►
Рассмотрим примеры.
48. Доказать:
/ 2 \ / 2 \ 71
1) если zn -+ 0 при п -+ оо, то ( 1 + — ) —> 1; 2) если zn 1 при п —► оо, то (1-1—— 1 —* е.
X п ) \ П /
◄ 1) Оценим разность (1 + ^-)" - 1. Поскольку (1 + ^) =1 + ^3то
С=1
nln(l+^?4 , |z„ 1+0 (4}
= е х 1=е — 1 —> 0 при п —♦ оо.
Следовательно, (1 + ► 1.
2) Полагая w„ = zn — 1, получаем, на основании 1), что (1 + —» 1 при п —> оо. Так как
Гл. 2. Комплексные числа и функции комплексного переменного z
49. Доказать, что последовательность (argzn) может расходиться, если последовательность
(zn) сходящаяся и lim zn # 0.
п —’оо
◄ Рассмотрим последовательность (zn), где zn = -1 + i. Она сходится, и lim zn = — 1.
п —’ОС
Поскольку z2k = -1 + ^2, = -1 - , то argz2fc = тг - arctg^, argz2fe-i = -тг +
arctg ',,2. Так как lim arg^ = тг, lim argz2fc-i — -л, то последовательность (arg^n) имеет
fc^oo fc—’ос
две предельные точки, в силу чего является расходящейся.
0 последовательность (arg2n) может расходиться. Пусть,
Заметим, что и в случае lim zn =
n—юе
например,
z„ =-------------------------, где
п
( если п = 2к,
1 j, если п = 2к — 1.
Тогда
lim zn = 0, lim p2fc =
П—’ОО fc—’ОО 4
7Г
Um P2fc-i = т,
fc—’ос о
т. е. последовательность (р„) расходящаяся. ►
п
50. Пусть }\рк -+ Too при п —> оо, где рг, > 0. Доказать, что если последовательность
fe=i
, . ' PlZl +P2Z2+ ••• +pnzn
(zn) комплексных чисел сходится к z, то и последовательность Zn = -----------------------
Pl + Pl + • • • + Рп
сходится К Z.
Ч Оценим \Zn — z|. Имеем
_z\ = Pl^‘ ~Z^+P^Z2 -z)+ ... +Pn(zn -z) < Pi|z, - z|+p2|z2 - z| + ... + p„|z„-z|
Pi +p2 + ... + pn p,+p2+...+pn
t. e.
n
^PkP^k, z)
p(Zn, z) ^4-----------•
52 Ph
fc=I
n
Так как +oo, то по теореме Штольца для последовательностей действительных чисел
fc=i
^,PkP(zk,z)
,. 4 = 1 ,. Pn+lP(zn+i, Z)
lim ------------= lim ------------— = 0.
Tl^OO n-»oo Pn+1
Z^Pk
k=l
Следовательно, p(Zn, z) = o(l), t.e. lim Zn = z. ►
n—>00
«1 TT - / , (™)k
3i. Наити предел последовательности (гп), где zn — У ------.
z—t fc!
4=0
◄ Докажем, что последовательность (zn) фундаментальная. Пусть е > 0, п 6 N, р Е N. Тогда
irk
при всех достаточно больших п и Vp G N, поскольку числовой ряд > , сходится соглас-
П=1
но признаку Д’Аламбера, и сумма его остатка г„ стремится к нулю при возрастании п. Ранее
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области
55
было показано (см. теорему 1, п. 2.3), что сходимость последовательности комплексных чисел
равносильна сходимости последовательностей ее действительной и мнимой частей. Поскольку
1Г2 — -тг" тг2 "-1 п-1
Rezn = 1 - у + ... + (—1)2 —, если п четное, и Rezn = 1 —^- + ... + (—1) 2 *, если п
3 71 — 1 3 71 t 71
нечетное, Im zn = тг~~ — 4- ... +(-1) 2 , если п четное, Imzn = тг--у +... +(-1) 2
если п нечетное, то
lim Re zn = cos тг = — 1, lim Im z„ = sin тг = 0.
n—»oo n—*oo
Следовательно, lim zn = — 1. ►
/ a\n
51. Найти lim zn, если zn = 1 4— I , a = a + i{3.
n —oo \ П/
◄ Записывая zn = xn + iyn = rn(cos^n + zsin^„), имеем
/ a \ (fit aX1
<pn = arg zn = n arg 1 + - = n arctg - 1 + -
\ n) \n \ n /
так как при больших значениях п точка zn находится в правой полуплоскости Z = {z б С |
Rez > 0}. При п — ос 1 + ^- + ~ 1 + 2“
J 1 n nz 71 ’
Следовательно,
lim rn = exp (lim — • - ) = е“, lim <pn = fi, lim zn = e“(cos/3 + isin/3) = e°+'^. ►
n—\n—n 2 / П—»OC 71—»oo
53. Пусть последовательность (zn) комплексных чисел такая, что последовательность (w„),
где w„ = z„ - ?zn_|, |9| < 1, сходится. Доказать, что последовательность (zn) сходится, и найти
ее предел.
◄ Поскольку последовательность (ш„) сходится, то она ограничена (см. п. 2.3), т. е. ЭС > 0 :
Vn б N |w„| С. Пусть М = max{|zo|, С}. Докажем, что Vn б N
Оценим Z,. Из условия примера получаем
zi = w,+qzo, IzJ |wi| + |д| |z0| < С + |9| |z0| М(1 + |9|).
Пусть к б N, к > 1, и справедливо неравенство
Ы^М(1 + |д|+ ... +|д|Ч (2)
В силу высказанного предположения имеем
l-Zfe+il sS |wfcI + |g| ]zfcI M + |g|M(1 + |g| + ... + |g|fc) = M(1 + |g| + ... + |g|fc+1) (3)
Методом математической индукции доказано, что Vn б N выполняется оценка
м
fc=0
Неравенство (1) установлено.
Из соотношений
Z„ = + qzn_i = w„ + 9w„_[ + 92Z„_2 = wn+qw„_t + 92W„_2 + 93z„_3 = ...
56 Гл. 2. Комплексные числа и функции комплексного переменного
имеем V(n € N, р п — 1)
р
wn_kqk + qp+lz„_p_l. (4)
fc=0
Принимая во внимание, что последовательность (wn) сходится, и обозначая w = lim wn, полу-
n—♦оо
чаем:
wn_kqk + qp+lzn_p_i-w'^2/qk = '^(wn_k-w)qk +qp+i z,__p_,-w qk. (5)
fc=0 k=0 k=0 k=p+l
Поскольку |g| < 1 и |z„| to
i P+1 , .\q\p+l „
\q zn_ । 0 при p-+ oo,
1 ~ l?l
t. e. qp+lzn_p_i = o( 1). Так как |w| g R и ряд qk сходится, то сумма его остатка гр = 57 qk -+ О
fc=O /с=р+1
при возрастании р. Следовательно, w 52 <1к = °(1)- Каким бы ни было фиксированное р 6 N,
к=р+1
Vs > О Эп£ Е N : Vn ns справедлива оценка
р
- w)qk
к=0
Р Р ос
|Wn-it - w| |g|fc < г У2 |g|fc < £ |g|fc = £---------------— = г,,
fc=O fc=O fc=O
p
t. e. - w)gfc = 0(1), так как lim wn = w. Таким образом,
fc = O 71 —* OG
w w
z„ - ------- = o(l), lim zn = -------------. ►
1 — q 1 — q
п 6 N.
2) Из условий задачи следует, что
= arg П f 1 + ar& Г1 + = Ё arctg
k=i \ / k=i \ / k=i
откуда непосредственно следует равенство
/ d
рп+\ -<рп= arctg 4 / ---
V “n+l
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области
57
Поскольку arctg х ~ х при х —> 0 и lim
то
7^77 при п —> оо. Поэтому
a t
1 arctg
1 +--------1
®п + |
V’n+l ~
◄ Пусть Z,
(72 \ n
1 + i —;- ) .
П1 - 1 /
J , тогда
n2
(n2 - I)2
argz,
п
= п arctg —5—-
nL — 1
2
Поскольку
lim
lim |zn| = e1*-”
= 1,
n
arctg—— -----—
n - 1 nL — 1
п
lim п arctg —--------
i—П* — 1
n2
lim —-----= 1,
.-ос П2 - 1
п
то lim zn = cos 1 + i sin 1 = el. ►
n—*oc
56. Выяснить, при каких значениях комплексного параметра а сходятся последовательно-
а 71
сти (z„) и (<п), где zn = а", <п =
1 + ап
◄ Если |а| < 1, то из равенства \zn\ = |ар следует, что lim |zn| = 0 и lim zn = 0. Если
тг—‘©с n-’x
|а| > 1, то |z„| —» +со и zn —► оо, т. е. последовательность расходящаяся.
Пусть |а|= 1, тогда а = е’*’, ip -- arga и z„ = an = е”**’. Поскольку |zn| = 1, то lim |zn| = 1.
n—»ос
Последовательность (nip) при р # 0 предела не имеет, а при р = 0 lim nip — 0. В последнем
случае a = 1, zn = 1, lim zn = 1.
n—‘ОС
Таким образом, последовательность (zn) сходится лишь для |a| < 1 и а = 1.
Для последовательности (£п) рассмотрим те же случаи значений параметра а, которые изу-
чены выше.
Если |a| < 1, то lim а" = 0, lim (1 + а") - 1, lim 777т- = 0, т. е. lim — 0.
п—»ое п—‘ос п—‘оо п—+оо
Пусть |а| > 1. Тогда lim а" = 00 и lim = 0. Записывая общий член последовательно-
п—»оо п-^оо
сти (<п) в виде
1 _ 1 1
~ 1 1 + ап ~ 1 “ ап 1 4- -L ’
а’*
находим: lim <„ = 1.
п—*ое
Пусть теперь |a| = 1 и Vn е N an # -1. Тогда а = е'*’, <р = arga, an = е”**’ и cosnp # —1.
Для указанных значений а имеем
einv ein»’(l +е-'"*’) einv + 1 2 (cos2 + «sin cos_ 1 nip
+ein*’ ~ (l + ei"*’)(l + e-*n»’) ~ 2(1 + cos пр) ~ 4 cos2 “ 2 + ‘ *8 2
Последовательность (tg2^) сходится лишь при <р = 0, т.е. a = 1. При этом получаем
lim С„ = 5 - Следовательно, последовательность (^„) сходится, если |a| < 1, |а|>1иа=1.^
58
Гл. 2. Комплексные числа и функции комплексного переменного
57. Доказать сходимость последовательности ((„), где
п + 1 + nz + (п — l)z2 + ... + zn
Cn : ; j
1 + п
если |z| I и z # 1. Найти ее предел.
Ч Рассмотрим последовательность (г/п), где = zQn Vn g N, и образуем разность г/п — (п =
(1-z)(i+n) - * • Тогда (п — (1_г)2(1+„) + 7Т7 •
( п+2__ \ п+2_
~1 _Ij2~у ограничена и lim (1_z)2(1+n) = 0.
Поэтому последовательность ((„) сходится и
1
Um G = ------- ►
П-.СО 1 - Z
58. Доказать, что все предельные точки последовательности (ап), где
принадлежат окружности 7={zgC:|z| =
Ч Из очевидного неравенства
следует, что все предельные точки последовательности (е1‘1П") принадлежат окружности радиуса 1
с центром в начале координат, а
Поскольку I 12 = , то все предельные точки последовательности (а„) принадлежат окруж-
ности 7. Здесь воспользовались тем, что функции комплексного переменного можно интегри-
ровать по известным правилам интегрирования функций действительного переменного: если
/(х) = /i(x) + ifi(x), fi g R[a, 6], /2 € Л[а, 6], то / € R[a, 6] и наоборот, т. е. f € Я[а, 6] <=>
fi g Л [а, Ь] Л /2 € _К[а, Ь]. Если F — любая первообразная функции /, то
ъ
f(x)dx = F(x)|
I х—а
Функция х н-> 7—7 является первообразной функции х
59. Пусть ЛСС, ВСС, где A={zgC:z=^ + i^; р € Z, q g Z, m g N, n € N} ,
,B={z€C:|z2-1|<1}. Найти предельные точки этих множеств, замыкания и границы. Уста-
новить также, будут ли эти множества открытыми, замкнутыми и областями.
Ч Точки множества А на плоскости R2 имеют каждая обе рациональные координаты. Из
анализа известно, что множество Q всюду плотно в R. Поэтому в каждой окрестности O«(z)
точки z g С имеется бесконечное множество точек из А. Поэтому А' = С, где А' — множество
предельных точек А. Следовательно, А = С. Отсюда следует, что множество А незамкнуто.
Поскольку множество всех иррациональных чисел также всюду плотное в R, то ни одна точка
множества А не является внутренней. Поэтому А не является открытым множеством, а значит
не является областью.
Установлено, что Vz g С в каждой ее 5-окрестности Og(z) есть точки множеств А и С\А,
т. е. 9 А = С.
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области
59
Полагая х = Rez, у = Im z, множество В зададим в виде
В = {(х, у) б R2 : (ж2 + у2)2 < (х2 - J/2) }•
Перейдя к полярным координатам, получим: В = {(р, р) g R2 : рг < 2cos2y>}. Граница этого
множества дВ = {(р, у>) G R2 : р2 = 2 cos — лемниската Бернулли. Поэтому множество В
есть внутренность этой лемнискаты. Пусть (р0, <ра) € В, тогда pl < 2cos2p0> pj - 2cos2<p0 < 0.
Поскольку функция р »-♦ р2 - 2cos2p непрерывная, то по свойству устойчивости строгих не-
равенств для непрерывных функций существует окрестность O«(po, Ро) С В, в которой строгое
неравенство сохраняется. Поэтому В — открытое множество. Пусть В = Bt U В2, где Bt —
множество всех точек из В, принадлежащих левой полуплоскости, В2 — множество всех точек
из В, принадлежащих правой полуплоскости плоскости R2..Точка (0, 0) не принадлежит множе-
ству В. Поэтому любую пару точек zt и z2, где Z| £ В(, z2 6 В2, нельзя соединить ломаной, все
точки которой принадлежат множеству В. Поэтому В не является областью. ►
60. На примерах множеств В, = {z € С : 0 < |z| $ j } и В2 = С убедиться в существенности
условий теоремы Бореля—Лебега (см. теорему 3, п. 2.4).
◄ Множество В| не замкнуто, поскольку ему не принадлежит его предельная точка z = 0.
Полагаем Vn € N Gn = {z g С : < |z| < yr}. Семейство (G„)n£N открытых множеств Gn
покрывает множество B|. Однако, никакое конечное семейство (Gj)Jgx (Л — конечное мно-
жество) не покрывает множество В,, поскольку их объединение (J Gj не содержит множества
ЗСА
Bjm) = {z g С : |z| < ртгтт}, где т g N — максимальный элемент множества А. Следовательно,
условие замкнутости в теореме Бореля—Лебега играет существенную роль.
В2 = С — замкнутое, но не ограниченное множество. Открытые множества семейства
(G,,),,^, где Gn = {z g С : |z| < п}, покрывают множество В2. Вместе с тем, никакое конечное
семейство (<?п)п£д не образует покрытия комплексной плоскости С. Таким образом, условие
ограниченности множества в условиях теоремы Бореля—Лебега является существенным. ►
61. Определить кривые, заданные следующими уравнениями
1) z = 1 — it, 0 t 2;
3) z = t2 + it4, -оо < t < +оо;
5) z = t + —оо < t < 0;
7) z = —t + i\/\ - t2, — 1 t 0;
2) z = t + it2, —oo < t < +oo;
7Г ЗтГ
4.) z = a(cost + isin<), — t C —, a > 0;
6) z = t + i y/1 — t2, — 1 t 1;
8) z = a(t -I-1 - ie 11), -oo < t < +oo, a > 0;
9) z = ia + at - ibe a, -oo < t < +oo, a > 0, b > 0.
4 1) Пусть z = x + iy. Тогда x = 1, у = -t, -2 у 0. Кривая, заданная уравнением
z = 1 - it, 0 t 2, есть отрезок у = {(x, у) g R2 : x = 1, — 2 у 0}.
2) Если z = x + iy = t + it2, to x = t, у = t2, т. e. у = x2, -oo < x < +oo. Уравнение
определяет параболу с вершиной в начале координат и осью симметрии — лучом 7, = {z g С :
Rez = 0, Imz 0}.
3) По аналогии с предыдущим х = t2, у = t4 = х2, 0 х < +оо. При изменении параметра t
от -оо до 0 подвижная точка (x(t), y(t)) пробегает всю правую ветвь параболы сверху вниз, а
при изменении параметра t от 0 до +оо она пробегает ту же самую ветвь снизу вверх. Уравне-
ние определяет две противоположно ориентированные непрерывные кривые с одним и тем же
множеством точек 7 = {zgC:0^Rez< +оо, Imz = х2}.
4) Уравнение определяет левую полуокружность, заданную параметрически: х = a cost,
у = asin t, у t < —.
5) Пусть z = х + iy. Тогда х = t, у = | = у, -оо < х < 0. Уравнение определяет гиперболу
(одну ее ветвь, лежащую в третьем квадранте плоскости хОу).
6) Из условий примера следует, что у = х/1 — х2, |х| 1. Уравнение определяет верхнюю
полуокружность радиуса 1 с центром в точке z = 0.
60
Гл. 2. Комплексные числа и функции комплексного переменного
7) Из условий примера следует, что
у = уЧ - х2, 0 х 1. Уравнение
определяет четвертую часть окружности
радиуса 1 с центром в точке z = 0. Все
точки кривой принадлежат первому ква-
дранту плоскости хОу.
8) Уравнение определяет плоскую
трансцендентную кривую — циклоиду,
являющуюся траекторией точки окруж-
ности, катящейся по прямой линии без
скольжения (рис. 24). Ее параметричес-
Рис. 24
кие уравнения имеют вид х = a(t - sint), у = а(1 - cost), t g R. Исключив параметр t, получим
уравнение циклоиды в декартовых прямоугольных координатах
х = a arccos
Циклоида — периодическая кривая, ее пе-
риод (базис) OOi = 2тга. Точки О, Ок =
(2йтга, 0), к 6 Z, — точки возврата. Точки
А, Ак = ((2k + 1)ла, 2а) — вершины.
9) Из уравнения находим:
< Ь \ ( b \
х = a I t--sin t , у = а I 1-----cos t ) .
\ а ' * \ а /
Если Ь > а (Ъ < а), то кривая описывается
точкой, лежащей вне (внутри) окружности,
которая катится по прямой. В первом случае
Рис. 25
ее называют удлиненной циклоидой (рис. 25), а во втором — укороченной циклоидой (рис. 26).
Иногда их называют трохоидой. Параметрические уравнения трохоиды записываются в виде
х = at — d sint, у = а - dcost, где d — расстояние точки М от центра катящейся окружности. ►
га
ia
ati
га
at2
Рис. 27
га
at3
х
- 22
Z — Z2
- 22
21 -Z2
62. Какая кривая определяется уравнением —
21
◄ Очевидно, что Im = 0, = а, а € R. Поэтому z = z2 + a(zi — z2). Уравнение
определяет прямую, проходящую через точки zt и z2. ►
63. Какие кривые определяются уравнениями
1) z = ia + at, а > 0, —оо < t < +оо;
2) z = —i6(cost — i sin t), Ь > 0, —оо < t < +оо?
•< 1) Рассматривая вектор z с началом в точке z = 0, замечаем, что его конец описывает
прямую, параллельную действительной оси (рис. 27).
2) Конец вектора z = 6(cos t+i sin t) с началом в точке z = 0 описывает окружность радиуса Ь в
положительном направлении. Вектор z = b(cost—isint) симметричен вектору z и, следовательно
§3. Непрерывные и гладкие кривые. Односвязные и многосвязные области 61
точка г, = -iz — результат поворота вектора z на угол -у, пробегает указанную окружность в
направлении движения часовой стрелки. ►
64 . Для отображения w = z2 требуется:
1) найти образы линий а) х = с, б) у = с, в) х = у, г) |z| = R, д) argz = а и выяснить, какие
из них преобразуются взаимно однозначно;
2) найти на z-плоскости прообразы линий u = с, v = с (w = и + iv).
◄ Пусть z = х + iy, тогда z1 = х2 — у1 + i2xy. Таким образом, и — х2 - у1, v = 2ху.
а) и = С2-!/2, v = 2Су г/= u = если С / 0. Это уравнение параболы. Если
С = 0, то и = — у2, v = 0. Получили множество точек полуоси 7 — {(u, v) € С : и 0, v = 0}.
б) и = х2 - С2, v = 2Сх => х = и = ^2 — С2, если С / 0. Линия у = С (С / 0)
отображается на параболу в плоскости ш. Если С = 0, то tz = х\ v = 0. Множество 7 =
{(и, к) € С : и 0, v = 0} является положительной полуосью. В случаях а) и б) отображения
взаимно однозначны, если С # 0.
в) у = а: => и = 0, v = 2х2. Множество 7 = {(u, v) 6 С : и = 0, v 0} — положительная
полуось. Отображение не взаимно однозначно, так как лучи, находящиеся в первом и третьем
квадрантах, переходят в одну и ту же полуось.
г) Если |z| — R, то z = Ле'*1, <р Е Aigz, z2 = R2e2"p, |w| = R2. Окружность радиуса R
с центром в точке z — 0 отображается на окружность радиуса Д2 с центром в точке w = 0.
Отображение не является взаимно однозначным.
д) Образом луча argz = а является луч arg w — 2а. Отображение взаимно однозначное.
2) Пусть и — С, тогда получим при С # 0 уравнение гиперболы хг - у1 = С. При С — 0
имеем пару прямых у = ±х. Если v = С, то 2ху = С. При С # 0 получаем уравнение гиперболы
у = , а при С = 0 — пару прямых ж = 0 и у = 0. ►
z2 Z
65. Найти lim f(z), если: a) /(z) = —; б) f(z) = -.
г—*0 Z Z
Ч а) Если zn = хп + гу„, то f(z„) = = zn и так как |1 = 1, то |/(z„)| = |zn| -+ 0
при zn —> 0. Поэтому lim ^- = 0.
z—>0 г
б) Пусть z„ = хп —> 0 при п —» оо. Тогда f(zn) = 1, f(zn) —► 1 при п —> оо. Если
< = iyn, Уп 0 при п -> оо, то f(z'n) = = “I, lim /«) = -1- Множество Ef(0)
частичных пределов функции f в точке z = О содержит больше одного элемента, поэтому f не
имеет предела в этой точке. ►
,, Rez z Rez2 zRez
66. Функции /|(z) = -----, f2(z) = —, /3(z) = -7-7Г’ А(г) = —— определены на
_ |z| \z\2 |z|
множестве Z = ОД0)\{0}, где O6(0) = {z G С : |z| < 6; 6 > 0}. Можно ли продолжить их на
множество ОДО) так, чтобы эти продолжения были непрерывными в точке z = 0?
◄ Пусть zn = (£, О) , z’n = (О, £). Тогда последовательности (z„) и (z'n) при достаточно
больших n G N принадлежат множеству ОДО) и lim zn = lim zn = 0. Из равенств /i(zn) = 1 и
Л(4) = 0, /2(zn) = 1 и /2(z;> = г, /3(zn) = 1 и f3(z'n) = -1 следует, что функции fj (j= 1, 2, 3)
не имеют пределов в точке z = 0 и поэтому не могут быть продолжены на множество ОДО) так,
чтобы полученные функции были непрерывными при z = 0. Рассмотрим функцию /4. Пусть
(z„) = (х„ + iyn) — произвольная последовательность точек множества ОДО), zn —> 0 Л Vn € N
zn / 0. Тогда —► 0 и з/п —> 0 при п —» оо. Поскольку |/Дг„)| = |хп| -+ 0 при п —» со, то
lim /4(zn) = 0. Следовательно, функция ОДО) Л С, где
п—»оо
,./гч _ f Mz), если Z 6 ОД0)\{0},
~ | 0 при z = 0,
непрерывна в точке z = 0. ►
62 Гл. 2. Комплексные числа и функции комплексного переменного
67. Будут ли функции /i(z) = ЛОО = Dfi = Dfl = {z е С : \z\ < 1}
непрерывны, а также равномерно непрерывны?
4 Пусть zq € Dft — любая точка. Тогда 1 -z0 / 0 и по теореме о непрерывности частного двух
непрерывных функций ft непрерывна на множестве D/,. Аналогично, функция f2 непрерывна
Vz g Dj2. Таким образом, обе функции непрерывны в области определения. Исследуем их на
равномерную непрерывность. Пусть z'n = 1 — 1, z" = 1 - £. Тогда
p(z'n, z") = |z" - z'„\ = - -+ О прип->00.
п
Вместе с тем
. II p(z' Zn) п
P(Ji(zn)> /1(гп)) = = - - -Юо при п —ос.
11 zn | 11 zn I z
Следовательно, функция /1 не является равномерно непрерывной на множестве Dу,.
Пусть z'n = i (1 - 1), z" = i (1 - £). Тогда
p(z'n, z") = - — 0 при n — oo, p(fr(z'n), f2(zty = »2i = 7 +oo при n — oo.
n |1 T Zn I + Zn I 2
Функция f2 также не является равномерно непрерывной на множестве
68. Функция / : С —» С, Df — {z С : \z\ < 1} равномерно непрерывная в области
определения. Доказать, что для любой точки ( на окружности 7 = {z g С : |z| = 1} и любой
последовательности (z„) точек zn g Df, сходящейся к (, существует предел lim /(z„). Доказать
п —
также, что этот предел не зависит от выбора последовательности (z„) и что функция, доопреде-
ленная на границе круга при помощи предельного перехода, будет непрерывна во всем замкнутом
круге К = {z g С : |z| < 1}.
4 Из определения равномерно непрерывной функции следует, что
Ve > 0 36 > 0 : V(z, g Df, z2 g Df)(p(Zl, z2) < 6) => р(/(г1), /(z2)) < e.
Пусть C g 7, zn — < Л Vn g N zn g Df. Сходящаяся последовательность (zn) являет-
ся фундаментальной, поэтому для указанного в условиях (1) 6 > 0 существует такое п6 g N,
что V(n р g N) выполняется условие p(z„, zn+p) < 6. Тогда, согласно условиям (1),
p(/(zn), /(zn+p)) < е, т. е. последовательность (/(zn)) фундаментальная и поэтому сходится.
Пусть lim f(zn) = А. Если z'n -+ (, то, как доказано выше, последовательность (/(z^)) схо-
п—
дится. Обозначим lim f (z'n) = В и предположим, что А / В. Смешанная последовательность
п—>оо
zb z{, z2, z2, ... сходится к точке (, а последовательность f(z{), /(zj), f(z2), /(z2) ... является
фундаментальной и поэтому сходится. Обозначим С = lim _f(z"), где z„ — общий член сме-
п—юо
шанной последовательности. Поскольку последовательности (zn) и (z'n) являются подпоследова-
тельностями смешанной последовательности, то Л = С и В = С, т е. А — В. Таким образом,
lim f(zn) существует и не зависит от выбора последовательности (zn). Доопределяя функцию
п—*оо
f на окружности 7 предельными значениями в ее точках, получим непрерывную на компакте К
функцию. ►
69. Пусть f(z) — е *2, Df = {z g С : 0 < |z| Л}. Является ли функция f равномерно
непрерывной?
4 Функция f непрерывна, как композиция двух непрерывных функций. Для исследования
ее на равномерную непрерывность полагаем z = x + iy. Тогда
1
1 _ х2 — у2 — i2xy
х2 - у1 + i2xy (х2 + у2)2
__1_ *2~1>2 12»у
е г2 = е (®2+i/2)2 е(а2+к2)2.
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость
63
Пусть z'n = (о, , z" = (о, -у—) Тогда Vn g N z'n e Df, z" £ Df,
p{z'n, z'^) = \ -----—------► 0 при n -too,
V Inn ln2n
P(/(4), /(4')) = eln271 - elnn = 2n - n = n -+ +00.
Следовательно, функция f не является равномерно непрерывной. ►
§ 4. Дифференцируемые функции
комплексного переменного.
Связь между С-дифференцируемостью
и R2-дифференцируемостью.
Аналитические функции
4.1. Определение дифференцируемой функции. Правила дифференцирования.
Определение. Пусть f : С —> С и z0 С Df. Функция f называется дифференцируемой в
точке z0, если существует такая непрерывная в точке z0 функция <р : С —> С, Dv — Df, что
Vz € Df выполняется равенство
f(z) - f(zQ) = (z- zQ)<p(z). (1)
Если zq — предельная точка множества Df, то число <p(z0) называется производной функции f
в точке z0 и обозначается символом /'(z0), т. е.
/'(z0) = y>(z0). (2)
Теорема 1. Пусть f : С —» С, z0 € Df и z0 — предельная точка множества Df. Если
функция f дифференцируема в точке zo, то существует
Df3z—*zq Z Zq
◄ Согласно формуле (1), имеем
Hz) - f(z0) ,
lim -------------= lim y?(z) = <p(za) = f (z0). ►
Df3z—>z0 Z — Zq
Пусть, например, /(z) = 7^2, z g C\{—i, i}. Вычислим f'(z0), z0 g Df. Поскольку
Z Z0 1 - ZZ0 1 — ZZq 1 — Zo
1 + z2 “ 1 + z2 =(2-Zo)(1 + zo2)(1+z2)’ (1+z2) (1+z2)’ V(2o) “ (1 + z2)2 ’
TO
1 — z2 1 — z2
= И Vz&D' /(2) = (Г+Pj2 ‘
Теорема 2 (о производной композиции). Пусть функция /:С-»С дифференцируема
в точке гй, а функция g : С —> С дифференцируема в точке Если z0 = ff(Co) и Со — предельная
точка множества D fog, то композиция fog дифференцируема в точке (0 и выполняется равенство
(J ° 9)' (Со) = /'(-so)ff'(Со)- (4)
◄ Согласно определению дифференцируемости функции f в точке z0, существует такая не-
прерывная в этой точке функция <р : С -» С, Dv — Df, что Vz € Df f(z) - f(zQ) = (z - za)<p(z).
Пусть ( g DfQg. Тогда g(£) G Df м при этом выполняется равенство
/(3(0) - №(Со)) = <3(0 - 3(Со)) <Р(3(С))- (5)
64
Гл. 2. Комплексные числа и функции комплексного переменного
Поскольку функция д дифференцируема в точке , то существует такая непрерывная в этой
точке функция гр : С —♦ С, D^ = Dg, что € Dg
д(О - s(Co) = « - Co)V-(z).
Равенство (5) принимает вид
(/ ° 5) (С) - (/ ° д) «о) = (С - Co)V-(C) (ч> ° <?)«)- (6)
Из равенства (6) следует дифференцируемость композиции f о д в точке (о, причем
(7 ° р)'(Со) = V«o) (<р ° д) (Со) = g'(Q>)v>(zo) = f'(zQ)g'(Q)). ►
Теорема 3 (о линейности операции дифференцирования). Пусть функции /:С—»С
и д : С -* С дифференцируемы в точке z0, являющейся предельной для множества Df(~\Dg, Л G С,
р € С. Тогда функция Xf + pg дифференцируема в точке z0 и справедливо равенство
(Xf + pg)' (z0) = Xf'(z0) + pg'(zo). (7)
◄ Согласно определению дифференцируемости функций fug, найдутся такие непрерывные
в точке zQ функции <р и ф, что = Df, Пф = Dg и
/(•г) - /(z0) = (z - z0)<p(z), g(z) - g(za) = (z - га)ф(г).
Следовательно,
(А/ + Щ) (z) - (Xf + pg) (z0) = (z - z0) (X<p + рф) (z).
По определению, функция Xf + pg дифференцируема в точке z0 и
(А/ + pg)'(z0) = (Х<р + рф) (z0) = A/'(z0) + pg'(z0). ►
Теорема 4 (о непрерывности дифференцируемой функции). Если функция f:C—>C
дифференцируема в точке га, то она непрерывна в этой точке.
• < Из определения дифференцируемости функции f в точке z0 следует равенство
7(z) = /(z0) + (z - z0)<p(z).
По теореме о непрерывности в точке z0 суммы и произведения непрерывных функций f является
непрерывной при z = z(l. ►
Обратное утверждение неверно: существуют непрерывные недифференцируемые функции.
Например, пусть f(z) = z, z 6 С. Функция / непрерывная. Согласно определению производной
В рассматриваемом случае
f(z + h) - f(z) _ z + h - z
h - h '
Пусть z = x + iy, h = £ + ig. Тогда = j2—. Если g = 0, £ —» 0, to —> 1;
если £ = 0, g -» 0, to /(г+^~А<г) _, _[ функция f не имеет производной в каждой точке
непрерывности.
Теорема 5 (о дифференцируемости произведения бесконечно малой диффе-
ренцируемой функции и непрерывной функции). Пусть функция / : С —> С диффе-
ренцируема в точке z0 и /(z0) = 0. Если g : С —» С непрерывна в точке z0 и z0 является предельной
для множества Df П Dg, то функция fg дифференцируема в этой точке и справедлива формула
(fg)' (z0) = /'(z0)g(z0). (8)
◄ Согласно определению дифференцируемости функции /, существует такая непрерывная
в точке za функция <р, что Dv = Df и f(z) = (z - z0)^(z) (принято во внимание, что f(zQ) = 0).
Следовательно,
(fg) (z) - (fg) (zo) = (z - za) <p(z)g(z),
что означает дифференцируемость функции fg в точке z0. При этом
(fg)' (zo) = V>(zo)g(2o) = f'(za)g(zo)- ►
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость
65
Следствие (правило дифференцирования произведения функций). Если функ-
ции f : С —» С, g : С —+ С дифференцируемы в точке z0, являющейся предельной для множества
Df Л Dg, то функция fg дифференцируема в этой точке и справедлива формула
(fg)' (г0) = /'(го)р(го) + g(z0) f(z0). (9)
◄ Доказательство следует из тождества
f(z)g(z) = (f(z) - f(z0))g(z) + f(z0)g(z) VzEDfn Dg
и теорем 3, 5. ►
Теорема 6 (о производной частного). Пусть / : С —> С, g : С -+ С — дифференцируемые
функции в точке z0, являющейся предельной для множества Df П Dg. Если g(zn) # 0, то функция
t дифференцируема в точке zfl и справедлива формула
/V . . /'(^o)j(z0) - g'(z0)/(z0)
- (г0) = -------z~—---------- (Ю)
g J 92(го)
◄ Воспользуемся правилом дифференцирования произведения функций и теоремой о про-
изводной композиции функций. Получим
( f\' ( х\' ' 1 АЛ'
- (г0) =(/-) (го) = f (го)—— + /(г0) - (г0) =
\9 / \ 9/ 9(?о) \9 /
- + f(z ) ( 3'{z^ - f'(zo>9(zo) ~ д'(г0)/(г0)
д(г0) 0 \ g2(z0)) д2(г0)
Теорема 7 (о производной обратной функции). Пусть функция / : С —> С обратима,
z0 6 Df и является предельной точкой множества Df, w0 = f(zB). Если существует f'(z0) / 0
и обратная функция непрерывна в точке w0, то она дифференцируема в этой точке. Если,
дополнительно, — предельная точка множества Ef = Df-i, то
По определению дифференцируемости функции / в точке z0, существует такая непрерыв-
ная в этой точке функция <р, что = Df и Vz S Df
f(z)-f(z0) = (z-z0)ip(z). (12)
Поскольку из равенства (12) и взаимной однозначности функции / следует, что ip(z) / 0 при
z / z0 и <p(z0) — f'(z0) / 0, то, полагая w = f(z), имеем
f~1(w)-f~‘(w0) = (w-w0)— 1 (13)
y>(/-‘(w))
Так как функция непрерывна в точке w0, то по определению функция f~' дифференциру-
ема в точке и>о. Если w0 — предельная точка множества Ef = D} -1, то на основании определения
производной получаем
( "‘V _ 1 1 _ 1
U ) ^(/-’(wq)) 9?(z0) /'(го) *
Заметим, что в случае, когда множество Df является компактом и функция f непрерывная,
то непрерывность обратной функции следует из теоремы п. 6.3, гл. 1.
В теории функций комплексного переменного дифференцируемые функции принято назы-
вать моногенными. Точнее, функция f : С —* С, определенная на множестве Е С С, называется
моногенной (относительно множества Е) в конечной неизолированной точке z0 6 Е, если она
имеет в этой точке конечную производную f'E(zo) по переменной z g Е:
. .. 7(г)-/(«о)
/в(го) - lim -------------.
•ЕЭ*-*«о Z — Zq
66
Гл. 2. Комплексные числа и функции комплексного переменного
Функция, моногенная в каждой неизолированной точке множества Е, называется моногенной
на Е. Если Е = G — область комплексной плоскости С, то функция, моногенная на G, назы-
вается аналитической функцией в области G.
4.2. Дифференциал функции.
Пусть функция / : С —» С дифференцируема в точке z0 G Df, предельной для множества D f.
Тогда по определению Vz € Df ее приращение в точке z0 записывается в виде
Д/(г0) = /(г) - /(г0) = У’(г) (г - г0), (1)
где 9? — непрерывная в точке z0 функция и <p(z0) = f'(z0). Записав равенство (1) в виде
Д/(г0, Дг) = р(га) Az + a(z0, Az) Az, Az = z - z0,
где a(z0, Az) = <p(z) - p(z0) = ^(z0 + Az) - ^(z0), делаем вывод, что приращение дифференциру-
емой в точке г0 функции / равно сумме двух слагаемых, одно из которых f'(z0) Az, а второе —
a(z0, Az) Az, где а — непрерывная функция, обращающаяся в нуль при z = z0, т. е. бесконечно
малая при z -+ z0. Обозначим a(z0, Az) = о(1), a(z0, Az) Az = o(l) Az = о(|Дг|). Функция
о(1Дг|) имеет высший порядок малости по сравнению с |Az| при z -+ z0, т.е. lim = 0.
z-го Z
Таким образом, равенство (1) принимает вид
Af(z0, Az) = /'(z0) Az + о(|Дг|). (2)
Прежде чем^нализировать формулу (2), рассмотрим линейное отображение С—>С.
Определение 1. Функция С —► С называется линейной, если V(z! Е С, t С, A t С)
выполняются условия'.
1) L(zt + z2) = L(zi) + T(z2) {свойство аддитивности)',
2) L(Xzi) = AL(zt) (свойство однородности).
Из условий 1) и 2) следует, что £(0) = 0 и Vz 6 С L(z) = az, а = L(\) = const.
Теорема. Пусть / : С —> С, г0 С Df — предельная точка множества Df. Если существует
такое линейное отображение (линейная форма) £-•£. L(z) = az, что Vz € Df выполняется
равенство
Af(z0, Az) = a Az + o(\Az\), (3)
то функция / дифференцируема в точке z0 и f'(z0) = а.
Ч При выполнении условий теоремы существует
Дг—0 AZ
Принимая во внимание равенство (2) и доказанную теорему, видим, что условие (3) может
быть принято в качестве определения дифференцируемой функции / в точке z0.
Определение 2. Если функция / : С —> С дифференцируема в точке z0 G Df, предельной для
множества Df, то линейная форма С-—С, удовлетворяющая условию (3), называется дифферен-
циалом функции f в точке z0 и обозначается символом df(z0). Для любого h Е С имеем
L(h) = df(z0) (h) = f'(z0)h. (4)
Таким образом, приращение функции / : С —» С, дифференцируемой в точке z0 € Df,
предельной для множества Df, состоит из суммы двух слагаемых, первое из которых есть значе-
ние дифференциала d/(z0) при h = Az, а второе является функцией вида a(z0, Дг) = о(1)Дг,
Da = Df, где о(1) — непрерывная бесконечно малая при z —» z0 функция, значение которой в
точке za равно нулю.
Пусть Vz € С g(z) = z. Тогда Vh € С имеем
dg(z) (h) = dz(h) = z'h = h, (5)
t. e. значения дифференциалов dz функции z >-> z в любой точке комплексной плоскости С
равны друг другу при выборе фиксированного h € С. Поскольку
df(za) (h) = f'(z0)h = f'(z0) dz(h), (6)
TO
df(z0) = f'(z0)dz. (7)
67
§4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость
Формула (7) определяет дифференциал функции / в точке z0 как линейную форму
с^’с.
(8)
Принимая во внимание, что производную функции / : С -» С можно рассматривать как
частное дифференциалов функции и независимого переменного, принято обозначение
df . d/(z0)
f = 7-, f (*o) = ——•
az az
Для приближенного вычисления значений дифференцируемой функции / в точках из не-
которой 6-окрестности точки z0 6 Df при достаточно малом 6 > 0 пользуются приближенной
формулой
Д/(г0, Дг) ~ <7/(z0)(Az) = f'(z0) Az,
(9)
т. е.
/(z) ~ /(z0) + /'(z0) Az, Az = z — z0.
(Ю)
4.3. Критерий дифференцируемости функции комплексного переменного.
Если функция f : С -» С дифференцируема в точке z0 6 Df в смысле определения п. 4.1,
то будем называть ее С-дифференцируемой в этой точке. Функцию g : R2 —* R, дифференци-
руемую в точке (ж0, уф, будем называть R2-дифференцируемой (напомним, что ее приращение в
точке (х0> уф имеет вид Ад(ха, уф = Да:+ Ау+ар, где р = у/Ах2 + Ау2, а -+ 0
при р —» 0). Поскольку функцию комплексного переменного можно записать в виде
/(z) = и(х, у) + iv(x, у), z = (х, у),
то естественно возникает вопрос о связи С-дифференцируемости функции f с R2 -дифференци-
руемостью функций и и у в точке z0 = (х0, уф). Эту связь устанавливает следующее утверждение.
Теорема (критерий дифференцируемости функции / : С —» С). Пусть функция
f : С —» С, где f(z) = и(х, у) + iv(x, у), определена в некоторой окрестности точки z0 = х0 + iy0.
Для дифференцируемости функции f в точке z0 необходимо и достаточно, чтобы функции и и у были
R2 -дифференцируемы в точке (х0, у0) и чтобы их частные производные в этой точке были связаны
соотношениями
ди(х0, уф) _ ду(ха, уф ди(х0, уф) _ dv(x0, уф
дх ду ’ ду дх
Соотношения (1) принято называть условиями Коши — Римана.
◄ Необходимость. Пусть функция / С-дифференцируема в точке z0 — (х0, уф. Тогда ее
приращение в этой точке имеет вид
Af(z0, Az) = ф'(гф Az + a(z0, Az) Az, a —> 0 при Az —> 0. (2)
Отделяя в этом равенстве действительную и мнимую части й обозначив /'(z0) = а + ib, получим
при х -> z0, у -+ у0
Аи(х0, уф = а Ах - Ь Ау + а\Ах + 01 Ау, с*| —> 0, 0i -+ 0 при Дх —>• 0, Ду —> 0,
Дv(x0, уф = Ь Ах + а Ау + а2 Ах + 02 Ду, аг 0, 02 ~* 0 при Ах —> 0, Ау —» 0.
Из R2-дифференцируемости функций и и v в точке (х0, уо) следует, что
ди(ха, уф dv(xa, уф ди(х0, у0) dt>(z0, уф
а = --------=--------—, о —------------=----------.
дх ду ду дх
Достаточность. Пусть функции и и v R2-дифференцируемы в точке (х0, уф и выполня-
ются условия (1). Обозначим = А, = В. Запишем приращения функций и и v
в точке (х0, уф, приняв во внимание условия (1). Имеем
Ди(х0, у0) = Л Дх - В Ду + a V Дх2 + Ду2, a —» 0 при х ~* хо> У —» Уо, (3)
Дц(®о, Уо) = В Ах + ААу + 0у/Ах2 + Ду2, Д —» О при х —> х0, у —► у0. (4)
68
Гл. 2. Комплексные числа и функции комплексного переменного
Умножив обе части равенства (4) на г и складывая полученное с равенством (3), находим:
Д/(г0, Дг) = Ди(х0, yo) + i Sv(x0, у0) = А(Дх + i Ду) + B(i Дх - Ду) + (а + г/З) у^Дх2 + Д’/2- (5)
Поскольку Дх + г Ду = Дг, г Дх - Ду = г Дг, то равенство (5) принимает вид
Д/(г0, Дг) = (4 + гВ) Дг + о(|Дг|), (6)
т. е. функция f С-дифференцируема в точке г0. ►
Соотношения (1) впервые изучались еще в XVIII столетии Д’Аламбером и Эйлером, поэтому
их следовало бы называть условиями Эйлера—Д’Аламбера—Коши—Римана.
Сделаем несколько замечаний.
1. В процессе доказательства теоремы установлена связь между производной f'(z) и частными произ-
водными действительной и мнимой частей функции f в виде
, ди dv ди ди ди ди ди ди
дх дх дх ду ду ду ду дх
2. Из курса математического анализа известно, что для IR2-дифференцируемости функций и и и доста-
ди ди dv dv
точно существования и непрерывности частных производных ~ в некоторой окрестности
точки. Поэтому для дифференцируемости функции f = и + iu в точке г = (х, у) достаточно, чтобы
3u(x,v) du(x,v) dv(x, и) dv(x.v) „
частные производные —i —gj * > —gx ? > —Qy * существовали в некоторой окрестности точ-
ки (х, у), были непрерывны в ней и удовлетворяли условиям Коши—Римана.
3. Введем в рассмотрение дифференциальные операторы и , полагая
df def 1 / df &f\ 1 / ди du\ i / ди ди \
dz 2 \ дх ду / 2 \ дх ду ) 2 \ дх ду / ’
df def 1 / df 1 / ди ди \ i / ди ди \
dz 2 \дх + ду / 2 \<?х ду ) 2 \<Эх + ду )
Тогда условия Коши—Римана можно записать как одно комплексное равенство
Если и и и — R2-дифференцируемые в точке (хд, уд), то
Д/(го, Дг) =
df(zg)
dz
&.Z +
Az + o(|Az|).
dz
(Ю)
Полагая в (10) Дг = |Дг|е'9, получим
Д/(г0, Дг) Э/(г0) df(za) _пв
----X------= “7— + '"'я- е +
Дг dz dz
(И)
Из соотношения (11) следует, что предел отношения при Дг -> 0 существует тогда и только тогда,
когда 5 = 0.
4.4. Аналитические функции.
Определение 1. Функция w = f(z), определенная в некоторой области G С С, называется
аналитической в G или голоморфной, если 'fz € G она дифференцируема.
Определение 2. Функция w = /(г) называется аналитической в точке г € С, если она
аналитическая в некоторой окрестности этой точки.
Определение 3. Функция w = f(z) называется аналитической на кривой у С С, если она
аналитическая в некоторой области, содержащей эту кривую.
Определение 4. Функция w = /(г) называется аналитической на открытом множе-
стве ЕСС, если она аналитическая в каждой точке г 6 Е.
Определение 5. Функция w = /(г) называется аналитической на произвольном мно-
жестве М С С, если она аналитическая на некотором открытом множестве Е D М.
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость 69
В частности, функция w — f(z) называется аналитической в замкнутой области G, если она
аналитическая в некоторой области D s> G. _
Понятие аналитической функции можно распространить и на области из С, если дать соот-
ветствующее определение аналитичности в бесконечно удаленной точке. _
Определение 6. Функция f, определенная в расширенной комплексной плоскости С, называется
аналитической на бесконечности, если функция р : z f аналитическая в точке z = 0.
Отметим некоторые свойства аналитических функций.
1) Сумма, разность, произведение и частное (при условии, что делитель # 0) двух аналитичес-
ких функций также являются аналитическими функциями. Отсюда следует, что множество функ-
ций {/}, аналитических в области G, образует кольцо. Обозначим его символом A(G).
2) Композиция fog аналитических функций есть аналитическая функция.
Свойства 1) и 2) следуют из теорем о дифференцируемых функциях, рассмотренных в п. 4.1.
Примером функции, аналитической в любой области G С С, служит произвольный много-
член
P„(z) = aoz" + a{zn 1 4- ... 4- a„_,z 4- ап.
Рациональная функция
Pn(z) aozn + ai2n-1 + ... + a„_|Z + an
f(z) = ----- = ------------:-----------------
<?m(z) 6oim+bl^m + • • • + bm_:Z + Ьт
аналитическая в каждой области G, не содержащей нулей знаменателя.
3) Если f € A(G) и Vz € G |/'(z)| / 0, то на множестве Ef = f(G) определена функция f~',
являющаяся аналитической. При этом, если w0 = /(z0), то
Ч Обратимость отображения w = и + iv означает, что уравнения и = и(х, у), v = v(x, у)
можно разрешить относительно х, у в области G. Поскольку функция / аналитическая в обла-
сти G, то Vz(l = (z0, j/o) С G выполняются условия Коши—Римана (1), п.4.3, вследствие которых
якобиан
du(:ro, у0) ди(ха, у0)
-Р(ц; V) , . _ дх ду
D(x, у) Ж°’ Уо) ~ dv(xo, Уо) dv(x0, у0)
дх ду
ди(х0, у0)\ 2 / dv(x0, у0)\ 2
дх ) \ дх I
du(z0, Уо) , ,dv(x0, уо)
1- г
дх----------------дх
2
= |/'(г0)Р
отличный от нуля в точке z0, поскольку Vz 6 G |/'(z)| / 0. По теореме о неявной функции в
некоторой окрестности точки ш0 = (и0, v0) существует z = f~x(w). Существование и непрерыв-
ность производной (/“')' доказываются так же, как в теореме 7, п. 4.1. ►
4) Пусть и — действительная часть функции f € A(G). Тогда мнимая часть v этой функции
определяется с точностью до аддитивной постоянной.
Действительно, в силу условий Коши—Римана, по известной функции и однозначно опре-
деляется полный дифференциал неизвестной функции v:
dv dv ди ди
dv = — dx 4-----dy =------- dx 4-dy.
дх ду ду дх
Это позволяет восстановить функцию v по известной формуле
VI
(*, V)
f Эи(£, rf) ди^у)
J —дГ^—дГ^0-
<=о. vol
5) Пусть f € A(G), f = и 4- iv, и(х, у) = С, v(x, у) = С — линии уровней функций и и
и. Вычислим Vz = (х, у) 6 G gradu и gradt,: grad u = (|^, , gradv = Считая
пространство R2 евклидовым, получим, принимая во внимание условия Коши—Римана:
, . , ди dv ди dv du du du du
dx dx dy dy dx dy dy dx
70
Гл. 2. Комплексные числа и функции комплексного переменного
Так как вектор-градиент функции ортогонален ее линии уровня, то семейства кривых и(х, у) ~ С
и v(x, у) = С взаимно ортогональны.
4.5. Геометрический смысл производной функции комплексного переменного.
Понятие конформного отображения.
Пусть f € A(G) и Zq € G — произвольная точка. Проведем через нее гладкую жорданову кри-
вую 7 С G. Функция / отображает область G комплексной плоскости z на некоторую область D
комплексной плоскости w. Пусть w0 = /(zo), 7* — образ кривой 7 при отображении f и w0 € 7*
(рис. 28).
Рис. 28
Если подвижная точка z стремится к z0 по кривой 7, то ее образ w стремится к w0 = /(z0)
по кривой 7*. Предположим, что /'(г0) # 0. Тогда f'(za) = |/'(z0)|e'“, а = arg/'(z0). Полагая
Az = z - z0 = Дге’^, Aw = Дре,в, имеем
|/'(z0)| = lim arg/'(z0) = lim (0 - р) (1)
Лг-0 ДГ Дг—*0
Пусть — параметрическое представление гладкой кривой 7. Тогда композиция являет-
ся параметрическим представлением гладкой кривой 7*. По теореме о производной композиции
дифференцируемых функций в точке t0, в которой V’(^o) — zo, получаем
(/ ° V-)' (io) = /(^oWo) # 0. (2)
Следовательно, у>'(<0) / 0. Обозначим через ^(| и 0О углы наклона к осям Ох и О'и касательных
к кривым 7 и 7* соответственно в точках z0 и w0 = /(z0). Тогда ip0 = lim <р, 6а = lim 6 и
Дг—*0 Дг—*0
второе соотношение в (1) примет вид
arg/'(z0) = 0О - 9?о (3)
Таким образом, угол, на который поворачивается кривая 7 в точке z0 6 G при отображении
w = /, не зависит от вида и направления 7. Считаем, что направления осей Ох и О'и, Оу и
О'и совпадают, и под углом поворота понимаем угол между первоначальным и отображенным
направлениями. Из равенства (3) следует, что а = arg/'(z0) равен углу поворота в точке z0 при
отображении w = f(z). Итак, отображение f имеет свойство сохранения углов: угол между двумя
произвольными гладкими кривыми в точке z0 равен углу между их образами в точке w0 = _f(z0).
Пусть z = € 7. Вследствие гладкости кривых 7 и 7* величины |Дг| и |Aw| при t —> t0
бесконечно малые и эквивалентные соответственно длинам As и Де* дуг 7 и 7*, отвечающих
сегменту [t, tol- Поэтому соотношение
Um — = l/'(zo)|
Дх^О |Д^|
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость
71
можно записать в виде
, , , Дз* ds’
|/ (z0)| = lim — = —. (4)
t—*tQ Лз as
Следовательно, с геометрической точки зрения |/'(z0)| есть коэффициент растяжения дуги 7 в
точке z0 при отображении f. Поскольку 7 — произвольная гладкая кривая, то все дуги растяги-
ваются одинаково в точке z0. Поэтому отображение f имеет в точке z0 так называемое круговое
свойство', оно отображает малые окружности с центром в точке z0 в кривые с центром в точке
и?о = /(z0), которые отличаются от окружностей на бесконечно малые высшего порядка. Заметим
также, что круговое свойство остается в силе и в случае, когда f'(z;i') = 0, однако принимает
вырожденную форму, тогда коэффициент растяжения равен нулю.
Определение 1. Отображение f называется конформным в точке zB € G, если оно локально
гомеоморфное в этой точке и имеет в ней свойство сохранения углов.
Из геометрической интерпретации аргумента производной /' следует, что отображение, осу-
ществляемое аналитической функцией, конформное в каждой точке z 6 G, в которой /'(z) / 0.
Определение 2. Если отображение f : С —» С конформное в каждой точке области G, то оно
называется конформным в этой области.
Преимущественно понятие конформного отображения включает в себя гомеоморфизм обла-
сти G (см. п. 6.6, гл. 1).
Замечание 1. При конформном отображении углы сохраняются не только по величине, но и по напра-
влению отсчета. Поэтому его также называют конформным отображением первого рода, в отличие от
конформного отображения второго рода, при котором углы сохраняются лишь по величине, а направле-
ние их отсчета изменяется на противоположное.
Замечание 2. Отображение, осуществляемое аналитической функцией с отличной от нуля производной,
характеризуется также и постоянством коэффициента растяжения в точке. Очевидно, что отображение,
обладающее этими двумя свойствами, в предположении, что коэффициент растяжения отличный от бес-
конечности, является аналитическим.
Замечание 3. Пусть функции и и v имеют непрерывные частные производные. В этом случае элемен-
тарными методами можно показать, что из конформности отображения f = -и + iv необходимо следует
его аналитичность, а если отображение f имеет постоянный коэффициент растяжения, то оно является
конформным первого или второго рода.
Можно также доказать, что при непрерывном однолистном отображении / : С -> С, Df = G, из
условия консерватизма углов следует аналитичность функции f.
Для изучения геометрических свойств отображения / : С —> С условимся о таком опреде-
лении величины угла, под которым пересекаются кривые в точке z = 00: этот угол считается
равным углу пересечения образов этих кривых (при этом величину последнего берем с обратным
знаком) в точке С = 0 при отображении ( = |.
В связи с понятием конформного отображения в расширенной комплексной плоскости С
дадим следующие определения.
Определение 3. Функция f конформно отображает окрестность Oz<s точки z0 на окрестность
точки w — оо, если функция w = конформно отображает OZa на окрестность точки w = 0.
Определение 4. Функция f конформно отображает окрестность Ох точки z = оо на окрест-
ность Owo точки w0, если функция w = f (|) конформно отображает окрестность точки £ = 0
на OW!S.
Определение 5. Функция f конформно отображает окрестность Ох точки z = оо на окрест-
ность О'х точки w = оо, если функция w — у конформно отображает окрестность точки
С = 0 на окрестность точки w = 0.
4.6. Плоские физические поля и их связь с аналитическими функциями.
Пусть в некоторой области G е С задано плоскопараллельное векторное поле F = (Fx, Fy).
Функции Fx = Ее(х, у), Fy = Fy(x, у) считаем дифференцируемыми в области G. Пусть поле F
потенциальное, т. е.
„ 9Fy 9FX л
rotF = —*• - -т-^- =0,
дх ду
(1)
Гл. 2. Комплексные числа и функции комплексного переменного
и соленоидальное, т. е.
dFx dFv
divF= —- + —— =0.
дх ду
(2)
Из (1) следует, что дифференциальная форма
Fx dx + Fydy = u (3)
является полным дифференциалом некоторой функции и = и(х, у), которую называют потенци-
алом поля F.
F = Vu = gradu. (4)
Из (2) получаем
~Fy dx + Fxdy = dv (5)
Функция v = v(x, у) называется функцией тока. Рассмотрим функцию
w = /(г) = и(х, у) + iv(x, у). (6)
Из (3) и (5) имеем
ди dv ди dv
= = ру = 7Г = -7Г-
дх ду ду дх
Следовательно, f € A(G).
Таким образом, всякому потенциальному и соленоидальному плоскопараллельному вектор-
ному полю F соответствует аналитическая функция, полностью определяющая это поле. Эту
функцию называют комплексным потенциалом векторного поля F.
Наоборот, каждой аналитической в области G функции f соответствует плоскопараллель-
ное векторное поле F, для которого f является комплексным потенциалом. Имеем очевидное
равенство ______
F = f(z). (8)
Векторное поле F может иметь различную природу. Рассмотрим некоторые конкретные поля.
1. Гидродинамическая интерпретация векторного поля. Пусть F — поле скоростей стаци-
онарного плоскопараллельного потока несжимаемой жидкости, плотность которой ц = const.
Это поле потенциальное и соленоидальное. Его соленоидальность означает, что в данной обла-
сти G отсутствуют источники жидкости, другими словами, поток жидкости через произвольный
замкнутый контур Г С G равен нулю:
j) Fn ds = -Fy dx + Fxdy = 0. (9)
г г
Потенциальность поля скоростей жидкости означает, что циркуляция жидкости вдоль про-
извольного замкнутого контура Г С G равна нулю:
FT ds = (j) Fx dx + Fy dy = 0. (10)
г г
2. Электростатическая интерпретация векторного поля. Рассмотрим плоское электростатичес-
кое поле, заданное вектором напряженности Е. Известно, что оно потенциальное, т. е.
E = -V<p, (11)
где tp — потенциал электростатического поля. Для произвольной замкнутой гладкой или кусочно-
гладкой кривой Г С G имеем
ETds = Q, (12)
г
поскольку этот интеграл равен работе по перемещению единичного заряда вдоль контура Г.
Интеграл
Ends (13)
г
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость 73
согласно теореме Гаусса равен 2тг, умноженному на алгебраическую сумму зарядов, содержа-
щихся в области, ограниченной контуром Г. Отсюда следует, что в области, в которой заряды
отсутствуют, поле Е будет соленоидальным.
Таким образом, при изучении плоскопараллельных электростатических полей в областях, в
которых отсутствуют заряды, удобно пользоваться аппаратом аналитических функций.
4.7. Неравенство Лагранжа.
Пусть материальная точка движется прямолинейно. Если ее начальное и конечное положения
совпадают, или направления движения в начальный и конечный моменты времени противопо-
ложны, то она должна иметь в какой-то момент времени скорость равную нулю, т. е. обязана
остановиться. В математике эти простые физические явления описываются классическими те-
оремами Ролля и Дарбу. Справедливы ли классические теоремы Ролля, Дарбу и Лагранжа для
функций вида f : R —► С? Физическое истолкование производной как скорости движения мате-
риальной точки в плоскости С позволяет ответить на поставленный вопрос. Двигаясь на плос-
кости, материальная точка может вернуться в исходное положение без остановки в какой-либо
момент времени, и в этом состоит одно из принципиальных различий движений на плоскости
и на прямой. Примером, подтверждающим сказанное, является вращение материальной точки
вокруг неподвижного центра, математической моделью которого служит функция f : R —> С, где
f(x) = егх, Df = [0, 2тг]. Действительно, /(0) = /(2%) Л f'(x) = ie'x / 0 Ух € [0, 2тг]. Поэто-
му существуют такие функции / : R -+ С, для которых утверждения теорем Ролля и Лагранжа
несправедливы.
Теорема Дарбу была основана на том факте, как отмечалось выше, что при прямолинейном
движении материальной точки для изменения его на противоположное требуется, чтобы скорость
в какой-то момент времени обратилась в нуль. Подтверждением того, что, двигаясь на плоскости,
материальная точка может изменить направление движения на противоположное, имея в каждый
момент времени ненулевую скорость, служит пример движения точки по полуокружности, зада-
ваемого функцией f : R —* С, где f(x) = ie'x, Df = [0, тг]. Векторы скорости /'(0) и /'(тг)
противоположно направлены, и тем не менее вектор f (х) ненулевой Ух G [0, тг]. Следовательно,
утверждение теоремы Дарбу для функций из R в С несправедливо.
Физическое истолкование производной указывает правильный аналог теоремы Лагранжа для
функций / : R —> С. Если /(а) — начальное положение движущейся материальной точки и ее
скорость по модулю не превосходит числа v = ||/'|| = sup |/'(ж)|, то за время t = Ь - а она не
f
может попасть за пределы окружности 7 = {w € С : |w - /(а)| = v(b — а)}.
Теорема (Лагранжа). Пусть функция [а, 6] С непрерывна на [а, 6] и дифференцируема в
каждой точке интервала (а, 6). Тогда справедливо неравенство
|/(6)- Да)|^||/'||(Ь-а), (1)
где ||/'|| = sup |/'(х)|.
г£(а, Ъ)
4 Пусть <р G Arg(/(6) - /(а)). Тогда
1/(6) —/(а)| = е_’*’(/(6) —/(а)) = (e"i'l’/)(6) — (е“’¥’/)(а). (2)
Полагаем e~'v f(x) — и(х) + iv(x) Ух € [а, 6]. Имеем
1/(6) - /(а)| = (“(b) + iv(6)) - (и(а) + w(a)) = u(6) - u(a) + i(v(b) - v(a)).
Начало цепочки равенств показывает, что ее конец является действительным числом. Поэтому
v(b) — v(a) = 0. По теореме Лагранжа для функции и существует такая точка £ 6 (а, 6), что
1/(6) - /(а)| = “'«) (6 - а) < |/'(е)|(6 - а) ||/'||(6 - а). ►
Рассмотрим примеры.
70. Доказать, что функция w = z2 + 2z + 3 однолистная в области G = {z g С : |z[ < 1}.
•4 Пусть |zj| < 1, |z2| < 1 и z, /z2. Покажем, что w(zD # w(z2), т.е. |w(zi) — w(z2)| > 0.
Действительно,
|w(zi) - w(z2)| = |z? + 2z1 - 2z2 - z2| = |Z| - z2| |z] + z2 + 2| |zt - z2| (2 - |zt| - |z2|) > 0. ►
74
Гл. 2. Комплексные числа и функции комплексного переменного
71. Доказать, что функция
w(z) = <
4 5 5 4
X 3 J/3 . х з уз
— 1 -1" —
ж2 + у2 х2 + у2
О
если z Ф О,
при z — О,
не дифференцируема в точке z = 0.
◄ Покажем, что lim не существует, откуда и будет следовать справедливость утвержде-
z—»0
НИЯ.
Пусть z = ж + iy, тогда
w(z)
Z
7 5 5 7
ЖЗуЗ + хЗуЗ
(ж2 + у2)2
0
8 4 4 8
,ХЗуЗ — хЗуЗ
+ г (х2 + у2)2
если z # О,
при z = 0.
Пусть у = ж -+ 0, тогда z —> 0 и lim = lim 77 = ч. Если z — х —» 0, то lim = 0.
Z—0 Z 2—в’* 2 Z -*0 Z
Следовательно, lim не существует и функция и не дифференцируема в точке z = 0. ►
z—*0 z
72. Доказать, что функция w = ж3-Зжу2 + г(Зж2у — у3 — 1), Dw = С, является аналитической.
◄ Действительно, функции и = ж3 - Зху2, v = Зх2у - у3 — 1 дифференцируемы, и условия
Коши—Римана выполняются:
-> dv , , ди , dv '
Зх ~ Зу , — = Зж2 - Зу , — = -бжу, —- = бху.
ду ду дх
ди dv 1
— + г — = Зж - Зу + гбху.
\J •£ (J JD
73. Функция w = f(z) = u(x, у) + iv(x, у) имеет в точке z g Df свойства:
1) и и v — дифференцируемые функции;
Дш
2) существует lim -- .
д2—о Дг
Доказать, что либо /, либо f дифференцируема в точке z.
◄ Поскольку Дш = Ди + г Ди, Дг = Дж + г Ду, то
Дт
д7
Ди2 + Ди2
Дж2 + Ду2
По условию существует lim ^7 . Этот предел не зависит от способа стремления Дг к нулю.
Дх.—»0
Взяв Дг = Дж, получим
lim
Az—0
Ди;
Дг
Если Дж = i Ду, то
Следовательно,
ди
дх
Дю
lim -----
Az—*0 Дг
dv\2
ду )
2
+
(1)
§ 4. Дифференцируемые и аналитические функции. С- и R2 -дифференцируемость
75
Из дифференцируемости функций и и v в точке z = (х, у) следует, что их приращения в
этой точке имеют вид
Ди = du + о(х/Дж2 + Ду2) = Ах + Ду + о(у/ Дг2 + Ду2),
дх ду
/--------- dv dv /---------
Av = dv + o(v/Ax2 + Ду2) = — Ax 4----Ду + o(v Ax2 + Ду2).
дх ду
Выражение записывается в виде
Ди2 + Ля2
Ах2 + Ду2
Q)2 + (В)2) ((fj)2 + (I;)2) ^2 + 2(В + f?), о(Дх2 + Ду2)
Дх2 + Ду2 Дж2 + Ду2
Принимая во внимание равенство (1), имеем
Дн2 + Ду2 = ( ди\2 ( dv V 2 + Дж Ду
Дж2 + Ду2 удх J \дх J Дж2 + Ду2
Поскольку lim | -^| = + (fi)'> то
ди ди dv dv
— — 4" — — = 0.
дх ду дх ду
Последнее возможно лишь в случаях: а) |^- = |^, = -fj; б) = -fj, fi = fi- В
случае а) функция / дифференцируема, так как для нее выполняются условия Коши—Римана^
В случае б) условиям Коши—Римана удовлетворяет функция f. Таким образом, либо /, либо /
дифференцируема в точке z. ►
74. Пусть f(z) — и(ж, у) + гТ(ж, у) — аналитическая в области D функция. Доказать, что
если 'iz € D и2 + uv + v2 = а (а = const), то f = const в D.
◄ Продифференцируем тождество и2 + uv + v2 = а по ж и по у. Получим
ди dv ди dv
(2u + v)---I-(u + 2г>)—= 0, (2u + v) ——1- (и + 2v) — = 0. (1)
дх дх ду ду
Допустим, что существует точка z0 g D, в которой /'(z0) 0. Тогда система уравнений (1)
относительно 2и + v, и + 2v имеет лишь тривиальное решение Vz g OZ(i, т. е. и — v = 0, что
противоречит предположению. Следовательно, Vz 6 D f'(z) = 0, т. е. /(z) = const в D. ►
75. Пусть функция f является аналитической в области G. Доказать, что если |/(z)| = const
в G, то функция / также постоянна в G.
◄ Если |/(z)| = 0 для всех z 6 G, то /(z) = 0 в каждой точке области G, т. е. /(z) = const.
Пусть |/(z)| = С Vz 6 G, С / 0 и /(z) = и(ж, у) + iv(x, у) У(ж, у) g G. Тогда в области G
выполняется тождество
и2(ж, у) + ц2(ж, у) = С2,
которое с помощью функции /(z) = и(ж, y)-iv(x, у) запишется как произведение /(z)/(z) = С2
Vz g G. Из последнего равенства следует, что /(z) / 0 для всех z G G, вследствие чего функция
/(•?) = является аналитической в области G. Условия Коши—Римана для функций f и f
приводят к равенствам
ди ди dv dv
дх dy дх ду
в каждой точке области G. Значит, функции и и v постоянны в области G, следовательно f
также постоянна в G. ►
76
Гл. 2. Комплексные числа и функции комплексного переменного
76. Пусть f : С —> С, Df = G, G — область, /(г) = и(х, у) + г«(х, у) и функции и, и
дифференцируемы в точке г0 = (х0, уа) € G. Доказать, что множество всех предельных значений
Д/(г0 Дг)
частного ---------- при Дг —+ 0 есть либо точка, либо окружность.
Дг
Ч Если / дифференцируема в точке г0, то lim _ у'(2о) и /'(г0) — единственное
Дг—О
предельное значение указанного частного при Дг —» 0. Пусть f не дифференцируема в точке г0.
Поскольку в этой точке дифференцируемы функции и и и, то
Д/(г0, Дг) _ Ди(ж0, у0) + tAti(t0, у0) _
Дг Дг
1 (ди(ха, уо) . , ди(х0, уо) Л г / ди(х0, у0) . , dv(x0, у0) . , ,Л
= — -----X-----Дг +---s--Ду + о Аг + 7“ (--------я----Лг +---п--------ДУ + ) =
Дг \ дх ду / Az \ дх ду )
1 / \ о(|Дг|)
= — (АДх + ВДу) + -^-Л
Дг 4 7 Дг
где А = + i е"(р°'Уо), В = + Поскольку Дх = , Ду = , то
** дх дх ’ ду ду J 2 ’ & 2г ’
после несложных преобразований получим:
Д/(г0, Дг) Дг о(|Дг|)
----- = А, + В,, — + —------, (1)
Дг------------------------------------------------------Дг Дг
где А] и В1 — некоторые комплексные числа. Так как | | = 1, то = е~‘21*’, у? € Аг§Дг.
Запишем соотношение (1) в виде
Д/(г0, Дг) _;2 о(|Дг|)
------ At=Bte v + —--. (2)
Дг------------------------------------------------------Дг
Поскольку lim = 0, то при каждом фиксированном р (0 р 2тт) получим
Дг—*0
Д/(г0) Дг)
lim-------------А
Лг—о Дг
= |В.|,
Д/(zn, Дг)
т. е. все частичные пределы частного J —i принадлежат окружности
7 = {г е С : |г - А,| = IB^}. ►
77. Записать уравнения Коши—Римана для функции f — и + iu в полярных координатах
х — г cosу?, у = г sinр, г — -у/х2 + у2.
Ч Применяя правило дифференцирования сложных функций, имеем
ди ди дх ди ду дг дх дг ду дг ди ди — cos р + — sin р, дх г ду
ди ди дх ди ду др дх др ду др ди ди г sin р 4 г cos р. дх ду
Решив эту систему относительно и , находим:
ди ди ди sin у? — = — cosy? - — •, дх дг др г ди ди ди cosy? — = — sin у? + . ду дг др г
Аналогично ди ди ди sin и — = — cosy? - , дх дг др г ди ди ди cosy? — = — sin у? + . ду дг др г
Теперь запишем условия Коши—Римана:
ди ди sin у? — cos р — = дг др г ди ди cos у? — sin у? + , дг др г (1)
ди ди cos у? — sin р + = дг др г ди ди sin у? cos у? + дг др г (2)
§4. Дифференцируемые и аналитические функции. С- и R2-дифференцируемость
77
Умножив (1) на cos</?, (2) — на siny? и складывая полученное, имеем
ди 1 dv
= (3)
dr г dtp
Умножая (1) на — sinyj, (2) — на cosр, сложим полученные результаты. Находим:
1 ди dv
= <4>
г др дг
Таким образом, уравнения Коши—Римана для функции f = и + iv в полярных координатах
имеют вид
ди 1 dv 1 ди dv
= - л-= ~ л-'► (5)
дг г др г др дг
78. Доказать, что функция w = /(г) = z Re г, Df = С дифференцируема только в точке
z = 0. Найти /'(0).
◄ Поскольку /(г) = и + iv = х2 + ixy, то и = х2, v = ху, = 2х, ~ = х, = 0, = JE
Следовательно, О х = 0, О у = 0, т.е. условия Коши—Римана выполнены
лишь в точке г = 0. По определению
, f(z) (х2 + ixy)(x — iy) х2 + ixy х2 — ix2y + ix2y + ху2
/'(0) = lim — = lim ------------— = lim --------- = lim -----y--------— = lim x = 0. ►
z—0 z »-.o XL + ?/ »-o X + iy xl + y1 г—0
у—0 у—0 y-.o
79. Доказать, что для функции /(z) = -^Ixy), Df = С в точке z = 0 выполняются условия
Коши—Римана, но производная не существует.
◄ Если рассматривать функцию f : С —► С в виде /(z) = и(х, у) + iv(x, у), то в данном
случае и = у/\ху\, v = 0. По определению частных производных функции двух независимых
переменных имеем
ди(0, 0) и(х, 0) — и(0, 0) Зи(0, 0) и(0, у) — и(0, 0)
—-----= lim----------------= 0, — ------= lim----------------= 0.
дх х—о х ду у—о у
Так как v = 0, то = 0. Следовательно, в точке z = 0 выполняются условия
Коши—Римана. Рассмотрим отношение , т. к. Д/(0, Дг) = f(z)~ /(0) = у/\ху\,
Az = z- 0 = x + iy. Если г = (ж, 0), х —» 0, то Дг -+ 0 и lim ДЖД11 = о. Пусть х —» 0, х > 0
Дг^О
и у = х. Тогда Дг -+ 0, если х —» 0 и д’Дг> = * —* -Ц2. Таким образом, lim
а ’ Дг х(1+г) 2 г ’ д._() Дг
не существует и функция f не имеет производной в точке г = 0. Здесь нет противоречия с
теоремой о необходимом и достаточном условии дифференцируемости функции / : С —> С в
фиксированной точке. Поскольку функция и(х, у) = у/’|хг/| не дифференцируема в точке (0, 0),
то не выполнено одно из условий упомянутой теоремы. ►
80. Доказать следующие утверждения:
/ Дм \
1) если у функции w = f(z) в точке г существует предел lim Re- I, то частные про-
Дг—о у Ьл )
ди dv
изводные — и — существуют и равны между собой;
дх ду
( tiMi \ ди dv
2) если существует предел пт ( 1т--- , то существуют частные производные — и ——,
Дг—о у Дг у dy dx
du dv
причем — =------;
ду дх
3) если заранее предположить, что функции и и v дифференцируемы, то существование лю-
бого из пределов, указанных в п.п. 1) и 2), обеспечивает существование другого и, следовательно,
дифференцируемость функции /.
78
Гл. 2. Комплексные числа и функции комплексного переменного
◄ 1) Пусть j(z) = и(х, у) + iv(x, у), z = х + iy. Тогда
Af(z) Aw Au + iAv (Ди + i Av) (Ax — i Ay) Au Ax + Av Ay . Av Ax —Au Ay
Az Az Ax + i Ay Ахг + Ауг Ахг + Ay1 Ax2 + Ay1 ’
Aw Au Ax + Av Ay Aw Av Ax —Au Ay
Az Ax2 + Ay2 ’ Az Ax2 + Ay2
Поскольку lim Re существует, то он не зависит от способа стремления Az к нулю. Взяв
Az—О
Az = Ах и Az = i Ay, соответственно получим
Aw Аи ди Av dv du dv
lim Re---= lim — = — = lim — = —, t. e. — = —.
Az—о Az Дг—о Ax дх Дк—о Ay dy dx dy
2) Рассуждая аналогично, имеем
Aw Av dv —Au du du dv
lim Im = lim — = — = lim —— = , t. e. — = .
Дг—о Az дг—о Ax дх Да—о Ay dy dy dx
3) Пусть функции и и v дифференцируемы и существует lim Re . Тогда, по доказанному,
Az—О
“ = . Приращения Ди и Av дифференцируемых функций и и v имеют вид
Ди = — Да? + — Дг/ + о(| Az |), Av = — Ах + — Ау + о(| Дг|).
дх ду дх ду
Тогда
Дю Д-и Дг + Дv Ди 1 / ди ) dv >( ди dv\ , \
Re д— = —. 2 2— = — , , . 2 ТГ Лз: + Дг/ + ( -J- + Т- ) Д* Ду + (Az + Ау)о( |Az|)) .
Дг Дг2 + Д?/2 Дг~ + Ду2 \дх ду \ду дх / /
Поскольку , то
Aw
Re---=
Az
ди (ди dv\ Ах Ay (Ах + Дг/)о(|Дг|)
дх \ду дхJ Ах2 + Ау2 Ах2 + Ау2
Из существования предела Re при Az -+ 0, который равен следует, что (f^ + fj) = О,
т. е. = lim Im ~. Поскольку для функции / выполнены условия Коши—Римана в
точке z, то f дифференцируема в этой точке. ►
о< az + b
<51. Найти множество точек Z плоскости С при отображении w = -------, с / 0, для
cz + d
которого: 1) коэффициент растяжения равен единице; 2) угол поворота равен нулю.
•< 1) Имеем
|w'(z)| =
ad - be
(cz + d)2
откуда
|ad — 6c | = \cz + d|2, или
-y/|ad-6c|
|c|
d
z + —
c
Таким образом,
Z={2eC:|z + f| = ^H}
•t/|ad — bcl d
— множество точек окружности радиуса -——1 с центром в точке z =
2) По условию argw'(z) = 0, т. е. arg(ad — 6с) — arg(cz + d)2 = 0. Отсюда получаем
(cz + d)2 = (ad - Ьс)т, т > 0.
Таким образом,
d Vad - be
z =--------------------------------1--------1, — oo <t< +oo.
c c
Множество Z — это множество точек прямой, заданной уравнением (1). ►
(1)
Упражнения для самостоятельной работы
79
82. Пусть функция w = f(z) аналитическая в точке z0, /'(z0) # 0, а гладкие кривые 7! и
72 имеют свойство: |w(z)| = |w(z0)|, если z € 71, arg w(z) = argw(z0), если z g 72. Доказать, что
кривые 7! и 72 пересекаются в точке z0 под прямым углом.
Ч Из условия задачи следует, что образом кривой 7t при отображении / является дуга окруж-
ности Г = {w g С : |w| = |w(z0)|}, а образом кривой 72 — отрезок луча, выходящего из начала
координат под углом argw(z0). Отсюда следует, что образы 7! и 72 пересекаются в точке w(z0)
под прямым углом, следовательно, кривые 7! и 72 также пересекаются в точке z0 под прямым
углом. ►
83. Потенциальные линии заданы уравнением |z — а| = Ь, а = а, + га2, Ъ > 0. Найти
комплексный потенциал /(z) потока жидкости, а также скорость.
Ч Имеем
In \z - а| = In b = const,
или Reln(z - a) = const. Таким образом
----- 1 1
/(z) = ln(z - a), v = /'(z) = v(2a) = -. ►
z — a a
84. Пусть функция f : C —+ С является аналитической в замыкании области D, a G — образ
области D при отображении /. Доказать, что если отображение / в области D однолистно, то
для площади //(G) области G справедлива формула
p(G) = УУ l/(z)|2 dx dy.
D
Ч Пусть z = х + iy, w = /(z) = и + iv, z g D, w g G. Тогда функции и = Re/, v — Im f
осуществляют с помощью уравнений
u — u(x, y), v = v(x, y) (1)
биективное отображение области D на G (см. п. 4.4). Из курса математического анализа известно,
что мера (площадь) жорданова множества G вычисляется по формуле
У f D(u, v)
р(О= тй—< dxdy’
J J D(x,y)
D
(2)
где n*-1-11* — якобиан преобразования (1). В п. 4.4 показано, что I '77(х, «)| = |/'(z)|2. Следо-
вательно, p(G) = ff |/'(z)|2 dx dy. ►
D
85. Найти площадь /z(G) образа G области D = {z g C : 1 < |z| < 2, |argz| < 7}.
Ч По доказанной в предыдущем примере формуле получаем:
M(G) = JУ |3z2|2 dxdy = 9 УУ (х2 + у2)2.
D D
Полагая х = pcos^>, у = psin^5, имеем J 1 < р <2,
7Г
7 2
12 /я [ 1Й 1 6 Р~
dpj pdp=13-- -p
о 1 р~
189тг
4
Упражнения для самостоятельной работы
1. Упростить выражение
а) (a:eR); б)
х — 1х/1+®
, если z = e*9.
80
Гл. 2. Комплексные числа и функции комплексного переменного
2. Доказать, что для произвольного комплексного числа z / 0 существует такое единственное
число ш, что |w| = fc|z| (fc > 0) и argw = - argz. Найти это число.
3. Доказать, что ни при каких значениях т (т € R) комплексное число вида
log2(m2 - 13m + 44) - 2 + i^/log2 m - 3
не может быть чисто мнимым.
4. Доказать тождества:
a) |z1 + z2|2 -Г — z2|2 = 2Qzi|2 + |z2|2) ;
6) |1 - 2tZ^|2 — |z, — Z2|2 = (1 + |Z|Z2|)2 - (|z,| + |z2|)2;
в) |z + ±|2 + i |z+ ||2 - (1 + i)|z|2 - 1(1 + t) = z;
r) + z3| + | - z3| = |zi| + |z2|, если ztz2 = z32;
д) Е|1 + |Г + Ё|1-7Г = 2н^,если |z2| = n, n£N;
k—l fc=l
e) =г,если |z,| = |z2| = |z3| = r;
ж) П (е^ - i) = (-1)"“' • n (n G N).
fc=l '
____ n
5. Пусть zk (к = 1, n) и zQ — произвольные комплексные числа и z = - ^zk. Доказать
fc=i
равенство
~ 52 l^o ~ zk\2 = l-^o- z\2 + ” 52 \z& ~ z\2•
fc=i fc=i
6. Пусть при всех z, |z| < 1, wfz) = z2 + 2z + 5. Доказать, что
w(zQ = w(z2) о z, = z2.
7. Пусть ни одно из чисел Z|, z2 и z3 не совпадает с z4. Доказать, что если из чисел
£uz£2 Z3~Z| два — чисто мнимые, то таковым является и третье.
Z3-Z4’ Z]-Z4’ Z2-24 г
Указание. Воспользоваться соотношением
|z3 - z4|2 Re + |z! - z4|2 Re + |z2 - z4|2 Re = 0.
8. Доказать, что
а) если z / -1 и |z| = 1, то z - где t — некоторое действительное число;
б) всякое действительное число а представимо в виде а = где z — некоторое ком-
плексное число, причем |z| = 1 и z Ф 1.
9. Представить в тригонометрической форме число z — (1 — cos а + isina)n, где п — целое
число, не равное нулю.
10. Найти суммы
С ___ 1 । sin х । sin 2х । , sin пх __ i . cost , cos 2т . , cos nx
TL sin x sin2 x • • sin71 x ’ 71 ' sinx ’’ sin2 x ' sin™ x '
Указание. Вычислить an +i(Sn - 1).
11. Пусть b G R, a € С и а # 0. Доказать, что
а) расстояние от начала координат до прямой az + az — 2b равно ;
б) расстояние от точки za G С до прямой az + az = Ь равно 1 •
12. Доказать, что точки zb z2 и z3 лежат на одной прямой тогда и только тогда, когда
Zi zt
z2 z2
z3 z3
1
1
1
= 0.
13. Пусть zb z2, z3 — соответственно вершины треугольника ABC, вписанного в единичную
окружность. Доказать, что АС = АВ (т. е. треугольник является равнобедренным) тогда и только
тогда, когда z2 = z2z3.
Упражнения для самостоятельной работы
81
14. Доказать, что V(n g N, zk : |г^| < 1) выполняется неравенство
П(! ~zk) 1- Ы.
к=1 к~1
15. Доказать, что
а) |1 + z2| > 2(Rez)2 Vz:-1 Rez 1;
б) Re 7^+it ~efRe~J;11 > если 2| С, z2 g С, Rez2 > 0.
16. Решить систему уравнений
z3 + w5 = 0
z2-w4 = 1.
17. Показать, что корни квадратного уравнения az2 + bz + с = 0 с действительными а, Ь, с и
отрицательным дискриминантом образуют пару взаимно сопряженных комплексных чисел.
18. Доказать, что корни Z| и z2 уравнения z2 + 2pz + q = 0 (р g С, q g С, q # рг) лежат на
прямой, проходящей через начало координат, в том и только в том случае, когда или р = 0, или
р # 0, а т- g R и < 1.
г р р‘
19. Найти множество точек z в комплексной плоскости С, удовлетворяющих следующим
соотношениям:
a) |z - a| = R; б) Rez + Imz = 1; в) argz = a, a g (—к, тг]; г) |y=4| = 1;
д) Re(z2 - z) = 0; e) |z - г| + |z + i| = 4; ж) Re(l + z) — |z| = 0.
20. Написать в комплексной форме уравнения следующих линий:
а) ху = 1; б) х2 + (у + I)2 = 1; в) х2 - у2 = |; г) у2 = 2х + 1; д) р = .
21. Найти множества точек z на плоскости С, которые определяются условиями:
а) г < [z —z0| < R; б) |^|| 1; в) а < Rez < 6; г) | < Re |+ Im | < |; д) 0 < arg < у.
22. Среди комплексных чисел z, удовлетворяющих условию |z — 25г | ^15, найти то, главное
значение аргумента которого наименьшее.
23. Доказать, что отличные от О и N точки Д(г,) и A(z2) сферы Римана диаметрально про-
тивоположны тогда и только тогда, когда точки zj и z2 плоскости С связаны условием z, z2 = -1.
24. При каких значениях параметра а следующие окружности комплексной плоскости С
отвечают большим кругам на сфере Римана:
a) |z - a| = a (a > 0); б) |z — у | = а (а > 0); в) |z — г| = а (а > 0); г) |z — 2аг| = а (а > 0).
25. Найти: _____
а) lim (п2 (1 — cos у) + i(Vn2 + 1 - >/n)sm у) ;
б) lim (1 + 2z + 3z2 + ... + nz”-1), если |z| < 1.
n—*oo
n
26. Доказать, что предельные точки последовательности (сп), где cn = (1 + у) лежат на
fc=i
окружности 7 =
27. Пусть а и Д (a# Д, |а| < 1, |Д| < 1) — заданные комплексные числа, а последователь-
ность (z„) определена рекуррентными соотношениями
z„ = (а + Д)г„_1-аДгп_2 Vn > 2.
Доказать, что lim z„ = 0.
п—*оо
28. Пусть Z[ = a, z-> = b (а # 0, Ь # 0, a # 6) и — = —-1-—. Доказать, что lim z„ = 0.
2" г"-' г" + 1 П-.ОО
29. Доказать, что если области D\ и D2 плоскости С имеют общую точку, то U £>2 также
является областью. 2
30. Дана функция f : С —* С, где f(z) = —, z = е’*’ и р — произвольное дей-
ствительное число; а) доказать, что f — действительная функция от <р; б) найти образ отрезка
7 = € К • 0 д } при отображении f.
31. Для отображения w = | (ш = и + iv, z = х + iy) найти:
z g С : |z| =
1) w = Imz; 2) w = z; 3) w =
82 Гл. 2. Комплексные числа и функции комплексного переменного
а) образы линий: 1) х = С; 2) у = С', 3) х + у = 1; 4) argz = а; 5) \z + t| = 1; 6) у = |х|;
б) образы множеств: 7) полосы, заключенной между прямыми х = 0 и х = 1; 8) полосы,
заключенной между прямыми у = 0 и у = 1;
в) прообразы линий: 9) и = С; 10) v = С.
32. Для отображения w = найти прообразы множеств:
a) W = {w € С : |w| < 2}; б) W = {ш € С : |w| 1}.
33. Доказать, что функция w = z1 + 2z + 3 однолистна в круге К = {z € С : |z| < 1}.
34. Определить кривые и построить их графики:
1) z = z0 + ae’f + (0 t тг; а g R, /3 € R);
2) z = ate'1, 0 t < +оо, а g R;
3) z = t2 + 4, 0 < t < +оо;
4) z = (а + Д)е*‘ — ре 0 , где 0 < t < +оо, а, р — положительные постоянные.
35. Найти (если существуют) пределы:
1) lim—; 2) lim 3) lim 4) Пт^Ч; 5) lim (~^ + 2i\;
' . z—г ’ ' г+г ’ ' z—2г ’ ' г4 — I ’ ' Л \ + /
Z—>1 z—‘ОС Z—‘ОС z—>i Z—»и X 17 /
6) lim z; 7) lim argz; 8) lim 4; 9) lim .
z^l-i z^-1 z^O г z—.0 lmz
36.Исследовать на непрерывность в областях существования следующие функции:
х + iy, если х или у рациональные,
0, если хну иррациональные.
4) w = 7^4’ 5) w = tg(argz).
37. Пусть функции и = и(х, у), v = v(x, у) дифференцируемы в области D и f(x + iy) =
и(х, у) + iv(x, у) для всех (х, у) g D. Доказать, что для дифференцируемости функции f в
точке z0 = х0 + iy0 g D необходимо и достаточно, чтобы выражение du(x0, у0) + г dv(x0, у0) было
пропорционально dz = dx + г dy.
38. Пусть функции и — и(х, у), v = v(x, у) дифференцируемы в области D, f{x 4- iy) =
и(х, у) + iv(x, у) для всех z = s + ij/g£>HVu = (f^, f^) , Vu = (||, fj) — градиенты
соответственно функций и и v. Доказать, что условия дифференцируемости функции f как
функции комплексного переменного z g С выражаются равенствами
(Vu, Vv) = 0, |Vu| = |Vv|,
где (Vu, Vv) — скалярное произведение градиентов, a |Vu|, |Vv| — их длины.
( Ху2(а:-Н1>) еСЛИ Z Ф 0
39. Доказать,что функция /(z) = < з-2+»4 ’ ’ непрерывна в окрестности
0 при z = 0
точки z = 0, пределы lim существуют, если z стремится к нулю вдоль произвольной
z-,0 Z
прямой, и равны между собой, однако / не дифференцируема в точке z = 0.
40. Исследовать на аналитичность в областях определения функции:
1) f(x + iy) = х + + i (у- ; 2) f(z) = |z|2 + 2z; 3) /(z) =
41. Пусть все корни многочлена P(z) лежат в некотором круге. Доказать, что в этом же круге
лежат и все корни его производной P’(z).
42. Доказать, что если функции / и д являются аналитическими в точке z(1 и /(z0) =
g(za) = 0, но g'(za) / 0, то lim = АЧЧ Найти lim АЧл-
и/ ’ с? \ и/ / ’ z—+z 9 \zQt z—*i 1 +
43. Пусть функция f — аналитическая в области D, и = Re f, v = Im f. Доказать, что линии
и — const всегда пересекают линии v = const перпендикулярно в тех точках, где f'(z) = 0.
44. Определить аналитические функции f, если
а) и = х2 - уг + 2х, f(i) — —1 + 2г; б) v = е1 sin у + 2ху + 5у, f(0) = 10.
Глава 3
Элементарные функции
в комплексной плоскости
В этой главе рассматриваются элементарные функции комплексного переменного, их основные
свойства и конформные отображения, осуществляемые ими.
§ 1. Дробно-линейные функции и их свойства
1.1. Определение дробно-линейной функции. Конформность отображения.
Дробно-линейными называются функции вида
где а £ С, b Е С, с € С, d € С и выполняется условие ad — be # 0. Это условие исключает случай
вырождения функции (1) в постоянную величину. При с = 0, d # 0 функция (1) становится
линейной:
а b
w — —z -I— = Az + В.
d d
Дробно-линейная функция w определена для всех г € С, за исключением двух точек: г, = — ^
и z2 = оо._ При с = 0 эти точки совпадают. Продолжим функцию w на всю расширенную
плоскость С, полагая w(zt) и ш(оо) равными предельным значениям w в этих точках:
а
w(zt) = оо, w(oo) =
с
Тогда^дробно-линейная функция станет непрерывной в С, осуществляя непрерывное отображе-
ние С на С. Рассматривая (1) как уравнение и решив его относительно z, получим
dw + Ь
z =-------- (2)
cw — а
Получили опять дробно-линейную функцию, определенную в плоскости С, поскольку z = оо
при ш = и z = - j при w = оо согласно с принятым выше условием. Таким образом, получили
теорему.
Теорема 1. Всякая дробно-линейная-функция (1) осуществляет гомеоморфное (т.е. взаимно
однозначное и непрерывное) отображение С на С.
Производная дробно-линейной функции
dw ad —be
dz (cz + d)2
не равна нулю и конечна для всех z € C\{zb z2}. Поэтому отображение, осуществляемое дробно-
линейной функцией w, является конформным для всех z 6 C\{zb z2}. Чтобы установить свой-
ство конформности также в точках zi и z2, введем в рассмотрение понятие угла в бесконечно
удаленной точке.
84
Гл. 3. Элементарные функции в комплексной плоскости
Определение. Под углом в точке z = оо между двумя путями 71 и проходящими через
бесконечность и имеющими в своих сферических изображениях касательные в полюсе У, понимаем
угол между образами Г, w Г2 этих путей при отображении z >-» Г = Z в точке Z = 0 (при условии,
что Г1 и Г2 имеют касательные в точке Z = 0) (рис. 29).
Пусть 71 и 72 — два пути, проходящие через точку z = и пересекающиеся в ней под
углом а (считая, что пути имеют касательные в этой точке). Их образы Г* и Г2 при отображении
(1) будут проходить через бесконечно удаленную точку. Угол между ними в бесконечности по
определению равен углу между их образами ? иГ; при отображении W = Поскольку
cz + d
W=------,
az + b
(3)
то пути и Г2 можно рассматри-
вать как образы 7! и 72 при отобра-
жении (3). Это отображение являет-
ся дробно-линейным с производной
dW Ьс - ad
dz (az + b)2 ’
отличной от нуля в точке z = — ,
т. е. отображение (3) конформное в
точке z = - и угол между Г] и Г2
в точке W = 0 равен а. Отсюда
имеем, что угол между Г[ и Г2 на бесконечности равен а. Конформность отображения (1) в
точке z = доказана. Для доказательства конформности отображения (1) в точке z = оо при-
меним приведенные выше рассуждения к обратной функции (2) в точке w = В результате
получим следующую теорему.
Теорема 2. Дробно-линейное отображение конформное везде на С.
Непосредственной проверкой можно убедиться в том, что композиция дробно-линейных ото-
бражений опять есть дробно-линейное отображение. Поэтому справедливо следующее утвержде-
ние.
Теорема 3. Совокупность Л всех дробно-линейных отображений образует группу, если за груп-
повую операцию принять композицию отображений.
Доказательство состоит в непосредственной проверке групповых аксиом (ассоциативность,
существование единицы и существование обратного элемента).
1.2. Геометрические свойства дробно-линейных отображений.
Рассмотрим следующие четыре частных случая дробно-линейных отображений:
1) параллельный перенос на вектор h
w = z + h;
2) поворот вокруг начала координат на угол в
{в
w = е z;
3) подобие с коэффициентом подобия г (г > 0) и центром подобия в точке z = 0
w = rz;
4) обратное отображение
1
w = -.
Z
§ 1. Дробно-линейные функции и их свойства
85
Покажем, что любое дробно-линейное отображение можно получить в результате композиции
нескольких отображений, каждое из которых является одним из четырех рассмотренных:
az + b а Ь — — а
w = ----- = - Н---= - + w4
cz + а с cz + а с
(ad\ 1 / ad\
b----I ----= I b---I w3
c J cz + d \ c J
1 1
cz + d w2
w2 = cz + d = W[ + d
w, = cz
(параллельный перенос);
(подобие и поворот);
(обратное отображение);
(параллельный перенос);
(подобие и поворот).
Итак, свойства, справедливые для указанных четырех отображений, можно в ряде случаев пе-
ренести на общее дробно-линейное отображение. Таким образом получается, например, круговое
свойство дробно-линейных отображений.
Теорема / (круговое свойство). Любое дробно-линейное отображение преобразует каждую
окружность на С в окружность на С, где под окружностью на С понимаем всякую окружность или
прямую на комплексной плоскости.
◄ Для отображений поворота, подобия, параллель-
ного переноса круговое свойство очевидное. Докажем его
справедливость для обратного отображения.
Каждую окружность на плоскости С можно задать
уравнением
А(х2 + уг) + Вх + Су + D = 0. (1)
Полагая z = х + iy, z — х — iy, перепишем (1) в виде
Azz + B\z + C\Z + D — 0, (2)
где Вг = |(В - iC), Ci = |(В + iC).
Чтобы получить уравнение образа окружности (2)
при обратном отображении, полагаем в (2) z = . По-
лучим
X
А + Btw + C|W + Dww = 0. ри 30
Это уравнение вида (2) и, следовательно, является уравнением окружности на плоскости С. ►
Чтобы сформулировать второе геометрическое свойство дробно-линейных отображений, вве-
дем в рассмотрение понятие симметричных точек относительно окружности.
Определение 1. Точки z иг* называются симметричными относительно окружности
(конечного радиуса) на С, если они лежат на одном и том же луче, выходящем из центра окруж-
ности z0, а произведение их расстояний от центра равно квадрату радиуса R2 данной окружности
(рис. 30),
Имеем
arg(z - г0) = arg(z' - z0), |z - z0||z* - z0| = R1,
a, *0 — >------Гc — .---------: <-----Г — • •
|z-z0| fz-zole-'^-^ z - z0
Отсюда
p2
z’ = z0 +------ (3)
Z - z0
В частности, при z0 = 0, R = 1 получаем z* = ~.
Определение 2. Точки z и z* назовем симметричными относительно прямой (т.е.
окружности бесконечного радиуса), если они лежат на одном и том же перпендикуляре к этой прямой,
на одинаковом расстоянии от нее, но с разных сторон.
Докажем основное свойство симметричных точек, полностью характеризующее их.
Гл. 3. Элементарные функции в комплексной плоскости
Теорема 2. Для того чтобы точки z и z* были симметричными относительно окружности Г,
необходимо и достаточно, чтобы любая окружность 7 на С, проходящая через них, была ортого-
нальна Г.
◄ Необходимость. Пусть точки z и z" симме-
тричны относительно окружности Г и 7 — произвольная
окружность, проходящая через z и z* (рис. 31).
Проведем через точку z0 касательную к окружно-
сти 7. По известной теореме квадрат длины отрезка этой
касательной — z0|2 равен произведению длины отрезка
секущей |z*-z0| на длину его внешней части \z- z0|, т. е.
|£ - z0|2 = \z - z0||z* — z0|. Так как z и z* симметричны
относительно Г, то |£ - z0| = R. Таким образом, отрезок
касательной к 7 является радиусом окружности Г, т.е. 7
ортогональна Г.
Достаточность. Пусть точки z и z* имеют свой-
ство: любая окружность 7, проходящая через них, орто-
гональна Г. Тогда:
1) точки z и z' лежат на одном луче с вершиной z0 —
центром окружности Г. Это следует из того, что в каче-
Рис. 31
стве 7 можно взять прямую, которая должна быть ортогональной Г и, следовательно, проходит
через центр z0 окружности Г.
2) |z - z0||z* - z0| = К — zo\2 = R2, т.е. точки z и z* симметричны относительно Г. ►
Из доказанного свойства симметричных точек вытекает, что в случае, когда окружность Г
вырождается в прямую линию, симметрия относительно окружности превращается в обычную
симметрию.
Доказанная теорема предоставляет возможность дать другое определение симметричных то-
чек.
Определение 3. Точки z и z* называются симметричными относительно окружно-
сти Г на плоскости С, если любая окружность 7, проходящая че-их, ортогональна Г.
Отображение z >-» z* называется инверсией.
Теорема 3 (об инвариантности симметричных точек при дробно-линейном
отображении). Произвольное дробно-линейное отображение переводит каждую пару точек z и z*,
симметричных относительно некоторой окружности Г С С, в точки w и w*, симметричные отно-
сительно окружности Г*, являющейся образом окружности Г при данном отображении.
◄ Проведем через точки шиш" произвольную окружность 7*. Ее прообраз 7 в плоскости z,
согласно теореме 2, ортогонален окружности Г. В связи с конформностью дробно-линейного ото-
бражения окружности 7* и Г* ортогональные. Тогда, по теореме 2, точки шиш* симметричные
относительно Г*. ►
1.3. Дробно-линейные изоморфизмы и автоморфизмы.
В формулу, задающую дробно-линейное отображение L
az + 6
cz + d
(1)
входит четыре комплексных параметра а, b, с, d. В действительности же, отображение (1) за-
висит от трех параметров, поскольку числитель и знаменатель (1) можно разделить на один из
отличных от нуля параметров. Поэтому естественно ожидать, что посредством дробно-линейного
преобразования три заданные точки единственным образом преобразуются в три_заданные.
Теорема 1. Какими бы ни были три разных точки zi € С, гг € С, z3 6 С и три разных
точки Ш] е С, ш2 6 С, ш3 € С, существует, и притом единственное, такое дробно-линейное
отображение L, что L(zk) = wk (k = 1, 2, 3).
Ч Существование: а) Пусть zk € С, wk G С (k = 1, 2, 3). Рассмотрим дробно-линейное
отображение, переводящее точки zlt z2, z3 и Ш|, ш2, ш3 соответственно в точки 0, 00, 1 плоско-
§ 1. Дробно-линейные функции и их свойства
87
сти
Z - Zx Z3 - Z2 w - w} - w2
•И : £ — ------------, h2 : Q-------------------.
z — z2 z3 — Z[ W — W2 W3 — WI
Очевидно, что отображение L = L3' о L\ является искомым, L : w = w(z), w(zfc) = wk. Его
можно найти из соотношения
z — z( z3 — z2 w — wt w3 — w2
z — z2 z3 — Zt W — W2 W3 — W,
б) Если одна из точек z, или w, или одна точка z, и одна точка Wj (i, j = 1, 2, 3) бесконечно
удаленная, то формула (2) остается в силе. В этом случае лишь требуется числитель и знаменатель
дроби, где появляется эта точка (каждая точка z; и wj входит в (2) дважды: один раз в числитель,
второй раз — в знаменатель), заменить единицей. Например, пусть z3 — w, = оо. Тогда (2)
примет вид
z3 — z2 w3 — w2
z — z2 w — w2
Единственность. Пусть кроме отображения L существует такое дробно-линейное ото-
бражение А, что A(zfc) = шк. Рассмотрим дробно-линейное отображение L = L2 ° А ° . Оно
оставляет неподвижными точки 0, оо, 1. Из L(oo) = оо => L(z) = az + b, из L(0) = 0 => b = О,
из £(]) = 1 => а = 1. Следовательно, L(z) = z, т.е. Ь2 о А о = Е, где Е — тождественное
отображение. Отсюда имеем А = L^L] = L. ►
Следствие. Любую окружность 7 С С можно посредством дробно-линейного отображения
преобразовать в любую другую окружность У С С.
Действительно, для этого достаточно перевести три точки окружности 7 в три точки окруж-
ности 7*. Из кругового свойства дробно-линейного отображения, а также из того, что три точки
определяют единственную окружность, следует утверждение.
Дробно-линейное отображение области D на область D* называется дробно-линейным изомор-
физмом, а области D и D*, для которых такой изоморфизм существует, называются дробно-линейно
изоморфными. _ _
Область К С С называется кругом, если ее граница является окружностью на С. Следо-
вательно, это может быть круг в обычном понимании, или внешность такого круга, а также по-
луплоскость. Любая окружность 7 плоскости z разделяет С на два круга К, и К2. В свою очередь
окружность 7* = Д(7) плоскости w разбивает С на два круга Кf и К2. Из топологических сообра-
жений ясно, что возможны два случая: a) L(Kt) = Kf, L(K2) = К2; 5) L(Kt) = К2, L(K2) = .
Чтобы выяснить, какой из этих двух случаев выполняется, достаточно найти образ любой
точки круга Д’, (или круга К2). Можно также воспользоваться так называемым правилом обхода,
которое состоит в следующем.
Зафиксируем на окружности 7 три точки z3, z2, z3. Их образами соответственно будут точки
W|, u?2, w3. Три точки на окружности устанавливают на ней вполне определенное направление
обхода. Используя свойство сохранения углов при конформном отображении, можно показать,
что при обходе окружности 7 и 7* в направлениях, определенных точками z; и Wj (г, j = 1, 2, 3),
области, соответствующие друг другу, будут размещены с одной и той же стороны. Теперь легко
убедиться в следующем. _
Теорема 2. Любые два круга на плоскости С дробно-линейно изоморфны.
Найдем, например, все дробно-линейные изоморфизмы верхней полуплоскости Z+ = {z g С:
Imz > 0} на единичный круг К = {w g С : |w| < 1}.
Пусть a (Im а > 0) — точка верхней полуплоскости Z+, которая при данном отображении
переходит в центр круга К w = 0. Точка а, согласно с инвариантностью симметричных то-
чек, перейдет при дробно-линейном отображении в точку w = 00, симметричную точке w = 0
относительно окружности 7 = {w € С : |to| = 1}. Очевидно, что искомое отображение имеет вид
z — а
w — к----(3)
z — а
При z = х имеем |z — а| = |z - а|. Для того чтобы ось Ох отображалась на единичную
окружность, необходимо, чтобы |А| = 1, т. е. к = е'в.
Гл. 3. Элементарные функции в комплексной плоскости
Итак, все дробно-линейные изоморфизмы верхней полуплоскости Z* на единичный круг
определяются формулой
(4)
ie z ~ а
w = е -----
z — а
где а — произвольная точка верхней полуплоскости (Im а > 0), а 9 — произвольное действи-
тельное число. Имеем также w(oo) = е'в.
Установлено, что вся совокупность дробно-линейных изоморфизмов верхней полуплоскости
на единичный круг зависит от трех действительных параметров, а именно 9, Rea и Im а.
Дробно-линейный изоморфизм области на себя назовем дробно-линейным автоморфизмом.
Очевидно, что совокупность всех дробно-линейных автоморфизмов какой-нибудь области обра-
зует группу, которая является подгруппой группы Л всех дробно-линейных отображений. Так,
1) совокупность всех дробно-линейных автоморфизмов С совпадает с Л,
2) совокупность дробно-линейных автоморфизмов С совпадает с подгруппой (целых) линей-
ных преобразований z az + 6;
3) подгруппа автоморфизмов единичного круга К = {w € С : |ш| < 1} имеет вид
if> z~a I,/,
z н-» е -a| < 1
1 — az
и зависит от трех действительных параметров: двух координат точки а и числа 9.
(5)
Рассмотрим примеры.
1 z + ia
1. Найти образ оси Оу при отображении w =------, а # 0, а £ R.
~z + га
•4 Имеем w(0) = 1, w(<x>) = - I, w(ia) = оо. Три точки —1, 1, оо на плоскости w определяют
действительную ось. ►
2. Найти образ отрезка с концами в точках z, = — 1 4- 2г', z2 = 1 4- 2г' при отображении
2z -f- г
w = .
гг 4- 2
4 Поскольку u>(z,) = —5 — 2г, w(z2) = 5 - 2г, го(2г) = оо, то образом прямой у = 2, которой
принадлежит данный отрезок, будет прямая Imir = -2. Конечный отрезок [z,, z2] переходит в
отрезок, содержащий бесконечно удаленную точку, с концами иц = — 5 — 2г, w2 = 5 — 2г. ►
ч , .. , V2(z - 1 - г')
э. Наити линию z -плоскости, образом которой при отображении w = — ---;— является
единичная окружность 7 = {w £ С : |w| = 1}.
4 Имеем |w| = 1 => ww = 1. Исходя из этого, получаем ~ 1’ 0ТКУда zz = 1,
т.е. искомый прообраз — единичная окружность 7' = {z £ С : |z| = 1}. ►
4. Доказать, что |а| = |с| > 0 является необходимым и достаточным условием того, что
dz - Ь
функция w =------ переводит окружность 7={z£C:|z| = 1}b прямую.
а — cz
4 Необходимость. Пусть заданная функция переводит окружность 7 в прямую. Про-
образом точки w = оо является точка z = |, поэтому | ~ | = 1.
Достаточность. Пусть |а| = |с| > 0. Дробно-линейная функция z = переводит оо в
точку |, которая, согласно условию, лежит на единичной окружности. А поскольку точка, лежа-
щая на единичной окружности, перешла в бесконечность, то прообразом единичной окружности
является прямая. ►
5. Построить дробно-линейный автоморфизм верхней полуплоскости, при котором точки
z = 0, z = — 1 остаются неподвижными.
•4 Пусть w = L(z) — искомый автоморфизм. Имеем L(0) = 0 и £(— 1) = — 1. Пусть, далее,
L(a) = b (а £ R, b € R). Тогда, по правилу обхода, а и 6 должны удовлетворять одному из
следующих условий: 1) {а, 6} £ [—1, 0]; 2) {а, &} € [-1, 0].
По формуле (2), п. 1.3, получаем /
(а + l)bz
w =-----------------. ►
(а — b)z + а(&+ 1)
$ 1. Дрооно-линеиные функции и их свойства 39
6. Найти образ единичного круга К = {z 6 С : |z| < 1} и его верхнего полукруга при
3 - 2z
отображении w = -—.
Ч Согласно данной формуле ш(-Г) = ш(1) = Поскольку коэффициенты дробно-
линейного отображения действительные числа, то действительная ось перейдет в действительную
ось. Образом единичной окружности будет окружность, для которой отрезок является
диаметром. Принимая во внимание, что ш(0) = |, единичный круг отображается на круг
Kt = {w G С : |w - || < .
По правилу обхода устанавливаем, что образом верхнего полукруга будет нижний полукруг. ►
7. Найти функцию, отображающую круг К = {z G С : |z| < 1} на круг К* = {w G С :
|w — г| < 1} и переводящую точки 0 и 1 соответственно в точки и 0.
Ч По формуле (3), п. 1.2, находим точку w*, симметричную точке w = |:
. 1
w = г +....... = —г.
Искомое отображение находим по соответствию трех пар точек
w(0) = г~,
w(l) = 0, u>(oo) = -i.
Окончательно получаем
г — iz
и = -------
z + 2
8. Построить дробно-линейную функцию, переводящую точки множества Z = {-1, г, 1 -I- г}
соответственно в точки множества W = {г, оо, 1}. Найти образ области
P={zGC:|z-^|> У|}.
Ч По формуле (3), п. 1.1, имеем
z + 1 1 + г — i w — i
z — i 1 + i + 1 1 - i
Отсюда
(1 + 2i)z + 6 — 3i
w =----------------.
5(2 - i)
Принимая во внимание, что точки zx = -1, z2 = i, z3 = 1 + i лежат на окружности 7 =
|z £ С: |z - ^1 = -^/i} и ОКРУЖНОСТЬ 7 переходит в прямую и + v = 1, по правилу обхода
устанавливаем, что образом области D является полуплоскость Р = {(u, v) € R2 : и + v > 1}. ►
9. Найти дробно-линейную функцию , отображающую правую полуплоскость без круга К =
{2 G С : |z — h\ R}, h> R на кольцо Kt = {w G С : p < |w| < 1} так, что мнимая ось переходит
в единичную окружность. Найти р.
Ч Найдем точки х и х* действительной оси плоскости z, симметричные одновременно отно-
сительно мнимой оси и окружности дК. Очевидно, что х* = —х. Считая х > 0, по формуле (3),
п. 1.2, при z = х и х* = —х находим х = Vh2 — R2. Строим искомое отображение как дробно-
линейную функцию, переводящую точки х и х* соответственно в 0 и оо:
z-Vh2- R2
W = К ----
z + Vh2- R2
90
Гл. 3. Элементарные функции в комплексной плоскости
\h - R - Vh2 — R2\
\h-R + Vh2-fi2|
Из условия |w(zj/)| = 1 находим, что |fc| = 1. Принимая во внимание, что образ точки z = h — R
лежит на окружности 7 = {ш 6 С : |w| = р}, имеем
(Л - R)2 - 2(Л - R)Vh2 - R2 + h2 - R2
(h - R)2 — h2 + R2
(h - R)(h - Vh2 - R2) Vh2 - R2 - h
R(R - h) ~ R
h-Vh2- R2
R
10. Найти общий вид дробно-линейной функции, имеющей две неподвижные точки z, и z2.
Ч 1) z\ = 0, z2 = оо, тогда w = Az, А € С.
2) Полагая W = , Z = и принимая во внимание 1), находим:
W — Z{ Z — Zi
---------= А----------.
W — Z2 Z — Z2
11. При каких значениях А дробно-линейное отображение с двумя неподвижными точками
и z2 (см. пример 10) переводит саму в себя любую окружность, проходящую через неподвижные
точки, с сохранением направления обхода? Показать, что при этом любая окружность, ортого-
нальная к окружности, проходящей через неподвижные точки, переходит в окружность также с
сохранением направления обхода.
◄ Для того чтобы отображение w = Az переводило прямые у = кх сами в себя с сохране-
нием обхода, очевидно, необходимо и достаточно, чтобы выполнялось неравенство А > 0. Это
же условие сохраняется и для общего случая, о чем свидетельствует общий случай 2) в приме-
ре 10. Второе утверждение задачи непосредственно следует из конформности дробно-линейных
отображений, а именно, свойства сохранения углов по величине и направлению отсчета. ►
«т „ iz+2
LA. Доказать, что прямая, проходящая через неподвижные точки отображения w = -------
z — г
переходит в себя.
4 Неподвижные точки отображения w являются решениями уравнения z2 — 2iz — 2 = 0,
z12 = ±1 + i. Точка i, которая указанным отображением переводится в оо, лежит на прямой,
проходящей через неподвижные точки zit z2. ►
13. Последовательность (zn) определена так: za — известное, zn+1 = f(zn), п € Zo, где f —
дробно-линейная функция с двумя неподвижными точками. Исследовать ее на сходимость.
Ч Пусть а G С, р € С — неподвижные точки отображения /. Принимая во внимание
формулу, полученную в примере 10, имеем
zn+\ .2:n—о 2 zn~i— о .п+1 *0 — а । . ,п+1 Цп+1)0 — а а .
zn+i-p z„-p zn-i-p Ze-0 zQ-p
Следовательно,
zn+i - « f 0, если I Al < 1,
n-,00 zn+i -p [оо, если | A| > 1,
ИЛИ
.. f а, если |Л| < 1,
lim zn = < a 4 L. 1
n-oe n [ P, если |A| > 1.
При |A| = 1 lim zn не существует. ►
п—>OO
1
14. Найти центр w0 и радиус R окружности, на которую функция w = ----, Imz2 О,
z-z2
отображает действительную ось.
Ч Из того, что w(z2) = оо, следуют равенства w0 = w(z2) = Поскольку w(oo) = 1, то
точка w = 1 принадлежит окружности и, следовательно, R = |w0 — 1| = 2pmZ'2| • ►
§2. Степенная функция w = zn (п 6 N, п 2). Многозначная функция w = J/z 91
15. Единичный круг отображается на себя так, что точка z0 # О переходит в центр круга. До-
казать, что при этом единичная полуокружность отображается на полуокружность тогда и только
тогда, когда ее концы лежат на диаметре, проходящем через точку z0.
Ч Отображение единичного круга на себя имеет вид
Диаметр окружности 7 = {z € С : |z| = 1), проходящий через точку z0, переходит в диаметр
окружности 7' = {w € С : |ш| = 1} согласно тому, что w(z0) = 0, = 00. Итак, единич-
ная полуокружность, концы которой лежат на диаметре, проходящем через точку z0, перейдет в
полуокружность, поскольку ее концы также лежат на диаметре. Любой другой диаметр, не прохо-
дящий через точку z0, будет отображаться на дугу окружности конечного радиуса. Таким образом,
полуокружности с концами на этом диаметре уже не будут отображаться на полуокружности. ►
16. Найти симметричный образ относительно окружности 7 = {zgC:|z-l| = l} линии
7' = {z € С : \z - 2| = 2} (окружности 7').
◄ Преобразование симметрии относительно окружности 7 полностью определяется функци-
ей w = 1 + ~-=А=,- (см. формулу (3), п. 1.2), откуда z = 1 + —. Поэтому нужно охарактеризовать
те и только те точки, для которых 11 + -==— 21 = 2, или | ш — 2| = 2|w — 11. Это множество точек,
отношение расстояний которых от двух данных точек есть величина постоянная. Оно является
окружностью Аполлония относительно точек 1 и 2. ►
§ 2. Степенная функция
w = zn (п G N, п 2).
Многозначная функция w = J/z
и ее поверхность Римана
2.1. Степенная функция.
Функция
w = z”, z € С (1)
аналитическая в плоскости С. Поскольку = п:"’1 / 0 Vz / 0, то отображение, осуществля-
емое степенной функцией, конформное в каждой точке z € С\{0}.
Пусть z = re’*’, w = ре’*. Тогда
р = г”, V = nV - argz). (2)
Из (2) видно, что отображение (1) увеличивает в п раз углы с вершиной в точке z = 0. Итак,
отображение (1) не является конформным в точке z — 0.
Отображение (1) однозначное, но не взаимно однозначное, поскольку любые две точки
zi g С\{0}, z2 € С\{0} с одинаковыми модулями |zj = \z2\ и аргументами, отличающимися
на целое кратное
2тг
arg z\ = arg z2 + к—, ktz.,
n
переходят в одну точку w. Следовательно, отображение (1) не является однолистным в С. Други-
ми словами, вершины каждого правильного п-угольника с центром в начале координат переходят
при отображении в одну точку на плоскости w. Область плоскости z, не содержащая никаких двух
разных вершин правильного п-угольника с центром в точке z = 0, является областью однолист-
ности функции z •—* zn. Очевидно, что областью однолистности будет любая область, целиком
92
Гл. 3. Элементарные функции в комплексной плоскости
лежащая внутри угла величиной с центром в начале координат. В частности, внутренность
любого угла
2тг
а < ip < а 3--, абй (3)
п
является областью однолистности степенной функции и будет отображаться на всю плоскость w
с выброшенным лучом па € Arg w.
2.2. Многозначная функция w = и ее поверхность Римана.
С помощью лучей <р = а + к^ всю плоскость z
можно разбить на п областей однолистности степенной
функции (к = 0, п — 1).
Пусть а = 0. Тогда такими областями будут внутрен-
ности углов
2Лтг 2(к + 1)тг
-----< <р <
п----п
(1)
т. е. бесконечные секторы.
Попытаемся теперь построить такой геометрический
образ, чтобы степенная функция (1), п. 2.1, устанавлива-
ла взаимно однозначное и взаимно непрерывное соответ-
ствие между точками всей плоскости z и точками этого
образа.
Рассмотрим первый угол 0 < <р < . Он отобража- 32
ется на всю плоскость w с выброшенной положительной
полуосью. В нее переходят два луча: р = 0 и р = . Чтобы сберечь взаимную однозначность
множества D = {г € С : 0 |z| < +оо, 0 argz } и плоскости w, проведем на плоскости
w вдоль действительной положительной полуоси разрез и в соответствии с правилом обхода счи-
таем, что луч р = 0 переходит в верхний берег разреза, а луч р = — в нижний. Изготовляем
п экземпляров плоскости w с разрезами вдоль положительной части действительной оси, являю-
щихся образами бесконечных секторов, определяемых условиями (1), подкладываем их друг под
друга и склеиваем так, чтобы сохранить непрерывность и взаимную однозначность соответствия.
Для этого нижний берег разреза первого листа склеиваем с верхним берегом второго (находя-
щегося под ним) листа, нижний берег разреза второго листа с верхним берегом разреза третьего
листа и т.д. и, наконец, нижний берег разреза n-го листа с верхним берегом разреза первого
листа (рис. 32).
Полученный геометрический образ называется поверхностью Римана функции z = l/w. По-
верхность Римана наглядно помогает лучше понять природу отображения, совершаемого степен-
ной функцией.
Выше отмечалось, что область плоскости z является областью однолистности функции z z”
тогда и только тогда, когда она не содержит двух разных вершин правильного п-угольника с
центром в точке z = 0. Ясно, что область, содержащая точку z = 0 или z = оо, этому условию не
удовлетворяет. Заметим также, что эти точки являются неподвижными , т. к. 0" = 0, (оо)" = оо.
Пусть теперь D* — любая односвязная область плоскости w, не содержащая точек 0 и оо.
В такой области можно определить п разных функций (однозначных), для каждой из которых
функция w = z" является обратной. Эти функции называются однозначными ветвями много-
значной функции z = y/w. Пусть z = re'*’, w = ре'в. Тогда г = ^/р, р = Угол 6 опре-
деляется однозначно для каждой ветки и каждой точки из области D*, а именно, берем любую
точку Wo € D*, фиксируем в ней какое-нибудь определенное значение 0 = в0 и в дальнейшем
считаем, что при непрерывном перемещении точек w в D* угол 6 изменяется непрерывно. По-
скольку область В* не содержит точки 0 и оо, то значение 9 для каждой точки множества D*
.— в_
будет однозначно определено и равенство z = « будет определять однозначную функцию
в области D*. Если теперь положить для ш0 6 D* в = 6й + 2тг, то получим другую ветвь, при
0 = 0о + 4тг — третью ветвь и т.д. Таким образом, фиксируя значение 0 в точке wo разными
способами, полагая 0 = 0О + 2fc?r (к = 0, п — 1), получаем п функций, для каждой из которых
§2. Степенная функция w = z" (n GN, n 2). Многозначная функция w = y/z
93
стеленная функция w = z” является обратной. Объединение этих функций (однозначных ветвей)
назовем многозначной функцией z = y/w.
Точка, при обходе которой в достаточно малой ее окрестности совершается переход от одной
ветви многозначной функции к другой ее ветви, называется точкой разветвления этой много-
значной функции. Причем, если после п-кратного обхода в одном и том же направлении опять
возвращаемся на начальную ветвь, то говорят, что это точка разветвления (п — 1)-го порядка, в
противном случае — бесконечного порядка. Точки разветвления конечного порядка называются
алгебраическими точками разветвления. Точки w = 0 и w = оо являются алгебраическими точками
разветвления (п — 1)-го порядка функции z = Уш. В этих точках сама функция принимает по
одному значению: Уб = 0, Уоо = оо. На поверхности Римана они будут концевыми точками
разрезов, общими для всех листов. Каждая ветвь функции z — y/w является аналитической в
области D* с производной
d - г- 7 п
-- у/W = 5= 0.
dw nw
Таким образом, отображение, осуществляемое каждой ветвью, конформное в любой области D*
(0 £.0* и оо £Р*).
Рассмотрим примеры.
17. Найти образы следующих областей при отображении w = z2:
а) внутренности правой ветви гиперболы х2 - у1 = а2;
б) области, ограниченной правой ветвью гиперболы х2 — у2 = 1 и лучами argz — ±j;
в) полуплоскости Р = {z g С : Imz с; с = const > 0}.
◄ а) правая ветвь гиперболы переходит в прямую и = а2. Принимая во внимание, что
х > 0, по правилу обхода устанавливаем, что внутренность правой ветви гиперболы переходит в
полуплоскость Q = {w 6 С : Rew > а2}.
б) Лучи argz = ±~- являются асимптотами гиперболы х2 — у2 = 1. При отображении w = z2
лучи переходят в мнимую ось, а правая ветвь гиперболы х2 — у2 = 1 — в прямую Rew = 1.
Образом заданной области является полоса Af={wgC:0<Rew< 1}.
в) При у = с имеем и = х2 - с2, v = 2сх, х G R. Исключив х, находим: и = - с2.
Принимая во внимание, что с > 0, по правилу обхода устанавливаем: образом полуплоскости Р
является внешность параболы и = — с2 (т. е. область, ограниченная этой параболой и такая,
что ей не принадлежит фокус параболы). ►
18. Построить конформное отображение области, ограниченной двумя параболами у2 =
4(z + 1), у2 = 8(z + 2) на полосу М = {w € С : 0 < Rew < 1}.
◄ Образом прямых Im W — с в плоскости z = W2 являются параболы у2 = 4с2(х + с2)
(см. предыдущий пример). Следовательно, функция W = yfz (УТ = 1) отображает заданную
область на полосу М' = {PF € С : 1 < ImW < 2}. С помощью отображения w = — (У2+1)(г1Г+1)
полоса М' перейдет в полосу М. Окончательно имеем
w = —(У2 4- V)(iy/z + 1). ►
19. Найти образ области G — {z € С : Imz > 1, |z| 2} при конформном отображении
( z + УЗ — г \ 3
w = - ------=---
\z — УЗ — i J
◄ Область G — круговая луночка. Точки zt = —УЗ + », z2 = Уз 4- г — ее угловые точки. С
помощью равенств W|(I) = —1, wt(2i) = устанавливаем, что функция w, = 4Д41 отобра-
жает луночку G на внутренность угла тг < argwt < |тг. Отображение w = — w2 переводит точки
внутренности угла в множество Р = {w € С : Im w > 0}, являющееся образом области G. ►
20. Найти отображение области (луночки) G = {z G С : |z| > 2, |z — У5| < У2} на верхнюю
полуплоскость.
◄ Найдем точки пересечения окружностей 71 = {z € С : |z| = 2} и 72 = {z € С : |z — у/2\ =
У2}: z1 = У2-1У2, z2= У5 + гУ2.
94
Гл. 3. Элементарные функции в комплексной плоскости
Функция
z — Z\ (л/2 — 1)(—1 + г) , г-
w, =--------w,(2) = --------Ц=------, W) (24/2) = i
z - z2 2-4/2 '
отображает луночку G на внутренность угла у- < argW[ < а функция w = wf отображает
внутренность угла на верхнюю полуплоскость Р = {w £ С : Im w > 0}. Следовательно, искомое
отображение имеет вид
z-4/2(1-») V
z-72(1 +г)/ ’ *
21. Конформно отобразить плоскость с разрезом вдоль промежутков (-оо, -|], +оо)
на круг К = {w £ С : |w| < 1} так, чтобы 0 <-» 0.
◄ Искомое отображение находим посредством следующей цепочки отображений:
Z| + 1 ,___ z-l — i
21(г) = 22, Z2(Zj) =------, Z3(z2) = y-Z?, Z2(-l) = I, V)(z3) = е-—, w(l') = 0.
2] — 1 23 + г
Окончательно имеем
1 - '/I - 4z2
w = е ------------. ►
22
22. Найти конформное отображение плоскости с разрезом вдоль интервала (-оо, —1) на
круг К = {ш £ С : |ц>| < 1}, при котором z = 0 <-> w = 0.
◄ При отображении wt = 4/z + 1, шДО) = 1, заданная область переходит в правую полуплос-
кость Р = {u)| € С : Reu?! >0}. При отображении w2 = iwt = г'4/z + 1 правая полуплоскость Р
переходит в верхнюю полуплоскость Р' = {ui2 6 С: lmw2 >0}, w2(0) = i. С помощью форму-
лы (4), п. 1.3, при а = г окончательно получаем:
w2 - i y/z + 1 - 1
w = e ------= e , ---. ►
w2 + г yjz + 1 + 1
23. Найти образ области G = {2 £ С : |z| < l,Rez > 0, Imz > 0} при отображении
= , 1 ,, \/1 + г2| = 1-
71 + z2 L=o
•< Отрезок [0, 1] отображается функцией w в отрезок М=, 1 , а отрезок [0, г] — в луч
[1, +оо). Дуга г = е*‘
(О $11 у) перейдет в кривую w =
1
л/1+(е'‘)2
или w = u + iv =
cos — г sin
у/2 cos t
Исключив параметр t, получим, что дуга окружности переходит в часть гиперболы и2 - v2 — |,
и > 0, v < 0. В соответствии с правилом обхода, искомым образом является область
D = {(и, v) £ R2 : и2 + V1 > |, v < 0} . ►
§ 3. Показательная функция w = ez
и многозначная функция z = Lnw.
3.1. Показательная функция w = ez.
Показательную функцию z н е!, z € С определим соотношением
w = u + iv = ег = ех+,у = ех(cosy + isin у). (1)
Для действительных z = х это определение совпадает с обычным. Чтобы установить этот
факт, полагаем в формуле (1) у = 0.
§3. Показательная функция w = ez и многозначная функция z = Lnw.
95
Функция w = ez аналитическая Vz g С. Действительно,
ди dv ди dv х
— = —- = е cos и, — — = = е sin у,
дх ду ду дх
т. е. Vz g С функции и и v удовлетворяют уравнениям Коши—Римана. Дифференцируя функ-
цию w, Vz g С имеем
d z ди . dv х х , z
—е = -—I- г — = е cosy + ге sin у = е .
dz дх дх
Для функции z н-» ег сохраняется теорема сложения
Z I Zf Z1 +zi
е 1е - = е 1 .
(2)
(3)
(4)
Действительно, пусть z\ = xt + iyt, z2 = x2 + гу2. Тогда
eZ|eZ2 = eZ | (cosy, + isin yi)e’:(cosy2 + isiny2) = ex,+x2 (cos(y[ + y2) + isin(yj + y2)} = eZ|+Z2.
Функция w = ez периодическая с чисто мнимым основным периодом 2тгг. Действительно,
пусть ez+'" = ez, w = а + i/З. Умножим обе части этого равенства на e~z. Получим
е = е cos р + ге sin Д — 1
или
eacos/3=l, е“ sin/3 = 0.
Отсюда находим: а = 0, /3 = 2ттг, w = 2т~г, т.е. 2тгг — основной период функции w.
Функция w определена в С и не имеет предела при z —» оо, так как
lim ez = оо, lim ez = 0.
г=х>0 z=x<0
Показательная функция не принимает в С нулевого значения, т. е. начало координат не
принадлежит образу плоскости С при отображении z >-+ ez. Чтобы доказать это, полагаем в
формуле (4) Z| = z, z2 = —z. Тогда eze~z = 1, или e~z = . Отсюда и следует утверждение, так
как если бы в какой-нибудь точке показательная функция обратилась бы в нуль, то в точке —z
она не была бы определена, что противоречит ее определению.
Покажем, что любая другая точка плоскости w (т. е. w # 0) принадлежит образу плоско-
сти С при отображении (1). Пусть w — произвольная точка плоскости С, отличная от нуля и
бесконечности. Найдем по w такое z, что ez = w. Имеем
|w| = ех => х = In |w|, у g Argw.
Следовательно,
z = x + iy = In |w| + iy = In |w| + i(arg w + 2/гтг), к g Z. (5)
Замечаем, что существует бесконечное множество прообразов точки w g С Л w ф 0. Все они
лежат на прямой, параллельной оси Оу, на расстоянии 2тг один от другого. Таким образом,
w = ez : С —» С\{0}.
Это отображение однозначное, но не взаимно однозначное, поскольку каждая точка w g С\{0}
имеет бесконечное множество прообразов.
Любая область, не содержащая двух разных точек, в которых действительные части совпадают,
а мнимые отличаются на 2/гтг, fc g Z, будет областью однолистности показательной функции
z ez. Так, областью ее однолистности будет полоса М = {z g С : b < Imz < b + 2тг}.
Ее образом будет вся плоскость w с выброшенным лучом, выходящим из начала координат под
углом Ъ.
Пусть w = регв. Тогда из равенства регв = е1е,у имеем р = ех, 0 = у, т.е. прямые у = const
функция w = ez переводит в лучи, а отрезки у = {(я, у) g R2 : х = const, Ь < у < Ь + 2тг} — в
окружности с выброшенной точкой, лежащей на луче 0 = Ъ.
Каждая горизонтальная полоса шириной 2тг
Мк = {z g С : 2А=тг < Imz < 2(к + 1)тг}, к g Z,
отображается показательной функцией на множество
= {(/>, <р) g R2 : 0 < р < +оо, 2Лтг < 0 < 2(к 4- 1)гг},
т. е. на плоскость w с разрезом по положительной действительной полуоси.
96
Гл. 3. Элементарные функции в комплексной плоскости
3. 2. Многозначная функция z = Ln w.
Разобьем всю плоскость z на области однолистности функции w = ez, например, прямыми
у = 2кл, к б Z. Для каждой из этих областей возьмем свой экземпляр плоскости w, являющийся
ее образом при отображении z >-> ez. Чтобы сохранить взаимно однозначное отображение области
вместе с границей, каждую из этих плоскостей разрезаем вдоль положительной действительной
полуоси. Подкладывая эти листы друг под друга и склеивая их надлежащим образом (например,
нижний берег разреза каждого листа с верхним берегом разреза находящегося под ним листа),
построим поверхность Римана многозначной функции z = Ln w, являющейся обратной к пока-
зательной w = ег. Согласно (1), п. 3.1, имеем
Lnw = In |w| + i(argw + 2кя), k£Z. (1)
Для функции w н+ In w точки 0 и оо являются точками разветвления бесконечного порядка. В
любой односвязной области D*, не содержащей точек 0 и оо, можно построить счетное множество
однозначных функций, по отношению к которым функция z ь-» ez будет обратной. Эти функции
назовем однозначными ветвями функции z = Lnw. Для того чтобы выделить в D* одну какую-
нибудь ветвь, фиксируем точку w0 и задаем 90 € Arg w0. При этом считаем, что при непрерывном
изменении w в D* в £ Argw изменяется непрерывно. Тогда, принимая во внимание, что 0 £ D*
и оо i D*, для каждой точки w £ D* 9 £ Argw будет определен однозначно и мы получим в D*
однозначную функцию
z = In |w| + i9. (2)
Изменив значения 0О на + 2тг (0О - 2тг), получим с помощью предыдущих рассуждений
вторую ветвь и т.д. Ветвь функции z = Lnw, для которой 9 = argw, называется ее главной
ветвью.
Рассмотрим примеры.
24. Доказать, что функция w = ez отображает полосу М = {z£C:O<Imz<y} на
первый квадрант w-плоскости.
◄ Сторона у = 0 полосы М переходит в положительную часть действительной оси: |w| = еТ',
argw = 0, —оо < х < +оо. Сторона у = у переходит в положительную часть мнимой оси:
|w| = ех, argw — у, -оо < х < +оо. Используя правило обхода, получаем первый квадрант
w-плоскости. ►
25. Отобразить плоскость с разрезом вдоль положительной действительной полуоси на по-
лосу М = {w€C:0<Imw< 1}.
◄ В плоскости w1 = Inz (In 1 = 0) получим полосу М' = {w1 £ С : 0 < Im W! < 2тг}. Функция
w = гуш, = уу- осуществляет указанное отображение. ►
26. Найти конформное отображение луночки G = {г £ С : |z | < 1, |z — 11 < |} на верхнюю
полуплоскость Р = {w £ С : Im w > 0}.
◄ Цепочка функций
1 1 г 1 — iz тт(1 — iz)
= --------- и>2 =----------------=------------, w3 = ---------------,
z — г z — i 2 2(z - г) z — i
w = eW3
отображает G соответственно на полосу М( = {W| € С : 0 < Imw! < 1}, на полосу М2 =
{w2 £ С : 0 < Im w2 < |}, на полосу М} = {w3 £ С : 0 < Imw3 < тг}, на верхнюю полуплос-
д-(1—ix)
кость Р. Таким образом, w = е . ►
27. Отобразить на верхнюю полуплоскость полосу, ограниченную прямыми у = х и у =
х + h, h > 0.
◄ Находим ширину полосы d = . Искомое отображение получаем посредством компози-
ции следующих отображений:
-i— |-£
1) Wj = е 4 z = ~^z — поворот на угол — у;
2) w2 — yW| = — подобие с коэффициентом подобия
ТГ-fi т(1-£)г
3) W = е*"2 3 = е~ = е я . >
§ 4. Общая степенная и общая показательная функции
97
Простейшие конформные отображения, осуществляемые показательной функцией w = ez,
приведены на рис. 33.
Рис. 33
§ 4. Общая степенная
и общая показательная функции
4.1. Общая степенная функция.
Согласно правилу возведения комплексного числа в произвольную действительную степень,
имеем при р £ R
w = zp — |z|'’(cospyj + isinpy>) = |z|'>e*'>’’, <p 6 Argz. (1)
Если p = n (n£N), то функция w аналитическая в С. Она изучена в § 2.
98
Гл. 3. Элементарные функции в комплексной плоскости
Если р — произвольное рациональное число и р = £ (р и q — взаимно простые), где
р € Z, q € N\{1}, то функция w в каждой точке z € С Л z / 0 имеет q разных значений и
в любой односвязной области, не содержащей нуля и бесконечности, можно выделить q одно-
значных ветвей. Следовательно, нуль и бесконечность — точки разветвления (q - 1)-го порядка
Е
многозначной функции w = z я .
Если р — иррациональное число, то в каждой точке z / 0, z ф оо существует сколь угодно
много значений zp. В любой односвязной области, не содержащей точек 0 и оо, существует
бесконечное множество однозначных ветвей многозначной функции w — zp.
Объясним, какой смысл вкладывается в понятие комплексной степени z°, а € С.
Запишем равенство (1) в виде
,Р — _ р1п|г|+»р^ _ pLnz
£ ““ I *** I - с 5
и обобщим это равенство на комплексную степень. А именно,
Заметим, что степень с произвольным показателем, вообще говоря, не подлежит правилу
сложения показателей при умножении степеней, а также правилу умножения показателей при
возведении степени в степень. Так
z
а
<*2 ___ оц Ln z «2 Ln z _____ a j Ln z+Q2 Ln z / (a i+aj) Ln г _________ a i+<*2
Z c £ —— G ~r~ G %
^za yi3 _ Ln z y'i _ Ln z+2kzri)
4.2. Общая показательная функция.
Общая показательная функция w = az (а 0) определяется формулой az = ezLna. Что-
бы получить определенную однозначную ветвь, следует зафиксировать одно из значений Ln а,
например, Ln a = b. Тогда az = ebz € A(C) — везде дифференцируемая функция (напомним
читателю, что символом А(В) обозначается множество функций, аналитических в области D).
Рассматривая все возможные значения Ln а, получим все возможные однозначные ветви мно-
гозначной функции z ь-> az. Поскольку два значения Ln а отличаются на слагаемое вида Ikiti,
то две ветки функции w — az отличаются множителем вида c'2klrz, который является однознач-
ной функцией со значением 1 лишь для целых значений z. В рассматриваемом случае ветви
многозначной функции w = az существенно отличаются от ветвей всех ранее рассмотренных
многозначных функций. А именно, в исследованных ранее случаях на плоскости С существуют
точки разветвления, перемещаясь вокруг которых по замкнутым кривым и требуя непрерывного
изменения значений функции (ее определенных ветвей), имели возможность непрерывно переве-
сти одну ветвь в другую. В данном случае картина иная. Здесь каждая ветвь является однозначной
функцией в С. Двигаясь по любому замкнутому пути при возвращении в начальную точку полу-
чим то же самое начальное число z, возможно, с другим значением аргумента, а значит и то же
самое значение ebz.
Таким образом, многозначная функция w = az не имеет точек разветвления и ее однознач-
ные ветви не могут непрерывно переходить одна в другую. Это позволяет рассматривать их как
самостоятельные, не связанные друг с другом функции:
। । g1 2’n° z I ) g^(lna+2?ri) gZ(lna—2irt)
Фиксируя одну из этих ветвей (т. е. значение In а = Ь), можем рассмотреть функцию, обрат-
ную по отношению к этой ветви, которая является логарифмом w по основанию а:
1 Lnw
z — - Ln w = ----= Loga w.
о Ln a
§ 5. Функция Жуковского
§ 5. Функция Жуковского
99
5.1. Определение функции Жуковского. Конформность.
Отображение
(1)
называется функцией Жуковского. Она аналитическая в С\{0}. Ее производная 77 = | (1 ~ р)
отлична от нуля везде в этой области, за исключением точек z = ±1. Следовательно, отображе-
ние (1) конформное в С, за исключением, возможно, точек 0, 1, —1.
Докажем, что в точке z = 0 отображение конформное. Принимая во внимание, что w(0) = 00,
рассмотрим
1 2z d / 1 \ _ 2(1 - z2)
w z1 + 1 ’ dz у w J (z2 + I)2
Поскольку (2.) [ # 0, то, согласно определению угла между кривыми на бесконечности,
имеем конформность в точке z = 0. Из равенства w(z) = w следует конформность также в
точке z = оо.
Чтобы убедиться в том, что в точках z = ±1 отображение (1) не конформное, рассмотрим его
как композицию отображений
2-1 2 W2 + I
Wj = ——W2=Wt, w=--------
Z + 1 1 - W2
Первое и последнее отображения дробно-линейные, а значит конформные в С. Отображение w2
удваивает углы в точках 0 и оо, которым отвечают точки z = ± 1. Поэтому функция Жуковского
удваивает углы в точках ±1, в силу чего не является конформным отображением в этих точках.
Установим условия однолистности этой функции. Пусть Z\ и z2 — две разные точки из С, в
которых значения функции Жуковского равны, т. е.
1 ( 1 \ ( 1
Z| +------I Z2 + — I — Zi — Z2 I —-
Z1 \ 22 } \Z]
— ) = (zi - z2) ( 1-----— ) = 0.
Z2 / \ ZsZj/
При Zi # z2 имеем z\z2 — 1. Следовательно, для однолистности функции Жуковского в какой-
нибудь области необходимо и достаточно, чтобы она не содержала никакой пары точек zb z2,
для которых Z]Z2 = 1. Примерами таких областей служат множества
G1 = {z € С : |z| < 1}, G2 = {z е С : |z| > 1}, G3 = {z € С : Imz > 0}, G4 = {z 6 С : Imz < 0}.
Единичная окружность с центром в начале координат делит плоскость z на две области од-
нолистности: Gi и G2. Полагая z = re'v, w = u + iv, запишем функцию Жуковского в виде
1
2
1
v = -
2
sin ip.
(2)
Из (2)'следует, что окружность 7 = {z € С : |z| = г0 # 1} отображается функцией Жуковского
в эллипс с полуосями а = | (г0 + и Ь = | |г0 - i | с фокусами в точках ±1 (с2 = а1 - Ь2 = 1).
Между точками окружности 7 и эллипса существует взаимно однозначное соответствие. При
го > 1 направления их обхода совпадают, а при го < 1 они противоположны. При г0 —► О
(г0 -+ оо) а —юо, Ь -+ оо, а при г0 -»1 а -+ 1, Ъ -> 0. _
Отсюда устанавливаем, что образом области G2, как и области Gi, является вся плоскость С с
выброшенным отрезком [—1, 1], в который переходит единичная окружность 7. Чтобы установить
взаимно однозначное соответствие точек окружности 7 и отрезка [—1, 1], делаем разрез вдоль
100
Гл. 3. Элементарные функции в комплексной плоскости
отрезка. Взаимно однозначное соответствие точек окружности и разреза устанавливаем согласно
правилу обхода (рис. 34).
Рис. 34
Функция, обратная к функции Жуковского, имеет вид
Z = W + yw2 — 1
(3)
и является многозначной с точками разветвления первого порядка w = ±1. Ее поверхность
Римана изображена на рис. 35.
Рассмотрим примеры.
28. Доказать, что любая окружность, проходящая через точки ± 1, делит плоскость С на две
области однолистности функции Жуковского.
◄ Пусть 7 — любая окружность, проходящая через точки ±1 и пусть точки zb z2 не лежат
на 7, причем ztz2 = 1. Докажем, что одна из этих точек лежит внутри круга с границей 7, а
другая — вне окружности 7. Рассмотрим отображение i 1
z + i |.| . / /W
W = E7------77 > * = Ь / 1 / /
«(z — 1) / 1 / /
переводящее одну из областей z-плоскости, ограниченных 7, на / Т II
верхнюю полуплоскость. Тогда / / Il
kw +1 / / / /
kw — 1 I о I I
Принимая во внимание условие ztz2 = 1, получим / ~1 [ I
(kwt + l)(fcw2 + 1) I II
Z|Z2 = ------------------ = 1, / II
(fcw[ — l)(fcw2 — 1) I--j- ---- ----------- I I
или *-----------------------'
k2W[W2 + fc(wt + w2) + 1 = fc2w1w2 - k(wj + w2) + 1. Рис- 35
Отсюда имеем wi = —w2. По свойству взаимно однозначного отображения прообразы точек w,
и w2, т.е. точки zj и z2, лежат с разных сторон 7. ►
а:2 у2
29. Найти конформное отображение внешней части эллипса —+ = 1 (а > Ь) на внешнюю
а2 Ъ2
часть единичного круга с центром в начале координат.
◄ В плоскости W, = U[ + = . г получаем внешнюю часть эллипса
уа2-Ь2
«1 у? _ 1 - = а 1 _ Ъ
а2 Ь2 ’ \/а2 — Ь2' \/а2 — Ъ2‘
а в плоскости w2 = wt + y/w2 — 1 (w2(oo) = 00) — внешнюю часть круга радиуса R:
!а + Ъ
G -- {w2 G С : |ш2| > й}, R = а + у/ а2 — 1= .
а2 + Ъ2
§ 6. Тригонометрические и гиперболические функции
101
В ПЛОСКОСТИ W =
л
получим область 2? = {wgC:|w|>l}. Таким образом,
w =
R
V а2 — Ь2 I z
а + b I х/а2 + д2
z2 \ 1
-7= - 1 = ---
'Уа2 — Ь2 I а + Ь
30. Найти функцию, конформно отображающую область, заключенную между ветками ги-
х2 у2
перболы — - — = 1, на верхнюю полуплоскость Р = {w g С : Im w > 0}.
а2 о2
◄ Рассмотрим преобразование подобия = . z , переводящее заданную гиперболу в
уа2 + Ь2
гиперболу
г? а
4 = 1, а =
Ь2
± _ ____________________________
б2 Ъ2 ’ Va2 + b2’ Va2 + Ь2’
а заданную область — на область, размещенную между ее ветвями. В плоскости
Ь
Ь =
«2
1 (w2(oo) = °о)
получаем внутренность угла а < argw, < тг - а, а = arctg |, в плоскости w3 = e~zaw2
внутренность угла 0 < arg < тг - 2а. Искомое отображение имеет вид
W = W
= (е ,“и>2)’г-2“
е
х/а2 + 62
z2 — а2
тг — 2а
е
Va2 + Ъ2
z2 — а2
2 arctg —
§6. Тригонометрические
и гиперболические функции
Тригонометрические функции z sin z и z i-> cos z определим через показательную функцию
z нег по формулам Эйлера
е*2 — е-’2 ezz+e~zz
----—----, cos z = --------
2г 2
Из свойств показательной функции следует:
1) при z = х sin z и cos z совпадают с тригонометрическими функциями х i-> sin х и х cos х
действительной переменной г;
2) sin z и cos z дифференцируемы в С и при этом
(sinz)' = cosz, (cosz)' = — sinz;
3) выполняются основные тригонометрические соотношения, такие, например, как
sin2 z + cos2 z = 1, sin z = cos (z — — ) ,
теоремы сложения и др;
4) sinz и cosz — периодические функции с основным периодом 2тг;
5) z и-» sin z — нечетная функция, z f-» cos z — четная функция.
С тригонометрическими функциями z f-» sinz, z ь-» cosz тесно связаны гиперболические функ-
ции z <-> shz, z i-t- chz, определенные формулами
, '<т е2 - е~2 def е2 + е-2
shz =---------, chz = ---------. (2)
2 2
Их связь с тригонометрическими функциями выражается равенствами
sh z = — i sin iz, ch z = cos iz,
(3)
sinz = —ishiz, cosz = chiz.
102
Гл. 3. Элементарные функции в комплексной плоскости
Из формул (1) следует, что отображения, осуществляемые синусом и косинусом, являются
композицией изученных ранее отображений. В частности, отображение w = cos z есть компози-
ция поворота на угол j и отображений, осуществляемых показательной функцией и функцией
Жуковского:
Рис. 36
Используя этот факт, рассмотрим простейшие конформные отображения, осуществляемые
функцией w = cosz (рис. 36).
§ 6. Тригонометрические и гиперболические функции
103
Из формулы
следует, что отображение w = sin z является композицией отображений
тг 1/1
1) W[ = z - —; 2) = iwi, 3) w3 = eW2, 4) w = - I w3 4-
2 2 у w3
В качестве примера найдем образ полосы G = {г G С : -у < Rez < у} (см. рис.37).
Из рассмотренных конформных отображений следует, что вертикальные полосы, ширина
которых равна тг, являются областями однолистности функций z sinz и z м cosz.
Рассмотрим более детально отображение полосы D = {z € С : -тг < Rez < 0}, осуществляе-
мое функцией w = cosz. С помощью теоремы сложения и формул (1)—(3) находим:
w = и + iv = cos z = cos(z + iy) = cos x ch у — i sin x sh y,
или
и = cos x ch y, v = — sin x sh y.
Найдем образ прямой x = xQ = const (-тг < x0 < 0 Л x0 / -’Д)- Имеем
(4)
и = cos x0 ch y, v = — sin Xq sh y.
Отсюда находим:
cos2 x0 sin2 го
При -у < x0 < 0 прямая х — а:0 переходит в правую ветвь этой гиперболы. При -т < х0 < — у
она переходит в левую ветвь гиперболы. Прямая х = 0 (мнимая ось) переходит в разрез вдоль
действительной оси от точки 1 до +<х>, а прямая х = —к переходит в разрез вдоль действительной
оси от точки —I до -оо, прямая же х = у переходит в мнимую ось. Образом полосы D является
вся плоскость w с выброшенным отрезком действительной оси и от — I до I через бесконечность.
Разбивая всю плоскость z прямыми х = ктг, к € Z на вертикальные полосы — области одно-
листности функции w = cosz и взяв для каждой из них свой экземпляр w-плоскости, путем их
склеивания можно получить поверхность Римана многозначной функции z = Arccosw, которая
является обратной к функции w = cos z и имеет вид
z = Arccos w = - Ln(w + \/w2 — 1)-
1
Точки разветвления этой функции: ±1, оо.
Тангенс и котангенс в комплексной плоскости определяются формулами
tgz =
sinz
cosz’
ctgz =
cosz
sinz ’
или
tgz =
e" - e-*2 . eiz + e~'z
, Ctg Z = I —r----—.
е"+е-,г e’2 - е~,г
(5)
(6)
(7)
104 Гл. 3. Элементарные функции в комплексной плоскости
Эти функции дифференцируемы всюду в С, за исключением тех точек, в которых знаменатели
дробей в (7) обращаются в нуль. Найдем, например, нули знаменателя дроби, определяющей ctgz:
е*г — e~'z = 0, е,г = е~'г, iz = -iz + 2kiri, z = ктг, kEZ.
Функции z «tgz, z h+ ctgz периодические, с действительным основным периодом тг. Для них
сохраняются известные из анализа формулы дифференцирования и основные тригонометричес-
кие соотношения.
Отображения, осуществляемые этими функциями, являются композицией уже изученных
отображений. Так, отображение
есть композиция таких отображений:
1) W] = 2zz; 2) w2 = eW|; 3) w3 — —---; 4) w = -iw3.
w2 + 1
Используя этот факт, рассмотрим простейшие конформные отображения, осуществляемые
функцией w = tgz (см. рис. 38).
Рис. 38
Изучая отображения w = tgz и w = ctgz, приходим к выводу, что области однолистно-
сти этих функций — вертикальные полосы шириной тг. Разбивая всю плоскость z прямыми
х = ктг (к £ Z) на области однолистности тангенса и взяв для каждой из них свой экземпляр
§6. Тригонометрические и гиперболические функции 105
w-плоскости с разрезом по отрезку [-г, г], путем склеивания их можно построить поверхность
Римана многозначной функции
1 1 + iw
z = Arctg w = — Ln-------.
2г 1 - iw
Функция Arctg w имеет две точки разветвления: ±i.
Рассмотрим примеры.
31. Найти образ прямоугольника Р = {z ё С : 0 < Re г < тг, 0 < Imz < 6} при отображении
W — COS Z .
•< Пусть z — х + iy, тогда
cos z = cos х ch у — г sin х sh у, Im w = — sin x sh у 0.
Следовательно, образ прямоугольника P принадлежит нижней полуплоскости плоскости ш.
При z = х
w — cos ж, 0 < х < тг;
при Z = тг + iy w = — chy, 0 < у < b -,
при Z = iy
w = chy, o <y <b;
при Z = х + ib
w = и + iv = cos x ch b — i sin x sh b, 0 < x < тг.
т. е.
u = cos х ch b, it = - sin ж sh b, —?—I-r—= 1.
ch2 b sh2 b
Таким образом, прямоугольник P отображается на нижнюю половину эллипса с полуосями ch b
и shb. Заметим, что в угловых точках z = 0, z = тг нарушается конформность отображения, а
именно, прямые утлы перешли в углы, равные тг, в фокусах эллипса ±1. В этих точках (cosz)1 =
— sin z = 0. ►
32 . Доказать, что функция w = tg2 j отображает полосу D = {z€C:0<Rez< у} на круг
К = {иг £ С : |w| < 1} с разрезом вдоль отрезка [-1, 0].
◄ Заданное отображение является композицией отображений
.г - 1 . 2
W] = е , Ц>2 = ---, w3 = —iw2i w = u>3-
W| + 1
При последовательном выполнении этих отображений заданная полоса преобразовывается в обла-
сти, указанные на рис. 39. ►
33. Доказать, что на сторонах квадратов с вершинами в точках ir(n + ^)(±1 ± г), п 6
выполняется неравенство | cosec z | 1.
106
Гл. 3. Элементарные функции в комплексной плоскости
◄ Из определения функции z н-+ cosec z = получаем:
, 1 1 1
I cosec z I = ——- = —-z = — ..=
Islnz! ch2 у - cos2 x sh2 у + sin2 x
На горизонтальных сторонах прямоугольников z = z±i(n+|)7r имеем
cosec ±
1 \
- 1 тг + гг/
На вертикальных сторонах г = ±(п+|)тг + гу выполняется равенство
1 _ 1
^/sh2 г/ + sin2 (n + |) тг \/sh У + 1
из которого следует очевидное неравенство | cosec (± (п 4- тг 4- гу) | < 1. ►
Рассмотрим теперь разные примеры, относящиеся ко всем разделам этой главы.
34. Найти общую форму целого линейного преобразования, переводящего:
1) верхнюю полуплоскость на себя;
2) верхнюю полуплоскость на нижнюю полуплоскость;
3) верхнюю полуплоскость на правую полуплоскость;
4) правую полуплоскость на себя.
Показать, что во всех случаях преобразование однозначно определяется заданием одной пары
соответственных внутренних точек или двух пар граничных.
Ч 1) Рассмотрим функцию w = az 4- b, являющуюся целым линейным отображением. Для
того, чтобы она переводила верхнюю полуплоскость на себя, требуется, во-первых, чтобы дей-
ствительная ось перешла в действительную, т. е. w(z) 6 R, если z € R. Поэтому а и Ь должны
быть действительными числами. Во-вторых, для выполнения поставленного требования должно
выполняться также условие w'(z) = а > 0. Таким образом, функция w = az 4- b, a g R, b € R
и a > 0, отображает верхнюю полуплоскость на себя.
2) Очевидно, что таким отображением является w = —az 4- b, agR, b g R Л a > 0.
3) Для решения поставленной задачи отобразим верхнюю полуплоскость на себя, а затем
применим преобразование поворота на угол -у. В итоге получаем: w = -i(az + b), a g R,
bgRAa>0.
4) Здесь чисто мнимым значениям z должны соответствовать чисто мнимые значения w, где
w = az + ib, a g R, b g R. Для того чтобы правая полуплоскость переходила в себя, требуется вы-
полнение условия w'(z) = a > 0. Поставленному требованию удовлетворяет функция w = az + ib,
agR, b g R Л a > 0.
Для однозначного определения преобразования требуется задать соответствие двух пар точек:
либо двух пар граничных точек, либо пары внутренних точек, поскольку другая пара определится
по свойству симметричных точек. ►
35. Найти общую форму целого линейного преобразования, переводящего:
1) полосу П = {z g С : 0 < Re z < 1} на себя;
2) полосу G — {z g С : -2 < Imz < 1} на себя;
3) полосу, ограниченную прямыми у = хиу = х— 1,на себя.
Выяснить, какие пары точек могут при этих отображениях соответствовать друг другу и в
каком случае это соответствие будет однозначно определять отображение.
Ч 1) Искомое преобразование имеет вид w = az + b. Поскольку оно должно перевести
полосу D в себя, то прямые х = 0 и х = 1 должны перейти в прямые и = 0 и и = 1. Возможны
два случая: 1') а: = 0 —> и = 0, х = 1 —>и=1;2')ж = 0-+и=1,а: = 1 —> и = 0. Рассмотрим их
в отдельности.
1') При z =,iy w = iv, iv = iay + b, в частности, при у = 0 iv = Ъ, следовательно, b = ibi,
b[ g R, agR. При z = 1 -I- iy w = 1 + iv, 1 4- iv = a(l + iy) 4- ib. Отсюда находим a = 1. Таким
образом, искомое преобразование имеет вид w = z + ib, b g R.
§ 6. Тригонометрические и гиперболические функции
107
2') При z = iy w = 1 + iv, 1 + iv = iay + b, в частности, при у = 0 1 + iv = Ь. Следовательно,
b € С и Ь = 1 + ibi, bi € R, а € R. При z = 1 + iy w = iv, iv = a(l + iy) + 1 + ibi. Отсюда находим
a = -1. Окончательно получаем w = —z + 1 + bi, b € R.
В случае 1') прямые x = с, параллельные граничным прямым, переходят сами в себя, а в
случае 2') соответствуют друг другу параллельные прямые, симметричные относительно средней
линии полосы х = |. Отсюда ясно, что для однозначного определения отображения следует
задавать соответствие пары точек либо лежащих на одной и той же прямой х = const # |,
либо на прямых, симметричных относительно прямой х = |. Отображение не будет определено
однозначно, если соответствующие точки будут лежать на средней линии полосы. Таким образом,
w = z + ib или w = —z + 1 + ib, b g R.
2) Отображение zi = - j(z + 2г) переводит полосу G в полосу D. Согласно результатам,
полученным при рассмотрении случая 1), отображение W! = zv+bi, b g R, или w2 = -Zi + 1 + bi
переводит полосу D саму в себя. Пусть w — искомое отображение полосы G в себя. Тогда
отображение w3 — — |(ш + 2г) переведет полосу G в D. Таким образом, отображение w находим
из условий: = W|, или w3 = u>2, т. е.
—~(w + 2г) = + 2г) + Ы, или - -(w + 2г) = -(z + 2г) + 1 + Ы.
В первом случае w = z — 3b = z + € R, во втором случае имеем
w = —z — i — 3b = —z — i + b2, b2 g R.
Относительно соответствия точек для однозначного определения отображения рассуждения
аналогичны, поскольку мы свели случай 2) к случаю 1).
3) Ширина полосы равна cos у = -^. Рассмотрим отображение
21
= v/2e' » z = Vi ( —= 4—— I 2 — (1 4- i)z.
\Vi ViJ
Оно переводит заданную полосу в полосу D. Если w — искомое преобразование, то, аналогично
рассмотренному случаю 2), (14- i)w - (1 + i)z 4- bi, или (1 4- i)w = -(1 4- i)z + 1 + bi, b g R. В
первом случае получаем
b . ™
w — z 4- — (1 + i) — z 4- bj(l + i), b3 g R,
а во втором случае имеем
b+1 b-1 b+1 i(b - 1) b-1
w — -z4—-—hi—-— = — z+14— ---------14---- = -z+14—-—(l+г) = —z+l+b(l+i), b g R.
Поскольку и случай 3) сводится к случаю 1), то прежние рассуждения о соответствии точек
для однозначного определения отображения остаются в силе. ►
36. Найти целую линейную функцию w = w(z), отображающую полосу, заключенную между
данными прямыми, на полосу J9 = {wgC:0<Rew< 1} при указанной нормировке:
1) х = а, х = а + h; w(a) = 0;
2) х = а, х = а + h; w (a + у) = | + г, Im w (a + у + г) < 1;
3) у = кх, у = кх + Ь; ш(0) — 0;
4) у = кх + Ьь у = кх + b2; w(ibt) = 0.
•< 1) Ширина полосы равна й. Отображение zx = (z - а) £ переводит заданную полосу в
множество D из примера 35. Согласно решению этого примера, отображение w = zx + bi, b g R
переводит полосу D в себя. Из условия нормировки w(a) = 0 получаем, что b = 0. Таким
образом, w = zzzs.
2) Функция w = + bi, или функция w = — + 1 + bi, b g R отображает указанную
полосу на множество D (см. пример 35). Здесь первое условие нормировки задано на средней
линии полосы, поэтому искомое целое линейное преобразование задается неоднозначно. Второе
условие Im w (a + у + ») <1 приводит к случаю 2') примера 35, т. е. прямая х = а переходит в
108 Гл. 3. Элементарные функции в комплексной плоскости
прямую и = 1 и прямая х = а + h переходит в прямую и = 0 (обходы прямых в плоскостях z и
w противоположны). Поэтому
z — а ( h \ 1 1
w(z) =--------1-1+ib, w | а-|— I = —\-ib = —Fг,
h \ 2 J 2 2
откуда Ь = 1. Следовательно, w = a~^+h + i — искомое целое линейное отображение.
3) Найдем ширину полосы в плоскости z, Поскольку tga = к, то
Ъ Ь 1 Vl + fc2
h = b cos a = — - = —r= и — = -----------.
у/ \ + tg2 a Vl + k2 h b
Повернув полосу на угол - (f + arctg fc) и умножив результат на получим полосу D из при-
мера 35:
х/1 + fc2 -i(y+arctgfc)
b
Условие нормировки выполняется.
4) Этот случай сводится к предыдущему. Полагая z, = z - ibt и принимая во внимание, что
tg а = к, получим
+ fc2 ( y+arctgfc)
w = -------e \2 ) (z - tbi).
bi - t>l
Условие нормировки выполняется. ►
37. Найти целую линейную функцию, отображающую круг JTi = {z б С : |z| < 1} на
круг KR = {w € С : |w - w0| < 7?} так, чтобы центры кругов соответствовали друг другу и
горизонтальный диаметр переходил в диаметр, образующий с направлением действительной оси
угол а.
◄ Полагаем w = az + b. По условию z = 0 -+ w0, 1 —* w0 + Re'a Из этих данных находим:
w0 = b, а + w0 = w0 + Re'a , откуда a = Re'a. Окончательно имеем
w = Re'az + w0. ►
38. Для функции w = | найти образы следующих линий:
1) семейства окружностей х2 + у1 = ах;
2) семейства окружностей х2 + у2 = by ;
3) пучка параллельных прямых у — х + Ъ;
4) пучка прямых у = кх;
5) пучка прямых, проходящих через заданную точку z0 # 0;
6) параболы у = х2.
•< 1) Пусть z = х + iy, w = и + iv, тогда
1 и v
х + гу = --— = —------ - i—--------
и + tv и1 + V1 и2 + V1
Отсюда имеем
U V 2 2 1
х — -----7> У = —;--------т, х + У = —;-----т
и2 + v2 и2 + v2 и2 + V2
Поскольку ах = , то из уравнения семейства окружностей следует, что
1 аи
и2 + v2 и2 + V2
— уравнение семейства образов. Искомое семейство образов имеет вид и = 4. Это семейство
прямых, параллельных мнимой оси в плоскости w. Сама мнимая ось в это семейство не входит.
2) Очевидно, что искомое семейство — прямые v = — |, параллельные действительной оси в
плоскости w, причем сама действительная ось в это семейство не входит.
3) Уравнение пучка образов имеет вид
V и
---5--7 = ~ч-----3 4- Ъ.
и2 + V2 и2 + V2
§ 6. Тригонометрические и гиперболические функции
109
Его можно записать в виде 6(u2 4- t>2) + и 4- v = 0, или
1 V / 1 У 1
lb) + у + 2b J ~ 2b1'
Получили семейство окружностей радиуса , с центром в точке ( ^, . Окружности это-
го семейства касаются в начале координат прямой v = — и. Сама эта прямая также входит в
семейство, что соответствует значению параметра Ь = 0.
4) Запишем уравнение пучка образов данного семейства. Оно имеет вид
v ки
—;----7 = —:---г, т. е. ки + v = 0.
и2 + V2 и2 + V2
Получили пучок прямых V = —ки.
5) Уравнение пучка прямых, проходящих через заданную точку z0 = (ж0, у0), имеет вид
У - Уо = к(х - х0).
Уравнение семейства образов этого пучка
V / и \
---ГГЛ - Уо = к ( 2 . 2 - х»)
и2 + V2 \и2 + V2 /
после очевидных преобразований запишем в виде
(кх0 - j/o)(“2 + v2) = ки + V.
Получили пучок окружностей, в который входит также прямая, проходящая через точки w = 0 и
w = ~ (образ прямой, проходящей через начало координат).
6) Поскольку
U2 4- и2 (и2 + и2)2
является образом параболы у = х2 при отображении w, то остается лишь упростить полученное
уравнение. Имеем
V3
и2 = —v(u2 + v2), u2(l 4- v) = —II3, u2 =-----.
1 + V
Кривая, заданная полученным уравнением, называется циссоидой. ►
39. Выяснить, во что функция w =----------F h переводит:
Z - Zo
1) прямоугольную сетку х = С, у = С ;
2) полярную сетку |z - z0| = R, arg(z - z0) = а.
◄ 1) Пусть z = х + iy, w = и + iv, h = hi 4- ih2. Тогда
1
w(z - z0) = 1 4- h(z — zq), Zq — Xi, + iy0, z(w — h) = 1 4- z0(w — /i), z'= -- + z0,
w — h
, . , . , 1 , . , (u - hi) - i(y - h2)
х + гу = х0 + гу0+ ---- ----------— = x0 4- гу0 4- ----- --------у
(u - hi) + t(v - h2) (u - hi)2 4- (v — h2)
и — hi v — h2
(u - ht)2 4- (« - h2)2 (u - hl)1 4- (v — h2)2
Подставляя вместо x и у С, получим два семейства окружностей
(С - x0)((w - hi)2 4- (v — h2)2) -(и- hi) = 0, (С - yo)(.(.u - hi)2 4- (v - h2)2) 4- (w - h2) = 0.
Первое семейство проходит через тбчку w = h и касается в ней прямой, параллельной мнимой
оси, причем эта прямая входит в семейство. Второе семейство касается в точке w = h прямой,
параллельной действительной оси. Прямая также принадлежит этому семейству.
2) Поскольку z — z0 = Re'a и w = 4- h, то w — h = •^e-*". Получено семейство
окружностей радиуса Т с центром в точке w = h. Очевидно, что arg(w — h) = —а — семейство
лучей, выходящих из точки w = h. ►
но
Гл. 3. Элементарные функции в комплексной плоскости
40. Во что преобразуется квадрант G = {z е С : Rez
z — i
ПОМОЩЬЮ функции W = -----;?
> 0, Im 2 > 0} при отображении с
х — i
w = и + iv = --------
х2 — 1
X1 + 1
1х
х2 - 1 х2 - 1
—----= lim —--------= 1.
X2 + 1 х-» + оо X2 + 1
1, v < 0. Поскольку |w| = 1, то часть границы
sup
v = 0.
Рис. 40
Функция х н-» неубывающая,
х2 - 1 х2 - 1
inf ——- = lim ——- = -1,
0<х<+оо xL + 1 Х-.+0 г2 + 1
Поэтому в рассматриваемом случае -1 < и <
квадранта 7l = {z g С : 0 < Re z < +оо, Imz = 0} переходит в нижнюю полуокружность радиуса 1
с центром в точке w = 0. Пусть z = iy, 0 < у < +оо. Тогда
iy - i у-1 у-\
w(z) = и + iv = ----= -----, и = ------,
гу + г у + 1 у + 1
Луч у > 0 перешел в интервал -1 < и < 1. Таким образом, функция w отображает множество G
на множество D = {ш € С : |w| < 1 Л Im w < 0}. ►
41. Во что преобразуется полукруг D = {z g С : \z\ < 1 Л Im z > 0} при отображении с
Iz — i
помощью функции W =--------?
2 + iz
◄ Дробно-линейная функция w = —отобража-
i+r
ет единичный круг G = {z С С : |z| < 1} на себя.
Выясним, во что отобразится верхняя полуокружность
7 = {z € С : \z\ = 1 Л Imz > 0}. Возьмем три точ-
ки: Zj = -1, z2 = i, z3 = 1. Они отобразятся в точки
u)| = - | - г^, w2 = i, w3 = I - Следовательно, полу-
окружность 7 отображается в верхнюю часть дуги окруж-
ности с концами в точках ± | — i |. Найдем теперь образ
интервала -1 < х < 1 при отображении w. По свойству
дробно-линейного отображения это будет дуга некоторой окружности. Найдем ее по трем точкам:
Z[ = -1, z = 0, z3 = 1. Раньше мы определили, что точки zx и z3 переходят в точки wx = -1 - i |,
w3 = | — i j. Точка z переходит в точку w = — \. Ясно, что центр искомой окружности лежит на
мнимой оси. Пусть ы0 = (0, Ь) — центр этой окружности, R — ее радиус. Ее уравнение имеет
вид и2 + (v - Ъ)2 = R2. Воспользуемся тем, что точки wx и w3 принадлежат ей: | + b) = R2.
Поскольку точка также принадлежит дуге искомой окружности, то + б)2 = R2. Получили
систему двух уравнений для определения Ь и R. Решив ее, находим: Ь = — |, R = Итак,
образом интервала (-1, 1) является дуга окружности Г = {wgC:|w + i|| = |},a весь полу-
круг D отображается на луночку, содержащую точку w = 0 и ограниченную дугами окружностей
I\ = {w £ С : |w| = 1} и Г (см. рис. 40). ►
42. Во что отображается внутренность угла 0 < <р <
z
____?
z — 1
◄ Сначала найдем образ луча z = х (х 0). Точка
предельных соотношений lim = — оо, lim 777 =
х—♦!—0 х—>1+0
жутку [0, 1) в плоскости ш соответствует промежуток (—оо, 0]. Если принять во внимание, что
lim 7^-j- = 1, то приходим к выводу, что промежутку (1, +оо) в плоскости w соответствует
промежуток (1, +оо). Следовательно, при отображении w луч z = х (х 0) переходит в дей-
ствительную ось плоскости w с выброшенным интервалом 0 < u < 1. Луч <р = 7 по свойству
7Г
— дробно-линейной функцией w =
4
х = 0 перейдет в точку w — 0. Из
+оо становится ясным, что проме-
§ 6. Тригонометрические и гиперболические функции
111
дробно-линейных отображений перейдет в дугу некоторой окружности, уравнение которой в об-
щем случае имеет вид (и - а)2 + (v - b)2 = R2. Для того, чтобы найти а, b и R, определим образы
трех точек, лежащих на луче у = z Эти образы будут принадлежать упомянутой окружности
и однозначно определять ее. Ищем образы точек z{ = 0, z2 = ег 4 , z3 = оо. После неслож-
ных вычислений находим: Wi = 0, w2 = | — 2(5д_1)Т w3 = 1. Поскольку все эти точки лежат
на искомой окружности, то для определения а, Ь и R получаем систему трех уравнений с тремя
неизвестными:
«2 , к2 _ г>2
а + о = л ,
«Ь + ») ’ = я1.
(1 - а)2 + Ь2 = R2.
Ее решением являются а = \ , b = - R = . Получаем искомую окружность:
Рис. 41
Таким образом, дробно-линейная фун-
кция w = отображает внутренность
угла 0 < р < на область, получен-
ную из нижней полуплоскости плоско-
сти w удалением находящейся в этой
полуплоскости части круга
1 i
2 2
(см. рис. 41). ►
43. Во что преобразуется полоса £> = {z€C:0<Rez< 1} при отображении с помощью
z — 1
функций: 1) w = -------
Z
z — 1
2) w = -------?
z - 2
◄ 1) Найдем образ
бражении w:
11/ - 1
W = --------
гу
мнимой оси при ОТО-
t
= 1 +
У
Прямая х = 0 перешла в прямую u = 1. Най-
дем образ прямой х = 1. Он ортогонален к
действительной оси, так как заданное отобра-
жение переводит действительную ось в дей-
ствительную ось. Следовательно, этим обра-
зом является окружность с центром на дей-
ствительной оси, уравнение которой имеет вид
(u—a)2+v2 = R2. Точка z = 1 переходит в точ-
ку w = 0, а точка z = оо — в точку w = 1. Для
определения а и R получаем систему уравне- Рнс-42
ний а2 = R2, (1 — а)2 = Я2, решениями которой являются а = |, R = Уравнение искомой
окружности имеет вид |ш — || = |. Таким образом, полоса D в рассматриваемом случае ото-
бражается на область, ограниченную прямой, уравнение которой Rew = 1, и касающейся ее
окружностью r={w€C:|w-5^=|} (рис. 42).
2) Образы прямых х = 0 и х = 1 — окружности с центрами на действительной оси, так
как действительная ось переходит в действительную ось, а углы сохраняются. На прямой х = О
возьмем две точки: zi = 0 и z2 = oo.
Их образами являются точки w = | и w = 1. Пусть уравнение образа прямой х = 0 имеет
вид (и — а)2 4- v2 = R2 (поскольку этот образ окружность). Константы а и R находим из системы
112
Гл. 3. Элементарные функции в комплексной плоскости
уравнений - а)2 = R2, (1 — а)2 = R2. Решив ее, находим: а = R = |. Прямая х = О
переходит в окружность, уравнение которой |w - 11 = j.
Найдем теперь образ прямой х = 1. Обра-
зами точек & = 1, & = оо являются точ-
ки Wj = 0 и w2 = 1. Поскольку указанная пря-
мая отображается на окружность, то точки wt
и w2 принадлежат ей. Так как ее центр лежит
на действительной оси, то уравнение окруж-
ности имеет вид (и - at)2 + v2 = R2. Для нахо-
ждения чисел и Л1 получаем систему урав-
нений а2 = R2, (1 - Д|)2 = 7?2. Решив эту си-
стему, имеем а1 = 7?! = |. Уравнение данной
окружности записывается в виде | w - 11 = |.
Следовательно, полоса D отображается функ-
цией w ~ на область, ограниченную каса-
ющимися друг друга окружностями, уравнения
которых |w- || = | и |w - 5| = | (рис.43).
44. Во что отображается кольцо К = {z € С | 1 < \z\ < 2} функцией w =----?
Ч Точке z=l соответствует точка w = оо, следовательно, окружность
7, = {z € С : Izl = 1}
переходит в прямую, ортогональную действительной оси (при данном отображении действитель-
жат ей. Точкам z\ и z2 отвечают точки wj = | и
ная ось переходит в действительную ось).
Точке z = — 1 соответствует точка w — |.
Таким образом, окружность 7! отображает-
ся на прямую, уравнение которой и = |.
Образом окружности
72 = {z 6 С : |z| = 2}
будет некоторая окружность в плоскости w
с центром на действительной оси. Ее урав-
нение записывается в виде
(и — а)2 + V2 = R2.
Образы точек zi = -2 и z2 = 2 принадле-
w2 = 2. Для определения а к R получаем
систему двух уравнений с двумя неизвестными
- a)2 = R2 и (2 — а)2 = R2. Решив ее, имеем
а = 5, R = |. Окружность 72 отображается на окружность Г = {w € С : |w - 11 = |} - Кольцо
К отображается на двусвязную область, граница которой состоит из прямой, уравнение которой
Rew = 5, и окружности Г (рис.44).
45. Отобразить на вертикальную полосу 72 = {w€C|0<Rew< 1}:
1) полуплоскость Р = {z 6 С | Rez > 0} с выкинутым кругом К = {z € С : |z - | |;
2) двуугольник, заключенный между окружностями
7i = {z G С : |z - iL| = , 72= {z € С : |z- (d, < d2);
3) внешность кругов К, = {z e С : |z + 1 < }, K2 = {z 6 C : |z — | } так, чтобы
w(d2) = 0.
4 1) Функция W] = | отображает множество P\K на полосу G = {w, € С10 < Re w( < 4 },
а отображение w2 = dwt = переведет полосу G в полосу G' = {w2 € С | 0 < Rew2 < 1}.
Согласно решению примера 35, 1), общий вид искомого преобразования определяется функцией
w = w2 + ih = i + ih, или w = — w2 + 1 + ih = - j + 1 4- ih, где h — любое действительное число.
§ 6. Тригонометрические и гиперболические функции
ИЗ
2) Функция W] = отображает двуугольник на полосу Dt = {w, € С| £ < Re wt < jj-}.
Ширина полосы равна = dj~^ Функция w2 = (w, — отображает полосу Dx
на полосу Di = {w2 €C|0<Rew2<l},a отображение w = w2 + ih или отображение
w = —w2 + 1 + ih, h € R, переводит полосу D2 в себя, т.е. в полосу D (см. пример 35, 1)).
Окончательно получаем, что w = ddJd - 1) + ih, или w = d-^d- - 1) + 1 + ih, h € R —
произвольное (см. рис. 45).
3) Композиция цепочки отображений wj = |, w2 = w1 —
w — --------w
di + d2
(i i
W = “W3 =-----------I----------
d\ И- t^2 \ Z ^2
d\
d\ + ^2
d1 ( z - d2
z \ + d2
приводит к требуемому результату (см. рис. 46). ►
46. Найти дробно-линейные функции, переводящие точки -1, г, 1 + г соответственно в
точки 1) 0, 2г, 1 — г; 2) г, оо, 1.
◄ 1) Для наглядности запишем условие в виде таблицы
Z -1 i 1 + г
W 0 2i 1 — г
Искомая функция имеет вид w4= к-^. Точка —1 переводится в точку w = 0. Для определе-
ния к и Ь получаем в соответствии с таблицей систему уравнений
1 + г
2г = к---------,
г — 6
l-i = fc
2 + г
1 4- г — Ь'
114
Гл. 3. Элементарные функции в комплексной плоскости
Разделив друг на друга левые и правые части уравнений системы, получаем уравнение относи-
тельно Ь:
2г _ (1 + г)(1 — 6 + г)
1 - i ~ (г — Ь)(2 + г)
После несложных преобразований находим:
t 3 + 2г
о =---------.
2(г - 1)
Подставив найденное значение в первое уравнение системы, получим:
к = ~-
2
Окончательно имеем
2i(z + 1)
w =----------------
4г - 1 - 5г
2) При виде таблицы
Z -1 i 1 + г
W i 00 1
становится ясным, что искомое дробно-линейное отображение следует искать в виде
z — а
w = к-----.
z — г
Условие г >-» оо выполнено. Неизвестные к и а определяются из системы уравнений
1 + а
= к----г,
— 1 — а
i = к-------
-1 — г
1 = к
= fc(l + г — а).
Решив ее, находим:
, 1
а = Зг, к =
(1 + 2i)z + 6 - Зг
-----, w = . >
1 - 2г-5(z - i)
47. Найти дробно-линейные функции, переводящие точки -1, оо, г соответственно в точки:
1) г, 1,1 + г; 2) оо, г, 1; 3) 0, оо, 1.
•4 Способ решения примера тот же, который применяли при решении примера 46: с помощью
таблицы определяем общий вид дробно-линейной функции, а затем находим два неизвестных
числа из системы уравнений.
1) Поскольку
Z -1 00 г
W г 1 1 + г
то w = . При этом оо 1. Из системы уравнений
— 1 — а 1 + а
х “ -1-6 “ 1 + 6’
г — а
1 + г = т—
г — 6
находим: а = — i — 2, 6 = г — 2. Таким образом,
z + i + 2
w =----_—
z — г + 2
2) С помощью таблицы
§ 6. Тригонометрические и гиперболические функции
115
z -1 oo i
w 00 i 1
определяем, что искомое дробно-линейное отображение имеет вид w = Тогда — I >—> оо,
оо I-+ i. Осталось найти а. Для этого воспользуемся условием, что i н-> 1. Из уравнения относи-
тельно неизвестного а
находим: а = -1 + 2г. Следовательно,
2 + i(z + 1)
w =----------------
3) Судя по таблице
z -1 oo i
w 00 00 1
искомая функция имеет вид w = az + Ь. Из условий 0 = — а + Ь, 1 = ia + Ь. получаем: а = Ь,
а = Таким образом,
1 — г
w = -у- (z + 1). ►
Заметим, что составлять таблицы соответствия точек полезно, но не обязательно.
48. Найти дробно-линейные функции по следующим условиям:
1) точки 1 и г неподвижны, а точка 0 переходит в точку —1;
2) точки 5 и 2 неподвижны, а точка | + г'| переходит в оо;
3) точка i является двойной неподвижной точкой, а точка 1 переходит в оо.
◄ 1) Ищем дробно-линейную функцию w в виде = kj^j. Поскольку 0 —1, то
= т+7 = 7 ’ откуда h = -^. Следовательно,
w — 1 2г z — 1 , х
-----7 = ;-:----7, ш((1 + i)(z - г) + 2г( 1 - z)) = 2(z - 1) + (1 + i)(z - г),
w — г 1 + г z — г х
z ч (3 + г)г - 1 - г
w(z(l - г) + г + 1) = z(3 + г) - 1 - г, w=-- .
4 ' (1 — г)г + г + 1
2) Определяем функцию w из условий = к^~. Тогда
2w — 1 2z — 1
-----= к------,
w — 2 z — 2
(2w - l)(z - 2) = fc(2z - l)(w - 2),
z(l - 4k) + 2k - 2
2z(l — fc) + fc — 4 ’
При z = | |г знаменатель последней дроби обращается в нуль, поскольку | + |г н-+ оо. Из этого
условия определяем к:
/5 Зг\
( 2 + ?) (l-fc) + fc-4 = 0.
Решив это уравнение, получим к = i. Окончательно имеем
г(1 — 4г) + 2(—1 + г)
V~ 2z(l —г) + г —4
3) Определим функцию w условиями — -^i+h — 1—. Тогда z-i = (w-i)(l+hz—ih),
w ~ ' Так как 1 i-» оо, то h 4- 1 - ih = 0, h = ~ Окончательно находим
w =
z(3 - i) - (1 + г)
(l+i)(l — z)
116
Гл. 3. Элементарные функции в комплексной плоскости
49. Найти дробно-линейную функцию, переводящую точки -1,0, 1 соответственно в точки
1, г, — 1 и выяснить, во что при этом отображении переходит верхняя полуплоскость.
◄ Для наглядности воспользуемся таблицей
Z -1 0 1
W 1 i -1
Согласно теореме 1,_п. 1.3, какими бы_ни были три разные точки z, € С, z2 g С, z3 € С и
три разные точки 6 С, € С, w3 6 С, существует, и притом единственное, такое дробно-
линейное отображение L, что L(zk) = wk (к = 1, 2, 3). Его можно найти из соотношения
Z — Z[ Z3 — Zj W — Wi w} — w2
Z — Z2 Z3 — Zi W — W2 Wy — Wi
Поскольку = |, = Ц1, то соотношение (1) принимает вид = (1 + i)y^V-, откуда
z — i
Функция w отображает верхнюю полуплоскость Р = {z £ С | Imz > 0} на единичный круг
К = {w € С : |w| < 1}. При этом точка i переводится в точку и = 0 — центр круга К. ►
50. Найти общий вид дробно-линейного преобразования, переводящего:
1) верхнюю полуплоскость на себя;
2) верхнюю полуплоскость на нижнюю полуплоскость;
3) верхнюю полуплоскость на правую полуплоскость.
•< Согласно теореме 1, п. 1.1, любая дробно-линейная функция w = осуществляет го-
меоморфное отображение С на С. Поскольку w' = °, то в случае 1) должно выполняться
условие ad —be > 0, в случае 2) — условие ad-bc < 0. В случае 3) дробно-линейное преобразова-
ние имеет вид w = i Л ad - be < 0 (умножением на i нижняя полуплоскость поворачивается
в положительном направлении на угол у, т. е. переходит в правую полуплоскость). Согласно
общему определению дробно-линейной функции, числа a, b, с, d — действительные. ►
51. Найти отображение верхней полуплоскости на себя при указанной нормировке:
1) w(0) = 1, w(l) = 2, ш(2) = оо; 2) w(0) = 1, w(i) = 2г.
◄ 1) По теореме 1, п. 1.3, имеем
z w - 1 2
------= , w = .
2(z — 1) w - 2----------2 — z
2) Составляем таблицу
Z 0 i
W 1 2i -2i
Точка —г переходит в точку -2г, так как г переходит в 2г (симметричные точки переходят в
симметричные). Снова применяем теорему 1, п. 1.3:
2z 4г w - 1 2z + 1
=------- , w = —2 -. ►
z — г--------------------------------2г+ 1 w — 2г-z — 2
52. Найти функцию w = w(z), отображающую круг KR = {z € С : |z| < Л} на правую
полуплоскость Р = {w € С | Re w > 0} так, что w(R) = 0, w(—R) = оо, w(0) = 1. Каков при этом
отображении образ верхнего полукруга?
◄ Функция w имеет вид w = к^£, поскольку w = 0 при z = R и w —> оо при z —» -R. Из
условия w(0) = 1 получаем, что к = — 1. Таким образом, w =
§ 6. Тригонометрические и гиперболические функции
117
Функция w отображает действительную ось Ох на действительную ось О'и. Следовательно,
интервал —R < х < R переходит в луч — положительную действительную полуось, а полуокруж-
ность 7 = {z € С : |z| < R Л Imz > 0} отображается в луч, выходящий из начала координат
под углом — у. Пользуясь правилом обхода и свойством сохранения углов по величине и на-
правлению при конформном отображении, приходим к выводу, что образом верхнего полукруга
является четвертый квадрант D = {(u, v) е R2 : и > 0, v < 0}. ►
53. Найти точки, симметричные с точкой 2 + i относительно окружностей:
1) 7i = {z € С : 121 = О; 2) 7з = {z е С : |z - г| = 3}.
Ч Согласно формуле (3), п. 1.2, имеем
Z* = Zo + (1)
z - z0
где z0 — центр окружности, R — ее радиус.
В случае 1) z0 = О, R = 1, следовательно, z* = 4 = -=- = = |(2 + г).
В случае 2) z0 = г, R = 3, z* = г + | + г. ►
2+i—i
54. Найти симметричный образ относительно единичной окружности 7 = {г£С:|г| = 1}
следующих линий:
1) 71 = {z е С : |z| = 1} ; 2) Ъ = {z € С : |z - 1| = 1}; 3) у = 2.
х — г'2 х2 + 4 х2 + 4
Поскольку х = ”, то, подставив это значение
несложных преобразований получим:
‘2 ( * 1V 1
(х ) + Ь/ " 7 = 77-
◄ Воспользуемся формулой (1) из примера 53.
1) Очевидно, что z — . Тогда z = = 2ег — точки окружности радиуса 2, с центром в
начале координат.
2) Поскольку z = 1 + е'в, то z* = |+ | \ tg f. Симметричным образом является
прямая, уравнение которой х = |.
3) Прямую, заданную на плоскости уравнением у — 2, представим в виде 7 = {z € С | —оо <
Rez < +00, Imz = 2}, т. е. z = х + г2.
Тогда
2 . _ х . _ 2
х2+4’ х2 4- 4’ х2 + 4
в правую часть равенства х* = , после
г 2 1
Т'е' Z“4 ~16’
z = х + гу
В данном случае симметричным образом является окружность радиуса j с центром в точке
55. Функция w
единичный круг.
Z- Р
Z-P
(Р = а + ib, Ъ > 0) отображает верхнюю полуплоскость на
1) Найти argw(x) = 0(х); 2) найти 3) выяснить, какая часть верхней полуплоскости
при этом отображении сжимается и какая растягивается.
◄ 1) Очевидно, что arg w(x) = а+ 2 arg(z - /3), так как arg(z -/?) = - arg(z - /3);
2) Дифференцируя w(x), получим:
w'(z)
z - /3 - z + Р
(z - P)2
P-P
(z-p)2
_ Щ »2b
6 (z-Д)2'
Подставив в полученную формулу z = /3, имеем
и>'(/3) = е'“
i2b
(i2b)2
2b
118
Гл. 3. Элементарные функции в комплексной плоскости
3) Поскольку |w'(z)| = > то ПРИ х/2Ь < \z - /31 происходит сжатие, а при \/2Ь > \z — Д| —
растяжение. Из равенства |z — /3| = |(z - а) + i(y - b)| следует, что
inf |z - ,fl| = у/(х - а)2 + (у + Ъ)2
>0
у=0
Из неравенства У2Ь < Ъ получаем, что при b 2 вся полуплоскость сжимается. Если Ъ < 2,
то область, лежащая внутри круга К = {z € С : \z - р\ < \/2Ь}, растягивается. ►
56. Отобразить верхнюю полуплоскость Р = {z € С | 1ш z > 0} на единичный круг К =
{ш € С : |w| < 1} так, чтобы:
1) ш(г) = 0, argw’(i) = — —; 2) w(2i) = 0, arg w'(2i) = 0;
3) w(a 4- ib) = 0, arg w'(a + ib) = 0 (b > 0).
4 1) Согласно формуле (4), п. 1.3, отображение верхней полуплоскости на единичный круг
осуществляется функцией w = • Из условия ш(г) = 0 следует, что а = г. Таким образом,
w = е*9 -^4. Дифференцируя функцию w, получаем
'i \ т е i ie 1 ’(9~т)
w (z) = 2г-------, w (г) = — е = - е ' 2 > .
(z + i)2’ 2 2
Из условия arg и/(г) = -у = в — у следует, что 0 = 0. Окончательно имеем
z — г
w = ------.
z + i
2) В общей формуле w = е’9ууу полагаем а = 2г, тогда w = е,9у=у-. Поскольку
, 4г' , е (в 2) я-
w(z) = e ; ; , w(2i) =---------, argw (2г) = 0- - = О,
(z + 2г)2 4 2
то 9 = у и
z - 2г
w = г-----.
z + 2г
3) По аналогии с 1) и 2) записываем функцию w в виде w = е*9’ Тогда
, ,д 2ог , г е \ 2 > , тг
w(z) = e9' --------—, w(a + bi) = - — е 91 =--------—-----, arg w (а + Ы) = 0t - - = 0,
(z - (а — bi))2 2b 2b 2
откуда 0t = у + 0. Окончательно получаем
•(?+») z — (a + bi)
tu = е \ 2 / ---------.
z — (а — Ьг)
57. Отобразить верхнюю полуплоскость Р = {z € С | Imz > 0} на круг К = {ш € С :
|w — wol < R} так, чтобы точка i перешла в центр круга, а производная в этой точке была
положительной.
◄ Сначала отобразим полуплоскость Р на единичный круг K'1 = {w6C:|w|<l} так,
чтобы точка i перешла в его центр w = 0. Согласно решению примера 56, 1), wt =
причем w'(i) = 2 ) . При 0 = у w'(i) = I > 0. Следовательно, = е*Т = iyy|. Теперь
совершаем преобразование подобия и переноса w = Rwi + w0. Окончательно получаем:
z — г
w = Ri----: + w0. ►
z + г
§ 6. Тригонометрические и гиперболические функции
119
58. Отобразить круг К = {z £ С : \z\ < 2} на полуплоскость Р = {w £ С | Rew > 0} так,
, тг
чтобы w(0) = 1, arg w (0) = —.
◄ Поскольку при дробно-линейном отображении симметричные точки переходят в симме-
тричные и 0 и I, то х « - 1.Из таблицы
Z 0 оо
W 1 -1
видно, что дробно-линейная функция, отображающая К на Р, имеет вид
z — а
w = к-------------------------------------------.
z — Ь
Из условий нормировки находим: к = -1, Ь — -а. Поэтому
z - а
w —-------.
z + а
Дифференцируя, получаем
, 2а , • 2 , / 2 \ тг
w = ~Z--------гг, w (0) = —, argw (0) = arg-----I = тг - arga = —,
(z + a)2 a \ ° / z
откуда arga = у, Следовательно, a = iat (at > 0) и w = Пусть w = и + tv. Граница
круга К переходит в мнимую ось плоскости w, т.е. 2е*9 iv, iv = — В частности,
при v = 0 имеем 2е*® — iat = 0. Это равенство выполняется при условии, что 0 = у, at = 2.
Окончательно находим:
59. Отобразить круг К = {z € С : \z - 4г| < 2} на полуплоскость Р = {(и, г») £ R2 | v > и}
так, чтобы центр круга перешел в точку —4, а точка окружности 2г — в начало координат.
◄ Сначала отобразим круг К на единичный крут Kt = {ц\ С С : |wj < 1} с помощью
функции wt = у — 2г. Тогда w, = 0 н w = -4, w, = —i 0. Так как точка w = -4г
симметрична относительно прямой v = и точке —4, то w, = оо >—> —4г. Составляем таблицу
W, 0 —г оо
W —4 0 -4г
и определяем искомое отображение общей формулой дробно-линейного преобразования
W| — а
w
Wi — Ь
Согласно условиям
откуда
Таким образом,
и имеем
ка
-4= —,
Ь ’
а + i
к----; = 0, —4г = к,
6=1, к =—4i.
у — 2г + г iz 4- 2
w = — 4г --------------= — 4-------------—
у — 2г — 1 z — 2 — 4»
а =
60. Найти функцию, отображающую верхнюю полуплоскость на себя так, что w(a) = Ь,
argw'(a) = a (Ima >0, Imb > 0).
◄ Пусть w = w(z) — искомое отображение. Тогда функция
w — b ie „ п
w i-t----= е . 0 Е R — произвольное,
w — Ъ
120
Гл. 3. Элементарные функции в комплексной плоскости
отображает верхнюю полуплоскость плоскости w на единичный круг с центром в начале коорди-
нат. На этот же круг функция
z — а
z >->-- е , <р € R — произвольное,
z — а
отображает верхнюю полуплоскость плоскости z. Таким образом,
w - Ь iez - а
----= = е 1----0! = р - 0 — произвольное.
w — b z — а
Дифференцируя обе части этого равенства, получаем:
1ш6 , гв Ima
(^Р^ш(г) = е
Полагая здесь z = а и принимая во внимание, что w(a) = 6, имеем
,, , Im 6 iffl
w (а) =----е .
Im а
Так как > 0, то argw'(a) = 0|. Полагая 0) = а, получим:
w(z) — b i z — a ,
———==е ----------; argw(a) = a. ►
w(z) — b z — a
01. Отобразить верхнюю полуплоскость на нижнюю так, чтобы w(a) = а и arg w (а) = — —.
◄ Пусть w = w(z) — искомое отображение. Полагая wt = e,rw = -w, получим верхнюю
полуплоскость. При этом а н+ -а. Согласно предыдущему примеру
tri + a ie z — а
------= е -----т
z — a
0 6 R — произвольное.
+ a
Заменив w, на -w, получим:
w — а
----= е
w — а
iez-a
z — а
е1в
(z - а)2'
Дифференцируя это равенство, имеем
w'(z)
(w(z) - a)2
Подставив сюда z = а, находим (приняв во внимание, что w(a) — a):
и/(a) = — егв.
Следовательно, argw'(a) = 0±тг = — у (по условию задачи). Из двух значений 0! = -|тг, 02 = у,
подходит значение 0 = у, поскольку
—тг < argw'(a) тг. Окончательно имеем
w — a z — а
-----= i----►
w — a z — а
(|а| < 1) отображающей единичный круг на себя:
S') ГГ Л. ia Z а
OZ. Для функции w = е -------—
1 — az
1) найти argw(e**’) = 0(^т);
2) найти ш'(0) и w'(a);
3) выяснить, какая часть единичного круга при этом отображении сжимается и какая растя-
гивается;
dw
dz
eiv -a
dw
4) найти max и min
dz
◄ 1) При z = е*’’ получаем
eltfi — а
ta
w = е ---------— = е — z —-
1 — ae**’ е**’(е-”’- a)
Пусть a = Ae’e’. Тогда
= . е ~ °
е-**’ - а
„ io , sin и — A sin 0i
в(<р) = a — + 2 arctg(e — a) = a — ip + 2 arctg---------------------
cos p — A cos 0]
§ 6. Тригонометрические и гиперболические функции
121
2) Дифференцируя, находим:
,, ч ial-az + a(z-a) ia 1 - |а|2 ia 2 , е'“
w(z) = e ----------—-------= е ------—w (0) = е (1 - а ), w (а) = -------------у.
(1 - az)2 (1 - az)2 1 - |а|
3) Если | [ > 1, то соответствующая часть круга растягивается; если | 1 < 1, то
соответствующая часть круга сжимается. Решив эти элементарные неравенства, получим, что
множество внутренних точек крута G = |z € С.: |z - || < - 1} растягивается, а мно-
жество внешних точек круга Z> = ^z€C:|z-y|> - 1} сжимается. Окружность 7 =
{z 6 С : \z - | J = — 1J — изометрическая. Если а = 0, то |w'(z)| = 1.
4) Из оценок |1 - az\ 1 - |a||z| 1 - |а|, |1 — az\ 1 + |a||z| 1 + |а|, для производной
w'(z) находим max |w'(z)| и min |w'(z)|:
|2|^1 |z|^l
I ,, 1 + |a| . , 1 - |a|
max w (z) = -——, min w (z) = ►
|z|^i 1-a |z|^i 1 + a|
63. Отобразить круг К = {z g С : |z| < 1} на круг Ki = {to g C : |w| < 1} так, чтобы:
1) w (I) = 0, argw' (I) = 0; 2) w (|) = 0, argw' (f) = f;
3) w(0) = 0, argw'(O) = -y; 4) w(a) = a, argw'(a) = a.
4 1) Воспользуемся решением задачи 62, полагая в 2) а = |. Получим:
^га
arg w' ) = arg------р = 0 => a = 0.
1 — 4
Тогда
2) По аналогии с предыдущим полагаем а = \. Тогда
= argw'(i) = y=>«=^.
Следовательно,
z - \ 2z — i Hz + 1
w = е 2---4- = i------- = -----.
1 + У 2 + iz 2 + iz
3) В задаче 62, 2) показано, что w'(a) = Полагая здесь a = 0, получим w'(0) = е’“. Из
условия argw'(0) = -у следует, что а = -у. Тогда
w = е-1Т z = — iz
(в общую формулу w = е*“ ууу подставляем a = - у, а = 0).
4) Пусть w = w(z) — искомое отображение К на Kt. Функции z 1-» и w >—» е*у 2°
отображают соответственно круги К и Ki на себя ((? g R, 99 g R — произвольные). Поскольку
argw'(а) = а, то, по аналогии с решением задачи 60, имеем
aw 1 — az
64. Отобразить круг К = {z € С : |z| < 2?i} на круг Ki = {w & С : |w| < Л2} так, чтобы
w(a) = Ь, argw'(a) = а (|а| < Rt, |Ь| < Л2).
< Функция
Z
122
Гл. 3. Элементарные функции в комплексной плоскости
отображает К на единичный круг, а функция
ieWj-W|(a) ieD z — a
w2 = e ---=-----= e ——= e R, —5——
1 - w!(a)wi 1 - я] R2 - az
отображает этот единичный круг на себя. Пусть w = w(z) — отображение круга К на круг Ki.
Тогда функция
w — Ъ
w3 = е^Яз -г-^-
R2 — bw
также отображает единичный круг на себя. В полученных формулах 0 € R, € R — произволь-
ные. Таким образом,
w — b
R2 —т—=—
R2 — bw
Продифференцировав это равенство, получим:
w'(z)(R2 - |Ь|2) _ R2 - |a|2 {(e_v)
2 (Я2 — bw(z))2 1 (Я2 — az)2
Полагая z = a и принимая во внимание, что w(a) = b, находим:
1, ч Я| Я2 — |Ь| це-р)
' ’ •') = 5;'5ж
R]-az
Ri I, ч Ri
SFw"(“,=
Я?-
„ д. К2-|Ь|2
Поскольку
> 0, то взяв 0 — <р = а, получим, что argw'(а) = а. Окончательно имеем
w - Ь { z — a
—з—=— = е Я, —з--. ►
Я2 — bw R\ — az
65. Отобразить круг К = {z g С : |z| < 1} на круг At = {w € С : |w - 1| < 1} так, чтобы
w(0) = 5 и w(l) = 0.
Ч Полагаем W! = w - 1. Тогда IwJ — |w — 1| С 1. Отображение единичного круга К на
единичный круг A2 = {w1GC:|w1|<1}b общем случае имеет вид
-а z — а
W{= е °---0 € R.
1 — az
Рассмотрим таблицу нормировки
Подставив во второе уравнение системы е'в = ±, получим:
1 — а = — 2a + 2|a|2 или а = 2|a|2 — 1.
Поскольку (2|а|2 — 1) € R, то а — действительное число и а = а. Для определения а получаем
квадратное уравнение а1 — у — | =0, корни которого a, = 1 и а2 = — |. Так как | — ae*e| = |а| = |
§ 6. Тригонометрические и гиперболические функции
123
(см. первое уравнение системы), то а = Таким образом, а = — е'в = -1. Подставив эти
значения в формулу для W|, получим:
Окончательно имеем
1 — z
W = Wi + 1 = -----. ►
2 + z
66. Отобразить круг К = {z 6 С : |z - 2| < 1} на круг Ki = {w € С : |w - 2г| < 2} так, чтобы
w(2) = i и argw'(2) = 0.
Ч Полагаем W[ = z - 2 и w2 = . Задача свелась к отображению круга К2 = {w, € С :
|ш|| < 1} на круг К2 = {w2 € С : |ш2| < 1} при условиях w2(0) = —ш2(0) = 0. Воспользуемся
решением задачи 64, полагая там Ri = R2 = 1, а = 0. Получим:
w2 + i wi - у z-2-i 2z - 4 - i
----— Wl, w2 = ------= -------:--— = .
1 - \w2 1 + jit)! 1 + j(z — 2) 2 + i(z-2)
Принимая во внимание связь между ш2 и w, имеем
( 2z - 4 - i \ z — 2 + i
w = 2(w2 +») = 2 —+ « ) = 2 т——-——. ►
y2 + i(z-2) J tz + 2 - 2г
67. 1) Отобразить кольцо К = {z £ С | 2 < |z| < 5} на кольцо Ki = {w £ С | 4 < |w| < 10}
так, чтобы w(5) = —4.
2) Отобразить кольцо К = {z Е С | 1 < |г-2г| < 2} на кольцо К} = {wgC | 2 < |w-3+2г| < 4}
так, чтобы ш(0) = — 1 — 2г.
Ч Воспользуемся теоремой: для того чтобы существовало конформное отображение кольца
К’ = {z € С | г, < |z| < г2} на кольцо К" = {w € С | Rt < |w| < Д2}, необходимо и достаточно
выполнения условия . При этом отображающая функция может быть только двух видов:
а
w = az или w ~ а £ С.
z
Отображение однозначно определяется заданием одной пары соответствующих друг другу гра-
ничных точек.
1) Очевидно, что в данном случае отображающая функция имеет вид w = |, так как по
условию внутренняя окружность кольца К должна перейти во внешнюю окружность кольца Ki.
Из соответствия точек находим: —4 = а = -20. Следовательно,
20
w =----.
Z
2) Полагаем wt = z — 2г, w2 = w - 3 + 2г. Тогда 1 < IwJ < 2 и 2 < |w2| < 4. Задача
свелась к отображению одного концентрического кольца на другое, причем 5 = f. При этом
W! = -2г >-> -4. Здесь внешняя окружность одного кольца переходит во внешнюю окружность
другого кольца, поэтому w2 = aw{, т. е. w - 3 + 2г = a(z - 2г). Постоянную а находим из условия
-4 = -2га, откуда а = —2i. Окончательно получаем:
w = 3 — 2i — 2i(z — 2г) = 3 - 2г - 2iz — 4 = — 2iz — 1 — 2i = -(2iz + 1 + 2i). ►
68. Полуплоскость P — {z g C : Rez > 0} с выкинутым кругом К = {z € С : \z - h\ < R}
(h > Д) отобразить на кольцо К’ = {w 6 С : р < |w| < 1} так, чтобы мнимая ось перешла в
окружность 7 = {w € С : |w| = 1}. Найти р.
◄ Найдем точки ±а, симметричные одновременно относительно окружности дК = {z g С :
\z — h| = Д} и мнимой оси. Они удовлетворяют условию (h — a)(h + а) = Д2, т.е. /г2 — а2 = Д2,
О| 2 = ±л/Л2 — Д2. Отображение w ищем в виде
iez-V^-R2
w = е-------, ,
z + Vh2 + R2
0 g R.
124
Гл. 3. Элементарные функции в комплексной плоскости
При z — iy имеем
ie iy - Vh2 - R2 ie iy - Vh2 - R2
e -------Iw = e ---------------------.
iу + Vh2 - R2 iy + y/h2 — R2
Следовательно, мнимая ось отображается в окружность 7. По-
скольку точка h + R лежит на окружности дК (см. рис. 47), и
эта окружность переходит в окружность радиуса р с центром в
точке w = 0, то
h + R - Vh2 - R2 y/h + R - Vh^R
P = -------,...- . = —..... ; =
h + R + Vh2 - R2 y/h + R + y/h-^R
Рис. 47
h — y/h2 — R2
R
h
R
69. Полуплоскость P = {z £ C | Re z > 0} с выкинутым кругом К = {z £ С : \z - h\ < 1}
(Л > 1) отобразить на кольцо К' = {w € С | 1 < |w| < 2}. Найти h.
◄ Воспользуемся решением предыдущего примера. Поскольку должно выполняться условие
|ш| = 2, то
z - Vh2 - 1
w = е #2----- - .. 6 g R. (1)
z -I- y/h2 — 1
Полагая в формуле для определения р в предыдущем примере р = 1, R = 1, находим:
1 = 2 (ft - y/h2 - 1) , h =
(предварительно умножив правую часть формулы на 2, принимая во внимание (1)). Подставив
в (1) h = |, окончательно получим:
70. Эксцентрическое кольцо, ограниченное окружностями 7! = {z £ С : \z - 3| = 9},
72 = {z £ С : |z - 8| = 16} отобразить на кольцо К' = {w £ С | р < |w| < 1}. Найти р.
◄ Находим точки а и а*, симметричные относительно 7t и 72:
(3 — а)(3 — а*) = 81,
(8 - а)(8 - а*) = 256.
Решив эту систему, получаем а = 0, а* = -24. Дальше можно решать задачу двумя способами.
1) Отображаем а = 0 н» w = 0, а* = -24 и = оо. Тогда окружность 72 перейдет в
окружность 7J = {w £ С : |ш| = 1}. Следовательно,
Поскольку точка z = 24 £ 72 отображается на окружность 72, то 1 = |fc|, |fc| = 2, к — 2е‘в,
0 = R. Функция w = w(z) принимает вид
Так как точка z = 12 £ 7j отображается на окружность радиуса р, то
ie 2 12 24 2
к 12+24 36 3
2) Точку а = 0 отображаем в w = оо, а точку а* = -24 — в w = 0. Тогда окружность 71
перейдет в окружность 7'. Имеем
, z + 24 ,36 е'в
w = k——, 1 = |fc| —, fe=—, <?6R.
§ 6. Тригонометрические и гиперболические функции
125
Окончательно имеем
ie z + 24 24 + 24 2
w = е -------, р = --------= —
3z ’ ' 3-24 3
(точка z = 24 € 72 отображается на окружность радиуса р с центром w = 0). ►
При решении некоторых задач, связанных с применением дробно-линейных функций, целесообразно
пользоваться так называемой нормальной формой дробно-линейного отображения с двумя неподвижны-
ми точками.
Всякая дробно-линейная функция L : z , отличная от тождественного отображения w = z,
имеет не более двух неподвижных точек, т. е. точек, которые при отображении L переходят сами в себя.
Действительно, уравнение
az + Ь
z = ------
cz + d
имеет корни
а - d ± -^/(а — d)2 + 46с
Они совпадают между собой, если (а - d)2 + 46с = 0, а в противном случае имеем две неподвижные
точки.
Если неподвижной точкой будет оо, то это возможно лишь в случае, когда с = 0, т.е. когда L —
целая линейная функция. Если же обе неподвижные точки сливаются с бесконечно удаленной точкой,
то с = 0 и d — а, что соответствует параллельному переносу.
Пусть L — дробно-линейная функция с двумя различными неподвижными точками Z\ и z^. Для
удобства будем изображать z и w = Z(z) точками в одной плоскости. Рассмотрим также вспомогательную
плоскость, в которой будем изображать переменные v и 0 Полагаем
w - Zl z - Zi
v — ------ = S(w), С = ------ = S(z).
w - zi z - z2
В случае zi = ос v = w — z<L = S(w), ( = z — z, = 5(z).
Из формул v = S(w), w = L(z), z = S~ '(£) получаем:
v = (5o£o 5-‘)(0.
Для дробно-линейной функции S°LoS~', устанавливающей зависимость между » и (, неподвижными
точками являются 0 и оо, в силу чего эта зависимость имеет вид v = к(, где к — некоторая комплексная
постоянная. Следовательно, данное линейное преобразование L можно задать в виде
W — Z2 z — Z2 ’
или, в случае Z2 = оо, w — z, = k(z — z,).
Формулу (1) называют нормальной формой дробно-линейного отображения с двумя неподвижными
точками. Поскольку
fc=w-z, Z-Z2 (2)
W - Z2 Z — Z[
Л Ь
не зависит от z, то, полагая z ~ 0, w = получим:
а + d — \/(а — d)2 + 46с
к = ------V —. (3)
а + d + у/ (а — d)2 + 46с
Если z = оо, то к = 5.
а
Различают три случая: 1) к > 0; 2) к = егв (0 / 0); 3) к = ге'в (в / 0, г # 1). В случае 1) отображе-
ние (1) называется гиперболическим, в случае 2) — эллиптическим, в случае 3) — локсодромическим.
71. 1) Отобразить внутренность угла 0 < argz < тг-а (0 < а < 2) на верхнюю полуплоскость.
ТГ ТГ
2) Отобразить угол---< argz < — на верхнюю полуплоскость так, чтобы ш(1 — г) = 2,
4 ‘ 2
w(i) = -1, w(0) = 0.
j.
◄ 1) Очевидно, что w = z&
4
(t — \ 3 - i —
ze 4 1 = z з e з переводит внутренность угла на верхнюю полуплос-
кость. Рассмотрим условия нормировки, которые удобно записать в виде таблицы
126
Гл. 3. Элементарные функции в комплексной плоскости
полученную выше:
W + 1 U>! + 1 W!
-----= к------’ откуда W = —— ---------—.
W Wi (К — 1)Ш! + к
Осталось найти к. Воспользуемся тем, что w! = \/4 w = 2. Имеем
2 + 1, ^4 + 1 3^4 , 3^4-2
2 ^4 2(^4+1) 2(v4+l)
4 . w
Подставив w1 = z з е’ з в формулу для w, получим:
2(v/4 + 1)е'~з гз
w =-----------__-------. k
(^4-2)е‘згз +3^4
72. Найти функцию w, отображающую полукруг К = {z € С : \z\ < 1 Л Imz > 0} на
верхнюю полуплоскость при условиях:
1) w(—1) = 0, w(0) = 1, w(l) = сю; 2) w(±l) = ^1, w(0) = oo; 3) w Q) = t, argw' Q) = - — .
◄ Из свойств функции Жуковского следует, что функция W| = (z + отображает по-
лукруг К на верхнюю полуплоскость. В каждом случае будем находить требуемое отображение w
по условиям нормировки.
1) Запишем условия нормировки в виде таблицы
Z -1 0 1
W| 1 оо -1
w 0 1 00
Ясно, что функция w = w(z) имеет вид
- 1 ( z + 1
w =------= I -----
W1 + 1 \Z - 1
2) Условия нормировки имеют вид
W = 1 + fc(Wi - 1).
ффициент к наход W 3) Поскольку z = им из условия -1 = 1 + fc(-l - 1), откуда к = 1. Окончательно имеем , Л 1 / 1\\ 1 ( 1\ z2 + l — 1 | 1 “Ь 1 2 “Ь 1 ) = I 2 + ) = \ 2 \ z J J 2 у z J 2z | W| = w = t, то, согласно решению задачи 60, w-* dw(2») ^ . = e * ., a = arg u» + t wi + jt dwi
§ 6. Тригонометрические и гиперболические функции
127
Дифференцируя w как сложную функцию, получим:
dw dw dwi dw Q) dw (|t) dw, Q)
dz dwt dz ’ dz dwt dz
откуда
Таким образом,
dw GO , , /;\ я-, *
arg—------= argw - argw, (J = --±тг = -.
dwi v/ v ' 2 2
w — i . w, — 4w, + 3 — Iz1 4- 3z — 2
w + i Zw, + |i’ W 4w, - 3 2z24-3z4-2
73. Найти функцию w(z), отображающую полукруг К = {z € С : |z| < 1 Л Im z > 0} на круг
К' = {w £ С : |w| < 1} при условиях:
1) w(±l) — ±1, w(0) = -i; 2) w Q) = 0, argw' (= •-.
Ч Сначала отобразим полукруг К посредством функции w, = — | (•? + |) на верхнюю по-
луплоскость плоскости w,, а затем построим отображение верхней полуплоскости на единичный
круг при выполнении условий нормировки.
1) Составим таблицу нормировки. Она имеет вид
z 1 -1 0
w. -1 1 00
w 1 -1
Искомая функция w имеет стандартный вид:
w, - а
w = е -----
w, — а
Из условий нормировки получаем:
в € R.
1 &
1 = е
1 + а
1 + а’
-1 = е
ie 1 ~а ie
• --------- —г = е
1 — а
Постоянную а находим из системы уравнений
или
1 4- а = —*(1 + а)
1 - а = i(l — а).
Ее решения: а = i, а = —г. Искомая функция w имеет вид
_ (г + - i _ . z + j + 2i z2 + 2iz + l _ z2 + 2iz 4- 1
l-|(z + |)+i l-z-^+2i * —z2 4-2iz — 1 iz2 4- 2z + i'
2) Поскольку z = j »-» w, = h+ w = 0, to
* ie wi ~ J* ie - 3i
w = e ------г- = e ------—.
w, + 4w, + 3г
Дифференцируя функцию w по переменной w,, получим:
dw _ 24ieie dw (|t) _ 24ie*a _ 2 . ie dw (|i) _ jr
dw, (4w, 4- 3i)2 dwi —36 3 *e ’ ,dw, 2
128 Гл. 3. Элементарные функции в комплексной плоскости
С другой стороны, как показано в предыдущей задаче,
dw (|i) , ,.. / / \
arg —-----= argw (1) - argw, (- ) .
dw.
Подставив в это равенство
dw (|») тг , z , тг , , •,
arg—------= --+в, argw ( J =-, argw, (5 ) = ±тг,
dw, 2 4 ' 2 ' ’
и выбирая argw', = -тг (так как -тг < argw' Q) - argwj Sj тг), имеем
тг тг
--+0=-- 0 = о.
2 2
Таким образом,
4w, - 3i —2 (z + — 3i 2z2 3 4 5 + 3iz 4- 2
W 4w,+3i -2(z+2)+3i 2z2-3iz + 2'^
74. Найти функцию w(z), отображающую область G = {z € C : |z| > 1 Л Imz > 0} на
верхнюю полуплоскость.
◄ Такое отображение осуществляет функция Жуковского w = | (z + |). Можно также
воспользоваться дробно-линейной функцией, отображающей область G на первый квадрант, а
затем возвести в квадрат полученное. Полагаем w, = . Тогда ? = 1 w w, = 0, z = -1 >-»
w = 00. При z = i получаем w,(z) = — zV.z9. — j Убедились в том, что функциям,
отображает G на первый квадрант. Следовательно,
2 / islV
W = W, = ---- I . ►
у Z + 1 J
75. Отобразить на верхнюю полуплоскость:
1) сектор S = {z 6 С : |z| < R, 0 < argz < тга} (0 < a iC 2);
2) область D = {z £ С : |z| > R, 0 < argz < тга} (0 < а 2).
Ч 1) Функция w, = zl/o отображает, очевидно, сектор S на верхний полукруг радиуса Я °
с центром в точке w, = 0. Рассмотрим функцию
w,+Я,/а
W1 ~ w, - К'/“ '
Тогда w, - -Rl/a >-+ w2 = 0, w, — Rl/a w2 = 00, w2 (Я|/иг) = |(1 4-i)2 = i. Следовательно,
функция w2 отображает указанный полукруг на первый квадрант плоскости w2. Поэтому искомое
отображение имеет вид
2 /г'/“+Я,/“\2
W = W2= '
2) Функция w, = * 1/г.+д1/о отображает область D на область D' = {w, 6 С : |w,| > R^a Л
Imw, > 0}. Согласно решению задачи 74, имеем
/zi/q-K1/q\2
W ~ \z'/“ +R'/a ) ' К
76. Отобразить на верхнюю полуплоскость следующие круговые луночки (двуугольники):
1) £>, = {z & С : \z\ < 1} П {z £ С : \z - :| < 1};
2) Р2 = {z £ С : |z| < 1} П {z Е С : |z - i| > 1};
3) D3 = {z £ С : |z| > 1} П {z £ C : |z - t| < 1};
4) = {z £ C : |z| > 1} П {z € C : |z - :| > 1};
5) Di = {z 6 C : |z| > 2} П {z 6 C : |z - ?2| < Vi}.
§ 6. Тригонометрические и гиперболические функции
◄ 1) Находим граничные угловые точки, являющиеся точками пере-
сечения окружностей, заданных уравнениями |z| = 1 и \z—»| = 1. Полагая
z = е'в, получим: 1 = \е'в — *|, или
1 = |cos6 + i(sin# - 1)| = -^/2(1 - sin#).
1 i- i —
Отсюда находим: sin# = j, в = , zx = e 6 , z2 = e 6 (рис. 48). Строим
дробно-линейное отображение, переводящее точку z2 в нуль, а точку zx —
в оо:
z -I—у — x 2z + V 3 — i
w = ------L.--- - ------ ---.
z _ V3 _ • 2z - %/3 - i
* 2 2
Принимая во внимание, что wt(0) = , W|(i) = — 1+^*,
строим образ луночки D, в плоскости w< (рис. 49). Дальнейшие пре-
-i — 2
образования очевидны: w2 — е зад, — поворот на угол и
3
w = w2 . Окончательно получаем:
з
/2z + \/3-i\ 2
W = — I ----—---- |
2) Граничные угловые точки луночки D2 те же, что и у луноч-
ки D,: zj = е’6 , z2 = е 6 . Взяв функцию ш, = , снова
получим на плоскости внутренность угла, образованного лучами,
выходящими из начала координат, с углом при вершине у (рис. 50).
Полагаем далее w2 = е * з ш,,
3
w = w2 = —
3) Функция W] = 77777=77 отображает луночку D2 на внутренность угла (рис. 51). Очевидно,
что искомая функция w имеет вид
3
W
4) Как и в предыдущих случаях, граничными угловыми точками луночки (см. рис. 52)
являются
Zt = е 6 , z2 = е 6 .
130
Гл. 3. Элементарные функции в комплексной плоскости
2я/3
Вспомогательная функция wt — прежняя. Поскольку
1 »%/з 1 17з
«Л(2г) = ----Wi(-»)=- + —,
то функция wi отображает луночку Л4 на внутренность утла, изображенно-
го на рис. 53. Применив преобразование поворота на угол j w2 = егз ц>15
окончательно получим:
W = Wj2
2
Рис. 53
z - 72(1 + 1)
2 и z = 272 на плоскости и)!. Имеем
1-1 (72 - 1 + I)2
Рис. 55
5) Найдем граничные угловые точки луночки D5 (рис. 54). Для этого
полагаем z = 2егв и рассматриваем уравнение относительно в
|2е’в - Т2|2 = 2,
откуда после несложных выкладок получаем:
1 я iX / 1 1 \ г-
cos# = —в = —, = 2е 4 = 2 I — Ч—— I = 72(1 + 1).
72 4’ \72 72/
Очевидно, z2 = ?| = 72( 1 - г). Полагаем по аналогии с предыдущим
? — ?2 2 — 72(1 - 1)
«Й = ----- -
Z — Z\
Установим образы точек z =
_ 2 - 72(1 - 1) 72 - 1 -
W 1(2) = --7=----- = ---- = 7=----------- —
2-72(1+1) 72- 1-1 (72-1)2+1
2 - 272 + 21(72 - 1) 1-1
~ 4-272 “
Точка z = 2 переводится в точку, лежащую на биссектрисе второго коор-
динатного угла. Далее,
272-72(1-1) 2-(1-1) 1 + 1 .
272-72(1 + 1) 2 —(l+i) l-i
т. е. образ точки z = 272 принадлежит мнимой оси плоскости wt. Луноч-
ка Dj отображается на внутренность угла, образованного положительной
мнимой полуосью и биссектрисой второго координатного угла (рис. 55).
Функция w2 = w:e~'~2 отображает указанное множество на внутрен-
ность угла, образованного положительной действительной полуосью и
биссектрисой первого координатного угла в плоскости ш2 Очевидно, что
искомая функция имеет вид
1
4
W = w2 =
4 _ Л-л/2(1 -i)V
\z - л/2(1 + 1)/
77. Отобразить на верхнюю полуплоскость плоскость с размером по отрезку [-1, 1].
Ч Рассмотрим функцию wt = Тогда z = — 1 i-+ = 0, z = 1 i-> = оо. Поскольку
Wi(0) = -1, то становится ясным, что функция отображает плоскость с разрезом по отрезку
[—1, 1] на плоскость с разрезом по отрицательной действительной полуоси. Функция w2 = — W|
отображает плоскость с разрезом вдоль отрицательной действительной полуоси на плоскость с
разрезом вдоль положительной действительной полуоси. Искомое отображение имеет вид:
W
Z + 1
1 — Z
§ 6. Тригонометрические и гиперболические функции 131
78. Отобразить на верхнюю полуплоскость плоскость с разрезом по отрезку [-г,»].
◄ Полагая Wi = —iz, получим плоскость с разрезом по отрезку [—1, 1], т.е. сведем задачу к
предыдущей. Таким образом,
79. Отобразить на верхнюю полуплоскость плоскость с разрезом по отрезку [zb z2],
4 Рассмотрим целую линейную функцию w{ = az + Ъ и потребуем, чтобы zt н-» — 1, z2 1.
Для определения а и Ь получаем систему двух уравнений с двумя неизвестными:
( — 1 = azt + b
1 1 — az2 + 6.
Ее решения: а = —-—, b = -г,+гг . Задача свелась к отображению плоскости с разрезом вдоль
z2 zl Z1 z2
отрезка [-1, 1] на верхнюю полуплоскость, (см. задачу 77). Следовательно,
80. Отобразить на верхнюю полуплоскость плоскость с разрезами по лучам (-оо, — Л],
[Я, +оо) (R > 0).
4 Функция Wi = отображает указанную плоскость с разрезами на плоскость с разрезом
вдоль положительной действительной полуоси. Следовательно,
— искомое отображение. ►
81. Отобразить на верхнюю полуплоскость плоскость с разрезом по расположенному в пер-
вом квадранте лучу, выходящему из точки i параллельно прямой у = х.
4 Функция W, = z — i отображает указанную плоскость с разрезом на плоскость с разрезом
вдоль биссектрисы первого координатного угла с вершиной разреза в начале координат, т. е. в
точке W] = 0. Функция w2 = е'^ wt отображает плоскость гщ с разрезом вдоль биссектрисы пер-
вого координатного угла на плоскость с разрезом вдоль положительной действительной полуоси.
Искомое отображение, очевидно, имеет вид
82. Отобразить на верхнюю полуплоскость плоскости w полуплоскость
Р = {z € С : Imz > 0}
с разрезом по отрезку [0, г/i] (h > 0).
4 Функция W] = z2 отображает указанную полуплоскость с разрезом на плоскость с разрезом
вдоль отрезка [—h2, 0]. Полагая w2 = wt + h2, получим отображение плоскости iz)t с разрезом
вдоль отрезка [—h2, 0] на плоскость с разрезом вдоль отрезка [0, /г2]. Следовательно,
w = y/w^ = у/z2 + h2
— искомое отображение. ►
83. Отобразить на верхнюю полуплоскость плоскости w полуплоскость
Р = {z € С : Imz > 0}
с разрезом от ih до оо вдоль положительной мнимой полуоси.
132
Гл. 3. Элементарные функции в комплексной плоскости
◄ В плоскости w1 = z2 образом заданной области будет плоскость с разрезами на действи-
тельной оси по лучам (-оо, — h2) и (0, +оо). Дробно-линейное отображение u>2 = пе-
реводит ее в плоскость с разрезом по положительной действительной полуоси. Окончательно
получаем
, Vz2 + h2
W = y/w? = -------. ►
z
84. Отобразить на верхнюю полуплоскость:
1) круг К = {z 6 С : |z| < 1} с разрезом по радиусу [0, 1] ;
2) внешность единичного круга с разрезом по лучу [1, +оо).
◄ 1) Функция W, = y/z отображает заданную область на верхний полукруг (при соответству-
ющем выборе ветви x/z). Тогда
W] + 1 \ 2
Wi — 1 у
л/z + 1 \
xjz- 1)
— искомое отображение.
2) Функция = yfz (при соответствующем выборе ветви л/с) отображает заданную область
на верхнюю полуплоскость с выброшенным верхним полукругом радиуса 1 с центром иц = 0.
Тогда функция
2
W =
— искомая. Внешне функции w в 1) и 2) одинаковы, а выбор ветвей y/z в них разный. ►
85. Найти отображение круга К = {z € С : |z| < 1} на и)-плоскость с разрезом по лучу
(-оо, при условии, что w(0) = 0, w'(0) > 0.
Пусть z = z(wt) — отображение верхней полуплоскости плоскости Ш| на круг К. Тогда
z = , к = е,в, 0 € R. Отсюда находим:
W, =
z/З — кр
z — к
Искомое отображение имеет, очевидно, вид
2 1
w = —W.-----
4
гД — к/3 \ 2 1
z — к J 4
(1)
Поскольку w(0) = 0 = —Д2 — | и 1тД > 0, то Д = j. Подставив это значение в формулу (1),
получим после несложных преобразований:
1 ((z + к\г
w = - -----
4 I \ z - к )
Дифференцируя w, имеем
(z + fc)
(z-fc)3’
Из условия w'(0) > 0 следует, что | > 0. Так как |fc| = 1, то к = е'в > 0 при 0 = 0, т.е.
к = 1. Окончательно получаем:
w'(z) = -к
z
W = -------т. ►
(1 - Z)2
86. Найти преобразование полярной сетки |z| = R, argz = а с помощью функции Жуков-
1 / 1\
СКОГО W = - Z Ч— .
2 \ z /
\ kz
1 / (2 - fc)2'
§ 6. Тригонометрические и гиперболические функции
133
◄ Подставив в формулу для w значение z = Re'a, получим:
Таким образом,
1 ( „ ia 1
w = и 4- iv = - I Re 4------------e
2 \ R
cos а 4- i ( R -
r) sma
1 ( 1 \
и = - Я + — cos a,
2 \ Я /
1 / 1 \
- Я — — sma.
2 \ R
Из равенств (1) находим:
2u 2V
cos a =----г, sin a = --r
Я+ ± R-±
Ji ti
4u2
. 1
4v2
(1)
(2)
Из (2) следует, что окружностям 7n = {z 6 С : |z| = Л} соответствуют софокусные эллипсы.
В частности, окружности 71 = {z € С : |z| = 1} соответствует отрезок 7 = {w€C:-l^Rew^l,
Im w = 0} (см. § 5).
Записав первые два уравнения в (2) в виде
и 1 f 1
------“ 1^3- —
cos а-2 \ R
v 1 ( 1
—=Т й--
sina 2 \ Я
(3)
и возведя левые и правые части полученных равенств в квадрат, а затем складывая соответственно
квадраты левых и правых частей, получим
и2 v2
—--------~ = k
cos2 a sin а
Равенство (3) показывает, что лучам arg z = а соответствуют ветви софокусных гипербол. В
частности, лучу argz = О соответствует луч = {w € С : Rew 1, Imw = 0}. Действительно,
при а = 0 из (2) получаем, что v = 0, и = =1. Аналогично устанавливаем, что
лучу argz = тг соответствует луч = {w € С : Re w — 1, Im w = 0}, а лучам arg = ±у — ось
Re w = 0. ►
87. Пользуясь функцией Жуковского, отобразить:
1) внешность отрезка [—с, с] (с > 0) на внешность единичного круга при условии, что
w(oo) = оо, argw'(oo) = а ;
т2 у2
2) внешность эллипса — 4—- = 1 на внешность единичного круга так, чтобы w(oo) = оо,
а1 Ь1
arg w'(oo) = 0;
х2 у2
3) верхнюю полуплоскость с выкинутым полуэллипсом — 4—- 1, у > 0, на верхнюю
а2 &2
полуплоскость.
Ч 1) Полагаем wt = При этом отрезок [-с, с] перейдет в отрезок [—1, 1]. Теперь применим
к функции w] отображение, обратное функции Жуковского:
U)2 = W] +
Дифференцируя функцию w2, находим:
? = l+
awi
1.
Поскольку w^oo) = OO, TO
dw->(oa)
arg —-------= arg 2 = 0.
aw]
Взяв w = w2e'a, получим
dw(oo) е
dz ।
z
Vz2 — c2
-e*'
c
dw(oc)
arg—-----
dz
v
134
Гл. 3. Элементарные функции в комплексной плоскости
Таким образом,
е’“ / /—---г\
w = --- + V z1 — с2 j
— искомое отображение.
2) Проведем преобразование подобия точек так, чтобы фокусами эллипса были точки (—1, 0)
и (1, 0):
z
W1 — —===.
Va2 — Ь2
Определим радиус г окружности, в которую функция Жуковского преобразует данный эллипс
2 2
“1 «1
! 1 ! -- = 1
/------------------------\ 1-/-\ 2
I а 1 । ь \
\ \/а2 — Ь2 / \ у/ai'—b2 J
Обозначим а — . а . Тогда находим г из уравнения а = | (г + -) или г2 - 2аг +1=0, откуда
г = а + \/а2 - 1 (берем перед радикалом знак “+”, поскольку должно быть г > 1). Имеем
а / Ь2 а + Ь
у/ а2 — Ь2 V а2 — Ь2 у/а2 — Ь2
Далее применяем функцию, обратную функции Жуковского, полагая w2 — W| + a/w2 - 1. Тогда
искомая функция w определяется равенством
w2 у/a2 -Ь2 ( z / z2 \ 1 / /—-----------—\
г а + b I Va2 - Ь2 у а2 - b2 j a + Ь \ v /
3) Воспользуемся решением предыдущей задачи. Отобразим данную область на верхнюю
полуплоскость с выброшенным единичным полукругом:
= -----(z + у/z2 - (а2 — b2)).
а + Ь
Теперь связь между функциями wt и w устанавливается функцией Жуковского
1 / 1 \ 1 / z + у/ z2 — (а2 - Ь2) а + Ь \
w = - I и»! Н-= - -----------------;---------1-----; = =
2 \ v>\ J 2 у а + Ь z + у' 22 _ (а2 _ J
_ 1 / z+y/z2- (а2 - Ь2) + У (^ ~ а/^2 ~ (а2 - &2)) \ _ az -Ьу/z2- (а2 - b2)
2 I а + Ь а2 — Ь2 I а2 — Ь2
88. Отобразить двусвязную область, ограниченную софокусными эллипсами
х2 у2 , х2 у1
+ = ^ + Ь^ = 1
на концентрическое круговое кольцо с центром в начале координат и найти модуль данной дву-
связной области (каждая двусвязная область, границы которой не вырождаются в точки, может
быть конформно отображена на концентрическое кольцо с вполне определенным отношением ц
радиусов внешней и внутренней окружностей. Число ц называется модулем двусвязной области).
◄ Преобразование подобия wi = —преобразует заданный эллипс в эллипс с фокусами
V а^—Ъ^
в точках ±1 и осями а = 7 ° , Ъ = .
у/а2-Ъ2 у/а2-Ъ2
Теперь с помощью функции, обратной функции Жуковского, отображаем эллиптическое
кольцо на круговое:
w2 = Wj + a/w? - 1 = -у--1 (z + у/z2 - (а2 - Ь2Й .
vaz — b2 \ /
§ 6. Тригонометрические и гиперболические функции
135
Если совершить преобразование поворота и подобия, то снова получим концентрическое кольцо.
Таким образом, в общем случае искомое отображение w имеет вид
w — х (z + a/z2 - (а2 - Ь2)
х 6 С — произвольное.
Модуль области равен отношению радиусов окружностей концентрического кольца. В плос-
кости Wt большими полуосями эллипсов являются
а _ /а2 + к2
°* ~ Va2 - Ь2 ’ Л2~ У а2 — Ь2’
Следовательно,
° _1_ / а2 _ 1
И у/а^-ь2 "Е V °2-ь2 а ± 6 а — Ь
r2 / a2+k2 , / a2+k2 7 у/a2 + к2 ± у/Ь2 + к2 ’ Va1 + к2 — у/Ь2 + к2
V а2~Ь2 Х V а2 — Ь2 1
89. Найти область, на которую функция Жуковского отображает круг К = {z 6 С : \z| < 1}
с разрезом по отрезку [а, 1] (-1 < а < 1). Рассмотреть случаи а > 0 и а < 0.
◄ Пусть а > 0. Поскольку функция Жуковского отображает единичный круг на всю плос-
кость с разрезом по отрезку [-1, 1], в который переходит граница круга, то она отображает за-
данную область на всю плоскость w с разрезом по отрезку [—1, 7 (а + £)] .
Пусть а < 0. Функция Жуковского w = | (z + j) переводит точку а в | (а + |) < -1, точку
-1 в -1. Пусть z = х. При z —> -0 | (а: + —► -оо, а при х —» +0 | (®+ j) —> +сю. Таким
образом, в рассматриваемом случае функция Жуковского отображает заданную область на всю
плоскость w с разрезами по лучам (-оо, | (а + £)] и [—1, +оо). к
90. Отобразить на верхнюю полуплоскость круг К = {z 6 С : |z| < 1} с разрезом по отрезку
М-
◄ Функция Жуковского W, = | (z + |) отображает заданную область на всю плоскость wi
с разрезом по отрезку [—1, |]. Получили задачу 79, в которой z1 = = —1, z2 = w{2) = |.
Следовательно, искомое отображение — функция
91. Отобразить на верхнюю полуплоскость круг fc = {z€C:|z|<l}c разрезами по радиусу
[-1, 0] и отрезку [а, 1] (0 < а < 1).
◄ Функция Жуковского wt — I (г + |) отображает заданное множество на всю плоскость
w( с разрезом по лучу (-сю, | (а + |)). Действительно, | (о+ “) \Ja‘ а = 1, z = х —> -оо
при х -* -0, а окружность 7 = {z € С : \z\ = 1} переходит в разрез по отрезку [-1, 1]. В итоге
получаем плоскость с разрезом по лучу 7' = (-00, | (а + £)). Функция ш2 = | (а + |)
отображает плоскость с разрезом по лучу 7' на всю плоскость w2 с разрезом вдоль отрица-
тельной действительной полуоси. Функция w3 = — w2 отображает плоскость ш2 с разрезом вдоль
отрицательной действительной полуоси на всю плоскость w3 с разрезом вдоль положительной
действительной полуоси. Следовательно, требуемая функция —
136
Гл. 3. Элементарные функции в комплексной плоскости
92. Отобразить на верхнюю полуплоскость верхнюю половину круга К = {z g С : |z| < 1} с
разрезом по отрезку [0, to] (0 < а < 1).
◄ Функция w, .= z2 отображает заданное множество на единичный круг с разрезом вдоль
отрезка [-а2, 1]. Функция Жуковского w2 = | (и>| + у) отображает этот круг с разрезом на
всю плоскость ш2 с разрезами вдоль лучей (-оо, (а2 + ^)) и [0, +со), а функция
^ + И“2 + ^)
Ц)3 - --------------
ш2
отображает эту плоскость с двумя разрезами на всю плоскость с разрезом вдоль положительной
действительной полуоси. Следовательно, w = y/w^ — искомое отображение. Таким образом,
w =
93. Отобразить на верхнюю полуплоскость верхнюю половину круга К = {z € С : \z\ < 1} с
разрезом по отрезку [ai, i] (0 < а < 1).
Функция W| = z1 отображает заданное множество на единичный круг с разрезами по
отрезкам [-1, -а2] и [0, 1]. Функция Жуковского w2 = 5 (ш, + отображает этот круг с
двумя разрезами на всю плоскость w2 с разрезом вдоль луча [-1 (а2 + у) , +оо) Функция
отображает плоскость w2 с указанным разрезом на всю плоскость ш3с разрезом вдоль положи-
тельной действительной полуоси. Следовательно,
— требуемое отображение. ►
94. Отобразить круг К = {z ё С : |z| < 1} с выкинутым отрезком [(1 - h)e'“, е’“] на
единичный круг плоскости w.
◄ Функция w, = ~ отображает заданную область на единичный круг с разрезом по
отрезку [(1 - Л)е*“, е'“], а функция w2 — | + у) отображает этот круг на всю плос-
кость ш2 с разрезом по отрезку [-1, hj, где h, — - (1 - h+ ' Д’111143 этого
отрезка равна (уу7у + 1 = Возьмем половину длины этого отрезка и рассмотрим чи-
сло Л, - уту = 4(121_h). Осуществим преобразование переноса так, чтобы разрез [-1, hj стал
симметричным относительно начала координат, полагая
Л2
ШЗ = ^-4(Г^-
Функция w3 отображает плоскость ш2 с разрезом по отрезку [-1, h|] на всю плоскость w3 с
разрезом по отрезку j^-*2"^, • Рассмотрим в плоскости w единичный круг К\ = {w g С :
|w| < 1}, на который отображается круг К. Функция ш = (w + отображает круг Kt на всю
плоскость ш с разрезом по отрезку [-1, 1]. Полагая
(2-Л)2 h2 \ Д . h2 \ 1 / 1
цл = ------w - ------ I (j = 1 ] 4- --- I — 1 w 4* —
4(1 -h) 4(1 -h)J 4(1 -h)J 2 \ w
§ 6. Тригонометрические и гиперболические функции
137
и подставив в это равенство
h2 1 ( ( 1 \
«-’З = ------— = - W, + —
4(1 — Л) 2 у у wt )
h2
2(1 - h)J
h2
2(1-h) J ’
получим после сокращения на | _•
Л2 \
4(1 -h))
h2
2(1-Л)'
95. Отобразить на внешность единичного круга: 1) всю плоскость с разрезами по отрезкам
[-1, 1] и [-г, г] (внешность креста); 2) всю плоскость с разрезами по лучам (-оо, -1], [1, +оо),
(-ioo, —г], [г, +гоо).
◄ Для решения задачи сформулируем, не вникая в подробности, принцип симметрии Рима-
на—Шварца, который рассмотрим подробно в главе 7. Суть его состоит в следующем: пусть
область G С С ограничена замкнутой жордановой кривой Г, в состав которой входит дуга I
окружности L расширенной комплексной плоскости. Пусть функция f определена и непрерывна
на G U /^аналитическая в G, а на I принимает значения, принадлежащие некоторой окружно-
сти С С С. Тогда / продолжается через дугу I в область G*, симметричную с G относительно L
до функции, аналитической в G U I U G*. Такое продолжение (через /) единственно и определя-
ется следующим свойством продолженной функции /: если точки z G G и z* € G* симметричны
относительно L, то точки w = f(z) и w* = f(z*) симметричны относительно С. В частности,
если L я С совпадают с действительной осью плоскости С, то f(z) = f(z) при z € G и I и G*.
1) Внешность креста изображена на рис. 56.
Применим принцип симметрии Римана—Шварца: отображаем верхнюю полуплоскость с раз-
резом [0, г] на верхнюю полуплоскость, полагая
W[ = \/ z2 +1.
Функция «J, вместе с ее аналитическим продолжением, ко-
торое также обозначим w,, осуществляет отображение внеш-
ности креста на всю плоскость ш, с разрезом вдоль отрезка
[—\/2, у/2]. Функция
отображает плоскость иц с указанным разрезом на всю плос-
кость w2 с разрезом по отрезку [-1, 1]. Функция
w = w2 + \/w2 — 1,
обратная функции Жуковского, осуществляет отображение плоскости w2 с разрезом по отрезку
[-1, 1] на внешность единичного круга. Окончательно получаем:
x/z2 + 1
V2
x/z2 + 1 — 2
d-------------
V2
2) Функция ц)| = 2 осуществляет отображение заданного множества на внешность креста из
предыдущей задачи. Поэтому искомое отображение ш определяется формулой
w = (Vw2 + 1 - - 1) = -J—
V Z \ / у 2 ‘ 2
1 + z2 + -\/1 - z2^ . ►
96. Отобразить верхнюю полуплоскость с разрезом по отрезку / = {z 6 С : Re z = а > О, О
Imz Л} на верхнюю полуплоскость.
Ч Искомая функция w является композицией элементарных преобразований:
= z — a, w2 = ш2, w3 = w2 + h2, w = у/йЦ = у/ (z — a)2 + h2.
138 Гл. 3. Элементарные функции в комплексной плоскости
Легко видеть, что аналитическая ветвь w, осуществляющая заданное отображение, определяется
условием w(0) < 0 (см. рис. 57). ►
97. Отобразить на верхнюю полуплоскость и на внешность единичного круга внешность
креста, состоящего из отрезка [—а, Ь] действительной оси и отрезка [-«, сг] мнимой оси (а О,
Ь 0, с 0, а2 4- Ъ2 + с2 / 0) (рис. 58). ______
Ч Согласно решению задачи 96, функция Wi = •/ z2 + с2 z—x
конформно отображает верхнюю полуплоскость с разрезом 1
по отрезку [0, ci] на верхнюю полуплоскость, причем рас-
сматривается та ее ветвь, которая характеризуется условием Г1 ci
1^(0) < 0. При этом прямолинейный отрезок границы
L = {z G С : —оо Rez -a, Imz = 0} и -------1 ►
U{z£C:6^Rez^ +оо, Imz = 0} I
отображается на отрезок LJ — С1
L' = {wt 6 С : —оо Rewj — \/а2 + с2, Imu^ = о} U
U {wi £ С : 0 < \/b2 + с2 Re W! +оо, Im w, = oj-. Рис. 58
Согласно принципу симметрии Римана—Шварца, функция ш, допускает аналитическое про-
должение в нижнюю полуплоскость через отрезок L. При этом образом внешности креста в
и>! -плоскости является внешность отрезка
I — G С : -у/а2 + с2 SJ Reu>i \/б2 + с2, Imwj = oj- .
Согласно решению задачи 79, функция
Wi + у/а2 + с2 / у/ z2 + с2 + у/а2 + с2
ш=\ —. ----= л / —. ---- ------. (1)
у у/Ь2 + с2 — Wj у у/Ь2 + с2 - у/ z2 + с2
отображает внешность отрезка I, следовательно, и внешность креста, на верхнюю полуплоскость.
Решим вторую часть задачи. Обозначим длину отрезка [-у/а2 + с2, у/Ь2 -I- с2] через 2/3 и
подберем такое а £ R, чтобы выполнялись условия
—у/а2 + с2 + а у/Ь2 + с2 + а
_ = -1, • = 1,
2 2
что равносильно уравнениям
2 (у/Ь2 + с2 + а) 2 (—у/а2 + с2 + а)
у/Ь2 + с2 + у/а2 + с2 ’ у/Ь2 + с2 + у/а2 — с2
Решением этих уравнений является а = У/°2+с2-'/к2.+52.
§ 6. Тригонометрические и гиперболические функции
139
Функция w2 = ^(w(+a) отображает плоскость w । с разрезом по отрезку [—л/a2 + с2, х/62 + с2]
на всю и?2 — плоскость с разрезом по отрезку [—1, 1]. Для получения требуемого отображения
плоскости w2 с указанным разрезом применим функцию, обратную функции Жуковского:
у/а2 + с2 - Vb2 + с2 т/а2 + с2 + л/Ь2 + с2
где
98. Плоскость с разрезами по лучу [—а, +оо) (а 0) и отрезку [—сг, ci] (с > 0) отобразить
на верхнюю полуплоскость.
Ч Функция wi = у/z2 + с2 отображает заданную область на всю wi -плоскость с разрезом по
лучу [~\/а2 + с2, +оо). Требуемое отображение w получим после применения операции сдвига
вправо на Va2 + с2 и извлечения затем квадратного корня:
w
а2 4- с2. ►
99. Отобразить на верхнюю полуплоскость внешность единичного круга с разрезами по
отрезкам [г, Ы], [-Ы, -г], [1, a], [-а, -1] (а > 1, b > 1).
Ч Функция Жуковского w1 = | (z + |) отображает внешность единичного круга с указан-
ными разрезами на внешность креста, состоящего из отрезка | (а + | (а + ~)] действи-
тельной оси и отрезка [- (b — |) г, (b - |) »’] мнимой оси. Получили частный случай задачи 97,
где а заменено на | (а + ^) , Ъ — на | (а + ~) , с — на | (b — |). Следовательно, можно вос-
пользоваться формулой (1) задачи 97, заменив в ней a, Ь и с выражениями, указанными выше.
Тогда получим искомое отображение ш:
w =
Рис. 59
100. Отобразить на верхнюю полуплоскость внутренность правой ветви гиперболы
д2 _ у2 _ j
, cos2 a sin2 a
Ч Пусть А — вершина правой ветви гиперболы, F — ее фокус (рис. 59).
Проведем разрез по лучу [4, +оо). При решении задачи 86 было показано, что функция
Жуковского w = и + iv = | (z + |) отображает лучи argz = а На софокусные гиперболы
и2 v2
•2
cos2 a
sin2 а
140
Гл. 3. Элементарные функции в комплексной плоскости
Поэтому функция wi = z + \/z1 - 1, шДоо) = оо, обратная функции Жуковского, осуществляет
конформное отображение верхней половины области на сектор 0 < argu?! < a, |w,| > 1 (рис. 60).
ТГ
Рис. 60
Функция = w“ отображает этот сектор на верхнюю полуплос-
кость с выброшенным верхним полукругом радиуса 1, а функция
и»з = | (wj + отображает полученную область на верхнюю
полуплоскость, причем лучу [Л, +оо) соответствует луч (—оо, — 1].
Применив принцип симметрии Римана—Шварца и затем допол-
нительное отображение w = г у/1 + w2, получим, что w — иско-
мая функция. Возвращаясь по цепочке от ш3 до z, окончательно
получим:
1
101. Отобразить на верхнюю полуплоскость внешность правой ветви гиперболы
cos2 a sin2 а
◄ Пусть А — вершина правой ветви гиперболы (рис. 59).
Проведем разрез по лучу (-оо, Л]. Функция wt = z + x/z2 - 1,
wl(oo) = oo, отображает верхнюю половину заданной области на
7Г
область, изображенную на рис. 61. Функция w2 = (e~lawt) ^~а
отображает указанную область плоскости w, на верхнюю полу-
плоскость с выброшенным верхним полукругом радиуса 1, а функ-
ция Жуковского w3 = | отображает эту область на
верхнюю полуплоскость плоскости ш3, причем лучу (—оо, А] соот-
ветствует луч [1, +оо). Применив принцип симметрии, получим,
что функция отображает внешность правой ветви гиперболы
на всю плоскость с разрезом по лучу [1, +оо). Следовательно,
w = \ — требуемое отображение. После несложных пре-
образований получим:
102. Отобразить область, заключенную между ве-
твями гиперболы
х2 у2 —
----— = 1,
а2 Ь2
на верхнюю полуплоскость.
•4 Проведем разрез по отрезку [4Ь А2] (рис. 62) и
заметим, что функция ш, = ~(г + Vz2 - с2), где с =
х/а2 + 62 отображает верхнюю половину заданной обла-
сти на сектор а < arg w2 < л—а, |иц | > 1, где а = arctg |.
По принципу симметрии Римана—Шварца эта же
функция конформно отображает всю заданную область
на весь сектор а < arg wt < тг — а. Следовательно, функ-
ция
w = (е ,awi)^-2a =
§ 6. Тригонометрические и гиперболические функции
141
осуществляет отображение заданной области на верхнюю полуплоскость. Поскольку
... Ь а
тг — 2а = 2------arctg - = 2 arcctg - = 2 arctg -,
- ' ~ Ь
тг
2
то полученную формулу можно записать в
/ _;<х z + Vz2 - с2\ Р
w = е --------------- , где
= 2 arcctg - = 2 arctg -
а Ь
виде
Ь
а = arctg -,
а
V = ----------, с =
2 arctg |
У
sin2
Для приведения уравнения гиперболы к виду
с = х/а2 + Ь2. Тогда a = arctg |. ►
103. Выяснить, во что преобразуются при отображении
1) прямоугольная сетка х — С, у = С\
2) полоса G = {z € С : 0 < Im2 < тг};
3) полуполоса D = {z € С : Re z < 0, 0 < Im z < тг}.
◄ 1) Пусть
ez + е
w = и + iv =------
2
взяли cos а = -, sin а —
С ’
ch z\
gX + iy e~x~iy j
---------------= - (ex(cos у + i sin y) + e~x(cost/ - i sin t/)) —
= cos у ch x + i sin у sh x.
а
X
1
ъ
w =
Тогда и = cos у ch х, v = sin у sh х. Если х = С, то
u2 v2
и = cos у ch С, t) = sinyshC, —:---1---;— = 1.
ch2 С sh2 С
Получили семейство софокусных эллипсов с фокусами в точках Rez = ±1. Если у = С, то
и = cos С ch х, v — sin С sh х, —=---------=— = 1.
ch2 С sh2 С
Прямые у = С преобразуются в семейство софокусных гипербол с фокусами в точках Re z = ± 1.
2) При у = 0 и = chx, v = 0, а при у = тг u = -chx, v = 0. Функция w = chz отображает
полосу G на всю плоскость с разрезами по лучам (—оо, —1], [1, +оо).
3) Поскольку w(0) = 1, ш(гтг) = -1, то отрезок [0, гтг] переходит в отрезок [-1, 1] и напра-
влению движения от точки 0 к точке гтг соответствует движение по направлению от точки 1 к
точке — 1. При этом точки плоскости w по правилу обхода находятся слева, т. е. принадлежат ниж-
ней полуплоскости. При z = х, х -+ —оо луч (-оо, 0] переходит в луч [1, +оо), а при z = х + гтг,
х -+ —оо функция w(z) — — chx имеет предел -оо и луч 7 = {z С С : Rez 0, Imz — гтг}
перейдет в луч (-оо, -1]. В соответствии с правилом обхода полуполоса D отображается функ-
цией w = ch z на нижнюю полуплоскость. ►
104. Отобразить на верхнюю полуплоскость полуполосу
G = {z 6 С : Re z < 1, 0 < Im z < h}.
◄ Композиция отображений wi = z - 1, w2 = пе-
реводит полосу G на полосу D из примера 103, 3). Поэтому
функция w3 = ch w2 отображает заданную область на нижнюю
полуплоскость. Следовательно,
(z - 1)тг
w = —ш3 = — ch----------. ►
h
105. Отобразить на верхнюю полуплоскость полосу, огра-
ниченную прямыми у = х и у = х + "h.
◄ Пусть d — ширина полосы. Тогда, очевидно, d =
(см. рис. 63). Композиция отображений
решает поставленную задачу. .►
тг
ш2 = -ш,,
a
w = е“2
ш, = е 4 z
= е
Рис. 63
142
Гл. 3. Элементарные функции в комплексной плоскости
106. Отобразить на верхнюю полуплоскость круговую луночку, ограниченную окружностями
Г = {z € С : \z\ = 2} и 7 = {z g С : \z - 1| = 1}.
◄ Функция W| = 73^ отображает круговую луночку на вертикальную полосу G = {wi £ С :
0 < Re-ич < 5}, а функция w2 = 2?riwl отображает полосу G
на горизонтальную полосу D = {w2 Е С : 0 < Imw2 < л-}
(см. рис. 64)
lirix
Тогда функция w = е”'2 = е 1 = е отображает луночку
на верхнюю полуплоскость (см. свойства показательной функ-
ции). ►
107. Отобразить на верхнюю полуплоскость область, огра-
ниченную окружностями Г — {z g С : |г| = 2}, 7 = {z Е С :
\z - 3| = 1} (плоскость с выброшенными кругами).
◄ Искомое отображение w является композицией w = е1'"-,
где w2 = ywt, u>i = (см. рис. 65).
Таким образом,
г 2L.
w = е 3 z-2. ►
108. Отобразить на верхнюю полуплоскость область, определенную неравенствами
(верхняя полуплоскость с выкинутыми полукругами).
Функция ш1 = ~ отображает заданную область на полуполосу G = {w, Е С : 0 < Re wt < 2,
Imwt < 0}, а функция w2 = переводит G в полуполосу D — {w2 Е С : 0 < Rew2 < %,
§ 6. Тригонометрические и гиперболические функции
143
Im w2 < 0}. Из свойств функции ( н~» cos ( следует, что функция w = cos w2 = cos —
искомая, (см. рис. 66) ►
109. Отобразить на верхнюю полуплоскость полуполосу G = {zgC:0<Rez< +оо, — 1 <
Imz < 1} с разрезами по отрезку [0, 1] и лучу [2, 4-оо).
◄ Требуемое отображение w определим с помощью композиции элементарных преобразо-
ваний: W| = ttz, w2 = eW|, w2 = J (w2 + , w4 = , w = y/w^. Последовательные
преобразования отражены на рис. 67. к
Рис. 67
110. Найти функцию w(z), отображающую область, ограниченную окружностью Г =
{z G С : |z| = 1} и прямой 7 = {z € С : Imz = 1} (полуплоскость G = {z € С : Im |z| < 1} с
выброшенным кругом К = {z € С : |z| < 1}) на круг К = {w € С : |w| < 1} с нормировкой
ш(—Зг) = 0, argw'(—Зг) = у.
< Функция wi = отображает множество G на вертикальную полосу
D = {wi € С : 0 < Reu»! < 1},
а функция w2 = — у переводит D на полосу |
Z»'= {w2 е С :-у < Rew2 <-} .
144
Гл. 3. Элементарные функции в комплексной плоскости
Полагая
тг\ (z + Зг)
— = tg тг-------,
4 ) 6 4(z -»)
получим отображение полосы D' на единичный круг с центром в начале координат (см. рис. 68).
Подставив в w3 z = —Зг, получим w3(-3i) = 0. Дифференцируя w3(z), находим:
, гтг , тг , тг
w3(z) =----------------т-гг-г, Wj(-3i) = i—, argw3(-3t) = —.
(z-i)2cos2f (^)’ 16’ * 2
Далее полагаем w = w(w3) и требуем выполнения условия нормировки argw'(-3i) = у. Диффе-
ренцируя w по переменной z, имеем
dw dw dw3 dw(z)
— =------------, arg--------
dz dw3 dz dz
dw(w3)
= arg —----
dw3
+ arg
wj=0
dw3(z)
dz
или
ТГ , ТГ , ТГ ТГ ТГ
- = argw (0) + откуда argw (0) = - - - -
3 2 3 2 о
Функция w = w(w3) должна удовлетворять условиям w(0) = 0, argw'(O) = - f • Следовательно,
тг f z + 3i\ у/З - i тг f z + 3i\
w = e <• w3 = e 6 tg - ------ = ——— tg - --------г
4 у z - i у 2 4 у z - i /
Принимая во внимание равенство tgz = —ithtz, можно представить w(z) в виде
1 + iyf3 vi(z + Зг)
w =----------th--------. ►
2 4(z - г)
111. Отобразить на верхнюю полуплоскость полосу G={z6C:0<Rez<l}c разрезом
вдоль отрезка 7 = {z 6 С : 0 < Re 2 < h, Im 2 = 0} (h < 1).
◄ Функция W| = гтг отображает полосу G на полосу D = {w, € С : 0 < Rew, < тг}, а
функция w2 = cosw, отображает полосу D на всю плоскость с разрезами по лучам (—сю, -1] и
[cosrrh, +00). Тогда
/w2 — COS nh у COS 7Г2 — cos тгЛ
V w2 + 1 V 1 + COS ТГ2
— требуемое отображение. ► '
112. Отобразить на верхнюю полуплоскость полуполосу G = {z € С : 0 < Re 2 < тг, Im 2 > 0}
с разрезом вдоль луча 7 = {z G С : Rez = у, h Imz < +00} (h > 0).
Ч Полагая w( = cos 2г, получим отображение множества G на всю плоскость с разрезами
по лучам (—оо, — сЬ2Л] и [—1, 4-оо). Функция w2 = отображает плоскость с указанными
Упражнения для самостоятельной работы
145
разрезами на всю плоскость с разрезом по лучу [0, +оо). Следовательно,
W = a/w} =
cos 1z + ch 2h
cos 2z + 1
— искомое отображение. ►
113. Отобразить на верхнюю полуплоскость область, ограниченную мнимой осью и окруж-
ностью Г = {z g С : |z - 11 = 1}, с разрезами вдоль отрезка 71 = {z g С : 2 < Rez a, Imz = 0}
и вдоль луча 72 = {z € С : b Rez < +00, Imz = 0} (а < b).
◄ Полагая Wi = 7, получим отображение указанной области на вертикальную полосу G =
€ С : 0 < Rewi < |} с разрезами по отрезкам [б, |] и |]. Функция иь = 27rw,
отображает множество G на вертикальную полосу D — {w2 g С : 0 < Re w2 < тг} с разрезами
по отрезкам [О, 77] и тг], а функция w3 = cos гл, отобразит полосу D на всю плоскость с
разрезами по лучам (-00, cos^1] и [cos 77, +00). Полагая
cos w, — cos 77
«М = -----------ST’
COS W2 — cos —
получим всю плоскость с разрезом по положительной действительной полуоси. Таким образом,
w = у/йЦ =
cos - cos 77
COS 77 - cos 77
— требуемое отображение. ►
Упражнения для самостоятельной работы
1. С помощью отображения w = z2 найти образ круга K = {zgC:|z — 11 < 2}.
2. Доказать, что если точка z описывает окружность 7 — {z g С : |z| = 2}, то точка
w = z — 2г + I
описывает эллипс с главными осями, равными 5 и 3.
3. Найти образ первого квадранта z-плоскости при отображении
-=Ш-
4. Доказать, что функция w = (777)2 взаимно однозначно и конформно отображает область
G = {z С С : |z| < 1, Imz > 0} на область D = {w g С : Im гл > 0}.
5. Найти образ области G = (z g С : |z| < |} при отображении
w = (тт) •
6. Найти образ области G = {z g С : |z| < 2, 0 < argz < j } при отображении
/ . \ 2
7. Найти образ множества G = {z g С : Rez 0,Imz 0} при отображении
z2-i
w = -ТТ7-
8. Множество D = {z g С : |z| 1, Rez > 0} отобразить с помощью функции
9. Доказать, что функция
_ (i+z3)2-m-^)2
W (l+z3)2+i(l-z3)2
однолистно и конформно отображает область G = {z g С : |z| < 1, 0< argz < j} на область
D = {w g С : |w| < 1}.
146
Гл. 3. Элементарные функции в комплексной плоскости
10. Найти образы указанных областей при заданных отображениях:
a) G = {г € С : |z| < 2, Imz > 1}, w = — >
6) G = {z 6 C : |z| > 2} П {z € C : \z - < Л}, w =
в) G = {z ёС: |z| < l}n{z €C: |z + i| > 1}, w = -
11. Найти степенную функцию, отображающую взаимно-однозначно и конформно внутрен-
ность угла 0 < arg z < у на всю комплексную плоскость w с разрезом по лучу arg w = -.
12. Найти функцию, отображающую однолистно и конформно внутренность угла
О < arg(z - г - 1) < f
на область
G = {w £ С : Rew > 0}.
13. Найти функцию, отображающую взаимно однозначно и конформно внутренность угла
- f < arg(z — i) < на верхнюю полуплоскость.
14. Найти функцию, осуществляющую взаимно однозначное и конформное отображение
внутренности угла — f < arg(z - а) < у на область G = {w G С : Im w > 0}.
15. Найти функцию, отображающую однолистно и конформно область G = {z g С : Re z > 0,
Imz > 0} на область Z> = {w € С : Rew > 1}.
16. Найти целую линейную функцию, отображающую треугольник с вершинами в точках
0, 1, г на подобный ему треугольник с вершинами 0, 2, 1 + г.
17. Найти целое линейное преобразование с неподвижной точкой 1 + 2г, переводящее точку г
в точку —г.
18. Для указанных преобразований найти конечную неподвижную точку z0 (если она суще-
ствует), угол поворота вокруг нее 0 и коэффициент растяжения к. Привести эти преобразования
к каноническому виду w — z0 = A(z — z0).
1) w — 2z + 1 — 3г';
2) w = iz 4- 4;
3) w = z -I- 1 - 2г;
4) w — W[ = a(z — Zj) (a / 0);
5) w = az + b (a 0).
19. Дана функция w = .
1) Доказать, что прообразом семейства <r = {w g С : |w| — A (0 < A < +oo)} является се-
мейство окружностей (окружности Аполлония). Для данного А найти радиус и положение центра
соответствующей окружности в z -плоскости.
2) Найти прообразы лучей argw = в.
3) Построить сетку в z-плоскости, соответствующую полярной сетке в w-плоскости.
4) Найти область z-плоскости, соответствующую полукругу К = {w g С : |w[ < 1, Im w > 0}.
20. Найти общий вид дробно-линейной функции w = w(z), отображающей круг К = {z g С :
|z| < 1} на правую полуплоскость Р = {w g С : Rew > 0} так, чтобы w(z^ = 0, w(z2) = оо, где
z, и z2 — заданные точки на окружности дК и такие, что argzi < argz2.
21. Найти центр w0 и радиус R окружности, на которую функция w = отображает
действительную ось (Im z2 7= 0).
22. Найти общий вид дробно-линейной функции w = w(z), отображающей круг К = {z 6 С :
|z| < Я} на себя при следующих условиях:
1) w(a) = 0 (|а| < Л);
2) w(a) = Ь (|a| < R, |Ь| < Я);
3) w(±R) = ±R.
23. Отобразить круг К = {z g С : |z| < 1} на себя так, чтобы заданные точки z,, z2 внутри
круга перешли в точки ±а (0 < а < 1).
24. Отобразить круг К = {z 6 С : |z| < 1} на себя так, чтобы отрезок действительной
оси 7 = {z € С : 0 Rez а (а < 1), Imz = 0} перешел в отрезок действительной оси,
симметричный относительно начала координат. Найти длину преобразованного отрезка.
Упражнения для самостоятельной работы
147
25. Доказать, что при отображении круга на круг линейное преобразование однозначно опре-
деляется заданием образов одной внутренней и одной граничной точек.
26. Доказать, что если линейное преобразование имеет две неподвижные точки, то произве-
дение производных в этих точках равно единице.
27. 1) Выяснить, для каких значений т функция w — R(z + mz"), где n g N, осуществляет
конформное отображение круга К = {z £ С : |z| < 1} на некоторую область, и найти эту область.
2) Выяснить эти же вопросы для отображения внешности круга К при помощи функции
w = R (z + и внутренности того же круга при помощи функции w = R + mz").
28. Полуплоскость Р = {z е С : Im z > 0} с разрезом по дуге окружности 7 = {zgC:|z| = l}
от точки z = 1 до точки z = ега, где 0 < а < тг, отобразить на верхнюю полуплоскость.
29. Отобразить на верхнюю полуплоскость внутренность угла 0 < argz < тг/3, где 0 < р < 2,
с разрезом по дуге окружности 7 = {z € С : |z| = 1} от точки z = 1 до точки z = ега, где
0 < а < /3.
30. Отобразить на верхнюю полуплоскость внешность единичного верхнего полукруга с раз-
резом по отрезку [0, —г] (внешность лопатки).
31. Найти преобразование полярной сетки с помощью функций:
D w = l(z-|);
2) w = i (* + т) (а > 0);
3) w = | (z + у) > с = |c|e’7 (0 Sj 7 < тг).
32. Отобразить на верхнюю полуплоскость внешность единичного круга с разрезами по от-
резку [-а, -1] и лучу [1, +оо), где а > 1.
33. Круг К = {z g С : |z| < 1} с разрезом по отрезку [а, 1], 0 < а < 1, отобразить на
круг К' = {w € С : |w| < 1} так, чтобы w(0) = 0, w'(0) > 0. Найти w'(0) и длину дуги,
соответствующей разрезу. При каком значении а разрез перейдет в полуокружность?
34. Круг К = {г £ С : |z| < 1} с разрезами по отрезкам [а, 1], [-1, —6] (0 < а < 1, 0 < b < 1)
отобразить на круг К' = {ш € С : |w| < 1} так, чтобы w(0) = 0, w'(0) > 0. Определить w'(0) и
длины дуг, соответствующих разрезам.
35. Отобразить внешность единичного круга G = {z С С : |z| > 1} на w-плоскость с разрезом
по дуге arg = /3 (0 < |/3| < тг) так, чтобы w(oo) = 00, argw'(oo) = а.
36. Выяснить, во что преобразуются при отображении w = ег :
1) прямоугольная сетка х = С, у = С ;
2) прямые у = kx 4- Ъ ;
3) полоса а<у<р(0^.а<р^. 2тг) ;
4) полоса между прямыми у = х, у = х + 2тг ;
5) полуполоса х < 0, 0 < у < а 2тг ;
6) полуполоса х > 0, 0 < у .< а 2тг ;
7) прямоугольник (а, р) х (7, <5) (б - 7 2тг).
37. Выяснить, во что преобразуются при отображении w — In z :
1) полярная сетка |z| = Я, argz = в ;
2) логарифмические спирали г = Aek,f (Л > 0) ;
3) угол 0 < arg z < а 2тг ;
4) сектор S = {z € С : |z| < 1, 0 < argz < а 2тг} ;
5) кольцо К = {z 6 С : г, < |z| < г2} с разрезом по отрезку [гн г2].
38. Выяснить, во что преобразуются при отображении w = arcsin z :
1) верхняя полуплоскость;
2) плоскость с разрезом по действительной оси вдоль лучей (—оо, —1], [1, +оо) ;
3) первый квадрант; .
4) полуплоскость Р = {z 6 С : Rez < 0} с разрезом по действительной оси вдоль луча
(-оо, -1].
39. Выяснить, во что преобразуются при отображении w = tg z :
1) прямоугольная сетка х = С, у = С ;
2) полуполоса Р = {z е С.: О < Rez < тг, Imz > 0} ;
3) полоса G = {z е С : 0 < Re z < тг} ;
148
Гл. 3. Элементарные функции в комплексной плоскости
4) полоса D = [z Е C:0<Rez<^} ;
5) полоса £>' = {гбС:-^<Кег<^} ;
40. Выяснить, во что преобразуются при отображении w = cth z :
1) полоса Р = {z € С : 0 < Im z < тг} ;
2) полуполоса Р' = {z € С : Rez > 0, 0 < Imz < %}.
41. Отобразить на верхнюю полуплоскость область, заключенную между софокусными пара-
болами у2 = 4(х + 1), у2 = 8(г + 2).
42. Найти функцию w — w(z), отображающую область, ограниченную окружностью 7 =
{z£C:|z| = 1}h прямой, уравнение которой Imz — 1 (полуплоскость Р = {z 6 С :1m z < 1} с
выкинутым кругом):
1) на круг К = {и £ С : |w| < 1} с нормировкой w(-3I) = -у2-, argw'(-3i) = 7.
2) на верхнюю полуплоскость с нормировкой w(-3«) = 1 + г, argш'(-Зг) = тг.
43. Отобразить на верхнюю полуплоскость полосу G = {z £ С : 0 < Re z < 1}с разрезами
вдоль отрезков {0 х /г,, у = 0} и {1 - /г2 < х 1, у = 0} (ht + < 1).
44. Отобразить на верхнюю полуплоскость полуполосу D — {z € С : 0 < Rez < тг, Imz > 0}
с разрезами вдоль отрезка
7t = {z £ С : Rez = 7,0 Imz /11}
и вдоль луча
72 = {z £ С : Rez = 7, Л.2 Imz < +00} (h2 > h,).
45. Отобразить на верхнюю полуплоскость область, ограниченную окружностями
7i = {z € С : |z - 1| = 1}, 72 = {z £ С : |z + 1| = 1}
с разрезом по лучу
7з = {z £ С : 2 Rez < +00, Imz = 0}.
46. Отобразить на верхнюю полуплоскость область, ограниченную окружностями
71 = {z € С : |z - 1| = 1), 72 = {z £ С : |z - 2| = 2}
с разрезом вдоль отрезка
73 = {z £ С : 2 Re z a, Im z = 0} (а < 4).
47. Отобразить на верхнюю полуплоскость область, ограниченную окружностями
7t = {z £ С : |z - 1| = 1}, 72 = {z £ С : |z - 2| = 2}
с разрезами вдоль отрезков
7з = {z £ С : 2 Re z a, Im z = 0} и 74 = {z £ С : b Re z 4, Im z = 0} (а < b).
48. Отобразить на верхнюю полуплоскость область, ограниченную окружностями
7! = {z £ С : |z - 1| = 1}, 72 = {z £ С : |z + 1| = 1}
с разрезом по отрезку
7з = {z £ С : Re z = 0, -а Im z /3} (а 0, /3^0).
Глава 4
Интегрирование
в комплексной плоскости.
Интегралы
Ньютона—Лейбница и Коши
Главное внимание в этой главе уделяется интегральной теореме Коши, одной из основных тео-
рем всей теории аналитических функций. С ее помощью устанавливаются глобальные свойства
аналитических функций.
Вместо неопределенного интеграла рассматривается интеграл Ньютона—Лейбница, обладаю-
щий многими достоинствами. Операция интегрирования в смысле Ньютона—Лейбница является
обратной по отношению к операции дифференцирования.
§ 1. Интеграл Ньютона—Лейбница
1Л. Первообразная.
Определение 1. Пусть f : С —> С и множество Dr не имеет изолированных точек. Функция
F : С —> С называется первообразной функции f, если DP = Df nVz € Df F'(z) = f(z).
Пусть F — первообразная функции f. Так как V(z С Df, С С С) (T’-I-C)'(z) = F'(z), то F+C
также является первообразной функции /. Поэтому первообразная определена неоднозначно и
специального обозначения не имеет.
Исследуем характер неоднозначности первообразной. Нам понадобятся понятие кусочно-
гладкого пути (см. определение 6, п. 2.9, гл. 2) и неравенство Лагранжа (см. п. 4.7, гл. 2).
Определение 2. Множество Z С С называется линейно-связным, если для любых то-
чек zt б Z, z2 € Z существует кусочно-гладкий путь, соединяющий их и лежащий в множестве Z.
Теорема 1. Пусть / : С -+ С и Df — линейно-связное множество, содержащее более чем одну
точку. Если 4z £ Df f'(z) = 0, то функция f постоянная.
◄ Пусть z( g Df, z2 6 Df. По определению линейно-связного множества существует
кусочно-гладкий путь, соединяющий точки zb z2 и лежащий в множестве Df. Следовательно,
найдется такая непрерывная функция [a, b] Df, что <^(а) = Z|, ^(Ь) = z2 и <р'(Г) существует
всюду, кроме конечного множества точек. Занумеруем их в порядке возрастания
£о — о < < • • • < — Ь-
Согласно неравенству Лагранжа, имеем
К/ ° V>)(M ~(f ° ?)(«fc-i)l С IIУ' • v'lKtfc - tfc-i) = 0 (fc = Т^)
Таким образом,
(J ° <?)(М = /Си) = (/ ° ~ f(z2). ►
Теорема 2. Пусть Ft и F2— первообразные функции / : С —> С, определенной на линейно-
связном множестве, содержащем более одной точки. Тогда существует такая постоянная С 6 С,
что Vz £ Df F2(z) = Ft(z} +'C. ►
150 Гл. 4. Интегрирование в комплексной плоскости.
◄ Рассмотрим функцию F = F2- Ft. Так как Vz € Df F'(z) — F2(z)~F[(z) = 0, то, согласно
теореме 1, функция F постоянная. ►
Предлагаем читателю составить таблицу первообразных основных элементарных функций.
1.2. Интеграл Ньютона—Лейбница.
Определение. Пусть f : С —+ С и Df — линейно-связное множество, содержащее более одной
точки. Функция f называется интегрируемой в смысле Ньютона — Лейбница, если она
имеет первообразную. При этом Va Е Df
(z \
F(z) = у /(Od< j (F(a) = 0 A Vz e DfF'(z) = /(z)) . (1)
a
Функция F в (1) называется интегралом Ньютона—Лейбница с фиксированным нижним преде-
лом интегрирования а и переменным верхним пределом. Ее значение F(b) называется определенным
ь
интегралом Ньютона—Лейбница и обозначается J /(()d0 где ( — переменная интегрирования,
от выбора которой величина интеграла не зависит, т. е.
ь ь ь
У /(О dC = У /(«) du = У f(w) dw = ....
а а а
z
Запись J /(z) dz не имеет смысла, поскольку буква z используется для обозначения верхнего
a
предела интегрирования.
Теорема 1 (формула Ньютона — Лейбница). Пусть / : С —> С, Df — линейно-связное
множество, содержащее более одной точки. Если функция f интегрируема в смысле Ньютона—
ь
Лейбница и Ф — ее первообразная, то V(a 6 Df, b € Df) интеграл J f(C)d( существует, определен
a
однозначно и справедлива формула Ньютона—Лейбница
ь
У Д0^ = Ф(д)-Ф(а) = Ф(0|^. (2)
a
◄ Полагаем Vz £ Df F(z) = Ф(г) - Ф(а). Тогда
F(a) = 0 A Vz € Df F\z) = Ф'(г) = f(z).
Согласно определению, имеем
ъ
У /(()</( = Г(Ь) = Ф(Ь)-Ф(а).
a
Убедимся в том, что интеграл определен однозначно. Пусть
&
У /<№ = ф(Ъ), Wa) = 0bVzeDf i/>'(z) = f(z).
а
По теореме 2, п. 1.1, существует постоянная С : Vz € Df ф(г) = F(z) + С. Полагая z — а,
получим, что С = 0. Следовательно, ф(Ъ) = F(b), т. е. интеграл определен однозначно. ►
§ 1. Интеграл Ньютона—Лейбница
151
Теорема 2. Пусть f : С —»СиР/ — линейно-связное множество, состоящее более чем из одной
точки. Если функция f интегрируема в смысле Ньютона—Лейбница, то справедливы равенства:
b а
( f(z)dz = ~ J f(z)dz V(a € Df, b е Df),
ь
b
J f(z)dz =
c b
У f(z)dz + / f(z)dz
V(a € Df, b € Df, c € Df),
V(z € Df,b g Df).
(3)
(4)
(5)
(6)
Пусть Ф — первообразная функции f. Согласно формуле Ньютона—Лейбница (2), имеем
f(z)dz = Ф(Ь) - Ф(а) = —(Ф(а) - Ф(Ь)) = - / f(z)dz,
ь
У f(z)dz = Ф(Ь) - Ф(а) = Ф(Ь) - Ф(с) + Ф(с) - Ф(а) =
= (Ф(2) - Ф(О))' = Ф'(2) = /(Z),
= (Ф(Ь) - Ф(2))' = -Ф'(2) = -/(2).
Равенство (3) называется правилом перестановки пределов интегрирования, равенство (4) —
аддитивностью интеграла относительно пределов интегрирования, формулы (5) и (6) — правилами
дифференцирования интеграла по верхнему и нижнему переменным пределам интегрирования.
1.3. Линейность интеграла.
Замена переменных и формула интегрирования по частям.
Теорема 1 (о линейности интеграла). Пусть Z —линейно-связное множество, содержа-
щее более одной точки. Если функции f : С —* С, g : С —> С, Df = Dg — Z, интегрируемы в смысле
Ньютона—Лейбница и А Е С, р € С, то функция Xf + pg также интегрируема и справедливо
равенство
ь ь ь
J(Xf + pg)(z) dz = А У f(z)dz + p J g(z)dz V(aEZ,b€Z). (1)
a a a
◄ Пусть F, G — первообразные функций f и g. Тогда V2 6 Z
(XF + /iG)'(z) = XF' (z) + pG’(z) = Xf(z) + pg(z).
152
Гл. 4. Интегрирование в комплексной плоскости.
Следовательно, функция А/ + рд имеет первообразную и по определению интегрируема в смысле
Ньютона—Лейбница. Пусть
Z Z
F(z) = У /(QdC, G(z) = У д(О
а а
Тогда (ЛК -Ь рб) (а) = 0, и по определению интеграла получим
ь ь ь
У\\f + Hg)(z)dz = (AF + рв) (6) = XF(b) + pG(b) = А У f(z)dz+p j g(z)dz. ►
a a a
Теорема 2 (о замене переменной). Пусть /:С—»С, <р:С—>С, Z = DfQI(, — линейно-
связное множество, содержащее более одной точки. Если функция р дифференцируема в каждой
точке z Е Z, а функция интегрируема в смысле Ньютона—Лейбница, то функция (f ° р)р'
также интегрируема и справедливо равенство
ь ^(Ь)
У f (p(z))v'(z)dz = у /(0 d( V(a&Z,beZ). (2)
а <^(а)
◄ Пусть F — первообразная функции f !<?(£), а € Z, Ъ £ Z н F(<p(a)) = 0. Так как Vz 6 Z
имеем
(F О sp)' (2) = F'(<p(z))<p'(z) = /(<p(z))<p'(z) = ((/ о р)р} (z),
то функция (/ о <^)у/ интегрируема в смысле Ньютона—Лейбница, и по определению интеграла
справедливо равенство
6 95(b)
У/(?(*)) /(z)dz = F(p(6)) = У /«)</<•►
a ^(а)
Теорема 3 (об интегрировании по частям). Пусть f : С —» С, g : С —+ С, Df ~
Dg = Z, — линейно-связное множество, состоящее более чем из одной точки. Если функции fug
дифференцируемы в каждой точке множества Z и функция f'g интегрируема в смысле Ньютона—
Лейбница, то функция fg' также интегрируема и справедлива формула интегрирования по частям
ь ь
У f(z)g’(z)dz = f(z)g(z)\Zz=ba- J f'(z)g(z)dz V(aEZ,b€Z). (3)
◄ Поскольку (/g)'(z) = /'(z)g(z) + /(z)g'(z) Vz € Z, to = (fg)' - f'g. По определе-
нию функция (fg)' интегрируема в смысле Ньютона—Лейбница. Согласно свойству линейности
интеграла, функция fg' также интегрируема по Ньютону—Лейбницу и
6 ь
У f(z)g'(z)dz = J(fg)'(z)dz
а а
Ь Ь
У f'(z)g(z)dz = f(b)g(b) - f(a)g(a) - J f'(z)g(z)dz. ►
a a
Из определения первообразной следует, что она принадлежит классу аналитических функ-
ций. Напомним читателю, что символом A(G) обозначается класс функций, аналитических в
области G.
Если функция f определена на линейно-связном множестве Z, то определение 1, п. 1.1, мож-
но сформулировать следующим образом: функция F С A(Z) называется первообразной функ-
ции f на множестве Z, если Vz 6 Z F'(z) = f(z).
§ 2. Производные и интегралы Ньютона—Лейбница любых порядков
153
Вычислим в качестве примера интегралы
z i
/1(2) = J С(1 - I2 = J(г - i)e-z dz.
i о
Полагая в I\ 1 — ( = w, получим: d( = — dw,
= 1 (1 - z)98 - 1 (1 - - 1 (1 - if + 1(1- i)99 =
98 99 98 99
o8 / 1 1 \ 1 , ^,98 1 / ^\99 _;»z.
= (1 - z)--------(1-2)------(V7) e ‘ 4 + — (V2) e 4 =
\98 99 ) 98 v ' 99 y J
q8 / 1 1 \ 248 49 ( 1 + i \
=(i-U-(1 _z))+2 Ы)-
Для вычисления интеграла 1г применим формулу интегрирования по частям:
г
Т2 = (z — i)e~z j + У e~z dz = —i + e~z | = — i + 1 — e * =
о
= — i + 1 — (cos 1 — i sin 1) = I — cos 1 + (sin 1 — l)i.
§ 2. Производные и интегралы
Ньютона—Лейбница любых порядков
2.1. Определение n-производной и п-интеграла.
Пусть область определения функции / : С -* С не имеет изолированных точек. Назовем ее
\-дифференцируемой, если Vz € Df она имеет производную Функция z >-+ f'(z) называ-
ется 1-производной функции f и обозначается через /(1). По индукции определим производную
функции f любого порядка.
Определение 1. Пусть п € N. Если функция fln! дифференцируема, то ее производная (f'nl)
называется п+ 1-й производной функции f и обозначается через При этом функция f
называется (п + \)-дифференцируемой.
Для упрощения записи считаем /(0) = /. Приведем примеры.
Пример 1. Пусть /(z) = е* Vz € С. Тогда
/'(z) = ez, /2)(z) = e% ... ,/(n)(z) = ez V(z € C, n € N).
Пример 2. Пусть /(z) = sinz Vz g С. Тогда
f'(z) = cosz = sin(z + —), fm(z) = - sin z = sin (z + 2—) , ... , /(n)(z) = sin (z + n—)
V(z € C, n € N).
Пусть область определения функции f есть линейно-связное множество, содержащее более
одной точки и пусть а € Df. Назовем функцию f интегрируемой, если Vz € Df существу-
Z 2
ет J f(t)dt. Отображение z f f(t)dt, z € Df, называется 1-интегралом функции f с нижним
а а
пределом интегрирования a g Df . По индукции определим интеграл произвольного порядка
функции f с нижним пределом интегрирования а 6 Df.
154
Гл. 4. Интегрирование в комплексной плоскости.
Определение 2. Если функция f интегрируема, п 2, то полагаем
Рассмотрим примеры.
/(")
dt У (а € С, z € С).
Последовательно интегрируя, получим
г (4)
Пример 5. Вычислить—/ sintdt, z g С.
о
Последовательно интегрируя четыре раза, получим
2.2. Формула Ньютона—Лейбница. Производные по пределам интегрирования.
Теорема 1 (формула Ньютона—Лейбница для n-интеграла). Пусть / : С —» С,
Df — линейно-связное множество, содержащее более одной точки, и п g N. Если существует
F :\/z g Df Fin\z) = f(z), a g Df mo'iz g Df существует
/ f(t)dt = F(z) - 22 Fw(a)
J L-П
(1)
§ 2. Производные и интегралы Ньютона—Лейбница любых порядков
155
◄ Применим метод математической индукции. Для п = 1 утверждение доказано в п. 1.2.
Предположим, что формула (1) справедлива после замены в ней п на п — 1. Так как (F')<n-1) =
_р(п) = у jTO по предположению
Согласно определению 2
dt =
Mfc) (z~a>)k
/ f(t)dt = F'(z)-22(F') W
J k=o
a
из n. 2.1, имеем
’.т j dt = f (F\t) - ^2 fc;a) j dt =
/ ^ \ k=0 /
a
n-2 n—1 /
= F(z) - F(a) - ^(fc+,>(a) = F(z) - E
k=0 k=Q
т. e. справедлива формула (1). ►
Теорема 2. (о производной n-интеграла по пределам интегрирования). Пусть
f : С —* С, Df — линейно-связное множество, содержащее более одной точки. Если функция f
интегрируема, то справедливы равенства
Va 6 Df
(2)
(3)
◄ Равенство (2) очевидно. Докажем справедливость формулы (3). Пусть F : С —♦ С и
Vz € Df Fin\z) = f(z). Тогда, согласно формуле (1), получим
х I ь
П~1 /к ,\к \ ,\п-1 /-(п-1)
F(b) - F(fc)(z) I = -F(n)(z) = -/(z) / dt
t—t kl I (п - 1)! J
к=й /
(см. пример 3 из п. 2.1).>-
Теорема 3 (Дирихле). Пусть f : С —► С, Df — линейно-связное множество, содержащее
более одной точки, и a g Df,b g Df. Если функция f интегрируема, то
ь
/»(п)
(Ь - 0(п~
(п - 1)!
dt.
(4)
◄ Согласно формуле (1) и теореме 2, имеем
//«)
а
(Ь - 0п~‘
(п - 1)!
dt =
156
Гл. 4. Интегрирование в комплексной плоскости.
2.3. Формула Тейлора.
Пусть выполнены все условия теоремы 1, п. 2.2. Тогда из формулы (1) того же пункта следует
равенство
"-1 , v
^) = EF<fc)(a)^4r
k=0
dt
V(a e Df, z e Df),
(1)
которое называется формулой Тейлора для функции F с остаточным членом, записанным посред-
ством п-интеграла. Функция
^\а)
к=0
(z - а)к
к'.
z
называется многочленом Тейлора.
Частные случаи формулы (1) встречаются в элементарной физике.
Пусть материальная точка движется прямолинейно по оси Оу с постоянной скоростью
v = F'(a). Если известно ее начальное положение F(a), то положение F(x) в момент време-
ни х можно найти по формуле
, (х — а)
F(x) = F(a) + v(x — а) = F(a) + F (а) ,
являющейся частным случаем равенства (1) при п = 2, а также при п = 1. Пусть снова матери-
альная точка движется прямолинейно по оси Оу с изменяющейся скоростью, но с постоянным
ускорением F"(a), т.е. равноускоренно или равнозамедленно. Если известны ее начальное по-
ложение F(a) и начальная скорость v0 = F!(a), то положение точки F(x) в момент времени х
можно определить по формуле
,, (х - а)2 , (х - а) ,, (х — а)2
Fix) = F(a) + v0(x — а) + F"(a) 2 = F(a) + F'(a) + F"(a) ,
являющейся частным случаем равенства (1) при п = 3, а также при п = 2. Таким образом,
равенство (1) является дальнейшим обобщением этих важных формул элементарной физики.
Из формулы (1) следует, что функция F является многочленом тогда и только тогда, когда
ее п-производная всюду равна нулю при некотором значении п Е N. Формула бинома Ньютона
является частным случаем формулы Тейлора.
Применив к n-интегралу формулу Дирихле (см. п. 2.2), получим формулу Тейлора с остаточ-
ным членом в интегральной форме'.
F(z.) = Ef<fc)(a)(2
К'.
k=0
lz~t)n-' м
----------at.
(п - 1)!
(2)
§ 3. Производная Ферма—Лагранжа.
Формула Тейлора—Пеано
3.1. Производная Ферма—Лагранжа.
Производная, определенная в п. 4.1, гл. 2, допускает следующее обобщение по индукции.
Определение. Пусть / : С —> С, z0 € Df, п € N. Функция f называется п-диффе-
ренцируемой в смысле Ферма—Лагранжа в точке z0, если существует такая (п — 1)-
дифференцируемая в смысле Ферма—Лагранжа в точке z0 функция <р, что Tz € Df
f(z) - f(z0) = (z- za)y>(z).
Если дополнительно za является предельной точкой множества Df,mo число n^(n-1)(z0) называется
п-производной Ферма — Лагранжа функции f в точке z0 и обозначается f^lzo)
как и прежде, считаем функцию f 0-дифференцируемой в смысле Ферма—Лагранжа в точ-
ке z0, если она непрерывна в этой точке. При этом f(S)(zQ) = f(z0).
§3. Производная Ферма—Лагранжа. Формула Тейлора—Пеано 157
Пример 1. Пусть п £ N и /„ : R-»R где
{z” sin—, если z£R\{0},
хт
О, если х = 0.
Доказать, что функция fn (п — 1)-дифференцируема в смысле Ферма—Лагранжа в точке х = 0
Vm е N.
Воспользуемся методом математической индукции. Если n = 1, то
1
lim /i(z) = lim a: sin — = 0 = /ДО),
х^О х^О хт
т. е. функция /1 О-дифференцируема в смысле Ферма—Лагранжа в точке х = 0 Vm £ N. До-
пустим, что функция /П(п - 1)-дифференцируема в смысле Ферма—Лагранжа в точке х = 0
Vm £ N. Согласно предположению, имеем
fn+i(x) - /п+|(0) = xfn(x) Vz € R.
По определению функция /п+1 п-дифференцируема в смысле Ферма—Лагранжа в точке х = 0
Vm g N.
Пример 2. Указать в примере 1 значение m t N, при котором функция /п не имеет 2-произ-
водной в точке х — 0 в классическом смысле.
Если х ф 0, то
/1 / \ n—1 • 1 п — m — 1 1
„(х) = пх sin------тх cos---------.
Полагая т = п - 1, получаем, что функция /,', разрывна в точке х = 0, вследствие чего /п не
п-дифференцируема в классическом смысле в этой точке при п 2.
Из примеров 1 и 2 видим, что Vn 2 существуют функции, п-дифференцируемые в смысле
Ферма—Лагранжа в фиксированной точке и не имеющие в ней второй классической производ-
ной.
3.2. Теорема Тейлора—Пеано и ее обращение.
Понятия п-дифференцируемости и п-производной Ферма—Лагранжа используются при изу-
чении локальных свойств функций. Очевидно, что если функция / п-дифференцируема в смысле
Ферма—Лагранжа в точке z0 £ Df, являющейся предельной для множества D f, то Vm = 0, п
существуют m-производные Ферма—Лагранжа /<m)(z0).
Теорема 1 (формула Тейлора—Пеано). Пусть / : С —► С, z0 — предельная точка
множества Df и z0 £ Df. Если функция f п -дифференцируема в смысле Ферма—Лагранжа в
точке z0, то справедлива формула Тейлора—Пеано
" (z - z )ь
f(z) = 12/<fe)(Z|1) fc! ~ + £"(г)(г ~го)" VzeDf’ (D
k=o
где еп — непрерывная в точке z0 функция и en(z0) = 0.
Ч Применим метод математической индукции. Если п = 0, то утверждение очевидно при
Eo(z) = /(z)—/(z0). Предположим, что утверждение теоремы справедливо после замены п на n— 1
и что функция / п-дифференцируема в смысле Ферма—Лагранжа в точке za. Согласно опреде-
лению, существует такая п — 1 -дифференцируемая в смысле Ферма—Лагранжа в точке z0 функ-
ция <р, что Vz € Df
f\z) - = (z- z0)<p(z). (2)
По предположению
n—I / \fe
¥>(2) = ^2¥><fc)(z0) —----н e„-i(z)(z - zo)—, (3)
k-Q
158
Гл. 4. Интегрирование в комплексной плоскости.
где en_i — непрерывная в точке zQ функция и e„_|(z0) = 0. Из равенств (2) и (3) получаем
(П—1 / xfc \
^2 V(k4za} +en_i(z)(z - zq)-1 j =
fc=0 ' /
^/(fc+1’(z0) (z — z0)‘
fc=0
------+en_i(z)(z-z0)n,
k\
что равносильно формуле (1) при en = е„_|. ►
Следующее утверждение является обращением теоремы 1 и объясняет важность понятия п-
производной Ферма—Лагранжа.
Теорема 2 (об обращении формулы Тейлора—Пеано). Пусть f : С -> С, z0 —
предельная точка множества Df и za Е Df. Если
(z — Z0)fc n
/(z) = >2 ----г----+ e(z)(z-z0) VzE-Dy, (4)
*—' fc!
k=0
где aj. 6 C \fk = 0, n, e(z0) = 0 и e — непрерывная в точке z0 функция, то функция f п-дифферен-
цируема в смысле Ферма—Лагранжа в точке z0 и ak = /(fe,(z0) Vfc = 0, п.
Ч Применим метод математической индукции. Если п = 0, то равенство (4) имеет вид
/(z) = a0 + e(z) Vz € Df и поэтому функция f непрерывна в точке z0 (т. е. О-дифференцируема
в смысле Ферма—Лагранжа в этой точке) и f<0)(z0) = /(z0) = а0. Пусть теорема справедлива при
замене п на п - 1 и выполняется равенство (4). Так как /(z0) = аа, то
/ n (z - z )fc-1 \
/(z) - /(z0) = (z - z0) I 52 ----+ £^z ~ zo)n-1 I
\k=l /
Полагаем
= E т (2(fc-°i)! + е(2)(г -
fc= I
В силу предположения, функция р (n — 1)-дифференцируема по Ферма—Лагранжу в точке z0 и
~ = p<fc-1)(zo) Vfc = 1, п. По определению функция / п-дифференцируема в смысле Ферма—
Лагранжа в точке z0 и /(fc)(z0) = kp>'k~x\zl)) = ак Vk = 1, п. ►
Доказанная теорема может применяться для вычисления производных Ферма—Лагранжа.
Приведем пример.
Пусть R R, где
{е~~Л если х € R \ {0},
0, если х = 0.
Вычислить /<п)(0) Vn £ N.
Найдем
е'Л tn
lim —-— = lim — = 0
х-,0 xin t—+oo e‘
(применяем n раз правило Лопиталя). Полагаем
En(®) = <
если х € R \ {0},
если х — 0.
Функция еп непрерывна в точке х = 0 Vn 6 N. Так как f(x) = х2пеп{х), то, согласно
теореме 2, /<fc>(0) = 0 Vfc = 1, 2п. В силу произвольности п /<|!)(0) = 0 Vfc 6 N.
§4. Криволинейные интегралы 159
§ 4. Криволинейные интегралы
4.1. Интегрирование функций по ориентированной гладкой кривой.
Непрерывная функция f : С —> С может не быть интегрируемой по Ньютону—Лейбницу
на линейно-связном открытом множестве. Поэтому возникает потребность в новом понятии —
криволинейном интеграле. В §3, гл. 2, определены понятия простой гладкой кривой или тра-
ектории и эквивалентных параметрических представлений кривой (см. определение 2), понятие
ориентации и ориентированной гладкой кривой Г = (7, 7ор) (см. определение 3), а также понятие
кусочно-гладкой кривой Г = (Г,, Г2, ..., Г„) (см. определение 6).
Определение 1. Пусть Г = (7, 7ор) — гладкая ориентированная кривая, <р € 7ор — параметри-
ческое представление кривой 7 и D^, = [а, t>]. Если f : С —> С и Df 2) 7, то криволинейным
интегралом функции f по Г называется число
ь
J f(z)dz = J f(<p(t»<p’(t)dt, (1)
Га
если оно существует.
Из правила замены переменной в интеграле следует независимость правой части формулы (1)
от выбора параметрического представления р 6 7ор.
Мы будем рассматривать криволинейные интегралы лишь по жордановым гладким и кусочно-
гладким кривым, не оговаривая этого в каждом случае.
Формулу (1) можно записать также в виде
ь ь
У f(z)dz = J Re(№(t))/(O)<tt + i J Im(/(y,(i))¥>'(t))d*. . (2)
Га а
Поскольку криволинейный интеграл (1) сводится к интегралу Римана, то он обладает свой-
ствами линейности и аддитивности:
1)
V(a € С, /3 € С) J (af + [3g')(z)dz = a J f(z)dz+f3 J g(z)dz, (3)
Г г г
2) если Г = (Гь Г2, ..., Гп) — кусочно-гладкая кривая, то
У f(z)dz = ^j f(z)dz. (4)
г k=l rfc
Если Г“ = (7, 7^) — противоположно ориентированная кривая по отношению к Г — (7, 7ор),
то выполняется равенство
У f(z)dz = - У f(z)dz, (5)
г- г
т. е. при изменении ориентации кривой на противоположную интеграл изменяет знак.
Интеграл в определении 1 называют криволинейным интегралом второго рода, отличая его от
следующего криволинейного интеграла первого рода.
Определение 2. Пусть 7 — простая гладкая кривая, функция [а, 6] -^*7 — ее параметрическое
представление. Если / :С-> С «7 С Df, то криволинейным интегралом первого рода
от функции f по кривой у называется число
ъ
У f(z)\dz\ = У /(^(t))l¥>'(t)|dt, (6)
если оно существует.
160
Гл. 4. Интегрирование в комплексной плоскости.
Из теоремы о замене переменной в определенном интеграле следует, что правая часть фор-
мулы (6) не зависит от параметрического представления кривой 7. Если Г = (7, 7ор) — ориенти-
рованная гладкая кривая, то по определению полагаем
У/(.г) |d.z| = J f(z)\dz\. (7)
г 1
Из оценки модуля определенного интеграла следует важное для дальнейшего изложения не-
равенство
У f(z)dz I |/(z)| |dz|, (8)
г г
справедливое для любой непрерывной функции f.
Рассмотрим несколько примеров на вычисление криволинейных интегралов.
Пример 1. Пусть f = 1. Тогда, согласно формуле (1), имеем
ь
J f(z)dz = j <p'(t)dt = ip(b) — >р(а).
Г а
Пример 2. Пусть /(z) = z. Применив формулу (1), получим
ь ь
J f(z)dz = J zdz = У V(t)v'(t)dt=i- У d(^2(/)) = .
Г Г а а
Примеры 1 и 2 показывают, что оба интеграла не зависят от выбора гладкой ориентированной
кривой Г, а зависят лишь от ее концов у>(а) и f(b).
Если Г — замкнутая ориентированная кривая, то будем называть ее контуром или петлей,
а для обозначения криволинейного интеграла по контуру Г от функции f будем пользоваться
записью
У /(z)dz.
г
В силу замечания о зависимости интеграла лишь от концов кривой, получим:
У dz = У z dz = 0. (9)
г г
Легко также убедиться в справедливости равенства
У г” dz = -i-j- (y>n+1(b) - ^n+‘(a)) .
г
Пример 3. Доказать, что
Г dz Г dz
/ — = in, I — = -itt,
П r2
где Г । и Г2 — соответственно верхняя и нижняя полуокружности радиуса 1 с центром в начале
координат. Начальная точка кривых z = 1.
Выбор начальной точки кривой определяет ее ориентацию. Параметрические представле-
ния ориентированных кривых имеют соответственно вид <p(t) ~ еа, 0 t тг и ip(t) = еа,
—тг t 0, yj(O) = ^>(0) — 1. Согласно определению, имеем
Г dz f ie'1 f dz f ielt
I — — I —— dt = iir, I — = / dt = —ITT.
J z J e'* J z J e'*
Г[ о гг 0
§4. Криволинейные интегралы
161
Пример 4. Вычислить f z dz, где Г — произвольная замкнутая положительно ориентирован-
г
ная жорданова кривая.
Поскольку z = х - iy, dz = dx + i dy, z dz = x dx + у dy + i(—y dx + x dy), to
xdx + ydy + i
—ydx + x
dxdy = i 2|D|
(в силу формулы Грина), где |О| — площадь фигуры, ограниченной кривой Г.
Пример 5. Вычислить интеграл J 4=, Г = (7, 7ор), где 7 = {z G С : |z| = 1, Imz 0}, когда
г
а)УТ=1;б)\/1 = ги начальная точка кривой Г z = 1.
а) Параметрическое представление кривой 7 — функция <p(t) = elt, 0 t тг. Согласно
формуле (1) получим:
f 4
= i I e * dt = -
J 3
0
б) Функция tp(t) = e,(t+2’r,1 0 t
Поэтому
dz _ Г iei{t+2n} dt
J e*<M>
г 0
тг, является параметрическим представлением кривой 7.
Из свойства аддитивности криволинейного интеграла следует, что интеграл по контуру
(j) f(z) dz
г
не зависит от выбора начальной точки интегрирования.
4. 2. Гомотопия двух кривых (путей).
Пусть [а, Ь] 70, [а, Ь] — параметрические представления простых непрерывных
на на
кривых 7о и 7Н GCC — открытое множество, G D 70, G □ 7Ь
Определение 1. Гомотопией (или деформацией) кривой 70 в кривую 71 называется не-
прерывное отображение [а, х [а, fi] С, где [а, /3] С R — такой отрезок, что Vt 6 [а, Ь]
<p(t, а) = <p0(t) и <p(t, fi) = <pi(t).
Из определения следует, что V£ £ [а, /3] отображение t <p(t, £) есть параметрическое пред-
ставление непрерывной кривой в G.
Обычно в определении гомотопии вместо прямоугольника [а, Ь| х [а, fi] рассматривают ква-
драт К = [0, 1] х [0, 1]. Этого всегда можно добиться с помощью замены переменных. В даль-
нейшем считаем, что Dvo = DVi = [0, 1], [a, fi] = [0, 1] и рассматриваем гомотопию К —> С,
причем Vt € [0, 1].
<p(t, 0) = <p0(t), <p(t, 1) = p^t). (1)
Пусть кривые 70 и 7t имеют одно и то же начало ^о(О) = pi (0) и один и тот же конец
¥>о(1) = Pi (1 )• В этом случае отображение р называется гомотопией с фиксированными началом и
концом, если выполнены соотношения (1) и если V£ € [0, 1]
¥>(0, О = ¥>о(0), ¥>(1, О = pod). (2)
Иначе говоря, мы требуем, чтобы V£ G [0, 1] кривая 7^ имела то же начало, что и 70 с 7Ь и
тот же конец, что и 70 с 71.
Если 7о и 7! — замкнутые кривые, то говорят о гомотопии замкнутой кривой у0 в замкнутую
кривую 71.
Мы будем, как правило, рассматривать гладкие или кусочно-гладкие пути и их гладкие или
кусочно-гладкие гомотопии.
162
Гл. 4. Интегрирование в комплексной плоскости.
Определение 2. Область DCC называется односвязной, если любая замкнутая кривая в ней
гомотопна точке, т. е. постоянному пути.
Следовательно, в односвязной области любую замкнутую кривую можно стянуть в точку.
§ 5. Теорема и интеграл Коши
5.1. Существование локальной первообразной аналитической функции.
Пусть функция f : С —> С определена в области G. Согласно определению 1, п. 1.1, функ-
ция F Е A(G) называется первообразной функции / в области G, если Vz € G F'(z') = f(z).
С понятием первообразной связано определение интеграла Ньютона—Лейбница.
Выясним, при каких условиях функция f, определенная в области G С С, имеет первообраз-
ную. При рассмотрении замкнутых областей их границам приписывают определенную ориента-
цию. Будем говорить, что граница 9G области G обходится в положительном направлении, если
при ее обходе внутренние точки z g G остаются _слева. Противоположное направление обхо-
да называется отрицательным. Пусть, например, G — замкнутый треугольник с вершинами в
точках a, z, z + Дг на плоскости С, tp\ — параметрическое представление отрезка [a, z], <р2 —
параметрическое представление отрезка [z + Дг, z], <р3 — параметрическое представление от-
резка [а, г + Дг] с соответствующими областями определения. Обозначим через Г1; Г2, Г3 их
положительные ориентации, соответствующие возрастанию параметра (рис. 69, а)). Положитель-
но ориентированной границей треугольника G назовем упорядоченный набор
дв= (rbr2-,r3-)
(рис. 69, б)).
Теорема 1 (достаточные условия существования первообразной в круге).
Пусть функция f непрерывна в круге К = {г £ С : |z — а| < г} и интеграл от нее по ориенти-
рованной границе любого треугольника G <ё К равен нулю, т. е.
f(z)dz = 0. (1)
0G
Тогда функция
F(z)= j f(QdC, (2)
(а, г]
где интегрирование проводится no прямолинейному отрезку [a, z] С К, является первообразной функ-
ции f в круге К, т.е. F — аналитическая функция в К и F'(z) — f(z) ^z € К.
◄ Пусть G — треугольник с вершинами в точках a, z, z + Дг, где г € К — любая точка
и (г + Дг) 6 К. Тогда G ® К (рис. 69, а)). Ориентируем границу треугольника в положительном
§ 5. Теорема и интеграл Коши
163
направлении (рис. 69, б)), соответствующем направлению движения против хода часовой стрелки.
Согласно условию теоремы и свойству аддитивности интеграла, имеем
У /«)<*£ = У /(С) + У /(0<*С + У /(0йС = К(г)-Г(г + Дг) + j
Г2*
= О,
8G
Г|
откуда
Г2
Рассмотрим выражение
F(z + Дг) - Г(г)
Дг
(/(O-/(z))dC
Поскольку функция f непрерывная, то Vs > 0 36 > 0 : |/(0 - /(г)| < г, если |Дг| < 6 и
£ € [г, г + Дг]. Принимая во внимание неравенство (6), п.4.1, получаем оценку
F(z + Дг) - Г(г)
-/(г) <щг£|Дг|=£’
Дг
откуда следует, что F'(z) = f(z). ►
Теорема 2. Если f € A(D), то интеграл от f по ориентированной границе 9G любого тре-
угольника GeD равен нулю.
◄ Применим метод доказательства от противного. Допустим, что теорема неверна. Тогда
существует такой треугольник G <s D, что
dz
= М,
(3)
30*
Разобьем треугольник G средними линиями на четыре тре-
угольника и ориентируем границу 9G* и границы составных тре-
угольников так, чтобы их обход совершался в положительном напра-
влении (см. рис. 70). Пусть 9Gj (j = 1, 2, 3, 4) — положительно
ориентированные границы составных треугольников. Тогда, очевид-
но, выполняется равенство
4 . „
f(z)dz,
Рис. 70
3~'dGj 0G*
так как интегралы вдоль средних линий берутся дважды в противоположных направлениях и при
сложении взаимно уничтожаются. _
В силу неравенства (3) среди составных треугольников Gj существует по меньшей мере один
(обозначим его G,) такой, что
М
~4
aGl
Треугольник G* опять разобьем средними линиями на четыре треугольника. Тогда, в силу при-
веденных выше рассуждений, среди них найдется по меньшей мере один такой треугольник Gi,
что
М
OG-
164
Гл. 4. Интегрирование в комплексной плоскости.
Продолжая этот процесс разбиения на составные треугольники, получим последовательность
вложенных друг в друга треугольников (Gn), для которых выполняются неравенства
М
dz
(4)
9G'
Согласно теореме Кантора (см. §4, гл. 1) существует точка z0, принадлежащая всем треуголь-
никам. Поскольку z0 £ G , то z0 С D. Так как функция f аналитическая, то Vz € D выполняется
равенство
(5)
/(•z) = /(Zo) + /'(z0)(z - z0) + a(z)(z - z0),
где a0 при z —► z0, t. e. Ve > 0 3<5(г) > 0 : |z - z0| < 6 => |a(z)| <
Пусть Ks = {z € C : |z - z0| < <5}. При достаточно больших nt К Gn <s Kg. Принимая во
внимание примеры 1 и 2 из п. 4.1, получим:
/'(z0)(z - za)dz +
dz =
as*
не-
откуда следует оценка
dz <e\9G*n\2,
где |<Э(7* | — периметр треугольника G*, т.к. \z - z0| < |3G* |. Согласно построению имеем
следовательно, выполняется оценка
dz
|c>G*|2
(6)
HG-
Сопоставляя неравенства (4) и (6), получаем оценку
М |<9G*|2
— < е--------,
Дп Дп. '
откуда следует неравенство М < е|5(7*|2. В силу произвольного выбора € > 0 М = 0. Получили
противоречие, источник которого в предположении, что
эа
Из теорем 1 и 2 получаем следствие, которое сформулируем как теорему.
Теорема 3. Если f € A(D), то в любом круге КТ = {z 6 С : |z — z0| < г} С D она имеет
первообразную
1*0, *1
где интеграл берется по прямолинейному отрезку [z0, z] С Кг.
Теперь покажем, как из локальных первообразных аналитической функции можно склеить
первообразную, действующую вдоль заданной кривой (пути).
§ 5. Теорема и интеграл Коши
165
5.2. Первообразная вдоль кривой (вдоль пути).
Пусть функция f определена в области D С С, 7 С D — простая непрерывная кривая,
tp — ее параметрическое представление, Dv = [а, 6] = I. Тогда f определена в каждой точке
z = <p(t) 67, t 6 I.
ф
Определение. Функция I —> С называется первообразной функции f вдоль кривой
(пути) у, если выполняются следующие условия'.
1) Ф непрерывная на сегменте I;
2) для каждой точки tQ g I существует окрестность OZIS точки z0 = p(t0), в которой функция f
имеет первообразную F, причем F(p(t)~) = Ф(<) Vt g О,,. С I, где OtlI — некоторая окрестность
точки to в топологии I.
Примечание 1. Если f имеет первообразную F во всей области D. то функция t F(tp(t)) будет,
очевидно, первообразной функции / вдоль кривой 7. Вообще говоря, в определении первообразной
вдоль кривой не требуется существование первообразной во всей области D, а лишь в окрестности каждой
точки z0 = p(to) € 7.
Примечание 2. Если p(t|) = ip(ti), ti / ti, то первообразные функции /, одна из которых соответствует
окрестности Ot , другая — окрестности Ot2, могут не совпадать. Две первообразные одной и той же
функции f в окрестности одной и той же точки p(t|) = ^>(t2) могут отличаться лишь на постоянное сла-
гаемое. Это является свидетельством того, что первообразная вдоль пути, являясь функцией параметра t,
может не быть функцией точки z.
Теорема 1. Для любой функции f g A(D) и любой непрерывной кривой ~ CD первообразная
функции f существует и определена с точностью до постоянного слагаемого.
Ч Пусть <р — параметрическое представление кривой 7, D,f = [а, 6] = I. Разобьем отре-
зок I на п отрезков Д = [Д, t'fc] так, чтобы два соседних отрезка пересекались: Д < Д+1 < t'k.
ti = a, t'n = b. По теореме Кантора функция <р равномерно непрерывна на сегменте I. Поэтому
сегменты Д можно выбрать настолько малыми, чтобы VA: = 1, п образ 9?(Д) содержался в кру-
ге Kk С D, в котором функция f имеет первообразную. Существование первообразной следует
из аналитичности функции f (теорема 3, п. 5.1).
Семейство первообразных, определенных в круге , имеет свойство: первообразные отли-
чаются друг от друга на постоянное слагаемое. Выберем из этого семейства какую-либо одну
первообразную и обозначим ее через Д. Затем рассмотрим семейство первообразных, опреде-
ленных в круге К^. Среди них существует одна (обозначим ее через F2 ), совпадающая на множе-
стве K't Л К? ф0 с F|. Продолжая этот процесс, в каждом круге Кк выберем первообразную Fk
так, чтобы Fk = Fk_t на множестве K'k_I Л Кк. Таким образом, функция t Ф(£) = Fk(<p(t)),
t € 1к (к = 1, п) является первообразной функции f вдоль кривой 7.
Докажем, что функция Ф определена с точностью до постоянного слагаемого.
Пусть Ф, и Ф2 — первообразные функции f вдоль кривой 7 и пусть ф(1) = ФДД — $2(t).
Возьмем произвольную точку ta g I. В ее окрестности Ota имеем ф(1) = Fm(<p(t)) - Fm(<p(t)),
где Fm и F(2) — две первообразные функции f, определенные в окрестности точки zQ = (p(t0).
Они могут отличаться лишь на постоянное слагаемое, поэтому ф(1) = const в Otfj. Функция ф
определена на связном множестве I и является локально постоянной. Но непрерывная локально
постоянная в каждой точке связанного множества функция является постоянной на всем множе-
стве. Докажем это утверждение.
Обозначим через Е С I множество точек, в которых ф(Т) = ^(Д): Е = {t € 11 ф(£) = ^(Д)}.
Поскольку Д € Е, то Е ^0. Из того, что функция ф локально постоянная, следует, что
Е — открытое множество в топологии I (см. теорему 7, п. 6.4, гл. 1). Из непрерывности функ-
ции ф следует, что множество Е также замкнуто в топологии I. Действительно, пусть t* —
предельная точка множества Е. Тогда существует такая последовательность (tn) точек из Е,
что t„ —» t* и ФН„) = ф(М, т.е. lim фПп) = фП0). Поскольку функция ф непрерывная, то
п-*оо
lim фП„) = ФИ’). Следовательно, ф(1") = фН0), т.е. t* g Е. Множество Е одновременно от-
крытое и замкнутое в топологии I. Согласно теореме § 3, гл. 2, Е = I, или ф(1) = фПо). Поэтому
Vt g I ФДО - Ф2(О = const. ►
166
Гл. 4. Интегрирование в комплексной плоскости.
Теорема 2. Если 7 — кусочно-гладкая кривая и f — непрерывная на у функция с первообразной
Ф вдоль 'у, то
J /(z)dz = Ф(Ь) — Ф(а), (1)
г
т. е. интеграл вдоль ориентированной кусочно-гладкой кривой Г = (Г|, Г2, ..., Г„) вычисляется по
формуле Ньютона—Лейбница.
Ч 1) Пусть Г = (7, 70р) — ориентированная гладкая кривая, ф € 7ор — непрерывно диф-
ференцируемое параметрическое представление кривой 7, = [а, 6], ф(а) — начало кри-
вой 7, и пусть 7 целиком лежит в области, в которой функция / имеет первообразную F. Тогда
Ф(4) = Г(ф(<)) + С, Ф'«) = Г(ф(/))ф'(«) = /(ф(О)ф'(О и
ь ь
j f(z)dz = У = У Ф'(4)Л = Ф(Ь)-Ф(а).
Га а
2) В общем случае 7 = U г = (Гь Г2, ... ,ГП), Г*. = 7^) , <Pk 6 7оР — непрерывно-
fc=l
п
дифференцируемые на сегментах [afc, 6fc] функции, [a, 6] = (J [afc, 6fcJ. По определению,
fc=l
/(z) dz.
Принимая во внимание 1), получим:
n
f(z)dz = 52(ф(Ьк) - Ф(ао) = Ф(Ь) - Ф(а),
ь=1
где Ф — первообразная функции f вдоль кривой Г. ►
Замечание. Посредством формулы Ньютона—Лейбница можно определить интеграл от аналитической
функции вдоль любой непрерывной кривой, поскольку аналитическая функция имеет первообразную
вдоль нее. В учебной литературе слова “кривая” и “путь” употребляют как синонимы.
5.3. Теорема Коши.
В этом пункте докажем основную интегральную теорему теории аналитических функций.
Теорема 1 (об инвариантности интеграла при гомотопиях пути интегриро-
вания). Если функция / : С -+ С аналитическая в области D, а и — две гладкие кривые,
гомотопные в области D как пути с общими концами, или как замкнутые пути, то справедливо
равенство
У f(z)dz = У f(z)dz, (1)
Го г,
где Го = (7о> 7оР)> Г1 = (71, 7°р) — ориентированные кривые с общей начальной точкой.
Ч Пусть фо € 7оР, Ф1 6 7°Р — параметрические представления гладких кривых 70 и 7Ь
К = [0, 1] х [0, 1] D — гомотопия кривой 70 в кривую 71. Тогда Vt € [0, 1] ф(г, 0) = ф0(£),
ip(t, 1) = и V£ £ [0, 1] отображение t <p(t, 0 есть параметрическое представление непре-
рывной кривой 7{ в G (см. п. 4.2).
Если 7о и 71 гомотопны как кривые с общими концами, то
G [0, 1] ф(0, 0 = ф0(0) = ф1(0) = а, ф(1, 0 = фоО) = Ф1(1) = Ь.
Если 7о и 71 гомотопны как замкнутые кривые (контуры), то
€ [0, 1] Ф(0, 0 = ф(1, 0.
§ 5. Теорема и интеграл Коши
167
Пусть (Knrn)n — семейство таких квадратов, покрывающих квадрат К, что каждый из
них пересекается со всеми примыкающими к нему. Поскольку функция <р равномерно непрерыв-
на в квадрате К, то квадраты Кпт можно выбрать настолько малыми, что образ р(К,гт') будет
принадлежать кругу K'nrn С D, в котором функция f имеет первообразную. Зафиксируем п и
далее поступаем так же, как и при доказательстве теоремы о существовании первообразной вдоль
кривой.
Рассмотрим совокупность первообразных в круге К'п1, отличающихся друг от друга, как из-
вестно, на постоянное слагаемое, и зафиксируем одну из них, которую обозначим через Fnl.
Среди первообразных, определенных в круге К'п2, выберем ту (обозначим ее через Г„2), ко-
торая равна на множестве К'п[ П K'ri2 В точности так же подбираем первообразные
N
Fn}, ... ,Fnm. Затем на множестве Кп = |J Кпт определим функцию Фп равенством
т=1
*n(t, О = Fnm(<p(t, 0), (t,0£K„m.
Очевидно, что функция Фп непрерывна на множестве Кп и определена с точностью до постоян-
ного слагаемого.
Функцию Ф1 (t, 0 выберем произвольно, а функцию Ф2(4, 0 выберем так, чтобы Ф2 = Ф]
в Ki П К2. Такой выбор возможен, поскольку функция Ф1 - Ф2 как локально постоянная и
непрерывная на связном множестве Kt П К2 является постоянной. Затем выберем Ф3 так, что-
бы Ф3 = Ф2 в К2 П К?, и т. д. В результате построим непрерывную функцию (t, () Ф(1, 0,
определенную равенством Ф(£, () = Фп(4, £), (t, £) 6 Кп.
Очевидно, что при фиксированном £ € [0, 1] функция Ф(£, 0 является первообразной функ-
ции / вдоль кривой с параметрическим представлением <p(t, 0. Поэтому, согласно формуле
Ньютона—Лейбница, имеем
У /(0</г = Ф(1,0-Ф(О,0 (2)
Рассмотрим два случая.
1) Пусть 7о и 71 имеют общие концы. Это означает, что € [0, 1] у>(0, 0 = у>о(0) = у>1(0) = а,
у>(1, О = V’o(l) = V’i(l) = Ъ. Отсюда следует, что Ф(0, 0 и Ф(1, 0 локально постоянные в каждой
точке £ € [0, 1], следовательно, постоянные на отрезке [0, 1]. Действительно, пусть (0, G Кп1.
Тогда Ф(0, 0 = Fnl(y?(0, 0) = Fnl(a) = const. Таким образом, Ф(0, 0 = const для всех таких £,
что (0, £) е Кп1. Локальное постоянство Ф(1, $) доказывается аналогично. Следовательно, спра-
ведливы равенства Ф(0, 0) = Ф(0, 1), Ф(1, 0) = Ф(1, 1), и по формуле (2) получаем
У f(z)dz = У f(z)dz, Го = (7о, 7о°Р), Г! = (71, 7^)-
г» Г|
2) Пусть кривые 70 и 7] замкнутые, т. е. 6 [0, 1] 9ДО, 0 = у?(1, 0. Аналогично предыду-
щему показываем, что разность Ф(1, 0 - Ф(0, 0 локально постоянная в каждой точке 4 6 [0, 1],
следовательно, постоянная на сегменте [0, 1]. В частности, Ф( 1, 1) - Ф(0, 1) = Ф(1, 0) - Ф(0, 0),
т. е. по формуле (2) имеем
У f(z)dz = (j) f(z)dz. ►
Го Г!
Следствие 1. Если f € A(D), 7 — гладкая замкнутая кривая, гомотопная нулю в области D,
то
У /(z) dz = 0, Г = (7, 70р).
г
◄ Напомним, что путь 7 с параметрическим представлением t/>, = [0, 1], гомотопен нулю
в области D, если существует непрерывное отображение К = [0, 1]х[0, удовлетворяющее
условиям
¥>(0, 0 = ¥»(1, 0, ¥>(*, 0) = V(O, ¥>(*, 1) = const.
168
Гл. 4. Интегрирование в комплексной плоскости.
Отсюда следует, что существует замкнутая гладкая кривая 7( с параметрическим представле-
нием <рх, DVI = [О, 1], гомотопная кривой 7 в D и содержащаяся в некотором круге К' CD.
Функция f имеет первообразную-F в этом круге. Поэтому функция Ф, где Ф(£) = F(<pt(t)),
является первообразной функции f вдоль пути 7,. При этом
Ф(0) = F(9?,(0)) = F(a), Ф(1) = Г(^(1)) = F(a),
откуда
У f(z)dz = У f(z)dz = F(a) - F(a) = 0, Г, = (71, 7°р). ►
Г г.
Следствие 2. Если функция f : С —» С аналитическая в односвязной области D, 7 С D —
любая гладкая замкнутая кривая, то
jf(z)dz = 0, Г = (7, 7оР).
г
Ч Утверждение следует из следствия 1, если принять во внимание, что в односвязной области
каждая замкнутая кривая гомотопна нулю (см. п. 4.2). ►
Примечание 1. Следствие 2 — это классическая формулировка теоремы Коши. При дополнительных
условиях, когда f' непрерывна в D, а 7 — гладкая жорданова кривая, классическая теорема Коши
доказывается элементарно с помощью формулы Грина.
Ч Пусть G С С — область, 9G — ее положительно ориентированная граница. Тогда получим:
У f(z)dz = У udx—vdy+i У vdx+udy = dxdy+i*У = *
OG dG 9G G G
в силу условий Коши—Римана, выполняющихся для аналитической функции f = и + iv. ►
В теореме 1 и следствиях из нее вместо гладких кривых можно брать кусочно-гладкие.
Примечание 2. Классическую теорему Коши можно сформулировать иначе: если функция f : С —» С
аналитическая в замыкании D = D и 9D, где D — односвязная область, и 3D — кусочно-гладкая
кривая, то
У /(z)dz = 0.
8D
Такую формулировку теоремы Коши можно обобщить. Оказывается, достаточно потребовать, чтобы
f € A(D) и чтобы / была непрерывной на замыкании D.
Теорема 2 (обобщение интегральной теоремы Коши на случай, когда функ-
ция не является аналитической на контуре интегрирования). Пусть область D
представляет внутренность кусочно-гладкой замкнутой кривой 7 и f — функция, непрерывная в
замкнутой области D и аналитическая в области D. Тогда выполняется равенство
J f(z)dz = 0, Г = (7,7ор). (3)
г
Ч Предположим сначала, что 7 — звездный контур, т.е. существует такая точка z0 € D, что
любой луч с вершиной в этой точке пересекает 7 в одной и только одной точке (см. рис. 71). На-
пример, звездными являются границы выпуклых многоугольников (в частности, треугольников)
или кругов.
Пусть pit) = z0 + A(t), 0 t 2тг — параметрическое представление контура 7. Согласно
предположению, функция А имеет кусочно-непрерывную производную A'(t). Преобразование
подобия С = z0 + pA(t), 0 < р < 1, отображает ориентированный контур Г на контур Гр с той же
§ 5. Теорема и интеграл Коши
169
ориентацией в направлении против хода часовой стрелки (рис. 71). Поскольку контур 7Р лежит в
области D, то по интегральной теореме Коши (следствие 2) имеем
2тг
У 7(0 < = У 7(*о + M(t))pA'(t) dt = 0,
Гр о
откуда
2тг
У 7(zo + pA(t))A'(i)^ = O.
следовательно,
2тг
У17(*o + A(t)) - 7(z0 + pA(t))| |A'(t)l dt.
о
Так как функция f по теореме Кантора равномерно непрерывна в D, то
Ve > 0 35 > 0 : V(z' € D, z" Е D) (\z -z"\<6): |/(z') - 7(z")| < e.
Пусть
sup | A(i)| = a, sup | A'(t)l = P-
teio, 2ir| teio, 2tt]
Тогда выполняется неравенство
|(zo+A(t))-(zo+pA(t))| < (l-p)a < 6, если 1 - p <
и поэтому
У f(z)dz < ер 2тг.
г
В силу произвольности е > 0 отсюда следует, что
У f(z)dz = 0.
г
Пусть 7 — произвольная кусочно-гладкая замкнутая Рис 72
кривая. Если она имеет точки возврата, то мы выбросим
из области D круги малого радиуса е с центрами в этих точках так, чтобы граница полученной
области Dc не имела таких точек (рис. 72). Проводя внутри линии 7*. (fc = 1, ш), эту область
можно разбить на части Pfc, ограниченные звездными кривыми у'к (к = 1, т).
По ранее доказанному
7(0 dz = 0, Г*. = (71, 71°Р), к =
170
Гл. 4. Интегрирование в комплексной плоскости.
где r'fc ориентированы в положительном направлении (см. рис. 72). Так как общие части границ
смежных областей проходятся дважды, притом в противоположных направлениях, то
Рис. 73
У f(z) dz = У f(z) dz = 0, Гг = (7г, 7е°р),
р.
где ГЕ — положительно ориентированная граница обла-
сти DE. Поскольку 7 и 7е отличаются лишь на конечное
число малых дуг, а функция f ограничена, то ее инте-
грал вдоль этих дуг, который обозначим через I, допус-
кает оценку
|Т| < 2тгМг,
где М > 0 — некоторая постоянная. Таким образом,
интеграл по кривой Г сколь угодно мало отличается от
интеграла по кривой ГЕ, равного нулю, вследствие чего
У /(z)dz = 0. ►
г
Из теоремы Коши для односвязной области легко получить теорему о существовании перво-
образной аналитической функции, заданной в односвязной области. Эта теорема носит глобаль-
ный характер.
Теорема 3. Любая аналитическая в односвязной области D С С функция f имеет в этой
области первообразную.
◄ Если функция / аналитическая в односвязной области D, то, согласно следствию 2 из
теоремы 1, для всех простых (жордановых) гладких кривых 7, лежащих в этой области и имеющих
общие концы, интеграл f f(z)dz, где Г = (7, 7ор), имеет одно и то же значение. Действительно,
г
пусть Г[ и Г2 — ориентированные гладкие или кусочно-гладкие кривые, с концами в точках za
и z, лежащие в области D (рис. 73).
Рассмотрим упорядоченный набор Г = (Гь Г^), являющийся замкнутой положительно ори-
ентированной кусочно-гладкой кривой. Тогда имеем
f(z)dz = 0,
откуда
У f(z)dz = — У f(z)dz = У f(z)dz.
ri г~ г2
Поэтому криволинейный интеграл в рассмотренном случае можно обозначить так же, как и ин-
теграл Ньютона—Лейбница
Z
У /«)<*<•
zo
Пусть а Е D — начало гладкой или кусочно-гладкой кривой 7, z G D — произвольная точка,
являющаяся концом кривой 7. Тогда в области D определена функция F, где
F(z) = / /«)df.
§ 5. Теорема и интеграл Коши
171
Пусть (г + Дг) € D. Тогда получим:
F(z + Дг) - F(z) 1 Г
~f{z}=^z J
(4)
Дг
В связи с замечанием о независимости интеграла от выбора пути, соединяющего две точ-
ки, в правой части равенства (4) считаем, что путь, соединяющий точки г и г + Дг, явля-
ется прямолинейным отрезком. Поскольку функция f непрерывна в области D, то Ve > 0
3<5(е) > 0 : |Дг| < 6 => \f(z + Дг) - /(г)| < е. Оценивая интеграл в равенстве (4), получим
для | Дг| < 6 ;
F(z + Дг) - Г(г)
-/(г) <Щ|£|Дг| = г-
Дг
Следовательно, Vz G D F'(z) = /(г). ►
В классической теореме Коши существенным является требование односвязности области.
В неодносвязной области не каждый путь гомотопен нулю, а по н'егомотопным нулю кривым
интеграл от аналитической функции может не быть равным нулю. Рассмотрим пример.
Пусть D = {г € С | 1 < |г| < 2}, /(г) = |. Очевидно, что f € A(D). Возьмем замкнутую
кривую (окружность) с параметрическим представлением <p(t) = pelt, 0 t 2тт, 1 < р < 2.
Тогда 7 С D. Рассмотрим интеграл
dz,
dz =
г
где Г = (7, 7„р) — ориентированная в направлении против
хода часовой стрелки окружность радиуса р с центром в
начале координат. По определению криволинейного инте-
грала второго рода вдоль гладкой кривой Г имеем
2тг 2тг
Г ip в'1 dt
dt = I -----— = 2тгг / 0.
J pelt
го о
Однако, классическая теорема Коши обобщается и на
случай неодносвязной области. Рассмотрим это обобще-
ние.
Пусть даны (п+1)-связная область D С С, ограничен-
ная гладкими или кусочно-гладкими кривыми 7о (внеш-
няя граница), 71, 7г, ... ,7„ (внутренние границы), функ-
ция / аналитическая в замкнутой области D (рис. 74),
Го = (7о, 7оР)> Г, = (7,, 7°р), ..., Гп = (7„, 7°р) — ори-
ентированные кривые, при обходе которых область все время остается слева.
Теорема 4. При выполнении всех перечисленных выше условий справедливо равенство
Рис. 74
/(г) dz = О,
ао
Го
где 9D — положительно ориентированная полная граница области D, состоящая из контуров
Го.Гь ...,Г„.
◄ Проведем разрезы 71, 7г> > 7п> превращающие область D в односвязную область D’.
Обозначим через Г' положительно ориентированную полную границу области D'. Так как область
D' односвязная и f аналитическая в замкнутой области Р , то по теореме Конт имеем
0.
172
Гл. 4. Интегрирование в комплексной плоскости.
Поскольку берега разрезов 7п 7ц • • •, 7^ при интегрировании будут проходиться дважды в
противоположных направлениях, то в силу свойств криволинейного интеграла второго рода по-
лучим
dz =
/(z) dz = О
(входящие в сумму интегралы по берегам разрезов взаимно уничтожаются). ►
Теорема 4 остается в силе, если функция f аналитическая в области D и непрерывная в
замыкании D.
5.4. Интегральная формула Коши.
Эта формула определяет аналитическую функцию в области через ее значения на границе
области. _
Теорема. Пусть D С — область, f — аналитическая функция в замыкании D, 9D —
положительно ориентированная граница области D, состоящая из одной или конечного числа кусочно-
гладких кривых. Тогда iz Р D выполняется равенство
f(z) =
1 Г /«) ,,
2тгг / < - z
дО
(1)
« Пусть г е D — любая точка, Кр = {z 6 D : \z' - z\ < р} <s D. Рассмотрим множество
Dp = D\KP (рис.75).
Поскольку функция F, где F(Cj = ^7, аналитическая в
замыкании Dp, то по теореме Коши 4, п. 5.3, имеем
= 0,
откуда
= о,
во дКр
где дКр — положительно ориентированная граница круга Кр.
Получаем, что
(2)
ЭО
ОК.
В равенстве (2) перейдем к пределу при р —> 0, приняв во внимание, что его левая часть не
зависит от р. Правую часть равенства (2) запишем в виде
[ ™ яг tl' f л. f ™ ~ „
J i-z J C.-Z J C-z
дКр вКр вКр
После замены переменной Q — z = ре'1, 0 t 2тг, получим:
Г f(O f ipeit:dt Г i(f(ре'1 + z) - f(z)}pe'* Г
J J -~й- + J 3---------------------dt = 2^if(z) + i J (fipe^+zy-f^dt.
дкР oo о
§ 5. Теорема и интеграл Коши
173
Поскольку аналитическая функция / является непрерывной, то Vs > 0 3<5 > 0 : |Дг| < <5 =>
|/(z + Az) - /(z)| < е. Взяв р <6, получим оценку
2тг 2тг
» / + Z>> ~ М f + “/<z)| d< < 27Г£-
0 0
В силу произвольности € > О
.. / /«) - /(г) „ .
lim / -----------dC = 0.
J C-z
и к,,
Окончательно имеем
f /(О .. ,. [ /«) .
/ -----d( = lim / --------d( = 2тгг /(z),
J < - г p-о J ( - z
9D 9KP
откуда следует формула (1). ►
Следствие (теорема о среднем). Пусть / — аналитическая функция в замкнутом кру-
ге KR = {г € С : |z - z0| R}. Тогда справедливо равенство
2?т
Ж)=^- [ f^ + Re^dt, (3)
2тг J
о
т. е. значение функции f в центре круга равно среднему арифметическому ее значений на окружности.
◄ Согласно формуле (1) имеем
.. , 1 f /(О
7----d^
J С- z
OKR
Произведя замену переменной по формуле ( = z0 + Re'*, 0 t 2тг, получим
2тг 2тг
1 Г it Re'*idt 1 Г it
f^)= — f(z0 + Re ) = — / f(z0 + Re )dt.*
2тгг J Re'1 2tt J
о о
Интеграл в правой части равенства (1) называется интегралом Коши.
Считаем полезным напомнить читателю, что положительная ориентация контура при его об-
ходе соответствует направлению движения против хода часовой стрелки. При положительной
ориентации границы области, состоящей из нескольких контуров, внешний контур обходится в
направлении против хода часовой стрелки, а внутренние обходятся в направлении по ходу часо-
вой стрелки. Это принято во внимание при доказательстве теоремы 4, п. 5.3, и теоремы Коши
этого пункта.
Рассмотрим задачи.
Г dz
1. Доказать, что / = 0, где Г = (7, 7ор), 7 = {z 6 С : |z| = 2}.
г
Ч Пусть Г, = (7_,, 7°р) — положительно ориентированные границы окружностей радиуса
р с центрами в точках —1, 1, —г, г, не пересекающиеся друг с другом. Применив формулу (1),
получим:
[ * _ /(u-iXz'+l))-' Г ((, + !)(,’-К) '
J ~,-J —гл—d' + J —~----------------------------------d‘ +
г г, г2
f ((z2-l)(z-f))_1 w f ((z2-i)(z + i))-1 _ ( 1 1 J 1\
+ I — .--------------dz+ I -----------:-----dz = 2iri ( — 7 + 7 + 7-7 - 77 ) =0. ►
J z + г J z — 1 \44 4i4i/
Гз r4
174
Гл. 4. Интегрирование в комплексной плоскости.
2. Пусть 7 = {z 6 С : \z\ = г} и |а| / г. Доказать равенство
1 = / ^ = 2’ГГН-ГТ
•^ Поскольку на окружности 7 выполняется равенство z = re'*, 0 р С 2тг, то
; idz irdz
dz = ire dtp,-------— dp, |dz| = r dp =--------,
то интеграл I сводится к интегралу второго рода по ориентированному в положительном напра-
влении (против хода часовой стрелки) контуру Г = (7, 7ор):
Г dz Г dz Г dz
I — —ir I ----------— —ir I --------=- = — ir I ----------2—
J Ф - a\2 J z(z - a)(z -a) J z(z - a)(z - a)
Г Г г
Так как z = r2z-1, то
ir [ dz
d J (z-a)(z- £)
Если контур Г окружает точку а, то по формуле Коши (1) получим:
I =----— = —2ят(|а|2 — г2) = 2тгг(г2 — |а|2)
Если |а| > г, то контур Г окружает точку и в силу формулы (1) имеем:
2тгг fг2 \ /, .2 2\->
I =----— I —— а I = 2тгг (|а| — г )
а у a ) '
Объединив обе формулы в одну, получаем:
I = 2тгг | |а|2 - г2| 1. ►
3. Вычислить интеграл
Т = У zsin zdz, Г = (7, 7оР), 7 = [z g С : \z\ = у, Imz > О},
г
◄ Поскольку / 6 А (С), где /(z) = z sin z, то в любой односвязной области, содержащей кри-
вую 7, функция f имеет первообразную T’(z) = -zcos z + sin z. Применив формулу Ньютона-
Лейбница, получим:
I z—irjl.
/= (-zcos z+ sin z)|i=_^/2 = 2
Параметрическое представление кривой имеет вид р = уе'4, -л t 0. Тогда а =
= -у — начальная точка кривой Г, b = уе’° = у — ее конечная точка. ►
4. Пусть функция f аналитическая в конечной т-связной области D, ограниченной замкну-
тыми кусочно-гладкими кривыми 71, 72, •••,7m- Доказать, что для существования первообразной
функции f в области D необходимо и достаточно, чтобы выполнялись равенства
J f(z)dz = 0 (fc=l, m-1), Tfc = (7*,, 7°р). (1)
◄ Необходимость. Пусть функция / имеете области D первообразную. Тогда
У f(z)dz = 0, Г = (7,7оР), (2)
Г
где 7 С D — любая замкнутая кусочно-гладкая кривая.
§ 6. Интеграл типа Коши
175
Для данного 1 к т — 1 выберем кусочно-гладкую замкнутую кривую 7 так, чтобы
функция / была аналитической в двусвязной области с положительно ориентированной границей
Г U (или Г- U Г). Тогда по теореме Коши для неодносвязной области имеем
j f(z)dz = 0.
rfc
Достаточность. Равенство (2) для любой замкнутой ориентированной кривой Г = (7, 7ор),
7 С D следует из равенств (1) и применения теоремы Коши для односвязной или неодносвязной
области. ►
5. Пусть f 6 A(D), D = {z g С : |z| < R} и f непрерывна в замыкании D. Вычислить
интеграл
Т= // f(z)dxdy.
r<\z\<R
Ч Применив теорему о среднем, получим
R 2тг 2 2
I - J pdp j ftpe^dip = = irf(Q)(R2 - r2). ►
г 0
§ 6. Интеграл типа Коши
В теории функций комплексного переменного значительное место занимает интеграл типа
Коши, являющийся обобщением интеграла Коши.
6.1. Определение и основное свойство интеграла типа Коши.
Интегралом типа Коши называют интеграл вида
(1)
2тп J С - z
г
где Г = (7, 7„р) — ориентированная гладкая или кусочно-гладкая кривая, / — непрерывная
функция Vz g 7. Если 7 — спрямляемая кривая, то требуем, чтобы f была суммируемой на 7
(кривая 7 называется спрямляемой, если ее параметрическое представление у> является функцией
ограниченной вариации на отрезке Dv — [а, Ь]).
В случае, когда путь 7 замкнут, a f — аналитическая функция в замкнутой области, ограни-
ченной контуром 7, то интеграл типа Коши совпадает с интегралом Коши, т. е.
F(z) = /(z).
Следовательно, интеграл Коши является частным случаем интеграла типа Коши.
Основное свойство интеграла типа Коши сформулируем в виде теоремы.
Теорема. Интеграл типа Коши имеет производную любого порядка в любой точке z g С, не
принадлежащей кривой 7, и эти производные определяются следующими равенствами
<2>
г
(т. е. их получают формальным дифференцированием под знаком интеграла (1)).
176
Гл. 4. Интегрирование в комплексной плоскости.
◄ Применим метод математической индукции. Пусть z g С — произвольная точка и z ^7.
Покажем, что F'(z) существует и вычисляется по формуле (2) при п = 1. Рассмотрим выражение
Г(г+Дг)-р(г) =—. — / ло (_1______________q =
Az 2iri Az J s \<-z-Az f-z/ 4
г
= 1 1 [ f(w<K =_L f
2тгг Az / « - z - Az)(( - z) 2%t J (£ - z)« - z - Az)'
г г
Оценим модуль разности
F(z + Az) - f(z) 1 Г /(0d£ =
Az 2тгг У (C - z)2
Г
= J_ f f(n ( 1__________1_\ „bf Л0<К
2«y y^\(C-z)((-z-Az) (C-z)2; 2iri J (C-z)2(C-z-Az) '
г г
Выберем |Az| настолько малым, чтобы (z + Az) £ 7. Очевидно, существуют такие числа
р0 > 0 и М > 0, что
р(Ъ z) = inf |< - z\ р9, р(у, z + Лг) = inf К - z - Az\ ро, |/«)| < М У< € 7.
сет Сет
Тогда Уе > О справедлива оценка
F(z + Az) - F(z) _ 1 Г f(Q M|Az|£
Az 2тгг У (C - z)2 2irpl £’
г
если |Az| < 7^, где L — длина кривой 7. Таким образом,
(2) = — / 77---й d(-
2тг» J (С - г)2
г
Предположим, что утверждение справедливо для п = к и покажем, что из этого предположе-
ния следует справедливость утверждения для п = к + 1. Имеем
Fw(z + Az)-Fw(z) = к'. Г / 1_____________1_\
Az 2;riAz J у (£ - z — Az)fc+’ (( — z)fc+I J
г
= *! f f(C) (< -z)fc+l - - г - A*)fe+1
2тггДз J - z — Az)fc+l(( — z)fe+l
г
r «-z^-^-iyc^JC-z^-'Az2'
fc! I j=o
= 2iriAz J - z - Az)fc+1« - z)fe+1 =
Г
i:(-iyc2:;(c-z)fc->Az>
fc! Г j=i fc! Г j=o
= 2Й7 У (<-z-Az)fc+,(C-2)*;+1 = 2iti J «-z^+^C-z-Az)fc+1
Г г
Оценим выражение
§ 6. Интеграл типа Коши
177
F{k\z + Дг) - F{k\z) _ (к + 1)! Г
Az 2iri J (( — z)k+2
г
fc!
2тгг
/ k
7=0______________________
(<-z)fc+1(C-z - Az)k+l
fc+ 1
« - z)k+2
<K
E(-l)JCj£i(< - z)k+l~jAz^ - (fc + 1)« - z - Az)k+'
fc! f j=o
2iri J (( — z)k+2(£ — z — Az)k+i
dC
(k +1) (<c - z)k+' - (c - z - Az)fc+1) + E(-iyc^!« - *)fc+1~j д?
fc! f . 7 = 1
2тгг J (C - z)k+2(£ — z — Az)k+'
г
(k + 1) Е(-1У+1^+1(С - z)k+'-jAz2 + E(-DJ'OC - z)k+,~2Azj
(C - z)k+4C ~ z- Az)k+l
k'.L\Az\MN , , , , e
—-—— = В|Дг| < e, если |Дг| < -.
2я-Ро В
В полученном неравенстве N — постоянная, зависящая лишь от к и р0.
Таким образом, формула (2) справедлива при п = к + 1, а значит и Vn € N. ►
Следствие. Аналитическая в области В С С функция f имеет производную любого порядка
/(п,(г) Vz € D.
◄ Пусть z0 € D — любая точка. Рассмотрим ее <5-окрестность Ks = {г € D : |г—г0| < 6} <s D.
Согласно интегральной формуле Коши, имеем
„ . 1 [ /(О .. w с „
/(г) = — / ---------Vz € К6.
2tti J £-z
9Kt
Поскольку интеграл Коши является частным случаем интеграла типа Коши, то функция /
имеет производные всех порядков в точке г0. Поскольку г0 € D — произвольная точка, то
V(zei>, n€N) 3/(n)(z). ►
Полученное следствие можно кратко записать в виде
/ € A(D) => V(z g D, n € N) 3/(n,(z) Л /<n)(z) € A(D).
Рассмотрим некоторые факты, непосредственно следующие из свойства бесконечной диффе-
ренцируемости аналитической функции.
6.2. Гармоничность действительной и мнимой частей аналитической функции.
Восстановление аналитической функции по ее действительной (мнимой) части.
Определение. Дважды дифференцируемая функция u : R2 —♦ R, D = G, называется гармони-
ческой в области G, если она удовлетворяет в G дифференциальному уравнению Лапласа
178
Гл. 4. Интегрирование в комплексной плоскости.
Дифференциальный оператор Д = -gg 4- -gg называется оператором Лапласа.
Пусть f = и + iv, f € A(D), D <s C — односвязная область. Из бесконечной дифферен-
цируемости функции f следует, что функции и и v имеют в каждой точке области D частные
производные любых порядков. Запишем условия Коши—Римана
ди dv ди dv
— = —, — =-----------• (2)
дх ду ду дх
Продифференцируем первое равенство в (2) по х, второе — по у и сложим полученное,
приняв во внимание, что Имеем
д2и д2и
ди = + = °.
dx1 ду1
Аналогично получаем равенство Дг = 0. Следовательно, действительная часть и и мнимая часть
v аналитической в области D функции / являются гармоническими функциями. Функцию v
принято называть гармонически сопряженной с функцией и.
Пусть в односвязной области D задана гармоническая функция и. Найдем сопряженную ей
гармоническую функцию v. Из условий (2) получаем:
dv dv ди ди
dv = — dx 4------dy = — — dx 4------dy,
дх ду ду дх
откуда
(*> у)
Г ди ди
v(x, у) = I---------dx Ч-----dy 4- С, С = const, (io, уо) € D, С Е. R. (3)
J ду дх
(«0, !/о)
Подынтегральное выражение в этом криволинейном интеграле является полным дифферен-
циалом, вследствие чего интеграл не зависит от выбора пути интегрирования.
Таким образом, аналитическая функция / в односвязной области D определяется ее дей-
ствительной частью с точностью до аддитивной постоянной iC по формуле
<=е, У~>
[ ди ди
f(z) = u(x,y) + i / - — dx Ч- — dy 4- iC. (4)
z J ay dx
(XQ,yQ)
Формула
(®, y)
f dv dv
f(z) = / — dx - — dy + C + iv(x, y) (5)
J dy dx
(^o, l/o)
восстанавливает аналитическую функцию f по ее мнимой части с точностью до произвольной
аддитивной действительной постоянной С.
6.3. Теоремы Лиувилля и Морера.
Теорема 1 (Лиувилля). Если функция f аналитическая во всей плоскости С и ограниченная,
то она постоянная.
Ч Согласно условию, Vz € С |/(z)| М = const. Пусть zQ G С — произвольная точка.
Рассмотрим круг KR = {z е С : |z( < R}, где R > |z0|. Согласно формуле производной от
интеграла Коши имеем
_ 1 f /Ю
/(Zo) 2тг» J (C-z)1
OKR
f ifiRe^Re1'
J (Re» - zo)1 ’
о
§ 6. Интеграл типа Коши
179
откуда при достаточно больших R получим Ve > О оценку
, 1 MR2ir
2тг (R - |z0|)2
В силу произвольности выбора е > 0 f'(zo) = 0. Поскольку z0 £ С — произвольная точка, то
f(z) = const. ►
Теорема 2 (Морера). Если функция f непрерывная в области D С С и интеграл от нее вдоль
ориентированной границы 9G любого треугольника G <s D равен нулю, то f € A(D).
Ч Пусть z0 Е D — любая точка. Рассмотрим круг Kz, = {z € С : \z - z0| < г} С D. Тогда по
теореме 1, п. 5.1, функция F, где
F(z) = У" /(С)^С,
(го. Z1
является первообразной функции / в круге Kza, т.е. Vz € KZI. F'(z) = f(z). Отсюда следует, что
/ б А(К,п), следовательно, f £ A(D) в силу произвольности Kzt!. ►
6.4. Главное значение и предельные значения интеграла типа Коши.
Согласно теореме п. 6.1, интеграл типа Коши
F(z) =^~ [ <*С, Г = (7, 7оР), (1)
2кг J Q-z
г
где / — непрерывная функция, Г — положительно ориентированная гладкая или кусочно-
гладкая кривая, является аналитической функцией в любой точке z Е С, не принадлежащей
кривой 7.
Функцию £ н-» /(С) называют плотностью, а функцию £ •-> ^7 — ядром Коши. Если z Е 7,
то интеграл в правой части (1) в обычном понимании не существует, однако при некоторых
дополнительных ограничениях, налагаемых на плотность /, ему можно придать определенный
смысл.
Считаем, что 7 — замкнутая гладкая кривая Жордана и Со £ 7. Пусть Lc = {z £ С : |z—Col = е},
где е > 0 — произвольное, как угодно малое число, не превышающее стандартного радиуса
кривой 7 (гладкие замкнутые кривые Жордана 7 имеют важное свойство: V7 Збо > 0 такое, что
Vz0 £ 7 окружность с центром в этой точке радиуса б < би ровно два раза пересекает кривую 7;
число б0 называется стандартным радиусом кривой 7).
Часть кривой 7, лежащей вне окружности L,, обозначим 7е. Интеграл
*Ж)= ^-7 (2)
2лч J С - G
Ге
очевидно, существует в обычном понимании.
Определение. Если существует lim Fz(£o), то этот предел называют интегралом в смы-
г —+0
еле главного значения по Коши, или главным значением интеграла типа Коши в
точке Со и обозначают Е'(Со)-
Обозначение главного значения интеграла типа Коши совпадает с обозначением интеграла
типа Коши, поскольку, как правило, если интеграл не существует в обычном понимании, то
рассматривают его главное значение.
Для существования интеграла типа Коши в понимании главного значения VCo € 7 достаточ-
но, чтобы функция f удовлетворяла на кривой 7 условию Гельдера с показателем 0 < h Sj 1 и
постоянной М:
(ЗМ > 0): V (ф € 7, Сз € 7) 1ЛС1) - /(0)1 < АГ 10 - 01^- (3)
Действительно, запишем f£(Co) в виде
Ге Ге
180
Гл. 4. Интегрирование в комплексной плоскости.
Принимая во внимание условия (3), легко доказать существование равномерно сходящегося не-
собственного интеграла
1 /"/(С)-/(Со) 1 Г /(С) - /(Со) ,z
/ —7—;------<*С = lim — / —-—-------d(.
2m J С - Со е-о 2m J с - Со
Г ге
Пусть L't — часть окружности £е, находящаяся вне области D, ограниченной кривой 7, т —
касательная к кривой 7 в точке (о (рис. 76). Имеем
С “Со
Г [
hm / 7—7
J С, ~ Со
re
= lim
с->0
V>2
Г eelt
= liri — lim I i —- dt =
J eelt
v>i
= 2тгг - i lim(^2 - Vi) = 2тгг - тгг = тгг.
t-0
de
= 2тгг — lim .
Е-° J С “ Со
Таким образом,
lim F,
f - /(Со) , . /(Со)
г
Следовательно, главное значение интеграла типа Коши определяется равенством
г
/(С) - /(Со)
С-Со
<К, г = (7, 7ор).
Замкнутая кривая Жордана 7 делит всю плоскость С на две области: конечную D+ и D~,
содержащую бесконечно удаленную точку. В каждой из этих областей интеграл типа Коши опре-
деляет аналитическую функцию. Пусть Со € 7 — произвольная точка. Возникает вопрос о суще-
ствовании пределов
lim F(z') и lim F(z).
г—<0 z—Cq
z£D+ ziD~
Эти пределы, если они существуют, называются соответственно предельными значениями инте-
грала типа Коши в точке слева от кривой 7 и справа от нее и обозначаются 7?+(Со), F~(C,o)-
Если указанные предельные значения существуют, то желательно установить связь между ними
и главным значением интеграла типа Коши FtQ,). Мы найдем эту связь при дополнительном
предположении, что функция / аналитическая на кривой 7.
Выберем г > 0 настолько малым, чтобы круг К, = {( £ С : |( - Col е} содержался в полоске
аналитичности функции /. Обозначим через 6е часть кривой 7, принадлежащей кругу Ке. Имеем
(в каждом из интегралов перешли к пределу под знаком интеграла, поскольку кривые, по которым
производится интегрирование, не содержат точку &)• Таким образом, справедливо равенство
^+(Со) = К~. [
2m J
Гс
/(С)
С-Со
dc +
/(С)
С-Со
<*С,
§ 6. Интеграл типа Коши
181
выполняющееся для любого как угодно малого е > 0. Поэтому в нем можно перейти к пределу
при е —> 0. Получим:
lim^r [ =
-'-о 2тгг J ( - <0
гс
так как
1
lim —
Е—о 2тгг
lim
7(C) —/(Co) . /(Co) .
Г'
Окончательно имеем
.. f
hm / -—~ = 7гг,
Е —о J С ~ Со
Г/(О-/(Со) .
lim / ----------= 0.
г'
<-<о
F+«o) = ^ + F«o).
Аналогично получаем
F'((o) = -^+W
последнего равенства вместо L'c берем L" — часть окружности Lc, со-
При доказательстве
держащуюся в D+. Тогда
.. 1 f d<
lim----- / --------= —тгг.
£-o 2тп J < - (о
Равенства
F±«o) = ±^+J’(Co)
в учебной литературе носят название формул Сохоцкого. Их открыл в 1873 г. русский математик
Ю. В. Сохоцкий (1842—1927). Формулы Сохоцкого справедливы при более общих предположениях
относительно функции /.
6.5. Формулы Шварца и Пуассона.
Пусть 7д = {С € С : |^| = 7?}, С, = Яе*‘, 0 t 2тг, и0 — функция, заданная на окружно-
сти 7д, где
«о(0 = «о (Де*‘) = йо(0, йо(0) = й0(2тг).
Формулой Шварца называется равенство
2тг
1 Г , 1 ( С + 2 dC
/(z) = — / и0 (Яе ) —---------dt= — и0(С) ;--- —, (1)
2тг J х ' Rext - z 2тгг J ~z Q
о rR
а интеграл в (1) носит название интеграла Шварца.
Рассмотрим свойства функции /.
1) Запишем формулу (1) в виде
1 Г 2dC 1 ЖоЮ
f(2) = mJ “°(0 (2)
ГН гв
Второй интеграл в формуле (2) является постоянной величиной, а первый — интеграл типа Коши.
Поэтому f — аналитическая функция в любой области, не содержащей точек кривой -yR и, в
частности, / Е A(KR), где KR = {z € С : \z\ < Я}.
182
Гл. 4. Интегрирование в комплексной плоскости.
2) Пусть и0(С) = 1, тогда
/(*) =
1 у 2d< 1 гас
2ri J ( - z 2iri J C '
гк гд
Если z 6 KR, то f(z) — 2 — 1 = 1.
3) Найдем Re f(z), считая, что z = re"f‘ € KR. Имеем
Re /(z) = Re —
2rr
2tf
0
Re'1 + re**°
Relt — re**’
2тг
0
(.Re44 + re4”) (йе-’4 — re-’*3)
(Леи-ге1*) (_Re-lt - re-**1)
1 Г R2 - г2 + Rr (е1**3 4) — е 4>) 1 Г , {t, R2 - г2 + 2iRr sinfjp - t)
Re — /u0 (Re'*) ------------------)-------------------(-dt = Re— u0 (Re ) —:----------=------------—------- dt =
2лJ ' ' R2 4- r2 — Rr (ег^~^ + е~г^~^Л ' R2 + r2 — 2Rr cos(t —
о 0
2тг
= — [ u0 (Ле*4) -у—т-5------------------------dt = и (re**3) .
2тг J ' ' R2 + r2 — 2Rr costt — ip) ' •*
о
Равенство
2тг 2 2
u(r, <p) = u(rev) = -i- / u0 (Де14) p Л. Г—------------------- dt (3)
2тг J 4 ' R2 + r2 - 2R r cos(t - p)
о
называется формулой Пуассона. Интеграл в правой части формулы (3) называется интегралом
Пуассона.
Из свойства 2) функции / следует равенство
2тг
1 Г R2 -г2
--- / -z----;-----------------dt = 1, (4)
2ir J R2 4- г2 - 2R r cos(t — р)
о
выполняющееся Vz g KR, z = re'4.
4) Покажем, что функция (г, р) ы- u(r, р) непрерывна в замыкании KR и что u(R, р) =
и0(Яе**’), т.е. u(r, р) =3 u0(Re'*) при z = г егч> —> С = Re'1 вдоль любого пути, лежащего в KR.
Для этого нам понадобится следующее утверждение.
Лемма. Пусть функция U: С —> R, U = U(z, (), где z = re**3, С = Ле’4, 0 г < R,
0^у><2тг, О С t < 2тг, удовлетворяет следующим условиям'.
1) она непрерывна и неотрицательна',
2тг
2) Vz выполняется равенство f U(z, Qdt = 1;
о
3) при z -» (о = Де*4° «о — любая точка окружности 7д) и С / Со функция U стремится
к нулю равномерно относительно С (т.е. Ve > 0 Э(р < R, б > 0)(г > R — р Л \<р — t0| < д)
(Vt: |t -10| < 26): 0 V(z, С) < е).
Тогда для любой функции и : С —» R, где и = и(С), кусочно-непрерывной с точками разрыва
первого рода, в любой точке ее непрерывности Со существует предел
2?г
Ит 2- I u(Q)U(z, Qdt = и(Со).
С-♦Со 2тг J
о
§ 6. Интеграл типа Коши
183
◄ Из условия 2) следует, что и(0) можно представить в виде
2тг
u«o)= [ u(0)U(z,0dt.
2п J
о
Оценим
2тг
д =
dt.
о
Из непрерывности функции и в точке 0 следует, что Ve > 0 3 6 > 0 : |t—to! <26 => |u(0—u((0)| < e
(см. рис. 77). Имеем
Д=~ / (u(O-^o))U(^0dt+^ У (ti
|t-to|<26 (e—e0|>2<s
где интегралы берутся по дугам окружности yR, для аргумен-
тов точек которых выполнены соответствующие неравенства.
Оценим 11:
dt = е.
2тг
I11'2тг f |“(0-«(<о)|*Ж У
|е—10|<2<5 о
Теперь предположим, что \р - t0| < 6. Тогда для всех t,
удовлетворяющих неравенству |t — t0| > 2<5, получим, что
\<р —1| > 6 и в силу условия 3) найдется такое число р < R,
что для указанных t и г > R — р выполняется неравенство
t7(z, 0 < е. Таким образом, для всех z из области, заштри-
хованной на рис. 77, для которых \р — i0| < 6 и г > R — р,
получаем:
— Л +11-,
± /
2т J
М = sup |«(0|, IД| < (1 + 2М)е.
сети
В силу произвольности е > 0 имеем
е
dt < — • 2М(2т - 26) < 2Ме,
2т
2тг
lim / u(0[7(z, 0dt = u(Co).
С-Со 2тг J
О
Полагая в условиях леммы
R2 - г2
U(z, 0 =
R2 + г2 - 2Лг cos(t - tp) ’
получим свойство 4).
Проведенные исследования показывают, что формула Шварца определяет аналитическую
функцию в круге KR по значениям ее действительной части на границе круга. Формула Пуас-
сона дает решение задачи Дирихле для уравнения Лапласа в круге KR, состоящей в нахождении
решения уравнения Лапласа в круге KR, непрерывного в замыкании KR и принимающего на
границе круга dKR заданное непрерывное значение «о(0-
Рассмотрим примеры.
184
Гл. 4. Интегрирование в комплексной плоскости.
6. Пусть f — функция, аналитическая в круге Kr = {z g С : \z — а| < Л}. Доказать, что
при 0 < г < R
2тг
/(<»)= — [ P(e)e-ied0,
’Г’’ J
о
где Р(в) — Ref(a + ге'в).
◄ По теореме Коши
2тг
0= f(z)dz = ir J / (а + гегв) ее df),
qkr о
откуда
2тг
°= 2^/ f(a + reie)e-ieM.
о
С другой стороны, по формуле производной от интеграла Коши, получаем:
2 т
/(а)= J_ //(а + ге,в) e-*ed0.
2тгг J v '
о
Из последних двух формул имеем
2т
/'(а) = — / P(e)e~iedO.
тгг J
о
Аналогично
2т
f’(a) = — / Q(0)e-ied6, Q(0) = Im f (a + re~ie) . ►
1ГГ J 4 7
0
cos z 2iri dr
--------- dz — -------- cos z
(z — t)3-2! dz2
7. Вычислить
cos z
;----rj dz, Г = (7, 7oP), 7 = {z £ C : \z - t| = 1}.
(z - i)J
г
◄ Согласно формуле (2), п. 6.1, находим:
= — iri cos i = —iri ch 1.
8. Вычислить интеграл
2т
/sin nip
-—-—:------- dtp, -1 < a < 1, n € N.
1-2a sin 93 +a2
0
◄ Воспользуемся формулой Пуассона. Получим:
(l-a2)sinn^ 2ir 1
1 — 2acos (у - + a2 1 — a2 lit
о 0
7Re(-iein”) (1 — a2) dy? _
/ 1 — 2a cos (? — + a2
§ 6. Интеграл типа Коши
185
J^Re(-,aV"i)
2rran nir
-----2 sin — =
1 — a2 2
О,
если п = 2к
2тг . 2Jt+, (fc 6 N). ►
-------(-l)fco2,=+1 если n = 2А + 1
I — а2
9. Вычислить интеграл J \z\zdz, где Г = (7, 7ор) — кусочно-гладкая, положительно ориен-
г
тированная кривая, 7 = 7] U 72, 7i = {z € С | —1 Rez 1, Imz = 0}, 72 = {z € С : |z| = 1,
Imz > 0}.
◄ Кривая 7 замкнута, а положительная ориентация кривой Г означает, что при возрастании
параметра (на отрезке 71 это х, а на верхней полуокружности 72 это i) подвижная точка пробегает
кривую 7 в направлении, противоположном ходу часовой
стрелки. На отрезке 71 \z\z = |г|а;, а на полуокружности 72
z = е*‘, 0 t тг. Следовательно,
г
ванная граница полукольца, изображенного на рис. 78. Рис- 78
•< При интегрировании по замкнутой кривой выбор начальной точки не играет роли. Пусть
это будет точка z = -2. Получим, принимая во внимание, что на действительной оси z = z = х,
на нижней полуокружности z = elt, на верхней — z = 2elt, 0 t тг:
-10 2 ir
У - dz = У dx+J ie'3t dt + j dx+J i2e'3t dt — 1+ - e'3t
Г —2 тг 10
11. Вычислить интеграл J (z - a)n dz, n € Z; Г = (7, 7„p):
г
1) по полуокружности 7 = {z € C : |z — a| = R, 0 arg(z — a) тг} (начало пути в точке
z = а + R);
2) по окружности 7д = {z € С : |z - а| = R} -,
3) по периметру квадрата с центром в точке а и сторонами, параллельными осям координат.
◄ 1) Выбор начальной точки кривой 7 определяет ее ориентацию, следовательно, кривая L
ориентирована в направлении, противоположном направлению хода часовой стрелки. В интеграле
произведем замену переменной, полагая z — а — Relt, 0 t тг. Пусть п # -1. Тогда
У (z - a)n dz = ERn+l У e’<n+1)t dt
L 0
t = 1r pn+1
= —T«-1)n+1 -D-
П + 1
Если n = -1, то
pn+1
Л____i(n+Dt
П + 1
2) Если n / — 1, то подынтегральная функция аналитическая в односвязной области, огра-
ниченной окружностью 7д, являющейся гладкой кривой. По теореме Коши (см. п. 5.3) имеем
(z — а)" dz = 0.
186
Гл. 4. Интегрирование в комплексной плоскости.
Если п = — 1, то, произведя ту же замену переменной, что и в предыдущем примере, получим:
2%
Г dz Г iRe'*
I ----- ~ I г, ; = ,2,г-
J z-a J Rea
L 0
3) Если п Ф — 1, то функция z 1-» (z-а)п аналитическая в односвязной области, ограниченной
кусочно-гладкой кривой и по теореме Коши
dz = 0.
Пусть п = -1. Тогда подынтегральная функция не является аналитической в области, огра-
ниченной сторонами квадрата. Из теоремы 4, п. 5.3, следует, что криволинейный интеграл второго
рода по замкнутой кусочно-гладкой кривой не зависит от ее вида. Поэтому вместо границы ква-
драта возьмем окружность с центром в точке а и радиуса, большего половины длины диагонали
квадрата. Задаф2елась к случаю, рассмотренному в 2). Поэтому
Г dz
/ -----= г2тг. ►
./ z — a
12. Вычислить интеграл I = / Lnzdz, Г = (7, 7ор), где:
г
1)7 — единичная окружность и Ln 1 = 0;
тгг
2) 7 — единичная окружность и Ln i = —;
3) 7 — окружность: 7 = {z G С : \z\ = 2?} и LnR = InR;
4) 7 — окружность; 7 = {z € C : |z| = R} и LnH = 1пЛ + 2?ri.
Ч Многозначная функция w = Ln z имеет следующие однозначные ветви:
Wfc = In |z| + i argz + 2ктг i, k^Z.
При интегрировании следует выбирать соответствующие ветви, определяемые дополнительными
условиями. В каждом из случаев 1)—4) окружности положительно ориентированы и ориента-
ция их соответствует возрастанию параметра. В случаях 1) и 2) параметрические представления
окружностей имеют вид соответственно z = y?(t) = elt, 0 t 2тг, z = ip(t) = е11, у t |тг,
а в случаях 3) и 4) — z = tp(t) = Re'*, 0 < t 2тг, z = ip(t) = Re'*, 2тг C t 4тг. Произведя в
каждом из рассматриваемых интегралов замену переменной, получим:
dt = ihtR-,
4тг
I = Ri J (In тг -Ь Ц)е“ dt = —R
2ir
t=4tr
= iKiell| = i2itR. >
t=2?r
§ 6. Интеграл типа Коши
187
13. Вычислить интеграл I = J znLnzdz, Г = (7, 7ор), п € Z, 7 = {z € С : \z\ = 1}, где:
г
1) Ln 1 = 0; 2) Ln(—1) = iri.
4 Рассуждая аналогично (см. предыдущий пример), получим:
1) Пусть п / 1. Тогда
2ir
I = - [ tei(n+,)t dt = — .
J l(n + l)z
tei(n+Df
t=2ir
о х
Пусть п = — 1. Тогда получим:
(n + l)i J
0
2тг
f ei<n+1)t dt
(n + l)
t=2ir
t=0
2л!
n + 1
2it
I=-
t2
tdt= -
2
= -2л2.
2) Пусть n / — 1. Имеем
Зтг
= - f tei{n+l)t dt = te
J n + 1
—------(Зтге
n+ 1 v
— ire
2лг
—7(-D
п + 1
Если n = -1, to
Зтг
t2
tdt = —
2
= -4л2. ►
4=3тг
14. Показать, что если путь интегрирования не
начало координат, то
= In r + iip + 2л ik,
проходит через
где к — целое число, указывающее, сколько раз путь интегрирова-
ния обходит начало координат (z = ге**’).
4 Пусть путь интегрирования не проходит через начало координат. Согласно теореме 3,
п. 5.3, интеграл от аналитической функции ( н+ | в односвязной области, не содержащей начала
координат, не зависит от выбора пути, соединяющего точки ( = 1 и ( = z = ге’*’. Пусть
Г*! — ориентированный отрезок [1, г] с параметрическим представлением z = <pi(x) — х, Г2 —
положительно ориентированная дуга окружности ут = {z € С : \z\ = г} с параметрическим
представлением ^2(t) — rclt, 0 t <р. Тогда упорядоченный набор Г = (1*1, Г2) является
кусочно-гладкой положительно ориентированной кривой с началом в точке ( = 1 и концом в
точке £ = z = ге*’’. Интегрируя по кривой Г, получим
Z r ф
Г dC Г dC f dx [ ire'1
J -. = J — = J — + J —dt = lnr + t<p.
L I I 0
Пусть r3 — гладкая или кусочно-гладкая кривая с началом в точке z и концом в точке 1, охва-
тывающая начало координат (рис. 79). Тогда положительно ориентированная замкнутая кусочно-
гладкая кривая Г = (Гь Г2, Г2) окружает начало координат и в силу однозначности функции
< |-» ( интеграл f не зависит от выбора кривой Г и его можно заменить, согласно теоре-
г
ме Коши, интегралом по любой замкнутой гладкой или кусочно-гладкой кривой, например, по
te’(n+1)f
0
1 = -
188
Гл. 4. Интегрирование в комплексной плоскости.
окружности радиуса 1 с центром в начале координат и направлением обхода против хода часовой
стрелки. При этом получим
г о
После такого полного обхода по кривой Г путь из точки ( = 1 в точку ( = z состоит из
объединения кривых Г и Г, т. е. кривая Г будет пройдена два раза, и при этом имеем
Теперь становится ясным, что при обходе начала координат к раз получим равенство
— = In г 4- i!-P 4- 2тгг к, к 6 Zo.
Пусть J"
— f Тогда J 4- J = —2тгг, откуда
Г" ГГ г~
- 2л г = In г + i<p - 2тгг.
г-
При обходе начала координат к раз в направлении хода часовой стрелки получим
ЛС.
— = In г 4- гу> - 2л ik,
к 6N.
Объединив полученные результаты, имеем
= In г 4- г<р 4- 2л ik,
15. Показать, что если путь не проходит через точки
±», то
= — + кл,
4
где к — целое число.
◄ Поскольку то
о о
Если путь интегрирования не охватывает точки ±i, то интеграл не зависит от его выбора и можно
интегрировать, например, по отрезку [0, 1]. Тогда получим:
х=1 Л
х—0 Д
к G Z. ►
о
о
4- Г2
О
о
§ 6. Интеграл типа Коши
189
Пусть кривая, по которой проводится интегрирование, охватывает точку i и состоит из за-
мкнутой кривой и отрезка [0, 1], ориентированных в положительном направлении (рис. 80, а).
Вместо произвольной гладкой или кусочно-гладкой ориентированной кривой можно, согласно
теореме Коши, взять положительно ориентированную единичную окружность с центром в точке
i (рис. 80, б). Пусть Г = (Гt, Г2) — положительно ориентированный путь, состоящий из упомя-
нутой ориентированной единичной окружности и отрезка [0, 1]. Тогда получим:
как интеграл от аналитической функции по замкнутой гладкой кривой, а
1
i f d( if ielt f dx тг
2 J C -i 2 J e1' 7r’ J 1 + X2 4
г 0 0
Пусть Г(1) = (Г, г;), Г(2) = (Г(1), Г). Тогда
J 1+С2 J 1 + С2
Г(1) г<2>
ТГ
----F 2тг.
4
Интегрирование по Г(2) соответствует полному обходу точки i в положительном направлении
два раза и одному интегрированию по отрезку [0, 1]. Полагая Г(3) = (Г<2), Г^*), Г(4) = (Г(3), Г),
находим:
Г!*)
ТГ
=-------1- Зтг.
4
Продолжая этот процесс, после к полных обходов точки i, получим:
df тг
—77 = 7 + ^7Г>
о
Если к полных обходов точки i совершаются в направлении хода часовой стрелки, то
тг
-----&ТГ,
4
кек
о
Оба случая объединяются в один:
тг
= — + Лтг,
4
kez.
J 1 + <2
о
Аналогичный результат получим в случае, когда замкнутая кривая окружает точку — £. ►
190
Гл. 4. Интегрирование в комплексной плоскости.
16. Показать, что если Г = (7, 7ор) — произвольный простой замкнутый контур, не прохо-
дящий через точку а, и п — целое число, то
' 0, если п # -1,
J (z - a)n dz = < 2лг, если п = — 1, а — внутри 7.
г 1 °- если п = — 1, а — вне 7.
◄ Если п / — 1, то по теореме Коши заменяем кривую 7 произвольной окружностью уг =
{z € С : |z — а| < г}, содержащуюся во внутренности или во внешности кривой 7. Тогда получим,
полагая z — а = ге'1, 0 Sj t 2л:
Коши
У (z - a)n dz = i У rn+'ei(n+1)f м = rn+1
г о
ei(n+l)t
П + 1
t~2ir
= 0.
Пусть п = -1, а — вне 7. Тогда функция z >-♦ (z - а) 1 является аналитической и по теореме
Если п = — 1, а — внутри 7, то, заменив кривую 7
окружностью 7г с центром в точке а, принадлежащую вну-
тренности 7, получим
17. Доказать, что
__ j.2 у ТГ _ь-
е cos 2bxdx = —е
2
◄ Пусть L — положительно ориентированная кусочно-гладкая кривая, состоящая из отрез-
ков, параллельных осям координат (рис. 81). Функция_г ь+ е~2 аналитическая в области D,
ограниченной этой кривой и непрерывна в замыкании D. По теореме Коши имеем
У е z dz = 0.
L
Воспользуемся свойством аддитивности криволинейного интеграла второго рода:
— R
о
о
§ 6. Интеграл типа Коши
191
Пусть
После замены х = — t в первом интеграле, получим
cos2bz dx,
R ь R
j e~x dx — 2i e~R +y sin2Rydy — 2eb j e~x cos 2bz dz = 0.
— RO 0
Интеграл
ь
J e'R +y sin 2Ry dy —> 0 при 7? —>+oo,
о
def
dx =
dx = х/тг
(это известный интеграл Эйлера—Пуассона),
Таким образом, перейдя к пределу в (1) при R —> +оо, получим:
х/л — 2е J" е~х cos2bxdx — 0
о
откуда
/ -*2 л -ь2
/ е cos 2ох dx = ---е . ►
J 2
о
ю Г dz
1о. Вычислить интеграл / —-----, Г = (7, 7ор), 7—замкнутая гладкая или кусочно-гладкая
J z + 9
г
кривая, если:
1) точка Зг лежит внутри кривой 7, а точка -Зг вне ее;
2) точка —Зг лежит внутри кривой 7, а точка Зг вне ее;
3) точки ±3г принадлежат внутренности кривой 7.
◄ Поскольку тщ = | (тЬ - гЫ, то
1) Так как точка —3i принадлежит внешности кривой 7, то по теореме Коши
/А=«-
J z + 3t
Г
В интеграле
Г dz
J 2-3»
г
192
Гл. 4. Интегрирование в комплексной плоскости.
вместо кривой 7 можно взять окружность 7r = {z£C:|z — 3i| = г}, принадлежащую внутрен-
ности 7. Тогда получим, после замены z — 3i = re'*, 0 С t С 2тг:
2тг
if dz _ 1 уre _ 2% _ *• f dz
6 J z - 3i 6 J re'* 6 3 ’ J z2 + 9 3
г о г
2) По аналогии с предыдущим, имеем
i Г dz тг Г dz тг
б/ z + 3i~ ~3’ J z2 + 9 ~ Т
г г
3) Применим теорему 4, п. 5.3, к интегралу по положительно
ориентированной полной границе области, состоящей из контуров
Г, Гь Г? (см. рис. 82). Получим, принимая во внимание случаи 1)
и 2):
f dz f dz Г dz тг тг
J z2 + 9 J z2 + 9~J z2 + 9 3 3
Г г, г2
in f z dz
19. Вычислить интеграл / ~Г — (7, 7op), 7 = {z € C : fz - a| = a}, (a > 1).
г
4 . fc-тг
◄ Функция z n z4+l имеет нули в точках zk = vl = e' 2 , fc = 0, 1, 2, 3. Кривая 7 окружает
лишь точку z0 = 1. Записав подынтегральное выражение в виде
z А , Bz2 + Cz + D
z4 - 1 - z-1 + (z + l)(z2 + 1)
легко найдем Л:
В силу свойства аддитивности
f zdz
J ^-'1 =
1
A = lim-------;---=
z->i (z + l)(z2 + 1) 4
интеграла, имеем
1 f dz fBz2 + Cz + D
4/ гл+у (z + d(z2 +1)
г г
л 1 f dz
dz = - ---
4./ z +
z
так как по теореме Коши
f zdz
J -?4-l
г
Г Bz2 + Cz + D „
I --------------dz = 0.
J (Z + l)(z2 + I)
г
Произведя в интеграле замену переменной по формуле z - I = re'*, 0 t С 2%, находим:
2тг
I Г ire'* 2iri tri
= - I —-dt =--------= —. ►
4 J re'1 4 2
0
ez dz
—-----Г = (7, 700), если замкнутая кусочно-гладкая кри-
z2 + а2
г __
вая 7 окружает круг Ка = {z б С : |z| а}, т. е. Ка D, где D — область, 0D = Г.
◄ Разлагая функцию z i-> zf~a2 на простые дроби, получим:
1 _ i_________________i
z2 + a2 2a(z + ie) 2a(z — t'a) ’
20. Вычислить интеграл
§ 6. Интеграл типа Коши
193
Таким образом,
— = ± [ ieZ-dz-± f ie dz.
2тгг J z1 + a3 2~i J 2a(z + ia) 2тгг J 2a(z — ia)
г г г
Применив интегральную формулу Коши (см. п. 5.4), находим:
sin а
е а 1 ( ~t‘
/ ------7 dz - — (е
J z2 + а1 2а '
г
а
1 Г zez
21. Вычислить интеграл ----- / --------dz, Г = (7, 7оР), если точка а принадлежит вну-
2тгг J (z - а)3
г
тренности кусочно-гладкой замкнутой кривой 7.
Ч Пусть
dt.
г
Согласно формуле (2), п. 6.1, имеем
/ ie*
/ --------;dt,
J V- *)3
г
а по интегральной формуле Коши f(z) = zez. Следовательно,
/•л 1 I с ил
LL. Вычислить интеграл ---- / ----------dz, Г = (7, 7„„), 7 — кусочно-гладкая замкнутая
2тгг J z(l — zy
г
кривая, если:
1) точка 0 принадлежит внутренности кривой 7, а точка 1 — ее внешности;
2) точка 1 принадлежит внутренности кривой 7, а точка 0 — ее внешности;
3) точки 0 и 1 принадлежат внутренности кривой 7.
Ч Записав подынтегральную функцию в виде суммы
ег e*(-z2 + 3z — 3)
7+ (z - I)3 ’
получим:
1 fezdz 1 Г е*(—z2-I-3z — 3)
ут /--------h —: / ------------у-----dz — Ii + I2.
2лч J z 2тп J (z - I)3
г г
1) По интегральной формуле Коши 2) = е° = 1. Поскольку подынтегральная функция в
интеграле 12 аналитическая, то 12 — 0 и, таким образом,
1 Г ezdz
2тгг J z(l — z)3
г
2) В рассматриваемом случае Л = 0, поскольку функция гм у аналитическая. Пусть
.. . 1 [ (—t2 + 3t — 3)е*
/(•?) = у? / ----------~.---------
2тг» J t — z
dt.
г
194
* Гл. 4. Интегрирование в комплексной плоскости.
Применив формулу (2), п. 6.1, получим:
(-t2 + 3t - 3)е‘ dt
(t - z)3
Поскольку /(z) = (—z2 + 3z — 3)e2, to
((—z2 + 3z — 3)e2)"
3) Рассуждая так же, как и при решении примера 18, 3), и принимая во внимание результаты,
полученные при решении задач в случаях 1) и 2), можем сразу записать:
1 Г ez е
--- / ----------7 dz — 1 . ►
2тгг j z(l — z)3 2
г
23. Функция f — аналитическая в области, ограниченной простым замкнутым контуром 7,
окружающим начало координат. Доказать, что при любом выборе ветви Ln z
~ f f'(z)Lnzdz = f(zo)-f(O), Г = (7, 7ор),
2?ri J
г
где z0 — начальная точка интегрирования.
4 Интегрируя по частям, получим:
1 Г чт я 1 << м I 1 f
— / /(z)Lnzdz = —/(z)Lnz - — / ---------------dz.
2тгг J 2тгг 11 2?гг J z
г г
Поскольку Lnz|r = 2тгг, то ^/(z)Lnz|r = f(zo). По интегральной формуле Коши
1 f /(z)
— / J—dz = f(0).
2?ri / z
Следовательно,
Lnzdz = /(zo)-/(O). ►
24. Вычислить интеграл I = /—-------------, Г = (7. 7O„), 7 = {z £ С : |z| = 1}, в
J (z-a)n(z-by
г
зависимости оттого, будет ли 1) |а| < |Ь| < 1; 2) |а| < 1 < |Ь|; 3) 1 < |а| < |Ь|.
◄ 1) Точки а
теорему 4, п. 5.3:
и Ь принадлежат внутренности окружности 7, в силу чего можно применить
f dz Г(г — Ь)~" f (z - а)~п
I ---------------= I ----------dz + I -----------dz,
J (z - a)"(z -b)n J (z - а)" J (z - b)n
Г Га ГЬ
и Гь — положительно ориентированные окружности с центрами в точках а
где, например, Г,
и Ь достаточно малых радиусов. Применив формулу (2), п. 6.1, получим:
f(z-bYn 2vi' dn-1
J (z ~ a)n (n — 1)! dzn~l
Га
27Г1~ ( 1)"-1(2п~2)!
(п—1)!' (п-1)!
(а-Ь)2""1’ (1)
Г (z — а)~п 2тг« Д2П-2)!
/ ---------az =-------I—1) -------
J (z-Ь)” (n — l)j (п-1)!
гь
Из (1) и (2) следует, что в этом случае 1 = 0.
(Ь — а)2п-1
(2)
e
2
г
1
1
195
Упражнения для самостоятельной работы
2) Пусть |а| < 1 < |Ь|, т.е. внутренности кривой 7 принадлежит лишь точка а. Тогда
Г^-аГп , А r , ,ч„_। 2tri(2n —2)!
/ —----------dz ~ О, I = / ----------dz = (—1) --------;----------.
у (z-б)” J (z ~ а)" ((П- I)!)2 (а - &)2—1
Гь га
__ 3) При 1 < |а| < |Ь| подынтегральная функция является аналитической в замыкании К, где
К — {z € С : |z| 1}. Тогда по интегральной теореме Коши I — 0. ►
25. Согласно теореме Лиувилля, функция f, аналитическая и ограниченная во всей плос-
f f(z)dz
кости, является постоянной. Доказать эту теорему, вычислив интеграл / -------------, Гл =
У (2 - a)(z - Ъ)
I'll
(Тл, 7д), где 7д = {z € С : |z| = Я} (|а| < R, |Ь| < R) и произведя его оценку при R -+ оо.
◄ Пусть Га и Гь — положительно ориентированные окружности с центрами в точках а и b
достаточно малых радиусов. Применив интегральную формулу Коши (см. п. 5.4), получим:
У ^~adz + J ~bdZ = 27tl[^-b + ^)
Гд Га ГЬ
/(Ь)-/(а)\
b — а у
Поскольку справедлива оценка
/(z) dz
(z — a)(z - Ь)
max |/(z)|
Ц|=я
—Ц-;-----------гт • 2тгй,
(Л - |а|)(Я - |Ь|)
где max |f(z)| М, М = const, то
f f(z)dz . (f(b) - /(а)\
hm / --------------= 0 = 2тгг ----------- ,
J (z — a)(z — b) у b — a j
Гд
откуда V(a € С, b € С) /(а) = /(&), т. е. Vz £ С /(z) = const. ►
Упражнения для самостоятельной работы
1. Вычислить интегралы:
a) f\z\2dz, Г = (7, 7ор), 7 = {z £ С : |z| = 1};
Г
б) J Rezdz, Г = (7, 7ор), 7 = {z € С : |z - 1| = 1}.
Г
2. Вычислить интеграл f е2 dz, где
г
а) Г = (7, 7оР), 7 — ломаная, соединяющая точки 0, 1 и 1 + i;
б) 7 — ломаная, соединяющая точки 0, i и 1 + i.
1
3. Вычислить J|z|dz, если путями интегрирования служат: а) прямолинейный отрезок;
-1
б) верхняя половина единичной окружности; в) нижняя половина единичной окружности.
4. Вычислить интегралы вдоль отрезка Г прямой с началом в точке z\ = 0 и концом z2 —
| + i^ от следующих функций: a) z ►-+ е,х| Rez; б) z >-+ ег Rez; в) z >-> 7^.
5. Вычислить f tgzdz, Г = (7, 70р), где 7 — дуга параболы у = х2, соединяющая точки
г
Z| = 0 и z2 = 1 + i.
6. Вычислить J , г = (7, 7оР)> 7 = {z £ С : |z| = 1}, V4z*+4z + 3\ > 0.
р V*z*+4z+3 •« = !
196
Гл. 4. Интегрирование в комплексной плоскости.
7. Пусть функция f непрерывная при |z - z0| > г0 и г • max |/(z)| —> 0 при г —► +оо.
|z-z0|=r
Доказать, что lim J f(z)dz = О, Г = (7, 7ор), 7 = {z € С : |z - z0| = г}.
т—» + оо р
8. Пусть функция / непрерывна при 0 < |z - z0| < R и г • max |/(z)| —> 0 при г —> 0.
|2-z0| = r
Доказать, что lim f f(z) dz = 0, Г = (7, 7ор), 7 = {z € С : |z - z0| = г}.
r-^° г
9. Пусть функция f непрерывна на окружности 7 = {z £ С : |z| = 1}. Доказать равенство
/ /(z) dz = - f dz, Г = (7, 7оР)
Г г
10. Пусть а € С, а функция f — аналитическая в круге К = {z 6 С : |z| 1}, Доказать, что
/(г) ( 2тгг/(0), ______ если |а| < 1,
ак ~ ( 2"1 > если Н > !•
11. Путем вычисления интеграла тЛ Г---------41—г = (7, 7ор), 7 = {z £ С : |z| = 1},
доказать, что при 0 < а < 1
2тг
Г ____dt___ ___ 2тг
J 1+а2 — 2а cos £ 1—а2 ‘
0
12. Вычислить интеграл J sln zz2^~'} dz, Г = (7, 7ор), 7 = {z g С : |z| = 2}.
г
13. Пусть R(.z) — правильная рациональная дробь, 7 - кусочно-гладкая замкнутая кривая,
охватывающая все нули этой дроби, а точка z лежит во внешности 7. Доказать формулу
; да = m г = (7,7оД
г
14. Пусть функция / — аналитическая в некоторой области D с жордановой границей 9D,
непрерывна в замыкании D и постоянна на 9D. Доказать, что она постоянна и в D.
15. Найти интегралы типа Коши:
а) Л2) = 277 f Г = <7. 7ор), 7 = {z € с : ICI = О;
б) g(z) = 277 / f(2C2+5C+2)(C-2) ,2?={z€C.|z|<1H |z + 3 I > 3 }.
od
16. Пусть функция f — аналитическая в круге KRl = {z € С : |z| < R[} и |a| < R < R].
Доказать, что
i
Л<*) = Г = (7, 7оР), 7 = {2 е С : |z| = R}.
г
Вывести отсюда формулу Пуассона
Нге’Л — — Г <д2~г2)/<Де“<’)<;у (0 < т < R}
JVe > - 2тг J R^—2Rr cosffl-^+r2 Г Л>-
о
17. Пусть функция f — аналитическая в круге KR = {z е С : \z - а\ < R}. Доказать формулу
2тт
/'(а) = ± f Ref (а + reie)e-iedd.
о
18. Доказать, что
f chzctgzdz - 2iri- ^sh (n € N), Г = (7, 7op), 7 = {z € C : |z| = (n + |) ?r} .
г 2
Глава 5
Ряды аналитических функций.
Изолированные особые точки
В этой главе изучаются равномерно сходящиеся ряды, членами которых являются аналитические
функции. Основное внимание уделяется разложению аналитических функций в ряды Тейлора и
Лорана, а также классификации изолированных особых точек аналитических функций, основан-
ной на разложении их в ряд Лорана.
§ 1. Ряд Тейлора
1.1. Общие сведения о рядах.
Числовой (функциональный) ряд можно интуитивно понимать как последовательность (zn)
комплексных чисел (последовательность (/„) функций), которые строятся по определенному за-
кону и последовательно складываются. В соответствии с этим числовой (функциональный) ряд
записывают в виде
Zi + гг+ ... + z„ + ... или ^2 zn
П=1
/1(*) + fl(z) + ... + fn(z) + ... или У2 fn(zH , (1)
п= 1
где zn (fn) называют общим членом ряда, а число (функцию)
n z П х
5„ = 52^ Vn € N (z » Sn(z) = ^2fk(z) Vn e N
fc=l ' b=l '
— его частичной суммой. Предел последовательности (Sn) частичных сумм ряда, если он суще-
ствует, называется суммой ряда и обозначается тем же символом
О© / оо
(е;/п(2)
71=1 71 = 1
что и ряд (1).
Обозначения ряда и его суммы различают по смыслу текста, в котором они встречаются. В част-
ном случае, когда члены ряда — действительные числа, его суммой могут быть символы +оо
и —оо. Однако, числовой ряд называется сходящимся, если у него существует сумма и она конеч-
ная, т. е. является действительным или комплексным числом. В остальных случаях, когда сумма
числового ряда не существует или является бесконечной, ряд называется расходящимся.
Для функциональных рядов рассматриваются понятия поточечной и равномерной сходимо-
сти, о чем речь пойдет позже.
В некоторых книгах по математическому анализу появилось формальное определение ряда
как пары последовательностей
ОО z / П \ \ / СЮ ✓ /71 \ \\
j2zn=4(Zn)„eN, (£>) ) = (52^(2)) ))’ (3)
п=1 ' 4=1 AgN / Х„=1 X Ч=| AgN / /
но для ряда и его суммы сохраняется одно и то же обозначение.
Определение ряда равенством (3) не является единственно возможным.
198
Гл. 5. Ряды аналитических функций. Изолированные особые точки
В настоящей книге ряд будем обозначать специальным символом 57 zn (57 fn) и определять
не как пару двух последовательностей, а как последовательность чисел (функций) вида (2):
е-=(е^ Y
\ k=l Лем \ \ j,=1 Лен /
Для суммы ряда, когда она существует, сохранено прежнее обозначение
ОС п / О© п \
=f lim E2fc ( = lim
n = l fc = l n=I fc=l
(4)
(5)
Таким образом, символы 57 zn и 57 zn имеют различный смысл. Первый из них обозначает
тг= 1
ряд, а второй — сумму ряда, когда она существует. Здесь проводится аналогия с обозначениями
функции f и ее значения f(z).
Теорема 1 (необходимый признак сходимости ряда). Если ряд сходится, то после-
довательность его членов стремится к нулю.
◄ Пусть ряд 57 zn (57 /п) сходится, S — его сумма (5(г) — его сумма в точке z 6 Ds),
(Sn) ((Sn(z))) — последовательность его частичных сумм. Тогда
zn=Sn- Sn_! S - S = 0 (/„(г) = Sn(z) - 5n_t(z) -+ S(z) - S(z) = 0). ►
Теорема 2 (критерий Коши).
тогда и только тогда, когда
Ряд 57zn (57 /п) сходится (сходится в точке z € Dfn)
(Ve > 0)(Эпг € N)(V(n пс, р 6 N))
п+р
Е-
fc=n+l
(6)
< е
е
< Условие теоремы означает, что последовательность (Sn) ((Sn(z))) частичных сумм ряда
фундаментальна. Поэтому утверждение следует из критерия Коши для числовой последователь-
ности. ►
Если числовой ряд сходится абсолютно, т.е. сходится ряд 57 lznl, то его сумму будем обо-
значать символом 57 zn, подчеркивая этим, что любая перестановка ряда имеет ту же сумму, что
пек
и сам ряд. Этим свойством не обладают условно сходящиеся ряды.
Поскольку последовательность комплексных чисел может рассматриваться как ряд, то они
являются различными названиями для одного и того же объекта — отображения множества N
в С. Поэтому с рядами можно производить те же операции, что и с последовательностями.
1.2. Последовательность функций и функциональный рад. Поточечная сходимость.
Определение 1. Отображение Ф множества N в множество всех функций называется функ-
циональной последовательностью. Значение отображения Ф(п) = /„ называется ее п-ным
членом.
Для последовательности функций примем обозначение (/„).
Определение 2. Пусть / : С —> С, /„ : С —> С и Vn € N Dfn = Df = Z. Последователь-
ность (fn) называется поточечно сходящейся к функции f, если Vz £ Z f(z) = lim f„(z).
п —»оо
Если последовательность (/„) поточечно сходится к функции /, то пишем fn~* /• В случае,
когда важен сам факт поточечной сходимости и не играет роли функция /, будем писать /„ —
Определение 3. Пусть (/„) — последовательность функций fn : С —► С, Dfn = Z. Функци-
п
ональная последовательность (Sn), где S„(z) — 57 fk(z) € Z, называется функциональным
k=i
рядом и обозначается символом 57 /» Функция S„ называется п-частичной суммой ря-
да 57 fn, и f„ — его п-членом.
§ 1. Ряд Тейлора
199
Определение 4. Поточечной суммой ряда J3 /п на множестве Z называется поточеч-
ный предел его частичных сумм, если он существует. Ряд называется поточечно сходящимся,
если его поточечная сумма существует и является конечной.
Поточечная сумма ряда УЗ fn обозначается символом УЗ /„. Таким образом,
Т1=1
ОО \ п
V /„ ) (2) = lim V Л (2) Vz € Z.
* / п—»оо
п=1 7 fc=l
Пусть -D.sn = Z Vn Е N. Тогда последовательность функций (5П) можно рассматривать
как ряд — S„_|), где S0(z) = 0 Vz € Z. Следовательно, функциональные ряды, подобно
числовым, представляют собой особую форму изучения последовательностей функций.
1.3. Равномерная норма функции.
Равномерная сходимость последовательности функций и функционального ряда.
Введем в рассмотрение равномерную норму функции, обобщающую модуль числа и совпада-
ющую с ним, когда функция постоянная. Это новое понятие используем при построении равно-
мерного предела функциональной последовательности.
Определение 1. Число
sup |/(z)|, (1)
z£Df
конечное или бесконечное, называется равномерной нормой функции f и обозначается ||/||.
Отметим основные свойства равномерной нормы функции.
Теорема 1. Для любых функций f : С —» С, g : С —♦ С и VA € С справедливы соотношения:
1) II7II = 0 => / = 0;
2) ||А/|| = |А| ||/||;
3) II/4-3'11 < 11/11 + 1Ы1, если Df П Dg £0.
◄ 1) Ц/H = 0 => sup |/(z)| = 0 =+ |/(z)| = 0 Vz € Df =+ /(z) = 0 Vz € Df => / = 0;
2) ||A/|| = sup |A/(z)| = sup |A| |/(z)| = |A| sup |/(z)| = |A| ||/||.
3) Пусть z E Df П Dg #0. Тогда
I/O) + </(z)| |/(z)| + |<7(z)| C sup |/(OI + sup ]p(T)| = H/Ц + ||p||.
t£Df r£Dg
Согласно определению точной верхней грани имеем
sup |/(z) + <z(z)| II/II +||з1|, Т.е. II/ + i?|| 11/11 + ||р||. ►
Теорема 2. Функция / : С -+ С ограничена тогда и только тогда, когда ||/|| < +оо.
Ч Действительно,
П/П = sup |/(z)| < +оо О ЗМ Е R : Vz g Df |/(z)| C. M О / — ограниченная. ►
z£Df
Для модулей чисел z g С, ш 6 С справедливо равенство |zw| = |z| |w|. Для равномерных
норм такого равенства не существует, например, пусть /(z) = 1, если |z| < 1, /(z) = 0, если
|z| 1, a g = 1 -/. Тогда fg = 0, ||/р|| = 0, ||/|| = 1, ||р|| = 1, т.е. ||/р|| ||/||||з||.
Однако справедливо утверждение.
Теорема 3. Пусть f : С —» С, g : С —» С. Если Df П Dg ft0, то
11/3II 11/11 • Нз11 (2)
◄ Пусть z G Df п Dg. Тогда |/(.z)<7(2)l = |/(^)| |p(^)l 11/11 НрН- Из определения точной
верхней грани следует неравенство
sup \f(z)g(z)\ Н/Н ||<?||, т.е. ||/з1| ^ ||/||||р||. ►
Определение 2. Пусть Z = Dy — Df„ Vn € N. Последовательность функций (/„) называется
равномерно сходящейся к функции f на множестве Z, если ||/„ — /|| —► 0 при п —» оо.
200
Гл. 5. Ряды аналитических функций. Изолированные особые точки
При этом функцию f называем равномерным пределом последовательности (fn) и пишем
f„ =4 f, или f„ =4 f на Z.
Теорема 4. Если fn=if,mofn-^f.
◄ Пусть Z — Df = Dfn Vn € N и z £ Z. Тогда при n —► oo имеем
l/(z) - /„(*)1 С ||/ - mi - 0,
Следовательно, /п -+ / • ►
Следствие. Если последовательность функций (/„) сходится равномерно, то ее равномерный
предел — единственный.
Теорема 5 (о линейности равномерного предела). Если fnz3f,gnzz$g,Z = Df =
Dg = Dfn = DSn Vn e N, mo VA £ C fn + Xgn =3 f + Xg.
◄ Имеем при n —> oo:
ll(/„ + Xgn) - (/ + Ap)|| ||/n - /Ц + |A) ||Sn - g\\ - 0,
следовательно, /„ + Xgn =3 / + Xg. ►
He все теоремы о пределах сходящихся числовых и равномерно сходящихся функциональных
последовательностей аналогичны друг другу. Это объясняется тем, что равномерная норма, в
отличие от модуля числа, может принимать значение +оо.
Приведем пример двух равномерно сходящихся последовательностей функций, произведение
которых сходится неравномерно.
Пусть V(n £ N, z € С) /n(z) = z, /(z) = z, g„(z) = Тогда /п =$ /, <Zn =) 0. Одна-
ко, V(n £ N,z £ О (/np„)(z) = J, ||/npn - 0|| = ||/np„|| = sup И = +oo, т.е. сходимость
zee
неравномерная.
Определение 3. Пусть f„:C—♦ С и Vn € N Dfn = Z. Последовательность (/„) называется
равномерно фундаментальной, если (Vs > 0) (Зпе 6 N) (V(n ne, р £ N)): ||/„+р - /п|| < е.
Числовую последовательность можно рассматривать как частный случай последовательности
постоянных функций, при этом понятия фундаментальности и равномерной фундаментальности
совпадают.
Теорема 6 (критерий Коши). Последовательность (frl) равномерно сходится тогда и толь-
ко тогда, когда она равномерно фундаментальна.
◄ Необходимость. Пусть /п д / и г > 0. Пользуясь определением равномерной схо-
димости, найдем такой номер nE £ N, что Vn пе ||/„ - /|| < f. Тогда V(n n£, р € N)
||/п+р - /II < f - Следовательно, V(n пг, р £ N) ||/п+р - /„|| ||/п+р - /|| + ||/ - /„|| < е, что
означает равномерную фундаментальность последовательности (/„).
Достаточность. Пусть последовательность (/„) равномерно фундаментальная и z € Z.
Тогда из оценки
1/п+Р(-г) - /„(z)| < ||/п+р - /„||, (3)
справедливой V(n £ N, р £ N), следует фундаментальность числовой последовательности (/n(z)).
Согласно критерию Коши, для последовательности комплексных чисел существует lim fn(z),
п—ИЗО
который обозначим через /(z). Пусть е > 0. Поскольку последовательность (/п) равномерно
фундаментальная, то существует такое ne £ N, что V(n ne, р € N) выполняется неравенство
ll/n+p - /nil < е. В силу неравенства (3) V(n пе, р £ N, z £ Z) имеем
1/п+р(«) ~ /n(z)| < е.
Перейдем в этом неравенстве к пределу при р —> оо. Получим V(n п,, z £ Z) неравенство
l/(z)-/n(z)|Ce.
Согласно определению точной верхней грани, Vn пе ||/ — /„|| е, откуда следует, что /п гЗ /
на Z. ►
Определение 4. Пусть /„ : С —► С, Dfn = Z Vn € N. Ряд называется равномерно
сходящимся, если последовательность его частичных сумм сходится равномерно.
Сумму равномерно сходящегося ряда назовем равномерной суммой.
§ 1. Ряд Тейлора
201
Определение 5. Пусть /п : С —> С, Dfn — Z Vn 6 N. Ряд удовлетворяет рав-
номерному условию Коши, если последовательность его частичных сумм является равномерно
фундаментальной.
Критерий Коши, доказанный для равномерно фундаментальной последовательности, сфор-
мулируем в терминах теории функциональных рядов.
Теорема 7 (критерий Коши для функционального ряда). Пусть /п : С -+ С,
D;n = Z Vn € N. Ряд УУ fn сходится равномерно тогда и только тогда, когда он удовлетворяет
равномерному условию Коши.
1.4. Нормальная сходимость функционального ряда.
Признаки Вейерштрасса, Абеля и Дирихле
равномерной сходимости функциональных рядов.
Определение 1. Пусть f„ : С С, Dfn — Z Vn € N. Ряд f„ называется нормально
сходящимся, если сходится ряд УУ ||ЛП-
Если все члены ряда УУ fn постоянны, то его нормальная сходимость равносильна абсолют-
ной сходимости числового ряда.
Теорема 1. Пусть fn :С-» С, Dfn = Z Vn £ N. Если ряд УУ /п сходится нормально, то он
является равномерно сходящимся.
◄ Из сходимости числового ряда УУНЛП следует, что он удовлетворяет критерию Коши:
(Ve > 0) (Зпе 6 N) (V(n > nE, р G N)): УУ ИЛИ < £•
Из неравенства
fc=n+1
п+р
Е А
Jc=n +
п+р
Е
k=n+l
выполняющегося V(n € N, р € N), и теоремы 7, п. 1.3, следует равномерная сходимость ря-
да уу fn. ►
Следствие (мажорантный признак Вейерштрасса равномерной сходимости
функционального ряда). Пусть fn : С —> С, Dfn = Z Vn g N. Если существует такой
сходящийся числовой ряд УУ ап, что Vn g N ||/„|| ап, то ряд УУ Л сходится равномерно.
В качестве примера исследуем на равномерную сходимость ряд УУ/„, где /п(х) = 1+,
0 х < -t-оо.
Поскольку Л(0) = 0 и lim /„(ж) = 0, то функция /п имеет Vn G N локальный максимум,
1- 4 2
являющийся одновременно ее равномерной нормой. Решая уравнение /„(ж) = = О,
получаем: жп = ~2, ИЛИ = Л(®п) = • Так как числовой ряд УУ сходится, то по теореме 1
ряд УУ fn сходится равномерно. Если взять ап = Л, то ||Л11 < ап и ряд УУ Л равномерно
сходится по мажорантному признаку Вейерштрасса. ____
Пусть fk : С —> С (к = 1, n), : С —» С (к = 0, n), Djk = DSk = Z. Тогда Vz G Z
справедливо тождество Абеля
п п — I
Е -Л-1Л)) = fn(z)gn(z)- ЛЛ)ЗоЛ) - Е(^+1^ “ ЛСО)^)-
fe=l fc=l
(1)
Действительно,
Ел(эь -gt-i) = Л(^1 - до) + fi(g2 - gi) + + f„(gn -gn-i) =
h=l
n— 1
fi9o H" (/i fi)9i И- • • • *1" (fn~i i 4* fn9n fn9n f\9o ~~ ^(/fc+i fk)9k‘
fc=i
Тождество (1) является источником получения признаков равномерной сходимости функци-
ональных рядов.
202
Гл. 5. Ряды аналитических функций. Изолированные особые точки
Теорема 2 (о равномерной равносходимости функциональных рядов, связан-
ных преобразованием Абеля). Пусть последовательность функций (fngn) сходится равно-
мерно на множестве Z. Тогда функциональные ряды, сходящиеся поточечно на множестве Z,
У /п(Рп - 5n-i), 5о = О, (2)
22<Ш„+1-Л) (3)
сходятся равномерно или неравномерно одновременно.
Ч Пусть ряд (3) равномерно сходится на множестве Z. Согласно теореме о линейности
равномерного предела и тождеству Абеля
п п — 1
У -gt-i) = /„g„ ~ У д^(Л+1 - A) VneN, (4)
k=i k=i
ряд (2) сходится равномерно на множестве Z. Аналогично ряд (3) равномерно сходится, если
ряд (2) является равномерно сходящимся. ►
Определение 2. Последовательность комплексных чисел (zn) называется бимонотонной, если
i(n е N, р € N)
п+р
У lZ* + l 2
fc=n + l
п+р
У (Zk+l - Zk)
k=n +1
(5)
Смысл термина “бимонотонность” поясняет следующее утверждение.
Лемма. Пусть Vn € N zn = хп + iyn. Если последовательности (хп), (уп) монотонны, то
последовательность (z„) является бимонотонной.
Ч Имеем V(n С N, р € N)
п+р п+р п+р
У l-Zfc+1 - Zfcl 2 У |zfc+1 - XCfcl + У ll/fe+1 - 9k\ =
fc=n + l fc=n+l fc=n + l
n+p
n + p
n+p
У (xk+t - xk) + У (yk+l - yk) < 2 У (zk+l - zk) . ►
Теорема 3. Если 'iz € Z последовательность комплексных чисел (fn(z)) бимонотонная и
sup llsdl sup [|/fc - fn\\
то ряд 52.9„(/„+i ~ fn) сходится равномерно.
Ч Пусть z C Z. Тогда
n+p
У 9k(.z)(fk+dz) - fk(z)) <7
fc=n + l
(6)
n+p
У(Л+1(г) - fk(z))
п+р
У, 1р*=(-г)| 1Л+1 (z) - fk(z)\ < sup ||pt||2
k>n
2 2 sup ||sfc|| |/„+p+i(z) - /„(z)| 2 sup |Ы| sup \\fk - fn||. (7)
fc^n fc J>n
Из оценки (7) и критерия Коши для функционального ряда следует утверждение теоремы. ►
Теорема 4 (Абеля). Пусть 'iz g Z последовательность комплексных чисел (f„(z)) бимоно-
тонная. Если ряд 52 ipn сходится равномерно и ||/„|| = 0(1), то ряд 52 fn<pn является равномерно
сходящимся.
оо п
Ч Пусть Ф = 52 Уп- Полагаем дп = 52 Vk - Ф 'in € N. По условию ||д„|| = о(1). Поскольку
n=l k = l
sup ll^ll sup ПЛ - /„II = o(l)O(l) = 0(1) и 'in 2 <pn = g„ - g„_i, то выполнены все условия
k^n
теоремы 3. Поэтому ряд 22p„(/„+i - /„) равномерно сходится. Так как ||/„р„|| 55 ||/„||||р„]| =
О(1)о(1) = о(1), то по теореме 2 ряд 52 /„¥>„ равномерно сходится. ►
§ 1. Ряд Тейлора
203
Теорема 5 (Дирихле). Пусть Vz
нотонная. Если
£ Z последовательность комплексных чисел (fn(z)) бимо-
= 0(1) и НДЦ = о(1),
(8)
Так как sup |Ы1 ' sup ||Д - /п|| = О(1)о(1) = о(1) и
fc=l
fe=i
то ряд У fnpn равномерно сходится,
п
◄ Полагаем Vn £ N gn = У Vk •
k=t
Vn^ 2 gn -gn-i = Vn, то, согласно теореме 3, ряд У5n(/n+i - fn) сходится равномерно. Кроме
того, ||/„р„|| ||/„|||Ы| = о(1)О(1) = о(1). По теореме 2 ряд У/п(ап сходится равномерно. ►
Пример 1. Исследовать на равномерную сходимость ряд У , если ф„(х) = УУ V(n £ N,
х Е (0, +оо)).
Воспользуемся признаком Дирихле, обозначив V(n 6 N, х £ (0, +оо)) fn(x') = <рп(х) -
(-1)". Последовательность (/п(ж)) является монотонной Vx S (0, +оо) и тем самым бимонотон-
п
ной. Далее, ||/п|| = £ = о(1), У Vk = 0(1)- Следовательно, выполнены все условия признака
ь=1
Дирихле, т.е. ряд сходится равномерно.
Пример 2. Доказать, что ряд У', у- сходится равномерно в интервале (-1, 0), а ряд У | У |
в этом же интервале сходится, но не равномерно.
На рассматриваемом множестве ряд имеет вид У (-1)" . Числовой ряд У сходится,
а поскольку его члены не зависят от х, то эта сходимость равномерная. При каждом х £ (-1, 0)
последовательность (|х|п) монотонная и ограниченная. По признаку Абеля ряд У у сходится
равномерно на интервале (-1, 0).
Исследование ряда У |у | на равномерную сходимость на интервале (—1, 0) равносильно
исследованию ряда У У на равномерную сходимость на интервале (0, 1). Сумма его п-остатка
rn = n^i~j —* О п₽и п °°- Оценим ||г„ - 0|| = ||гп||. Поскольку точка х„ = 1 - принадлежит
интервалу (0, 1) Vn > 1 и гп(хп) = (1 - ^)"+' —> е~1, то ||гп|1 т4» 0 при п —» оо и ряд сходится
неравномерно.
(П+j ч Z П \
У Д I называется п-остатком ряда У f„= ( У Л )
A:=n+1 ZjgN 4 = 1 ZngN
Если ряд У fn сходится равномерно, то, очевидно, его п-остаток равномерно сходится к
нулю.
1.5. Функциональные свойства равномерной суммы функционального ряда.
Теорема 1. Если функциональный ряд У /п сходится равномерно в области G С С и все
его члены являются непрерывными функциями в точке Zq Е G, то его сумма S будет непрерывной
функцией в этой точке.
◄ Пусть е > 0. В силу равномерной сходимости ряда У /п найдется такое n£ Е N, что
fc = n+l
Выберем h > 0 из условия Kk C G, где Kh = {z Е С : |z — z0| h}, рассмотрим Vz E Kh
разность
S(z)-S(z0) = S(z')-Sn,(z) + Snc(z)-Snt(zo)+Snc(zo)-S(zQ)= 5? fk+Snt(z')-Snc(z0) + ЛОо)
204
Гл. 5. Ряды аналитических функций. Изолированные особые точки
и оценим ее. Получим
\S(z) - S(z0)| <
ОО
Е fk (г)
k~ne+ 1
оо
52
к—пе+1
+ |5пе (г) - Snc (z0)| <
ОО
Е
fc = n + l
«S 2
2
+ |5Пе (z) - Snc (z0)| < -е + |5Пе (z) - S„e (z0)|.
Поскольку члены ряда являются непрерывными функциями в точке z0, то и их конечная
сумма Snc непрерывна в этой точке. Поэтому по заданному г > 0 найдется такое <5 > 0, что из
условия h < <5 Vz € выполняется неравенство |5ne(z) - S„c (z0)| < f- Объединяя полученные
оценки, имеем: Ve > 0 35 > 0 такое, что h < 6 => Vz G Kh |5(z) - S'(z0)| < e, т.е. сумма S
равномерно сходящегося функционального ряда является непрерывной функцией в точке z0. ►
Следствие. Если члены ряда 5У /„ непрерывны в области G и ряд сходится равномерно в G,
то его сумма S является непрерывной функцией в этой области.
Теорема 2 (о почленном интегрировании равномерно сходящегося функцио-
нального ряда). Пусть члены ряда 5У /п являются непрерывными функциями в области G С С,
7 С G — гладкая или кусочно-гладкая жорданова кривая и ряд сходится равномерно в G. Тогда его
можно интегрировать почленно вдоль кривой Г = (7, 7ор) и при этом
У S(z)dz = ^ У fn(z)dz. (1)
г п=| г
Ч Поскольку п — остаток равномерно сходящегося ряда равномерно сходится к нулю, то
Ve > 0 Зпг € N: Vn > n, ||r„|| = ||5 - Sn|| < е. По теореме 1 сумма ряда S является непрерывной
функцией в каждой точке кривой 7, поэтому интеграл J S(z)dz существует. Из оценки
г
l-S(z) - Sn(z)| |dz|
где I — длина кривой 7, следует, что
г
г
ffc(z) dz —► 0 при п —> оо, т. е.
справедлива формула (1). ►
Теорема 3 (Вейерштрасса). Пусть (fk) — последовательность функций, аналитических в
некоторой области D СС и ряд 5У fn равномерно сходится на любом компактном подмножестве
этой области. Тогда:
1) сумма ряда f аналитическая в D;
2) ряд можно почленно дифференцировать в каждой точке области D сколько угодно раз;
3) все продифференцированные ряды равномерно сходятся на любом компактном подмножестве
области D.
Ч 1) Пусть z0 € D — любая точка. Рассмотрим круг КТ = {z € С : \z - z0| < г} <s D.
Согласно условию теоремы ряд fn равномерно сходится в круге Кг и по теореме 1 его сумма f
является непрерывной функцией Vz G Кг. Пусть 9G — положительно ориентированная граница
треугольника G С Кт. Поскольку ряд 5У fn равномерно сходится на 9G, то согласно теореме 2
его можно почленно интегрировать:
OG
f(z}dz
Е У /„(z)dz.
n=1 OG
§ 1. Ряд Тейлора
205
По теореме Коши Vn g N f fn(z)dz = 0, вследствие чего f f(z)dz = 0. Функция / удовле-
8G 8G
творяет условиям теоремы Морера (см. п. 6.3, гл. 2), поэтому является аналитической в круге Кг.
В силу произвольности Kr С D приходим к выводу, что f g A(D).
2) Пусть zq € D — произвольная точка и Кт = {z g С : \z - z0| < г} <s D. Для каждой точки
z g дКт и k g N выполняется условие
fc!
2tti(z — z0)'c+1
fc!
2?rrA:+1
< +oo.
(2)
Из равномерной сходимости ряда 5? fn и условия (2) следует равномерная сходимость ряда
22 у.......(3)
2iri ^>(z- z0)fc+1 k ’
Пусть f — равномерная сумма ряда 52 А- Так как ряд (3) можно почленно интегрировать по
кривой дКт и его сумма равна , то
2L [ А0 я _ v* fe! f
2тгг J (z- z0)k+l 2tri J (z - z0)t+1 W
9Kr SK,
Принимая во внимание формулы для производных от интеграла Коши, имеем
ОО
/<fc,(z0) = £/<fcW. (5)
nz=l
Поскольку zo € D — произвольная точка, то формула (5) справедлива Vz g D.
3) Пусть К — произвольное компактное подмножество области D и z0 g К — любая точка.
Выберем число d > 0 так, чтобы выполнялось включение K2d = {z g С : |z - z0| < 2d} <s D. Ряд
57 fn сходится равномерно на окружности dK2d = {z g С : \z — z0| = 2d}, т. e. Ve > 0 3nr g N:
V(n Jne,zg dK2d}
У? fm (0
< г
(6)
(n-остаток ряда 52 А равномерно сходится к нулю). Имеем Vz g K2d :
ОФ
,, . SAW
V/-’(z)=— / тГ ^dl}. (7)
Z—' 2тгг J (; - z)**1
m~n я
Пусть z g Kd = {z g C : \z — z0| < d} и £ g dK2d. Оценим n-остаток ряда 52 f™}- Приняв во
внимание, что |£ — z| > d, а также неравенство (6), получим V(n пс, ( g dK2d) оценку
fc!4?rde 2fc!e
2irdk dk ’
(8)
не зависящую от z g Kd Следовательно, ряд 52 fi^ сходится равномерно в круге Kd, т. е. в не-
которой окрестности точки z0. Поскольку любое компактное подмножество области D согласно
теореме Бореля—Лебега может быть покрыто конечным семейством окрестностей, в каждой из
которых по доказанному ряд 52 /т* сходится равномерно, то он сходится равномерно на таком
множестве. ►
Пример. Доказать, что ряд удовлетворяет условиям теоремы Вейерштрасса в обла-
сти D = {z 6 С : | Imz| < 1пЗ} и найти /’(0).
206 Гл. 5. Ряды аналитических функций. Изолированные особые точки
Очевидно, что Vn € N /„ g A(D), где fn(z) = . Принимая во внимание равенство
| sinz|2 = sin2 х + sh2 у, при \у\ 01пЗ, 0 0 < 1, получаем оценку
lAC2)! 3-п + 3-п<1-в),
из которой по мажорантному признаку Вейерштрасса следует равномерная сходимость ряда 5? fn
в области D. Сумма ряда / является аналитической функцией в области В и по доказанной
теореме его можно почленно дифференцировать, т. е.
, х—' и cos nz . v—' Ц 3
П = 1 п = 1
Применим теперь теорему Вейерштрасса к рядам определенного вида.
1.6. Степенные ряды.
Ряд J2/„, где fn(z) = an(z - z0)n, п € Zo, ап € С, ап = const, z0 € С, z € С, называется
степенным. Частичные суммы этого ряда являются алгебраическими многочленами, и поэтому
ОО
его сумму ^2 an(z — -о)” можно рассматривать как дальнейшее обобщение понятия многочлена.
71=0
Члены степенного ряда являются аналитическими функциями во всей плоскости С. При
определении степенного ряда возникает вопрос, в какой области он сходится равномерно и, сле-
довательно, по теореме Вейерштрасса определяет аналитическую функцию.
Каждый степенной ряд 52 a„(z - z0)n обладает замечательным свойством: с ним связано
число 0 R +<х>, называемое его радиусом сходимости. Зная это число, можно ответить
на вопросы о поточечной, равномерной и нормальной сходимости, указать свойство его членов
(ограниченность, стремление к нулю). Наиболее простой задачей является исследование членов
ряда
Y^an(z - z0)" (1)
на ограниченность. Ее решение служит основой определения радиуса сходимости степенного
ряда.
Определение 1. Радиусом сходимости степенного ряда (1) называется число
R = sup{r 0 | апгп = 0(1)}. (2)
Поскольку {г 0 | апгп = 0(1)} #0, то точная верхняя грань этого множества в R суще-
ствует.
Теорема 1. Пусть R> 0 и 0 < г < R. Тогда ряд (1) сходится нормально в круге Kr = {г € С :
\z - ZO\ < г}.
Ч По определению точной верхней грани существует такое г1; что г < п Л anr" = 0(1).
Пусть V(z S Кг, п 6 N) fn(z) = a„(z - z0)n. Тогда
Ш1 = Ыгп = Кг?|(-0 =О((^) )
Так как 0 < < 1, то по признаку сравнения числовых рядов ряд 5? ||/nII сходится, что по
определению означает нормальную сходимость ряда J2 fn, т. е. степенного ряда (1) в круге Кг. ►
Следствие 1. Пусть R > 0. Тогда ряд (1) поточечно сходится в круге KR. Если R < +оо, то
ряд (1) расходится поточечно вне круга KR, т.е. в тех точках z € С, для которых \z — z0| > R.
Следствие 2. Пусть R > 0 и \z — z0| < R. Тогда an(z — z0)n = 0(1). Если R < +oo и
\z - z0| > R, mo an(z - z0)n / 0(1).
Следствие 3. Пусть R > 0 и \z — z0| < R. Тогда an(z — z0)n = o(l). Если R < +00 и
|z - z0| > R, mo an{z - z0)" 0 o(l).
Следствие 4. Пусть R > 0 и \z — z0| < R. Тогда ряд (1) сходится абсолютно в круге Кя. Если
R < +оо и \z - z0| > R, то ряд (1) не будет абсолютно сходящимся.
Следствие 5. Если R>0u0<r<R,mo ряд (1) сходится равномерно в круге КТ.
§ 1. Ряд Тейлора
207
Теорема и следствия из нее не содержат никакой информации о свойствах степенного ряда
на окружности 7д = {z € С : |z - z0| = R}- В силу формул Эйлера ряд (1) на окружности -yR
превращается в тригонометрический ряд. Вопрос о поведении степенного ряда на границе круга
сходимости KR требует в каждом конкретном случае специальных исследований. Может слу-
читься, что в некоторых точках z g 7д ряд сходится, а в некоторых — расходится. Существуют
также степенные ряды, сходящиеся или расходящиеся в каждой точке z g 7д.
Теорема 2 (первая теорема Абеля). Пусть числовой ряд
У^ап(21 - г0)п
(3)
сходится и Z[ z0. Тогда степенной ряд (1) сходится в круге К = {z €'С : |z - z0| < \zt — z0|}.
-< Поскольку ряд (3) сходится, то, согласно следствию 1, \z{ - z0| < R. Следовательно,
К С KR, где KR — круг сходимости ряда (1). ►
__ Из теоремы 2 и следствия 5 получаем, что ряд (1) сходится абсолютно и равномерно в круге
КТ = {z € С : |z - z0| г}, где г < |zi - z0|.
Теорема 3 (Коши — Адам ар а). Пусть R — радиус сходимости ряда (1) и I = lim \/|ап|.
Тогда R= у, причем R = +оо, если I = 0 и R = 0, если I = +оо.
< Очевидно, что
lim y/\a„(z - z0)n| = l\z - z0|.
(4)
Если Z = 0, то по радикальному признаку Коши Vz g С ряд (1) сходится абсолютно. Согласно
следствию 4 из теоремы 1, R = +оо.
Если I = +оо, то Vz / z0 a„(z - z0)" / 0(1). Согласно следствию 2 из теоремы 1, R = 0.
Пусть 0 < Z < +оо. По радикальному признаку Коши из равенства (4) следует, что Vz g
Kt = [z £ С : |z - z0| < |} ряд (1) сходится абсолютно. Следовательно, Kt С KR и f R.
Если \z — z0\ > j, то из равенства (4) получаем, что a„(z — z0)n / о(1). Согласно следствию 3 из
теоремы 1, | R. Таким образом, R = |. ►
Если Vn € N |а„| > 0 и существует lim то, как известно из курса математического
п—*ос
анализа, lim = lim 1I • В этом случае радиус сходимости степенного ряда (1) можно
п —»ОС П —»ОС 71
найти по формуле
R = lim
(5)
Теорема 4 (вторая теорема Абеля). Если степенной ряд (1) с конечным радиусом схо-
димости R > 0 сходится в некоторой точке z1 g yR = {z € С : |z — z0| = J?}, то его сумма
f(z) = 57 an(.z ~ zoY1 стремится к f(zt) при подходе к точке zl вдоль радиуса [z0, zj.
< Не ограничивая общности можем считать, что zt = (R, у0), чего можно достичь пре-
образованием w = ze'a при некотором a g R. Тогда Vz € [z0, zi] z = (x, y0), x0 < x < R,
z - z0 = (x- xa, 0), |z - z0| = I® - Xo| и Vz g [z0, zj
/(•z) = ^2ап(х-жо)" = д*0)
(6)
По условию теоремы числовой ряд 57 ап Дп сходится, что равносильно его равномерной
сходимости. Последовательность ((£^4) ) монотонно возрастает на отрезке [я0, Я] и огра-
ниченная, так как Va; g [а?0, Я] 1£г£»1 = 1. По признаку Абеля (см. теорему 4, п. 1.4)
ряд 57“"(2 - 2о)п сходится равномерно на отрезке [z0, zj, в силу чего его сумма f является
непрерывной функцией на этом отрезке (см. теорему 1, п. 1.5 и следствие из нее). Поэтому
/(zt) = lim /(z). ►
1*0,
208
Гл. 5. Рады аналитических функций. Изолированные особые точки
Немецкий математик А. Прингсхейм (1850—1941) доказал, что при выполнении условий те-
оремы сумма рада / непрерывна в точке zx вдоль любой жордановой кривой 7, лежащей внутри
какого-либо угла раствора, меньшего тг, с вершиной в точке г, и с биссектрисой, совпадающей
с радиусом [z0, zj].
При исследовании некоторых проблем с применением степенных радов над ними производят
арифметические операции, в том числе операцию умножения степенных радов.
В курсе алгебры произведением многочленов
п тп
p(z')~'^2akzk, Q(z) =
к=0 j-0
называется многочлен
m-f-n
E(z) = ^2c,z1', (7)
I/=O
и ____
где cv = 52 (" = 0, п + m).
Т=о
Это определение согласуется с правилом умножения конечных сумм в том смысле, что Vz € С
P(z)(?(z) = B(z).
Сформулируем правило умножения степенных рядов, обращаясь с ними, как с многочленами.
Определение 2. Произведением степенных рядов
ao + '^2an(z - z0)n, Ьо + 57 bn(z - z0)n (8)
называется степенной ряд
Со + ^Сп(г - z0)n, (9)
п
где с„ = 52 aibn-j Vn € Zo-
j=o
Полагая в радах (8) и (9) z - z0 ~ 1, получим правило Коши умножения числовых рядов.
Пусть KRt и KR1 — соответственно круги сходимости рядов (8), а их произведение (9) имеет
радиус сходимости R. Тогда R min{P|, Я2} и Vz € KR, П KR1
57 с"<2 - го)’1 = f57a"(z ~ г«)п J f 57Ь"<г - z0)"
пЕ^о 7i£Z{j n£Zo
Так как каждый степенной ряд 52ап(г - z<j)" с ненулевым радиусом сходимости абсолютно
сходится в круге сходимости, то любая его перестановка имеет ту же сумму, что и сам рад. Этот
факт отмечается записью 52 an(2 " zo)n-
По первой теореме Абеля степенной ряд 52 an(z~zo)” сходится равномерно в любом замкну-
том круге КТ — {z € С : \z —z0| г} С KR. Поскольку любое компактное подмножество К круга
сходимости KR принадлежит ему, то для степенного рада в круге сходимости выполняются все
условия теоремы Вейерштрасса (теорема 3, п. 1.5). Следовательно, в круге сходимости KR сумма
степенного ряда /(z) = 52 an(z — zo)" является аналитической функцией, ряд можно почлен-
но дифференцировать сколько угодно раз и при этом степенные рады, получаемые в результате
дифференцирования, имеют тот же радиус сходимости R.
1.7. Теорема Тейлора.
В предыдущем пункте было показано, что сумма степенного рада является аналитической
функцией в круге сходимости. Вполне естественно поставить вопрос о возможности разложения
в степенной ряд аналитической функции. Ответ на него содержится в следующем утверждении.
§ 1. Ряд Тейлора
209
Теорема (Тейлора). Аналитическую в области D функцию f можно в окрестности каждой
точки z0 G D представить суммой степенного ряда
f(z) = - z0)n,
п=0
радиус сходимости которого не меньше расстояния d от точки za до границы области D.
◄ Рассмотрим круг КТ = {z € С : \z - г0| <r}, г < d, Kr 1= D. По интегральной формуле
Коши Vz € Кт имеем
.. . _ 1 [ f(Qd<; _ j_ Г /(0^ ...
2« / C-z 2тг1 / ( ) Л
дКг 6КГ S ' \ <-*0 /
Для каждой фиксированной точки z 6 Кг выполняется неравенство
z - ZQ
С - zo
l-z - -?ol
г
если ( g дКт.
прогрессии:
Поэтому выражение —можно рассматривать как сумму геометрической
С-zo
1
(2)
Ряд (7^77) равномерно сходится на дКт, поэтому его можно почленно интегрировать. При-
нимая во внимание (1) и (2), получим
, <4 1 f f(O<K
f(z) = / - zo) 7-^ / 77----77ТТ. (3)
2тг J (C-z0)"+1
"=0 эк,.
Таким образом,
f(z) = ^2<in(z - z0)n, (4)
71=0
где
_ 1 [ /(0rf< _ /(n)(zo) _
2vi J (( — z0)n+1 n!
3Kr
/ _ \ n
Поскольку ряд У2 ( JT77 1 Для каждой фиксированной точки z G Кт сходится равномерно
относительно £ € дКт, а коэффициенты ап одни и те же для всех г, где 0 < г < d, то радиус
сходимости R степенного ряда 5? an(z - z0)n не меньше чем d. Действительно, предположив,
что R < d, получим противоречие с определением радиуса сходимости этого ряда, так как в
качестве г можно взять число, большее R. ►
Ряд У2 an(z ~ zo)n > коэффициенты которого вычисляются по формуле (5), называется рядом
Тейлора функции f.
Следствие 1. Каждый сходящийся степенной ряд ^2 an(z — zo)n является рядом Тейлора своей
суммы
оо
/(z) = ^2an(z - Zo)",
n=0
вследствие чего его коэффициенты определены однозначно и вычисляются по формуле
210
Гл. 5. Ряды аналитических функций. Изолированные особые точки
Следствие 2 (оценка Коши для коэффициентов степенного ряда). Пусть функ-
ция f аналитическая в замкнутом круге Kr = {z 6 С : |z — z0| С г}' и М = max |/(z)|. Тогда
zedKr
коэффициенты ряда Тейлора функции f по степеням z — z0 удовлетворяют неравенствам
М
|а„| — (п g Zo). (6)
Гп
Действительно
1 Г М-Ткг_М
п 2тгг J (( — z0)n+l 2тггп+1 г"
дКГ
Напомним разложения основных элементарных функций в ряды Тейлора по степеням z.
Для целых функций z ь» ег, z ь» sinz, z н cosz, z i-+ shz, z chz имеем соответственно
сходящиеся во всей плоскости С разложения:
' п! п=0 00 2п—1 00 _2п sinz = \ (—1)п+1 , cosz — \ (-1)" ’ (2п-1)! (2п)! П=1 71 = 0
00 2n—1
sh z = \ ,
(2п - 1)!
тг= 1
chz
В каждой точке z G С соответствующие ряды сходятся абсолютно, их можно почленно диф-
ференцировать сколько угодно раз и V)? > 0, R < +оо они сходятся равномерно в круге
KR = {z е С : |z| R}.
Главная ветвь w = ln( 1 + z) многозначной функции w = Ln(l + z) в круге Кх = {z G С :
|z| < 1} также допускает представление в виде ряда Тейлора
zn
ln(l+z) = V(-l)n-1—•
п
п= 1
Пусть (1 + z)“ = ealn<1+z>j т.е. рассматриваем главную ветвь многозначной функции w =
(1 + z)“ . Тогда в круге Ki справедливо разложение
(1 + гГ = 1 + £
71=1
а(а - 1) ... (а - п + 1)
п<
Если z 6 Ks, то
1
1 -z
1.8. Теорема единственности.
Из представления аналитической функции степенным рядом следует одно из важнейших
свойств аналитической функции, выражаемое следующей теоремой единственности.
Теорема. Если функции ft и fi аналитические в области D, совпадают в ней на бесконечном
множестве точек Е, имеющем предельную точку в D, то эти функции тождественно равны друг
другу в области D.
4 Пусть z0 € D — предельная точка множества Е, а последовательность (zn) точек множе-
ства Е сходится к точке z0. Представим функции fi и f2 в окрестности точки z0 с помощью
степенных рядов:
ОФ ОФ
Л (-2) = 52 “п С* -• л (г) = 52a"(z “ г°)"'
П = 0 71=0
Поскольку lim zn = z0, то начиная с некоторого номера п все zn лежат в круге
П—*ОФ
кр = {z е С : \z - za\ < р}, p^d,
§ 1. Ряд Тейлора 211
где d — расстояние от точки z0 до границы области D, т. е. d = inf p(z0, z). В силу этого имеем
zeao
ОО оо
^2a'n(z„ - z0)" = ^2<i"(z„ - z0)n.
n=0 n=0 '
Переходя к пределу при п —» оо, получим, что aj, = а". Таким образом, справедливо равенство
^2«'п(гп - гоГ-1 = 52«n(zn - го)"-1.
П=1 71 = 1
При п оо получим, что а', = а". Продолжая эти операции предельного перехода, убеждаемся
в том, что Vti € N а'п = а" (применив метод математической индукции). Следовательно, Vz € Кр
/i(z) = A(z).
Пусть z* б D — любая точка. Рассмотрим жорданову кривую 7 С D, соединяющую точки z0
и z*. Пусть ро > 0 — расстояние от кривой 7 до кривой 9D, т. е. р0 = inf p(z, (). Очевидно,
что ро р. Пусть pi < ро — некоторое положительное число. Разделим кривую 7 на дуги
точками z0, zi, ... , zn_H zn = z* так, чтобы \zk - zt_|| = pi - Рассмотрим круги = {z £ С :
|z - zfcI < ро} (fc = 0, n — 1). Очевидно, что K(pk0~l) П K(PJ и центр круга К'р,- принадлежит
кругу В круге Кр..' fi = f2. Центр zt круга Кр^ является предельной точкой множества,
на котором /1 = /2, и, таким образом, повторяя предыдущие рассуждения, получим, что /i = f2
в<’-
Продолжая этот процесс, после конечного числа шагов достигнем круга К^, т.е.
VzgK^ /,(z) = /2(z)
и, в частности, f\(z*) = f2(z*). Поскольку z* £D— произвольная точка, то Vz £D /i(z) =/2(z). ►
Определение. Пусть А € С — произвольное конечное число, f — аналитическая в некоторой
области D функция. A-точками функции f называются корни уравнения f(z) = А.
Из теоремы единственности следует, что в случае, когда /(z) Л. множество A-точек не
может иметь ни одной предельной точки, принадлежащей области D, поскольку допустив про-
тивное, получили бы, что /(z) = А. Отсюда, в частности, следует, что любой компакт К С D
может содержать лишь конечное число А-точек для фиксированного А. Действительно, пред-
положив, что К содержит бесконечное множество А-точек, получим, что это множество имеет
предельную точку, принадлежащую К.
Пусть zo — какая-нибудь A-точка функции /, т.е. /(z0) = А. В окрестности точки z0 имеем
г, ч /<п)(2о)
/(z) = А + > -------— (z - z0) ,
n!
n = l
или
/<n>(z0)
/(z) - A = > -------—• (z - z0) . (1)
n!
n=i
Если /(z) А, то среди коэффициентов правой части равенства (1) найдутся отличные от
нуля. Пусть (z — Zq)4 — младшая степень z — z0, коэффициент при которой отличен от нуля.
Тогда равенство (1) принимает вид
/(z) - А = (z - zo)* 52 (z - zoy-fc, (2)
j=fc 3'
где y<fc)(z0) 0. Число k £ N называется порядком или кратностью А-точки z0.
В случае, когда k = 1, A-точка называется простой, в случае, когда к > 1, — кратной.
Простая точка характеризуется тем, что для нее /(z0) = А и /'(z0) # 0. Кратная А-точка
порядка к 2 характеризуется соотношениями
/(z0) =.А, /'(z0) = 0, ... , /''“‘’(zo) = 0, /<fc)(z0) # 0.
212
Гл. 5. Ряды аналитических функций. Изолированные особые точки
Если А = 0, то точка z0 называется нулем функции f. Она называется нулем кратности п,
если
/(Zo) = /'(zo) = .. • = /(n-,)(zo) = 0, /(n)(z0) / о.
В последнем случае разложение функции f в ряд Тейлора в окрестности точки z0 имеет вид
/(z) = УУ ajz - z0)fc,
k—n
откуда
/(z) = (z - z0)n9?(z),
где
¥>(z) = УУ аУ2 ~ 2оУ~п- W
j=n
Из формул (3) и (4) следует, что аналитические функции обращаются в нуль как целые сте-
пени z — z0, а из теоремы единственности получаем, что отличные от тождественного нуля ана-
литические функции не могут иметь нулей бесконечного порядка.
Рассмотрим примеры.
1. Найти область сходимости ряда УУ ---
◄ При |z| г < 1 имеем |-ртг | кддг = ап. Ряд ап сходится. Следовательно, иссле-
дуемый ряд абсолютно и равномерно сходится на любом компактном подмножестве единичного
круга К\ = {z € С : |z| < 1}. ►
2. Доказать, что если радиусы сходимости степенных рядов У ' anz
ственно равны Я,, Я2, то:
1) радиус сходимости R степенного ряда У \nbnzn удовлетворяет неравенству R R\R2',
2) радиус сходимости R' степенного ряда У"^ — zn
I -Rj
r^r~2’
3) радиус сходимости Ro степенного ряда У /апЬр +
неравенству Ra min{.Ri, Я2}.
◄ 1) Поскольку
соответ-
(Ьп / 0) удовлетворяет неравенству
+ ... + aobn)zn удовлетворяет
Um V|anbn| = -
ТО
-- -п , т.е. R R{R2-
R R\R2
Воспользовались неравенством1* lim хпуп lim хп lim уп, выполняющимся V(zn > 0, уп 0).
п—»оо п—»оо п—*ос
2) Так как ап = • Ь„, то по доказанному в 1) Я( й'Я2, откуда R'
3) Оба ряда абсолютно и равномерно сходятся в замкнутом круге Kr = {z 6 С : |z| г},
г < гшгДЯ.,, Д2}. Тогда радиус сходимости Ro ряда
(УУ anzn) (УУ 6nzn) = УУ(а„Ь0 + + ... + bnaa)zn
не может быть меньше min{fib Я2}. ►
* 1 См., например, И. И. Ляшко, А. К. Боярчук, Я. Г. Гай, Г П. Головач. Справочное пособие по высшей математике, Москва,
“УРСС”, 1995, т. 1, гл. 1, пример 106.
§ 1. Ряд Тейлора
213
3. Доказать, что когда сумма f степенного ряда an(z — Ь)п, b 6 R, принимает действи-
тельные значения в некоторой действительной окрестности точки Ь, то все ап действительные.
Ч Очевидно, а0 = f(b) g R. Поскольку
/(Ь + Дг)-/(Ь) /(Ь + Дг)-/(Ь)
а, = f (о) = lim ---------------= lim ------------------,
Az—o Дг Дх—*о Дг
то а! € R. Предположим, что ап = /<П,(Ь) € R. Тогда
/(п)(& + Дх) -/(п)(6) , „+п
а„+1 = lim -— ------——-—— = /<n+1)(b) е R.
Дх—о Дг
Утверждение доказано с помощью метода математической индукции. ►
4. Доказать, что для коэффициентов степенного ряда , anzn с радиусом сходимости R > 0
справедлива формула
2тг тг
а„ = ----- / и(г, р)е^'п<р dp -I-/ v(r, <г)е~'п*’ dip, (1)
тггп J irrn J
о 0
где 0 < r < R, f(z) = u + iv = ' a„z" — сумма ряда.
71 = 0
◄ Пусть у, = {z (E С : |г| = г}, Гг = (уг, 7°р) — положительно ориентированная гладкая
или кусочно-гладкая жорданова кривая. Тогда
1 f 1 re^idip _ 1 f
2iri J C+1 2тгг J ^Гв rn+iei(n+i)^ 2тгг'1 J ^Гв 6 <f>’
Гг о о
Применив интегральную формулу Коши при п 1, получим:
2тг
J f(OC~'<K = / /(rel*’)rne,n*’id<^ = 0,
гг о
или
2тт
—[ f(re"fi)en'fi dip = 0. (3)
2ятп J
о
Складывая и вычитая (2) и (3), имеем
2тг 2тг
ап = —/ f (ге>,р) cos nip dip =-----/ sin пр dp.
7ГГ" J ЯГп J
о 0
Отсюда, полагая an = an + i/3n, находим:
2?г 2tt
1 f 1 Г
rnan = — / u(r, p)cosnpdp = — I v(r, p) sin np dp,
J J
о 0
2тг 2тг
„ 1 f If
г /3„ = — / v(r, у>) cos ny; =----/ u(r, p) sin npdp.
о о
С помощью этих равенств получаем формулы (1) Vn € N. В случае п = 0 формулы (1) получаем
сразу из (2). ►
214
Гл. 5. Ряды аналитических функций. Изолированные особые точки
5. Пусть сумма степенного ряда f(z) = anzn с кругом сходимости Кх = {z 6 С : |z| < 1}
п=0
удовлетворяет условию Re/(z) > 0 Vz € Доказать, что Vn £ N |an| 2и0, где u0 = Re/(0).
< Согласно формуле (1) предыдущей задачи имеем
2тг
а„ = —f u(r, <р)е~'п'/’ dip.
~rn J
о
Оценим ап. Получим
2тг
, , 2 Г 2u0
|ап| z—- / «(г, p)dp = —.
2тггп J rn
о
Принимая во внимание, что г € (0, 1) — произвольное, имеем
|an| < 2и0. ►
6. Найти первые четыре члена, отличные от нуля, разложения функции z f(z) = Ccosz
(/(0) = 1) в окрестности точки z = 0. Найти радиус сходимости ряда.
◄ Воспользуемся представлением функции / в виде
,_______________________ . .I 1
/(z) = x/cosz = (1 - (1 — cosz)J 2 = (1 — w)2 .
Тогда Vz E С получим:
z2 z4 z6 z8 1 w 1 , 1 j 5 4
w = l_coss = __w __w H<1>
1 /z2 z4 z6 \ 1 /z2 z4 V 1 (z1 V
2 \ 2 24 720 ) 8 \ 2 24 ) 16^2 J
1 (гг z* z6 \ 1 / z4 z6 \ 1 /z6 \
~1_2\ч‘Г~24 + 720_”78\4’~24+”7~16\'8’”’'7+"' =
_ i _ f! _ fl 12f! _
~ 4 “ 96 ” 5760
Очевидно, что R = у, т. к. точка z = у — ближайшая к точке z = 0, в которой нарушается
аналитичность функции /. Заметим, что первые четыре члена разложения функции / в ряд
можно получить непосредственно, вычисляя ее производные в точке z = 0. ►
7. Разложить в
радиус сходимости.
Z
ряд Тейлора функцию z >-+ /(z) =------- в окрестности точки z = 0 и найти
е2 - 1
◄ Имеем
z 1
Д - п+| — ~ ~ Д 7й
z 4- у- + ... + + ... 1 + д + ЗГ + ••• + щП)! + ••
Пусть разложение функции / в окрестности точки z = 0 имеет вид
/(•z) =
п=0
Тогда
-> ( z z1, zn \
(а0 + axz + a2z + ... + a„zn + ...)1 1 + ^ + д7 + ••• + 7—Т~Д7 +•••)= 1.
\ Z! j! {п -г 1J. 1
Приравняв коэффициенты при одинаковых степенях z, получим:
11 1
«о7—-"тг: + в! — + ... + a„_i — + ап = 0, п Е N.
(п + 1)! п! 2!
§ 1. Ряд Тейлора
215
Полученные уравнения позволяют последовательно находить числа ап. Обозначим Вп = п\а„
Коэффициенты Вп называются числами Бернулли. Для их определения имеем
1 В, Вг Вп
1’ (п + 1)! + 1!п! + 2!(п — 1)! nil!
Умножив обе части последнего равенства на (п + 1)! и замечая, что fc,(<^'l'2!fc)i = С^+1, получаем:
1 + BiC^+i + + ... + BnCn+l =0 (ng N).
С помощью последней формулы находим:
11 1
В[ — —, By — ~, В} — 0, В4 —-----------,
2’ 6 30
Искомое разложение имеет вид
Радиус сходимости этого ряда R — 2л, так как ближайшие к началу координат точки, в
которых нарушается аналитичность функции f — z — ±2ггг. ►
8. Найти радиус сходимости и исследовать поведение на границе круга сходимости следую-
щих степенных рядов:
а) У (- 1)п------ (п > 1); б) \ ' — zkn, k = const, к g N.
' Inn п
◄ а) Очевидно,
( (-1)” ,
I -------, если к = Зп - 1, _ 1
ак = < Inn R= — k ,---------- = lim (lnn)3"-i = 1.
I 0, если fc/3n-l, llm vlad
к—>-oc
На границе круга сходимости z = e*e ив этих точках получаем числовой ряд
/ 1 \п „гтг(3$ —тг)
V — е’(3"-1)9 = е-*в V -_____________•
4—' In п In п
Если 30 — тг = 2тл (т g Z), то ряд расходится. Если Зв — тг / 2тл, то ряд сходится по признаку
Дирихле.
б) Здесь
{4П
—, если т = кп, _ _ 1 _ 1 _ 1 _ 1
П . ,,, j ~ j. .— •
0, если т / кп, im Vam ц /4^\ Гп 4? V4
m \ п /
71—»ОС
’ 0 < л, _ t А: п 0
На границе круга сходимости, т. е. при z — 7— получаем числовой ряд У J-. Если кд — 2?тг
п
(j g Z), то он расходится, поскольку превращается в гармонический ряд. Если кв 2ул, то ряд
сходится по признаку Дирихле. ►
9. Существуют ли функции /, аналитические в точке z = 0, удовлетворяющие условиям:
*)/(£) = /(4) = ^; 6)/U)=/H) = 3^n?
◄ а) Существует, это функция z i-> z2.
б) Применим метод рассуждения от противоположного. Предположим, что функция f с ука-
занным свойством существует. Рассмотрим функцию /1; где /i(z) = Она удовлетворяет
условию ft (^) = т.е. совпадает с функцией f на бесконечной последовательности то-
чек (ж„), где хп = i > 0 при п —► оо. По теореме единственности f(z) = /i(z) в окрестности
точки z = 0. Однако, . Получили противоречие, источник которого в предполо-
жении, что функция f с указанным свойством существует. ►
216
Гл. 5. Ряды аналитических функций. Изолированные особые точки
10. Найти радиусы сходимости следующих степенных рядов:
'> з>
4) У7(3 + (-l)n)nzn; 5) zn cosin; 6) ^~~^(n + gn)zn.
< 1) Применим формулу (5), п. 1.6. Получим
n! (n + l)n+1 / 1 \"
R = lim — —-----------—- = lim 1 + - = е.
п—Пп (П “Ь 1)! п —>х \ Т1 J
k I 1, если к = п!,
2) Степенной ряд имеет вид > , akz , где ак = < Q’ если fc п!’
следовательно,
1
-=--------= 1.
lim y/Ok
fc—+ос
3) Аналогично случаю 2) имеем R = 1.
4) Поскольку lim ^/(3 + (-1)п)" = 4, то, согласно формуле Коши—Адамара, R = |.
П —ЮО
5) ап = cos in = . Согласно формуле Коши—Адамара
R = = 1 = 1.
lim u е е
п—►оо 1
П —♦ОС 2 71.
_____________ ________ f 1 ргтги Ini <- 1 Г 1} если |а| 1,
6) Так как lim \/|п + а"| = < ,, то R = < t
„_«= v 1 ( 14 если |а| > 1, I если |а| > 1.
11. Исследовать поведение на границе круга сходимости степенных рядов:
» 3> 3>
◄ 1) Согласно формуле (5), п. 1.6, R = lim = 1. На границе круга сходимости получаем
71—»ОО
числовой ряд
Е(— 1)пегп<? -л cos пО \—\ sinn#
——=£<-» —+iE<-» — •
Если в = тг, то ряд расходится. Для всех остальных значений в ряд сходится, так как оба числовых
ряда сходятся по признаку Дирихле. Поскольку на границе круга сходимости | (-1)п z | = £, то
ряд в этих точках абсолютно расходится.
2) Записав ряд в виде 57 akZk , видим, что его коэффициенты равны
( 1
I —, если fc = п!,
a-k = < п2
0, если fc / п!,
следовательно,
R — ____1-----= пт Пу/п* — j.
Нт п—»оо
fc—*оо
На границе круга сходимости |afczfc| = поэтому в точках указанной границы ряд сходится
абсолютно.
3) По формуле Коши—Адамара
R =
1
Km
= 2.
На границе круга сходимости получаем числовой ряд 57 п, очевидно, расходящийся. ►
§ 1. Ряд Тейлора
217
12. Найти сумму ряда У nz\ |z| < 1, п 6 N.
4 Пусть f(z) = ^nzn. Рассмотрим функцию где <p(z) = zn = Дифференцируя
71=1 П = 0
функцию <р в круге сходимости, получим </(z) = 57 nzn~'' = (1_'г-р . Умножая левую и правую
71=1
части полученного равенства на z, имеем:
/(z)=z/(z)=?r^.»-
Л
13. Найти сумму ряда > —.
у-—' п
Ч Радиус сходимости ряда R = 1. Если |z| < 1, то ln(l — z) = — 57 Следовательно,
71 = 1
°° гп
V — = -ln(l-z). ►
п
п=1
___22п+1
14. Найти сумму ряда У ' -——-.
Ч Радиус сходимости ряда R = 1. Если |z| < 1, то
°° / п’1-!.71 00
1п(1 + г) = У2----------> ln(l-z) = -V—
Z—/ п х—/ п
П=1 п=1
Тогда
г2п+1
ln( 1 +z)-ln(l - z) = 2^7 - .
< 2п + 1
Т1= I
Таким образом,
°° ~2п+1 1 1 । _
EZ 1 1 + Z
--------= - In----. ►
In + 1 2 1 - z
71 = 1
15. Разложить в степенной ряд функцию z к-» sin2 z.
Ч Воспользуемся равенством sin2 z = 1-с”2г и разложением в степенной ряд функции
z »-» cosz в п. 1.7. Получим:
sin2 z = -
2
%2п
(2п)!
22п— 12^тг
(2п)!
16. Разложить в степенной ряд функцию z i-> ch2 z.
Ч Принимая во внимание равенство ch2 z = ‘+c2h2z и разложение функции z ch z в сте-
пенной ряд в п. 1.7, имеем
1 1 00 о2п_,2тг t °° -)2n—I 2п
2 11 2 Z 1 у—\ 2 Z
ch z = 2 + 2 Ху (2п)! “ 2 + Ху (2п)! *
71=0 п=0
17. Разложить в степенной ряд функцию z >-> y/z +1.
При выполнении неравенства |z| < 1 получим (см. п. 1.7):
218
Гл. 5. Ряды аналитических функций. Изолированные особые точки
18. Разложить в степенной ряд функцию z i->--.
az + о
Ч При |z| < | £ | имеем
—1— = 1-----L_ = 1 ►
az + b b l + ?z b^> bn
b n=0
19. Разложить в степенной ряд функцию z .
z2 - 4z + 13
◄ Раскладывая функцию на простые дроби, получим:
z _ z / 1 1 \ _ г / 1 1 1 1 \
z2 - 4z + 13 6г у z — 2 — Зг z - 2 + Зг J 6г у 2 + Зг 1 — 2 — Зг 1 - уА- у
При выполнении неравенства |z| < vT3, имеем
Z _ Z ( 1 z"
z2 -4z+ 13 ~ 6г \ ~2 + Зг 2^ (2 + Зг)" + 2-31 Z-' (2 - 31)" / ”
\ п=0 п=0 /
= z" у> \ = 1 V (2 + 3у+' -(2~3г')П+1 гп+1 =
611 (2 + 31)"+1 (2 - Зг)"+1 / 6г13n+1 Z
\ п=0 п=0 / п=0
1 (2 - 31)" - (2 + 31)" „
6 2^ 13" z
n = l
г2
20. Разложить в степенной ряд функцию z н->-—.
(1 + z)2
◄ При jzj < 1 имеем = 22(-l)"z". Дифференцируя, получим:
п=0
1
(1+Z)2
(1+z)2
21. Разложить в степенной ряд функцию z Arctg z.
Имеем при |z| < 1
/г J4 Г 00 00 Г °° _2п+1
тт?=/Л=Е<-»* ]
о о п=0 п=0 о п=°
Z
22. Разложить в степенной ряд J е4 dt.
о
◄ Очевидно,
/, f 00 t2n 00 _2п+1
е‘ dt = / У —~dt=y^ —-------------—, R = оо. ►
/ n! n!(2n + 1)
о о "=0 ”=0
§2. Рад Лорана и изолированные особые точки аналитических функций 219
~~ f sint
Zj. Разложить в степенной ряд / -у- at.
о
Ч Имеем
/-• л р f 3 °° /2п-1 \ °° 2п—I
/ 7£<->'-'=£<->"-'Cn-w-„-►
О О ' n=1 7 "=1
§ 2. Рад Лорана и изолированные особые точки
аналитических функций
2Л. Теорема Лорана.
Среди функциональных рядов, отличных от степенных, наиболее близким к степенному явля-
ется ряд вида ^2 —Го)" ' Его область сходимости — внешность круга радиуса г = lim ^/|сп |
с центром в точке z0, которая при г = оо вырождается в бесконечно удаленную точку, при
О < г < jx) — это внешность круга в собственном смысле слова, а при г = 0 совпадает с плос-
костью С, из которой выброшена точка z = z0. Если г < оо, то ряд сходится абсолютно и
равномерно внутри области D = {z 6 С : \z - z0| > г}. Следовательно, его сумма / является
аналитической функцией в D и /(оо) = с0. При этом говорят, что функция / аналитическая в
бесконечно удаленной точке.
Теорема 1 (Лорана). Любую функцию /, аналитическую в кольце
Vr, R = {z € С | г < \z - z0| < R}, r 0, R oo,
можно представить в этом кольце как сумму сходящегося ряда
= an(Z - го)П, (1)
п = —ОС
где ап определяются по формулам
1 f яг
= — / 77-----—ту <К, neZ, (2)
2яг J « - z0)n+'
Гр
ГР = (7р, 7рР), 7р = {z € С : |z - z0| = />}, г <p<R.
◄ Фиксируем любую точку z е Vr R и рассмотрим кольцо
Vr,,R, = {z е С | г' < \z - z0| < R'} Vr, R-
По формуле Коши имеем
, 1 f /(О .. 1 Г /(О „ 1 f /(О ..
f(z) = — / 7------dC = — / 7-----d<-— ----df, zeVT,:Rl. (3)
2%i J C ~ z 2тгг J С, — z 2tti J ( — z
rK, rr,
Здесь кривые Гд- и Гг» положительно ориентированы. Для любой точки С е yR'
Z - z0 |z - z0|
---- = ------= а < 1.
С - z0 R'
Отсюда получаем: 1 _ 1 (<-го)(1-£ха) ОО =Е 71=0 (Z-ZQ)" (С - Zo)"+1 • (4)
Ряд (4) абсолютно и равномерно сходится по € 7д/.
220
Гл. 5. Ряды аналитических функций. Изолированные особые точки
Если £ € 7Г/, то
z - z0 \z - z0|
Отсюда
i = -1 = _ V (С ~zo)n
(z-z0)(l-^)
Ряд (5) равномерно сходится относительно £ € 7,'. Подставив (4) и (5) в (3), получим:
(5)
ОС
/(z) = ^(г - z0)”
п=0
ГК'
(С - Zo)n+1
/(Qd<
(С - 2о)-п
или
/(z) = an(z - z0)n + 5У ak(z - z0)k,
где
а„
(С ~ z0)n+1
(n € Zo),
1 [ ЖМС
2тгг J (C - z0)fc+i
Гг'
(-fc 6 N).
По теореме Коши интегралы по ориентированным окружностям Гд, и ГР/ можно заменить
интегралами по любой положительно ориентированной окружности Гр = (7Р, 7°₽), где 7Р =
{z е С : \z - z0| = р}, г' < р < R1. *
Ряд (1), коэффициенты которого вычисляются по формулам (2), называется рядом Лорана
функции f в кольце УР, д.
Рассмотрим отдельно те два ряда, из которых состоит ряд (1). Первый из них
- г°)"
есть обычный степенной ряд. Его областью сходимости является круг KR = {z € С : \z — z0| < R},
где -g = lim \/|an|. Второй ряд
n—>oo
y2a-n(z - zo)
n=l
является степенным относительно z' = . Выше было указано, что его областью сходимости
является внешность круга радиуса г = lim ^/|a_n|.
п—>со
о©
Если г R, то область сходимости ряда 52 an(z — z0)n есть пустое множество. Если
п = — оо
же г < R, то его областью сходимости является кольцо VTi R = {z € С | г < \z - z0| < R}. Из
теоремы Абеля следует, что ряд Лорана сходится равномерно на любом компакте, принадлежа-
щем кольцу К, r Согласно теореме Вейерштрасса, сумма ряда Лорана является аналитической
функцией в этом кольце.
Ряд 52 a„(z — z0)n называется правильной частью ряда Лорана, а ряд 52 а-п(,z — zQ)~n носит
название его главной части.
Пусть /(z) = 57 c„(z-z0)" и ряд 52 cn(z-z0)n = 52 c_n(z-z0)_n + 52 cn(z“zo)" сходит-
n= — oo n£Z nGN nGZo
oo
ся равномерно в кольце Vr_R. Умножив на (z-z0)-fc_| обе части равенства/(z) = 52 с»(г—го)”
п=-оо
§2. Ряд Лорана и изолированные особые точки аналитических функций 221
и интегрируя полученный ряд почленно по ориентированной окружности Гр = (7Р, 7°р), 7Р =
{z € С : \z - z0| = р}, г < р < R, получим:
г п= —оо г
1 р L р
Принимая во внимание, что
2тг
f .n-k-1 , f n-k £(n-k)t. ,. J о, если n/fc,
J(z-z0) dz = J p e если n = fcj
Гр 0
имеем
1 f я
2тгг J (z - zo)*'1’1
Гр
Мы доказали следующее утверждение.
Теорема 2. Любой ряд c„(z - г0)" = с-«(г ~ го)-п + У? cn(z _ го)" в кольце сходимо-
n£Z n£N n£Zo
emu Vr, R является рядом Лорана своей суммы.
Из этой теоремы, в частности, следует, что разложение аналитической функции / в коль-
це К, r в ряд по целым степеням z — z0 единственное.
Формула (2) для коэффициентов ряда Лорана на практике применяется редко, поскольку
требуется вычислять интегралы. Поэтому для получения лорановских разложений можно вос-
пользоваться любым законным приемом.
2.2. Классификация изолированных особых точек в С.
Определение. Точка а 6 С называется изолированной особой точкой функции f, если
существует такая проколотая окрестность этой точки, т.е. кольцо V), д = {zgC | 0 < |z—а| < R}
с нулевым внутренним радиусом, в котором функция f аналитическая.
Пусть z = а € С — изолированная особая точка функции /. Рассмотрим разложение функ-
ции f в ряд Лорана в кольце VOi R
= У? с«(г -a)n. (1)
П = —ОС
В зависимости от вида разложения (1) различают три типа изолированных особых точек.
1) Если в разложении (1) отсутствует главная часть, т.е. члены с отрицательными степенями,
то точка z = а называется устранимой особой точкой функции f.
2) Если в разложении (1) главная часть содержит конечное число членов, то точка z = а
называется полюсом функции f. При этом, если с_! = с_2 = ... = с_(п_!) = 0, а с_п # 0, то
число п называется порядком полюса. Полюс первого порядка называют также простым полюсом.
3) Если в разложении (1) главная часть содержит бесконечное число членов, то точка z = а
называется существенно особой точкой.
Пример 1. Функция z <-♦ /(z) = аналитическая в кольце V0 oo = {z € С | 0 < |z| < оо}.
Ее разложение в ряд имеет вид
sin z z2 z4 z6
~ = 1~3!‘+5!’~7!’+’“’
из которого следует, что z = 0 — устранимая особая точка функции f.
Пример 2. Функция z >-> /(z) = ИМеет две изолированные особые точки zi = 2i,
Zi = -2i. Разложим функцию f в ряд Лорана в проколотой окрестности точки z, Vo( * = {z 6 С |
О < \z — 2i| < 4}. Получим:
1 » » i 1 _ i -А (-«')"
z2 + 4 4(z - 2t) + 4(z + 2») ” 4(z - 2i) + 16 (1 + ~ 4(z - 2i) + 4n+2
x 4» / n=0
222 Гл. 5. Ряды аналитических функций. Изолированные особые точки
Отсюда заключаем, что точка z = 2г является простым полюсом функции f.
Аналогично получим разложение функции / в ряд Лорана в проколотой окрестности точки
z2 = {z в С | 0 < |z + 2г| < 4}, с помощью которого убедимся в том, что точка z2 = -2i
также является простым полюсом функции f.
Пример 3. Функция z ь+ /(z) = sin аналитическая в проколотой окрестности Vo> ,х =
{z € С | 0 < |z - 11 < сю}. Разложение этой функции в ряд Лорана в V0>oc имеет вид
1 1 1
sin-----=------------------- + ... ,
z — 1 z — 1 3!(z — I)3
из которого следует, что z = 1 — существенно особая точка функции /.
2.3. Поведение аналитической функции при подходе к изолированной особой точке.
Поведение аналитической функции в окрестности устранимой особой точки полностью опи-
сывается следующими двумя утверждениями.
Теорема 1. Если при подходе к изолированной особой точке z = а функция f ограниченная или
имеет порядок роста меньше единицы, то z — а — устранимая особая точка.
Пусть функция / в окрестности точки z = а удовлетворяет неравенству
О а < 1.
, м
!/(*)! < ;---------
Тогда Vn € N получим:
тУ / /(z)(z - а)” 1 dz
2тгг /
Т1 —а —и Г П — Ос
Г~Р 2~р = Мр
2тг
Принимая во внимание, что п - а > 0, а р можно выбрать как угодно малым, имеем с_п = О
Vn € N . Следовательно, z — a — устранимая особая точка. ►
Теорема 2. При подходе к устранимой особой точке z = а функция f имеет конечный предел,
и если его принять в качестве значения функции в точке z = а, то f становится аналитической
функцией в точке а.
4 При z € Vo,я = {z 6 С | 0 < |z - а| < 2?} /(z) = с0 + ^2 c„(z ~ а)п> откуда lim /(z) = с0.
„=1
Доопределим функцию f в точке z = а равенством /(а) = с0. Тогда разложение /(z) =
Со + сn(z - а)п будет справедливым в круге KR = {z € С : |z - а| < Я}. Ряд Лорана пре-
п,— I
образуется в ряд Тейлора, а функция f становится аналитической в круге KR и, в частности, в
точке z = а. ►
В дальнейшем, как правило, будем считать устранимые особые точки точками аналитичности
соответствующих функций.
Поведение функции в окрестности полюса устанавливается следующей теоремой.
Теорема 3. Изолированная особая точка z = а функции f является полюсом тогда и только
тогда, когда
lim /(z) = оо. (1)
z—»а
Ч Необходимость. Пусть z - а — полюс функции / порядка р. При z € Vo, д имеем
/(*) = + / C ptl-i + • ~ ~ аЛ с-р^О-
(z - а)р (z - а)Р 1 г
П = — Р
Отсюда
ко = <7^ Ё _ а). = _Д_ /1М, (2)
п=—р п=0
где /| — аналитическая в круге KR = {z 6 С : |z — а| < R} функция, /Да) = cj = с_р 0. Из (2)
следует (1).
§ 2. Ряд Лорана и изолированные особые точки аналитических функций 223
Итак, при подходе к полюсу функции f она стремится к бесконечности, и чем выше порядок
полюса, тем быстрее это стремление.
Достаточность. Пусть z = а — изолированная особая точка функции / и lim f(z) = со.
z —»а
Очевидно, существует проколотая окрестность точки а, в которой f (z) / 0. Поэтому точка z — а
является изолированной особой точкой функции z i-> y>(z) = и lim y>(z) = 0, т. е. а —
устранимая особая точка функции <р. Устраним ее, полагая у>(0) = 0, и пусть z = а — нуль
функции <р кратности р. Тогда согласно формуле (3), п. 1.8., имеем
<p(z) = (z - a)py>i(z),
где pi(z') / 0 в окрестности точки z = а. Следовательно,
(z-a)P<p,(z) (z-a)P^^’
где — аналитическая в точке z = а функция и гр (а) / 0. Представим ее в окрестности точки
z = а рядом Тейлора:
У'(г) = У^сп(г-а)п, со = ^(а)#О.
п=0
Тогда
/(г) = £cn(z - а)п~р,
71 = 0
т. е. точка z = а — полюс функции f порядка р. ►
Следствие. Точка z = а является полюсом функции f порядка р тогда и только тогда, когда
функция р = у (ip 0) аналитическая в точке а, и точка а — ее нуль кратности р.
Из проведенных выше рассуждений следует такое утверждение.
Теорема 4. Для того чтобы изолированная особая точка z = а функции f была ее существенно
особой точкой, необходимо и достаточно, чтобы f не имела предела при z -+ а.
Углублением и уточнением теоремы 4 является следующее утверждение.
Теорема 5 (Сохоцкого). В окрестности существенно особой точки аналитическая функция
принимает значения как угодно близкие любому наперед заданному числу расширенной комплексной
плоскости. Другими словами, если z = а — существенно особая точка функции f, то УД € С
найдется такая последовательность (z„), zn —» а, что lim f(z„) = А.
п—
◄ 1) Пусть А — оо. Функция / не может быть ограниченной в окрестности точки z = а,
поскольку в противном случае точка а была бы устранимой особой точкой. Поэтому в проколотой
окрестности 70, я = {? € С | 0 < |z - a| < R} найдется такая точка Z|, что |/Oi)| > 1. Возьмем
проколотую окрестность V |Z|_a|={z£C|0<|z - a|< —} . В ней найдется такая точка zi,
что |/(z2)| > 2 и т. д. В проколотой окрестности У ={z€C|o<|z — a|< } найдется
такая точка zn, что |f(z„)| > п. Очевидно, что z„ —> а и lim |/(zn)| = +оо.
П —'ОС
2) А Ф оо. Здесь возможны два случая: 1') 4-точки функции / имеют а своей предельной
точкой. Тогда, очевидно, найдется такая последовательность (zn), z„ —» а, что f(zn) —> А при
п —* оо. Следовательно, утверждение справедливо. 2') существует проколотая окрестность точки
z = а, в которой /(z) / А. Тогда для функции z >-> <p(z) = точка z = а является
изолированной особой точкой. Установим ее характер. Рассмотрим возможные случаи. Допустим,
что а — устранимая особая точка функции <р. Тогда >р имеет конечный предел при подходе к ней:
lim </?(z) — В и Нт /(z) = 4+ -g. Отсюда следует, что если В -Д- 0, то z = а является устранимой
«—»а г—»а
особой точкой функции /, а при В = 0 точка z = а — полюс функции /. Обе возможности
противоречат условию теоремы. Следовательно, z = а не может быть устранимой особой точкой
функции <р.
224 Гл. 5. Ряды аналитических функций. Изолированные особые точки
Допустим теперь, что z = а — полюс функции <р, т.е.
lim 9?(z) = оо Л lim f(z) = А.
z—z —
Следовательно, z ~ а — устранимая особая точка функции f, что снова противоречит условию
теоремы. Таким образом, остается единственный возможный случай, что z = а — существенно
особая точка функции р. Тогда, согласно доказанному в 1), существует такая последователь-
ность (z„), zn —» а, что lim ^(zn) = сю Л lim f(zn) = А. ►
П—*ОО П—»оо
Рассмотрим пример.
1 гс
Пусть f(z) = е* = 22 z б Vo,к = {-z € С | 0 < |z| < оо}. Здесь а = 0 — существенно
п=0
особая точка функции f. С помощью очевидных соотношений
X 1
lim ег =оо, lim ег =0
z=®>0 г=х<0
х—>0 х—>0
проверяем утверждение теоремы Сохоцкого для А = оо и А = 0. Пусть А # { Д . Решим
1
уравнение е‘ = А:
1 11 1
— = Ln A, Z = ----=--------------= -----;------------- п € 1.
z Ln A In | А| + i Arg A In |А| + i(arg А + 2птг)
Пусть
___________1________
In | А| + г (arg А + 2птг)
1 1
Очевидно, что zn —> О, е*п = А, следовательно, lim ез„ = А.
П—»ОО
Характерным в этом примере является то, что за исключением значений 0 и оо, все остальные
значения А достигаются не в пределе, а на целой последовательности. Оказывается, что это не
случайность, а общая тенденция. Об этом свидетельствует теорема Пикара, уточняющая теорему
Сохоцкого и утверждающая, что в окрестности существенно особой точки функция / принимает,
причем бесконечное число раз, любое конечное значение, за исключением, может быть, одного.
1
Этим случаем для е г является нуль.
2.4. Бесконечная изолированная особая точка.
Пусть / — аналитическая функция в области Vri00 — {z 6 С | R < |z| < оо}. Это означает,
что точка z = оо является изолированной особой точкой функции f. Представим функцию f в
окрестности бесконечности рядом Лорана
ОО
/(z) = УД cnzn. (1)
п=—оо
Члены ряда 52 cnzn с неположительными степенями z образуют его правильную часть, а с
положительными — его главную часть.
Характер особой точки z = оо определяется, как и в случае конечной особой точки, главной
частью ряда Лорана, а именно: точка z = оо является соответственно устранимой особой точкой,
полюсом или существенно особой точкой в зависимости от того, отсутствует ли главная часть в
разложении (1), содержит ли главная часть конечное или бесконечное число членов.
Например, функция z i-+ /(z) = | имеет на бесконечности устранимую особую точку, функ-
ция z ►-+ ip(z) = z имеет на бесконечности полюс первого порядка, а функция
°° г2п+1
z^z^sinz^C-ir^^^
п=0
имеет на бесконечности существенно особую точку.
§ 2. Ряд Лорана и изолированные особые точки аналитических функций 225
Замечание 1. Все сказанное в п. 3.2 о поведении аналитической функции вблизи конечной изолированной
особой точки справедливо и в случае, когда г = оо является изолированной особой точкой.
Замечание 2. Если z = оо является изолированной особой точкой функции f, то ( = 0 — изолированная
особая точка функции ( >-♦ = / ( j) > лорановское разложение которой в окрестности ( = 0 получаем
из разложения (1) заменой z = |.
Замечание 3. Поведение аналитической функции при подходе к изолированной особой точке полностью
определяет характер особенности этой точки. Это свойство можно положить в основу классификации
изолированных особых точек, а именно, если при подходе к изолированной особой точке z = а функция
имеет конечный предел, то эта точка называется устранимой особой точкой. Если предел существует и
равен бесконечности, то z = а называется полюсом. Если же при подходе к точке z — а функция предела
не имеет, то эта точка называется существенно особой.
Рассмотрим примеры.
24. Разложить в ряд Лорана в кольце V12 = {0 < \z — 1| < 2} функцию z н-» /(г) = —---.
Z\Z — 3)
◄ Очевидно, справедливо разложение функции f на простые дроби
1111
z(z - З)2 ” 97 ~ 9(z - 3) + 3(z — З)2’ (1)
После некоторых преобразований дроби в правой части равенства (1) можно рассматривать как
суммы бесконечно убывающих прогрессий. Имеем
z ~ (z-l)+l “ (г — 1) (1" 7^1 Й(-1) (z " 1}
х г-1 > п=0
= ^(-1Г(г - = ^(-l)n-1(z - 1)", \z - 1| > 1,
n=0 тг= —I
1 1 1 1 1 1 1Чп _ (-Z - 1)"
z — 3 ~ (z - 1) - 2 ~ 2 ’ 1 - “ 2 2П 1 z—2n+1 ’ 2 <2,
2 П = 0 71=0
I ОО оо
= = I--и<2,
2 ' J J 2п+2
П=1 71 = 0
1 ( 1 1
(Z - З)2 " ” U-3}
1 =
z(z - З)2 9
1
9.2n+1
п + 1 \
Г2^) (2-1)
(-1)1
9
ЕЗп + 5
„ „ (z - 1) Vz е Vt
Q.2^+2 ' ' ‘
п=0
25. Найти множество
Обозначим
ОО
л-) = Е
точек
z
3^
п=0
Ez
—--, n € Z.
3-" + 1 zn +
z
предполагая, что функции /1 и f2 определены на некотором множестве. Ряд 57 сходится в
круге KR = {z 6 С : |z| < Ж}, где
R =-------. = lim \/3n + 1 = 3.
lim \/з^Т
71—»ОО
226
Гл. 5. Ряды аналитических функций. Изолированные особые точки
Областью сходимости ряда 57 3-п+1 • рг является множество D = {z 6 С : |z| > г}, где г =
lim л / 3_^+| = 1. Таким образом, заданный ряд сходится в кольце Vi, 3 = {z € С | 1 < |z| < 3}. ►
п—>оо V
26. Функцию z ь-> f(z) = z2 sin тг —+ разложить в ряд Лорана в кольце Vo = {z € С |
z
О < |z| < оо}.
Ч Имеем
2 . Z ~г 1 2 . / , 1
z sm тг--------— z sin тг I 1 H—
z \ z
2 . 7Г
= —z sin — =
z
(-l)n
(2n+ 1)!
= -^+52
71 = 1
(-l)n+1TT2n+1
(2n + 1)!
27. Функцию Бесселя 1-го рода п-го порядка Jn(z) при целых п можно определить как ко-
эффициент при (п разложения в ряд Лорана функции ( >-> е2 k С2 в кольце Vo, оо = {С € С |
О < [<| < оо}:
Доказать, что
/ cos(n0 - z sin 0) d6 — У
о к=°
(-1/
k'.(n + k)'.
2k+n
Ч По формуле (2), п. 2.1, имеем
1 Ге^С'^
Jn(z} С+' °<р<°°-
При р — 1 получаем:
Jn(z)=~ [ е2 х|- [ e*zsin9е~'пвid0 = — f ei{zsiae~ne)d6 =
2ттг J (n+l 2яч J 2тг J
Гр —7Г -IT
— [ cos(z sin 0 - nd) d6 -I- — / sin(z sin 6 — nd) de = — / cos(n# - z sin 0) dO.
2tt J 2tt J % J
— 7Г — 7Г 0
28. Найти главную часть ряда Лорана в окрестности точки z0 = оо функции
z >-> (2z3 + z) In---------------------------------,
1 - z
если выбранная ветвь логарифма действительна на верхнем берегу радиуса [О, 1].
§ 2. Ряд Лорана и изолированные особые точки аналитических функций
227
4 Имеем
(2z3 + z)In = (2z3+z)ln
= <2z3 + z)
= (2z3 + z) In ^1----------J + •«
= (2z3 + z) (iir + - + -—7 + -Д- + ...') = 2tTrz3 + inz + 2z2 + ... ►
\ z 2z2 3zj /
29. Найти особые точки функции z i-+ /(z) = sin--j-, установить их характер и исследовать
cos ~
Z
поведение функции f на бесконечности.
Для функции ( и-* sin £ точка ( = оо является в С единственной особой точкой, а именно,
существенно особой точкой. Следовательно, особые точки функции f определяются равенством
cos 7=0. Таким образом, функция f имеет бесконечное множество существенно особых точек
{z„ = ,, п 6 Z|. Точка z = 0 — предельная для указанного множества. Далее, lim /(z) =
sin 1, поэтому z = oo — устранимая особая точка функции f. ►
30. Пусть z = а является изолированной особой точкой функции f и lim(z — a)f(z) = 0.
z—»а
Доказать, что:
1) f(z')dz = 0, где Г = (7, 7ор) — произвольный замкнутый положительно ориентирован-
г
ный жорданов путь, лежащий в проколотой окрестности точки a Vo, я = {z 6 С | 0 < |z — а| < Л}.
2) /(Z) = -Д [ d(, z € {z 6 С I 0 < |z - а| < г < Я}, Гг = (7р, 7°Р), 7г = {z Е С :
2?ri J Q - z
Гг
\z - а| = г}.
◄ Точка а — устранимая особая точка функции /. Поэтому 1) следует из теоремы Коши, а
2) — из формулы Коши. ►
31. Доказать, что когда f является аналитической функцией в окрестности точки a KR =
{z € С : |z — а| < Я} и не принимает в этой окрестности значений, находящихся в круге
Кт = {ш € С : |w — Wo! < г}, то точка z = а либо устранимая особая точка, либо полюс.
◄ Справедливость утверждения следует из теоремы Сохоцкого. ►
32. Доказать, что функции z w ch z и z shz в окрестности бесконечности принимают
все значения из С.
◄ Пусть А 6 С. Решим уравнение chz = А:
ez — А + А2 — 1 /0, z = Ln + \/-^2 ~
Пусть zn = In | А + у/ А — 1| + t (arg(A + хЛА2 — 1) + 2птг) , n Е Z. Имеем
lim zn = оо, ch zn = A. ►
71—*ОФ
33. Определить характер особой точки z = 1 следующих функций:
z2 — 3z + 2 z2 - 3z + 2 _!_
а) ——7—Г-7; 6) ——о , в) (z -
z2 - 5z 4- 4 zl - 2z + 1
◄ а) Поскольку lim -5- 3zt; = lim = |, то z = 1 — устранимая особая точка для данной
х—*1 г ~5г+4 г_1 3
функции.
б) В достаточно малой проколотой окрестности Уо, е точки z = 1
z2 - 3z + 2 _ (z - l)(z - 2) _ z - 2
z2 — 2z + 1 (z — l)2 z — 1 ’
поэтому z = 1 — простой полюс заданной функции.
228 Гл. 5. Ряды аналитических функций. Изолированные особые точки
в) Разложение данной функции в ряд Лорана в окрестности точки z = 1 имеет вид
I оо оо
(z - 1)е ’ 1 - (z - 1) 52 n!(z _ - 52 n!(z - I)"-1 “ 1 + Z ~ 1 + 2!(z - 1) + ' ’' + n\(z - 1)
п=0 п=0
Главная часть ряда Лорана содержит бесконечное множество членов, поэтому z = 1 — суще-
1
ственно особая точка функции z н+ (z - 1)ег-> . ►
34. Определить характер точки z = оо для следующих функций:
z1 + 2 , 1 у
а) —m; б) z cos -; в) z е
z10 + 2 z
◄ Полагая z = |, получим:
z2 + 2 £8(1 + 2(2) 4 1 cos<
z10 + 2 ~ 1 + 2(10 ’ г со% - (4 •
а) Точка С = 0 является нулем восьмого порядка функции Q С , следовательно, точка
z = оо — нуль восьмого порядка заданной функции.
б) Точка < = 0 — полюс четвертого порядка функции Q , поэтому точка z = оо
является полюсом четвертого порядка для данной функции.
в) Разлагая заданную функцию в степенной ряд, получим
Таким образом, z = оо — существенно особая точка функции z г2е-2г. ►
35. Пусть степенной ряд ' anz" имеет своим кругом сходимости единичный круг, и на
окружности 7 = {z€C: |z| = l} его сумма / не имеет никаких других особенностей, кроме
полюсов первого порядка. Доказать, что последовательность (ап) ограничена.
Ч Так как сумма / ряда имеет на окружности 7 своими особенностями лишь простые полю-
сы, то этих полюсов может быть лишь конечное число, поскольку в противном случае / имела бы
на границе круга сходимости и неизолированную особую точку. Обозначим эти полюсы через Sj ,
(j = 1, m) и рассмотрим функцию
m
z <p(z) = f(z) - У2 Cj ,
Z—4 Z - Zi
где — главная часть ряда Лорана функции / в окрестности точки zj, (j = 1, т). Каждая
точка Zj является для функции правильной, вследствие чего аналитическая как внутри кру-
га К — {z € С : |z| < 1}, так и на окружности 7, т.е. в некотором круге KR, R > 1. Поэтому
справедливо представление
тп оо
/(г) = 52 С] + 52 ь"гП’ где lim < г
* "" Z — Z* * ~ п—»оо
j=l J n=0
Тогда
°о оо , т п„+1„ \
п=0 n=0 '
Отсюда получаем Vn 0:
тп тп
= (-1)п+152 “£+т+ьп> i°ni 52^+м = c°nst- ►
,=iZj j=i
Упражнения для самостоятельной работы
229
V—\ sin nt
ДО. Для всех значений t £ (0, 2тг) найти сумму ряда у
◄ Обозначив сумму ряда через f, получим:
sin nt 1 уЧ eint - e~int
'«> = £ — = 5Z—
, п е N.
п!
z“ — z
пГ
где z = elt, t e (0, 2тг). Полученный ряд Лорана сходится в кольце V"o, = {z € С | 0 <
|z| < оо}, содержащем окружность -у = {z g С : |z| = I}, а его сумма совпадает с функцией
. / t \
z ( ez - е? I Vz g Уо,^. Следовательно,
1 / it
- ee
2г \
г sin t _ —i sin t
----------------= ecos 1 sin(sin t). ►
2г
Упражнения для самостоятельной работы
1. Найти радиус сходимости каждого из следующих степенных рядов:
а)Е^П; 6)£n!^; В)£П:="ЛпО
г> Е (z^+ni> д) Е(«2 + *cos п^)(г -1 +2»)”•
2. Найти круг сходимости каждого из следующих степенных рядов:
а)Е^; в)Е^3"; г)^)"2-"/;
Д) Е(3г)”!; е) Е(4 + (-1)п)"г"; ж) £ ; з)
3. Исследовать поведение на границе круга сходимости следующих степенных рядов:
a)ES б> Е^г"; в)Е^; од) E5bn-
4. Разложить в ряд Тейлора в окрестности точки z = 0 следующие функции:
а) z ; 6) z Н-+ —уг~‘ ; в) z -— 1 г) z и-» chzcosz.
' (1 — zby ’ 7 4zx — 2z + l ’ 7 (1 —z4)(l + z + z2 + zJ) ’ 7
5. Коэффициент при n -й степени в тейлоровском разложении по степеням z функции z >-»
/(-) = ЕлЬ (|t| 1) называется полиномом Чебышева и обозначается Tn(t). Доказать, что
Tn(t) — cos(narccost), n € N, и T0(t) = 1.
6. Разложить в степенные ряды по степеням z следующие функции:
a) /(z) = j (in y^)2 ; б) /(z) = J е‘3 dt.
о
7. По методу неопределенных коэффициентов найти первые три отличные от нуля члена
разложения следующих функций в ряд Тейлора в окрестности точки z — 0:
a)/(z)=,, 6)/(Z) =
' 7 (I —z2)sinz ’ 7 J ' 7 ln(l+z)
8. Найти разложение в ряд Тейлора в окрестности точки z = 0 функций f, аналитических в
точке z = 0 и удовлетворяющих условиям:
а) (1 + z2)f'(z) = 1, /(0) = 0; б) f"(z) + zf(z) = 0; /(0) = 1, /'(0) = 0;
в) (1 - z2)f"(z) - 5zf'(z) - 4f(z) = 0; /(0) = 1, /'(0) = 0.
9. Пусть f и g — аналитические функции в области D, причем Vz g D выполняется равен-
ство f(z)g(z) = 0. Доказать, что тогда либо f(z) = 0 всюду в D, либо g(z) = 0 всюду в D.
10. Доказать, что если f — аналитическая функция в круге KR = {z € С : |z| < R} и
0 (к е Zo), то в этом круге справедливо неравенство |/(z)| /(|z|).
11. Доказать, что для п € N и z g С
к_(1 + д)п|<еИ_(1 + 1Д)^еыН
230
Гл. 5. Ряды аналитических функций. Изолированные особые точки
12. Доказать, что если функция f(z) = 52 является аналитической в круге К = {z € С :
п=0
|z| < 1} и непрерывна на окружности 7 = {z g С : |z| = 1}, то ряд У', |ап|2 сходится.
13. Пусть а # 0. Найти области сходимости следующих рядов Лорана:
a) £anzn = ^anzn+^a~nz-n; б) = £>-n2zn +
в) = ^a~nzn + ^a-nz~n.
14. Найти разложения в ряды Лорана в соответствующих областях по степеням z — za следу-
ющих функций:
a) z z0 = 1; б) z И-» cos^ + TTf, z0 = 0; в) z z0 = 0.
15. Разложить в ряды Лорана в указанных областях следующие функции:
а) z ~ (Л^-в ПРИ 1 < |^| < 2; б) z ~ пРи |г| > 2;
в) z ctgz при 0 < |z| < тг; г) z >-» ctgz при тг < |z| < 2тг.
16. Показать, что при всех z: 0 < |z| < 00
a) ch (z + I) = Др + 52 a« (2" + рг), где a„ = f ch(2cost?)cos
n = l 0
б) ег+2г2 = 52 an2", гДе a« = J cos(csin0(l - cos#) - n#)ec(cose+cos2в) M.
n = -x 0
17. Показать, что область сходимости ряда 52 ГпД-'й состоит из внутренности и внешности
единичной окружности, и что в каждой из этих частей ряд представляет одну функцию.
18. Определить характер точки z = 0 для следующих функций:
а) е2^-; б) --pS в) (е2 - 1 - z)ctg3 z; г) ——22 т; д)е*2-*.
smz-z + ~- cosz—1+ —
19. Определить характер точки z = 00 для следующих функций:
а) 4т1; 6)cosz-sinz; в) г)
20. Найти особые точки следующих функций:
а>Й 6)-^;
21. Пусть сумма / степенного ряда 52 Дп^п имеет на границе круга сходимости только одну
особую точку z0 — простой полюс. Показать, что в этом случае —* z0 и, следовательно,
| 2221 Я, где Я — радиус сходимости ряда.
22. Доказать, что когда точка z — а является существенно особой точкой функции /, то
она остается существенно особой точкой и для функции z >-> P(/(z)), где P(w) — многочлен
(P(w) const).
23. Доказать, что функциональное уравнение
f(z) = f(kz), к * 1,
не имеет решений, аналитических в точке z — 0 и отличных от тождественной постоянной.
24. Пусть радиусы сходимости рядов 52 enzn и 52 Reanz:n равны единице и Rea„ 0
Vn € Zq. Доказать, что точка z = 1 является особой для сумм этих рядов.
25. Пусть функция f — аналитическая в области G за исключением конечного числа полюсов
и А € С. Доказать, что функция z (логарифмическая производная функции f - Л)
имеет простые полюсы во всех полюсах функции f и во всех Л-точках этой же функции и не
имеет никаких других особых точек.
Глава 6
Аналитическое продолжение
Аналитическое продолжение является одним из основных и важных понятий комплексного ана-
лиза. Оно позволяет лучше понять природу функций комплексного переменного и наиболее
естественно определить многозначные аналитические функции.
Выясним, какие данные являются достаточными для определения аналитической функции
во всей области ее существования, и как по этим данным можно построить аналитические выра-
жения, определяющие функцию в этой области.
В случае целой рациональной функции степени п достаточно знать ее значения в п+1 точках,
чтобы определить ее на всей плоскости.
Для определения дробно-линейной функции, являющийся отношением двух целых много-
членов степени тип, достаточно задать т -I- п + 1 ее значений.
Но уже в случае целой трасцендентной функции недостаточно задать ее значения даже на
бесконечном множестве дискретных точек. Например, условие f(z) = 0 при z = ктг (fc g Z)
может относиться к функциям f(z) = 0, f(z) = sinz, /(z) = Asinz, А = const.
В случае целой трансцендентной функции достаточным является, например, задание значе-
ний функции и ее производных всех порядков в любой точке z0, поскольку по этим данным
можно построить степенной ряд
п!
сходящийся во всех точках плоскости и, таким образом, определяющий в ней функцию f.
Для определения функции, аналитической в замкнутой области, достаточно, согласно фор-
муле Коши, знать ее значения на контуре.
Для определения непрерывной функции недостаточно знать даже все ее значения в какой-то
области. Например, функцию [а, Ь] -+ R можно продолжить за сегмент [а, Ь] неограниченным
количеством способов, не нарушая при этом непрерывности функции.
Рассматривая класс аналитических функций, который выделяется из совокупности всех не-
прерывных функций требованием их дифференцируемости в области, мы увидим, что он имеет
такое свойство, которое позволяет определить аналитическую функцию во всей области ее суще-
ствования, зная:
а) “элемент” этой функции, т. е. степенной ряд
/<n)(z0) .
(z - Zo) ,
' п!
определяющий ее в круге сходимости, или
б) значения этой функции в как угодно малой области, или, наконец,
в) значения ее на как угодно малой дуге некоторой кривой.
После установления этого обстоятельства естественно поставить вопрос о том, как, имея
аналитическую в некоторой области D функцию /, расширить область определения функции,
т. е. построить новую область, содержащую область D, и определить в ней такую аналитическую
функцию, сужение которой на область D совпадало бы с f.
Такое расширение области определения аналитической функции называется процессом ее
аналитического продолжения, а полученное при этом аналитическое выражение, определяющее
функцию в новой области — ее аналитическим продолжением.
Необходимость такого расширения области определения функции возникает, например, при
нахождении решения дифференциального уравнения в виде ряда, сходящегося внутри некоторого
круга.
232
Гл. 6. Аналитическое продолжение
§ 1. Основные понятия.
Аналитическое продолжение вдоль пути
1.1. Свойство единственности аналитической функции.
Определение аналитического продолжения.
Теорема. Если функция f аналитическая в некоторой области D и обращается в нуль в неко-
торой ее части D\, то f = 0 во всей области D.
◄ Допустим, что / отлична от нуля в точке z = Ь той
части области D, которая лежит вне области Dt. Соединим эту
точку с любой точкой а & Di некоторой кривой 7, лежащей
в D (рис. 83).
На некоторой дуге этой кривой, примыкающей к точке а,
f(z) = 0, а на некоторой дуге, примыкающей к b, f(z) # 0.
Тогда существует такая точка z0 G 7, что Vz € az'o f(z) = 0,
а на дуге zr,b есть точки, как угодно близкие к z0, в кото-
рых f(z) / 0. Поскольку функция f непрерывная, то должно
выполняться равенство /(z0) = 0, т.е. z0 является неизолиро-
ванным нулем функции f. Это последнее обстоятельство воз-
можно лишь тогда, когда разложение функции f в ряд Тейлора Рис- 83
в окрестности с центром в точке z0 тождественно равно нулю. Но тогда /(z) будет равно нулю
и на некотором отрезке дуги zob , примыкающем к точке z0, что невозможно в силу свойства
ТОЧКИ Zq. ►
При доказательстве теоремы можно было бы ограничиться требованием, чтобы функция /
обращалась в нуль на некоторой кривой, лежащей в D, поскольку тогда она обращается в нуль и
в некотором круге с центром в одной из точек этой кривой.
Следствие. Если две функции /у и fi, аналитические в некоторой области, принимают оди-
наковые значения на некоторой части этой области или на отрезке кривой, лежащей в области,
то fi = Л во всей области.
Таким образом, задание элемента функции, аналитической в некоторой области, или, вооб-
ще, задание ее значений в как угодно малой области или на кривой, а также на бесконечном
множестве точек, имеющем предельную точку, полностью определяет функцию в области ее ана-
литичности.
Определение 1. Пусть функция f0 определена на некотором множестве М СС.Аналитиче-
ским продолжением функции f0 в область ПЭМ называется аналитическая в области D
функция f, сужение которой f\M = /0.
Примеры:
1) /о(®) = М = R; /(z) = ez = еЭ cos у + iex sin г/, D = С;
2) №) = £ z", M = {z e C : |z| < 1}; /(z) = -^, П = C\{1}.
n=0
Расширим понятие аналитического продолжения.
Определение 2. Аналитическим элементом Р называется упорядоченная пара Р = (П, /),
состоящая из области П С С и аналитической в этой области функции f.
Определение 3. Два аналитических элемента Pi = (Z>i, /() и Р2 = (П2, f2), области которых
удовлетворяют условию О П2 0, являются непосредственным аналитическим продолжением
друг друга через область А — связную компоненту множества Di П П2, если везде в A fi = f2.
Заметим, что значения функций fi и f2 в других связных компонентах пересечения jDt П П2
не обязательно должны совпадать.
Пример 1. Пусть
Di = {z 6 С | z = re'v, —тг < <р < тг, г > 0} ,
П2 = {z Е С | z = ге**’, у < <р < |?г, г > О} ,
/i(z) = л/ге* 2 , —тг < тг,
htf) = , f < <р < %.
§ 1. Основные понятия. Аналитическое продолжение вдоль пути
233
Элемент Pt = (Dj, fi) определяет в z-плоскости с разрезом вдоль отрицательной действительной
полуоси функцию fi, аналитичность которой следует из таких рассуждений. Очевидно, что w1 =
fi(z) = re'*5 = z, так что /i(z) = y'z. Поскольку дает однолистное отображение области D{
на правую полуплоскость плоскости w, то существует f'(z) 4z € Dx и эту производную можно
найти по правилу дифференцирования обратной функции:
' 1 _ 1 1
Таким образом, функция fi аналитическая в области Di. Аналогично убеждаемся в том,
что Рг = (Di, /г) также является аналитическим элементом.
Пересечение Di П D2 / 0 состоит из двух связных компонент Aj и Д2, представляющих
собой соответственно второй и третий квадранты z-плоскости.
Из определения функций /1 и /2 следует, что при z g Д[ /i(z) = f2(z) и f[(z) # /2(z),
если z g Д2.
Следовательно, элементы Р, и Р2 являются аналитическими продолжениями друг друга через
второй квадрант Дь
Определение 4. Элементы Р = (D. f) и Q = (G, д) являются аналитическими продолжениями
друг друга через области Др (v = 0, п — 1), если существует такая цепочка элементов Р„ = (D„, /„)
(и = 0, п), что'.
1) Ро = Р, Р„ = Q '
2) области D,, и D.,+i имеют непустое пересечение и Д„ является одной из компонент этого
пересечения',
3) элемент Pv+i является непосредственным аналитическим продолжением элемента Р„ че-
рез Д„.
Пусть, например,
D = {z g С | z = re**’, — у < tp < у, г > О} , /(z) = v/re,‘2, — у < <p < у,
G = {z 6 C | z = re**”, у < tp < yy r > 0} , g(z) = yfre 2 , у < <p < y\
Как и в примере 1, устанавливаем, что пары Р = (D, f) vi Q = (G, g) являются аналитическими
элементами. Цепочка элементов Ро, Pt, Р2, где Ро = Р, Р2 = Q, а р = (Ру /1) определяется
равенствами
.Di = {z g С | z = relv, 0 < tp < к, г > 0}, /i(z) = у/ге’^, 0 < <р < тг,
показывает, что элементы Р и Q являются аналитическими продолжениями друг друга в смысле
определения 4. При этом До —.первый квадрант, а Д1 — второй квадрант z-плоскости.
Для простоты последующих рассуждений конкретизируем понятие аналитического элемента.
Определение 5. Каноническим элементом с центром в точке a g С назовем пару
Ра = (KRa, fa), где fa — сумма сходящегося степенного ряда, a KRri — круг сходимости этого
ряда с центром в точке z = а:
KRa = {z g С : |z - а| < Ра}, /Q(z) = c„(z - а)п.
п=0
Круг KRa называется кругом сходимости элемента Ра.
Приведенные выше определения 3 и 4 для канонических элементов упрощаются, так как
их области (круги) всегда пересекаются по связным множествам, и поэтому нет необходимости
оговаривать, через какие компоненты пересечения Д„ совершается продолжение.
Рассмотрим еще несколько моментов, связанных с понятием канонического элемента.
1) Пусть Ра = (KRa, fa) и Рь = (KRb, /ь) — два канонических элемента, являющихся не-
посредственным продолжением друг друга, и пусть b g KRa. Тогда, очевидно, продолжение
элемента Ра сводится к переразложению суммы степенного ряда /„ в ряд по степеням z — Ь:
00 1
ACO = V-^’CbXz-b)". (1)
' п!
71=0
234
Гл. 6. Аналитическое продолжение
2) Если два канонических элемента Ра и Рь являются не-
посредственным продолжением друг друга, то их круги KRa
и KRb не могут компактно принадлежать друг другу. Действи-
тельно, пусть, например, KR, <s KRa , fb G A(KRb) и fb = fa
в KRb, однако fa 6 A(KRa). Отсюда получаем, что функ-
ция Д аналитическая в большем круге, чем KRb, и, таким
образом, KRb не может быть кругом сходимости.
Из последнего утверждения следует, что кривые dKRa и
dKRb обязательно имеют общую точку, и справедливо нера-
венство (см. рис. 84)
|Ла-Ль| |Ь - а|.
(2)
3) Пусть элементы РЬ\ и РЬ2 являются непосредственным
аналитическим продолжением одного и того же элемента Ра. Тогда РЬ1 = Рьг. Действительно,
пусть Rbl < Rb2. Тогда функции fbi и fb2 аналитические в круге KRbl и совпадают в нем,
поскольку fbl — fa и fb2 = fa на пересечении KRa П KRb*. Теперь очевидно, что Rb\ = Rb2 и,
следовательно, РЬ1 = РЪ2.
1. 2. Аналитическое продолжение вдоль пути.
Пусть Ро = (KRa, /о) — канонический элемент с центром в точке z = а, 7 — непрерыв-
ная жорданова кривая с параметрическим представлением ip, = I = [0, 1] и началом в точ-
ке р(0) = а, Г = (7, 7ор).
Определение. Канонический элемент Ро аналитически продолжается вдоль кривой (пути) Г, если
существует семейство элементов (Pt)tei = ((-Кд,, A))fgJ с центрами в точках at = ip(t) и ненуле-
выми радиусами сходимости, удовлетворяющее условию: для каждой окрестности O't., точки t0 € I,
'p(Ota) С KRto => Vt € Otll элемент Pt является непосредственным аналитическим продолжением
элемента Pta.
Если канонический элемент Ро продолжаем вдоль пути Г, то говорят, что элемент Р[ с цен-
тром в конечной точке 9?(1) = Ь получен из Ро аналитическим продолжением вдоль Г.
Следующая теорема устанавливает единственность аналитического продолжения вдоль пути.
Теорема 1. Если канонический элемент Рц продолжить вдоль пути Г, то полученный в резуль-
тате его аналитического продолжения элемент не зависит от выбора семейства, осуществляющего
это продолжение.
◄ Применим метод доказательства от противного. Пусть Р[ — элемент, полученный из Ро
продолжением вдоль пути Г с помощью семейства Pt, a Qj — элемент, полученный из Ро про-
должением вдоль Г с помощью семейства Qt. Имеем Ро = Qo.
Рассмотрим множество точек t из интервала I, для которых Pt = Qt \ Е = {t € 11 Pt = Qt}-
Очевидно, Е # 0, поскольку t = О € Е. Покажем, что Е — открытое множество. Пусть
to € Е : Pt„ = Qt0- Обозначим через Oto С I такую окрестность точки to, что <p(Ot!i) С KRl.,
где KRli — общий круг сходимости элементов Pta и Qto. Тогда Vt € Oto элементы Pt и Qt по-
лучаются непосредственным аналитическим продолжением одного и того же элемента Pto = Qtg
Отсюда Pt = Qt (см. замечание 3, п. 1.1), т.е, Oto С Е и Е — открытое множество.
Теперь докажем, что Е — замкнутое множество в топологии I. Пусть ta — предельная точка
множества Е. Обозначим через Кн,я меньший из кругов сходимости элементов Pto и Qto, и пусть
Otl. — такая окрестность точки t0, что <p(Oto) С Kr((| . Поскольку to — предельная точка множе-
ства К, то в окрестности €>to обязательно найдется точка tt g Е и, следовательно, Pti = Qt,. В
силу замечания 3, п. 1.1, имеем Pto = Qt„, т. е. to € Е и Е — замкнутое множество. Таким обра-
зом, непустое множество Е, являющееся подмножеством множества I, одновременно открыто и
замкнуто в топологии I. Поэтому Е = I (см. теорему § 3, гл.2) и, в частности, Pi = Qi. ►
Нас будет интересовать следующий вопрос. Мы имеем определения аналитического продол-
жения вдоль цепочки элементов (определение 4, п. 1.1) и определение аналитического продолже-
ния вдоль пути. Как они связаны между собой?
§ 1. Основные понятия. Аналитическое продолжение вдоль пути
235
Лемма. Пусть R(t) — радиус элемента Pt из семейства элементов, осуществляющего ана-
литическое продолжение вдоль жорданова пути Г, и пусть, далее, все круги KRt имеют конечные
радиусы сходимости. Тогда R(t) — непрерывная функция на отрезке I = [0, 1].
Ч Пусть to g I — любая точка. Существует такая окрестность Ofo точки t0, что Vt g Otg
элемент Pt является непосредственным аналитическим продолжением элемента Ptg. Согласно
неравенству (2), п. 1.1, имеем
\R(t) - R(t0)\ \?(t) - <p(t0)\,
где <р — параметрическое представление жордановой кривой Г. Поскольку отображение <р не-
прерывное, то R(t) является непрерывной функцией на сегменте I. ►
Теорема 2. Пусть элемент Q получен из элемента Р посредством аналитического продолжения
вдоль жорданова пути Г. Тогда Q является аналитическим продолжением в понимании определения 4,
п. 1.1.
Ч Пусть (Pt)te/ — семейство элементов, осуществляющее аналитическое продолжение вдоль
кривой Г (Ро — Р, Pi = Q). Радиус семейства R(t) является непрерывной функцией на сег-
менте I, и Vt € I R(t) > 0. Отсюда следует, согласно свойству непрерывных функций, что
Vt £ I R(t) > е для некоторого г > 0. Поскольку параметрическое представление <р жордановой
кривой Г есть равномерно непрерывная функция на сегменте I, то существует такое разбиение
П = {t*.; к = 0, п} сегмента I, где 0 = t0 < ti < ... < tn = 1, что
ISP(tfe) — 9?(#fe_i)| < £ (fc = l, n).
Тогда <p(tk) £ Кв^ , и, согласно определению 3, п. 1.1, элементы Pv(tk) и Pv(tk_t) явля-
ются непосредственным аналитическим продолжением друг друга, а элементы Р = и
Q = Pv<tn; — аналитическим продолжением друг друга вдоль цепочки элементов PV(tk > (к = 0, п),
т. е. элемент Q является аналитическим продолжением элемента Р в смысле определения 4,
п.1.1. ►
Рассмотрим, например, семейство элементов
Pt = (KRW, ft), tei =[o,i],
где
KRW = {z e C : \z - e,,rt| < 1}, ft=Vre'”, - у + vt < <p < у + xt.
Очевидно, w" = /"(2) = z, поэтому в каждой точке z е KRlt) существует f't(z) =
и fl(z) —> 00 при z —» 0. Получаем, что функция ft аналитическая в круге KRm. Представляя ее
рядом Тейлора в окрестности точки e”rt, получим степенной ряд с кругом сходимости KRW.
Таким образом, элементы Pt = (KR,t), ft) при t € [0, 1] образуют семейство канонических
элементов, осуществляющее аналитическое продолжение элемента Ро в элемент Р( вдоль по-
луокружности 7 = {z е С | z = e,lrt, 0 t 1}. Очевидно, элемент Р[ можно также получить из
элемента Ро аналитическим продолжением с помощью цепочки элементов Ро, Pi, Р\.
2
1. 3. Инвариантность аналитического продолжения вдоль пути
относительно гомотопных деформаций этого пути.
Пусть/ = [0, 1], К = 1x1, К-^С —гомотопияжордановойкривой 7о вжорданову кривую 71
с общими началом и концом, I 70, I 71 — параметрические представления кривых 70
на на
и 7t. Тогда V£ £ I tp(O, £) = у>0(0), у>(1, £) = ^о(1)> т.е. любая кривая 7^ с параметрическим
представлением £ i-» tp(t, £) имеет то же начало, что и 70 с 7, и тот же конец, что и 70 с 71
(см. п. 5.1, гл. 4).
Теорема 1. Пусть жордановы кривые 70 и 71 гомотопны как кривые с общими концами, а
элемент Р аналитически продолжается вдоль любой кривой 7^ с параметрическим представлением
f yj(t, £), 0 t 1, где у> — гомотопия кривой 70 в кривую 71. Тогда результаты аналитического
продолжения элемента Р вдоль кривых Го и Г] совпадают, где Го = (70, 7^р), Г! = (71, 7°₽).
М Согласно условию, аналитическое продолжение элемента Р вдоль любой жордановой кри-
вой 1\, имеющей общие концы с кривыми Го и Гь существует. Обозначим через Q( резуль-
тат аналитического продолжения, осуществляемого семейством элементов (Р/)ее/ вдоль пути
236
Гл. 6. Аналитическое продолжение
= (7^, 7^р). Пусть Е = {£ € 11 = Q0}. Множество Е непустое, так как $ = 0 € Е. Пусть
£о € Е. По лемме п. 1.2 существует такое г > 0, что радиусы R(t) семейства элементов ,
осуществляющего аналитическое продолжение вдоль кривой Г^о, удовлетворяют Vt € I нера-
венству R(t) е. Поскольку гомотопия tp является равномерно непрерывным отображением на
компакте К, то в К найдется такая окрестность О^0 С I, что V(£ € Ofn, t Е I) выполняется
неравенство
е
О- 01 < -• (1)
Выберем точки tk € I (fc = 0, п) так, чтобы Vfc р'[. = р(£0, О) удовлетворяли неравенству
I О О I ,
и элементы Р^°, , были непосредственным аналитическим продолжением друг друга. Обо-
значим tk) и заметим, что при £ б О^, согласно (1) и (2), выполняется неравенство
1^1 - Vk-II -Vk\ + \<Pk - < £ (3)
Очевидно, что элементы Р? и р/° являются непосредственным аналитическим продолжени-
ем друг друга (так как Pt°° и Р^ являются непосредственным аналитическим продолжением друг
друга согласно (3), и также Р^ и Р^11 являются непосредственным аналитическим продолжением
друг друга, и все три элемента Р^, Pf°, Р^1 имеют общую часть). Аналогично показываем, что
элементы Р^ и Р/ являются непосредственным аналитическим продолжением друг друга и т. д.
Наконец, Р/п и Р?° являются непосредственным аналитическим продолжением друг друга и, кро-
ме того, имеют общий центр, вследствие чего совпадают: pfn = СР = Pt?° = . Итак, CPri С E,
т.е. E — открытое множество.
Пусть £0 — предельная точка множества Е и О(о — окрестность этой точки, рассмотренная
выше. В этой окрестности найдется такая точка £ € Е, что продолжение элемента Р вдоль
кривой Г? приводит к элементу Qf- = Q°. Повторяя приведенные выше рассуждения, получим,
что аналитические продолжения вдоль кривых и Го приводят к одному и тому же элементу
_ q( — qQ т е с е, откуда следует, что Е — замкнутое множество. Следовательно,
Е = I и, в частности, Ql = Q°, что и требовалось доказать. ►
Замечание. Если хотя бы вдоль одного из путей , определяемого гомотопией <р, элемент Р аналити-
чески не продолжается, то результаты его продолжения вдоль кривых Го и Г| могут оказаться разными.
Для иллюстрации сказанного вернемся к примеру, рассмотренному в конце п. 1.2. Элемент Ро можно
продолжить вдоль нижней единичной полуокружности 71 = {z Е С | z = t Е [0, 1| = Г} с
помощью семейства элементов Pt' = /4'), где = {z Е С : \z - < 1}, /tl = ^re'n ,
— j -itt < tp < j — irt. Тогда Pg = Pg, но Pj1 P], хотя их круги сходимости одинаковые. Рассмотрим,
например, значения fi(z) и /,(г) в точке z = — 1: /i(—1) = е*" , /((—1) = е ’ п , /1(-1) # Д (—1). Это
объясняется тем, что гомотопию 7 и 71 можно осуществить лишь в области, содержащей точку z = 0,
однако аналитическое продолжение элемента Ро вдоль пути, проходящего через точку z = 0, невозможно
(в конце п. 1.2 показано, что ft(z) —» 00 при z —> 0).
Теорема 2 (о монодромии). Пусть Р = (К, f) — некоторый аналитический элемент,
К С D, где D — такая односвязная область, что элемент Р аналитически продолжается вдоль
любой жордановой кривой, лежащей в D. Тогда совокупность всех аналитических продолжений опре-
деляет в области D аналитическую функцию.
◄ Прежде всего заметим, что любые две жордановы кривые с общими концами, лежащие в
области D, гомотопны вследствие односвязности области D. Пусть z € D — произвольная точка.
Рассмотрим множество всех жордановых кривых, лежащих в D, с общими концами а и z, где
а — центр заданного элемента Р. Результаты аналитического продолжения вдоль этих кривых
по теореме 1 совпадают. Значения этих продолжений в точке z сопоставим ей. Этот закон и
определит, в области D аналитическую функцию. ►
§ 2. Полные аналитические функции 237
§ 2. Полные аналитические функции
2.1. Понятие полной аналитической функции.
Определение 1. Полной аналитической функцией назовем совокупность всех каноничес-
ких элементов, получаемых из одного какого-нибудь элемента Р аналитическими продолжениями его
вдоль всех жордановых кривых, начинающихся в центре а элемента Р, для которых такие продол-
жения возможны.
Покажем, что понятие полной аналитической функции не зависит то выбора начального
элемента Р. Действительно, пусть Q — любой другой элемент полной аналитической функ-
ции, определенной начальным элементом Р. Это означает, что Q получаем из Р продолжением
вдоль некоторой кривой Г = (7, 7ор). Тогда Р можно получить из Q продолжением вдоль кри-
вой Г“ = (7“, 70“).
Пусть теперь элемент Ф получаем из элемента Р продолжением вдоль пути Tt = (7,, 7°р).
Тогда, очевидно, получаем Ф из Q продолжением вдоль пути Г- U Г[. Принимая во внимание
теорему о единственности аналитического продолжения вдоль пути, естественно дать следующее
определение.
Определение 2. Две полные аналитические функции считаются равными, если они имеют хотя
бы один общий элемент.
Теорема 1. Объединение кругов сходимости элементов, принадлежащих полной аналитической
функции, образует область.
Ч Пусть D — это объединение. Оно открытое как объединение открытых множеств, т. е.
если z0 £ D, то € К — кругу сходимости некоторого элемента и К С D. Пусть а и Ь —
произвольные точки множества D. Тогда найдутся элементы, для которых а и Ь являются цен-
трами. Эти два элемента получаем аналитическим продолжением друг друга вдоль некоторого
пути Г = (7, 70р), соединяющего точки а и Ь. Ясно, что 7 С D. Следовательно, D является связ-
ным открытым множеством, т. е. областью. Она называется естественной областью определения
полной аналитической функции, или областью ее существования. ►
Заметим, что полная аналитическая функция может не быть в области D функцией в об-
щепринятом понимании, поскольку не будет однозначной. Сколько значений функции сопо-
ставляется фиксированной точке из области Z)? Ответ на поставленный вопрос содержится в
следующем утверждении.
Теорема 2 (Пуанкаре — Вольтерра). Полная аналитическая функция может иметь не
более чем счетное множество разных элементов с центром в фиксированной точке.
4 Пусть полная аналитическая функция определяется начальным элементом Ра с центром
в точке а, и z — произвольная точка из области определения D полной аналитической функ-
ции. Пусть Pz — один из элементов с центром в точке z, принадлежащий полной аналитичес-
кой функции. Его можно получить из элемента Ра с помощью конечной цепочки элементов с
центрами в точках zb z2, ... , zn_b z, в которой каждый следующий элемент является непосред-
ственным аналитическим продолжением предыдущего. Не ограничивая общности можно считать,
что точки zi, z2, ... , zn_l имеют рациональные координаты. Действительно, пусть сначала цен-
тры z[, z'2, ... , z'n_i произвольные. В как угодно малой окрестности точки z'k (fc = 1, п — 1)
возьмем точку zk с рациональными координатами и заменим элемент Pz' элементом Pz, . Со-
fc
гласно теореме об инвариантности аналитического продолжения вдоль пути относительно гомо-
топных деформаций путей, при достаточно малых [z'k — zk \ результат продолжения по новой це-
почке будет совпадать со старым. Множество непосредственных аналитических продолжений PZl
с рациональными центрами элемента Ра счетное, точно так же счетное множество и элемен-
тов PZ2, ... , PZn_t. Задание и точки z однозначно определяет элемент Pz. Следовательно,
число различных Pz не более чем счетное. ►
Вводя в рассмотрение понятие полной аналитической функции, не обязательно пользоваться
лишь каноническими элементами. Можно брать произвольные элементы, рассматривая полную
аналитическую функцию как совокупность аналитических элементов (£)„, /«), где а пробегает
некоторое множество индексов А. При этом каждый из этих элементов получаем из любого
другого элемента аналитическим продолжением.
238
Гл. 6. Аналитическое продолжение
2.2. Примеры полных аналитических функций.
Функции, аналитические в С, а также аналитические в С за исключением счетного множества
особых точек, являются, очевидно, полными аналитическими функциями.
Приведем также пример полной аналитической функции, состоящей из одного каноничес-
кого элемента.
ОО
Рассмотрим канонический элемент Р = (К, f), где К = {z € С : |z| < 1}, /(z) = zn'.
n= 1
Покажем, что этот элемент не может быть продолжен ни по какому пути с началом в точке z = 0.
Если бы такое аналитическое продолжение существовало, то некоторая дуга окружности
7 = {z6C:|z| = l} состояла бы полностью из точек аналитичности функции f. Однако на
любой такой дуге содержится бесконечное множество точек вида z0 = е ч , где р и q — целые
положительные числа, которые не могут быть правильными точками функции f. Действительно,
положим z = pz0, 0 < р < 1. Тогда получим:
д-1 °°
/(z) = £z- + £^.
n=l n—q
Для любого натурального числа N > q имеем
N д-1
l/(z)l > 5? р1' ~ УЗ lzln! ><N ~q + ^)pn' ~(q~ О-
n=q n=l
Отсюда, в силу произвольного выбора N > q, приходим к выводу, что функция f при приближе-
нии к точке z0 по радиусу стремится к бесконечности. Следовательно, z0 не может быть точкой
аналитичности функции f.
Изученные в главе 3 многозначные функции ^/z и Ln z, которые рассматривались нами как
объединение конечного или бесконечного (однако счетного) множества однозначных аналитиче-
ских функций, являются полными аналитическими функциями.
Определяя ^/z с помощью канонических элементов, можно в качестве начального взять эле-
мент Qa с центром в точке z = 1, состоящий из круга Ко = {z g С : \z - 1| < 1} и аналитической
в нем функции
1 Д 1 1 /1 \ / 1 \ k
z g0(z) = (1 + (z - l))n = 5 — ---------1 ) ... I--k + 1 ) (z - 1) . (1)
к! n \ n / \n j
k=0 4 ' 4 '
При z = x функция g0 является биномиальным разложением действительной функции
х ух на интервале (0, 2), a g0(z) является аналитическим продолжением этой функции в
крут Ко. Элемент Qo аналитически продолжается вдоль любого пути с началом в точке z — 1, не
содержащего точку z = 0 (см. пример п. 1.1). Итак, областью определения полной аналитической
функции \fz, порожденной элементом Qo, является область D = С\{0}.
Функцию 1/z можно также определить как совокупность аналитических элементов Ра =
(Da, fa), а е R, где
Da = {—тг + а < <р < тг + a}, fa(z) = vre « , —тг + а<^<тг + а.
Действительно, в круге Ко = {z g С : |z — 1| < 1} функция /o(z) элемента Ро = (Do, /о)
совпадает с функцией g0(z), определенной формулой (1). Это означает, по определению 2 из пре-
дыдущего пункта, что полные аналитические функции, определенные элементами Q = (Ко, до)
и Ро = (Dq, /о), совпадают.
Аналогично, полная аналитическая функция Ln z может быть определена с помощью кано-
нических элементов, или как совокупность аналитических элементов Ра = (Da, fa), а € R.
В первом случае исходным может быть выбран элемент Q = (Ко, до), где
°° (z - Dn
g0(z) = V(-l)n-‘-----p-, tf0 = {zeC:|z-l|< 1}. (2)
n!
n=l
§ 2. Полные аналитические функции
239
Функция д0 является аналитическим продолжением в Ко из интервала (0, 2) действительной
функции х Inх = 1п( 1 + (х - 1)).
В другом случае возьмем
Da = {-тг + а < ip < тг + a}, fa(.z) = In г + itp, —ir + a<p<ir + a.
Область определения Ln z совпадает с областью определения 'Цг:
D= (J Da = С\{0}.
Примером полной аналитической функции также является общая степенная функция w — zp,
р € R (см. п. 4.1, гл. 3). Однако общая показательная функция (см. п. 4.2, гл. 3), определенная
равенством
z z Ln а
w = а = е ,
не является полной аналитической функцией, поскольку ее отдельные элементы не являются
аналитическим продолжением друг друга (az есть совокупность различных аналитических в С
функций wk = fk(z) = fc е Z).
2.3. Особые точки полной аналитической функции.
Определение 1. Точки границы области определения полной аналитической функции называются
ее особыми точками.
Наибольший интерес представляют собой изолированные особые точки.
Пусть z = а — изолированная особая точка полной аналитической функции /, Va — ее
проколотая окрестность, расположенная в области D определения f.
Лемма. Если какой-нибудь канонический элемент Ро, принадлежащий f, при аналитическом
продолжении вдоль некоторого замкнутого пути Го = (70, 7о'Р)< 7о С Va, не изменяется, то и любой
элемент Р, полученный из Ро аналитическим продолжением в Va, не изменяется при продолжении
вдоль любого пути Г = (7, 7ор), если жордановы кривые 70 и 7 гомотопны в Va.
◄ Пусть Г' = (7', 7оР) — путь в Va, переводящий Ра в Р. Упорядоченный набор Г" =
(Г Го, Г') является ориентированной замкнутой кривой, совпадающей с Го. Поэтому кривые
7~ U 7о и 7' и 7 гомотопны в Va. Согласно теореме 1, п. 1.3, аналитические продолжения
элемента Р по путям Г" и Г совпадают. Но аналитическое продолжение вдоль Г" не изменя-
ет элемента Р, поскольку Г ~ переводит Р в Ро, Г о не изменяет Ро, а Г' переводит Ро в Р.
Следовательно, элемент Р не изменяется при аналитическом продолжении вдоль Г. ►
Из леммы следует, что аналитические продолжения вдоль путей, гомотопных нулю в V,., не
изменяют элементов, поскольку такие пути стягиваются в пути, лежащие в круге любого элемента,
аналитическое продолжение вдоль которых не изменяет элементов. Поэтому в дальнейших на-
ших исследованиях рассматриваются лишь аналитические продолжения вдоль замкнутых путей,
негомотопных нулю в Va.
Определение 2. Пусть z = а — изолированная особая точка полной аналитической функции f,
Va — ее проколотая окрестность, принадлежащая области определения f, и 70 С Va — замкнутая
жорданова кривая, охватывающая точку z = а. Тогда, если: 1) обход по кривой Го = (70, 7п’Р) приво-
дит к исходному элементу, то z = а называется особой точкой однозначного характера ’,
2) обход Го приводит к элементу, отличному от исходного, то z = а называется особой точкой
многозначного характера или точкой разветвления.
В первом случае легко убедиться, что аналитическое продолжение исходного элемента вдоль
любого пути Г' = (7', 7оР), 7' С Va, ведущего в фиксированную точку z Е Va, приводит к
одному и тому же элементу, и, следовательно, аналитическое продолжение начального элемента
вдоль путей, лежащих в множестве Va, определяет аналитическую (однозначную) в Va функцию,
являющуюся ветвью полной аналитической функции, которую рассматриваем. Для этой ветви
точка z = а будет, согласно классификации (см. п. 2.2, гл. 5) либо устранимой особой точкой, либо
полюсом, либо существенно особой точкой. Заметим, что если начальный элемент канонический,
то случай устранимой особой точки исключается, поскольку она уже с самого начала является
устранимой.
240
Гл. 6. Аналитическое продолжение
Определение 3. Пусть z = а является точкой разветвления полной аналитической функции f,
и 7о С Кх — замкнутая жорданова кривая, охватывающая точку z = а. Тогда, если: 1) существует
такое целое число п 2, что п-кратный обход Го = (70, 7^) в одном и том же направлении при-
водит к исходному элементу, то z = а называется точкой разветвления, а именно, (п— 1)-го
порядка, если п является наименьшим из всех целых чисел, имеющим указанное свойство', 2) целого
числа, указанного в 1), не существует, т. е. обходы Го в одном направлении приводят все к новым и
новым элементам, то z = а называется точкой разветвления бесконечного порядка или
логарифмической точкой разветвления.
Замечание. Легко проверить, что порядок разветвления не изменится, если кривую 70 заменить любой
жордановой кривой 7, гомотопной 70 в Va. Этим подтверждается корректность определения 3.
В качестве примера заметим, что точки z = 0 и z = 00 являются точками разветвления
(п - 1)-го порядка для функции w = ^/z и логарифмическими точками разветвления для функ-
ции w = Ln z.
2.4. Существование особой точки на границе круга сходимости степенного ряда-
Пусть степенной ряд У^ a„(z — z0)" имеет ненулевой радиус сходимости R. При R = оо
его сумма есть аналитическая функция в С и, таким образом, имеет единственную особую точ-
ку на бесконечности (граница круга сходимости). Пусть R < оо. Тогда пара (KR, fa), где
Kr = {z £ С : \z — z0| < R} — круг сходимости степенного ряда, /о(^) = У? an(z - z0)n опреде-
п=0 *
ляет аналитический элемент Ро, порождающий некоторую полную аналитическую функцию /,
которая, в частности, может совпасть с /о (см. пример в п. 2.2).
Рассуждая от противного покажем, что на окружности 7д = {z £ С : \z - z0\ = R} лежит
по меньшей мере одна особая точка функции /. Пусть Гд = (7д, 7д) = dKR, yR С D, где
D — область определения функции /. Тогда каждую точку z £ 7д можно рассматривать как
центр некоторого элемента Pz, являющегося непосредственным аналитическим продолжением
элемента Ро = (KR, fa). Объединение круга KR с кругами сходимости элементов Pz, z £ yR,
определит область D' С D, при этом KR § D', а функции этих элементов определят в D'
аналитическую функцию. Разлагая ее в ряд Тейлора в окрестности точки z0, мы, очевидно,
получим степенной ряд с радиусом сходимости, большим чем R. Полученное противоречие и
доказывает, что на границе круга сходимости степенного ряда всегда найдется по меньшей мере
одна особая точка полной аналитической функции, порожденной этим рядом.
§ 3. Принципы аналитического продолжения
В связи с понятием аналитического продолжения возникают вопросы, когда оно существует
и как его находить на практике. В решении этих вопросов важная роль принадлежит принципам
аналитического продолжения.
Теорема 1 (принцип непрерывности). Пусть две области Dt и D2, П D2 = 0,
имеют общий участок границ, содержащий замкнутую или незамкнутую гладкую дугу Жордана 70.
Тогда, если функции fa и fa аналитические соответственно в областях D\ и D2 и непрерывны вплоть
до 7о, причем Vz € 70
fa(z) = fa(.z), (1)
то функция fa где
{/i(z), если z € Л],
/2(z), если z G D2, (2)
/1(2) = fa(z), если z £ 70,
аналитическая в области D = Dt U D2 U 70.
◄ Пусть Kfazn) = {z £ С : \z — z0| < <5} — некоторая окрестность произвольной фик-
сированной точки z0 £ 70, K6(za) С D, причем считаем, что б меньше стандартного радиуса
§3. Принципы аналитического продолжения 241
кривой 7о (гладкие замкнутые кривые Жордана имеют свойство: для каждой такой кривой суще-
ствует число <50 > О, называемое ее стандартным радиусом и имеющее свойство, что окружность
радиуса S < 6г, с центром в любой точке кривой ровно два раза пересекает кривую).
Интеграл типа Коши
= f <з>
2тгг J Q ~ z
8K6(z„)
определяет в окрестности К6(г0) аналитическую функцию. Пусть, далее, и 72 соответственно
границы областей D' — Dt П Ks(z0) и D" = _О2 П Ke(z0). Принимая во внимание (1) и (2),
формулу (3) запишем в виде
. 1 ffdOdC 1 Г f2(OdC г t ор. г . ора
— mJ Г| = (7"7|)' Г1 = <7-7'7
Г1 г2
С помощью обобщенной теоремы и формулы Коши получаем равенства
1 f fi (Qd( _ ( /1(2), если z g D', 1 f _ f 0, если z g £>',
Im J < - z ~ [ 0, если z g D", 2тсг J £ - z ~ ( Л(х), если z g Z>",
г, r2
из которых следует, что Vz € Ki(z0) F(z) = f(z). ►
Теорема 2 (принцип симметрии Римана — Шварца). Пусть область D содержит в
составе своей границы некоторую дугу окружности -у и не содержит одновременно обеих симметрич-
ных относительно 7 точек и пусть, далее, f является аналитической функцией в D, непрерывной
вплоть до у и принимает на 7 действительные значения. Тогда существует аналитическое продол-
жение функции f в область D*, симметричную области D относительно 7, и для его получения
требуется, чтобы в точках, симметричных относительно 7, функция f принимала сопряженные
значения.
◄ Не ограничивая общности можем считать, что 7 совпадает с отрезком действительной оси,
а область D лежит в верхней полуплоскости (этого всегда можно добиться с помощью дробно-
линейного отображения). Точки области D* будем обозначать через г*. Каждой точке г* g D*
поставим в соответствие точку z g D по закону z = z* и определим в области D* функцию
z* f(z*) равенством
f(z’) = J(zj, z = z^.
Имеем ___________________
f*(z* + A.z*) - f(z*) _ f(z + bz)-f(z) _ //(г +Дг)-/(г)\
Дг* Дг \ Дг J
Отсюда, перейдя к пределу при Дг —> 0 (Дг* —> 0), получим, что функция /* дифференцируема
в О* и Г'(г*)=?7(1).
Таким образом, /* — аналитическая в области D* функция и, при условии доопределения
ее на Г равенством /*(ж) = f(x), непрерывная в D* и 7. Теперь к f и f* можно применить
принцип непрерывности. ►
Рассмотрим задачи.
1. Доказать, что элементы
Pi= (Кь^г"), = {г € С : |z| < 1},
И
/ 1 /г - г-
Рг= [К2, —/Е\ —i) )’ K2 = {zeC:\z-i\<V2},
являются непосредственным аналитическим продолжением друг друга.
◄ Оба ряда представляют функцию z >-» в кругах К, и К2. ►
242
Гл. 6. Аналитическое продолжение
2. Доказать, что элемент
(°° 1 /1 — \ п\
Кх, 1п2 - 52 - J J , Кх = {z е С : \z - 1| < 2},
является непосредственным аналитическим продолжением элемента
/ 00 \
Ро- , tf2 = {z€C:|z|<l}.
\ п /
х 71 = 1
◄ Оба ряда определяют разложение функции z н+ ln(l + z) и К2 С К-,. ►
3. Доказать, что элементы
Рх = (кь V— \ Кх = {z et: \z\ < 1},
71 = 1
И
/ °° (-1)" \
Р2 = ( К2, -Ki + -—— (z - 2)" , К2 = {z е С : |z - 2| < В,
\ п )
П=1
не имеют общей области сходимости, однако являются аналитическими продолжениями друг
друга в понимании определения 4, п. 1.1.
Ч Элементы Р1 и Р2 являются аналитическими продолжениями друг друга вдоль любого
пути, лежащего в верхней полуплоскости с концами в точках 0 и 2. Эти продолжения определяют
в верхней полуплоскости функцию z i-> - ln(l - z). ►
4. Доказать, что сумма д степенного ряда У', z2 является полной аналитической функцией.
Ч Имеем g(z) = У z2 . В точках zkm = е27Г”п2 ( плотно размещенных на окружности
тг=О
7 = {z € С : |z| = 1}, являющейся границей круга сходимости ряда, функция д не имеет
конечного радиального предела. ►
5. Привести пример полной аналитической функции /, областью определения которой явля-
ется единичный круг К = {z € С : \z\ < 1}, непрерывный в замыкании К.
Ч Такой функцией является z /(z) = У Если бы f аналитически продолжалась за
71 = 0
единичный круг, то такое же свойство имела бы и ее производная /', что противоречит задаче 4. ►
6. Доказать, что когда радиус сходимости степенного ряда У anzn равен единице и все
а„ 0, то такой ряд не может быть продолжен в точку z = 1 (теорема Прингсхейма).
Ч Пусть /(z) = У a„zn. Рассуждаем от противного. Пусть существует такое число h 6 (0, 1),
71 = 0
что ряд У f nXh)(z - h)n сходится в круге Кт = {z g С : |z - h\ < г} и h + г > 1. Согласно
равенству |/(n)(/ie*e)| = ряд У —Дг — he'e)n будет сходящимся для каждого 0 в
круге K’r = {z € С : |z — helfl| < г}, а сама функция f, следовательно, будет аналитической в
круге К — {z € С : |z| < h-t-r} радиуса, большего единицы, что противоречит условию задачи. ►
7. Доказать, что функция /, определенная рядом
“есх(0)
является непосредственным аналитическим продолжением функции
а ( z
f(z) = ------ (1-4--------4- ... +
а — z \ а — z
Упражнения для самостоятельной работы 243
◄ Функция д является суммой степенного ряда с кругом сходимости К = { z 6 С : \z | < }
и этот ряд является рядом Тейлора функции z >-> в окрестности точки z = 0. Область сходи-
мости первого ряда определяется неравенством | | < 1 и представляет собой полуплоскость D,
содержащую начало координат, ограниченную срединным перпендикуляром к отрезку [0, а]. На-
ходим сумму ряда в точке z Е D :
z \" \ а 1 а
------) + • ) =----------- —----т- ’
a — z) / а — z I — a — zz
Таким образом, К С D и /(г) = g(z) Vz Е К. ►
8. Привести пример функций /1 и /2, аналитических соответственно в областях D\ и Г2,
причем П Р2 = D = А] и Д2 и /Дг) = /2(z), если z € Ai, /i(z) # /2(z), если z € Д2.
◄ Пусть fi(z') = In |z| + iargz, Di = [z E С |—тг < argz < ~ }, /2(z) = In |z| + rargz,
D2 = {z E C |o < argz < }, Aj — первый квадрант, Д2 — третий квадрант z-плоскости
(см. также пример перед определением 4, п. 1.1). Функции /, и /2 удовлетворяют поставлен-
ным требованиям. ►
9. Доказать, что когда функция f £ 4(C) удовлетворяет условиям
ImMy=O = Re-Mz=O = 0’
то она нечетная, т.е. f(-z) = -f(z).
◄ Принимая во внимание равенство Im/(z)|j,=o = 0, по принципу симметрии имеем
/(z) = /(!)• (1)
Введем в рассмотрение функцию
z н. F(z) = if(z).
Тогда
IniF(z)|i=0 = Re/(z)|x=o = 0)
и, принимая во внимание, что точки z и —z симметричные относительно мнимой оси, получаем
F(z) = JW),
или
/(z) = -7PI). (2)
Из (1) и (2) следует нечетность функции f. ►
10. Построить четыре элемента функции с центрами в точках z = 1, z = i, z = -1,
z = —i и выяснить, какие из них являются непосредственными аналитическими продолжениями
друг друга.
◄ Непосредственно получаем четыре разложения
1 °° 1 °°
- = 5j-D"(z-i)n, k-i|<i; - = 52*—‘(z-i)", |z-i|<i;
n=0 n=0
°Q OO
- = - + 1)", |z + 1| < 1; - = ^2(-i)n~‘(z + i)n, |z + i| < 1.
n—Q n=0
Второе из этих разложений является непосредственным аналитическим продолжением пер-
вого, третье — второго, четвертое — третьего и первое — четвертого. ►
Упражнения для самостоятельной работы
1. Функцию х >-> /(г) = с интервала (-1, 1) С R аналитически продолжить методом
степенных рядов сперва в круг К == {z 6 С : |z| < 1}, а затем в круг К' = {z € С : |z — < 2}.
2. Пусть 2>i = {z € С | 1 < |z| < 2 Л Imz > 0}, a /(z) = Inz = ln|z| + :argz. Найти
аналитическое продолжение функции f из Di в область Р2 = {z € С | 1 < |z| < 2 Л Imz < 0}
через интервалы (—2, —1) и (1, 2).
244 Гл. 6. Аналитическое продолжение
3. Пусть С — комплексная плоскость с разрезом вдоль отрицательной части действительной
оси, К = {z € С : \z — 1| < 1},
z оо _ I
/1(г) = f & Z е С, f3(z) = £ - 1)п- Z € к.
1 П=1
Доказать, что fi и /2 являются аналитическими продолжениями одной и той же функции.
4. Пусть функция ip аналитическая в кольце Кгц = {z 6 С | г 5} |z| R}. Доказать, что
функцию f, определенную в круге Kr = {z € С : \z\ < г} соотношением
/U) = ih (mCZ), Гг = (7г17гор), 7r = {<€C:|z|= 1},
г,-
можно аналитически продолжить в круг К'д = {з€С:|г|<Я}и что это аналитическое
продолжение F(z) можно задать формулой
F(S) = £- J(C-z)XC)^ (meZ), Гл = (7н, 7°яр), 7д = {( € С : |(| = Л}.
гл
5. Доказать, что функции
z >-+ /i(z) = 52 гП (И < О и “ fit2) — f e“t<1-z)dt (Rez < 1)
n=0 0
являются аналитическими продолжениями друг друга.
6. Найти аналитическое продолжение функции х arcsina: из интервала (-1, 1) С R в круг
К = {z € С : |z| < 1}.
7. Пусть на интервале (—1, 1) определена функция f, где
_ J е х2, если х # О,
Г 0, если х = 0.
Можно ли аналитически продолжить ее в С?
8. Доказать, что функции
2 <-> Д2) = Е и 2”Дг)= fr'e^dt
п=0 О
являются аналитическими продолжениями друг друга.
9. Какие функции определяются рядом
^^НЕ^ЧИт^-^) (new)
в областях К6 Х = {z € С | 0 < е < |z| < 1} и К = {z G С : |z| > 1}? Являются ли они
аналитическими продолжениями друг друга?
10. Пусть
Ж) = /еС+?Д, Г = (7, 7ор), 7 = К € С : |С| = 1}.
г
Доказать, что эту функцию можно аналитически продолжить в С.
11. Доказать, что функцию /, где
Д2) — f (l+<2)(f+ez С)
о
можно аналитически продолжить в область D = {z £ С : | arg z] < тг}.
12. Доказать, что если функция / является аналитической в единичном круге и в каждой
точке его границы, то она аналитически продолжается и в некоторый круг Кр = {z G С : |z| < р},
где р > 1.
13. Пусть f — аналитическая в окрестности точки z = 0 функция, а последовательность
(/(n)(z)) сходится там равномерно и lim /<п)(0) = 1. Доказать, что предельная функция этой
п—КЭО
последовательности аналитически продолжается в С.
Глава 7
Вычеты и их применения
§ 1. Определение вычета. Основная теорема
1.1. Вычет относительно изолированной конечной точки.
Определение. Вычетом аналитической функции f относительно ее изолирован-
ной особой точки z — а € С называется коэффициент с.-, при первой отрицательной степени
разложения функции f в ряд Лорана в окрестности этой точки.
Обозначение вычета1’:
с_! = res/(z).
а
Принимая во внимание формулу (2), п. 2.1, гл. 5 для коэффициентов ряда Лорана, имеем
KSf(z)=~. [ f(z)dz, Гр=(тР, 7рР), (О
a 2.ТТ1 J
Гр
где 7Р — окружность радиуса р с центром в точке : = а, СО,, (Оа — окрестность точки а).
Заметим, что в случае, когда z = а — устранимая особая точка, res/ = 0. Если z = а —
полюс первого порядка, то res / Ф 0. В остальных случаях res/ может быть равным, а может и
не быть равным нулю, например:
sin z 1 -L
res ---= 0, res ----= 1, res е=2 =0.
О Z 2 z — 2 о
Получим формулы для вычисления вычета относительно полюса.
Пусть z = а — полюс функции / порядка р. Разложение функции / в ряд Лорана в проко-
лотой окрестности точки z = а имеет вид
/(*) = С~Р + ... + cn(z - а)п.
(z — а)р z — a
п=0
Отсюда получаем:
/(z)(z - а)р = с_р + c_p+1(z - а) + ... + c_t(z - а)р-‘ + сп(г - а)п+р,
п=0
dp-l ~
(f(^)(z: - а)р) =с_\(р- 1)! + сп (п + р)... (n + 2)(z - а)"+1,
71 = 0
lim ——r (/(2)(z - а)р) = с_,(р - 1)!.
z—*а CLZ^
Имеем формулу для вычисления вычета функции / относительно полюса р-го порядка:
1 <У~1
Т /(г) = - О • (2)
res — начальные буквы слова residu (франц.) — вычет.
246
Гл. 7. Вычеты и их применения
В частности, при р = 1 формула (2) принимает вид
res f(z) = lim f(z)(z — a),
a z—>a
(3)
На практике оказывается полезной небольшая модификация последней формулы.
Пусть функция f в окрестности простого полюса z — a имеет вид
f (z) =-------,
J
(4)
где р и ip — аналитические в точке z = а функции, причем <р(а) У- 0, ip(d} = 0, 1р'(а) / 0. В
соответствии с формулой (3) имеем
res f (z) — lim
a z—>a
t. e.
y>(z)(z - a) ¥>(z) 99(a)
-----------= lim -7-.' .—77—- =---,
ip(z~) z—a ip'(a)
ip(a)
KSf(z)=^-. (5)
Например, resctgz = res = 1.
К7Г kir
В случае, когда функция f определена формулой (4), а функции р и ip имеют в точке z = а
нули порядка выше первого, для вычисления вычета удобно заменить функции р и ip несколь-
кими членами разложения их в ряд Тейлора.
Например,
sin3z - 3sinz 3z - ^z3 + ... - 3z + -4z3 + ...
_______£_______________£__ — ra, ________ — Э/1
0 sinz(sinz —z) 0
1.2. Вычет относительно бесконечности.
Пусть z = oo — изолированная особая точка функции f. Разложение функции / в окрест-
ности бесконечности Ох = {z € С : г < |z| < 00} имеет вид
/(z)= 57 cnzn.
п~ — оо
Проинтегрируем это равенство по окружности Г" — (7”, 7д~), ориентированной в напра-
влении хода часовой стрелки (при этом бесконечность остается слева). Тогда получим:
У /(z)dz= 57 Сп J zn dz =-2iric_i, (1)
р — 73, ——ОС Г"
так как
У z" dz = 0 при n / 1.
г-
Определение. Вычетом функции f относительно бесконечности называется коэф-
фициент при первой отрицательной степени разложения функции f в окрестности бесконечности,
умноженный на —1.
Принимая во внимание (1), имеем
res/(z) = -с_, = -7 / f(z)dz. (2)
00 2тг» J
г-
Заметим, что в соответствии с данным определением res /(z) определяется коэффициентом
ОО
правильной части ряда Лорана и поэтому может быть отличным от нуля и в том случае, когда
бесконечность является устранимой особой точкой функции /, например, res | = — 1.
§ 1. Определение вычета. Основная теорема
247
Пусть бесконечность является устранимой особой точкой функции f. Введем обозначение
lim f(z) = /(оо). Тогда
2—»ОС>
res/(z) = lim z (/(оо) - /(z)) . (3)
ОО 2 —»ОО
Действительно, разложение функции f в ряд в окрестности бесконечности в этом случае
имеет вид
оо
/(z) = /(оо) + 57 c_kz~k,
к=1
откуда
оо
z(/(z) - /(оо)) = 57 C-kZ"k+l.
k=l
Совершив в последнем равенстве предельный переход при z —> оо, получим формулу (3).
Легко можно получить следующую формулу
res/(z) =-р'(0), (4)
где <р ( j) = /(z) и ip(z) — аналитическая функция в точке z = 0.
1.3. Теорема о вычетах.
Теорема 1 (Коши). Если функция f аналитическая в D U dD С С, за исключением некоторо-
го множества изолированных особых точек к = 1, п}, принадлежащих области D (но не 9D),
то справедливо равенство
п
f(z)dz = 57res/(z)- О)
< Рассмотрим окружности 71, 7г, ,7n ( A 7k
4=i
радиуса рк с центром в точках ак,
причем рк выбираем настолько малыми, чтобы круги КРк с границами ук компактно принад-
лежали области D. Рассмотрим область D \ {КРк; к = 1, п} и применим формулу Коши для
неодносвязной области (см. теорему 4, п. 5.3, гл. 4):
2 /* __________। /* ____
— / /(z)dz = 57 ~ / /(z)dz = 57res/<2)> = (7fe, 7Г) • ►
2тгг / £—' I ak '
* k=i * k=i
OD K 1 Гк 1
Эта теорема имеет большое принципиальное значение. Она сводит вычисление глобальной
величины, которой является интеграл от аналитической функции по границе области, к вычи-
слению величин локальных вычетов функции в ее особых точках. Например, вычислим интеграл
Г dz
OD
Подынтегральная функция / аналитическая в замыкании D, за исключением точек zj = 1
(полюс второго порядка), z2 = i (полюс первого порядка). С помощью формулы (1) получаем:
/dz ( \ ( 1 1 \ тгг
u-i>4z4.i)= 2” (7/<2)+= “ Н + V = “
0D
Справедливо следующее утверждение. ______
Теорема 2. Пусть / € А (С \ {а4; к = 1, п}). Тогда сумма вычетов функции f во всех ее
конечных особых точках и вычета на бесконечности равна нулю'.
Vres/(z) + res/(z) = 0. (2)
*:=! °°
248
Гл. 7. Вычеты и их применения
Ч Пусть = {z £ С : |z| = R} — окружность столь большого радиуса R, что она охватывает
все конечные особые точки ак. Тогда согласно формуле (1) и формуле (2), п. 1.2, получим:
/ f(z)dz = = — res/(z). ►
2тгг / < ак оо
„ ь=1
1 R
Доказанная теорема может оказаться полезной при вычислении интегралов по контуру. В
качестве примера рассмотрим интеграл
1 = f z^_ 2у Г = (7. 7ор) , Т = {2 6 С : |z| = 2}.
г
Согласно теореме 1 имеем
( 1 -Д 1 \
1 = |^Ч S * * * * + Ь ’
где (к (fc = 1, 10) — корни уравнения z10 - 2 = 0, или, воспользовавшись формулой (2),
Рассмотрим примеры.
Найти вычеты указанных функций относительно всех изолированных особых точек и отно-
сительно бесконечно удаленной точки (если она не является предельной для особых точек).
. z2 + Z — 1
1. f(z)= —------.
z2(z - 1)
◄ Особыми точками функции / являются zi = 0, z2 = 1, z3 = оо. По формуле (2), п. 1.1,
находим:
d , 2 \ d / z2 + z — 1\ z2 — Iz
res/(z) = lim — (z /(z)) = lim — ----------— = lim ---— = 0
о о dz ' ' z—n dz у z — 1 J z—o (z — I)2
(принято во внимание, что точка = 0 — полюс второго порядка функции /).
Точка z2 = 1 является полюсом первого порядка функции /, поэтому для вычисления вычета
в этой точке применим формулу (3), п. 1.1. Получим
z2 + z - 1 _
72 = L
res /(z) = lim f(z)(z - 1) = lim
Согласно формуле (2), п. 1.3, имеем
res /(z) + res /(z) + res /(z) = 0,
z = 0 z = l oo
откуда
res/(z) = -1. ►
2. /(;) = —
sinz
◄ В точках zk = ктг (fc € Z) функция f имеет простые полюсы. Воспользуемся формулой (5),
п. 1.1, в которой = 1, $(z) = sinz. Тогда res /(z) = = (-1)*- Бесконечно
удаленная точка является предельной для особых точек. ►
1
3. f(z) = cos —
Ч Точка z = 2 — существенно особая для функции /. Ее разложение в ряд Лорана в
окрестности точки z = 2 имеет вид
~ (_1)П / 1 V" 1 / 1 V
= >2 ттт—d = 1~d—й + ....
(2п)\ \z — 2 J 2 \ z — 2 J
п—0
§ 1. Определение вычета. Основная теорема
249
Коэффициент при (z — 2) 1 равен нулю, следовательно, res f(z) — 0.
2
Согласно формуле (2), п. 1.3, res f(z) + res f(z) = 0, откуда res f(z) = 0. ►
2 oo oo
4. f(z) = z3 cos --
z - 2
< Как и в предыдущем примере, z = 2 — существенно особая точка для функции f. По-
скольку
z3 = (2 + (z - 2))3 = 8 + 12(z - 2) + 6(z - 2)2 + (z - 2)3,
1 ^(-pn f i У" , i < i V, 1 < 1 у
C0S z -2 (2n)! I z-2 ) 2! \z - 2 J + 4! \z -2 J
n=0
TO
?cos_^ = (8 + №_2) + №_,). + (;-2)’)(1-5^ + ;^-...).
Очевидно, что коэффициент при (z - 2)“1 равен -6 + . Следовательно, res /(z) = - —.
Согласно формуле (2), п. 1.3, resf(z) + res f(z) = 0, откуда resj(z) = . ►
2 ос оо
5. /(z) = zn sin - (n € Z).
z
◄ Точка z = 0 — существенно особая для функции f. Ряд Лорана функции f в окрестности
точки z = 0 имеет вид
)= "V (-1)" 1 = V 1
z nk + z2k+l 2^ (2fc +1)! z2i:-"+l’
k=0 k=0
Равенство 2к - n + 1 = 1 невозможно, если n < 0 или если п С Z — нечетное. В указанных
случаях res/(z) = res/(z) = 0.
0 оо
Если п = 2т (т 0), то главная часть ряда Лорана функции f будет содержать член
(-1Г (-1Д
(2т+1)!г (п + 1)! Z
тг
Следовательно, для всех четных п € Zo res/(z) = В частности, при п = 0 res/(z) = 1.
0 (П+Р- 0
Применив формулу (2), п. 1.3, получим, что для всех четных п 6 Zo
д + 1
(-1)2
res/(z) = -res/(z) = ———.
оо О (п+1)!
В частности, при п = 0 res f(z) — -1. ►
r 15z3 - Hz2 + 4z + 6
”• =-----7~27Л—П-------•
2z2(z2 - 1)
◄ Представляя функцию f в виде суммы простых дробей, получим:
2 3 4 3
/(г) --------j —Z7 + э7----Г?
z z2 z +1 2(z — 1)
Особыми точками функции f являются z1 = 0, z2 = —1, z2 = 1, z4 = оо. Поскольку точки
zH z2 и z3 — простые полюсы функции /, то res f(z) = 2, res/(z) = 4, res f(z) = |. Согласно
о -i i
формуле (2), п. 1.3,
res /(z) + res /(z) + res /(z) + res /(z) = 0,
0 -I t oo
откуда
res /(z) = — I res /(z) + res /(z) + res /(z) I = —7,5. ►
250
Гл. 7. Вычеты и их применения
7. Найти вычеты всех ветвей многозначной функции
1
/(2) ~ ЛЛ +ЛТТ
во всех ее конечных точках однозначного характера.
◄ Из представления функции
/(г) =
— \/ z + 1
z - I
видно, что она четырехзначная и что конечной особой точкой однозначного характера для ка-
ждой из ее ветвей является простой полюс Zi = 1. Точки z2 = 0 и г3 = -1 являются точками
разветвления, т. е. особыми точками неоднозначного характера.
Выделим четыре однозначные ветви функции / в области С (плоскости С с выброшенной
отрицательной действительной полуосью) их значениями в фиксированной точке, например, в
точке z = 2:
/1(2) = 2 - Л,
/2(2) = -2 - Л,
/з(2) = 2 + Л,
М2) = -2 4- Л.
Тогда получим:
. . . 1 ( ггг~.( argz . . argz\ г—— Г arg(z + 1) . . arg(z + l)\\
/Л) =-------- I V2H I C0ST~ +г5т~Г“ 'Л + Щ cos—;— + isin —:— I ) r
Z 1 \ \ 2, f \ 2. x / /
. . . 1 ( r^-.( argz . . argz\ , — / arg(z +1) . . arg(z + l)\\
/2(2) = I ~v 2H ^cos^f” +rsm-^— J - Vk + 1| I cos----------------------b г sin------ I 1 ,
/3(2) = -/2(2), Л(г) = -/i(z).
Таким образом,
res fi(z) = lim(z — l)/i(z) = Л - Л = 0, res fi(z) = lim(z — l)/2(z) — - Л - Л = -2Л,
1 z —»I I z —»I
res /3(z) = 2Л, res Mz) = 0. ►
1 1
8. Доказать, что если z„ является полюсом функции z >-+ f(z) = —--, то res/(z) =
z — a1 4а4
Ч Воспользуемся формулой (3), п. 1.1, и правилом Лопиталя раскрытия неопределенностей
вида 2. Получим:
z z(z-z„) 2z - z„ 1 2z2 - zvz 12z2-z2 z2
res —:---7 = Inn —--------r- = lim ——:— — - lim —------------- = -----— = —. ►
г» z4-e4 z4 - a4 z^z„ 4z3 4 z4 - a4 + a4 4 a4 4a4
e2z e*z •
9. Найти: a) res ---—; 6) res —---- (a e R).
□o (z - I)3 00 z1 + a1
◄ а) Согласно формуле (2), п. 1.3, имеем:
e2z e2z 1 d2 2, ,
res - —- = - res - — = - - lim — e = -2e .
00 (z - l)3 1 (z — l)3 2 z—1 dz2
б) Аналогично,
e*z / e’z e*z \ / e*z eiz \
------r = - I res -5--т + res -z----z ) = - I lim -------— + Um ------— I =
52 + a1 \z=ia Zl + a2 z=-ia Zl + dLJ z-.-ia Z - la/
/ e~° _ e^\ _ 1 ei(io) - e-i<ie> _ sin ia
\ 2ia 2ia J a 2i a
§ 1. Определение вычета. Основная теорема
251
10. Найти вычеты следующих функций относительно всех конечных изолированных точек
и на бесконечности, когда она является изолированной особой точкой:
Z
a) = sin ——;
Z “г 1
6)/w= /, 1 Л (л#о);
z (1 - e-ftz)
в) /(г)Ч(1 + ГТ7 + (ГТ^ + -'-+(Г^)'
< а) Воспользуемся формулой (3), п. 1.2:
res sin--= lim z (sin 1 - sin-- ) = lim Iz sin —cos —=
oo Z 4“ 1 z —oo \ Z 4" 1 / z —oo 2 2
(Z \ Z
1-----I = cos 1 lim -- = cos 1.
z -Ь 1 / z—»o© z 4- 1
Согласно формуле (2), п. 1.3, имеем
z z
res sin---- = — res sin-----= — cos 1.
— i z 4- 1 oo z 4- 1
б) Особыми точками функции / являются zk = (к € Z). Точка z = 0 — полюс второго
порядка, а точки zk при к 0 — полюсы первого порядка. Применив формулу (2), п. 1.1,
получим:
res/(z) = lim ~
о г—о dz \ 1 — е Л /
1 -e~hl(\ + hz)
— lim------------5—-
г~° (1- e-hz}
1 - (1 4- hz) (1 - hz + ^z2 + o(z2)) j _ j + hiz2 _b^L+
lim------------------------------5---------= lim-----------—r—-----—г----------
z-o (1 - 1 + hz + o(z))2 г-0 h2z2 + o(z2)
1
2
Для вычисления вычетов функции f в точках zk (к / 0) воспользуемся формулой (5), п. 1.1,
полагая <fi(z) = |, V'(-z) = 1 - e~hz. Тогда
res/(z) =
V>'(*)lz=zfc
i _ i
^he~^h ~ 2k™
к /0.
в) При \z 4- 1| < 1 имеем |
— i-(z+d — 52(1+ ’
к=й
/1 / i 1 \\
res [-114- ----h ... 4- ----— I I —
-1 V \ 1 + 2 (1 4-z)n//
= res( (-1-(1 + z)- (1 + z)2-...) (1 + -J- + ... + --4 И =
-1 \ 14- z (1 +z)n/ /
( 1 2 п \
-1 \ (14-z)n (1+z)""1 1+z J
Далее,
252
Гл. 7. Вычеты и их применения
11. Вычислить интегралы:
й) / Гк = (7л>Т'я), 7В ={г£С: |z| = Л}, п<Я2 <n+1, n6N;
б) /
Г г = (7r, 7°р), 7r = {z € С: |z| = г}, г > 2 И при больших |z|
vzS? = 1 + °(1)-
◄ Окружность 7r охватывает 4n + 1 полюса подынтегральной функции: точку z = 0 и на
каждой окружности = (z € С : |z| = \/fc} (fc = 1, п) лежит четыре полюса zm = Vke 2
(m = 0, 1, 2, 3). Согласно формуле (1), п. 1.3, получим:
/ п 3 \ / \
/ 1 \ 1 1 . / 1 П \
2тгг — + } > , = 2тгг — И-----------= 2n + 1
\ 2ттг -4—' 4—< 4тгге(_|) 2,Г"& / \ 2тгг тг )
\ к~\ тп=0 /
б) Воспользуемся формулой (2), п. 1.2:
12. Доказать равенство
(z4 + l)dz _ . г8 + 64
z2(z-a)(b-z) 2™ Ь4г2(Ь - а)
Здесь Гг = (7Г, 7°р), уТ = {z g С : \z\ = г}, 0 < |а| < г < |Ь|.
◄ Поскольку z G 7Г => zz — г , z — , то
1= Г (z4+l)dz
J (г2 — az)(bz — г2)
Подынтегральная функция имеет два простых полюса zj =
охватывается кривой уг. Поэтому
z4 + 1 2тгг z4 + 1
I = 2тг res —-----—-------5- = — lim -5--------
r2 (г2 — az)(bz — г2) Ь г2 г2 — az
Т
Т2 т2
— И Zj = у , причем ПОЛЮС Zj
г8 + Ь4
%г &4г2(Ь - а)
13. Вычислить
dz
(z-3)(z5-l)’
Г = (7, 7оР), 7 = {z 6 С : |z| = 2}.
Ч Окружность 7 охватывает одну особую точку подынтегральной функции |z| = 1, следова-
2Ьтг ___
тельно, точки zk = е s (fc = 0, 4) — ее простые полюсы. Согласно формуле (1), п. 1.3,
(z - 3)(z5 - 1) 2,Г152 г®5 (Z - 3)(Z5 _ J) '
§ 1. Определение вычета. Основная теорема
253
Поскольку
4
El 1 1
res--------;------h res------:-------1- res----г----= О,
<Z - 3)(z5 - 1) 3 (z - 3)(z5 - 1) eo (Z - 3)(z5 - 1)
*=0
TO
r dz c i i \
I -------------= — 2iri I res----:-------1- res------:----
J (г - 3)(z5 - 1) \ 3 (Z - 3)(z5 - 1) сю (z - 3)(z5 - 1) J
Г
В окрестности z — оо имеем
i \ ( ъ /з\2 V . 1 . A
(z — 3)(z3 — 1) ~ 7 11 + 7 + J +"'J у + + ”/ ’
следовательно, res -—< ,, = 0, поэтому
x (г-3)(г3-1)
/dz dz 1 2тгг тгг
-------:----- = —2rrires------------= -2rri lim -7--=--------=-----.
(z - 3)(z5 - 1) 3 (z - 3)(z5 - 1) z-3 z5 - 1 242 121
г
Применив формулу (2), п. 1.3, мы избежали громоздких вычислений. ►
14. Вычислить I = f _ Z^Z_ , Г = (7, 7ор) , 7 = {z £ С : |z - 2| = |}.
J \Z 1)\Z Z)
Г
◄ Окружность 7 охватывает одну изолированную особую точку z = 2 подынтегральной функ-
ции /, являющуюся ее полюсом второго порядка. Следовательно,
d ( {z — T^z \ d ( z \ —1
1 = 2тгг res f (z) = 2тгг lim — -------- — 2~i lim — ------) = 2rri lim-------- = -2тгг. ►
2J z—*2 dz \(z - l)(z - 2)2/ z-.2dz\z-\J г—»2 (Z — I)2
15. Вычислить I = J 2z^+\ ’ Г = Ь> 7°p) 7 = {2 € C : |z| = 1}.
Г
◄ Подынтегральная функция / имеет простые полюсы в точках
1 тг + З/гт
zfc = ^=e’~^r- (Л = 0, 1,2, 3).
Согласно формуле (1), п. 1.3, имеем
з
I = 2тгг У ' res /(z).
fc=0
3
Поскольку res/(z) + res/(z) = 0, то I = -2Trires/(z). Из разложения
fe=0 ~
1 / 1 \ 1 / 1 \
/(г) - 2z V + Л / 2^ \ ~ 27 + ’/
\ 2z* / x /
следует, что res/(z) = —c_! = (см. формулу (2), n. 1.2). Следовательно, I = tti. ►
e
16. Вычислить 1=1 e2 _ dz, Г = (7, 7op) , 7 = {z € C : |z| = 1}.
J Z \Z V)
г
4 Подынтегральная функция f имеет полюс второго порядка в точке Z| = 0 и простые
полюсы в точках z2 = -3, z3 = 3, однако окружность 7 охватывает лишь точку zj, поэтому
т —о • \ „ ... d ( ех \ ex(z2 — 2z — 9) 2jri
I — 2%ires/(z) = 2тг: hm — ( ——- I = 2iri lim-—-——5---= ——. ►
0 Z~odz\z2-9j г-o (z2 — 9)2 9
254
Гл. 7. Вычеты и их применения
17. Вычислить I = [ sin - dz, Гг = (7,., 7°р) , 7Г = {z € С : |z| = г}.
2тг1 J z 4
Гг
4 Точка z = О является существенно особой для подынтегральной функции. Поскольку
(-D’
Slnz (2n+l)!z2n+1’
п=0
то res/(z) = 1,1 = res/(z) = 1. ►
о о
18. Вычислить I — J" sin2 - dz, Г = (yr, 7°р) , 7r = {z € С : |z| = г},
г,.
Ч Поскольку в разложении в ряд Лорана
1
Z
1
2
sin
2
1 - cos -
z
2^ (2n)! \z
n=l x
2
отсутствует член вида c_,z *, то res sin2 - = 0, I = res sin2 - = 0. ►
0 o’
19. Вычислить I = -—Jzndz, n £ Z, Гг — (7,., 7°p) , yr = {z g C : |z| = r}.
rr
◄ Поскольку
00 -1.
n.2 V" 2
Z Z k'zk~n'
fc=0
2_ ->n+l 2.
то при n = к — 1, fc g Zq, т. e. при n -1 reszne« = 7, а при n < -1 resz’le- = 0.
0 (n + l). 0
Следовательно,
f2«+ 1
--------, если n > —1,
(n+1)!’
0, если n < -1. ►
2тг
20. Вычислить 1=1 ——— (a > 1).
J a + cos if
0
◄ Произведем в интеграле замену переменной е**1 = z. Тогда
d<f —
dz
iz'
1 _ 2z
a + cos f z1 + 2az + 1 ’
dz
z2 + 2az + 1 ’
г
Г = (7, Top) , 7 = {z € C : |z| = 1}.
Уравнение z2 + 2az +1=0 имеет корни z^j = — a ± Va2 — 1, причем лишь точка Z\ = — a +
Va2 - 1 охватывается окружностью 7 (т. к. I Va2 — 1 ~ a | =-7=т= < b- По формуле (1),
1 1 I a+va2-l I
п. 1.3, имеем
I
- 2iri res -р— ------- = 4ir------—-
» л, z2 + 2az + 1 2z + 2a
г=г1
2я-
s/a2 — 1
255
§ 1. Определение вычета. Основная теорема
/ —V <° > ь > °>-
/ (a + bcos^)2
о
•4 Воспользуемся решением предыдущего примера. Для этого представим интеграл I в виде
2тг 2тг 2-тг
1 f adp if dp b f cospdp
a J (a + bco&p)2 a J a + bcosp a J (a + 6cosp)2
0 00
21. Вычислить I
2тг
О
2тг
-^— + <4 Z
а + о cos ab J
о
Согласно решению примера 20 имеем
2?г 2тг
f dp 1
J ^+cos<? Ь
о
[ dlp -
J a + bcos<p
о
2тг
2тг
Va2 — b2 ’
2тг
- /
db J a + b cos 9?
о
dp
d / 2тг
db
\/а2 — Ь2
2тгЬ
(а2 -Ь2)2
I - - I 27Г
<2 \ Va2 — b2
2тгЬ2
(а2 — Ь2)г ) а(а2 — Ь2)2
2тг
2тга
(а2 — 62)2
2тг
22. Вычислить 1=1
dp
(а + bcos2 р)2'
о
◄ Аналогично предыдущему, представим I в виде
2тг 2тг
cos2 р dp
(а + b cos2 р)2
f dp b
J a + b cos2 p a J
о 0
2 т
f dp
J а + Ь cos2 р
о
2-тг
Г
adbj
о
dp
а + b cos2 р
/ 2тг
1 / /
dtp
a I J а + b cos2 р
\ о
2 т
f dp
J a+ b cos2 p
0
Полагая 2р = t, получим:
2тг 2тг
4тг
[ = 1 [ - dt—, где А = а+Ь-,В=Ь-.
J a + bcos2p J A + Bcos2p 2 J 4 + Bcost 2 2
00 0
Принимая во внимание решение предыдущего примера, а также то обстоятельство, что при
изменении t от 0 до 4тг замкнутый контур, охватывающий полюсы подынтегральной функции,
обходится два раза, получим
4тг
1 Г dt
2 J A + Bcost ~ у/А2 - В2 ~
О
2тг
2%
2ir
ь\2 p Va2 + ab
’ 2) ~ T
Поскольку
2 т
ь± Г____________
db J а + Ь cos2 р
о
d [ 2тг
= Ь — I - ——
db \ ya2 + ab
irab
(а2 4- ab) 2
256
Гл. 7. Вычеты и их применения
то
тг аЬ
1 / 2тг тгаЬ \ тг , , тг (2а + Ь)
I = - 7^-^------------г = ----------Г (2(“ + а6> ~ аЬ) = "Г--Т
а yva + ао (a2+ab)i/ а(а2 + а6)2 а2(а + 6)2
23. Вычислить I =
— sin <p)dip (п g Z).
гиф е । — ।
е е +е е
0
4 Воспользуемся формулами Эйлера для преобразования подынтегральной функции. Имеем
COS OS / . 1 coses 7 i(n«s~sin e>) . — i(nus— sin cs)
e cos(nip — sintp) = -e {^e + e
Произведя в интеграле замену е**5 = t, получим:
— 1 1 . <—п—1
е t + t е
Г=(э, 7op), 7 = {< € C : |i| = 1}.
Согласно формуле (1), п. 1.3, находим:
Е = 0,
I = тг res (tn~'et +t~n
о X
24. Вычислить I =
dx.
если п < О,
если п 0. ►
е
о
Ч Преобразуем подынтегральную функцию с помощью формул Эйлера:
gi(x + ia) _ g~i(i+ia) । xlx _ ^2a
tg(x + iot) = —;----------------r* = - —7-------Г-.
i (^(х+га.) _|_ e-i(x4-ia)\ | gi2x g2a
Полагая e'2x = t, после замены переменной в интеграле получим:
1 Г t - е2а , ч
'='5/ Г=(^’-) 7 =
Если а > 0, то окружность у охватывает лишь точку t = 0 — простой полюс подынтегральной
функции. В этом случае имеем
t - e2a t - e2a
I = —iri res------;— = -Tri lim----— = Tri.
о t(t 4- e2“) i.a/ + e2t>
Если a < 0, то кроме полюса t = 0 кривая 7 охватывает и полюс t = -е2а подынтегральной
функции. В этом случае
t-e2a t- е2“ 2е2“
res —----с— = lim —-— =----------— = 2,
-e2“t(t + e2“) t —e2a
( t-e2a t-e2a \
I = -тгг res —---— + res —-------— = - iri(~ I + 2) = -Tri.
\o t(t + e2“) _e2= t(t + e2“)/
Оба рассмотренных случая объединяются в один: I = Trisgna.
При а = 0 данный интеграл рассматриваем в смысле главного значения:
/7-' ' х
ж=0
х=
I = v.p / tgxdx =
о
о
tgxdx I — lim ( IncoszT L +lncosa:|I 2
I e—*+0 \ lx=7-e lz=*
2
z > / / — sin е \ \
= lim (— in sine + ln(- sine)- ln(-l)) = lim ( In ( —: ] — ln(—1) I = ln(-l)-ln(-l) = 0. ►
e-.+ov 7 e-.+o \ \ sine ) )
§ 2. Целые и мероморфные функции 257
§ 2. Целые и мероморфные функции
2.1. Целые функции.
Определение. Функция f, аналитическая во всей плоскости С, называется целой.
Из определения следует, что целая функция не имеет конечных особых точек. Точка z = оо
является изолированной особой точкой целой функции. Если z = оо — устранимая особая точка,
то по теореме Лиувилля целая функция является постоянной.
Пусть г = оо — полюс целой функции J. Тогда ее разложение в ряд Лорана в окрестности
бесконечности имеет вид
ОО оо
= cnzn + ... +ctz + Со + y^c_nz~n = Pn(z) + 57c_nz~n.
n=i n=l
Функция f — Pn удовлетворяет условиям теоремы Лиувилля, так как
lim (/(z) - Pn(z)) = 0.
Z—»ос
Отсюда имеем f(z) — Pn(z) = 0, или /(z) = Pn(z).
Итак если функция f целая и имеет на бесконечности полюс, то она является многочленом,
т. е. целой рациональной функцией.
Целые функции с существенной особенностью на бесконечности называются целыми транс-
цендентными функциями. Примерами таких функций являются z i-+ ez, z i-> cosz, z i-+ sinz.
2.2. Мероморфные функции. Теорема Миттаг-Леффлера.
Определение. Функция f, аналитическая в С, за исключением лишь полюсов, называется ме-
роморфной.
Из определения следует, что у мероморфной функции f в плоскости С нет никаких иных
особенностей, кроме полюсов.
Целые функции образуют подкласс класса мероморфных функций. Поскольку каждый полюс
является изолированной особой точкой, то мероморфная функция f не может иметь в С более
чем счетное множество полюсов. Действительно, в каждом круге KR = {z £ С : |z| < Р},
R = const, полюсов может быть лишь конечное число, в противном случае существовала бы их
конечная предельная точка, которая была бы неизолированной особой точкой, а не полюсом.
Таким образом, все полюсы мероморфной функции можно пересчитать, например, в порядке
возрастания их абсолютных величин.
Рассмотрим два случая. Пусть функция f имеет:
1) конечное множество полюсов;
2) бесконечное (счетное) множество полюсов. ____
В случае 1) бесконечность является изолированной особой точкой. Пусть {bj; j = 1, m} —
множество полюсов функции f, fy — порядок полюса Ь3,
с«> C-L
— ----7“ + ---TTJ + • • • + ----g-; ,
z — bj (z — fy)2 (z-fy^i
— главная часть лорановского разложения функции / в окрестности полюса bj. Рассмотрим
функцию
m
z <p(z) = /(z) - 57 Sj(z)>
j=i
которая является целой, поскольку ее устранимые точки bj можно считать устраненными. Так
как
7П
цт = °>
Z—»оо
7=1
то функции / и ip при подходе к бесконечности ведут себя одинаково.
258
Гл. 7. Вычеты и их применения
Пусть f (а значит и <р) имеет на бесконечности устранимую особую точку или полюс. Тогда
п п т
P(z) = £ekz‘, f(z) = ^“kzk+ ^9j(z) =-~
f '' * rilZI
к=0 к=0 j=l
где Р[ и Р2 — некоторые многочлены.
Доказано следующие утверждение.
Теорема 1. Если мероморфная функция f имеет на бесконечности устранимую особую точку
или полюс, то она является рациональной функцией.
Если же у мероморфной функции f бесконечность является существенно особой точкой, то
такую функцию можно представить в виде
/(г) = у(?) + У^д,(г), (1)
j = i
где <р — некоторая целая функция, отличная от полинома.
Рассмотрим теперь случай 2), когда мероморфная функция f имеет бесконечное множество
полюсов. Такими функциями, например, являются z >-» tg z, z >-+ ctg z. Покажем, что и в этом
случае для функции / можно получить формулу, аналогичную (1).
Определение. Ряд мероморфных функций 52 .Уп называется сходящимся (равномерно схо-
дящимся) на множестве М С С, если лишь конечное число членов этого ряда имеют полюсы на М
и после устранения этих членов ряд сходится (равномерно сходится) на М.
Теорема 2 (Миттаг-Леффлера). Какой бы ни была последовательность точек (bi),
lim bi — оо, |Ь|| |Ь2| С и последовательность функций (gi) вида
г—*ос>
б,
(2 - bi)” ’
существует мероморфная функция f, имеющая полюсы в точках bi с главными частями в них, рав-
ными gi(z).
4 Не ограничивая общности считаем, что bi # 0. Функция д, является аналитической в
круге К = {z £ С : \z\ < |bj} и, следовательно, может быть представлена в нем степенным рядом
9d2) =
fc=0
<Ао)
W.
(2)
k
z .
Фиксируем q € R, где 0 < q < 1. Круг Kj = {z € C : |z| < компактно принадлежит кругу К,
в силу чего ряд (2) сходится в нем абсолютно и равномерно. Поэтому существует такое nj € N,
что
1
2>
Vz е Kj.
Обозначим
fc! Z ‘
fc=0
Тогда
|& (?) - Pj (z) | < — Vz 6 Kj.
Рассмотрим ряд 52(9j ~ ?j)- Он равномерно сходится на любом компакте Л'ССв смысле
данного выше определения. Действительно,
VK С С ЭЯ € N : Vn N К С К„ = {z 6 С : |z| < д|&„|}.
Рассмотрим ряд 52 (Sj — Pj), j N. Его члены являются аналитическими функциями на К
и мажорируются геометрической прогрессией 52 j N- Следовательно, его сумма /n(z) —
аналитическая функция в круге К.
§ 2. Целые и мероморфные функции
259
Пусть функция f определена равенством
N-1
f(z) = ^(gj-Pj) + fN(z).
3 = 1
Функция f аналитическая в круге К, за исключением полюсов bj (j = 1, N - 1) и имеет в bj
главные части gj(z). Поскольку К — произвольный компакт, то функция f мероморфная, имеет
в С заданные полюсы bj с главными частями gj. ►
Следствие. Любую мероморфную функцию f можно представить суммой ряда
ОО
/(z) = h(z) + ^(ffn(z)-Pn(z)), (3)
П=1
равномерно сходящегося на каждом компакте, где h — целая функция, дп — главные части ло-
рановских разложений / в окрестности Ьп (полюсы Ь„ занумерованы в порядке возрастания их
абсолютных величин, / 0), Рп — некоторые многочлены.
◄ По теореме Митгаг-Леффлера строим функцию /0, где
, оо
/o(2)=^2(Pn(2)-P„(z)).
П = 1
Она имеет те же полюсы и те же главные части в них, что и f. Следовательно, f — fо — h —
целая функция. ►
Замечание. Если функция f имеет полюс в точке z = 0 с главной частью до, то в наших рассуждениях
везде f заменим на f - до-
Иногда термин “мероморфная функция” используется в более общем понимании. Именно,
функцию f называют мероморфной в области, если f не имеет в ней кроме полюсов других
особенностей. Такая функция также не может иметь более чем счетное множество полюсов.
Если это множество бесконечное, то предельные точки множества полюсов принадлежат границе
области.
2.3. Разложение мероморфных функций на простейшие дроби.
Пусть ( /(£) — любая мероморфная функция, 7 — замкнутая жорданова кривая, окру-
жающая начало координат и не проходящая через полюсы функции /. Пусть {&*,; k = 1, п} —
множество полюсов функции /, принадлежащее внутренности 7, Vfc = 1, п Ък Ф 0, дк — глав-
ные части лорановских разложений функции f в окрестности полюса Ьк. Если ( = 0 — полюс
функции f, то главную часть лорановского разложения в его окрестности обозначим да (если
( = 0 не является полюсом, то считаем д0 = 0).
Пусть z — любая фиксированная точка, принадлежащая внутренности 7. Рассмотрим функ-
цию
ЕЫО
. k=o
С-г
Она рациональная в С, имеет на бесконечности по меньшей мере нуль второго порядка и, сле-
довательно, ее вычет на бесконечности равен нулю.
Воспользуемся теоремой Коши для неодносвязной области, а также определением вычета на
бесконечности. Получим
1 / Ь=0 ,, 1 / Ь=0 ,, k=0 -
V~: / —------= т—: / —----------= - res —--------- = 0
2яч J С ~ z 2rrt J (— z 00 — z
r rB
260
Гл. 7. Вычеты и их применения
(здесь Гк = (ув, 7°р), = {( 6 С : |£| = R} — окружность, охватывающая 7). Отсюда следует
равенство
j ..... j /ю-Еыо
l^LdQ= — ------------------d<, Г = (7,7оР).
2яч J C-z 2тп J (-г
Г г
п
Функция f — дк аналитическая в области, ограниченной кривой 7 (устранимые особен-
t=o
ности этой функции считаем устраненными). Согласно теореме Коши
1 / _________fc=0
2тгг J Q~z
г
В результате получим равенство
= f(z) ~
fe=0
/(*) = ъ
k=Q
f /(<) яг
/ 7—d^-
J C-z
г
(1)
Допустим, что существует последовательность (7„г) замкнутых жордановых кривых, окружа-
ющих начало координат и не проходящих через полюсы функции /, с такими свойствами:
1) Vm £ N 7„г принадлежит внутренности 7m+i;
2) гт —+ оо при т —> оо, где гт — расстояние от начала координат до кривой 7т.
Из этого, в частности, следует, что V7? > 0 существует такое т0 £ N, что круг KR = {£ £ С :
|£] < R} Vm > шо(Л) принадлежит внутренности ут.
3) lim f = 0, Гт = (7т, 7™Р), |z| < R.
m—J Q — Z
Г„г
(2)
Запишем формулу (1) для Г,„. Обозначим через пт число полюсов, охватываемых кривой ут.
Получим:
f(z) = У~'дь(х) + — / --------d£, m>mn(R). (3)
I m
Перейдем в (3) к пределу при т —<• оо. Принимая во внимание формулу (2), имеем
пт
f(z)= lim Y\t(z). (4)
т—>оо ' *
fc=l
Таким образом, функция f в круге Kr представлена в виде предела последовательности сумм
главных частей ее лорановских разложений относительно полюсов, принадлежащих внутренно-
сти 7т.
Укажем достаточные условия справедливости формулы (2). Из оценки
1
2тг(гт - R)
2%i J £ — z
гт
следует, что для выполнения соотношения (2) достаточно, чтобы
М,
(5)
Покажем, что разложение функции / можно получить и при более слабых ограничениях,
чем (2).
§ 2. Целые и мероморфные функции
261
Пусть существует такое целое неотрицательное число р, что
Д”«2й/ = W<B- <«
г„,
Достаточным условием соотношения (6) является следующее:
[
т—►оо 27Г J
(р+1
|d([ < оо.
(7)
При |z| < |(| имеем
Подставим полученное разложение в (3):
Пщ Р
f(z) = +
fc=O n=0
zp+'
(p+l((-*)‘
f(Qd<;
(n+1(( ~гУ
Принимая во внимание равенства
имеем
n"‘ n”‘ Р _р+1 Г flr\
/(z> = ,.<«) + £ 4"*" + у- / «К,
k=Q fc=O n=0 /
1 in
ИЛИ
zp+1 f 7(0
M + Р.Ы) + — J d(, .
p
где PJt(z) = У7 — многочлен степени не выше р.
п=0
Переходя в (8) к пределу при т —» оо и принимая во внимание (6), имеем
П,п
/(z) = lim 57(yfc(z) + pk(z)), \z\ < R.
k=Q
(8)
(9)
Равенство (4) (или (9)) и является искомым разложением мероморфной функции на простые
дроби.
Пример. Найти разложение функции z i-> ctg z на простые дроби.
Имеем bk = кл (fc € Z), дк = -Д -. Пусть -ут — границы квадратов с центрами в начале
координат и сторонами длиной (2m + 1)тг, параллельными координатным осям. Оценим ctgz на
сторонах квадрата: 1) параллельных мнимой оси; 2) параллельных действительной оси.
1) z = ±(2т + 1)у + iy,
e±i(2m+l)«-e-2s + ] _ j _ e-2V
e±t(2m+l)xe-2» _ J J g-2y < 1’
2) Z = X ± i (m + j) 2Г,
е2^еТ(2т+1И + 1 eT(2m+l)>r + j 1 +
| CtgZ| — e2i»eT(2m+l)ir _ | < |eq:(2m+l)ir _ j| J _ e~ir '
+ 1
e2iz - 1
|ctgz| =
262
Гл. 7. Вычеты и их применения
Принимая во внимание, что > 1, получаем:
1 +е"’
I ctgz| < --z е (10)
1 — е
Условие (7) выполняется для ctgz при р — 0. Действительно,
f |ctgz| 1 + е-х 4(2т+1)тг 8(1 + е-,г)
/ ——- dz -----г-----> —------- при т —> оо.
J М l-e-77 (т+|)тг 1-е-
Tni
Таким образом, Pk(z) являются постоянными (многочлены нулевой степени):
п / \ 4» Ctg^
Pk(z) = Ak = res —
fc тг £
Отсюда
Po(2) = O, Pfe(z)=-^-.
fc?T
По формуле (9) получаем разложение ctg z на простые дроби
1 (( 1 1 \\
ctgz = - + hm / . I --------— + — ,
Z m—оо \ \z — К1Г К1Г J I
\k = — m /
ИЛИ
1 ( 1 1 A
ctgz = - + ( ---— + — I (11)
Z \ Z — klC К7Г /
fc = —oc
(символ 22 указывает, что к принимает все значения из множества Z, за исключением к — 0).
Принимая во внимание абсолютную и равномерную сходимость ряда (11), последнюю фор-
мулу можно также записать в виде
1 \ 2z
ctg2 = - + > —-------(12)
Z zL — nl1CL
n = l
Замечание. В качестве 7m можно было взять окружности 7m = {z€C:|z|=m + |}. При этом оцен-
ка (10) остается прежней.
Рассмотрим задачи.
25. С помощью теоремы Миттаг-Леффлера найти общий вид мероморфной функции f,
имеющей полюсы второго порядка в точках Ьк = fcir (fc G Z) с главными частями в них
1
5п(^) = -----rj.
(z — nicy
◄ Очевидно, ряд из главных частей п е Равномерно сходится на любом ком-
пакте (в смысле определения п. 2.2.), так как мажорируется в любом круге KR = {z € С : |z| < Я}
сходящимся рядом У~: (пд.1Д)2 • Поэтому по формуле (3), п. 2.2, полагая в ней Pn (z) = 0, получаем:
оо 1
/(z) = h(z)+ V -----------j. ►
(z — птг)2
п——оо
26. В условиях задачи 25 найти функцию h, если f(z) = —.
sin z
оо
•< Функция z i-> ft(z) = —— У: (7-п7)^ периодическая, с периодом тг. Изучим ее в
п=—ОО
полосе G = {z € С : 0 < Rez тг}. Имеем Vn 6 N
|z — птг| П7Г — |z| 2Г(п — 1).
§ 2. Целые и мероморфные функции
263
Следовательно,
1
(z — гиг)2
1 <4 1 л V- 1
< + Z 1---------о +2 Z 7-------0 ПРИ z -> оо.
|z|2 2—< |z — птгр ' (п — 1)2%2
n = — т n=m+l
Поскольку |sin2z\ = sin2ж + sh2т/ —» оо при z оо, 0 < Rez < тг, то функция h ограничена в
полосе G и, в силу периодичности, она ограничена и в плоскости С. Согласно теореме Лиувилля,
h(z) = 0. Таким образом,
1
sin2 z
1
(z — пт)2
27. С помощью теоремы Миттаг-Леффлера найти общий вид мероморфной функции /,
имеющей полюсы первого порядка в точках Ьп = п (п 6 N) с вычетами в них соответственно
равными п.
◄ Имеем
а)2._______....... г2
1 — J п(п — z) n(z — п)
Принимая во внимание, что
~~—; Г( 1 Vz е {г € С : 121 < ’
n(z - п) у/П(П — -Уп) 1 J
делаем вывод о том, что ряд УР равномерно сходится на любом компакте К С С в смысле
определения п. 2.2. Итак, согласно формуле (2),п. 2.2, имеем
28. Доказать равенство
1
sinz
n = i
/(z) = h(z)+y'-----►
n(z — n)
71— 1
= - + ^nTT(neZ)
z z2 — п2я2
◄ Функция z h-> ~~ имеет простые полюсы в точках bn = птг (n G Z),
Pn(z) =
(~1)п
z — птг
В качестве возьмем границу квадрата с вершинами в точках (т + тг(±1 ± i). Оценим
j2-;: 1) на сторонах квадрата, параллельных мнимой оси; 2) на сторонах квадрата, параллельных
действительной оси. Имеем
264 Гл. 7. Вычеты и их применения
Таким образом, оценка (7), п. 2.3., выполняется при р = 0, Pn(z) = А°п = res 7I7. Отсюда
П7Г
Р0(г) = 0, Pn(z) = 77. По формуле (9), п.2.3, находим:
JL = 1 + ((~1)П + ± V 1 + у' ±1221
sin Z Z \ Z - П7Г П7Г J Z Z1 — П2ТГ2
П= —ОО П=1
29. Доказать справедливость разложения
°° Л 2
Z Z ZZ
е2 - 1 1 2 + z2 + 4п2тг2
П = 1
•< Заменив в (12), п.2.3, z на iz и сократив на -г, получим:
cthz =
2z
Z1 + П2ТГ2
Отсюда следует, что
z
ег - 1
Z Z Z
- - + - cth - =
2 2 2
z \ 2z2
2 + + -2-* z1 + 4п2тг2
п= I
30. Найти разложение мероморфной функции z i-» /(z) = rrctgrrz без использования фор-
мулы (12), п. 2.3.
◄ Рассмотрим ряд Фурье функции х ip(x) = cosax, -тг < х < Имеем
cos аж =
а0 v~^
у + 2^ап cosnx,
п= I
где а„
1 Г „2а
— I cosax cos пх ах = (-1) —
тг J тг
sinarr
а2 — п2 ’
п € Zq.
Поэтому
sinarr
cosax =-----------h
атг
2а sinarr
cosnx
a2 ~ n2
При х = тг получаем:
cos атг 1 1
7rctgQ7r = тг------= —F 2a > —-------------
sinaTr a —
n=l
Если продолжить аналитически это соотношение с действительной оси в комплексную плос-
кость, то получим решение задачи в виде
§3. Бесконечные произведения
Изучение функций в комплексной плоскости позволяет установить не только новые, иногда
неожиданные их свойства (например, связь между показательной и тригонометрическими функ-
циями), но и выделить отдельные классы функций. Целесообразность выделения таких классов
должна быть подтверждена их значением для развития самой теории функций и ее применений.
§ 3. Бесконечные произведения
265
3.1. Числовые бесконечные произведения
Предполагается, что читатель знаком с понятием бесконечного произведения действительных
чисел и некоторыми результатами соответствующей теории.
Пусть (zn) — произвольная последовательность комплексных чисел.
Определение 1. Бесконечное произведение
n<1+zn) (1)
называется сходящимся, если последовательность (Р„) частичных произведений, где
п
рп=П(1+Zk)’
k=l
сходится к конечному и отличному от нуля предельному значению Р : Р„ —* Р, 0 < \Р\ <. оо, которое
называется значением бесконечного произведения (1) и обозначается через Pf(l+z„).
П=1
Если среди множителей (1 + z„) есть конечное число равных нулю, то бесконечное произ-
ведение называется сходящимся или расходящимся в зависимости от того, каким является бес-
конечное произведение, полученное из данного путем извлечения из него нулевых множителей.
В случае, когда среди множителей (1 + zn) есть бесконечное множество нулевых, бесконечное
произведение называется расходящимся.
В соответствии с данными определениями исследование сходимости бесконечного произведе-
ния сводится к исследованию сходимости бесконечного произведения, все сомножители которого
отличны от нуля. Очевидно, для сходимости бесконечного произведения (1) необходимо, чтобы
lim z„ = 0. Действительно, lim (1 + zn) = lim = £ = 1, следовательно, z„ — 0.
n —»oc n —► OO n —♦ ОС П ~ '
Теорема 1 (о равносходимости бесконечного произведения и числового ря-
да). Бесконечное произведение Y[(l + zn) и ряд 22 ln(l +zn), —тг < Imln(l+z„) С it, одновременно
сходятся или расходятся.
◄ Пусть бесконечное произведение P[(l +zn) сходится. Тогда lim Рп = Р, Р # 0, Р ф оо,
п
п
где Рп = 22(1 + zfc), Р = те’*’. Если Р„ = rne’Vn , —к < <^п зг, 1 + zk = рке'вк , it < 0k ^ir,
k — 1
п
то ipn —* <р, 6к —» 0 при zk —* 0. Обозначим Sn = 22 ln( 1 + zk) Тогда
t=i
Sn = 1пР„ + 2mniri, (2)
где mn — целое число. Очевидно, 2пгптг = + в2 + • • + — <рп и, таким образом,
2?г(тп+1 - тп) = 0п+| - (9зп+1 - <рп).
Поскольку 0п+1 —> 0, ipn+l - <рп -+ 0, то |2тг(тп+1 - пг„)| < 2тг при достаточно большом п.
Поэтому mn+1 = т„ = т для указанных п и Sn = 1пР„ + 2miti. Следовательно,
ОО
lim Sn = \ ln(l -I- zn) — 1пР + 2пгтгг,
п—»оо
71 = 1
т. е. ряд 22 ln( 1 + zn) сходится.
ОО
Пусть 22 1п(1 + z„) — S. Из равенства (2) получаем es" = Рп, откуда
П=1
lim Р„ — exp ( lim Sn ) = es = Р,
TI —»оо \п—*оо /
т.е. бесконечное произведение JJ(1 +zn) сходится.
Если бесконечное произведение fj(l + zn) расходится, то и ряд 221п(1 + zn) расходится.
Допустив, что этот ряд сходится, получили бы противоречие с доказанным выше. Аналогично, из
расходимости ряда 22 ln( 1 + z„) следует расходимость бесконечного произведения JJ(1 + z„). ►
266
Гл. 7. Вычеты и их применения
Определение 2. Бесконечное произведение (1) называется абсолютно сходящимся, если бес-
конечное произведение
П(>+м <з>
сходится.
Бесконечное произведение (1) и ряд 57 zn одновременно абсолютно сходятся или расходятся.
Действительно, из оценки 1 + |zj следуют неравенства, выполняющиеся Vn € N:
|z,| + |z2|+ ... + |z„|< (l + k|)(l + |z2|) ... (l + |zn|) ^e|z'l+|zil+-+|zn|. (4)
n n
Частичные произведения fl (l + kd) и частичные суммы 57 kJ соответствующих бесконечного
fc=l fe=l
произведения и числового ряда образуют монотонно возрастающие последовательности, которые,
согласно неравенствам (4), одновременно ограничены сверху или неограничены.
Теорема 2. Абсолютно сходящееся бесконечное произведение сходится.
< Пусть бесконечное произведение (3) сходится, Рп — его n-частичное произведение,
Рп —» Р. Для частичных произведений бесконечного произведения (1) имеем
Pn -Pn-l =P„-\Zn,
|P„-Pn-il = |Pn-ilk„| = ll+zj |l+z2| • • |l+-z„-i| knl < (1 + kll) ... (1 + kn-il) knl = P„-P„_,,
так как
n
Pn = JJ(1 + Ы), Pn-Pn-1 = (1 + |Z1|) ... (1 + kn-il)knl, n^2.
fc=l
Поскольку P„ —> P, то ряд 57 (Pn ~Pn-i) (« 2) сходится и, согласно теореме сравнения рядов,
будет сходящимся ряд 57(Pn — P„-i) (п 2). Это означает, что Рп —» Ро, Ро / оо. Осталось
доказать, что Ро # 0.
Согласно теореме 1, ряд 57 knl сходится. Поскольку начиная с некоторого номера модули
|1 + zn\ ограничены снизу, то ряд 57 , ТТ7“ I сходится. Поэтому, по теореме 1, бесконечное
произведение fj (1 + | I) сх°лится> а вместе с ним и бесконечное произведение f]i д„, где
qn = fl I 1 - I (чтобы убедится в этом, полагаем выше Р„ = qn, Р^ = fj (1 + ) ).
Таким образом, существует lim qn = g0 # 0. Так как qn = ~, то _Pn —► Po # 0. ►
n —* oo n
Значение абсолютно сходящегося бесконечного произведения не зависит от порядка сомно-
жителей. Действительно, в этом случае сходится ряд 57 knl (по теореме 1). Пусть е = Тогда
существует такое n, € N, что Vn n, |zn| < | (т.к. |z„| —» 0 в силу необходимого условия
сходимости ряда) . Для указанных п получаем оценку
ln(l + zn)
Z-a
1 / Z2 Z3
— I z„-----------
Zn\ 2 3
^n Zn <
T + т_
1111
1+2 2 + 4 3
1
2 + 22
= 2,
из которой следует, что Vn пс |ln(l + zn)| < 2|zn|. Следовательно, ряд 57*n(l +zn) абсолютно
сходится. Теперь утверждение о независимости значения абсолютно сходящегося бесконечного
произведения (1) является следствием равенства
ОО ✓ оо
JJ(1 + Z„) = exp ( ^2 ln(i + z")
n=l Xn=l
(см. теорему 1), поскольку для абсолютно сходящихся рядов выполняется свойство коммутатив-
ности.
§ 3. Бесконечные произведения
267
3.2. Равномерно сходящиеся бесконечные произведения
Пусть (/„) — последовательность функций /„ : С —> С, и Vn € N Dfn = G, где G С С —
некоторая область. Тогда Vz 6 G можно рассматривать бесконечное произведение JJ(1 + /„(z)).
В случае его сходимости оно называется поточечно сходящимся в области G. При этом оно опре-
деляет в G некоторую функцию z i-» P(z). Если последовательность (Р„) частичных произведе-
ний Рп — fj(l -t- fk) равномерно сходится на любом компакте К С G к функции Р (Рп Р), то
fc=i
бесконечное произведение JJ(1 + /„) называется равномерно сходящимся в области G. Согласно
теореме 6, п. 1.3, гл. 5, бесконечное произведение fj(l + /п) сходится равномерно в области G
тогда и только тогда, когда последовательность (Рп) его частичных произведений равномерно
фундаментальная в G.
Теорема (достаточные условия равномерной сходимости бесконечного про-
изведения). Для равномерной сходимости бесконечного произведения £J(1 -I- /п) достаточно су-
ществования такой числовой последовательности (ап), чтобы выполнялись условия:
1) Vn € N ||/„|Юп
2) бесконечное произведение fj(l + ап) сходится.
◄ Поскольку бесконечное произведение J~J(1 +а„) сходится, то последовательность (Р„) его
п
частичных произведений Рп = П (1 + afc) фундаментальная:
fc=i
п z n+p s
Vs > 0 Зпг е N : V(n п£, р € N) Рп+р - Р„ = ]Г[(1 + ak) ( (1 + ак) - 1 J < е.
= l А:=п+1
Оценим
п+р п
П(1 + А)-П(1 + А)
к = 1 fc=I
для п пе и всех р G N. Из свойств равномерной нормы имеем
П z П+р
П<1 + А)( П a + A)-i
к = 1 fc=n+l
п+р
П a + A)-i
fc = n+1
Обозначим Рп = П(1 + fk)- Принимая во внимание условие 1), получаем V(n ne, р € N):
к-\
П z П+р х
||Р„+р-Р„|| ^П(1+°4)( П <l+afc) - 1) <е,
к — 1 /с=п + 1 '
т. е. последовательность (Р„) равномерно фундаментальная и бесконечное произведение
П<1 + А)
сходится равномерно в области G. ►
3.3. Представление целой функции в виде бесконечного произведения.
Пусть задана некоторая последовательность (an), модули членов которой образуют неубыва-
ющую последовательность, причем lim а„ = оо, ап # 0 и среди чисел а„ может быть конечное
множество равных друг другу.- п—«=
268
Гл. 7. Вычеты и их применения
Рассмотрим бесконечное произведение Р, где
где числа рп € Zo такие, что ряд
(2)
абсолютно и равномерно сходится в любом круге KR = {z € С : |z| < Я} (в качестве рп можно
взять, например, рп — п - 1).
Покажем, что бесконечное произведение (1) равномерно сходится на любом компакте К С С.
Введем в рассмотрение функцию дп, где
При | 1 q < 1 получаем оценку
|ln$n(z)| <
Рп+1
Z
(3)
Для любого компакта К С С найдется такой номер п0, что Vn п0 К С Кп = {z g С :
|z| Sj g|a„|}. Следовательно, ряд
У^1п^„(г) (п n0)
мажорируется на компакте К равномерно сходящимся рядом (2), и поэтому его сумма является
аналитической функцией gnQ.
Отсюда следует сходимость бесконечного произведения
ОО
nSnW = W*) = es"tW,
(4)
где f„0 — аналитическая функция на компакте К, отличная от нуля. Бесконечное произве-
по-1
дение (1) отличается от fna(z) множителем gn(z), который обращается в нуль в точках
П=1
аь а2, ... , апо_! и только в этих точках. Поскольку К — произвольный компакт, то z P(z) —
целая функция с нулями {ап; n € N}, ап 0 0, причем кратность нуля функции Р в точке а*,
такая же, как и количество членов последовательности (а„), равных числу ак. Бесконечное про-
изведение (1) называется бесконечным произведением Вейерштрасса.
Очевидно, функция z >-+ <p(z) = zxP(z) является целой, имеющей в точке а0 — 0 нуль
кратности А и последовательность нулей (ап), а„ # 0, lim ап = оо.
п—><30
Теперь легко доказать теорему Вейерштрасса о представлении целой функции в виде беско-
нечного произведения.
§ 3. Бесконечные произведения
269
Теорема (Вейерштрасса). Любую целую функцию f, имеющую бесконечное множество нулей,
причем z = О — нуль порядка А и (ап) — последовательность остальных нулей, lim ап = оо, можно
п—>-ОО
представить бесконечным произведением, соответствующим ее нулям:
(5)
где h — некоторая целая функция, а числа рп выбраны так, чтобы сходился ряд (2).
◄ Поскольку функция z tp(z) = zAP(z) является целой и ее нули совпадают с нулями
функции /, то функция £ также является целой (ее устранимые особые точки считаем устра-
ненными) и не имеет нулей в плоскости С. По теореме монодромии (см. теорему 2, п. 1.3, гл. 6),
функция z <-» h(z) = In также является целой и, следовательно,
f(z) = eh{z\(z) = zAe'*(z)P(z). ►
3.4. Разложение sin z в бесконечное произведение.
В качестве примера получим разложение целой функции z и» sinz в бесконечное произ-
ведение. Она имеет простой нуль в точке z = 0, а также простые нули в точках ап = пк
(п = ±1, ±2, ...). Поскольку ряд У', сходится на любом компакте, то в бесконечном про-
пио
изведении (1), п. 3.3, можно взять Vn Р„ = 1. Таким образом, согласно формуле (5), имеем
где h — некоторая целая функция. Символ обозначает отсутствие множителя, отвечающего
значению п = 0.
Пусть К СС — произвольный компакт, не содержащий нулей синуса. Для z С К получаем:
In sin z = h(z) + In z +
V' (in (1 + —)+—)>
< \ \ ПК / ПК /
d i I v—'1 ( 1 1 \
— In sin z = ctg z = h (z) 4---1- У I------------1----- I .
dz z \ z — пк пк )
Сравнивая полученное равенство с разложением ctgz на простые дроби (формула (И), п.2.3.),
имеем h(z) = const. Таким образом,
sinz = Cz
Из предельного соотношения lim — 1 находим: С = 1. Искомое разложение sin z в беско-
z~0 2
нечное произведение окончательно принимает вид
В связи с абсолютной сходимостью ряда У (1 — появилась возможность объединить мно-
жители с индексами — п и п._
270
Гл. 7. Вычеты и их применения
3.5. Род и порядок целой функции.
Пусть последовательность (ап) нулей целой функции /, ап # 0, lim ап = оо такая, что
п—«ОС
ряд (2), п. 3.3, сходится при рп = р, где р — некоторое неотрицательное целое число, причем
оно наименьшее из всех неотрицательных целых чисел, при которых ряд сходится. Тогда это
число р называется родом бесконечного произведения
(формула (1), п. 3.3, при рп = р). При этом формула (5), п. 3.3, принимает вид
В случае, когда h — полином степени р\, говорят, что функция f является функцией конечного
рода, и этот род равен max{p, pi}.
В случае отсутствия нулей ап род функции / равен р\, т. е. степени полинома h.
Например, sin z является целой функцией первого рода (р ~ 1, рх =0).
В других случаях, когда h — целая трансцендентная функция или ряд |о ‘р+1 не сходится
ни при каком неотрицательном р, функция / называется целой функцией бесконечного рода.
Пусть М(г) = max |/(z)|. Если /(z) const, то по теореме Лиувилля lim М(г) = оо.- Для
|z|=r r — oo
целых функций конечного рода некоторое представление о характере стремления к бесконечности
содержится в следующей теореме, выходящей за рамки книги.
Теорема 1 (Пуанкаре). Если f — целая функция рода р и а — произвольное положительное
число, то для всех достаточно больших г выполняется оценка
М(г) < еатР+'. (2)
В случае, когда число нулей функции f конечное, оценка (2) очевидна.
называется порядком целой функции.
Из определения верхнего предела следует, что если q конечное, то Ve > 0 Зг0 > 0 такое, что
Vr 7? г0 справедлива оценка
M(r)<eri . (4)
Связь между родом и порядком целой функции / устанавливает следующая теорема.
Теорема 2. Если род р целой функции / конечен, то конечен и ее порядок q, и наоборот, причем
р^д^р+1. (5)
Справедливость первой части утверждения и неравенства1^ q st р + 1 непосредственно
следует из определения порядка целой функции и из неравенства (2) при а — 1. ►
З.б. Мероморфная функция как отношение двух целых функций.
Пусть F — мероморфная функция, а функция z t-> <p(z) = zAP(z) — целая, представленная
бесконечным произведением, нули которой и их кратность совпадают с полюсами и, соответ-
ственно, их порядками функции F (А — порядок полюса F в точке z = 0; если z0 = 0 — точка
аналитичности функции F, то полагаем А = 0).
Функция ф = Ftp является целой, поскольку полюсы функции F устраняются нулями функ-
ции <р. Поэтому-
ф
F=-.
V
Полное доказательство этой теоремы, а также теоремы Пуанкаре заинтересованный читатель найдет в книге Бичадзе Л. В.,
“Основы теории аналитических функций комплексного переменного”, М., “Наука”, 1972.
§ 3. Бесконечные произведения
271
Итак, любая мероморфная функция является частным двух целых функций. Очевидно, справед-
ливо и обратное утверждение: частное двух целых функций есть мероморфная функция. Отсюда
следует второе определение мероморфной функции (первое определение дано в п. 2.2): функция F
называется мероморфной, если она является частным двух целых функций.
Рассмотрим примеры.
°° / °°п3 — 12
31. Доказать равенства: а) Т| ( 1 -I-1=2; б) 1 | —:----= -.
А А \ п(п + 2) J А1п3+1 3
n=i ' n=2
◄ а) Поскольку
P — TT (i + 1 _ TT + I)!)2'2 _ 2(n + 1)
n “ 11 + fc(fc + 2) / H k(k + 2) “ n!(n + 2)! “ n + 2 ’
TO
00 / 1 \
nl 1 +------------- I = Um Pn = 2;
\ П(П + 2)/ n-oo
n= 1
б) Имеем
nfc3 — 1 т-r (k — l)(fc2 + k + 1) 2(n — 1)! -i—r fc2 + fc + 1 2 n2 + n + 1
fc3 + 1 “11 (fc + l)(fc2 - fc + 1) ~ (n + 1)! 11 (fc - I)2 + (fc - 1) + 1 ~ n(n + 1) 3 ’
n=2
lim Pn
n—*oc
2
3'
32. Исследовать на сходимость произведения J J (1-1—
◄ Согласно теореме 1, п. 3.1, указанные бесконечные произведения сходятся или расходятся
вместе с рядами
Поскольку ряд
Y)lnfl + -^
сходится (in (1 + ^i) ~ 7т) , а ряд
Е arctg -
п
расходится (arctg 2. ~ 1) , то первое бесконечное произведение расходится, а второе — сходит-
ся. ►
33. Найти области сходимости бесконечных произведений:
а)П(1 + ^); + в)П(1 + йе-"-
◄ а) Поскольку lim (|)” # 0, если |z| 3, то для этих значений z бесконечное про-
изведение расходится. Если |г| < 3, то указанное бесконечное произведение сходится аб-
солютно, так как ряд 22 сходится. При этом сходимость равномерная в любом круге
КТ = {z g С : |z| < г < 3}. Следовательно, данное бесконечное произведение определяет в
круге Кг аналитическую функцию Р.
б) Бесконечное произведение сходится в С и является целой функцией. Это следует из абсо-
лютной и равномерной сходимости ряда 52 в любом круге KR = {z g С : |z| SJ R 1}.
в) Данное произведение является бесконечным произведением Вейерштрасса при а„ = —п и
р„ = 1. Следовательно, оно сходится в С и является аналитической функцией в С. ►
Til
Гл. 7. Вычеты и их применения
34. Исследовать на абсолютную сходимость бесконечное произведение
◄ Согласно теореме 1, п. 3.1, данное бесконечное произведение сходится или расходится
абсолютно вместе с рядом
1
1
Этот ряд по степеням сходится лишь при |г| > 1. Следовательно, областью абсолютной
сходимости бесконечного произведения является множество D = {z g С : \z\ > 1}. ►
35. Доказать, что бесконечное произведение jTJ ------е* абсолютно сходится при
всех z, если только с не является отрицательным целым числом.
Ч Пусть z 6 С — фиксированное. При больших п получаем асимптотическую формулу
z ( 1 \\
—0 ( ~ ) ) —
п \ п1 1 j
z
1-----------
1 -
Z
с + п
Z / 1
- + О I —
п \ п1
Iczl ( 1
7- —- + О,
|п + с|п
Если с не является отрицательным целым числом, то ряд
абсолютно сходится, поскольку сходится ряд
у |п + с|п + уп2 ) )
Согласно теореме 1, п. 3.1, данное бесконечное произведение абсолютно сходится, если с # — п,
п £ N. ►
36. Пусть (zn) — последовательность комплексных чисел, удовлетворяющая условиям:
б) ряд
(1)
сходится.
Доказать, что бесконечное произведение
11 l~ZZn
(2)
сходится в круге К = {z € С : \z\ < 1} и представляет в этом круге аналитическую функцию Р,
обращающуюся в нуль лишь в точках zt, z2, ... и удовлетворяющую неравенству |P(z)| < 1.
◄ Рассмотрим в круге K\Zk। = {z € С : \z\ < |zfc|} функцию
z
— z
~т~ z,
(3)
Все сомножители в (3) отличны от нуля. Из оценки
l«n(z)| =
(Zn ~ z)zn
1 ~ zz„
1 ~ |z„|2 < 2(1 —|zn|)
|l-zzn| 1 - |zfc|
и сходимости ряда (1) делаем вывод о том, что бесконечное произведение (3) равномерно схо-
дится к функции, аналитической в круге и отличной от нуля в этом круге, а бесконечное
§ 3. Бесконечные произведения
273
произведение (2) является функцией Р, аналитической в круге A'|2fc|, обращающейся в нуль лишь
в точках Zi, z2, ... ,zfc_,. Так как lim zk = 1 (это следует из сходимости ряда (1)), то Р явля-
к—*оо
ется функцией, аналитической круге К = {z € С : \z\ < 1}, обращающейся в нуль лишь в
точках Z), Zi, ....
Оценим модуль произвольного сомножителя бесконечного произведения (2) при |z| < 1:
~ -z _
1 - 2 А, г’
< |г„| < 1.
Следовательно, |P(z)| < 1 Vz € К. ►
37. Доказать равенство
eaz - еЬг = (а — b)ze
4гг2л"2 J
•< Воспользуемся формулой разложения синуса в бесконечное произведение (см. п. 3.4). По-
лучим после некоторых преобразований:
а+Ь _ / а-Ь .. а-Ъ \ о+6 а~Ъ а+Ъ (а — b)iz
= е 2 ( е 2 -е 2 ) = 2е 2 sh —-— z = — 2ie ъ sin
(a — b)2z2 \ г±ьх-1
=(a~b)Ze 2 J
az bz
е - е
а±ьгг(а-Ь)
= —2ге 2 ------z
(a - 6)2z2
4п2я2
1
Пусть а2„_! = —, а2.
у/п
сходится, а ряды расходятся.
◄ Если a2n_[ = О (-Й , а2п = О ( 4=
38.
---— + —. Доказать, что бесконечное произведение ТТ(1 +а„)
s/п п
= О при п —» 00, то
а„ = О , а„ = О (£) при п -+ оо и ряды а„, 5Z расходятся по признаку сравнения
с гармоническим рядом.
Необходимое условие сходимости бесконечного произведения f][(l + я„) выполнено. Оно
сходится тогда и только тогда, когда сходится JJ(1 + a2„_i)(l + а2п). Поскольку
1
(1 + a2n-l)(l + “2п) — -7=
> а2п-1
и ряд сходится, то вместе с ним сходится и данное бесконечное произведение. ►
39. Найти порядок функции z <-+ f(z) = cos az2, где a € С.
◄ Поскольку
M(r) = max | cos az2
(2п)!
п=0
_ j area
и в точке z0 = Vire г /(zo) = ch |a|r , то
00 |л|2п_4п л|<1|г2 । л~|а|г2
Е|а| г е1 1 +е 1 1 2
-------=----------------= ch а г
(2п)! 2 1
п=0
e1 |r -t-e
M(r) =--------—
Поэтому, применив формулу (4), п. 3.5, получим:
q = lim
2
111 Г
-----1п(|а|г2 + 1п(1 + е“2|а|г ) - In 2)--„
hm------------------------------------------- 2. ►
r-^оо inr
2
2
274
Гл. 7. Вычеты и их применения
§ 4. Применение вычетов
для вычисления интегралов и сумм рядов
4.1. Применение вычетов для вычисления определенных интегралов.
Основная теорема о вычетах (см. теорему 1, п. 1.3) позволяет свести вычисление интеграла
по замкнутой кривой к вычислению суммы вычетов подынтегральной функции относительно ее
особых точек, охватываемых кривой. Иногда с помощью этого же метода удается вычислять ин-
тегралы по незамкнутым кривым и, в частности, некоторые определенные интегралы от функций
действительной переменной. При этом специальными преобразованиями вычисление таких ин-
тегралов сводится к вычислению интегралов по замкнутым кривым, к которым можно применять
теорему Коши о вычетах.
1) Пусть (я, у) R(x, у) — рациональная функция от х и у, не имеющая особых точек на
окружности 7 = {(г, у) € R2 : х2 + у2 — 1}. Тогда справедлива формула
2тг
J R(sint, cost)dt =
(1)
где {zk; к = 1, п} — полюсы функции
размещенные в единичном круге K = {zgC:|z|<l}.
Для получения формулы (1) следует в интеграле перейти к комплексному переменному ин-
тегрирования z = elt. Тогда
Г = (7, Тор)-
Осталось применить теорему Коши о вычетах, в результате чего получим формулу (1).
2) Пусть функция f аналитическая в верхней полуплоскости, включая и действительную ось,
за исключением конечного множества точек {zj.; к = 1, п], лежащих в верхней полуплоскости
(Imzfc > 0 Vfc = 1, п). Пусть, далее
7„ = {z € С : z = Relt, О < t тг}, M(R) = max |/(z)|, R > max \zk|'
и
lim RM(R) = 0. (2)
Я-.00
Тогда справедлива формула
n
J(x) dx = 2тгг \ res/(z). (3)
* Zl,
fc=l
< Пусть 7 = [-Я, Я] U 7И, Г = (7, 7ор) = (Г^ Гн) —
положительно ориентированная кусочно-гладкая замкнутая
кривая (рис. 85). Согласно основной теореме о вычетах вы-
полняется равенство
R
f(z) dz = 2тг£ \ res f(z).
Zk
Г -R гк к=1
Перейдем в этом равенстве к пределу прй R —» +оо, приняв во внимание соотношение (2).
Получим формулу (3). ►
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
275
3) Лемма (Жордана). Пусть функция f аналитическая в верхней полуплоскости Z+ —
{z g С : Im z 0} за исключением конечного множества изолированных особых точек и
lim M(R) = Q.
R—»ос
(4)
(или lim M(Rn) = 0, где (Rn) — такая последовательность чисел, что полуокружности 7д„ с
Rn~»ео
центром в начале координат не содержат особых точек функции /). Тогда VA > 0 выполняется
предельное соотношение
lim
dz - 0,
Ч Оценим интеграл в левой части формулы (5), используя известное равенство sin £
выполняющееся VZ € [о, у]. Имеем
dz
J f(Reil)eiXRmt
О
— XR sin t т* it • j,
e Re i at
^RM(R) / e~XRsmtdt =
2
/ — AJtsint
/ е
f 2ЛЯ 7ГМ(Я)
/ е чг dt =-------
0 0
Из условия (4) и полученной оценки следует справедливость соотношения (5). ►
Замечание 1. Анализируя доказательство леммы Жордана, убеждаемся в том, что условие аналитичности
функции / не является существенным.
Замечание 2. Лемма Жордана, доказанная для верхней полуплоскости, может быть сформулирована и
доказана без всяких затруднений и для других полуплоскостей.
Считая во всех случаях Л > 0, а полуокружность 7Я лежащей в соответствующей полуплос-
кости, запишем формулу (5) для случаев:
а) Z = {z £ С : Im z С 0}, lim / R-^J гн f(z)e~iXz dz = 0; (6)
б) Zn = {z € С : Rez 0}, lim ( R^xJ f(z)e~Xz dz = 0; (7)
в) Zn = {z g С : Rez 0}, lim [ /(z)eAz dz = 0. (8)
Если функция / удовлетворяет условиям леммы Жордана и имеет в полуплоскости Zn конеч-
ное множество особых точек {afc; k = 1, n}, Imafc > 0, то, повторяя рассуждения, проведенные
в 2), получим VA ; > 0 формулу +°° n [ f(x)e,Xx dx = 2iri res (/(z)e*Az ) . (9) J k=, “fe —o©
Отсюда + oo n [ f(x) cos Ax dx = Ref 2тг£ res (/<z)e*Ax) J, (10)
— OQ
276
Гл. 7. Вычеты и их применения
+оо
У J(x) sin Xxdx = Im
— ОО
(11)
Пример.
4-ос
/х sin Аж ze'Xz 2iri ie~x _Л
------— dx = Im 2тгг res------ = Im----—-----= те
1 + x2 i 1 + z2 2г
4) Пусть функция f удовлетворяет условиям 2) и, сверх того, имеет конечное множество
простых полюсов {&_,•; j = 1, т} на действительной оси, т.е. Im 6,- = 0. Тогда справедлива
формула
/ /(ж) dx = 2тгг I Х'' res f(z) + - Х^ res f(z) 1, (12)
J \ ,, ak i ~ bi /
fc=l J=1
где интеграл вычисляется в смысле главного значения относительно всех точек Ъ, и оо.
◄ Рассмотрим замкнутую жорданову кривую
т т
7Rr = [-R, Я] \ U (ЬУ -г <х < bj + г) и 7и U Tir,
з=1 i=1
где — верхняя полуокружность радиуса г с центром в точке Ь, и г достаточно малое, 7R —
верхняя полуокружность с центром в начале координат и R достаточно большое, а кривая 'fRr
охватывает все особые точки ак (k = 1, п). Рассмотрим кусочно-гладкую положительно ориен-
тированную замкнутую кривую ГДг = (Г1; Г["г, Г2, ... , Г“г, Гт+,, Гк), состоящую из упорядо-
ченного набора ориентированных гладких кривых (рис. 86).
Применив теорему Коши о вычетах, имеем
/(z)dz = ^ J /(z)dz + ^~2 J f(z)dz + J f(z) dz = 2ггг res /(z).
3=1 rj >=,r-_ rB A=‘
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
277
Перейдем в полученном равенстве к пределу при R —* оо и г —> 0. Принимая во внимание
предельные соотношения
lim / f(z)dz =—res/(z),
r-oj 2 ъ5
получаем формулу (12). ►
Аналогично может быть обобщена и формула (9), которая при наличии у функции / простых
полюсов 6j (j = 1, т) на действительной оси принимает вид
f(x)e’Xx dx = 2rri \esf(z)e
Z * a 1.
Пример. Главное значение интеграла
(t >0)
равно iri res -— = тгг.
о z
5) Пусть f — рациональная функция,
{at; k = 1, п}
— множество ее полюсов, ни один из которых не
лежит на действительной положительной полуоси.
Пусть, далее, р и q — такие целые числа (р < q),
что
/(z) = O(^), г —> 0,
; . : (14)
f(z) = O[^) , z^oo.
Рассмотрим функцию z^zQ-1/(z), где p<a<q
не равно целому числу в z — плоскости с разрезом вдоль луча (0, +оо) и при этом ветвь z“-1
фиксируется равенством
z“ 1 = exp ((a — l)(ln |z| + i argz)), 0<argz<2Tr.
Упорядоченный набор гладких ориентированных кривых (рис. 87) ГЛт. = (Гц Гл, Г^, Г“)
является кусочно-гладкой положительно ориентированной замкнутой кривой, охватывающей
точки ак (к = 1, п). Применив основную теорему о вычетах, получим:
f(x)dx + J za 'f(z)dz + J xa lf(x)ela I)2,r' dx + J za ‘f(z)dz =
rR R r-
= 2iriX^ resz“ ’j(z).
t=i °fc
Перейдем в этом равенстве к пределу при R —► +<х> и г —> 0. Из условий (14) следует, что
lim / za~'f(z)dz—0, lim / z"-1/(z) dz = 0,
Я—»+oo J r —»0 J
r« rp
278
Гл. 7. Вычеты и их применения
вследствие чего имеем
j/" z“-1/(a:)dz = —е<“-1)2,г'У = 2тг£ \esza~l f(z).
о о fc=1
+оо
Таким образом, интеграл f ха~1 f(x)dx существует и
о
+ сс
/2тгг ж
xa~'f(x)dx = ——— ^resz“-7(z). (15)
1 — е аь
Ь=1
о Л 1
+ оо
Пример. Вычислить 1=1' 3=~. , . Здесь р = О, 0 = 2, а = и условие р < а < а
J у/х(х*+4) *
О
выполняется. Согласно формуле (15) имеем
4.2. Применение вычетов к вычислению сумм рядов.
Пусть / — мероморфная функция, имеющая конечное множество полюсов {а*.; к = 1, п},
среди которых нет целых чисел. Пусть, далее, (7т) — последовательность замкнутых жордановых
кривых, окружающих начало координат и не проходящих через целые точки z = п, а также через
полюсы функции f и таких, что гт —> оо при т —> оо, где гт — расстояние от начала координат
до кривой -ут. Тогда, если
lim [ f(z)ctgirzdz = O, Гт = (ут, 7m), (1)
m —оо J
Г,„
ИЛИ
lim
т—>oo
Г>н
и соответствующие ряды сходятся, то справедливы соответственно следующие равенства:
оо п
52 /(") =-’rV'res/(z)ctg7rz, (3)
* а к
П = —ОО fc = l
f(z)dz
sinyrx
52(-1)"/(п) = -’r52res^~- w
Z—' Z--/ ak Sin 7TZ
n=l *=1
◄ Докажем справедливость формулы (3). Для простоты считаем, что кривая 7т симметрич-
ная относительно мнимой оси. Выберем т настолько большим, чтобы все полюсы ак (к = 1, п)
охватывались кривой ~/т, и обозначим через 2Рт количество целых точек, охватываемых этой
кривой. Тогда, согласно теореме о вычетах, имеем
л 71 Рт п Рт
; / f(z) ctg nzdz — У res tt/(z) ctg irz + у res ?r/(z) ctg ttz = 5 res irf(z) ctg ttz + > /(J)-
P k — 1 J — ~Pm fc — 1 J — ~Pm
Im
Перейдя в этом равенстве к пределу при т —► оо и приняв во внимание соотношение (1),
получим формулу (3).
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
279
Формулу (4) получим аналогично с помощью соотношения (2), приняв во внимание, что
resito^ = Условия (1) и (2) выполняются, если /(z) = O(z2) при z —» оо, а =
j
{z€C:|z| = m+ |}, так как в этом случае Vz 6 7m
, , l+e-*
|ctg7Tz|^
Пример. Найти сумму ряда ^2 <;1+Lb)2 ’ " 6 z-
Имеем /(z) = , z = — полюс второго порядка функции /,
1 тг ctg nz
_________ — — fgg ___________
(а + nb)2 _ д (а + bz)2
ъ
a ZirctgTrz • (z + ^)2\ тг d Л-2
m — I -------------—;---- I = - lim -r — ctgTrz = —---;.
dz I (a + bz)2 I Z_ib2dz ft2 sin2 t2-
ь \ / ь о
Рассмотрим задачи.
40. Доказать равенство
2тг
dt
J a — ibcost
о
если
если
2тг
у/а2 + Ь2'
2тг
у/а2 + Ь2’
◄ В соответствии с формулой (1), п. 4.1, рассмотрим функцию
1____________ 2» _ 2»
/ 2+±\ bz2 + b + i2az b(z — z\)(z — z2)'
z I a — ib • -у5- 1
где z1 — | (-а + Va2 + b2) , z2 — (-а - у/а2 + Ь2) .
Если а > 0, то точка z1 охватывается окружностью 7 = {zgC:|z| = I},a точка z2 лежит
вне 7 и по формуле (1), п. 4.1, получаем
2тг
Г dt 2i 4тгг 2тг
/ -----------= 2тг res-----------------=-----------= .
J a —ibcost z, b(z — zt)(z - z2) b(zt — z2) va2 + b2
о
Если a < 0, то точка z1 находится вне окружности 7, а точка z2 охватывается ею, в силу чего,
применив упомянутую формулу, имеем
2тг
/dt 4rri 2тг
a —ibcost b(z2 - zj у/а2 + b2
о
41. Вычислить интеграл
/cos mx . ,
----------- dx, a € R, a # 1, m € N.
1 - 2acosa: + a2
◄ Поскольку функция x i-i ip(x) = = 7Г> ,г1> нечетная, то f <p(x)dx = 0, в
силу чего
e'm*dx
1 — 2a cos x + a2'
280
Гл. 7. Вычеты и их применения
С помощью замены переменной е'х = z преобразуем интеграл I в интеграл по положительно
ориентированной окружности Г = (7, 70р), 7 = {z 6 С : |z| = 1}:
- * f zmdz
а J (z - a)(z - |)
г
Если |a| < 1 , то
i liria™ lira™
a a — - 1— a2
a
Если |a| > 1 , то
I
~am(a2—1)"
42. Вычислить интеграл
2тг
I = J ecos ® cos(sin ж) cos nx dx, n 6 N.
0
2тг t
•4 Поскольку I € R, I\ € R, где I\ = f ecosx cos(sinir) sinnx dx, to
о
2тг 2тг 2тг
г , • т / cos х / • гпх j „ 1 / cos x+inx ( i sin x . — i sin x \ >_ / inx / e'1 . e tx A »_
I+ili ~ I e cos(sinx)e ax — ~ I e ^e Ч-e jdx — - / e |^e +e j dx.
0 0 0
Легко убедиться в том, что 1\ = 0. Полагая в интеграле е,х = z, получим:
I = Yi У z"^l(gZ +eT)dz, Г = (7,7ор), 7 = {z е С : |z| = 1}.
Г
Так как функция z zn~'ez аналитическая, то по теореме Коши
У zn~ie2 dz = 0,
г
поэтому
I = — [ zn~le^ dz.
г
По основной теореме о вычетах имеем
п-1 7Г
I — л res z е* = — .►
о п!
43. Вычислить интеграл
+оо
[ х6 dx
I = J
о
◄ Функция z »-» /(z) = имеет в плоскости С восемь простых полюсов
(2<:+1)х ____
Zk = е s (fc = 0, 7),
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
281
из которых первые четыре принадлежат верхней полуплоскости. Применив формулу (3), п. 4.1,
6
получим (приняв во внимание четность функции <р(х) = D^, = (-оо, +оо)):
X6 z6
--------- dx = iri > res--------
1 + z8 1 + г8
k—0
rri 1 « / -i
= TL; = 7(e
4=0
тг _ • Зтг _ . 5ir _ • 7tt
8 + e 1 8 + e ' 8 + e 1 8
) =
44. Вычислить интеграл
cos az
————- dx
X4 + X2 + 1
(a > 0).
◄ Находим особые точки функции z н-> t, принадлежащие верхней полуплоскости:
1 \/3 1 хЛ
zi — е з = - + г —, г2 = еЗ=--+г —.
2 2 22
По формуле (10), п. 4.1, получаем:
1 Т cos az 1 Т e’al ( eiaz eiaz
I = - I —;----;--dx = - / —-----------dx = iri res —---------h res —:-;---
2 J z4 + z2 + 1 2 J x4 + z2 + 1 \ г ' 1 ' ’ a . .
eiaz' eiaZ2 \ _ тге~^
4z\ + 2^t + 4zj + 2zj у 2
Функция z I-» J(z) = имеет в верхней полуплоскости один простой полюс z\ = ib и
один простой полюс z2 = 0 на действительной оси. По формуле (13), п. 4.1, получим:
I = j bn(2x»res/(z) + jr«res/(z)) — i lm(2irie~ab + тт»(—1)} = тге~аЬ — —. ►
282
Гл. 7. Вычеты и их применения
46. Вычислить интеграл
/х - sin х
г3(х2 + а2)
о
◄ Функция х <р(х} = р, Уг., Dv = (-00, +оо)
1 Г x - sin x 1
- / ---------------dx = - .
2 J x3(x2 + a2) 2 J x3(x2 + a2)
Действительно,
cos х — 1
7----г- dx = О,
х3(х2 + а2)
— четная, в силу чего
x + i(e'x - 1)
dx.
Рис. 88
так как подынтегральная функция нечетная, поэтому ра-
венство (1) справедливо.
Применим формулу (13), п. 4.1:
./ z + i(e -1) 1 z + i(e — 1)\
I = Tri | res —7—5-----—F - res —7-—-----7— 1 =
y.a z3(z2 + a2) 2 0 z3(z2 + a2) J
. fi(a + e~a + 1)
= -------------------
V 2a4
i \ тг (а2
^)=2^(-2+1-а-е
1 - ei2mz
4/. Интегрируя функцию z 1-+ f(z) = ——7-------7- (a > 0, m > 0) по границе полукольца
z2(z2 + a2)
доказать, что
f Sin2 mxdx _ 1Г (..-lam ,4
I --------ТГ = 12am + e ~ 1 )
J x2(x2 + a2) 4а3 ' '
о
◄ Пусть г < a < R, 7b={z€C:z = Re'1, 0 t тг}, yT = {z € C : z = re,f, 0 t тг}.
Рассмотрим упорядоченный набор гладких ориентированных кривых Г = (Г1; Гк, Г2, Г“),
являющийся кусочно-гладкой положительно ориентированной замкнутой кривой (рис. 88). Функ-
ция f имеем в точке z = ia простой полюс, причем z € KRr. Согласно основной теореме о
вычетах, получаем:
R -г
/Г 1 _ р»2"1® Г 1 _ p»2m* Г 1 _ р'2тх Г 1 _ i2mz
f(z) dz = I —z-~i--57 dx + I -г—:-j- dz + / -7—5---57 dx + I -y—---— dz =
J x2(x2 + a2) J z2(z2 + a2) J x2(x2 + a2) J z2(z2 + a2)
гл -я Г7
1 - ei2rnz
г
. _ тг(е-2т“ - 1)
= 2тг» res —г—т--г- =---------5-----
ia z2(z2 + а2) а3
Устремляя R в бесконечность, ar — к нулю и принимая во внимание, что
Г 1 — е’2тг
lim I -----------r- dz = О,
n—oo J z2(z2 + a2)
гк '
§ 4. Применение вычетов для вычисления интегралов и сумм рядов 283
[ 1-е2тг 1 Г ( Нт г (4 3 2т\ \
lim / ----тг dz = lim -т / |---------1- 2m 4-1 I - m 4------ \ z + ... I dz =
r-oj z2(z2 4-a2) r—o a2 J \ z \3 a3 ) }
Г,- Гт
7Г
if/ /4 , 2m \ \ 2mir
= lim — / I -2m 4- i2m2re v 4- i ( - m3 4------ ) ir2e 2v + ... I dtp =---
r-^oa2 J у y3 a3 / у a2
о
получим:
I - ei2mz 2таг
dz =-.
z2(z2 4- a2)---------a2
Г7
f 2 - 2cos2mz f sin2 та: аг(е 2тп“ — 1) 2mar ar(e 2тпа - 1 4- 2ma)
J x2(x2 + a2) d J x2(x2 + a2) X a3 a2 a3
о о
48. Вычислить интеграл
+oo
f Inz
I = / -TT~i dx (“ > °)-
J xl 4- a2
о
f Inz
/ ~5-----7 dz =
J z2 4-a2
гт
◄ Интегрируя функцию z /(z) = 77^7 (Inz = In|z| 4- iargz) по кривой Г (см. рис.88),
получим Va 6 (г, R):
R -г
Г ч f Ina: f Inz f Ina:
I f(z) dz = I —------- dx 4- I ---r dz 4- / -5--5 dx 4-
J J x2+a2 J z2 +a2 J x2 +a2
Гк -R
r
Inz
= 2тгг res —------7 =
ia z2 4- a2
Замена переменной x = — t (t > 0) в интеграле
/Inxdx
x2 4- a2
-R
приводит к интегралу
R
f In t + ITT
11^dt-
После этой замены перейдем в равенстве
аг
2
г
к пределу при R —► 4-оо и г —> 0. Получим
/In z dx Г In х 4- »'аг
z2 4- а2 + J х2 + а2 dX
о о
откуда
/In zdz
-----7 4- (аг
х2 + а2
о
/dz аг »аг2
—------7 = - 1п а 4- —,
х2 + а2 а 2а
о
In zdz
аг
--------т = — In а.
z2 4- а2 2а
о
284
Гл. 7. Вычеты и их применения
Если а = 1, то
/inxdx
^2+T = 0’>
0
49. Вычислить интеграл
f x1 dx
<«>»>
0
◄ Функция z /(z) -
плоскости С. Так как
имеет полюс второго порядка z — ia в верхней полуплоскости
If x2 dx
2 J (x2 + a2)2 ’
то можем применить формулу (3), п. 4.1. Имеем
d z2(z — ia)2 d
---------— = тгг lim —
dz (ZJ + aJ)J z—*iadz
i z2
I = 2;ri res-----------гт = кг Ит
ia 2 (z2 + a2)2 z—ic
2 2iaz ' it
= ttj lim --------;—г = —
z —-ia (z + ia)’ 4a
50. Вычислить интеграл
Г dx
J (X2 + 1)"
(n e N).
◄ Функция z i-> /(z) = ^2J1)n имеет полюс n-го порядка в точке z = i, лежащей в верхней
полуплоскости z-плоскости. Поскольку
1 Т dx
2J (х2+1)"
то по формуле (3), п. 4.1, получим:
тгг dn~’ (z — г)п тгг dn~' 1
I = тгг res /(z) =------- lim-----г • —-------=----------------r--------.
z=i (n - 1)! z~i dzn~l (z2 + 1)" (n — 1)! dz"”1 (z + г)"
Так как + i)~n = (—l)kn(n + 1) ... (n + к - l)(z Ч- г) ~fn+fc), то
dn-1 1 „ , 1
-----Г--------= (-l) 'n(n + 1) ... (2n - 2)----------;
dzn-1 (z +г)п (z + i)2n-1
r dn~' 1 _ (~l)n~'n(n +1) ... (2n-2)
™ dzn~l (z + г)2п~‘ ~ i2n-‘ • 22n-‘ ’
гтг (—1)”-1я(п + 1) ... (2n — 2) irn(n + 1) ... (2n — 2)
“ (n - 1)! t-2n-i22n-i ~ („_ 1)! - 22”-1 =
it (2n — 2)! rr (2n — 2)! it (2n — 3)!!
- 2 ((n- l)!)2(2"-‘)2 “ 2 ((2n - 2)!!)2 = 2 (2n-2)!!’
Если n = 1, то
+oo
0
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
285
51. Вычислить интеграл
dx
(х2 + а2)(ж2 + Ь2)
(а > О, Ь > 0).
< Поскольку функция z >-> /(z) — , 7, , д, имеет в верхней полуплоскости два простых
(Z тй тО )
полюса Zj = ia, z2 = ib, то, применив формулу (3), п.4.1, получим:
I = 2?ri(res J(z) + res J(z)) = 2тгг ( lim - - -j-,-~2. + Hm t~ • )
ia ib yz—*га (z + га)(г2 + o~) z^ib (zl + a2)(z + го)j
( 1 1 \ _ тг / i _ 1 \
\2ia(b2 — a1) 2ib(b2 - a2)) b2 — a2 ya b)
7Г
ab(a + b)
52. Вычислить интеграл
•4 Очевидно,
1 =
dx.
1 T г2 + 1
2 J х4 + 1
dx.
1 =
Так как функция z ь-+ /(z) = имеет в верхней полуплоскости два простых полюса z} = е1 4
г ^7Г
и z2 = е 4 , то по формуле (3), п.4.1, имеем
53. Вычислить интеграл
х cos х dx
х2 — 2х + 10
◄ Применим формулу (10), п. 4.1, приняв во внимание, что функция z н+ имеет в
верхней полуплоскости простой полюс zi = 1 + Зг:
r zeiz (1 + 3t)e’<1+3i)
I = Ке2згг res f(z) = Ке2тгг lim ----------------г = Ке2тгг-----------------=
z=z, z-un z - 1 + Зг 6г
= Re(l + 3i)e~3(cos 1 + г sin 1) = j e'3(cos 1 - 3 sin 1). ►
54. Вычислить интеграл
х sin х dx
х2 + 4х + 20
— ОО
286
Гл. 7. Вычеты и их применения
Функция z f(z) = имеет в верхней полуплоскости простой полюс zt = —24- £4.
По формуле (11), п. 4.1, находим:
ze*2 (-2 4- £4)е'<-2+*4)
I = 1т2тг£ res f(z) = 1т2тг1 lim --------------= 1т2тг£
z~Z{ z—*—2+>4 Z 4" 2 4“ £4
= 1т — (-2 4- 4£)e~4(cos2 - £sin2) =
55. Вычислить интеграл
8£
— е 4(2sin2 + 4cos2) =
4
— е 4(sin 2 4- 2 cos2). ►
/cosax
-r~ridx
х2 4- b2
о
◄ Поскольку функции х н+ tp(x) =
соответственно четная и нечетная, то
х ~ v-w = +°°)
—-----г dx.
х2 4- Ъ2
Функция z н-» /(г) = имеет в верхней полуплоскости простой полюс zx = Ы, поэтому
iaz _•
I = ni res/(z) = тт£ lim ----- = — е(,“)<,Ь) - — е~аЬ. ►
ы z-^ыг+Ьг 2bi 2b
56. Найти главное значение интеграла
sinz
—------------dx.
(х2 + 4)(х - 1)
< Интеграл I расходящийся, так как при х —» 1 подынтегральная функция имеет одинаковый
порядок роста с функцией х i-+ 777 •
Поскольку функция z н+ /(z) = _-[) имеет в верхней полуплоскости простой полюс
z( = 2£, а также простой полюс z2 = 1 на действительной оси, то воспользуемся формулой (13),
п. 4.1:
е
I = Im(2Trires/(z) 4- Tri res /(z)) = Im I 2тг£ lim -:-------F iri lim -7-- )
v Z| 1 ' \ (z 4- 2t)(z - 1) Z_iz24-4y
( e."2 e' \ (тг e-2 ?r£
= Im 2,r' П T = Im I \ V-—7 + V <cos 1 + 2 sin
\ 4z(2z — 1) 5/ \2 2i-l 5
1 —2 1 / —2
= Im I — e (-1 - 2i) + — cos 1 — — sin 1 j = у (cos 1 - e
57. Вычислить интеграл
/sin ax
x(x2 + b2) X
(a > 0, b > 0).
◄ Очевидно,
sin ax
x(x2 + b2) ’
cosax
x(x2 4- &2)
dx = 0,
1
1
2
2
eiax
---------r~ dx.
x(x3 + b2)
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
287
Функция zw f(z) = дтщгу имеет два простых полюса в точках z{ = Ы и Zi = 0 соответственно
в верхней полуплоскости и на действительной оси. Применив формулу (13), п. 4.1, получим:
е*“г тг е’“2 е~аЬ л
2(2 + Ы) + 2 22 + Ь2 = "^267 + 2d2
w -at
= ^(1"e
I = л! res /(2) + — i res f(z) — % lim
zj 2 zj z—*bi
58. Доказать равенства:
e
------dx =
1 + ex
f Г'1 Л
/ -----dt = ------
J 1 + t sin атг
о
(1)
IX 7Г
/ ------dx — -------
/ 1 + xn nsin —я
J n
0
◄ Рассмотрим функцию z >-> /(2) = и проинтегрируем ее по положительно ориенти-
рованной границе прямоугольника Р с вершинами в точках (-R, 0), (Д, 0), (Д, 2л), (-Д, 2л),
(рис. 89):
(2)
f(z)dz =
дР
Г,
Г2
г?
[ е<1Х<1х
J 1 + е*
-R
2тг
/^aR+iay
1 + eR+‘v
0
&ах+г2тга
---------dx
1 + е'
О
/e~aR+iay
1 -t-e-я+.у dy~
2тг
R
/-. г2тга^ / ®
= (1 -e
2тг
------dx + i
1 + ex
e.a^
l+eRe^ l+e-Re'y
e~aR
dy. (3)
— R О
Точки zk = (тг + 2Лгтг): (к € Z) являются просты-
ми полюсами для функции f. Однако, внутри прямо-
угольника Р находится лишь один полюс zQ = тгг. По
основной теореме о вычетах имеем
eaz
I = 2?rtres/(z) = 2тгг —
zq ег
В равенстве (4) перейдем к пределу при R —+ +оо, при-
няв во внимание предельные соотношения
eaR e~aR
= -2лге
(4)
lim -----= lim ------------
Я-.+00 I + eRe,v я—+се 1 +e~Re'y
При этом получим:
тг
sin ал
sin атг
= -ти2т-------з—
2 sin2 атг
e
l + ex
2nieia* 2Trieia,r(l - e'i2,ra) iri(eia* - e~iav)
dx =---------rz— =-----------------=----------=---------------=--------
1 - e*2’r“ 4sin2arr 2 sin2 ал
R
В интеграле f dt произведем замену переменной, полагая
о
рассмотренный интеграл
t = ех. При этом получим
е тг
--------dx = ----------,
1 + ех srn ал
что доказывает равенство (1).
288
Гл. 7. Вычеты и их примейения
+оо
В интеграле Л = J г dx (0 < т < п) произведем замену переменной по формуле хп = t.
о
При этом получим:
»>• ,
1 f t п 1 ТГ , ,
Л = - / --------dt—-------— (о < ^ < 1). ►
п J 1+t П sin “7Г ' п >
V П
О
Читатель, вероятно, заметил, что при 0 < а < 1
+ое
7Г
— dt = B(a, 1 — а) = Г(а)Г(1 — а) = -----.
1+t sin атг
о
59. Доказать, что
и подынтегральная функция имеет устранимую особую точку х — 0. Функция
/1 1 \ 1
Z /(z) =1------— -
у z sh z / z
также имеет устранимую особую точку z = 0. Кроме того, она имеет простые полюсы в точ-
ках zfc = Ttfci (fc g Z\{0}). Рассмотрим последовательность (_Rn) положительных чисел, где
Л„ = (п + тг, а также последовательность областей KRn = {z € С : |z| < Яп; Imz > 0}
Рис. 90
с положительно ориентированными границами dKRn = (Г„, ГДп) (рис. 90). Интегрируя функ-
цию f по кривым dKRn , имеем
[ f(z)dz — f f(z)dz+ [ f(z)dz= f f ~ ~ ~T~') — + [ f ~ ~ ~
J J J J \x shx/ x J \z shz/ z
ГЯп -Rn ГдЛ
§ 4. Применение вычетов для вычисления интегралов и сумм рядов
289
n п
sh z — z
res /(z) = 2тгг > res —:---------------
feKi ' fciri z2shz
A=l fc=t
n
2^52
fe=l
sh z - z
2zshz + z2chz
z — k-ni
" -feTTi _ 2y(-n* =2y(-l)t+l
2—< — fc27r2 ch(fcTTi) ' к 2—t k
k=l k = l k=l
При n oo Rn -+ +oo, поэтому по лемме Жордана
60. Доказать, что при -1 < а < 3 выполняется равенство
Г ха dx _ тг 1
J (1 + х2)2 4 cos ~
о
◄ Здесь можно применить формулу (15), п. 4.1, где f(z) = (1+Ь~2’ а = а + 1- Условия,
рассмотренные в случае 5), п. 4.1, для функции f выполняются при р = 0, q = 4. Принимая во
внимание, что 0 < а + 1 < 4, по формуле (15), п. 4.1, имеем
f ха 2тгг С za za \
/ --------dx ~ ------------------- । геч------------4- res-------------- I
J (1 + Т2)2 1 _ е>2т(а+1) (1+z2)2 -£ (1 + Z2)2 /
2тгг / d za d za \ 2iri (2ia(a-\) 2(-г)°(а - 1)\
----т— lim------------ + lim-----------r = -------—-------------1------------=
1 — e’2™ > dz (z + г)2 t--.dz (z — г)2 J 1 — е*2,га у —8» 8г J
2rri а - 1 /z ,ах _ тг(1—а) , Uxox тг(1 - а) 1
1 — ei2,ro 4г ' ’ 1 ' 2(1 - е,2’п) в ' 4 cos3—'
61. Найти сумму S ряда > —-------- (n g N).
—2 п4 - а4
◄ Применив формулу (4), п. 4.2, получим, полагая /(z) = )2а<:
S
(~1)п
п4 - а4
1 Я" A /(z) , /(z) , /(z) , /(г) А
—т-------res-----------1- res--------1- res--------1- res----- =
2a4 2 у a sinTrz ia sinjrz -ia sin irz -a sin ttz у
1 тг
2a4 4a3
1 1
---------T—
sin it a sh it a
62. Доказать, что
S =
n—~OQ
1 2tt tt\/5
-----------7 = “F th
n2 + n + 1 л/З 2
◄ По формуле (3), п. 4.2, имеем
„ I CtgTTZ CtgTTZ
S = -гг res —------------------1- res —----------
\ -i+iv5 z2 + z + 1 -1-173 z1 + z + 1
2 2
290
Гл. 7. Вычеты и их применения
63. Найти сумму ряда Х' -----—, п € Z.
' (а + п)2
Ч В примере, рассмотренном в п. 4.2, показано, что
(а + пЪУ b2sin2^'
п = —оо 0
Следовательно, при b = 1 получим рассматриваемый ряд и при этом
1 тг2
(а + n)2 sin2 тга
Е(— 1)п
ГХ-—у’п
◄ Очевидно,
(~1)П _ 1 1
(а 4- п)2 (а + 2п)2 < (а + 2п — I)2
п = —ос п = —ос п = —оо
Ряды 52 (а+2пр ’ S (o^-ir “ частные случаи ряда 52 (a+Lp > сумма которого известна
(см. равенство (1) в примере 63). Полагая в (1) Ь = 2, получим:
1
(а + 2п)2 4 sin2
Для вычисления суммы ряда 52
а - 1:
в указанном равенстве полагаем Ъ = 2 и вместо а берем
_______________ _ тг2
(а + 2п - I)2 4sjn2i(2_:
тг2
Д 4 cos2 4г
Окончательно имеем
(-1)"
(а + п)2
тг2
Т \shT^ cos22y
тг2
т
cos тга
sin2 cos2
тг2 ctg тга
sin тга
1
1
65. Найти сумму ряда \ -------, п € Zo.
< (2n + I)2
◄ Запишем сумму ряда в виде
1
1
1
у____J__
(2п + I)2
п=0
1
(2n+ I)2
(1 - 2п)2
(2n + I)2
(2n - I)2
о° оо оо
Е1 V Л 1 1 *
(2n + I)2 ~ (2n + I)2 “ 2 (2п + I)2 ’
Получили частный случай суммы ряда 52 (О+7Д)Т
Таким образом,
у—!— = 1
(2n + I)2 2
71=0
при а = 1, Ъ = 2.
ТГ ТГ
4sin2 ~ 8 '
Упражнения для самостоятельной работы
291
66. Найти сумму ряда V'' —;-7, п € Zo.
z—2 п2 + а2
◄ Воспользуемся формулой (3), п.4.2, полагая /(z) = г2^а2 '
ч Л 1 11 Л 1 1 ТГ
г п2 + а2 2а2 2 п2 + а2 2а2 2
п=0 п= —оо
CtgTTZ
res —-------
z=ia Z2 + a2
4- res
z~ — ia
CtgTTZ
z2 + a2
1
2a2
67. Найти сумму ряда
тг / ctgitra
2 у 2ia
(-l)n
2 , 2 , n ez0.
n2 + a2
ctg гтга \ _ 1
2ia / 2a2
тг cth ira 1
—----------- — (1 + тга cth тга). ►
2a 2a2
◄ Очевидно,
(-Dn i i y- (-Dn
n2 4- a2 2a2 2 n2 4- a2
n=0 n= —oo
1 11 v* 1
2a2 + 2 \ (2n)2 + a2
1 ТГ / CtgTTZ CtgTTZ CtgTTZ CtgTTZ \
= 2^ " 2 I 4z2 4- a2 + z rcsia 4z2 + a2 + (2z - I)2 + a2 + (2z - I)2 4- a2 ) =
\ 2 2 2 z~ 2 /
= _ 7Г / Ctg^ Ctg^ + Ctg(j+tV) + Ctg(f-^)\ =
2a2 2 I 4ia 4ia 4ia — 4ia I
1 тг тга тг гтга 1 тг тга тг тга 1 тг / тга тга\
= —т 4----cth-----1---tg----= —- 4----cth--------th — = —г 4------cth-----th — =
2a2 4a 2 i4a 2 2a2 4a 2 4a 2 2a2 4a \ 2 2 /
1, г /ch! у - sh2 y '\ 1 тг 1
2a2 + 4a V sh ch ~ 2a2 + 4^ ' sh ch
Упражнения для самостоятельной работы
1. Найти вычеты следующих функций в особых точках:
а) /(г) = (п 6 N); б) /(z) = ууутг (n € N); в) /(z) = cosz - sinz;
г)/(г) = zV (n е N); д) f(z) = е)/(z) = ег In —.
2. Найти вычеты в конечных особых точках следующих функций:
а) f(z) = si.n2V.2; 5)f(z)=^^.
3. Найти res - (1 4- + ... + —1—.) (n € N).
4. Найти вычет функции /(z) = (x/T = 1).
5. Пусть fug — аналитические в точке z = a функции, причем /(a) / 0, a g(z) имеет в
точке z — а нуль второго порядка. Доказать, что:
/Ц) _ 6/,(a)g”(a)-2/(a)g'"(a)
reS S(z) “ 3S"(a)2
a
Если же точка z = а — простой нуль функции д и f(a) / 0, то
/(z) _ /'(а)д'(а)-/(°)9"(д)
r®s 9Ы s'(a)2
6. Доказать, что:
X z
^^ = ^(06^); б) res -^=е 2 , ^^-=e^(feeZ);
a
>, z3" _ <3")l
В) res (-j+2)„ —
292 Гл. 7. Вычеты и их применения
7. Пусть функция / имеет в бесконечно удаленной точке полюс порядка к. Доказать, что
res/(z) = lim (zfc+2/fc+1>(z)).
ОО Z —»сс
8. Вычислить интегралы:
а) / тйг? Г = <7> 7ор)> 7 = {г 6 с : |z - г'| = 3};
б) /z3 sin | dz, Г = (7, 7„р), 7 = {z & С : \z\ = 1};
Г
в) J (sin 72 + ez2 cosz) dz, Г = (7, 7ор), 7 = {z 6 С : |z| = |}.
Г 4 7
9. Доказать равенства:
а) / Д;7^т~ =2n+i, Гв =(7К,7°Р), 7л = {z 6 С : |z| = R}, n<R<n+\, m€N, n€N;
1 R
б) / Г- = (7r, Г°Р), 7r = {z € C : |z| = r}, r > | и при больших |z|
10. Вычислить интегралы от всех ветвей подынтегральных многозначных функций-:
/ Ln(z-2)+iH ’ Г = (7, 7оР); 7 = {г € С : |z - 1| = j };
б) / vH + z4dz, Г = (7, 7ор), 7 = {z е С : jz| = 2};
Г
в) / sinp+v'T) ’ Г = (7, 7°р), 7 = {г € С : |z - 2| = j}.
г
11. Вычислить интегралы отданных однозначных ветвей многозначных функций:
а) J (Lnz|z=_e = 1 - тгг), Г = (7, 7ор), 7 = {z € С : |z + 2| = |;
б) /(2+УТИ)sinz ('/?Т7Я=о = Г = (7,7оР), 7={z6C:|z| = l}-
Г
12. Доказать, что f = ^== (а > 0).
13. С помощью теоремы Митгаг-Леффлера найти общий вид мероморфной функции /, име-
ющей полюсы второго порядка в точках Ьп = п с главными частями в них gn(z) = .
14. Доказать равенство:
-г--1- = -7 + 7TZ2 У' П 1— 1 , Z Ф птг(±1 ± г).
chz— COS Z z2 t sh 7ГП 1 г4+п47Г4 ’ ' ' '
n=l 4
15. Доказать равенства:
•> П0-^) = Ь »> пО + ^Г)»!.
п = | П = 1 4 7
16. Найти области сходимости бесконечных произведений:
°°/ „2 \ се / к / / \ 2 / \3\
а) П (1 + (1 + £) ^П); б) П (1 - ехР +1 (^) +1 (т-г) ) •
17. Доказать, что функция /, где /(z) = ((1 - exp | («)*)) является Целой.
Найти нули этой функции и их кратность.
18. Получить теорему Вейерштрасса (п. 3.3) из теоремы Миттаг-Леффлера (п. 2.2).
Упражнения для самостоятельной работы
293
19. Доказать равенства:
a) chz — cosz = г2 П П + б)
в) thz
20. Доказать равенства:
п=2 п = 2
21. Доказать равенства:
2тг
a) Г ;----ттг-----(agR, b g R, cER; с2 - 62 - a2 > 0);
7 J (a cos x + b sin x+c)- 2 ' ’ ' ’ /J
0 (c2 —a2-b2)2
2tt
Д) f = if (a - Va^^b2), 0 < b < a.
r ' J a + b cos x b2 4 75
0
22. Вычислить интеграл:
2тг
I— f ea cos x sin(a sin x) sin nx dx (n g N).
о
23. Доказать равенства:
i) 7 -s,2 = 2) 7 7^6 = f; 3) J 4fr = J’rsinf cos
' J (x^+lRx^ + a2)2 2a2(l+a4)2 ’ ' J l + x° 3 ’ 7 J x3 + l 5 5 ->
-oc 0 0
24. Интегрируя функцию z >-+ f(z) = — тг < a < тг, по границе прямоугольника с
вершинами в точках (-R, 0), (й, 0), (й, г), (-Й, г), доказать равенства:
a) f ^H^=sec^; /3) f ^dx = sec^.
' J Сп7гх 2 ’ ~' J ch 7ГХ 2
25. Доказать равенства:
«) J = c>°’ -1 < a < 3 и не равно целому числу; Д) f dx =
0 о 2с 2
+ оо +ос
7) f 7 ^,2 dx = S') f dx = у sec -1 < а < 1.
1 ' J (х + с)1 L\/c ’ J l + x^ 2 Z ‘
о о
26. Интегрируя функцию z м- /(z) = 7—7 по границе кругового сектора
5= {z g С :0 < |z| < й, 0 < argz < },
доказать равенства:
\ Г dx 2тг>/3. cz\ С & dx 1г\/3
а> J 7771 = —> б> J Й76 = ~•
о о
27. Интегрируя функцию z 1-+ /(z) = по границе кругового сектора
S = {z g С : г < |z| < й, 0 < argz < у } ,
доказать, что:
а) Г ds^dx = -^-, б) Г ^Лгг2 =
7 J 1+х4 8 * 7 J ж4+1 8
0- 0
294
Гл. 7. Вычеты и их применения
28. Доказать равенства:
оо оо /22
1) Ё СТ = ^4 - ^(ctga-a + cthтга); 2) £ 4- тгаcthтга - 2
П=1 71=1
Глава 8
Некоторые общие вопросы
геометрической теории
аналитических функций
Эта глава посвящена изучению некоторых общих топологических свойств аналитических функ-
ций. В ней рассмотрены геометрические принципы и общие вопросы теории конформных ото-
бражений. Последний параграф посвящен конформным отображениям многоугольников.
§ 1. Принцип аргумента. Теорема Руше
1.1. Вычисление интеграла
1 [
---- / -----------dz.
2тгг J f(z) — A
8D
Пусть D C — область, / — аналитическая в замыкании D функция, за исключением
конечного множества полюсов, лежащих в D (но не на 9D) и 9D — непрерывная положительно
ориентированная кривая. Пусть, далее, А — такое произвольное (конечное) комплексное число,
что функция f не имеет Л-точек на границе 9D, а. — произвольная аналитическая в замыка-
нии D функция. Рассмотрим в области D функцию z F(z~) = Ее возможные особые
точки в D — это А-точки и полюсы функции f.
Пусть {а*; к = 1, т} — A-точки функции / в D кратностей соответственно аь а2, ... , ат,
a {6j; j = 1, n} — полюсы соответственно порядков /3], /32, • • , Рп • Изучим функцию F в окрест-
ности точки ац.. В соответствии с формулой (3), п. 1.8, гл. 5, имеем
/(z) - А = (z - ak)akf0(z), f0(ak) Ф 0.
Тогда
/'(z) = ak(z - ак)°к lf0(z) + (z - ак)ак f^z),
. ,.(z-ak)ak l(akf0(z) + (z - ak)fo(z)) akf0(z) + (z-ak)f£(z)
F(z) = ip(z)--------------------------------= w(z)---------------------
(z - ak)a^f0(z) (z-ak)f0(z)
откуда
res F(z) = ak<p(ak).
<*k
Аналогично, рассмотрим функцию F в окрестности точки bj:
/'(z) = -Pj
7(*)-A = (z-b>’ /o(b>)#0’
(z -b^+t + (z - V)^ = (z - MZ) + Z°(Z)(Z “ bj^’
F(z) = <p(z)
-PjMz) + f'0(z)(z-bj)
(z - bj)f0(z)
296
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
откуда
resF(z) = -fijplb.j).
bj
По основной теореме о вычетах имеем
1 Г f(z)dz
w J = Ев^<а*>- Е^м- (1>
а о J-1
В дальнейшем каждую Л-точку засчитываем столько раз, какова ее кратность. Аналогично,
каждый полюс засчитываем столько раз, каков его порядок. При таком соглашении правая часть
формулы (1) выражает разность между суммой значений, принимаемых функцией <р в А-точках
функции / и суммой значений, принимаемых той же функцией в полюсах функции f, лежащих
в области D.
Рассмотрим частные случаи.
1) При <p(z) = z формула (1) принимает вид
1 Г f'(z)dz
Z f7~\--Л = ~ <2)
2тгг J f(z) — А
до k=i J = 1
В правой части формулы (2) стоит разность между суммой А-точек функции / и суммой ее
полюсов, размещенных в D.
2) При <p(z) = 1 имеем
1 У /'(•?)
Г~ / /Л 7fe = Eat~E^- <3)
2ттг J f(z) — A /
вв fc=l J = 1
В правой части формулы (3) стоит разность между числом A-точек и числом полюсов функ-
ции /, помещенных в области D.
1.2. Теорема о логарифмическом вычете.
Пусть теперь А = 0, т. е. А-точки функции f являются ее нулями в области D.
т
Введем в рассмотрение следующие обозначения: а*. = N — число нулей функции f в
к=\
п
области D, ~ Р — число полюсов этой же функции в D. Тогда
7 = 1
1 f f'W ;
2тгг J f(z)
дв
= N — Р.
(1)
Интеграл, находящийся в левой части этого равенства, называется логарифмическим вычетом
функции f относительно dD, а само равенство выражает смысл следующей теоремы о логариф-
мическом вычете.
Теорема. Пусть D <s С — область с положительно ориентированной границей dD, и множе-
ство точек границы является кривой Жордана. Тогда, если функция f аналитическая в замыкании D,
за исключением полюсов, размещенных в D, и f не обращается в нуль на dD, то логарифмический
вычет функции относительно dD равен разности между числом нулей и числом полюсов функции f,
размещенных в области D.
1.3. Принцип аргумента.
Теореме о логарифмическом вычете можно придать геометрический оттенок.
Первообразной функции в окрестности любой точки z € dD, в которой нет ни нуля,
ни полюса функции /, является функция z F(z) = lnf(z), где In обозначает любую ветвь
логарифма, поскольку F'(z) —
§ 1. Принцип аргумента. Теорема Руше
297
Пусть dD = (7, 70р), [а, /3] 7 — параметрическое представление кривой 7. Тогда пер-
вообразной функции Д вдоль кривой 7 является функция t 1-» Ф(£) = 1п/(уз(<))- Поскольку
кривая 7 замкнута, то In |/(<р(/3))| = In |/(9?(а))|. Принимая это во внимание и применив форму-
лу Ньютона—Лейбница (см. формулу (1), п. 5.2, гл. 4), получим:
[ ^^dz = Ф(/3) - Ф(а) = j(arg/(y?(/3))-arg/(y,(a))). (1)
J J\z)
&d
Введем обозначение
Дао arg / = arg /(<р(/Д) - arg /(<?(<*))
и запишем равенство (1) в виде
1 f f'{z) b6Daxzf
-- I dz = ,
2тгг J f(z)---------2ir
8D
или, принимая во внимание теорему о логарифмическом вычете, в виде
N-P= ^--ASDarg/. (2)
Z7T
Последнее равенство выражает принцип аргумента, который можно сформулировать следую-
щим образом.
Принцип аргумента. Пусть D <s С — область и множество 7 точек ее границы dD является
кривой Жордана. Тогда, если функция f аналитическая в замыкании D, за исключением конечного
числа полюсов, размещенных в D, и f не обращается в нуль на кривой у, то разность между числом
нулей N и числом полюсов Р функции f в области D равна деленному на 2тг приращению аргумента f
при обходе точкой z границы области D в положительном направлении один раз.
Очевидно, что Д Д0В arg/ — это число полных оборотов вокруг точки w = 0, совершаемых
вектором /, когда подвижная точка z обходит положительно ориентированную кривую dD один
раз в направлении, противоположном ходу часовой стрелки. В связи с этим принцип аргумента
можно сформулировать по-другому, а именно:
Принцип аргумента {альтернативная формулировка). Пусть D С — область и мно-
жество 7 точек ее границы dD является кривой Жордана. Тогда, если функция / аналитическая в
замыкании D за исключением конечного числа полюсов, размещенных в D, и f на границе области D
не обращается в нуль, то разность N—Р равна числу полных оборотов, совершаемых вектором w = f
вокруг точки w = О при обходе точкой z границы области D в положительном направлении один
раз.
1.4. Теорема Руше.
Из принципа аргумента следует такое утверждение. _
Теорема (Руше). Пусть функции р и ф аналитические в замыкании D, где D is С —
область с положительно ориентированной границей dD, множество точек которой является кривой
Жордана, и пусть Vz € dD |^(z)| > |^(z)|. Тогда функции р и р + ф имеют в области D одинаковое
количество нулей.
◄ Из неравенства |^(z)| > |^(г)|, выполняющегося Vz € dD, следует, что функции р и р + ф
не имеют нулей на dD. Действительно, поскольку Vz 6 dD |y>(z)| > |^(z)| 0, то
|p(z) + ф{г)\ > |$p(z)| - |^(z)| > 0.
Пусть — число нулей функции + ф в области D. В соответствии с принципом аргумента
имеем
1 1 ( ф\ 1 ( ( Ф^\\
N = т- Дао arg(y> + ф) — — ДЭр arg у? ( 1 + — ) = — I AdD arg уз + Дэг> arg 1 4- — ) .
Z7r \ Р \ \ у? / /
298 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Принимая во внимание, что | | < 1, вектор w = 1 + ~ при обходе точкой z границы 9D не
может совершить оборот вокруг точки w = 0, поскольку точка w = 1 + все время движется
внутри круга К = {w € С : |w — 1| < 1},не содержащего точки w = 0. Следовательно, arg (1 + ^ )
при полном обходе границы 9D возвращается к первоначальному значению и
/ гЬ \
Да£> arg 1 + - ) =0.
\ V J
Таким образом,
N = — Дао arg уз,
Z7T
т.е. — число нулей функции <р в области D. ►
Теорема Руше имеет многочисленные применения. Она используется, в частности, для опре-
деления числа нулей функции.
Пусть, например, требуется определить количество нулей многочлена P(z) — z5 - 5z3 + 2, ле-
жащих в круге К = {z € С : \z\ < 1}. Полагаем P(z) = ip(z) + ^(z), где y?(z) = -5z3, ip(z) = z5 + 2.
Если |z| = 1, то |y?(z)| = 5 > |z5 + 2|, так как |z5 + 2| |z5| + 2 = 3. Функция <p имеет в единичном
круге К три нуля. Поэтому, по теореме Руше, многочлен Р имеет в круге К три нуля.
С помощью теоремы Руше очень просто доказывается основная теорема алгебры'.
Основная теорема алгебры. Любой многочлен степени п
Pn(z) = aoz" + a1zn“1 + ... + an_{z + an
имеет в комплексной плоскости ровно п нулей.
◄ Полагаем Pn(z) = <p(z) + y>(z), где y?(z) = aazn. Многочлен <p имеет в комплексной плос-
кости ровно п нулей, т. к. z = 0 является нулем n-го порядка функции <р>, а при подсчете числа
нулей каждый из них засчитывается столько раз, какова его кратность. В качестве области D
возьмем круг KR = {z € С : \z\ < R}, а R выберем настолько большим, чтобы Vz € DKr выпол-
нялось неравенство |yj(z)| > |^(z)|, где ^(z) = a^"-1 + ... + an_(z + a„. Для этого достаточно
взять R = 1 + |я|| + |а2| + ... + |ап|. Тогда по теореме Руше число нулей функций и Р в
круге KR одинаково, т. е. многочлен Р имеет п нулей. ►
Рассмотрим задачи.
1. Определить число нулей многочлена P(z) = z5 — 12г2 + 14:
а) в кольце Vi = {zeC|l<|z|<|};
б) в кольце V2 = {z G С | 1 < |z| < 2};
в) в правой полуплоскости D = {z G С | Re z > 0}.
◄ а) Пусть
P(z) = <p{z) + p(z)-—z5, = — 12z2 + 14.
При \z\ = | имеем
3125 21
lp(z)| = = 97 -, |^(2)| I - 12z2| + 14 = 89,
t. e. |^(z)| > |^(z)|. По теореме Руше все пять нулей многочлена Р лежат в круге К5/2 =
{zGC:|z|<|}. Определим, сколько из них имеют модуль меньший единицы. С этой целью
полагаем
P(z) = y>i(z) +V’i(z), y>1(z)=14, V'iGO = z5 - 12z2.
При |z| = 1,
KP1O)I = 14, IV-1(Z)| < 13,
следовательно, по теореме Руше в круге К = {z G С ; \z\ < 1} нулей многочлена Р нет. Таким
образом, все пять нулей многочлена Р размещены в кольце V,.
б) Пусть
P(z) = y?3(z) + i/>3(z), <p3(z) = — 12z2, 4>3(z) = z5 + 14.
§ 1. Принцип аргумента. Теорема Руше
299
При |z| = 2
l¥>3(z)| = 48, Ш-z)! С |z5| + 14 = 46.
По теореме Руше число нулей многочлена Р в круге Кг = {z € С : |z| < 2}, следовательно и в
кольце V2 равно двум, т. е. столько, сколько их у функции у>3.
в) Из неравенства P(iy) = iy5 4- 12г/2 4- 14 следует, что многочлен Р не имеет нулей на
мнимой оси, поскольку действительная и мнимая части P(iy) не обращаются одновременно в
нуль. Применив принцип аргумента к полукругу К = {z £ С : |z| < R, Rez > 0}, получаем, что
число .У нулей многочлена Р в правой полуплоскости определяется равенством
1 / \
lim (ДцЯ, _;Д| aig P(z) 4-Дг arg P(z)),
2тг К—сю \ I - I н /
где Гд = (7д, 7д), 7д = {z £ С | z = Relt, -7 * «S 7 }.
При больших R > 0 имеем
Дця, -1Я| argP(z) = Д!/6[д1 -R^iy^ + 12г/2 4- 14) =
у3 . г/5 гг гг „_______।
= Д-/е1Я,о1 arctg ^4 Ду6|о,-к| arctg ]4 = - - - - +О(Я ) = -гг + O{R ),
< f 11 —12z2\
ДГд argP(z) = ДГд argz5 4- ДГк I 1 4-----—---- I = 5тг + O(R ).
Таким образом,
N = — (-гг + 5гг) = 2. ►
2тг
2. В каких квадрантах находятся корни уравнения
z 4- z3 4- 4z 4- 2z 4-3 = 0?
◄ Очевидно, что уравнение не имеет неотрицательных корней. Покажем, что оно не имеет
отрицательных корней. Действительно, полагая z = — х, получим уравнение
х4 — х3 4- 4г2 — 2х 4- 3 = 0.
При 0 < х 1 сумма первых трех членов, а также сумма двух последних членов положительны.
При х > 1 сумма первых двух членов, а также сумма трех последних членов положительны.
Следовательно,
Vz > 0 х4 - х3 4- 4а:2 — 2х 4- 3 > 0.
Подставим в уравнение z = iy. Тогда оно примет вид
у4 — iy3 — 4у2 4- 2iy 4-3 = 0.
Действительная и мнимая части этого уравнения не обращаются одновременно в нуль, в силу
чего исследуемое уравнение не имеет и чисто мнимых корней.
Число его корней, размещенных в первом квадранте, определяется равенством
N = -5- lim (Aj-gio, д| arg(a:4 4- х3 4-4а:2 4- 2х 4- 3) 4- Д„е|я,о| arg (г/4 - iy3 - 4у2 4- 2iy 4- 3) 4-
Z7F К-*ос \
4- Д z=Reil arS(^4 + 4" 4z2 4- 2z 4- 3)) .
Имеем
Дх61о, ki arg(x4 4- x3 4- 4x2 4- 2x 4- 3) = 0,
, , , —y3 4- 2y
Ay6[K,oiaig(y — 4y 4- 3 4- i(-у 4- 2y)) = Дуе[Л,0| arctg y4 _ 4y2 + 3 •
Числитель дроби под знаком арктангенса обращается в нуль при у = х/2 и у = 0, а ее знаме-
натель — при у = у/з и у = 1. Изменение этой дроби при изменении у от R до 0 можно
охарактеризовать следующей таблицей:
300 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
У R х/З V2 1 0
-у3 + 2у
у4 - 4«/2 + 3 O(R *) - оо + 0 ОО + 0
с помощью которой легко заметить, что
Д^я.о] arg(?/4 - 4j/2 + 3 + г(-г/3 + 2г/)} = -2ir + O(B_1).
Далее,
4 3 2 4 ( 4" 4z2 + 2z -Ь 3 \ I
Д I=Rtn arg(z4 + z + 4z2 + 2z + 3) = Д г=Леи arg г4 I 1 3------------- I = 2тт + O(R~ ’)
В результате получаем:
= -1- (0 - 2тг + 2тг) = 0,
2тг
т. е. рассматриваемое уравнение не имеет корней в первом квадранте. Поскольку корни уравнения
распадаются на пары сопряженных, то корней нет и в четвертом квадранте, а во втором и в третьем
имеем их по два. ►
3. Пусть f G А(К), где К — {z G С : |z| sj 1}. Доказать существование такого числа р > 0,
что для всех w из круга Кр = {w € С : |w| < р} уравнение z = wf(z) имеет в круге К ровно один
корень.
◄ Запишем уравнение в виде p(z) + ^>(z) = 0, где y>(z) = z, ip(z) — При |z| = 1
|92(z)| = 1, |w/(z)| |w|M, где M = max|/(z)|. При |w| < -А- выполняются условия теоремы
Руше. ►
4. Доказать, что уравнение (2z + l)ez = 2z + 3 не имеет решений с положительной действи-
тельной частью.
◄ Запишем уравнение в виде
2z + 3
p(z) + ф(г) = -—— —е ' = 0.
2z + 1
В полуплоскости Л] = {z G С | Rez > -1} выполняется неравенство |9?(z)| = | | > 1, а в
полуплоскости D2 = {z G С | Rez > 0} — неравенство |^>(z)| = | — е~г\ — е-1 < 1. Таким
образом, на границе полукруга KR = {z G С : |z| < R. Rez > 0} |^(z)| > |^(z)| VA > 0. ►
§2. Сохранение области
и локальное обращение
аналитической функции
2.1. Принцип сохранения области.
Теорема 1. Если функция f аналитическая в области D и не равна тождественно постоянной,
то образ области D при отображении f также есть область.
◄ Пусть D D*. Покажем, что D* — связное открытое множество.
1) Пусть w, и и>2 — Две любые точки множества D*, z, — один из прообразов z2 —
один из прообразов w2 при отображении /: /(z() = иц, f(z2) = w2, z, G D, z2 G D. В си-
лу связности D существует жорданова кривая 7, соединяющая точки z{ и z2, лежащая в D.
Пусть [«, в] 7 — параметрическое представление кривой 7. Тогда Vt G [а, /3] <p(t) G D
на
и <р(а) = Z], у(Д) = z2. Так как функция / непрерывная, то композиция ф = f ° у>, D^ = [а, /3],
§2. Сохранение области и локальное обращение аналитической функции 301
является параметрическим представлением непрерывной кривой 7* CD*, соединяющей точки
V’(a) = (/ 0 <р) (а) — f(zi) = wi и v(p) = (/ ° р) (р) = /(z2) = w2- Следовательно, множество D*
является линейно-связным, так как любые две его точки можно соединить путем, состоящим из
точек D*.
2) Покажем, что D* — открытое множество. Пусть wn € D* — любая точка и z0 — один
из ее прообразов: /(z0) = wQ. Так как D — открытое множество, то существует окрестность
Or(z0) = {z €. С : \z — z0| < г} <g D. Выберем г настолько малым, чтобы в замыкании Or(z0) не
содержалось ш0-точек функции / (кроме точки z0). Очевидно, такой круг существует, поскольку
у аналитической функции / const ее w0 -точки изолированы. Пусть 7 = {z g С : \z — z0| = г)
и р = min|/(z) - w0|. Очевидно, fi > 0 (т. к. в противном случае, т.е. при р = 0 непрерывная
функция z |/(z) - w0|, достигающая на замкнутом множестве своего наименьшего значения,
обратилась бы в нуль в некоторой точке z' g ~fT, а это означало бы, что на кривой есть w0-точка
функции /, что противоречит выбору 7Г). Теперь покажем, что
= {w g С : |w - ш0| < fi} С D*.
Действительно, пусть w{ g — любая точка. Имеем
/(г) - w, = (/(z) - w0) + (wa - Wi),
причем |/(z) - ц)0| Р на кривой yr, a |wi - wq| < р. По теореме Руше функция z и-» /(z) —
имеет внутри 7Г столько же нулей, сколько их имеет функция z f(z) — w0. Последняя имеет в
окрестности Or(z0) по меньшей мере хотя бы один нуль, следовательно, функция z /(z) — wt
также имеет в этой окрестности по крайней мере один нуль, т.е. существует такая точка zj g Or(zo),
что f(zt) = wt, откуда следует, что wi g D*. В силу произвольности выбора w, g KIL делаем
вывод, что Кр С D*, т.е. D* — открытое множество.
Из 1) и 2) следует, что D* — область. ►
Замечание 1. Непрерывные отображения, оставляющие инвариантными открытые множества, называ-
ются открытыми отображениями. Ясно, что любое открытое отображение оставляет инвариантными
также и области. Следовательно, отображения, осуществляемые аналитическими функциями, являются
открытыми.
Замечание 1. Открытое отображение А-^В называется внутренним, если для любой точки b g В множе-
ство /-1(6) ее прообразов (/-1(t>) С А) не содержит никакого континуума. Очевидно, что отображения,
осуществляемые аналитическими функциями, являются внутренними, так как V6 6 В множество /~*(6)
состоит лишь из изолированных точек.
2.2. Локальное обращение аналитических функций.
Пусть w = /(z) — аналитическая функция в точке z0. Рассмотрим два возможных случая.
а) Пусть f'(zo) / 0 и /(г0) = w0- Так же, как и в теореме о сохранении области, выбе-
рем круг Or(z0), компактно принадлежащий окрестности аналитичности функции / и не со-
держащий других Шо-точек функции /, кроме центра г0. Пусть, далее, ц = min |/(z) — w0|,
«етг
7r = {z g C : |z — z0| = r}, fi > 0. По теореме Руше получим, что функция / принимает в кру-
ге Or(z0) любое свое значение столько раз, сколько раз она принимает значение ш0. Однако, это
значение она принимает только в точке г0 и притом однократно, так как /'(го) / 0. Таким обра-
зом, функция / принимает в круге Or(z0) любое значение из круга Kfl = {w g С : |w — w0| < р}
и притом только один раз. Иными словами, / — локально однолистна в точке z0. Тем самым в
круге Кр определена функция z = g(w), обратная функции /: ff(wo) = z0 и (/ о g)(w) — w. Из
однолистности / следует, что Дш / 0 при Дг # 0. При этом
До Дг 1 1
Дщ Дщ /'(г)
в окрестности точки z0. Таким образом, д € А(КР).
302
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Пусть
z - g(w) = ZO + a^w - w0) + e2(w - w0)2 + ... ,
g(n)(w0) _ 1 f g(w)dw
n\ 2тп J (w~w0)n+1
ж,
a.
Заменим в интеграле переменную, полагая z = g(w) (w = /(z)). Тогда получим:
f zf'(z)dz ____________1 f z^_ ( 1 \ dz _
J (f(z)-w0)n+l 2irin J Z dz \(f(z) - w0)n J
Г,. Г,-
Z - Zq
dzn~l f(z) — w0
1 Г dz 1 / d’
2itin J (f(z) - w0)n n!
Таким образом,
El ( d f z-z0 \ \
-7 ТТГТ T7T--------- (w - w0) . (1)
n! ydz"”1 \f(z)-w0J J
n=l 4 4 2~2<T
•
Ряд (1) называется рядом Лагранжа.
Рассмотрим обобщение формулы (1), а именно, получим разложение в окрестности точки w0
функции F°g, где F — произвольная аналитическая функция в области, компактно содержащей
круг Or(z0).
Пусть
(F °g)(w) = F(z0) + "^2bn(z - z0)n.
n= 1
Повторяя предыдущие преобразования, получим:
1 f F(g(w)) j 1 f F(z)f'(z)dz 1 1
--- / -----------7 dw = -- I ------------- =------/ F(z)— ( -------------
2tti J (w - w0)"+ 2iri J (/(z) - w0)"+1 2тггп J dz \(/(z)-w0)n
акр г,. г,-
1 f F(z)dz 1 C dn~l z-z0
= ---- / ----------- = — -------- F (z) ----------
2тггп J (/(z) - w0)n n! \dzn 1 у \J(z)-Wq
r,.
Следовательно,
\ \ 1 / dU 1 ( . ( Z — Zq \ \ \
(F о 3)(w) = F(z0) + \ — —— F (z) —---------- ) (w-w0).
z—' n! I dz"”1 k \ f(z) - w0 / / /
n—1 4 4 4 / / / z-z0
(2)
При F(z) = z получаем формулу Лагранжа.
б) Пусть f'(z0) = /”(z0) = ... = /(p-l)(z0) = 0, /<p)(z0) / 0 (p > 1). Повторим прежние
соображения. Выберем круг Or(z0) так, чтобы в нем кроме центра z0 не было других w0-точек
функции /, и чтобы Vz € Or(z0) \ {z0} /'(z) # 0. Как и ранее, выберем р > 0 и покажем, что
в круге Or(z0) любое значение w из круга функция / принимает столько раз, сколько она
принимает в нем значение w0, т.е. р раз. При этом, если w # w0, то все значения w функция f
принимает в разных точках, поскольку в них /'(z) # 0. В таком случае функцию f называют
р-листной в круге Or(z0). Если z € Or(z0), то
w = /(z) = wQ + (z - z0)p<p(z), ip(z0) / 0,
V>(z) = (Z - Zq) x/p(z) = K/w -Wq.
Под ^/p(z) понимаем здесь какую-либо ветвь. Эту ветвь можно разложить в ряд Тейлора в
окрестности точки z0, свободный член которого не равен нулю, следовательно, V (zo) / 0 и, со-
гласно пункту а), в окрестности нуля существует функция, обратная функции < = ф(г): z = ^-1(С)-
§ 2. Сохранение области и локальное обращение аналитической функции 303
Запишем ее разложение в окрестности точки ( = 0 в ряд Тейлора
z = za+a^ + аг(2 + ... = za + апС-
71= 1
X
Заменив здесь £ на (w - wq)p , получим разложение, обращающее функцию f в обобщенный
степенной ряд
Z = g(w) = z0 + '^an(w - и>0)р . (3)
n=l
Легко убедиться в том, что коэффициенты ап разложения (3) определяются по формулам
Анализируя разложение (3), приходим к выводу, что g(w) является в круге А'м элементом
полной аналитической функции, для которой точка w0 является точкой разветвления (р — 1)-го
порядка.
Из рассмотренных случаев а) и б) следует такое утверждение.
Теорема 1. Неравенство f'(zg) ф 0 является необходимым и достаточным условием локальной
однолистности аналитической функции f в точке zg.
Заметим, что из выполнения условия локальной однолистности функции f в каждой точке z
области D не следует, вообще говоря, ее однолистность в D. Пусть, например, f(z) = ez. Тогда
Vz 6 С f'(z) = ег yt 0. Однако функция z ег не является однолистной в любой области,
содержащей хотя бы одну пару таких точек Z\ и z2, что zY — z2 = 2тг/гг. Следовательно, f'(z) / 0
в D является необходимым условием однолистности f в D, но не достаточным.
Теорема 2 (принцип однолистности). Пусть функция f аналитическая в области D и
—— -у ж
непрерывна в замыкании D С С, 9D — положительно ориентированная кривая Жордана и D —* D ,
на
причем отображение dD на 9D* является взаимно однозначным. Тогда f — однолистная функция
в области D.
◄ Пусть w0 G D* — произвольная точка. Определим, сколько раз функция z >—► f(z) — wg
обращается в нуль в области D. Согласно теореме о логарифмическом вычете имеем
f(z) - wg
(5)
во
где N — число нулей функции z >-+ /(z) — w0 в D. Поскольку между точками границ 9D
и 9D* существует непрерывное и взаимно-однозначное соответствие, то в (5) можно перейти к
интегрированию по кривой 9D*, полагая w = f(z), dw = f'(z)dz:
1 f dw
N=— ------ = 1,
2тгг J w — wg
OD*
что и требовалось доказать. ►
Рассмотрим задачи.
5. Разложить по степеням w функцию z = g(w), определенную в окрестности точки w = 0
уравнением Кеплера z — а = wsinz (а ф 0, ±тг, ±2?г, ...).
◄ Здесь z0 = а, wg = 0, /(z) = . По формуле Лагранжа (1) получаем:
°° 1 / dn~' \
z = g(w) = a + '£~, w". ►
„ = 1 \ / z=a
304 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
6. Разложить по степеням w функцию eb9<w) (Ъ # 0), где функция z = д(ы) является обратной
функции w = zeaz (а # 0).
◄ Здесь z0 = w0 = 0, /(z) = ze~az, /'(0) # 0, F(z) — ebz. Согласно формуле (2) имеем
еь9<«) = 1 + у 1 /= j +bX^ (Ь+-а.^---------------------------w".
п! \ dz"”1 v ' п!
п=1 4 ' z=° п=|
Радиус сходимости полученного степенного ряда находим по формуле Коши—Адамара:
R=----------^= =-------------
Щп л/ |Ь+°Т~- lim |ь+°-п|' " -#= е|“'
V n! _ n vn!
п—+оо * п—>ос
Полагая Ь = а, находим:
. z p(w)
F(^) = e = —(Fo^(w) =-------------.
/(z) w
Итак,
g(w) ixV n(n+l)n ' n
w ' n!
n—1
ff(w) = w + yy wn+l = у an (n+D-1 wn+1 k
4—' n! 4—< n!
n=l n=0
7. Пусть функция <p аналитическая в замкнутом круге Кт = {z 6 С : |z - z0| г} и не
обращается в нем в нуль. Доказать, что Vw 6 {w g С : |w — w0| < тг}, где М = max |w(z)|
1 ’ г£8Кг
уравнение z — zo = (w — w0)^(z) имеет одно и только одно решение, принадлежащее кругу Кг.
◄ Запишем уравнение в виде w = w0 + yfy-. Функция z и-» /(z) = w0 + аналитическая
в круге Кт, f’(z) / 0 и /(z0) = w0. Согласно рассмотренному выше случаю а), уравнение
w = /(z) Vw g {w g C : |w - w0| < , j, = min|/(z) - w0|, имеет единственное решение
g(w), принадлежащее кругу Кт. По формуле Лагранжа (1) его можно представить суммой ряда
___ । — 1 \
g(w) = z0 + V — ( ——-j- (<p(z))n I (w-wo)n. ►
2—nl \ dzn~l J
n=l 4 7 z~-z<*
§ 3. Экстремальные свойства
модуля аналитической функции
3. 1. Принцип максимума модуля аналитической функции.
Теорема 1 (первая формулировка принципа максимума модуля). Если функ-
ция f аналитическая в области D и ее модуль |/| достигает локального максимума в некоторой
точке z0 g D, то f = const в области D.
◄ Применим метод доказательства от противного. Пусть f const и /(z0) = w0. Пусть, далее,
D-^D*. Тогда w0 € D* и D* является областью. Следовательно, существует круг Ки = {w g С :
|w — w0| < р} С D*, и в нем, очевидно, найдется такая точка wt, что |wj > |w0|. Тогда в не-
которой окрестности точки z0 найдется такая точка z,, что /(z,) = иц и |/(z,)| > |/(z0)|. Это
неравенство противоречит тому, что |/(z0)| является локальным максимумом функции /. Источ-
ник противоречия — в предположении, что f const. Следовательно, Vz g D f(z) = const. ►
§ 3. Экстремальные свойства модуля аналитической функции
305
Следствие (вторая формулировка принципа максимума модуля). Если функ-
ция f аналитическая в области D и непрерывна в замыкании D, то |/| достигает максимума
только на границе 9D области D.
Ч Справедливость утверждения следует из первой формулировки и свойств функций, непре-
рывных на компакте. ►
Утверждение, аналогичное теореме 1, для минимума модуля |/| несправедливо. Пусть, на-
пример, /(z) = z, Df = К = {z € С : \z\ < 1}. Функция f аналитическая и / const, однако
минимум |/(z)| = 0 достигается во внутренней точке области Df z = 0. Здесь, видимо, дело
состоит в том, что функция f обращается в нуль в области аналитичности. Поэтому справедливо
следующее утверждение.
Теорема 2. Если f G A(D) и Vz G D f(z) / 0, то |/| может достигать в D локального
минимума лишь в том случае, когда f = const.
< Для доказательства достаточно применить теорему 1 к функции g = |, аналитической в D,
так как Vz G £> f(z) / 0. ►
3. 2. Лемма Шварца.
Следующее утверждение принадлежит Шварцу.
Лемма (Шварца). Пусть функция f аналитическая в круге К = {z G С : \z\ < 1} и
удовлетворяет в нем условиям /(0) = 0, |/(z)| 1. Тогда Vz G К выполняются неравенства
l/И |z|, |/'(0)| 1. (1)
При этом, если выполняется равенство |/,(0)| = 1 или равенство |/(z)| — |z| хотя бы в одной
точке z # 0, moVz Е К |/(z)| = |z|, т. е. функция f будет иметь вид
f(z) = e’“z, а € R.
Ч Рассмотрим функцию z <p(z) = . Из условия /(0) = 0 следует, что <р G А(К)
и у>(0) = /'(0) (устранимую особую точку считаем устраненной). Исследуем функцию <р в кру-
ге Кр = {z € С : |z| < р}, где р < 1. По принципу максимума модуля |у>| достигает максимума
на кривой = {z е С : |z| = р}. Поскольку Vz 6 К |/(z)| 1, то Vz G 7Р |p(z)| = j.
Следовательно, Vz G Кр |y?(z)| si Зафиксировав точку z 6 К и устремив р к единице, получим
неравенство |p(z)| 1 или |/(z)| |z|. Очевидно, что в качестве z можно взять любую точку
из круга К. Пусть, в частности, z = 0. Тогда |^(0)| = |/'(0)| 1. Предположим теперь, что
в некоторой точке za G К выполняется равенство |^(z0)| = 1. Это означает, что |р| достигает
максимума в точке z0. Следовательно, по теореме 1 tp = const и, так как |уз(г)| = 1, z € К,
то <p(z) = e'az, agR. ►
Лемма Шварца имеет простой геометрический смысл. Она утверждает, что при отображении
с помощью функции w = J(z) любая точка z G К или приближается к началу координат, или
отображение представляет собой вращение вокруг начала координат. Другими словами, образ
любой окружности 7r = {z G С : |z| = г} либо лежит внутри круга K'r = {w € С : |w| < г}, либо
совпадает с его границей.
Лемма Шварца имеет много обобщений. Выделим простейшее из них. Если точка z = 0
является нулем функции f кратности А, то, рассмотрев функцию z получим неравенства
|/(z)| < |z|A Vz G К и
/<А,(0)
< 1,
причем равенства в них возможны лишь в случае, когда /(z) = e‘AzA.
Рассмотрим задачи.
8. Доказать, что если P(z) — многочлен степени п, то линии уровня его модуля |P(z)| = R
(лемнискаты) могут распасться не более чем на п связных компонент.
◄ Любая связная компонента представляет собой границу некоторой области D и модуль ана-
литической в ней функции Р на ее границе постоянный. Отсюда, согласно принципу максимума
модуля, в D найдется хотя бы одна точка z, в которой P(z) = 0. В противном случае P(z) = const
в D. ►
306
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
9. Если функция / const аналитическая в круге KR = {z g С : |z| < R}, то функция
М(г) = sup |/(z)| строго возрастает на интервале (0, R).
Н=г
4 Утверждение является прямым следствием из принципа максимума модуля. ►
10. Доказать, что если функция / const аналитическая в области D = {z € С : |z| >7?},
имеет конечный предел при |z| —► оо, а |/| — непрерывная функция в D, то |/| достигает
максимума на окружности 7д = {z € С : |z| = Л}, а функция М(г) = sup |/(z)| строго убывает
|z|=r
на интервале (R, +оо).
◄ Функция ( <£(() = / (1) аналитическая в круге K\/R = {( € С : |£| < (устра-
нимую особую точку С = 0 считаем устраненной) и ее модуль непрерывен в замкнутом круге
Ki/R. Согласно принципу максимума, |<р| достигает максимума на окружности dK\/R, а |/| —
на окружности yR. Из задачи 9 следует, что sup |у>(0| строго возрастает на интервале (0, -g).
1С1=₽
Следовательно, М(г) = sup |/(z)| строго убывает на интервале (R, +оо). ►
|z|=r
11. Пусть P(z) = z" + сцг”-1 + ... + а„. Доказать, что если P(z) z”, то хотя бы в одной
точке окружности 7 = {z g С : |z| = 1} выполняется неравенство |P(z)| >1.
Ч Функция z~2_P(z) удовлетворяет условиям задачи 10 и, следовательно, ее модуль дости-
гает максимума в D = {z £ С : |z| 1} на окружности 7 = {z € С : |z| = 1}. Пусть
М = max lz~nP(z)l <( 1. Тогда, согласно утверждению задачи 10, либо |z-7lP(z)| = 1,
|z|=l
т.е. P(z) = zn, либо \z~nP(z)| < 1 Vz g D = {z g C : |z| > 1}. Последнее неравенство
невозможно. ►
12. Пусть P(z) — многочлен степени п, a M(r) = max |P(z)|. Доказать, что при 0 < г, < г2
|z| = r
выполняется неравенство
М(Г|) > М(г2)
гГ " Г2 ’
причем знак равенства хотя бы для одной пары значений г, и г2 возможен только для многочлена
вида P(z) = az”.
◄ Функция z аналитическая в области D = {z g С : |z| > 0} и, таким образом,
удовлетворяет условиям задачи 10 при любом R > 0. ►
13. Пусть P(z) — многочлен степени п, для которого на отрезке [-1, 1] справедлива оцен-
ка |P(z)| sC М. Доказать, что в любой точке z, лежащей вне этого отрезка, выполняется неравен-
ство |P(z)| М(а + 6)", где а и 6 — полуоси эллипса, с фокусами в точках -1, 1, проходящего
через точку z.
◄ Функция w >-» <p(w) = w~nP (|(w 4- w~')) аналитическая на множестве D = {w € С :
|w| 1}. Поскольку образом окружности 7 = {w € С : |w| = 1} при отображении z = |(w + w-1)
является отрезок [—1, 1], то, принимая во внимание условия задачи, получаем, что
Vw € 7 l¥>(w)| С М.
Согласно решению задачи 10, последнее неравенство справедливо и при |w| 1:
Vw € D
С M|w|".
Пусть za — любая точка, не принадлежащая отрезку [—1, 1] и a, Ъ — полуоси эллипса с фокусами
в точках ±1, который проходит через точку zn. Его образом при отображении w = z + — 1
(w(oo) — 00) является окружность 7' — {w 6 С : |w| — а + 6}. Окончательно имеем
|Р(2о)1 =
М|w0|n = М(а + 6)". ►
§ 3. Экстремальные свойства модуля аналитической функции
307
14. Пусть функция f — аналитическая в правой полуплоскости G = {z € С | Rez 0},
при Rez = 0 удовлетворяет неравенству |/(z)| М и обращается в нуль в точках zb z2, ... , zn
(Rezj. > 0; к = 1, n). Доказать неравенство
I// м ~zli|z -Z2| ... |z —zn|
l/(*)l Af ---- -7 (Re z > 0).
|z + z,| |z + z2| ... |z + z„|
◄ Функция z I-» ^^(z) = устанавливает конформный изоморфизм полуплоскости
G' = {z g C | Rez > 0} и единичного круга К = {w g С : |w| < 1}, т.е. \<fik(гг/)| = 1 и <Pk(.Zk) = 0.
Таким образом, функция F, где F(z) = f(z) (jj , является аналитической в полуплос-
кости G’ (ее устранимые особые точки zk (к = 1, п) считаем устраненными) и |F(iy)| М,
следовательно, согласно принципу максимума модуля, |F(z)| Vz g G.t.е.
|/(z)|^Af JJ|^(z)| VzgG'. ►
fc=l
15. Пусть функция f аналитическая в круге KR = {z € С : |z| R} и |/(z)| М. Доказать,
что Vz g KR = {z g С : |z| < Л}
f(z) - /(0)
M2 - 7(0)/(z)
И
RM ’
◄ Функция f >-+ y>(0 = аналитическая в круге К = g С : |0 1} и |р(0| 1.
Принимая во внимание общий вид автоморфизма единичного круга (формула (5), п. 1.3, гл. 3),
устанавливаем, что функция
/ ~ у(0)
1 - р(О)р(0
удовлетворяет условиям леммы Шварца и, таким образом,
у(0 - у(0)
1 - ^(0)^(0
10 при |<| 1.
Полагая здесь £ = и принимая во внимание, что (jj) = , получаем требуемое неравен-
ство. ►
16. Пусть / g А(К), К = {z g С : |z| 1} и Vz g К |/(z)| М. Доказать, что
М|/(0)| 5= М2 - |/(0)|2.
◄ Функция z >-> F(z) = удовлетворяет условиям леммы Шварца, следователь-
но, |F'(0)| 1. В равенстве
»Ж = ^(м2_Ш))
перейдем к пределу при z —> 0. Получим:
М/'(0) = Р'(0)(М2-|/(0)Р).
Отсюда, принимая во внимание неравенство |F'(0)| 1, получим доказываемое неравенство. ►
17. Доказать, что если Q(z) — многочлен степени п и при z = х g [—1, 1] выполняется
неравенство |xQ(a;)| < М, то Vz g К = {z g С : |z| < 1} |Q(z)| M(1 + \/2)n+l.
◄ Пусть P(z) = zQ(z), E — эллипс с полуосями a = V2, b = 1 и фокусами =F1- Тогда
(см. задачу 13) Vz g E выполняется неравенство
|P(z)| «:м(1 + х/2)п+1.
Применив лемму Шварца к функции z >-> > получим оценку
|P(z)| = |z(?(z)| М(1 + ^)n+1|z|. ►
308 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
§ 4. Принцип компактности.
Функционалы
на семействах аналитических функций
4.1. Равномерно ограниченные и равностепенно непрерывные семейства функций.
С равномерной непрерывностью функции f свяжем новое понятие — равностепенную не-
прерывность семейства. Это понятие появляется в результате следующих рассуждений.
Функцию f : С -+ С можно одновременно рассматривать и как функцию / : R2 —» С, если
считать z = х + iy = (х, у). Пусть Z = Df, Z,, Z2 — первая и вторая проекции множества Z,
а /[(г), Z2(y) — его сечения посредством х и у (см. п. 1.7, гл. 1). Поставим в соответствие
функции f два семейства функций из R в С:
(/|,х)жЕД|5 (fl, у )у Е Z2 1
где
Df.:, = Zi(x), Df2v=Z2(y-),
fi.xty') = f(x, y)Vy € -Zi(z), Л,у(ж) = f(x, y) Vx e Z2(y). (I)
Обычно говорят, что функция /1>а. получается из f фиксированием первой переменной х,
а функция /2у — фиксированием второй переменной у. Из определений следует, что если
функция / : С-» С равномерно непрерывная, то все функции семейств (Д iks.?,; (f2,y)yez2
равномерно непрерывные. Это свойство проще формулируют следующим образом: равномерная
непрерывность функции по совокупности переменных влечет за собой равномерную непрерыв-
ность по каждой из них в отдельности. Однако существуют разрывные по совокупности перемен-
ных функции, равномерно непрерывные по каждой из них в отдельности, о чем свидетельствуют
следующие примеры.
Пример 1. Пусть
{ху
х2 + у2’
0,
если |г| 1, |у| 1 и х2 + у1 # 0,
если х2 + у2 = 0.
Тогда Z = [-1, I]2, Zi = Z2 = Zi(x) = Z2(y) = [-1, 1] V(x e [—1, 1], у € [-1, 1]). Если x # 0,
то функция Д х является рациональной на сегменте [-1, 1]. По теореме Кантора она равномер-
но непрерывная. Этим же свойством обладает и функция Ду Vy 6 [-1, 1] \ {0}. Если х = 0
или у = 0, то функции До и До равны нулю и являются равномерно непрерывными. Таким
образом, функция f равномерно непрерывна по каждой переменной в отдельности. По совокуп-
ности переменных функция f : С —► С является разрывной в нулевой точке. Действительно,
следовательно, множество Ef(0) частичных пределов функции f в нулевой точке содержит более
одного элемента и lim /(z) не существует.
х—*0
Пример 2. Рассмотрим произвольную функцию /, заданную на единичной окружности
7 = {z € С:|z| = 1}.
Тогда Г, = Г2 = [-1, 1], ГДх) = {-УГ^?, vT^?}, Г2(у) = {-^/f-yi, у/1-y2}.
Множество ГДж) при каждом значении х 6 Г! содержит не более двух точек. Этим же свой-
ством обладает множество Г2(у) Vy 6 Г2. Поэтому семейства функций (Дх) и (Д у) состоят из
равномерно непрерывных функций. Поскольку функция f — произвольная, то она может быть
разрывной в каждой точке окружности 7.
Поиски условий, налагаемых на семейства (/i1I)a:gz1 и (Ду),,е.г2, обеспечивающих равно-
мерную непрерывность функции f по совокупности переменных, приводят к понятию равносте-
пенной непрерывности.
§ 4. Принцип компактности. Функционалы на семействах аналитических функций 309
Определение 1. Пусть ЭЛ —множество функций f : С —+ С. Оно называется равностепенно
непрерывным, если Ve > 0 > 0:
v(/ е ЭЛ, z € Df, z" е D}) (|z' - z"\|/(z') - f(z")| < г.
Если А — множество, то семейство функций (fa)aeA считается равностепенно непрерывным
в случае, когда множество ЭЛ = {fa | а € А} — равностепенно непрерывное. В частности,
можно говорить о равностепенной непрерывности последовательности (/„) функций /„ : С -+ С.
Термин “равностепенная непрерывность” связан с тем, что 6 в определении выбирается лишь по е
и может быть использовано для обоснования свойства, требуемого в определении равномерной
непрерывности любой функции / € ПЛ.
Определение 2. Множество ЭЛ функций f : С —> С, заданных в некоторой области D, назы-
вается равномерно ограниченным внутри D, если для любого компакта К D существует
такая постоянная М = М(К), что € ЭЛ, z € К) |/(z)| М.
Семейство функций (/„)с, gx считается равномерно ограниченным внутри D в случае, когда
множество ЭЛ={/а | a g А} является равномерно ограниченным внутри D.
Определение 3. Множество W функций f : С —> С, заданных в области D, называется равно-
степенно непрерывным внутри D, если Ve > 0 « для любого компакта К <s D Э<5 = 6(е, К) :
V(/ (Е ЭЛ, z' £ К, z” 6 К) (Iz’ - z"\ < б) =>\f(z’) - f(z")\ < е.
Семейство функций считается равностепенно непрерывным внутри области D, если
таковым является множество ЭЛ = {/„ | а 6 А}.
Теорема. Если множество ЭЛ функций / : С —» С, аналитических в области D, равномерно
ограничено внутри D, то оно равностепенно непрерывное внутри D.
◄ Пусть К D. Обозначим через 2р расстояние между множествами К и dD, т.е.
2р = _inf p(z, 0.
= ел', сеэо
Очевидно, что р > 0, так как К и dD — замкнутые непересекающиеся множества. Рассмотрим
множество
К{р} = (J {z € С : \z - z0| < р},
которое иногда называют р-раздутием множества К. Очевидно, что D к, следовательно,
существует такая постоянная М(К(р)), что V(z € f € ЭЛ) |/(z)| М. Пусть z и z" — две
любые точки из К, для которых \z' - z"| < р. Поскольку Кр = {z g С : \z — z'\ < р} С К(р),
то Vz € Кр выполняется неравенство |/(z) - /(z')| 2М. Функция ( = i(z - z') отображает
круг Кр на единичный круг Кх = {( € С : |£| < 1}. Рассмотрим функцию
s(O = -pO-f(z')), geAdKt), 5(0) = о, Ш1 < 1.
Она удовлетворяет условиям леммы Шварца, согласно которой
Vf G Ki |5(0| < ICI,
ИЛИ
4т|/<г'-Х)-7(г')| <ICI, < = -(z-z'), |/(z)-/(z')| < — \z-z'\ VzeKp.
zM ' ' p p
Выберем 6 = min [p, }. Тогда V/ g ЭЛ |/(z") - f(z’)\ < s. ►
4.2. Принцип компактности.
Определение. Множество ЭЛ функций / : С —* С, заданных в области D, называется ком-
пактным в D, если из каждой последовательности (/„) этого множества можно выделить под-
последовательность (fnk), равномерно сходящуюся на любом компакте К <s. D.
Теорема (признак компактности Монтеля). Если множество ПЛ функций, аналити-
ческих в области D, равномерно ограничено внутри D, то оно компактное в D.
◄ 1) Докажем сначала, что если последовательность (/„) сходится в каждой точке некоторого
множества Е С D, всюду плотного в D, то она сходится равномерно на каждом компакте К <i= D
310
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
(напомним, что множество Zo С Z называется всюду плотным в множестве Z, если каждый
элемент z € Z является точкой прикосновения множества Zo). Пусть е > 0 и К <g D. По
теореме п. 4.1 множество функций ОТ равностепенно непрерывное внутри области D, в силу чего
область D можно с помощью прямых, параллельных осям координат, разбить на столь мелкие
квадраты, что V(z' g К, z" € К), принадлежащих одному и тому же квадрату, а также V/ € ОТ
будет выполняться неравенство
|/(z')-/(z")| < |. (1)
Множество К покрывается конечным числом таких квадратов. Пусть их количество равно р.
Поскольку множество Е всюду плотное в области D, то в каждом упомянутом выше квадрате
найдется точка zk (fc = 1, р). Так как последовательность функций (/п) сходится на множестве Е,
то существует такое пе 6 N, что V(m > пЕ, п > пе, к = 1, р) выполняется неравенство
(2)
Пусть z € К — любая точка, принадлежащая fc -му квадрату, в котором зафиксирована точ-
ка zk g Е. При т > пе, п > п„ имеем
|/m(z) - 7n(z)| |/m(z) - fm(zk) | + \fm (zk) - /„(zfc)| + | fn(zk) - /„(z)| < | + ^ + | = £ .
в силу неравенств (1) и (2). Таким образом,
ll/m - /nil = sup l/m(z) - /n(z)l e V(m > ne, n > nJ,
z^K
t. e. последовательность (/n) равномерно фундаментальная на множестве К и /п =4.
2) Теперь докажем, что из любой последовательности (/„) функций из множества ОТ можно
выделить подпоследовательность (fnk), сходящуюся в каждой точке некоторого множества Е,
всюду плотного в области D. В качестве Е выберем множество точек z из К, у которых
действительная и мнимая части рациональные, Е = {zk, fc g N}. Рассмотрим последователь-
ность (/„(zi)). Так как она ограничена, то по теореме Больцано—Вейерштрасса из нее можно вы-
делить сходящуюся подпоследовательность (/nt(Z|)). Пусть f„k(z} = fki(z) и рассмотрим после-
довательность (/ы(г2)). Она также ограничена и из нее можно выделить сходящуюся подпоследо-
вательность (/„ti(z2)). Пусть f„ki = fkl. Из последовательности (/b2(z3)) можно извлечь сходя-
щуюся подпоследовательность (/„t2(z3)) и т.д. Аналогичное построение можно продолжить не-
ограниченно. При этом получим последовательность последовательностей (Ai(z)), (/k2(z)), ....
Выберем теперь диагональную последовательность /n(z), /22(z), .... Очевидно, она сходится в
любой точке множества Е. Действительно, если взять любую точку zp € Е, то все члены после-
довательности (/„„(z)), начиная с /pp(z), выбраны из последовательности (fnp), сходящейся в
точке zp.
Поскольку 2) => 1), то принцип компактности доказан. ►
4.3. Функционалы, определенные на множествах функций.
Определение 1. Пусть ЗЕ — множество функций f : С —» С, определенных в области D.
Отображение ОТ —» С называется функционалом.
По определению каждой функции / g ОТ ставится в соответствие комплексное число 1(f).
Определение 2. Функционал I называется непрерывным на элементе f0 g ОТ, если для любой
последовательности (/„) функций из множества ОТ, равномерно сходящейся к функции f0 на любом
компакте К <е D, выполняется равенство
lim I(fn) = Г(/о).
п—*оо
Пусть, например, ОТ — множество всех функций, аналитических в области D, 1(f) = ^Рр>!<°-,
а g D — фиксированная точка. Докажем непрерывность этого функционала. Пусть последова-
тельность (fn) функций из множества ОТ сходится равномерно к функции /0 на любом компак-
те К <ё D. По теореме Вейерштрасса fo € A(D). Пусть К = 7, = {z € С : \z - а| = г} С D.
§ 4. Принцип компактности. Функционалы на семействах аналитических функций
311
Тогда Vs > 0 Зп£ 6 N : V(n n£, z € 7Г) |/„(z) - /o(z)l < £ Применим неравенство Коши для
коэффициентов степенного ряда (см. формулу (6), п. 1.7, гл. 5):
|ЛА)-К7о)| = |Л/п-/о)| <
Это и означает непрерывность функционала I.
Определение 3. Компактное множество функций ЯЛ называется компактным в себе, если
предел любой последовательности (/„) функций из ЭЛ, равномерно сходящейся на любом компак-
те К <s D, принадлежит множеству ЯЛ.
Таким образом, множество ЯЛ функций f : С -+ С называется компактным в себе, если из
любой последовательности (/„) функций из ЯЛ можно выделить подпоследовательность (/пь),
равномерно сходящуюся на любом компакте К <ё D к некоторой функции из ЯЛ.
Примером компактного в себе множества функций является множество аналитических в обла-
сти D функций, равномерно ограниченных в D.
Теорема. Если функционал I непрерывный на компактном в себе множестве ЭЛ функций
f : С —> С, то его модуль |Т(/)| достигает своей точной верхней грани, т.е. существует такая
функция f0 G ЯЛ, что V/ G ЯЛ |Т(/)| |Т(/о)|.
◄ Пусть а = sup |Т(/)|, (еп) —бесконечно малая последовательность положительных чисел,
/еал
По свойству точной верхней грани Vn G N 3/п € ЯЛ:
а - е„ < |Д/„)| а,
откуда lim |Т(/„)| = а. Таким образом, существует последовательность (/п) функций из множе-
ства ЯЛ : lim |Г(/П)| = а.
Поскольку множество ЯЛ компактное в себе, то существует подпоследовательность (fnk),
равномерно сходящаяся на любом множестве К (s D к некоторой функции /0 € ЯЛ. В силу
непрерывности функционала I, lim |T(/nt)l = 1Д/о)1 = а. Отсюда следует, что а < оо и V/ G ЯЛ
1Д/)1 1Л/о)|. ►
4.4. Теорема Гурвица.
Следующее утверждение принадлежит А. Гурвицу (1859—1919).
Теорема (Гурвица). Пусть последовательность (/„) функций, аналитических в области D,
равномерно сходится к функции f const на любом компакте К <ё D. Тогда, если f(za) = 0, z0 G D,
то в любом круге КТ = {z G С : \z — z0| < г} С D все функции fn, начиная с некоторой, также
обращаются в нуль.
Ч По теореме Вейерштрасса f 6 А(£>). Так как f 0, то существует проколотая окрестность
точки z0 Op(z0) = {z € С | 0 < \z - z0| < p} C D, в которой f / 0 (нули аналитических функций
изолированы).
Пусть р = min |/(z)|, р > 0, где 7„ = {z € С : \z - z0| = р}. В силу того, что f„ f в
области D, существует np € N: V(n nM, z g 7Р) |/n(z) - /(z)| < д и Vz G 7Р /„ = / + (/„ - /).
По теореме Руше число нулей у функций f и /п внутри одинаково, но f имеет по меньшей
мере один нуль, следовательно, все функции /п при п пм также имеют нули внутри ~[р. ►
Следствие. Если последовательность функций (/„), аналитических и однолистных в обла-
сти D, сходится равномерно на любом компакте К <s D, то предельная функция либо однолистна,
либо постоянна.
Ч Пусть lim /„ = f и f const. Допустим, что существуют две различные точки z{ G D,
z2 е D и /(zi) = /(z2). Рассмотрим последовательность функций (дп), где gn(z) = fn(z) — fn(z2)
и круг Kr = {z 6 С : \z — zi\ < г}, г С \zi — z2|. Имеем
lim <Z„(z) = /(z) - f(z2) = g(z), g{zi) = 0.
n—»00
Отсюда, согласно теореме Гурвица, получаем, что все функции дп, начиная с некоторой, также
обращаются в нуль в круге КТ. Это противоречит свойству однолистности функций . ►
312 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
§ 5. Существование и единственность
конформного отображения
5.1. Конформные изоморфизмы и автоморфизмы.
Конформное отображение f области Dt на П2 назовем конформным изоморфизмом D\ на jD2.
а области Dt и D2 — конформно-изоморфными. Конформный изоморфизм области на себя на-
зывается конформным автоморфизмом. Совокупность автоморфизмов произвольной области D
образует группу, которая называется группой автоморфизмов этой области и обозначается симво-
лом A(D). В качестве групповой операции берут композицию (р2 ° pt)(z) = ?2(^i(z))> единицей
является тождественное отображение е : z —► z, а обратным элементом к р является обратное
отображение z = p~x(w).
Замечание. Слово “конформный” в выражении “конформный изоморфизм (автоморфизм)” часто будем
для простоты опускать.
Теорема. Если D\ D2 — какой-нибудь фиксированный изоморфизм, то совокупность всех
на
изоморфизмов Dt на D-. определяется формулой
f = V°fo,
где р — произвольный автоморфизм области D2.
◄ 1) Очевидно, что V^ € Л(Р2) композиция р о /0 является изоморфизмом Dt на D2.
2) Пусть f — любой изоморфизм Dt на D2. Рассмотрим композицию р = f о f~x. Очевидно,
что р € Л(Р2), f = ро f0. >
5.2. Примеры автоморфизмов.
1) D = С. Пусть р — любой автоморфизм С. Тогда существует единственная точка z0 6 С,
такая, что p(z0) = оо. Поэтому функция z к-» p(z), аналитическая на множестве С \ {зп}, в
точке z0 имеет полюс первого порядка (полюса выше первого порядка не может быть, поскольку
функция р должна быть однолистной). Поэтому по теореме Лиувилля имеем
А
p(z) =-----1- В.
Z - г0
при z0 ф оо и p(z} — Az + В при Zq = оо. Таким образом, совокупность всех дробно-линейных
отображений образует группу автоморфизмов С.
2) D = С. Рассуждая аналогично, получим, что группу Л(С) образует все множество целых
линейных функций p(z) = Az + В.
3) D = К = {z е С : \z\ < 1}. Пусть р — произвольный автоморфизм единичного круга К и
пусть у?(0) = ш0. Построим дробно-линейный автоморфизм А круга К:
w — w0
A(w) = -—=—, A(w0) = 0.
1 - wow
Рассмотрим композицию f = Хор. Очевидно, |/(z)[ < 1 Vz € К, /(0) = 0. Следовательно, f
удовлетворяет условиям леммы Шварца и Vz € К
|/(z)| < |z|. (1)
Рассмотрим обратное отображение /-1(w) = z. Оно также удовлетворяет условиям леммы Швар-
ца и, таким образом, |/-1(w)| С |w|, или
|z| < |/(Z)| Vz 6 А”. (2)
Из (1) и (2) получаем равенство |/(z)| = |z|, т.е. /(z) = e’“z — простейшая линейная функция,
а р = A-1 of — дробно-линейная функция. Следовательно, любой автоморфизм круга К является
дробно-линейным и, таким образом, имеет вид (формула (5), п. 1.3, гл. 3):
z — g, dw
w = е'а----|а| < 1, а 6 R, а = arg —
1 — az az
z=a
§ 5. Существование и единственность конформного отображения
313
(3)
Получили, что автоморфизм единичного круга К зависит от трех действительных параметров:
двух координат точки а и а.
Покажем теперь, что, подбирая эти параметры, можно найти один и только один автомор-
физм А € Л(7С), удовлетворяющий следующим условиям нормировки:
А(а) = b, argA'(a) = a,
где а и Ь — любые фиксированные точки из К, а а — любое действительное число.
Действительно, построим два автоморфизма круга К
z — a w — Ъ
< = p(z) = е ----С = i/(w) = ------=-
1 — za 1 — bw
и рассмотрим автоморфизм А = и-1 ° р. Имеем
А(а) = Ъ, X'(z) = \ arg А1 (а) = arg//(а) — argi/(b) = а - 0 = а.
v (.0
Таким образом, мы построили автоморфизм единичного круга А = р-1 о р, удовлетворяющего
условиям (3). Рассмотрим композицию
f = v о А[ о р-1,
где А] — другой автоморфизм круга К, удовлетворяющий тем же условиям. Очевидно, /(0) = 0,
arg/'(О) = argр'(д) + argAj(a) — argp'(a) = 0 + a- a = 0. Следовательно, A|(0) = 0, argA,(0) = 0
и по лемме Шварца f = e — тождественное отображение, т. e.
e = v ° A[ о p-1 => A1 = и-1 ° p = A.
5.3. Существование и единственность изоморфизмов областей,
изоморфных единичному кругу.
Отметим следующее: поскольку группа автоморфизмов единичного круга зависит от трех дей-
ствительных параметров, то и группа автоморфизмов любой области D, изоморфной единичному
кругу, также зависит от трех действительных параметров.
Следующая теорема устанавливает существование и единственность изоморфизмов областей,
изоморфных единичному кругу.
Теорема. Если области D, и D2 изоморфны единичному кругу К, то совокупность изомор-
физмов Dt на D2 зависит от трех действительных параметров. В частности, существует одно и
только одно отображение Di -^->D2, нормированное условиями
на
/(z0) = w0, arg/'(z0) = 6, (1)
где z0 € Di, € D2 — произвольные точки, в g R — произвольное число.
◄ Пусть £>[ -^+ К, D2 К. Тогда отображение f0 = /Г1 о Л является конформным изо-
на на
морфизмом D, на D2. По теореме п.5.1 совокупность всех отображений П, на В2 определяется
формулой
f =V ° /о,
где <р — произвольный автоморфизм области В2. Поскольку группа Л(Р2) автоморфизмов обла-
сти D2 зависит от трех действительных параметров, то и совокупность конформных отображе-
ний Dy на D2 также зависит от трех действительных параметров. Таким образом, первая часть
теоремы доказана.
Пусть
/i(z0) = a, arg/[(z0) = 0i, A(w0) = Ь, arg f2(wa) = 02, (2)
a A — автоморфизм единичного круга К с нормировкой
А(а) = b, argA'(a) = 0 + 02 — 0!, (3)
(такой автоморфизм, как мы уже знаем, определяется единственным образом).
Рассмотрим следующий изоморфизм на D2:
f = f2' °Xofi.
314 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Ймеем
/(z0) = w0, arg/'(z0) = -arg/2(w0) + argA'(a) + arg/i'(z0) = -02 + 0 + 02 - 0i + 0| = 0.
Таким образом, доказано, что существует изоморфизм на D2, удовлетворяющий условиям
нормировки (1). Теперь докажем единственность такого изоморфизма.
Пусть существует изоморфизм Di —► D2, удовлетворяющий условиям (1). Тогда
на
= € Л(Дг), ^(wo) = wo, aigy>'(w0) = arg/'(z0) - aigp'(z0) - 0.
Рассмотрим автоморфизм единичного круга К д = /2 ° V ° /2-1 - Имеем
ц(Ъ) = b, arg//(b) = argy>'(w0) + arg/2(w0) - arg/2(w0) = 0.
Отсюда следует, что /г = е и, следовательно, р = е, т. е. / о д~' = е, или д = f. ►
5.4. Теорема существования.
Теперь естественно возникает вопрос: какие области конформно изоморфные единичному
кругу, а значит и конформно изоморфны друг другу? Ответ на поставленный вопрос содержится
в следующей теореме.
Теорема (Римана). Любая односвязная область, граница которой содержит более одной тон-,
ки, конформно изоморфна единичному кругу AT = {zgC:|z|<l}.
Замечание 1. Ограничение, наложенное на границу области, существенное. Расширенную комплексную
плоскость нельзя конформно отобразить на круг, плоскость С даже не гомеоморфна кругу К (сфера
не гомеоморфна кругу). Если взять С с выколотой точкой, то можно дробно-линейно отобразить ее
на С, но С отобразить конформно на круг К нельзя. Действительно, если бы отображающая функция
существовала, то она была бы целой и ограниченной по модулю единицей, а такая функция по теореме
Лиувилля тождественно равна постоянной.
Замечание 2. Если граница односвязной области содержит более одной точки, то она обязательно будет
содержать бесконечное множество точек, поскольку она связная.
◄ 1) Покажем, что в области D существует по крайней мере одна аналитическая однолистная
функция, ограниченная по модулю единицей. Пусть а € dD, b € 9D и а / Ь. Рассмотрим
полную аналитическую функцию z i-> ip(z) = , допускающую выделение в области D двух
однозначных ветвей z >-» y?i(z) и z i-+ ^2(z), так как Vz 6 D / { X • ® каждой точке z 6 D их
значения отличаются знаком. Покажем, что каждая из этих функций однолистна в D. Допустим,
что это не так. Пусть = <Pk(z2) (fc = 1, 2). Тогда <pl(zt) = <pl(z2), что эквивалентно
равенству
Zi - a z2~ а
-----= -------. (1)
Z| - b z2 — b
Отсюда, в силу однолистности дробно-линейной функции, получаем равенство Zi = z2.
Пусть D Pi, D D2. Покажем, что Р> и D2 не имеют общих точек. Предполо-
на на
жим, что Di и D2 имеют общие точки. Это означает, что в D имеется пара точек z, и z2 ,
для которых <pi(zi) = <p2(z2). Из этого равенства следует (1), а из (1) — равенство z2 = z\,
т.е. <pi(z!) = tp2(,Zi). Принимая во внимание, что 9?i(zi) = -<p2(zt), получаем равенства - 0
(fc = 1, 2), которые невозможны, т. к. Vz € Р ‘fik(x) # 0.
Пусть круг Кр = {w € С : |w — w0| < р} С D2 такой, что функция не принимает значений
в этом круге, т.е. Vz € Dx |y?i(z) - w0| p. Поэтому функция z i-» g(z) = U;_W(), очевидно,
аналитическая и однолистная в Р и Vz 6 Р |j(z)| Sj 1.
2) Пусть ЯН — множество всех аналитических и однолистных в области Р функций, огра-
ниченных по модулю единицей. Оно непустое, поскольку g € ЯП. Согласно принципу ком-
пактности, это множество компактное в Р. Пусть а — некоторая фиксированная точка обла-
сти Р. Обозначим через ЯН| часть множества ЯН, состоящую из всех функций f € ЯП, для
которых |/'(а)| |</(а)| > 0 (последнее неравенство является следствием однолистности функ-
ции д). Покажем, что множество компактное в себе. Пусть последовательность (/„) функций
§ 6. Соответствие границ и принцип симметрии при конформном отображении
315
из множества ЭЯ! равномерно сходится на любом компакте К <s D и lim fn = f0. Поскольку
П—’ОС
Vn € N |g'(a)|, to |/o(a)| |g'(a)|. Кроме того, согласно следствию из теоремы Гурвица,
либо /о — const, либо /о однолистна в D. Случай /0 = const исключается в связи с последним
неравенством. Следовательно, /0 Е Э311-
Рассмотрим на множестве функций ЭЯ! функционал !(/) = Поскольку он непрерывен
на компактном в себе семействе функций ЭЯ, (см. §4), то его модуль достигает своей точной
верхней грани, т.е. существует такая функция h € ЭЯ1, что V/ € 9Я| выполняется неравенство
|/'(a)| < |h'(a)|.
Рассуждая от противного, покажем, что Л(а) = 0. Действительно, при Л(а) / 0 функция
z H(z) =
h(z) - h(a)
1 - h(a)h(z)
и
Я <а>1 ~ <а)1’
1 - |Л(а)|2
что противоречит экстремальному свойству функции h.
3) Покажем, что D-^K. Допустим, что это не так. Пусть h(z) не принимает в D некоторого
значения b € К. Поскольку h(a) = 0, то Ь / 0. Очевидно, что функция h не принимает в D также
и значения Ь* = |, так как |Ь*| > 1. Тогда можно выделить в D однозначную ветвь
Обозначим ее через ф(г). Очевидно, функция V>(z), как и функция
Ф(г) =
1 - ф(а)ф(г)
принадлежит множеству ЭЯ. Непосредственным подсчетом находим:
h'(z)(l-|b|2) V’Wl-k'(a)!2)
ф (z) = ---------2------2’ Ф = ------------------г-
2^(г)(1 - bh(z)) (l-V’(a)V'(z))
Отсюда
Ф (а) = ——
1 - IV>(a)l2
h'(a)(l-|b|2) ч, |h'(a)| (1 + |b|) ,
= —=--------—, Ф (а)| =------------—------ > \h (a)|.
2vzzb(l-|b|) 2v/ib|
Следовательно, Ф € ЭЯ, и > |h'(a)|.
Последнее неравенство противоречит экстремальному свойству функции h. ►
Следствие. Любые две односвязные области, границы которых содержат более чем по одной
точке, конформно изоморфны друг другу.
§ 6. Соответствие границ и принцип симметрии
при конформном отображении
6.1. Теорема о соответствии границ.
В теореме Римана ничего не сказано о соответствии границ при конформном отображении, о
поведении отображающей функции на границе области. Ответ на затронутые вопросы содержится
в следующем утверждении.
Теорема (Каратеодори). Если границы областей D и D' являются кривыми Жордана, то
конформное отображение D -?-> D’ можно продолжить на границу области D до гомеоморфизма
на
замыканий D и D .
Доказательства теоремы здесь не приводим. Заметим только, что условия, налагаемые на гра-
ницы областей, существенны. Можно показать на примерах, что утверждение теоремы становится
неверным, когда границы областей не являются жордановыми.
316 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Установлено также несколько более точных результатов о граничном поведении конформного
отображения с жордановыми границами при дополнительных предположениях об этих кривых.
Укажем два из них1’.
1) Результат Шварца. Если границы областей D и D' — аналитические жордановы кривые,
то конформное отображение D —> D' продолжается до аналитической функции в D.
2) Результат Линделёфа. Если границы областей D и D' являются гладкими жордановыми
кривыми, a f осуществляет конформное отображение D наб', то arg/'(z) продолжается до не-
прерывной функции в D, причем € dD arg/'(0 = 6’ — 0, где 9 и О' — углы наклона касательных
к кривым 9D и 9D' в точках ( и /(0 соответственно.
В случае конформного отображения областей, ограниченных кривыми Жордана, условия
единственности отображения можно определить по соответствию трех пар граничных точек. А
именно, пусть а, Ъ, с — три произвольные точки границы 9D, а!, Ь', с — три произвольные
точки границы 9D', которые устанавливают одинаковые направления их обходов относительно
областей D и D'. Тогда существует такой изоморфизм D D', для которого выполняются
на
условия:
/(а) = а', f(b) = Ь', f(c) = c. (1)
Действительно, пусть D -^+ К, D' К, К = {z € С : |z| < 1}. По теореме о соответствии
границ fi осуществляет гомеоморфизм замыканий D и К, а /2 — гомеоморфизм замыканий D
и К. Пусть
71(a) = а, /i(b) = /3, /[(с) =7, /2(а') = а', /2(Ь') = Д', /2(с') = 7'.
Существует, и притом единственный, автоморфизм единичного круга К А : К —» К, удовлетво-
ряющий условиям
А(а) = а', А(Д) = Д', Л(7) = 7'.
Очевидно, что отображение / = /2-1 о А о /, является конформным изоморфизмом D на D',
удовлетворяющим условиям (1). Пусть теперь кроме / существует еще изоморфизм D D’,
на
удовлетворяющий условиям (1):
д(.а) = а', д(Ь) = b', д(с) = с.
Очевидно, что <р = / о д~1 является автоморфизмом области Р2, удовлетворяющим условиям:
р(а) = а , у’(Ь') = Ь1, у’(с') = с .
Рассмотрим следующий автоморфизм единичного круга К:
М = /2°<ро/2-1,
удовлетворяющего условиям
ц{а) = а, = р', = у
и, таким образом, являющегося тождественным отображением е. Из вида отображения р следует,
что и <р = е, т. е. д = /.
6.2. Принцип симметрии.
Следующая теорема устанавливает применение принципа симметрии Римана—Шварца ана-
литического продолжения функций к конформным отображениям.
Р Читателя, интересующегося поведением конформного отображения на границе области, отсылаем к книгам: Карате-
одори К. Конформное отображение. — ГТТИ, 1934; Гмузин Г.М. Геометрическая теория функций комплексного
переменного, М.—Л., 1967.
§ 6. Соответствие границ и принцип симметрии при конформном отображении
317
Теорема. Пусть и В2 — две области с жордановыми границами, причем дВ\ содержит дугу
окружности у], a дВ2 — дугу окружности ~f2. Пусть, далее, D1 и D2 — области, симметричные В{
и В2 относительно и у2 соответственно. Тогда, если функция f конформно отображает Dt
на В2 и 7! ~^+72> то она допускает аналитическое продолжение в В' и продолженная функция
конформно отображает область D| U 7| U В* на область В2 U 72 U В2. Предполагается, что
Di П В* =0, В2 П В2 =0.
Ч He ограничивая общности можем считать, что 7t
и 72 — отрезки действительной оси, a Bi и В2 — обла-
сти, лежащие в верхней полуплоскости (рис. 91). Этого
всегда можно добиться с помощью дробно-линейного ото-
бражения. Пусть D\ В2. По теореме о соответствии
на
границ функция f будет непрерывной в замыкании В L и
устанавливает гомеоморфизм В\ на В2. При этом, в силу
условий теоремы, f непрерывна на 7 и принимает на 7
действительные значения. Согласно принципу симметрии
Римана—Шварца функция / аналитически продолжается
в В* по закону f(z) = f(z), а это и означает, что про-
долженная функция конформно отображает Di U 71 U В,
на В2 U 72 U В2. ►
Рассмотрим задачи.
18. Построить конформное отображение области В,
} (к = 0, п — 1) (рис. 92) на
представляющей собой внешность единичного круга с
разрезами по отрезкам 7r={zGC|1^|z|^ a, argz =
внешность единичного круга.
Ч Согласно принципу симметрии, задача сводится к построению конформного отображения
области Gt = {z € С| 1 < \z\ < 00, 0 < argz < (рис. 93) на себя так, чтобы лучи Го =
{z € С : |z| a, argz = 0} и Г( = [z € С : |z| a, argz = ~ } переходили соответственно в
лучи Го = {z € С : |z| 1, argz = 0} и Г( = {z € С : |z| 1, argz = ^}. Это отображение
находим как композицию следующих отображений:
2. 1 / _1Ч W2
Wt = z 2 , w2 = - («Ц + Wj ), -----5-,
2 j(a2+a'2)
w4 = w3 + y/wj — 1,
Отображающая функция имеет вид:
2
w = w".
318 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Очевидно, что функция w1 отображает сектор на верхнюю полуплоскость с выброшенным полу-
кругом, ш2 (функция Жуковского) отображает верхнюю полуплоскость с выброшенным полукру-
гом на верхнюю полуплоскость, причем точки At и А2 переходят в точки -t-oTT ). Функ-
ция w3 отображает верхнюю полуплоскость на верхнюю полуплоскость, а точки ±| (аТ + оГ 2 )
переходят в точки ±1. Функция w4 (обратное отображение функции Жуковского) отобража-
ет верхнюю полуплоскость на верхнюю полуплоскость с выброшенным единичным полукругом.
Функция w отображает верхнюю полуплоскость с выброшенным единичным полукругом на сек-
тор G|. ►
19. Отобразить на верхнюю полуплоскость внешность правой ветви гиперболы
cos2 a sin2 а
Ч Согласно принципу симметрии задача сводится к построению конформного отображения
верхней половины заданной области на первый квадрант, при котором луч (-оо, cos а) перехо-
дит в положительную мнимую полуось. Это отображение находим как композицию следующих
отображений:
у----- ТГ
иц = z + yz2 — 1, ui2 = ,
1
w3=-
Множитель роли не играет, поскольку преобразование w' = kw при к > 0 отображает
верхнюю полуплоскость на себя. ►
§ 7. Конформное отображение многоугольников.
Интеграл Кристоффеля—Шварца
7.1. Отображение верхней полуплоскости на многоугольник.
Пусть требуется отобразить верхнюю полуплоскость z-плоскости на внутренность некоторо-
го многоугольника М <ё С, лежащего в плоскости w (рис.94). По теореме Римана отображаю-
щая функция существует и по теореме о соответствии границ, когда границы рассматриваемых
§7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца 319
областей жордановы кривые, устанавливает гомеоморфизм замкнутых областей. Вершинам мно-
гоугольника Аь А2, ... , Ап будут соответствовать точки «ц, а2, , ап действительной оси. Не
ограничивая общности, можно считать, что Vfc = 1, п ак € С (в противном случае следует приме-
нить такой автоморфизм верхней полуплоскости, чтобы бесконечность переходила не в вершину
многоугольника).
Рис. 94
Пусть w = f(z') — искомая отображающая функция. Отрезок [аь а2] она переводит в отре-
зок [А], А2]. Следовательно, по принципу симметрии она продолжается в нижнюю полуплоскость
через [а1; а2], и это продолжение будет устанавливать отображение нижней полуплоскости на
многоугольник, симметричный данному относительно прямой, проходящей через точки Ai и А;.
Аналогично можно построить аналитические продолжения и через другие отрезки [<ц, а^+|]. Та-
ким образом, полная аналитическая функция, определяемая /, не будет иметь особых точек в
нижней полуплоскости и во всех точках действительной оси, за исключением, быть может, мно-
жества {ак; к = 1, п}. Следовательно, ак (к = 1, п) — возможные особые точки продолженной
функции / как полной аналитической функции.
Величины внутренних углов многоугольника обозначим соответственно через а|7г, а2тг, ...,
а„7г. Имеем
тг
= П - 2, 0 < ак < 2.
fc—I
Рассмотрим f(z) в верхней полуокрестности точки ak. Функция (ее ветвь фиксируется)
1 . (3k
z >-<• u(z) = (f(z) - Ак) ак е
переводит полуокрестность точки ак в полуокрестность начала координат, причем граничный от-
резок действительной оси также переходит в граничный отрезок действительной оси (см. рис. 95).
Рис. 95
Следовательно, w(z) по принципу симметрии аналитически продолжается в полную окрестность
точки ак, и это продолжение отображает окрестность точки ак в окрестность начала координат
320 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
взаимно однозначно. Таким образом, ш — аналитическая функция в точке ак и ы'(ак) # 0.
Представим ее в окрестности точки ак рядом Тейлора:
ui(z) = (e~il3(f(z) - Ак)) = Cr(z - ак) + C2(z - ак)2 + ... = (z - аМ),
Щак) = Ci = ы'(ак) ф 0, e",/3(/(z) - Ак) = (z - afc)afc(f2(z))ai: = (z - ak)tp(z),
где 9?(z) — однозначная ветвь функции (Q(z))“t. Далее,
f(z) = Ак +(z~ak)ak<pi(z), tf>i(ak)^O,
/'(2) = ak(z - ak)c‘k~lif>i(z) + (z - ak)ak /j(z) = (z - ak)ak(aktpi(z) + (z - aJfe)y?'1(z)) = (z - afc)“t-1$(z),
Ф(аь)#0,
/"(z) = (afc - 1) (z - aj“^-4(z) + (z - ak)ak~l<S>'(z),
f"(z) _ (z-afc)at- ~2((afc -l)$(z) + (z-afc)$'(z)) _ - 1)ф(г) + (z - at)$'(z) _ ak - 1 Ф'(г)
/'(z) (z - ак)ак-'Ф(г) (z-ak)$(z) z - ak + Ф(г) '
Из полученного следует, что точка ак является полюсом функции -у? с вычетом ак - 1.
II п
Рассмотрим функцию z $(z) = . Это — целая функция и lim Ф(г) = 0.
k=i г z~°°
Действительно, разложение функции f в окрестности бесконечности имеет вид
/(z) = а + У7
с,
Z'
и тогда
f"(z)
/'(2)
0
при z —» 00.
Кроме того, очевидно, что У7 -----> 0 при
к=1
По теореме Лиувилля Ф = 0. Таким образом,
z —► 00.
/"(-?) _ vp at ~ 1
/'(г) “ z - ak
K = l
d
= 7" 1П/ (2),
n n n
ln/'(z) = ^(ak - l)ln(z - ak) 4-lnG = InC, JJ(z - акГк~\ f\z) = G JJ(z - ak)ak~
k=l fc=l fc=l
/(2) = G J
+ C2.
(1)
Равенство (1) называется формулой Кристоффеля—Шварца, а интеграл в ее правой части —
интегралом Кристоффеля—Шварца.
Посмотрим, как изменится вид формулы Кристоффеля—Шварца, если прообраз одной из
вершин многоугольника, например, вершины 4„, равен бесконечности. С этой целью строим
следующий автоморфизм верхней полуплоскости плоскости z:
1 1
Z| =----—, z - а„----.
an~z Z|
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца
321
Тогда получим:
<1п-----) = /1(*|) =
•И /
О *=>
'd<+C2 = C, к ^-+с2
1 4=1 1
(в интеграле произведена замена ( = ап — d~). После очевидных несложных преобразований под
знаком интеграла , имеем
А п-1
= Сх I J J (Ci(an — ak) ~ 1)
d(i + С2 —
О к~1
+ с’2 = с’х [ П(С, - dG + С2. (2)
о fc=‘
Здесь а’к = — образы точек ак в плоскости zi.
В процессе получения формулы (2) множитель
исчез в связи с тем, что
*: = !
Полагая в предпоследнем интеграле формулы (2) нижний предел интегрирования равным нулю,
а не мы изменяем лишь постоянную С2. Заменив обозначения zx на z и /ДгО на f(z),
получим формулу
}{^) = Сх l'Y[(C-ak)^-ldC + C2.
Интегралы в формулах (1) и (3) называются соответственно интегралами Кристоффеля—
71
Шварца первого и второго рода. Разница между ними очевидна: в обоих случаях ^ак = п - 2,
fc=i
(3)
хотя в формуле (3) множитель (( - под знаком интеграла отсутствует.
Формулы (1) и (3) получены в предположении, что точки ак известны. Однако в задачах на
конформные отображения задают лишь вершины Ак многоугольника, а точки ак остаются неиз-
вестными. Согласно п.6.1 три из них можно задать произвольно, а остальные ак вместе с С, и С;
должны определятся из условий задачи. Это обстоятельство является главным затруднением при
практическом использовании формулы Кристоффеля—Шварца. Существуют различные методы
их определения. Постоянная С2 определяется заданием размещения одной из вершин много-
угольника. Для определения постоянных ак и можно иногда воспользоваться известными
длинами сторон многоугольника
|/'(ж)| dx (fc = 1, п— 1),
однако на практике осуществить это удается не всегда. Существуют также приближенные методы
определения постоянных ак и Ct.
322
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
7.2. Случай многоугольника, имеющего вершины в бесконечности.
Пусть вершина Ак n-угольника лежит в бесконечной точке (рис. 96). Возьмем на лучах
и АкАк+1 произвольно по точке А'к, Ак, и соединим их отрезком прямой. В результате
получим (п + 1)-угольник. Функция, отображающая верхнюю полуплоскость на этот многоуголь-
ник, имеет вид
Z
f{z) = Cv Уа,)"'"1 ...«-<)<-*«••• (C-a„)Q"-'d( + C2, (1)
О
где а'ктг и акк — значения углов при вершинах А\. и А"., а а'к и ак — точки оси Ох, соответ-
ствующие этим вершинам.
Пусть отрезок А'кАк удаляется в бесконечность, оставаясь параллельным самому себе. При
этом точки ак и а'к сливаются в одну точку ак, соответствующую вершине Ак. Обозначим че-
рез -ak" значение угла пересечения лу-
чей 4*. _ [4^ и 4j.+14fc в конечной точке
4J. Тогда из треугольника АкАкАк имеем
a'j. + a'j'-aj, = 1, т.е. а'к + ак -2 = ак -1 и
формула (1) принимает обычный вид фор-
мулы (1), п.7.1.
Ясно, что эти рассуждения можно про-
вести и в случае, когда в бесконечности ле-
жит несколько вершин многоугольника.
Таким образом, формула (1), п.7.1,
остается в силе и для многоугольников, у
которых одна или несколько вершин лежат
в бесконечности, если при этом угол между
двумя прямыми с вершиной в бесконечно-
сти определяется как угол в конечной точ-
ке их пересечения, взятый со знаком ми-
нус.
Заметим, что при таком определении
угла в бесконечности остается в силе соот-
ношение
п
= п - 2
fc=l
для суммы углов многоугольника.
Рис. 96
7.3. Отображение верхней полуплоскости на внешность многоугольника.
Проводим рассуждения, аналогичные проделанным в п. 7.1. Функция / имеет теперь в неко-
торой точке а верхней полуплоскости полюс первого порядка. Функция же р- наряду с простыми
полюсами {afc; k = 1, п} будет иметь еще простые полюсы в точках а, а с вычетами в них, рав-
ными -2. Таким образом,
/"(г) _ у- % ~ 1 _ 2 _ 2 ,j.
f'(z) z - ak z — a z — a
fc=l
Отсюда
z
™ = C, / П« - + C, <2>
0 fc=1
n
Здесь аьтг — значения внешних углов многоугольника, ак = n+2, ak — точки действительной
оси, соответствующие его вершинам.
§7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца
323
7.4. Отображение верхней полуплоскости на прямоугольник.
Отобразим верхнюю полуплоскость на прямоугольник Р с вершинами в точках ±w, ±w + гш,
(рис. 97). Применим принцип симметрии. Пусть функция f отображает первый квадрант на
правую половину прямоугольника Р так, что мнимая полуось переходит в отрезок [0, ги? । ] мнимой
оси. Зададим соответствие трех пар граничных точек:
Z 0 1 оо
W 0 (Jj
Этим соответствием отображающая функция определяется единственным образом. Некоторая
точка { > 1 (fc < 1) перейдет в вершину ш + гш, прямоугольника, к — неизвестно. По принципу
симметрии функция / продолжается во второй квадрант и продолженная функция (обозначим
ее также f) осуществляет отображение верхней полуплоскости на весь прямоугольник. При этом
имеем
/(-l) = -w, / (-|) = -ш + го?!.
Вид функции f определяется формулой Кристоффеля—Шварца. Получим:
= | (*=1,4), {afc; * = 1,4} = -1, 1,1
2 к k
w = f(z) = С f == (1)
J x/d - С2)(1 - Л2С2)
о
Фиксируем ветвь корня УТ = 1. Тогда, принимая во внимание, что /'(z)| = С, получаем,
что С > 0, так как положительное направление действительной оси при отображении не изме-
няется.
Полученная формула содержит два неизвестных параметра С и fc.
Рассмотрим функцию
z^F(z,k) = [ .... dC (2)
J х/(1 - С2)(1 - *2С2)
о
где 0 < fc < 1 считается известным. Она определяется эллиптическим интегралом первого рода, fc —
его модуль. Из предыдущего изложения ясно, что F(z, к) осуществляет конформное отображение
324
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
верхней полуплоскости на прямоугольник со сторонами 2ш0 и ш'а, где
= = К(к)
J ^/(i-c2)(i-fc2c2)
о
— полный эллиптический интеграл первого рода с модулем к,
1 1
к к
, . , f dC , . f
J x/d - C2)(l - fc2C2) J VK2- D(i-fcV)
Следовательно,
X
к
, f dC
J у«2 - 1)(1 - fc2O
Заменив в интеграле переменную по формуле
1 — fcfr2
получим:
1
, Г dr
4,= / ::== =K(fcl).
У д/(1 - т2)(1 - fcjr2)
Итак, мы получили, что эллиптический интеграл первого рода отображает верхнюю полуплос-
кость на прямоугольник со сторонами 2К(к) и K'(fc'l).
Вернемся к нашему случаю:
/(г) = С f —=JL==,
J х/(1 - <2) (1 - fc2<2)
о
к, С — неизвестные стороны прямоугольника, 2ш и ш' — известны.
На основании только что рассмотренного имеем
ш = СК(к), ш' = СК(к').
Эти равенства являются системой трансцендентных уравнений относительно С и к. Она может
быть решена с использованием таблиц эллиптических интегралов первого рода. Действительно,
пусть
_ ш _ К(к)
Т ~ К(к')
Тогда по заданным т по таблицам можно найти К (к), а затем и С — тгтт,-
1\ \К)
7.5. Эллиптический синус и его двоякая периодичность.
Как установлено выше, эллиптический интеграл первого рода z = F(w, fc) осуществляет кон-
формное отображение верхней полуплоскости G+ = {w g С | Im w > 0} на прямоугольник Ро с
вершинами ±К, ±К + iKt, при этом в вершины прямоугольника переходят точки ±1 и ± | дей-
ствительной оси. Обращение эллиптического интеграла первого рода называется эллиптическим
синусом, его обозначение: w = sn(z, fc). Эллиптический синус является аналитической функцией
в прямоугольнике Ро и отображает его на верхнюю полуплоскость G+ = {w € С | Im w > 0}. В
силу гомеоморфизма замкнутых областей, функция sn переводит отрезок [К, К + i-K)] в отре-
зок [1, . Следовательно, к ней применим принцип симметрии, по которому она аналитичес-
ки продолжается в прямоугольник Рь симметричный с Ро относительно отрезка [К, К + iKi],
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца
325
причем продолженная функция (мы снова обозначим ее через sn) отображает Pi на нижнюю
полуплоскость G_ = {ш 6 С | Im w < 0} (рис. 98). Продолженная функция также удовлетворяет
условию принципа симметрии и по этому принципу аналитически продолжается в прямоуголь-
ник Р2, симметричный с Pi относительно отрезка [ЗК, ЗК + iK\ ] и отображает его снова на
верхнюю полуплоскость. При этом
sn(z + 4К) = sn z Wz € PQ.
(1)
Более подробно: точка zi, симметричная с z относительно отрезка [7f, К + гЛ)], переходит в
точку snz, а точка z2 = z + 4К. симметричная z{ относительно отрезка [ЗК, ЗК + г'К|], — снова
в точку sn z.
Точно так же можем продолжить функцию snz в прямоугольник Р{, симметричный с Ро
относительно отрезка [—К + iKit К + iKi], только это продолжение будет иметь в точке iKt
полюс первого порядка. Продолженная функция sn отображает Р{ на нижнюю полуплоскость
и аналитически продолжается в прямоугольник Р2, симметричный с Р[ относительно отрез-
ка [—К+i2Ki, K+i2Kt], и этот прямоугольник она снова отображает на верхнюю полуплоскость.
Как и выше, получим, что
sn(z + 2iKi) = snz Vz g Ро- (2)
Рассуждая в точности так же и далее, мы можем продолжить эллиптический синус на всю
плоскость С. Продолженная функция будет мероморфной: в точках iKi + 4Кт + 2iK{n, где т
и п — любые целые числа, она имеет полюсы первого порядка. Формулы (1) и (2), очевидно,
будут выполняться для любых точек z € С. Это свидетельствует о том, что функция sn имеет два
независимых периода = 4 К и Т2 = 2iKt: для любых целых тип справедливо соотношение
sn(z + 4Кт + 2iKtn) = snz. (3)
Мероморфная двоякопериодическая функция, отношение периодов которой является строго
комплексным числом (не действительным), называется эллиптической функцией. Проведенные
исследования показывают, что sn z является эллиптической функцией.
Равенство (3) свидетельствует также о том, что функция sn z инвариантна относительно груп-
пы линейных преобразований вида
z >-» z + 4Кт + 2iKtn (т € Z, п £ Z).
Функции, обладающие свойством инвариантности относительно некоторой группы дробно-ли-
нейных преобразований, называются автоморфными'^.
Для автоморфных функций существует отдельная хорошо разработанная теория, с которой можно ознакомиться, напри-
мер, по книге: Л. Р. форд. Автоморфные функции, ОНТИ, 1936.
326
Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
7.6. Отображение единичного круга на многоугольник.
Найдем общий вид функции, осуществляющей конформное отображение единичного круга
на многоугольник. Для этого отобразим единичный круг на верхнюю полуплоскость, а затем
воспользуемся формулой (1), п. 7.1.
Отображение верхней полуплоскости G+ = {z g С | Im z > 0} на круг К = {zt € С : IzJ < 1}
имеет вид
z — b
Z\ =----=, Im 6 > 0.
z — 6
откуда находим отображение К на G+:
(1)
bzi — b
z —--------.
Z! - 1
Подставив в формулу (1), п. 7.1, вместо z правую часть равенства (2), получим:
5z । —ь
(2)
Полагая в интеграле £ =
(bzi — b\
=/1(г1) = С1
Zi — 1 у
, находим:
1 dC + С2.
о fc=1
b
Ь
d<i
(Ci -1)2
УП((Ь-<1ОС1-(Ь
Ь
ъ
— Як
fc=i
dCi
(Cl - I)2
Поскольку
П(с> - D1'
fc=l_________
(Cl - I)2
= (г, -1)
(так как п - — 2 = 0), то
k=i
fi(zl) = Cl f H((b-afc)Ci-(b-afc))
{ fc=l
5
dCi + Ci —
= 1
d(l + c2 = c{ (Cl -4)“l-'dCi + G,
ь K=‘
5
(3)
5
где а'к — точки единичной окружности, в которые переходят точки ак.
Если в интеграле, входящем в формулу (3), изменить нижний предел интегрирования, полагая
его равным нулю, то изменится лишь постоянная С2, а общий вид формулы останется прежним:
/i(^i) = с{ f JJ(Ci - 4)“
о *='
dCi + С2.
(4)
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца
327
Заменяя z( на z, а'к — на ак, fl — на /, получим общий вид функции, осуществляющей
конформное отображение круга К = {z € С : |z| < 1} на многоугольник :
Z п
f(z) = Ct + |afc| = 1. (5)
о
Для отображения единичного круга на многоугольник общий вид формулы Кристоффеля—Швар-
ца не изменился.
В качестве примера рассмотрим отображение единичного круга на правильный многоуголь-
ник. Считаем, что центр многоугольника находится в точке w = 0. Этого всегда можно добиться
линейным преобразованием заданного многоугольника. При построении отображения восполь-
зуемся принципом симметрии.
Пусть
. 2(fe - 1)7Г __
Ак = А{е « (Л — 2, п).
Обозначим через / функцию, осуществляющую конформное отображение сектора единичного
круга S = {z g С : |z| < 1, 0 < argz < на треугольник OAtA2 (рис.99) при условиях:
/(0) = 0, Д1) = Д1( /(е^)=Д2.
Г 21L1 f
Очевидно, что 10. е* [0, Л2]. Согласно принципу симметрии, функция f аналити-
чески продолжается в сектор S' = {z 6 С : |z| < 1, ~ < argz < , причем ее продолжение
(которое также обозначим через /) отображает его на треугольник ОА2А2. Рассуждая анало-
гично, продолжим / на весь единичный круг. Продолжение функции / будет аналитической
функцией в единичном круге К = {z £ С : |z| < 1}, осуществляя конформное отображение его
/ 2(fc—1)тг К __ . 2(fe — 1)тг
на весь многоугольник, причем f I е' п ) = Ак (к = 1, п), т. е. точки е’ п = ак являют-
п
ся прообразами вершин многоугольника. Поскольку = па = п - 2, то ак = а = 1 — и
k-i
П(С — = (£п — 1) n f в силу того, что ак являются корнями n-й степени из единицы и
/г = 1
По формуле (5) получаем:
Z
/(z) = C [(l-C)’"dC
О
328 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Определим константу С из условия
1
/(1) = су(1-Г)-" <*с = л„
О
откуда
jd-o-ndc
о
1 1-1
Полагая в интеграле (п = t, получим: d( = ~tn dt,
1 i
(l-C)-"d(=- [ l-£),
n J n
о о
где В — бета-функция Эйлера. Окончательно имеем
(l-f)~"<K
О
Замечание. Поворотом плоскости z на угол а вокруг начала координат можно добиться того, что про-
образом вершины А] будет любая заданная точка ега единичной окружности.
Из формулы (2), п. 7.3 с помощью дополнительного дробно-линейного изоморфизма плоско-
сти z легко получаем формулу отображения внутренности единичного круга на внешность мно-
гоугольника
7(2) = Ciyf[«-a)t)“fc-1^ + C2. (6)
о fc=1
Здесь предполагается, что центр круга переходит в бесконечно удаленную точку.
Рассмотрим задачи.
nA,
w = /<г) = „zi .
20. Отобразить верхнюю полуплоскость G+ = {z G С | Imz > 0} на ромб в w-плоскости с
углом тга при вершине А и стороной d (рис. 100). Соответствие точек задано схемой
ш(А = 0, В = d, С = d(l + е*’"), D = de™a) -* z(0, 1, oo, -1).
Обосновать возможность такого отображения.
◄ Пусть функция w = f(z) осуществляет конформное отображение первого квадранта на
треугольник АВС. При этом
/(0) = А, /(1) = В, /(оо) = С.
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца 329
Согласно свойству соответствия границ, прообразом стороны АС будет мнимая полуось z = iy
(у > 0). По принципу симметрии функция f аналитически продолжается на всю верхнюю по-
луплоскость и это продолжение осуществляет конформное отображение верхней полуплоскости
на ромб. При этом /(-1) = D. По формуле (3), п. 7.1, имеем
Z
о
Постоянную с находим из условия
i
/(1) = d = су Г-1(1 - <2)”“ = | В (f, 1 - а) ,
о
откуда с = —J Окончательно получаем:
Z
т=в(Л пх [ r-'d-C2)-“dC.>
В (у, 1 - a) J
о
21. Найти конформное отображение верхней полуплоскости G+ = {zgC|Imz>0}Ha
область, содержащую первый квадрант, граница которой состоит из полупрямых 71 = {w g С |
Rew sj 0, Imw =1}, 72 = {w g С | Rew 0, Imw = —1}, а также из отрезка [—г, г]. Соответ-
ствие точек задано схемой
w(z, —г, оо) -+ z(— 1, 1, 00).
◄ Согласно формуле (3), п.7.1, при = —1, а2 = 1, а3 = 00, = |, а2 = j имеем
22. Найти конформное отображение верхней полуплоскости G+ = {z g С | Imz > 0}
на верхнюю полуплоскость D+ = {w g С | Imw > 0} с разрезом вдоль луча 7 = {w g С |
Rew 0, Imw = я}.
Ч Область в плоскости w является треугольником с двумя вершинами Аь А3 на бесконеч-
ности (рис. 101) и углами: 077г, a2v, a3v, где
07 =0, а2 = 2, а3 = —1.
Полагаем а{ = 0, а2 = —1, а3 = оо. По формуле Кристоффеля—Шварца получаем:
Z
w = f(z) = С\ J£-1(1 + C)dC + гтг = Ci(z + 1 + Inz — iv) + гтг. (1)
330 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Для определения С, воспользуемся тем, что при обходе точкой z полуокружности = {z g С :
|z| — г, 0 < argz < тг} по часовой стрелке функция w, определенная равенством (1), получает
приращение —гттС\ + О(г). С другой стороны, при этом обходе соответствующая точка w перехо-
дит с луча А|Л2 на луч А|.43. Следовательно, приращение функции Дш мало отличается от -гтг.
Таким образом, С| = 1. Окончательно имеем
w = /(z) = z + 1 -f- Inz. ►
23. Найти конформное отображение верхней полуплоскости G+ = {z € С | Im z > 0} на tv —
плоскость с разрезами вдоль лучей 71 = {w € С | Re w < 0, Imw = -тг} и 72 = {w 6С [ Rew < 0,
Im w = тг} (рис. 102), при котором точки z = ЯР 1 переходят соответственно в точки w = ±тгг.
◄ Введем в рассмотрение вспомогательную ( -плоскость. Функция w = <^(() = ( + 1 + 1п(
отображает верхнюю полуплоскость плоскости ( на верхнюю половину области в w-плоскости
(см. предыдущую задачу). При этом действительная положительная полуось 7 = {( € С |
Re( > 0, Im( = 0} переходит в действительную ось w-плоскости. По принципу симметрии
функция ( ь-» аналитически продолжается через эту полуось в нижнюю полуплоскость и это
продолжение конформно отображает (-плоскость с разрезом по отрицательной действительной
полуоси на всю заданную в w-плоскости область. Отобразив (-плоскость на верхнюю полуплос-
кость G+, окончательно получим:
w = —z2 + 1 + 2Inz — гтг. ►
24. Найти образ верхней полуплоскости G+ = {z G С | Im z > 0} при отображении
w = /(z) = f-------------= (0 < а < Ь).
а
Найти расстояние между параллельными полупрямыми для каждой из пар, составляющих границу
области.
< По виду функции / заключаем, что искомая область является четырехугольником с двумя
вершинами на бесконечности: СЦ = 0, ац = 0, At = 00; а2 = а, аг = Аг = 0; а3 = Ь, а3 = 0,
Аз = оо; а4 = оо, а4 = |, А4 — требуется найти.
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца
331
Исследуем поведение производной f'(z) на интервале (а2, а3). Имеем
/'(г) = ~i---J < 0 е аз)’
z(z — о) \/z — а
т.е. arg /'(г) = тг и образом интервала (а2, а3) является отрицательная действительная полуось.
Принимая во внимание, что а2 = j, образом интервала (а15 а2) будет отрицательная мнимая
полуось. Теперь очевидно, что вершина А4 принадлежит третьему квадранту, а сама область
имеет вид, изображенный на рис. 103.
Чтобы найти hi, рассмотрим приращение функции Дш при обходе точкой z полуокружности
7г = {z С С | z = ге'*1, 0 < < тг}:
dC тг
—>=- + О(г) = -—+ О(г),
tby/aQ Ьу/а
Гг = (7г, 7гР).
Следовательно, ht = . Аналогично находим h2, определяя приращение функции w при обходе
точкой z полуокружности с центром в точке Ь:
При b = 2а, ht = h2. ►
25. Найти конформное отображение круга К = {z £ С : \z\ < 1} на внутренность п-конеч-
ной звезды — 2п-угольника, стороны которого, а также углы (через один), равны.
◄ Пусть тупой угол звезды равен тг( 1 + А), тогда ее острый угол равен тг (1 —А - . Ис-
пользуя принцип симметрии, считаем, что прообразы вершин острых углов являются корнями
n-й степени из единицы, а прообразы вершин тупых углов — корнями n-й степени из -1. По
формуле Кристоффеля—Шварца получаем:
w = f(z) = С
(1+Г)А dC
(1-Г)Л+"’
2
0 < А < 1 — —.
п
о
Принимая во внимание, что /(1) = Alt находим С. ►
26. Найти вид функции, осуществляющей конформное отображение внешности единичного
круга на внешность произвольного n-угольника с внешними углами а*.тг.
◄ Требуемую функцию получим с помощью формулы (5), п. 7.6, заменой z — d-, отобража-
ющей единичный круг на его внешность:
332 Гл. 8. Некоторые общие вопросы геометрической теории аналитических функций
Заменив переменную интегрирования, полагая £ = и приняв во внимание равенство
= п + 2,
к=1
преобразуем полученную формулу к виду
Г "
w = = + С2. ► (1)
)t=i
г0
27. Найти конформное отображение внешности круга К К1 = {z £ С : |z| > 1}на внешнюю
.2тг(А:-1) ____
часть правильного n-угольника с вершинами в точках Ак = е* п (к = 1, п), которые остаются
неподвижными при этом отображении.
◄ Отображающая функция определяется формулой (1) предыдущей задачи при ак = 1 +
ак = Ак, С2 = 1, z0 = 1, a определяется из равенства At = ft(At):
2 тгг тгг
, е п — 1 е п 2г sin - п sin -
С =-----------------=--------------------=-----------------. ►
1 ЦГА 2тт 2’2
-inм
1 о
Упражнения для самостоятельной работы
1. Доказать, что при А > 1 уравнение zeA-z = 1 имеет в круге К = {z 6 С : |z| 1} лишь
один и притом действительный корень.
2. Сколько корней имеет в круге К — {z £ С : |z| < 1} уравнение ez - 4zn + 1 = 0 (n £ N)?
3. Доказать, что уравнение ez = azn (п £ N) при а > е имеет в круге К = {z £ С : |z| < 1}
п корней.
4. Сколько корней имеет в круге K' = {z£C:|z|<l} уравнение
zn + aoz2 + ajz + а2 = О,
если |a0| > |ai| + |а2| + 1 (n £ N)?
5. Доказать, что уравнение z4 + az + b = 0 (а > О, b > 0) имеет в первом квадранте один и
только один корень, и его аргумент больше .
6. Доказать, что уравнение (z—l)ez — z—2 не имеет решений с отрицательной действительной
частью.
7. Доказать, что уравнение P(z) = Ь, где F(z) = , |aj.| < 2 Vfc = 1, n и |b| < 2~n
k = l
имеет в круге К = {z £ С : |z| < 2} п корней.
8. Разложйть в ряд по степеням w функцию z = д(ш), определенную уравнением w =
e~oz(ez - 1), а € N и условием д(0) — 0. Найти радиус R сходимости полученного степенного
ряда.
9. Доказать, что внутри области, ограниченной линией уровня модуля функции f (т. е. лини-
ей, во всех точках которой |/(z)| = const) и компактно принадлежащей области аналитичности /,
найдется хотя бы один нуль этой функции (/ ^ const).
10. Доказать, что когда P(z) — многочлен степени п и |P(z)| М Vz € К = {z £ С : |z| 1},
то Vz € К' = {z € С : |z| > 1} |P(z)| sC M\z\n.
11. Пусть P(z) — многочлен степени n, Ei, E2 — два софокусных эллипса с полуосями аь Ь|
и а2, Ь2 (в! < а2, bi < b2) и пусть, далее, Mi = max |P(z)|, М2 = max |P(z)|. Доказать, что
Ml Мг
(<Х[+Ь|)” (а2+Ь2)" •
Упражнения для самостоятельной работы
333
12. Пусть функция / аналитическая в круге KR = {z € С : |z| < R}, удовлетворяет
при \z\ = R неравенству |/(z)| С М и обращается в нуль в точках zit z2, ... , zn этого кру-
га. Доказать неравенство
!/(*)! м П ггап (Н<Л)-
13. Пусть функция f аналитическая в круге Кк = {z G С : |z| < Я} и удовлетворяет Vz G KR
неравенству |/(z)| С М, а /(0) = 0. Доказать, что |/'(0)| С , причем знак равенства возможен
только для функции
/(z) = Me’V5, pCR.
п
14. Пусть -оо < в! < а2 < ... < ап < +оо, 0 < ак < 1 (к = 1, n), 57 = п - 2. Доказать,
4=1
что любая ветвь функции
z^7(z) = /n«-“4)“fc-1^
О 4=1
в полуплоскости G+ = {z G С | Imz > 0} однолистная в этой полуплоскости и конформно
отображает ее на конечный выпуклый п -угольник.
15. Найти область, на которую функция
(1+С")Л rfC
+Л ’
z н-» w(z) = J
о
ы'(0) >0, -1 < А < 1 - |
отображает единичный круг К = {z G С : \z | < 1}.
16. Отобразить верхнюю полуплоскость на область, указанную на рис. 104 (дуга АС — полу-
окружность) при заданном соответствии точек
w(A = аг, В = оо, С = 0) —* z(0, 1, оо).
17. Отобразить верхнюю полуплоскость G+ = {z € С | Imz > 0} на область w-плоскости,
указанную на рис. 105, при условии
w(A = —h, В = оо, С ±= h, D = оо) —> z(—1, 0, 1, оо).
Ответы
Глава 2
I 2sinTt+2 х —2 sin71 + х cos x+sin71 х—sin(n + l)x sin x+sin nx
sin” x 1 — 2 sin x cos x+sin2 x
1. а) г; б) sin# - |. 2. w = kz. 10. S„ =
_ 1 sinn+2 x—sin7l + 1 x cos x—sin x cos(n+l)x+cos nx 1 О о) * г| ^2~22^1~^^(г2~г1) . gx _ z2~z] ('z~~~Z~'}
sinn x 1 — 2sinx cos x+sin2 x ' " *2 — z] ’ z2~z\
16. Z\ = -1, Wi = 1. 19. а) Окружность с центром в точке а радиуса R \ б) прямая х+у = 1; в) луч,
выходящий из начала координат и образующий с положительным направлением действительной
оси угол а; г) действительная ось; д) гипербола (х - - у2 = |; е) эллипс у + \ = 1;
ж) парабола у2 = 2х + 1. 20. a) Imz2 = 2; б) Im | в) z2 + z2 = 1; г) Re(z + 1) = |z|;
д) |z| + Rez = 1. 21. а) Кольцо с центром в точке z0 и радиусами г и R ; б) правая полуплоскбсть,
включая мнимую ось; в) полоса между прямыми х = а и х = Ь; г) область, заключенная между
окружностями (х - I)2 + (г/ - I)2 = 2 и (х — 2)2 + (у - 2)2 = 8; д) правая половина единичного
круга с центром в точке z = 0. 22. z = 12 4- 16г. 24. а) Ни при каких а; б) у=; в) V2; г) ни
при каких а. 25. а) | + г; б) _'г)2. 30. б) Отрезок |]. 31. 1) Окружность и2 + и2 -
~ = 0, если с / 0; при с = 0 — ось и = 0; 2) окружность и2 + у + =0, если с # 0; при
с = 0 — ось v = 0; 3) окружность (u—|)2 + (и + 0 = |; 4) луч arg го = -а; 5) прямая
v = |; 6) v = —|и|; 7) полуплоскость и > 0 без крута и2 + г>2 — и 0; 8) полуплоскость t> < 0
без круга и2 + v2 + v 0; 9) окружность х2 + у2 - | = 0, если с 0; при с = 0 — ось х = 0;
10) окружность х2+у2 + * = 0, если с 0; при с = 0 — ось у = 0. 32. а) Внешность круга |z| 2;
б) замкнутая полуплоскость, расположенная слева от прямой Rez = 2,5, z 1. 34. 1) Эллипс;
2) спираль Архимеда; 3) одна ветвь гиперболы; 4) циклоиды. 35. 1) оо; 2) 1; 3) оо; 4) 5) не
существует; 6) 1 + г; 7) не существует; 8) не существует; 9) не существует. 36. 1) Непрерывная;
2) непрерывная; 3) всюду разрывная; 4) непрерывная всюду, кроме z = 2г; 5) непрерывная
всюду, кроме прямых argz = ±у. 40. 1) Аналитическая в С\{0}; 2) не аналитическая в каждой
точке z 6 С, но дифференцируемая в точке z — 0; 3) не аналитическая в каждой точке z £ С.
42. |. 44. a) /(z) = z2 + 2z; б) /(z) = ez + z2 + 5z + 9.
Глава 3
1. Линия Rew = 4cosy>(2cosy> + 1) — 3, Imw = 4 sin y>(2 cos ip + 1), 0 <p 2тт. 3. Круг
|w| < 1. 5. Круг |w| < 4. 6. Полуплоскость Imw > 0. 7. Круг |w| 1. 8. Круг |w| 1.
10. a) Imw > 0; 6) Imw > 0; в) Imw < 0. 11. w = e'^z3. 12. w = —i(z-l-i)2. 13. w = i(z-l)2.
14. w = 1+12 — (z — a)2. 15. w = -iz2 + 1. 16. w = (1 + »)(1 — z). 17. w = (2 + i)z -I- 1 - 3i.
18. 1) z0 = -1 + Зг, 6 = 0, к = 2, w + 1 - 3г = 2(z + 1 - 3г); 2) z0 = 2 + 2г, # = f, к = 1,
w — 2 - 2г = i(z — 2 — 2г); 3) конечной неподвижной точки нет; 4) если а = 1, то конечной непо-
движной точки нет; если а # 1, то z0 = - , # = arga, к = |a|, w — = a (z - ;
5) если a = 1, то конечной неподвижной точки нет; если а # 1, то z0 = 6 = arga, к = |а|,
=а(г-гУ .19. Уравнение семейства окружностей Аполлония относительно точек zx
и z2 имеет вид = А. 20. w = kexp 1 | I тг + arg J г j • где fc > 0. Лучам, выходя-
Ответы
335
щим из точки w = 0 в полуплоскости Rew > 0, соответствуют в z-плоскости дуги кружностей,
лежащие внутри круга \z\ < 1 и проходящие через точки zlt z2. Лежащим в полуплоскости
Rew > 0 полуокружностям с центром в точке w = 0 соответствуют находящиеся внутри кру-
га |z| < 1 дуги окружностей Аполлония относительно точек z{ и z2. 21.
22. 1) w = R2e'a ~^~a ; 2) ътпг- = e‘° g2~- ; 3) w = R2 Д~а , где a — действительное чи-
' Я2-аг ’ ' /tz-bw R^-az ’ ' RL — az ’
ело и |а| < R. 23. ,w~° — e"? , где tp = тг — arg ,г;7г| , a = —----—I*2"*1' .
1 1 l-ziz* Г 6 1-2|!;> |i_£1Z2| + x/(1_|21|2)(1_|Z2|2)
24. w = ± az.-l+2^1~al p = 227. 1) lm| < Область ограничена удлиненной
(l-VI-a!)2-a Г “ n
эпициклоидой, т.е. траекторией точки, находящейся на расстоянии mR от центра круга ра-
диуса катящегося извне по кругу радиуса —у/0; 2) |ш| В первом случае внешность
единичного круга, а во втором случае его внутренность, отображаются на внешность “укоро-
ценной” гипоциклоиды. 28. w =
. 29. w =
30. w =
Г~/ 2 2 \ _______________
= ) + 1. З2.«,.уи + Н«+Л 33. » + i = S& (*+9-2^
V \ (1-2)3 +(l + z)3 / '
w'(0) = П+°) . Длина дуги, соответствующей разрезу, равна 2arccos она равна тг при
4G (I •f’G )
= 3-а/8. 34. w + ^ = 2
W
(о+±)+(ь+1)
а+1+Ь+1
w (0) = —2-^—-. Длины дуг, соответ-
п \ а / X b J Л П \ V V ОЕ w —1
ствующих разрезам, равны Загссоз-у1—। \ / , \ , 2тг - zarccos—/ > \ / 1 \ • 35. =
\a+a/ + V+bJ \ +“/ \ +Ь/
/ ze-+.exp(4) V
= ( —:/ я\ , гае 7 = а, если /3 > 0, и 7 = a + тг, если (3 < 0. 36. 1) В полярную сетку
у zel~r+i ехр(-г у j J
е-ь
р = const, 0 = const; 2) в спирали р = е (при fc = 0 в лучи 0 = Ь); 3) в угол а < 0 < /3 (при
а = 0 и {3 = 2тг — в плоскость с разрезом по положительной части действительной оси); 4) во
всю плоскость с разрезом по спирали р = е9; 5) в сектор р < 1, 0 < 0 < а (при а = 2тг — в
единичный круг с разрезом по радиусу v = 0,0^u^1);6)b область р>1,О<0<а (при
а = 2тг — во внешность единичного круга с разрезом по лучу v = 0, 1 и < оо; 7) в область
е“ <р<е/3,,у<0<6 (при <5 — 7 = 2тг эта область является концентрическим кольцом с
разрезом по отрезку 0 = 7, е“ / р / е'9). 37. 1) В прямоугольную декартову сетку и = с, v = с;
2) в прямые; 3) в полосу 0 < v < a; 4) в полуполосу и<0,0<и<а;5)в прямоугольник
1пГ1 < и < 1пг2, 0 < v < 2тг. 38. 1) В полуполосу -у < и < у, и > 0; 2) в полосу -у < и < у;
3) в полуполосу 0 < и < у, v > 0; 4) в полосу -у < и < 0. 41. w = exp ( |(У? - «)) •
Глава 4
1. а) 0; б) тгг. 2. а) е(2 - e-i - 1); б) 1 + е~\е - 2). 3. а) 1; б) 2; в) 2. 4. а) £fl(l + iV3);
б) |(1 — г-/3) fexp f—j 4- 1/2^ — ' 5- ~ In -\/sh21 + ch2 1 + iarctg(tg 1 • th 1). 6. iri. 12. 0.
336
Ответы
15. a) f(z) =
если
если
И < 1,
М> 1;
6) ff(z) =
2z ’
___1_
2z ’
2z+5
2(2z2+5z+2) ’
если
если
если
И > I,
zED.
Глава 5
1. a) j; б) 1; в) 1; г) УЗ; д) 1. 2. a) |z + i| < 1; б) \z - 1 - г| < 3; в) \z\ < 1; г) \z\ < 1; д) \z\ <
е) \z\ < ж) \z\ < +оо; з) если а — целое неотрицательное, то \z\ < +оо; для остальных
а — круг |z| < 1. 3. а) Сходится во всех точках окружности \z\ = 1; б) сходится во всех точках
окружности |z| = j, кроме z = |; в) сходится во всех точках окружности |z| = 1, кроме z = — 1
и z = j ± i^; г) сходится во всех точках окружности |z| = 1, кроме z = 1 и z = ±г; д) сходится
ОО
во всех точках окружности |z| = 1, кроме z = 1 и z = ±г. 4. а) Е (п+1)(п+2>гбп, |г| < j.
п=0
оо оо оо
б) Ё(-1П23л+!г+2 — 23nz3n), |z| < 1; в) £(n+l)(z8n -z8n+1), |z| < 1; r) E(-l)n22n^,
тг=0 n=0 n=0
oo oc 2
|z| <+oo. 6. a) E (1 +!+•••+I^K1;6) E(I^Wn+i)' И <+00. 7. a) 1 + 2z +
n=2 n=0
+ -^z2 + ..., |z| < 1; б) 1 + | — + ..., |z| < 1. 8. a) E(~l)n ln+i > lzl < — Гз +
n= 1
+ 2.3.5.6 _ 2-3-5-6-8-9 + • • •> lzl < +°°; B) E 2 (2^p~z2n 1 lzl < 1- 13. а) Пустое множество; б) кольцо
n=0
О < |z| < 00 при |а| > 1 и пустое множество при |а| 1; в) кольцо < |г| < |а| При |а| > 1 и
пустое множество при |а| 1. 14. a) е2 I + Е ( Ъ + (?Г+Т>!) (z _ ) ПРИ 0 < |z - 1| < оо;
V n=o ' J
б) Е (2n)!^" ~ E*n+1 при о < |z| < 1 или Е (2%‘р- + ЕЕ при |z| > 1; в) Е(-1)п+1п-гП при
71 = 0 71 = 0 71 = 0 71 = 0 71=1
оо / ОС ОО \ сс
|z| < 1 или Е при |z| > 1. 15. а) I Е + Е ЩЕ2" ) ; б) | Е ; в)
П=0 \п=1 71=0 / п = 2
оо оо оо 2 оо ОС
— 2 Е М2п’', где an = Е Vn G N; г) |+2 Е Е^-2 Е “n^1, ап = Е Е N.
n = l fc = l п=1 п=1 к=2
18. а) Правильная точка; б) полюс 5-го порядка; в) простой полюс; г) полюс 3-го порядка;
д) существенно особая точка. 19. а) Существенно особая точка; б) существенно особая точка;
в) полюс 4-го порядка; г) нуль 4-го порядка. 20. a) z = 1 — существенно особая точка, z =
= 2kiri (fc G Z) — простые полюсы, z = oo — неизолированная особая точка (предельная точка
множества полюсов); б) z = — j + ктг (к Е Z) — простые полюсы, z = оо — неизолированная
особая точка; в) z = (2fc + 1)тгг (fc G Z) — простые полюсы, z = оо — неизолированная особая
точка.
Глава 6
оо
1. F(z) = E(-1)n (i+7)"+i ’ z € К> 2. ЛСО = ln|z| + 2тгг + гargz, /2(z) = In |z| 4- iargz, z G Z>2-
71 = 0
OO
6. z+E 2"n"(27+i)z2n+1 Нет. 9. Сумма ряда совпадает с z при 0 < б < |z| < 1 и соответственно
71=1
с 2 при |z| > 1; нет.
Ответы
337
Глава 7
1. a) res/(z) = , где zfc = е*2 n+l,r (fc = 0, п - 1); res/(z) = I еслип=1’ б)гез/(2) =
= (-l)n+'c"n+1; res f(z) = (-l)nc"n+1; в) res/(z) = 0; г) res/(z) = 0; д) res/(z) = res/(z) = -±;
e) res/(z) = e6-ea. 2. a) res/(z) = sh2; res/(z) = -|i(e+2e-1); 6) res/(z) = — resj(z) = 0.
oo — i £ 0 —
2 2
3. -n. 4. -2e,2k,ra. 8. a) 2(1 - e~*)тгг; 6) 0; в) 0. 10. а) -2?гг, если Ln(z - 2)|2=1 = —тгг и О
для остальных ветвей; б) 0 для всех ветвей; в) 0, если = 1 и — 4тгге, если Vz|z=i =
11. а) 0; б) ^(1 + 2г). 13. f(z) = h(z) + £ . 16. а) £> = {z е С : |z| < е-1}; б) С.
Глава 8
2. п. 4. 2. 8. g(w) = С2п~', Я = |(а - 1)“-'1а-а|. 15. На многоугольную звезду с углами
П=1
тг — — Атгитг + Атг попеременно, с центром в начале координат и одной из вершин первого
_2 r(^-±)r(l±A)sin^
вида углов в точке w(l) = 2 п —А- si„ г-7—----. 16. ш = ^ , где £ = - (7271 + In 777) ,
___ п
t — . 17. w = (Vz2 - 1 + arcsin .
Литература
1. БицадзеА.В. Основы теории аналитических функций комплексного переменного. — М.:
Наука, 1972.
2. Волковыский Л. И., Лунц Г. Л., Араманович И. Г. Сборник задач по теории функций ком-
плексного переменного. — М.: Наука, 1970.
3. Грищенко А. Е., Нагнибида Н.И., Настасиев П.П. Теория функций комплексного перемен-
ного, — Киев: Вища школа, 1986.
4. Евграфов М.А. Аналитические функции. — М.: Наука, 1965.
5. Евграфов М.А. Сборник задач по теории аналитических функций. — М.: Наука, 1969.
6. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — М.:
Физматгиз, 1958.
7. Ляшко И. И., Емельянов В. Ф., Боярчук А. К. Основы классического и современного матема-
тического анализа. — Киев: Вища школа, 1988.
8. Маркушевич А. И. Краткий курс теории аналитических функций. — М.: Физматгиз, 1961.
9. Mitrinotic D. S. Kompleksna analisa: Zbornik zadataka i problema. — Beograd: Nauchna kniga,
1972.
10. Привалов И. И. Введение в теорию функций комплексного переменного. — М.: Наука, 1967.
11. Соколов Ю.Д. Елементи теори функцш комплексно'! змшно'!. — Киев: Радянська школа,
1954.
12. Титчмарш Е. Теория функций. — М.: Наука, 1980.
13. Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1976.
Предметный указатель
Настоящий предметный указатель призван облегчить поиск терминов по алфавитному
признаку. Для поиска терминов по тематическому признаку пользуйтесь подробно соста-
вленным оглавлением.
В настоящем предметном указателе, как правило, приводятся ссылки на страницу, где
термин определяется. Составитель указателя не ставил своей целью отследить все упоминания
приведенных терминов в книге. Исключение составляют термины, описывающие методы,
приемы, практические результаты: для них в некоторых случаях указаны также задачи, в
которых они используются. Номера задач указаны курсивом по схеме “число:число”, где
первое число — номер главы, второе — порядковый номер задачи.
А
Абеля
— теорема, 202
---вторая, 207—208
--- первая, 207
— тождество, 202
абсолютное значение
— в поле, 11
— в теле, 11
автоморфизм конформный, 312
аддитивность
— интеграла относительно пределов интегрирования,
151
— криволинейного интеграла, 159
аксиома индукции, 5
аксиомы
— абсолютного значения, 11
— векторного пространства, 11
— длины, 11
— метрики, 12
— модуля, 11
— нормы, 11
Аполлония окружность, 41
аргумент комплексного числа, 28
— , главное значение, 28
Архимеда спираль, 40
Б
Бернулли
— лемниската, 59
— числа, 215
Бесселя функция, 226
бета-функция Эйлера, 328
Больцано—Вейерштрасса теорема, 47
Бореля—Лебега теорема, 48 2:60
в
Вейерштрасса
— беконечное произведение, 268
— мажорантный признак равномерной сходимости
функционального ряда, 201
— теорема, 50, 204—205
---о представлении целой функции в виде
бесконечного произведения, 269
вектор-функция, 50
векторное пространство над полем, 11
векторы, 11
ветви многозначной функции однозначные, 92
ветвь многозначной функции Lnw главная, 96
Виета теорема, 2:21, 2:40, 2:41
внешность простой замкнутой кривой, 52
внутренность
— множества, 15
— простой замкнутой кривой, 52
вычет
— аналитической функции относительно се
изолированной особой точки, 245
— функции
---логарифмический, 296
---относительно бесконечности, 246
г
Гаусса утверждение, 37
Гейне определение
— непрерывности отображения в точке, 21
— предела отображения, 21
Гельдера условие, 179
главное значение
— аргумента комплексного числа, 28
— интеграла типа Коши в точке, 179
гомеоморфизм, 25
гомотопия
— замкнутой кривой в замкнутую кривую, 161
— кривой в кривую, 161
— с фикисрованным началом и концом, 161
граница множества, 17, 45
график отображения, 8, 9
группа, 10
— абелева, 10
— автоморфизмов области, 312
— аддитивная,10
— коммутативная, 10
— мультипликативная, 10
Гурвица теорема, 311
д
Д’Аламбера признак, 2:51
действительная часть
— комплексного числа, 27
— функции, 48
деформация одной кривой в другую, 161
диаметр множества, 14
Дирихле
— теорема, 155, 203
— признак, 5:8, 5:11
дифференциал функции в точке, 66
дифференцируемость вектор-функции на сегменте, 51
длина в векторном пространстве, 11
долгота, 31
дополнение одног(6жества в другом, 6
ж
Жордана
— лемма, 275, 7:59
— теорема, 52
340
Предметный указатель
Жуковского функция, 99, 318, 3:28, 3:72, 3:74, 3:87—93,
3:95, 3:97, 3:99, 3:100, 3:101
3
замыкание множества, 16, 45
знаки
— включения, 5
— принадлежности, 5
значение
— аргумента комплексного числа главное, 28
— бесконечного произведения, 265
— интеграла типа Коши в точке
---главное, 179
---предельное слева от кривой, 180
---предельное справа от кривой, 180
— отображения, 9
и
изоморфизм
— дробно-линейный, 87
— конформный, 312
— множества на множество, 10
интеграл
— Ньютона—Лейбница
---определенный, 150
---с фиксированным нижним пределом и
переменным верхним пределом интегрирования,
150
— в смысле главного значения по Коши, 179
— Коши, 173
— криволинейный функции по кривой, 159
---второго рода, 159
---первого рода, 159
— Кристоффеля—Шварца, 320
---второго рода, 321
---первого рода, 321
— типа Коши, 175
, значение в точке
главное, 179
предельное
слева от кривой, 180
справа от кривой, 180
— Шварца, 181
— Эйлера—Пуассона, 191
— эллиптический первого рода, 323
---полный, 324
1-интеграл, 153
п-интеграл, 154
к
Кантора теорема, 18, 25
Каратеодори теорема, 315
Кардано формулы, 2:41
квантор
— общности, 4
— существования, 4
кольцо, 10
— коммутативное, 10
— унитарное, 10
компакт, 18, 47
комплексная плоскость, 27
комплексные числа, 27
комплексный потенциал, 72, 2:83
композиция отображений, 9
компонента упорядоченной пары
— вторая, 7
— первая, 7
компоненты связные, 52
континуум, 52
— линейный, 52
контур, 160
координата упорядоченной пары
— вторая, 7
— первая, 7
Коши
— интеграл, 173
— критерий, 46, 198, 200
----для функционального ряда, 201
— определение
----непрерывности отображения, 22
----предела отображения, 22
— теорема
----интегральная, 166—167
-------, обобщение на случай функции, не
являющейся аналитической на контуре
интегрирования, 168—170
----о вычетах, 247, 7:42, 7:47
----, обобщение на случай неодносвязной области,
171-172
— формула интегральная, 172—173
— ядро, 179
Коши—Адамара
— теорема, 207
— формула, 5:10, 5:11, 8:6
Коши—Римана условия, 67, 2:72, 2:73, 2:75, 2:77—80
кривая
— гладкая
----, ориентация, 51
----ориентированная, 51
----, параметрическое представление, 51
----простая, 51
— жорданова, 51
----замкнутая, 51
— замкнутая, 51
— канторова, 52
— кусочно-гладкая, 52
— непрерывная, 51
— ориентированная
----противоположно по отношению к данной, 51
— , параметрическое представление, 51
— простая, 51
----замкнутая
-------, внешность, 52
-------, внутренность, 52
Кристоффеля—Шварца
— интеграл, 320
----второго рода, 321
----первого рода, 321
— формула, 320, 8:22, 8:25
критерий
— дифференцируемости функции / : С С, 67, 2:79
— компактности в себе, 47—48
— Коши, 46, 198, 200
----для функционального ряда, 201
круг сходимости аналитического элемента, 233
круговое свойство дробно-линейных отображений, 85
л
Лагранжа
— ряд, 302
— теорема, 73
Ландау символы, 11
Лапласа оператор, 178
лемма
— Жордана, 275, 7:59
— Шварца, 305, 8:15—17
леммы
— Паскаля, 5
лемниската Бернулли, 59
Линделёфа результат, 316
линейное пространство над полем, 11
линейность криволинейного интеграла, 159
Лиувилля теорема, 178—179, 4:25
Лопиталя правило, 7:8
Лорана теорема, 219—220
Предметный указатель
341
М
мера жорданова множества, 79
метод
— математической индукции, 5—6, 2:53
— от противного, 4
метрика, 12
— сферическая, 43
Миттаг-Леффлера теорема, 258—259, 7:25, 7:27
мнимая часть
— комплексного числа, 27
— функции, 48
многочлен Тейлора, 156
множества
— изоморфные, 10
— нспересекающиеся, 6
— равные, 5
множество
— внешних точек данного множества, 15
— , внутренность, 15
— вполне ограниченное в метрическом пространстве, 18
— , граница, 17, 45
— , диаметр, 14
— жорданово
---, мера, 79
---, площадь, 79
— замкнутое, 16, 45
---связное, 45
— , замыкание, 16, 45
— значений отображения, 9
— компактное, 20
---в метрическом пространстве, 18
---в себе, 18, 47
---относительно метрического пространства, 18
— линейно-связное, 149
— , образ при отображении, 9
— ограниченное, 14, 44
— определения отображения, 9
— открытое, 14, 45
---связное, 45
— , покрытие, 18
— , прообраз при отображении, 9
— пустое, 5
— связное в метрическом пространстве, 20
— точек кусочно-гладкой кривой, 52
— функций
компактное
-------в данной области, 309
-------в себе, 311
---равномерно ограниченное внутри данной области,
309
---равностепенно непрерывное, 309
-------внутри данной области, 309
модуль
— в поле, 11
— в теле, 11
— комплексного числа, 26
Монтеля признак компактности, 309—310
Морера теорема, 179
Муавра формула, 29, 2:17
н
направление обхода границы области положительное,
162
непрерывность
— отображений взаимная, 25
— отображения, 21, 23
---в точке, 23
-------в смысле Гейне, 21
-------в смысле Коши, 22
---равномерная, 24
— функции в точке, 48
неравенство треугольника
— для абсолютного значения, 11
— для метрики, 12
— для модуля, 11
— для нормы (длины) в векторном пространстве, 11
норма
— в векторном пространстве, 11
— вектора, 11
— функции равномерная, 199
---, свойства, 199
нуль функции, 212
— кратности п, 212
Ньютона—Лейбница формула, 150
— для п-интсграла, 154—155
о
области
— дробно-линейно изоморфные, 87
— конформно-изоморфные, 312
область, 20, 45
— бесконечносвязная, 53
— замкнутая, 20, 45
— значений отображения, 9
— компактная, 53
— многосвязная, 52
— неодносвязная, 53
— односвязная, 53, 162
---относительно комплексной плоскости, 52
---относительно расширенной комплексной
плоскости, 52
— определения
---отображения, 9
---полной аналитической функции естественная, 237
— отправления отображения, 8
— прибытия отображения, 8
— существования полной аналитической функции, 237
образ множества при отображении, 9
обращение отношения, 8
объединение множеств, 6
окрестность
— множества, 15
---открытая, 15
— точки в множестве, 53
6 -окрестность точки, 13
е -окрестность бесконечно удаленной точки, 44
е -окрестность точки, 44
окружность Аполлония, 41
оператор Лапласа, 178
операции над множествами, 6—7
операция
— обращения отношения, 8
— сложения комплексных чисел, 26
— транспонирования отношения, 8
— умножения комплексных чисел, 27
ориентация
— гладкой кривой, 51
---противоположная, 51
п -остаток ряда, 203
отношение
— бинарное
---между элементами множеств, 7
---обратное, 8
---, проекция
------- вторая, 8
-------первая, 7
---функциональное, 8
— , обращение, 8
— , транспонирование, 8
отображение
— биективное, 9
— взаимно однозначное, 9
— гиперболическое, 125
— , график, 8, 9
— дробно-линейное
---, нормальная форма, 125
342
Предметный указатель
— заданное параметрически, 9
— , значение, 9
— из множества в множество, 8
— конформное
---в области, 71
---в точке, 71
— локсодромическое, 125
— множества в множество, 9
— множества на множество, 9
— , множество значений, 9
— , множество определения, 9
— непрерывное, 21, 23
---в точке, 23
-------в смысле Гейне, 21
-------в смысле Коши, 22
— , область значений, 9
— , область определения, 9
— , область отправления, 8
— , область прибытия, 8
— обратимое, 9
— обратное, 9
— открытое, 301
---внутреннее, 301
— равномерно непрерывное на множестве, 24
~ разрывное в точке, 21
— эллиптическое, 125
отображения
— взаимно непрерывные, 25
— , композиция, 9
отрезок
— на комплексной плоскости, 45
— , параметрическое представление, 45
п
пара упорядоченная, 7
— , вторая компонента (вторая координата), 7
— , первая компонента (первая координата), 7
параллель, 31
параметр, 9
Паскаля леммы, 5
первообразная функции, 149
— вдоль кривой, 165
— вдоль пути, 165
пересечение множеств, 6
петля, 160
Пикара теорема, 224
плоскость
— комплексная, 27
---расширенная, 29
— экваториальная, 30
плотность, 179
площадь жорданова множества, 79
подмножество, 5
— максимально связное, 52
подпространство метрического пространства, 17
показательная форма записи комплексного числа, 28
покрытие множества, 18
поле, 11
— нормированное, 11
полином Чебышева, 229
положительное направление обхода границы области,
162
полумеридиан,31
полюс
— северный, 31
— функции, 221
---простой, 221
— южный, 31
порядок
— полюса, 221
— связности, 53
— Л-точки, 211
— целой функции, 270
последовательность
— векторов
---фундаментальная, 12
— комплексных чисел
---бимонотонная, 202
— сходящаяся, 46
— точек метрического пространства
---сходящаяся, 13
---фундаментальная, 13
---(С, р), 45
— функциональная, 198
---поточечно сходящаяся к данной функции, 198
---равномерно сходящаяся к данной функции на
данном множестве, 199
---равномерно фундаментальная, 200
— числовая, 9
— элементов множества, 9
потенциал комплексный, 72, 2:83
правила дифференцирования интеграла
— по верхнему переменному пределу интегрирования,
151
— по нижнему переменному пределу интегрирования,
151
правило
— дифференцирования произведения функций, 65
— Лопиталя, 7:8
—- перестановки пределов интегрирования, 151
предел
— отображения, 21
---в смысле Гейне, 21
---в точке в смысле Коши, 22
---частичный, 21
— последовательности, 45
---векторов в нормированном пространстве, 11
---точек в метрическом пространстве, 13
---частичный, 47
— функции в точке, 48
---частичный, 48
— функциональной последовательности равномерный,
200
представление параметрическое
— гладкой кривой, 51
— естественное, 51
— кривой, 51
— натуральное, 51
— нормальное, 51
— обобщенной непрерывной кривой, 52
— отрезка, 45
представления параметрические экивалентные
— гладкой кривой, 51
— непрерывной кривой, 51
признак
— Вейерштрасса равномерной сходимости
функционального ряда мажорантный, 201
— Д’Аламбера, 2:51
— Дирихле, 5:8, 5:11
— компактности Монтеля, 309—310
— сходимости ряда необходимый, 198
Прингсхейма теорема, 242
принцип
— аргумента, 297
— двойственности, 7
— исключенного третьего, 4
— максимума модуля, 8:8—10, 8:14
---вторая формулировка, 305
---первая формулировка, 304
— непрерывности, 240—241
— однолистности, 303
— симметрии, 317, 8:18, 8:19
---Римана—Шварца, 137, 241, 3:95
— сохранения области, 300—301
продолжение функции, 9
— аналитическое, 232
Предметный указатель
343
проекция
— бинарного отношения
---- вторая, 8
---- первая, 7
— стереографическая, 30
произведение
— бесконечное
----Вейерштрасса, 268
----, значение, 265
----сходящееся, 265
----абсолютно, 266
----равномерно в области, 267
— многочленов, 208
— множеств
---- декартово, 7
----прямое, 7
— степенных рядов, 208
1-производная, 153
п-производная Ферма—Лагранжа функции в точке, 156
n+ 1-производная, 153
производная вектор-функции, 50
прообраз множества при отображении, 9
пространства метрические гомеоморфные, 25
пространство
— банахово, 12
— векторное
----над полем, 11
----нормированное, 11
— линейное над полем, 11
— метрическое, 12
----полное, 13
---- связное, 20
— нормированное полное, 12
— топологическое, 45
----, свойства, 45
Пуанкаре теорема, 270
Пуанкаре—Вольтерра теорема, 237
Пуассона формула, 182, 4:8
р
равенство
— множеств, 5
— упорядоченных пар, 7
радиус сходимости степенного ряда, 206
р-раздутие множества, 309
разность множеств, 6
расстояние
— индуцированное, 17
— между точками метрического пространства, 14
— хордальное, 44
расстояния
— топологически эквивалентные, 25
— эквивалентные, 25
расширенная комплексная плоскость, 29
результат
— Линделёфа, 316
— Шварца, 316
Римана
— сфера, 30, 2:43—47
— теорема, 314—315
Римана—Шварца принцип симметрии, 137, 241, 3:95,
3:97, 3:100, 3:102
род бесконечного произведения, 270
Руше теорема, 297—298, 8:1, 8:3
ряд
— Тейлора, 209
— Лагранжа, 302
— Лорана функции в кольце, 220
— мероморфных функций сходящийся, 258
----равномерно, 258
— функциональный, 197, 198
----степенной, 206
----сходящийся нормально, 201
---сходящийся поточечно, 199
---сходящийся равномерно, 200
---удовлетворяющий равномерному условию Коши,
201
— Фурье, 7:30
— числовой, 197
---расходящийся, 197
---сходящийся, 197
с
свойства
— аналитической функции, 69—70
— векторного пространства, 11
— нормы функции равномерной, 199
— показательной функции, 28
— стереографической проекции, 30
— топологического пространства, 45
северный полюс, 31
f-сеть множества, 18
сечение
— второе, 8
— первое, 8
символ
— дизъюнкции, 4
— импликации, 4
— конъюнкции, 4
— отрицания, 4
— эквивалентности,4
символы Ландау, 11
синус эллиптический, 324
след кусочно-гладкой кривой, 52
сопряженное число, 27
Сохоцкого
— теорема, 223—224
— формулы, 181
спираль Архимеда, 40
стереографическая проекция, 30
— , свойства, 30
структура математическая, 10
сужение функции, 9
— на множество, 9
сумма ряда, 197
— функционального
---поточечная на данном множестве, 199
---равномерная, 200
---частичная, 198
— частичная, 197
сфера, 13
— Римана, 30, 2:43-47
т
Тейлора
— многочлен, 156
— теорема, 209
— формула с остаточным членом, записанным
посредством п-интеграла, 156
Тейлора—Пеано формула, 157—158
тело, 10
— нормированное, 11
теорема
— Абеля, 202
---вторая, 207—208
---первая, 207
— алгебры основная, 298
— Больцано—Вейерштрасса, 47
— Бореля—Лебега, 48, 2:60
— Вейерштрасса, 50, 204—205
---о представлении целой функции в виде
бесконечного произведения, 269
— Виета, 2:21, 2:40, 2:41
— Гурвица, 311
— Дирихле, 155, 203
— Жордана, 52
344
Предметный указатель
— Кантора, 18, 25
— Каратеодори, 315
— Коши
---интегральная, 166-167
-------обобщение на случай функции, не являющейся
аналитической на контуре интегрирования,
168-170
---о вычетах, 247, 7:42, 7:47
---, обобщение на случай неодносвязной области,
171 — 172
— Коши—Адам ара, 207
— Лагранжа, 73
— Лиувилля, 178-179, 4:25
— Лорана, 219-220
— Миттаг-Леффлера, 258—259, 7:25, 7:27
— Морера, 179
— о биективных и непрерывных отображениях, 52
— о вычетах основная, 247, 7:42, 7:47
— о дифференцируемости произведения бесконечно
малой дифференцируемой функции и непрерывной
функции, 64
— о достаточных условиях
---равномерной сходимости бесконечного
произведения, 267
---существования первообразной в круге, 162—163
— о замене переменной интегрирования, 152
— о линейности
---интеграла, 151-152
---операции дифференцирования, 64
---равномерного предела, 200
— о логарифмическом вычете, 296
— о монодромии, 236
— о непрерывном образе компакта, 21, 50
— о непрерывности
---дифференцируемой функции, 64
---композиции
-------отображений, 21
-------функций, 49
---нормы, 11
---обратного отображения, 22
---сужения отображения, 23
— о почленном интегрировании равномерно
сходящегося функционального ряда, 204
— о пределе композиции функций, 49
— о производной
---n-интеграла по пределам интегрирования, 155
---композиции, 63—64
---обратной функции, 65
---частного, 65
— о равномерной равносходимости функциональных
рядов, связанных преобразованием Абеля, 202
— о равносходимости бесконечного произведения и
числового ряда, 265
— о среднем, 173
— о существовании первообразной аналитической
функции, заданной в односвязной области, 170-171
— об инвариантности
---интеграла при гомотопиях пути интегрирования,
166-167
---симметричных точек при дробно-линейном
отображении, 86
— об интегрировании по частям, 152
— об обращении формулы Тейлора—Пеано, 158
— об ограниченности компакта, 47
— Пикара, 224
— Прингсхейма, 242
— Пуанкаре, 270
— Пуанкаре—Вольтерра, 237
— Римана, 314-315
— Руше, 297-298, 8:1-3
— Сохоцкого, 223—224
— Тейлора, 209
— Фреше, 19
— Хаусдорфа, 19
— Штольца, 2:50
тождество Абеля, 202
топология, 44
— метрического пространства, 25
— относительная, 53
точка
— бесконечно удаленная, 29
— кривой
----конечная, 51
----• кратная, 51
----начальная, 51
— множества
------- внешняя, 15
------- внутренняя, 15, 45
— — граничная, 17, 45
------- изолированная, 17
----предельная, 17, 45
— особая
----аналитической функции, 239
— — изолированная, 221
----* многозначного характера, 239
----однозначного характера, 239
----устранимая, 221
— последовательности предельная, 47
— прикосновения, 16, 45
— разветвления, 93, 239, 240
----(п - 1)-го порядка, 93, 240
----алгебраическая, 93
-------(п - 1)-го порядка, 93
----бесконечного порядка, 93, 240
----логарифмическая, 240
— существенно особая, 221
— устранимого разрыва, 21
А-точка функции, 211
— кратная, 211
— , кратность, 211
— , порядок, 211
— простая, 211
точки
— метрического пространства, 12
— симметричные
----относительно окружности, 85, 86
----относительно прямой, 85
траектория
— гладкая
----простая, 51
— непрерывная, 51
транспонирование отношения, 8
тригонометрическая форма записи комплексного числа,
28
трохоида, 60
У
угол между путями в точке, 84
упорядоченная пара, 7
уравнение деления круга, 35
условие Гельдера, 179
условия Коши—Римана, 67, 2:72, 2:73, 2:75, 2:77—80
утверждение Гаусса, 37
ф
форма
— дробно-линейного отображения нормальная, 125
— записи комплексного числа
----показательная, 28
----тригонометрическая, 28
формула
— Коши интегральная, 172—173
— Коши—Адамара, 5:10, 5:11, 8:6
— Кристоффеля—Шварца, 320, 8:22, 8:25
— Муавра, 29, 2:17
— Ньютона—Лейбница, 150
Предметный указатель
345
---для п-интеграла, 154—155
— Пуассона, 182, 4:8
— Тейлора с остаточным членом, записанным
посредством п-интеграла, 156
— Тейлора—Пеано, 157—158
— Шварца, 181
формулы
— Кардано, 2:41
— Сохоцкого, 181
— стереографической проекции основные, 30, 2:43—47
— Эйлера, 101, 7:23, 7:24
Фреше теорема, 19
функции
— аналитические равные, 237
— гиперболические, 101
— тригонометрические, 101
функционал, 310
— непрерывный на данном элементе, 310
функция
— авторморфная, 325
— аналитическая
---в бесконечно удаленной точке, 219
---в замкнутой области, 69
---в области, 68
---в точке, 68
---на бесконечности, 69
---на кривой, 68
---на открытом множестве, 68
---на произвольном множестве, 68
--- полная, 237
---, свойства, 69—70
— Бесселя, 226
— гармоническая в области, 177
— гармонически сопряженная с данной, 178
— голоморфная, 68
— С-дифференцируемая, 67
— -дифференцируемая, 67
— 1-дифференцируемая, 153
— п -дифференцируемая в точке в смысле
Ферма—Лагранжа, 156
— п -I- 1-дифференцируемая, 153
— дифференцируемая в точке, 63
— дробно-линейная, 83
— Жуковского, 99, 3:28, 3:72, 3:74, 3:87~93, 3:95, 3:97,
3:99-101, 8:18
— 1-интегрируемая, 153
— интегрируемая в смысле Ньютона—Лейбница, 150
— кусочно-линейная, 45
— линейная, 66
— ломаная, 45
— мсроморфная, 257, 271
---в области, 259
— моногенная, 65
— непрерывная в точке, 48
— неявная, 10
— обобщенно-непрерывная, 50
— ограниченная на множестве, 50
— однолистная, 48
— показательная, 28, 94
---общая, 98
---, свойства, 28
— , продолжение, 9
--- аналитическое, 232
— степенная, 91
---общая, 97-98
— , сужение
---на множество, 9
---с множества на множество, 9
— тока, 72
— целая, 257
---бесконечного рода, 270
---конечного рода, 270
---трансцендентная, 257
— эллиптическая, 325
Фурье ряд, 7:30
X
Хаусдорфа теорема, 19
ц
циклоида, 60
— удлиненная, 60
— укороченная, 60
ч
часть ряда Лорана
— главная, 220
— правильная, 220
Чебышева полином, 229
числа
— Бернулли, 215
— комплексные, 27
число комплексное сопряженное данному, 27
член
— ряда общий, 197
— функционального ряда, 198
— функциональной последовательности, 198
ш
шар
— замкнутый, 13
— открытый, 13
Шварца
— интеграл, 181
— лемма, 305, 8:15—17
— результат, 316
— формула, 181
широта, 31
Штольца теорема, 2:50
э
Эйлера
— бета-функция, 328
— формулы, 101, 7:23, 7:24
Эйлера—Пуассона интеграл, 191
элемент
— аналитический, 232
— группы
---единичный, 10
---нейтральный, 10
--- нулевой, 10
---обратный данному, 10
— канонический с центром в данной точке, 233
ю
южный полюс, 31
я
ядро
— Дирихле, 35
— Коши, 179
Оглавление
Предисловие.........................................................3
Глава 1. Основные структуры математического анализа.................4
§ 1. Элементы теории множеств и отображений.........................4
Некоторые логические символы (4) Обозначения, используемые в теории множеств (5) На-
туральные числа. Метод математической индукции (5) Простейшие операции над множества!
ми (6) Упорядоченная пара и декартово произведение множеств (7) Бинарные отношения. Про-
екции и сечения бинарного отношения. Обратное бинарное отношение (7) Функциональное
бинарное отношение. Функция и простейшие понятия, связанные с нею (8) Обратная функция.
Композиция отображений (9) Параметрическое и неявное отображения (9) Изоморфизм (10)
§2. Математические структуры......................................................10
Группа (10) Кольцо (10) Тело (10) Поле (11) Векторное пространство над полем К. Нормиро-
ванное пространство (11)
§ 3. Метрические пространства......................................................12
Аксиомы метрики. Предел последовательности точек метрического пространства (12) Шары,
сферы, диаметр множества (13) Открытые множества (14) Внутренность множества (75) За-
мкнутые множества, точки прикосновения, замыкание множества (16)
§4. Компактные множества..........................................................18
§ 5. Связные пространства и связные множества......................................20
§ 6. Предел и непрерывность отображения
из одного метрического пространства в другое.......................................20
Предел и непрерывность отображения (20) Непрерывность композиции отображений (21) Не-
прерывность обратного отображения (22) Предел и непрерывность отображения в смысле Ко-
ши. Некоторые свойства непрерывных отображений (22) Равномерно непрерывные отображе-
ния (24) Гомеоморфизмы. Эквивалентные расстояния (25)
Глава 2. Комплексные числа и функции комплексного переменного.......26
§ 1. Комплексные числа и комплексная плоскость.....................26
Определение комплексного числа (26) Аргумент комплексного числа. Тригонометрическая и
показательная формы его записи. Умножение и деление комплексных чисел. Операция из-
влечения корня из комплексного числа (28) Стереографическая проекция и ее свойства (29)
Примеры (31)
§ 2. Топология комплексной плоскости. Последовательности комплексных чисел.
Свойства функций, непрерывных на компакте............................................43
Топология комплексной плоскости (43) Замкнутые множества, отрезок и ломаная. Связные
множества (45) Последовательность комплексных чисел и ее предел (45) Свойства компакта
К С С (47) Предел и непрерывность функции комплексного переменного (48) Арифмети-
ческие операции над пределами и непрерывными функциями (49) Предел и непрерывность
композиции функций (49) Свойства функций, непрерывных на компакте (50)
§ 3. Непрерывные и гладкие кривые. Односвязные и многосвязные области...............50
Примеры (53)
Оглавление
347
§ 4. Дифференцируемые функции комплексного переменного.
Связь между С-дифференцируемостью и R2 -дифференцируемостью.
Аналитические функции...................................................63
Определение дифференцируемой функции. Правила дифференцирования (63) Дифференциал
функции (66) Критерий дифференцируемости функции комплексного переменного (67) Ана-
литические функции (68) Геометрический смысл производной функции комплексного пере-
менного. Понятие конформного отображения (70) Плоские физические поля и их связь с ана-
литическими функциями (71) Неравенство Лагранжа (73) Примеры (73)
Упражнения для самостоятельной работы .......................................79
Глава 3. Элементарные функции в комплексной плоскости........................83
§ 1. Дробно-линейные функции и их свойства...................................83
Определение дробно-линейной функции. Конформность отображения (S3) Геометрические
свойства дробно-линейных отображений (84) Дробно-линейные изоморфизмы и автоморфиз-
мы (86) Примеры (88)
§2. Степенная функция w = zn (n G N, n 2).
Многозначная функция w = %/z и ее поверхность Римана....................91
Степенная функция (97) Многозначная функция w = y/z и ее поверхность Римана (92) При-
меры (93)
§ 3. Показательная функция w = ez и многозначная функция z = Ln w............94
Показательная функция w = ег (94) Многозначная функция z = Lnw (96) Примеры (96)
§ 4. Общая степенная и общая показательная функции...........................97
Общая степенная функция (97) Общая показательная функция (98)
§ 5. Функция Жуковского......................................................99
Определение функции Жуковского. Конформность (99) Примеры (100)
§6. Тригонометрические и гиперболические функции...........................101
Примеры (105)
Упражнения для самостоятельной работы.......................................145
Глава 4. Интегрирование в комплексной плоскости.
Интегралы Ньютона—Лейбница и Коши......................................149
§ 1. Интеграл Ньютона—Лейбница..............................................149
Первообразная (149) Интеграл Ньютона—Лейбница (150) Линейность интеграла. Замена пере-
менных и формула интегрирования по частям (151)
§2. Производные и интегралы Ньютона—Лейбница любых порядков................153
Определение n-производной и п-интеграла (153) Формула Ньютона—Лейбница. Производные
по пределам интегрирования (154) Формула Тейлора (156)
§ 3. Производная Ферма—Лагранжа. Формула Тейлора—Пеано......................156
Производная Ферма—Лагранжа (156) Теорема Тейлора—Пеано и ее обращение (157)
§4. Криволинейные интегралы................................................159
Интегрирование функций по ориентированной гладкой кривой (759) Гомотопия двух кривых
(путей) (161)
§ 5. Теорема и интеграл Коши................................................162
Существование локальной первообразной аналитической функции (162) Первообразная вдоль
кривой (вдоль пути) (165) Теорема Коши (166) Интегральная формула Коши (172) Приме-
ры (173)
§6. Интеграл типа Коши.....................................................175
Определение и основное свойство интеграла типа Коши (175) Гармоничность действитель-
ной и мнимой частей аналитической функции. Восстановление аналитической функции по
348
Оглавление
ее действительной (мнимой) части (777) Теоремы Лиувилля и Морера (178) Главное значе-
ние и предельные значения интеграла типа Коши (779) Формулы Шварца и Пуассона (181)
Примеры (184)
Упражнения для самостоятельной работы.........................................195
Глава 5. Ряды аналитических функций.
Изолированные особые точки................................................197
§ 1. Ряд Тейлора..............................................................197
Общие сведения о рядах (197) Последовательность функций и функциональный ряд. Пото-
чечная сходимость (198) Равномерная норма функции. Равномерная сходимость последова-
тельности функций и функционального ряда (799) Нормальная сходимость функционального
ряда. Признаки Вейерштрасса, Абеля и Дирихле равномерной сходимости функциональных
рядов (201) Функциональные свойства равномерной суммы функционального ряда (203) Сте-
пенные ряды (206) Теорема Тейлора (208) Теорема единственности (210) Примеры (212)
§2. Ряд Лорана и изолированные особые точки аналитических функций............219
Теорема Лорана (279) Классификация изолированных особых точек в С (221) Поведение ана-
литической функции при подходе к изолированной особой точке (222) Бесконечная изолиро-
ванная особая точка (224) Примеры (225)
Упражнения для самостоятельной работы.........................................229
Глава 6. Аналитическое продолжение............................................231
§ 1. Основные понятия. Аналитическое продолжение вдоль пути...................232
Свойство единственности аналитической функции. Определение аналитического продолже-
ния (232) Аналитическое продолжение вдоль пути (234) Инвариантность аналитического про-
должения вдоль пути относительно гомотопных деформаций этого пути (235)
§2. Полные аналитические функции.............................................237
Понятие полной аналитической функции (237) Примеры полных аналитических функций (238)
Особые точки полной аналитической функции (239) Существование особой точки на границе
круга сходимости степенного ряда (240)
§ 3. Принципы аналитического продолжения......................................240
Примеры (241)
Упражнения для самостоятельной работы....................................... 243
Глава 7. Вычеты и их применения...............................................245
§ 1. Определение вычета. Основная теорема.....................................245
Вычет относительно изолированной конечной точки (245) Вычет относительно бесконечно-
сти (246) Теорема о вычетах (247) Примеры (248)
§ 2. Целые и мероморфные функции..............................................257
Целые функции (257) Мероморфные функции. Теорема Миттаг-Леффлера (257) Разложение
мероморфных функций на простейшие дроби (259) Примеры (262)
§ 3. Бесконечные произведения.................................................264
Числовые бесконечные произведения (265) Равномерно сходящиеся бесконечные произведе-
ния (267) Представление целой функции в виде бесконечного произведения (267) Разложение
sinz в бесконечное произведение (269) Род и порядок целой функции (270) Мероморфная
функция как отношение двух целых функций (270) Примеры (271)
Оглавление
349
§ 4. Применение вычетов для вычисления интегралов и сумм рядов................274
Применение вычетов для вычисления определенных интегралов (274) Применение вычетов к
вычислению сумм рядов (278) Примеры (279)
Упражнения для самостоятельной работы..........................................291
Глава 8. Некоторые общие вопросы
геометрической теории аналитических функций................................295
§ 1. Принцип аргумента. Теорема Руше..........................................295
Вычисление интеграла Дт [ у.(г)/ д dz (295) Теорема о логарифмическом вычете (296)
lift J j (z) А
8D
Принцип аргумента (296) Теорема Руше (297) Примеры (298)
§ 2. Сохранение области и локальное обращение аналитической функции...........300
Принцип сохранения области (300) Локальное обращение аналитических функций (301) При-
меры (303)
§ 3. Экстремальные свойства модуля аналитической функции......................304
Принцип максимума модуля аналитической функции (304) Лемма Шварца (305) Примеры (305)
§ 4. Принцип компактности. Функционалы на семействе аналитических функций.... 308
Равномерно ограниченные и равностепенно непрерывные семейства функций (308) Принцип
компактности (309) Функционалы, определенные на множествах функций (310) Теорема Гур-
вица (311)
§ 5. Существование и единственность конформного отображения...................312
Конформные изоморфизмы и автоморфизмы (312) Примеры автоморфизмов (312) Существо-
вание и единственность изоморфизмов областей, изоморфных единичному кругу (313) Теорема
существования (314)
§ 6. Соответствие границ и принцип симметрии при конформном отображении........315
Теорема о соответствии границ (315) Принцип симметрии (316) Примеры (317)
§ 7. Конформное отображение многоугольников. Интеграл Кристоффеля—Шварца .. 318
Отображение верхней полуплоскости на многоугольник (318) Случай многоугольника, имею-
щего вершины в бесконечности (322) Отображение верхней полуплоскости на внешность мно-
гоугольника (322) Отображение верхней полуплоскости на прямоугольник (323) Эллиптичес-
кий синус и его двоякая периодичность (324) Отображение единичного круга на многоуголь-
ник (326) Примеры (328)
Упражнения для самостоятельной работы.........................................332
Ответы........................................................................334
Литература....................................................................338
Предметный указатель..........................................................339
Боярчук Алексей Климентьевич
Справочное пособие по высшей математике. Т. 4: Функции комплексного переменного:
теория и практика. — М.: Едиториал УРСС, 2001. — 352 с.
ISBN 5-354-00020-3
«Справочное пособие по высшей математике» выходит в пяти томах и представляет собой новое,
исправленное и существенно дополненное издание «Справочного пособия по математическому анализу»
тех же авторов. В новом издании пособие охватывает три крупных раздела курса высшей математи-
ки — математический анализ, теорию дифференциальных уравнений, теорию функций комплексной
переменной.
Том 4 является логическим продолжением трех предыдущих ориентированных на практику томов
и содержит более четырехсот подробно решенных задач, но при этом отличается более детальным
изложением теоретических вопросов и может служить самостоятельным замкнутым курсом теории
функций комплексного переменного. Помимо вопросов, обычно включаемых в курсы такого рода,
в книге излагается ряд нестандартных — таких, как интеграл Ньютона—Лейбница и производная
Ферма—Лагранжа.
Пособие предназначено для студентов, преподавателей и работников физико-математических,
экономических и инженерно-технических специальностей, специалистов по прикладной математике,
а также лиц, самостоятельно изучающих высшую математику.