М.В. Лурье
ГЕОМЕТРИЯ
Техника решения задач
Учебное пособие
4-е издание, стереотипное
унц ди
Москва 2004
УДК 373.167.1:514
ББК 22.151
Л86
Л86 Лурье М.В.
Геометрия. Техника решения задач. Учебное пособие. -4-е изд., стер. - М.: Издательство УНЦ ДО, 2004. - 240 с. -(Серия «В помощь абитуриенту»)
ISBN 5-88800-222-4
Выделяются и рассматриваются классы геометрических задач, объединенные общей идеей, приемами и методами решения. Показывается, как решение весьма сложных экзаменационных задач по геометрии раскладывается зачастую в последовательность более простых и стандартных задач, обладающих установившимися подходами и методами решения.
Большое количество примеров, заимствованных в основном из письменных работ, предлагавшихся на вступительных экзаменах по математике в Московском государственном университете, демонстрирует разнообразие идей, лежащих в основе геометрических задач, и вместе с тем достаточную стандартность приемов и методов их решения.
Книга предназначена прежде всего школьникам и абитуриентам вузов, учителям, а также широкому кругу читателей, любящих решать математические задачи.
Рецензент: Левинтова Н.Е., учитель средней школы № 707 г. Москвы
ISBN 5-88800-222-4
© Лурье М.В., 2002
© Учебно-научный центр
довузовского образования, 2002 © Оформление. УНЦ ДО, 2003
ПРЕДИСЛОВИЕ
Посвящается памяти Б. И. Александрова
Настоящая книга представляет собой учебное пособие, предназначенное учащимся старших классов и лицам, окончившим школу и готовящимся к поступлению в высшие учебные заведения. Предметом книги является достаточно сложный раздел школьной программы — геометрия, которая, как показывает практика, представляет собой наибольшую трудность при сдаче вступительных экзаменов. Главные цели пособия — систематизировать знания, полученные учащимися в школе, выделить общие методы и приемы решения геометрических задач, указав в них стандартные элементы, продемонстрировать технику решения как простых, так и относительно сложных задач, дать поступающему достаточное количество материала для закрепления приобретённых навыков.
В отличие от большинства других руководств, не носящих методического характера, данное пособие ставит своей целью обучить поступающего методам и приемам решения геометрических задач. Для этого из всего многообразия геометрических задач выделяются классы, объединенные общей идеей и стандартной техникой решения. Объясняется, в чем именно состоит идея задач того или иного класса и какова методика их решения. Такой подход определил как расположение материала, так и подборку задач для самостоятельных упражнений, приведенных в конце каждого параграфа. Поскольку в книге рекомендуется определенная последовательность изучения материала, то во многих случаях для решения задач определенного раздела необходимы знания и умения, приобретенные в предыдущих разделах. Показывается, как во многих случаях решение весьма сложных экзаменационных задач как бы «расщепляется» на более простые элементы, анализ которых осуществляется по стандартной методике. В книге приводится большое число однотипных задач, решение которых должно закрепить полученные знания.
Множество примеров из экзаменационной практики, основанной главным образом на письменных работах по математике, предлагавшихся в Московском государственном университете, демонстрирует разнообразие идей, лежащих в основе геометрических задач, и вместе с тем достаточную стандартность методов и приемов их решения.
Автор будет благодарен всем, кто сочтет необходимым прислать свои отзывы и замечания о книге.
Проф. М.В. Лурье
Глава L ПЛАНИМЕТРИЯ
§ 1.	ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ
Отметим прежде всего теоремы и формулы планиметрии, наиболее часто используемые при решении геометрических задач. Список таких теорем и формул дополним некоторыми полезными утверждениями и соотношениями, указав, естественно, их доказательство.
Признаки равенства треугольников. Два треугольника равны, если выполняется одно из условий:
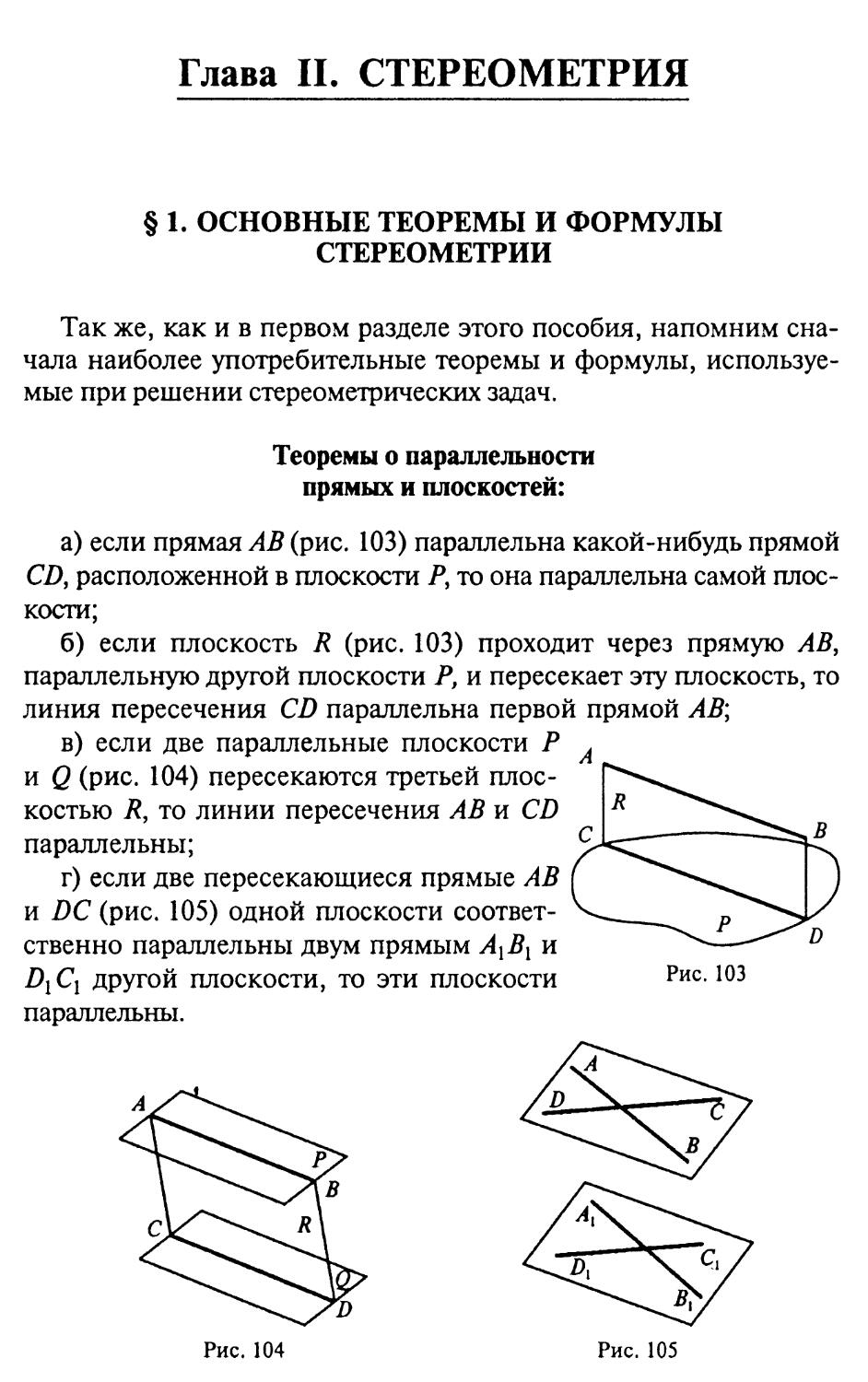
а)	две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу, заключенному между ними, другого треугольника (рис. 1я);
б)	два угла и прилежащая к ним сторона одного треугольника соответственно, равны двум углам и прилежащей к ним стороне другого треугольника (рис. li);
в)	три стороны одного треугольника равны трем сторонам другого треугольника (рис. 1с).
На рис. \а,Ь,с жирными линиями выделены элементы, равенство которых определяет равенство треугольников.
в	в	в
а	Ь	с
Рис. 1
Биссектриса внутреннего угла треугольника — это отрезок прямой, заключенный внутри треугольника и делящий данный угол на две равные части.
Биссектриса обладает следующими важными свойствами:
а)	Биссектриса — есть геометрическое место точек, равноудаленных от сторон угла1 * *;
1 Геометрическим местом точек, обладающих некоторым свойством, назы-
вается такое множество точек, которое содержит все точки, обладающие
этим свойством, и не содержит ни одной точки, не обладающей им (см. § 8).
6
ГЛАВА I. ПЛАНИМЕТРИЯ
б)	во всяком треугольнике биссектрисы пересекаются в одной точке О (рис. 2), являющейся центром окружности, вписанной в треугольник (т.е. касающейся всех его сторон);
в)	биссектриса AD (рис. 2) любого угла А треугольника АВС делит противоположную сторону на части CD и BD, пропорциональные прилежащим сторонам АС и АВ треугольника:
СР = АС
BD ~ АВ'
Доказательство. Легко видеть, что площади треугольников ACD и ABD, имеющих общую вершину А, относятся как длины их оснований, т.е. SACD: SABD = CD: BD.
A	С другой стороны, эти площади относят-
Жся как длины сторон Ь: с (Ь = АС, с = АВ),
1
поскольку SACD = - b - I • sin (а/2), SABD-
1
и и а В = 2 с' sin (а/2), где / — длина биссектрисы Рис. 2 AD, а а - величина угла А и, следовательно, SACD : $abd = 7>: с. Из сравнения полученных пропорций и вытекает доказываемое утверждение;
г)	длина 7 биссектрисы AD (рис. 2) угла А треугольника АВС, равного а, заключенного между сторонами АС и АВ, определяется по формуле:
_ 2 с • cos а/2 _ 2 cos а/2
“ ~Ь + с ~ l/b + 1/с'
Доказательство. Запишем площадь треугольника АВС двумя различными способами — один раз через стороны АС, АВ и угол а, заключенный между ними, другой раз — через сумму площадей треугольников ACD и ABD\
С	1 А
SABC =-*£c-sina;
SABC = sacd+sabd = | i • 7 • sin a/2 +1 • с • 7 • sin a/2.
Приравнивая эти выражения друг другу, получаем:
b • с • sin a = (b + c)l • sin a/2,
£ 1. Основные теоремы и формулы планиметрии
7
ИЛИ
2Ьс • sin а/2 • cos а/2 = (Ь + с)1 • sin а/2,
откуда и следует указанная выше формула для вычисления длины биссектрисы.
Медианой треугольника называется отрезок прямой, проведенной из вершины треугольника, лежащей внутри треугольника и делящий противоположную сторону на две равные части:
а)	медиана — есть геометрическое место точек, являющихся серединами отрезков прямых, заключенных внутри треугольника и параллельных той его стороне, к которой проведена медиана (рис. 3);
б)	во всяком треугольнике медианы пе
ресекаются в одной точке К, называемой центром тяжести треугольника. Эта точка отсекает от каждой медианы третью часть, считая от соответствующей стороны (т.е. делит медиану в отношении 1:2, считая от соответствующей стороны);
в)	длины медиан треугольника вычисляются через длины его сторон по формулам:
та = 72Z?2 + 2с2 - а2;
ть = ^2а2 + 2с2 -Z>2;
тс = - л/2а2 + 2Ь2 ~с2.
с 2
Доказательство. Достроим треугольник АВС до параллелограмма, проведя BG^AC и CG^AB (рис. 3). Легко видеть, что середина D стороны ВС треугольника АВС будет являться точкой пересечения диагоналей параллелограмма ABGC, Следовательно, длина диагонали AG будет равна 2та, где та — длина медианы треугольника АВС, проведенной к стороне ВС из вершины Л. Используя теорему о том, что сумма квадратов длин диагоналей параллелограмма равняется сумме квадратов всех его сторон (следствие теоремы косинусов), будем иметь равенство
4т2 + а2 = 2Ь2 + 2с2,
откуда следует первая из доказываемых формул. Аналогично доказываются и остальные формулы. В них ть и тс — длины соответствующих медиан треугольника АВС.
8
ГЛАВА I. ПЛАНИМЕТРИЯ
Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону или ее продолжение.
Три высоты треугольника пересекаются в одной точке, назы-~	2
ваемои ортоцентром .
Срединный перпендикуляр — перпендикуляр, восстановленный к стороне треугольника из ее середины.
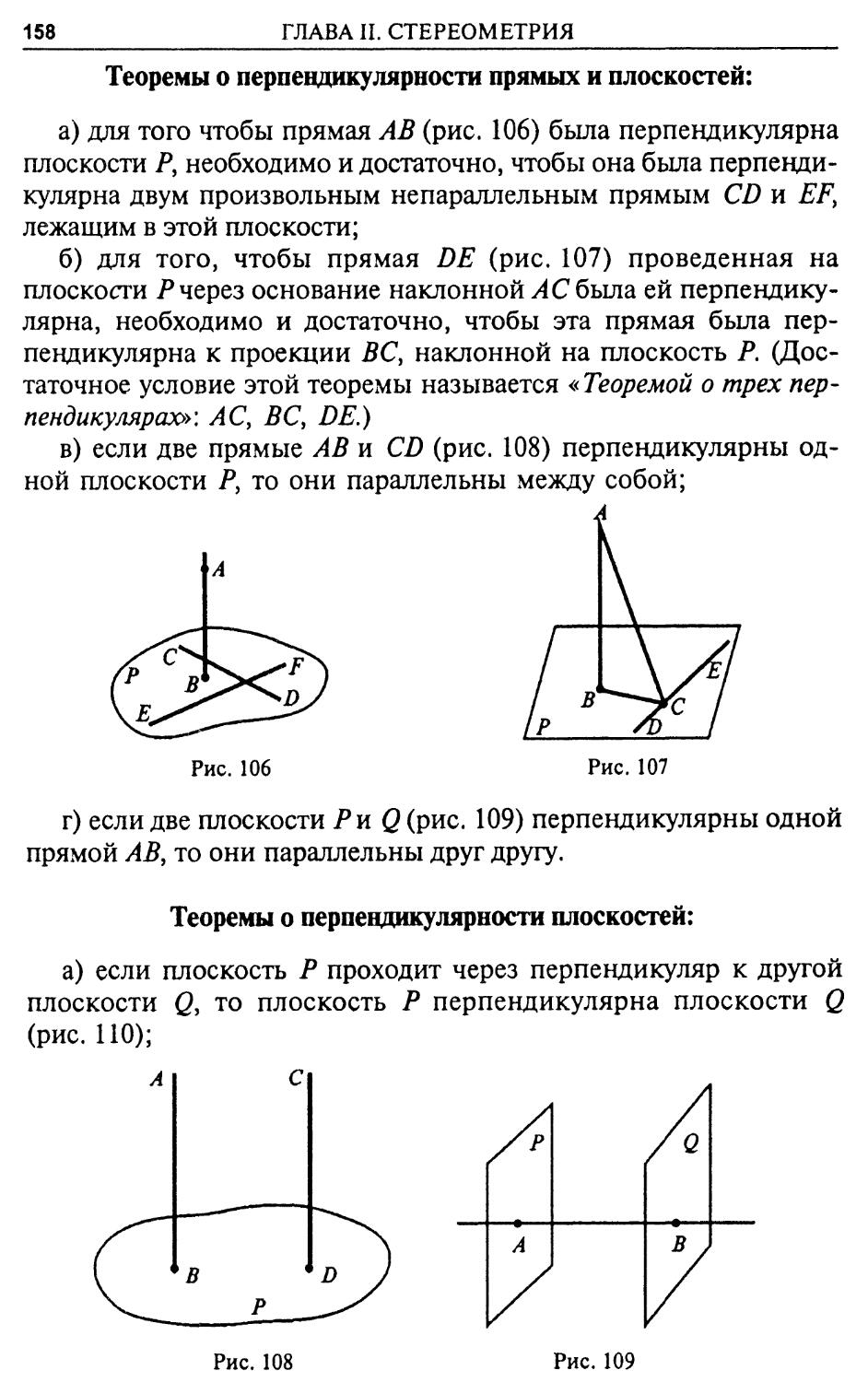
Все три срединных перпендикуляра пересекаются в одной точке О, являющейся центром окружности, описанной вокруг треугольника, т.е. проходящий через все его вершины (рис. 4).
Если треугольник остроугольный, центр описанной окружности лежит строго внутри треугольника (рис. 4а).
Если треугольник, прямоугольный, центр описанной окружности лежит в середине гипотенузы (длина гипотенузы равна диаметру этой окружности) (рис. 46).
Если треугольник тупоугольный, центр описанной окружности лежит вне треугольника (рис. 4в).
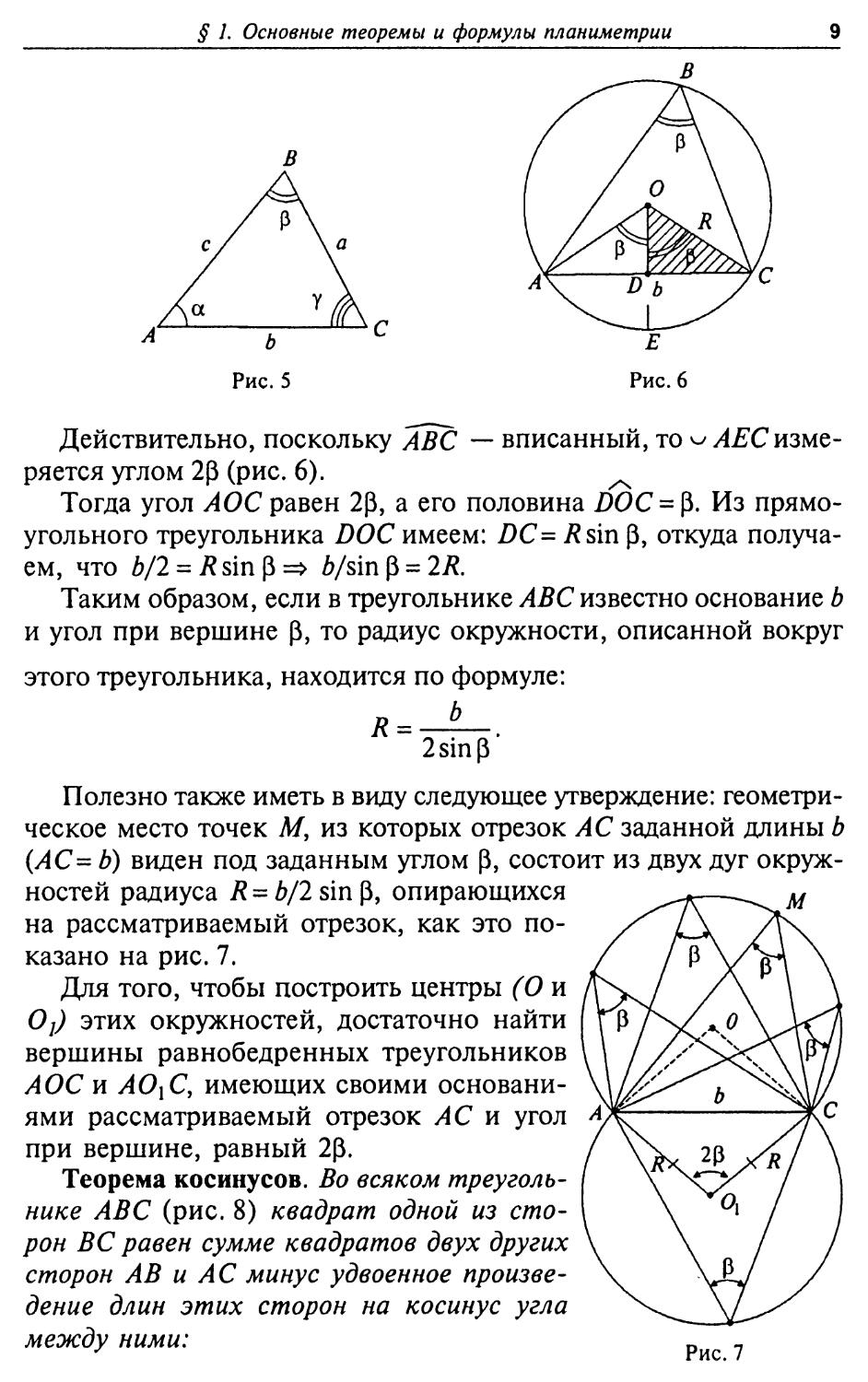
Теорема синусов. Во всяком треугольнике АВС (рис. 5) отношение любой стороны к синусу противоположного ей угла есть постоянная для данного треугольника величина, т.е.:
а _ b _ с
sin a sin(3 sin у’
£4С = а, АВС = $, ВСА = у, ВС= а, АС= Ь, АВ = с. Если R — радиус окружности, описанной вокруг треугольника АВС, то
sin a smp sin у
2
Термин «орто» означает «перпендикулярность».
£ 7. Основные теоремы и формулы планиметрии
9
Рис. 5
Действительно, поскольку АВС — вписанный, то ЛЕС измеряется углом 20 (рис. 6).
Тогда угол AOC равен 20, а его половина DOC = 0. Из прямоугольного треугольника DOC имеем: DC= Asin 0, откуда получаем, что Ь/2 = R sin 0 => d/sin 0 = 2R.
Таким образом, если в треугольнике АВС известно основание b и угол при вершине 0, то радиус окружности, описанной вокруг этого треугольника, находится по формуле:
R = ——.
2 sin р
Полезно также иметь в виду следующее утверждение: геометрическое место точек М, из которых отрезок АС заданной длины b
(АС=Ь) виден под заданным углом р, состоит из двух дуг окруж-
ностей радиуса R = b/2 sin р, опирающихся на рассматриваемый отрезок, как это показано на рис. 7.
Для того, чтобы построить центры (О и Oj) этих окружностей, достаточно найти вершины равнобедренных треугольников А ОС и АОjC, имеющих своими основаниями рассматриваемый отрезок АС и угол при вершине, равный 2р.
Теорема косинусов. Во всяком треугольнике АВС (рис. 8) квадрат одной из сторон ВС равен сумме квадратов двух других сторон АВ и АС минус удвоенное произведение длин этих сторон на косинус угла между ними:
Рис. 7
10
ГЛАВА I. ПЛАНИМЕТРИЯ
В
Рис. 8
ВС2 = АВ2 + АС2 - 2АВ • АС • cos ВАС.
Теорема Пифагора. В прямоугольном треугольнике АВС (рис. 9) квадрат гипотенузы равен сумме квадратов его катетов:
ВС2 = АВ2 + АС2.
Подобие плоских фигур. Две плоские фигуры (например, треугольники АВС и AtBt Ct) называются подобными, если существует отображение одной на другую, при котором расстояние между образами любых двух точек и Xj относится к расстоянию между прообразами этих точек Хи У как одно и то же число к. Число к называется коэффициентом подобия (рис. 10).
Подобие треугольников. В частности, два треугольника являются подобными, если углы одного треугольника равны углам другого треугольника, а противолежащие равным углам стороны пропорциональны (рис. 10).
ААХ=АА,АВ^АВ,АСХ = АС, =	=
Признаки подобия треугольников
По трем сторонам. Для того, чтобы два треугольника были подобны, необходимо и достаточно, чтобы три стороны одного треугольника были пропорциональны трем сторонам другого треуголь-
l*i Г, | = Л • | АУ|
Рис. 10
§ 1. Основные теоремы и формулы планиметрии	11
По двум углам. Для того, чтобы два треугольника были подобны, необходимо и достаточно, чтобы два угла одного треугольника были равны двум углам другого треугольника.
По двум сторонам и углу. Для того, чтобы два треугольника были подобны, необходимо и достаточно, чтобы две стороны одного треугольника были пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, были равны.
Следствия
1.	В подобных фигурах (например, треугольниках) углы между любыми сходственными линейными элементами равны, а длины этих элементов относятся как коэффициент подобия к.
Так, например, длины сходственных сторон АВ и АХВХ, биссектрис 1Х и I, медиан тх и т, высот hx и й, периметров Pj и Р, радиусов вписанных гх и г и описанных Rx и R окружностей относятся как к:
АВ I т h Р г R
2.	В подобных фигурах площади любых сходственных элементов относятся как квадрат коэффициента подобия к?.
Так, например, для площадей SA в с и SABC подобных треугольников справедливо соотношение:
54AC| г !:2 $АВС
Площадь треугольника. Для нахождения площади треугольника со сторонами ВС=а, АС=Ь, АВ=с и противолежащими им углами ВАС = а, АВС = р, ВСА = у (рис. 5) наиболее употребительны следующие формулы:
а)	5 = \aha = ^bhb =^chc>
где ha, hb, и hc — длины высот треугольника, проведенных к соответствующим сторонам;
б)	S = — Z>c sin а = -асsinР = -aZ>sin г.
2	2	2
в)	формула Герона: S = 7 р(р - а)(р -Ь)(р-с), где р = (а + b + с) —
полупериметр треугольника.
12
ГЛАВА I. ПЛАНИМЕТРИЯ
Кроме того, справедливы формулы, выражающие площадь треугольника через его стороны и радиус вписанной или описанной окружности;
Г) s = р • г
Доказательство. Действительно, площадь треугольника АВС (рис. 2) можно представить как сумму площадей трех треугольников О АВ, ОАС и О ВС, имеющих общую вершину в центре О вписанной в треугольник АВС окружности. Каждый из этих треугольников имеет своим основанием какую-либо сторону треугольника АВС и одинаковую высоту, равную радиусу г вписанной окружности. Поэтому
$АВС = $ОАВ + $ОАС + $ОВС ~ ~	~ ДГ = р • Г,
что и требовалось доказать. Очевидно, что такая же формула верна и для произвольного выпуклого многоугольника, если только в него можно вписать окружность;
Доказательство. Действительно, S = 1/2 • Ьс • sin а. С другой стороны, по теореме синусов a/sina = 27?, или sina = a/2/?. Подставляя это выражение в формулу для площади S, получим рассматриваемое соотношение.
Как уже отмечалось, если треугольник АХВХСХ получается из треугольника АВС преобразованием подобия с коэффициентом подобия к, то 5^^ сх = $авс- Полезно иметь в виду более общее утверждение;
е) Теорема. Если в треугольнике АВС одну из сторон АВ изменить в к раз (АВХ =к- АВ, рис. 11), а другую — в т раз (АСХ = т • АС), оставив без изменения угол между ними, то площадь получившегося треугольника АВХ Q изменится в к - т раз (т.е. SAB^ = к - т- SABC).
Действительно,
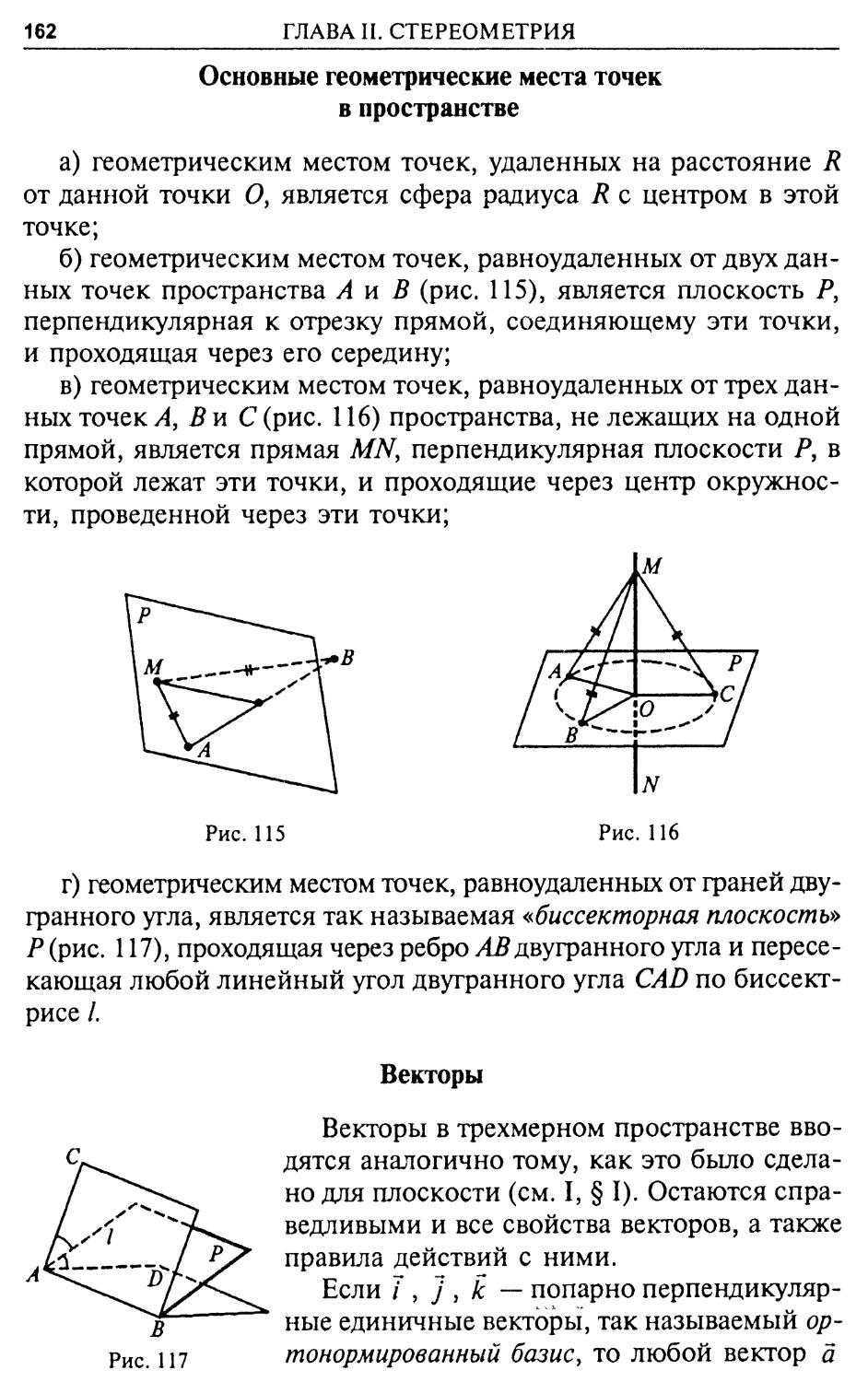
SAB[Ci = ^ЛВХ • АСХ • sin a = ^(к - АВ)(т • AC)sin a = = к m SABC.
Очевидно также, что при к=т треугольник АВХСХ получается из треугольника АВС преобразованием подобия с коэффициен-
§ 1. Основные теоремы и формулы планиметрии
13
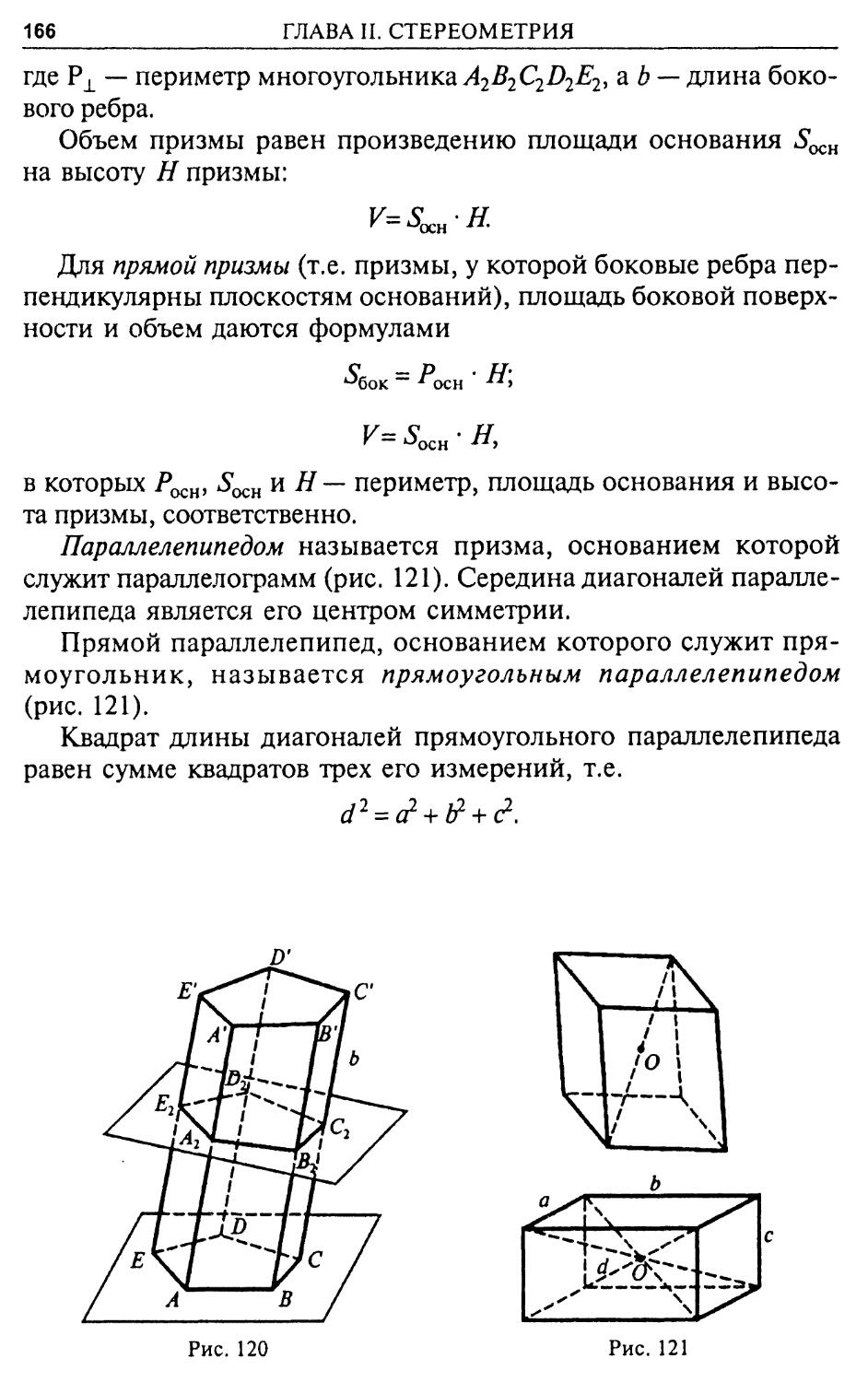
том к. При этом полученная формула переходит в уже известную формулу SAB^ = Л2 • SABC для площадей подобных треугольников.
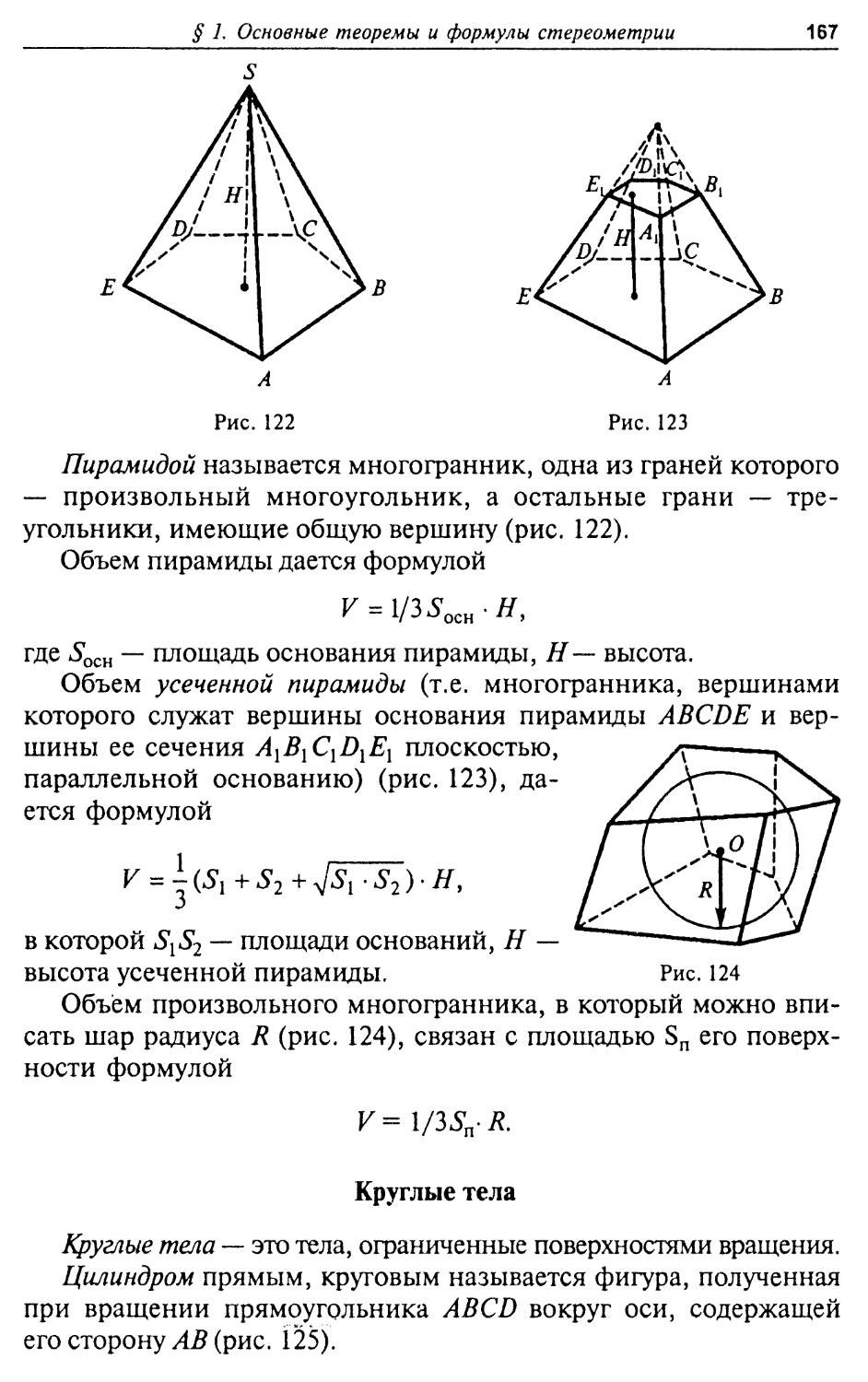
Четырехугольники. Четырехугольник называется выпуклым, если он расположен по одну сторону от любой из своих сторон (рис. 12).
Если диагонали выпуклого четырехугольника равны dx и d2 и образуют угол а, то площадь четырехугольника дается формулой:
Середины сторон произвольного четырехугольника К, L, М, N являются вершинами некоторого параллелограмма. Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника (рис. 13).
Средние линии (т.е. отрезки прямых, соединяющие середины противоположных сторон) четырехугольника в точке своего пересечения делятся пополам.
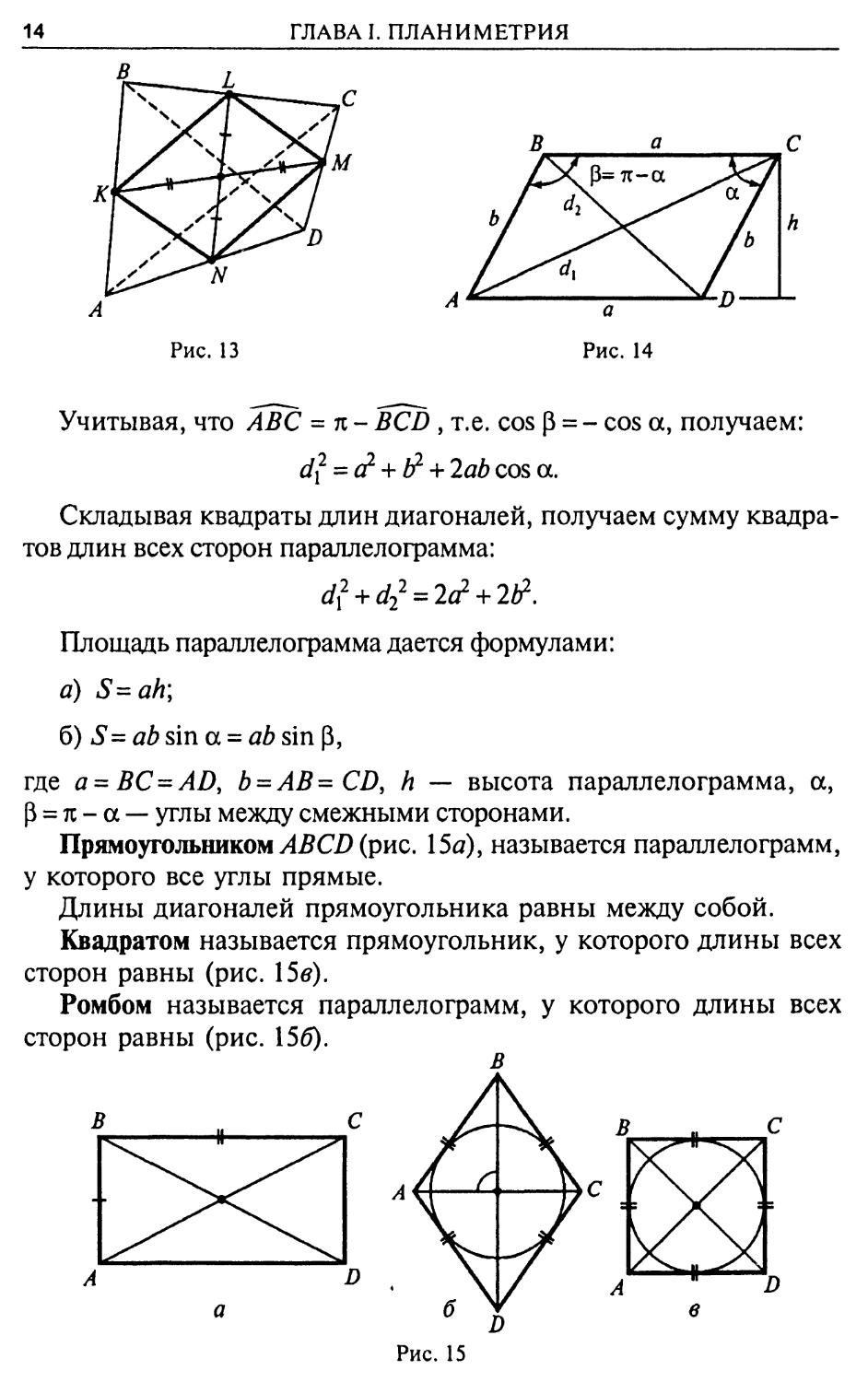
Параллелограмм — это четырехугольник ABCD (рис. 14), у которого противоположные стороны попарно параллельны. Длины противоположных сторон равны.
Теорема 1. Для того, чтобы выпуклый четырехугольник был параллелограммом, необходимо и достаточно, чтобы его диагонали в точке пересечения делились пополам.
Теорема 2. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (рис. 14).
Доказательство. По теореме косинусов из треугольника BCD следует:
d2=c? + b2 - lab cos а.
По той же теореме из треугольника АВС находим: dx =£ + &- lab cos р.
14
ГЛАВА I. ПЛАНИМЕТРИЯ
Учитывая, что АВС = л - BCD , т.е. cos р = - cos а, получаем: df = а2 + & + 2ab cos а.
Складывая квадраты длин диагоналей, получаем сумму квадратов длин всех сторон параллелограмма:
df + d-? = 2(? + 2l?.
Площадь параллелограмма дается формулами:
a)	S=ah\
б)	S=ab sin а = ab sin р,
где а = BC = AD, b = AB- CD, h — высота параллелограмма, а, р = л - а — углы между смежными сторонами.
Прямоугольником АВ CD (рис. 15а), называется параллелограмм, у которого все углы прямые.
Длины диагоналей прямоугольника равны между собой.
Квадратом называется прямоугольник, у которого длины всех сторон равны (рис. 15в).
Ромбом называется параллелограмм, у которого длины всех сторон равны (рис. 156).
в
Рис. 15
£ 1. Основные теоремы и формулы планиметрии
15
Диагонали ромба и квадрата взаимно перпендикулярны.
В ромб и квадрат можно вписать окружность, центр которой находится в точке пересечения диагоналей.
Трапеция — это выпуклый четырехугольник ABCD (рис. 16), у которого две противоположные стороны (основания) параллельны, а две другие не параллельны.
Средняя линия трапеции EF — отрезок, А соединяющий середины не параллельных сторон, параллельна ее основаниям. Длина средней линии равна полусумме длин оснований. Площадь трапеции с основаниями AD= а, ВС= b и высотой h дается формулой:
а + b , 5-—*.
Теорема 1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы длин противоположных сторон были равны друг другу (рис. 17а).
Теорема 2. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны л (рис. 176).
Рис. 17
О ГЕОМЕТРИИ ОКРУЖНОСТИ
Окружность геометрическое место точек, удаленных на одно и то же расстояние R от заданной точки О, её центра.
Круг — часть плоскости, ограниченная окружностью:
а)	длина окружности С=2лЯ;
б)	площадь круга 5 = яЯ2.
16
ГЛАВА I. ПЛАНИМЕТРИЯ
Угол между двумя радиусами окружности называется центральным углом (рис. 18). Если а — число радианов* в центральном угле, то:
а)	длина / дуги, на которую опирается центральный угол, равна l=a-R;
б)	площадь S центрального сектора OADB круга с углом а при вершине Сдается формулой:
5 = - Я2а;
2
в)	площадь сегмента ADB определяется как разность площади сектора OADB и площади треугольника ОАВ
1 э
5 = ~Т?2(а - sin а),
где R ~ радиус окружности.
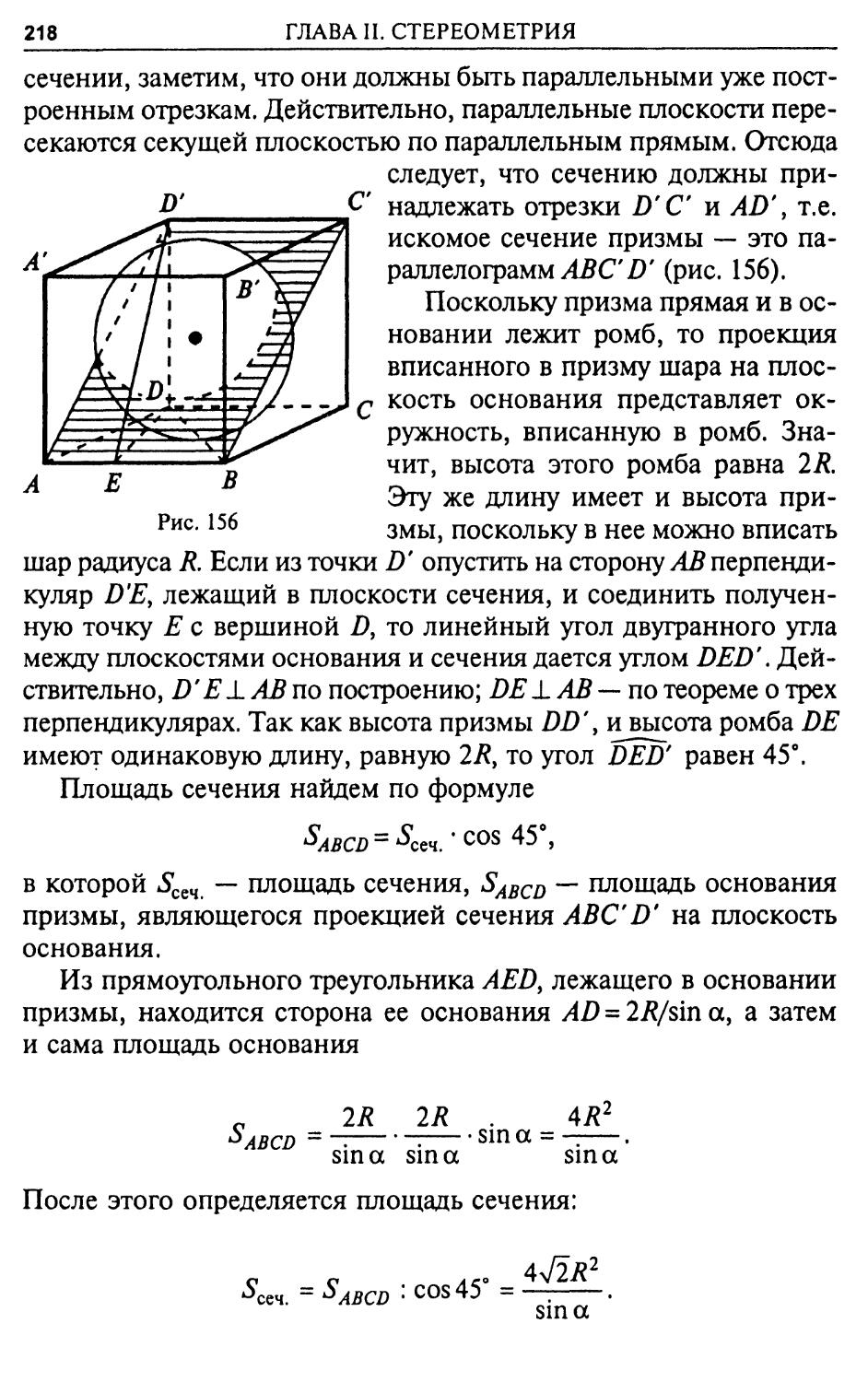
Угол АС В, образованный двумя хордами СА и СВ, исходящими из одной точки С окружности (рис. 19), называется вписанным. Величина вписанного угла р равна половине величины центрального угла а, опирающегося на ту же дугу окружности
Р = а/2.
Угол, образованный хордой, стягивающей дугу АВ окружности с центральным углом а и касательной AD к окружности, проведенной через один из концов хорды, также равен а/2 (рис. 19).
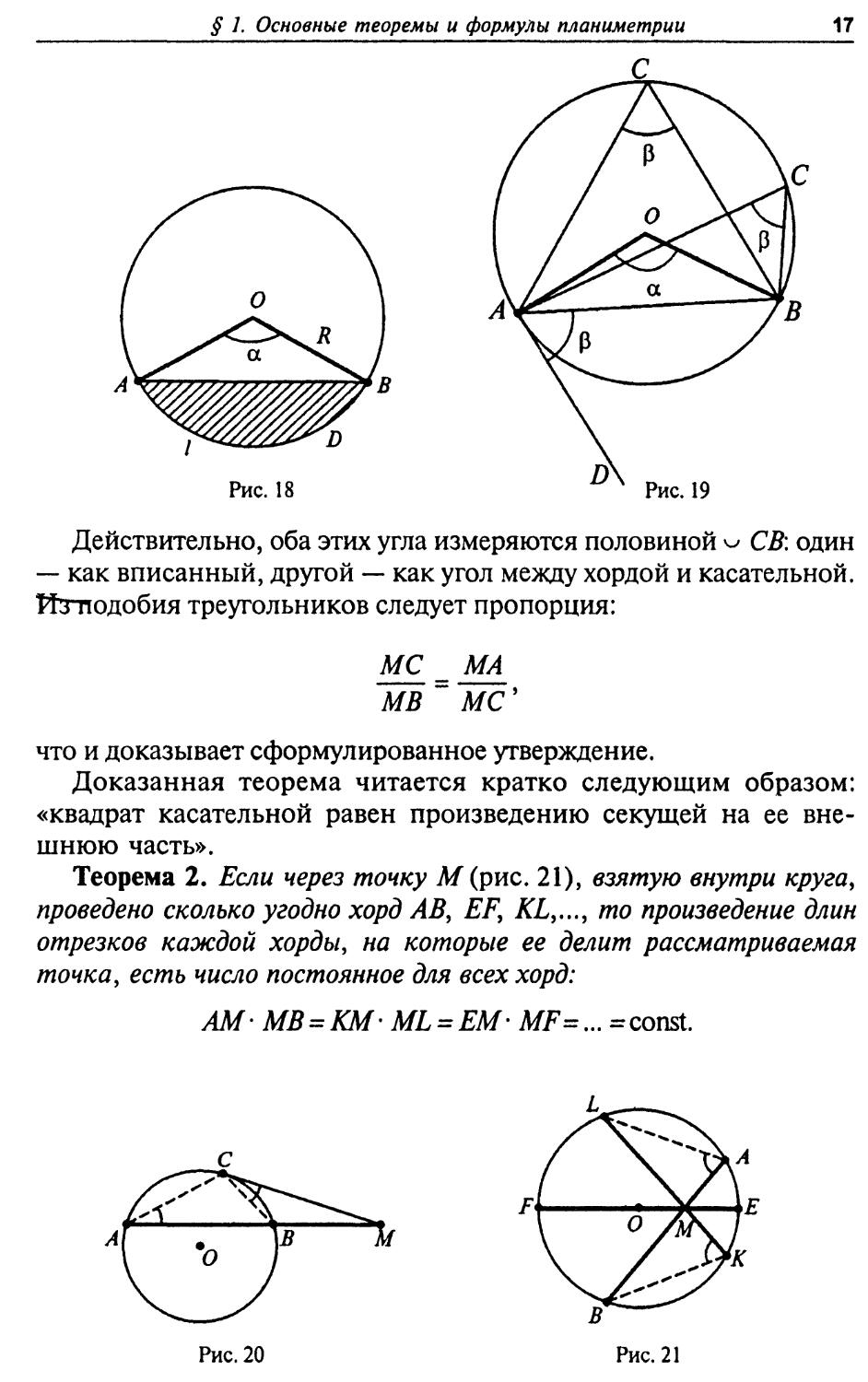
Касательные, проведенные к окружности из одной точки, имеют одинаковую длину.
Теорема 1. Если из одной точки М (рис. 20), взятой вне круга, проведены к нему какая-нибудь секущая МА и касательная МС, то произведение длины секущей на длину ее внешней части МВ равно квадрату длины касательной:
МС2 = МА- МВ.
Доказательство. Соединим точку Сотрезками СВ и СА с точками В и А. Треугольники^ВСМ и АСМ подобны: у них угол СМВ — общий, а САМ = ВСМ .
Радиан — это центральный угол, опирающийся на дугу окружности, длина которой равна ее радиусу. В полном развернутом угле — 2л радиан.
§ 1. Основные теоремы и формулы планиметрии
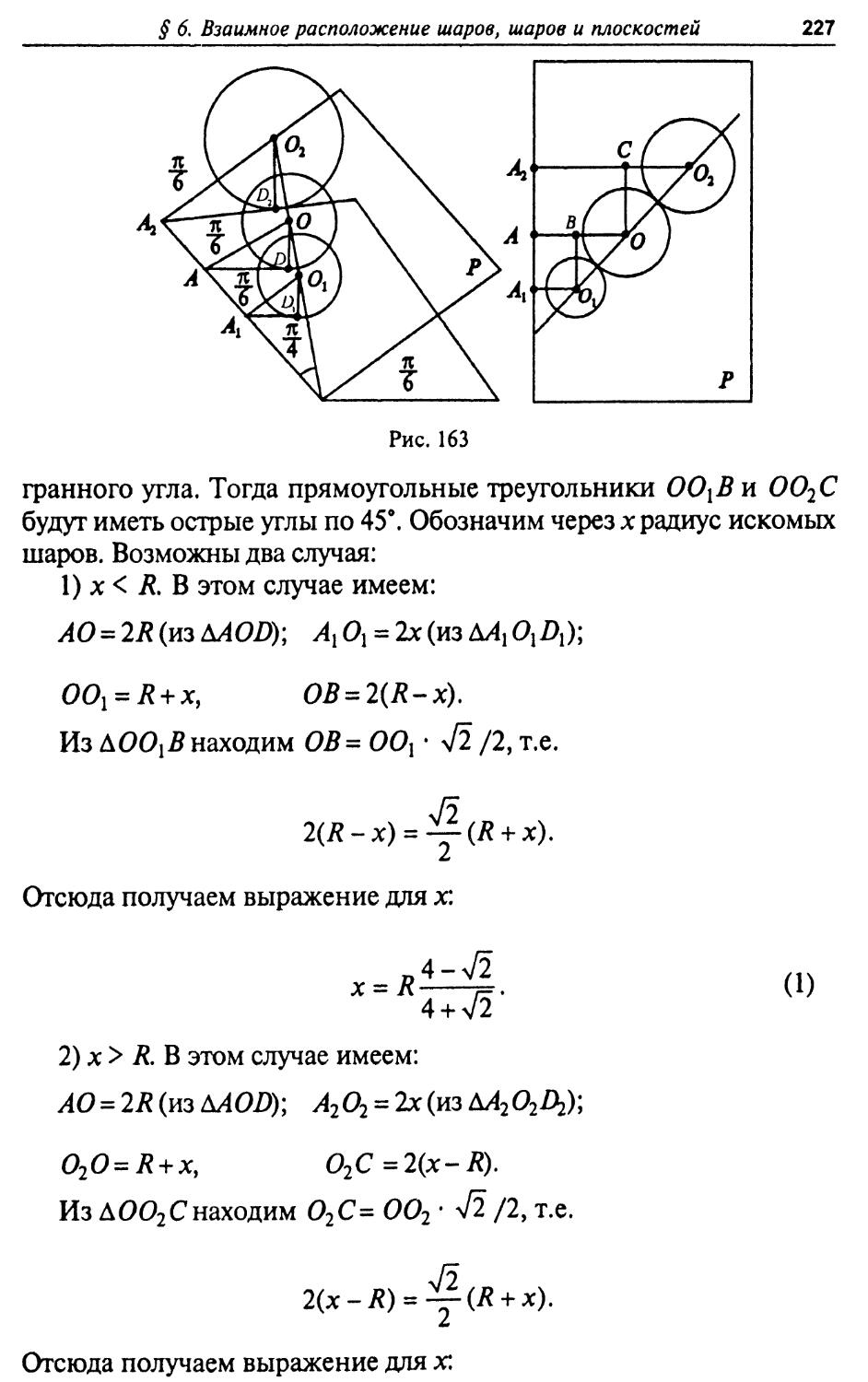
17
Действительно, оба этих угла измеряются половиной СВ: один —- как вписанный, другой — как угол между хордой и касательной, йтподобия треугольников следует пропорция:
МС = МА МВ МС'
что и доказывает сформулированное утверждение.
Доказанная теорема читается кратко следующим образом: «квадрат касательной равен произведению секущей на ее внешнюю часть».
Теорема 2. Если через точку М (рис. 21), взятую внутри круга, проведено сколько угодно хорд АВ, EF, KL,,.., то произведение длин отрезков каждой хорды, на которые ее делит рассматриваемая точка, есть число постоянное для всех хорд:
AM- МВ = КМ-ML = EM- MF=... = const.
Рис. 20
Рис. 21
18
ГЛАВА I. ПЛАНИМЕТРИЯ
Доказательство. Соединим точки А и L, К и В отрезками прямых. Треугольники ALM и КМВ подобны. Углы AML и КМВ равны как вертикальные, а углы MAL и МКВ — как вписанные и опирающиеся на одну и ту же дугу LFB. Из подобия этих треугольников следует пропорция:
AM = ML
КМ МВ'
или AM - МВ^КМ' ML, что доказывает утверждение теоремы.
Векторы. Упорядоченная пара А, В несовпадающих точек определяет направленный отрезок с началом А и концом В. С помощью этого отрезка задается преобразование плоскости — параллельный перенос, при котором каждая точка М отображается на такую точку Мх, что луч ММХ сонаправлен с лучом АВ и расстояние ММХ равно расстоянию АВ (рис. 22).
Это преобразование называется вектором.
Вектор изображается направленным отрезком и обозначается символом АВ или а .
Один и тот же параллельный перенос можно задать с помощью бесконечного количества направленных отрезков. Все такие отрезки имеют одинаковую длину, называемую длиной или модулем вектора | ЛВ| = |й |, параллельны (или лежат на одной прямой) и направлены в одну сторону. Поэтому два вектора считаются равными, если они изображаются отрезками, лежащими на одной или параллельных прямых, имеющими одинаковую длину и направленными в одну сторону.
Если векторы АХВХ и А2В2 (рис. 23) изображаются отрезками, лежащими на одной или параллельных прямых, то они называются коллинеарными.
Для каждой точки А можно построить единственную точку В такую, что АВ = а (рис. 24). Это построение называется откладыванием вектора а от точки А.
Рис. 22
Рис. 23
Рис. 24
§ 1. Основные теоремы и формулы планиметрии
19
Рис. 25
Сумма и разность векторов. Два вектора складываются по правилу параллелограмма. Для этого оба вектора откладываются из одной точки и строится параллелограмм, сторонами которого являются вектора (рис. 25я).
Чтобы получить сумму большего числа векторов, нужно отложить от произвольной точки А первый вектор а , а каждый последующий вектор b , с , d отложить от конца предыдущего. Суммой будет вектор, начало которого совпадает с началом (точка А) первого, а конец — с концом (точка Е) последнего вектора (рис. 256).
Разностью двух векторов а и b называется такой вектор с , который, будучи сложенным с вектором b , дает а . Разность двух векторов b и а представляется направленным отрезком, соединяющим концы этих векторов и имеющим направление «к концу того вектора, из которого вычитают» (рис. 26).
Если для вектора b ввести противоположный ему вектор (-6), который колли
неарен вектору b , имеет тот же модуль, но направлен в противоположную сторону, то разность векторов а и b представляется как сумма вектора а и вектора (~Ь ), т.е. с = а + (-5).
Сумма противоположных векторов равна 0: £ + (-£) = б.
Под произведением X а вектора а на число X понимается такой вектор, который коллинеарен вектору а , имеет модуль [ X I I а | и направлен в ту же сторону, что и а — если X положительно, и в противоположную — если X отрицательно. Геометрически умножение вектора на число означает растяжение или сжатие вектора и,
20
ГЛАВА I. ПЛАНИМЕТРИЯ
возможно, перемену его направления на противоположное (рис. 27). Имеют место равенства:
(Х + |1)я = Ха +ця ,
Х(д + b) = Ха + X Z?,
в которых X и ц — произвольные действительные числа.
Вектор с = Ха +цЬ называется линейной комбинацией векторов а и b . Если А, и ц — произвольные действительные числа, а а и b — неколлинеарные вектора, то, варьируя эти числа, можно получить произвольный вектор плоскости.
Если ОА = а и ОВ = Ь — два_неколлинеарных вектора, отложенные от точки О, то вектор ОС, оканчивающийся в середине отрезка АВ, равен полусумме векторов а и b , т.е.
2
Вообще, вектор точки F, делящий отрезок АВ в отношении X: ц (X, ц — положительные числа) и начинающийся в точке О, дается формулой (рис. 28):
Рис. 28
£ 1. Основные теоремы и формулы планиметрии
21
ОР -	+
Х + ц
РАЗЛОЖЕНИЕ ВЕКТОРА НА КОМПОНЕНТЫ. КООРДИНАТЫ ВЕКТОРА
Рис. 29
Если а и b — два неколлинеарных вектора в плоскости, а z — произвольный вектор в той же плоскости, то всегда существуют такие числа аир, что z -аа +р5.В этом случае говорят, что вектор z разложен по векторам а и b . На рис. 29 все три вектора отложены от одной точки О,
Если Т и j — неколлинеарные единичные векторы (т.е. векторы, модуль которых равен единице I i I = I j I = 1), то произвольный вектор плоскости может быть представлен в виде АВ = a =axi + a2j. В этом случае говорят, что вектор АВ имеет в системе i , j координаты {aXi а2}.
Если векторы / и j взаимно перпен
дикулярны, причем вектор J может быть получен из вектора i поворотом против часовой стрелки, то говорят, что прямые, в которых лежат векторы i и j , образуют декартову прямоугольную систему координат, а числа {ах, а2}, называются декартовыми координатами вектора а.
Пусть точка А с координатами (xj,^j) — начало вектора а , а точка В с координатами (х2, у2) ~ его конец (рис. 30). Тогда координаты вектора связаны с координатами точек А и В формулами:
вх=х2-хъ a2 = y2-yb
т.е. декартовы координаты вектора равны разности соответствующих координат конца вектора и его начала.
Декартовы координаты вектора а являются проекциями этого вектора на соответственные оси системы координат:
= прх а , а2 = пру а .
Пусть вектор а имеет координаты {аь а2}, что записывается в виде а {я15 а2}, а вектор b — {b[f b2}, или b {bXi b2}.
22
ГЛАВА I. ПЛАНИМЕТРИЯ
Тогда:
1)	(5 4- Ь ) {#i 4- Z>|, а2 +Ь-^}
2)	(а - Ь) {Д] - Ь}, а2 - Ь2]\
3)	\а {Хаь Ха2};
4)	(Хя 4-	) {Xtfj 4- p,Z>j, \а2 4- pZ>2},
т.е. действиям с векторами отвечают идентичные действия с их координатами.
Докажем, например, что вектор а + b
имеет координаты {ах + Ьъ а2 4- Ь2}, Действительно, векторы а и b
можно записать как
а = axi +a2j, b = bj + b2j.
Сумма этих векторов представляется в виде: a + b = (ax + b{)T + (a2 + b2)J.
Отсюда следует, что числа а} 4- Ьх и а2 4- Ь2 являются координаторами вектора а 4- b .
Модуль вектора а определяется через его декартовы координаты посредством равенства:
| а | = yjal+aj, а единичный вектор ё, имеющий с вектором а одинаковое направление, записывается в виде ё = а/\ а | и имеет координаты: + а} , а2Ца^ + а}}.
Скалярное произведение векторов. Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними*. Иными словами, скалярное произведение векторов — это число.
Если через <р обозначить угол между векторами а и b , а через a b — их скалярное произведение, то
а • b = | а | \Ь I cos ср.
Углом (р между векторами а и b называется угол между их направлениями.
§ 7. Основные теоремы и формулы планиметрии
23
Необходимым и достаточным условием перпендикулярности двух ненулевых векторов является равенство нулю их скалярного произведения:
а ± b <=> а b = 0 (а * О, b * 0).
Свойства скалярного произведения:
1)	а b = Ь-а (переместительныйзакон);
2)	(ka)b =(kab) (сочетательный закон);
3)	а (Ь + с) = а b + а с (распределительный закон).
Скалярное произведение выражается через координаты сомножителей по формуле:
a b — ахЬх + #2^2*
Доказательство. Действительно, представим векторы а и b равенствами:
а = axi + л2Л b = bxi + b2J.
Используя свойства скалярного произведения, находим:
ab = (ах1 + а2])(Ьх1 + Ь2]) = = axbx(i 1) + axb2(i J) + bxa2(Ji) + a2b2(J J).
Поскольку скалярные произведения (ij) (Ji) равны нулю вследствие перпендикулярности векторов i и j , а скалярные произведения (it) (]]) равны единице, то из последнего равенства получаем формулу: ab = ахЬх + а2Ь2.
Отсюда, в частности, следует:
(аа) = а2 = | а || a |cos0 = | а |2 =ах +а2, I а | = 7«i2+<*22.
Необходимым и достаточным условием перпендикулярности ненулевых векторов а {дь а2} и b {/>] Ь2} является равенство:
°1 ^1 + а2 = 0.
24
ГЛАВА I. ПЛАНИМЕТРИЯ
Зная скалярное произведение векторов, можно определить угол между векторами:
ab cos ф =--пт
I «I\ь
или в координатной записи:
ci\b\ + djbj COS ф = -===^=-.
Val2 + д2 • 7612 + *2
Поскольку косинус острого угла положителен, а косинус тупого угла — отрицателен, то, если скалярное произведение положительно, векторы образуют острый угол, а если отрицательно — тупой.
На этом закончим обзор основных теорем и формул планиметрии. Задачи, которые приведены ниже, дополняют предложенный список, поэтому они снабжены решениями; ознакомление с ними весьма полезно.
ЗАДАЧИ
Задача 1. (Теорема о свойстве биссектрисы внешнего угла треугольника). Пусть BD — отрезок биссектрисы внешнего угла треугольника АВС (рис. 31), заключенный между вершиной В треугольника и точкой D пересечения биссектрисы с продолжением основания АС. Тогда отношение расстояний точки D до вершин треугольника при его основании пропорционально боковым сторонам треугольника, т.е.
/	АР = АВ
CD СВ ’
/ЧЦ	Решение. Обозначим АВС = а, тогда
/	\	внешний угол при вершине В будет равен
у!	С	р л - a, a CBD = л/2 - а/2.
Рис. 31	Легко видеть, что площади треугольни-
ков ABD и CBD, имеющих общую вершину В и лежащих на одной прямой основания, относятся как длины этих оснований, т.е. SABD: Scbd-AD : CD.
£ 7. Основные теоремы и формулы планиметрии
25
С другой стороны, площади треугольников ABD и CBD можно записать в следующем виде:
SABD =\АВ .5Z)sinfa + ^-^l = -Л5- BDcos-, 2	2 2	2	2
SCBD = X-CB-BDsm\^-^\=X-CB- BDcos^.
Отсюда видно, что SABD: SCBD = АВ: СВ. Сравнивая последнее отношение площадей с полученными ранее, заключаем, что
AD: CD = AB: СВ.
Задача 2. Доказать, что треугольник, в котором равны длины: а) либо двух высот’, б) либо двух медиан’, в) либо двух биссектрис, является равнобедренным.
Решение, а) пусть сначала в треугольнике равны длины двух каких-нибудь высот, например ha = hc. Покажем, что треугольник — равнобедренный. Для этого запишем площадь 5треугольника АВС двумя различными способами:
с 1 , 1 ,
5 =	 ha =-c-hc,
где с = АВ, а = СВ. Поскольку ha = hc то АВ = СВ и треугольник АВС — равнобедренный;
б) пусть теперь равны длины двух медиан, например та = тс. Воспользовавшись формулами, выражающими длины медиан через стороны треугольника, получаем:
4/я02 + a2 = 2Z?2 + 2с2,
4/я2 + с2 = 2b2 + 2a2.
Поскольку та = тс, то почленная разность этих равенств дает а2 - с2 = 2(<? - о2),
откуда следует, что а = с и треугольник АВС — равнобедренный;
в) наконец, рассмотрим случай равных биссектрис. Пусть 1а = 1С. Используя формулу, выражающую длину биссектрисы через длины сторон треугольника и заключенный между ними угол, получим:
26
ГЛАВА I. ПЛАНИМЕТРИЯ
2iccosa/2 __ 2я й-cos у/2 b + c a + b
или
cos a/2 __ cos y/2 1/Й + 1/С ” \/Ь + \/а'
Предположим противное, т.е. что треугольник АВС не равнобедренный: а * с, пусть, например, а > с. Тогда 1/й + 1/с > \/Ь + \/а, а поскольку написанные выше дроби равны, то необходимо, чтобы и cos a/2 > cos у/2. Заметим далее, что функция у = cos х в первой четверти монотонно убывает. Поэтому из неравенства cos a/2 > cos у/2 следует неравенство a/2 < у/2 или a < у.
Таким образом, мы получили противоречивое утверждение: в треугольнике АВС против большей стороны а лежит меньший угол а. Поскольку этого не может быть, то наше исходное предположение а >с неверно. Аналогично доказывается, что а не может быть и меньше с. Остается единственный вывод: а = с и треугольник АВС — равнобедренный.
Задача 3. (Теорема тангенсов). Если b и с — две стороны треугольника, а р и у — противолежащие им углы, то имеет место соотношение
ь-с^щ-т b + c tg[(P+y)/2]’
называемое теоремой тангенсов.
Решение. Так как согласно теореме синусов
— = — = 2R, sin р sin у
то b = 2R sin р, с = 2R sin у, где R — радиус окружности, описанной вокруг треугольника. Далее имеем:
b-c _ 27?(sin р - sin у) _ 2 cos (р + у)/2 sin (Р - у)/2 b + c 2A(sin р + sin у) 2 sin (Р + у)/2 cos (р - у)/2 ’
или
b-c = tg(p — у)/2 b + c tg(p + y)/2’
что и требовалось доказать.
§ 1. Основные теоремы и формулы планиметрии
27
Применение теоремы тангенсов позволяет иногда упрощать вычисление неизвестных элементов треугольника. Пусть, например, в треугольнике заданы две стороны Ь, с и угол а, заключенный между ними. Тогда остальные углы треугольника р и у можно найти, используя соотношение
Р +у _ л-а _ л _ а 2” 2 и, таким образом,
tg (Р + у)/2 = tg (л/2 - а/2) = ctg а/2, tg(P-y)/2 = |^ctga/2.
Ь + с
Поскольку Ь, с и а известны, то легко вычисляются сумма углов (р + у) и их разность (р - у).
Конечно, эту задачу можно решить с помощью теорем косинусов и синусов, однако вычисления, производимые в случае использования теоремы тангенсов, проще.
Задача 4. Доказать следующие утверждения:
1.	Угол, вершина которого расположена вне круга, измеряется полуразностью дуг окружности этого круга, заключенных внутри угла;
2.	Угол, вершина которого расположена внутри круга, измеряется полусуммой дуг, которые высекают из окружности круга стороны угла и их продолжения;
3.	Угол, образованный касательной к окружности и хордой, исходящими из одной точки окружности, измеряется половиной дуги, заключенной внутри этого угла.
а	б	в
Рис. 32
28
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение, а) пусть угол АХМВХ с вершиной_в точке Мвне круга равен ф (рис.32а), а центральные углы АХОВХ = а и А2ОВ2 - р • Тогда
<р = |(а-р).
Действительно, = «/2 и А2ВХВ2 = р/2. Поскольку угол АхА2Вх — внешний угол треугольника МА2ВХ, то его величина равна сумме величин двух несмежных с ним углов АХМВХ и т.е. а/2 = ф + р/2 или ф = (а - Р)/2, что и требовалось доказать.
б)	пусть угол АХМВХ с вершиной в точке Мвнутри круга равен Ф (рис. 326), а центральные углы А^ОВХ = а и A^Ofy = р. Тогда
Ф = |(а + Р).
Действительно, АХА2В} =а/2 и А2ВХВ2 = Р/2. Тогда внешний к треугольнику МА2В} угол <р равен а/2 + р/2, что и требовалось доказать.	___
в)	пусть угол АМВ с вершиной в точке М, лежащей на окружности, равен <р (рис. 32в), а центральный угол МОА = а. Тогда
Действительно, q = n/2-0MA, ОМА = (п-а)/2 и <р = я/2 -- ОМА = а/2, что и требовалось доказать.
Задача 5. Доказать, что высоты АР, BQ, CR треугольника АВС являются биссектрисами углов треугольника PQR.
Решение. Пусть точка О — ортоцентр треугольника АВС, т.е. точка пересечения его высот (рис. 33).
Тогда можно построить три окружности с в	центрами в точках Оь О2 и О3, являющихся
серединами отрезков АО, ВО и СО, соответ-ственно, причем точки А, О, R, Q лежат на \ первой из этих окружностей, точки С, О, Р, ( /'$4/	С — на второй и точки В, О, Р, R — на тре-
X-Jr ~ ус тьей окружности. Действительно, проведем, v	например, через точки А, О и R окружность.
Рис. 33	Понятно, что ее центр Ох должен совпадать с
серединой отрезка АО, поскольку угол ARO — прямой и, следовательно, должен опираться на диаметр. Кроме того, точка Q также должна лежать на этой окружности, посколь
£ L Основные теоремы и формулы планиметрии	29
ку угол AQ0 — прямой. Если бы точка Слежала внутри круга, этот угол был бы тупой, а если — вне круга, то угол был бы острый (см. задачу 4 этого параграфа). Аналогично доказываются и утверждения относительно двух других окружностей.
Рассмотрим первую окружность. Углы RAO и RQO являются вписанными и опирающимися на одну и ту же дугу, поэтому их величины равны. Аналогично, равны величины углов PQO и РСО, поскольку эти углы также являются вписанными и опирающимися на одну и ту же дугу в окружности с центром О2. Кроме того, равны величины углов РАО и РСО, поскольку эти углы входят в прямоугольные треутольникиу!5Р и BCR с общим углом АВС. Отсюда следует, что RQO = PQO и, следовательно, BQ — биссектриса угла PQR.
Аналогично доказывается, что две остальные высоты являются биссектрисами углов QRP и RPQ треугольника PQR.
Заметим, наконец, что в том случае, когда треугольник АВС — тупоугольный и точка пересечения высот лежит вне треугольника, приведенное доказательство не претерпевает существенных изменений.
Задача 6. Доказать, что в прямоугольном треугольнике сумма длин катетов равна сумме диаметров вписанной и описанной окружностей:
a + b = 2r+2R,
при этом между острым углом а треугольника и отношением радиуса вписанной окружности к радиусу описанной к окружности существует зависимость:
1 г sin а + cos а = 1 + —, где а-ВС и Ь- АС — катеты треугольника, г и R — радиусы вписанной и описанной окружностей соответственно.
Решение. Пусть О — центр вписанной окружности, а Р, Q, R — точки ее касания со сторонами A^JBC и АС соответственно, величину угла G42? обозначим через а (рис. 34). А Так как центр О вписанной окружности находится в точке пересечения биссектрис, то в прямоугольных треугольниках RAO и
РАО\ RAO-PAO , а в треугольниках РВО и QBO\ PBO-QBO. Поэтому ^RAO-^PAO и ^PBO-^QBO. Отсюда следует, что AR-AP, BP=BQ и далее: AR + BQ-AB-2R.
Рис. 34
30
ГЛАВА I. ПЛАНИМЕТРИЯ
То, что центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы следует из теоремы о вписанных углах.
Прямой угол при вершине прямоугольного треугольника может опираться только на диаметр описанной окружности, поэтому длина гипотенузы всегда равна 2R.
Четырехугольник ORCQ — квадрат. Во-первых, у этого четырехугольника все углы — прямые. Кроме того, OR = OQ = г. Таким образом, ЯС= CQ=r и RC+ CQ=2r.
Далее имеем:
AR+BQ = AB=2R,
RC+CQ = 2r.
Складывая почленно эти равенства, получаем:
(ЛЯ + RC) + (BQ + CQ) = 2г+2 R, т.е. a+b = 2r+2R.
Разделив обе части последнего равенства на 2R и заметив, что a/2R = sin a, b/2R - cos а, получаем sin а + Cos а = 1 + r/R, откуда следует, что углы прямоугольного треугольника определяются отношением радиусов вписанной и описанной окружностей и, наоборот, отношение радиусов этих окружностей однозначно определяется углом прямоугольного треугольника.
Полученное соотношение можно преобразовать следующим образом:
sina + cosa = V2sin(a + Jt/4) = 1 + ~.
R
Отсюда следует
~ = V2 sin(a ч- л/4) -1.
Поскольку максимальное значение синуса равно единице, то наибольшее значение, которое может принимать отношение радиусов вписанной и описанной окружностей, равно V2-1 (в данном случае при а = л/4). Отсюда видно, что отношение r/R удовлетворяет неравенству:
Задача 7. Доказать, что трапеция может быть вписана в окружность в том, и только в том случае, когда она равнобочная.
£ 1. Основные теоремы и формулы планиметрии
31
Решение. Пусть трапеция ABCD — равнобочная (ВС || AD, АВ = CD). Покажем, что ее можно вписать в окружность.
Проведем через точки А, В и С окружность. Ее центр, как точка, равноудаленная от точек Ви С, должен лежать на срединном к отрезку ВС перпендикуляре. Поскольку, однако, такой перпендикуляр должен являться срединным и для отрезка AD равнобочной трапеции, то центр окружности должен быть также равноудален от вершин А и D. Следовательно, точка D также лежит на рассматриваемой окружности и трапеция ABCD вписана в эту окружность.
Обратно, пусть трапеция ABCD вписана в окружность. Покажем, что она — равнобочная. Согласно теореме о вписанных четырехугольниках, суммы противоположных углов трапеции равны 180°. Однако такой же величине равны и суммы углов при каждой боковой стороне трапеции (ВС || AD). Это может быть только в том случае, когда углы при основании трапеции равны, т.е. трапеция является равнобочной.
Задача 8. В произвольной трапеции через точку пересечения диагоналей параллельно ее основаниям проведена прямая. Доказать, что отрезок этой прямой, заключенный внутри трапеции, делится точкой пересечения диагоналей пополам, причем длина каждой части равна
ab а + Ь'
где а и Ь — длины оснований трапеции.
Решение. Пусть ABCD — произвольная трапеция с основаниями AD = a, ВС=Ь (рис. 35). Отрезок EF проходит через точку О пересечения диагоналей трапеции: EF\\ BC^AD.
Покажем сначала, что ЕО = FO. Для этого обозначим высоту трапеции через Н, а расстояние между прямыми ВС и EF— через h. Из подобия треугольников ЕВО и ABD следует, что
ЕО h
AD Н ’ или
EO = AD-^. н
Аналогично из подобия треугольников FCO и ACD следует
32
ГЛАВА I. ПЛАНИМЕТРИЯ
ИЛИ
FO h
AD Н ’
FO = AD-^~. н
Сравнивая эти пропорции, заключаем, что EO=FO, т.е. точка О делит отрезок EF пополам.
Обозначим длину каждого из отрезков ЕО и FO через х. Из подобия треугольников ОВС и OAD имеем:
ВО b	ВО ВО b
— = — или -----------=----=-----.
DO а ВО + DO BD a + b
Из подобия треугольников ОВЕ и ABD имеем:
ВО х
BD а'
Сравнивая эти две пропорции, получаем выражение для величины х:
х _ Ь а а + Ь
ab или х =-----.
а + b
Следствие. Середины оснований трапеции и точка пересечения ее диагоналей лежат на одной прямой.
Действительно, все три указанные точки являются серединами отрезков прямых, проведенных параллельно основанию треугольника ADM (М — точка пересечения боковых сторон трапе-
§ 1. Основные теоремы и формулы планиметрии
33
Рис. 37
ции ABCD (рис. 36), поэтому они принадлежат медиане этого треугольника, проведенной из вершины М к основанию AD.
Задача 9. {Теорема Л. Эйлера). Доказать, что сумма квадратов длин сторон произвольного выпуклого четырехугольника равна сумме квадратов его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей (рис. 37а).
а2 + Ь2 + с2* d2 = 5\2-ь 522 + 4р2.
Эта теорема обобщает известное утверждение, верное для параллелограммов и состоящее в том, что сумма квадратов сторон параллелограмма равна сумме квадратов длин его диагоналей. Действительно, в параллелограмме диагонали, пересекаясь, делятся пополам, поэтому расстояние р между их серединами равно нулю, и мы получаем наше утверждение как частный случай при р = 0 теоремы Эйлера.
Решение. Введем следующие векторы (рис. 376):
а - АВ, b=BC, c=CD, d = DA, 5j = AC, S2 = BD, p = MXM2.
Тогда AM\ = 5i/2, M2D = Si/2.
Очевидны (см. рис. 376) следующие векторные равенства:
а + b = 5*!, с + d = -5j, d + а — —52,
— 5i + рн—-5з + = 0.
2	2
34
ГЛАВА I. ПЛАНИМЕТРИЯ
Эти равенства можно разрешить относительно векторов а , b , с и d
5 = -1si_1s2-p;
2	2
b = 1.У1 + ^S2-p;
2	2
1	C	1 c -
C = --S1 +	+P-
2	2
Обозначим буквами без стрелочек длины векторов, т.е.
а=|а|, b =| Ъ |, с=|с|, d =\d |,	=| Si |, S2=|S2|, р =| р |.
Вычислим квадраты длин векторов а, b , с , d , для чего каждое из полученных равенств умножим скалярно само на себя.
Имеем:
й2 = - 5]2 + - Si + р2 - - S\S2 + 5jp - 52р,
ь2 = Isi +1 si + р2 +1 ад - s,p - s2p,
с2 = 1 s,2 +1 si + р2 - ±ад - s,p + s2p, 4	4	2
J2 = ~ 52 + ~ Si + р2 + - SXS2 + З^р + 52р.
Складывая почленно эти уравнения, находим:
a2 + Zz2 + ? + J2 = 5124-522 + 4р2,
что и составляет утверждение теоремы Эйлера.
Задача 10. (Теорема о четырехугольнике, вписанном в окружность), Произведения расстояний от любой точки окружности, описанной около выпуклого четырехугольника, до его противоположных сторон или их продолжений равны между собой (рис. 38);
ab^cd.
£ 1. Основные теоремы и формулы планиметрии	35
Решение. Пусть S — произвольная точка окружности, описанной около выпуклого четырехугольника ABCD, расположенная на AD, не содержащей вершин четырехугольника (рис. 38).
Точки Р, С, М и //являются основаниями перпендикуляров, опущенных из S, соответственно, на стороны AD, ВС, АВ, CD или на их продолжения. Длины этих перпендикуляров обозначим через а, Ь, с и d соответственно. Нужно доказать, что ab = cd.
Рассмотрим две пары подобных треугольников:
SAPS оо sCNS и SAMS оо SCQS.
Первая пара треугольников подобна
л Л'-***’ потому, что, во-первых, они — прямоу-
гольные, а во-вторых,jjmciot по равному острому углу (SAP = SCN = р , как углы, опирающиеся на одну и ту же дугу SD /-ач окружности).	/р^у /
Вторая пара прямоугольных треуголь-
ников также подобна, так как QCS = MAS.	_____
Действительно, обозначим угол BAD	м &Т...С£1
четырехугольника ABCD через а. Тогда	Рис. 38
BCD = к - а , поскольку_этот четырехугольник вписан в окруж-ность. Следовательно, QCS = л - а - р , в то время как угол MAS также равен л - ос - р, поскольку он дополняет угол В AS , равный а + р, до л. Таким образом, QCS = MAS . Из подобия треугольников следует:
а _ AS с _ AS d~CS’ l^CS'
откуда заключаем, что а/d = c/b или ab = cd, что и требовалось доказать.
§ 2. РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
В этом параграфе рассмотрим простой, но важный для приобретения практических навыков, метод решения задач, объединяемых общим названием «решение треугольников». Речь пойдет о расчете одних, неизвестных, элементов треугольника через другие, заданные.
Под элементами треугольника АВС мы будем понимать его стороны — а, Ь, с, противолежащие им углы — а, р, у, биссектрисы внутренних углов треугольника — lai lbi 1С, медианы — та, mbpnci высоты — йд, hb, hc> радиусы — г и R вписанной и описанной окружностей, соответственно, периметр треугольника — 2р, его площадь — 5, а также другие линейные или квадратичные параметры, характеризующие треугольник.
Произвольный треугольник определяется, вообще говоря, тре
мя независимыми параметрами, например, длинами трех его сторон или двух сторон и заключенным между ними углом, или одной стороной и величинами двух прилежащих к ней углов, или двумя сторонами и радиусом вписанной окружности и т.д. Сформулируем три основные задачи «решения треугольников».
Задача 1. В треугольнике даны длины двух сторон и величина заключенного между ними угла. Рассчитать остальные элементы треугольника.
Задача 2. В треугольнике даны длина одной стороны и величины двух прилежащих к ней углов. Рассчитать остальные элементы треугольника.
Задача 3. В треугольнике даны длины трех его сторон. Рассчитать остальные элементы треугольника.
Приведем решения каждой из этих задач.	Д
Как будет видно из дальнейшего, эти реше-
ния являются постоянными элементами ре- с/ \ а шения других, более сложных задач.	/	\
Решение задачи 1. Итак, в треугольнике	у\
АВС (рис. 39), даны длины двух сторон:-------------~ь--
АС=Ь и АВ = с, а также величина угла Рис 39
£ 2. Решение треугольников
37
ВАС = а между ними. Требуется рассчитать остальные элементы треугольника.
Длину а третьей стороны ВС треугольника находим по теореме косинусов:
а = ВС =	+ с2 - 2Z>ccosa.
Углы р и у треугольника АВС можно вычислить либо по теореме синусов: b а . п b . ----------------------=-------=> sin р = — sin a, sinp sin a--------------------a
с a . c . ----=-------=> sin у = — sin a, sin у sin a-a
либо по теореме косинусов:
b2 = c2 +a2 — 2ac cos p => cos p = (с2 + a2 - b2)/2ac, c2 = a2 +b2 - 2ab cos у => cos y = (a2 + b2 - c^/lab,
и далее n c - b cos a COS P =-------------------------------,
a
- c cos a cos у =---------.
a
Во всех этих формулах следует использовать уже найденное выражение для длины стороны а.
Если с - 6 cos a > 0, т.е. проекция отрезка АС на прямую АВ меньше длины отрезка АВ, то угол р — острый, в противном случае он — тупой. Аналогично, если b — с cos a > 0, т.е. проекция отрезка АВ на прямую АС меньше длины отрезка АС, то угол Y — острый, в противном случае он — тупой.
Вычисление углов р и у по формулам, получаемым на основе теоремы косинусов, более предпочтительно, поскольку эти формулы сразу позволяют записать углы р и у через обратные тригонометрические функции: о	c-bcosa
р = arccos--------,
а b - с zQsa у = arccos--------,
а
38
ГЛАВА I. ПЛАНИМЕТРИЯ
в то время как форма записи этих углов через значения их синусов, получаемых по теореме синусов, зависит от того, острые или тупые эти углы.
Наконец, углы р и у могут быть вычислены на основании теоремы тангенсов, как это сделано в задаче 3, приведенной после § 1:
tg = ctg а/2,
В - у b - с tg = ----------ctg а/2,
2 Ь + с
откуда находим:
P + y=2arctg [ctg(a/2)]=n - a, 'b-c a A \b + c	2
Р “ у = 2arctg
Длина 1а биссектрисы угла ВАС = а находится по формуле:
. _ 2Accos(a/2) a~ b + ~c
(см. § 1). Длины lb и lc остальных биссектрис находятся по этой же формуле заменой А, с и а соответственно на с, а и р или а, b и у.
Длина тс медианы, проведенной к стороне А В из вершины С, находится по теореме косинусов из треугольника АЕС (АЕ= ЕВ) (см. рис. 3):
z х2
т2 = I — I + Ь2 - 2 — • b cos a, 2	2
т,. = — vc2 + 452 - 4/?с cosa. 2
Это же выражение следует также и из общих формул § 1 для длин медиан, если только в них величину а заменить полученным для нее значением. Аналогично:
mh ~ ~ >12а2 4- 2с2 - b2 = — VЬ2 + 4с2 - 4bc cos a, b 2	2
£ 2. Решение треугольников
39
та = yfab2 + 2с2 - а2 = ± ylb2 + с2 + 2bc cos а.
Площадь SABC треугольника дается формулой:
3АВС= | b-c-smo..
Высоты треугольника находятся из равенств:
$авс=\ b-c-sina=^ ha-a=^ hb-b=^ hc-c, откуда	,
hb = c sin a, hc = b sin a и ha = —- • sin a.
a
В последнюю из этих формул, разумеется, нужно подставить найденное для а выражение через стороны Ь, с и угол а.
Радиус г вписанной окружности проще всего найти по формуле:
$авс = Р' г> откуда
r _ sabc = Ьс  sin a р а + b + c
Радиус R описанной вокруг треугольника окружности находится по теореме синусов:
R - а -	+ с2 ~^с cos a
2 sin a	2 sin a
Этим завершается решение первой задачи. Обратимся к решению второй задачи.
Решение задачи 2. По условию известна длина стороны АС= b и величины двух прилежащих к ней углов: ВАС =а и АСВ = у. Требуется рассчитать остальные элементы треугольника (рис. 40).
Прежде всего ясно, что АВС = р = л - (a + у). Отсюда sin р = sin (a + у). Из теоремы синусов находим:
sin(a + у) sin a sin у
40
ГЛАВА I. ПЛАНИМЕТРИЯ
Поэтому длины d и с двух оставшихся сторон треугольника и радиус R описанной окружности находятся из равенств:
, sina , siny n b 1 a = b_____?	‘} ft-----------1
sin(a+y) sin^c+y) 2 sin^c+y)
Длины lai lb и lc биссектрис треугольника определяются уже известными соотношениями:
_'lbccGsal'l - lacvysfllZ _2аЬсо^у/2 b+c ’ ь а л-с ’ с а+Ь
в которых а, с и р заменяются найденными для них выражениями.
Медианы та) ть и тс определяются по характерным для них формулам через длину известной стороны b и найденные длины двух других сторон а и с.
Высоты ha и hc легко находятся по формулам:
ha = b sin у; hc-b sin a.
Третья же высота hb может быть определена различными способами. Можно, например, воспользоваться равенствами:
,	. .sin a • sin у
hb = #sin у = b~—------
sin(a + y)
а можно, рассмотрев два прямоугольных треугольника ABD и DBC, где D — основание высоты, опущенной из вершины В на сторону АС (рис. 41), получить для hb уравнение:
hb ctg a + A^ctg у =b.
Из этого уравнения находим:
. b , sin a sm у hb --------------= ь —---------J.,
ctg a + ctg у sin(a + y)
Необходимо отметить, что данная формула имеет место независимо от того, острые ли углы а и у, как это показано на рис. 41, или хотя бы один из них — тупой.
Аналогичным приемом можно воспользоваться и для вычисления радиуса вписанной окружности (рис. 42). Поскольку ее центр
§ 2. Решение треугольников
41
О лежит в точке пересечения биссектрис треугольника, то из прямоугольных треугольников АОЕ и СОЕ (Е — точка касания вписанной окружности и стороны АС) следует:
г ctg (а/2) + г ctg (у/2) = Ь, или
г =b= b sin(q/2) • sin(у/2) ctg (а/2) 4-ctg (у/2) sin(a/2 + у/2)
Площадь треугольника АВС вычисляется по формуле:
$авс~ 2 '^ь~ 2	‘
sin a • sin у sin(a + y)
Рассмотрим решение последней, третьей задачи.
Решение задачи 3. Теперь известны длины а, Ь, с всех сторон треугольника. Вычислим остальные его элементы.
Углы треугольника вычисляются на основании теоремы косинусов.
л 7 ,2 эд	с2+Ь2-а2
er = cr + b - 2bc -cos a => a = arccos-—-
2bc
b2 = a2 + c2 - 2ac -cos В => В = arccos —-------—
2ac
2 l2 2 n l	b2 + Cl2 — C2
c=b+ a - 2ab -cos у => у = arccos ———------------
2ab
Площадь треугольника находится по формуле Терона
SABc = р(р - а){р - b){p - с),
в которой р = (а + Ь + с)/2 — полупериметр.
Рис. 41
Рис. 42
42
ГЛАВА I. ПЛАНИМЕТРИЯ
Радиус вписанной окружности равен:
г _ $АВС
Р
Радиус описанной окружности находится по формуле:
я—
4$АВС
Длины медиан вычисляются через стороны треугольника по формулам, приведенным в § 1.
Длины высот определяются равенствами:
7 ^"^АВС 1	АВС 1	АВС
ha = —; hb = —; hc =---------,
а	b	с
в которых площадь SABC треугольника уже вычислена.
Длины биссектрис вычисляются через стороны треугольника и заключенные между ними углы по неоднократно использовавшимся формулам (§1).
Пример 1. Найти отношение радиусов окружностей, вписанной в треугольник АВС и описанной около него, если известны отношение двух его сторон АВ: АС=т: п и угол ВАС = а, заключенный между этими сторонами.
Решение. Пусть длина стороны АВ равна с, а длина стороны АС - Ь, с: Ь = т: п. Тогда решение данной задачи сводится к расчету величин г и R по двум сторонам и углу, заключенному между ними.
Определяем сначала по теореме косинусов третью сторону треугольника:
ВС2 = Ь2 + с2 - 2bc -cos а, откуда
ВС = yjb2 + с2 - 2facosa.
Затем находим радиус г вписанной окружности:
г ^$авс = fa sin a
Р b + c + Jb2 + c2 - 2facosa
§ 2. Решение треугольников	43
После этого вычислим радиус R описанной окружности:
_ ВС ylb2 + с2 — 2Ьс cos а 2 sin а	2 sm а
Наконец, вычисляем их отношение:
г __________________2fecsin2a___________________
К (b + c + y/b2 +с2 -2bccosa)ylb2 + с2 -2bccosa ’
Разделив числитель и знаменатель дроби на Ь2, получим:
г ___________________________2.(с/Ь) sin2 а_______________________
(1 + c/Z> + ^/1 + (c/b)2 - 2 c/Z> cos a)-Jl + (c/b)2 - 2 c/Z> cos а
_____________________________2(лп/п) sin2 a_______________________
(1 + т/п + -Jl +(w/n)2 - 2 m/n cos a)-/l + (m/ri)2 - 2 m/n cos a
Пример 2. Вычислить площадь круга, вписанного в треугольник АВС, у которого АС =5 м, ВАС =30°, ВСА =45°.
Решение. Из прямоугольных треугольников ОАЕ и ОСЕ (рис. 42), находим:
откуда
г • ctg 15° + г • ctg 22,5° = 5,
5
Г ~ ctg 15° + ctg 22,5° ’
где г — радиус вписанного круга. Легко видеть, что
2	. cos215° l + cos30° 2 + v3 .	/г2
ctg2 15 =	"2,-------------^7 = -—7t = (2 + V3) ,
sin215	1-cos 30	2-V3
2	cos2 22,5° l + cos4.5°	2 + V2	r-,2
ctg2 22,5 =-------1-7 =----------- =---7= = (1 + V2)2.
&	sin2 22,5	l-cos45	2-V2
Отсюда
ctg 15° = 2+ V3, ctg 22,5° = 1+ V2 .
44
ГЛАВА I. ПЛАНИМЕТРИЯ
Таким образом,
3 + V2+ Л ’
а площадь круга S равна:
__	2__	25тг	. 2\
iS 7Г К	I—	।— (М ).
14 + 6V2+6V3+2V6
Пример 3. В треугольнике АВС известны стороны АВ = 3, ВС = 5, ЛС= 7. Найти длину биссектрисы угла АВС треугольника.
Решение. Вычислим сначала величину р угла АВС. Для этого воспользуемся теоремой косинусов. Имеем:
АС1 2=АВ2+ВС2 - 2АВ ВС cos АВС,
ИЛИ
49 = 9 + 25 - 30cos р,
откуда получаем, что cos р = —1/2 или р= 120°.
Далее, воспользовавшись формулой
/ - cos ь"	АВ+ВС	’
где 1Ь — длина биссектрисы, делящей пополам угол между сторонами АВ и ВС, получаем:
1	2 3  5 1/2 _ 15
ь~	3 + 5	" 8 ‘
ЗАДАЧИ
1. В треугольнике АВС. АВ=2, АС-1, ВАС =60°. Найти ha, высоту треугольника, опущенную на сторону ВС.
Ответ. 7/ТГз .
2. Длины сторон АВ и АС треугольника АВС соответственно равны 4 и 5 см, а величина угла, заключенного между ними, — 60°. Найти длины отрезков касательных, проведенных из вершины В к окружности вписанного в треугольник круга.
§ 2. Решение треугольников
45
Ответ: 711-721/2 см-
3.	В треугольнике АВС со сторонами 5С= а, AC- b и углом а между ними вписан полукруг с диаметром, лежащим на стороне, противоположной этому углу. Найти радиус этого полукруга.
Ответ: ab • sin а/(я + Ь).
4.	В треугольнике АВС известны АВ- с и АС = Ь. Величина угла ВАС вдвое больше величины угла АВС. Найти длину третьей стороны треугольника.
Ответ: yjb(b + с) .
5.	Найти расстояние между центрами вписанной и описанной окружностей для равнобедренного треугольника с основанием, равным а, и боковой стороной Ь.
Ответ: b \ a - b\ /у14Ь2 -а2, причем b > а/2.
6.	Найти длину биссектрисы прямого угла треугольника, если его катеты равны а и Ь.
Ответ: abjl /(а + Ь).
7.	Стороны треугольника АВС равны 5, 7 и 8 см. Найти площадь круга, описанного вокруг этого треугольника.
Ответ. 49л/3 см3.
8.	Существует ли треугольник, у которого все высоты меньше 1 см, а площадь — больше 100м2?
Ответ: Существует.
9.	Доказать неравенство
(р - а)(р - b)(p - с) < 1 abc,
8
в котором а, b и с — длины сторон треугольника, р — его полупериметр.
Указание. Воспользовавшись неравенством “среднее арифметическое неотрицательных чисел х и у больше или равно их среднему геометрическому”, поочередно принимая за эти числа разности p-а, р — b и р — с.
46
ГЛАВА I. ПЛАНИМЕТРИЯ
10.	Доказать, что во всяком треугольнике отношение радиуса вписанной окружности к радиусу описанной окружности не может превышать 1/2.
Указание. Воспользоваться результатом решения предыдущей задачи.
§ 3. РАСЧЕТ ЭЛЕМЕНТОВ ТРЕУГОЛЬНИКА МЕТОДОМ СОСТАВЛЕНИЯ УРАВНЕНИЙ
Задачи, изложенные в предыдущем параграфе, позволяют проиллюстрировать стандартный метод решения задач более широкого класса, также связанных с расчетом элементов треугольника, а именно — «метод составления уравнений». Как ясно уже из самого названия, этот метод основан на введении одного или нескольких неизвестных, которыми являются те или иные элементы треугольника, и последующем составлении для них необходимых уравнений.
Рассмотрим сначала простой пример.
Задача. В треугольнике АВС длина стороны АВ равна 4 см, длина стороны АС равна 5 см, радиус окружности, описанной вокруг треугольника, составляет V7 см, (рис. 43).
Определить площадь треугольника АВС.
Если бы в треугольнике АВС кроме сторон АВ и АС был известен угол ВАС между ними, то задача была бы «стандартной», одной из тех, решение которых рассматривалось в предыдущем параграфе. Однако угол треугольника неизвестен, вместо него дан другой элемент, а именно — радиус описанной окружности.
Чтобы свести эту задачу к решению «стандартной», введем в качестве неизвестного недостающий угол ВАС. Если А принять теперь, что в задаче известны две стороны и угол между ними, то стандартным методом можно вычислить как радиус описанной окружности, так и
площадь треугольника. Причем, прирав-	Рис 43
нивая полученное выражение радиуса описанной окружности данному для негюзначению, получим уравнение, определяющее величину угла BACL
Решение. Обозначим величину угла ВАС через х Тогда В С находится по теореме косинусов:
ВС2=АВ2+АС2 - 2АВ-AC COSX,
48
ГЛАВА I. ПЛАНИМЕТРИЯ
ИЛИ
ВС = л/16 + 25 - 2 • 4 • 5 • cos х = 7?! - 40 cos х.
Используя затем теорему синусов, получаем для радиуса R описанной окружности выражение:
D ВС 741 - 40 cos х к =--------=----------------
2 sin х 2 sin х
Поскольку 77 , то получаем для х уравнение:
741 - 40 cos х
2 sin х
77.
Решим это уравнение:
41 - 40 cos х= 28 sin2x
или
28 cos2x-40 cosx+ 13 = 0.
Отсюда:
1. cosx= ~ , X! =~ (sinxj = 77 /2);
2. cosx = y|, х2 = arccos 13/14 (sinx2 = зТз /14).
Таким образом, решение задачи не однозначно. Существуют два треугольника, имеющих по две равные стороны, но с разными углами между ними, причем оба таких треугольника вписаны в одну и ту же окружность с радиусом 7?= 7?.
Из чертежа на рис. 43 видно, что такими треугольниками могут быть Д/15С и ДЛ Вх С, где Вх — точка, симметричная с точкой В относительно диаметра окружности, проходящего через вершину А треугольника.
Соответственно найденным значениям Xj и х2 получаем значения площади треугольника:
$АВс= | АВ • AC sin Xi = |  4 • 5 • -у = 5 7з (см2);
SABlc= | лв\ •АС sin х2 = | • 4'5 • ~~~ = 15 Л /7 (см2).
$ 3. Расчет элементов треугольника методом составления уравнений 49
Этот пример наглядно показывает, в чем состоит суть излагаемого метода. Отказавшись от «неудобного» условия задачи, которое непосредственно не могло быть использовано (в нашем случае — от радиуса R описанной окружности), мы ввели неизвестную, но «удобную» величину, которая дополнила исходные данные до «стандартного» набора параметров (в рассматриваемом случае —угол х треугольника). Эти параметры позволили известным образом вычислить любой элемент треугольника, в том числе и тот элемент, от которого мы временно отказались. Формула для вычисления этого элемента служила уравнением для определения введенного неизвестного.
Рассмотрим еще одни пример.
Задача. Один из углов треугольника составляет 60°, а длина высоты, опущенной на одну из сторон, образующих этот угол, равна Зм. Найти площадь треугольника, если радиус вписанного в него круга равен \м.
Решение. Пусть в треугольнике ЛЯС (рис. 41, 42) угол ВАС = я/3. Кроме того, известны длина высоты: = 3, опущенной из вершины В, и радиус: r = 1.
Введем две неизвестные: длину стороны АС обозначим х, а ВАС - у. Будем считать далее, что в треугольнике ЛЯС даны сторона и два прилежащих к ней угла. Тогда, согласно идее рассматриваемого метода, следует выразить через эти данные радиус вписанного круга и высоту. Воспользовавшись для этого стандартным приемом «решения треугольников», получим систему уравнений:
A(ctg а + ctg у) = х, r(ctg а/2 + ctg у/2) = х
с двумя неизвестными х и у. Далее имеем:
л/з + 3 ctg у = х, 7з + ctg у/2 = х
Исключив х, получим уравнение:
ctg у/2 = 3 ctg у,
или
ctg у/2 = 3
ctg2y/2 -1 2ctg у/2
50
ГЛАВА I. ПЛАНИМЕТРИЯ
Отсюда находим ctg у/2 = 7з , у/2 = л/6 или у =
я
3 ’
Таким обра-
зом, треугольник АВС — равносторонний. Далее получаем:
x=3ctg у + л/З =2а/3 ,
и, наконец, определяем площадь треугольника:
5^С=^ = ЗЛ(М2).
В отличие от решения предыдущей задачи, здесь оказалось удобным ввести не одну, а две неизвестные. В остальном же решения этих задач принципиально не отличаются друг от друга.
Рассмотрим еще один пример решения задач подобного типа.
Задача. Найти углы треугольника, если высота и медиана, проведенные из одной и той же вершины, образуют с боковыми сторонами углы, равные а.
Решение. Прежде всего отметим, что в этой задаче не задан ни один линейный элемент, т.е. элемент с размерностью длины, и „	требуется определить только безразмерные
А\	величины — углы треугольника. Отсюда
/I \	легко заключить, что наряду с любым тре-
TaV -Д угольником, отвечающим условиям зада-/ /	\ чи, им же отвечает любой другой треуголь-
/	/	\ ник, подобный данному. Поэтому одну из
/\х	/ А сторон треугольника АВС (рис. 44), мож-
D Е но задать произвольно, например, принять Рис. 44	___ ________
АС= 1. Обозначим ВАС = х, ВСА = У- Тогда в треугольнике АВС будут как бы заданы сторона и два прилежащих к ней угла.
Согласно общему методу, нужно записать через введенные неизвестные два условия:
а)	высота ^треугольника ЛВС образует со стороной ВС угол а;
б)	медиана BD треугольника АВС образует со стороной АВ угол а.
Первое из этих условий приводит к простому уравнению:
л
а = 2 ”
(1)
§ 3. Расчет элементов треугольника методом составления уравнений 51
Второе условие можно записать следующим образом. Пусть т — длина медианы BD. Очевидно, что AD = 1/2, DC- 1/2, DBC -х-у~а = я-(х+у + а). Тогда, используя теорему синусов в и &DBC, имеем:
AD т	1/2 т
	~	 ил и 	=----; sina---------------------------sinx-sina-sinx
DC	m	1/2
------------~ —— или —_—l-------- sin(?r -x-y-a) sin у sin(x + y + a)
m
sin у
Исключая m, получаем:
sin(x + у + a) = sin у sin a sin x
Таким образом, приходим к системе двух уравнений с двумя неизвестными х и у.
Исключая из второго уравнения у с помощью первого, получаем:
cos х _ cos a sin a sin x ’
или
sin 2x = sin 2a.
Отсюда имеем:
1)	2x=2a => x = a;
TC
2)	2x = 7t - 2a => x= - -a.
Первое равенство дает решение: х = а, у = я/2 - а, т.е. х + у ~ я/2, (треугольник АВС — прямоугольный).
Второе равенство приводит к решению: х = у = к/2 - а, т.е. треугольник АВС — равнобедренный (медиана BD совпадает с высотой BE).
В качестве последнего примера этого параграфа рассмотрим следующую задачу.
Задача. Хорда АВ стягивает дугу окружности, равную 120е. Точка С лежит на этой дуге, а точка D лежит на хорде АВ. При этом AD = 2, BD= 1, DC= V2 . Найти площадь треугольника АВС.
52
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение.* Обозначим угол ACD буквой х (рис. 45). Тогда угол CDB = тс - х и площадь S треугольника АВС дается формулой:
5=1- AD • DC • sin х + - • BD- DC • sin(7t - x)
2	2
или
c 1 n nz .	1 . я •	3>/2 .
5 = - • 2V2 sinx+ - • 1 • v2 sinx =	- sm x.
Таким образом, задача сводится к отыс-канию неизвестной х.
По условию задачи угод АСВ равен лт-----——i"r 120°. Значит, это условие нужно исполь-
’	зовать в составлении уравнения для х. Для
Рис’45	этого используем теорему косинусов в
&АВС, выразив предварительно АС и ВС по этой же теореме из треугольников ADC и BDC.
АС2 = AD2 + DC2 - 2 AD • DC cos x,
BC2 = BD2 + DC2 - 2BDDC cos (tc-x) или
AC2 = 6 - 4^2 cos x,
BC2 = 3 + 2 V2 cos x.
Наконец, используя равенство
AB2 = AC2 + BC2 - 2AC-BC cos 120°, получаем уравнение для определения величины х:
9 = (6 - 4 V2 cos х) + (3 + 2 >/2 cos х) + +л/б-4>/2 COSX • V3 + 2V2 COSX или
2V2 cos х = 7б-4-/2 cosx •	+ 2-/2 cosx.
Здесь, как и во многих других задачах, приводится один из возможных путей решения. В данном случае выбранный путь решения демонстрирует возможности излагаемого метода. По-другому эту задачу можно решить, используя теорему о произведении отрезков хорд, пересекающихся в одной точке круга (см. § 1).
3.	Расчет элементов треугольника методом составления уравнений 53 Отметив, что cos х > 0, получим:
8 cos2x= 18 - 16 cos2x,
2	3
cos x= - .
4
Поскольку cos х > 0, то cos х= л/з /2 или х= 30°. Отсюда находим, что sin х = 1/2 или 5= 3 V2 /4.
Для приобретения навыков решения задач рассмотренным методом рекомендуется самостоятельно решить следующие задачи.
задачи
1.	Биссектриса одного из острых углов прямоугольного треугольника в шесть раз короче гипотенузы. Найти острые углы этого треугольника.
Ответ: 2 arccos 3/4, л/2 - 2 arccos 3/4.
2.	В остроугольном треугольнике ЛВС дано: ВАС = а, ВСА проведенная из вершины В медиана имеет длину т. Вычислить площадь треугольника АВС.
т2 sin a sin ysin(a + у)
Ответ: -----й----й------й-----.
4sin asin у + sin (а - у)
3.	В треугольнике АВС угол ВСА равен 60°, а радиус круга, описанного вокруг этого треугольника — 2 >/з . На стороне АВ взята точка D, так, что AD^l-DB и при этом CD- V2 . Найти площадь треугольника АВС.
Ответ: 3 V2 .
4.	Найти площадь треугольника ЛВС, если ЛС=3, ВС =4, а медианы АК и BL взаимно перпендикулярны.
Ответ: VTF.
5.	В остроугольном треугольнике ЛВС угол ВАС равен а. На стороне ВС, как на диаметре, построена окружность. Эта окружность пересекает сторону Л С в точке В, а сторону ЛВ — в точке Q. Найти отношение площади треугольника APQ к площади треугольника ЛВС.
Ответ: cos2 a.
54
ГЛАВА I. ПЛАНИМЕТРИЯ
6.	В треугольник АВС со сторонами ВС=а, АС=2а и углом
ВСА = 120° вписана окружность. Через точки касания этой окружности со сторонами АС и ВС и через вершину В проведена вторая окружность. Найти ее радиус.
Ответ: а^6,5 - 2 77.
7.	В треугольнике АВС из вершины угла А на сторону ВС опущена медиана, длина которой равна половине среднего геометрического длин сторон АВ и АС. Угол ВАС равен а. Найти углы а! и а2, на которые медиана делит угол ВАС, считая, что cq > а2. Исследовать, при каких значениях а задача имеет решение.
Ответ: cq = а/2 + 1/2 arccos (2 sin2a + cos а),
а2 = а/2 - 1/2 arccos (2 sin2a + cos а).
Решения существуют при 2тс/3 < а < я.
8.	В треугольнике АВС длина стороны ВС равна среднему арифметическому длин сторон АВ и АС. Угол ВАС равен а. Найти углы АВС и ВСА, считая, что АВС > ВСА. Исследовать, при каких значениях а задача имеет решение.
Ответ: АВС = (я - a)/2 + arccos (2 sin а/2),
ВСА = (я - а)/2 - arccos (2 sin а/2).
Решения существуют при 0 < а < я/3.
9.	В треугольнике АВС сторона АВ имеет большую длину, чем сторона ЯС, а угол ВАС равен а. На стороне АВ взята точка D так, что BD = AC Пусть Е— середина отрезка AD, a F— середина отрезка ВС. Найти угол BEF.
Ответ: а/2.
10.	В равнобедренном треугольнике АВС (АВ = АС) проведены биссектрисы AD, BE, CF. Найти длину стороны ВС, если известно, что АС= 1, а вершина А лежит на окружности, проходящей через точки D, Е, Е
Ответ: (V17 - 1 )/2.
§ 4. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ТРЕУГОЛЬНИКЕ
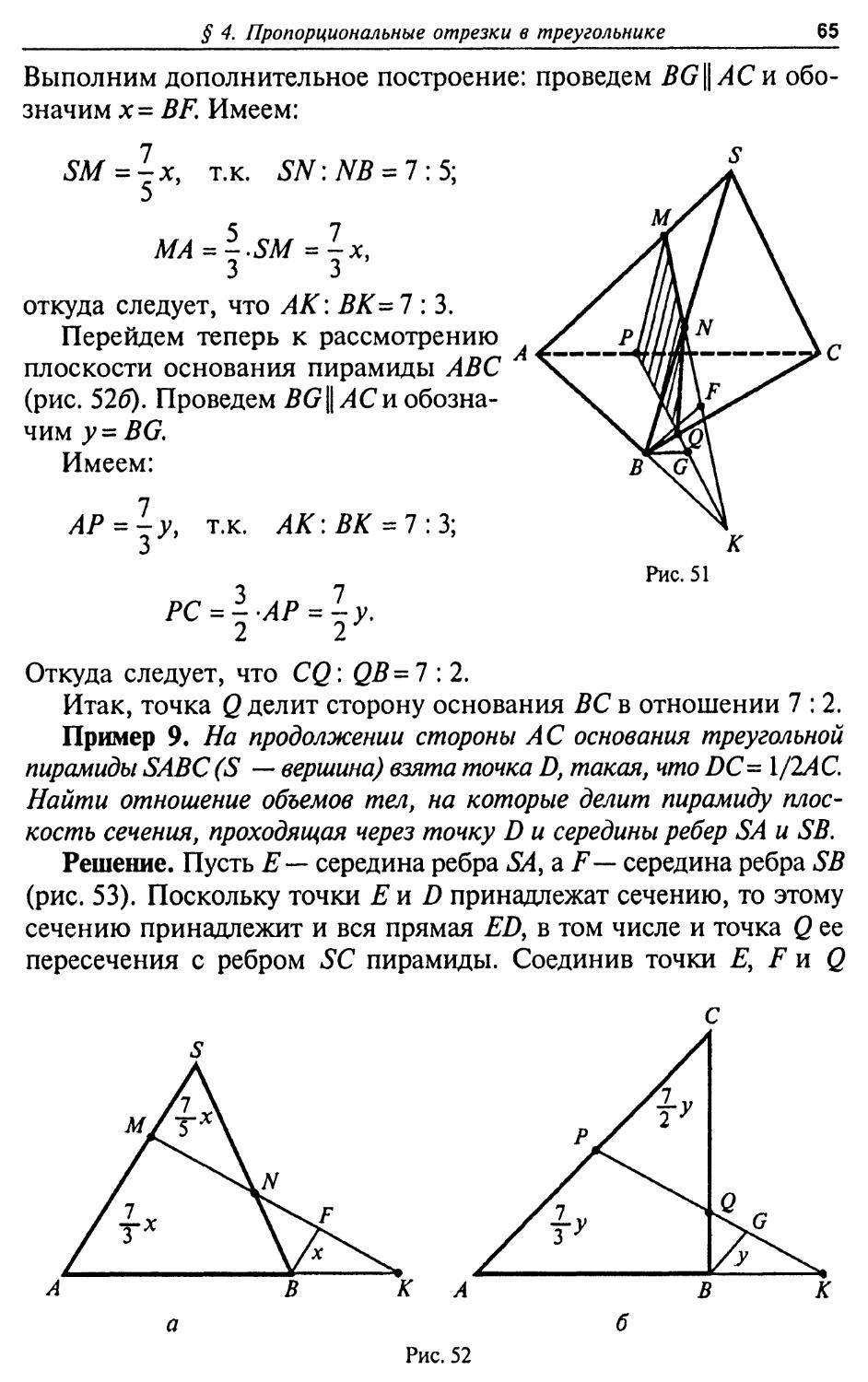
В этом параграфе приводится решение одной полезной планиметрической задачи, связанной с пропорциональным делением отрезков в треугольнике, и основанный на ней метод решения большого количества других задач, в том числе и стереометрических.
Рассмотрим следующую основную задачу:
В треугольнике АВС (рис. 46) из вершин А и В к сторонам ВС и АС, соответственно, проведены отрезки AD и BE, делящие эти стороны в заданном отношении, т.е.
BD _ т АЕ _ р
~DC~~n' ~EC~~q	(1)
Определить, в каком отношении делятся эти отрезки точкой их пересечения, т.е. найти отношения:
BQ и QE QD’
Иными словами, известно, в каком отношении отрезки AD и BE делят противоположные вершинам А и В стороны треугольника; требуется определить, в каком отношении они делятся между собой.
Оказывается, что эти отношения не зависят ни от вида треугольника, ни от его сторон, ни от его углов, а определяются лишь отношениями, в которых делятся соответствующие стороны треугольника точками D и Е, т.е. пропорциями (1).
Решение 1. Найдем сначала первое из искомых отношений (рис. 46а). Для этого выполним вспомогательное построение, характерное для всех задач подобного типа. Проведем отрезок EF\\ ВС (точка F лежит на AD) и обозначим его длину через х, т.е. положим EF-x.
Поскольку &ACD °° &AEF, причем коэффициент подобия, согласно второй из пропорций (1), равен (р + ^)/р, то
56
ГЛАВА I. ПЛАНИМЕТРИЯ
а
Рис. 46
DC = P^.EF = ^.x. Р	Р
Используя затем первую из пропорций (1), находим:
BD = m/n DC или
л р
Наконец, из подобия треугольников BDQ и EFQ находим:
т р + q
BQ = BD = п р	= rn	q.
QE FE~ х п	р'
Таким образом, BQ: QE=m/iv(\+q/p),
Решение 2. Аналогично находится отношение AQ: QD (рис. 466). Для этого проводится ЛАГ|| АС (точка Улежит на ВЕ\ KD = y). Из подобия треугольников ЕСВ и KDB с коэффициентом подобия (т + ri)lm имеем:
EC^^-KD^^-.y. т	т
Далее находим АЕ, используя вторую пропорцию (1):
АЕ = ^ЕС = Р.^.у. q q т
Наконец, из подобия треугольников AEQ и KDQ вычисляем отношение AQ: QD.
§ 4. Пропорциональные отрезки в треугольнике
57
р т + п
AQ _ АЕ _ д т Л _|_ JL) QD~ KD~ у - q { пг
т.е. AQ: QD-p/q -(1 + п/т). Таким образом,
если В® - т - Р_ DC п ’ ЕС q ’
то
QE п р QD q т
Рассмотрим несколько примеров.
Пример 1. Найти отношение, в котором делятся медианы треугольника точкой их пересечения.
Решение. Для рассматриваемого случая m = n=p = q=\. Поэтому BQ: QE= 2 и AQ: QD = 2. Это означает, что медианы делятся точкой их пересечения в отношении 2:1, считая от вершин треугольника.
Пример 2. На стороне ВС треугольника АВС взята точка D, такая, что BD: DC =2 : 5, а на стороне АС — точка Е так, что АЕ= 1/3 Л С. В каком отношении делятся отрезки BE и AD точкой Q их пересечения.
Решение. Обратимся к рис. 46а и 46£. Учитывая, что АЕ: ЕС= 1 : 2, имеем:
KD=y, ЕС=1у/2\ АЕ^у/4.
Поэтому AQ: QD = АЕ: у = 7/4 = 7 : 4 (в частности, AQ = 7/11 • AD).
Аналогично этому имеем:
EF=x' CjD=3x; BD = 6/5-х.
Поэтому BQ: QE= 6/5 = 6: 5 (в частности, BQ = 6/11 • BE).
Пример 3. В треугольнике АВС длины сторон АВ, ВС и АС относятся как 2:4:5, соответственно. Найти, в каком отношении делятся биссектрисы внутренних углов треугольника точкой Q их пересечения.
Решение. Используя свойство биссектрисы делить противоположную сторону треугольника на части, пропорциональные заключающим ее сторонам, находим (рис. 47):
58
ГЛАВА 1. ПЛАНИМЕТРИЯ
= ЯО = 2. AG
ЕС ~ 4 ’ DC ” 5 ’ GB ” 4 ’
Используя затем результаты решения основной задачи этого параграфа, получаем:
|ЛЯ|:|ЯС|:1ЛС| = 2:4:5
Рис. 47
Пример 4. В треугольнике АВС, площадь которого равна 18 м2, проведены отрезки BE и AD, причем точки Е и D лежат соответственно на сторонах АС и ВС и делят их в отношении АЕ: ЕС =3:4 и BD: ЛС= 2 : 7. Найти площадь четырехугольника CEQD, где Q — точка пересечения отрезков BE и AD.
Решение. Площадь SCEqD четырехугольника CEQD (рис. 466) равна разности площадей SACD треугольника ACD и SAEQ треугольника AEQ, т.е.
$CEQD = $ACD “ $AEQ’	(4)
С = АЕ AQ с
AEQ~ACADSacd’
(5)
поскольку EAEQ образуется из треугольника ACD путем уменьшения его сторон АС и AD соответственно в АЕ/АС и AQ/AD раз. Известно, однако (см. § 1), что в этом случае площадь треугольника уменьшается в {АЕ' AQ)/(AC- AD) раз.
Кроме того, очевидно равенство:
$аво : ^acd = 2:7,	(6)
поскольку треугольники ABD и ACD имеют общую вершину А и основания, лежащие на одной прямой. Отсюда следует, что их площади относятся как длины оснований BD и CD, т.е. как 2:7.
Таким образом,
>ACD “ 1 $АВС'
9
§ 4. Пропорциональные отрезки в треугольнике
Из равенств (1)—(3) следует:
59
$CEQD ~ $ACD ~ $AEQ “ $ACD (1 “ Тг~~АГ\ ” А С- • AJJ
2f AEAQ'\t,	( AEAQ}
9^ AC AD)abc	[ AC AD)
Учитывая, что по условию АЕ:ЕС=3:4 или АЕ-3/1 • АС, получаем:
^Од2д~4(1 - 7 ’	)
и задача сводится к вычислению отношения AQ/AD, Последнее легко осуществляется рассматриваемым методом. Имеем:
KD=y\ ЕС=1у\ АЕ=1.2.у = —у.
27	4 2Л 8 Л
Поэтому AQJQD = AE/KD = 27:8 или AQ-HL- AD. После этого находим:	35 5 * * * * * * * * * * * * * * * * * *
5	-4Г1 3 —} - 2 166
5с^~4(1~Г35}	245’
Пример 5. Каждая из сторон произвольного треугольника АВС
разделена на три равные части так, что точки деления D, Е и F,
лежащие на его сторонах АС, ВА и СВ соответственно, отсека-
ют по 1/3 длины каждой стороны
(AD=\/3AC, ВЕ=1/ЗВА, CF=l/3CB)
(рис. 48). Вершины треугольника АВС со-
единены с точками деления отрезками	\
прямых AF, BD и СЕ, которые, пересека- /	\
ясь, образуют треугольник PQR. Какую /	/
часть площади треугольника АВС зани- / ^гггТнР^
мает треугольник PQR?	A&rtxmlliL----------А,
Решение. Заметим сначала, что сум-	Рис 48
марная площадь заштрихованных на
рис. 48 треугольников APD, BRE и Справна площади треуголь-
ника PQR, Действительно, с одной стороны, площадь каждого из
треугольников ACF, ВСЕ и ABD равна 1/3 площади всего тре-
угольника АВС.
60
ГЛАВА I. ПЛАНИМЕТРИЯ
С другой стороны, эти треугольники размещены внутри треугольника АВС таким образом, что площади заштрихованных треугольников перекрываются дважды, в то время как треугольник PQR не покрывается ни разу.
Поскольку
$АВС = $ACF + $ВСЕ + $ABD И
$АВС = №сГ + $ВСЕ + $АВЕ>) + $PQR “ ($APD + $BRE + ^CQF)>
то очевидно, что
SpQR ~ $APD + $BRE + $CQF'
Найдем теперь, какую часть площади треугольника, например, ACFсоставляет площадь заштрихованного треугольника APD. Имеем:
с AD АР с _ 1 АР 1 Q 5apd~ACAF^acf = 3AF"35abc’
с _ 1 с APD ~ 9 ~AF АВС’
и задача сводится к отысканию отношения AP/AF
Согласно основной задаче, излагаемой в этом параграфе, можно положить т/п = BF: FC=2 : 1;p/q = AD: DC= 1: 2. Тогда искомое отношение определяется формулой
АР .= 1 fi  1 V 3 /4F"2|41 + 2j 4’
или ЛР= 3/7 ’ AF. Отсюда следует:
$apd = — $авс-
21
Аналогично находим:
$BRE = ^CQF- $АВС-
Таким образом, площадь треугольника PQR равна 1/7 площади всего треугольника АВС:
Spqr = 3 J_ SABC = 1SABC.
§ 4. Пропорциональные отрезки в треугольнике
61
Рассмотрим теперь решение задачи, которую можно назвать
обратной по отношению к рассмотренной выше. Основной ее
вопрос можно сформулировать следующим образом: найти, в каком отношении отрезки AD и BE, проведенные из вершин А и В треугольника АВС к сторонам ВС и АС, соответственно, делят эти стороны, если известно, в каком отношении отрезки AD и BE делятся между собой?
в
Рис. 49
Задача. В треугольнике АВС проведены отрезки AD и BE, пересекающиеся в точке Q (рис. 49) так что известны отношения:
aq_
QD
QE и
Найти, в каком отношении делятся стороны АС и ВС точками Ей D, т.е. найти отношения:
АЕ	BD
--- и -----.
ЕС	DC
Решение. Воспользуемся результатами решения основной задачи, изложенной в этом параграфе. Обозначим искомые отношения через p/q и т/п, соответственно. Тогда имеем систему уравнений:
? i+" U, н п) т(. q\
— I 1 + — = ц. п I Р I
Перепишем эту систему в виде:
1	Р/Я
1	я	1
1+-=Ц----7-.
р	т/п
или
Отсюда легко находятся искомые
P/я т/п
1 1
-Г + Н--7-Р/Я т/п
отношения, а именно:
62
ГЛАВА I. ПЛАНИМЕТРИЯ
р __ Хц-1 т _ Х|1-1 q 1 + |i п 1 + X
Очевидно, что решение обратной задачи существует при условии цХ> 1.
Пример. В треугольнике АВС отрезки AD и ВС, проведенные из вершин А и В к сторонам ВС и АС, соответственно, делятся между собой в следующем отношении:
Я2 = 3 BQ
QD ~ 2' QE ~ 5
(Q — точка пересечения отрезков AD и ВС). В каком отношении точки Е и D делят стороны треугольника?
Решение. Воспользуемся полученными формулами (или проделаем те построения, которые описывались в начале этого параграфа). Тогда находим:
р^З/2-4/5-1 = 1 q 1 + 4/5	9’
тл ^3/2 4/5-1 = 2 п 1 + 3/2	35’
Таким образом, АЕ/ЕС- 1 : 9, BD/DC=2 : 25.
Пример 7. В треугольнике АВС отрезок AD, проведенный из вершины А к стороне ВС, делит последнюю в отношении 2:3, т.е. BD : DC= 2:3. Из вершины В к стороне АС проведен отрезок BE, который пересекается с отрезком AD в точке Q так, что BQ = 2 • QE. Найти, в каком отношении точка Е делит сторону АС.
Решение. В этой, смешанной, задаче заданы отношения:
BD 2 BQ __ 2
DC 3’ QE Г
Требуется найти отношение АЕ/ЕС. Обозначим отношение АЕ/ЕС через p/q и введем неизвестную величину X, равную отношению отрезков AQ/QD.
Тогда имеем систему уравнений:
2J
-(1+^
3l PJ
= 2,
§ 4. Пропорциональные отрезки в треугольнике	63
из которой легко определяем, что p/q = 1/2 и X = 5/4. Это означает, что сторона АС треугольника АВС делится точкой Е в отношении 1 :2.
Отметим теперь еще две задачи, которые условно назовем «задачами о внешних пропорциональных отрезках».
Задача. На сторонах АВ и ВС треугольника АВС (рис. 50) взяты соответственно точки Du Е так, что BD: DA=p\ q и BE: ЕС = т.п (p/q^m/n). Через точки D и Е проведена прямая до пересечения в точке Q с прямой АС. Найти отношение QA : QC.
Таким образом, по известному отношению отрезков, на которые делятся боковые стороны треугольника, требуется найти отношение расстояний от точки пересечения прямой, проходящей через точки деления боковых сторон, с основанием до вершин этого основания.
Решение. Аналогично решению предыдущих задач этого параграфа выполним дополнительное построение: проведем отрезок CF параллельно стороне АВ (рис. 50). Обозначим длину этого отрезка через х, т.е. положим CF=x.
Из подобия &BED и &CEF с коэффициентом т/п имеем:
BD = - • CF = ™ • х. п п
Учитывая, что BD: DA = p/q, находим DA.
DA = -- BD = — — x.
Р пр
Наконец, из подобия &QAD и &QCF получаем искомое отношение:
(24 _ т/п>д/р-х _т £
QC х пр
64
ГЛАВА I. ПЛАНИМЕТРИЯ
Отсюда вытекает, что QC-AC/Cnqjnp - 1). Попутно следует отметить, что если p/q < т/п, т.е. mq > пр, то точка Q лежит на продолжении основания треугольника за точку С, в то время как при mq < пр эта точка лежит на продолжении основания за точку А.
Задача. На продолжении основания АС треугольника АВС за точку С взята точка Q такая, что QA : QC=X, а на стороне АВ— точка D такая, что BD . DA~p. q (рис. 50). В каком отношении отрезок DQ, пересекаясь в точке Е со стороной ВС, делит эту сторону?
Эта задача является фактически обратной предыдущей.
Решение. Воспользовавшись результатами решения предыдущей задачи, можем записать:
где т/п = BE: ЕС. Отсюда находим:
£ ЕС q’
что дает ответ в этой задаче.
В качестве примера рассмотрим несколько задач из стереометрии.
Пример 8. В треугольной пирамиде SABC (S — вершина) на боковых ребрах SA, SB и стороне основания АС взяты соответственно точки М, N и Р такие, что
5М 3 ^- = 1	= l
МА~ 5 ’ NB “ 5 ’ PC ~ 5 ’
Найти, в каком отношении делит сторону основания ВС плоскость, проходящая через эти точки.
Решение. Чертеж к этой задаче представлен на рис. 51.
Продолжим прямую MN, лежащую в плоскости грани AST? до ее пересечения в точке Ко продолжением стороны основания АВ. Поскольку прямая MNлежит в плоскости, проходящей через точки М, N и Р, то и точка К лежит в этой плоскости. Соединим точки Р и К, принадлежащие плоскости основания пирамиды, отрезком прямой, пересекающимся со стороной основания ВС в точке Q. Так как точки Р и К лежат в плоскости, о которой идет речь в задаче, то этой плоскости принадлежит и точка Q; четырехугольник MNQP — сечение пирамиды этой плоскостью.
Найдем сначала, где на основании АВ находится точка К. Для этого вынесем плоскость грани ASB на отдельный чертеж (рис. 52л)«
J 4. Пропорциональные отрезки в треугольнике	65
Выполним дополнительное построение: проведем 2?<7|| ЛСи обозначим х = BF. Имеем:
5Л/ = |х, т.к. SN:NB = 7:5;
5	7
MA = -SM = -х, 3	3
откуда следует, что АК: ВК= 7:3.
Перейдем теперь к рассмотрению плоскости основания пирамиды АВС (рис. 526). Проведем Z?C?||JC и обозначим = BG,
Имеем:
7
АР = -у, т.к. АК.ВК = 7:3\
3
Рис. 51 3	7
РС = ±.АР = ^у.
2	2
Откуда следует, что CQ : QB-7 : 2.
Итак, точка Q делит сторону основания ВС в отношении 7 : 2.
Пример 9. На продолжении стороны АС основания треугольной пирамиды SABC(S — вершина) взята точка D, такая, что DC- 1/2АС. Найти отношение объемов тел, на которые делит пирамиду плоскость сечения, проходящая через точку D и середины ребер SA и SB.
Решение. Пусть Е — середина ребра SA, a F— середина ребра SB (рис. 53). Поскольку точки Ем D принадлежат сечению, то этому сечению принадлежит и вся прямая ED, в том числе и точка Q ее пересечения с ребром SC пирамиды. Соединив точки £, F и Q
Рис. 52
66
ГЛАВА I. ПЛАНИМЕТРИЯ
попарно отрезками прямых, получим сечение пирамиды, о котором идет речь в задаче.
Нетрудно заметить, что объем треугольной пирамиды SEFQ, получаемый из треугольной пирамиды SABC путем изменения длин ее боковых ребер соответственно в к. т и п раз, составляет ктп-ю часть объема пирамиды SABC, т.е.
^sefq-кт п- VSABC.
Поскольку ES:	1/2, FS: BS= 1/2,
то к = т = 1/2 и для применения последней формулы необходимо знать п, т.е. в каком отношении точка Q делит ребро SC.
Рассмотрим боковую грань ASC пирамиды. Как обычно, выполним дополнительное построение, состоящее в проведении СК\\ AS, Имеем х = СК. Далее находим: АЕ=Зх, поскольку AD:DC=3, ES=AE- Зх. Из подобия треугольников QES и QCK получаем: SQ \ QC=3 : 1. Следовательно, SQ= 3/4 • SC. Имеем:
113	3
Vsefq = 2 2 4 ^sabc = Тб ^авс>
или Vsefq • ^efqabc- 3:13.
Пример 10. На продолжении стороны АС треугольника АВС отложена точка D, такая что DC-\/2- АС, а на стороне ВС — точка Е, которая делит эту сторону в отношении BE : ЕС= 1 : 2. Точка D соединена с серединой F стороны АВ отрезком прямой, которая пересекает АЕ в точке Q. В каком отношении точка Q делит отрезок АЕ?
Решение. Проведем СК^АВ и примем СК=х. Тогда АГ=Зх, поскольку AD= 3 * CD (рис. 54).
Поскольку, однако, AF-FB, то и FB-3x.
Из подобия треугольников GBFm GCK, где (7 — точка пересечения отрезка DF со стороной ВС, получаем:
BG\ CG=3:1
или BG= 3/4 • ВС. По условию ВЕ-- 1/3 • ВС\ значит, EG= 5/12 • ВС.
§ 4. Пропорциональные отрезки в треугольнике	67
Проведем далее отрезок CL парал-
лельно отрезку АЕ и примем CL-y. 3x/\F
Тогда имеем: AQ=3y, поскольку
AD=3 • CD, а из подобия треугольни-ков GQ& и GKC с коэффициентом а* 'y^D подобия 5/12 : (1 - 1/3 - 5/12) = 5 : 3	Рис. 54
следует, что QE= 5/3 • у.
Составляя отношение AQ к QE, получаем:
QE 5/3-у
ЗАДАЧИ
1.	В треугольнике АВС на стороне АВ взята точка К так, что АК: ВК = 1: 2, а на стороне ВС взята точка L так, что CL \ BL = 2 : 1. Пусть Q точка пересечения прямых AL и СК. Найти площадь треугольника АВС, если дано, что площадь треугольника BQC равна 1.
Ответ: 7/4.
2.	В треугольнике АВС, площадь которого равна 6, на стороне АВ взята точка К, делящая эту сторону в отношении АК: ВК= 2:3, а на стороне А С —- точка L, делящая АС в отношении AL: £С= 5 : 3. Точка Q пересечения прямых СК и BL удалена от прямой АВ на расстояние 1,5. Найти длину стороны АВ.
Ответ: 6,4.
3.	В треугольнике АВС на стороне АС взята точка К так, что АК = 1, КС = 3, а на стороне АВ взята точка L так, что AL : LB = 2 : 3. Пусть Q — точка пересечения прямых ВК и CL. Площадь треугольника A QC равна 1. Найти длину высоты треугольника АВС, опущенной из вершины В.
Ответ: 3/2.
4.	На продолжении стороны АВ треугольника АВС отложен отрезок AD так, что AD: АВ = а. На продолжении медианы BE отложен отрезок £FTaK, что EF'. ВЕ=$. Найти отношение площадей треугольников BDF и АВС.
Ответ: (а - 1)(0 + 1 )/2.
5.	На стороне А В треугольника АВС между точками А и В взята точка D так, что AD: АВ- а(а < 1). На стороне ВС между точками
68
ГЛАВА I. ПЛАНИМЕТРИЯ
Ви С взята точка Е так, что ВЕ\ 2?С=р (Р < 1). Через точку Е проведена прямая, параллельная стороне АС и пересекающая сторону АВ в точке F. Найти отношение площадей треугольников BDE и ВЕЕ
Ответ: (1 - а)/р.
6.	Дан треугольник АВС. На стороне АС берется точка К, а на стороне ВС — точка А/таким образом, что
_ 5 $кмс _ 5
$лкмв 6
Найти СМ: МВ.
Ответ: 6/5.
7.	Дан треугольник А ВС, площадь которого равна 1. На медианах АК, BL и CN треугольника АВС взяты соответственно точки Р, Q и R так, что
АР , BQ = l	CR	5
РК	’ QL 2’ RN 4'
Найти площадь треугольника PQR.
Ответ: 1/12.
8.	На сторонах выпуклого четырехугольника ABCD, площадь которого равна 1, взяты точки: К на А В, L на ВС, М на CD и N на AD. При этом
Я£ = 2	= 1 £^. = 1 DN _ 1
КВ ’ LC 3’ MD ’ NA 5’
Найти площадь шестиугольника AKLCMN.
Ответ: 11/12.
9.	На сторонах АВ, ВС и СА треугольника АВС взяты соответственно точки Р, Q, R такие, что АР= 1/k-AB, BQ= 1/т • ВС и CR= \/п • СА, где к, т,п — натуральные числа, превосходящие 1. Точка А соединена с точкой Q, точка В — с точкой R, точка С — с точкой Р. Найти отношение площади треугольника, вершинами которого служат точки пересечения отрезков AQ, BR и СР, к площади треугольника АВС.
£ 4. Пропорциональные отрезки в треугольнике
Ответ: \-\/к- \/т - 1/п +--Ц;---+------Ц----+------Ц----.
(т - \)к2 +к (к- \)т2 + т (п- \)т2 + т
10.	На продолжении ребра SC треугольной пирамиды SABC (S — вершина) отложена точка D, такая, что CZ>= 1,5-SC, а на ребрах SA и SB взяты соответственно точки EnF, причем SE= 1/3 • SA и SF= 2/3 • SB. В каком отношении делит объем пирамиды плоскость, проходящая через точки D, Е и F?
Ответ: 472/815.
§ 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ОКРУЖНОСТЕЙ, УГЛОВ И ТРЕУГОЛЬНИКОВ
В предыдущих параграфах уже шла речь об окружностях, кругах и их основных элементах. В частности, отмечалось, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис, а центр окружности, описанной около треуголь
ника, — на пересечении срединных перпендикуляров к его сторонам. Там же приводились наиболее используемые формулы для
вычисления радиусов окружностей.
Остановимся теперь на решении различных задач, связанных
с расположением окружностей друг относительно друга, а также окружностей, углов и треугольников. Задачи подобраны таким
образом, чтобы их решения демонстрировали основные приемы
и элементы решения других, более сложных задач.
Задача. Центр Ох окружности радиуса г удален на расстояние т от центра второй окружности О2 радиуса R (R > г, т> r+ R). Найти длины общих касательных к этим окружностям.
Решение. Известно, что при условии т> г+ R окружности имеют четыре общие касательные (две внешние и две внутренние) с попарно равными длинами (рис. 55).
Длины внешних касательных, напри-
Рис.55	мер, (K{i К2), находятся следующим об-
разом. Проводим 0{А || КХК2 и рассматриваем прямоугольный треугольник О1ЛО2 (рис. 55а). Из него находим: ОХА2 = ОХО2 - О2^.
Очевидно, что О2А ~ R - г. Поэтому
КХК2 = 0хА = Jm2 -(R-г)2 = ^(т +R-r)(m +г - R).
Длина внутренней касательной, например, МХМ2, находится почти аналогично. Строится О2А\\МХМ2 и рассматривается прямоугольный треугольник ОХАО2 (рис. 556). Из него находится:
§ 5. Взаимное расположение окружностей, углов и треугольников 71 О2А2=ОХО22 - ОХА2.
Поскольку OxA = R + r, то
МХМ2 = О2А = у]т2 -(R + r)2 = 7(w + R + r)(m-r-R).
Рассмотрим еще одну задачу о взаимном расположении двух окружностей.
Задача. Центр Ох первой окружности радиуса г удален на расстояние т от центра О2 второй окружности радиуса R(R> г). Найти длину дуги первой окружности, заключенной внутри второй окружности.
Решение. Определим сначала, при каких т задача имеет решение (рис. 56).
Если т > R+r, то окружности, как это имело место в предыдущей задаче, не пересекаются; при т = R + r они касаются внешним образом друг друга, а при
R- r< т< R + r окружности пересекаются в двух точках. При
0< т<R-г меньшая из окружностей целиком попадает внутрь второй окружности.
Таким образом, задача имеет решения при R - г <т < R + r.
и
Пусть Е и F — точки пересечения округлостей. Длина EF искомой дуги равна удвоенной длине дуги ЕК , т.е.
EF = 2ЕК = 2осг,
где а — величина центрального угла ЕО{К.
Для нахождения а используем теорему косинусов. Из треугольника 01Е02 имеем:
ЕО2 = ЕО2 + 01О22 - 2Е0{ • Oj O2 cos а или
R2 = r2 + m2 - 2т cos а,
cos а =
г2 + m2 - 7?2 2гт
72
ГЛАВА I. ПЛАНИМЕТРИЯ
Таким образом:
п г2 + т2 - R2
EF = 2г • arccos---------.
2гт
При этом, если т = г + Л, то EF =0; если т = R - г, то EF = 2пг, т.е. длине первой окружности.
Задача. Найти площадь общей части двух кругов радиусов г и R (R> г), центры которых находятся на расстоянии т друг от друга (R - г< т £ R + r).
Решение. Аналогично предыдущей задаче (рис. 56) находим:
cq = arccos
г2 л-т2 -R2
2гт
а2 = arccos
R2 л-т2 - г2 2Rm
где ot] иа2- половины углов EOXF и EO2F соответственно.
По формуле для площади сегмента, см. § 1, получаем, что площадь S общей части кругов выражается суммой:
1 о	1 э
S = -г2(2щ - sin ) ч-— 7? (2а2 -sin2a2)-
Здесь sin 2их можно вычислить по формуле:
„2 , р2	2 , ™2 р2
~ п	п г л-т — к	г л-т —к
sm 2ai = 2 cos ai • sm ai =2-------smarccos-----------=
1	2rm	2rm
_ r2 + m2 -R2 L _ ' r2 + m2 -R2 rm V 2rm
>	\	J
Аналогично
. _ R2 + m2 - r2 [. f R2 +m2 - г2 V Rm V I ^rm J
В обеих задачах ответ значительно упрощается, если окружности имеют одинаковые радиусы, т.е. R = r.
§ 5. Взаимное расположение окружностей, углов и треугольников	73
Пример. Около прямоугольного треугольника описана окружность. Другая окружность того же радиуса касается катетов этого треугольника так, что одной из точек касания является вершина треугольника. Найти отношение площади треугольника к площади общей части данных кругов.
Решение. Обозначим радиус окружностей через R. Тогда = ВОХ = COj = R (рис. 57). Поскольку точка О2 — центр окружности, касающейся катетов АВ и ВС, то (ВО{) — биссектриса прямого угла треугольника, (АО2) ± (АВ), (АО2) ± (ВС). Следовательно, угол АВО2 равен 45° и AB = AO2 = R.
Так как АВ = АО{ = ВО{ = R, то ЛАВО{ равносторонний и его высота EOi равна Ял/з/2. Кроме того, АЕ= R/2,
Проведем OXF\\AB. Тогда О1/’=Л£=Л/2; O2F=R -- Ry/3 /2 = Л(2->/3)/2 . Следовательно,
Таким образом, эта задача свелась к предыдущей, поскольку теперь известны не только радиусы окружностей, но и расстояние между их центрами. Площадь общей части двух кругов находится по формуле, полученной в предыдущей задаче, если в ней положить r= R. Имеем:
1	/З
Sabc=±AB •/4C-sin6O°
S=R* (2а-sin 2а), и отношение площадей SABC/S равно:
$авс _
S	2а - sin 2а ’
где а = arccos m/2R.
Рассмотрим теперь несколько задач, в А которых речь пойдет об окружностях, ка- / сающихся друг друга, а также некоторой ' прямой.
Задача. Дее окружности с радиусами г и R касаются друг друга и некоторой пря
Рис. 57
74
ГЛАВА I. ПЛАНИМЕТРИЯ
мой. Найти радиус третьей окружности, касающейся первых двух и данной прямой.
Решение. Очевидно, если гф R, то °4 К	задача имеет два решения (рис. 58).
уч	Одна из окружностей вписана в
\ ч.	криволинейную область КХВК2, дру-
\ ч.	гая касается данных окружностей и
\Р2	прямой внешним образом.
/ ч^О, \ Пусть Oj и О2 - центры двух ок-G '	2	/ Py^H0CTen (примем, что Л > г), а О3
н ' у	~ центР тРетьей (меньшей) окруж-
а------с ности, причем радиус этой после-
рис 5g3	дней обозначим рР Расстояние меж-
ис’	ду центрами О{ и О2 равно r+ R. Ана-
логично: О1О3 = г+р1 и О2О3 = Л + р1.
Рассмотрим прямоугольный треугольник Ох O2D, где D — проекция точки Ох на перпендикуляр О2К2 к прямой АС.
Идея решения состоит в том, чтобы, записав длину отрезка Ох D двумя различными способами (один раз через г и R как сторону прямоугольного треугольника ОхO2D, другой — через г, Ли Pi как длину равного ему отрезка EF), получить уравнение для нахождения радиуса рР
Из прямоугольного треугольника имеем:
OiD = 7(Л + г)2 -(Л-г)2 = l4rR.
Из прямоугольных треугольников О|О3£и O2O3Fнаходим:
О3Е = 27р^г, O3F = 27pjA.
После этого составляем уравнение:
2-УгЛ = 2\frpi + 2yjRpl, или
'ГгК =	+ JR).
Находим радиус искомой окружности:
гЛ
P1 = (V7 + W
£ 5. Взаимное расположение окружностей, углов и треугольников
75
Аналогично находим радиус р2 большей окружности. Ее центр обозначим О4, а проекции точек О1 и О2 на перпендикуляр, опущенный из центра О4 на прямую АС — через Н и G соответственно.
Очевидны следующие равенства:
OiН = 7(Рг +г)2 “(Рг ~r)2 = 27ру->
O2G = 7(р2+Л)2-(р2-Т?)2 = Z'faR,
OiD =	+ A)2 - (r - Л)2 = 2jrR.
Поэтому уравнение для определения р2 запишется следующим образом:
2yfrR = 2y]p2R - 2\[(W’
откуда находим:
rR
р2 = (Л?-77)2‘
Особый класс представляют задачи, в которых две касающиеся друг друга окружности вписаны в некоторый угол. Оказывается, величина такого угла определяется только отношением радиусов данных окружностей. Справедливо и обратное утверждение: при заданной величине угла отношение радиусов таких окружностей однозначно определено.
Задача. В угол ВАС, величина которого равна а, вписаны две окружности, касающиеся друг друга и сторон угла. Определить отношение радиусов этих окружностей.
Решение. Легко видеть, что центр любой окружности, вписанный в угол ВАС лежит на биссектрисе этого угла, поскольку именно биссект-риса является геометрическим местом точек, равноудаленных от сторон угла.
Поэтому точка О, центр данной окруж-ности, и точка Оь центр любой окруж-ности, касающейся ее сторон и угла	Рис 59 .
(очевидно, что таких окружностей будет две) лежит на биссектрисе угла ВАС
76
ГЛАВА I. ПЛАНИМЕТРИЯ
Проведем OD^AC, где точка D лежит на перпендикуляре, опущенном из центра окружности О1 на сторону АС (рис. 59).
Основным приемом, позволяющим связать радиусы окружностей с величиной угла, в который они вписаны, является использование соотношения в прямоугольном треугольнике 00{D: гипотенуза в этом треугольнике равна сумме радиусов окружностей, поскольку те касаются друг друга, один из катетов, а именно OjD, равен разности этих радиусов, поскольку окружности касаются прямой (АС), а острый угол равен -а/2, так как центры окружностей лежат на биссектрисе.
Имеем
ОО} = А, R - г, б^ОЬ = а/2.
Отсюда следует:
. a R-r	.а 1-r/R
sin — =---- или sin — = ------— .
2 R + r	2 1 + r/R
Разрешая это уравнение относительно r/R, получаем:
г _ 1 - sin(a/2)
R 1 + sin(a/2) ’
Таким образом, отношение радиуса меньшей окружности к радиусу большей зависит только от величины угла, в который эти окружности вписаны. Поэтому радиус меньшой окружности, касающейся сторон угла ВАС и данной окружности, относится к радиусу данной так же, т.е. как
/1	• a .	•	\
(1 - sin -)/(!+sin 2 )•
Пример. В треугольнике АВС размещена система бесконечного числа кругов, причем первый из них вписан в треугольник АВС, а каждый следующий круг касается предыдущего и сторон угла АВС. Какую площадь занимает система кругов, если стороны АВ и ВС треугольника соответственно равны 1 и 2, а угол, заключенный между ними, составляет 60°?
Решение. Прежде всего можно заметить, что радиусы кругов, а значит, и их площади, образуют бесконечно убывающую геометрическую прогрессию. Действительно, решение предыдущей задачи показывает, что отношение радиусов последовательных кругов одно и то же и равно:
§ 5. Взаимное расположение окружностей, углов и треугольников
77
rk+l _ 1 - sin(g/2) _ 1 - sin 30° _ £ rk l + sin(a/2) 1 +sin 30° 3’
где rk — радиус k-ro круга. Таким образом, площади кругов и Sk, относящиеся как квадраты их радиусов, относятся как 1:9, т.е.
$к+1 -	$k>
9
aS — сумма площадей всей системы кругов определяется выражением:
5= «S', + Л + +...= ——— ~ — Si • 1-1/9 8 1
Здесь использована формула для суммы членов бесконечно убывающей геометрической прогрессии со знаменателем 1/9.
После этого остается вычислить площадь St круга, вписанного в треугольник АВС.
По теореме косинусов вычисляем третью сторону треугольника:
ЛС2= 12+22 - 2 • 1 • 2 cos 60° = 3,
АС= -Л.
Затем находим площадь треугольника АВС:
1	1	>/з л/з
Sabc = -АВ • ВС • sin 60° = 4 • 1 • 2 ~ = 3L1
2	2	2	2
Вычисляем радиус вписанного круга:
r .Sabc V3/2	1
1 Р (1 + 2 + ТЗ)/2 1 + >/3
и его площадь:
После этого суммарная площадь кругов определяется выражением:
S = —9я ~ 32 + 1б7з 
78
ГЛАВА I. ПЛАНИМЕТРИЯ
Рассмотрим теперь несколько задач, в которых речь идет об окружностях, касающихся только одной из сторон угла и пересекающих другую его сторону в различных точках.
Задача. На луче АВ, являющемся одной из сторон угла ВАС, даны две точки Р и Q. Построить окружность, проходящую через точки Р и Q и касающуюся другой стороны АС угла.
Решение. Пусть такая окружность построена (рис. 60), иМ-точка ее касания с лучом АС. Поскольку точки Р и Q заданы, то можно считать известными расстояния АР и AQ.
По теореме о касательной AM п секущей AQ, проведенных к окружности из одной точки А, имеем:
AM2 = AQ АР, т.е. квадрат длины касательной равен произведению секущей на ее внешнюю часть. Отсюда находим:
AM = ^AQ-АР,
т.е. длина отрезка АМявляется средним геометрическим длин отрезков AQ и АР.
Построить отрезок AM можно следующим образом: отложим на прямой последовательно отрезки КХК2 и К2К3, равные по длине отрезкам АР и A Q; затем с помощью циркуля и линейки разделим отрезок пополам; принимая середину отрезка за центр окружности, опишем эту окружность радиусом 1/2 • КХК3\ из точки К2 восстановим перпендикуляр к КХК3 до его пересечения с окружностью в точке L. Длина отрезка ЬК2 и будет средним геометрическим длин отрезков АР и AQ.
Действительно, &KXLK3 — прямоугольный, поскольку угол KXLK3 опирается на диаметр окружности. Тогда отрезок ЬК2, являющийся по построению высотой прямоугольного треугольника, будет иметь длину, равную среднему геометрическому длин отрезков гипотенузы, на которые ее делит точка К2, т.е.
LK2=^KiK2 K2K3 или LK2=jAQ AP, что и требовалось доказать.
Отложив на луче АС от точки А расстояние, равное AM ~ЬК2, получим третью точку, через которые должна проходить искомая окружность, ее центр находится как точка пересечения срединных перпендикуляров к отрезкам PQ, QM или РМ.
£ 5. Взаимное расположение окружностей, углов и треугольников
79
Рис. 60
Таким образом, соотношение длин отрезков, высекаемых на стороне угла окружностью, и отрезка касательной, образуемой на другой его стороне, регулируется теоремой о касательной и секущей.
Пример 1. Центр окружности, касающейся стороны ВС треугольника АВС в точке В и проходящей через А, лежит на отрезке АС, Найти площадь треугольника АВС, если известно, что ВС =6, ЛС=9.
Решение. Пусть окружность с центром О проходит через точку А треугольника АВС и касается стороны ВС в точке В (рис. 61); D — вторая точка пересечения стороны АС с окружностью.
По теореме о касательной и секущей, проведенными из одной точки к окружности, находим:
AC CD = ВС?,
9 - 00=36 =* CD = 4.
Следовательно, АО =5; радиус R = 2,5.
Площадь треугольника АВС можно определить по формуле:
лвс =	* sin АСВ.
Соединив центр О с вершиной В, получим прямоугольный треугольник ОВС, из которого найдем:
5шЛСЯ = Л-
13
Подставив значения АС и ВС из условия задачи и найденное значение синуса в формулу для площади треугольника АВС, получим:
80
ГЛАВА I. ПЛАНИМЕТРИЯ
Пример 2. Каждая из боковых сторон АВ и ВС равнобедренного треугольника АВС разделена на три равные части, и через четыре точки деления на этих сторонах проведена окружность, высекающая из основания АС хорду DE. Найти отношение площадей треугольников АВС и BDE, если АВ = ВС =3 и А С=4.
Решение. Чертеж к этой задаче представлен на рис. 62.
Пусть F — середина стороны А С, a L и М — точки деления боковой стороны АВ, так что AL - 1 и AM =2. Обозначим, кроме того, AD = х.
По теореме о касательной и секущей имеем:
ALAM=ADAE, или
1-2 = х(4-х).
Отсюда находим, что
x=2-V2 ,
поскольку, очевидно, что х< 2. Следовательно, DE-2 • DF-2^2 . Треугольники АВС и BDE имеют одинаковые высоты, поэтому их площади относятся как длины оснований, т.е. SABC: SBDE-2 : V2 .
Пример 3. В треугольнике АВС: АВ = V14 , ВС = 2. Окружность проходит через точку В, через середину отрезка ВС, через точку Е на отрезке АВ и касается стороны АС. Найти отношение, в котором эта окружность делит отрезок АВ, если DE — диаметр этой окружности.
Решение. Пусть F — точка касания окружности со стороной АС треуголь-\\ ника (Рис< 63)- Поскольку угол EBD опи-./'у Jрается на диаметр окружности, то он .s'	— прямой, и треугольник АВС — пря-
а	F с моугольный. Его гипотенуза находится
РнС бз	по теореме Пифагора: АС= Зл/2 .
По теореме о касательной и секущей, в данном случае проведенных из точки С, легко найти длину отрезка FC. Имеем:
FC2 = CD • СВ или FC2 = 1 • 2 => FC= V2 . Тогда
AF=AC-FC=3J2 - 72 =2^2.
$ 5. Взаимное расположение окружностей, углов и треугольников 81
Обозначим АЕ=х. По той же теореме для касательной AF и секущей АВ получаем:
AF2=AE-АВ
ИЛИ
(2Л)2 = х714,
откуда находим х = 4 V14 /7. Тогда
ЕВ= V14 -х=3>/14/7.
Таким образом, АЕ: ЕВ=4 : 3.
ЗАДАЧИ
1.	Центры двух кругов с одинаковыми радиусами, равными 2, находятся на расстоянии 2^3 один от другого. Найти площадь той части каждого из этих кругов, которая не принадлежит другому кругу.
Ответ: (8л + бТЗ)/3.
2.	Сторона АВ треугольника АВС является хордой некоторой окружности. Стороны АС и ВС лежат внутри окружности, продолжение стороны АС пересекает окружность в точке D, а продолжение стороны ВС —в точке Е, причем АВ = АС= CD = 2, ЕС = V2 • Чему равен радиус окружности?
Ответ: 45.
3.	На стороне ВС треугольника АВС как на диаметре построена окружность, пересекающая отрезок АВ в точке D. Найти отношение площадей треугольников АВС и BCD, если известно, что АС= 15, ВС= 20 и АВС = ACD.
Ответ: 25: 16.
4.	Окружность касается стороны ВС треугольника Л2?Св ее середине, проходит через точку А, а отрезки АВ и АС пересекает в точках D и Е, соответственно. Найти величину угла ВАС, если известно, что ВС= 12, AD= 3,5 и ЕС = 9/45 .
Ответ: 90°.
5.	А, В, Си D — последовательные вершины прямоугольника. Окружность проходит через точки А и В и касается стороны CD в
82
ГЛАВА I. ПЛАНИМЕТРИЯ
ее середине. Через точку D проведена прямая, которая касается той же окружности в точке £, а затем пересекает продолжение стороны АВ в точке К. Найти площадь трапеции BCDK, если известно, что АВ = 10 и КЕ: КА = 3:2.
Ответ: 210.
6.	Сторона АВ квадрата ABCD имеет длину 1 см. Она же является хордой некоторой окружности, причем все остальные стороны квадрата лежат вне этой окружности. Длина касательной СК, проведенной из вершины С к той же окружности, равна 2 см. Чему равен диаметр окружности?
Ответ: V10 см.
7.	Гипотенуза АВ прямоугольного треугольника АВС имеет длину 2 см и является хордой некоторой окружности. Катет АС равен 1 см и лежит внутри окружности, а его продолжение пересекает окружность в точке D, причем CD-3 см. Чему равен радиус окружности?
Ответ: 2 см.
8.	В прямоугольном треугольнике АВС с катетами АВ- 3 и ВС- 4 через середины сторон А В и АС проведена окружность, касающаяся стороны ВС. Найти длину отрезка гипотенузы АС, который лежит внутри этой окружности.
Ответ: 1,1.
9.	Три окружности расположены на плоскости так, что каждая из них внешним образом касается двух других. Радиусы окружностей относятся как 1:2:3. Вычислить углы треугольника, вершины которого расположены в точках касания.
Ответ: я/4; arctg 2; arctg 3.
10.	Центры трех окружностей различных радиусов расположены на одной прямой, а центр четвертой находится на расстоянии d от этой прямой. Найти радиус четвертой окружности, если известно, что каждая из этих окружностей касается трех других.
Ответ: d/2.
§ 6. ТРАПЕЦИИ, ПАРАЛЛЕЛОГРАММЫ, ПРОИЗВОЛЬНЫЕ ЧЕТЫРЕХУГОЛЬНИКИ
Изучение этой группы фигур начнем с трапеции. Как уже отмечалось, трапеция —это выпуклый четырехугольник, две стороны которого (основания) параллельны друг другу, а две другие стороны (боковые) — непараллельны. Сумма внутренних углов, прилежащих к каждой боковой стороне трапеции, равна 180°; точка пересечения диагоналей трапеции лежит на прямой, соединяющей середины оснований; длина средней линии трапеции равна полусумме длин оснований, а площадь трапеции — произведению полусуммы длин оснований на высоту (§1). Если в трапецию можно вписать окружность, то сумма длин боковых сторон равна сумме длин оснований, причем справедливо также и обратное утверждение: если сумма длин боковых сторон трапеции равна сумме длин оснований, то в трапецию можно вписать окружность. Для того, чтобы трапецию можно было вписать в окружность, необходимо и достаточно, чтобы она была равнобочной (см. задачу 7, § 1).
Установим прежде всего число параметров, необходимое для того, чтобы задать трапецию. Покажем, что вообще говоря, таких параметров четыре. Чтобы пояснить сказанное, рассмотрим следующие три задачи на построение.
Задача 1. Построить трапецию по четырем сторонам (а и b —основания трапеции, с и d— боковые стороны).
Решение. Предположим, такая трапеция построена (рис. 64). Имеем: AD = a, BC=b, АВ-с, CD=d.
Пусть, например, а> Ь. Возьмем на AD точку £, такую, что jBjE'H CD. Тогда AE=a-b, ВЕ= CD = d. Следовательно, в треугольнике АВЕ известны длины всех сторон и, значит, его можно построить. Очевидно, как построенный треугольник достроить до трапеции.
84
ГЛАВА I. ПЛАНИМЕТРИЯ
Построение осуществляется в следующей последовательности. Сначала (известным способом) по трем сторонам с, d и (а-А) строится треугольник АВЕ. Затем на продолжении отрезка АЕ за точку Е откладывается отрезок ED длиной Ь, наконец, через точки В и D проводятся прямые ВС и CD, параллельные прямым ED и ЕВ. Четырехугольник ABCD есть искомая трапеция.
Действительно, ВС || AD по построению, а АВ и CD —непараллельны. Следовательно, ABCD — трапеция. Далее: АВ=с, BE- CD=d, ВС-ED-b — как стороны параллелограмма.
Очевидно, что задача имеет единственное решение, если только а, Ь, с и d таковы, что по трем отрезкам с длинами с, d и - Ь\ можно построить треугольник.
Решение этой задачи показывает, что знание четырех сторон трапеции полностью задает ее и, следовательно, достаточно для расчета всех ее элементов.
Задача 2. Построить трапецию по двум основаниям и двум углам при одном из них.
Решение. Пусть ABCD — искомая трапеция, а и b — ее основания, а а и у - углы при основании AD (рис. 65).
Продолжим боковые стороны АВ и CD до их пересечения в точке Е. Очевидно, что получившийся треугольник AED можно построить, поскольку известны его основание AD и два прилежащих к нему угла. Осталось построить отрезок ВС, параллельный основанию AD и равный по длине Ь.
Если на AD отложить отрезок AF, длина которого равна Ь, и провести прямую FC, параллельную боковой стороне АВ, то длина отрезка ВС, проведенного через точку С параллельно основа-
Е нию AD, будет как раз равна Ь, т.е. трапе-Л ция ABCD будет построена полностью.
/ \	Таким образом, построение состоит
п/ ъ \с из следующих процедур. Сначала по ос-/ н А нованию а и двум прилежащим к нему
/	/ \ углам строим треугольник AED. Затем на
/	/	\ его основании откладываем отрезок AF,
/п / у А такой, что AF-b, и проводим ГС||ЛВ.
Через точку С проводим отрезок ВС, параллельный основанию AD треуголь-Рис’ 5	ника AED. Трапеция ABCD — искомая.
Действительно, как основание, так и прилежащие к нижнему основанию углы по построению равны заданным. Таким образом, задача имеет единственное решение. Решение показывает,
§ 6. Трапеции, параллелограммы, произвольные четырехугольники
85
что и в этом случае четыре элемента (хотя и отличные от элементов предыдущей задачи) полностью задают трапецию.
Задача 3. Построить трапецию по двум основаниям и двум ее диагоналям.
Решение. Пусть ABCD — искомая трапеция, а и Ь — ее основания, rfj и d2 — диагонали (рис. 66).
Проведем прямую BE, параллельную АС, и рассмотрим получившийся треугольник BDE. В этом треугольнике известны длины всех сторон: BE=dx, BD = d2n DE-a + b, следовательно, такой треугольник можно построить. После этого решение задачи
становится очевидным, поскольку до-
строить треугольник BDE ж трапеции	и- с
ABCD легко: достаточно провести че-рез точку В прямую, параллельную ос-	\
нованию AD, и отложить на ней отре-зок ВС, равный Ь.
Доказательство того факта, что тра-	Рис 66
пеция ABCD — искомая, также очевидно. Из построения ясно, что ее диагонали и основания равны заданным величинам. Ясно также и то, что построение возможно тогда, когда по трем отрезкам dx, d2 и (a + b) можно построить треугольник.
Как и в предыдущих случаях, решение этой задачи показывает, что произвольная трапеция определяется, вообще говоря, четырьмя независимыми параметрами. В данном случае такими параметрами являются ее основания и диагонали.
Рассмотрим решение нескольких «производных» задач.
Пример 1. Найти площадь трапеции, если ее основания равны 5 и 2 см,а боковые стороны— 3 и 1 см.
Решение. В условии задачи даны четыре элемента, по которым трапецию можно построить, см. задачу 1 (рис. 64). Используя метод построения, нетрудно предложить и способ решения этой задачи. Найдем сначала площадь треугольника АВЕ по трем сторонам: ЛВ=3, ВЕ=\ и Я£-5-2 = 3. Для этого воспользуемся формулой Герона:
С п--------------и-----й?------?	/7 1 1 5 >/35
Sabe =	- а)(Р - b)(p - с) = J- • - • -• - = ——.
f	Хг X» £*	i
Площадь параллелограмма BCDE равна удвоенной площади треугольника ECD. Поскольку треугольники АВЕ и ECD имеют
86
ГЛАВА I. ПЛАНИМЕТРИЯ
одинаковую высоту, а основание DE треугольника ECD равно 2 см, то
с _2 С	-V35. с	_ V35
ECD “ у ' АВЕ - ~ > ^BCDE “ “J“
Следовательно, площадь трапеции ABCD равна:
с _ е г _ V35 -У35 _ 7л/35
ABCD - АВЕ • ° BCDE “	+ ~у" “ '	.•
Пример 2. Длины оснований трапеции равны 4 см и 2 см, а один из углов при большем основании составляет 60°. Известно, что в трапе-
цию можно вписать окружность. Найти радиус этой окружности.
Решение. В условии этой задачи присутствуют почти все элементы, необходимые для того, чтобы ее можно было построить стандартным способом, см. задачу 2 этого параграфа. Не хватает только величины второго угла при основании. Вместо этого в задаче имеется условие — в трапецию можно вписать
окружность — равносильное условию равенства сумм длин противоположных сторон трапеции, т.е. условию:
AB+CD-AD+BC-6 (рис. 67).
Поэтому для решения задачи зададим угол BAD, обозначив его величину через а; кроме того, длины сторон АВ и CD назовем х и у. Тогда получим систему уравнений:
xsina = у sin 60°,
х cos а + 2 + у cos 60° = 4,
х + у = 6.
Первое из этих уравнений получено путем выражения высоты трапеции двумя различными способами из треугольников АВЕ и CDF\ второе — путем проектирования ломаной ABCD на прямую AD, причем вид этого уравнения не зависит от того, острый или тупой угол а; третье — отражает условие, что в трапецию можно вписать окружность.
§ 6. Трапеции, параллелограммы, произвольные четырехугольники
87
Из первых двух уравнений находим х и у. Имеем:
2\/3	4 sin а
X —	, у —	-=	,
sin а + л/З cos а sin а + V3 cos а
Подставляя этот результат в третье уравнение системы, получаем:
2 sin а + Уз _ sin а + Уз cos а
sin а + 3 Уз cos а = Уз .
Решив это уравнение, найдем, что sin а = 4Уз/7, cos а= 1/7.
После этого определяем величину у:
-	4 sin а _	4 - 4Уз / 7	_ 16
sin а + Уз cos а ” 4-Уз/7 + -УЗ/7	5’
Поскольку 2г=у sin 60° = у 7з /2, где г — радиус вписанной в трапецию окружности, то г=4Уз /5 см.
Пример 3. Трапеция ABCD с основаниями ВС=\ и AD = 3 такова, что в нее можно вписать окружность и вокруг нее можно описать окружность. Определить, где находится центр описанной окружности, т.е. расположен ли он внутри, вне или же на одной из сторон трапеции ABCD. Найти также площадь описанного круга.
Решение. Пусть трапеция ABCD — такая трапеция (рис. 68). Поскольку в трапецию можно вписать окружность, то суммы ее противоположных сторон равны между собой, а поскольку трапецию можно вписать в окружность, то она — равнобочная. Следовательно, АВ= CD-0,5(BC+AD) = 2 и в t с в ней известны длины всех сторон.	/	^Т\
Для того, чтобы определить, где ле- /	\
жит центр описанной вокруг трапеции //	\
окружности, достаточно выяснить — А -------------L-----AD
острый или тупой угол ACD. Если он 3 Е
~	Рис. 68
острый, то центр окружности лежит внутри трапеции; если он тупой, то центр окружности лежит вне трапеции.
Углы трапеции легко определяются по ее сторонам (см. задачу 1 этого параграфа). Проводим СЕ^АВ, тогда С£= CD = ED =2. Следовательно, угол ADC равен 60°.
88
ГЛАВА I. ПЛАНИМЕТРИЯ
Угол ACD можно рассчитать с помощью теоремы косинусов, примененной к треугольнику ACD. Сначала находим диагональ АС. Имеем:
AC2=CD2+AD2 -2 CD AD cos 60° = 7; АС=Л.
Затем вычисляем угол ACD, равный а:
AD2 = AC2+CD2 -2 AC- CD cos а,
АС2 + CD2 - AD2 7 + 4-9 cos а =------------= —f= = —.
1ACCD 277-2	14
Отсюда, во-первых, видно, что угол а — острый, поскольку cos а > 0; во-вторых, можно найти sin а, который в сочетании с теоремой синусов, примененной к треугольнику ACD, позволяет вычислить радиус описанной вокруг него окружности. Имеем:
2 • sin а ’
где sin а = 71 - cos2 а = 3771 /14. Получаем: R = 771 / 3 .
Площадь описанного круга равна 7тс/3, его центр находится внутри трапеции.
Равнобочная трапеция, с которой мы встретились в последней задаче, имеет ось симметрии, проходящую через середины оснований; центр описанной вокруг нее окружности лежит на этой оси, а в том случае, когда в трапецию можно вписать окружность, на этой оси лежит и центр вписанной окружности. Равнобочная трапеция определяется меньшим числом параметров, чем произвольная трапеция; в общем случае таких параметров три.
Задача. Доказать, что если диагонали трапеции равны, то она — равнобочная.
Решение. Используем построение, выполненное на рис. 66 и состоящее в том, что через вершину Л трапеции ABCD проводится прямая BE, параллельная диагонали АС. Поскольку ВЕ= BD, то треугольник EBD — равнобедренный. Следовательно, угол BED равен углу BDE, а также углу CAD.
Аналогично доказывается, что угол ВАС равен углу BDC. Для этого нужно только провести через точку D прямую, параллельную диагонали BD.
§ 6. Трапеции, параллелограммы, произвольные четырехугольники
89
Таким образом, величина угла BAD равна величине угла CDA и, следовательно, трапеция ABCD — равнобочная.
Пример 4. В трапеции ABCD: AD = 7, длины диагоналей равны V37 , а угол BAD составляет 60°. На диагонали BD расположена точка М так, что ВМ: MD = 3:5. Узнать, какую из сторон трапеции—ВС или CD— пересечет продолжение отрезка AM?
Решение. Поскольку длины диагоналей трапеции равны, то она —равнобочная (см. предыдущую задачу). Из треугольника ABD легко найти длины боковых сторон трапеции. Обозначим их через х (рис. 69). По теореме косинусов имеем:
BD2 = ^ + AD2 - 2x AD cos 60°, или х2-7х+12 = 0,
откуда находим два значения х: jq = 3 и х2 = 4. Таким образом, при заданных условиях возможны два варианта рассматриваемой фигуры.
Пусть Q — точка пересечения диагоналей трапеции. Легко понять, что если Q лежит на отрезке ВМ, то продолжение AM пересечет сторону ВС', если же Q принадлежит отрезку MD, то продолжение AM пересекает сторону CD трапеции.
Из подобия треугольников BQC и AQD видно, что
BQ: QD=BC:AD, т.е. BQ: BD = ВС: (ВС + AD).
Рассмотрим случай, когда боковая сторона трапеции равна 3. В этом случае отрезки АЕ и FD равны 3 cos 60°, т.е. 3/2. Тогда верх-
нее основание трапеции равно 4. Искомое отношение BQ: BD равно 4/11, т.е. меньше, чем 3/8. Значит, в этом случае продолжение AM пересечет боковую сторону CD трапеции.
Во втором случае АВ= CD = 4. Дна- а
логично находим, что верхнее основа-	рис 69
ние трапеции имеет длину, равную 3.
Тогда отношение BQ к QD составляет 3/10, т.е. опять меньше
3/8. И в этом случае продолжение отрезка AM пересекает сторо-
ну CD трапеции.
Пример 5. Дана равнобочная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно V2 /V3 . Найти
углы трапеции.
90
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение. Чертеж к этой задаче дан на рис. 70.
Обозначим угол при большем основании трапеции через а, высоту — Я, радиус описанной окружности — R. Будем искать величину R как радиус окружности, описанной вокруг треугольника АВС, с углом В при вершине, равным (я-а). По теореме синусов имеем:
R_ АС АС 2 sin(7t - а) 2 sin а ’
Вычислим стороны А4ВС. Учитывая, что центр вписанной окружности лежит на
пересечении биссектрис углов трапеции (а также и на оси ее симметрии), получаем
Н sin а ’
АВ =
пт? Я а ^-ytgy;
ВС = 2ВЕ = Я16а/2.
По теореме косинусов находим:
АС2=АВ2+ВС2-2АВВС cos (л-а),
.„2 Н2 „2. а п Н2 „ а
ЯС2 = —=— + Я tg — + 2 -— tg — cos а, sin2 а 2 sina 2
и далее:
4 sin2 a - R2 = Я2(—Jy— + tg2 ~ + 2tg~ • ctga). I^sin a 2	2 J
Поскольку H/R= 72/3 , to R2/H2 = 3/2. Имеем:
A . 2	3	1	2 a a +
4 sin a • - = -r-y- + tg2 - + 2tg— ctga, 2 sin a 2	2
т.е. уравнение для определения острого угла а. Полученное уравнение после упрощений дает:
4 . 2	1	1
6 sin a = —5— + 1, sin a
£ 6. Трапеции, параллелограммы, произвольные четырехугольники 91
6 sin4 а - sin2 а - 1 = О,
Поскольку sin а > 0, то sin а = >/2 /2 и а = тс/4.
Таким образом, углы трапеции равны 45° и 135°.
Рассмотрим теперь выпуклые четырехугольники, у которых имеется не одна, а две пары параллельных сторон — параллелограммы. Напомним, что при этом условии параллельные стороны будут еще иметь и равные длины.
Диагонали параллелограммов в точке их пересечения делятся пополам. Если стороны параллелограмма имеют равные длины, то это — ромб. Диагонали ромба взаимно перпендикулярны. Если длины диагоналей параллелограмма равны, то это — прямоугольник. Прямоугольник с взаимно перпендикулярными диагоналями — квадрат.
Задача 4. Доказать, что параллелограмм, в который можно вписать окружность, есть ромб.
Решение. Поскольку в описанном четырехугольнике суммы длин противоположных сторон равны друг другу, то в случае параллелограмма это условие равносильно равенству длин смежных сторон. Следовательно, такой параллелограмм — ромб.
Задача 5. Доказать, что параллелограмм, вокруг которого можно описать окружность, есть прямоугольник.
Решение. Поскольку во вписанном четырехугольнике суммы противоположных углов равны 180°, то в случае параллелограмма, у которого величины таких углов равны между собой, это условие равносильно тому, что каждый угол составляет 90°, и данный параллелограмм — прямоугольник.
Следствие. Параллелограмм, в который можно вписать окружность и вокруг которого можно описать окружность, является квадратом.
Произвольный параллелограмм полностью определяется заданием трех параметров, например, длин сторон и угла между ними, или длин его диагоналей и угла между ними, или. одной стороны, одной диагонали и угла между сторонами и т.д. Поэтому многие задачи, связанные с расчетом элементов параллелограмма, можно решать как задачи на составление уравнений, аналогично тому, как это делалось в § 3.
92
ГЛАВА I. ПЛАНИМЕТРИЯ
Рассмотрим следующий пример.
Пример 6. В параллелограмме ABCD со стороной AD -а и острым углом BAD = а (а > л/6) высота, опущен-В_____ С ная из вершины В на сторону AD, вдвое /	меньше диагонали АС. Найти площадь па-
х/	/х роллелограмма.
* Х/	Решение. В условии задачи содержатся
—J два из Трех параМетров, «удобно» опре-
Рис 7|	деляющих параллелограмм, это а и а.
Вместо третьего параметра указано соотношение между длинами одной из высот и диагональю параллелограмма.
Введем в качестве третьего параметра длину стороны АВ параллелограмма, обозначив ее х, и запишем условие, что 2?£= = 1/2’ЛС (рис. 71).
Имеем:
1. ВЕ=х- sin а
2. АС* 1 2=АВ2+ВС2-2 АВ ВС cos- АВС
или
АС2 = х1 + а2 - 2а - х- cos (л-а).
Далее составляем уравнение:
х2 sin2 а - ^(х2 + а2 + 2-а  х cos а) или
^(1 - 4sin2 а) + 2 • а  х • cos а + а2 = 0.
Дискриминант 3 sin2 а этого уравнения положителен, поэтому уравнение имеет действительные решения. Поскольку а > л/6, то sin а > 1/2, и первый коэффициент уравнения отрицателен. Так как свободный член уравнения положителен, то по теореме Ви-етта корни уравнения имеют разные знаки. Берем, естественно, положительный корень уравнения:
Уз sin а + cos а 4 sin2 а -1
Заметив, что
V3sina + cos a = 2sin (а+ 7), 6
£ 6. Трапеции, параллелограммы, произвольные четырехугольники
93
4 sin2a - 1 = 4(sin a - sin - )(sin a + sin 7 ) = 4 sin(a - - )sin(a + - ), 6	6	6	6
получим:
a
2sin(a - л/6) ’
Площадь параллелограмма:
с 1
5 = — ax sm a =
2
2 • a sm a
4 sin(a - я / 6) ’
Конечно, этот же результат можно получить^фоще. Из прямоугольного треугольника A CF находим, что CAD = я/6 (отсюда ясно, почему а должно быть больше тт/6). Кроме того, известно, что ADC = я-а, следовательно, ACD = а-я/6. По теореме синусов, примененной к треугольнику ACD, имеем:
а	СР
sin(a - к / 6) sin п / 6 ’
откуда находим длину стороны CD = х:
_______а_____
2sin(a-л/6) ’
Пример 7. В параллелограмме со сторонами aub и углом а проведены биссектрисы четырех углов. Найти площадь четырехугольника, ограниченного биссектрисами.
Решение. Покажем сначала, что четырехугольник, ограниченный биссектрисами внутренних углов параллелограмма, — пря-
моугольник.
Действительно, биссектрисы противолежащих углов паралле-
лограмма попарно параллельны, следовательно, ограниченный
ими четырехугольник KLMN (рис. 72), будет параллелограммом.
Кроме того, все углы этого параллелограмма — прямые. Треугольники ALD, BNC, CMD и АКВ — прямоугольные. Например, в треугольнике АЫ)\ LAD = 1/2 BAD-а/2; LDA = 1/2 • • ADC = (я - a)/2, следовательно, ALD =я-а/2-(я/2-а/2) = я/2. Таким образом, KLMN— прямоугольник.
94
ГЛАВА 1. ПЛАНИМЕТРИЯ
Стороны прямоугольника находим следующим образом. Пусть а >Ь. Заметив, что &CDE — равнобедренный^ЕСЕ = DCE — по условию, так как СЕ — биссектриса; ДЕС = ВСЕ — как накрест лежащие; следовательно, DCE = DEC), получим: АЕ= а - Ь. Тогда из прямоугольного треугольника AEF находим, что EF= KN= (a- b) sin а/2. Аналогично находим, что GD=a-b и GH= MN= (а - b) sin (л/2 - а/2) = (а - b) cos а/2.
Площадь S прямоугольника KLMN вычисляем по формуле:
S=KN- MN=(a-b)2
•	OL	fit.	1	/	l\2
sin	—	cos	_	=	-	(a -	b)	sin a.
2	2	2
Пример 8. Вычислить площадь общей части двух ромбов: диагонали первого равны 2 и 3, а второй получается поворотом первого на 90° около его центра.
Решение. Чертеж к этой задаче представлен на рис. 73. Очевидно, что площадь общей части двух ромбов складывается из четырех площадей фигуры АЕА'О. В свою очередь площадь четырехугольника АЕА' О — есть часть площади прямоугольного треугольника АВО так, что
$аеа'о- $аво ~ Лева1-
Площадь треугольника ЕВА' легко найти, заметив, что этот треугольник получается из треугольника АВО уменьшением двух из его сторон в ОВ/А'В и АВ/ЕВ раз. Поэтому (см. § 1 и 4):
3 ЕВ
2 ’ АВ
S = S
ДД °АВО’ °АЕА'О ° АВО
_ А'В ЕВ „	1/2 ЕВ
ЕВА' ОВ АВ ^аво	1/3 ' АВ
Следовательно, $ =^-° ЕВА' 2
Таким образом, задача сводится к отысканию отношения ЕВ: АВ. Для этого воспользуемся методом, изложенным в § 4. Через точку А проведем HF|| ОВ.
Из подобия треугольников AFD’ и ОА’ D’ с коэффициентом подобия 1 : 3 следует, что AF= 1/3 • ОА’ = 1/3.
§ 6. Трапеции, параллелограммы, произвольные четырехугольники
95
Из подобия треугольников AFE и А'BE с коэффициентом подобия AF: А'В = 1/3 : 1/2 = 2 :3 следует, что ЕВ= 3/2 • ЕА или ЕВ = = 3/5 • АВ. Следовательно, ЕВ: АВ= 3 : 5.
Имеем:
$АЕА'О — $ АО В
fi-- -l--fi-—1=— f1 2*5 J 4|/ 10 J 40’
Поэтому площадь общей части двух ромбов равна 3/10.
В заключение этого параграфа рассмотрим несколько задач, в
которых речь идет о произвольных четырехугольниках или мно-
гоугольниках.
Пример 9. Площадь четырехугольника, вершинами которого служат середины В сторон выпуклого четырехугольника ABCD, равна S. Найти площадь четырехугольника ABCD.
Решение. Четырехугольник KLMN (рис. 74), вершинами которого являются середины сторон произвольного вы
пуклого четырехугольника — параллелограмм (см. § 1), посколь-
ку его стороны попарно параллельны диагоналям четырехугольника ABCD. Длины сторон этого параллелограмма равны dx/2 и д?2/2, как длины средних линий соответствующих треугольников, а угол между ними равен углу между диагоналями четырехугольника. Поэтому
с» г»	d\ dy .	1 (1 , ,
S = sklmn =y ysma = - -J^sma
где a — угол между диагоналями четырехугольника ABCD.
Поскольку площадь произвольного четырехугольника равна полупроизведению диагоналей на синус угла между ними, то
$abcd ~ d2 sin a
2 и
Sabcd = 2S-
Пример 10. Четырехугольник ABCD обладает тем свойством, что около него можно описать и в него можно вписать окружности. Диагонали этого четырехугольника перпендикулярны, АВ = CD и радиус вписанной окружности равен 1. Чему равна площадь четырехугольника ABCD?
96
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение. Поскольку в окружности, описанной вокруг четырехугольника ABCD, хорды АВ и CD имеют равные длины, то равны длины стягиваемых ими дуг. Отсюда следует равенство углов DAC, DBC, АСВ и ADB, опирающихся на эти дуги. Если к тому учесть, что треугольники ВСЕ и ADE — прямоугольные, можно заключить, что упомянутые углы составляют по 45° (рис. 75).
Таким образом, установлено, что четырехугольник ABCD — равнобочная трапеция. Обозначим длины оснований ВС=и, AD=v, а боковых сторон — х. Тогда очевидны соотношения:
1)	и + о = 2х;
2)	(и/42 )2 + (v/42 )2 = х1;
3)	u/2 + v/2 = 2.
Первое из них следует из условия, что в четырехугольник ABCD можно вписать окружность, второе — из теоремы Пифагора, примененной к треугольнику АВЕ, третье отражает тот факт, что EF= и/2, EG= u/2, а весь отрезок FG является диаметром вписанной окружности.
Разрешая эти соотношения, получаем: w = u = x=2, т.е. устанавливаем, что четырехугольник ABCD — квадрат. Следовательно, его площадь равна 4.
Пример 11. Пятиугольник ABCDE вписан в окружность. Расстояния от вершины Е до сторон АВ, ВС и CD (или их продолжений) соответственно равны а, b и с. Найти расстояние от вершины Е до диагонали AD.
Решение. В § 1 была сформулирована в виде задачи следующая теорема: «произведение расстояний от любой точки окружности, описанной около выпуклого четырехугольника, до его противоположных сторон или их продолжений, равны между собой» (см. задачу 10 § 1) (рис. 38). Поэтому, приняв за точку S вершину Е пятиугольника, можно записать уравнение
ас = Ьх,
в котором х — расстояние от вершины Е до диагонали AD пятиугольника. Отсюда легко следует, что х= ас /Ь.
§ 6. Трапеции, параллелограммы, произвольные четырехугольники
ЗАДАЧИ
97
1.	В равнобочную трапецию, верхнее основание которой равно 1, вписана окружность радиуса 1. Найти площадь трапеции.
Ответ: 5.
2.	Дана трапеция ABCD с основаниями AD= 8, ВС-4 и стороной АВ = V28 . Кроме того, известно, что угол CDA составляет 60°. Через точку С проходит прямая, делящая трапецию на две равновеликие фигуры. Найти длину всего отрезка этой прямой, находящегося внутри трапеции.
Ответ: 6.
3.	В трапеции ABCD длина большего основания AD равна 19, А В =13, а другая боковая сторона CD= 12 и перпендикулярна основаниям. Биссектриса острого угла BAD пересекает прямую DC в точке М. Определить, где лежит точка М, на отрезке DC или вне его?
Ответ: Точка Млежит вне отрезка DC\ DC: MD=38 : 3.
4.	Основание АВ трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали Л С равна а, а длина боковой стороны ВС равна Ь. Вычислить площадь трапеции.
Ответ: ЗаЬ/4.
5.	Дана равнобочная трапеция, в которую вписана окружность и около которой описана окружность. Площадь описанного круга в 12 раз больше площади вписанного круга. Найти углы трапеции.
Ответ: arcsin (1/3); я - arcsin (1/3).
6.	Дан параллелограмм ABCD, у которого АВ- 1, ВС =2 и угол АВС — тупой. Через каждую из точек В и D проведено по две прямые, одна из которых перпендикулярна стороне АВ, а другая перпендикулярна стороне ВС. В пересечении этих четырех прямых получился параллелограмм, подобный параллелограмму ABCD. Найти площадь параллелограмма ABCD.
Ответ: 6/5.
7.	А, В, Си D ~ последовательные вершины прямоугольника. Окружность проходит через точки А и Ви касается стороны CD в ее середине. Через точку D проведена прямая, которая касается
98
ГЛАВА I. ПЛАНИМЕТРИЯ
той же окружности в точке Е, а затем пересекает продолжение стороны АВ в точке К. Найти площадь трапеции BCDK, если известно, что АВ- 10 и что КЕ\ КА- 3 : 2.
Ответ: 210.
8.	В выпуклом четырехугольнике ABCD утлы при вершинах А и В — прямые, величина угла при вершине D равна 45°. Длина стороны ВС равна 1 м, длина диагонали BD равна 5 м. Найти площадь этого четырехугольника.
Ответ: 7,5 м2.
9.	В выпуклом четырехугольнике длины диагоналей равны 1 и 2 м. Найти площадь четырехугольника, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны.
Ответ: 1 м2.
10.	В трапеции длины диагоналей равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции.
Ответ: 6.
§ 7. ЗАДАЧИ НА ОТЫСКАНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР С ЭКСТРЕМАЛЬНЫМИ ЭЛЕМЕНТАМИ
Обратимся теперь к особому классу геометрических задач, а именно к задачам, в которых требуется найти фигуру или ее элементы с экстремальными, т.е. наибольшими или наименьшими значениями тех или иных параметров. В задачах этого класса, как правило, речь идет о том, чтобы среди всех фигур, обладающих определенным свойством, найти фигуру, у которой тот или иной параметр принимает наибольшее или наименьшее значение.
Рассмотрим простейший пример.
Задача 1. Среди всех прямоугольников, периметр которых равен 2р, найти прямоугольник с наибольшей площадью.
Решение. Произвольный прямоугольник определяется двумя параметрами: х и у — длинами его сторон. Однако в данном случае эти параметры не являются независимыми, поскольку между ними существует связь, выражаемая уравнением
2х+2у = 2р
и вытекающая из условия, что у всех рассматриваемых прямоугольников один и тот же периметр. Поэтому площадь S такого прямоугольника 5=ху = х(р-х), является функцией только одной переменной — х, причем 0 < х < р.
Таким образом, задача сводится к отысканию максимума квадратичной функции 5(х) = х(р-х) в интервале хе [0;р]. Поскольку парабола х(р-х) направлена ветвями вниз, то, очевидно, что ее максимум достигается в вершине, т.е. при х=р/2. Поэтому в прямоугольнике с наибольшей площадью одна из сторон равна р/2. Отсюда сразу же следует, что у - х=р/2, т.е. прямоугольник — квадрат.
Итак, среди всех прямоугольников с заданным периметром наибольшей площадью обладает квадрат.
Практической интерпретацией полученного результата служит вывод о том, что максимальная площадь прямоугольного участка, который можно огородить забором заданной длины, у квадрата.
100
ГЛАВА I. ПЛАНИМЕТРИЯ
Задача 2. Среди всех прямоугольников вписанный в треугольник АВС таким образом, что две вершины прямоугольника лежат на основании АС,а две другие— на боковых сторонах АВ и В С,соответственно. Найти прямоугольник: 1) с наибольшей площадью; 2) с наи-
меньшей диагональю.
Решение. Обозначим длину основания Л С треугольника через а, а высоты BD — через h (рис. 76). Пусть KLMN— вписанный прямоугольник со сторонами, длины которых равны LM-х, KL = у.
1. Найдем сначала среди прямоугольников тот, у которого наибольшая площадь.
Как и в предыдущей задаче, площадь
А К D N С выражается формулой S=xy, причем Рис. 76	между величинами х и у существует связь.
Действительно, из подобия треугольников ЬВМм АВС следует пропорция
LM АС
BE	х h-у
--- или — =---—
BD	ah
откуда вытекает, что х = (й - у) • a/h. Это позволяет заключить, что площадь любого вписанного прямоугольника равна:
S=xy= ^y(h-y)
Площадь является функцией только одной переменной у.
Поскольку парабола S(y) = y(h - y)a/h направлена ветвями вниз, то в интервале ]0; h[ она имеет максимум, причем этот максимум достигается в точке y-h/2. Отсюда легко следует, что х= а/2.
Таким образом, среди всех вписанных прямоугольников будет обладать наибольшей площадью тот, у которого одна из сторон является средней линией треугольника. При этом x/y-a/h.
2. Найдем теперь прямоугольник с наименьшей диагональю. Обозначим ее длину d. Тогда:
J2 = ? + y2=^2 + h
или
§ 7. Задачи на отыскание геометрических фигур ...
101
Z х2	/ \2
rf2 = y2[l + f £ I ] -2Лу| £ | + а2 [hJ	[hJ
т.е. длина диагонали прямоугольников является также функцией только одной переменной.
Нетрудно видеть, что для параболы f(y), направленной ветвями вверх, минимум достигается при у = у*, где у* — координата вершины этой параболы:
1 + (я/Л)2
Этому значению у* соответствует х*, равное а/[1 + (a/h)2]\ х*/у> - h/a, т.е. отношение сторон прямоугольника, у которого длина диагонали будет наименьшей из всех возможных, равно h/a. Заметим, что отношение сторон полученного прямоугольника обратно по отношению к прямоугольнику с наибольшей площа-
дью, вписанному в этот же треугольник.
Задача 3. На окружности дана точка М. Провести хорду АВ
параллельно касательной к окружности в точке М так, чтобы пло-
щадь треугольника АМВ была наибольшей.
Решение. Пусть О — центр данной окружности, R — ее радиус, АВ — произвольная хорда, параллельная касательной к окружности, проведенной в точке М, С — середина этой хорды (рис. 77).
Прежде всего заметим, что положение хорды АВ определяется всего лишь одним независимым параметром — расстоянием этой хорды от точки М или, например, углом АМВ , под которым эта хорда вид
на из точки М. Поэтому площадь треугольника ЛАЛ? также должна зависеть от этого параметра. Выберем в качестве такого параметра величину угла АМВ , назвав ее а.
Имеем:
1.	СТ? =7? sin а, AS = 27? sin а.
2.	ОС = 7? cos а, (если а > я/2, то С лежит выше О).
3.	A/C=7?+7?cosot = 7?(l +cosа).
102
ГЛАВА I. ПЛАНИМЕТРИЯ
Таким образом,
5(a) = АВ • МС = R2 sin а(1 + cos а) = A2(sin а + у sin 2а).
Найдем теперь, при каком значении а функция 5 (а) принимает свое наибольшее значение (а е [ 0; я ]). Для этого вычислим производную S' (а), приравняем ее к нулю и найдем соответствующие а:
5'(а) = R 2(cos а + cos 2а) = R 2(2 cos2a + cos а - 1),
S'(a) = 2R 2(cos а + l)(cos а - 1/2) = 0,
cos а = -1; cos а= 1/2.
С учетом интервала, в котором меняется а, находим, что a = я/3. Очевидно, что в точке а = я/3 производная 5'(а) меняет знак с «+» на «-», что свидетельствует о максимуме функции 5(a) в этой точке.
Таким образом, среди треугольников, вписанных в окружность
и имеющих основания, параллельные одной и той же прямой,
наибольшей площадью обладает равносторонний треугольник.
Задача 4. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
Решение. Аналогично тому, как это делалось в предыдущих задачах, выразим интересующий нас элемент, в данном случае периметр вписанного в полуокружность прямоугольника (рис. 78), че
рез один параметр.
Этим параметром может быть одна из сторон прямоугольника, например, AD-x. Тогда длина другой стороны CD равна
2 - х2 /4 , а периметр Р выражается формулой:
Р = 2х + 2.1 А2 - — = 2х + V4A2-x2.
V 4
Таким образом, периметр Р является функцией только одной переменной х. Найдем максимум функции Р(х). Вычислим производную Р'(х)\
£ 7. Заданы на отыскание геометрических фигур ...
103
Р'(Х\ - ? +	~2х	- 2^47?2 ~%2 ~х
Приравнивая Р'(х) нулю, находим необходимое условие экстремума
2д/47?2 - х2 = х, откуда х = 47? / V5.
Нетрудно увидеть, что при x<47?/V5 производная Р' положительна, а при х>47?/>/5 , производная Р' отрицательна. Следовательно, в точке x = 47?/V5 функция Р(х) имеет наибольшее значение. Другая сторона CD равна R/45 .
Таким образом, среди всех прямоугольников, вписанных в полуокружность, максимальный периметр имеет тот прямоугольник, у которого стороны равны 47?/ и 7?/V5 .
Теперь можно сформулировать последовательность действий, которой мы придерживались при решении всех рассмотренных выше задач. Сначала определялись независимые параметры, через которые можно было бы выразить интересующий нас элемент произвольной фигуры, принадлежащей к данной совокупности. Затем величина этого элемента записывалась как функция выбранного параметра (переменной). Наконец, с помощью того или иного приема (например, с использованием производной) отыскивался экстремум этой функции и значение экстремального элемента.
Однако имеются задачи, которые допускают чисто геометрическое решение при нахождении фигур с экстремальными свойствами или использующие алгебраические методы частично. Более того, решение этих задач алгебраическим методом было бы связано с громоздкими математическими выкладками и трудностями при истолковании полученных результатов, в то время как геометрическое решение дает ясный и простой ответ. Рассмотрим примеры таких задач.
Задача 5. Две точки А и В расположены по одну сторону от прямой MN. Найти на прямой MN такую точку Q, чтобы сумма ее расстояний от точек А и В была минимальной.
Решение. Пусть Q — произвольная точка, лежащая на прямой MN (рис. 79). Решение задачи легко находится, если заметить, что расстояние от точки Q до точки В равно расстоянию от этой же точки до точки В' симметричной точке В относительно пря-
104
ГЛАВА I. ПЛАНИМЕТРИЯ
Рис. 79
мой MN и лежащей, следовательно, с точкой А по разные стороны прямой MN.
Таким образом, задачу можно переформулировать как задачу о минимуме суммы расстояний QA и QB', которая, очевидно, будет минимальной, если точка Q лежит на прямой АВ', являющейся, как известно, кратчайшим расстоянием между точками А и В'.
Задача 6. Внутри угла А дана точка М. Через точку М провести прямую, отсекающую от этого угла треугольник наименьшей площади.
Решение. Пусть такая прямая проведена,
а точки В и С — точки ее пересечения со сторонами данного угла. Покажем, что если площадь треугольника АВС — наименьшая из всех возможных, то длины отрезков МВ и МС равны (рис. 80).
Обозначим МВ-а, МС-b и предположим противное, что а^Ь, например, а>Ь. Проведем через точку М еще одну прямую, пересекающуюся со сторонами угла в точках В' и С', и так, чтобы АВ' < АВ. Подсчитаем, насколько при этом изменится площадь отсекаемого треугольника:
$АВ‘ С' = $АВС ~ $МВ’В + ^Л/С'С»
т.е. изменение площади этого треугольника происходит за счет уменьшения при отбрасывании площади &МВ' В с одновременным увеличением за счет присоединения площади &МС' С. Имеем:
SMB’b= - а ’ МВ' ’ sin Ф, ^л/с'с= - ’ МС' * sin Ф> 2	2
где ср — угол между прямыми ВС и В' С' (рис. 80<з).
Рис. 80
§ 7. Задачи на отыскание геометрических фигур ...
105
Поскольку а > Ь, то вследствие непрерывности изменения длин отрезков МВ и МС при повороте прямой ВС вокруг точки М, угол ср можно выбрать столь малым, что МВ' > МС'. Отсюда следует, что прямую (В' С') можно провести так, что площадь SMB'В будет больше площади SMC' С, т.е. площадь треугольника SAB' С' будет меньше площади треугольника SABC. Это противоречит условию, согласно которому площадь SABC выбрана наименьшей из всех возможных. Следовательно, а не больше Ь. Аналогично b не может быть больше а. Следовательно, а = Ь. Это означает, что данная точка М должна быть серединой секущего отрезка ВС.
Нетрудно показать, что если искомая прямая ВС проведена через точку М так, что МВ=МС, то SABC будет иметь наименьшую площадь. Действительно, проведем любую прямую В' С', например, как это сделано на рис. 805, и CD || АВ. Фигура В'BCD — параллелограмм, поскольку отрезки ВС и В'D, являющиеся его диагоналями, делятся в точке пересечения пополам. Отсюда следует, что площади треугольников МВБ' и МСС' равны. Следовательно, SMCC'> SMBB- и, значит, площадь треугольника АВ'С' больше площади треугольника АВС.
Построение прямой ВС осуществляется следующим образом. На продолжении отрезка AM за точку М откладываем точку А' так, чтобы АМ= МА'. Затем через точку Л' проводим прямые А 'В и А'С, параллельные соответствующим сторонам угла А. Вершины В и С получившегося параллелограмма АВА'С определяют положение искомой прямой.
Рассмотрим, наконец, пример задачи, в которой алгебраический метод используется лишь частично.
Задача 7. Среди всех треугольников, имеющих при вершине угол р и длину основания, равную Ь, найти треугольник, у которого сумма квадратов боковых сторон наибольшая.
Решение. Известно (см. § 1), что вершины всех треугольников, имеющих одинаковое основание и равные по величине углы при вершине, лежат на одной из дуг окружности, опирающейся на данный отрезок (рис. 7). Этим определяется совокупность рассматриваемых треугольников.
По теореме косинусов, примененной к треугольнику АМС, имеем
АС2 = АМ2 + СМ2-2 •AM- CMcosp, откуда находим интересующую нас сумму квадратов боковых сторон:
106
ГЛАВА I. ПЛАНИМЕТРИЯ
ЛМ2+СМ2 = ЛС2 + 2-ЯМ- CMcosp = i2 + 2-HM- CMcosp.
Поскольку площадь 5 треугольника АМС равна 1/2 -AM- CM sin р, то сумму квадратов боковых сторон можно выразить через площадь S треугольника:
AM2+CM2 = b2 + 4S ctg 0.
Таким образом, сумма квадратов боковых сторон оказалась функцией только одной переменной — площади треугольника S, причем функцией монотонно возрастающей.
Очевидно, что среди всех треугольников, имеющих одно и то же основание и разную высоту, наибольшей будет площадь того треугольника, у которого наибольшая высота. Следовательно, &АМС - равнобедренный.
ЗАДАЧИ
1.	Среди всех прямоугольников с заданной площадью 5 найти прямоугольник с наименьшим периметром.
Ответ: Квадрат со стороной 4s .
2.	В данный сегмент круга вписать прямоугольник наибольшей площади.
Ответ: Высота прямоугольника равна
(л/8Я2 + Л2 -ЗА)/4,
где h — расстояние хорды, стягивающей дугу сегмента, от центра, R — радиус круга.
3.	Каков должен быть угол при вершине равнобедренного треугольника заданной площади, чтобы радиус вписанного в этот треугольник круга был наибольшим?
Ответ: 60°.
4.	Из круга вырезан сектор с центральным углом а. Из сектора свернута коническая поверхность. При каком значении угла а объем полученного конуса будет наибольшим?
Ответ: 2пу[2/3 .
5.	Даны две параллельные прямые и точка М между ними, лежащая на расстоянии а от одной прямой и на расстоянии b от другой. Точка М служит вершиной прямых углов прямоугольных треугольников, две другие вершины которых Р и Q лежат на
§ 7. Задачи на отыскание геометрических фигур ...
107
каждой из параллельных прямых. Какой из треугольников имеет наименьшую площадь? Найти эту площадь.
Ответ: ab.
6.	На стороне угла даны две точки А и В. Найти точку М, лежащую на другой стороне угла и такую, что угол АМВ наибольший из всех возможных.
Ответ: Точка М расположена так, что окружность, проходящая через точки А, В и М, касается стороны угла.
7.	Найти внутри треугольника точку, сумма квадратов расстояний от которой до вершин треугольника была бы минимальной.
Ответ: Искомой точкой является точка пересечения медиан треугольника.
8.	Найти длины сторон равнобедренного треугольника, площадь которого равна 5, а сумма квадратов боковых сторон минимальна.
Ответ'. V45, V25,
9.	В трапеции ABCD боковая сторона CD перпендикулярна основаниям. Кроме того, длина основания AD равна 1 см, а площадь трапеции — 3 Тб /2 см2. Какими должны быть стороны трапеции, чтобы диагональ BD имела наименьшую длину?
Ответ: Основания — 1 и 2 см, боковые стороны — Тб и V? см.
10.	По данному основанию и высоте построить треугольник, имеющий минимальный периметр.
Ответ: равнобедренный треугольник.
§ 8. ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК И МЕТОД КООРДИНАТ
В дальнейшем пойдет речь о «геометрическом месте точек» т.е. множестве точек плоскости, каждая из которых обладает одним и тем же определенным свойством, причем множестве, содержащем все точки, обладающие этим свойством.
Например, геометрическим местом точек, равноудаленных от двух заданных точек А и В, является срединный перпендикуляр к отрезку АВ. Такой вывод можно сделать по двум причинам: во-первых, любая точка этого перпендикуляра равноудалена от точек А и В, во-вторых, любая точка, не принадлежащая срединному перпендикуляру, будет ближе к одной из точек А или В в зависимости от того, по какую сторону от срединного перпендикуляра эта точка лежит. Следовательно, этот перпендикуляр содержит все точки, равноудаленные от точек А и В, т.е. действительно является геометрическим местом точек.
Приведем несколько примеров геометрических мест точек.
Геометрическим местом точек, удаленных от данной точки О на расстояние R, является окружность с центром в точке О и радиусом R.
Геометрическим местом точек, равноудаленных от сторон угла, является биссектриса этого угла.
Геометрическим местом точек, из которых данный отрезок виден под данным углом р, служат дуги двух одинаковых окружностей, в которых данный отрезок является хордой, видной из центров окружностей под углом 2р (рис. 7).
Геометрическим местом середин отрезков, проведенных параллельно основанию треугольника и ограниченных его боковыми сторонами, служит медиана треугольника, проведенная к основанию.
Геометрическим местом середин отрезков, имеющих начало на одной из параллельных прямых, а конец — на другой прямой, служит прямая, параллельная первым двум и находящаяся от них на равном расстоянии.
Рассмотрим несколько задач на нахождение геометрических мест точек.
§ 8. Геометрические места точек и метод координат	109
Задача 1. На плоскости найти геометрическое место оснований перпендикуляров, опущенных из заданной точки А на произвольные прямые, проходящие через данную точку В.
Решение. Пусть точка М— основание одного из таких перпендикуляров (рис. 81). Тогда угол АМВ — прямой. Аналогично прямым будет и любой другой угол АМВ, получающийся при проектировании точки А на прямые, проходящие через точку В.
С другой стороны, известно, что геометрическим местом точек М, из которых заданный отрезок АВ виден под прямым углом, является окружность, проходящая через точки А и В и имеющая отрезок АВ своим диаметром. Таким образом, искомым геометрическим местом точек является окружность с диаметром АВ.
Задача 2. Найти геометрическое место точек плоскости, симметричных данной точке А относительно произвольной прямой, проходящей через данную точку В.
Решение. Очевидно, что сама точка А принадлежит искомому геометрическому месту. Действительно, если прямая, проходящая через точку В, выбрана так, что она проходит и через точку А, то симметричная точке А относительно этой прямой точка А' совпадает с точкой А (рис. 82).
Пусть точка М — точка, симметричная точке А относительно произвольной прямой, проходящей через точку В. Тогда очевидно, что ВА = ВМ. Это означает, что точка М лежит на окружности с центром в точке В и радиусом ВА. Таким образом, необходимым условием, чтобы точка М принадлежала искомому геометрическому месту точек, является условие принадлежности ее указанной окружности.
Покажем теперь, что любая точка окружности с центром в точке В и радиусом ВА принадлежит искомому геометрическому месту.
Рис. 81
Рис. 82
110
ГЛАВА I. ПЛАНИМЕТРИЯ
Пусть М — произвольная точка такой окружности. Проведем к хорде МА срединный перпендикуляр, который, очевидно, проходит через центр окружности, точку В. Тогда точки Ми А оказываются симметричными относительно этой прямой, что и доказывает высказанное утверждение.
Таким образом, геометрическим местом точек плоскости, симметричных данной точке А относительно произвольной прямой, проходящей через другую данную точку В, является окружность с центром в точке В и радиусом ВА.
Задача 3. На плоскости даны два отрезка АВ и CD. Найти геометрическое место середин отрезков, у которых один конец лежит на отрезке АВ, а другой — на отрезке CD.
Решение. Рассмотрим подмножество отрезков, соединяющих точки отрезков А В и CD, такое, что один конец этих отрезков находится в точке Л, а другой — в любой точке отрезка CD (рис. 83).
Это множество принадлежит пучку лучей, исходящих из точки Л, и ограниченно отрезками ЛС и AD. Очевидно, что середины этих отрезков образуют отрезок KL, являющийся средней линией АЛСД параллельный CDn равный по длине 1/2 • CD.
Аналогично, отрезок MN служит множеством середин отрезков, начинающихся в точке В отрезка АВ и оканчивающихся в точках отрезка CD, причем MN\\ CD и MN= 1/2 • CD.
Пусть Е — произвольная точка отрезка АВ. Рассмотрим середины отрезков, исходящих из точки Е и оканчивающихся в точ
ках отрезка CD. Они образуют отрезок PQ, являющийся средней линией &ECD, параллельный CD и равный по длине, как и предыдущие отрезки, 1/2 • CD.
Покажем, что точки Р и Q принадлежат отрезкам КМ и LN соответственно. Действительно, точка Р является серединой одного из отрезков, исходящих из точки С и оканчивающихся в точках отрезка АВ. Следовательно, эта точка принадлежит средней линии КМ треугольника САВ, которая параллельна АВ и равна по длине 1/2 • АВ. Аналогично показывается, что точка Q принадлежит отрезку LN, который также параллелен АВ и равен по длине 1/2 • АВ.
Рис. 83
§ 8. Геометрические места точек и метод координат	111
Таким образом, фигура KLMN— параллелограмм со сторонами, параллельными отрезкам АВ и CD и длинами сторон, равными половинам длин этих отрезков. Геометрическим местом середин отрезков, начинающихся в точках отрезка АВ и оканчивающихся в точках отрезка CD, является множество точек, лежащих внутри или на границе этого параллелограмма.
Заметим, что метод решения этой задачи показывает, что ни одна из точек, лежащая вне параллелограмма KLMN, не может быть серединой какого-либо из рассматриваемых отрезков.
Метод координат
Во многих случаях для отыскания геометрических мест точек удобно использовать метод координат. Напомним основные положения этого метода.
Прямоугольными декартовыми координатами точки на плоскости называются координаты проекций этой точки на оси координат. Между точками М плоскости и парами чисел (х, у) существует взаимно однозначное соответствие, т.е. соответствие, при котором каждой точке соответствует одна пара чисел и каждой паре чисел соответствует некоторая точка плоскости, причем разным точкам соответствуют разные пары. Записывают это так: М(х, у).
Если числа х и у произвольно меняются от 0 до то соответствующая точка М может лежать в любом месте плоскости. Если же точки таковы, что между их координатами существует определенное соотношение, то они лежат не произвольно, а образуют на плоскости некоторое множество. Например, совокупность точек М(х, у), у которых х > 0 и у > О, образуют «первый квадрант», или «первую четверть» плоскости; точки, у которых х< О, у > 0, лежат во «втором квадранте»; совокупность точек, координаты которых связаны неравенством х2 ч-у2 < R2, представляет собой круг с радиусом R и центром в начале координат; совокупность точек, координаты которых удовлетворяют уравнению х = у, является биссектрисой первого и третьего квадрантов и т.д.
Квадрат расстояния d между двумя точками Л(хь у^ и Дх2, у2) выражается через координаты этих точек формулой:
J2 = (x, -хг)г + (у\-у2)г.
Середина отрезка АВ имеет при этом координаты 1/2 • (xj + х2);
Отыскание геометрических мест с помощью метода координат удобно, потому что каждое свойство, которое выделяет геометри
112
ГЛАВА I. ПЛАНИМЕТРИЯ
ческое место точек, алгебраически выражается одним или несколькими соотношениями между координатами точек, принадлежащих этому геометрическому месту. С другой стороны, всякое соотношение (или система соотношений) между координатами хи у точек плоскости определяют множество, которое можно рассматривать как геометрическое место точек, обладающих свойством, выражаемым этим соотношением.
Для иллюстрации сказанного рассмотрим несколько задач.
Задача 4. Каким соотношением между координатами точек, образующих окружность с центром в точке О и радиусом R, записывается это геометрическое место?
Решение. Введем систему координат так, что точка О получит координаты (х0, у0). Пусть М(х,у) — произвольная точка окружности. Тогда расстояние ОМ равно R. Имеем:
d2 = ОМ2 = (х-х^)2 + (у-у0)2.
Поскольку в рассматриваемом случае d = R при любых х и у, то координаты точек окружности должны удовлетворять соотношению
(х - До)2 + (у - Уо)2 = R2,
которое и представляет собой координатную запись данного геометрического места точек. Это соотношение называется «уравнени-
ем окружности» с центром в точке О(х§, у0) и радиусом R.
«х,у)	Задача 5. На плоскости даны две точки
А и В. Найти геометрическое место то-
—► чек, расстояние от каждой из которых до точки Ав к раз больше, чем расстояние до точки В.
_	Решение. Введем на плоскости систему
Рис. 84	-
прямоугольных координат так, чтобы точ-
ки А и В лежали на оси абсцисс, а начало координат, точка О, находилось в центре отрезка АВ (рис. 84). Если обозначить при этом длину отрезка АВ через 2а, то точки А и В получат координаты: Я(-а,0), В(а,0).
Пусть М(х, у) — произвольная точка, принадлежащая искомому геометрическому месту. Тогда
Л/Л2 = (х+ а)2 + У2,
Л/В2 = (х— а^+у2
£ 8. Геометрические места точек и метод координат
113
и соотношение, определяющее геометрическое место точек, имеет вид:
(х + а)2 + у2 .2
(х - а)2 + у2 или более просто:
х2^ - 1) +Л*2 - 1) - 2xa(J<? + 1) = а2 (1 - к2).
Если &= 1, то отсюда следует, что х=0. Это показывает, что геометрическим местом точек, равноудаленных (&= 1) от точек А и В, является срединый перпендикуляр к отрезку АВ, ось ординат.
Если к* 1, то можно разделить обе части уравнения на Р- 1. Получим:
2 п Р + 1	2	2
х1 - 2ха —=--+ у = -а2.
Р-1
Дополняя первые два члена левой части этого уравнения до полного квадрата разности двух чисел, перепишем его в следующем виде:
х - а
Р+Г
Р-1
7
+/ =
2ак Т
P-1J '
Это уравнение описывает окружность с центром в точке Ор
k2 + 1 л
Ox a—z--, О
1 Р-1
и радиусом R-2ak/(k2 - 1).
Полученную окружность называют «окружностью Аполлония». Она представляет геометрическое место точек, расстояния от которых до двух заданных точек плоскости относится как к. Окружность Аполлония легко построить, приняв во внимание, что ее центр лежит на прямой, проходящей через заданные точки, а сама окружность делит отрезок между ними внутренним и внешним образом на части в отношении к \ 1.
Задача 6. Даны окружность и точка А вне ее. Найти геометрическое место середин отрезков АВ, где В — произвольная точка данной окружности.
114
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение. Пусть М (х, у) — произвольная точка, принадлежащая геометрическому месту точек. Начало системы координат удобно выбрать в центре О1 окружности, а ось абсцисс направить вдоль прямой, проходящей через точки Oj и А так, что О^О, 0), А(а, 0), где а — расстояние от точки А до центра окружности (рис. 85).
Пусть В(хьух) — произвольная точка окружности такая, что точка М является серединой отрезка АВ. Числа Xj и связаны между собой уравнением окружности х2 + у2 = R2, где Rx —- радиус этой окружности. Поскольку х= 1/2(х! + а) и у = 1/2 • то находим соотношение между координатами точки М:
'i	2	(R]
(2х - а)2 + (2у)2 = R2 или * ~ у I + У = у
Это уравнение также представляет окружность. Ее центр находится в точке О^а/1, 0), а радиус Т?2 равен 1/2 • Rx. Таким образом, искомое геометрическое место точек найдено. Заметим, что окружность О2 получается из данной окружности преобразованием подобия с центром в точке А и коэффициентом подобия 1/2.
Задача 7. Найти геометрическое место точек, равноудаленных от заданной прямой и данной точки, лежащей вне этой прямой.
Решение. Примем заданную прямую за ось абсцисс, а ось ординат направим так, чтобы она проходила через заданную точку (назовем ее F). Точка F имеет координаты 0 и d, где d — расстояние от точки F прямой (рис. 86).
Рис. 85
§ 8. Геометрические места точек и метод координат	115
Пусть М(х, у) — произвольная точка искомого геометрического места. Тогда
7*2 + (у-^)2,
МА = | у I
и числа хп у удовлетворяют уравнению
7х2 +(у-J)2 = | у |.
После преобразований и упрощений получим уравнение параболы
Таким образом, искомым геометрическим местом точек является парабола, направленная ветвями вверх и делящая отрезок OF пополам.
Указанные в определении геометрического места прямая и точка носят названия директрисы параболы и фокуса параболы, соответственно.
Задача 8. На плоскости даны две точки Fx и F2i расстояние между которыми равно 2f. Найти геометрическое место точек, сумма расстояний от каждой из которых до точек Fx и F2 равна одному и тому же числу 2а(а > f).
Решение. Введем систему координат таким образом, чтобы ось абсцисс проходила через точки Fx и F2, причем начало координат находилось бы в середине отрезка FXF2 (рис. 87). Имеем: Fx(-j\ 0),
Пусть М(х, у) — произвольная точка, принадлежащая геометрическому месту. Тогда
Рис. 86
Рис. 87
116
ГЛАВА I. ПЛАНИМЕТРИЯ
MF!2 = (x+/)2 + Z MF22 = (x-/)2 + y2
и свойство точек, принадлежащих геометрическому месту, записывается в виде уравнения
yl(x + f)2+y2 + 7(х-/)2 ту2 = 2а.
Преобразуем это уравнение:
7(х + /)2 +/ = 1а - J(x - f)2 + у2, a2 -xf = a^(x-f)2 + y2, х2(а2 - /2) + а2у2 = а2(а2 - /2).
Разделив обе части уравнения на его правую часть, имеем:
и, наконец, обозначив разность a2-f2 через Ь2, получим:
Кривая с таким уравнением называется эллипсом, а числа а и b — его полуосями (рис. 87). Если поочередно полагать в уравнении х = 0 и у = 0, то можно видеть, что точки А и В имеют координаты (а, 0) и (0, Ь), соответственно, т.е. длины отрезков АО и ВО равны а и Ь, соответственно.
Точки Fx и F2 называются «фокусами» эллипса, точка О — «центром» эллипса, а точки А и В — «вершинами» эллипса. Оси ОХ и OY служат осями симметрии эллипса.
Если /=0, т.е. точки F{ и F2 совпадают, то длины полуосей эллипса равны между собой (а = b = R), и уравнение эллипса переходит в уравнение окружности с центром в начале координат:
§ 8. Геометрические места точек и метод координат
117
Величина t-f/a, характеризующая относительное удлинение эллипса, называется его «эксцентриситетом». Очевидно, е < 1. Для окружности е - 0.
Задача 9. На плоскости даны две точки Fx и F2, расстояние между которыми равно 2 f Найти геометрическое место точек, для которых разность расстояний (взятая по модулю) до то- Z чек Fx и F2 есть постоянная величина, равная 2а(а < f).
Решение. Введем систему координат таким образом, чтобы ось абсцисс проходила через точки F} и F2, причем начало координат находилось бы в середине отрезка F{F2 (рис. 88).
Имеем: F^-f, 0), F2(f 0).
Пусть М (х, у) — произвольная точка, принадлежащая искомому геометрическому месту. Тогда
Л/Г^^х+уУ + У2,
MF22 = (x-/)2 + /
Свойство точек, входящих в геометрическое место, записывается следующим образом:
| 7(* + /)2 + У2 - >l<x-f)2+y2 | = 2а.
После упрощений, аналогичных предыдущей задаче, получим уравнение
*2 V , a2 f2-a2
Поскольку/> а, то разность/2 - а2 можно обозначить через Ь2. Окончательно имеем:
1 а2 Ь2
Кривая с таким уравнением называется «гиперболой». При указанном выборе системы координат оси координат являются ося
118
ГЛАВА I. ПЛАНИМЕТРИЯ
ми симметрии гиперболы, а начало координат — ее центром симметрии. Точка F{ и F2 называются «фокусами» гиперболы.
Гипербола пересекает одну из своей осей; точки пересечения называются «вершинами» гиперболы. Прямоугольник со сторонами 2а и 2Ь, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется «основным прямоугольником гиперболы». Диагонали основного прямоугольника являются «асимптотами гиперболы».
Число е = f/a называется «эксцентриситетом» гиперболы. Очевидно, с> 1. Если а-b, то уравнение гиперболы имеет вид х2 - у2 = а2. Такая гипербола называется равносторонней. Если оси координат ОХ и ОУповернуть на 45° вокруг начала координат, то в новых осях уравнение гиперболы будет иметь привычный вид: ху = к, где к = а2/2, выражающий обратную пропорциональность двух величин. Можно показать, что график любой гиперболы получается из графика обратной пропорциональности двух величин путем растяжения или сжатия координатных осей и параллельного переноса в ту или иную точку плоскости.
Последние задачи этого параграфа показали, что геометрические свойства фигур и соотношения между их элементами могут быть выражены с помощью алгебраических уравнений между координатами. Изучение геометрических фигур этим способом составляет предмет аналитической геометрии.
ЗАДАЧИ
1.	Найти геометрическое место точек, расстояния которых от сторон данного острого угла имеют одно и то же отношение т : л; (т < п).
Ответ'. Биссектриса этого угла, если т = п; два луча, лежащие внутри угла и исходящие из его вершины, если косинус данного угла больше, чем т/п; четыре луча, исходящие из вершины данного угла, притом два из них лежат внутри угла, а два другие — вне угла, если косинус данного угла меньше, чем т/п.
2.	Найти геометрическое место середин хорд, проведенных в окружности через данную внутри нее точку.
Ответ: Окружность.
3.	Найти геометрическое место середин хорд окружности, образованных прямыми, проходящими через данную точку вне окружности.
§ 8, Геометрические места точек и метод координат	119
Ответ: Дуга окружности.
4.	Найти геометрическое место точек, сумма расстояний которых до двух данных пересекающихся прямых постоянна.
Ответ: Контур прямоугольника.
5.	Найти геометрическое место точек, для которых сумма квадратов расстояний от двух данных точек есть величина постоянная.
Ответ: Окружность с центром в середине отрезка между данными точками.
6.	Найти геометрическое место точек, для которых разность квадратов расстояний от двух данных точек есть величина постоянная.
Ответ: Перпендикуляр к прямой, проходящей через заданные точки и делящий отрезок между ними в определенном отношении.
7.	На плоскости дан луч [ОА) с вершиной в точке О. Найти геометрическое место точек М, расстояние которых до точки О численно равно углу между лучами [ОХ) и [ОМ).
Ответ: Развертывающаяся спираль («спираль Архимеда»).
8.	На плоскости дан луч [ОА) с вершиной в точке О. Найти геометрическое место точек Л/, для которых расстояние от точки О численно равно косинусу угла между лучами [ОА) и [ОМ).
Ответ: Окружность.
9.	На плоскости дан луч [ОА) с вершиной в точке О. Найти геометрическое место точек Л/, для которых расстояние от точки О численно равно косинусу утроенного угла между лучами [ОХ) и [ОМ).
Ответ: Трилистник.
10.	На плоскости дан луч [ОА) с вершиной в точке О. Найти геометрическое место точек М, для которых расстояние от точки О равно а(1 - cos ср), где а — длина данного отрезка, а ср — величина угла между лучами [ОХ) и [ОМ).
Ответ: Кривая, имеющая форму сердца («кардиоида»).
§ 9. ПРЯМЫЕ НА ПЛОСКОСТИ. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Если на плоскости введена система декартовых прямоугольных координат XOY, то каждая точка М плоскости получает пару координат (х, у), а любая прямая может быть записана уравнением
Ax+By+C=Q,	(1)
выражающим линейную связь между координатами составляющих ее точек. Обратно, каждое линейное уравнение указанного вида определяет прямую на плоскости (предполагается, что числа А и В одновременно не равны нулю).
Уравнение у~кх+Ь прямой пропорциональной зависимости между величинами (у- Ь) и х является частным случаем первого уравнения, поэтому оно также определяет прямую на плоскости.
Величина к называется угловым коэффициентом прямой: & = tga, где a — угол накло-напрямой к оси абцисс; параметр b — координата точки, в которой рассматриваемая прямая пересекает ось ординат (рис. 89).
С помощью уравнения у = кх + Ь записывается не всякая прямая плоскости. Прямые, перпендикулярные оси абцисс, образуют с ней угол а, равный л/2, поэтому для них tg а не
существует. В то же время уравнение общего вида (1) определяет любую прямую плоскости, в том числе и вертикальную.
Если а^л/2, то В*0 и уравнение (1) можно переписать в следующем виде:
Рис. 89
А С у—вх-~в-
В этом случае угловой коэффициент определяется формулой:
к = tg a = - —, а
а параметр b равен -С/В.
£ 9. Прямые на плоскости. Элементы аналитической геометрии 121
Если а = я/2, т.е. прямая вертикальна, то 5 = 0. Поскольку при этом А * 0, то уравнение (1) дает х = -С/Л, являющееся уравнением прямой, перпендикулярной оси абцисс и проходящей через точку с координатой Х--С/А. Таким образом, с помощью уравнения (1) можно записать любую прямую плоскости, поэтому оно называется «общим уравнением прямой».
Если на плоскости дана точка у15), то через нее можно провести бесчисленное множество прямых. Уравнение любой такой прямой имеет вид
Л(х-х1) + 5(у-у1) = 0,	(2)
где А и В — произвольные коэффициенты. Действительно, уравнение (2) — линейное, следовательно, оно определяет прямую на плоскости. Кроме того, координаты точки Р, числа хх и уь удовлетворяют этому уравнению. Значит, прямая проходит через данную точку. Если такие прямые не параллельны оси ординат, то В* 0 и, вводя угловой коэффициент к--А/В, уравнение (2) можно записать в другой форме:
y-y}=k(x~xi).	(2')
Если на плоскости даны две точки Р(х15 у0 и Q(x2, у2), то они определяют уже единственную проходящую через них прямую. Если х^х2) т.е. такая прямая не вертикальна, то из уравнения (2') можно найти ее угловой коэффициент. Для этого достаточно подставить в уравнение прямой, проходящей через точку Р(хр у^, координаты точки Q. Имеем:
к = УШ1> х2 -X,
и уравнение прямой, проходящей через две заданные точки плоскости Р(х1,у1) и С(х2,у2), имеет вид
У-У1 = - ~У1 (х-х,), х2 - Xi
ИЛИ
у2 - У1 х2 - X!
Пример 1. Написать уравнение прямой, проходящей через точки Р(1,3) и б(-1,4).
122
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение. Согласно уравнению (3), имеем:
у-3_ х — 1
4^У“ -1-1
или
Эту же задачу можно было бы решить другим способом, а именно с помощью векторов (см. § 1).
Пусть М(х, у) — произвольная точка прямой (5,0. Тогда векторы РМ и ~PQ коллинеарны. Координаты этих векторов таковы:
5М{х-1; у-3}, 50 {-1 -1; 4-3}.
Поскольку координаты коллинеарных векторов пропорциональны, имеем
у - 3 _ х -1 4^3 “ (-1)4” т.е. приходим к тому же уравнению прямой: у = -0,5х + 3,5.
Пример 2. Написать уравнения прямых, являющихся сторонами треугольника АВС, в котором вершины А, В и С имеют координаты Л(0,0), 5(1,-2), С(3, 5).
Решение. Используя уравнение (3), имеем:
(АВ):	У~° =	=» 2х + у = 0;
v '	-2-0 1-0
(ВС): У - 2). =	7х_ 2^-11 = 0;
4	5-(-2)	3-1
(СА):	=	^=>5х-3)> = 0.
0-5	0-3
Пример 3. Написать уравнение медианы AD треугольника АВС, у которого Л(0, 0), 5(1, -2) и С(3, 5), а точка D — середина отрезка ВС.
Решение. Координаты середины отрезка ВС находятся как среднее арифметическое координат точек 5 и С:
1 + 3 п -2 + 5 3 ^= — = у
§ 9. Прямые на плоскости. Элементы аналитической геометрии 123
Уравнение прямой, проходящей через точки А и Z), имеет вид:
у-о
3/2-0
х - 0 о Л л ~Зх ~ 4у - 0.
2-0 л
Для геометрической интерпретации коэффициентов А и В, входящих в общее уравнение прямой (I), рассмотрим следующую задачу.
Задача. Написать уравнение прямой, проходящей через данную точку Р(х^у$) перпендикулярно заданному вектору п , координаты которого {А, В}.
Решение. Прежде всего заметим, что условие задачи определяет единственную прямую. Действительно, через данную точку в заданном направлении (перпендикулярном вектору п ) можно провести только одну прямую.
Пусть М(х, у) — произвольная точка этой прямой (рис. 90). Тогда вектор РМ колинеарен этой прямой при любом положении точки М, Отсюда следует, что вектор РМ перпендикулярен вектору п с координатами {А, В}.
Так как необходимым и достаточным
условием перпендикулярности векторов (п 0, Л2 + 52 0) является условие равенства нулю их скалярного произведения (см. § 1.), т.е. условие
(п • РМ) = 0, то сумма произведений координат соответствующих векторов равна нулю. Заметив, что вектор РМ имеет координаты {х- х$, у~Уо}, получим:
Л(х-хь) + Ду-у0) = 0 или
Ах+ Ву+ С=0, где
С=-Лх0-Ву0.
Решение этой задачи показывает, что коэффициенты А и В, стоящие при х и у в общем уравнении прямой (1), можно трактовать как координаты вектора, перпендикулярного данной прямой.
124
ГЛАВА I. ПЛАНИМЕТРИЯ
Пример 4. Написать уравнение прямой, проходящей через точку Р с координатами (-3, 1) перпендикулярно вектору п {2 - 3}.
Решение. Согласно общей формуле, такое уравнение будет иметь вид:
2(х+3)-3(у-1) = 0 или
2х-Зу + 9 = 0.
Пример 5. Дан треугольник АВС с вершинами /1(1, 3), ДО, 4) и С(-1, 2). Написать уравнение высоты треугольника, опущенной из вершины В на сторону АС.
Решение. Очевидно, что вектор АС перпендикулярен искомой прямой. Его координаты находятся как разности координат точек С и А, т.е. {-2, -1}. Тогда уравнение высоты будет следующим:
-2(х-0)-1(у-4) = 0 или
2х+у-4 = 0.
Угол между прямыми. Будем называть углом между прямыми тот из двух углов между этими прямыми, который не превосходит прямого.
Пусть даны две прямые своими уравнениями
Ахх+ Вху + Сх~0 и А2х + В2У+ С2 = 0.
Поскольку угол между перпендикулярными им векторами пх {Д, Д} и п2 {А2, В2} равен по величине углу ср между самими прямыми или дополняет его до 180°, то косинус этого угла можно вычислить через скалярное произведение векторов пх и п2 и их длины (см. § 1):
cos Ф1 =	,
ЫЫ д/4 + 4 • 74 + 4
(4)
где ср! — величина угла между векторами пх и п2.
Если Л1Я2 + ДД>0, то угол <pj — острый, и угол ср между прямыми равен срр
Если Л1Л2 + ДД = 0, то прямые взаимно перпендикулярны, ср = 90°.
§ 9. Прямые на плоскости. Элементы аналитической геометрии 125
Если А\А2 + ВхВ2< 0, то угол <pj — тупой, и ср = я- ср|. Пример 6. Вычислить угол между прямыми, заданными своими уравнениями
Зх-4у + 1 = 0, х+у-5 = 0. Решение. Для первой прямой вектор п имеет координаты {3,-4}, для второй — {1, 1}. Поэтому
1.3 + 1•(-4) Л
COS Ср 1 =	--- Г  ,
^З2 +(-4)2 -Vi2 + 12	10
откуда
72	41
cpj= 7c-arccos(-—) = arccos(—).
Пример 7. При каких значениях параметра т прямые тих+2у-3 = 0 и
х+ (т- 1)у+ 1 =0 перпендикулярны ?
Решение. Условие перпендикулярности прямых записывается следующим образом:
АХА2 + ВХВ2 = 0.
Поэтому необходимо, чтобы
т • 1 + 2(т- 1) = 0.
Отсюда находим, что /л = 2/3.
Пример 8. Вывести условие, которому должны удовлетворять коэффициенты прямых для того, чтобы эти прямые были параллельны.
Решение. Для параллельных прямых | cos <р | = 1. Используя формулу (4) этого параграфа для косинуса угла между прямыми, получим
| аха2 + вхв21 = Ах + вх • \Ja2 + в2.
После упрощений находим искомое условие:
126 ГЛАВА I. ПЛАНИМЕТРИЯ
~ ^2^1 = О’	(6)
Если для двух прямых, записанных в виде
у = крс+ Ь{ иу= к2х+ Ь2, известны угловые коэффициенты к{ и к2, то угол ср между прямыми определяется по формуле
tg ф=	.	(7)
v 1+kfa	4 7
Признаком параллельности двух прямых является равенство их угловых коэффициентов
= ^2-	(8)
Признаком перпендикулярности двух прямых является соотношение
ИЛИ ^2="*Т”-	(9)
Соотношения (7)—(9) могут быть получены из общих формул (4)-(6), причем соотношение (7) может быть преобразовано к виду:
Из него, в частности, следует условие параллельности прямых (6), если ср положить равным нулю.
Пример 9. Написать уравнение прямой, проходящей через точку М (1, 4) параллельно прямой 2х - Зу + 5 = 0.
Решение. Уравнение прямой, проходящей через точку М(1, 4), имеет вид
у-4 = Л(х-1),
поэтому остается определить только угловой коэффициент к. Для параллельных прямых, согласно формуле (8), коэффициенты кх и к2 равны. Следовательно, к-- 2/3. Итак, у = 2/3(х-1) + 4.
Пример 10. Написать уравнения прямых, проходящих через точку М(1, -1) под углом 45° к прямой Зх-2у + 1 =0.
Решение. Очевидно, что таких прямых две. Поскольку каждая из них проходит через точку М, то их уравнения можно записать в виде
§ 9. Прямые на плоскости. Элементы аналитической геометрии 127 уч-1 -к{х- 1).
Воспользуемся формулой (7) для тангенса угла между прямыми. Для данной прямой угловой коэффициент равен 3/2, поэтому имеем уравнение для определения к:
tg 45° =1 =
к-3/2 1+(3/2)-к
Отсюда находим к} = -5, к2 = 1/5. Следовательно, искомые прямые имеют уравнения у = -5х ч- 4 и у = х/5 - 6/5.
Расстояние от точки до прямой. Пусть дана точка P(xq, yQ) и прямая Ах ч- By ч- С= О (рис. 91). Вычислить расстояние от данной точки до данной прямой.
Поскольку вектор п с координатами {А, В} перпендикулярен данной прямой, то для подсчета расстояния h от точки Рдо прямой достаточно спроектировать вектор РМ (рис. 91) на направление этого перпендикуляра. Здесь М(х,у) — произвольная точка данной прямой.
Заметим, что скалярное произведение двух векторов а и ё, из которых вектор ё — единичный (т.е. имеет длину, равную единице), равно как раз проекции вектора а на направление вектора ё.
Действительно, имеем
(а ё) = | а 11 ё | cos а ё = | а | cos а ё = проекция^,
т. к.| ё |= 1.
Единичный вектор ё получим в данном случае из вектора п , разделив его на |л |, т.е.
п - А	В
ттгг =	-===
|л|	[7л2 ч- В2 у1а2 ч- В2
Кроме того, имеем PM {x-xQ, у-у0}. Находим расстояние h:
h - \ РМ  ё \ -I	I
Л(х-х0) + Д(у-у0)
128
ГЛАВА I. ПЛАНИМЕТРИЯ
ИЛИ
Л =
AxQ+ByQ-(Ax + By) \1а2+в2
Поскольку точка М(х, у) лежит на прямой, то Лх + By + С = 0 и Ах + By = -С, Заменяя сумму Ах + By в последней формуле ее значением -С, получаем формулу для расстояния от точки Р(х0,у0) Д° прямой:
_ | ^хр + Др + С | у/а2+в2		(11)
Пример 11. Найти расстояние от точки Р(3, 1) до прямой Зх-4у + 2 = 0.
Решение. Воспользовавшись формулой (11), имеем:
| 3-3-41+2 | _ 7
а/з2+(-4)2	5'
Пример 12. Найти высоту треугольника АВС, опущенную из вершины А на сторону ВС, если А(2, 1), Д-З, 4) и <7(1, 1).
Решение. Запишем сначала уравнение прямой ВС, проходящей через две точки В и С. Имеем
у - 4 _ х - (-3)
1-4	1-(-3)
или
Зх+4у-7 = 0.
По формуле (11) находим длину высоты треугольника:
|3-2 + 4-1-7| 3
5-
Взаимное расположение прямых на плоскости. Пусть две прямые плоскости заданы своими уравнениями
А}х+ В{у+ С{ = 0,
у^зХ + В2у + С2 = 0,
причем Ау + 52 * 0, А2 + В2 * 0.
Эти прямые могут пересекаться, быть параллельными или совпадать. Если выражение
129
(13‘)
(13”)
(12’)
$ 9. Прямые на плоскости. Элементы аналитической геометрии А^Л^-А^О,	(12)
то прямые не параллельны, следовательно пересекаются в единственной точке.
Если
А = АХВ2-А2ВХ = 0,	(13)
то прямые либо параллельны, либо совпадают.
Последние случаи можно отличить друг от друга, проверив, равно или не равно нулю одно из двух выражений А1=Л1С2~ -А2СХ или Д2 = ВхС2- В2Сх. Если они не равны нулю, то прямые параллельны; если же А! = А2 = 0, то прямые совпадают.
В тех случаях, когда соответствующие коэффициенты в уравнениях прямых отличны от нуля, условие параллельности прямых означает простую пропорциональность этих коэффициентов __ .
4	^2 Q
условие совпадения прямых —
л2	в2	с2
а условие пересечения прямых —
Л2 В2
Пример 13. Какие из трех данных прямых 2х+Зу-4 = 0, 4х-- 2у + 1 = 0, 2х + у + 4 = 0 параллельны прямой 4х + 2у - 7 = 0?
Решение. Прямые2х + у + 4 = 0и4х + 2у-7 = 0параллельны, поскольку только для них выражение А -АХВ2 -А2ВХ равно нулю. Очевидно также, что эти прямые не совпадают.
Пример 14. При каких значениях т прямые тх + (т - 1)у + 2 = 0 и Зх+ (т - 1)у + 1 = 0 пересекаются?
Решение. Подсчитаем выражение А = АХВ2 - А2ВХ, Имеем: А = т(т - 1) - 3(т - 1) = (т - 3)(m - 1). Отсюда находим, что А 0, если т * 1 и т * 3. Именно при таких т прямые пересекаются.
Пример 15. При каких значениях т прямые тх + Зу + 1 = 0 и (w + 2)x+3wy+2 = 0 совпадают?
Решение. В случае совпадения прямых А = 0. Следовательно, необходимым условием совпадения прямых является уравнение
130
ГЛАВА I. ПЛАНИМЕТРИЯ
А = т~ Зт - 3(т + 2) = 0
ИЛИ
т2 - т - 2 - 0.
Отсюда находим тх = -1, т2 = 2.
При Ш--1 имеем два уравнения: -х+3у + 1 =0 и х-Зу + 2 = 0. Очевидно, что эти прямые параллельны, но не совпадают.
При w = 2 имеем: 2х+Зу+1 = 0 и 4х+6у+2 = 0, т.е. прямые совпадают.
ЗАДАЧИ
1.	Стороны треугольника АВС заданы уравнениями 4х + Зу - 5 = 0, х-Зу+10 = 0их-2 = 0. Найти координаты его вершин.
Owee/л; (2,-1); (-1,3); (2,4).
2.	Даны уравнения двух сторон параллелограмма 8х + Зу + 1 = 0, 2х + у- 1 = 0 и уравнение одной из его диагоналей Зх+ 2у + 3 = 0. Определить координаты вершин этого параллелограмма.
Ответ: (1, -3); (-2, 5); (5, -9); (8, -17).
3.	Дана прямая 2х+Зу + 4 = 0. Составить уравнение прямой, проходящей через точку Р(2,1): а) параллельно данной прямой; б) перпендикулярно данной прямой.
Ответ: а) 2х + Зу - 7 = 0; б) Зх - 2у - 4 = 0.
4.	Даны вершины треугольника АВС: А(2, 1), 5(-1, -1) и С(3, 2). Составить уравнения его высот.
Ответ: 4х+3у- 11 = 0; х + у + 2 = 0; Зх+2у-13 = 0.
5.	Составить уравнение прямой, проходящей через точку Р(3,5) на одинаковых расстояниях от точек Л(-7, 3) и 5(11, -15).
Ответ:х+у~ 8 = 0; 11х-у-28 = 0.
6.	Даны уравнения сторон треугольника Зх + 4у-1=0; х- 7у - 17 = 0; 7х + у + 31 = 0. Вычислить углы треугольника и доказать, что он равнобедренный.
Ответ: л/4; л/4; л/2.
7.	Составить уравнения сторон треугольника АВС, если даны одна из его вершин Л(1, 3) и уравнения двух медиан х- 2у + 1 = 0 и у - 1 =0.
Ответ:х + 2у-7 = 0; х-4у-1=0; х-у + 2 = 0.
§ 9. Прямые на плоскости. Элементы аналитической геометрии 131
8.	Даны вершины треугольника: Л(-10, -13), В(-2, 3) и С(2, 1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
Ответ: 4.
9.	Составить уравнения прямых, параллельных прямой Зх - 4у - 10 = 0 и отстоящих от нее на расстояние d= 3.
Ответ: Зх-4у - 25 = 0; Зх - 4у + 5 = 0.
10.	Составить уравнения прямых, которые проходят через точку Р(2, -1) и вместе с прямыми 2х-у+5 = 0иЗх + 6у-1=0 образуют равнобедренные треугольники.
Ответ: х-Зу-5 = 0; Зх + у- 5 = 0.
§ 10. ЗАДАЧИ НА ПОСТРОЕНИЕ
Задачи на построение — это задачи, в которых с помощью циркуля и линейки требуется выполнить то или иное построение, изобразив определенную геометрическую фигуру по ее заданным элементам. Решения таких задач состоят из четырех частей.
Анализ задачи. В этой части, полагая, что задача решена, т.е. требуемая геометрическая фигура построена, разыскивают такие зависимости между ее элементами, которые позволили бы свести данную задачу к другим, известным ранее.
Построение. Выполняется согласно найденному плану решения.
Доказательство. На основании известных теорем производится доказательство того, что построенная фигура удовлетворяет всем условиям задачи.
Исследование. Производится определение условий, при которых задача имеет решение, определяется число существенно различных решений, исследуются особые случаи.
Отметим простейшие построения, которые служат основой для выполнения других, более сложных.
1.	Построить отрезок, равный данному.
2.	Построить угол, равный данному.
3.	Разделить данный отрезок пополам.
4.	Разделить данный угол пополам.
5.	Через данную точку провести прямую, параллельную данной прямой.
6.	Из данной точки, не принадлежащей данной прямой, опустить на эту прямую перпендикуляр.
7.	Из данной точки, лежащей на прямой, восставить к этой прямой перпендикуляр.
8.	Построить треугольник по трем сторонам (т.е. построить треугольник, стороны которого были бы равны трем заданным отрезкам).
9.	Построить треугольник по двум сторонам и заключенному между ними углу (т.е. построить треугольник, две стороны кото
£ 10. Задачи на построение
133
рого и угол, заключенный между ними, были бы равны двум заданным отрезкам и заданному углу соответственно).
10.	Построить треугольник по стороне и двум прилежащим к ней углам (т.е. построить треугольник, сторона которого и два прилежащих к ней угла были бы равны отрезку и двум заданным углам соответственно).
Кроме того, напомним решения еще двух задач, требующих построить отрезок, длина которого х удовлетворяла бы уравнениям:
ах= Ьс, £-ab,
где а,Ь и с — длины трех заданных отрезков. Решение первого из этих уравнений позволяет разрешить пропорцию
решение второго — найти «среднее геометрическое» двух заданных отрезков
х = Jab.
Решение первой задачи понятно из рис. 92. На одной из сторон произвольного угла от его вершины А откладываются последовательно отрезки АВ и ВС, равные заданным отрезкам с длинами а и Ь. На другой стороне угла откладывается отрезок AD, равный третьему отрезку с длиной с. Затем про-водится прямая BD и через точку С — прямая СЕ || BD. Получающийся при этом отрезок DE будет искомым, поскольку его длина х должна с/\	\
удовлетворять пропорции АВ: ВС-AD: DE или Q	-
а: b = с: х в силу известной теоремы Фалеса (об рис 92 отрезках, отсекаемых параллельными прямыми на сторонах угла).
Заметим, что длина х отрезка DEпрямо пропорциональна длинам b и с и обратно пропорциональна длине а. Поэтому рассмотренный метод решения позволяет строить отрезки как пропорциональные, так и обратно пропорциональные данным. Например, имеется множество отрезков с длинами
Ь\, 1>2, Ь3,..., Ьп и требуется построить им пропорциональные отрезки с длинами такие, что
134
ГЛАВА I. ПЛАНИМЕТРИЯ
h. = h. = А.
*1 Х2 "'х„'
Очевидно, что взяв два произвольных отрезка с длинами а и с, можно построить множество искомых отрезков указанным методом пр формуле
Xj =	, где z= 1, 2, 3, п.
а
В случае необходимости построить множество отрезков, длины	которых обратно пропорциональны длинам
b}, b2, Ь3,..., bn, опять задаемся двумя произвольными отрезками с длинами о и с и выполняем требуемое построение по формуле
у,. = а - где i- 1, 2, 3,..., п.
1 ь;
Решение второй задачи о построении среднего геометрического двух отрезков иллюстрируется рис. 93. На прямой последовательно откладываются два отрезка АВ и ВС такие, что АВ= а и ВС~Ь. Затем на отрезке Л С как на диаметре строится окружность радиуса (а + Ь)/2 и из точки В восстанавливается перпендикуляр
_____с к прямой АС до его пересечения в точке Е с окружностью. Поскольку КАЕС — пря-
Z / \\ моугольный (Z АЕС — опирается на диа-^2 /z Х метР и БЕ - его высота, то по извес-тной теореме BE2=АВ- ВС, т.е. BE = \/ab . Таким образом, очевидно, что следует
Рис. 93	принять х = BE.
В дальнейшем будем ссылаться на эти простейшие задачи как на известные.
Рассмотрим ряд задач на построение.
Задача 1. Построить треугольник по периметру 2р и двум углам, величины которых равны а и р.
Решение. Анализ задачи. Пусть АВС — искомый треугольник, в котором АВ+ВС+ СА = 2р и ВАС =а, ВСА =р (рис. 94).
Если на продолжении основания АС за точку А отложить отрезок DA, такой, что DA = AB, а за точку С —- отрезок СЕ, такой, что СЕ= СВ, то длина всего отрезка DE будет равна как раз периметру 2р.
£ 10. Задачи на построение
135
Соединив точки D и Е с вершиной треугольника В, получим два равнобедренных треутольника^ДЛ и ЕВС. В этих треугольниках ADB = ABD^ а/2 и СВЕ = СЕВ = р/2 , поскольку внешние углы ВАС и ВСА равны сумме двух с ними несмежных углов соответствующих треугольников. Таким образом, в треугольника DBE известны длина основания DE-2p и величины углов при основании а/2 и р/2. Следовательно, &DBE можно построить известным способом. Далее при вершине В известным способом мож-	а/2	р/2
но^построить углы DBA - а/2 и	R/2
СВЕ - р/2 . Стороны этих углов	р\
определят две другие вершины А	—1
и С искомого треугольника АВС.	94
Построение. По данным в усло-
вии_ задачи элементам строим &DBE (DE=2p, ДИдЕ = а/2 , ВЕР = Р/2 ). Затем при вершине В строим углы DBA = а/2 и ЕВС = Р/2 ; получаем точки Аи С. Треугольник АВС— искомый.
Доказательство. Действительно, периметр треугольника АВС равен 2р, поскольку треугольники ABD и СВЕ — равнобедренные по построению, т.е. в них AD-AB и СВ=СЕ\ следовательно, АВ + ВС + СА = AD+СЕ+СА = DE=2p.	___
Угол ВАС = а как внешний угол к треугольнику ABD\ ВСА = р, как внешний угол к треугольнику СВЕ.
Анализ задачи. Задача имеет решение, если а + р < я. Очевидно также, что это решение единственное с точностью до положения треугольника АВС на плоскости.
Задача 2. Построить треугольник по трем медианам (т.е. построить треугольник, у которого медианы были бы равны трем заданным отрезкам).
Решение. Анализ задачи. Предположим, что задача решена и искомый треугольник АВС построен, AM, BN и СР — его медианы, причем AM = та, BN= ть, СР- тс (рис. 95).
Рассмотрим &ВЕС. Точка М— середина его основания, а боковые стороны BE и СЕ таковы, что BE =2/3 • ть, СЕ =2/3 • тс. Если продлить медиану AM за точку М на отрезок MFc длиной 1/3 • та, соединить точку F с вершинами В и С, то получившийся четырехугольник BECF будет, очевидно, параллелограммом, поскольку его диагонали, пересекаясь, делятся пополам (ВМ- МС, ЕМ- MF= 1/3 • та). В таком случае BF= ЕС- 2/3 • тс.
136
ГЛАВА I. ПЛАНИМЕТРИЯ
После этого анализа становится ясно, что в &BEF известны длины всех сторон — каждая из них равна 2/3 длины соответствующей медианы треугольника АВС, Значит, &BEF можно построить известным способом. Продлив затем его основание ЕРзъ точку Е на расстояние EF, мы получим вершину А, а продлив его медиану ВМ за точку М на расстояние ВМ~ вершину С ААВС, т.е. построим искомый треугольник.
Построение. Построим треугольник BEF по трем сторонам с длинами 2/3 • та, 2/3 • ть, 2/3 • тс. Для этого сначала с помощью пропорционального деления разделим каждый из трех заданных в условии отрезков на три
равные по длине части и возьмем по две части каждого. Затем на продолжении отрезка EF за точку Е отложим отрезок ЕА {ЕА = 2/3 • та), построив тем самым точку А. Разделим отрезок EF пополам, проведем прямую ВМчерез его середину Ми отложим на ней отрезок МС {МС= ВМ), построив тем самым точку В. Наконец, соединив точки Л, Би С отрезками прямых, получим треугольник АВС.
Доказательство. &АВС — искомый. AM — медиана, поскольку ВМ- МС — по построению. Точка Е — центр тяжести треугольника АВС, поскольку ЕМ- 1/3 • та, АЕ =2/3 • та — т построению. Следовательно, отрезки СР и BN будут двумя другими медианами &АВС. Кроме того, BECF — параллелограмм по построению. Следовательно, ЕС=BF- 2/3 • тс и BE =2/3 • ть — по построению. Это означает, что BN= тьи СР= тс, что и требовалось доказать.
Исследование. Анализ задачи и построение показывает, что она имеет решение тогда и только тогда, когда длины данных отрезков та,ть и тс позволяют построить по ним треугольник, т.е. тогда, когда выполняются известные неравенства та + ть > > тс, ть + тс> таи та + тс> ть. В этом случае задача имеет единственное решение с точностью до расположения треугольника на плоскости.
Задача 3. Построить треугольник по трем высотам {т.е. построить треугольник, у которого высоты были бы равны трем заданным отрезкам).
Решение. Анализ задачи. Предположим, что задача решена и искомый треугольник АВС построен, AM, BN и СР — его высоты, причем AM = ha, BN= hb, CP= hc (рис. 96).
£ 10. Задачи на построение
137
Обозначим длины сторон треугольника а, b и с, соответственно. Очевидно, что aha = bhb = сЛс = 25, где S — площадь треугольника. Отсюда следует, что длины сторон треугольника а, b и с обратно пропорциональны длинам его высот hahb и hc\
. 2S 25 25
Поэтому можно построить, хотя и не единственным способом, три отрезка, длины которых а', Ь' и с будут обратно пропорциональны высотам искомого треугольника и, следовательно, прямо пропорциональны его сторонам (как это делается, было показано выше). Значит, треугольник со сторонами а\ Ь'н с'будет подобен искомому.
Пусть Д/Г В 'С' — треугольник со сторонами а', Ь' и с построен. Тогда определятся его высоты — /Га, h'bn h'c. Очевидно, что коэффициент к подобия этого треугольника искомому определяется отношениями
k =	= —
ка hb hc ’
Поэтому, имея треугольник А'В'С', нетрудно достроить его до искомого треугольника АВС.
Построение. Построим сначала указанным выше способом три отрезка, длины которых а', Ь' и с были бы обратно пропорциональны длинам ha, hb и hc, соответственно. Затем построим треугольник Л'Б'С' по трем сторонам с длинами а', Ь' ис'. Из одной из вершин треугольника Л'В' С', например, из вершины В', опустим на его основание Л' С' высоту В'N. На получившемся перпендикуляре к основанию в точке N отложим отрезок NB, такой, что NB= hb. Через полученную точку В проведем прямые, параллельные боковым сторонам треугольника Л'В' С\ а именно: ВЛ || В'Л'
Рис. 96
138
ГЛАВА I. ПЛАНИМЕТРИЯ
и ВС || В'С' до пересечения их с основанием Л'С' в точках А и С. Треугольник АВС — искомый.
Доказательство. Во-первых, ясно, что построенный треугольник подобен искомому. Действительно, его стороны по построению параллельны сторонам треугольника А'В’С, а следовательно, он подобен этому треугольнику. В свою очередь последний подобен искомому, поскольку его стороны пропорциональны сторонам искомого треугольника. Таким образом, построенный треугольник подобен искомому. Во-вторых, коэффициент подобия построенного и искомого треугольников равен 1, поскольку высоты, опущенные из вершины В в этих треугольниках, имеют равные длины (также по построению). Следовательно, эти треугольники равны, и высоты построенного треугольника имеют заданные длины.
Исследование. Задача может быть решена в том случае, если по трем отрезкам, длины которых обратно пропорциональны заданным отрезкам ha, hb и hci можно построить треугольник, причем задача имеет единственное решение.
В последней задаче искомый треугольник был построен с помощью преобразований подобия, примененного к другому треугольнику, подобному искомому. Этот метод можно использовать и во многих других задачах на построение. Рассмотрим несколько частных примеров.
Задача 4. В данный треугольник вписать прямоугольник с заданным отношением т : п сторон (предполагается, что две вершины такого прямоугольника должны лежать на основании треугольника, а каждая из двух других— на боковой стороне данного треугольника).
Решение. Анализ задачи. Пусть задача решена и прямоугольник
MNPQ, вписанный в данный треугольник АВС (рис. 97), имеет требуемое отношение сторон MN\ MQ = т: п.
Можно заметить, что преобразование подобия с центром в вершине А треугольника, примененное к рассматриваемому прямоугольнику, отображает вершины M,Nyl Qwl соответствующие вершины MX,NX и Qx подобного ему прямоугольника MXNXPXQX, лежащие на сторонах того же треугольника, причем, естествен
§ 10. Задачи на построение
139
но, отношение сторон прямоугольника сохраняется. Единственно, что при этом вершина Р прямоугольника MNPQ отображается в вершину Рх подобного прямоугольника MXNXPX Qx уже не лежащую на стороне данного треугольника. Однако именно это обстоятельство открывает следующую возможность решения задачи: построить внутри угла С прямоугольник MXNXPXQX, три вершины которого лежат на сторонах этого угла, причем MXNX: MxQx = m\ nfa затем подобным преобразованием увеличить (или уменьшить) его до таких размеров, при которых и четвертая вершина Р оказалась бы лежащей на сторонах треугольника АВС. Для этого достаточно провести прямую АРХ до пересечения ее со стороной ВС треугольника АВС в точке Р. Коэффициент к = АР\АРх и определит искомый коэффициент подобия.
Построение, Из произвольной точки Мх основания АС треугольника АВС восставим перпендикуляр MXNX. Построим отрезок MXQX, длина которого равна т/п • MXNX (используя для этой цели уже указанный выше прием, основанный на теореме Фалеса), и достроим фигуру до прямоугольника MXNXPXQX. Затем через точки А и Pj проведем прямую до пересечения в точке Р со стороной ВС треугольника. Из точки В проведем прямые PN || АС и PQ || NM. Из точки допустим перпендикуляр на основание АС. Фигура MNPQ — искомый прямоугольник.
Доказательство. То, что фигура MNPQ — прямоугольник, следует из построения. Из подобия треугольников APXNX и APN, а также АРХ Qx и APQ следует
PN = АР . PQ = АР PXNX " АРХ ’ PXQX " АРХ ’
Отсюда находим:
PQ = PxQx = т PN PXNX п ’
Следовательно, отношение сторон построенного прямоугольника равно т : п, что и требовалось доказать.
Исследование. Задача имеет единственное решение при любом отношении чисел т : п.
Задача 5. Внутри угла ВАС дана точка М. Построить окружность, касающуюся сторон данного угла и проходящую через точку М.
140
ГЛАВА I. ПЛАНИМЕТРИЯ
Решение. Анализ задачи. Предположим, что искомая окружность построена (рис. 98). Очевидно, что ее центр О лежит на биссектрисе угла BA С.
На этой же биссектрисе лежит центр и любой другой окружности, касающийся сторон данного угла, однако такие окружности, вообще говоря, не проходят через заданную точку М. Рассмотрим одну из таких окружностей с центром в точке Ох (рис. 98). Очевидно, что она может быть получена из окружности О преоб-в разованием подобия с центром в точке Л, причем заданная точка М отобразится в yf	одну из двух точек Мх или М2, получаю-
щихся в результате пересечения луча с * окружностью Ор Таким образом, нетруд-------------------У но построить комбинацию фигур, подоб-А-----------------С ную искомой. Если затем увеличить (или
уменьшить) ее линейные размеры путем преобразования подобия с коэффициентом к = АМ/АМх, то получится искомая фигура.
Построение. Построим сначала биссектрису AD утла ВАС, на которой должен лежать центр искомой окружности. Приняв любую точку Ох этой биссектрисы за центр окружности, подобной искомой, впишем эту окружность в угол ВАС.
Соединим точки М и А лучом AM, получив тем самым на окружности Ох две точки Мх и М2, которые в результате преобразования подобия могут отобразиться на заданную точку М, т.е. служить ее прообразом. Соединим точку Мх или точку М2 с центром Ох вспомогательной окружности.
Если теперь с помощью преобразований подобия увеличить (или уменьшить) линейные размеры треугольника АМ1О1(АМ2О1) в АМ/АМХ (или AM/AM-i) раз, то точка Ох отобразиться на некоторую точку О, которая и будем центром искомой окружности. Известно, что каждая прямая в результате такого преобразования отображается на параллельную ей прямую, поэтому для построения точки О достаточно провести через точку М прямую, параллельную ОХМХ или (О^М^. Пересечение такой прямой с биссектрисой AD дает центр О искомой окружности.
Доказательство. Покажем, что окружность с центром в точке О (или О*) и радиусом ОМ (или 0*М) касается сторон данного угла. Поскольку ОХЕХ = ОХМХ по построению, а искомая окружность по-
§ 10. Задачи на построение
141
лучена из окружности Ох преобразованием подобия, то ОМ = ОЕ. Это ясно и из пропорций:
ОМ = АО ОЕ АО
ОХМХ ЛЦ О\ЕХ ЯЦ
Так как ОХЕХ = то ОЕ= ОМ.
Исследование. Очевидно, что если точка М лежит строго внут-
ри заданного угла, то задача имеет ровно два решения.
Рассмотрим еще несколько характерных задач на построение.
Задача 6. Построить окружность, касающуюся данной окруж-
ности и данной прямой в заданной на этой прямой точке {данные
окружность и прямая не пересекаются).
Решение. Анализ задачи. Пусть задача решена и искомая окруж-
ность (ее центр обозначим 00 построена (рис. 99). Эта окружность касается данной окружности (с центром в точке О) в точке В, а данной прямой MN — в заданной на ней точке А.
Прежде всего ясно, что расстояния 0{А и Отравны, поскольку точка Ох должна быть равноудалена от точек Аи В. Отсюда следует что расстояние Ох О между центрами окружностей больше длины перпендикуляра ОХА к прямой MN на величину R радиуса данной окружности. Значит, если отложить на продолжении от-
резка ОХА за точку А отрезок А02, такой, что А02 = R, то расстояния Ох О и Ох 02, будут равны между собой. Таким образом, точка Ох равноудалена от точек О и 02 и является центром окружности, касающейся прямой MN в заданной на ней точке А.
Построение. Проведенный анализ показывает, что центр Ох искомой окружности может быть построен как пересечение двух геометрических мест точек (см. § 8): одного из них — множества точек, равноудаленных от двух _ данных точек О и 02 (срединный м перпендикуляр к отрезку 002) и другого —- множества центров окружностей, касающихся данной
прямой в заданной на ней точке А (перпендикуляр к прямой MN в точке А). Каждое из геометрических мест строится известными способами.
142
ГЛАВА I. ПЛАНИМЕТРИЯ
Доказательство. ОХА ± MN — по построению, следовательно, окружность с центром в точке Ох и радиусом ОхА касается прямой MN. ОХО2 = ОХО— по построению, следовательно, ОХВ= Ох О-- R- ОХО2 - R- ОХА. Значит, эта окружность касается данной окружности.
Исследование. Очевидно, что задача всегда имеет решение и притом только одно.
Нахождение искомой точки как результата пересечения двух геометрических мест может быть использовано и в других задачах на построение. Проиллюстрируем это еще одним примером.
Задача 7. Построить треугольник по основанию, противолежащему ему углу при вершине и высоте (т.е. построить треугольник, у которого основание, высота, опущенная на него из противолежащей вершины, и угол при этой вершине были бы равны двум заданным отрезкам и данному углу).
Решение. Анализ задачи. Пусть искомый треугольник АВС построен (рис. 100а). В нем длина основания АС равна а, высота равна Л, угол АВС = а.
Из вершины В треугольника отрезок АС виден под углом а, значит, точка В должна принадлежать геометрическому месту точек, о котором уже шла речь (см. § 1, рис. 7), т.е. лежать на
Рис. 100
§ 10. Задачи на построение
143
окружности радиуса А, опирающийся на данный отрезок. Радиус этой окружности определяется теоремой синусов:
2 sin а
Кроме того, поскольку вершина А удалена от основания треугольника на расстояние Л, то она должна принадлежать соответствующему геометрическому месту точек, состоящему из двух прямых, параллельных основанию АС, и отстоящих от него на расстояние Л. Значит, вершина В принадлежит пересечению этих геометрических мест и может быть построена таким способом.
Построение. Имея в виду, что построить две прямые MXNX и M2N2, параллельные АС и отстоящие от нее на расстояние h, нетрудно, покажем только, как строится геометрическое место точек, из которых данный отрезок АС виден под данным углом а (известно, что это две симметричные дуги окружностей с радиусами R).
Из середины D отрезка АС восставим к прямой АС перпендикуляр. Возьмем на этом перпендикуляре произвольную точку Р и проведем через нее прямую PQ под заданным углом а и к восставленному перпендикуляру.
Через вершину А треугольника проведем прямую АО, параллельную прямой PQ до пересечения ее в точке О с перпендикуляром DP. Точку О примем за центр первой окружности, а симметричную ей точку — за центр второй окружности (рис. 1006). Фигура AECFA — искомое геометрическое место.
Точки В,В{,В2 и пересечения двух построенных геометрических мест определяют возможное положение вершин искомого треугольника.
Доказательство. Любой из построенных треугольников АВС, АВХС, АВ2С или АВ3С (а они все равны) будет искомым. Действительно, основание и высота каждого из них имеют, по построению, заданные длины а и h, соответственно.
Покажем, что угол при вершине каждого треугольника, например &АВС, равен а. Поскольку угол AOD равен по построению углу OPD и равен а, то центральный угол АОС равен 2а. Поэтому любой вписанный в окружность угол, как, например, углы АВС, АВХС, АВ2С или АВ3С, опирающийся на хорду АС, равен половине центрального угла, т.е. а.
144
ГЛАВА I. ПЛАНИМЕТРИЯ
Исследование. Очевидно, что с точностью до равенства треугольников задача имеет единственное решение. При этом оно существует только в том случае, если длина h высоты треугольника не больше длины отрезка DE (рис. 100), т.е. удовлетворяет неравенству h < R 4- R cos а или h < R( 1 + cos а). Отсюда получаем:
h < я(1 + cos а)/2 sin а.
Задача 8. Построить треугольник по медиане, биссектрисе и высоте, проведенным к стороне из противоположной ей вершины (т.е. построить треугольник, в котором медиана, биссектриса и высота, выпущенные из какой-либо вершины, были бы равны трем заданным отрезкам).
Решение. Анализ задачи. Пусть АВС — искомый треугольник
(рис. 101). Длины его медианы BD, биссектрисы BE и высоты BF обозначим через т, I и h, соответственно.
Установим сначала немаловажный факт: во всяком треуголь-
нике биссектриса лежит между медианой и высотой, проведенными из той же вершины. Для доказательства опишем вокруг &АВС
Рис. 101
окружность (ее центр — точка О), так что угол АВС окажется вписанным, а основание АС— хордой этой окружности. Поскольку биссектриса BE делит угол АВС пополам, то ее продолжение ЯЯд^угжно разделить пополам дугу АС, на которую опирается рассматриваемый угол (ABH = СВН). Поскольку далее D — середина основания &АВСи, следовательно, середина хорды АС окружности, то срединный перпендикуляр
к отрезку Л С должен прсугги как через центр О окружности, так и через середину Я дуги АС. Треугольник DHE— прямоугольный, причем угол DEH — острый. Поэтому дополнительный для него угол DEB — тупой. Следовательно, &DEB — тупоугольный. Отсюда следует, что высота BF, опущенная из вершины В острого угла
тупоугольного треугольника на основание, попадает на продолжение этого основания, т.е. точка £ лежит между точками Z) и F, что и доказывает сформулированное утверждение.
Построение. Из произвольной точки Упрямой восставим к ней перпендикуляр FB, такой, что FB~h. Из точки В, приняв ее за вершину искомого треугольника, растворами циркуля т и I опи
£ 10. Задачи на построение
145
шем дуги окружностей до пересечения их в точках Ли Ес выбранной прямой. Примем, что BD и BE — это медиана и биссектриса искомого треугольника, соответственно. В точке D восставим перпендикуляр к прямой до пересечения его в точке Нс прямой ВН, продолжением биссектрисы BE за точку Е. С одной стороны, центр описанной окружности должен лежать на срединном перпендикуляре к отрезку АС, т.е. на перпендикуляре DH. С другой стороны, он равноудален от точек В и Я, следовательно, он лежит на срединном перпендикуляре к отрезку ВН. Пересечение этих двух перпендикуляров дает точку О. Описав из точки О, как из центра, окружность радиуса ОВ, получим точки А и С ее пересечения с исходной прямой. Приняв эти точки за вершины треугольника, получим треугольник АВС.
Доказательство. Треугольник АВС — искомый. В нем высота BF имеет длину h по построению. BD — медиана, поскольку точка D — середина отрезка АС, также по построению. Ее длина равна т. Наконец, отрезок BE является биссе^рисой, поскольку его продолжение попадает в середину дуги АС и, следовательно, угол АВЕ равен углу СВЕ . Кроме того, по построению длина этого отрезка равна 7.
Исследование. Задача имеет единственное решение, которое возможно при условии h<l<m.
В заключение этого параграфа рассмотрим несколько задач о построении отрезков, длины которых выражаются той или иной алгебраической формулой. Следует отметить, что многие задачи на построение допускают прием решения, при котором некоторый элемент геометрической фигуры сначала рассчитывается аналитически и находится формула, выражающая его величину через заданные длины и углы. Затем указывается способ, как построить этот элемент (по полученной для него формуле) с помощью циркуля и линейки. Задачи о построении отрезков по формулам являются одним из этапов указанного пути.
Задача 9. Заданы отрезки длиной а,Ь,с и d. Построить отрезок, длина которого выражается формулой jabcd .
Решение. Корень четвертой степени из произведения отрезков может быть представлен в следующем виде:
У abed ~ у] Jab • Vcrf.
Поскольку известно, как построить среднее геометрическое двух отрезков, то сначала можно построить отрезок с длиной = Jab ,
146
ГЛАВА I. ПЛАНИМЕТРИЯ
затем — отрезок с длиной х2 = 4cd , наконец — искомый отрезок с длиной 7*1*2 •
Задача 10. Заданы отрезки длиной а и Ь. Построить отрезок, длина которого выражается формулой ^2а2 + 7Ь2 .
Решение. Построим сначала отрезок с длиной Xj = ^2а2 , представив его как среднее геометрическое отрезков с длинами а и 2а, т.е. Ja 2а . Затем построим отрезок с длиной х2 = 7?Z>2 , предста-вив его как среднее геометрическое отрезков b и 7Ь, т.е. х2 = \lb • 7Ь . Наконец, построим искомый отрезок, представив его в виде гипотенузы прямоугольного треугольника с катетами Xi и х2, т.е.
yl2a2 + 7b2 = 7*? + *2 •
Задача 11. Заданы три отрезка, длины которых а, b и с. Построить отрезок х, с длиной, выраженной формулой
1
с
£ х
1 1
— + — а b
Решение. Построим сначала отрезок у, длина которого выражается формулой
1	1	1
— _ —।—, у	а b
Для этого запишем последнюю формулу в виде (а + Ь)/а = b/у. Тогда становится очевидным, что у можно найти как четвертое пропорциональное для отрезков а + Ь, а и Ь. На одной из сторон произвольного угла от его верши-р/	ны последовательно откладываем
отрезки а + b и а; на другой стороне — отрезок Ь. Через концы отрезков проводим параллельные прямые А~Га-------------а ' (рис. 102). В результате построения
получаем отрезок DE с длиной у.
Рис*102	После того как отрезок DE пост-
роен, нетрудно построить искомый отрезок. Очевидно, что
1 1 1
X у с
поэтому отрезок с длиной х строится аналогично предыдущему.
§10. Задачи на построение
147
ЗАДАЧИ
1.	Построить прямоугольный треугольник: а) по гипотенузе и отношению катетов; б) по катету и отношению другого катета к гипотенузе.
2.	Построить треугольник: а) по основанию, высоте и медиане, проведенной к боковой стороне; б) по двум сторонам и углу, противолежащему одной из них.
3.	Вписать в данный сегмент квадрат.
4.	Вписать в данный сегмент прямоугольник с заданным отношением сторон.
5.	Построить треугольник по стороне, противолежащему ей углу и разности двух других сторон.
6.	Дана прямая и две точки по одну сторону от нее. Построить окружность, проходящую через данные точки и касающуюся данной прямой.
7.	Провести через точку М, находящуюся вне круга, прямую, на которой окружность высекает отрезок заданной длины а.
8.	Через данную точку, лежащую внутри данного угла, провести прямую так, чтобы она отсекала от угла треугольник наименьшей площади.
9.	Провести через точку Мвнутри круга хорду заданной длины а..
10.	Заданы отрезки с длинами а, Ь, с и d. Построить отрезки, длины которых выражаются следующими формулами:
а) \llab + led, б) \1а2 + Ь2 - с2 -d2,
в)^]а31Ь + c3/d, г) yfa^b,
Z)(Jfa + tfb)4 е) (a4 +b4)/(a3+b3).
§ И. РАЗНЫЕ ЗАДАЧИ
1.	Даны две концентрические окружности. Касательная к меньшей окружности делит длину дуги большей окружности в отношении 1 : 5. Найти отношение площадей кругов, ограниченных этими окружностями.
Ответ. 4: 3.
2.	Дан ромб с острым углом ос. Какую часть площади ромба составляет площадь вписанного в него круга?
Ответ, я sin а/4.
3.	В окружность вписана трапеция ABCD, причем ее основания АВ- 1 и DC-2. Обозначим точку пересечения диагоналей этой трапеции через F. Найти отношение суммы площадей треугольников ABF и CDF к сумме площадей треугольников AFD и BFC.
Ответ. 5/4.
4.	В прямоугольной равнобедренный треугольник АВС с прямым углом при вершине В вписан прямоугольный треугольник ЛВУСтак, что MNC =90°, точка Долежит на АС, а точка М —• на стороне АВ. В каком отношении точка Nдолжна делить гипотенузу АС, чтобы площадь треугольника MNC составляла 3/8 от площади треугольника АВС?
Ответ. 3/4.
5.	В треугольнике ЛВС длины боковых сторон АВ и ВС равны а, угол АВС= 120°. В треугольник ЛВС вписана окружность, касающаяся стороны АВ в точке D. Вторая окружность имеет центром точку В и проходит через точку D. Найти площадь той части вписанного круга, которая находится внутри второго круга.
Ответ. - 4 7з )(5я - 6 7з )/24.
6.	На стороне Л С остроугольного треугольника ЛВС взята точка В так, что AD- 1, ВС= 2 и BD является высотой треугольника ЛВС. Окружность с радиусом 2, проходящая через точки Л и D,
§11. Разные задачи
149
касается в точке D окружности, описанной около треугольника BDC. Найти площадь треугольника АВС.
Ответ. 3>/15 .
7.	Дан квадрат ABCD, длина стороны которого равна а, и построены две окружности. Первая окружность целиком расположена внутри квадрата ABCD, касается стороны АВ в точке Е, а также касается стороны ВС и диагонали АС. Вторая окружность имеет центром точку А и проходит через точку Е. Найти площадь общей части двух кругов, ограниченных этими окружностями.
Ответ. - 1)[(2Л - 1)я-4]/8.
8.	В треугольнике АВС биссектриса АК перпендикулярна медиане ВМ, а угол ХВС равен 120°. Найти отношение площади треугольника АВС к площади описанного около этого треугольника круга.
Ответ. 3 V13 (V13 - 1)/32л.
9.	В треугольнике АВС биссектриса АН делит медиану BE в отношении ВК'. КЕ=2,а угол АСВ равен 30°. Найти отношение площади треугольника ВСЕ к площади описанного около этого треугольника круга.
Ответ. 3/14л.
10.	В трапеции ABCD диагонали АС и DB взаимно перпендикулярны, ВАС = CDB , Продолжения боковых сторон АВ и CD, пересекаясь в точке К, образуют угол AKD , равный 30°. Найти площадь треугольника AKD, если площадь трапеции равна 5.
Ответ. 35/2.
11.	Дана равнобочная трапеция, у которой верхнее основание вдвое меньше нижнего. Определить, в каком отношении делит нижнее основание трапеции прямая, которая параллельна диагонали, проходит ниже ее и отсекает треугольник площадью, в 4 раза меньшей площади трапеции.
Ответ. 4/Тб - 1.
12.	Дана трапеция ABCD, сторона АВ которой перпендикулярна основаниям ВС и AD. На стороне АВ как на диаметре построена окружность радиуса Тб , которая касается стороны CD. Другая окружность радиуса V2 касается сторон AD и CD и пересекается с
150
ГЛАВА I. ПЛАНИМЕТРИЯ
первой окружностью, имея с ней общую хорду длины Тб . Центры обеих окружностей расположены по разные стороны от общей хорды. Найти площадь трапеции ABCD.
Ответ. 12V2/^/3(V3-1).
13.	В параллелограмме ABCD со сторонами AD = 5 и АВ=4 проведен отрезок EF, соединяющий точку Е стороны ВС с точкой F стороны CD. Точки Е и F выбраны так, что ВЕ\ ЕС =1:2, CF\ EF= 1 : 5. Известно, что .точка М пересечения диагонали АС с отрезком J577делит EFb отношении MF: МЕ= 1: 4. Найти диагонали параллелограмма.
Ответ. AC- V45 , BD = V37 .
14.	Трапеция ABCD имеет основания AD- 7, ВС = 4 и боковые стороны АВ- 5, CD = 4. Окружность радиуса V2 с центром в точке 5, лежащая в плоскости трапеции, пересекается со второй окружностью, центр которой лежит внутри трапеции ABCD и которая проходит через точки А и D. Известно, что касательные, проведенные через одну из точек пересечения окружностей, взаимно перпендикулярны. Найти радиус второй окружности.
Ответ. V197/4.
15.	Отрезок АВ есть диаметр круга, а точка С лежит вне этого круга. Отрезки АС и ВС пересекаются с окружностью в точках D и М, соответственно. Найти угол CBD, если площади треугольников DCM и АСВ относятся как 1 : 4.
Ответ, л/6.
16.	В треугольнике АВС проведены биссектриса BD угла АВС и отрезок AM. Точки D и Млежат соответственно на АС и ВС, К — точка пересечения BD и AM. Площади треугольников AKD и АМС относятся как 1 : 6. Найти длину стороны АВ, если АВ+ ВС- 3 и АВ+МВ = 2.
Ответ. 1.
17.	На отрезке АВ длины R как на диаметре построена окружность. Вторая окружность такого же радиуса, что и первая, имеет центр в точке А. Третья окружность касается первой окружности внутренним образом, второй окружности — внешним образом, а также касается отрезка АВ. Найти радиус третьей окружности.
Ответ. Ry[3/i.
§11. Разные задачи
151
18.	Дан правильный треугольник АВС, сторона которого имеет длину а. Окружность проходит через центр треугольника и касается стороны ВС в ее середине М. Прямая, проведенная из вершины Л, касается окружности в точке Е, так что ВАЕ < 30°. Найти площадь треугольника АЕМ.
Ответ. а*\[б /40.
19.	В треугольнике АВС известны длины сторон АВ-6, ВС-4, АС= 8. Биссектриса угла С пересекает сторону АВ в точке D. Через точки A,D, С проведена окружность, пересекающая сторону ВСъ точке Е. Найти площадь треугольника ADE.
Ответ. 3 V15 /2.
20.	В треугольнике АВС косинус угла АСВ равен 2/3, АС=3, ВС =9. Точка D лежит на стороне ВС, так, что CD- 3. Найти отношение площади круга, описанного около треугольника ACD, к площади круга, вписанного в треугольник ABD.
Ответ. 9(11 +4^6 )/50.
21.	В прямоугольном треугольнике АВС длины катетов равны 3 и 4. Из вершины С прямого угла проведена высота CD. Найти расстояние между центрами окружностей, вписанных в треугольники ACD и BCD.
Ответ. V2 .
22.	Дан прямоугольный треугольник АВС с прямым углом при вершине С. Угол САВ равен а. Биссектриса угла АВС пересекает катет АС в точке К. На стороне ВС как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке М. Найти угол AM К.
Ответ, arctg (1/cos а).
23.	Дан параллелограмм ABCD со сторонами АВ = 2 и ВС=3. Найти площадь этого параллелограмма, если известно, что диагональ АС перпендикулярна отрезку BE, соединяющему вершину В с серединой Е стороны AD.
Ответ. V35.
24.	Около окружности с радиусом г описана равнобочная трапеция ABCD. Ей К — точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием АВ и боковой сторо
152
ГЛАВА I. ПЛАНИМЕТРИЯ
ной AD трапеции равен 60°. Доказать, что ЕК параллельна АВ и найти площадь трапеции АВЕК.
Ответ. 9 7з ^/4.
25.	В окружность с радиусом R вписан равнобедренный треугольник АВС с углом при вершине С, равным 120°. D — середина меньшей из дуг, соединяющих А и С, Е — середина меньшей дуги из соединяющих С и В. Доказать, что DE параллельна АВ, и найти площадь трапеции ABED.
Ответ. R2/2.
26.	В треугольнике Я^С угол А равен 45°, а угол С — острый. Из середины стороны ВС опущен перпендикуляр NMw& сторону АС. Площади треугольников NMC и АВС относятся соответственно как 1:8. Найти углы треугольника АВС.
Ответ. 45°, 45°, 90°.
27.	В трапеции ABCD углы А и D при основании AD равны соответственно 60° и 90°. Точка N лежит на основании ВС, причем BN: ВС =2 : 3. Точка М лежит на основании AD, прямая MN параллельна боковой стороне АВ и делит площадь трапеции пополам. Найти отношение АВ: ВС.
Ответ. 4:3.
28.	Три окружности расположены на плоскости так, что каждая из них касается двух других внешним образом. Две из них имеют радиус 3, а третья — радиус 1. Найти площадь треугольника АВС, где А, В и С — соответственно точки касания трех окружностей.
Ответ. 9^7 /16.
29.	Даны утлы АВС и ВСА треугольника (АВС * ВСА ). Найти котангенс острого угла, который образует медиана, выходящая из вершины Я, со стороной ВС.
Ответ. | ctg АВС - ctg ВСА | /2.
30.	В треугольник АВС с заданными углами Я и В из вершины Я опущена высота AD. Точка Р делит сторону АВ пополам. Через точку Р проведена окружность, касающаяся стороны ВС в точке D. Определить радиус окружности, если длина стороны ВС равна а.
Ответ. a/4sin2 2?[ctg В - ctg (Я + Б)].
§11. Разные задачи
153
31.	В параллелограмме со сторонами 2 и 4 проведена диагональ длиной 3. В каждый из получившихся треугольников вписано по окружности. Найти расстояние между центрами окружностей.
Ответ. V51/3.
32.	Даны два одинаковых пересекающихся круга. Отношение расстояний между их центрами к радиусу равно 2т. Третий круг касается внешним образом первых двух и их общей касательной. Определить отношение площади общей части первых двух кругов к площади третьего круга.
Ответ. 32(arccos т - т V1 - т2 )/п т4.
33.	В выпуклом четырехугольнике ABCD заключены две окружности равного радиуса г, касающиеся друг друга внешним образом. Центр первой окружности находится на отрезке, соединяющем вершину А с серединой F стороны CD, а центр второй окружности находится на отрезке, соединяющем вершину С с серединой Е стороны АВ. Первая окружность касается сторон АВ, AD и CD', вторая окружность касается сторон АВ, ВС и CD. Найти АС.
Ответ. 2>/5.
34.	Точка Е стороны ВС и точка У7 стороны AD выпуклого четырехугольника ABCD расположены так, что BE-2'ЕС и AF= 2 - FD. На отрезке АЕ находится центр окружности радиуса г, касающейся сторон АВ, ВС и CD. На отрезке ВТ7 находится центр окружности того же радиуса г, касающейся сторон АВ, AD и CD. Найти площадь четырехугольника ABCD, зная, что указанные окружности внешним образом касаются друг друга.
Ответ. 8г2.
35.	В треугольнике ЛВС сторона ВС служит основанием полукруга, площадь которого равна площади треугольника АВС. Угол ВАС равена. Найти величины углов АВС и ВСА, считая, что АВС > ВСА . Исследовать, при каких а задача имеет решение.
Ответ. АВС = (л - а)/2 + 1/2 • arccos (л/2 • sin а - cos а);
BG4 = (л - а)/2 - 1/2 • arccos (л/2 • sin а - cos а);
О < а < 2 arcsin (1/7л2/4 + 1).
36.	Четырехугольник ABCD вписан в окружность радиуса R и описан вокруг другой окружности, которая касается сторон че
154
ГЛАВА I. ПЛАНИМЕТРИЯ
тырехугольника в точках К, L, М и N. Найти площадь четырехугольника ABCD, если известно, что она в три раза больше площади четырехугольника KLMN, а угол между диагоналями АС и BD равен у.
Ответ. 4R 2sin у/3.
37.	В четырехугольник ABCD можно вписать и вокруг него можно описать окружность. Диагональ ЯС делит площадь четырехугольника пополам. Найти длину диагонали BD, если радиус вписанной окружности равен г, а периметр четырехугольника равен 2р.
Ответ. 2rp/yjp2 -2гр.
38.	Центры трех окружностей различных радиусов расположены на одной прямой, а центр четвертой находится на расстоянии d от этой прямой. Найти радиус четвертой окружности, если известно, что каждая из этих окружностей касается трех других.
Ответ, d/2.
39.	В прямоугольном треугольнике АВС длина гипотенузы АВ равна с, а угол при вершине А равен а. На продолжении гипотенузы АВ через точку В взята точка М, а на продолжении катета Л С через точку С взята точка Nтаким образом, что ВМ- СМ. Найти длину общей хорды двух окружностей, описанных около треугольников АВС и AMN.
Ответ, с sin а/2.
40.	В окружность вписана трапеция ABCD, причем AD || ВС и AD > ВС. На дуге др), не содержащей вершин Ви С, взята точка S. Точки Р, Q, М и N являются основаниями перпендикуляров, опущенных из 5 соответственно на стороны AD, ВС, АВ и CD или на продолжения этих сторон. Известно, что SP-a, SQ-b, SN = с. Найти отношение площади треугольника MQS к площади треугольника NQS.
Ответ. аЬ/З’.
41.	В треугольнике АВС известно, что АВ-20, АС= 24. Известно также, что вершина С, центр вписанного в треугольник АВС круга и точка пересечения биссектрисы угла ВАС со стороной ВС лежат на окружности, центр которой принадлежит отрезку АС. Найти радиус окружности, описанной около треугольника АВС.
Ответ. 12,5.
§11. Разные задачи
155
42.	В прямоугольном секторе АОВ из точки В как из центра проведена дуга ОС (С — точка пересечения этой дуги с дугой АВ) радиуса ВО. Окружность S, касается дуги АВ, дуги ОС и прямой и
ОА, а окружностьS2 касается дуги АВ, прямой ОА и окружности Найти отношение радиуса окружности^ к радиусу окружности S2.
Ответ. 4(2 + 7з )/3.
43.	В треугольнике АВС угол при вершине В равен л/4, а угол при вершине С — л/З. На медианах BMw CN, как на диаметрах, построены окружности, пересекающиеся в точках Р и Q. Хорда PQ пересекает среднюю линию MN в точке F. Найти отношение длины отрезка NF к длине отрезка FM.
Ответ. 7з.
44.	В трапеции ABCD точки К и М являются соответственно серединами оснований АВ и CD, причем АВ =5, С0=3. Найти площадь трапеции, если треугольник АМВ — прямоугольный, а DK — высота трапеции.
Ответ. 8.
45.	В прямоугольном треугольнике АВС из вершины прямого угла ВСА проведены биссектриса CL и медиана СМ. Найти площадь треугольника АВС, если LM= а и СМ - Ь.
Ответ. Ь2^- а2)/^2 + о2).
46.	В окружность с центром О вписана трапеция ABCD, в которой ВС || AD. В этой же окружности проведены диаметр СЕ и хорда BE, пересекающая AD в точке F. Точка Я — основание перпендикуляра, опущенного из точки В на СЕ, S — середина отрезка ЕО, М — середина отрезка BD. Известно, что радиус окружности равен R, а СН = 9Я/8. Найти длину отрезка SM.
Ответ. 3 V2 7?/4.
47.	Окружность радиуса 1 вписана в треугольник АВС, в котором косинус угла АВС равен 0,8. Эта окружность касается средней линии треугольника АВС, параллельной стороне АС. Найти длину стороны АС.
Ответ. 3.
156
ГЛАВА I. ПЛАНИМЕТРИЯ
48.	Два равных правильных треугольника АВС и CDE со стороной 1 расположены на плоскости так, что имеют только одну общую точку С, и угол BCD меньше, чем л/3. Точка К — середина АС, точка L — середина СЕ, точка М —середина отрезка BD. Площадь треугольника KLMр.пвн i 7з /5. Найти длину отрезка BD.
Ответ. (2-V3)/V5 .
49.	Два равных равнобедренных треугольника АВС и DBE (АВ= BC-BD- BE) имею ! общуь вершину Л и лежат в одной плоскости так, что точки .и С ik. одятся по разные стороны от прямой BD, а отрезки АС и DL ле, осекаются в точке К. Известно, что АВС = DBE - а < л '2, АК1 - р < а. В каком отношении прямая Выделит угол АВС 1
Ответ, (а - Р)Дис + р).
50.	В треугольнике ЛВС известно, /то АВ = АС и угол ВАС — тупой. Пусть точка D — это тс жа пер сечения биссектрисы угла ЛВС со стороной АС, М— основание перпендикуляра, опущенного из вершины Л на сторону ВС, Е — основание перпендикуляра, опущенного из D на сторону ВС, Через точку D проведен также перпендикуляр к BD до пересечения со стороной ВС в точке F. Известно, что ME =FC- а. Найти площадь треугольника ЛВС.
Ответ. 25 V7 ^/Yl.
Глава II. СТЕРЕОМЕТРИЯ
§ 1.	ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ СТЕРЕОМЕТРИИ
Так же, как и в первом разделе этого пособия, напомним сначала наиболее употребительные теоремы и формулы, используемые при решении стереометрических задач.
Теоремы о параллельности прямых и плоскостей:
а)	если прямая АВ (рис. 103) параллельна какой-нибудь прямой CD, расположенной в плоскости Р, то она параллельна самой плоскости;
б)	если плоскость R (рис. 103) проходит через прямую АВ, параллельную другой плоскости Р, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой АВ;
в) если две параллельные плоскости Р А и Q (рис. 104) пересекаются третьей плос- Г костью R, то линии пересечения АВ и CD параллельны; г) если две пересекающиеся прямые АВ ( и DC (рис. 105) одной плоскости соответ-ственно параллельны двум прямым А}В{ и D{C{ другой плоскости, то эти плоскости параллельны. /0^	R __	— — Рис. 103 /
Рис. 104
Рис. 105
158
ГЛАВА II. СТЕРЕОМЕТРИЯ
Теоремы о перпендикулярности прямых и плоскостей:
а)	для того чтобы прямая АВ (рис. 106) была перпендикулярна плоскости Р, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости;
б)	для того, чтобы прямая DE (рис. 107) проведенная на плоскости Р через основание наклонной ЯС была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции ВС, наклонной на плоскость Р. (Достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: АС, ВС, DE.)
в)	если две прямые АВ и CD (рис. 108) перпендикулярны одной плоскости Р, то они параллельны между собой;
г)	если две плоскости Ри Q (рис. 109) перпендикулярны одной прямой АВ, то они параллельны друг другу.
Теоремы о перпендикулярности плоскостей:
а)	если плоскость Р проходит через перпендикуляр к другой плоскости Q, то плоскость Р перпендикулярна плоскости Q (рис. 110);
Рис. 108
Рис. 109
$ 1. Основные теоремы и формулы стереометрии
159
б)	если две плоскости Р и Q (рис. НО) взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.
Теоремы о скрещивающихся прямых:
а)	угол а между скрещивающимися прямыми ABnCD (рис. 111) определяется как угол между одной из этих прямых (например, CD) и любой прямой АХВХ, проходящей через ее произвольную точку Е параллельно другой прямой;
б)	расстояние h между скрещивающимися прямыми АВ и CD (рис. 111) определяется как кратчайшее расстояние между точками этих прямых и может быть найдено как расстояние от одной из этих прямых (например, АВ) до плоскости Р, проходящей через другую прямую CD параллельно первой.
Двугранные углы
Определения. Пересечение двух полупространств, границами которых служат непараллельные плоскости Р и Q (рис. 112) называется двугранным углом.
Ограничивающие двугранный угол плоскости Р и Q называются его гранями, а прямая АВ, являющаяся общей границей этих плоскостей — ребром двугранного угла.
Пересечение двугранного угла и плоскости S, перпендикулярной к его ребру, называется линейным углом двугранного угла (рис. 113). Величиной <р двугранного угла называется величина его линейного угла, т.е. величина угла между прямыми CD и СЕ, перпендикулярными ребру АВ двугранного угла.
Величину меньшего из двугранных углов, определяемых двумя пересекающимися плоскостями, называют углом между этими плос-
Рис. по
Рис. 111
160
ГЛАВА II. СТЕРЕОМЕТРИЯ
костями. Если плоскости параллельны, то угол между ними равен 0; если они перпендикулярны, то угол между ними равен л/2.
Трехгранные углы
Объединение всех лучей, имеющих общее начало S (рис. 114), и пересекающих данный треугольник АВС, называется трехгранным углом.
Величина каждого плоского угла трехгранного угла меньше суммы величин двух других его плоских углов:
а<р + у,р<а + у;у<а + р.
В трехгранном угле сумма величин всех его плоских углов меньше 2л; (а + р + у< 2л). Двугранные углы <р, у и 0, образованные гранями трехгранного угла, выражаются через плоские углы a, р и у при его вершине формулами:
cos у - cos а • cos В cos ф =--------------,
sin а -sin Р
cos В - cos у•cos а cos \|/ =--——’------,
sin у • sin а
л cosa-cosBcosy cos 0 =--------------,
sin р * sin у
где ф — величина двугранного угла, противолежащего грани с
плоским углом у; v — грани с плоским углом Р; 0 — грани с плоским углом а (рис. 114).
Доказательство. Покажем, например, справедливость первой из этих формул. Отложим на ребре SB отрезок SK, такой,
§ 1. Основные теоремы и формулы стереометрии
161
что SK= 1. Из точки допустим перпендикуляр КМ на плоскость грани SAC, а из полученной точки М проведем ML ± SA, продолжив его до пересечения с ребром SC в точке N. Соединим точку К с точками L и N отрезками прямых.
По теореме о трех перпендикулярах, KL будет перпендикулярна прямой SA, поскольку эта последняя перпендикулярна ее проекции LN на плоскость SAC. Поэтому угол KLN будет линейным углом
двугранного угла между плоскостями SAB и SAC и его величина как
раз равна ср.
Из прямоугольных треугольников SKL и SNL находим:
SL = cos a; KL- sin а;
г \т	. п Г»АГ COSOt
LN- cos а • tg Р; SN - -.
cosp
После этого из &SKN по теореме косинусов можно вычислить:
KN2
cos2 а cos2 р
-21-
cos а cosp
cosy.
Квадрат длины KN можно найти также и из &KLN'.
KN2 = sin2 а + cos2 а • tg2 р - 2cos а tg р sin а cos <р.
Приравнивая друг другу эти выражения, получаем уравнение для определения cos<p:
sin2 а + cos2 а • tg2p - 2 • cosatgpsin acoscp =
= 1 +
cos2 a _cosa
---5--2-----cosy, cos2p cosp
откуда получаем первую из приведенных формул. Остальные формулы получаются аналогично.
162
ГЛАВА II. СТЕРЕОМЕТРИЯ
Основные геометрические места точек в пространстве
а)	геометрическим местом точек, удаленных на расстояние R от данной точки О, является сфера радиуса R с центром в этой точке;
б)	геометрическим местом точек, равноудаленных от двух данных точек пространства А и В (рис. 115), является плоскость Р, перпендикулярная к отрезку прямой, соединяющему эти точки, и проходящая через его середину;
в)	геометрическим местом точек, равноудаленных от трех данных точек А, В и С (рис. 116) пространства, не лежащих на одной прямой, является прямая MN, перпендикулярная плоскости Р, в которой лежат эти точки, и проходящие через центр окружности, проведенной через эти точки;
г)	геометрическим местом точек, равноудаленных от граней двугранного утла, является так называемая «биссекторная плоскость» Р (рис. 117), проходящая через ребро АВ двугранного угла и пересекающая любой линейный угол двугранного угла CAD по биссектрисе /.
Векторы
Векторы в трехмерном пространстве вво-дятся аналогично тому, как это было сдела-/	но для плоскости (см. I, § I). Остаются спра-
L/'l ведливыми и все свойства векторов, а также 4^._____правила действий с ними.
Если Г , J у к — попарно перпендикуляр-ные единичные векторы, так называемый ор-Рис. 117	то нормированный базис, то любой вектор а
§ 7. Основные теоремы и формулы стереометрии	163
пространства может быть единственным образом разложен по этим векторам, т.е. представлен в виде
а = axi + a2j + а3к.
Числа {ах.а2, а3} называются декартовыми координатами вектора а в базисе i , J , к . Декартовы координаты вектора являются проекциями этого вектора на соответственные оси системы коор-
динат:
ах = прха ; а2 - пруа \а3-пр2а .
Если все числа ax.a2ia3 отличны от нуля, то а можно изобразить с помощью диагонали прямоугольного параллелепипеда, у которого длины ребер равны | ах |, | ^21 и | а31 (рис. 118).
Рис. 118
Если вектор а отложен от точки А с координатами (хХ) уХ)гх)и кончается в точке В с координатами (х2, Уз» гз)>то координаты век-
тора определяются через координаты начала и конца вектора по формулам:
ai = x2-Xi; а2 = у2-ух, a3 = z2~ гх,т.е.
ЛВ{х2-Хх;у2-У1-, zj-zJ.
Если а {а1? а2, а3} и b {Ьх, Ь2, Ь3} —два произвольных вектора, то: а) координаты суммы векторов равны сумме соответствующих координат слагаемых
а + b = {#i + bx\ а2 + b2\ а3 + b3}\
б)	координаты разности векторов равны разности соответствующих координат этих векторов
а-Ь —	— Ьх\ #2””^2» ^3—63};
в)	координаты произведения вектора на число X равны произведению соответствующих координат вектора на данное число
Хе — X#2j Ха3};
г)	линейной комбинации с =ка +ц£ векторов а и Ь , где X иц— произвольные числа, соответствуют координаты
с ={Ха1+ц/>1; Хд2 + цй2; ка3 + ц£3}.
164
ГЛАВА II. СТЕРЕОМЕТРИЯ
Скалярное произведение векторов определяется как
(а • b) = 15|-|&|- cos ср, где ср = (я • Ь),
Величина скалярного произведения определяется через координаты векторов по формуле
(а Ь) -а^ + а2Ь2 + а3Ь3.
Длина вектора а с координатами {аъ а2, а3} дается формулой
а = 7^i2 +^2 + •
Угол между векторами а и Ь определяется из равенства
™ ,п _	+ а2^2 + а3^3
yja} + а2 +а3 <	+Ь2 +Ь3
Всякое линейное уравнение
Ах + Ву + Cz + D = Q, связывающее координаты х, у, z, определяет множество точек пространства, лежащих на плоскости, и, наоборот, каждую плоскость можно задать линейным уравнением с тремя переменными, имеющим по крайней мере один ненулевой коэффициент при переменных.
Вектор п с координатами {А, В, Q перпендикулярен плоскости Ах + By + Cz + D = 0.
Доказательство. Действительно, если A/qC^o,Уо, го) ка" кая-либо точка плоскости, то Ах$ + byQ + CzQ + Z) = 0. Отсюда следует, что уравнение данной плоскости можно переписать в виде
А(х - х0) + В(у - у0) + C(z - z0) = 0, или как скалярное произведение
векторов п={А,В, С} и ММо - {х - х0, у - у0, z - z0}, где Af(x, у, z) — произвольная точка данной плоскости. Поскольку 0, то равенство нулю скалярного произведения означает перпендикулярность перемножаемых векторов, т.е. п1ММ^.
§ 1. Основные теоремы и формулы стереометрии	165
С другой стороны, известно, что если прямая перпендикулярна хотя бы двум пересекающимся прямым плоскости, то она перпендикулярна самой плоскости.
Таким образом, коэффициенты А, В, С при переменных х, у, z в уравнении плоскости можно рассматривать как координаты вектора, перпендикулярного данной плоскости.
Угол (р между двумя плоскостями Ахх+Вху + Cxz + Dx =0 и Л2х+ В^у + C2z + D2 = 0 находится как угол между перпендикулярными им векторами пх = {Ах, Вх, Q} и п2 = {А2, В2, С2}, т.е. по формуле
cos<p =
^1^2	+ ^1^*2
Ja?+bI+c? -JaI+bI+cI
Расстояние h от точки Afo(xo, у0, z0) до плоскости Ах + By + Cz + + Z)= 0 дается формулой
Ja2+b2+c2
Площадь ортогональной проекции многоугольника
Площадь Snp ортогональной проекции многоугольника на плоскость равна площади Бф проектируемого многоугольника, умноженной на косинус угла ср между плоскостями многоугольника и его проекции (рис. 119):
5пр = 5'ф-со5ф.
Многогранники
Многогранником называется объединение замкнутой многогранной поверхности и ее внутренней области.
Призмой называется многогранник, две грани которого п — угольники, лежащие в параллельных плоскостях, а остальные п граней — параллелограммы (рис. 120).
Площадь 56ок боковой поверхности призмы равна произведению периметра перпендикулярного сечения на боковое ребро (рис. 120):
‘^бок - Л.'
166
ГЛАВА II. СТЕРЕОМЕТРИЯ
где Р± — периметр многоугольника	a Z> — длина боко-
вого ребра.
Объем призмы равен произведению площади основания 5^ на высоту Н призмы:
Для прямой призмы (т.е. призмы, у которой боковые ребра перпендикулярны плоскостям оснований), площадь боковой поверхности и объем даются формулами
о _ р . и.
‘“'бок ~ л осн
И=5ОСН-Я,
в которых 50СН и Н — периметр, площадь основания и высота призмы, соответственно.
Параллелепипедом называется призма, основанием которой служит параллелограмм (рис. 121). Середина диагоналей параллелепипеда является его центром симметрии.
Прямой параллелепипед, основанием которого служит прямоугольник, называется прямоугольным параллелепипедом (рис. 121).
Квадрат длины диагоналей прямоугольного параллелепипеда равен сумме квадратов трех его измерений, т.е.
J2 = ^ + d2 + c2.
Рис. 120
Рис. 121
§ 1. Основные теоремы и формулы стереометрии	167
Пирамидой называется многогранник, одна из граней которого — произвольный многоугольник, а остальные грани — треугольники, имеющие общую вершину (рис. 122).
Объем пирамиды дается формулой
И = 1/35осн • Я,
где 50СН — площадь основания пирамиды, Н~ высота.
Объем усеченной пирамиды (т.е. многогранника, вершинами которого служат вершины основания пирамиды ABCDE и вершины ее сечения А{В{СЦ)ХЕХ плоскостью, параллельной основанию) (рис. 123), дается формулой
v={-(sx+s2 + Js^s;)-H,
в которой ~ площади оснований, Н —
высота усеченной пирамиды.	Рис. 124
Объем произвольного многогранника, в который можно вписать шар радиуса R (рис. 124), связан с площадью Sn его поверхности формулой
И= 1/35п R.
Круглые тела
Круглые тела — это тела, ограниченные поверхностями вращения.
Цилиндром прямым, круговым называется фигура, полученная при вращении прямоугольника ABCD вокруг оси, содержащей его сторону АВ (рис. 125).
168
ГЛАВА II. СТЕРЕОМЕТРИЯ
Площадь боковой поверхности цилиндра и 5Ц — его полной поверхности даются соответственно формулами:
^бок ~ 2лЯЯ;
= ^бок + 2^осн ~ 2 л ЛЯ + 2лА2,
в которых R — радиус основания цилиндра, Н — его высота, 5^ — площадь основания. Объем цилиндра равен Иц = kR2H.
Конусом (прямым, круговым) называется фигура, полученная при вращении прямоугольного треугольника АВС вокруг оси, содержащей его катет АВ (рис. 126).
Площадь 5бок боковой поверхности конуса и 5К0Н — его полной поверхности даются соответственно формулами
^бок =
^кон “ ^^бок ^осн ~	>
в которых R — радиус основания конуса, L — длина его образующей, Лосн — площадь основания.
Объем Икон конуса равен
ИКОН = 1/35ОСН-Я,
где Н — высота конуса.
Площадь Syi бок боковой поверхности и объем Vy> бок усеченного конуса (рис. 127) определяются формулами:
бок = 7t(^! + RfiL',
Иу,бок=1/3№+^+7ад)-^>
Рис. 125
Рис. 126
§ 1. Основные теоремы и формулы стереометрии
169
в которых Rx и R2 — радиусы оснований усеченного конуса; = яАД S2 = кТ?22 — площади его оснований, L — длина образующей, Н — высота.
Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр AD (рис. 128).
Сфера — это поверхность шара, геометрическое место точек, удаленных от некоторой точки пространства (центра шара) на заданное расстояние R (R —- радиус сферы, шара).
Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку (рис. 128). Радиус, проведенный в точку касания, перпендикулярен касательной плоскости.
Касательной прямой к сфере (шару) называется прямая, имеющая со сферой единственную общую точку (рис. 128).
Если из точки Л/, лежащей вне сферы, проведены к сфере две касательные (рис. 128), то отрезки МВ и МС этих касательных, заключенные между точкой М и точками касания В и С, имеют одинаковую длину (МВ-МС).
Площадь S поверхности шара и его объем Vопределяются формулами?
5=4п/?2, И=1лЛ3,
3
где R —- радиус шара.
Сегментной поверхностью (рис. 129) называется часть шаровой поверхности, отсекаемая от нее какой-нибудь плоскостью Р, Отрезок МК радиуса, перпендикулярного плоскости сечения, называется высотой сегментной поверхности.
Шаровым сегментом (рис. 129) называется часть шара, отсекаемая от него какой-нибудь плоскостью Р,
Площадь 5сег сегментной поверхности и объем Ксег шарового сегмента определяются формулами:
Рис. 127
Рис. 128
170
ГЛАВА II. СТЕРЕОМЕТРИЯ
5сег = 2л/?Я; Исег = nH\R- 1 • Н),
3
где А — радиус шара, Н= МК— высота сегмента.
Шаровым поясом (рис. 129) называется часть шаровой поверхности, заключенная между двумя параллельными секущими плоскостями Ри Q. Расстояние Я между этими плоскостями называется высотой шарового пояса.
Шаровым слоем (рис. 129) называется часть шара, заключенная между двумя параллельными секущими плоскостями Р и Q.
Площадь поверхности 5Ш п шарового пояса определяется формулой
Хц.п. = 2nRH,
в которой Н — высота шарового пояса (рис. 130).
Объем шарового слоя находится как разность объемов двух шаровых сегментов.
Шаровым сектором (рис. 130) называется фигура, полученная при вращении Кругового сектора COD вокруг диаметра АВ, не пересекающего ограничивающую его дугу.
Объем Кш сек шарового сектора определяется формулой
Иш.сек,= 1^ш.п.Л=-2
3	3
где Н — высота соответствующего шарового пояса.
Рис. 129
Рис. 130
£ 1. Основные теоремы и формулы стереометрии
171
ЗАДАЧИ
1.	Дана прямая, параллельная плоскости. Параллельна ли эта прямая любой прямой, лежащей в плоскости? Может ли эта прямая пересечь хотя бы одну из таких прямых?
Ответ: Нет. Нет.
2.	Найти угол между двумя скрещивающимися прямыми, одна из которых содержит диагональ куба, а другая — диагональ боковой грани.
Ответ: 90°.
3.	Найти угол между двумя скрещивающимися прямыми, содержащими диагонали граней куба.
Ответ: 60°.
4.	Доказать, что если угол АОВ спроектировать ортогонально на плоскость, параллельную его биссектрисе ОС, то биссектриса проекции угла АОВ будет параллельна ОС.
5.	Доказать, что биссекторные плоскости трех внутренних двугранных углов трехгранного угла проходят через одну прямую.
6.	На двух скрещивающихся прямых I и лежат отрезки АВ и CD. Доказать, что объем тетраэдра ABCD не меняется, если отрезки АВ и CD произвольно перемещать по данным прямым.
Ответ: Объем указанного тетраэдра равен 1/6 • abh sin а, где а = АВ, b = CD, а — величина угла между скрещивающимися прямыми, а й — кратчайшее расстояние между ними; отсюда следует сформулированное утверждение.
7.	Теорема. Если ребро 5Л произвольной треугольной пирамиды SABC (S — вершина) изменить в к раз, ребро SB — в т раз, ребро SC — в п раз, т.е. перейти к пирамиде SAXBXCX такой, что
SAx = k SA\ SB^m SB ; SC^n -SC, то объем пирамиды изменится в ктп раз, т.е.
VsAiBfa = ктп VSABC-
S
Рис. 131
172
ГЛАВА II. СТЕРЕОМЕТРИЯ
Числа к, т, п могут быть меньше или больше единицы (рис. 131).
Доказательство. Представим объем каждой из пирамид по формулам:
^SAlBlCl = J ^5Д|С|  ^1 >
V$ABC = J $SBC 
где hi и h — длины высот каждой из пирамид, опущенных на боковые грани из вершин Л[ и А, соответственно (рис. 131). Составляя отношение объемов пирамид, находим
^SA^Cj _	hj
^SABC $SBC
Очевидно, что отношение площадей треугольников 551С1 и SBC равно
^sb1ci _ 1/2 • SBi  SC[ • sin а _ SBi • .SC] _
SSBC ~ 1/2 -SB -SC-sina ~ SB- SC ~ тП’
поскольку эти треугольники имеют общий угол а при вершине S.
Отношение высот hi: h равно к. Это следует из рассмотрения подобных треугольников Л^^и ADS.
Таким образом,
'SABC
и утверждение доказано.
Следствие. Если к = т = п = к§, то пирамида 5АХВХС{ подобна пирамиде SABC и объемы этих пирамид относятся как куб коэффициента подобия, т.е.
Кул, ад •’ Vsabc - Ц-
8.	На продолжении ребра SA пирамиды SABC отложена точка М такая, что AM = 5  SA, а на ребрах SB и SC —точки N и Q такие, что SN = 1/3 • SB и SC = QC. Найти объем пирамиды SMNQ, если объем пирамиды SABC равен V.
£ 1. Основные теоремы и формулы стереометрии
173
Ответ: 4 V (см. решение предыдущей задачи).
9.	Доказать, что объемы цилиндра, конуса, усеченного конуса, шарового сегмента и шарового слоя можно вычислить по формуле
V=IL (S{ + S2 + 450), 6
в которой Н — высота тела, 51 и S2 — площади его оснований (для конуса и шарового сегмента одна из этих площадей равна нулю), а 50 — площадь сечения тела плоскостью, параллельной основаниям и проходящей через середину высоты.
10.	Задача. Найти площадь сферического треугольника, углы которого равны а, р и у, который расположен на сфере радиуса R (рис. 132).
Решение. Определение. Сферическим рис. 132 треугольником называется часть сферы, ограниченная дугами трех ее больших кругов. Углом АВС сферического треугольника называется линейный угол двугранного угла, образуемого плоскостями больших кругов сферы, высекающими на ней данный угол сферического треугольника (рис. 132).
Заметим сначала, что площадь части сферы, высекаемой из нее гранями двугранного угла величиной а, ребром которого является диаметр сферы, равна а5/2л, где S — площадь поверхности сферы.
Пусть теперь АВС — произвольный сферический треугольник. Так как его стороны — дуги больших кругов, то, проводя, например, через сторону АЬ плоскость, заключаем, что она пройдет через центр сферы, а сферический треугольник АВС окажется расположенным на одной из полусфер, на которые данная сфе^а разделится проведенной плоскостью (рис. 132). Дугами АС и ВС, продолженными за точку С, полусфера разделится на 4 части, площади которых обозначим через х, у, г и и (х — искомая площадь). Можно написать следующие уравнения:
174
ГЛАВА II. СТЕРЕОМЕТРИЯ
x + y = ^-S = 2aR2-,
2л
х + г = -&-5 = 2рЛ2;
2я
х + и = —S = 2уЛ2.
2л
Кроме того,
x + j + z + и = 2лЛ2.
Решая составленную систему уравнений, находим
х=(а + р + у-л) • Л2.
Отсюда следует, что
а+р+у=л+ , R2
т.е. сумма углов сферического треугольника больше л (180°) на величину, равную отношению площади этого треугольника к квадрату радиуса сферы, на которой расположен этот треугольник.
§ 2. РЕШЕНИЕ ПРАВИЛЬНЫХ ТРЕУГОЛЬНЫХ И ЧЕТЫРЕХУГОЛЬНЫХ ПИРАМИД
Так же, как и в первом разделе пособия, рассмотрим сначала геометрические фигуры частного вида — правильные пирамиды и в первую очередь правильные треугольные и четырехугольные пирамиды.
Пирамида называется правильной, если ее основанием является правильный многоугольник, а вершина проектируется в центр основания.
Правильная пирамида может быть задана двумя параметрами. В качестве таких параметров можно взять сторону основания и высоту пирамиды; сторону основания и длину бокового ребра пирамиды; или длину бокового ребра пирамиды и величину плоского угла при ее вершине и т.д.
Под «решением правильных пирамид» будем понимать расчет одних, неизвестных, элементов пирамида через другие, известные.
Рассмотрим сначала правильную треугольную пирамиду (рис. 133). По определению — это такая пирамида, в основании которой лежит правильный треугольник АВС, а вершина 5 проектируется в его центр, точку О.
На рис. 133 показаны основные элементы правильной треугольной пирамиды:
а — длина стороны основания пирамиды (а = АВ-ВС- С4);
Ъ — длина бокового ребра пирамиды (b-AS-BS-CS)\
Н — высота пирамиды; h — апофема боковой грани пирамиды (например, h-SE)\
а — величина угла между боко- л вым ребром пирамиды и плоскостью ее основания, определяемого как угол между боковым ребром и его проекцией на плоскость основания (О < а < л/2);
В
Рис. 133
176
ГЛАВА II. СТЕРЕОМЕТРИЯ
Р — величина угла между плоскостью боковой грани и плоскостью основания. Поскольку SE ± ВС и АЕ ± ВС (Е — середина ВС), то угол AES есть линейный угол двугранного угла между рассматриваемыми плоскостями (0 < р < л/2);
у — величина угла между боковыми ребром пирамиды и ее высотой (0 < у< л/2);
6 — величина плоского угла при вершине пирамиды (0 < 0 < 2л/3).
Длина отрезка АО находится как 2/3 высоты основания правильной пирамиды, а ОЕ — как 1/3 этой высоты, т.е.
= ОЕ = ^-.
3	6
Кроме того, справедливы следующие соотношения между основными элементами пирамиды:
2	2
,? rrl в 1 2 rr2 #	71
Ь1 = Нг+ —; h£=Hl+ —; а + у = -;
3	12	2
H = bcosy,	= 2»siny = icosa;
Я = /шпР; ^-^ = AcosP; a = 2Z>sin-.
3	2
Двугранный угол <р между боковыми гранями пирамиды находится следующим образом. Из двух вершин основания пирамиды (например, В и С) опускаются перпендикуляры BFn CF на боковое ребро AS. В силу равенства треугольников ABS и ACS эти пер-
пендикуляры, естественно, попадают в одну и ту же точку F, лежащую на ребре AS пирамиды, поэтому получившийся угол BFC есть линейный угол двугранного угла между боковыми гранями пирамиды (рис. 134).
Из равнобедренного треугольника BFC по теореме косинусов находим:
a2 = 2- CF2-2- CF2cos<₽
ИЛИ
Рис. 134
§ 2. Решение правильных треугольных и четырехугольных пирамид
177
costp =
2CF2-a2 2CF2
Этот же угол можно найти и по-другому. Из прямоугольного треугольника CEF следует, что
. о а/2
Sin-J =
2 CF
Высота CF боковой грани A CS находится из уравнения b • CF= ah. Следовательно:
CF^, Sin5 = 4.
b ’	2 2h
Плоскости ASE и BSD, проходящие через высоту пирамиды и, следовательно, перпендикулярные плоскости основания, играют важную роль при решении многих задач, связанных с правильной треугольной пирамидой. Каждая из этих плоскостей делит соответствующий двугранный угол между боковыми гранями пирамиды пополам, т.е. служит биссекторной плоскостью такого угла.
Полезно отметить, что в правильной треугольной пирамиде скрещивающиеся ребра взаимно перпендикулярны AS ± ВС, BSLAC, CSLAB (это следует из теоремы о трех перпендикулярах), а длина отрезка EFдает кратчайшее расстояние между этими ребрами (рис. 134):
EF
а43 .
=-----sin а.
2
Вокруг всякой треугольной пирамиды можно описать сферу. В правильной пирамиде центр К этой сферы лежит на высоте пирамиды или на ее продолжении за точку О, ведь прямая SO, содержащая высоту пирамиды, есть геометрическое место точек, равноудаленных от вершин основания пирамиды.
Радиус R описанной сферы удобно находить из равнобедренного треугольника AKS (рис. 133):
D b D b
A cos у - - или R = ---- (SK-R; AS=b)
2	2cosy’'	’	'
а)	Если R < Н, т.е. а > п/4, центр описанной сферы лежит внутри пирамиды;
178
ГЛАВА II. СТЕРЕОМЕТРИЯ
б)	если R=H, т.е. а = я/4, центр описанной сферы лежит на основании пирамиды, в его центре;
в)	если R> Н, т.е. а < я/4, центр описанной сферы находится вне пирамиды.
Во всякую треугольную пирамиду можно вписать шар. В правильной пирамиде центр вписанного шара находится на высоте пирамиды в точке ее пересечения с биссектрисой угла AES (рис. 133). Действительно, центр вписанного шара должен быть равноудален от всех граней пирамиды, т.е. должен принадлежать пересечению биссекторных плоскостей всех внутренних двугранных углов пирамиды.
Радиус г вписанного шара удобно находить из прямоугольного треугольника ЕКХО\
а^З В ( . _ Н а
г = -г-^, sinp = —, cosp = —- . 6	2	h	bn
Рассмотрим теперь несколько типовых задач на решение правильных треугольных пирамид.
Задача 1. Правильная треугольная пирамида SABC (рис. 133) задана двумя элементами: длиной а сторон основания и длиной Н ее высоты. Вычислить все остальные элементы пирамиды: а, р, у, 0, <р, b, R, г и V.
Решение. Вычисляем: 1) угол а наклона боковых ребер пирамиды к плоскости ее основания и длину b бокового ребра из SAOS.
t SO Н Ну/з t н4з
tga = —— = —=— =-------, a = arctg-----;
АО а-/3/3 а	а
ь = >Iao2+so2 = у]а2/3+Н2;
2)	угол р наклона боковых граней пирамиды к плоскости ее основания и длину h апофемы боковой грани — из &EOS\
t „ SO Н 2Ну!з а t 2//Тз
tgP = 777=	=-----> P = arctg-----;
ЕО а\3 / 6 а	а
h = JeO2+SO2 = 7°2/12+Я2;
3)	угол 0 при вершине S пирамиды — из ABCS :
179
§ 2.	Решение правильных треугольных и четырехугольных пирамид a2 = 2Z/-2/^05 0,
откуда
COS0 =
6Я2-472 . 6Я2 + 2д2’
4)	угол ср между боковыми гранями — из &CEF, (рис. 134):
. ф СЕ а sin — = — =-----,
2 CF 2CF
Так как b  CF- ah, то CF = а^Н2 + а2/12 /^Н2 +а2/3,откуда
• Ф sin — =
2
13Я2 +д2 . ПН2 + а2’
5)	объем V пирамиды по формуле
1 а27з „ а2нЛ ~	-- п =------:
3	4	12
6)	радиус R описанного вокруг пирамиды шара — из SDKS:
о b D b 7?cosy = -, R =------.
2 2cos у
Поскольку cos у = OS/AS - H/b, то R = Ь2/2Н, следовательно:
D 3H2+a2
7)	радиус г вписанного в пирамиду шара — из SEKXO\
г Р
ОЕ tg2’
W3 t р
T'tg2’
где р = arctg (27/^3 /а)- Радиус г можно найти также по объему V пирамиды и площади ее полной поверхности S по формуле г = 3 V/S.
Задача 2. В правильной треугольной пирамиде известны: b — длина бокового ребра и ф — двугранный угол между ее боковыми гранями. Вычислить сторону основания а и высоту Н пирамиды.
180
ГЛАВА II. СТЕРЕОМЕТРИЯ
Решение. Известно, что плоские углы 0Ь 02 и 03 при вершине произвольного трехгранного угла определяют двугранные углы этого же трехгранного угла по формулам
cos0i - cos02 cos03 cos <p =--1-----------,
sin02 sin03
в которой ср — двугранный угол между гранями с углами 02 и 03
(см. гл. 2, § 1). В данном случае 0j = 02 = 03 = 0, поэтому
cosф = cose ~ cos2 в _ cos 0(1 ~ CQs 0)
sin20	l-cos20
или
Отсюда находим:
_ СО5ф COS 0 =----—.
1	- COS ф
Поскольку для правильной треугольной пирамиды л/3 < ф < л, то | cos ф/(1 - cos ф) | < 1, и полученная формула всегда позволяет определить угол 0 при вершине пирамиды.
Зная cos 0, нетрудно вычислить искомые величины а и Н:
1)	а/2 = Asin 0/2, а = 2Аsin 0/2 = by/'2(\- cos0);
2)	Н = у]ь2-а2/3, Н = *71 - 2/3(1 - cos 0).
Задача 3. Известны длина а стороны основания правильной треугольной пирамиды и радиус г вписанного в нее шара. Вычислить высоту Н пирамиды.
Решение. Прежде всего, из &ЕКХО (рис. 133) вычислим угол р наклона боковой грани пирамиды к плоскости ее основания
t Р _ Г _ г _ 2гЛ
2	ОЕ аТз/6 а
После этого вычисляем Н из &ESO'.
Н = OFtgp = ^tgp
О
§ 2. Решение правильных треугольных и четырехугольных пирамид
181
ИЛИ
н = 2tgP/2 2а2г
6 l-tg2p/2 а2-12г2
Если в правильной треугольной пирамиде длина бокового ребра равна длине стороны основания (а = Ь), то правильная пирамида представляет собой правильный тетраэдр.
На рис. 135 изображен правильный тетраэдр. Эта фигура обладает всеми свойствами правильной треугольной пирамиды. Кро-
ме того, полезно знать и дополнительные ее свойства:
1) правильный тетраэдр имеет центр, точку К. В этом центре пересекаются все высоты тетраэдра, отрезки, соединяющие середины скрещивающихся ребер (бимедианы тетраэдра), а также в нем находятся центры вписанной и описанной вокруг пирамиды сфер (шаров);
2) центр К правильного тетраэдра делит каждую высоту тетраэдра в отношении 3:1, считая от вершины SK: КО=3: 1;
3) радиус описанного шара составляет 3/4 высоты тетраэдра, а радиус вписанного шара — 1/4 его высоты:
R=1H,	г=±Н;
4	4
4) сечения правильного тетраэдра, параллельные скрещивающимся ребрам, представляют собой прямоугольники, а то из них, которое проходит через середину ребра, — квадрат (DE'D'Е).
Задача 4. Пусть сторона правильного тетраэдра равна а. Проверить справедливость следующих формул:
высота Н тетраэдра: Н = aj2/3 ;
угол а между ребром и плоскостью основания: а = arcsin ^2/3 ;
2V2
углы Р = (р между боковыми гранями: р = arcsin -у- ; радиус г вписанного шара: г = ~ • Дл/2/3 ;
182
ГЛАВА II. СТЕРЕОМЕТРИЯ
3	.--
радиус R описанного шара: R = -~ aJ2/3 .
4
Решение. Высота Н тетраэдра находится из ДА05 (рис. 135):
н = Jas2 -ао2 = .а2
Отсюда находятся г и R:
г=1Я;Я=2я. 4	4
Углы а и р = ср вычисляются соответственно из треугольников A OS и EOS.
Правильная четырехугольная пирамида. На рис. 136 изображена правильная четырехугольная пирамида SABCD, В основании такой пирамиды лежит квадрат, а вершина пирамиды проектируется в его центр.
Основные элементы пирамиды: а — длина стороны основания; b — длина бокового ребра пирамиды;
h — длина апофемы боковой грани;
Н — высота пирамиды;
а — величина угла между боковым ребром пирамиды и плоскостью основания пирамиды, 0 < а < тг/2;
Р — величина угла между плос
костью боковой грани и плоскостью основания пирамиды, О < р < тг/2;
0 — величина угла при вершине пирамиды, 0 < 0 < я/2;
Ф — величина угла между боковыми гранями пирамиды, л/2 < ф < л;
г — радиус вписанного шара;
R — радиус описанного шара.
Нахождение большинства элементов правильной четырехугольной пирамиды аналогично нахождению тех же элементов правильной треугольной пирамиды. При вычислении этих элементов
£ 2. Решение правильных треугольных и четырехугольных пирамид
183
основную роль играют треугольники, расположенные в плоскостях симметрии ASC, BSD, ESMпирамиды, проходящие через ее высоту SO и, следовательно, перпендикулярные плоскости основания. Рассмотрим следующий пример.
Задача 5. В правильной четырехугольной пирамиде SABCD (рис. 136) известны: а — длина стороны основания пирамиды и Н — длина ее высоты. Найти остальные элементы пирамиды, т.е. а, р, 0, <р, Ь, г и R.
Решение. Вычисляем:
1)	угол а наклона боковых ребер пирамиды к плоскости ее основания и длину b боковых ребер из SAOS:
SO Н нЛ
АО аЛ/2 а
а = arctg
Ял/2. а
ь = Jao2+so2 = 7я2+а2/2;
2)	угол р наклона боковых граней пирамиды к плоскости ее основания и длину h апофемы боковой грани из SEOS:
tgp=~ = —, p = arctg —; h = yjEO2+SO2 = Ja2/4 + H2-, EO a	a
3)	угол 0 при вершине пирамиды из SDSC: а2 = 21?-2b1  cos0,
откуда
а 2Я2 Л	2Я2
COS 0 =-:---7, 0 = arccos “3-7;
2Я2+а2	а2+2Я2
4)	угол <р между боковыми гранями пирамиды из ЛАСЕ (АЕ± SB, СЕЛ. SB):
. <р АО a-j2 2 smn =Т? = —Tn-’ 2 AF AF
где b  AF= ah, т.е. AF = а^Н2+а2/4 /^H2 + a1/2,
• Ф sin — =
2
\2H2 +a2, 4Я2 + a2 ’
184
ГЛАВА II. СТЕРЕОМЕТРИЯ
5)	радиус г вписанного в пирамиду шара из &ЕКХО (ЕК{ — биссектриса угла OES):
г , Р	л В
— = tg-, r = --tgr, ОЕ 2	2 2
где р = arctg (2Н/а). Радиус г можно найти также по объему Ипира-
миды и площади S ее полной поверхности: г= 3 V/S\
6)	радиус R описанного вокруг пирамиды шара из &KLS (KL — высота равнобедренного треугольника AKS):
Поскольку cosy= OS/AS= H/b, то R-b2/2H и
_ а2+2Н2
Задача 6. В правильной четырехугольной пирамиде SABCD даны длина а стороны основания и угол ср между боковыми гранями. Вычислить высоту пирамиды Н.
Решение. Из прямоугольного треугольника (рис. 136) находим его катет FO:
FO = АО  ctg^  dg^.
Поскольку плоскость треугольника ACFперпендикулярна ребру BS, то отрезок FO также перпендикулярен этому ребру и является высотой треугольника BOS. Из прямоугольного треугольника ВОР находим:
FO . <р .л ср л, sin а = —— = ctg-J, (-<^<-),
ВО 242 2
где а — угол между боковым ребром пирамиды и плоскостью ее основания. После этого из прямоугольного треугольника BOS находим Н:
Н = ВО-tga = —• ,	.
2 Vl-ctg29/2
£ 2. Решение правильных треугольных и четырехугольных пирамид
185
ЗАДАЧИ
1.	Величина угла между боковым ребром и плоскостью основания правильной треугольной пирамиды равна а. Найти отношение радиусов вписанного в пирамиду и описанного около нее шаров.
Ответ: 1/2 • cos а (71 + 4tg2a -1).
2.	Вычислить расстояние между центрами вписанного в правильную треугольную пирамиду шара и шара, описанного около нее, если известно, что длина стороны основания пирамиды равна 3 7з см, а длина ее высоты — 9 см.
Ответ: (17 - У37 )/4 см.
3.	Доказать, что если центры вписанного и описанного около правильной треугольной пирамида шаров совпадают, то эта пирамида — правильный тетраэдр.
4.	Длина стороны основания правильной треугольной пирамиды равна а, а величина плоского угла при ее вершине — 0. Найти расстояние между боковым ребром пирамиды и скрещивающейся с ним стороной основания.
Ответ: aVl -I- 2 cos 0/2.
5.	В шар радиуса R вписано множество правильных треугольных пирамид. У какой пирамиды может быть наибольший объем и чему равна максимальная величина объема?
Ответ: 0 = л/3; наибольший объем — 8ТзЛ3/27.
6.	Плоский угол при вершине правильной четырехугольной пирамиды равен 0, а длина высоты — Н. Найти объем пирамиды.
Ответ: 2/3 ' Я3(1 - cos 0)/cos 0.
7.	Объем правильной четырехугольной пирамиды равен И, а длина стороны основания —• а. Найти радиус вписанного в пирамиду шара.
Ответ: 1/12 • (7збИ2 +а6 - а3) • a/V .
8.	Доказать, что боковое ребро правильной четырехугольной пирамиды перпендикулярно скрещивающейся с ним диагонали основания.
186 ГЛАВА II. СТЕРЕОМЕТРИЯ
9.	Найти плоский угол при вершине правильной четырехугольной пирамиды, если величина двугранного угла между его боковыми гранями равна ср.
Ответ: arccos ctg (<р/2), л/2 < ср < п.
10.	В шар радиуса R вписываются правильные четырехугольные пирамиды. При каком значении угла при вершине пирамиды ее объем будет наибольшим? Указать величину этого объема.
Ответ: 9 = arccos 2/3; наибольший объем равен 32/?3/81.
§ 3. РАСЧЕТ ЭЛЕМЕНТОВ ПИРАМИД МЕТОДОМ СОСТАВЛЕНИЯ УРАВНЕНИЙ
Задачи, рассмотренные в предыдущем параграфе, позволяют стандартным методом рассчитывать различные элементы правильных пирамид через заданные. При этом такие пары элементов, как, например, сторона основания и боковое ребро; боковое ребро и угол при вершине пирамиды; сторона основания и высота и т.д., можно назвать «удобными параметрами», потому что через них особенно просто рассчитываются многие другие элементы пирамиды. В то же время в ряде задач требуется рассчитать тот или иной элемент пирамиды при более сложном виде исходных условий. Например, требуется найти объем правильной треугольной пирамиды, в которой высота пирамиды равна Н, а площадь поверхности описанного около нее шара в 4раза больше площади сечения этого шара плоскостью, содержащей основание пирамиды.
В этой задаче известен только один из «удобных» элементов пирамиды — длина Нее высоты. Другое же условие сразу использовать в стандартных расчетах затруднительно. Поэтому поступают следующим образом. Вводят в качестве неизвестного еще один «удобный» элемент, например, длину х стороны основания пирамиды. Тогда искомый объем V пирамиды выражается простой формулой
1 Х^у/З у = 3-.±Л±.н.
3	4
Таким образом, задача сводится к отысканию величины х. Как же она определяется?
Для нахождения величины х служит условие задачи, говорящее, что площадь поверхности описанного около пирамиды шара в 4раза больше сечения этого шара плоскостью, содержащей основание пирамиды. Запишем это условие в виде уравнения. Поскольку
5Ш = 4ЛЯ2; 5сеч = л
3
188
ГЛАВА II. СТЕРЕОМЕТРИЯ
то уравнение имеет вид:
4л А2 лх2 /3
откуда находим R = х/х/З .
Радиус R описанного шара выражается через длину b бокового ребра пирамиды и ее высоту Н по формулам
2Я
ИЛИ
Я2 + х2/3 г ЗЯ2 + х2 2Н 6Н
Отсюда получаем квадратное уравнение для определения х
ЗН2+х2 6Н
X
ТУ
с
Рис. 137
единственным решением которого является х, равное НТ. После этого находим объем пирамиды: V = Н3 • V3/4.
Метод расчета, основанный на введении неизвестных и составлении для них соответствующего числа уравнений, применим во многих других задачах. Рассмотрим конкретные примеры.
Задача. В правильной треугольной пирамиде расстояния от центра основания до плоскости боковой гра-В ни и до бокового ребра равны соответственно р и q. Найти объем пирамиды.
Решение. В этой задаче обе заданные величины pvtq следует отнести к разряду «неудобных». По
этому введем два более «удобных» параметра х = а и у = Я — длину стороны основания и длину высоты (рис. 137). Тогда очевидны следующие соотношения:
1) из &AOS : AS = 7яО2 +О52 = ^х2/'3 + у2. Поскольку АО - 05= =AS • q, то имеем первое уравнение:
£ 3. Расчет элементов пирамид методом составления уравнений
189
Хл/З IX22
—У = ^у+У ;
2) из SDOS: DS = JdO2+OS2 = Jx2/12+y2.. Поскольку DO  OS= = DS  p, то имеем второе уравнение:
Х>/3 IX2 2 ~ry=ph+y
Таким образом, для определения двух неизвестных имеем систему двух уравнений.
После возведения в квадрат обеих частей каждого уравнения получаем:
х2у2 =(х2 + 3y2)q2, х2у2 = (х2 + Г2у2)р2.
Поделив каждое уравнение на х2/, представим эту систему в виде двух линейных уравнений относительно двух неизвестных 1/х2 и 1/у2:
3 1 _1_ х2 у2 q2 '
12	=
2 + 2	2 ‘
х у р
Отсюда находим:
* = 3pq/ >/q2-p2, у = J3pq / ^4p2-q2 (p<q<2p).
После этого вычисляем объем пирамиды:
у = 1	= 9 А3
3 4	4 (42-Р2)74/’2-?2
Задача. Объем шара, вписанного в правильную четырехугольную пирамиду, относится к объему всей пирамиды как л : 8. Найти плоский угол при вершине пирамиды.
190 ГЛАВА II. СТЕРЕОМЕТРИЯ
Решение. Прежде всего заметим, что по данным задачи пирамида не определяется однозначно. Любая пирамида, подобная той, которая удовлетворяет условию задачи, также удовлетворяет этому условию. Поэтому ясно, что ни один размерный элемент рассматриваемой пирамиды не может быть определен однозначно; в то же время угловые (и любые безразмерные) элементы пирамиды определяются однозначно. Все это позволяет принять какой-нибудь линейный элемент пирамиды, например, длину а стороны ее основания, за 1.
Обозначим угол наклона боковой грани пирамиды к плоскости ее основания через р и постараемся составить уравнение для его определения. Считая р заданным и полагая а= 1, находим:
1)	'• = |tg|, Иш =|лг3 =£tg3|;
2	2	3 о 2
2)	tf = |tgp, Кпир =|.l |tgp = |tg₽.
Приравняв отношение объемов шара и пирамиды заданному числу, получим уравнение для определения р.
л/6  tg3p/2 _ л l/6-tgp ~8
В развернутом виде это уравнение имеет вид tg2p/2  (1 -tg2p/2)= 1/4.
Здесь использована формула для тангенса двойного аргумента.
Из полученного уравнения находим единственное решение tg2P/2= 1/2 и затем
tgp = 2V2.
После того как угол р найден, в нашем распоряжении имеется уже два «удобных» элемента: сторона основания 1 и угол р. Поэтому можно стандартным приемом (см. гл. 2, § 2) вычислить величину искомого угла при вершине пирамиды. Имеем (рис. 136):
# = |tgp = V2, й = х/О52+О£2 =^2 + | =-|,
§ 3. Расчет элементов пирамид методом составления уравнений
191
*^2—8(1/3).
Z jl	э/2 j
что и требовалось найти.
ЗАДАЧИ
1.	Длина стороны основания правильной треугольной пирамиды равна а, а высота, опущенная из какой-нибудь вершины основания на противоположную ей боковую грань, равна h. Определить объем пирамиды.
Ответ: 1 /12а3 А />/Зд2 -4й2.
2.	Из основания высоты правильной треугольной пирамиды опущен перпендикуляр на боковое ребро. Его длина равна р. Найти объем пирамиды, если величина двугранного угла между плоскостью боковой грани и плоскостью основания пирамиды равна р.
Ответ: 1/24р3 tg р (12ctg2 р + З)1,5, 0 < р < л/2.
3.	Объем правильной треугольной пирамиды равен 1/6 куба длины бокового ребра. Найти величину плоского угла при вершине пирамиды.
Ответ: л/2.
4.	Длина высоты правильной четырехугольной пирамиды равна Я, а плоские углы при вершине равны 0. Определить объем пирамиды.
Ответ: 4/3 Н3 • sin2(0/2)/cos 0.
5.	В правильной четырехугольной пирамиде точка Р лежит на высоте и делит ее в отношении 1:3, считая от основания. Расстояние от Р до бокового ребра равно р, а до боковой грани — q. Определить площадь поверхности пирамиды.
Ответ: 32^2 p3q2 /[9(р2 -q2)y]2q2 -р2].
6.	Высота правильной треугольной пирамиды равна Н, Точка пересечения высот каждой из боковых граней и вершина пирамиды лежат на поверхности шара радиуса А. Найти объем пирамиды.
Ответ: 1/2Я2 Л (Я- 2Я), Я> 2R.
192
ГЛАВА II. СТЕРЕОМЕТРИЯ
7.	Дана правильная четырехугольная пирамида SABCD (5 — вершина) с длиной стороны основания а и длиной бокового ребра а. Сфера с центром в точке О проходит через точку А и касается ребер SB и SD в их серединах. Найти объем пирамиды OSCD,
Ответ: 5а3>?2 /96.
8.	В правильной шестиугольной пирамиде длина высоты равна 6, радиус описанного шара равен 19. Найти радиус вписанного шара.
Ответ: 12>/5 - 24 .
9.	Стороны оснований правильной шестиугольной усеченной пирамиды имеют длины а и За. Расстояние между двумя параллельными ребрами, лежащими в плоскостях различных оснований и в различных боковых гранях, равно h. Вычислить площадь сечения пирамиды плоскостью, проходящей через указанные параллельные ребра.
Ответ: 6ah.
10.	В правильной четырехугольной пирамиде длина высоты равна 1, а отношение квадрата длины бокового ребра к квадрату длины стороны основания равно х. Найти зависимость объема пирамиды от х.
Ответ: V= 1/3(х- 0,5)~1, х > 0,5.
§ 4.	СЕЧЕНИЕ ПИРАМИДЫ ПЛОСКОСТЬЮ
Решение большинства стереометрических задач сводится в конечном счете к решению ряда планиметрических задач. При этом «расчленение» каждой пространственной задачи на последовательность плоских задач чаще всего связано с построением различного вида сечений рассматриваемой пространственной фигуры, в частности пирамиды, плоскостью.
Построить сечение — это значит указать линии пересечения секущей плоскости с гранями рассматриваемого многогранника, в том числе точки её пересечения с ребрами многогранника.
Для построения сечений используются следующие правила:
а)	через три точки фигуры, не лежащие на одной прямой, можно провести единственное сечение;
б)	если две какие-либо точки принадлежат сечению, то принадлежит сечению и прямая, проходящая через эти точки. В том случае, когда точки лежат на одной из граней многогранника, эта прямая является линией пересечения грани с сечением;
в)	параллельные грани многогранника (или вообще параллельные плоскости) пересекаются сечением по параллельным прямым.
При построении сечений многогранников, в том числе и пирамид, как правило, выполняют дополнительные построения. Весьма часто эти построения связаны с продолжением линий пересечения секущей плоскости с гранями многогранника за пределы этой грани. Рекомендуется сохранять эти построения, поскольку они используются для обоснования чертежа, и для последующих расчетов.
Рассмотрим несколько типовых задач на построение сечений пирамиды плоскостью.
Задача 1. Построить сечение произвольной треугольной пирамиды SABC (S — вершина) плоскостью, проходящей через три точки М, N, Р, взятые на ее ребрах SA, SB и SC или на их продолжениях, если дано, что
SM , SN SP
=	~^ = т’ ^г=п-
SB *50-
194
ГЛАВА II. СТЕРЕОМЕТРИЯ
Найти, в каком отношении эта плоскость делит объем пирамиды.
Решение. 1) Пусть сначала все три числа к, т, п меньше 1. Тогда Me SA, п е SB, Ре SC (рис. 138). След от сечения пирамиды плоскостью, проходящий через три точки, строится простым соединением точек М, ТУи Р отрезками прямых, лежащих в соответствующих боковых гранях пирамиды, так, что SMNP представляет искомое сечение.
Отношение объема пирамиды SMNP, получаемой из пирамиды SABC изменением длин ее ребер в к, т и п раз, к объему всей пирамиды SABC, как известно (см. задачу 5 после § I гл. II), равно
VsMNP -	’ VsABC >
поэтому отношение объемов частей, на которые делит пирамиду секущая плоскостью, равно ктп : (1 - ктп).
2) Пусть теперь одно из чисел к, т, п, например, п, больше 1 (т.е. О<А?<1,О</п<1,л/>1). Это означает, что точка Р лежит на продолжении ребра SC за точку С (рис. 139).
В этом случае сечение представляет собой четырехугольник MNRQ. Для его построения в плоскости грани SAC проводится прямая МР, причем отрезок MQ дает первую из сторон искомого четырехугольника; в плоскости грани SBC проводится прямая NP, причем отрезок NR дает другую сторону четырехугольника; наконец, точки М и N соединяются отрезком MN в плоскости грани ASB, a Q и R — отрезком QR в плоскости грани АВС. Таким образом, сечение замыкается.
Особо отметим, что пирамида CPQR (С — вершина), полученная в результате дополнительных построений, очень важна для последующих расчетов.	s
Рис. 138
Рис. 139
£ 4, Сечение пирамиды плоскостью	195
Вычислим отношение объемов, на которые делится пирамида SABC. Для этого заметим, что объем части пирамиды, расположенный выше плоскости сечения, представляет разность объемов пирамид SMNP (S — вершина) и CPQR (С — вершина).
Пирамиду SMNP — можно рассматривать как пирамиду, получающуюся из пирамиды SABC изменением длин ее ребер, исходящих из вершины S, в к, т и п раз, поэтому
VsMNP^kmn Vsabc-
Пирамиду CPQR также можно рассматривать как пирамиду, получающуюся из исходной (обозначим ее теперь CABS, С — вершина) изменением длин ее ребер в CP/CS, CQ/CA и CR/CB раз, поэтому
r	СР CQ CR v
CPQR	CS СА СВ VsABC'
Одно из этих отношений, а именно CP/CS, известно, оно равно (и - 1); два других требуется найти. Как это делается, подробно показано в § 4 гл. 1, где шла речь о пропорциональных отрезках в
треугольниках.	$
Найдем, в каком отношении точки Q хп /\ и Л делят стороны основания. Обратимся	п-\ -J
к рис. 140, на котором отдельно пред-	/\
ставлена плоскость грани ASC. Так же, хп(1-к) / X \ как и в других подобных задачах (см. § 4, к(п-1)/	\. \
гл. 1), сделаем дополнительное построе-ние — проведем CD | SA и обозначим длину отрезка CD через х.	\
Из подобия SPSM и &PCD с коэффициентом PS: РС=п/(п- 1) следует,	Рис. 140
что SM = хп/(п - 1). Поскольку SM: AM - £(1 - к), то АМ= хп (1 - к)/к(п - 1). Наконец, из подобия S.QCD и SQAMнаходим отношение CQ: AQ. Оно равно х: хл(1 - к)/к(п - 1). Имеем:
CQ к(п-1)
AQ п(1-к)’
откуда получаем
CQ _ _ к(п -1) СА п-к '
196
ГЛАВА II. СТЕРЕОМЕТРИЯ
Аналогично находится отношение CR: СВ. Получается формула:
CR т(п -1) СВ п-т '
Учитывая оба эти результата, вычисляем объем пирамиды CPQR'.
VCPQR=(n-tf {n_^n_m}VSABC.
Затем находим объем отсекаемой части пирамиды SABC, лежащей выше плоскости сечения:
^SMNRCQ
- VsMNP “ ^CPQR
- тпк
1 (я-I)3
п(п - к)(п - т)
KsABC-
3) Если два из трех чисел к, т, п больше единицы (к> 1, т < 1, п > 1), то сечением пирамиды опять будет треугольник NRQ (рис. 141). От пирамиды SABC отсекается пирамида BNRQ (В — вершина). Можно считать, что она получается из исходной пирамиды изменением ее ребер (исходящих из вершины В) в BN/BS, BQ/BC и BR/BA раз. Поэтому
BN BQ BR bnrq bs ВС BA SABC'
Отношение BN/BS известно по условию, оно равно (1-тя), поэтому нужно найти два других отношения. Проводя такие же
Рис. 141
построения, как и в предыдущем пункте, находим:
BQ = п(1-т) BR = к(1-т)
ВС п-т ' ВА к-т ' откуда получаем для объема отсекаемой части выражение
VBNRQ = ктП т(1^	’ VSABCу
т(к - т)(п - т)
что и завершает решение задачи.
§ 4. Сечение пирамиды плоскостью
197
В заключение заметим, что использованный при решении этой задачи метод, основанный на расчете пропорциональных отрезков в треугольниках, применим в большинстве задач «на сечение мно-гогранников».
Задача 2. Дана правильная четырехугольная пирамида SABCD (S ~~ вершина). На продолжении стороны АВ основания за точку А взята точка М, такая, что AM=АВ; на другой стороне CD основания взята точка N, причем DN: CN~ 1 : 2; третья точка Р взята на боковом ребре SB пирамиды в ее середине. В каком отношении делит объем пирамиды плоскость сечения, проходящего через точки М, N и Р?
Решение. Построим сначала сечение пирамиды. Обратимся к рис. 142. Точки М и N, лежащие в плоскости основания пирамиды, принадлежат этому сечению, поэтому принадлежит сечению и вся прямая MN, причем отрезок QN служит одной из сторон многоугольника, по которому сечение пересекается с поверхностью пирамиды.
Точка R пересечения прямой MN с продолжением стороны ВС основания лежит в плоскости грани BSC, поэтому в ней лежит и вся прямая PR, проходящая через точки Ри R. Отрезок PL этой пря
мой служит другой стороной искомого многоугольника. Соединяя точки L и N в плоскости грани CSD, получаем третью сторону многоугольника.
Точки Мн Р, принадлежащие сечению, соединим прямой МР, которая пересекается с боковым ребром AS пирамиды в точке Т. Отрезки ТР и TQ, принадлежащие граням AS В и ASD, замыкают искомый многоугольник. Таким образом, сечение пирамиды представляется пятиугольником PLNQT.
Для расчета отношения объемов, на которые делится пирамида плоскостью сечения, используем дополнительные построения (рис. 142). Объем V{ части пирамиды, лежащей ниже плоскости сечения, представим как разность объемов пирамиды PMBR (Р — вершина) и двух пирамид: TMAQ (Т — вершина) и LCNR (L — вершина):
Q В
Рис. 142
я
" VpMBR ~ VtMAQ ~ VlCNR'
198
ГЛАВА II. СТЕРЕОМЕТРИЯ
Объем каждой из этих трех пирамид зависит от площади ее основания и высоты. Определим эти параметры. Найдем, в каком отношении точки Q, N, R, L и Тделят соответствующие ребра пирамиды.
На рис. 143 изображены отдельно плоскости граней ABCD, ASB и BSC пирамиды. Треугольники MAQ, QND и CNR подобны (рис. 143а), причем коэффициент подобия первого ко второму равен 3 • (AM = 3 • DN), а третьего ко второму — 2 • (CN = 2 • DN). Отсюда находим Л 0=3/4, СЯ = 2 • QD = 1/2, BR = 3/2 и затем — площади:
5 -А.2.2-1
MBR 2 2 3	2>
MAQ 2*4 8
-1 1 1-1
”*2 3 2~6
Длина стороны основания пирамиды принята за 1.
Пусть Н — длина высоты пирамиды SABCD. Тогда высота пирамиды PMBR равна Н/2, так как Р — середина ребра BS. Найдем длины высот двух других пирамид: TMAQ и LCNR. Для этого определим, в каком отношении точки Т и L, делят ребра AS и CS пирамиды. Используем метод, изложенный в § 4, гл. 1.
На рис. 1436, где вынесена плоскость грани ASB, проведем дополнительно Я£|| BS и примем АЕ=х. Тогда РВ=2х (так как МВ= 2 • МА, по условию) и PS= 2х (так как Р — середина PS). Из
Рис. 143
£ 4. Сечение пирамиды плоскостью
199
подобия SAET и &PST находим ST: АТ= PS: АЕ=2х : х = 2, т.е. АТ= 1/3 • AS. Следовательно, длина Н2 высоты пирамиды TMAQ равна Н/3.
Аналогично находим длину Я3 высоты пирамиды LCNR. На рис. 143е, изображена плоскость грани BSC. Проводим CF|| BS и полагаем CF=y. Тогда ВР= Зу (так как BR = 3 • CR, PS= Зу, а из подобия треугольников LPS и CFL находим: CL: LS= 1 : 3, т.е. CL = 1/4 • CS. Следовательно, высота Н3 пирамиды LCNR равна Н/4.
Теперь вычислим объемы всех пирамид:
Ksabco = у ’$abcd = Н =—,
„	_ 1	Н_1 3 Н Н
'pmbr - J ’^mbr	"2	2	~2 ~~4'
v _ 1 „	И _	\	3	Н _Н
VTMAQ - J • ^MAQ	"з" -	3” 8	"У - 24 ’
v _1„	Н _	\	\	Н _Н
К£СТЛ’з стя'7'з'б"4 ~т1'
Объем Vx части пирамиды, лежащей ниже плоскости сечения, равен:
у =IL-^L_IL = UL
1	4 24 72	36 ’
Объем К2 части пирамиды, лежащей выше плоскости сечения, равен:
Н 1Н 5Н
2	3	36	36 ‘
Отношение И]: V2 равно 7 : 5.
Рассмотрим еще две характерные задачи.
Задача 3. Дана правильная треугольная пирамида SABC (5— вершина), сторона основания которой имеет длину а, а боковое ребро — длину Ь. Изучить сечения этой пирамиды плоскостями, параллельными скрещивающимся ребрам пирамиды (например, AS и ВС), показать, что эти сечения — прямоугольники; вычислить площадь сечения, являющегося квадратом.
Решеиие. В отличие от предыдущих задач здесь не указаны точки, через которые проводится сечение; условие, задающее такое
200
ГЛАВА II. СТЕРЕОМЕТРИЯ
сечение, сформулировано в виде требования его параллельности определенным прямым, а именно, скрещивающимся ребрам AS и ВС (рис. 144).
Пусть М— произвольная точка, принадлежащая стороне АС основания пирамиды. Проведем искомое сечение через эту точку. По-
скольку плоскость такого сечения должна быть параллельной ребру ВС, то и линия MQ его пересечения с плоскостью основания пирамиды должна быть параллельной ВС, т.е. MQ || ВС. Аналогично, линия пересечения MN плоскости сечения с боковой гранью ASCдолжна быть параллельной боковому ребру AS пирамиды. Отрезок прямой NP, являющийся пересечением плоскости сечения с другой боковой гранью BSC, также должен быть параллелен ВС.
Наконец, соединив точки Р и Q, получим отрезок PQ, замыкающий сечение. Поскольку плоскость сечения параллельна ребру AS, то линия ее пересечения PQ с гранью ASB, содержащей ребро AS, должна быть параллельной этому ребру, т.е. PQ || Л5. Таким образом, MN\\ PQ || AS и MQ || NP || ВС, т.е. фигура MNPQ — параллелог-
рамм.
Далее имеем: A/7V|| Л5, MQl ВС, но AS± ВС, как скрещивающиеся ребра правильной пирамиды. Следовательно, MN± MQ, т.е. параллелограмм MNPQ — это прямоугольник, что и доказывает
первую часть утверждения.
Будем перемещать точку Мпо ребру Л С (рис. 144). Если приближать ее к вершине А, то прямоугольник MNPQ, лежащий в сечении, будет «вытягиваться» вверх, если же точку М приближать к вершине С, то основание MQ прямоугольника будет увеличиваться, а высота MN — уменьшаться, прямоугольник будет как бы сплющиваться. Поэтому нетрудно видеть, что существует такое положение точки Мна ребре АС, при котором получающаяся в сечении фигура будет квадратом. Найдем его сторону.
Пусть АМ=х. Из подобия SCMNn A CAS имеем:
MN CM	MN а-х
----—----- т.е, -----—------.
AS	СА	b а
Кроме того, очевидно, что MQ-AM=x, поскольку SAMQ —-равносторонний, а так как сечение MNPQ — квадрат, то MN- MQ = х.
4. Сечение пирамиды плоскостью
201
Имеем уравнение:
х а - х	ab
— =-----, т.е. я =-----.
b а	а + b
Итак, сторона квадратного сечения имеет длину ab/(a + Ь), а его площадь равна сМДа + й)2.
Рассмотрим аналогичную задачу для правильной четырехугольной пирамиды (рис. 145).
Задача 4. Дана правильная четырехугольная пирамида SABCD (S — вершина). Длина стороны ее основания равна а, длина бокового ребра — Ь. Изучить сечения пирамиды плоскостями, параллельными боковому ребру пирамиды и скрещивающейся с ним диагонали основания {например, SD и АС). Найти те из них, в которые можно вписать окружность.
Решение. Сечения, о которых идет речь, могут иметь различную форму. Поскольку плоскость сечения параллельна диагонали АС, то, указав точку, через которую его следует провести, мы определим такое сечение однозначно. В качестве таких определяющих точек возьмем точки другой диагонали - BD.
Пусть N — произвольная точка диагонали BD, принадлежащая ее части BE, где Е — центр основания (рис. 145). Построим сечение, проходящее через эту точку. Поскольку его р плоскость должна быть параллельна АС, то отрезок Lx L3, по которому
эта плоскость пересекается с основанием пирамиды, должен быть также параллелен АС. С другой стороны, искомая плоскость пересекается с плоскостью BSD диагонального сечения пирамиды по отрезку NL2. Этот отрезок лежит в той же плоскости, которая содержит другую прямую SD, параллельную искомому сечению. Следовательно, NL21| SD. Соединив точку Ь2 с точками Lx и £3, получим треугольник LxLqL3, представляющий искомое сечение. Поскольку NL21| SD, LXL3\\AC и, кроме того, AC1SD, то NL21LXL3 т.е.
— равнобедренный, a NL2 — его высота.
Перемещая точку N между двумя крайними положениями BylE, каждый раз будем получать в сечении равнобедренный треугольник. Естественно, что в любой из них можно вписать окружность.
Рис. 145
202
ГЛАВА II. СТЕРЕОМЕТРИЯ
Пусть теперь N принадлежит другой половине диагонали BD, а именно, лежит внутри отрезка ED, В дальнейшем будем обозначать эту точку буквой М. Проведем через точку М сечение, параллельное АС и SD. Отрезок КХК2 проходящий через точку Мпараллельно диагонали АС, служит линией пересечения искомой плоскости с
основанием пирамиды. Поскольку плоскость сечения параллельна боковому ребру SD, то отрезки КХК2, МК3 и К3К4, лежащие соответственно в плоскостях ASD, BSD и CSD, также параллельны
этому ребру, а значит, и друг другу. Соединив точку К3 с точками
Рис. 146
К2 и К4, получим пятиугольник представляющий искомое сечение. Ясно, что КХК21КХК3 и К5К4 ± КХК3, поскольку SD 1АС. Кроме того, К2К3-К4К3, т.е. фигура, представляющая сечение, напоминает «домик с равноскатной крышей» (рис. 146).
Перемещая точку М между двумя
крайними положениями Ей D, мы можем либо увеличивать осно-
вание этого «домика», уменьшая высоту его «стен», либо умень
шать основание, увеличивая высоту его «стен».
Заметим, что искомое сечение КХК2К3К4К5 можно построить и другим способом. Продолжив отрезок КХК3 до пересечения со сторонами основания ВА и ВС в точках Р и Q соответственно, можно построить равнобедренный треугольник РК3 Q. Точки К2 и К4 пересечения его сторон с боковыми ребрами SA и SC пирамиды дают вершины искомого сечения (рис. 145 и 146).
Не во всякий пятиугольник КХК2К3К4К5 можно вписать окружность. Действительно, с одной стороны, эта окружность должна быть вписана в равнобедренный треугольник PK3Q (рис. 146); с другой стороны, перпендикуляры К2КХ и К4К5, опущенные из точек К2 и 7^, должны касаться окружности. Найдем, при каких условиях это выполнимо, т.е. укажем, где должна лежать точка М, чтобы в проведенное через нее сечение можно было бы вписать окружность.
Обозначим расстояние ВМчерез х (рис. 145). Тогда DM- а\[2 - х и КХМ- DM-а>/2 -х. Поскольку длина радиуса г вписанной окружности должна равняться половине основания сечения KXK2K3K4KS, т.е. КХМ, то г=а41 -х. С другой стороны, этот же радиус можно найти как радиус окружности, вписанной в треугольник РК3 Q. Для этого достаточно воспользоваться формулой
£ 4. Сечение пирамиды плоскостью
203
S=рг, где S — площадь треугольника PK3Q, ар — его полупериметр. Найдем величины 5 и р.
Сначала заметим, что РМ= ВМ=х, поскольку &PBQ — равнобедренный и прямоугольный. Затем найдем длину отрезка МК3, являющегося высотой треугольника PK3Q. Из подобия треугольников ВМК3 и BDS, лежащих в плоскости диагонального сечения BSD пирамиды (рис. 145), имеем:
МК3 ВМ	МК3 х
DS	BD b	aj2,
откуда MK3 = bx / a41. Наконец, по теореме Пифагора вычисляем длину стороны SPK3Q.
РК3 = yjPM2 + МК32 = у]х2+х2Ь2/2а2 = х^1 + Ь2/2а2.
Площадь треугольника 5 и его полупериметр р вычисляем по формулам
х2Ь
S = РМ мк3=~, аЛ
р = РМ + РК3=х{\ + -jl + b2/2а2}.
Отсюда находим длину г радиуса вписанной окружности
S xb
г = —  ------=========.
Р а\[2+>J2a2 + Ь2
Составляем уравнение для определения х путем приравнивания друг другу двух выражений для величины г:
/х	xb
а\12 - х =---,... -	,
aj2 + \2а2 + Ь2
откуда находим х = ау[2 (а^2 + 72л2 + Ь2)/(b + а^2 + ^2а2 + Ь2\, определяющее положение точки М на диагонали BD.
Приведем еще несколько примеров, в которых требуется определить те или иные параметры построенного сечения.
Задача 5. В основании треугольной пирамиды SABC лежит пря-
моугольный треугольник АВС с катетами СА = 4, СВ=3. Вершина
204
ГЛАВА II. СТЕРЕОМЕТРИЯ
R
Рис. 147
пирамиды S проектируется в точку С, причем SC-Л. На ребрах пирамиды взяты точки: М — на СА, N — на СВ, Р — на SA, причем МС- 1, NC- NB, SP-РА. Найти величину угла, образуемого плоскостью сечения пирамиды, проходящей через точки М, N и Р, с плоскостью основания.
Решение. Чертеж к этой задаче представлен на рис. 147. Сначала построим искомое сечение. Поскольку точки Р и М лежат в плоскости боковой грани ASC пирамиды, то в этой плоскости лежит и вся прямая МР, проходящая через данные точки, в том числе и точка R ее пересечения с продолжением ребра 5Сза точку С. Таким образом, в плоскости BSC другой бо-
*' Т ковой грани пирамиды известны уже две точки — Nw R. Прямая NR, проходящая через них, дает в пересечении с гранью BSC отрезок NQ, являющийся следом от пересечения секущей плоскости с поверхностью пирамиды. Проведя отрезки MN в
плоскости АВС и PQ — в плоскости ASB, получим четырехугольник MNPQ, представляющий искомое сечение.
Затем построим угол между плоскостью сечения и основанием пирамиды. Для этого из точки Р опустим на основание пирамиды перпендикуляр РК (точка К попадает, естественно, на АС), поскольку грань ASC перпендикулярна плоскости основания, из точки К опустим высоту на прямую MN и соединим получившуюся точку L пересечения с точкой Р.
Угол PLK есть линейный угол двугранного угла между сечением и основанием, величину которого нужно определить. Действительно, РК — перпендикуляр к плоскости основания, NL1. KL — по построению, следовательно, на основании теоремы о трех перпендикулярах можно заключить, что NL ± £Р.
Обозначим PLK = а. Тогда tg ос - PK/LK. Величина РК известна. Она равна 1/2, т.к. Р — середина AS, РК\\ 5С и РК — средняя линия треугольника ASC. Величину LK можно найти, рассмотрев подобные прямоугольные треугольники MCN и MLK в плоскости основания пирамиды. Имеем:
LK = МК
NC MN’
£ 4. Сечение пирамиды плоскостью
205
NC=BC/2 = 3/2, MK=AC/2-MC=l, MN2 =МС2 + NC2 =1 + 9/4, откуда MN= 713 /2. Таким образом, LK: 3/2 = 1: ТГз /2, откуда LK= 3/ 713 . Окончательно находим: tg а = 1/2 : 3/ ТГз = 713 /6 и а = arctg(713 /6).
2-й способ. Уместно отметить и другой способ решения этой задачи, основанный на использовании системы координат и скалярного умножения векторов.
Взаимно перпендикулярные ребра пирамиды CS, СА и СВ позволяют связать с ними прямоугольную систему отсчета, поместив ее начало в вершине С. Тогда плоскость сечения проходит через три точки, координаты которых известны, а именно Л/(1,0,0), 7V(0, 3/2,0), и Р(2, 0,1/2) (рис. 147).
Уравнение плоскости, проходящей через эти точки, будем искать в виде
х у 2 ,
а о с
Это так называемое «уравнение плоскости в отрезках». Числа а, b и с — это координаты точек пересечения плоскости с соответствующими осями координат, точнее говоря, координаты этих точек имеют вид (а, 0, 0), (0, Ь, 0) и (0, 0, с).
Подставляя в это уравнение последовательно координаты точек М, N и Р, получим три уравнения для определения чисел а, b и с:
3/2
b
2 + 1/2
а с
Отсюда находим а=1, b = 3/2, с = -1/2, т.е. секущая плоскость имеет уравнение
—+ —4~ + ——= 1 или 3x +2y-6z-3 = 0.
1 3/2 -1/2
Известно далее, что коэффициенты {3, 2, -6}, стоящие при х, у и z, в уравнении плоскости, можно рассматривать как координаты
206
ГЛАВА И. СТЕРЕОМЕТРИЯ
вектора п , перпендикулярного этой плоскости. Аналогично, координаты вектора к , перпендикулярного плоскости z = 0 основания пирамиды, равны {0, 0, 1}. Поэтому, используя формулу для выражения косинуса угла между векторами через их скалярное произведение и длины, можно вычислить этот угол, который как раз и равен углу между рассматриваемыми плоскостями. Имеем:
t	<13
tgoc^—-о
+ 22 + (-6)2
D
Рис. 148
.	. 13-0 +2 0 + (-6)• 11 6
732 + 22 + (-6)2	7
т.е. a = arctg(Vf3/6).
Задача 6. В правильной четырехугольной пирамиде SABCD с вершиной S проведена секущая плоскость Р, параллельная стороне АВ проходящая через точку касания вписанного шара и грани SAB, а также через точку этого шара, ближайшую к вершине S. Найти площадь сечения пирамиды плоскостью Р, если АВ = 1, SA- V5 /2.
Решение. В отличие от предыдущих задач секущая плоскость задана не тремя точками, принадлежащими ребрам пирамиды, а более сложно. Поэтому построим сначала искомое сечение.
Пусть К — точка касания вписанного шара (О — центр) с боковой гранью SAB (рис. 148). Секущая плоскость должна пересекаться с этой гранью по отрезку MR, параллельному стороне АВ.
Таким образом, становятся известными две точки М и R, лежащие на ребрах пирамиды и принадлежащие сечению.
Обратимся к плоскости ЗТ^симмет-рии пирамиды, проходящей через апофемы боковых граней. В этой плоскости также известны две точки К и О2, G принадлежащие сечению (О2 — точка шара, ближайшая к вершине). Следовательно, принадлежит сечению вся прямая О2К, пересекающаяся с гранью SCD в точке L и с плоскостью основания в точке G. Отрезок NQ, по которому плоскость сечения пересекается с гранью SCD, должен быть параллельным CD, поскольку плоскость сечения параллельна АВ и, следовательно, CD. Соединив точки Nc М и Q с R, получим четырехугольник MNQR, представляющий искомое сечение.
§ 4. Сечение пирамиды плоскостью
207
Четырехугольник MNQR — равнобочная трапеция (MR и NQ — основания). Действительно, MR | NQu MR* NQ. Кроме того, MN= RQ в силу симметрии. Заметим попутно, что плоскость этой трапеции, параллельная АВ, перпендикулярна плоскости SEF, а отрезок LK — высота трапеции, соединяющая середины L и А'ее оснований.
Площадь 5трапеции MNQR равна:
S = ^(MR + NQ)LK,
поэтому нужно найти MR, NQ и LK. Из подобия &SNQ и &SCD, &SMR и &SAB заключаем:
NQ = ^, MR = ^ (АВ = \). ОГ	JE
Чтобы вычислить эти отношения, обратимся к плоскости &SEF. В этом треугольнике: SE = SF = >IaS2 - АЕ2 = 1 = ЕЕ Следовательно, этот треугольник равносторонний. Такое обстоятельство значительно облегчает решение.
Точка К— середина отрезка SE. Следовательно, MR = 1/2. Точка О2 делит высоту 50] в отношении 1: 2, считая от вершины. Поскольку LKLNQ, то LK составляет 1/2 высоты равностороннего треугольника со стороной, равной 1. Значит, LK- 43 /4, а точка L отсекает от апофемы SF ее четвертую часть: NQ = 1/4. Таким образом, 5 = 1/2( 1/2 + 3/4) • 7з /4 = 3 Уз /32.
ЗАДАЧИ
1.	В треугольной пирамиде проведена плоскость сечения, параллельная основанию и делящая площадь ее боковой поверхности пополам. В каком отношении эта плоскость делит объем пирамиды?
Ответ-. 1 : (2 V2 - 1).
2.	Дана правильная четырехугольная пирамида SABCD с вершиной 5. На ребрах SA и SC взяты точки Р и Q, соответственно, причем АР: PS= 1: 3, CQ-SQ. Найти отношение, в котором делится ребро SB плоскостью, проведенной через точки D, Р и Q.
Ответ: 3 :4.
208
ГЛАВА II. СТЕРЕОМЕТРИЯ
3.	Плоскость проходит через вершину А треугольной пирамиды SABC, делит пополам медиану SKтреугольника SAB, а медиану SL треугольника SAC пересекает в точке D, такой, что SD= 1/2 • DL, В каком отношении эта плоскость делит объем пирамиды?
Ответ: 1 : 14.
4.	Дана правильная четырехугольная пирамида SABCD с вершиной 5. Через точки А, В и середину ребра SC проведена плоскость. В каком отношении эта плоскость делит объем пирамиды?
Ответ: 3 : 5.
5.	Через одну из сторон основания правильной треугольной пирамиды проведена плоскость, делящая боковую поверхность пирамиды пополам. В каком отношении эта плоскость делит объем пирамиды?
Ответ: 1:3.
6.	В правильной шестиугольной пирамиде длина стороны основания равна а, а высоты — Н. Вычислить площадь сечения, проходящего через середины двух не смежных и не параллельных сторон основания и через середину высоты.
Ответ: 25а^4Н2 + 3а2 /64.
7.	Ребро правильного тетраэдра SABC имеет длину а. Через вершину А параллельно ребру ВС проведена плоскость так, что величина угла между прямой АВ и этой плоскостью равна 30°. Найти площадь сечения.
Ответ: Зл/2а2 /25.
8.	Через сторону основания правильной треугольной пирамиды и центр вписанного в нее шара проведена плоскость. В каком отношении эта плоскость делит объем пирамиды, если длина ее бокового ребра в 3,5 раза больше длины стороны основания?
Ответ: 1:4.
9.	В правильной четырехугольной пирамиде SABCD с вершиной S сторона основания имеет длину 4 см. Через сторону CD основания проведено сечение, которое пересекает грань SAB по средней линии треугольника SAB, Площадь сечения равна 18 см2. Найти объем пирамиды SABCD,
Ответ: 32 7з см3.
§ 4. Сечение пирамиды плоскостью
209
10.	На основании правильной треугольной пирамиды, длина высоты которой равна Я и радиус круга, вписанного в основание — г, лежит шар, касающийся основания в его центре. Найти радиус шара, если плоскость, проведенная через вершину пирамиды и середины двух сторон основания, касается этого шара.
Ответ: Hr /(г + \1г2 + 4Я2
§ 5. КУБ И ЕГО СВОЙСТВА. СЕЧЕНИЕ КУБА ПЛОСКОСТЬЮ. ПРИЗМЫ
Кубом называется прямоугольный параллелепипед, у которого длины всех ребер равны между собой (рис. 149). Куб — это правильный многогранник, все грани которого квадраты.
Куб обладает рядом свойств, которые полезно иметь в виду при решении стереометрических задач. Укажем основные из них:
а)	диагональ куба перпендикулярна любой скрещивающейся с ней диагонали граней куба В'D ± AC; B’Dl. CD' и т.д.;
б)	диагонали непараллельных граней куба образуют между собой угол величиной 60° (А'В и А'С, ВС и DC и т.д.);
в)	сечение куба плоскостью (А'С В) или (AD'C), проходящей через концы ребер куба, исходящих из одной вершины (В' или D), является правильным треугольником;
г)	плоскости треугольников Я' С'Б и AD' С параллельны друг другу, перпендикулярны диагонали куба B'D и делят эту диагональ на три равные по длине части В'L = LK= KD;
д) сечение куба плоскостью, перпендикулярной диагонали куба и проходящей через центр куба, представляет собой правильный шестиуголь
ник. Этот шестиугольник пересекается с ребрами куба в их серединах (Д> Д, Д, Д, Д, Д).
Решение многих экзаменационных задач связано с плоскими сечениями куба. Как правило, в каждой из них требуется построить сечение куба плоскостью, задаваемой теми или иными условиями, например, тремя точками, лежащими на поверхности куба, или двумя точками и условием параллельности плоскости сечения той или иной прямой, или одной точкой и условием параллельности плоскости сечения другой плоскости и т.д. Построение таких сечений и последующие расчеты в принципе не отличаются от решения аналогичных задач для пирамид, о кото
£ 5. Куб и его свойства. Сечение куба плоскостью. Призмы
211
рых говорилось в предыдущем параграфе. Рассмотрим несколько
примеров.
Задача 1. Дан куб ABCDA' В' С D', где АА', ВВ', СС и DD' — боковые ребра. Найти площадь сечения этого куба плоскостью, проходящей через вершину А и середины ребер В'С' и С'D'. Ребро куба имеет длину, равную 1.
Решение. Сначала построим сечение. Начнем с точек Кн L, являющихся серединами ребер В' С и CD' (рис. 150). Эти точки лежат в плоскости верхней грани куба, поэтому прямая (KL),
проходящая через эти точки, есть линия пересечения секущей
плоскости с указанной гранью куба, а отрезок KL — одна из сторон многоугольника, представляющего сечение.
Продолжив KL до ее пересечения с продолжением ребер куба A’D’ и А’В’, получим точки Е и F, лежащие соответственно в гранях ADD1 А' нАА'В'Вкуба. Тогда в каждой из этих граней будут известны уже по две точки, принадлежащие сечению. Это А и Ев плоскости грани ADD'А'
Рис. 150
и А и F в плоскости грани
АА ’В'В. Поэтому прямые АЕ и AFпринадлежат сечению, а отрезки AN и AM этих прямых — стороны многоугольника, представ-
ляющего сечение.
Соединив точки Nn Кв плоскости грани ССD'Dn точки L и Мв плоскости грани ВВ' С С, получим весь пятиугольник AMLKN, представляющий сечение куба рассматриваемой плоскостью.
Заметим, что пятиугольник AMLKN получается из треугольника AEF отсечением от него двух равных треугольников MLF и NKE. Это дает возможность определить площадь сечения по формуле
$amlkn~ $aef ~ ^$nke-
Площадь равнобедренного треугольника AEF найти нетрудно. Для этого заметим, что из подобия треугольников B'LF, С'KL и D’КЕс коэффициентом подобия 1 (т.е. фактически, из равенства этих треугольников) следует:
Л'£ = 3/2, A'F = 3/2.
212
ГЛАВА II. СТЕРЕОМЕТРИЯ
откуда
з г-	ТГз
EF = ~J2, AE = AF = —, 2	2
поэтому длина h высоты &AEF, опущенной из вершины А на сторону ЕД равна ^АЕ2 -1/4 EF2 = V34 / 4, а площадь SAEF равна 3V17/8.
Поскольку &NKE можно получить из tuAEF изменением длины его стороны EF ъ EK/EF= 1/3 раза, а длины стороны ЕА — в EN/EA раз, то
_	_ 1 EN _	_ V17 EN
Snke=~3~EASaeF=~V~EA-
Осталось найти отношение EN/EA. Из подобия AED'N и &AND с коэффициентом подобия ED'/АО= 1/2 заключаем: EN\AN= 1: 2, откуда находим интересующее отношение EN\ £4=1:3. Итак, SNKE =	/^- Окончательно имеем:
„ ЗЛУ _Л7 7V17
SAmlkn= — -2— = —.
Заметим, что к этому же результату можно было бы прийти другим способом, а именно: найти площадь проекции пятиугольника AMLKN на плоскость основания куба (она равна 7/8), а затем разделить эту площадь на косинус угла проектирования, т.е. на косинус угла между плоскостью сечения и плоскостью основания куба. Метод определения этого угла понятен из рис. 151. Имеем: cos (р = 3/ >/17 . Тогда искомая площадь равна 7 V17 /24.
Еще один пример подобной задачи.
Задача 2. Дан куб ABCDA'В'С'D', где АА', ВВ', СС и DD’ — боковые ребра. В каком отношении делит объем куба плоскость, проходящая через вершину А, середину ребра ВС и центр грани DCCD'?
Решение. Построим плоскость сечения. Начнем с точек Ли Е (Е — середина ребра ВС). Проведем через них прямую АЕ до ее пересечения в точке F с продолжением ребра DC. Отрезок АЕ служит одной из сторон многоугольника, лежащего в сечении куба (рис. 152).
Теперь в плоскости грани ССD'D куба известны две точки О и Д принадлежащие сечению. Следовательно, прямая OF также
$ 5. Куб и его свойства. Сечение куба плоскостью. Призмы
213
принадлежит плоскости сечения. Отрезок LNee пересечения с гранью (СС D' D) служит другой стороной искомого многоугольника.
Рис. 152
Соединив точки А и N в грани AA’D’D и — Е и L в грани ВВ' С С, получим искомый четырехугольник ANLE, представляющий сечение куба.
Объем Ичасти куба, лежащей ниже плоскости сечения, вычисляется как разность объемов двух треугольных пирамид DANF (D — вершина) и CELF(C — вершина).
Из подобия &.FEC и &FAD с коэффициентом 1/2 имеем: CF- 1 (если длину ребра куба принять равной 1). Аналогично, из подобия &FCL и MFOO\ с коэффициентом 2/3 получим CL = 2/3 • ОО\ = 1/3, где Ot — проекция центра О грани ССD' D на ребро куба CD. Наконец, из подобия &FCL и &FDN с коэффициентом подобия 1/2, получим DN= 2 • CL-2/3.
Имеем:
r _ 1 DADF DANF ~ j j
1	2
• DN = 4 • 1 • 2 • - =
6	3
2.
9’
_1 CECF 'CELF ~ j	“
1 1 1=—• б'г ^'з зб’
И
- Vdanf - Ycelf - g ~3g "3g-
Итак, отношение объемов частей, на которые секущая плоскость делит объем куба, равно 7 : 29.
Задача 3. Через три точки О, Ей F, лежащие на поверхности куба ABCDA'B'C'D' (АА', ВВ', СС', DD' — боковые ребра), проведена плоскость сечения. Построить это сечение и найти величину угла, образуемого его плоскостью с плоскостью основания куба, если изве
214
ГЛАВА II. СТЕРЕОМЕТРИЯ
Рис. 153
стно,что О— центр грани АА'В'В куба,Е и Fпринадлежат ребрам C'D'u ВС, соответственно, причем С'Е=\/3 C'D' и BF= FC.
Решение. В отличие от предыдущих задач в этой задаче из трех данных точек О, Ен Fникакие две не лежат в плоскости одной и той же грани куба, так что сразу провести линию пересечения секущей плоскости с поверхностью куба нельзя (рис. 153).
Поступим следующим образом: спроектируем точки Ен О на плоскость основания куба ABCD и получим точки Ех и Ох, соответственно лежащие на ребрах DCylAB. Через точки Е и О, а также через их проекции Ех и Ох проведем прямые ЕОи ЕХОХ, которые должны пересечься, поскольку одна из них есть наклонная, а другая — проекция этой наклонной на плоскость основания куба. Пусть К — точка их пересечения. Естественно, она лежит в плоскости основания куба, поэтому в плоскости основания известны уже две точки, принадлежащие сечению: Ки F. Следовательно, принадлежит сечению и вся прямая
KF, содержащая эти точки. Отрезок MF— одна из сторон искомого многоугольника, лежащего в сечении (Л/ — точка пересечения прямой KFс ребром ВС).
Пусть L — точка пересечения прямой KFс продолжением ребра DC. Соединим точки ЬмЕ. Отрезок ЕР — это еще одна из сторон многоугольника, лежащего в сечении куба. Соединим точки F и Р в грани ВВ' С С, Мн О-в грани АА'В'В, N и Е — в грани А'В'СD' (N — точка пересечения прямой ОМ с ребром А'В'), получив остальные стороны пятиугольника ENMFP, представляющего сечение куба.
Если из точки Е в плоскости треугольника EKL опустить на его основание KL высоту (рис. 153), то угол между секущей плоскостью и основанием куба будет равен углу наклона этой высоты к плоскости основания. Обозначим его величину через а.
Получим:
К
tga =
ЕЕХ EXQ'
§ 5. Куб и его свойства. Сечение куба плоскостью. Призмы
215
Пусть ребро куба имеет длину, равную 1. Тогда ЕЕХ = 1. Найдем длину отрезка EXQ. Этот отрезок — высота треугольника KEXL (рис. 154). Из прямоугольного треугольника EXLQ находим: EXQ = EXL- cosLEiQ_=ElL  cosLFC (поскольку LFC = LEXQ как углы с взаимно перпендикулярными сторонами).
Обозначим МВ - х. Тогда CL = х (так как треугольники MBFw CLFравны); 0{М-\/2-х‘, ExL = 20xM= \-2х, Ех С- EXL - CL = 1 - Зх. Но по условию ЕХС= 1/3, следовательно, х=2/9. Тогда EXL = 1 -2х = 5/9. __
Далее находим: 1&LFC =CL/CF= = 2/9:1/2 = 4/9 или cos LFC = 9/797. После этого имеем: EXQ= EXL  cos LFC = = 5/797. Следовательно tga = 797/5, a = arctgT97 /5.
Так же, как и в задаче 5 предыдущего параграфа, косинус искомого
угла можно найти иначе, а именно с использованием метода координат. Приняв за начало системы координат вершину 7? куба, направим ее оси х, у и г соответственно по векторам ВА, ВС и ВВ'. Тогда точки Е, О и F, через которые проводится сечение, имеют координаты, Е (1/3,1,1), 0(1/2, 0,1/2), /'(0, 1/2, 0).
Запишем уравнение плоскости, проходящей через эти точки. Будем искать его в виде
х у z ,
- + Y + - = 1, а b с
где а, Ьм. с — неизвестные коэффициенты. Подставив в это уравнение последовательно координаты всех трех точек, получим систему уравнений
1111.
--+-+-=1 sabc
1111,
2 а 2 с
1.1 = 1,
2 Ь
216
ГЛАВА II. СТЕРЕОМЕТРИЯ
откуда находим а - 2/9, b = 1/2, с = -5/2. После этого уравнение плоскости можно записать следующим образом:
9х + 4у - 5г - 2 = 0.
Числа {9, 4, -5} можно рассматривать как координаты вектора, перпендикулярного проведенной плоскости. Угол между плоскостью сечения и плоскостью основания куба равен углу между векторами, перпендикулярными этим плоскостям, т.е. углу между векторами {9; 4; -5} и {0; 0; 1}. Имеем:
90 + 4-0-51 cos а = —, .....	=-
>/81 + 16 + 25
5
V122 ’
Отсюда видно, что а — тупой угол Острый угол (л - а) между плоскостями записывается как п - arccos (-5/ V122) = arccos (5/ V122) или как arctg (V97 /5). Как видно, в данном случае этот способ приводит к результату гораздо быстрее, чем предыдущий.
Рассмотрим теперь несколько задач на сечение призм.
Задача 4. Дана треугольная призма АВСА'В' С' (АА*, ВВ', СС — боковые ребра). Плоскость пересекает ребра А' В', В' С и ВС соответственно в точках М, N и Р, Найти, в каком отношении делит эта плоскость объем призмы, если известно, что В' М.А' В' -1:2, В'#:5'С' = 2:ЗиЛР:С5=1:3.
Решение. Чертеж к этой задаче представлен на рис. 155. Сечение строится в следующем порядке. Точки N и М соединяются
отрезком MN\ через точки N и Р в плоскости боковой грани ВВ’С С проводится прямая NP до ее пересечения в точке К с продолжением ребра ВВ’. Через две точки Мп К, лежащие в плоскости боковой грани АА'В'В, проводится прямая КМ, точка Q ее пересечения с ребром АВ призмы соединяется отрезком PQ с точкой Р, Четырехугольник MNPQ — искомое сечение (MNPQ — трапеция, поскольку MN\\ PQ).
Учитывая, что пирамида KPQB (К — вершина) подобна пирамиде KNMB' (К — вершийа) с коэффициентом подобия 1/2 (действитель
§ 5. Куб и его свойства. Сечение куба плоскостью. Призмы
217
но, из подобия треугольников КРВ и KNB' следует, что КВ . КВ' = = РВ: NB', т.е. как 1:2), находим:
^kpqb - 2	' ^KNMB’
или объем И] части призмы, лежащей правее плоскости сечения (рис. 155), равен 7/8 объема VKNUB- пирамиды KNMB'.
Сравним объем пирамиды KNMB' с объемом Ипризмы. Имеем:
V - $лвс ’ Н; Vknmb' - j' $nmb' • 2Н, где Н — высота призмы, SABC — площадь ее основания; 2Н — высота пирамиды KNMB', SNMB- — площадь ее основания. Далее:
_	_ NB' МВ' _
^NMB-^^^ABC
2.1 с U
3 2 ^лвс - 2^авс
(см. § 1, гл. 1). Следовательно,
Vknmb’ = з ’ з ’	' 2Я = - И.
Отсюда объем отсекаемой части равен
7	7 2	14
о	о У	/ Z
Следовательно, объем призмы делится в отношении 14: 58 или 7:29.
Наконец, рассмотрим последний пример задачи подобного типа.
Задача 5. В прямую призму ABCDA’ В’ CD’, основанием которой является ромб ABCD, а АА', ВВ', СС' и DD’ — боковые ребра, вписан шар радиуса 2R. Найти площадь сечения призмы плоскостью, проходящей через вершины А, В и С', если известно, что BAD =а.
Решение. Покажем сначала, как проходит упомянутая в условии задачи плоскость сечения. Поскольку ей принадлежат точки А, В и С, то сторона AS основания и диагональ ВС боковой грани будут линиями пересечения секущей плоскости с поверхностью призмы. Чтобы построить остальные стороны многоугольника, лежащего в
218
ГЛАВА II. СТЕРЕОМЕТРИЯ
сечении, заметим, что они должны быть параллельными уже построенным отрезкам. Действительно, параллельные плоскости пересекаются секущей плоскостью по параллельным прямым. Отсюда следует, что сечению должны принадлежать отрезки D'C' и AD'} т.е. искомое сечение призмы — это параллелограмм ABCD' (рис. 156).
Поскольку призма прямая и в основании лежит ромб, то проекция вписанного в призму шара на плоскость основания представляет окружность, вписанную в ромб. Значит, высота этого ромба равна 2R. Эту же длину имеет и высота призмы, поскольку в нее можно вписать
шар радиуса R, Если из точки D' опустить на сторону АВ перпендикуляр D'E, лежащий в плоскости сечения, и соединить полученную точку Е с вершиной D, то линейный угол двугранного угла между плоскостями основания и сечения дается углом DED'. Действительно, D'El. АВ по построению; DE 1 АВ —по теореме о трех перпендикулярах. Так как высота призмы DD', и высота ромба DE имеют одинаковую длину, равную 2А, то угол DED' равен 45°.
Площадь сечения найдем по формуле
$ABCD = ^сеч. ’ COS 45°,
в которой 5сеч — площадь сечения, SABCD — площадь основания призмы, являющегося проекцией сечения ABCD' на плоскость основания.
Из прямоугольного треугольника AED, лежащего в основании призмы, находится сторона ее основания AD = 2A/sin а, а затем и сама площадь основания
$ABCD
2R sin а
2R sin а
•sin а
4Я2 sin а ’
После этого определяется площадь сечения:
^сеч. “ $ABCD
COS 45°
4y[2R2 sin а
£ 5. Куб и его свойства. Сечение куба плоскостью. Призмы
ЗАДАЧИ
219
1.	Дан куб ABCDA 'В' С’D' с боковыми ребрами АА', ВВ', СС’ и DD'. На продолжении ребер АВ, АА', AD отложены соответственно отрезки ВР,А' Q, Д/? длиной 1,5 • Абтак, что АР=AQ=АВ =2,5 АВ. Через точки Р, Q и R проведена плоскость. В каком отношении эта плоскость делит объем куба?
Ответ: 1 :47.
2.	Дан куб ABCDA'В'СD’ с боковыми ребрами АА', ВВ', СС и DD’. В каком отношении делит ребро СВ' точка Е, которая принадлежит плоскости, проходящей через вершину А и центры граней А 'В'C'D' и В'С'СВ?
Ответ: 2:1.
3.	Дан куб ABCDA'В'СD', где АА', ВВ', СС и DD' — боковые ребра. Найти площадь шестиугольника, который получается в сечении куба плоскостью, проходящей через центр куба и середины ребер АВ и ВС. Ребро куба имеет длину, равную 1.
Ответ: зТз / 4.
4.	Длина ребра куба ABCDA'В’ CD' (АА' ] ВВ’ Ц СС || DD’) равна 1. На ребре АА' взята точка Етак, что длина отрезка АЕравна 1/3; на ребре ВС взята точка /’так, что длина отрезка BFравна 1/4. Через центр куба и точки Е и F проведена плоскость. Найти расстояние от вершины В до этой плоскости.
Ответ: 117170/170.
5.	Дан куб ABCDA 'В' C'D (АА' || ВВ' || СС || DD’), причем длина его ребра равна а. Точка Е' — середина ребра CD', точка F' — середина ребра В' С. Найти радиус сферы, проходящей через точки Е’, F, А, С.
Ответ: а>/4 \ /8.
6.	Найти площадь сечения куба ABCDA'В'СD' (АА', ВВ', СС, DD' — боковые ребра) плоскостью, проходящей через вершину D и середины ребер А 'В' и В'С. Ребро куба имеет длину, равную а.
Ответ: 7a2 ТГ7 /24.
7.	Дана правильная треугольная призма АВСА В С с боковыми ребрами АА', ВВ', и СС. На продолжении ребра А'В' взята точка М так, что ВМ' = 1/2 • А 'В' (А'М= 3/2 • А 'В'). Через точку М и се
220
ГЛАВА II. СТЕРЕОМЕТРИЯ
редины ребер А' С и В' В проведена плоскость. В каком отношении эта плоскость делит объем призмы?
Ответ: 49:95.
8.	Дана прямая призма, у которой основанием служит правильный треугольник. Через одну из сторон нижнего основания и противоположную вершину верхнего основания проведена плоскость. Величина угла между этой плоскостью и плоскостью основания призмы равна а, а площадь сечения призмы равна S. Определить объем призмы.
Ответ: л/3(5 cos а)312.
9.	Дана прямая треугольная призма АВСА'В' С',АА' || ВВ' || СС', у которой АС=6, АА' = 8. Через вершину А проведена плоскость, пересекающая ребра ВВ' и СС соответственно в точках М и N. Найти, в каком отношении эта плоскость делит объем призмы, если известно, что ВМ=МВ', a AN является биссектрисой угла САС.
Ответ: 7/17.
10.	Дан куб ABCDA' В' С D' с ребром, длина которого равна 1. На продолжении D'Рза точку D взята точка Ртакая, что DP= 1/2. Через точку Р и середины ребер АА' и СС проведена плоскость. Найти площадь получившегося сечения.
Ответ: 3>/3 / 4.
§ 6. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ШАРОВ, ШАРОВ И ПЛОСКОСТЕЙ
Рассмотрим некоторые типовые задачи, в которых речь идет о взаимном расположении шаров или шаров и плоскостей. Во мно
гом приемы их решения схожи с приемами, используемыми при
решении задач на взаимное расположение окружностей, о которых речь шла в § 5 гл. 1.
Пусть, например, в пространстве даны четыре одинаковых шара, имеющие радиус R, и попарно касающиеся друг друга внешним образом, как это показано на рис. 157. Пусть требуется найти радиус пятого шара, содержащего данные шары внутри себя
и имеющего с каждым из них внутреннее касание.
Ключом к анализу подобной комбинации пространственных тел может служить рассмотрение многогранника	с вершинами
в центрах данных шаров. Если вспомнить, что расстояние между центрами любой пары касающихся внешним образом шаров равно сум-
ме их радиусов, то станет ясно, что длины всех ребер такого многогранника будут известны. Так, например, центры Olf 02, 03, 04 данных шаров являются вершинами правильного тетраэдра с длиной ребра 2А. С другой стороны, если шары касаются друг друга внутренним образом, то точка их касания принадлежит линии, соединяющей центры, а расстояние между центрами равно разности радиусов этих шаров. Для рассматриваемой конфигурации центр пятого, описанного, шара находится в центре правильного тетраэдра Oj С?2О3С?4. Этот центр, как известно, делит высоту тетраэдра в отношении 3:1, считая от вершины.
Обозначив через х радиус искомого шара, а через Л, — высоту тетраэдра O}O2O3O4i получим уравнение
х - R = 4  h.
4
222
ГЛАВА II. СТЕРЕОМЕТРИЯ
Если учесть, что длина высоты тетраэдра с ребром 2R равна 2Ry]2/3, то радиус пятого шара определится выражением
х = Х + у/1 = Я + ~2Х,- = Я
4	4 V 3
Аналогично решаются и другие задачи.
Задача 1. Три одинаковых шара радиуса R попарно касаются друг друга и некоторой плоскости внешним образом. Четвертый шар радиуса R лежит с той же стороны плоскости, что и первые три шара, и касается каждого из них. Найти расстояние от точки четвертого шара, максимально удаленной от плоскости, до этой
плоскости.
Решение. Нетрудно заметить, что искомое расстояние Н скла-
дывается из суммы двух радиусов и длины h высоты пирамиды О1О2О3О4 (рис. 157). Таким образом, //= 2R + h или 27 = 2Я( 1 +V6 /3).
Задача 2. Внутри прямого кругового конуса расположены четыре шара одинакового радиуса R, попарно касающиеся друг друга внешним образом, причем три из них лежат на основании конуса и касаются его боковой поверхности, а четвертый — только боковой
поверхности конуса. Найти высоту конуса.
с	Решение. Очевидно, что высота тако-
го конуса содержит высоту правильного тетраэдра	образованного цен-
трами данных шаров (рис. 158). Рассмотрим сечение конуса и вписанной в него системы шаров плоскостью, проходящей через высоту конуса и центр одного из шаров, например, первого, т.е. рассмотрим одну из плоскостей симметрии данной пространственной конфигурации тел. Это сечение изображено на рис. 158. Нетрудно понять, что окружности с центрами в точках и О4, получившиеся вследствие пересечения плоскости симметрии и первого и четвертого ша
ров, касаются образующей АС конуса. Поэтому Oj О41| АС.
Длина высоты СЕ конуса равна сумме длин трех отрезков: СЕ= СО4 + O4Z) + DE, причем O4D = h = 2Ryj2/3 — высота тетра-
§ 6. Взаимное расположение шаров, шаров и плоскостей	223
эдра О1О2О3О4, С04 = Л/sin а, где а= АСЕ — угол при вершине конуса, DE = R.
Синус угла а определяется отношением длин отрезков 0^ и 0104:
причем длина отрезка 0\D равна 2/3 длины высоты основания тетраэдра OjOjOjQi— O1Z>=2/3 • 2R- 41 /2 = 2А%/3 /3. Таким образом,
sin а =
2Л>/3/3 _ Уз
2R 3 ’
С04
R
Уз/з’
С£ = Л +2ЯУ2/3+ЗЛ/УЗ = Л(1+ 2Уб/З + Уз).
Задача 3. Три одинаковых шара радиуса R касаются некоторой плоскости и друг друга внешним образом. Четвертый шар касается каждого из трех данных шаров и той же плоскости. Найти его радиус.
Решение. Рассмотрим правильную треугольную пирамиду ОХО2О3ОА с вершинами в центрах шаров, причем 04 ~ центр четвертого шара (рис. 159). Длины сторон основания этой пирамиды равны 2Я, а длины боковых ребер — (Я + х), где х — радиус четвертого шара. Очевидно, что расстояние от плоскости основания правильной пирамиды О1О2О3О4до данной плоскости равно Я, поэтому высота пирамиды равна (Я-х).
Запишем выражение для связи высоты правильной пирамиды, высоты ее основания и длины бокового ребра:
(R + x)2 = (R-x)2 +
3	2
откуда находим: х= R/3.
Подобный прием можно использовать и при решении следующей задачи.
224
ГЛАВА II. СТЕРЕОМЕТРИЯ
Задача 4. Три шара радиуса г лежат на нижнем основании прямо-
го кругового цилиндра, причем каждый из них касается двух других и боковой поверхности цилиндра. Четвертый шар лежит на этих трех шарах, касаясь поверхности цилиндра и его верхнего основания. Опре
делить высоту цилиндра.
Решение. Так как три шара имеют одинаковые радиусы и ле-
жат на нижнем основании цилиндра, то их центры О15 О2 и О3
(рис. 160) находятся в одной плоскости я, параллельной плоскости основания цилиндра. Поскольку четвертый шар касается боковой поверхности цилиндра и верхнего основания, то его радиус равен радиусу основания цилиндра R.
Центр шара О4 лежит на оси цилиндра и проектируется в точку О — центр сечения цилиндра плоскостью
Рис. 160
я. Это сечение представлено отдельно на том же рисунке. Легко усмотреть, что высота цилиндра Я= r+ h + R, где h = ОО4.
Рассмотрим пирамиду О1О2О3О4. Очевидно, что эта пирамида правильная, длины сторон основания равны 2г, длины боковых ребер — (г+7?), следовательно, вершина пирамиды, точка О4, проектируется в центр треугольника ОХО2О3. Теперь легко под
считать, что
2\[3 D пп 3 + 2л/3
ООХ = —— г, R = 00] + г =---------------г.
1	3	3
Высоту h определяем из прямоугольного треугольника ООХ О4:
h = y/OiOl-OOl = J(R + г)2 - |r2 = |r^9 + 6V3
Окончательно находим
Н = |г(з + 7з+79 + б7з).
Во многих задачах рассматриваются один или несколько шаров, вписанные в двугранный угол, т.е. касающиеся плоскостей, образующих этот угол. В частности, речь может идти о шарах, касающихся двух, трех или большего числа граней какого-либо много-
£ 6. Взаимное расположение шаров, шаров и плоскостей
225
гранника. При решении таких задач удобно использовать следую-
щее соображения: центр шара, касающегося сторон двугранного угла,
лежит в его диссекторной плоскости L, т.е. в плоскости, каждая точка которой равноудалена от граней Рта С этого угла (рис. 161);
если шар вписан в трехгранный угол, то центр такого шара лежит на прямой, являющейся пересечением биссекторных плоскостей составляющих его двугранных углов;
если в двугранный угол вписана пара шаров, касающихся друг друга, то между радиусами этих шаров и величиной а двугранного
угла существует простое соотношение
. a R-r . a \-r/R sin — = —— или sm — =  .
2 R + r	2 1 + r/R
Как получается последнее соотношение, видно из рис. 161. Из непг следует, в частности, что величина а двугранного угла определяет
отношение радиусов вписанных в угол и касающихся друг друга шаров и наоборот, отношение радиусов таких шаров определят ве-
личину двугранного угла а.
В качестве примера рассмотрим следующую задачу.
Задача 5. Два одинаковых шара радиуса R касаются друг друга и граней двугранного угла, величина которого равна а. Найти радиус
меньшего из двух шаров, касающихся граней двугранного угла и обоих данных шаров.
Решение. Поскольку все шары касаются граней Р и Q двугранного угла, то их центры О], О2и Оз принадлежат биссек-торной плоскости L, причем треугольник Oj ОгО3 — равнобедренный (рис. 162). Длина О] О2 его основания равна 2R, а длины боковых сторон — (/? + г), где г— радиус
Рис. 162
искомого шара. Шары О1 и О2 имеют одинаковый радиус R, поэтому их центры равноудалены от ребра MNдвугранного угла и, следовательно, О1021| MN, а высота О2В равнобедренного треугольника 0]020з, где В — точка взаимного касания шаров Ot и О2, перпендикулярна этому ребру.
226
ГЛАВА П. СТЕРЕОМЕТРИЯ
Спроектируем точки О3 и В на одну из граней двугранного угла (например, Р), получим точки Du Е. В плоскости проектирования проведем О3 С || DE. Рассмотрим прямоугольный треугольник О3ВС. Имеем:
. а ВС R-r
Sm2~O^B~~OyB'
Высота О3В треугольника О]О2О3 находится по теореме Пифагора из треугольника Ot О3В:
О3В = ^O^-OiB2 = y](R + г)2 - R2 = 7г(2Я + г).
Используя выражение для О3В через г, получим уравнение для определения г:
.a R-r
sin—• = -7==
2 Vr(2A + r)
или
г2 cos2 - 2Rr\ 1 + sin2 |+ R2 = 0.
2	2 1
Меньший корень этого уравнения имеет вид:
г = R + sin2 а/2-sin а/2	+ sin2 а/2 j/cos2 а/2.
Заметим, что болыг(а/2рРен(а/2^нения 01(а/2)ляет Р(а/2/ другого, большего шара, также касающегося граней двугранного угла и данных шаров, но лежащего «за» этими шарами (рис. 162).
В качестве последнего примера рассмотрим следующую задачу.
Задача 6. В двугранный угол величиной 60’ вписан шар радиуса R. Найти радиус шара, вписанного в тот же угол и касающегося данного шара, если известно, что прямая, соединяющая центры обоих шаров, образует с ребром двугранного угла угол 45’.
Решение. Как и в предыдущих случаях, центры шаров лежат в биссекторной плоскости Р (рис. 163). Нетрудно заметить, что задача имеет два решения. На прямой, проходящей через центр данного шара и образующей угол 45’ с ребром двугранного угла, можно выбрать две точки О( и О2 для центров искомых шаров. Радиус одного из этих шаров будет меньше R, радиус другого шара — больше, чем R. Проведем С^Вя ОС параллельно ребру дву-
§ 6. Взаимное расположение шаров, шаров и плоскостей
227
Рис. 163
гранного угла. Тогда прямоугольные треугольники ОО^В и ОО2С будут иметь острые углы по 45’. Обозначим через х радиус искомых шаров. Возможны два случая:
1) х < R. В этом случае имеем:
ЯО=2/?(изДЛО2>); А^ = 2х (из ДА^О^)-,
OOi = R + x, 0B = 2(R-x).
Из ДOOj 2? находим 0В= 00} • V2 /2, т.е.
2(Я-х) = ^(Я + х).
Отсюда получаем выражение для х:
х = R
4-Л
4 + V2’
(1)
2) х > R. В этом случае имеем:
АО = 2R (из ДЛОО); А2О2 = 2х(из bA&DJ;
O2O=R + x,	O2C=2(x-R).
Из ДОО2Снаходим 02С= 002 • V2 /2, т.е.
л/2
2(х-А) = у(й + х).
Отсюда получаем выражение для х:
228
ГЛАВА II. СТЕРЕОМЕТРИЯ
x = R^~.	(2)
4-V2
Формулы (1) и (2) дают решения задачи.
ЗАДАЧИ
1.	Три шара радиуса R лежат на нижнем основании правильной треугольной призмы, причем каждый из них касается двух других шаров и двух боковых граней призмы. На этих шарах лежит четвертый шар, который касается всех боковых граней и верхнего основания призмы. Определить высоту призмы.
Ответ: R[б + V3 + ^27 + 12>/з)/3.
2.	Три шара касаются плоскости треугольника АВС в его вершинах и попарно между собой. Найти радиусы шаров, если известны
длина с стороны АВ и прилежащие к ней углы А и В
Ответ: гх = с • sin В /2 sin A , r2 = c sin A /2sin В,
г3 = с * sin A sin В/2 sin2 (А + В).
3.	В шар вписан прямой круговой цилиндр. Во сколько раз объем шара больше объема цилиндра, если известно, что отношение радиуса шара к радиусу основания цилиндра вдвое меньше, чем отношение поверхности шара к боковой поверхности цилиндра?
Ответ: 16:9.
4.	Две одинаковые сферы касаются друг друга и граней двугранного угла. Третья сфера, меньшего радиуса, также касается граней этого двугранного угла и обеих данных сфер. Дано отношение т радиуса меньшей сферы к радиусу одной из одинаковых сфер. Найти величину а двугранного угла. В каких пределах может меняться параметр т?
Ответ: а = 2arcsin^(l -m)/jm2 + 2wJ; 0,25 <m<l.
5.	В прямом круговом конусе угол при вершине осевого сечения равен 60°. В этом конусе расположены три одинаковых шара радиуса R, касающиеся изнутри боковой поверхности конуса, плоскости основания конуса и попарно друг друга. Найти площадь боковой поверхности другого конуса с той же вершиной,
§ 6. Взаимное расположение шаров, шаров и плоскостей	229
высотой и плоскостью основания, которого данные шары касаются внешним образом.
Ответ: 26nR\/21г.
6.	На плоскости лежат, не пересекаясь, два шара радиусов ruR. Расстояние между центрами шаров равно р. Найти минимально возможный радиус шара, который лежал бы на этой плоскости и касался заданных шаров.
Ответ: (р + R- г) (р + г- R) /4 (4И + 4г) .
7.	В правильную треугольную пирамиду помещены три шара так, что первый шар касается всех боковых граней пирамиды и второго шара, второй шар касается боковых граней и третьего шара, третий шар касается боковых граней, основания пирамиды и второго шара. Какую долю объема пирамиды занимают три шара, если ее боковые грани наклонены к основанию под углом а?
Ответ: 4 л л/З (tg3a/2 + tg9a + tglsa/2) / 9tg a.
8.	В прямой круговой конус, у которого образующая составляет с осью угол а, помещены три шара так, что первый шар касается боковой поверхности конуса и второго шара, второй шар касается боковой поверхности, первого и третьего шаров, а третий шар касается боковой поверхности, основания конуса и второго шара. Какую долю объема конуса занимают все три шара?
Ответ: 4 (tg3a/2 + tg9a/2 + tgI5a/2) / tg a.
9.	Три одинаковых прямых круговых конуса, радиусы оснований которых равны г, а высоты равны 4г/3, расположены по одну сторону от плоскости Р, а их основания лежат в этой плоскости. Окружности оснований каждых двух из этих конусов касаются. Найти радиус шара, лежащего между конусами и касающегося как плоскости Р, так и всех трех конусов.
Ответ: 2г (2 43 - 3) /3.
10.	В правильной четырехугольной пирамиде расположены два шара О1г и О2. Шар О} вписан в пирамиду и имеет радиус 2, шар О2 касается внешним образом шара Oj и боковых граней пирамиды. Радиус шара О2 равен 1. Найти площадь боковой поверхности пирамиды и величину двугранного угла при боковом ребре пирамиды.
Ответ: 96; 2 arcsin (45/3).
§ 7. РАЗНЫЕ ЗАДАЧИ
1.	Определить синус угла между двумя высотами, опущенными из двух вершин правильного тетраэдра на противоположные грани.
Ответ: 2>/2/3 см3.
2.	Основанием пирамиды служит равнобедренный прямоугольный треугольник, катет которого равен 8 см. Длина каждого бокового ребра составляет 9 см. Найти объем пирамиды.
Ответ: 74.
3.	Основание пирамиды — правильный треугольник с длиной стороны, равной 6. Одно из боковых ребер перпендикулярно плоскости основания; его длина равна 4. Найти радиус шара, описанного вокруг пирамиды.
Ответ: 4.
4.	Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда наклонены к плоскости основания под углами, величины которых равны аир. Найти величину угла между этими диагоналями.
Ответ: arccos (sin а • sin Р).
5.	Площадь боковой грани правильной шестиугольной пирамиды равна S. Вычислить площадь сечения, проходящего через середину высоты пирамиды параллельно боковой грани.
Ответ: 25/16 • S.
6.	В основании пирамиды лежит равносторонний треугольник с длиной стороны, равной а. Высота пирамиды проходит через середину одного йз ребер основания и имеет длину За/2. Найти радиус шара, описанного вокруг пирамиды.
Ответ: а 4? /3.
7.	Через сторону оснований правильной треугольной пирамиды и центр вписанного в нее шара проведена плоскость. В каком
£ 7. Разные задачи
231
отношении эта плоскость делит объем пирамиды, если ее боковое ребро в 3,5 раза длиннее стороны основания.
Ответ: 4:1.
8.	Плоскость пересекает боковые ребра SA, SB и SC треугольной пирамиды SABC в точках К, Ln М, соответственно. В каком отношении эта плоскость делит объем пирамиды, если известно, что SK: КА = SL: LB= 2, а медиана SN треугольника SBC делится этой плоскостью пополам.
Ответ: 7:29.
9.	В треугольной пирамиде SABC ребро SA перпендикулярно плоскости грани АВС, двугранный угол с ребром SCравен 45°, SA = BC= а и угол АВС прямой. Найти длину ребра АВ.
Ответ: aVV2 -1.
10.	Основанием треугольной пирамиды служит равносторонний треугольник. Три другие грани образуют с основанием двугранные углы, величины которых равны а, р и у, каждый меньше л/2. В пирамиду вписан шар. Определить отношение радиуса шара к высоте пирамиды.
Ответ: (ctg а + ctg р + ctg у) / (ctg а/2 + ctg р/2 + ctg у/2).
11.	Определить объем параллелепипеда, у которого длины всех ребер равны 1, а все плоские углы при одной из вершин имеют величину <р (<р < 90°).____________
Ответ: sin <р  7sin2 <р - cos2 ф • tg <р / 2.
12.	Ребра треугольной пирамиды, выходящие из вершины О, попарно перпендикулярны, и их длины равны а, b и с. Найти объем куба, вписанного в эту пирамиду так, что одна из его вершин совпадает с вершиной О.
Ответ: а3Ь3<?/(аЬ + ас + Ьс)3.
13.	Усеченный конус и правильная шестиугольная призма расположены так, что верхнее основание усеченного конуса вписано в верхнее основание призмы, а нижнее основание усеченного конуса описано около нижнего основания призмы. Известно, что длина высоты усеченного конуса равна сумме длин радиусов его оснований. Найти отношение боковых поверхностей этих фигур.
Ответ: п>/14 /12.
232
ГЛАВА II. СТЕРЕОМЕТРИЯ
14.	Длина стороны основания правильной треугольной призмы АВСА\В{ Сх равна а. Точка D — середина ребра АВ, точка Е принадлежит ребру Ах Прямая DE образует углы аире плоскостями АВС и ААХСХ С, соответственно. Найти высоту призмы и радиус шара с центром на отрезке DE, касающегося плоскостей АВС и AAtCj С
Ответ: а4з /4 • sin a/sin р; а л/З /4 • sin a/(sin a + sin P).
15.	Все ребра правильной треугольной призмы АВСА&Су имеют длину а. Рассматриваются отрезки с концами на диагоналях ВСХ и СА{ боковых граней, параллельные плоскости АВВ^. Один из этих отрезков проведен через точку М диагонали ВСХ такую, что ВМ: BCi = 1:3. Найти его длину. Найти также наименьшую д лину всех рассматриваемых отрезков.
Ответ: 45 а/3', а/45 .
16.	В прямоугольном параллелепипеде ABCDAxBxCiDx, длины ребер АВ, ВС и ВВх равны соответственно 2а, а и а. Точка Е — середина ребра ВС. Вершины Ми Nправильного тетраэдра MNPQ, лежат на прямой СХЕ, вершины Р и Q — на прямой, проходящей через точку В{ и пересекающей прямую AD в точке F. Найти длину отрезка DF и расстояние между серединами отрезков MN и PQ.
Ответ: а; 4а/3 45 .
17.	Длина ребра куба ABCDAXB} СХОХ равна а. Точка Е —середина ребра AD. Вершины Ми Nправильного тетраэдра MNPQ лежат на прямой ED{, а вершины Р и Q, — на прямой, проходящей через точку А{ и пересекающей прямую ВС в точке R. Найти отношение длин BR: ВС и расстояние между серединами отрезков MNn PQ.
Ответ: 2; 2а/ -УЗО .
18.	Ребро куба АВСОАхВхСхОь имеет длину а. На ребрах АВ и ССХ взяты соответственно точки М и ТУтак, что прямая MN образует угол 30° с плоскостью ABCD и угол arcsin 1/3 с плоскостью ВВХ Ct С. Найти длину отрезка MN и радиус шара с центром на отрезке MN, касающегося плоскостей ABCD и ВВХ Сх С.
Ответ: 6а/ 423 ; 6а/5 423 .
19.	Основанием прямой треугольной призмы АВСА^Су является равнобедренный прямоугольный треугольник с катетами
£ 7. Разные задачи
233
ЛС = ВС— а. Вершины Ми N правильного тетраэдра MNPQ лежат на прямой CAlf а вершины Р и Q — на прямой АВ{. Найти объем призмы и расстояние между серединами отрезков MN и PQ.
Ответ: 4/2; а/ Тб .
20.	Дан правильный тетраэдр SABC, длина ребра которого равна а. Через точки С, Е, М и S, где Е — середина ребра АВ, а М — середина ребра АС, проведена сфера. Найти радиус этой сферы.
Ответ: а 422 /8.
21.	Дан куб ABCDA'В'С'D' с нижним основанием ABCD и боковыми ребрами АА', ВВ', СС' и DD'. Длина ребра куба равна (4 - 2 V2 )/ (423 -42-3). Первая сфера касается нижнего основания ABCD, боковой грани ВВ’СС и плоскости АА'С'С. Вторая сфера с центром в точке А' имеет радиус вдвое больший, чем радиус первой сферы, и касается первой сферы внешним образом. Найти радиус первой сферы.
Ответ: 1.
22.	В треугольной пирамиде SABC (S — вершина) грань SAC перпендикулярна грани АВС. Кроме того, SA = SC- 1, а угол при вершине 5 треугольника А8С-- прямой. Шар касается плоскости основания пирамиды в точке В, а грани SAC — в точке S. Найти радиус шара.
Ответ: 42 /2.
23.	Дана пирамида SABC (S — вершина), в которой ребро АС перпендикулярно грани SAB. Шар касается грани ASC в точке S, а грани АВС — в точке В. Найти радиус шара, если АС=1, АСВ = BCS = 60°-
Ответ: 4б /2.
24.	Длина стороны основания правильной четырехугольной пирамиды SABCD с вершиной S равна 1, а длина ее высоты — 41 . На ребрах SA и SC взяты точки К и М, соответственно, причем АК: KS- 1/3; СМ = SM. Найти отношение, в котором делится ребро SB плоскостью, проведенной через точки D, К и М.
Ответ: 4:3.
25.	В прямой круговой цилиндр с радиусом основания, равным 3/2, и высотой 6(72-1) вписаны четыре одинаковых шара так,
234
ГЛАВА И. СТЕРЕОМЕТРИЯ
что они касаются верхнего основания цилиндра и его боковой поверхности и каждый из шаров касается двух из трех других шаров. Найти площадь боковой поверхности прямого кругового конуса, основание которого совпадает с нижним основанием цилиндра и который касается всех четырех шаров.
Ответ: 15л/4.
26.	Дан куб ABCDA' В' С D', длина ребра которого равна 1. На ребрах АА', ВВ', и DD' взяты соответственно точки К, Р и М так, что АК: А'К= 1:3, BP:B'P=3:l, DM:D’M=3 :1. Найти объем пирамиды, у которой основанием служит сечение куба плоскостью, проходящей через точки К, Р и М, а вершина находится в точке Л'.
Ответ: 7/32.
27.	В основании треугольной пирамиды ABCD лежит правильный треугольник АВС. Грань BCD образует с плоскостью основания угол 60°. На прямой, проходящей через точку D перпендикулярно основанию, лежит центр сферы единичного радиуса, которая касается ребер АВ, АС и грани BCD. Высота пирамиды DO в два раза меньше длины стороны основания. Найти объем пирамиды.
Ответ: 9 7з /8.
28.	На основании правильной треугольной пирамиды, высота которой равна Н, а радиус вписанного в основание круга — г, лежит шар, касающийся основания в его центре. Найти радиус шара, если плоскость, проведенная через вершину пирамиды и середины двух сторон основания, касается этого шара.
Ответ: Hr /{г + Vr2 + 4Я2).
29.	В прямой круговой конус вписан шар, поверхность которого равна площади основания конуса. В каком отношении боковая поверхность конуса делится линией касания шара и конуса?
Ответ: 4:25.
30.	Величина угла в осевом сечении прямого кругового конуса равна а. Через его вершину под углом р к оси конуса (Р < а/2) проведена плоскость. Найти величину угла между двумя образующими конуса, по которым проведенная плоскость пересекает его поверхность.
J 7. Разные задачи
235
Ответ: 2 arctg ^7s>n(a / 2 + 0) sin(a / 2 - 0) I cos a / 2j.
31.	Прямой круговой цилиндр описан около шара радиуса R. Точка С расположена внутри цилиндра на его оси и удалена на 3/4 • R от нижнего основания. Через эту точку проведена плоскость Р, имеющая с окружностью нижнего основания только одну общую точку. В шар вписан прямой круговой конус, основание которого лежит в плоскости Р, а вершина расположена выше этой плоскости. Найти объем этого конуса.
Ответ: 48лЯ 3/125.
32.	В прямом круговом конусе угол при вершине осевого сечения равен 60°. В этом конусе расположены три одинаковых шара радиуса г, касающиеся изнутри боковой поверхности конуса, плоскости основания конуса и попарно друг друга. Найти площадь боковой поверхности другого конуса с той же вершиной, длиной высоты и плоскостью основания, которого данные шары касаются внешним образом.
Ответ: 26л/27 • г2.
33.	Треугольная пирамида ABCD, все ребра которой имеют длину а, вложена в прямой круговой конус так, что вершина А лежит на окружности основания конуса, ребро AD лежит в плоскости основания конуса, ребро ВС параллельно основанию конуса, а вершины В и С лежат на боковой поверхности конуса. Величина угла между высотой конуса и его образующей равна a (a < л/6). Определить высоту конуса.
Ответ: а  a[tg 2a/(l -y]2tga)].
34.	В правильную треугольную пирамиду SABC, все ребра которой имеют д лину а, вписана сфера. Высота SD пирамиды опущена на основание АВС. На ребре Л С взята точка М так, что МС = 2 • AM, а на высоте SD — точка ?7так, что ND= 2 • NS. Прямая MN пересекает сферу в двух точках Р и Q. Найти длину отрезка PQ.
Ответ: 2а/3 V1T.
35.	В правильную четырехугольную пирамиду с вершиной S и основанием ABCD вписана сфера. Длина стороны основания пирамиды равна а, а длина бокового ребра — а 45 /2. На апофеме SE грани DSC взята точка М так, что SM = ME. Найти расстояние
236
ГЛАВА II. СТЕРЕОМЕТРИЯ
между точками, в которых прямая AM пересекает сферу, вписанную в пирамиду.
Ответ: а/2.
36.	Три прямых круговых конуса имеют общую вершину, и каждый из них касается внешним образом двух других. Вычислить величину углов между линиями касания боковых поверхностей этих конусов, если у первого конуса величина угла между осью и образующей равна а, у второго — Р, у третьего — у.
Ответ:
( 2	-2	cosQ, -COSQi cosQ> 'I
arccos cos а + sin а---——-——— ,
sin Q2 sin 03 J
(	2a, -2a cos0г -COS01 cosQ3 "1
arccos cos p + sin p---—------—-----— ,
4	sin 0i sin Оз
( 2	-2 COS Оз-COS 01 COS O2
arccos cos y + sin у---—------=-----— I,
sin 0i sin O2	j
где Oi = P + T> (?2 = а + Г> Сз = а + Р-
37.	В прямом круговом конусе с вершиной S величина угла между образующими SA и SB равна а, а между их проекциями на плоскость основания — р. Вычислить величину угла между биссектрисами углов OSA и OSB, где точка О является центром круга, служащего основанием конуса.
Ответ', arccos [cos2 (р/2) + sin (р/2) /1 / 2(cos а - cos а / 2)].
38.	Шар радиуса г, касается всех ребер треугольной пирамиды. Центр шара лежит внутри пирамиды на ее высоте на расстоянии г-у/З от вершины. Доказать, что пирамида правильная. Найти длину ее бокового ребра.
Ответ: 4г /3.
39.	Шар касается всех боковых граней треугольной пирамиды в центрах описанных около них окружностей. Каждый из трех плоских углов при вершине пирамиды имеет величину а. Сумма длин боковых ребер пирамиды равна ЗЬ. Доказать, что пирамида правильная. Найти радиус шара.
Ответ: b tg (а/2) /sin(a/2) / 2Vsin(3a/2).
J 1. Разные задачи
237
40.	Боковая поверхность треугольной пирамиды равна S, а периметр основания За. Шар касается всех трех сторон основания в их серединах, а середины боковых ребер лежат на поверхности шара. Доказать, что пирамида правильная. Найти радиус шара.
Ответ: 71 б№ + 45а4 / 24а.
41.	Длина ребра куба равна а. Найти объем прямого кругового цилиндра, вписанного в куб так, что осью его является диагональ куба, а окружности оснований касаются тех диагоналей граней куба, которые не имеют общих точек с диагональю куба.
Ответ: л 7з а3/18.
42.	Высота правильной четырехугольной пирамида равна л/2 , а длина стороны основания 1. В каком отношении делится объем пирамиды поверхностью шара, центр которого расположен в вершине пирамиды, а радиус основания равен 1?
Ответ: (8<р - 2л): (72 - 8<р + 2л), <р = arctg (75 /2).
43.	В центре шара помещена вершина правильной треугольной пирамиды, длина стороны основания которой равна радиусу шара, а объем относится к объему шара как 3 :16л. В каком отношении делится объем пирамиды поверхностью шара?
Ответ: (3<р-л): (3/4-3<р + л), <р = 2 arcsin jlO/37.
44.	В треугольной пирамиде SABC середины всех ребер лежат на поверхности шара радиуса 2. Известно, что АВ= 3, АС= 4. Ребро SA перпендикулярно к плоскости основания АВС. Доказать, что отрезки, соединяющие середины противоположных ребер пирамиды, являются диаметрами указанного шара, и найти объем пирамиды.
Ответ: 2 739 .
45.	Шар радиуса R касается всех боковых граней треугольной пирамиды в серединах сторон ее основания. Отрезок, соединяющий вершину пирамиды с центром шара, делится пополам точкой пересечения с основанием пирамиды. Найти объем пирамиды.
Ответ:
46.	В пирамиде SABC произведения длин ребер каждой из четырех граней равны одному и тому же числу. Длина высоты пирами
238
ГЛАВА II. СТЕРЕОМЕТРИЯ
ды, опущенной из точки S на грань АВС, равна 2^/102/55, а величина угла САВ равна arccos (\/34 /12). Найти объем пирамиды SABC, если
5И2 + 5Б2-5-5С2 = 60.
Ответ: 34 >/б /3.
47.	Точка О — общая вершина двух равных конусов, расположенных по одну сторону от плоскости а, так что только одна образующая каждого конуса (ОА для одного конуса и ОБ для другого), принадлежит плоскости а. Известно, что величина угла между высотами конусов равна р, а величина угла между высотой и образующей конуса равна <р, причем 2<р < р. Найти величину угла между образующей ОА и плоскостью основания другого конуса, которой принадлежит точка В.
Ответ: л/2 - arccos [ cos <р - 2sin2(P/2)/cos <р ].
48.	На сфере радиуса 11 расположены точки А,АХ, В, Вх, Cvt Сх. Прямые ААХ, ВВХ и ССХ взаимно перпендикулярны и пересекаются в точке М, отстоящей от центра сферы на расстояние V59 . Найти длину отрезка ААХ если известно, что длина отрезка ВВХ равна 18, а точка Мделит отрезок ССХ в отношении (8 + V2 ): (8 - V2 ).
Ответ: 20.
49.	В правильную шестиугольную пирамиду вписан прямой конус, и около нее описан прямой конус. Дана высота пирамиды Н и радиус основания описанного конуса R. Найти разность объемов описанного и вписанного конусов.
Ответ: tcHR 2/12.
50.	Прямоугольные проекции плоского четырехугольника на две взаимно перпендикулярные плоскости являются квадратами с длиной стороны, равной 1. Найти периметр четырехугольника, зная, что одна из его сторон имеет длину ^3/2 .
Ответ: 4 д/3 / 2 .
СОДЕРЖАНИЕ
Предисловие...........................................................3
Глава I. ПЛАНИМЕТРИЯ
§	1.	Основные теоремы и формулы планиметрии.......................5
О геометрии окружности...........................................15
Разложение вектора на компоненты. Координаты вектора.............21
Задачи...........................................................24
§	2.	Решение треугольников.......................................36
Задачи...........................................................44
§	3.	Расчет элементов треугольника методом составления	уравнений.47
Задачи...........................................................53
§	4.	Пропорциональные отрезки в треугольнике.....................55
Задачи...........................................................67
§	5.	Взаимное расположение окружностей, углов и	треугольников....70
Задачи...........................................................81
§	6.	Трапеции, параллелограммы, произвольные четырехугольники....83
Задачи...........................................................97
§ 7.	Задачи на отыскание геометрических фигур с экстремальными элементами.......................................99
Задачи..........................................................106
§	8.	Геометрические места точек и метод координат...............108
Задачи..........................................................118
§	9.	Прямые на плоскости. Элементы аналитической	геометрии.....120
Задачи..........................................................130
§	10.	Задачи на построение.....................................132
Задачи..........................................................147
§11.	Разные задачи.................................................148
Глава II. СТЕРЕОМЕТРИЯ
§ I.	Основные теоремы и формулы стереометрии........................157
Теоремы о параллельности прямых и плоскостей....................157
Теоремы о перпендикулярности прямых и плоскостей................158
Теоремы о перпендикулярности плоскостей.........................158
Теоремы о скрещивающихся прямых.................................159
Двугранные углы.................................................159
Трехгранныс углы............................................ 160
Основныегеометричсскиеместаточеквпространстве............... 162
Векторы...................................................   162
Площадь ортогональной проекции многоугольника............... 165
Многогранники............................................... 165
Круглые тела................................................ 167
Задачи...................................................... 171
§ 2.	Решение правильных треугольных и четырехугольных пирамид... 175
Задачи...................................................... 185
§ 3.	Расчет элементов пирамид методом составления уравнений..... 187
Задачи...................................................... 191
§ 4.	Сечение пирамиды плоскостью................................ 193
Задачи.......................................................207
§ 5.	Куб и его свойства. Сечение куба плоскостью. Призмы.........210
Задачи.......................................................219
§ 6.	Взаимное расположение шаров, шаров и плоскостей.............221
Задачи.......................................................228
§ 7.	Разные задачи...............................................230
Учебное пособие
Лурье Михаил Владимирович
ГЕОМЕТРИЯ. Техника решения задач
Серия «В помощь абитуриенту»; 4-е изд., стер.
ИД № 00545 от 06.12.1999
Издательство УНЦ ДО
117246, Москва, ул. Обручева, 55А Тел./факс (095) 718-6966, 718-7785 e-mail: izdat@abiturcenter.ru http://www.abiturcenter.ru/izdat
Гигиенический сертификат № 77.99.02.953.Д.001743.03.03 от 11.03.2003 г. Налоговые льготы - Общероссийский классификатор продукции ОК-005-93, том 1 - 953000
Подписано в печать 13.09.2003. Формат 60x90/16.
Бумага газетная. Усл. печ. л. 15.
Тираж 3 000 экз. Заказ Ns 8445.
Отпечатано в полном соответствии с качеством предоставленных диапозитивов в Тульской типографии.
300600, г. Тула, пр. Ленина, 109 .