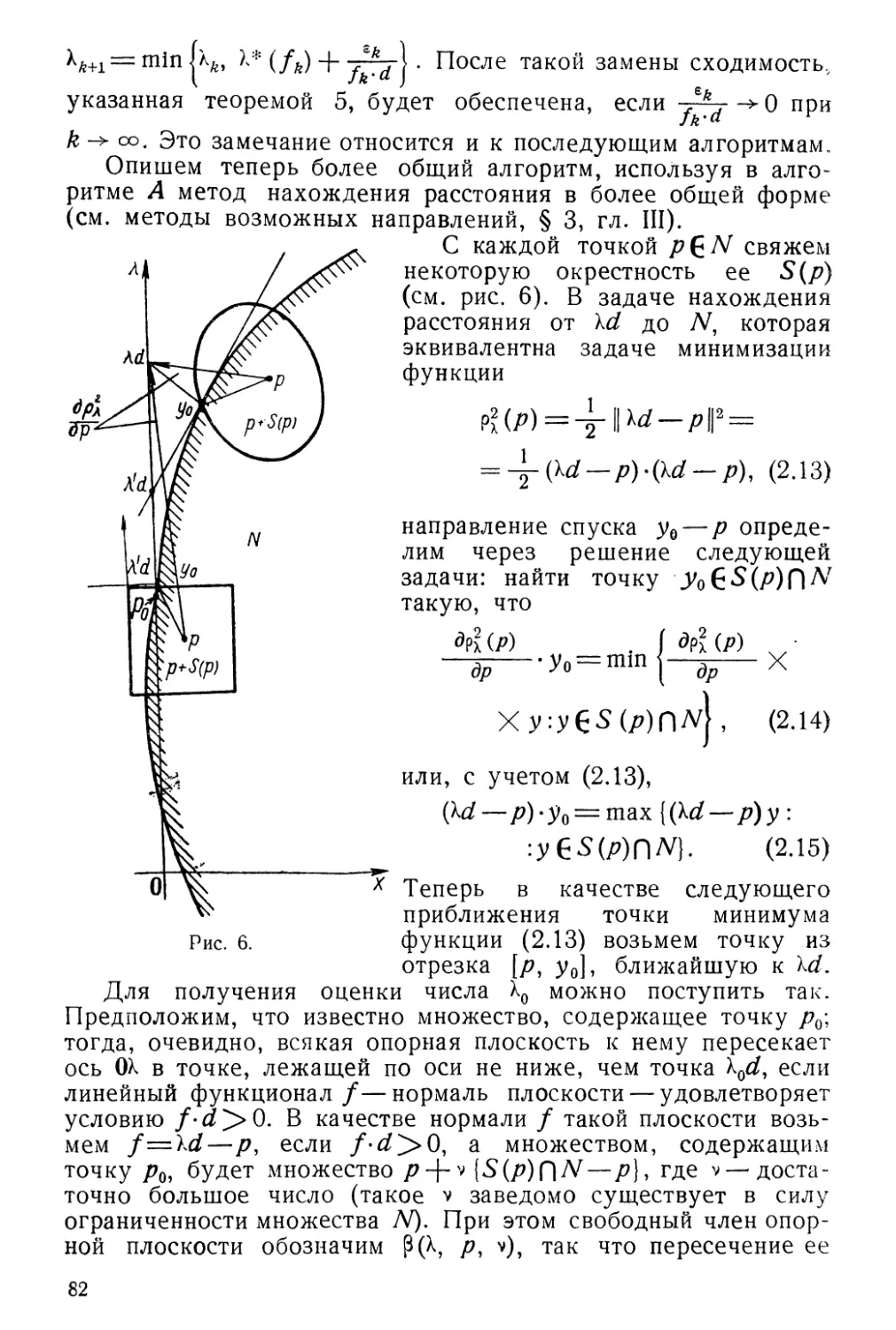
Текст
Н. Е. КИРИН
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
ТЕОРИИ
ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
ЛЕНИНГРАДСКИЙ ОРДЕНА ЛЕНИНА ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ имени А. А. ЖДАНОВА
Н. Е. КИРИН
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
ТЕОРИИ
ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Под редакцией В. В. Хоменюка
ИЗДАТЕЛЬСТВО ЛЕНИНГРАДСКОГО УНИВЕРСИТЕТА
1968
Печатается по постановлению
Редакционно-издательского совета
Ленинградского университета
Работа посвящается теоретическим и численным
аспектам математической теории оптимальных про¬
цессов. Вслед за геометрической интерпретацией
условий оптимальности («принципа максимума»
J1. С. Понтрягина) ставится экстремальная задача
для множителей Лагранжа, входящих в условие
экстремума исходной экстремальной задачи. На ос¬
нове связи этих задач излагаются методы их реше¬
ния. Общие методы демонстрируются на конкретных
классах задач автоматического регулирования и не¬
которых других задач на условный экстремум.
Работа предназначается для широкого круга ин¬
женеров и научных сотрудников, работающих в об¬
ласти применения математических методов исследо¬
вания к анализу и синтезу систем управления.
2—2—4
77—67
ВВЕДЕНИЕ
Настоящая работа содержит описание некоторых численных
методов решения задач на условный экстремум, возникающих в
теории оптимального управления. Эти методы используются в
первую очередь при решении вариационных задач, необходимые
условия экстремальности в которых выражены «принципом мак¬
симума» JI. С. Понтрягина. Отметим сразу же, что речь пойдет
о построении отдельных оптимальных траекторий, точнее, о при¬
ближенном построении соответствующих оптимальных управле¬
ний как функций времени. Методы более полного решения зада¬
чи синтеза оптимального управления (построения его как функ¬
ции информации о текущем состоянии управляемой системы) мы
здесь не рассматриваем (им посвящены, например, работы [2, 3,
19, 29, 32, 35]).
Остановимся кратко на содержании работы.
В известных методах получения признаков экстремальности
в задачах на условный экстремум можно выделить два приема.
Первый прием — вариационный — основывается на сравнении
точки экстремума с «близкими» к ней точками (уравнение Эйле¬
ра). Второй прием заключается в использовании признаков от¬
делимости множеств, представляющих собой образы «допусти¬
мых» и «запретных» изменений искомых параметров задачи
(условия Куна — Таккера). Описанию этих приемов посвящена
глава вторая.
В главе третьей рассматриваются прямые методы построения
последовательных приближений оптимальных элементов, осно¬
ванные на существовании производной оптимизируемого функ¬
ционала. Здесь излагаются модификации метода градиентного
подъема применительно к задачам выпуклого программирования
и оптимального регулирования.
В четвертой главе приводятся методы решения общей задачи
на условный экстремум, основанные на экстремальных свойсг-
з
вах решения исходной задачи и связанных с этим решением мно¬
жителей Лагранжа. Дано описание этих методов применительно
к решению линейных задач управления.
Пятая глава посвящена задаче об оптимальном быстродейст¬
вии. Методы решения этой задачи также состоят в отыскании эк¬
стремальных свойств множителей Лагранжа, определяющих ре¬
шение исходной задачи, и построении последовательных прибли¬
жений этих множителей.
Изложение в основном ведется в терминах теории нормиро¬
ванных пространств. Поэтому в первой главе приводятся опреде¬
ления некоторых понятий и факты этой теории.
Описываемый материал лег в основу курса лекций, прочи¬
танных автором для инженеров, студентов вечернего отделения
математико-механического факультета ЛГУ.
Автор не ставил своей целью дать сколько-нибудь полную
библиографию по затрагиваемым в книге вопросам и цитировал
минимальное количество работ. Поэтому в книге остались неупо¬
мянутыми многие параллельные исследования, перечень кото¬
рых читатель может найти в статье «Теория оптимальных упра¬
вляемых систем» юбилейного сборника «Механика в СССР за
50 лет» (изд. «Наука», Тематический план 1968 г.).
Автор пользуется случаем выразить благодарность своим то¬
варищам В. И. Валяеву, Б. К. Кирпичникову, В. И. Лукиной,
Ю. В. Малееву, оказавшим большую помощь в подготовке ру-'
копией.
ГЛАВА I
НЕКОТОРЫЕ ПОНЯТИЯ ТЕОРИИ НОРМИРОВАННЫХ
ПРОСТРАНСТВ
§ 1 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [22]
1°. Определение нормированного пространства
Пусть имеется некоторое непустое множество X элемен¬
тов х.
Определение 1. Множество X называется линейным (век¬
торным) пространством, если указаны правила сопоставления:
1) каждому* х£Х и любому числу а сопоставляется эле¬
мент из X, который записывается так: ах;
2) каждой паре элементов а:, у из X сопоставляется эле¬
мент из X, который записывается так: х-\-у. Кроме того, пра¬
вила 1, 2, называемые соответственно „умножением элемента
на число* и „сложением элементов*, должны удовлетворять
следующим аксиомам:
а) х-\-у = у -\-х;
б) хуz = х-\-{уz)\
в) существует элемент 0£Х такой, что CU = 0 (0—число);
г) (a-f-Р) х = ах-\-§х (а, р— числа);
д) a (х -f- у) = ах ay;
е) (а^) Х = а (8х);
ж) \х = х.
Элемент 0 в аксиоме в) называется нулевым элементом или
нулем линейного пространства X. Чтобы подчеркнуть принад¬
лежность нулевого элемента пространству X иногда вместо О
пишут Ох.
Говоря о числе, будем иметь в виду вещественное число.
В связи с этим, определенное выше линейное пространство
следует называть вещественным линейным пространством.
Ниже слово „вещественное* в этом названии будем опускать.
* Запись „х^Хи читается так: „х принадлежит Xй или „х, принадлежа¬
щий Xй в зависимости от контекста.
5
Примером (точнее сказать, прообразом) линейного простран¬
ства является множество всех вещественных чисел. Будем
обозначать это пространство буквой R. Другое важное линей¬
ное пространство определяется на множестве всех упорядо¬
ченных наборов чисел по п чисел в каждом (ft натуральное
число). Всякий такой набор (аь а2, ..., ап) (а/ — числа)^назы¬
вается ^-мерным вектором (точкой) и обозначается одной бук¬
вой, скажем, х. Числа аь а2, ... , ал называются компонентами
вектора х. Множество /z-мерных векторов будет линейным
пространством (обозначим его Rn), если для любых векторов
•* = (аь ••• I ал) и У = (Pi, . • • , Рл) операции сложения и умно¬
жения на число определить так:
1) \х = (каи . . . , Хал);
2) A:-}-y = (ai + Pi, ал + Рл).
По примеру пространства Rn элементы любого линейного про¬
странства называют также точками или векторами.
Определение 2. Линейное пространство X называется нор¬
мированным, если в нем определена функция, сопоставляющая
каждому элементу х£Х число, которое называется нормой
элемента х и обозначается \\х\\, причем эта функция такова,
что для любых числа а и элементов х, у из X выполняются
следующие соотношения:
1)
2)
3)
х\\>0; [|аг|| = 0 тогда и только тогда, когда х = 0\
ал;|| = | а и л: | (положительная однородность нормы);
* + >1 <1*11+ 11УII (неравенство треугольника).
Пространство Rn будет нормированным, если норму опре¬
делить, например, одним из следующих способов:
О 1*1= у 2a/ = ljcl;
И) Iл;|| = max {|а, |, ... , |ал| ) = \\х\\
Р гт
in) 1*1 = 1/
р = \\х
V
i= 1
Таким образом, на одном и том же линейном пространстве
норму можно ввести различными способами, получая при этом
различные нормированные пространства. Для того чтобы раз¬
личать их, делают различие в обозначениях нормы, что и сде¬
лано в примерах норм I, II, III. Ниже, говоря о пространстве
Rn, будем иметь в виду, что в нем введена норма I.
Геометрический смысл нормы I — это длина вектора л:.
Длину вектора х —у в Rn называют расстоянием между точ¬
ками л; и у. По аналогии вводится понятие расстояния между
элементами произвольного нормированного пространства. С по¬
нятием расстояния связаны следующие определения.
6
Определение 3. Говорят, что последовательность элемен¬
тов* хг, хъ , хп£Х, /1=1, 2, , сходится в себе, если
по любому е>0 найдется номер п0 такой, что для номеров
/, у, ббльших га0, будет \xt — Xj||<е.
Определение 4. Говорят, что последовательность {хп} схо¬
дится в X, если существует элемент х£Х такой, что после¬
довательность чисел (||~ * II) сходится к нулю. При этом
пишут lim хп = х и элемент х называют пределом последова-
Л-»- оо
тельности {хп}.
Как известно, всякая последовательность чисел, сходящаяся
в себе, сходится, т. е. в R определения 3 и 4 эквивалентны.
В произвольном нормированном пространстве это не всегда так.
Определение 5. Нормированное пространство, в котором
всякая сходящаяся в себе последовательность сходится, назы¬
вается полным или ^-пространством.
Определение 6. Множество V С X называется компактным
в X, если из любой последовательности \хп) его элементов
V) можно выделить сходящуюся в X последовательность.
Определение 7. Шаром радиуса р > 0 с центром в точке
х0£Х называем множество всех элементов х£Х, удовлетво¬
ряющих неравенству || х — х01| < р. Обозначим это множество
через S9 (х0). Множество S9 (х0) называют еще открытой сферой.
Определение 8, Окрестностью точки х0£Х называется вся¬
кое множество V такое, что существует число р>0, при ко¬
тором SP (х0) с V.
Определение 9. Точка х0 множества V называется внутрен¬
ней точкой этого множества, если оно является ее окрест¬
ностью.
Определение 10. Множество, все точки которого внутрен¬
ние, называется открытым.
Определение 11. Точка х0 называется предельной точкой
множества V, если существует последовательность точек хп
из V, сходящаяся к х0, причем хпФ х 0, п= 1, 2, ....
Определение 12. Точки множества V и его предельные
точки составляют замыкание множества V, которое обозна¬
чается V.
Определение 13. Множество V называется замкнутым, если
оно совпадает со своим замыканием V=V.
* Ниже последовательность записывать будем так: {хп}“^ или {хп}.
Укажем еще формы записи множества элементов. Пусть каждому элементу
v множества V можно взаимно однозначно сопоставить элемент а множе¬
ства А. Тогда следующие записи считаются эквивалентными
К= lv\ я = U v= \v-a£А].
1 а е Л 1 * 1
Здесь знак тождества „ = “ читается так: „равно по определению". Если из
контекста ясно, каково множество А, то пишут V = {^а}.
7
2°. Гильбертово пространство
Определение 14. Линейное пространство X называется ли¬
нейным пространством со скалярным произведением, если каж¬
дой паре элементов х, у из X сопоставлено число, обозначае¬
мое х-у и называемое скалярным произведением, причем
правило сопоставления удовлетворяет аксиомам:
1) х-х^О; х-х = 0 тогда и только тогда, когда х = 0;
2) х-у=у-х\
3) (x + y)-z = x-z + y-z;
4) (ах)-у = л (х-у).
Определение 15. Нормированное пространство X называет¬
ся унитарным, если в нем можно ввести скалярное произведе¬
ние, связанное с нормой соотношением
\\х\\ = ]/гх- х.
Определение 16. Полное унитарное пространство называет¬
ся гильбертовым.
Пространство Rn — гильбертово, если для его точек у =
п
= Р„) И х = (аъ ... , ап) положить л; • у = 2 <*$/.
/= 1
(Будем знаком * обозначать транспонирование конечномерных
векторов и матриц. Тогда, считая векторы х и у вектор-столб-
цами и пользуясь правилом умножения матриц [40], их скаляр¬
ное произведение запишем в виде х-у = х*у).
§ 2. ОПЕРАЦИИ В ФУНКЦИОНАЛЬНОМ ПРОСТРАНСТВЕ [22]
1°. Определения операций
Определение 1. Пусть U и X два множества элементов
произвольной природы. Всякое правило Q сопоставления лю¬
бому элементу и из U некоторого элемента x=Q{u) из X
называется операцией, отображающей U в X. При этом опе¬
рацию обозначают либо тем же символом, что и элемент
Q(u)(< X, либо одной буквой Q.
Множество операций, отображающих U в X, обозначают
символом [U^X], Принадлежность операции Q(u) этому
множеству записывают так: Q£{£/->.Y}.
Определение 2. Пусть U и X — линейные пространства.
Операция называется линейной, если для любых
элементов и2 из U и любых чисел а, {3 справедливо равенство
Q (a%~b (te2) = aQ (^i) PQ (^2) •
Линейную операцию Q (и) мы будем чаще записывать в ви¬
де Q-u.
Определение 3. Пусть U и X — нормированные простран¬
ства. Операция называется непрерывной в точке
u0£U, если сходимость в U к точке и0 последовательности {ип}
влечет сходимость в X к точке Q (и0) последовательности
\Q(un)}' Если операция x = Q(u0) непрерывна во всех точках
u£U, то ее называют непрерывной.
В условиях определения 3 справедлива теорема: если
Q{u) — линейная операция, непрерывная хотя бы в одной
точке, то она непрерывна, при этом существует число
С > О такое, что
IIQ (я) II <С• ||и|| при всех u£U.
Ниже под линейной операцией мы будем подразумевать ли¬
нейную непрерывную операцию.
Определение 4. Если в определении 1 X — множество чисел,
то операцию Q называют функционалом (или функцией).
Нетрудно убедиться, что множество всех линейных функ¬
ционалов, определенных в нормированном пространстве U,
является линейным пространством, если для любых линейных
функционалов f\{u), /2(&) и чисел а, р положить: a/i + P/2
есть функционал, значения которого в произвольной точке
и£И таковы: (a/1 + P/2)(^) = a/i(^) + P/2(^)- Это пространство
функционалов будет и нормированным, если принять
Последнее пространство называется сопряженным к простран¬
ству U и обозначается U*. Чтобы подчеркнуть линейность
функционала /, иногда будем записывать его значения в виде
/•и. Здесь /—элемент из U*.
Нам понадобится следующее предложение.
Теорема 1. В гильбертовом пространстве U все линей¬
ные функционалы / исчерпываются функционалами вида
f-u = v-u,
где v — некоторый элемент из U\ v-и—скалярное произведе¬
ние. При этом
ll/ll/. =SU|> -рг,|^=Ф \\и-
Таким образом, отождествляя линейные функционалы /
с соответствующими элементами v гильбертова пространства U,
можно написать (J=U*.
2°. Производная операции
Пусть X и U— полные нормированные пространства,
а Q(#) — операция из U в X. Фиксируем некоторую точку
и0 G U.
Определение 5. Производной операции Q(u) в точке и0
называется такая линейная операция L, отображающая U в X,
для которой при любом q^U справедливо соотношение
9
lim
т-0
I 0 (uo + ZQ) — 0 (wo) iL'q ||^
= 0,
или
lim - [Q (u0 + xq) - Q (m0)] =L-q.
(2.1)
При этом будем обозначать
L =
dQ (up)
du
Определенную таким образом производную называют произ¬
водной Гато, или слабой производной, а элемент L • q € X — диф¬
ференциалом Гато.
Если стремление к нулю переменной величины под знаком
предела в (2.1) равномерно относительно множества единич¬
ных векторов q£U, ||tf||=l, то операцию Q называют диффе¬
ренцируемой в точке и0, а линейную операцию L — производ¬
ной Фреше или сильной производной. Таким образом, для
производной Фреше справедливо соотношение
II dQ (а0)
Q («о + я) - Q («о) — —52—-я
lim J — = 0
II я Ну-о 11 я 1!г/
Соотношения (2.1) и (2.2) можно переписать в виде
Q iuo~\~x4) = Q (ио) •^’ + 0(т, q),
dQ («о)'
(2.2)
Q(uo 4~я) — Q К) ■
да
•^+o(ki
(2.3)
(2.4)
где
0(т, q)£X- 0(М)€*;
11° О. я) \х п п
■ при т -э- 0;
ii 0 (|1? II) Цх
о
0 при I q I -> 0.
Равенство (2.4) назовем разложением (представлением) опера¬
ции Q(«) в точке и0 в ряд Тейлора с точностью до линейных
членов. Заметим, что элемент 0(т, q) (0(||^||)) зависит от вы¬
бора точки и0 и от элемента u^^-xq {u-Q-\-q). В случае надоб¬
ности эти элементы будем включать в аргументы операции
0(S q) (0(|| q I)).
Определение 6. Говорят, что операция Q(u) непрерывно
дифференцируема в U, если производная Фреше суще¬
ствует в каждой точке u£U и
dQ (и + &и)
да
dQ {а)
да
■0
dQ(u)
да
I II dQ
при
I Ди|
0.
10
В частности, если \(и) — непрерывно дифференцируемая
функция, то, согласно (2.4), имеет место представление
Х(и+Д«) = Цй)+-^.Д» + о(|Ди|, и). (2.5)
Здесь функция о(|Д«|, и) непрерывна по и, Ди и при каждом
фиксированном и является величиной более высокого порядка
малости, чем ||Дк||
1°(}дц1|1|’ ~*° ПРИ IIIIО-
§ 3. ВЫПУКЛЫЕ МНОЖЕСТВА [14]
.Будем рассматривать множества полного нормированного
пространства X.
Определение 1. Множество VdX называется выпуклым,
если вместе с любыми его двумя точками х, у ему принадле¬
жит и весь отрезок, соединяющий эти точки, т. е.
х*+(1_х)Уе1л [о,1].
Определение 2. Множество V называется ограниченным,
если существует конечное число р > 0 такое, что
KcSp (0).
Определение 3. Множество V называется линейным мно¬
гообразием, если вместе с любыми двумя точками х, у ему
принадлежит и вся прямая, проходящая через эти точки, т. е.
х —(— X (у/ — -^) G 1^ при Х£ (— оо, —|— оо ).
Определение 4. Множество К С.Х называется конусом
с вершиной в точке х0, если вместе с любой точкой х(<К,
х ф х0 множеству К принадлежит и весь луч, исходящий из
точки х0 и проходящий через точку х, т. е.
•*о “Ь ^ (х ~ хо) 6 К при X > 0.
Определение 5. Пусть f-x— линейный функционал в X
и р — некоторое число. Множество всех точек х £Х, удовлет¬
воряющих уравнению
/•* = Р, (3-1)
называется гиперплоскостью (или плоскостью) в *Y.
Нетрудно проверить, что гиперплоскость является и выпук¬
лым множеством, и линейным многообразием, и конусом с вер¬
шиной в любой точке ее.
Определение 6. Плоскость (3.1) называется опорной к мно¬
жеству V, если число р равно либо sup {f-x: х(« V], либо
inf {f-x :х£ V).
В дальнейшем с каждым линейным функционалом f-x бу¬
дем связывать одну опорную плоскость, в уравнении которой
f-x=Hf,V) (3.2)
и
свободный член р(/, V) = sup {f-x :х£ V}. При этом функцио¬
нал / будем называть внешней нормалью опорной плоскости,
и вместо (3(/, V) писать Р(/), считая, что из контекста ясно
к какому множеству V построена опорная плоскость.
Точка х £ 1/, лежащая на опорной плоскости, то есть удов¬
летворяющая уравнению (3.2), называется точкой опоры.
Говорят, что опорная плоскость отделяет точку опоры от
множества. Вообще, если точка х0 такова, что для функцио¬
нала f-x будет f-x^ k3 ^ р (/), то говорят, что плоскость
f<x = $ разделяет (или отделяет) точку х и множество V.
В дальнейшем большое значение будут играть следующие
предложения [14].
Теорема об опорной плоскости. Пусть V — выпуклое мно¬
жество в нормированном пространстве X, имеющее внут¬
ренние точки и х0 — точка из X, не являющаяся внутрен¬
ней точкой V. Существует ненулевой линейный функционал
f такой, что множество V лежит по одну сторону от
плоскости f-x = f-xQ, проходящей через точку х0, т. е.
p(/) = sup/-x</-A:0. (3.3)
х е V
В условиях теоремы при конечномерном пространстве X тре¬
бование существования внутренних точек множества V можно
опустить.
Нам понадобится также следующая теорема.
Теорема об отделимости. Если V — замкнутое выпуклое
множество в нормированном (вещественном) пространстве
и точка х0 не принадлежит V, то существует такой ли¬
нейный функционал f, что
Hf) = sup f-x<f-x0. (3.4)
лге V
Приведем доказательство последнего предложения для слу¬
чая, когда X—гильбертово пространство, а ^—ограниченное
множество. Схема этого доказательства будет использована
при доказательстве сходимости описываемых в последующих
главах методов последовательных приближений решения задач
на экстремум.
Доказательство. Поскольку точка х0 не принадлежит
замкнутому множеству, то расстояние от до V больше
нуля, т. е.
inf I л:0 — х || = р > 0. (3.5)
jce V
Введем функцию
о (х) — II л0 — л; II2 = (х0 — х) ■ (х0 — х). (3.6)
Возьмем последовательность точек {х^} из V, реализующих
расстояние (3.5), и, обозначив fk = xo~~xki рассмотрим функ¬
ционалы fk-x. Если будет доказано, что
lim sup /*•(■* — хо) < 0, (3.7)
k-yoc хе V 7
12
то этим и будет доказана теорема, так как (3.7) означает су¬
ществование функционалов, для которых sup fk-{x — х0) <0,
хе V
что эквивалентно (3.4).
Предположим, что (3.7) не имеет места. Это означает, что
существует подпоследовательность номеров {/} последователь¬
ности {k} и бесконечная последовательность точек xi£V, для
которых \\mfi\xi — х0)^ 0. Следовательно, для любого s из
i-y оо
промежутка ^0, -yj при достаточно больших i будет
- S < (Л0 — X,) • (+■ — А'0) = (х0 - xj) ■ {Xi — Xj) — II А0 — Xt If2.
Отсюда
(*0 — */) ■ [xi — Xi) > II x0 — Xi f — 8 > P2 — e > . (3.8)
Рассмотрим точки Aj(pO —0 — p)x-t + fix;, где p.£ [0, 1]. Сог¬
ласно определению (3.6), имеем
3 (*/GO) = (*o — */ — t* (*/ - *i))j (*o — xi ~ - xi)) =
= II *o — xi ||2 — 2p (a0 — xi) ■ {х( — xi) -f p.21 xi — Xi f • (3.9)
Поскольку последовательность {л:,-} ограничена, то sup||jc/—а,-||=
г
= г<+оо. Найдем минимум по ^£[0, 1] функции (3.9). Не¬
трудно вычислить с учетом оценки (3.8), что этот минимум не
превосходит величины
к-*,г-4' +--<:4*'> <'
»{= , хЛ
||х0 — Xi|р — -у р2 в противном случае.
Выбирая i столь большим, чтобы было
II *о - xif < р2 + у min |ра, ,
получим при некотором р£[0, 1]
= Ы)<ао<Ра>
но это противоречит определению р как расстояния от х0 до
V, ибо точка в силу выпуклости этого множества
и принадлежности ему точек xit xt. Теорема доказана.
ГЛАВА II
УСЛОВИЯ ОПТИМАЛЬНОСТИ
В известных методах получения признаков экстремальности
в задачах на условный экстремум можно выделить два приема.
Первый прием — вариационный — основывается на сравнении
точки экстремума с «близкими» к ней точками (уравнение
Эйлера). Второй прием опирается на признаки отделимости
множеств, представляющих собой образы „допустимых44 и „за¬
прещенных" изменений искомых параметров задачи (условия
Куна—Таккера).
При изложении этих приемов в настоящей главе, кроме
классических результатов вариационного исчисления [5, 11]
и математического программирования [21, 44], использованы
сравнительно недавние работы академика Л. С. Понтрягина
и его школы [38], А. Я. Дубовицкого и А. А. Милютина [15],
Г. Ш. Рубинштейна [39], L. W. Newstadfa и Н. Halvin’a [49]
и других советских и зарубежных ученых.
§ 1. ПЕРВАЯ ПОСТАНОВКА ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
И УСЛОВИЯ ОПТИМАЛЬНОСТИ В ПРОСТРАНСТВЕ АРГУМЕНТА
(УСЛОВИЯ ОТНОСИТЕЛЬНОГО ЭКСТРЕМУМА)
1°. Постановка задачи
В некотором пространстве U элементов и определена функ¬
ция X {и) и фиксировано множество М*. Обычно ставится сле¬
дующая задача на условный экстремум.
Задача 1. Найти максимум функции Х(и) на множестве Ж*,
т. е. найти элемент и0£М такой, что
Х(гг0)=г max(X(a) : u£M%}. (1.1)
Элемент и0 в задаче 1 будем называть оптимальным элемен¬
том или оптимальным значением аргумента задачи 1, а число
14
X (и0) — оптимальным значением функции Ъ(и) задачи 1 или
значением оптимума. Множество M^dU назовем множеством
допустимых элементов.
Перейдем к выводу условий оптимальности. Перепишем (1.1)
в виде
ПРИ любом и£М*. (1.2)
Если нет никакой информации о свойствах функции 'к(а)
и множестве М*, то естественно, что, кроме (1.2), нельзя
получить никакой информации о признаках элемента и0. Обычно
предполагается, что возможно построение некоторой оценки
функции Х(и), если не на всем множестве М*, то на некотором
его подмножестве. Включая далее эту оценку в (1.2) и поль¬
зуясь ее более простой структурой по сравнению с функ¬
цией Х(и)у получают некоторое необходимое условие на щ,
возможность проверки которого обусловливается конструктив¬
ностью оценки.
В качестве подмножества, на котором строится оценка,
чаще берется некоторая „окрестность44 элемента и0 (или эле¬
мента и, испытываемого на оптимум).
Пусть U — полное нормированное пространство. Будем рас¬
сматривать точки u£U, близкие к щ по норме пространства U.
Вариация по направлению
Очевидно, близкие по норме к и0 точки можно представлять
в виде u = u0-\-\iq, где q£U, a ja — достаточно малое число.
Элемент q£U называется допустимым направлением в точке
и0, если существует последовательность элементов
представимых в виде
= йо + Ра? + О(Р*), £ = 1, 2, ..., (1.3)
где ^>0, ^->0, J.P. 11 —> Q ПрИ k —^ оо, Элемент ^+0([а)
из последовательности (1.3) назовем допустимой вариацией
элемента и0 по направлению q. Понятно, что если q — допу¬
стимое направление, то vq (при v>0) также допустимое на¬
правление. Так что множество допустимых направлений есть
конус с вершиной в нулевом элементе 0*/ £ U. Обозначим этот
конус К(а0). Считая 0и£К {н0), будем иметь конус К(и0) всегда
непустым множеством.
Предположим теперь, что для любой последовательности
вида (1.3) имеет место неравенство
— >Л“о) >*(<!, (?) + <>* («о. uk), (1.4)
где з(<7, |лА) > 0 и -» 0 при к -> оо. В силу (1.2) левая
а \Чу ik)
часть неравенства (1.4) неположительна, так что, поделив (1.4)
на а(<7> l1*) и перейдя к пределу при &со, получим
0 >h{q).
Это неравенство есть необходимое условие оптимальности
точки и0.
Теорема 1. Пусть и0— оптимальный, элемент в задаче 1,
К (и0) —конус допустимых направлений в точке и0 и пусть
имеют место■ неравенства (1.4) для всех последователь¬
ностей допустимых вариаций по направлению. Тогда
0~^t-h(q) для всех q£K(u0). (1.5)
Предположим, что функция Цм0) непрерывно дифферен¬
цируема в точке и0. Тогда в качестве оценки (1.4) можно взять
представление (см. гл. 1, формулу (2.5))
*■(»*) —Ч«о) = нЩйГ’Я + °(ик, Ио).
Поскольку в этом случае функция h(q) = -q линейна по q
и Оц (и0), то соотношение (1.5) можно переписать в виде
max axgoЦ = 0. (1.6)
9бЛ'(и0) °а
Следствие А. Если и0 — внутренняя точка множества М#,
то допустимыми направлениями являются все векторы q£U.
Тогда при любом q должно быть • q = 0- Это означает,
что линейная функция ^ “0^ • q тождественно равна нулю
д\(и0) —Л
= (1.7)
Следствие Б. Если множество М.А: выпуклое, то в каче¬
стве допустимого направления можно взять любой вектор q
вида q — u — UQ, где ибо при любом ц£[0, 1] точки
+ Для множества таких векторов q также спра¬
ведливо соотношение типа (1.6), которое можно записать
так [12, 42]:
д\ (и0) , ч ~
max \„ '{и — и0) = 0
иеМ* оа
ИЛИ
^.Ио = тах^).и. (1.8)
^ 0 ивм. ди V '
Геометрически необходимое условие (1.6) означает, что пло¬
скость • q = 0 является опорной к конусу К(и0) в точке О,
„ дХСио)
а в следствии Б плоскость ■ ^ = -ii0 опорная к мно¬
жеству 714* в точке и0 (см. рис. 1, где элементы и0, q,
; (Ur))
/0 = ^ — двумерные векторы
16
Следствие В. Пусть й0 — внутренняя точка М:{; и функция
Х(й) имеет оценку
X (ц) > X(ц0) -f [Q-(и - и0)] • (й — й0) + о(||и — й0[|2)
где Q — билинейная операция. В этом случае имеем при
любом q£U
°(<I, V)h{q) = ]?(Q-q)-q,
и неравенство (1.5) означает неположительность операции Q
[Q-q]-q< о.
Дальнейшее изучение условий оптимальности может основы¬
ваться на изучении конуса допустимых направлений К (я0)>
который в свою очередь зависит от определения множества М%.
Другие классы вариаций
Можно рассматривать отличные от приведенного выше
способы выбора последовательностей элементов {uk) и соот¬
ветственно оценки функций \(и) на этих последовательностях.
В общем случае будем считать, что имеется некоторый класс
D(u0) вариаций в точке и0, если: а) существуют некоторое
множество 3 элементов g и отображения и = и(Ь, (< £/,
^->0 при k-+co; б) имеется оценка
Х(й)>Х(й0) + а(?, + Е), (1.9)
где а (I, > 0; ■ °0; и==и^’ В этом СЛУ‘
чае можно точно так же получить соотношение типа (1.5)
sup/z(€)<0. (1.10)
£es
Необходимые условия оптимальности, полученные в этом
параграфе, основаны на сравнении точки оптимума и0 с близ¬
кими к ней по норме точками пространства U. Поэтому
2 Н. Е. Кирин 17
понятно, что этим условиям удовлетворяют также точки и0,
являющиеся при некотором е > 0 решением следующей задачи:
найти точку и0 такую, что
х(и0) = тах {Х(и) :||й —и0||<е; и, «„СМ*). (1.11)
Такие точки и0 называются точками относительного (локаль¬
ного) максимума функции 'к (и) на множестве Ж*.
§ 2. ВТОРАЯ ПОСТАНОВКА ЗАДАЧИ НА УСЛОВНЫЙ ЭКСТРЕМУМ
И УСЛОВИЯ ОПТИМАЛЬНОСТИ В ПРОСТРАНСТВЕ УСЛОВИЙ
(УСЛОВИЯ АБСОЛЮТНОГО ЭКСТРЕМУМА)
В задаче 1 предыдущего параграфа условность экстремума
определялась только множеством Ж*. В каждой конкретной
задаче это множество может определяться большим количе¬
ством соотношений. Среди этих соотношений могут быть такие,
удовлетворить которым сравнительно легко, и такие, разре-"
шение которых может составить самостоятельную задачу.
Поэтому представляется целесообразным уже при постановке
задачи сделать различие „простых“ и „сложных14 условий.
1°. Постановка задач
В некотором пространстве U фиксировано множество Ж
элементов и, на котором определены функция 1(и) и операция
х(и) в пространство X. В X фиксировано множество Х0.
Обычно ставится следующая задача на условный экстремум.
Задача 2. Найти максимум функции к(и) при условиях:
ц£Ж, х(и)£Х0.
Пример 1. Для переформулировки в термины задачи 2
задачи линейного программирования: найти
тах{с*_у: Ау
где А матрица т X и, у, с — п-мерные, а Ь — т-мерный век¬
торы, можно положить
U=Rn, и = у, M=U, \(и) = с*у,
x(u) = Ay-b, .Y0 ={* = ($,,
Пример 2. Рассмотрим задачу вариационного исчисления:
найти максимум интеграла
0
при условиях: у = /г(у, и), у(0)=у0, у(Т)=уи где u(t) —
кусочно-непрерывная функция, \ и\ 1. Для переформулировки
этой задачи в термины задачи 2 можно положить: U— про¬
18
странство кусочно-непрерывных ограниченных функций и (t),
определенных на промежутке [О, Г]; М - множество функ¬
ций u(t)£U, по модулю не превосходящих единицы;
т
X (гг) = J ср (t, у (t; и)) dt
о
(здесь у (t; и) — решение дифференциального уравнения
у = /г (у; &) с начальным условием 3/(0; гг) = у0);
х(и) = у(Т- и)-ух;
Л" — пространство векторов _у, содержащее векторы у1} у(£; ^);
Х0 = [х:х = 0}.
Замечание. Представление задачи на условный экстремум
в форме задачи 2 не однозначно.
Пусть и0 — решение задачи 2. В практических задачах
почти всегда невозможно, да и нет необходимости точно
решать задачу 2. Достаточно уметь решать ее с наперед
заданной точностью, например, по любому е>0 уметь нахо¬
дить такой элемент ие£М, что х(иг)^Х0 и X(uQ) — X (иг) < г.
Кроме того, не всегда обязательно требовать, чтобы точки х(иг)
принадлежали множеству Х09 а достаточно получить точку х(ие\
„близкую" к Х0, т. е. если АГ — нормированное пространство
с нормой ||.*||^, то достаточно потребовать, чтобы
inf {II х (и6) — х \\х: х£Х0}< е.
При этом норма ||л;||х выбирается соответственно тому, как
понимается близость элементов л; из природы задачи. В связи
со сказанным, наряду с задачей 2 будем рассматривать следую¬
щую задачу.
Пусть А"—полное нормированное пространство и Ж* — мно¬
жество последовательностей \uk), uk£M, таких, что последо¬
вательность расстояний
г (X (ик), Х0) = ini {|| х (ик) -х\\:х£Х0\ — -* 0. (2.1)
Последовательность {и*} («Ж* называется допустимой.
Задача И. Найти допустимую последовательность
такую, что
НтХ(и®)=Х0> (2.2 >
Л-> ОО
где
Х0= sup_limX(afe). (2.3)
{uk}eM* h~y00
Будем считать, что^ решение задачи II существует, если \
существует (то есть Ж* — не пусто) и конечно. Задача II,
вообще говоря, не эквивалентна задаче 2 в том смысле, что
2* 19i
из существования решения задачи 2 может не следовать суще¬
ствование решения задачи II и наоборот (см. пункт 3°). Если
решения обеих задач существуют, то очевидно Х0>Х(и0).
В тех случаях, когда Х0 = Х(и0), задачу II можно рассматривать
как задачу приближенного решения задачи 2. Независимо от
существования решения задачи 2 задача II может представлять
и самостоятельный интерес.
2°. Каноническая форма задач
Прежде чем формулировать условия оптимальности, приведем
задачу 2 к специальному виду. Рассмотрим множество {— Х0}
в 26. Понятно, что если при некотором z£{— Х0] будет
х (и) 4- г = 0, то это означает, что х(и)£Х0. И наоборот, если
х(и)£Х0, то существует z — х(и)^\— Х0], при котором
x(u)-\-z — 0. Таким образом, условие х{и)£Х0 эквивалентно
условиям
jc(»)+z = 0,
Основываясь на этом, можно построить такую задачу, экви¬
валентную задаче 2. ..... „ , .
Задача 2'. Найти пару элементов и'=(и, z)GM'=Mx[-X0}
такую, чтобы функционал
к' (и') = Х(«)
принимал наибольшее возможное значение при условии, что
л;' (и') х (u)-\-z — Ох = Х'0.
Формально задача 2' отличается от задачи 2 тем, что все ее
компоненты „штрихованные", а множество Х0 состоит из един¬
ственного элемента 0^. Задачу 2 назовем канонической.
В дальнейшем будем считать, что задача 2 уже имеет канони¬
ческую форму, т. е. множество А0 в ней состоит из единствен¬
ного элемента 0. Соответственно каноническая форма задачи II
будет такой. ,
Задача II. Среди последовательностей {«*} множества
Af„ = {{»*i :||-*(«*)1 -*-° ПРИ (2.4)
найти ту последовательность для которой
lim X (и°) =Х0,
k 00
где
Х0= sup_ lim X (И*).
Замечание. Описанный выше способ приведения задачи
к каноническому виду не единственный.
3°. Геометрическая интерпретация условий оптимальности
Пусть решение задачи 2 существует. Рассмотрим прямое
произведение пространств R X Х = Р, т. е. множество векторов
вида (X, х), где X —число, a xQX. Пространство Р будем счи¬
тать полным нормированным, положив, например, для /7=(Х, х)
\\Р\ Р = 1Ч2 + № (2-5)
Пусть 0Р = (0, 0Х) — нулевой элемент пространства Р, a d=.
— (1> 0Х) — единичный орт — направление вещественной оси
(будем ее обозначать ОХ), точки которой можно записать в виде
Ы, Х£( — со, -L- со). (2.6)
Введем обозначение р(и) — (К(и), х(и)) и рассмотрим в Р
множество
N= \р{и) :и£М\. (2.7)
Элемент р (и) есть образ элемента и в пространстве Р, и соот¬
ветственно TV —образ множества М (см. рис. 2,а). Возьмем
допустимый элемент и^М*, т. е. такой, что х(и) = Ох. Тогда
его образ р(и) = {Х(и), 0Х) принадлежит оси ОХ. Теперь ясно,
что пересечение оси ОХ и множества N есть образ множества
допустимых элементов М*, а образ оптимального элемента к0 —
точка р(и,0) гн (Х(м0), л:(«0)) —есть „верхняя" точка, этого пере¬
сечения, т. е. точка, из TVflOX с наибольшим значением веще¬
ственной компоненты. Понятно, что точка р (м0) не может быть
внутренней точкой множества N, ибо в противном случае
нашлась бы точка из N, лежащая на ОХ выше точки р(и0),
что противоречит оптимальности элемента и0. Точка р{и0) —
граничная точка множества N. Опираясь на это обстоятельство,
с точкой р(и0) можно связать некоторые экстремальные задачи,
отличные от задачи 2, что может оказаться полезным для
отыскания ее и ее прообраза и0.
21
Для задачи II геометрическая интерпретация будет отли¬
чаться только тем, что вместо множества N надо рассматривать
множество N, являющееся замыканием множества N в метрике
пространства Р. При этом образ оптимальной последователь¬
ности — последовательность {р (#£)} — будет сходиться
к граничной точке /?0 множества N, являющейся верхней точ¬
кой пересечения N с осью ОХ (см. рис. 2,6). Рис. 2,6 иллюст¬
рирует связь задач 2 и II, отмеченную в пункте 1°. На этом
рисунке граница множества N не принадлежит ему, за исклю¬
чением точки р{ио).
4°. Двойственная задача. Условия оптимальности
Случай выпуклого множества N
Будем здесь считать, что множество N— замкнутое и
выпуклое. Ниже будем также считать выполненным следующее
условие.
Условие А. Пусть линейный функционал / такой, что
sup {/ (р): Р 6 N] = Р (/) < + оо. Тогда, если последователь¬
ность {pL} точек из N реализует верхнюю грань Р(/), т. е.
Иmf{pi) = $(/), то последовательность [Pi) сходится в себе.
/ ' =с
Предположим, что множество N удовлетворяет условиям,
которые налагаются на множества V в теореме об опорной
плоскости (глава 1, § 3). Пусть решение задачи 2 существует.
Как отмечалось в конце пункта 3°, образ оптимального эле¬
мента—точка р(и0) не является внутренней точкой множества N.
Тогда, согласно теореме об опорной плоскости, необходимо
существует опорная плоскость к множеству N, проходящая
через точку р(и0), т. е. существует ненулевой линейный функ¬
ционал /0 такой, что
l0p(uQ) = max {l0p :p£N} =Hl), (2.8)
причем в силу условия А для рфр{и0), p£N будет l0-Po>K'Р-
Таким образом, если функционал /0 известен, то задача отыска¬
ния р(и0) сводится к отысканию максимума (2.8), а построение
и0 — к отысканию максимума
V Р (Щ) = тах [10-р(и):и£М\. (2.9)
Итак, соотношения (2.8) и (2.9) являются необходимым усло¬
вием оптимальности. Теперь возникает вопрос: как найти
функционал /0, какими отличительными признаками он обла¬
дает? Такие признаки есть.
Обозначим через F множество тех линейных функциона¬
лов, для которых:
22
а) существует конечная верхняя граница
?(/) = sup {/•/?:/?6ЛМ; (2.10)
б) 0. (2.11)
Покажем, что F— непусто. Действительно, поскольку число
к(и0) существует и конечно, то для любого Х>Х(&0) точка Ы
оси ОХ не принадлежит замкнутому множеству N, и по теореме
об отделимости существует линейный функционал /х такой,
что /х*(Xd) > 1\'р для любой точки p£N. Это дает: /x(X-d)^
>т > hp{uQ), т. е. р (к) — конечное число. В то же время
^ = и 4u0)-d£N,
так что
/x-d = rrx^[/x(X.rf)-/x-(XK)-rf)]>0.
Можно показать, что функционал /0, о котором идет речь
в (2.8), может быть выбран из множества F. Для этого рас¬
смотрим множество
S={s=p — p(u0) — ld:p£N, Х>0).
Точка 0р не принадлежит 5, ибо при любом Xj>0 точки
(p(uo)~\~'M)£N. В силу выпуклости множества S' по теореме
об опорной плоскости существует функционал /0 такой, что
/0-0р = 0> l0-s при любом s£S, что дает:
1) 0 >10 •(р — р (и0) — Ы) при любом p£N, следовательно,
0 > Иш 10 -(р--р (и0) — Щ = 1Лр—р («о)).
х-о
т. е. Цр(ий)^ 10р, а значит, р (/0) — конечное число и /0 удо¬
влетворяет соотношениям (2.8), (2.9);
2) 0 ^ l0(p (и0) — р (uQ) — ~kd) = — Х/0 - of, что в силу положи¬
тельности означает l0-d>0. Итак, /06^ и удовлетворяет
соотношениям (2.8), (2.9).
Возьмем некоторый функционал l£F и будем считать, что
l-d> 0. Найдем точку пересечения опорной плоскости
i-p=m (2-12)
с осью Ох (см. рис. 2, в). Если эту точку обозначить У*{1) d,
то нетрудно получить, подставляя \*(l)d в уравнение (2.12),
что
<2лз)
Условимся считать в случае l-d = 0, что Х:-: (/) = X (г/0), если
ось ОХ лежит в плоскости (2.12), и что Х*(/) = +оо в про¬
тивном случае. Когда решение задачи 2 не существует, при
l*d = 0 положим Х*(/) = —оо.
23
Таким образом, на множестве F мы определили функцио¬
нал Х*(/), причем при любом l£F, если и0 существует, то
Х*(/)>Х(и0), (2Л4>
так как в случае l-d = 0 либо X* (1) = \(и0), либо Х*(/) = -[-со,
а в случае l-d> 0 по (2.13)
Х*(1)=Ш>Ь1М± = -к{и())_
Геометрически это означает, что точка р(и0) пересечения
плоскости 10-р = $(1о) с осью ОХ самая «низкая» по сравнению
с точками пересечения оси ОХ другими опорными плоскостями
(2.12) при /(*/\ Этот отличительный признак функционала /0
и можно положить в основу его построения. Для этого введем
следующую задачу, называемую двойственной к задаче 2.
Задача 2*. Найти
X*(/0)=min{x* (/):/£?} • (2.15)
Функционал I называется двойственной переменной, а функ¬
ционал X* (/) —двойственным функционалом.
В соответствие задаче II сопоставим такую двойственную
задачу.
Задача II*. Найти последовательность функционалов .{/&}
из множества
F={l:l£F, l-d> 0) (2.16)
такую, что
ИшХ*(/л)=Х*, (2-17)
k -*■ ОО
где
X* = inf{X*(/) :l£F\.
В силу полноты пространства Р и замкнутости множества
N будет N — N и, следовательно, Х(м0)=Х0. Тогда поскольку
FczF, то из неравенства (2.14) следует, что X* > Х0. Нетрудно
убедиться, что "Х* = Х0. Для этого достаточно рассмотреть
последовательность функционалов /х, которые строились выше
при доказательстве непустоты множества F, когда X -> Х0 + 0.
Таким образом, мы убеждаемся в необходимости условий сле¬
дующих предложений.
Теорема 2. Пусть N —замкнутое выпуклое множество
полного нормированного пространства Р. Пусть также
множество N удовлетворяет условиям, которые налагают¬
ся на множества V в теореме об опорной плоскости
(глава /, § 3). Тогда: I. для того, чтобы, существовало ре¬
шение задачи 2 (II), необходимо и достаточно, чтобы су¬
ществовало решение задачи 2* (II*);
24
2. если решение хотя бы одной из задач 2, 2* (II, II*)
существует, то элементы и0, /0({#£}, (М) — решения этих
задач — связаны соотношением
Ч«о) = **(*<>), (2.18)
(lim'k^u0^ = ^о = = ИшХ* (/#) = lim l^'P (^)j- (2.19)
Равенство (2.18) можно рассматривать как необходимое и до¬
статочное условие оптимальности элементов
/0ел ((4! ем*, (4),
соответственно в каждой из задач 2,2* (II, II*).
Доказательство достаточности условий теоремы 2 будет
являться следствием более общей теоремы 3 следующего раз¬
дела. Отметим, что для пары задач II, И* теорема 2 справед¬
лива без предположений о замкнутости множества iVn о вы¬
полнении условий теоремы об опорной плоскости относительно
этого множества, сделанных в начале этого пункта.
Общий случай
Уже в случае не строго выпуклого множества построение
функционала /0, входящего в (2.8), может оказаться практи¬
чески недостаточно эффективным. Дело в том, что уравнению
(2.8) может удовлетворять не только точка р(и0), но целое
и довольно обширное множество точек из N. Так что даже
если функционал /0 известен, то нужно еще находить способ
выделения из решений уравнения (2.8) точки р (и0), что часто
не просто. Вопрос тем более осложняется, когда /0 не изве¬
стен. В этом и более общем случае можно рассмотреть вместо
линейных функционалов I нелинейные. Ограничимся ниже
рассмотрением задачи II.
Опишем один из возможных способов распространения
подхода раздела I на вывод условий оптимальности. Пусть
решение задачи II существует, т. е. число Х0 существует и ко¬
нечно. Как отмечалось выше, предел образа искомой после¬
довательности {Uu} — точкар0 = (Х0> 0*) — не является внутрен¬
ней точкой замыкания множества N. И если, проводя анало¬
гию с разделом I, попытаться найти функцию, которая дости¬
гала бы максимума на N в точке р0 и только в ней, то
в качестве такой функции можно взять /0 (р) = — \р — /?0||*
Ограничиться рассмотрением только этой функции вряд ли
эффективно с конструктивной точки зрения (р0 — не известно
заранее), поэтому рассмотрим однопараметрическое множество
функций
fJp) = -\\P-^dI, +«)■ (2-20)
25
В силу оптимальности точки p0 — \d при |а > Х0 будет pd£N,
так что
р (/J = sup {/„(/>):/>е ЛГ}<0. (2,21)
Множество функций у* (р) при р. > Х0 обозначим через F.
Через функции этого множества, как и через линейные функ¬
ции l-p £F в предыдущем разделе, можно получить оценки
сверху оптимума V Геометрически такая оценка дается ко¬
ординатой «нижней» точки пересечения сферы Д(р) = —
— \\р — pd\ = + р (/р.) с осью ОХ (см. рис. 3, а). Пусть это
точка X* (у^) d, где, как нетрудно вычислить,
^*(Л) = 1* + РСЛ). (2.22)
В силу неположительности Р(Д) (см. (2.21)) при р > Х0 будет
*>* (Л) <С Н-- С другой стороны, — (3 (/ц) есть расстояние от pd
26
до N, так что на интервале (X* (fv.) d, pd) нет точек множест¬
ва N и, следовательно, X* (/,,.) > Х0. Поскольку ia может быть
взято сколь угодно близким к х0, ясно, что
X* = infX*(A) = X0. (2.23)
/ eF
(J-
Последнее соотношение завершает аналогию с предыдущим
разделом, если функцию /р. назвать двойственной переменной,
функционал Х*(/Д определенный в (2.22), — двойственным
функционалом, а задачу нахождения нижней границы его зна¬
чений — двойственной задачей к задаче II.
Приведенные построения являются основанием для следую¬
щей схемы вывода условий оптимальности. Пусть N не пусто.
Если множество Ж* допустимых последовательностей не
пусто, то положим
Х= sup_ \im^(uk)' (2.24)
{ик}вм* k-*~
В противном случае положим \= — со. Очевидно, в случае
существования решения задачи II Х = Х0 (см. (2.3)). Пусть
имеется некоторое множество Ф непрерывных функций (функ¬
ционалов) /(/?), определенных в Р. Обозначим через F мно¬
жество тех из них, каждая из которых удовлетворяет сле¬
дующим двум условиям:.
а) существует конечная верхняя граница
Р (/) = sup {/(/>) :p£N)- (2.25)
б) существует пересечение поверхности уровня
f(P) = Hf) (2.26)
с осью ОХ не «ниже» точки Ы.
Поясним условие б. Пусть F не пусто и /£/\ Тогда су¬
ществует конечное число Х*(/) такое, что точка /? = Х* (f)d
удовлетворяет уравнению (2J26) и Х*(/)^Х. Таким образом,
непустота F означает, что Х< + °°. Итак, закрепив за каж¬
дой функцией f£F одно из чисел Х*(/), тем самым опреде¬
лим на F функционал Х*(/). Ясно, что если решение задачи II
существует и F не пусто, то при любом f£F будет
Х*(/)>Х=Х0, (2.27)
т. е.
= (2.28)
Может оказаться, что Х* = Х0. В этом случае задачу нахож¬
дения точки p0=(XQd, Ох), т. е. фактически числа Х0> можно
заменить нахождением числа 7*, т. е. решением следующей
задачи.
27
Задача И*. Найти последовательность [fk\, такую,
что
lim X* (Л) = Х* = inf {X* (/) :/€Л. (2.29)
к-*- оо
Эта задача называется двойственной задачей для задачи II.
Под существованием решения задачи II* будем понимать
непустоту множества F и конечность числа X*. Укажем условие,
при котором будет Х* = Х0.
Условие В. Будем говорить, что выполнено условие Б,
если для любого числа Х>Х найдется функция /£Б такая,
что № (/) < X.
Очевидно, в случае существования решения задачи II вы¬
полнения условия В достаточно для равенства Х* = Х0, ибо
если взять последовательность чисел {Х^}, сходящуюся к Х0
справа, и по каждому числу Х^ найти функцию /&£/% су¬
ществующую по условию В[\ь > Х0 = Х) и такую, что Х*(/^)<
< ХЛ, то получим
Х0 = ИтХ*(/Л)>Х*,
k-+ оо
что вместе с (2.28) дает Х* = Х0. Этим завершено доказатель¬
ство необходимости условия теоремы, аналогичной теореме 2.
Теорема 3. Пусть выполнено условие В. Для того чтобы
существовало решение задачи II (II*), необходимо и доста¬
точно, чтобы существовало решение задачи II* (II). При
этом
Х0 = X*. (2.30)
Доказательство достаточности теоремы 3.
Пусть существует решение задачи II*, т. е. число X* в (2.29)
существует и конечно. В силу условия В будет Х*=Х. Но,
согласно определению числа X, оно конечно тогда, когда за¬
мыкание N имеет непустое пересечение с осью ОХ, т. е. су¬
ществует хотя бы одна точка 1'd = \imp{uk), и^^М, причем
&-VOO
X есть верхняя граница таких чисел X'. Следовательно, Х = Х0,
т. е. существует решение задачи II. На этом доказательство
можно считать законченным, ибо соотношение (2.30) вытекает
из существования решения задачи II, т. е. из условия, при
котором справедливость этого равенства показана выше.
Доказательство достаточности условий тео¬
ремы 2. Заметим, что множество F линейных функций /,
•введенное в разделе I, удовлетворяет условию В при выпук¬
лом множестве N (достаточно вспомнить линейные функции
/х-/?, для которых выше показано, что фактически X* (k) < X
и X может быть взято сколь угодно близким к X). Поэтому
факт существования решения задачи II из существования ре¬
шения задачи IP раздела I является частным случаем доста-
28
точности условий теоремы 3. Существование решения задачи
2* в силу определения функционала Х*(/) в разделе I также
означает существование конечной точки р0, т. е. точки пере¬
сечения множества N и оси ОХ с наибольшей координатой X.
В силу замкнутости N эта точка принадлежит N и, следова¬
тельно, существует ее прообраз который и является
решением задачи 2.
Равенство (2.30) выражает собой необходимое условие
оптимальности в каждой из задач II, II*, т. е. если последо¬
вательности и |/fe), lk£F есть соответственно ре¬
шения задач II, II*, то
\ — lim X (и°л = lim X* (fk) = X*. (2.31)
оо k^oo
Это равенство является и достаточным признаком оптималь¬
ности в том смысле, что если последовательности и {/ft},
таковы, что
||х(^)||->0 и limX (#£) = lim X* (/fe), (2.32)
то эти последовательности являются решениями задач II, II*.
Для определения оптимальности последовательностей {й°}, \lk)
вместо проверки соотношений (2.32), можно проверять со¬
отношение
И<)-х*(ЛН1г-лго. (2.33)
В заключение этого параграфа укажем примеры множеств
Фи F, для которых будет выполнено условие В.
Основным условием справедливости приведенного в теоре¬
ме 3 необходимого и достаточного критерия существования
решения задачи II и оптимальности допустимой последователь¬
ности является наличие определенного условиями а) и б)
(стр. 27) множества F и выполнение для него условия В.
Что касается существования такого множества, то в этом нас
убеждает построенное выше F из функций f^{p) (см. (2.20)).
Это универсальное множество можно назвать тривиальным.
Другим универсальным множеством является множество F,
состоящее из единственной функции /0(я)> одна из поверхно¬
стей уровня которой совпадает с границей множества N (при
этом предполагается, что внутри N значения /0(я) строго
меньше, чем на границе). Такое множество следует называть
идеальным. Преимущество его состоит в том, что оно инва¬
риантно относительно некоторых изменений параметров задачи
II, геометрически выражающихся в переносе начала координат
пространства Я, что типично, например, для задач синтеза
оптимального регулятора по начальным данным. «Промежу¬
точные» между названными множества двойственных функций
могут строиться также на основе оценки (приближений) гра¬
29
ницы множества N. Такими «оценками» границы являются,
например, опорные плоскости выпуклого множества.
Приведем еще один пример достаточно универсального
множества двойственных функций, известных под названием
„функций штрафа" или „функций нагружения44. Для
/? = (Х, х)£Р положим
/’(/0 = b-v||*r. (2-34)
Здесь v — вещественное число; т — натуральное число. За
множество Ф можно принять
ф= i/v (Р): VG (~ 00, + °°)}.
Если при некотором v() окажется, что
sup {f° •(/?): р £ N) = Э < + со, (2.35)
то в качестве F можно принять
/7={/v(^):v>v0}. (2.36)
В частности, если функция X (и) ограничена на М сверху, то
можно взять v0 = 0.
Убедимся, что множество (2.36) удовлетворяет условиям
а), б) (стр. 27) и условию В. Действительно, если v^>v0, то
/■' (р) = 1 — v II * Тт = /• — v0 IIX \fm + (v0 — v) I! X If2'" < /'»(/?),
что в силу (2.35) и означает конечность числа £ (/•’ (р)). Далее.
Пересечением поверхности уровня f ‘(p) = ${f ‘(P)) с осью ОХ
является единственная точка X* (/') d, где
Ь*(Л = Р(/’) (2.37)
(см. рис. 3, б, где поверхности уровня функций /' (р) есть
параболы, а поверхности уровня_/v (P) = P(/V (Р)) есть пара¬
бола, „касающаяся" множества N).
Если Х = —оо, то очевидно, что условие б) выполнено.
Если же Х = Х0, то условие б) также удовлетворено
у (Л = Р (Я >Р (Ро) = К - v II0Х IP-=V
Равенство Х= + оо невозможно, так как это противоречит
конечности числа P(/V°) = P в (2.35).
Проверим, выполнено ли условие В. Требуется показать,
что при любом Xf>X найдется число v v0 такое, что
Р(Л < X. Очевидно, если X>(3(/vо), То в качестве такого v
можно взять v0. Пусть X<p(/vo). Поскольку Х>Х, то най¬
дется е > 0 такое, что точки рd при р-^Х — е не принадле¬
жат N, так что расстояние от множества таких точек до N
больше нуля
Г2 = inf (II \xd —pf:p£N, i^>X-s) >0.
30
Определим координату X точек р—(\ х) пересечения цилинд¬
ра ||-*|1 = г с „параболой" /v° (р) = р (/*). Нетрудно вычислить,
что Х==р (/v») + v0r2m. Выберем числа v и с так, чтобы „пара¬
бола" /v (р) = с имела вершиной точку (X — г) и пересекала
цилиндр ||х|| = г на уровне Х = Х (см. рис. 3, б). Для этого
достаточно положить с = X — е и v = к ^ - . Возьмем число
v = шах {v0, v) Н- 1 и убедимся, что это число требуемое. Дей¬
ствительно, „парабола" f‘(p) = X лежит „строго выше" 7V,
т. е. X > р (/v (/?)) = Х* (/'), ибо для любой точки р' = (У, х') £ N
будет
У < X — s, если У < X — s,
/v (/) = X'-v||x,|rz<
< X' - v01! x' f» - p (/«.) 4- x - e < X - s,
если У — s.
Выполнение условия В доказано.
Если условия оптимальности, выраженные теоремой 3, не
являются достаточно эффективными, то расшифровку призна¬
ков оптимальности можно продолжить. Для этого можно
вместо множества N рассмотреть некоторое его подмножество
(например, пересечение N с некоторой окрестностью точки
р0 — образа оптимального элемента и0). Очевидно, такое под¬
множество также должно отделяться от точек луча Д>
>м. Условия отделимости этого подмножества и луча L
могут дать дополнительную информацию о точке р0 (элемен¬
те и0). Часто подмножество заменяют некоторым его прибли¬
жением. Например, если MdU, а £/, Р— полные нормиро¬
ванные пространства и операция р (и) дифференцируема
в точке и0, то вместо точек р{и0-{- Д#) при малых прираще¬
ниях Ди рассматривают р(и0)-\-ор, где Ьр — линейная по Ди
часть приращения р{и^ + Аи) — р (и0). Полученное таким
образом подмножество {/?0 + °/?} линейно зависит от Д&. Если
это подмножество выпукло и условие отделимости его от
луча L остается необходимым условием оптимальности точки
й0, то, как мы видели выше, условие отделимости может быть
выражено в терминах самых простых функций — линейных,
что делает простой его проверку.
ГЛАВА III
МЕТОДЫ ОПТИМИЗАЦИИ В ПРОСТРАНСТВЕ
АРГУМЕНТА
В этой главе будут изложены некоторые методы решения
задачи на условный экстремум, тесно связанные с постанов¬
кой задачи 1 в § 1 предыдущей главы. Построения последо¬
вательных приближений оптимального элемента, согласно этим
методам, ведутся в пространстве элементов и — пространстве
аргумента задачи.
В основе методов лежит идея градиентного подъема
(спуска), развитая применительно к задачам выпуклого про¬
граммирования (методы возможных направлений [18]) и зада¬
чам оптимального регулирования (методы подходящих вариа¬
ций [13, 24, 43]).
§ 1. ЭКСТРЕМУМ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
1°. Постановка задачи
В этом параграфе будем заниматься следующей задачей.
Задача 1. Найти
max (Х(и) :и^(—оо, + оо)). (1.1)
Из курса математического анализа известно, что необхо¬
димым условием максимума гладкой функции i-(u) является
равенство
(1.2)
в котором и0 — точка максимума функции Х(и), так что в слу¬
чае гладкости функции Х(и) задачу (1.1) можно заменить за¬
дачей нахождения корней уравнения (1.2). Однако во многих
d\(u)
практических задачах даже вычисление производной —
сопряжено с большими трудностями. В связи с этим укажем
32
некоторые известные методики приближенного решения зада¬
чи (1-1), использующие только вычисление функции Х(д)
в отдельных точках. При этом мы заранее не предполагаем
ни дифференцируемости функции Х(и), ни даже непрерывности
ее. Сначала напомним некоторые определения.
Определение I. Точка и0 называется точкой максимума
вещественной функции Х(и) на множестве MdR (/? = (—оо,
-j- оо)), если и0£М и Х(и0) = sup Щи):и£М\.
Такую точку и0 будем обозначать и0(М) и иногда назы¬
вать также точкой абсолютного (глобального) максимума на М.
Определение 2. Точка щ называется точкой относительного
(локального)- максимума вещественной функции Х(и) на мно¬
жестве MC.R, если и0£М и существует открытый интервал
(и0 — s, «о + е), е > 0, такой, что «0 является точкой максимума
на множестве МП(м0 —в, w0 + s), т. е.
X (ы0) = sup (X (и): и 6 М П («о — е, «о + е)) •
Определение 3. Функцию Х(и) назовем строго квазивогну-
той на промежутке [а, Ь\, если существуют числа а и р
(а<[а<1[3-<6) такие, что функция Х(ц) на промежутке [а, а]
строго возрастает, на [Р, b] строго убывает, на интервале (а, р)
постоянна и равна sup (Х(и) :и£(а, Ь)\.
Возможно а = а = — оо, b = р = -(- со.
Полезно отметить и другое эквивалентное определение
строго квазивогнутой функции.
Определение 3'. Функция X (и) называется строго квазивог-
нутой на <а, 6>, если на любом отрезке [а', Ь'\ из <А #>
ее значения не меньше меньшего из значений на концах этого
отрезка:
+ Х(б')}, ?£[0, 1].
При этом если X (аг) ф \ (й'), то на интервале (а\ Ь') значения
к (и) строго больше, чем min{X(a'), X (&')}.
Легко убедиться, что все точки локального максимума
строго квазивогнутой функции на промежутке <#, Ь^> являются
точками абсолютного максимума на том же промежутке. Не¬
трудно также проверить, что для того, чтобы непрерывная
функция была строго квазивогнутой, необходимо и достаточно,
чтобы множество точек ее локального максимума было вы¬
пукло.
Отметим, что вогнутая (не обязательно строго) функция
является строго квазивогнутой, однако множество всех строго
квазивогнутых функций существенно шире множества вогну¬
тых (квазивогнутая функция может быть и кусочно-непре¬
рывной [2, 4]).
Перейдем к описанию алгоритмов решения задачи (1.1).
3 Н. Е. Кирин
33
2°. Метод простой итерации
Пусть фиксирована некоторая точка их и известно, что точки
максимума и0 лежат правее их (т. е. м0 > щ). Зададимся числом
Л > Оибудем вычислять значения функции в точках иъ uk + h,
к = 1, 2, , до тех пор, пока последовательность чисел
{Х(м^)1 строго возрастает. Ту первую точку и^ в последова¬
тельности {«*.}, для которой будет X [п-^)~^к(и^-\-к), примем
за приближение точки максимума. В какой связи находятся
точки и£ и и0? На этот вопрос можно ответить следующей
леммой.
Лемма 1. Обозначим max и_— /г| = и_. а) Если к (и) —
непрерывная функция, то на отрезке \и.., u_-j- /г| имеется
точка локального максимума функции к {и) на множестве
Mj, оо). б) Если L — константа Липшица функции к (и) на
их,
|L > sup 11X (и') — X (и") |/| и/ — и" |: и’, и" 6 р^, и_ + AJ | j ,
то
h
X^H_j />тах jX («) : и(« ргь и_ -f- AJ| --- L .
в) Если функция к (и) строго квазивогнута на [иъ
то на | м_ -f- /zj находится точка максимума и0.
3°. Методы уточнения максимума на отрезке
Пусть к (и) непрерывна на [а, Ь\. Возьмем на интервале
(а, Ь) точки а ир(а<^). Если Х(а)^Х(р), то на промежутке
[а, (3) непременно имеется точка локального максимума функ¬
ции Х(и) на [а, Ь\. Если же Х(а)X(j3), то точка локального
максимума имеется на промежутке (а, Ь]. Аналогичные заклю¬
чения относительно точки максимума можно сделать в случае
строго квазивогнутой функции к(и).
Итак, вычисление функции Х(и) в двух точках интервала
(а, Ь) позволяет уточнить местоположение точки локального
максимума. Опишем два алгоритма последовательного уточне¬
ния точки локального максимума, основанных на этом свойстве.
Эти алгоритмы могут быть использованы как продолжение
метода простой итерации.
Метод деления отрезка пополам
Построим последовательность точек {«*), \bk}, (cft), k = 0,
1, 2, ... .следующим образом. Пусть ak, bk, ck — (ak + bk)• 2-1
уже построены,
34
Х(а*)<Х(с*), Ц6*)<Х(с*). (1.3)
Тогда точки аш, bk+1, ck+1 строятся так. Возьмем точку
= -йк Ск- и вычислим X (aft). Если Х(<**).>Х(сй), то положим
«*+1 —= с*’ с*+1 = **• Если же x(aft)<x(c*). то возьмем
точку Pft = -Ски вычислим X(E3ft). Если X(рА)^X(с*.), то по¬
ложим aft+i = с*, ftft+i = bk, ck+1 = % ■ Если же X (pfc) < X (ск), то
положим ak+1 = ah, bk+1 =Рл, tft+i = £*. Очевидно, для выбран¬
ных таким образом точек ак+и Ьк+и Cfc+i имеют место неравен¬
ства (1.3), где, разумеется, номер k заменен на fe-f-1, и, сле¬
довательно, построение можно продолжить. В качестве на¬
чальных точек следует взять а0 = а, Ь0 = Ь, с0 = . Спра¬
ведлива
Лемма 2. Пусть Х(и) непрерывка на [a, b] или строго
квазивыпукла. Если неравенства (1.3) имеют место при
k — О, то последовательности (аД, \Ьк}, (сД таковы, кто
на промежутке [ак, Ьк\ имеется точка и локального ма¬
ксимума на [а, Ь\ функции Х(и), причем
\ск-и\<^щ-. 0-4)
Следствие. Согласно сделанному на стр. 33 замечанию,
в случае строгой квазивогнутости функции Х(и), точка и в (1.4)
есть точка абсолютного максимума функции Х(и) на [а, Ь].
Замечание. Метод деления отрезка пополам несложно
доопределить и для случая, когда неравенства (1.3) не имеют
места. В частности, если X (a?i) > X (ск) ^ X (Ьк), то следует по¬
ложить ак+1 = ак, bk+1 = ск.
Для нахождения максимума с высокой точностью более
эффективным является следующий метод, предложенный
Джонсоном [2,4].
Метод Джонсона
Пусть для функции Х(и), определенной на [а, Ь], по значе¬
ниям ее в любом конечном числе точек известен некоторый
способ, позволяющий указать промежуток (по возможности
наименьшей длины), в котором содержится точка максимума.
При этом упомянутый способ не использует значений X (а) и
Задача А. Найти точку и0 максимума функции Х(и) на
[а, b] с точностью до е > 0 за наименьшее число вычислений
функции Х(и).
Задаче А сопоставим следующую задачу.
3* 35
Задача А. Для каждого я (я = 0, 1, 2, ... ) указать наи¬
большую длину промежутка с произвольным началом и спо¬
соб выбора я точек на нем, сравнение значений функции Х(я)
в которых позволит найти точку максимума на этом проме¬
жутке с точностью до е = 1.
Отметим, что наибольший промежуток, о котором идет
речь в задаче А, может не существовать. Однако может су¬
ществовать верхняя граница длин промежутков, на которых
за я вычислений функции X (я) можно найти точку максимума
с точностью до единицы. Эту верхнюю границу обозначим
через Ln, и последовательность \Ln\ будем считать решением
задачи А.
Для класса строго квазивыпуклых функций Х(«) Джонсон
[2, 4] предложил для построения Ln применить метод матема¬
тической индукции. Опишем это построение.
Пусть я^ 2 и L0, Lx, ..., Ln_x найдены. Очевидно Ln ^ Ln_x ^
^... Возьмем число L >Ln_х. Можно считать, что на¬
чало промежутка совпадает с нулем. Пусть 0<а<р<£. Как
отмечено выше, ввиду строгой квазивогнутости функции Х(и)
после вычисления Х(а) и Х(Р) можно заключить, что либо
Яо€ [О- PL либо и06 [а, L\. Рассмотрим первый случай: я0(. [0, (3].
Очевидно, значение Х(Р) не может повлиять на выбор точек
в интервале (О, Р), ибо какую бы точку т€(0, Р) ни взять,
и при X(y)>-X(P), и при Х(т)<Х(р) заключение может быть
только одно: и0 6 (О, Р). Точка а может быть выбрана с самого
начала произвольно на (О, Р) i , следовательно, на [О, Р] должно
быть выбрано я — 1 точек из условия определения точки мак¬
симума с точностью до единицы. Значит, должно быть р < Ln_v
Поскольку а может быть любым положительным числом,
меньшим р, то можно считать а ближайшей точкой к р из тех
я—1 точек, которые должны быть взяты на (0, р), согласно
решению задачи А для я —1. Понятно, что тогда точка а
играет на интервале (О, Р) такую же роль, какую р — на (О, L),
т. е. должно быть а < Z„_2.
Для случая и0£[а, L) аналогичным образом можно полу¬
чить неравенства L — а^/.л_ь Z. — р^/,я_2. Оставляя из этих
неравенств независимые, приходим к заключению, что
Ln = sup {L : L a a Ln_2),
a
т. e. -
Ln ~ Lfi^i -f- Ln__2. (1.5)
Таким образом, последовательность {Ln} может быть вы¬
числена по рекуррентной формуле (1.5), если известны два
первые члена этой последовательности. Очевидно, L0 = 1, Ьг = 1.
36
Решая теперь разностное уравнение (1.5) с начальными усло¬
виями L0 = \, Z.i=l, получим
1 Г/1 + /5\«+1 /1-/5
'« “ /5 LI 2■ J ■ [ 2
(1.6)
Укажем теперь последовательность действий для решения
задачи А.
I. Найдем наименьшее п, при котором (b — a)<eZ,„.
II. Вычислим отношение-^7^ и точки
Ln
«й = Ь-±^{Ь-а), $0 = a + ±f+(b-a). (1.7)
П
III. Положим для однородности обозначений а = а$\ b = Ь^0п\
Опишем общий шаг дальнейших построений. Пусть полу¬
чены точки а< ak < pk < Вычислим X (ak), X (Pk). Если
окажется, что X (aft) X (РА), то положим = ak, = b£\
an+i = Pk. Pft+i = bin) ~ (Pk — aft)- Если окажется, что X (ak) > X (рд
то положим = а[п\ b^ = рк, «к+1 - а» + (рк - aft), Рк+1 = ак.
Поскольку для £ = О точки atf\ btf'*, a0, р0 определены, то,
проделав операцию III для к = 0, 1, 2, .. . , п — 2, получим
промежуток (л^.1, #п"2,) длиной меньше е, содержащий точку
и0.
Для начала построения по описанному методу требуется,
как видно из (1.7), знать отношение , зависящее от е и
Ltl
числа (b — а). Если число —■ а достаточно велико, то прибли¬
женно это отношение можно найти, пользуясь формулой (1.6).
Поскольку -~~*~2^Гв ~ 1,62 > 1 > ^ l--f5 , то при достаточно
больших п будет Ln ^ -т=(1,62)л+1, а, значит, ~ - —^-5 •
У 5 Ln ^
Это отношение носит название золотого сечения.
Лемма 3. Пусть функция X (и) непрерывна или строго
квазивогнута на [а, Ь\. Тогда последовательности {//,},
таковы,
Л") 4- йМ
/2 — 1 + fl— 1
<ттг- (L8)
где и0 — тонка абсолютного максимума на [а, Ь], если X (и)
строго квазивогнута, и и0 — тонка локального максимума
на [а, b], если Х(и) непрерывна.
37
§ 2. ГРАДИЕНТНЫЕ МЕТОДЫ ПОИСКА БЕЗУСЛОВНОГО
ЭКСТРЕМУМА
1°. Максимизирующие последовательности
Пусть требуется максимизировать функцию Х(ц), опреде¬
ленную в полном нормированном пространстве U, т. е. найти
Х0 = шах (Х(м): и £ U}. (2.1)
Возьмем произвольный элемент иX£U и зададимся целью
отыскать такой элемент м2, чтобы было
X(m2)>X(«x).
Предположим, что функция Х(ц) непрерывно дифференцируема
всюду в U. Тогда (см. гл. I, § 2) справедливо представление
X (и) = X (йх) + (и - иг) + о (||м — «j||). (2.2)
Здесь —• и ~ линейный функционал по м,
о (1 и — «Л )/|| и — «] |i -> 0 при I и — их I -► 0. (2.3)
Предположим, что -и — не равный нулевому функцио¬
нал. Тогда существует элемент qx£U такой, что
Если взять w = «! + p?i, то в силу (2.3) найдется ех > 0 такое,
что при (J. ^ (0, sx) будет
о(1ю.|)<4^-М.,
и тогда из (2.2) получим
X(«1 + p<7i) > X(мj) + (2.4)
г. е. любую точку u1-{-\>.q1 при р6(0, ei) можно взять в ка¬
честве искомой точки «2- В случае | — 0 положим и2 — их.
Пусть точка и2 на луче их -f \iqx, |j.£(0, + оо) уже выбрана
так, что X(«2)^X(mj). Для точки й2 можно повторить те же
построения, что и для их. Продолжая этот процесс, можно по¬
строить последовательность
мх, и2, Mg, ... (2.5)
такую, что
Х(м1)<Х(м2)< ....
Такая последовательность называется максимизирующей.
38
Изучим свойства последовательности (2.5). Итак, пусть
uk+i = uh + [Lkqk, k = 1,2,..., (2.6)
d^-qh>0, Х(и,+1)>Х(иЛ).
Пусть также рь — точка максимума функции ^(«ft + ^ft) пере¬
менной р на J^O, |, А> 0. Обозначим Xft = X [ик + £*?,,)•
Лемма 1. Пусть для некоторой подпоследовательности
{м(.J последовательности (2.6) выполнены условия:
1?Д «>о.
v dX(Ul) > д ах (Ц;)
а> ди Ч1^'а\ ди
||^. 1=0 тогда и только тогда, когда
<?х (щ) II _ п.
ди ~ и'
б)
X (Ц;-и) — X (Uj)
— X (й;)
I Х(м) о<
[ и(.} вместе с нормой
^ ^ 0, При X. =^= Х(м*) ;
(2.7)
(2.8)
в) функция X (м) ограничена на подпоследовательности
ад || >
1 ’
г) функция Х(м) равномерно дифференцируема на после¬
довательности {«г}, т. е. в разложении
дЦи)
х(« + Ди) = x(w) ч ди
последнее слагаемое таково, что
Дм + о (I Дм||, и)
(2.9)
Iо(||Д«|Ь «)|
-|ММ U
(Дм I
равномерно относительно м6{и,}. Тогда
дХ (щ)
да
lim
= 0.
Доказательство. Предположим, что заключение леммы
не имеет места. Это означает с учетом ограниченности ПОСЛе-
dA (ui) )
1 существование подпоследовательности
d> 0.
довательности
дХ (uj)
да
IUj) последовательности [ut\ такой, что lim
j-+ оо
Согласно условию г) леммы, по числам a, d найдем число
е>0 такое, что в разложении (2.9) будет |о(||Ди||, и)|<
<-4—||Дм|| при IДм||^е и uf*{Uj}. Подставляя теперь в (2.9)
« = uj, Дм = \x.qj, где |С =
II Я] II
и учитывая неравенство
(2.7), получим при достаточно больших номерах у, что
^ [UJ + PjQj) ^^(му) + -^-ads. Очевидно можно считать с са¬
39
мого начала, что е</г, так что полученное неравенство озна¬
чает Ху > X (uj) + -j- adce. Тогда неравенство (2.8) дает
X («у+1) — X (uj) > -j- acfce. (2.10)
Теперь для элемента и- последовательности [uj\ с достаточно
большим номером у будет
x(wr+i) = x(»i)+2 ixK+i)_xK)]>x^)+
ft=i
+ ^ [>' (иу+i) - («у)] > < 7-Уо > “Г acfcs- (2Л ^
j
Здесь у0 — первый номер последовательности номеров (у), на¬
чиная с которого справедлива оценка (2.10), а символ <j — у0> —
количество членов подпоследовательности {иу}, номера ко¬
торых не меньше у'0 и не больше у. Поскольку подпоследова¬
тельность [uj] имеет бесконечное число членов, то <j — у0>->-
-> + со при у -»• со. Тогда из (2.11) следует, что Х(иу+1) с»,
но это противоречит ограниченности функции X(и) на подпо¬
следовательности (иу) (условие в)). Полученное противоречие
доказывает лемму. _
Следствие I. Пусть и—предельная точка последователь¬
ности (2.6) и {иг} — сходящаяся к ней подпоследовательность
последовательности (2,6). Если для подпоследовательности j у}
выполнены условия а), б) леммы 1, то
д\ (а) =р
да
Это равенство следует из заключения леммы 1, условия в), г)
которой выполнены вследствие непрерывной дифференцируе¬
мости функции Х(«) в точке и —и, которая обусловлена пред¬
положением, сделанным в начале этого параграфа.
На основе леммы 1 сформулируем некоторые признаки
сходимости последовательности {Х(ий)} к верхней границе (2.1).
Признак 1. Пусть X (и) = а (х(и)), где х (и) — дифференци¬
руемая операция, определенная в полном нормированном
пространстве U, со значениями в полном нормированном
пространстве X; о (х) — непрерывно дифференцируемая функ¬
ция в X. Пусть выполнены следующие условия.
1. Точка u(*U такова, что множество Х0 = (х : а (л;) >
^ а [х («))}c2f — компактно.
40
2. Производная операции х(и) удовлетворяет во всех
iпочках и множества Q = {« :Х(м)^х(и)| условию
<1Ая\>\*^яг'ч\>йАя\>Ъ, Ikll^O. (2.12)
Операция х (и) равномерно дифференцируема на Q.
3. В каждой точке и множества Q существует обрат-
1дх(и)\~1 . „ дх (и)
ная операция ^ 1 к линеинои операции ^ .
4. Норма линейной операции обращается в нуль
только в точках абсолютного максимума функции <з(х) в X.
Тогда последовательность (2.6), максимизирующая функ¬
цию Х(и) = а (л: (к)), имеющая первым членом элемент u^Q
и удовлетворяющая условиям а) б) леммы 1, реализует
верхнюю границу функции Х(и), т. е.
lim л. (мП = supX(«). (2.13)
х ’ aeU
Доказательство. Рассмотрим последовательность точек
xk = -«(ий), k = 1, 2, ... . По построению xk£X0, k — 1, 2, ... .
В силу компактности множества Х0 существует подпосле¬
довательность {*•} последовательности {xk} такая, что limx; =
= л:^Лг0. Так как функция о (х) непрерывна и конечна в точке
х = х, то последовательность {X (щ) = о (х(мг))) ограничена.
Кроме того, производная -^г- непрерывна, так что
< Z. < со. Теперь, учитывая (2.12), получим
дХ (щ) I
II да (Xi)
дх (tii)
ди \
J дх
да
да 03 || ^
дх
Таким образом, для последовательности {и,| выполнено усло¬
вие в) леммы. Убедимся, что условие г) также выполнено.
Справедливы равенства
. Х(и + Ди)-X(w) —Ди = о(||Ди||, и) =
= а(х(и + Дм)) — а(х(и)) - =
= д1Щи)1.0jc(tAuit и)+Оа(Цх(и + Аи)-х(и)П, х(и)), (2.14)
где Ож (1 ДМ ||, и) = х(и+Аи)-х(и) — ^р--Аи;
0Л1Д*1> •*)=°С*+ ДЛ—^'Ax-
Поскольку х(и) равномерно дифференцируема в Q, то по
е > 0 найдется 8 >0 такое, что при любом / будет
||0^(11д«11, w/)||<illd«ll- ПРИ 11ди||<8- (2.14)'
41
Далее, поскольку производи^ ^.непрерывна, то она равно¬
мерно непрерывна на замкцуТом КОМПактном множестве Х0.
Пользуясь формулой конечных приращений с остаточным чле¬
ном для функции ° (х) [22, СТр ^ п0лучим
I (IIх (и1 + д и) ~ |, xt) | < I х (м + Дм) — xt I X
(Xj + 6 (лц^. Дв) _ Xi)) _ (И (х.) I!
дх
X sup
o<e<i
Можно считать, что здесь при цд^ц^б первый множитель
меньше 2^1||Ди||, второй мецЬще
ыл
так что левая часть не¬
равенства будет меньше 2 Цд^Ц. Подставляя эту оценку и
iU«1<8 ииР(йВ1 (чт^4ознаПч°йЛУЧИМ |о(М’ И)К811Д«11 при
II и1|< икс{м/), что означает равномерную дифференцируе¬
мость функции а(х(м)) на последовательности (м.). Применяя
заключение леммы 1, получим
д\ (ид
дх 0 при i-*co. (2.15)
получим
= II а8^.^(и,)|
ди
По определению нормы операции и в силу оценки (2.12)
имеют место неравенства r J
да
(xk)
дх
<
da(xk)' дх (Uk)
дх * дц
ди
ди
<
Отсюда
дх (uk) \-i
ди )
"дх (uk)
х ди
<
<
дз (хк) дх (ц )
дх с)ц
>d9
дз
дх
дз
дх
Учитывая здесь (2.15), прих0дим к ВЫВОДу, чт0 Iim
= | ^ дх ^ = П° УСЛ0В^ 4 доказываемого признака это
означает, что х — точка абсоД10тного максимума функции о (х)
и, следовательно, ]1ш«(^%8ираМ и/и fim о (х (и,)) =
supo(x(M)). Учитывая монотонное возрастание последова¬
тельности {о(х(мА))}, делае^, заключение о справедливости
соотношения (2.13).
Следствие. Пусть о (л).— вогнутая гладкая функция в
конечномерном пространстве х и при ||х|К со функция а(х)
неограниченно убывает: а(х) Пусть дифференцируемая
операция х(и) удовлетворяет условиям 2, 3 признака 1. Тогда,
42
если максимизирующая последовательность (2.6) для функции
у (и) = о (х(и)) удовлетворяет условиям а), б) леммы 1, то
lim X (%) = sup X (и).
h-+oo ueU
Признак 2. Пусть для функции \(и) справедливо разло¬
жение
Х(и + де) = Х(и) + ^-^.;^ + о(|л)о(и, д), (2.16)
где -2-^- -> 0 при р -» 0; о (и, q) -- ограниченная снизу функ¬
ция на множестве
a6Q = {a:X(a)>x(»)}, q£[q :|| ?||< 1).
Пусть, кроме того, норма производной функции Х(и) удовлет¬
воряет неравенствам
1 >||т||>^(8ииР>'^ “ Х(м)) ’ <2Л7)
где ср (а) — монотонно возрастающая функция и ср (а) > О при
а о. Тогда, если £ Q и последовательность (2.6) для функ¬
ции Х(ц) удовлетворяет условиям а), б), в) леммы \, то эта
последовательность реализует верхнюю границу функции
Х(и) на U.
Проверка. Разложение (2.16) обеспечивает выполнение
условия г) леммы 1. Поскольку условия а), б), в) выполнены,
то в силу леммы 1 будет
—■—ч0. Подстановка этого соот-
ди
ношения в (2.17) дает <р ^sup Х(м) — X (и*)|.0 при k оо, что
означает supX(a) = lim Х(«^).
II k -+ оо
2°. Методы наискорейшего подъема
Приведенный выше метод построения последовательности
(2.6), удовлетворяющей условиям а), б) леммы 1, называется
градиентным методом подъема. Укажем способы выбора на¬
правлений q в этом методе, удовлетворяющих условию
а) леммы 1.
Всякий элемент q£U, II <7II ^0 называется направлением
подъема для функции Х(и) в точке и, если
>(“+^гм',) >°- <2-18>
Пользуясь дифференцируемостью функции Х(и), (2.18) можно
переписать так:
1 ах (и) . Л
Направление подъема qtl называется направлением наиско¬
рейшего подъема, если при q — qlt предел (2.18) принимает
наибольшее значение, или
1 д\(и) 1 д\(и)
— —max —
q 6 U
ii—п—з <7„ —- шах -й—г—q. (2.19)
II «'Ы II dU 4U ||д,|| ди Ч \ /
Кривая и (t) (однопараметрическое множество в U вещест¬
венного параметра t(t~^0)) называется кривой наискорейшего
подъема, если при 0
Иш ц^ + 8)-цС0 = ш {t) qu ^ (2.20)
где ш(*)>0 — вещественная непрерывная функция. Обозначая
предел в (2.20) через -jjuit), соотношение (2.20) можно запи¬
сать в виде дифференциального уравнения
^ = (2-21)
Теперь всякий метод интегрирования уравнения (2.21) назовем
методом непрерывного наискорейшего подъема в задаче (2.1).
Если в уравнении (2.21) qu заменить другим направлением
подъема, то решение этого уравнения можно назвать кривой
подъема, а метод интегрирования получившегося уравнения —
методом непрерывного подъема. В общем виде это уравнение
можно записать так:
=f (и щ -*Ц“Ж, ^ . (2.22)
Здесь элемент таков, что
*)>а||*Ц£М
а > 0.
\ / | ~ и*
Таким образом, изучение сходимости непрерывных методов
подъема сводится к изучению поведения интегральных кривых
уравнения (2.22).
В отличие от непрерывных методов подъем-а метод построе¬
ния последовательности (2.6) называется дискретным методом
подъема. При этом построение последовательности (2.6) назы¬
вается дискретным методом наискорейшего подъема, если
Чъ.= Ч(ик) — направление наискорейшего подъема и \х = рк при
h ■— —{— оо.
Отметим, что определение (2.19) направления наискорейшего
подъема существенно зависит от нормы пространства U. Это
видно на следующем простом примере.
Пусть U—Rn, Ъ(и) — непрерывно дифференцируемая функ¬
ция. Будем считать, что \\uf = u*Cu, где С — положительно
определенная симметричная матрица, а запись и*Си означает
скалярное произведение векторов-столбцов и, Си. Решим за-
44
дачу (2.19): найти max Я '■ q*Cq = l|. Применяя правило
множителей Лагранжа, найдем
Ч- = ((Ir)*^1 ж)"с" т =' (“)с- ТГ1' <2-23>
д\ (и)
7^0.
Здесь С-1 — обратная матрица для С; v(m)>0 при,,—
Убедимся, что положительно определенную симметричную
матрицу С можно выбрать так, чтобы_ qu совпадал по направ¬
лению с наперед заданным вектором q, имеющим положитель¬
ную проекцию на вектор ф 0 [q* дк^ > oj. Для этого
возьмем векторы qh i= 1, ..., и —1, составляющие вместе
с вектором ортогональный базис пространства Rn. Оче¬
видно, векторы qx, ... , qn_v q также составляют базис Rn.
п— 1
Теперь положим С-1 =2 qq*• Это — положительно оп-
<=1
ределенная симметричная матрица, так что она имеет обратную
положительно определенную матрицу, которую и примем за С.
Кроме того, согласно (2.23),
Можно убедиться, что если в (2.6) ^„ — направления наиско¬
рейшего подъема, то для последовательности {и^} имеет место
условие а) леммы 1. Приведем более общее предложение.
Лемма 2. Пусть с каждой, точкой иk последовательно¬
сти (2.6) связано ограниченное множество Gk<zU, содержа¬
щее внутри себя пересечение некоторой сферы радиуса
гь, > 0 с центром в точке 0 и полупространства —j~—q > 0.
Обозначим через рь радиус сферы., содержащей множество
Gk. Пусть sft>0,
sup =
и направления qk в (2.6) таковы, что qk£Gk и
д\ (и*)
ди
'Ян ^ Pfc sfc-
Ik , л Ik
дХ(ак) -■ р
0, —■/>() при & оо, то
Тогда, если Sft-s-О, -
Pft|| W
для некоторой подпоследовательности {«,•) последовательно¬
сти (2.6) выполнено условие а) леммы. 1.
Проверка. Возьмем подпоследовательность {#/}, для ко¬
торой — >с> 0. Можно считать, что
<ЭХ (и,)
ди
М=0, в против¬
ном случае неравенство (2.7) было бы выполнено при любом
числе а> 0 (и этим лемма 2 была бы доказана). Учитывая
д1 (и)
определение нормы линеинои операции •у, имеем
дХ (tt;) ^ ^ dX (w)
• а. ^ 3; — s. > sup ■ -■> ■ -q
ди 1 ‘ 1 и»7
дХ (и)
да
Г; — г;
Заменяя здесь г. на меньшую величину ср^сЦ^.Ц и считая /
, получим требуемое не-
^ 1
столь большим, ЧТО 6. <—ср.
равенство
дХ(и) ^
ди
ди
ди 1р «'li-
Итак, в условиях леммы 2 для определения направления
подъема в точке uk можно решать задачу
дЦиь)
sup
ди
q:q£Gh
(2.24)
Решение этой задачи (точное или приближенное) и назовем
направлением подъема во множестве Gk. Будем его обозначать
qu{Gk) или просто qa.
Каждому множеству Gk соответствует (возможно, не одно¬
значно) свое направление подъема (см. рис. 4, а). Выбором
множеств Gk, удовлетворяющих условиям леммы 2, можно
распорядиться в каждой конкретной задаче, обеспечивая доста¬
точную простоту решения задач (2.24). Приведем несколько
примеров таких множеств и решения задач (2.24) построения
направлений наискорейшего подъема при Gft = G, ah — u.
Пример 1. Пусть U—Rn,
a) G={q — (ть
П
l*qu = sup l*q = г ^ I //1
(=i
х,- = r sign ...
d\ (a)
du
•• - xn) '■ I ' 1 I < ГЬ
отсюда qu={-u ... , v)>
n (считаем sign 0 = 0).
6) G= [q : q*Cq <>}, С — положительно определенная симмет¬
ричная матрица. Как уже указывалось, в (2.23)
Обозначим через i0 номер, для которого | /,0| = шах |//|; тогда
q-tt=(*:I, , %), где Т; = 0 при i^=i0, xio — г sign lk.
r) G={q:Aq^g, аг<х;<Тг, i= 1, . . . , n).
Здесь A — матрица, строки
которой — линейно незави¬
симые векторы, g — вектор
с положительными компо¬
нентами, <*г- < 0, тг>0. За¬
дача (2.24) является зада¬
чей линейного программи¬
рования и решать ее можно
численно известными мето¬
дами [46].
Приведем аналог этого
примера в функциональном
пространстве.
Пример 2. Пусть U —
пространство кусочно-не¬
прерывных функций «(/),
определенных на проме¬
жутке [0, 1], а линейная
дХ (и)
операция ^ •q имеет вид
д\ (и)
ди
•? = j/ (t)q(t)dt +
О
п
+Yiliq{ti)- (2-25)
i=i
Здесь l(t) — непрерывная
функция; /, — числа; //£ [О,
1], /= 1, ... , п; при
i*J-
а) G={q(t):\q(t)\^rt},
б)
Я и *7а(0:
0 =
\rsign/(/), если /=== 1, ..
г sign //, если t = t(, i = 1, ..
j? (*) : j Я2 (*) с (t) dt < ru £ ciq2 (//) < r,
ti.
где с (/)> a >0 — непрерывная функция, c,-> 0. Нетрудно,
вычислить, что аналогично примеру 1 б)
47
Решим задачу (2.24) при данном множестве G, считая, что
в функционале (2.25) /; = 0, /= 1, п. Введем в рассмотре¬
ние множества
u)(v)={2f:|/(0|>v, *£[0, 1]), v > 0.
Рассмотрим интеграл 8 (v) = r2 J dt. Пусть существует v0—наи-
ш (v)
меньшее из чисел v, при которых Теперь направле¬
нием наискорейшего подъема в множестве G будет функция
п /A — f^sign l{t), если *6M(vo);
Ч и \L) i Л j. F~ / \
0 , если t
§ 3. МЕТОДЫ ПОДХОДЯЩИХ ВАРИАЦИЙ
1°. Методы возможных направлений
Рассмотрим задачу: найти
sup {Х(й) :и£М*}. (3.1)
Здесь М* — множество в полном нормированном пространстве
U\ \(и) — функция, определенная на N.1*. Возьмем некоторый
элемент иг и зададимся целью найти такой элемент
^26^*, ДЛЯ которого будет Х(^1)<Х(^2). Будем считать, что
функция 'к(и) непрерывно дифференцируема на М*.
Направление q£U будем считать допустимым в точке иг,
если найдется отрезок ^£[0, р] такой, что иг-\-при
Iх 6 [о, у]; Iх > о.
Пусть <7—допустимое направление в точке их и — -<?^>0.
Тогда, повторяя вывод формулы (2.4), придем к заключению,
что при достаточно малых |^б[0> Iх] будет + >M«2)>
и в качестве точки и2 можно взять любую из таких точек
ux-{-)xq. Таким образом, аналогично (2.6) можно построить на
множестве Ж* максимизирующую последовательность {tik}
функции \(и)
-J-k 1, 2.... (3.2)
Здесь ^—допустимое направление в точке 0;
pk таково, что йы-i^* и х («fc+О > ^ (и*); 1^ = 0, если
?tS!^-qk = 0. Характер поведения такой последовательности
ди
определяется не только выбором направлений qk и чисел
но и структурой множества М%.
Приведем некоторый аналог леммы 1 § 2. Прежде всего
А
отметим способ выбора направления подъема. Пусть К (uk) —
множество всех допустимых направлений в точке ик таких,
что Uh + pqQM# при [0, 1]. Пусть Gk — некоторое ограни¬
ченное множество, для которого 0 — внутренняя точка. Обоз¬
начим
Pft = SUP 'Я -Я е К (UО n Oft). (3.3)
/ч
Определим направление qk£K (uh) Г\ Gk подъема в точке ик
как решение неравенства
<3-4>
✓Ч
Обозначим через Х& максимальное значение функции ^(«*+1^)
на множестве j*£[0, 1].
Теорема I. Пусть последовательность (3.2) такова, кто
/Ч
а) qk — вектор из множества К {ик) П Gk —решение неравен¬
ства (3.4);
б) ^(“*+l)~X(“*)>c>0 (при Xh^X(ttft)). (3.5)
Ч — ь («*) к }
Пусть также выполнены условия:
в) функция \(и) ограничена сверху на множестве М*
1(и) = |-^Т|<1<оо при и 644*;
г) в представлении
Х(и + Ди) = Х(и)4--^^Ди + о(|Ди||> и)
величина 0 ^ || д“ —>0 при ||Ди||->0 равномерно на множе¬
стве Af*;
д) последовательность множеств Gk удовлетворяет условиям
~ц^>е>0, t> 1, р*<р<оо, k = \, 2,... , (3.6)
где г и —радиус сферы с центром в точке 0, содержащейся
в Gk\ pk = sup {|«| \u^Gk]—радиус сферы с центром в точ¬
ке 0, содержащей Gk.
4 Н. Е. Кирин 49
Тогда при, любом первом элементе их последовательности
(3.2), взятом из множества М*, и при любом шсле р > О
будет
Доказательство. Пусть отношение (3.7) не имеет
места. Это означает существование таких чисел р > 0, а > О
и последовательности элементов |^г}, q&KiUi), Ц^Л^Р ({“«} —
подпоследовательность последовательности (гг*)), для которых
^М-Гь>,> 0, (3.8)
Поскольку <^=min jl, -^J <7,60, (") К {и.,), то из (3.8) получаем
• fi ri ) ^ dX(lli) ' ^ о
Отсюда с учетом первого неравенства (3.6) следует, что
^ > min |a, ‘ 'е 11 > 0. (3.9)
Из неравенства pft <р< со, &=1, 2, ... , в (3.6) и ограничен¬
ности нормы производной (условие в) теоремы) выте¬
кает ограниченность последовательности {р(), так что, не ума¬
ляя общности, можно считать lim^ = p'>0. Теперь неравен-
/-> оо
О
ство (3.4) для достаточно больших номеров i дает || <7* ^ ^ > 0-
ft'
Обозначая h — 1, ad — , далее можно почти дословно повто¬
рить доказательство леммы 1 § 2, начиная со слов: „Согласно
условию г) ...“ на странице 39. Полученное в доказательстве
леммы 1 противоречие доказывает и данную теорему.
Следствие. Пусть X(и) — вогнутая непрерывно дифферен¬
цируемая функция и Ж* — выпуклое ограниченное множество.
Тогда при выполнении условий теоремы последовательность
(3.2) такова, что
lim l(uk) — sup (Х(и) £Ж*}. (3.10)
ft-oo
Проверка. Предположим, что (3.10) не имеет места»
Тогда существуют элемент #£Ж* и число v>0, для которых
при любом номере k будет
V < цй) — Х(и*) = — uk) + Q (I и — ик I) < (« - uk).
50
Поскольку в силу выпуклости множества М* направление
Ъ. = и — Uk—допустимое, то при р = р, ч = min 11, --Д Л будет
_ I 2 II Як IIJ
чЯь. 6 К (ик) ПС» и
(щ) ‘ ^}к1Г>
>^-min|2, 1 | [sup (!|й— и|: и£М*}]-1 > О,
/ч
т. е. ^-/->0 при &->оо, что противоречит утверждению тео¬
ремы.
Остановимся на некоторых видоизменениях построения
последовательности (3.2), определенного условиями теоремы 1.
1. Проверка отношения (3.5) часто затруднительна. В этих
случаях в (3.5) можно заменить \k числом. X [uk-\-^kqk)=^k.
Здесь р.Д[0, pj таково, что | \>-к — pfe | ||<7j< <«2 (A* — X (ик)), а
число [0, pk] таково, что X (uk -f- \xkqh) = V Теперь построе¬
ние числа можно проводить методами § 1 настоящей главы.
2. Пусть М* — выпуклое множество. Тогда множество
К (и^ всех допустимых направлений q можно представить
в виде
К {Uk) = {q = u — uh : и£М:,}.
Теперь направление подъема в точке Uk определяется как ре¬
шение неравенства, аналогичного (3.4),
ди 2 '
где
]>а = sup j дКЦк) ; q:q = u-uh, и£М*,
В частности, если Ж* — ограниченное множество, то при до¬
статочно большом числе г будет Ж* с Ok -+- uk и тогда [12, 42]
Pfc = sup (и ~ иа):«€Ж*|.
3. В случае, когда множество М* ограничено, очевидно,
пересечение {Gk + uk} Г) будет ограниченным, и в условиях
теоремы числа pk можно заменить на диаметр сферы, содер¬
жащей множество М*. Теперь множество Gh можно задать,
например, в виде
Gk= Я = и — ик, и £Ж*, V> oj.
4* 51
На рис. 4, б приведены примеры 1—5 построения направле¬
ний подъема q при различных типах множеств Gh.
Способы выбора множества Gk определяют способы норма¬
лизации направления подъема qk [18]. Методы рассмотренного
типа названы в монографии Г. Зойтендейка [18] методами воз¬
можных направлений. Этим и объясняется название настояще¬
го пункта.
Понятие допустимого направления, использованное в пре¬
дыдущем пункте, связано с возможностью построения точек
вида Uk + pq множества М*, близких к точке ик при фиксиро¬
ванном направлении q и сколь угодно малом числе \> > 0.
В тех случаях, когда практическое построение таких измене¬
ний pq точки ик затруднительно или недостаточно, целесооб¬
разно рассмотреть более общее понятие вариации и, пользуясь
дифференциальными свойствами функции X(и), найти точку и,
близкую к точке ик, „почти* принадлежащую множеству М*
и доставляющую функции к\а) большее значение, чем к{ик).
Приведем одну модификацию метода предыдущего пункта,
имея в виду вариационную задачу следующего параграфа.
Рассмотрим задачу: найти
Здесь М С U; U — полное нормированное пространство элемен¬
тов и; К—полное нормированное пространство элементов у;
к (у) — непрерывно дифференцируемая функция в У; х(у, и) —
непрерывно дифференцируемая операция из У X U в полное
нормированное пространство X. Будем считать, что величины
равномерно по (и, у) стремятся к нулю при ||Ду||->0 на всяком
ограниченном множестве.
В терминах задачи (3.1) здесь М* = {(и, у): и£Му х(у, ц) = 0}.
Возьмем (их, yJE^W* и зададимся целью найти способ построе¬
ния сколь угодно близких к (uv ух) по норме пространства
ОхУ элементов (^-J-Д&, Ух + дУ) таких, что
1) &!-[-
2°. Метод подходящих вариаций
max (X (у): и £ У14, х(у, и)— Ох}.
(3.11)
Х(у + Ау)-Х(у)--^-.Ду
II Ду II
(3.11)'
дх (у, и)
X (у + Ду, и) — л: (у, и) — ^ • Ду
1)0(11 Ау И) Д
11 АУ11
II ДУ II
2) |*(.У, + Ду, «1 + Аи)|| = о(Ди, Ду),
3) Х(ух) <Цу1 + Д_у).
52
Сформулируем задачу 1)—3) более четко. Введем некото¬
рые определения.
Всякий элемент Aj/£K назовем вариацией элемента ух.
Элемент А и назовем вариацией элемента иъ если их-\- ки^М.
Множество Q пар вариаций (Ау, \и) назовем множеством до¬
пустимых вариаций, если выполнены два условия:
а) при любом (х > 0 множество Qa = {(А,у9 ки): (А у, А и) £ Q,
Ди| <(*> 1Ау|0} непусто;
б) для (Aj/, Am)6Q,, будет
И-кСУх+ДУ, «1 + д«)II = о GO,
r-K liil+i^il " ° "Р" М + М-О.
Множество Q допустимых вариаций назовем множеством
подходящих вариаций, если
lim sup 1 - ~ Х ^у^ = XQ (ul9 УО > 0. (3.12)
^+0 (АУ, Ли) е №
Множество Q подходящих вариаций назовем наилуяшим, если
ему соответствует наибольшее значение предела (3.12) среди
всех значений пределов (3.12), соответствующих множествам
подходящих вариаций.
Поставим задачу: найти наилучшее из множеств Q подхо¬
дящих вариаций. Пользуясь дифференцируемостью функции
Х(_у), непрерывностью операций х(у, и), дх ^ ^ - А у и равно¬
мерной малостью величин (3.11)', получим:
^ = + = + (3.13)
Ьх^х^ + Ау, и, + Ди)~х(уи и,) =
~ х(у1-\-Ау> и1-(-Дм) —м, —|— Ди) —J—
+ х(У1, и1 + &и)гх(у1, иг)= (3.14)
дх(ул, и} -4-Дм) а I г / мм« + Лм I /\ \
;= •АУ+[х(у1, мд)]Ц1 + о(Лу) =
= ~ '%и{)-Ьу+\х{Уи M"fiU + 0(Ay, Дм).
Здесь 1| 0(1^^)|1 - ГЛ ->0 при || Ду||->0 I Дм||^0.
Рассмотрим задачу: для каждого у > 0 найти вариации А_у,
А и из условий
дх(уд)’ Ц|)-Ау+[х(У1, М,)]“;+4В = о, (3.15)
II II || р., и-\- Аи£М, (3.16)
величина -^^—-Ау — максимальна. (3.17)
53
Будем ниже считать выполненным условие (С), состоящее
в том, что любому счетному множеству Q подходящих вариа¬
ций (Дуг, Дк,) произвольной точки (у, и) 6 Y X М соответствует
счетное множество Q вариаций (Ду/, Дм,-), удовлетворяющих
уравнению (3.17) при «i = m, j/x = y и таких, что
II ДУ/—Ху/II/II Ду/И + |Ду)|1 -»■ О
при i оо — расстояние между Ду/, Ayt есть величина более
высокого порядка малости, чем || А_у/1| +1| [|. Нетрудно убе¬
диться, что условие (С) выполнено, если, например, для любой
пары (у, и) линейная операция дх ^ и- • Ау имеет на X ли¬
нейную правую обратную операцию.
Теперь, если решение (Ду^, А и ) задачи (3.15)—(3.17) су¬
ществует при любом достаточно малом [^>0, то нетрудно
показать, что множество вариаций Q^JA^, Ди ) и есть наи¬
лучшее. Задача (3.15)—(3.17) — задача выпуклого программи¬
рования. Ее решение можно проводить, например, непосред¬
ственно методами возможных направлений или методами сле¬
дующей главы.
Пусть задача (3.15) —(3.17), в которой элементы- uv ух
заменены на ик, yk, решена приближенно, при любом
точнее: построено множество вариаций Qk = {Ay[}/) Ди^}, кото¬
рые удовлетворяют условиям (3.15), (3.16) при и{ = ик, ух~ ук
и при соответствующих значениях и при этом
' Л-И* ^где 1 > °>
Pe = sup{^^--Ay:.(Ay, Ди)6<(3.15)-(3.16)>}.
Здесь символом (3.15)—(3.16) обозначено множество всех пар
(Ду, Аи), удовлетворяющих условиям (3.15), (3.16) при дан¬
ном [х. Если = 0, при любом малом ^>0, то положим'
Уk+\= Ую uk+\==uk' Пусть pg>0 при любом малом р>0.
Возьмем достаточно малое число > 0. Найдем число ^>0
такое, чтобы было
а) ||*(yft + Дyv.k, uk+ Ди^ )-x(yk, и,)|< rkht
б) ^(л + %)-Чл)>т^-
Положим yk+l =Уъ + ик+1 = ак+Аи^к. Проводя такие
построения для k = 1, 2, .. . , получим последовательности эле¬
ментов {&£}, {у*}, для которых справедливо следующее пред¬
ложение, аналогичное теореме I.
54
Теорема II. Пусть
а) 0 < r0 < rk < г ;
б) > I > о, fj.ft <; [J. < оо, ^> 1, = Phfe/!V
К
в) выполнено условие (С); д\(>) дх( и)
г) функция Х(у) м нормы производных Х-0у U
ограничены сверху на последовательностях {yk), \{yk, и*)):
ЧУаХЧ,
Л (У*)
<4,
*с(у*, «*) II ^ /
• ду Х^2-
<>У
Тогда, есуш последовательности \uk\, {yk} ограничены, /по
fc-i
а) 14(Л, мй)||<14(^1, «01 + 2
1 = 1
А
б) я/ж любом ^>0 будет при >оо, (3.18)
PR = supJ^!*L Ду: (Ду, A«)£Q, ||Д_у||<у, 14«1|^} •
Здесь верхняя граница определяется по всем множествам Q
подходящих вариаций в точке (у*,, ид.).
Доказательство теоремы очень близко к доказательству
теоремы I, поэтому не будем_его проводить.
Замечание I. Если у, и — предельные точки последова¬
тельностей {у*}, {п*1, то в условиях теоремы соотношение
(3.18) означает, что задача (3.15)—(3.17) при и1 = и, ух=у
имеет нулевое решение: Д« = 0у, Ду = 0г.
Замечание 2. Сформулированный метод построения по¬
следовательностей {и*}, \уь) является возможным вариантом
общей схемы вычислительной процедуры решения задачи
(3.11). Конкретная реализация такой схемы требует неко¬
торых уточнений.
§ 4. ПОСЛЕДОВАТЕЛЬНАЯ ОПТИМИЗАЦИЯ СИСТЕМ
РЕГУЛИРОВАНИЯ
В этом параграфе будет рассмотрено приложение метода
подходящих вариаций к задачам оптимального управления
объектами, поведение которых описывается системами обыкно¬
венных дифференциальных уравнений. Этот метод разраба¬
тывался многими авторами. Из широко известных работ отме¬
тим работы Дж. Брайсона [6, 13], Г. Келли [24], Л. И. Шат-
ровского [43].
1°. Постановка задачи
Пусть объект регулирования описывается системой обыкно¬
венных дифференциальных уравнений, записанной в векторной
форме,
y = f(y,w,c). (4.1)
55
Здесь у — я-мерный вектор фазовых координат объекта, изме¬
няющихся с течением времени t; w — функция времени; с =
— {°i, •••> £5) — постоянный вектор; f(y\ w, ^ — вектор-функ¬
ция, определенная на Rn X R X Rs и непрерывная по совокуп-
df(y\ w, с) df (у\ w, с)
ности аргументов вместе с ^ —- — матрицами
частных производных от вектор-функции /(у; w, с) по ком¬
понентам вектора у и вектора с; точкой* обозначено диффе¬
ренцирование по времени.
Пусть фиксировано начальное состояние системы у(О) = у0.
Функцию w(t), кусочно-непрерывную и принимающую значе¬
ния в ограниченном множестве & с R, назовем управлением.
Из теории обыкновенных дифференциальных уравнений сле¬
дует, что каждому управлению w(t) и вектору с соответ¬
ствует единственное решение системы (4.1) с начальным зна¬
чением уф)=Уо. Будем это решение обозначать y{t\ w^ с).
Управление w (t) и вектор с назовем допустимыми, если
в некоторый конечный момент t, вообще говоря, зависящий
от w, с, вектор фазовых координат у (t; w, с) выходит на
многообразие
¥/(у) = 0, i = 1, s, (4.2)
т. е.
<Р/(У (*; W, С)) = о, i=l, s. (4.3)
Здесь ^/(y)—непрерывно дифференцируемые функции в R".
Допустимое управление w и вектор с будем называть допу¬
стимой. парой (w, с). Число t, фигурирующее в (4.3), будем
иногда обозначать t (w, с) и называть временем перехода си¬
стемы (4.1) на многообразие (4.2) при допустимой паре (w, с).
Допустимую пару (w0, с0) назовем оптимальной, если
% (У {t (w0, с0))) = шах <р0 (у (t (w, с))). (4.4)
(W, С)
Здесь ?0 (у) — функция, непрерывно дифференцируемая в /?",
и максимум вычисляется по всем допустимым парам.
Задача А. Найти оптимальную пару (w0, с0).
Возьмем произвольную допустимую пару (wv сх) и зада¬
димся целью построить другую допустимую пару (w2, с2), ко¬
торой соответствует большее значение функции <р0(У(^ w, с))•
Для решения этой задачи воспользуемся идеей построения
подходящих вариаций, описанных в предыдущем параграфе.
Для переформулировки задачи А в терминах задачи (3.11)
следует положить (далее в левых частях равенств стоят тер¬
мины задачи (3.11), в правых — задачи А): у={у, с), и =
= (да, t)
Чу) = <РоОО, х(У. a)={Ti(y), • ... ?т(У)> У—У(*)>
у-/(у, w, с), у (0) -Jf0}.
56
Однако в силу единственного соответствия паре (w, с) реше¬
ния y(t; w, с) и возможности строить это решение (скажем,
численно интегрируя систему (4.1)) можно рассматривать
только вектор-функции вида y{t) = y(t; w, с). Тогда послед¬
ние три компоненты введенной операции х(у, и) будут тожде¬
ственно нулевыми и норма элемента х(у, и) определится
только первыми т компонентами. Тогда для переформули¬
ровки задачи А в терминах задачи (3.11) (в которой, правда,
предварительно следует заменить X (у) на X (у, и)), положим:
У = с, u = (w, t), Х(у, u) = <o0{y(t; W, с)),
х(У, и) = {срЛуУ; w, С)), . . ., Чт(У(*\ W> С))> '°
2°. Уравнение в вариациях
Для получения подходящих вариаций построим теперь
вспомогательную задачу (3.15)—(3.17). Поскольку y{t) —
— у (t\ w, с), то под вариацией Ду в точке ух —у (^; с^)
следует подразумевать
Дy{t) = y{t\ w -|- Д w, с -f- Дс) — у (t; w, с). (4.6)
При составлении уравнения аналогичного (3.15) не будем
удерживать члены порядка выше чем || Ду (£)||-j-|| ДС1~Н| Д1^ (011-
Тог да и саму вариацию (4.6) достаточно найти приближенно,
т. е. нужно найти такую вектор-функцию 8у(0> чт0
Ду (t) = оу (^) + 0 (Ду, Дте», Дс, t), (4.7)
где
II 1у\+||Дда|| + ||1с|| ^ 0 ПрИ ИАУ11 + 11А«1 + 1| Ас1К°-
При этом желательно, чтобы вектор-функция 8у (t) вычислялась
достаточно просто. Найдем такую вектор-функцию 8у(^).
В силу сделанных предположений о вектор-функции
f(t; w, с) и управлении w(t) можно воспользоваться теоре¬
мой о непрерывной зависимости решения у {t\ w, с) системы
(4.1) от параметров w, с. Эта теорема гласит, что если
|| Дс||= |Дс| = ]/‘(Дс)»Дс -*0,
г 1 (4.8)
I Aw || = || Aw \\L = J \Aw(t)\dt-> 0,
о
TO
II by || = || Ду||c = max Vby*(t)-by (t)(4.9)
t e [0, T)
Здесь [0, T] (Г>0) — ограниченный промежуток существо¬
вания вектор-функции ky(t) из (4.6),* означает транспониро¬
вание матрицы, в частности замену вектор-столбца вектором-
строкой, а запись у'у" — скалярное произведение вектор-
столбцов У, у".
57
Дифференцируя тождество (4.6), заменяя производные
вектор-функции y{t), согласно системе (4.1), и учитывая соот¬
ношения (4.8), (4.9), получим
Ду= д/()ц(0^а>1 (/), Сд) | |
+ /(Ух(0, гМ0+д®(0. СО—/(Л (О, Щ, Cj) +
-}-0(Д.у, Дс, Aw, t). (4.10)
Здесь вектор-функция 0(Д.у, Дс, Aw, t) такова, что при лю¬
бом t на любом конечном промежутке [0, Т] величина
t
j || 0 (Ду + Дс, Дw, t) || dt
ii Ду ii+ii дс ii+ii д® 1 ^4•10),
равномерно по ^£[0, Г] стремится к нулю при || Ду || +1| Дс || +
+ ||Дда||0. Для краткости далее будем опускать аргументы
уУ), w^t), с1 в матрицах уравнения (4.10) и записывать его
в виде
by = -^by + %bc-\-b{t, Дда) + 0(Ду, Дс, Aw, t), ^ ^
Ду (0) = 0.
Здесь принято обозначение
b(t, Дw)=f(y1(t), w1{t) + b.w(t), с,)—/СуДО, «ДО. fi). (4.11)
Определим теперь вектор-функцию 8+ (t) как решение урав-
нения
8у = ^'8у+|Дс + Й(^ Д®), 8у(0) = 0. (4.12)
Убедимся, что для такой вектор-функции 8у(£) имеет место
равенство (4.7). Для этого воспользуемся известной формулой
Коши для представления решений уравнений (4.10"), (4.12).
Согласно этой формуле, имеем
t
Д.у {t) = F {t) J F~l (x) Дc + b (t, Aw) + 0 (Ду, Ac, Aw, *)} dx,
0
t
by it) = Fit) J F~x (x) {|Дc + bit, AW)}rfx.
(4.12)'
Здесь F(t) — матрица фундаментальных решений системы z —
= F(0) — E (F — единичная матрица). Из полученных
представлений с учетом равномерной малости величины (4.10/
получаем оценку
58
ЦАУ — оуЦс
F(t) | F 1(х)0(Ду, Дс, Дw, t) dx
IIДУ11 +II Ac II+ 11 Aw II
I max || F(t) F'
0)
II Ay 11 + 11 Дс 11+ II Да»[|
t
110 (Ay, Дс, Дw, t)\dx
о
^ II д>-1| + II Дс ft + II i
В силу непрерывности неособой матрицы F{t) норма
Ц/ДО F~x ("5)| ограничена во всяком конечном квадрате и,
следовательно (см. 4.10'), норма ||Ду— 8у |с является величи¬
ной более высокого порядка малости, чем | Ду||-|-||Дта;||-f-ЦДсЦ.
Этим справедливость формулы (4.7) для выбранной вектор-
функции §у(t) доказана. Далее всюду с точностью до вели¬
чин высшего порядка малости, чем величина р = ||Ду|| +
+1| ДдаI-J-! Дс||, будем заменять вектор-функцию Дy (t) вектор-
функцией 8у(£). Вектор-функцию SyOO называют первой ва¬
риацией траектории у (t,' щ, с,), а уравнение (4.12) — уравне¬
нием в вариациях.
3°. Вспомогательная задача
Будем считать, что 2 = 2 и функция w1(t) равна w(^i) при
t^>tx. Возьмем независимую вариацию bt. Будем также считать
функцию wl + Aw определенной на промежутке [0, тах{^,
^i + 8£}] и непрерывной в точке tx (непрерывной слева, если
«<0, и непрерывной справа, если Ы > 0).
Полагая Ы малым числом, можем написать
<Рг(У(*1 + 8^; П + Дс)) — ?/(y(^i. ®'i. П)) =
= у(У|))»(8y(^)-j-/(yi> «Д^ + ДтеД^), c,)W)-f О,».
Обозначим ■ = //, i — 0, ..., т. Теперь задача (3.15)—
(3.17) принимает вид: найти функцию Aw(t), число М и век¬
тор А с из условий:
а) ||Aw(*)IL Oi> ||^L<^ т<Ы (4-13)
б) hw (t)Щ (t) £ £ при * £ [0, max(^, + &£)],' функция
(t)Wi(t) непрерывна в точке tx (непрерывна слева, если
<0, и непрерывна справа, если Ы > 0);
в) имеют место равенства
+ wVJ+bwitJ, Cj)U = 0, i = 1, ..., т, (4.14)
в которых вектор 8у(£) есть решение системы в вариациях
(4.12);
г) величина
(*i) + /о/(+ь ® &) + (Д), с0 и (4.15)
максимальна.
59
Эту задачу назовем вспомогательной. Она является зада¬
чей выпуклого программирования. Для построения ее реше¬
ния можно применить методы последовательных приближений,
например, методы возможных направлений и методы, с по¬
мощью которых непосредственно отыскивают множители Ла¬
гранжа, соответствующие этой задаче. Через эти множители
несложно представить ее решение (см. главу IV, § 3).
4°. Квадратичная вспомогательная задача
Укажем случай, когда множители Лагранжа во вспомога¬
тельной задаче можно выразить аналитически, и решение
(приближенное) вспомогательной задачи представляется в явном
виде через решения и интегралы от решений так называемой
сопряженной системы. Для простоты будем считать, что
в исходной задаче А поставлено условие, состоящее в том,
что при всех допустимых парах (w, с) должно быть t(w, с) =
= Г>0. Это условие можно учесть, положив во вспомога¬
тельной задаче Ы — 0, tx= Г. Пусть вместо ограничений (4.13)
заданы такие неравенства:
т
ЦД«>(*)Р = J (Дw{t))2 nf, !! Дс[|2 = (Дс)* дс < vl (4:16)
о
Такая замена хотя и меняет само решение вспомогательной
задачи, но не меняет характера его: решения задачи при раз¬
личных значениях р1? р2 составляют множество подходящих
вариаций.
Пусть в условии б) вспомогательной задачи Q = ( — оо, со)
и b(t, Aw(t)) — b(t)kw(t). Исключим из левых частей равенств
(4.14), (4.15) вектор 8у(^). Для этого заменим вектор 8у(£,)
его представлением (4.12)'. Обозначим в получившихся инте¬
гралах вектор-функции [l*F(T) F~l (Щ* через Ф/(£). Нетрудно
проверить, чтоФ/(£) есть решение системы, называемой со-
df
пряженной к системе z =
h=~ (Wf*1’ = h, i = U m. (4.17)
T
Положим fo(t) = J^(x)rfx = ^
i= 0, ..., m. Теперь равенства (4.14) примут вид (8£ = 0)
т
q*Ac-\- j (т) Д-ге; (т) Л = 0, i— 1, ..., m. (4.18)
о
60
Условие г) перепишется так: величина
т
^оАс +1 °0 (т) Lw (х) dl (4.19)
О
максимальна. Теперь задача (4.16), (4.18), (4.19) может быть
решена методом множителей Лагранжа.
Возьмем пока неопределенные числа v0 > 0, v1? ..., vm.
Обозначим
m m
2 = Я\ 2 W (x) = aV(T)-
/=o ;=i
Умножая выражения в (4.18)—(4.19) на соответствующие числа v£-
и складывая их почленно, придем к задаче: найти максимум
суммы
т
q*Ac + j av (Д w (т) d'z
о
при ограничениях (4.16). Используя здесь результат приме¬
ров I б) и II б) из § 2, получим решение этой задачи. С точ¬
ностью до положительных множителей это решение таково:
Дс — kxql, Aw = &2av (т). (4.20)
Подставив (4.20) в равенство (4.18) и обозначив
г
Т/у = Я*Яр hj = j °/(х) зу(х)> dt, I, j = 0, m, (4.21)
о
получим линейную алгебраическую систему для множителей
^0 5 * • • 5 V/7l
m
2 (ftiT<7 + vy = °> f = 1, • • •, m. (4.22)
/=0
Для решения этой системы можно принять отношение ^ = k
заданным (это отношение определяется неявно отношением
чисел р,, jjl2; поскольку решением вспомогательной задачи
важно получить множество подходящих вариаций, то можно
считать отношение Pi/p2 априори не заданным и определять
его, фиксируя некоторое отношение &i/&2). Найдем решение
системы (4.22), положив v0 = l. Не умаляя общности, можно
считать, что уравнения в (4.18) линейно независимы, так что
определитель получившейся из (4.22) системы (определитель
Грамма) не равен нулю и искомое решение существует. Теперь,
когда решение системы (4.22) найдено, положим в (4.20)
К = ftp, ft2 = р, р > 0. (4.22)'
Как отмечалось в методе подходящих вариаций, решение
вспомогательной задачи нужно строить при сколь угодно ма¬
лых iAb ja2, чтобы была возможность остановиться на допусти¬
мом элементе, для которого равенства (4.3) достаточно точно
выполнены. Полученное решение (4.20), (4.22)' удовлетворяет
этой цели: уменьшая число ^ в (4.22)', можно удовлетворить
неравенствам (4.16) при любых значениях ^>0, [*2>0 и при
этом однажды найденные числа v0, ..., не меняются. Дру¬
гими словами, элементы (4.20), (4.22)' представляют собой
множество подходящих вариаций.
5°. Игольчатые вариации
Обратимся к вспомогательной задаче пункта 3°. Исключим
из рассмотрения параметры с, т. е. положим §£=0. Пусть
множество Sc/? ограничено и решена задача а)—г) без учета
ограничения Это решение можно получить сколь
угодно точно методами следующей главы (см. §3). Пусть при этом
найдены соответствующие множители Лагранжа v0, v1# ..., vm.
Укажем теперь, как построить множество подходящих ва¬
риаций.
Согласно определению множителей Лагранжа, задача а), в),
г) сводится к максимизации суммы
т
2 V*I8yi(*1)+/(J'; «'+*«'(*1), Щ (4.23)
на множестве всех управлений ££[0, max {^, + таких,
что ^(г1)-)-Aw(t)£Q, |«|<(х3. Как и в предыдущем пункте,
введением сопряженной переменной б (£)
т
■ = ^>=2 nh (4.24)
/=0
сумма (4.23) приводится к виду
jV(*W, bw{t))dt + r (ti)f(yi, w^Aw^bt. (4.25)
о
Теперь ясно, что для нахождения максимума (4.25) необхо¬
димо найти максимум подынтегральной функции (4.25) при
(почти) всех ^£[0, ty)
шах б* (£)(?(£, Aw). (4.26)
Aw + W^t) € 2
Обозначим значения Aw, на которых достигаются максимумы
(4.26) при различных t через Aw(t). В силу определения
вектор-функции b(t, Aw) будет b(t, 0)=0. Поэтому макси¬
мальное значение интеграла (4.25) неотрицательно.
62
Положим Дw (z^) таковым, что
Ф*(^)/(Уь ®'1 + Д«'(А)) — max ^*{tx)f(yь w),
w е 2
= p3-sign'!;*(z‘1)/(,p1, да1 + Дда(г1])).
Теперь построим такую вариацию Дда^), 8^» чтобы при всех
р£(0, 1) с точностью до величин высшего порядка малости,
чем I II “Ь Ш»- И~ II ДУи-II (A)V = y(*. Wi + Д^)— y{t, даО), вы¬
полнялись равенства
<Р/СУ(*1 + 8*и. Wi + ДтаУ)) = (1 — Iх) ?i (У (*i, ®i)) +
+ №(Ж + ^, ®1 + Д™)). (4.27)
i — 0, 1, m.
Для этого вариации Дда^ (t), Д^ выберем так, чтобы значения
функций в (4.14) и в (4.15) при разных р. отличались только
множителем р (с наперед заданной точностью). Понятно, что
при таких вариациях норма операции (4.5) будет равна нулю
с точностью до величины высшего порядка малости, чем
l|A®Vl|-M4*l + llAJVll. а приращение функции (4.4) будет_ поло¬
жительным, если (4.25) было положительно при Дге> = Д«у. Кон¬
струкция До^. определяется леммой § 3 следующей главы
(стр. 95). Вот она:
| Дw(t), если t£[sd, (s + t1)^);
Д®v(0—| Л ’ +г.\1г\,лн (4-28)
О , если £(i[(s + p)c?, (s+1)^),
h
d
s = 0, 1, 2, ..., ^, t£[tu ^ + 8^], Д®|1(0 = Дда(^1),
*€[*ъ ^i + ад.
Здесь d — достаточно малое число, вообще говоря, завися¬
щее от р (при d-*■ 0 равенства (4.14) будут выполнены сколь
угодно точно); можно считать, что -j — целое число.
Вариацию (4.28) иногда называют игольчатой. В качестве
можно взять
a^=p8f. (4.29)
Из (4.28) видно, что
||Ди;,,. (OKpft + h) max max (Ди;: Дда(0 + Щ (t) £ Q),
t е [0, t\
поэтому в силу ограниченности множества Q выбором ма¬
лого р норма функции Дда,*^) может быть сделана сколь
угодно малой.
Итак, множество вариаций (4.28), (4.29) при р£(0, 1),
является множеством подходящих вариаций.
Замечание. Если в задаче А равенства (4.2) отсутствуют,
то при построении множества подходящих вариаций ^w^(t)
можно не придерживаться конструкции (4.28). Ее можно за¬
менить, например, следующими конструкциями (t(w, £) = £,).
1. Возьмем произвольное число различных точек ^/£(0, tl))
i — 1, ..., s, в которых __
У (tj) b (//, Aw (£/)) >р sup [ф* (0 ^ (*v ],
'•|0'''1 />€(0,1),
и положим
Л*Л0=( 4”й) ”ри S> («O'
1 0 При ££(£/— (J-, 1 1, •••, 5.
При достаточно малом ц так построенная вариация .опреде¬
ляется однозначно, норма ее имеет порядок р, интеграл в (4.25)
положителен, если он положителен при Aw = Aw, и имеет
порядок малости pp.
2. Воспользуемся результатом примера II в), приведенного
на стр. 48 параграфа 2. Введем множество
со (v) — [t: ty* (t) b (£, Aw (0) ^ v* ^ 6 [0> ^i]}*
Считая meso)(v) непрерывной функние]^ 0T положим
ц£(0, со).
При р -> 0 норма || Awp. || стремится к нулю, и интеграл в (4.25)
Выше дана конструкция множеств подходящих вариаций
в точке (иъ съ ^). Пусть существует ненулевое решение вспо¬
могательной задачи (ненулевое в том смысле, что при этом
решении значение функционала (4.15) вспомогательной задачи
положительно). В конструкциях подходящих вариаций возьмем
достаточно малое р такое, чтобы норма операции х(и) в (4.5)
при w, + Aw„, * + Д^, + ^ была достаточно мала, а значе¬
ние функционала (4.4) „существенно больше“, чем его значение
в точке w = wx, c = cL, t = tv Положим w2 = Aw„ + wb
= ^1 + ^C,,, t2 = tx -f- Wu И при ^ = ^2» С = СЪ t = ВНОВЬ
решим вспомогательную задачу. Продолжая эту процедуру,
получим последовательность управлений {w*}, векторов {ск}
и чисел [tk). Пусть последовательность этих элементов выби¬
ралась так, что были выполнены условия а), б), в) теоремы 2
из § 3 (при этом условие г) будет также выполнено в силу
предположений о дифференциальных свойствах вектор-функции
/(У, с), функций <р* (у) и управления ^(г), если считать,
что||с*|)<с, при k=\y 2, •••)• Тогда имеет место и
имеет порядок меры множества «>
6°. Максимизирующая последовательность
64
заключение этой теоремы, которое в данном случае означает,
цто максимальное значение функционала вспомогательной
задачи стремится к нулю при всяком фиксированном р. При
этом из (4.25) следует, что по любому е > 0 найдется номер k0
такой, что если k > k0, то на промежутке [0, 4] будет
max &w)s^s (4.31)
A w + WfrityeQ
для всех 7£ [0, 7/,], кроме точек t множества меры порядка е.
Учитывая выражение (4.11)" для b(t, Дда) и обозначая
Я(ф, у, с, = w, с), неравенство (4.37) можем пере¬
писать так:
ск, !Wh(t))>max yk{t), ck, w) — e. (4.32)
W 6 2
Здесь (t) — решение сопряженного уравнения (4.24), соответ¬
ствующее паре ск), числу tk вместо tx и множителям
v0, vb ..., vft как решению вспомогательной задачи при w{=Wkf
С^ = Cfi, — tk.
Следствие к теореме 2 означает, что если w (t) — предель¬
ная функция последовательности [wk(t)), с—предельный век¬
тор последовательности \cht — предельная_точка последова¬
тельности {tk}, то для траектории у (t, w, с) при ££[0,_ t\
выполнены условия „принципа максимума4* (при этом (w, с)—
„почти44 допустимая пара: согласно, заключению а) упомянутой
теоремы 2 будет Цл: [и] || < lim-рЛ .
i —*• °о J
7°. Задача с ограничениями на фазовые координаты
Пусть в исходной задаче добавлено еще одно условие
? O'(ОКО, *6 [о, t],
где ср (у) — гладкая функция. Это условие приводит к добав¬
лению во вспомогательной задаче дополнительного соотношения
д) |^8У(0<0 при г?£3.
Здесь 3—множество таких чисел / £ [о, Д при которых
? (У\ (0)^0, в —достаточно малое фиксированное число,
которое должно меняться при переходе к новой вспомогатель¬
ной задаче. Пусть в* — значение этого параметра в в k-й вспо¬
могательной задаче. Для выполнения условий теоремы 2 ек
должно быть величиной более высокого порядка малости,
чем РЕ. Решение (приближенное) вспомогательной задачи
о условием д) может быть получено методом § 3 следующей
г л а вы.
5 Н. Е. Кирнн
ГЛАВА IV
МЕТОДЫ ОПТИМИЗАЦИИ В ПРОСТРАНСТВЕ УСЛОВИИ
В этой главе будут изложены некоторые методы решения
задачи II, поставленной в главе II (§ 2,2°). В основе этих
методов лежит связь двойственных задач, отмеченная теоре¬
мой 3 (гл. II, § 2,4°). Ниже будем считать, что условие тео¬
ремы 3 выполнено и решение задачи II существует.
Напомним постановку задачи II. В нормированном простран¬
стве U выделено множество М элементов и. На множестве М
определены функция X(и) и операция х(и) в нормированное
пространство X. Ставится
Задача 2. Найти максимум функции 'к(и) на можестве М
при условии х(и) = Ох.
Вместо задачи 2 предлагается решать другую задачу, тесно
связанную с задачей 2.
Последовательность элементов \ик), uk£M называется допу¬
стимой, если
II x(uk) ||->0 при kСО .
Множество допустимых последовательностей обозначается УН*.
Задача II. Найти допустимую последовательность
такую, что
lim X («"} ■ sup_ lim X(wh) == Х0.
С задачей II связывается другая экстремальная задача —
задача И*. Рассмотрим нормированное произведение пространств
Р — Р X X и в нем множество N= [р (и) = (Ми), х{а))\ и(*М}.
Пусть а! = (1, 0Х) £Р — орт вещественной оси ОХ в Р. Построим
задачу II для случая, когда точка X0d=/70 = lim/?(«£) является
ft-»- оо
„наивысшей“ (с наибольшим значением параметра X) точкой
пересечения вещественной оси Ок и замыкания выпуклой обо-
66
лочки множества N. Рассмотрим множество F линейных функ¬
ций / в Р
F={f:f-d> 0, зир[/-/7(«):и6^]^Р(/)<оо}.
Для f£F построим точку пересечения X*(f)d плоскости
= с осью ОХ. Координату этой точки
1*</)=-т5-. (*)
как функцию от функции /, назовем двойственным функцио¬
налом.
Задача II*. Найти последовательность {/*},/*£Атакую, что
lim X* (/j = inf X* (/) = X*.
ft-* °о /б F
Теорема 2 главы II гласит, что из существования решения
задачи II следует существование решения II*, при этом
Последнее равенство позволяет для построения точки р0 заме¬
нить решение задачи II решением двойственной задачи II*.
В конкретных алгоритмах решение задачи II*, как правило,
содержит и решение {и°} задачи II.
Отметим, что в этих алгоритмах в отличие от максимизи¬
рующих последовательностей, получаемых в методе возможных
направлений, элементы последовательности не обязательно
должны быть допустимыми, т. е. удовлетворяют не всем огра¬
ничениям исходной задачи 2 (*(#*) 0), а только части огра¬
ничений (u°k£M}.
Если решение щ задачи 2 существует и оптимальные зна¬
чения функционалов задач 2 и II равны, элементы будем
называть слабыми приближениями оптимального элемента и0
задачи 2, имея под этим в виду отношения
Х(й0) = НтХ(в°к), НтЦл: (и°)|| = 0.
Эти отношения можно переписать в виде
р(и0) = lim/7 («£). (**)
Здесь сходимость последовательности понимается по норме
пространства Р. Пространство Р будем называть пространством
условий задачи 2 (1Ь. Этим термином и характером прибли¬
жений оптимального элемента в (**) объясняется название
настоящей главы.
Ниже излагаются примеры алгоритмов построения решений
задачи II* (и задачи II), когда задача II* имеет своим функ¬
ционалом функционал (*).
Абсолютный характер сходимости этих алгоритмов основы¬
вается на выпуклости функционала (*) на плоскости
f'd — const > 0.
5* 67
В § 1 приводится условие, при котором функционал (*)
имеет производную (условие регулярности), и формулируется
метод наискорейшего спуска для решения задачи II*. В § 2
дается более общий метод, основывающийся только на воз¬
можности построения оценки верхней границы
P(/) = supJ/-p(«):»€M}.
В § 3, 4 указываются приложения общих алгоритмов к реше¬
нию задач построения оптимальных программ в системах регу¬
лирования, описываемых дифференциальными уравнениями.
§ 1. ГРАДИЕНТНЫЕ МЕТОДЫ В ДВОЙСТВЕННОЙ ЗАДАЧЕ
В этом параграфе будут выяснены условия, при которых
функционал двойственной задачи IP имеет производную, и на
основании этой производной сформулирован метод наискорей¬
шего спуска для решения задачи II*.
1°. Свойства двойственного функционала
Сначала изучим свойства функции
Р (/) = sup (/{р) :p£N\. (1.1)
Как было определено в § 2 главы II, функция Р(/) определена
и конечна в каждой точке множества Fa Ф (Ф — нормирован¬
ное пространство непрерывных функций /(/?)).
Лемма 1. Пусть функция Р(/) определена и конечна
в точках fu /2. Тогда она определена и конечна на отрезке
[/„ /*] и является выпуклой функцией на нем.
Проверка. Возь.мем точку А —(1 —р)Л+р/2, р-€ [0» !]•
Пусть
lim A (Pi) = Р (Л).
оо
Переходя к пределу в неравенстве
А(л) = (i — p)/i(a) + kA(a)<(i — А Р(Л)-1-рР(Л).
получим требуемое
Р(АХО-1-) Р (Л) + (h) < «• (i -2)
Следствие. Множество, где функция Р(/) определена
и конечна, выпуклое, и функция р (f) — выпуклая функция
на нем.
Лемма 2. Пусть функция р(/) определена и конечна
в точках /', /". Тогда функция <p(ji.) = p (/'-|-[а (/" —/'))
непрерывна на интервале О < 1.
Проверка. Согласно лемме 1, функция <рА) определена
и конечна на интервале (0, 1). Возьмем произвольное число
fi0£(0, 1). Пусть s > 0 — достаточно малое число. Полагая
в неравенстве (1.2)
68
f*=f' + (H + *)(r-f), «* = 4-*
получим
[*0*0 — e) + tP(lAo + s)]. (1.2У
Устремляя здесь е к нулю, будем иметь
<рЫ<4[ llin <p(f»0 —е)+ lim <p(|i0 + e)]. (1.2)"
L U-+0 e— -hO J
С другой стороны, если в (1.2) положить /i =/'+ (*о(/" —/')»
(j. = ei f2=f" и /2“-/' и устремить е к нулю, то получим
при е = е(1 — р.0) и e = eji0
Jim <р ((*0+-8)<?Ы и Jim <р (р0 —e)<9(l*o)- (1.2)"'
е -*■ +0 е -> +0
Очевидно, неравенства (1.2)" и (1.2)'" совместны только в слу¬
чае, если
lim ср (jx0 — е) = ср (1Ац) = Ит ср ([х0 + е).
е-*ф0 £-*-+0
Остается заметить, что
ср+ = lim ср (у0 — е) = lim ср (|Л0 + s) = ср-.
е-° 6-0
Действительно, неравенство ср+>ср- означало бы существование
таких (для определенности положительных) чисел 0<е'<[е'/<е"/,
что
ср = max (ср ([Х0 + е'), ср (fi0 + е'")} < <Р (p-q + е").
Но, в силу выпуклости функции cp(pi) должно быть
<Р (1*0 + е") < Е т (н-о + О + ■ 1~_? (1*0 + в"') < ?.
Лемма проверена.
Условие регулярности. Будем говорить, что в задаче
11—11* выполнено условие регулярности, если для любой
функции /G/7 всякая последовательность, реализующая
sup \f(p) -Р G W}, сходится в себе.
Из условия регулярности и полноты нормированного про¬
странства Р следует, что существует единственная точка р'
(обозначим эту точку р' через р (/)) такая, что
f(p (/)) = sup/(/>). (1.3)
peN
Далее будем считать, что N = N.
69
Признак регулярности. Предположение замкнутости
множества N означает также, что существует элемент
и'£М такой, что p(f)=p(u') Будем обозначать этот
элемент иг через u(f). Единственность u(f) естественно
является достаточным, но не необходимым условием для
выполнения условия регулярности.
Теорема 1. Пусть условие регулярности выполнено, и
точки а£[— а, а], а>0 принадлежат F. Тогда
в точке / существует производная функции р (/) по направ¬
лению q:
,„M±^sWI=,(p(/)). (,.4)
Доказательство. Существование правосторонней про¬
изводной функции ср (а) = р (/-Ьа<7) следует из выпуклости этой
функции [36]. Наша задача установить представление (1.4)
для ее производной.
Пусть /а = /+ <*q. Обозначим p(fa)=pai aG [О, aj. Согласно
определению (1.1) функции Р(/) и определению точки р (/)
(см. (1.3)), имеем
Р (/+ ая) = f(pj + уя (Ра) > f {р0) + аР (р0) • (1.5)
I. Убедимся, что ра->р0 при а-> 0. Предположим, что
ра-/-+ Р0 при а-> 0. Тогда существуют число е>0 и последо¬
вательность чисел {a,.}, az>0, af. -> 0 при /-> оо такие, что
|/70 —ра |>е. Поскольку функция Р(/+а<7) непрерывна по a
при а = 0 (лемма 2) и f[pa) < В (/) =f(p0), то, переходя
к пределу в (1.5) при а = а,-» 0, получим
/(р„) < Йт/(Л,) + Й™ аП (AJ- (1-6)
В силу условия регулярности и неравенства ||/?0 — ра_ || > е, при
некотором 5 > 0, будет
/(A)</(A.)-S- (1.7)
В самом деле, если бы при любом 8у>0 нашелся номер у,
при котором f(pa^>f{Po) — bj, то это означало бы вместе
с неравенством /(Я) >/(Д,у). что /(р ) jjz^fiPo), т. е. по¬
следовательность^} реализует Р(/). Но по условию регу-
лярности такая последовательность должна сходиться к /?0, что
противоречит неравенству Ц/?0 — /?а.| > е > 0. Теперь, учитывая
(1.7) в (1.6), заключаем, что lim a;-<7 (ра) > о > 0, т. е. сущест-
/ -»- оо \ у/
70
вует подпоследовательность номеров {s} с {/) такая, что
asq[pa )>-2“>0- Из чисел as, s оо выберем последователь¬
ность чисел х? так> чтобы было при г^О. Тогда,
as
переходя к пределу в неравенстве
Р(/+ТЛ) >/(Д) +™(P't)=f(P'S) + ^(<w (ks)) =
=Hf+w)-w(kt) W) =
= P (/+ M) + M ( К) (тг -!) > P (/+ ^) + 4 (V -!)
получим 0>-(-co. Из этого противоречия заключаем, что
рй -*Ро ПРИ а^°-
II. Вычитая из (1.5) почленно равенство р (/) =/(Д,) и деля
полученное равенство на а, получим
+ = + ^ (18)
Убедимся, что
f(Pa)—f(-Po) п п /л м
— —1 > 0 при а -»• 0. (1.9)
Предположим, что
ш /(Л)-/(А) = 1|m/(P-.)-/W=a_
п а а
а-0 а-*0
Поскольку f[pa) <f[Po) , ТО ДОЛЖНО быть а+^0. Но из (1.5)
следует, что
/(Р«)~/>Р.!. > д (Д0) _ д (Л). (1.10)
Так как функция q(p) непрерывна и ра -> /?0, то переходя
к пределу в (1.10), получим Следовательно, а_=а+=0,
и соотношение (1.9) доказано.
III. Для доказательства представления (1.4) остается перейти
к пределу в (1.8). Теорема доказана.
Следствие. Пусть выполнено условие регулярности и / —
внутренняя точка множества F. Тогда для любой функции q
нормированного пространства Ф найдется число а>0 такое,
что f-{-oiq^F при а^[—а, а]. Теперь для любой функции q
(1.4) можно переписать так:
■я=я(р(Л), О-11)
да ел
df
Т. е. функция Р(/) имеет производную (Гато) в точке /.
71
Будем говорить, что функция (3(/) имеет производную
(Гато) по множеству F в точке /, подразумевая под этим
справедливость соотношения (1.4) для всех функций <7£Ф,
удовлетворяющих условиям теоремы 1. Теорему 1 перефор¬
мулируем теперь следующим образом: функция (3(/) имеет
производную (Гато) по множеству F. Эту производную будем
записывать в виде (1.11), имея в виду, что в (1.11) рассматри-
ваются_только функции q, для каждой из^ которых при неко¬
тором а> 0 б\ дет /+ 'ЯЪ.Р при о. £ [— а, а].
Обратимся теперь к функционалу Ь*(/) задачи II*. Рас¬
смотрим случай, когда множество F есть множество в про¬
странстве Ф линейных функций fif'd > 0) и функционал двой¬
ственной задачи имеет вид
Нетрудно проверить, что множество F— открытое выпуклое.
Считая, что f-{-a-q£F при а-> 0, с помощью (1.4) продиффе¬
ренцируем по а функцию ^*(/+а<7). Это приводит к следую¬
щему предложению.
Теорема 2. Функционал (1.12) имеет производную (Гато)
по множеству F
Здесь <7—линейная функция такая, что существует число а>0>
для которого ПРИ аб[—а> <*]•
2°. Метод наискорейшего спуска в двойственной задаче
Будем рассматривать задачу II* для функционала (1.12).
Основываясь на производной (1.13) можно сформулировать
методы спуска для построения минимизирующей последователь¬
ности функционала Х*(/). Сформулируем метод наискорейшего
спуска для решения задачи II*.
Под методом спуска для минимизации функционала X* (/)
понимается метод подъема для ммкеимизации функционала
— ^* (/). Методы подъема (методы подходящих направлений)
были изложены в § 2 и 3 предыдущей главы.
Ниже будем читать, что N — ограниченное множество.
В этом случае для любой линейной функции /£Ф верхняя
граница Р(/) конечна, так что множество F совпадает с полу¬
пространством /-rf>0 и является открытым множеством.
Направлением наискорейшего спуска в точке /С/7 функ¬
ционала а*(/) является такая непрерывная функция qf из про¬
странства Ф = Я*, что
(1.12)
d\*(f)
df
72
или, с учетом (1.13),
?)(£(/)-*>*(/)<*) = mlnq-(p(f) — \*(f)d), (1.14)
II?,11=1.
В частности, если Р — гильбертово пространство, то минимум
(1.14) существует, и поскольку элементы пространств Р и Р*=Ф
отождествляются, то
4f= p{f)\c, о = \)* f)d~p{f)l\ (1.15)
Если решение задачи II существует, то, как было показано
в § 2 главы II, функционал X* (/) ограничен снизу на F'X*(f)^\y
так что для f£F
inf X* С/+а<7) >Х0. (1Л6)
feF
Теперь опишем операции, выполняемые на одном шаге
метода наискорейшего спуска. Предположим, что в каждой
точке f£F существует направление наискорейшего спуска qf
функционала л*(/). Зададимся последовательностью положи¬
тельных чи>*ел \ek\f в£>0, гк -> 0 при &-*оо. Пусть после к
шагов известен некоторый элемент /*£/% ||/л[|=1. Операции
к-f- 1-го шага метода таковы:
I) найдем точку pk = p(fk), согласно формуле (1.3);
II) вычислим = к* (/*» =fk-Pk(fk'd)~l (см. (1.12));
III) построим направление спуска qk = qfk\
IV) положим fa=fk-\-oiqk и найдем а>0 такое, что
Л и *■*(/;)< inf ^*(/a) + sft;
f**F
a>0
V) положим
/ = (’если х* ^ ^<
1л, если X* (/-) > 1-*(Л)
и перейдем к следующему шагу.
Таким образом, выбирая в качестве /, произвольную функ¬
цию из F, можно построить последовательности |pk\,
(Л)- Будем считать, что одновременно построены и элементы
uk = u(fk) такие, что p{u(fk)) — pk. Приведем без доказатель¬
ства достаточные условия, при которых последовательности
(ЛЬ \uk\ являются решениями соответственно задач II*, II.
Теорема 3. Пусть Р—гильбертово пространство и реше¬
ние задачи II существует. Будем считать выполненным
расширенное условие регулярности: для любой функции /фОр*
из замыкания F множества F будет р(/) < со и сходи¬
мость последовательности (Р(/) — /(Л)Ь=1> влечет
°ходимость последовательности \pi\- Тогда последователь-
73-
поста (X.*), \fk\, [pk\, \nk\> построенные согласно операциям
I—V описанного выше метода, таковы, что если последова¬
тельность [pL\ ограничена, а последовательность {/£} ком¬
пактна, то:
1. X^->X0-f-0 при &->oo, \fk)—решение задачи IP,
2- ||Pk ““Mil 0 при &->оо, [uk\—решение задачи II.
В приведенном алгоритме можно ввести модификации,
указанные после теоремы I, параграфа 3, главы III.
Подчеркнем, что ограниченность множества /V, предполо¬
женная выше, не является необходимым условием сходимости
приведенного выше алгоритма. Приведем пример, когда
несмотря на неограниченность множества N для подпоследова¬
тельностей [pk\, \lk\, построенных по описанному выше алго¬
ритму, имеет место сходимость, указанная в заключении
теоремы 3. Рассмотрим следующую задачу выпуклого програм¬
мирования: найти
max (Х0 (_v): \ (у) ^ 0, г = 1, ...,от). (1.17)
Здесь Му) — гладкие строго вогнутые функции, определенные
в конечномерном пространстве Rn векторов у = (£ц ..., Ея)
и такие, что
Л(У) — 00 при IIУII-* °°, i = 0, 1, ..., от. (1.18)
Для приведения этой задачи к виду задачи 2 положим и=(уу v)y
где г>== (г>ь ..., vm) в V=[v = (vt, ..., vj: i= 1, ... от);
М =Rn X V; Х(и)=\(у); х (и) = (Хг (у) - <?,)“,.
Будем решать полученную задачу 2 приближенно, положив
т / т \
X (и) = Х0 (у) + е0 2 г»2, х (и) = |^..., \ (y)-vt -f- е, 2 v), ...j;
здесь е/<0, / = 0, ..., т достаточно малые числа.
Используя известные результаты математического програм¬
мирования [31, 44] или прием, аналогичный приведенному на
странице 23, основанный на построении функций 4, можно
установить, что в качестве множества F, удовлетворяющего
условию В теоремы 3, параграфа 2, главы II, можно взять
F=[f = (v о, v„ ..., vm) : v„ > 0, v^O, /= 1, 2, ..., т\.
Выполнение расширенного условия регулярности обеспечи¬
вается тем, что верхняя граница
У** S
VG V
т
4- £ W
/ = 1
j-1 _
достигается (вследствие (1.18)) и в единственной точке
(У (/). • ••> vm(f)) ^вследствие строгой вогнутости функ-
74
ций М.У) и условия 2IV/I^° • Компактность последователь¬
но /
ности F следует из конечномерности векторов / и ограничен¬
ности их совокупности. Нетрудно проверить также ограничен¬
ность соответствующей последовательности векторов pk, по¬
строенных по формулам I—V приведенного алгоритма.
Доказательство теоремы 3. Предположим, что ПРИ
> оо. Тогда учитывая оценку (1.16) и невозрастание после¬
довательности {Хл| заключаем, что существует ПтХл = Х'>Х0.
к-*°о
Это влечет за собой соотношение
1 /?ft — >[j -/-> 0 при £-5-00. (1.19)
В самом деле, если — X0d|| 0, то qk-d = (lkd — ph) X
X dI^kd — pk||-1 -»■ 1. Учитывая это в неравенстве fk+\-d>
> min [fk'd, qk-d\ (см. операции IV, V), заключаем: \lm fk-d=.
k^O
= a>0. Теперь получим: Хд, = (fk'Pk){fk'd)~l -> X0, что про¬
тиворечит предположению В силу компактности
последовательности {/*|. Найдется подпоследовательность номе¬
ров |/( последовательности номеров \к\ такая, что существует
предел lim/, =/'. Не умаляя общности можно считать, что либо
/->ос
lim/-d=0, либо lim/.-rf>0. Рассмотрим первый случай. Убедим-
ОО I* оо
ся, что последовательность чисел {Р {f)—f-Pi} сходится. Дейст-
вительно Hf')>f'-Pi=f-P'+ {f -fi)-(Pi — p') + fr(P-P')>
't^§{f)—\f'—fi\‘\Pi — P'\- Поскольку {/^ — ограниченная
последовательность, то здесь второе слагаемое в правой части
стремится к н\лю, что обеспечивает требуемое. Так как /'£/%
то по расширенному условию регулярности pt р'. С другой
стороны,
/' -р, = (/ - /,)-р,+/,• д - (Г - /,)•/>, + /,-М “ (/' - п-р, +
+fi'Po + (\ — \) fi'd I.
Так как первое и последнее слагаемое стремится к нулю, то
f'-p'=hmf-p, — \ixaf-p0. В силу расширенного условия ре-
I— оо I оо
гулярности и принятого обозначения \d = /?0 это означает,
что р' = р0 и ||/^ — X0d|| -> 0. Но это противоречит соотношению
(1.19). В случае limfpd >0, так же как и в следствии леммы 1
i-f оо
\дНА)
i-o| V
ствие (1.15) ||/?f — j| -5- 0, чего не может быть: h'd£N. Пред¬
положение соотношения приводит к противоречию.
параграфа 2, главы III должно быть lim
= 0, т. е. вслед-
Этим заключение 1 теоремы доказано. Второе заключение
теперь следует немедленно, ибо как и выше для всякой пре¬
дельной точки f последовательности (/*} будет Po==P(ff) и
f ■p0 = \im.fi-pi. Но в силу расширенного условия регулярно-
i— оо
сти это может быть лишь в случае р.->р0 при /оо. Тео¬
рема доказана.
§ 2. МЕТОД РАЗДЕЛЯЮЩИХ СФЕР
1°. Общая схема метода
Будем решать задачу II, считая, что решение ее сущест¬
вует. В качестве множества двойственных переменных возь¬
мем однопараметрическое множество
Ф = {/х(/»)=-И-^11}хв(—,+-)• (2-1)
Как установлено в § 2 главы II, для этого множества
выполнено условие В, достаточное для выполнения соотношения
Х0 = X* infX* (/*)> (2.2)
X > Х0
где
X* (/*) = X + р (/х) = \ — inf {II Id — р II: р б N\. (2.3)
Соотношение (2.2) обеспечивает получение сколь угодно точ¬
ного приближения числа Х0 построением приближений нижней
грани X*, указанной в (2.2). Приближения числа X* можно
строить по следующему алгоритму. Возьмем некоторое число
xi > Х0 в качестве начального приближения числа X*. После¬
дующие приближения Хл+1 строятся по предыдущим прибли¬
жениям X*, k= 1, 2, ..., так.
I. Найдем расстояние pft от точки bk = \kd до множества N.
II. Положим \+i =\ — Pk- Геометрическая интерпретация
этого алгоритма дана на рис. 5, а. Последовательность (Хл}
можно также задать реккурентным соотношением
Ч*, = Ч + Р(А0’* = '. 2 (2.4)
Теорема 4. Если решение задачи II существует, то по¬
следовательность (2.4) такова: >£ -> X* - Х0.
Очевидная проверка справедливости теоремы 4 фактически
содержится в проверку выполнения условия В для подмно¬
жества Р= {/х(/?)'Д > X} функций из (2.1). Эта проверка была
приведена в § 2 главы II.
Следствие. Если последовательность элементов {^А}>
ик£М такова, что
I у*-/>(«*) И о,
то — решение задачи II. Здесь {Хй) — из теоремы 4.
76
Практически такие элементы uk содержатся в построениях
по формуле (2.4). Это — прообразы точек р{и), реализующих
(возможно приближенно) расстояние от X&d до N.
Основной операцией сформулированного метода является
нахождение расстояния от точки до множества. Это самостоя¬
тельная экстремальная задача, правда, содержащая меньшее
число ограничений, чем исходная задача II. Понятно, что эту
задачу не нужно решать
точно на каждом шаге.
Процесс приближений
точки точками мно¬
жества N можно прекра¬
тить сразу же, как толь¬
ко будет получено число
Х'£[\), М* После этого
нужно положить >^+1 = //.
Примеры таких модифи¬
каций алгоритма (2.4) и
будут приведены ниже.
2°. Алгоритмы
Пусть N — выпуклое
ограниченное множество
в гильбертовом простран¬
стве Р. Предположим, что
имеется некоторый метод
последовательных при¬
ближений для решения
задачи нахождения рас¬
стояния от произвольной
точки оси ОХ до множе¬
ства N. Если Х^ > Х0, то
из определения числа Х0
следует, что £ N. Если
теперь точка P^N яв¬
ляется достаточно близ¬
кой к \^d (по сравнению
с другими точками из /V),
то, как было показано в
Доказательстве теоремы
об отделимости (глава I,
§ 3), линейный функцио-
нал frP, где f. = \hd —
PL, определит опорную
плоскость, разделяющую
fK=\Kd-pK
Рис. 5.
77
точку Ikd и множество N, т. е. будет
(2.5)
Из (2.5), в частности, следует, что fi-\d>fi-\d, поскольку
\d£M. Это соотношение дает (Xft —Х0)fl-d^>0, откуда/f-d> О
и, следовательно, f-^F. Убедимся, что X* (/.) d — точка пере¬
сечения оси ОХ и опорной плоскости fi-p = $[fl) — лежит „ни¬
же" по оси ОХ, чем точка Xftd. Действительно, из (1.15) и Д.5)
имеем
Следовательно, число X* (/;) является более "точной оценкой
Х0, чем число Xft, и его можно взять в качестве следующего
приближения Хй+1.
Итак, если имеется способ построения последовательности
точек PL£N, i = 1, 2, ... , реализующих расстояние от ХЛо( до
N, то за конечное число шагов будет построен функционал
/(., для которого
Теперь возникает задача построения последовательности
{/?.}. Если для каждого линейного функционала / известен
алгоритм построения одной из точек р (/) £ N, реализующих
верхнюю границу Р(/), то можно указать метод последова¬
тельных приближений для решения задачи минимизации рас¬
стояния от точки до выпуклого множества [12, 42] (см. также
гл. III, § 2). Приведем алгоритм решения задачи II, каждый
шаг которого состоит из одного шага в задаче минимизации
расстояния по упомянутому методу и проверки неравенства (2.6).
Пусть перед началом k-ro шага построены элементы: число
Xft > Х0 и точка pk£N. Опишем операции, выполняемые на k-м
шаге (см. рис. 5, б).
I. Вычислим функционал fk = \hd—pk.
II. Найдем точку опоры p{J^ = p плоскости fh-p = Р (/ft)
на множестве N.
III. Если fk'd> 0, то найдем точку №(fk)d пересечения
плоскости fk9P = $(fk) с осью ОХ
и положим Х^+1 = min {X*, X* (/*)}. Если fk'd < 0, положим
(2.6)
Алгоритм А
(Л)=Р (Л) (Л -аУ1 = Л-Р (Л • аУЛ
IV. Найдем расстояние от точки )^+\d до отрезка [рк> р\-
Точку, которая реализует это расстояние, обозначим рк+1.
Она определяется формулой
Pk+i = VP+ (1 -v-)ph, (2J>
где
- IГ" „ • (W-Л
V- = рЛ если и-6 1°’ 1]’ V- =-л-т= ГТ^ ч—;
10, если р' < 0. \р рм\Р Рь)
Теорема 5. Пусть решение задачи II существует. Тогда
для последовательностей элементов {phj справедливы
отношения:
a) Xfe —» 0; б) pk -+р0 при k оо.
Доказательство. Поскольку в операции III определено
Xft+1 = min {V X* (Д)}, то последовательность jX^J не возра¬
стает. Кроме того, она ограничена снизу числом Х0, которое
существует в силу предположения в теореме о существовании
решения задачи II. Ограниченность последовательности {Х^}
проверяется индукцией так: — по выбору по опре¬
делению двойственного функционала Х*(/^)^Х0>_ отсюда
xft>xh+i = min {К Х*(Л)) >хо- 2* ••• •
Итак, существует
limXfc = x'>X0. (2.8)
Л-*- ОО
Убедимся, что хотя бы одна подпоследовательность \pj\
последовательности |/?Л} реализует расстояние от точки X'd
до множества /V, т. е., что
lim || Vd - pj || = inf {I Vd - p ||: p £ N) = p'. (2.9)
k->-oo
Предположим, что (2.9) не имеет места, т. е. существуют
число 8>. 0 и подпоследовательность {p.} последовательности
{/>*}> для которых
lim — рЛ = р' + 8 = inf I!/?ft — Vflfj. (2.10)
i-»- oo k
Пусть p£N точка, для которой \^'d — р\ < р' + • Будем
рассматривать столь большие номера г, для которых ||X'd -^||>
7
>р' + —о. Рассмотрим функции, равные квадратам расстоя¬
ния от точки k'd до точек отрезков [/ь, /?],
о. (ц) = I I'd -Р1-г{р- Pl) If, (X G [0,1 ].
73
Поскольку это выпуклые гладкие функции, то
dij (»
d\i
ii=p.-
и, в частности, при ^' = 0, ц" = 1 бу ает
d\i
^<аД1) —о.(0)<р'+ -I_S_p'_ -Ls = 48- (2.11)
Учитывая представление нормы через скалярное произведе¬
ние, имеем
а. (ц) = (;K'd — pt —v- (р—Р^) • (У -pt-p(p-Р^),
Теперь, принимая во внимание (2.11), получим
- 2(k'd-р^- [р-PiX,- -|-8
или, при достаточно больших /,
(М ~Pi){p-Pi)>jQb-
Отсюда
sup (\d —Pi) [р —Pi) > 4-8.
peN lb
Будем здесь считать, что всем величинам в операции IV
присвоены индексы номера шага. Теперь, согласно формулам
операции IV, при достаточно больших номерах i получим
, . = (х«+1 d~Pj) (Pj-Pj) ^(h+x -\)d-[P,-P,) , 5$
‘ (Pi-pi)(Pi-Pi) ^ \\Pi-Pi\\' i6||рг-Pif ‘
Поскольку множество N ограничено, то ||р—pt ||<(г<;со; кро¬
ме того, jjpi—р^^аУО и Х.+1 — Х; 0 при гоо, так что
при достаточно больших i будет р/ > — “Г * Теперь очевидна
справедливость неравенства
II ы+xd—Pi — \н (Pi —/7г) II2 = i h+xd — PiII2- 2tx/Vi \Pi —Pi 1Г +
+ (Pif II Pi — Pi IP = II h +xd—Pi I3 - p? 1 pi—pif <
<\\h+xd—Pi I2 —T5tV (2-12)
Согласно определению числа |Аг в формуле (2.7), в силу того,
| g ,
что p’i^-j- 72 >° р1-/-+°° при i-> со, будет ц* > О, [*/< у«,
—7- -/> 0 при i-y 00.
Pi
80
В силу выпуклости нормы имеем, с учетом (2.12),
1:К ♦-р,+, Г < (1 —f) II:\ «<* ■- р> Г +
+ # I \+,d-pt - р; (Я - f < 1 \+id~Pi Г - й 4" •
Pi
Перейдя здесь к пределу при /-> оо, получим
Иш ЦХ^—/7.+1|2<р'4-8,
г-»»
что противоречит определению числа р'-|-8 в (2.10). Следо¬
вательно, сделанное предположение противоречиво и суще¬
ствует подпоследовательность {р}\, реализующая расстояние
(2.9) от Vd до N.
Предположим теперь, что в (2.8) X'> Х0. Возьмем под¬
последовательность \pj), существование которой только что
показано. Используя неравенство (2 6), в котором число Xft
следует заменить на X', получим Х*(/;.) < У, что, с учетом
монотонности последовательности (Xft), дает Х*(/у) <Х'<;Х;..
Тогда, согласно операции 111 алгоритма А, должно быть
Xy+1 = min{Xy, X* (fj)) = Х* (fj) <Х'. Но это противоречит моно¬
тонности (Xft). Следовательно, в (2.8) Х' = Х0. Этим утвержде¬
ние а) теоремы доказано.
Докажем утверждение б). Убедимся, что последователь¬
ность чисел
v* = l|Xo^ Xft+1rf||-f-||Xft+1cf Pk\i k=\, 2, ...,
монотонно убывает. Действительно, поскольку на каждом
шаге число р* в операции IV выбирается' так, чтобы точка
pk+1 из всех точек отрезка [pk, р\ была ближайшей к точке
K+1d, то ||X*+1d— A+1|K|Xfe+1af—pk\\. Теперь имеем
Д ^ II \d — Xft+2rf I -f-1| Xft+2d — Xft+) d || Д-1| Xfe+1rf—P k+\ II ^
>1| >-0d — Xft+2d || Д-1| Xmrf — pk+i I = vft+1.
Выше доказано, что хотя бы одна подпоследовательность {pi\
сходится к точке yd = K0d. Очевидно, для этой подпоследо¬
вательности V,- 0, что вместе с монотонностью последователь¬
ности (v;) дает следовательно
/blfcZSO.
Теорема доказана.
Замечание 1. Нетрудно видеть, что подпоследователь¬
ность функционалов {/;} последовательности {/*}, для которой
Х;+1 = X* (ft), есть решение задачи II*.
Замечание 2. Пусть число Р(/Д вычислено в операции
II с точностью до ek > 0. Тогда для того, чтобы было Xft+1^X0,
в операции III вместо Xft+1 = min{Xft, Х*(/А)} следует брать
6 Н. Е. Кирин
^A+i = mln|^A> (fk) + jk,Д | • После такой замены сходимость.,
О при
указанная теоремой 5, будет обеспечена, если -~j
k -> со. Это замечание относится и к последующим алгоритмам.
Опишем теперь более общий алгоритм, используя в алго¬
ритме А метод нахождения расстояния в более общей форме
(см. методы возможных направлений, § 3, гл. III).
С каждой точкой p£N свяжем
некоторую окрестность ее S(p)
(см. рис. 6). В задаче нахождения
расстояния от Ы до N, которая
эквивалентна задаче минимизации
функции
?UP) = ±-W-pf=
= -^{M — p)-(ld — p), (2.13)
направление спуска у0—р опреде¬
лим через решение следующей
задачи: найти точку _Уо€5(/>)П^
такую, что
ар* О»)
др
"Уо
= min |-
т (р)
др
X
X у (p)r\Nj , (2.14)
или, с учетом (2.13),
(Id—р)-у0 = шах {(Xd—р)у :
:yeS(p)nN}. (2.15)
Теперь в качестве следующего
приближения точки минимума
Рис. 6. функции (2.13) возьмем точку из
отрезка [/?, у0], ближайшую к М.
Для получения оценки числа Х0 можно поступить так.
Предположим, что известно множество, содержащее точку /?0;
тогда, очевидно, всякая опорная плоскость к нему пересекает
ось ОХ в точке, лежащей по оси не ниже, чем точка \d, если
линейный функционал /—нормаль плоскости — удовлетворяет
условию f-d^> 0. В качестве нормали / такой плоскости возь¬
мем f=kd—/?, если f-d^>0, а множеством, содержащим
точку /?0, будет множество /7 + v{S{p)C\N — р}, где v — доста¬
точно большое число (такое v заведомо существует в силу
ограниченности множества N). При этом свободный член опор¬
ной плоскости обозначим р(Х, /7, v), так что пересечение ее
82
f-d
X — р-а
Считая, что число v для каждой точки р определяется, при¬
ведем формулы алгоритма для решения задачи II* с учетом
указанного метода нахождения расстояния.
Алгоритм В
Пусть построены число и точка pk£N.
I. Составим разность Л = ^—Pk и найдем точку у0, как:
решение задачи (2.15) при X = Р = Рь ^(p) — Sk(pk). За¬
фиксируем числа Та = (М — Рк)'Уо, = Рь va)-
II. Если fk-d=(Kk—то положим ХА+1-—Х^,. Если
fk-d> 0, тогда вычислим X' = <ok (А-^)-1 и положим Xft+1=-
= min{Xft, X'}, если точка у0 не внутренняя точка множества
S(p)- Если у0 — внутренняя точка множества S(pk), (Л*^>0),
то положим Х&+1 = тт{ХЛ, Х'# ^}.
III. Найдем pk+l как точку на отрезке [pk, у0], ближайшую
к точке h+id. Она вычисляется по формуле (2.7), где следует
заменить р на у0. Перейдем к следующему шагу.
Замечание 1. Для справедливости теоремы 5 относи¬
тельно построенных по алгоритму В последовательностей
{ХД, \Pk\ окрестность S(p) = Sk(pk) не должна стягиваться;
в точку быстрее, чем \pk—/?0|—>0 при &->оо. Поскольку точ¬
ка Ро — неизвестна, то норму jpk—р01| ^ожно оценить, заменив
точку р0 на точку X^d. Укажем достаточный признак для
выполнения этого необходимого условия сходимости.
Пусть rk — радиус сферы, которая целиком находится
в Sk(pk), с центром в точке pk. Тогда для сходимости метода
указанной теоремой 5, достаточно, чтобы было rk-\\kd —
— Pk 1Г17^ О ПРИ k со.
Замечание 2. Поскольку точки р множества N пред¬
ставляются в виде р{и), и£М, то в задаче (2.15) надо также
иметь в виду, что у=у{и). Пусть М — выпуклое множество
в полном нормированном пространстве U и р(а) — непрерывно
и равномерно на М дифференцируемая операция. Пусть G(u) —
окрестность точки и такая, что
S(p(u))<Zd-^-G(u).
Тогда задачу (2.15) заменим построением элемента <706:
6Mf\G(u) такого, что
Ы —р (и))• • q0 = шах {(Х</—р (и))• д-^~-q:q^Mf]G(м)| ...
Оценка (2.16) сохраняется, если р{и) — линейная операция.
Часто в практических задачах получение точек р{и) по
элементу и сопряжено с большими вычислениями (например,
6*
интегрированием больших систем дифференциальных уравне¬
ний). В таких случаях на k-u шаге целесообразно использо¬
вать точки Pi (i^k), полученные на предыдущих шагах для
построения точки pk+v Их, например, можно использовать
для лучшего определения расстояния от точки \d до мно¬
жества N. Опишем шаг такого алгоритма.
Алгоритм С
Пусть в N известны точки р\, р\, ... , psk.
I. Рассмотрим выпуклую оболочку точек \р1к)8._х
S S
P—^jdPiPk’ (2.17)
i=l 1 = 1
и найдем расстояние от точки до этой оболочки. Пусть
оно реализуется в точке р.
II. Составим вектор fk — ^kd—Р и> как в алгоритме Л,
найдем Pfc = sup \fkP-P£ Щ и точку p(fk) такую, что Д X
хр (fk) = h-
III. Выберем ^+i так же, как в операции III алгоритма А.
IV. Положим
Рк+1=р(/к). PLi=P’
Pi+i = Pi+2’ i=l, 2, s — 2.
Перейдем к следующему шагу.
Замечание 1. Операция I — нахождение расстояния от
выпуклой оболочки (2.18) до точки есть задача выпуклого
программирования в s-мерном пространстве. Учитывая выра¬
жение расстояния через скалярное произведение, ее можно
привести к следующей форме. Найти
min I ^ v-iV-jO-i) T 2 ^ 4~ (2.18)
U/=i г-i J
S
при условиях 2^“!’ 1. Здесь аи=pftj, at=—Ъ^'Рь
г=1
ad=xL Функция в (2.18) выпуклая. Задачу (2.18) можно при¬
вести к виду задачи II, если положить
^ = (Нч» • • •» tO» N1 = ... , ^л)’. О ^ ^ 1, i 1,..., 5},
$ £ S
\(и)= 2 PiV‘jaijJC^Aa№i-{'a0> —1.
I, у=1 г-1 1 = 1
Такая задача может быть решена непосредственно методом
сфер.
84
Замечание 2. В операции IV можно принять другой
способ выбора точек {р1^ • Например, източек/?&, i— 1, 2 ..., s
исключить не точки р\, р\, а две наиболее удаленные от точ¬
ки X^rf или те, для которых проекции fk{pik—p)j\pik — p\ на¬
именьшие.
Замечание 3. Для последовательностей { Xfe}, {/?£}, по¬
строенных в алгоритме В, имеет место сходимость, указанная
теоремой 5.
Выше всюду предполагалось, что N—выпуклое множество.
Однако для решения задачи II по алгоритмам А, В, С доста¬
точно предполагать, что точка р0 остается верхней точкой
пересечения оси ОХ с замыканием выпуклой оболочки мно¬
жества N.
Требование ограниченности также можно опустить. При
этом множество F линейных функций / уже не будет совпав
дать со всем полупространством f-d> 0 и потому уточнять
оценку числа Х0 (в алгоритмах — число X7) можно только тог¬
да, когда /£Д
Распространение схемы метода сфер в случае, когда вместо
множества (2.1) взято произвольное множество двойственных
функций, будет дано в § 4 главы V.
§ 3. ЗАДАЧА ОПТИМИЗАЦИИ В СИСТЕМАХ РЕГУЛИРОВАНИЯ,
ОПИСЫВАЕМЫХ ОБЫКНОВЕННЫМИ ДИФФЕРЕНЦИАЛЬНЫМИ
УРАВНЕНИЯМИ
1°. Постановка задачи
Пусть поведение объекта регулирования описывается линей¬
ной системой дифференциальных уравнений
y(t) = Ay(t) + bw(t). (3.1)
Здесь, как обычно, t — время; y(t) = (y-y(t), ..., yn(t)) — век¬
тор фазовых координат; w(t) — функция управляющих воздей¬
ствий (управление). Пусть W — некоторое множество управле¬
ний таких, что при любом w (< W существует решение системы
(3.1) при w = w, проходящее в момент 0 через точку y0£Rn--
Это решение будем обозначать у да), ££[0, Т] и называть
траекторией. Т > 0 — конечное фиксированное число.
Управление w£ W и траектория y(t-, w) называются допу¬
стимыми, если фазовая точка у (t; w) во время движения
остается в области, определяемой неравенствами
Оу {t, w) -f-c*w(t) + £<0, t £ [0, Г], (3.2)
85
згде g, с — 5-мерные векторы; G—матрица размерности s X п.
Пусть, наконец, на траекториях системы (3.1) и управлениях w
определен некоторый функционал, зависящий в конечном счете
от управления; обозначим его через ср (w).
Допустимое управление w0(<W называется оптимальным,
•^если оно доставляет функционалу ср (w) наименьшее значение
по сравнению со всеми допустимыми управлениями.
Задача А. Найти w0.
Поставим теперь задачу приближенного решения задачи А.
Сначала сформулируем ей эквивалентную (см. 2°, § 2, глава II).
Пусть а = (аи ... , as) — вектор, который ограничивает (по¬
компонентно) снизу левую часть неравенства (3.2) при любом
управлении w(* W. Введем множество V дополнительных
управлений v (t) = (v1 (t), vs (t)), удовлетворяющих неравенствам
О v* (t) < — au j = 1,2,..., 5.
Понятно, что неравенства (3.2) эквивалентны следующему
соотношению:
z(t\ w, v) = Gy{t\ w)-\-cw-\-v{t)Jrg = Q,
v{t)=V, t G [О, T]. (3.3)
Обозначим u = (wy v)y U= W X V. Теперь задачу А можно
переформулировать так.
Задача А'. Найти элемент u = (wy v) (w(*Wt v£V)y для
которого вектор-функция z(t\ w, v) тождественно равна нулю
на [О, Г] и значение функционала y(w) — наименьшее воз¬
можное.
Практически часто нет надобности, чтобы неравенства (3.2)
или равенства (3.3) выполнялись точно, и при этом можно
указать, в каком смысле и в каком „количестве44 допускаются
погрешности в выполнении этих условий. Пусть, например,
достаточно, чтобы неравенства (3.2) выполнялись в среднем
по некоторому весу с малой погрешностью ^0^>Оу а в опре¬
деленные моменты tL £ (О, Г), i = l, 2, ..., г, — с заданными
погрешностями > 0. Это требование можно выразить нера¬
венствами
т
jz*(£; w, v) Г (t) z (t; w, v)dt< e0,
z*(t„ w, v) TiZ (th и, 5)<s„ / = 1, 2, ... r, (3.4)
где Г(*), гг — положительно определенные симметричные
матрицы; матрица Г (t) непрерывна на [О, Г]; * означает за¬
мену вектор-столбца вектор-строкой, а запись z*z2—скалярное
цроизведение векторов zlt z2. Поскольку значения е, могут
быть заданы сколь угодно малыми и меняться в процессе
исследования, целесообразно поставить следующую задачу.
Рассмотрим элемент
z(w, v) = (z(t- w, v), z(ta w, v), z(tr; w, v)),
56
первая компонента которого есть вектор-функция, заданная
на [О, Г], остальные компоненты — s-мерные векторы.
Введем на множестве таких элементов z понятие расстоя¬
ния р, положив для z' = z(w', v'), z" = z(w", v"):
pv, z") — I! z’ — z"||, (3.5)
где
r
|| z(w, v) f = j z* (t\ да, v)T(t)z{t; да, v)dt-\-
+ £ 2* (tда, v) T.Z (ti; да, v). (3.6)
i=i
Обозначим через U* множество последовательностей
{и*«»)}“„,, да* 6 W, vk£V
таких, что
II 2(w*. »0. (3.7)
ft-* oo
Соотношение_(3.7) означает, что для каждой последователь¬
ности {и*} (< U* при любых е^О, / = 0, ... г, найдется номер
к0 такой, что для всех k > k0 выполнены неравенства (3.4)
при w — wk, v = vk, т. е. управления да* являются допустимы¬
ми „с точностью до 1®/)“. Последовательности {и*)£./И* будем
называть допустимыми. Обозначим I (и) = ср (да). _
Задача II. Построить последовательность {и°=(да°, т>”)} £ U*
такую, что
lim Х(и*) = Х0,
U-+ оо
где
Х0 = inf _ НтХ(и*). (3.8)
Если решение да0 исходной задачи А существует и функцио¬
нал (да) ограничен на множестве W, то существует и реше¬
ние задачи II, при этом Х0 <; <р (да0). Действительно, для управ¬
ления да=да0 и y = y(t; да0) выполнены неравенства (3.2) и,
следовательно, равенства (3.3) при
щ {t) = — Gy{t\ да) cw g, (3.9)
так что множество U* непусто (оно содержит элемент и0 =
= (да0, г>0). Поэтому нижняя граница Х0 в (3.8) существует и,
вследствие ограниченности (да), эта граница—конечное число,
не большее Х(и0) = 9(да0).
2°. Алгоритм А
Построим двойственную задачу. Будем считать компоненты
матриц А, О и векторов Ъ, с, g кусочнонепрерывными огра¬
ниченными функциями на [О, Т\. Множество W управлений да
87
будем считать состоящим из кусочнонепрерывных ограничен¬
ных в совокупности функций. Тогда компоненты решения
y(t\ w) системы (3.1) и левых частей неравенств (3.2) также
будут кусочнонепрерывными ограниченными в совокупности
на промежутке [О, Г] функциями. Теперь из равенства (3.3)
ясно, что в качестве вектор-функций v(t) множества V доста¬
точно рассмотреть тоже кусочнонепрерывные ограниченные
в совокупности вектор-функции. В данной задаче пространство
условий Р должно содержать элементы вида
р(и) = (\(и), z(a)), (3.10)
где = y(w)\ z(u) = z(w, v). Дополним множество таких
элементов до полного нормированного пространства Р с нормой
M=V\W+W>
где I z|| совпадает с определением нормы (3.6) для z = z(u).
Построенное таким образом пространство Р будет гильберто¬
вым пространством, если скалярное произведение определить
через норму так:
р'-р"= т [ \\р'+р” ¥■- \\р'-р" II2] •
Будем считать, что W—выпуклое множество, а ср(^) —
линейный функционал. Тогда в силу линейной зависимости от
w и у соотношений (3.1), (3.2) множество N векторов вида
(3.10) будет выпуклым и в силу сделанных предположений
ограниченным. Следовательно, в качестве двойственных функ¬
ций достаточно рассмотреть линейные функционалы, опреде¬
ленные в Я, и для решения задачи II применить алгоритмы
А — С предыдущего параграфа. Остановимся на применении
алгоритма А для случая, когда у (w) = l*y(T, w), I — заданный
вектор. Основной операцией этого алгоритма является опреде¬
ление опорной плоскости /£•/? = р(/А) и точки опоры р. Пока¬
жем как это сделать, учитывая, что все точки р множества N
представляются через элементы #£УкГ, так что Pk—P{uk)>
р=р{й).
Согласно определению скалярного произведения, имеем
г
fk-p (и)=(К—<р («»*))• v М—р* (*; wk> vk)г (*) * (*; ®)dt —
0
— wk, "Vk)T^(t; W, v). ' (3.11)
/= 1
Зададимся целью в представлении (3.11) исключить z и полу¬
чить явную зависимость от (w, v). Для этого можно выписать
решение уравнения (3.1) по формуле Коши и подставить
в (3.10) и затем интегрированием по частям избавиться от
повторных интегралов. Тот же результат можно получить*
проведя операции в несколько другом порядке. Этот послед¬
ний способ основывается на известной теореме Грина. Напом¬
ним его.
Возьмем некоторую (пока неопределенную) кусочнонепре¬
рывную, кусочно дифференцируемую на [О, Т] вектор-функцию
<!>(£). Перенесем все слагаемые в уравнении (3.1) в левую
часть и полученное векторное равенство умножим скалярно
на (t), а затем возьмем интеграл от скалярного равенства
в пределах от 0 до Т. Этот интеграл по построению равен
нулю, так что, добавив его в (3.11), мы не изменим величины
fk-p(u). Измененное так равенство (3.11) будем обозначать
Ч+\
(3.11)'. В (3.11) возьмем по частям интегралы J b*(t)y(t)dt,
Ч
i — 0, 1, ..., г, ^0 = 0, tr+1 = T, считая, что вектор-функция
Ф(£) кусочно дифференцируема внутри интервалов (th ti+1),
т
J
0 /=о
j w) dt — ^
b*(ti+1-0)-y(ti+1, w)-
ti+1 .
w)— j Ф* (^)-Vw)dt
4
= Г(Т)у(Т, W) + £ [ф(^_0)-ф(^ + 0)]*у(^; w)-
i=1
T
— +*(0)y(0; w)—~y*f* {t) y(t\ w)dt. (3.12)
о
T
Заменив в (3.11)' интеграл Jф* (Л)_j>(^; w)dt по формуле (3.12)
0
и собрав затем коэффициенты при y(t; w), w(t), v(t), получим
/*•/>(«)=-{ [<К*)+л*(*Ж*) +
+ G*T(t)z(t; wk, vk)]*y(t; a,)-f-£[_G*r,z(*,; wk, vh) +
/=1
+ Ф (— 0) — ф (^i + 0)]* у (t\ w) ([Хл — cp (wk)\ / + ф (7"))* X
т
Xy{T\w)—ty*(0)y{0)—^ [ф* (t) b—z* {t; wk, vk)-T(t)c]w{t)dt—
о
- 2 j (z* № wk, ^k)v{t))j^j{t)dt —
j= 10
89
~s{z*(7': Wk' vk)'Ticw(ti) — 2 wkt Vk) ■ T)jvj (tj) —
J* [z* (t‘, wkt vk)-r(f)g]dt—yz*(ti\ wk, Vk)-Yig. (3.13)
0 /=1
Приравняем здесь коэффициенты, стоящие при y{t; w), нулю
(исключая точку £ = 0)
b = -A*-b~G*.T(t)-z(t-, wk, vk), (3.14)
Ф(Л = ['Р(^) — h] I, М*/ + 0) — ф(*/) = — Q*Ylz{ti\ wk, vk).
(3.15)
Эти формулы однозначно определяют кусочнонепрерывную
и кусочно дифференцируемую вектор-функцию ^(0. Теперь
(3.13) принимает вид
г
fk'P(*) = J(*•(*; wk, vk)T (t)c-b*b)-w(t) dt —
T 0
— V j (d(t; wk, Vk)-T)jV/(t)dt — yz*(ti; wk> vk) Yfw{t^ -
7=1 0 /=1
_ 2 51 (z* ^ Wk' Vk) Ю + 0 — ф (°)Уо- (3.16).
i=1 /=1
Здесь через а обозначены два последних слагаемых в (3.13),
не зависящих от у, w, v.
Предположим теперь, что множество управлений W опре¬
деляется, как множество всех кусочнонепрерывных функций,
удовлетворяющих ограничению
\w(t)\<U *G[0, Т]. (3.17)
Из (3.16) видно, что верхняя граница (3.11) в этом случае
такова:
Р(Л) = sup {/*•/>(W):®G W, v£V\ =
т
— max fk-p(w)— Г\z*{t\ wk, Vk)-Y(t)c — Ф*6| +
+ J] I z* (^; wk, vk) Г.с | — £ j (г* (t; wk, vk) Y (*)), v, {t) -
/= 1 7 = 10
- 2 2 (2*(f,; w*. ®*)ri},Vjiti) — a — Ф(0)y0. (3.18)
<=i /=i
Здесь
i-aj, если (z*(f; wk, г»*) Г (^<01
- 0, если (z*(t; wk, vk)T(t))j>Q} i = l’ ••• • Г;тдч
W- _a., если (г*(^; гдг,)у<01 * = *t> ^
0, если {z*{tL\ wk, vk)Tl)j>0\ l — X' ••• » r-
90
Обозначим
^ ('sign (г* (г^; wk, vk) Г (t)c — ф* (t)b), если t=^th
«(<) = i=1’"(3.2r0)
I—Sign(z*(f; wk, vk) Ггс), если t — th i = 1, r.
(Условимся^ считать sign0_==0.) Теперь, если положить гг =
= (w, v)Lv = [v1{t), ..., то можно записать ?(/*) =
=fh (р {и)), т. е. точки р (гг) реализуют верхнюю границу
?(/*)• Итак, получение функционала fk связано с вычислением
функции z(t; vk), т. е. фактически с интегрированием
исходной системы (3.1), а получение величины ?(/*) = ?* —
с интегрированием сопряженной системы.
Как видно из формул (3.15), для получения вектор-функ¬
ции ф(£) нужно интегрировать систему (3.14) от Г к нулю
(в обратном по времени направлении), в то время как началь¬
ное условие для исходной системы (3.1) задано на левом конце
при £=0, и систему (3.1) для получения вектор-функции
z(t; Wk, v^) нужно интегрировать от 0 к Г (пока неизвестен
вектор у(Т, Wk)). В связи с этим выполнение операций алго¬
ритма А (В, С) целесообразно разбить на две группы.
Приведем описание одного шага алгоритма А. Для этого
предварительно запишем правую часть (3.18) через диффе¬
ренциальное уравнение. Если (3.18) записать в виде (■)(/*) =
г
= ^df(t), где 7 (t) — функция ограниченной вариации, и поло-
0
_ г _ _
жить 7 (t)= J ^т(х) и 7 (Г) = 7 (Т—0) = 0, то
t
7 (t)=-\z*(t\ wk, vk)Y(t)c — +*ft| +
-f-J z*(t; wk, г/*)Г (t)Vj-j-z*(t; wk, Vk) Г (t) g
J-i
при ti=tif i = 1, 2, .. . , r;
7 Vi + 0) — T № — 0) = 2* (tr, wk, vk) T, {cw (t{) +
4-£ + ^(^)). г'=1> 2, ... , г, т(+0) — т(0) = Ф*(0)у0- (3-21)
Проинтегрировав уравнение (3.21) от Т до 0, получим 7(0) =
К началу k-ro шага алгоритма в памяти ЭВМ хранятся
функции wh(t)£W, vh(t)£V, вектор ук=у(Т, wk), число
и число <?к = 1*у(Т; wk). Операции k-ro шага можно
разбить на две последовательные группы.
91
I. Параллельно интегрируются от Т до 0:
а) система (3.1) при w — с граничным условием
У{Т)=Ук,
б) система (3.14)—(3.15) с граничным условием ф(7')==
= — (Xft— <pft) I и уравнение (3.21).
При этом функция w(t) и вектор-функция v (t), Л
запоминаются. После выполнения интегрирования полагаем,
что Л+1 = ХЙ5 если и ).k+l = max {Хъ /.}, где Х =
= T(0)[<Pft-X;]-\ если<?к<0.
II. Параллельно интегрируются от 0 до Т:
а) система (3.1) при да = дад,(£), у(0)=у0;
б) система (3.1) при w = w(t), у(0)=у0;
в) -^ = z*(0r[i(£)_z(O],-*(0) = 0,
•/. (tt + 0) — у. (tt — 0) = 2* (ti) Г,- (z (ti) — г (*/)), i = 1, ... , r,
-;2(t) = (z(t)-z(t)T{z(t)-z(t))),_ v2(0) = 0,
v (*/ + 0) - Vi (tt - 0) = (2 (tt) - 2 (t)T Tt (z (ti) - 2 (t)),
где
z(f) = z(t; wk, vk); z(t) = z(t; да, v).
После интегрирования вычисляются величины
4 — l*y{T;w),
«.S-rf+MDH (3.22)
(<P — 9 k) +^(r)
_ I 1, если Op—<Pfe)2 + v2 (7') = 0,
P=| min (1, p'), еслир'>0Ь- \a , wrw n
[ 0, если ^<0/^-^ +v,(7)>0.
Далее принимается, что даk+l = wk -|- ^ (да— даД vk+1 = vk -j-
+ |л(г> — vk), Ук+1 = УкЛ'\>-(У (T; wk)—yk), fk+i — 4k~\~ (*■(?—?*)•
Для выполнения первого шага можно взять произвольные
w1 (t) £ W, (t) £ V и достаточно малое число <рх.
Замечание. Если собственное движение системы (3.1)
(в (3.1) ® = 0) устойчиво, то для меньшего влияния погреш¬
ностей вычислений на значения y(t; да) интегрирование на
ЭВМ системы (3.1) целесообразней проводить в положитель¬
ном по времени направлении. Чтобы избежать интегрирования
системы (3.1) от Г к нулю в операциях группы I алгоритма,
следует предварительно провести интегрирование этой системы
от нуля к Т, параллельно вычисляя и запоминая (приближен¬
но) вектор-функцию z(t; да^, Vh), которая потребуется при
интегрировании системы (3.14). В случае отсутствия фазовых
ограничений (3.2) внутри интервала [0, Г] необходимость такого
интегрирования отпадает.
92
Если идею метода наискорейшего спуска, реализованную
алгоритмом_А, заменить идеей простого градиентного метода,
т. е. число |х в группе операции II считать заранее выбранным
(или выбранным, согласно некоторому итерационному методу
минимизации функции Цх^д? — рЫи-{-pin — и/J) || одной пере¬
менной р), то в группе операций II остается интегрирование
только одной системы а).
Для последовательностей, построенных в алгоритме А, спра¬
ведлива теорема 5 предыдущего параграфа, из которой в част¬
ности следует
Теорема 6. Пусть существует хотя бы одна допустимая
последовательность в множестве М#. Тогда последователь¬
ность [щ] есть решение задачи II.
3°. Одна дискретная система
Пусть система (3.1) заменена на следующую:
у = Ay(kh) -\-bw (kh) при t£[kh, (й + 1)Л), (3.23)
k = 0, — 1, h = ~, y(0)=y0, |w|<l.
k
Требуется найти управление w (£), (|^(^)|<Д), переводящее
систему (3.23) к моменту Т в точку уг (т. е. должно быть
у (Г, и) = ух) при соблюдении условия
Gy(t) + cw+-g< 0, t£[0, Т], (3.24)
при этом интеграл
7
ср (w) = j* w2 (t) dt
о
должен принимать наименьшее значение.
В качестве нормы соответствующего пространства Р можно
взять функцию, определенную в (3.6), где положить Г/ = О,
£ = 1, ..., г и добавить еще слагаемое у(Т)Ту(Т), Г > О
(этим членом как бы придается особый вес условию попадания
в точку j/J. Для максимизации соответствующего (3.11) линей¬
ного функционала в Р вида
f-p (W) = V j W* (t) dt + j 2* (t) Г (t) [Oy (t) +
+ cw + v(t) + g (0] dt + ч*Г (У(Т)-У1) (3.25)
применим вновь метод функций Грина (здесь считаем Гг = 0).
Возьмем вектор-функцию ф (0. имеющую разрывы в точках
kh, & = 1, , k — 1 и абсолютно непрерывную вне этих то¬
чек на [О, Г]. Очевидно равенство
93
f p (те») = V j w-2 (t) dt + J (t) V (t) [Gy (t) +
+ с*те» + г» (0 + g (01 dt + 4*G(y(T)-yi) +
T
+ j Ф*(0 [у —Ay (kh) — bw(kh)\ dt. (3.26)
о
Учитывая здесь (3.12) и полагая
if(t) = G*T(t)z(t)
при t£(kh, (k-\-\)h\
<К*Л + 0) —Ф(ЛА —0) = - j A*to(t)dt, k = \,...,k-l,
kh
Ф(7’) = -1’Ч
функцию (3.26) приведем к виду
т г
f.p (w) = v J те»2 (t) dt -f j [a (t) те»(t) + q* (t) те (7)] dt -f
0 0
ft-1 I
£ akw (kh) + г* (t) V (t) g (t) dt — 6* (0)y0, (3.27)
Ь —П X
h=0
где
(k+\) h
*(t) = z* (t)Y(t)c, q*(t) = z*(t)V(t)t ak = - f b*(t)bdt.
kh
Из (3.27) легко заключить, что управления те», те, доставляю¬
щие максимум функционалу (3.25), определяются формулами
sign a (£), если v>0|
— /j.\ , ,~l а(») k = 0, 1, ... , k—1,
те» — те» (t) = ( sut | если v<0J
sign а,- при t — kh, £ = 0, 1, ..., k—1;
v = v(t) = (v(A)(t), ..., те^(^));
(a;. если (,(^>0 f_
_ _ ’ если
Подставив те», те в (3.27), получим величину {!(*:). Теперь для
решения задачи можно использовать алгоритм предыдущего
пункта.
4°. Нелинейная зависимость управляемой системы
от аддитивно входящей функции от управления
Здесь мы укажем случай более сложной зависимости си¬
стемы (3.1) от управления, которая «почти» не нарушает вы¬
пуклость множества достижимости (множества векторов у (t; те»)
94
при всех со£Ц7, t фиксировано). Приведем вспомогательное
предложение.
Лемма, Пусть Q<zRm произвольное множество, W =
z=z{w(t)) — множество кусочнонепрерывных вектор-функций
w(t) со значениями в множестве Q; gfc, w)— ограниченная
непрерывная п-мерная вектор-функция на [О, Т] X 2. Тогда
при любом фиксированном t множество
s (t) = {| g (S w (X)) Cfx = p (w): w e wj (3.28)
плотно в своей выпуклой оболочке, т. е. для любого век¬
тора р из выпуклой оболочки множества S(t) и числа s > О
найдется управление we(t)£W такое, что
\\p-p{w,)\\<z. (3.29)
При этом если вектор р по определению выпуклой оболочки
приближенно представляется комбинацией векторов
p{Wj), Wi£W, i — \, 2, ..., р<«, т. е.
У v-iP (Щ) - Р
где
i=i
Pi
<4-
/-1
то управление wt(t) можно построить так:
, h | k -f У p-|-
(3.30)
k = 0, 1, ..., k-\- A = -f.
k
Здесь k — достаточно большое целое число, определяемое
величиной е.
Из леммы, в частности, следует, что если имеются два
вектора p(w') и р(w") и требуется с точностью до е предста¬
вить точкой из 5 (г1) вектор р =_рр (w')-f- (1 — (А)/?('ге,,,)> [0, 1],
то при достаточно большом k такое представление дает век¬
тор p(wc), где
wt(t) =
( w'(t), если t£[kh, (k + y)h), k = 0, 1,
\ w" (t), если ^6[(А + р)А, (A+1)A).
Доказательство леммы основывается на свойстве интеграла
как линейной операции на множестве значений подынтеграль¬
ной функции. Мы не будем его здесь приводить [33, 3, 10].
95
(3.31)
Приведенная лемма позволяет сделать небольшое обобще¬
ние системы (3.1). Заменим в (3.1) слагаемое b-w на слагаемое
b(t; w(t)), где b (t; w) — непрерывная функция своих аргу¬
ментов. Тогда, пользуясь интегральной формой Коши для
представления решения уравнения (3.1), получим
Г 1
У (t) — F(t) y0 + $F~l(x)b(x,w{x))th
о
Отсюда видно, что замыкание множества значений вектора
y(t) при всевозможных управлениях w(t) так же, как и мно¬
жество S(t) в (3.28), выпукло. Теперь в задаче пункта 2° за¬
мыкание соответствующего множества N в пространстве Р
будет выпуклым, если в неравенстве (2.2) положить с = 0.
Это позволяет применить алгоритм пункта 2°, в котором фор¬
мулу (3.20) следует заменить на
w{t) = [w. — б* (t) b (t; w) = max <h* (t) b {t\ w)\.
I |®|^1 >
Кроме того, в конце операции II (fe-f-l)-e приближение опти¬
мального управления следует строить по формуле (3.31),
в которой нужно положить w'(ъ) = тк(ъ), w" (т) — w(t), е =
— гк, Iх — Р1* Для сходимости алгоритма необходимо, чтобы
sk 0 при k со.
5°. Программная оптимизация линейных систем
с последействием
Пусть в задаче пункта 1° система (3.1) имеет вид
y(f) = A1y(t) + A,y(t — Ai(*))-f c(t, w{t)) +
+ d{t, w(t — h2(t)). (3.32)
Здесь hx{t)^0, h2(t) >0 — кусочнонепрерывные кусочно диф¬
ференцируемые на [0, Г] функции; w (t) — m-мерная кусочно¬
непрерывная вектор-функция со значениями в ограниченной
области 2с/?т; вектор-функции c(t; w), d(t; w) — кусочно -
непрерывные, ограниченные на [0, Г] X 2.
Задано начальное состояние объекта
У (х) = У о (т) при т^0. (3.33)
Пусть решение системы (3.32) с начальным условием (3.33)
существует на [0, Г] для каждой кусочнонепрерывной вектор-
функции w(t) со значением в 2. Будем считать в (3.2) с = 0
и рассмотрим задачу' пункта 2°. Используя лемму предыду¬
щего пункта, можно показать, что множество N в этой задаче
выпукло и использование алгоритма А дает решение соответ¬
ствующей задачи II. _
Выведем соотношения для управления w(t), доставляющего
максимум линейного функционала (3.11). Для меньшей гро¬
моздкости выкладок будем считать, что Г<- = 0, £ = 0.
96
Пусть промежуток [О, Г] разбит точками 0=7о < <^2 < • • •
... < tr < tr+l = T так, что на каждом интервале (£/, 7Ж) функ¬
ция 9i(7)=7— h\{t) непрерывно дифференцируема внутри и
непрерывна справа в точках t( и пусть на четных интервалах
\ti, ^+1) (i + 1 — четное число) | У (7) | > &'0 > 0, а на нечетных
d' (t) = 0. Для определенности считаем г нечетным числом. По¬
скольку при i четном для t£ (tit ti+l) будет &х(£) = 0(^) = &it то
*i+l ( li+\ \
j Ф*(0— Ах(^)); w)dt=[ J ^(О'Мм.У^)- (3.34)
U ' U '
Вектор-функцию <1* (7) будем считать имеющей разрыв в точ¬
ках &г, i четное. Тогда формула (3.12) примет вид
т
jt*(0T(z‘; w)dt = ty* (Т)у(Т; w) -f-
0
+ 2 im - о)-И&/+он* у &)-
i четное
T
- Ф* (0) у (0) - J (t) у (f; w) dt. (3.35)
0
Для нечетного i обозначим
ftr = min{»& + 0), ft&+1-0)},
bt— max |d(^-f 0), &(*m—0)}.
Поскольку производная $'(£) на [th tiArl\ строго отделена от
нуля, то справедлива следующая замена переменной в инте¬
гралах:
*;
&+
1+1
j Ф*(*М»У(М0. w)dt =
= jV (»Г‘ (*Жу (t; w) dt. (3.36)
ЙГ
/=1, 3, 5, ..., г.
Здесь &Г'(0— функция, обратная функции &,(£) на (ti, 7m).
Учитывая теперь в (3.11) равенства (3.34), (3.35), (3.36), соби¬
рая затем коэффициенты при у (£; w) и приравнивая их нулю,
получим
fk-p{w) = — ] {t){d{t\ w(t-h2{t)))-\-c(t, w(t))) dt +
0
T
+ j 2* (t- wk, vk) V (t) vj(t) + a. (3.37)
0
7 H. E. Кирин 97
Здесь а — сумма интегралов, не зарисящих от y(t\ w) при
t^> 0, и функций w(t), $(t). Вектор-функция однозначно
определяется соотношениями:
+ (О=-Ant) - V ЛИ »г‘ (0) +
iel(t) V * '
+ С*Г (*)*(*; да*, vk), t G[0, T), t=hvu
(Г) = —9 (wk) A (A\ = Al{vT\t))), (3.38)
U+l
Ф(»< + 0)-ф(»(-0)= j' Al(t)^(t)dt, i = 1, 3, r-1.
fi
Здесь /(^) — множество тех нечетных индексов i из множества
{1, 3, г}, для которых £б[®Г,®Г]. Поскольку §Tl
то (3.38) — система с опережающим аргументом, и вектор-
функцию ф(^) удобнее получать интегрированием этой системы
от Г к нулю.
Теперь рассмотрим функцию a(t) = t — h2(t) и поступим
с ней так же, как с функцией &(0- Пусть [т., т/+1) — интер¬
валы постоянства функции c(t) при i четном, а при i нечет¬
ном на интервалах т/+1) будет ||а7 (£)|| > о' > 0. Тогда при
четном i будет
Xi+1 Xi+1
j rit)b{t- w(t-hi{t)))dt= j r{t)b{t,wo{^)dt=bUw*{^)-
xi xi
(3.39)
При i нечетном обозначим через зГ1 (t) функцию, обратную
к о (t) при хг+1) и определенную на промежутке [зг, о+]>
где
<j,- = mln{o(x/ + 0), o(xm — 0)),
о+ = тах{о(х, + 0), о(х/+1 — 0)).
Теперь можно сделать замену переменной
T;+i
j’ w(t—h2(t)))dt =
ц
вТ
— j Ф* (°Г‘ (0) d (о-1 (t), да (t)) -g—-i {t)y dt• (3-4°)
Подставляя (3.39), (3.40) в первый интеграл формулы (3.37),
приведем его к виду
т
- j Зф (t, да (*)) dt + 2 8? (*/))• (3.41)
То *
98
Отсюда ясно, что для максимизации первого интеграла сум¬
мы (3.37) достаточно положить
_ | да:8ф(^, ®0 = тах {Вф(^, ад):®/^}, если t^^j,
^ j w: 8; (®>) = max (oj1 (t, w): ®>£ 2}, если t = Vj.
i — четное
Здесь
To— min (o(^) :t£ [0, 7’]};
Ъ* (t, w{t)) =
= г(а-мо)^(^чо^(0){t}) +№'<:(*,
16 и (0 \ i )
H{t) — множество нечетных индексов i, для которых t £ [ат*? 0+] •
суммирование во втором слагаемом (3.41) проводится по чет¬
ным номерам i.
§ 4. ОПТИМИЗАЦИЯ СИСТЕМ С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
1°. Постановка задачи
Пусть процесс нагревания стержня описывается соотноше¬
ниями [8]
db(t,i) d4(t,t)_ мп
dt
&(0, 1) = М1), = о, (4.2)
[а* (*)-»*(*, 1)]+«ч[и(0-»(^ 1)], (4-3)
й-<й(0<й+, *6 [О, Т], ?б[0, 1]. (4.4)
Здесь &(£, |) — распределение температуры стержня единичной
длины в момент времени t\ и (t) —температура нагревателя; а^О,
а2^0 — константы. Будем называть кусочнонепрерывную функ¬
цию u(t)y удовлетворяющую ограничению (4.4), управлением.
Пусть &(/\ £, и) — решение краевой задачи (4.1)—(4.3),
соответствующее управлению u{t) [17]. Управление, при ко¬
тором стержень к моменту Т принимает заданное распреде¬
ление температуры
Ь{Т, I и) = Ьз(Е), (4.5)
назовем допустимым. Ставится задача: найти программу изме¬
нения температуры нагревания, при которой к моменту Т
стержень имеет заданное распределение температуры при наи¬
меньшем расходе энергии нагревателя, или: найти допустимое
управление, доставляющее минимум интегралу
т
X(u) = j u2(t)dt. (4.6)
О
7* 99
Поставленная задача есть задача типа задачи 2 главы II, если
принять: М — множество управлений u(t), 1(и) =Х(и), х(и)--=
= 5, и), X — пространство непрерывных (точнее, сумми¬
руемых с квадратом) функций на [0, 1]. Поставим задачу II.
Для недопустимых управлений и£М за критерий близости
к множеству допустимых управлений примем величину инте¬
грала
1
j [0(Г, 5, и)-М&)]*<« = 1*(7\ S, «)-»з(5)Г. (4.7)
О
Последовательность управлений {uk), ик£М назовем допусти¬
мой, если
и*)-»,(£) 1-0. (4.8)
к-> *
Множество допустимых последовательностей управлений обо¬
значим через Л4*.
Задача II. Найти допустимую последовательность {#*}, для
которой
ИшХ(и^)= inf lim X(uk). (4.9)
2°. Линейный случай
Предположим, что в (4.3) «1=0. Тогда все соотношения
(4.2) —(4.3) линейны по и и ft и в силу выпуклости мно¬
жества М функций u(t), удовлетворяющих ограничению (4.4),
будет выпуклым множество функций ft (Г, Е, и). Метрику
в линейном пространстве, содержащем функции ft (Г, Е, и),
можно определить через интеграл (4.7). Тогда полученное
пространство (£2(0, 1)) будет гильбертовым, если за скаляр¬
ное произведение двух функций ft'(E) и ft"(§) взять
1
]>(£)Г(£)^.
и
Пространство Р или произведение R X X тоже можно счи¬
тать гильбертовым. В данном случае соответствующее мно¬
жество N векторов р{и) = (X (и), ft (Г, Е, и)) нельзя считать
выпуклым ввиду нелинейности по и функционала к (и). Однако
этот функционал выпуклый и можно показать, что в простран¬
стве линейных функционалов Я* подмножество F= (/: /# > 0},
удовлетворяющее условию В теоремы 3 из § 2 главы II (смотри
также § 2, пункт 3° настоящей главы). Следовательно, к ре¬
шению задачи можно применить алгоритмы § 1 и 2.
Рассмотрим задачу построения опорной плоскости. Согласно
принятым в § 1 обозначениям, имеем
100
Л • (р (и)) = (h — х (и*)) Ч«) ~
1
- f [» (7\ ?, «*)-», (?)] * (Т, 6, и) dl (4.10)
б
Преобразуем функционал (4.10) так же, как и функционал
(3.11) в предыдущем параграфе, с целью получения явной
зависимости его от функции и {t). Для этого умножим урав¬
нение (4.1) на пока произвольную почти всюду на прямо¬
угольнике [0, Т\ X [0, 1] непрерывно дифференцируемую по t и
дважды дифференцируемую по £ функцию ф(£, £). Возьмем
интеграл от полученного произведения и добавим его к (4.1 ).
Видоизмененную так формулу (4.10) обозначим (4.10)' и бу¬
дем интегрировать по частям в этой формуле слагаемые, со¬
держащие производные функций &(£, £), взятые во внутрен¬
них точках прямоугольника [0, Т] X [0, 1]. После этого собе¬
рем коэффициенты при &(^, |) и приравняем их нулю за счет
выбора функции ф (£, £). Тогда получим
т
fk'Р (и) = 1 КХА — х Ы «2 (*) — ««ф (*, 1) » (*)1 dt -
о
1
— J Ф (0, 6)»o(6)rf6, (4.11)
о
где ф(£, £)— решение следующей краевой задачи:
^-^ + ^-^ = 0. ^€[0, п, 56[0, 1], (4.12)
ф(7\ «) = »(Г, g, а*)-Мб), ^§-^ = 0, ^Li) = _a.v(^fi).
Из (4.11) видно, что максимум _fk-{p (и)) на множестве
управлений М достигается при u — u(t), где
u(t) =
ис — Ид sign (и — ис), если \ — МиА) > 0,
uc-\-Ub.s\gn(u —ис), если \ — Ци*)<0, |и — ис|>ис,
и , если — Чи*)<0, |и — ис|=^ис,
ис— ид sign (ajJ) (t, 1)), если — \(uk) — 0.
Члегь и — “- + «+ ~ а2ф(/, 1) _ «н. -
ддесь Ис— 2 , И 2 (ХА — X («*)) ’ д — 2
Приведем теперь описание общего шага алгоритма Л.
К началу k-ro шага известны числа управление
к*(^)> функция Ь(Т, ?, и*) и числа Х(иА). Операции &-го шага
проводятся в два этапа.
I. Параллельно интегрируем от Г к нулю:
а) уравнение (4.12);
101
б) уравнение
й р = - (V- к («*)) • »* (*) + “2 • Ht, 1)«(О, Р (П = О;
в) уравнение
S=-»s(0, °(0=о.
Уравнения в б) и в в) являются дифференциальной записью
соответственно первого интеграла (4.11) и интеграла (4.6).
Функцию u(t), попутно вычисляемую по формулам (4.13), за¬
поминаем для интегрирования системы (4.1) на следующем
этапе. На последнем шаге интегрирования вычисляем интеграл
1 1
]Ч(0, и число р* =fk'P («) = Р(0) — j4(0, I) X
о о
Далее, если Xft— Ц«*)^0, то полагаем Xftf, = Xft.
Если же Xft — Х(ий)< 0, то полагаем Xft+1 = max |хъ ^(и^) — хА) •
II. Параллельно интегрируем от 0 к Г:
а) уравнение (4.1) с краевыми условиями (4.2) —(4.3) при
u = uk(t);
б) уравнение (4.1) с краевыми условиями (4.2)—(4.3) при
a = u(t).
На последнем шаге интегрирования вычисляем интегралы
1
*=- j (ft (Г, Е, «*)-М$))(&(7\ €. «*)-» (Г, 5, и*))
1
v = J[»(7't I, и) — Ь(Т, Е, «ft)]2^i.
О
После этого вычисляем
/ (Wi — ^ (J <Q) — ^ (ц&)) 4- *
^ — (з (0) — х (ыЛ))2 + V
0, если ц'<0 или (а(0) — X(#ft))2-f-v = 0,
jj/, если p'G [0, 1],
1, если у/ > 1,
\й(t) при ££ [ih, (i + ^)A),
И‘и_и*(0 при + (/ + 1)А).
г = 0, 1,,.. , /0. h—T/i0,
х (%fi) = (1 — I1) ^ («а) + t10 (°).
»(Л 5, «**,) = ft(7\ g, и*) + р(*(7\ 5, ик)-Ь(Т, Е, «*)).
102
3°. Нелинейный случай
Рассмотрим теперь случай, когда передача тепла от на¬
гревателя к стержню описывается нелинейным законом (4.3),
где аг Ф 0. В этом случае можно применить идею градиентных
методов (см. главу III). Для этого возьмем некоторое допусти¬
мое управление ux{t) и найдем соответствующее ему решение
&(£, £, их) краевой задачи (4.1) —(4.3). В окрестности этого ре¬
шения построим линейное приближение для малых отклоне¬
ний процесса АО-, соответствующих малым в метрике L откло¬
нениям А& управления иг, и оптимизируем функционал
| (tii -f- А и)2 dt при ограничениях: j | A# | dt е и Aft является ре-
о о
шением краевой задачи
Si dW = Q' ^ = 0’ —di— = 0’ ^ =
^|Л = а1[(М1 + Д^ + ^-4»3(^ 1)] +
+ а2 [Аи— А&(^ 1)].
Это задача типа построенной в предыдущем пункте и может
быть решена (сколь угодно точно) с помощью алгоритма А.
Далее решение этой задачи (линеаризированной) обозначим
через Аих и положим и.2 = и1ф^и1. С управлением и2 поступаем
так же, как с управлением и,ъ и т. д. Такой процесс обычно
заканчивают на том шаге &, которому соответствует малое
уменьшение оптимизируемого функционала. Как известно
{гл. Ill), оптимизируемая последовательность в градиентном
методе может сходиться к точке относительного минимума и
даже стационарной точке. Поэтому, если полученный результат
неудовлетворителен, то повторяют процесс, начиная с другого
допустимого управления.
ГЛАВА V
ЗАДАЧА ОБ ОПТИМАЛЬНОМ БЫСТРОДЕЙСТВИИ
В этой главе изложены методы приближенного определе¬
ния множителей Лагранжа в задаче линейного быстродействия.
Поиск этих множителей связывается с решением некоторой
экстремальной задачи, содержащей меньшее число ограниче¬
ний, чем исходная задача оптимального быстродействия. В при¬
веденных ниже методах вместе с построением множителей
Лагранжа строятся и приближения оптимального по быстро¬
действию управления. В главе использованы известные резуль¬
таты Н. Н. Красовского [28,29] по применению теории 1-про¬
блемы моментов в экстремальных задачах, методы решения
задачи быстродействия, впервые предложенные Л. Нойштадтом
[51] и Дж. Итоном [48].
§ 1. ОДНОРОДНАЯ ЗАДАЧА ОБ ОПТИМАЛЬНЫХ ЛИНЕЙНЫХ
БЫСТРОДЕЙСТВИЯХ
1°. Постановка задачи. Условия оптимальности
В теории регулирования типичная задача оптимального
быстродействия может быть сформулирована так. Имеется си¬
стема п л нейных дифференциальных уравнений (запись в
векторной форме)
х= Ах + Ьи, (1.1)
где х, b - /г-мерные векторы; А — м: трица размерности пХп.
Компоненты матрицы А и вектора b — аналитические функции.
Задано начальное значение вектора x(t)
х (0) = х0 =^= 0. 0-2}
Всякая кусочнопостоянная функция u(t), удовлетворяющая
ограничению
U(0I<1, (1.3)
104
x (t (ti), и) =F(t)
называется управлением. Управление u(t) называется допусти¬
мым, если существует конечное число такое, что
соответствующее этому управлению u\t) решение x(t, и) си¬
стемы (1.1) с начальным условием (1.2; попадает в момент
t=t(u) в начало координат, т. е.
x(t(u), и) = 0.
Задача состоит в нахождении допустимого управления, кото¬
рому соответствует наименьшее число t(u). Такое управление
и0 назовем оптимальным, а соответствующее ему время
t(u0) — t0 — временем оптимального быстродействия. (Иногда
в этом названии слово «оптимального» будем опускать.) Ста¬
вится задача: найти оптимальное управление.
Пусть и (т) допустимое управление со временем t{u) — t.
Тогда, пользуясь известной формулой представления решения
системы (1.1) с начальным условием (1.2), имеем
*0 + j F"1 (х) Ь (х) и (х) dx =0. (1.4)
о
Здесь F(t)— фундаментальная матрица решений уравнения
х=Ах, Е(0) = Е (Е—единичная матрица). Поскольку
det F(t) Ф 0, то равенство (1.4) дает
t
Х° = 1 ^ ^ ^ U ^ ^
о
Умножая это векторное равенство скалярно на вектор / из
плоскости 1*х() = — 1, получим
t t
1 = j l*f-i (x) ь (x) и (x) dx< j I l*F-1 (x) b (x)I rfx. (1.6)
Неравенство (1.6) является необходимым и достаточным усло¬
вием существования оптимального управления [28]. Точнее,
справедлива
Теорема Н. Н. Красовского. Для того чтобы в постав¬
ленной задаче существовало оптимальное управление, необхо¬
димо и достаточно, чтобы при некотором конечном t^> 0
неравенство
l<j\l*F~1Wb(*)\dx (1.6)'
0
имело место для всех векторов I из плоскости 1*х0 = — 1.
Для дальнейшего это предложение удобно сформулировать
несколько в других терминах. (В работе [28] эта теорема дана
в более завершенном виде. Часть заключения теоремы, выра¬
жающая связь между оптимальным управлением и вектором
/о, доставляющем минимум интегралу в (1.6) при наименьшем
значении t> 0, отнесена нами в нижеследующую теорему 1°.)
юг>
Введем функции
<F (/. х) = |/*^Ч(т)6(х)|, Р(/, 0 = f<p(/, x)rfx. (1.7)
О
Теперь неравенство (1.6) можно переписать так: р(/, t)^\.
Учитывая это неравенство и то, что (3(/, 0) = 0, из непрерыв¬
ности по t функции р (/, t) заключаем, что существует
t £ [0, t] такое, что
р(/, ?) = !. (1.8)
Число t, удовлетворяющее уравнению (1.8) при фиксирован¬
ном векторе /, является функцией /; обозначим ее через t* (I).
Итак, доказана необходимость условий сле дующего >твержде-
ния.
Теорема 1. Для того чтобы существовало оптимальное
управление, необходимо и достаточно, чтобы Функция t*(l)
была определена и ограничена на плоскости /*х0= — 1.
Приведем переформулировку теоремы 1, выражающую связь
экстремума функции t* (I) и оптимального управления. Эта
теорема (в несколько отличной формулировке) впервые дана
Л. Нойштадтом [51].
Теорема 1°. Для того чтобы существовало оптимальное
управление, необходимо и достаточно, чтобы существовал
вектор /0 из плоскости 1*х0 = *— 1 такой, что существует
конечное число t* (/0) и
t* (/о) = шах t* (/), 1*х0 = — 1.
i
Вектор /0 связан с оптимальным управлением #0(х) так:
t(u^ = t* (/о),
^(T) = sign(/oF-1(x)6(x)). (1.9)
Аналитическая функция t0F~l (т) Ь (т) ф 0, ибо по определению
t(lo)
t* (I) следует, что j | /о^-1(х)^ (х) I ^х = 1- Поэтому в формуле
о
(1.9) функция не определена только в конечном числе точек
на промежутке [0, £*(/0)], где ее можно доопределить, поло¬
жив, например, равной нулю.
Вектор определяющий оптимальное управление по фор¬
муле (1.9), может быть не единственным. Как будет ясно из
теоремы 2 следующего пункта, построение приближений к мно¬
жеству таких векторов позволит определить через формулу (1.9)
приближения оптимального управления. Для построения после¬
довательности приб ижений векторов /0 можно использовать
экстремальное свойство этих векторов, отмеченное теоремой 1°,
а именно искомой последовательностью будет последователь¬
ность, реализующая верхнюю грань функции t* (/) на плоскости
106
l*x0=— 1. Задачу отыскания этой грани назовем двойствен¬
ной задачей (по отношению к исходной задаче об оптималь¬
ном быстродействии). Вектор / и функцию /*(/) назовем соот¬
ветственно двойственной переменной и оптимизируемым функ¬
ционалом двойственной задачи. *
Перейдем к методам решения двойственной задачи.
2°. Метод наискорейшего подъема в двойственной
задаче
Д~я построения приближений решения двойственной задачи
можно применить методы градиентного подъема. Если опти¬
мальное управление существует, то сходимость этих методов
можно обеспечить выполнением условий аналогичных тем,
которые приведены в главе II. Опишем метод, основан!-,ый на
том свойстве функционала /*(/), что все стационарные по I
точки функции р(/, t) при / = /*(/) ^точки, где норма произ¬
водной ^ ^t}. обращается в нуль^ являктся точками абсолют¬
ного максимума функции /*(/) (здесь имеется в виду, что
вектор / изменяется только в плоскости /*л;0~ — 1).
Вычислим производную функции Р(/, /).
Лемма 1. Если функция t* (/) определена и ограничена в
окрестности точки V ф 0, то она и непрерывна в этой
точке.
Проверка. Обозначим /*(/') через t'. Предположим, что
утверждение леммы неверно. Тогда существует последова¬
тельность {/*}, сходящаяся к Г, такая, что существует
l = Y\mtkj=t\ tk = t*{lk).
k^OO
По определению tk, ? имеем
* k
О = р (/*, tk) - р (/', Г) = j | rhF-' (х) Ь (х) | dx +
г
+ J {|rft/^-i(x)6(x)|- |/'*/7-»(x)6(x)|}dx. (1.15)
о
Очевидно, что последовательность функций lkF~l (х) b (х) равно¬
мерно на [0, t'\ сходится к Г*/7-1 (х) b (х), та с что второй ин¬
теграл в правой части тождества стремится к нулю Поскольку
jl/'*/7"1 {x)b{x)\dx=£0, то аналитическая функция l’*F~x (x)b(x)
О
* Теперь теорема 1° может быть приведена в форме теоремы 3 главы II:
Аля того чтобы существовало решение исходной (двойственной) задачи, не¬
обходимо и достаточно, чтобы существовало решение двойственной (исход¬
ной) задачи, при этом t (и0) — t* (/0).
107
не равна тождественно нулю ни на каком положительной длины
интервале из [о, max {t\ t}\ , а тогда
fk 7
lim j | l*kF~l (т) b (т) |Л = j| V*F~X (t) b (t) | 0,
fc'*00r1
что противоречит предельному переходу в (1.15 .
Лемма 2. функция t* (/) определена и ограничена в
окрестности точки 1'=?=0, то направление убывания в точ¬
ке I' для функции (3(/, t* (/')) является направлением возра¬
стания в точке V функции
Доказательство. Пусть вектор q— направление убы¬
вания функции 8 (/, t* (/')) в точке / = /', т. е. при достаточно
малых [х > 0 = р (/'-f-t* (/')) — ^*(//))<0- Обозна¬
чим £* (lrjrvq) = tv., t*(l') = t'. Согласно неявному определению
функции t* (/) уравнением (1.8), имеем
Р(/'+м, g-P(/' + w, <o = -p(/' + w, о + № о=-др.
Поскольку интеграл в левой части этого равенства вычисля¬
ется от неотрица ельной функции | <р(/'+1^, *01, то из усло¬
вия Ар<0 следует A t = t^ — t' > 0, что и требовалось пока¬
зать.
Следствие. Вычислим градиент функции (3(/, t') по пере¬
менной I в точке 1 = 1'=£0. Возьмем малое число р > 0 и
обозначим через со ((а) множество тех чисел [0, tr\, при ко¬
торых
sign (/' + А/)*/7-1 (т) Ь Ф sign l'*F~x (т) b,
если ЦД/Ц^р. Поскольку функция l'*F~l(x)b имеет конечное
число нулей на промежутке [0, £'], очевидно, мера mes ш (ja)
множества ^ ((а) стремится к нулю при (а —> 0. Возьмем произ¬
вольный вектор q, II<7||=1. Согласно определению функции
Р(/, t) в (1.7), имеем
др = Р(/' + м, n = j + X) — <р С/'. т)}Л =
о
= J ■q*F~i (t) sign (x) b)dt +
|0.
+ J {<p (/' +1*-^, x) — ? (/' X)} flfx.
CO ({J.)
Обозначим через k наибольшее значение евклидовой нормы
\F-U*)bl на [0, t'}. То да второй интеграл в полученном
представлении для приращения др оценивается по модулю ве¬
личиной 2&[i.mesu)((A). Учитывая эту оценку и переходя к пре-
делу при (а у 0 в отношении — , получим
р*
108
ар(Г + н-<?, п
dv-
i
= f q*F~l (x) b sign (l'*F-1 (x) b) dx.
= +o J
и
Полагая здесь q = ex, e2, . . . , en (^- — единичные орты про¬
странства Rn), получим вектор частных производных
W (/', П
j F~l (х) b sign {l'*F~x (х) b) dx.
61 ~
о
т- II (l't О || г\ О
Если —- Ы= 0, то, согласно лемме 2, направление
является направлением возрастания функции t* (/)
в точке 1 — V. Если составляющая этого направления, ортого¬
нальная вектору х0, не равна нулевому вектору, то она будет
направлением возрастания функции t* (I) в точке / = /' по пло¬
скости /*х0 - —1 (при условии, что V*x^= — 1). Основываясь
на этом, опишем следующий алгоритм решения двойственной
задачи.
Построим последовательность векторов {1р} и чисел [tp} по
следующим формулам:
/х — любой вектор из плоскости /*л:0= — 1,
lP*\=lP + V-iK' 2’ ••• ’ (,л°)
где
а°п = ар- тйг II II* = <*<>; (1-11)
ап =
ip
(tp, tp)
р ||jc0||2 °’ " 011 — 0^0 5
>
j F-'(x)b(x)sign(i;F-'(x)b(x))dx; (1.12)
dl
tp = t*(L);
P * V V '
V*p — такое число, что
tp^=t{lp + vpa°)= max t(lp + \ia0). (1.13)
— oo<(j.< + oo
Теорема 2. Пусть существует оптимальное управление.
Тогда:
а) построения по формулам (1.10)—(1.13) возможны;
б) существует \imtp = t0 и t^ —время быстродействия;
Р -у оо
в) последовательность функций
Мх) = signl/pf-^x) 6 (х)\ /7 = 1,2,... (1Л4)
сходится на [0, t{)] /го к оптимальному управлению (1.9).
Доказательство теоремы 2. Допустим, что построено
несколько векторов /х, ... , 1р. Рассмотрим Np = L {a°)f=1 —
линейная оболочка соответствующих векторов а? и пусть для
простоты первые k (1 ^ k < п) векторов a°v . .. , a°k — базис Np.
100
Предположим, что размерность Np больше нуля. Покажем
тогда, что
infPte, tk)=h{Np)> О, (1.16)
Q
где q£Np, ||^||=1. Дей твительно если h(Np) — 0, то в силу
непрерывности подфункции (3(9, tk) и замкнутости множества
векторов q£Np, ||9l| — 1 найдется вектор q, ||?||=1, для ко-
торого Р (9, £л)=0. Так как р(у, £л)= j | 9*/7-1 (х) b (т) | дГт, то,
_ о _
очевидно, для q будет 9*/7"1 (т) Ь (т) =0, а тогда q*ax = . ..
... = q*ap = 0. Следовательно, вектор q орто онален jVp, но
q£Np, и, значит, 9=0, что противоречит равенству ||^|| = 1.
Поэтому в (1.16) A(yVp)> 0.
Обратимся теперь непосредственно к доказательству су¬
ществования [1р\. Пусть построено р{р^ 1) вектор в 1р. Если
|а°| = 0, то, как видно из (1.10), 1р+1 = 1р. Пусть Ца^Ц Ф 0. Тогда
Np — L {^)/7_i имеет ненулевую размерность. Интегрируя от
0 до tp очевидное неравенство
| (/,+ (х) & (х) | > | Н |а°;р-' (х) Ь (х) | - | fpF-' (х) b (х)1
и учитывая затем (1.16), получим
Н1Р + ^а% ^)>1нрк* *р)-тР, tP)>
II ар II
Отсюда заключаем, что при |[х| > а^ = 2 [/г(УУр)|а^||] будет
р(/р + ца£, tp)> 1, или t* [lp + pa0p)<tp, т. е. внутри отрезка
функция t* (1р +ра°р) достигает больших значений,
чем вне его и, следовательно, (в силу непрерывности) дости¬
гает своего максимального значения на этом отрезке. Этим
существование максимума в (1.13) доказано, а значит, и су¬
ществование последовательностей [lp|, {tp\.
Убедимся, что [1р\ — ограничена. Действительно, если на
i-м шагу ||а°|| = 0, то при всех р > /, lp = lh Пусть при всех i
||а?|=5^0. Рассмотрим множество Nm = L и пусть k —
номер последнего вектора в базисе Nвыбранного из векто¬
ров Из построения последовательности \1р) ясно, что
любой вектор 1р может быть представлен в виде = 4 +
где 9р£М», II 9pll = 1» vp — некоторое число. Поскольку для
любого вектора вида
* = /* + *?, (?№, ||91| = 1)
справедливо неравенство, аналогичное (1.17),
Р(/, **)>M*W*,)-1,
110
то заключаем, что для таких векторов /, находящихся вне
ограниченного замкнутого множества
Q = |/ : / = lk~\~ v</; ||?|| = 1, v < - h ^ ^ J ,
будет t*(l)<Ctk. Так как последовательность t1^t2< ... мо¬
нотонна, то векто ы 1р при p^k должны оставаться в этом
множестве, что и означает ограниченность {1р\.
Выберем сходящуюся подпоследовательность (для простоты
оставляем прежнюю нумерацию) Иmlp = lQ. Покажем, что для
Р -*• оо
соответствующей подпоследовательности \ар) будет limар =
р-го
= а° = 0. Обозначим \\mtp = tQ. (Предел lim tp существует в
силу монотонности последовательности tx ^ ... и огра¬
ниченности ее: 0 tk t («<>)•) Поскольку почти всюду
<р (/0, -с)# 0, так как (3(/0, £0) = 1, то подпоследовательность
|sign(/*.F_1 (p)b (x))J сходится почти всюду на [0, £0]. Этим су¬
ществование вектора а0 доказ но.
Предположим, что || а01| ф 0. Рассмотрим тождество
Р(^+К* + *р) =
=?(tP, д-Р(/Р+к. tPy
Обозначив t* (lp-\-v-a°p, т) через t , при малом по модулю ^
будем иметь
1Р'1-
f т) Р (А>» 4) — Р [h~\~Va°> А>) = — На°1РЧ“
'р
Выберем в этом соотношении достаточно малое по модулю
< 0 так, чтобы правая часть в соотношении при ^ = 1* была
положительна. Тогда в последнем соотношении интеграл слева
будет стремиться при [а = [а к некоторому положительному
числу. А это значит в силу неотрицательности подынтеграль¬
ных функций
ч{1р + *) - | {1Р + (*) Ь (т) |,
что при достаточно большом р будет t ~> tp, и, поскольку
функции {<р (/p-f-fJ-^p, T)}~_j равномерно ограничены на всяком
конечном промежутке, то t — tp -/•> 0 при /?—>со. Тогда най¬
дется е>0 такое, что какое бы р0 ни взять, можно указать
Р>Ро> Для которого будет — Так как lim tp=t0,
р-*- 00
то по ~y найдется рй такое, что при всех р> р0 будет t0 — tp<C
< -у-. Тогда для р, соответствующего этому р0, имеем
или
f (I- + ? a,) > t, > t7t, = __max+_ i(/, + !>s7).
Полученное неравенство противоречиво. Следовательно, ||а°|| = 0.
*
арХ о
Заметим, что lim = — 1. Это следует из предельного
перехода в равенстве ап*1р = ф (lp, tp) +j^p, полученном ска¬
лярным умножением (1.11) на 1р (по построению l*px0= —1).
Переходя теперь к пределу в (1.11), получим
f (х) & (X)slgn (Й/7-1 (х)) йГх Н- ЛГ0 = 0. (1.18)
0
Это означает (см. (1.5), (1.4)), что функция (1.9) — допустимое
управление со временем t0. Покажем, что оно оптимально.
Допустим, что существует допустимое управление u{t) со
временем Умножая (1.5) и (1.18) скалярно на /0, полу¬
чим
1 = [ /0>1 (х) b (х) и (х) rfx = j | (х) 6 (х) | rfx, (1.19)
О о
откуда j | Z*/7-1 (х) 6 (х) j di < 0, что может быть только при
t
t^t0 (напомним, что функция |<р(/0, х) | имеет конечное число
нулей на [0, t0], и, следовательно, интеграл ее по любому
промежутку положительной меры положителен).
Осталось доказать чретье утверждение теоремы, в). Пред¬
положение несходимости последовательности (1.14) означает
существование сходящейся подпоследовательности , для
которой существуют е>0 и о>0 такие, что мера множества
(х : I sign (i;F-1 (X)b (х)) - и0 (X) | > 6} > 8. (1.20)
Управление и (х) = sign (Z*/7”1 (Ч) b (х)), где / = lim lPk является
k -*■ зо
оптимальным, ибо выше в качестве сходящейся подпоследова¬
тельности {1р) можно было взять данную подпоследователь-
ность {У •
Из (1.20) следует, что
о < J I l*0F~l (х) ^ (О | • I йо СО - sign {TF-1 (О Ь (X)) | rfx =
О
= j (х) ь (X) {UQ (x) - sign 7*/7-1 (X) 6 (x)}.
0
112
Это противоречит равенству (1.19) при допустимом управлении
а(*) =sign (*)&(*)} со временем t0. Теорема 2 доказана.
Замечание 1. Относительно вычислений заметим, что
Z*/7'1 (т)— решение системы У = — A* Y с начальным условием
К(0) = / и, следовательно, <р(/, т) модуль линейной комбина¬
ции компонентов этого решения с коэффициентами, являю¬
щимися компонентами вектора Ь. К нахождению максимума в
(1.13) можно применить методы параграфа I главы III, поскольку
функция t* (/) строго квазивогнута. Действительно, пусть
хе(о, 1), = (1 -Dn
и пусть для определенности f = t* (/') ^ t* (/"). Из легко по¬
лучаемого неравенства
р(/'х+(1 -Х)Г, П+(1-МР(^ *')<*+(1->0 = 1
следует, что т. е. что на всяком отрезке функция
/*(/) принимает значения, не меньшие меньшего из ее значе¬
ний на концах этого отрезка. При £'<£*(/") будет
3°. Некоторые обобщения
Убедимся сначала в справедливости теорем 1 и 1°. В ка¬
честве доказательства достаточности условий теоремы 1 можно
буквально повторить доказательство теоремы 2, ибо из пред¬
положения существования оптимального управления в теореме 2
мы использовали только факт ограниченности функции t* (I)
на плоскости = — 1, что и содержится в условиях тео¬
ремы 1. Этим доказательство теоремы 1 завершено.
Необходимость условий теоремы 1° есть следствие теоремы 2,
ибо в качестве вектора /0, фигурирующего в теореме 1°, можно
взять вектор /0, построенный в доказательстве теоремы 2.
Достаточность проверяется так: если условия теоремы 1° вы¬
полнены, то это означает ограниченность t* (I) на плоскости
l*x0 = — 1, а тогда по теореме 1 существует оптимальное
управление.
Можно сделать некоторые обобщения в постановке задачи
пункта 1°.
Пусть уравнение (1.1) имеет вид
X (т) = А (-с) Х(т) + В(х) U(*), (1.21)
где U (т) = (т), , um(i))—tn-мерная вектор-функция, а
В (т) — матрица размерности пХт, заданные на интервале [0, t].
Пусть далее вектор-функция U(b)£Gt, здесь t 0 — неко¬
торое конечное число, a Gt— одно из нормированных про¬
странств, определяемых, например, следующими нормами:
j_
t
а) ||^)|0< = max (j | Щ (т) |Vx) , а > 1;
\о J
8 Н. Е. Кирин
6) II^MIIo = vraimax . P>1;
t xe[Of /1 i /
ге[0, /]
1
Обозначим через Ht нормированное пространство такое, что
Ht = Gt1 Ht — сопряженное пространство с Ht. Будем считать
коэффициенты матрицы А (т) суммируемыми на достаточно
большом промежутке [О, Т], а коэффициенты матрицы В(ъ)
такими, что 1*Е~1{ъ) В (%) £ Нь < Г + °° (/ —я-мерный
вектор).
Теперь для задачи быстродействия (1.1 —1.3), в которой
(1.1) заменено на (1.21), а ограничение (1.3) имеет вид
справедлива
Теорема 3. Для того чтобы существовало оптимальное
управление, необходимо и достаточно, чтобы функция t* (/)
была ограничена на плоскости /*х0 = — 1.
Здесь t*(l)—наименьшее из чисел ^£[0, Т], удовлетво¬
ряющее равенству, аналогичному (1.8)
Доказательство необходимости буквально совпадает с дока¬
зательством необходимости условий теоремы 1, доказательство
достаточности требует некоторых уточнений, которые мы не
будем здесь приводить. Несложно также сформулировать
аналог теоремы 1°.
Простым следствием теоремы 1 (теоремы 3) является
известная
Теорема 4. Если существует допустимое управление, то
существует и оптимальное.
Действительно, при доказательстве необходимости условий
теоремы 1 (теоремы 3) использовалось только существование
допустимого управления, а тогда по теореме 1 (теореме 3)
существует и оптимальное.
<i,
4°. Геометрическая интерпретация
Следуя [50, 51], рассмотрим в я-мерном пространстве
множество
Нетрудно видеть, что это выпуклое ограниченное множество.
Можно убедиться, что S(t) замкнуто [50]. Очевидно также,
что при будет S (?) D S (£"). Кроме того, в силу
ограничения |и|^1 и непрерывности интегралов (1.22) по
верхнему пределу множество S(t) „непрерывно" меняется
о
с изменением t, т. е. каждая точка z£S(t) есть предел неко¬
торой последовательности {гл}“=1, £ S ^ ±.
Равенство (1.5) означает, что — x0£S(t), если t—время
перехода системы (1.1) в начало координат при некотором
допустимом управлении (см. рис. 7,а). Задача оптимального
быстродействия состоит, следовательно, в нахождении наимень¬
8* 115
шего t, при котором — лг0£5(^). Если этот наименьший момент
существует (он обозначается t0)y то, используя отмеченные
только что свойства переменного множества S (£), молено
показать, что — х0 является граничной точкой множества S(t0)y
а тогда по теореме об опорной плоскости существует ненуле¬
вой вектор /0 такой, что
Верхнюю границу (1.23) можно вычислить, т. е. можно найти
то управление и(т) и соответствующий вектор z(t0y и), при
которых — l*0z (tQy и). Обозначим искомое управление
и(у, /0) и найдем его. По определению (1.22) имеем
Отсюда, очевидно, и(х9 /0) — sign IIF"1 (т) b. Если определенное
таким образом и (т, /0) единственное управление, то в силу (1.23)
будет
Обозначим через #(т, I) управление, определенное равен¬
ством (1.24), в котором /0 заменено на /. Из построения #(т, /)
ясно, что точки z(ty &(т, /)) являются точками опоры на S (t)
плоскостей с внешней нормалью /. Будем обозначать их z(l, t).
Итак,
Согласно формуле (1.24) решение задачи во многом (если не
полностью) определяется вектором /0. Чтобы найти его, выясним
отличительные признаки этого вектора от прочих векторов /.
Возьмем некоторый ненулевой вектор / и рассмотрим
опорную плоскость
/*г = Р(/, t). (1.25)
Если 1*(—х0) = 1, то уравнение р (/, t) = 1 определяет момент
t = t*(l), когда опорная плоскость (1.25) содержит точку —х0,
или когда множество S (t) впервые „касаетсяа плоскости
l*z — I* (— л0). Если / Ф /0*}, то, как отмечается теоремой 1°,
t* (/) < t* (/0), и, следовательно, — х0 £ S (t* (/)).
*) Вектор /0, удовлетворяющий соотношению (1.23), может быть не един¬
ственным. Тогда соотношение I Ф /0 означает, что вектор / не совпадает ни
с одним из векторов /0.
— l*0X0— sup /*2.
zeS(/0)
(1.23)
О
/**(/, t) = sup{l*z:z£S(t)} = Р(/, t).
116
Пусть фиксирован некоторый вектор 1ХФ /0 и найдено
соответствующее ему число t*(lO = tx. Теперь ввиду отноше¬
ния t* (/т) < t* (lQ) вектор /0 следует искать среди тех векто¬
ров /, для которых Покажем, что такие векторы I
можно искать среди векторов, для которых соответствующие
опорные плоскости к множеству S(^) строго разделяют мно¬
жества S(tx) и точку — х0. В самом деле, если найден такой
вектор 1(1*х0 =— 1), то
I* (- *0) > sup [l*z :z£S(*,)} == p(/,
но это и означает, что р (/, t() < 1, то есть t*(l) > tv В методе
пункта 2° такие векторы / получаем изменением 1У в сторону
антиградиента функции Р(/, ^), или направления возрастания
функции ^*(/). В общем случае (когда, например, компоненты
матриц -А (х), b произвольные кусочнонепрерывные функции)
такого антиградиента может не существовать. Тогда в выборе
очередного приближения вектора /0 можно ориентироваться
на построение плоскостей, разделяющих точку — х0 и множе¬
ство S(tk), где tk приближение снизу числа t0.
Пусть имеется некоторое приближение времени быстродей¬
ствия tk<J0, т. е. — £S{tk). Тогда для построения разде¬
ляющей плоскости достаточно найти расстояние между — х0
и S(tk) (см. рис. 7,6). В самом деле, если zk = z(tk, ик)—точка
множества S(tk), ближайшая к точке — х0) то, положив
lk+1 = — х0 — zk, будем иметь
— ll+ix0>max{ll+iz:z£ S(£*)}• (1.26)
Из этого неравенства легко следует, что —1%+1^0!>0, так как
0£5(^),и после нормировки (т. е. домножения lk+1 на число v>0
такое, что v/^+1x:0 = — l) будем иметь
tk+i — (v^+i) > tk-
Для построенных так последовательностей [tk), {/*}, z(tk, uk)
справедлива
Теорема 5. Если решение задачи существует, то при Л-» оо
будет:
1. tk -> t0 — 0;
2- z(tk, ик)-*х0;
3. x(t0, uk) -> 0.
Так что \uk)—последовательность (слабых) приближений
оптимального управления.
Доказательство этой теоремы несложно. Это доказательство
так же, как и доказательства следующих теорем о сходимости
методов, фактически содержится в доказательствах теорем
о сходимости методов главы IV. Потому не будем их при¬
водить. Теорема 5, в частности, является аналогом теоремы 4
главы IV (§ 2).
117
Итак, каждый шаг описанного алгоритма состоит в построе¬
нии точки zk множества S(tk), ближайшей к точке — х0. Это
задача на условный экстремум, которую можно решать, используя
идеи градиентных методов (методов возможных направлений).
Конечно, эти методы не дадут точное построение точки zky
но в этом и нет необходимости: разумно переходить к следую¬
щему шагу сразу же, как только будет получена разделяющая
плоскость, т. е. вектор /Л+1, удовлетворяющий строгому нера¬
венству (1.26).
Перейдем к точному описанию алгоритмов.
5°. Общий метод решения двойственных задач
Прежде всего установим метод нахождения расстояния.
Для этого воспользуемся идеей метода наискорейшего спуска.
Метод нахождения расстояния (метод минимизации
выпуклой функции на выпуклом множестве)
Итак, нам надо найти
( f \2
р2(0= 4- min U> + • (J-27)
1 J J
Здесь под (z)'1 понимается квадрат длины вектора z — скаляр¬
ное произведение z*z. Обозначим множество всех управлений
через М.
Пусть фиксировано некоторое управление uk(t). Как изве¬
стно, для проведения метода наискорейшего спуска следует
прежде всего установить направление q(t) спуска в простран¬
стве функций и(х)у позаботившись, чтобы: 1) это направление
не выводило из множества Ж, т. е., хотя бы при малых ц->0,
было
*€[0, *]; (1.28)
2) в направлении q (т) из точки tik (т) функционал
t Ч 2
*0 + J F-1 (т) Ьи (т) di J (1.29)
о /
уменьшался бы при достаточно малых точнее, если
= *)> то <р; (0) < 0. (1.29)'
Обычно под направлением наискорейшего спуска в точке uk
понимается такое направление „единичной длины44 ^(^О,
которое среди всех „единичных44 направлений q (т) доставляет
минимум производной <р^(0) в (1.29)'. Следовательно, прежде
всего требуется ввести понятие „длины44 направления q{y),
118
р(и(х), t) = ±-
В нашей задаче за такую „длину" естественно принять норму
функции q(x) в пространстве непрерывных на отрезке [0, t]
функций
II ? СО II= max | ^ (х) |.
те[0, /]
Для общности можно считать
|?(т)Ц= sup k(x)l
те [О, t]
(ибо управления а (Ч). являются кусочнонепрерывными ограни¬
ченными функциями).
Однако если при таком выборе „длины“ найти направление
наискорейшего спуска qk(z), то для qk{^) не гарангируется
выполнение условия (1.28). Чтобы учесть это, за множество
^единичных" направлений примем множество (г>0)
Ok (г) = 1<7 (х): IЯ (х)! < г, I ин (х) + Я (х) I < 1 }•
Нетрудно проверить, что Gk (г) — выпуклое множество, ибо оно
является пересечением выпуклых множеств
(<?(х) :|?(х)1 <''1 и М — ик{х).
Множество Gk{r) можно записать так:
Ok (г) = {q (х): а (х)< q (х)< р (х)},
где
а(х) = шах {— 1, ик{х) — г), р(х) = min {1, tik{x)-\-r\.
Теперь вычислим производную функционала р(и(т), t) в точке
ик{х). Эта производная есть
Ф3 (ик 00. О
ди
, t ч* t
•?vx) = l Jf0+ \F~l{')btlk{x) j j Z7'1 (x) bq (x) dx. (1.30)
\ 0 /0
t
Обозначим вектор -v0+ j* Z7"1 {^)Ьик[^) через hk, тогда (1.30)
o
можно переписать так:
t t
6? iuk(z), t) q (^) _ ^ * j* F_x (^) bq ^ ^ _ j ^ ^ ^ dX'
о 0
Теперь нетрудно и найти направление спуска, вычислив
t
min Ф>(ц* 0О' О .?(х)=: min Г_у*(х, hk)bq{x)dx.
q(z)6(3k(r) оа J
я (J
Отсюда видно, что минимум функционала (1.30) на множестве
направлений Ок(г) достигается при q {x) = qk(x), где
a(t), если .У*(х)£>0,
Як (х)== ■ Р(х), если у* (х) b < 0,
. ?6[«(х). Р(Х)Ь если у* (х)й = 0.
119
•*0 + F~l (x) b (lh (x) +1Wk (x))dx =
Для завершения тага метода осталось найти на выбранном
направлении точку, в которой функционал (1.29) принимает
наименьшее значение, т. е. найти число ^£[0,1] такое, что
^ / t \ 2
"2-1-0
\ о
( f \2
= \ |*о + jF~x (х)b («а + Ми (х))dxJ ■
Это задача нахождения минимума функции одной переменной
на отрезке. Причем это гладкая выпуклая функция, так что
задачу легко решить: вычислить производную по р, приравняв
ее нулю, найти корень pk получившегося уравнения и затем
установить tv Это уравнение таково:
[hk + Ра j F~l (х) ьЧн (х) dx j j F~1 (x) b4k (x) ^x = 0.
Отсюда
П=— Д*(х> hk)b4k(z)dx j (x)b(fk(x)d^j ■
Теперь, если точка р*6[0, 1 ], т. е. минимум (1.29) достигается
в точке множества М, то положить = если же jift£ [0, 1],
то взять в качестве число из отрезка [0, 1], ближайшее к [с*.
Таким образом,
10, если < 0,
Pfe, если 0Ср*С1,
1, если и-* > 1*
На этом описание шага метода закончено. Полагая иш =
— uk "Ьн-fe^A, можем переходить к следующему шагу, поступив
с иА+1 (т) так же, как с и*(х)-
Замечание 1. В описанном методе минимум по ^ ищется
на отрезке [0, 1], а не по всему лучу как в класси¬
ческом варианте этого метода. Это обусловлено тем, что при¬
ближения Kft(x) должны находиться в множестве
М={и(т):|й(т)|<1}.
Однако может оказаться, что и при некоторых [л > 1 функция
и (т) = (т)-j- (х<7Дт) будет лежать в М. Эго будет так, если,,
например, | uk (т) | < 1—е, е>0, а г — достаточно малое число
(0<r< min \\uk(t)—1 |, |йл(х)+1|П. Так что малое г будет
V *ce|0, t] I
„сдерживать" скорость приближения к минимуму. С другой
120
стороны, большое значение г (г ^2) хотя и обеспечит полное
использование направления qk(t) (если г ^2, при ^ > 1 функ¬
ция tik(4.)-\-\xqk(4) в примере не принадлежит /И), но сходимость
метода может оказаться малой из-за плохого выбора <7ь(т)>
который зависит от г. Положим г = 2. Тогда, очевидно, Gk(r)=M.
Соответствующее этому Gk(r) направление спуска обозначим
через ^(т)(см. рис. 8,а). Далее положим г <2. Тогда соот¬
ветствующее направление спуска есть qkG). Из рисунка видно
(с учетом его условности), что в первом случае следующее
приближение u'k+l ненамного уменьшает расстояние до и{)—точки
абсолютного минимума функционала (1.29), в то время как
во втором случае приближение Uk+1 дает искомый минимум.
Вывод из этого примера такой: выбором величины г следует
разумно распоряжаться. Видимо, г следует уменьшать особенно
при приГлижении к искомому минимуму.
Можно рассмотреть вопрос о быстроте сходимости в случае,
когда г не константа, а функция г(т).
121
Замечание 2. Следует упомянуть также возможность
построения аналогов s-шаговых методов спуска в решении
линейных алгебраических уравнений [40]. Примером такого
метода может быть следующий s-шаговый метод при s = 2.
Пусть на каждом шагу известно 3 точки множества S(t):
z\k' z2k> z3k> т- e* известны три управления и™ (т), ^2)(т), и{£\т)
такие, что
zik = j F 1 (%) bUk] (x) dx | (n) | < 1, / = 1,2,3.
0
Найдем точку zk треугольника с вершинами в точках z]k, z2k>
z3k (см. рис. 8,6), ближайшую к точке — х0. (Это простая задача
аналитической геометрии.) Далее положим, fik+1 = — х0 — zk
и найдем соответствующую точку z(hk+x, t) опоры плоскости
с нормалью hkи к множеству S(t). Теперь выберем одну из
точек zlk, z2k, z3k, обозначим ее zk и перейдем к следующему
шагу, положив
Z\, ft + l — Zh' Z2, fe + l = Z ip'h+l » 0’ Z3, k + l = zh-
Можно рассмотреть метод, в котором сохраняется значи¬
тельно большее число точек zik и следующая точка ищется,
как и выше, как точка „касания* S(£) плоскостью с нор¬
малью — х0 — zk, где zk — ближайшая к — х0 точка выпуклой
оболочки векторов, построенных на предыдущем шаге,
^ S S
^=2V7A> ai > °- 2*/ = 1-
у-1 J=1
Метод решения задачи быстродействия
Теперь можно рассмотреть такой метод решения поставлен¬
ной в начале задачи быстродействия.
Пусть на ft-м шагу получены число tk^Ct0 и точка zk =
= z(tk, uk). Сделаем 1 шаг по одному из методов решения
задачи (1.27) при t = tk, взяв uk за начальное приближение.
Пусть z — точка, ближайшая к — х0, из полученных за этот
шаг точек. Составим вектор h= — x0— г. Если Л* (— х0) ^0,
то, положив tk+i = tkJ zk+l = z, перейдем к следующему шагу.
Если Л* (—- xQ) у> 0, то пронормируем /г и найдем t* {h). Положим
/Л+1 = max {£*, t*(li)\. В качестве zk+l можно взять точку
отрезка [z, z(hk, tk+l ] , ближайшую к точке — х0.
Теорема 6. Если решение исходной задачи существует,
то последовательность чисел tk сходится к t0, zk-> — х0
122
при k-+coy последовательность [uk(i)) является последова¬
тельностью слабых приближений оптимального управления.
Эта теорема является аналогом теоремы 5 главы IV.
Замечание. В процессе построения точки zk могут быть
получены без прообраза uk(y) :zk = z{tk, uk). В этом случае
для построения слабых приближений решения задачи быстро¬
действия достаточно найти такие управления uk(т), чтобы было
Дальнейшие модификации алгоритмов этого параграфа
можно проводить, основываясь на построении более точных
приближений границы множества S(^), чем опорные плоскости.
Примеры таких модификаций приведены в [47J.
§ 2. НЕОДНОРОДНАЯ ЗАДАЧА ОБ ОПТИМАЛЬНЫХ ЛИНЕЙНЫХ
БЫСТРОДЕЙСТВИЯХ
1°. Постановка задачи
Пусть поведение управляемого объекта определяется
системой
x = Ax-\-bu-\-fy (2.1)
которая отличается от системы (1.1) свободным членом /.
Компоненты матрицы А и векторов Ь, / считаем кусочно-
непрерывными ограниченными функциями времени t на [0, оо).
Ставится задача о построении управления u(t), удовлетворяю¬
щего ограничению
|И(*)|<1
и такого, что управляемый объект переходит под его воздей¬
ствием из начального состояния х{) в некоторое фиксированное
положение xf.
Для решения этой задачи можно с некоторым уточнением,
предложенным Дж. Итоном [48], использовать подход преды¬
дущего параграфа. В § 1 все построения велись не в фазовом
пространстве (пространстве значений вектора x(t) как решения
уравнения (2.1)», а в пространстве, отличающемся на некоторое
линейное преобразование (F~l(t)). Это преобразование позво¬
лило свести все построения в основном к интегрированию
сопряженной системы в положительном по времени направле¬
нии. В случае неустойчивости этой системы (и в некоторых
других случаях) такое интегрирование нежелательно. Тогда
аналогичные построения можно весги в фазовом пространстве.
При этом интегрирование сопряженной системы можно про¬
водить большей частью в обратном по времени направлении.
Ниже будет приведен пример такого алгоритма.
123
2°. Метод последовательных приближений
Пусть u{)(t)— решение задачи, a t0 — время перехода
системы. Тогда
to
xf = F(tо) х0+ 1К(Х)+/} dx = x(t0u0).
о
Здесь F(t) — матрица фундаментальных решений системы
х = Ах.
Введем в рассмотрение множество
S(О = {*(*, и) :|и|< 1}.
Ясно, что t0 есть наименьшее число t > 0, при котором
*,6 SW-
Рассмотрим следующую процедуру. Возьмем вектор
l1 = xf — xQ и найдем число t^ = t* (lu 0) как первое число
после'нуля, при котором опорная плоскость к S(t ) с нормалью
(l*F~l (ti))* содержит точку xft т. е.
l*F-' W) xf = max I*F"1 fa) х (tl9 a). (2.2)
|И|<1
Пусть максимум в (2.2) достигается при ^ (т) = й (т, /х). Для
нахождения tx и их(т) надо интегрировать уравнения
f (х) = —Ф (о) = /i, (23)
ш = ф*(т)&м(т, /,)-)-<|>*(х)/, <о(0) = 0
до того момента, когда впервые будет
Р (t) = <j>* (t) xf — 1гх00.
Этот момент и есть t1 = t*(ll, 0). В формуле (2.3)
и(т, /j) = sign^* {т)Ь. (2.4)
Теперь с управлением и1(х)=й('с, 1г) проинтегрируем систему
х = л;(0) = л:о
и вычислим xl = x(t1, их). Если окажется, что xx = xf, то
ux(t) — оптимальное управление; tx — время оптимального
быстродействия. Если же хх ф xf} то следует, например, так
изменить вектор /2, чтобы было t* (l2, tx)^tx и в множестве
t})) найти точку jc2, более близкую к точке xf, чем
точка х}. Покажем, как это можно сделать.
Пусть в пространстве векторов х введена норма
\\х\\2 — фх*Ох,
124
где G — положительно определенная симметричная матрица.
Расстояние между векторами х', х" определим так:
г(х\ х") = \х' — х”\. (2.5)
Обратимся к геометрической интерпретации случая х^фхJe
Очевидно, в силу х^фх^ и того, что плоскость
CxF^it,) х = £р~1 (tjxf
опорная, точка xf не является внутренней точкой множества
S(^) и, следовательно, существует опорная к 5(^) плоскость,
разделяющая 5(^) и точку xf. В частности, чтобы построить
такую плоскость, достаточно найти расстояние от xf до мно¬
жества S(A). Пусть это расстояние реализуется в точке
xl=x(tl, иJ множества 5(^). Тогда, если xf = xx, то их —
оптимальное управление. Если х^фхъ то вектор l2 — xf — х±
может служить нормалью, разделяющей плоскости
l*2x= l\xf > max l\x иъ и).
|И|<1
Далее найдем момент t2 как первый после tu в который
опорная к S(t2) плоскость с нормалью llF(t{)F~x (t2) содер¬
жала точку Xf. Такой момент t2 так же, как и момент tu
существует, если существует решение поставленной задачи.
На множестве S{t2) можно опять найти точку х2, ближайшую
к xf, и т. д. Итак, если решение поставленной задачи су¬
ществует, то последовательность точек |лД сходится к xfy
tL t0, а последовательность управлений {ut (х)} таких, что
x[ti, щ(у)) = Xi слабо сходится к оптимальному управле¬
нию (аналог теоремы 5).
Описанный алгоритм включает в себя на каждом шагу
определения расстояния от точки xf до множества S(tj), что
является самостоятельной экстремальной задачей, которая
может быть решена методом последовательных приближений.
Поэтому общий алгоритм мы составим так, что на каждом
этапе построения оценки // числа t0 будем выполнять только
один шаг по методу, с помощью которого решается задача
определения расстояния.
Пусть Х( — некоторая точка множества Градиент
функции расстояния (2.5) в этой точке есть
Теперь на направлении qt надо найти точку множества £(£/),
ближайшую к Xf. В данном случае проще найти точку х,
являющуюся опорной точкой плоскости с нормалью <7/ на мно¬
жестве S(ti). Как мы видели выше, для построения такой
точки надо:
1) проинтегрировать от ^ к 0 сопряженную систему
ф = -А*у, Wi) = 9t, (2.6)
попутно запомнив управление
й (х) — sign if* (x)b;
2) проинтегрировать от 0 до ^ систему
х = Ах -f- Ьи (т) -\-f,x (0) = xQ.
В результате последнего интегрирования получим точку х (tft
такую, что вектор х (t;) — х (t{) можно взять в качестве на¬
правления спуска в задаче минимизации функции расстояния
r2{x, xt) и искать на отрезке [*(£/), x^tf)J минимум этой
функции. Но посмотрим, нельзя ли прежде уточнить число t0
(т. е. заменить tt на число 1, более близкое к t0). Для этого
рассмотрим величину
bi = ql(xf— x(tj).
Если то точка Xf и множество S(tj) лежат по одну
сторону от плоскости
<ftx = qix[tt). (2.7)
В этом случае положим ti^\ = ti. Если ^>0, то точка Xj и
множество S(ti) лежат по разные стороны от плоскости (2.7)
и можно продолжать интегрирование сопряженной системы
(2.6) от ti в положительную сторону до тех пор, пока не будет
Plf)<0. (2.8)
Здесь
р (*) = Ф* (t) xf — qlxjti) — <0 (t),
®(0 = 1Г(‘')*1 + Г/, “(*/) = О- (2.9)
Тот момент, при котором впервые (после tL) выполнится не¬
равенство (2.8), обозначим ti+\.
Параллельно с интегрированием уравнений (2.9) запомним
на [£;, 7,+i] функцию
a(^) = slgn«l»*(x)-6,
а по окончании интегрирования — вектор x{ti +1). Затем про¬
интегрируем от ti до ti+1 уравнение
х '=■ Сх —J— Ьи {t) —{- f, х {ti)г= Х[.
126
Теперь на отрезке [x(^,+i), ,*(£i+i)J найдем точку, ближай¬
шую к xf. Для этого вычислим
,_(*/-■*( */+0)*о(*( *<+i)-*(*i+i))
2г[х( ^+0- *('/+0)
и примем
II, если j/ > 1,
[а, если ц/6 [0, 1],
О, если р' < 0.
Положим
и /т\_ [иг-(т) + р.(«(т:) — ui(i)) при ^ [0, ti),
<+1 UW при т е [tb ft+i].
Очевидно, что
xt+l = x(tl+1, »/+1) = Jc(^+I) + {tU(^+i) —л(^+1)) .
Итак, получены величины tl+v xi+v с которыми можно
поступить так же, как здесь мы поступили с th xh т. е.
можно перейти к следующему шагу. Для построенных так
последовательностей (^), {^}, {^(т)} справедлива теорема,
аналогичная теореме 5.
3°. Нелинейная зависимость фазовых координат от аддитивно
входящей в уравнение (2.1) функции управления
В задачах этого и предыдущего параграфов в уравнениях
движения можно заменить слагаемое bui'i) на нелинейную
вектор-функцию b(t, u(t)). Поскольку множество S(t) при
фиксированном t есть множество интегралов от этой вектор-
функции, то, как следует из леммы § 3 главы IV, замыкание
этого множества выпукло, если вектор-функция b (t, и) при
почти всех t непрерывна по своим аргументам, а кусочно¬
непрерывная (измеримая) функция и (у) принимает значения
в произвольном ограниченном чисел Sc(— оо, + оо). Заменяя
во всех построениях множество S(t) на замыкание S(t)r
можно построить аналогичные приведенным выше алгоритмы.
Отличие этих алгоритмов будет состоять в том, что теперь
вместо нахождения простого та х^(^)Ьи нужно искать
|и|<1
sup б* (т) b (t, и). Это самостоятельная экстремальная задача.
U €2
Приближенное решение ее обозначим и(т, I) (ср. (2.4)). Для
приближенного нахождения точки на отрезке можно восполь¬
зоваться конструкцией, приведенной в упомянутой выше лем¬
ме главы IV. Поскольку решение задачи оптимального быстро¬
действия в этом случае может не существовать (даже если
127
существует допустимое управление), то с самого начала нуж¬
но ставить задачу о переводе объекта в сколь угодно малую
окрестность конечного состояния xf за возможно меньшее
(наименьшее может не существовать) время (задача II гла¬
вы II). Для практических задач такая постановка вполне
приемлема. Алгоритмы этого параграфа как раз и дают ре¬
шение такой задачи.
§ 3. ОПТИМАЛЬНЫЕ ЛИНЕЙНЫЕ БЫСТРОДЕЙСТВИЯ С УЧЕТОМ
ОГРАНИЧЕНИЙ НА ФАЗОВЫЕ КООРДИНАТЫ
Модифицируем для решения этой задачи метод, описанный
в предыдущем параграфе. Рассмотрим этот метод на конкрет¬
ном примере фазовых ограничений.
1°. Постановка задачи
Пусть движение управляемого объекта описывается систе¬
мой уравнений
х А. х -|— bit, (3.1)
На параметры движения объекта заданы ограничения:
М<1> (3.2)'
Ka^ + a^Kl, (3.2)"
л„>0. (3.2)"'
Здесь хъ хп — первая и п-я компоненты /г-мерного вектора х.
Начальное состояние задается точкой
л:(0) = х0. (3.3)
Задача. Достигнуть за наименьшее время заданного линей¬
ного многообразия
Gx — g = О
на движениях (3.1) из начального состояния (3.3) при ограни¬
чениях (3.2) (G — матрица г X п\ g — r-мерный вектор).
2°. Эквивалентная задача
Перепишем (3.2)", (3.2)'" в виде
<Pi (ДЛ + 0*0 + vi) = 4" + а*и + ^)2 = °> (з-4)
К1<1, (3.5)
?2 (Хп + V2) — ~2 V=
2<0. (3.7)
128
Здесь h — достаточно большое число. Будем равенства (3.4),
(3.6) на временном промежутке [0, t\ понимать в интеграль¬
ном смысле, т. е.
t
г (t, и, v) = J{ с! (х) ?1 (агХ! 4- а2и + г\) +
О
+ С2 (х) <р2 (хп -J- Я'г)} dt = 0, (3.8)
(х) Ф О, С2 (х) =4= 0.
Теперь будем решать задачу пункта 1°, но требование удо¬
влетворить ограничениям (3.2)', (3.2)" заменим требованием
равенства (3.8), где vu v2 из промежутков (3.5), (3.7), a t —
конечный момент движений.
Итак, новая задача состоит в нахождении функций и(х),
i'i(x), t>2(t) таких, что при наименьшем t выполняется равенство
p(t, и, v) = (Gx(t, u) — g, r(t, и, v)) — 0. (3.9)
Здесь и) — решение системы (3.1) с начальным условием
(3.3), соответствующее данному управлению и (х). Очевидно,
что вектор Gx(t, и) — g будет равен нулевому вектору тогда
и только тогда, когда квадрат нормы его равен нулю:
a(t, u) = -^-[Gx{t, и) — g\* [Gx(t, и) — g]=0
(* — знак транспонирования), так что (3.9) можно переписать
в виде
p(t, и, v) = a(t, u)-\-r(t, гг, v) = 0. (3.10)
3°. Метод решения
Этот метод, как и метод предыдущего параграфа, заклю¬
чается в том, что зафиксировав некоторое число t19 не боль¬
шее времени оптимального быстродействия tQ, мы будем ми¬
нимизировать по и функционал p(tu гг, v) одним из градиент¬
ных методов. Если после некоторого числа шагов станет
ясно, что p(tl9 и, v) не может быть равным нулю, то заменим
t1 на t2, удовлетворяющее неравенствам t2> tu t2^t0.
Вычислим градиент по (и, v) функционала (3.10) в точке
(гг, v). Для этого сначала найдем приращение функционала
Др = р(^ и-\- Дгг, <V-\-kv) —p(t, и, ^) = Да -j- Дг =■
= [Gx(t, и) - g] * GAx (t) + j | c\ (x) ^ {aiXl (z' u) + a*u (t) +■ X
0
X (#j Дхх (x) -}- a2ku (x) -j- + (3.11)
+ С* (x) дъ{Xn (Axn (4 + bv2) } dx + о (Ди, Дг», Дх).
9 Н. E. Кирин
129
Здесь вектор Дл;^) является решением уравнения
Дx(i)=AAx-{-bAti\ Ах (0) = 0, (3.12)
где А и b — матрица и вектор из уравнения (3.1). В силу (3.12)
при любой кусочнонепрерывной вектор-функции ф (т) будет
t
J ф* (х) [ Д ;с (х) - ААх (t) - ЬАи, (х)] rfx == о.
0
Добавляя этот интеграл в (3.11), интегрируя слагаемое
ф*(т)Дд;(т) по частям и собирая коэффициенты при Дя(^),
получим, опустив величину 0(Ди, Av, Ах),
t
[О* (Gx (t, и) - g) + о (/)] * д* (0 - J [ ф (х) + «М - d (X)]* X
О
t
X Ах (х) di — j* [ф* (b) — г (х)] Дм (х) dx = (3.13)
о
t
= ДР — j (С1 (т) Лг;1 (х) + °1 (х) w (4) fa-
о
Здесь приняты обозначения:
rf(x) = (^(x), rf2(x), ...^.Дх), rf„(x)),
dl (X) = cl (х) о, Шал + w + vj =
— с? (х) аг (atxx (х, и) + а2и (х) + г»х (х)),
^2(х) = ... =d„_1(i) = О,
dn (т) = с2 (,) ^2(^(Х. «) + 1>2(х» = с2 (х) ( ^ (Х) и) + ^ (х))>
г (х) = Д (х) а2 ») + ^(;)+^Д1) = rfi (х) £l .
Положим
О = — Л*ф + rfx, 6 (/) = — G* [Gx (t, и) — g].
Тогда (3.13) можно переписать в виде
t t
Др = -|[^-г(х)] Att(x)rfx4-J[C2^A^.-i-^g-2Ax/2]rfx. (3.14)
о о
Вычислим минимум интеграла (3.14) по AvxAv2Aи при огра¬
ничениях | Д^| -С 1, Av2£(— А, О), | Дм|<Д. Ясно, что этот
минимум достигается при
Дм = sign [ф' (х) b — г (х)] = и (х),
— ду'2
— Л, если > О,
^2=*>2 = i дП
О, если ^<0.
Теперь в качестве направления изменения и, vu v2 для умень¬
шения р(*г, t) примем направление
q(t) = u(x) — u^),
h1(t)=v1^)-vi (х),
hi(t) = v2(r)-vz(x).
Найдем на этом направлении точку минимума функционала
p(t, U, V), т. е.
minp(£, и + p-q, v + р/г), р^=0.
Поскольку функционал p(t, и, v) выпуклый по и, vx, v2 и диф-
ференцируемый, то минимум его достигается там, где
dp (« + м> v + t) _ п
ф — и*
Пользуясь (3.11), это можно записать так:
[Gxy. {t)~g\ * ОДх, (*) + j {с? (х) {аМч (х) +
0
+ а2е? + еЛх (х)) + ^2(х)^а%^1 (ДхП1Л(х) +>Л, (х))} rfx = 0. (3.15)
Здесь приняты обозначения:
Дл;,, (х) = s [х (х, и) — х(х, и)],
Д x(t) = x(t, и) — X (t, и),
(х) = X (х, м)-f-J. (х(х, и) — х(х, и)).
Подставляя эти представления в (3.15) и сокращая на е, получим
t
[Gx (t)-g + pGAx (t)}' GAx (t) + j* [c? (x) ^ (axAx + a2q +
0
_L ,h (x)) + c\ (x) (AXn (x) + ^ (,))} dx = 0.
Здесь
= axxj,* -f a2uv. + vx (x) == ax {xx + рДл^) + a2 (u + pq) + vx (e) -
+ (*) = йл + a2u 4- Vj + p (a^ + a2? + hx (x))=ex (x) + p^ (t)\.
7& = (x) + v2 (x) + p (Axn + h2 (x)) = 62 (x) + pT2 (x).
9* 131
Теперь из (3.15) находим
t
[Gx (t) — g]’ GAx (t) + J [ c\ (x) 0x (x) {axAxx + a%q -f hx (x)) +
[Дх {t)]*G*GAx (t) -f | [ c\ (x) Tl (x) (a1Ax1 -f a2q + ht (x)) +
0
+ 4 (x) 92 (x) (Ax„ (x) + hj (x))] dz
+ 4 (x> Y2 (*) (bxn (x) -f h2 (x))] dz
Здесь введены обозначения:
01 (x) = «1-^1 (x, «) + (x) + ®1 (x).
02 (x) = xn (x, и) + г», (x) - xn,
Ti(x) = «i(^i (x, к) (x, гг) + a2q (x) + hx (x)),
T2(x) = x„ (x, гг) — л:„(х, и) + /г2 (х),
kx(t) — x{t, u) — x(t, гг).
Теперь положим, что
о
х (&) = J { С1 (х) 0i (х) Ti (х) + с2 (х) 02 (х) Т, (х)} dz,
v = I ( С1 121 (х) + С1 (х)т1 (х)) dz.
о
Тогда (3.16) можно переписать так:
[Gx(t) -g]'GAx (Q + »(Q
[д.*:(г)]*о*од.*:(г)-|^(г) •
Таким образом, для вычисления у. надо от 0 до г? проинте¬
грировать системы уравнений для х(х, гг), х (х, гг), х(х), v(x).
Теперь остается проверить, является ли выбранная точка ми¬
нимума допустимой, т. е. удовлетворяют ли функции гг + pq,
vt + \iAt, i — 1, 2, соответственно ограничениям (3.2), (3.5),
(3.7). Для этого достаточно проверить, что jj-G[0. 1]. Если же
ц.(« [0, 1], то вместо fi следует взять тело равное 0 или 1
в зависимости от того ^<0 или jj- > 1.
Приведем сводные формулы алгоритма.
Алгоритм. Перед началом k-то шага заданы числа tk > 0,
Р* и функции 'Hi(x), ^(х), т;?(т), v\(z), uk(х), uk(z), определен¬
ные на [0, £*].
1а. Интегрируем от 0 до tk систему уравнений
x = Ax-\-bukt х(0) = д:0,
х = Ах -f Ьак, х(0)=л:0,
X==C101, kTl, ft “Ь С2®2, Д 2, ft’ х(0)=0,
'^=сЫк + сгг!,*. v(0)=0.
132
16. Если pfe < 0, то переходим к выполнению операций
пункта 1в, положив tk+l=tk, если же РА>0, то с момента tk
вместе с уравнениями пункта 1а интегрируем
ф = _ Ац + dk(x), ф (tk)=_G* (g - Gx (tk)),
p = — I <b*b — rk (t) I + kVi + C%b2, hV2, p (tk) = pft,
P = c\*l k + clbl h, P(tk) = 0, A = IA || Д +1 b% д (tk) = 0.
Параллельно запоминаем функции tik —tik, v* = vfv2 = V2 при
т > tfoy вычисляемые по приводимым ниже формулам (3 17),
(3.18), в которых индекс k-\-\ заменен на k. Интегрирование
ведем до тех пор, пока не будет
Р (х) - -г р (х) - А (х)IIФ (h) ~ Ф (х) II+■** (tk) (ф (х) - Ф (tk)) < 0.
Этот момент обозначим через z^+1 и перейдем к следующему
этапу вычислений.
1в. После интегрирования запоминаем х(^+1), л(^+1), v(tk+1)>
*(^+i) и затем вычисляем
. (Gx (t) - g)* G (x (t) — x (tj) + ■/. (t)
(x (t) - x (0)* G*G (x (t) - x (0) + v (t)
1, если p > 1,
p., если p6[0, 1]
О, если р<С0 или р. не определено,
+1 = £l - р) VI + p.vl v%+l = 0 - р) v\ + р^,
uk+\ = I1) wft “Ь -*7г+1 = о I1) x(t\i+\) + p^^ft-t-l)*
Полученные иА+1, v£+1 засылаем в память ЭВМ.
II. Интегрируем от tk+l к 0 системы уравнений
Ф = — Л *ф + dh+1 (т), ф (4+I) — G*{g — Gxk+i),
х — Ах + Ьик+1, x(th+i) = xk+u
p = I G*b — ^fc+l(x) I — Cnh, h+iVi+1 — C2&2, ft+1^2 + 1, P(^h+l)=0,
P =— Ci&tfc+I — clbl, h+i, p(4+i)= [GXh+1 — g]* [Gx:*+1 — g].
Здесь
vi+1 = — sign&i, k+\,
v\+x = {-^ если d2,fe+i>0, (3 17j
1 0. если &2, ft+i<0.
Параллельно запоминаем функции t>i + 1(x), г'2+1(т),
«А+i (x) = sign [ф* (x) b - rk+1 (t)] (3.18)
и число pft+i = p(0) — ф*(0)х0 j-p(O). Теперь можно пере¬
ходить к следующему шагу.
133
Теорема 7. Пусть решение задачи пункта 1° существует.
Тогда построенные выше последовательности управлений
ilk (т) и чисел tk таковы: по любому г > 0 найдется номер k0
такой, что для k > &0 за время t^y не превосходящее вре¬
мени оптимального быстродействия управляемый объект
переходит в заданное многообразие с точностью до е>0:
IIGx{tk, ИлСс))-г||<е,
и фазовые ограничения выполняются при этом в среднем
с точностью до е;
гк
j uk{i)) + a2uk{t)) + H%{xn{t, и* (*)))} Л <е.
о
Здесь
/ | а I при М > 1,
1 1 0 при | а| ^ 1;
//,(«) = •
— а при а < О,
О при а > О.
§ 4. ОБЩАЯ ЗАДАЧА БЫСТРОДЕЙСТВИЯ
Схему решения задачи об оптимальном быстродействии,
использованную в предыдущих параграфах, можно распро¬
странить и на случаи более общих моделей движения управ¬
ляемого объекта. В настоящем параграфе кратко описывается
возможный вариант такого распространения.
1°. Постановка задачи
Объект регулирования описывается дифференциальным
1зекторным уравнением
x(t)=f{x{t), u{t)). (4.1)
Здесь t — время; x (t) — «-мерная вектор-функция фазовых
координат объекта; u(t)-m-мерная вектор-функция управ¬
ляющих воздействий (управление). Пусть М— некоторое мно¬
жество управлений u(t), определенных для Г>0.
Будем считать, что для любого управления и (t) из М опре¬
делено на [О, Т) кусочно-дифференцируемое решение x(t)
системы (4.1) с начальным условием х(0) = х0. Будем обозна¬
чать такое решение, соответствующее данному управлению
и (t), через x(ty и(ъ)) или x(ty и).
Управление u(t)£M называется допустимым, если суще¬
ствует число t{u)£[О, Т), при котором выполнены условия
g(x(t, и), и (ОХ 0, t £ [О, Г), (4.2)
m(x(t, и), и (ОХ 0, t£\t(u\ Т\ (4.3)
Здесь и) и т(ху и) — заданные 5-мерные вектор-функции.
134
Допустимое управление u0(t) называется оптимальным,
если соответствующее ему число t — t{ii0) — наименьшее из
возможных. Число t(uо) называется временем оптимального
быстродействия или просто временем быстродействия.
Задача I. Найти оптимальное управление.
Эту задачу можно интерпретировать так: найти управле¬
ние u(t), при котором фазовая точка x(t), находясь в неко¬
тором фиксированном множестве, определяемом неравен¬
ствами (4.2), за наименьшее время достигнет данного множе¬
ства, определяемого неравенствами (4.3), и останется в нем.
Обычно такую задачу решают в два этапа: сначала находят
множество G0 состояний системы, для каждого из которых
строят управление, удерживающее систему в множестве (4.3),
затем строят управление, переводящее систему за наимень¬
шее время в G0. При описанном ниже подходе такого раз¬
биения не делается, что имеет свои преимущества, например,
в случае невтономных систем, в задаче частичного синтеза
и т. д.
Поставим задачу приближенного решения описанной проб¬
лемы. Для этого напомним сначала, что условия (4.2), (4.3)
введением дополнительных управлений могут быть записаны
в виде равенств. Предположим, что это уже сделано, и усло¬
вия (4.2), (4.3) имеют вид
g{t\ u) = g{x(t\ и), и (^)) = 0, ^ 6 [о, Т), (4.4)
тп(г1; u) = m{x{t; и), u(t)) = 0, t£[t{u), Т). (4.5)
Определим «меру нарушения» этих условий следующим обра¬
зом. Поскольку вектор-функции g(t, и), m(ty и) определены
для любого U{t) из УИ, составим вектор-функцию с компо¬
нентами g,_m\p{t\ и, t) = (g(t, и), m(t,ji)), где m{t, и) = О
при *€[о, О, m(t, u) = m(t, и) при t^[t, Т\.
Пусть Р—некоторое полное нормированное пространство,
содержащее вектор-функции p{t\ и, t). Теперь за «меру на¬
рушения» условий (4.4), (4.5), где t(u) заменено на t, для
произвольного и£М примем норму ||p(t; и, £)|| вектор-функ¬
ции p(t; a, t) как элемента пространства Р. Для определен¬
ности для p=p(t) = (g(t), m(t))£P можно положить
г
IIР (*) II2 = 5 [s'* (0 8 (0 + m* (t)m (0] dt. (4.6)
О
Последовательность элементов [uk)y uk£M назовем допус-
тимой, если при некотором числе t = t {{uk))£[ О, Т) будет
\р[*> «*» *)1 —> 0 при &->оо. Допустимую последовательность
ju°k} назовем оптимальной, если соответствующее ей число
{\u°k}) — наименьшее возможное. Это число обозначим че¬
рез t0.
Задача II. Построить оптимальную последовательность.
Отметим, что задача II шире задачи I в том смысле, что
из существования решения задачи I следует существование
решения задачи II, причем Обратное не всегда
имеет место, но и тогда задача II представляет. самостоя¬
тельный интерес. Перейдем к ее решению.
2°. Двойственная задача
Будем обозначать вектор-функцию p_[t\ и, 1) через р{и, t),
подразумевая одновременно под р(и, t) операцию сопостав¬
ления управлению и£М и числу t вектор-функции p{t\ и, t)
пространства Р. Для каждого ££[О, Т) введем в рассмотре¬
ние множество
S(t) = {р(и, ~t):u£M) а Р. (4.7)
Очевидно, что в задаче I время быстродействия есть наимень¬
ший момент t, при котором нулевой элемент 0 пространства Р
принадлежит множеству S(i), а оптимальным управлением
является всякое управление и0£М, для которого р{щ, t) =0.
Будем считать выполненными в этом пункте и в пункте 3°
следующие условия.
Условие А. Пусть на параметры задачи (вектор-функции
/С*. и)> S(x, и), тп{х, и), множество управлений и) нало¬
жены условия, при которых
а) множества S(t) при всех ££[0, Т) компактны и замк¬
нуты;
б) однопараметрическое семейство множеств S(t) непре¬
рывно по t в том смысле, что при любом ^£[0, Т) величины
Pi (*, 8) = sup inf {|/> —?||:/?6S(*), ^€5(^ + 8)},
Я Р
Р2 (t, 8) = sup inf (||/? — <71|£ S (t), q£S(t + 8)}
P Q
стремятся к нулю при 80. Такие условия можно сформули¬
ровать на основе известной теоремы А. Ф. Филиппова [37].
Поскольку 0 £5(0, если t < t, то существует непрерывная
функция /(/?), определенная на элементах пространства Р и
такая, что /(0)>/(р) для всех p£S{t) (t фиксировано).
(Действительно, в качестве такой функции всегда можно взять
функцию расстояния до точки 0 :/(/?) = —1|/?||.) Такую функ¬
цию назовем строго отделяющей множество S(t). Предполо¬
жим, что мы умеем вычислять функцию
Р(/, 4 = max {/(/>) :/>65(х)} (4.8)
для всех х £ [О, t ]. Нетрудно убедиться, что при выполнении
условия А, Э(/, т) — непрерывная функция т и в силу нера¬
136
венств Р(/, 0 </ (0) < Р(/> *) существуют числа t£(t, i\,
для которых /(0)<;р(/, t). Нижнюю границу таких чисел t
обозначим через t* (/, t). Итак, вычислением функционала
(/> можем получать оценку снизу времени быстродей¬
ствия t.
Пусть имеется некоторый класс Ф непрерывных функций
f(p). Обозначим через F(t) множество функций /из Ф, строго
отделяющих S(^). Для уточнения введенной выше оценки
естественно искать число
**(*) = sup (**(/, t):f£F{t)). (4.9)
(Если F(t) пусто, положим t* (t) равным t.) Если способ вы¬
числения функции t* (t) известен, то можно строить последо¬
вательность [tk\ оценок снизу числа t по следующей формуле:
= **(**)> ^i = °-
Поскольку t)^t для f£F(t), t^.i, то имеют место
неравенства 0 ^ tx ^ t и, следовательно, существует
lim tk — t*^t. Закономерен вопрос: когда t* = i?
k -*■ оо
Теорема 8. Пусть решение задачи I {II) существует, и при
любом ^б[0, t ) множества F{t) непусты. Тогда t* = t0 — i.
Итак, при сделанных предположениях указан способ нахо¬
ждения времени быстродействия, состоящий в построении на
[О, Т) наименьшего неотрицательного корня t* уравнения
** = *•(**) = sup {**(/, t*) \f£F{t*)).
Нахождение этого корня назовем двойственной задачей II*
к задаче 1(11) и соответственно функционал £*(/, t) — двой¬
ственным функционалом, а функцию f{p) — двойственной
переменной.
Отметим, что при выполнении условия непустоты множеств
при t£ [0, t*) (а это зависит от выбранного множества функ¬
ций Ф) существование решения одной из задач II и II* является
необходимым и достаточным условием существования реше¬
ния другой, а конструктивным признаком выполнения этого
условия является ограниченность последовательности [tk).
3°. Методы одновременного решения прямой и двойственной
задач
Посмотрим, как связаны аргументы и и / решений двой¬
ственных задач.
Будем говорить, что функция f (р) удовлетворяет условию В
по отношению к множеству S{t), если максимум (4.8) реали¬
137
зуется на единственном элементе p(f, t)£S(t). Если усло¬
вию В по отношению к множеству S(t) удовлетворяют все
функции / из Ф(/г(^)), то будем говорить, что S(t) регулярно
относительно Ф {E(t)).
Теорема 9. Пусть {Д}—решение двойственной задачи,
т. е. Д € B(tk), tk+l = t* (Д, tk)-+t\ Если функции fk равно¬
степенно непрерывны, lim Д = / и /, fk удовлетворяют уело-
k~> <х>
вию В относительно соответствующих множеств S(t*),
S(tk),mo последовательность {р (/*, 4+i)} ->0(<Pnpuk^ оо,
т. е. если управления Uk(*M таковы, что \p(fk, tk+1) —
—p(uk,tM)I—>0, то последовательность {и* } есть решение
k -*■ 00
задачи II.
В теореме 9 соотношение НтД=/ достаточно понимать
ft-* 00
00
как lim /. (/?)=/(/?) для всех p£S(t*)\J S (tk). Условия тео-
ft- 00 к k=1
ремы 9 можно ослабить.
Итак, в условиях теоремы 9 для получения решения за¬
дачи II можно решать двойственную задачу, основным эле¬
ментом решения которой является нахождение верхних гра¬
ниц (4.8) и (4.9). В связи с этим полезно отметить некоторые
свойства функционалов £*(/, t) и Р(/, t) при ££[0, i).
Пусть множество Ф функций /—нормированное простран¬
ство и в Ф определено понятие сходимости, связанное с нор¬
мой так, что сходимость последовательности функций {/*}
к функции /0 означает, что fL{p) /0 (р) при i -> оо равно¬
мерно относительно р из любого компактного множества.
Лемма 1. Функционал р(/, t) — выпуклый по / при фик¬
сированном t и непрерывен по обоим аргументам.
Следствием этой леммы является следующее предложение,
проверка которого аналогична доказательству, проведенному
в замечании 1 пункта 2° первого параграфа.
Лемма 2. Функционал t* (/, t) является строго квази-
вогнутым по f на множестве F(t), т. е. при любых /ь /2
из F(t) и р£(0, 1)
ЩрЛ + а—р) Л. *)>*ц = mm t), t)\,
причем знак ревенства имеет место только, если
/х=/2 или если tl<2i есть максимум функционала t* (/, t) на
прямой Д +(Л —Л). Е-G(—оо, +«>).
Лемма 3. Пусть S(t)—регулярно относительно Ф и
f(p) £Ф — непрерывная функция. Тогда функционал |3* =
= Р(/> t)—/(0) имеет производную
(£р*(Л t))-q=q{p(f, t))-q{0). (4.10)
138
Эта лемма аналогична теореме 1 в § 1 гл. IV. Всякая функ¬
ция q, доставляющая отрицательное значение дифференциалу
(4.10), является направлением спуска по / для функционала
В*(/, t) в точке / и направлением возрастания функционала
t* (f> если t = t* (/, t), и потому ее можно использовать
для направленного поиска максимума функционала t*(f, t),
например, следующим образом. Пусть q (р, t) £Ф —такое еди¬
ничное направление, на котором значение производной (4.10)
в точке /—наименьшее. Под f(\i) будем иметь в виду одно¬
параметрическое множество функций /, т. е. кривую в про¬
странстве Ф. Пусть условия леммы 3 выполнены при всех
*<>]• Обозначим через i(p) непрерывную при р >0
функцию, удовлетворяющую уравнению t (у-) = i (р)),
i(0) = t* (/(0), t>), где /(р) — непрерывная кривая в Ф. Пусть
/ (!А)— решение уравнения
= ч*))) (4.11)
при начальном условии / (0)(*F(t'). Тогда функция Ц^) воз¬
растает до тех пор, пока при некотором (V не будет t ([*') = t0.
Уравнение (4.11) — непрерывный аналог метода спуска. Ко¬
нечно, для сходимости процесса в (4.11) не обязательно брать
Я (Р, t\ можно брать и другие направления спуска для функ¬
ционала [3(/, t) (подъема для t* (/, t)), а также строить дру¬
гие кривые непрерывного спуска (подъема).
Остается упомянуть еще о вычислении £*(/, t), т. е. фак¬
тически Р(/, t). Согласно (4.8), это тоже экстремальная задача,
решение которой чаще всего составляет процесс последова¬
тельных приближений. Здесь очень важно подобрать такой
класс Ф, при котором этот процесс приближений можно осу¬
ществить.
Практически шаг общего метода можно составить из одного
или нескольких шагов в каждой вспомогательной задаче (4.8),
(4.9). Примеры реализации такого алгоритма были приведены
в §§ 1-3.
4°. Замечания
I. Условия, в предположении которых выше излагался под¬
ход к решению задачи быстродействия, можно ослабить. На¬
пример, можно опустить требование выполнения условия Л,
которое было наложено в основном для краткости написания
идеи метода. Тогда можно будет включить в эту схему задачи
с неограниченным множеством траекторий системы (4.1),
а также дискретные системы. В нее можно также включить
задачи для систем с распределенными параметрами, систем
с последействием.
139
II. Как было отмечено в начале раздела 2°, задача состоит
в нахождении наименьшего t, при котором существует реше¬
ние уравнения р(и, t)= 0. Напомним два других подхода
к решению этой задачи.
Пусть u£U, где U—нормированное пространство. В ра¬
ботах [13, 24, 43], а также в главе III рассматривается гра¬
диентный метод минимизации времени перехода t(u) допу¬
стимого управления и на множестве допустимых управлений.
Основные этапы одного шага этого метода таковы.
1. Найдем некоторое допустимое управление их со време¬
нем = т. е. О и их связаны уравнением
р(иъ tx) = 0.
2. Построим вариацию операции р (и, t) в окрестности
точки «1 и числа tx
8 др(^8 ,^Л)8
^ ди 1 dt
3. Найде1М Ьа и Ы как решение следующей задачи выпук¬
лого программирования:
o£ = min,
8/7 = 0, |8и|<в1, 1«|<в8. (4.12)
4. Пусть Ьах, btx — решение задачи (4.12). Положим и2 =
= и1-|-8м1, 0=0 + 80 и перейдем к следующему шагу. В ре¬
зультате получается так называемая минимизирующая после¬
довательность допустимых управлений. Отметим, что в общем
случае даже в линейной задаче такая процедура может при¬
вести к точке локального минимума, что не может случиться
в описанном выше алгоритме.
Другой подход состоит в замене операций р(и, t) после¬
довательностью операций \pk(u, 0). более простых с точки
зрения решения уравнения Pk(u, t) = 0 и сходящихся в под¬
ходящем смысле к операции р(и, t). Существуют алгоритмы,
использующие комбинацию упомянутых трех подходов.
III. В пункте 2° рассмотрена довольно общая схема экстре¬
мальной задачи; найти наименьший параметр t, при котором
множество 5(0 из однопараметрического семейства множеств
{5(0} содержит заданную точку. В такую схему укладываются
многие экстремальные задачи [18, 39]. Например, задача;
найти
max [g'o (•*): gi (-0 ^ 0, / = 1, ...т, x£Rn}
сводится к задаче пункта 2° так: надо положить
и = (х, v), v = (0, vx ... vm), vi>0,
d = ( 1, 0 ... 0)6Rm+1, g(x) = (g0(x), gm(x))y
p(u, t) = g(x)-{-v + (t1 — t)d,
S(t) =\P(u, 0:^i>0, л6^я].
где 0 — достаточно большое число.
140
ЛИТЕРАТУРА
1. Н. И. А х и е з е р, М. Г. Крейн. О некоторых вопросах теории мо¬
ментов. Харьков, ГОНТИ, 1938.
2. Р. Б е л л м а н. Динамическое программирование. М., ИЛ, I960.
3. Р. Беллман, И. Гликсберг, О. Гросс. Некоторые вопросы
математической теории процессов управления. М., ИЛ, 1962.
4. Р. Б е л л м а н, С. Дрейфус. Прикладные задачи динамического
программирования. М., изд. «Наука», 1965.
5. Г. А. Блисс. Лекции по вариационному исчислению. М., ИЛ, 1962.
6. Д. Брайсон, В. Денхэм. Решение задач оптимального програм¬
мирования методом быстрейшего подъема. «Прикл. мех.», № 2, 1962.
7. Н. Б у р б а к и. Топологические векторные пространства. М., ИЛ, 1958.
8. А. Г. Бутковский. Теория оптимального управления с распределен¬
ными параметрами. М., изд. «Наука», 1965.
9. Р. Г а б а с о в. К оптимальным процессам в связанных системах.
«Автом. и телемех.», т. XXIII, вып. 7, 1962.
10. Р. В. Г а м к р е л и д з е. О скользящих оптимальных режимах. До¬
клады АН СССР, т. 143, № 6, 1962.
11. И. М. Гельфанд, С. В. Фомин. Вариационное исчисление. М.,
Физматгиз, 1961.
12. В. Ф. Демьяно в. Построение программного управления в линей¬
ной системе, оптимального в интегральном смысле. «Автом. и телемех.»,
т. XXVII, вып. 3, 1963.
13. В. Денхэм, Д. Брайсон. Задача оптимального программирова¬
ния при наличии ограничений типа неравенств, II. «Ракетная техника и кос¬
монавтика», № 1, 1964.
14. М. М. Дэй. Нормированные линейные пространства. М., ИЛ, 1961.
15. А. Я. Д у б о в и ц к и й, А. А. Милютин. Задача на экстремум при
наличии ограничений. Ж. вычисл. математики и матем. физ., т. V, вып. 5, 1965.
16. А. И. Е г о р о в. Об оптимальном управлении процессами в распре¬
деленных объектах. «Прикл. матем. и мех.», т. 27, № 4, 1963.
17. Ю. В. Егоров. Некоторые задачи теории оптимального управления.
Ж. вычисл. математики и матем. физ., т. III, еып. 5, 1963.
18. Г. 3 о й т е н д е й к. Методы возможных направлений. М., ИЛ, 1963.
19. В. И. Зубов. Теория оптимального управления. Л., изд. «Судострое¬
ние», 1966.
20. С. И. Зуховицкий, Л. И. Авдеева. Линейное и выпуклое
программирование. М., изд. «Наука», 1964.
21. Л. В. К а н т о р о в и ч. Об одном эффективном методе решения не¬
которых экстремальных проблем. ДАН СССР, т. XXVIII, № 3, 1940.
22. Л. В. Канторович, Г. П. Акилов. Функциональный анализ
в нормированных пространствах. М., Физматгиз, 1959.
23. Л. В. Канторович, В. А. 3 а л г а л л е р. Расчет рационального
раскроя промышленных материалов. Лениздат, 1951.
24. Г. Д. Келли. Метод градиентов. В кн.: Методы оптимизации с при¬
ложениями к механике космического полета. Под ред. Дж. Лейтмана. М.,
изд. «Наука», 1965.
25. Н. Е. Кирин. Об одном численном методе в задаче о линейных бы¬
стродействиях. В сб.: «Методы вычислений», вып. II, Изд. ЛГУ, 1963.
141
26. Н. Е. К и р II н. Программная оптимизация линейных систем с после¬
действием. «Автом. и телемех.», т. XXVI, вып. 1, 1965.
27. Э. Коддингтон, Н. Левинсон. Теория обыкновенных диффе¬
ренциальных уравнений. М., ИЛ, 1958.
28. Н. Н. К р а с о в с к и й. Об одной задаче оптимального регулирования.
«Прикл. матем. и мех.», т. XXI, вып. 5, 1957.
29. Н. Н. Кр асов с кий. Оптимальное управление в динамических
системах. УМН, т. XX, вып. 3, 1965.
30. В. Ф. Крото в. Методы решения вариационных задач на основе до¬
статочных условий абсолютного минимума. I и II. «Автом. и телемех.»,
т. XXIII, вып. 5, 1963.
31. Г. П. Кюнци, В. Крелле. Нелинейное программирование. М.,
изд. «Советское радио», 1965.
32. А. М. Летов. Аналитическое конструирование регуляторов. «Автом.
и телемех.», т. XXI, вып. 4, 5, 6, 1960, т. XXII, вып. 4, 1961.
33. А. А. Ляпунов. О вполне аддитивных вектор-функциях. Изв. АН
СССР, серия матем., 3, 1940.
34. Методы оптимизации с приложениями к механике космического поле¬
та. Под ред. Дж. Лейтмана. М., изд. «Наука», 1965.
35. Н. Н. Моисеев. Методы динамического программирования теории
оптимальных управлений. I, II. Ж- вычисл. математики и матем. физ., т. V,
вып. 1, 1965, т. VI, вып. 3, 1966.
36: И. П. Натансон. Теория функций вещественной переменной. М.,
Гостехиздат, 1957.
37. Л. Ньюстад, Б. Пайевонский. Синтез оптимальных управле¬
ний. Труды II Международного конгресса ИФАК. Изд. АН СССР, 1965.
38. Л. С. П о н т р я г и н, В. Г. Болтянский, Р. В. Г а м к р е л и д з е,
Е. Ф. Мищенко. Математическая теория оптимальных процессов. М., Физ-
матгиз, 1961.
39. Г. Ш. Рубинштейн. Двойственные экстремальные задачи. ДАН
СССР, т. 152, № 2, 1963.
40. Д. К. Фаддеев, В. Н. Фаддеев а. Вычислительные методы ли¬
нейной алгебры. М., Физматгиз, 1960.
41. А. Ф. Ф и м и н г о в. О некоторых вопросах теории оптимального ре¬
гулирования. М., Вестник МГУ, серия матем., вып. 2, 1959.
42. В. В. X о м е н ю к. Градиентные методы оптимизации нелинейных
систем автоматического регулирования. В сб.: «Прикладные задачи техниче¬
ской кибернетики». Изд. «Советское радио», 1966.
43. Л. И. Ш а т р о в с к и й. Об одном численном методе решения задач
оптимального управления. Ж. вычисл. математики и матем. физ., т. II, вып. 3,
1962.
44. К. Дж. Эрроу, Л. Г у р в и ц, X. У д з а в а. Исследования по ли¬
нейному и нелинейному программированию. М., ИЛ, 1962.
45. Л. Э. Э л ь с г о л ь ц. Введение в теорию дифференциальных уравне¬
ний с отклоняющимся аргументом. Изд. «Наука», 1964.
46. Д. В. Юдин, Е. Г. Гольдштейн. Линейное программирование.
М., Физматгиз, 1963.
47. Computing methods in optimization problems, ed. by A. Balakrishian,
L. Neustadt, N.—L., Acad. Press, 1964.
48. E a t о n J. H. An iterative solutions to time optimal control. J. Math.
Anal. Appl., vol. 5, No 2, 1962.
49. H a 1 v i n H., L. Neustadt. General necessary conditions for opti¬
mization problems. Univ. of South. Calif. School of Engng., Techn. Rep., 1966.
50. La S a 11 e J. P. The time optimal control problem. Reprinted from:
Contributions to the theory of nonlinear oscillations, vol. 5 (RIAS, 7212, Bellonu
Avenue Baltimore 12, Md).
51. Neustadt L. W. Synthesizing time optimal control systems. J. Math.
Anal. Appl., vol. 1, No 3-4, 1960.
52. О g u s t б r e 1 i M. N. Optimal pursuit strategy process with retarded
control systems. I. SIAM Control, ser. A, vol. 2, No 1, 89—105, 1964.
142
ОГЛАВЛЕНИЕ
Введение .
Глава I. Некоторые понятия теории нормированных пространств
§ 1. Нормированные пространства [22] ....
§ 2. Операции в функциональном пространстве [22] .
§ 3. Выпуклые множества [14]
Глава II. Условия оптимальности
§ 1. Первая постановка задачи на условный экстремум и условия опти¬
мальности в пространстве аргумента (условия относительного эк¬
стремума) .
§ 2. Вторая постановка задачи на условный экстремум и условия опти¬
мальности в пространстве условий (условия абсолютного экстре¬
мума)
Глава III. Методы оптимизации в пространстве аргумента
§ 1. Экстремум функции одной переменной ....
§ 2. Градиентные методы поиска безусловного экстремума .
§ 3. Методы подходящих вариаций . ....
§ 4. Последовательная оптимизация систем регулирования
Глава IV. Методы оптимизации в пространстве условий
§ 1. Градиентные методы в двойственной задаче
§ 2. Метод разделяющих сфер
§ 3. Задача оптимизации в системах регулирования, описываемых обык¬
новенными дифференциальными уравнениями . . .
§ 4. Оптимизация систем с распределенными параметрами
Глава V. Задача об оптимальном быстродействии
§ 1. Однородная задача об оптимальных линейных быстродействиях
§ 2. Неоднородная задача об оптимальных линейных быстродействиях
§ 3. Оптимальные линейные быстродействия с учетом ограничений на
фазовые координаты
§ 4. Общая задача быстродействия
Кирин Николай Ефимович
Вычислительные методы теории оптимального управления
Редактор Н. Н. Васильева
Техн. редактор Е. Г. Учаева Корректоры С. К. Школьникова, Е. К. Лелякова
М 11420. Сдано в набор 21 XII 1967 г. Подписано к печати 1 IV 1968 г.
Формат бум. 60x90Vi6- Бум. тип. № 1. Уч.-изд. л. 9,1. Печ. л. 9.
Бум. л. 4,5. Тираж 6000. Заказ 837. Цена 91 коп.
Издательство ЛОЛГУ им. А. А. Жданова
Типография ЛОЛГУ. Ленинград, Университетская наб., 7/9,