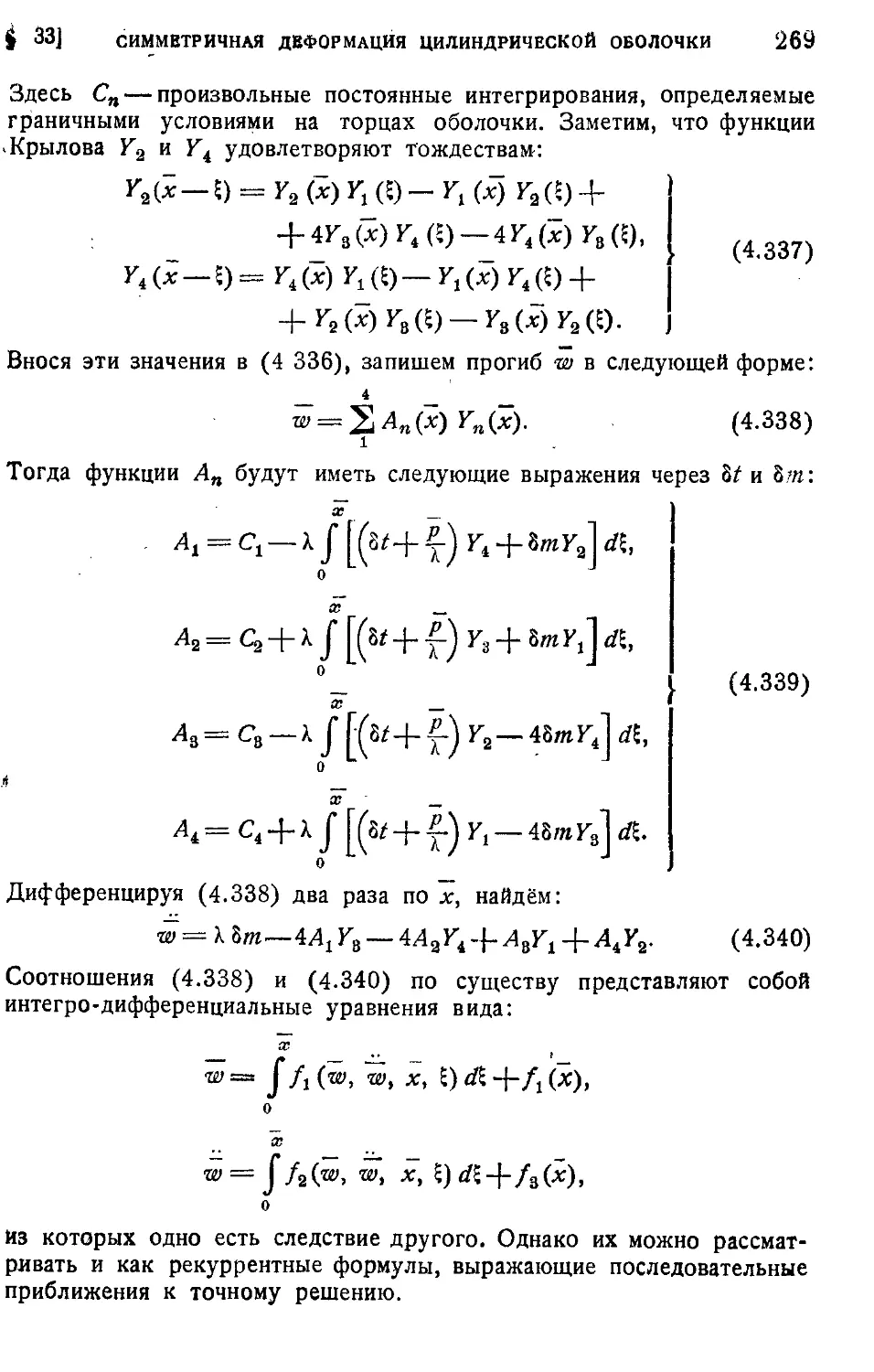Текст
А. А. ИЛЬЮШИН
ПЛАСТИЧНОСТЬ
ЧАСТЬ ПЕРВАЯ
УПРУГО-ПЛАСТИЧЕСКИЕ
ДЕФОРМАЦИИ
ОГИВ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 19 4 8 ЛЕНИНГРАД
12-5-4
Редактор И. К. Снитко.
Техн, редактор А. И. Сипелёва.
Подписано к печати 23/IV 1948 г. 23,5 печ. л. 27,8 уч.-изд. л. 47 312 тип. зн. в печ. л.
Тираж 5000 экз. A-0I799. Цена книги 17 р. Переплет 2 р. Заказ № 3138.
4-я типография им. Евг. Соколовой треста «Полиграфкнига» ОГИЗа
i при Совете Министров СССР. Лена^нщр-ад, Измайдовский: пр., 29
s
ОГЛАВЛЕНИЕ
Предисловие.............................................................. б
ГЛАВА I.
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ.
§ 1. Предварительные замечания................... 7
§ 2. Пластические свойства, выявляемые при растяжении-сжатии ,
образца ..................................................... 9
§ 3. Напряжённое состояние тела........................• . 17
§ 4. Девиатор напряжений и интенсивность напряжений. 24
§ 5. Малая деформация тела.......................... 31
§ 6. Направляющие тензоры и гиперболоиды напряжений и деформа-
ций; случай простой деформации.............................. 44
§ 7. Закон Гука; сжимаемость тела и условие пластичности.. 50
§ 8. Экспериментальное изучение законов пластичности при сложном
напряжённом состоянии....................................... 57
§ 9. Различные теории пластичности...................................... 80
глава п.
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ МАЛЫХ
УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ.
§ 10. Законы активной упруго-пластической деформации и разгрузки 97
§ 11. Работа напряжений и потенциальная энергия; потенциалы .... 104
§ 12. Постановка задачи теории пластичности,’ вариационное уравне-
ние и уравнения равновесия..................................108
§ 13. Теорема минимума работы внутренних сил.............................112
§ 14. Теорема о простом нагружеици.......................................115
§ 15. Теорема о разгрузке............................................... 118
§ 16. Дифференциальные уравнения равновесия в перемещениях и
метод упругих решений'......................................121
ГЛАВА Ill.
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ.
§ 17. Изгиб и растяжение бруса.......................................... 126
§ 18. Устойчивость сжатого стержня . . . ................................132
§ 19. Кручение стержня круглого сечения..................................135
4
ОГЛАВЛЕНИЕ
§ 20. Деформация полого шара под действием внутреннего и наруж-
ного давления ............................................. 138
§ 21. Симметричная деформация толстостенной трубы............144
ГЛАВА IV.
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК.
§ 22. Предварительные замечания..............................153
§ 23. Законы пластичности при плоском напряжённом состоянии . . . 154
§ 24. Связь между внутренними силами, моментами и деформациями
оболочки .................................................. 156
§ 25. Потенциал сил и моментов и постановка задачи о равновесии
оболочек....................................................168
§ 26. Конечное соотношение между силами и моментами и постановка
задачи о несущей способности оболочек......................170
§ 27. Деформация пластинок в их плоскости....................182
§ 28. Изгиб пластинок........................................195
§ 29. Некоторые задачи об изгибе пластинок............• ... 209
§ 30. Приближённые решения задач изгиба пластинок .... • . . . 222
§ 31. Несущая способность пластинок..........................232
§ 32. Безмоментная симметричная деформация оболочек вращения . . 246
§ 33. Симметричная деформация цилиндрической оболочки........263
§ 34. Несущая способность цилиндрической оболочки............275
ГЛАВА V.
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК.
§ 35. Выражения сил и моментов через деформации серединной по-
верхности при потере устойчивости............................282
§ 36. Устойчивость пластинок.................................291
§ 37. Приближённое решение задачи устойчивости пластинок.....303
§ 38. Устойчивость цилиндрической оболочки...................314
§ 39. Числовые данные для мягкой стали, применённой в опытах Кар.
мана.........................................................319
ГЛАВА VI.
ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ
НЕСЖИМАЕМОГО ПЛАСТИЧЕСКОГО ТЕЛА.
§ 40. Предварительные замечания..............................323
§ 41. Плоская деформация идеально пластического тела.........324
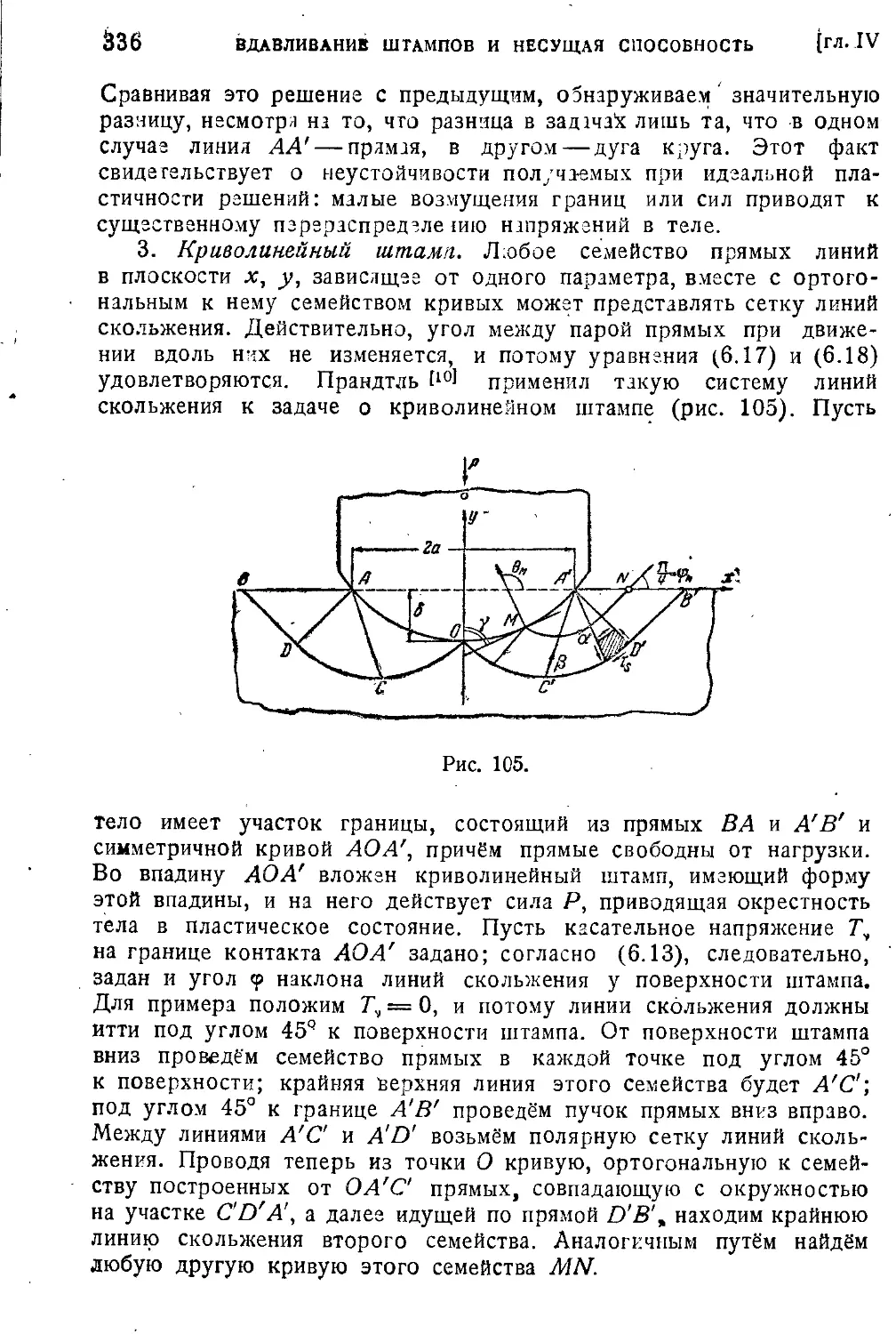
§ 42. Плоская задача о вдавливании штампов..............333
§ 43. Осесимметричные штампы.................................339
ОГЛАВЛЕНИЕ 5
ГЛАВА VII.
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ.
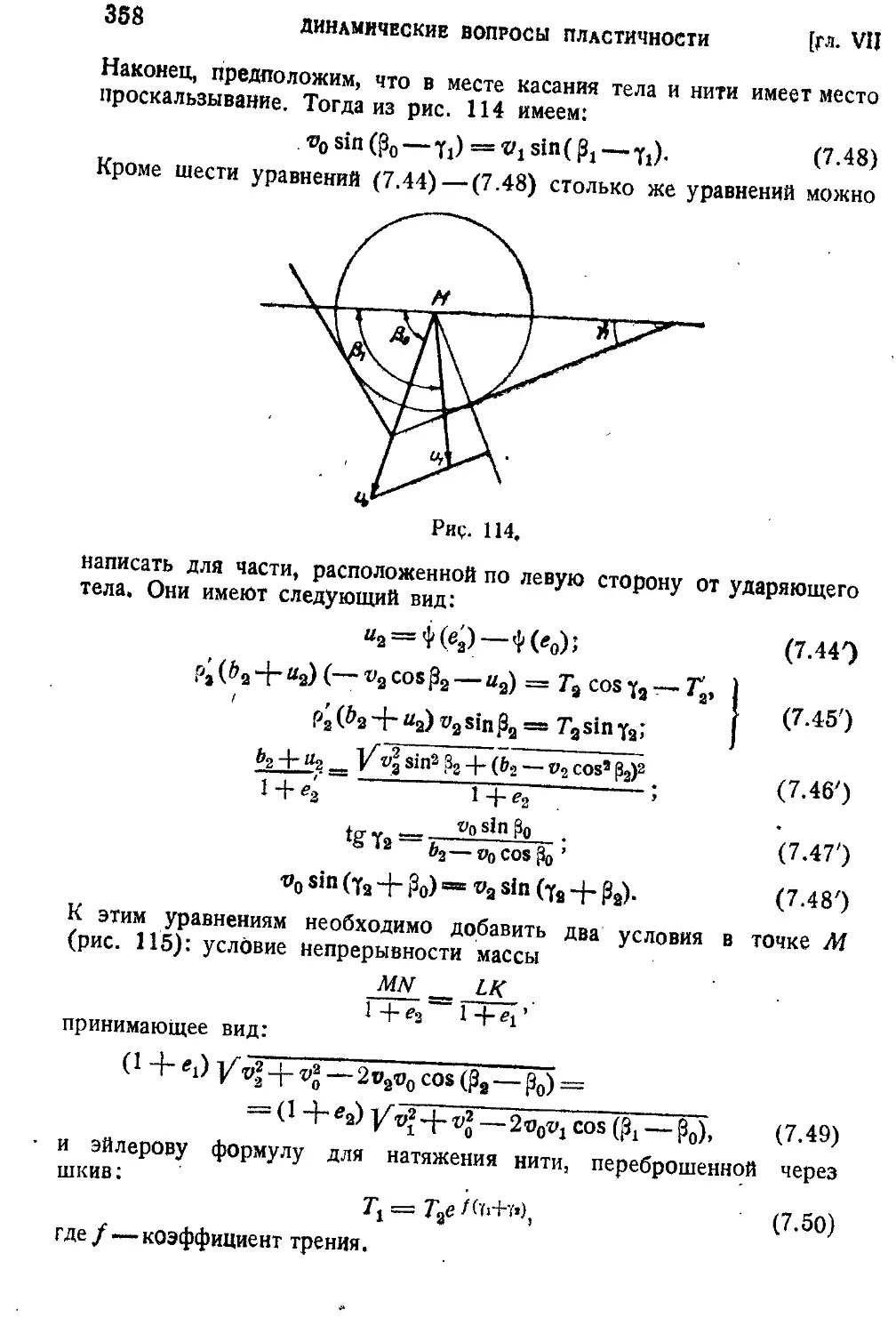
§ 44. Распространение плоских нелинейных воли.................345
§ 45. Упруго-пластическая волна Рахматулина...................349
§ 46. Распростраиеиие волн, возникающих при поперечном ударе по
гибкой деформируемой нити.....................................355
§ 47. Полярио-симметричиая задача.............................367
Литература....................................................370
. ПРЕДИСЛОВИЕ.
В этой книге освещается один из трёх разделов механики
пластических деформаций—теория упруго-пластических деформа-
ций. Три основных механических свойства металлов за пределами
упругости: нелинейность зависимости между напряжениями и дефор-
мациями, упрочнение в процессе деформаций и различие законов
нагружения и разгрузки — находят отражение в этой теории.
Влияние времени на механические свойства металлов, ползучесть,
релаксация, усталость, зависимость сопротивления от скорости и
течение при больших скоростях и высоких давлениях в ней не рассмат-
риваются; они составляют два других самостоятельных раздела теории
пластичности, впрочем, тесно связанных с первым.
Инженер, который будет читать эту книгу, вправе требовать
постановки и решения задач или, по крайней мере, обоснованного
толкования всех тех механических явлений при пластических дефор-
мациях тел, которые могут быть объяснены тремя указанными
свойствами металлов.
Теоретик вправе ожидать математически строгой и чёткой поста-
новки задачи теории пластичности и доказательства эксперименталь-
ной обоснованности принятых в ней законов.
Автор стремился удовлетворить указанным требованиям в той
мере, в какой это возможно при современном состоянии теории
пластичности. Он основывался при этом на своих исследованиях*
которые позволили, повидимому, выразить в единой теории пластич-
ности многочисленные разрозненные теории.
Автор выражает благодарность сотрудникам Лаборатории испы-
тания материалов Московского университета Ю. А. Цвибак и И. М. Тюне-
евой за помощь при подборе материала и его оформлении; он ценит
также заботу и участие О. К. Ильюшиной.
А. А. Ильюшин,,
ГЛАВА I.
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ.
§ 1. Предварительные замечания.
Способность твёрдых тел деформироваться под действием при-
ложенных к нему внешних сил и получать постоянные или времен-
ные остаточные (пластические) деформации при устранении сил
называется пластичностью. Основное свойство пластических дефор-
маций состоит в том, что между напряжениями и деформациями,
возникающими в теле, не С)пцествует взаимно однозначной зависи-
мости, т, е. по данным напряжениям нельзя найти деформаций и,
обратно, по данным деформациям нельзя найти напряжений.
Не следует думать, что пластическими свойствами обладают лишь
некоторые особые материалы и только при достаточно больших
деформациях; все реальные твёрдые тела при каких угодно дефор-
мациях обладают этими свойствами в большей или меньшей мере.
Конечно, при некоторых условиях пластическими свойствами дел
можно пренебречь, как это делается в теории упругости.
Идеализация реального тела, находящегося в определённых усло-
виях, т. е. сохранение за ним лишь основных механических свойств
и отбрасывание второстепенных, была всегда основой прогресса
механики; достаточно вспомнить роль абсолютно твёрдого тела
в динамике, идеальной жидкости и газа в аэро- гидродинамике, иде-
ально упругого тела в строительной механике и др. Но расчёты и
заключения, основанные на этих теориях, будут верны до тех пор, пока
они не выходят за пределы опытов, при которых установлена воз-
можность идеализации. Пусть, например, стальная балка с пределом
упругости, равным 2000 кг/см2, лежит на двух опорах и находится
под действием груза 1 т, который вызывает в ней максимальное
напряжение изгиба 1 000 кг/см2 и прогибает её на 1 мм. Принято считать,
что расчёт такой балки методами теории упругости или сопроти-
вления материалов даёт достаточно точные результаты как для макси-
мального напряжения, так и для величины прогиба (ошибка может
составлять лишь доли процента). Но каковы будут прогиб и напря-
жение в ней через 1 год, 5 лет и 30 лет после приложения груза?
8 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Теория упругости даёт неизменный ответ: 1 мм и 1000 кг]см*.
Однако уже из простых рассуждений станет ясным, что прогиб по
прошествии ряда лет будет в несколько раз большим начального,
а максимальное напряжение на десятки процентов меньшим. Расхож-
дение теории и опыта происходит здесь оттого, что весьма малая
пластическая деформация, не учитываемая законом Гука, непрерывно
возрастает со временем и совершенно изменяет как первоначальный
вид изогнутой оси балки, так и распределение напряжений по попе-
речному сечению. С точки зрения теории пластичности такое пере-
распределение напряжений и деформаций с течением времени есть
результат последействия и релаксации. Эти свойства особенно сильно
сказываются в материалах"'при высоких температурах; они носят
общее название: ползучесть. Первоначальное упругое состояние тела,
описываемое термо-упругими уравнениями Дюгамеля-Неймана, вслед-
ствие ползучести существенно изменяется уже за очень короткие
интервалы времени и потому практически мало интересно для инженеров.
Мы привели пример, когда весьма малая пластическая деформа-
ция, не учитываемая законом Гука, приводит к весьма существенному
изменению напряжённого состояния тела, вследствие продолжитель-
ности действия нагрузки. Можно привести аналогичный по резуль-
татам пример изменения напряжённого состояния тела и даже его
разрушения, вследствие большого числа циклов периодически меня-
ющейся во времени нагрузки. Такое йроявление пластических свойств
называется усталостью. Затухание свободных упругих колебаний тел,
связанное с внутренним трением или с явлением гистерезиса, также
является результатом неточности закона Гука и проявления пласти-
ческих свойств материала. Но при средней продолжительности вре-
мени действия нагрузок, средних скоростях деформаций, среднем
числе циклов колебаний и нормальной температуре *) твёрдые тела
с достаточной точностью можно считать упругими до тех пор, пока
возникающие в них напряжения и деформации не превосходят опре-
делённых значений. В области, где напряжения и деформации выше
этих пределов, твёрдые тела получают бдльшую или меньшую
пластическую деформацию; можно добиться значительного роста
пластических деформаций от нагрузки, прибегая либо к чисто
механическим воздействиям (давление), либо к нагреванию. Поэтому
следует говорить не столько об упругом или пластическом теле,
сколько об упругом и пластическом состояниях твёрдого тела. Эти
понятия в отличие от общепринятых, например, в отличие от приведён-
ного выше определения пластичности, являются вполне определёнными
и строгими. ®
Упругим состоянием твёрдого тела называется такое его со-
стояние, когда для каждой температуры тела независимо от времени
*) Все эти средние и. нормальные величины можно определить только
из опыта.
§ 2] ПЛАСТИЧЕСКИЕ СВОЙСТВА ПРИ РАСТЯЖЕНИИ-СЖАТИИ ОБРАЗЦА 9
существует взаимно однозначная зависимость между напряжениями
и деформациями. Эта зависимость обычно является линейной и
выражается законом Гука.
Пластическим называется такое' состояние твёрдого тела, при
котором для данной температуры связь между напряжениями и дефор-
мациями в каждый данный момент времени становится взаимно одно-
значной, если известны все (или хотя бы одно) предшествующие
напряжённые и деформированные его состояния и соответствующие
значения температуры; в противном случае эта связь является не-
определённой.
§ 2. Пластические свойства, выявляемые
при растяжении-сжатии образца.
Рассмотрим основные явления пластичности на простейшем при-
мере растяжения-сжатия цилиндрического образца. Для определён-
ности будем предполагать, что материал образца обладает качественно
такими же упруго-пла-
стическими свойствами,
как сталь, алюминий, медь,
никель и другие метал-
лы, причём до начала
опыта он является изо-
тропным и имеет оди-
наковый предел текуче-
сти на растяжение и сжа-
тие. Через а здесь будем
обозначать растягиваю-
щее напряжение в образ-
це, а через е— относи-' >
тельное удлинение.
Нелинейность диа-
граммы растяжения.
Если растягивать образец с
разрывной машине, то можно
называемый диаграммой растяжения (рис. 1). До некоторого пре-
дельного напряжения ае, называемого пределом упругости, образец
обнаруживает свойство упругости, состоящее в том, что если при
любом а<ае прекратить растяжение и начать разгрузку образца,
то диаграмма разгрузки совпадёт с первоначальной прямой ОЕ.
Упругое состояние образца описывается законом Гука: а = Ее. Диа-
метр образца при растяжении будет уменьшаться пропорционально
относительному удлинению, и коэффициент Пуассона v будет по-
стоянной величиной. Относительное изменение плотности материала
образца в пределах упругости будет равно (1—2v)e, т. е. будет
прямо пропорционально удлинению. Для стали при напряжении
постоянной скоростью на обычной
получить график зависимости а от е,
10 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
порядка 2000 кг/см* относительное изменение объёма образца
будет порядка О,О4°/о.
Продолжая опыт на растяжение при напряжениях выше предела
упругости, мы обнаруживаем значительное искривление линии а-е,
так что при изменении деформации от предельной упругой до
(2 — 3)|,- тангенс угла наклона касательной к линии а-е изменяется от
величины = Е до величины, в десятки раз меньшей модуля упру-
гости Е, или даже становится, равным нулю. В последнем случае
говорят, что материал имеет площадку текучести, и соответствую-
щее значение напряжения называют пределом текучести ag. Очень
часто материалы не имеют площадки текучести, и угловой коэффициент
касательной к кривой монотонно убывает по мере роста дефор-
мации *). Во многих случаях вся диаграмма, исключая малую область
_ da ~
быстрого изменения может быть заменена схемой в виде лома-
ной, состоящей из двух участков прямой линии; при этом пределом
текучести можно назвать напряжение ag, при котором происходит
перелом прямой а — Ее. При а > а8 в такой схеме = Е'
будет также постоянной величиной, называемой модулем упрочнения.
Для сталей модуль упрочнения в 10—50 раз меньше модуля
JOnra. Иногда вводят ещё понятие модуля пластичности Е" — . Для
всех известных материалов Е^> Е Е" >0. '
Дальнейшее растяжение образца за пределом текучести даёт
монотонный рост напряжения вместе с деформацией, причём на диа-
do
грамме а-е возможен участок, где — несколько возрастает, однако,
не достигая величины Е, и затем уже монотонно убывает, асимпто-
тически приближаясь к некоторому постоянному значению. При
некоторой величине напряжения а==аь происходит разрыв образца,
и потому аь называют пределом прочности или временным сопро-
тивлением материала. Говорят, что материал является хрупким',
если разрыв образца происходит при сравнительно малых деформа-
циях, и ему не предшествует образование заметной шейки. В против-,
ном случае материал называется пластичным. Несмотря на то, что
Металлы могут получать очень большие деформации порядка 5—20—100
и более процентов, их плотность изменяется лишь очень незначи-
(гельно (порядка долей процента). Поэтому ясно, что «коэффициент
J) Тогда взамен предела текучести определяют некоторый условный
предел пропорциональности как напряжение, при котором, например,
=* 0,5 Е.
de
$2] ПЛАСТИЧЕСКИ! СВОЙСТВА ПРИ РАСТЯЖЕНИИ-СЖАТИИ ОБРАЗЦА 11
Пуассона» по мере роста деформаций за пределом упругости материала
довольно быстро возрастает, приближаясь к максимальному значе-
нию 0,5.
Влияние скорости. На испытательных машинах обычно получается
скорость растяжения-сжатия порядка 0,01—г-1°/0 в минуту 10-5-+-
-н 10-2l/сек). Так как диапазон изменения скоростей довольно велик,
то представляется весьма существенной оценка влияния скорости
растяжения на вид диаграммы растяжения. Прежде всего отметим,
что упругие свойства тел остаются неизменными даже в гораздо
более широком интервале изменения скоростей деформации. Доста-
точно сказать, что модуль Юнга и коэффициент Пуассона, определя-
емые, с одной стороны, статически, т. е. на разрывных машинах,
с другой стороны, динамически — путём замера частот колебаний и
скоростей распространения упругих волн— практически совпадают.
Очень важно, что и за пределами упругости в указанном диапазоне
скоростей (а для сталей даже значительно большем) диаграмма
растяжения практически не зависит от скорости, и потому можно
сравнивать диаграммы, полученные на различных испытательных
машинах. Прандтль 14 в 1928 году предложил следующую логариф-
мическую зависимость предела текучести металлов от скорости
. de
деформации — = е :
. . е
° = 3о + 311п^>
ео
где а и а0 — пределы текучести, соответствующие скоростям е и еа,
а а( — постоянное для каждого металла и весьма малое сравнительно
с <з0 напряжение порядка 1% от <?0. Если интересоваться малым
диапазоном изменения скоростей, так что \е— е0| < I е01 — влияние
скорости на предел текучести можно оценить более простой линей-
ной зависимостью, как это было сделано нами в связи с изучением
вопроса устойчивости растяжения И:
а == 2k Зр.е.
Совпадение этой формулы с формулой Прандтля обнаружится, если
воспользоваться разложением в ряд Тейлора и положить
2й = а0 — Oj и 3 р. =-V-.
Величина для сталей оказалась порядка 0,2 ч- 0,4 кг • сек/см2 при
скорое 1ях деформаций порядка 10s- Х/сек. Чем больше скорость
растяжения, тем выше идёт диаграмма растяжения, но повышение
является очень незначительным, и им, как говорилось, можно пре-
небречь в достаточно большом диапазоне изменения скоростей.
Разгрузка и повторная нагрузка за пределом упругости. Если
в некоторой точке А .диаграммы, т. е. при значении напряжения ад
12 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
(рис. 1) прекратить дальнейшее растяжение образца и произвести
разгрузку, то график зависимости напряжения от деформации в про-
цессе разгрузку будет представлять прямую линию АО', параллель-
ную начальному упругому участку ОЕ, причём, когда осевое напря-
жение в образце будет полностью снято, относительное его удлинение
будет в масштабе диаграммы равно отрезку 00'. Удлинение образца,
которое он сохраняет при полной разгрузке, называется остаточной
деформацией или пластической деформацией, соответствующей напря-
жению «д. Как видим, остаточное удлинение ерд равно разности
между полным удлинением ед, соответствующим напряжению <зд, и
упругим -g-.
Состояние образца при полной разгрузке (характеризуемое на
рис. 1 точкой О') можно принять как бы за новое естественное его
состояние. Если образец вновь подвергнуть растяжению, т. е. про-
извести вторичную нагрузку, то график сначала пойдёт по той же
линии О'А, которая описывает процесс разгрузки. В самом деле,
модуль Юнга Е является для каждого металла вполне стабильной
константой, независимо от того, каким способом из него был изго-
товлен образец; при определении Е обычно мы даже не интересуемся
тем — подвергался ли металл предварительной осадке или вытяжке,
получен ли он прессованием или прокаткой, т. е. обладает он анизотро-
пией или нет, имеет какую-либо остаточную деформацию или не
имеет; модуль Юнга металла во всех этих случаях оказывается одним
и тем же с достаточной степенью точности. Поэтому совпадение
прямой АО' для разгрузки и прямой О'А для повторной нагрузки
является вполне естественным. Так как при повторной нагрузке пря-
мая О'А определяет зависимость <з-е включительно до точки А,
можно утверждать, что разгрузка и повторная нагрузка являются
чисто, упругими процессами. Поскольку напряжение больше пер-
воначального предела упругости ое, мы отмечаем, следовательно, по-
вышение предела упругости по мере роста пластической деформации
образца. Материал упрочняется или наклёпывается, и потому отме-
ченное явление называется упрочнением или наклёпом. Как видим,
этот эффект будет тем большим, чем больше угол наклона кри-
вой <з-е.
Продолжая процесс вторичного нагружения выше точки А, мы
увидим, что график а-е совпадёт с участком кривой АВ, которая
получилась бы при непрерывном растяжении образца с постоянной
скоростью *), т. е. образец как бы забудет про. то, что он подвер-
гался разгрузке.
Точка А есть совершенно произвольная точка на диаграмме растя-
жения, и потому можно считать, что всякому напряжению о на кри-
!) Могут быть незначительные отклонения от этого правила, вследствие,
старения и релаксации Р).
I 2] ПЛАСТИЧЕСКИЕ СВОЙСТВА ПРИ РАСТЯЖЕНИИ-СЖАТИИ ОВРАЗЦА 13
ой а-е соответствует деформация е, состоящая из двух частей:
пластической или остаточной деформации ер и упругой деформации
ee = -gr; таким образом:
в = ер “I- ее.
Поэтому деформацию е называют полной, общей или упруго-плас-
тической деформацией. Благодаря наличию упругой части дефор-
мации ев наряду с величиной работы деформаций W, представляющей
собой площадь диаграммы а-е, т. е.
е
W = J a de,
О
говорят о потенциальной энергии деформации 1Ге, которая может
быть освобождена путём разгрузки:
й2 1
Вследствие наличия упрочнения, потенциальная энергия We будет
тем больше, чем больше пластическая деформация ер.
Эффект Баушангера Ю. Выше мы рассмотрели только такой
процесс разгрузки, который заканчивался уменьшением действующего
напряжения до нуля (точка О'). Представляет интерес продолжить
этот процесс путём приложения напряжений обратного знака, пере-
ходом от растяжения к сжатию. Практически это требует нового
опыта, поскольку длинные образцы, применяемые при растяжении,
теряют устойчивость при сжатии. Обычно из растянутого образца
вырезают короткий цилиндрический образец, который и подвергают
сжатию. Однако результаты его испытаний можно нанести на преж-
нюю диаграмму (рис. 1) и вести все рассуждения так, как если бы
образец оставался одним и тем же.
Приложение к образцу напряжения обратного внака, т. е. в на-
шем случае сжимающего, прежде всего вызывает упругую деформа-
цию сжатия, причём связь между напряжением и деформацией
устанавливается в виде прямой линии О'А', которая является про-
должением прямой АО'. После того, как в образце будет дости-
гнуто сжимающее напряжение ал-, он станет получать вторичную
пластическую деформацию, и процесс будет иттй, согласно кривой
А'В', примерно параллельной АВ, причём точке А', являющейся
новым пределом упругости, будет соответствовать напряжение ад>, по
модулю меньшее величины а^, а зачастую меньшее предела текучести
растяжения а$, найденного при первом нагружении. Итак, приложе-
ние к наклёпанному образцу напряжений обратного знака с перехо-
дом при этом за предел упругости, влечёт за собой разупрочнение
материала; новый предел упругости падает. Это явление подробно
исследовано Баушингером и носит его имя.
14 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЙЕСКЙХ ДЕФОРМАЦИЙ (гл. 1
Релаксация, последействие, ползучесть. Повторим опыт растя-
жения образца с постоянной скоростью и, достигнув точки /И на диа-
грамме о-e, быстро прекратим нагружение, оставляя в дальнейшем
деформацию постоянной (рис. 2, а). Напряжение ом начнёт убывать сна-
чала быстрое а затем
всё медленнее, асимп-
тотически стремясь к
2* значению < <зм.
Процесс самопроизт
вольного уменьшений
внутреннего напряжен
ния с течением време-i
ни при неизменной де-|
формации называется
рис 2. релаксацией. Харак4
тёр явления релакса-
ции представлен кривой типа ММ' на рис. 2, б. Для математического
описания процесса релаксации Максвелл [Б] предложил следующую
зависимость:
da р de а
dt~ £ di Т ’
где / — время, е — деформация, отсчитываемая от точки О', и Т—
постоянная, зависящая от температуры и называемая временем релак-
сации. При е — const,
имеем закон измене-
ния напряжения с те-
чением времени:
о == ом ехр (—у) >
который для металлов,
таких, как сталь, не
подтверждается опы-
том. При нормальных
температурах пониже-
ние напряжения вслед-
ствие релаксации является очень незначительным. Если в любой момент
времени прекратить процесс релаксации и продолжить растяжение
образца с постоянной скоростью, напряжение быстро достигнет зна-
чения оя, и далее ход кривой а-е будет таков, как если бы
в точке М остановки опыта не происходило.
Рассмотрим теперь другой опыт: в некоторой точке W диа-
граммы а-е, описывающей растяжение с постоянной скоростью,
быстро прекратим изменение нагрузки и оставим напряжение по-
стоянным (рис. 3, а). Окажется, что деформация в# не будет по-
I 2J ПЛАСТИЧЕСКИЕ СВОЙСТВА ПРИ РАСТЯЖЕНИИ-СЖАТИИ ОБРАЗЦА 15
Стоянкой, а начнёт сначала быстро и затем всё медленней возрастать,
цока не достигнет конечного значения. e’N. Характер возрастания
деформации со временем изображён на рис. 3, б. Процесс самопро-
извольного роста деформации с течением времени при постоянном
напряжении называется последействием. формулы Максвелла, при
а = const. имеем е = const., что при нормальных температурах стали
также не соответствует опыту. Однако для свинца, например, как
релаксация, так и последействие при нормальной температуре каче-
ственно верно отражаются формулой Максвелла.
Если из точки N' вновь продолжить процесс растяжения образца
с постоянной скоростью, большей чем скорость процесса последей-
ствия, напряжение быстро возрастёт до значения, соответствующего
деформации еи> на кривой растяжения, получаемой безостановочным
процессом деформирования. Эффект последействия, как и релакса-
ции, для сталей при нормальных температурах весьма мал.
Подобно тому как у свинца последействие и релаксация очень
существенны при нормальных температурах, у сталей они приобре-
тают большое значение при высоких температурах порядка 500° С.
Последействие, релаксация и всякие другие изменения механических
свойств металлов при высоких температурах иногда объединяются
более правильно, чем
ползучести, могут быть
вытекающий из приве-
термином . ползучесть. Примерами
формула Максвелла, описывающих
либо логарифмический закон, по
дённой выше формулы Прандтля:
de 1 da _
Ht~ Е di~S°e °’
отсчитываемая от точки О', и а0, е0, Е—по*
от температуры, либо закон гиперболического
формул,
процесс
существу
где е — деформация,
стоянные, зависящие
синуса Надаи I6':
de 1 da п ,в
— — -с- Ti — 2е0 s“ _ •
dt b. dt 0 a0
Выводы из опытов на растяжение. Уже перечисленные выше
явления, обнаруживаемые в материалах при простом растяжении
образца, показывают, насколько сложен процесс пластической дефор-
мации. Мы оставили без рассмотрения такие проявления пластичности,
как усталость, старение, восстановление и другие. Большинство из
названных эффектов ещё недостаточно хорошо изучено, и потому
понятно, что в настоящее время не существует общей теории пла-
стичности, позволяющей рассчитывать напряжения и деформации
в телах сложной формы при произвольных заданных нагрузках
с учётом всех этих эффектов. Не существует, например, достаточно
удовлетворительной теории ползучести металлов даже при первона-
чально упругих напряжениях, хотя имеется большое количество ра-
бот в этом направлении 1’1; эффект БауТшингера при сложных на-
16 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
пряжённых состояниях вовсе не изучен; не существует никакой
теории усталости металлов, если не иметь в виду те полуэмпири-
ческие формулы, которые применяются при расчёте простейших
деталей машин (81.
Поскольку цель настоящей книги — дать теорию пластических
деформаций металлов, при нормальной или постоянной температуре,
причём, за счёт сужения границ применимости теории, формулировать
законы пластичности так, чтобы они были достаточно полно проверены и
подтверждены опытом, ибо только в этом случае имеют практическое
значение выводы, получающиеся из теории, постольку из всех рас-
смотренных в § 1 свойств тел мы сохраним лишь те, которые,
с нашей точки [зрения, окончательно установлены не только при
простом растяжении, но и при сложном напряжённом состоянии тел.
К числу таких свойств относятся следующие.
1) Нелинейность зависимости напряжений от деформаций при
пропорциональном возрастании внешних сил или, применительно
к рассмотренному образцу, криволинейность диаграммы а-е при
растяжении с некоторой скоростью. Зависимость а-е, установленную
диаграммой растяжения, будем записывать в виде:
а — Ф (с) = Ее[1 — (<?)]>
причём функция Ф обладает следующим свойством,'
т. е. материал, вообще говоря, обладает упрочнением. Если кривая
Ф(е) допускает с достаточной точностью замену её ломаной с коор-
динатами точки перелома os, es = J- os и модулем упрочнения Е", то
аналитическое выражение функции ш таково:
ш = 0, е св;
при этом параметр к имеет выражение
. Е — Е"
К==-~Ё~-
2) Упругость процесса разгрузки и повторной нагрузки. Если
разгрузка начинается при значениях напряжения а = а* и деформации
е<=е*, то текущее напряжение а и деформация е определяются зако-
ном Гука или в дифференциальной форме:
d<s = Ede,
или в виде
в — а* =ж Е (е — е*),
§ 3J НАПРЯЖЁННОЙ СОСТОЯНИЕ ТЕЛА 17
или, наконец, с помощью пластической деформации ер\
<з = Е(е — е>),
* ’*
р —— р ф ..I. _
е*> е Е
При этом будем предполагать, что в процессе разгрузки никогда не
возникает вторичная пластическая деформация, связанная с эффектом
Баушингера, и потому в результате повторной нагрузки вновь всту-
пает в силу зависимость а = Ф (е), как только напряжение достигает
исходного значения а*. Явлениями релаксации и последействия будем
пренебрегать, как мало изменяющими указанные выше факты !)•
Переходим к исследованию сложного напряжённого и деформиро-
ванного состояния тела.
§ 3. Напряжённое состояние тела.
Пусть рассматриваемое нами тело некоторым образом ориентиро-
вано в прямоугольной системе координат х, у, г. Его напряжённое
состояние становится известным, если напряжения определены в ка-
ждой его точке на произвольным образом ориентированной площадке.
Проводя через произвольную точку тела (х, у, г') три плоскости,
параллельные координатным, и пересекая их одной наклонной пло-
скостью, достаточно близкой к точке (х, у, г), мы получаем элемент
тела в виде тетраэдра. Грани, соответствующие первым трём пло-
скостям, называем основными площадками, четвёртую грань — наклон-
ной или’косой площадкой (рис. 4). Взаимодействие рассматриваемого
О Более подробные сведения о проявлениях пластичности в простых
опытах даны в специальной литературе Р1.
2 Зак. 3138. А. А. Ильюшия.
18 ОСНОВНЫЕ ЗАКОНЫ УПУУГО-ПЛАбГИЧЕбКИХ ДЕФОРМАЦИЙ [гл. I
элемента с телом осуществляется через напряжения по граням. В слу-
чае идеально жидкого тела напряжения по граням представляют давле-
ние, нормальное! к площадкам. Для твёрдого деформируемого тела они
суть векторы, вообще говоря, не перпендикулярные площадкам.
Обозначим вектор напряжения на площадке, нормаль к которой
совпадает с осью х, через $х и на двух других основных площадках
соответственно Sy, Ss- Разлагая каждый из них по осям х, v, г,
получаем:
Sx = Xxi + YJ + Z^t
Sy = Xvi+Yyj-\-Zyk,
S^Xj+YJ + ZJt,
где i, j, k— единичные векторы по осям х, у, z соответственно,
причём Хх, Yy, Zz суть нормальные напряжения на основных пло-
щадках, а
{Yx, Zx\ {Ху, Zy), (Хг, Y,)
— касательные напряжения.
Касательные напряжения удовлетворяют закону парности: проекция
на ось у касательного напряжения на площадке, нормальной оси х,
равна проекции на ось х касательного напряжения на площадке,
нормальной оси у; то же верно для пар осей х, z и у, z:
— Zx — Xe, Zv~Yz.
Таким образом напряжение в точке (х, у, z) на трёх основных
площадках определяется шестью величинами:
Хх, У„, Z., Хи, К, Zx.
Я’ yr Я' J/
Напряжение на наклонной площадке может быть выражено
через напряжения на основных, поскольку тетраэдр должен находиться
в равновесии. Обозначая через у единичный вектор нормали к косой
площадке
у = Н -j- mJ nk,
где I, т, п — направляющие косинусы нормали у с осями х, у,
определяющие ориентацию косой площадки:
Z = cos(v, х), т = cos (v, v), « = cos(v, z),
мы получим из уравнений равновесия тетраэдра выражения проекций
напряжения S, на оси х, у, z:
X^Xxl^-Xytn-YXzn,
Y^YJ+Yym^Y'n,
Z, = Zxl Zym -j- Zzn.
(1-1)
§ 3J НАПРЯЖЁННОЕ СОСТОЯНИЕ ТЕЛА 1§
Вес и силы инерции тетраэдра не входят в эти формулы, потому
что наклонная площадка предполагается проходящей бесконечно
близко к точке (х, у, г), и потому объёмные силы имеют более
высокий порядок малости, чем силы поверхностные.
Проектируя напряжение S, на нормаль у, мы получаем значение
нормального напряжения на косой площадке:
с., = Х.,1 Y рп —Z.tn =
= ХхР + Yym? 4- ггп* + 2Ху1т 4- 2Ypnn 2Zxnl. (1.2)
Обозначим координатную ось в направлении нормали у через х' и выбе-
рем в плоскости наклонной площадки две другие ортогональные
координатные оси у', z’. Тогда, следуя нашим обозначениям, а., будет
одно из основных напряжений, а именно Хх< в новой системе коор-
динат х’, у', z', повёрнутой произвольно относительно старой х, у, г:
—- Ххг.
Проектируя напряжение на оси у', z', мы получим напряжения
Yx/, ZX’, а рассматривая площадки, перпендикулярные осям у', г',
найдём также и другие напряжения Yy, ZZ’, Yz>, причём формулы
будут аналогичны (1.2), но в них войдут также косинусы углов осей
у', z' с осями х, у, z. Эти формулы называются формулами пре-
образования напряжений при повороте осей координат. Они приво-
дятся в большинстве курсов теории упругости. Напряжения на основ-
ных площадках новой системы координат х', у', z' будут вообще
отличны от напряжений Хх ... Zx первоначальной системы х, у, г,
несмотря на то, что напряжённое состояние в точке (х, у, z), являю-
щейся общей для обеих систем, остаётся неизменным. Подобно тому,
как скорость некоторой точки тела есть вектор, не зависящий от
системы координат, в которой он определён, хотя проекции этого
вектора и будут различны в разных координатных системах, так и
напряжённое состояние есть некоторая величина, не зависящая от
выбора координатных осей. Эта величина называется тензором напря-
жений, а величины Хх... Zx — его компонентами в осях x,y^z,
точно так же, как величины Х^. . .Z& — компонентами в осях х', у’, z'.
Соотношения типа (1.£) называются формулами преобразования ком-
понент тензора напряжений при повороте координатных осей. Заме-
тим, что вообще всякая физическая величина, определяемая шестью
компонентами, которые удовлетворяют формулам преобразования при
пово1роте осей координат типа (1-2), называется симметричным тен-
зором второго ранга. Примерами таких величин являются деформация
тела, инерция твёрдого тела с одной неподвижной точкой и другие *).
Как числа и как векторы, тензоры можно складывать, вычитать, умно-
*) Желающим ознакомиться со свойствами тензоров можно рекомен-
довать книгу Н. Е. Кочина (101.
2*
20 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл.
жать. Суммой двух тензоров называется новый тензор, компоненть
которого равны суммам соответствующих компонент слагаемых тен
зоров. Умножить тензор на скаляр (число)—значит умножить на этс
число каждую его компоненту.
Мы будем пользоваться для краткости изложения словами «тензор
напряжений», «тензор деформаций», «тензор скоростей деформаций»,
хотя можно было бы обойтись и без них, так как никакими спе-
циальными сведениями тензорного анализа мы пользоваться не
будем. Впрочем, многие свойства тензоров второго ранга уясняются
сами собой по мере изучения напряжённого и деформированного
состояний тела.
Итак, напряжённое состояние в некоторой точке тела определяется
шестью компонентами тензора напряжений в какой-нибудь системе
координат, например х, у, г, причём в любой другой системе компо-
ненты определяются формулами преобразования или формулами (1.1).
Тензор напряжений будем обозначать (5) и записывать его в
осях х, у, z в виде:
Ху Хя\
(5)= Yy Уг . (1.3)
\ZX zy zj-
Здесь по главной диагонали расположены нормальные напряжения
у у 7
Замечательно, что в каждой точке тела при данном напряжённом
состоянии существуют три взаимно перпендикулярные площадки, на
которых действуют только нормальные напряжения, касательные же
равны нулю. Нормали- к этим площадкам называются главными осями
напряжений (или тензора напряжений), а сами напряжения — главг
ными напряжениями. Ясно, что как главные направления, так и
величины главных напряжений определяются только напряжённым
состоянием в рассматриваемой точке, но не системой координат
(х, у, z или х', у', z'y, такие величины называются инвариантами
при повороте осей координат.
Предположим, что косая площадка с нормалью v является главной.
Обозначая о, — напряжение на этой площадке, легко получим, что
проекции его на оси х, у, z будут:
Внося эти значения в формулы (1.1), получим уравнения, определяю-
щие как неизвеетное нам значение av, так и направление главной
площадки, т. е. Z, /га, я:
(Хх — av) I + Хут 4- ХЙп = О,
У^+(^--а,)^+Угп==0,
zxi zym 4- (za—о,) п = о,
(1-4)
; § 3J
НАПРЯЖЁННОЕ СОСТОЯНИЕ ТЕЛА
21
( причём I, т, п связаны также очевидным соотношением:
е P-j-m2-j~n9== 1.
Так как система уравнений (1.4) является однородной относитель-
но'/, т, п, а все направляющие косинусы одновременно не могут
равняться нулю, то детерминант из коэффициентов уравнений (1.4)
должен равняться нулю:
ху
Ух У у у. = 0. (1-5)
Zx zy
Мы получили кубическое уравнение относительно неизвестной а,;
в развёрнутом виде оно пишется так:
— °v + 3a^+S2^ + K=0. С1-6)
причём мы обозначили:
О = | (^+^ + 2,), )
} (17)
а через значение детерминанта (1.5), если в нём вычеркнуть
величину о,. Уравнение (1.6) всегда имеет три действительных решения:
°v = ol> = 32> ач ~ °3>
которые и являются главными напряжениями. Для каждого из них
уравнения (1.4) дают направление соответствующей главной пло-
щадки. f
Так как корни уравнения (1.6) суть инварианты при преобразо-
вании осей координат, то и коэффициенты его также суть инвари-
анты. Итак, тензор напряжений имеет три независимых инварианта:
линейный, называемый средним нормальным напряжением (или сред-
ним гидростатическим напряжением):
з = | (А’а,1|-Уг, + 2г) = |(а1 + а84-аД (1-П
квадратичный, имеющий выражение через главные напряжения:
2г = °132 + 3з31, (1.7")
и кубический, равный произведению главных напряжений:
= °102°з-
В теории напряжений-деформаций изотропных сред инварианты
напряжений и деформаций имеют основное значение, поскольку лишь
22 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
они могут определять физические закономерности; компоненты же,
связанные с осями координат, являются вспомогательными.
Наглядное представление о напряжённом состоянии тела в неко-
торой точке, т. е. о напряжениях по различным образом ориенти-
рованным косым площадкам, даёт поверхность напряжений Коши.
Она может быть построена, если известны компоненты тензора на-
пряжений в какой-нибудь системе координат. Пусть, например, известны
главные оси напряжений и сами главные напряжения <з2, <за.
Тогда, согласно (1.2), на наклонной площадке, имеющей нормаль
v (Z, т, п), нормальное напряжение равно
av — 4- бащ2 4- о8/г3,
а проекции полного напряжения на оси 1, 2, 3 будут, согласно (1.1),
Отложим на направление нормали v произвольного масштаба отре-
зок имеющий проекции на главные оси 6, vj, С Тогда, очевидно,
,5 к; £
R ’ т~R ’ n~"R ’
Приравнивая некоторой постоянной величине произведение нормаль-
ного напряжения а, на квадрат радиуса вектора /?, мы получим
уравнение центральной поверхности второго порядка
2Ф($, т), + + (1.8)
причём, как легко видеть,
<? — 1*1 с —11 с -11
di ’ ^~R дц ’ R X ’
23
I
f* § 3J НАПРЯЖЁННОЕ СОСТОЯНИЕ ТЕЛА
I или в векторном виде:
S,=:l-grad<£>,
т. е. оказывается, что вектор напряжения S, направлен параллельно
нормали к поверхности в точке пересечения её радиусом-вектором /?.
Если направление его известно,
и проекция на нормаль к пло-
щадке также известна:
_ С
— £2 >
то простым геометрическим по- _________
строением находится как вели-
чина вектора напряжения
так и касательное [напряжение
(рис. 5):
,_____________________
S = Рис. 6.
Другой метод наглядного геометрического представления напря-
жённого состояния в точке тела, более удобный для вычисления, но
менее общий, дают круги Мора (или диаграмма Мора). Рас-
смотрим призму, две боковые грани которой совпадают с глав-
ными плоскостями напряжений (1.3) и (2.3), так что главное на-
правление 3 есть ось призмы, третья же боковая грань имеет нор-
маль v, лежащую в плоскости (1.2) и составляющую с осью 1
произвольный угол а (рис. 6). Высоту призмы примем равной еди-
нице. Нормальное и касательное напряжения имеют следующие
известные выражения через главные напряжения alt з2:
+ °-у?- cos 2а,
т, = sin 2а.
(1-9)
Откладывая для разных углов а по оси абсцисс диаграммы нормаль-
ное напряжение о, и по оси ординат касательное т.,, мы получаем круг
. радиуса (^ —о2) с центром на оси абсцисс на расстоянии foH-Og)
от начала координат. Если из центра Ot провести луч под углом 2а
к оси абсцисс, то координатами точки пересечения его с кругом
будут нормальное и касательное напряжения' на косой площадке
(рис. 7). Наибольшее касательное напряжение действует на пло-
щадке, расположенной под углом 45° к главным, и равно полураз-
Ности главных напряжений.
24
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
[гл. I
Аналогичное построение на той же диаграмме можно сделать для
косых площадок, нормаль к которым лежит ‘в плоскости (2.3)
и затем (3.1). Диаграмма Мора, следовательно, представляет собой
совокупность трёх касающихся попарно между собой кругов. Ради-
усы этих кругов пред-
ставляют собой экст-
ремальные касатель-
ные напряжения. По-
этому величины
называются главными
касательными напря-
жениями.
Подобно тому, как
направленный отрезок
прямой является геометрическим образом вектора (например, вектора
(1.Ю)
перемещения точки), поверхность напряжений Коши и диаграмма Мора
суть геометрические образы тензора напряжений в некоторой точке тела.
§ 4. Девиатор напряжений и интенсивность напряжений.
Особую роль для построения теории пластичности (и вообще
теории движения любой сплошной среды) играют девиатор напряже-
ний (£>g) и его второй инвариант. Девиатором напряжений назы-
вается тензор, представляющий собой разность тензора напряжений (5)
и тензора гидростатического напряжения (о), иногда называемого
шаровым тензором1):
/а 0 0\
(о) = I О а 0 1
\0 0 о/
Обозначим SX3>y Syy, S^S^, Syil, компоненты девиатора на-
пряжений:
(S&x $а>у
Syas Syy Syss ь (1.11)
„ Sxx $zy Szz'
!) Поверхность напряжений Коши для этого тензора есть сфера, имеющая
уравнение а (;2 iq2 -f- = const.
§ 4j ДЕВИАТОР НАПРЯЖЕНИЙ И ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙ 25
Компоненты, следовательно, равны:
• $а!а>== Х-в о, §ху= -^4/>
$уу ~ Yy °’ $У2
$гг % г °, ^г® = ^®>
(1-12)
причём на основании (1.7) сумма диагональных элементов (т. е. пер-
вый линейный инвариант девиатора напряжений) равна нулю:
^ + ^ + ^ = 0. (1.13)
Таким образом напряжённое состояние в каждой точке тела можно
представить себе как равномерное всестороннее растяжение с на-
пряжением о, на которое наложено
напряжённое состояние (1.12), опреде-
ляемое девиатором напряжений. Нор-
мальное напряжение о стремится из-
менить объём элемента тела, 'а компо-
ненты девиатора — изменить форму
этого элемента без изменения объёма.
Поверхность напряжений Коши для
девиатора напряжений (Dg) есть всег-
да гиперболоид (рис. 8). В самом деле,
обозначим главные.компоненты девиа-
тора напряжений буквами S13 S2, Ss;
через главные напряжения они выража-
ются формулами:
—3; )
52 = о2—°; | (1Л4)
^3 = °з °- J
Тогда, согласно (1.8), уравнение поверхности Коши будет
+ М’Ч- S3C2 = const. (1.15)
Это — гиперболоид, так как сумма коэффициентов при квадратах ко-
ординат равна нулю, и потому знаки этих коэффициентов различны.
Поверхность Коши для девиатора напряжений называется гипер-
болоидом напряжений.
Очевидно, главные касательные напряжения и вообще касатель-
ные напряжения на любой площадке не зависят от среднего нормаль-
ного напряжения, т. е. они определяются только девиатором напря-
жений. Так, формулы (1.10) можно переписать в виде:
Si — S2 . _ Si—S3 . _ S3 — Si
т12-------— t t23 — g , t81 — .
26 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Диаграмма Мора для девиатора напряжений отличается той осо-
бенностью, что расстояние центра малого круга Мора от начала
координат равно по абсолютной величине сумме расстояний центров
большого и среднего кру-
гов, причём центры по-
следних расположены все-
гда по одну сторону от
оси ординат (рис. 9).
Для теорий пластично-
сти представляет интерес
второй инвариант девиатора
напряжений который,
по аналогии с формулой
(1.7), можно записать через
компоненты девиатора на-
пряжений:
Sa “ $хх$уу $уу$гв
Sze^xx Ч" 4“
+ + (1-16)
Первый трёхчлен правой части (1.16), имеющий выражение
- (*х-(Уу~ °) - (Уу - °) (?г - о) - (Z3 —я) (X,— а),
после замены величины о её выражением (1.7) и перемножения
преобразуется к виду:
-|(Л5+ Y* + Z2z-XxYy- YyZa-ZzXx}^
= “4 + (Уу- +(z - ад.
Следовательно,
6S2 = (Xx - Yy? + (Yy-ZeY + (Z,-Xxy +
+ 6(^+^ + Z^). (1.17)
Последняя формула показывает, что второй инвариант девиатора
напряжений 2а есть величина, всегда положительная, причём она
не зависит от среднего нормального напряжения о.
Интенсивностью касательных напряжений называется положи-
тельное количество, квадрат которого с точностью до числового
множителя равен второму инварианту девиатора напряжений:
=4 V(Хх- Y^(YV-Zz)2+(^-^)2+6(4+ (118),
Механический смысл этой величины раскрывается интерпретацией
§ 4] ДЕВИАТОР НАПРЯЖЕНИЙ И ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙ 27
Роша и Эйхингера; назовём площадкой результирующих напряжений
которая имеет нормаль, равным обра-
осям напряжений. Очевидно, эта пло-
осях равные отрезки (рис. 10), а на-
в данной точке тела такую,
зом наклонённую к главным
щадка отсекает на главных
правляющие косинусы её
нормали равны
7 1
I — т=^П — —;= .
/3
Вектор напряжения $„ на
такой площадке согласно
(1.1) имеет компоненты:
и, следовательно, нормальное
напряжение на ней по (1.2), равно
среднему нормальному напряжению:
°, = + = у (°i + °2 + аз) ~
а касательное напряжение т, будет:
Внося в последнюю формулу значение
получим окончательный результат:
| У (31 - 32)2 + (32 — Зз)2 + (38 — а1)2- (119)
Правая часть (1.19) есть не что иное, как величина (1.18), написан-
ная через главные напряжения. Следовательно, интерпретация Роша
гласит: интенсивность касательных напряжений есть касательное
напряжение на площадке результирующих напряжений. Величину
называют ещё октаэдрическим напряжением, поскольку оно оди-
наково для всех восьми площадок результирующих напряжений,
которые можно провести во всех октантах; если отрезки, отсекае-
мые площадками на главных осях 1, 2, 3, одинаковы во всех октан-
28
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
[ГЛ. I
тах, то совокупность площадок результирующих напряжений пред-
ставляет замкнутую восьмигранную фигуру—оК’гаэдр (рис. 11).
Октаэдрическое напряжение мало отличается от максимального
касательного напряжения, причём всегда меньше последнего. Для
доказательства этого утвержде-
ния рассмотрим разность
R ~~~ ”тах
Максимальное касательное на-
пряжение, как уже доказано
выше, равно наибольшему по
модулю главному касательному
напряжению. Пусть главные на-
пряжения расположены в следую-
щем порядке:
°1<°3<<53>
так что
т „__<< О т _________°2~g3 л
Чэ-----§ т23 — 2
Т31----9 > U.
причём максимальным касательным напряжением будет т81,т. е.
“'max — Т31 > О’
Октаэдрическое напряжение, согласно (1.19), выражается через глав-
ные касательные напряжения формулой
= g" ]/T12“f~'r23~l“'C31- (1.20)
Исключая в (1.20) величину т12 на основании тождества
Т12'4_Т23~ЬТ31 — 0,
(1.21)
мы получим для разности R выражение
Чтобы найти экстремум этой величины по т23, приравняем нулю
производную ‘
3R _____ Vs________-4- 2ти________
3 1/7® Хт , т2
+ ^23
Отсюда имеем;
_____1
Т?3 g
§ 4] ДЕВИАТОР НАПРЯЖЕНИЙ И ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙ 29
и, следовательно, максимальное значение разности R будет:
Так как по условию т23 не положительно, то минимальное значение
К будет при т23 = О и т23 = — ттах:
2/2^
3 у ^виг
Таким образом, отношение октаэдрического напряжения xt к макси-
мальному касательному ттах удовлетворяет неравенству:
0,941 (1-22)
у ттах *
Наряду с поверхностью напряжений Коши и диаграммой Мора,
характеризующими распределение напряжений по различным пло-
щадкам, проходящим через одну и ту же точку тела, для теории
пластичности представляют интерес
ещё другого типа поверхности, а имен-
но такие, которые устанавливают за-
висимость между напряжёнными состоя-
ниями в различных точках тела. В ка-
честве координатных осей возьмём пря-
моугольные и на осях за переменные
примем главные напряжения о,, а2, а3
(рис. 12).
Призма Кулона определяется ура-
внением:
= (1-23)
где С — некоторая постоянная для раз-
личных точек тела. Легко убедиться Рис. 12.
в том, что уравнение (1.23) предста-
вляет шестигранную призму, ось которой, проходя через начало ко-
ординат, одинаково наклонена к положительным направлениям коор-
динатных осей, а каждая из граней параллельна одной из осей и со-
ставляет угол в 45° с двумя другими осями. В самом деле, если
оз<°2<°1> т0 мы имеем
'Стах — т31»
и, следовательно, (1.23) даёт уравнение пары параллельных плоско-
стей
°1 °з — — С-
(1.23')
На рис. 12 изображён кусок призмы, продолжающейся до бесконеч-
30 ОСНОВНЫЙ ЗЛК0НЫ£уШ>Уг6-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
ности вдоль её оси, причём плоскости (1.23') суть АА'ВВ' и
DD'EE'.
В случае, если о2 < < Og, то мы имеем
ттах== т23>
и потому из (1.23) получаем уравнение новой пары параллельных
плоскостей:
а8 — а2 = ±С. (1.23")
Эти плоскости суть ВВ'СС и EE'FF'. Наконец, в случае, если
°1 < °3 < °2>
то мы имеем:
^паах ^12>
и, следовательно, уравнением пары плоскостей CC'DD' и FF'AA1
будет:
а2 — ?1=±С. (1.23"')
Вполне очевидно, что все рёбра граней (1.23) параллельны линии,
равнонаклонённой к осям координат; уравнением этой линии является
а1 = а2 = аз- (1.24)
Так как (1.24) не удовлетворяет уравнениям (1.23) со штрихами, то
грани (1.23) и линия (1.24) не пересекаются. Из чертежа ясно также,
что линия (1.24) есть ось призмы Кулона.
Цилиндр Губера-Мизеса определяется уравнением: \
— const.
Вместо величины октаэдрического напряжения или интенсивности
напряжений сдвига мы в дальнейшем часто будем рассматривать
эквивалентную ей величину, отличающуюся только числовым множи-
телем, а именно величину которую будем называть интенсивно-
стью напряжений'.
V~ +(^-^а+6 (^ + ^+®
уу К(31 — 32)2 + (°2 — Зз)2+ (а3 — а1)2- -25)
Уравнение цилиндра Губера-Мизеса напишем в виде:
а<=С, (1.26)
где С—та же самая постоянная, что и в уравнении призмы Кулона.
В развёрнутом виде уравнение (1.26) запишем так:
(°! - »2)2 + 02 - *з)2 + 03 - 31)2 = 2С2. (1.26')
Из неравенства (1.22) вытекает, что поверхность (1.26) по крайней
$ 5]
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
31
мере почти параллельна призме Кулона, причём ясно, что она нигде
не пересекает линию (1.24). Но так как а< = С есть поверхность вто-
рого порядка, то это может быть только цилиндр, параллельный приз-
ме Кулона, и линия (1.24)
есть его ось. В плоскости
(ар а2), т. е. при а3 = 0,
уравнение (1.26') предста-
вляет эллипс, описанный
около шестиугольника Ку-
лона:
°!—°i°2 + °2:=c’2- (1.27)
На рис. 13 в плоскости (ар
<з2) изображены шестиуголь-
ник Кулона тдаах = у С и
описанный около него эллипс
Губер-Мизеса af = С. Около
этого эллипса можно опи-
Рис. 13.
сать шестиугольник, парал-
лельный первому; из (1.27)
2
следует, что, когда одно из напряжений ар а2 имеет максимум С,
другое равно —С; на описанном шестиугольнике, следовательно,
у 3
максимальное касательное напряжение равно:
= (1-28)
так как на плоскости (ор а2) оно равно(oj — а3) или (а2—а3),
а <з3 = 0. Таким образом цилиндр Губера-Мизеса (1.26) является
описанным около призмы Кулона (1.23) и впи’санным в призму (1.28)
§ 5. Малая деформация тела.
Деформация тела вполне определяется, ес; ’ известен вектор пере-
мещения w каждой его точки (рис. 14). Обозначим проекции пере-
мещения точки М с координатами х, у, z на направления осей через
и (х, у, z, t), v(x, v, z, t), w(x, у, z, t),
так что:
w = uivjwk. (1.29)
Чтобы определить деформацию тела в окрестности точки М, рассмо-
трим соседнюю точку положение которой относительно М опре-
деляется вектором р с проекциями 5, т], С:
р =W+V4-^,
32 обнойныЕ законы УПРУГо-ПлАбтичвбких деформаций [гл. I
и координатами точки будут
x1==x + $, £-1==^+C.
Отрезок р можем считать материальным волокном, длина которого
сколь угодно мала. Перемещением точки Mt будет:
w' = u(Xl, ylt Zj)i + v(xv vp zJJ-j-wtXi, ylt zjk,
и потому относительное перемещение точки Afj относительно Л1 най-
дём как разность:
80 = «/—w. (1.30)
Если из точки М брать волокна р различных направлений, то ясно,
что относительные перемещения чх концов 80 будут вполне опреде-
лять деформацию тела в
г окрестности точки М. Из
рис. 14 явствует, что новое
Ру''//9 положение и длина волокна
Р в результате деформаций
\ / определяются вектором
-f ’ p' = p + S0. (1.31)
fc//
В дальнейшем мы будем
М(х,ул) рассматривать лишь настоль-
. ко малую деформацию, что
/ квадратами удлинений и
сдвигов можно пренебречь.
Угол поворота волокна р и
' его относительное удлине-
ние, следовательно, являют-
ся также весьма малыми ве-
личинами. В таком случае абсолютное удлинение р равно проекции
вектора 80 на направление р, т. е. их скалярному произведению
р • 8о
- - , а относительное удлинение его будет:
= 0-32)
Г
Обозначая через 80iB, 80j/, 80г проекции относительного перемещения
80 по осям, получим:
&0 — 4“ ®0у/ 4- 8оЛ
Из уравнения (1.30) имеем:
80а, = «(х-Н, + * + £) — и(х, у, г),
80у = ^ (* 4~ У’ + 'П, г4-С) — v(x, v, z),
8о« = «'(* + £> j + *4" О—«'(*» V, г)-
(1.33)
§6J
МАЛАЯ ДЕФОРМАЦИЯ ТЁЛА
33
Поскольку длина волокна р, а, следовательно, и его проекции 5, т], С
сколь угодно малы, правые части выражений (1.33) можно разло-
жить в ряды по степеням 5, т], Си ограничиться только линейными
членами:
j ди t . ди . ди г
s dv t , dv . dv г
„ dw t । dw i dw
(1.34)
Входящие здесь производные от перемещений берутся, конечно,
в точке х, у, z.
Гельмгольцу принадлежат следующие преобразования формул
(1.34): добавляя и вычитая в правой части первого равенства
1 dv
2 дх
1 dw
2 дх
и
в правой части второго равенства
1 ди
2 ду
1 dw
2 ду
и
и в правой части третьего равенства
1 ди .. 1 dv
2"dz^ и Т’аГ71’
формулы можно переписать следующим образом:
8о® = 8а,—+
So» = 8y —+
8ог = 8г— e’^+‘Vb
(1.35)
где через wx, шг обозначены компоненты вектора углового вра-
щения <о:
1 / dw dv \ 1 f ди dw \
<°!В~'2\ду dz)’ &У~~2\дг г/’
__ 1 / dv ди \
2 \дх ду )'
(1.36)
i через Ъу, 8г — компоненты вектора 8, смысл которого будет
установлен ниже:
8® г== “Ь ~2 "4* "2”
8г/ 2 еу^ ~b" еуу^ “Ь 2 еУг^‘’
(jz — 2 2 ^гУ^ ~
(1.37)
£4 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Здесь введены обозначения, которые называются формулами Коши:
______ ди ________ ди , ди )
ех^-~ е^и~еу^~~ду "г IF’ I
_____ ди _________ ди , dw I
еуу ~ ~ду ’ еУг ~ — ~дГ ' ~ду ’
dw dw । ди
— ~dz' — дх' ~дГ~
(1.38)
Как увидим, величины (1.38) представляют собой компоненты дефор-
мации. Соотношения (1.35) можно написать в векторном виде:
8о = 3 + w X Р,
из которого явствует, что векторное произведение w X р предста-
вляет поворот всей окрестности точки М, т. е. любого волокна на
Рис. 15.
один и тот же угол м и
потому не связано с дефор-
мацией материала в такой же
мере, как и переносное пе-
ремещение w всей окрест-
ности точки М. Путём пово-
рота осей координат на
угол — to можно добиться
того, что вектор относи-
тельного перемещения 60 бу-
дет совпадать с вектором 3,
откуда ясно, что вектор 3
определяет чистую дефор-
мацию материала в окрестно-
сти точки М. Заметим, что
исключить переносное движение и поворот окрестности при заданных
для всего тела перемещениях (1-29) можно только для одной произволь-
ной точки тела, и потому вектор 3 можно принять за вектор отно-
сительного перемещения только для изучения перемещений в окрест-
ности этой точки. Но поскольку вектор 8 определяет чистую дефор-
мацию, ясно, что напряжения, возникающие в теле, могут зависеть
только от него, но не от переносных векторов w и to. Итак, для
изучения перемещений и деформаций материала тела в окрестности
любой точки можно считать, что вектор 6 с его проекциями (1.37)
есть вектор относительного перемещения. Оси координат х, у, z
поместим в изучаемую точку (рис. 15).
Пусть направляющие косинусы волокна р будут:
Z = cos(p, х); щ = соз(р, у); n = cos(p, г).
Они. очевидно, выражаются так:
, 1 t 1 1 г
Р Р Р
§ 51
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
35
Формулы ’(1.37) теперь можно переписать в виде:
, I 1 ,1
р ехх^~\~ 2 ехут ~2 ^хгп>
2 £УХ ~Ь еУУт ~Ь ~2 еугп>
6, 1 1 I 1 .
~ ~ У ezJ- + у ezym +
(1.39)
Сравнивая эти формулы с формулами (1.1) для проекций напряже-
ний на косой площадке, мы видим полную их аналогию с той лишь
разницей, что вместо касательных напряжений стоят половины соот-
ветствующих деформаций. Этот факт свидетельствует о том, что
совокупность величин (1.38) не является тензором. Между теорией
напряжений и деформаций была бы полная аналогия, если бы через
деформации еху, еуг, егх были обозначены половины величин, стоя-
щих в правых частях (1.38). Однако обозначения (1.38) общепри-
няты, и потому тензор деформаций (Е) записывают в форме:
(£) =
ехх 2 е<вУ 2
1 £
2 еухеуу 2 еУ:<
1. 1
2 &ZX 2
(1.40)
Входящие в него величины являются компонентами тензора деформаций.
Впрочем, для краткости и величины (1.38) называют компонентами
тензора деформаций, подразумевая необходимость соответствующих
поправок'в тех случаях, когда какие-нибудь формулы деформаций
желают написать без вывода по аналогии с соответствующими фор-
мулами теории напряжений.
Согласно (1.32), относительное удлинение волокна р равно:
г г
= ехх1* + еуут* + + ехц1т + еугтп + ezxnl.
(1-41)
Эта формула соответствует формуле (1.2) для нормального напря-
жения о,.
Чтобы выяснить геометрический смысл величин ехх, eyyt eZK,
направим сначала вектор р по оси х, т. е. рассмотрим волокно, рас-
положенное вдоль оси х. В таком случае 7 = 1, т — п — 0 и из
(1.41) имее^‘ ер = ехх. Рассматривая волокно вдоль оси у, т. е.
полагая Z = п — 0, т = 1, из той же формулы получим е? = еуу.
Наконец, направляя вектор р по оси z и замечая, что для него
7 = z» = 0, л = 1, мы находим ер = егг. Следовательно, величины
eyw> являются относительными удлинениями волокон, взятых
в точке х, у, z в направлении осей х, у, z соответственно.
3*
36 основные ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гЛ. I
Геометрический смысл трёх других величин группы (1.38) станет
ясным, если рассмотреть изменение угла между двумя волокнами р/
и р2 в результате деформации тела (рис. 16). Пусть направляющие
косинусы этих волокон будут соответственно (Z1( nJ и (/2, пг2, nJ.
Согласно (1.39) перемещения концов волокон рп р2 будут:
и
== Pl Ч" 2*еа>У™1 Ч" ~2 >
= Р1 (^2 еУх^ Ч~ еуут\ Ч" ~2 eyzni) >
^1г = Pl ezaJl Ч~ е^Ут1 4“ ezznl) >
^2ж Р2 (ехх^2 Ч* ~2 ехут2 Ч* ~2" ехг^2^ >
^2у = Рй ("д’ eyJ-2 Ч~ еуут2 Ч" ~2 еугП2^ t
®2г ~ Р2 (~2 ezx^2 Ч~ ~2 ееут2 4“ еггп2\ •
Найдём косинус угла между этими волокнами после деформации.
Начальные положения век-
торов р! и р2 и угол &12
между ними и их изменения
в результате деформации по-
казаны на рис. 16, причём,
очевидно:
Pi == Pi Ч~ ^1>
₽2 = р2 Ч~ s2-
Косинус угла между и р2
равен отношению их скаляр-
ного произведения к произ-
ведению их модулей:
Аналогично для угла &'а после деформации получаем соотношение:
гп<! а' __(Pi + 8i) • (Рг + 8а)
COS Vi2 —----------1--Г >
Pi • ?г
причём, очевидно:
Pi = °i (1 4“ ерР> Рг = Рг (1 4“ ef)‘
§ 5]
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
37
Перемножая входящие в выражение cos9^2 двучлены и отбрасывая
малые величины порядка 82 в числителе, получим:
cos 912 =
cos &12
Р1?2
в знаменателе последнего слагаемого отброшено произведение малых
величин, поскольку числитель есть величина малая.
Рассмотрим теперь случай, когда волокна рг и р2 взаимно перпен-
дикулярны, а 912 = тг/2. Тогда
Р1®2 + ₽2S1
cos via ==--------,
P1P2
или через проекции:
Pi +
₽2 = Ра(У+ /«a/ + M),
и через 81а,,..82гв,...:
. P1P2 COS ^2 = (Z1S2® + m&Ly + »182з) Pl + MA® + m£ly + «281г) P2-
Окончательно имеем:
cos = 2 + eyytn^-f-e^npi^ -f- exy (1рп.2 Ц-1^-f-
+ ^г («1«2 4- ^2«i) 4- ezx Wa 4- «2^1)- (1-42)
Направим теперь вектор pi по оси х, вектор р2 по оси у и рассмо-
трим косинус угла между соответствующими волокнами. При этом
имеем:
’4а= zi = I« ^ = ^ = 0, /2 = п2 = 0, w2=l.
Из формулы (1.42) получаем cos 9^ = еху. Но деформация предпо-
лагается малой, и потому ’ «/2 — есть весьма малый угол, для
которого
cos 9Ж^ = sin (тс/2 9Ж^) = тг/2 9^ = '
Следовательно, деформация еХу есть относительный сдвиг или изме-
нение прямого угла элемента в виде прямоугольного параллелепипеда
с гранями, параллельными плоскостям (х, z) и (у, г) (рис. 17).
Совершенно аналогично докажем, что еуг и егх есть деформация
сдвига или’изменения прямых углов между плоскостями (_у, х), (z, х)
и (г, _у), (х, у) соответственно.
В каждой точке тела существует три взаимно перпендикулярных
направления, называемых главными осями деформаций которые
38 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
[гл. I
обладают следующими свойствами: волокна, направленные по ним,
испытывают только изменения длин, но не поворачиваются, т. е.
сдвиги в главных осях де-
формаций равны нулю. Пусть
будут I, т, п неизвестные
направляющие косинусы глав-
ного направления и е? — от-
носительное удлинение глав-
ного волокна. Тогда переме-
щение конца волокна р будет
р • е?, а его проекции на
оси
*>х = Рер1 2>
^у---Р^РМ}
8, = рерп.
Внося эти значения в формулы (1.39), мы получим однородную
систему уравнений относительно направляющих йосинусов:
(.ехх ^р) 4~ ~2 еа>у™ ~2 О’
~2 еух^ ^fiyy ер) “F ~2 eyzn~ 0, О>43)
g" “1“ ~2 еруМ 4“ ^р)
откуда получаем кубическое уравнение для определения ер:
_ 1 2.
ехх е? 2 2 еяХ1
1 1 л
2 еух еуу ер 2 еуч О’
1 1 _
2 ezx 2 вгУ ^гг
Развёртывая детерминант по степеням ер, получим:
— е3Р + Зе/р-Ь£^р-ЬЕз = О, (1.44)
причём коэффициенты:
е — з (ехх 4~ еуу 4~ егг) >
fa = ~ ?Х»^УУ — eyyezz— ezaexx +"4 (е®У eyz ~Г е2®)»
(1-45)
§51
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
39
и коэффициент Е3 являются инвариантами преобразования осей коор-
динат при повороте, поскольку корни уравнения (1.44) не связаны
с направлением осей координат х, у, г. Три действительных корня
кубического уравнения:
== ^2> ~ е3’
*
представляют собой три главных удлинения по трём главным осям.
На основании формул (1.43) и очевидного соотношения:
Р /п9 и3 = 1
можно доказать, что главные направления взаимно ортогональны.
Инварианты е, Е3, Е3 могут быть записаны через главные удлинения:
е = 4 “Ь £з)>
£2 —------^1^2-----------еЗеЪ
Е3 = е^е^е^.
(1-45')
Величина е представляет среднее относительное удлинение, а 0 = Зе
относительное объёмное расширение элемента. Это ясно из рис. 18,
где в главных осях (7, 2, 3)
изображён куб со стороной 1
до деформации, а пунктиром —
параллелепипед после -деформа-
ции; стороны его равны
1 + е1> 1+^21 1 + ез-
Так как первоначальный объём
элемента равен 1, то относитель-
ное его изменение будет
(1 "Г ei) (1 "Г ез) (1 + ез) — 1»
или, развёртывая произведение и
отбрасывая малые второго и
третьего порядков,
в = е1 “Ь е2 + е3'
Рис. 18.
Поверхность деформаций Коши строится следующим образом:
пусть волокно р имеет направляющие косинусы I, т, п относительно
главных осей (х1; у1г zj, и пусть радиус-вектор R произвольного
масштаба взят в том же направлении
m=i=4-,
р R р к
С Z
П = —=~О-
? R
40 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Относительное удлинение волокна р выражается, согласно (1,41),
формулой:
ее — ei^ + ечт^ + ез"2>
а перемещение конца вектора р, согласно (1.39), имеет проекции:
— е1рЛ — ез?,п> = ^аР”-
Пользуясь выражениями для I, т, п через х, у} г, R, перепишем
эти формулы в виде:
Ва = е2>^-, Ь3 = е5г-^.
Полагая
R2e? — const,
получим уравнение центральной поверхности второго порядка:
2Ф(х, у, г) = Ц-e8z2 = const., (1.46)
которая в случае, если е2, е3 одного знака, есть эллипсоид,
в противном случае гиперболоид (рис. 19). Замечая, что проекции
перемещения 3 пропорциональны частным производным функции Ф:
х _ рдФ s ____ р дФ s ___ р ОФ
1 7? дх ’ 2"~ 7? ду ’ 7? дг ’
заключаем, что вектор перемещения конца волокна р направлен
параллельно градиенту (нормали) поверхности (1.46) в точке пере-
§ 5]
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
41
сечения её радиусом
8 = -^-grad Ф.
Итак, удлинение любого волокна р обратно пропорционально квад-
рату радиуса вектора R поверхности Коши, а направление перемеще-
ния конца его совпадает с нормалью к поверхности. Этих данных
вполне достаточно для построения всей геометрической картины
деформаций и перемещений в окрестности точки О.
Подобно тому как строится для напряжений по различным косым
площадкам диаграмма Мора, она может быть построена и для
деформаций. Рассмотрим призму с прямоугольным основанием ABCD,
грань АВ которой имеет нормаль, наклонную под углом а к главной
плоскости (1.3), остальные же расположены, как показано на рис. 20.
После деформаций сечение примет вид A'B'C'D', причём относитель-
ное удлинение сторон AD и ВС в направлении нормали к АВ
будет ер, и сдвиг, т. е. уменьшение угла при вершине А будет ур.
Если удлинения по главным осям е2 заданы, то величины ер,
можно найти путём простых геометрических построений. Но в этом
нет необходимости, так как в результате мы получим формулы (1.9)
$ заменой в них о, на е?, т„ на у fp и о2 на
Ср = £ф?+£ЦрС08 2а,
^ — (ei — sin 2a,
(1-47)
42 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
На рис. 21 построена диаграмма Мора для деформаций, причём
на оси абсцисс отложены относительные удлинения волокон е,„ а на
1 р
оси ординат половины углов сдвига Кроме круга (1.47) построе-
ны ещё два круга, соответствующих главным плоскостям (2,3) и (3,1).
Не повторяя всех рассуждений о кругах Мора, которые приведены
в теории напряжений и остаются верными здесь, отметим лишь
формулы для главных сдвигов в плоскостях (1,2), (2,3) и (3,1),
которые аналогичны формулам (1.10):
Ъ2 = е1~е2> 723 = е2—ез‘> Ъ1 —ез~е1- С1-48)
Девиатором деформаций называется тензор:
ехх е 2 £хУ 1 2 вя!г
(Рв)= 1 2 еУг еуу е j 2 еУг
1 2 егх 2_ 2 егу ezn е
(1.49)
Его нормальные компоненты, следовательно, суть разности соответ-
ствующих относительных удлинений и среднего нормального удлине-
ния е, а касательные компоненты — половины соответствующих
сдвигов. Первый его инвариант, т. е. сумма элементов главной
диагонали, равен нулю. Второй инвариант, согласно (1.45), равен:
^2== {.ехх е) (еуу е) (еуу е) (^гг е)
(егг е) (,ехх Ю "Г (.еху 4“ еуг 4” егх)-
Не повторяя вычислений, которые были проделаны в § 3 для пре-
образования величины 23, мы перепишем величину Е2 в виде:
6^2 == (е^ — е^У -J- (ew — егг)2 _j_ (егг— exxf +
4“ ~2 (рхц 4" 4" (1-50)
откуда вытекает, что она существенно положительна.
Интенсивностью деформаций сдвига называется положительная
величина, квадрат которой с точностью до множителя равен второму
инварианту девиатора деформаций:
= 3 (ехх еуу)2~Ь(еуу егг)24~(егг ео;®)24"2 (e®2/4~eys4~ea»)- U-51)
2
Множитель перед корнем выбран так, чтобы для величины
имела место интерпретация Роша и Эйхингера: интенсивность дефор-
§5]
МАЛАЯ ДЕФОРМАЦИЯ ТЕЛА
43
маций сдвига есть удвоенный угол сдвига площадки результирующих
сдвигов; при этом площадкой результирующих сдвигов называется
такая, которая равным образом наклонена к главным осям деформа-
ций. Нормаль к площадке результирующих сдвигов у имеет
направляющие косину-
сы (рис. 22)
. 1
1 = т — п = —==.
/3
Перемещение конца
волокна р, взятого на
направлении нормали у
и имеющего длину пер-
пендикуляра, опущен-
ного на площадку из
начала координат, со-
гласно (1.39), имеет
проекции на главные
оси:
= etpZ, 8а == е2р/п,
8а = е3рл.
* Проекция этого перемещения на нормаль будет:
8V = 8^ -J- Ъат 83я »-у р (е, еа е3) = ре,
а на касательную к площадке:
— V 82 — 8,”=р -g- (el 4" es 4* ез) — §- (ei 4~ еа 4“ ез)2-
Угол сдвига площадки получим, как отношение
.
₽
=4 У'(Ъ - е3)9 4- (еа - е3)2 + (е3 - е^.
Так как это выражение есть половина интенсивности деформаций
сдвига ft, записанного через главные удлинения, то интерпретация
Роша доказана. В дальнейшем вместо величины ft мы часто будем
пользоваться величиной:
3 егг^+^гг—е0!®)2+ ^(е1у+е£+ега)~
= У ~ ~ ’
О
(1.52)
которую мы будем называть интенсивностью деформаций', эти две
величины отличаются только числовым коэффициентом
е*~ (1-53)
44 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. I
Подобно тому, как строится гиперболоид напряжений, являющийся
поверхностью Коши1 для девиатора напряжений, можно построить
поверхность деформаций для девиатора деформаций (De). Эта поверх-
ность по аналогии с (1.46)
имеет уравнение:
(ej — е) х2 -j- (е3 — е) />-}-
-j- % — е)г3 = const,
и называется гиперболоидом
деформаций.
В теории пластичности на-
ряду с тензором деформаций
рассматривается ещё тензор
скоростей деформаций (Е) и со-
ответствующий девиатор (£>е).
В случае малых деформаций
компоненты тензора скоростей
деформаций суть частные про-
изводные по времени или вообще по параметру, монотонно возра-
стающему и зависящему только от времени, от компонент тензора
деформаций:
- ____
~ dt ’
в _____ дегя.
~ dt ’
де
dt
(1.54)
Второй инвариант девиатора скоростей деформаций имеет вид:
8< = "IF (S*y+Syz+SD •(! -55)
Вся теория тензора скоростей деформаций (Е) тождественна с тео-
рией тензора деформаций (£), изложенной выше, если компоненты
вектора перемещений точки тела заменить на компоненты вектора
скорости, а величины на s^.. .ssx. Однако главные оси
скоростей деформаций, вообще говоря, не совпадают с главными
осями деформаций, и сами главные скорости деформаций е15 е2, е3
не равны производным по времени от главных деформаций е1( еа, е3
так же, как и =/= . Это ясно хотя бы потому, что направле-
ния вектора перемещений и вектора скорости точки, вообще говоря,
не совпадают.
§ 6. Направляющие тензоры и гиперболоиды напряжений
и деформаций; случай простой деформации.
Во всех известных теориях пластичности, не учитывающих явле-
ний релаксации-последействия в телах и предполагающих, что тела
являются квазиизотропными, механическое состояние элемента мате-
риала характеризуется тензорами напряжений (5), деформаций (£) и
§ 6] НАПРАВЛЯЮЩИЕ ТЕНЗОРЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 4S
их дифференциалами, а механические свойства тела, в простейшем
случае даваемые диаграммой растяжения-сжатия образца, определяются
соотношениями между этими четырьмя тензорами. Как будет доказано
ниже, имеющиеся в настоящее время экспериментальные материалы
с полной надёжностью позволяют формулировать законы упругости
и пластичности лишь для случая так называемой простой упруго-
пластической деформации, причём они могут быть экстраполированы
и на близкие к простому состояния.
При приложении нагрузки к телу и последующем её увеличении
в каждой точке тела механическое состояние изменяется. Каждая из
действующих внешних сил, т. е. как сила поверхностная, так и
объёмная, является функцией координат и ещё только одного пара-
метра, например, времени или какой-нибудь другой монотонно воз-
растающей во времени переменной. Поэтому и механическое состоя-
ние в любой точке тела будет кроме координат точки зависеть
только от одного параметра. Изменения тензоров (S) и (Е), связан-
ные с бесконечно малым приращением этого параметра, мы и назы-
ваем их дифференциалами d(S), d(E). Механические свойства раз-
личных сплошных сред обычно представляются функциональным
соотношением между тензорами (S), (Е) их дифференциалами раз-
личных порядков и интегралами различной кратности по параметру.
Рассмотрим любой симметричный тензор второго ранга (П). Его
можно представить -в виде суммы шарового тензора (р) и девиа-
тора (Dj,):
(П) = (р) + (ЯД (к56>
где р есть линейный инвариант (П), равный среднему значению чле
нов главной диагонали, а
/Ри Р12 Р13\
(рр) = ( Р21 Р22 Р23 ) » (1.57)
'Рз1 Рз2 Pss'
где ртп — компоненты девиатора в осях х, у, 2, причём
Ри + Р22+Р33 == °- (1.58)
Второй инвариант девиатора, который назовём интенсивностью (£>р),
запишем в виде:
Pi = (/’11-Р2а)2+(/’2а-Р33)2+(/?33-Р11)2+6(^2 + Р13+ PL)- (159)
Умножая и деля девиатор (Dp) на скаляр р4 и обозначая отношение
любой его компоненты ршп к р{ через ртп, т. е.
Р,™ = ^-. /я, « = 1,2, 3, (1.60)
мы получим:
(7^>) —Pi {Рр)*
(1-61)
(1.63)
46 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Вводя ещё единичный тензор (/), перепишем тензор (П) в следую-
щем виде:
(П) = р(/) + Р<(5р). (1.62)
Назовём тензор (£>„) направляющим тензором для (П), а его
поверхность Коши — направляющим гиперболоидом. Ясно, что глав-
ные оси тензора (П) совпадают с главными осями (О^).
Направляющий тензор (£>р) определяется только четырьмя неза-
висимыми компонентами, т. е. тремя главными его направлениями,
которые относительно выбранной системы координат определяются,
например, тремя углами Эйлера, и значением одной из главных его
компонент или отношением любой пары главных компонент. В самом
деле, если главные направления заданы и главные его компо-
ненты суть ри ря, р3, то, согласно (1.58) и (1.59), мы имеем:
Р1 + /’2 + Рз = 0>
(F1—Р2)а + (р2—Рз)2+(/’з—Р1)2 = 9.
Зададим ещё одно отношение между компонентами в виде ’):
~ = [г. (1.64)
Pi—Рз Pi— Рз
Решая совместно уравнения (1.63), (1.64), находим:
. 3 —- . 2р. ~~ 3 -4- р. /, /? с \
rl /2(3-)-^) Г2 У2(3-Ьр2) ^/2(3 + р2) К У ’
Обозначим через jq, х8, х3— прямоугольные координаты по глав-
ным осям тензора (П), тогда направляющий гиперболоид опреде-
лится уравнением:
PlXi “Ь р2х3 Н” Рзх3 = — const.
Постоянная может быть выбрана так, чтобы одна из трёх полуосей
гиперболоида была равна 1; для этого необходимо в качестве посто-
янной взять одну из главных компонент направляющего тензора
отличную от нуля; тогда получим:
Р1*1 ~Ь Рах2 + Рвхз ~-Рп- (1.66)
На рис. 23 изображён направляющий гиперболоид, причём предпо-
лагается, что — 3<р.<0, поэтому принято pn — pi. Уравнение
этого гиперболоида таково:
(1-67)
1) Можно взять любое независимое от (1.63) соотношение, но мы выби-
раем это, следуя На дай и Лоде.
§ 6j НАПРАВЛЯЮЩИЕ ТЕНЗОРЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 47
а размеры полуосей равны: _______________
1 г. /~ 3 — р.
а — 1, <& = 1/ -----,
’ Г — 2р.
(1.68)
При рассечении гиперболоида плоскостями хг = const, получаются,
эллипсы, а плоскостями х2 = const, и х3 = const.—гиперболы. На
рисунке показана также ориента-
ция главных осей (х1г х2, х3)
относительно осей (х, у, г).
Предположим теперь, что тен-
зор (П) является функцией неко-
торого параметра X, например
времени:
Ртп ==Ртп (Ч> /5 доч
Л = ( • }
(т, п = 1, 2, 3).
Направляющий гиперболоид и его
ориентация относительно непо-
движных осей (х, у, z), вообще
г ,
Рис, 23.
говоря, будут изменяться с изме-
нением А, причём тензор (II) каждый раз становится вполне опре-
делённым, как только известны инварианты р и pt и направляющий
тензор (Ор), т. е. ориентация осей направляющего гиперболоида и
число у..
Зависимость тензора (II) от параметра X называется простой
в том случае, если от X зависят только инварианты р и р{, а напра-
вляющий тензор (Dp) от него не зависит, т. е. если направляющий
гиперболоид при изменении X остаётся неподвижным. Относительно
тензора (П) в этом случае имеет место следующая теорема: если
зависимость (П) от X является простой и если символом L обозна-
чен любой линейный оператор по X, например,
х
А(П)=Л(П) + В-^(П)+[ С(ПЖ+..., (1.70)
о
где А, В, С...—функции инвариантов, то тензор (Q) = L(H)
имеет направляющий тензор (Dg), тождественно совпадающий с (DA,
а втодрй инвариант девиатора (Dq) равен оператору L от pt. По
определению имеем:
(Q) = ^(/) + ^(Da), (1.71)
причём
q = L (р), ==: 2, 3),
+ + ’ (1-72)
48 основные законы Упруго-пластических деформаций (гл. 1
Поскольку [рр) не зависит от А, из (1.62) имеем:
L (И) = (Q) = L (р) (/)+L (pt) (Ьр).
Сравнивая последнее выражение с (1.71), получаем;
74(О2) = £(Л)(ОР). (1.73)
Так как (Dp) не зависит от X, то, по свойству пропорций, Имеем:
. Z, __________________ Ртп _ 7, (ртп)_ Ятп
Ртп=~ р{ ~ L(pi} - L(pi} ,
откуда
L (Pi)
Qmn — pt Ртп'
Поэтому, внося значение qmn в выражение для qt согласно (1.72),
находим:
4i = L(pi), (1.74)
а на основании (1.73) получаем:
(5,) = (5p). (1.75)
Все определения и рассуждения, проведённые для тензора (П),
справедливы в отношении тензоров напряжений и деформаций. На-
пряжённое состояние тела в каждой точке характеризуется средним
нормальным напряжением о, октаэдрическим напряжением (или
интенсивностью напряжений а{) и направляющим тензором напряже-
ний (О8):
/Sj 0 0 \
W=^0S80 (1.76)
* \о о sj
или направляющим гиперболоидом напряжений
+ 6’2^2 J- 53xs = zb Sn. О-??)
Если главные оси напряжений известны, то (£>g) определяется только
одним числом [л:
., 2S2— S,— S3 3S2
------(к78)
Деформированное состояние тела характеризуется средним учине-
нием е, октаэдрическим сдвигом (или интенсивностью деформа-
ций е,) и направляющим тензором деформаций (Ьв)
(е1— е 0 0\
0«2-е 0 1 (1.79)
О Ов) — е/
§ 6] НАПРАВЛЯЮЩИЕ ТЕНЗОРЫ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 49
или направляющим гиперболоидом деформаций, j Если главные оси
деформаций известны, то (Ое) определяется только одним чи-
слом v:
v == — gi — 63 — 3 (g8 — g) zj 8q\
>1 — ga gi — ga V '
Зависимость между девиаторами напряжений и деформаций во всех
известных теориях пластичности, не учитывающих явлений ползу-
чести материала, укладывается в одну формулу:
L(D8)=L'’(De), (1.81)
где L, L' — линейные операторы типа (1.70).
На основании данной выше теоремы можно утверждать, что
в случае, когда деформация элемента тела является простой, т. е.
направляющие тензоры напряжений (Z)8) и деформаций (Ое) по мере
возрастания напряжений и деформаций остаются неизменными, все
теории, изображаемые формулой (1.81), совпадают между собой
и, по существу, утверждают, что направляющие тензоры напряже-
ний и деформаций равны
(Ds) = (5e), (1.82)
и что интенсивность напряжений есть определённая функция интен-
сивности деформаций
°/= $(*<)• . (1-83)
Кроме того, во всех теориях пластичности считается, что объёмная
деформация происходит упруго, т. е.
<з = 3 Ке. (1.84)
Формулы (J.82), (1.83), (1.84) и представляют собой основные
законы простейшей из теорий пластичности — теории малых упруго-
пластических деформаций. Эта теория, строго говоря, справедлива
только в тех случаях, когда направляющий тензор напряжений (Ds),
различный в разных точках тела, не зависит от параметра к, что,
как увидим, имеет место, если произвольные внешние силы, дей-
стгующие на тело, возрастают от нуля пропорционально одному
параметру. Такую нагрузку мы называем простой. Если нагружение
тела является сложным, т. е. возрастание во времени одной из дей-
ствующих сил не сопровождается пропорциональным возрастанием всех
остальных сил, направляющий тензор напряжений (£)8) будет изме-
няться со временем и, строго говоря, излагаемая ниже теория малых
упруго-пластических деформаций будет несправедлива, хотя при слабой
4 Зак. 3138. А. А. Ильюшин
5б ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСГИЧЁСКЙХ ДЕФОРМАЦИЙ
[гл. t
зависимости (Ds) от К результаты её будут приближённо верными.
Однако эксперименты по изучению сложного нагружения ещё недоста-
точны для того, чтобы с достаточной уверенностью остановиться
на какой-нибудь теории пластичности типа (1.81) при сложном на-
гружении.
§ 7. Закон Гука; сжимаемость тела и условие пластичности.
Если к телу прикладывается нагрузка, то до некоторых пределов
в нём имеет место упругая деформация, подчиняющаяся закону Гука.
Закон Гука можно формулировать в виде следующих трёх поло-
жений:
1. Направляющие тензоры напряжений и деформаций или напра-
вляющие гиперболоиды в каждой точке тела совпадают:
(DJ = (De).
(1.85)
2. Линейные инварианты тензоров напряжений и деформаций
пропорциональны или, иначе, изменение объёма элемента тела прямо
пропорционально среднему нормальному напряжению
о = 3 Ке,
(1.86)
причём К называется модулем объёмной деформации.
3. Квадратичные инварианты девиаторов напряжений и деформа-
ций пропорциональны или, иначе, октаэдрическая деформация (интен-
сивность деформаций et-) прямо пропорциональна октаэдрическому
напряжению (интенсивности напряжения о*)
o,= 3Gef, (1.87)
причём Q называется модулем сдвига. В такой форме закон Гука
имеет гораздо более наглядный механический смысл, и его инвариант-
ность для различных координатных осей более ясна, чем в обычной
форме шести соотношений. Разрешая (1.85) относительно тензора
деформаций, получим:
= <1-88)
Отсюда в проекциях на оси х, у, г находим:
еуу = ~Ё [ УУ ~~ т ’
fa? ~ ^х >
р = X
сху Q^y'
е =— У
СУЯ (J Z’
еЯХ Q
(1.89)
§ 7) ЗАКОН ГУКА; СЖИМАЕМОСТЬ ТЕЛА. Й УСЛОВИЕ ПЛАСТИЧНОСТИ
51
Здесь модуль Юнга Е и коэффициент Пуассона — выражаются
через G и К формулами:
9GK 1 _ ЗК— 2G
£ 3K+G ’ т 4(3K+G)'
Разрешая (1.85) относительно тензора напряжений, получим:
(S) = 20(E) ф-(3^2б)е(/). (1.90)
Отсюда в проекциях на оси х, у, 2 имеем:
Хх = Х9 ф-- 206™, Ху = Ge
Л/ I <4/(4/' у d/ff'
Г^ХОф-20^ Yz=Geyz,
Zz — Х9 ф- 20вга, Zx = dezx,
(1.91)
где 6 = Зе — относительное объёмное расширение и X — постоянная
Ляме:
2
X = К—4 G.
. о
Наконец, уравнение (1.85) в проекциях на оси даёт
5в? = 20зв?, (1.92)
(а, = х, у, г),
где 5а?, эа6— компоненты девиаторов (Da) И (Ое) В осях х, у, 2,
причём: 1
1 Эаав== ехх $ху == еху>
__ 1 эуу еуу е’ эу^~~ 2 еУ^' (1.93)
_ __1_ — егг е> 3zx 2 егх-
Найдём выражение работы упругих напряжений, приходящейся
на единицу объёма тела. Эта величина в теории упругости называется
эластическим потенциалом или потенциальной энергией'.
21Г=Ла,еа,а. 4" ¥уеуу + + ^уеху + ^Xxz + Y'Xyz- (1-94)
Её можно переписать в виде:
2 IT = (Sxx ф- а) (эхх ф- е) ф- (Syy -ф- а) (эуу ф- е) ф- (Sss ф- о) (зг2. ф- е) ф-
ф~ 28хуэху ф— ^Syz9ys ф- 2SZX9ZX,
откуда после перемножения и приведения подобных членов находим:
2Г=а9ф-2^а₽. (1.95)
а?=а:, г/, г
4*
§2 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Так как первое слагаемое правой части, т. е. о8 представляет собой
удвоенную работу, идущую на изменение единичного объёма тела,
то второе выражение представляет собой удвоенную работу формо-
изменения (т. е. идущую на изменение формы элемента тела без
изменения объёма).
Итак, мы получили следующие результаты. 1. Работа компо-
нентов шарового тензора напряжений на компонентах шарового
тензора деформаций или скалярное произведение1) шаровых тензоров
напряжений и деформаций представляет собой удвоенную упругую
работу внутренних сил, идущую на изменение объёма, т. е.:
(о) (е) = <зе (Z) (/) = о8. (1.96)
2. Работа компонентов девиатора напряжений на компонентах девиа-
тора деформаций, т. е. скалярное произведение девиаторов напряже-
ний и деформаций, представляет собой удвоенную работу внутрен-
них сил, идущую на изменение формы (без изменения объёма):
(о,)(ле)^2^ = 2и7-з0 = 2ц/Ф- О-97)
«, ₽ = ®> У, « ,
Укажем теперь на следующую интерпретацию второго инва-
рианта девиатора напряжений или октаэдрического напряжения, дан-
ную Генки Гп1; второй инвариант девиатора напряжений или квадрат
октаэдрического напряжения с точностью до множителя равен упругой
работе внутренних сил, идущей на изменение формы элемента
тела, т. е. , '
(1.98)
Для доказательства выразим Ц7ф через напряжения Sa?. На основа-
нии (1.92) имеем:
2 ^ = 53- S Ъ
a у, г
Вычтем из правой части величину
д-— (*^хх "4~
О С/ ' XX 1 у у I ££* •
которая, как известно, равна нулю. После простых преобразований
получаем:
2 П = ± [(S^ - Syy)* + (Syy - 5зг)2 + (Ss2 - +
+ 6(^+^ + -^)1. 9 *
9 Скалярное произведение тензоров, как и векторов, есть скаляр, рав-
ный сумме произведений соответствующих компонентов.
§ 7] ЗАКОН ГУКА; СЖИМАЕМОСТЬ тела и условие пластичности 53
или, сравнивая с (1.18), имеем:
2Гф = -^, (1.99)
откуда и следует интерпретация Генки.
Попутно получаем ещё и другую интерпретацию величин а{ и е<\
интенсивности напряжений и деформаций представляют приведённое
напряжение и приведённую деформацию, полупроизведение которых
равно энергии формоизменения элемента. В самом деле, найдём про-
изведение
4°а-
Величины о4-, связаны с октаэдрическим напряжением и дефор-
мацией соотношениями:
а 1
= (1.100)
Пользуясь закром (1.87) и формулой (1.99), непосредственно
получаем:
: (1.Ю1)
С этой точки зрения величины о4-, ^представляют собой как бы
простое растягивающее напряжение и простое удлинение фиктивного
образца, заменяющие сложное напряжённое и деформированное
состояние тела.
Закон Гука, отображающий упругие свойства тел, вообще говоря,
теряет силу, как только начинают возникать остаточные деформации.
Условие, которому должны удовлетворять напряжения в некоторой
точке тела, чтобы в ней появились первые остаточные деформации,
называется условием пластичности. Чтобы не различать разные трчки
тела, мы будем предполагать пока, что деформация его и напряжённое
состояние являются однородными, т. е. они одинаковы во всех
точках тела, которое также предполагается однородным и квази-
изотропным.
Вполне очевидно, что условие пластичности должно быть инва-
риантно в отношении преобразования осей координат х, у, z путём
поворота, и потому оно должно выражаться только через инварианты
тензора напряжений. В самом общем случае оно, следовательно,
должно иметь вид:
/(31, а2, а3) = 0, (1.102)
где о3, о3 — главные напряжения и /—некоторая функция. Как
уже говорилось в § 1, при простом растяжении образца материала
(а^ = а3 = 0) условие пластичности имеет вид:
31 ~ ’’у
(1.103)
54 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
где <з8 — постоянная для каждого материала величина, которую
в дальнейшем будем называть пределом текучести при растяжении1)
и считать, что при растяжении и сжатии она имеет одинаковое зна-
чение.
При кручении стержня круглого поперечного сечения наибольшее
касательное напряжение возникает на поверхности стержня, причём,
если индексу «2» приписать главное направление осёй напряжений,
совпадающее с радиусом, то, как показывает опыт, условием начала
образования пластических деформаций будет:
x = (1.104)
так как кручение соответствует случаю чистого сдвига (а2=0, а3 =
=— Oj). Здесь т8, называемая пределом текучести материала при
сдвиге, также представляет собой физическую постоянную. Три
основных опыта: на простое растяжение, на сжатие и на кручение
(чистый сдвиг) уже давно наводили исследователей на мысль объ-
единить три частных условия начала возникновения в материале
остаточных деформаций в единое условие пластичности типа (1.102).
Следует заметить, что в курсах сопротивления материалов часто
смешивают условия пластичности и условия прочности, называя их
теориями прочности; вообще говоря, между условиями прочности и
условиями пластичности нет ничего общего: возникновение в теле
пластических деформаций вовсе не означает потери прочности и чаще
всего сопротивление тела при переходе его за пределы упругости
возрастает. Теории прочности в этой книге не излагаются, поскольку
они ещё недостаточно установлены для различных материалов, хотя
при решении частных задач мы и будем пользоваться некоторыми
более или менее очевидными условиями прочности ДО.
Сен-Венаном I12), на основании опытов Треска по истечению
металлов через отверстия, было предложено условие пластичности,
состоящее в том, что тело переходит за пределы упругости, как
только максимальное касательное напряжение достигает некоторого
определённого значения т8
= V (1.105)
Сен-Венан рассматривал задачу о плоском деформированном пласти-
ческом состоянии и шёл по пути обобщения уравнений движения
вязкой жидкости Навье-Стокса. Вскоре Леви 1131 предложил это же
условие для пространственной задачи пластичности, формально обоб-
щив теорию пластичности Сен-Венана. Впрочем, идея такого условия
пластичности принадлежит Кулону. Геометрический смысл уравнения
(1.105) в прямоугольных координатах оп оа, о3 нами уже выяснен
в § 3: оно представляет шестигранную призму Кулона. Аналитическая
J) По определениям § 1 она является пределом пропорциональности, что
ы и будем иметь в виду.
§ 7] закон гука; сжимаемость тела и условие пластичности 55
запись условия пластичности Кулона-ХЗен-Венана-Леви через все шесть
компонентов тензора напряжений оказалась чрезвычайно сложной и
неудобной.
Губером ПЛ, а затем Мизесом I161 и Генки I16) было предложено
новое условие пластичности — условие постоянства энергии формо-
изменения. Как уже показано в § 3, октаэдрическое напряжение
оказывается почти постоянный, если максимальное касательное напря-
жение постоянно, и это. является достаточным основанием для замены
уравнения (1.105) новым уравнением пластичности:
т4 = const.
В координатах о2, о2, з3 оно представляет цилиндр Губера-Мизеса.
Для того чтобы это условие совпадало с (1.103) в случае простого
растяжения, постоянная должна быть выбрана определённым образом,
и условие Мизеса приобретает вид:
(1.106)
Оба указанных условия пластичности в настоящее время можно
считать достаточно правильно отражающими начало пластических
деформаций в телах. При решении частных задач теории пластич-
ности можно остановиться на том из них, которое математически
упрощает решения. Впрбчем, по существу обнаружилась большая
точность условия Мизеса. Это становится очевидным уже из сравнения
результатов опытов на растяжение и кручение. Применяя к опыту
на растяжение (<з2 = <з3 — 0, о4 = з8) условие пластичности Сен-Венана,
находим ts = 0,5о8. Применяя его теперь к кручению, заключаем, что
пластичность при кручении наступает тогда, когда максимальное
касательное напряжение тгаах достигает значения 0,5 as. Опыты, о ко-
торых будет речь в следующем параграфе, показывают, что пласти-
ческие деформации при кручении появляются, когда тмах достигает
несколько большей величины порядка 0,56 ~ 0,6 os. Из условия
Мизеса (1.106) для случая кручения:
о.-» = 0, а3 — — а. = гг
имеем:
= °>5 77аа,
т. е. величину, хорошо совпадающую с опытной.
Основная особенность формулированных выше условий пластич-
ности Сен-Венана (1.105) и Мизеса (1.106) состоит в том, что они,
так сказать, нечувствительны к равномерному всестороннему давлению
или растяжению. В самом деле, если все главные напряжения о1г оа, о3
увеличить или уменьшить на одну и ту же произвольную величину,
условия пластичности останутся прежними. Математически это ясно,
так как интенсивность напряжений о4 выражается только через ком-
56
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
[ГЛ. I
поненты девиатора напряжений (Ds), а максимальное касательное
напряжение есть полуразность главных. В связи с этим интересно
отметить некоторые факты, связанные с поведением металлов при
высоких всесторонних давлениях.
При действии высоких всесторонних давлений плотность металлов
возрастает очень незначительно, причём изменение объёма является
упругим. Отсылая интересующихся этим вопросом к книге Бридж-
мена tnI, мы приведём лишь некоторые описанные в ней результаты.
При давлениях порядка до 15 000 атмосфер и более Бриджмен даёт
следующую зависимость между всесторонним равномерным давлением р
и относительным изменением объёма в:
где К—модуль объёмного сжатия, выражающийся через модуль
Юнга Е и число Пуассона т формулой:
у_ тЕ
л ~3(т — 2) ’
и Кх — вторичный модуль, значение которого для различных металлов
можно найти в указанной книге. Некоторые значения этих модулей
в кг/см* при нормальной температуре приведены в табл. 1.
Таблица 1 Значения модулей К и Ki в кг!см\ Снятие давления, как пра- вило, не сопровождалось появлением остаточной.объ- ёмной деформации. Таким образом, при всесторонних равномерных давлениях по-
Металл К кх
Железо .... Медь Алюминий . . . Свинец 1,70-106 1,38 -10» 0,75-106 0,42 • 106 2,80-106 2,71 -105 3,82 • 10® 1,37-105 рядка предела текучести ме- талла ag отклонение формулы (1.107) Бриджмена от за- кона Гука (1.86) составляет величину порядка 1%, и им
вполне можно пренебречь. Более того, изменение объёма металла при таких давлениях составляет величину порядка 0,1°/ои потому соответствующее равномерное удли- нение е = -i 9 будет порядка 0,03%. Если рассматривать пластические
деформации, значительно превосходящие величину , то из сказан-
ного ясно, что изменением объёма вообще можно пренебречь и счи-
тать материал несжимаемым. Поэтому вместо закона Гука (1.86)
в теории пластичности чаще всего берут условие несжимаемости'.
6 = Зе = ei + ea + e3 = 0, (1.107')
хотя закон (1.86) более точен и содержит условие (1.107') как
частный случай, соответствующий К=<х>.
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 57
Влияние всестороннего равномерного давления на условие пластич-
ности, как показывают рпыты, является очень слабым, на пластич-
ность же очень значительным. Первое может быть учтено, если
в условиях (1.105), и (1.106) предел текучести считать функцией
инварианта а. Однако опыты Шлейхера 1181 и недавние опыты Бридж-
мена 1191 показывают, что не только при средних давлениях порядка
предела текучести металла, но и при значительно больших давлениях
влиянием среднего равномерного напряжения на условие пластичности
можно пренебречь. Это влияние становится заметным у сталей при
давлениях порядка ста тысяч атмосфер. Но пластичность материалов
под действием высоких всесторонних давлений значительно возрастает,
и даже’ самые хрупкие тела, не разрушающиеся при действии равно-
мерного всестороннего давления, могут получать достаточно большие
остаточные деформации.
§ 8. Экспериментальное изучение законов пластичности
при сложном напряжённом состоянии.
Этому вопросу с начала нашего столетия и до последнего времени
уделяется основное внимание исследователей в области теории пластич-
ности. Не останавливаясь на ранних исследованиях частного характера,
мы укажем лишь на те работы, в которых проблема изучалась
с достаточной широтой и общностью и в которых получены резуль-
таты достаточно общего характера.
В докладах 2-го Международного конгресса по прикладной механике
1926 года имеются, две фундаментальные работы, относящиеся к этому
вопросу: 1) Надаи и Лоде l20!, выполненная в Геттингене при участии
Прандтля; 2) Роша и Эйхингера 1211. В этих работах заложена основа
современных методов изучения пластичности при сложных напряжён?
ных состояниях путём растяжения и кручения тонкостенных труб и
дано подтверждение основных законов пластичности. Необходимо
иметь в виду, что за два года до Конгресса была опубликована
теория пластичности Генки, лежащая в основе теории малых упруго-
пластических деформаций, и имелась некоторая ясность в том, какие
именно факты должны быть подвергнуты экспериментальной проверке.
В опытах Надаи и Лоде окончательно установлено условие пластич-
ности Мизеса, причём показано его преимущество перед условием
наибольших касательных напряжений и рассмотрен вопрос о подобии
напряжённого и деформированного состояний. В опытах Роша и
Эйхингера рассмотрено влияние упрочнения материала на условие
пластичности Мизеса и установлена связь между октаэдрическим
напряжением и деформацией. Тэйлор и Квини 1221 в 1931 году опубли-
ковали свои опыты, посвящённые уточнению опытов Надаи и Лоде.
Они также приходят к подтверждению условия пластичности Мизеса,
устанавливают совпадение главных осей напряжений и скоростей
деформаций и приближённое подобие распределения напряжений и
58 ОСНОВНЫЕ законы УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
скоростей деформаций в условиях, сильно отличающихся от условий
простой пластической деформации. В 1932 году опубликованы опыты
Шмидта Р81, в которых рассмотрены те же вопросы и использованы
некоторые идеи работы Гогенемзер и Прагера они интересны
как положительными, так и отрицательными для теории пластичности
Генки-Мизеса результатами. Несколькими годами позднее в лабора-
тории Ленинградского университета проверкой законов пластичности
занимался Смирнов-Аляев, причём в общем дал подтверждение основ-
ных гипотез. В последующие годы появилось большое количество
Рис. 24.
экспериментальных исследований явления пластичности при сложном
напряжённом состоянии и особенно в области упрочнения металлов
и при конечных деформациях. В них нет противоречий с теми выво-
дами из перечисленных выше работ, которые нам необходимы для
установления основных законов излагаемой здесь теории пластичности
и, скорее наоборот, чем тщательнее делались опыты с изотропными
металлами, тем лучше подтверждаются эти законы. Однако, как это
отмечает и Прагер 12Б1, из новых опытов пока нет возможности
прлучить достаточно обоснованные экспериментальные законы более
общего характера, хотя теоретические возможности здесь очень
велики. Поэтому, в качестве примера, мы остановимся лишь на двух
работах, которые в лаборатории Надаи и, видимо, под его руковод-
ством были выполнены Дэвисом I261.
Характер испытаний при сложном напряжённом состоянии.
Испытание тонкостенных круглых труб на одновременное действие
растягивающей силы Р, внутреннего давления р и крутящего момента М
представляет возможность установления и полной проверки законов
пластических деформаций в общем случае плоского напряжённого
состояния. Исключая влияние крепления -концов трубы в машине,
можно считать, что напряжённое состояние в трубе является одно-
родным, если однороден металл и достаточна точность при её изго-
товлении. Направляя ось х по оси трубы, ось у по касательной
к окружности и ось z по радиусу и считая толщину стенки h. малой
сравнительно со средним радиусом /?, мы вправе полагать все основные
§ 8]
ЭКСПЕРИМЕНТАЛЬНОЕ изучение законов пластичности
59
напряжения постоянными по толщине, исключая Zz, которое в случае,
когда действует равномерное внутреннее давление р, изменяется от
нуля на наружной до р на внутренней поверхности и, следовательно,
в общем очень малд сравнительно с основными напряжениями Хх,
Yy, Ху (рис. 24). Компоненты тензора напряжений, как легко видеть',
определяются следующими формулами:
Yy = p^, Zz=0, |
М I <1108)
, = = j
где F=2TtRh — площадь живого сечения трубы. Таким образом,
отличными от нуля и вполне произвольными оказываются все три
компоненты напряжений плоского напряжённого состояния. Среднее
нормальное напряжение <з равно: .
о =
(1.109)
и потому компоненты девиатора напряжений (Og) имеют
значения:
следующие
2Р
F
— к _ _ 1 / _
* луу г у а з (
хх ^х
Z.. — <3 =
с ___.у ___ М
ху лу ftp »
= S..z — 0.
Октаэдрическое напряжение равно:
•4 =
а рр
(1.110)
(1-111)
Вычисляя отношение компонентов девиатора (Os) к октаэдрическому
напряжению х{, находим компоненты направляющего тензора (Z>8):
_____ $хх
^хх = — >
X $ху
О ___ Syy F I_____^гг
•^УУ— т. > — >
* »
с ____ с — п
(1.112)
60 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ' ДЕФОРМАЦИЙ [гл. I
Как уже указывалось, тензор (Ds) определяется его главными напра-
влениями (которые мы выберем так, чтобы главные оси хи х9
лежали в плоскости развёртки нашего цилиндра, а х3 — г, поскольку
ось г является главной) и одним числом у.. Найдём главные напра-
вления и главные компоненты (£>s). ! Пусть ср—угол, составленный
нормалью п косой площадки с осью трубы х (рис. 25) и пусть
Sn — нормальная составляющая (£>s) на этой площадке. Из условия
равновесия призмы имеем:
cos2T + SM,Sln2T + ^ + S» .
Разыскивая экстремум этой величины по ср, т. е. полагая
dSn __ А
-U’
находим главные направления (рис. 25) по формуле:
182ср = _2Ц_^ 2^ (L113)
^уу х 1У
из которой следует, что одно направление (xt) составляет с осью х
угол ср, другое (х2)— угол ср-ф-у. Внося значение ср в выраже-
ние Sn, а именно:
cos 2ср = zt ... '
V(SXX — Syy)2 + 45^
sin 2ср = zt -. ------------- . ,
r $уу^ +
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 61
причём знак (-]-) для первого главного направления (Xj) и (— ) —
для второго, получаем главные компоненты (D8):
$1 = у Н- ~Ь у ($хх — + 4
52= |(^ + ^)-|Г(5ж;с-5о)2 +4S^, <1Л14>
S, = $zz-
Уже доказывалось, что из трёх главных компонентов (£>s) независим
только один, так как имеют место соотношения:
5i + S2 + 3s = 0,
& - S2)2 + (S2- S3)2 + (Sj -SJ2 = 9;
поэтому кроме угла ср тензор (£>s) определяется только одним пара-
метром (1.78):
ч _____ 2Scp — Sma — Smi 3SCp
Sma— Smi Sma—S mi
который в опытах с трубами имеет такое выражение через главные
напряжения aj, а2, о3:
2<Тср — ffma — Omi
u.=------£------------
Ста — ffmi
(1.115)
где ота, бпй, оСр — максимальное, минимальное и среднее напряжения
из aj, о2, а3; при этом:
= у + Yy) 4-1 V(Хх~ Уу)2 + 4.Y2,
°2 = | (Хх + У у) - 4
(1.116)
Деформация трубы определяется тремя компонентами: продольным
удлинением еХХ) тангенциальным удлинением еуу и углом сдвига еху,
так как сдвиги exz — eyz — 0, a ezz можно определить из условия
несжимаемости:
ezz ехх еуу
Таким образом, сам тензор деформаций является девиатором (Е) =
~(De). Направление главных осей деформаций определяется углом
и для него, согласно (1.113), имеем:
tg2<p = —
КХХ----------- vyy
(1.117)
(>2 ОСНОВНЫЙ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гЛ. 1
Главные удлинения
^1> ^2’ ^3 == ^2>
определяются формулами, аналогичными (1.116):
е1 — 2 еуу) ~Ь 2 (ехх еуу? Н- еху >
е2 = ~2 (ехх 4“ еуу) (ехх еуу) ~Ь еху-
(1.118)
Октаэдрический сдвиг, согласно (1.51), равен:
Ъ =
I 2
ехх еуу “Г еУУ
(1.119)
Направляющий тензор деформации (Ое), кроме угла определяете3
только одним числом v (1.80):
Можно себе представить два основных типа опытов с трубами.
Первый осуществляется на машинах, в которых по произволу экспе-
риментатора могут быть заданы сила Р, давление р и крутящий мо-
мент М. В таком случае, постепенно увеличивая определённым обра-
зом эти величины, можно измерять возникающие в трубе деформации,
а именно: её осевое удлинение
_ Д/
ехх I )
изменение диаметра
е = **
УУ R
и угол закручивания <о на длине I:
R
еху = ^-
Затем, обрабатывая результаты по формулам (1.113), (1.111), (1.115),
(1.117), (1.119) и (1.120), можно искать зависимость между напря-
жениями и деформациями. Направляющие тензоры напряжений и де-
формаций будут равны между собой, если = и p. = v для любой
комбинации внешних сил Р, р, Ж.
Второй тип опытов может быть осуществлён на машинах, позво-
ляющих произвольным образом менять деформации трубы, а именно:
её осевое удлинение А/, радиальное удлинение Д7? и угол закручива-
ния ш. Тогда приборы должны регистрировать возникающую силу Р,
давление р и крутящий момент М. Обработка результатов останется
прежней. Можно представить себе и опыты комбинированного типа.
Обычно делались опыты первого типа и притом частного характера.
Например, труба подвергалась действию только внутреннего давления
§ 8] . ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 63
и осевой силы. В таком случае из условий симметрии ясно, что
кручение не возникает:
= °> Ху = °>
и потому совпадение главных осей о = ф обеспечивается автомати-
чески. Таким образом, опыты без кручения позволяют найти связь
между величинами р и v. В других случаях применялось только
растяжение и кручение. Они позволяли найти связь между ® и ф,
а также между р и v.
Диапазон изменения угла 9 и параметра р, исчерпывающий все
возможные случаи при плоском напряжённом состоянии, таков:
(1-121)
В самом деле: 1) в случае равномерного растяжения в двух напра-
влениях, когда
°1 = 32 > °, =
имеем
Згаа = °i, 3mi О,
аср = а2, и потому р = 1; 2) в случае растяжения в одном направле-
нии, когда
Хх °1 == Yy = <?2 = О3 = <Jmj = <70р == О,
и потому ;i = —1; 3) в случае сдвига, когда
== 0, oma’=(3i, °mi — "ср = О,
и потому р = 0; 4) в случае осевого сжатия р=1 и, наконец,
5) в случае равномерного сжатия по двум направлениям
°ma = 0> °mi — °ср =а1 — °2>
и потому р = — 1. Совпадение значений р в первом и четвёртом,
а также во втором и пятом случаях очевидно, так как они отлича-
ются только на величину равномерного всестороннего давления и растя-
жения (добавляя, например, в первом случае равномерное давление
со всех сторон, равное—aj, получим четвёртый случай и т. д.).
Если ещё принять во внимание, что механические свойства рассма-
триваемых металлов при растяжении и сжатии одинаковы, можно
ограничить диапазон изменения величин ® и р значениями:
- 1<р<0. (1.122)
Все имеющиеся опыты при сложном напряжённом состоянии
с точки зрения излагаемой теории пластичности следует разбить на
две группы. К первой группе будем относить опыты, в которых
осуществлялось простое нагружение трубы, т. е. для каждой данной
64 ОСНОВНЫЕ ЗАКОНЫ УПРУГО^ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ (гЛ. t
трубы проводилось только одно испытание, в котором соотношение
между прилагаемыми силами оставалось постоянным всё время, т. е.
было постоянно и отношение главных напряжений Щак как напра-
вление главных осей напряжений при этом не могло изменяться отно-
сительно тела, то из простых условий симметрии ясно, что главные
оси деформаций совпадали в главными осями напряжений. При этом
совершенно несущественно — упрочняется ли в процессе деформации
материал или не упрочняется. Итак, в случае простого нагружения
условие:
? = Ф
выполняется автоматически. Вполне очевидно, что выполняется
и условие р. = v во всех пяти перечисленных выше частных случаях,
если нагружение являлось простым. В самом деле: 1) при равномер-
ном растяжении в двух направлениях из условий симметрии ясно,
что
== ^2 0, Cmi = бср = йша,
и потому из (1.120) v = |t = 4-l; 2) в случае растяжения в одном
направлении
== ^ор ^mi :==: 0,5
и потому v — р == — 1; 3) в случае чистого сдвига утолщение или
утоньшение стенки не происходит, и потому еср = 0, т. е. v.= р = 0;
4) при простом сжатии в одном направлении
emi — еОр —2^ — е2, ^та —* emt еСр,
и потому у = р = 1; 5) при равномерном двустороннем сжатии
у = р = — 1. Таким образом, в опытах при простой деформации усло-
вие 41 = v подлежит проверке только для р, не равных 1,0 и — 1.
Все эти значения могут быть достигнуты при испытании труб без
кручения, и потому опыты на совместное действие растяжения и внут-
реннего давления при простом нагружении являются исчерпывающими.
В самом деле, полагая
Х~ — °i > О, Y == з2 > О, Z, — а3 = О,
мы имеем из (1.115):
P = 2^-l, (1.123)
и потому при простом растяжении (р—0, с2 = 0) имеем р=—1;
при условии а1 = 2о2, т. е. при /5=4л7?2р имеем, р = 0 и, наконец,
при равномерном двустороннем растяжении, т. е. при Oj = а2 или
при Р = 2тг/?2р имеем р = 1.
Опыты с простым нагружением математически можно определить
условием, что в каждом отдельном испытании направляющий тензор
I
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 65
напряжений остаётся неизменным, т. е. что все внешние силы (по-
скольку напряжённое состояние является однородным) в каждом испы-
тании возрастают, пропорционально одному параметру А:
Р = кР, р = Хр, Af==AM, (1.124)
причём величины Р, р, М меняются только при переходе от одного
испытания к другому. При этом и все напряжения оказываются про-
порциональными А, в том числе и октаэдрическое напряжение ~{ = A zit
ибо т{ будет функцией только Р, р, М. Отметим следующее свойство
таких опытов: если v = p. при всех значениях Р, р, М, а октаэдри-
ческое напряжение есть функция только октаэдрической деформа-
ции 7/, т. е.:
т< = Ф(ъ),
то зависимости aj от eY и а2 от е2 отличаются между собой и от
т4 = Ф(7<) только масштабом, характерным для каждого опыта.
В самом деле, из (1.123) и при р == v имеем:
1 п ч 2р.
'3»=2- 0 +н)°Р e2 = J^el>
а потому, согласно (1.111) и (1.119), получаем:
^ = 11/2(3 + ^)^, 7f = ^L-/2(3 + v«)q. (1.125)
Так как т{, отличаются от ег только масштабом, то указанное
свойство становится очевидным.
Если материал трубы в результате деформации при одном испы-
тании получает упрочнение, т. е. становится анизотропным, как это
следует из эффекта Баушингера, второе испытание трубы при новом
значении р, вообще говоря, будет находиться в противоречии с пер-
вым. Поэтому, если необходимо проводить весь цикл испытаний
с одной и той же трубой, то её каждый раз следует путём термо-
обработки приводить в одинаковое начальное состояние. Только тогда
результаты различных испытаний будут сопоставимы.
Вторая группа испытаний может быть названа испытаниями при
сложном нагружении и характеризуется тем, что число р и угол <р
изменяются в процессе опыта с одной и той же трубой. Например,
можно себе представить частично простые испытания, состоящие в том,
что число р оставляют постоянным в течение части общего времени
испытания Af (р = р') и находят соответствующие деформации Aej,
А^2, а число у' и угол ф' находят по формулам:
у' =----tg2(?, =.
2А е + А е А е — А е
Ша * vp vZzvv Му
5 Зак. 3138. А. А. Ильюпшк
66 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧВСКИХ ДЕФОРМАЦИЙ [ГЛ. t
Затем нагрузку полностью снимают и, проводя следующее частичное
Испытание в течение времени Д% сохраняют постоянным другое
число у." и находят добавочные деформации Aei, Де2, а также число v"
и угол-ф" и т. д. Таким образом, за каждый промежуток времени Д/W,
сохраняя постоянным находят прирост деформаций Д Д4П)
и соответствующие угол ф(га) и число vW:
ЗД /п) Д е(п)
V(n) =____---------- fa 2<!А) =_______________
2Д + д 4») ’ Ig д е(п) __ Д е(п)
Шс1 1 bp tCUz уу
Затем сравнивают между собой углы ®W и ф(п) и числа и vW.
Если <р(?1) = ф(п), значит совпадают между собой главные оси тензора
напряжений и тензора скоростей деформации. Если, кроме того,
р,(п) _ v(n)> значит направляющий тензор напряжений совпадает
с направляющим тензором скоростей деформаций, т. е. девиаторы их
подобны.
В обеих группах опытов производится разгрузка трубы, причём
в первой один раз, во второй многократно. Если разгрузку произ-
водить пропорциональным снятием всех сил, т. е. так, чтобы число у.
и угол оставались постоянными и равными их значениям в послед-
нем частичном испытании, — можно очень просто проверить законы
разгрузки. Во всех опытах, о которых будет идти речь ниже,
оказывается, что процесс разгрузки подчиняется закону Гука для
деформаций, которые отсчитываются от их значений при полной
разгрузке.
Опыты Надаи-Лоде. Испытанию на совместное действие растя-
гивающей силы Р и внутреннего давления р были подвергнуты
тонкостенные трубы, изготовленные из литого железа (причём для
уничтожения анизотропии они прокаливались в электропечах при
температуре 950°), медные трубы (прокалка при 500^650°) и одна
никелевая труба (температура прокалки 920°). Размерь? железных
труб таковы: h = 1 мм, 2г ~ 26 мм, длина 300 мм, измеряемая
длина 150 мм. Опыты велись методом частичных испытаний и имели
целью сравнить условие пластичности Мизеса с условием пластичности
Кулона-Сен-Венана, а также найти соотношение между числами у
и v, так как, по условию опыта, главные оси их совпадали. Опыт
с каждой трубой содержал 10—20 частичных испытаний, причём
частичные испытания сопровождались удлинениями по оси трубы
от 0,2 до 0,6%. Предел текучести ая для каждого частичного
испытания определялся следующим образом: через определённое
число частичных испытаний, отличных от простого растяжения,
производилось частичное испытание на простое растяжение, при
котором [J. = — 1, таким образом в опыте с каждой трубой последних
было несколько; далее строилась кривая зависимости 2тти = р1 — а3
от удлинения по оси трубы еи которое представляет сумму пред-
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 6?
шествующих частичных значений Де^ (рис. 26), причём точки, соот-
ветствующие простому растяжению (у = — 1), соединялись плавной
кривой (пунктир). Так как кривые частичных испытаний не совпадали
с этой кривой, то значение Oj—а3 = а0, соответствующее пределу
текучести, определялось как точка на кривой частичного испытания,
для которой её наклон равен наклону кривой у =— 1; наконец,
на самой кривой у = — 1 под найденной точкой определялся предел
ния на простое растяжение (у = — 1) пунктирная кривая «невиди-
мому, близко совпадает с кривой напряжение — удлинение непреры-
ваемого испытания на растяжение», и потому её ординаты могут
быть приняты за предел текучести ag. По условию пластичности
Кулона-Сен-Венана
2ттах = <3S,
поэтому частичные испытания должны были совпадать с кривой
предела текучести (т. е. пунктирной кривой). По условию Мизеса,
должно иметь место соотношение:
2 .22
°1--3^2 -J- 02 = ®S-
' 2-t
Таким образом, откладывая по оси ординат величину —2352, а по оси
абсцисс величину у:
у = 2——1,
мы должны получить по условию Кулона-Сен-Венана горизонтальную
прямую
°1 — °з J
а по условию пластичности Мизеса — кривую
°i~ Дз_____2
=s Уз + у2’
к*
68
ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ
[гЛ.
совпадающую при р. = rt 1 с первой и имеющую при р. = 0 максимум
2
р== 1,154. На рис. 27 построены эти зависимости, и помещены
экспериментальные точки . Несмотря на разбросанность
точек, ясно, что условие Мизеса лучше согласуется с опытом.
Следует заметить, что, стремясь к уточнению результатов, авторы
опытов не считали, как это делаем мы для большей ясности изло-
Рис, 27.
жения, что третье главное напряжение а3 равно нулю, а принимали
-1
для него среднее значение а3 = -у р; но эта величина составляет
D
только около 2°/0 от а2 — Р •у > и так как °i > °2» то влияние её
на результаты, безусловно, было за пределом точности опытов.
Величина у при частичных испытаниях определялась согласно (1.126):
ЗДеС”>
у(») = ---------7—
Результаты сравнения величины у. и v даны на рис. 28, причём опыт-
ные данные для всех испытаний даны точками, а жирная прямая
изображает уравнение
li = v.
Таким образом, авторы приходят к выводам, что условие пластич-
ности Мизеса хорошо согласуется с опытом и имеет явное преиму-
щество перед условием постоянства максимального касательного
напряжения и что скорости сдвигов пропорциональны соответствую-
щим касательным напряжениям.
По поводу опытов Надаи-Лоде заметим следующее: они являются
первым обстоятельным экспериментальным исследованием законов
пластичности при сложном напряжённом состоянии и позволяют
считать, что выводы авторов оправдываются удовлетворительно.
Однако разброс точек на рис. 27 и 28 свидетельствует о недостаточ-
§ 81
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ
69
ной их точности. Если считать, что в измерениях деформаций не име-
лось заметных погрешностей, причины такого разброса можно усмотреть
в следующем: как видно из рис. 27, материалы труб обладали
заметным упрочнением, и потому при последующих частичных испы-
таниях анизотропия всё время менялась. Пунктирная кривая, вероятно,
заметно отличается от диаграммы непрерывного растяжения образца,
которую авторы не строили. Доказательством этому является большой
разброс опытных точек на рис. 28 при у. = — 1, т. е. при частичных
испытаниях на простое
растяжение, включаемых
после других частичных
испытаний. Если бы ани-
зотропия здесь не сказы-
валась, совпадение ц и v
при р.== — 1 было бы не-
пременным.
Опыты Роша и Эй-
хингера. Тонкостенные
трубы из литой стали бы-
ли подвергнуты испы-
таниям • на растяжение,
сжатие и кручение, а так-
же на совместное дейст-
вие всех этих нагрузок,
причём от начала до кон-
ца каждого опыта с опре-
делённой трубой авторы
сохраняли постоянными
главные оси напряжений.
Таким образом, условие
совпадения осей напряже-
ний и деформаций ® = Ф
Рис. 28.
выполнялось автоматически. Цель их работы состояла в установлении
закона упрочнения при сложном напряжённом состоянии. В каче-
стве определяющих величин ими были приняты октаэдрическое напря-
жение и октаэдрический сдвиг ft. В результате исследования ими
был формулирован следующий закон: октаэдрическое напряжение
х{ является вполне определённой для каждого материала функцией
октаэдрического сдвига ft независимо от характера сложности напря-
жённого состояния, если только последнее от начала до конца опыта
изменяется подобным образом:
Ч = Ф (Т»)-
Опыты Тэйлора и Квинн. Основная задача этих опытов состояла
в проверке опытов Надаи-Лоде и, кроме того, в установлении
взаимной ориентации главных осей напряжений и деформаций (точнее
70 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
скоростей деформаций); последняя, вследствие симметрии в опытах
Надаи-Лоде, не могла быть ими установлена. Испытанию на совмест-
ное осевое растяжение и кручение были подвергнуты медные трубы
(медь высокой проводимости с содержанием не более 0,2°/о примесей),
которое подвергались 36-часовому отжигу при 650°С, отожжённые
алюминиевые трубы (с содержанием 99,7 — 99,8°/0 алюминия) и трубы
из мягкой стали (отожжённые в пустоте при 920° С). Длина труб
11,5 дюйма, наружный диаметр—0,25
л и толи*ина стенки 0,036 дюйма. Изме-
рение деформаций труб при прило-
E=ai жении нагрузок производилось очень
точно, а именно, осевое относитель-
ное удлинение измерялось теле-
скопом, радиальная ^ = «3 и тан-
генциальная еуу деформации путём изме-
рения внутреннего объёма труб, ко-
торые наполнялись водой, вытесняемой
через капиллярную трубку; малейшие
изменения объёма давали значитель-
3 S ное перемещение мениска в капилляре.
^з****^^' Угол закручивания (следовательно, иде-
I формация сдвига еху) измерялся угло-
I 7 А мерой. Схема установки изображена на
о - рис. 2®’
Испытания Тэйлора и Квини, также
1|/у* являясь частичными, отличались тем,
что в каждом частичном испытании от-
1 ношение осевой нагрузки Р к крутящему
моменту М не было постоянным. Ис-
- в пытания состояли в следующем: труба
ставилась на прибор, и к ней прикла-
Рис. 29. дывалаеь только одна осевая сила Ро,
которая вытягивала трубу за предел
упругости; затем производилась неполная разгрузка до значения
силы Р = тР0, где т < 1. На диаграмме сила — удлинение разгрузка
шла по прямолинейному ’ закону, и потому значение осевого напря-
жения, соответствующее силе Ро, являлось пределом текучести ag
данного частичного испытания: ss~Pq!F. Затем, сохраняя силу
р = тР0 постоянной, т. е. постоянным и напряжение Xx = PIF,
прикладывали постепенно возрастающий крутящий момент М, т. е.
касательное напряжение Xy — M/PF, причём напряжения в трубе
вновь выходили за предел упругости. Удлинение ехх и угол закручи-
вания возрастали, и можно было построить графики .момент — удли-
нение и момент—угол закручивания. Так как переход за предел
упругости при этом не являлся столь же резким, как при разгрузке,
то значение 7И = Ms, соответствующее переходу трубы в пласти-
§ 8]
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ
71
ческое состояние, бралось условно: график момент — удлинение
продолжался назад до значения удлинения, с которого началось
приложение момента (пунктиры на рис. 30). Таким образом, по силе
р = тР0 находится соответствующий момент Ма а, следовательно,
и напряжение Ху, причём комбинация этих напряжений Хх, ^ соот-
ветствует пределу текучести og == Pq/F. В каждом таком испытании
измеряются удлинение еха) = дг/г, угол закручивания со и изменение
внутреннего объёма трубы, причём за начало отсчёта их берётся
тот момент времени, в который к трубе прикладывается постепенно
возрастающий крутящий момент. На этом первое частичное испыта-
ние заканчивается, и нагрузки полностью снимаются. Каждое следую-
щее частичное испытание проводится так же, как и первое, с той
только разницей, что число т имело уже другое значение. В резуль-
тате пяти-семи таких частичных испытаний каждой трубы получается
пять-семь значений числа т, соответственно каждому из которых
находятся величины cg, P = mPQ и Afg, а следовательно, и напряже-
ния Хх, Ху.
Диаграммы момент — удлинение и угол закручивания — удлинение
для стальных труб • даны на рис. 30 и 31. Величины со и Д/ все-
гда были пропорциональны. Заметим ещё, что материал труб в каж-
дом частном испытании обнаруживал вполне заметное упрочнение.
Обработка результатов опытов производилась следующим образом:
по известным напряжениям Хх, Ху, Yy = 0 находились углы наклона
осей главных напряжений по формуле:
tg2<p=^,
72 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. I
максимальное касательное напряжение >
и величина [i, которая после определения главных напряжений о2
по формулам (1.116) и подстановки их в (1.115) при условии
зОр = а3 = 0 получается равной
(1 == — cos 2о.
Относительное изменение внутреннего объёма трубы при дефор-
мации будет
+ , 2 _ _ 2д
IP XX I / •
Величина f измерялась в каждом частичном испытании с помощью
капиллярной трубки. Поскольку
ехх \уу Н- ezz = 0>
то, как следствие,
— _ 1 f _ £
&хх &хх> ^zz <^^х ъ jt ^уу — 2 йа!® ~Г /’
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 73
и потому наклоны главных осей деформаций определяются из усло-
вия (1.117):
Подсчитывая главные деформации (1.118), находим затем по фор-
муле (1.120) величину v (при еор=ег):
По условию пластичности Кулона-Сен-Венана должно быть:
2'тах = V X2 4- 4Ху =as,
а по условию Мизеса:
Так как в каждом частичном испытании
то по первому должно быть:
(ху\2 _ 1 — т2
“ 4 ’
а по второму —
/Х?\з _ 1 — та
~ 3 ‘
На рис. 32 в качестве примера приведены/ эллипсы, соответствую-
щие этим уравнениям для меди, причём ясно видно преимущество
условия пластичности Мизеса. Сравнение вычисленных углов <р и
показало, что разница их не превосходит 2° и в среднем имеет
значение rt 0,64°, вследствие чего можно считать, Мто направления
главных осей напряжений и скоростей деформаций совпадают:
? = '{'•
Сравнение величин р. и v, необходимое для проверки условия
подобия направляющих гиперболоидов напряжений и скоростей
деформаций, дано на рис. 33. На этом графике помещены также
точки, соответствующие испытаниям стеклянных трубок при сложном
напряжённом состоянии и повышенной температуре- Анализируя
этот график, автор считает, что зависимость
74 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. I
хорошо согласуется с данными опытами для материалов, подобных
стеклу, которое ведёт себя как очень вязкая жидкость; для метал-
Рис. 32.
По поводу опытов Тэйлора и Квинн заметим следующее: мате-
риалы труб обладали довольно заметным упрочнением, в пределах
одного частичного испытания дающим увеличение момента на 10—20°/0,
вследствие чего неизбежно должна была возникать анизотропия и
сказываться эффект Баушингера. Поскольку в процессе опытов наи-
более сильно наклёпывались именно стальные трубы, как это явст-
вует из графиков, данных в их работе (по типу рис. 30), для этих
труб следует ожидать наибольшие отклонения экспериментальных
§8]
ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ
75
данных от условия пластичности Мизеса и от равенств <р = ф и
как это и есть на самом деле.
Опыты Шмидта. Вслед за Рошем и Эйхингером Шмидт поста-
вил задачу: исследовать зависимость напряжений от деформаций для
материалов, обладающих упрочнением. Тонкостенные трубы из литого
железа, а также медные, подвергались испытанию на совместное
действие растягивающей силы Р и крутящего момента М, а также
и на раздельное их действие. Часть опытов была проведена по ме-
тоду простого нагружения, т. е. сила и момент увеличивались про-
порционально, и потому от начала до конца каждого опыта отноше-
X я
ние оставалось постоянным. При этом оказалось, что для любого
ху
значения этого отношения зависимость октаэдрического напряжения
it от октаэдрической' деформации отмеченная Рошем и Эйхинге-
ром, имеет место, и отклонения экспериментальных точек от ней
составляют не более 3—5°/0 для железа и значительно меньше для
меди. Предположение, что упрочнение металла при всяком сложном
напряжённом состоянии может быть характеризовано одной и той же
зависимостью ттах от утах, имеет уже меньшую точность, и отклонения
экспериментальных точек могут быть порядка 7% и более. Другая
часть опытов проведена так, что условие пропорциональности Р и М
в каждом отдельном опыте не соблюдалось: прикладывались сила и
момент поочерёдно, причём каждый раз производилась разгрузка.
Таким образом, главные оси напряжений поочерёдно менялись на
максимальную величину 45°. Кроме того, произведены были опыты
на растяжение железной полосы, из которой затем вырезался обра-
зец в поперечном направлении и вновь подвергался растяжению. Все
опыты с попеременным нагружением показали, что прежняя зави-
симость xt от -fa уже не имеет места, что вполне естественно, если
принять во внимание эффект Баушингера.
Опыты Дэвиса (1943—1945 гг.). Испытанию на совместное дей-
ствие осевого растяжения и внутреннего давления подвергались мед-
ные и стальные тонкостенные трубы, причём последние изготовлялись
из стали со средним содержанием углерода и были нормализованы.
Каждое испытание было простым, т. е. отношение величины растя-
гивающей силы к внутреннему давлению оставалось постоянным и
изменялось от опыта к опыту, так что были охвачены все промежу-
точные состояния от простого растяжения по оси до растяжения
одним лишь внутренним давлением. Каждое испытание доводилось
до разрушения образца. Так как деформации при этом достигали
значительных величин, то при обработке результатов по методу,
указанному выше, вместо относительных деформаций elt е2 брались
истинные относительные деформации, которые, согласно предложе-
нию Генки, определяются формулами:
In (1 4-е,), 1п(1+е8).
76 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
По этим величинам вычисляется *и октаэдрическая деформация у{.
Напряжения также брались истинные, и по ним вычислялось окта-
эдрическое напряжение х{. Аналогично вычислялись максимальное
касательное напряжение ттах и максимальный сдвиг утах. Результаты
испытания медных труб изображены на рис. 34 и 35. Несмотря на
конечность деформаций, отклонение экспериментальных точек от пря-
мой |i = v ие превосходит обычных для малых деформаций преде-
лов Обе возможные зависимости,' отражающие закон упрочнения:
Ф "шах ~~ Ф1 (Ттах)’
достаточно хорошо согласуются с 'опытными данными, причём при
малых деформациях закон упрочнения лучше отражается первой из них,
а при конечных—второй.
На рис. 36 изобра-
жены аналогичные зави-
симости для стали, при-
чём, как и на рис. 35,
левые кривые относятся
к тем образцам, которые
получали кольцевую тре-
щину, а правые — про-
дольную. Сплошные ли-
нии на рис. 35 изобра-
жают опыт на одноосное
растяжение без внутрен-
него давления и та-
ким образом представ-
ляют диаграмму растяже-
ния образца, выражен-
ную связью х{—и
"шах ~ Тпшх- Й3 РИС- 36
видно, что зависимость:
= Ф (Т<)
очень хорошо отражает закон упрочнения при сложном напряжён-
ном состоянии, причём зависимость:
Ттах Ф1 (Ттах)>
которая также может быть принята, уступает первой по точности.
Выводы из опытов на сложное напряжённое состояние. Ана-
лизируя все имеющиеся опыты по изучению сложного напряжённого
состояния, можно установить закономерности, степень точности кото-
рых является вполне определённой и достаточной для тех случаев,
когда нагружение тела при однородном напряжённом состоянии
является простым. Поскольку все опыты с частичными испытаниями
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 77
относятся к процессам сложного нагружения и также имеют некото-
0.0 О,/О 0,20 азо 0,00 О,SO ОБО
Рис. 35.
Частичные испытания показывают, что условие пластичности Ми-
зеса правильно отражает начало текучести; при этом пределом
текучести называется напряжение для той точки диаграммы простого
растяжения, которая соответствует началу разгрузки при сложном
напряжённом состоянии. Этот результат показывает, что закон про-
?8 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСГИЧВСКИХ ДЕФОРМАЦИЙ [гл. t
стого нагружения:
о &оч ш мг м иго о.гч о,гв о,зг ojs о,ю
вляющий гиперболоид напряжений
цессе опыта, и его главные оси
несколько деформируется в про-
меняют свои направления на не-
§ 8] ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ ЗАКОНОВ ПЛАСТИЧНОСТИ 79
большие углы. Сравнение чисел ц и v в частичных испытаниях мате-
риалов, обладающих малым упрочнением, показывает, что равенства
у. = v и (р = <}» приближённо имеют место, т. е. направляющий тен-
зор напряжений приближённо совпадает с направляющим тензором
скоростей деформаций. Как уже указывалось в предыдущем пара-
графе, этот вывод в применении к процессам простого нагружения
означает, что направляющие тензоры напряжений и самих дефор-
маций совпадают, а для процессов, мало отличающихся от простых,
что разница между указанными тензорами будет малой. Равенство
для материалов, обладающих упрочнением, лучше выполняется в опы-
тах при простом нагружении. Так как главные оси напряжений и
скоростей деформаций при сложном нагружении (или главные оси
напряжений и деформаций при простом нагружении) совпадают (в пер-
вом -случае, согласно опытам, во втором для изотропных материалов из
определения простой деформации) и числа р. и v равны при у. = 1 = у,
при y = 0 = v и при у =—l=v, то наибольшее несовпадение
направляющих тензоров соответствует значению у. между 0 и 1 или
между 0 и — 1. Характерным наибольшим отклонением от зависи-
мости u. = v в опытах Дэвиса является точка у =— 0,52; v =— 0,38.
В соответствии с формулами (1.65) мы можем найти главные ком-
поненты направляющего тензора напряжений (Ds):
__ 3 — у ______2р. _________3 -4- у.
1 /2(ЗТР) ’ 2— У 2(3 + у2) ’ /2(3 + у.2)’
и направляющего тензора деформаций (De):
— 3 — у — 2у — 3 4-1
----------------------, Эл------------------ --г-;— — > Э*.. ~
1 /2(3-4-72)-/2(34-72) d /2(3-4-72)
Произведя вычисления этих величин, находим:
/1,37 0 0 \ /1,35 О О
(53) = | 0 —0,406 О ), (5в)=1 0 —0,304 о
\ 0 о —о,97/ \ 0 0 —1,04
и разность этих деваигоров равна
/0,02 0 0 \
(De) —(Ое) = 1 0 —0,102 0 .
\ 0 О 0,07/
Таким образом, большие полуоси направляющих гиперболоидов прак-
тически совпадают, малые же разнятся на величину порядка 7%
80 ОСНОВНЫЙ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. t
размера большой полуоси.. Такое сравнение результатов опытов более
наглядно и более правильно оценивает погрешность гипотезы о совпа-
дении направляющих тензоров напряжений и деформаций, ибо наи-
большая разница между числами у. и v характеризует наибольшее
расхождение между наименьшими по модулю компонентами этих тен-
зоров. Но если последние приближаются к нулю, то каково бы ни
было их отношение, на связь между напряжённым и деформирован-
ным состоянием они не влияют. Именно поэтому ясно, что степень
точности гипотезы о равенстве направляющих тензоров напряжений
и деформаций значительно больше, чем степень точности равенства
[1 = v. Если вторая характеризуется погрешностью максимально в 30%,
то первая — погрешностью порядка не более 7%.
Опыты при сложном напряжённом состоянии, как и при простом
/растяжении или кручении, показывают, что процесс разгрузки тела
подчиняется закону упругости, причём, если процесс нагружения
является простым и сопровождается несколькими простыми разгру-
жениями и нагружениями одного и того же характера (так что отно-
шение между Собой напряжений всё время остаётся одним и тем же),
то зависимость от является одной и той же, характерной для
’ данного материала. Для построения этой зависимости достаточно про-
извести только один опыт, например, на растяжение образца или на
кручение трубы. Если материал считать несжимаемым и пренебрегать
изменением его плотности при деформации, то зависимость между интен-
' сивностью напряжений oi и интенсивностью деформаций et:
V(Хх - YyY + (% -ZJ* + (Z2 - .%)2-]- 6 + r:+zj),
= —j/”еуу) ~\~^еуу exx) “Г "g (,e‘xy 4' eys 4' eax)
в точности совпадает с диаграммой простого растяжения образца,
поскольку при простом растяжении а/ равна растягивающему напря-
жению, a et—относительному удлинению образца.
§ 9. Различные теории пластичности.
Выше приведены результаты лишь таких опытов, из которых можно
। извлечь подтверждения основных законов теории малых упруго-пла-
[стических деформаций или отвергнуть эти законы. Поскольку такая
теория развивается для первоначально квазиизотропных тел и притом
в предположении, что деформация их в любой точке'является простой
или близка к простой, мы не приводили опытов, неудовлетворяющих
этим условиям. Например, мы не рассматривали опытов Гогенемзера
и Прагера (241, в которых трубы сначала выводились за предел упру-
гости путём кручения, а затем при постоянном угле закручивания
к ним прилагалась возрастающая осевая сила и измерялось удлинение;
§ gj Различные теории Пластичности 81
не приводим результатов на поочерёдное растяжение и кручение
Шмидта и т. д. Опыты Гогенемзера и Прагера, по существу, подобны
ойытам Тэйлора и Квинн, но ставят уже новый вопрос о влиянии
предшествующих деформаций на соотношение напряжение — дефор-
мация при сложном нагружении. Такие опыты вообще немногочис-
ленны, они имеют очень большое значение для развития теории пла-
стичности на случай сложного процесса деформирования, но из них
пока ещё нет возможности вывести законы сопротивления тел при
сложном нагружении, не говоря уже об установлении законов упроч-
нения материала.
В настоящее время известно много различных теорий пластичности,
причём в самое последнее время предложены новые теории. Отчасти
они изложены в книге Лейбензона (271. Чтобы понять причины много-
образия теорий пластичности, необходимо уяснить цели, какие они
преследуют. Задача теории упругости, например, совершенно ясна:
по заданным нагрузкам найти деформации (знание которых необхо-
димо инженерам для суждения о пригодности той или иной конструк-
ции в практике), а также найти в теле напряжения для того, чтобы
знать, не возникнут ли в нём нежелательные остаточные деформации
или, в случае хрупких материалов, не произойдёт ли разрушение.
Поскольку нет ничего лучшего, — по упругим напряжениям и различ-
ным эмпирическим фактам инженер судит о возможности усталостных
разрушений и других эффектах, поскольку они тесно связаны с дей-
ствующими упругими напряжениями и имеющимися деформациями.
Задача теории упругости в принципе легко решается благодаря чрез-
вычайной простоте закона Гука.
Посмотрим, каковы же основные задачи теории пластичности. Мы
не будем рассматривать задач пластичности, связанных с изучением
вопросов ползучести, релаксации, последействия, гистерезиса, вязкости
(зависимости сопротивления от скорости), т. е. всех тех, в которых
само время протекания процесса существенно сказывается на механи-
ческих свойствах тела. Эти вопросы выходят за пределы данной книги.
Мы остановимся только на тех теориях пластичности, в которых меха-
нические свойства тел от времени не> зависят.
В таком случае перед теорией пластичности с точки зрения
механики могут стоять две задачи. Первая основная задача ана-
логична задаче теории упругости: по заданным внешним силам стати-
ческого и динамического характера или вынужденным деформациям
некоторых частей тела или по тому и другому найти деформации;
найти остаточные деформации, если нагрузки полностью или частично
сняты; найти изменённые в результате пластической деформации меха-
нические свойства материала тела и установить, каковы будут его
деформации, если приложены вторичные нагрузки; найти нагрузки,
при которых происходит разрушение (трещина) в какой-нибудь части
тела и т. п. Вполне очевидно, что соответствующая теория пластич-
ности должна учитывать основной факт — зависимость напряжений от
6 Зак. 5138. А. А. Илъюшиж-
28 основный законы УпрУго-пластических деформаций [гл. 1
предшествующих деформаций тела, т. е. свойство упрочнения. Такая
теория в простейшем случае может допускать, что деформация тела
является сравнительно малой; . /
Вторая основная задача в некотором смысле аналогична задаче
гидродинамики: по заданному движению абсолютно твёрдого (или де-
формируемого) тела в среде или на поверхности среды, обладающей
пластическими свойствами, найти её сопротивление и распределение
давления по поверхности тела, а также механическое состояние самой
среды. Эта проблема может быть ещё усложнена некоторыми из тре-
бовайий первой основной задачи. В простейшем случае соответствую-
щая теория пластического течения может и не учитывать зависимости
сопротивления среды от предшествующих деформаций и, напротив,
при очень больших давлениях учитывать зависимость его от величины
давления. Но такая теория должна быть верной при конечных дефор-
мациях и потому в некотором смысле быть подобной гидродинамике.
Все основные известные теории пластичности, как отмечал уже
Прагер I24!, и в том числе его теория, основаны на некоторых ланей-
, ных соотношениях между тензорами, полученными путём дифферен-
цирования и интегрирования девиаторов напряжений и деформаций
и кроме того на некоторых скалярных соотношениях между их ин-
вариантами. Вводя параметр X, как это сделано в § 5, и обозначая
через L интегро-дифференциальный оператор согласно (1.70), мы
можем записать основное соотношение:
L(D,)=Z/(De),
х
L (Ds) == A (Da) + В t (D.) + f С (Da) d\ + ..., (1.127)
о
к
L'(De) = A' (De) + В' ± (£)е) + f С (De) Л + ...
6
Если теперь отбрасывать различные слагаемые в (1.127), делать
частные предположения о коэффициентах
А, В, С... А', В', С'...
-ч и добавлять скалярные соотношения, мы будем получать различные
теории пластичности.
Теория Сен-Венана, Леви и Мизеса 12®1 получается, если сохранить
отличными от нуля А и В', которые выбрать так, чтобы A (Ds),
B'^(De) стали направляющими тензорами напряжений и скоростей
деформаций, т. е. положить:
§ Э] Различные теории ПлАстичНоСгй
8$
Кроме того, принимаются условие несжимаемости материала и условие
пластичности Мизеса:
sxx ~f“ 4~ ®гг 0> °< Зв — Const.
(1.128)
В скалярном виде связь между напряжениями и скоростями деформа-
ций получается следующей:
— Ъ, 2ия $ау = Xy = ¥ } 3Ч ЯУ>
Q _ ЧГ ° Syy» 3г,-
С =7 ° «г — 2u8 ° “' Зч®гг’ Згх e Зег г«-
(1.129)
Поскольку эти соотношения означают только равенство направляю-
щих тензоров напряжений и деформаций, ясно, что по заданным
напряжениям они не позволяют найти скоростей и деформаций. \
Теория пластичности Прандтля Рейса получается, если
в (1.127) сохранить только А, В и В', причём положить В'»=1,
о 1
В = 2ОИ
2s3 х * — 2иа ^яя^хя 4“ $УУ~УУ 4“
+ ^ггегг 4" ^^хугху 4" ^yisys 4“ ^^ях9г<У) • (1-130)
гВ скалярной форме равенство (1.127) теперь даёт:
sxx — 2Q д)Х ^^яя~’ 3яУ О ~I~2ASxV>
р______1 д$УУ | 4<? . ------dSys годе
syy — 2G дк ^ УУ’ еУг~~ G дК
e» = 2G ега?—□
(1.131)
Здесь остаются в силе соотношения (1.128). Заметим, что Прандтль
рассматривал плоский случай и условие пластичности брал в несколько
иной форме.
Теория Прагера с точки зрения выбора членов уравнения (1.127)
совпадает с предыдущей, отличаясь лишь выбором коэффициента А,
но сохраняя соотношения (1.128). Ниже мы рассмотрим несколько
другую его теорию.
Теория пластичности Генки - Надаиполучается из (1.127),
если сохранить коэффициенты А и А1, т. е. вместо скоростей дефор-
6*
Й4 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЁСКИХ ДЁФОРМАЦИЙ [гл. I
маций, как у Сен-Венана-Мизеса, взять сами деформации. В скаляр-
ной форь[е основные соотношения примут вид:
с л\ с °3 .
^хх — \гхх — Зе< С^У'
S — — fe ° УУ~ 3ef \еуу е)> Syz = ^-е Зе{ еУ‘' (1.132)
с — (е _ °22 Зе,- Угг So —2— Р
Таким образом имеет место условие пластичности Мизеса, но материал
предполагается сжимаемым упруго в отношении объёма:
а = 3№.
Перечисленные и все другие теории, основанные на условии
пластичности Мизеса:
= const.,
не отвечают некоторым очень важным требованиям первой основной
задачи теории пластичности, поскольку при заданных внешних силах
и найденных, согласно этим теориям, напряжениях деформации
остаются неопределёнными, и никаких свойств упрочнения материала
в них 'не отражено. Таким образом для них остаются лишь те
вопросы,_ при постановке которых оказываются заданными как внеш-
ние силы, так и перемещения на границе области пластичности, что
бывает очень редко.
Представляют интерес и, принципиально говоря, вероятно, могут
быть решены с помощью таких теорий задачи, которые решаются
только в напряжениях 1321. Укажем два типа задач. Первый харак-
терен тем, что здесь всё тело или часть тела, примыкающая к гра-
нице, предполагается перешедшей в пластическое состояние, и напря-
жения в этой части определяются' только теми силами, которые
действуют на соответствующей части внешней границы. В таком
случае ясно* что все теории пластичности для несжимаемого мате-
риала при плоской деформации должны совпадать со статиче-
ской теорией Сен-Венана (или очень мало от неё отличаться), по-
скольку одно только условие пластичности Мизеса делает задачу,
статически определимой и потому характер связи между напряжениями,
и деформациями не играет роли. Такого рода вопросы можно назвать
задачами о несущей способности тела. Они состоят в том, что по
заданному характеру распределения внешних сил, пропорциональных
одному параметру, нужно найти их значение, т. е. величину э£ого па-
раметра, при котором возможно состояние пластического равновесия.
Другой тип задач относится к тем случаям, когда в основном нужно
определить сопротивление упругого тела, если в нём возникают
малые области пластичности. Трудность решения таких задач заста-
вляет пользоваться и даже искать наиболее простую теорию пластич-
РАЗЛИЧНЫЕ ТЕОРИИ ПЛАСТИЧНОСТИ
85
§ 9]
ности, может быть, и не отражающую всех тонкостей игры пласти-
ческих деформаций, но более или менее правильно характеризую-
щую распределение возникающих на границе области пластичности
напряжений. Во многих случаях вполне удовлетворительные резуль-
таты решения подобных задач получаются по методу упругих реше-
ний на основании излагаемой ниже теории малых упруго-пластиче-
ских деформаций. При этом первое или, во всяком случае, второе
приближение оказывается достаточным.
Если обратиться ко второй основной задаче теории пластичности
и исключить случай определения несущей способности, то в ней,
вследствие возникновения в телах конечных деформаций, упругие
деформации типа (по их малости сравнительно с общими
деформациями), видимо, не играют никакой роли. Гораздо большее
значение здесь приобретает объёмная сжимаемость тел, и может быть
зависимость «постоянной» as от величины давления (— а). В таком
случае остаётся пригодной только одна, с нашей точки зрения удо-
влетворительная теория, в основном совпадающая с теорией Сен-Ве-
нана-Мизеса.
Переходя к теориям пластичности, в которых учитывается эффект
упрочнения материала в Цроцессе деформации и которые, следова-
тельно, позволяют по внешним силам определять деформации тела
и потому отвечают полностью требованиям первой основной задачи
теории пластичности, заметим, что их строят также, исходя из
уравнения (1.127), подбирая соответствующим образом коэффициенты.
Однако для случая сложного нагружения тела пока ещё нет доста-
точных оснований считать хотя бы и самую общую из них удовле-
творительной. Трудности экспериментального изучения законов упроч-
нения при сложном процессе нагружения и, в частности, трудности
обобщения эффекта Баушингера, весьма велики, а имеющийся
экспериментальный материал совершенно недостаточен.
Теория Прагера 1331, учитывающая эффект упрочнения при слож-
ном напряжённом состоянии, в основных чертах такова: сохраняют
в (1.127) отличными от нуля коэффициенты А, В и В' и полагают
В = 1, В'= 2G (О— упругий модуль сдвига), и
для случая, когда ^>-0,[или А =0для < 0; в скалярной форме
О А ок
получаются уравнения:
2G8eiBa, = 85a,a,4-g(ai) 8^5^, )
08^ = 85^-}-g-(а,) 8^5^, | (1.133)
...........................• J
86 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
Функция g (а<) должна быть определена экспериментально. К уравне-
ниям (1.133) следует добавить условие несжимаемости
^еах + + ^гг == °>
Для определения функции g воспользуемся диаграммой растяжения
образца (§ 1); в этом случае = ee№ = el = ei'.
n 1 2
з-°1 = з°1-
Уравнения (1.133) дают:
2G8e1 = -| 3^ -j-g- (aj yOjSaj,
и поэтому
3G^1—1 30-^-
X
По диаграмме растяжения величины или X могут быть выражены
через ср и потому функция g (aj = g (aj найдена ВД.
Все изложенные теории пластичности обладают теми или иными
недостатками, на которых мы подробно не останавливаемся. Например,
теория Сен-Венана-Леви-Мизеса построена в предположении, что
направляющий гиперболоид напряжений определяется только мгновен-
ным гиперболоидом скоростей деформаций, т. е. материал как бы
мгновенно забывает предисторию деформаций, что не совсем верно.
Теория Прандтля-Рейса предполагает, что гиперболоид скоростей
деформаций зависит только от двух бесконечно близких (по пара-
метру XI значений девиатора напряжений; это также не совсем верно,
ибо история деформирования сказывается более сильно. Теория
Генки-Надаи предполагает, что деформации в некоторый момент
определяются только мгновенными значениями напряжений, что неверно
хотя бы потому, что напряжения можно изменять скачком, но дефор-
мации должны изменяться непрерывно. Теория упрочнения Прагера
в основном обладает тем же недостатком, что и теория Прандтля-
Рейса, но учитывая эффект упрочнения по простому опыту, не свя-
зана со специальным опытом для учёта эффекта Баушингера.
Для наглядного представления различных теорий' пластичности
в применении к плоскому случаю Прагер l85! предложил интересную
модель. Рассмотрим деформацию тонкостенной трубы, на которой
и делались все фундаментальные опыты, причём предположим, что
внутреннее давление отсутствует. Напряжения и деформации её
§ 9]
РАЗЛИЧНЫЕ ТЕОРИИ ПЛАСТИЧНОСТИ
87
исследованы в § 7. Максимальное касательное напряжение и макси-
мальный сдвиг определяются формулами:
= + 7max = /’+
Рассмотрим плоскость переменных и, v (рис. 37). Деформированное
состояние определяется точкой Е с координатами
3
ив - еху> g" ехх-
Напряжённое состояние будем изображать точкой 5 с координатами
us — ив Q ’ из « 20
Тогда векторы е — ОЕ и S = SE представляют соответственно fmax
причём угол наклон? вектора $ к оси v, определяемый из
, 2°
Формулы
2ф = = “а~~ - = tg у,
Хх ve — va
равен удвоенному углу наклона
оси главного напряжения с осью
трубы, а угол вектора е с той же
осью равен удвоенному углу на-
клона главной оси деформации с
осью трубы 2 ______
Вектор S = SE, с другой сто-
роны, отображает упругую дефор-
мацию трубы:
р(в) *х . (2) Ху
хх — Е > кху-------Q- >
и так как при условии несжимае-
мости Е = 3G, то проекция $ на и
даёт е^у, а проекция его на v
даёт ~ е^х- Теперь очевиднр, что вектор OS изображает остаточную
(или пластическую) деформацию:
№ — е ~L(e _ _®\
ху — сху q > 2 Схх — 2 \хх Е ) '
Итак, с одной стороны, векторы е = ОЕ и S = SE изображают
7т*х и 'max и наклоны главных осей деформаций и напряжений,
а с другой они представляют деформацию, причём е = ОЕ — полная
деформация, SE = $ — упругая деформация, a OS — пластическая или
88 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
остаточная деформация. На рис. 37 отображено такое состояние
тела, когда тензоры полной, остаточной и упругой деформаций не
совпадают по направлению, и потому гиперболоиды напряжений и
деформаций имеют различную ориентацию.
До тех пор пока деформация тела является упругой, вектор OS
равен нулю, т. е. точка S совпадает с О. Как только напряжения
достигают величин, удовлетворяющих условию пластичности, которое
в изображающей диаграмме Прагера удобно взять как условие
постоянства максимального касательного напряжения
= const- = k,
тело выходит за предел упругости. Процесс деформирования изобра-
жается движением точек Е и S, причём как только вектор SE
k с
достигает размера -g-, точка о выходит из начала координат и начи-
нает двигаться вслед за Е, причём расстояние между S и Е остаёт-
ся постоянным. Условия постоянства отрезка SE при движении
точки Е, конечно, недостаточно для определения движения точки S;
необходима ещё, например, связь между углами а и ф.
Отметим, что изображающая диаграмма Прагера является только
качественной. Во-первых, вместо условия пластичности Мизеса
в ней берётся условие Кулона-Сен-Венана; во-вторых, она не вос-
производит полностью тензорного характера напряжений и дефор-
маций. Но она очень наглядна и удобна для изображения некоторых
теорий пластичности.
Для того чтобы ясно представить себе движение точки S по
заданному движению точки Е, вообразим отрезок SE материальным
§ 9]
РАЗЛИЧНЫЕ ТЕОРИИ ПЛАСТИЧНОСТИ
89
н&изгибаемым линейным элементом (стержень—нить), длина которого
может быть или меньше или равна А/G; в первом случае точка 5
совпадёт с точкой О, во втором — точка S может быть на окруж-
ности радиуса /? = kj G, описанном из центра Е. До тех пор, пока
отрезок ОЕ меньше R, имеет место упругая деформация, н одно
только положение точки Е вполне определяет напряжённое и дефор-
мированное состояние тела. Таким образом, если точка Е лежит
внутри круга радиуса R = k/G, описанного из точки О' (рис. 38, а),
деформация тела является упругой, и точка S совпадает с О. Если
же | SE | > R, деформация является упруго-пластической, причём,
в зависимости от того, какова теория пластичности, точка S может
занимать различное положение на окружности радиуса R описанной
около Е. Если точка Е движется по некоторой кривой ЛЕВ, т. е.
деформированное состояние тела изменяется, точка 5 также будет
перемещаться, но для её движения имеется всегда одна степень
свободы (положение на соответствующей окружности). Направление
касательной к кривой АЕВ в точке Е характеризует скорость
полной деформации.
Рассмотрим теперь теорию пластичности Сен-Венана-Леви-Мизеса
(рис. 39,а). Согласно этой теории очевидно, что направление
отрезка SE, проекции которого характеризуют напряжения в теле,
всегда должно совпадать с направлением касательной в точке Е
к линии АЕВ, как только SE > R. Поскольку сами деформации
в этой теории остаются неопределёнными, не следует обращать
внимание на длину отрезка OS. Если в некоторый момент времени
направление движения точки Е изменяется скачком, то проекции SE
на оси, т. е. напряжения, изменяются скачком.
Теория Рейса-Прандтля имеет следующую интерпретацию. Пусть
в некоторый момент положение отрезка SE известно, и пусть
точка Е в данный момент переходит в близкую точку Е' по напра-
влению'ЕЕ'. Тогда точка S переходит в S', расположенную на пред-
шествующем направлении отрезка S'E', т. е. на SE (перемещение ЕЕ'
нужно считать бесконечно малым). Это изображено на рис. 39, в. Пре-
90 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
рывному изменению направления движения Е здесь соответствует
непрерывное изменение как наклона SE, так и перемещения S. Если
точка Е движется по кругу, описанному около 5, то OS остаётся
неизменным, т. е. такое деформирование происходит за счёт только
упругих составляющих деформации.
Теория Генки-Надаи имеет следующую интерпретацию: точка 5
всегда расположена на луче ОЕ на расстоянии ES = E’S’ = R,
т. е. главные оси напряжений (или упругих деформаций), остаточ-
ных деформаций и полных деформаций совпадают.
Легко видеть, что если точка Е всё время движется по одному
и тому же лучу, выходящему из начала координат, точка 5 также
движется по этому лучу, какую фы из названных теорий пластич-
ности мы ни приняли. Этот случай относится к простому нагружению.
Нагружение можно назвать близким к простому, если точка Е дви-
жется по кривой, мало отклоняющейся (мало искривлённой) от луча,
соответствующего простому нагружению. Легко видеть, что и в этом
случае все теории пластичности мало отличаются между собой.
На рис. 40 изображён случай деформирования, резко отличаю-
щийся от простого; к трубе сначала приложен только крутящий
момент, и она закручена на некоторый угол, так что достигнут
предел текучести. При этом точка Е по оси абсцисс вышла на окруж-
ность в положение а точка осталась в положении О. После
этого угол закручивания оставлен постоянным, и труба растягивается
силой, приложенной по оси. Точка Е при этом переходит из Е1
в Е2. По теории Сен-Венана точка S при движении Е из Ех в Еа
будет на прямой Е2ЕЪ и потому (рис. 40, а) в трубе касательные
напряжения исчезнут и будут одни только нормальные, так как
проекция SE на ось и равна нулю. Когда точка Е движется по
§ 9] РАЗЛИЧНЫЕ ТЕОРИИ ПЛАСТИЧНОСТИ • 91
прямой EtEs, точка S описывает трактрису (рис. 40, б), если
принять теорию Прандтля-Рейса, и конхоиду (рис. 40, в) согласно
теории Генки-Надаи. Наклон S2Ea к оси v, следовательно, меньше
всего по первой теории (он равен нулю), больше по второй и ещё
больше по третьей. Все три теории утверждают в согласии с опытом,
что касательные напряжения убывают, но по первой оно исчезает
сразу при приложении осевой силы, по второй очень быстро и по
третьей медленнее.
Сравнивая три указанные теории пластичности, Прагер приходит
к выводу, что первая теория даёт совершенно недопустимые резуль-
таты: получается скачок точки 5 при переходе точки Е с прямой ОЕГ
на прямую EtE2, т. е. скачок остаточной деформации. Но правиль-
нее этот дефект отнести к самой диаграмме Прагера, поскольку
в теории Сен-ВФ1ана-Мизеса, как и других, принимающих условие
пластичности (ттах = const. или а{ = const.), пластические и общие
деформации по величине остаются неопределёнными, и только упругие
составляющие деформаций и напряжения определяются вполне. Далее,
ссылаясь на свои опыты, а также на опыты Рейса и Гогенемзера
по кручению с последующим растяжением, Прагер, обрабатывая
результаты опытов на диаграммах а, б, в, рис. 40, приходит к вы-
водам в пользу теории Генки-Мизеса. Впрочем, через два года,
в связи с обсуждением уравнений (1.133), Прагер приходит к про-
тивоположным выводам из чисто теоретических соображений.
Случай простого нагружения, основные особенности которого/
/состоят в том, что направляющий тензор напряжений остаётся посто-*
янным, направляющий гиперболоид напряжений — неподвижным, глав-
ные оси напряжений не меняют своей ориентации относительно*
материальных частиц элемента тела, является исключительным. Если)
не рассматривать явлений ползучести, релаксации и последействия,
все теории пластичности, вытекающие из уравнения (1.127), то-
ждественно совпадают между собой. Это утверждение вытекает из
теоремы, доказанной в § 5: если зависимость девиатора некоторого
тензора от параметра А является простой, т. е. направляющий тен|
зор от него не зависит, то девиатор, получающийся из данного путём
любой линейной операции, имеет тот же самый направляющий тензор,!
и девиаторы относятся как их интенсивности. Совпадение теорий)
пластичности в том случае, когда главные оси деформаций неподвижны, (
уже было проиллюстрировано на диаграмме Прагера. Теперь мы;
поясним его на основе только что приведённой теоремы 1341.
Если направляющий тензор напряжений (Z)g) в некоторой точке
тела не зависит от параметра А (А — время или другая величина,
определяющая последовательные значения напряжений, например,
характерная нагрузка), то из определения fZ)g) имеем:
(D8) = -^(D8) = const.,
92 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. I
т. е. для любой компоненты (£>g) имеем:
£— — Cofist.
Компоненты $т, как и их интенсивность xit зависят от X, т. е.
изменяются с течением' времени, вследствие изменения внешних сил
от момента их приложения до любого рассматриваемого момента.
Пусть Хь Х2, ..., кп . X — промежуточные значения X. Тогда имеем:
(Х2) ___ _Suv (Хга)__ Suv __
^(Xi) т,(Х2) S(X„) — — cuns,‘-
По свойству таких пропорций имеем:.
Suv __aiSuv (X2)4~. . ~\-nnSuv (Xn) -|- aSuv __ ,
Ч al~i (Xj) + (X2) + • • + ^n~-i ('- и) 4* fl"ti ’’
где a1( Oj, ...,an, a — любые величины, могущие зависеть как
от ХИ! так и от X. Выбирая, например, разность соседних значений X
весьма малой и полагая:
fl-j * ” 1Т2 — " ... i — - О, CL -—- — Х^ ' сП,
получаем:
dSuv
Suv dX
di.
Беря отличными от нуля три бесконечно близких значения X, легко
получим аналогичную формулу для вторых производных и т. д.
Полагая, например,
®ra^d(Xm, X) (Хи1 Xm),
и переходя к пределу
Хщ pi ~~ Хиа *= —> 0, п -* со,
получим:
^uv
i
1
J*g (X, Xm) Suv (X,m) d\m
_____________________________
x
J*cl (X, X^j) (Xm) dXwi
X»
§ 9] РАЗЛИЧНЫЕ ТЕОРИИ ПЛАСТИЧНОСТИ 93
Таким образом, вообще для всякой линейной операции L (Suv)
типа (1.127) имеем:
ъ- — 7-Сч)
Величины
quv — L(Suv) (u,v=x,y,z)
представляют собой девиатор (Dq), так как сумма элементов главной
диагонали равна нулю. Их интенсивность будет равна:
—^)2+ • • • 4~6(^-Ь^г + <7га;)-
Но из пропорций
$иу___Quv
Ъ Lbi)
величины qm. можно выразить формулой:
и, поставив их в qit получить:
т. е. ^ = Л(т{). Таким образом, имеем:
(De) = (Dg),
т. е. направляющий гиперболоид левой части (1.127) совпадает
с направляющим гиперболоидом напряжений и, согласно (1.127),
является направляющим гиперболоидом правой части (1.127):
L(Ds') = ^-(Ds) = Ll(De).
Так как компоненты (De) суть: ехх— е=эхх, .. ., еху = эху,
то теперь имеем:
= const,
Pi 4i
§4 ОСНОВНЫЕ ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ (гЛ. I
\
где
Pi = I VW (^) - L' (^Я2 + .. . + 6 {[£' (^)12 + ...}.
Обозначим через L' линейную операцию, обратную Л', т. е. позво-
ляющую по данной L' (эмв) найти эИ1):
Тогда по свойству пропорций:
Яиу L (Зир) (^ № (&иг>)] __ 3uv _______const
<li Pi L'tPi)
находим:
L' (з ) — э ,
X 4417/ livi г / \ '
L'(Pi)
а, вычисляя получим:
или
Г (р{) »== ^ =« J
Таким образом мы получили:
(De) = (Dg),
а, следовательно, получили и:
(Д) = (5в).
ч
Это значит, что направляющие тензоры напряжений и деформаций
тождественно совпадают.
Таким образом, в случае простого нагружения всякая теория
пластичности типа (1.127) приводит к соотношению
11 2
(1.134)
It
§ 9] различные теории пластичности 95
т. е. все известные теории пластичности совпадают между собой.
Все известные опыты, проведённые при условии простого нагруже-
ния и близкие к простому нагружению, подтверждают соотношение
(1.134): главные оси напряжений и деформаций совпадают, и напра-
вляющие тензоры напряжений и деформаций равны между собой.-
Кроме того, имеет место закон упрочнения материала: интенсив-
ность напряжений есть всегда определённая функция интенсивности
деформаций, характерная для данного материала.
Как уже отмечалось, наибольшая неточность теории, основанной
на соотношении (1.134), составляет около 7°/0 и вытекает из срав-
нения величин [1 и V. Эта неточность не может быть ликвидирована,
если оставаться в рамках линейных соотношений между тензорами
напряжений и деформацийг). Поэтому Прагер 1361 предлагает
нелинейное тензорное уравнение:
(De) = Q (Ds) + С3 (Z)s)3 + Сй (Ds)5 + ...,
которое из соображений независимости деформаций от среднего
нормального напряжения и некоторых теорем тензорного анализа
должно иметь вид:
(£>e)=/(S3, S3)h(Sa, Sl)S3(r) + ^(S2, S^)(De)].
Здесь S2, S3 — второй и третий инварианты (Z)g); тензор же (7)
имеет выражение через квадрат (£)g) и единичный тензор:
(T) = (Ds)a-C22(/),
а р и q—однородные полиномы. Теория, основанная на этих урав-
нениях, получается чрезвычайно сложной и является обобщением
теории, основанной на соотношении (1.134). Учитывая малость
ошибки последнего, его можно считать главной частью истинного
закона. Поэтому уточнение результатов с помощью указанных соот-
ношений Прагера возможно после того, как задача пластичности
будет решена, исходя из (1.134). Этими поправками мы заниматься
не будем.
Возникает ещё вопрос: простое нагружение возможно в случае,
если напряжённое состояние в теле является однородным, т. е.
напряжения одинаковы во всех точках тела; но возможно ли оно,
если тело имеет произвольную форму, а поверхностные и объёмные
*) Уравнение (1.127) является линейным тензорным уравнением, хотя
связь между компонентами тензоров, благодаря входящим в него инвариан-
там, является, конечно, нелинейной.
96 основные ЗАКОНЫ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл I
внешние силы, произвольным образом распределены по телу. На
этот вопрос отвечает теорема следующей главы: в каждой точке
произвольного по форме тела деформация будет простой при любом
значении параметра А, если произвольные внешние силы от начала
их приложения возрастают пропорционально одной из них, которая,
например, и может быть выбрана в качестве параметра X. Тем
самым полностью устанавливается область применения излагаемой
теории пластичности. Поскольку она применима и при состояниях,
близких к простому, круг вопросов, решаемых этой теорией, оказы-
вается очень большим; "г
ГЛАВА II.
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ МАЛЫХ
УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ.
§ 10. Законы активной упруго-пластической деформации
и разгрузки.
Простую деформацию элемента тела в данный момент будем назы-
вать активной в том случае, если интенсивность напряжений имеет
значение, превышающее все предшествующие её значения. Если
меньше хотя бы одного её предшествующего значения, деформацию
элемента называем пассивной. Таким образом в случае активной
деформации элемента тела за пределами упругости пластическая
деформация его возрастает, а в случае пассивной она остаётся по-
стоянной. Активную деформацию будем также называть процессом
нагружения, пассивную иногда — разгрузкой 14.И,
Объёмное напряжение элемента тела подчиняется закону Гука
и является упругим как при активной, так и при пассивной дефор-
мации:
o = ^0 = 3№> ' (2.1)
причём:
• = j
3 j- (2.2)
О == Зе = ехх -{- еуу Ц- е22. j
В случае, если упругой деформацией можно пренебречь, вследствие1
её малости сравнительно с ехх или по каким-нибудь другим' соображе-
ниям, модуль всестороннего сжатия /< следует положить равным
бесконечности и, так как среднее напряжение а является конечным,
вместо (2.1) будем иметь:
6 = Зе = ехх -ф- еуу -|- ею = 0. (2.1')
Направляющие тензоры напряжений и деформаций совпадают:
» и
8ак. МЭ8. ▲. ▲. Едькмдаи
98 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. II
или, если произвести замену:
i—
Т/==е4 у 2,
получим
(°.)-
В проекциях на оси х, у, z это равенство даёт:
• = 3^- (еуу е)> Yz = еуг>
*7 Z \ ^9
Zz а== 3^(егг — б)> Z®= з^7ег®-
(2.37
(2-3)
Закон равенства направляющих тензоров иначе может быть форму-
лирован так: главные оси напряжений и деформаций совпадают,
и отношения главных касательных напряжений к соответствующим
главным сдвигам для данного элемента тела постоянны:
Ti2 _ тгз __ т31 __ °, С2
Tn Таз Tai Зе( ’ \ /
Так как сумма трёх первых уравнений (2.3) даёт тождество
0 = 0, система (2.3) вместе с уравнением (2.1) представляет пять
уравнений, содержащих шесть деформаций и шесть напряжений.
Шестое уравнение даёт третий закон активной упруго-пластической
деформации. Интенсивность напряжений:
* = ТГ V Й»- ^у)2+( Ky-Zg)®+ (Z-X^Q (J^+ r^+zp (2.4)
для каждого материала является вполне определённой и не зависящей
от характера напряжённого состояния функцией интенсивности дефор-
маций:
(e^-eyv)a+(e.yy-e2z^ (2.5)
Эту функцию мы будем обозначать двояко; либо по (1.83):
°< = Ф(е/), (2.6)
либо, выделяя упругую часть:
ai = 3Ge4[l — <й(е£)1, (2.6')
причём в последнем случае функция <а выражается через Ф согласно
уравнению: z
§ 10] ЗАКОНЫ АКТИВНОЙ УПРУГО-ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ 99
Кривая может быть получена как из опыта на растяжение образца,
так и из опыта на кручение тонкостенной трубы или на чистый сдвиг.
В последнем случае, пользуясь диаграммой кручения, имеем:
т = Ф2(1),
где т — касательное напряжение, 7 — сдвиг. Принимая во внимание,
что в этом случае
Ху=х, Хх—Yy = Zz = Xz—Yz — G
и аналогично
exy=zt> хх~~ еуу = ezz== exz== eyz~®>
И потому
0( = г/з; е, = ^,
кривую a{-et получаем из диаграммы кручения:
а< = /ЗФ2(е</з) = Ф(е<),
т. е. путём увеличения ординат в ]/3 и уменьшения абсцисс в такое
же число раз. В случае опыта на растяжение образца наряду с диа-
граммой растяжения '
а1 = Ф1(е1),
где <з1— осевое напряжение, et— удлинение, необходимо в процессе
опыта определить коэффициент Пуассона ~^- = — ; он будет по-
„ . / 1 А
стоянен при упругой деформации (для стали— = -3), а за пределом
упругости будет возрастать, приближаясь к значению-^ =§-• Таким
образом из опыта на растяжение будет получена также кривая
т = т (ej.
Поскольку в этом опыте
ехх е1> еуу — ezz— т е^-' е<хгУ — e'Us — £гх—
а потому
Из диаграммы растяжения получим:
°. = Ф.[т4”2м,,) г.]=ф<><).
100 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. II
мацию тела можно считать упругой
Поскольку за пределом упругости т 2, то зависимость прибли-
жённо совпадает с диаграммой простого растяжения образца.
Относительно кривой = Ф (е4) будем предполагать, что она
удовлетворяет неравенству
(рис. 41)
3G > > -р > 0.' (2.8)
Функция представляет
собой отношение отрезка
УИТИ' к отрезку АГ'ЛГ. Она
равна нулю, пока деформа-
ция является упругой и удо-
влетворяет следующему не-
равенству, вытекающему из
(2-8):
1 <о -ф- ~ О,
J 1 di’i '
S>°- <2-9>
Отмеченные свойства функ-
ций а{ и и соответствуют
данным опыта и очень важны
для теории пластичности.
Обозначая через <з8 и ея
точку, 'до которой дефор-
(оя . мы будем называть про-
сто пределом текучести и es — деформацией текучести), для функ-
ций (о имеем:
<“ = 0, et<es,
ш ш (*<) >0, ег > е8.
(2.Ю)
В том случае, когда кривую — ф (^) можно заменить ломаной
ОАМВ (рис. 41), величины ag, es будут соответствовать точке пере-
лома, будет постоянна, а для функции в> получим:
u€i
to = 0, ^<cs, )
— \ I (2.11)
= ei>c^' j
причём постоянная к в дальнейшем будет обозначать величину *)
Х=1—.
Зю d£j.
’) Её не следует и в дальнейшем не будет возможности смешивать
с параметром X предыдущей главы, где к означала, например, время.
§ 101
ЗАКОНЫ АКТИВНОЙ УПРУГО-ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
101
В дальнейшем мы часто будем иметь дело с отношением ~ , кото-
рое, согласно (2.6), можно мыслить себе уже выраженным либо
только через et, либо,только через поскольку неравенство (2.8)
гарантирует возможность решения уравнения а{=Ф (ef) относительно е{-
те случаи, когда постоянна, т. е. Материал не обладает упрочне-
нием, будут каждый раз оговариваться особо.
Таким образом, подразумевая, что <з4 уже выражена через еь мы
можем считать, что уравнения (2.1) и (2.3) устанавливают полно-
стью зависимость между напряжениями и деформациями. Для того
чтобы написать йх в форме, аналогичной закону Гука, перенесём
величину <з=ЗКе в правую часть. Тогда получим формулы:
\
X = — е
ЛУ Зе{ ХУ'
(2-12)
Если et < es, то эти соотношения совпадают с обычным законом Гука
в форме Ляме.
Можно выразить также и деформации через напряжения; для этого
заменим е = и разрешим (2.3) относительно деформаций:
Зе* v (Зе; 1 5
р — —* V I Л —- ] а
2зг х \2а< ЗК)
е = —4 X
ху а,- У'
(2.13)
причём следует считать, что - - выражено через Это возможно,
конечно, только в том случае, если материал обладает упрочнением.
Общая деформация элемента тела состоит из упругой и пла-
стической (остаточной). Припишем компонентам упругой деформации
индекс «е», а компонентам пластической — индекс «у?»1)
Г-да/'— еху Т еху >
Д Такое разложение предложено Генки н имеется, например, в работах
Падай (31, Беляева W и др.
102 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. II
Компоненты упругой деформации выражаются через напряжения по
закону Гука:
е
(б) ___ 1 у
ху — Q и'
(2.15)
Здесь v — обычный упругий коэффициент Пуассона и Е — модуль
Юнга. Компоненты пластической деформации найдём как разности
компонентов полной и упругой деформаций:
/*9 _ е _ й,е1 _ Р _____
схх — аХХ схх • • • , Ъху -кху---к&у • • •
Пользуясь формулами (2.13) и (2.15), .имеем:
Но между постоянными _Е, G, v, К существуют соотношения, отме-
ченные в § 6:
__ Е у____ Е
2(1+у) ’ л 3(1— 2у) ’
и потому:
J___J____2^ . 2__ £
Е 9/С~ Е ' 9№ЗО’
Следовательно, формулы для пластических деформаций принимают
вид:
р'Р')— 'iSz< j Гу _J (у I у
где функция <р, аналогичная функции со, имеет выражение:
3Gef —= (а
• 1 — ш
(2.17)
а на рис. 41 представляется отношением отрезков ММ’ к ММ".
§ 10) ЗАКОНЫ АКТИВНОЙ УПРУГО-ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ ЮЗ
Как видно из (2.16), тензор пластических деформаций есть девиатор:
е^ + ^)+4> = 0. (2.18)
Подобно тому, как из деформаций ехх ... еху составляется интен-
сивность деформаций et (2.5), можно составить интенсивность упру-
гих и интенсивность пластических деформаций. Если в формулу
Де) 1^2 /~,е „е \2 , ✓ е L I /Де)» । Де>* । Дв)*\
= -g- (ехх — еуу) -j- (еуу—ezz) . .-{-^(еа^ ~т~еуг 4~егж )
подставить значения деформаций е^... .е(ху. .. согласно (2.15) и при-
нять во внимание (2.4), легко получим:
4e) = £j- (2.19)
ОС*
Аналогично для пластических деформаций будем иметь согласно (2.16):
~3G — 30(1 — ш) 0<I (2-20^
Складывая (2.19) и (2.20) и принимая
во внимание (2.6'), получаем интерес-
ный результат:
et = e^ + e(f\ (2.21).
т. е. сумма интенсивностей упругих и
пластических деформаций равна интен-
сивности полной деформации.
Поскольку интенсивности общих,
упругих и пластических деформаций
обладают такими же аддитивными свой-
ствами, как и сами деформации (2.14),
мы имеем право считать диаграмму at-et
эквивалентной диаграмме растяжения образца (рис. 1) не только при
активной пластической деформации, но и при разгрузке (рис. 42);
если, начиная с некоторого значения а4 в точке /И диаграммы
интенсивность напряжений начинает убывать и принимать значение
то разгрузка следует прямой МО' параллельной первоначаль-
ному прямолинейному участку ОС и
a4 = 3G(7<-^)) = 3G7^.
(2.22)
Чтобы получить все необходимые законы разгрузки, к этому необхо-
димо добавить условие пропорциональности девиаторов напряже-
ний— (£>в) и упругих деформаций (£>«):
(Ов) = ^)(О:) (2.23)
104 УРАВНЕНИЯ ТВОРИ И МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. [I
и закон упругости объёмных деформаций:
7=ЗЛХ
(2.24)
Волной наверху обозначены напряжения и деформации, соответствую-
щие точке 7И в стадии пассивной деформации. Как видим, закон Гука
в стадии разгрузки записывается так же, как при первоначальных
упругих деформациях на участке ОА с той только разницей, что
деформации отсчитываются от нового начала О' и предел пропор-
циональности является повышенным. В дальнейшем для нас будет
более'удобной следующая форма закона Гука при разгрузке, экви-
(валентная указанным выше соотношениям:
= А (0 - 0) + 2G (ехх-7хх),
А$ Ху — G (еХу
(2.25)
Здесь через А и Q обозначены обычные упругие постоянные Ляме,
причём:
A = /<—|g. i (2.26)
о /
Полагая в этих соотношениях
Хх=±...=Х„=...=0, (2.27)
мы можем найти остаточные деформации полностью разгруженного
элемента:
ехх = №, ...,еху = е^ ... (2.28)
§ 11. Работа напряжении и потенциальная энергия;
потенциалы.
Работа напряжений, совершаемая при переходе элемента тела
единичного объёма из недеформйрованного состояния О в деформи-
рованное М определяется, как сумма элементарных работ в проме-
жуточных состояниях:
м
Г= J{ХхЪехх^ Y-^y + Z^ + X^-Y (2.29)
о
Нокажем, что подинтегральное выражение в (2.29) есть полный
дифференциал, т. е., что W зависит только от начального и конеч-
ного состояний. Обозначим подинтегральное выражение через 6'IF и
§ 11J РАБОТА НАПРЯЖЕНИЙ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 105
заменим напряжения Хх .. . через компоненты девиатора напряжений
Хх — Sxx -ф ”, а деформации через компоненты девиатора дефор-
маций:
&хх &хх "Ф ei • • • > ^ху '== %&ху • • • (2.30)
Тогда после перемножения получим:
8'№" = Sxafiэхх -ф...-ф 25га,оэга. -ф з ($эхх-ф Ъэуу -ф 8,9,.,.) -ф'
+ ($хх + Syy ^гг) 8е 4~ 3<з8е.
Множители, стоящие в скобках при а и 8е, равны нулю. Пользуясь
формулами (2.1) и (2.3), мы можем 8'UZ йаписать в виде:
= (Эхх^хх + ЭууЬЭуу + э^>эгг + 25^8.9^ +
-ф 2^28з^2-ф 2^8,9^)-ф а 86. (2.31)
Шестичлен, стоящий в круглых скобках, есть полный дифференциал
функции
т>- (5жж + эуу ~г Эзз + Ъдху -ф 2Эуа -ф 2эг2ж),
3 2
которая, аналогично показанному в § 6, преобразуется в Таким
образом имеем:
8'1Г=<з48^-фо80.
полный
у знака
Поскольку зг = Ф(с{) и а =/С6, то 8 W—действительно
дифференциал, и потому можно написать (опуская штрих
вариации):
W=W (et, в)=\Р(ехх... =
О
г1Г = вЛ'зе, + ^!в_ »8<.га+ ... + »S<.„+...
(2.32)
Следовательно, функция W, представляющая работу внутренних сил,
одновременно является потенциалом напряжений:
dW dW
dW
(2.33)
dW
Потенциальной энергией единичного элемента тела называется та часть
работы W, которая будет возвращена элементом при полной разгрузке.
106 * УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. М
Таким образом, она равна работе напряжений Хх ... на упругих
деформациях ..,, т. е.:
= "2 + • • • + ^уеху +•..)= у °<4е) -|- ~2
причём, так как <з1 = ЗО4е) и а = /С0, она имеет выражение:
+ '2 М>
Необратимая часть работы внутренних сил будет равна:
ч
Wp = W— We - Jа4 det — ^ .
Если разгрузка элемента является неполной, а именно, напряжения
и деформации Хх ..., ехх уменьшаются до значений Хх..., ехх...,
то остающаяся в нём потен-
циальная энергия будет равна:
<Т» = ^+^.<2.35)
Величина
ч
J* <з4 de( = W—а0
о
f представляет собой площадь
диаграммы о4-е4, заключённую
между кривой о4-Ф (ef), оёью
абсцисс и ординатой е(, т. е.
3). Потенциальная энергия формо-
изменения элемента
Гф=Ге—|о0
равна площади треугольника О'ММ" О', а остающаяся энергия формо-
О'ММ"О'.
до прямо-
изменения элемента выражается площадью треугольника
Площадь фигуры OSMO"О, дополняющую OSMM"O
угольника ОО"ММ"О, обозначим W — тогда:
ч Ч
№' — ^<30 = 0^ — I 0{^= fetrfa{.
(2.36)
о о
§11] РАБОТА НАПРЯЖЕНИЙ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 107
Нетрудно видеть, что функция W представляет собой потенциаль-
ную функцию для деформаций, т. е. для неё имеют место формулы
Кастильяно:
е е (237)
хх'~дХх’ хУ~дХу'
Последняя из. формул (2.37) очевидна. Для проверки, остальных
найдём, например, первую:
dW dW dot , 1 v , v .
dXx da( dXx^~e za) + ^ —
3(^-4) , д
Хл 04 v W
после чего, согласно (2.3), имеем -^- = ехх.
и-Х-х
Следует заметить, что полная разгрузка элемента тела теорети-
чески всегда возможна, но она, вообще говоря, не имеет места при
полной разгрузке тела, т. е. при снятии с него всех нагрузок. В нём
получаются остаточные напряжения Хх .. ., Ху . , остающиеся де-
формации ехх . .. , еху ... , отличные от пластических ех2 ... ,
, поэтому оно сохраняет в себе некоторую остающуюся по-
тенциальную энергию. Это обстоятельство нередко забывают при
расчётах.
Полную работу деформаций всего тела обозначим V. Она пред-
ставляет сумму работ всех элементов
ei
у= JJ J = J J + (2.38)
О
причём d~ = dx dy dz — элемент объёма тела, т — его объём, и
интегрирование распространено по первоначальному объёму тела
в предположении, что внешняя форма тела как бы вовсе не измени-
лась. Такое приближение возможно при малых деформациях и обще-
принято в теории упругости. Случаи, когда это допущение является
невозможным, будут оговариваться особо.
Потенциальная энергия тела согласно (2.34) будет
/ J J / <2'39*
а остающаяся потенциальная энергия равна:
=П / f JЛ+2Т? / / ,РЛ- *2Л0>
108 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. II
§ 12. Постановка задачи теории пластичности,
вариационное уравнение и уравнения равновесия.
Пусть дано тело, некоторым образом ориентированное в прямо-
угольной системе координат:
х = х1, у = х2, z = x3.
В некоторый момент времени оно находится под действием за-
данных сил: поверхностных A',, Zv и массовых — X, Y, Z. Ме-
ханические свойства тела определяются его упругими характеристи-
ками, кривой <з(-е{ и законами, изложенными выше. Требуется
найти напряжения и деформации в теле.
Для решения задачи воспользуемся вариационным уравнением
равновесия Лагранжа, причём в случае движения к массовым силам
будем добавлять силы инерции. Пусть
и = их (х, у, z, t\ v = u2 (х, у, z, f), rw — и3 (х, у, г, f) (2.41)
будут компоненты перемещения произвольной точки тела под дей-
ствием заданной системы сил. Виртуальным или возможным переме-
щением будем называть всякую изохронную вариацию 8zzn, совместимую-
со связями, наложенными на тело и его части. Вариации деформаций
и скоростей определяются из формул:
ди
— dU1 •
dt ’
у2 =
du3
dt ’
ди2 .
dt ’
^з =
причём знаки дифференцирования и
лять:
варьирования можно перестав-
5 ди д J
8 з- = з- оа,
дх дх
Пусть функция V, согласно (2.38), выражена через компоненты
деформации ef и 6, а следовательно, через ехх , .. еху. Вариацион-
ный принцип равновесия Лагранжа гласит следующее: вариация работы
внутренних сил при виртуальных перемещениях частиц тела равна
работе внешних сил и сил инерции на вариациях перемещений
’“Ш
8^(^, •
р (Х5и -ф- Ydv -|- Z8w) d~ Ц-
§ -j— Zv0w) ds.
(2.42)
Первый интеграл правой части распространён по объёму, второй — по
поверхности тела. Это уравнение называется вариационным уравне-
нием равновесия. Оно содержит в себе как дифференциальные уравне-
ния равновесия элемента тела в перемещаниях, так и граничные условия.
§ 12] ПОСТАНОВКА ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
109
Преобразуем вариацию ЗИ следующим образом:
8Н7 J - / J7 8-+ +^8-+• • У-
заменяя
_____ди _, ду dW________у
e^~dx’ ' вхУ~ ду~^~ дх д~ех.х~'Аа: "
получим:
( v div . „ oBv . „ dozA . / dbw . <5Bw . 58«A1
+ <Y”777 + Yy ~dy + 77) + [Z*777 + zv~d~y + z* ~d7)\ dx-
Воспользуемся теперь формулами преобразования Грина:
и т. п., где двойной интеграл распространён по поверхности тела и
1, т, п — направляющие косинусы нормали к поверхности. Тогда по-
лучим:
ЗУ== J J № + Хут-± Хгп)Ъи -И- • + (•• -)8w] ds -
- /// [(^ + ^‘+те')8“+<-->+(-)»•]*
Скобки с многоточиями получаются из предыдущих скобок путём
круговой перестановки х, у, z и Z, т, п. Собирая теперь все мно-
жители при вариациях З'гд в уравнении (2.42), получим:
J J7 [(^+^+т&+Н8”+<- -Н
J J К- + Xyi) 8« + (...)3^ +
bw]ds — 0. (2.43)
Вариации перемещения любой точки тела должны быть только не-
прерывны, но они совершенно независимы, и потому равенство (2.43)
возможно только при том условии, если все коэффициенты при
вариациях равны нулю. Таким образом мы получаем уравнения равно-
весия :
дХх , дХу д_Х
дх ду ‘ dz
_ц , ^7
дх 1 ду ‘ dz
dZx i 1
дх Т йу '"di
(2.44)
110 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. II
и граничные условия:
4“ ХгП — Ху,
*V+ = И,
Zxl-\- Zytn -f- Zzn = Z,.
(2.45)
Этих уравнений достаточно для решения задачи пластичности, и их
следует понимать, как уравнения равновесия в перемещениях, поскольку
предполагается, что напряжения выражены через деформации по
формулам (2.33) и, следовательно, на основании формул Коши через
ври компонента перемещения а, г», vo.
Если систему (2.44) рассматривать как уравнения равновесия
в напряжениях, она недостаточна для определения напряжений, и
к ней необходимо добавить ещё условия совместности деформаций,
которые получаются известным в теории упругости образом из фор-
мул Коши (1.38)
&*еХУ _ ^ехХ I д2еуу
дхду ду2 ' дх2 ’
о д~ехх __ д /___I I &еху\
ду dz дх \ дх ду ‘ дг )
(2.46)
причём остальные четыре формулы получаются путём круговой пере-
становки х, у, z. Вместо деформаций в (2.46) должны быть поста-
влены их выражения (2.13) через напряжения, поэтому они приобре-
тают довольно сложный вид:
причём остальные четыре уравнения снова получаются из (2.47) кру-
говой перестановкой х, у, z.
Таким образом можно формулировать три основные постановки
задачи теории пластичности при активном процессе нагружения.
1. Найти три функции: a, v, чо— такие, чтобы для произволь-
ных непрерывных с непрерывными производными вариаций За, 8г», Zw
имело место вариационное уравнение равновесия (2.42). В таком
случае для решения задачи, например, можно применить метод Ритца:
§12] ПОСТАНОВКА задлчи ТЕОРИИ ПЛАСТИЧНОСТИ 111
подбирая для области, занятой телом, полную систему функций
fn (*» .У> г) и представляя перемещения u, v, на рядами
= (2-48>
найдём вариации перемещений в виде:
8г’= 2^»» 8гг,= 2^8с»-
Подсчитывая теперь работу внутренних сил, найдём:
== ^п)
и её вариацию:
ЗУ = У (^-Ъап+Zbn + 8ся ),
^\дап п 1 дЬп п 1 дсп п)'
а сравнивая коэффициенты при вариациях Sa„, Zbn, 8сп левой и
правой частей уравнения (2.42), найдём формулы типа:
ж;=ШрХ'»л+ <2-49>
причём их будет столько, сколько неизвестных ап, Ьп, сп входит
в выражения и, v, w; поэтому, принципиально говоря, они могут
быть найдены, если функция = Ф (^) удовлетворяет некоторым
условиям, о которых уже сказано выше.
2. Найти три функции и, v, w, удовлетворяющие дифференциаль-
ным уравнениям (2.44), выраженным через перемещения, причём эти
функции должны удовлетворять условиям на границе (2.45). Эта за-
дача при произвольных внешних силах может иметь решений только
в тех случаях, если система дифференциальных уравнение (2.44)
будет эллиптического типа. Условия разрешимости системы (2.49)
тождественно совпадают с указанным требованием, поскольку первая
и вторая постановки задачи совпадают межд} собой на основании
преобразований, приведённых выше, и аналогичных обратных пре-
образований системы (2.44) в уравнение (2.42) при соблюдении
условий (2.45). Для решения задач пластичности во второй поста-
новке ниже будет указан общий эффективный метод упругих ре-
шений.
3. Найти шесть компонентов напряжений Хх . .., Ху . .., удовле-
творяющих уравнениям равновесия (2.44) в напряжениях и условиям
Совместности деформаций (2.47), причём на границе тела они должны
удовлетворять условиям (2.45).
Легко убедиться, что поставленная задача имеет единственное
решение. Пусть «„ wlt Хх1, ..., Гг1 и «2, vB, ®2, Х^, два
различных решения системы (2.44) при одинаковых внешних силах
и одинаковых значениях перемещений на границе тела. Обозначим
112 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. II
и, v, w, Хх, . . . , Yg разности соответствующих значений, так что на
границе тела и = v — w = Q, а внутри напряжения Хх ... удовле-
творяют уравнениям (2.44) без массовых сил.
Умножая эти уравнения на и, v, w соответственно, складывая м
интегрируя по объёму тела, получим:
Применяя формулы Грина, получим:
/ = J J J (Лд, ехх + • • • + Л eyz) d-c ~0.
Заменим здесь Хх — XQi — XXi, ... ехх = eXXt — е Xi . .. и затем вос-
пользуемся выражениями напряжений через деформации; получим:
/ Л Л"-+•**-1 (ч+Л/* ** ] *+
+ J J J(°a ——
Но согласно неравенству Шварца И:
S < ]/" Е Е =4
поэтому:
/ [(% — %) О.~ Ч) + (°2 — °1) (>2 — ?i)Idz.
Так как зависимость ог-рг удовлетворяет неравенству (2.8), то
под интегралом при <зи + ci2> 'l Ф =2 будет всегда положительная
величина; но /= 0, и потому эта величина должна равняться4 нулю,
т. е.
= °1 = °2>
откуда и вытекает теорема единственности.
§ 13. Теорема минимума работы внутренних сил.
Пусть тело находится в равновесии под действием только по-
верхностных сил Х„, Pv, Zv, и пусть перемещение любой точки Гела
при этом определяется вектором w
W = iи -j-jv-j-k w.
Компоненты тензора деформаций через этот вектор определяются по
формулам Коши, а компоненты напряжений по формулам (2.12)
^de^-K^ — ^dz.
§13]. ТЕОРЕМА МИНИМУМА РАБОТЫ ВНУТРЕННИХ СИЛ 113
Кинематически возможным состоянием тела назовем состояние,
определяемое вектором w':
w1 = w Ц- 8 w,
причем — виртуальное перемещение, кроме непрерывности обла-
дающее ещё тем свойством, что на границе тела оно обращается
в нуль. Напряжения и деформации, соответствующие кинематически
возможному состоянию тела, определяются через iv' теми же фор-
мулами, что и для основного состояния равновесия.
Теорема минимума работы внутренних сил состоит в следующем:
истинное состояние равновесия тела отличается от всякого кинемати-
чески возможного его состояния тем, что работа внутренних сил
имеет минимум. Для доказательства этого воспользуемся выражением
работы внутренних сил (2.38) в виде:
е.
V(e.fl) = J Ц I’ о4 de.- 1 KW^d-.
s
найдём разность:
*1
ei
Поскольку в — линейная функция перемещений, её можно для кине-
матически возможного состояния записать в виде:
6' = 0-f- gQ,
и потому разность 6'2 — 68 может быть точно вычислена:
6'11—6«= 2086 + 862.
Величина ef, как уже упоминалось, может быть записана в виде:
«,₽ = х,у,г
и, так как
5 aS = 3 Зф
то для возможного состояния равновесия имеем:
= с22 (з«з + 8^«?)а = e2i -f- Зе4 с2^ S
8 Зак. ®L98. А. А. Ильюшин
114 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. 11
причём Зе4— обычная первая вариация е{:
2 Зе4 = 2 с»2' эвЭ 8эа?.
Разлагая теперь интеграл
»
ei
J det
е.
г
в ряд по степеням е'. — eiy получим:
ei
J dei = аДе: — ег) + у g (е. — ^)».
ei
Но поскольку имеем
= Ке* + 2 ^3^ + ^ 8 =
= ^ + 8е* +А 1^28^-(Ч)2]+ • • •>
то предыдущий интеграл будет выражаться формулой
ег
Г , .4,1 Г s сЧ2эаДэа?)2 1 ,
J 9< de^ = 9<f>et + [c2^6 M---------Ц------J + у ^"W2±
»i
+ ... =0(Se<+ 2eiS^t [(SsM(S8l’b)_(Ss-»a’-»)’h +
+ jg(Ma+-.-
Если мы теперь напишем разность V'.— V в виде
У(е'Л) — УСе^б) = 3V4-32V4- ..
то первое Слагаемое будет обозначать обычную первую вариацию
работы внутренних сил
8У = зЛ|1Г</т,
которая при отсутствии массовых сил и при условии на границе
тёла :
Зи = 8tf = 3w = О
обращается в нуль на основании вариационного уравнения равновесия
(2.42). Тем самым цз (2.42) непосредственно вытекает, что в поло-
§14]
Ieopema о Простом нагружении
115
жении равновесия функция V имеет экстремум. Вторая вариация V
имеет выражение:
+~ к (39)а 4-... ] dz.
На основании неравенства Шварца l6! первое слагаемое положительно,
поскольку положительны et и третье слагаемое под интегралом
также положительно, поскольку положительно К', второе слагаемое
будет положительно при условии >0, и потому имеем:
32V>0, £i>0.
’ de(
(2.50)
Таким образом, теорема минимума работы внутренних сил имеет место
для тел, материал которых обладает упрочнением.
§ 14. Теорема о простом нагружении.
В предыдущей главе путём анализа экспериментальных данных
было показано, что основные законы пластичности при активном
процессе деформаций, выражаемые формулами (2.3) и (2.6), имеют
место по крайней мере в том случае, когда деформация элемента
тела является простой или близка к простой. Возникает вопрос,
существуют ли такие нагрузки, прилагаемые к телу произвольной
формы, чтобы от момента их приложения и в течение всего времени
их возрастания до заданных окончательных значений направляющий
тензор напряжений или направляющий гиперболоид напряжений
в любой данной точке тела оставался постоянным, будучи различным
в разных точках тела. Иначе говоря, существует ли для тела сложной
формы и нагрузок данного типа (любого) такой способ их возраста-
ния от нуля до заданных значений, чтобы главные оси напряжений,
различные в разных точках тела, не изменяли своей ориентации
относительно материальных частиц за всё время возрастания нагрузки,
и чтобы отношение между собой главных касательных напряжений
оставалось постоянным .(но, вообще говоря, различным для разных
точек тела).
Если напряжённое состояние тела является однородным, то ответ
на поставленный вопрос очевиден: поскольку напряжения не зависят
от координат тела, то и деформированное состояние, согласно (2.13),
тоже является однородным; дифференциальные уравнения равновесия
и условия совместности деформаций выполняются тождественно,
и массовые силы должны отсутствовать. Таким образом, напряжённое
состояние определяется только граничными условиями, т. е. только
я*
116 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [гл. 11
поверхностными силами. Ясно, следовательно, что деформация тела
будет простой, если все нагрузки возрастают от момента их приложения
пропорционально одному общему параметру, например, пропорциог
I нально одной из нагрузок, и, кроме того, совершенно независимо!,
I может изменяться постоянное внешнее давление. J
Для того чтобы ответ на поставленный вопрос был дан в общем
случае неоднородного напряжённого состояния тела произвольной
формы, необходимо решить следующие задачи. Пусть X есть пара-
метр, определяющий последовательные значения приложенных к телу
внешних сил (например, время), так что внешние силы суть функции
координат точки тела и этого параметра:
Xv = Х.,(к,х,у, г).. ., Х==Х(Х, х,у,г)..., (2.51)
причём пусть при X = О, X.t = У, = Zv — Х~ Y ~ Z — 0. Необходимо
определить: 1) какова должна быть зависимость (2.51) по А для того,
чтобы решение задачи пластичности обладало бы тем свойством, что
в любой точке тела направляющий гиперболоид напряжений не за-
висел от X? 2) если внешние силы пропорциональны А, т. е.
X, = X X* (х,у, г), ... Х= X X* (х, у, г),..., (2.52)
то какова будет зависимость направляющего гиперболоида от пара-
метра X? 3) каковы должны быть свойства зависимостей линейного
инварианта напряжений а и интенсивности напряжений af от соответ-
ствующих инвариантов деформаций е и et, если при условии (2.52)
направляющие тензоры (или гиперболоиды) напряжений во всех точках
тела неподвижны относительно материальных частиц, т. е. не зависят
от параметра X? Общего решения этих задач ещё не дано. Мы укажем
ограниченное решение третьей задачи 181, которое позволяет форму-
лировать следующую теорему о простом нагружении.
Для того чтобы направляющие гиперболоиды напряжений, а следо-
/вательно, и деформаций, были неподвижны во всех точках тела
' произвольной формы при произвольных внешних силах, возрастаю-
f щих по мере их приложения пропорционально общему параметру X
(2.52),—достаточно, чтобы зависимость (2.6) в интересующем
I нас диапазоне деформаций тела могла быть представлена в виде
\ степенной функции:
'i^Ae* «<е.<<), (2.53)
где А и х — произвольные постоянные, и чтобы зависимость а-е
(2.1) была заменена условием несжимаемости материала (2.1).
Доказательство этой теоремы вполне элементарно; предположим,
что для какого-нибудь определённого X, например Х = 1, задача пла-
стичности решена. Это значит, что найдено решение системы диф-
ференциальных уравнений (2.44) при граничных условиях (2.45).
Отметим звёздочкой наверху все величины, определённые этим ре*
§14]
ТЕОРЕМА О ПРОСТОМ НАГРУЖЕНИИ
117
шением: Л*. а* е*. Таким образом имеем тождества:
+'-*=°' ^‘+х>+х'.’'-<• 1»
..............................................I
1 __ 2 ехв *у __£ еХу
* о ♦“ » « о • > \ >
°i 6 ei °i J ei
Здесь в формулах (б) а! и е\ будем считать выраженными через на-
пряжения Х*х,... и деформации е*ж,... соответственно.
Кроме того, имеем соотношения:
О а да* I dv* . dw* _ ,
3е$ = ^- + 1Г + ^=г0’ (в)
< = (г)
Попытаемся найти решение задачи для X,
в виде:
^“^хх" ' ' ’ еху Es ^ху ’
и =1= рИ* . , . , V = pt/* ,
отличного от единицы,
а,. = Ха?,
«i = .
•w = pw*,
(2.54)
где р— пока неопределённая функция одного Л. В таком случае из
уравнений (2.44) и (2.45) по сокращении на X получаем тождества
(а); т. е. уравнения равновесия в напряжениях и граничные условия
удовлетворяются. Аналогичным образом из (2.3) и (2.1) по сокраще-
нии величии X и р получим тождества (б) и (в). Последнее уравне-
ние, которому необходимо удовлетворить, чтобы убедиться, что (2.54)
есть решение задачи пластичности при произвольных силах-.вида (2.52),
есть (2.53); из него имеем:
Ха* =я рх А (е()х-
Это равенство также станет тождеством, если величину р определить
соотношением:
Итак, формулы (2.54) действительно дают решение, и оно обладает
тем свойством, что компоненты направляющего тензора напряжений
V с
• • • ‘-’хг/’ • • •
не зависят от X, а, следовательно, направляющие гиперболоиды на-
пряжений и деформаций в каждой точке тела неподвижны.
Заметим, что возможность представления зависимости а=Ф(е1)
в виде (2.53) есть достаточное, но не необходимое условие непо-
118 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. II
движности направляющих гиперболоидов напряжений в каждой точке
тела. В целом ряде частных случаев, как увидим далее, условия
формулированной выше третьей задачи выполняются при совершенно
произвольном виде функции а* = Ф(е*), если только нагрузки изме-
няются во'времени пропорционально общему параметру X.
Теорема о простом нагружении дает ограниченное решение и пер-
вых двух задач. Таким образом, решение задач пластичности, согласно
уравнениям § 11, для тела произвольной формы при произвольных
внешних силах, удовлетворяющих условию (2.52), будет физическим,
т. е. будет также согласно с опытом, как согласуются с ним основ-
ные законы пластичности при однородном напряженном состоянии
цилиндрических образцов, тонкостенных труб и др., если в интере-
сующем нас диапазоне деформаций закон (2.6) может быть апрокси-
мирован зависимостью (2.53). Легко видеть, что в области пласти-
ческих деформаций формула (2.53) может достаточно хорошо апро-
ксимировать закон а1 = ф(е4) для большинства материалов: прих = 0
она дает условие пластичности Мизеса at = const., при малых х даёт
кривые с малым упрочнением и при х = 1 — закон Гука.
В связи с тем, что выше были указаны только достаточные усло-
вия неподвижности направляющих гиперболоидов во всех точках тела,
находящихся в области пластических деформаций; что опыты, описан-
ные в гл. I, подтверждают основные законы пластичности (2.1) и
(2.3) также по крайней мере в тех случаях, когда при больших
изменениях X направляющий тензор напряжений изменяется мало; что
в области пластичности формула (2.53) с достаточной степенью точ-
ности апроксимирует опытные кривые cj-ei для многих материалов;
что в области упругих деформаций закон Гука имеет место незави-
симо от того, подвижен или неподвижен направляющий гипербо-
лоид напряжений; наконец, что решения большого числа частных
задач пластичности при произвольной зависимости at-et дают либо
независимость, либо слабую зависимость направляющего тензора
напряжений от параметра Xj— в связи со всем этим можно высказать
следующий постулат: теория малых упруго-пластических деформа-
ций даёт правильные (согласные с опытом) результаты по край-
ней мере в том случае, когда процесс нагружения тела является
простым, т. е. внешние силы от начала их приложения возра-
стают пропорционально общему параметру.
§ 15. Теорема о разгрузке.
Пусть для некоторого тела, находящегося при некотором значе-
нии параметра X под действием заданной системы сил X..., Xv...,
задача пластичности решена, т. е. напряжения Хх,..., деформации
ежа.... и перемещения a, v, w найдены во всех точках тела. Рас-
смотрим процесс разгрузку тела. Разгрузка элемента тела, под-
§15)
ТЕОРЕМА О РАЗГРУЗКЕ
119
чиняющаяся закону Гука (2.22), наступает с того момента, когда
интенсивность напряжений ai начинает убывать. Разгрузкой всего
тела будем называть процесс изменения внешних сил, при котором
во всех областях тела, где имела место пластическая деформация,
интенсивность напряжений начинает убывать одновременно.
Таким образом разгрузка тела характеризуется тем, что тело из
стадии активной деформации переходит в стадию пассивной деформа-
ции. Отметим волной наверху все величины, которые относятся к раз-
грузке; тогда при Х = Х имеем:
Хх == > ^хх =s хх * • •
Разгружение, подобно нагружению тела, можно назвать простым,
если внешние силы в стадии пассивной деформации тела удовлетво-
ряют соотношениям (2.52); в таком случае состоянием разгрузки можно
назвать такое, при котором X < X. Отсюда, кстати говоря, видно,
что параметр X, являющийся всегда функцией времени t, не обязательно
есть время, поскольку он может и убывать, но только в стадии
пассивной деформации тела.
Для разгрузки уравнения равновесия (2.44) принимают вид:
дХх . дХ„ , дХ, .
дх ‘ ду Т- дг '
рХ—О,
(2.56)
а граничные условия (2.45) переписываются в форме:
AJ, —J- ХуТк —Ху = Хч, 1
(2.57)
Вычитая теперь из уравнений (2.44) соответствующие уравнения
(2.56) и пользуясь законом Гука (2.22), получим уравнения Ляме:
(А+О)-^-(9 —0)4-2GV8 («—«) +р(А—А) — О,
(A4-G)-^(0-6)4-2GV2(®-«) + p(K-r) = O, (2.58)
(А 4- G)~ (0— Jj-[-2Gv2 (w-w) + p(Z-Z) = 0.
Аналогично из (2.45) и (2.57) получим граничные условия:
(Хх - Хх)1 + {Ху — Ху) т + (Хг-Х,)п = Х,-Х„ |
(Г.-У4Ч4- (K2/-yy)m_|_(ri-Q«=rv-y;, j (2.59)
(Z^ — ZJ I + {Zy — Zy) tn + (Z, — Z2) n = Zv — Z,, |
120 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ [ГЛ. II
причём в последних уравнениях нужно считать, что разности напря-
жений, входящих в левые части, выражены через разности перемеще-
ний, согласно (2.22). Уравнения (2.58) с граничными условиями (2.59)
имеют единственное решение, которое может быть найдено по мето-
дам теории упругости:
и—u — ul, v — 1»?=^!, w—№ = ©,,
~ _ dut ~ _ дих ; дих
ехх — дх • • еху — еху — 77 “Г 77 > • • • (2 60)
= Хх — Хх = /Л 4- 2Gexxl,...
Xyl Ху Ху ^^xyl > • ’ •
Таким образом доказана следующая теорема о разгрузке: перемеще-
ния точки тела в некоторый момент стадии разгрузки отличаются
от их значений в момент начала разгрузки на величины упругих
перемещений, которые возникали бы в теле, если бы в естественном
(ненапряжённом и недеформированном) состоянии к нему были при-
ложены внешние силы, равные разностям внешних сил, действующих
на тело в указанные моменты. То же относится к деформациям и
напряжениям. Отсюда, как следствие, имеем теорему об остающихся
в теле напряжениях, деформациях н перемещениях при полном снятии
всех внешних сил: если для тела решена задача пластичности и
заданным значениям внешних сил X,.. ., Х„. . . соответствует истин-
ное состояние равновесия (S) и если, кроме того, для тела решена
задача теории упругости, т. е. тем же внешним силам .соответствует
фиктивное состояние упругого равновесия (SJ, то в результате
полной разгрузки тела в нём остаются перемещения, деформации и
напряжения, равные разностям их значений в истинном и фиктивном
состояниях. При этом, конечно, предполагается, что остающиеся
напряжения в результате разгрузки вторично не выходят за предел
упругости.
Поясним указанные теоремы примером. Пусть толстостенная
труба находится под действием внутреннего давления р. Упругие
напряжения и деформации её определяются известными формулами
Ляме. Предположим, что давление р столь велико, что материал
трубы частично или полностью выходит за предел упругости. При-
меняя формулы Ляме, мы найдём фиктивные деформации и напряже-
ния в трубе. Истинные напряжения и деформации можно найти
путём применения уравнений пластичности, считая при этом, что
процесс нагружения трубы является простым, поскольку все внеш-
ние силы сводятся только к давлению р, которое и можно выбрать
в качестве параметра X. Если теперь давление р снято полностью,
в трубе останутся напряжения, равные разности напряжений истин-
ного и фиктивного состояний; так же могут быть подсчитаны и
остаточные деформации (гл. III, § 20).
§ 16] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ В ПЕРЕМЕЩЕНИЯХ 121
§ 16. Дифференциальные уравнения равновесия
в перемещениях и метод упругих решений.
Выражения напряжений через деформации, а, следовательно, и
перемещения даны формулами (2.12). Прибавляя к ним и вычитая
из них соответственные величины тензора (S') фиктивных упругих
напряжений:
х;=де+20^, х; = ор.^, (2.бп
где А — упругая постоянная Ляме:
2
А == К- - G,
О
мы после несложных преобразований на основании формулы (2.6)
получим:
*х =• — 20ш У хх — <0>
Xv = Х'и ~
(2.62)
или, короче:
(S) = (S') — 2Gco (DeY (2.62')
Ради краткости письма мы применим для перемещений и, v, vo
обозначения й2, и8 и для координат х, у, z обозначения xt, ха, х3.
В таком случае компоненты деформаций ; удобно обозначить
э12. .., причём:
—е.... -9.0 = -•—!-4--з-i....
11 dxt ’ 13 2 1 дху ’
9 = -^ 4- । диз
(2.63)
Интенсивность деформаций е* определяется формулой:
« 3 'яп
ni,n = \, 2, 3
(2.64)
Дивергенцией тензора (S) называется вектор, компоненты которого
по осям х, у, z представляют дивергенции векторов напряжений на
соответствующих основных площадках (§ 2):
div (S) = i div Sx -\-j div Sy -j- k div Ss.
Пользуясь этим определением, мы можем написать уравнения равно-
весия (2.44) в виде:
div(S)-(-pF=O. (2.65)
122 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ (ГЛ. II
Тензор (S'), компоненты которого определяются законом Гука,
удовлетворяет тождеству:
div (S') s= (Д G)grad 6 -f- Gv3w, 1 66)
причём grad обозначена векторная операция:
, . д - . д . . д >
grad^—+j —
Согласно (2.62') уравнение равновесия (2.65) принимает следующий
вид:
div (S') - 2 G« div (De) — 2 G grad ® (De) + pF = 0,
причём по аналогии c (2.66) имеем:
2Gdiv(De)= — у G-f-О ) grad 6-J-GV3®-
Нам остаётся подсчитать вектор grad <о (De), представляющий скаляр-
ное произведение вектора grad а> на тензор (De). Поскольку
i °*
о>= 1 —57Л-,
3G<?$
то grad ш можно переписать в виде:
grad а> = —1— №. — grad е'
6Ge{ \е$ de^
Деля теперь уравнение равновесия на G и замечая, что
A -f- G_____т
G т — 2 ’
где т — число Пуассона, получаем:
f--------—grad 6-[-(1 —а>) V3® —
\п — 2 3 '
~Ч7^(”~?-)&Гас1еИОе)+^'=0. (2.67)
3Gei \е( dei/ ’ G
Это и есть векторная форма уравнений равновесия, выраженных
через компоненты перемещения и15 п2> “з- В проекции на ось
як(А=1, 2, 3), согласно (2.63) и (2.64), получим:
/ т ш \ <Э0 , . _<>
"А—
3
^7—-+^ = °. (268>
9G^ dej 3 дхтдхп G
3).
§16] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ В ПЕРЕМЕЩЕНИЯХ 123
Если вместо эт11 ввести компоненты направляющего тензора дефор-
мации (De):
» __^этп ____этп^2
’’ап >
It
а <з< выразить через о>, то уравнения принимают вид:
(----п---5- ) 3---Г (1 ®) —
\т — 2 3) дхк 14 / к
з
—4^4^ У эпт У -~s-%— -ь -?Д == о, (2.69)
3 1 det jU Кт 1,1 дхтдхп 1 G ’ 1 7
И,П=1|2,3 1—1
причём величины этп удовлетворяют соотношениям:
з
23,nni = ®’ S5*»n = 3> (2.70)
m = l т, п = 1, 2, з
а <о и т неравенствам:
1 >• со ei ш 0, оо>»1>2. (2.71)
Условие (2.71) при тождествах (2.70) достаточно и необходимо для
того, чтобы уравнения (2.69) были эллиптического типа. Особый
случай имеем при со = 1, когда уравнения (2.69) вообще теряют
смысл, так как формулы (2.13) при этом не позволяют выразить
напряжения через деформации. В случае со = 0 уравнения (2.69) со-
впадают с известными уравнениями теории упругости в форме Ляме.
Обозначим через Rk (k = 1, 2, 3) сумму всех членов уравнения (2.69),
которые обращаются в нуль вместе с со:
3 ’»« з (2-72>
т, я,=1,2, 3; I ~ 1,2,3
и перепишем их в виде:
(Л + 0)^ + 0\72«а + р^-7?л.О, (£ = 1,2,3). (2.73)
Для решения задачи пластичности при активной деформации необхо-
димо найти интегралы уравнений (2.73), соблюдая граничные усло-
вия на поверхности тела(2.45). Последние, согласно (2.62), можно
переписать в следующей векторной форме:
v(S') = Fv + G/?„ (2.74)
где v (S') — вектор напряжения на границе, подсчитываемый через
перемещение w по закону Гука (2.61), F,— вектор поверхностной
внешней силы и /?,— вектор, обращающийся в нуль вместе с со:
/?, = 2соу(7)й). (2.75)
124 УРАВНЕНИЯ ТЕОРИИ МАЛЫХ УПРУГО-ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ {^Л. II
В проекциях на оси уравнение (2.7’4) даёт:
/С9 cos (v, + 2G 2 э*т cos хт) = х>к + (2.76)
т = 1, г, з
(*=1, 2, 3),
причём проекции /?„ определяются формулами:
flvfc = 2o> 2 5*mcos(v, х„), (fe = l, 2, 3). (2.77)
«=1, 2 ,3
Для решения задач пластичности можно применить следующий общий
метод, называемый методом упругих решений 14. Положим в первом
приближении а>0 — 0, так что = 0. Тогда из (2.73) и (2.76)
имеем уравнения теории упругости в форме Ляме и граничные усло-
вия в напряжениях, т. е. в первом приближении имеем обычную
задачу теории упругости. Предположим, что для данных массовых Хк
и поверхностных Х.,к сил она решена, и найден вектор перемеще-
ния с его проекциями По формулам (2.63) и (2.64) нахо-
дим деформации и по формулам (2.62) — напряжения в первом при-
ближении;
9(4 уп ^i) v(t) ..
тг t ’ св ’
а по значению еФ из (2.7) находим а>(°). Формулы(2.72)и (2.77) по-
зволяют теперь найти второе приближение для векторов R и
/?Ф, /?Ф; они являются известными функциями координат, и потому
в (2.73) величину рХк — GRW можно рассматривать как массовую
силу, а Х.,к 4- GR§> как поверхностную силу:
ъХу = ?Хк — GRW,
х$ = хчк+аячк.
Решая задачу теории упругости для этих сил, мы найдём вектор
перемещения адФ с его проекциями и£> во втором приближении,
после чего, повторяя все вычисления по формулам (2.72) и (2.77),
найдём третье приближение величин <оФ, R!£>, RW и, следовательно,
новые значения рХ^\ Х&; таким образом из (2.73) и (2.76) полу-
чаем задачу теории упругости для новых внешних сил и. т. д. Про-
должая этот процесс решения последовательных задач теории упру-
гости, мы для А7-го приближения будем иметь из (2.73) и (2.76):
(Л + G) + GV2 + рЛ^-0 = 0, (2.73')
cos (v, хк) 4- 2G24m C0S <*> Хт) = Х^~^, (2.76')
(А=1, 2, 3).
§ 16] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ В ПЕРЕМЕЩЕНИЯХ 125
Процесс такого решения задач теории упругости может быть
закончен, как только разница между последовательными прибли-
жениями окажется желаемой точности или будет в пределах
точности вычислений. Величины остающихся в теле перемещений,
деформаций и напряжений, согласно теореме о разгрузке, можно
найти как разности соответствующих величин в Мм и 1-м прибли-
жениях, причём напряжения, соответствующие деформациям 1-го при-
ближения, следует брать по формулам (2.61):
Hfe =
6 = 0W — 0(1),
7 -W -а) ]
#тп — ^тп !
X — A£v>—да. f
(2.78)
Доказательства сходимости последовательных приближений, получае-
мых методом упругих решений в общем случае пространственной
задачи, пока не дано, хотя условия (2.71) её обеспечивают во всех
рассматриваемых ниже случаях. Более того, вычисления показывают
очень быструю сходимость приближений, так что, даже в случае дей-
ствия на тело сосредоточенных сил, третье приближение даёт вполне
удовлетворительные результаты. Строгое доказательство сходимости
метода упругих решений применительно к пластинкам и оболочкам
при условии (2.71) дано Панферовым П1. Попутно им доказывается
существование и единственность решения, а также конечность числа
и ограниченность размеров областей пластических деформаций
в телах бесконечных размеров.
ГЛАВА ill.
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ.
§ 17. Изгиб и растяжение бруса.
В теории упругости простейшими называют такие задачи, в кото-
рых напряжения суть линейные функции координат, и потому усло-
вия совместности деформаций при их решении рассматривать не
нужно. Здесь к числу простейших мы отнесём различные задачи для
тел простой формы и при простом характере нагрузки, так что
решение их будет сравнительно элементарным. К числу простейших
относятся задачи о чистом изгибе бруса, о поперечном изгибе в при-
ближённой постановке, о продольном изгибе, о кручении стержня
круглого поперечного сечения, о деформации полых труб под дей-
ствием внутреннего давления и другие.
Рассмотрим сначала случай чистого изгиба бруса, сечение кото-
рого обладает двумя осями симметрии, причём изгиб происходит
в одной из этих плоскостей. Пусть оси х, у будут осями симметрии
поперечного сечения, ось z—центральная продольная ось бруса
и (у, z)— плоскость изгиба. Обозначим через х— кривизну цен-
тральной оси бруса в результате изгиба, Ь(у) — ширину и h — вы-
соту’сечения (рис. 44). Удовлетворяя условиям совместности дефор-
127
§ 17] ИЗГИБ И РАСТЯЖЕНИЕ БРУСА
маций (2.46), положим для всего сечения:
_____________1
ехх — еуу — 2
еху ~ еХ2 “ eyz == 0-
(3.1)
Таким образом для всего сечения принято значение коэффициента
Пуассона 0,5. Этим упрощением мы в дальнейшем будем часто поль-
зоваться, поскольку оно незначительно влияет на результаты. Заме-
тим, что если такого допущения не сделать и в строгом соответствии
с опытом считать коэффициент Пуассона в области пластических
деформаций переменным, то благодаря условиям совместности дефор-
маций (2.46) задача о чистом изгибе становится чрезвычайно слож-
ной, и в такой постановке она не решена.
На основании (3.1) имеем, очевидно, = и потому из (2.3)
находим:
X^Y^X^X^Y^Q, (а)
Из(2.6') теперь получаем зависимость от е1:
о>(^)]. (3.2)
Легко проверить, что эти напряжения удовлетворяют уравнениям
равновесия (2.44). Вследствие симметрии сечения .ясно, что продоль-
ная сила в брусе отсутствует:
Л/2
Ja1&((y = O.
—Л/2
Таким образом вся задача решается одним только соотношением -
между изгибающим моментом и кривизной, которое получается, если
написать выражение момента внутренних напряжений и приравнять
его изгибающему моменту М:
h/i
М = 2 J atby dy. .(3.3)
о
Это уравнение на основании (3.2) и (3.1) перепишем в виде:
л
Л/2
М = £7х — 2Е j we^by dy, (б)
о
где 7 — момент инерции сечения. Функция ш (et) в упругой зоне
деформаций равна нулю; обозначая через у8 ординату плоскости,
128 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ.П1
y=ys, разделяющей область упругих и пластических деформаций
сечения, и имея в виду, что на этой границе:
q = = Ув=^, (в)
мы можем уравнение (б) переписать в виде:
Л/2
М = ЕЬ. — 2Е Jчье^Ьу dy.
Введём следующие обозначения для безразмерных величин:
, Mh , xh у ei -
*=*.• у.=т = '< Тг^у
Тогда уравнение (б') принимает окончательный вид:
к
(з-5)
1
причём, как только конкретные свойства материала бруса w(s) и форма
сечения b (у) заданы, оно позволяет по заданной кривизне бруса х
или приведённой кривизне, k найти изгибающий момент М или его.
приведённое значение k0 и обратно. Пластическая деформация возни-
кает в брусе в том случае, если et es при у , т. е. при усло-
вии
А>1, Ао>1-
Если материал не обладает упрочнением, то теоретически наиболь-
шее значение изгибающего момента получается при бесконечно боль-
шой кривизне: k—co, причём ш = 1, и
(3.6)
где Sx— статической момент верхней половины площади попереч-
ного сечения относительно оси х. Выражение (3.6) получается пре-
дельным переходом из (3.5). Величина изгибающего момента
А«т.х = -^-АОшах (3.6')
называется несущей способностью бруса при изгибе.
Если брус, получивший найденные выше деформации и напряже-
ния, освободить от действия изгибающего момента, в нём возникнут
остаточные деформации и напряжения. Для определения их .восполь-
зуемся теоремой о разгрузке и прежде всего найдём фиктивную кри-
' § П]
ИЗГИБ И РАСТЯЖЕНИЕ БРУСА
129
визну х' или её приведённое значение k', которую получил бы брус,
если бы деформация была упругой. Из (3.5) ясно, что k' ~ k0.
Упругие фиктивные напряжения выражаются формулой «ь — Ежу =
— °в^оУ- Таким образом, остающиеся кривизна х и напряжение
находятся по формулам:
i.h ~ , I
= « = « — «л. I
2₽в °’ } (3.7)
~ а _ _ |
°i = °8 I (k — ko)y — кУшЪ J
причём величина co(ej) = u) (у) при y<iys обращается в нуль,
а при у > ys определяется через деформацию eliS=^fc_y.
Рис. 45.
Проведём более подробные вычисления для стержня, материал
которого характеризуется диаграммой в виде ломанной (2.11)
и сечение прямоугольное. Полагая в (3.5):
получим:
(3.5')
Остаточные напряжения, согласно (3.7), будут:
°i = °s(£—Л)Л
01= ~ [(*о — (!— W)y~ \1»
(3.7')
1
У >ys =у
На рис. 45 показано распределение напряжений до разгрузки (слева)
и после разгрузки (справа). Остаточные напряжения в точках 5 и Й
суть:
°8 , (о1)„= ~os[A0 —(1—Х)А —X].
* •* \ 'Л
9 Зак. ЗЦВ6. А, А. Ильюдше.
130
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
(гл. Ш
Для оценки порядка получающихся величин приводим в табл. 2
значения k, k0,(^) > при = 0,95 (сталь).
Легко видеть, что остаточные напряжения при полной разгрузке
всегда являются упругими, т. е. напряжения в точках S и Н по абсо-
лютной величине меньше ав.
Приближённое решение задачи о поперечном изгибе может быть
основано на применении зависимости между кривизной х и изгибаю-
щим моментом М при чистом изгибе. Как это и делается в сопро-
тивлении материалов, можно пренебречь влиянием на изгиб касатель-
ных напряжений Хг, Уг, поскольку они в длинных брусьях всегда
Таблица 2. Оценка остаточных напряжений. малы сравнительно с напря- жением а,. Таким образом, разрешая соотношение (3.5) относительно k, мы по-
йа 1 1,29 1,406 1,60 лучаем дифференциальное
k 1 1,59 2,00 4,0 уравнение изогнутой оси балки в виде:
1 г 11 0 0,21 0,594 2,40 h <Pv ,
% — | 05 1 0 0,140 0,297 0,60 2^ ~ * ~~ = — (3.8)
р \ ~ 1 0 — 0,265 — 0,356 — 0,45 Решение этого уравнения в случае статически опреде-
Уа~ ~k ,1 0,666 0,50 0,25 лимых задач изгиба балок весьма элементарно и ничем
не отличается от решения
обычных задач теории упругости. Несколько сложнее оказываются
статически неопределимые задачи, поскольку места возникновения
зон пластичности оказываются заранее неопределёнными. По этому
вопросу имеется большая специальная литература 14.
Задача о совместном действии, изгибающего момента и растяги-
вающей силы Р в общем решается так же просто, как и задача
чистого изгиба. Полагая все деформации сдвига равными нулю, а
удлинения равными:
С::>: — е1 — е0 + V>
_ _______________1_
еуу еха: ’ 2 ^гг’
где е0— постоянная по толщине, мы тем самым удовлетворяем усло-
виям совместности деформаций (2.46). Напряжения определяются
формулами (а) и (3.2), причём они удовлетворяют уравнениям равно-
весия и граничным условиям на боковой поверхности бруса. Таким
образом по заданным Р и М остаётся только вычислить удлинение
е0 центрального слоя- (v = 0) и его кривизну х. Для этого служат
§ 17] ИЗГИБ И РАСТЯЖЕНИЕ БРУСА 131
уравнения равновесия сил и моментов. Имеем;
Л/2 Л/2
Р— J <3lbdy = EeSjF—Е J* be^dy,
“й/2 -й/2 (3.9)
М== J atbydy = EIv.— Е J be^ydy,
— Л/2 —Л/2
где F—площадь сечения бруса. Поскольку функция о> отлична от
нуля только в зоне пластических деформаций, интегралы, входящие
в (3.9), распространены фактически только по этой зоне. Как и в
случае чистого изгиба, удобнее считать заданными не Р и 7И, а дефор-
мации е0 и х. Тогда значение Р и М через них выражены явно.
Следует различать три случая. 1) Если
।
е0 -1 О~ ^35
то < es всюду, и потому ш = О по всему сечению. Тогда всё сече-
ние остаётся в области упругих деформаций, и мы имеем:
P — Ee0F, M = EJx. (3.9')
2) Если
, 7-Л ..
ео П 2" ?s’
то существует упругая и пластическая зоны сечения, причём граница
между ними определяется формулой:
и потому нижним пределом интегралов, входящих в (3.9), будет уа.
Наконец, 3) если
•>.h .
ео 2”
то функция «о будет отлична от нуля по всему сечению. Вычисления
интегралов (3.9) для стержня прямоугольного сечения при условии,
что материал его подчиняется закону ломаной (2.11), не представляют
никакого труда, и потому мы их опускаем. Остаточные деформации
бруса при полной его разгрузке, согласно теореме о разгрузке, будут:
~ Р ~ М
ео — ей *— * £/ •
9*
132 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИЙ ПЛАСТИЧНОСТИ [ГЛ.Ш
§ 18. Устойчивость сжатого стержня.
Пусть стержень, сечение которого обладает двумя осями симмет-
рии, сжат силой Р, причём напряжение больше ''предела текучести
Р .
01=_>0s.
Относительное удлинение
места простое нагружение.
его определяется кривой <3f-et, которая
в данном случае совпадает с кривой про-
стого сжатия образца из материала стер-
жня (рис. 46):
О1=:ф(г1).
Допустим, что после того, как сила Р уже
приложена, на стержень начинает действо-
вать пара сил в плоскости наименьшего
момента инерции сечения, и пусть мо-
мент пары М будет бесконечно мал. За-
дача определения деформаций стержня при
этом существенно отличается от рассмот-
ренной выше, поскольку здесь не имеет
Обозначим дополнительные деформации оси
стержня через е0 и х, причём е0 — сжатие оси стержня, х — искрив-
ление её в плоскости пары М. Эти величины' будут также бесконечно
малыми. Пусть пара М приложена так, что наиболее удалённые в сто-
рону положительной оси у» волокна лежат на стороне вогнутости бруса.
Результирующая дополнительных напряжений Soj, вследствие неиз-
менности силы Р, должна обращаться в нуль:
ft/2
J" 8о1 b dy = О,
— Л/2
(3.10)
и потому ясно, что Scj должно менять знак в области сечения.
Поскольку плоские сечения бруса вследствие симметрии должны
всегда оставаться плоскими, то дополнительное укорочение волокон,
расположенных на расстоянии у от центральной плоскости (х, z),
будет равно:
8гх — е0 ху/, 4 (З.П)
поэтому граница, где напряжения 8ах меняют знаки, будет плоскостью,
определяемой равенством:
Ц = о, = <ЗЛ2>
Волокна, получающие при приложении М дополнительное сжатие
(8^! > 0), будут получать активную пластическую деформацию, и
потому сжимающее напряжение их возрастёт. Согласно кривой
§18]
УСТОЙЧИВОСТЬ СЖАТОГО СТЕРЖНЯ
133
рис. 46 точка Ри характеризующая напряжённое состояние стержня
до приложения пары, для этих волокон перейдёт на бесконечно
малое расстояние РМ. Волокна же, получающие удлинение (8q < 0),
находятся в стадии разгрузки и, согласно закону разгрузки, для них
точка Р, перейдёт в положение М' на прямой РО', параллельной
упругому участку OS. Таким образом дополнительные напряжения
8ot будут равны:
Stjj = — Scj,
1 aet 11
8т1 = ESgj,
8ех > 0, )
8ex<0. |
(3.13)
Уравнение (3.10) позволяет теперь найти одно соотношение между
е0 и х. В самом деле, согласно (3.13) имеем:
Ус Пр
Е J pei&dy = O,
— Л/2 у с
или на основании (3.11) и (3.12):
Л/2 Л/2 Й'З
Fo = J" bdy, S0 = J by dy, F = j" bdy.
Уь у „ — л/2
(3-14)
Величины Fo и So суть площадь и статический момент площад#части
сечения, в которой изгиб вызывает дополнительное сжатие волокон
(область активных деформаций). Если только сечение бруса конкретно
задано, уравнение (3.12) позволяет определить единственную входя-
щую в него неизвестную уа. Заметим, что у0 < 0, так как Ь’о > у0 Fo.
Напишем теперь выражение изгибающего момента через момент
внутренних напряжений:
Л/2
М = — J* 8at by dy.
— пр
Замечая, что
8^ = x(j—Уо),
и пользуясь формулами (3.13) и (3.14), находим:
-(г-| гр-р].
Пр
/0 = j by*dy,
У»
Л/2
/= f by*dy.
-пр
(3.15’)
134 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [гл. Ш
Величина:
=в[1 -(1 j (3.1б)
называется модулем Кармана. Поскольку /o>JoSo. то модуль Кар-
мана меньше модуля Юнга или равен ему. Связь между изгибающим
моментом М, сжимающей силой Р — Еа1 и кривизной стержня имеет
следующий вид:
М = — KJ*. (3.15)
Величина Р входит сюда- постольку,. поскольку модуль упрочнения
do, „ г, Р
~ на кривой сжатия должен быть взят в точке Р, где о, = .
a^i k г
Уравнение (3.15) отличается от обычного уравнения изгиба упругой
оси балки только тем, что вместо модуля Юнга берётся модуль
Кармана. х
Пренебрегая весьма малыми касательными напряжениями Хг, Yx,
формулу (3.15), строго справедливую только для чистого изгиба,
можно применить к изучению устойчивости сжатых стержней, т. е.
к случаю, когда бесконечно малый изгибающий момент является пере-
менным по длине стержня. Поэтому значения критических сил для
стержней с различными условиями закрепления концов при пласти-
ческих деформациях будут определяться соответствующими формулами
Эйлера с заменой в них Е на Kv Так, для стержня со свободно
опёртыми концами будем иметь:
'Л кР /2 »
или, деля на площадь р и решая это уравнение относительно гибкости
стержня:
'^7=* /(зл7)
Для каждого данного сечения стержня и кривой сжатия материала
Oj-ej, согласно (3.17), можно построить зависимость критической
гибкости от сжимающего напряжения о,.
Для стержня прямоугольного сечения имеем:
z С ы. г , /й \
F = bh, 1 = ^2, F0 = b
с _ „г) г _ b з\
°0 2\4 У°)' 'о — У (У — У°)>
и потому из (3.14) находим у0, а из (3.16) — выражение модуля
Кармана:
19]
КРУЧЕНИЕ СТЕРЖНЯ КРУГЛОГО СЕЧЕНИЯ
135
Изложенное выше решение задачи устойчивости стержня за пре-
делом упругости, по существу, принадлежит Энгессеру 121 и Кар-
ману I* 8!. Последний провёл также большое экспериментальное иссле-
дование устойчивости стержней за пределом упругости и обнаружил
хорошее подтверждение данной выше теории. В частности, для мате-
риалов, имеющих ярко выраженную площадку текучести на диа-
грамме им в хорошем согласии с формулами (3.17), (3.18)
обнаружена полная потеря устойчивости даже весьма коротких стоек.
§ 19. Кручение стержня круглого сечения1).
Решение задачи об упруго-пластическом кручении вала круглого
поперечного сечения (рис. 47) можно найти, предполагая, что пло-
мы ищем в перемещениях,
необходимо удовлетворить только уравнениям равновесия (2.44) и
граничным условиям (2.45). Согласно (3.19), все компоненты дефор-
маций будут равны нулю кроме двух:
ди , dw . и '
^=•^7+-^ = — ^ sin в, eyz = trcosf),
которые эквивалентны простому сдвигу в направлении перемещения п9
e0s = eyz cos 6 — ea,3sin6='tr. (3.20)
Таким образом из (2.3) следует, что и все компоненты напряжений
равны нулю, за исключением одного касательного напряжения
Решение задачи о кручевии стержней некругового сечения дано Падай
В книге «Пластичность».
136
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
[ГЛ. III
которое направлено по окружности радиуса г. Связь между 50г и еЦг
найдём из закона (2.6) а< = Ф(е4). Интенсивности напряжений и де-
формаций равны:
е. — ЛГ „л — _____________
* ~ 3 V 2 9г ~ Уз ~
<з4=30е4 [1—®(е<)].
I1
(3.21)
Уравнения равновесия (2.44) при этом удовлетворяются тождественно
и, поскольку касательное напряжение 50г направлено по окружности,
на боковой поверхности оно также удовлетворяет условию отсутствия
внешних сил. Напряжение SSe теперь может быть найдено по диа-
грамме если только крутка т задана. Задача сводится к опре-
делению зависимости крутки т от крутящего момента Л4. Для этого
выразим М через момент касательных напряжений:
М = J*2irr3drS0a
о
или на основании (3.21):
ха
vт
л/г 6" Г з , (3.22)
М = J <V< det.
о
Если кривая задана графически, то графически же можно
вычислить и интеграл (3.22) и таким образом получить связь между М
и х.. Если воспользоваться функцией <о, то формула (3.22) примет
вид:
М = de„ <3-22')
•«
г , гса4
где 1р— полярный момент инерции сечения, 1р~ -у, a £s— предел
текучести на диаграмме
Если зависимость о<-е< принять в виде ломаной, то, согласно
(2.11), получим:
М =.хО1р — ^^-esSpx* /3 +-| rcefj, (3.22")
§ 19) КРУЧЕНИЕ СТЕРЖНЯ КРУГЛОГО СЕЧЕНИЯ
137
причём Зр — статический момент площади поперечного сечения:
с — 2ка3
Ojo — з »
a rs—радиус упругой области при кручении. Если материал стержня
в области пластических деформаций не обладает упрочнением (А=1),
то связь между крутящим моментом и круткой упрощается
(Oe = 3G6s):
М — . (3.22"')
Y3 2"3
Величина момента:
Моа(3-23)
получается при т == со и называется несущей способностью вала на
кручение. Практически она достигается при величине крутки т3^>
.. /е«\3 *
, т‘ е' Уже ПРИ очень небольших углах закручивания.
Остаточная крутка, согласно теореме о разгрузке, будет
Распределение .напряжений по радиусу изображено во втором
квадранте (рис. 47); в третьем изображено распределение остаточных
напряжений:
~ м *
5дг = S9s J- Г.
Формула (3.22) позволяет на основании опыта на кручение сплош-
ного стержня круглого сечения строить диаграмму зависимости
материала стержня. В самом деле, пусть на основании опыта построен
график зависимости крутящего момента М от крутки х. Из него
можно построить зависимость х3М (т), от т после чего, согласно (3.22),
получаем:
Здесь и относятся к наружному волокну, для которого
Следовательно, в результате графического дифференцирования по т
т/ 3 о
функции х3М, умножая её на и деля на е< = —g-, мы получим
зависимость от х, а значит,, и от
ах
es ~ I— •
Уз
138
- простейшие ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
[гл. III
§ 20. Деформация полого шара под действием
внутреннего и наружного давления.
Полый шар наружного радиуса Ь и внутреннего а находится под
действием наружного рь и внутреннего ра равномерного давления
(рис. 48). Главными осями напряжений и деформаций, по условию
симметрии, будет направление центрального радиуса г и два любых,
перпендикулярных к нему направления на сфере г — const. Послед-
ним двум направлениям придадим индексы «1», «2», а радиальному
- 26----
Рис. 48.
направлению индекс «3». Тогда
радиальные напряжения и дефор-
мации можно обозначить о3 и г3,
а тангенциальные соответственно
а2 —Oj и = Радиальное пе-
ремещение точки А на сфере ра-
диуса г обозначим w(r), танген-
циальное её перемещение будет
равно нулю вследствие симметрии.
Формулы Коши в данном случае
дают следующие выражения для
деформаций в точке А:
dw w
ез — > е2 — ei — ~ > (3.25)
и потому имеем:
F) == Зг = е3,
2
?i = "з — ез) s’gn <3.26)
Постоянная величина sign w есть единица со знаком величины w,
т. е.
причём знак её совпадает со знаком разности (е1—е3), и потому е{,
согласно (3.26), действительно положительная величина. За незави-
симые величины напряжений возьмём теперь и — о2; имеем,
очевидно,
а4 = (а1 —<j8)signw, (3.27)
так как знак разности <зх — <з3, согласно (2.3), совпадает со знаком
ei — ез’ т- е- с sign w. Таким образом получаем:
з3 —— SjSignw, )
1 . , । . 1 } (3.28)
’ = -3 (31-f-°3+ °з) = °1 — J^Slgnw. v ’
§20]
ДЕФОРМАЦИЯ ПОЛОГО ШАРА
139
Поскольку, согласно (2.1) и (2.6),
о ==/<8,
= Ф (еР,
то, согласно (3.28), все три напряжения: а1==о2, о3 являются функ-
циями одного только перемещения w, и потому для решения задачи
необходимо составить только одно уравнение равновесия и соблюсти
граничные условия при г—а и г^= Ь. Но мы дадим другое решение.
Уравнения равновесия (2.44) в данной задаче сводятся только
к одному, получающемуся из проектирования всех напряжений, дей-
ствующих на элемент, на направление радиуса. Оно имеет вид:
-$+|-(^--’1)t=0. (3.29')
На основании тождества
°3 = °3--°1 + °1
и пользуясь (3.27), перепишем eto в виде:
ensign да —0. (3.29)
dr \ dr ' г b ’
Мы дадим решение задачи в напряжениях, и потому к уравнению
(3.29) необходимо добавить условие совместности деформаций типа
(2.46), выраженное через напряжения. Для получения его отметим
тождество:
9 s= 2^i -j- ё3 = 3^ — у sign да,
и напишем закон Гука для объёмных деформаций а = А'0, принимая
во внимание выражение а через <з1 и а,- (3.28):
а, — у <зг sign да = З/С у — у Ке^ sign да. (3.30)
Дифференцируя последнее равенство по г и замечая, что
d tw\ 1 fdw w\ 1 , . 3 .
-Tr\T)^y\-d7—7)^—Г^-вз) = —27*<s>gnw, ,
получаем:
Исключая из уравнений (3.31) и (3.29), получаем:
2 d~t । 2 । 3 de$ । 9 tz f\
3 ~dF + 7 + T K~dT + 2 K V = °
140 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ.Ш
Но это уравнение имеет интегрирующий множитель; умножая его
на г3 и интегрируя, получим:
9 с
^+1^ = ^--. <3-32)
Произвольная постоянная с может быть выражена через размер сферы,
давление и перемещение поверхности. Для этого вычтем из обеих
2
частей равенства (З.ЗО)-^-assignw и, учитывая (3.28) и (3.32), пе-
репишем его в виде:
। „ .,w 2с. , .
— =3 73- sign w. (а)
При г == а давление задано равным а3 = — р2; тоже при г — Ь,
а3 = —рь; поэтому из (а) имеем:
с ~ "1Г О’» + 3/С ’V’) sign w Ц Ил + 3/<'Дг) sign w’ (3’33)
или
3/C(6awft — a2wa) = а3ра—bspb. (3.34)
Последнее равенство, впрочем, может быть просто выведено из ин-
тегрирования по объёму тела формулы a = КВ, если принять во вни-
мание, что на основании (3.29'), (3.25) и (3.26):
30Г2 = ^_(гЗ°з)) Г20 -±(r2W).
Соотношение (3.32) вместе с законом
0< == Ф (е<) (б)
С т->
позволяет выразить <st и е{ через . В самом деле, имеем уравнение
для ер.
= (в)
и потому (б) определяет of. Уравнение равновесия (3.29) мы можем
переписать в виде:
~ Sign <W
dr Г2 dr v v 6
и проинтегрировать:
°i = + 2 J si£n (r)
о
§2OJ Деформация полого шара 141
На основании (3.28) теперь находим:
Г
О8 = (2 I* ^~+Cl)si§nW- (Д)
а
При г = а имеем а8 = —ра, и потому:
Г
°з+а» = 2 | -^signw. (3.35)
а
Полагая ещё г=^Ь, о3 = —рь> получаем:
ь
Ра — Ръ = 2 J ~~ sign <w- (3.36)
а
Это уравнение определяет постоянную с, которая на основании (б)
и (в) входит в выражение af = (уз) > и потому задач» может счи-
таться решённой. Напряжение а3 при любом г определяется по фор-
муле (3.35), а <з1 = а2—по формуле (3.28). Как ^Ледует из (3.36),
знак величины -ш совпадает со знаком разности ра—рь:
sign да = sign (ра—рь).
Для определения радиального перемещения различных точек тела
воспользуемся формулой (а):
(3.37)
а
В частности, перемещение wa внутренней поверхности (г = а) нахо-
дим по формуле:
ЗАаэдаа = у с sign да—раа9- (3.38)
Рассмотрим сначала случай чисто упругой деформации, причём
всем искомым величинам в этом случае припишем штрих наверху.
Уравнение (б) имеет при этом вид:
Of = 3Ge,,
(б')
поэтому из формулы (в) находим:
' с' 1
— / 3 \ г3 ‘
3(С + 4/С)
Д42 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. III
Значение постоянной с' находим из соотношения (3.36):
з(о + -|-1с)(рв-рь) а’63
------2О(»з-аз)--------sign^,
(3.36')
и потому распределение упругих напряжений, согласно (3.35) и (3.28)
определяется формулами Ляме:
°3 = —Ра +
01' = —Ра +
(ря—.Pbl^Lh___
&з_аа гз;>
(Ра—Ръ) ЬВ
Ь3— а3
(3.35')
Если давление внутри и снаружи шара снято, то возникающие в нём
остаточные напряжения определяются разностями
°i ~ °i — °i >
°з — °з — °з
и остаточное перемещение внутренней поверхности будет
I ЗКа2и?а = — (с — с') sign w. (3.38х)
Рассмотрим теперь случай, когда полый шар, материал которого
удовлетворяет соотношению (2.11), целиком переходит в пластическое
состояние. Во всей его толще закон (б) будет выражаться так:
ч= 3 G [(1 — X) е{ -f- XeJ,
и согласно (в) находим:
0(1—1.) с . 4 ^’в
Ч * гЗ “Г о
С(1-Х) + ТАГ G (1 - X) + £ К
(б")
(3.39)
Постоянная с, согласно (3.36), теперь приобретает следующее выра-
жение:
3 [ О (1 - X) + | d (Ра - Ръ) а*Ь3
----2О-(1-Х)(63-аз)--------
_ 1п 2 ,3 40)
40(1 — Х)(й3— аЗ)1п а '
Дальнейшее определение напряжений не представляет никакого труда.
Найдём одно только перемещение wa, т. е. увеличение внутреннего
радиуса шара. Из (3.38) и (3.40) имеем:
аб3 Г bl
W<t 4G(i-^(b3-a3) — Ръ — 2Ч in sign «, J +
{авРа — Ь3ръ}а
' 3K\b3 — a3)
(3.41)
§20)
ДЕФОРМАЦИЙ ПОЛОГО ШАРА
143
Для того чтобы вся толща шара перешла за предел упругости, не-
обходимо, чтобы наименьшее значение интенсивности напряжений а*
при г—Ь было больше as. Из (3.39) и (3.40) находим следующее
условие:
\Ра~ Ръ\>
2 (1-Х) (О+ 4 *)(*’-«’)
2[0(1-Х) + 4**| 3 [ G(1 - X) +А /С] «3
(3.42)
Если материал шара не обладает упрочнением (А = 1), то несу-
щая его способность или наибольшая разность внутреннего и наруж-
ного давления, которую он способен удержать, находится из условия
конечности wa или равенства (3.42):
\Ра—Ръ Lax = 2agln- .
(3.43)
Решение задачи о деформации полого шара является совершенно
элементарным в том случае, если материал его считать несжимаемым.
Полагая в (3.26) 9 = 0, находим:
а2
w — -w„ ,
° г- ’
и потому
2w„a2
закон а{ = Ф (е{) позволяет сразу в квадратурах писать выражение Oj
и Од из уравнения равновесия (3.29), после чего из граничных усло-
вий находится постоянная ша и другая константа интегрирования.
В формуле (3.41) второе слагаемое как раз представляет поправку
к такому простому решению за счёт сжимаемости материала. Условие
полного перехода тела в область пластических деформаций (3.42) тоже
зависит от сжимаемости, поскольку в него входит модуль объёмного
сжатия К. Однако влияние сжимаемости оказывается достаточно
малым.
Рассмотрим следующий пример: стальной полый шар с отношением
радиусов = 2, с параметром А = 0,95 и пределом текучести
= 4000 кг)см’ находится под действием внутреннего давления
ра = р, (рь — 0). Из (3.42) находим, что вся толща его выходит за
предел упругости при ^=2G:
р l,65as,
а при /С=оо, т. е. при условии несжимаемости:
1,55ав.
144 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. Ш
Разница в условиях, как видим, весьма незначительна. Найдём дефор-
мациюна внутренней поверхности при р = 1,7ав = 6800 кг/см2;
имеем при G = 0,8 • 10е кг)см2:
= 0,01092 -4- 0,00020,
причём второе слагаемое, происходящее за счёт сжимаемости мате-
риала, в 55 раз меньше основного, получающегося из условия ЛГ= оо.
Роль сжимаемости повышается, если брать меньшие давления. Возь-
мём минимальное значение, при котором на наружной поверхности
тела впервые возникает пластическая деформация, p=l,65as =
= 6600 кг/см-; получим:
=0,00950 + 0,000194.
Влияние сжимаемости остаётся попрежнему малым. О влиянии сжи-
маемости, впрочем, можно легко судить на основании соотношения
(3.34), которое имеет место для любой диаграммы а4 = Ф(е,) и лю-
бого отношения радиусов. При условии ЛГ=оо из него имеем:
b2wb — a2wa = 0
pR
и, следовательно, сжимаемостью можно пренебрегать всегда, если -+
К
мало сравнительно с перемещением wa сферы радиуса R; здесь
р—‘характерное значение давления на тело.
§ 21. Симметричная деформация толстостенной трубы.
Напряжения и деформации толстостенной трубы, находящейся под
действием внутреннего и наружного давлений, а также под действием
осевой силы Р для простоты рассмотрим, исходя из условия несжи-
маемости материала. Сохраняя обозначения предыдущего параграфа,
осевое направление будем отмечать индексом «1». Формулы Коши
для выражения деформаций через перемещение w дают:
„ . w dw
= const, е2 = ~, е& = ~, (3.44)
причём постоянство осевой деформации вытекает из того, что давле-
ния ра, рь и осевая сила Р постоянны по длине. Условие несжимае-
мости :
dw . w
_+_i=_ei
даёт такое выражение для перемещения w:
1 г
— (3.45)
§21] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТОЛСТОСТЕННОЙ ТРУБЫ 145
Интенсивность деформаций, а следовательно, и интенсивность напря-
жений теперь становятся известными функциями радиуса и зависят от
двух произвольных постоянных е1 и с:
= г = Ф(^).
(3.46)
Формулы (2.3) дают два соотношения между тремя напряжениями:
(3.47)
В этой задаче мы можем написать два уравнения равновесия: одно
представляет условие равновесия элемента трубы в проекции на
радиус
I °3 ~ °2
dr ' г
(а)
а другое — условие равновесия трубы в проекции на её ось
ь
Р — 2тг J* rojdr.
а
(3.48)
Первое из этих уравнений на основании (3.47) можно проинтегри-
ровать
°з ~ъ~ f —ir~ dr с,
3 3 J г^е{ 1 1
и заменить интегрирование по г интегрированием по et, поскольку
^-^-^-K^Fsignc, ---(3.49)
ei е1
Тогда получим:
°8=С1
Согласно (3.49), между значениями величины е4 на внутренней
и наружной поверхностях и значением её при любом г существует
соотношение:
(*|о - ф = (^ = Р - 4), (3.50)
eia > е1Ъ-
Ю Зав. 3138. А. А. Ильюши»
146 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [гл. III
Полагая в предыдущем уравнении, что при г » a, et — eia, а3 = — ра,
находим распределение радиальных напряжений:
‘ 1 > и
«8 = -рв+^= f —fi^signc, (3.51)
ei
а из условия г = Ь, а8 = — рь находим одно соотношение между
двумя неопределёнными постоянными eia и :
%
J ₽|^rsi5"c: <3'52)
вп
при этом постоянные с и eib выражаются также через е{а и е1г
согласно (3.50); попутно из (3.52) устанавливаем, что знак постоян-
ной с совпадает со знаком разности ра—ръ:
sign с = sign (ра— ръ).
Напряжения а2 и а1 теперь будут иметь следующие выражения:
2с,-
е2 sign с,
°2 °8 е{ /з г
(Уе2 — е2 sign с /з ).
О-
(3.53)
Уравнение (3.48) позволяет найти второе недостающее соотношение
между постоянными eia и еР Замечая, что согласно (3.50)
а 2У^-<
г2 = а2 — —, rdr =
2 (е2_е2)7. (3,54)
У^4
Д2
мы получаем:
ла®
г е*а
Г f ^ejdej ,
ia 4J +
eib
е‘“
r /з J 4
eib
ei /3
de., .
§21] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТОЛСТОСТЕННОЙ ТРУБЫ 147
Подставляя сюда значение а3 из (3.51) и применяя формулу Дирихле
для преобразования двойного интеграла, а именно:
eia eia
Jejdej г aidej
eib eib
Ча! -I 1 \
J —4 ——4) / 4
eib
окончательно получим следующий результат:
вга
Р—к(а^а — т/р~—f °idei (3-55)
= «11% \ J (е2_е2)%-
е1Ь
При заданном законе а4 = Ф(е4) формулы (3.50), (3.52) и (3.55)
определяют все константы ег, eia, eib, с, и потому напряжения
в трубе вполне определены формулами (3.51) и (3.53), а перемеще-
ние w — формулой (3.45). Из (3.55) видно, что если осевая сила Р
отсутствует, то благодаря действию одного только внутреннего
давления труба укорачивается; если действует одно наружное давле-
ние— она удлиняется по оси.
Рассмотрим случай, когда материал трубы подчиняется закону (2.11):
<з4 = ЗСеД1—w),
<о = 0, (ei<es), a>=a(l--g-), (ei>es). (б)
Предположим, что цилиндрическая поверхность г — r,f разделяет
зоны упругих и пластических деформаций. Поскольку е,-— монотонно
убывающая функция при переходе от внутренней к наружной поверх-
ности цилиндра, существование упругой и пластической зон будет
обеспечено, если
(3.56)
причём радиус зоны пластичности, примыкающей к внутренней поверх-
ности цилиндра, согласно (3.50), будет определён условием е/ = г3:
Прежде всего составим уравнения для определения постоянных eia
и ег Для уменьшения числа параметров, входящих в эти уравнения,
10*
148 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [ГЛ. III
обозначим
f = A = S1 (3.58)
&8 е8
и заметим, что 3Oes = as есть предел текучести материала. Уравне-
ние (3.52) при законе (б) принимает вид:
еш „
I ___ I 3G г ejdej _____________ 3GX г (e{ — es)dei .
“ Иь /3 J /3 J ’
eib es
после вычисления интегралов и несложных преобразований со-
гласно (3.50) и (3.58) оно даёт первое соотношение между sia и г/
. 1 г 2 2
(’-‘-О =
1 + V 1 — Ч
(3.52')
Аналогичным образом из (3.55) получаем второе соотношение
в следующем виде:
(-3
C3.ss')
Соотношения (3.52') и (3.55') позволяют построить серию графиков
величин
\Ра— Pb\ Уз „ Р— — Ь2Рь) (пх
Р ~ a, ’ Р r.tfcs ' W
в зависимости от e1( sia и графиков обратных зависимостей при
различных значениях отношения и параметра к. Распределение
напряжений по толщине стенки теперь может быть найдено из (3.51),
(3.53), но сами напряжения ар о2, а3 особого интереса не пред-
ставляют, так как при найденных е., sfa по значениям:
eia — es®«a> е1 ~~ ^sel’
мы знаем распределение интенсивности напряжений а4 = Ф (е4) и осе-
вую и радиальную деформации трубы, а также радиус зоны пластич-
ности
§ 21] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТОЛСТОСТЕННОЙ ТРУБЫ 149
Перемещение -ш любой точки трубы, согласно (3.45), (3.50), мы
можем записать в виде:
= — 61 е1 -^-^"(Ра-Ръ)- (3-59)
Рассмотрим более подробно частный случай, когда et — 0.
При этом имеет место плоская деформация трубы. Из (3.52') полу-
чаем трансцендентное уравнение для определения efo:
х + (1 — X — Я2) sia + X In ei0= р', (3.52")
где <х = -^--отношение радиусов цилиндра; теперь из. (3.55') мо-
жем найти силу Р, возникающую в направлении оси трубы;
открывая встречающуюся здесь неопределённость, получаем:
Р" = О, Р = * (с?ра — ЬРрь). (3.53")
Переход трубы за предел упругости происходит при eia = es или
£^а=1, что соответствует предельному упругому состоянию трубы.
Таким образом, при упруго-пластическом состоянии
= . •> 1 п'— ^Ра~Ръ \ У~3 1 2
Деформация трубы в нашем случае будет выражаться простой фор-
мулой :
w t / \ 2ar ^(Ра Ръ\ (3.59')
г*~а ]А<в.
Найдём ещё остаточную деформацию трубы после снятия нагрузки.
Поскольку решение задачи об упругой деформации трубы получается
из данного выше при Х = 0, значение eia в упругом случае,
согласно (3.52"), будет:
= _Р—
~ia 1____a2 ’
и потому фиктивная упругая деформация при е1 = 0 имеет по (3.59)
следующее выражение;
w' Р'а УЗ . , ч
На основании теоремы о разгрузке находим остаточную деформацию:
4-^(4 - т^г “•) <3-60>
50
ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ
[гл. Ill
аХ/3 / г; г*
aes ~ 2 (1 — а2) г \ 1 ‘ а3 Z а
Если мы воспользуемся соотношениями (3.52") и (3.59'), то сможем
выразить w в функции радиуса зоны пластичности г*:
sign (ра—рь),
а отношение остаточной деформации к общей выразить в виде:
w _ X Л а2 а"" . г* \
w “l-а2 г2 Г1 п а2 )
На рис. 49 дан график зависимости величины —— — от
построение сделано по координатам точек, вычисленным из
и помещённым в табл. 3.
(3.61)
г* .
а ’
(3.61)
Координаты к рис. 49.
Т аблица 3
Г* а 1 1,2 1,4 1,6 1,8 2,0 2,2 ОО
1 — a2 w X w 0 0,052 0,147 0,241 0,348 0,403 0,467 1
Как видим, у толстостенных труб, имеющих а <0,5 при значи-
тельном радиусе пластической зоны, на 20—40% превосходящем
внутренний радиус трубы,
остаточная деформация со-
ставляет 4 ~ 10% от общей
деформации.
Предположим, что мате-
риал трубы обладает резко
выраженной пластичностью и
при малых деформациях не
имеет упрочнения, т. е.
X = 1. В таком случае ясно,
что существует некоторое
Максимальное значение на-
грузок ра, рь и Р, при ко-
торых труба находится в
предельном состоянии равно-
весия, так что дальнейшее увеличение их невозможно. Соотношение
между величинами ра, рь, Р в этом случае определяет несущую спо-
собность трубы, а зависимость такого типа в дальнейшем будем на-
§21] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТОЛСТОСТЕННОЙ ТРУВЫ 151
зывать конечным соотношением между силами. Конечное соотно-
шение между величинами р' и р", определяемыми формулами (в),
можно найти из (3.52') и (3.55'), положив в них 1=1 и
е2ь = е2 + а4(£2а-е2)=1>
поскольку вся толща трубы должна перейти за предел упругости
Но можно его получить и прямо из (3.52) и (3.55), поло-
жив в них а( = as = const. Вычисляя простые интегралы и обозначая
х = 22-^= у, 8=А- = А, (г)
г J 1 а а ' '
имеем
, . x+Vx*— 1
р = In---
a2y+Va^ — l
р" = ~х-\~у.
(д)
К этим уравнениям нужно добавить соотношение, вытекающее
из (3.50):
х2—_У2 = Р4—1. (е)
Решая совместно второе уравнение (д) и (е), находим:
__ _^2 + |34_1 _ ^ + Р«-1
Чр" > У— 2р"
а подставляя эти значения в первое из уравнений (д), получаем
искомое конечное соотношение:
р' = In Г -р"2 + Е4 -1 + /(-р"2 + Р4 — 1)а- 4р"2 1 (3 62)
Р L ^(р'^ + р4—1)+Vra*(p"2-|-p*—1)2—4р"2 J ’
Величины eia, eib и е1г как следовало ожидать, остаются неопре-
делёнными, и известно лишь их отношение между собой. В случае
плоской деформации трубы, когда вдоль оси она не имеет возмож-
ности удлиняться (т. е. ег = 0), конечное соотношение распадается
на два отдельных равенства:
р" = 0, р' = 2 In р,
которые запишем в явном виде
\Ра— A>l = yjlnT’ Р==^(^Ра~ Ь2Ръ)- (3-63)
Анализируя эти формулы, заключаем, что путём неограниченного
увеличения толщины стенки трубы или, что то же, уменьшения
внутреннего радиуса, можно достигнуть того, что труба будет выдер-
живать неограниченно большие внутренние или наружные давления;
если её концы закреплены и не могут приближаться или удаляться
152 ПРОСТЕЙШИЕ ЗАДАЧИ ТЕОРИИ ПЛАСТИЧНОСТИ [гл. Ш
один от другого, то при действии наружного давления (ра=0)
возникает сжимающая осевая сила Р =— ъЬ*Рь> а ПРИ действии
внутреннего давления — растягивающая сила /э = тга2р0.
При плоской деформации трубы (ег — 0), материал которой
полностью перешёл за предел упругости и не обладает упрочне
нием (1=1), силы, определяемые формулой (3.63), дают следующе
распределение напряжений ап а2, а3 по радиусу
, 2а„ , г . , .
«з = - Ра + у=- 1" — sign (ра—рь\
°2 = -Pa + ^=(l+ln-£-)sign(p0— рь), [ (3.64)
«1 = - Ра + (4 + In -7) Slgn — Рь~)•
у о \ ** /
В частности, если наружное давление отсутствует (рь = 0), имеем
следующий закон распределе-
ния напряжений:
~"4)- <3.64')
Если р<е = 2,7183, то тан-
генциальные напряжения а2 по-
ложительны по всей толщине
стенки, если же е, то при
b
г = ~ напряжение а2 меняет
знак, являясь положительным
на наружных и сжимающим на
рис go внутренних слоях трубы. Рас-
пределение общих и остаточных
(после снятия давления) напряжений о2 и а2 по толщине стенки показано
на рис. 50. Пунктиром показан закон распределения упругих напря-
жений а'. Как видим, характер распределения напряжений при пла-
стических деформациях труб прямо противоположен распределению
упругих напряжений, и наиболее тяжёлые условия для прочности
материала возникают, видимо, на наружном слое трубы. Бриджмен 1*1,
применяя очень высокие давления, показал, что разрушение сталь-
ной трубы начинается именно с поверхности.
ГЛАВА IV.
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК.
§ 22. Предварительные замечания.
Решение проблемы равновесия пластинок и оболочек при упруго-
пластических деформациях, как и при чисто упругих, основывается
на двух основных постулатах Кирхгоффа-Лява. Первый состоит
в том, что совокупность материальных частиц, расположенных на
нормали к серединной поверхности оболочки до деформации, рас-
положена также на нормали к серединной поверхности её после
деформации, и потому деформированное состояние оболочки опре-
деляется только деформированным состоянием её серединной поверх-
ности. Этот постулат, по существу, говорит о том, что каждый
кусок оболочки, размеры серединной поверхности которого малы
сравнительно с общими её размерами (и соизмеримы с толщиной),
находится в условиях, весьма близких к чистому изгибу и кручению,
наложенным на растяжение и сдвиг без изгиба и кручения. Второй
постулат состоит в том, что все компоненты напряжений, имеющие
направление нормали к серединной поверхности, весьма малы срав-
нительно с другими. Оба эти постулата находятся в согласии друг
с другом и означают, что всякий тонкий элементарный слой мате-
риала, парадлельный серединной поверхности оболочки, находится
в условиях плоского напряжённого состояния или, точнее, напряже-
ния, действующие в его плоскости, значительно больше других
напряжений. В справедливости такого предположения можно убе-
диться из анализа порядка различных компонентов напряжений в тон-
кой оболочке, исходя из уравнений равновесия.
Кроме постулатов Кирхгоффа-Лява в дальнейшем мы будем поль-
зоваться предположением, что материал оболочки можно считать
несжимаемым. Степень точности такого предположения заранее
является довольно определённой, поскольку хотя бы из теории
упругих оболочек известно, как влияет коэффициент Пуассона на
деформации и напряжения. В теории упруго-пластических деформа-
ций оболочек гипотеза о несжимаемости вносит значительные упро-
щения.
154
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
§ 23. Законы пластичности при плоском напряжённом
состоянии.
Пусть тонкая пластинка находится под действием сил, приложен-
ных в её плоскости (х, у). В таком случае компоненты напряже-
ний Хг, Kg, Zz малы сравнительно с Хх, Yy, Ху, а последние мало
изменяются по толщине, и потому можно рассматривать их средние
значения *).
Интенсивность напряжений а4- будет иметь следующее прибли-
жённое выражение (см. § 8):
о, = (4.1)
Поскольку
первые три формулы (2.3) примут вид:
с — v____________________L у — 2L о — , 1
*°аз 2 1У — ^хх* I
s = Y _____— X = — е = — э У • Г4 2^
°у !у 2 х W уу {
<? х с, — 21. а • I
^ху — ^у— зе. еху ~~ 3 ^ху’ I
остальные формулы (2.3) дадут выражение деформации ег2:
^гг '= ехх вуу’
и два соотношения, показывающие, что деформации ехг, еуе относи-
тельно ехх, еуу, еху имеют тот же порядок малости, как напряже-
ния Хг, Yz относительно Хх, Yy, Ху. Поэтому интенсивность дефор-
мации е{ будет иметь следующее выражение:
2 _ 2 I I 2 I 1 2
---у еах ~Г еххеуу ~Г еУУ -Г е®у —
— У^^хх -\-эххЭуу 4- эуу Эху. (4.3)
Величины и et связаны между собой законами (2.6) или (2.17):
°» = Ф(^) — £еИ1 —<0(^)1, }
I (4,4)
г) Мы имеем в виду обобщённое плоское напряжённое состояние.
§23] ЗАКОНЫ ПЛАСТИЧНОСТИ ПРИ плоском состоянии
155
Второе соотношение (4.4) не имеет смысла в том случае, если ма-
териал пластинки не обладает упрочнением, т. е. если имеет место
условие пластичности Мизеса:
Xl — XxYy + Y2y + 3^ = ot (4.5)
В дальнейшем мы часто будем иметь дело с однородной квадра-
тичной формой Р трёх аргументов:
хх = ^1» ^2> ^ху = Р1Э» I , . g.
Ри = ul + и±и2 + ul + ^12> J
которая положительна при любых действительных значениях аргу-
ментов Un. Из (4.3) следует, что
Ра = ^е1 (4.7)
Составим согласно (4.6) и (4.2) квадратичную форму Ра. Для этого
заметим, что если ,
U1 = ах1 Ьуг, U2 = ах2 + Ьу2, 17i2 = axi2 by 12, (4.8)
то Ри = а*Рх 4- 2аЬРау 4- Цг vG 1 1 Ъ^Ру, (4.9)
гДе Рху — билинейная форма: Px,y = x1y1-\-^xiy2^- ^x2yl^-x2y2-\-xl2yi2. (4.10)
Полагая получим теперь ® = 1, b = , хj = Хх, У1 == Yyt у2 — Хх, = Ху, р — р р J- р = 1 a * х ху\ у = Уу, У12 = 0> |4. (4.11)
Составим ещё дифференциалы форм Р3, Ра; имеем, очевидно,
dPM = 2PM(d„. (4.12)
Теперь из (4.7) и (4.11) легко видеть, что
» Pg, 8а •••• ““ - ) i /з Vp8 ’ 2 Р 8а<=-—(4.13) /з Vps
156
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
Квадратичные формы Рв и Ра обладают ещё следующими свой-
ствами:
у - 2 v дР^ у 1 дР8
3 dSx ' 3 dSy ' ЛУ '2 dSxy ’
1 1 дР3 1 j дР8
эх<в + -2 эт — ’ 3^ + ~2 эхх = 2дэ^>
1 дРа
2 дэху ’
и потому формулы (4.2), связывающие напряжения и деформации,
можно переписать в виде:
иоа?
иаУУ
vaxy * иоху
(4.14)
причём зависимость а, от et заменяется зависимостью
Ps= Ф'(Р8).
§ 24. Связь между внутренними силами, моментами
и деформациями оболочки 14.
Пусть дана оболочка толщины h. Серединной поверхностью обо-
лочка называется поверхность, делящая толщину её всюду пополам.
Предполагается, что всюду, исключая, может быть, некоторые точки
или линии на ней, серединная поверхность является непрерывной
с непрерывно изменяющейся касательной и кривизнами, причём все её
геометрические характеристики изменяются весьма плавно. Выберем
на серединной поверхности главную ортогональную систему" криво-
линейных координат •»]. Под плавным изменением некоторой геоме-
трической характеристики будем понимать такое, когда при переходе
от точки (£, г]) к точке ($', ?]'), расположенной на расстоянии
порядка толщины оболочки h, она имеет относительное изменение
порядка (где R—радиус кривизны) или меньше1). В точке
с координатами (?, т() серединной поверхности проведём касательную
плоскость. Подвижной трёхгранник Дарбу (х, у, г) расположим так,
чтобы начало координат (х=у — г — 0) совпало с точкой (;, г|),
оси х, у были направлены соответственно в сторону возрастания $ и <],
а ось г — к центру кривизны линии $. Таким образом оси х, у сов-
J) Как известно, можно несколько расширить это требование И.
§24] СВЯЗЬ \1ЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ 157
падают с главными направлениями поверхности в точке ($, г|). Элемент
серединной поверхности оболочки образуем линиями Е = const.,
т] = const, и = const-> = const., а элемент оболочки
проведением через указанные линии нормальных её сечений. На
рис. 51 изображён элемент оболочки и показаны напряжения, дей-
ствующие на слой элемента, расположенный на расстоянии z от се-
рединной поверхности. Как уже говорилось, напряжения Zx, Zy и Zz
малы сравнительно с остальными напряжениями, и потому напряже-
ния и деформации элемента связаны между собой формулами § 23.
Относительные удлинения и сдвиг элемента серединной по-
верхности в результате деформации оболочки обозначим:
®1 — (eaxc)z=0>
®2 == (еуг<)г=О>
1 / ч
®12 2 '^®г/)г=О>
а изменения нормальных
кривизн его и кручения,
которые в целом будем
называть искривлениями
оболочки вследствие де-
формации, обозначим со-
ответственно:
_ 1 1
54 т?; R'C
Рис. 51.
(4.15)
Если компоненты вектора перемещения точки серединной поверх-
ности по осям х, у, г заданы как функции координат (Е, г|), то де-
формации еп е2, е12 выражаются через них по известным формулам,
содержащим производные от перемещений йе выше первого порядка, а
искривления хп х2, х12 — не выше второго порядка (31. Мы приведём эти
выражения для тех частных задач, которые будут рассмотрены ниже.
Согласно первой гипотезе Кирхгоффа-Лява нормальные сечения
оболочки до деформации остаются также нормальными к серединной
поверхности' после деформации, и потому деформации слоя, распо-
ложенного на расстоянии г от серединной поверхности, будут:
эхх == ^хх == ®1 >
эуу ~’еУУ ~ S2 '?Z2>
^эху ~ еху ~ (Sja
(х12 = т).
(4-17)
158
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК f
[ГЛ. IV
Эти формулы вполне определяют правило знаков для искривлений.
Например, величина Xj считается положительной в том случае, если
волокно, параллельное оси х и расположенное со стороны положи-
тельных значений z вследствие искривления Xj укорачивается; кру-
чение т = х12 положительно, если угол между волокнами, парал-
лельными х и у и расположенными со стороны положительных z,
увеличивается.
Интенсивность деформаций, согласно (4.7), будет:
или, на основании (4.8), (4.9), в которых нужно положить
ft = 1, Ь хп — у п = хп,
е< = 2гР6Х + ^Рх.
Напряжения в слое О'тп, согласно (4.2), будут:
Sx = Хх — 4 Yy = - J (е, - г-zj,
Sy^Yv— — ^2). ’
$ху = *у :== 3^”(е12 ^х12)»
(4-18)
(4.19)
(4.20)
причём а4 есть определённая функция ef; напряжения Xz, Кг, Zz малы
сравнительно с основными.
Всё упрощение, вносимое в теорию оболочек гипотезами Кирх-
гоффа-Лява, состоит в том, что вместо шести компонентов напря-
жений можно ввести пять компонентов усилий и три компонента
момента, действующих на элемент оболочки в целом, причём эти
восемь величин будут функциями только двух независимых перемен-
ных Е, т); для их определения в конечном счёте достаточно одних
уравнений равновесия элемента, если только связь между усилиями,
моментами и деформациями и искривлениями будет установлена.
Пять компонентов усилий определяются, как равнодействующие
всех напряжений по двум взаимно перпендикулярным граням эле-
мента, длины дуг которого в серединной поверхности равны единице.
Если оболочка достаточно тонка, так что отношением толщины её
к характерному радиусу кривизны можно пренебречь сравнительно
с 1, мы получим следующие пять выражений для усилий:
Л/2
Т1 = J X„dz,
— Л/2
Л/2
-Л/2
Л/2
Лг = J* Ху dz,
-№
Л/2 Л/2
М = J* zx dz, — J Zy dz.
— Л/2 — Л/2
(4-21)
§24]
СВЯЗЬ МЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ
159
Перерезывающие силы N2, несмотря на малость напряжений Zx, Zy,
не равны нулю, и они определяются только из уравнений равно-
весия.
Аналогично можно написать формулы для изгибающих и крутя-
щего моментов
Л/2
Afj = J* Xxz dz,
— Ъ,/2
Л/2
м2 == J Yyz dz,
— Л/2
Л/2
Ml2=$Xyzdz. (4.22)
—w
Поскольку напряжения, приложенные
няются результирующими усилиями и
мент оболочки заменить элементом
рис. 52 изображён элемент
серединной поверхности
оболочки, и показана схема
действующих на него сил.
Силы 7\ и Т2 растягивают
его в направлении осей х
и у, сила Т12 создаёт сдвиг
внутри поверхности; поло-
жительные их направления
в осях х, у таковы же,
как и направления напря-
жений Хх, Yy, Ху. Поло-
жительные направления пе-
ререзывающих сил Nt, Х2
совпадают с положительными
Изгибающие моменты М2
к элементу,
моментами,
серединной
таким путём заме-
можно и сам эле-
поверхности.
Ha
Рис.
52.
7
направлениями напряжений
считаются положительными, если
стремятся дать выпуклость оболочке в сторону положительной оси z.
Крутящий момент М12 положителен в том случае, если со стороны
положительной оси х он стремится закручивать элемент по часовой
стрелке.
Для упрощения
ввести их линейные
Z^.
они
вычислений вместо сил 7\, Т2, Т12 удобно
комбинации
Л/2
Si = 7\— ~Т2=^ $Sxdz,
— h/2
Л/2
5а=7’2-|г1 = J Sydz,
— Л/2
Л/2
У ^12 = Лг ~ j* $ху dz,
— Л/2
(4.23)
160
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
а вместо моментов Aflt /И2, /И12 их комбинации
h/2
Н1 = М1 — y/W2= I* Sxzdz,
-h/2
h/2
Н2 = М2—~МХ=- | Syzdz,
— h/2
h/2
2 Г
-д’ = ^12 = I $xyz dz-
-h/2
Из (4.23) и (4.20) теперь имеем:
h/2 h/2
S. — е, f — dz — -z. i — zdz,
1 J et J ei
— h/2 -h/2
' h/2 h/2
S2 = a2 I ~ dz — -z2 I - z dz,
J e* J
—h/2 — h/2
h/2 h/2
«Sia = ei2 |* ~^dz *12 j* ~^zdz,
-h/2 - ii/1
а из (4.24) имеем:
h/2 h/2
H< =г, f — zdz — z. / — z2 dz,
J ei J ei
— h/2 - h/2
h/2 h/2
= e.2 f — zdz — x2 i — z2 dz, ;
I I
— h/2 —h/2
h/2 h/2
^12 = ^2 [<T2dz — x12 I ~Z*dz.
— h/2 —h!2
(4.24)
(4.23')
(4.24')
В формулах (4.23') и (4.24') встречаются три типа интегралов,
распространённых по толщине оболочки:
h/2
У1= pzidz,
J ei
-h/2
h/2
| — z dz,
J ei
-h/2
h/2
Js= J* dz. (4.25)
— Й/2
§24]
СВЯЗЬ МЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ
161
Через них силы и моменты выражаются просто:
Так как в (4.25) есть данная функция от е,-, причём конкретно
вид её для каждого материала становится известным в частных зада-
чах, естественно избавиться от интегрирования по z и, на основании
соотношения (4.19), перейти к интегрированию по et. Умножая
на Ре, на •—2PSX и Js на Рх и складывая результаты, получим:
Л/2
ЛРв-2/2Р,х + /3Рх= J (4.28)
Дифференцируя (4.19) по z, находим:
О
4- eidei = (zP, — Р6Х) dz. (4.29)
Умножим теперь на —Рех и J2 иа Рх и сложим результаты; тогда
получим:
ч л
-АРех+У2Рх = | j
(4.30)
Найдём выражение г2 через е4; для этого необходимо решить квад-
ратное уравнение (4.19)
22Рх-2гРех + Ре = |^,
корнем которого, не противоречащим соотношению (4.29), является
Р.х , /3 .. / 2 4 Р.Р-, — Р* . , о п ,
|/ е,-з
11 Зак. 31М- А; А. Ильюшин.
162
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
причём необходимо брать всегда положительное значение квадрат-
ного корня. Дифференцируя (4.31), получим:
dz
УЗ_________ejdej sign de{_______
2 I - 4 '
V ‘ 3 рг
(4.32)
de ‘
Знак величины zPA— Ре7, согласно (4.29), совпадает со знаком ,
а так как в интересующих нас интервалах dz всегда положительно
h . h j
при изменении г от — -% до + , то интегрирование по de{ должно
выполняться так, чтобы det тоже возрастало, т. е. необходимо инте-
грировать по de* sign fife*.
Рассмотрим значения интенсивности деформаций в трёх точках,
расположенных на оси z:
где
(4.33)
Обозначим их соответственно:
(4.34)
Как видно из (4.29), точка z = z0 есть точка минимума ef, так как
^-^>0. Следовательно, всегда имеют место неравенства
(4.34')
Будем говорить, что деформации растяжения и сдвига середин-
ной поверхности s1, е2, s12 соизмеримы или малы сравнительно
. - , , h , h , h
с деформациями изгиба оболочки ±-^-х1я ±у*2, ±ух12 или что
последние являются доминирующими, если точка z0 не выходит за
пределы толщины оболочки, т. е. если
Деформации серединной поверхности будем называть большими
или доминирующими сравнительно с деформациями изгиба, если
§24] СВЯЗЬ МЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ 163
точка z0 расположена вне толщины оболочки, т. е. если имеет место
одно из неравенств
(4.36)
В случае соизмеримых деформаций
от всякой положительной величины
ходимо вычислять по формуле:
растяжения и изгиба, интеграл
R по толщине оболочки необ-
Rdz —
eii
Г
Ч ’ t0
Re ide;
(4.35')
В случае несоизмеримых или больших деформаций растяжения такой
интеграл следует вычислять по формуле:
Л/2
J /? =
— Л/2
%
V^sign Г Rsjdej
2 yp; J /g<-< ’
eH
(4.36')
Введём теперь обозначения основных в теории оболочек величин:
Л — Ао,
A = AV
В — Во, С — Со,
B = Blt с=сп
(4-37)
где величины Ао, Во, Со относятся к
маций изгиба и равны:
случаю доминирующих дефор-
11*
е<1 ei,
Со = J Ve2i—eia de{ + J а4 Ve^ — e^ deiy
eh eh J
• (4.37')
164
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
а Д15 Blt относятся к случаю доминирующего растяжения сре-
динной поверхности и равны:
До = Д2 = J
eh
ej,
Bi = Г —== sl£n (еъ — eh) >
J
eii
eh ________
Q = J Of /4 _ el dSi sign (e,a — eh).
% *
(4.37")
Интегралы J2, Js, входящие в формулы (4.23'), (4.24'), (4.26)
и (4.27), можно выразить через основные величины Д, В, С, зави-
сящие от основных квадратичных форм Ре, Рп, согласно фор-
мулам (4.37). Для этого заметим, что интеграл на основании
формул (4.25) и (4.35'), (4.36') непосредственно выражается-через
функцию В\ после чего из (4.30) находим J2 через А и В и затем
из (4.28) получаем J3 через Д, В, С. Таким путём находим следую-
щие формулы:
1
I
ЗР„ л
--5"
2Pf
2^* ‘
(4.38)
Л
причём величинам Д, В, С нужно приписать индекс «0» и вычис-
лять их по формулам (4.37'), если доминирует деформация изгиба,
или же приписать индекс «1» и вычислять согласно (4.37"), если
доминирует растяжение-сжатие серединной поверхности.
Исключительный случай, когда формула (4.32) и все последую-
щие вычисления теряют смысл, представляет безмоментное напря-
жённое состояние, при котором величина е,-, а следовательно, и af
постоянны по толщине. В этом случае
Л. = Л.в = 0, (4.39)
и интегралы JY, J%, J.A можно вычислить непосредственно. Из фор-
мул (4.25) имеем:
А = ^, /,-0. (4.40)
§24] СВЯЗЬ МЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ 165
причём поскольку равенство = О возможно только при xt = х2 —
= х12 = 0, то изгибающие моменты все равны нулю:
Afj = Af3 == Af12 = О,
а силы находятся из простых соотношений:
Л A =51==/z^S1,
Га-уЛ =58 = Л2-е3)
х j
7„-p„=^5, J
(4.41)
Легко видеть, что формулы (4.41) получаются простым умножением
на h формул (4.2), имеющих место при плоском напряжённом состоя-
нии, причём
T^hX^ T2 — hYy, T^hXy. (4.42)
Соотношения (4.23'), (4.24') или (4.26), (4.27) дают выражения
сил и моментов, действующих на элемент оболочки, через три квад-
ратичные формы Ре, Рх, Рт:
2 м I 2 । 2 \
Рг = ei 4- ®1га + + ai2, I
Рх =’t! + x1x2+x2 + x?2, I (4.43)
Рех = zl*l + ®2Х2 + | ®1’Z2 + J ®2Х1 + XI2®I2 J
и шесть компонентов деформаций и искривлений
®1> ®2> ®12> х2> х12>
а следовательно, через три компонента вектора перемещения w
точки серединной поверхности
w = iu jv + kw,
поскольку деформации и искривления имеют определённые диффе-
ренциальные выражения через и, v, w.
Покажем, что и обратно все деформации и искривления можно
выразить через силы и моменты. Для этого прежде всего найдём
выражения квадратичных форм (4.43) через аналогичные квадратич-
ные формы от сил и моментов. Согласно выражениям S и Н, через
166
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
Т и М (4.23), (4.24) имеем тождества:
Ps = S! + S,S2 И- S2 + = 4 ( Л2 — Л Т2 + Tl + 3 Т?2),
Рн = Hl + HtH2 + | (ЛА-М^+М^-ЗМн),
Psh = + S2H2 + 1 5^2 + 4 + S12H12 =
= у + 7-2Ma - ± T\M2 - ± T2Mt + 3T12Af12).
(4.44)
Интересно отметить, что величины Р„ Рх с точностью до множителя
и обозначений по форме совпадают с. квадратом интенсивности
деформаций, а величины Ps, Рн по форме и с точностью до множи-
теля совпадают с квадратом интенсивности напряжений.
Составим теперь квадратичные формы Ps, Рн, Psh согласно
соотношениям (4.23') и (4.24'), предварительно заменив входящие
в них интегралы обозначениями (4.25) через Jlt J2, Js. Для этого
необходимо воспользоваться свойством (4.8), (4.9) квадратичной
формы Ри и аналогичным свойством билинейной формы Puv. Из
группы уравнений (4.23') имеем:
Ps = №* + JlP„ (4.45')
Аналогично из группы уравнений (4.24') находим:
Рн = №* — 2J2JsP„ + (4.45")
Составляя, наконец, из обеих групп уравнений (4.23'), (4.24') били-
нейную форму Р$н''
PsH — (Jizl-^2Х1)(А®1 АХ1) + (Ч®2 АХз) (^2®2 Ч7’) Ч~
Ч* (4S1 ЧХ1) (Ч®2 ^3Xs) Ч ~2 ЧХ1) (Ч®2 Чха) Ч"
Ч" 1®12 J2х1з) (Ч®12 JЗх1г)>
а затем, собирая коэффициенты при произведениях Ч, J2 и J2) J3,
получаем:
Psh = Р— (ЧА+Л2) ЛхЧ-ЛЛА- (4.45"')
Поскольку левые части соотношений (4.45) являются известными
функциями (4.44) сил и моментов, а правые зависят только от Pv
Рх, Ptx, так как J2, Js через них выражаются по формулам (4.38),
(4.37), (4.34), то соотношения (4.45) представляют три алгебраиче-
ских уравнения, из которых формы Pt, Рх, Ptx можно выразить через
Ps, Рн, Psh- ,
P*=fi{Ps, Рн, Psh), P^—fikPs, Рн, Psh),
Pn=fs(Ps, Рн, Psh). (4.46)
§24]
СВЯЗЬ МЕЖДУ ВНУТРЕННИМИ СИЛАМИ И ДЕФОРМАЦИЯМИ 167
Фактически это можно выполнить, конечно, только после того, как
дана конкретная характеристика материала оболочки, т. е. будет
задан вид функции а{ == Ф (^). Предполагая, что выражения (4.46)
уже найдены, мы легко можем найти выражения деформаций е, х
через силы Т, М или 5, Н. Для этого необходимо подставить (4.46)
в (4.38) и выразить Jlt Ja, Js через Pg, Ргг, Pgs, после чего решить
уравнения (4.23'), (4.24') относительно г, х. Например,
откуда
е2^2 Х1^3 “ 7^1,
__ S1J3 — НУъ
3 ' ’ 7g
S1J2 — PjJi
J1J3 — J%
Таким образом получим окончательные формулы:
S1 ~ д’ (^1А ^1Л)>
е2 == д' 3 Н
s12 — д'(^12^3
Д=/Л—Jl
В исключительном случае безмоментного напряжённого состояния,
когда формулы (4.32)—(4.38) теряют смысл или, лучше сказать,
приводят к неопределённостям, выражение деформаций через напря-
жения можно найти непосредственно из соотношений (4.41). Для
этого достаточно только из кривой а{ — Ф (ef) найти обратную зави-
симость — а величину
°* = Vx2x—XxYv+Yl + 3X2y
умножением на —— заменить, согласно (4.44), на
Ps=^ha°i-
Тогда найдём:
Уз /2 /Рс \ /3 / 2 \
—L—ф-1 —е2 = - j—- ф-1 - 5а,
2/Ру \нУЗ/ ^VPS \hV3j
Уз ( 2 У1\
8 2 yps
(4.48)
Д12-
Эти соотношения, впрочем, могут быть найдены и из (4.47), если
совершить предельный переход, стремя к нулю Р, как х2 и Рп как
х, и открыть неопределённости.
168
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
{ГЛ. IV
§ 2S. Потенциал сил и моментов и постановка задачи
о равновесии оболочек.
В § 11 уже было показано, что напряжения, возникающие в теле
при активной упруго-пластической деформации, имеют потенциал,
причём последний представляет собой работу внутренних сил. В слу-
чае несжимаемого материала работа внутренних сил, приходящаяся
на единицу объёма тела, равна
ei
W= f о, de,.
о
Естественно ожидать, что силы Т и моменты М, возникающие в обо-
лочках, также имеют потенциал, который представляет работу внут-
ренних сил, приходящуюся на единицу площади серединной поверх-
ности её
Л/2
U = [ Wdz.
— Л/2
Вариация функции U, соответствующая вариациям деформаций 8гд,
8s2> 8е12 и искривлений 8х15 8х2, 8х12, должна равняться работе сил
Л, Л2 и моментов /Й2, Л412 на вариациях деформаций и
искривлений:
877 = EjSsj -j- 7’28$2~|-27'126sJ2— AfjSxj — Л428х2— 2Л4128х12. (4.49)
Если вариацию 877 подсчитать
по формуле
Л/2
8(J = J" о48е4 dz,
— Л/2
(4.19), то мы получим новый
причём е, взять по формуле
выражения сил и моментов через деформации и искривления:
т __ди т _________ ди
д^’
.. ди ди
Что формулы (4.51) точно совпадают
диться путём вычисления вариации 8е4 согласно (4.19):
у e48ef = 8Ре — 2гВРеч + г28Р,
(4.50)
способ
(4.51)
т ди
12 2 ’
1 dU
с (4.26), (4.27), легко убе-
и подстановки её в (4.50); принимая обозначения (4.25), получаем:
877= |8РЛ - 18PSXJ24-| 8РЧ/3. (4.52)
§25] ПОТЕНЦИАЛ СИЛ И МОМЕНТОВ 169 .
Отсюда, между прочим, видим, что величины
Р Р Р
можно принять за обобщённые перемещения, а величины
________________________________*Lj г
3 р 3 2’ 3 3
— за соответствующие им обобщённые силы, причём
2 r _ dU 4 . _ ди 2 _ди ,, еоч
3J1~dPt’ 3J*~dPxe’ 3Js~~dPx' ( }
Если вычислить вариации 8PS, ЬРСХ, %РХ, согласно выражениям
(4.43), и заметить, что:
8Pe = 2PS(5s, 8Рех = Р8„х + Р„8х, 8Рх = 2Рх,8х, (4.54)
то, собирая коэффициенты при вариациях одних и тех же деформа-
ций и искривлений в (4.52), получим, например, при
4 r Z . 1 \ 4 , / , 1 \
^7 ~ 3 71 V*1 + 2 ®2/ 3 М*1 + 2 Ха7’
что, согласно (4.26), совпадает с Т1; аналогично убеждаемся в спра-
ведливости всех остальных формул (4.51).
Возможны три основные постановки задачи о равновесии пла-
стинок. 1) Постановка задачи в усилиях и моментах; для этого необ-
ходимо написать уравнения равновесия элемента оболочки и к ним
присоединить условия совместности деформаций и кривизн, выражен-
ные через усилия и моменты, согласно (4.47). Уравнений равновесия
будет, вообще говоря, пять: три уравнения равновесия проекций
сил Тр Т2, Т]2, А73 на оси х, у, г и два уравнения равновесия
моментов Л4р М2, М12 и моментов сил Nlf N2 около осей х и у,
недостающие уравнения находятся из условия совместности шести
величин гр е2, е12, -х2, -х12 (4.47), которые выражаются через
три компонента перемещений и, v, vd. 2) Постановка задачи в пере-
мещениях получается, если из уравнений равновесия исключить пере-
резывающие сйлы Nr, N2, а остальные усилия и моменты выразить
согласно (4.26), (4.27) через три компонента перемещения. 3) На-
конец, возможна постановка задачи без уравнений равновесия эле-
мента в виде вариационного уравнения равновесия оболочки. Для
этого необходимо составить вариацию работы внутренних сил всей
оболочки
8У = j" Jsc/dE, (4.55)
где интеграл распространён по всей серединной поверхности £, а 6/7
имеет выражение (4.49) или (4.52); затем составить работу поверх-
ностных сил на вариациях перемещений 8«, 8ц, и работу краевых
170 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
обобщённых сил на соответствующих им вариациях четырёх обоб-
щённых перемещений, составленных из 6«, 8®, 8w, и их производных
по координатам; обозначая эту работу 8'Д, получим вариационное
уравнение равновесия
8У = 8'Д,
решение которого можно искать, например, методом Ритца.
Ввиду громоздкости выражений деформаций ех, е2, е12 и искрив-
лений хх, х2, х12 через перемещения «, v, w, а также пяти уравне-
ний равновесия элемента для оболочки произвольного очертания, мы
не будем их выписывать, отсылая интересующихся к книге Лява.
В конкретных же задачах, которые будут рассмотрены ниже, мы
будем пользоваться частным видом всех этих соотношений.
§ 26л Конечное соотношение между силами и моментами
и постановка задачи о несущей способности оболочек.
Если интенсивность деформаций ef (4.19) любого слоя оболочки
достаточно велика по сравнению с пределом текучести es, т. е.
• 2 ]rpe-2^Pex + ^Px = е, ^>ев, (4.56)
Г ’Э
и материал её не обладает упрочнением, то закон = Ф (е,-) совпа-
дает с условием пластичности Мизеса:
а* = os = const., (4.57)
или приближённо может быть заменён условием пластичности Сен-
Венана-Кулона:
'Imax = -7^:= conSt. (4.58)
V °
Покажем, что в этом случае между силами и моментами существует
конечное (не дифференциальное) соотношение. По формулам (4.37),
вынося за знаки интегралов постоянную а,-, мы можем вычислить
значения функций А, В, С.
В случае доминирующих деформаций изгиба формулы (4.37')
принимают вид:
^о = аз(ей —
В„=01„
‘-'о S —--------7)------- ,
с.=У - j ча,
(4.59')
$ 26] КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ И МОМЕНТАМИ 171
1 в случае доминирующих удлинений серединной поверхности из
формул (4.37") находим:
Л1 = °8(Ч — еп)’
В обоих случаях величины eiv eh, eia выражаются формулами (4.34).
Рассматривая последние как уравнения относительно трёх квадра-
тичных форм Рх, PeyL, Ре, перепишем их в виде:
м 3
Ре4- Р, = 4 е-?,
* I 8* I 4 Х 4
Pt — hPn-\-^-Px=ie^.,
8 ех I 4 х 4
Р Р — Ра — —е2Р
v* 4 io -е
Решение их относительно квадратичных форм весьма несложно и
приводит к следующим результатам:
йРех = 4(е.2_е2),
ех 8 v Н
Рх = — е~ =t У~еа —
4 х 16 *1 •» ' г» *</
(4.60)
Для того чтобы определить знак в последней формуле, воспользуемся
неравенствами (4.35) и (4.36). В случае доминирующей деформации
изгиба из (4.35) имеем:
Л2 Л2
-2Л-Рх</гРех<2.4-Рх.
Легко проверить, что это неравенство будет иметь место, если
в формуле (4.60) для Рх в скобках взять знак (-]-). Аналогичным
образом убедимся, что неравенство (4.36) будет иметь место, если
для Рх в скобках взять знак (—).
Ниже во всех формулах, имеющих два знака, верхний знак будет
относиться к случаю доминирующего изгиба оболочки, а нижний —
к случаю доминирующего растяжения-сжатия её.
Введём два основных параметра 1 и у следующим образом:
(4-61)
172
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
(4.62)
(4.63)
принять
Эти параметры удовлетворяют условиям:
0<Х>р<1, (4.61')
поскольку eia—:есть минимальное значение интенсивности деформа-
ций в данной точке оболочки. Тогда формулы (4.60) можно'пере-
писать в виде:
Зе; ф
р_____h А2 Р________- АЛ
4^3 *ех
Л=-^(4н9+Д2),
где Aj и Д обозначают следующие функции:
Д1= | /Г^Г2 ± /Л2 — [Г2 |, д = 1~-. '
Вид формулы (4.62) для Pt станет вполне понятным, если
во внимание тождество:
4р2 4- Д2 == 1 -j- Ха -j- 2р2 + 2/ (1— р.2) (X2 — р.2).
Пользуясь обозначениями X, р и установленным правилом примене-
ния двузначных формул, можно теперь переписать выражения функ-
ций А, В, С (4.59) в виде:
X = ag«/i<p(X, р),
В = !*)> (4.64)
V2JX(X, р) —р2<Ь(Х, р)],
причём функции ф, 4 и у определяются так:
<р = Х— 1,
ф = (In 1+^EZ ± 1П Л+|, (4.65)
у = | /1 — p2~ ± X /X2 —p2 | .
Пользуясь формулами (4.62) и (4.64), теперь мы можем убедиться
в том, что квадратичные формы Pg, Рн и Psh, согласно формулам
(4.45) и (4.38), не зависят от величины е{1 и являются функциями
только параметров X и р. В самом деле, слагаемые (4.45') имеют
общий множитель а2 /г2, но не зависят от е{, .так как J2 обратно про-
порционально е^, а Р* прямо пропорционально е2, и потому J2 Pz
не зависит от eir. Аналогично убедимся, что слагаемые (4.45") имеют
общий множитель а2 /г*, а et в них сокращается и, наконец, что
слагаемые (4.45"') не зависят от eit и имеют общий множитель a2 hs.
§26J
КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ И МОМЕНТАМИ
173
В связи с
значения сил
этим естественно ввести обозначения для характерного
Гр Т2, Т12 и моментов Ми М2, М12:
Ts
asA2
Т~
(4.66)
М
Как увидим, величины Ts и Ms соответственно в задачах о безмо-
ментных деформациях оболочек и задачах о чисто моментных дефор-
мациях их играют такую же роль, как предел текучести as в задаче
о плоском напряжённом состоянии. Поэтому целесообразно ввести
обозначения для безразмерных сил и моментов:
t — —1 у > t -Ь. 'Г > 1 S f Tvt f12 — ~f~ 1 s
Afj _ M12
m'2~ W12 Ms
(4.67)
а вместо квадратичных
формы от безразмерных
форм (4.44) рассматривать
квадратичные
сил и моментов:
Qm = m\ — mtm2 -f- 3m22
(4.68)
Qtm = ^т1 — 2- — 2 + 3^12^12-
Последние связаны c Pg, Рн, Psh очевидными соотношениями:
4Pff
4/\ 4Pff 4PSH
Qt = T^' Qm~~3My Qtm==3f^Ts-
(4.69)
Произведя довольно громоздкие преобразования правых частей урав-
нений (4.45), а именно возведение в квадрат многочленов и пере-
множение, и собирая затем коэффициенты при
4'9> ?2> ФЧ*» Z'b Х2>
получим следующие уравнения:
Q# = -4 W + <p2),
Qtm = -J- (н2^9+Д'?2 + нМ 4- ?х),
Qm = (н2+д2 И2 + (4^2+д2) ?2 +
2р.2Д®<р — 2|*2<рх + 2Д«Х + Х21 •
(4.70')
174
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Поскольку правые части уравнений (4.70'), согласно (4.63) и (4.65),
являются функциями только двух параметров X и у., то в трёхмер-
ном пространстве с переменными Qt, Qm, Qtm они представляют
поверхность
f{Qt, Qm, Qtm'i — 0’ (4-70)
а (4.70') является параметрическим уравнением этой поверхности.
Получаемая таким образом связь между квадратичными формами (4.68)
называется конечным соотношением между силами и моментами,
действующими в оболочках. Конечное соотношение было получено
из гипотезы Мизеса а( = и потому оно является обобщением усло-
вия Мизеса1) 14.
Существование конечного соотношения между силами Т и момен-
тами М в случае идеальной пластичности, т. е. при условии Мизеса
и при малости упругих деформаций, вытекает и непосредственно из
формул (4.23') и (4.24'), поскольку при этом они являются одно-
родными нулевой степени относительно шести величин е1( еа, е12,
х2, х12. Отношение любой деформации к et, согласно (4.19),
может быть выражено через пять независимых параметров. В самом
делех пусть, например, Xj ф 0; обозначая/пять соотношений
мы можем выразить правые части уравнений (4.23') и (4.24') через
Ci
эти пять параметров, так как —- или
• fl.
2 ’ 2 ’ 2
*1 Xj xx
будут зависеть только от них. Но если шесть величин .Sj, S12,
Н2, Н12 являются функциями только пяти параметров, значит,
между ними существует одно конечное соотношение, и оно пред-
ставляет поверхность в пространстве с шестью переменными Т1г Т2, Т12,
/Ир М2, М12. Поверхность (4.70) представляет трёхмерный образ
указанной поверхности шестимерного пространства.
Переходим к более подробному анализу конечного соотноше-
ния (4.70'). Прежде всего отметим три частных случая конечного
соотношения.
1. Безмоментное напряжённое состояние имеет место при хх =
= х2 = х12 = 0; при этом и Pez = 0 (4.68). Конечное соотношение
получим из (4.70'), если положим, что деформации волокон по тол-
щине оболочки одинаковы:
ец = е<-, = 4> Х = р.==1.
!) Заметим, что конечное соотношение, выведенное нами из уравнений
теории малых упруго-пластических деформаций, будет иметь такой, же вид
и согласно теории течения Сец-Венана-Мизеса.
§26] КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ И МОМЕНТАМИ 175
В формулах (4.63), (4.65) можно взять нижний знак и затем открыть
неопределённости в формулах (4.70'). Тогда найдём, очевидно, усло-
вие Мизеса:
= = Q,= l, (4.71')
или в развёрнутом виде:
1\Т2+ 71+37* =7*. (4.71)
2. Чисто моментное напряжённое состояние имеет место при
отсутствии удлинений серединной поверхности. Квадратичная форма
Р, = 0, а потому Рп — 0. Как следует из формулы (4.19), интен-
сивность деформаций ег есть чётная функция z и, согласно (4.34),
имеем:
eia = $, X=l, u. = 0.
В формулах (4.63), (4.65) следует брать нижний знак, так как из
(4.33) имеем z0 — Q; таким образом получаем:
Aj=2, Д = 0, ср == 0, ф = 2 1п2, Х=2.
Конечное соотношение (4.70') принимает такой вид:
QZ = Q#M = O, Qm=l, . (4.72')
ИЛИ
М2_ММ Л-Af2 + 3Af2 — Ml (4.72)
3. Простейшее сложное напряжённое состояние оболочек при
Р., ф0, Р-. ф 0 имеет место, если билинейная форма Ргу обращается
в нуль:
T’sz = Z1 ^S1 + 2’ e2j + ‘Z2 + "2 Sl) + z12®12 = (4.73)
Оно может иметь место, например, в случаях,
а) 'с12 = ха = °> «14=0, 8j = — -|s2;
Ь) 512 = 62 = °, ®1 ф 0» Z1 = “7Z2
и многих других.
Из (4.60) при этом имеем:
, =~= , X = 1, [t 1,
т. е. налицо доминирующая деформация изгиба. Находим:
Д = ? = о, Дх = х = 2 /1 —-х2 , ф = 2 In -+ — 1x2 ,
Р’
176
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
и после несложных преобразований конечное соотношение принимает
вид:
с 1—р.2
1 + Vi —
Iх
Qto = o,
Qm —
Г"----2 1П
1 --|Х2
1 + /1 И2
Iх
(4-74)
Оно даёт линию пересечения поверхности (4.70) с плоскостью Qtm~
— 0. Поскольку Qt, Qm существенно положительны, вся поверхность
расположена между плоскостями Q( = 0 и Qm = 0, а линия (4.74)
между положительными направлениями осей Qt, Qm, т. е. в первом
квадранте плоскости QZm = 0. Точка Qm = 0,' Q( = l, соответствую-
щая безмоментному состоянию оболочки, получается из (4:74) при
у = 1, а точка Qt — 0, Qm=l, соответствующая чисто моментному
состоянию оболочки, получается при р. = 0. Последнее очевидно,
поскольку [j. In у. = 0 при у. = 0. Уравнение (4.74) можно преобра-
зовать к другому виду, если произвести замену параметра
_ Iх2
“ 1—(J.2’
Н==
Iх!
1 +Н1 ’
причём изменению у. от 0 до 1 соответствует изменение pj от 0
до оо. Если воспользоваться тождеством
In 1 1п Г1 + н + .1... >
У Iх I 2 V 1 + Iх! — 1
то (4.74) примет вид:
Qt = ’ ^InaЕ 1+ixt+_L
* 4^ /1+^-1 ’
2т -= н in /г+кГ
(4.74')
Кривую QfQm можно построить по точкам, координаты которой
внесены в табл. 4.
Таблица 4.
Координаты кривой QfQm-
Iх! 0 0,01 0,02 0,04 0,1 0,25 0,5 1 2 3 8 ОО
Iх 0 0,10 0,141 0,196 0,301 0,447 0,578 0,707 0,815 0,865 0,944 1
Qt 0 0,09 0,141 0,214 0,342 0,522 0,660 0,782 0,875 0,908 0,960 1
Qm i 0,95 0,917 0,861 0,746 0,574 0,416 0,275 0,168 0,122 0,050 0
26] КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ И МОМЕНТАМИ 177
На рис. 53 изображена кривая (4.74) и прямая
Qt Ч- Qm —1 >
(4-75)
которая довольно хорошо апроксимирует её. Максимальное отклоне-
ние прямой составляет около 9%.
Поверхность (4.70) симметрична относительно плоскости Qtm — 0.
В этом нетрудно убедиться, если рассмотреть значения параметра >
в окрестности Х = 1. Для этого введём новые параметры:
= = = Т (4.76)
A ‘'It Л
и будем рассматривать значения квадратичных .форм Qt) Qm, Qtm
при значениях
Х<1, у- < X и у. < X', X' < 1,
обозначив значения форм в последнем случае через Q', Q'm, Q'
Произведя замену X, у. на Х'р/, согласно (4.76), получим:
Внося эти значения в (4.70'),
получим:
Qf Qt’ Qm ~ Qm'
Qtm Qtm'
откуда вытекает симметрия
поверхности (4.70) относи-
тельно плоскости Q(,„ —0.-
Таким образом достаточно иметь представление о поверхности (4.70),
только в первом октанте систему координат Qt, Qm, Qtm. Можно
убедиться в том, что на линии X = 1 в плоскости (Qt, Qm) вели-
чины Qt, Qm имеют максимум. Если ещё воспользоваться неравен-
ством Шварца В1,«.которое в отношении квадратичных форм Qt, Qm,
Qtm гласит:
Ofm QfQm'
то можно заключить, что величина Qtm по модулю также ограни-
чена.
12 Зак. ЗИ8. А. А. Ильюшин
1^8
РАВНОВЕСИЕ ПЛАСТИЙОК И ОБОЛОЧЁ1< ' [гл. IV
Таблица 5 даёт координаты некоторых точек поверхности на
л'иниях X = const., причём против каждого значения X даны: в первой
строке во второй — Qm и в третьей — Qtm.
Наибольшие значения Qtm будут в случае, когда неравенство
Шварца превращается в равенство
= <¥?„> (4-77)
причём оно возможно только тогда, когда величины t и т пропорцио-
нальны:
-^1 = — = (4 77'\
mt т2 т12 ‘ \ )
Покажем, что гиперболический параболоид (4.77) пересекается
с поверхностью (4.70) по линии у. = 0. Из (4.65) при р = 0 имеем:
<р == — 1 -} X, •£ = 1 zt X2, u/i = 0, j
Л1 = 1±„, 4 = J=J. |
(4.77")
Внося эти значения в уравнения (4.70), получим:
5(д?+•/•)’ = (4-78)
Отсюда в -случае доминирующего растяжения оболочки (при ниж-
нем знаке в (4.77")) имеем:
Qt ~ 4, Qtm ~ Qm ~
т. е. линия и. = 0 вырождается в точку.
В случае доминирующего изгиба оболочки получаем:
О о -- 4М!~М о _ (4 79м
Qt — U+xp Т+х)3 ’ ~ (1 + хр ’
откуда следует (4.77). Кроме того, из последних уравнений легко
находим другое соотношение:
Qw==(l—Q«)a> (4.79)
а, комбинируя его с (4.77), находим ещё:
\Qtm\ = (y-Qt}VQt. (4.80)
Отсюда заключаем, что линия р. = 0, определяющая наибольшие
по модулю значения билинейной формы Qtm, представляет собой
линию пересечения двух параболических цилиндров, из которых
цилиндр (4.79) проходит через точки:
Qt=l> Qm==0, Qtm== 0 И Qt = 0, Qm = l, Qmt’^^t
Таблица 5.
Координаты точек поверхности (4.70).
р' X С 0,1 0,2 0,3 0,4 0,6 0,8
Х= 1 0 1 0 0,09047 0,9494 0 0,21998 0,9379 0 0,4674 • 0,6204 0 0,6789 0,3996 0 0,8539 0,1887 0
X = 0,8 0,0123 0,9760 — 0,1095 0,2596 0,8131 — 0,07067 0,5287 0,56t;6 — 0,0с 84 0,7519 0,3109 — 0,018.3 0,9651 0,0472 — 0,0022
X = 0,6 0,0695 0,8770 — 0,2340 0,3424 — 0,7107 — 0,1375 0,6349 0,4457 — 0,0642 0,9289 0,0)91 f 9 — 0,01015
X - 0,4 0,1850 0,6660 — 0,3510 0,3229 0,5339 — 0,2610 0,5909 0,5171 — 0,1729 0,6748 0,3658 — 0,0988 0,8959 0,1264 — 0,02502
X = 0,2 0,445 0,310 — 0,372 0,6053 0,2359 — 0,2454 0,8856 0,1197 — 0,0512 8
§ 25] КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ Й МОМЕНТАМИ 179
isb
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
{гл. IV
Рнс. 54.
имея образующие, параллельные координате Qtm, цилиндр же (4.80)
имеет образующие, параллельные координате Qm, и проходит через
те же точки. Линия у = 0, ограничивающая кусок поверхности
(4.70) для доминирующего изгиба, на котором значения Qt, Qm, Qtm
имеют механический смысл, показана на рис. 54J). Максимальное значе-
ние ординаты Qtm по
модулю будет при
Qi="з ’ Q“ = <г
и имеет значение
2
I Qtm lmax £ yy •
Таким образом, конеч-
ное соотношение ме-
жду силами и моментами в случае доминирующего изгиба может
быть приближённо представлено, как пара плоскостей, проходящих
через линию (4.75") и через точки
1 4 2
Qf== — , Qm = — > Qtm — — -------•
* 3 9 зуз
Они имеют уравнение:
Qt + Qm 4“ T/T I Qi»» I — 1 ‘
Переходим к постановке задачи об определении несущей способ-
ности оболочек. Если предположим, что силы и моменты или
квадратичные формы Qt, Qm, ~Qtm заданы и удовлетворяют конечному
соотношению (4.70), то по ним любые два уравнения (4.70) позволяют
найти параметры
(4.81)
}.=
еч
еч
а затем, согласно (4.62) и (4.38), найти Jt, J%, J3. При этом вели-
чина е/, останется неопределённой,
Л==т-Л(^
ч
Г. (Q>_,
и мы получим:
Qm’
Qm’
Qtm)>
Qtm)i
Qtm)’
(4.82)
где Fn будут вполне определёнными функциями сил и моментов.
!) Эта линия нанесена на развёртке параболического цилиндра (4.79).
§26] КОНЕЧНОЕ СООТНОШЕНИЕ МЕЖДУ СИЛАМИ И МОМЕНТАМИ 181
Если эти значения интегралов J2, J3 внести в формулы (4.23')
(4.24'), то одно из получающихся таким образом шести уравнений
будет следствием пяти других, так как силы Т и моменты М
удовлетворяют конечному соотношению (4.70). Решая эти шесть
уравнений относительно шести деформаций и искривлений, мы получим
уравнения (4-47), которые, согласно (4.82), принимают вид:
_ S^-H.F, ®1 Д'- *1 =
. — H$F2 еа — " д' ‘ > х2 = «и
®Г2 — еЧ Д' х12~еЧ
Д'
S^F2 — 1
Д'
^12^ 2 H)2FI
Д'
(4.83)
(Д' = 7^3-/ф,
причём одно из них есть следствие пяти других, если е,, имеет
значение (4.34); в этом нетрудно убедиться, если составить из выраже-
ний (4.83) соответствующие квадратичные формы.
Поскольку шесть компонентов деформациий и искривлений вы-
ражаются с помощью дифференциальных операций по криволиней-
ным координатам через три компонента вектора перемещения w
точки серединной поверхности, они должны удовлетворять уравне-
ниям совместности деформаций. В общем случае уравнения совмест-
ности можно выразить только через силы Т и моменты М, но в случае
(4.83) они будут содержать ещё одну функцию координат е41. Та-
ким образом дифференциальных уравнений равновесия и условий
совместности деформаций будет недостаточно для определения сил
Тц Т2, Г12, моментов Л42, М12 и неизвестной функции etl.
Недостающим уравнением и будет конечное соотношение (4.70')
между силами и моментами. В виду того, что это соотношение
не дифференциальное и из него следует, что силы и моменты и
даже их квадратичные формы Qt, Qm, Qtm ограничены по вели-
чине, ясно, что при произвольных внешних силах равновесие обо-
лочки невозможно.
Несущей способностью оболочки называется то предельное значе-
ние внешних сил, при котором внутренние силы Т и моменты М
удовлетворяют конечному соотношению (4.70'), уравнениям равно-
весия, условиям совместности деформаций и граничным условиям.
В некоторых частных случаях благодаря конечному соотношению
задача о равновесии становится статически определимой и не требует
условий совместности деформаций. Тогда вопрос о несущей способ-
ности оболочки решается сравнительно просто. Он ещё более
упрощается, если силы и моменты могут быть выражены через внеш-
ние силы только с помощью уравнений равновесия, что имеет место,
например, в безмоментной теории оболочек; в таком случае конечное
соотношение (4.70') определяет несущую способность.
182
РАВН0В6СЙЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
Условия совместности деформаций делают задачу об определении
несущей способности весьма сложной и потому важное значение
имеют приближённые методы её решения. Энергетический метод
решения состоит в следующем: задаются подходящей формой дефор-
мированной поверхности оболочек и, составляя выражения вариации
работы внутренних сил и работу внеших сил на вариациях перемеще-
ний, сравнивают их. Приближённое предельное значение внешних
сил получится, если упрочнение материала положить равным нулю,
а деформации неограниченно увеличивать или, что то же, сохраняя
постоянным предел текучести ag = 3Geg, О стремить к бесконеч-
ности, a es — к нулю. Хар и Карман ввели понятие полной пластич-
ности, по существу, заменяющее одно условие пластичности Мизеса
двумя условиями и тем самым расширили класс статически определи-
мых задач; об этом будет сказано в связи с изложением задачи
о штампах.
§ 27. Деформация пластинок в их плоскости.
Если внешние силы приложены к пластинке в её плоскости, мы
имеем случай плоского напряжённого состояния. Искривления отсут-
ствуют, и поэтому:
Р-l = ^ez. ~ Qm = Qtm “ О-
Квадратичная форма Pt связана в этом случае простым соотноше-
нием с
2 г—
Силы Tt, Т2, Г12 получаются умножением на толщину h напряже-
ний Хх, Y„, Ху-.
T\ — hXx, T2 — hYy, T12 = hXy-,
поэтому
П+Зхг, <4-84)
Пусть и (х, у), v(x, у) будут компонентами вектора перемеще-
ния точки пластинки по осям х, у. Деформации определяются
формулами Коши:
_ дм ди ди , ди о_.
дх ’ evv ду ’ = ду дх * (4.85)
причём, согласно (4.2) и (4.4), они могут быть выражены через
напряжения, если материал пластинки обладает упрочнением. Обо-
значая рХ, pY— массовые силы, действующие в плоскости пластинки, мы
можем написать дифференциальные уравнения равновесия элемента
+ ^+^-|_рУ==о. (4.86)
§27] ДЕФОРМАЦИЯ ПЛАСТИНОК в их .плоскости 183
Если .на границе пластинки заданы напряжения А",, К,, то граничные
условия задачи принимают вид:
Xal-Y Хут Х„ Yxl+ Yym = (4.87)
причём через I, т — обозначены направляющие косинусы нормали
с осями координат. Если на границе известны смещения точек
и = (х, у), v = v4 (х, у), (4.86')
то задачу о нахождении деформаций и напряжений, возникающих
в пластинке, удобнее, решать в перемещениях, т. е. воспользоваться
уравнениями (2.69), положив в них
и = и(х,у),' v = v(x, у),
т. е.
з™, = э„, = О, X-,=* Y,= Z. = 0.
Задача при заданных на контуре напряжениях (4.87) может быть
сведена к интегрированию одного дифференциального уравнения.
Предположим, что массовые силы отсутствуют, и введём функцию
напряжений Эри:
X —дгр V — d'F X — d2F (4 RR\
—Yv~ dx^ ХУ~ дхду ’ (4.88)
В таком случае уравнения равновесия будут удовлетворены. Интен-
сивность напряжений будет иметь следующее выражение через Ft
a, = Vf2 — F F 4-F2 +3F2 ; (4.89)
г V XX хх уу • уу 1 ху’ > '
поэтому, согласно (4.2) и (4.4), деформации будут равны:
^В + тМ^ЧЙ).
= <4'90’
Ь,—3[l+?Wl4
Дифференциальное уравнение, определяющее функцию напряжений F,
найдём из условия совместности деформаций:
I £уу __ л
д_у2 дх2 дх ду
Выпишем явно только главную часть этого уравнения, содержащую
высшие производные от Ft
«+К - 6V« ®^+2«+*аЧ^);₽5;=-
~6SAs^+«+sl>ey+z=<l- <4'91)
184
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Здесь у— квадратичная функция третьих производных от F, а 6
имеет выражение:
л — 4- ?)
\ . rfy
d^i
Если величина аг меньше предела текучести оа, то ® = 0, и по-
тому <р = 0°- Уравнение (4.91) в этом случае совпадает с обычным
бигармоническим уравнением плоской задачи теории упругости.
При уравнение (4.91) всегда эллиптического типа, так
как уравнение характеристик 151 приводится к виду
HP2+l)2 + (V+5js = 0.
Рассмотрим частный вид зависимости интенсивности напряжений аг
от интенсивности деформаций (4.4), близкий к закону ломаной:
Of / Л \
= -Ъ-ЗНк-! , (4.92)
2(1 — л) \ as /
причём к = 0, если и 0 <^к < 1, если >> ss. Функция (<з$)
в этом случае имеет вид:
, л \
2(1—к)\а^ /’
причём постоянная величина к определяется так:
при X==1- = (4-93)
при О/ < к = 0.
На рис.' 55 дана кривая (4.92) при к = 0,95. Функция i, входящая
в левую часть уравнения (4.91), в данном случае имеет следующее
выражение:
?=-2Г-°« +-2-=<, (4-94)
т. е. с точностью до постоянной слагаемой представляет собой одно-
родную квадратичную форму от вторых производных функции
напряжений F. Функция у, входящая в уравнение (4.91) при законе
(4.92), имеет, пожалуй, также простейший вид:
у = 3S (-®3 4- 3SX (—г Y+(зя 4- ~ s ) (тДС-Y 4-
' v \ дх3) 1 х \ ду3 ) 1 \ ® 1 2 У)\ дх2ду) 1
_L(\ I Ч d'<F V о.у ( d3F. ffJF I d*F дзр \ I
~Г ( у "Г 2 х ду2} У V дх3 дх2ду ду3 дх ду2/ *~
, 3 „ &F d3F , 3 у d3F d3F ,
>" 2 Лх дх3 дх ду2 "г 2 УУ ду3 дх2ду
। 3 „ d3F d3F d3F d3F (
"t 2ЛУ.ду»дх3 1{>ЛУ дх2ду дхду2' { }
§27]
ДЕФОРМАЦИЯ ПЛАСТИНОК В ИХ ПЛОСКОСТИ
185
Она представляет однородную кубическую форму вторых и третьих
производных от F. Таким образом дифференциальное уравнение для
функции напряжений в области пластических деформаций является
линейным относительно четвёртых производных и кубическим отно-
сительно всех входящих в него производных от функции напряжения.
За исключением простейших слу-
чаев, а именно: задачи о растяже-
нии-сжатии полосы, когда функ-
ция F зависит только от одной
переменной, задачи о чистом из-
гибе и других простейших
задач, никаких решений плоской
задачи для пластинок, материал
которых обладает упрочнением,
нам не известно.
Рассмотрим теперь задачу о
несущей способности пластинок
в их плоскости. Так как при этом
имеФг место условие пластичности
Мизеса или Кулона-Сен-Венана,
ними и, в частности, неопределённой является функция ср в форму-
лах (4.90). Предположим, что напряжения в пластинке, удовлетво-
ряющие уравнениям равновесия (4.86), условию пластичности и
некоторым условиям на границе пластической области, найдены. Тогда
из условия совместности деформаций (4.90) можно составить следующее
дифференциальное уравнение для функции ср:
о v । <? д2<? [ dsn о дхгЛ i
S'dx2 й У дх ду ' х ду2 ' дх к дх" ду )~т
3^-') + (1+ср)('^4 —3й^ + -у¥) = 0- (4-96')
• ду \ ду дх ) 1 v 1 у \ ду2 дхду 1 дх2 )
Поскольку для данных напряжений легко найти функцию напряже-
ний F, мы можем упростить дифференциальное уравнение (4.96') и
написать его в виде
деформации являются неопределён-
s4 й — Й" + Й + 2 Й й ( V 2 Л +
дх2 У дхду 1 х дх2, ’ дх дх 4 ' 1
+ (V2n + d +<p)V4F = 0. (4.96)
Чтобы выяснить тип этого уравнения, напишем дифференциальное
уравнение для характеристик И:
5«Ш+3*»-Й-+^=°-
Отсюда находим корни:
<4'97>
186
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Легко видеть, что под корнем в правой части находится выражение,
инвариантное относительно преобразования осей координат. Введём
главные напряжения:
°1> °2’ °3 == == ®
и главные касательные напряжения (1.10):
12 —Т-’
^2 а3
т28 = —2~ >-2^’ Tsi = " ’
(4.98)
Напряжение
формулой:
т12 через компоненты Хх, Yy, Ху выражается известной
Выражение, стоящее под корнем в правой части уравнения (4.97), как
легко видеть, может быть выражено через т12
и = (1.20):
Д = 9X# — 4S*Sv = — <4, (4.99)
откуда следует, что Д есть инвариантная величина.
Предположим сначала, что максимальным касательным напряжением
является именно т12. Это будет при условии ajaa < 0, т. е. когда aj
и а2 различны по знаку. Теперь из неравенства (1.22) следует:
12тЦ1—Д<12тЦ1— |),
(4.100)
2
и потому Д не только положительно, но и почти постоянно, поскольку
вместо условия пластичности Мизеса можно с известной точностью
взять условие постоянства максимального касательного напряжения:
(4.101)
Характеристики уравнения (4.96) будут действительными и имеют
следующее уравнение:
£Уд_ _ Xy±2czs
dx ‘IYy —Хх
(4.102)
где величину с можно считать постоянной, поскольку она изменяется
в пределах:
0,91455 А < с 0,935. (4.102')
Уравнение (4.96) будет при этом гиперболического типа.
Если напряжения а1( а2 одного знака, так что их произведение
положительно
°1°г > °!
§27]
ДЕФОРМАЦИЯ ПЛАСТИНОК В ИХ ПЛОСКОСТИ
187
то максимальным будет одно из напряжений т23, т31. Предположим
для определённости, что | at | > | с2|. Тогда из (4.99) имеем:
R+’]-
откуда следует, что, если
0<-|^<0,5, (4.103)
то А > 0, и уравнение (4.96) будет гиперболического типа, а харак-
теристики (4.97) будут действительными. Если же
1>Л->0,5, (4.104)
то А < 0, характеристики будут мнимыми, а уравнение (4.96) для
функции <р будет эллиптического типа. Для определения деформаций
в любой точке той области пластинки, где имеет место условие (4.104),
величина <s или интенсивность деформаций et или любая из дефор-
маций ехх, еуу, еху должна быть задана на всей границе этой области,
причём это может быть совершенно произвольная однозначная
функция дуги контура.
Соотношения между напряжениями и деформациями (4.90) в главных
осях эквивалентны пропорции:
= 3£1_ = 05,
ах — а2 2oj — а2 2а2 — '
На основании (4.98), (4.103) и (4.104) мы заключаем, что уравне-
ние (4.96) будет эллиптического типа в том случае, если
ete2 > 0, (4.106)
и гиперболического типа, если
ete2 < 0. (4.107)
В случае «jC2 = 0 оно будет им'еть параболический тип.
Покажем теперь, что дифференциальные уравнения равновесия:
дХх г _ Q дУх . dYy __ Q
Ох ' ду ’ дх ' ду ’
при условии пластичности Мизеса
' Х2х — ХхУу+У2у + ?>Х2у = га
или при условии постоянства наибольшего касательного напряжения
(после соответствующей замены величины а4 на ттах) всегда имеют
характеристики, совпадающие с характеристиками (4.97), и потому
188
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
тип их совпадает с типом уравнения (4.96). Для этого, дифференцируя
условие Мизеса по х и по у:
__ Ч У __ С I С 1g
ЛУ дх дх дх , .
□ у дХу __ с дХх , „ дУу
6ЛУ ду ~~^x ду "г ^У ду
и подставляя значения производных напряжения Ху в уравнения
равновесия, перепишем их в виде:
Sx — зх. 4- sn = °’
х дх У ду 1 У дх
С ______ О у ^Хх । с dYy ___ Q
sx ду 6лу дх -уЪу ду —и.
(4.108)
Отсюда видно, что уравнение характеристик системы (4.108) точно
совпадает с (4.97'); исключая же, например, Yy из (4.108), получим
уравнение,, аналогичное (4.96):
о д2Лд. „ у. д*Хх I q д*Хх । р___„
ЬУ~дХ* 6ЛУдхду^ х ду* ~УГ— и’
где г зависит от напряжений и их первых производных.
Таким образом уравнения, определяющие несущую способность
пластинок и деформации её, будут эллиптического типа, если макси-
мальный сдвиг частиц материала происходит по поверхностям,
наклонённым под углом 45° к пло-
скости пластинки, и, наоборот,
они будут гиперболического типа,
если максимальные сдвиги проис-
ходят по поверхностям, пересе-
кающим пластинку под прямым
углом, причём сами максимальные
сдвиги происходят параллельно
плоскости пластинки. Решение ура-
внений пластичности при 'стах=т1.г,
когда они имеют гиперболический
тип, будут рассмотрен^ в главе
VI, в связи с изучением плоской
деформации тел.
Рассмотрим некоторые свой-
Рис. 56.
ства решения уравнений равнове-
сия при условии пластичности ттах = const, в том случае, когда главные
напряжения а2 имеют одинаковый знак, так что aj а2 > 0. В таком
случае максимальное касательное напряжение действует по площадкам,
наклонённым к плоскости пластинки под углом 45°, и оно лежит
в плоскости, перпендикулярной к пластинке. Проведём траектории
главных нормальных напряжений (рис. 56); они образуют ортого-
§27]
Деформация пластинок в их плОСКОСТЙ
183
нальную криволинейную систему координат ($п $2), причём будем
считать, что координаты $2 изменяются соответственно в напра-
влениях действия главных напряжений а„ а2. Пусть элемент дуги dS
имеет следующее выражение:
dS*=ldSl+d£=Aldll+Ald&, (4.109)
так что коэффициенты первой квадратичной формы Alt А2 суть
известные функции координат В1; $а. Кривизны линий $2, очевидно,
определяются уравнениями:
——- Aj dS% —
i______i JL —___________________
AjAg d&a f AiA2’
dS?
представляют изменения углов наклона, каса-
#2
или, поскольку
1
(4.110)
Величины ,
тельных к линиям £а при Переходе из точки 0 по соответствующей
координате. Поэтому легко непосредственно вывести уравнения
равновесия
в точке 0,
элемента dSj, dS2, проектируя силы на направления
имеем:
(ai dS£) dSr a2
на направление S2:
(a2 dSJ dS2 - 01 dS2 = 0.
После некоторых преобразований получаем:
d°i । <?i — у?_г.
<?Si^ /?2 ’
• д»2 [ О2--О'!_
dS2"r /?i “и-
Условие пластичности ттах — const. = k в рассматриваемом нами слу-
чае имеет вид:
f7 = °:
аналогично
если | Qj |
или
тогда из первого
(4.1115
(4.112')
о2 = ±2Л, (4.112")
Предположим для определённости, что |aj | > | о2|;
уравнения системы (4.11) имеем:
— 26 — а2 __п
/?2 “U’
(4.113)
190
РАВНОВЕСИЕ ПЛАСТИНОК и оболочек
[гл. IV
откуда получаем два решения. Первое даёт:
О2 = а1==±2А. (4.113')
В этом случае оба уравнения равновесия удовлетворяются тожде-
ственно. Решение (4.113') соответствует равномерному всесторон-
нему растяжению или сжатию пластинки, причём растягивающее
или сжимающее напряжение а на контуре имеет проекции:
X, == 2kl, У, = ± 2km.
Второе решение
/?2 = со (4.113")
означает, что траектории, на которых действует постоянное главное
напряжение, суть прямые линии, а линии, вдоль которых оно дей-
ствует, суть ортогональные траектории к этим прямым.
Таким образом, если вся пластинка полностью находится в пла-
стическом напряжённом состоянии, и главные напряжения ап а2
всюду имеют одинаковый знак, несущая их способность опреде-
ляетсй элементарно с по-
мощью уравнений (4.113')
или (4.113"); одна из систем
траекторий главных напря-
жений представляет семей-
ство прямых линий, причём
нормальное к этим прямым
напряжение постоянно и рав-
но -±z2k. Величина 2k за-
ключена в пределах
^>2А>а8, (4.114)
Рис. 57.
поскольку условие пластич-
ности Мизеса
2 ,-22
°1 — aja2 а2 — ag
вписанный и описанный около него
в плоскости а„ а2 изобра-
жает эллипс (рис. 57), а
шестиугольники изображают
условие 2ттах = 2А. Несущая способность пластин, рассчитанная по
описанному шестиугольнику, для которого:
_2?s_
Гз ’
2k =
является завышенной, а по вписанному (2A = as) — заниженной.
Давая постоянной k значения —i-. и -у >
у и 2
мы, следовательно, будем
§27]
ДЕФОРМАЦИЯ ПЛАСТиНОк В ИХ ПЛОСКОСТИ
191
Рис. 58.
. получать верхнюю и нижнюю границы' несущей способности пла-
стинки.
Пусть геометрическое место центров пересечения семейства прямых
дано кривой LM (рис. 58), а само семейство прямых — линии,
нормальное напряжение
на которых постоянно
и равно ±2/г. Тогда
каждая кривая ортого-
нального к прямым се-
мейства будет эвольвен-
той кривой LM. Всё се-
мейство эвольвент состоит
из параллельных кривых.
Если задана одна из эволь-
вент, например, кривая
1т, то простым геометри-
ческим построением мож-
но найти геометрическое
место центров кривизны
её (эволюту), а также и
всё семейство эвольвент.
Рассмотрим пласти нку,
положительную кривизну (рис. 59), и пусть, отвер-
стие в ней образовано кри-
вой (//) параллельной (/).
Построим эволюту этих
кривых LM и обозначим
через R' и R" радиусы
кривизны кривых (/) и (//)
в точках М' и М"
ограниченную замкнутым контуром (/),
имеющим всюду
Рис. 59.
Я' = ММ',
R" = ММ",
так что Н = R' — R"
представляют постоянную
всюду ширину кольца.
Радиусы R' и R", следо-
вательно, известны в ка-
ждой точке внутреннего и
наружного контуров. Ре-
шим следующую задачу:
растягивающее нормальное
(/) пластинки, чтобы при
р (или
контуру
быть давление-
по внешнему
каково должно
напряжение—р)
свободном от нагрузок внутреннем контуре (//) пластинка полностью
перешла в пластическое состояние? Согласно рисунку 59 имеем
1&2 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
•Oj = — 2k. Условие равновесия элемента М'Mi Mi Mi' даёт непо-
средственное
PM' m'i = 2k(MM1 — м" Mi),
и, так как
м'м[ R’
м"м’[ ~ R" ’
то искомое давление равно:
р=2*(1-^ = 2%^. 6.115)
Если аналогичное уравнение написать для кривой, параллельной
контуру и имеющей в точке М эволюты радиус кривизны R, то
для напряжения а2 получим:
с2=-2б(1—^), (4.116)
откуда убеждаемся, что напряжение а3 действительно имеет тот же
знак, что и Oj в любой точке пластинки. Давление р, как видим,
Рис. 60.
вообще говоря, не является постояннымлпо контуру (I) и должно
изменяться 'обратно пропорционально радиусу кривизны R'. Однако,
если размер пластинки весьма велик, и в бесконечности она сжи-
мается давлением р, то максимальное значение этого давления будет
равно 2k, какова бы ни была форма отверстия (//). На рис. 60
показаны некоторые примеры определения несущей способности
пластинок, не требующие особых пояснений. Заметим ещё, что если
на внутреннем контуре (//) также действует давление q, то вместо
формулы (4.115) получим:
а вместо (4.116) — следующий закон распределения тангенциальных
напряжений оа:
О// / П'/ \
’2=-<7^-2*(1 —^=-2k-Y(2k-q)^.. (4.116')
§27]
ДЕФОРМАЦИЯ ПЛАСТИНОК В ИХ ПЛОСКОСТИ
193
Наибольшее значение давления q будет 2k, так как мы предпола-
гаем |ci| > |а2|. Если q отрицательно, т. е. на^внутреннем контуре
приложено растяжение, то на-
пряжение с2 становится положи-
тельным при любом q, и по-
тому формулы (4.115) и (4.116)
не имеют смысла.
Так же просто решаются
задачи о несущей способности
пластин, находящихся под дей-
ствием массовых сил опреде-
ленного характера. Пусть мас-
совая сила, действующая на
каждую точку пластинки, имеет
постоянный знак и направлена
по касательной к эволюте кон-
тура, например от эволюты Рис. 61.
(растягивающая сила). Обозна-
чим ее через g, а плотность материала — через о. Из рис. 61 имеем:
R
2kH <70—a2/?fif0 — JpgRdfidR-!rqR"d^ = O,
R"
ИЛИ .
R
о2=2^—1 ^'pgRdR+q-^-, (4.117)
В"
где q — растягивающее напряжение а2 на внутреннем контуре. Если
растягивающее напряжение а2 на внешнем контуре равно р, то имеем
такое уравнение, определяющее несущую способность:
P+XR7 \?gRdR = 2k-^ + q^r. (4.118)
R"
Рассмотрим ещё некоторые частные задачи о несущей способности
круглого диска постоянной толщины с отверстием.
1. Диск вращается в своей плоскости около центра с угловой
скоростью <о, на. внешнем контуре приложено растягивающее напря-
жение р, на внутреннем—q. Массовая сила g в этом случае равна
/ g = R<^,
и потому из (4.118) имеем:
/>+^(*3-«3)-?т=2*-Ц:^ <4119)
13 Зак. 3138. А. А. Ильюшжя
194 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
где а, b — внутренний и наружный радиусы. В частности, для
сплошного диска находим:
/> + < = 2/.
^Если к нему не приложено растягивающее напряжение р, то ско-
рость v = bm, при которой весь он переходит в пластическое
состояние, равна:
о = -,/'6^.
" ₽
2. Диск с отверстием растягивается внешним напряжением аа — р,
(R = b), и на внутреннем контуре действует давление ^:а2 =—q,
Поскольку на внутреннем контуре ata2<0, то условие
пластичности принимает вид:
<з1— аа=2й, (4.120)
и из уравнений равновесия имеем:
1 с2 а1 __ п
dR ' R ~~
Решая это уравнение при условии (4.120), получаем:
<3^ — 2k\v^~ — q. (4.121)
Если наружный радиус b удовлетворяет неравенству
а
b ае2к ,
то из условия а8 = р при г = Ь имеем формулу для несущей спо-
собности:
Р = 2k 1п 4 +<7,
по существу, совпадающую с формулой для несущей способности
трубы. Если же
Ь>аЛ, <4122>
то решение (4.121) при /?>/?*, где
а
АД = ае-к ,
не имеет смысла, так как напряжения а2 будут уже одного знака.
Поскольку при /? = /?#, с2 = 0, а при а2 > 0, то
§28]
ИЗГИБ ПЛАСТИНОК
195
согласно (4.119), где нужно положить <u=0, q = 0, а = К*, имеем:
„, Ь — /?*
р = 2£----
и потому при условии (4.122) несущая способность пластинки
определяется формулой:
ч
p-\-2k^e2k = 4k. (4.123)
Как видим, во всех рассмотренных выше случаях деформации
пластинок в их плоскости внешние нагрузки не являлись произволь-
ными и каждый раз определялись из решения задач. Это совершенно
естественно, поскольку мы предполагали, что материал не обладает
упрочнением. Возникает вопрос, каково же будет напряжённое
состояние пластинок, если внешние силы отличны от указанных выше.
В общем на него можно ответить так: в этих случаях невозможно
плоское пластическое напряжённое состояние пластинок, при котором
напряжения а2 будут одного знака. Следовательно, в ней могут
возникать упругие области, а также области, где уравнения пла-
стичности будут гиперболического типа (глава VI).
§ 28. Изгиб пластинок.
Рассмотрим вопрос об изгибе пластинки под действием сил,
распределённых по её поверхности и направленных по оси z (рис. 62).
Так как в плоскости пластинки внешниХ'Сил нет, естественно пред-
положить, что результирующие силы 7\, Т2, Т12 всюду равны нулю.
Из уравнений (4.26) имеем:
а12^1 х12^2 —
(4.124)
196
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
где г„— удлинения, — кривизны серединной поверхности. Этим
равенствам можно удовлетворить единственным способом, а именно,
необходимо положить e1 = s2 = s12 = 0, и так как ф 0, to»J2 = 0.
В самом деле: поскольку s„ = 0, то квадратичная- форма Ps = 0,
а следовательно, и Pez = 0. В таком случае из (4.19) имеем следую-
щее выражение интенсивности деформаций в слое пластинки, рас-
положенном'на расстоянии z от серединной поверхности:
; = (4.125)
и согласно (4.34)
^ = ^2 = ^/Л., ^о = О, (4.126)
т. е. имеем случай доминирующего изгиба. Функции Ао, Вс, Со, со-
гласно (4.37'), будут равны:
(4.126')
%
C0 = 2j ^ае{,
О
и потому функции Jj, J2, согласно (4.38), будут:
.л,- eil
о
т. е. действительно уравнения (4.124) выполняются тождественно.
Обозначая
(4.127')
мы из (4.27) получаем следующие формулы, выражающие изгибаю-
щие и крутящий моменты I6':
Л41 = -(х1 + 1-ха)/(Рх),
/И2 = ~ (*2 + ф *1) J (Л). (4.127)
^12 — ~2 7'1а^ У3*)•
§28]
ИЗГИБ ПЛАСТИНОК
197
Напомним, что Р.л представляет квадратичную форму от кривизн:
Рц — *14~хг-<2‘4 -j-y-is. (4.128)^
Если w(x,y) есть прогиб серединной поверхности пластинки в точке
(#,У), то кривизны х2, -х12 имеют следующие известные выраже-
ния П1;
d"w d2w „ d-w
- Z1 Эх2 ’ *Za ' ду2 ’ Х1а дхду ’
(4.129)
и потому есть функция вторых производных от w. Обозначим
квадратичную форму моментов
4 Ph = Qm — Mi — .(4.130)
О
Тогда формулы (4.45') и (4.45'") обращаются в тождества, а из
(4.45") находим связь между Р7 и
ЛЛ(Л) = 4<2аь (4.131)
О
откуда при известной J (Р ,') находим выражение Р., через и J
через Qu- Уравнения (4.127) теперь можно разрешить относительно
кривизн и написать обратные зависимости: <
xi 2 ^а / ’
4 / 1 \
”2 = — 37^2—2^4» > (4.132)
2 ЛЛ
х12 — j ^412-
Вариация работы внутренних сил, приходящейся на единицу площади
пластинки, может быть вычислена по формуле (4.52):
S77 = lj(^)8Px,
поэтому вариация работы для всей пластинки будет:
ЗУ = A Jр (PJ ЗР7 dx dy.
(4.133)
(4.134)
Выведем основное уравнение равновесия элемента пластинки/ Если
через q(x,y) обозначим распределённую по площади нагрузку, то
условие равновесия сил, действующих на элемент (рис. 62), в проек-
ции на ось z даёт:
dNx , dN2
дх 1 ду
198
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
(ГЛ. IV
а условия равновесия моментов дают следующие выражения для пере-
резывающих сил:
_дМ, , |
1 дх "I" ду ’ J
N _дМ2 сШ12 | (4Л35>
"2— ^'дх J
Внося эти значения в уравнение равновесия сил, получаем основное
уравнение:
ЗШт . пс>Ш,2 . д*М2 , _
дх* •" дхду' ду*^ч~^
(4.136)
Граничные условия в задачах об-изгибе пластинок при упруго-
пластических деформациях совпадают с обычными в теории упруго-
9
Рис. 63.
сти условиями. На краю могут быть
заданы (рис. 63) либо перемещение
w и его производная по нормали v:
CJ-*=/2(s). (4.137')
либо приведённая перерезывающая
сила и изгибающий момент:
(4-13Г>
либо смешанные условия, типичным
примером которых являются условия
на свободно опёртом краю:
w = 0, 7И„=0. (4.137"')
Можно указать три основные
постановки задачи о равновесии пла-
стинок при изгибе: 1) постановка задачи с помощью дифферен-
циального уравнения в частных производных четвёртого порядка отно-
сительно перемещения w; уравнение получается из (4.127) и (4.136)
при граничных условиях (4.137); 2) постановка задачи с помощью
вариационного уравнения равновесия; 3) постановка задачи с помощью
трёх дифференциальных уравнений относительно моментов /И2,
М12, получающихся из (4.132) и (4.136) при граничных условиях
(4.137). Рассмотрим вопрос детально.
1. Первая постановка задачи о равновесии пластинки и общее
решение. Воспользуемся представлением зависимости через
функцию со: • '
ai — Eei [1 — со (<?*)], О
со <б_
1,
§28]
ИЗГИБ ПЛАСТИНОК
199
и вычислим интеграл J:
%
J = £)(l—2), 2 =
(4.138)
о
известным.
Eh3
Здесь Г) = -г?г7-,-st — обычная цилиндрическая жёсткость пластинки;
12(1 —-t1)
функция 2 (Рх) вполне определяется, как только конкретный вид
характеристики материала пластинки становится
В случае закона ломаной, т. е.
со = О,
со
&s'
(4.139)
, . 1 d^i ।
л = 1-----—i-= const.;
E dei
функция 2 имеет следующее выражение:
2 — 0, е{ —
1 Уз
I
(4.140)
3’
Таким образом пластинка разбивается на две области: область чисто
упругих деформаций (2 = 0) и область упруго-пластических дефор-
маций X 2 0, причём
уравнение границы между
этими областями будет:
3d
е(1=е8, Рг = (4.141)
В области упруго-пласти-
ческих деформаций по тол-
щине пластинки имеют место
Рис. 64.
две пластические зоны, при-
мыкающие к её поверхности
(г — ± h/2), и одна упругая зона, содержащая серединную плоскость
(г = 0). Граница между этими зонами представляется двумя поверх-
ностями, уравнение которых будет ei = es или, согласно (4.125):
z = za —
es
(4.142)
2 У Л
। । / h
z ' < —
I * i 2 •
На рис. 64 изображено сечение пластинки вертикальной плоскостью
и заштрихована зона пластических деформаций упруго-пластической
области пластинки. Вполне понятно, чГо как бы ни были велики
200
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
деформации пластинки, в ней всегда будет существовать зона упру-
гих деформаций, и только при -> со эта зона будет уменьшаться
до нуля (zs->0). Этот факт математически выражается в том, что
даже при а,- — ag = const., (Х = 1) уравнения равновесия пластинок
имеют эллиптический тип.
Пользуясь выражением (4.138) функции J.2, и подставляя значе-
ния моментов согласно формулам (4.127) в основное дифференциаль-
ное уравнение равновесия (4.136), мы получим:
V4®» = Ч- ^5 [a (xj + у х2)] + (2х1а) 4-
(4Л43)
Для того чтобы убедиться, что (4.143) представляет дифференциаль1
ное уравнение эллиптического типа, и потому при граничных усло-
виях (4.137) оно должно иметь решение, выпишем явно его главную
часть, т. е. члены, содержащие четвёртые производные прогиба ни.
Согласно (4.127), имеем;
___(d*w , 1 <Pw \ . dJ f , 1 Г дР-, . дР* дЧз
дх2 I дх4 2 дх2ду2/ * дРу[У1 ‘ 2 |_ dxj дх2 ах2дх2 ’
, дРх д2%121 ,
’ d%i2 дх2 J ‘ • • • ’
ЭШ2 ' fd4w , 1 d4w ) , ' dj / , 1 АГдЛд2*! . дР., ,
Оу2 ~ J \ду4 "Г 2 дх2 dy2J + dPx V2 ‘ 2 ХМ [ c?/.i ду* ’ дх2 ду2 '
, дР.дЧ^ ,
1 ^12 ду2 ] ’
, d4w t d.J_, f дР., (p-t-i । дР, с2ч.2 । дРу й2-/-12,
дхду ' дх2ду2 ‘ [ dv-i дхду д/.2 дхду дх12 дхдуJ “г ’ ’ ’
В этих формулах опущены слагаемые, содержащие производные от
•w ниже четвёртого порядка. Пользуясь тождествами вида:
а также формулами (4.129) и вытекающими из (4.127) соотноше-
ниями вида:
( . 1 \ dPz о AfjM,
1Х1+27-2^^2^-’
напишем основное уравнение (4.136):
9=[лйЙ + + 2 (Л, А + rft) +
+4л’:«'и.вд+4л’Ле^.]+--- <4:144>
§ 28] ИЗГИБ ПЛАСТИНОК 201
Для того чтобы выяснить тип квазилинейного дифференциального
уравнения в частных производных п-го порядка по двум независимым
переменным с главной частью
V Ar dnw
к дхкдуп~к'
л- = о
где Ак — функции х,у и всех производных от w ниже zz-ro порядка,
необходимо установить, имеет ли нули однородная форма /z-ой сте-
пени от двух аргументов $, тр
с = 2 (а)
* = о
при каких-нибудь действительных значениях £, 7]. Если имеет, то диф-
ференциальное уравнение будет гиперболического типа; если же с = 0
только при комплексных значениях £, 7], то уравнение относится
к эллиптическому типу.
В нашем случае коэффициенты Ак равны
= = Ji м12м2, д8 = 2/+^-'(Жгм2+л«!д
As=~M12Mv = (б)
Приведём квадратичную форму Р., к главным осям деформированной
поверхности:
где х', х"— главные кривизны в точке (х, у). Поскольку главные
оси кривизн поверхности w(x, у), согласно (4.127), совпадают с глав-
ными осями изгибающих моментов (т. е. при х12 = 0, Д412 = 0), то
квадратичная форма Qm преобразуется к виду:
qm = M'2—-М'М"±М"2. (в)
Фбрма с при этом преобразуется к виду:
с = ДД^+'2Д27|2;2 + Д4«), (г)
где коэффициенты А' имеют выражения:
А0=\-\-^М"2, А\=1-^2-у3 М'2.
Пользуясь соотношением (4.131), мы перепишем эти коэффициенты
в следующем виде:
Ao— 1—z/zzzj, Д2=1—dmtm2, Ai—l—dm}, (д)
202
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
где обозначены:
М' М" . х
т‘=Уй’ "S=W <е)
И
. 2J' ЗРХ dj .
d~~ -J3 Qm— ~2J dpx>°- (4.145)
Форма с теперь принимает вид:
с =J [(nq-f- S)2 — d (m2ti + ffijO2]-
Приравнивая её нулю и обозначая через р отношение 5/t], получим
1-}*Р2 = —(/«2 ZKjP2),
или
г = (4.146)
1 у dmt
Согласно формуле (в) и обозначениям (е) величины /я1т2 ограни-
чены и связаны соотношением:
/«I — 1, (4.147)
причём максимальное значение каждой из них по модулю есть 2/У"3.
Отсюда следует, что если
d<|, (4.148)
то р2 будет отрицательно, и форма с будет определённо положитель-
ной при любых $, Т), т. е. уравнение равновесия пластинки будет
эллиптического типа. ,
Подсчитаем величину d согласно обозначениям (4.126), (4.145):
4 J de^’
и запишем неравенство (4.148) в виде:
1 de{
Согласно (4.127z) окончательно преобразуем его:
%
рй^>°- (4Л4.4 * * * * 9>
о
Поскольку верхний предел всегда положителен и В области пла-
стинки может иметь произвольное значение, неравенство (4.149) будет
§28]
ИЗГИБ ПЛАСТИНОК
203
выполнено, если для любого ef
daj
deg
О,
ввиду того, что для е( es,
^- = Е. Таким образом уравнение изгиба
пластинки (4.143) будет эллиптического типа даже при условии пла-
стичности Мизеса с.г = ag, поскольку в нём учитывается упругая
деформация упруго-пластической зоны (| z | < j zs |) и становится гипер-
болическим только при es = 0.
Приведённое выше исследование показывает, что выражение, стоя-
щее в правой части уравнения (4.143), хотя и содержит главные
члены, но коэффициенты при них меньше соответствующих коэффи-
циентов бигармонического оператора '74та, стоящего в левой части.
Отсюда при интегрировании уравнения (4.143) вполне законно вели-
чину
1'=£ [а (*+-W]+Я2 Ь+?)]+<4 15»>
рассматривать как нагрузку, т. е. применить метод упругих реше-
ний.
Покажем, что если для пластинки с определёнными граничными
условиями известна функция Грина упругой задачи, т. е. известно
решение упругой задачи
тае, — £г(л, у, 5, т]) (4.151)
для сосредоточенной силы Р, приложенной в точке с координатами
(£, т]), то вычисление её прогиба, удовлетворяющего дифференциаль-
ному уравнению упруго-пластического изгиба (4.143), при действии
распределённого давления q ($, т]) по методу упругих решений сво-
дится к квадратурам. Решение уравнения
по определению функции Г можно записать в виде 1®1:
w = J J [q(i, т])]Г(х, у, s, t^did^
или
(4.152)
<w = w(e) -4- та,
где
та(е) = -i У У q (;, 7]) Г (х, У, ц) di dr[
(4.153)
204 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
есть упругое решение задачи изгиба пластинки под действием на-
грузки q, а
w = J f q’(i, т])Г(х, у, В, (4.154')
На основании теоремы о разгрузке w = w— •w^ представляет оста-
точный прогиб пластинки в любой точке после освобождения пла-
стинки от нагрузки q. В формулах (4.153) и (4.14') интегралы рас-
пространены по всей пластинке:
Внося значение (4.150) в (4.154'), мы получим интегралы типа
/2
Такой интеграл преобразуется по формулам Грина к виду:
J jf 2 (*i +<-2 х2) did-t] -f-
4 /1 4 [2 (xi 4 y "''2)] Г — 2 G1 4 ЗГ Z2) } cos
причём второй интеграл берётся по контуру пластинки; индексы,
приписываемые функции Г, означают производные
Г — г —
di ’ ds2
В результате вычислений получим следующее выражение остаточного
прогиба:
w = f f [xi (Г& + трГ-гл) + xi2^ + х2 4 УГк)] 2 &(4.154)
Здесь опущен контурный интеграл
/ {Г [ 2 (*1 4 у х2) cos vx 4-1 4 Sz12 cos vx 4-
д . 1 A 1 1 d „ 7
' +<42lX2+ 2 XVC°SVJ4- 2 Sx12cosvyj —
— 2 [(xi 4- j- *2) r;cos« 4 4 ziAcos +
4 G2 4 2 X1) Гпcos 4 4 X12 rE cos vx j I ds,
который обращается в нуль на основании граничных условий; мы не
будем приводить этому доказательства, ибо оно тождественно совпа-
дает с доказательством обращения в нуль такого контурного инте-
грала при упругом изгибе пластинки. Например, в случае защемлён-
ного края на контуре Г = Ц = Г^ = 0 и т. д.
§28]
ИЗГИБ ПЛАСТИНОК
205
Таким образом (4.152) представляет интегро-дифференциальное
нелинейное уравнение относительно прогиба:
® = w(e) + 11 + 4-^Г^Н-
+^,Т) fr.„ 4- } Г J] 2 d.' d-q, (4.155)
в котором 2 есть функция (4.138) от Р„ а
г> 2 . ,2,2
Функция Грина Г в точке x = t, y = 'i\, как известно, имеет особен-
ность вида г2 In г, а именно:
Г = ^г21пл+/(х,л е, Tj),
где f—правильная всюду бигармоническая функция и
г2 = (х — £)2 -|- (у — т])2.
Поскольку вторые производные Г имеют особенность вида In г, то
интеграл w существует ' и конечен всюду; в точке х = у — ц он
имеет особенность логарифмического потенциала.
Метод упругих решений в применении к уравнению (4.155) пред-
ставляет следующий процесс последовательных приближений: пола-
гая в первом приближении 2t — 0, находим Wj = w(e) и затем
7.;1* — > , Р*\ e<i\ а по формуле (4.138) находим 22. Под-
ставляя эти значения в (4.154), находим первое приближение ос-
таточного прогиба и второе приближение общего прогиба
w2 = wty -j- Wj. Повторяя вычисления, определяем xi , ..., 23 и затем
-w2 и т. д, ’
2. Вариационное уравнение равновесия пластинки. Работа поверх-
ностной силы q на возможном перемещении Sw определяется
интегралом ч
8'А — f f qSwdx dy.
Сравнивая её с вариацией работы внутренних сил (4.134), получаем
вариационное уравнение равновесия:
~ J J (P.,)lP.,dx d$ «= J J qbwdxdy, (4.156)
или на основании (4.138):
~ J J (1—2) 8РХ dx dy — J" q&w dxdy. (4.156')
206 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
Выберем систему функций gn(x, у), удовлетворяющих граничным
условиям, и положим
® = 2 = 2
Р* будет однородной квадратичной формой по постоянным сп-
Сравнивая коэффициенты при вариации 8сп в (4.156), мы получаем
систему уравнений, определяющих постоянные сп, и потому дающую
решение задачи:
J J qgn dx dy 4- J J iOw3 4- M2 + 2M12 ) dx dy = 0,
« = 1, 2 ...
Здесь моменты Mlt Mi2, предполагаются выраженными через
по формулам (4.127).
Приближённое решение задачи об изгибе пластинки всегда может
быть найдено следующим образом: предположим, что упругая задача
решена, т. е, известно:
— у), (4.157)
где w — известная функция координат и q0 — постоянное - характер-
ное значение нагрузки q:
q = qQq(x,y)t (4.158)
и а — характерный размер пластинки. •
Представим прогиб w одночленной формулой:
w = ^w(x, у), (4.159)
где с — неопределённая постоянная; такой вид прогиба пластинки за
пределом упругости является всегда подходящим, поскольку, как пра-
вило, он удовлетворяет граничным условиям и отражает особенности
нагрузки. Подсчитаем квадратичную форму Р,:
п .<(д*и>\2 I d2wd‘“w | /д2иА2 । / с)2и , 1ДП'
р* = D^P^ р,- = «4{ J + ж W + \д7ду) Г (4-160)
Поскольку
J. atwhc „„ п - Рха8
8w = —D"’ ^ = 2с8с-^-,
(4 161)
(4.161')
§ 28] ИЗГИБ ПЛАСТИНОК
то из уравнения (4.156) находим:
— £ И аУ
D $ \ q w dx dy ’
или через функцию 2:
_ И dx dy ~ Л dx dy
J J* q w dx dy
Функция 2 (Px) отлична от нуля только в области упруго-пласти-
ческих деформаций пластинки, и потому интеграл, стоящий вторым
слагаемым в числителе правой части уравнения (4.161'), распростра-
нён по этой области. Граница её определяется уравнением (4.141),
имеющим в нашем случае вид:
- Зе2 О2
~ ’ (4.162)
Линии
Р, = const.,
к числу которых принадлежит граница (4.162) между упругой и упруго-
пластической областями пластинки, можно назвать линиями постоян-
ной напряжённости пластинки. Их можно использовать для вычисле-
ния интеграла:
j* J QPyix dy,
если кривая материала аге{ задана графически, или если квадра-
тура оказывается сложной. Для этого поступаем следующим образом:
находим максимум функции Рх согласно (4.160); это будет точка,
линия или конечное число точек или линий на пластинке, из кото-
рых начнут распространяться области упруго-пластических деформа-
ций при переходе пласУинки за предел упругости. Из всех возмож-
ных максимумов Р, выбираем абсолютный максимум Рх гаах и, согласно
(4.162), находим значение постоянной с — са, при которой ещё вся
пластинка будет деформирована упруго:
I с I_ е»Р -if_____3
1 ' ath. V -р
(4.163)
'х max
Для всякого значения | с| < | cs | из (4.161') имеем линейную зави-
симость между нагрузкой и прогибом:
с = 7о> (4.164)
как это видно из сравнения величин (4.157) и (4.159), и потому:
ffdxdy _ х .
ffqwdxdy
208
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
Поскольку эта дробь не зависит от с, она всегда остаётся равной 1,
вследствие чего формулу (4.161') можно переписать в виде:
7о с I 1 —
f f QP., dx dy
П qwdxdy
(4.165)
Найдём еще абсолютный минимум Р., = Р., Тогда, согласно(4.141),
найдём максимальное значение постоянной с, при которой ещё су-
ществует в виде точки или линии зона чисто упругих деформаций
пластинки:
a3h
min
(4.166)
Если постоянную с изменять в пределах | cs| [ с | | cs |, то зона
упруго-пластических деформаций будет увеличиваться от бесконечно
малой до заполняющей всю пластинку. Наконец, если давать зна-
чения постоянной |c|>|cs|, то области чисто упругих деформаций
на пластинке не будет, и вся она будет деформироваться за пределом
упругости.
Вычисление зависимости между характерной нагрузкой qQ и ха-
рактерной деформацией с можно произвести следующим образом:
при |с | <| cg| имеем прямую (4.164). Возьмём какое-нибудь значе-
ние с — ск, заключённое между
cs и cg, и построим (рис. 65)
серию линий постоянной на-
пряжённости:
(Л)о =
(Л)х =
(Р. )N =
з^2о2
c^aV
Зе^О2
2^^
9 4.2
Cftirh
рис. 65. Измеряя площадь кольца, за-
ключённого между двумя сосед-
ними линиями (Р.,)п и (Px)n+i, и обозначая её через Fn, мы можем считать,
что в пределах кольца Рп величина постоянна и равна, например,
(Р^)п; функция Q(PX) будет также постоянна:
2 = 2п
Д2 (Р*)а
,П^ЛГ.
(4.167)
§29]
НЕКОТОРЫЕ ЗАДАЧИ ОБ ИЗГИБЕ ПЛАСТИНОК
209
Нагрузку q0N, соответствующую деформации сц, найдём по формуле
(4.165), заменив интеграл суммой:
W-1
S Qn(PJnFn
J)__________
wdxdy
(4.168)
4oN~Cn
Ниже будут даны примеры расчёта пластинок по этой формуле
и сравнение результатов с точными решениями задач об изгибе
пластинок.
3. Постановка задачи равновесия пластинки с помощью диф-
ференциальных уравнений для изгибающих моментов. Условия
совместности кривизн Xj, х2, х12, согласно (4.129), можно записать
в виде двух уравнений:
__дх18 дъ din
ду~~ дх • дх ду ’
и, пользуясь соотношениями (4.132) и (4.131), выразить их через
моменты:
д 2Л41 — М2 ___„ д Mi2
ду J(Qm) дх J(Qm) ’
д 2М2 — М, _ _д_ Mi2
дх ' J (Qm) ду J(Qm)
(4.169)
Эти уравнения совместности моментов вместе с основным уравне-
нием равновесия в форме (4.136) позволяют искать решение задачи
непосредственно в моментах, не обращаясь к прогибу пластинки,
если только граничные условия имеют вид (4.137").
§ 29. Некоторые задачи об изгибе пластинок.
1. Изгиб круглых пластинок. Круглая пластинка с наружным
радиусом а и круговым вырезом радиуса b находится под действием
равномерно распределённой по внутренней окружности перерезы-
вающей силы интенсивности Р на единицу длины окружности и сим-
метричного давления q(r). На рис. 66 изображён разрез такой коль-
цевой пластинки.
Перерезывающая сила ДГ на окружности радиуса г определяется
непосредственно:
г
J"qrdr = O, (4.170)
ь
причём ясно, что это уравнение является интегралом уравнения
(4.136) в полярных координатах при осевой симметрии. Обозначая
14 Зак. 3138. А. А. Ильюшин.
210
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
М1 — радиальный, Л42— тангенциальный изгибающие моменты и при-
нимая во внимание, что вследствие симметрии крутящий момент
будет равен нулю, из рассмотрения условия равновесия моментов,
действующих на элемент кольцевой пластинки, легко вывести сле-
дующее выражение для перерезывающей силы
—
dMt
dr
(4Л71)
Это уравнение может быть получено также из (4.135) путём пре-
Рис. 66.
образования моментов к полярным координатам. Из (4.170) и (4.171)
имеем основное уравнение равновесия:
dMj
dr
Mi — Л42
7 Р~Т hrdr-
(4.172)
Радиальная и тангенциальная х2 кривизны пластинки при симметрич-
ной деформаций имеют следующие известные выражения через
прогиб w(r):
d2w 1 dw
1 dr2 2 г dr
причём
<4-173')
I
Согласно (4.127) и (4.138), получаем формулы для изгибающих
моментов:
М, = - D (1 - 2) 4- 1 (1_^,
M2 = —D(l—2) (х2-Ц =
Q = Q (Рх), Р.л = 3 [4 + -x2r + г2 .
(4.173)
§ 29] НЕКОТОРЫЕ ЗАДАЧИ ОБ ИЗГИБЕ ПЛАСТИНОК 211
Таким образом уравнение (4.172) может быть выражено только
через одну неизвестную функцию х2:
Г
= ™+i>fardr- <4-174)
ъ
Это — квазилинейное обыкновенное дифференциальное уравнение
второго порядка относительно х2. Его решение при произвольном
законе распределения нагрузки q по радиусу может быть найдено
одним из известных методов численного интегрирования; при этом
характеристика материала пластинки о>(^), а, следовательно, функция
2 (Рх) (4,138) может быть задана любым образом. С целью проверки
точности дальнейших приближённых решений, ' рассмотрим более
подробно случай изгиба кольцевой пластинки только от действия
перерезывающих сил Р, распределённых по контуру. Полагая
в (4.174) <7 = 0, и замечая, что
d dt^ d
г -у-=Г-~ — ,
dr dr dv.°
мы перепишем уравнение (4.174) в виде:
dxg d I /. / dXg t 3 1/1 \ dXg РЬ
;773d(I~S|(^+lHl + T<1-S)r<F = D
Если ввести обозначения безразмерных величин
х2Л h dx2 dx
~ = — х, —-г—s = = — r-т-,
2es ’ 2е, dr dr
(4.175)
где ea—предел текучести материала по деформации и h — толщина
пластинки, то это уравнение становится уже уравнением первого
порядка Относительно о:
«^[(1 —S)(3x —2©)] + (1—2)© = р. (4.176)
Постоянная р имеет значение:
ЬЬР
P==D^'
(4.177)
Отношение интенсивности деформаций ец (4.126) к ее, т. е.
Х2~х^ + у®2 (4.178)
14*
21S
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
при упруго-пластических деформациях пластинки есть величина
порядка 1 или больше. Функция 2 зависит только от е и, в частно-
сти, согласно (4.140), имеет выражения:
2 = 0, (г<1); 2 = + Й (е>П- (4.179)
Разрешим уравнение (4.176) относительно производной
4(1_2)_(3Ч_2»)
dv ' ' дх v j, ч
=------------.------. =/(Х)
2(l-2)+(3x-2p)g
(4.180)
Здесь частные производные функции 2, согласно (4.179) и (4.178),
выражаются формулами:
f = S(2—
(4.181)
Поставленная задача тетерь решается хотя бы методом конечных
разностей. Для этого заменим dx, dv конечными малыми прираще-
ниями Дх, Дт/ и напишем формулу для Д®:
Д©=/(х, -»)Дх. (4.180')
Она содержит два постоянных параметра: характеристику материала
, , 1 dzt
А = 1—E~dei и хаРактеРистикУ нагрузки р, а потому позволяет
представить решение частных задач в виде серии графиков. Для
этого необходимо начальное условие Коши.
Для определённости предположим, что изгибающие моменты
при г —а и г = Ь равны нулю, т. е. наружный и внутренний кон-
туры свободно опёрты. Тогда, согласно (4.174) и (4.175), имеем:
г — а ]
r=b I 3z— 2,a = 0> e = ’z> (4.182)
т. е., по существу, мы имеем краевую задачу, а не задачу Коши.
Однако её легко привести к задаче Коши. Заметим, что по смыслу
задачи кривизны Xj и х2 имеют противоположные знаки и потому Xj
и х2 можно считать положительными при положительных р. При
переходе от наружного края пластинки (/•== а) к внутреннему (/• = &),
х возрастает, т. е. Дх>0. Следовательно, если при некоторых
числовых значениях р и X мы дадим величине х начальное значение
х0^-1 и соответствующее начальное значение v = v0 возьмём из
3 X
(4.182): va—^-x0, то, давая величине х малые положительные при-
§ 29] НЕКОТОРЫЕ ЗАДАЧИ ОБ ИЗГИБЕ ПЛАСТИНОК 213
ращения, согласно (4.180'), найдём кривую » = ©(/), которая при
некотором значении х==хп пересечётся с прямой Зх— 2® = 0. Тем
самым будет найдено решение следующей задачи: по данному зна-
чению силы Р и интенсивности деформаций е на краю пластинки
найти отношение наружного радиуса её к внутреннему. Изменяя зна-
чения р и х0, мы получим серию графиков для пластинок различных
размеров; тем самым задачи будут решены столь же общо, как
и в прямой постановке. Отношение радиусов контуров пластинки
согласно (4.175) находится по значению х0 и с помощью кривой
v = и (х) из формулы
Inf-JI*, (4.183)
X»
а связь между кривизной х и текущим радиусом г — из формулы
(4.183')
После этого прогиб пластинки на окружности радиуса г относительно
наружного края выражается квадратурой, вытекающей из (4.173),
(4.175):j
а 1
2е, Г , 2е„а2 (“ г , г , П4.
®=-rJvrdr= -тг J <4-184>
г г[а
В табл. 6 дано численное решение задачи об изгибе кольцевой пла-
стинки, материал которой обладает упрочнением = 0,05£(А=0,95),
Таблица 6.
Решение задачи об изгибе пластинки.
X 1 1.5 2 2,5 3 3,5 3,8 3,9 4
V 1,5 2,1968 2,9305 3,6804 4,4431 5,2179 5,6880 5,8455 6,0034
Зх—2v 0 0,1064 0,1390 0,1392 0,1138 0,0642 0,0240 0,0090 —0,0032
е 1 1,5016 2,0000 2,5014 3,9008 3,5002 3,8090 3,9000
1 — 2 1 1 . 0,8749 0,7029 0,5892 0,5073 0,4460 0,4164 0,4074
<32 0 0,3634 0,2859 0,2019 0,1457 0,1083 0,0925 0,0861
Э2_ dv 0 —0,0160 -0,0124 -0,0071 — 0.0035 — 0,0013 — 0,0004 -0,0001
&V 0,1333 0,1459 0,1488 0,1513 0,1541 0,1563 0,1575 0,1579
г а 1 0,7512 0,6141 0,5251 0,4640 0,4090 0,3870
214 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [гЛ. IV
причём находится отношение у при значении р — 2 в случае, когда
на наружном контуре впервые получается пластическая деформация:
г —а, х0==е0=1, о0= 1,5. Сила Р вы-
ражается через параметр р по формуле:
De
Р^^Р-, (4.185)
прогиб внутреннего контура (г = &) отно-
сительно наружного (г— а) имеет выра-
жение:
1
2esa- — — Г г , г
wb = -~fr^b, (4.186)
b;a
Ход вычислений различных величин от
Зх—2^ = 0 на наружном крае (г = а)
до Зх — 2v = о на внутреннем, которые
в ходе исследования велись через Дх=0,1,
дан в таблице с некоторым сокращением.
На рис. 67 дан график зависимости х
и v от у . Поскольку величина Зх — 2v
обращается в нуль при у = 0,387, то
внутренний радиус пластинки равен
b = 0,387а. Прогиб wb получаем путём
численного интегрирования данных таб-
лицы :
wb = 0,732.
Подобные расчёты, однако, следует делать
уже в связи с практическими требованиями
свойств материалов пластинок, поведение
и с учётом механических
которых явится необходимым изучить.
Для сравнения приведём известное упругое решение задачи об
изгибе кольцевой пластинки. Полагая в (4.174) 2 = 0, q — О, нахо-
дим первый интеграл этого уравнения:
d%2__РЬ । с
rdr~^D~^Ti'
после чего находим:
§ 29] НЕКОТОРЫЕ ЗАДАЧИ ОВ ИЗГИБЕ ПЛАСТИНОК 215
Определяя произвольные постоянные с, с' согласно условиям
г = Ь, Зх2-}- — О,
г —а, Зх2 4-2г = О,
’ 2 1 dr ’
получим:
1 dw РЬ(2 . . Зуб2 । . А \ , о„<
г dr Ха—’ г2 "Ь111"?/’ (4-.187)
где 7—функция отношения радиусов:
1 = I- 0.188)
Прогиб w любой точки пластинки относительно наружного её края
будет:
®’ ==~1х2гг/г==^’[(к + 1Г)(1 “?) + 6т1п7_51п'7]; <4-189)
т
в частности, прогиб внутреннего контура
— PbcPfl а1, — &2 , с . а\ 1 оп>\
^ = 1о (б--^-+6^1птЬ <4-189)
Если воспользоваться обозначениями (4.185), (4.186), то для вели-
чины wb при упругом изгибе получим:
»‘=Шй?+611п£>- <4Л89">
Для сравнения найдём упругий прогиб wb при значениях р = 2,
=0,387, принятых в данном выше расчёте, приписав ему индекс
е наверху:
^’=0,311.
Остаточный относительный прогиб внутреннего края пластинки будет
равным разности и
, — rwb> = 0,421,
и потому остаточный прогиб wb для рассматриваемого значения на-
грузки и размеров пластинки, а именно, при
Р = — = 0,387,
bh ’ а
216
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОДОЧЕК
[ГЛ. IV
I
имеет следующее значение:
w = (wb — wfi) =±= 0,842 .
Как видим, прогибы, найденные по формуле упругого изгиба,,
оказываются сильно заниженными против действительных прогибов,,
даже при сравнительно небольших нагрузках.
Рассмотрим ещё задачу об изгибе сплошной круглой пластинки
радиуса а, нагруженной распределённой осесимметричной нагрузкой..
Вместо радиуса г введём переменную р:
, с
р = In — , г=се~?,
г г ’ ’
(4.190)
и, пользуясь обозначениями (4.175) и (4.181), перепишем уравнение
(4.174) в виде двух дифференциальных уравнений первого порядка:
dv
.- — Т)
d?
=
rfp
4(l_Q)_(3x-2»)g-|e-2p
2(l-Q) + (3x-2»)^
(4.191)
где
. ^=^в2Р Г°21Р)е-2р^2р> (4.192')
ZegU J q0
р
a q0— характерное постоянное значение распределённой нагрузки q
(например, q0 = 9max). В случае равномерной нагрузки q = q0 из
(4.192') имеем:
— аксъ
4
(4.192)
В центре пластинки (г = 0, р=оо) кривизны х2 и отрицательны
и равны между собой, вследствие чего о = 0 из (4.173') и относи-
тельная кривизна х = -|- х0 положительна. Через х0, следовательно,
мы обозначаем положительную величину
(4.193)
Интенсивности деформаций на верхней z = -f- у и нижней z = —~
плоскостях в центре пластинки согласно (4.178) будут:
(4.194)
§ 29] НЕКОТОРЫЕ ЗАДАЧИ ОБ ИЗГИБЕ ПЛАСТИНОК 217
и потому пластическая деформация в центре пластинки будет при
хо > "2 •
Решение уравнений (4.191), удовлетворяющее условиям
р = оо, х == х0, v — О,
представим в виде:
х = х04-сае-2р+ .. .,
v = -т- = —2сае 2р •
dp * 1
(4.195')
Внося эти значения в (4.178) и разлагая получающиеся выражения
в ряд, найдём:
е = 2х0 + ...
Из (4.179) получим:
4а> ' 1бх^
Вычисляя ещё по формулам (4.181) производные:
32 _ ЗХ
““ 16xJ "1 • • • ’
(4Х2— п 4-
32л*1 0 ’
подставляя найденные выражения во второе из уравнений (4.191)
и приравнивая коэффициенты при е-2? в левой и правой частях,
получим:
са —
— g__________
16(1-X) + ^+^s ’
'О 4-z.q
а потому решения (4.195') в окрестности р = со, (г = 0) примут
вид:
х = х0
________0______
16(1-Х)+^ + ^
*о 4xq
2g
.. . ЗХ
(4.195)
16(l-k)+g + ^
*0 4*jj
*0
218
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Эти
вать
формулы необходимы для того, чтобы численно проинтегриро-
уравнения (4.191), которые перепишем в конечных разностях:
Дх = v Др,
Дц = <р(х, и) Др. (4.196)
этого дадим радиусу г малое значение гь а, следовательно, вели-
и найдём из (4.195) соответ-
Для
чине р — большое значение ра ==1п —
ствующие значения хх и причём — х0 и должны быть малыми
величинами ' —
приращение
сравнительно с 1. После этого величине pi даём малое
Д?! = ра—?! и из (4.196) находим:
ха — Xj = Axj — ^jApi,
= Д®1 =?(’'•!> ®1)ДР1-
вычисления сводятся к повторению вычислений после-
= а,
(4.197)
Дальнейшие
довательных значений
Дхй = х3 — ха, Дц2 = ц3—
по данному Дра = р3—ра и т. д.
Предположим, что край пластинки свободно опёрт:
Р = Ра==1п^> Зх —2я==0
(если он защемлён, то условие будет р = 0, х = 0). Тогда при неко-
тором значении р == f может оказаться, что величина е, непрерывно
убывающая от значения 2х0, станет равной единице: e.f = 1; функция 2
при этом обратится в нуль. Это значит, что достигнута граница
упруго-пластической области, и она имеет радиус гт = се-т. При
r>rT деформация пластинки будет упругой, и в дальнейших вычи-
слениях необходимо считать
Ох ОО
Если же условие (4.197) будет выполнено при (е)р=0^>1, значит,
упруго-пластическая область распространилась на всю пластинку.
Рассмотрим сначала упругое решение задачи. Полагая в (4.191)
2 = 0, имеем:
dv.
dp
— О®____Едй-2р
dp 2 qe *
=
Интеграл этих уравнений, удовлетворяющий условию р = оо,х = х0,
имеет вид:
х = х0 — о==-|-е-2!>. (4.198)
§ 29] НЕКОТОРЫЕ ЗАДАЧИ ОВ ИЗГИБЕ ПЛАСТИНОК 219
Условие (4.1 #7) позволяет найти:
xo = ^7e-2₽“ = jG)c=a- (4.199)
Отсюда следует, что произвольная постоянная с несущественна
и может быть принята равной а; с~а, ра = 0. При
— - 24
?<у = 3,43
(2х0<1) _ (4.200)
деформация пластинки будет упругой, а при значениях q > 3,43 в ней
будет возникать упруго-пластическая зона. Для определения прогиба
w заменим в (4.198) х её выражением через w согласно (4.175) и
(4.173) и проинтегрируем полученное уравнение в предположении,
что прогиб w = 0 при р = 0, (г —а); тогда получим:
_Л_^==Х = _£<7 —Зе-2?)
2^ dP Х_ 48 )> (4 201)
ад=-^1(Ц_14е-2Р-фЗе-4Р).
Если прогиб в центре пластинки р = оо, г = 0 представить в виде,
аналогичном (4.186):
®о = 2-Т®о. < (4.202)
то величина w0 будет иметь значение
— 11g
192 ’
(4.202')
и прогиб в любой точке представится формулой:
14 . 3
(4.203)
В качестве примера, иллюстрирующего способ решения задачи
при упруго-пластической деформации пластинок, рассмотрим следую-
щий: пусть в центре пла-
стинки пластическая зона
деформаций достигла по-
ловины толщины (рис. 68);
поскольку интенсивность
деформаций е< пропор-
циональна расстоянию
Рис. 68.
точки, для которой она вычисляется, от нейтральной плоскости
(е< = то величина е (4.178) в центре пластинки должна иметь
значение:
е0 — 2х0 = 2, х0—1.
220
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
нагрузки q,
Параметр q, зависящий от произвольной постоянной с и
возьмём равным 5:
qhc?__—___ 9 qc2 ____
2^0 ~ q ~ Т ~~ °'
Модуль упрочнения материала пластинки за пределом упругости возьмём равным 1/20 Е, и потому Х = 0,95. Начало вычислений будем вести по формулам Таблица 7. (4.190) и (4.195), которые Расчёт пластинки по уравнениям (а). принимают вид:
Р СО 3 2 1.5 © = 2,068е-2?, х = 1 — 1,034е~аР,
(а)
Г с 0 0,0498 0,1353 0,2231 1 С Q =3 In — . г Г
1 2 1 « S ьэ « 1 0 3 0,9974 0,00512 0,9811 0,0379 0,9480 0,1030 Пользуясь выражениями (а), вычисляем данные, приводи- мые в табл. 7. Дальнейшие вычисления хи© произве-
дём по формулам (4.196), причём функция ® определится вторым из уравнений (4.191) и (4.178), (4.179), (4.181).- Начальные значения величин х, ©, р берём из табл. 7:
Р1 = 1,5 ^ = 0,948 ©==0,103.
В первой строке табл. 8 помещаем значения р==1п— через интер-
вал . Др = 0,1, во второй и третьей х и ©, в четвёртой е, пятой
разность Зх — 2©,- пропорциональную изгибающему моменту Мх.
Таблица 8.
Продолжение расчёта пластинки.
Р 1,5 1,4 1,3 1,2 1,1 1,0
* 0,9480 0,9356 0,9208 0,9033 0,8828 0,8591
V 0,1030 0,1242 0,1482 0,1752 0,2054 0,2368
е 1,7940 1,7484 1,6955 1,6093 1,5647
Зх — 2v 2,6380 2,5584 2,4660 2,3595 2,2076
Р 0,9 0,8 0,7 0,6 0,5 0,4
% 0,8319 0,8011 0,7657 0,7272 0,6857 0,6413
V 0,2717 0,3078 0,3536 0,3851 0,4149 0,4441
е 1,4877 1,4009 1,3066 1,1953 1,0921 0,9993
3* — 2» 2,1037 1,9523 1,7877 1,5899 1,4114 1,2273
§29] .
НЕКОТОРЫЕ ЗАДАЧИ ОВ ИЗГИБЕ ПЛАСТИНОК
221
При р = 0,4 величина е = 1, и потому при р < 0,4 деформация
пластинки будет чисто упругой. Полагая в (4.151) 2 = -^- = -^- = 0,
находим уравнения:
dx dv п 5 о '
-~7- = v, —г- = 2ц—о-е-2?; (б)
dp ’ dp 2 ’ v '
интегралы их, получающие значения х = 0,6413, v = 0,4441 при
р = 0,4, имеют вид:
v = 0,0733^4- 0,625г-2?, )
х = 0,69760,0365е2Р —0,3125е-2Р. j
Величина Зх — 2 г» обращается в нуль при р = ра = 0,03, и поскольку
это соответствует наружному краю пластинки (г = а), то из соот-
ношения:
In - = 0,03
а
находим постоянную с:
с = 1,03а «а. (г)
Радиус зоны пластичности г = г* найдём из условия:
е=1, 1п —— = 0,4, г* = 1,03ае-°'4яа0,67а. (д)
г*
Прогиб пластинки в центре, согласно (4.186), будет:
2ева2 — , ,
= (е)
причём
1 со
w0 = j Jxe-2Prfp. (ж)
О о
Этот интеграл разбиваем на три интеграла:
0,4 1,5 со
w0== j* xe-2Pflf(oJ" xe-2Pdp-f- J* xe_2?rfo, (з)
О 0,4 1,5
причём первый из них относится к упругой области и равен
0,4 0,4
Jx^-2?rfp = J (0,697б4~0,0365е2Р —0,3125е-2Р) e~2Prfp = 0,144;
о о
222
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
второй вычисляется, согласно таблице:
1.5
j"'ze-2Pdp = 2х»е-2рАр = 0,154,
0,4
и, наконец, третий по формулам (а):
оо со
J* xe~2?dp = J* (1 — 1,034е-2Р)е~2Рй?р = 0,0243. (и)
1,5 < 1,5
Таким образом при q = = 5
-И1О== 0,322. (к)
Упругий фиктивный прогиб, соответствующий нагрузке q = 5, со-
гласно (4.202') будет w0$ — 0,286, поэтому остаточный прогиб
равен:
— 2/* д2
w — w0 — w0$ = 0,036 ,
т. е. составляет около 11% от общего.
§ 30. Приближённые решения задач изгиба пластинок.
Приближённый расчёт пластинок по формуле (4.165) § 28
является совершенно элементарным и даёт удовлетворительные резуль-
таты не только для оценки прогиба, но, как увидим дальше, и для
оценки величины предельной нагрузки. В качестве примеров на
определение зависимости прогиба пластинки от нагрузки рассмотрим
круглую и прямоугольную пластинки.
1. Круглая опёртая пластинка под действием равномерной
нагрузки. Точное решение этой задачи путём численного интегриро-
вания уравнения равновесия указано в предыдущем параграфе.
Обозначая здесь через р отношение текущего радиуса пластинки г
к её наружному радиусу а\
мы можем упругий прогиб её (4.203) записать в форме (4.157):
= (4.204)
причём w имеет выражение:
§ 30]
ПРИБЛИЖЁННЫЕ РЕШЕНИЯ ЗАДАЧ ИЗГИБА ПЛАСТИНОК
223
или, так как согласно (4.202)
(е) Tlfffl4
то
®’ = W(11-14P2 + 3p9. (4.205)
Представим теперь упруго-пластический прогиб пластинки при дей-
ствии нагрузки q в виде:
w==^-w. (4.206)
Тогда, согласно (4.165), для определения постоянной с имеем
уравнение:
f
о
9 = с
(4.207)
поскольку нагрузка q постоянна, и элемент площади пластинки
можно представить в виде 2zr dr — а22тер dp. Квадратичная форма
(4.160) в нашем примере имеет выражение:
£>2 р _____р _____/ d2w \2 , 1 dw d^w , /_1_ dw \2
с2а4 х * \ dp2 / ' р dp dp2 ' \ р dp ) ’
или, на основании (4.205):
^ = i-2(W-252p2+147);
поэтому относительная интенсивность деформаций е равна:
‘ = ZF5 = 7/49 - 84p’ + 3V,
где е0 — значение е в центре пластинки при г = 0, т. е.
____ Tccflh __ 21ся2
е° ~~ 48Дё; — Тб^й2 ’
Вычисляя интеграл
С — , 1/11 14 , 3 \ 5
J wprfp — 1921 2 4'6/ 384 ’
о
(4.208)
(4.209)
224
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
и умножая обе части равенства (4.207) на
его к виду:
мы преобразуем
1
= го [1 - го J <49 ~ 84Р2 + 39?‘)• <4-210)
о
Вычисления проведём для пластинки, материал которой обладает
линейным упрочнением, и потому, согласно (4.179), имеем:
2 = 0, (е<1); 2 = х(1-1 + 2.), (е>1).
Рассмотрим сначала случай, когда часть пластинки, заключённая
внутри окружности радиуса г* < а, деформируется упруго-пластически,
а вне его — упруго, так что:
0<р<7 = ^, е>1; 1 > р > Т, е<1. (4.211)
Ввиду того, что на границе областей р =-у, е== 1, то между у и е0
существует соотношение
1 == -^/49 — 84/ 4- 39/,
или
___________7_________
0 — /49 — 84т2 + 39ji '
(4.212)
Отсюда видим, что если величина е0 изменяется в пределах
то граница областей г* изменяется в пределах Вычисляя
интеграл, входящий в (4.210), получаем:
21^ Г, 1 ' । 1 , 1 >1
—_еор_х,?+_+__х)|,
•?=^(49—42,’4-13-г*),
। 343 1п /49 — 84Т2 + 39р + 39/ — 42
Ч 40 /39 7 /39 — 42
1
>(4.213)
X = 8УЛЗ [(13/“ 14) /49 — 84/ + 39т1 + 98] -/1 /
Поскольку т выражается через е0 формулой (4.212), эти соотноше-
ния устанавливают связь между нагрузкой и прогибом.
§ So] ПРИЁЛИЖЁННЫЕ РЕШЕНИЯ ЗАДАЧ ИЗГИБА ПЛАСТИНОК 225
Если вся пластинка переходит в упруго-пластическое состояние, то
ео ~2 ~
Интеграл, входящий в (4.210), в этом случае берётся от 0 до 1
при 2^-0. Зависимость нагрузки от е0 найдём из (4.213),, если
в функциях <р, X положим 7=1:
. , S43 , 2/39 — 3 о оп 126 . 3 , о
а = 1, 6=-------— In—---------= 2,39, у = -^ 4- = 2,22.
40 /39 7(/39 —6) А 65 1 26 ' ’
Таким образом для е0^>3,5 имеем:
/ -gg=(l-X)e0 + 2,22X-^. (4.214)
8 Cq
Зависимость параметра
а = (4.215)
характеризующего, нагрузку, от относительной интенсивности дефор-
маций в центре пластинки е0 изображена на рис/69. Кривая k*eg
построена по формуле (4.214) для е0>3,5, по формулам (4.213
для 1 / et 3,5 и по условию q = c или, согласно (4.209):
k = eQ, *?0<1.
15 Зик 3138 А. А. Ильюшин.
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [rX.1V
- Прогиб пластинки в центре найдём по формулам (4.206), (4.205):
или, заменяя постоянную с её выражением через е0 (4.209):
Wo = 28-^eo- (4.216)
Сравним прогиб пластинки, найденный путём численного интегри-
рования уравнений (4.191) в § 29. При А = 0,95, е0 = 2 и
Там было найдено значение прогиба в центре:,
9/,
- w0 = 0,322^#-.
0 ’ h
Найдём, какая нагрузка и интенсивность деформаций в центре
пластинки соответствует этому прогибу по приближённому расчёту.
Для этого приравняем прогибы
о 329 2е«а3— 11
h 28 h \
и найдём 5О=1,64. Отличие этого результата от е0 = 2 составляет
18%; такое же отличие получается в кривизнах, а следовательно,
и напряжениях. Из (4.212) находим границу между упругой и
упруго-пластической областями:
3974_84^ + 49(1-^ = 0, .
72 = 0,467, 7 = 0,683.
Отклонение от 7 = 0,67, найденного в§ 29, составляет менее 2%.
По формулам (4.213) находим теперь ©, ф, /:
® = 0,7352, ф = 0,6876, /= 1,3372
и находим параметр, определяющий нагруку:
Л = 1,4974. ‘
При численном интегрировании уравнений равновесия эта величина
равна 1,46, и потому отклонение приближённой зависимости нагрузки
от прогиба от точной составляет 1,5%.
Кривая k-e0 (рис. 69) при к = 1 имеет асимптоту
^« = ^^==2,22, (4.217)
§ 30] приближённые решения задач изгиба ПЛАСТИНОК 227
которая определяет несущую способность пластинки. Ниже мы увидим,'
' что эта величина достаточно хорошо совпадает с точным значением
несущей способности.
2. Квадратная опёртая пластинка под действием равномерной
нагрузки. На рис. 70 изображена
квадратная пластинка со стороной
2а, начало координат х, у помеще-
но в центре пластинки. Отнесём
координаты точки к размеру а и
обозначим:
Прогиб пластинки при упругой де-
формации зададим в виде (4.157),
а при упруго-пластической — в виде
(4.159):
—
w = .
Причём
W =/И COSCOS 7| (4.218)
удовлетворяет граничным условиям
По формуле (4.160) находим:
S (з coS2 е cos2 ~ 7] + sin® “ $ siП2у , (4.219')
или
Рх = + cos ^5-]- cos тет] 2cos cos тет]). (4.219)
Число т должно быть выбрано так, чтобы выполнялось равенстве
(4,164'):
' ,f Г К di a fl
f f W d; di} *
откуда следует:
« = §• (4-220)
Как и в предыдущих задачах, введём относительную интенсивность
Деформаций:
е —— Jell - 1/ р cha?
es es /3 V * e3D/3
2Й8 РАВНОВЕСИЙ ПЛАСТИНОК И ОБОЛОЧЕК (гЛ. IV
или согласно (4.219):
е$ , /к 144 ся2
) в У 6“ ’ е° тс* с3 /г2 ’
R = 2 -f- cos тс; -|- cos ttf\ -j- 2 cos тс; cos тст].
(4.221)
144 <9 2
Умножим обе части равенства (4.165) на и обозначим пара-
•рис. 71. Вычисляя интеграл
метр, характеризующий нагруз-
ку на пластинку, через k:
к=^г' <4-222)
Тогда получим:
k=e0 I-'-’ '• ). (4.223)
\ J J w di d<\ j
Вследствие симметрии рассматри-
ваемой задачи, входящие в послед-
нюю формулу интегралы можно
вычислять лишь по четверти квад-
рата: 0 1, 0 т; 1; эта
часть пластинки изображена на
от ® и выражая через /?, имеем:
Уравнение (4.223) теперь принимает вид:
1 1 ,
k = е0 (1 — 1 j* j* /?2 dl difr (4-224)
о о
Дальнейший расчёт произведён для пластинки, материал которой
обладает линейным упрочнением, так что
' 2 = 0,(е<1); ' 2 = Х(1 — + (*>!)•-
Поскольку е0 есть максимальное значение интенсивности деформаций
(в центре пластинки), то при е0 < 1 изгиб пластинки будет упругим
(2 = 0):
k = e0, е0< 1. (4.225)
Построим линии уровня поверхности /?, совпадающие с линиями
уровня Рх. На поверхности:
Р = 2 cos тс$ -j- cos тст] —j- 2 cos nJ cos тст]
§ 30] ПРИБЛИЖЁННЫЕ РЕШЕНИЯ ЗАДАЧ ИЗГИБА ПЛАСТИНОК 229
в первом квадранте расположены две прямые: c = и , па-
3 '
раллельные плоскости 5, ц; па них R — -%, и потому они являются
линиями уровня. Плоскость ; = т] пространства ;, -q, R является
плоскостью симметрии поверхности R. Некоторые значения R даны
в табл. 9.
Таблица 9.
Значения величины R.
1 0 0,134 0,500 1,00 1,53 1,87 2,00
5/о 0,432 1,53 1,77 1,87
‘/в 1,53 1,50 1,53 1,53 1,53 1,50 1,50
8/б 3,00 2,00 1,53 1,00
2/в 4,53 3,59 1,5) 0,50
Ve 5,63 5,23 1,53 0,134
0 6,00 5,63 4,50 3,00 1,50 0,402 0,00
0 7в 3/в 4/в 7в 1
На рис. 72 показана поверхность R и на ней нанесены линии уровня
при значаниях iq, принятых в таблице. Кроме абсолютного макси-
мума R = 6 в центре пластинки имеются ещё относительные максимумы
R — 2 в углах. Так как в случае упругой деформации квадратичная
форма Р* с точностью до множителя совпадает с потенциальной
энергией деформаций пластинки, приходящейся на единицу площади,
а Р* пропорционально R, поверхность R характеризует закон рас-
пределения упругой потенциальной энергии. Сргласно (4.221), вели-
чина R пропорциональна квадрату интенсивности деформаций наруж-
ных слоёв пластинки, и потому поверхность R позволяет указать,
В какой последовательности и какие именно области пластинки
230 РАВНОВЕСИЕ ПЛАСТИНОК и оболочек [гл. IV
выходят sa предел упругости. Обозначим через Fo, Ft . . . , FQ пло-
щади областей части пластинки, заключённой в первом квадранте
(5 О, т] 0). Эти площади ограничены прямыми линиями, прибли-
жённо совпадающими с проекциями линий уровня R на плоскость
£., tj, причём они заполняют всю пластинку, т, е.
в
о
Средние значения Rn на этих площадях выберем в соответствии
с приведённой выше таблицей, причём так, чтобы
в
S/?nFn = 2,
о
Это условие вытекает из равенства
1 1
J J R d^dti = 2.
о о
Тогда получим табл. 10 значений Fn, Rn и .
Таблица 10.
Значения Fn, Rn и еп1е$. . .
п 0 1 2 3 4 5 6
Fn 1/зв 7зв 5/з6 7/зв ' 4/зв 12/зв 4/зз
Fn 5,5 4,7 3,3 2,1 1,8 1,1 0,2
enJe0 С 0,955 0,881 0,742 0,591 0,546 0,429 0,184
Если е0 > 1 и упруго-пластическая область пластинки охватывает
площадь Fo, F^ ... ,Ftf(N^. 6), значит, еу = 1 и потому е0 должно
быть найдено из соотношения
причём значение следует взять в таблице при п = N. Формулу
(4.224) перепише,м в следующем виде:
я
= 5оА' (1 о" ^«) >
Z 0
#30]
ПРИБЛИЖЁННЫЕ РЕШЕНИЯ ЗАДАЧ ИЗГИБА ПЛДСТИНОК
231
или, заменяя Qn его выражением через еп и затем получим:
„ N N
[1 -4(2 R'.F. V w] •
Обозначим
N N г z- у _
0 Q ' Q
Тогда найдём окончательную форму зависимости нагрузки от дефор’
мации:
ь » А Х?лг> г Z/w Х<Ь? (Л. 99ГП
«№= CoWl 1 - 9“ Н" "9 2^2~ (4,220)
V * 7 * ON
Функции <pw, И Con (,eN — 1) даны в табл. 11.
Таблица II,
Значения функций фу, <ру, yN и e^N.
N 0 1 2 3 4 5 ’ 6
’ <?N 0,153 0,545 1,004 1,412 1,612 1,978 2,000
XN 0,240 0,901 1,828 2,865 3,412 4,697 4,883
hr 0,087 0,371 0,932' 1,918 2,528 4,858 5,043
eoN 1,045 1,133 1,35 1,69 - 1,83 2,33 5,43
Если е0~^> еОб = 5,43, то величины -%N, фд принимают макси-
мальные значения согласно таблице, и потому зависимость k — е0
имеет вид:
А = (1^Х)е0 + 2,44Х—е0> 5. (4.227)
о
По мере возрастания нагрузки и интенсивности деформаций е0 сначала
за предел упругости выходит центральная часть’ пластинки (площадь
Fo на рис. 71), затем последовательно в порядке удалённости от
центра получают пластические деформации площади F2, F3;
после этого возникает пластическая деформация в углах пластинки
(площадь Г4 на рис. 71). При e0N = 2,33 упруго-пластическая область
охватывает почти всю пластинку, исключая окрестности середин её
сторон; в точках Е = 0, т] = 1 и Е = 1, т| = 0 пластическая дефор-
мация возникает теоретически лишь при бесконечно'большом еначе-
нии в0, но практически уже при е0>5 можно считать, что она воз-
никает всюду.
232
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Если материал пластинки не обладает упрочнением, то Х=1, и
при ‘достаточно больших прогибах (е0>5) зависимость (4.227) прини-
мает вид:
9 52
А = 2,44-^, Атах = 2,44. (4.227')
о
Значение ^=2,•44 определяет несущую способность квадратной
пластинки. Заметим, что дро'ь 144/~2, входящая в выражение k
(4.222), отличается от дроби 21/16, входящей в выражение k для
круглой пластинки, только на 4°/0; сравнивая значения k для круглой
(4.217) и квадратной (4.227) пластинок, заключаем, что 1 если
радиус первой равен полустороне второй, то максимальное равномер-
ное давление, которое они могут выдержать, примерно одинаково.
Для квадратной пластинки имеем:
/;2 £ __ j 7g J-s
Чтах 144 «2» гетах— ’ д2 ’
а для круглой (4.217)
„ 16 1 . - - q
"max' 21 a2 ’ К“и ' 1,Da e2
Приведём ещё формулу для прогиба в центре квадратной пластинки:
еа4 —
wo-
Заменяя постоянную с её выражением через е0 (4.221) и учитывая,
что согласно (4.218) и (4.220). <шс — 64Д6, получим:
4 а-е
(4-228)
Задача об определении прогиба по данной нагрузке q решается
с помощью формул (4.228) и (4.225) или (4.226) или (4.227), так
как и k оказываются выраженными в функции одного параметра
«0. 3 виду простоты такого метода можно не производить построе-
ния кривых k-e, как это было сделано для круглых пластинок.
§ 31. Несущая способность пластинок.
Как уже показано на примерах предыдущих параграфов, макси-
мальная нагрузка, которую может выдержать пластинка, определяется
вариационным уравнением равновесия (1.156') или (1.165) при условии,
что материал её не обладает упрочнением
§31]
НЕСУЩАЯ СПОСОБНОСТЬ ПЛАСТИНОК
233
а упругая деформация еа пренебрежимо мала сравнительно с общей et.
Если воспользоваться выражением функции 2(РХ) для материала
с линейным упрочнением:
2 = Лр — f + =
( 2е 1 2е3/ е8 е8Уз v
то, полагая К — 1 и совершая предельный переход
ел-+ О, Е -> со, (Ees)-+ og,
из (1.156') получим
2-7>/x,<>'= J J" ,i^dxdy-
Обозначая через a характерный размер пластинки и через q0 хара-
ктерное значение нагрузки q:
q = qrf, (4.229)
мы запишем вариационное уравнение равновесия в виде:
s Г Г С /^7 — - ^~k~ Ч™} dx dy = °- (4.230)
Так как
= ’'j + *3 + '4 + Х12,
уравнение (4.230) относительно w является однородным квазилиней-
ным. Моменты и перерезывающие силы выражаются через прогиб и
его произвочные в виде однородных функций нулевой степени; в самом
деле, из (4.127), (4.138) имеем:
J,= Z)(1— Q)=JL А ма = ^,
V 3 У ’ 8 4
(4.231)
Таким образом граничные условия для прогиба и его производных
будут всегда однородными и квазилинейными. Следовательно, вариа-
ционное уравнение (4.230) может иметь решение лишь при некото-
рых определённых значениях параметра k; минимальное из них и
234 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [гл.IV
определяет максимальную нагрузку или несущую способность пла-
стинки. Разрешим уравнение (4.230) относительно k:
(4.232)
2 V 3 J f q aw dx dy
Для нахождения несущей способности согласно этому уравнению
нужно найти такое w(x, у), чтобы величина k имела минимум,
т. е. решить задачу, в"некотором смысле экологичную задаче опре-
деления упругой критической силы по методу Тимошенко.
Для примера возьмём прямоугольную пластинку с отношением
сторон а — а/b, свободно опёртую по контуру и нагруженную равно-
мерным давлением q — q0. Направляя оси х, у, по сторонам а и b
и полагая, согласно граничным условиям:
, т.х . гуа
w = с sin — sin ,
a a
имеем: >
T n >---
7= ____________________________________________________________
= (l-l-a8)3— (14-a4)^cos~~ + cos~^') + (1 -[~a2)acos^^cos^^.
Поскольку вариации 8w и 8 P* берутся по с и пропорциональны
8c, знак вариации в числителе и знаменателе (4.232) можно сокра-
тить вместе с с. Задача сводится к вычислению одного интеграла:
а
а а
k= а^~ f f Tdxdy.
16За2,J J
00
Другая постановка задачи о несущей способности получается
с помощью конечного соотношения между моментами (4.72):
Mi— Л41Л42 + Л42 + ЗЛ1?2 = Л1в. (4.233)
Основное уравнение равновесия пластинок имеет вид:
^+2^ + ^42+^0. / (4.234)
дх- 1 дх ду 1 ду2 17 ’
К нему необходимо присоединить условия совместности деформаций
(4.169), в которых, однако, функция J уже не может быть выра-
жена через моменты и Должна считаться неизвестной. Воспользуемся
обозначениями (4.24) и перепишем (4.169) так:
д (Hi\ 3 3 /Mis\ д (Н.Л 3_ д
ду \ J ) 2 дх ( J ) ' дх \ J ) 2 ду \ J )'
§31]
НЕСУЩАЯ СПОСОБНОСТЬ ПЛДСТИНОК
235
Из них можно исключить функцию J следующим образом; производя
дифференцирование, имеем:
н^- 1 ду dz Н*дх 3 .. dz dHi 2 12 дх ду 3 .. dz дН 2 12 ду дх 3 2 дх ’ 3 дМ12 2 ду ’
где z = In J. Решим эти уравнения относительно производных
функции 2'.
1 дх 2 ( 12 ду * ду j 1 дх 4 12 дх
dz 3 г.. dHi г, dM!2\ . „ dHr 9 .. dM^ \Ъу-2 X2 H, dx ) + H2 ду 4 Л41а ^dy .
Теперь обозначим
(4.234')
и исключим из последних уравнений г. Тогда получим дифферен-
циальное уравнение:
д д / Hi \ д
дх L "Д~ дх \ Л412 / J ду L
L ( М
ду \ Ми /
2 „ д /1 дНЛ 2 „ д (1 дНЛ
3 1 с(_у1 Д дх J 3 2 dr I Д ду) ’
(4.235)
Система уравнений (4.234), (4.235) вместе с конечным соот-
ношением (4.233) определяет несущую способность пластинки.
Вместо моментов Мг, М2,
ТИ]2 и их линейных комби-
наций
Яа == Л43 — -i-
удобно ввести новые неиз-
вестные. Для этого обозна-
чим через 9 удвоенный угол,
составленный нормалью к
одному из главных напра-
влений деформированной поверхности с осью х (рис. 73). В главных
осях (1.2) крутка поверхности и крутящий момент равны нулю; глав-
ные изгибающие моменты обозначим через М', М". Тогда из условий
236
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
|ГЛ.1¥
равновесия элемента имеем:
. М' -\-Мп М'- М" „
----------г-----cos 9,
„ М' + М" , М' — М" а
Мя =------2-----1----2-----со 9>
.. М’ — М" . п
----------------sin9-
(4.236)
Подставляя эти значения моментов в конечное соотношение, получим:
Л4'3 —Л4'ЛГ + ЛГ2==Л41. (4.237)
Условию (4.237) можно удовлетворить, введя новую переменную ср;
М' =s sin fc₽ 4- £),
, • 2М
М — —TLsin
(4.238)
после чего из (4.236) найдём выражение трёх моментов Mlf Л42, Л413
через две функции ср и 9:
М1 , 1 „
— = siп ср--— cos ср cps 9,
М, т уз ‘
Д4о . 1 п
~ = Sin Ср 4--— COS ср cos 9, •
Ms Уз .т
—• —, _L_ cos ср sin 9,
уз у
(4.239)
а также выражения Ни Н.2 и Д:
= cos3 ср — \ .
Л42 4
Уравнения (4.234) ,и (4.235) теперь можно записать через функции ср
и 9, и вместе с граничными условиями они будут определять несущую
способность пластинок.
Рассмотрим простейшую задачу о несущей способности круглых
пластинок при симметричной нагрузке. Решение её позволит оценить
ещё раз степень точности приближённого определения максимальных
нагрузок вариационным методом. Вместо уравнения (4.234) восполь-
зуемся более простым уравнением равновесия в. полярных коорди-
натах (4.172):
У
dM, । Mi — М, b г. 1 г , ,.
. -^ + -±7-^=-7/’-7j ^г-йГг> (4-24°)
ь
$31j
НЕСУЩАЯ СПОСОБНОСТЬ ПЛАСТИНОК
237
причём /Ир Л12— радиальный и тангенциальный изгибающие моменты
являются Главными, и потому согласно (4.238):
'М^б’
М^.ЛГ'^^зи^,
V $
(4.241)
Основные граничные условия
является свободно опёртым, то:
,/Wi = 0,
= (я = 0,1). (4.242)
Если край защемлён (х2 = 0),
то:
п,, , 2М,
2М2 = М, = ± ,
= «ir — — (« = 0,1). (4.243)
Эллипс, изображающий конеч-
ное соотношение (4.237) или
(4.241), дан на рис. 74; на нём
указаны значения параметра <!>
для различных М1ГМ2, приво-
димые в табл. 12.
Вместо эллипса можно взять тачже описанный или вписанный
имеют следующий вид: если край
в него шестиугольник.
Таблица 12.
Значения ф, т^, и т«.
ф — л 5 6 ~ 2 ~ з-11 1Г ~ 2 те ~ 3 It “ '6 0 те "6 У те У 2я 3 5.т те
мг Ш1 = -— Ма 0 1 УЗ — 1 2 Уз — 1 1_ УЗ 0 1 /3" • 1 2 Уз 1 1 Уз 0
<Nl * II с« g 1 1 Уз 0 1_ Уз — I 2 Уз 1 2 УЗ 1 1 Уз 0 1 Уз —1
238
РАВНОВЕСИЕ ПЛАСТИНОК и оболочек
[гл. IV
1. Кольцевая пластинка, нагруженная перерезывающей силой Р.
Предположим сначала, что наружный край защемлён (рис. 75, а). На
внутренней границе г = Ь, = 0, и так как кривизна ха отрица-
тельна, то Л42 = -J- Ма; на наружной границе г —а, согласно (4.243),
= 2М2 — — Следовательно, возрастанию радиуса от b до а
соответствует движение по эллипсу (рис. 74) от =— тс до ф = — у
против часовой стрелки или движение по шестиугольнику по АР’С'Е'.
Обозначим
Мх
т, = тА-, т2 = ^г-,
.ЬР . ЬР
Мя—^ h^a ~
(4.244)
и положим q — 0. Из (4.240) имеем:
г - -jp + nii-^m2= -kv
(4.245)
На линии AFC' шестиугольника имеем т2 — тг =* 8, причём 8 — 1
2
для вписанного в эллипс шестиугольника и 6 = —-= для описанного
t ; V3
шестиугольника. Интегрируя (4.245), получим:
/Я1 = (8—^)1пу. (4.246')
На участке шестиугольника от точки С' до £' имеем тг = — 8,
поэтому отрезок £'£' соответствует наружному контуру. Полагая
Несущая Способность пластиной
239
в (4.246х) г —а, т = — 8, находим несущую способность пластинки:
1 + 1пТ / 2\
А = 8 -----(1 < 8 < (4.246)
1 1ПЛ ч /зЛ
п ь
Отсюда полная сила, приложенная к внутреннему контуру, имеет
следующее максимальное значение:
i + ln4
2^^max = $max = 7 ------— • (4’246")
1п7
ЁозьМём теперь конечное соотношение согласно эллипсу (4.241):
= m2 = Y^sinV?+-з;> —л-
Уравнение (4.245) приводим к виду:
r_sn4?_ --^coscp — ^,
и, инДегрируя в пределах от ^<р= — ft + ^J до /* = ^»
( 71 ।
1<р=—у “г е' /> получим:
(4.247х)
< «
— л ч------
* 6
Квадратура, входящая в это уравнение, легко вычисляется, и мы на-
ходим следующую формулу, определяющую несущую способность
пластинки:
, а Л1У”3 Г . ЛЛАТ+З .
1П » —Г- = - [arc,S (.У 47=1 с|8 nJ -
, / 1 _ 1 \-| f 1 1 2^14- 3 .. пл*1\
-«rclg^y ^ijJ+^" (4.247)
Значение А,, даваемое этой формулой, заключено между значе-
2
ниями Ац согласно (4.246), при 8=1 и 8 = -^==, так что расчёт по
описанному шестиугольнику даёт верхнюю границу Несущей способ-
240 РАВНОВЕСИЕ ПЛАСТИНОЙ И ОЙОЛОЧЕЙ (гл- IV
ности, а по вписанному — нижнюю границу её. В самом деле, урав-
нение (4.245) можно записать в виде:
«и
in £ = _ f dmi
а b J kt — (m* — mi) ’
«•la
У”3 ‘
причём в нашем примере т1а—---------лг1Ь = О; замена эллипса
описанным шестиугольником означает, что разность т2 — mi заме-
няется большим значением, благодаря чему и интеграл получается
большим, т. е. при заданном величина получается большей, чем
если бы расчёт вёлся согласно эллипсу. Замена -еллипса вписанным
шестиугольником приводит к обратному результату.
Рассмотрим теперь другие случаи граничных условий пластинки,
причём для простоты -вычислений расчёт произведём только по шести-
угольнику. -
Если внутренний и наружный края свободны от изгибающих мо-
ментов (рис. 75, б), так что
г —а, г — Ь, 2И, = 0, М2 = -\-Ма,
то решению задачи на шестиугольнике соответствует одна точка А,
и потому имеем из (4.245):
^ = 0, m2 — Z, Aj = 8. (4.248)
Если внутренний край (г = Ь) защемлён (рис. 75, в), а внешний
нагружен только перерезывающей 1илой Р, то при \
г==6, -z2 = 0, 2zW2 = Afj — + Ма;
на наружном контуре ^=0, и так как х,2 < 0, то М2 —Ма.
Таким образом для решения задачи необходимо использовать на шести-
угольнике участок ЕВ Л. На ВА т2 = Ъ, и потому из (4.245) имеем:
OTj = 8 — kr 1 — у),
причём удовлетворено условие г — Ь, т1 = Ъ. Отрезок ЕВ шести-
угольника соответствует внутреннему контуру пластинки.. Полагая
на внешнем контуре r = a, т1 » 0, находим:
(4.249)
a
Интересно отметить, что на внутреннем контуре имеет место скачко-
образное изменение /па от значения у до 8; ясно, что если вместо
§31]
НЕСУЩАЯ СПОСОБНОСТЬ ПЛАСТИНОК
241
шестиугольника для расчёта воспользоваться эллипсом, этот скачок
не имел бы места и в окрестности внутреннего контура происхо-
дило бы очень резкое изменение т2.
Последний случай, когда оба края пластинки защемлены (рис. 75, г),
можно рассчитать следующим образом: от г — Ь до г = г*, при ко-
тором т1 — 0, имеет место предыдущее решение:
г*
т г = г* до г = а имеет место первый из рассмотренных случаев,
и потому, заменяя в (4.246) радиус b на г*, имеем:
Исключая из этих уравнений г*, находим несущую способность пла-
стинки: \
. _\
= 4. (4.250)
В табл. 13 даём значения у, соответствующие различным значе-
ниям у для рассмотренных четырёх случаев нагружения.
Таблица 13
Значения alb в зависимости от Aj/8.
О ' 1 ’ 1.25 1,5 1,75 2 2,5 3 4 5 ОО
\bk ". об I 54,6 7,39 3,79' 2,72 1,95 1,65 1,39 1,28 1
Й И со^ не существуют
„ . 5 3 2,33 2,00 1,67 1,50 1,33 1,25 1
\ О /г - j273 22,2 8,83 5,44 3,25 2,48 1,86 1,61 1
На рис. 76 построены графики несущей способности кольцевых
.. ki
пластинок, причём по оси ординат отложена величина у, выражаю-
16 Зак. S138. А. А. Ильюшин.
242 РАВНОВЕСИЕ ПЛАСТИНОК Й 0Ё0Л0ЧЕК (гл* IV
щаяся через результирующую силу Q, приложенную к внутреннему
или наружному контуру: v
8 лй2а38 \ "|ЛЗ /
2. Сплошная круглая пластинка, нагруженная давлением.
Пусть qQ— максимальное значение нагрузки q = qtf]. Обозначим
k=.^- о = - 1
₽ > (4.251)
/(р) = / ?Р<*Р.
о J
а уравнение (4.240) запишем в виде:
p^-4-mi-/«2 = -4V(p). (4.252)
Относительно функции / (р) (нагрузки q (г)) будем предполагать,
что она монотонна или такова, что прогиб не меняет знака и моно-
тонно изменяется от центра к краю пластинки. В центре, по условию
симметрии, оба момента одинаковы: /и1 = /и2 = 8, и потому ему со-
ответствует точка В на шестиугольнике или ф = на эллипсе (рис. 74).
О
§ 31 j несущая способность пластинок 243
Если пластинка свободно опёрта, то при г —а, (р = 1),
т1 = 0, /я2 = 8» т. е. краю пластинки соответствует в этом слу-
чае точка А шестиугольника или ф = 0 эллипса. Следовательно,
согласно шестиугольнику на пластинке всюду конечное соотно-
шение имеет вид: т2 = 8. Интегрируя уравнение (4.252), имеем:
₽
у f /(р) ^Р + у,;
или, определяя сг по условию
/«1 = 0, р = 1, получаем:
т1 = 8 —s
+ 7 J/(P)^P. (4-253)
р
Несущую способность пластинки
находим из условия р = 0, т1 = 8:
р
т. е.
& = _—2----. (4.254)
4 f /(р) dp
о
Рассмотрим, в частности, случай симметричной равномерной на-
грузки, распределённой по кругу радиуса с^а (рис. 77, а). Со-
гласно (4.251) имеем:
/(р) = 4, 1р <-£.,
Лр)=4£’ р>4’
/яр)^=14(3-2т)’
о
и потому максимальная нагрузка определяется формулой:
а2
3 -V
k = —-----—? 8. (4.255)
2(3-2—)
\ а /
16*
244
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК I™- IV
При с = а .равномерная нагрузка распространяется по всей пла-
стинке, причём:
= = (4.255')
г, Л2 2 ’ ' ’
Эта задача была решена приближённо вариационным методом, при-
чём несущая способность согласно (4.217) определена формулой:
== — о 22 — 1 677
Сравнивая эту величину с (4.255')» снова убеждаемся в очень боль-
шой степени точности приближённого решения вариационным мето-
дом. Интересно отметить, что приближённое значение 1,677 заклю-
чено между двумя точными решениями по описанному и вписанному
около эллипса шестиугольнику, и потому оно почти точно совпа-
дает с решением задачи, при котором конечное соотношение между
/Wj и ТИ2 берётся в виде эллипса.
Если пластинка защемлена по наружному контуру, то при р = 1,
2/я2 — т1 — — 8 (точка Е' на шестиугольнике рис. 74). Следовательно,
в пределах 0 < о < 7 < 1 имеет место решение предыдущего случая:
«1 = 8 (1 - -j- у- J /(р) do,
р
которое при р == 0 даёт:
78 = 4*//(p)rfp. (4.256)
о ,
В пределах 7 р 1 имеет место соотношение
та — = 8,
благодаря которому из (4.252) имеем:
р .
«1 = 81п-^-4А ^/(p)rfp,. (4.257)
7
причём произвольная постоянная выбрана так, что т1 — 0 при р = 7-
Отрезок С’Е' шестиугольника соответствует границе пластинки,
в чём нетрудно убедиться, если допустить обратное, т. е. что ему
соответствует некоторая граничная кольцевая область. Поэтому, по-
лагая р = 1 и т1 — — 8, из (4.257) имеем:
1
8 fln|+l) = 44 J l/(p)dp. (4.258)
§ 31] несущая способность пластинок 245
Исключая k из (4.251) и (4.258), получаем уравнение, опреде-
ляющее 7:
т 1
(14-Ini) J/(p)rfp = 7 j ^/(Р)йр, (4.259)
о t
после чего находим параметр k, определяющий несущую способность
&«= J. (4.260)
4 f/(p)dP .
о
В качестве примера рассмотрим случай постоянной нагрузки, рас-
пределённой по всей площади пластинки (рис. 77, б). Вычисляя
интегралы:
|/(р)с?р=^-, J у/1р)^р= №)>
о '<
из (4.259) имеем:
5— 4Т Ш 4-= 0,
ул ’ у« '
откуда находим у = 0,731, т. е. зона пластинки, примыкающая
к-центру, в которой изгибающий момент Л42 = /Иа постоянен, зани-
мает почти диаметра. Из (4.260) определяем несущую способ-
ность:
& = А=2,88. (4.260')
Она почти в два раза больше, чем у свободно опёртой по контуру
пластинки.
Полученные выше точные решения позволяют в большом числе
случаев подтвердить тот факт, что приближённое определение несу-
щей способности вариационным методом даёт весьма близкие к истин-
ным значения предельных нагрузок, особенно в тех случаях, когда
в качестве формы изгиба берётся прогиб w (х, у), определяемый
упругим решением соответствующей задачи. Определение же несущей
способности по приближённому методу сводится всего лишь в вы-
числению по заданному w(x, у) квадратичной формы Р* и вычисле-
нию двух квадратур, входящих в формулу (4.232). Необходимо
отметить, что граничные условия закрепления пластинок имеют весьма
существенное влияние на величину предельной нагрузки,
246
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[г.'. IV
§ 32. Безмоментная симметричная деформация
оболочек вращения.
Если распределённая нагрузка, действующая на тонкую оболочку,
изменяется достаточно плавно по её поверхности, то, исключая
границу, вблизи которой возможен краевой эффект, напряжённое
её состояние можно считать безмоментным. Нагрузка, вообще говоря,
произвольная, не должна, однако, вызывать геометрических изгиба-
ний, т. е. деформаций, не сопровождающихся удлинениями элементов
серединной поверхности. Например, любая плавно изменяющаяся по
образующей и постоянная по круговым сечениям нагрузка, прило-
женная к оболочкам вращения, допустима при безмоментном напря-
жённом их состоянии.
Мы рассмотрим некоторые частные вопросы безмоментной теории
осесимметричных оболочек, имеющие практический интерес: во-пер-
Рис. 78.
оболочки и обозначены 00 —
вых, задачу об определении об-
щих и остаточных деформаций
оболочки при произвольной на-
грузке и об определении несущей
способности оболочки; во-вторых,
вопрос о том, насколько увели-
чивается прочность оболочки, ес-
ли ей дать определённую конеч-
ную деформацию; наконец, в-тре-
тьих, задачу об опрессовывании
оболочки с помощью осесиммет-
ричной матрицы.
1. Определение деформаций
по заданным нагрузкам', несущая
способность. На рис. 78 изобра-
жено сечение куска симметричной
ось симметрии, R%— главные
радиусы кривизны серединной поверхности, г — радиус поперечного
кругового сечения, h — толщина оболочки и 6 — угол между нор-
малью к поверхности и осью 00. Внешние силы представим в виде
двух величин: внутреннего давления р и результирующей силы Р,
растягивающей оболочку в направлении оси 00; последняя является
проекцией на ось внешних сил, действующих на часть оболочки,
расположенную справа или слева от рассматриваемого сечения. Ввиду
того, что напряжённое состояние оболочки является безмоментным,
меридиональная растягивающая сила Т\ и тангенциальная Тя связаны
с соответствующими напряжениями avo2 простыми формулами:
Ti = c1h, Тя = аяй.
Известные уравнения равновесия сосудов имеют вид:
= А 2^TlSin6=P,
(4.261)
§32]
БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК
247
и потому напряжения а2 определяются формулами:
С __ ^*^2 С ______ ^?2 _____ ^?2 с
1 2прг3 ’ 2 Г /?1 Р
Интенсивность напряжений определяется формулой
(4.263)
Таким образом, в случае малых деформаций оболочки одних лишь
уравнений статики достаточно для того, чтобы полностью определить
напряжённое состояние. Если материал оболочки не обладает упроч-
нением, то из условия Мизеса
находим предельную нагрузку данного характера распределения,
т. е. несущую способность оболочки:
|р I . (4.264)
Если действующая в некотором сечении нагрузка меньше предель-
ной, т. е. левая часть равенства (4.264) меньше правой, то дефор-
мация оболочки в этом сечении является упругой; в противном слу-
чае равновесие сил невозможно.
Для оболочек, материал которых обладает упрочнением и харак-
теризуется диаграммой <з4 = Ф(е4), или
af = Eef(l — ш), Е^ = ^(1-}-<?),
так что по диаграмме определена функция ф (аД — по задан-
ным силам р, Р или напряжениям а1, а2 легко найти меридиональ-
ную и тангенциальную деформации серединной поверхности:
si=^-(ai ~ 7аа). ®а = ^(а2—j (4.265')
или согласно (4.262):
е — d+<P)pr /„ с )
ei “ Eh ^2’/’
2—’ Eh 2
Компоненты вектора перемещения точки рассматриваемого сечения
по направлениям внешней нормали и образующей в сторону воз-
растания угла 0 обозначим соответственно те» и а. Тогда можем «а.
248 РАВНОВЕСИЕ ПЛАСТИНОК И ОВОЛОЧЕК [гл. IV
писать следующие формулы, выражающие деформации через пере-
мещения:
w , du ' w sin 0 4-и cos 0 пйсх
== ’ г* = '--------г-----• <4-26б)
Перемещение и. будем считать равным нулю в сечении, где в = ~,
т. е. где образующая оболочки параллельна её оси. В таком случае,
интегрируя дифференциальное уравнение для перемещения а, кото-
рое получается из (4.266) путём исключения щ», находим:
в
« = sin© f df),
J sin 0
u< — s.2/?a— u ctg 0.
Внося сюда значения s1; ea, получаем окончательные выражения
перемещений:
9
и = f В-L
Е J h
re
T
w ~ i S^ — uctgfE
Здесь функция ср предполагается выраженной через af, которое,
в свою очередь, определяется через известные величины по формуле
(4.263). Поскольку упругие перемещения (в случае, если а; < оя)
получаются по формулам (4.267), в которых нужно положить ср = О,
то ясно, что остаточные перемещения и, и>, которые сохраняются
после снятия нагрузки, получаются также из формул (4.267), если
в них вместо I-}-? сохранить лишь величину ср.
Для оболочек, материал которых обладает линейным упрочнением,
функция ср (af) имеет следующее выражение:
(4.268)
Здесь обычный параметр А = 1 -—. Если воспользоваться этим
выражением <р и, заменяя в нём <з{ его выражением (4.263), подста-
вить в (4,267), можно получить явные выражения общих и остаточ-
ных деформаций оболочек. Однако интеграл, входящий в (4.267),
может быть вычислен лишь после того, как будут заданы конкретно
форма и размеры оболочки, а также нагрузка.
§ 32] БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 249
2. Нагартовка оболочек. Нагартовкой называется процесс упроч-
нения оболочки путём сообщения ей предварительной пластической
деформации сравнительно большой величины. Если материал обо-
лочки обладает значительным упрочнением, так что, например, истин-
ное сопротивление при разрыве образца в два раза больше предела
текучести, то путём нагартовки можно значительно увеличить .проч-
ность оболочки. Среди вопросов, которые в связи с этим могут
быть решены методами теории пластичности, находятся такие, как
вопрос о том, какова должна быть исходная форма оболочки и как
нужно прикладывать деформирующие заготовку силы, чтобы полу-
чить в результате оболочку данной формы. Мы ограничимся про-
стейшими примерами нагартовки сферической и цилиндрической обо-
лочек, толщина которых в исходном состоянии постоянна, а также
задачей о прочности круглой пластинки с большим прогибом.
В случае сферической оболочки, начальный радиус которой /?0
и толщина стенки. h0, а конечные размеры соответственно /? и h,
имеем:
__ __ __р/?
— °2 —— 2А >
причём р — конечное значение внутреннего давления. Деформации е15 г2
одинаковы и определяются формулой:
<4-2И>
где через р обозначено отношение конечного радиуса R к началь-
ному Rq. Из формул (4.265') имеем:
Р~ 1 = -£—(-1 — • <4-270)
Из условия неизменяемости массы оболочки имеем:
A-rtR^h = 4л/?5Л0, (4.271)
и потому выражение интенсивности напряжений (4.269) можем пре-
образовать к виду:
= <4.272)
Поскольку характеристика упрочнения материала a(at) известна, то
уравнение (4.270) определяет давление р, которое способна выдер-
жать сильно деформированная сферическая оболочка. Воспользуемся
законом линейного упрощения (4.268) и определим это давление;
(4.273)
250
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
где ра — давление, при котором начинается текучесть заготовки, и
т — параметр, зависящий от удлинения еа — ^~ и от А:
2й0 2(1— X)
(4.273')
Определяя максимум р по р, находим, что соответствующее значение
деформации рт — ~ будет:
*м>
__ 3 т — 1
ри,—• 2 ~~пГ'
а максимальное сопротивление упрочнённой оболочки равно
4/п3
Рт~Ра — •
(4.273")
Дальнейшая нагартовка нецелесообразна потому, что она сопровож-
дается утоньшением стенки, которое ослабляет оболочку сильнее,
чем она упрочняется за
счёт наклёпа материала.
Заметим, что максималь-
ная прочность, даваемая
формулой (4.273"), для
металлических оболочек
не всегда достижима, так
как деформация р,„ может
оказаться большей той,
при которой происходит
разрыв. Но формула
(4.273) показывает, что
нагартовка, даже и незна-
чительная, весьма эффек-
тивно повышает проч-
ность. Например, для ста-
ли, имеющей А —0,98, es = 2,10-3, имеем/и = 20; раздутие сфери-
ческой оболочки всего лишь на 5%(р = 1,05) даёт р=\,7ра, т. е.
повышает её предел упругости на 70%.
В случае цилиндрической оболочки, которая деформируется равно-
мерным внутренним давлением, так что а2, соответствующие
формулы имеют вид:
/
1 4-fft(p 1)
Р2
Р Л *" » РЪ **" ** ч >
* Яо/3 Xes/3
(4.274)
§ 32] БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 25!
причём наивыгоднейшая нагартовка определяется формулами:
Р.-bP.f^- (4.274Э
Рассмотрим теперь задачу о деформации круглой пластинки
радиуса а под действием постоянного давления р в случае, когда
прогиб её является значительным. На рис. 79 показана изогнутая
пластинка и её размеры в деформированном состоянии, г0 — начальное
расстояние какой-нибудь точки М от оси, r — rQ-\-u— её расстояние
после деформации и®»— прогиб;/?!, /?2 — главные радиусы кривизны
поверхности после деформации. Приближённое решение задачи можно
получить для как угодно больших прогибов, если сделать очень веро-
ятное предположение, что изогнутая поверхность будет частью сферы.
Однако мы рассмотрим задачу в обычных для теории упругости пред-
положениях, которые делаются при изучении больших прогибов мем-
бран: выражения деформаций возьмём не абсолютно строгие, но при-
ближённые с сохранением квадратичных членов:
Напряжения и а2 можно определить по формулам (4.262), если
заметить, что осевая сила в сечении радиуса г будет:
Р =
а для упрощения выкладок ввести обозначения:
р = -а, (4.276)
При этом получим:
°i=Ap> = (4.277)
так как
1 ^rfsiaO d (х\^ 1 d (х\
dr0 ' ' drQ dro \ ~ a dx\?J
Наклон касательной к меридиану поверхности в точке г определяется
формулой:
dw^ г0 х
dr0'"' р ’
(4.278)
и потому согласно (4.275) можно написать следующее уравнение
совместности деформ аций:
d . . 1 I dw
252
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл.IV
или, согласно (4.276) и (4.278):
2 (е2- S1) + 2*-> - 0- (4-279)
Если деформации еп s2 выразить через напряжения elt о2 (4.277)
по законам пластичности:
е< / 1 V ei / 1
2°зЛ е2=^(°2-
то получатся следующие формулы:
2s‘=^4(p“x®« |
2ва = рав-^(2х^ + Р;, ।
причём:
(4.280)
(4.281)
Как только характеристика материала — Ф (е<) задаётся конкретно,
уравнение (4.279), нелинейное 2-го порядка относительно р(х), может
быть проинтегрировано. Так как нас интересуют большие прогибы,
и потому вся пластинка находится в пластическом состоянии, для
многих металлов зависимость а{ = Ф (е() можно взять в виде степен-
ной функции (2.53), которую мы запишем так:
а. \2и 4-1
(4.282)
где п — целое число на' — постоянная, при я — О равная модулю
Юнга Е, а при п > 0 определяемая путём обработки диаграммы рас-
тяжения образца. Обозначим:
2» 4-1
— _L J7® _ -1Л1
а / а ’ 2Л.' г а ’
ф = 2ае2 - f 2х £ + р )[ Р2 + рх £ + х2(^)2]'1
6 e 2а (е3 - £[) = Зх [р2 + рх 4- х*^]п
(4.283)
и перепишем уравнение (4.279) в виде:
р2(Х:Й + '’'; + аха=:=0- (4.284)
Контур пластинки неподвижен, и потому граничное условие имеет
вид:
Х = 1, 2х^ + р = 0 (е9 = 0). (4.285)
§32] БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 2ЙЗ
Поскольку в центре Rt — R% имеет максимум, функция р(х) пред-
ставляется чётным рядом по степеням х:
<х>
р ==р0 —с2х2— cixi— • • — 2C2b»x2w- (4.286)
Внося этот ряд в (4.283), получим:
ф =
СО
Ро- 2 (1 +4//i)c2m№'1! I po+ 2
m = 1 JI m-l
—2р0(Л1-|-Ос2т4-
т — 1 - I | п
-4- 2 (1 -j- 2k — 4А2 + Amk) с2т_2кс2к J ,
fc=i J)
—6 2 mc3rnx2mJ | РО + 2 x2m
m—1
4~ 2 ~Ь 2/г—4/г2 -f- 4mk) ^2т-2кс2к
к=1
2po "1 1) ^2m i
. ' pi
(4.283')
co / m —-1 \
p2 == Po + 2 x2’"( — 2РоС2>» -t 2 с2т~2кс2к ) •
m=l ' Л-—1 '
Внося эти выражения в уравнения (4.284) и приравнивая нулю коэф-
фициенты при различных степенях х, получим:
с __ Роа____________ е (8п2 Ц- 29л -J- 8) а2р0 (4 2874
8 8(л + 2)р^ + з ’ 4 384(я + 2)3р2(2и+3)’'
Для определения постоянной р0 имеем из (4.285) следующее уравне-
ние х =>= 1, ® = 0):
._________5а________3 (8л1 + 29л + 8) а2 '
8(л + 2)рд”+3 128(я + 2)3р|(2”+з) ••==‘
Ограничиваясь выписанными здесь членами, находим
?+^з = [/(«)]2”+3 =
= 40(/i + 2)* / /-~24(8n2 + ^9H + 8)_ '
3(8л2 + 29л + 8) ' 100(л + 2) J ' { >
Прогиб w найдём из уравнения (4.278), предполагая, что он обра-
щается в нуль при х — 1:
[2 —
Со 1 f Со \ 1
1 — х2 4-^(1 —х‘)-4 —4+.^КI-**)'+•• , (4.289')
2р0 Зро ’ Ро • ‘ 4
254 равновесие пластинок и ойойоЧек (гл. IV
причём максимальный прогиб в центре (х —0) определяется сле-
дующей формулой:
2п+1
Л2Л»/ (4 289)
f („\ _ 1 f („\ h 4- 1 Z/„x2» + 3 ,8л« +35л+ 20.2 (2и+3)1
— 2/(«) [I + 1б(л + 2) J W + 9 -128(п + 2)з/п ]•
Для примера рассмотрим случай я = 1 (я = 0 соответствует закону
Гука, при котором получается известный результат Генки, но при
коэффициенте Пуассона 0,5); при этом характеристика материала
изображается кубической параболой. Из (4.238) находим /(я) = 1,25
и из (4.289) (л) = 0,678, а для прогиба в центре получаем фор-
мулу:
«'о = 0,678а
Коэффициенты ряда (4.286) имеют значения: с3 = 0,127 р0,
с4 = 0,004 р0, поэтому он быстро сходится:
^1 = р = р0(1 — 0,127+ —0,004.+— .. .).
Напишем ещё формулу для радиуса кривизны
А « 1.р (1 _ 0,381х2 4- 0,045+ —...).
4х\ р /
Как видим, радиусы кривизны заметно изменяются только при зна-
чениях х, близких к 1, т. е. у края пластинки; в остальной части
они почти постоянны и равны между собой, вследствие чего изо-
гнутая поверхность пластинки мало отличается фт сферы 91.
3. Обжатие, раздача , и волочение труб1). На рис. 80 показаны
четыре различных процесса конечной деформации трубы, имеющей
первоначальный средний радиус а и толщину стенки hQ. Эти про-
цессы часто применяются в практике, причём иногда трубы-заготовки
предварительно нагреваются. На рис. 80, а, б показаны процессы
обжатия или раздачи трубы с целью получения утолщённой оживаль-
ной части заданной формы или утоньшённой горловины. На рис. 80, в
показан процесс волочения трубы, иногда применяемого для получе-
ния трубок с капиллярными отверстиями; рис. 80, г показывает об-
ратный процесс. Задача расчёта этих процессов сводится к нахожде-
нию закона распределения давления р по поверхности матрицы,
Г) Приводимое здесь решение не содержит приближённой гипотезы,
которая была принята в нашей работе 1940 г. [1<Ч и в аналогичной работе
Надаи 1942 г., о которой он сообщил в 1945 г. на сессии АН СССР.
§ 321 БЕЗМОМЕЙТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 2а5
определению необходимых усилий прессования или волочения, а также
толщины стенки и удлинений изделия в различных сечениях.
Во всех случаях давление р оболочки на матрицу будем считать
положительным. Напряжения (по образующей), <з2 (тангенциаль-
ные) определяются формулами (4.262):
.. Р/?2
~ 2лг2Д ’
РРг .
~h
(4.290)
причём сила Р в любом сечении г равна:
Р = — 2nahoqa zt 2я j* гр dr.
а
(4.291)
В этих формулах верхний знак относится к случаям (б, г), когда
труба расширяется (й>д), нижний же к случаям (а, в), когда
диаметр её уменьшается (£<;«); таким образом для всех случаев
± 2я j* p rdr^-G.
а
На левом конце (г=а) сила Р равна:
Р — — 2~ahbqa,
на правом же (г = й):
ь
Р — — 2vahoqb ±: 2я J* гр dr = 2nbhbqb,
а
256
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
причём считается положительным, если оно сжимающее, ^—-поло-
жительным, если оно растягивающее (<7а = 0 в случаях в, г; <7;, = 0
в случаях а, б).
Для простоты решения задачи конечное соотношение
2 .22
°1 — 3132 ± °2 = °8,
изображаемое эллипсом Мизеса, заменим условием пластичности Сен-
Венана, изображаемым шестиугольником. Тогда для случаев (а, г),
когда а2 одного знака, имеем всюду: ч
*2
±aso,
f 2_
для случаев же (б, в), когда оп о2 различны по знаку, имеем:
-°1 = —°.8-
Эти условия можно записать в виде одной общей формулы:
а2 —(2—Е2)о!
(4.292)
где постоянные величины Ех, Е2 имеют следующие значения в раз-
личных случаях, которые указываются в скобках:
Е, — 1 (б, г), Е.2 — 2 (а, г,), 1
р 1 А а р 1 /а ; и-293)
tj = —1 (а, в), Е2 — 1 (б, в). J
Из (4.290) и (4.292) находим следующее соотношение:
(4.294)
в котором вместо неизвестного давления р введена новая перемен-
ная г:
/г,л„о
Р = -~г. (4.295)
Из первой формулы (4.290) и из (4.291), исключая Р, находим следую-
щее уравнение:
+ «296)
Обозначим безразмерные величины:
~а=7’ Й =
(4.297)
§ 32] ВЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 257
так что qa — неизвестная постоянная величина удельного давления
или нуль, 7—относительный радиус, ср и ф — неизвестные функции
радиуса г и у (г)—неизвестная функция, характеризующая закон из-
менения толщины стенки в зоне деформаций трубы. Теперь мы мо-
жем уравнения (4.294), (4.296) перевисать так:
- , „ г 1 (4.298)
— <7О+ Ei г?<Е- = • ~=
/ Х^)
В них входят три неизвестные функции координаты г: напряжение
Oj, давление z и относительная толщина стенки у. Недостающее
уравнение найдём из условия неизменяемости объёма материала и из
связи напряжений с деформациями. Для этого по (4.265') найдём
относительное удлинение элемента 'трубы в направлении меридиана:
Учитывая, что тангенциальное относительное удлинение еа равно:
(4.299)
и заменяя а2 его выражением (4.292), преобразуем формулу для гх
к виду:
81 = (7— 1)-----—. (4.300)
(3-2£2)г1 + 2£! >
Относительное удлинение элемента оболочки в направлении её нор-
мали представляет относительное изменение толщины 7г0:
•=7г-7' ' <4'301)
Условие несжимаемости объёма материала трубы при конечных де-
формациях имеет вид;
П + г1) О 4" sa)(l sa) — 1 >
или, согласно (4.299), (4.300), (4.301):
rf 1 + (7—1)-------------1 = х. (4.302)
L 1 4 7 (3 —2£2)aI + 2£'1 J л 7
Это и есть недостающее для определения неизвестных функций ура-
внение. Дифференцируя второе уравнение системы (4.298) по г, имеем:
> = - (4.303)
<f dr \ X / ‘
17 8ак. 5138. А. А. Ильюшин.
258 РАВНОВЕСИЕ ПЛАСТИНОК И ОВОЛОЧЕК [гл. IV
а исключая z и у из первого уравнения, находим дифференциальное
уравнение, определяющее закон распределения напряжения вдоль
образующей оболочки:
Е = -£- = У[(2+Ф—g^ + £iH(3 —+2E,] /4 3()4ч
11 dr V X J r[(3 — 3E24-rE2)a1 + (3 — r)£i] ’
Для интегрирования этого уравнения необходимо знать конкретно
форму матрицы, с помощью которой производится деформация трубы,
поскольку функции <р (г) и ф (г) зависят от формы. Если разрез ма-
трицы дан графически, так что для каждого значения г известны <э
и ф, то уравнение (4.304) можно проинтегрировать численно. Для
этого воспользуемся условием, что на одном конце трубы напряже-
ние з1 = 0. В случаях (а, б) имеем:
в случаях же (в, г) имеем:
г= 1
— 0,
?= ?o>
ф = фо;
5i — o>
? = ?o>
(4.305)
(4.306)
Давая радиусу г малые приращения Дг, из формулы (4.304) будем
находить соответствующие приросты Д(г«а1) и таким образом по-
строим распределение напряжения Sj вдоль образующей. Одновременно
находится и величина г, т. е. закон распределения давления обо-
лочки на поверхность матрицы (4.295). Формулу, определяющую за-
кон изменения толщины стенки оболочки, найдём из (4.297) и (4.302):
1-* - =--------(3-^)5+ а, .
X hfj г[(3 — 3EjrEa) aj + (3—г) £)]
При численном интегрировании уравнения (4.304) эта величина на-
ходится в процессе промежуточных вычислений.
Нам остаётся найти ещё усадку’ или вытяжку трубы в процессе
деформаций. Пусть в матрицу подан кусок цилиндрической трубы
радиуса а и длины Lo. Длина образующей изделия, получающегося
из этого куска, будет
L = Lo + J* si ds,
о
§32]
БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК
259
причём относительное удлинение et следует взять по формуле (4.300),
а элемент длины дуги:
dr
/ 1 — Cf2
ds = Ех
Таким образом получаем:
' Р _ _
_ Г (r-l)(E2ai-£i) dr
L Lo — ^a J _ tf2f(3_2f2)O1 + 2E1] ‘
(4.308)
Рассмотрим частный случай, когда матрица является конической, так
что угол наклона её постоянен (6). В таком случае имеем:
= оо, ф = 0,
ср = = sin 9 = const. > 0.
Основные уравнения (4.304) и (4.307) принимают вид:
d /год (2—Е2) 4-fi
dr \ X / х (г)
= -(3 - 3£, + гЕа) at + (3 -г) Ei
* (3-2Е.)^ + 2Е,
(4.309)
Дадим решение следующей задачи: найти максимальную степень
обжатия или расширения трубы, т. е. величину
b
Эта задача, безусловно, имеет решение, поскольку, если степень
деформации задать слишком большую, то в случаях (в) и (г) потре-
буется настолько большая сила натяжения правого койца трубы, что
произойдёт разрыв; а в случаях (а) и (б) надавливающая на левый
конец сила достигнет такого значения, что выступающий конец трубы
начнёт течь. Математически величина Зта1 находится из того условия,
что напряжение на том конце трубы, где прилагается внешняя,
сила, достигает максимального значения rtag8, а именно:
' = ь Т, = _А-=-1 (а. б),
(4.310)
' = ?. = г>-
Числовое интегрирование произведём для случая (а) — обжатия
трубы. Согласно (4.293) имеем Et =— 1, £2 = 2, и начальное усло-
вие (4.310) имеет вид:
7=1, 01 = —1.
17*
260
РАВНОВВСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
{гл. IV
Уравнения (4.309) переписываем в конечных разностях:
+ 2[2г+ -4- (3 — г) (1 + gj)]
7(3—2г) + 2(3 — г)(14- gt) ’
1_ _ ___2 °i_____
X Т[3—7 + (3 —2r) gj ’
(4.311)
.Г
г
и заметим, что давление на матрицу согласно (4.295) можно опре-
делить по формуле:
2 s hn
Р==Р^-^, Ра = =£~. (4.312)
Формулу (4.308) для усадки оболочки напишем в виде:
1
• + (1 —r) (2°i + 1) . р /г\
а ' 2+?!
, \а — Я
h ~ cos 0 ‘
(4.313)
Величину г уменьшаем ступенями через Дг = — 0»1, —0,05, —0,01.
Вычисления необходимых величин по формулам (4.311), (4.312)т
(4.313) даны в табл. 14.
Таблица 14.
Расчёт трубы на обжатие.
Г 1 0,9 0,8 0,7 0,6 0,5 0,40 0,35 0,3472
— 1 0.8 0,6697 0,5491 0,4309 0,2954 0,125 0,0081 0
ж 1 1,169 1,317 1,458 1,609 1,7856 1,9972 2,162 2,171
Z 1 1,2988 1,646 2,082 2,6816 3,5712 4,993 6,177 6,252
ру> 0 — 0,050 — 0,051 — 0,0203 + 0,0352 +0,120 +0,2399 0,3005 0,3264
Г • Z 1 1,0521 1,0536 1,0206 0,965 0,893 0,7989 0,7567 0,7538
Поскольку при г ==0,34 напряжение ог изменило знак, а оно должно
обращаться в нуль при г = р, мы имеем, следовательно:
₽ = 0,347.
Давление на стенку матрицы возрастает от pa<?, (r= 1) до максимума
6,25 р,ср, (г == 0,347). Толщина стенки изменяется примерно так
§ 32] БЕЗМОМЕНТНАЯ СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК 261
же, как и удельное давление. Вычисляя интеграл от функции Л (г),
находим вытяжку:
L — До = 0,109
а
У1 —
Она весьма мала. Величина, помещённая в последней строке таблицы,
представляет
собой произведение местной толщины стенки на ра-
диус, отнесённое к йоа,
т. е.
Если бы осевое удлине-
ние ej всюду равнялось
нулю, это произведение
равнялось бы 1. Как ви-
дим, отклонение его от 1
составляет приблизительно
±25%. Этим в известной
мере оправдывается воз-
можность приближённого
расчёта изучаемого про-
цесса на основании гипо-
тезы rft=const. На рис. 81
изображены кривые, опре-
деляющие изменение на-
пряжения удельного
р
давления толщины Стен-
ая
h
ки -г- в зависимости от
й®
Рис. 81.
" радиуса г.
Дадим теперь полное решение задачи о волочении трубы через
конечную матрицу (случай в, рис. 80). В этом случае имеем = — 1,
£2 = -f-l, и потому уравнения (4.309) принимают вид:
= —-
dr \7. / гу ’
___1 —Jj __ (1 —др (2 —др
г~ 1 = 7(3 —г—г?1) ’
(4.314)
Давление на стенку матрицы попрежнему выражается формулой
(4.312), а вытяжка, согласно (4.308), может быть подсчитана по
1 h
262
РАВНОВЕСИЕ ПЛАСТИНОК И ОБСЛОЧЕК
[ГЛ. IV
формулам:
1 /1 _?2 _ J F (г) dr = F, (P), (4.315)
F (Й =(i-7) 2 —ai
Начальное условие (4.306) для г=1 имеет вид:
г = 1, aj = О,
и потому численное интегрирование уравнения (4.314) можно вести
для любого значения ~, однако не может быть меньше некото-
рого значения £min, при котором = 1 для г = ^min. Весьма простые
вычисления полностью приведены в табл. 15.
Таблица 15.
Решение задачи о волочении трубы.
r 1 0,9 0,8 0,7 0,6 0,5 0,40 0,35 0,33 0,3215
0 0,1 0,2063 0,3271 0,4550 0,6012 0,7759 0,8917 0,9597 1,00
1/X ' 1 1,0503 1,1017 1,1539 1,2106 1,2719 1,3366 1,3543 1,3395 1,3205
l/x“ 1 l,lb7 1,3771 1,6484 2,0176 2,5438 3,3415 3,8694 4,059 4,1073
F 0 0,0579 0,1345 0,2379 0,3767 0,5723j 0,870 1,1094 1,2620 1,357
Величина р может быть принята равной любому значению г в этой
таблице, причём значения величин Opl/y, г/г, F для г<^ будут
давать распределение напряжений, изменение толщины стенки, распре-
деление давления на матрицу; при г — р величина определяет
необходимое напряжение волочения qb = ((3) ag • 8. Таким образом
для различных из данных табл. 15 имеем возможность определить
вытяжку (табл. 16).
Таблица 16.
Определение Fr (3).
0,8 0,7 0,5 0,4 0,3215
Qb agB 0.2C63 0,3271 0,6012 0,7759 1,00 '
A (?) 0,0125 0,0305 0,1075 0,1845 0,2105
§ 33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
263
Минимальное значение соответствующее максимальной сте
пени обжатия, возможной при волочении трубы, таково:
1
чение величины -я-, согласно
А
таблице, равно 1,354, т. е. максимальное увеличение толщины стенки
получается равным 35,4% при волочении через матрицу, дающую
а — Ь
степень обжатия по диаметру —-—=1—р = 0,65.
§ 33. Симметричная деформация цилиндрической оболочки.
Цилиндрическая оболочка радиуса а находится под действием
осесимметричного внешнего давления р, причём осевая сила отсут-
ствует. На рис. 83 показан элемент оболочки и силы, действующие
на него. Ось х направлена по образующей серединной поверхности,
ось .у—по окружности и z — по радиусу внутрь цилиндра. Деформа-
ция оболочки в данном случае характеризуется радиальным перемеще-
нием -ш, которое считается положительным, если оно направлено
внутрь (в сторону положительного направления оси г), и осевой
деформацией элемента серединной поверхности Деформации эле-
мента, расположенного на расстоянии г от серединной поверхности,
будут:
еаа — г1 г ,
1S3 W W
еУУ а — z а 2 а? ’
причём второе слагаемое выражения е^у так относится к первому,
264
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. IV
Z
как —,
а
отброшено. Второе слагаемое выражения е.
если прогиб
Л . .
т. е. это отношение меньше следовательно, оно может быть
'хх будет порядка ~,
w и его производные существенно изменяются при
переходе от сечения х к сечению
где I — значительно меньше а,
а именно I—порядка y~ah. Если
же I порядка а или больше, то вто-
рое слагаемое в выражении ехх так-
же должно быть отброшено; в этом
случае состояние оболочки будет
безмоментным, и оно уже рассмотре-
но в предыдущем параграфе.
Пользуясь обозначениями (4.17),
в случае моментного состояния ци-
. линдрической оболочки, имеем:
__ 1
X1 — ~ах* ’ |
е _ ® >(4.316)
®2 —~ V’
ехх-------- ,г'Х1
еуу — s2>
= 0.
Силы Т2 и моменты Ж2 выражаются через деформации
и кривизны по формулам (4.25), (4.26), (4.27).
Условие отсутствия осевой силы
Т^О
будет выполнено в том и только в том случае, если
I 1 n w
^+2^ = °' S1=2^-
(4.317)
В самом деле: интенсивность деформаций е{ согласно (4.19) можно
записать в виде:
поскольку
т"> 2
Л =
/,.z = ^i + 7sa)’{i==o.
(4.318)
г* 2 « 12
(4.319)
Таким образом е4, а следовательно, и есть чётная функция г, и
потому из (4.25) получаем J2 = 0 и, следовательно, из (4.26) Г1 = 0.
§ 33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
265
Это ясно также из (4.38) и (4.37'), так как, вследствие чётности
функции по г имеем:
(4.320)
и потому Ао = О, Рп — 0 и /2 = 0.
Для того чтобы выразить силу Т'2 и моменты М1г Л42 через де-
формации, найдём величины Во, Со (4.37'):
ей
Во = 2 |
®io
cidei
со = 2 J /4 — 4» dSi, (4.321)
после чего на основании (4.38) и (4.26), (4.27) имеем:
Л = о,
w До /З
а 2 VT\ ’
Ср УТ
dx* 2РХ ’
M2 = ±.MV
Поскольку согласно (4.319), (4.317)
/(Pw\2 р _ З/w У
\dx2) ’ 4 \а ) ’
(4.322)
(4.323)
и потому eio, е(1, а следовательно, и Во, Со зависят только от един-
ственной неизвестной функции w (x), то формулы (4.322) дают зави-
симость силы Г2 и момента от прогиба.
Дифференциальные уравнения равновесия элемента (рис. 83)
имеют вид:
^+^Гз+Р = 0, 2V = ^, (4.324)
поэтому для прогиба w получается уравнение:
^-1+|7’2 + Р = 0. (4.324')
Зависимость представим в виде ломаной
cg
c{ = Eei(l —<о),
<о=0, е{ < es,
ei>
es,
и найдём явные выражения Т2, через прогиб w. Чтобы упростить
дальнейшие вычисления, введём безразмерные переменные:
- 2z - х ./3
(4.325)
266
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
и безразмерные функции:
(4.326)
В зависимости от характера нагрузки д'(х) п0 длине оболочки может
возникнуть некоторое число упругих, упруго-пластических и пласти-
ческих областей, причём ме-
жду двумя соседними упру-
гими областями, заключаю-
щими пластическую, сле-
дует различать три участка
(рис. 84): I — пластический,
в котором при любом
z е( > es; 11 — упруго-пласти-
ческий, в котором некото-
рая часть толщины стенки,
примыкающая к поверхности,
деформируется пластически
(е{ > es), часть же, вклю-
чающая серединную поверхность, деформируется упруго (е4 < es),
и потому их разделяет поверхность = es; Ш — упругий, в котором
для любого z, < е8.
В новых обозначениях интенсивность деформаций имеет выражение:
2
с2 4- 4-
О
е8
(4.327)
где две точки наверху w означают вторую производную по
и момент т представим в виде:
t — —
4
m = —w-I-
0*0
x. Силу t
(4.328)
и тогда, вычисляя квадратуры (4.321), получим:
В области I (пластической):
(4.329)
§ 33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
267
На границе области I минимальное по толщине значение интенсивности
деформаций равно е8; обозначая через х0 координату этой границы,
имеем из (4.327) при г = 0:
х — х0,е—1. (4.329')
В области II (упруго-пластической) интегралы (4.321) вычисляются
по участкам: 1) от z = 0 до г = г0 (т. е. от e = |w| дое = 1)при
^ — Еер, и 2) от г = г0 до г=1 при
= Е (1 — X) et ;
в результате получим:
8/= 4w — ~^—V 1 — w2 sign w —
w УЗ
8® y3lw-)-y w2-j--KW
— rr—-In- ------X==-----V
®У3 2(1 + V1 — w sign w)
8m = w 4* 1 у j — ^2 sign w—Ij
3 У3 w2 w
(4.330)
4w2 , уЦ»+У w2-j--5-«
T------ In 4 '________±_
ws У 3 2 (1 + /1—w?signw)
Граница этой области с пластической есть х = х0, граница же её
с упругой областью (III) определяется тем условием, что максимальное
nq, толщине значение интенсивности деформаций (при z= 1) равно е8:
x~xt, е~ 1, w94— 1 • (4.330')
В области III (упругой) имеем:
t =— -w, т = —-|-w, (4.331)
X ’J
причём она примыкает к области II.
Дифференциальное уравнение (4.324) на основании обозначений
(4.326) и уравнений, (4.328) перепишем в виде:
^4-4w=p4-U/4-k^, (4.332)
dx4- 1 1 dx2 \
причём через p обозначена величина, пропорциональная нагрузке:
4ар
(4.333)
268
РАВНОВЕСИЕ ПЛАСТИНОК И ОВОЛОЧЕК
(гл.IV
Если вместо Ы, Ът в уравнение (4.332) внести их значения (4.329)
или (4.330), получится довольно сложное нелинейное дифференциаль-
ное уравнение 4-го порядка относительно iso. Как бы ни была
проста нагрузка р, проинтегрировать его в конечном виде не удаётся,
и' оно специально написано в форме, удобной для применения метода
упругих решений.
Общее решение задачи о деформации цилиндрической оболочки
по методу упругих решений можно получить через функции Крылова I11!:
Yt = ch х cosx;
К2 = у (ch х sin х -f- sh x cos x),
гч = -к shxsinx,
a 2 ’
(4.334)
K4 = -y (ch x sin x — cos x sh x).
При нулевом значении аргумента (х = 0) значения этих функций
и их производных до третьего порядка определяются таблицей 17,
Таблица 17. причём они обладают сле-
Значения функций (4.334). дующими свойствами:
п к„(0) Уп (0) К»(0) Уп (0) и/Ъ v dx ~ Yl‘ dY,K v
1 2 3 4 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 -г = у» dx 3 ^=-4У4. dx * (4.335)
Если бы правая часть уравнения (4.332) была известной функ-
цией х, его решение определялось бы формулой
4 а?
w = + ^)к4(х—E)rfE.
о
Поскольку момент т и перерезывающая сила, пропорциональная
— , непрерывны на границах различных областей, интегрированием
dx
по частям формулу можно преобразовать к виду:
w = 2 CnYn (х) + f р&К4(х— 0Л +
1 _ о
/ X
+ X f [3(К4 (х — S) 4- (х — ;)] dl.
о
(4.336)
S 33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ цилиндрической оболочки 269
Здесь Сп — произвольные постоянные интегрирования, определяемые
граничными условиями на торцах оболочки. Заметим, что функции
-Крылова У2 и У4 удовлетворяют тождествам:
К2(х-0 - У2 (х) Y. G) - Y, (X-) Уа(5) +
+ 4К3(х)К4(0-4К4(х)У8($), (4 337)
У4 (x-S) = У4 (х) ^(0— Y. (х) УД?) +
+ К2(х)К8($)-У3(х)У2(0-
Внося эти значения в (4 336), запишем прогиб да в следующей форме:
w = £xn(x) Уп(х). (4-338)
Тогда функции А„ будут иметь следующие выражения через bt и Bm:
я? _ 41 = С1 — X К4 + 8»гУ2]^, 0
X _ А2 == С2 + к f 4- f) Ya + 8m yj л, 0 яг — 43= C8 - X J K2- 48m K4] 0 if a? X4 = C4 + X J + f) У, - 48/и У31 Л. 0 (4.339)
Дифференцируя (4.338) два раза по х, найдём:
да = Х8от—44^8 —4ДаГ1-{-Л8К14-Д4У2. (4.340)
Соотношения (4.338) и (4.340) по существу представляют собой
интегро-дифференциальные уравнения вида:
а? }
да== J/j (да, да, х, £)
О
X
w = f2(w, да, х, 5)с?$-]-/3(х),
о
из которых одно есть следствие другого. Однако их можно рассмат-
ривать и как рекуррентные формулы, выражающие последовательные
приближения к точному решению.
270
РАВНОВЕСИЕ ПЛАСТИНОК И ОЙОЛОЧЕК
(гл. IV
Поскольку моментное напряжённое состояние существенно отли-
чается от безмоментного только в том случае, если нагрузка р(л) су-
щественно изменяется при изменении х на величину / = О(]/аЛ), т. е.
меньше радиуса а, постольку представляет интерес случай, когда
нагрузка р вообще распространяется только на небольшой участок.
Впрочем, формулы (4.338), (4.340) позволяют построить решение и
в общем случае. Для этого достаточно определить призвольные
постоянные Ста.из граничных условий и затем последовательно приме-
нить метод упругих решений.
Рассмотрим случай сосредоточенного кольцевого давления, прило-
женного по внешней окружности в сечении х = 0. Пусть Р будет
интенсивность этого давления, т. е. сила, приходящаяся на единицу
длины окружности сечения х — 0. Безразмерные прогиб и кривизну
образующей в сечении х — 0 обозначим соответственно:
а=<ш(0) = ^-,
<4 341’
Считая оболочку безграничной в обе стороны, мы можем написать
граничные условия, определяющие произвольные постоянные, в виде
х = 0
(4.342)
X — со
причём связь между прогибом а и силой Р найдём из того условия,
что перерезывающая сила N в сечении х — 0 равна половине силы Р
с обратным знаком. Интегрируя уравнение (4.324') по х от 0 до оо
и замечая, что
о
так как М» = 0,
между Р и а:
а также, что для х > 0, р = 0 получим связь
(4.343)
где величина Р связана с силой Р соотношением:
P = 2ah 1/" ^Р.
• г За
(4.344)
§33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 271
Полагая в (4.338) w(0) = a, а также после дифференцирования
w(0)=0, находим две постоянные:
С^а, С2= 0: (4.345)
Условия (4.342) на бесконечности позволяют определить и_две^другие
произвольные постоянные. Для этого заметим, что при х>хн ко-
торое определяется из (4.330') 8Z— 8т = 0, и потому при x>Xj вели-
чины Лп Л2, Л3, Л4 будут постоянными. Отметим штрихом наверху
эти постоянные значения функций Лга и перепишем формулу (4.338)
для х>х4 в виде:
•ш == 2- е -Аг + Atj cos х -f-
4“ Аг — 2 Аз -j- A^j sin xj
Т е+Х Т — Т cos х + ('2 ^2 4“ у Ч~ f &) sin хj .
Для того чтобы условия при х = со выполнялись, необходимо, чтобы
коэффициенты при cosx и sinx второго слагаемого обращались
в нуль. Отсюда и из (4.345), (4.339) имеем:
X = a —A j* (8/У4-|-8тУ2)<Й,
ЯТ1
Аг — А [ (8/У3-ртУ^сЙ,
Аз = — 2 (Л1 -{- Л2),
Ai —2 (2Al -|- Л2).
(4.346)
Постоянные С3, С4 теперь исключаются, и функции Ап становятся
вполне определёнными:
Л1'= А’14- A J (3/У4 -ф-ЪтУ2) di,
X
«1
Л2 = Аг— А | (8/Уг Ц-ЗотУ,)
X
л3 = Аз 4- A JУа — 48/йУ4) di,
X
(4.347)
Л4 = Ai — А |(8^ — 48m yg) di.
X
2l2
рАвновВсие пластинок и оволочкк
(гл. IV
Величина р опущена, так как она отлична от нуля только при
х = 0, но эта точка исключена из рассмотрения. Теперь формулы
(4.338), (4.340) позволяют строить последовательные приближения
решения задачи.
1. Первое приближение и упругое решение. Полагая в первом
приближении А = 0, что соответствует упругому изгибу оболочки, из
(4.346) имеем:
41 = а, Аг —0, Ag—— 2а, Л4 = 4а;
из (4.338), (4.340) имеем:
w = a (cos sin х) е~х= аКБ (х),
w=—2а (cos х — sinx')e-x = — 2аК6(х).
(a)
(б)
Переход материала оболочки за предел упругости происходит при
том значении а, при котором условие (4.330') выполняется в сечении
х—0. Поскольку К5(0) = 1 и К6 (0) = 1, условие (4.330') даёт:
4а2 = 1, а = 1,
а из (4.343) находим для аС-^~:
Р = а(а<1),
Р = 2а.
(4.348)
Это — известное решение задачи об упругом изгибе оболочки кольце-
вым давлением.
Первое приближение значений координа^ х0, xL, определяющих
границы между I — II и II — III областями, при упруго-пластической
деформации (а > 0,5) находим из условий (4.329'), (4.330'):
(*о) =4 ’ 3 (*!) = i • <В)
Кроме значений а < 0,5 ниже мы рассмотрим ещё три значения
<х : 1; 2; 3; при этом каждое а при трёх различных значениях А
(кроме A = 0):k = 0,5; X = 0,75; Х = 1. Каждому числовому зна-
чению а соответствует первое приближённое значение х0, хп полу-
чающихся из (в). Формулы (4.348) для этих значений а представляют
первое приближение решения задачи.
2. Второе приближение. На основании формул (б) и (4.329),
(4.330) при числовом значении а строим графики изменения вели-
чин 8/ и в зависимости от х (в пределах от 0 до х0 и от х0
до Xi) и, графически выполняя квадратуры (4.346), находим постоян-
§ 33] СИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 273
Рис. 85.
ные А'; одновременно строим графики функций А№(х) согласно (4.347).
После этого по формулам (4.338), (4.340) строим графики для про-
гиба ‘W и кривизны w и, графически вычисляя квадратуру (4.343),
находим второе приближение значения силы Р, соответствующей
взятому а. После этого из (4.329') и (4.330') находим второе при-
ближение значений координат границ х0, хР Второе приближение
кривизны находим из
(4.340) при х = 0:
? = к8/я(0)4-Л3(0). (г)
3. Третье и после-
дующие приближения.
Вычисление третьего при-
ближения отличается от
предыдущего только тем,
что функции w и ®, со-
гласно второму прибли-
жению, заданы графи-
чески, тогда как прежде
они определялись форму-
лами (б); следовательно,
мы снова строим графики
величин 3/, от, при новых
пределах х0, xt вычис-
ляем квадратуры (4.346),
находя постоянные А',
и строим графики функ-
ции Ап по формулам (4.347). Поскольку с графиками прихо-
дится совершать лишь алгебраические операции и интегрирование,
но не дифференцирование, вычисления производятся с большой сте-
пенью точности. Формулы (4.338) и (4.340) позволяют построить
графики w и w в третьем приближении, после чего из (4.343)
находим третье приближение силы Р.
Сходимость процесса вычисления последовательных упругих ре-
шений получается очень сильная. Так для любого а при /. = 0,75
и меньше третье приближение практически не отличается от второго
и только при X = 1 оно даёт заметную поправку величин Р и р для
больших значений а (2 и 3). Но случай X = 1 относится уже к за-
даче о несущей способности оболочки, и для него будет дано точное
решение; оно показывает, что третье приближение величины Р, най-
денной по методу упругих решений, хорошо совпадает с точ-
ным.
18 Зак. 3138. А. А. И.тыошии.
274
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Результаты вычисления третьего приближения при различных
значениях а и X даны в таблице 18х).
Таблица 18.
Третье приближение в расчёте оболочки.
а к Р 3
0,5 1 2 3 0,5 1 2 3
0 0,5 1 2 3 1 2 4 6
0,5 0,5 0,974 1,595 2,143 1 2,28 4,523 6,553
0,75 0,5 0,962 1,400 1,738 1 2,39 4,784 6,830
1 0,5 0,950 1,107 1,262 1 2,52 5.С45 7,106
Йри а 0,5 имеют место формулы (4.348), каково бы ни было
число X. Результаты, указанные в таблице, позволяют построить
графики зависимостей:
X), р = р(а, X).
Графики изображены на рис. 85 и дают окончательное решение
задачи для оболочек произвольной толщины h радиуса а.
Наибольшие напряжения получаются в сечении х = 0. Распре-
деление их по толщине на основании формул:
— у ^ei (1 tt>) 2“ еуу) ’
= з" ^ei (1 “) ^УУ "2" ’
соотношений (4.316), (4.317) и обозначений (4.341), определяется
зависимостями:
= (1 — Х-f- \ , I
°8 \ Узр’г» + 4а2/ I
= —аУ1—X-}- .|
°8 И3₽222 + 4а2/ J
(4.349)
причём г == 0 соответствует серединной поверхности, z = 1 — внутрен-
ней и z = — 1 — наружной поверхностям оболочки.
Исходя из формул (4.338), (4.339) и (4.340) и подчиняя про-
извольные постоянные Сп соответствующим граничным условиям,
аналогичным способом может быть решена любая другая задача
о деформации цилиндрической оболочки.
!) Они выполнены в Лаборатории испытания материалов МГУ под руко-
водством С. М. Попова с большой степенью точности.
§ 34] НЕСУЩАЯ СПОСОБНОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 275
§ 34. Несущая способность цилиндрической оболочки.
Если материал оболочки деформируется достаточно сильно и
перестаёт упрочняться или не обладает упрочнением, то существует
максимальное значение внешних сил, при которых ещё возможно
равновесие. Как и прежде, такое значение внешних сил мы называем
несущей способностью оболочки. Сила Т2 и момент в этом слу-
чае удовлетворяют конечному соотношению, которое уже найдено
в § 26. Поскольку при изгибе цилиндрической оболочки поперечными
силами согласно (4.319) Реа.= 0, конечное соотношение имеет фор-
му (4.74). Пользуясь уже введёнными выше обозначениями:
Ж8 = ^, Ts = v3h,
(4.350)
из (4.67) мы имеем:
/j = 0, = t, t12 = 0,
1 n
m1 = m, wi2 = y/ra, wi12 = 0,
а потому согласно (4.68):
Qt = t2, Qm = ^, Qtm = o.
Таким образом конечное соотношение (4.74) можем записать в виде:
Ki-P и I
mVS = р 1 + 1 I
2 1—у.2 [х у 1 — (х2 ’ J
или согласно (4.74") в виде: ,
t? -j- ~ m? — 1.
(4.351')
(4.351)
Сохраним обозначение (4.325) для безразмерной координаты х, а
также (4.333) для безразмерной нагрузки р и обозначим безразмер-
ную перерезывающую силу в сечении х:
dm 4N 2а
dx has " 3h
(4.352)
N =
Теперь уравнение равновесия (4.324) можно переписать в виде:
О о
(4.353)
18*
276
РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК
[ГЛ. IV
Вместе с конечным соотношением (4.351) это уравнение позволяет
решать различные задачи о несущей способности оболочек. Конечное
соотношение в плоскости т, t изображается эллипсом с полуосями
> 2
1 (вдоль t) и (вдоль т). Он показан на рис. 86.
у 3
Рассмотрим наиболее интересные случаи, когда на оболочку
действуют сосредоточенные кольцевые силы и б промежутках между
ними равномерное давление (р = const.). Пользуясь преобразованием
Рис. 86.
d гу г-, dN
tn = —N=N —,
dx dm
напишем первый интеграл уравне-
ния (4.353):
т
— f tdm —
ma
— ^p(m—moy, (4.354)
здесь No — значение перерезываю-
щей силы в сечении, где действует
изгибающий момент т0. Интеграл
J*/ dm = F(т, т0) (4.354')
т„
представляет собой часть площади эллипса, заключённую между
ординатами т — т0 и т и, таким образом:
№ = —^F(m, т0) — ^р(т— т0). (4.354")
Указанное преобразование не имеет смысла, если изгибающий момент
всюду постоянен. Но в этом
случае из (4.353) имеем
и из конечного соотношения
получаем уравнение, определя-
ющее несущую способность:
(|)2 + 4^о = 1- (4-355)
На рис. 87 показана цилиндрическая оболочка с нагрузкой, для ко-
торой справедлива формула (4.355); по краям приложены одинаковые
§ 34] НЕСУЩАЯ СПОСОБНОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 277
изгибающие моменты
Мо = Мат0,
а поповерхности равномерная нагрузка р. Если = 0, то из (4.355)
получаем уже известный результат, полученный по безмоментной
теории (§ 31):
— . h
Заменяя в формуле (4.354) W его значением:
7V—
dx ’
и интегрируя это уравнение, получим:
dm
----------4---------- - (4’356)
М — ~ F (т, т0) — -^р(т-тд)
причём предполагается, что т — т0 в сечении х = 0. Рассмотрим не-
сколько частных задач.
1. Бесконечно длинная труба с кольцевым сосредоточенным
давлением (рис. 88); р = 0. Перерезывающая сила в сечении х = 0
равна, очевидно, половине кольцевой
нагрузки Р, и потому из (4.352)
имеем ( N — —
Рис. 88.
совпадающая с (4.357),
2 V 2а о
= (4.357)
Эта задача для оболочки, материал
которой обладает упрочнением, была
решена по методу упругих решений
в предыдущем параграфе, причём для
силы Р была получена формула (4.344),
если обозначить
8 ‘
Как видно из графика (рис. 85), при л — 1 и при изменении а от
1 до 3 величина Р имеет среднее значение:
Рор = 1(0,950+ 1,107 + 1,262) = 1,106.
Теперь мы можем найти точное значение этой величины при Х=1.
278 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. IV
Заметим, что согласно (4.322) Л/ обращается в нуль вместе
cftw
с а 7'2—вместе с w. Поскольку, как это видно из рис. 88,
форма изогнутой поверхности оболочки невозможна без точки пере-
гиба, и сила Та— отрицательна, на эллипсе (рис. 86) нашей задаче
соответствует нижняя половина (ADC). На некотором расстоянии
х = I от силы прогиб оболочки обратится в нуль, и перерезывающая
сила также будет равна нулю. Таким образом:
х = I, х — хг, t — 0, N = Q
и, следовательно:
, 2
х = I, ш< —----=
1 /з •
Из (4.354) при х = 1 имеем:
тл 16„/ 2 \
'''““з'Ч-уГ “»)•
Наибольшее значение этой величины получим при
причём площадь полуэллипса:
р(----ХД = -Д=-
\ /3 /3/ /3
и потому
= (4.358)
ИЗ /3
Коэффициент Р при этом значении No равен:
Р = 1,167.
2 у 3/3
Как видим, эта величина отличается от среднего значения, найденного по
методу упругих решений, всего на 5%, откуда вытекает достаточная
точность третьего приближения в § 33 даже для значения X = 1.
• Найдём ещё расстояние, на которое в обе стороны от силы Р
распространяется деформация оболочки. Формула (4.356) принимает
вид:
/з С__________dm__________
Xl~ 4 J /f (mlt m0) — F (m, m0)
§ 34] НЕСУЩАЯ СПОСОБНОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 279
Для вычисления этого интеграла положим:
2
т —------— cos©, t — — sin©,
/3 •’
после чего получим:
я
— У2 Уз" Г sin<?d<(>
Xl~~ 2 J У2'?—sin2? = 2>43-
0
Из (4.352) находим длину /(x = Z, x — x^\
l = ^V2ah .
1/3
(4.359)
(4.360)
(4.360')
Эта величина также мало отличается даже от первого приближённого
значения х, при котором прогиб не обращается в нуль в решении
предыдущего параграфа. Как видно из
формулы (б) § 33, упругий прогиб
•w — 0 при х = 2,36.
Размер порядка ah является, как
известно, типичным в теории краевого
эффекта оболочек при упругой дефор-
мации. Он же является типичным и при
пластических деформациях, и потому
характер убывания краевого эффекта
является одинаковым в обоих слу-
чаях 1121.
2. Краевой эффект. Пусть полу-
бесконечно длинная труба находится
под действием краевого момента 7И0(/и0) и перерезывающей силы
А/о (А/р) (рис. 89). При выбранном направлении Af0 и No момент т
2 —
в конце области деформации х = I будет тх = -^= ; — 0 и =. 0.
Из (4.354) имеем конечное соотношение:
г-,2 16 2 \
т°)-
В частности, если действует только перерезывающая сила No (т0 — 0),
/2 х
то F I —— > 0) есть четверть площади эллипса в первом квадранте
(4.361)
рис. 86:
wi0
280 РАВНОВЕСИЕ ПЛАСТИНОК И ОБОЛОЧЕК [rfl.IV
и потому максимальное значение перерезывающей силы будет:
= (4.362)
° /6 уз 2 « Гз
Такая перерезывающая сила с обратным знаком действует в точке
перегиба деформированной поверхности бесконечно длинной трубы,
которая была рассмотрена выше. Если воспользоваться преобразова-
ниями (4.359) и заметить, что значению т — т0 соответствует
к 2
% =-----у > значению же т = т1=^^ соответствует «j — — -, то
. т0) = ^~г , F(m, »i0) = ^~-(^ + 2«> — sin2<?).
Формула (4.356) даёт следующий размер х2(при х = 1) области дефор-
маций:
п
—___ У^УЗ С sin 9 ___
1 2 J У2т--г2<? — sin2’p
— п
п
= .К2_УЗ t —?^l£l= = 2,03. (4.363)
2 J У2? — sin 2ср \
о
Если, наоборот, на краю действует только изгибающий момент 7И0,
а перерезывающая сила Ng = 0, то максимальное значение момента
будет:
2 2
= = (4.364)
причём, поскольку t0 — 0, деформация заканчивается в бесконечно
узкой зоне, примыкающей к краю х — 0. Заметим, что и упругое ре-
шение задачи в этом случае даёт очень узкую зону заметной дефор-
мации, значительно меньшую, чем величины хг, найденные выше.
3. Оболочки конечной длины. Если под действием рассмотренных
выше нагрузок находятся оболочки, длины которых конечны, но
больше соответствующих размеров хг, определённых формулами
(4.260), (4.263) и вообще (4.356), то их можно считать бесконечно
длинными, поскольку за предел размера I деформация не распростра-
няется. Если же длина оболочки L порядка y/zo: или меньше, то
несущая способность её будет меньше, чем у длинной оболочки.
Например, если весьма короткая оболочка со свободными краями
в центре нагружена кольцевым давлением Р, напряжённое состояние
её будет соответствовать малой окрестности эллипса возле точки D
/
§ 34] НЕСУЩАЯ СПОСОБНОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 281
(рис. 86), если Р — сжимающая сила, или—возле точки В, если
Р — растягивающая сила. В этом случае несущую способность найдём
непосредственно из (4.353), если проинтегрируем это уравнение по
х от — xl до xl и заметим, что на концах
т = 77 = О,
a t всюду приблизительно равно — 1:
pdx,
2Z./??,
а
Если длина оболочки порядка I найденного выше, то решение раз-
личных задач даётся формулами (4.354) и (4.356), поскольку крае-
вые значения N и т известны.
Как и в задачах о несущей способности пластинок, в задачах
о несущей способности цилиндрических оболочек можно применить
вариационный метод и написать формулу для несущей способности
в виде, аналогичном (4.322), и, пользуясь упругой формой изгиба,
определить максимальные нагрузки. Однако в этом нет необходимости,
ввиду общности и простоты указанного выше точного решения,
представленного формулами (4.354) и (4.356).
ГЛАВ A V.
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК 11 2 81.
§ 35. Выражения сил и моментов через деформации
серединной поверхности при потере устойчивости.
Пусть под действием заданной системы сил оболочка или пластинка
находится в безмоментном состоянии равновесия; оно определяется
Рис. 90.
деформациями имеют место
методами, которые уже рассмо-
трены в главе IV, и потому на-
пряжения и деформации в этом
состоянии мы будем считать из-
вестными. Таким образом в эле-
менте оболочки (рис. 90) нам
известны напряжения Хх, Ху, Yy
и деформации ехх, еуу, е^.
Плоскость (х, у) является каса-
тельной к серединной поверхности
оболочки в рассматриваемой точ-
ке 0; оси х, у направлены по
ортогональным криволинейным
координатам на серединной по-
верхности и ось z—по нормали
к ней. Между напряжениями и
соотношения (4.2) § 23, которые мы
выпишем снова:
*х 2 ^У ei
с __ у______L у ___-
Jy У 2 х ei уу
<? — у — о
иху ^у %е. сху
(5.1)
Интенсивность напряжений
(5-2)
§ 35] ВЫРАЖЕНИЯ СИЛ ЧЕРЕЗ ДЕФОРМАЦИИ 283
и интенсивность деформаций
е,==7Т/ еХХ + еХХеуу + еуу + ~4еХу (5,3)
связаны между собой зависимостью (4.4):
а, = Ф (с4).
Поскольку состояние равновесия элемента оболочки является безмо-
ментным, все выписанные величины , постоянны по толщине оболочки
и являются вполне определёнными функциями криволинейных коорди-
нат точки fio поверхности (а, р) и заданных внешних сил.
Явление неустойчивости характеризуется тем, что при некоторых
значениях внешних сил наряду с данным (безмоментным) состоянием
равновесия оказываются возможными и другие состояния равно-
весия.
Рассмотрим бесконечно близкое к данному деформированное со-
стояние оболочки, характеризуемое удлинениями ехх-\-еуу-\-Ъеуу
и сдвигом _еху-{- Ъеху в слое АВС, расположенном на расстоянии z
от серединной поверхности; вариациям деформаций Ъехх, Ъеуу, Ъеху
соответствуют вариации напряжений ьХх, ЪХу, которые можно
вычислить на основании законов пластичности. Поскольку в данном
случае речь идёт о действительных вариациях деформаций, а не о
виртуальных, как в вариационном уравнении равновесия, необходимо
различать два возможных случая: случай нагружения и случай раз-
грузки, поскольку формулы, связывающие напряжённое и деформи-
рованное состояние, при этом различны.
Область нагружения характеризуется тем, что в ней за счёт ва-
риаций Ъехх,.. . , .. . интенсивности деформаций и напряжений
возрастают; в области же разгрузки эти величины убывают. Поверх-
ность, пересекающая толщу оболочки и разделяющая области нагру-
жения и разгрузки, определяется, следовательно, из условия равенства
нулю вариации интенсивности деформаций или интенсивности напря-
жений. Ввиду того, что вариация работы внутренних сил в единичном
объёме оболочки, согласно (2.31), равна
= ^х^ехх + ^еуу + ХуЪеху, (5.4)
т. е. пропорциональна то уравнение указанной поверхности будет
ALBCj.j, = 0. (5-5)
Оу iLiL I у уУ I У •by X /
Оно может быть получено непосредственно путём варьирования фор-
мулы (5.3) и простых преобразований согласно (5.1) и (5.2).
В области нагружения вариации напряжений можно найти путём
дифференцирования формул (5.1), так как они имеют место как
284
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОВОЛОЧЕК
[гл. V
в основном, так и в близком состоянии оболочки:
85® s 8>Y® 2-3 Yy ~ £ 8<?^ + dei (ё}) Qgi’
— ЪХх = -Ъеуу-\- еуу-^^-А^Ъе^
^Sxy 55 8Л/ = Zel ^ХУ + "3 ехУ Те} (?,’) 8е’’’
(5.6)
причём <st и г; связаны диаграммой растяжения az = Ф (е{), так что
/°г\ _ _ L(a±
(5.7)
В области разгрузки вариации напряжений и деформаций подчи-
няются закону Гука, и связь между ними находится из (5.6), если
положить az = Ее{:
85ж = Д8ггж, 85?/ = Д8^, 8^ - ~ЕЪеху. (5.8)
Как и в обще! теории оболочек, будем исходить из основной
гипотезы Кирхгоффа, а именно предполагать, что вариации дефор-
мации слоя оболочки АВС (рис. 90) выражаются линейными зависи-
мостями через вариации деформаций серединной поверхности и через
её искривления:
8^® = ei—2~л1, 8<W = s2~ ^2> 8^2/ = 2(г3 —г7.3), (5.9)
причём здесь через ер е3, 2s3 обозначены бесконечно малые гариации
деформаций серединной поверхности, a х1; х2, z3 = t— бесконечно
малые вариации её кривизн и кручения.
Для удобства вычислений введём обозначения безразмерных величин:
чертою над величиной напряжения отметим отношение этого напря-
жения к интенсивности напряжений а4:
0< “Л®> а{ — *У' ЛУ’ а( р.10)
Эти величины являются известными; вместо искривлений и ординаты z
введём безразмерные величины:
Л - h h — 2z - z- 11 ч
~2 'Z1— zi> ~2 z2 — x2> "2'z3~'z3’ д—zi (°-11)
где h — толщина оболочки. Формулу (5.4) теперь напишем в виде:
6г,- = s — z'/. — s. — zt., (5.12)
§35]
ВЫРАЖЕНИЯ СИЛ ЧЕРЕЗ ДЕФОРМАЦИИ
285
где
s == ^xsl + ^s2 4“ 2^®з>
7. = ХхХ1 + YyV.^ -j- 2Ху*ъ,
h
X= у X.
(5.13)
Если теперь через г0 обозначить ординату поверхности, разделяющей
области нагружения и разгрузки, то согласно (5.5) и (5.12) получим:
s — г
= г0=-=.
'• 7.
(5-14)
Для определённости будем предполагать, что область нагружения
примыкает к внешней поверхности оболочки z — -j- . В таком слу-
чае для z > имеют место формулы (5.6), причём согласно принятым
обозначениям безразмерных величин они могут быть переписаны
в виде:
= (Й - г?,) + я- - х>?)’
is, = g +
=ё - *<г - <'•~ ’•
(5.15)
Формулы (5.8), имеющие место в области разгрузки г< z0, запишем
так:
85а. = £(г1— х^),
— Е (®2 х2^)>
8^ = 4e(S8-x34).
(5.16)
Как видим из сравнения формул (5.15) и (5.16) на границе областей
нагружения и разгрузки (z~z0) вариации напряжений, вообще говоря,
не являются непрерывными функциями z. Бесконечно малые скачки
их пропорциональны разности
Е —
т. е. они исчезают, если материал оболочки лишь очень немного вышел
за предел упругости относительно величины интенсивности деформа-
ций et (при этом,
очевидно, ~ может быть сколь угодно малой).
Разрывность напряжений исчезает также тогда, когда вариация напря-
286
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. V
жённого состояния является простой, т. е. если вариации напря-
жений пропорциональны действующим напряжениям; в этом случае
на границе областей нагружения и разгрузки они обратятся в нуль
z - вместе с вариацией интенсивности напряжений 8а* (или интенсивности
деформаций Ъе{), так как будут пропорциональны 8а*. Таким обра-
зом, принципиально говоря, разрывность величин оХх... на границе
z = z0 будет иметь место в тех случаях, когда потеря устойчивости
оболочки сопровождается сложным нагружением элементов материала,
т. е. разрывность или непрерывность напряжений может быть уста-
новлена после того, как задача об устойчивости оболочки будет
решена. Отсюда ясно, что степень точности решения задачи устой-
чивости оболочек, понимая под точностью степень соответствия
математического решения опытным данным, будет вполне достаточ-
ной, если величины скачков вариаций напряжений на границе z = z0
будут малы сравнительно с вариациями напряжений на поверхности
оболочки (z = ± у 1, в противном случае необходима эксперимен-
тальная проверка решений. Трудность, с которой мы здесь сталки-
ваемся, является неизбежной не только в рамках теории малых
упруго-пластических деформаций, но и с точки зрения любой другой
теории пластичности, поскольку, как уже отмечалось в главе I, законы
пластичности при сложном нагружении ещё не установлены. Отметим,
что скачкообразное изменение вариаций напряжений при переходе
через границу г = га есть неизбежное следствие непрерывности
деформаций, их интенсивности и интенсивности напряжений, ввиду
того, что переход материала из пластического состояния в упругое
при неизменной интенсивности напряжений связан с перераспределе-
нием напряжений.
Формулы (5.15), (5.16) показывают, что вариации напряжений
являются линейными функциями ординаты z, причём в отличие от
случая упругой потери устойчивости они зависят не только от дефор-
маций и механических характеристик материала оболочки, но и от
действующих перед потерей устойчивости напряжений, а следова-
тельно, и от сил. В этом состоит специфическая особенность явления
потери устойчивости оболочки за пределом упругости.
§ 35] ' ВЫРАЖЕНИЯ СИЛ ЧЕРЕЗ ДЕФОРМАЦИИ
287
Для того чтобы иметь возможность написать дифференциальный
уравнения устойчивости, необходимо найти выражения вариаций сил
и моментов, действующих на элемент оболочки, поскольку они выте-
кают из уравнений равновесия элемента. По определению сил и
моментов имеем:
+Л/2
87\ — у 8 Га = J 83ж dz,
— h/2
+h/2
ЪТ2 —1 8 7\ = ZSydz,
—Л/З
+Л/2
83 = J bXydz,
— h/2
+ЛД
SAfj— ~ 8Af2= J bSxzdz,
— h/2
(5-17)
+ Л/2
8Af,= J bSyZdz,
— h/2
ZXyZdz.
Для вычисления этих интегралов прежде всего необходимо разбить
оболочку на следующие три зоны: в первой зоне (рис. 91) предпо-
лагается упругое состояние оболочки *), и потому согласно (5.16),
(5.17) для этой зоны имеем:
iss=b.
^(8Afa-|8Af1)=-xa
— 8Н = —д-х3.
Здесь через D обозначена обычная цилиндрическая жёсткость
D —
Eh?
12(1—v2; ‘
(5.19)
!) Если до потери устойчивости в некоторой зоне оболочки состояние
является упругим, то при бесконечно малых вариациях оно, вообще говоря,
останется упругим.
288 устойчивость пластинок и оболочек 1гл- V
Вторая зона характеризуется тем, что до потери устойчивости мате-
риал оболочки в ней деформирован пластически, а после потери
устойчивости часть толщи переходит в упругое состояние, т. е.
в этой зоне имеют место и область активной пластической дефор-
мации (нагружения) и область разгрузки. Каждый из интегралов (5.17)
в этой зоне должен быть разбит на две части: от г =— у до г=г0
, h
и от z = г0 до z — 4 -у, причем первый следует вычислять согласно
формулам (5.16), а второй — согласно (5.15); например:
87i_~ 2'872 = -2 J (ег — ^z} dz
—1
1 1
(^7 ~ dei) ~~ zo) dz + у ~ J (si zi2') dz.
^0
Таким образом при вычислении мы встречаемся с простейшими
интегралами типа
$dz — z, J г = у га, Jz2 dz — у z3.
Воспользуемся обычными обозначениями известных величин:
<0=1—А = 1—(5.20)
£ <?г ’ £ dei 4 '
Тогда, вычисляя первую группу интегралов (5.17), получим выра-
жения для вариаций сил:
= 2 (2 — <0 <ог0) Sj to (1 — z о) Zj (л — <о) Sx (1 — z,,)2 z,
_ -f (5-21)
=2(2—<0 шг0).=2 -j- <o (1 — z0) (k — <d)Sy (1 — z0)2 z,
2У 8S = 4 (2 — <o 4* "^o) ез 4- 2w (1 — го) z3 -ф-
4-3(k-<o)^(l-J0)2 -z.
§35]
ВЫРАЖЕНИЯ СИЛ ЧЕРЕЗ ДЕФОРМАЦИИ
289
После вычисления второй группы интегралов находим формулы для
вариаций моментов:
-^(8iW1—y84f2) = — 2(2 — <u + co4)x1-f-
-}- (X — <о) (1 — г0)2 (2 -J- г0) 5жх — ~ (1 — zfa,
^8Ма — 8aQ == — 2(2 — <о -1- <о4) х2 +
+ (к - со) (1 - г0)2 (2 +70) - ^ (1 - J2) е2,
= — 4 (2 — <и шг'о) х3 -|-
+ 3(Х-<о)(1 — г0)2(2 + 70)^х-^(1-^)е3.
(5.22)
В третьей зоне оболочки пластическая до потери устойчивости
деформация оболочки остаётся пластической и после потери устой-
чивости, т. е. область разгрузки отсутствует. Поэтому выражения
вариаций сил и моментов получаются из (5.17) согласно форму-
лам (5.15):
1(87'1-1S7'S) = (1-<U) ^-(Х-ш)^,
( 8Г2 -1 87^ = (1 - ш) е2- (X - со) 8уг,
1^8^=~(]. — <u)e3 — (X — <о) Хуг,
^8Af, — 2- 87И2) = — (1 — <u) Xj -ф- (X — <u) 8xv.,
& (8М2 -18М= -(1 — <о) х2 + (X — ш) ^х,
(5.23)
(5.24)
з_1 8Я = —|- (1 - <о) х 3 -f- ( X - ®) Хуг..
Формулы (5.18), (5.23), (5.24) для 1-й и 3-й зон устанавливают -
линейные однородные зависимости между вариациями сил и момен-
тов, с одной стороны, и деформаций серединной поверхности и её
искривлений, с другой. Однако в зоне упруго-пластических дефор-
маций (2-й) эти зависимости не являются линейными, оставаясь одно-
родными. Это видно из формул (5.21), (5.22), в которые входит
величина z0, являющаяся дробнолинейной функцией нулевой степени
относительно еп и хп:
z ~ 4~ 2А^е3
Xjr*i + У+ 2Ау/.3
(5.14')
19 Зак. 3(138. А. А. Ильюшин
290
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гЛ. V
Очень существенно, что в этом выражении г0 можно исключить
деформации еп, выразив их через вариации сил 8ГП 85. Умно-
жая первое уравнение группы (5.21) на Хх, второе на Yy и третье
на Ху и складывая их, видим, что деформации гп входят в получаю-
щееся уравнение только в виде комбинаций е (2.13); но так как из
(5.14) в — г0?., то, исключая эту величину, получим:
k (1 — г0)2 4г0 — 4 —-———--------------«Х- = 0. (5.25)
Eh-f.
Обозначим через <₽ безразмерную величину, входящую в это уравне-
ние и зависящую от вариаций сил и кривизн:
к 5Ж8 Л + Syb Т2 + 3X^65
У 1—'Л Efrt.
Решая квадратное уравнение (5.25), находим:
г = l--f(l-k) (1 + ?)
к ’
причём С есть отношение толщины пластического слоя оболочки
к общей её толщине (рис. 91):
Z = = , 70 = 1—2С. (5.28)
Таким образом в формулах (5.21), (5.22) под г0 мы можем под-
разумевать либо выражение этой величины (5.14') через деформации,
либо выражение её через, вариации сил и искривлений (5.28).
Выражения сил и моментов в зоне упруго-пластических дефор-
маций оболочки несколько упрощаются, если перед потерей устой-
чивости пластическая деформация мала сравнительно с упругой.
Отбрасывая в (5.21), (5.22) малые порядка <и сравнительно с 1 и
заменяя г0 по формуле (5.28), получим:
Й(г7’‘-Т87'»)=ч+¥^Л
K(s^"T87'-)“«»+rsX.’.
— -1 8Ж2) = — *! Н- Х5>2 (3 — 2С) X,
(зм2 -18Л/,) = - х2 + Х5/,2 (3 — 2Q х,
Аш=-1 хз+<з -2С) *•
(5.29)
(5.30)
§ 36] устойчивость Пластинок 291
Принципиальное упрощение основных соотношений (5.21), (5.22)
происходит в тех случаях, когда из каких-либо соображений вели-
чина С, т. е. относительная толщина пластического слоя во второй
зоне, может считаться известной функцией координат точки поверх-
ности. Действительно при этом указанные соотношения, как и соот-
ношения (5.23), (5.24), становятся линейными и однородными отно-
сительно силовых факторов деформаций и искривлений, и потому
задача об устойчивости оболочек за пределом упругости в матема-
тическом отношении будет немного сложнее соответствующей упру-
гой задачи.
Мы не будем выписывать здесь дифференциальные уравнения
равновесия элемента оболочки произвольной формы, поскольку они
ничем не отличаются от уравнений, принятых в теории упругой
устойчивости оболочек, и ограничимся лишь некоторыми замечаниями.
В общем случае это система пяти дифференциальных уравнений пер-
вого порядка относительно сил ST^, 8 Т2, 85, моментов 8/Wj, 8/И2, 8Я
и перерезывающих сил ЗА/), W2; первые три уравнения получаются
из условия равновесия проекций сил ST;, ЬТ2, 85, 8Л\, на направле-
ния осей х, у, z основного трёхгранника (рис. 90); последние два
уравнения суть уравнения равновесия моментов сил относительно
осей х, у-. Ввиду того, что компоненты деформации en е2, s3 и
искривления х2, х3 выражаются по известным формулам Лява
через три компонента перемещения точки серединной поверхности
и(а, Р), v(a, (3), та (а, (3), выведенные выше формулы (5.18), (5.21),
(5.22), (5.23) и (5.24) позволяют выразить величины <37\, 8Т2, 8S и
8Mj, 8М2, 8Я через «, v, w и потому пять уравнений равновесия
будут содержать пять неизвестных функций: 8ЛГ1Г и, v, w. К ним
нужно присоединить граничные условия, из которых статические гра-
ничные условия сводятся к тому, что вариации внешних сил на гра-
нице оболочки равны нулю, поскольку потеря устойчивости оболочки
должна происходить при неизменных внешних силах. Другая поста-
новка задачи устойчивости сводится к тому, что на основании соот-
ношений типа (5.21), (5.22) и выражений еп, /.п через и, v, та
составляются дифференциальные уравнения совместности деформаций,
выраженные через силовые факторы 87\, 8Т2, 8S, SAfj, 8/Й2, 8/У;
к этим уравнениям присоединяют пять уравнений равновесия и гра-
ничные условия. Наконец, третья постановка задачи сводится к при-
менению вариационного уравнения равновесия или теоремы о мини-
муме энергии. Все эти методы ниже будут проиллюстрированы на
частных задачах.
§ 36. Устойчивость пластинок
Имея в виду в первую очередь дать точную постановку задачи
об устойчивости пластинок за пределами упругости и найти некото-
рые точные решения, мы несколько упростим дальнейшие формулы,
исходя из предположения, что перед потерей устойчивости пласти-
19*
292
УСТОЙЧИВОСТЬ ПЛАСТИНОЙ Й ОБОЛОЧЕЙ
[гл. V
ческая деформация пластинки всюду мала по сравнению с упругой.
При этом в формулах (5.23), (5.24) можно положить о> = 0 и вместо
формул (5.21), (5.22) пользоваться формулами (5.29), (5.30).
Обозначая w (х, у) прогиб пластинки при потере устойчивости, а
проекции перемещения точки серединной плоскости в результате
потери устойчивости на направление осей х и у соответственно
«(х,у), т/(х,у), имеем выражения для кривизн v.v х2, х3 и дефор-
маций Sj, s2, s3:
d2w _______d2w ______ d2w 1
dx2 ’ 7'2 dy2 ' 7'3 dx dy ’
__du __dv ________ 1 (du । dv\
S1 dx ’ sa dy ’ 83 2 \dy dx)'
(5.31)
Силы, действующие в серединной плоскости пластинки перед
потерей устойчивости, можно записать в следующем виде:
Т\ = h<3iXx, Т2 = ha<Yy, S = hViXy,
а их проекцию на ось z после потери устойчивости в виде:
ЛХ1 + Г2У2 + 25х3 =
Поэтому условие равновесия всех сил, приложенных к элементу,
в проекции на ось z даст:
= <5-32>
Условия равновесия сил, лежащих в серединной плоскости, после
потери устойчивости будут:
ЙЦ dBTj.dBS
Наконец, условие совместности деформаций имеет вид:
^ + ^_2^. = о. (5.34)
dy2 1 dx* dxdy ' 1
Совокупность дифференциальных уравнений (5.32), (5.33) и (5.34)
необходима и достаточна для решения задач устойчивости, если
поставить соответствующие граничные условия. В самом деле, со-
гласно (5.23) или (5.30) и (5.28) деформации еп е2, г3 можно выра-
зить через силы 37^, 8Т2, 8S и кривизны хп (прогиб w), после чего
моменты ЗУИ!, 87И2, <>Н станут функциями тех же четырёх аргумен-
тов. Таким образом задача сводится к четырём дифференциальным
уравнениям с четырьмя неизвестными функциями, причём (5.32) —
§36]
УСТОЙЧИВОСТЬ ПЛАСТИНОК
293
типа уравнения Брайана, а (5.33) и (5.34) — типа уравнений плоской
задачи. '
Для области чисто пластических деформаций (т. .е. такой, где
пластическое по всей толщине состояние до потери устойчивости
переходит также в пластическое после потери устойчивости) система
дифференциальных уравнений разбивается на две независимые. Для
простоты рассмотрим лишь случай начала текучести. Внося значе-
ния SAfj, 8Д42, 8// согласно (5.24) в (5.32), получим дифференциаль-
ное уравнение типа Брайана для прогиба w:
has 3 f ds ху i Э2 -r; i „ \
V —-- —рг- x = ~т ( ч—«-4— s—p Yy -4— 2 5—5—(5.35)
D 4 \dx2 x 1 оу2 У 1 дхду v} ’ 4 '
где в соответствии с (5.13) и (5.31):
х _ Хх Й + У:„ Й+ • <5-36)
х дхг 1 У ду2 1 У дх ду 4 '
Два граничных условия, налагаемых на прогиб vu, совпадают
с обычными граничными условиями для уравнения Брайана. Разрешая
уравнения (5.23) относительно деформаций, получим:
+ ^8 Г2 + 3^8$),
®а = Ёл (8г2 г'87"1) + +
+ ^8Т2+3^,85),
2гз=i85+тга)£л <^8Г1+ W + 3W
Уравнениям (5.33) удовлетворим, вводя функцию напряжений
8 7j d*F 8 Г2 _ 8S __ _ д*Е
Eh дуг ’ Eh дх? ’ Eh дхду’
после чего, обозначая через t выражение, аналогичное (5.36):
д2р чР д2р
’х ду2 “1“ У дх2 У дх ду ’
(5.37)
F:
(5.38)
(5.39)
получим условие совместности деформаций в виде:
3 (5.40)
® 1 ()х2 у дх ду у J1 — л '
Чтобы написать граничные условия для этого уравнения, необходимо
подсчитать вариации нормальной 8Г, и касательной 8SV сил на неко-
тором криволинейном контуре, проведённом в серединной плоскости
294
УСТОЙЧИВОСТЬ ПЛАСТИНОК и оболочек [гл. V
пластинок. Если внешняя нормаль v и касательная s к этому контуру
образуют систему координат такую, что путём вращения можно совме-
стить положительное направление оси v с у, a s с х, и если угол
нормали с осью х обозначить через а (рис. 92), то интересующие
нас величины имеют известные выражения:
й ® 7) 8 । 8 7) — 8 о iso* о 1
оТ, — ——%---i п--------- cos 2а о S sin 2а,
' - 'р_у. р (5.41)
SS, = ——— sin 2а — 83 cos 2а.
ЧистО пластическая область пластинки может быть ограничена кон-
туром, часть которого совпадает с границей пластинки, другая же
часть примыкает к упруго-пластической
области. При формулировке задачи
устойчивости в первой области гранич-
ные условия имеют вид:
8Г, = 83., == 0, (5.42)
во второй же величины 8Т„ 83„ должны
быть непрерывны.
Легко показать, что при потере
устойчивости вся пластинка не может
остаться в чисто пластическом состоя-
нии, т. е. что область упруго-пласти-
ческих деформаций обязательно суще-
ствует. В самом деле, допуская обратное, мы будем иметь одно-
родные граничные условия (5.42) на всём, внешнем контуре пластинки.
Но дифференциальные уравнения (5.33) и (5.34) при условиях (5.37)
будут также линейными и однородными, и потому имеют единствен-
ное решение:
87; = §Т2 = 83 = 0.
Из (5.37) следует, что и е1 = е2 = е3 — 0, откуда на основании (5.13)
и (5.14) вытекает г0 — 0. Но г — г0 есть граница между упругой
и пластической зонами по толщине пластинки, и условие z0 = 0
означает, что серединная плоскость есть как раз эта граница. Зна-
чит, данная область пластинки является не чисто пластической, а
упруго-пластической, что противоречит предположению. Таким обра-
зом при потере устойчивости пластинки за пределами упругости она
либо полностью переходит в упруго-пластическое состояние, либо
в ней останутся чисто пластические области, однако не распростра-
няющиеся на всю пластинку. В области упруго-пластических дефор-
маций пластинки уравнение (5.32) на основании выражений (5.30)
преобразуется к виду:
у<„ _%, = |+ Y, + 2 Л,) (3 — 2QX, (5.43)
36]§ УСТОЙЧИВОСТЬ ПЛАСТИНОК - " 295
пфчём, как и в уравнениях (5.35), (5.40), оператор, стоящий
в круглых скобках правой части, относится к множителю, стоящему
справа от него.
Условие совместности деформаций (5.34) на основании (5.29)
принимает вид:
<5-44>
где функция напряжений F определена согласно формулам (5.38).
Величина С, равная отношению толщины Апл пластического слоя
к толщине пластинки, входит в уравнения (5.43) и (5.44), поэтому
они оказываются совместными; эта величина выражается форму-
лой (5.27), причём функция <?, если воспользоваться обозначением (5.39),
равна:
2 X t
? —тгт—г — • (5.45)
Уравнения (5.43), (5.44) совпадают с соответствующими уравне-
ниями (5.35) и (5.40) на границе чисто пластической и упруго-пла-
стической областей. В самом деле, на этой границе, кроме непрерыв-
ности величин сил 8 Тч, 8S,„ моментов 87И,, (где 8Н, есть при-
ведённый крутящий момент согласно граничным условиям Кирхгофа),
прогиба w и наклона касательной плоскости, должно иметь место
ещё условие
Лпл = й, С = 1. (5.46)
Т» , I (1 -------X) %Й *
Из (5.27) при этом условии имеем<р = — Хи t — —------— , после
чего отмеченное совпадение уравнений нетрудно доказать. Гранич-
ными условиями для уравнений (5.43), (5.44) на части контура
упруго-пластической области, совпадающей с контуром пластинки,
являются обычное требование 8 Г, = 8SV = О, а также два условия,
налагаемые на прогиб w.
Условие (5.46) или
/ = -(1 (5.47)
представляет собой уравнение границы между чисто пластической
и упруго-пластической областями.
Возможность возникновения наряду с упруго-пластической также
чисто пластической области вытекает из того, что величина С,
согласно (5.27) и (5.45), может принимать значения, не лежащие
в интервале 1 С 0. Ниже приводятся некоторые примеры точных
решений задач устойчивости пластинок и, в частности, задачи о сжа-
тии свободно опёртой по двум сторонам пластинки; края пластинки
вблизи свободных опор после потери устойчивости остаются в чисто
пластическом состоянии.
296 УСТОЙЧИВОСТЬ ПЛАСТИНОК и ОБОЛОЧЕК (гл. V
Рассмотрим примеры точных решений задачи устойчивости пласти-
нок. Интегрирование системы дифференциальных уравнений (5.43)
и (5.44) в упруго-пластической области и (5.35), (5.40) в пласти-
ческой при неопределённой границе между ними, определяемой
соотношением (5.46), связано со значительными математическими труд-
ностями. Как было указано выше, задача устойчивости упрощается,
когда вариация сил, лежащих в серединной плоскости, всюду равна
нулю. В этом случае относительная толщина пластического слоя t,
оказывается известной функцией координат, так как, согласно (5.26),
<р = 0 и, следовательно,
C = Y(1-VT=I). (5.48)
Если ещё напряжённое состояние пластинки перед потерей устой-
чивости является однородным, величина будет постоянной, так как
в (5.29) будет одинаково для всей пластинки. Приближённым
решением задачи устойчивости мы называли такое, при котором
вариации сил 87), ЪТ2, 8S тождественно равны нулю. При этом
удовлетворяются уравнения равновесия (5.33) и граничные усло-
вия (5.42), но, за исключением частных случаев, не удовлетворяется
условие совместности (2.34). Исключительная простота такого реше-'
ния объясняется тем, что в основном уравнении (5.43) величина С
известна и выражается формулой (5.48), вследствие чего это урав-
нение становится линейным с постоянными или переменными коэф-
фициентами. В развёрнутом виде оно очень напоминает уравнение
упругой устойчивости анизотропных пластинок.
Точные решения системы (5.43), (5.44) представляют несомнен-
ный самостоятельный интерес, но для нас они существенны ещё
и потому, что позволяют оценить степень точности приближённых
решений. Мы укажем некоторый класс точных решений задачи
устойчивости для равномерно сжатых пластинок произвольной формы
и решения , для прямоугольных пластинок в тех случаях, когда
возможна цилиндрическая форма потери устойчивости.
1. Устойчивость равномерно сжатых пластинок произвольной
формы в плане (рис. 92). В этом случае напряжённое состояние
пластинок перед потерей устойчивости является однородным и опре-
деляется формулами:
^=^--00 ^ = о, (5.49)
где а( — сжимающее напряжение по контуру и одновременно интен-
сивность напряжений в любой точке пластинки. Приведённые напря-
жения, согласно (5.10) и (5.1), будут:
V=V=-1, J„ = 0, ^„=5 = — 1. (5.50)
w if ’ у ’ х У 2 f
§ 36] УСТОЙЧИВОСТЬ ПЛАСТИНОК 297
Величины х и t согласно (5.36) и (5.39) имеют выражения:
x = -V2w> J_v2F. (5.51)
Уравнение (5.44) принимает вид:
V2(/ — ^(?х) = 0. (5.52)
Опуская гармоническую функцию, получаем класс точных решений:
/ = (5.53)
вследствие чего величина ® (5.45) выражается через С, и из (5.27)
находим:
1-т) = С0П5к (5.54)
Основное дифференциальное уравнение устойчивости (5.43) теперь
становится линейным с постоянными коэффициентами и имеет простой
вид:
[1— 5c2(3-2C)]v4w-f-^ V2w = 0. (5.55)
Его решение хорошо изучено для различных видов контура и раз-
личных граничных условий, хотя бы в связи с изучением упругой
устойчивости равномерно сжатых пластин. Значение С (5.54) мало
отличается от приближённого (5.48) и характеризует степень откло-
нения точных решений от приближённых. В общем случае (5.52)
имеем
^ = ^(хС2 + Г1), (5.56)
где 1\ — произвольная гармоническая функция. Для сплошной круглой
пластинки, например, Г! — постоянная величина. Согласно (5.45) и
(5.27) теперь получаем выражение С через х:
(5-57)
после чего уравнение (5.43), имеющее в данном случае вид:
V2[l—^С2(3-2С)]х+ ^х = 0, (5.58)
содержит уже одну только искомую функцию х. Учитывая соотно-
шения (5.51), его можно ещё раз проинтегрировать:
l_3?iE;2(3_2Q]v2® + ^-® = r2. (5.59)
298 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК [гл- V
J
где Г2 — новая гармоническая функция для сплошной круглой пла-
стинки, представляющая собой также постоянную величину, поскольку
в центре прогиб w и У2да должны быть конечны. Учитывая (5.57),
уравнение. (5.59) может быть разрешено относительно после
чего задача сводится к интегрированию только^одного линейного
относительно производных дифференциального уравнения второго
порядка (для круглых пластинок):
V2-sy = Ф (ьу, Гп Г2).
Функция напряжений F определяется теперь согласно (5.56) и (5.51)
дифференциальным уравнением Пуассона:
V2F= —^(x^ + rj. (5.60)
Как видим, задача устойчивости для круглых пластинок сравнительно
просто может быть решена до конца. Детали подобного расчёта
будут выяснены ниже на
примере прямоугольной
пластинки, сжатой в одном
направлении.
2. Устойчивость пря-
моугольной пластинка
при условии плоской де-
формации (рис. 93). Та-
кой случай имеет место,
если прямоугольная пла-
стинка ширины I сжимает-
ся в направлении оси х,
причём перемещения кра£в
её в направлении оси у
исключены вследствие на-
личия ограничивающих стенок, расположенных в плоскостях у = 0
и у = Ь. Плоскость х = 0, изображённая на рис. 93, будет, оче-
видно, плоскостью симметрии деформаций. Форма потери устой-
чивости предполагается цилиндрической. В таком случае по условию
задачи имеем напряжения перед потерей устойчивости:
(5.61)
После потери устойчивости:
ц) = р)(х\ е3=сз = О,
§36]
УСТОЙЧИВОСТЬ ПЛАСТИНОК
299
Из уравнений (5.30) имеем:
8S = 0, 87'2 = |87’1.
Так как, согласно уравнениям равновесия, 8^ = const, а ЗТ^зО
I
из условия на краю х = -^, то мы имеем случай, когда 87) =
= S7'a = 8S==0. Приближённое решение, отмеченное выше, в дан-
ном случае, следовательно, является точным. Относительная толщина
пластического слоя С постоянна и определяется формулой (5.48).
Уравнение устойчивости (5.43) принимает вид:
diw , hp <Pw_________„ .
dxi О [1 — Ц2(3 — 2£)]dxz ' '
Если ввести в рассмотрение относительный модуль Кармана, обоб-
щённое выражение которого есть
А =----------- = —4(1^1L , (5.63)
то из (5.48) получим:
к = 4 (1 ~ VJ). C=l— -Vk, (5.64)
(2— У k)2 2 у '
после чего можем упростить выражение параметра в уравнении (5.62):
у —------------------— -1L /5 65)
* D [1 — XI2(3 —2С)] Dk' у.о.'оо)
Так как до предела упругости k — 1, а на площадке текучести
материала k — Q и так как характеристические значения параметра у
в упругой и пластической задачах одинаковы, то из (5.65) вытекает,
что критическое напряжение, соответствующее площадке текучести,
равно нулю.
Интересно отметить, что задача Кармана может рассматриваться
как предельный случай устойчивости сжатой в одном направлении
прямоугольной пластинки, размер b которой весьма мал, причём
параметр у будет иметь выражение
* 3W
и, следовательно, на площадке текучести материала критическое
напряжение будет равно нулю. Как видно из предыдущего и сле-
дующих примеров точных решений, полная потеря несущей способ-
ности пластинок, получающаяся в задаче Кармана, вообще говоря,
не имеет места,
300
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. V
3. Устойчивость прямоугольной пластинки, сжатой в одном на-
правлении (рис. 93). Будем рассматривать цилиндрические формы потери
устойчивости прямоугольной пластинки, достаточно длинной в напра-
влении оси у, предполагая, что сжимающее напряжение приложено
только вдоль оси х. В этом случае:
Хх— °i> Yy— ]
^ = -1, sy = ^, X,==-i> ^==ху = о. j (566)
По условию задачи, всякое поперечное сечение пластинки плоскостью
у = const после потери устойчивости остаётся плоским, и потому
имеем:
е3 = 0, е2 = const, (5.67)
на основании чего из (5.30) получаем 8S = 0. Кроме того, из гра-
ничного условия 87'1 = О на краях x = rt-^-/ и, следовательно, из
уравнения (5.33) следует, что 87^ = 0 повсюду. Так как никаких
сил вдоль оси у не приложено, то должно выполняться условие
J bT2dx = 0.
(5.68)
Из второго уравнения системы (5.44) имеем:
d‘!F ВГ2 Хй„9
4Czi>
(5.69)
так как х =— хг Нетрудно убедиться, что (5.69) есть интеграл
уравнения (5.44). Функция <р, с помощью которой согласно (5.27)
определяется величина С, в данном случае имеет вид:
? (1—Х)^2^” (1 — X) ft*! ~+~ 4(1 — X) * (5-70)
Изп^бающий момент в произвольном сечении равен:
8Л11== — £>£1 — |-Ца(3 — г^хр (5.71)
и потому граничные условия на сторонах х — zd ~ I суть Xj = 0.
Из формулы (5.70) ясно, что хх не может равняться нулю в упруго-
пластической области, так как г2 ф 0 (последнее вытекает из того,
что величина C2Xj знакопостоянна, а именно — положительна вдоль
РСей пластинки, поэтому условие (3.68) требует е? ф 0). Таким образом
§36]
УСТОЙЧИВОСТЬ ПЛАСТИНОК
301
упруго-пластическая область не доходит до краёв пластинки и закан-
чивается в сечениях х = ± 2_с. Примыкающие к краям области будут
целиком пластические. В самом деле, так как величина положи-
тельна, то и s2 положительна. Из (5.37) следует, что в чисто пла-
стической и чисто упругой областях сила имеет тот же знак,
что и еа, т. е. является растягивающей. Но если к пластинке, сжа-
той за пределом упругости в одном направлении (х), приложить
растягивающую силу в другом (у), то она останется в пластическом
состоянии. Формально в этом можно убедиться путём вычисления
величины согласно (5.12), которая на концах равна — Sj, но удли-
нение 6%, согласно (5.37), отрицательно, и потому величина
будет положительной, т. е. пластическая деформация до потери
устойчивости остаётся пластической и после.
Из (5.27) и (5.70) теперь имеем:
£г = Й)’ (5.72)
Отсюда находим нижнюю границу величины С(р>0):
*-Н <5-7з>
*
Основное дифференциальное уравнение устойчивости (5.43) прини-
мает вид:
£ [1 - 4 W - 2ф + § = 0. (5.74)
Вводя обозначения
Q(C)=4 — 9/.:? + 6/Л3, $ = а = у, (5.75)
уравнение (5.74) представим в виде:
где [а — основной параметр, определяющий критическое напряжение
р2 = Д^. (5.77)
Интеграл уравнения (5.76) можно получить в квадратурах. Вводя
обозначение:
D Ю - 9 4-12С + 12С»-ЗХСЗ
а (У—2 (4_8С + ЗХС«)2 ’ (5./8)
получаем последовательно
^'2<5га>
причём штрих наверху означает производную по С.
302 УСТОЙЧИВОСТЬ.ПЛАСТИНОК И ОБОЛОЧЕК [гл. V
/
В чисто пластической области, согласно полученным выше резуль-
татам и (5.66), имеем для силы оГ2 и для момента SMj выражения:
Вг’=Т^Г- (5.80)
Основное дифференциальное уравнение становится таким:
Решение последнего уравнения, удовлетворяющее условию Xj = 0
на конце С = 1, запишем в виде:
Х1 = 8эСд sin , (5.82)
причём, вследствие симметрии прогиба относительно плоскости х — 0,
в дальнейшем будем рассматривать лишь правую половину пластинки
(х^>0). Для определения пяти неопределённых постоянных, а именно
трёх произвольных постоянных интегрирования cv с2, с3, коорди-
наты границы областей а и критического числа у. мы можем, кроме
уравнения (5.68), написать ещё четыре условия:
условие симметрии:
$ = 0, ^ = 0; (5.83)
условие наличия границы областей: ,
£ = а, С=1. (5.84)
Два условия непрерывности: момента и перерезывающей силы, которые
согласно (5.72) и (5.82) принимают вид:
. р. (1 —а) 4
С» Sin ? = -i-rr;---,
/4 — ЗХ h (4 — ЗХ)
__Р*з___cos Р- (1 — 4P'(i) fdZ\
/4 — ЗХ /4 —ЗХ “ ЙР2 \rfUa
(5.85)
Постоянная s2 несущественна и в указанные условия не входит,
поскольку от неё не зависят отношения и — . Выполняя пе-
е2 е2
речисленные условия и вводя новую неизвестную Со — относительную
толщину пластического слоя в сечении х = 0, получим для вели-
чин 1 — а (относительной длины чисто пластического участка) и у.
следующие формулы:
\ ХЛ1 , (4 — ЗХ) L
у. — — ------, 1 — а = —------—-—
(1— X)-/'2 ХА4
(5.86)
§ 37] Приближённой решение задачи Устойчивости 303
где L и М суть интегралы:
R Ы
L = J
Ж1)
1-2С + цг dR
Vr^q)—r& ’
R М
M== f
J VR^)-R(Z)
RW
(5.87)
причём величина Co определяется соотношением:
ctg2 (1 -.% - 2 (4 - ЗХ) [7? Co) -7? (1)] (5.88)
\(i — a; у /
Как уже установлено, величина 1—а положительна, поэтому инте-
грал L должен быть положителен, а для этого необходимо 1 —2С04"
т. е.
^о<т(1-/1-X).
(5.89)
Учитывая оценку (5.83), справедливую и для Со, видим, что эта
величина заключена в узких пределах и близка к приближённому
значению (5.48). Отсюда вытекает, что и критическая сила будет
мало отличаться от приближённого её значения.
§ 37. Приближённое решение задачи устойчивости
пластинок.
Тимошенко [И, БлейхК!, Геккелер 161 и другие авторы предло-
жили приближённый приём, решения задач об устойчивости пласти-
нок и оболочек за пределом упругости, основанный на допущениях,
которые мы рассмотрим применительно к частной задаче устойчи-
вости прямоугольной пластинки, сжатой в одном направлении равно-
мерным давлением интенсивности Р. В пределах упругости эта задача
приводится к интегрированию известного уравнения Брайана:
r.fdiw , о d*w , d*w\ . D d2w „ /с
D^ + 2d^*+~w) + P-dxT=:0- (5-90>
Поскольку сжатие происходит в направлении оси х, и поскольку
при сжатии стержня в направлении оси х прогиб его за пределами
упругости удовлетворяет уравнению Кармана 1’1:
где k — отношение модуля Кармана к модулю Юнга, в уравне-
ние (5.90) вносят поправку, умножая первое слагаемое в круглых
скобках на А; поскольку в направлении оси у сила не действует,
d*w
т. е. материал пластинки как бы остаётся упругим, слагаемое
304 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОВОЛОЧЕК [гл. V
оставляют неизменным; смешанную производную умножают на сред-
нее геометрическое поправочных множителей для крайних слагаемых,
т. е. на Получающееся в результате уравнение:
+ + = 0 (5-91)
\ дх* 1 ' дхг оуъ 1 ду*} 1 дх2 4 '
и применяют к решению задач устойчивости за пределом упругости.
Произвольность таких рассуждений очевидна, поскольку нельзя гово-
рить о том, что материал пластинки может в одном направлении (х)
переходить за предел упругости, а в другом (у/) оставаться упругим.
Кроме того, указанные и аналогичные рассуждения не дают общего
метода составления дифференциального уравнения устойчивости
в общем случае, когда на пластинку действует сложная система сил и
не отражают тот бесспорный факт, доказанный в §§ 37 и 38, что
действующие силы существенным образом влияют на величины жест-
костей, т. е. на коэффициенты уравнений, связывающих изгибающие
моменты с кривизйами.
Приближённое решение задачи устойчивости йластинок можно
получить, исходя из результатов предыдущих параграфов,! предпо-
лагая, что вариации сил 371,, 8Т9, 8S, две однородные линейные
комбинации которых согласно (5.42) обращаются в нуль на контуре,
тождественно равны нулю всюду:
8T1 = 87’2 = SS = O. (5.92)
Такая гипотеза может быть принята по следующим причинам: во-
первых, как увидим ниже, получающиеся на основании этой гипотезы
значения критических сил хорошо согласуются с точными решениями,
которые указаны в § 36; во-вторых, имеющиеся опытные данные
дают удовлетворительное подтверждение результатов, получающихся
согласно этой гипотезе; в-третьих, она удовлетворяет тождественно
главному условию при постановке задачи устойчивости, а именно
тому, что вариации внешних сил равны нулю; в-четвёртых, она
строго выполняется в том случае, когда деформация пластинки
является упругой, т. е. пластинка не имеет второй и третьей зон
деформаций. Заметим ещё, что если бы в области пластинки могли
существовать только 1-я и 3-я зоны деформаций, то вследствие
линейности и однородности соотношений (5.18) и (5.23) и граничных
условий (5.42) гипотеза (5.92) также выполнялась бы тождественно.
Согласно гипотезе (5.92) из (5.26) имеем <р = 0, и потому отно-
сительная толщина пластического слоя в зоне упруго-пластических
деформаций пластинки равна:
( = —г0=1—2С. (5.93)
Она точно совпадает со значением, найденным Карманом при реше-
нии задачи о Продольном изгибе стержня. Полагая теперь в фор-
§37] ПРИБЛИЖЕННОЙ РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ 305
мулах (5.21):
6T1==8T2 = 3S = O,
и выражая деформации sn через кривизны хга— найденные значения sn
можем подставить в формулы (5.22) для изгибающих моментов и
собрать подобные члены. В результате этих преобразований получим:
а = - и _ф) Х1+(1 - ф-k)
QLJ \ *• !
А(8Д1а _ 18уИ1) = - (1 — ф) х2 + (1 -ф - А) ^х,
^8Н= -2(1—<ь)х3+(1
(5.94}
где обозначены:
Сравнивая величину k с модулем Кармана К (3.18), видим полную
аналогию, поэтому называем его обобщённым относительным моду-
лем Кармана
поскольку вместо осевого напряжения и осевой деформации et
бруса в эту величину входит интенсивность напряжений ai и интен-
сивность деформаций et. Параметр ф обращается в нуль вместе с ш
и потому в случае, если пластинка лишь незначительно выходит за
предел упругости, его можно отбросить.
Подобно тому как это делается в теории изгиба анизотропных
упругих пластинок, разрешим уравнения (5.94) относительно момен-
тов и результат запишем в виде:
oAlj = Z)]1x1 Т)]2х22Z9]3x3;
оЛ42 — ^ajXj Z)22x2 2Z)23x3,
o// = Z)32xa 2Z)33x3.
(5.97)
20 Зак. 3138. А. А. Ильюшин
306
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. V
Величины Dmn можно назвать жёсткостями при потере устойчивости
пластинок за пределом упругости. Они имеют следующие выражения:
= D [1 | (1 -«J— k) У*] ,
Аз = 1д[1-ф-3(1-<
£>13 = ^>31 = Т (1 -'Р - ,
^23 = Аа = т D (1 -ф-k) ?уХу.
(5.98)
Формулы (5.98) показывают, что жёсткости зависят как от механи-
ческих свойств материала пластинки, а именно, от обычной упругой
цилиндрической жёсткости D, модуля Кармана К и степени пласти-
ческой деформации о>, так и от действующих перед потерей устой-
чивости напряжений Хх, Yy, Ху.
Внося значения Dmn в уравнения (5.97), получим:
=- (1 -ф) +4 х2)+4 (1 -Ф-хХ7.,
= _(1 _ф)+ |+|(1 __k) Yyv,
~-Р *з + 4 (1 - Xyv..
(5.99)
Отсюда заключаем, что моменты имеют потенциал:
г) Г 4 1
= -f [(1 - 4) 04+w+'4+хр —J (i - 7-2] , (5.100)
так что
dW ... dW 1 dW
oM.= —, о/И2 = —-з- , —o-v-. (5.101)
1 д-/-1 ’ J d-м 2 дч.3 v 7
Метод Тимошенко, широко применённый им в исследованиях
упругой устойчивости пластинок и оболочек, вполне применим и
в задачах устойчивости пластин за пределом упругости, поскольку
зависимости (5.99) между моментами и кривизнами являются линей-
ными, и работа внутренних сил при изгибе согласно (5.100) является
однородной квадратичной формой параметров Xj, х2, х3. Метод со-
§37]
ПРИБЛИЖЁННОЕ РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ
307
стоит в следующем: пусть под действием заданной системы контур-
ных сил, действующих в плоскости (х, .у), пластинка находится
в плоском напряжённом состоянии, определяемом напряжениями:
== У- ' ^ъ^У’ ХУ == ^г^у' •
Пусть по каким-либо причинам
лое выпучивание, определяемое
пластинка получила бесконечно ма-
прогибом w (х, у) и кривизнами:
d2w , _______ d"w
~дх? ’ 'Z2 — "ду2 ’
д-w
X» = 5-^- •
6 дхду
При этом внутренние силы (моменты) совершают работу:
V= J J Wdxdy.
(5.102)
Поскольку за пределом упругости потеря устойчивости сопрово-
ждается деформациями серединной поверхности вп в2, в3, то силы
Т\, Т2, S совершат работу:
Vi= j* f T^2-\-2Sis)dx dy,
которая согласно вариационному уравнению равновесия равна ра-
боте внешних сил на перемещениях контура, соответствующих
деформациям Sj, е2, г3. Кроме работы А1г контурные силы совер-
шают работу А на перемещениях точек контура в плоскости (х, у)
за счёт выпучивания пластинки. Последняя, как известно, равна:
. h Ifff / dw\2 , / dw\2 i oc dw dw) , ,
Л=2Л -=-2] J +2S^^\dxdy =
= — yj si[Xx'W2x-^Yy'wl-]r‘2Xy'Wxw,J\dx dy. (5.103)
Здесь ‘Wx> Wy суть частные производные от -w по х и у.
Если работа внутренних сил V-|- Vr больше работы внешних
сил А~1~А1, то плоское состояние пластинки является устойчивым;
если меньше — то неустойчивым. Таким образом критическое значе-
ние внешних сил определяется равенством этих работ. Так как = Уг,
то уравнение, определяющее критические силы, имеет вид:
V = А,
или, согласно (5.102) и (5.103):
/ / [ W + Т °* + У^2у + 2^^)] dx dy = 0. (5.104)
20*
308 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК [гл. V
Обозначим через I какой-нибудь характерный размер пластинки
в плане и назовём гибкостью пластинки I величину
Z = 4/12(1->2) = 4Z.
При ч — 0 эта величина представляет собой обычную гибкость балки-
полоски длиной / и толщиной h, причём ширина её равна 1. Умно-
жим уравнение (5.104) на X и, замечая, что перед af образуется
множитель
-а
D ~ Е ’
разрешим его относительно гибкости:
/2£ f Г — + *1*2 + + *з) — т (! — 4'—fe) *21 dx dy
а2 = —---------------------------—-----------J----. (5.105)
~ff°i + rywy + 2xywxwyl dx dy
Это и есть основное уравнение, определяющее критические нагрузки
или критическую гибкость по методу Тимошенко. Оно очень удобно
для решения задач и особенно в тех случаях, когда имеется прибли-
жённое решение. Задавая прогиб -ш в виде ряда
®=2vb(*,a
который удовлетворяет граничным условиям на контуре пластинки,
и вычисляя величины:
X
• ^fn
п дх2
., Х = \Cn(xJ^-\
’ ® дх2 1
у Wn
1 Уду2
1~2Х
У дхду)у
х 2л п^х ’ • • >
после подстановки их в (5.105) получим:
jy S S атпРтСп
(5.106)
причём в числителе и знаменателе находятся однородные положи-
тельные квадратичные формы по коэффициентам Ст, а аяа)г, —
определённые постоянные величины, выражающиеся через размеры
пластинки в плане, через механические характеристики материала и
через внешние силы. Разыскивая минимум величин г2 из уравнений:
dl^
-^- = 0 (тп = 2,3,...)
(коэффициент С1; ввиду однородности дроби (5.106), можно считать
заданным и отличным от нуля, т. е. его не варьировать), мы находим
критическую гибкость I.
§37]
ПРИБЛИЖЁННОЕ РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ
309
Если разыскивать минимум гибкости I согласно выражению (5.105),
то можно получить дифференциальное уравнение устойчивости пла-
стинок. Для этого перепишем его [на ^основании (5.100) и (5.103)
следующим образом:
РЕ f f Wdxdy
fl =----LL---------1 (5.107)
и вариацию i2 приравняем нулю:
8fl = ^{A' J J bW'dxdy — 84' J J W
или, согласно (5.107):
PE J j* ZW'dxdy — PbA' = Q.
Но согласно (5.100) и (5.101) имеем:
8 W' = 8 U7 = — [(8Af j) 8xr + <8Ma) 8xa + 2 (8/7) 8x3];
0,
(5.108)
при этом знак вариации, о которой идёт речь, относится к кривиз-
нам, у моментов же символ 8 связан с принятыми выше обозначе-
ниями моментов, вследствие чего для определённости величины мо-
ментов 84fj, 8/И2, 8/7 и взяты в скобки.
Знаки варьирования и дифференцирования по координатам можно
переместить:
* <, <Pw д2 <, <, д j
ох. = о= з-^о-да, ..., о-даж=з—8-да, ...,
1 дх2 дх2 ’ ’ х дх ’ ’
после чего уравнение (5.108) перепишется в следующем развёрнутом
виде:
J J [(8^1) 8™ + (8Л42) З-да 2 (8/7) 8-да] dx dy +
+ f f йо Г^/_8^ + г/^А8^ +
II * x dx dx 1 v dy dy 1
+ ?«(^i8”+Ss78»’)]‘'x'i-v = 0' <5,M>
Интегрируя эти выражения по частям и принимая во внимание
уравнения равновесия сил, действующих в серединной плоскости
(5.33), получим:
f С гд^Мл , „ дЧН . \ j . . .
J J W+23T^ + ^+Mto,fa‘i-,'+
+ J ((84i„)aw.+(UUS«^— KW,)/+(SN,)»> +
4- (^W;r4- YyWy)} 8-®} ds = 0,
310
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. V
где I, т — направляющие косинусы нормали к контуру, по которому
распространён второй интеграл и
(8Afvl) = (87H1)ZH-(8/7)m, (8ATJ = ,
(Ж2) = (8W) /+ (8Af2) т, (8AQ - 5? + -~2
Контурный интеграл обращается в нуль на основании граничных
условий, и потому двойной интеграл, распространённый, как и во
всех предыдущих случаях, по всей площади пластинки, равен нулю.
Но при произвольной вариации ста такое равенство возможно лишь
в том случае, если подинтегральное выражение равно нулю, т. е.
если имеет место уравнение (5.32). Таким образом эквивалентность
условия минимума выражения (5.105) и дифференциального уравне-
ния устойчивости (5.32) доказана.
Если напряжённое состояние пластинки перед потерей устойчи-
вости не является однородным, то величины <u, ф, k и напряжения
з ависят от координат х, у и потому жёсткости Dmn являются пере-
м енными. Подстановка выражений моментов (5.99) в уравнение (5.32)
Приводит к линейному дифференциальному уравнению четвёртого
порядка с переменными коэффициентами почти общего вида, поскольку
в него входят все возможные производные по двум переменным от
второго до четвёртого порядка включительно.
Рассмотрим наиболее простой и интересный случай, когда напря-
жения Хх, Yy, Ху всюду постоянны. Согласно (5.32) и (5.99) полу-
чаем следующее дифференциальное уравнение с постоянными коэф-
фициентами :
/ 3 । _ 6—k d*w , J. 3 1-i-K- I о v2)l diw ।
— Г 1 - ф "Хх) + 2 [1 — Т“Г-Ф Wy-r^Xy) j +
। з i — ф—k 1 — Ф—-kx diw । v 6iw \
4 ;1 — Ф v) dy* 2 1 —У\ хдх^ду' у dx dyi)
(1 — Ь\Хх дх^^ХУ дх ду^ Yy dy2/ °' <5’110)
Так как рассматриваемое напряжённое состояние пластинки перед
потерей устойчивости является однородным, главные оси напряжений
всюду имеют одинаковые направления, и потому образуют декартову
систему координат. Если в качестве осей х, у взять именно глав-
ные оси, то уравнение (5.110) упростится, поскольку касательное
напряжение Ху в этих осях равно нулю; члены, содержащие нечётные
степени дифференциалов координат, исчезают, и уравнение устойчи-
вости становится вполне аналогичным известному уравнению Брайана.
Множитель, стоящий перед последним трёхчленом уравнения (5.110)
на основании (5.104) можно выразить через гибкость z;
hat ____
D ' ' 1:1-
(5.111)
§37] ПРИБЛИЖЁННОЕ РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ 311
и принять за параметр, критическое значение которого определяется
при решении задачи устойчивости пластинок. Рассмотрим несколько
частных примеров.
1. Устойчивость сжатой, полосы. Полоса, длина которой I зна-
чительно больше ширины Ь, сжата в направлении оси х напряже-
нием— Хх, два других напряжения равны нулю, и потому
сь= — Ху, 1, Х„=К„ = О.
Ч, ’ и и
Так как крутящий момент оН и поперечный изгибающий равны
нулю на длинных сторонах полосы, то, вследствие малости ширины Ь,
они равны нулю всюду, и потому из (5.99) имеем (х = — xj:
Х2 = — Xt, J = — k D/.x.
Из уравнения (5.32) получаем:
64w . 4<т,:/а 6‘:w „
Подчиняя решение этого уравнения:
w = A cos ух -}- В sin ух,
^7
граничным условиям на концах полосы, находим критическое значе-
ние параметра у = 7,:р, а отсюда получаем и критическую гибкость
1^-.. (5.112)
Эта формула соответствует результату Кармана и отличается от него
лишь постольку, поскольку вместо жёсткости балки здесь входит
цилиндрическая жёсткость пластинки. Для полосы со свободно опёр-
ТС 1
тыми краями, как известно, критическое значение у равно у, и фор-
мула (5.П2) даёт:
(5. ИЗ)
2. Цилиндрическая форма потери устойчивости прямоугольной
пластинки. Если размер b прямоугольной пластинки длины I (рис. 93)
соизмерим или больше I, и она сжата в направлении *оси х напря-
жением— Хх, постоянным в направлении оси у, то основная форма
потери устойчивости будет цилиндрической, и потому w —w(x).
Полагая в (5.И0):
Хх= — oit ^= — 1, X=Y=O,
CU Uz ' О О ’
312
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧ8К
[ГЛ. V
/получим дифференциальное уравнение:
rf4te> . й т - 2г 1/ а<
dxi ‘ ' dx* и’ I У £(!—ФН-Зй) '
Подчиняя решение этого уравнения граничным условиям, находим ^кр,
«после чего определяем критическую гибкость:
Для пластинки со свободно опёртыми концами, как и в предыдущем
случае, увр = тт/Z, и потому критическая гибкость будет:
(8Л15)
3. Устойчивость равномерно сжатых пластинок произвольной
формы в плане (рис. 92). Полагая в (5.110):
^=^=-1,
получим:
74та -f- TaV2w = 0,
~l V £(1 — ф+3£) '
Это дифференциальное уравнение
совпадает с дифференциальным
уравнением упругой устойчивости равномерно сжатых пластин, отли-
чаясь лишь выражением Поскольку кинематические граничные
условия, а также все основные статические условия для упругих
я пластических деформаций пластинки одинаковы, то и характеристи-
ческие числа укр одинаковы ц потому непосредственно получаем
выражение критической гибкости:
1 ,,/£(! —d- + 3£)
------• (5.116)
Например, для круглой пластинки радиуса I, защемлённой по контуру,
.. 3,8317
известное упругое решение даёт fBp =—j—, поэтому:
13= 1,9158 + (5.117)
4. Свободно опёртая прямоугольная пластинка, сжатая в одном
направлении (рис. 94). В этом случае имеем:
Yv=Xy = Q, Хх=-^, Ха=-1,
§37]
ПРИБЛИЖЁННОЕ РЕШЕНИЕ ЗАДАЧИ УСТОЙЧИВОСТИ
313
(5.118)
и потому уравнение (5.110) преобразуется к виду:
1 — ф 4- 3k d*w „ d*w . d*w . d2w
4 дх* ' дх*ду* * ду* 'ЕР дх2
Сравнивая это уравнение с применяемым обычно уравнением (5.91),
обнаруживаем разницу в первых двух слагаемых, причём она является
принципиальной, поскольку при 6 = 0 в (5.91) они исчезают,
а в (5.118) остаются, что означает, что при напряжении, равном
пределу текучести, жёсткость пластинок не обращается в нуль и
потому существует отличная от нуля критическая гибкость. Для
разнообразия критическую гибкость найдём по методу Тимошенко.
В соответствии с граничным условием положим:
. я v , тг.х
w - с sin —j- sin--
b a
и, подставляя в уравнение (5.105) значения:
(тпл\2 . я у . тг.х /л\2 . г.у . тпх
-- ) SinSin------, Х2 =-----С т) Sin-f- sin----,
а ) Ь а ' * \b/ b а '
тгР лу т~х тг. . лу т лх
“ ab b а х а Ь а
(5.119)
-----7. = 7.
после сокращения с и вычисления простых квадратур, найдём:
»+’*)”>’+<U—»Giw+^)]- <5Л2О>
Рассмотрим сначала бесконечно длинную пластинку (а = со); так как
число волн в направлении оси х будет бесконечно велико, а длина
полуволны конечна, обозначим её через а'-.
а
и в качестве характерного размера возьмём 1 — Ь. Переходя в (5.120)
к пределу (а-> со, т-> со), получим:
/ — ^-./^и-ф) П-ф + ЗЛ/ 6\з
V °i L 4(1—ф>
Это выражение имеет минимум при
4/’1
4(1-ф) ’
(5.121)
а
причём критическая гибкость бесконечно длинной пластинки равна:
1 — ф + 3k
4(1-ф)
(5.122)
314 УСТОЙЧИВОСТЬ ПЛАСТИНОК и ОБОЛОЧЕК [гл. V
Если размеры а и b соизмеримы, то наименьшее значение /, со-
гласно (5.120), получается при числе полуволн т, определяемом
неравенством
m-[-l>-^>wi, (5.123)
где а' имеет значение (5.121). В частности, для квадратной пла-
стинки, полагая а — b — I, имеем т = 1, поэтому
[13 (1-^ + 3^. (5.124)
Устойчивость опёртой пластинки, сжатой в двух направлениях, можно
получить аналогичным образом, полагая
. JTV . П1~Х
w = с sin —=5- sin-.
b а
Заметим, что указанные решения не изменятся, если вместо метода
Тимошенко воспользоваться для их определения дифференциальным
уравнением (5.110), поскольку в пределах исходного предположе-
ния (5.92) они являются точными.
§ 38. Устойчивость цилиндрической оболочки.
1. Цилиндрическая форма потери устойчивости цилиндрической
оболочки, сжатой внешним давлением р и осевой силой Q (рис. 95).
Выберем оси координат х, у, как
показано на рис. 95. Ввиду того,
что внешние силы постоянны по
оси х и оболочка является круго-
вой цилиндрической, напряжения
в ней всюду постоянны и равны:
Y = — р —
у ‘ h ’
Y Q
х~ 2n.Rh ’
Ху — 0. (5.125)
Задача об устойчивости такой оболочки может быть точно решена:
прогиб w является функцией только угла 6, и потому W:
n 1 /d-w , \
х1=х8 = 0, -z2 = —( —4-.
(5.126)
Кроме того, из уравнения равновесия вариаций сил, .действующих
на элемент вдоль оси х, и условия неизменности напряжённого
состояния по оси х следует:
8Г1==85 = 0.
§38] УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 315
В самом деле, ввиду того, что оболочка в направлении х предпо-
лагается достаточно длинной, поперечные её сечения остаются плоскими
всегда, и потому сдвиг s3 отсутствует; из третьего уравнения группы
(5.21) имеем 85 = 0. Следовательно, уравнение равновесия сил
в направлении оси х имеет вид:
^i = 0, 87’1=О.
dx ’ 1
Дальнейшие выкладки аналогичны тем, которые были проделаны
при точном решении задачи об устойчивости прямоугольной пластинки
в § 36. Однако они значительно упрощаются в одном частном слу-
чае, когда сила Q равна:
Q = *R*p,
т. е. когда на донья оболочки действует то же самое равномерное
давление, что и на боковую поверхность. В этом случае
/„ = 2^, Sx = Xx — У„ = 0, (5.127)
т. е. деформация перед потерей устойчивости является плоской,
а потому она останется плоской и после потери устойчивости, т. е.
удлинение Sj будет равно нулю (sx = 0). Из первого уравнения
группы (5.21) при этом имеем:
8Г2 = 0,
а из второго можем найти деформацию е2, которая, однако, в даль-
нейшем уже не понадобится. Таким образом гипотеза (5.92) в рас-
сматриваемой задаче выполняется, и потому уравнения (5.22) пре-
образуются к виду (5.99) и дают следующее выражение для
тангенциального изгибающего момента:
3M2=-Z)[1 — —1(1—б — &)уф2, (5.128)
или, так как при условии (5.127)
а2 _ A Y2 Y =--------2=
г 4 у> у "КЗ
ТО
8М2 = —&£>х2. (5.129)
Интересно отметить, что из всех возможных значений Yy при усло-
вии (5.127) получается наименьшая жёсткость оболочки. Если дей-
ствующие на оболбчку нагрузки не удовлетворяют условию (5.127),
то выражение момента о/И2 формулой (5.128) можно принять как
п оиближённоэ. Кроме того, из условия равновесия внутреннего
момента 8М2 и момента внешнего давления р в любом сечении 6
имеем _
87И2 = pRw -j- с = с — h'iYyW. (5.130)
316
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОВОЛОЧЕК
[гл. V
Сравнивая это выражение с (5.128), получаем дифференциальное
уравнение
tPw ।
— Yvi<&h
-----------2^- } и = t,
i-bf(i-bt)d)
причём с и с' — связанные между собой произвольные постоянные.
Наименьшее значение выражения, заключённого в фигурные скобки и
^3
соответствующего периодическому по о изменению w будет . Таким
образом, пользуясь попрежнему выражением гибкости i и выбирая
в качестве характерного значения размера I длину окружности
2к7? (/ = 2тг7?), получаем критическое значение:
3^ 4(1 —ф) —3(1 ——Л)
Yy
В частности, при условии (5.127):
, /"б V3Ek
При отсутствии осевой силы (Ха. = 0, Yy= — a(} имеем:
— *
/в=1сУ “(1—Ф + з*)-
(5.131)
(5.132)
(5.133)
2. Осесимметричная форма потери устойчивости цилиндри-
ческой оболочки, сжатой осевой силой и боковым давлением (рис. 96).
Напряжения перед потерей устойчи-
L вости выражаются формулами (5.125).
I Из условия симметрии и уравнения
I I I I I равновесия в направлении оси х сле-
I I I I I 1 дует:
~~ — 85 = 87'1 = 0,
” ! " р е3 = х3 = 0.
— -----------f-Z/?---- —
! Точное решение поставленной задачи
* I " получим для того случая, когда осевое
—Л I — сжимающее напряжение в два раза
больше тангенциального
Рис. 96. Xx = ZYy, Q = 4vR*p. (5.134)
В этом случае SJ, = 0, и потому из формулы (5.26) имеем ср = О,
т. е. относительная толщина пластического слоя С постоянна; фор-
мулы (5.27), (5.28) и (5.95) дают:
i0=l — 2С = — 1-ф- (5.135)
§38]
УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
317
Из (5.21) найдём аТ2 и
^J==2(2—<o + <oF0)ea + y (1 — г*)ха +
—"2 (2 — a> + «W0> (si + y ег) =
(1 -г’5)(xt +1 ха) + 4(Х-«>)^(1 -i0)ax] .
(5.136)
Эти формулы несколько упрощаются при 8у = 0; при г0= — 1 -j- ]/А
их можно рассматривать как приближённые и для произвольного
значения Sy. Из первых уравнений группы (5.22) имеем выражение
для изгибающего момента
^ = —2(2—®+®^)(xi+4xa) +
+ 4 (А -ш)(1 - V (2 + (1 -Ч2) (*1 + 4 %) • (5‘ 137>
Обозначим через <ш (х) прогиб оболочки; тогда искривления хн ха
я тангенциалйная деформация еа будут иметь выражения:
d"w , ________ w __________ w
Х1 = ~dx? ' х2 — ^5 ’ е2 Г ’
х = ^а?х1 “И г/х2 = (х1 ~Ь “2 Хя) + ^г/Х2'
(5.138)
Исключая Si-j-g- s2 из (5.137), находим следующие выражения SAfj
« ЪТ% через ж
Wi /d2a> । w \ , T7 77 w
~D~ (1 \dx- “Ь 2T?2/ ’
Ц = _(1_ш + 1шу-й)®+|Л(и|<й(2-/й)^+ (5.139)
+ 4 h (A - ш)-(2 - Vk^Sy (X S +Л ^2) >
причём функция <}> имеет прежнее значение (5.96), а у имеет зна-
чение:
а = А (2 - Г1 + V ------------------------------
I 4(1-ш+А-<0 /Л)
(5.140)
318
УСТОЙЧИВОСТЬ ПЛАСТИНОК и оболочек [гл. V
Формулы (5.139) значительно упрощаются при условии (5.134),
когда Sy = О, Y = — X =-:
у ’ » 2 Уз
,., , „ (dtw . да \ )
оМ = — kD\ 4- ,
1 \dx2 1 2/?2/ ’ !
/ 1 ( (5.141)
ZT^ = -Eh[l^j
Для решения задачи об устойчивости нам остаётся написать диф-
ференциальное уравнение равновесия W:
d^Af i , т . 57~3_______
dx2 ‘ 1 dx2 R — и‘
(5.142)
Оно легко интегрируется как в общем случае, когда оТИ, и ST2
определяются формулами (5.139), так и, особенно, в случае Sy—0.
Внося значения (5.141), получим:
d* *w . 2^ d”w (1 " + 2 ю
dx* "t" kER? УЗ dx- "T~ R*k
(5.143)
где через i обозначена «гибкость» x):
3/?
h
Если длина оболочки велика сравнительно с радиусом и концы
свободно опёрты, то прогиб чю можно взять в виде:
w — С sin ах,
причём наименьшее значение критической силы получается из условия
(5.144)
Исследование других случаев устойчивости основано на применении
либо уравнения (5.143), либо (5.142) при значениях 844,, 8442
согласно (5.139); оно вполне аналогично исследованию соответствую-
щих упругих задач, поскольку дифференциальное уравнение (5.142)
является линейным и содержит только чётные производные от w.
Виды функций и»(х) и все вычисления для подобных уравнений даны
в книге Тимошенко !41.
h
*) При этом отброшены члены порядка -=- сравнительно с 1.
/\
§39] ЧИСЛОВЫЕ ДАННЫЕ ДЛЯ МЯГКОЙ СТАЛИ В ОПЫТАХ КАРМАНА 319
§ 39. Числовые данные для мягкой стали,
применённой в опытах Кармана.
Как уже упоминалось в главе III, Карманом I7' были поставлены
опыты по проверке его формул, определяющих устойчивость стержней
за пределом упругости. В качестве материала была взята мягкая
сталь, причём на диаграмме а — е этой стали имеется резко выра-
женная площадка текучести. Основные её данные таковы:
Е = 2,17 - 106, аь = 6800, as = 3250, <^ = 2600 (кгсм2).
Поскольку, как уже установлено в главе I, диаграммы зависимости
напряжения и деформации образца и интенсивностей — е{ совпадают,
на основании диаграммы сжатия образца стали, имеющейся в указан-
ной работе Кармана, можно составить следующую таблицу'(19):
Таблица 19.
Характеристики сталей.
et 103 4- Ю-e dei CO k
2600 1,20 2,17 0,000 1,000 0,000
2800 1,31 1,98 0,014 0,940 0,007
3000 1,43 ' 1,54 0,034 0,825 0,017
3100 1,51 1,12 0,054 0,685 0,026
3240 1,92 G,06 0,212 0,0805 0,149
3250 2,1 2,7 0,00 0,285-0,445 0,000 0,285—0,445
3260 2,90 0,042 0,482 0,055 0,360
3300 3,30 0,117 0,540 0,141 0,369
3500 4,70 0,14) 0,657 0,16? 0,456
4 J00 8,80 0,115 0,790 . 0,139 0,605
Произведём вычисления критических гибкостей in при различных
значениях сжимающих напряжений для рассмотренных выше случаев.
Все формулы, определяющие in:
. __3Z_
h 1
совпадают с известными в теории упругой устойчивости, если в них
положить = ф = 0 и модуль Кармана й=1. Для сравнения инте-
ресно рассчитать не только найденные нами значения критической
гибкости, но и значения их при упругом законе деформации. Этим
последним припишем два штриха сверху. Если в них заменить модуль
Юнга Е на модуль Кармана kE, получим приближённые значения in,
которыми нередко пользуются при расчётах. Этим величинам при-
пишем штрих "сверху.
320
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
[гл. V
Таким путём получаем формулы для следующих случаев.
1. Стержень Кармана и узкая полоса:
,/"Л£
z,=z, =1г1/ -, I, = ~ I/ — .
11 Г ц 1 г <ч
2. Широкая пластинка с двумя свободными краями (цилиндриче-
ский изгиб: 1 = а, =— Хх, Yy = Ху = 0):
-Г £(1 —^4-3fe)
г 4ц
3. Круглая пластинка, защемлённая по контуру (l—R, Xx=Yy =
“ — +' ,
/З = 3,84 т/~—1+^L , z'" = 3,84 1/"+, z; = 3,84 тЛ—•
3 г 4ц ’ 3 г ц 3 г ц
4. Длинная узкая прямоугольная пластинка, опёртая по всему краю
и сжатая вдоль длинной стороны (ширина 1 — Ь, Хх =— <ц, Yy=*
= ^ = 0):
2£(1—ф) Г. , Л1—64-З/Я
|/ ц L 4(1—ф) J ’
5. Квадратная свободно опёртая пластинка, сжатая в одном на-
правлении (/ == а = Ь, Хх= — а;, Yy = Ху = 0):
.* —. Г1 Q / 1 1 \ I 9 Ы ______ 1 1/ 12f
6. Труба под внешним давлением при отсутствии осевой силы
(l = 2*R, Хх = Ху = 0, Уу = -., = ^р^-
= 4+36), г-; = кул+^, =
r ° г <з< ь г
7. Продольная устойчивость трубы при осевой силе и боковом
давлении (l — R, Xx = 2Yy =
2 \
iri = Vi jA36(l — <0 + 1(0 У ky i’i = Ly^
§ 39] ЧИСЛОВЫЕ ДАННЫЕ МЯГКОЙ СТАЛИ 3 ОПЫТАХ КАРМАНА 321
Т а б ли ц а 20. ,
Критические гибкости.
«1 l2 й г’з гв
90,8 90,8 111,9 181,6 181,6 314 1440
2600 { 93,8 9\8 111,0 181,6 181,6 314 1440
90,8 90,8 111,0 181,6 181,6 314 1440
84,8 85,4 104,0 193,0 173,0 296 1290
2830 | 84,8 84,8 103,6 173,0 175,0 293 1300
88,5 88,5 108,0 177,0 177,0 306 1340
76,8 78,7 96,1 166,0 166,0 273 1120
3000 | 76,8 76,8 91,3 161,0 161,0 266 ИЗО
84,5 84,5 103,0 v 169,0 169,0 293 1250
69,0 72,4 88,4 162,0 160,0 251 984
3100 j 69,0 69,0 84,2 151,0 152,0 239 1000
83,2 83,2 101,5. 166,4 165,4 289 1210
23,0 ' 42,2 51,6 132,0 136,0 14S 295
3240 | 23,0 23,0 28,0- 46,2 105,0 80,5 328
81,5 81,5 99,5 163,0 . 163,0 283 1155
0 34—30 41,5—36,6 119-105 123—119 118-104 0
3250 0 0 0 0 81,3 0 0
81,3 81,3 99,4 162,6 162,6 282 1150
19,3 36,5 44,5 114,0 118,0 126 206
3260 j 19,3 19,3 23,6 38,5 100,0 66,5 271
81,1 81,1 99,3 162,2 162,2 281 1145
30,3 41,6 50,9 116,5 119,0 144 318
3300 | 30,3 30,3 37,0 60,5 110,5 105 425
80,5 80,5 98,3 161,0 151,0 279 ИЗО
31,6 39,7 48,5 Юб.о 108,0 138 298
3500 | 31,6 31,6 . 38,6 63,2 109,5 109 432
78,3 78,3 95,5 155,6 156,6 271 1070
27,3 33,0 40,2 85,5 87,0 114 210
4000 | 27,3 27,3 33,4 54,6 100,0 95 350
73,2 73,2 89,5 146,4 146,4 254 935
21 з»к. 3128. А. А. Ильюши»
$22 УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОЁОЛОЧЕК (гл. V
Приведённая выше таблица характеристик стали позволяет
вычислить все эти величины. Результаты даны в табл. 20, причём
против каждого значения напряжения а{ указаны три значения
гибкости: верхнее — in, второе — I' и третье — г".
Из этой таблицы видно, что приближённые значения tn, а тем
более упругие in — довольно сильно отличаются от установленных
в этой главе значений гибкостей in, причём, как правило, прибли-
жённые значения in дают заниженные величины. Например, на пло-
щадке текучести все in, за исключением одного случая (*6), равны нулю,
в то время как в ряде случаев in отличны от нуля, т. е. оболочки
не‘полностью теряют жёсткость.
ГЛАВА VI.
ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ
НЕСЖИМАЕМОГО ПЛАСТИЧЕСКОГО ТЕЛА.
§ 40. Предварительные замечания.
Если материал тела не обладает свойством упрочнения или из
каких-нибудь соображений упрочнением можно пренебречь, пласти-
ческое состояние тела невозможно при произвольных нагрузках. Для
того чтобы возникла область пластических
деформаций, необходимы нагрузки доста- А-
точно большие; однако, если всё тело пе-
решло в пластическое состояние, то вслед- < .... " ... 1 1 'f
ствие отсутствия упрочнения этому со- / |
стоянию соответствуют некоторые пре- / б,
дельные нагрузки, и дальнейшее увеличение /
их невозможно, так как сопротивление '___________,,__________
тела исчерпывается, и равновесие при 0 *
больших нагрузках оказывается невозмож- рис д7
ным. Тело, материал которого не обладает
упрочнением и является несжимаемым (объём элемента остаётся по-
стоянным при деформации), называют идеально пластическим. Диа-
грамма зависимости -е{ такого материала изображается ломаной
с горизонтальным участком SE (рис. 97).
Все основные задачи, аналогичные задачам, которые ставятся
в теории упругости, для идеально пластического тела теряют смысл,
например:
1. По заданным силам найти перемещение точек тела и деформа-
ции. Для рассматриваемого тела в пластическом состоянии эта задача
принципиально не может быть решена, так как зависимость о, = Ф (^)
(рис. 97) неразрешима (даёт неопределённое значение) относительно
деформации.
2. По заданным внешним силам найти напряжения; такая задача
в общем случае не имеет решения, так как при произвольно задан-
ных внешних силах упруго-пластическое равновесие идеально пласти-
ческого тела (его элементов) невозможно.
324 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ |гл. 1V
3. По заданным внешним силам, при которых всюду возможно
пластическое равновесие тела, на ти напряжение. Такая задача раз-
решима, но практически мало интересна. И в самом деле, напряжение
обычно находят для того, чтобы судить о прочности тела. Но в дан-
ном случае заранее известно, что интенсивность напряжений всюду
постоянна и равна пределу текучести. Таким образом условие проч-
ности должно выражаться не только через напряжения, но и через
деформации, которые, как уже сказано, для идеально пластического
тела являются принципиально неопределёнными, если известны только
внешние силы.
Как отчасти мы уже видели в предыдущих главах, для идеально
пластического тела имеют смысл задачи совершенно иного типа.
1. Задача о несущей способности тела. Дано тело конечных
размеров односвязное или многосвязное; найти все возможные типы
поверхностных нагрузок, при которых тело будет всюду находиться
в состоянии пластического равновесия. Задача имеет двоякий практи-
ческий интерес: а) решение её выясняет предельные нагрузки, отно-
сительно которых может быть целесообразно выбран запас прочно-
сти; б) решение её даёт необходимые данные для решения смешан-
ной упруго-пластической задачи. Последняя же интересна потому,
что отвечает на вопрос: насколько уменьшается жёсткость тела,
если некоторая его область выходит за предел упругости. Заметим,
что вопрос о возможности разрушения в этой области остаётся
открытым, так как деформации в них, вообще говоря, не могут быть
определены.'
2. Задача о вдавливании штампа. Дано тело, некоторая часть
поверхности которого свободна от нагрузки, и именно на этом
участке поверхности в него внедряется жёсткий штамп определённой
формы; найти распределение давления на контактной поверхности и
величину силы в зависимости от глубины вдавливания.
3. Задача о течении среды, подобном течению жидкости.
§ 41. Плоская деформация идеально пластического тела.
Поскольку в области пластических деформаций идеально пласти-
ческого тела интенсивность напряжений постоянна
°* = <’g> (6.1)
связь "между напряжениями и деформациями устанавливается извест-
ными шестью соотношениями:
ЛЛ “^8 TZ ‘’Q
Лл>-~ 0 = з^ еж' лУ = з^ехщ
Yy — a = ^e^, Yg = ^s-eu„
У 3ci УУ’ z 3ei У*'
7 ___а = Z = -^-е
“ 3ei х Зе4 г®’
(6-2)
§ 41] ПЛОСКАЯ ДЕФОРМАЦИЯ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО ТЕЛА 3^5
из которых только четыре являются независимыми, так как, составляя
выражение:
= yf Yyy+ (Yy-Zf+iZ^'X^ + 6 + Y* + Z2),"
получим тождественно а* = ав; кроме того, сумма трёх первых
равенств (6.2) даёт тождественно 6=0, так как:
ехх~Уеуу~Уеег — °* (6.3)
Деформация тела называется плоской и происходит в плоскости х, у,
если все компоненты деформации, имеющие индекс «г», равны нулю:
= еХ2 = Суг = 0. (6-4)
Плоская деформация может иметь место в цилиндрическом теле, ось
которого направлена по г, причём нагрузки, действующие по поверх-
ности, должны быть постоянны вдоль образующей, и торцевые сече-
ния, как и все другие поперечные сечения, должны оставаться непо-
движными (w = 0).
Из третьего, пятого и шестого уравнений группы (6.2) имеем:
Хг = Ys = 0,
А = (6-5)
и потому интенсивность напряжений
<з4 будет иметь следующее выраже-
ние через напряжения:
= + (6.6)
Таким образом условие пластичности
(6.1) принимает вид:
, 4Л
(Дф,—Уф)2 + 4Ху = 4т;, (6.7)
где тя = у^— предел текучести при сдвиге. Найдём главные напря-
жения Cj, и максимальное касательное напряжение тшах в плоско-
сти (х, у). На косой площадке, нормаль которой v составляет угол 6
с осью х, а ось г> выбрана так, что путём поворота можно v со-
вместить с х, а 5—с у (рис. 98), нормальное ДА и касательное Т,
напряжения равны: >
N., = Аф cos2 9 -ф- Yy sin2 0 -ф- 2Ху sin 0 cos 9 =
= с-ф.cos 20х„sin 20,
(6-8)
T, = (- Xx ф- Yy) sin 0 cos 0 -4- Xy (cos2 9 — sin2 9) =
в — sin 29 -ф- Xy cos 20. \
328 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОВНОСТЬ [гл. VI
Находя экстремум М, по 6, получим для главных осей напряжений:
Таким образом главные напряжения равны /V7> = c2):
°i=»+4 / (АГ- гу)2+4^, '
О2 = 0 —— 4-4X2.
напряжение <з3 = 2Гг = <з, и потому ясно, что оно
Третье главное
будет средним между и <з2. Отсюда видим, что максимальное каса-
тельное напряжение при пло-
ской деформации всегда будет
равно полуразности напряже-
ний а1э <за:
_lst —g8l
Lmax | 2 I
= 4 r(^-K2/)2 + 4Xj.(6.i°)
Сравнивая c (6.6), имеем:
a.-
<Г — — *Г
атх уд 8>
т. е. условия пластичности Ми-
зеса и Сен-Венана совпадают.
Найдём направления площа-
док, на которых действуют ма-
ксимальные касательные напря-
жения. Параметры аир будем
рассматривать, как криволинейные координаты, соответствующие на-
правлениям v и s (рис. 98), а угол линии a (v) с осью х обозначим
для этой площадки через 6а. Разыскивая максимум Тч (6.8) по б,
получим:
от
+гг 26 „ = Хх ~ Yy = —. А
g e-₽ ЧХу tg,O1(2 ’
(6.11)
откуда находим уже известный результат:
т. е. линии я. и [3 наклонены под углом 45° к главным осям. В даль-
нейшем буквой о (рис. 99) будем обозначать угол наклона линии я,
на которой действует максимальное касательное напряжение, с осью х.
9« = ?> % = ? + 4> 0! = ?—р = +
§41]
ПЛОСКАЯ ДЕФОРМАЦИЯ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО ТЕЛА 327
На рис. 99 показана взаимная ориентация произвольного элемента
OMPN, на который действуют напряжения Хх, Yy, Ху главного
элемента 0132, на который действуют главные напряжения, и эле-
мента скольжения ОАСВ, на гранях которого нормальные напряже-
ния одинаковы и равны сред-
нему а, а касательные на-
пряжения одинаковы, макси-
мальны и постоянны по всем
четырём граням. В каждой
точке тела имеются два
взаимно перпендикулярных
направления граней элемента
скольжения аир, причём
угол наклона их ®, вообще
говоря, плавно изменяется
при переходе от одной точки
тела к соседней. Таким обра-
зом линии а, р образуют
криволинейную ортогональ-
ную сетку, и в области пла-
стических деформаций они
Рис. 100.
называются линиями скольжения (рис. 100). Экспериментально они
обнаруживаются в виде линий Людерса при травлении шлифованных
образцов, вырезанных из деформированного тела Г1!.
Все напряжения можно выразить через среднее напряжение а и
угол ®. Из (6.11) имеем:
Xx-Yy^-2Xyig^,
и потому из условия пластичности (6.7) находим:
. Х„ — cos 2®,
а, следовательно:
Xx—Yy = qz 2ts sin 2<p.
Решая последнее уравнение вместе с (6.5), находим:
Хх = aqz sin 2ср, rj/ = o±Tesin 2<p.
Выбирая во всех этих формулах верхний знак (он произволен), полу-
чим формулы Леви i2i:
Хх = а — ts sin 2<f>,
r^ = <3 + Ts sin2?.
Xy = "s cos 2cp.
(6.12)
Условие пластичности-(6.7) при этом обращается в тождество.
Если на какой-либо площадке, лежащей на границе или внутри
тела, известно нормальное и касательное напряжения и Т,, то
328 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [ ГЛ. V
известными оказываются и все другие напряжения и, в частности,
величины а и ср. Пусть нормаль к этой площадке составляет угол 9
с осью х. Тогда справедливы формулы (6.8). Внося в них значения
напряжений (6.12), получим:
cos 2 (9 — ср) = —4 ,
^8
а = — tg sin 2 (9 — ср),
(6.13)
скольжения (рис. 100).
откуда и находится ср и а.
Рассмотрим дифференциальные уравнения равновесия элемента
Этот элемент в увеличенном виде показан на
рис. 101. Пусть в криволиней-
ных координатах а, Р элемент
дуги da имеет выражение:
/?$2 = Л2 (а, р)й’а2-{-
+ В2(а, В) d^, (6.14)
так что dSx — Ada и dS2 —
= Вd^ — линейные элементы
линий аир. Если линии а (на
которых р — const.) в рассма-
триваемой точке имеют возра-
стающий наклон и расходятся
при возрастании а, то линии р,
вследствие ортогональности при
должны сходиться. Дифферен-
выбранном направлении возрастания а,
циал угла ® наклона касательной к линии а в точке 0 при переходе
в точку'Л, очевидно, равен:
, д-р , ВС—ОА
d!? = -^da =------0-в—
Аналогично получаем:
т др г А да г
Проектируя все силы на направление а, получим:
dS.2 — о dS^' - tsdS2 d<f = 0.
Аналогично в направлении р:
-dsrrf^+
Внося сюда значения dS1, dS2 и tfcp, dep' и учитывая, что ср'= ср-}-у,
и потому
д (Л da) _ —1 дА ,
Вд$ ~~ В д$
ду' _____ дер дер' ____________др_
д« да ’ д$ d'i '
§41]
ПЛОСКАЯ ДЕФОРМАЦИЯ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО ТЕЛА
329
после сокращений получим:
Оа * да
4_ о-r — О
(6.15)
Интегрируя эти уравнения, получаем соотношения, которые другим
путём впервые были получены Генки (31 и называются интегралами
Генки:
а + 2-t3<p = Е (a) ts, 1
о —2vp = ^(P)Ts- ) (6Л6)
Если бы линии скольжения а, 0 были нам известны, то интегралы
Генки представляли бы общее решение задачи о плоской деформа-
ции идеально-пластической среды. Из них ясно, что нагрузки на
контуре тела не могут иметь произвольное значение. В самом деле,
пусть известна одна линия скольжения семейства а, начинающаяся
и кончающаяся на границе тела в точках М и L. Так как на этой
линии 0 постоянно, то значения а и <р в точках М и Д связаны соот-
ношением: '
ац — 2-scp;n = a£—2т8с?£.
Если в точках 7И и L действуют только нормальные напряжения, тЬ
последнее уравнение вполне определяет одно через другое.
Класс во.зможных линий скольжения ограничен. Обозначая согласно
рис. 101 через и радиусы кривизн линий а и 0:
1 ___ do________1 дА
R^ ~ ~Ada ~ ~АВ ~д?~ ’
1 ___ d-f' __ 1 дВ
В d'i АВ да ’
и замечая, что, согласно (6.15):
получаем:
(6-17)
(6.18)
Уравнение (6.17) показывает, что угол Щр (рис. 101) между сосед-
ними линиями скольжения 0 остаётся постоянным при движении вдоль
этих линий, так же как d<f' остаётся постоянным при движении вдоль а.
Этот факт позволяет очень просто геометрически построить всю сетку
линий а, 0, если известно по одной линии каждого семейства. Построе-
ние принадлежит Каратеодори и Шмидту и также дано в книге Михли-
на с большим числом примеров. Основные семейства линий скольже-
330 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОВНОвТЬ [ГЛ. VI
ния были указаны Прандтлем М. Мы приведём их в связи с рассмо-
трением частных задач.
Дифференциальные уравнения равновесия в координатах х, у
(при отсутствии массовых сил)
>-f-.^ = 0, = ° (6.19)
дх * 1 ду ду 1 дх v 7
вместе с условием пластичности (6.7) позволяют решать задачи
в напряжениях, не обращаясь к деформациям. Впервые они были
даны Сен-Венаном И, причём он исходил из гидродинамического пред-
ставления течения металла. Это означает, что в правых частях
равенств (6.2), вместо деформаций еХ!В ... , подразумевались ско-
рости деформаций, что совершенно не изменяет системы уравне-
ний^.?), (6,19).
' Дальнейшие преобразования уравнений (6.19) на основании (6.12)
в основном принадлежат Леви. Обозначим удвоенный угол наклона
линии скольжения
2ср = ® (6,20)
и внесём значения (6.12) в (6.19):
да ( д<о , . ди> \ п
,----То I COS <0-5--н sin <0 -5— = О,
дх я\ дх 1 ду) ’
да / . д<о д<0\ _
-5----То sin <0 -5------cos со = 0.
ду ®\ дх ду)
(6.21)
Исключая а, получим для со уравнение гиперболического типа:
. _ , . Г/д<о\2 * ( д<о \21 о 3<о д<о л „
4— 2 ctg со 5-5- 4- ctg <0 3—) —(-5— ) — 2 д—=0. (6.22)
1 ь дхду 1 ь L\<?y/ \дх) J дх ду ' 7
В самом деле (см. гл. IV), уравнение характеристик его имеет вид:
dy^ — dx- 4- 2 ctg <0 dx dy =s 0,
откуда имеем два решения:
-^ = tg<f>, -JL==_ (6.23)
х dx 6Т’ dx tg 9 4 * * >
Отсюда ясно, что оба семейства характеристик совпадают с семей-
ствами линий скольжения а, {3 и имеют те же уравнения а = const.,
р = const., или, согласно (6.16):
5== const., 7j = const.
Поскольку а и <о являются функциями х, у, то и обратно можно
считать х и у функциями а, а>. Пользуясь правилом дифференциро-
§41] ПЛОСКАЯ ДЕФОРМАЦИЯ ИДЕАЛЬНО ПЛАСТИЧЕСКОГО ТЕЛА 331
вания функций от функций, имеем четыре уравнения;
дх __1____ дх_ да . дх dw дх ___g__ дх да . дх dw
дх да дх' д<о дх ’ ду да ду ~1~ dw ду ’
ду __q____ ду да . ду dw ду ___j___ ду да . ду dw
дх да дх' dw дх ’ ду да ду ' dw ду ’ .
откуда можем выразить производные от а и <о через производные
от х и у по а и <о:
да___ 1 ду dw ______ 1 ду да____ 1 дх dw 1 дх гс
дх dw ’ дхв Д даду A dw ’ ду да ' ' '
и подставить в (6.21), если Д ф 0. Получим:
— -ф cos <о — — т8 sin <о ~ ==. О,
0(0 I * 0(5 « 05 ’
, л л (6.25)
дх , дх . . ду _ 4 ’
---5 Г COS <0 -5-Н Тв SIH <0 = 0.
0(0 *-8 . 05 1 8 OS
Как видим, это — линейные дифференциальные уравнения первого
порядка с переменными коэффициентами. Если вместо <о и а ввести
переменные $, т; (6.16), то вместо уравнений (6.24) получим:
d£tg?-^=o,. г]),
tg? = O, ает^-(Е + т]).
drj 1 оц ° ’ 2 v *. u
(6.26)
Эти дифференциальные уравнения определяют линии скольжения
в параметрическом виде: х = х(£, г;), у =у (?, »]).
Если ца некоторой части контура тела АВ, уравнение которого
j=/(x)
(хь>х>ха),
(6.27)
задать значения а и да, т. е. нормальные и касательные напряжения
N.„ 7, (6.13), так что при y—f(x):
E = V(x), )
<р=Д(х), ti = *i(x), j
(6.28)
и потребовать, чтобы в окрестности этой части контура тело нахо-
дилось в пластическом состоянии, то, как уже сказано выше, для этого
необходимо приложить силы в других частях контура или сечениях
тела, причём последние будут некоторыми функциями сил Тч.
Для определения этих неизвестных сил имеем следующую задачу
Коши П1: в плоскости $, т; (рис. 102) уравнение (6.28) изображает
кусок кривой ab, соответствующий участку АВ контура тела, причём
332 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [ГЛ. VI
каждой точке линии ab' соответствуют' определённые] значения
x,y=f(x) согласно (6.28). По этим значениям дифференциальные
уравнения (6.26) позволяют найти х, у во всех точках внутри тре-
угольника abca, образованного кривой ab и прямыми т] = т]о, В=56.
Значения х, у в точке С могут оказаться такими, что соответствую-
щая им точка С (х, у) окажется вне контура тела, и линии АС и ВС
пересекут его в точках А'В'; тогда значениям х, у на участке кон-
тура А'В' будут соответствовать определённые значения $, т; (ли-
ния а'Ь', пунк!ир), а следовательно, и с, ср; из уравнений (6.13)
после этого находятся силы 7'v, N4, которые действуют на А' В',
и вместе с силами, данными на ДВ,' вызывают пластическое состоя-
ние в четырёхугольнике АВВ'А'. Если же точка С окажется
внутри тела, то нагрузка на всей остальной (исключая АВ) части
контура остаётся неопределённой. Они, однако, не произвольны,
так как аналогичное построение решения для них привело бы,
вообще говоря, к пересечению линий скольжения не под. прямыми
углами, т. е. к противоречию. Линии АА' и ВВ' являются, конечно,
линиями скольжения разных семейств $ = т; — f\a.
Для определения значений х, у в различных точках треуголь-
ника abc (плоскости ц) можно либо применить функцию Римана П),
либо численное интегрирование Массо. Поскольку наиболее интерес-
ные практически частные задачи решены Прандтлем в простой зам-
кнутой форме, мы не будем излагать названных выше способов
решения уравнений (6.26), отсылая интересующихся к работам Хри-
стиановича 181 и Соколовского I0J; последним даны многочисленные
примеры построения характеристик, относящиеся как к плоской
задаче пластичности, так и к задаче кручения.
Мы выскажем теперь следующие довольно очевидные предложе-
ния, имеющие, однако, существенное значение при решении частных
задач: а) обращение нагрузки: если при заданных на определённом
участке контура напряжениях N4, Д внутри определённой области
тела возможно пластическое состояние материала, то при напряже-
§ 42] ПЛОСКАЯ ЗАДАЧА О ВДАВЛИВАНИИ ШТАМПОВ $3$
ниях обратного знака (— AQ, ( — Г,) система линий скольжения не
изменится, и все напряжения в теле изменят знаки на обратные;
б) наложение равномерного давления (растяжения): если внутри части
тела найдены линии скольжения, соответствующие данным на участке
кснтура напряжениям N,., Т\, то от добавления любого постоянного
на этом участке контура давления или растягивающегЬ напряжения р
сетка линий скольжения и все касательные напряжения в соответ-
ствующей области тела не изменятся, а все нормальные изменятся
на постоянную р. В справедливости этих утверждений легко убе-
диться, если снова просмотреть все выкладки этого параграфа. Заме-
тим, что предложение б) справедливо вообще для всякой несжимае-
мой среды.
§ 42. Плоская задача о вдавливании штампов.
1. Начало вдавливания плоского штампа. Декартовы и поляр-
ные координаты могут представить сетки линий скольжения. В самом
деле, для декартовых координат:
ds2 — dx2 dy2, а'—х, (3'=_y, Д = В—1, /?s = /?g = co,
и потому ® —const. =0, вследствие чего уравнения (6.17) или (6.18)
удовлетворяются. -Для полярных координат:
ds2=*dr2‘-]-r2d№, з" = г, Д = 1, В = г, /?а=оо,
Яр = г.
Угол <р = &, и потому уравнения (6.17) или (6.18) удовлетворяются.
Прандтль применил эти сетки линий скольжения задачам о вда-
Рис. 103.
вливании плоского штампа при отсутствии силы трения на границе
контакта (рис. 103, а, б). Рассмотрим более общий случай (<?):
в равнобедренном прямоугольном треугольнике АА'С построим пря-
334 ВДАВЛИЙАНЙЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ (гл-
моугольную сетку линий скольжения под углом ±2 45° к оси х:
со = тг/4, <р' = -тс/2 тг/4. Из (6.13) при Т, = 0 и 9—0 следует ® = к/4
(в аналогичных , треугольниках ABD и A'B'D' на гранях тела по-
строим такие же сетки линийпод углом zt 45° к граням АВ и А'В'-,
вследствие того, что на этих гранях нормальное 2V7 и касательное Т.,
напряжения должны отсутствовать, линии скольжения должны распо-
лагаться под углом 45° к ним). В треугольниках ADC и A'D'C'
проведём полярную сетку линий скольжения. Таким образом в окрест-
ности действия давления р мы получим всюду. ортогональную сетку
линий скольжения, вдоль которых величины S, т; (6.16) остаются
постоянными. Рассмотрим заштрихованный на рис. 103, б квадрат:
касательные напряжения т8 действуют, очевидно, так, как указано
стрелками, и потому, сравнивая с рис. 101, заключаем, что к семей-
ству а принадлежат линии, поднимающиеся от грани В'А' к АА',
а к семейству р— линии, опускающиеся от АА' к грани АВ. Углы
наклона линий а (р = const’.) будут: == 3^/4-j-углы
наклона нормалей к граням А'В' и А А' с осью х будут: 9^ —у,
9^ = 1т/2. Из условия р == const, (на линии а) имеем т] = const., т. е. из
интегралов Генки:
=Л1--2т/5М — Од,-------2т/Х>^.
Но согласно (6.13) в точке М имеем:
т;=М = о,
а в точке 7V:
т, = о, ч = -р,
и потому:
= —Ts sil’2(9Jr—?дг) = -тв,
°№~т, 81п2(9лг—?х)—р = —
Таким образом из условия const, имеем:
Р = 2?8(1 + у). , (6.29)
В частности, при у = тс/2’ (рис. 103, а) имеем:
р-?8(2 + О. (6.29')
Прандтль называет эту величину «давлением врезания», предполагая,
что при таком значении давления штамп начинает врезаться в тело.
Опыты, обработанные Надаи (И, показывают, что указанная система
линий скольжения наблюдается в действительности. Построенное
решение кажется несколько искусственным и ничего не говорит
о распределении напряжений ниже линии BDCD'B'. Однако оно
единственно, поскольку единственно упомянутое выше решение
задачи Коши.
§ 42) ПЛОСКАЯ ЗАДАЧА О ВДАВЛИВАНИИ ШТАМПОВ 335
2. Давление у дна контейнера при начале прессования. Нало-
жим на область BAA'B'DCD (рис. 103) равномерное растягивающее
напряжение а ——р = — 2т8(1-|-у) и затем обратим получив-
шуюся нагрузку. Получим решение задачи о давлении металла на
стенку контейнера при прессовании (рис. 104). При этом трение
по участкам АВ и А'В' предполагается равным нулю. Давление
определяется формулой (6.29) и, в частности, для контейнера,
имеющего плоское дно (2у — к), формулой (6.29). Распределение
давления выше точек В, В' и полная сила Р остаются неопределён-
ными и требуют дальнейших построений линий скольжения.
Рис. 104.
Другое решение почти той же задачи (рис. 104,6) получим,
предполагая, что линия АА' — дуга круга радиуса а. Если трением
на поверхность контейнера пренебречь, получим простейшую осесим-
метричную задачу: радиусы и окружности суть главные направле-
ния. Разность главных напряжений равна
°1 — °2 = 2т8,
и потому из уравнения равновесия получаем:
d~i । Д1 — __л.
dr । 2 “ ’
удовлетворяя условию == 0 при г = а, имеем:
°1 = 2т81П-^, а2=-р = — 2тв(1-|-1п
Здесь р есть давление на стенку контейнера. Независимо от угла -у
при г —а имеем /? = 2т8. Линии скольжения пересекают главные
направления под углом 45°, и потому это — логарифмические спирали.
336 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [ГЛ. IV
Сравнивая это решение с предыдущим, обнаруживаем ‘ значительную
разницу, несмотря на то, что разница в задача'х лишь та, что в одном
случае линия АА'— прямая, в другом—дуга круга. Этот факт
свидетельствует о неустойчивости получаемых при идеальной пла-
стичности решений: малые возмущения границ или сил приводят к
существенному пэрераспредэле аию напряжений в теле.
3. Криволинейный штамп. Любое семейство прямых линий
в плоскости х, у, зависящее от одного параметра, вместе с ортого-
нальным к нему семейством кривых может представлять сетку линий
скольжения. Действительно, угол между парой прямых при движе-
нии вдоль них не изменяется, и потому уравнения (6.17) и (6.18)
удовлетворяются. Прандтль l10! применил такую систему линий
скольжения к задаче о криволинейном штампе (рис. 105). Пусть
тело имеет участок границы, состоящий из прямых ВА и А'В' и
симметричной кривой АОА', причём прямые свободны от нагрузки.
Во впадину АОА' вложен криволинейный штамп, имеющий форму
этой впадины, и на него действует сила Р, приводящая окрестность
тела в пластическое состояние. Пусть касательное напряжение Тч
на границе контакта АОА' задано; согласно (6.13), следовательно,
задан и угол ср наклона линий скольжения у поверхности штампа.
Для примера положим Д = 0, и потому линии скольжения должны
итти под углом 45Q к поверхности штампа. От поверхности штампа
вниз проведём семейство прямых в каждой точке под углом 45°
к поверхности; крайняя верхняя линия этого семейства будет А'С;
под углом 45° к границе А'В' проведём пучок прямых вниз вправо.
Между линиями А'С и A'D' возьмём полярную сетку линий сколь-
жения. Проводя теперь из точки О кривую, ортогональную к семей-
ству построенных от ОА'С прямых, совпадающую с окружностью
на участке C'D' А, а далее идущей по прямой D’B\ находим крайнюю
линию скольжения второго семейства. Аналогичным путём найдём
любую другую кривую этого семейства MN.
142} ПЛОСКАЯ ЗАДАЧА О ВДАВЛИВАНИИ ШТАМПОВ
337
Поскольку металл из-под штампа должен вытекать вверх, каса-
тельные напряжения тя будут направлены, как указано на заштри-
хованном элементе, и потому за семейство линий скольжения а
следует взять линии MN. Пусть у есть острый угол, составленный
касательной к поверхности штампа в точке М. с осью штампа. Изме-
нение угла наклона ® линии /AN при переходе от М к М равно
®,v—®лг = у. Так как угол наклона нормали к поверхности тела
в точке М будет 0дг == к — у, а в точке N, 0№=к/2, то из (6.13)
(Г, == 0) имеем:
. п те
3.v = — Т8 sin 2 - = — т4,
Олг= _0 — t8sin2(it —х ——p-f-t,.
Из условия у; — const, на линии а получаем:
ода — w= 2ts («лг—®у), р = 2т3 (1 -f-y). (6.30)
Эта формула точно совпадает с (6.29), что вполне понятно, так
как только изменение угла ® определяет разность ад — оу. Значе-
ние силы Р, приходящейся на всю
поверхность штампа (вдоль оси г
берётся единица длины), опреде-
ляется интегралом
а
Р = 2 § pdx~
о
а
, (6.31)
= 4rs(a -f- J ^dx
о
где 2а—ширина криволинейной
части тела.
Указанное решение, повидимо-
му, можно применять для расчёта
процесса вдавливания штампа в тело, имеющее плоскую или слабо
искривлённую (сравнительно с кривизной штампа) поверхность;
однако при этом необходимо, чтобы выдавливаемый металл ничтожно
мало искажал границу, т. е. чтобы он имел малую кривизну, и глубина
вдавливания была весьма мала. Но в таком'случае поверхность
его может быть охарактеризована соприкасающимся кругом радиуса R
или параболой
22 3<и. Ш8. А. А. Илыошжж.
338 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [гл. VI
а сила Р определится по формуле:
Р — 4rs (1 + —2^) а — 4*8 (1 +у — С6-31')
4. Сжатие пластического материала между- шероховатыми
плитами (рис. 106). Из уравнений равновесия (6.19) можно полу-
чить уравнение:
/ Л2 Л2 \ ffl
— (*« — К„) = 0,
\ду- дх^) v ' дхду к х У
и из условия пластичности (6.7) внести сюда значение разности
Хх—'Yy', тогда получим:
/ Л2 Л1 \ tfl ----------
<6-32)
Простейшее решение, зависящее только от одной переменной, ука-
зано Прандтлем:
- —t Z у —с_____- —
8 Л ’ ' 3 h ’
с — *8-£-+ 2ts 1 —^j-.
(6.33)
Пусть сечение .г = 0 свободно от нагрузки:
^Xxdy — jfc + 2-г, уЛ 1 — ^dy = 0, с = —^-
—h —h
Среднее давление, возникающее в сечении х, определяется инте-
гралом
' л
9сР == 2Й / Xxdy ~Xa~h'>
-h
касательное напряжение на стенках плит постоянно (ts), а давле-
ние— Yy — P меняется по линейному закону:
л . X \
Р — "^
Линиями скольжения в этом случае являются циклоиды, а границы
y = ±h — их огибающими 14. Некоторые другие случаи равновесия
идеально пластического тела рассмотрены Соколовским ДО.
§43]
ОСЕСИММЕТРИЧНЫЕ ШТАМПЫ
339
§ 43. Осесимметричные штампьь
Пусть штамп, представляющий собой тело вращения, вдавли-
вается в плоскую границу среды. Предполагая, что плоскость пер-
пендикулярна к оси штампа и пренебрегая трением на поверхности
контакта, мы получаем задачу с осевой симметрией. На элемент
среды в цилиндрических координатах г, г, б (рис. 107, рис. 107, а)
действуют нормальные напряжения сг, аг и в меридиональной'
плоскости касательное напряжение' т. Координата <]>, вследствие
симметрии, совпадает с главным направлением, и потому напряже-
ние <3ф = о2 является главным. Два других главных напряжения а8
выражаются через а2, аг, тина оси z(r = 0) равны:
Г = 0, аа — а3, аг =р= вр
Траекторию максимальных касательных напряжений в меридиональ-
22*
340 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ (ГЛ. Vi
ной плоскости равных:
max 2 *
будем называть линией скольжения а, а угол её с осью обозначать
через © (другая линия 0 имеет угол ©' = © -ф- тс/2).
Предположим, что от давления штампа (силы Р) в окрестности
поверхности контакта среда находится в пластическом состоянии,
причём попрежнему она является несжимаемой и не обладает упроч-
нением. Тогда из условия Мизеса имеем:
(°1 — °2)2 + (32 — -з)2 + (°з~ °1)2 = 2гД
Вследствие симметрии на оси z имеем ar = a^ или а2=«а8, и потому
из условия Мизеса следует:
З'тах^З — = (6-34)
°2 = -S’ /
Хар и Карман I11! в 1909 году предложили эти два уравнения как
условие полной пластичности. Генки 131 применил формулы (6.34)
к решению осесимметричной задачи, считая, что в этом случае они
имеют место. Замена условия Мизеса двумя соотношениями (6.34)
даёт значительное упрощение осесимметричной задачи, так как она,
как и плоская, становится статически определимой и не требует
выражения напряжений через деформации. Йшлинский решил задачи
о вдавливании плоского и сферического штампа 112Г Поскольку
опыты дают удовлетворительное подтверждение следствий такой
гипотезы, применение её к некоторым осесимметричным задачам,
повидимому, столь же законно, как и замена эллипса Мизеса
шестиугольником (гл. IV).
Угол наклона главного направления «1» с осью z равен ©—ir/4
(рис. 107), и потому напряжения аг, сг и т выражаются через глав-
ные напряжения а8 по формулам:
a, = ZlJp4.J?qpsin2©,
t — —cos 2«.
Введём обозначение:
в'ж=у(014-°з)в01 + у0« (6.35)
i 43]
ОСЕСИММЕТРИЧНЫЕ ШТАМПЫ
341
и перепишем полученные формулы согласно (6.34) в виде:
, 1
аг — о' — у ag sin 2?,
аг = о' -]- °s sin 2?,
* = + cos 2?.
(6.36)
Для определения неизвестных в' и ? напишем дифференциальные
уравнения равновесия элемента (рис. 107):
| Эт | gy--Стф
dr ' "dz •” г
^ + ^ + ±==0
dz 1 dr 1 г
(6.37)
и внесём в них значения (6.36). В результате преобразований,
подобных тем, которые были сделаны в задаче о плоской деформа-
ции при выводе уравнений (6.15), получим:
<Sr==^^7-(sin;?-cos^’ <б-38>
где обозначены;
e'4-ag<s = -l оД ]
! > (6.39)
о'—s8’J= j j
a dSr, dS2 — дифференциалы дуг семейства a (dSi^Ada) и
Р (dS2 = Bd$).
Если линии скольжения известны, то из (6.38) получим:
$ == (а) — J (cos ? — sin ?) ,
^=/2(.8)— f (cos ® — sin ?)-——-.
(6.40)
Эти интегралы получены Генки I81. Предположим, что построена
линия скольжейия MiN, на которой 0 == const. Разность значений т)
в точках М и N, согласно (6.39) и (6.40), даёт связь между а' и ?
в этих точках:
N
<z’n—о'и — °g(®w—®м) —— J*(cos? — sin?)—у-. (6.41)
м
342
ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [гл. VI
Если угол наклона касательной
с отрицательным направлением
через y> то:
к поверхности штампа в точке М
оси z обозначим, как и гГрежде,
W—?лг = -~г
В точке М главное напряжение равно давлению на штамп с обрат-
ным знаком: — — р, и потому
' I •
•вМ — — р-Г~2 >
в точке N имеем:
<за=*0,
°1 = —”»> °№=
Таким образом:
N
/> = (1 + т) о, I" (sin 7—cos®)-—. (6.42')
й
Если уравнение рассматриваемой линии скольжения дано в виде:
т = /(г),
то, поскольку
dr = dSr sin ®,
dz =w= dSA cos <p,
уравнение (6.42') запишем в виде:
(в-42)
м
где Гу, гу — расстояния точек ДГ и Л4 от оси.
Замечая, что:
— П)
и значения $, q заданы на поверхности контакта, заключаем что
линии скольжения могут, быть построены на основании урав-
§ 43] ОСЕСИММЕТРИЧНЫЕ ШТАМПЫ 343
нений (6.38) путём численного интегрирования. Генки пред-
ложил в качестве линий скольжения брать те, которые полу-
чаются в соответствующей плоской задаче и построение
которых, как было установлено в предыдущем параграфе,
элементарно. Пучков <131 доказал, что такой выбор линий
скольжения приводит к весьма хорошим результатам, практи-
чески не отличающимся от тех, которые получаются при интегриро-
вании системы (6.38). Для этого он использовал результаты Ишлин-
ского, относящиеся к вдавливанию сферического штампа, и построил
другие точные решения системы уравнений (6.38), а затем сравнил
их с приближёнными, получающимися на основании применения
формулы (6.42) и линий скольжения плоской задачи. При этом
выяснилось, что давление по поверхности штампа независимо от его
формы с достаточной точностью является линейной функцией орди-
наты е’м точки поверхности штампа:
, Ро — Ра jo-,
Ри — Рл Ч-------j---звь <6.43)
где рл, Ро — давления в точках А и О и 8 — глубина вдавли-
вания штампа.
Давление рА, как видно из (6.42), всегда известно (гог = гя,
точки М и N совпадают):
Ра = ae (1 -f- 7д),
и потому задача сводится только к определению р0. Для этого
строится линия скольжения, проходящая через точку О следующим
образом (рис. 107): на участке контакта АО проводим семейство
прямых под углом y к дуге АО с наклонением прямых влево
(линии ОО', АА', ММ' и т. д.); проводим прямую АА", наклонён-
ную под углом я/4 к прямой АВ вправо. Теперь, начиная от
точки О, строим графически кривую, пересекающую лучи ОО',
ММ' и т. д. АА' под прямым углом; продолжением её между
линиями АА' и АА" будет дуга круга с центром в А. От луча АА''
в точку В продолжаем эту линию в виде прямой. Получившаяся
кривая ОВ будет искомой линией скольжения r=f(z). Так как
в точке О, ^0 = ~ , то из (6.42) имеем:
з
(, , я । 1 f dr—dz
‘+2 "i”2 J--------г—
о
Поскольку в точке О при гладком штампе dr = dz, интеграл, вхо-
дящий здесь, всегда сходится и легко вычисляется графически.
344 ВДАВЛИВАНИЕ ШТАМПОВ И НЕСУЩАЯ СПОСОБНОСТЬ [ГЛ. VI
Давление р& на поверхность штампа состоит из постоянное®
слагаемого р0, которое даёт равнодействующую Ррд, и слагаемого,
пропорционального глубине, которое даёт равнодействующую
о
где Р—.площадь круга и V—объём отпечатка; результирующая
сила давления штампа, следовательно, равна:
P = V. (6.44)
Эта простая формула получена Пучковым 1131.
ГЛАВА VII.
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ.
§ 44. Распространение плоских нелинейных волн.
В предыдущих главах изучались исключительно статические за-
дачи теории упруго-пластических деформаций; или, лучше сказать,
задачи, в которых колебаниями и связанными с ними силами инерции
можно пренебречь. Пренебрегалось также и влияние времени и ско-
рости деформирования на зависимость at-eif о чём уже было ска-
зано в главе I.
Основное предположение, которое принимается при решении всех
излагаемых ниже вопросов динамики тел, таково: между интенсив-
ностью напряжений <з( и интенсивностью деформаций в изучаемом
диапазоне скоростей деформаций существует определённая зависи-
мость:
»< = $(*<) (7.1)
такога же типа, как и при. малых скоростях деформации, причём
закон разгрузки остаётся прежним. Следует, однако, помнить, что
зависимость между инвариантами напряжений и деформаций при усло-
вии простого нагружения, строго говоря, является более сложной
и в неё в первую очередь входят среднее нормальное напряжение
у (°1 + б2 + °з).
связанная с ним сжимаемость и интенсивность скоростей деформа-
ций е4. Недавние опыты Бриджмена 14 показали, что при высоких
всесторонних давлениях сопротивление сдвигу больше, чем при нор-
мальных давлениях. Вопрос о том, стремится ли величина af при не-
ограниченном возрастании давления к определённому пределу или
также неограниченно возрастает, остаётся пока открытым и имеет
первостепенное значение в теории прочности. Скорость деформации
также увеличивает сопротивление сдвигу. Поэтому излагаемые ниже
результаты расчётов, основанные на предположении а4 = Ф (е4), сле-
дует подвергать экспериментальной проверке и рассматривать как
приближённые.
346
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ
[гл. VII
Постановка и решение основных задач динамики при упруго-пла-
стических деформациях тел принадлежит Рахматулину. Его исследо-
вания главным образом и излагаются ниже.
Рассмотрим вопрос о распространении плоских волн вдоль стержня,
к концу которого в начальный момент времени приложено напряже-
ние р (0), изменяющееся с течением времени по данному закону р (£).
Осевое напряжение в сечении х обозначим а (х, t) и осевую дефор-
мацию е (х, /), причём под а понимаем условное напряжение,
т. е. напряжение, отнесённое к первоначальной площади поперечного
сечения стержня Fo; величины а, е будем считать положительными
в случае растяжения. Смещение сечения х обозначим через и (х, t),
так что
е = -^- = Иа,, о=о(е) = а(иа,). (7.2)
Зависимость а==а(е) определяется на основании кривой (7.1). На
рис. 108 изображены два состояния стержня: нижнее соответствует
моменту / = 0, верхнее — моменту t >0. Координата сечения х в мо-
мент t будет х' — х-\-и, длина элемента dx равна dx' = (\-\-^jdx.
Из условия неизменяемости массы элемента имеем:
есть местная скорость звука, зависящая от деформации, поскольку
зависимость <з-е не является линейной. Уравнение (7.3) представ-
ляет частный вид известного дифференциального уравнения Монжа-
Ампера, которое легко интегрируется методом характеристик. Для
этого введём начальные условия:
= Й = (7’3')
означающие, что при t — 0 стержень находился в покое* введём также
граничное условие:
х = 0, а(йа,)=р(0 или ма, = е(/). (7.3")
% 44]
РАСПРОСТРАНЕНИЕ ПЛОСКИХ НЕЛИНЕЙНЫХ ВОЛН
347
Характеристики уравнения (7.3) суть:
dut =
(7.4)
(7.4')
Уравнение (7,4') можно проинтегрировать:
ди , , , , ,
ut~~df — — Ф (йш) + ci-2,
изв
Ф (««)=]* а{их)<1ия.
о
Удовлетворение начальных условий:
t — 0, иа, = нг = 0,
(7-5)
связано с решением задачи Коши, и это решение даёт нуль для вся-
кого х<и(0)/, так как а(0), согласно кривой а-е, имеющей моно-
тонно убывающий (не возрастающий) угол наклона, есть максималь-
ная скорость распространения волн, и перед её фронтом напряжённое
состояние не возникает.
Рассмотрим• две плоскости: (х, t) и (мж, мг) (рис. 109). Из ска-
занного следует, что области между осью х и характеристикой
х а (0) t плоскости (х, t) соответствует начало координат плоско-.
сти ия, ut (ия — иь — 0), причём все характеристики (7.4') для этой
области будут прямолинейными:
d [х-4-а(0)Л =0, d{x— а (0)/] = 0.
Найдём теперь решение задачи за фронтом волны, идущей со ско-
ростью а (0), т. е. между осью t и характеристикой х = а (0) t плоскости
348 ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ [гл. VI1
• (х, /). Ия граничного условия для любой точки zn8 на оси Ot внаем
' wa,==s(0> т- е- в плоскости (иж, Uf) знаем точку ЛГ3 пересечения
прямой их — г (/) с характеристикой отрицательного наклона
ut = —ф (мж)- (Предполагается, что напряжение р (£) сжимающее, так
| что р < О и е < 0.) Рассмотрим точку/и4, получающуюся пересечением
1 характеристики m3mi положительного и mimi отрицательного на-
! клона. Поскольку характеристике отрицательного наклона плоскости
i (х, t) соответствуют такие же характеристики плоскости (их, ut)
| и поскольку точки Afj М2 совпадают, ясно, что точке т± в плоско-
। сти (их, ut) соответствует точка Л14, совпадающая с М3. Значит, ,
I любой точке характеристики m2mi соответствует одна и та же
I ’ точка ttx, ut, т. е. характеристика — есть прямая линия. Отсюда
следует, что все характеристики плоскости (х, t), имеющие положи-
тельный наклон, прямолинейны, т. е.
х = а(«а!) {t — *о). (7.6)
где — любая точка на оси t, для которой согласно (7.3")
известно
«*==*('<)) (7.7)
Исключая из этих двух уравнений t0, получаем функциональное урав-
нение
К нему необходимо добавить уравнение характеристики положитель-
ного наклона
(7-9)
Формулы (7.8), (7.9) дают решение поставленной задачи, в чём легко
убедиться путём проверки граничного и начальных условий уравне-
ния (7.3). Это решение принадлежит Рахматулину Р1.
Если давление p(t), а следовательно, и деформация конца стержня
е (/) возрастают в интервале времени t0 < t < tY и затем остаются
постоянными, то семейство характеристик будет состоять из наиболее
быстро распространяющейся волны хо = а(0)£, волны (7.6) с моно-
тонно убывающей скоростью (прямые уменьшающегося к оси t угла
наклона показаны на рис. ПО, а) и, наконец, семейства волн, рас-
пространяющихся с минимальной скоростью, соответствующей постоян-
ному значению деформации (параллельные прямые выше t — tt на
оси t).
Уменьшая до нуля, получим случай мгновенного приложения
к концу стержня постоянного давления р. Семейство волн перемен-
I 45] УПРУГО-ПЛАСТИЧЕСКАЯ волна рахматулина 349
ной скорости распространения при этом собирается в пучок прямых,
проходящих через начало координат (рис. 110,6). Эти волны Рахма-
тулин назвал волнами Римана. Решение задачи при мгновенном при-
ложении постоянного давления получим из уравнений
«(«ж) = у, «< = -*(«<»). (7.10)
из которых следует, что перемещение и зависит только от отноше-
ния -у. Этот факт можно выяснить также из соображений размер-
йости.
§ 45. Упруго-пластическая волна Рахматулина и.
Значительный интерес представляет случай, когда давление р (/)
на- конце стержня имеет ударный характер, т. е. мгновенно возра-
стает до некоторого значения и затем монотонно убывает. В момент
удара от конца стержня пойдёт пучок волн Римана, вызывающих
значительную пластическую деформацию в стержне, но после этого
начнётся падение нагрузки на конце и уменьшение напряжений. По-
скольку закон (1.7), связывающий напряжение а с деформацией е
при нагружении (возрастании напряжений) и разгрузке (падении напря-
жений), различен (рис. 111), вслед за пучком волн Римана должна
итти волна разгрузки, разделяющая область стержня, в одной из
которых происходит возрастание напряжений, в другой же разгрузка.
На фронте этой волны, открытой Рахматулиным, имеет место разрыв
вторых производных смещения и, первые же непрерывны вместе с на-
пряжением а.
На рис. 112 показаны волны Римана и волна разгрузки. В обла-
стях ниже волны х = а (0) t и между этой линией и волной Рахма-
тулина имеет место дифференциальное уравнение (7.3). Пусть г0(х)
350 ' ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ [гл. VII
будет деформация стержня , на фронте волны разгрузки и а0—соответ-
ствующее напряжение. После прохождения через сечение х волны
разгрузки связь между напряжением и деформацией в нём будет
а = о0 — Е(е0 — е), (7.11)
причём о0 = Ф (<?0)—данная кривая, но е0(х)— неизвестная функция.
Уравнение движения элемента стержня будет:
<71S>
Прямая задача об определении волны разгрузки по заданному значе-
нию давления на конце стержня не сводится к известным задачам
математической физики. Пусть будет b (х) — скорость распростране-
ния волны разгрузки и она опрёделяется уравнением
(7.13)
Общее решение уравнения (7.12) имеет вид:
+ «0 = ^(0); (7.14)
а
ио(х)~--Ё^^о — еоЕ:)ах- (7.15)
О
Из условия непрерывности первых производных и на волне разгрузки
следует:
ео £ 7ч [aof(x) -|-х] — F2 [aof (х) — х] = е0,
«о F'i [яо/0) + *1 4~ ао & [aof(x) — х] == — ф (<>0),
откуда:
F2 [aof(.x) - х] « -1 [ g 4- .
§ 451 УПРУГО-ПЛАСТИЧЕСКАЯ ВОЛНА РАХМАТУЛИНА 3^j
Дифференцируя эти равенства по х, 'находим:
к/'W +1) Л' [«./« 4-Л1 1)£,
(7.16)
Найдём из (7.14) изменение во времени деформации е = и!В(в обла-
сти за фронтом волны разгрузки):
Й = dffe = ао 1 z+ *> — F2 («</— х)].
На волне разгрузки согласно (7.16) имеем:
де _ д2и __а anf -j- 1 rfg0
dt tit dx a2f _____________________i dx ‘
(7-17)
Отсюда следует, что если скорость распространения волны разгрузки
, . де
меньше скорости распространения звука, т. е. о < а0, то знаки
den
и —совпадают:
ах
. де , den
sign a-z = sJgn^.
Найдём теперь знак этой величины. Из (7-Ю) имеем:
а (е0) =--------
v 07 J (х)
или после дифференцирования по х:
de& 1 — af 1 . dx f da' (7.18)
de
так как скорость а а < Ь'. убывает с ростом | e , TO отсюда имеем для
o' d V A ©i ц о; Ts Ь3 Ts |ts o* o“ A V © © Ч) 4) (7.19)
Внося значение (7.18) в (7.17), получаем:
де __ dtu _ a 1
dt “ dtdx^ «2 — 62 / da ' (7.20)
de
Отсюда следует, что в некоторой окрестности волны разгрузки имеем
для растягивающего удара, «0 > 0, убывание деформации растяжения,
352 ДИНАМИЧЕСКИЕ ВОПРОСЫ пластичности (гл. VII
а для давления, (е0 < 0), убывание деформации сжатия, т.
случаях процесс разгрузки:
е0>°>
е. в обоих
(7.21)
^<о.|
^>0- I
каждой заданной волне
а0, соответствует ударная нагрузка,
разгрузки,
Эти неравенства показывают, что
удовлетворяющей условию а < b <
приложенная к концу стержня и убывающая по соответствующему
закону. Таким образом доказано существование волны разгрузки.
Картина деформации некоторого элемента стержня, находящегося на
расстоянии х от конца, получается такая: возмущение от места удара’
. х
приходит к . этому элементу через t = —, после чего деформация
^0
возрастает до момента прихода волны Рахматулина (Z = /(x)], после
прохождения этой волны напряжение элемента убывает.
Приведём решение прямой задачи: по данному закону убывания
взрывного давления на конце стержня найти напряжённое и дефор-
мированное состояние стержня. Основная трудность сводится к нахож- .
дению волны Рахматулина. ,
Предполагая, что кривая о-е состоит из трёх характерных
частей: упругой (<з —Ее), пластической с резким падением ^и пла-
стической с почти постоянным наклоном Е’ = , следует сделать
заключение, что волны Римана также будут состоять из трёх групп:
—
и вызывает возрастание деформации е от 0 до е8 (условного предела
текучести); вторая группа волн идёт с резко переменной скоростью,
убывающей от а0 до — и почти не изменяет деформации
" Ро
элемента; наконец, третья группа волн идёт почти с постоянной ско-
ростью аг и вызывает значительные деформации от еа до етах. Поэтому
естественно заменить кривую <з-е ломаной, которая уже неодно-
кратно применялась выше.
На волне разгрузки пластическая деформация достигает максимума
в каждом сечении, и потому она пересекается третьей группой волн
Римана; следовательно, на ней
/—/(х) — а’ (Ь =
Замечая, что согласно принятой схеме:]
°o = <5s+£'i (е0 —ев)>
<(»(«) =а0ев4-а1.(г —е,),
(7.22)
§ 45] УПРУГО-ПЛАЙТИЧЕЙКАЯ волна ра^матулинд * 353
уравнения для F'v F’a и F", F" (7.16) напишем в виде:
Пусть закон изменения давления р (/) на конце стержня дан степен-
ным рядом:
Р = (7.25)
Так что р0 — максимальное значение давления:
Ро — I °о 1 ®=° — °о (0) >
(7.26)
еа (0) “
I ро —
£1
Согласно (7.11) для концевого сечения имеем деформации в лю-
бой момент времени:
С другой стороны, из (7.14), (7.15)-имеем:
(Й)я=о = “ 5 + е°(0) + (М ~ W)' (7-28'}
Заменяя в (7.23) аргументы функций F', на aot, т. е. заменяя
в F'x аргумент х на
Д0Д1 2
^ + «1’
а в F2 — на
gogi
«о — Д1
и внося в (7.28'), получим:
(Й)„о=-т+с«(°>+:г^+
+ Hr-S)««(^;')+T(f4-7:)«»Gv^0- <7-28>
23 Зак. BL3S. А. А. Ильюшив,
3§4
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ
(гл. VI t
Сравнивая значения (7.27) и (7.28), получаем функциональное уравне-
ние для определения функции е0. Из него ясно, что е0(х) предста-
вима степенным рядом:
<7-29)
Сравнивая коэффициенты при одинаковых степенях t, имеем:
ь ______£»____
п АвР—Вф* '
А е Л Дет—f-1_________________
2 \а0 ' Е J ’ ° 2 Е J ’
а == а°а< 0 __ а1яо
яо—а1 ’ ° aiH~ao
Таким образом решение ’задачи найдено. В частности,
известным распределение остаточных деформаций:
7==e0-cg0 = k(2Mn-^
(7.30)
становится
(7.31)'
Здесь к — обычный параметр == —g—к J •
Рассмотрим частный случай удара- жёсткого тела массы т по
концу стержня. Из уравнения движения этой массы, пользуясь разло-
жением (7.29), получим рекуррентные формулы для Ьп:
— nbn (Dot^-Ч- С8"-1) m С(п — 1) (В'а”“1 — 4>-J),
Где обозначены:
и'_ __аЛ R' -г- (а1 .1
2 U a*J> 2 Uo^ag/’ ~ л/
° 0 (7.32')
2 2 ' 7
С D а — ,д0 + Д1
2 Ло -f* 5 2 tjg —
Отсюда все Ьп можно выразить через Ьо. Коэффициент Ьо находится
из начального условия t = 0, ^1 ^t»0:
OX I x=XQ
= aoes 4~ ei (^o — йз)» (7.33)
поскольку eo(O)=do — начальная деформация конца стержня. Из
(7.32) находим:
а_____.7W
---, 2/ а •; я\~ • V *d4)
§46) РАСПРОСТРАНЕНИЕ волн при поперечном ударе по нити 358
Зная коэффициенты b0, bt, можно сказать, как расклёпывается конец
стержня при ударе. Если начальный радиус круглого сечения стержня
обозначить г0, то из условия несжимаемости имеем значение г после
удара:
и тангенс угла наклона образующей —
' 2(1—e)“z.’
На основании (7.34) имеем:
tgy ----------. (7.35)
Чта20 а{ (в® + в*)(1 — е)*1г
Из (7.33) ясно, что деформация конца стержня зависит только от
скорости удара v0, но не от массы т, в то время как угол наклона
образующей зависит главным образом от массы ударяющего тела.
Приведённые результаты принадлежат, Рахматулину И. Дальней-
шее развитие проблемы продольного упруго-пластического удара дано
в работах Шапиро 14, который рассмотрел случай произвольной
зависимости а-е и произвольного закона изменения давления на конце
стержня. Он дал прямой численный метод определения волны Рах-
матулина.
§ 46. Распространение волн, возникающих при поперечном
ударе по гибкой деформируемой нити.
Приводимая ниже задача о поперечном ударе твёрдого тела по
натянутому упруго-пластическому гибкому стержню поставлена и ре-
шена Рахматулиным 14.
Пусть тело весьма большой массы движется с постоянной ско-
ростью v0 и в некоторый момент под углом р0 встречает неограни-
ченно длинную натянутую нить. Пусть $0 — начальное расстояние
любой точки нити от места удара, а х, у — смещения этой точки
в направлении первоначальной прямой, по которой была расположена
нить, и перпендикулярно к ней в сторону удара. Обозначая через р0
начальную плотность (массу единицы длины нити) и Т—натяжение
в любом сечении s0 в момент /, можем написать следующие диффе-
ренциальные уравнения движения элемента:
д2х___ д Г Т 7т । । дх\|
‘J° dfi dsa [1 еу•’"Г dsjJ ’
d2y____dj T dyl
P° dfi [1 e ’
(7.36)
23*
356
ДИНАМИЧЕСКИЕ вопросы ПЛАСТИЧНОСТИ
[гл. VII
где через. в обозначено относительное удлинение элемента нити, т. е.
Введём новые переменные:
X у
(7,37)
(7.38)
Эти величины являются безразмерными и потому могут зависеть
только от безразмерных параметров, которые можно составить из
всех встречающихся в задаче величин. Кроме длины $0, можно со-
ставить лишь единственную величину vot, имеющую размерность
длины, и потому ясно, что х и у будут зависеть от их комбинации;
z
___
,
«О*
(7.39)
Внося значения х. у согласно (7,38) в уравнения движения и при-
нимая во внимание сказанное выше, получим два обыкновенных диф-
ференциальных уравнения:
: Роп2(1+^)У' + rqh. Id +*') +
, , d Г Т 1
1 </₽[р»2(1 +<?)] ' '
(7,40)
Это — линейные и однородные относительно х", у" уравнения, и по-
тому допускают решение;
у" = х" = 0. (7.41)
Отсюда и из (7.38) следует, что соответствующие перемещения
х, у являются линейными функциями координаты s0 и времени /:
ду дх ду дх
= = ~dt~C*' ~dt==c^’
(7-42)
отсюда же вытекает возможность прямолинейного состояния и равно-
мерного движения частей нити.
Покажем, что интегралы (7.42) дают решение поставленной задачи
и приводят к следующей системе распространения волн (рис. 113);
вправо и влево от места удара идут две системы волн, одна из ко-
торых— система волн Римана, — распространяющаяся по прямоли-
нейному (начальному) направлению» другая же—волна сильного
§ 46] РАСПРОСТРАНЕНИЕ волн при поперечном ударе по нити 357
разрыва, являющаяся границей продольного и поперечного движе-
ний частиц нити. Толщина нити и её изменение по длине показаны
на рис. 113 утрированно: на фронте волн Римана деформации нити
малы, в областях же I, I', II, II' они значительны. Принятые обо-
значения таковы: То, е0—начальные натяжение и деформация нити
(до удара); Oj, pn v2, р9— скорости и их направления для частиц
нити на участках 1 и //; «t, w9— скорости частиц на участках /' н
II' (максимальные); blt b2 — скорости распространения сильных раз-
рывов (точек перелома); у2— углы наклона участков нити; ev е2,
e'lt е'—удлинения на соответствующих участках; р0— угол встречи
тела и нити при ударе. Из перечисленных величин заданы: г»0, е1}, Тд
и упруго-пластическая характеристика нити —
Г(е). (7.43)
Пользуясь обозначением (7.5) для функции «р» имеем:
«1 = («о)- (7+4)
Теорема количества движения в применении к элементу длиной
(&х -j-ut)dt, расположенному справа от точки перелома нити, даёг:
Pi (&i + «1) C°i cos pi — «О = 7\ cos Ti —• Гр
P't (*i + “i) vi sin Pi ® Ti sin T1,
(7.45)
где p' — плотность, Tr—натяжение нити на участке Г и ^ — натя-
жение её на участке I.
Условие неизменяемости массы элемента длиною bt dt на участке /'
у точки перелома, переходящего на участок I согласно постоянному
направлению скорости vlt даёт соотношение:
»i + «i VA sin2 01 + (*1 + »1 cos
—;== ---------------(7.46)
1 + el 1 + el
' Поскольку скорости v0, vit bl и угол p0 постоянны, из рис. 113
имеем кинематическое соотношение:
taY——(7.47)
358
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ [ГЛ- VII
Наконец, предположим, что в месте касания тела и нити имеет место
проскальзывание. Тогда из рис. 114 имеем:
v0 sin (ро —Ti) = sin( ₽i — 71)- (7-48)
Кроме шести уравнений (7.44) — (7.48) столько же уравнений можно
написать для части, расположенной по левую сторону от ударяющего
тела. Они имеют следующий вид:
(7.44')
“2=Ш)—Ж);
(*>2 4- «2) (— ^2 cosРя — “2) = Та cos 7а —
Ps(62 + “2)u2sinp2 = T’asin72;
<>2 + “2 _ sin2 За + (fe-2 — Ра cos8 fe)a.
1 4* e2 1 + e2 ’
tp-Y ^sinfo .
a 12 —VocosPo’
°0 sin (72 + ?o) “ v2 sln (7a + ₽a)-
необходимо добавить два условия
(7.45')
К этим уравнениям
(7.46')
(7.47')
(7.48')
в точке М
(рис. 115): условие непрерывности массы
MN _ LK
1 + 1 + «1 ’
принимающее вид:
(1 + «1) V— 2w2t>0 cos (Р9—р0) ==
= (1 + e2)yv2 v2 — 2'00z'i cos (Pj — p0), (7.49)
и эйлерову формулу для натяжения нити, переброшенной через
шкив:
Т1 = Гае/О.+-г*)1 (7.50)
где/—коэффициент трения.
§ 46} распространение волн при поперечном ударе по нити 35§
Всего мы получили 14 уравнений со столькими же неизвестными,
которые и следует выразить через v0, р0, е0. Покажем, что макси-
мальная деформация в области Г равна деформациям частиц нити,
принадлежащих области I, т. е.
Умножая первое уравнение (7.45) на sin^,- второе на — cos^i и
складывая результаты, имеем:
р{(^х + "х) sin (Т1 — Зх) — «1 sin Til == — 7^ sin Tj. (7.51)
С другой стороны, из (7.47) имеем:
MnT1 = fosin(i%--T1)-
Следовательно, на основании (7.48) получим:
sin (Pi — Tj) == bi sin-ф
Подставляя последнее в (7.51), найдём:
р;(^ + «1)2=Л(0- (7.52)
Так как и1 = «1(еО» то уравнение (7.52) устанавливает связь между
скоростью bi и деформацией Далее из уравнения (7.46)
(&!“)-И1)®(1 2 I о А о | .о
——!—— = V2 -4- %Vibi cos 8. -f- b2
(1+q)2 1 ' 1 t 1
Из'(7.45) находим:
’ • ь TisinTi
Vi Sin Pi = -r~---— ,
имеем:
(7.53)
6 „ Г1cos 71
C0S rl p' И1) P1 ф K1)
Tjcosfi
(7.54)
360
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ
(гл. Vii
Возведя эти уравнения в квадрат и складывая результаты, имеем:
2___ 7"i TjCOSTfi 2
V} —• 1л"" " “““ f ......... "'"I vb
Pl (6t + “l)2 Pl (t>l + 111)
Подставляя в (7.53) выражение и cosp,, получим:
(h+iiM-Hi)8
(1 + <Р
Г2
(7-55)
---------2г.,-£с<м*-+г,;+2», —2Й+»?.
Р1(^1 + И1)2 Pl (&14-«1) P1(61+“1)
Произведя приведение подобных- членов в правой части этого
уравнения и имея в виду (7.52), найдём:
г'2 Г2
------— —-------- е = £а.
(1 + efr (1 + etf 1
(7.56)
Заметим, что из уравнений (7.44) — (7.47) можно определить вели-
чины vlt через elt ро, v0.
Выведем ряд соотношений, имеющих место для областей 77 и II'.
Из уравнений-(7.45') следует:
P2(^a+«a)(T'2sin(pa + 72)-f «2з1пта]= T^sin^. (7.57)
Но из (7.47) имеем:
»2 sin уд == vQ sin (po -f- ya).
у
Следовательно, из (7.48) найдём:
ра sin (р2 4- Ya) = Z>2 sin y2-
Подставляя это выражение в (7.57), Получим:
Ра (^2 4* иа)2 “ Та-
Возведя в квадрат обе части уравнения (7.46'), имеем:
(14- <?2)2 (*2 + «2)2 2 9. о । /2
-----т— г— — — -‘"г г2 1* 42.
Из уравнений (7.45'), имея в виду (7.58), легко получить:
о 71 TicosYj . Trosts
v2 COS p2 7= -7—--------и-------)---------- ---------------,
Ps + йа) ?2 + ut) Рг (^2 + ua)
ioasinp2=..7.^i.HJ2. ,
P2 (6a + И2)
(7.58)
(7.59)
(7.60)
§ 46] РАСПРОСТРАНЕНИЕ волн при поперечном ударе по нити 361
Отсюда следует:
2 , А2 COSTS
-У2 = —-------------п 02-----•‘0О ~7—----------- •
р22 (^2 + ыг)2 Рг № + «г)
(7.61)
Подставляя полученное выражение в (7.59), имеем:
(»2+ы2)2(1+^ т22-
(1 + е2 )2 ?2 (&2 + ы2)2'
или, имея в виду (7.52), найдём:
Т'2
(1 + ^)2
т2
(1+^)2
(7-62)
/
ИЛИ ^2 = ^2-
Уравнение (7.62) выражает равенство деформаций перед и за фрон-
том волны сильного разрыва, двигающейся влево со скоростью Z»2.
1. Случай удара без трения. Если коэффициент трения /=0,
то из (7.50) получим, что Т1==Т2—Т‘, поэтому и ег — еъ т. е.
деформации в областях / и II одинаковы. Таким образом уравнение
(7.49) примет вид:
2 .2
у2 — V1 =
= 2-v0 {[г/2 sin р2—VjSinPj sin^-J-]^005^-cos?il cosPob (7-63)
Так как в рассматриваемом случае согласно (7.44) и1 = и2 = й, то:
(’i ^2 — Pi= Рг — р — утру *
Поэтому из (7.54) и (7.59) получим:
V2 — v} = 2b (cos Tj — cos Та).
Аналогично из (7.54) и (7.60) имеем:
v2 sin р2 — Vi sin (sin — sin Ъ),
v2 cos p2 — Vi cos Pj = 2 b — p(^M) (cos t2 — cos ft).
Таким образом уравнение (7.63) можно преобразовать так:
b (cos ъ — cos Та) = г'о {(sin Ъ — sin Ti)sin ₽о +
2&р(& + и) cospo_(cosl2_c05Ti)cospo}i
Определим v0cosp0, vosinpo. Из (7.47) и (7.47') имеем:
Vqsin ₽0 = cosр . (Le4)
° ™ tgTl + ‘gT2 ’ ° ™ tgE + tgT2 4 ’
$62 ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ [гл. VII
Следовательно, окончательно уравнение (7.63) будет иметь вид:
(cos 7! — cos у2) (tg Ti tg у2) = 2 (sin y2 — sin T1) tg T1 tg Ta +
+ (X — cosT1 — cos?2) (tgy2 — tgTi). (7.65)
Это и есть основное уравнение, решающее задачу о косом ударе
без трения. В него входит только один параметр X, зависящий от
вида функции Т— Т (е) и начального натяжения е0, так как:
,__ 26р'(6-}-«) _ 2&
Л ~ ‘ Цё) b + и ’
р0 (6-(-и)2 = (1 -|-е) Т, и = j"a(e)de. (7.66)
Кроме того, из (7.64) получим:
аг?0=4№г1-с18-г,). (гл?)
Уравнения (7.65), (7.66) и (7.67) позволяют решить до конца задачу
об определении возникающих при косом ударе деформаций по задан-
ным скорости удара и углу ]30. Для этого следует составить таблицу
значений Х = Х(е, е0) на основании зависимостей (7.66). С помощью
значений X можно составить таблицу изменения v0 для различ-
ных значений e = ^=e2 и р0. Для этого, задаваясь значе-
ниями fl при фиксированном |30 из второго соотношения (7.67), опре-
деляем значения у2. Затем из (7.65) определяем X; по значениям X
упомянутой таблицы Х = Х(е, е0) находим е для фиксированного е0.
Зная же е, определяем из (7.66) значение b и по (7.67) скорость
удара v0.
2. Случай нормального удара. В силу симметрии в этом случае
деформации слева неправа от точки удара будут одинаковыми; поэтому
уравнение (7.50) заменится уравнением:
Т= Т\ — Т2, (ех = е2 = е)
— д2 = Ь.
Уравнение (7.49) так же, как и в предыдущем пункте, примет вид
(7.65). Из симметрии движения можно заключить, что 71 = у2 = у и,
следовательно, уравнение (7.65) преобразуется к виду:
X = 2cosy. (7.69)
На основании первого соотношения (7.66) получим:
b = (Ь -|- и) cos 7. (7.70)
Из первого уравнения (7.64) имеем
i)0 = Mg7. * (7.71)
§ 46] РАСПРОСТРАНЕНИЕ ВОЛН ПРИ ПОПЕРЕЧНОМ УДАРЕ ПО НИТИ 363
Таким образом в рассматриваемом случае задача свелась к решению
уравнений (7.69), (7.70) и (7.71). Например, если положить Т=Ее,
то из соотношений (7.66) найдём:
и = а0(е—е0), Ь = а0Уе(1-\-е) — ^0(е — е0). (7.72)
Уравнения (7.70) и (7.71) дают:
62 = -j*. и)2 = fl2 (1 е) е>
v0 = jA (е — е0) /е (1 + е) + (е — е0)2 (7 73)
или
(е—е0)Уе,
где v0 = — . Отсюда в случае отсутствия начального натяжения:
4 2
з ~ "з" 1
Ь^^—, или &«О,8^ао3. , (7.74)
V4 у 2 к
Пользуясь (7.71), находим:
з<“
tg т 1,251/
61 ’ Г а0
Уравнение (7.75) показывает, что угол у имеет большую величину
даже при малых скоростях. Найдём величину скорости, которая для
железной проволоки вызывала бы предельные упругие деформации.
Пусть es = 0,002. Тогда (7.74) даёт:
_ — А А
v0s = ]Z2es4 =1,4 (2 ХЮ’8)4 =0,011,
или
vOs = 0,011 а0 да 55 м/сек.
Таким образом для перехода материала проволоки за предел упру-
гости требуются значительные скорости. При ударе по сильно натя-
нутой нити с малыми скоростями можно принять е$&еа. В этом
случае из формулы (7.72) имеем:
b = a0^=-i/'^ =1/^. (7.75)
Как и следовало ожидать в этом случае, скорость распространения
волны сильного разрыва оказалась равной скорости звука в натянутой
струне. Заметим, что при ударе по струне вдоль неё также побежит
волна продольного растяжения. В обычной теории колебания струны
эта волна не принимается во внимание.
3. Косой удар при отсутствии скольжения. Если скольжение
отсутствует, то частицы нити в областях / и II должны иметь одина-
ковую скорость, равную скорости удара, а именно:
?i = Pa=Po> Vi = T/2 = v0. (7.76)
364
ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ
(гл. VII
В силу этого уравнения (7.48) и (7.48') обращаются в тождества.
По смыслу постановки задачи уравнения связи (7.46) и (7.47) не
должны приниматься во внимание, так что для решения задачи имеем
десять уравнений и соответственно 10 неизвестных. Нетрудно видеть,
что уравнения (7.44), (7.47), (7.52) и (7.54) будут иметь место и
для рассматриваемого случая. Из них можно определить величины
Ьг, е1г их, fj. В предельном случае для — 0, т. е. при чисто про-
дольном ударе, из уравнений (7.54) получаем:
Л
ъ — о, vt = —,—-----------Ьг.
Pi (^i + wi)
Тогда на основании (7.52) получаем; как и следовало ожидать, v1~u1.
4. Случай косого удара по нити, когда диаграмма растяжения
может быть представлена ломаной. Полученные результаты по-
зволяют подсчитать не только принципиально, но и практически,
возникающие в нити деформации, когда по ней ударяется тело
достаточно большой массы. Приведём конкретные расчёты, предпо-
лагая, что материал нити удовлетворяет условиям:
е < es, Т = Ее,
e>es, Т= Ts-\-Ex (е— еа).
(7-77)
Предположим, что трение
отсутствует. В силу (7.77) имеем:
e<es, и = а0(е — е0) )
e>es, и~ао [ея — e0 + ai(e — es)]. J
Рассмотрим случай деформаций, выходящих за пределы упругости,
т. е. при е > es. В этом случае из уравнений (7.66) будем
иметь: k = =, 1 b + es — f0 + «i(e— es) 1(7.79)
[* + *s — *o + ai(e — «8)12 = (1 +*) К + (е — еа)], }
где
«1
ао
Нетрудно найти выражение для b:
~Ь = У(1 + е) [е„ + a'i (е—^)] — [(<?s — е0 (е — /?8)(. (7.80)
Из (7.79) и (7.80), исключая Ь, получаем квадратное уравнение от-
носительно е:
(Х2 _ 4Х) а21е + [(2 — Х)2 (% — а! еа + е0) — 8а (еа — е0) + 8 и* <?,] +
+ (2 — X)2 (es — ales) — 4 (es — <?0)2 -f- 8е, (e, — e0) — 4af e] = 0.
§ 46] РАСПРОСТРАНЕНИЕ ВОЛН ПРИ ПОПЕРЕЧНОМ УДАРЕ ПО НИТИ 365
Таблица 21.
Значения
>< 10° . 13° 18’ 23° 30° 35’ 40° 50° 55’
90° 10°09' 13’00' 18’00' 23’00' 30°00' 35’00' 40°00’ 59°
70° 8’59' 11’10' 14’40' 18’00' 22°10' 24’50' 27’30' 32’30' —
59° 7°40' 9’20' 11’50' 14’00' 16’20' 17’50' 19’10' 21’40' —
30° 6°10' .7’20' 8’40' 9’40' 10’50' 11’30' 12’10' 13°00' 13°30'
Обозначим решение этого урав-
нения через
е = е(Х). (7.81)
Из (7.67) получим:
ctg Т! = 2 ctg ₽0'+ ctg т2. (7.82)
Из (7.65) находим:
* ~ tg Т2 — tgTi I Т1 +
+ tgla) (созъ —COS72) —
—2 (sin т2—sin 71) tg 7! tg T2] %-
-j- cos fl -}- cos 72. (7.83)
Для скорости удара, со-
гласно (7.64), будем иметь:
.. __ 2frtgTi-tgT» z7R4x
0 sin Ро [tg T1-Hg т2] ' ’
Пользуясь приведёнными фор-
мулами, можно получить зави-
симость e — e(v0). В табли-
це 21 приведены значения
для фиксированных значений р0,
Рис. 116.
но для различных значений 72. Для этих значений углов по форму-
лам (7.83) можно вычислить соответствующие значения X, а затем
по формулам (7.81) подсчитать соответствующие значения деформа-
ций е. Зная деформации по формулам (7.80), можно вычислить соот-
ветствующие значения b и, наконец, по формуле (7.84) вычислить
соответствующие значения скорости удара.
В таблице 22 дана зависимость деформации е и скорости волны
сильного разрыва b от безразмерной скорости удара для различных
значений угла ро; вычисления проведены для es~ 0,002, а? = 0,05
при начальных деформациях е0 = 0,001 и ео = 0. На рис. 116 дан
график зависимости e = e(v) для значений £ = 30% 50°, 70°, 90°.
366 ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ [ГЛ. VII
Таблица 22.
Значения |?0 = 93е, ? — О, — 0,05.
»0 0,0135 0,0167 0,0192 0,0245 0,0347 0,045
е 0,002 0,006 0,01 0,02 0,04 0,600
~Ъо 0,0426 0,0441 0,0453 0,0481 0,0530 0,05696
V» 0,0518 0,64 0,0661 0,0742 0,085
С 0,08 0,1 0,12 0,14 0,16
А) 0,06045 0,0656 0,0655 0,068 0,0707
Ро = 9О°, ей = 0,001, = 0,05
»е 0,00978 0,01295 0,0164 0,02035 0,0228
е 0,002 0,006 0,01 0,016 0,02
Ъо 0,0436 0,0451 0,0463 0,0481 0,0491
»о 0,0283 0,0331 0,0381 0,0423 0.0511
е 0,03 0,04 0,05 0,06 0,08
Л) 0,0518 0,054 0,0563 0,0579 0,0614
₽о = 7О°, е0 = = 0,001, -2 Ц — 0,05
V0 0,0139 0,0182 0,0254 0,0311 0,0376 0,0554
е 0,006 0,01 0,0219 0,0326 0,0444 0,0787
*0 0,0450 0,0464 0,0499 0,0525 0,0551 0,0612
₽о = 50°, еа~ = 0,001, «1 = 0,05
v0 0,0113 0,0148 0,0188 0,02426 0,0286 0,0337 0,0423
е 0,0002 0,0042 0,008 0,0146 0,0207 0,0323 0,0455
5о 0,0431 0,0445 0,0458 0,0478 0,0496 0.С0525 0,0555
?о = 50°, е = 0,001, *1 = 0,05
Vo 0,0142 0,0183 0,0217 0,0263 0,0297
е 0,0004 0,0023 0,0058 0,0082 0,0114
Ъо 0,043 0,0439 0,0446 0,0458 0,0472
Vo 0,0332 0,036 0,0388 0,0425
е 0,015 0,0185 0,0223 0,029
' 0.0487 0,049 0,051 0,0517
§47]
ПОЛЯРНО-СИММЕТРИЧНАЯ ЗАДАЧА
is?
§ 47. Полярно-симметричная задача.
рассмотрена задача о статической' деформации полого
48). Сохраняя основные обозначения для напряжений
В § 20
шара (рис.
и деформаций, рассмотрим соответствующую волновую задачу. Пусть
в начальный момент времени t~ 0 размеры шара будут а.д, Ьо, ко-
ордината некоторой сферы г0 (рис. 48), а плотность материала всюду
постоянна и равна р0. Увеличение радиуса г0 сферы в момент £>0
обозначим w (z0, f). Тогда тангенциальные и радиальная деформации
элемента тела будут:
w ' . dw
— es~
Изменение объёма элемента при конечных деформациях равно:
(7-85)
— 1 ,
(7.86)
и потому плотность р в момент времени t равна:
п - Ро
Интенсивность деформаций согласно (3.26) будет:
2 Zw dw\ .
— -5-1-----5— sign w.
* 3 Vo dra/
Среднее нормальное напряжение
° = 4 + аз)
и интенсивность напряжений (3.27)
о«==(С1 — °s)signw
будем считать известными функциями 6 и et-.
a = F(6), о< = Ф(^,8).
(7.87)
(7.88)
(7.89)
(7.90)
(7.91)
Вместо перемещения w(rof) введём r(r0,t)— значение радиуса г0
в момент t и, в частности, размеры а, Ь:
z‘(/'o’0 = /'o + w(ro>0> а — ао 4" w (ао> = 4~ (^о> (7-92)
Тогда формулы (7.86) и (7.88) перепишутся в виде:
2 / г дг \ .
'V''»
(7.93)
368 ДИНАМИЧЕСКИЕ ВОПРОСЫ ПЛАСТИЧНОСТИ (гл- VII
Дифференциальное уравнение движения элемента тела в лагранжевом
представлении имеет вид:
дая . 1 дг , ч ро dr д'-г
d7o+“^(s“ oi)=IT0<W (7,94)
Заменяя здесь разность — a8 согласно (7.90) и
°з.= °— ~ 0< sign г> (7.95)
Получим
(da 2 . \ 36 2 3^ dei: . 1 дг
\35~ 3 design г )дГ0 — assign г — yg^signr ==
Ро дг дгг
~ 1 + 0 dr0 dfl '
На основании (7.93) окончательно имеем:
о Гдгг , f, дг . 1 <Рг ,
с Ld^+/(r’^o)J = ^’ <7-96)
где обозначены:
с2
4 д~( 1
9 det ] ’
2 (da 2 dsj .\ г dr ( dr r\ 4 dat f dr r \ 1 dr _ • '
\d0 3 39 s‘gnr/rgd77(dr0~r07~~9r0dg7(dr0 7у~~ 3r^ °* slSn r
r3 (da 2 dai •) , 4 daj
(S 3 dQ si8n rJ 9 det
Если рассматривать только малые перемещения частиц тела и пред-
полагать, что упрочнение материала является линейным, т. е.
Р =3G (1 —П = const.,
de{ 4 7
то скорость распространения волны будет постоянна
‘“/^[Л+у00-4]’ (7Л,)
и дифференциальное уравнение (7.96) будет линейным:
d2w । г (dw ®\ 1 aj sign w _ 1 diw Г/
+ K+4Lo 0_x)~^ ' •
так как в этом случае линейная функция (7.88).
§ 47] ПОЛЯРНО-СИММЕТРИЧНАЯ ЗАДАЧА 369
Если внутри полости покоящегося тела происходит взрыв, то
фронт упругой волны будет перемещаться со скоростью а0 = а 11=0
(7.98), а за ним с меньшей скоростью будет перемещаться
граница области пластических деформаций.
Случай, когда упрочнение материала отсутствует и на внутренней
поверхности дан закон изменения перемещения w со временем, рас-
смотрен Альтшулером П1. Бахшиян 181 рассмотрел случай, когда
на внутренней поверхности задано давление. Общее решение урав-
нения (7.99) при А = 1 (a( = ag) он берёт в виде:
го!п'о+ —
— + + Го)1> (7.100)
(7? = а0-j-с/),
где с?! и ®2 — произвольные функции. Задачи исследования уравне-
ния (7.100) аналогичны упругим волновым задачам, и на них мы не
останавливаемся.
24 Зак, 0138. А. А. Илыешия
ЛИТЕРАТУРА.
К главе I.
Р] Prandtl L., Zs. f. angew. Math. u. Meeh. т. VIII, 1928.
P] Ильюшин А. А., Учёные записки Моск, госуд. университета, Меха-
ника, вып. 39, 1940.
[3] Давиденков Н. Н., Некоторые проблемы механики, Лениздат, 1943.
[*] Bauschinger, J. Mitt. Meeh. Techn. Lab., Miinchen, т. XIII, 1886.
I5] См. библиографию:
a) First report on viscosity and plasticity, prepared by the Committee for
the study of viscosity of the Academie of Sciences of Amsterdam. Verh,
d. Kon. Nied. Acad. d. Wes., 1935.
6) Second report on viscosity and plasticity, prepared by the Committee
for the study of viscosity of the Academie of Sciences of Amsterdam. Verh,
d. Kon. Nied. Acad. d. Wes., 1938.
в) Бро некий А. П., Прикл. математ. и мех., том V, № 1, 1941.
г) Allen N. Р., Nature, Apr. 1946.
[в] N a d a i A., Contrib. to the Meeh, of solids dedicated to Steph. Timoshenko,
Maximillian C°, 1938.
PJ Одинг И. А., Современные методы испытания металлов, Металлург-
издат, 1944.
Серенсен С. В., О прочности деталей машин при действии перемен-
ных нагрузок. Изд. АН СССР, 1938.
Фридман Я. Б., Механические свойства металлов, Оборонгиз, 1946.
К очин Н. Е., Векторное исчисление и начало тензорного исчисления,
ГОНТИ, 1938.
Н е n с к у Н., Zs. f. angew. Math. u. Meeh. t. 4, 1924.
Saint-Vena nt B., J- d. Math, pures et appl. ser. IL t. 16, 1871.
Levy M-, J. d. Math, pures et appl. ser. II, t. 16, 1871.
Huber M. T., Czasopismo tech. t. 22, 1904.
Mises R„ Nachr. d. Geselt. d. Wiss. zu. Gottingen, Math. Pys. Klasse, 1913.
H e n с к у H„ Zs. VDI, t. 69, 1925.
Бриджмен П., Физика высоких давлений. ОНТИ, 1935.
Schleicher F., Zs. f. angew. Math. u. Meeh. t. 6, 1926.
Bridgman P. W., J. Appl. Phys. № 2, 1946.
Lode W., Mitt. u. Forschungsheft VDI № 303, 1938.
RosM. u. Eichinger A., Proc. II Intern. Congress of Appl. Meeh.
Zurich, 1926.
22 T а у 1 о r G. I. a. Q u i n п e у H., Phil. Trans. Roy. Soc., London, A230, 1931.
23 S c h m i d t R., Ingenieur Archiv, t. 3, вып. 3, 1932.
24 Hohenemser К- u. Prager W„ Zs. f. angew, Math. u. Meeh. 'v. 12,1932.
25 ] Prager W., Mechanique des solides isotropes au dela du domaine elasti-
que. Memorial de Sciences Math., вып. LXXXVII, 1937.
[26] Davis E. A., J. Appl. Meeh., t. 10, № 4, 1943. J. Appl. Meeh., t. 12, 1945,
ЛИТЕРАТУРА
ait
р7] Лейбензон Л. С., Элементы математической теории пластичности
Гостехиздат, 1943.
"8
29'
.10
Г'
Г
33
34
35
Зв
Mises R., Gottingen Nachrichten, 1913.
Prandtl L. Zs. f. angew, Mith. u. Meeh. t. 1,1921 и т. 3, 1923.
Reuss A., Zs. f. angew. Math. u. Meeh. t. 10, 1930.
На да и А. Пластичность. ОНТИ, 1936.
H а а г А. и Th. v. Karman, Gottingen. Nachr., Math.-phys. Klasse, 1909.
H*a ndelman G. a. Prager W., Прикл. математ. и мех., т. XI, № 3, 1947.
Ильюшин А. А., Прикл. математ. и мех., т. XI, № 2, 1947.
Prager W., Journ. Appl. Phys. 15, № 1, 1944.
Prager W., Journ. Appl. Meeh. 16, № 12, 1945.
К главе II.
ИльюшинА. А., Прйкл. матем. и мех., т. VII, № 4, 1943,
2] Gleizal A., Journ. Appl. Meeh. 13, № 4, 1946.
3 См. [3I] к главе I.
Ч Беляев Н. М., Изв. АН СССР, ОТН, № 1, 1937.
s] Курант Р. и Гильберт Д„ Методы математической физики, т. I,
ОНТИ, 1933.
[в] Ильюш ин А. А„ Прикл. матем. и мех., т. X, № 3, 1946.
р] Панфёров В. М., О методе упругих решений в задачах пластичности
для цилиндрической оболочки, Диссертация, 1946.
К главе III.
[*] Гвоздев А. А., Труды конференции по пластическим деформациям.
Изд. АН СССР, 1938.
Бернштейн С. А., Работа статически неопределимых ферм в упруго-
пластической стадии. Госстройиздат, 1938.
Жудин Н. Д., Сборник трудов Киевского строительного института,
вып. 2, 1935.
Р] Engesser F., Schweiz. Bauzeitung, 1895.
[3J Karman Th. v„ Mitt. Forschungsarb. a. d. Geb. d. Ingenieiirwesens,
вып. 81, 1910.
P] Cm. литературы к главе I.
К главе IV.
П И дью шин А. А., Прикл. матем. и мех., т. IX, № 3, 1945.
’J Работнов Ю. Н., Прикл. матем. и мех., т. X, № 5—6, 1946.
8 Ля в А., Математическая теория упругости, ОНТИ, 1936.
4 См. [5] литературы к главе II.
“1 Курант Р. и Гильберт Д., Методы математической физики, т. II,
ОГИЗ, 1945.
[в] См. литературы к главе II.
[7] Ф и л о н е н к о-Б о р о д и ч М. М., Основы теории упругости. Госстрой-
издат, 1932.
Г8] Ильюшин А. А., Учёные Записки Моск. Гос. университета, вып. XXIV,
кн. 2, 1938.
[9] Смирно в-А л я е в Г. А., Исследования по теории пластичности, Сбор-
ник III, ГОНТИ, 1939.
P°j Ильюшин А. А., Инж. сборн., т. I, в. № 1, 1941.
pi] Крылов А. Н., О расчёте балок, лежащих на упругом основании,
Изд. АН СССР, 1931.
Р2] Ильюшин А- А., Прикл. матем. и мех., т. VIII, № 1, 1944.
24*
372
ЛИТЕРАТУРА
К главе V.
Ч Bijlaard Р. Р., Proc. Кбп. Ned. Akad. Wet. 41, № 7, 1938.
-J Ильюшин А. А., Прикл. матем. и мех., т. VIII, Ns 5, 1944.
3 Ильюшин А. А., Прикл. матем. и мех., т. X, Ns 5—6, 1946.
Ч Тимошенко С. П., Устойчивость упругих систем. Гостехиздат, 1946.
5] Блейх Ф., Теория и расчёт железных мостов, Гострансиздат, 1931.
в] Геккелер И., Статика упругого тела. ГТТИ, 1934.
’] См. [3] литературы к главе 111.
К главе VI.
1
5
3J
'4
О
в
7
В
Г9]
10
11
12
13
См. [3] литературы к главе II.
Levy М., Comptes Rendus, т. LXXIII, № 16, 1871.
Не nek у Н., Zs. f. angew. Math. u. Meeh. 3, вып. 4, 1923.
Михлин С. Г., Основные уравнения математической теории пластич-
ности. Изд. АН СССР, 1934.
Prandtl L., Zs. f. angew. Math. u. Meeh. 1, вып. 1, 1921.
См. P2] литературы к гл. I.
См. [e] литературы к главе II.
Христианович С. А., Математич. сборник, нов. серия, т. I (43),
вып. 4, 1938.
Соколовский В. В., Теория пластичности. Изд. АН СССР, 1946.
Prandtl L., Zs. f. angew. Math. u. Meeh. t. 3, вып. 6, 1923.
См. [32J литературы к главе I.
Ишлинский А. Ю., Прикл, матем. и мех., т. VIII, № 3, 1944.
Пучков В. М., О вдавливании жёсткого штампа в пластическую среду.
Диссертация, 1946.
К главе VII.
Ч См. р9] литературы к главе I.
2 Р а х м а т у л и н X. А., Нелинейные волны, рукопись, 1945.
’] Рахматулин X. А., Прикл. матем. и мех;, т. IX, Ns 1, 1945.
4 РахматулинХ А., Прикл. матем. и мех., т. X, Ns 3, 1946.
Ч Шапиро Г. С., Прикл. матем. и мех., т. X, № 5—6, 1946.
в] РахматулинХ. А., Прикл. матем. и мех., т. IX, № 4, 1945.
7 А л ь т ш у л е р Л. В., Доклады АН СССР. № 3, 1946.
в Б ах шиян Ф. А., Прикл. матем. и мех., т. XII, № 3, 1948.
ИМЕННОЙ УКАЗАТЕЛЬ.
Альтшулер 369
Баушиигер 13
Бахшиян 369
Блейх 303
Бриджмен 56, 57,
345
Геккелер 303
Гельмгольц 33
Генки 52, 55, 101,
340, 341, 342
Гогенемзер 58
Губер 55
Дэвис 58, 75
Ишлинский 340
Каратеодори 329
Карман 182, 319, 340
Квини 57, 69
Кулон 54
152 Леви 54, 330
’ Лоде 57, 66
Максвелл 14
Мизес 55
Надаи 57, 66, 135, 334
Панфёров 125
Попов 274
Прагер 58, 82. 86, 91, 95
Прандтль 11. 57, 83, 330,
333, 334, 336, 338
Пучков 342, 344
329,
Рахматулин 346, 348,
349, 355
Рош 57, 69, 75
Сен-Венан 54, 330
Смирнов-Аляев 58
Соколовский 332, 338
Тимошенко 303
Тэйлор 57, 69
Хар 182, 340
Христианович 332
Шапиро 355
Шлейхер 57
Шмидт 58, 75, 329
Эйхингер 57, 69, 75
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.
Баушингера эффект 13
Вдавливание штампа 324
Волна Римана 349
— упруго-пластическая Рахматулина
349
Волочение трубы 254, 262
Время релаксации 14
Вытяжка трубы 254, 262, 263
Генки интегралы 329
Генки-Надаи теория пластичности 83,
86, 90, 91
Гибкость пластинки 308
Гиперболоид деформаций 44
— направляющий 46
— напряжений 25
Гогенемзера и Прагера опыты 81
Губера-Мизеса цилиндр 30
Гука закон 50, 53
Давление врезания 334
Девиатор деформаций 42
— напряжений 24
— скоростей деформаций 44
Деформация активная 97
—безмоментная симметричная обо-
лочек вращения 246
— доминирующая изгиба серединной
поверхности 162
---растяжения серединной поверх-
ности 162
— малая 31
— остаточная 12
— пассивная 97
— пластинок в их плоскости 182
— пластическая 12
— плоская 325
— полная 13
— полого шара 138, 143
— простая 49
— симметричная толстостенной тру-
бы 144
---цилиндрической оболочки 263,
272, 273
Деформация текучести 100
-г-упруго-пластическая 13
Диаграмма Мора для деформаций 41
для напряжений 23
— Прагера 86, 88
— растяжения 9
Дивергенция тензора 121
Дэвиса опыты 75
Жёсткость при потере устойчивости
пластинок за пределом упругости
306
Закон Гука 50, 53
Законы пластичности при плоском
напряжённом состоянии 154
Изгиб квадратной опёртой пластин-
ки 227
— кольцевой пластинки 213, 214
— круглой пластинки 209, 216, 222
— поперечный 130
— упругий оболочки 272
— чистый бруса 126
Интегралы Генки 329
Интенсивность деформаций 43, 154
— касательных напряжений 26
-----, интерпретация Роша и Эй-
хннгера 27
— напряжений 30, 154
— сдвига 42
Искривление оболочки вследствие
деформации 157
Кармана модуль 134
---относительный 299
-----обобщённый 305
Кирхгоффа-Лява постулаты 153
Компоненты тензора деформаций 35
---напряжений 19
Коши поверхность деформаций 39
---напряжений 22
— формулы 34
Круги Мора 23, 41
Предметный указатель
37g
Кручение стержня круглого сече-
ния 135
Кулона призма 29
Леви формулы 327
Линия постоянной напряжённости
пластинки 207
— скольжения 327, .339, 342
Материал пластичный 10
— хрупкий 10
Метод упругих решений 124, 125
Модуль Кармана 134
---относительный 299
------обобщённый 305
— объёмной деформации 50
— пластичности 10
— сдвига 50
— упрочнения 10
Мора диаграмма для деформаций 41
---для напряжений 23
Нагартовка оболочек 249
Нагружение близкое к простому 90
Нагрузка повторная за пределом
упругости 11
— простая 49
Надаи-Лоде опыты 66
Наклёп 12
Напряжение безмоментное 246
— нормальное на косой площадке 19
— октаэдрическое 27
— условное 346
Напряжения главные 20
---касательные 24
Обжатие трубы 254, 260
Опыты Гогенемзера и Прагера 81
— Дэвиса 75
— Надаи-Лоде 66
— при сложном напряжённом состоя-
нии 58, 76
— Роша и Эйхингера 69
— Тэйлора и Квини 69, 70, 74
— Шмидта 75
Оси главные деформаций 37
---напряжений 20
Перемещение возможное 108
Пластичность 7
— полная 182
Площадка косая 18
— основная 17
— результирующих сдвигов 43
Поверхность деформаций Коши 39
— напряжений Коши 22
— серединная оболочки 156
Ползучесть 8, 15
Последействие 15
Постулаты Кирхгоффа-Лява 153
Потенциал эластический 51
Прагера диаграмма 86, 88
— теория пластичности 83, 85
Прандтля-Рейса теория пластичности
83, 86, 89, 91
Предел Прочности 10
— текучести 10, 54, 77, 100
— упругости 9
Призма Кулона 29
Процесс нагружения (см. деформа-
ция активная) 97
Равновесие пластинок в перемеще-
ниях 169
---в усилиях и моментах 169
---при изгибе 198, 206, 209, 222
Разгружение простое 119
Разгрузка 97, 119
— за пределом упругости 11
Работа напряжений 104
Релаксация 14
Римана волны 349
Роша и Эихингера опыты 69
Сен-Венана — Леви — Мизеса теория
пластичности 82, 8 5, 89
Сжатие пластического материала
между шероховатыми плитами 337
Состояние пластическое твердого
тела 9
— разгрузки 119
— тела кинематически возможное 113
— упругое твёрдого тела 8
Способность несущая бесконечно
длинной трубы 277
---бруса при изгибе 128
---вала на кручение 137
---кольцевой пластинки 238
— — круглого диска постоянной тол-
щины с отверстием 193
---круглых пластинок 236, 242
---оболочек 180, 181, 182
---пластинок в их плоскости 185,193
---тела 84, 324
---цилиндрической оболочки 275,
277, 279, 280, 281
---------, краевой эффект 279
Сумма двух тензоров 20
Тело идеально пластическое 323
Тензор деформаций 35
— направляющий 46
— напряжений 19, 20
— симметричный второго ранга 19
— скоростей деформаций 44
— шаровой 24
376
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Теорема минимума работы внутрен-
них сил 113, 115
— о простом нагружении 116, 118
— о разгрузке 120
Теория пластичности Генки-Надаи 83,
86, 90,91
----Прагера 83, 85
----Прандтля-Рейса 83, 86, 89, 91
----Сен-Венана — Леви — Мизеса
82, 86, 89
Тэйлора и Квини опыты 69, 70, 74
Удар поперечный по гибкой дефор-
мируемой нити 355, 361, 362, 363,
364
Упрочнение 12
Уравнение вариационное равнове-
сия 168
------оболочки 169
------пластинки 205
Условие несжимаемости 56
— пластичности 53
— — Мизеса 55, 57, 77, 174
----Сен-Венана 54
Усталость 8
Устойчивость оболочек 286
— пластинок 291
----, приближённое решение 303,
311, 312
— прямоугольной пластинки при усло-
вии плоской деформации 298
Устойчивость прямоугольной пла-
стинки, сжатой в одном направ-
лении 300
— равномерно сжаты? пластинок про-
извольной формы 296, 312
— свободно опёртой прямоугольной
пластинки, сжатой в одном напра-
влении 312
— сжатого стержня 134, 135
— сжатой полосы 311
Форма цилиндрическая потери устой-
чивости прямоугольной пластинки
---------цилиндрической оболочки
314
— осесимметричная потери устойчи-
вости цилиндрической оболочки 316
Формулы Коши 34
— Леви 327
Цилиндр Губера-Мизеса 30
Шмидта опыты 75
Штамп криволинейный 336
—осесимметричный 338
— плоский 333
Энергия потенциальная 51
----единичног-о элемента тела 105
----деформации 13
Эффект Баушингера 13
Опечатки
Стра- ница Строка Напечатано Должно быть По вине
60 2 снизу ~syv ~svv Тип.
170 3 снизу — еа ei1 — «41 •
176 19 сверху V1 + H1+1 Vi + ni + i »
230 11 сверху Rdt | d-ц Rdkd^ 1»
257 2 сверху Г Г »
315 1 снизу т У •
Л.Л. ИЛЬЮШИН
ПЛАСТИЧНОСТЬ