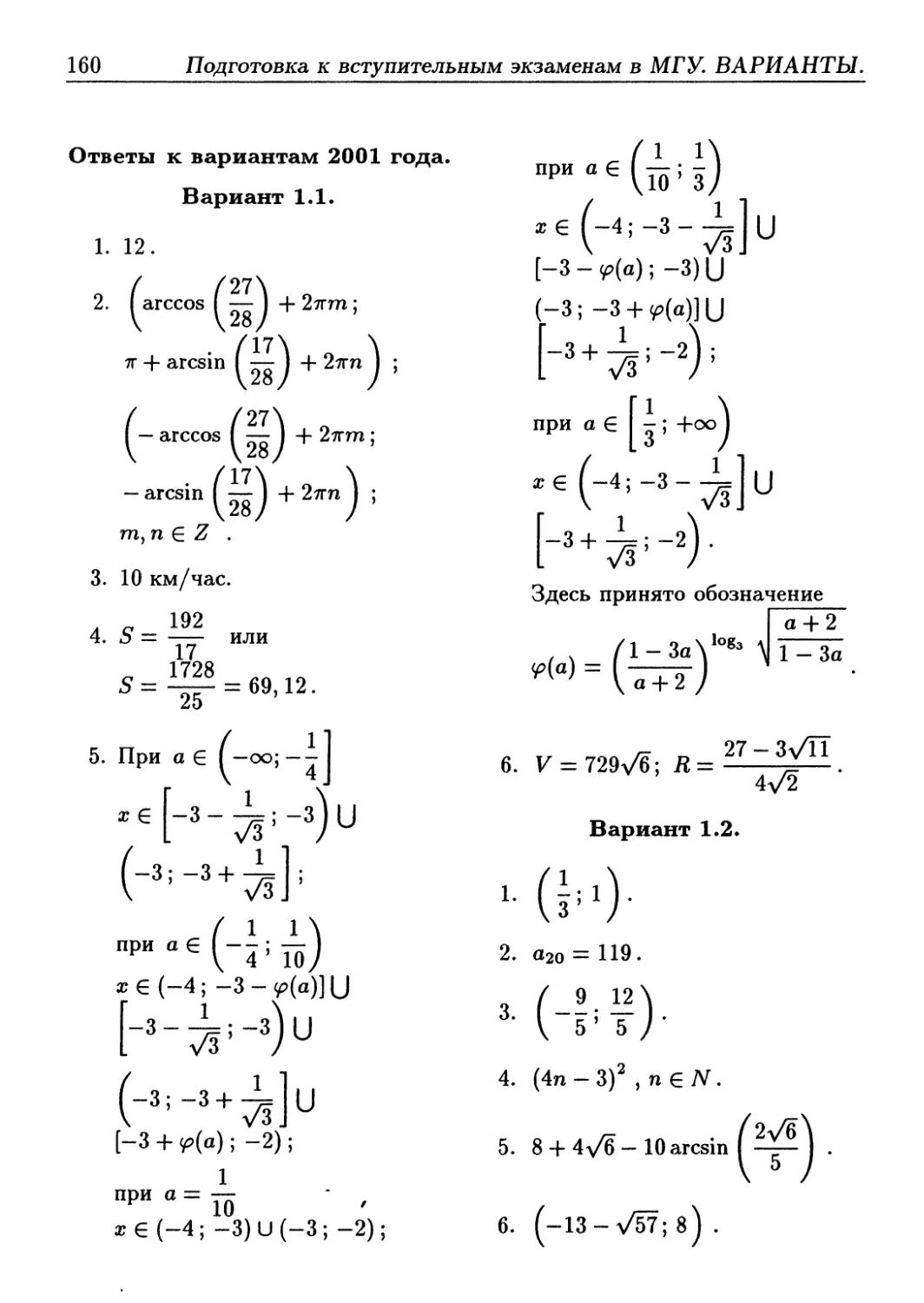МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им.
М.В.ЛОМОНОСОВА
ФАКУЛЬТЕТ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ и
КИБЕРНЕТИКИ
ПОДГОТОВКА К ВСТУПИТЕЛЬНЫМ
ЭКЗАМЕНАМ В МГУ
ВАРИАНТЫ
письменных экзаменов
по математике
2001-2005 годов
Москва
2006
УДК 51
ББК 22.14я729
П44
П44 Подготовка к вступительным экзаменам в МГУ.
Варианты письменных экзаменов по математике 2001-2005
годов./ составитель М.В.Федотов. - М.: факультет ВМК МГУ, 2006.
- 195 стр.
ISBN 5-89407-233-6
Издательский отдел факультета Вычислительной математики и кибер-
нетики МГУ им. М.В. Ломоносова (лицензия ИД №05899 от 24.09.2001)
Настоящий сборник содержит около 150 вариантов письменных вступи-
тельных экзаменов и олимпиад по математике в МГУ им.М.В.Ломоносова
за 2001-2005 годы. Приведены по одному варианту с каждого факультета
МГУ, где есть вступительный экзамен по математике.
Сборник может быть полезен абитуриентам при подготовке к поступ-
лению как в МГУ, так и в другие Вузы, где есть вступительный экзамен
по математике.
УДК 51
ББК 22.14я729
Печатается по решению редакционно-издательского совета факультета вы-
числительной математики и кибернетики МГУ им. М.В. Ломоносова
ISBN 5-89407-233-6
© Факультет Вычислительной математики и
кибернетики МГУ им. М.В.Ломоносова, 2006 г.
© М.В.Федотов, 2006
Содержание
3
Настоящий сборник содержит варианты письменных вступительных эк-
заменов и олимпиад по математике в МГУ им.М.В.Ломоносова за 2001-
2005 годы. Он составлен на основе ежегодных сборников, выпускаемых
факультетом ВМК[1], механико-математическим факультетом[2] и спра-
вочников для поступающих в Московский университет[3]. Приведены по
одному варианту с каждого факультета МГУ, где есть вступительный эк-
замен по математике.
Сборник может быть полезен абитуриентам при подготовке к поступ-
лению не только в МГУ, но и в другие Вузы, где есть письменный экзамен
по математике.
При составлении данного сборника была использована следующая ли-
тература:
1.	Задачи вступительных экзаменов по математике (2001 - 2005 гг.).- М.,
факультет ВМиК МГУ.
2.	Варианты вступительных экзаменов по математике в МГУ (2001 - 2005
гг.).- М., Механико-математический факультет МГУ.
3.	Справочник для поступающих в Московский университет (2002-2006 гг.).
СОДЕРЖАНИЕ.
Программа вступительных экзаменов по математике
для поступающих в МГУ им. М. В. Ломоносова.............4
Варианты 2001 года....................................10
Варианты 2002 года....................................40
Варианты 2003 года....................................72
Варианты 2004 года...................................108
Варианты 2005 года...................................134
Ответы к вариантам 2001 года.........................160
Ответы к вариантам 2002 года.........................167
Ответы к вариантам 2003 года.........................174
Ответы к вариантам 2004 года.........................183
Ответы к вариантам 2005 года.........................189
4
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
ПРОГРАММА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ
ПО МАТЕМАТИКЕ ДЛЯ ПОСТУПАЮЩИХ
В МГУ им. М. В. ЛОМОНОСОВА.
Настоящая программа состоит из трех разделов. В первом разделе пе-
речислены основные математические понятия, которыми должен владеть
поступающий как на письменном, так и на устном экзамене.
Второй раздел представляет собой перечень вопросов теоретической ча-
сти устного экзамена. При подготовке к письменному экзамену целесооб-
разно познакомиться с формулировками утверждений этого раздела.
В третьем разделе указано, какие навыки и умения требуются от по-
ступающего на письменном и устном экзаменах.
Объем знаний и степень владения материалом, описанным в програм-
ме, соответствуют курсу математики средней школы. Поступающий может
пользоваться всем арсеналом средств из этого курса, включая и начала
анализа. Однако для решения экзаменационных задач достаточно уверен-
ного владения лишь теми понятиями и их свойствами, которые перечис-
лены в настоящей программе. Объекты и факты, не изучаемые в общеоб-
разовательной школе, также могут использоваться поступающими, но при
условии, что он способен их пояснять и доказывать.
В связи с обилием учебников и регулярным их переизданием отдельные
утверждения второго раздела могут в некоторых учебниках называться
иначе, чем в программе, или формулироваться в виде задач,-или вовсе
отсутствовать. Такие случаи не освобождают поступающего от необходи-
мости знать эти утверждения.
I.	Основные понятия
1.	Натуральные числа. Делимость. Простые и составные числа. Наи-
больший общий делитель и наименьшее общее кратное.
2.	Целые, рациональные и действительные числа. Проценты. Модуль
числа, степень, корень, арифметический корень, логарифм. Синус,
косинус, тангенс, котангенс числа (угла). Арксинус, арккосинус, арк-
тангенс, арккотангенс числа.
3.	Числовые и буквенные выражения. Равенства и тождества.
4.	Функция, ее область определения и область значений. Возрастание,
убывание, периодичность, четность, нечетность. Наибольшее и наи-
меньшее значения функции. График функции.
5.	Линейная, квадратичная, степенная, показательная, логарифмиче-
ская, тригонометрические функции.
Программа вступительных экзаменов по математике
5
6.	Уравнение, неравенства, система. Решения (корни) уравнения, нера-
венства, системы. Равносильность.
7.	Арифметическая и геометрическая прогрессии.
8.	Прямая на плоскости. Луч, отрезок, ломаная, угол.
9.	Треугольник. Медиана, биссектриса, высота.
10.	Выпуклый многоугольник. Квадрат, прямоугольник, параллелограмм,
ромб, трапеция. Правильный многоугольник. Диагональ.
11.	Окружность и круг. Радиус, хорда, диаметр, касательная, секущая.
Дуга окружности и круговой сектор. Центральный и вписанный уг-
лы.
12.	Прямая и плоскость в пространстве. Двугранный угол.
13.	Многогранник. Куб, параллелепипед, призма, пирамида.
14.	Цилиндр, конус, шар, сфера.
15.	Равенство и подобие фигур. Симметрия.
16.	Параллельность и перпендикулярность прямых, плоскостей. Скре-
щивающиеся прямые. Угол между прямыми, плоскостями, прямой
и плоскостью.
17.	Касание. Вписанные и описанные фигуры на плоскости и в простран-
стве. Сечение фигуры плоскостью.
18.	Величина угла. Длина отрезка, окружности и дуги окружности. Пло-
щадь многоугольника, круга и кругового сектора. Площадь поверх-
ности и объем многогранника, цилиндра, конуса, шара.
19.	Координатная прямая. Числовые промежутки. Декартовы координа-
ты на плоскости и в пространстве. Векторы.
II.	Содержание теоретической части устного экзамена
Алгебра
1.	Признаки делимости на 2, 3, 5, 9, 10.
2.	Свойства числовых неравенств.
6
Подготовка к вступительным экзаменам в МГУ. ПАРИ АНТЫ.
3.	Формулы сокращенного умножения.
4.	Свойства линейной функции и ее график.
5.	Формула корней квадратного уравнения. Теорема о разложении квад-
ратного трехчлена на линейные множители. Теорема Виета.
6.	Свойства квадратичной функции и ее график.
7.	Неравенство, связывающее среднее арифметическое и среднее гео-
метрическое двух чисел. Неравенство для суммы двух взаимно об-
ратных чисел.
8.	Формулы общего члена и суммы п первых членов арифметической
прогрессии.
9.	Формулы общего члена и суммы п первых членов геометрической
прогрессии.
10.	Свойства степеней с натуральными и целыми показателями. Свой-
ства арифметических корней n-й степени. Свойства степеней с раци-
ональными показателями.
11.	Свойства степенной функции с целым показателем и ее график.
12.	Свойства показательной функции и ее график.
13.	Основное логарифмическое тождество. Логарифмы произведения, сте-
пени, частного. Формула перехода к новому основанию.
14.	Свойства логарифмической функции и ее график.
15.	Основное тригонометрическое тождество. Соотношения между три-
гонометрическими функциями одного и того же аргумента. Формулы
приведения, сложения, двойного и половинного аргумента, суммы и
разности тригонометрических функций. Выражение тригонометри-
ческих функций через тангенс половинного аргумента. Преобразо-
вание произведения синусов и косинусов в сумму. Преобразование
выражения a sin х 4- Ь cos х с помощью вспомогательного аргумента.
16.	Формулы решений простейших тригонометрических уравнений.
17.	Свойства тригонометрических функций и их графики.
Программа вступительных экзаменов по математике
7
Геометрия
1.	Теоремы о параллельных прямых на плоскости.
2.	Свойства вертикальных и смежных углов.
3.	Свойства равнобедренного треугольника.
4.	Признаки равенства треугольников.
5.	Теорема о сумме внутренних углов треугольника. Теорема о внешнем
угле треугольника. Свойства средней линии треугольника.
6.	Теорема Фалеса. Признаки подобия треугольников.
7.	Признаки равенства и подобия прямоугольных треугольников. Про-
порциональность отрезков в прямоугольном треугольнике. Теорема
Пифагора.
8.	Свойство серединного перпендикуляра к отрезку. Свойство биссек-
трисы угла.
9.	Теоремы о пересечении медиан, пересечении биссектрис и пересече-
нии высот треугольника.
10.	Свойство отрезков, на которые биссектриса треугольника делит про-
тивоположную сторону.
11.	Свойство касательной к окружности. Равенство касательных, прове-
денных из одной точки к окружности. Теоремы о вписанных углах.
Теорема об угле, образованном касательной и хордой. Теоремы об уг-
ле между двумя пересекающимися хордами и об угле между двумя
секущими, выходящими из одной точки. Равенство произведений от-
резков двух пересекающихся хорд. Равенство квадрата касательной
произведению секущей на ее внешнюю часть.
12.	Свойство четырехугольника, вписанного в окружность. Свойство че-
тырехугольника, описанного около окружности.
13.	Теорема об окружности, вписанной в треугольник. Теорема об окруж-
ности, описанной около треугольника.
14.	Теоремы синусов и косинусов для треугольника.
15.	Теорема о сумме внутренних углов выпуклого многоугольника.
8
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
16.	Признаки параллелограмма. Свойства параллелограмма.
17.	Свойства средней линии трапеции.
18.	Формула для вычисления расстояния между двумя точками на коор-
динатной плоскости. Уравнение окружности.
19.	Теоремы о параллельных прямых в пространстве. Признак парал-
лельности прямой и плоскости. Признак параллельности плоскостей.
20.	Признак перпендикулярности прямой и плоскости. Теорема об общем
перпендикуляре к двум скрещивающимся прямым. Признак перпен-
дикулярности плоскостей. Теорема о трех перпендикулярах.
III.	Требования к поступающему
На экзамене по математике поступающий должен уметь:
1.	выполнять (без калькулятора) действия над числами и числовыми
выражениями; преобразовывать буквенные выражения; производить
операции над векторами (сложение, умножение на число, скалярное
произведение); переводить одни единицы измерения величин в дру-
гие;
2.	сравнивать числа и находить их приближенные значения (без каль-
кулятора); доказывать тождества и неравенства для буквенных вы-
ражений;
3.	решать уравнения, неравенства, системы (в том числе с параметрами)
и исследовать их решения;
4.	исследовать функции; строить графики функций и множества точек
на координатной плоскости, заданные уравнениями и неравенствами;
5.	изображать геометрические фигуры на чертеже; делать дополнитель-
ные построения; строить сечения; исследовать взаимное расположе-
ние фигур; применять признаки равенства, подобия фигур и их при-
надлежности к тому или иному виду;
6.	пользоваться свойствами чисел, векторов, функций и их графиков,
свойствами арифметической и геометрической прогрессий;
7.	пользоваться свойствами геометрических фигур, их характерных то-
чек, линий и частей, свойствами равенства, подобия и взаимного рас-
положения фигур;
Программа вступительных экзаменов по математике
9
8.	пользоваться соотношениями и формулами, содержащими модули,
степени, корни, логарифмические, тригонометрические выражения,
величины углов, длины, площади, объемы;
9.	составлять уравнения, неравенства и находить значения величин, ис-
ходя из условия задачи;
10.	излагать и оформлять решение логически правильно, полно и после-
довательно, с необходимыми пояснениями.
На устном экзамене поступающий должен дополнительно уметь:
11.	давать определения, формулировать и доказывать утверждения (фор-
мулы, соотношения, теоремы, признаки, свойства и т.п.), указанные
во втором разделе настоящей программы;
12.	анализировать формулировки утверждений и их доказательства;
13.	решать задачи на построение циркулем, линейкой; находить геомет-
рические места точек.
10
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Варианты 2001 года
Варианты 2001 года
11
1. Факультет ВМК.
Вариант 1.1 (Олимпиада, апрель 2001 г.)
1.	Сумма первых трех членов арифметической прогрессии равна 27, а
сумма первых пяти членов равна 80. Сумма какого числа первых
членов прогрессии равна 486 ?
2.	Найдите все решения системы уравнений
{3 sin х 4- cos у = 0 ,
6 cos х — 2 sin у = 7 .
3.	Из пункта А в пункт В выехал первый велосипедист. Одновременно
с ним с такой же скоростью из В в А выехал второй велосипедист.
Через некоторое время первый велосипедист увеличил скорость на 10
км/час. Если бы первый велосипедист сразу двигался с увеличенной
скоростью, то его встреча со вторым велосипедистом состоялась бы
на три часа раньше. Известно, что расстояние между А и В равно
180 км, в момент изменения скорости первым велосипедистом рас-
стояние между ним и вторым велосипедистом было меньше 70 км, на
весь путь из А в В первый велосипедист затратил 15 час. Найдите
первоначальную скорость велосипедистов.
4.	В параллелограмме ABCD диагонали пересекаются в точке О, дли-
на диагонали BD равна 12. Расстояние между центрами окруж-
ностей, описанных около треугольников AOD и COD, равно 16.
Радиус окружности, описанной около треугольника АОВ, равен 5.
Найдите площадь параллелограмма ABCD.
5.	Для каждого значения параметра а решите неравенство
За — 1 — (8а — 5)  3 *	< 3(а + 2) • |« + 3|’.
6.	Сфера касается всех боковых рёбер правильной шестиугольной пи-
рамиды SABCDEF, причём рёбер SA и SB она касается соответ-
ственно в точках К и L. Точки К, L и S лежат по одну сторону
от плоскости, которая касается сферы в точке М, принадлежащей
грани SAB, и пересекает рёбра SA и SB в точках G и Н соот-
ветственно. Прямые КМ и LM делят апофему грани SAB натри
равных отрезка. Известно, что АВ = 9 и GH — 3\/Г1- Найдите объём
пирамиды SABCDEF и радиус сферы.
12
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 1.2 (июль 2001 г.)
1.	Решите систему уравнений
Г 2 • 51-у = log3 (а;-2),
[	4- log3 х = 4.
2.	Сумма первых четырех членов арифметической прогрессии равна
56. Все члены этой прогрессии - натуральные числа. Двенадцатый
член больше 67, но меньше 74. Найдите двадцатый член этой про-
грессии.
3.	Среди всех решений системы
( у 4- Зя < -3 ,
[ х2 4- у2 4- 4х 4- 2у < 11
найдите такое, при котором выражение х2+у2—6х—81/4-25 принимает
минимальное значение.
4.	Решите уравнение
cos(7r(z 4- 7у/х)) • sin (^(4я 4-	= 1 •
5.	Трапеция с основанием у/8 и высотой \/34-\/2 вписана в окружность
радиуса . Каждый из четырех отсекаемых сторонами трапеции
сегментов отражен внутрь трапеции симметрично относительно от-
секающей его стороны. Найдите площадь фигуры, состоящей из тех
точек трапеции, которые не принадлежат ни одному из отраженных
внутрь нее сегментов.
6. Функция f(x) определена, возрастает и отрицательна на всей число-
вой прямой. Решите неравенство
2 • /(а;2 - 2а; - 112) + |/Q2 - 2а; - 112) - 3 • /(-2аУ32 - 2х)|
(3 • /'(-2а;Л/32 - 2а; - 112) - 2 • /(-2aV32 - 2а:))6 7
Варианты 2001 года
13
Отделение прикладной информатики.
Вариант 1.3 (июль 2001 г.)
1.	Решите систему уравнений
log2 у/у = -З1 х ,
3* + log2 у = 1.
2.	Сумма первых девяти членов арифметической прогрессии больше
119, но меньше 133. Все члены этой прогрессии - натуральные чис-
ла. Третий член равен 10. Найдите сумму первых ста членов этой
прогрессии.
3.	При всех значениях параметра а решите неравенство
|2ж 4- а| < х -Ь 2 .
4.	Среди всех решений системы
Зу 4- 2х > 2,
х2 4- У2 — 2х — 4у < 4
найдите такое, при котором выражение a?24-j/24-4«4-6j/-f-13 принимает
минимальное значение.
5.	Решите уравнение
cos(?r(« 4- 3\/я)) • cos(?r(2« — у/х)) = —1.
6.	Пусть [ж] означает целую часть числа ж, т.е. наибольшее целое число,
не превосходящее х. Найдите все корни уравнения
7.	Вокруг трапеции с основаниями у/8 и \/28 описана окружность ра-
диуса 3 с центром, находящимся внутри трапеции. Каждый из четы-
рех отсекаемых сторонами трапеции сегментов отражен внутрь тра-
пеции симметрично относительно отсекающей его стороны. Найдите
площадь фигуры, состоящей из тех точек трапеции, которые не при-
надлежат ни одному из отраженных внутрь нее сегментов.
14
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
2. Геологический факультет.
Вариант 2.1 (Олимпиада, май 2001 г.)
1.	Решите неравенство
2.	Решите неравенство
3.	Решите уравнение
|х-3| + 2
|2х - 3| - 5 - '
\/а:2 — 8x + 12 > х — 5.
|оёз (~г)	_ j
log9 (-5» - 4)
4.	Найдите все решения уравнения
cos х — cos 2х — sin 2х = 1,
расположенные на отрезке
Зя* 7Г
Т’ “б
5.	Окружность, проходящая через вершину А треугольника АВС, ка-
сается стороны ВС в точке М и пересекает стороны АС и АВ со-
ответственно в точках L и К, отличных от вершины А. Найдите
отношение АС : АВ, если известно, что длина отрезка LC в два
раза больше длины отрезка КВ , а отношение СМ : ВМ = 3:2.
6.	При проведении опыта раствор А был получен растворением ненуле-
вого объема кислоты в воде. Раствор В был получен из раствора А
добавлением некоторого объема воды, при этом концентрация раство-
ра (отношение объема кислоты к общему объему раствора) уменьши-
лась на 40%. Раствор С получен из раствора В добавлением нового
количества воды, в два раза большего по объему, чем было добав-
лено к раствору А при получении В . Во сколько раз концентрация
раствора В больше концентрации раствора С ?
7.	При каких значениях у уравнение
|2я + 6| + |2ж — 8| = ух 4-12
имеет единственное решение х ?
8.	Найдите радиус сферы, описанной около правильного тетраэдра, две
вершины которого лежат на диагонали куба с ребром 2, а две другие
- на не пересекающей эту диагональ куба диагонали его грани.
Варианты 2001 года
15
Вариант 2.2 (июль 2001 г.)
А-1
1. Решите неравенство	— > 0 .
х — 7
Найдите неотрицательные решения уравнения
,	. „	( Зх ЗаЛ2
1 -Ь sin 7х = I cos —— sin — I
\	" J
2.
х—2
3.
4.
5.
6.
7.
8.
Решите уравнение	= нВ ‘
Прямая, проходящая через вершину основания равнобедренного тре-
угольника, делит его площадь пополам, а периметр треугольника де-
лит на части 5 и 7. Найдите площадь треугольника и укажите, где
лежит центр описанной окружности: внутри или вне треугольника?
ХУ >	5	= 5
2 2х 4- у — ху ’
2х + у ----= 4 4- ху.
ху
Пункты Ап В расположены на двух различных дорогах, представля-
ющих собой две взаимно перпендикулярные прямые, пересекающие-
ся в пункте С. Два мотоциклиста одновременно начинают движение:
первый из пункта А по направлению к С, а второй из В по направ-
лению к С. Через какое время после начала движения расстояние
между мотоциклистами будет наименьшим и каким, если скорость
первого мотоциклиста равна 44 км/час, второго - 33 км/час, а каж-
дое из расстояний от пункта А до пункта С и от пункта В до пункта
С равно 275 км ?
Сфера с диаметром AD = л/3 касается плоскости треугольника АВС
в точке А. Отрезки BD и CD пересекают сферу в точках М и N
соответственно. Найдите длину отрезка MN, если АВ = 3, АС =
3^5, a Z.BDC = J.
и
При каких значениях параметра a > 1 уравнение
/4 \
sin I — х I • tg х = О
\13 ) ь
имеет ровно шесть различных корней на отрезке [2атг; (a2 + 1) тг] ?
Укажите эти корни.
Решите систему уравнений
16
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
3. Экономический факультет.
Отделение экономики.
Вариант 3.1 (июль 2001 г.)
1.	Решите неравенство
|я2 — 8х + 15| < 115 — ж2|.
2.	Брокерская фирма приобрела два пакета акций, а затем их продала
на общую сумму 7 миллионов 680 тысяч рублей, получив при этом
28% прибыли. За какую сумму фирма приобрела каждый из пакетов
акций, если при продаже первого пакета прибыль составила 40%, а
при продаже второго - 20% ?
3.	На координатной плоскости заданы точки 4(0; 2), В(1;7), €7(10;7)
и Z>(7; 1). Найдите площадь пятиугольника ABODE, где Е - точка
пересечения прямых АС и BD.
4.	Решите неравенство
log2 (2* - 3) • logyj (4®+2 - 12 • 2®+3 + 144) < 32.
5.	Решите уравнение
л/З cos ( 7г у/х • \/-х — 4 I 4- 3 sin ( яг ж • а/—-1 I = у/12 .
\ ух J I V х2 х /
6.	Центры двенадцати шаров равных радиусов совпадают с середина-
ми ребер правильной шестиугольной пирамиды. Найдите величину
двугранного угла при ребре основания пирамиды, если известно, что
шар, вписанный в пирамиду, касается всех двенадцати данных ша-
ров.
7.	Найдите наибольшие целочисленные значения и и v, для которых
уравнение
364 а2и — 55 v = -20020 а4
выполняется ровно при четырех различных значениях а, два из ко-
торых относятся как 3:5.
Варианты 2001 года
17
Вечернее отделение.
Вариант 3.2 (июль 2001 г.)
1.	Решите уравнение
7 sin х — 6 sin 2х 4- v 7 sin Зя = 0.
2.	Решите неравенство |ж2 — 13х + 36| > |36 — я2|.
3.	Вследствие неблагоприятных погодных условий план сбора свеклы
на первом поле был недовыполнен на 20 %, а на втором - на 15 %.
При этом общий урожай с двух полей составил 328 тонн свеклы, что
составляет 82 % общего плана. Определите план сбора свеклы с каж-
дого поля.
4.	На координатной плоскости заданы точки А(1; 3), В(1; 9), С(6;8) и
Е(5; 1). Найдите площадь пятиугольника ABCDE, где D - точка пе-
ресечения прямых АС и BE.
5.	Решите неравенство
logys (5® - 2) • logs (25’+1 - 20 • 5*+1 + 100) > 24.
6.	Решите уравнение
л/7 cos (—	• д/6ж2 4- 6я3	— ж4) 4- д/7 sin	f -Д= • \/ба?2 4- 6ж —	ж3 )	= \/14.
\х	/	\ух	/
7.	Центры восьми шаров равных радиусов совпадают с серединами ре-
бер правильной четырехугольной пирамиды со стороной основания
a — 2 и боковым ребром I = \/б. Девятый шар того же радиуса с цен-
тром внутри пирамиды касается всех восьми данных шаров. Найдите
радиус шаров.
18
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Отделение менеджмента.
Вариант 3.3 (июль 2001 г.)
1.	Решите уравнение cos х 4- cos Зж = л/З cos 2х .
2.	Решите уравнение |ж2 — 8х 4- 151 = 115 — я2|.
3.	Антикварный магазин приобрел два предмета, а затем продал их на
общую сумму 39900 рублей, при этом прибыль составила 40%. За
сколько магазин купил каждый предмет, если при продаже первого
предмета прибыль составила 30%, а при продаже второго - 55% ?
4.	На координатной плоскости заданы точки А(1; 9), (7(5; 8), Z>(8; 2) и
£(2; 2). Найдите площадь пятиугольника ABODE, где В - точка пе-
ресечения прямых ЕС и AD.
5.	Решите неравенство
log3 (3* - 1) • log9 (9®+2 - 6 • Зт+3 + 81) < 3.
6.	Решите уравнение
Варианты 2001 года
19
4- Институт стран Азии и Африки.
Вариант 4.1 (июль 2001 г.)
1.	Решите неравенство
у/2х2 - 5ж - 3 > 0
6 + Зу/Зх - 2х2 “
2.	Найдите все решения уравнения
5 sin2 2х 4- 8 cos3 х = 8 cos х ,
удовлетворяющие условиям
- 7Г < X < 2тг.
2 ~ “
3.	Из пункта А в пункт Б, расстояние между которыми равно 10 км,
отправились в разное время пешеход, всадник и велосипедист. Из-
вестно, что их скорости постоянны и образуют в указанном порядке
арифметическую прогрессию. Первым из А вышел пешеход, которо-
го в середине маршрута обогнал велосипедист, выехавший из А на
50 минут позже пешехода. В пункт Б пешеход прибыл одновременно
с всадником, выехавшим из А на 1 час 15 минут позже пешехода.
Определите скорости участников маршрута.
4.	Решите неравенство
(1 + log3 я) •
5.	В треугольнике АВС даны длины сторон АВ — л/2, ВС = у/5 и
АС = 3. Сравните величину угла ВОС и 112,5°, если О - центр
вписанной в треугольник АВС окружности.
6.	Найдите все значения параметра а, при каждом из которых система
уравнений
( а (х 4- 2) 4- у — За ,
| а 4- 2ж3 = у3 4- (а 4- 2) х3
имеет не более двух решений.
7.	Решите уравнение
3 cos х 4- 2 sin х cos 2х cos х + sin х / -     ——----5 7
-------------= —— +----------------V3 4- 2х - 2у 4- 2ху - я2 - г/2 .
COS X	COS2 X cos X
20
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
5. Факультет Государственного управления.
Вариант 5.1 (июль 2001 г.)
1. Решите уравнение
sin х + sin Зя — л/3 sin 2х.
2. Решите уравнение
|я2-13я + 36|=|36-я2|.
3.	В магазине одежды проводилась распродажа. Костюмы продавались
со скидкой 20%, плащи - со скидкой 40%. Покупатель купил костюм
и плащ за 9180 рублей в сумме, заплатив на 32% меньше их суммар-
ной первоначальной цены. Найдите первоначальные цены костюма и
плаща.
4.	На координатной плоскости заданы точки Л(9; 1), В(2;0), D(l; 5) и
1?(9; 7). Найдите площадь пятиугольника ABCDE, где С - точка пе-
ресечения прямых AD и BE.
5.	Решите неравенство
log4 (4® - 1) • log16 (16r+1 - 8 • 4®+1 + 16) > 12.
6.	Решите уравнение
arccos
i + c°s
-х2 + 2х+П
х2 + 4х + 7
т = °-
^7Г
Варианты 2001 года
21
6. Черноморский филиал МГУ (г. Севастополь).
Вариант 6.1 (Олимпиада, май 2001 г.)
1.	Определите все целые значения х, для которых дробь
х2(х2 - 35)(я2 - 10)
(я2 -64)(я2 - 100)
является неположительной.
2.	Решите неравенство
|ж — 1| |ж — 1|
3 — х ~ 3 — 2х
3.	Решите неравенство
1g (4- -5) - 1g (5 —2x)>lg2.
4.	Найдите все пары (ж; у), удовлетворяющие условию
(|х| - 2ж) у2 < 18x (6 - 2j/).
5.	Решите уравнение
4 sin х — 3	_
у/1 sin х 4- 3 cos х
6.	Решите неравенство
7.	В трапеции ABCD стороны BCtfAD, ВС < AD, диагональ BD
в 4/3 раза больше радиуса окружности, описанной вокруг трапе-
ции. Найдите отношение CD к радиусу, если площади треугольников
ABD и BCD относятся как 5:1.
8.	Решите уравнение
2|®34'2а;| ।	। ^—2х—х%-}-1 _
9.	Для каждого значения а решите неравенство
22
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 6.2 (июль 2001 г.)
1.	В коробке находятся красные и синие шары, причем синие шары со-
ставляют 1% от общего числа шаров. После того, как из коробки
взяли часть красных шаров, доля синих от общего числа оставших-
ся в коробке шаров составила 2%. Найдите отношение числа взятых
красных шаров к первоначальному общему числу шаров в коробке.
2.	Решите уравнение
, . । 1
| sm х | — cos х 4- - .
3.	Решите неравенство
|ж _ ц _ |2ж-Ц|
- 2| - |2х + 2| - ’
4.	Решите неравенство
1g (5х — х2) — 1g (ж2 — Зх) < 1g (х2 — 13х 4- 40).
5.	Выясните, при каких значениях а уравнение имеет решения и найдите
эти решения:
х2 + 1	х2-1
2	4- 2 х2 = a .
6.	В треугольнике АВС радиус вписанной окружности равен 1. Из-
вестно, что ВС : АВ = 3:2, АС : АВ = 2:1. Найдите высоты
На, Нв и Нс , опущенные из вершин А, В и С соответственно.
7.	Решите уравнение
8 |д/3 sin 2х — cos 2х| = cos 18х 4- 12 cos 9х 4- 27.
8.	Решите уравнение
4/2«’+2i: • 5*2-5®+5 _ 50 = ^/24-®3 • 52»’-2*+1 _ 50.
9.	В параллелограмме проведены биссектрисы всех внутренних углов.
Четырехугольник, полученный при пересечении этих биссектрис, име-
ет площадь, равную 2/3 площади исходного параллелограмма. Най-
дите отношение большей стороны параллелограмма к меньшей.
Варианты 2001 года
23
7. Механике-математический факультет
Вариант 7.1 (Олимпиада, март 2001 г.)
1.	Решить уравнение
Зх - 2|х - 2| = Зг/Зх 4- 18 - 2|д/3х4-18 - 2|.
2 Решить неоавенство	(? х) 1
2.	Решить неравенство	+ 4ж _	< 4’
3.	В трапеции ABCD с боковой стороной CD = 30 диагонали пересека-
ются в точке Е, а углы AED и BCD равны. Окружность радиуса 17,
проходящая через точки С, D и Е, пересекает основание AD в точке
F и касается прямой BF. Найти высоту трапеции и её основания.
4.	Можно ли подобрать числа А, В, 0, так, чтобы выражение
sin (х - уj + 2j 4- А cos(x -f- ф) 4" В sin(2x 4" ф)
принимало при всех х одно и то же значение С? Если да, то какие
значения может принимать константа С?
5.
4
Основанием прямой призмы АВСА'В'С' с высотой - служит тре-
3
угольник АВС, в котором АВ = ВС = 1 и АС = у. Через точку
4
пересечения диагоналей грани АСС'А' на расстоянии — от точки А
проводится плоскость, делящая объём призмы пополам. Какова наи-
большая площадь сечения призмы такой плоскостью?
6. Найти все значения а, при которых система
( (а — 1)х2 4- 2ах 4- а 4- 4 < О,
[ ах2 4- 2(а 4- 1)х 4- а 4-1 > О
имеет единственное решение.
24
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 7.2 (Олимпиада, май 2001 г.)
1.	Решить неравенство 26* 4- 27 > 9(6 — VTO)® 4- 3(6 4- \/10)*.
2.	При каких значениях х числа
log2(2a?2 4- 4ж), log2(8 — х2 — 19ж) и log2(ж2 — 15ж 4- 7.5)
являются длинами сторон некоторого равнобедренного треугольни-
ка?
3.	Две окружности с центрами О и Q, пересекающиеся друг с другом
в точках А и В, пересекают биссектрису угла OAQ в точках С и D
соответственно. Отрезки OQ и AD пересекаются в точке В, причем
площади треугольников ОАЕ и QAE равны 18 и 42 соответственно.
Найти площадь четырёхугольника OAQD и отношение ВС : BD.
4.	Решить уравнение
Зтг
|cos2«sin6«| 4- |cos6xsin2z| = sin —.
5.
Основанием треугольной пирамиды SABC служит треугольник со
сторонами АВ = ВС = 15 и АС = 18. Двугранные углы при рёбрах
АВ и ВС равны по arctg у, а при ребре АС— %. Сфера, центр которой
лежит в плоскости АВС, касается боковых граней в точках К, L и М.
Найти радиус сферы, описанной около пирамиды SKLM.
6. Найти все значения параметра а, при каждом из которых графики
функций
Зх 4-1	4ж 4- За — 7
У =------ и у -----------------—
х	ax — 1
разбивают координатную плоскость ровно на пять частей.
Варианты 2001 года
25
Вариант 7.3 (июль 2001 г.)
1.	Решить неравенство
ж > log2(101 • 10® - 102+2*) - logs(101 • 2х - 52+® • 22+2®).
/Зтг \
2.	Имеет ли уравнение 12 cos ( “Tj" + ж ) =|4 — 5 cos ж|
хотя бы одну пару корней, расстояние между которыми не превосхо-
Дит - ?
3.	Через вершины А, В, С параллелограмма ABCD со сторонами АВ =
3 и ВС = 5 проведена окружность, пересекающая прямую BD в точке
В, причем BE = 9. Найти диагональ BD.
4.	Найти все трехзначные натуральные числа, каждое из которых боль-
ше суммы квадратов своих цифр ровно на 517.
5.	Найти все числа, которые не могут быть корнями уравнения
4\/2ж4 4- х3 = a\/4 — а4(х + 4ж2 — 8)
ни при каком значении параметра а.
6.	Основание ABCD прямоугольного параллелепипеда ABCDА'В'СD'
повернули в плоскости АВС на угол 30° вокруг точки пересечения
диагоналей АС и BD (вершина А повернулась в направлении вер-
шины В), а боковые грани заменили гранями АА'В, А'В'В, ВВ'С^
В'С'С, CCD, CD'D, DD'A и D'A'A. Найти все значения, которые
может принимать периметр и площадь сечения полученного много-
гранника плоскостью, параллельной плоскости АВС, если периметр
прямоугольника ABCD равен 26, а его площадь равна 42.
26
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
8. Физический факультет
Вариант 8.1 (Олимпиада, март 2001 г.)
П D	2® 4- 5ж — 18
1.	Решить неравенство ------------< 5 .
х — 2	“
2.	Решить уравнение
2 sin 2х • cos(5z2) — sin(5a?2 4- 2ж) = 0.
3.	Решить уравнение 18* — 9*+1 — 2*+2 4-36 = 0.
4.	В треугольнике ABC AN и СМ— медианы, АВС = 120° Окруж-
ность, проходящая через точки А, М, 7V, проходит также через точку
С. Радиус этой окружности равен 7. Найти площадь треугольника
АВС.
5.	Решить неравенство
^/21og9(3a:2 — 4) > log3 л/Зх2-4.
6.	В правильной треугольной пирамиде SKLM, все ребра которой рав-
ны 8а, на ребре SK взята точка А так, что SA : АК = 1:3. Через
точку А проведена плоскость, параллельная ребру SM и высоте KN
треугольника KLM. Найти периметр сечения пирамиды этой плос-
костью.
7.	Для любого значения а решить неравенство
3(2ж — а) 4- Ьа>/2х — а — 2а2 > 0.
8.	На стороне острого угла КОМ взята точка L (L между О и К).
Окружность проходит через точки К и L и касается луча ОМ в точке
М. На дуге LM, не содержащей точки К, взята точка N. Расстояния
от точки N до прямых ОМ, ОК и КМ равны соответственно т, к и
I. Найти расстояние от точки N до прямой LM.
Варианты 2001 года
27
Вариант 8.2 (Олимпиада, май 2001 г.)
1.	Решить уравнение cos 3z = -у- cos х — - sin х .
(\\Х~х 1
2.	Решить неравенство 1-1	• 5V х > — .
3.	Решить неравенство
log3(z3 + х2 - 2х) - 2 log9(z2 - ж) < log3 5.
4.	В треугольнике АВС угол В— тупой, продолжение высот AM и CN
.—--------------------------- ----------
пересекаются в точке О, ВАС = а, ВС А = у, АС = Ь. Найти рассто-
яние от точки О до прямой АС.
5.	Решить систему уравнений
{. Icosd
sin • sin у = --------,
cos X
| cos x — 1|2 + | sin y\2 = 4.
6.	В правильной треугольной пирамиде SAB С высота равна 4, а сторо-
на основания равна 2. Шар, вписанный в пирамиду, касается граней
AS С и С SB соответственно в точках М и N. Найти длину отрезка
MN.
7.	Для каждого целого значения m найти все решения уравнения

= m2 + 1.
8.	На прямой взяты три различные точки L, М, N (М между L и N,
LM / MN). На отрезках £7И, MN и LN как на диаметрах построены
полуокружности, середины которых - соответственно точки А, В и С.
Точка С лежит по одну сторону, а точки А и В— по другую сторону от
прямой LN. Найти отношение площади фигуры, ограниченной этими
тремя полуокружностями, к площади треугольника АВС.
28
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 8.3 (июль 2001 г.)
1.	Решить уравнение tg(x + 1) • ctg(2x 4- 3) = 1.
no	11
2.	Решить неравенство —т== > ------.
у/з^х Х-2
3.	Решить уравнение 43®’+® — 8 = 2 • 8Ж з .
4.	В трапеции KLMN LM\\KN, KLM = тг/2, LM = I, КМ = k, MN =
а. Окружность проходит через точки М и N и касается прямой KL
в точке А. Найти площадь треугольника AMN.
5.	Решить неравенство
log2
ж2 + 2а: 4-1
х2 — 2х + 1
6.
В пирамиде S АВС АВ = 7, ВС = 8, С А = 9. Высоты боковых гра-
ней, проведенные из вершины S', являются касательными к сфере,
л/5
вписанной в пирамиду. Радиус этой сферы равен . Найти объем
пирамиды.
7.	Для каждого значения а найти все решения уравнения
cos 2x4-2 sin2 (х 4- а) 4- 2 — sin а = О,
принадлежащие промежутку тг < х < 2тг .
8.	В треугольнике АВС ВАС = тг/4. Прямая, параллельная стороне
АС, пересекает стороны АВ и ВС соответственно в точках М и N.
На отрезках AN и СМ как на диаметрах построены окружности. Их
общая хорда пересекает отрезок MN в точке MD : DN = у/З : 1.
Найти величину угла ВС А.
Варианты 2001 года
29
9.	Химический факультет
Вариант 9.1 (Олимпиада, май 2001 г.)
п р	1*-1|	1ж+1|
1.	Решить уравнение	-----г = ---г.
|*-2|	|я4-2|
2.	Решить неравенство 2lg^2""1^ > (ж 4- l)lg2.
3.	Решить уравнение
1оёу2+Уз+У5 ж + 1о8х(^ + \/3 - л/5) = - + logj.(2\/6).
4.	Решить уравнение arcsin ------= 2тг — тгж.
2х — 1
5.	В выпуклом шестиугольнике ABCDEF все внутренние углы при вер-
шинах равны. Известно, что АВ = 3,ВС = 4, СР = 5 и EF = 1.
Найти длины сторон DE и AF.
6.	Для каждого значения параметра а решить уравнение
sin2«4-sin2 2x4-sin2 Зя —2а(sinx4-sin 2s4-sin Зя) 4-cos я—cos Зя4-2а2 = 0.
7.	Последовательность чисел ах, аз, аз,... устроена следующим образом:
ai = 1, каждое последующее число равно удвоенной сумме предыду-
щих чисел, т.е. аз = 2ах,аз = 2(ai 4-«2) и т.д. Найти произведение
всех чисел от ах до 02001-
30
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Химический факультет,
Высший колледж наук о материалах
Вариант 9.2 (июль 2001 г.)
. т.	1	1
1.	Решить неравенство ------г > -----
|х-1|	|ж4-1|
2.	В равнобедренном треугольнике с основанием АС проведена биссек-
триса угла С, которая пересекает боковую сторону АВ в точке D,
Точка Е лежит на основании АС так, что DE ± DC. Найти длину
А£>, если СЕ = 2.
3.	Решить уравнение
tg х 4- tg 2х 4- tg х • tg 2х • tg Зж = tg Зж 4- tg 4х .
4.	Решить уравнение
\/4х — х2 4- \/4х — х2 — 3 = 3 4- \/2х — х2 .
5.	Решить уравнение
|я - 1| 4- к + 1| 4- к “ 2| 4- к 4- 2| + ... 4- к - Ю0| 4- к 4- Ю0| = 200ят.
6.	Найти все значения параметра а , при каждом из которых система
( х3 — (а 4- 3)ж2 4- (За 4- 2)х — 2а > О,
( х3 — (а 4- 3)ж2 4- Заж < О
имеет единственное решение.
7.	Функция /(ж) для всех х удовлетворяет уравнению:
f(x 4- 1) = /(ж) 4- 2х 4- 1.
Найти /(2001), если /(0) = 0.
Варианты 2001 года
31
10.	Высший колледж наук о материалах
Вариант 10.1 (май 2001 г.)
1.	Решить неравенство
2.	Решить уравнение
3.	Решить уравнение
-----4-2 <--------.
х — 2 х 4-4
3 cos 2х — 6 sin х — 2 = 0.
4.	Учительница принесла в класс счётные палочки. Дети раскладывали
их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то
осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик,
и тогда осталось 7 лишних палочек. Когда же палочки разложили по
9 штук в пакетик, то лишних палочек не осталось. Сколько, самое
меньшее, было счётных палочек?
5.	Решить неравенство
| loga.+2(x3 + 5.5а:2 4- 10.2а: 4- 6.385) < 1.
и
6.	В призме Q = ABCA^BiCi с основанием АВС тангенс угла между
плоскостями АА\С и АСС\ равен л/З, АВ перпендикулярно плос-
кости АА\СУ АВ = 1, AAi = 1. Известно, что в призму Q можно
поместить шар, касающийся всех его граней. Вычислить синус угла
АССъ
32
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
11. Биологический факультет и
факультет фундаментальной медицины
Вариант 11.1 (июль 2001 г.)
1. Решить неравенство
у/х2 + 5я — 84 >
х — 7	~
2. Решить уравнение
— sin х =
3. Решить неравенство
log2 ж — 3
61og,2-l- ’
1
2 ’
4.	Из аэропорта одновременно вылетают два самолета и сразу набирают
скорость и высоту. Они летят по замкнутым круговым маршрутам:
первый - по окружности радиуса Я, а второй - по окружности ра-
диуса г. Предполагается, что самолеты летят безостановочно с оди-
наковыми постоянными скоростями, и каждый из них облетает свою
окружность за целое число часов. Кроме того, не ранее, чем через 43
часа и не позднее, чем через 49 часов после вылета произошли сле-
дующие события: первый самолет облетел свою окружность 4 раза, а
второй облетел свою окружность 5 раз, и разрыв во времени между
г
этими событиями составил не менее 2 часов. Найти отношение — .
R
5.	В треугольник АВС со сторонами АВ = 6, ВС = 5, АС = 7 вписан
квадрат, две вершины которого лежат на стороне АС, одна на стороне
АВ и одна на стороне ВС. Через середину D стороны АС и центр
квадрата проведена прямая, которая пересекается с высотой ВН тре-
угольника АВС в точке М. Найти площадь треугольника DMC.
6.	Найти все значения параметра а, при каждом из которых система
уравнений
sinx — cos(xy/§ — 2а2),
/	2 \
cos х = ( а — - ) sin(x\/6 — 2а2)
имеет ровно одно решение на отрезке [0;2тг].
Варианты 2001 года
33
12.	Факультет почвоведения
Вариант 12.1 (Олимпиада, май 2001 г.)
1.	Решить уравнение sin х = 2 ctg х .
2.	Решить уравнение |2х 4- 3| — х2 .
3.	Решить уравнение х2 — cos 2х2 + 1=0.
4.	Найти арифметическую прогрессию, в которой сумма членов, сколь-
ко бы, начиная с первого, их ни взять, всегда равна утроенному квад-
рату числа этих же членов.
5.	Решить уравнение в целых числах:
Зя2 4- 5ху 4- 2у2 = 7.
6.	В равнобедренной трапеции средняя линия равна ш, а диагонали вза-
имно перпендикулярны. Найти площадь этой трапеции.
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 12.2 (июль 2001 г.)
1.	Решить уравнение 2 + cos 2х = 4 cos2 х .
2.	Решить уравнение у/5 — х2 = 1 — х .
3.	Решить неравенство logr_2 х < loga._2 4.
4.	В треугольнике АВС боковые стороны АВ и ВС равны, основание
АС равно 2, а угол при основании равен 30°. Из вершины А к бо-
ковой стороне ВС проведены биссектриса АЕ и медиана AD. Найти
площадь треугольника ADE.
5.	Решить неравенство
2 logjr (sin х) • log^ (sin 2х) — log£ (sin 2x) < log£ (sin x).
6.	Дано задание: на прямоугольном участке земли размером 1 м на 4 м
посадить три дерева, одно из которых должно быть в углу участка.
Расстояние между любыми двумя деревьями не должно быть меньше
2,5 м. Можно ли выполнить это задание? Ответ обосновать.
Варианты 2001 года
35
13.	Географический факультет
Вариант 13.1 (Олимпиада, май 2001 г.)
1.	Решить систему уравнений
( 9 • 2Г • 5У - 5 • Зх+у = 3х • 5У ,
। 2Х~~2 • 3y_r+1 •	— 1
2.	Решить неравенство |х — 6| + у/Зх + 1 < 5 .
3.	Из пункта А в пункт В одновременно выехали велосипедист со ско-
ростью 25 км в час и мотоциклист. Доехав до пункта В, мотоциклист
развернулся и сразу направился к пункту А, через некоторое вре-
мя встретив велосипедиста. Если бы скорость мотоциклиста была на
37.5% меньше, то расстояние от места встречи до пункта В уменьши-
лось бы в 3 раза. Найти скорость мотоциклиста.
А п	Зтг . 4
4.	Сравнить два числа: — и arcsin - .
10	5
5.	Найти все целые значения параметра ку при каждом из которых гра-
фики функций
у = log 1 (х ~ 2k) и у — log2(x — 2&3 — 3&2)
х/з
пересекаются в точке с целочисленными координатами.
6.	На одной стороне угла О взяты точки	а на другой - точки
P,Q,R так, что KQ ± PR,PL ± KM,LR ± PQ.QM ± KL. От-
ношение расстояния от центра описанной вокруг четырёхугольника
17
К PRM окружности до точки О к длине отрезка К Р равно —. Найти
величину угла О.
36
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 13.2 (июль 2001 г.)
1. Решить неравенство 1°£узТ-У21(х2
3.	Числа а, 6, с в указанном порядке образуют арифметическую прогрес-
сию, а числа a — с, с — 6, 2а в указанном порядке образуют геометри-
ческую прогрессию. Какое минимальное значение может принимать
число 2а2 — 462 — с2 + 46с 4- 6а?
4.	Стороны ромба EFGH являются гипотенузами равнобедренных пря-
моугольных треугольников EAF, FDG, GCH, НВЕ, причем все эти
треугольники имеют общие внутренние точки с ромбом EFGH. Сум-
ма площадей четырёхугольника ABCD и ромба EFGH равна 12.
Найти GH.
5.	Решить уравнение
4arcsin(2r — 7) — arccos(5® — 124) = —
6.	При каких целых значениях параметра к система неравенств
х2 + у2 _ 2х + 4у < к2 + ЮАг 4- 20,
5х2 4- 5j/2 — 2кх 4- 4ку <5 — к2
имеет хотя бы одно решение?
Варианты 2001 года
37
Ц- Филологический факультет
Вариант 14.1 (июль 2001 г.)
1.	Решить уравнение 3 cos 2х 4- 4 sin х = 1.
пт.	111
2.	Решить неравенство -----—------ > -----1- ---.
log_L(2x2 —1) logi х logi х
3.	В трапеции ABCD стороны АВ и CD параллельны и CD = 2 • АВ.
На сторонах AD и ВС выбраны соответственно точки Р и Q так,
что DP : РА = 2, BQ : QC = 3:4. Найти отношение площадей
четырёхугольников ABQP и CDPQ.
4.	Писатель-западник (3) и писатель-славянофил (С) опубликовали по
одной книге. 3 употребляет букву ”ф”в среднем на страницу текста
на 75% чаще, чем С. Тираж книги писателя С на 5% больше, чем
тираж книги писателя 3. Количество страниц в книге у 3 на 10%
меньше, чем количество страниц в книге у С. На сколько процен-
тов в опубликованных текстах 3 букв '^"больше или меньше, чем в
текстах С?
5.	При каких значениях параметра а на плоскости (ж, у) существует
круг, содержащий все точки, удовлетворяющие системе неравенств:
2у — х < 1 у
< у 4- 2х < 2,
у 4- ах > — 1.
38
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
15.	Факультет психологии
Вариант 15.1 (июль 2001 г.)
1.	Решить уравнение у/х 4- 2 4- V8 — х = л/15 .
2.	Решить неравенство
Зят + 4
3.	Решить уравнение
3 sin2 х — 3 cos х — 6 sin х 4- 2 sin 2х 4- 3 = 0 .
4.	В трапеции BCDE основание BE = 13, основание CD = 3, СЕ = 10.
На описанной около BCDE окружности взята отличная от Е точка А
так, что С А = 10. Найти длину отрезка В А и площадь пятиугольника
ABCDE.
5.	При каждом значении параметра а решить неравенство
ах4 4- х3 4- (2а 4- За3)я2 4- 2х 4- ба3 > 0 .
Варианты 2001 года
39
16.	Социологический факультет
Вариант 16.1 (июль 2001 г.)
1.	Решить неравенство---------F — > 2.
х 4- 1 И “
2.	Решить уравнение logsina. (3 sin х — cos 2х) = 0 .
3.	В городе N за последний год численность населения уменьшилась
на 4%, а число безработных увеличилось на 5%. Сколько процентов
от общего числа жителей составляют безработные, если год назад их
было 8%?
4.	Диагональ АС выпуклого четырёхугольника ABCD является диа-
метром описанной около него окружности. Найти отношение Sabc и
Sacd, если известно, что диагональ BD делит АС в отношении 2:1
(считая от точки А), а ВАС = 30°.
5.	Найти все значения параметра а, при каждом из которых расстояние
между корням уравнения
ах2 4- (2а 4- 2)ж 4- а 4- 3 = О
больше 1 .
6. Решить уравнение
2 4- х з/2 — 6ж
х
х
40
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Варианты 2002 года
Варианты 2002 года
41
1. Факультет Вычислительной математики
и кибернетики.
Вариант 1.1 (Олимпиада, апрель 2002 г.)
1.	Найдите площадь фигуры, заданной на координатной плоскости Оху
условиями
Зт/ Ч- ж > -5,
< 6 V3/+ 1 < 6 — 4?/,
х < 0.
2.	Решите неравенство
|б - log2 (4ж2 - 20ж + 25) | • log5_2a;
3.	Даны две окружности. Первая из них вписана в треугольник АВС,
вторая касается стороны АС и продолжений сторон АВ и ВС. Из-
вестно, что эти окружности касаются друг друга, сумма кубов их
радиусов равна 152, а угол ВАС равен arccos . Найдите радиус
окружности, описанной вокруг треугольника АВС.
4.	Найдите tg |ж|, если известно, что
sin х + 3 cos х +
0.
5.	При каких значениях параметра а система
( sin (2тг \/а2 — х2) = 0 ,
[ 2 • 3|аа?1 + 32-|ar| < 19
имеет наибольшее число решений ?
6.	Рассматриваются всевозможные параллелепипеды с четырьмя реб-
рами длины 4 и остальными ребрами длины 3, в которые можно
вписать шар. Найдите максимальное значение радиуса такого шара.
42
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 1.2 (июль 2002 г.)
1.	При каких значениях параметра b уравнение
Ь4х + Ь2 + (2 + у/2)Ь + 2л/2 = b2(b + V2) + 4х
имеет бесконечно много корней ?
2.	Решите неравенство
2 cos(arcsin х) — sin Г arccos х ) < 0.
3.	Дан прямоугольный параллелепипед ABCDA1B1C1D1 , у которого
AD = 6, АВ = 3 и AAi = 2. Найдите угол между прямой ACi и
прямой, проходящей через середины ребер AAi и BiCi .
4.	Из пункта А в пункт В в 8 часов утра вышел пешеход. Спустя два
часа из пункта А вслед за пешеходом по той же дороге выехали вело-
сипедист и мотоциклист. Известно, что скорость мотоциклиста в три
раза больше скорости велосипедиста. Не позднее чем через 15 минут
после своего выезда из пункта А мотоциклист обогнал пешехода и
продолжил путь в пункт В. Велосипедист обогнал пешехода спустя
не менее 45 минут после обгона пешехода мотоциклистом. Пешеход
прибыл в пункт В в 14 часов того же дня. Найдите время прибытия
мотоциклиста в пункт В.
5.	Решите систему уравнений
{</13 cos х 4- 98 sin у — </13 cos х 4- 28 sin у = 4,
2</13cos х 4- 28 sin у — </70 sin г/ 4- 8 = 2 .
6.	Биссектриса угла А треугольника АВС пересекает сторону ВС в
точке D. Окружность радиуса 35, центр которой лежит на прямой
ВС, проходит через точки А и D. Известно, что АВ2 — АС2 ==
216, а площадь треугольника АВС равна 90\/3. Найдите радиус
окружности, описанной около треугольника АВС.
Варианты 2002 года
43
Отделение бакалавров
(прикладной информатики).
Вариант 1.3 (июль 2002 г.)
1.	Решите уравнение sin 2х — 7 sin х = 0 .
2.	При каких значениях параметра b уравнение
9х + Ь2 - (2 - V3)b - 2л/3 = b4x - b2(b + Л)
не имеет корней ?
3.	Решите неравенство
__ у . 2^4*2
4.	Решите неравенство
sin (arccos х) — л/З • cos arccos < 0.
5.	Дан прямоугольный параллелепипед ABC DAiBiCiDi, у которого
AD = 4, АВ = 5 и AAi = 6. Найдите угол между прямой АС\ и
прямой, проходящей через середины ребер AAi и BiCi.
6.	Из пункта А в пункт В в 10 часов утра стартовал первый бегун.
Спустя 30 минут из пункта А вслед за первым бегуном по тому же
маршруту в пункт В одновременно стартовали еще два бегуна. Из-
вестно, что скорости второго и третьего бегунов относятся как 5:6.
Не позднее чем через час после своего старта из пункта А третий бе-
гун обогнал первого. Второй бегун обогнал первого спустя не менее
часа после обгона первого бегуна третям. Первый бегун финиширо-
вал в пункте В в 13 часов того же дня. Найдите время финиша в
пункте В третьего бегуна.
7.	Биссектриса угла А треугольника АВС пересекает сторону ВС в
точке D. Окружность радиуса 56, центр которой лежит на прямой
ВС, проходит через точки А и D. Известно, что АВ2 — АС2 = 135, а
радиус окружности, описанной около треугольника АВС равен 7л/3-
Найдите площадь треугольника АВС.
44
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
2. Геологический факультет.
Вариант 2.1 (Олимпиада, май 2002 г.)
1.	Решите неравенство —-------r Н-----< 0.
|2 — ж| х — 5 “
2.	Решите неравенство
\/бж — ж2 — 8 — \/1 — 2х > y/Sx — ж2 — 15.
3.	Решите уравнение
| log^-i (ж - 5)4 - 8 + 4 logg.,, (6® - х2 - 5) = 0.
4.	Решите систему уравнений
2 sin(2a? + у) sin у = cos 2х ,
sin 2х — sin 2у = л/2.
5.	В треугольнике АВС угол С - прямой, отношение медианы СМ к
биссектрисе CN равно у/$ : 1, высота СК = 2. Найдите площади
треугольников CNK и АВС.
6.	На полевых работах геологу нужно собрать образцы типов А и Б.
Вес одного образца типа А равен 3 кг, а типа Б - 4 кг. По каждому
из образцов типа А требуется провести 5 видов анализов, а по каж-
дому из образцов типа Б - 7 видов. Известно, что вес всех собранных
образцов не должен превышать 149 кг, а общее число всех проведен-
ных анализов должно быть не менее, чем 249. Какое минимальное
и максимальное суммарное количество образцов обоих типов можно
собрать при указанных условиях ?
7.	При каких положительных значениях параметра а неравенство
а + 2ж 5
------- > — выполнено для всех х > 10 f
ах — 4 х
8. В правильной треугольной пирамиде SABC с вершиной S и основа-
нием АВС длина стороны основания равна УЗ, расстояние между
з^/з
ребрами SA и ВС равно ——. Сфера проходит через точки С, S и
середины сторон АВ и АС. Найдите отношение площади поверхности
сферы к площади боковой поверхности пирамиды.
Варианты 2002 года
45
Вариант 2.2 (июль 2002 г.)
1.	Решите неравенство —!------(- 1 > х .
х — 2
f 1о = 2
2.	Решите систему уравнений <	2	1
[ х + у = ху+1.
( г-\2~2х	/1\^2+г-2-3
3.	Решите неравенство З2 ^Ч-б-^уЗу > 1-1
4.	Пункт С расположен между пунктами А и В, АС — 2ВС. Из пунк-
тов С и В одновременно навстречу друг другу вышли два поезда.
Время, затраченное вторым поездом на путь от В до А, не менее
чем в 6 раз превосходит время, затраченное первым поездом на путь
от С до В. Третий поезд, скорость которого равна разности скоро-
стей первых двух, затратил на путь от А до В не менее, чем в 9 раз
больше времени, чем первый поезд затратил на путь от С до места
встречи со вторым. Чему равно отношение скоростей первого и вто-
рого поездов?
5.
Найдите все решения уравнения
| sin 2ж| + cos х = 0 ,
принадлежащие отрезку
6.	В равнобедренном треугольнике АВС с основанием АС проведены
биссектриса CD и прямая DE, перпендикулярная CD (точка Е ле-
жит на прямой АС). Найдите площадь треугольника АВС, если
СЕ — 4 м, С А — 3 м.
х2
7.	При каких значениях параметра а периметр плоской фигуры, задан-
ной на координатной плоскости Оху системой
больше, чем 4 + 2л/2 Ч- ~ ?
8.	В кубе ABCDА'В'СD' с длиной ребра, равной 1, на вертикальном
ребре АА' и на горизонтальном ребре АВ взяты точки М и N со-
1	3
ответственно, при этом AM = -, AN = -. Через точки М и N
проведена плоскость, параллельная диагонали АС нижнего основа-
ния куба. Чему равна площадь получившегося сечения ?
46
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
3.	Экономический факультет.
Отделение экономики.
Вариант 3.1 (июль 2002 г.)
1.	Докажите или опровергните следующее утверждение: периметр ром-
ба с диагоналями длины 1 и 3 больше длины окружности радиуса
1.
✓	2	\ 7+11®-6®3
2.	Решите неравенство (1-------)	> 1.
\	5 /
{у — ху — х = 11,
2	2 __ on
ху — х у — Ом •
4.	Бригада рабочих выполняет задание за 42 дня. Если бы в бригаде
было на 4 человека больше и каждый рабочий бригады работал бы
на 1 час в день дольше, то это же задание было бы выполнено не
более чем за 30 дней. При увеличении бригады еще на 6 человек и
рабочего дня еще на 1 час все задание было бы закончено не ранее
чем через 21 день. Определите наименьшую при данных условиях
численность бригады, а также продолжительность рабочего дня.
5.	Решите уравнение
log2 (cos 3 ( — х^ • log2 (cos 2х) 4- log2 (sin 5х 4- sin х) = 0 .
6.	Найдите все значения а, при которых неравенство
х2 — бах 4- Юа2 4- V^3 4- бая — х2 — 10а2 >
> yJVba 4- 24 -	4-	— л/2а2| 4- |г/ - v^3a|
имеет единственное решение.
7.	Равные кубы А и В, имеющие общую вершину, расположены так,
что ребро куба А лежит на диагонали куба В, а ребро куба В лежит
на диагонали куба А. Найдите объем общей части этих кубов, если
длина их ребер* равна 1.
Варианты 2002 года
47
Вечернее отделение.
Вариант 3.2 (июль 2002 г.)
g
1.	В треугольнике АВС сторона АС равна 4, а сторона ВС равна -^= ,
Найдите площадь треугольника АВС, если известно, что угол АВС
равен 45°.
/Зя	\4а?3~ 19x4-21
2.	Решите неравенство I —------1)	< 1.
3.	Решите систему уравнений
Г х 4- ху + у = -1,
( х2у 4- ху2 = —12 .
4.	Звено тракторов вспахивает поле за 28 дней. Если бы в звене было на
2 трактора больше и каждый трактор работал бы на 1 час 30 минут
в день дольше, то это же поле было бы вспахано за 20 дней. При
увеличении звена еще на 3 трактора и рабочего дня еще на 1 час 30
минут все поле было бы вспахано за 14 дней. Определите количество
тракторов в звене и продолжительность рабочего дня.
5.	Решите уравнение
log2 cos х * log2 tg х 4- log4 (1 - cos 2я) 4- | = 0 .
6.	Найдите все значения 6, при которых неравенство
\/7Ь2 — 56я 4- ж2 4-	— я2 — 7b2 4- 5bx >
> ^60 - 2^66 + |у - 362 - л/6*>| 4- 13/ 4-	— 61
имеет единственное решение.
7.	Двугранный угол между плоскостями оснований двух равных пря-
моугольных параллелепипедов равен 120°. Найдите объем их общей
части, если известно, что эти параллелепипеды имеют общую диаго-
наль, длина ребер их оснований равна 1, а длина всех других ребер
равна
48
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Отделение менеджмента.
Вариант 3.3 (июль 2002 г.)
1. В треугольнике DEF угол DEF равен 60°. Найдите площадь тре-
g
угольника DEF , если известно, что DF = 3, EF =	.
2. Решите уравнение
о X За?2 4-17г 4-20
=i.
з J
3.	Решите систему уравнений
х 4- ху - у = 1,
ху2 — х2у = 30.
4.	Бригада рабочих выполняет задание за 42 дня. Если бы в бригаде
было на 4 человека больше и каждый рабочий бригады работал бы
на 1 час в день дольше, то это же задание было бы выполнено за
30 дней. При увеличении бригады еще на 6 человек и рабочего дня
еще на 1 час все задание было бы закончено за 21 день. Определите
численность бригады и продолжительность рабочего дня.
5.	Решите уравнение
log^/2 sin х * l°gy2 ct£ х +	(1 + cos 2ж) = 0 .
6.	Найдите все значения а, при которых неравенство
\/ж2 — бая 4- Юа2 + \/3 4- бах — ж2 — 10а2 >
> уд/За 4- 24 — —= 4- р — л/2а21 4- |г/ - У3а|
имеет единственное решение.
Варианты 2002 года
49
4- Институт стран Азии и Африки.
Вариант 4.1 (июль 2002 г.)
1.	Решите неравенство
2.	Решите уравнение
2* - 2
>0.
. л Л .	5х	ж
sm 4х 4- 2 sin	—	cos	—	= 0.
£	z
3.	Решите неравенство
х у/2 — х < х2 — х ~ 2 — \/2 — х.
4.	Решите неравенство
1°&г+1 2 + l°g2
X + 1
4
log2 (4® + 4) + ^ж+1 2
5.	В треугольнике АВС даны длины сторон АВ = 8, ВС = 6 и биссек-
триса BD = 6 . Найдите длину медианы АЕ.
6.	Решите систему уравнений
{. я*
arccos 2у 4- arcsin Зх = т ,
4
• л	п 5тг2
arcsm 2у • arccos Зх = —- .
64
Для каждого решения (ж; у) определите, какое из чисел больше:
2у — Зх или ^2 — 0.5 .
7.	Найдите все значения параметра а, при каждом из которых система
( х2 + у2 - 6 |®| - 6 |j/| + 17 < 0,
1 X2 + у2 - 2у = а2 - 1
имеет хотя бы одно решение.
50
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
5. Факультет Государственного управления.
Вариант 5.1 (июль 2002 г.)
1.	Из деревни в город вышел турист. Первую половину пути он шел
пешком со скоростью 5 км/ч, а затем оставшуюся часть пути ехал
на автобусе. Найдите среднюю скорость движения туриста на всем
маршруте, если скорость автобуса равна 45 км/ч.
2.	Решите уравнение 4х — 3 • 2г+2 — 8 = 0.
3.	Решите неравенство	—g—< 3 — х.
4.	На окружности радиуса 5, описанной около правильного треугольни-
ка, взята точка D. Известно, что расстояние от точки D до одной из
вершин треугольника равно 9. Найдите сумму расстояний от точки
D до двух других вершин треугольника.
5.	Одна труба наполняет бассейн на 2 часа, а другая на 4 часа 30 минут
дольше, чем наполняют этот бассейн обе трубы, открытые одновре-
менно. За сколько часов может наполнить бассейн каждая труба в
отдельности?
6.	Найдите все значения а, при которых система уравнений
Г (з-Уф|+ |у| - з) (|®| + 3|j/| - 9) = о,
{ (х — а)2 4- у2 = 25
имеет ровно три решения.
7.	Пять пиратов делят 10 слитков золота. Процедура дележа устроена
так: сначала старший пират предлагает дележ по своему выбору. Ес-
ли больше половины пиратов его отвергает, второй по старшинству
пират предлагает новый дележ добычи среди оставшихся четырех
(старший пират никакого участия в дальнейшем дележе не принима-
ет). Если новый дележ отвергается большинством голосов, то пред-
лагавший его пират от дальнейшего участия в дележе устраняется,
и процедура повторяется для трех пиратов. Как будут распределены
слитки золота, если каждый пират из двух данных дележей предпо-
читает тот, в котором его доля золотых слитков больше?
Варианты 2002 года
51
6. Черноморский филиал МГУ (г. Севастополь).
Вариант 6.1 (Олимпиада, май 2002 г.)
1.	Решите уравнение
2.	Решите неравенство log х (ж2 — 1)з < - .
Уз	3
3.	Самолет летает по маршруту Москва - Симферополь - Москва. Ско-
рость самолета 450 км/ч. На сколько процентов изменится длитель-
ность полета по маршруту Москва - Симферополь - Москва в без-
ветренную погоду по сравнению с полетом при наличии ветра, когда
на участке Симферополь - Москва скорость самолета уменьшается
на 50 км/ч, а на участке Москва - Симферополь увеличивается на
50 км/ч?
4.	Решите неравенство (4x+1 4- 2r+1 — 1) х х > 1.
5.	Решите систему уравнений
tg х + ctg х = 2 sin (1/ + ^) >
tg у 4- ctg у = 2 sin	•
6.	Решите неравенство х4 4- х3 + х + 1 > 18ж2 .
7.	При всех значениях а решите систему уравнений
f 2 sin х • cos 2у = (а — I)2 ,
8.	Найдите наименьшее значение функции
у = \/12 — х2 4- 4х — \/з — ж2 4- 2х.
9.	В выпуклом четырехугольнике ABCD стороны АВ и ВС равны а.
Известно также, что радиус вписанной в четырехугольник ABCD
окружности равен г и угол АВС - прямой. Найдите AD и DC и
определите значения а и г, при которых решение возможно.
52
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 6.2 (июль 2002 г.)
1.	Решите неравенство ---------j—:--> 1.
х I	““
2.	Решите уравнение arccos х = arctg х .
3.	В банк кладется 1000 руб. В каком случае вкладчик получит через
год больше денег: если банк начисляет 6% от имеющейся суммы один
раз в год или если вклад через каждые три месяца увеличивается на
1.5% ?
4.	Решите уравнение 4	4-10 = 7 • 4sin3r .
5.	Решите уравнение
sin х — у/2 cos х — у/2
\/2 cos х — 1	д/2 sin х — 1
6.	Решите неравенство
logi (2 х/г — sin х — 2 sin х) > — 1
для х из отрезка [0; тг].
7.	Непараллельные стороны трапеции перпендикулярны друг другу. Од-
на из них, равная 3, составляет с диагональю угол в 40° , а другая
наклонена под тем же углом к нижнему основанию. Найдите сред-
нюю линию трапеции.
8.	Определите все значения параметра a, при которых уравнение
log3 (ж2) + a • <0og3 fa8) + a + 1 = °
имеет ровно два решения. Найдите эти решения.
9.	Ребро куба равно a. Найдите радиус прямого кругового цилиндра,
осью которого служит диагональ куба, если известно, что поверх-
ность цилиндра касается ребра куба.
Варианты 2002 года
53
7. Механико-математический факультет
Вариант 7.1 (Олимпиада, март 2002 г.)
1.	Решите неравенство
logy^G — х — х2) + log2(x2 — 2х + 1) 4- 2 > 2 log* (я2 — 4х 4- З)2 .
2.	Точка О лежит на диагонали АС выпуклого четырёхугольника ABCD.
Известно, что ОС = OD и что точка О одинаково удалена от прямых
DA, АВ и ВС. Найти углы четырёхугольника, если АО В = 110° и
СОВ = 90°.
3.	Сумма первых четырнадцати членов арифметической прогрессии рав-
на 77. Известно, что её первый и одиннадцатый члены - натуральные
числа. Чему равен восемнадцатый член прогрессии?
Основанием пирамиды служит правильный шестиугольник
ABCDEF) а её боковое ребро SA перпендикулярно плоскости основа-
4.
ния. Расстояния от точек В и С до прямой SD равны соответственно
V 14 И V 14’ Чему Равна плоп™ь треугольника ASD7. Найти от-
ношение наименьшей из площадей треугольных сечений пирамиды,
проходящих через ребро 5D, к площади треугольника ASD.
5. Решить систему
{ — — Уху = 2 ,
---9yz = 6,
L
----3zx = 2.
z
6. Найти все значения параметра а, при каждом из которых все решения
уравнения
6 sin ^2х — ^|тга) 4- 6 sin	+ За3 — 7а2 4- За 4- 1 =
2(3а2 — 4а — 1) cos — ^тга^ + 6(а ~ 1) s*n х >
будучи отложенными на тригонометрической окружности, образуют
на ней ровно четыре точки, причём эти точки являются вершинами
трапеции.
54
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 7.2 (Олимпиада, май 2002 г.)
, и Л	tgatg/3tg7	sin a sin/3 sin 7
1.	Найти дроби -------— ----- и ——-----------г, если числа ot.fi
tga + tg/? + tg7 sin (а + fi + 7)
и 7 выбраны так, что обе дроби положительны и одна из них втрое
больше другой.
2.	Решить неравенство
yj^x — ху/х — 1 4- \/х 4- ^1 — 2# < 0.
3.	Точка М лежит на боковой стороне CD трапеции ABCD. Известно,
_________________________ 5
что BCD = CBD — ABM = arccos - и АВ = 9. Найти ВМ.
4.	Найти все значения параметра а, при каждом из которых уравнение
l°gd+i х + l°gr(19 - 8а) - 2
имеет по крайней мере два корня и при этом произведение всех его
корней не меньше 0, 01.
5.	Сфера высекает на рёбрах АВ, СВ, AS и CS треугольной пирамиды
SABC равные отрезки KL, NM, K1L1 и NiMi соответственно (точ-
ки К и Ki лежат ближе к А, чем L и £х, а точки N и Ni лежат ближе
к С, чем М и Mi). Известно, что MMi — 2KKi и 2KN = 3£хMi,
ZLSBA = Z.SBC и Z-KK1N1 = 90°. Найти отношение объёмов пира-
мид SABC и MiKLMN.
СП	С	ж2 + 4х - 1	1-х
6.	При каких ж оба числа, —г— ----- и ----, целые:
н	’ 7х2-6х-5	1 + х’
Варианты 2002 года
55
Вариант 7.3 (июль 2002 г.)
1.	Решите неравенство
1 х 1 х +1
2.	Три сферы, радиусы которых соответственно равны у/б, 1 и 1, по-
парно касаются друг друга. Через прямую, содержащую центры А и
В второй и третьей сфер, проведена плоскость у так, что центр О
первой сферы удалён от этой плоскости на расстояние 1. Найти угол
между проекциями прямых О А и ОВ на плоскость у и сравнить его
4
с arccos - .
5
3.	Из пункта А в пункт С выехал с постоянной скоростью велосипедист.
За два километра до промежуточного пункта В он решил, что необ-
ходимо ехать быстрее, и увеличив скорость в пункте В, продолжил
движение с постоянной скоростью вплоть до пункта С. Приехав в С,
велосипедист обнаружил, что время движения с каждой из скоро-
стей было прямо пропорционально соответствующей скорости и что
на первые 18 км пути он затратил времени в полтора раза больше,
чем на последние 18 км. Найти расстояние между пунктами А и В,
если известно, что расстояние между А и С равно 75 км.
4.	Четырёхугольник ABCD вписан в окружность. Точка X лежит на
3
его стороне причем ВХЦСВ и CX||BA. Найти ВС, если АХ = -
и DX = 6.
5.	Найти все значения параметра а, при каждом из которых сумма арк-
тангенсов корней уравнения
х2 + (1 — 2а)х 4- a — 4 = О
7Г
больше, чем — .
6.	Найти минимальное значение выражения (z4-j/-z)2 при условии, что
числа х, у и z одновременно удовлетворяют каждому из неравенств
4
1 < (х 4- у)2 < -, 8 < (у -4- z)2 < 9 и 10 < (z + х)2 < 11.
о
56
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
8.	Физический факультет
Вариант 8.1 (Олимпиада, март 2002 г.)
1.	Решить уравнение 2 sin2 4х • tg(sin х) 4- cos 8х = 1.
2.	Решить уравнение
28 * 1о&с+1 ((* + 1)(9г3+6а;+1)) _ 2(21о8з3)+1о6*+1(3®+1) 4-4 = 0.
\/9 + 4я - х2
3.	Решить неравенство ------------< 1.
3 х
4.	Точка С делит хорду АВ окружности радиуса 6 на отрезки АС = 4
и СВ = 5. Найти минимальное из расстояний от точки С до точек
окружности.
5.	Решить систему уравнений
(	~ 4х — Зу,
\ 4\j2x1 — у4 = Зх — 2г/.
6.	Конус вложен в двугранный угол так, что каждой грани двугранного
угла принадлежит только одна образующая конуса. Двугранный угол
равен /3, а угол в осевом сечении конуса при его вершине равен /3/2.
Найти угол между осью конуса и ребром двугранного угла.
7.	Для каждого значения а решить систему
Г 4 log2 X + 9 logs у < 4(а2 + а),
( log2 ху > 8(а2 + а).
8. Внутри прямоугольного треугольника АВС (С— прямой угол) взята
точка О так, что О А = OB = b. CD— высота треугольника АВС,
точка Е— середина отрезка ОС, DE = а. Найти СЕ,
Варианты 2002 года
57
Вариант 8.2 (Олимпиада, май 2002 г.)
log2(4a? - 3)	2
равнение ------------ =: ---.
1. Решить уравнение
log3 х log3 2 *
2.	Решить уравнение cos 8х • ctg х 4- 2 sin2 4х = ctg х .
3.	Решить уравнение 4 4- у/х 4- 9 = |а? 4- 5|.
4.	В треугольнике АВС известны стороны АВ = 14, ВС = 6, АС = 10.
Биссектрисы BD и СЕ пересекаются в точке О. Найти OD.
5.	Решить систему уравнений
2х+1 • log9 г/— 22* = 2,
9 • 2® • log27 у - Iog3 у = 9 .
6.	Окружность проходит через вершину В треугольника АВС, касается
стороны АС в ее середине D и пересекает стороны АВ и ВС в точках
М и N соответственно, АВ : ВС = 3:2. Найти отношение площади
треугольника AMD к площади треугольника DNC.
7.	Для каждого значения а решить неравенство
(ж2 4- 2а? — а2 — 4а — 3)(sin х 4- 2а?) > 0.
8.	В треугольной пирамиде SABC ребро SC перпендикулярно к грани
АВС, Z.ACB— прямой, АС = 1, ВС = 2, SC = 4л/5/5. Сфера ка-
сается плоскостей SCA, SCB и АВС, причем плоскости АВС она
касается в точке, лежащей на отрезке АВ, Найти:
а)	радиус сферы;
б)	радиус окружности, по которой пересекаются сфера и грань AS В,
58
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 8.3 (июль 2002 г.)
1. Решите неравенство
г	t _
cos эх — cos 15а? = —	§х'
2. Решить неравенство
д/2 - х
3-2я
4х”2	/3\х
3.	Решить неравенство 15 • ——— >1+1-1 .
4.	Около окружности радиуса 3 описана равнобедренная трапеция ABCD
(BC||AD), площадь которой равна 48. Окружность касается сторон
АВ и CD в точках К и L. Найти KL.
5.	Три числа, сумма которых равна 28, образуют геометрическую про-
грессию. Если к первому числу прибавить 3, ко второму числу приба-
вить 1, а от третьего числа отнять 5, то полученные числа образуют
арифметическую прогрессию. Найти эти числа.
6.	В пирамиде SBCD каждое ребро равно 3. На ребре SB взята точка
А так, что SA : АВ = 1:2. Найти радиус сферы, описанной около
пирамиды SACD.
7.	Для каждого значения а решить неравенство
logi(x2 — 6а? — а2 — 5а + 12) < —1.
и найти, при каких значениях а множество чисел а?, не являющихся
решениями этого неравенства, представляет собой отрезок числовой
оси, длина которого меньше 2\/3
8.	В треугольнике KLM отношение радиусов описанной и вписанной
окружностей равно 3. Вписанная окружность касается сторон тре-
угольника KLM в точках А, В и С. Найти отношение площадей тре-
угольников KLM и АВС.
Варианты 2002 года
59
9.	Химический факультет
Вариант 9.1 (Олимпиада, май 2002 г.)
За? х
1.	Решить уравнение 2 sin — cos — = sm х.
2.	Решить систему
' 3 tg х 4- 40 log3 у2 = 163,
<	л/2 _ sin (а? 4- |)
к log^ 9 cos х
3.	Решить неравенство
|43* _ 24*+2.3х+1 + 20 • 12* • 3* > 8 • 6* • (8*’1 4- 6*).
4.	В треугольнике АВС биссектрисы углов при вершинах А и С пересе-
каются в точке D. Найти радиус описанной около треугольника АВС
окружности, если радиус окружности с центром в точке О, описанной
около треугольника ADC, равен 6 и АСО = 30°.
5.	В усеченной пирамиде Ai А2А3А4А5А1А2А3А4А5 основания являют-
ся правильными пятиугольниками со сторонами А1А2 = 4,
А'^2 = 2. Найти объем усеченной пирамиды, если объем пирамиды
А1А{ Л2А3А4А5 равен V,
6.	При каждом значении параметра а решить уравнение
\/—z3 4- (а — 1)я2 4- (а — 1)ж 4-а = 2х2 + 3х + 2 — а.
60
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Химический факультет,
факультет наук о материалах
Вариант 9.2 (июль 2002 г.)
1.	Решить уравнение 4* — 5 • 22+® + 64 = 0.
2.	Решить систему
( И + |з/- 1| < 1,
I |х-2| + |г/-1|<1.
3.	Решить неравенство
Iogi7-г* (56 - х2 + 10а:) < |(^3+л/7(8 + Зд/7) + log3+7?2).
4.	Решить уравнение ^63 cos2 ~ — sin2 cos2 х = tg2 2х 4- sin2 х .
5.	Из точки С проведены две касательные к окружности. Точки А и В—
точки касания. На окружности взята произвольная точка М, отлич-
ная от А и В. Из точки М опущены перпендикуляры MN, ME,MD
на стороны АВ, ВС, С А соответсвенно. Найти площадь треугольника
MNE, если известно, что MN = 4,
MD = 2,ACB = 120°.
6.	Найти все значения параметра а, при каждом из которых уравнение
2~®2.4® _|_ sjn ™ + cos _ 2 — а3 — За2 4- а 4- д/2 .
4	4
имеет единственное решение.
Варианты 2002 года
61
10. Факультет наук о материалах,
факультет биоинженерии и биоинформатики
Вариант 10.1 (Олимпиада, апрель 2002 г.)
1.	Найти все значения ж, для которых точки графика функции
3
у — ---г лежат не выше соответствующих точек графика функции
х — 1
у = 2ж.
2.	Решить уравнение log3(x — 5)2 — 4 = logy^x — 1).
3.	Решить уравнение х1 — 3xt/4-t/2 4-1 + |2ж2 4- Ьху — 3t/2| = 0.
4.	Решить уравнение
/—	/	7Г\	/	7Г\	(	117Г \	/	7Г\
v3sin (Зя — — ) 4-2 sin	(8ж — — ) =	2 sin	I 2х 4- —) 4-3 cos (Зх	—	— )	.
х 5 /	\	3	/	\	15/	х	5 /
5.	Окружность радиуса 6-\/7 описана около остроугольного треугольни-
ка АВС. Через вершину В треугольника и центр окружности прове-
дена прямая, которая пересекает АС в точке D. Из точки D на сто-
роны АВ и ВС опущены перпендикуляры DK и DN соответственно.
------ 2
Найти KNb если AD : DC = 5 : 7, a sin АВС = —7=.
/7
6.	Найти все значения параметра а, при каждом из которых неравенство
4х 4- 4~х 4- 8|2Х 4- 2~х - а| 4- 11а < 26 4- 2а(2х 4- 2~х).
имеет хотя бы одно решение.
62
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
И. Биологический факультет,
факультет биоинженерии и биоинформатики
Вариант 11.1 (Олимпиада, май 2002 г.)
1.	Решить уравнение 2\/2 sin2 (х — —) — 5 sin ж 4- 5 cos х 4- 2д/2 = 0.
\	4/
2.	Решить неравенство	— 1)(\/4 • 2~12*~11 — 3 — 1) > 0.
3.	Окружность проходит через вершины Аи В треугольника АВС и ка-
--------------------------------------------------------------
сается прямой АС в точке А, Найти радиус окружности, если ВАС =
а, АВС = Р и площадь треугольника АВС равна S'.
4.	Решить неравенство
log2(\/2®2 - 1 + |®|) < log(iI.+3|(z2 - 1) • log2 I® + 3|.
5.	На ребрах AD и ВС куба ABCDAiB^CiDi соответственно взяты
точки Р и Q так, что АР : PD = 2:1, BQ : QC = 1 : 3. В каком
отношении делит объем куба плоскость, проходящая через точки Р, Q
и центр грани CCiDiD?
Варианты 2002 года
63
Биологический факультет,
факультет биоинженерии и биоинформатики,
факультет фундаментальной медицины
Вариант 11.2 (июль 2002 г.)
1.	Решить неравенство |ж — 2| > 2х 4-1.
2.	Решить уравнение sin2 2х + sin2 Зх = 1.
3.	Длины сторон треугольника АВС равны 4, 6 и 8. Вписанная в этот
треугольник окружность касается его сторон в точках D,E и F. Най-
ти площадь треугольника DEF.
4.	Решить неравенство
log2 |2х| — 5 log2 12х| 4- 2|ж| log2 |2ж| — 4|ж| 4- 6 > 0.
5.	Найти все значения параметра а, при каждом из которых уравнение
(ж24“2(а—2)х4-о2—4а)24-(а4-5)(х24-2(а —2)ж4“а2—4а)~а24-8а4-2 = 0.
имеет: а) единственное решение; б) ровно два различных решения.
64
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
12.	Факультет почвоведения
Вариант 12.1 (Олимпиада, май 2002 г.)
1.	Определить величину угла между часовой и минутной стрелками ча-
сов, показывающих 1 ч 10 мин, при условии, что обе стрелки часов
движутся с постоянными скоростями.
2.	Вычислить tg За, если sin а = 2 cos а.
3.	Решить неравенство
1
X - 1 ~ X2 *
4.	Найти все значения х из интервала (0; 2тг), при каждом из которых
наибольшее из двух чисел sin х и cos (ж 4- тг) равно - .
5.	Решить неравенство 6	<10^.
6.	Определить площадь фигуры, расположенной на координатной плос-
кости и состоящей из точек (x,t/), удовлетворяющих неравенству:
х2 + У2 < 2|ж| + 4|t/|.
7.	Основанием пирамиды является равносторонний треугольник со сто-
роной а, а высота, опущенная на это основание, равна 77, причем
все шесть ребер пирамиды касаются некоторой сферы. Найти радиус
этой сферы.
Варианты 2002 года
65
Вариант 12.2 (июль 2002 г.)
1.	Решить неравенство |5 — 7х| < 2.
2.	Вычислить cos .
8
3.	Пусть a = >/20 4- л/50. Доказать, что число а3 — 30а целое и найти
его.
4.	Решить неравенство log3 log4 х < log9 log2 Sx .
5.	Найти все значения ж, принадлежащие интервалу (-—тг; тг) и являю-
щиеся решениями уравнения:
1 /-^-----------
 .....— = у—2 cos х.
у—2 sin я
6.	Гипотенуза прямоугольного треугольника равна с, а один из острых
углов равен а. В треугольник помещены две окружности одинакового
радиуса, каждая из которых касается одного из катетов, гипотенузы
и другой окружности. Найти радиусы этих окружностей.
7.	Найти все значения параметра а, при каждом из которых уравнение
(х3 — 1)(ж2 — 16)
log10(15a - х)- log10(a: - a) '
имеет единственное решение.
66
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
13. Географический факультет
Вариант 13.1 (Олимпиада, май 2002 г.)
1.	Решить неравенство — < 2.
х
2.	Решить уравнение 22®4"1 — 15 • 2® 4-10 = 6 • 12®“1 — 1|.
3.	В треугольнике АВС точки Е и F являются серединами сторон АВ
и ВС соответственно. Точка G лежит на отрезке EF так, что EG :
АЕ = 1 : 2 и FG = BE. Найти:
а)	отношение площадей треугольников ABG и AGC\
б)	GCA, если AGC = 90°.
4.	Пункты А и В соединены двумя дорогами. Первая дорога в два раза
короче второй и проходит через пункт С. Одновременно по корот-
кой дороге из пунктов А и В выехали соответственно грузовик и
мотоцикл, каждый из которых, доехав до пункта С, вернулся в свой
исходный пункт и продолжил движение по другой дороге. Грузовик
прибыл в пункт В, а мотоцикл — в пункт А одновременно. Скоро-
сти грузовика и мотоцикла постоянные. Если бы грузовик двигался
со скоростью мотоцикла, а мотоцикл - со скоростью грузовика, то в
момент возвращения мотоцикла в пункт В, грузовик также прибыл
бы в этот пункт. Найти:
а)	отношение скоростей грузовика и мотоцикла;
б)	время движения грузовика с момента начала движения до встре-
чи с мотоциклом на второй дороге, если известно, что в пункт С он
добрался на 35 минут раньше мотоцикла.
5.	В треугольной пирамиде ABCD углы DAB и ADC - прямые, АВ = 3,
AD — 8, DC = 3, ВС > 9. Угол между прямыми, проходящими через
ребра АВ и CD, равен 60°. Найти радиус сферы, описанной около
пирамиды ABCD.
6.	Найти все значения параметра а, при каждом из которых уравнение
(а — 1) cos2 х — (а2 4- а — 2) cos х 4- 2а2 — 4а 4- 2 = 0
4тг'
имеет более одного решения на отрезке
Варианты 2002 года
67
Вариант 13.2 (июль 2002 г.)
1.	Решить уравнение |я — 2| — —.
х 2
2.	Решить уравнение
4 sin х — 3
4 sin2 х 4- sin х — 3
3.	Квадратное уравнение х2 — брх 4- q = 0 имеет два различных корня
х\ и Х2. Числа р, xi,x2,g— четыре последовательных члена геомет-
рической прогрессии. Найти xi и ж2.
4.	Тележка с передними колесами диаметром 30 см и задними колеса-
ми диаметром 40 см движется по прямой дороге, проходящей через
точки Ли В. Между точками АиВ ровно 100 метров. Точка А покра-
шена. Через точку А проезжают правые колеса тележки и в точках
соприкосновения с ней красятся. В свою очередь, при каждом сопри-
косновении с дорогой эти точки оставляют свой след в виде точек на
дороге. Никакие точки на дороге, кроме точки А, колеса не окраши-
вают. Тележка движется по направлению от точки А в сторону точки
В. Найти:
а)	наименьшее расстояние между соседними окрашенными точками;
б)	количество окрашенных точек на отрезке АВ,
5.	В треугольнике PQR точка Т лежит на стороне PR,
QTR = PQR, PT = 8,TR = 1. Найти:
а)	сторону QR;
б)	угол QRP, если радиус описанной около треугольника PQT окруж-
ности равен Зл/З.
6.	Решить систему
( х3 = 5х + у,
[ У3 =	+ х.
68
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Ц. Филологический факультет
Вариант 14.1 (Олимпиада, май 2002 г.)
2х + 1	4
1.	Решить неравенство ---— > -----.
х + 4 х + 1
2.	Полуокружность радиуса г разделена точками на 3 равные части, и
точки деления соединены хордами с одним и тем же концом диамет-
ра, стягивающего эту полуокружность. Найдите площадь фигуры,
ограниченной двумя хордами и заключенной между ними дугой.
3.	Автор и редактор вносят исправления в рукопись. При каждом про-
чтении автор увеличивает объем рукописи на 10 страниц, а редактор
каждый раз сокращает ее на 20%.
а)	Каким был первоначальный объем рукописи, если после того как
ее один раз прочитал автор, а потом дважды прочитал редактор, ее
объем составил 800 страниц?
б)	Каким был первоначальный объем рукописи, если после прочте-
ния автором, а затем редактором, и опять автором и редактором, ее
объем остался прежним?
4.	а) Решить систему
{у/З sin х > 2 sin у — cos х,
7Г
у~х= 6-
б)	Указать все решения этой системы, являющиеся одновременно ре-
шениями уравнения Vsinz • (1 — sin 2у) = 0 .
5.	Найти сумму корней уравнения
х + 1 = 2 log2(2* + 3) - 2 log4(2002 - 2~х).
6.	Для каждого значения параметра а решить уравнение
\/|ж| + 1 - i/N = а.
Варианты 2002 года
69
Вариант 14.2 (июль 2002 г.)
,	logr6 7г • arcsin f
1.	Решить неравенство ---------------- > 0.
sin \х — ) • у/х
2.	Окружность радиуса 3 проходит через середины трех сторон тре-
угольника АВС, в котором величины углов А и В равны 60° и 45°
соответственно. Найти площадь треугольника.
3.	Решить уравнение
1 4- tg2 х + л/2 sin f т ~	4* -\/3(cos х - sin х) = — - .
\4	/	ctg х
4. Положительное число а подобрано так, что меньший корень урав-
нения х3 4- 2х = 4х2 — 4 является одновременно одним из решений
неравенства а5 6®“4 > а~х +4х~4, Решить это неравенство.
5. В правильную четырехугольную пирамиду вписан шар радиуса 6, а
боковая грань составляет угол 45° с высотой пирамиды.
а) Найти площадь основания пирамиды.
б) В данную пирамиду вписан второй шар так, что он касается всех
боковых граней и первого шара; затем вписан третий шар, касающий-
ся всех боковых граней и второго шара и т.д. Найти сумму объемов
бесконечной системы вписанных шаров.
6. ”... Словарь людоеда из племени ”Мумбо-Юмбо”составляет 300 слов.
Эллочка Щукина легко и свободно обходилась тридцатью...”
Однажды людоед начал посещать проповеди миссионера, поэтому его
словарный запас стал, оставаясь целочисленным, увеличиваться на
некоторое число процентов за каждые полгода. Эллочка поступила в
вечернюю школу и каждый месяц стала узнавать целое число новых
слов, равное 50% от того количества слов, которое людоед знал к
концу первого полугодия. Однако через несколько месяцев Эллочка
бросила школу.
Какое наибольшее целое число месяцев могла проучиться Эллочка в
школе, чтобы при этих условиях словарь людоеда после одного года
посещения проповедей обязательно остался богаче словаря Эллочки?
70
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
15.	Факультет психологии
Вариант 15.1 (июль 2002 г.)
1.	Решить неравенство у/х + 1 > х — 2 .
2.	Решить неравенство logr+1(x2 + Зх — 10) > 2 .
3.	Решить уравнение 2^ + ( - J = 3.
4.	На катете АС прямоугольного треугольника АВС как на диаметре
построена окружность. Она пересекает сторону АВ в точке Е. На
стороне ВС взята точка G так, что отрезок AG пересекает окруж-
ность в точке F, причем отрезки EF и АС параллельны, BG = 2GC
и АС = 2V3. Найти GF.
5.	Решить уравнение cos 6х — 3 cos 5х 4- cos 4х — cos х 4- 5 = 0 .
6.	Решить уравнение
|х3 + 7ж2 - Их - 6| + |х3 - 12ж2 - 5х + 3| = 18ж2 - 2х - 13 .
Варианты 2002 года
71
16.	Социологический факультет
Вариант 16.1 (июль 2002 г.)
1.	Решить уравнение уЗх + 10 = х 4- 2.
2.	Решить неравенство
-L а-2 , д. _ 14(bgi (-ж2 + 5ш - 6)) < 0.
5 V л “г	•**	1“	4
3.	Определить угол А треугольника между сторонами 2 и 4, если меди-
ана, выходящая из вершины А, равна у/7.
4.	Куплен товар двух сортов: первого на 1200 руб. и второго на 1500
руб. Товара второго сорта куплено на 10 кг больше, чем первого и
по цене (за 1 кг) на 20 руб. меньше. Сколько куплено товара первого
сорта?
5.
В шар радиуса R вписана четырехугольная пирамида с квадрат-
ным основанием. Одно из боковых ребер пирамиды перпендикулярно
плоскости основания, а наибольшее боковое ребро образует с ней угол
а. Найти боковую поверхность пирамиды и вычислить ее значение
О р гг=
при а = arcsm —, R = V17.
6. Найти все значения параметра а, при каждом из которых уравнение
(1 4- а)х2 4- (1 — а)х 4- а 4- 3 = 0.
имеет по крайней мере один корень и все его корни являются целыми
числами.
72
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Варианты 2003 года
Варианты 2003 года
73
1. Факультет Вычислительной математики
и кибернетики.
Вариант 1.1 (Олимпиада, апрель 2003 г.)
1.	Сумма первых тридцати членов геометрической прогрессии с нену-
левым первым членом и ненулевым знаменателем равна удвоенной
сумме ее первых десяти членов. Найдите знаменатель этой прогрес-
сии.
2.	В равнобедренном треугольнике АВС (АВ = ВС) отношение рассто-
яний от центра вписанной в этот треугольник окружности до вершин
углов В и С соответственно равно k. Найдите углы треугольника
АВС. Каковы возможные значения k ?
3.	Найдите все решения системы неравенств
{V— sin х < \/cos3 х 4- sin2 х ,
7Г I 7Г I
— < |ж + —| < 2тг.
4.	В прямоугольном параллелепипеде KLMNK1L1M1N1 среди всех се-
чений, проходящих через точки Z, N и произвольную точку Л, лежа-
щую на ребре выбирается сечение наименьшей площади. Най-
дите диагонали этого сечения, если известно, что К Ку = a, KiNi = b
и LKi = d.
5.	Найдите все значения параметра а, при каждом из которых система
{2 Зж2 4- 2у2 4- 8х - 4у 4- 8 + 2 х2 4- 4у 4- 5 <
< 33 • 2 2x2 + У2 + 4ж + 4,
х2 4- у2 — Sx 4- Sy = а
имеет хотя бы одно решение, но среди этих решений нет удовлетво-
ряющих условию х 4- у = 0 .
6.	Решите неравенство
arcsin( sin х) 4- 3 arccos( cos х) > Зх — 18.
74
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 1.2 (июль 2003 г.)
1.	Решите неравенство log /з-г\ ( ------) > —1.
\~T~J \х 4- 1/
2.	Решите уравнение Vsin ж • sin Зх = cos х .
3.	Найдите множество значений функции
у = \4с2 — 3z 4- 2 — х .
4.	В правильную четырехугольную пирамиду SABCD вписана сфера
радиуса 2ч/б. Через точку касания этой сферы с боковой гранью
SAB параллельно прямой АВ проведена секущая плоскость Р, про-
ходящая через ближайшую к вершине S точку сферы. Известно, что
АВ = 12 \/2. Найдите площадь сечения пирамиды плоскостью Р.
5.	Найдите все значения параметра а, при каждом из которых система
неравенств	108 а-161
<	—	2 a — 3 ’
5.- 9 • 4У > 54
—
имеет решение.
6. Дан параллелограмм ABCD, у которого АВ = 3, AD = у/З 4- 1 и
Z.BAD = 60 . На стороне АВ взята такая точка /С, что АК : КВ =
2:1. Через точку К параллельно AD проведена прямая. На этой
прямой внутри параллелограмма выбрана точка Z, а на стороне AD
выбрана точка М так, что AM = KL. Прямые ВМ и CL пересека-
ются в точке N. Найдите величину угла BKN.
Варианты 2003 года
75
Отделения бакалавров
Вариант 1.3 (июль 2003 г.)
1.	Решите неравенство 3 |я 4- 2| — 4 |ж 4- 1| > 2 .
/ 12 \
2.	Решите неравенство log /1-2г\ ( ----- ) > —1.
\3z4-4/
3.	Решите уравнение у — cos х • cos Зх = — sin х.
4.	При всех значениях параметра с решите уравнение
4* + с • 25* = 3 • 10* .
5.	Найдите множество значений функции
у = \Лг2 4- 5я 4- 4 — х .
6.	Боковое ребро SA правильной четырехугольной пирамиды SABCD
равно 4\/5. Через точку касания с боковой гранью SAB вписанной
в эту пирамиду сферы параллельно прямой АВ проведена секущая
плоскость Р, проходящая через ближайшую к вершине S точку сфе-
ры. Известно, что АВ = 8. Найдите площадь сечения пирамиды
плоскостью Р,
7.	Дан параллелограмм ABCD, у которого АВ = 5, AD — 2л/3 4- 2 и
/.BAD = 30 . На стороне АВ взята такая точка К, что АК : КВ =
4:1. Через точку К параллельно AD проведена прямая. На этой
прямой внутри параллелограмма выбрана точка L, а на стороне AD
выбрана точка М так, что AM = KL. Прямые ВМ и CL пересека-
ются в точке N. Найдите величину угла BKN.
76
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
2. Геологический факультет.
Вариант 2.1 (Олимпиада, май 2003 г.)
1.	Решите уравнение sin (х —	) + 2 cos2 х — 1.
\ о/
2.	Решите неравенство
/ Зж \
log-2-я (-3 - 2®) > log-2-, - V •
3.	Целые числа A:, n, m в указанном порядке образуют геометрическую
прогрессию с целым знаменателем. Известно, что число т на 39 боль-
ше, чем А:, а прогрессия не является возрастающей. Чему равна сумма
чисел А,п и т?
4. Решите неравенство
у/х2 — 6ж — 7 х 4-1
ж —7	“ 3
5.
Окружность пересекает стороны угла ВАС в точках В, N, М и (7,
точка N находится между А и В, точка М - между А и С. Величины
7Г 7Г
углов АС В и ВМС равны — и — соответственно, BN = 2MN.
Чему равна величина угла ВАС ?
6.	При каких значениях параметра а уравнение
2тг2 (х — I)2 4- 4а cos(2ttx) — 9а3 = О
имеет единственное решение ?
7.	Решите систему уравнений
22-® = 4у V2,
\Хж2 + у2 + 1 — 2® + \/®2 + у2 — 6ж — 2у + 10 = у/5.
8.	Длина стороны правильного треугольника АВС равна у/3. На пер-
пендикуляре, восстановленном из вершины А к плоскости этого тре-
л/3
угольника, отложен отрезок AD = —-. Найдите расстояние между
о
прямыми АВ и DC.
Варианты 2003 года
77
Вариант 2.2 (июль 2003 г.)
х ~~~ 2 2х | 5
1.	Решите неравенство	Ч----ру < 0.
2.	Решите уравнение 4 ж 2 — 7х ~ 2 = 7 ж + 2 — 2 2а?+1.
3.	Два пешехода вышли одновременно навстречу друг другу из пунктов
А и В и, встретившись через 50 мин., без остановки продолжили
движение каждый в своем направлении. За какое время проходит
путь между А и В каждый из пешеходов, если известно, что первый
пришел в В на 4 час. раньше, чем второй пришел в А ?
4.	Решите систему уравнений
| 2 ж2 -у2 + 3 = 0,
| бу3- 18г/— 13а:3-Зх = 0.
5.	Прямоугольный треугольник АВС вписан в окружность. Из верши-
ны С прямого угла проведена хорда СМ, пересекающая гипотенузу
в точке К. Найдите площадь треугольника АВМ, если АК : АВ =
1:4, ВС = у/2, АС = 2.
6.	Решите уравнение \Zcos Зх • log4 I tg I х Ч- — 11=0.
7.	Найдите все значения параметра а, для каждого из которых суще-
ствует нечетное число п, удовлетворяющее равенству
Зап2 - За Ч-34"ап2 = 96п + 34'а.
8.	В правильной четырехугольной пирамиде SABCD с вершиной S от-
ношение высоты SO к длине стороны основания равно у/b. Через
точку М, лежащую на стороне основания ВС, и боковое ребро SA
проведена плоскость; при этом точка М выбрана так, что площадь
сечения пирамиды этой плоскостью является наименьшей. В каком
отношении эта плоскость делит объем пирамиды ?
78
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
3. Экономический факультет.
Отделение экономики.
Вариант 3.1 (июль 2003 г.)
1.	Решите неравенство \/5 — 4з? — z2 > — 2х — 1.
2.	Про числа а и b известно, что а + b = —12, а • Ь = 2. Вычислите
1 \ь\
значение выражения —
3.	Найдите все решения системы уравнений
4 • 49* - 4 •7*+i/iog73 + дУ _
49х 4-12 • 3х 1о6з 5 6 7+у - 4 •	= 9.
4.	На первом складе сахара было на 16 тонн больше, чем соли. За день
1	1
с первого склада вывезли — часть сахара и - часть соли, причем
т	3
сахара вывезли на 2 тонны больше, чем соли. На втором складе соли
было на 4 тонны больше, чем сахара. За день со второго склада вы-
1	1
везли также — часть сахара и - часть соли, причем сахара вывезли
т	5
на 3 тонны больше, чем соли. Сколько соли было на первом и втором
складах, если известно, что т - целое число? При каких т задача
имеет решение?
5. Площадь четырёхугольника PQRS равна 48. Известно, что PQ —
QR — 6, RS = SP, и ровно три вершины Р, Q и R лежат на окруж-
ности радиуса 5. Найдите стороны RS и SP.
6. Найдите все значения 6, при которых уравнение
3 • </Г+2 - 1662 • Ж 4- 32 =	4- Зж 4- 2
имеет единственное решение.
7. Найдите максимальный объём многогранника с пятью вершинами,
который можно поместить в шар радиуса 2\/3 .
Варианты 2003 года
79
Вечернее отделение.
Вариант 3.2 (июль 2003 г.)
1.	Решите неравенство V8 4- 2ж — ж2 < 2х + 1.
2.	Про числа а и b известно, что a + b = —18, a ♦ Ъ = 3. Вычислите
1 1
значение выражения —% — m—-%.
а3 |о| • Ъ2
3.	Найдите все решения системы уравнений
( 9х - Зх+1 • 2У - 4*'+1 = О,
( 9х + 3* • 2у+1 — 2 • 4У = 11.
4.	Под овес был выделен участок на 13 гектаров больший, чем участок
1	1
под пшеницу. За день засеяли — часть участка овса и - часть участка
71	3
пшеницы, причем овса посеяли на 3 гектара больше, чем пшеницы.
Какова площадь участка, выделенного под пшеницу, если известно,
что п - целое число? При каких п задача имеет решение?
5.	Найдите площадь четырёхугольника ABCD, если АВ = ВС = 3\/3,
AD = DC = а вершина D лежит на окружности радиуса 2,
вписанной в угол АВС, причем Z.ABC = 60°.
6.	Найдите все значения а, при которых уравнение
5 • v'z’+I - За2 •	- 16 =	+ ж - 6
имеет ровно два различных решения.
7.	Найдите минимальный радиус шара, в котором можно разместить
пару одинаковых круглых цилиндров, радиусы оснований которых
равны 3, а высоты 4.
80
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Отделение менеджмента.
Вариант 3.3 (Олимпиада, апрель 2003 г.)
1.	Решите уравнение 2 • 4х — 31 • 2х — 16 = 0.
2.	Для заготовки сена фермер три раза с интервалом в неделю скашивал
на заливном лугу одно и тоже количество травы. После трёх поко-
сов масса травы на лугу уменьшилась на 78,3% по сравнению с её
первоначальным значением до начала покосов. Определите, сколько
процентов от первоначальной массы травы на лугу составляет масса
всей скошенной травы, если еженедельный прирост травы составляет
10%.
3.	Высота правильного треугольника АВС со стороной 1 совпадает с
одной из сторон прямоугольного треугольника DEF, углы которого
составляют арифметическую прогрессию. При каком взаимном рас-
положении треугольников АВС и DEF площадь их общей части ока-
жется наименьшей? Найдите эту площадь.
4.	Решите уравнение
6х  д/1 - 9а:2 + 18а:2 - Зу/2х -1 = 0.
5.	Найдите все значения параметра 6, при которых уравнение
. /тг + 2	\	. 2 (	2
b sm I —-----х I + sin I -   — -  
k 2	J	\6+l 6+1
—by/4x2 4-8 — 8® = 3 4- arcsin |1 — ®|
имеет единственное решение.
Варианты 2003 года
81
Вариант 3.4 (июль 2003 г.)
1.	Решите уравнение -/5 — 4z — я2 = — 2х — 1.
2.	Про числа х и у известно, что х + у = 12, х • у = 6. Вычислите
1 1
значение выражения — Н—
х3 у5 6
3.	Найдите все решения системы уравнений
3 • 4х + 2r+1 • Зу - 9^ = О,
2 • 4х - 5 • 2* • Зу + 9У = -8.
4.	На складе сахара было на 10 тонн больше, чем соли. За день со склада
1	1
вывезли — часть сахара и - часть соли, причем сахара вывезли на 2
m	3
тонны больше, чем соли. Сколько соли было на складе, если известно,
что m - целое число? При каких m задача имеет решение?
5. Найдите площадь четырёхугольника ABCD, если АВ = ВС = 8,
= DC = 6, и ровно три вершины А, В и С лежат на окружности
радиуса 5.
6. Найдите все значения 6, при которых уравнение
3 • -УГ+4 - 762 • ^32® + 96 = v®2 + 7ж + 12
имеет единственное решение.
82
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
4. Высшая школа бизнеса.
Вариант 4.1 (Олимпиада, апрель 2003 г.)
1.	Решите уравнение 22 х2 4- 10 х — у/1276 х3 4- 364 а?2.
2.	После того, как 1500 новых вкладчиков открыли в банке счета на
общую сумму в 7 млн. 800 тыс. руб., средний размер вклада, состав-
лявший 6 тыс. руб., уменьшился на 10%. Определите число старых
вкладчиков банка.
g
3.	Решите неравенство \л/х + 4 — 2| > - .... .
ух 4- 4 — 3
4.	Найдите координаты центра и радиус окружности, описанной около
треугольника с вершинами К(—5; —1), £(—2; 0), М (2; — 2).
5.	Найдите область определения функции
/(») = J log 4 | - log2 (2ж) • log в | •
V Г	X &
6.	В трапеции ABCD (AD || ВС) биссектриса угла BAD пересекает
сторону CD в точке М. Найдите длину отрезка AM, если известно,
что ВМ = 8, ВС + AD = 17, а треугольники АСМ и ADM имеют
одинаковую площадь.
7.	Решите уравнение
(х — I)6 (sin 4х + sin 4) в 4- (я 4-1)6 (sin 2 — sin 2я)б = 0.
8.	Найдите все значения параметра р, при которых система уравнений
г (|®| + М - р)  (М + М +1® + у| - 2р) = о,
1	2 ।	2	1
я + У = -к
(	р2
имеет ровно 4 различных решения.
Варианты 2003 года
83
Вариант 4.2 (июль 2003 г.)
1.	Решите неравенство —----------------< 0.
2.	В банке общая сумма кредитов, выданных населению, составляет 25%
от суммы кредитов, выданных предприятиям. Какой процент от об-
щего объема кредитования в этом банке приходится на долю пред-
приятий ?
3.	Решите уравнение 2 ctg х • | sin ж| + 1 = 0.
4.	Решите систему уравнений
f 5 log32 (х + у) + log 1 (Зу - 8) = 0,
/ 2
( х2 + 2х + у2 + у = 12.
5. Найдите стороны параллелограмма ABCD, если известны координа-
ты двух его противоположных вершин А(—3;—6), С(5; 12) и точки
М(1;9), являющейся серединой стороны ВС.
6. Найдите все пары целых чисел (х; у), удовлетворяющих уравнению
2 х2 = 2 у2 -|- 3 ху + 7.
7. В равнобедренном треугольнике АВС (АВ = ВС) угол при вершине
В равен 80°, а точка М внутри треугольника расположена так, что
AM АС = 30°, a AM С А = 10°. Найдите величину угла ВМС.
8. Найдите все значения параметра а, при которых уравнение
25 х5 6 7 8 + 25 (а - 1) х3 - 4 (а - 7) х = 0
имеет ровно 5 различных решений, а сами решения, упорядоченные
по возрастанию, образуют арифметическую прогрессию.
84
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
5.	Институт стран Азии и Африки.
Вариант 5.1 (июль 2003 г.)
1.	Числа ж, у изменяются в пределах: 3 < я < 4 и 1 < у < 2. Найдите,
в каких пределах изменяется величина выражения
А = 4х 2у 1 - 4?/ 4- 4х - 4.
2.	Решите уравнение (|ж| — 5)2 — |5 — я| = 30.
3.	В правильный треугольник АВС со стороной а вписана окружность.
Эта окружность касается внешним образом трех других окружно-
стей того же радиуса в точках касания сторон треугольника. Цен-
тры внешних окружностей соответственно Oi, Оз, Оз- Найдите пло-
щадь шестиугольника, получающегося при пересечении треугольни-
ков АВС и O1O2O3.
4.	Найдите корни уравнения
tg (я 4-	+ 1 = 2 (у/2 4-1) ctg х ,
принадлежащие отрезку
7Г 7тг
4 ’ Т
5.	Решите неравенство
V(z2 +	4- 15) (256а?2 - 24а? - 1) >0.
6.	Функция у(х) = х2 4- 2(с — d)x 4~ Зс — d такова, что ?/(1) • г/(— 1) < 0 и
|с — d| > 1. Найдите величины с и <У, при которых длина промежутка,
представляющего собой множество значений функции f(x) = |t/(a?)|
на отрезке [—1; 1], наименьшая; укажите это множество значений.
Варианты 2003 года
85
6. Факультет Государственного управления.
Вариант 6.1 (июль 2003 г.)
1.	Автозаправочные станции Е и F расположены на расстоянии 3 км
одна от другой. Где наиболее выгодно разместить бензосклад, если на
АЗС Е ежедневно поставляется 8 тонн бензина, а АЗС F - 4 тонны?
2.	Решите неравенство |2я + 8| > 8 — |1 — х|.
3.	Три предприятия А, В и С на паритетных (равных) началах про-
кладывают необходимую им шоссейную дорогу длиной 16 км. Пред-
приятие А взяло на себя прокладку 10 км дороги, предприятие В -
остальных 6 км, а предприятие С внесло всю свою долю деньгами,
уплатив 16 миллионов условных денежных единиц. Как эти деньги
должны быть распределены между предприятиями А и В ?
4.	В прямоугольном треугольнике KLM проведен отрезок MD, соеди-
няющий вершину прямого угла с точкой D на гипотенузе KL так,
что длины отрезков DL, DM и DK различны и образуют в указан-
ном порядке геометрическую прогрессию со знаменателем при-
чем DL = 1. Найдите величину угла KMD.
5.	Для каждой пары чисел а и b найдите все решения неравенства
b • х2 + а < 0.
6.	Решите систему уравнений
f х + у + z = 2,
( 2ху — z2 = 4.
7.	Для того, чтобы успеть на последний электропоезд, семье из четы-
рех человек нужно перейти по пешеходному мосту быстрее, чем за 32
минуты. Одновременно по мосту могут идти не более двух человек,
причем ввиду темного времени непременно с фонариком. Если мост
проходят двое, то со скоростью того, кто идет медленнее. Успеют ли
на последний поезд все члены семьи, если известно, что в одиноч-
ку Анна может перейти мост за 2 минуты, Василий - за 4 минуты,
Игорёк - за 10 минут, Марья Ивановна - за 16 минут, а фонарик
только один.
86
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
7. Черноморский филиал МГУ (г. Севастополь).
Вариант 7.1 (Олимпиада, май 2003 г.)
1.	Найдите количество решений уравнения cos х = ——
Ответ надо обосновать.
2.	Бассейны Аи В одинаковой емкости заполняются водой через несколь-
ко труб. Через каждую трубу в бассейне А поступает на 20% меньше,
чем через каждую трубу в бассейне В. Количество труб, заполняю-
щих бассейн А, на 20% больше числа труб, заполняющих бассейн В.
Какой бассейн заполнится быстрее ?
3.	Треугольники BCD и BCiDi имеют общую медиану В А, Точка С±
лежит на отрезке АС. Найдите величину угла С, если ВС = 4, CiD =
2, В Di = 2^/3.
4. Решите неравенство
х2 — х — 2
я2 - 2я - 3
5.	Найдите такие числа а и 6, что при всех значениях х справедливо
равенство
(х2 + 5я + 6) (ж + а) = (х2 — 9) (х + Ь).
6.	Решите систему уравнений
(logy 2) • log2 (1-х) = -1,
х logy х _
4arctg2x	_ о
7.	Известно, что-------------F77rarctgx = 2тг х,
х
х2
Найдите -------------------.
х arctgx + arctg^x
8.	При всех натуральных значениях п решите неравенство
У(1 + 2»)2 - 1 — 4® > V(l-2r)2.
Варианты 2003 года
87
Вариант 7.2 (июль 2003 г.)
1.	Решите уравнение
у/ х2 — 4х + 4 — \/х2 + 2х + 1 = 3.
2.	В равнобедренную трапецию можно вписать окружность. Найдите
длину боковой стороны, если длина средней линии трапеции равна
3.
3.	Команда бегунов, состоящая из Тани и Миши, участвовала в эстафе-
те. Таня и Миша пробежали этапы равной длины, Миша со скоростью
8 м/сек, а Таня - 6 м/сек. Какова была средняя скорость команды?
4.	Найдите log54 84, если log7 12 = a, log12 24 = 6,
i	i
5.	Решите неравенство sin 4 (2ж) 4- cos4 (2а?) > 1.
6.	Решите неравенство
хз 2Г~2 । 21®~31+4 > х3 2	31+1 -|- 2r+1.
7.	Найдите все тройки чисел (ж; у; z), удовлетворяющие системе урав-
нений
( а; 4- 2t/ 4- z = 2 ,
[ 4ху — 4у — z2 = 1.
8.	Пусть в треугольнике АВС длины сторон ВС, АС и АВ равны а, b и
3
с соответственно, причем выполнено равенство а—Ъ = — с. Найдите
ЛВАС	Z.ABC
значение tg —------- ctg —---.
z	z
9.	Для всех значений параметра а Е (2; 4) найдите все целые числа х
и ?/, удовлетворяющие равенству
х2 4- Ьху 4- 6t/2 = a .
88
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
8. Механико-математический факультет.
Вариант 8.1 (Олимпиада, март 2003 г.)
1.	Найти первый член целочисленной арифметической прогрессии, у ко-
торой сумма первых шести членов отличается от суммы следующих
шести членов менее чем на 450, а сумма первых пяти членов превы-
шает более чем на 5 сумму любого другого набора различных членов
этой прогрессии.
_ _	/ 4а?7 — Юж3 о
2.	Решить неравенство \ -----х—- < х .
V 4х — х3 — 3 —
3.	На продолжении биссектрисы AL треугольника АВС за точку А взя-
та такая точка Z), что AD = 10 и В DC = BAL = 60°. Найти площадь
треугольника АВС. Какова наименьшая площадь треугольника В DC
при данных условиях?
4.	Найти площадь фигуры, заданной на координатной плоскости систе-
мой
( |г/ + log2 а?| + |t/ + 1 - 2Г'1| = |2т/ - 2х”1 + 1 + log2 а?|,
[ И 4- \у + 1| + 1з/ - 1| = х + 2-
5.	Точка О расположена в сечении АА'С'С прямоугольного паралле-
лепипеда ABCDA'B'C'D' размером 2x6x9 так, что ОАВ 4- OAD +
О А А' — 180°. Сфера с центром в точке О касается плоскостей А'В'С', АА'Н
и не имеет общих точек с плоскостью АА* D. Найти расстояние от
точки О до этой плоскости.
6.	Найти все значения а при каждом из которых расстояние между
любыми двумя соседними корнями уравнения
cos a cos За? — sin За cos х + 2 sin 2а cos 2a? = 3 sin а — cos 3a?
7Г
не превосходит
<5
Варианты 2003 года
89
Вариант 8.2 (Олимпиада, май 2003 г.)
1 п	1	11
1.	Решить уравнение ,-;-—г 4- г;—;-тг < г;-г.
|7 - log3 Зж| |4 - log9 9ж2| ~ | log9 81aj|
2.	Решить неравенство
х
cos —
2
5 cos(2x — тг) 4- 8 sin
X у---------
5 4- sin — • у 2 cos х = 0.
3.	В треугольнике АВС с углом В = 50° и стороной ВС = 3 на высоте
ВН взята такая точка D, что ADC = 130° и AD = л/З. Найти угол
между прямыми AD и ВС, а также СВЯ.
4.	Числа р и q подобраны так, что уравнение 21+® 4-p4-Q21“a7 = 0 имеет
ровно два различных корня, а их сумма равна 4. Найти произведение
всех различных корней уравнения
(х2 — 5х — 300) (ж2 — рж — q) = 0.
5.	Пирамида SABCD с боковыми ребрами AS — BS — CS = 2 вписана
5
в сферу радиуса -. Линия пересечения плоскостей ASD и BSC ка-
<о
сается сферы. Найти объем пирамиды, если
Q
АВ = ВС = -.
5
6.	Найти все значения а, при каждом из которых неравенство
logr
х — a . х — a — 1
--	4- log^ ——-
1 — ax-------------a 4- 1 — ax
> o
имеет хотя бы 3 целочисленных решения.
90
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 8.3 (июль 2003 г.)
1.	Решить неравенство
1у/х + 4 + \/х + 3	/у«4-4~	+ 3	/——г
5а / —===----——г + 4ч / —=------т= < 9л/ж 4- 4.
у у/ х 4- 4 — у ж -р 3 у 4- 4 4~	4“ 3
2.	Решить уравнение |5logx 122 — я1085® 4- 614| = 636 — 5logx 122 — £log5®.
3.	Первый член конечной геометрической прогрессии с целочисленным
знаменателем меньше последнего, но не более чем на 17, а сумма ее
членов со второго по последний не меньше 26. Найти знаменатель
прогрессии.
4.	Через вершины А и В треугольника АВС проведена окружность, ка-
сающаяся прямой ВС, а через вершины В и С - другая окружность,
касающаяся прямой АВ. Продолжение общей хорды BD этих окруж-
ностей пересекает отрезок АС в точке Е, а продолжение хорды AD
одной окружности пересекает другую окружность в точке F. Най-
ти отношение АЕ : ЕС, если АВ = 5 и ВС = 9. Сравнить площади
треугольников АВС и ABF.
5.	Найти значения а, при каждом из которых уравнение
sin arccos(5a) = a 4- arcsinsin(7« — 3)
имеет единственное решение.
6.	Высота АН тетраэдра ABCD пересекается с его высотой BE, но не
лежит в одной плоскости ни с одной из других его высот. На отрезке
НЕ = 4 взята точка О, равноудаленная от граней тетраэдра, обра-
зующая двугранный угол в 30° при ребре CD = 5. Найти площадь
сечения тетраэдра, проходящего через точку О и являющегося пря-
моугольником.
Варианты 2003 года
91
9. Физический факультет.
Вариант 9.1 (Олимпиада, март 2003 г.)
1.	Решить уравнение cos Зж — 2 sin 2х — cos х — sin х — 1 = 0.
2.	Решить неравенство 7 log3(2 4- ж)8 * * * < 8 log2(—x 4-1)7 ♦ log3 2.
3.	Решить неравенство (4* — 2 • 2х — 3) log2 х — 3 > 4^ _ 4х.
4.	В треугольнике АВС АВ = ВС, АС = 4л/3, радиус вписанной окруж-
ности равен 3. Прямая АЕ пересекает высоту BD в точке Е, а впи-
санную окружность - в точках М и ^(M между А и Е),
ED = 2. Найти EN.
5.	Решить систему
17	|	12	-з
2х2 4- 31/ Зж2 — 2у ’
6	I	34	-3
k Зж2 — 2у 2х2 4- 31/
и изобразить на координатной плоскости Оху ее решения.
6.	Площадь треугольника равна бл/б, периметр его равен 18, расстояние
А	.	2^42
от центра вписанной окружности до одной из вершин равно —-—.
Найти наименьшую сторону треугольника.
7.	Для каждого допустимого значения а в уравнении
у/х + \/— х — а
1)	найти число различных решений уравнения;
2)	найти эти решения.
8. В правильной треугольной призме АВСА\В\С\ (AAi||BBi||CCi), объ-
ем которой равен 4, проведено сечение плоскостью ACiB. В пирамиду
CiAAiBiB вписан шар. Найти:
1) площадь сечения ACiB;
2) радиус сферы, описанной около данной призмы.
92
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 9.2 (Олимпиада, май 2003 г.)
1.	Решить уравнение 2 sin(6 cos х cos 2х — 3 cos Зх) = 1.
2.	Решить систему уравнений
Г 9* • 72« = 27,
[	• 4r+1 = 32.
3.	Решить неравенство (log5(x2 — 5ж + 6)) 1 < log20 5.
4.	В треугольнике KLM даны стороны: KL = m,LM = Л,МК = I.
Биссектрисы КА и МВ пересекаются в точке О, диагонали четырех-
угольника AOBL пересекаются в точке С. Найти ВС : СА.
5.	Решить неравенство \/12ж2 + 42ж + 1 + |2ж2 + 7z| > 9.
6.	Окружность проходит через вершину угла АВС и отсекает на его
сторонах равные отрезки ВА и ВС, АВС = а. Другая окружность
касается отрезков ВА и ВС в точках М и N соответственно, а также
касается первой окружности. Найти MN : АС.
7.	Для каждого допустимого значения а решить неравенство
х/7 - loge х2 > loga х • (1 - 2 log^i a).
8.	Сфера касается плоскости основания АВС правильной треугольной
пирамиды SABC в точке С, а также касается бокового ребра SA в
точке М, SM : МА = 1:2, АВ = а. Найти радиус сферы.
Варианты 2003 года
93
Вариант 9.3 (июль 2003 г.)
1.	Решить уравнение tg2 х — 6 cos 2х = 6.
2.	Решить неравенство |ж2 4- Зж| + х2 — 2 > 0.
3.	Решить неравенство log25(5a? — 1) • log5(5®+2 — 25) < 4.
4.	В трапеции КLMN(LM\ \КN) LA— биссектриса угла KLM, точка
А— середина отрезка M7V, средняя линия равна \/5, КА = 4. Найти
LA.
5.	Решить систему уравнений
Г у/х - у = 9 - |ж 4- 2?/|,
[ х(х + 4у - 2) 4- у(4у 4- 2) = 41.
6.	В треугольнике KLM радиус описанной окружности равен Я,
К = а, точка О - центр окружности, вписанной в этот треугольник.
Прямая КО пересекает окружность, описанную около треугольника
KLM, в точке N. Найти ON,
7.	Для каждого значения а решить неравенство
я;2.212а-Ч-2x4-1
ж2 — (а — 2)ж — 2а
8.	В пирамиде SLMN даны ребра: LM = 5, MN = 9, NL = 10. Сфера
радиуса —= касается плоскости основания LMN и боковых ребер
4у14
пирамиды. Точки касания делят эти ребра в равных отношениях,
считая от вершины S. Найти объем пирамиды.
94
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
10.	Химический факультет.
Вариант 10.1 (Олимпиада, май 2003 г.)
1.	Найти все значения параметра а, при каждом из которых уравнение
ах2 4-(а4-1)#4-1 = 0 имеет единственное решение.
2.	Решить неравенство х log3 х 4-1 > log3 х • log2 3 4- х log3 2.
3.	Решить уравнение
(х 4- 1)тг	(х — 2)тг
Sin 4я2 - 4х + 2 ~ COS 4х2 — 4х + 2
4.	В треугольной пирамиде ABCD известны длины ребер:
AD = 3, CD = 5, а также углы: ABD = CBD — ВАС = тг/2; кроме
того, угол между гранями АВС и ADC равен тг/12. Найти объем
пирамиды.
5.	Найти все пары целых чисел (x,t/), удовлетворяющие системе нера-
венств:
Г у3 - Зх2 - 4у 4- 18х - 26 > О,
[ у3 4- х2 — 4у — 8х 4-14 < 0.
6.	В пятиугольник ABCDE вписана окружность, Р— точка касания
этой окружности со стороной ВС. Найти длину отрезка ВР, если
известно, что длины всех сторон пятиугольника есть целые числа,
АВ = 1 и CD = 3.
Варианты 2003 года
95
Вариант 10.2 (июль 2003 г.)
1.	Найти все значения параметра а, при каждом из которых множество
а
решений неравенства ---> 0, содержит точку х = 1.
х — a
2.	Решить уравнение cos2 8х 4- sin2 х = 2 sin2 х • cos2 Sx.
3.	Решить неравенство
1о6У2+Уз(2 - 1ж - i|) > l°g>/io(2:c - я2)
4.	Решить уравнение
Л +	• (i + -==Y(vT^7+лт^) = 8.
\	у1 — х J \	у 1 + х /
5.	Четырехугольник ABCD вписан в окружность. Известно, что пря-
мые АС и ВР перпендикулярны. Найти длину отрезка ВС, если рас-
стояние от центра окружности до стороны AD равно 2.
6.	При каких значениях параметра а система
( (х + л/2;?)2 + (у + y/2t)2 = 25 + 2aV25 - а2,
I х2 + у2 = а2,
имеет хотя бы одно решение?
96
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
11.	Факультет наук о материалах.
Вариант 11.1 (Олимпиада, апрель 2003 г.)
г -Ь 2
1.	Решить уравнение 2*5 * =100.
2.	Решить уравнение logi(l 4- (ж2 — Зя 4- 2)2) = \/я2 — 6я 4- 8.
4я
3.	Решить неравенство j---—----- > 3.
4.	Дан куб ABCDA\B\C\D\, Длина ребра куба равна За. Точки К и L
лежат на ребрах ВВ\ и DD\ соответственно, причем
ВК : KBi = DL : LD\ = 2:1. Через точки А, К, L проведена плос-
кость. Найти диагонали многоугольника, который образуется при се-
чении данного куба плоскостью AKL.
5.	Дана арифметическая прогрессия ai,...,a8i с первым членом ai =
7г/4, и разностью Зтг/10. Найти количество членов an этой прогрессии,
при каждом из которых система
( х sin ап 4- у cos an = 1,
| х tg ап - у ctg an = 1
не имеет решений.
6.	Автомобиль, двигаясь от пункта А до пункта В, проехал первую
треть пути со скоростью vi, а оставшиеся две трети - со скоростью г>2-
На обратном пути автомобиль половину всего времени движения от
В до А проехал со скоростью t>i , а вторую половину - со скоростью
t>2- Известно, что средняя скорость движения от А до В в а > 1 раз
больше средней скорости движения от В к А. Найти все значения а,
при которых задача нахождения отношения скоростей V2 и vi имеет
решение.
В июле экзамен по математике на факультете наук о материалах про-
ходил по варианту химического факультета
Варианты 2003 года
97
12.	Биологический факультет.
Вариант 12.1 (Олимпиада, апрель 2003 г.)
1.	Решить уравнение log2(1 4- 2х) = 14-2 log2 х.
2.	Решить неравенство 1 — у -—— < х.
3.	В симпозиуме по математическим проблемам в биологии, проходив-
шем в течении трех дней, участвовали биологи и математики. В пер-
вый день работы симпозиума в нем приняли участие ученые обеих
специальностей. На второй день в симпозиум прибыли дополнительно
специалисты по математике; при этом доля числа биологов в общем
числе участников симпозиума изменилась, и разность ее значений в
первый и во второй день составила 1/20. На третий день к работе
симпозиума присоединились специалисты-биологи, в результате чего
доля числа математиков в общем количестве участников изменилась,
и разность ее значений во второй и в третий день составила 7/100.
По окончании симпозиума оказалось, что первоначальная доля чис-
ла биологов больше окончательной доли числа математиков, причем
разность их значений равна 1/25. Найти долю числа биологов среди
участников симпозиума в первый день.
4.	Решить уравнение
4 • 32ж +	- 8 • 3® +	+ 2 = |4 • 3® + *7 - 1|.
5.	В квадрате ABCD точка М лежит на стороне ВС, а точка 7V— на
стороне АВ. Прямые AM и DN пересекаются в точке О. Найти пло-
щадь квадрата, если известно, что DN = 4, AM = 3, а косинус угла
DO А равен q.
6. Найти все значения параметра а, при каждом из которых система
уравнений	________
- /(«) = 0,
< у2 + (а - 5 • 106 * * *)у + 25 • 1О10 = О,
z2 + 5 • 103 • z + а = 0
имеет хотя бы одно решение, где /(я) = |х — 12| + |ж — 22| + ... + |ж —
2032|.
98
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 12.2 (июль 2003 г.)
1. Решить уравнение
2 cos2 f# + -7) + 3 cos (2х 4- тП = — 3.
\	4/	\	2/
2. Решить неравенство
4-2ж
3. Решить уравнение
у/2х • log4 х — —1.
4. Три мотоциклиста А^ВиС участвовали в показательном заезде, дви-
гаясь по трассе от старта до финиша с постоянными скоростями. Мо-
тоциклисты А и С стартовали одновременно, а мотоциклист В спустя
некоторое время. Первым к финишу пришел мотоциклист А. Мото-
циклист В через 1 час после своего старта догнал мотоциклиста С на
трассе и прибыл на финиш через 4 часа после старта мотоциклистов
А и С, и за 2 часа до финиша мотоциклиста С. Найти отношение
скорости мотоциклиста А к скорости мотоциклиста С, если известно,
g
что мотоциклист А двигался в - раза медленнее мотоциклиста В.
5
5.	В ромбе ABCD через точки А, В, С проведена окружность с центром
в точке Ох, а через точки А, В, О проведена окружность с центром
в точке Ог- Известно, что отношение длины отрезка O1O2 к длине
отрезка АО2 равно 4. Найти величину угла DAO2-
6.	Решить неравенство
(3 - х) log2(l + ^/7)«’+3«+2 > У2^Н<^3(8 +	.
Варианты 2003 года
99
13.	Факультет фундаментальной медицины.
Вариант 13.1 (Олимпиада, апрель 2003 г.)
1.	Решить уравнение log^1_a.j(4x 4- 25) = 2.
2.	Найти все значения ж, при которых числа sinz,tgx, —-— в указан-
cos х
ном порядке являются последовательными членами геометрической
прогрессии.
3.	Решить неравенство \/2 — х — у/4 4- х < л/х 4- 3.
4.	Из точки А, находящейся вне окружности с центром О, проведены
две касательные АВ и АС(В и С*— точки касания). Отрезок АО пе-
ресекается с окружностью в точке D и с отрезком ВС в точке F.
Прямая BD пересекает отрезок АС в точке Е. Известно, что пло-
щадь четырехугольника DECF равна площади треугольника ABD.
Найти угол ОС В,
5.	Найти область значений функции Iog(i6x-i2~4a;2)
6.	Найти все действительные значения параметра а, при каждом из ко-
торых не найдется ни одной такой пары чисел (иу v), чтобы функция
/(ж) = vx4 4- а(аи — 1)ж3 — 2и — 2 удовлетворяла одновременно двум
условиям /(—1) > —2и и /(1) < —2.
7.	Количество сотрудников корпорации ежегодно возрастало в геомет-
рической прогрессии и за 6 лет увеличилось на 20615 человек. Найти
первоначальную численность сотрудников корпорации.
В июле экзамен по математике на факультете фундаментальной меди-
цины проходил по варианту биологического факультета
|ж 4-1| 4- |я - 5|
3
100
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Ц. Географический факультет, факультет
биоинженерии и биоинформатики.
Вариант 14.1 (Олимпиада, май 2003 г.)
1.	Решить уравнение ctg (— 4х | 4- tg х — у/3 ( 1 — —| .
\ 2	/	\ ctg х J
2.	В треугольнике АВС проведены медиана ВМ и биссектриса ВК. Из-
вестно, что ABM = ~, CBM = АК = 6. Найти КМ.
4	о
3.	Решить неравенство: 2\/9 — х2 < х 4- 3(\/2 4-1) — |я 4- 3(\/2 — 1)|.
4.	Двум тракторам Ti и 7з необходимо вспахать два поля А и Б. Если
71 начнет вспахивать поле А и в то же время Тз начнет вспахивать
поле Б, то к моменту, когда Т\ закончит работу на А, трактору Тз
останется вспахать а гектар на поле Б. Если же, наоборот, одновре-
менно 71 начнет работать на Б, а Т2 на А, то к моменту, когда 7\
закончит вспахивать Б, трактору Т2 останется b гектар на А. Из-
вестно, что числа а и b различны, а разность b — а, уменьшенная на
25%, равна разности площадей полей А и Б, выраженной в гектарах.
Какова производительность трактора Т2 , если производительность
71 равна 9300 м2/день?
5.	Плоскость а параллельна оси цилиндра и делит границу каждого из
оснований на две части, длины которых относятся как 2:1. Сфера
касается боковой поверхности цилиндра, а также обоих его оснований
и плоскости а в точках, лежащих в одной плоскости с осью цилиндра.
Найти отношение объема цилиндра к объему сферы, если известно,
что оно больше 5 >/23-
6.	При каких значениях q числа
1
log_x_ 3’
243
\/16 — q2 cos Зх 4- <7 sin Зх; 15 — q • 21
существуют, но в указанном порядке не образуют арифметическую
прогрессию ни при каких х и у?
В июле экзамен по математике на факультете биоинженерии и био-
информатики проходил по варианту биологического факультета
Варианты 2003 года
101
1J. Географический факультет.
Вариант 14.2 (июль 2003 г.)
1.	Разность девятого и третьего членов знакочередующейся геометри-
ческой прогрессии равна ее шестому члену, умноженному на 24/5.
Найти отношение десятого к пятому члену прогрессии.
g
2.	Решить неравенство — > 7 + х.
И “
3.	Непустое множество X состоит из конечного числа N натуральных
чисел. Четных чисел в X меньше двух третей от N, а нечетных не
больше 36% от N. Какое минимальное значение может принимать
число N?
4.	Отрезки, соединяющие середины противоположных сторон выпукло-
го четырехугольника ABCD, перпендикулярны. Известно, что
——— -----—-
АС = 4, CAB+DBA = 75°. Найти площадь четырехугольника ABCD
и сравнить ее с числом 2^/15.
5.	При каких значениях параметра а уравнение
(sin х — log4 a) (sin х — 2 4- 2а) = О
7Г . 5тг ?
2;Т ’
имеет ровно два корня на отрезке
102
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
15. Факультет почвоведения.
Вариант 15.1 (Олимпиада, май 2003 г.)
1.	Решить уравнение logy^* — 1) — logy^* — 1) = 2.
2.	Решить уравнение V3sin 2х 4- 2 sin2 х = 1.
3.	Если двузначное число разделить на сумму его цифр, то в частном
получится 6, а в остатке 8. Если же число, написанное теми же циф-
рами, но в обратном порядке, разделить на разность между цифрами
десятков и единиц исходного числа, то в частном получится 15, а в
остатке 2. Найти это число.
4.	Найти все целочисленные решения уравнения
я2 4- Ьу2 4- 34z2 4- 2.ху —	— 22yz = 0.
5.	Решить неравенство log_4a?24.12a?_8 |4® — 5| > 0.
6.	Ребро куба ABCDA\B\C\D\ равно а. Найти периметр и площадь
сечения, проведенного через диагональ DC\ параллельно BD\.
Варианты 2003 года
103
Вариант 15.2 (июль 2003 г.)
1. Решить уравнение cos2 4х — 2 cos4« — 3 = 0.
2. Решить систему
/	+7®у = 1,
I 7^ + log7(® - у) = 1.
3. Решить неравенство
3 , , .
-ж 2 — |ж| > о.
4.	Найти наименьшее значение функции у = -у/За?2 + 5 — а/Зж2 на ин-
тервале [0; 3].
5.	В окружность радиуса 2 вписан угол QPR так, что PR— диаметр
3
окружности. В угол QPR вписана еще одна окружность радиуса -
так, что она касается большей окружности внутренним образом. Най-
ти величину угла QPR.
6.	Найти все значения параметра 6, при каждом из которых отрезок
[-3,-1] целиком содержится среди решений неравенства
х — 36
Ъ — 2х
< 0.
104
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
16. Филологический факультет.
Вариант 16.1 (Олимпиада, март 2003 г.)
1.	Решить неравенство (2r + 5)-1 < (2*4*3 — 2)”1.
2.	Сколько различных корней имеет уравнение sin 5тгж 4- cos 2тгж = О
на отрезке [—2; 0]?
3.	Даны такие арифметическая прогрессия {ап} и геометрическая про-
грессия {6П}, что «1 = 61,04 = 6з)^2Оз — &2 — 8. Найти разность
арифметической прогрессии.
4.	АС и BD— диагонали вписанного четырехугольника ABCD. Углы
DAC и ABD равны соответственно 7 и J, сторона CD = а. Найти
площадь треугольника ACD.
5.	Вовочка написал домашнее сочинение и допустил орфографические
и пунктуационные ошибки. Затем его сестра проверила сочинение и
исправила часть ошибок. В новом тексте количество пунктуационных
ошибок оказалось в пределах от 15, 5% до 18% от числа пунктуацион-
ных ошибок в старом тексте. Количество орфографических ошибок
уменьшилось втрое и составило 25% от числа пунктуационных оши-
бок в первоначальном тексте.
а)	Может ли в новом тексте содержаться ровно 6 ошибок?
б)	Какое наименьшее число ошибок могло содержаться в первона-
чальном тексте?
Варианты 2003 года
105
Вариант 16.2 (июль 2003 г.)
1.	Решить уравнение cos 4ж = cos4 х — sin4 х.
2.	Решить систему уравнений
f cos у • 3х +5 * * 8 = 27х +2х ♦ | cos г/|,
I 2 sin г/= log2 ж.
3.	В равнобедренном треугольнике АВС {АВ = ВС) медианы AM и
CN пересекаются в точке D под прямым углом. Найти все углы тре-
угольника АВС и площадь четырехугольника NBMD, если основа-
ние АС = 1.
4.	В двух группах учится одинаковое количество студентов. Каждый
студент изучает по крайней мере один язык: английский или фран-
цузский. Известно, что 5 человек в первой и 5 во второй группе изуча-
ют оба языка. Количество изучающих французский в первой группе
в 3 раза меньше, чем во второй. Количество изучающих английский
во второй группе в 4 раза меньше, чем в первой. Каково минимально
возможное количество студентов в одной группе?
5. Найти все значения параметра 6, при каждом из которых для любого
а неравенство
{х - a - 2b)2 + {у - За - Ь)2 < |
имеет хотя бы одно целочисленное решение {х,у).
106
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
17. Факультет психологии.
Вариант 17.1 (июль 2003 г.)
1.	Решить уравнение log3a._|_3 5 = 2.
2.	Решить уравнение sin3« • sin х = —
3.	Решить неравенство |3ж + 1| 4-	4- 4 < 3.
4.	В окружность радиуса л/? вписана трапеция с меньшим основанием
4. Через точку на этой окружности, касательная в которой парал-
лельна одной из боковых сторон трапеции, проведена параллельная
основаниям трапеции хорда окружности длины 5. Найти длину диа-
гонали трапеции и площадь трапеции.
5. При каких, значениях параметра а уравнение
2|ж — 9а| — 2а2 4- 35 4- х = О
не имеет решений? При каких (остальных) значениях параметра а
все решения этого уравнения принадлежат отрезку [—30,63]?
Варианты 2003 года
107
18. Социологический факультет.
Вариант 18.1 (июль 2003 г.)
1. Решить уравнение у/2х 4- 3 4- у/х — 2 =	4- 7.
3.	Четырехугольник ABCD вписан в окружность. Радиус окружности
равен 2, сторона АВ равна 3. Диагонали АС и BD взаимно перпен-
дикулярны. Найти CD.
4.	В городе N на должность мэра на выборах баллотировались 3 канди-
дата: Акулов, Баранов и Воробьев. В начале предвыборной кампании
предпочтения избирателей распределялись как 1 : 2 : 1. По окончании
предвыборной гонки 40% избирателей города N отказались участво-
вать в выборах, у остальных же предпочтения не изменились. Сколь-
ко процентов сторонников каждого кандидата отказались от голосо-
вания, если по окончании предвыборной гонки соотношение голосов
стало 3 : 3 : 3, 6?
5.	Двое рабочих изготовили 316 деталей, причем вторым сделано на 4
детали меньше, чем первым. Известно, что первый рабочий работал
на 3 дня дольше второго, при этом в день изготавливал на 2 детали
меньше. Сколько деталей в день делал каждый рабочий?
6.	Определить все значения параметра а, при каждом из которых три
различных корня уравнения
х3 4- (а2 — 9а)ж2 4- Sax — 64 — 0
образуют геометрическую прогрессию. Найти эти корни.
108
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Варианты 2004 года
Варианты 2004 года
109
1. Факультет Вычислительной математики
и кибернетики.
Вариант 1.1 (Олимпиада, апрель 2004 г.)
1.	Четыре числа а>, а2, «з и сц образуют в указанном порядке гео-
метрическую прогрессию. Если к ним прибавить 6, 7, 6 и 1 соот-
ветственно, то получатся числа, образующие в том же порядке ариф-
метическую прогрессию. Найдите числа ai, 02, аз и 04.
2.	Решите неравенство
3.	Найдите все целые п, при которых справедливо равенство
5"г+4",+ 13 = п -
п + 1
4.	Решите неравенство
9 log2 х 4- 36 <
А ( о 2 7Г(47 - 8х) о 7Г(47 - 8х)	\ ,
<41—8 cos2-----7------ 4- 8 cos —-— -- 4- 7 ) • log2 х.
~ \	45	45	/
5.	В параллелограмме ABCD угол между диагоналями АС и BD
равен 30°. Известно отношение АС : BD = 2 : \/3. Точка В\ сим-
метрична вершине В относительно прямой ЛС, а точка С\ сим-
метрична вершине С относительно прямой BD. Найдите отношение
площадей треугольника АВ\С\ и параллелограмма ABCD.
6.	При всех значениях параметра а решите уравнение
|ж — 3| — (1 — 2a) х2 4- (3 — 4a) ж 4- 6a — 4 =
= sin (|ж — 3| 4- 6a — 4) — sin ((1 — 2a) x2 — (3 — 4a) x) .
по
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 1.2 (июль 2004 г.)
1.	Решите уравнение
7 - 4^3 - 3 cos(аге tg(2V2)) + -тЛт) • х = 2,Og^3 - 6 * * 9-
2. Решите неравенство
х2 — 4
х/15 + 2а? — ж2 ~~
3.	Решите уравнение
2 cos2
4.	Окружность с центром в точке М касается сторон угла АОВ в точках
А и В. Вторая окружность с центром в точке N касается отрезка О А,
луча В А и продолжения стороны угла О В за точку О. Известно, что
ON : ОМ = 12 : 13. Найдите отношение радиусов окружностей.
5.	Для каждого значения параметра а найдите число решений уравне-
6. В основании прямой призмы ABCDA1B1C1D1 лежит равнобокая
трапеция ABCD (AD || ВС). Через точку Bi проведена плоскость
Р, пересекающая ребро AD в точке А”, а ребро CD - в точке N.
Прямые A Ai и С Ci эта плоскость пересекает в точках L и М со-
ответственно. Известно, что DN: DC = 3 :4, BC = DK и KN>DN.
Объем многогранника ABCNKLBiM относится к объему призмы
ABCDAiBiC\D\ как 49 : 144. Найдите отношение длины отрезка
DK к длине отрезка AD.
Варианты 2004 года
111
Отделения бакалавров
Вариант 1.3 (июль 2004 г.)
1. Решите неравенство
1оё4®-з (15 - 16ж) < 0.
2.	Решите уравнение
3. Решите неравенство
х2 — 4
—т=== < 1x1 — 2.
-/20 — х — х2
4.	При всех значениях параметра d решите неравенство
4х - d < 2х+2.
5.	Решите уравнение
6.	Первая окружность с центром в точке А касается сторон угла KOL
в точках К и L. Вторая окружность с центром в точке В касается
отрезка О/<, луча LK и продолжения стороны угла OL за точку О.
Известно, что отношение радиуса первой окружности к радиусу вто-
15
рой окружности равно —. Найдите отношение длин отрезков О В и
16
ОА.
7.	В основании прямой призмы KLMNK1L1M1N1 лежит равнобокая
трапеция KLMN (KN || LM ). Через точку Li проведена плоскость
Р, пересекающая ребро KN в точке А, а ребро MN - в точке D.
Прямые KKi и М Mi эта плоскость пересекает в точках В и С со-
ответственно. Известно, что ND:NM = 1:4, LM — AN и AD>ND.
Объем многогранника KLMDABLiC относится к объему призмы
KLMNK1L1M1N1 как 57 : 144. Найдите отношение длины отрезка
NА к длине отрезка KN.
112
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
2.	Геологический факультет.
Вариант 2.1 (июль 2004 г.)
Л — L	о
1.	Решите неравенство --------— < 4 — х ,
|ж — 2|
2.	Какие значения может принимать sin ж, если sin (ж 4- ~
3.	Решите неравенство -/441 — х2 < х 4- 21.
4.
В треугольнике АВС угол В прямой, точка М лежит на стороне
ЛС, причём AM : МС = 1 : 3-/3- Величина угла АВМ равна
6
ВМ = 6. Найдите величину угла ВАС и расстояние между центрами
окружностей, описанных вокруг треугольников ВСМ и ВАМ.
5.	Решите неравенство
l°g3-r (я2 “ Юж 4- 25) - 2 log3_r (4ж — ж2 4- 5) 4- 2 < 0 .
6.	Две группы геологов исследуют маршрут, проходящий от пункта А
через пункт В до пункта С. Первая группа проходит весь маршрут
за 2, а вторая - за 3 дня. Расстояние между А и В вдвое меньше рас-
стояния между В и С. Скорости движения групп на участках АВ и
ВС постоянны, но на участке АВ скорости обеих групп в т раз мень-
ше, чем их скорости на участке ВС. Группы выходят одновременно
из Л и С навстречу друг другу. Если первая группа выходит из Л,
а вторая из С, то они встречаются в В. Если же первая выходит из
С, а вторая из Л, то они встречаются в пункте D. Какую часть от
длины всего маршрута составляет расстояние между В и D ? Чему
равно значение т ?
7. Решите систему уравнений
8.
' sin х	1
cos(x + у) yft,'
cos у 1
. cos(r + у) ~ у/2'
Основанием пирамиды SABC является правильный треугольник АВС
со стороной длины 2-/2. Рёбра SB и SC равны, шар касается сторон
основания, плоскости грани SBC, а также ребра SA. Чему равен
СЛ
радиус шара, если SA = —— !
Варианты 2004 года
113
3.	Экономический факультет.
Отделение экономики.
Вариант 3.1 (июль 2004 г.)
1.	Вычислите произведение всех отрицательных корней уравнения
Зж3
2 sin
/-	f 13я \
= 2V5xtg ( — I .
2.	Решите неравенство 1 4- 2 sin2 (4тгж) • logi (11ж — 4ж2 — 7) < соз(8тгж).
з
3.	Окружность, пересекающая боковые стороны АС и СВ равнобедрен-
ного треугольника АС В соответственно в точках Р и Q, является
описанной около треугольника ABQ. Отрезки AQ и ВР пересекаются
в точке D так, что AQ : AD = 4:3. Найдите площадь треугольника
DQB) если площадь треугольника PQC равна 3.
4.	Решите неравенство
logr+3 (2a: + 5)-5 6 7 * * Iog4^+20x+25 (®2 + 2® +1) +log	Х (х2-ж-2) > 0.
\ 3 Зг+9 )
5. Паром грузоподъемностью 109 тонн перевозит джипы и грузовики.
Количество перевозимых на пароме грузовиков не менее чем на 20%
превосходит количество перевозимых джипов. Вес и стоимость пере-
возки одного джипа составляют 3 тонны и 600 рублей, грузовика - 5
тонн и 700 рублей соответственно. Определите наибольшую возмож-
ную суммарную стоимость перевозки всех джипов и грузовиков при
данных условиях.
6. Найдите наибольшее значение w, при котором имеет решение система
{о	2ж	о 2ж
4 sin2 у — w = 16 sin2 -4-9 ctg2 —,
(7г2 cos2 Зх — 2тг2 — 72)у2 = 2тг2(1 4- у2) sin Зж.
5
7. В правильную треугольную пирамиду с высотой h = - и стороной
4
основания а = л/15 вложены пять шаров одинакового радиуса. Один
из шаров касается основания пирамиды в его центре. Каждый из трех
других шаров касается своей боковой грани, причем точка касания
лежит на апофеме и делит ее в отношении 1 : 2, считая от вершины.
Пятый шар касается всех четырех шаров. Найдите радиус шаров.
114
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вечернее отделение.
Вариант 3.2 (июль 2004 г.)
1.	Вычислите сумму всех решений уравнения
л/3 . /14тг\	л/7
---Sin —- I 4------777—г — Х'
Х \ 3 / ctg
2.	Решите уравнение
о (7Г X \	_	. п	.	/ ч л • 2 f ^Х\
cos J • *°g2 (5 — х 4- 4х) — 4cos(ttx) = 4sm .
3.	На боковых сторонах PQ и QR равнобедренного треугольника PQR
взяты соответственно точки А и В так, что АВ : PR = 3 : 5 и вокруг
четырехугольника PABR можно описать окружность. Отрезки AR
и РВ пересекаются в точке С, причем площадь треугольника PCR
равна 10. Найдите площадь треугольника PQR.
4.	Решите неравенство
21ogr_2(7 - 2х)  log4a.2_28j.+49(x + 1) + log_r_i (х2 - 1) < 0.
2г-4	2
5.	Паром грузоподъемностью 126 тонн перевозит микроавтобусы и гру-
зовики. Вес и стоимость одного микроавтобуса составляют 5 тонн и 10
тысяч условных единиц, грузовика - 9 тонн и 8 тысяч условных еди-
ниц соответственно. Известно, что количество загруженных на паром
микроавтобусов составляет не более 70% от количества загруженных
на паром грузовиков. Определите наибольшую возможную суммар-
ную стоимость всех микроавтобусов и грузовиков, перевозимых па-
ромом при данных условиях.
6.	Найдите наименьшее значение v, при котором имеет решение система
{7T2V — 16ж2 = 167ГЖ,
2тг(1 4- |ж|) sin Зу = |ж|(2тг 4- 8 — ttcos23?/).
7.	В правильную четырехугольную пирамиду с боковым ребром I = у/5
и стороной основания a = у/2 вложены шесть шаров одинакового
радиуса. Один, из шаров касается основания пирамиды в его центре.
Каждый из четырех других шаров касается своей боковой грани в
точке пересечения ее медиан. Шестой шар касается всех пяти шаров.
Найдите радиус шаров.
Варианты 2004 года
115
Отделение менеджмента.
Вариант 3.3 (июль 2004 г.)
1.	Вычислите сумму всех решений уравнения
2.	Решите уравнение
2 sin2 (4тгж) • logi (11ж — 4ж2 — 7) = cos(8tfx) — 1.
з
3.	Площадь прямоугольного треугольника ABC (Z.C = 90°) равна 6,
радиус описанной около него окружности равен Найдите радиус
окружности, вписанной в данный треугольник.
4.	Решите неравенство
2I°gr+i(l - 2х) • l°gi-4®+4®’(a: + 3) +log 1 (ж2 4- 7х+ 12) < 0.
г 4-1
5.	Баржа грузоподъемностью 96 тонн перевозит контейнеры типов А и
Б при условии полной загрузки. Количество загруженных на баржу
контейнеров типа Б не менее чем на 25% превосходит количество за-
груженных контейнеров типа А. Вес и стоимость одного контейнера
типа А составляют 3 тонны и 5 тысяч рублей, контейнера типа Б
- 4 тонны и 2 тысячи рублей соответственно. Определите наиболь-
шую возможную суммарную стоимость всех контейнеров, перевози-
мых баржей при данных условиях.
6.	Найдите наибольшее значение и, при котором имеет решение система
{7г2и 4- 9?/2 = 9тг£/,
у2 (18 + 2тг2 — 7г2 sin2 Зж) 4- 2тг2(1 4- у2) cos Заг = 0.
116
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
4- Высшая школа бизнеса.
Вариант 4.1 (июль 2004 г.)
1 D	Х + 1	1
1.	Решите неравенство :-------? > 1.
|ж — 1| ~
2.	Решите уравнение
l°g3(3 sin х) + log 1 (cos х) = 1.
3.	Решите систему уравнений
( х + у — 20 = 0.
4.	Найдите периметр треугольника АВС, если известны координаты его
вершин Л(—3;5), В(3;—3) и точки М(6; 1), являющейся серединой
стороны ВС.
5.	Сколько времени в течение суток на электронном табло вокзальных
часов, которые показывают время в диапазоне от 00:00 до 23:59, при-
сутствует хотя бы одна цифра 3?
6.	Найдите все пары целых неотрицательных чисел (fc;m), являющихся
решениями уравнения
2k2 + 7k = 2mk 4- 3m 4- 36.
7.	Найдите наибольшее значение выражения Зж — 2у на множестве пе-
ременных ж, у у удовлетворяющих условию
4ж2 4- у2 — 16.
8.	Найдите все значения параметра р 6 [-—4; 4], при которых неравен-
ство
(р-2).((ж + 1)(р-3) + 2ж) > 0
выполняется при любых х > 0.
Варианты 2004 года
117
5. Институт стран Азии и Африки.
Вариант 5.1 (июль 2004 г.)
1.	Решите неравенство у/х2 ~ 25 • (ж 4- 3) < 0.
2.	Решите уравнение sin3 х — cos4 х = — 1.
3.	Решите систему уравнений
х2 4- у2 = xyz ,
У2 + z2 = xyz,
z2 4- х2 = xyz.
4.	Решите уравнение
(2 log4 (22® + 1) - х) • (log2 (2* + 2~х) - 2) = 8.
5.	Два круга, расстояние между центрами которых равно
д/3 4- 1, имеют радиусы л/2 и 2. Найдите отношение площади круга,
вписанного в общую часть данных кругов, к площади общей части.
6.
Найдите наибольшее и наименьшее значения выражения
у2 w2
25 + 144’
если величины ж, г/, z, w удовлетворяют системе
х2 + у2 4- 2ж 4- 4у — 20 = 0,
< z2 4- w2 - 2w - 143 = 0,
xw + yz — х 4- w 4- 2z — 61 > 0.
118
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
6.	Факультет Государственного управления.
Вариант 6.1 (июль 2004 г.)
1.	Тест, который должен пройти испытуемый, состоит из 26 вопросов.
За каждый неверный ответ у испытуемого вычитается пять очков, а
за каждый правильный - начисляется восемь очков. Испытуемый дал
ответы на все вопросы. На сколько вопросов он ответил правильно,
если в итоге сумма полученных им очков оказалась равной нулю?
2.	Решите уравнение sin 2х ~ 2 cos 4х 4- sin 6х = 2.
3.	Длины трёх сторон четырёхугольника, вписанного в окружность ра-
диуса 2^/2, одинаковы и равны 2. Найдите длину четвёртой стороны.
4.	Компания предложила 350 своим служащим выполнить сверхуроч-
ную работу, причем каждому мужчине предлагалось в виде возна-
граждения 20 долларов, а каждой женщине - 16 долларов 30 центов.
Все женщины согласились с этим предложением, а часть мужчин
отказалась. Общая сумма выплаченного вознаграждения составила
5705 долларов. Какова сумма вознаграждения, выплаченного всем
женщинам?
5.	Найдите все значения ж, удовлетворяющие неравенству
min (log3(3x + 5), \/х2 - х - 2) < 2.
6.	Каково минимальное число гирь, необходимых для того, чтобы взве-
сить любой груз массой от 1 до 39 килограммов на рычажных (ча-
шечных) весах, если известно, что этот груз может весить только
целое число килограммов?
7.	На плоскости Оху найдите наибольшее расстояние между такими
двумя точками с координатами (аг,?/), что х и у являются целыми
числами и удовлетворяют уравнению
4 - _ У. - 15
У х ху'
Варианты 2004 года
119
7. Черноморский филиал МГУ (г. Севастополь).
Вариант 7.1 (июль 2004 г.)
64ж3 - 27г/6
1. Сократите дробь
2.
3.
4.
5.
9г/4 — 16ж2
Окружность, центр которой лежит на гипотенузе прямоугольного
треугольника, касается его катетов. Найдите радиус окружности, ес-
ли длины катетов равны 3 и 4 см.
Решите уравнение sin 2х + 6 cos2 — = 3.
Три числа, которые являются последовательными членами геомет-
рической прогрессии, дают в произведении 8. Если их умножить со-
ответственно на 16, 5 и 1, то получатся три числа, являющиеся по-
следовательными членами арифметической прогрессии. Найдите три
исходных числа.
Таня и Миша отправились в 9 часов утра с одинаковой скоростью по
одному маршруту из Севастополя в Форос. Сначала они ехали на ве-
лосипедах, затем в разное время пересели на автобусы, при этом ско-
рость передвижения увеличилась в 5 раз. Известно, что Миша про-
ехал на автобусе и на велосипеде одинаковое расстояние. Таня ехала
на автобусе и на велосипеде одинаковое время. Когда Таня приехала
в Форос, если Миша приехал на 40 минут позже ?
6.
Решите систему неравенств л . 11 J с ’
( |ж 1| < э .
7.	Решите уравнение (з2я?4-з _ 3*4-1 _ j)2 _ 2 • 32я?+4 _|_ g . 3*4-1 _ j = q
8.	Найдите пару подобных треугольников, длины всех сторон которых
выражаются целыми числами, если известно, что две стороны одного
треугольника равны двум сторонам другого, а длины третьих сторон
отличаются на 61.
9.	Найдите все значения параметра а, при которых уравнение
cos2 х + cos х = 0.5| sin а| + 1.5 sin |а|
имеет ровно два решения на отрезке —тг/2 < ж < тг/2. Укажите эти
решения.
10.	Три окружности одинакового радиуса с центрами в точках Ci, Оз, Оз
проходят через одну точку О . В точках Л, В, С они пересекаются
попарно. Найдите площадь треугольника ЛВС, если известно, что
O1O2 — 2, O2O3 = 3 и O1O3 — 4.
120
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
8. Механико-математический факультет.
Вариант 8.1 (Олимпиада, март 2004 г.)
1.	Найти сумму тангенсов всех х 6 (—тг; тг) таких, что
sin 2х 4- 5 cos 2х = 3 .
2.	Решить неравенство З1обх^3я? +2*”1) < (ж2 4-x)logx 9.
3.	Найти все возможные значения суммы убывающей арифметической
прогрессии
_ 6m — т2 — 9	_ 6m — m2 — 12	_	—10
6m — m2 ’ °2 6m — m2 ’ ’ ’an 6m — m2 ’
где m— некоторое целое число.
4.	В выпуклом четырёхугольнике KLMN диагонали КМ и LN пер-
пендикулярны соответственно сторонам MN и KL, а длина сторо-
ны KN равна 4\/3- На стороне KN расположена точка А так, что
LAK = MAN, Известно, что MKN — KNL = 15°. Найти длину ло-
маной LAM и площадь четырёхугольника KLMN, если LA : AM =
1 : л/3.
5.	Найти все значения параметра а, при каждом из которых уравнение
arctg((3a — 1) sin2 or — (За3 —а2 4-За — 1) sin х 4-tg(aar —атг)) — ах 4-атг = О
имеет ровно три решения.
6.	Дана сфера радиуса 1 с центром в точке О. Из точки А, лежащей вне
сферы, проведены четыре луча. Первый луч пересекает поверхность
сферы последовательно в точках Bi и Сд, второй - в точках В2 и 6*2,
третий - в точках В$ и Сз, четвертый - в точках В4 и С4. Прямые
В1В2 и С1С2 пересекаются в точке Е, прямые В3В4 и С3С4 — в точке
F. Найти объём пирамиды OAEF, если АО = 2, ЕО — FO = 3, а угол
между гранями АОЕ и AOF равен 30°.
Варианты 2004 года
121
Вариант 8.2 (июль 2004 г.)
1.	Решить неравенство
log4(2 — ж) — log6(2 — ж) < д
log6 х - log9 х
2.	Решить неравенство
(х2 4- х 4-1)2 — 2|я3 4- х2 4-	— Зх2
Юж2 — 17а; — 6	~ ’
3.	Выпуклый многогранник ABCDFE имеет пять граней: CDF,
ABE, BCFE, ADFE и ABCD. Ребро АВ параллельно ребру CD.
Точки К и L расположены соответственно на рёбрах AD и ВС так,
что отрезок KL делит площадь грани ABCD пополам. Точка М яв-
ляется серединой ребра EF и вершиной пирамиды MABCD, объём
которой равен 6. Найти объём пирамиды EKLF, если известно, что
объём многогранника ABCDFE равен 19.
4.	Решить уравнение
V—3sin2x = —2sin2x — sinх 4- cosх — 1.
5.	Дорога проходит последовательно через пункты А, В, С и D. Рассто-
яние от А до В равно 24 км. Из А в D выехал с постоянной скоро-
стью автомобиль. Одновременно с ним из В в D отправились с посто-
янными скоростями велосипедист и мотоциклист. Когда автомобиль
догнал велосипедиста, мотоциклист обгонял их на 6 км. В пункте С
автомобиль догнал мотоциклиста, и, доехав до D, сразу поехал об-
ратно в А, встретившись с велосипедистом во второй раз в С. Найти
расстояние между В и С, если известно, что время от начала движе-
ния до момента повторной встречи автомобиля и велосипедиста в два
раза больше, чем время от начала движения до того момента, когда
автомобиль впервые догнал мотоциклиста.
6.	В остроугольном треугольнике АВС высоты пересекаются в точке Н,
а медианы - в точке О. Биссектриса угла А проходит через середину
отрезка ОН. Найти площадь треугольника АВС, если ВС = 2, а
разность углов В и С равна 30°.
122
Подготовка, к вступительным экзаменам в МГУ. ВАРИАНТЫ.
9. Физический факультет.
Вариант 9.1 (Олимпиада, март 2004 г.)
1.	Решить уравнение 6 sin
2.	Решить систему неравенств — 2 < —г---------- < — 1.
х* — х — 2
3.	Решить неравенство log32(#2 + Зя 4- 2)5 4- log2 (я2 — Зя 4- 2) < 2.
4.	Окружность с центром О вписана в ДЛВС, АВ = 4, ВС = 5,
АС = 6. Прямые ЛО, ВО и СО пересекают стороны ВС, АС и АВ в
точках K,Lia М соответственно. Найти отношение площади АВМК
к площади &CKL.
5.	Решить систему уравнений
Г |2* - 2^| + 2* + 3 • 2^ = 12^2,
| |2* + 2“у| + 2*-33 • 2“у = 0.
6.	В ДЛВС даны стороны АВ = 5, ВС = 6, АС = 7. Три окружности
попарно касаются друг друга внешним образом в точках Л, В и С.
Найти радиус наибольшей окружности.
7.	Для каждого значения а решить уравнение
logj ( -—— ) + 4(log4(a: - За)) log2 х - 8 log4 х = 0.
\ X )
8.	В правильной треугольной призме АВС А\В\С\ (ЛЛ1ЦВВ1ЦСС1)
ЛЛ1 : АВ = 4:3. На боковых ребрах ЛЛ1, BBi и CCi взяты точки
К, L и М соответственно, так что АК : КА^ =3:1, BL = LB\,
CM : MC\ = 1 : 3. Найти двугранный угол между плоскостями
KLM и ЛВС.
Варианты 2004 года
123
Вариант 9.2 (июль 2004 г.)
1.	Решить уравнение sin х • sin 4х + sin 5х • sin 2х — cos Зж = 0.
1х — 11
2.	Решить неравенство --------g--< —1.
1 ” к -1|
3.	Решить неравенство
log2((2 - 2х - х2)(х + 2)) - log8((4 + 4х + х2)(8х + 16)) + 1 > 0.
4.	В окружности с радиусом 4 через точку D диаметра ВС (BD : DC =
5 : 3) проведена хорда EF, перпендикулярная к этому диаметру. Най-
ти радиус окружности, касающейся отрезков ВD, DF и дуги BF.
5.	Решить систему уравнений
Г 3.2х~2у - у/2х - 2у = 24 - х,
( 2х~2у + 2д/2х — 2^/ = 2ят 4- 8.
6.	В трапеции BCDE (CD\\BE) BCLBE. BE =14,
LN— средняя линия (точка L на стороне ВС). Прямая, проходящая
через точку В и перпендикулярная к стороне DE, пересекает отрезок
LN в точке Af, LM : MN = 2:1. Найти площадь трапеции BCDE.
7.	При каких значениях а уравнение (1 + sin Sax)y/5irx — х2 = О
имеет ровно 5 различных корней?
8.	В правильной треугольной пирамиде SLMN с вершиной S проведена
медиана МР в треугольнике SMN и даны LM = 2, SL = 6. Через
середину К ребра SM проведена прямая КЕ, параллельная ребру
LN. Через точку L проведена прямая, пересекающая прямые МР и
КЕ в точках А и В соответственно. Найти длину отрезка АВ.
124
Подготовка к вступительным экзаменам в МГУ, ВАРИАНТЫ,
10.	Химический факультет.
Вариант 10.1 (июль 2004 г.)
1. Решить неравенство
10 4- Зя — х2
я2 — Зя 4- 2 “
2.	Решить уравнение у/1 4- sin х =1 — 2 sin х.
3.	Решить неравенство
0og5 х + 3 - yiog5 ж — 2 < yiog5 ж — 1.
4.	Известно, что трапеция ABCD— равнобедренная,
BCtfAD и ВС > AD, Трапеция ECDA также равнобедренная, при-
чем AEtfDC и АЕ > DC, Найти BE, если известно, что косинус
5.	Дан куб EFGHE1F1G1H1 с длиной ребра, равной 2. На рёбрах ЕН
и HHi взяты точки А и В такие, что ЕА : АН = 2:1, НВ : ВН\ =
1 : 2. Через точки Л, В, G\ проведена плоскость. Найти расстояние
от точки Е до этой плоскости.
6.	Найти все значения параметров а и 6, при которых среди корней
уравнения
cos2 х 4- (а2 — ab 4- Ъ2 — З)2 — (4а2 — 4 — 62 4- 2а6)(я 4- 1)2® = О
есть два различных корня с равными абсолютными величинами.
Варианты 2004 года
125
11.	Факультет наук о материалах.
Вариант 11.1 (Олимпиада, апрель 2004 г.)
1.	Для приготовления водного раствора кислоты взяли 4 литра 40%-го
и 6 литров 60%-го растворов кислоты. Затем часть полученной смеси
вылили и добавили такое же количество чистой воды, в результа-
те чего получился 39%-ный раствор кислоты. Сколько литров воды
было добавлено?
3	1
2.	Решить неравенство |3» + 1| + 2 + |3i+[|_2 < |3l+1| + 2 
3.	Решить уравнение
l°g2«’(4a;2 + 8 “ 8ж\/2) + log2r3(2®2 + 4 + ж\/32) = ^2х2 .
*°g8r3 2
4.	В треугольнике АВС прямые, содержащие высоты AP,CR и BQ
(точки Р, R и Q лежат на прямых, содержащих соответствующие сто-
роны треугольника ЛВС), пересекаются в точке О. Найти площади
треугольников АВС и РОС, если известно, что ЯРЦЛС, АС = 4 и
----------24
sin АВС = —.
25
5.	Решить уравнение \/sin ж 4- 2 cos 2х — \/2cos2x = 0.
6.	При каких значениях параметра а неравенство
(3 4- 2x/2f 4- (а4 4- 6 - 4а2)(3 - 2у/2)* 4- 22у - а • 2у+1 4- а2 - у/8 < О
имеет хотя бы одно решение (ж, у) ?
В июле экзамен по математике на факультете наук о материалах
проходил по варианту химического факультета
126
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
12.	Биологический факультет, факультет
фундаментальной медицины, факультет
биоинженерии и биоинформатики.
Вариант 12.1 (июль 2004 г.)
1.	Решить уравнение у/х 4- 2 = |я — 1|.
2.	Решить уравнение sin х • sin Зх = cos 2х • cos 4х .
3.	В равнобедренной трапеции с основаниями 1 и 4 расположены две
окружности, каждая из которых касается другой окружности, двух
боковых сторон и одного из оснований. Найти площадь трапеции.
4.	Решить неравенство
!og(2^ _ 2)2(4®+1 - 5 • 2r+2 + 24)-
-log(2,_2)-3 (2^-2-7-2-2 + -j>-.
5.	В шар радиуса 4 вписана правильная шестиугольная пирамида с вы-
сотой 6, а в неё вписан второй шар. Найти радиус второго шара.
Варианты 2004 года
127
13.	Факультет почвоведения.
Вариант 13.1 (Олимпиада, май 2004 г.)
1.	Вычислить sin 255°.
/- ------ о 1
2.	Пусть а = ylO - yll. Доказать, что число а 4—- является целым.
а2
3.	Решить неравенство 4® < 2®+1 + 3 .
4.	Решить уравнение	| cos ж — 2 sin ж | 4- cos ж = 0.
5.	Точки М и N находятся на боковых сторонах АВ и CD трапеции
ABCD, прямая MN параллельна AD, а отрезок MN делится диа-
гоналями трапеции на три равные части. Найти длину отрезка MN,
если AD = а, ВС = Ь, а точка пересечения диагоналей трапеции ле-
жит внутри четырёхугольника MBCN.
6.	Шарик радиуса г брошен в стакан, образованный вращением парабо-
лы у = Зж2 вокруг оси Оу. При каком наибольшем значении г шарик
достигнет дна стакана (точки О = (0,0))?
128
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 13.2 (июль 2004 г.)
1.	Найти наибольшее и наименьшее значение функции у = 2х2 — Зх при
х е [-1;3].
2.	Решить уравнение |5а? 4- 1| 4- 7а? 4-2 = 0.
3.	Решить уравнение
\/а?2 4- 5а? 4- 4 — \/а?2 — а? — 6 = — \/2а?2 4- 4а? — 2.
4.	Решить неравенство log0 5(2a;+1 — 3) > а? — 1.
5.	Найти все значения а?, удовлетворяющие неравенству 0 < х < 7Г и
являющиеся решениями уравнения
д/tg Зж = V- tg Ж.
6.	В окружность радиуса 5 вписан квадрат. На окружности отмечена
точка, расстояние от которой до одной из вершин квадрата равно 6.
Найти расстояние от этой точки до трёх других вершин квадрата.
7.	Доказать, что график функции
У = 4а: 4- log2
а?2 4- 5а?
а?2 4- За? — 4
имеет центр симметрии, и найти координаты (а:, у) этого центра сим-
метрии.
Варианты 2004 года
129
Ц. Географический факультет.
Вариант 14.1 (июль 2004 г.)
1.	Решить неравенство ---------—>0.
х — 3
Л _	sin Зж _
2.	Решить уравнение  --------;—— = 0 .
sm х 4- sm 2х
3.	Пункты А и В соединены двумя дорогами. Первая дорога разделена
паромной переправой с одним паромом. На второй дороге препят-
ствий нет. Переправа на пароме занимает полчаса. Паром работает
без перерывов. Из пункта А по первой дороге выезжает автомобиль,
скорость движения которого по дороге равна 60 км/ч. Одновременно
с ним из пункта В по той же дороге выезжает трактор со скоро-
стью 20 км/ч. Автомобиль без задержки переправляется паромом и
встречает трактор, ожидающий паром. После прибытия в пункт В
автомобиль без остановки возвращается по второй дороге и прибы-
вает в пункт А на 15 минут раньше трактора, затратив на обратный
путь на полчаса больше, чем на путь из А в В. Найти:
а)	разность между длинами второй и первой дорог, не учитывая дли-
ну переправы;
б)	длину второй дороги, если известно, что, поехав обратно по первой
дороге, автомобиль прибыл бы в пункт А одновременно с трактором.
4.	В выпуклом четырёхугольнике ABCD точки К, L, М, N— середины
сторон АВ, ВС, CD, DA соответственно. Отрезки КМ и LN пересе-
каются в точке Е. Площади четырёхугольников AKEN, BKNL и
DNEM равны соответственно 6, 6 и 12. Найти:
а)	площадь четырёхугольника СМ ЕЕ,
б)	отрезок CD, если АВ = 0,5.
5.	При каких значениях параметра а система
f |х - а| + \у - а| 4- |а 4- 1 - а?| 4- |а 4-1 - т/| = 2,
[ у 4- 2|а? - 5| = 6
имеет единственное решение?
6.	Сколько цифр содержится в десятичной записи 99991-го члена после-
довательности ап, если а\ — 0, ап_|_i = 2ап 4- 1024,
Ig 2 = 0,301029...?
130
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
15.	Факультет психологии.
Вариант 15.1 (июль 2004 г.)
1.	Решить уравнение 4Г — 12 • 2Г — 1 = 0.
х + 2
2.	Решить неравенство log х-2 ----< 1 •
2г—10	4
3.	Решить уравнение
V15 cos х • ctg х + \/5 cos x 4- V5 ctg x — 0
и найти сумму его различных корней, принадлежащих отрезку [—тг; тг].
4.	Окружность радиуса 3 проходит через вершины А и В прямоуголь-
ного треугольника АВС с катетом АВ = 5. Прямая CD касается этой
окружности в точке D. Найти величину угла ABD и длину второго
катета АС, если луч DA делит угол CDB пополам.
5.	Найти все значения параметра а, при каждом из которых уравнение
|®2 — 5|ж|| = а[х 4- 4)
имеет ровно три различных корня.
Варианты 2004 года
131
16.	Филологический факультет.
Вариант 16.1 (июль 2004 г.)
, „	2 2а - 1
1.	При каких значениях параметра а уравнение х 4- х 4--— = О
а 4- 5
не имеет решений?
(7Г \
Зх ~ 2/ ~ 1 = О
3.	Решить уравнение (ж 4- 4) (ж2 4- 4) = 5 — 2Х+4 — 16(л/2)* .
4.	Из точки М на плоскость а опущен перпендикуляр МН длины л/3
и проведены две наклонные, составляющие с перпендикуляром углы
по 60°. Угол между наклонными равен 120°.
а)	Найти расстояние между основаниями А и В наклонных.
6)	На отрезке АВ как на катете в плоскости а построен прямоуголь-
ный треугольник АВС (угол А— прямой). Найти объём пирамиды
МАВС, зная, что cos ВМС = — -.
5.	Криптографическая лаборатория получила задание расшифровать
три текста одинакового объёма. Капитан Иванов на расшифровку
первого и второго текстов в сумме затратил 40,5 минут, а на расшиф-
ровку второго и третьего - 37,5 минут. Оказалось также, что второй
текст он расшифровывал с такой же скоростью, как в среднем первый
и третий. За какое время капитан Иванов выполнил задание?
6.	Дана система уравнений
( у — а\х — За|,
[ |ж| = 6- |г/|.
а)	При каких значениях параметров а и b эта система относительно
неизвестных х и у имеет бесконечно много решений?
б)	На плоскости (ж, у) изобразить множество точек, координаты кото-
рых таковы, что система относительно неизвестных а и b имеет ровно
три решения.
132
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
17. Социологический факультет.
Вариант 17.1 (Олимпиада, апрель 2004 г.)
1. Решить уравнение
ж3 4- 7ж2 4- Юж — 3(ж2 4- 7ж) — 30 _
2.	Дана функция т/(ж) = |ж — 3| 4- |2ж — 4| 4- 1.
а)	Найти наименьшее значение функции у(х) .
б)	Решить неравенство у(х) > 8.
3.	На факультете X отличники составляют 10% от общего количества
студентов этого факультета, а на факультете Y—20%, а на факультете
Z— лишь 4%. Найти средний процент отличников по всем трём фа-
культетам, если известно, что на факультете Y учится на 50% больше
студентов, чем на факультете X, а на факультете Z— вдвое меньше,
чем на факультете X.
4.
В прямоугольном треугольнике АВС отрезок ВН является высотой,
опущенной на гипотенузу, a BL— медианой в треугольнике ВНС,
Найти угол LBC, если известно, что BL = 4 и АН =
9
2у/7
5. Найти все решения уравнения
sin -/Зж -4- тг = 0 ,
каждое из которых меньше любого решения уравнения
cos у/х — 4тг = 0 .
6. На плоскости Оху изобразить фигуру, все точки которой удовлетво-
ряют неравенству
211об2!/2 + 1
1
3| log3 ж2 + 1
Доказать, что её площадь S удовлетворяет неравенству 2 < S < 3.
Варианты 2004 года
133
Вариант 17.2 (июль 2004 г.)
1. Решить неравенство
ж2 + 8а: + 15
х2 4- 7х + 14 “
2. Решить уравнение
• *2	. (с\	\ л 2 /	\
4 sm Зж — 2 sm ^2ж — — J — 4 cos (я: — тг) = tg — • ctg у .
3. Популярность продукта А за 2002 год выросла на 20%, в следующем
году снизилась на 10%, а в конце 2004 года сравнялась с популярно-
стью продукта Б. Популярность продукта Б в 2002 году снизилась
на 20%, затем на протяжении одного года не изменилась, а за 2004
год выросла на 40%. Как изменилась популярность продукта А за
2
2004 год, если в начале 2002 года она составляла - от популярности
продукта Б?
4.
7Г
В треугольнике АВС угол при вершине В равен у, а длины отрез-
ков, соединяющих центр вписанной окружности с вершинами А и С
равны 4 и 6 соответственно. Найти радиус окружности, вписанной в
треугольник АВС.
5. Три числа, являющиеся длинами рёбер прямоугольного параллелепи-
педа с диагональю 6, образуют арифметическую прогрессию. Кубы
этих чисел тоже образуют арифметическую прогрессию. Найти эти
числа.
6. Для каждого положительного значения параметра с изобразить мно-
жество тех пар (6, а), для каждой из которых уравнение
Ьх2 4-аж — ~-|-с = 0
4
имеет два различных отрицательных корня, и указать все значения
параметра а, при каждом из которых множество соответствующих
значений b состоит из двух непересекающихся интервалов.
134
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Варианты 2005 года
Варианты 2005 года
135
1. Факультет ВМК
Вариант 1.1 (ВМК, отделение специалистов, июль 2005г.)
1.	Решите неравенство
.	/ж2 4- |ж — 3| 4- 3\2 и Л1 _
log2 -------—-----) - |log2 х - 21 > log2 x + 2.
у x 4- 1	/
2.	Решите уравнение	у/ctg ж + 1 = —/15 • sin х.
3.	Последовательности {ап}и {6n} , n = 1, 2, 3,..., являются арифмети-
ческими прогрессиями, оц = 32, 621 =43. Последовательность {сп}
определяется равенствами сп = (—l)n-an4-(—1)п • 6П- Сумма первых
сорока членов последовательности {сп} равна 100, а сумма первых
ее двадцати трех членов равна —60. Найдите 640 и сумму первых ста
членов арифметической прогрессии {ап}.
4.	На стороне АВ выпуклого четырехугольника ABCD выбрана точка
М так, что Z.AM D = Z-ADB и А АСМ = ААВС. Утроенный квадрат
отношения расстояния от точки А до прямой CD к расстоянию от
точки С до прямой AD равен 2, CD = 20. Найдите радиус вписан-
ной в треугольник ACD окружности.
5.	Найдите все значения параметра а, принадлежащие отрезку [0, тг],
при которых уравнение
зш5(3ж 4- а) = cos (тг ♦ [ж])
имеет на отрезке [1, тг] нечетное число решений. (Здесь [ж] - целая
часть числа ж, т.е. наибольшее целое число, удовлетворяющее нера-
венству [ж] < ж).
6.	На гранях ABC, ABD, ACD и BCD тетраэдра ABCD выбраны
соответственно точки К, L, М и N так, что KL || CD, КМ ||
BD, KN || AD. Отношение объема тетраэдра ABCD к объему тет-
раэдра KLMN равно 64. Известно, что
2 (AD • КМ 4- BD • KN) = AD • BD.
Найдите отношение площадей треугольников ABD и KMN.
136
Подготовка к вступительным экзаменам в МГУ, ВАРИАНТЫ,
Вариант 1.2 (ВМК, отделение бакалавров, июль 2005г.)
1.	В убывающей арифметической прогрессии разность девятого и чет-
вертого членов равна третьему, а сумма квадратов первого и второго
членов равна 4. Найдите сумму первых двадцати пяти членов этой
прогрессии.
2.	Решите неравенство
,	/ж2 + |2ж - 5| + 5\	(1	,
logys (----7+2------) ~'og3х ~ > og3х + L
3.	Решите уравнение д/б - ctg ж — 8 — -Д- •
sin х
4.	Найдите все решения системы уравнений
(х + у\	( 5ху\
arccos ( —-— I = arccos I —— I ,
\ 4 /	\ 24 /
x2 4- y2 - 13.
5.	На стороне AB выпуклого четырехугольника ABCD выбрана точка
M так, что Z.ADM = Z.ABD и ЛАСМ = Л АВС. Квадрат отноше-
ния расстояния от точки А до прямой CD к расстоянию от точки
С до прямой AD равен 2, CD = 28. Найдите радиус вписанной в
треугольник ACD окружности.
6.	Найдите все значения параметра а, принадлежащие отрезку [0, тг],
при которых уравнение
8ш3(Зж + а) = sin — тг • [ж])
имеет на отрезке [1, тг] ровно два решения. (Здесь [ж] - целая часть
числа ж, т.е. наибольшее целое число, удовлетворяющее неравенству
И < «)•
7.	На гранях ABC, ABD, ACD и BCD тетраэдра ABCD выбраны
соответственно точки A”, £, М и N так, что KL || CD, КМ ||
BD,KN || AD, Отношение объема тетраэдра ABCD к объему тет-
раэдра KLMN равно 50. Известно, что
- 2 (AD • КМ + BD • KN) = AD • BD,
Найдите отношение площадей треугольников ABD и KMN.
Варианты 2005 года
137
2.	Геологический факультет
Вариант 2.1 (геологический факультет, июль 2005г.)
1.	Решите неравенство	(|ж| — 1)(2ж2 4- х — 1) < 0.
2.	Решите неравенство	\/ —х2 — ж 4- 6 — х > 2.
3.	В треугольнике АВС угол С прямой, тангенс угла А равен медиана
4
BD равна л/5 - Найдите площадь треугольника ABD и радиус окруж-
ности, описанной вокруг треугольника ABD.
4.	Найдите наименьший корень уравнения
у/cos 2ж 4- ж — 11 = у/х — 15 — 5 cos ж.
5.	В арифметической прогрессии квадрат суммы третьего и четвертого
ее членов равен сумме второго и пятого ее членов. Чему равна сумма
первых шести членов этой прогрессии?
6.	Решите неравенство
1 ( И 1	/ 1\
logx I х + - 1 < logy55+3 ( х + з I •
7.	Найдите все значения, которые может принимать сумма х 4- а при
условии |2ж 4- 4 — 2а| 4-	— 2 4- а| < 3.
8.	В треугольной пирамиде SABC плоские углы АВС и SAB прямые,
(2У10
--Q--
О
Найдите длину высоты пирамиды, опущенной из вершины В на плос-
кость ASC, если ВС — 7, АВ = 4.
138
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
3.	Экономический факультет
Вариант 3.1 (Экономический ф-т, отд. экономики, июль 2005г.)
1.	Решите уравнение
log 1 ctg — +
9 У
^/logj. sin4# = 0.
2.	Найдите сумму всех целых значений, которые принимает функция
/»	~.2
X X Л
’=7Гго + в
при х е [ 2 ; 12].
3.	Вновь созданное акционерное общество продало населению 1000 сво-
их акций, установив скидку 10% на каждую пятую продаваемую ак-
цию и 25% на каждую тринадцатую продаваемую акцию. В случае,
если на одну акцию выпадают обе скидки, то применяется большая
из них. Определите сумму, вырученную от продажи всех акций, если
цена акции составляет 1000 рублей.
4.	Решите неравенство
1оё2+У5 (4 - ®) - log9_475 (4а;2 + 28» + 49)+
+ logV5-2 (®2 + х ~ 6)
5.	Вписанная в треугольник АВС окружность касается его сторон в
точках A", N и М. Известно, что в треугольнике KNM угол Z.M ра-
вен 75°, произведение всех сторон равно 9 + 6\/3, а вершина К делит
отрезок АС пополам. Найдите длины сторон треугольника АВС,
6.	Найдите все рациональные решения уравнения
\/у • (ж + I)2 - ж2 + Ж + 1 + log/|y+2|\ cos2iry = 0.
к 21 )
7.	Фигура F задается на координатной плоскости неравенством
о2 о • (у-х + 9\	/10+ 2х + 2у\
Зтг — 2 arcsm I -—- 1 • arccos I ----- I
\	13	/	\	18	/
I» - 4| • (|yW128-1>7 +	+ |y + 5|)
В каких пределах изменяются площади всевозможных кругов, цели-
ком принадлежащих F?
Варианты 2005 года
139
Вариант 3.2(Экономический ф-т, отд. менеджмента, июль 2005г.)
1.	Решите уравнение
x/log2 (х2 — ж — 5) 4- ^/logj. cos тгж = 0.
2.	Найдите произведение всех целых значений, которые принимает функ-
X2 X
у —----------;= 4- 4
12 УЗ
ция
при х е [ 2 ; 9 ].
3.	В целях рекламы новой модели автомобиля, автосалон установил
скидку 10% на каждый седьмой продаваемый автомобиль и 20% на
каждый одиннадцатый продаваемый автомобиль новой модели. В
случае, если на один автомобиль выпадают обе скидки, то приме-
няется большая из них. Всего было продано 516 автомобилей этой
модели. Определите выручку автосалона от продажи автомобилей
новой модели, если её базовая цена составляет 20000 условных еди-
ниц.
4.	Решите неравенство
1о61+>/2 (я + 4) + 2 log3+2>/2 (7 - 2®) + logyj-i (х2 - X - 6) < 0.
5.	Вписанная в треугольник АВС окружность радиуса 1 касается сто-
рон ЛВ, ВС и АС соответственно в точках К, М и 7V. Известно,
что углы Z.MKN и Л АВС оба равны 45°. Найдите длины сторон
треугольника АВС.
6.	Найти все целые значения параметра а, при каждом из которых все
решения уравнения
_ (4 _ 2V ^4 + 1-2=0
\a J	а
являются целыми числами.
140
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 3.3(Экономический ф-т, вечернее отд., июль 2005г.)
1.	Решите уравнение
v/log3 (х2 + х- 5) + у l°g| sin = 0.
2.	Найдите сумму всех целых значений, которые принимает функция
3.	В целях ускорения распродажи дубленок, магазин установил скид-
ку 15% на каждую четвертую продаваемую дубленку и 25% на каж-
дую шестую продаваемую дубленку. В случае, если на одну дубленку
выпадают обе скидки, то применяется большая из них. Всего было
продано 602 дубленки. Определите выручку магазина от продажи
дубленок, если базовая цена дубленки составляет 5000 рублей.
4.	Решите неравенство
1°б2+л/з (ж 4- 3) 4- 21067-1-4^/3	~ 2а?) 4- 1°б2->/з (а? — х — 2) > 0.
5.	Вписанная в треугольник АВС окружность касается сторон АВ, ВС
и АС соответственно в точках /<, М и N. Известно, что АС = 1,
а углы Z.MKN и Z.ABC равны соответственно 45° и 30°. Найдите
радиус окружности.
6.	Найдите все целые значения параметра 6, при каждом из которых
все решения уравнения
являются целыми числами.
7.	Фигура F задается на координатной плоскости неравенством
/Зж — Зз/4-9\	. /Зж4-3?/ —5\	9
arccos I ------- I • arcsm I -------I 4- ttz
-----------V-----~---i---4----------------> °-
|3® 4- 4| • (\3y — 51 4- 3® - \/36i/8-97h
В каких пределах изменяются площади всевозможных кругов, цели-
ком принадлежащих F?
Варианты 2005 года
141
4-	Московская школа экономики
Вариант 4.1 (Московская школа экономики, май 2005г.)
1.	Решите уравнение |2ж — 4| 4- 4 = 2х .
2.	Решите неравенство \/ж2 4- 2ж — х > 1.
3.	Решите уравнение
1 + log4 (х 4- 2)2 = log2 (2я + 8).
4.	Найдите все решения уравнения
С /15ЯА	(х\	,
6 cos I —— I • cos ) — COS X = 3,
принадлежащие отрезку [—2 ; 10, 99].
5.	Найдите четыре числа, которые образуют арифметическую прогрес-
сию, если сумма крайних равна 18 и второе число меньше третьего
на 20%.
6.	Найдите все целочисленные решения системы
Г (Ж - З)2-ь (з/- 4)2 < 5,
[ 4у < х 4- П .
7.	Окружность, вписанная в треугольник АВС, касается стороны ВС
в точке М. Найдите площадь треугольника АВС, если АС = 21,
ВМ = 9, а угол АВС равен 60°.
8.	При каких значениях параметра а уравнение
(а - 1) • 4х 4- (2а - 3) • 6х = (За - 4) • 9*
имеет единственное решение?
142
Подготовка к вступительным экзаменам в МГУ, ВАРИАНТЫ.
Вариант 4.2 (Московская школа экономики, июль 2005г.)
1.	Решите неравенство
2.	Решите уравнение
х/2ж1 2 - Зя - 1 = х - 1.
3.	Цена товара изменяется два раза в год: в апреле она повышается на
20%, а в сентябре снижается на 20%. Какова будет цена товара в
декабре 2005 г., если в январе 2004 г. она составляла 6250 руб.?
4.	Найдите множество определения функции
У = ^logi (2-9-* -3-®).
5. Найдите все значения
2тг
у;3.
, удовлетворяющие уравнению
х е
1 4- cos 2х = 4 sin х .
6. В равнобочной трапеции основания относятся как 3:2, диагональ
делит острый угол пополам. Найдите площадь трапеции, если длина
диагонали равна 4.
7. Найдите все значения параметра 6, при которых система уравнений
(я2 4- 1) b = у 4- cos 2х,
2lsin®l + |у| = 2
имеет единственное решение.
Варианты 2005 года
143
5.	Институт стран Азии и Африки.
Вариант 5.1 (ИСАА, июль 2005 г.)
1.	Решите неравенство
2.	Решите уравнение
3.	Решите уравнение
х2 — Зя — 4
х 4-1	“
cos 4х = 4 cos х • cos 2х — 1.
л/я 4- 1 4- V#2 + 4ж 4- 3 = У(я + 2)3
4.	Магазин закупил некоторое количество товара и начал его реализа-
цию по цене на 25% выше цены, назначенной производителем, что-
бы покрыть затраты, связанные с его транспортировкой, и другие
дополнительные расходы. Оставшуюся после реализации часть това-
ра магазин уценил на 16% с тем, чтобы покрыть только затраты на
закупку этой части товара у производителя и его транспортировку.
Сколько процентов от цены, назначенной производителем, составля-
ла стоимость транспортировки товара?
5.	Решите неравенство
log(4|®|+1)(6® + 2) - log (6® + 2)(4|аг| + 1) < 0.
6.	В выпуклом четырёхугольнике с вершинами в точках А, В, С, D за-
даны длины отрезков AD = 2, АВ = 2л/3, ВС — 2(л/3 — 1). Величины
7Г 7Г
углов DAB и АВС равны — и — соответственно. Вычислите все углы
6	3
четырёхугольника.
7.	Фигура на плоскости (ж, у) состоит из всех точек, через которые не
проходит ни одна из кривых, задаваемых соотношением
(р4 + 4р2 +16)2 + (х2 - у2)2 = 16(р3 + 4p)zj/ + 2(р4 + 12р2 + 16)(ж2 + у2)
при различных действительных значениях р. Найдите длину линии,
ограничивающей эту фигуру.
144
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
6. Факультет Государственного управления
Вариант 6.1 (ФГУ, июль 2005г.)
1.	Можно ли разделить сумму в 196 рублей на 16 разных частей так,
чтобы ближайшие по величине части отличались на 50 копеек?
у/2 (х — 4)
2.	Решите неравенство 1 < —======== .
у/х2 -	4- 17
3.	В четырёхугольнике ABCD найдите точку Е так, чтобы отношение
площадей треугольников ЕАВ и ECD было равно 1/2, а треугольни-
ков EAD и ЕВС — 3/4, если известны координаты всех его вершин:
А(—2, —4), В(-2,3), С(4,6), £>(4,-1).
4.	Решите систему уравнений
{sin х — sin 1 = О,
cos х — cos 1 = 0.
5.	Тёма сделал несколько мелких покупок в супермаркете, имея при се-
бе сто рублей. Давая сдачу с этой суммы кассир ошиблась, перепутав
местами цифры, и выплатила рублями то, что должна была вернуть
копейками, и, наоборот, копейками то, что полагалось вернуть рубля-
ми. Купив в аптеке набор пипеток за 1 руб. 40 коп., Тёма обнаружил
ошибку кассира и, пересчитав деньги, нашёл, что оставшаяся у него
сумма втрое превышает ту, которую ему должны были вернуть в су-
пермаркете. Какова стоимость всех покупок Тёмы?
6.	Найдите все значения а, для которых при любом положительном b
уравнение	.	А .	(1 Л\ .
alog/i \ 4 = log2 I ——21 - Ь
(--2)	/
)
, 1
имеет хотя бы одно решение, меньшее - .
7.	Для того, чтобы сделать полный круг по кольцевому маршруту, ав-
томобилю требуется 150 л бензина. На маршруте расположены пять
промежуточных пунктов, в каждом из которых имеется запас в 30 л
бензина. Покажите, что найдётся пункт, в котором автомашина с пу-
стыми баками и достаточным запасом пустых канистр может запра-
виться, стартовать и, пополняя запас бензина в четырёх встречных
пунктах, сделать полный круг.
Варианты 2005 года
145
7. Факультет Глобальных процессов
Вариант 7.1 (ф-т глобальных процессов, июль 2005г.)
1.	В турнире борцов участвуют 127 спортсменов. Борец выбывает из
соревнований сразу после поражения в поединке. Сколько поединков
требуется провести, чтобы выявить победителя турнира?
2.	Решите неравенство - 	 < т—~г-т •
к	2х2 + Зх ~ Зх - 2я3
3.	Решите неравенство
1°6(0,5-|2т2-5а?+2|) (0> 5 + |8ж2 — 2ж — 1|) > 1 .
4.	Найдите площадь трапеции ABCD (BC||AD), вписанной в окруж-
ность с центром в точке О, если ее высота равна 2, а угол COD равен
60°.
5.	Выясните, верно ли следующее утверждение:
множество значений функции у = cos 2х — 3 sin х принадлежит
отрезку [—4 ; д/5] . Ответ надо обосновать.
6.	Общий процент прибыли за весь товар, проданный в трех магази-
нах, расположенных в разных районах города, составил 26,8%. Че-
рез первый магазин было продано 60% всего товара, через второй -
40% оставшейся части товара. С какой прибылью продан товар через
третий магазин, если прибыль от продажи в первом составила 30%,
а во втором - 25% ?
7.	Верхняя грань ABCD куба ABCDA'B'C'D' (АА'ЦВВ'ЦСС' HDD'
- боковые ребра) является одновременно основанием правильной че-
тырехугольной пирамиды SABCD) у которой высота вдвое меньше
длины ребра куба. Найдите угол между прямыми А1 В и AS.
8.	Переменные ж, у связаны условием х2 + у2 — 6х+4у4-10 = 0. Найдите
все значения параметра а, при которых разность между наибольшим
и наименьшим значением выражения 2ах — Зу — 10 больше 12.
146
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
8. Черноморский филиал МГУ (г. Севастополь)
Вариант 8.1 (Черноморский филиал МГУ, июль 2005г.)
/ 1 \ ~2
1.	Сравните числа 105 и I— — I •2“3•55.
2.	Найдите множество значений функции у = у/2х — х2 +4.
3.	В равностороннем треугольнике АВС сторона ВС = 4 является диа-
метром окружности, пересекающей стороны АВ и АС в точках М и
N соответственно. Найдите периметр треугольника AMN.
4.	Решите уравнение х3 + 5ж2 = х2 4- 5 .
5.	Решите неравенство	log4( 16ж2) + \/log2 я 4-1 < 1.
6.	Решите неравенство
v-4- -1 - 1/-Л--1 > °-
V cos2 X V Sin2 X
7.	Диагонали выпуклого четырехугольника ABCD пересекаются в точ-
ке О. Найдите площади треугольников ADO и ВСО, если площадь
четырехугольника ABCD равна 15, а площади треугольников АВ О
и С DO равны 2 и 6 соответственно.
8.	Решите уравнение х2 4- [ж] = 4 , где [ж] обозначает наибольшее
целое, не превосходящее число х,
9.	Заданы числа А > 0 и О Е [0; тг]. Докажите, что графики функций
у — A cos х и у — sin (х — 0) для значений х из отрезка 0 < х < 2тг
пересекаются в двух точках. Найдите расстояние между абсциссами
этих точек.
10.	Пусть числа х и у удовлетворяют неравенствам
log ± (2® - 3) > log 1 у и log2 (ж2 + у2 - 4х - 2у + 5) < log2 5.
Найдите все а, для которых максимальное значение выражения ах+у
равно 4.
Варианты 2005 года
147
9. Механико-математический факультет.
Вариант 9.1 (мехмат, июль 2005 г.)
1. Согласно расписанию, автобус курсирует по маршруту из пункта А в
пункт В и обратно с постоянной скоростью и без остановок. На пути
из А в В автобус был вынужден на некоторое время остановиться,
поэтому на обратном пути он увеличил скорость на 25%. Приехав
в А с 10-минутным отклонением от расписания, он уменьшил свою
последнюю скорость на 24% и прибыл в В вовремя. Какова была
продолжительность вынужденной остановки?
Ilogys*’ -21og2®| + ||2- х| - (log2 ж|| < (х - 2) log8 х3.
3.	Решить неравенство ---------„—=---------=- > 0.
cos - cos “
4	4
4.	На основании ВС трапеции ABCD взята точка Е, лежащая на одной
окружности с точками А, С и В. Другая окружность, проходящая
через точки Л, В и С, касается прямой CD. Найти ВС} если АВ —
12 и BE : ЕС = 4:5. Найти все возможные значения отношения
радиуса первой окружности к радиусу второй при данных условиях.
5.	Пусть X— сумма корней уравнения
на промежутке [0; 2тг), a Y — сумма корней уравнения
a cos 2у — 2 sin 2у = а — 3 sin у
на том же промежутке. Найти все значения а, при каждом из которых
6.	Найти объём тетраэдра ABCD с рёбрами АВ = 3, АС = 5 и BD = 7,
если расстояние между серединами М и N его рёбер АВ и CD равно
2, а прямая АВ образует равные углы с прямыми AC, BD и MN.
148
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
10.	Физический факультет.
Вариант 10.1 (физический ф-т, июль 2005 г.)
1.	Решить уравнение 2 cos 2х • cos lx — cos 4® = 1.
2.	Решить неравенство \/bx — я2 + 6 < л/б — х.
3.	Решить уравнение — 5д/3 • 15*^ + 4 • з1*®'/*2 = 0.
4.	На окружности взяты последовательно точки P^Q^Rn S',
PQ = PS. Отрезки PRh QS пересекаются в точке Т, RQ = g, RS = s,
RT = t. Найти PT.
5.	Решить систему
( x + 4y/x - у = у + 12,
I |2(z+l) + ^| + 2|2z + (t/-1)| = 3.
6.	Вершина M прямого угла в ALMN лежит внутри окружности с цен-
тром О и радиусом 8, проходящей через концы гипотенузы UV, МН—
высота ALMN. На прямой LN взята точка К так, что КН = ОН.
Найти МК.
7.	Для каждого допустимого значения а решить неравенство
l°gar (^) • l°g<x*-2 (« ~ 1) < 0 •
8.	В правильной треугольной пирамиде SKLM с вершиной S', точка N—
середина отрезка KL, SN = л/17. Сфера, проходящая через точки Z,
М и ЛГ, касается ребра SK в точке Р такой, что
КР : PS =1:2. Найти высоту SH пирамиды SKLM.
Варианты 2005 года
149
11.	Химический факультет.
Вариант 11.1 (химический факультет, июль 2004 г.)
1.	Решить уравнение |2ж 4- 1| = |ж + 2|.
2.	Решить неравенство л/З • 4® < у/2 • 9*.
3.	Решить уравнение ctg х = tg 4х + cos 5х.
4.	Найти число п сторон выпуклого п—угольника, если каждый его
внутренний угол не меньше 143° и не больше 146°.
5.	Найти все целочисленные пары (ж, у), удовлетворяющие уравнению
у/2х -у-3 + у/2у - я + 3 = 2^/3 -х -у.
6.	При каких значениях параметра а уравнение
kl +
х 4- 1
Зх-1
= а
имеет ровно три решения?
150
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
12.	Биологический факультет, факультет наук о
материалах, факультет фундаментальной
медицины, факультет биоинженерии и
биоинформатики.
Вариант 12.1 (июль 2005 г.)
1.	Решить уравнение
2.	Решить уравнение
х2 4- 2|а?| — 3 = 0.
cos х — д/З sin х = л/2.
3.	Диагонали трапеции равны 12 и 6, а сумма длин оснований равна 14.
Найти площадь трапеции.
4.	Решить неравенство у/х — 1 < 3 — х .
5.	На беговой дорожке стадиона длиной 400 м одновременно со старта
в одном направлении начали забег два спортсмена на дистанцию 10
км. Каждый из них бежал со своей постоянной скоростью. Первый
спортсмен пришёл на финиш на 16 мин 40 с раньше второго и через
43 мин 20 с после того, как он второй раз на дистанции (не считая
момента старта) обогнал второго спортсмена. Известно, что скорость
первого спортсмена больше 100 м/мин. Сколько всего раз первый
спортсмен обогнал второго на дистанции после старта?
6.	Решить систему
у/х2 + у2 — 2х — 22у + 122 = 2-/37 - у/х2 + у2 + 2х + 2у + 2,
<
. logaH-l 4 + logy 4 = °-
7.	Задана функция /, причем f(x + у) = f(x) + f(y) для всех рацио-*
/ 2
нальных чисел ж, у. Известно, что /(10) = —тг. Найти / I — -
Ва/ныиты 2005 года
151
13. Факультет почвоведения.
Вариант 13.1 (факультет почвоведения, июль 2005 г.)
1.	Решить уравнение (6ж — 15)7 = (х — I)14 .
2.	Решить уравнение sin(\/3 arcsin х) = 1.
3.	Решить неравенство |ж — 1| < |я|.
4.	Грузовики трёх типов А, В и С возили кирпич. В первый день ра-
ботали по пять грузовиков каждого типа и выполнили весь объем
работы за 3 ч 12 мин. Во второй день за 6 ч 40 мин этот же объём
работы выполнили по два грузовика типов А и В и четыре грузовика
типа С. За сколько часов был бы выполнен весь объём работы, если
бы кирпич возили два грузовика типа А и два грузовика типа В.
5.	Для каких значений параметра р отношение суммы коэффициентов
многочлена (рх2 — 7)18 к его свободному члену минимально?
6.	На плоскости даны точки с координатами А = (1; 2), В = (2; 1),
С = (3;—3), D = (0;0). Они являются вершинами выпуклого че-
тырёхугольника ABCD. В каком отношении точка пересечения его
диагоналей делит диагональ АС1
152
1.
2.
3.
4.
5.
6.
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Ц. Географический факультет.
Вариант 14.1 (географический факультет, июль 2005 г.)
Решить систему
( 12 sin2 х — sin2 у = 3 ,
[ 6 sin х 4- cos у = —2 .
Произведение средней линии трапеции и отрезка, соединяющего се-
редины её диагоналей, равно 25. Найти площадь трапеции, если её
высота втрое больше разности оснований.
Решить неравенство logyy^-(l 4- 5ж) > — 2.
Найти периметр фигуры, точки которой на координатной плоскости
удовлетворяют системе
У > lk-2|- 1| ,
х2 + у2 < 4х 4- 2у — 3.
В цехе имелось N одинаковых станков, которые, работая вместе, вы-
тачивали в день 5850 деталей. После модернизации число производи-
мых в день каждым станком деталей возросло на 20%. Это позволи-
ло без сокращения общего объёма продукции цеха уменьшить число
станков максимум на 4. Найти ЛГ.
Угол между прямыми, каждая из которых содержит по одной об-
разующей конуса, равен 45°. Прямая, перпендикулярная обеим этим
образующим, пересекает плоскость основания конуса под углом
Найти угол боковой развёртки конуса, если он больше 270°.
7Г
8‘
Варианты 2005 года
153
15.	Факультет психологии.
Вариант 15.1 (Факультет психологии ,июль 2005 г.)
1.	Решить уравнение |х — 2| + 2|х + 1| = 9.
4* + 5
2.	Решить неравенство ----—- > — 1.
3.	Решить уравнение \/2cos2 х — л/3 + v^sin х = 0.
4.	В выпуклом четырёхугольнике ABCD диагонали BD и Л С равны
стороне АВ. Найти угол BCD и сторону АВ> если угол CD А прямой,
ВС = 4,AD = 5.
5.	Зенон не раз наблюдал забавную игру Ахилла с черепахой: Ахилл и
черепаха приближались друг к другу вдоль тропинки, стартуя с раз-
ных концов тропинки. Двигались они только навстречу друг другу,
причём, когда черепаха стояла, Ахилл шёл навстречу ей, а когда чере-
паха ползла навстречу Ахиллу, Ахилл стоял в течение всего времени
её движения. Продвигались они по тропинке друг к другу каждый со
своей постоянной скоростью, одной и той же в разных играх, причём
скорость идущего Ахилла была в 50 раз больше скорости ползущей
черепахи. Игра заканчивалась, когда Ахилл и черепаха сходились в
одной точке тропинки.
В первой игре, начав сближаться по первой тропинке, они сошлись
не ранее, чем через 15 мин. Во второй игре, сближаясь по второй
тропинке, они сошлись не позже, чем через 1,5 мин. В третьей игре
они сошлись по третьей тропинке за 11 мин, причём в ходе этой игры
Ахилл двигался в общей сложности в течение 1 мин, а черепаха - в
течение 10 мин. Известно, что сумма длин первой и третьей тропинок
равна длине второй тропинки.
Каково отношение расстояния, пройденного Ахиллом навстречу че-
репахе за время всех трёх игр, к расстоянию, на которое продвинулась
черепаха навстречу Ахиллу за время всех трёх игр?
6.	Найти все значения параметра а, при каждом из которых функция
ч 4 sin х -F а	ГЛ
f(x) — ----—---- принимает все значения из отрезка [0; 1].
154
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
16.	Филологический факультет.
Вариант 16.1 (июль 2005 г.)
1.	Решить уравнение |ж2 — 3|а?| + 1| = 1.
2.	На вступительном экзамене по математике 15% поступающих не ре-
шили ни одной задачи, 144 человека решили задачи с ошибками, а
число остальных абитуриентов, верно решивших все задачи, относит-
ся к числу не решивших ничего, как 5:3. Сколько человек экзаме-
новалось по математике в этот день?
3.	Решить неравенство log2(;r + 1) > log^+i 16 .
4.	Найти площадь круга, описанного около прямоугольного треуголь-
ника, катеты которого являются корнями уравнения
2ж2 —	4-1 = 0 .
5. Решить уравнение
х
2 + sin х = 3 tg — .
6.	Биссектриса CD угла АС В при основании ВС равнобедренного тре-
угольника ABC pfijiwr сторону АВ так, что AD = ВС. Найти длину
биссектрисы CD и площадь треугольника АВС, если ВС = 2.
7.	При каких целых а неравенство
2 log 1 а — 3 + 2х log 1 а — х2 < О
2	2
верно для любого значения ж?
Варианты 2005 года
155
17.	Социологический факультет.
Вариант 17.1 (Социологический факультет, июль 2005 г.)
1. Решить уравнение
\А?2 — 4ж 4- 9 = 3 .
2. Решить уравнение
3-81*-10-9* 4-3 = 0.
3.
Бесконечно убывающая геометрическая прогрессия содержит член
Ьп = Отношение суммы членов прогрессии, стоящих перед 6П, к
о
сумме членов, стоящих после 6П, равно 6. Найти п, если сумма всей
3
прогрессии равна
4.	Высота треугольника, равная 2, делит угол треугольника в отноше-
нии 2 : 1, а основание треугольника - на части, меньшая из которых
равна 1. Определить площадь треугольника.
5.	Решить неравенство log0 5(\/б — х — х 4- 1) > — 3 .
6.	Группа школьников решила купить музыкальный центр, при этом
каждый внёс одинаковую сумму. Однако в последний момент двое из
них забрали деньги назад, и каждому из оставшихся пришлось доба-
вить по 100 рублей. Сколько школьников первоначально участвовало
в покупке и какова цена музыкального центра, если известно, что она
заключена в пределах от 17000 до 19500 рублей?
156
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 18.1 (Олимпиада "Ломоносов-ЗООб”, май 2005г.)
1. Вычислить -------2
при х = 1, 2 .. . 22 ,
46
2. Решить неравенство
- у) (х4 - у4) _ 2ху(х3 - у3)
- у2	X2 + ху + у2
у =-2,^7,8.
45
3.21-® 4-1	1
2® - 1	- 1 - 2“® '
3.	Найти площадь трапеции ABCD с боковой стороной ВС = 5, если
расстояния от вершин А и D до прямой ВС равны 3 и 7 соответствен-
но.
4.	Решить уравнение log4 (4 sin2 2х) = 2 — log2 (—2 tg х).
5.	На окружности взята точка А, на ее диаметре ВС - точки D и Е, а
на его продолжении за точку В - точка F. Найти ВС, если Z.BAD =
ZACjD, Z.BAF = Z.CAE, BD = 2 BE = 5 и BF = 4.
6.	Решить неравенство 5 |ж| < х (Зж 4-2 — 2 y/S — 2х — х2).
1. Основанием пирамиды служит треугольник со сторонами 5, 12 и 13,
а ее высота образует с высотами боковых граней (опущенными из той
же вершины) одинаковые углы, не меньшие 30 . Какой наибольший
объем может иметь такая пирамида?
8.	Найти все значения а, при которых уравнение
4ж — |3ж — |а? 4- а|| — 9 |ж — 1|
имеет хотя бы один корень.
9.	Группа отдыхающих в течение 2 ч 40 мин каталась на моторной лод-
ке по реке с постоянной скоростью (относительно воды) попеременно
то по течению, то против: в каждую сторону - в общей сложности не
менее, чем по 1 ч. В итоге лодка прошла путь в 40 км (относительно
берега) и, отчалив от пристани А, причалила к прстани В на рас-
стоянии 10 км от А. В какую сторону течет река? Какова при этих
условиях максимальная скорость ее течения?
10.	При каждом натуральном п тело Фп в координатном пространстве
задано неравенством
3	4- |8t/|n 4- \z\n < 1,
а тело Ф - объединение всех тел Фп. Найти объем Ф.
Варианты 2005 года
157
Вариант 18.2 ("Покори Воробьевы горы-2005", заочный тур)
1.	Три брата возвращались с совместной рыбалки домой, где их ожи-
дал бочонок холодного кваса. Старший брат шел втрое медленнее
младшего и вдвое медленнее среднего. Придя домой, младший сразу
принялся за бочонок и выпил 7-ю его часть к приходу среднего брата,
который присоединился к младшему и стал поглощать квас с такой
же скоростью. Досталось ли кваса старшему брату?
2.	Решить неравенство \у/х 4- 3 — 2| + у/х 4- 3 4-|ж4-1|<2;4-3.
3.	Бригада землекопов должна была в 8 час» начать рыть траншею.
Однако, простояв в очереди за лопатами, они приступили к работе
позже: первый на 5 мин., второй на 10, а третий на 15 мин. и т.д.
Вырыв траншею в 12 час., они ушли на обед, ас 13 до 16 час. 30
мин. вырыли вторую такую же траншею. Сколько было землекопов?
4.	В четырехугольнике ABCD точки М и N - середины сторон АВ и
ВС соответственно, причем АВ = а, ВС = b, CD = с и AN = СМ.
Найти AD.
5.	Найти произведение всех действительных корней уравнения
J_ . 2log2 * = 2 72 <1О82 Х ~	2)
\/2
6.	В каждом подъезде нового дома одинаковое число этажей, а на каж-
дом этаже одинаковое число квартир. На восьмом этаже третьего
подъезда первая квартира имеет номер 106. Какой номер имеет вто-
рая квартира на третьем этаже шестого подъезда?
7.	Решить уравнение sin (х 4- sin х) 4- cos (ж 4- cos х) = 0 .
8.	Найти наименьшее значение выражения
У(ж - 9)2 + 4 + \/ж2 + у2 4- \/(у — З)2 + 9.
9.	Диаметром плоской фигуры называется максимальное расстояние
между точками этой фигуры. Для какого наименьшего положитель-
ного числа d можно разделить круг единичного радиуса на 7 частей
диаметром, не превосходящим d каждая?
10.	Существуют ли функции f и д, определенные на всей числовой пря-
мой и при каждом х удовлетворяющие равенствам:
/(у(ж))=х2, д (/(ж)) = ж3 ?
158
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 18.3 (ВМК, "Абитуриент-2005", отд. специалистов)
1.	Решите неравенство
6 log2a. X + 2 log4.yj(2a;) > 1.
2.	Найдите все решения системы уравнений
{sin 2(х -f- у) = 1,
ху = 9.
3.	Найдите все пары целых х и у, удовлетворяющие равенству
4ж2 — 2ху 4- 2у2 + у — 2х — 1 = 0.
4.	На сторонах АВ и ВС треугольника АВС взяты точки М и N
соответственно. Отрезки AN и СМ пересекаются в точке L. Пло-
щади треугольников AMLy CNL и ALC равны соответственно 1,
6 и 4. Найдите площадь треугольника MBN.
5.	Дана правильная четырехугольная пирамида SABCD с вершиной
S. Известно, что длина перпендикуляра, опущенного из основания
Н высоты пирамиды SH на грань SDC, равна л/б, а угол наклона
тг
бокового ребра SB к плоскости основания равен —. Найдите радиус
сферы, описанной около пирамиды SABCD.
6.	Решите уравнение
12 cos 2х 4- 8| sin х|д/З 4- | sin ж| — 3 cos 2ж = 11.
Варианты 2005 года
159
Вариант 18.4 (ВМК, ”Абитуриент-2005", отд. бакалавров)
1.	Решите неравенство	у/х — 1 < х — 3 .
2.	Решите неравенство	|ж2 — 2х — 4| < 11.
3.	Решите неравенство
2 l°g9.y^ 3 + 1оёЗа;2 ж < 1 •
4.	Найдите все решения системы уравнений
( cos(x2 + 2/2) = О,
1 2х — у = 10 .
5.	Найдите все пары целых х и ?/, удовлетворяющие равенству
х2 — ху 4- 2у2 — Зу — 2х 4- 2 = 0.
6.	На сторонах KL и LM треугольника KLM взяты точки А и В
соответственно. Отрезки КВ и МА пересекаются в точке С. Пло-
щади треугольников К АС, МВС и КСМ равны соответственно 3,
1 и 3. Найдите площадь треугольника ALC.
7.	Решите уравнение
2| cos ж|^/12 4- 6| cos ж| 4- 12cos2x — 12 cos 2х = 3.
160
Подготовка к вступительным экзаменам в МГУ, ВАРИАНТЫ.
Ответы к вариантам 2001 года.
Вариант 1.1.
1. 12.
/	/27\ о
larccos I — I 4-2тгт;
7г + arcsm I — I 4- 2тгп
\28 /
"р“-е(й4)
X е (-4; -3 - 4=] U
[-3 - у>(а); -3) и
(-3; -3 + ^(a)]|J
4- 2тгт;
— arcsin
т, n Е Z
3. 10 км/час.
Здесь принято обозначение
192
17
_ 1728
25
или
= 69,12.
р(«) =
1- 3a\log3
a 4“ 2 у
о 4" 2
\ 1 — За
и
6. V = 729л/6 ; R = ——.
4у/2
Вариант 1.2.
/ 1 1 \
х е (-4 ; -3 - (р(а)] (J
-з--4;-з)и
.	V	/
2. а20 = 119.
/ 9 12 \
\ 5’5/'
(“3;“3 + 7з]и
[-3 + р(а); -2);
1
ПРИ «=10	-	,
хЕ (-4; -3)U(-3; -2);
4. (4п - З)1 2 , п е W.
Г-	. ( 2л/6
5.8 + 4-\/б — 10 arcsm I ——
\ 5
Ответы к вариантам 2001 года
161
Вариант 1.3.
2. 51(Ю= Ю500.
Если a < 4,
то х Е
если a
если a > 4, то решений нет.
f А.
\ 13’ 13 7
5. (2n—I)2, n£N.
6. 0; 72.
7.4 + 4714 — 36 arcsin
Вариант 2.1.
I-	( 1;4).
13	\
2.	( оо; 2] U — ; +оо I .
2S	J
3.	( 4}.
л 3/г тг 5тг .1
4.	5 “ТГ ; —1-----arcsin —т=.
2’2’4	2>/2
5.	9:8.
6.	1,8 раза.
‘х>; —4]U[4; +oo)U
2 1 1
3’2/'
Вариант 2.2.
1.	(1; 2]U(7; 8).
Л тгп тг лк ,	„
2.	т-;т + тг; n,tEZ,n,t>0
5 4	2	“
3.	{3±7й}.
16
4.	a) S = — (м2), центр вне тре-
угольника;
b) S =	(м2), центр внут-
ри треугольника.
5.	{(1; 5);	: 2) } •
6.	7 час.; 55 км.
ч-
8. a G {3} U [л/10; 711).
Вариант 3.1.
15
1.	0; — U[4; -Foo) .
2.	2 млн. 400 тыс. рублей и 3 млн.
600 тыс. рублей.
3.	36.
4.	(log2 49 - 4; log2 7).
с 7356-12 7164-12
5-	—в——6—•
6.	arccos (6 — л/33).
7.	и =-187; v = —819.
8. К
1
72 ’
Вариант 3.2.
162
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
, лк .	~
1.	—, А: е Z.
о .	Г 72 13
2.	(-оо; 0] U —; — .
I 10	£1
3.	240 и 160 тонн.
4.	21.
(1°б5 ; log5 251 — 3) U
и (log5 27; +со).
„ 12+ >/239 12 + >/159
К ----------- • ----------
4.	(в; 0 U [3; 3^] .
5.	ZBOC = 112,5°.
6.
Ми(°4
U{-1;1}.
7. (тгп; тгп — 1); n Е Z.
Вариант 5.1.
Вариант 3.3.
irlc тг
1.	—; ±- + 2тгп, k,ne Z.
2	6
2	0‘—• —
’ 13 ’ 2
3.	5400 рублей и 8100 рублей .
4.	33.
, ТГ	irk	ТГ	,	„
1. -т + — ;	+ 2тгп, k,n£Z.
4	2	6
5.	(0; log4 257—4 )U( log4 65; +оо).
6.	-3; -2; 1.
Вариант 6.1.
3.	17100 руб. и 11400 руб.
4.	27.
5.	(log3 28 - 3; log3 4).
18+ >/503 18+ >/335
6	’	6
Вариант 4.1.
2.
Зтг
— : 2тг: 2тг — arccos
2 ’	’
2
5
3. 4 ; 8; 12 км/час.
1.	{0; ±4; ±5; ±9}.
2.	(-оо; 0]U{l}U Q; 3
3.	[log2 3; log25) .
4.	(х ; 6), где х < 0;
(0; у), где у Е R;
(* ; У), где х > 0,
у Е (—оо; 18 — 6\/6] U
U [18 + 6\/б; оо).
5.	тг (2п 4- 1), n Е Z.
Отцеп.) к вариантам 2001 года
163
/61 ’
8. -l±/2;-l±Jlog2 (б - /1з) .
9. При а<0 решений нет; при
О < a < 1 х Е [—а; а2 — а];
при а > 1
Г -1 +V4a-3
х Е -а; --------
2. (м/м-01(1).2)
(-3; 2 - 2/6) U (2 - 2/6; -2)U
(—2; 2) U (2; 2 + 2/б)и
(2 + 2/6; 7)
450 255 960
17 ’ 8 ’ 17 ‘
о
4. (м/м-01(1).4) да , С = -
5.
Вариант 6.2.
169
5292
/187.
1. 1:2.
6. (м/м-01 (1).6)
у7 — 1
2. ± arccos--------h 2тг&, k Е Z.
4
Вариант 7.2
3. ( —оо ; —4 )и[—2; О )и( 0; 4-оо).
1. (-оо; log6+yjQ 9]u[log6_v^Q 3;+оо).
5.
2. -8.
3. 200,3 : 7.
При a > 4
х = ± I log2
4.
. Зтг яп
±88 ± Т’" 6 Z
6. кл = 3; Кв = - ; hc = •
7. ~ + 2тгт, m Е Z .
Q 1	625
8‘ 1о*54/5 Зб--
Q _____
5. — V^21.
266
6. [0;1].
9. 3:1.
Вариант 7.1
1. (м/м-01(1).1) 6.
Вариант 7.3
1. (—оо; —2] U [0; 1g 101 — 2).
2. нет.
4. 618,659,698
164
5.
6.
1.
2.
3.
4.
5.
6.
7.
8.
1.
2.
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
(^4) и
26, L 253+ 84^'.
3.	(-2; О) и (1;3).
cos a cos 7
4.	b • -т-7---г-,
sm a + 7)
5.	x = ± arccos(l — л/З) 4- 2тгЛ,
7Г
у = — — 4- 2тгп, n, A: G Z.
Вариант 8.1
(2;3].
1 ± л/1 + 5тгп
-------------, n G Z, п > 0.
5
1°8з 2,2 log2 3.
7д/7.
6
7’
при
при
при
при
8. 7Г.
Вариант 8.3
1. —2 4- тгп,п 6 Z.
(13 + 2^/3)а.
„	„ 2 a
при а < О х > 2а +
а2 а
при a > О * > тх + х •
lo Z
mk
Т'
Вариант 8.2
5. (-оо;-2).
7Г
12 + ”“’
7Г irk . п
~24 + T^keZ-
7. При a = ~ 4- 2тгп, n 6 Z
Зтг
2 ’
при других а решений нет .
Огне гы к вариантам 2001 года
165
Вариант 9.1
1.	О, ±72.
2.	[2; -Foo)
3.	(72 + ТЗ + Т5)2,
(72 + 73 + 75)"’.
4
5.	6 и 8.
2тг& t _
о. тгп, -j-, п, к 6 Z при a = I
при а 0 корней нет.
у 22000.31999000
Вариант 9.2
1.	(0; 1) U (1; +оо).
2.	1.
3.	тгп, п G Z
4.	2.
5.	[100; ±оо)
6.	[3; +оо) •
7.	4004001.
Вариант 10.1
1. (-4;-l)U(-l;2).
\/15 — 3
2. (—l)narcsin--------F тгп,
6
п е z.
’44
4. 189 .
5. [—1.9; —1.7] U (—1; ±оо).
й 273-2
Вариант 11.1
1. {-12}U(7;+oo)
2. 7ГП,
, 7Г 7Г л	п
±—— — + 2л±, п, k £ Z.
3 о
и (1; 16] и (64; ±оо).
4.
3
4 '
. зТб
5. —•
в- -х,-|,±1,±л/5.
<5 и
Вариант 12.1
1.	± arccos(72 — 1) + 2тгп, п Е Z.
2.	3,-1.
3.	0.
4.	ai = 3,</=6.
5.	(5;-4),
(-13; 20), (-5;4), (13;-20).
6.	т2.
166
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 12.2
, 7Г 1ГП п
L 4+Т’"е Z>
2.	-1.
3.	(3;4].
Л 2^3-3
4
(1Г	\
2лп\ — + 2irnj ,n G Z.
6. Нельзя.
Вариант 13.1
5. 3.
6. к < —11 и к > —3, к Е Z.
Вариант 14.1
1.	~ 4- 2тгп,
(—1)* arcsin
п, к Е Z.
2.	(1;оо).
3.	1°.
44
4.	больше на 50%
1- (2;1).
Вариант 15.1
3.	50 км в час.
Л Зтг .4
4.	—- < arcsm - .
10	5
5.	0,-2.
Вариант 13.2
1.	[--ДО;-3) U (3; \/10].
2.	± arccos |-~) 4- 2тгп,
\ х/34-17
n G Z.
3.	-9.
4. 2л/3.
6 ± 5л/3
2
2. (—оо; —8] U (12;+оо).
3. 2тгп, + 2тгЛг,
Л 1 Л >
2 arccos -у= + 2тп,
_	1	7Г _
2 arccos —= — — 4- 2тгт,
у 5	2
п, m Е Z.
5. при a < —
нет;
при
Ответы к вариантам 2002 года
167
/ -1 - 71 - 12а4
х Е 1
3. Я = 8.
2а
-1 +V1 - 12а4
2a I ’
при a = 0 х Е (0; оо);
5. а е [-у/2; -1)и(1; V2] •
6. г = 1 .
(	-1 - л/1 - 12а4
х Е I —оо;
Вариант 1.2
2а
,/-1 +VI-12а4
U | ----------; оо
U
1. 6=-72.
2a
и{1}.
при a >
Вариант 16.1
4. 10 часов 40 минут того же дня.
1. (~1;О)и(о;2= .
2.	(-1)п-4-7гп,пе/.
6
3-	т%-
4
5.	(—2 - 2^2; 0) U (0; -2 + 2л/2).
Ответы к вариантам 2002 года.
( ± arccos + 2тгЛт;
\	5
4
(—l)n arcsin - -f- тгп
5
fc, n Е Z.
6. R = 7V3.
Вариант 1.3
Вариант 1.1
-4
59 Г
2 ’ 2
1.	{ irk, k&Z} .
2.	6=V3-
3.	(—оо; 3].
4.	{-1}U [-1; 1
2.
U
6. 12 часов 30 минут того же дня.
168
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
7. 5 = 9073-
6. ^715.
4
Вариант 2.1
1. (—оо; —1] U
7. a G (-оо; 1).
8. ^ТПз.
288
14-717
Л	(37Г	7Г
4-	T‘ + ’rp;~'5' + ’r9
\ о	о
тг	Зтг	,
ё + ’гр;--г- + 7г9);
о	о /
p,q е Z.
5.	Scnk = л/2; Здвс = 12.
6.	36 и 49.
7-
[5 2 J
61тг
О. ---7= .
9л/39
Вариант 3.1
1.	утверждение справедливо.
„ Г 1 J Г7 5\
2.	—; О U -; - .
2 ’ ] [ 3 2 у
3.	(—2;3), (-3;2), (-1;5), (-5; 1).
4.	20 рабочих, 6 часов.
тг Л , 5тг Л , ТГ
5.	—- + 27гЛг, — 4-2тг/, — 4-2тгтп,
о	о 18
17тг _	, .
—- 4- 2тгп ; к, I, m, п 6 Z.
18
7. |(2-Л).
О
Вариант 2.2
Вариант 3.2
1. 8.
3.	(-1;-3), (-3;-1),
(-1;4), (4;-1).
4.	10 тракторов, 9 часов.
тг	1
5.	— 4- 2тгАг, arctg - 4- 2тгп;
о	Z
k,n € Z.
3
Ответы к вариантам 2002 года
169
6. -л/6.
Вариант 3.3
1
2
2.	-4; -3;
3.	(1;6), (—6;—1),
(1;-5), (5;—1).
4.	20 рабочих, 6 часов.
7Г л .	1
5.	— 4- 2тгк , arcctg 4- 2тгп ;
Ar, п 6 Z .
6.	а=/|.
Вариант 4.1
1.	(—оо ; 1) U [2 ; 4-оо ) .
2.	— , п G Z.
3
3.	(—оо; —1 ] U {2} .
/ 1 с; 1	\
4-	I -ттт; - 1 )U( у/2-1; 15).
\ 16 ’ 42	)
г 4190
5-	—•
( х/2-У2 у/2-у/2\
6.	------
первое из чисел больше.
7.	[-6; 1 — х/1з]и[д/Тз — 1; 6j .
Вариант 5.1
1. 9 км/ч.
л-
3.	(-оо;-417) и (-4;-3)и
(-3; 3) U (417; 5].
4.	9.
5.	5 часов и 7 часов 30 минут.
6.	—4; 4; 6.
7.	(8,0,1,0,1).
Вариант 6.1
1. 0; —2; -2+4=.
Vo
2- (vT-'/5) 
3. полет при ветре продолжитель-
нее на 1, 25%.
4. [—1; 0] U [ 1; 4-оо) .
5.
Зтг	Зтг
— 4- 2тгп ; —-4- 2тгЛг;
4	4
n, k Е Z .
170
7.
8.
9.
1.
2.
3.
4.
5.
6.
7.
8.
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
при a / 0 решений нет;
при a = 0 решения
(ТГ ТГ	. ТГ 7Г . ,	. \
т +	+ n); R + т(2^ - п)) >
4 Z	0	4	/
k,Tl £ Z .
УтпЛп — V 3 .
а (2г2 — 2аг + а2)
а2 - 2г2
(\/2 < < 2+ Л) .
Вариант 6.2
9.
a
/2
Вариант 7.1
2. 50°, 90°, 110°, 1Ю°.
3. -5.
и(0; +оо) .
второй вариант выгоднее.
„ /1	1	„ \
5- I , tg«, ztg2a,tg4a I ,
\ о	о	/
, тг 2я , Зя
где а = ±у,±у,±у.
1 4 _£ £ 18
6’ 3 ’ 3 ’ 11 ’ 1Г 11 '
тг irk ,	„
4 + Т- ‘ez.
5тг
— 4- 2тгЛг, k Е Z.
4
Вариант 7.2
*4
0; arcsin—--- I U
(	. Vb-1
I тг — arcsm —-— ; тг
3
2 sin 10° sin 40° *
1 - y/$	З-л/5
при a = —-—	x = ±3 4
2. {0}u[l;l]u
3 + У5
2	;°°
3. 15.
5. 32 : 5.
6. 1,
1	1	3
3’-2’~4 ’
при a G (-00; -1)	Вариант 7.3
x = ±3“2 “ a 5/6(2 “ a “ 1 “	.	1. (0; 2].
Ответы к вариантам 2002 года
171
300
13 км
4. 3.
з.
4. у/7.
5. (1;27).
5. (2; оо).
6. |(3 + V8 — \/1Т)2.
Вариант 8.1
7Г71 /	ч jl	. 7Г
1.	—1) arcsin — + 7гя;
4	4
n, k G Z .
2.	1.
3.	[2 - У13; 0) U (3; 2 + ^/13] •
4.	2.
5.	(0; 0), (2>/7; v'T) -
л  ( Х \
6.	arcsm ( --; - 7-Г I .
\2cos(/?/4) /
7.	При a G (—оо; —1) U (0; оо)
х = у = 22У<а3+а)/2 и
X = У = 2-2V(«’+“)/2;
при a Е {—1; 0} х = у = 1;
при a Е (—1; 0) решений нет.
Вариант 8.2
1. 3.
2.	4- 7гп, 4- тгк\ п,к Е Z .
4	2
6.
4
9 ’
7. (а 4-1; 0) U (—а — 3; 4-оо)
при a < —3;
(а 4- 1; —а — 3) U (0; 4-оо)
при a Е (—3; —2);
(0; 4-оо) при a — —2;
(—а — 3; а 4-1) U (0; 4-оо)
при а е (-2; -1);
(—а — 3; 0) U (а 4-1; 4-оо)
при a > — 1.
О 2 4У15
8’ 3’ 15 ’
Вариант 8.3
1.
10 + 5 4 ' 15 + 5 ’
п, к Е Z.
/3
2. (-оо;1)и(д;2
3. (0;log±4) .
ч-
5. 4, 8, 16; 16, 8, 4.
Зл/6
172
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
7. а) х £ R при a Е (—3; —2);
(—оо; 3 — \/а2 + 5а + 6) U
(3 + у/а2 + 5а Ч- 6; +оо)
при a Е (—оо; —3] U [—2; +оо);
Г -5 + Лз\
2 /
8. 6.
Вариант 9.1
, КП _
1.	— ,n е z.
2.	(— 4- 7гп; 9^) , n Е Z .
\4	/
3.	(—оо; 0) U jjogi 4; logi 7^ U
jtogi 12; +oo) .
4.	6.
5.	7V.
6.	—1 ± у/a при a > 0;
нет решений при a < 0.
Вариант 9.2
‘ й-
2.	(1,1).
3.	(-4;-3, 9] U (4; \/17).
2тгп 2тгт
4.	—,-^-, где
п ф 11, m 9l,n,m,l Е Z .
5.	8.
6.
Вариант 10.1
3. (1; 2), (—1; —2).
4_____I--------+_____I---•
’ 45	3 ’ 25	6	5’
n, k Е Z.
5. 20.
6. (-8;4)U(7;+oo).
Вариант 11.1
1.	+ (-1)”^-+ я-n, п Е Z.
9 /с sin(a + /?)
у 2 sin a sin Д
4. (-оо;-4) U (-4;-3) U
(—3; — 1 - л/3] U [1 -Ь \/3;+оо).
г 133
5 • ---.
803
Вариант 11.2
Ответы к вариантам 2002 года
173
л 7Г 7ГП _
2’ io + T’neZ‘
, 15л/15
’	32 *
4. (—оо; —2]U[—1; 0)U(0; 1]и[2; 4-оо).
5. а) 2 4- \/2;
б) (-оо;2-\/2)и{1}и
(2 + \/2; 4-оо).
Вариант 12.1
1. 25°.
3.	(—оо; 0) U (0; 1) U {2} .
, я 4тг
4-	6’ Т-
5.	{0} U [1g15 6; +оо).
6.	Ютг+16.
7.	-^= (Jh2 + ^-^ .
Нл/з\У 3 2J
Вариант 12.2
3. 70.
4. (1;64].
Птг 7тг
12’ ~12'
6’ 2 + ctgf+ctgd-f)-
Вариант 13.1
1.	(—оо;0) U Q;+°°) •
2.	3; log2(3 - л/7).
3.	а) 1 : 3; б) arcsin .
4.	а) 2 : 3; б) 2 часа 48 минут .
5.	5.
/1 3 "
6' (-з!й]и{1)-
Вариант 13.2
1.	3.
2.	(— 1)п+1тг + яп,п е Z.
о
3.	(—3; 9), (2;4).
4.	а) Ютг; б) 160.
5.	а) 3; б) ± arccos - .
3	6
6.	(0;0),(±2;т2),(±х/б;т?6))
/у/З + у/7 л/3-
у 2	’	2	J	’
/з/3-Т7 \/3 + \/7\
\	2	’	2	/	’
174
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
1.
Вариант 14.1
3. а) 1240; б) 40.
(7Г\
ж; ж , х G R;
о /
_ / 7Г л 7Г л \
б) (12+27Гп;4 + 2 / ’
(7Г \
7гАг; — + irk) ,k,n G Z .
5. log2ll.
6.
при a G (0; 1] x = ±
при остальных a решений нет.
Вариант 14.2
1.	(0;l)U(^;2] .
2.	9(3 4- л/3).
_ тг	5тг	Л
3.	— 4-	+ 2тг&; п, k G Z .
4	6
6. 2.
Вариант 15.1
1.	[-1;^
’	2
2.	(11;+оо).
3.	0.
4.	1.
5.	2тгп, n 6 Z.
6.	2.
Вариант 16.1
1.	2.
2.	(2;|)и (|;з) .
3.	60°.
4.	15 кг.
5.	V2R2 cos a •
• (2 sin a 4- V2 + 2 sin2 a) = 54 .
6.	-3; -1;
Ответы к вариантам 2003 года.
Вариант 1.1
5. а) 432 + 288>/2;
б) 144тг(5У2 + 7)
Ответы к вариантам 2003 года
175
2. ZA = ZC = a, ZB = тг — 2а,
. У8РП-1
a = 2 arcsm-—-: к
4k
0.
4.
4. л/б2 + d2 ;
/а2 + 62+^3)(°а-.ЬР_2
уа -t-o -I-	(а2+Ь2)2
5. a е (44- 24^5 44 + 24у/2) .
2- (4;-1)иМ) 
3.
5тг л , 7тг ,	„
— + 2тгАг; — + 2тгп; к, п G Z.
при с < 0
, З + ИГ^к
х = l°g 2 ----------;
5	*
9
при 0 < с < -
,	3±л/9^к
х = l°g 2 ------- *
5
9
при С = - X = log 2
4	5
9
при с > - решении
3
2’
нет.
6.
/	4л-+ 18
-°°; —г—
\
[8?г- 18; 18 — Зтг]
U
5.
5 \
1; 2 ) и14;+°°)-
Вариант 1.2
1. (-1; 1)U[2; 3).
6. бд/З.
7.
12
2. ±у + 2я*, *6Z.
4
3 \
3. -2;--J U[-l;+oo).
4. 27\/3.
Вариант 1.3
Вариант 2.1
7Г л , 7Г	27ГП _	„
1.	- + 2лгЛ, -- + —; к, п G Z.
о	а о
2.	(-oo;-6]U(-3;-2).
3.	39.
4.	(—оо; —2]U {—1} U (7; 8].
5.	/.ВАС = arctg
7Г	v/З
/ВАС = - - arctg V
4	5
176
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 2.2
1. [-7; -2) U ( —2; -1].
3. Первый пешеход прошел путь
за 1 час, второй - за 5 часов.
4. (0; л/3), (0;-V3),
. . тг	тг	v3 „ ,
6.	±- + тгп; —---— + 2тгЛг;
6	4	2
k,n е Z.
7.	log3 (18±9\/3); log3 (10±л/19).
8.	Vsabm : Vsamcd = 1:41.
Вариант 3.1
1-	[-2; 1].
2.	-207.
3.	(log73; 2) ; (log7^;-l ) .
у о /
4.	24 и 80 тонн; m = 4.
5.	4^13.
с ( 1 1 11
6.	-оо;------7=	U --; - U
\	2 Л J	I 4 4 J
’ 1	\
L2s/2	J
7.	36 .
Вариант 3.2
1. [1;4].
2. -210.
„ /3,	„	1\
\ 2 °®3 ~ 2 / ’
4. 3 га; п = 4.
5. Зл/З.
7. 5.
Вариант 3.3
1. 4.
2. 90%.
Л У2 + ^/б
6 ’	12
5. Ь = 3.
Вариант 3.4
1- {-2}-
Ответы к вариантам 2003 года
177
2. 7.
5.	АВ = 12; ВС = 10.
6.	(3; 1); (-3; -1).
7.	70е.
8.	а = -2.
4. 6 тонн; m = 4.
Вариант 4.1
1. Ае Г^; 12 .
I 10
Вариант 5.1
1. 0; 2.
2.	500.
3.	[-4; 5)U(21;+oo).
4.	центр в т. (—2; —5), R = 5.
5.	(4; 8) U {2}.
6.	AM = 15 .
7.	— 1;	— 1 + тгп, п € Z.
8.	ре{^2}и(-^;1 .
Вариант 4.2
1.	(—оо ; —5) U {3} .
2.	80%.
о 2тг
3.	— 4- 7гп, n Е Z.
4.	(-2; 3).
. 7Г	у2 Зтг
4. -;^ + arctg—
5.
(—оо ; —5] U
И
1 32 ’ 8 J
6. отрезок [0; 2] при
с = 0,
d=l
Вариант 6.1
1.	в пункте Е.
2.	(—оо; —5] U [—1; 4-оо).
3.	14 млн у.е. для предпр. А и
2 млн у.е. - для В.
А 1
4.	arccos —7= .
л/З
178
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
5. нет решений при a > О, b > О;
( —оо ; 4-оо) при a < О, Ь < 0 ;
при a < 0, b > 0 .
6. (2; 2;-2).
7. Успеют.
1.	(—оо;—1].
2.	3.
п 48	,
3.	— м/сек.
7	'
4 а 4" 1
* а (8 — 56) ‘
I- Г	1	ГТ
5. 7ГП ; — 4- 7ГП j , n G Z.
6. (—оо ; 2] U [3 ; 4-оо) .
Вариант 7.1
1.	2 решения.
2.	Бассейн В.
3.	ZC = 60° .
/	5
4.	(—оо;—1)U (-1; -
5. a = — 3 ; b — 2 .
log2
2"-(У5-1)»\ 0
2n + (V5-l)n / ’
если п - четное число;
9. (3; -2), (-3; 2),
(7; -2), (-7; 2).
Вариант 8.1
1.	54.
2.	{0} U
3.	25г/3,75\/3.
4.	2.
5.	3.
6.	7ГП, п Е Z.
2П-(У5-1)П
2” + (У5-1)п
Вариант 8.2
1. (0; 3~4) U (3~4; 1].
если п - нечетное число.
2.
Вариант 7.2
7Г	2	Л ,
— 4- тгп, — arccos - 4- 2тгА:,
2	5
n, k е z.
Ответы к вариантам 2003 года
179
3. 90°, 20°.
4. 4800.
с 96>/3
' 125 ’
6 ЬЧ)-
Вариант 8.3
1.	-3.
2-	й-
3.	2 .
4.	25 : 81; одинаковы.
6.	5.
7.	При a = Ох = 0;
при a Е (0; 1) решений нет;
при a Е 1; 2з)
a ± \/2у/а — а2
2
при а = 2з х = 2“ з ;
2
при а > 2з решений нет .
. 5л/3 2л/б
8-	~ ~
Вариант 9.2
t .	тг
1. ± arccos — 4- 2тгп,
18
± arccos — 4- 2тгЛг, п, к Е Z.
18
6. 10(2- </3).
Вариант 9.1
_* + 2,rM-l)n+1
к,п Е Z.
7Г 7ГП
12 + Т’
2. ( оо; 2) U ( 2;
3.
U[log2 3; +оо).
л 1 + Узз
4- ~т—
5. (—2; 3), (2;3).
(—оо; -2) U
Л.5 + у5\
\ ’ 2 )
U (7; 4-оо).
U
I 4“ гп
Т+~к'
5. (—оо;— 4] U
g ___________
1 4- sin у
7. при а Е (0; 1)
х Е (а3; 1) U (1; 4-оо) ;
при а > 1 х Е (0; 1) U (1; а3).
180
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
Вариант 9.3
5. (3;0), (3;2), (3;-2).
Ч-
7Г
1.	±— 4- 7ГП, п Е Z.
о
Л /	2
2.	I —оо; —
к 3
и |;+ooj.
3.	(log5 626-4; log5 26).
Вариант 10.2
1.	(0; 1).
Л тг	~
2.	— + тгп, n Е Z.
3.	(0;2).
4.	2.
4. 0 .
11
3
5.	4.
6.	[-5; 5].
6. 2R sin —.
2
7. При a < — 2
х Е (—оо; а) U (—2; 4-оо);
Вариант 11.1
1.
2, log2 5.
при a G
х Е (—оо; —2) U (а; +оо);
2.
2.
3.
при a = ;
(1;4-оо).
я 1125
’ 224 ’
;1 U
4.
5.
6.
1.
2.
3.
4.
Вариант 10.1
О или 1.
(0; log2 3] U [2;+оо).
1.

8.
(1; 18 — 12х/2].
Вариант 12.1
2
11	2
3
2’
10
2.
3.
51
100’
7
4
Ответы к вариантам 2003 года
181
4 ^^±^^2-1
144g2
5.		.	.
25 - 240 - q2
6.	[2101608; 4000000]U
[6000000; 6250000].
Вариант 12.2
7.	1984.
Вариант 14.1
„ ТГ	ТГЛ	~
1- Т7 + Т’ П
15	5
2. 3(л/2- 1).
U(0;3].
Л	ГУ
1. — 4- 7гп, п Е Z.
4
2. (—оо; -у/2] U [>/2; 2) U
8 + У10	\
---------; 4-оо I .
4.	3100 м2/день.
5.	24 : 1.
6-	Н;1).
-1-д/ЗЗ
3. 2	2
4. 15:8.
Вариант 14.2
5
1.	-5~3.
5.
arcsin
х/б — 2
2
2.	(—оо; —6] U [—1; 0) U
3.	14.
Вариант 13.1
4.	2д/2(\/3 + 1); меньше.
1	. —4.
2	.-4- тгл, п Е Z.
4
„	-1 -2л/29 '
з	- —е-----;2
S. (Н)и)1)и(1;4
Вариант 15.1
1. 1.
4. 30°.
2.
5. (—оо; 0) U
7Г 7ГП „
и + — ,nez.
3. 74.
6. (-1;2].
6. -1.
4. (In, 3n, 2n), n E Z.
182
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
5.
6. а(Л+Т5),
Вариант 15.2
3.	А = С = arctg 3,
В = тг — 2 arctg 3;
4
4.	28.
5.	b/^,kez.
а
1.
7Г 7Г71	_
4 + T’”6Z-
Вариант 17.1
2. (0; —1), (1; 0).
3.
2
~°°;~з
и{о}и
75-3
3
2.
4.	472- ЗТЗ.
г „	1
5.	2arctg-.
6.	(-оо; — 6) U ( — Ч-оо
\ о
, 1	1-7Й
±- arccos-------F тгп,
2	4
n G Z.
( 41
3- 1-аГиН;0]-
I и I
4.
97573
196 ‘
Вариант 16.1
1.	(—2;0).
2.	9.
3.	±2.
a2 sin 6 ♦ sin(7 4- <5)
2 sin 7
5. а) нет; б) 21 .
Вариант 16.2
L
7ГП _
—, п Е Z.
о
/ 5 \	9-72П. 5
\ 2’7’	2	’2
U{7}.
Вариант 18.1
1.	1.
2.	(0;3].
3.	77.
4.	25%; 62,5%; 10%.
5.	первый —10, второй —12.
6.	а = 7; Xi = 2, «2 = 4, ®з =
2.
/1 7Г
(1, 2тг&); I — — 4- 2тгт
(4 + 2™),
Ar, m, n G Z.
Ответы к вариантам 2004 года
183
Ответы к вариантам 2004 года.
Вариант 1.2.
Вариант 1.1.
1.	2, 4, 8,	16.
2.	2; 3.	
3.	-15.	
4.		
5.	1 - или 4	5 4
6. При аЕ(—oo;0)U ^;4-оо
при a Е
решений нет;
3 — \/з\
0; —-— I два ре-
шения:
a
х =
при a =
х
3 — V3
—-— три решения:
я:=24-л/3 и х= 1±#12;
(3 — у/3 1 \
—-—; - I четыре
решения:
2(а - 1) ± V~8a2 + 12а - 3
Х~	2а- 1
/ a
У 1 - 2а ’
1
при a = - три решения: х =
— 1 , х — 3 , х = 5 ;
Л
a Е I -; - J два решения:
\ О " /
I a
2(а - 1) - л/-8а2 + 12а - 3
2а- 1
2.	(-3; -2] U [2; 5) U
Гз-л/зТ. л/23 — 1
U 2’2
3.	— + 2irk; к 6 Z.
16
4.	65 : 144.
/	5\
5.	При	а Е	I —оо; — - ) одно ре-
\	4 /
шение;
5
при а = — два решения;
4
/ 5	\
при а Е -- ; —1 I три реше-
\ 4	/
ния;
при а Е J—1 ; 1 — два ре-
шения;
при а = 1 — д/2 одно реше-
ние;
при а Е (1 — л/2 ; 5^ два ре-
шения;
при а Е [ 5 ; 4-оо) одно реше-
ние.
6. DK : АР=1 :2.
при
2. R.
Вариант 1.3.
х
х —
184
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
3.
4. нет решений при d 6 (—оо; —4);
х = 1 при d = —4 ,
и
23тг
- 4-	2тгт; m € Z > .
14	J
6.	4 : 5.
7.	WA:K4V=1:2.
Вариант 2.1.
1. [-?5; 2).
3.	{-21} U [0; 21].
4.	arctg 3 ; 10.
5.	[1; 2).
6.	j; m = 3.
„ (тг л	Зтг л , \
7.	I — + 2тгт; — + 2ттАг I ;
\4	4	/
/ ТГ	ТГ	л ,\
(—— 4~ 2тгтп; т 4- 2тгАг) ;
\ 4	4	/
Ar, m G Z.
8.	1.
Вариант 3.1
ЧИ
з4
4-	U (2; 3].
5.	17100 рублей.
6.	-14.
ч
Вариант 3.2
•Л
2. {1; 3}.
3. 40.
< И).
5. 150 тысяч у.е.
6. -3.
Вариант 3.3
1. л/3.
5 31
4 ; 2 J
3. 1.
5. 90 тысяч рублей.
Ответы к вариантам 2004 года
185
6. 2.
Вариант 4.1.
1.	[0; 1) U (1; 4~оо).
2.	| 4- 2тгп, n Е Z | .
14	J
3.	{ (26;—6); (-9; 29) }.
4.	32.
5.	8 час 15 мин,
6-	{(9; 9)}.
7.	10.
8.	р&[-4; 1] U (3;4].
Вариант 5.1.
1.	(—оо ; —5 ).
_ Г	7Г	'I
2.	<7гп;— — + тгл; п,л Е Z >.
V	&	)
3.	(0;0;0); (2; 2; 2); (2;-2;-2);
(-2; 2;-2); (-2;-2; 2).
4.	(Iog2 (8 ± л/бЗ)
г 3тг(3-Ь л/2 — л/3 — л/6)
5.	------------------——— .
7тг-6(у/3+ 1)
4201	x/60T
' 3600 ± 30 ‘
Вариант 6.1.
3.	5.
4.	2445 долларов.
/ 5
5.	и[2;3).
\
6.	Четыре. Например, это гири мас-
сой 1, 3,9,27 кг.
7.	2^/65-
Вариант 7.1.
16а?1 2 * 4- 12я?г/2 4- 9j/4
4х 4- Зг/2
п тг	_
3.	— 4- тгп , п Е Z .
4.	(1; 2; 4), Q; 2; 1б) .
5.	9 час 50 мин.
6.	( 2—л/б ; 2—л/2 )U( 2+V2 ; 4 ).
1. 10.
{7Г 7гЛ? ,	„ 1
4 + -2-; k € z у-
8. ( 64 ; 80 ; 100 ) , ( 80 ; 100 ; 125 ).
9. При значениях а, удовлетворя-
ющих условиям
2тгЛт < |а| < тг 4- 2тг к, |а|	4-
2тг£, к = 0, 1, 2, ••• ,
решения
(-1 + х/1 + 4р(а)\
х = ± arccos I ---------------J
г х 1  • I 3 . . .
где g(a) = - | sin а| 4- - sin |а|.
186
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
10. ^У15.
4
Вариант 8.1
1
3
2. |V2-l;l)U(l;+oo).
3. (—v/5; -2) U (-1; 0)U
U(0; 1)0(2;^)-
21	11
’	5 ’ 4 ‘
4. >/б(л/3 + 1), 3(3 + \/3).

/5 3\ /7 , . „ 1 ,	\
5- \2’2/’ \2 ~ °®2 3’2 + °g2 / '
7. Если a = 0, to x > 0;
8.
если 0, to x =
arctg -.
«5
3a + \/9a2 + 4
2
Вариант 8.2
1.	(0; 1)U(1;2).
2.	(-оо; -2 - д/З] U
U (-0,3; -2 + %/3) U
U {1} U (2; +оо).
3.	13.
4-	J + (-l)"+1J + ™,
£ + (-1Г+1£ + ™,
n, m G Z.
5.	16 km.
2Л+1
У15
Вариант 9.1
Вариант 9.2
7Г	7ГЛ 7Г
L + о +
12	6	2
n, k G Z.
2.	(-5; -1) U (3; 7).
3.	(-2;-l + v^).
4.	-3 + yf2A.
c (1 + У13 - 5 + -Дз\
к*-!—5—/'
6. 96.
[_И_2Л| if 11.If
'	30’ 30/^130’30
Ответы к вариантам 2004 года
187
Вариант 10.1
1. (—оо; —1] U (1; 2) U [4; 4-оо).
2. 7гп, п 6 Z.
т 3±v^3
2
7Г
2+™’
7Г тгАг . п
io + T;n’*eZ-
4. (—oo;0)U log2
9 + У13
2
6. (а, 6) = (1,2), (-1,-2),
Вариант 11.1
1. 2,5.
3. ±1,±2.
4.
16	21	„	112
— и — или 3 и —
3	25	75
5. nk, (-1)п+1^ + тгп,
1 — у/5
(—l)m arcsin-------F 7гт;
4
&,п,т Е Z .
6. л/2.
Вариант 12.1
Вариант 13.1
х л/6 4-^/2
4
2.	42.
3.	(—oo;log23).
Зтг
4.	— — 4- 2тгп, тг 4- 2тгАг; п, к Е Z .
Заб
‘ а 4- 2 6 ’
6' 5-
Вариант 13.2
2-	4-
3.	-4.
4-	(log2|;l •
188
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
6. 8,Т2,7л/2.
7. (-2,-8).
Вариант 14.1
1.	{±2} U (3;+оо).
2.	±- + 2тгп, n Е Z.
о
, х	195
3.	а) 60 км; 6) -у- км.
4.	а) 12; 6) |.
5.	2,У.
О
6.	30103.
Вариант 15.1
1.	log2(6 + Л7).
2.	[-1; 2) U (5; 6] U (8; +оо).
о 7Г 5яг л	_ 5тг
3.	— + 7гп, — 4- 2тг&, n, k Е Z; —.
2	6	6
.	. 5 225
4.	arcsm ----==.
6’ 16л/П
5.	0,1.
Вариант 16.1
/д \
1. (-оо; —5) U I+оо I .
2- (-1)"й+Т’пе7-
3.	—4.
4.	а) 6; б) 3^5 
5.	58,5 минут.
6.	а) (±1;3);
Вариант 17.1
1.	3.
/14
2.	а) 2; б) (-oo;0)U I — ;+оо
\
3.	14% .
„	23
4.	arccos —= .
4д/37
7Г 7Г2 — 7Г 4?Г2 — 7Г
' ~3’~ ’	3	'
Вариант 17.2
1.	[—5;—3].
л , 7Г лк , п
2-	±? + T,iGZ.
и О
о гх	500„,
3.	Выросла на -т-% •
У
. 6^3
4.	—;= .
У19
5.	2х/3,2д/3,2л/3.
6.	a G (0; 2с].
Ответы к вариантам 2005 года
189
Ответы к вариантам 2005 года.
Вариант 1.1
, |-з:
3. Sabd = 1; R =
4. 5тг.
2.	тг 4- arcctg 2 4- 2тгп, п 6 Z.
3-	51оо = 15 050 ; 640 = 81.
4.	4710 - 2715.
5-“фт-’
и(^-6; £_9].
\ 2	2 J
6. 32.
5. S6 Е {0 ; 3}.
Вариант 3.1
Вариант 1.2
{Отт
—(41: + 1), k G Z
8
1. -150.
2. 18.
2.	(0; 1).
3.	{arcctg 3 4- 2тгп, п G Z) .
, (-13- 7481 -13 + Т481\
4.	-----------; ----------
у ю 10	/
/-13 + 7481 -13 - 7481
I 10	’	10
3. 962 500 руб.
5. 4714-277.
7. 25.
5. 273 + 4, 273 + 4, 473 + 6.
6.
Вариант 2.1
1- {-1} и | ; 1
I GZ, // -5,-2, 1, 4.
190
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
1.	(0 ; 16тг).
Вариант 3.2
1- {-2}.
2.	60.
3.	10 миллионов 2 тысячи у.е.
5.	6; 8; 10; 12.
6.	(2;3); (3;2); (3; 3);
(4;3); (5; 4).
7.	5=9073.
Г 51
8.	a Е (-оо ; 11 U < - > U
I 4 I
5. 2 + х/2, 2 + 72, 272 + 2.
6. а = 2.
Вариант 3.3
1. -3.
2. 18.
3. 2 миллиона 810 тысяч руб.
6. 6=1.
Вариант 4.2
1.	{0} U (1; 4-оо).
2.	{2}.
3.	5760 руб.
4.	[0; log3 2).
5.	{ тг —а ; 2тг+а ; Зтг — a },	где
a = arcsin (72 — 1).
6.	5 = 2715.
7.	6=2.
Вариант 5.1
1. (-оо ; —1) и (—1 ; 5].
Вариант 4.1
1.	[1 ; +оо).
2.	(—оо;—2].
3.	-3.
4.	-
тг тг
2 ’ 2'
2. ± arccos —-------1- 2тгЛ;
тг тгп ,	„
4 + ~2~ > n> £ Z.
-3 + 75
4. 5%.
Ответы к вариантам 2005 года
191
7Г 7Г 7?Г 117Г
' а' 6’1’12’ ТГ ’
тг 2тг
2 ’ Т; “’ Т ~а
л/З
где а = arccos-	.
2V4-л/З
6.	20%.
_ 7Г
7.	arccos
2
7. 1272.
Вариант 8.1
Вариант 6.1
1.	Можно. С 8 руб. 50 коп. по 16
руб. 00 коп. включительно.
2.	(5 ;+оо).
3.	Е(0;0).
4.	{ 1 + 2тгп, п 6 Z}.
5.	69 руб. 43 коп.
6.	а > 0.
7.	Найдется.
Вариант 7.1
1. 126.
4. Sabcd — 4л/3.
5. Утверждение верно.
1.	Числа равны.
2.	[ 0 ; Тб].
3.	6.
4.1^.
„ ( ТГ . ТГ , \
6.	- + як ; - 4- лк ) U
( тг , Зтг
U ( — + лк ; — + лк
\ “	nt
к G Z.
7.	3 и 4.
8.	-W, \/3.
9.	тг.
10.	а = 2 д/Т0 — 6.
Вариант 9.1
1.	28.
2.	-1.
3.	[1; 2) U (2; 75].
192
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
4.	18;£le
Г 2	\ о /	\	3 /
5.	0;4+2УЗ.
6.	4д/б.
4.	10.
5.	(2;0).
6.	2.
Вариант 10.1
7Г 7ГП 2тГ& 27Г771
4 + Т’ ~1~’
n,k,m 6 Z.
1. 2,5.
Вариант 11.1
2. [—1;0).
3. ±1,±2.
16	21	„	112
— и — или 3 и ——.
3	25	75
7.	Если a = 2, то решений нет;
если a G \/3), то х >
a
если a 6 (А 2) U (2,-f-oo), то
х е (о,-
\ a
я
8-	“Г-
Вариант 11.1
1. ±1.
5. кк, (—1) +1 — + кп,
6
1 — \/5
(—l)m arcsin — -----1- кт;
k,n,m Е Z.
6. V2.
Вариант 12.1
1.	±1.
2.	—— i — + 2тгп, n € Z.
3.	16\/5.
4.	[1;2).
5.	4.
Ответы к вариантам 2005 года
193
7. —
35
Вариант 13.1
1. 4.
о • V3
2. sin —-7Г .
6. 1:3, считая от точки А.
Вариант 14.1
1.	((— 1)п+’1~ + 2тгп; 2тгЛг^ ,
n, k G Z .
2.	150.
з-	[!’)•
4.	^ + 2у/2.
у/2
,	5	‘	л-	4л/22
4.	arccos -	+	—;	—=-.
8	2	ЛЗ
5.	5.
6.	[-2; 0) U (0; 2].
Вариант 16.1
1.	0, ±1,±2,±3.
2.	240.
/	3	\
3.	I—0 I U (3;+оо).
4.	2тг.
5.	+ 2тгп,n Е Z.
6-	2; tgy.
7.	1,...,7.
Вариант 17.1
1. 0;4.
5. 26.
Вариант 15.1
1. ±3.
2. (—оо; 1] U (log2 11; -Ьоо).
3.
тг л 11тг л ,
-12 + 2 *’ГП’—1Г + 2я*’
п, k G Z.
3. 2.
1 + -/17
2
6. 20; 18000.
Вариант 18.1.
1.	64.
194
Подготовка к вступительным экзаменам в МГУ. ВАРИАНТЫ.
2.	(О ; log2 3].
3.	25.
, тг	„
4.	— — + тгп, n Е Z .
5.	ВС = И.
„ ’ „ 27101-25 ' fnl
6.	-4;-^—-------- U{O}U
Г 23 „1
U — ; 2 .
13 ’
7.	15073.
8.	о 6 [—8 ; 6].
9.	Река течет от А к В; макси-
мальная скорость ее течения 8
км/ч.
10.	1.
Вариант 18.2
1.	Не досталось.
2.	[-1; 1].
3.	11 землекопов.
Вариант 18.3.
L (0; iVMib |)и[1;+оо).
Л /	7Г	\
2.	Жп ; Т 4- КП - хп ;
\	4	/
n Е Z, п / —2, —1,0,1,
7Г 7ГП
Где Жп = -+т±
± 1^ + ™)2_36.
3.	(0	1).
4 9	-	15
4.	bMBN —
£
5,Л=^?.
О
\/3 -Ь 1
6. ± arcsin----|- тгп ; п € Z.
Вариант 18.4
1. [5 ; +оо).
2. [-3 ; 5].
3.
U [27; +оо).
з
5.	2^2.
6.	218.
7.	— 4- тгп, n £ Z .
8.	13.
9.	1.
10.	Таких функций не существует.
4.	(хп; 2жп — 10); п € N, п > 6,
. . I(^n + 1) тг — 40
где хп = 4 ± у-----------—---------
5.	(2 ; 2).
6-	Salc = 3.
,	3(721 + 1)
7.	± arccos----—------ + тгп ,
п Е Z.
195
Учебно-методическое пособие
Подготовка к вступительным экзаменам в МГУ.
Варианты письменных экзаменов по математике 2001-2005 годов
Составитель Федотов Михаил Валентинович
Издательский отдел факультета Вычислительной математики и
кибернетики МГУ им. М.В. Ломоносова
(лицензия ИД >05899 от 24.09.2001)
Подписано в печать 04.08.2006. Формат 60x88/16.
Печать офсетная. Бумага офсетная № 1.
Печ. л. 12,25. Тираж 1000 экз. Заказ № 551.
Отпечатано в ООО «МАКС Пресс».
105066, г. Москва, Елоховский пр., д. 3. стр. 2.
Тел. 939-38-90, 939-38-91. Тел./факс 939-38-91.