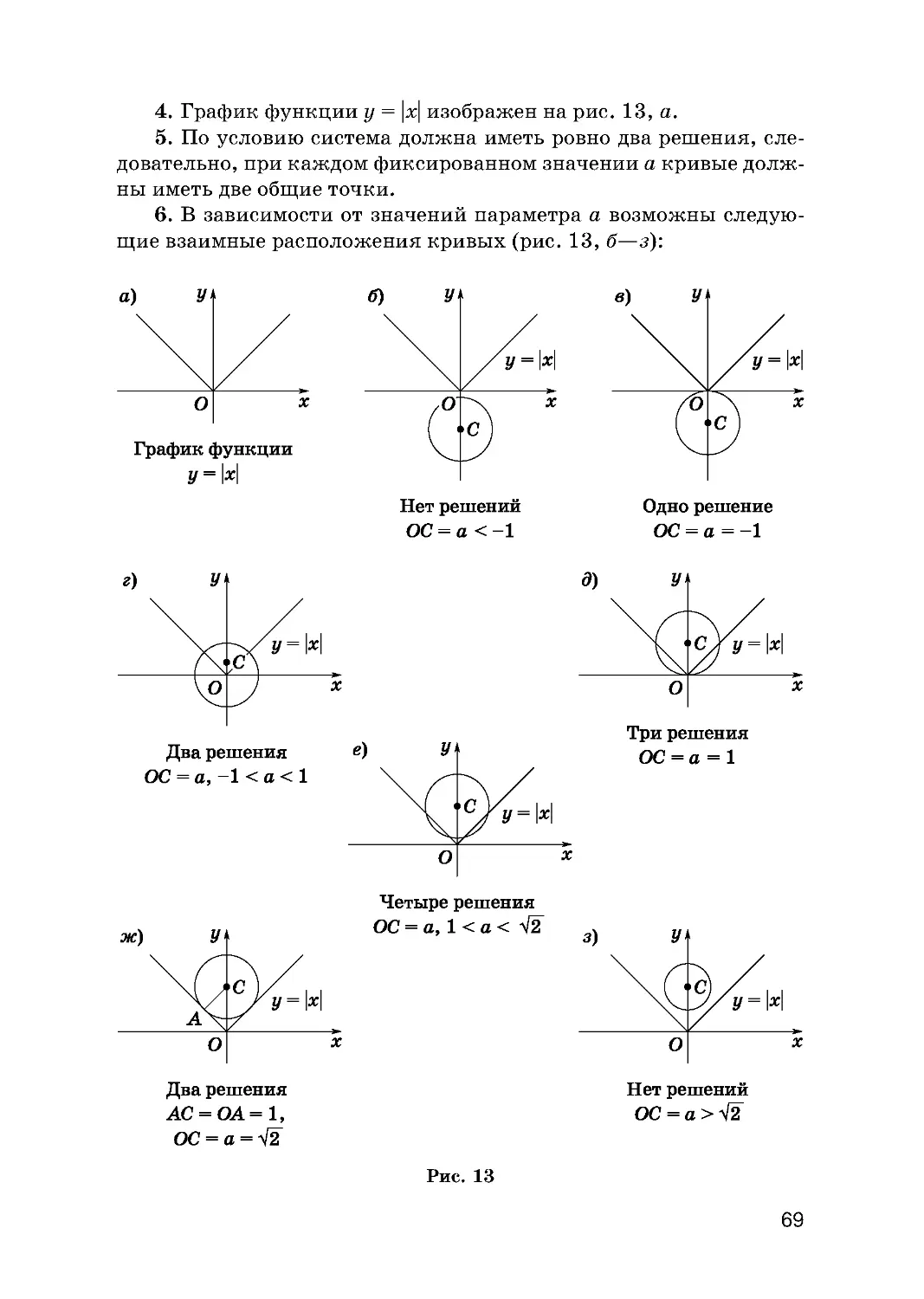
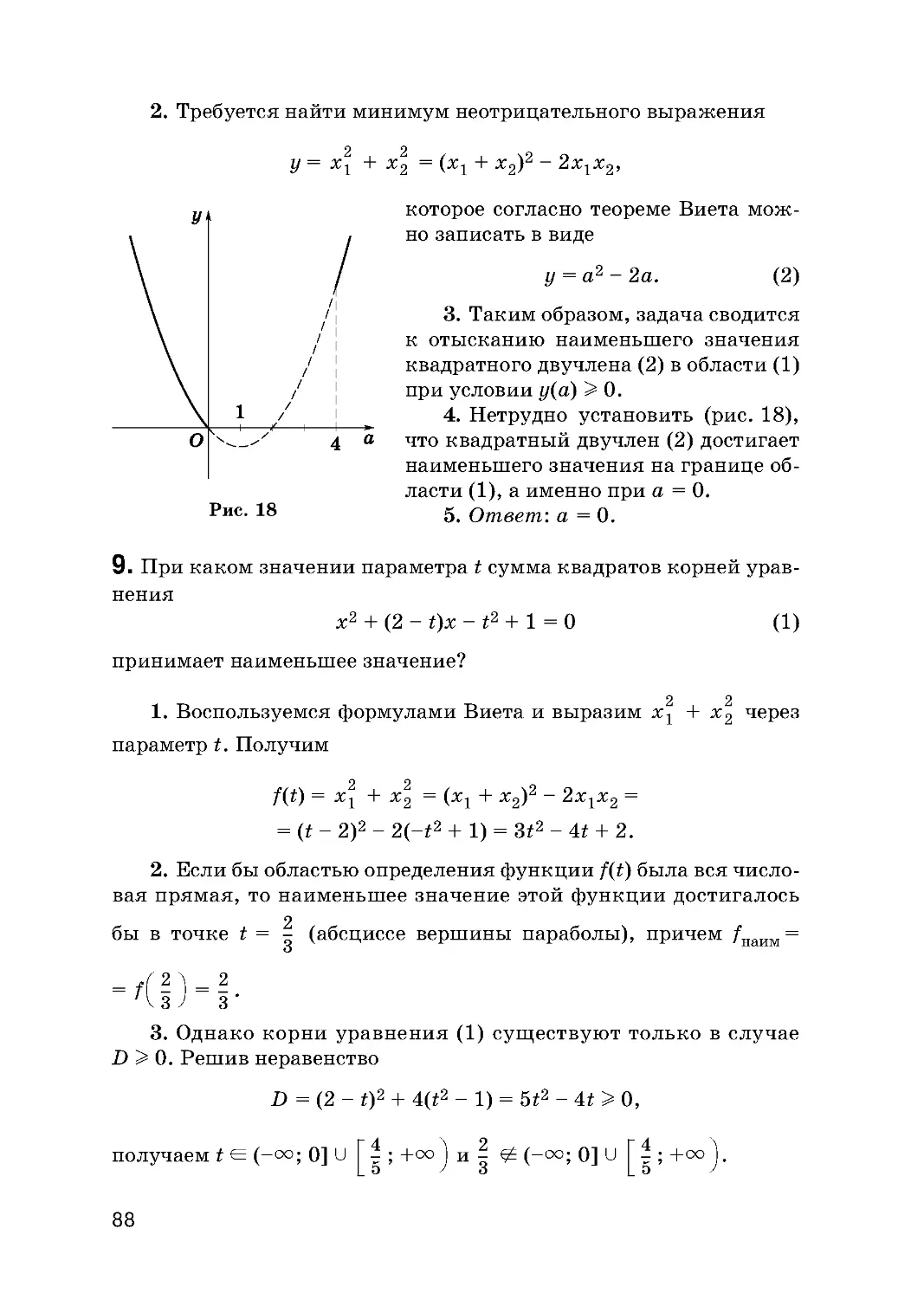
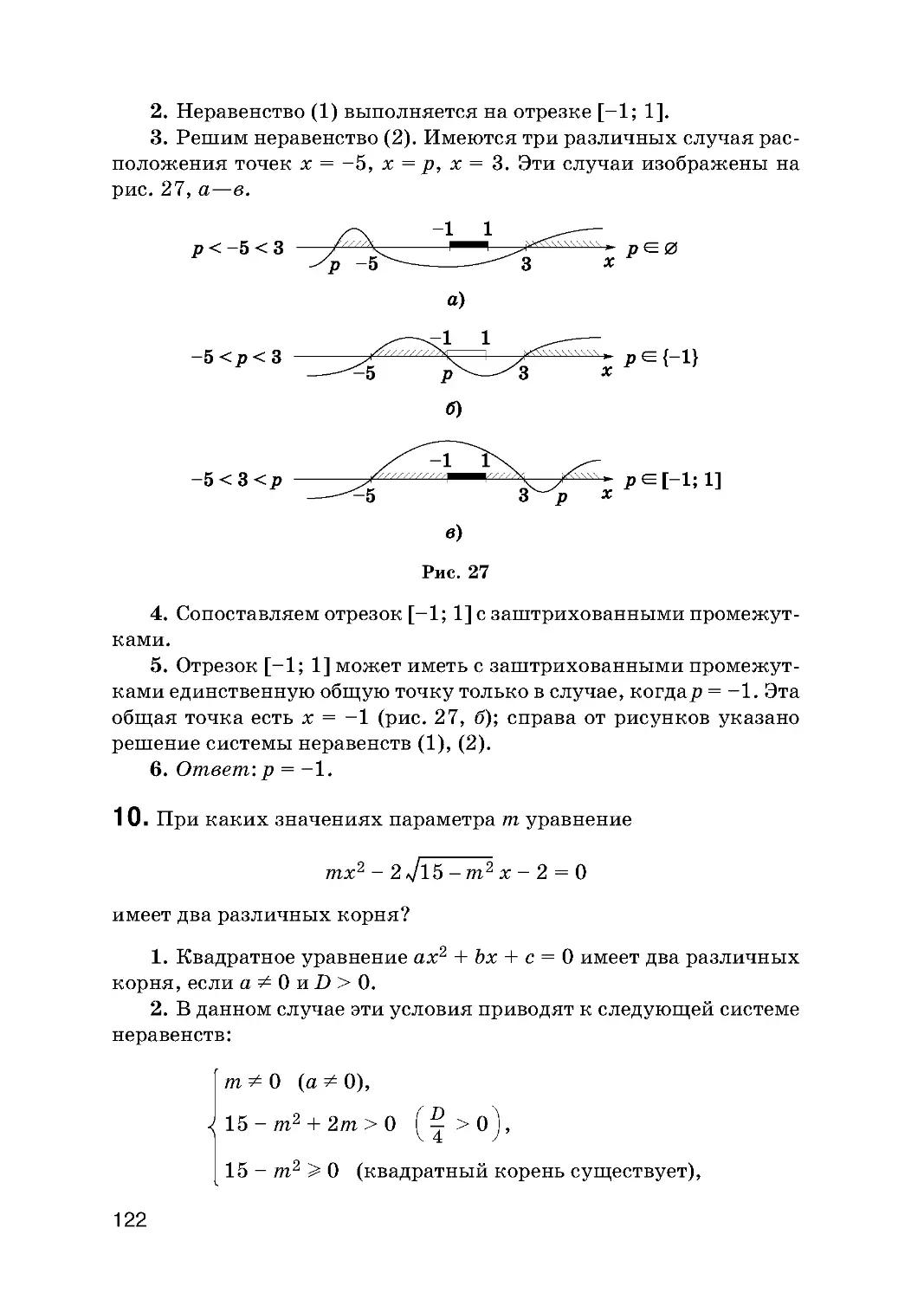
Текст
ШКОЛЬНЫЙ КУРС МАТЕМАТИКИ
В. С. Крамор
ЗАДАЧИ
С ПАРАМЕТРАМИ
N МЕТОДЫ ИХ РЕШЕНИЯ
Москва
ОНИКС • Мир и Образование
2007
УДК 512(075.3)
ББК 22.14я72
К78
Крамор В. С.
К 78 Задачи с параметрами и методы их решения / В. С. Крамор. — М.:
ООО «Издательство Оникс»: ООО «Издательство «Мири Образование»,
2007. — 416 с.: ил. — (Школьный курс математики).
ISBN 978-5-488-01066-6(000 «Издательство Оникс»)
ISBN 978-5-94666-362-5(000 «Издательство «Мир и Образование»)
Цель книги — научить школьников и абитуриентов вузов самостоя-
тельно решать задачи с параметрами и помочь прочно усвоить различ-
ные методы их решения.
Пособие содержит около 350 типовых задач с методическими указа-
ниями и 300 задач для самостоятельного решения и ответы к ним.
Книга может быть использована при подготовке к выпускным экза-
менам в средней школе, к сдаче ЕГЭ и вступительным экзаменам в вуз.
УДК 512(075.3)
ББК 22.14я72
Учебное издание
ШКОЛЬНЫЙ КУРС МАТЕМАТИКИ
Крамор Виталий Семенович
ЗАДАЧИ С ПАРАМЕТРАМИ
и методы их решения
Редактор А М. Суходский. Младший редактор Н. А Карасева
Техн, редактор Е. А Вишнякова. Компьютерная верстка Е. Ю. Пучковой
Подписано в печать 26.02.2007. Формат бОхЭО1/ . Гарнитура «Школьная».
Печать офсетная. Усл. печ. л. 26,00. Тираж бЬОО экз. Заказ №
Общероссийский классификатор продукции ОК-005-93, том 2; 953005 — учебная литература
ООО «Издательство Оникс».
127422, Москва, ул. Тимирязевская, д. 38/25. Почтовый адрес: 117418, Москва, а/я 26.
Отдел реализации: тел. (495) 119-02-20,110-02-50. Internet: www.onyx.ru; e-mail: mail@onyx.ru
ООО «Издательство «Мир и Образование».
Изд. лиц. ИД №05088 от 18.06.2001.109193, Москва, ул. 5-я Кожуховская, д. 13, стр. 1.
Тел./факс: (495) 120-51-47, 129-09-60, 742-43-54. E-mail: mir-obrazovanie@onyx.ru
ISBN 978-5-488-01066-6 (ООО «Издательство Оникс»)
ISBN 978-5-94666-362-5 (ООО «Издательство «Мир и Образование»)
© Крамор В. С., 2007
© Оформление переплета. ООО «Издательство Оникс», 2007
ПРЕДИСЛОВИЕ
Задачи с параметрами являются одними из наиболее трудных
задач курса элементарной математики. Их решение по существу пред-
ставляет собой исследование функций, входящих в условие зада-
чи, и последующее решение уравнений или неравенств с числовыми
коэффициентами. При решении уравнений (неравенств) с парамет-
рами необходимо выяснить, при каких значениях параметра задан-
ное уравнение (неравенство) имеет решение, и найти все эти реше-
ния. В том случае, когда хотя бы одно из допустимых значений па-
раметра не исследовано, задание не считается полностью решенным.
В течение многих лет задачи с параметрами включаются в эк-
заменационные билеты по математике для абитуриентов высших
учебных заведений, а в последние годы такие задачи предлагаются
и при сдаче ЕГЭ.
Как правило, немногие абитуриенты могут решить подобные
задачи, что приводит к снижению оценки за письменную работу,
и часто именно из-за этого нехватает нужного количества баллов
при зачислении в вуз.
Общеобразовательная школа по многим причинам не может
научить своих учеников решать задачи с параметрами. Это очень
трудный материал, требующий большого количества времени; кро-
ме того, прежде чем приступать к решению подобных задач уча-
щийся должен в совершенстве овладеть общим курсом математики.
Цель данной книги состоит в том, чтобы попытаться научить
выпускников средней школы и абитуриентов вузов самостоятель-
но решать задачи с параметрами и прочно усвоить различные мето-
ды, применяющиеся в процессе их решения.
Весь учебный материал разбит на 18 тем, имеющих одну и ту
же структуру. Каждая тема (за исключением тем 10 и 11) содер-
жит: справочный материал; задачи с решениями; задачи для са-
мостоятельного решения и ответы к ним. Кроме того, имеются два
приложения: «Текстовые задачи на составление уравнений и нера-
венств» и «Разные задачи».
3
В общей сложности книга содержит около 350 задач с решения-
ми и около 300 задач для самостоятельного решения.
В разделе «Справочный материал» приводятся формулировки
определений, правил, теорем и т. д.
Теоретические сведения изложены конспективно в той же по-
следовательности, что и при изучении их в школе. Указанный раз-
дел является весьма важным, поскольку в случае затруднений при
анализе решений задач или при их самостоятельном решении уча-
щийся может получить необходимые консультации, обращаясь
к справочному материалу.
В разделе «Задачи с решениями» приводятся решения задач
с параметрами, относящихся к заданной теме. Этот раздел содер-
жит большое количество задач, решения которых основаны, с од-
ной стороны, на общих теоретических сведениях из школьного
курса математики (определениях, правилах, теоремах, следствиях),
а с другой — на специфических особенностях задач, содержащих
параметры (умении определенным образом классифицировать зна-
чения параметра, переходе от исходной задачи к равносильной ей,
использовании наиболее рационального метода решения, умении
мыслить логически и т. д.). Каждая задача из этого раздела реша-
ется подробнейшим образом, каждое действие в процессе решения
нумеруется, поскольку оно несет определенную смысловую нагруз-
ку. В качестве заключительного действия любая задача сопровож-
дается подробным ответом, в котором для каждого допустимого
значения параметра записывается соответствующее этому значе-
нию решение задачи.
Раздел «Задачи для самостоятельного решения» предназначен
для тех учащихся, которые уже усвоили предыдущий раздел и хо-
тят закрепить свои знания и умения самостоятельно.
Книга завершается двумя приложениями. Приложение 1 со-
держит текстовые задачи на составление уравнений и неравенств
с параметрами, а Приложение 2 — разные задачи, не только анало-
гичные тем, что и в уже рассмотренных темах, но и такие, которые
по тем или иным причинам в эти темы не вошли.
В конце книги приводится обширный список литературы, ко-
торой пользовался автор при подготовке настоящего издания. Мно-
гие задачи, взятые из указанных пособий, входили в экзаменаци-
онные билеты для поступающих в различные вузы страны.
В заключение несколько слов о том, как пользоваться этим
пособием. По мнению автора, не следует начинать с анализа тех ре-
шений, которые приведены в книге. Прежде всего нужно в совер-
шенстве владеть методами решения примеров и задач, не содер-
4
жащих параметры. В частности, усвоению таких методов может
способствовать книга: В. С. Крамор. Повторяем и систематизируем
школьный курс алгебры и начал анализа (М.: ОНИКС, Мир и Обра-
зование, 2007). Из упомянутой книги следует усвоить только один
раздел: «Упражнения с решениями». Лишь после этого можно пе-
реходить к анализу решенных в настоящей книге задач с парамет-
рами. Сначала попробуйте самостоятельно решить какую-либо за-
дачу, а в случае затруднений обращайтесь к ее решению, приведен-
ному в книге. Усваивайте приемы, использованные при решении
этой задачи, так как в дальнейшем тот или иной прием может ока-
заться полезным.
Успехов вам, школьники и абитуриенты!
Автор
н
4.
5.
6.
атуральные числа
2. Простые и составные числа
3. Обыкновенные дроби. Правильные и неправильные
дроби I
Множество целых чисел, множество --------
рациональных чисел 2ZZZZZZZ
Модуль числа I I I I I I I I I I I I IT ""22
Возведение рациональных чисел в степень . . . . .
с натуральным показателем U - - -
- - -7. Свойства степени с натуральным показателем U
2 2 'ф^Числовые выражения. Выражения с переменными
- - Тождественно равные выражения |||||||j
2 2^9. Одночлены. Многочлены ZZZZZZZZZ
- - tp. Формулы сокраще>|н|)г|э---------------------
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Натуральные числа
1°. Понятие натурального числа относится к простейшим,
первоначальным понятиям математики и не определяется через
другие, более простые понятия.
2°. Натуральные числа возникли в результате счета предметов.
В порядке возрастания их можно записать как ряд чисел 1, 2, 3,
4, ... , т. е. это целые положительные числа.
3°. Множество натуральных чисел обозначают N.
2. Простые и составные числа
1°. Число а называют простым, если его делителями являют-
ся только единица и само число а.
6
2°. Число а, имеющее более двух натуральных делителем (кро-
ме 1 и а), называют составным.
3°. Заметим, что число 1 не относится ни к простым, ни к со-
ставным числам.
3. Обыкновенные дроби. Правильные и неправильные дроби
1°. Одну или несколько равных частей единицы называют
обыкновенной дробью.
2°. Обыкновенную дробь записывают с помощью черты и двух
натуральных чисел.
3°. Число, записанное под чертой и показывающее, на сколько
равных частей разделена единица, называют знаменателем дроби.
4°. Число, записанное под чертой и показывающее, сколько
взято таких равных частей, называют числителем дроби.
5°. Дробь, в которой числитель меньше знаменателя, называют
правильной.
6°. Дробь, в которой числитель равен знаменателю или больше
его, называют неправильной.
7°. Основное свойство дроби. При умножении числителя и зна-
менателя дроби на одно и то же число, отличное от нуля, значение
дроби не меняется.
4. Множество целых чисел, множество рациональных чисел
1°. Числа натуральные, им противоположные, а также число
нуль составляют множество целых чисел. Его обозначают Z.
2°. Множество натуральных чисел, дополненное нулем, называ-
ют множеством целых неотрицательных чисел и обозначают Zo.
3°. Объединение множеств целых и дробных чисел (положи-
тельных и отрицательных) составляет множество рациональных
чисел. Его обозначают Q.
5. Модуль числа
1°. Модулем {абсолютной величиной) действительного числа
а называют:
а) само это число, если а > 0;
б) противоположное число {-а), если а < 0.
2°. Модуль числа а обозначают |а|.
7
3°. Итак,
II \ а, если а > 0;
а' (~а), если а < 0.
4°. Геометрически |а| означает расстояние на координатной
прямой от точки, изображающей число а, до начала отсчета.
6. Возведение рациональных чисел в степень
с натуральным показателем
1°. Степенью числа а с показателем k, где k — N, a — Q, назы-
вают произведение k множителей, каждый из которых равен а:
ak = а а а а .
k раз
2°. Число а называют основанием степени, а число k — пока-
зателем степени.
1. Свойства степени с натуральным показателем
1°. При умножении степеней с одинаковыми основаниями по-
казатели складываются, а основание остается прежним:
ak а1 = ak + 1, где k, 1‘— N.
2°. При делении степеней с одинаковыми основаниями показа-
тели степеней вычитаются, а основание остается прежним:
ak : а1 = ak ~ 1, где k, N.
3°. При возведении степени в степень показатели степеней пе-
ремножаются, а основание остается прежним:
(ак)1 = аы, где k, I — N.
4°. Степень произведения равна произведению степеней мно-
жителей:
(аЪс)к = акЪкск, где k-— N.
5°. Степень частного равна частному степеней делимого и дели-
теля:
(s )‘
8
8. Числовые выражения. Выражения с переменными.
Тождественно равные выражения
1°. Из чисел, знаков действий и скобок можно составить раз-
личные числовые выражения.
2°. Примерами выражений с переменными являются выраже-
а + 3 о . о
ния , + у - 2 и т. д.
«э
3°. Значение выражения, содержащего переменную, зависит
от значения переменной.
4°. Множество значений переменных, при которых выражение
с переменными имеет смысл, называют областью определения
этого выражения.
5°. Выражение 3 „ при х = 5 не имеет смысла, так как при
х - о
х = 5 знаменатель дроби обращается в нуль.
6°. Два выражения называют тождественно равными, если
при всех значениях входящих в них переменных, принадлежащих
общей области определения, соответственные значения этих выра-
жений равны.
7°. Равенства, верные при всех допустимых значениях пере-
менных, называют тождествами.
9. Одночлены. Многочлены
1°. Выражение, представляющее собой произведение чисел, пе-
ременных и их степеней, называют одночленом.
2°. Одночлены, отличающиеся только числовыми коэффици-
ентами или равные между собой, называют подобными.
3°. Алгебраическую сумму одночленов называют многочленом.
4°. Преобразование многочлена в произведение двух или не-
скольких многочленов (среди которых могут быть и одночлены),
называют разложением многочлена на множители.
10. Формулы сокращенного умножения
1°. х2 - у2 = (х - у)(х + у) (разность квадратов).
2°. (х + у)2 = (х + у)(х + у) = х2 + у2 + 2ху (квадрат суммы).
3°. (х - у)2 = (х - у)(х - у) = х2 + у2 - 2ху (квадрат разности).
4°. х3 + у3 = (х + у)(х2 + у2 - ху) (сумма кубов).
9
5°. х3 - у3 = (х - у)(х3 + у3 + ху) (разность кубов).
6°. (х + у)3 = х3 + у3 + Зх3у + Зху3 (куб суммы).
7°. (х - у)3 = х3 - у3 - Зх3у + Зху3 (куб разности).
8°. (а + х + у)3 = а3 + х3 + у3 + 2ах + 2ау + 2ху.
9°. (а - х - у)3 = а3 + х3 + у3 - 2ах - 2ау + 2ху.
ЗАДАЧИ С РЕШЕНИЯМИ
1 . Найти все действительные решения уравнения
8а4(х4 + у4) - 4а2(х2 + у3) +1 = 0.
(1)
1. Данное уравнение содержит параметр а и две переменные
X и у.
2. Преобразуем уравнение (1) так:
а) разделив уравнение (1) на 2, раскроем скобки и получим
4а4х4 + 4а4у4 - 2а3х3 - 2а3у3 + 1 = 0; (2)
б) в уравнении (2) представим | как | |;
в) сгруппируем члены 4а4х4 - 2а3х3 + | и 4а4у4 - 2а3у3 + |;
тогда уравнение (2) примет вид
4^а2х2-|^ + 4^а3у3 - ± =0; (3)
г) разделив уравнение (3) на 4, получим
(^а3х3 - i ) + (^а3у3 - i ) =0. (4)
3. Левая часть уравнение (4) есть сумма двух неотрицательных
слагаемых. Поэтому уравнение (4) может иметь место только при
условиях
а3х3 - i = 0,
4
а3у3 - - = 0.
4
(5)
10
4. Решив систему (5), находим |ах| = \ау\ = |, откуда |х| = |у| =
= щ-[ (при условии, что а 0).
5. Ответ: если а = 0, то решений нет;
если а 0, то х, = — , у, = — ; х.
1 2а 2а
„ _ 1 _ 1
2 2а ’ ^2 2а ’
х3 = 2~а ’ Уз = ~2а Х4 = ~2а ’У1 = 2~а-
2. Пусть т и п — натуральные числа, причем — — правильная не-
сократимая дробь. На какие натуральные числа можно сократить
, Зп - т ,,
дробь -----— , если известно, что она сократима?
5п + 2т
1. Так как — — правильная дробь, то т < п и потому (Зп - т) —
натуральное число.
2. Пусть р (р > 1) — натуральное число, на которое можно со-
Зп - т
кратить дробь -----— .
5п + 2т
3. Это значит, что натуральные числа Зп - т и 5п + 2т делятся
нар, т. е. существуют натуральные числа N и М такие, что Зп - т =
= pN и 5п + 2т = рМ.
4. Отсюда следует, что
lln =p(2N + М), 11т =р(ЗМ - 5N),
т. е. числа 11п и 11т делятся нар.
5. Так как дробь — несократима, т. е. числа п и т не имеют
п
общих делителей, то 11 делится нар.
6. Поскольку р > 1 и 11 — простое число, отсюда следует, что
р = 11.
7. Ответ: 11.
3. Найти все значения параметра а, для каждого из которых су-
ществуют четыре натуральных числа х, у, и, v, удовлетворяющих
равенствам
(х + у)(х + у + 20) = (140 - а)(а - 80), (1)
a(8u2 + 2v2 -а) = (4н2 - и2)2. (2)
11
1. Преобразуем равенство (2) следующим образом:
2а(4н1 2 + и2) - а2 = (4и2 - и2)2;
-а2 + 2а(4н2 + и2) - (4и2 + и2)2 = (4и2 - и2)2 - (4и2 + и2)2;
-[а - (4и2 + и2)]2 = (4и2 -и2- 4и2 - и2)(4и2 - и2 + 4и2 + и2);
-(а - 4и2 - и2)2 = -2и2 8и2; \а - 4и2 - v2\ = 4uv;
а = (2и ± и)2. (3)
2. Так как и и v — натуральные числа, то число а должно быть
точным квадратом некоторого натурального числа (или же нулем).
3. Левая часть равенства (1) положительна. Поэтому (140 - а) х
х (а - 80) > 0, т. е. а должно удовлетворять двойному неравенству
80 < а < 140. В этом интервале существуют три числа, являющие-
ся точными квадратами целых чисел: 81, 100 и 121.
4. Из равенства (1) для суммы (х + у) получаем квадратное
уравнение, которое, очевидно, должно иметь целые решения. Од-
нако только при а = 100 это условие выполняется. Итак, решением
задачи служит число 100.
5. Ответ: а = 100.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все действительные решения уравнения:
а) (х2 + 4у2) - - (х - у) + 5 = 0;
az а
б) х6 + а2у® + 4а(х3 * * - у3) + 4(а2 + 1) = 0.
2. Установить, при каких значениях параметра а существуют
четыре натуральных числа х, у, и, v, удовлетворяющих равенст-
вам:
а) ху(40 + ху) = (150 - а)(а - 90),
а(8н2 + 18и2 - а) = (4н2 - 9и2)2;
б) х2 + у2 = (107 - а)(а - 91),
54(н2 + v2) = а(15и + 3v - а).
Ответы
1. а) Если а = 0, то решений нет (уравнение не имеет смысла); если
а 0, то х = 2а, у = -0,5а; б) если а = 0, то решений нет; если а 0, то
х = 1/2“ , у = ЗР . 2. а) а = 100; б) а = 99.
12
ажения
- - 4* 1 Дробь
"2. Целые и дроби
- - 3. Понятие об иррациональном числс| I I I I I
”4. Числовые промежутки _ Z
15. Корень А?й степени из действительного числа1
№ реобразования арифметических корней
гепень с целым и дробным показателем
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Дробь
1°. Дробью называют выражение вида | (Ъ 0), где буквами
аиЬ обозначены числовые выражения или выражения с перемен-
ными.
2°. Область определения дроби — это множество чисел, при
которых дробь имеет числовое значение. Следовательно, областью
определения дроби является множество пар чисел (а; Ъ), где
Ъ е (-оо; 0) U (0; +°о).
3°. Дробь | равна нулю тогда и только тогда, когда а = 0 и & 0.
2. Целые и дробные выражения
1°. Целыми выражениями называют:
все числовые выражения;
выражения с переменными, содержащие операции сложения,
вычитания, умножения и возведения переменных в натуральную
степень.
13
2°. Выражения 4ab 3; не являются целыми, так как они со-
держат операции возведения в целую отрицательную степень и де-
ления на переменную.
3°. Одночлены и многочлены являются целыми выраже-
ниями.
4°. Если в выражении с переменными, кроме операций сложе-
ния, умножения, вычитания и возведения в натуральную степень,
производится и операция деления на переменную, то такие выра-
жения называют дробными выражениями.
3. Понятие об иррациональном числе
1°. Любое рациональное число вида — , где п * 0, можно пред-
п
ставить в виде конечной или бесконечной периодической дроби.
2°. Иррациональным числом называют бесконечную десятич-
ную непериодическую дробь, например, 0,31133417... .
3°. Объединение множества рациональных чисел и множества
иррациональных чисел (бесконечных десятичных непериодиче-
ских дробей) дает множество R действительных чисел.
4. Числовые промежутки
Для числовых промежутков вводятся следующие обозначе-
ния:
1°. [а; Ь] или а < х < Ъ — замкнутый промежуток (или отре-
зок) с началом а и концом Ь.
2°. (а; Ь) или а < х < Ъ открытый промежуток (или ин-
тервал).
3°. (а; &]; [а; Ь) или а < х Ь; а х <Ь — полуоткрытые про-
межутки (полуинтервалы).
4°. [а; +оо) или х > а, (-°°; Ь] или х < Ъ — лучи.
5°. (а; +°°) или х> а, (-°°; Ъ) или х < Ъ — открытые лучи.
6°. (-о°; +°°) = R — числовая (координатная) прямая.
5. Корень fe-й степени из действительного числа
1°. Корнем k-й степени, где k е N и k 1, из действительного
числа а называют действительное число Ъ, k-я степень которого
равна а.
14
2°. Корень k-й степени из числа а обозначают символом kJa.
Согласно определению, 0]а)к = а.
3°. Число k называют показателем корня, число а — под-
коренным выражением.
4°. Заметим, что 2nJa , где п е N и а < 0, не существует.
5°. Корень нечетной степени извлекается и из отрицательного
числа.
6°. Определение арифметического корня: арифметическим кор-
нем k-й степени из неотрицательного числа а (а 0) называют не-
отрицательное число Ь, k-я степень которого равна а, где k > 1 —
натуральное число.
Замечание. В школьном курсе (и в этой книге) рассматри-
вается только арифметическое значение корня, т. е. kJa имеет
смысл лишь при а > 0 и принимает только неотрицательное зна-
чение.
6. Преобразования арифметических корней
1°. \[аЬ = kJa • kJb , где а > 0, & > 0 (правило извлечения корня
из произведения).
/л \J~CL
2°. k - = — , где а > 0, & > 0 (правило извлечения корня из
Чь kJb
Дроби).
3°. kJ^/a = kcJa , где а 0, k N, k > 1, с > 1 (правило извлече-
ния корня из корня).
4°. (KJa)m = kJa™, где а > 0 (правило возведения корня в сте-
пень).
5°. kJa™ = knJam ’ п , где а 0, т N, п N, т. е. показатель
корня и показатель подкоренного выражения можно умножить на
одно и то же число.
6°. Если щ > а2 > 0, то kJa[ > > т. о- большему положи-
тельному подкоренному выражению соответствует и большее зна-
чение корня.
Замечание. Все указанные выше формулы часто применя-
ют в обратном порядке (т. е. справа налево).
15
7. Степень с целым и дробным показателем
1°. Если/, = 0, то а° = 1 (при а 0).
2°. Если/) < 0, то аР = — (при а 0).
а -п
Р
3°. Выражение aq в общем виде имеет смысл только при а > 0.
р
Если а > 0, р Z, q r— N, то по определению aq = l/aP .
ЗАДАЧИ С РЕШЕНИЯМИ
1. Известно, что
2
Ja3 + л/b3 . a\Ja? - 7b3) = у
Va2(a - b)2 b 2 У а - Ь
Во сколько раз значение параметра а больше значения пара-
метра Ь, если оба эти числа положительны?
1. Имеем (л/о® + )(Ja3 - Jb3 ) = a3-b3 = (a- b)(a2 + ab + b2).
2. Выполнив дальнейшие тождественные преобразования ле-
вой части исходного выражения, получим
2
(a-b)(a2 + ab + b2)a3 = a2 + ab + b2 = А а А 2 + а +1 = 7
37a2(a-b)2b23/^—b 62 UJ b
3. Пусть х = . Решив квадратное уравнение х2 + х + 1 = 7,
находим х1 = -3; х2 = 2.
4. Так как по условию а>0и&>0, тох = ^ >0. Значит, хг =
= -3 является посторонним корнем. Итак, а = 2Ь.
5. Ответ: в 2 раза.
2. В зависимости от параметров тип найти значение выражения
А= , где х =
16
Sis
1. Так как и имеют арифметические значения, то
> 0, т. е. тп > 0.
2. Возведем выражение х = — + /—в квадрат: х2 = — +
А/ п Ц т п
Тогда получим
^2-4 = 1(т-п)2 = \т-п\ .
У тп Jnin
3. Пусть т > 0, п > 0. Упростим выражение А:
Sis a|S
Учитывая, что
\т - п\ = т - п при т > п, \т - п\ = ~(т - п) при т < п,
находим:
\ л 2п(т-п)
а) если т > п, то А = ---— = т - п;
т + п - т + п
,л 2п(п-т) п(п-т)
б) если т < п, то А = ---— = —-------.
т+п-п+т т
4. Пусть т < 0, п < 0. В этом случае, преобразуя выражение А,
надо учесть, что
Поэтому
2п\т - п\
(- т - п) - \т - п\ ’
откуда находим:
\ л 2п(т-п)
а) если т > п, то А =----—
-т-п-т+п
п(п - т) .
т ’
, л 2п(п-т)
б) если т < п, то А = ---— = т - п.
-т-п-п+т
17
5. Ответ: если 0 < п < т, то А = т - п;
А . п(п - т)
если 0 < т < п, то А = —i;
т
, м . п(п - т)
если п < т < 0, то А = —i;
т
если т < п < 0, то А = т - п.
3. Определить все такие целые числа а и Ь, для которых один из
корней уравнения
3xs + ах2 + Ьх + 12 = 0 (1)
равен д/3 + 1.
1. Для того чтобы многочлен Ps(x) = 3xs + ах2 + Ьх + 12 в левой
части уравнения (1) имел своим корнем число J3 + 1, необходимо,
чтобы выполнялось равенство Р3(л/3 + 1) = 0, т. е.
3(73 +1)3 + а(л/3 +1)2 + &(73 + 1) + 12 = 0. (2)
2. После упрощения равенство (2) примет вид
(4а + Ь + 42) + ТЗ(2а+&+18) = 0. (3)
3. Так как а иЬ — целые числа, то целыми числами будут так-
же выражения, записанные в круглых скобках в равенстве (3).
4. Эти выражения должны быть равны нулю, иначе придем
к противоречию: целое число равно иррациональному числу.
5. Итак, необходимо, чтобы
J 4а + Ь + 42 = О,
12а + Ь + 18 — О,
откуда находим а = -12,& = 6.
6. Ответ: а = -12, Ъ = 6.
4. Число а подобрано так, что уравнение
Jx - ,J3 + а2х2 + 2ах(л/б - д/З ) = 6л/2 - 9 (1)
имеет решение. Найти это решение.
1. Пусть х0 — действительное число, являющееся решением
уравнения (1).
18
2. Тогда справедливо равенство
Jx(l - л/3 + а* 1 2 * х® + 2ax0(j6 - */3 ) - 6 л/2 + 9 = 0. (2)
3. Равенство (2) можно переписать в виде
или, выделив полный квадрат относительно а, в виде
4. Отсюда ясно, что одновременно справедливы два равенства:
5. Из второго равенства получаем х0 = ; тогда из первого ра-
венства следует, что а = 1 - л/2 .
6. Легко установить, что при найденном значении а = 1 -
число х(} = д/3 действительно есть корень исходного уравнения.
7. Ответ: д/3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти зависимость между значениями параметров а и Ь,
если известно значение заданного выражения:
1 + JL
а) 2 а + Ъ (1 + а2 + &2~4 (а + Ъ + 2)-2 = |, а * 0, Ъ * 0, а * -Ь;
1 IV 2ab J 6
2 а + Ь
1 1 А-1
а2 + Ь2
1
2аЬ2 '
= 8, а > 0, b > 0;
< 2Ьа2 >
19
3 3 1
„2 + b2 b2
в) —---j : (a - b) + —--j = 5, a > 0, b > 0, a + b.
cfi + &2 + &2
2. Найти все целые числа а и Ъ, для которых один из корней
уравнения:
а) х3 + ах2 + Ъх - 8 = 0 равен 1 - д/З ;
б) ах2 + Ъх2 - 12х + 5 = 0 равен д/б - 1.
Ответы
1. а) Ь = - ; б) Ь = - ; в) Ь = 0,8а. 2. а) а = 2, Ь = -10; б) а = 2, Ь = 3.
а а
I.I
№а3
уравнения с одной переменной ___________
. Понятие о равносильности уравнений I I I I I I I I I I 1_
. Свойства числовых равенств и теоремы о равносильности
уравнений
. Линейное уравнение с одной переменной, содержаще* - -
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Уравнения с одной переменной
1°. Пусть заданы функции Дх) и <р(х). Если относительно равен-
ства /(х) = ф(х) поставлена задача найти все значения переменной,
при которых получается верное числовое равенство, то говорят,
что задано уравнение с одной переменной.
2°. Значение переменной, обращающее уравнение в истинное
равенство, называют корнем уравнения.
3°. Решить уравнение — значит найти множество его корней
или доказать, что их нет. Это множество называют также решени-
ем уравнения.
4°. Множество всех х, при которых одновременно имеют смысл
выражения /(х) и <р(х), называют областью определения уравнения.
5°. Для того чтобы установить область определения уравнения,
необходимо найти пересечение множеств, на которых определены
данные функции /(х) и <р(х).
2. Понятие о равносильности уравнений
1°. Два уравнения называют равносильными (или эквивалент-
ными) на данном числовом множестве, если каждое решение (ко-
рень) одного уравнения является решением (корнем) другого, и
наоборот.
2°. Заметим, что если оба уравнения не имеют решений на дан-
ном числовом множестве, то их также считают равносильными на
этом множестве.
21
3°. Например, уравнениях2 + 3 = 0их4 + 2 = 0равносильны на
множестве действительных чисел, так как множество решений
каждого из них пустое.
3. Свойства числовых равенств и теоремы о равносильности
уравнений
1°. Числовое равенство не нарушится, если к обеим его частям
прибавить или отнять одно и то же число.
2°. Если к обеим частям уравнения /(х) = ф(х) прибавить одну
и ту же функцию А(х), имеющую смысл при всех допустимых зна-
чениях переменной, то получится новое уравнение /(х) + А(х) =
= <р(х) + А(х), равносильное данному.
3°. Любое слагаемое можно перенести из одной части уравне-
ния в другую, изменив знак этого слагаемого на противоположный.
4°. Числовое равенство не нарушится, если обе его части умно-
жить или разделить на одно и то же число, отличное от нуля.
5°. Если обе части уравнения /(х) = ф(х) умножить (или раз-
делить) на одну и ту же функцию А(х) 0, имеющую смысл для
любого х из области определения, то получится новое уравнение
А(х) • /(х) = А(х) • <р(х) или , равносильное данному.
Л(х) Л(х)
4. Линейное уравнение с одной переменной,
содержащее параметр
1°. Пусть дано уравнение вида
f(a, Ъ, с, ... , k, х) = ф(а, Ь, с, ... , k, х), (1)
где а, Ъ, с, ... , k, х — переменные величины.
2°. Переменные а, Ь, с, ... , k, которые при решении уравнения
(1) считаются постоянными, называют параметрами, а само урав-
нение называют уравнением, содержащим параметры.
3°. Решить уравнение (1) — значит указать, при каких значе-
ниях параметров существуют значения х, удовлетворяющие дан-
ному уравнению.
Замечания.
1. В дальнейшем уравнение
F(x, а) = 0 (2)
условимся понимать не как уравнение с двумя переменными, а как
уравнение с одной переменной х и одним параметром а.
22
2. Решить уравнение (2) — это значит решить (на множестве
действительных чисел) семейство уравнений, которые получаются
из уравнения (2) при различных действительных значениях пара-
метра а.
3. При решении уравнения с параметром (параметрами) стре-
мятся выделить «особые» значения параметра (иногда их называ-
ют «контрольными»), в которых или при переходе через которые
происходит качественное изменение уравнения.
ЗАДАЧИ С РЕШЕНИЯМИ
1. В зависимости от значений параметра а решить уравнение ах = 0.
1. Это уравнение содержит параметр а (переменную, которая в
условии данного примера сохраняет одно и то же значение).
2. а) Пусть а = 0; тогда 0 • х = 0, т. е. х е R.
б) Пусть а 0; тогда х = =0.
3. Ответ: если а = 0, то х е R;
если а 0, то х = 0.
2. В зависимости от значений параметра а решить уравнение ах = а.
1. Данное уравнение содержит параметр а.
2. а) Пусть а = 0; тогда 0 • х = 0, т. е. х е R.
б) Пусть а 0; тогда х = - =1.
3. Ответ: если а = 0, то х е R;
если а 0, то х = 1.
3. В зависимости от значений параметра а решить уравнение
х + 2 = ах. (1)
1. Данное уравнение содержит параметр а.
2. После упрощения уравнение (1) примет вид х - ах = -2, т. е.
х(1 - а) = -2. (2)
3. а) Пусть 1 - а = 0, т. е. а = 1; тогда получим уравнение х 0 =
= -2, которое не имеет корней.
б) Пусть 1 - а 0, т. е. а 1; тогда уравнение (2) имеет единст-
2
венный корень х =-- .
а -1
23
4. Ответ: если а = 1, то нет корней;
, . „ 2
если а 1, то единственный корень х =--- .
а -1
Замечание. Как понимать выражение: «уравнение имеет
единственный корень»?
Это означает, что каждому допустимому значению а соответст-
вует единственное значение х.
Например, если а = 0, то х = -2; если а = 2, то х = 2 и т. д.
4. В зависимости от значений параметра а решить уравнение
(а2 - 1)х = 2а2 + а - 3. (1)
1. Приведем уравнение (1) к виду
(а- 1)(а+ 1)х = (2а + 3)(а - 1). (2)
2. а) Пусть а = 1; тогда уравнение (2) примет вид 0 • х = 0. Его
решением является любое действительное число, т. е. х '- R.
б) Пусть а = -1; тогда уравнение (2) примет вид 0 • х = -2. Это
уравнение не имеет решений.
в) Пусть а/-1 иа/ 1; тогда уравнение (2) имеет единственное
решение
3. Ответ: если а = 1, то х е R;
если а = -1, то нет корней;
, 1 , 1 2а + 3
если а -1, а 1, то х =----— .
а+ 1
5. Решить уравнение
2а(а - 2)х = а - 2. (1)
1. Пусть а = 0; тогда уравнение (1) примет вид 0 • х = -2. Это
уравнение не имеет решений.
2. Пусть а = 2; тогда уравнение (1) примет вид 0 • х = 0. Корнем
этого уравнения служит любое действительное число.
3. Пусть а / Оиа / 2; тогда из уравнения (1) следует, что х =
а-2 1
= ’ откуда находим х = — .
2а(а-2) 2а
24
4. Ответ: если а = 0, то корней нет;
если а = 2, то х е R;
если а 0, а/2, тох = .
2а
6. В зависимости от значений параметра а решить уравнение
а + х _ q
х2-5х - 6
1. По смыслу уравнения должно быть х2-5х-6?й0,т.е.х^-1,
X 5* 6.
2. При х/ -1 их / 6 данное уравнение имеет решение х = -а.
3. Из условий х/ -1 их / 6 следует, что а / 1 иа / -6.
4. Ответ: если а -6, а / 1, то х = -а;
если а = -6, а = 1,тох'-0.
7. При каких значениях параметра Ъ уравнение
ах - Ъ = 2а + Зх (1)
имеет решение для любого а?
1. Преобразуем уравнение (1) к виду
(а - 3)х = b + 2а. (2)
2. Пусть а 3; тогда уравнение (2) имеет решение
при любом значении Ъ.
3. Следовательно, единственным значением а, при котором мо-
гут отсутствовать решения уравнения (2), является а = 3. В этом
случае уравнение (2) примет вид
О • х = b + 6. (3)
4. Если Ъ -6, то уравнение (3) не имеет решений. Если же Ъ =
= -6, то любое х е R есть решение уравнения (3).
5. Итак, Ъ = -6 есть единственное значение параметра Ъ, при
котором уравнение (2) имеет решение для любого а (а именно, х = 2
для а / 3 и х -й для а = 3).
6. Ответ: b = -6.
25
8. В зависимости от значений параметра k решить уравнение
З/гх-5 , 3k-11 _ 2х + 7
(А - 1)(х + 3) k-1 х+3 ’ ( '
1. По смыслу уравнения должно быть (k - 1)(х + 3) 0, т. е. k 1,
х -3.
2. Упростив уравнение (1), получим
3kx - 5 + (3k -11)(х + 3) = (2х + 7)(k - 1),
или
(4А - 9)х = 31 - 2k. (2)
3. Из уравнения (2) при k | находим
31-2*
х = ----.
4fe-9
4. Теперь проверим, существуют ли такие k, при которых най-
денное значение х равно (-3). Имеем
31-2k _ _ о
4fe-9
, 2
откуда k = -- .
5
9 2
5. Таким образом, при к* 1, k^ -, k^ -- уравнение (1) имеет
31 -2k ,9 ,2
единственное решение х = ——— ; при k = - и при k = -- решении
4/г-9 4 5
нет; при k = 1 уравнение не имеет смысла.
„ г.^2,,.,,9 31 -2k
6. Ответ: если k -- , k 1, /г , то х = —-—— ;
5 4 4/г-9
, 2 , 9
если k = -- или k = - , то корней нет;
5 4
если k = 1, то уравнение не имеет смысла.
Замечания.
1. Необходимо иметь в виду, что если при каком-либо значении
параметра k = k0 данное уравнение не имеет смысла, то, разумеет-
ся, нет и его решения при k = k0.
26
2. Обратное утверждение неверно. Например, нельзя утверждать,
, 2
что при к = -- рассмотренное выше уравнение не имеет смысла.
2
3. Подставив в уравнение (1) значение k = -- , получим
6х + 25 , 61 _ 2х+7
7(х + 3) Т ” х + 3 ’ 1 '
2
Таким образом, при k = -- уравнение (1) имеет смысл. Однако
это уравнение не имеет корней, так как корень х = -3 уравнения
53х = -159, к которому сводится уравнение (3), является для него
посторонним.
9. Решить относительно х уравнение
а2 + х _ а2 - х _ 4аЬх + 2а2-2Ь2 ,
Ь2 - х Ь2 + х Ь4-х2 ’ 1 '
1. По смыслу уравнения х +Ь2.
2. Так как &4 - х2 0, то, умножив обе части уравнения (1) на
&4 - х2, получим
(а - Ь)2х = а2 - Ь2. (2)
3. Пусть а = Ь; тогда уравнение (2) примет вид 0 • х = 0, т. е.
оно удовлетворяется при любом действительном значении х, кроме
х = +Ь2.
4. Пусть а Ь; тогда уравнение (2) примет вид
= а2-Ь2 = а + Ь
Х (а-Ь)2 а-Ь'
5. Найдем теперь те значения а и Ъ, при которых выполняются
а + Ь , о а + Ъ , 9
равенства---- = Ъ2 и--- = -о2:
а-Ь а-Ь
а) = Ь2; а + Ъ = аЪ2 - Ь3, откуда а = + ;
а-Ь Ь2-1
б) а + Ь = _^2. + = -af)2 _|_ ьз 0ТКуда а = .
’ а-Ь ’ Ь2+1
27
СП -/ ь , &(&2 + 1) , Ь(Ь2 -1) а + Ь
6. Ответ: если а Ъ, а -Ц-----, а -Ц-----, то х = ---- ;
&2-1 &2+1 а-Ь
если а = Ъ, то х е R, кроме х = +Ь2;
b(b2+l) b(b2-l)
если а = -Ц------ или а = —Ц---- , то корней нет.
Ь2-1 Ь2 + 1
10. Найти значения параметра т, при которых уравнение
т2х - т2 + 6 = 4х + т (1)
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечное множество решений.
1. Приведем уравнение (1) к виду
(т2 - 4)х = т2 + т - 6. (2)
2. Уравнение (2) имеет единственное решение, если т2 -4^0,
т. е. если т ±2.
3. Уравнение (2) не имеет решений, если выполнены условия
[ т2 -4 = 0, \ т = ±2, „
< „ „ „ т. е. < , о , о откуда т = -2.
[ т2 + т - 6 0, [ т 2; т -3,
4. Уравнение (2) имеет бесконечное множество решений, если
и коэффициент при х, и правая часть одновременно равны нулю:
[ т2 -4 = 0, | т = ±2,
Ло „ „ т. е. < о о откуда т = 2.
[ т2 + т - 6 = 0, |тп = 2;тп = -3,
5. Ответ: а)т- (-оо; -2) U (-2; 2) U (2; +°°);
б) т = -2; в) т = 2.
11. В зависимости от значений параметра k решить уравнение
kx + 2 2х + k ’
1. Допустимыми значениями х и k являются те, при которых
kx + 2 0 и 2х + k 0, т. е. kx -2 и 2х -k.
2. Упростив уравнение (1) при допустимых значениях k и х, по-
лучим 4х + 2k = kx + 2, или
(k - 4)х = 2(k - 1). (2)
28
3. Пусть k = 4; тогда уравнение (2) не имеет решений.
гт и -а л 2(fe - 1)
Пусть k 4; тогда х = —.
4. Исключим теперь значения k, при которых kx = - 2 и 2х = -k.
a) kx = -2, т. е. = -2 или
k - 4
/г2 - k = -k + 4,
k 4,
откуда k = ±2, k 4.
б) Эти же значения k получим, решив уравнение 2х = -k. Дей-
о , 4(А-1) ,
ствительно, 2х = -k, т. е. —= - k или
k - 4
4А - 4 = -/г2 + 4А,
k 4,
откуда k = ±2, k 4.
5. Ответ: если k ±2, k 4, то х = ^4“—;
k - 4
если k е {+2; 4}, to.y‘-0.
1 2. В зависимости от значений параметров aub решить уравнение
ах -1 , b _ а(х2 + 1) _ л /-| \
“П” ГГ1 х2-1 1 ’
1. Уравнение имеет смысл при всех х ±1.
2. С учетом ОДЗ преобразуем уравнение (1) в равносильное:
(ах - 1)(х + 1) + b(x - 1) = а(х2 + 1),
или
х(а + b-l) = a + b+l. (2)
3. а) Пусть а + Ъ = 1; тогда уравнение (2) не имеет решений.
б) Пусть а + b 1; тогда х = а + .
4. Из условия х -1 следует, что а + Ъ + 1 -(а + Ъ - 1), т. е.
а + Ъ 0.
5. Равенство х = 1, т. е. а + Ь + 1 = а + Ь-1,не выполняется ни
при каких значениях а и Ъ.
6. Ответ: если а + & 0, а + &^1,тох = а + ^+ •
а+ Ь- 1
если а + Ъ = 0 или а + Ъ = 1, то .г - 0.
29
13. В зависимости от значений параметра а решить уравнение
а + 2х _ qv
1 + ах
1. В области определения данного уравнения, т. е. при 1 + ах О,
имеем
а + 2 х — 1 — ах /п \ 1
---—------ = 0, или (2 - а)х = 1 - а. (2)
Полученное уравнение (2) — линейное.
2. Если коэффициент при неизвестном в линейном уравнении от-
личен от нуля, то уравнение имеет корень и притом единственный.
Значит, если а 2, то уравнение (2) имеет единственный ко-
рень х = |—- . При этом для исходного уравнения (1) должно вы-
полняться условие 1 + ах 0, т. е.
1 + а • |0, откуда а ± .
3. Если коэффициент при неизвестном в линейном уравнении
равен нулю, а свободный член не равен нулю, то уравнение не име-
ет корней.
Этот случай для уравнения (2) реализуется при а = 2. Следова-
тельно, исходное уравнение (1) при а = 2 и при а = + J2 не имеет
корней.
4. Если коэффициент при неизвестном и свободный член в ли-
нейном уравнении равны нулю, то уравнение имеет бесконечное
множество корней.
Последний случай для уравнения (2) не имеет места ни при ка-
ких а.
5. Ответ: если а 2, а +J2 , то уравнение имеет единствен-
„ 1 - а
ныи корень х = --;
2 - а
если а = 2 или а = + J2 , то уравнение не имеет кор-
ней.
1 4. При каких значениях а уравнения х1 2 - а = 0 и Jx - а = 0 рав-
носильны?
1. Если а > 0, то первое уравнение имеет два корня, а второе —
только один, и в этом случае о равносильности речь идти не может.
30
2. Если а = 0, то решения уравнений совпадают.
3. Если а < 0, то ни первое, ни второе уравнения решений
не имеют. Как известно, такие уравнения считаются равносиль-
ными.
4. Ответ: а < 0.
1 5. Определить, при каких значениях параметра а уравнения
х2 + ах + 1 = 0, (1)
х2 + х + а = 0 (2)
имеют: а) один общий корень; б) два общих корня.
1. Пусть х1 — общий корень уравнений (1) и (2), т. е.
хх + ах} + 1=0, (3)
2
хх + хх + а = 0. (4)
2
Тогда из равенства (4) следует, что а = -хх - хх. Подставив это
выражение в равенство (3), получим
хх - хх(хх + хх) +1 = 0, или хх = 1,
откуда хх = 1 и, следовательно, а = -2.
2. Проверкой убеждаемся, что при а = - 2 уравнения (1) и (2)
имеют один общий корень х = 1.
3. Пусть уравнения (1) и (2) имеют два общих корня. Это имеет
место тогда и только тогда, когда коэффициенты уравнений (1) и (2)
пропорциональны:
1 = а = 1
1 1 а ’
т. е. когда а = 1.
4. При а = 1 уравнения (1) и (2) сводятся к одному уравнению
х2 + х + 1 = 0. Это уравнение не имеет действительных корней, т. е.
значение а = 1 не удовлетворяет условию задачи.
5. Ответ: а) один общий корень при а = -2;
б) нет двух общих корней ни при каких а.
31
16. При каких а уравнение ах = а2 равносильно неравенству
|х - 3| > а?
1. Если а 0, то уравнение ах = а2 имеет единственное решение
х = а, а неравенство |х - 3| > а — бесконечное множество решений.
2. Если а = 0, то решением как неравенства, так и уравнения
является множество всех действительных чисел.
3. Таким образом, требованию задачи удовлетворяет только
а = 0.
4. Ответ-, а = 0.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить уравнение:
а) а = 2; б) а + = а; в) а2х - а = 4х + 2;
’ х +1 ’ х-3 ’
г) 9&2х - 3& = 4х - 2; д) х + -^- = Д, (Эх + 1).
а3 а3
2. При каких значениях а имеет бесконечное множество реше-
ний уравнение:
а) 6(ах - 1) + а = 3(а - х) - 5;
б) | (х - 1) = | + а(3 - х)?
О о
3. При каких значениях а не имеет решений уравнение:
а) 2(3х - 2а) = 2 + ах\
б) а2х = а(1 + 5х) - 2 - 6х?
4. При каких значениях Ъ уравнение:
а) (а + 1)х = 2Ь - а;
б) (2а - 1)х = b + а - 1;
в) (а + 2)х = ЗЬ - а + 1
имеет решение для любого значения а?
5. Решить уравнение:
ч х - а г. а) х = 0; х + 2 х - 3 . 4 _ 2 б) Н- — Z ’ х + 2 а-1 (а-1)(х + 2)
. х , х + а , а .. в) - + + - = 1; а а + 3 3 х -а _ х + а• Г а + 2 а + 1 ’
— 2 , х — 1 । 2 /д Д) а2-2а +а-2 + « " Oi ч 5 + х - ах п е) —;—~ = °- 4-х3
6. При каких значениях а каждый корень уравнения 2(х - 2а) =
= 3 + а удовлетворяет условию х -[-1; 3]?
32
Ответы
а _ 2
1. а) Если а Z 0, то х = —— ; если а = 0, то нет корней; б) если а Z О,
а -5, то х = + 5 ; если а = 0, а = -5, то нет корней; в) если а -2, а 2,
1 2
то х = --- ; если а = -2, то х - R ', если а = 2, то нет корней; г) если b Z -- ,
2 1 ,2 Tt ,2 „ .
о Z , то х = ——- ; если о = - , то х G R; если о = - - , то нет корней; д) если
3 до + 2 3 3
а 0, а -3, а 3, то х = ------; если а = 3, то х е R; если а = 0, а = -3,
а(а + 3)
1 2
то нет корней. 2. а) При а = ; б) при а = . 3. а) При а = 6; б) при а = 3.
4. а) При b = -1; б) при Ь = 1 ; в) при b = -1. 5. а) Если а Z -2, то х = а; если
а = -2, то корней нет; б) если а -3, а 0,6, а 1, то х = ; если
а = -3, а = 0,6, а = 1, то корней нет; в) если а -3, а -1,5, а 0, то х =
а(а2 "Ь 3а — 9) о 1 к л ,j . / о
= - 4 —+ 3) ’ если а = ~ ", а = 1,5, а = 0, то корней нет; г) если а -2,
а -1, то х = -(2а2 + За); если а = -2, а = -1, то корней нет; д) если а -3,
а 0, а 2, то х = 6 ; если а = -3, а = 0, а = 2, то корней нет; е) если
5
а -1,5, а 1, а 3,5, то х = ---- ; если а = -1,5, а = 1, а = 3,5, то корней
а - 1
нет. 6. а ~ [-1; 0,6].
HffffH
гема 4
- -1. Понятие функции Hill - -
" 2. Монотонность функции । । । L Z Z
- - 3. Четные и нечетные функции Н-
" 4. Линейная функция и ее график
- - б. Квадратичная функция и ее график^
"6. Функция у = и ее график
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Понятие функции
1°. Зависимость одной переменной от другой называют функ-
циональной зависимостью.
2°. Зависимость переменной у от переменной х называют функ-
цией, если каждому значению х соответствует единственное значе-
ние у. При этом используют запись у = f(x).
3°. Переменную х называют независимой переменной (или ар-
гументом), а переменную у — зависимой переменной. Говорят,
что у является функцией от х.
4°. Значение у, соответствующее заданному значению х, назы-
вают значением функции.
5°. Все значения, которые принимает независимая перемен-
ная, образуют область определения функции.
6°. Все значения, которые принимает зависимая переменная,
образуют множество значений функции.
7°. Для функции f приняты обозначения:
a) D(f) — область определения функции;
б) E(f) — множество значений функции;
в) f(xo) — значение функции в точке х0.
2. Монотонность функции
1°. Функцию f(x) называют возрастающей на данном число-
вом промежутке X, если большему значению аргумента х е X со-
34
ответствует большее значение функции f(x), т. е. если для любых
х} и х2 из промежутка X таких, что х2 > хх, выполняется неравен-
ство f(x2) > /(хх).
2°. Функцию f(x) называют убывающей на данном числовом
промежутке X, если большему значению аргумента х е X соот-
ветствует меньшее значение функции /(х), т. е. если для любых
х1 и х2 из промежутка X таких, что х2 > хх, выполняется неравен-
ство /(х2) < /(хх).
3°. Функцию, только возрастающую или только убывающую
на данном числовом промежутке, называют монотонной на этом
промежутке.
3. Четные и нечетные функции
1°. Функцию у = f(x) называют четной, если она обладает сле-
дующими двумя свойствами:
а) область определения функции симметрична относительно точ-
ки О (т. е. если точка а принадлежит области определения, то точ-
ка (-а) также принадлежит области определения);
б) для любого значения х, принадлежащего области определе-
ния функции, выполняется равенство /(х) = /(-х).
2°. Функцию у = f(x) называют нечетной, если:
а) область определения функции симметрична относительно
точки О;
б) для любого значения х, принадлежащего области определе-
ния функции, выполняется равенство /(-х) = -/(х).
3°. График четной функции у = х2 изображен на рис. 1.
4°. График нечетной функции у = х3 изображен на рис. 2.
5°. Заметим, что не всякая функция является четной или не-
четной.
Рис. 2
35
4. Линейная функция и ее график
1°.Функцию, заданную формулой у = kx + Ъ, где k и Ъ — неко-
торые числа, называют линейной.
2°.График линейной функции у = kx + Ъ есть прямая.
3°.Коэффициент k характе-
ризует угол, который образует
прямая у = kx с положительным
направлением оси Ох, поэтому
число k называют угловым ко-
эффициентом. При этом:
а) если k > 0, то этот угол
острый;
б) если k < 0, то этот угол ту-
пой;
в) если k = 0, то прямая у =
= kx совпадает с осью Ох.
На рис. 3 изображены пря-
мые у = kx при k = - 1, k = |,
k = 1 и k = 2.
4°. Областью определения линейной функции служит множе-
ство R всех действительных чисел, так как выражение kx + Ъ имеет
смысл при любых значениях х.
5°. Уравнение вида kx + Ъ = 0 называется линейным.
5. Квадратичная функция и ее график
1°. Функцию, заданную формулой у = ах2 + Ъх + с, где х, у —
переменные, а, Ъ и с — заданные числа, причем а 0, называют
квадратичной.
2°. Областью определения квадратичной функции является
множество R.
3°. Графиком функции у = ах2 + Ъх + с является парабола. При
этом:
а) если а > 0, то ее ветви направлены вверх;
б) если а < 0, то ее ветви направлены вниз;
в) осью симметрии параболы служит прямая х = - — .
4°. Координаты вершины параболы находят по формулам
Ь , ч 4ас-Ь2
36
На рис. 4 изображены графики
функций у = х2, у = 2х2 и у = -i х2,
Z О
а на рис. 5 — графики функций у =
= х2 + 4х + 3иу = -2х2 + Чх - 5.
6. Функция у = - и ее график
X
1°. Если переменная у пропорци-
ональна переменной х, то такая зави-
симость выражается формулой у = kx,
где k 0 — коэффициент пропорцио-
нальности.
2°. Если переменная у обратно пропорциональна переменной х,
то такая зависимость выражается формулой у = - , где k 0 — ко-
эффициент обратной пропорциональности.
3°. Область определения функции у = - есть множество чисел,
отличных от нуля, т. е. х е R, х 0.
37
4°. Графиком обратной пропорциональности у = | является кри-
вая, которую называют гиперболой. Она состоит из двух ветвей,
симметричных относительно начала координат. При этом:
а) если k > 0, то ветви гиперболы расположены в I и III коорди-
натных четвертях (рис. 6, а);
б) если k < 0, то они расположены во II и IV координатных чет-
вертях (рис. 6, б).
Рис. 6
5°. Заметим, что гипербола не имеет общих точек с осями коор-
динат, а лишь сколь угодно близко к ним приближается.
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каком значении параметра а прямая у = 2ах - 3 проходит
через точку А(1; -6)?
1. Подставив х = 1, у = -6 в уравнение прямой у = 2ах - 3, по-
лучим -6 = 2а - 3, откуда а = -1,5.
2. Ответ: а = -1,5.
2. При каком значении параметра а параболы у = Зх2 + 2ах - 1 и
у = ах2 - 5х + 8 пересекаются в точке с абсциссой х0 = 3?
1. Подставив значение х0 = 3 в уравнения парабол, получим ра-
венство
3 • 9 + 6а - 1 = 9а-15+ 8,
откуда находим а = 11.
2. Ответ: а = 11.
38
3. Найти все такие а, что при любом b уравнение
ах + Ъ = |х|
(1)
имеет решение.
1. Наиболее рациональный подход к решению этой задачи —
геометрический.
2. Рассмотрим графики функций
у = |х| и у = ах + Ъ (рис. 7).
а) Если Ъ < 0 и |а| < 1, то графики не
пересекаются, а это значит, что урав-
нение (1) не имеет решений.
б) Если же Ъ > 0 и |а| < 1, то хотя
графики и пересекаются, это происхо-
дит не при любом значении Ъ, а только
при Ъ > 0.
в) Наконец, если |а| > 1, то графики
пересекаются при любом значении Ъ.
3. Ответ: |а| > 1.
4. При каких значениях параметра а расстояние между вершина-
ми парабол у = х2 + ах + | и у = Зх2 + 5ах + больше ?
1. Найдем координаты вершин обеих парабол. Для первой из
а а2 . 2 „ 5а а2
них х1 = , у1 = -— + - , для второй х2 = , у2 = - — .
Z 4 о О Z
2. Расстояние между вершинами парабол выразится так:
, М 5а . а}2 ( а2 а2 2^2 1 /„ 4 . с . 2 , ел
d= +l-2- + Z-3J =1279а +64“ +64’
3. Решив теперь неравенство
79а4 + 64а2+ 64 > ,
J. Z О
получаем а2 > 4.
4. Ответ: а (-°°; -2) U (2; +°°).
5. При каких значениях параметра а уравнение |х - 1|(х - 5) + а = 0
имеет ровно три решения? В ответе указать наибольшее целое зна-
чение а.
39
Рис. 8
1. Преобразуем заданное уравне-
ние к виду
|х - 1|(х - 5) = -а.
2. Построим график функции у =
= \х - 1|(х - 5) (рис. 8). При х > 1 —
эта часть параболы (х -1)(х-5) = х1 2 3-
- 6х + 5, а при х < 1 — часть параболы
(1 - х)(х - 5) = -х2 + 6х - 5.
3. График функции у = -а есть пря-
мая, параллельная оси Ох (рис. 8).
4. Из рисунка видно, что эта прямая
пересекает график функции у = |х - 1| X
X (х - 5) в трех точках, если -4 < а < 0.
5. Следовательно, а е (0; 4). Наи-
большее целое значение а из этого ин-
тервала равно 3.
6. Ответ: а = 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. При каких значениях а является четной функция:
а) у = (а - 3)х + 5а - 1;
б) у = -ах2 + (4а + 5)х + 3;
в) у = ------—----------?
(а+ 1)х2 - 2ах + За - 1
2. При каких значениях а является нечетной функция:
а) у = (2а - 1)х - 6а + 5;
б)у =
(7а - 3)х - 9 ’
в) У = + zAt ?
3. Найти значения параметра а, при которых заданная функ-
ция монотонно возрастает и монотонно убывает:
а) у = (а - 1)х + а2 -3;
б) у = (2а + 5)х2 + 4х + а - 1;
, 7 - За
в) У = ——;
\ _ 5
Г>У (4а-1)х‘
40
4. При каких значениях а множество значений функции:
а) у = х1 2 + 4ах + 5 - За2 есть промежуток [-9; +°°);
б) у = -4х2 + 12ах + 4а2 - 5а есть промежуток (-°°; 8]?
с тт , 2х + а -Зах + 1
5. При каком значении а функции у = ---р и у = -----j—
имеют одно и то же множество значений?
6. При каком значении параметра а прямая:
а) у = ах - 3 проходит через точку А(-2; 9);
б) у = Зх + а проходит через точку А(-1; 5)?
7. При каком значении параметра а параболы:
а) у = х2 - 4ах + 5 и у = -2х2 + Зах - 4 пересекаются в точке
с абсциссой х0 = -1;
б) у = ах2 - 7х + 3 и у = 0,бах2 - 4х + 3,5 пересекаются в точке
с ординатой у0 = 2?
8. При каких значениях параметра а уравнение (2 - х)|х - 8| + а =
= 0 имеет единственное решение? В ответе указать наименьшее це-
лое значение а.
9. При каких значениях параметра а уравнение |х + 3|(х - 3) +
+ а = 0 имеет ровно три решения? В ответе указать наибольшее це-
лое значение а.
Ответы
1. а) а = 3; б) а = -1,25; в) а = 0. 2. а) а = | ; б) а = $ ; в) а е R. 3. а) Если
а < 1, то функция убывает; если а > 1, то функция возрастает; б) если
а < -2,5, то функция убывает; если а > -2,5, то функция возрастает; в) ес-
7 7
ли а < - , то функция убывает; если а > - , то функция возрастает; г) если
а < | , то функция возрастает; если а > | , то функция убывает. 4. а) а =
= ± V2 ; б) а = 1; а = . 5. а = -| . 6. а) а = -6; б) а = 8. 7. а) а = ;
б) а = 3,25. 8. а = 10. 9. а = 8.
(емаэ
- -1. Квадратные уравнения I I I I I I I
"2. Теорема Виета I I I I I I I I I
- - 8. Уравнения с несколькими переменными
2 2 Системы уравнений
tf
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Квадратные уравнения
1°. Уравнение вида ах2 + Ъх + с = 0, где х — переменная, а, Ь,
с — некоторые числа, причем а 0, называют квадратным.
2°. Формула корней квадратного уравнения имеет вид
-b ± Jb2 - 4ас
X. 9 = ---.
х’2 2а
3°. Выражение Ь2 - 4 ас называют дискриминантом квадрат-
ного уравнения и обозначают буквой D.
4°. Если D < 0, то квадратное уравнение не имеет действитель-
ных корней.
5°. Если D > 0, то квадратное уравнение имеет два различных
действительных корня.
6°. Если D = 0, то существует только одно значение переменной,
удовлетворяющее уравнению ах2 + Ъх + с = 0. Условились говорить,
что в этом случае квадратное уравнение имеет два равных действи-
тельных корня, а само число ) называют корнем кратности два.
7°. Уравнение х2 + рх + q = 0, в котором первый коэффициент а
равен 1, называют приведенным.
8°. Формула корней приведенного квадратного уравнения имеет
вид
Р и- IfpV
*1,2 2 1 JU ~q-
42
9°. Уравнение вида ах4 + Ьх2 + с = 0 называют биквадратным.
С помощью замены переменной по формуле t = х2 оно приводится
к квадратному уравнению at2 + bt + с = 0.
2. Теорема Виета
1°.Теорема Виета. Сумма корней приведенного квад-
ратного уравнения х2 + рх + q = 0 равна второму коэффициенту,
взятому с противоположным знаком, а произведение корней рав-
но свободному члену, т. е. х1 + х2 = -р, хгх2 = q.
2°. Выражение вида ах2 + Ъх + с называют квадратным трех-
членом. Корни этой функции являются корнями соответствующе-
го квадратного уравнения ах2 + Ьх + с = 0.
3°. Если дискриминант квадратного трехчлена больше нуля
(D > 0), то этот трехчлен можно представить в виде
ах2 + Ьх + с = а(х - х^(х - х2),
где х1 и х2 — корни трехчлена.
4°. Справедлива теорема, обратная теореме Виета. Если чис-
ла р, q, х1г х2 таковы, что х1 + х2 = -р, хгх2 = q, то хги х2 — корни
уравнения х2 + рх + q = 0.
3. Уравнения с несколькими переменными
1°. Уравнение с двумя переменными хну имеет вид f(x, у) =
= ф(х, у), где / и <р — выражения с переменными х и у.
2°. Графиком уравнения с двумя переменными называют
множество точек, координаты которых служат решениями этого
уравнения. Например:
а) график уравнения ах + by + с = 0 есть прямая;
б) график уравнения у = ах2 + Ьх + с — парабола;
в) график уравнения ху = k (k 0) — гипербола.
3°. Графиком уравнения х2 + у2 = г2, где х и у — переменные,
г — положительное число, является окружность с центром в нача-
ле координат и радиусом, равным г.
4. Системы уравнений
1°. Если ставится задача найти множество общих решений двух
или нескольких уравнений с двумя (или более) переменными, то
говорят, что надо решить систему уравнений.
43
Систему двух уравнений с двумя переменными будем записы-
вать так:
/1(х, у) = фДх, у),
f2(x, у) = Ф2(х, у).
2°. Число переменных может, вообще говоря, не быть равным
числу уравнений.
3°. Решить систему уравнений — значит найти все ее реше-
ния.
4°. Систему называют:
а) совместной, если она имеет хотя бы одно решение;
б) несовместной, если она не имеет ни одного решения.
5°. Систему называют:
а) определенной, если она имеет конечное число решений;
б) неопределенной, если она имеет бесконечное множество ре-
шений.
6°. Две системы называют равносильными, если они имеют од-
но и то же множество решений.
7°. Графическое решение системы уравнений с двумя перемен-
ными сводится к отысканию координат общих точек графиков
уравнений.
8°. Как известно, прямые на плоскости могут пересекаться
в одной точке, быть параллельными или совпадать. Соответствен-
но этому система линейных уравнений с двумя переменными мо-
жет:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
9° . Пусть дана система линейных уравнений
аух + Ъху = с1(
а2х + Ъ2у = с2.
Не решая эту систему, можно определить число ее решений по
коэффициентам при соответствующих переменных.
а, ^1
а) Если — 5* —, т. е. коэффициенты при х и у не пропорци-
ей Ь2
овальны, то система имеет единственное решение. Это решение
графически иллюстрируется как точка пересечения двух прямых
(рис. 9).
44
Рис. 10
Рис. 11
h
b2
С1
— , то система не имеет решений. В этом слу-
с2
а-.
б) Если —
«2
чае прямые, являющиеся графиками уравнений системы, парал-
лельны и не совпадают (рис. 10).
а1 Ь1 с1
в) Если — = — = — , то система имеет бесконечное множество
а2 Ь2 с2
решений. В этом случае прямые совпадают друг с другом (рис. 11).
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра а отношение корней уравне-
ния х2 +ах+ а+ 2 = 0 равно 2?
1. Пусть хг и х2 — корни данного квадратного уравнения, причем
Xt
=2.
х2
(1)
1
2
2. Тогда —
т.
е.
X., 15
— = 2 + - = - . С другой стороны,
х -| Л Л
1
1
2
2
2
2
2
и,значит,
5
2 ’
1Л2
(2)
3. Для тех значений а, при которых выполнено соотношение (1),
должно также выполняться равенство (2).
45
4. Согласно теореме Виета, хг + х2 = -а, хгх2 = а + 2. Поэтому
равенство (2) можно записать следующим образом:
а2-2(а + 2) = 5 2 2 _ 9а _ 18 = 0
а + 2 2
а 3
откуда аг = 6, а2 = -- .
5. Ответ: = 6; а2 = -- .
2. В уравнении Зх2 - 7х + с = 0 найти значение параметра с, если
корни уравнения удовлетворяют соотношению
(х1+|)(х2-1)=1. (1)
1. Согласно теореме Виета, имеем
х1 + х2=^- (2)
2. Используя равенства (1) и (2), составим и решим систему
уравнений
_ 7
Х1 з х2’
Q “Х2 + |)(^2“1)=1>
или
_ 7
Х1 х2,
1 2 (3)
х2 - 4х2 + 4 = 0,
откуда х2 = 2.
7 1
3. Тогда из первого уравнения системы (3) найдем х} = - - 2 = - .
О о
4. Снова воспользуемся теоремой Виета и получим, что хгх2 =
С 1 С
= - ; тогда - • 2 = - ; т. е. с = 2.
О о о
5. Ответ: с = 2.
46
(4)
3. Найти все значения а, для которых разность корней уравнения
2х2 - (а + 1)х + а + 3 = 0 (1)
равна 1.
1. Пусть х1 и х2 — корни уравнения (1), причем х2 > х1.
2. Тогда х2 - х1 = 1, или (х2 - хх)2 = 1, т. е.
х2 - 2х2хг + хх =1. (2)
3. Упростив левую часть равенства (2), получим
х2 - 2х2хг + xf = (х2 + хх)2 - 2х2хг - 2х2хг =
= (х2 + хх)2 - 4х2хх = 1. (3)
4. По теореме Виета х2 + х1 = а + ; х2хг = Следовательно,
равенство (3) можно записать так:
Л а. + 1 Л 2 _ ' а + 3 _ ,
I 2 J ' ~2
5. Решив уравнение (4), получим ответ.
6. Ответ: а = -3; а = 9.
4. При каких значениях k уравнение
kx2 - х + 3 = О
имеет единственное решение?
1. Пусть k = 0. Тогда уравнение (1) имеет единственное реше-
ние х = 3.
2. Пусть k 0. Тогда уравнение (1) является квадратным, а его
дискриминант равен D = 1 - 12й. Так как уравнение должно иметь
единственное решение, то его дискриминант должен быть равен
нулю: 1 - 12й = 0, т. е. k = .
3. Ответ: k = 0; k = .
Замечания.
1. Следует обратить особое внимание на распространенную ошиб-
ку при решении задач такого типа.
(1)
47
2. Уравнение (1) нельзя считать квадратным. На самом деле это
уравнение имеет степень не выше второй.
3. При k = 0 получается линейное уравнение, а не квадратное.
5. Найти все значения параметра/,, при которых корни уравнения
(р - 3)х2 - 2рх + 6р = 0 (1)
действительны и положительны.
1. Предположим сначала, чтор * 3. Для того чтобы корни квад-
ратного уравнения были действительными, необходимо и доста-
точно, чтобы дискриминант D уравнения (1) был неотрицателен.
Так как
D = 4р2 - 24р(р - 3) = 4р(18 - 5р),
то неравенство D > О выполняется при
ОСрСЗ.б. (2)
2. Действительные корни х1 и х2 уравнения (1) положительны
в том и только в том случае, когда их сумма и произведение поло-
жительны, т. е.
г + г = ^р > 0 х х = > О
1 z р-3 1 z р-3
или
> о, (3)
р- о
^>0. (4)
3. Система неравенств (2), (3), (4) удовлетворяется при
3<р<3,6. (5)
4. Заметим теперь, что при/, = 3 уравнение (1) имеет единствен-
ный положительный корень х = 3 > 0. Поэтому все искомые значе-
ния/, определяются неравенствами (5) и равенством/, = 3.
5. Ответ: р е [3; 3,6].
6. Решить относительно х уравнение
х _ 2 _ 3 - а2 ,,,
а(х + 1) х + 2 а(х+1)(х + 2)’
1. При а = 0 уравнение (1) не имеет смысла; кроме того, значе-
ния х должны удовлетворять условиям х -1, х -2.
48
2. Умножив обе части уравнения (1) на а(х + 1)(х + 2) О, полу-
чим уравнение
х2 - 2(а - 1)х + а2 - 2а - 3 = О, (2)
равносильное данному.
3. Уравнение (2) имеет корни х1 = а + 1; х2 = а - 3.
4. Среди полученных корней могут оказаться и посторонние,
а именно такие, при которых (х + 1)(х + 2) = 0.
5. Чтобы обнаружить их, необходимо определить, при каких
значениях а корни х1 и х2 (или один из них) принимают значения
(-2) или (-1). Имеем:
а) х1 = а + 1 = -2 при а = -3; тогда х2 = а - 3 = -6;
б) х1 = а + 1 = -1 при а = -2; тогда х2 = а - 3 = -5;
в) х2 = а - 3 = -2 при а = 1; тогда х1 = а + 1 = 2;
г) х2 = а - 3 = -1 при а = 2; тогда х1 = а + 1 = 3.
6. Ответ: если а 0, а -3, а ±2, а 1, то х1 = а + 1, х2 = а - 3;
если а = -3, то х = -6;
если а = -2, то х = -5;
если а = 1, то х = 2;
если а = 2, то х = 3;
если а = 0, то уравнение не имеет смысла.
7. Решить относительно х уравнение
(fe + 2)x2 _ 2kx 5 12-k2-k m
(A + l)(x-2) (A-l)(x-2) k2 - 1 (fe2-l)(x-2)' 1 '
1. При й 5й ±1 их/2 уравнение (1) равносильно уравнению
(k + 2)(k - 1)х2 - (2k2 + 2k + 5)х + k2 + k - 2 = 0. (2)
а) Пусть k = -2; тогда x = 0.
б) Пусть k -2 и k ±1; тогда уравнение (2) имеет корни х1 =
=k + 2 =k-1
k-l’*2 k + 2'
2. Теперь необходимо проверить, нет ли таких значений k, при
которых корни х1 и х2 (или один из них) равны 2.
fe + 2
а) х} = -—j = 2 при k + 2 = 2k - 2, т. е. при k = 4; тогда х2 = 0,5;
б) х2 = + = 2 при k - 1 = 2k + 4, т. е. при k = -5; тогдах1 = 0,5.
49
3. Ответ: если k -2, k +1, k 4, k -5, то
_ k + 2 _ k-1
1 k-1’ 2 k + 2
если k = -2, то х = 0;
если k = 4 или k = -5, то х = 0,5;
если k = ±1, то уравнение не имеет смысла.
Замечание. Корни рассмотренных выше уравнений оказа-
лись рациональными относительно параметров и использованный
при этом способ проверки корней удобен и прост. Однако он может
оказаться слишком громоздким в случае, если корни квадратного
уравнения являются иррациональными относительно параметра.
8. Найти все значения параметра а, при каждом из которых урав-
нение
|1 - ах\ = 1 + (1 - 2а)х + ах2 (1)
имеет только один корень.
1. Пусть а = 0; тогда уравнение (1) запишется в виде 1 = 1 + х,
т. е. при а = 0 оно имеет только один корень х1 = 0. Следовательно,
а = 0 удовлетворяет условию задачи.
2. Пусть а 0. Положим z = 1 - ах и выразим х через z: х = -—- .
Подставив это выражение в уравнение (1), получим уравнение
|z| _ z2 + (2а — 3)г + 2 - а
3. Ясно, что при любом а 0 уравнения (1) и (2) имеют одина-
ковое число корней. Выясним, сколько корней имеет уравнение (2)
в каждой из областей z > 0 из < 0.
4. В области z > 0 уравнение (2) примет вид
z _ г2 + (2а - 3)z + 2 - а
а ’
или
z2 + (а - 3)z + 2 - а = 0. (3)
5. Квадратное уравнение (3) имеет два корня: zx = 1 и z2 = 2 - а.
При а = 1 эти корни совпадают, и, значит, при а = 1 уравнение (2)
имеет в области z > 0 единственное решение zx = 1. При всех а 1
корень zx лежит в области z > 0.
50
6. При а < 2 корень z2 также лежит в области z > 0. Следова-
тельно, все а такие, что а < 2, а 0, а 1, не удовлетворяют усло-
вию задачи.
7. При а > 2 уравнение (2) имеет в области z > 0 единственный
корень zx — 1. Таким образом, если а = 1 или если а > 2, то уравне-
ние (2) имеет в области z > 0 один корень zx = 1.
8. В области z < 0 уравнение (2) примет вид
_z _ z2 + (2а - 3)z + 2 - а
а ’
или
z2 + (За - 3)z + 2 - а = 0. (4)
Дискриминант этого уравнения D = (За - З)2 - 4(2 - а) при а > 2
положителен. Значит, уравнение (4) имеет два корня. Обозначим
меньший из них через z3, а больший — через z4.
9. При а > 2 свободный член уравнения (4) отрицателен (z3z4 =
= 2 - а < 0). Поэтому один из корней z3 или z4 лежит в области z < 0,
а уравнение (2) имеет в области z < 0 единственный корень.
10. Итак, если а > 2, то уравнение (2) имеет в области z > 0 один
корень zx = 1 и в области z < 0 также один корень z3 или z4. Значит,
все числа а > 2 не удовлетворяют условию задачи.
11. Если а = 1, то уравнение (4) не имеет корней в области z < 0,
так как D = -4 < 0. Поэтому при а 0 только а = 1 удовлетворяет
условию задачи.
12. Ответ: а = 0; а = 1.
9. Найти все значения параметра/,, при каждом из которых урав-
нение
(х— р)2(р(х-р)2-р - 1) = -1 (1)
имеет больше положительных корней, чем отрицательных.
1. Пустьр = 0; тогда уравнение (1) примет вид х2 = 1. Это урав-
нение имеет корни хх = 1 и х2 = -1. Следовательно, в этом случае
число положительных и число отрицательных корней одинаково
и такое значение р условию задачи не удовлетворяет.
2. Пустьр 0. Положим z = (х -р)2; тогда уравнение (1) примет
вид
pz2 - (р+ l)z + 1 = 0. (2)
Корнями уравнения (2) являются zx = 1 и z2 = - .
51
3. Пусть/, < 0; тогда исходное уравнение имеет два корня: х1 =
= р + 1 и х2 = р - 1. Легко установить, что если -1 <р < 0, то х1 > 0
и х2 < 0; если/» < -1, то х1 < 0 и х2 < 0, а если/, = -1, то х1 = 0 и
х2 = -2.
Следовательно, ни при каком/, < 0 исходное уравнение не име-
ет положительных корней больше, чем отрицательных, т. е. ника-
кие значения/, < 0 условию задачи не удовлетворяют.
4. Пусть р > 0; тогда исходное уравнение имеет четыре корня:
1 , 1 1
Хх=р+У,Х2=р-У,Хъ=р+— и х4 = р - — .
ЧР л/р
а) Если 0 <р < 1, то х1 > 0, х2 < 0, х3 > 0, х4 < 0, т. е. при любом
р таком, что 0 < р < 1, уравнение (1) имеет два положительных и
два отрицательных корня. Значит, никакие значения/, из проме-
жутка 0 <р < 1 условию задачи не удовлетворяют.
б) Если/, = 1, то х1 = 2, х2 = 0, х3 = 2, х4 = 0, т. е. уравнение (1)
имеет два положительных и ни одного отрицательного корня. Та-
ким образом, это значение/, удовлетворяет условию задачи.
в) Еслир > 1, то х4 > 0, х2 > 0, х3 > 0, х4 > 0, т. е. уравнение (1)
имеет четыре положительных и ни одного отрицательного корня,
т. е. все такие значения/, удовлетворяют условию задачи
г) Итак, условию задачи удовлетворяет любое значение/, > 1.
5. Ответ: р е [1; +оо).
10. Определить все значения а, при которых уравнения х2 + ах +
+ 1 = 0 и х2 + х + а = 0 имеют общий корень.
Замечание. Эта задача была решена ранее (см. пример 15,
тема 3). Здесь мы приведем другой способ решения.
1. Если при каком-либо а данные уравнения имеют общий ко-
рень х, то пара (а; х) является решением системы
х2 + ах + 1 = 0,
х2 + х + а = 0.
2. Система (1) равносильна двум системам:
ax-x+l-a = G,
х2 + ах + 1 = 0.
ах-х+1~а = 0,
х2 + х + а = 0.
52
3. Как получились системы (2) и (3)?
а) Первое уравнение обеих систем получено вычитанием второ-
го уравнения системы (1) из первого:
(х1 2 + ах + 1) - (х2 + х + а) = ах - х + 1 -а = 0. (4)
б) Второе уравнение систем — это первое или второе уравнение
системы (1).
4. Уравнение (4) после преобразования примет вид (х - 1)(а - 1) =
= 0, оно имеет единственный корень х = 1 при а‘-йиа?1,а вто-
рые уравнения систем (2) и (3) имеют этот корень х = 1 только при
а = -2.
5. Ответ: а = -2.
11. Даны уравнения
х2 - 5х + k = 0, (1)
х2 - 7х + 2k = 0. (2)
Определить значения k, при которых один из корней второго
уравнения вдвое больше одного из корней первого уравнения.
1. Пусть х — корень уравнения (1); тогда 2х должен быть кор-
нем уравнения (2). Составим систему
J х2 - 5х + k = 0,
] (2х)2 - 7 • (2х) + 2k = 0. (3)
2. Решим систему (3):
J х2 - 5х + k = 0, -2 J Зх - k = 0,
12х2 - 7х + й = 0 1 | х2 - 5х + й = 0.
3. Из системы (4) получаем
j х = 0, J х = 2,
\k = 0 или \k = 6.
Значение k = 0 не удовлетворяет условию, а значение k = 6
приводит к уравнениям х2 - 5х + 6 = 0 (с корнями х = 2 и х = 3)
и х2 - 7х + 12 = 0 (с корнями х = 3 и х = 4).
4. Ответ: k = 6.
1 2. Для каждого действительного а найти действительные корни
уравнения
ах2 + 2(а + 1)х + 2а = 0. (1)
53
1. Прежде всего рассмотрим случай а = 0 (при этом значении а
обычная схема решения квадратного уравнения неприменима).
Тогда уравнение (1) примет вид 2х = 0, откуда х = 0.
2. Пусть теперь а + 0. Существование и количество корней
квадратного уравнения (1) зависят прежде всего от его дискрими-
нанта.
3. Вычислим дискриминант:
D = 4(а + I)2 - 8а2 = 4(-а2 + 2а + 1). (2)
Корнями квадратного трехчлена (2) являются ar = 1 - л/2 иа2 =
= 1+72.
4. При D < 0 уравнение (1) действительных корней не имеет.
Это будет в том случае, когда < а < 1 - 72 или 1+72 < а +
5. При D = 0, т. е. при а = 1 - л/2 или а = 1 + л/2 , уравнение (1)
имеет один корень
а + 1
х = -----,
а
а именно: если а = 1 - л/2 , то х = л/2 ; если а = 1 + л/2 , то х = - л/2 .
6. При D > 0 (и а + 0) уравнение (1) имеет два корня:
_ -(а+1) + 7о _ -(а+1)-7о
•Аг 1 • И •
1 Л л
7. Ответ: если < а < 1 - л/2 или 1 + 72 <а < +°°, то.г‘-0;
если а = 1 - л/2 , то х = 72;
если 1 - л/2 < а < 0 или 0 < а < 1 + л/2 , то х = хг,
х = х2;
если а = 0, то х = 0;
если а = 1 + л/2 , то х = - л/2 .
1 3. При каких k уравнение
(А - 2)х2 + (4 - 2k)x + 3 = 0 (1)
имеет единственное решение?
1. Ясно, что решение надо начинать со случая, когда коэффи-
циент при х2 равен нулю: k - 2 = 0, т. е. k = 2.
2. При k = 2 уравнение (1) не имеет решений: -3 = 0.
54
3. Если k - 2 0, т. е. k 2, то уравнение (1) квадратное и воз-
можные искомые значения параметра — это корни дискриминан-
та: k = 2 или k = 5, но k = 2 не подходит (см. п. 2).
4. Ответ: k = 5.
14. При каких k уравнение
k(k + 3)х2 + (2k + б)х - 3k - 9 = 0 (1)
имеет более одного корня?
1. Начнем со случая, когда k(k + 3) = 0, т. е. k = 0 или k = -3.
2. При k = 0 уравнение (1) имеет единственное решение:
6х - 9 = 0, т. е. k = 1,5.
3. При k = -3 решением уравнения (1) служит любое действи-
тельное число: 0-х2 + 0- х + 9- 9 = 0.
4. Дискриминант квадратного уравнения (1) равен
4(А + З)2 + ±k(k + 3) • 3(k + 3) = 4(3* + 1)(A + З)2
и, очевидно, положителен при k > -- .
О
5. При записи ответа из промежутка (следует исклю-
чить точку k = 0.
6. Ответ: k = -3; < k < 0; k > 0.
О
1 5. Определить все действительные значения а, при каждом из ко-
торых уравнение
х4 - (а + 2)х2 - (а + 3) = 0
имеет действительные решения, и найти все эти решения.
1. С помощью подстановки х2 = t (t 0) рассматриваемое би-
квадратное уравнение приводится к смешанной системе
!t2-(a+ 2)t - (а + 3) = 0,
[t>0.
Корнями уравнения этой системы являются t1 = а + Зи f2 = -1
(не удовлетворяет условию t 0). Значит, система имеет решение
t = а + 3 при а > -3.
55
2. Воспользовавшись снова указанной подстановкой, получим
х2 = а + 3, а -3, откуда хг = - Jа + 3 , х2 = Jа + 3 .
3. Ответ: а -3; х = +*]а + 3 .
1 6. Найти все действительные значения параметра а, для каждого
из которых уравнение
Jx-a (х2 + (1 + 2а2)х + 2а2) = 0 (1)
имеет только два различных корня.
1. Решив уравнение (1), найдем три значения х} = а, х2 = -1,
х3 = -2а2, которые обращают в нуль или первый, или второй мно-
житель данного уравнения.
2. Заметим, что при а > О выполняются неравенства х2 - х} < О,
х3 - х} < 0, т. е. х2 - а < 0, х3 - а < 0. Поэтому если при а > 0 в
уравнение вместо х подставить х2 или х3, то множитель Jx - а не
имеет смысла. Следовательно, при а > 0 уравнение (1) имеет лишь
один корень х} = а.
3. Будем считать, что а < 0. При а = -1 имеем х1 = х2 > х3, т. е.
х3 ~ Х1 = хз ~ а < значит, х3 = -2а2 не является корнем уравнения
при а = -1; уравнение (1) имеет два совпадающих корня х1 = х2, что
не удовлетворяет условию задачи. При а = -2а2, т. е. при а = ,
имеем х2 - а = -1 + | < 0, т. е. х2 = -1 не является корнем уравне-
ния; уравнение (1) имеет два совпадающих корня х1 = х3, что так-
же не удовлетворяет условию задачи.
4. Рассмотрим теперь следующие три случая: 1)а - (-°°; -1),
а) В случае 1 имеем -2а2 < а < -1, т. е. х3 < х} < х2. Отсюда
следует, что х3 - х} = х3 - а < 0 и х3 не является корнем уравнения,
а х2 - х} = х2 - а > 0 и, значит, х2 является корнем уравнения.
Итак, при а е (-оо; -1) уравнение (1) имеет только два различных
корня х1 = а и х2 = -1.
56
б) В случае 2 имеем -1 < а и а < , т. е. а2 > или -2а2 < а.
Следовательно, х2 - х1 = х2 - а < 0 и х3 - х1 = х3 - а < 0, т. е. ни х2,
ни х3 не являются корнями уравнения; при а е (-1; ) уравне-
ние (1) имеет только один корень х1 = а.
в) В случае 3 имеем а > , следовательно, -2а2 > -1, т. е. х2 <
< х1 < х3; тогда х3 - х1 = х3 - а > 0, а х2 - х1 = х2 - а < 0. Таким
образом, х3 является корнем уравнения, а х2 не является его кор-
нем. Итак, при а|; 0 ) уравнение имеет два различных корня
х} = а и х3 = -2а2.
5. Ответ: если а е (-оо; -1), то х} = а, х2 = -1;
если а ; о) , то х} = а, х3 = -2а2.
17. Решить относительно х уравнение
х _1_ 2х _ ЗЬ-4
&+ 1 х-2 ~ (& + 1)(х-2) ’ 1 '
1. При (Ъ + 1)(х - 2) 5й 0 уравнение (1) равносильно уравнению
х2 + ЗЪх - ЗЬ + 4 = 0. (2)
2. Найдем корни уравнения (2):
хг = -b - Jb2 + 3& - 4 , х2 = -b + Jb2 + 3& - 4 . (3)
3. Необходимо проверить, нет ли таких значений Ь, при кото-
рых один из полученных корней равен 2.
4. Оказывается, что такое значение b имеется: если в уравне-
ние (2) подставим х = 2, то получим b = -8.
5. Подставив значение Ъ = -8 в выражения (3), находим х1 = 2
(посторонний корень), х2 = 14.
6. Итак, при Ъ = -8 уравнение (2) имеют один корень х = 14;
при Ъ -8, Ъ -1 — два корня.
7. Решив неравенство Ъ2 + ЗЪ - 4 > 0, заключаем, что эти корни
действительны при Ъ < -4 (Ь -8) и при & > 1; уравнение не имеет
корней при -4 < b < 1 (Ь -1).
57
8. При b = -1 уравнение не имеет смысла.
9. Ответ: если < ь < -8, -8 < b < -4, b > 1, то х1 = -Ь -
- л/b2 + 3& - 4 , х2 = —b + Jb2 + 3& - 4 ;
если Ъ = -8, то х = 14;
если b = -4, то х = 4;
если -4 < & < -1, -1 < Ъ < 1,то уравнение не имеет
корней;
если Ъ = -1, то уравнение не имеет смысла;
если Ъ = 1, то х = -1.
18. Решить на множестве действительных чисел уравнение
sJ(a + х)2 + 4^(а -я)2 = 5sJa2 - х2 . (1)
1. Если а 0, то х = а не является корнем уравнения.
2. Разделив обе части уравнения (1) на - х)2 , получим
(2)
3. Пусть t = з -—- ; тогда уравнение (2) примет вид t2 - 5t + 4 =
= 0, откуда = 1, t2 = 4.
а) Уравнение з/-- = 1 имеет корень х = 0.
„ а + х . 63а
б) Уравнение з/- = 4 имеет корень х = —— .
Ца-х 65
4. Если а = 0, то уравнение (1) имеет один корень х = 0.
5. Ответ: если а 0, то х-. = 0, х., = ;
1 z 65
если а = 0, то х = 0.
и П т. х2-2тх + тг-9 п
1 У. Решить уравнение----------- = 0.
1. Данное уравнение равносильно системе
х2 - 2тх + т2 -9 = 0,
х - 2 0.
(1)
(2)
2. Из уравнения (1) находим х = т ± 3, т. е. х1 = т - 3, х2 =
= т + 3.
58
3. Из условия х - 2 0, т. е. х 2, следует, что ттг — 3 2, ттг + 3
5й 2, откуда т 5, т -1.
4. Значит, х1 = т - 3 — корень данного уравнения, если т 5;
х2 = т + 3 — корень данного уравнения, если т -1.
5. Ответ: если т = -1, то х = -4;
если т = 5, то х = 8;
если т -1, т 5, то х1 = т - 3, х2 = т + 3.
20. При каком значении а сумма квадратов корней уравнения
х2-ах + а-1 = 0 (1)
будет наименьшей?
1. Уравнение (1) имеет корни при любом а, так как
D = а2 - 4(а - 1) = (а - 2)2 > 0.
2. При этом х1 + х2 = а, хгх2 = а - 1.
3. Найдем сумму квадратов корней уравнения (1):
х% + х2 = (х1 + х2)2 - 2хгх2 = а2 - 2а + 2 = (а - I)2 + 1 > 1.
Эта сумма минимальна при а = 1.
4. Ответ: а = 1.
21. Найти все пары значений параметров а и Ь, при которых урав-
нения
х2 - ах + а = 0 (1)
и
х2 + b2x - 8Ь = 0 (2)
равносильны.
1. Решение задачи основано на том, что если даны два уравне-
ния х2 + prx + qr = 0 и х2 + р2х + q2 = 0, то они равносильны только
в двух случаях:
а) когда дискриминанты Dy и D2 этих уравнений отрицатель-
ны, т. е. когда уравнения не имеют решений;
б) когдарх =p2,qx = q2.
2. В первом случае для уравнения (1) дискриминант D1 < 0, если
0 < а < 4. Для уравнения (2) дискриминант _О2 < 0, если -2'1/4 <
< b < 0.
59
3. Таким образом, в данном случае искомой парой является
любая пара значений параметров а и Ъ, где значение а выбирается
из интервала (0; 4), а значение Ъ — из интервала (-2?/4 ; 0).
4. Во втором случае приходим к системе
J -а = Ь2,
[ а = ~8Ъ.
Это система имеет два решения: а) а = Ъ = 0; б) а = -64, Ъ = 8.
5. Ответ: (0; 0); (-64; 8); (а; Ъ), где а (0; 4), Ъ (~23*/4 ; 0).
22. Для каждого k решить уравнение
х2 + \х\ + k = 0. (1)
1. Положим \х\ = у 0. Так как х2 = |х|2 = у2, то уравнение (1)
примет вид
у2 + у + k = 0. (2)
2. Решив уравнение (2), получим
-1 ± 71 -4А
У=-------2----’
где
f 1 - 4* > 0,
< п---т-г . , или < 4 ’ т. е. /г < 0.
71-4А >1, ] _
I [ k < 0,
а) При k > 0 уравнение (1) не имеет корней.
б) Очевидно, что ——< 0 при k < 0, поэтому уравнение
I I - 1 - л/1 - 4Л:
|х| = -------- не имеет корней.
ч тт 11-1 + 71-4А , 71-4А -1
в) Из равенства |х| =------- следует, что 2 = ±---------
при условии k < 0.
г) При k = 0 получаем х = 0.
3. Ответ: если k > 0, то уравнение не имеет корней;
если k = 0, то х = 0;
если k < 0, то уравнение имеет два корня: х1 =
_ 71 -4А 1 _ 1 71 -4fe
2 ’ Х2 2
60
23. Установить, при каких значениях параметра а уравнения
х2 - (2а + 1)х + а + 1 =0, 2х2 - (4а - 1)х +1=0
имеют общий корень. Найти соответствующий корень.
1. Пусть k — общий корень данных уравнений. Тогда справед-
ливы два числовых равенства:
k2 - (2а + l)k + а + 1 = 0, (1)
2k2 - (4а - 1)А + 1 =0. (2)
2. Умножив равенство (1) на (-2), имеем
- 2k2 + 2(2а + 1)А - 2а - 2 = 0. (3)
3. Сложив равенства (3) и (2), получим 3k - 2а - 1 = 0, откуда
, 2а + 1
k=~-
4. Подставив в любое, например в первое из данных уравнений,
вместо х найденное значение k, имеем
<2a + iy _(2а+1)2+а+1=0. (4)
V о J о
7
5. Решив уравнение (4), находим a, = 1, а2 = -- . Вычислим со-
О
ответствующие значения х:
ч , 2а+1 2-1 + 1 .
a) k = —— =-------— = 1 = Хр
О о
2 ’ + 1
, 2а+ 1 ^87 1
б)А’= — = ------з----- =-4 =Х2.
7 1
6. Ответ: а} = 1, х} = 1; а2 = -- , х2 = -- .
24. Решить уравнение
х4 + х3 - Зах2 - 2ах + 2а2 = 0, (1)
где а — положительный параметр.
1. Перепишем заданное уравнение в виде
2a2 - (Зх2 + 2х)а + х4 + х3 = 0. (2)
2. Решив уравнение (2) как квадратное относительно а, нахо-
X2
дим ах = — , а2 = х2 + х.
61
3. Таким образом, решение уравнения (1) сводится к нахожде-
нию корней уравнений:
а) х2 = 2а; б) х2 + х - а = 0.
4. Ответ: х1 = - J2a , х2 = J2a , х3 = ——+ ,
__ — 1 + л/1 + 4а
Х4 2 ’
25. Найти все значения параметра Ь, при каждом из которых сис-
тема уравнений
J Ьх + 2у = b + 2,
2Ъх + (Ъ + 1)у = 2Ъ + 4
имеет хотя бы одно решение.
1. Из первого уравнения системы следует, что у = ------.
Подставив это выражение во второе уравнение системы, приходим
к равносильной системе
Ъ(Ъ - 3)х = (Ъ + 2)(Ь - 3).
2. а) Если b = 0, то система (1) несовместна.
б) Если b = 3, то система (1) имеет бесконечно много решений
5-За ,
вида х = а, у = —-— , где а — любое число.
в) Если & ^0и&^3,то система (1) имеет единственное решение
Ь + 2 п
х = —— , у = 0.
Ь v
3. Следовательно, данная система имеет хотя бы одно решение
при любом Ь, кроме b = 0.
4. Ответ: b е (-оо; 0) U (0; +°°).
26. При каких значениях параметров а и & система
J 8х + (а2 + ab + Ъ2)у = 4, ....
[ (а - Ь)х + 26у = 2 J
имеет бесконечное множество решений?
1. На координатной плоскости хОу множество точек (х; у), удов-
летворяющих уравнениям системы (1), состоит из двух прямых.
62
2. Решением системы (1) являются точки пересечения этих
прямых. Поэтому данная система будет иметь бесконечное множе-
ство решений в том и только в том случае, когда эти прямые совпа-
дают.
3. В общем случае две прямые, заданные уравнениями у =
= krx + Ь1иу = k2x + b2, совпадают, если /г, = k2 и Ъг = Ъ2 (при кл k2
они имеют одну точку пересечения, при кл = k2 и Ъг = Ъ2 точек пе-
ресечения у них нет).
4. Следовательно, система (1) будет иметь бесконечно много ре-
шений, если совместна система
а-Ь _ 26 _ 1
“8 а2 + аЬ + Ь2 - 2 ’ 1 ’
где а / 0и & / 0.
5. Решив систему (2), получаем = -2, = -6 или а2 = 6, Ъ2 = 2.
6. Ответ: (-2; -6); (6; 2).
27. Найти значения параметра т, при которых система уравнений
\(т- 2)х + у = (т - 2)2, (1)
| х + (т - 2)у = 1 (2)
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечное множество решений.
1. Выразим х из уравнения (2) и подставим в уравнение (1):
х = 1 - (т - 2)у, (3)
(т - 2)(1 - (т - 2)у) + у = (т - 2)2. (4)
Упростив уравнение (4), получим
(1 - (т - 2)2)у = (т - 2) - (т - 2)2. (5)
2. Уравнение (5) (а, значит, и данная система) имеет единст-
венное решение, если коэффициент при у не равен нулю, т. е.
1 - (т - 2)2 0, т. е. если т 1 и т 3.
3. Система не имеет решений, если коэффициент при у в урав-
нении (5) равен нулю, а правая часть не равна нулю, т. е.
J 1 - (т - 2)2 = 0,
| (т - 2) - (т - 2)2 0,
что выполняется только при т = 1.
63
4. Система имеет бесконечное множество решений при усло-
виях
J 1 - (т - 2)2 = О,
[ (т - 2) - (т - 2)2 = О,
которые выполняются только при т = 3.
5. Ответ: a) mr— (-°°; 1) U (1; 3) U (3; +°°); б) т = 1; в) т = 3.
28. При каких значениях с и d система уравнений
J(c+1)2х - (с + 1)у =-с,
| (d - 1)х + (5 - 2d)y = с + d ' '
имеет единственное решение х = 1, у = 1?
1. Подставив значения х = 1, у = 1 в систему (1), получим
;С2 + 2С=°,
|c + 2d = 4. ()
2. Система (2) имеет два решения: а) с = 0, d = 2; б) с = -2; d = 3.
Таким образом, только при этих значениях с и d система (1) имеет
решение х = 1, у = 1, но это не означает, что найденные значения
параметров с и d обеспечивают единственность решения.
3. Мы установили пока только необходимое условие, которому
удовлетворяют искомые параметры.
4. Достаточность же этого условия должна быть установлена,
либо опровергнута в процессе проверки.
а) Если с = 0, d = 2, то получим систему
J х - у = О,
| х + у = 2,
которая имеет единственное решение х = 1, у = 1.
б) Если с = -2, d = 3, то получим систему
J х + у = 2,
| 2х - у = 1,
которая также имеет единственное решение х = 1, у = 1.
5. Ответ: с = 0, d = 2 или с = -2, d = 3.
64
29. При каких значениях а для любого b найдется хотя бы одно с
такое, что система
J 2х + by = ас2 + с,
\Ьх + 2у = с - 1
имеет по крайней мере одно решение?
1. Система (1) при b +2 и при любых а и с имеет единственное
решение
2ас2 + 2с - be + b 2с-2-аЬс2-Ьс
х = ----’ У = --------------------•
4:-Ь2 4:-Ь2
2. Если b = 2, то система (1) примет вид
2х + 2у = ас2 + с,
\2x + 2i,-c-l.
3. Чтобы система (2) имела решения, должно выполняться ус-
ловие ас2 + с = с - 1, т. е. ас2 = -1. Рассматривая последнее соотно-
шение как уравнение относительно с, замечаем, что оно имеет ре-
шение При ЛЮбыХ а £ (-ОО; 0).
4. Если b = -2, то система (1) примет вид
2х - 2у = ас2 + с,
\-2х + 2ц-с-1. <3)
5. Чтобы система (3) имела решения, должно выполняться ус-
ловие ас2 + с = 1 - с, т. е. ас2 + 2с - 1 = 0. Рассматривая последнее
соотношение как уравнение относительно с, замечаем, что оно име-
ет решения, если 1 + а > 0, т. е. а — [-1; +°°).
6. Таким образом, при а е [-1; 0) всегда найдется такое с, что
для любого значения Ъ заданная система имеет по крайней мере од-
но решение.
7. Ответ: а е [-1; 0).
30. При каких значениях aub системы уравнений
\х-Зу = Ь2-2,
\2х + у = 5 1 ’
И
[ 2х + 4&и = За + 2,
| х + 2у = 4 (2)
являются равносильными?
65
1 Ь2+13
1. Система (1) имеет единственное решение х(1 = —-— , у(1 =
9 _ 2Ь2
= —-— при любом значении параметра Ъ.
2. Поэтому если при некоторых значениях параметров an b за-
данные системы равносильны, то и система (2) должна иметь то же
самое единственное решение. Подставив это решение во второе
уравнение системы (2), получим
|(&2+13)+?(9-2&2) = 4,
откуда b2 = 1, или Ъ = ±1, х0 = 2, у0 = 1.
3. Из первого уравнения системы (2) найдем две пары значений
а и Ъ: а) а = 2, Ъ = 1; б) а = , Ъ = -1.
О
Полученные значения а и & выражают лишь необходимое усло-
вие, которому должна удовлетворять искомая пара значений а и Ъ.
Поэтому обе найденные пары подлежат проверке.
4. Пусть а = 2, Ъ = 1. Тогда система (2) примет вид
J 2х + 4у = 8,
। х + 2у = 4
и имеет бесконечно много решений. Следовательно, пара а = 2, Ъ = 1
не обеспечивает равносильность систем (1) и (2).
2
5. Пусть а = --,& = -1. Тогда система (2) примет вид
О
J 2х - 4у = О,
| х + 2у = 4
и имеет единственное решение х0 = 2, у0 = 1.
2
6. Ответ: а = -- , b = -1.
О
31. При каких значениях параметра k система уравнений
J (х + 2)2 + у2 = 1,
|(х - З)2 + у2 - 4у = й2 - 4
имеет единственное решение?
66
1. Первое уравнение системы (1) определяет окружность с цент-
ром в точке (-2; 0) и радиусом г = 1.
2. После упрощения второго уравнения системы (1) получаем
уравнение (х - З)2 + (у - 2)2 = k2, которое определяет окружность
с центром в точке (3; 2) и радиусом R = k.
3. Система (1) равносильна следующей:
](x + 2)2 + z/2 = 1,
|(х-3)2 + (у-2)2 = й2. (2)
4. Система (2) будет иметь единственное решение в двух случаях:
а) окружности касаются внешним образом;
б) окружности касаются внутренним образом.
5. Построим окружности для случая а). Из рис. 12 видно, что ок-
ружности I и II в точке N касаются внешним образом. В прямоуголь-
ном треугольнике ОХЛО2 гипотенуза ОХО2 равна сумме двух данных
радиусов 1 и k; поэтому (k + I)2 = 22 + 52, откуда йх 2 = + V29 - 1.
67
6. Построим окружности для случая б). Из рис. 12 видно, что
окружности I и III в точке М касаются внутренним образом. Ради-
ус окружности III равен О2М = O2N + 2, откуда следует, что ks 4 =
= +729 + 1.
7. Ответ: 2 = + 729 - 1; kg 4 = +729 + 1.
32. При каких значениях параметра а система
х2^2^2’ (1)
х + у + z = а
имеет единственное решение? Найти это решение.
1. Подставив выражение для z из первого уравнения системы (1)
во второе, получим х2 + х + у2 + у = а, или
(х+|)+(у+|)=а+|. (2)
2. а) Если а < , то уравнение (2) не имеет решений.
б) Если а > , то уравнение (2), а следовательно, и система (1)
имеет более одного решения.
в) Если же а = -- , то
1 А2
у + - J =0 только при
1
= У = ~2-
„ 1 11
3. Ответ: a = --:x = u= --,z = - .
2 2 2
33. При каких значениях параметра а система
J х2 + (у - а)2 = 1,
[ у = М
имеет ровно два решения?
1. С геометрической точки зрения количество решений систе-
мы — это количество точек пересечения кривых, заданных уравне-
ниями системы.
2. Первое уравнение системы является уравнением окружнос-
ти с радиусом 1 и с центром в точке (0; а).
3. Значение параметра а определяет положение окружности
относительно осей координат.
68
4. График функции у = |х| изображен на рис. 13, а.
5. По условию система должна иметь ровно два решения, сле-
довательно, при каждом фиксированном значении а кривые долж-
ны иметь две общие точки.
6. В зависимости от значений параметра а возможны следую-
щие взаимные расположения кривых (рис. 13, б—з):
График функции
у = Н
Нет решений
ОС = а < -1
Одно решение
ОС = а = -1
Четыре решения
ОС = а, 1 < а < ^[2
Три решения
ОС = а = 1
Два решения
АС = ОА = 1,
ОС = а = л/2
Нет решений
ОС = а > л/2
Рис. 13
69
7. Итак, система имеет два решения, если а е (-1; 1) U {„/2 }.
8. Ответ: а е (-1; 1)U {72}.
34. В зависимости от значений параметров aub решить систему
| х7у31 = а,
\х^ = Ь. (1)
1. Если а = Ъ = 0, то система (1) имеет следующие решения: х = О,
у — любое; х — любое, у = 0.
2. Если а = 0, Ъ 0, то система (1) не имеет решений.
3. Если а 0, Ъ = 0, то система (1) также не имеет решений.
4. Рассмотрим, наконец, случай а 0, Ъ 0. Возведя второе
уравнение системы в куб, получим уравнение
х&у27 = Ъ3.
Отсюда с учетом первого уравнения системы имеем
х7у31 = хбу27(ху4) = Ь3(ху4) = а,
т. е.
5. Подставив выражение (2) во второе уравнение системы (1),
находим
6. Ответ: если а = b = 0, то х = 0, у е R и у = 0, х е R;
если а = 0, Ъ 0 и а 0, Ъ = 0, то решений нет;
если а 0, Ъ 0, то х = адЬ 31, у = Ъ7а 2.
35. При каких значениях параметров а и Ъ система
х2 - у2 + а(х + у) = х - у + а, (1)
х2 + у2 + bxy = 1 (2)
имеет не менее пяти решений?
1. Перепишем уравнение (1) в виде
(х - у + а)(х + у -1) = 0. (3)
70
2. Тогда исходная система равносильна совокупности следую-
щих двух систем:
Г х + у - 1 = 0, 1х - у + а = О,
а) х2 + у2 + Ьху =1; х2 + у2 + bxy = 1.
Каждая из этих систем может иметь либо не более двух, либо
бесконечное множество решений, поэтому исходная система имеет
не менее пяти решений в том и только в том случае, когда хотя бы
одна из систем а) и б) имеет бесконечное множество решений.
3. Выразив из первого уравнения системы а) переменную у и под-
ставив это выражение во второе уравнение той же системы, полу-
чим уравнение
(2 - Ь)х2 + (Ь - 2)х = 0. (4)
4. При Ъ = 2 решением уравнения (4) является любое х - й.
При Ъ 2 уравнение (4) имеет не более двух решений.
5. Рассмотрим систему б). Поступая так же, как и в п. 3, при-
ходим к уравнению
(2 + Ъ)х2 + a(b + 2)х + а2 - 1 = 0,
откуда следует, что система уравнений (1) и (2) будет иметь не менее
пяти (а именно, бесконечное множество) решений в случае, ког-
да Ъ = -2, а = ±1.
6. Ответ: a — R, b = 2: а = ±1, Ъ = -2.
36. Найти все значения параметра а, для каждого из которых сущест-
вует только одно значение х, удовлетворяющее системе уравнений
J |х2 - 5х + 4| - 9х2 - 5х + 4 + 10х|х| = 0, (1)
| х2 - 2(а —1)х + а(а - 2) = 0. (2)
1. Решим первое уравнение системы. Для этого освободимся сна-
чала от знака модуля. Так как х2 - 5х + 4 = 0 при х = 1 и х = 4, то
разобьем числовую прямую на промежутки х<0, 0<хС1,1<хС4,
х > 4 и найдем решения уравнения в каждом из этих промежутков.
2. Пусть х < 0; тогда |х2 - 5х + 4| = х2 - 5х + 4, |х| = -х, а урав-
нение (1) запишется в виде
-18х2 - 10х + 8 = 0. (3)
Уравнение (3) имеет корни хх = -1 и х2 = |. В рассматриваемый
промежуток входит только хх = -1. Значит, в промежутке х < 0
уравнение (1) имеет один корень хх = -1.
71
3. Пусть 0 < х < 1; тогда |х2 - 5х + 4| = х2 - 5х + 4, |х| = х,
а уравнение (1) запишется в виде
2х2 - 10х + 8 = 0. (4)
Уравнение (4) имеет корни х3 = 1 и х4 = 4, из которых в рас-
сматриваемый промежуток входит только х3 = 1. Значит, в проме-
жутке 0 < х < 1 уравнение (1) имеет один корень х3 = 1.
4. Пусть 1 < х < 4; тогда |х2 - 5х + 4| = ~(х2 - 5х + 4), |х| = х,
а уравнение (1) равносильно тождеству 0 = 0, т. е. удовлетворяется
при любом значении х из промежутка 1 < х < 4. Поэтому любое
значение х из промежутка 1 < х < 4 является решением уравнения.
5. Пусть 4 < х < +оо; тогда |х2 - 5х + 4| = х2 - 5х + 4, |х| = х,
а уравнение (1) запишется в виде
2х2 - 10х + 8 = 0. (5)
Уравнение (5) имеет корни х5 = 1 и х6 = 4, ни один из которых
не входит в рассматриваемый промежуток. Значит, в промежутке
4 < х < уравнение (1) не имеет решений.
6. Собрав вместе все найденные вы-
। 4 ше решения, получаем, что решениями
—°-------<</////////>*-уравнения (1) являются х = -1 и все х
из промежутка 1 < х < 4.
₽ИС- На числовой прямой (рис. 14) отме-
тим решения уравнения (1).
7. Второе уравнение системы имеет два корня: х7 = а и х3 = а - 2.
Очевидно, что любого а решения уравнения (2) связаны соотноше-
нием х3 = х7 - 2.
8. Выясним теперь, при каких значениях а система уравнений
(1) и (2) совместна; для этого будем рассматривать различные зна-
чения а, двигаясь по числовой прямой слева направо.
9. Для любого а < -1 оба корня уравнения (2) лежат левее лю-
бого корня уравнения (1), а потому система (1), (2) несовместна.
10. Если а = -1, то, поскольку х3 лежит левее точки х = -1,
система (1), (2) имеет единственное решение х7 = -1.
11. Для любого а из промежутка -1 < а < 1 число х7 лежит меж-
ду корнями уравнения (1), а х8 лежит левее корня уравнения (1),
равного -1. Значит, система (1), (2) несовместна.
12. Если а = 1, то, очевидно, система (1), (2) имеет два решения
X 7 1 И Xg 1 •
72
13. Для любого а из промежутка 1 < а < 3 система (1), (2) сов-
местна. Ее решением является только х7 = а, так как х8 будет ле-
жать между числами -1 и 1.
14. Для любого а из промежутка 3 < а < 4 система (1), (2) имеет
два решения х7 = а и х8 = а - 2, так как оба эти числа лежат на
промежутке [1; 4].
15. Для любого а из промежутка 4 < а < 6 система (1), (2) сов-
местна, ее решением является х8 = а - 2, так как х7 будет находить-
ся правее отрезка [1; 4].
16. Для любого а > 6 система (1), (2) несовместна, поскольку
х7 > 6 и х8 > 4.
17. Так как нас интересуют лишь те значения а, для каждого
из которых система (1), (2) имеет единственное решение, то из пре-
дыдущего вытекает, что условию задачи удовлетворяют а = -1,
а также любые а из двух промежутков 1 <а<3и4<а<6.
18. Ответ: а = -1,1<а<3, 4<а<6.
37. Найти значения k, при которых решения системы
[ Зх - бу = 1,
] 5х - ky = 2
удовлетворяют условиям х < 0 и у < 0.
1. Из первого уравнения системы выразим х = | (1 + бу) и под-
О
ставим во второе. Получим 3z/(10 - k) = 1.
а) Если k = 10, то система не имеет решений.
б) Если k 10, то
12-й _ 1
х 3(10-й)’У 3(10 7г) '
2. Найдем теперь значения k, при которых х < 0 и у < 0. Для
этого решим систему неравенств
12-й
3(10 й)
1
3(10 й)
Из второго неравенства следует, что 10 - k < 0, тогда из первого
получаем 12 - k > 0, т. е. 10 < k < 12.
3. Ответ: k е (Ю; 12).
73
38. Найти все значения а, при которых система
j xs - ay3 = 0,5(а + I)2,
| х3 + ах2у + ху2 = 1 (1)
имеет хотя бы одно решение и всякое ее решение удовлетворяет
уравнению х + у = 0 (а, х, у — действительные числа).
1. По условию у = —х. Тогда система (1) примет вид
J х3 + ах3 = 0,5(а + I)2,
| х3 - ах3 + х3 = 1,
или
J х3(1 + а) = 0,5(1 + а)2, (2)
|х3(2-а)=1. (3)
2. Если а + 1 0, 2 - а 0, то выразим х3 из уравнений (2) и (3):
а)х3^2^)-2;б)х3^а.
3. Приравняв полученные выражения, приходим к уравнению
относительно а:
0,5(1 +а)2
1 + а
—— , т. е. а2 - а = 0.
2 - а
4. Ответ: а = 0; а = 1.
39. При каких а система уравнений
J х2 + z/2 = 2(1 + а),
\(х + у)2 = 14
имеет в точности два решения?
1. Пусть а — искомое значение параметра и (х0; у0) — решение
системы. Легко установить, что пары чисел (~х0; ~у0), (у0; х0),
(~у0; ~х0), также будут решениями системы.
2. Решения (х0; у0) и (~х0; -у0) различны, так как в противном
случае х0 = 0 и у0 = 0, и тогда пара чисел (х0; у0) не удовлетворяет
второму уравнению системы.
3. Решения (х0; у0) и (~у0; ~х0) также различны; в противном
случае х0 + у0 = 0 и снова не удовлетворяется второе уравнение
системы.
74
4. По условию система имеет в точности два решения, значит,
решения (~х0; -у0) и (~у0; -х0) должны совпадать, т. е. должно вы-
полняться равенство у0 = х0.
5. Подставив х0 вместо у0 во второе уравнение системы, по-
лучаем уравнение 4xq = 14, которое имеет два корня: (х0)' =
и <хо)” = -Д-
6. Значит, если при данном а пара (х0; у0) — решение исходной
системы, то либо х0 = у0= , либо х0 = у0 = - . В обоих случаях,
подставив (х0; у0) в первое уравнение системы, получим 2(1 + а) =
= \ \ , откуда а = |.
7. Таким образом, если а — искомое значение параметра, то
5
оно может принимать только значение - .
5
8. При а = - исходная система уравнений примет вид
х2 + у2 = 7,
(х + у)2 = 14.
(1)
9. Умножим первое уравнение системы (1) на 2 и вычтем ре-
зультат из второго уравнения системы (1). Получим систему
х2 + у2 = 7,
-(х - у)2 = О,
равносильную системе (1).
10. Система (2) в свою очередь равносильна системе
(2)
У = х,
2х2 = 7,
которая имеет в точности два решения:
5
2
Итак, действительно, а =
и только это значение удовлетворяет
условию задачи.
5
11. Ответ: а = - .
75
40. Найти множество значений а, при которых уравнение
х2 - (За - 4)х + 2а2 - 5а + 3 _р
л/х + 1
имеет единственное решение.
1. Находим ОДЗ: х > -1.
2. Данное уравнение может иметь единственное решение в двух
случаях: либо квадратный трехчлен в числителе имеет единствен-
ный корень (D = 0), принадлежащий ОДЗ, либо этот трехчлен име-
ет два корня (D > 0), один из которых принадлежит ОДЗ, а другой
не принадлежит ОДЗ.
3. Квадратное уравнение
х2 - (За - 4)х + 2а2 - 5а + 3 = 0
За - 4 ± (а - 2) о <> ,
имеет корни х} 2 = ---, т. е. х} = 2а - 3, х2 = а - 1.
4. Рассмотрим два случая:
1) D = 0 при а = 2, х1 = х2 = 1 > -1. Следовательно, а = 2 удов-
летворяет условию задачи.
2) D >0;
ч [2а-3<-1, [а<1, н
аЦа-1>-1 ^\а>0; а <0;
[ 2а - 3 > -1, [ а > 1,
б) < \ i\ a'—Z.
' \а - 1 < -1 1 а < 0
5. Ответ: а е (0; 1] U {2}.
41. При каких значениях а уравнение
(2х2 - (5а + 2)х + За2 + 3a)Jx^i = 0 (1)
имеет ровно два решения?
1. Очевидно, что уравнение (1) имеет одно решение х = 1 при
любом значении параметра а.
2. Уравнение (1) будет иметь ровно два решения при тех значе-
ниях а, при которых система
Г 2х2 - (5а + 2)х + За2 + За = 0, (2)
{х - 1 > 0 (3)
имеет только одно решение.
76
3. Возможны два случая.
а) Дискриминант уравнения (2) равен нулю и единственный ко-
рень этого уравнения больше 1. Так как D = (а - 2)1 2 3 4 5 6 = 0, если а = 2,
а единственный корень уравнения (2) есть х = 3 > 1, то при а = 2
исходное уравнение будет иметь ровно два решения.
б) Уравнение (2) имеет два корня, но один из этих корней мень-
ше или равен единице. Находим корни уравнения (2): х1 2 =
= 5а + 2 ± (а—2), Тф е_ , х2 = а + 1. Значит, система (2), (3)
будет иметь только одно решение, если а удовлетворяет следующей
совокупности систем неравенств:
3а < -| За >
J ~2 " ’ J ~2
| а + 1 > 1; | а + 1 < 1.
Решив первую систему, получим а е ( 0; | J, вторая система не
имеет решений.
4. Таким образом, уравнение (1) имеет ровно два решения, если
(0; U {2}.
5. Ответ: а е (о; | ] U {2}.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. При каких значениях а сумма корней уравнения х2 + (а2 -
- 4а - 5)х + а2 - 6а + 1 = 0 равна нулю?
2. При каких значениях а разность корней уравнения 2х2 -
-(а + 1)х + а-1=0 равна их произведению?
3. Найти значения а, при которых отношение корней уравне-
ния х2 - (2а + 4)х + а2 + 4 = 0 равно 5.
4. При каких значениях а имеют общий корень уравнения:
а) Зах2 - 5х + 2а = 0 и 2х2 + ах - 3 = 0;
б) х2 - (а - 1)х = 3 и 4х2 - (4а + 3)х + 9 = 0?
5. При каких значениях а один из корней уравнения х2 - 5х -
- За = 0 втрое больше одного из корней уравнения х2 - 6х + 4а = 0?
6. Найти все значения а, при которых квадратный трехчлен
(а2 - 1)х2 + 2(а - 1)х + 1 положителен для всех значений х.
77
7. При каких значениях а уравнение:
а) х2 - 7х + а = 0 имеет два равных корня;
б) х2 + х^а2 - 1 + а - 1 имеет два равных корня;
в) (а - 2)х2 - 2ах + 2а - 3 = 0 имеет единственный корень?
8. Решить уравнение:
а) а(а + 1)х2 + х - а(а - 1) = 0;
б) ах2 + (2а - 1)х + а - 2 = 0;
в) (а2 + а - 2)х2 + (2а2 + а + 3)х + а2 - 1 = 0;
г) (а2 - Ъ2)х2 - 2ах +1 = 0.
9. Решить уравнение:
а) - + 4 =2; б) - + | = 2;
х х-1 а х-1
Bjx_|_ . ч х2 - (а + 1)х - (а + 2) _ q
В Х х-2а х-2а’ Г (х + 2)(х-3а)
10. Найти все значения а, при которых система
I х2 + у2 = а,
[х - у = а
имеет единственное решение.
11. Найти все значения b такие, чтобы при любом а система
I 2х = а + Зу,
] ах = b - 4у
имела хотя бы одно решение.
12. Найти все значения а такие, чтобы при любом b нашлось
значение с, для которого система
Ъх = у + ас2,
(Ъ - 4)х = 1 - 2с - ЗЬу
имела хотя бы одно решение.
13. При каких значениях а система уравнений:
Г (а + 1)х - у = а,
а) ] (а - 3)х + ау = -9 имеет единственное решение;
а2х + (2 - а)у = 4 + а3,
, . к „ не имеет решений;
ах + (2а - 1)у = а° - 2
х + ау = 2а,
в) < 2х + 2ау = 5 имеет бесконечное множество решений?
78
14. При каких значениях а система
lax + 4у = -8,
х + lay = 49а1 2 * 4
имеет более одного решения?
15. Решить относительно х и у систему уравнений
х2 - 2ау - а2 = О,
у2 - 2Ьх - Ь2 = О
(х, у, а, b — действительные числа).
16. Найти значения а и Ъ, при которых заданная система имеет
бесконечное множество решений:
I ах + by = За + 5,
а) ] Ьх + 4ау = 6& - 5а;
J b2x + ay = 2Ъ2 + 8а,
| ах + а2у = 2,25 - 5а;
а2х - by = а2 + 2Ь,
J v ’
’ | 4&х - Ь2у = 4 - 3&.
17. Найти значения а,
ровно два решения:
Л \у\ = х,
а)[(х-а)2 + у2 = 4;
Л X = 5 - \у\,
ВЛ (х - а)2 + у2 = 9;
при которых заданная система имеет
\у = з - |х|,
"I х2 + (у - а)2 = 4;
\у = 7з |х|,
| х2 + (у - а)2 = 4.
Ответы
1. а = 5. 2. а = 2. 3. а = 1, а = 4. 4. a) а = -1, а = 1; б) а = 3. 5. а = 2.
6. я -[1; +°о). 7. а) а = 12,25; б) а = 1, а = 3; в) а = 1, а = 2, а = 6. 8. а) Если
а = -1, то х = 2; если а = 0, то х = 0; если а = -4= , то х = —-— ; если а =
л/2 л/2 - 1
1 1 -а 1 > , । 1 а а-1
= — , то х = ------; если а -1, а^О, а ± — , то х, = --------- , х9 = --;
л/2 л/2 + 1 л/2 а + 1 а
б) если а < -1, то нет корней; если а = -1, то х = -3; если а = 0, то х = -2;
1л л 1 - 2а ± л/4а + 1 , о
если -- < а < и или а > и, то х-, „ = -----——-------; в) если а = -2, то х =
4 z 2а
79
1 i л /о/1 1 - а 1+ а ,
= -- ; если а = 1, то х = 0; если а -2, а 1, то х-, = --, х9 = --; г) если
3 ’ ’ ’ 1 2 + а’ 2 1-а ’
а2 - Ь2 0, то х = — ; если а Z О, Ь = 0, то х = - ; если а = О, Ь = 0, то нет
2а а
корней; если а2 Z b2, b Z 0, то х1 = , х2 = 9. а) Если а Z 0, а Z 1,
то х4 = 0,5, х2 = а; если а = 0, а = 1, то х = 0,5; б) если а 0, а 1, то х4 = а,
х2 = а + 1; если а = 1, то х = 2; если а = 0, то нет корней; в) если Ь Z -2а,
то х = -Ь; если Ь = -2а, то нет корней; г) если а -4, а -3, а -1, а 1,
то Xj = -1, х2 = а + 2; если а = -4, а = -3, а = 1, то х = -1; если а = -1, то
х = | . 10. а = 0, а = 2. 11. Ь = . 12. а е ^-1; 1 ] . 13. а) а -3, а 1;
б) а = 1; в) а = 1,25. 14. а = -| . 15. Если а > 0, то х4 = а + J2ab , у1= b +
+ л/2аЬ , х2 = а - J2ab , у2 = b - J2ab ; если а < 0, то х4 = -а + J 2аЬ , у1 =
= -Ъ + 7 2ай , х2 = -а - J 2ab , у2 = -b - J 2аЬ . 16. а) а1 = — , Ь1 = - — ;
а9 = 10, &9 = 20; б) а, = -1,125, b, = 1; а9 = -1,125, &9 = -1; а, = 0,25, &, = 1;
а4 = 0,25, &4 = -1; в) а4 = -2, Ь1 = -4; а2 = -2, &2 = 0,5; а3 = 2, Ь3 = -4; а4 = 2,
&4 = 0,5. 17. а) а - (-2; 2) U {2 J2 }; б) a G (1; 5) U {3 - 2 J2 }; в) a G (2; 8) U
U {5 - 3 ^/2 }; г) а е (-2; 2) U {4}.
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Неравенства
1°. Запись х у (у < х) означает, что либо х > у, либо х = у,
и читается так: «х больше или равно у» или «х не меньше у».
2°. Запись, в которой два числа или два выражения, содержа-
щие переменные, соединены знаком >, с, > или С, называют нера-
венством.
3°. Неравенства, составленные с помощью знаков > или с, на-
зывают строгими; неравенства, составленные с помощью знаков >
или С, — нестрогими.
4°. Два неравенства вида а > Ъ и с > d называют неравенствами
одинакового смысла, а неравенства вида а > Ъ, с < d — неравенст-
вами противоположного смысла.
5°. Вместо двух неравенств х < а, а < у употребляется запись
х < а < у. Такое неравенство называют двойным.
6°. Если неравенство представляет собой истинное высказыва-
ние, то его называют верным.
7°. Неравенства, содержащие только числа, называют число-
выми.
2. Основные свойства неравенств
1°. Если к обеим частям верного неравенства прибавить одно
и то же число, то получится верное неравенство, т. е. если а > Ъ, то
а + с > Ъ + с.
81
2°. Если обе части верного неравенства умножить на одно и то
же положительное число, то получится верное неравенство.
3°. Если обе части верного неравенства умножить на одно и то
же отрицательное число и изменить знак неравенства на противо-
положный, то получится верное неравенство.
4°. Так как деление можно заменить умножением на число, об-
ратное делителю, то аналогичные правила справедливы и в отно-
шении деления.
3. Действия с неравенствами
1°. Неравенства одинакового смысла можно почленно склады-
вать. Например:
а) а > b б) а < b
с > d с < п
а + с > b + d; а + с < b + п.
2°. Неравенства противоположного смысла можно почленно
вычитать, оставляя знак того неравенства, из которого произво-
дится вычитание. Например,
а > Ъ
с < d
а - с > Ъ - d.
3°. Неравенства одинакового смысла с положительными члена-
ми можно почленно умножать. Например, если а >Ь,тоак> bk, где
а > О, b > 0, k е N.
Верно и обратное утверждение: если ak > bk, а > О, Ъ > 0, k е N,
то а> Ъ.
Замечание. Часто используют следующие важные нера-
венства:
а) —л/оЬ , если а >0и & >0.
Это неравенство означает, что среднее арифметическое двух не-
отрицательных чисел не меньше их среднего геометрического,
причем равенство достигается только в том случае, когда а = Ъ.
б) у + - >2, если а > 0 и b > 0.
Ь а
Это неравенство означает, что сумма двух взаимно обратных
положительных чисел не меньше 2.
82
4. Решение линейных и квадратных неравенств
1°. Линейным неравенством называют неравенство вида ах +
+ Ъ > 0 (или ах + Ъ < 0).
а) Если а > 0, то неравенство ах + Ъ > 0 равносильно неравенст-
ву х
б) Если а < 0, то неравенство ах + Ь > 0 равносильно неравенст-
ву х
2°. Квадратным неравенством называют неравенство вида
ах2 + Ьх + с > 0 (или ах2 + Ьх + с < 0), где а 0.
3°. Два неравенства называют равносильными, если множест-
ва решений этих неравенств совпадают.
4°. Пусть требуется решить неравенство ах2 + Ьх + с > 0.
В зависимости от знака дискриминанта D = Ъ2 - 4ас возможны
три случая:
а) Если D < 0, то график квадратного трехчлена f(x) = ах2 +
+ Ьх + с не пересекает ось Ох и лежит выше этой оси при а > 0
и ниже ее при а < 0. Тогда при а > 0 множество решений неравен-
ства есть вся числовая прямая (рис. 15, а), а при а < 0 оно является
пустым (рис. 15, б).
б) Если D > 0, то график квадратного трехчлена пересекает ось
Ох в точках х} и х2 (х1 < х2), служащих корнями уравнения ах2 +
+ Ьх + с = 0. Эти точки разбивают числовую прямую на три проме-
жутка: (-°°; хх), (хх; х2) и (х2; +°°). При этом знак квадратного
трехчлена совпадает со знаком коэффициента а во всех точках про-
«)
Рис. 15
83
Рис. 16
Рис. 17
межутков хх) и (х2; +°°) и противоположен знаку коэффици-
ента а во всех точках промежутка (хх; х2) (рис. 16, а и б).
в) Если D = 0, то график квадратного трехчлена касается оси
Ох в точке хх, являющейся единственным корнем уравнения ах2 +
+ Ъх + с = 0. Точка хх разбивает числовую прямую на два проме-
жутка: (-о°; хх) и (хх; +оо). Знак квадратного трехчлена совпадает
со знаком а при х хх (рис. 17, а и б).
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях а неравенство
(х - а)(х - 2) < 0
имеет единственное решение?
84
1. Легко догадаться, что если а = 2, то требование задачи удов-
летворяется. Действительно, при а = 2 получаем неравенство
(х - 2)2 < О,
имеющее единственное решение.
2. В случае, когда а 2, решением данного неравенства, оче-
видно, является отрезок.
3. Ответ: а = 2.
2. При каких значениях параметра т неравенство (т - 2)х2 - 2х +
+ т - 2 < 0 выполняется для всех х?
1. Пусть т 2. Тогда ветви параболы у = (т - 2)х2 - 2х + т - 2
должны быть направлены вниз и парабола не должна пересекать
ось Ох.
2. Для этого необходимо, чтобы выполнялись условия
[а<0’ [ т - 2 < О,
}-<0, т-е- 5 1 _ (т _ 2)2 < 0. (1)
[ 4 L
3. Решив систему неравенств (1), получим т < 1.
4. Пусть т = 2. Тогда данное неравенство примет вид -2х < 0,
т. е. оно выполняется только при х > 0. Поэтому значение тп = 2 не
удовлетворяет требованию задачи.
5. Ответ: т е (-оо; 1).
3. Найти все значения а, для которых выражение
(а2 - 1)х2 + 2(а - 1)х + 2 (1)
положительно при всех действительных значениях х.
1. Пусть а2 - 1 = 0, т. е. либо а = 1, либо а = -1. Тогда в случае
а = 1 выражение (1) равно 2 при всех х, а в случае а = -1 выраже-
ние (1) примет вид -4х + 2 и, значит, не будет положительным при
всех х.
2. Пусть а2 - 1 0. Тогда выражение (1) представляет собой
квадратный трехчлен, который положителен при всех значениях х,
если коэффициент при х2 положителен, а дискриминант квадрат-
ного трехчлена отрицателен:
[ а2 - 1 > 0,
j = (а - I)2 - 2(а2 - 1) < 0. (2)
85
3. Система (2) равносильна следующей:
а2 - 1 > 0, Г|а|>1,
а2 + 2а - 3 > О, ИЛИ [ (а - 1)(а + 3) > О,
откуда а > 1, а < -3.
4. Ответ: а (-°°; -3) U [1; +оо).
4. При каких значениях параметра т графики функций у = х2 +
+ тп2 + 12 и у = 2(т + 2)х пересекаются в двух различных точках?
1. Графики пересекутся в двух различных точках, если урав-
нение
х2 + т2 + 12 = 2 (т + 2)х
имеет два различных корня.
2. Преобразуем это уравнение к виду
х2 - 2(т + 2)х + т2 + 12 = 0.
3. Так как = (т + 2)2 - (т2 + 12) > 0, или т2 + 4тп + 4 - т2 -
- 12 > 0, то т > 2.
4. Ответ: т '~ (2; +°°).
5. При каких значениях параметра k графики функций у = 2kx + 1
и у = (k - 6)х2 - 2 не пересекаются?
1. Графики функций не пересекутся, если уравнение
2kx + 1 = (k - 6)х2 - 2 (1)
не будет иметь корней.
2. Преобразуем уравнение (1) к виду
(k - 6)х2 - 2kx - 3 = 0. (2)
3. Уравнение (2) не будет иметь корней, если < 0, т. е. k2 +
+ 3(/г - 6) < 0, откуда -6 < k < 3.
4. Ответ: k е (-6; 3).
6. В зависимости от значений параметра а решить неравенство
(а2 + а + 1)х - За > (2 + а)х + 5а. (1)
1. После упрощения неравенство (1) примет вид
(а2 - 1)х > 8а. (2)
86
2. а) Пусть |a| > 1; тогда неравенство (2) имеет решение х >
> 8а
а2 - 1 ’
б) Пусть |а| < 1; тогда неравенство (2) имеет решение х < .
а2 -1
в) Пусть а = 1; тогда неравенство (2) примет вид 0 • х > 8 и не
будет иметь решений.
г) Пусть а = -1; тогда неравенство (2) примет вид 0 • х > -8
и будет выполняться при любом значении х.
Sci
3. Ответ: если < а < -1 или 1 < а < +°°, то х > —г-;
а2-1
1 , , 1 , 8а
если -1 < а < 1, то х < —г-;
а2-1
если а = -1, то х е R;
если а = 1, то нет решений.
7. В зависимости от значений параметра а решить неравенство
56х2 + ах - а2 < 0. (1)
1. Найдем дискриминант квадратного трехчлена: D = 225а2 > 0;
а а
корнями трехчлена являются х1 = -- , х2 = g .
а
7
2. При а >
0 неравенство (1) имеет решение -
а
8 ’
< х <
3. При а < 0 неравенство (1) имеет решение - < х <
О
а
7 ’
4. При а = 0 неравенство (1) не имеет решений.
5. Ответ: если а > 0, то < х < |;
,,, а , , а
если а<0, TOg < х
если а = 0, то нет решений.
8. Пусть хг и х2 — действительные корни уравнения х2 - ах + а = 0,
где а — действительное число. Найти такое значение а, чтобы ве-
личина выражения х[ + х2 была наименьшей.
1. Уравнение х2 - ах + а = 0 имеет действительные корни при
условии неотрицательности его дискриминанта:
D = а2 - 4а > 0,
откуда
а < 0 и а 4. (1)
87
2. Требуется найти минимум неотрицательного выражения
у = х[ + ^2 = (Х1 + х2^2 ~ %Х1Х2
которое согласно теореме Виета мож-
но записать в виде
у = а2 - 2а. (2)
3. Таким образом, задача сводится
к отысканию наименьшего значения
квадратного двучлена (2) в области (1)
при условии у (а) 0.
4. Нетрудно установить (рис. 18),
что квадратный двучлен (2) достигает
наименьшего значения на границе об-
ласти (1), а именно при а = 0.
5. Ответ: а = 0.
9. При каком значении параметра t сумма квадратов корней урав-
нения
х2 + (2 - t)x - t2 + 1 = 0 (1)
принимает наименьшее значение?
2 2
1. Воспользуемся формулами Виета и выразим хг + х2 через
параметр t. Получим
f(t) = х2 + Xg = (хг + х2)2 - 2хгх2 =
= (t- 2)2 - 2(-t2 + 1) = 3f2 - 4f + 2.
2. Если бы областью определения функции f(t) была вся число-
вая прямая, то наименьшее значение этой функции достигалось
2
бы в точке t = - (абсциссе вершины параболы), причем /наим =
О
=сн-
3. Однако корни уравнения (1) существуют только в случае
D > 0. Решив неравенство
D = (2 - О2 + 4(f2 - 1) = 5f2 - 4f > 0,
получаем t е (-оо;
88
а) На промежутке (-°°; 0] функция
f(t) убывает и принимает наименьшее
значение при t = 0; /(0) = 2.
б) На промежутке [ |; +°°^ функ-
ция /(f) возрастает и принимает наи-
. 4 Л 4
меньшее значение при t = - ; /^ - J =
= ^ < 2 (рис. 19).
Рис. 19
4. Ответ: t = .
5
10. При каких значениях параметра t наименьшее значение квад-
ратного трехчлена
/(х) = 4х2 3 - 4tx + t2 - 2t + 2
(1)
на промежутке 0 < х < 2 равно 3?
1. При каждом фиксированном значении параметра t графи-
ком квадратного трехчлена (1) является парабола, абсцисса верши-
t
ны которой х = - .
2. В зависимости от положения вершины параболы требуемые
значения параметра t можно найти, рассматривая следующие три
возможных случая:
а)
/(0) = 3;
°< | <2,
Ц >2,
в) V
/(2) = 3.
б) 5
3. Решив каждую из этих трех систем с учетом того, что
/(0) = t2 - 2t + 2, /Q ) = -2t + 2, /(2) = t2 - lOt + 18,
заключаем, что в первом случае t = 1 - J2 ; во втором в треть-
ем t = 5 + Ло.
4. Ответ: t(1 - 72 ; 5 + 710).
89
11. При каких значениях параметра а вершины парабол у = 4х2 +
+ 8ах - а и у = 4ах2 - 8х + а - 2 лежат по одну сторону от прямой
У = -5?
1. Найдем координаты вершин обеих парабол.
а) Абсцисса вершины первой из них х1 = -а, ее ордината у} =
= -4а2 - а.
б) Абсцисса вершины второй параболы х2 = i , ее ордината у2 =
= -- + а-2.
а
2. Точки А1 (~а; -4а2 - а) и А2(^- ; + а - 2^ будут лежать по
одну сторону от прямой у = -5 тогда и только тогда, когда выпол-
няется неравенство
(-4а2 - а + 5)(-^ + а - 2 + б) > О,
т. е.
(1 - а)(а + | ^а(а - 1)(а + 4) > О,
или
а(а + 4)(а + | ^(а - I)2 < 0.
3. Решив это неравенство, получим ответ.
4. Ответ: а е (-оо; -4) и (-Ё ; о).
1 2. Решить уравнение \х - 3| = kx + 2.
1. Данное уравнение равносильно совокупности двух систем:
г - - г 3>0,
3 = kx + 2.
= 1
k + 1 ’
которых х} < 3. Из неравенства
< 3 находим k е (-оо; -1) и ; +°сЛ.
Й т 1 \_ О J
а) -х + 3 = kx + 2; б) | х -
2. Решим систему а). Имеем
Г х < 3,
| х = хг
Определим значения k, при
90
3. Решим систему б).
Имеем
х > 3,
5
X = х9 = ---- .
1 -k
хг 0 хг хг
-12x0 Iй
“3 2
Рис. 20
Так как х2 > 3, то —^Ц- > 3, откуда < k < 1.
J. — к о
4. На числовой прямой Ok изобразим промежутки значений k,
в которых уравнение имеет решение (рис. 20).
5. Ответ: если k е (-оо; -1), то одно решение хх = ;
если fce -1
2 А
- I, то решении нет;
о У
если k = , то х = 3 (получается из х2 при k =
3 J’
ис= ( 2 х А 1 5
если k е I - - ; 1 I то два решения хх = -—- , х2 = -—- ;
v о / /? "Ь 1 1 — k
если k = 1, то х = | (получается из ху при k = 1);
если +°°), то одно решение ху = .
13. При каких значениях параметра а все решения уравнения
2|х -а| + а- 4 + х = 0
удовлетворяют неравенству 0 < х < 4?
1. Данное уравнение равносильно совокупности двух смешан-
ных систем:
| 2(х - а) + а - 4 + х = 0; ' '
Ь-п<(),
| 2(а -х) + а- 4 + х = 0. ' '
2. Уравнение системы (1) имеет решение х = а + . Чтобы это
О
решение удовлетворяло условию х - а > 0, должно выполняться
d ”1” 4 Z-V Q
неравенство —— - а 0, откуда а ч 2.
о
91
3. Уравнение системы (2) имеет решение х = За - 4. Чтобы это
решение удовлетворяло условию х - а < 0, должно выполняться
неравенство За - 4 - а < 0, откуда а < 2.
4. Если а = 2, то исходное уравнение имеет одно решение х = 2,
удовлетворяющее неравенству 0 < х < 4.
5. Если же а < 2, то исходное уравнение имеет два решения,
которые удовлетворяют неравенству 0 < х < 4 при значениях а, яв-
ляющихся решением системы неравенств
J 0 < < 4,
I 0 < За - 4 < 4,
4 ,
т. е. при - ч а < 2.
О
6. Ответ: а — [ |; 2 ].
14. Решить относительно х неравенство
2х - 5 _ х + 7 < Зх - 2 а ч
а-1 3 " 2(а-1) ’ { '
1. Пусть а = 1. Тогда неравенство (1) не имеет смысла.
2. Пусть а > 1. Тогда неравенство (1) равносильно неравенству
6(2х - 5) - 2(а - 1)(х + 7) < 3(3х - 2а),
или
(2а - 5)х > -8(а + 2). (2)
а) Если а > 2,5, тох> ^(а + 2).
2а - 5
б) Если 1 < а < 2,5, то х < + 2).
2а - 5
в) Если а = 2,5, то неравенство (2) примет вид 0 • х > -36, т. е.
х — любое действительное число.
3. Пусть а < 1. Тогда, умножив обе части неравенства (1) на
(а - 1) и изменив его знак на противоположный, получим неравен-
ство
6(2х - 5) - 2(а - 1)(х + 7) > 3(3х - 2а),
или
(2а - 5)х < -8(а + 2),
равносильное неравенству (1). Отсюда х > ^(а + 2) , так как ПрИ
CL —
а < 1 имеем 2а - 5 < 0.
92
4. Ответ: если а < 1 или а > 2,5, то х > ^(а + 2).
2а - 5
если 1 < а < 2,5, то х < + 2);
2а - 5
если а = 1, то неравенство не имеет смысла;
если а = 2,5, то х е R.
1 5. При каких значениях k неравенство (k - 1)х + 2k + 1 > 0 верно
для всех значений х, удовлетворяющих условию |х| < 3?
1. Рассмотрим функцию /(х) = (k - 1)х + 2k + 1. Очевидно, она
является линейной при любом действительном значении k, т. е.
при любом k'—R графиком функции служит прямая (рис. 21, а—в).
2. Из этих рисунков видно, что для выполнения данного нера-
венства на отрезке [-3; 3] нужно, чтобы имела место система нера-
венств
/(-3) > О,
/(3) > 0.
(1)
3. Так как
/(-3) = -3(k - 1) + 2k + 1 = 4 - k,
/(3) = 3(k - 1) + 2k + 1 = 5k - 2,
то система (1) примет вид
4-A>0,
5k - 2 > 0,
откуда 0,4 < k < 4.
4. Ответ: k e [0,4; 4].
93
1 6. Найти все значения параметра а, при которых неравенство
(1)
выполняется для всех х таких, что 2 < х < 4.
1. Здесь требуется найти такие значения а, чтобы множество
чисел от 2 до 4 принадлежало множеству решений неравенства (1).
2. Сначала найдем решения данного неравенства. Рассмотрим
два случая.
а) Пусть а > 0; тогда 2а > . Поэтому решение неравенства (1)
имеет вид
-л <х<2а. (2)
4
б) Пусть а < 0; тогда 2а < <0. Таким образом, решение нера-
венства (1) имеет вид
2а < х < .
4
Очевидно, что случай б) можно не рассматривать, поскольку
в этом случае решения вообще не содержат положительных х, а,
значит, чисел х таких, что 2 < х < 4.
3. Для того чтобы все числа 2 < х < 4 входили в множество ре-
шений неравенства (2), необходимо выполнение неравенств < 2
и 2а > 4. Решив их совместно, находим 2 < а < 8.
4. Ответ: а е (2; 8).
17. При каких значениях параметра/, неравенство
* + ЗР - 5 > Q Q4
X + р
справедливо для всех х таких, что 1 < х < 4?
1. Данное неравенство равносильно неравенству
(х + Зр - 5)(х + р) > 0,
т. е.
х2 + (4р - 5)х + Зр2 - 5р > 0.
94
2. Рассмотрим квадратный трехчлен
f(x) = х2 + (4р - 5)х + Зр2 - 5р
и найдем его дискриминант:
D = (4р - 5)2 - 4(3р2 - 5р) = 16р2 - 40р + 25 - 12р2 + 20р =
= 4р2 - 20р + 25 = (2р - 5)2 > 0 прир 2,5.
Заметим, что прир = 2,5 исходное неравенство верно.
3. Требования задачи будут выполнены, если корни квадратного
трехчлена f(x) будут либо меньше 1, либо больше 4 (рис. 22, а и б).
4. Исходя из геометрической интерпретации трехчлена f(x),
заключаем, что искомые значения параметра/, удовлетворяют со-
вокупности двух систем неравенств:
[ - А < 1 [ 5 - 4р <
а) < 2 а ’ или J 2
|/(1)>0, 13р2-р-4>0;
|-А>4, АА£>4,
б) 4 %а ’ или <
[/(4)>0, Зр2 + 11р - 4 > 0.
5. Решив эти системы, находим р < -4;р > | .
О
6. Ответ: р (-оо; -4) и ; +оо^_
95
18. Найти действительные значения k, при которых неравенство
х2 - (k + 1)х + k + 1 > О
верно для всех значений х, удовлетворяющих условию |х| < 1.
1. Введем обозначение: /(х) = х2 - (k + 1)х + k + 1.
2. Найдем дискриминант квадратного трехчлена /(х): D =
= (k + I)2 - 4(А + 1) = (k + 1)(А - 3).
3. Имеем D < 0 при -1 < k < 3.
а) При этих значениях k знак /(х) совпадает со знаком коэффи-
циента при х2 для любых действительных значений х.
б) Поэтому при -1 < k < 3 неравенство /(х) > 0 выполняется на
отрезке [-1; 1].
4. Имеем D = 0 при k = -1 и при k = 3.
а) Если k = -1, то /(х) = х2, следовательно, /(х) > 0 при х 0. Это
означает, что неравенство /(х) > 0 выполняется не при всех х, удов-
летворяющих условию |х| < 1.
б) Если k = 3, то /(х) = (х - 2)2.
Так как (х - 2)2 > 0 при х 2, то неравенство /(х) > 0 верно на
отрезке [-1; 1].
в) Учитывая проведенное выше исследование, заключаем, что
неравенство /(х) > 0 выполняется для всех х, удовлетворяющих ус-
ловию |х| < 1, при -1 < k < 3.
5. Остается рассмотреть случай D > 0, который имеет место при
k < -1 и при k > 3.
Пусть хх их2 — корни /(х) при этих значениях k, причем хх < х2.
Чтобы неравенство /(х) > 0 выполнялось для всех х, удовлетво-
ряющих неравенству |х| < 1, достаточно потребовать, чтобы отрезок
[-1; 1] был расположен вне промежутка (хх; х2), т. е. чтобы выпол-
нялось одно из двух условий:
а) хх < х2 < -1 (рис. 23, а);
б) 1 < хх < х2 (рис. 23, б).
х-t + х2 k + 1
6. Еще нужно учесть, что —-— = .
7. Условие а) будет выполнено при всех значениях k, удовлет-
воряющих системе
т. е.
(k + 1)(А - 3) > 0,
1+й + 1+ й + 1>0,
fe+1 <
2
Данная система несовместна.
96
8. Условие б) будет выполнено при всех значениях k9 удовлет-
воряющих системе
> о [ (/г + - 3) > °’
т е J г _(А + 1) + А;+ г >0,
1 < , \k > 1.
Данная система имеет решение k > 3.
9. Итак, /(х) > 0 для всех х, удовлетворяющих условию |х| < 1,
если -1 < k < 3 или если k > 3, т. е. если -1 < k < +°°.
10. Ответ: k (-1; +°°).
1 9. Для каждого действительного значения k решить неравенство
х2 + kx + 1 > 0.
1. Находим D = k2 - 4.
2. Если D > 0, т. е. k < -2 или k > 2, то решением нера-
, ( -к- 7*2-4 А
венства является объединение промежутков ----J и
^-fe + 7fe^4;+oo^
3. Если D = 0, т. е. k = -2 или k = 2, то решение неравенства есть
объединение промежутков (-°°; ) и
4. Если D < 0, т. е. -2 < k < 2, то неравенство справедливо при
f а > 0,
х -й, так как л д < q
97
5. На рис. 24 изображены графики квадратных трехчленов
у = х2 + kx + 1 для различных k. Здесь ху = ——4 , х2 =
=---------- — корни трехчлена.
6. Ответ: если k < -2 или k > 2, то х е (-оо; ——4 ) и
и (-fe + 7^.+ooj.
если k = -2 или k =2,to.v- (-°°; ) и » +°°);
если -2 < k < 2, то х е (-оо; +оо),
20. При каких значениях параметра а неравенство
х2 + 4|х - а| > а2
справедливо для всех значений х‘1
1. Если х а, то данное неравенство равносильно неравенству
х2 + 4(х - а) а2, или
(х - а)(х - (-а - 4) > 0,
которое справедливо для всех рассматриваемых значений х при
а -а - 4, т. е. при а -2.
98
2. Если х < а, то приходим к неравенству
(х - а)(х - (4 - а)) О,
которое справедливо для всех рассматриваемых значений х при
а < -а + 4, т. е. при а < 2.
3. Ответ: а е [-2; 2].
21. При каких значениях параметра а множество решений нера-
венства
(а - х2)(а + х - 2) < 0 (1)
не содержит ни одного решения неравенства х2 < 1?
1. Пусть а < 0. Тогда неравенство (1) равносильно неравенству
а + х- 2>0,и требования задачи будут выполнены при условии
х > 2 - а 1,
т. е. при условии а < 0.
2. Пусть а = 0. Тогда из неравенства (1) следует, что -х2(х - 2) <
< 0, т. е. х > 2 и, значит, требования задачи выполнены.
3. Пусть а > 0. Перепишем исходное неравенство (1) в виде
(х - л/а )(х + Ja )(х - (2 - а)) > 0.
Нетрудно убедиться, что при Ja < 1, т. е. при 0 < а < 1, задача
не имеет решений.
4. При а > 1 рассмотрим следующие возможные случаи распо-
ложения точек ху = - Ja , х2 = Ja , х3 = 2 - а и отрезка х [-1; 1]
на числовой прямой, когда требования задачи могут быть выпол-
нены:
2 - а < - Ja ,2 - а = - Ja , - Ja < 2 - а < -1, 2 - а = -1.
5. Решив последовательно эти неравенства и равенства, соот-
ветственно находим а > 4, а = 4, 3 < а < 4, а = 3.
6. Объединив полученные результаты, запишем ответ.
7. Ответ: а (-°°; 0] и [3 ; +оо),
22. При каких значениях параметра а больший корень уравнения
х2 - а(а + 1)х + а2 = 0 больше | ?
1. Исходное уравнение имеет корни х} = а, х2 = а2.
99
2. Чтобы найти требуемые значения параметра, составим сис-
темы неравенств
а > а2, а2 > а,
1 б) < 2 I
а > - ; \а2 > - .
2 ’ [ 2
3. Решениями системы (а) являются все значения а такие, что
4. Решениями системы (б) являются все значения а такие, что
л/2
-оо < а < и 1 < а < +оо.
5. Ответ: а е (-оо; - ) и ( | ; 1) и (1; +оо).
23. Найти все значения х, при которых неравенство
(2 - а)х3 + (1 - 2а)х2 - 6х + 5 + 4а - а2 < О
справедливо хотя бы для одного значения параметра а из проме-
жутка [-1; 2].
1. Перепишем данное неравенство в виде
f(d) = а2 + (х3 + 2х2 - 4)а - (2х3 + х2 - 6х + 5) > О,
где переменную х считаем параметром.
2. Тогда требования задачи не будут выполнены, если отрезок
[-1; 2] лежит на числовой прямой между корнями трехчлена /(а),
т. е. если совместна система
J /(-1) = -Зх(х + 2)(х - 1) < О,
|/(2) = 3(х + 3)(х - 1) < 0.
Это будет иметь место при х е [-2; 0] U {1}.
3. Поэтому дополнение к записанному множеству и будет ре-
шением задачи.
4. Ответ: х (-оо;-2) U (0; 1) U (1; +оо),
24. При каких значениях а все решения уравнения
2а - 3 _ Зх - 1
х + 2 (х-2)2 + х-14
принадлежат отрезку [-3; 4]? В ответе указать наибольшее целое
значение а.
100
1. Упростив данное уравнение, получим
2а-3 _ Зх-1
х + 2 (х + 2)(х - 5) '
2. Решим уравнение (1):
(2а - 3)(х - 5) = Зх - 1,
х -2, х 5,
откуда
= 5а-8
а - 3 ’
-2, х 5.
3. Решения уравнения должны удовлетворять условиям
-3 < х < 4,
х -2,
или
о 5а - 8
d " ~а~Т
х -2.
(2)
< 4,
4. Решив систему (2), находим а е
[-4; 2) U (2;
5. Ответ: 1.
25. Для каждого неотрицательного значения параметра а решить
неравенство
а3х4 + 6а2х2 - х + 9а + 3 > 0. (1)
1. Если а = 0, то неравенство (1) примет вид -х + 3 > 0, а мно-
жество его решений есть промежуток < х < 3.
2. Пусть теперь а — фиксированное положительное число. Пре-
образуем левую часть неравенства (1) следующим образом:
а?‘х4 + 6а2х2 - х + 9а + 3 = а(а2х4 + бах2 + 9) - х + 3 =
= а(ах2 + З)2 - х + 3 = а((ах2 + З)2 - х2) + ах2 - х + 3 =
= а(ах2 + 3 - х)(ах2 + 3 + х) + ах2 - х + 3 =
= (ах2 - х + 3)(а2х2 + ах + За + 1). (2)
3. Дискриминант квадратного трехчлена а2х2 + ах + За + 1 ра-
вен Dr = -а2(12а + 3). Так как а > 0, то ясно, что Dr отрицателен.
Следовательно, квадратный трехчлен а2х2 + ах + За + 1 положите-
лен для любого значения х, т. е. исходное неравенство равносильно
неравенству
ах2 - х + 3 > 0. (3)
4. Дискриминант квадратного трехчлена ах2 - х + 3 равен D2 =
= 1 - 12а. Очевидно, если а > , то D2 неположителен, т. е. мно-
101
жество решений неравенства (3), а следовательно, и исходного не-
равенства, есть вся числовая прямая.
5. Если же 0 < а < , то множество решений неравенства (3),
а, значит, и исходного неравенства, состоит из двух промежутков:
1 - л/1 - 12а 1 + л/1 - 12а
-оо < х < -------- и --< х < +оо.
2а 2а
6. Ответ: если а = 0, то < х < 3;
п „ „ 1 1 - а/1 - 12а
если 0 < а < — , то -оо < х --------,
12 2а
1 + 71 - 12а
---< X < +оо;
2а
если а > ]~2 ’ то -о° < х < °°-
26. В зависимости от значений параметров а и п решить нера-
венство
а2(х2 + 1) + 6 > а2 + 2(п2х + 3). (1)
1. После преобразований неравенство (1) примет вид
п2х2 - 2п2х + п2 - а2 > 0. (2)
2. Найдем дискриминат квадратного трехчлена (2) и его корни.
Тт D о о , А п-а п + а , п
Имеем — = > 0, х, = - их, = ----, где п 0.
4 1 п z п
„ п , п а п + а
3. Ответ: если ап > 0, то х < - и х > ---;
п п
, , п + а па
если ап < 0, то х < -- и х > ---;
п п
если а = 0, п 0, то х е R, кроме х = 1;
если п = 0, то нет решений.
27. Найти все значения а, при которых неравенство
(х - За)(х - а - 3) < 0 (1)
выполняется для всех х таких, что 1 < х < 3.
1. Решением неравенства (1) является один из промежутков:
(За; а + 3) или (а + 3; За).
2. По условию каждый из этих промежутков должен содер-
жать отрезок [1; 3]. Возможны два варианта (рис. 25, а и б).
102
За 1 3a+3 x a+3 1 3 3a x
Рис. 25
3. Поэтому искомые значения параметра — это решения сово-
купности двух систем:
J За < 1, J а + 3 < 1,
аЦ 3 < а + 3; бЦ 3 < За.
4. Первая из них имеет решения 0 < а < |, а вторая не имеет
О
решений.
5. Ответ: а е (0; | ).
28. Корни хг и х2 уравнения х2 + kx + 1 = 0 удовлетворяют нера-
венству хх + х2 >1. Определить возможные значения, которые
может принимать параметр k.
1. Воспользуемся формулами, вытекающими из формулы
квадрата суммы:
а) х% + х2 = (х1 + х2)2 - 2ххх2;
4 . 4 z 2 2 .о о 2 2 zz о \9 о 2 2
б) хх + х2 = (хх + х2 )z - 2хг х2 = ((хх + х2у - 2xxx2)z - 2хх х2 .
2. Согласно формулам Виета, имеем
хх + х2 = -k, ххх2 = 1.
Неравенство хх + х2 > 1 можно выразить через k так:
/г4 - 4/г2 + 2 > 1, или /г4 - 4й2 + 1 > 0.
3. Решив неравенство /г4 - 4/г2 + 1 > 0, получаем k2 > 2 + д/З и
k2 < 2 - 7з •
4. Данное уравнение х2 + kx + 1 = 0 имеет два корня при усло-
вии D = k2 - 4 > 0.
5. Искомые значения k должны удовлетворять системе нера-
венств
\k2<2- J3,k2>2 + J3,
\k2 - 4 > 0.
6. Ответ: k e (-oo; -2] U [2; +°°).
103
29. В зависимости от значений параметра а решить уравнение
|х + 1| + а|х — 2| = 3.
1. В соответствии с определением модуля задача сводится к на-
хождению решений следующих уравнений:
(а + 1)х = 2а - 4, где х е (-оо;-1); (1)
(1 - а)х = 2 - 2а, где х е [-1; 2); (2)
(а + 1)х = 2 + 2а, где х е [2; +оо). (3)
2. Уравнение (1) имеет решения, если а -1. При этом условии
должно выполняться неравенство х = J < -1. Отсюда нахо-
а + 1
дим, что а е (-1; 1).
3. Рассмотрим уравнение (2). Отметим, что при а = 1 решением
уравнения является любое х е [-1; 2).
Если же а / 1, то х = —— = 2. Однако найденное значение
1 - а
х не принадлежит промежутку [-1; 2), поэтому при а 1 уравне-
ние (2) не имеет решений.
4. Рассмотрим уравнение (3). Здесь при а = -1 решением явля-
ется любое х -[2; +оо).
5. Ответ: если а < -1, то х = 2;
если а = -1, то х 2;
ч , , , с, 2 а — 4
если -1 < а < 1, то х, = 2, х9 = -— ;
1 2 а +1
если а = 1,то-1<х<2;
если а > 1, то х = 2.
30. В зависимости от значений параметра а решить уравнение
Jx - 4а + 16 = 2 Jx - 2а + 4 - Jx . (1)
1. Перенеся Jx в левую часть и возведя обе части уравнения
в квадрат, получим
Jx Jx - 4а + 16 = х - 2а. (2)
2. Далее, возведя обе части уравнения (2) в квадрат, найдем,
а2
что х = — — единственный возможный корень уравнения (1). Под-
ставив его в это уравнение, получим
Ja2 - 16а + 64 = 2 Ja2 - 8а + 16 - Ja2 ,
104
или, в силу того, что радикалы неотрицательны,
|а - 8| = 2|а - 4| - |а|. (3)
3. а) Пусть а > 8; тогда равенство (3) выполняется. Следова-
а2
тельно, уравнение (1) при этом условии имеет корень х = — .
б) Пусть 4 < а < 8; тогда равенство (3) не выполняется, посколь-
ку 8 - а 2(а - 4) - а.
в) Пусть 0 < а < 4; тогда равенство (3) примет вид 8 - а =
= 2(4 - а) - а и выполняется лишь при а = 0.
г) Пусть а < 0; тогда равенство (3) превращается в тождество
8 - а = 2(4 - а) + а, т. е. оно выполняется при всех а < 0.
4. Ответ: если а < 0 или а > 8, то уравнение имеет единствен-
а2
ный корень х = — ;
если 0 < а < 8, то корней нет.
31. Для каждого значения параметра а найти все значения х,
удовлетворяющие уравнению
\х + 3| - а\х - 1| = 4. (1)
1. Разобьем числовую прямую на три промежутка: 1) < х <
< -3; 2) -3 < х < 1; 3) 1 < х < +°°. Решим уравнение (1) в каждом
из этих промежутков.
2. Рассмотрим промежуток < х < -3. В этом промежутке
уравнение (1) примет вид
~(х + 3) + а(х - 1) = 4, или (а - 1)х = 7 + а. (2)
Отсюда видно, что при а = 1 уравнение (2) не имеет решений.
Если же а / 1, то уравнение (2) имеет один корень
3. Теперь следует выяснить, при каких значениях а этот ко-
рень удовлетворяет неравенству < х < -3.
а) Для этого надо решить неравенство
7 + a _q
б) Перепишем неравенство (4) в виде
4(а+1) <0
а - 1
(4)
(5)
105
в) Решением неравенства (5) является промежуток -1 < а < 1.
Следовательно, на множестве < х < -3 исходное уравнение име-
ет один корень (3) при любом значении а из промежутка -1 < а < 1
и не имеет корней при любом значении а, не принадлежащем это-
му промежутку.
4. Рассмотрим промежуток -3 < х < 1. В этом промежутке
уравнение (1) примет вид
х + 3 + а(х - 1) = 4, или (а + 1)х = а + 1. (6)
Отсюда видно, что при а = -1 решением уравнения (6) является
любое действительное число, так как 0 • х = 0.
Если же а -1, то уравнение (6) имеет один корень х = 1. Сле-
довательно, в рассматриваемом промежутке уравнение (1) имеет
единственный корень х = 1 при любом а -1, а при а = —1 его
решением будет любое число из промежутка -3 < х < 1.
5. Рассмотрим промежуток 1 < х < +°°. В этом промежутке
уравнение (1) примет вид
х + 3 - а(х - 1) = 4, или (1 - d)x = 1 - а. (7)
Отсюда видно, что при а = 1 решением уравнения (7) является
любое действительное число.
Если же а / 1, то уравнение (7) имеет единственный корень х = 1,
не лежащий в рассматриваемом промежутке. Следовательно, в про-
межутке 1 < х < исходное уравнение не имеет корней при лю-
бом а 1, а при а = 1 его решением является любое число из про-
межутка 1 < х < +оо.
6. Подводя итог, получаем, что при а = 1 решением исходного
уравнения (1) являются все значения х из промежутка 1 < х < +°°;
при а = -1 — все значения х из промежутка -3 < х < 1; при любом
значении а таком, что |а| < 1, исходное уравнение имеет два корня
х} = ? + & и х2 = 1; при любом значении а таком, что |а| > 1, исход-
ное уравнение имеет один корень х = 1.
7. Ответ: если а = 1, то х е (1; +оо);
если а = -1, то х е [-3; 1];
. . 7 + а
если а < 1, то х-. = -- , х9 = 1;
11 1 а -1 л
если |а| > 1, то х = 1.
32. При каких значениях параметра а уравнение
|х2 - 1| = 2х - х2 + а (1)
имеет единственное решение?
106
Замечание 1.
Приведем сначала решение задачи, которое часто дают абиту-
риенты.
1. Числовая прямая разбивается на три промежутка: х < -1,
-1 < X < 1 И X > 1.
2. В промежутках х < -1 и х > 1 имеем |х2 - 1| = х2 - 1 и урав-
нение (1) примет вид
2х2 - 2х - 1 - а = 0. (2)
3. Квадратное уравнение (2) имеет единственное решение при
условии, что его дискриминант равен нулю, т. е. = 1 + 2(а + 1) = 0,
3 1
откуда а = -- и, значит, х = - .
4. Однако значение х = | не принадлежат ни одному из проме-
жутков х < -1 и х > 1. Поэтому в данном случае задача не имеет
решений.
5. В промежутке -1 < х < 1 имеем |х2 - 1| = 1 - х2 и уравнение
(1) примет вид 2х + а = 1. Это уравнение имеет единственное решение
1 - а
2
(3)
6. Так как в данном случае должно выполняться ограничение
|х| < 1, то | | 1» откуда |1 - а| < 2, т. е. -1 < а < 3.
7. Отсюда делается вывод, что уравнение (1) имеет единствен-
ное решение х = а при любых а е [-1; 3].
Замечание 2.
1. Приведенное решение является неверным. Из него лишь
следует, что на отрезке [-1; 1] уравнение (1) имеет единственное
решение вида (3) при а е [-1; 3].
2. Однако это вовсе не означает, что при тех же значениях а
уравнение (1) не имеет других решений, отличных от (3), но прина-
длежащих промежутку х < -1 или х > 1.
3. Например, если а = 0, то из равенства (3) находим х = |,
а из уравнения (2) с учетом условия |х| > 1 получим х = 1 + .
107
4. Таким образом, при a = 0 уравнение (1) имеет два различных
1 1 + л/З
решения: х1 = - и х2 = —.
5. Это значит, что условие -1 < а < 3 является лишь необходи-
мым, но не достаточным условием единственности решения.
6. Для получения верного ответа среди значений а е [-1; 3]
нужно было отобрать такие (если они существуют), которые дают
единственное решение уравнения (1).
Замечание 3.
Приведем теперь правильное решение задачи.
1. Воспользуемся графическим методом как наиболее нагляд-
ным и эффективным в данном случае.
2. Для этого запишем уравнение (1) в виде
|х2 - 1| + х2 - 2х = а
и будем искать его решения как абсциссы точек пересечения гра-
фика функции
у = f(x) = |х2 - 1| + х2 - 2х
и семейства прямых у = а.
3. Чтобы построить график функции /(х), освободимся от зна-
ка модуля:
/W - л
1 - 2х, если |х| < 1.
4. График функции Дх) изображен на рис. 26.
5. Построив семейство прямых у = а, убеждаемся, что единст-
венная точка пересечения прямой у = а с графиком функции /(х)
существует только при а = -1 (прямая АВ). Тогда х = 1 — единст-
венное решение уравнения (1).
6. Ответ: единственное решение х = 1 при а = -1.
33. Найти минимум функции
у = ——-, если 0 < х < 1. (1)
v х(1 -х) ' ’
I способ. 1. Функция у(х) достигает минимума, когда выраже-
ние х(1 - х) максимально. Это имеет место при х = |.
108
У
Рис. 26
2. При этом значение выражения х(1 - х) равно i , а значение
данной функции (1) равно 4.
3. Ответ: = 4.
П11П
II способ. 1. Произведение х(1 - х) двух положительных мно-
жителей, сумма которых постоянна: х + (1 - х) = 1, максимально
при равенстве этих множителей, т. е. когда х = 1 - х.
2. Отсюда получаем, что при х = | произведение х(1 - х) мак-
1
симально и равно - .
3. Следовательно, z/min = 4.
109
Ill способ. 1. Будем искать наименьшее значение функции
У = х(1-х) (° < х У > °)
с помощью исследования множества ее значений.
2. Так как х и у связаны уравнением
х(1 - х)у = 1,
или, что то же самое, квадратным уравнением
ух2 - ух + 1 = 0 (у > 0), (2)
то отыскание множества значений функции (1) эквивалентно отыс-
канию множества всех значений параметра у, при которых уравне-
ние (2) имеет действительные корни.
3. Последнее условие выполняется тогда и только тогда, когда
дискриминант уравнения (2) неотрицателен:
D(y) = у2 - 4у > 0,
откуда у > 4.
4. Итак, z/min = 4.
34. Найти все значения параметра а, для каждого из которых чис-
ла х и у, удовлетворяющие системе уравнений
\ х + у = а,
I 2х - у = 3,
удовлетворяют также неравенству х > у.
1. Решив данную систему уравнений, находим
а + 3 2а — 3
X = —— , у = — .
3 ' 3
2. Следовательно, искомые значения параметра а являются ре-
шениями неравенства
а + 3 > 2а - 3
3 3 ’
которому удовлетворяют все а из промежутка < а < 6.
3. Ответ: а е (-оо; 6).
110
35. При каких значениях параметра а система
J у = х2 - 2х,
| х2 + у2 + а2 = 2х + 2ау
имеет решения?
1. Преобразуем исходную систему к виду
](х - I)2 = у + 1,
| (у - а)2 + (х - I)2 = 1.
2. Отсюда приходим к смешанной системе
J (У - а)2 + у + 1 = 1,
[У + 1 > О,
т. е. к системе
J у2 + (1 - 2а)у + а2 = 0, (1)
>>-1. (2)
3. Решив уравнение (1), получим
_ 2а - 1 ± Vi - 4а
У1,2 2 •
4. Требование задачи будет выполнено, если смешанная систе-
ма уравнений (1), (2) имеет хотя бы одно решение. Искомые значе-
ния а находим из неравенств
2а - 1 ± а/1 - 4а
У1,2= ------2------ >-1’
решив которые получаем ответ.
5. Ответ: а [-2; 0,25].
36. Найти все значения а, при каждом из которых существует хо-
тя бы одна пара (х; у), удовлетворяющая условиям
J х2 + (у + З)2 < 4,
| у = 2ах2.
1. Очевидно, что система имеет хотя бы одно решение тогда и
только тогда, когда существует хотя бы одно решение неравенства
х2 + (2ах2 + З)2 < 4, (1)
полученного подстановкой в данное неравенство 2ах2 вместо у.
111
2. Положим х2 = t и обозначим функцию t + (2at + З)2 через f(t).
3. Неравенство (1) будет иметь решение только в том случае,
когда наименьшее значение функции f(t) на множестве f > О будет
меньше 4. Вычислим это значение f(t).
а) Пусть а = 0; тогда /(f) = t + 9 и наименьшее значение /(f) на
множестве f > 0 равно 9, что больше 4. Следовательно, а = 0 не от-
вечает условию задачи.
б) Пусть а 0; тогда график функции /(f) = f + (2af + З)2 = 4a2f2 +
+ (12а + l)f + 9 представляет собой параболу, ветви которой направ-
лены вверх, а абсцисса вершины равна f0 = - 1 . Если f0 < 0,
т. е. если 12а + 1 > 0, а 0, то на множестве f > 0 функция /(f)
монотонно возрастает и, значит, ее наименьшее значение на этом
множестве равно /(0) = 9 > 4. Таким образом, все искомые значе-
ния параметра а лежат в области 12а + 1 < 0. В этом случае точка
f0 лежит в области f > 0 и наименьшее значение /(f) равно
/(f0) = 4а2(-Ц^ )2 - + 9 = .
4. Итак, все искомые значения параметра а являются реше-
ниями системы неравенств
[12а+1<0,
S _24а + 1 <4_ (2)
[ 16а2
5. Система (2) равносильна системе
J 12а + 1 < 0,
[ 64а2 + 24а + 1 > 0.
Квадратный трехчлен 64а2 + 24а + 1 имеет корни а, 9 = 3 ± ,
1 ’ I в
-3-75 „ 1 -3 + 75 1
причем а__
6. Итак, множество решений системы (2), а, значит, и множе-
ство значений параметра а, удовлетворяющих условию задачи,
„ -з-7б
есть промежуток а < —_ „
16
7. Ответ: а е -оо;
-з-7б А
16 )
112
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить неравенство:
а) а(3х - 1) > Зх - 2; б) (а2 - 2а - 3)х < а;
, х . х + 2 1 - Зх . 1.^1. ।
в) - > —— - —-— ; г) ах - Ъ > Ъх + а.
’а 4а 2 ’ ’
2. Решить неравенство:
а) х2 + 2ах + 4 > 0; б) х2 - 2(а + 1)х + 4а < 0;
в) (а2 - 1)х2 - 2ах + 1 < 0; г) х2 - Зах + 2а2 + а - 1 > 0.
3. Решить неравенство:
ч 2ах + 3 „ . I ах - 5 . I „ о
а) =--г- <4; б) —з— + х <3.
5х - 4а | 3 |
4. Найти все значения k, для которых при всех значениях х вы-
полняется неравенство:
а) х2 - (2 + k)x + 4 > 0; б) (k2 - 1)х2 + 2(/г - 1)х + 2 > 0;
в) (k2 - 1)х2 + 2(k - 1)х + 2 < 0; д) „ х2-8х + 20-- < Q
fex2 + 2(fe + l)x + 9fe + 4
5. Для всех а > 0 решить неравенство
(ах2 - х + 3)(а2х2 + ах + За + 1) > 0.
6. Найти все значения а, при которых уравнение
х2 - 2(а - 1)х + 2а + 1 = 0
имеет два положительных корня.
7. При каких значениях а каждое решение неравенства 2х + 3 >
> х2 является решением неравенства х2 - Зах - 6 - 2а < 0?
8. Найти все значения параметра а, при которых заданное не-
равенство справедливо для всех х е R, кроме, быть может, указан-
ного значения х0. Решить задачу, если:
а) (2 - а)х2 + (а + 2)х - а - 2 < 0; х0 = 2;
б) (а - 3)х2 - (а + 1)х + а + 1 > 0; х(1 = 2;
в) 3(1 - а)х2 - (За + 1)х - За - 1 < 0; х0 = -2.
9. Найти все значения а, при которых разность между большим
и меньшим корнями уравнения
ах2 + (а - 11)х - 2а - 33 = 0
не меньше 2 V5 .
10. Найти все значения параметра а, при каждом из которых
неравенство х а < 0 выполняется для всех х таких, что \х - 3| < 1.
ЭС о (L
113
Ответы
1. а) Если а < 1, то х <
—----— ; если а = 1, то х R: если а > 1, то х >
3(а -1)
3(Й) ; б) если а е (-оо; -1) и (3; +оо), то х < (а + 1)а(а_3); если а е (-1; 3),
то х > (а + 1)(а-3); если а = -1’ то х ~
е (—оо; 0) и Г 1 ; +оо\ ТО х < 2(1 ~ д)
\ / о у 4. — U)
если а = 0, а = , тохе 0; г) если а = b =
0; если а = 3, то х <е R; в) если а <е
, 1 . 2(1 -а)
; если а е (0; - ), то х > ;
= 0, тох - 0; если а = b > 0, то х <е 0;
,. п 1. а ', b , , , а + Ь
если а = о < 0, то х е R; если а > Ь, то х > ---- ; если а < Ь, то х < -- .
а -о а-Ь
2. а) Если |а| < 2, то х е R; если |а| х 2, то х - (-°°; -а - Ja2 - 4 ) U
U (-а + Ja2 - 4 ; + оо); б) если а е (-оо; 1), тох - (2а; 2); если а е (1; +оо),
тох'- (2; 2а); если а = 1, то х'- 0; в) если а <е (-оо; -1) U (1; +°°), то х -
1 если а е (-1; -1), тох'- । -оо; _J__ | и ( 1 д ; +°о |; если
а + Га-12’ v ’ X а-17 Ха + 1 )
а = -1, а = 1, то - ( -оо; -1 г) если а е (-оо; 2), то х'- (-оо; 2а - 1) и
U (а + 1; +°о); если а=2,тох - (-°°; 3) U (3; +°°); если а е (2; +°о), тох-
G (-оо; а + 1) U (2а - 1; +оо).
3. а) Если а < 10, то х'- (-оо; — 'l и ( 3 + ; +оо'); если а > 10, то
X 5 X 20 - 2а /
_ ( 3 + 16а 4а, лп т о,
х е I ол—5“ ’ “Е" J ’ если а = 10, то X - (-оо; 8); б) если а < -3, то х -
_ < 14 4 о <= f 4 14 А „
е ------- ; --- ; если а > -3, то х е --т-; -----т- ; если а = -3, то х е R.
Ха+З а+3J X а+3 а+37
4. a) k е (-6; 2); б) k е (-оо; -3) и (1; + оо); в) k е 0; г) k е (-оо; -0,5).
5. Если а = 0, то -оо < х < 3; если 0 < а < Д- , то -оо < х < -—~12а и
12 2а
+ ^2 ~ Х < +°°’ если а ]~2 > т0 ох: < х < +°°. 6. а £ [4; +оо). 7. а £
е [и ;5]’8, а) [т ;+°°);б) [т ;+°°);в) ;+°°).9. ае[-1;0)и(0; 11].
10. ае (0,5; 2).
Системы и совокупности неравенств
Решение рациональных неравенств методом
ТТТГ....................
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Системы и совокупности неравенств
1°. Если ставится задача найти множество общих решений
двух или нескольких неравенств, то говорят, что надо решить сис-
тему неравенств.
2°. Значение переменной, при котором каждое из неравенств
системы обращается в верное числовое неравенство, называют ре-
шением системы неравенств.
3°. Множество решений системы неравенств есть пересечение
множеств решений входящих в нее неравенств.
4°. Неравенства, входящие в систему, объединяются фигурной
скобкой.
5°. Иногда систему неравенств записывают в виде двойного не-
равенства.
’ можно записать так: 2 < Зх -
- 1 <8.
6°. Две системы неравенств называют равносильными, если
они имеют общее множество решений, удовлетворяющих этим не-
равенствам.
7°. Равносильность систем неравенств обозначается так же,
как и равносильность систем уравнений, т. е. с помощью зна-
ка <=>.
8°. Если ставится задача найти множество всех таких значений
переменной, каждое из которых является решением хотя бы одно-
го из данных неравенств, то говорят, что надо решить совокуп-
ность неравенств.
J Зх -
Например, систему <
115
9°. Значение переменной, при котором хотя бы одно из нера-
венств совокупности обращается в верное числовое неравенство,
называют решением совокупности неравенств.
10°. Множество решений совокупности неравенств есть объ-
единение множеств решений входящих в нее неравенств.
11°. Неравенства, образующие совокупность, объединяют
квадратной скобкой. Например, запись
неравенства образуют совокупность.
Зх - 5 < 1,
2х + 3 > 4
означает, что
2. Решение рациональных неравенств методом промежутков
Решение рациональных неравенств вида 777—;
> 0 или
Р(х) < л
(?(х)
, где Р(х) и Q(x) — многочлены, основано на следующем
свойстве непрерывной функции: если непрерывная функция обра-
щается в нуль в точках х} и х2 (х1 < х2) и между этими точками
не имеет других корней, то в промежутке (хх; х2) функция сохра-
няет знак.
2°. Поэтому для нахождения промежутков знакопостоянства
функции у = f(x) поступают так:
а) на координатной прямой отмечают точки, в которых функ-
ция f(x) обращается в нуль или терпит разрыв;
б) эти точки разбивают координатную прямую на несколько
промежутков, внутри каждого из которых функция f(x) непрерыв-
на и не обращается в нуль, т. е. сохраняет знак;
в) чтобы определить этот знак, достаточно найти знак функции
в какой-либо точке рассматриваемого промежутка координатной
прямой.
3°. Изменение знаков функции f(x) удобно иллюстрировать с по-
мощью волнообразной кривой, которую чертят справа налево.
4°. На тех промежутках, где кривая проходит выше координат-
ной прямой, выполняется неравенство f(x) > 0; на тех же проме-
жутках, где кривая проходит ниже, — неравенство f(x) < 0.
Замечания.
1. При установлении знака целой рациональной функции на
каждом из интервалов ее знакопостоянства необходимо учитывать
кратность корней.
116
2. В случае, когда кратность корня — четное число, функция
сохраняет знак при переходе через этот корень; в случае, когда
кратность корня — нечетное число, функция меняет знак.
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра k каждый корень уравнения
Зх = 3(2 - k) - k
удовлетворяет условию 2 < х < 4?
1. Преобразуем данное уравнение к виду
Зх = 6 - 4й,
6-4fe
откуда х = —— .
О
2. Решив двойное неравенство (систему неравенств)
2 < 6^1* < 4,
з
находим -- < k < 0.
3. Ответ: k — ; о] .
2. При каких значениях параметра а корни уравнения х2 -
- 2(а - 1)х + 2а + 1 = 0 имеют разные знаки, и оба по абсолютной
величине меньше 4?
1. Обозначим квадратный трехчлен в левой части данного урав-
нения через f(x). Тогда требования задачи будут выполнены, если
совместна система
[ /(-4) > 0,
/(0) < 0, (1)
[/(4)>0.
2. Выразив значения /(-4), /(0), /(4) через а, перепишем систе-
му (1) так:
[ 10а + 9 > 0,
J 2а + 1 < 0, (2)
[-6а + 25>0.
117
Системе (2) удовлетворяют все а такие, что < а < .
( 9 1 А
3. Ответ.-, а е __ ; J.
3. При каких а решением неравенства
(х - а)2(х -2)(х + 3) < 0 (1)
является отрезок?
1. Так как (х - а)2 > 0, то неравенство (1) равносильно системе
J (х - 2)(х + 3) < О,
| х = а. ' '
2. Решение неравенства этой системы есть отрезок -3 < х < 2.
Следовательно, при -3 < а < 2 решением системы (2) также будет
отрезок.
3. Ответ: а е [-3; 2].
4. Найти все значения параметра а, при которых система
J х2 + у2 + 2х < 1,
]х-у+а=0
имеет единственное решение. Найти соответствующие решения.
1. Данная система равносильна следующей:
! у = х + а, (1)
х2 + (х + а)2 + 2х < 1. (2)
2. Неравенство (2) преобразуется к виду
2х2 + 2(а + 1)х + а2 - 1 < 0. (3)
3. Неравенство (3) имеет единственное решение относительно х
тогда и только тогда, когда дискриминант квадратного трехчлена
в его левой части равен нулю:
(а + I)2 - 2(а2 - 1) = 0, или а2 -2а -3 = 0,
откуда
= 3, а2 = -1.
а) Если а = 3, то неравенство (3) примет вид х2 + 4х + 4 < 0, т. е.
х = -2, у = 1.
118
б) Если а = -1, то неравенство (3) примет вид х2 < 0, т. е. х = О,
у = -1.
4. Ответ: а = -1, х = 0, у = -1; а = 3, х = -2, у = 1.
5. Известно, что для некоторой квадратичной функции f(x) = ах2 +
+ Ьх + с выполнены неравенства /(-1) < 1, /(1) > -1, /(3) < -4. Оп-
ределить знак коэффициента а.
1. Так как /(-1) = а - Ъ + с, /(1) = а + Ъ + с, /(3) = 9а + ЗЪ + с, то
получаем систему неравенств
[ а - Ъ + с < 1,
J а + Ъ + с > -1,
| 9а + ЗЪ + с < -4.
2. Перепишем эти неравенства, умножив второе из них на (-2):
[ а - Ъ + с < 1,
J -2а - 2Ъ - 2с < 2, (1)
| 9а + ЗЪ + с < -4.
3. Так как все неравенства системы (1) справедливы, то, скла-
дывая почленно их правые и левые части, получим неравенство
8а < -1. Отсюда вытекает, что коэффициент а отрицателен.
4. Ответ: а < 0.
6. В зависимости от значений параметра а решить систему нера-
венств
(а + 3)х < 5а + 6,
х > 3.
1. Пусть а > -3; тогда система (1), (2) примет вид
5а + 6
а + 3
3.
(1)
(2)
(3)
(4)
2. Чтобы найти решение системы (3), (4), нужно сравнить чис-
ла + J* и 3 при а > -3. Имеем
а + 3
V 3; 5а + 6 V За + 9; 2а V 3; а V ?
а + 3 2
119
. 3 5а+ 6. о
Следовательно, если а > - , то -— > 3 и решением системы
Л а "Ь 3
/о \ / j \ г) 5 а “I- 6 о 3
(3), (4) является промежуток 3 < х <---— ; если же -3 < а ч - , то
а + 3 Л
5а + 6
—-j-g- < 3 и система (3), (4) не имеет решений.
3. Пусть а < -3; тогда система (1), (2) примет вид
5а + 6
а + 3 ’
3.
4/-Ч ОН ~ и
. Сравним числа---—
и 3 при а < -3. Имеем
(5)
(6)
'ia + J’ V 3; 5а + 6 Л За + 9; а Л |.
а + 3 2
Так как а < -3, то знак Л соответствует знаку <; следовательно,
5а + 6
—-j-g- > 3, т. е. решением системы (5), (6) при а < -3 является про-
ба + 6
межуток х > —-j-g-.
5. Пусть а = -3; тогда система (1), (2) примет вид
J 0 • х < -9,
| х > 3,
т. е. она не имеет решений.
6. Ответ: если а < -3, то х > + ® ;
а + 3
з
если -3 < а < - , то решений нет;
3 „ , ,5а + 6
если а> - , то 3 < х <-— .
2 а + 3
7. Найти множество значений а, при которых существует хотя бы
одно решение системы
J х2 + (а - 1)х - 2а2 + 4а - 2 > О,
] 2х + а - 4 = 0.
120
1. Из уравнения 2х + а - 4 = 0 выразим х = а и подставим
в данное неравенство:
а2~8а+16 - а2~5а + 4 - 2а1 2 + 4а - 2 > 0. (1)
4 2
2. Упростив неравенство (1) получим
-9а2 + 18а > 0, или а(а - 2) < 0.
3. Ответ: а е [0; 2].
8. При каких значениях а система неравенств
х2 + х- 2 < 0, (1)
х2 - 2(а - 3)х + а2 - 6а > 0 (2)
не имеет решений? Найти сумму всех таких целых значений а.
1. Неравенство (1) имеет решение
-2<х<1. (3)
2. Неравенство (2) имеет решение
х < а - 6 или х > а. (4)
3. Из неравенств (3), (4) и условия задачи следует, что
а-6<-2,
, т. е. 1 < а < 4.
а > 1,
4. Сумма всех целых значений а из этого интервала равна 5.
5. Ответ: а‘-(1; 4); 5.
9. Найти все значения параметра^, при которых область определе-
ния функции
у = JITP + 1х2 - (р + 3)х + Зр
4 х+5
состоит из одной точки.
1. Область определения данной функции задается системой не-
равенств
1 - х2 > 0, [ (х - 1)(х + 1) < 0, (1)
х2-(р + 3)х + 3р > 0 или < (х-р)(х-3) 0
х + 5 ’ х + 5
121
2. Неравенство (1) выполняется на отрезке [-1; 1].
3. Решим неравенство (2). Имеются три различных случая рас-
положения точек х = -5, х = р, х = 3. Эти случаи изображены на
рис. 27, а—в.
а)
Р^{-1}
-5<р<3
4. Сопоставляем отрезок [-1; 1] с заштрихованными промежут-
ками.
5. Отрезок [-1; 1] может иметь с заштрихованными промежут-
ками единственную общую точку только в случае, когдар = -1. Эта
общая точка есть х = -1 (рис. 27, б); справа от рисунков указано
решение системы неравенств (1), (2).
6. Ответ: р = -1.
1 0. При каких значениях параметра т уравнение
тх2 - 2 л/15 - пг2 х - 2 = 0
имеет два различных корня?
1. Квадратное уравнение ах2 + Ъх + с = 0 имеет два различных
корня, если а / 0 и Л > 0.
2. В данном случае эти условия приводят к следующей системе
неравенств:
т 0 (а 0),
15 - т2 + 2т > 0 > 0^),
15 - т2 > 0 (квадратный корень существует),
122
или
-V15 -3 О V15 5 х
т О,
(т - 5)(т + 3) < О,
(т - V15 )(m + V15 ) < О.
Рис. 28
3. Решение этой системы иллюстрирует рис. 28.
4. Ответ: т е (-3; 0) U (0; V15 ].
11. Найти наименьшее целое значение а, при котором корни урав-
нения
х2 + (а + 2)х + За + 1 = 0 (1)
действительны, а сумма их кубов меньше 5а - 2.
3 3
1. Выразим хг + х2 через сумму и произведение корней урав-
нения:
хг + х2 = (х, + Х2)(Х1 - хгх2 + х2) =
= (х1 + х2)((х1 + х2)2 - Зххх2). (2)
2. Согласно теореме Виета, для уравнения (1) имеем
х1 + х2 = -(а + 2), хгх2 = За + 1. (3)
3. Подставив выражения (3) в равенство (2), получим
хх + Х32 = -(а + 2)((а + 2)2 - 3(3а + 1)) = -(а + 2)(а2 - 5а + 1).
4. Найдем дискриминант уравнения (1):
D = (а + 2)2 - 4(3а + 1) = а2 - 8а.
5. Таким образом, приходим к системе
а(а - 8) > 0,
-(а + 2)(а2 - 5а + 1) < 5а - 2,
или
(а - 8)а > 0,
а(а - 4)(а + 1) > 0. W
6. Система (4) имеет следую-
щее решение: -1 < а < 0, а 8
(рис. 29).
7. Ответ: 8.
0 8
////////*________________________^\\\\\\\
А\\\\\\\\\\\\\\\\\\\\\\\
-10 4
Рис. 29
123
1 2. При каких значениях параметра/, система неравенств
_д<Х2-рХ-2 < 2
(1)
удовлетворяется для всех значений х?
1. Область определения системы (1) есть х е R.
2. Заменим систему неравенств (1) равносильной системой и
упростили ее:
х2-рх- 2
х2 - х + 1
х2-рх- 2
х2 - х + 1
< 2,
или
х2 + х(р- 2) + 4 .
X2 - X + 1
4х2 - х(р + 3) + 1
х2 - х + 1
(2)
3. Поскольку х2 - х + 1 > 0, система (2) равносильна следую-
щей:
X2 + х(р - 2) + 4 > О,
4х2 - х(р + 3) + 1 > 0. 1 ’
4. Так как коэффициенты при х2 в квадратных трехчленах ле-
вых частей неравенств (3) положительны, то сами трехчлены будут
положительны, если их дискриминанты отрицательны, т. е. при-
ходим к системе
(р - 2)2 - 16 < 0,
(р + 3)2-16<0. ’
5. Решив систему (4), получим -2 <р < 1.
6. Ответ: р е (-2; 1).
13. Решить неравенство ах2 + (а+1)х+1>0.
1. Если а = 0, то неравенство примет вид х + 1 > 0 и оно спра-
ведливо при ix-l.T-e.x- (-1; +°о).
2. Если а = 1, то левая часть неравенства есть полный квадрат.
Неравенство (х + I)2 > 0 выполняется при х е (-оо; -1) U (-1; +оо).
3. При остальных а (а 0, а 1) представим данное неравенст-
во в виде а(х + 1)( х + - ) >0. Знак левой части этого неравенства
124
б)
X G
и (-1; +ОО)
Рис. 30
определяется знаком и величиной а. Три различных случая изо-
бражены на рис. 30, а—в.
4. Ответ: если а < 0, то х е (-1; --
если а = 0,тох - (-1; +°°);
если а е (0; 1), то.г- (-°°; ) U (-1; +°°);
если а = 1,тох - (-о°; -1) U (-1; +°°);
если в --1,тох - (-о°; -1) U Г-i ; +оо\
14. Найти множество значений а, при которых уравнение
(Зх2 - (5а + 3)х + 2а2 + 2а)7-х2 - 4х - 3 = 0 (1)
имеет ровно три корня.
1. Корни уравнения (1) должны удовлетворять условию -х2 -
- 4х - 3 > 0, откуда х е [-3; -1].
2. Преобразуем исходное уравнение в равносильную ему сово-
купность:
Зх2 - (5а + 3)х + 2а2 + 2а = 0,
-х2 - 4х - 3 > 0,
-х2 - 4х - 3 = 0.
(2)
(3)
(4)
125
3. Очевидно, что уравнение (4) имеет два решения: х1 = -3 и
х2 = -1 любом значении параметра а.
4. Поэтому исходное уравнение будет иметь ровно три корня
при тех значениях параметра а, когда система (2), (3) имеет единст-
венное решение, отличное от значений х1 = -3 и х2 = -1.
5. Найдем дискриминант и корни уравнения (2):
D = (5a + З)2 - 12(2а2 + 2а) = (а + З)2,
х3 = а + 1, х4 = .
О
6. Рассмотрим два возможных случая, когда система (2), (3) бу-
дет иметь единственное решение.
1)D = 0, а единственный корень уравнения (2) принадлежит
интервалу (-3; -1). Очевидно, что D = 0 при а = -3, и при этом
х3 4 = -2 е (-3; -1). Следовательно, при а = -3 исходное уравнение
имеет ровно три корня: х е {-3; -2; -1}.
2) D > 0 и только один из корней уравнения (2) (х3 или х4) при-
надлежит интервалу (-3; -1). В этом случае возможны следующие
четыре варианта:
f а -3,
a) J х3 > -1, <ss>
Jх4 е(-3; -1)
а -3,
а + 1 > -1,
2а
т
3
2
а
т.е.ае[-2;-|);
а -3,
б) < хз ~ (_3; _1), <=>
\Х4 > -1
а 5й -3, г а 3,
-3 < а + 1 < -1, , а - С"4? -2)’
т. е. а — 0;
т. е. а —
-4
а -3,
в) < хз “3, <ss> <
х4 £= (-3; -1)
126
a -3,
г) хз ~ (_3; _1), <ts> <
X4 C —3,
a -3,
-3 < a + 1 <-l,
2a о
a -3,
-4 <a < -2,
t. e. a — 0.
7. Объединяя найденные множества значений параметра а, по-
лучим ответ.
8. Ответ: а ; -4] U {-3} U [-2;
1 5. При каких а все решения уравнения
а-1 _ 2х + 7
х + 6 (х + 2)2-х-22 1 '
неположительны?
1. После упрощений уравнение (1) примет вид
а-1 _ 2х+ 7
х + 6 (х + 6)(х - 3) ’
или
x(a-3)-3a-4
(х + 6)(х-3) ’
2. Перейдем к равносильной системе
[ х(а - 3) = За + 4, (2)
< х -6, (3)
3. (4)
3. Рассмотрим уравнение (2).
а) Ясно, что при a = 3 оно не имеет решений;
б) Если а 3, то х = +.
а-3
в) Так как нас интересуют только неположительные решения
уравнения (1), то искомые значения параметра а найдем, составив
и решив следующие две системы:
За + 4 </ q а - 3 ’ За + 4 а - 3 < 0
За + 4 , л» _6; За + 4 * 3
а - 3 а - 3
4. Ответ: a е ) U ( ; з).
127
1 6. Решить уравнение
||3х + 5| - 7х| = 9 - а.
1. Решение этого уравнения не столь сложное, сколь громозд-
кое, тем более если выбрать нерациональный путь решения.
2. Заметим сразу, что при а > 9 уравнение не имеет решений.
3. При а = 9 имеем
|3х + 5| - 7х = О,
т. е.
|3х + 5| = 7х.
Отсюда при х > 0 получаем следующую совокупность уравне-
ний:
Зх + 5 = 7х,
Зх + 5 = ~7х,
1
2
>0,
0.
5
Итак, при а = 9 уравнение имеет один корень х = - .
4. Теперь рассмотрим случай а < 9. Дальнейшее решение мож-
но выполнять двумя способами в зависимости от того, какой мо-
дуль раскрыть раньше — внутренний или внешний.
В данном примере лучше (короче) начинать с раскрытия внут-
реннего модуля.
5
5. Пусть х > - - . Тогда уравнение примет вид
О
|3х + 5 - 7х| = 9 - а,
т. е.
|4х - 5| = 9 - а.
Раскрывая модуль, приходим к совокупности уравнений (на-
помним, что правая часть уравнения положительна):
14 - а
г X = X, = ------
4х - 5 = 9 - а, 4
4х - 5 = -9 + а, Т’е’ а -4
L х = х9 = —— .
4
гт 5
Полученные корни должны удовлетворять условию х > - -.
128
ч 14 - а 5 - 62 ,
а) хг = —-— > -- при а ч — (корень х = — истинный при
4 о о
а < 9).
,ч а 4 .5 >8
б) х2 = —Г“ “ч ПРИ а > “о •
41 о о
5
6. Пусть х < -- . Тогда уравнение примет вид
О
|-Зх - 5 - 7х| = 9 - а, т. е. |10х + 5| = 9 - а.
Отсюда получаем совокупность
4 - а
г х = х.-,= , „ ,
10х + 5 = 9 - а, 3 Ю
10х + 5 = а - 9, Т’е’ _ _а-14
Х ~ Х4 - -^о“ ’
Остается решить еще два неравенства:
а) —— < - - при а > — (поскольку а < 9, этот случаи не имеет
J. U о о
места);
,ч а- 14 5 , 8
б)^(Г з приа<’з-
7. Все полученные сведения изобразим на рис. 31.
Под осью Оа записаны значения а, над ней — значения х. В ча-
о 5
стности, при а = 9 имеем х = - .
о 8 5 14-а а-14
8. Ответ: если а е |^-оо; -- J , то хх = —-— , х4 = ;
Г 8 14-а а - 4
если а ; 9 J, то хг= —-— , х2 = —— ;
о 5
если а = 9, то х = - ;
4
если а е (9; +°°), то нет решений.
О 9
Рис. 31
129
17. Определить значения k, при которых уравнение
(А - 2)х4 - 2(А + 3)х2 3 + k - 1 = О
имеет четыре действительных корня, отличных от нуля.
1. Если k 2, то данное уравнение является биквадратным,
т. е. квадратным относительно х2.
2. Следовательно, для того чтобы его корни были действитель-
ными, необходимо и достаточно, чтобы их квадраты были положи-
тельны, т. е. чтобы уравнение
(k -2)у2 - 2(А + 3)у + k - 1 = О
имело положительные корни. Для этого должны выполняться ус-
ловия
\D>0,
J У1 + у2 > °,
|У1У2 > °’
или
(k + З)2 - (k - 1)(А -2) > О,
2(fe + 3) „
< k-2
3. Решив последнюю систему, находим k > 2.
4. Ответ: k е (2; +оо).
1 8. При каких значениях параметра а система
х2 + 4ах + За2 > 1 + 2а,
х2 + 2ах < За2 - 8а + 4
имеет хотя бы одно решение?
1. Система (1) равносильна следующей:
х2 + 4ах + За2 - 2а - 1 > О,
х2 + 2ах - За2 + 8а - 4 < 0.
2. Квадратный трехчлен <р(х) = х2 + 2ах - За2 + 8а - 4 имеет
корни х1 = -За + 2 и х2 = а - 2, поэтому решением второго неравен-
ства системы (2) являются все значения х такие, что
min {хр х2} < х < max {хх, х2}.
3. Учитывая это, найдем все значения параметра а, при кото-
рых система (2) не имеет решений.
130
4. Именно, система (2) не будет иметь решений тогда и только
тогда, когда совместна система
/(хх) < О,
/(х2) < О,
где /(х) = х1 2 + 4ах + За2 - 2а - 1, а, значит,
/(хх) = -6а + 3 < О,
/(х2) = 8а2 - 14а + 3 < 0. (3)
5. Множеством решений системы (3) является отрезок
0,5 < а < 1,5.
6. Таким образом, исходная система (1) будет иметь хотя бы од-
но решение, если а < 0,5 или а > 1,5.
7. Ответ: а 0,5) U (1,5; +°°).
1 9. При каком значении р площадь фигуры, заданной на коорди-
натной плоскости неравенством |2х - у - 4| + |х + у - 2| < р, будет
равна 54?
или -2х + у + 4 + х + у- 2^р, откуда у <
1. Чтобы освободиться от знаков модуля, рассмотрим четыре
возможных случая:
j2x-z/-4<0,
аЦх+у-2>0
< х , р - 2
" 2 ’
J 2х - у - 4 > 0,
бЦх + у- 2>0
j2x-z/-4>0,
B)^x + z/-2<0
_ Р + 2 .
2 ’
или 2х-у-4+х+у-2 откуда х <
или 2x-z/-4-x-z/ + 2<p, откуда у > -
J2x-y-4<0,
г']х + у- 2<0
или -2х + у + 4- х- у + 2<,р, откуда х >
3 ’
2. Изобразим на плоскости хОу множества точек, являющихся
решением рассмотренных систем неравенств.
131
3. Из построения (рис. 32) видно, что прямые 2х - у = 4 и х +
+ у = -2 разбивают координатную плоскость на четыре области, каж-
дая из которых соответствует одному из рассмотренных случаев.
4. Принадлежность каждой области соответствующему случаю
можно определить методом пробной точки.
5. Возьмем, например, точку М(3; 0). Ее координаты удовлет-
воряют случаю б), следовательно, точки этой области являются ре-
шением системы неравенств, рассмотренной в случае б).
п г» х , р-2 х р + 2
6. Заметим, что прямые у = и у = - - , а также
р + 6 6-р
прямые х = и х = —£ попарно параллельны и ограничивают
О о
рассмотренные выше области.
7. Итак, заданная на координатной плоскости фигура является
параллелограммом.
8. Площадь построенного параллелограмма есть S = АВ CD.
9.
Найдем координаты точек А, В, С и D: а(
с( 0; ^ ), 1>(0; . Тогда ЛВ - |хв - xj - | Eli - SjE | - Ц
и CD = \yD - z/c| = | “^-77— _ j =P- Площадь параллелограмма S =
= -p = 54.
О
10. Ответ: p = 9.
132
20 . Найти все значения параметра а, при каждом из которых нера-
венство
3 > |х - а| + х2 (1)
имеет хотя бы одно отрицательное решение.
1. Пусть а — некоторое фиксированное число. Тогда неравен-
ство (1) можно переписать в виде |х - а| < 3 - х2. Отсюда следует, что
оно равносильно двойному неравенству -(3 - х2) <х-а<3-х2,
т. е. системе неравенств
х - а < 3 - х2,
-(3 - х2) < х - а.
2. Поэтому задачу можно переформулировать так: определить
те значения а, при каждом из которых множество решений систе-
мы неравенств
х2 + х- 3- а<0,
\х2-х-3 + а<0, (3)
х < 0
содержит хотя бы одно число.
3. Дискриминанты квадратных трехчленов х2+х-3-аих2-
- х - 3 + а равны соответственно 13 + 4а и 13 - 4а.
4. Следовательно, для того чтобы первое и второе неравенства
системы (3) имели решения, необходимо выполнение неравенств
13 13
13 + 4а > 0 и 13 - 4а > 0, т. е. < а < — . В дальнейшем будем
считать, что а удовлетворяет этим неравенствам.
5. Обозначим через хх, х2 и х3, х4 корни квадратных трехчле-
нов х2+х-3-аих2-х-3 + а соответственно. При этом будем
считать, что хх < х2 и х3 < х4.
6. Так как множества решений первого и второго неравенств
системы (3) имеют соответственно вид хх < х < х2 и х3 < х < х4,
причем хх < х4 и х3 < х2, то система (3) будет иметь решение тогда
и только тогда, когда хх < 0 и х3 < 0, т. е. когда
-1-713 + 4а
2
<
1-713-4а
(4)
(5)
133
7. Неравенство (4) выполнено для всех а из интервала <
8. Неравенство (5) равносильно на этом интервале неравенству
1 < Лз^ 4 а , или неравенству 1 < 13 - 4а. Множество решений
последнего неравенства есть промежуток < а < 3.
9. Итак, система (3) имеет хотя бы одно решение, если пара-
13 о
метр а принадлежит интервалу - — < а < 3.
10. Ответ: а е ; з).
21 . При каких значениях параметра а система
J х2 + 4х + 3 - а < О,
| х2 - 2х + 6а - 3 < О ( '
имеет единственное решение?
1. Система (1) может иметь решения только тогда, когда диск-
риминанты левых частей обоих неравенств неотрицательны, т. е.
когда
/1+а>0 2
^2 - За > О, или -1<а<-.
2. При а = -1 система (1) примет вид
J (х + 2)2 < О,
| х2 - 2х - 9 < О
и имеет единственное решение х = -2.
2
3. При а = - система (1) примет вид
О
х2 + 4х + <0,
J О
I (х - I)2 < 0
и является несовместной.
2
4. Пусть теперь -1 < а < - . В этом случае решениями первого
о
неравенства системы (1) являются значения х из промежутка х1 <
134
< х < х2, где хг = -2 - л/1 + « , х2 = -2 + ^/1 + а , а решениями вто-
рого неравенства — значения х из промежутка х3 < х < х4, где х3 =
= 1 - д/4 - 6а , х4 = 1 + д/4 - 6а .
5. Таким образом, система (1) имеет единственное решение
только в том случае, когда отрезки [хх; х2] и [х3; х4] имеют одну
общую точку.
6. Так как абсцисса вершины параболы у = х2 3 + 4х + 3- а равна
(-2), а абсцисса вершины параболы у = х2 - 2х + 6а - 3 равна 1, то
рассматриваемые отрезки имеют одну общую точку лишь при ус-
ловии х3 = х3, т. е. при условии
-2 + 71 + а = 1 - 74-6а . (2)
7. Решив уравнение (2), находим а = 0.
8. Ответ: а = -1; а = 0.
22 . При каких значениях а система неравенств
|х2 - 12х + 16| < 16,
|х - 2а| > 7
(1)
(2)
имеет единственное решение?
1. Неравенство (1) равносильно двойному неравенству -16 <
< х2 - 12х + 16 < 16 или системе
х2 - 12х + 32 > 0,
х2 - 12х < 0,
т. е.
(х - 8)(х - 4) > 0,
х(х - 12) < 0.
2. Решив полученную систему методом интервалов (рис. 33, а),
заключаем, что она выполняется на объединении двух отрезков:
х — [0; 4] U [8; 12].
3. Неравенство (2) равносильно совокупности
х - 2а > 7,
х - 2а < -7,
т. е.
х > 2а + 7,
х < 2а - 7,
которая выполняется на объединении двух лучей (рис. 33, б): х е
е (-оо; 2а - 7] U [2а + 7; +°о).
4. Исходная система имеет единственное решение в двух случаях:
J2а-7 = 0, \а = 3,5,
аП2а + 7>12, ] 2 • 3,5 + 7 > 12 (рис. 33, а), т. е. при а = 3,5.
135
2а-7 2а+7
в) ////////0-----« ///////
О 12
б) //////>----•---0////// -
2а-7 2а 2а+7 х
2а-7 2а+7
г) /////// »------0\\\\\\\\ -
О 12 а
Рис. 33
В этом случае промежутки из пп. 2 и 3 имеют единственную об-
щую точку: х = 0.
J 2а - 7 < 0, J а < 3,5,
бЦ 2а + 7 = 12, ^« = 2,5 (рис. 33, г), т. е. при а = 2,5.
В этом случае промежутки из пп. 2 и 3 имеют единственную об-
щую точку: х = 12.
5. Ответ: а = 2,5; а = 3,5.
23. При каких значениях параметра а система
у > х2 + а,
5 -^2 (1)
х > у6 + а
имеет единственное решение?
1. Заметим, что если (х0; у0) — решение системы (1), то и
(у0; х0) — также решение этой системы. Поэтому приходим к вы-
воду, что условие х = у необходимо для существования единствен-
ного решения системы (1).
2. Подставив у = х в систему (1), приходим к неравенству
х2 - х + а < 0,
которое имеет единственное решение только тогда, когда дискри-
минант его левой части D = 1 - 4а равен нулю, т. е. когда а = | .
3. Теперь подставим значение а = i в систему (1):
о 1
X2 + - < у,
о 1
у2 + - < X.
136
Складывая почленно эти неравенства, приходим к неравенству
1 \2 ( ]\2
- - J + [JJ ~ % О, которое имеет единственное решение х =
1
= У=2-
4. Ответ: а = - .
4
24. При каких значениях параметра а каждое решение системы
J у + 2х а,
\у - х 2а
является решением неравенства 2у - х > а + 3?
1. Прямые у + 2х = аиу-х = 2а пересекаются на координат-
ной плоскости хОу в точке А^-^ ; -у )•
2. Требование задачи будет выполнено, если точка А лежит вы-
ше прямой 2у - х = а + 3 (рис. 34); в этом случае область коорди-
натной плоскости, задаваемая исходной системой, будет содержать-
ся в области, задаваемой неравенством 2у - х > а + 3.
137
3. Аналитически условие того, что точкаА лежит выше прямой
2у - х = а + 3, записывается следующим образом:
2-|а-(-1а)>а + 3.
О О '
Решив это неравенство, находим а >
9
8 ’
4. Ответ: а е | ;
\ о
25. Решить уравнение |х + 4| + 2 = k\x + 1|.
1. Решим данное уравнение на трех промежутках: х < -4; - 4 <
< х < -1; х > -1.
\х < -4, 2-к
]-(x + 4) + 2 = -k(x + l); х ГТ
ту 2 - к 2 - к . .
Корень х = -—- должен удовлетворять неравенству -—j < -4.
2 2 2 - к
Решив его, находим - < k < 1. Значит, если - < k < 1, то хг = -—- .
о о К — 1
J-4Cx<-l, _ _fe + 6
’ х + 4 + 2 = -k(x + 1); х Х2 k+1'
Решив двойное неравенство -4 < < -1, которое равно-
сильно системе
< 4
к+ 1
k + 6 > ,
k + 1 '
, 2
получаем /г > - .
О
\х > -1, = =6-k
4- \x + 4 + 2 = k(x+l); х хз к~1 •
Неравенство |—j > -1 выполняется при k > 1.
5. Для записи ответа построим схему (рис. 35), на которой ука-
зано, какие корни получаются при тех или иных значениях k.
138
Хо— 0
О * 3 1 Рис. 35
2 6. Ответ: если k < - , О , то уравнение не имеет решений;
и 2 если k = - , о , то х = -4 (получается из х2 при k = | (
2 „ , если - < к О ,, 2 /г к +6 < 1, то х, = -—- и х9 = - -—- ; 1 k-1 2 k +1
если k = 1, <7 то х = - - (получается из х2 при k = 1);
если k > 1, к + 6 6 - к 2 k+1 3 k-1
26. При каких значениях а система неравенств
J х2 - (2а - 7)х + а2 - 7а < О,
[х2-7х-18>0
не имеет решений? Найти сумму всех таких целых значений а.
1. Исходная система равносильна следующей:
J (х - (а - 7))(х - а) < О,
((х + 2)(х - 9) > 0.
2. Для того чтобы система (1) не имела решений, нужно, чтобы
меньший корень первого неравенства был больше корня х = -2
второго неравенства, а больший корень первого неравенства был
меньше корня х = 9 второго неравенства (рис. 36). Так как а — 7?,
то а - 7 < а, поэтому должны выполняться условия л а < g
т. е. 5 < а < 9.
3. Сумма всех целых значений а из этого отрезка равна 35.
4. Ответ: а е [5; 9]; 35.
а-7 а
Рис. 36
139
27. При каких значениях а неравенство
(х - а)(х - а - 2) > 0 (1)
является следствием неравенства
х1 2 3 4 5 - 4х + 3 < 0? (2)
1. Решением неравенства (1) является объединение промежут-
ков (-о°; а) и (а + 2; +°°).
2. Решение неравенства (2) есть промежуток (1; 3).
3. По условию решения неравенства (1) должны содержать все
решения неравенства (2).
а) --•------—* б) ------------•—*
1 3 а х а+2 1 3 х
Рис. 37
4. На рис. 37, а и б показана графическая интерпретация этого
требования. Отсюда следует, что нужно найти решения совокуп-
а > 3,
пости неравенств а + 2 < 1
5. Ответ: а (-°°; -1] U [3; +°°).
28. Найти множество значений а, при которых существует хотя
бы одно решение системы
J (Зх - 2а + 3)(х - 4а + 1) < О,
| х2 + а2 = 10.
1. Для наглядности решения этой смешанной системы вос-
пользуемся геометрическими изображениями неравенства и урав-
нения (рис. 38, а).
2. Сначала в плоскости хОа построим прямую Зх - 2а + 3 = 0,
которая проходит через точки (1; 3) и (-1; 0).
3. Затем построим прямую х - 4а + 1 = 0; она проходит через
точки (3; 1) и (-1; 0).
4. Уравнение х2 + а2 = 10 определяет окружность радиуса л/10
с центром в начале координат. Точки Р(1; 3) и М(3; 1) лежат на
этой окружности.
5. Неравенство данной системы описывает некоторую область
на плоскости хОа, ограниченную построенными двумя прямыми.
140
6. Рассмотрим два случая:
j Зх - 2а + 3 > О,
। х - 4а + 1 < О,
или
(этой системе удовлет-
воряют точки дуги РМ);
j Зх - 2а + 3 < О,
б) }х - 4а + 1 > О,
-- Зх + 3
или К (этой системе удовлет-
воряют точки дуги NQ).
141
7. Найдем ординаты точек Q, Р, N, М окружности. Для этого
нужно решить две системы уравнений:
J Зх - 2а + 3 = О,
а) ] х2 + а2 = 10
_ 2а - 3
х з- ’
(2^3 у + а2 = Ю,
6 ± 33
откуда а =
27 о
т-е- а1 = -уз>а2 = 3-
I х - 4а +1=0, ( х = 4а - 1, 4+13
б) < о , 9 , „ у 1 г, 9 о откуда а = ——— , т. е.
}х2 + а2=10 1 17а2 - 8а - 9 = 0, 17
9 1
аз = -у7’а4= !•
8. Остается записать значения а, соответствующие дугам МР
и NQ. Эти значения а определяют вертикальные отрезки на оси Оа
(рис. 38, б).
9. Ответ: а Г-yZ ! “X I и П’ 3]-
L 1о 17 J
29. При каких значениях а корни уравнения
х2 - 2х - а2 + 1 = 0 (1)
лежат между корнями уравнения
х2 - 2(а + 1)х + а(а - 1) = 0? (2)
1. Находим корни уравнения (1):
х4 = 1 - |а|, х2 = 1 + |а|, х4 < х2.
2. Находим корни уравнения (2):
х3 = а + 1 - J1 + За , х4 = а + 1 + + За , х3 < х4.
3. Корни уравнения (2) являются действительными при условии
а > - |. Требуется найти такие а, чтобы выполнялись неравенства
О
а + 1 — л/1 + За < 1 — |а| С 1 + |а| < а + 1 + л/1 + За .
(3)
4. Пусть а < 0; тогда неравенства (3) примут вил
а + 1 — аУ 1 + 3 ст < 1 + а С 1 — £z<£z + l+ л/1 + За .
142
В этом случае достаточно, чтобы удовлетворялось лишь нера-
венство
1 — а < а + 1 + 71 + За ,
или
-2а < 71 + За ,
где -2а > 0.
5. Возводя в квадрат правую и левую части последнего неравен-
ства, после преобразований получим неравенство 4а2 - За - 1 < 0,
которое выполняется при а е (-0,25; 1). Так как а < 0, то постав-
ленная задача имеет решение при а е (-0,25; 0).
6. Пусть теперь а > 0; тогда неравенства (3) примут вид
а + 1 — 71 + За <1-а<1+а<а+1+ 71 + За .
В этом случае достаточно, чтобы удовлетворялось лишь нера-
венство
а + 1 - 71 + За < 1 - а,
или
2а < 71 + За ,
где 2а > 0.
7. Возводя в квадрат правую и левую части последнего неравен-
ства, после преобразований получим неравенство 4а2 - За - 1 < 0,
которое выполняется при а е (-0,25; 1). Так как в рассматривае-
мом случае а > 0, то поставленная задача имеет решение при а е
[0; 1).
8. Итак, корни уравнения (1) лежат между корнями уравне-
ния (2), если -0,25 < а < 1.
9. Ответ: а е (-0,25; 1).
30. При каких значениях параметра а существует единственная
пара целых чисел (х; у), удовлетворяющая смешанной системе
[ -15х2 + 11ху - 2у2 = 7,
<х<у,
2а2х + Зау < 0?
1. Перепишем уравнение данной системы в виде
(у - Зх)(5х - 2у) = 7. (1)
143
2. Так как по условию числа х и у должны быть целыми, то це-
лыми будут и числа у - Зх и 5х - 2у.
3. Поэтому все целые числа х и у, которые удовлетворяют урав-
нению (1), найдем из следующих четырех систем уравнений:
у - Зх = -1, 5х - 2у = -7; (2)
у - Зх = -7, 5х - 2у = -1; (3)
у - Зх = 1, 5х - 2у = 7; (4)
у - Зх = 7, 5х - 2у = 1. (5)
4. Решениями систем (2), (3), (4), (5) являются соответственно
пары чисел (9; 26), (15; 38), (-9; -26), (-15; -38).
5. Второму соотношению данной системы удовлетворяют пары
чисел (9; 26) и (15; 38).
6. Подставив значения х = 9, у = 26 в третье соотношение дан-
ной системы, придем к неравенству За1 2 + 13а < 0, решением кото-
13 п
рого являются все а такие, что - — < а < 0.
О
7. Подставив значения х = 15,у = 38 в третье соотношение дан-
ной системы, придем к неравенству 5а2 + 19а < 0, решением кото-
19 „ п
рого являются все а такие, что - — < а < 0.
5
8. Требованию задачи будут удовлетворять те значения пара-
метра а, которые удовлетворяют каждому из неравенств пп. 6 и 7.
<> /1 с ( 13 19 А
9. Ответ: а е ; - — .
V 3 5 7
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти значения а, при которых корень уравнения
а2(х - 3) - а(4х - 13) = 34 - 4х не меньше, чем 4.
2. Установить, при каких значениях а система неравенств:
[ 3 - Qx < 2х - 13,
а) < о , 9 , не имеет решений;
144
I -2(а + 4х) < х - 3,
б) < g _ gx > 2 + имеет хотя бы одно решение;
ч [ 2х - (а + 1)у > 2а + 2,
ВЦ (а - 5)х + 4у > а - 9 ИМееТ решеНие;
f у - х <2,
г) \ У ~ 2х > а, имеет единственное решение.
3. Решить систему неравенств:
J а(х - 2) > х - 3,
[ 8(а + 1)х > 8ах + 9; '
ах 2х + 3 , х - 1
а-2 4~ 3 ’
х(а2 10) + 6 > а(Х2+ 2) - 5х - а.
4. Установить, при каких значениях а неравенство:
а) (а - 3)х2 - 2ах + За - 6 > 0 выполняется для всех значений х;
^х ах 3
б) --- < - выполняется для всех значении х;
а2 + 4 2
в) (а - 1)х2 + 2(а+1)х + 2а-1<0 выполняется только для
одного значения х;
х х - 2а-1
г) „ „
О справедливо для всех х е [1; 2]?
5. При каком значении а уравнение |х2 - 2х - 3| = х + а имеет
ровно один корень?
6. При каких значениях а двойное неравенство
2 < х2 + ах - 2 < g
V _ 1 _
выполняется для всех значений х?
7. Найти все значения а, при которых корни уравнения
(а - 2)х2 - 2(а + 4)х + 4а = О
имеют одинаковые знаки.
8. Решить неравенство:
х а . о ,-х х 2а , 8а2
а) ---- > 3; б)----- - —— < .
2а-х х-а х + а х-ал
9. При каких значениях параметра а неравенство
2 - ах - х2
2
верно для всех значений переменной?
145
10. Найти множество значений а, при которых существует хо-
тя бы одно решение системы:
J 2х2 - (5а + 2)х + 2а2 - 2а - 4 < 0,
а)"|х-1-а-5 = 0;
J 2х2 + (а - 2)х < а2 + 2а;
бЦх + 2а - 1 = 0.
11. Найти все значения параметра/,, при которых неравенство
X2 + р2 -|
——> 1 выполняется для всех х, удовлетворяющих условию
- 1 < х < 1.
12. При каком значении q площадь фигуры, заданной на коор-
динатной плоскости неравенством:
а) |х - у + 2| + \х + 2у - 1| < q, будет равна 96;
б) |х + у + 2| + |2х - у - 2| < q, будет равна 6?
13. Найти множество значений а, при которых уравнение име-
ет ровно три корня:
а) (2х2 - (За - 6)х + а2 - За)7б + 4х - х2 = 0;
б) (2х2 - (За + 6)х + а2 + 3d)Jx2 + х-2 = 0;
в) (Зх2 - 2(2а - 3)х + а2 - 2а)д/2 + х - х2 = 0.
Ответы
1. а е [-3; 2) U (2; 6]. 2. а) а е (-оо; 5]; б) а е (-0,12; +<*>); в) а 3;
, _ ( 9 2а - 3 Л _ Г, 15 1 _
г) а = 2. 3. а) Если в < 1, то х £ ; -j- J; если а~ 1; — , то х -
<е ( | ; +оо); если а > у ,то.г:- 2а % ; +oo^j; б) если а е (-оо; -10) U (2; +°°),
то х с 52) ; если а е (-10; 2), то х > 5; если а = -10, то х - Л;
2(а + 10) ' ’ 2(а + 10)
если а = 2, то х е 0. 4. а) а е (6; +°°); б)а - (-6; 6); в) а = 5; г) а е (0,5; 1).
5. а = -3. 6. а£(-1; 2). 7. a G о) U (2; 8+^ J . 8. а) Если а < 0,
тох - у2а; — J; если а = 0, то решении нет; если а-О.тох- ; 2а j;
б) если а ' 0, то X - (За; а) U (-а; -2а); если а = 0, то решений нет; если
а - 0, тох - (-2а; -а) U (а; За). 9. а - [-1; 7]. 10. а) а - [1; 4]; б) а - [0; 1].
11. ре р + ; +оо). 12. а) 7 = 12; б) q =3.13. а) а е (-2; 2] и {6} и [8; 10);
б) а е {-6} U [-5; -4) U (-2; 2]; в) а е (-3; 1] U {3} U [4; 6).
146
Применение теоремы Виета к определению знаков корней
Г
квадратного трехчлена
2. Расположение корней квадратного трехчлена
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Применение теоремы Виета к определению знаков корней
квадратного трехчлена
1°. Как известно, между корнями х1 и х2 квадратного трехчле-
на ах2 + Ъх + с и его коэффициентами а, Ъ, с справедливы следую-
щие соотношения (теорема Виета):
. Ъ с
Xi + Хп — * X1Xп — •
1 z а 1 z а
С помощью этих соотношений можно исследовать знаки кор-
ней квадратного трехчлена.
2°. Теорема 1. Чтобы корни квадратного уравнения
(трехчлена) были действительными и имели одинаковые знаки,
необходимо и достаточно выполнение соотношений:
D = Ь2 - 4ас 0; х,х9 = - > 0.
При этом оба корня будут положительными, если дополнитель-
но выполняется условие
х, + х9 = -- >0,
1 а
и оба корня будут отрицательными, если выполняется условие
। ь А
х, + х9 = -- <0.
1 а
147
3°. Теорема 2. Чтобы корни квадратного уравнения
(трехчлена) были действительными и имели различные знаки,
необходимо и достаточно выполнение соотношений:
D = Ъ2 - 4ас > 0, х,х2 = - < 0.
1 а
При этом отрицательный корень будет иметь меньшую абсо-
। ь А
лютную величину, если х} + х2 = -- >0.
Если же х} + х2 = -- < 0, то отрицательный корень будет иметь
большую абсолютную величину.
2. Расположение корней квадратного трехчлена
1°. При решении многих задач требуется знание других важных
теорем и их следствий о расположении корней квадратного трех-
члена на координатной прямой.
2°. Пусть квадратный трехчлен f(x) = ах2 + Ьх + с имеет дейст-
вительные корни х} и х2 (где х} < х2), а х0 — какое-нибудь действи-
тельное число.
3°. Теорема 1. Чтобы оба корня квадратного трехчлена
были меньше, чем число х0 (т. е. лежали на координатной пря-
мой левее, чем точка х0), необходимо и достаточно выполнение
условий (рис. 39, а и б):
а> 0,
D>0,
а < 0,
D > 0,
или б) < _ Ъ
2а
f(x0) > 0
f(x0) < 0.
148
4°. Теорема 2. Чтобы оба корня квадратного трехчлена
были больше, чем число х0 (т. е. лежали на координатной прямой
правее, чем точка х0), необходимо и достаточно выполнение ус-
ловий (рис. 40, а и б):
а> 0,
D>0,
а < 0,
D>0,
а) <_Ъ_
2а
или
б) <_Ъ_
2а
/(х0) > 0
/(х0) < 0.
5°. Т е о р е м а 3. Чтобы один из корней квадратного трех-
члена был меньше, чем число х0, а другой больше, чем число х0
(т. е. точка х0 лежала бы между корнями), необходимо и доста-
точно выполнение условий (рис. 41, а и б):
J а> 0, \ а < О,
аЦ/(хо)<О или бЦ/(хо)>О.
149
6°. Следствие 1. Чтобы оба корня квадратного трехчле-
на были больше, чем число М, но меньше, чем число N (М < N),
т. е. лежали в интервале (М; N), необходимо и достаточно вы-
полнение условий (рис. 42, а и б):
а> О,
D>0,
а < О,
или б) ->
f(M) > о,
f(N) > О
М< - A <N,
2а
f(M) < о,
f(N) < О.
7°.Следствие 2. Чтобы только больший корень квадрат-
ного трехчлена лежал в интервале (М; N), необходимо и доста-
точно выполнение условий (рис. 43, а и б):
f а > О, [ а < О,
а) f(M) < О > или б) f(M) > о,
[f(N)>0 [f(N)<0.
150
8°. Следствие 3. Чтобы только меньший корень квадрат-
ного трехчлена лежал в интервале (М; N), необходимо и доста-
точно выполнение условий (рис. 44, а и б):
f а > 0, [ а < О,
а) f(M) > О > или б) f(M) < о,
[f(N)<0 [f(N)>0.
9°. Следствие 4. Чтобы один корень квадратного трех-
члена был меньше, чем М, а другой больше, чем N (М < N), т. е.
отрезок [М; ДГ] целиком лежал внутри интервала между кор-
нями, необходимо и достаточно выполнение условий (рис. 45,
а и б):
f а > О, [ а < О,
а) /(М) < О > или б) /(М) > о,
[Ж)<0 [/(7V)>0.
151
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра k корни квадратного уравнения
(k + 2)х2 + 2kx + k - 4 = О
имеют разные знаки?
1. Так как степень уравнения равна 2, то k + 2 0.
2. Уравнение имеет два различных корня при условии = k2 -
- (k + 2)(к - 4) > 0, причем произведение корней отрицательно:
/г
х-.х9 = -—- < 0.
12 к + 2
3. Итак, приходим к системе неравенств
k + 2 О,
Ь2 - (k + 2)(k - 4) > О,
I 4 < о.
[k + 2
4. Решив эту систему, получим -2 < k < 4.
5. Ответ: k е (-2; 4).
2. Найти все значения параметра а, при которых корни уравнения
(а - 2)х2 - 2ах + 2а - 3 = О (1)
действительны, и определить знаки корней.
1. Пусть а = 2; тогда уравнение (1) является линейным и имеет
один корень, равный 0,25.
2. Пусть а 2; тогда уравнение (1) имеет действительные кор-
ни, если дискриминант квадратного трехчлена неотрицателен, т. е.
=а2-(а-2)(2а-3)^0,
откуда, учитывая, что а 2, находим
1 <а<2,2<а <6. (2)
3. Для определения знаков корней воспользуемся теоремой
Виета:
. 2а
х, + х9 = --- ,
1 2 а-2
152
4. Корни имеют одинаковые знаки, если их произведение поло-
жительно. Если при этом положительна и сумма корней, то оба они
положительны. Таким образом,
2а - 3 п
лх2 = — > 0,
1 z а - 2
। 2 а А
1 + х2 = —- > 0,
1 2 а-2
откуда с учетом неравенств (2) находим 2 < а <6.
5. Если произведение корней положительно, а их сумма отри-
цательна, то оба корня отрицательны. Значит,
2а - 3 . п
ЛХ2 = Т > °’
1 z а-2
• 2 а - А
1 + х2 = —- < 0,
1 2 а-2
откуда с учетом неравенств (2) находим 1 < 1,5.
6. Если корни имеют разные знаки, то произведение корней от-
рицательно и выполняется неравенство
2а - 3 ,п
лх2 =-------— < 0
1 z а - 2
откуда с учетом неравенств (2) находим 1,5 < а < 2.
7. Если хотя бы один из корней уравнения равен нулю, то
ххх2 = % = 0, откуда следует, что а = 1,5. Так как при а = 1,5
сумма корней отрицательна, то другой корень отрицателен.
8. Ответ: корни уравнения действительны при 1 Са <6;
если 2 < а <6, то оба корня положительны;
если а = 2, то один положительный корень;
если 1,5 < а < 2, то корни имеют разные знаки;
если а = 1,5, то один из корней равен нулю, а другой
отрицателен;
если 1 Са < 1,5, то оба корня отрицательны.
3. В зависимости от значений параметра/, исследовать знаки кор-
ней уравнения
(р + 2)х2 - 2(р + 3)х + р + 5 = 0.
1. Согласно теореме Виета, для корней квадратного уравнения
ах2 + Ъх + с = 0 справедливы равенства х1 + х2 = , хгх2 = - .
153
2. Пусть х1 > 0, х2 > 0; тогда получим систему
или
-р - 1 > О,
р + 5
J ^+2
-2(р + 3) q
р + 2
О,
Решив эту систему (рис. 46, а), находим р е (-оо;-5) и (-2; -1).
3. Пусть х1 < 0, х2 < 0; тогда получим систему
или
-р - 1 > 0,
Р-Ц >0,
< Р + 2
-2(р + 3) > q
р + 2
Эта система не имеет решений (рис. 46, б).
4. Пусть х1 > 0, х2 < 0, х1 > |х2|; тогда получим систему
или
-р - 1 > О,
<0,
< р + 2
-2(р + 3) < 0
р + 2
Решив эту систему (рис. 46, в), находим р е (-5; -3).
5. Пусть х1 > 0, х2 < 0, х1 < |х2|; тогда получим систему
7 - < 0, или
а
-р - 1 > О,
р + 5
J ~2
-2(р + 3) > Q
р + 2
О,
Решив эту систему (рис. 46, г), находим р е (-3; -2).
6. Ответ: х1 > 0, х2 > 0 прир е (-оо; -5) U (-2; -1);
х1 > 0, х2 < 0, х1 > |х2| прир е (-5; -3);
х1 > 0, х2 < 0, х1 < |х2| прир е (-3; -2);
случай х1 < 0, х2 < 0 невозможен.
154
-1
///////////////////Л7/Л7—*
-5 -2
a) ?//////////*
—3 —2
-ШШШШ—A'///////// ~
-1
/////////////////Л7///Л7---*
-5 -2
б) 77////////>
-1
/////////////////////////<>-*
-5 -2
e) ------------------------------*
—3 —2
—/////////// >
-1
/////////////////////////7---j
-5 -2
г) -------////////////////--------*
-3 -2
Рис. 46
4. Найти все значения параметра с, при которых оба корня квад-
ратного уравнения
х2 + 4сх + 1 - 2с + 4с2 = О
действительны и меньше, чем (-1).
1. Здесь а = 1 > 0.
2. Применяя теорему 1 из п. 2, составим систему
D
4
>0,
-Д < -1>
2а
/(-1) > 0,
4с2 - (1 - 2с + 4с2) > 0,
т. е. < _2с < -1,
1 - 4с + 1 - 2с + 4с2 > 0.
(1)
3. Решив систему (1), находим с > 1.
4. Ответ: с‘-(1; +оо).
5. Найти все значения параметра k, при которых оба корня квад-
ратного уравнения
X2 - 6kx + 2 - 2k + 9/г2 = 0
действительны и больше 3.
155
1. Здесь а = 1 > 0.
2. Применяя теорему 2 из п. 2, получаем систему неравенств
~Га>3-
/(3) > о,
т. е.
[ 9/г2 - (2 - 2А + 9й2) > 0,
J 3k > 3,
[ 9 - 18А + 2 - 2k + 9/г2 > 0.
(1)
3. Решив систему (1), находим k >
11
9 ’
4. Ответ: k
6. При каких значениях параметра k один из корней уравнения
(/г2 + k + 1)х2 + (2k - 3)х + k - 5 = 0
больше 1, а другой меньше 1?
1. Здесь а = й2 + й + 1>0 при всех k.
2. Согласно теореме 3 из п. 2, имеем /(1) < 0, т. е.
k2 + k+ 1 + 2k - 3 + k - 5 < 0. (1)
3. Решив неравенство (1), находим
-2 - Jll < k < -2 + Jll .
4. Ответ: k e (-2 - ^/11 ; -2 + ,/lT).
7. При каких значениях параметра т корни уравнения
х2 - 2(т + 2)х + т2 + 12 = 0
принадлежат отрезку [-1; 4]?
1. Ветви параболы у = х2 - 2(т + 2)х + т2 + 12 направлены
вверх (так как а = 1 > 0). Эта парабола должна иметь:
а) точки пересечения с осью абсцисс;
б) вершину с абсциссой , принадлежащей отрезку [-1; 4];
в) неотрицательные ординаты /(4) и /(-1).
2. Указанным требованиям отвечает рис. 47.
156
3. Согласно следствию 1 из п. 2, за-
пишем и решим систему неравенств
Рис. 47
/(4) > О,
/(-1) > О,
т. е.
(т + 2)2 - т2 - 12 > О,
-1 < т + 2 < 4,
] 16 - 8(тп +2) + т2 + 12 > О,
1 + 2(т + 2) + тп2 + 12 > 0.
4. Ответ: т = 2.
8. При каких значениях параметра k корни уравнения
kx2 -(й + 1)х + 2 = 0
будут действительными и оба по абсолютной величине меньше 1?
1. Корни уравнения должны быть действительными и удовлет-
ворять условиям - 1 < х1 < 1 и -1 < х2 < 1.
2. Согласно следствию 1 из п. 2, получаем совокупность двух
систем неравенств для нахождения параметра k:
а> 0,
D>0,
<N,
f(M) > 0,
f(N) > 0;
а < 0,
D > 0,
Jm<-A <n,
2а
f(M) < о,
f(N) < 0,
т. е.
а) 5
k>0,
(k + l)2 - 8k > 0,
-1 < LL2 < 1,
2k
k + (k + l) + 2>0,
k - (k + 1) + 2 > 0;
k<0,
(k + l)2 - 8k > 0,
-1 < < 1,
2k
k + (k + 1) + 2 < 0,
A - (A + 1) + 2 < 0.
6) <
157
3. Решив систему а), находим й > 3 + 2 л/2 . Система б) не имеет
решений.
4. Ответ: k е [3 + 2 «/2 ; +°°).
9. При каких значениях параметра/, больший корень уравнения
рх2 + (2р - 7)х - Юр = 0 принадлежит интервалу (4; 6)?
1. Для того чтобы выполнялись требования задачи, нужно, что-
бы график квадратного трехчлена f(x) = рх2 + (2р - 7)х - Юр имел
вид, изображенный на рис. 48, а или на рис. 48, б.
2. Согласно следствию 2 из п. 2, получаем совокупность двух
систем неравенств:
f а > 0, [ а < О,
</(4) < О, </(4) > О,
|/(6)>0; |/(6)<0,
т. е.
f р > О, [р < О,
а) < 16р + 4(2р - 7) - Юр <0, б) < Юр + 4(2р - 7) - Юр > 0,
[ Збр + 6(2р - 7) - Юр > 0; I Збр + 6(2р - 7) - Юр < 0.
21
3. Из системы а) следует, что — < р < 2, а система б) не имеет
решений.
4. Ответ: р — f тт;; 2 Y
158
10. При каких значениях параметра/, меньший корень уравнения
(1 - р)х2 - (Зр - 8)х + р2 - 1 = 0
по модулю меньше 1?
1. По условию меньший корень уравнения должен принадле-
жать интервалу (-1; 1).
2. Поэтому квадратный трехчлен f(x) = (1 - р)х2 - (Зр - 8)х +
+ р2 - 1 должен иметь вид, изображенный на рис. 49, а или на
рис. 49, б.
3. Воспользуемся следствием 3 из п. 2 и запишем совокупность
двух систем неравенств:
[ а > 0,
/(-1) > о,
[/(1) <0;
[ а < 0,
/(-1) < о,
[/(!)> 0,
т. е.
1 - р > 0, 1 - р < 0,
а) < 1-р + Зр-8+р2-1>0, б) < 1-р + Зр-8+р2-1<0,
1-р-Зр + 8+р2-1<0; 1-р-Зр + 8+р2-1>0.
4. Система а) не имеет
решений, а из системы б) находим, что
1 <р<2.
5. Ответ: р — (1; 2).
159
11. При каких значениях k неравенство х2 + kx + /г2 + 6k < 0 вы-
полняется для всех 1 < х < 2?
1. Чтобы неравенство х2 + kx + /г2 + 6k < 0 имело место для всех
1 < х < 2, т. е. чтобы интервал (1; 2) лежал между корнями квад-
ратного трехчлена f(x) = х2 + kx + k2 + 6k, нужно, чтобы выполня-
лись требования следствия 4 из п. 2:
J /(1) < О,
2. Отметим, что здесь записаны нестрогие неравенства, посколь-
ку возможно не только расположение параболы, указанное на
рис. 50, а, но и расположения, изображенные на рис. 50, б—г. В по-
следних трех случаях один или оба корня квадратного трехчлена
могут совпадать с точками х1 = 1 или х2 = 2, но внутренние точки
интервала между корнями удовлетворяют неравенству 1 < х < 2.
3. Итак, имеем систему неравенств
J /(1) = 1 + k + k2 + 6k < 0,
[ /(2) = 4 + 2k + k2 + 6k < 0.
4. Решив эту систему, получим 7 ^3>/5 < < 2^3 - 4.
4. Ответ: k^ [-0,5(7 + 3^5); 2^3 -4].
160
1 2. При каких значениях а неравенство 4х2 - 9ах + 2а2 < 0 выпол-
няется для всех х таких, что \х - 3| < 1?
1. Сначала решим неравенство \х - 3| < 1, т. е. -1 < х - 3 < 1,
откуда х е [2; 4].
2. Рассмотрим функцию
f(x) = 4х2 - 9ах + 2а2. (1)
3. Чтобы функция (1) была отрицательной на отрезке [2; 4], до-
статочно выполнения условий
/(2) < О, 116 - 18а + 2а2 < 0, [ 1 < а < 8,
/(4)<0, ИЛИ ]б4-36а + 2а2<0, }2<а<16. (2)
4. Решив систему (2), находим 2 < а < 8.
5. Ответ: аг-[2; 8].
13. При каких значениях k один из корней уравнения
(k - 2)х2 - 2(k + 3)х + 4А = 0 (1)
больше 3, а другой меньше 2?
1. Согласно следствию 4 из п. 2, имеем совокупность двух сис-
тем неравенств:
Г а > О, Г а < О,
а) </(2) < 0, б) ?(2)>0,
[/(3) < 0; [/(3)>0.
2. Система а) в данном случае имеет вид
\k - 2 > О,
J /(2) = (k - 2) • 4 - 2(А + 3) • 2 + 4А < О,
| /(3) = (k - 2) • 9 - 2(А + 3) • 3 + 4А < О,
откуда 2 < k < 5.
3. Система б) не имеет решений.
4. Ответ: k е (2; 5).
14. При каких значениях параметра а абсолютная величина одно-
го из корней уравнения
а2х2 + ах - 2 = О
больше 1, а другого меньше 1?
161
1. Задача равносильна следующей: при каких значениях пара-
метра а один из двух корней квадратного трехчлена
/(х) = а2х2 + ах - 2 (1)
принадлежит интервалу (-1; 1), а второй расположен вне этого ин-
тервала и по модулю не равен 1?
2. Заметим, что ровно один корень трехчлена (1) принадлежит
интервалу (-1; 1) только тогда, когда числа /(-1) и /(1) имеют раз-
ные знаки (корни по модулю не равны 1). Поэтому требование за-
дачи выполняется только при условии /(-1)/(1) < 0, которое в дан-
ном случае примет вид
(а2 - а - 2)(а2 + а - 2) < 0. (2)
3. Решив неравенство (2), находим, что -2 < а < -1 или 1 < а < 2.
4. Ответ: а (-2; -1) U (1; 2).
1 5. Найти все значения с, при которых корни уравнения х2 + х +
+ с = 0 действительны и оба больше с.
1. Если оба корня квадратного трехчлена у = х2 + х + с больше с,
то его график имеет вид, изображенный на рис. 51.
2. Таким образом, должны выполняться условия теоремы 2 из
п. 2:
а) парабола у = х2 + х + с пересекает ось Ох в двух точках, т. е.
D > 0, где D = 1 - 4с;
б) абсцисса вершины параболы х0 = находится правее точ-
1
ки с, т. е. -- > с;
в) значение трехчлена у = х2 + х + с
в точке х = с положительно, т. е. у (с) > 0,
где у(с) = с2 + с + с = с2 + 2с.
3. В результате приходим к систе-
ме неравенств
1 - 4с > 0,
1
С 2 ’
с(с + 2) > 0,
Решением этой системы является
промежуток с < -2.
4. Ответ: с е (-оо;-2).
162
1 6. При каких значениях а оба корня квадратного трехчлена
(2 - а)х2 - Зах + 2а
действительны и больше | ?
1. Используя теорему 2 из п. 2, получим совокупность двух сис-
тем неравенств:
2 - а > О,
9а2 - 8а(2 - а) > О,
а) ( > -
’ | 2(2-а) 2 ’
i (2 - а) - За + 2а > 0;
4 2
2 - а < 0,
9а2 - 8а(2 - а) > 0,
За 1
2(2-а) 2 ’
i (2 - а) - За + 2а < 0.
4 2
б) <
2. Решив систему (а), находим
16
17
< а < 2; система (б) не имеет
решений.
3. Ответ: а
—; 2^
17 ’ )
17. При каких значениях k неравенство
(k - 1)х2 + (2k - 3)х + k - 3 > 0
(1)
выполняется хотя бы для одного значения х < 1?
1. Пусть k > 1. Положим f(x) = (k - 1)х2 + (2k - 3)х + k - 3.
Тогда, как видно из рис. 52, а—в, всегда найдется хотя бы одно
значение х < 1, при котором неравенство f(x) > 0 верно.
2. Пусть k = 1. Тогда неравенство (1) примет вид -х - 2 > 0. Оно
верно при х < -2. Значит, k = 1 удовлетворяет условию задачи.
Рис. 52
163
Рис. 53
3. Пусть k < 1. На рис. 53, а—в изображены графики функции
f(x) при D>0,D = 0hD<0. Условию задачи удовлетворяет только
случай а). Согласно теореме 1 из п. 2, получим систему
k- 1 <0,
D> 0,
-Л<1>
2а
/(1) < 0,
т. е. 4
k < 1,
(2А - З)2 - 4(А - 3)(А - 1) > 0,
3-2fe j
2(А-1)
k — 1 + 2/г — 3 + 7? — 3 < 0.
3
4
Решив ее, находим
<k< 1.
4. Ответ: k
3 ,
4 ’
18. Найти все значения k, при которых неравенство
kx2 - 4х + 3k + 1 > 0
(1)
выполняется для всех х > 0.
1. Понятно, что значения k должны быть положительны, так
как в противном случае всегда найдутся такие х > 0, для которых
функция у = kx2 - 4х + 3k + 1 принимает отрицательные значения
(при k < 0 ветви параболы направлены вниз; случай k = 0 также не
подходит).
2. При k > 0 возможны два случая, удовлетворяющие условию
задачи.
а) Квадратный трехчлен не имеет действительных корней, если
k > 0,
1б-4А(ЗА + 1)<0.
164
Решив эту систему, получим k > 1.
В этом случае неравенство (1) выполняется для всех х.
б) Корни квадратного трехчлена действительны, но оба меньше
или равны нулю: х1 < 0, х2 < 0.
Согласно теореме 1 из п. 2, составим систему
k > 0,
D > 0,
I <0,
3k + 1 > о,
которая несовместна. Таким образом, случай а) исчерпывает все
решения задачи.
3. Ответ: k (1; +°°).
1 9. Найти все значения k, при которых из неравенства
kx2 -x+l-k<0 (1)
следует неравенство
0<х<1. (2)
1. Прежде всего отметим, что одно неравенство является след-
ствием другого, если множество решений первого неравенства це-
ликом содержит множество решений второго. Например, если х
удовлетворяет неравенству |х| < 3, то х2 < 10, т. е. неравенство
х2 < 10 есть следствие неравенства |х| < 3. В самом деле, множество
решений (-710 ; «/10 ) неравенства х2 < 10 целиком содержит мно-
жество решений (-3; 3) неравенства |х| < 3.
2. Согласно условию, требуется найти все значения k, при кото-
рых любое число х, удовлетворяющее неравенству (1), удовлетво-
ряет и неравенству (2).
3. Это означает, что неравенство (1) достаточно для выполне-
ния неравенства (2), а неравенство (2) необходимо для выполнения
неравенства (1).
4. Покажем, что число k должно быть положительным.
а) Если k < 0, то квадратное неравенство (1) выполняется либо
при всех х (рис. 54, а), либо при тех х, которые лежат вне отрезка,
165
Рис. 54
содержащего корни квадратного уравнения kx2 -x + l- k = 0
(рис. 54, б).
б) В каждом из рассмотренных случаев обязательно найдутся
значения х, удовлетворяющие условию (1), но не удовлетворяю-
щие условию (2), т. е. в этих случаях условие (2) не является необ-
ходимым для выполнения условия (1).
в) Если k = 0, то из неравенства (1) следует, что х > 1, а это про-
тиворечит неравенству (2).
5. Итак, k > 0. Так как D = 1 - 4й(1 - k) = (1 - 2k)2 0 при
любых k, то решения неравенства (1) заключены между корнями
квадратного трехчлена.
6. В результате приходим к следующим выводам:
а) чтобы выполнялись требования задачи, нужно, чтобы корни
квадратного трехчлена принадлежали отрезку [0; 1] (см. решение
задачи 11);
б) последнее означает, что должны выполняться требования
следствия 1 из п. 2.
7. Составим систему уравнений
k>0,
D = (1 - 2k)2 > 0,
/(0) = 1 - k > 0,
/(1) = A- l + l- A>0,
1 / Ь 1
откуда находим - < k ч 1.
8. Ответ: k е |; 1 ] .
166
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить уравнение
(/г - 1)х2 - (2k - 1)х + k + 5 = 0.
Исследовать знаки корней в зависимости от k.
2. Установить, при каких значениях параметра k уравнение:
a) (k - 2)х2 + (2k - 3)х + k2 - 3k + 2 = 0 имеет два корня, один из
которых меньше (-1), а другой больше (-1);
б) х2 + (2k - 1)х + k2 - 6k + 8 = 0 имеет корни разных знаков;
в) kx2 - (3k + 2)х + 2(k + 1) = 0 имеет корень, больший, чем 1.
3. Установить, при каких значениях параметра k корни урав-
нения:
a) (k - 1)х2 - 2(k + 2)х + k + 13 = 0 больше 2;
б) х2 - 4/гх + 3 = 0 положительны;
в) kx2 - 2(k - 1)х + 3k - 2 = 0 отрицательны;
г) х2 + 2х + k = 0 больше й;
д) (k + 2)х2 + (k - 1)х - k = 0 удовлетворяют условиям х1 < 1,
х<£ + 3;
е) х2 - (2k - 2)х + k2 - 2k - 3 = 0 удовлетворяют условиям -3 <
< х1 < -1, 1 < х2 < 3;
ж) х2 - (3k - 2)х + 2k2 - k - 3 = 0 находятся между корнями
уравнения х2 - (5k - 1)х + 6/г2 - k - 2 = 0.
4. При каких k любое решение уравнения (k - 1)х2 - 2(k + 1)х +
+ k - 3 = 0 удовлетворяет условиям -1 < х < 5?
5. При каких k только один корень уравнения х2 + kx + 4 = 0
удовлетворяет условиям - 3 < х < -1?
6. Найти все значения параметра а, при которых заданное урав-
нение имеет решение на указанном интервале:
а) х2 + 2ах + 7а - 12 = 0; (-°°; 0);
б) х2 - 2ах + За - 15 = 0; (1; +°°);
в) х2 + 2ах + 6а - 8 = 0; (-°°; -1).
7. Найти все значения k, при которых квадратный трехчлен
х2 + (2k - 15)х + 7k - k2 отрицателен для всех значений х, удовлет-
воряющих неравенству 1 < х < 2.
8. Найти все значения параметра а, при которых уравнение
ах2 - (а + 5)х - 6а + 35 = 0 имеет два различных корня, причем
меньший из них принадлежит отрезку [-1; 8].
167
9. При каких значениях параметра а все решения неравенства
(а - 1)х2 + 4ах + За > 0 являются также решениями неравенства
х2 - 2х - 3 < О?
10. Дано неравенство х2 - (За + 1)х + а > 0. Требуется устано-
вить, при каких значениях а:
а) это неравенство выполняется для всех х > 1;
б) из этого неравенства следует неравенство х > 1.
Ответы
ь „ 1 1 „ г, 21 2Й-1 ± 721 - 20/г , .
1. Если к < 1 или 1 < k< — , то х, 9 = -; если к = 1, то
20 1>z 2(/г-1)
21 21
х = 6; если fe=—,тох=11; если k > — , то корней нет; х1 > 0, х2 > 0 при
k < -5 или 1 < k < |Z ; х1 < 0, х2 > 0 при -5 < k < 1. 2. a) k G (-оо; 1) U (2; 3);
б) /г- (2; 4); в) k G (-оо; -2) U (0; +оо). 3. а) /г- (1;
17 А г. г- ( 73 ,
-a- l;6)feG I ^-;+оо I;
0 2 \ Z /
|; ); г) к е (-оо; -3); д) к е (-2; ); е) к е (0; 2); ж) к е 0.
3 72 7 7 11 7
; ч-оо') и {1}. 5. /г ; 5) IJ {4}. 6. а) а - (Д ; 3] [4; +<х>);
о J V о 7 7
б) a G (Z ; 3] U [5; +оо); в) a G (Z ; 2] U [4; +оо). 7. /г- (-оо; 2) U ( 11 ;
+оо). 8. а _ (0; 0,1] U (5; 10]. 9. а - (-оо; -3]. Ю. а)в - (-оо; 0); б) a G 0.
й№
- - .1' Числовая последовательное™. ---------
"2. Арифметическая прогрессия ^"2222222
- - 3. Геометрическая прогрессия | | | | | | | | |
2 2 Сумма бесконечной геометрической прогрессии
- - - н fui Iqj
III Illi lllllllllll ни
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Числовая последовательность
1°. Бесконечной числовой последовательностью называют
функцию, определенную на множестве натуральных чисел.
2°. Числовую последовательность принято обозначать (хп), где
n^N.
3°. Последовательность (хп) называют ограниченной, если су-
ществуют два числа т и М такие, что для любого п е N справедли-
вы неравенства т < хп < М.
4°. Последовательность (хл) называют возрастающей, если каж-
дый ее член, начиная со второго, больше предыдущего, т. е. если
хп + 1 > хп для всех натуральных п.
5°. Последовательность (хп) называют убывающей, если каж-
дый ее член, начиная со второго, меньше предыдущего, т. е. если
хп+ 1 < * * * * * * * * * хп Для всех натуральных п.
2. Арифметическая прогрессия
1°. Числовую последовательность, каждый член которой, на-
чиная со второго, равен предшествующему члену, сложенному
с одним и тем же числом, называют арифметической прогрессией.
Обозначение: + аг, а2, а3, ... ап, ... .
2°. Из определения арифметической прогрессии следует, что
разность между любым ее членом и ему предшествующим равна
169
одному и тому же числу, т. е. а2 - а} = а3 - а2 = ... = ап - ап _ х = ... .
Это число называют разностью арифметической прогрессии и обо-
значают буквой d.
3°. Для того чтобы задать арифметическую прогрессию (ап), до-
статочно знать ее первый член и разность d.
4°. Арифметическая прогрессия является:
а) возрастающей, если ее разность — положительное число;
б) убывающей, если ее разность — отрицательное число;
в) постоянной (все ее члены равны между собой), если ее раз-
ность равна нулю.
5°. Характеристическое свойство арифметической прогрес-
сии. Последовательность (ап) является арифметической прогрессией
тогда и только тогда, когда любой ее член, начиная со второго, есть
среднее арифметическое предшествующего и последующего чле-
нов, т. е.
6°. Формула тг-го члена арифметической прогрессии имеет вид
ап = ах + d(n - 1). (2)
7°. Формула суммы п первых членов арифметической прогрес-
сии имеет вид
Sn= П (3)
ИЛИ
Sn = Za + d(n-l) п_ (4)
8°. Из определения разности арифметической прогрессии сле-
дует, что + ап = а2 + ап _ х = ... , т. е. сумма членов, равноотстоя-
щих от концов прогрессии, есть величина постоянная.
3. Геометрическая прогрессия
1°. Числовую последовательность, первый член которой отли-
чен от нуля, а каждый член, начиная со второго, равен предшест-
вующему члену, умноженному на одно и то же не равное нулю чис-
ло, называют геометрической прогрессией. Обозначение: н &х, Ь2,
bs, ... , bn, ... .
170
2°. Из определения геометрической прогрессии следует, что отно-
шение любого ее члена к предшествующему равно одному и тому же
числу, т. е. b2 : Ъг = bg : b2 = ... = Ъп : Ъп_ х = ... . Это число называют
знаменателем геометрической прогрессии и обозначают буквой q.
3°. Для того чтобы задать геометрическую прогрессию (&га), до-
статочно знать ее первый член Ъг и знаменатель q. Например, усло-
виями Ъг = 4, q = -3 (q < 0) задается геометрическая прогрессия
4, - 12, 36, -108... . Эта прогрессия не является ни возрастающей,
ни убывающей последовательностью.
4°. Если q > 0 (q 1), то прогрессия является монотонной после-
довательностью. Пусть, например, = -2, q = 3; тогда геометриче-
ская прогрессия -2, -6, -18, ... есть монотонно убывающая после-
довательность.
5°. Характеристическое свойство геометрической прогрессии.
Последовательность (&га) является геометрической прогрессией тог-
да и только тогда, когда каждый ее член, начиная со второго, есть
среднее геометрическое соседних с ним членов, т. е.
&L1 =brl-hrl 2,vnen-N. (1)
6°. Формула тг-го члена геометрической прогрессии имеет вид
= &i • qn -1, где п е N. (2)
7°. Формула суммы п первых членов геометрической прогрес-
сии имеет вид
b„q -Ь-,
S-=J^ (3)
ИЛИ
8°. Из определения знаменателя геометрической прогрессии
следует, что • Ьп = Ь2 • Ьп1 = ... , т. е. произведение членов, рав-
ноотстоящих от концов прогрессии, есть величина постоянная.
4. Сумма бесконечной геометрической прогрессии
при |g| < 1
1°. Пусть (хп) — геометрическая прогрессия со знаменателем q,
где |g| < 1 и хг 0. Тогда суммой бесконечной геометрической про-
грессии, знаменатель которой удовлетворяет условию |g| < 1, назы-
вается предел суммы п первых ее членов при п
171
2°. Обозначим сумму бесконечной геометрической прогрессии
через S. Тогда справедлива формула S =
Х1
Т~9'
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра а найдутся такие значения х,
что числа 51т + 51 т, |, 25х + 25 х, взятые в указанном порядке,
составляют арифметическую прогрессию?
1. Положим у = 5х + 5~х. Тогда 25ж + 25-ж = (5х + 5-ж)2 - 2 =
= у2-2.
2. Так как заданные числа должны составлять арифметиче-
скую прогрессию, то, согласно ее характеристическому свойству,
имеем
а _ у2 + 5у - 2
2 2 ’
т. е.
у2 + 5у - а - 2 = 0, (1)
откуда а = у2 + 5у - 2.
3. Заметим, что при любом х значение у > 2, откуда следует,
что а 12.
4. С другой стороны, дискриминант уравнения (1) должен быть
33
неотрицательным, т. е. D = 25 + 4(а + 2) > 0, или а — .
5. Из неравенств а> 12 иа> следует, что а 12.
6. Ответ: а [12; +°°).
2. При каких значениях параметра а корни уравнения
х3 + ах2 + 14х + 8 = 0 (1)
составляют геометрическую прогрессию?
1. Пусть xQ, xQq, xQq2 — корни уравнения (1), составляющие
геометрическую прогрессию, где q — знаменатель прогрессии.
172
2. Тогда
х2 3 * * + ах2 + 14х + 8 = (х - xQ)(x - xQq)(x - xoq2). (2)
3. Раскрывая скобки в правой части равенства (2), приводя по-
добные члены и приравнивая коэффициенты при одинаковых сте-
пенях х, получим систему
xQ + xQq + xQq2 = -а,
2 . 2 о . 2d .j л
\ x^q + x^q^ + x^q6 = 14,
Xqq3= -8.
4. Из первых двух уравнений этой системы следует, что axoq =
= -14. Из третьего уравнения вытекает равенство (ах0д)3 = -8а3.
Таким образом, а3 = 73, т. е. а = 7.
5. Ответ: а = 7.
3. Найти все значения параметра а, при которых множество реше-
ний неравенства
х(х - 2) < (а + 1)(|х - 1| - 1) (1)
содержит все члены некоторой бесконечно убывающей геометриче-
ской прогрессии с первым членом, равным 1,7.
1. Преобразуем неравенство (1) следующим образом:
х2 - 2х - (а + 1)|х - 1| + а + 1 < 0;
х2 - 2х + 1 - (а + 1)|х - 1| + а < 0;
|х - 1|2 - (а + 1)|х - 1| + а < 0;
(|х - 1| - 1)(|х - 1| - а) < 0. (2)
2. Левая часть неравенства (2) представляет собой квадратный
трехчлен (t - l)(f - а) относительно переменной t = |х - 1|. Корни
этого трехчлена равны 1 и а, причем ветви соответствующей ему
параболы направлены вверх.
3. Так как по условию х = 1,7 есть решение неравенства (1), то
1,7(-0,3) < (а + 1)( -0,3), или 1,7 > а + 1, т. е. а < 0,7.
Поэтому неравенство (2) равносильно следующему:
а<|х-1|<1. (3)
173
4. Пусть а < 0. Тогда неравенство а < |х - 1| верно при всех х.
Далее, неравенство |х - 1| < 1 равносильно неравенству -1 < х - 1 < 1,
т. е. оно выполняется для всех х из отрезка [0; 2]. Этот отрезок со-
держит все члены любой геометрической прогрессии с первым чле-
ном, равным 1,7, и знаменателем q е (0; 1). Таким образом, значе-
ния а < 0 удовлетворяют требованию задачи.
5. Пусть 0 < а < 0,7. В этом случае неравенство (3) равносильно
системе
Г |х - 1| < 1,
] |х - 1| > а,
решением которой является множество х таких, что х — [0; 1 - a] U
U [1 + а; 2]. Поскольку 1 + а < 1,7, отрезок [1 + а; 2] содержит число
1,7, т. е. первый член прогрессии. При этом знаменатель q > 0 про-
грессии всегда можно выбрать так, чтобы выполнялось неравенст-
во 1,7g < 1 - а (например, взять q = 0,1). Тогда все члены такой
бесконечно убывающей геометрической прогрессии, начиная со вто-
рого, будут принадлежать отрезку [0; 1 - а]. Следовательно, рас-
сматриваемые значения а также удовлетворяют требованию задачи.
6. Ответ: а (-°°; 0,7].
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Пусть х1 и х2 — корни уравнения х1 2 - Зх + а = 0, а х3 и х4 —
корни уравнения х2 - 12х + Ъ = 0. Известно, что числа х2, х3, х4
(взятые в указанном порядке) образуют возрастающую геометри-
ческую прогрессию. Найти а и Ъ.
2. При каких значениях параметра а уравнение х3 4 5 + Зх2 - 6х +
+ а = 0 имеет три различных корня, составляющих геометриче-
скую прогрессию? Найти эти корни.
3. При каких значениях параметра а корни уравнения х3 + 6х2 +
+ Их + а = 0 составляют арифметическую прогрессию? Найти эти
корни.
4. При каких значениях а существуют такие х, что числа 41 + х +
+ 41 ~ х, а, 16ж + 16 х, взятые в указанном порядке, составят ариф-
метическую прогрессию?
5. Произведение 2-го и 12-го членов арифметической прогрес-
сии равно 1, а произведение 4-го и 10-го членов равно а. Найти 7-й
член прогрессии.
174
6. Сумма квадратов 4-го и 10-го членов арифметической про-
грессии равнар, а сумма квадратов 5-го и 9-го членов равна 1. Най-
ти произведение 2-го и 12-го членов прогрессии.
Ответы
1. а = 2, Ь = 32. 2. а = -8; х1 = -1, х2 = -2, х.{ = -4. 3. а = 6; х1 = -1,
х2 = -2, х3 = -3. 4. а е [5; +<*>). 5. ± ^2Г)" ~9 , а е (1; +<х>). 6. 34~39р,
р е [1; 2,25].
ШИЦ
J 1111111 П1111111 m
Градусное и радианное измерение yr
irrTiiniiiiiiiiii
. Градусное и радианное измерение угловых величин - -
. Тригонометрические функции числового аргумента _ "
4Основные тригонометрические тождества I I I I I I ~ ~
. Формулы приведения | | | | I I I I I I Т~ ZZZZZZZZ
. Формулы сложения I 1111г" - -- -- -- -
. Формулы двойного аргумента^ 111111111111_ 2 2
. Преобразование произведения тригонометрических г -
функций в сумму 2 2
. Формулы суммы и разности одноименныхттттт~ - - -
тригонометрический функций I I I I I 1_ _ _
. Тригонометрические функции половинного аргумента-!^
. Выражение тригонометрических функций через тангенс
половинного аргумента ।
Темы 10 и 11 не содержат задач, а включают только справоч-
ный материал, в котором рассматриваются важнейшие тригоно-
метрические формулы, а также определения и свойства тригоно-
метрических и обратных тригонометрических функций. Однако
наличие этого материала необходимо для последующего решения
тригонометрических уравнений и неравенств с параметрами.
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Градусное и радианное измерение угловых величин
1°. Фигуру, состоящую из двух различных лучей с общим нача-
лом и ограниченной ими части плоскости, называют углом.
2°. Отметим на оси Ох справа от начала координат точку А и про-
ведем через нее окружность с центром в точке О (рис. 55). Радиус ОА
называют начальным радиусом.
3°. Условимся считать угол поворота:
а) отрицательным, если начальный радиус повернут около точ-
ки О по часовой стрелке;
176
Рис. 55
б) положительным, если начальный радиус повернут около
точки О против часовой стрелки.
4°. За единицу измерения углов и дуг принимают соответствен-
но угол в 1 градус и дугу в 1 градус (обозначают 1°).
5°. Рассматривают еще одну единицу измерения величины уг-
ла — 1 радиан.
6°. Угол в 1 радиан есть центральный угол, опирающийся на
такую дугу окружности, длина которой равна радиусу этой окруж-
ности (рис. 56).
7°. Если начальный радиус совершит один полный оборот, то
получится угол, равный 360° или 2л радианам.
8°. Радианная мера 1° равна
о OU
71
180 ’
2. Тригонометрические функции
числового аргумента
1°. Рассмотрим единичную окруж-
ность, т. е. окружность с центром в на-
чале координат и радиусом, равным 1
(рис. 57).
2°. На единичной окружности от-
метим точку Ро(1; 0). При повороте на-
чального радиуса около центра О на
угол а радианов точка Ро(1; 0) перей-
дет в некоторую точку Р . Обозначим
координаты этой точки ха и уа.
Рис. 57
177
3°. Определения:
а) синусом угла а называют отношение ординаты точки Ра к
радиусу; таким образом, sin а = = и,, (рис. 57);
Н
б) косинусом угла а называют отношение абсциссы точки Ра
ха
к радиусу; таким образом, cos а = — = хп (рис. 57).
п
4°. Каждому углу а соответствует единственная точка Ра(ха', уа)
и, следовательно, единственные значения синуса и косинуса этого
числа. Поэтому sin а и cos а являются функциями числового аргу-
мента.
5°. Основное соотношение между sin а и cos а выражается фор-
мулой
sin2 а + cos2 а = 1,
откуда следует, что
sin а = ± л/1 - cos2 а ,
cos а = ± 71 - sin2 а .
6°. Определения:
а) тангенсом числа а называют отношение ординаты точки Ра
к ее абсциссе (рис. 57); таким образом, tg а = — , причем tg а опре-
ла
делен, если cos а * 0;
б) котангенсом числа а называют отношение абсциссы точ-
ки Рп к ее ординате (рис. 57); таким образом, ctg а = — , причем
Уа
ctg а определен, если sin а^О;
в) секансом числа а называют величину, обратную cos а, т. е.
sec а = —3— , cos а * 0;
cos а
г) косекансом числа а называют величину, обратную sin а,
т. е. cosec а = —, sin а^О.
sin а
7°. Функции у = sin х, у = cos х, у = tg х, у = ctg х, у = sec х и
у = cosec х называют тригонометрическими функциями.
178
3. Основные тригонометрические тождества
Ранее были рассмотрены тождества:
1°. sin2 а + cos2 а = 1, а е R. (1)
2°. sin а = +л/1 - cos2 а . (2)
3°. cos а = ± а/1 - sin2 а . (3)
4°. tg а = , а ф " + лй. (4)
cos а 2
5°. ctg а = cos а , а лй. (5)
sin а
6°. sec а = —3— , а 5й + лй. (6)
cos а 2
7°. cosec а = Л , а nk. (7)
sin а
Добавим к ним следующие:
8°. Из формул (4) и (5) следует, что
tg а ctg а = 1, а у . (8)
9°. Из формулы (8) следует, что
j 1 , 71 k /f\\
tga=^’a^l-; (9)
ctga=t^’a7iT- <10>
10°. Разделив обе части равенства (1) на cos2 а, получим
tg2 a + 1 = —, а 2 + лй. (11)
cos^ a 2
11°. Разделив обе части равенства (1) на sin2 а, получим
ctg2 a + 1 = —3^— , а nk. (12)
sin2 a
4. Формулы приведения
1°. Формулами приведения называют соотношения, с помо-
щью которых значения тригонометрических функций аргументов
| + а, л + а, ± а, 2л ± а выражаются через значения sin a, cos a,
tg a и ctg a.
179
2°. Приведем правила:
а) при переходе от функций углов | ± а, ± а к функциям
угла а название функции изменяют: синус на косинус, тангенс на
котангенс и наоборот;
б) при переходе от функций углов л ± а, 2л ± а к функциям угла
а название функции сохраняют;
в) считая а острым углом (т. е. О < а < перед функцией
угла а ставят такой знак, какой имеет приводимая функция углов
± а, л ± а, ± а, 2л ± а.
5. Формулы сложения
1°. Формулы синуса суммы и разности двух аргументов:
sin (а + Р) = sin а cos Р + cos а sin р. (1)
sin (а - Р) = sin а cos Р - cos а sin р. (2)
2°. Формулы косинуса суммы и разности двух аргументов:
cos (а + Р) = cos а cos Р - sin а sin р. (3)
cos (а - Р) = cos а cos Р + sin а sin р. (4)
3°. Формулы тангенса суммы и разности двух аргументов:
1«(а + й-Йцг|т5' <5>
‘г'а-»-гп^- <6>
Замечание. Формула (5) справедлива при а + лй, Р
5й | + лй, а + Р 5й | + лй, а формула (6) — при а | + лй, Р | + лй,
а - Р 5й | + л/г (7г Z).
4°. Формулы котангенса суммы и разности двух аргументов:
ctg (а + Р) = ctg a ctgf 1 , (7)
ctg Р + ctg a
ctg(a-p)=ctg7tgf + 1. (8)
ctg P - ctg a
180
Замечание. Формула (7) справедлива при а nk, Р лй,
а + Р 5й nk, а формула (8) — при а * nk, Р nk, а - Р nk (k е Z).
6. Формулы двойного аргумента
1°. sin 2а = 2 sin a cos а, (1)
cos 2а = cos2 а - sin2 а, (2)
tg 2а = -2^- . (3)
1 - tg2 а
2°. 1 - cos 2а = 2 sin2 а, (4)
1 + cos 2а = 2 cos2 а. (5)
3°. Кроме перечисленных выше формул (1)—(5), полезно знать
и формулы
sin За = 3 sin а - 4 sin3 а, (6)
cos За = 4 cos3 а - 3 cos а, (7)
tg3a= 3tg(f 1 - 3tg2а (8)
7. Преобразование произведения тригонометрических
функций в сумму
1О . . о cos (а - В) - cos (а + В) х
1°. sin а sin Р = i1, (1)
2° cos а cos fi = cos(a+P) + cos(a-P) (2}
la • LUb LX LUb /
Li
3°. sin a cos P = Sin(q+P) + Sin(a-P), (3)
4“-tg“t8p=o‘*“iXV <4)
5°- °ct* p - XX SV <5>
Замечание. Формулы (4) и (5) справедливы при а^ у,
Р (k — Z). Кроме того, в формуле (4) должно быть ctg а +
+ ctg Р 5й 0, а в формуле (5) tg а + tg Р 0.
181
8. Формулы суммы и разности одноименных
тригонометрических функций
1°. Формулы суммы и разности синусов:
। • о и • + В 3 / "1 \
sin а + sin р = 2 sin • cos ; (1)
• • о г) • Ct — В ОС + В / о \
sin а - sin р = 2 sin • cos . (2)
2°. Формулы суммы и разности косинусов:
। о о ОС + В ОС В /о\
cos а + cos р = 2 cos - cos ; (3)
г\ л • ос В . ос + В / л \
cos а - cos р = -2 sin • sin . (4)
3°. Формулы суммы и разности тангенсов:
tg а + tg Р = sin ((f + Р) Где а ф Л + лй, р ф /г-Z; (5)
cos а cos р 2 2
tg а - tg Р = sin(a~P) где а 5й + лй, Р 2 + лй, /г'-Z. (6)
cos а cos р 2 2
4°. Формулы суммы и разности котангенсов:
ctg а + ctg Р = s*n | (f + , где а лй, Р лй, /г '-Z; (7)
sin а sin р
ctg а - ctg Р = s*n(P . а) где а * nk, Р nk, k — Z. (8)
sin а sin р
9. Тригонометрические функции половинного аргумента
X _|_ /1 — cos X
81П2 =±аН>—
2°. cos | = ±
3°. tg
4°. tg
5°. tg
X_____|_ 11 - COS X
2 — А/1 + cos x '
x _ sin x
2 1 + cos x ’
x _ 1 - cos x
2 sin x
(1)
(2)
(3)
(4)
(5)
182
10. Выражение тригонометрических функций через тангенс
половинного аргумента
0 4- Х
2tg„
1°. sin х =----— . (1)
1 + tg^
1 х 9 %
1 - tg2 о
2°. cos х =------. (2)
l+tg2|
Замечание. Область определения рассматриваемых функ-
ций: х л + 2лй, /г'-Z.
i-tg2f
4°. ctg х = --. (4)
Замечание. Формула (3) имеет смысл при х + лк, х^ л +
+ 2лк, kr— Z, & формула (4) при х лк, kr— Z.
гтг
ема
Фу1н1цЛ?
у = sin х
~ГТ2. Функция у = cos х "ZZ22222222222222
- - 3. Функция у = tg X | | | | | | | | | | | | | | | |~|~|~
Z Z : 4. Функция у = ctg х
- - 5. Нахождение периодовтригонометрическихфункций
2 216. Обратная функция I I I .
“ “ НФункция у = агс>1|1|л| | I I I I I I I I I I I I I I
_ _ . 8. Функция у = arccos х ...............
Z Z ' 9. Функция у = arctg х ZZZZZZZZZZZZZZ
- - 10. Функция у = arcctg х J_ _____
Z Z 1| । НёКбторые соотношения для обратных ' Z Z 2 2 2
- - тригонометрических функций |-|—| । । ।-
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Функция у = sin х
1°. Область определения — множество всех действительных
чисел.
2°. Множество значений — отрезок [-1; 1], т. е. синус — функ-
ция ограниченная.
3°. Функция нечетная: sin (-х) = -sin х при всех х е R.
4°. Функция периодическая с наименьшим положительным пе-
риодом 2л, т. е. sin (х + 2л) = sin х при всех х е R.
5°. sin х = 0 при х = л/г, k •— Z.
6°. sin х > 0 при всех х е (2лй; л + 2лй), k — Z.
7°. sin х < 0 при всех х (л + 2лй; 2л + 2лй), k е Z.
8°. Функция возрастает от -1 до 1 на промежутках + 2лй;
+2лА],Ае^.
184
9°. Функция убывает от 1 до
-1 на промежутках + 2лй;
+ 2nk^,k^Z.
10°. Функция принимает наи-
большее значение, равное 1, в точ-
ках х = + 2nk, k — Z.
11°. Функция принимает наименьшее значение, равное (-1),
в точках х = + 2nk, k — Z.
12°. График функции у = sin х изображен на рис. 58.
2. Функция у = COS X
1°. Область определения — множество всех действительных
чисел.
2°. Множество значений — отрезок [-1; 1], т. е. косинус — функ-
ция ограниченная.
3°. Функция четная: cos (-х) = cos х при всех х е R.
4°. Функция периодическая с наименьшим положительным
периодом 2л, т. е. cos (х + 2л) = cos х при всех х е R.
5°. cos х = 0 при х = + л/г, k
6°. cos х > 0 при всех х е (-5
7°. cos х < 0 при всех х е (5 -
8°. Функция убывает от 1 до -
k^Z.
9°. Функция возрастает от -1
2лй], k'-Z.
10°. Функция принимает наи-
большее значение, равное 1, в точ-
ках х = 2лй, /г'-Z.
11°. Функция принимает на-
именьшее значение, равное (-1),
в точках х = л + 2лй, k — Z.
12°. График функции у = cos х
изображен на рис. 59.
eZ.
+ 2лй; + 2лй^
I- 2лй; + 2л/г), k Z.
-1 на промежутках [2лй; л + 2лй],
до 1 на промежутках [-л + 2лй;
185
3. Функция у = tg X
1°. Область определения — множество всех действительных чи-
сел, кроме чисел вида х = + nk, kr— Z.
2°. Множество значений — вся числовая прямая, т. е. тангенс —
функция неограниченная.
3°. Функция нечетная: tg (-х) = -tg х при всех х из области оп-
ределения.
4°. Функция периодическая с наименьшим положительным пе-
риодом л, т. е. tg (х + л) = tg х при всех х из области определения.
5°. tg х = 0 при х = л/г, k — Z.
6°. tg х > 0 при всех х е (jtk; | + л/г), k е Z.
7°. tg х < 0 при всех х е (-Н + лй; л&), /г ‘-Z.
8°. Функция возрастает на промежутках
+ лй; + л/г^),
k^Z.
Рис. 60
9°. График функции у = tg х изображен на рис. 60.
4. Функция у = ctg х
1°. Область определения — множество всех действительных чи-
сел, кроме чисел вида х = л/г, k — Z.
2°. Множество значений — вся числовая прямая, т. е. котан-
генс — функция неограниченная.
3°. Функция нечетная: ctg (-х) = -ctg х при всех х из области
определения.
186
4°. Функция периодическая с наименьшим положительным
периодом л, т. е. ctg (х + л) = ctg х при всех х из области опреде-
ления.
5°. ctg х = 0 при х = + л/г, /г -Z.
6°. ctg х > 0 при всех х е , k е Z.
7°. ctg х < 0 при всех х е + лй; л&), k — Z.
8°. Функция убывает на промежутках (лй; л + лй), k е Z.
9°. График функции у = ctg х изображен на рис. 61.
5. Нахождение периодов тригонометрических функций
1°. Период функции:
а) у = sin х равен 2л;
б) у = cos х равен 2л;
в) у = tg х равен л;
г) у = ctg х равен л.
2°. Период функции, представляющей собой сумму непрерыв-
ных и периодических функций, равен наименьшему кратному пе-
риодов слагаемых, если оно существует.
6. Обратная функция
1°. Пусть функция у = f(x) монотонна в своей области определе-
ния D(f). Тогда каждому значению х е D(f) соответствует единст-
венное значение у е E(f) и обратно, каждое значение у е E(f) со-
187
ответствует единственному х е D(f). Значит, в этом случае можно
построить новую функцию, определенную на E(f) и такую, что каж-
дому у е E(f) ставится в соответствие х е D(f), удовлетворяющее
уравнению у = f(x). Эту новую функцию называют обратной по
отношению к функции у = f(x).
2°. Для нахождения функции, обратной данной у = f(x), надо
выразить х через у: х = g(y), а затем записать полученную функцию
в общепринятой форму у = g(x).
3°. Отметим, что если функции у = f(x) и у = g(x) являются взаим-
но обратными, то область определения функции f совпадает с множе-
ством значений функции g и, наоборот, область определения функции
g — с множеством значений функции /, т. е. D(f) = E(g) и D(g) = E(f).
4°. Графики взаимно обратных функций симметричны относи-
тельно прямой у = х (рис. 62).
5°. Рассмотрим, например, функцию у = х2, заданную на проме-
жутке (-°°; 0]. На этом промежутке функция убывает и принимает
все значения из множества [0; +°°). Следовательно, для данной функ-
ции существует обратная. Из уравнения у = х2 находим х= 4у или
х = _ 4у ; так как переменная х может принимать только неположи-
тельные значения, то искомая обратная функция имеет вид x = -Jy.
Поменяв обозначения х на у и у на х, получим формулу у = - Jx ,
где х > 0, с помощью которой и задается обратная функция.
Если же рассматривать функцию у = х2, заданную на проме-
жутке [0; +°°), то обратной для нее служит функция у = Jx , где
х > 0. На рис. 63 изображены график функции у = х2 при х > 0
и график обратной ей функции.
188
6°. Приведем другие примеры взаимно обратных функций.
а) Функция /(х) = 2х на промежутке (-°°; +°°) возрастает и при-
нимает все значения из множества (-°°; +°°). Поэтому она обрати-
ма. Графики функции f(x) = 2х и обратной ей функции g(x) =
ьэ I Н
изображены на рис. 64.
б) Функция f(x) = \[х на промежут-
ке [0; +°°) возрастает и принимает все
значения из множества [0; +°°). Зна-
чит, она обратима. Графики функции
/(х) = \[х и обратной ей функции g(x) =
= х4, где х > 0, изображены на рис. 65.
в) Функция /(х) = х3 + 1 на проме-
жутке (-°°; +°°) возрастает и принима-
ет все значения из множества (-°°; +°°).
Таким образом, функция /(х) обратима.
Графики функции /(х) = х3 + 1 и обрат-
ной ей функции g(x) = \]х - 1 изобра-
жены на рис. 66.
7. Функция у = arcsin х
1°. Функция у = sin х на отрезке | ] возрастает и прини-
мает все значения из отрезка [-1; 1] (рис. 67, а). Поэтому функция
у = sin х на отрезке | J обратима, т. е. имеет обратную функ-
189
Рис. 67
цию, которую называют арксинусом и обозначают у = arcsin х.
Геометрически arcsin х означает величину угла (дуги), заключен-
ного в промежутке J, синус которого равен х.
2°. График функции у = arcsin х изображен на рис. 67, б. Этот
график симметричен графику функции у = sin х, х‘— [“£ ; ] > от"
носительно прямой у = х.
3°. Отметим свойства функции у = arcsin х:
a) D(arcsin) = [-1; 1];
6)E(arcsin) = |
в) функция нечетная, т. е. arcsin (-х) = -arcsin х;
г) функция возрастающая.
8. Функция у = arccos х
1°. Функция у = cos х на отрезке [0; л] убывает и принимает все
значения из отрезка [-1; 1] (рис. 68, а). Поэтому функция у = cos х
на отрезке [0; л] обратима, т. е. имеет обратную функцию, которую
называют арккосинусом и обозначают у = arccos х. Геометрически
arccos х означает величину угла (дуги), заключенного в промежут-
ке [0; л], косинус которого равен х.
2°. График функции у = arccos х изображен на рис. 68, б. Этот
график симметричен графику функции у = cos х, х е [0; л], отно-
сительно прямой у = х.
190
3°. Отметим свойства функции у =
= arccos х:
a) D(arccos) = [-1; 1];
б) .E(arccos) = [0; л];
в) функция убывающая;
г) arccos (~х) = л - arccos х.
9. Функция у = arctg х
1°. На промежутке (
возрастает (рис. 69, а) и принимает все
числовые значения, т. е. -E(tg) = (-°°; +°°).
Поэтому функция у = tg х на промежутке
i ) обратима, т. е. имеет обратную
191
функцию, которую называют арктангенсом и обозначают у =
= arctg х. Геометрически arctg х означает величину угла (дуги), за-
ключенного в промежутке тангенс которого равен х.
2°. График функции у = arctg х изображен на рис. 69, б. Этот
график симметричен графику функции у = tg х, х | от-
носительно прямой у = х.
3°. Отметим свойства функции у = arctg х:
a) D(arctg) = (-°°; +°°);
6)E(arctg)= | );
в) функция нечетная, т. е. arctg (~х) =
= -arctg х;
г) функция возрастающая.
10. Функция if = arcctg х
1°. На промежутке (0; л) котангенс
убывает (рис. 70, а) и принимает все чис-
ловые значения, т. е. E(ctg) = (-°°; +°°).
Поэтому функция у = ctg х на промежут-
ке (0; л) обратима, т. е. имеет обратную
функцию, которую называют арккотан-
генсом и обозначают у = arcctg х. Геомет-
рически arcctg х означает величину угла
(дуги), заключенного в промежутке (0; л),
котангенс которого равен х.
192
2°. График функции у = arcctg х изображен на рис. 70, б. Этот
график симметричен графику функции у = ctg х, х е (0; л), отно-
сительно прямой у = х.
3°. Отметим свойства функции у = arcctg х:
a) D(arcctg) = (-°°; +°°);
б) .E(arcctg) = (0; л);
в) функция убывающая;
г) arcctg (~х) = л - arcctg х.
11. Некоторые соотношения для обратных
тригонометрических функций
1°. Записи у = arcsin х и х = sin у, < у < , равносильны.
Следовательно, для любого х, взятого на отрезке -1 < х < 1, имеем
-- ч arcsin х ч - ; (1)
sin (arcsin х) = х. (2)
2°. Записи у = arccos х и х = cos у, 0 < у < л, равносильны. По-
этому для любого х такого, что -1 < х < 1, имеем
0 < arccos х < л; (3)
cos (arccos х) = х. (4)
3°. Записи у = arctg х и х = tg у, - <у <^, равносильны. Зна-
чит, для любого х такого, что < х < +°°, имеем
< arctg х< (5)
tg (arctg х) = х. (6)
4°. Записи у = arcctg х и х = ctg у, 0 < у < л, равносильны. Та-
ким образом, для любого х такого, что < х < +°°, имеем
0 < arcctg х < л; (7)
ctg (arcctg х) = х. (8)
5°. Функции у = arcsin х, у = arccos х, у = arctg х и у = arcctg х
называют обратными тригонометрическими функциями (или
аркфункциями).
193
6°. Приведем еще некоторые формулы, позволяющие находить
значения тригонометрических функций от аркфункций.
Например, вычислим cos (arcsin х). Положим arcsin х = у. Тог-
да sin у = х, < у < ; нам нужно найти cos у.
а) Известно, что cos у = +J1- sin2 у .
б) Значит, cos у = +J1 -х2 .
в) Но - < у < , а на этом отрезке косинус принимает неотри-
цательные значения.
г) Таким образом, cos у = - х2 , т. е.
cos (arcsin х) = -х2 , где -1 < х < 1. (9)
7° . Выведем еще одну формулу. Так как tg у = , то из фор-
cos у
мул (2) и (9) следует, что
tg (arcsin х) = х , где -1 < х < 1. (10)
л/1 - X2
8°. Аналогично получаются следующие формулы:
ctg (arcsin х) = х ( Где -1 < х < 1; х 0; (11)
X
sin (arccos х) = - х2 , где -1 < х < 1; (12)
tg (arccos х) = х , где -1 < х < 1; х 0; (13)
X
ctg (arccos х) = , где -1 < х< 1. (14)
л/1 - X2
9°. Справедливы тождества:
a) arcsin х + arccos х = |, х е [-1; 1];
б) arctg х + arcctg х = |, х е R.
Решение тригонометрЫе^ккЦ^авнений вида sin х = а
Решение тригонометрических уравнений вида cos х = а
Решение тригонометрических уравнений вида tg х = а
решение однородных тригонометрических уравнений
ение систем тригонометрических уравнений
3
Ч
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Решение тригонометрических уравнений вида sin х = а
1°. Формула для корней уравнения sin х = а, где -1 < а < 1,
имеет вид
х = (-l)*arcsin а + nk, /г -Z.
2°. Частные случаи:
a) sin х = 0, х = nk, /г'-Z;
б) sin х = 1, х = + 2лй, /г - Z;
в) sin х = -1, х = + 2л/г, k — Z.
3°. Формула для корней уравнения sin* 1 2 х = а, где 0 < а < 1,
имеет вид
х = iarcsin Ja + л/г, k — Z.
2. Решение тригонометрических уравнений вида cos х = а
1°. Формула для корней уравнения cos х = а, где -1 < а < 1,
имеет вид
х = iarccos а + 2л/г, /г -Z.
2°. Частные случаи:
a) cos х = 1, х = 2л/г, /r-Z;
б) cos х = 0, х = | + nk, к — Z;
в) cos х = -1, х = л + 2л/г, /г Z.
195
3°. Формула для корней уравнения cos2x = а, где 0 < а < 1,
имеет вид
х = iarccos Ja + nk, kr— Z.
3. Решение тригонометрических уравнений BMflatg х = а
1°. Формула для корней уравнения tg х = а имеет вид
х = arctg а + nk, к1— Z.
2°. Частные случаи:
a) tg х = 0, х = nk, k‘— Z\
б) tg х = 1, х = + ~k, k r— Z;
в) tg x = -1, x = + v.k, k e Z.
3°. Формула для корней уравнения tg2 х = а, где а е [0; +°°),
имеет вид
х = larctg Ja + лй, /г ‘-Z.
4. Решение однородных тригонометрических уравнений
1°. Уравнение вида
a sin х + Ъ cos х = 0 (а 0, Ъ 0)
называют однородным уравнением первой степени относительно
sin х и cos х. Оно решается делением обеих его частей на cos х 0.
В результате получается уравнение вида atg х + Ъ = 0.
2°. Уравнение вида
a sin2 /(х) + Ъ sin f(x) cos f(x) + c cos2 f(x) = 0 (1)
называют однородным уравнением второй степени относитель-
но sin f(x) и cos f(x), если все три коэффициента а, Ь, с или какие-
либо два из них отличны от нуля. Считая, что а / 0, разделим обе
части уравнения на cos2 f(x) 0; тогда получим
a tg2 f(x) + b tg f(x) + c = 0. (2)
3°. Уравнение (2) равносильно уравнению (1), так как корни
уравнения cos2 /(х) = 0 не являются корнями уравнения (1).
4°. Однако если а = 0, то уравнение (1) примет вид
b sin /(х) • cos /(х) + с cos2 /(х) = 0.
196
Полученное уравнение решают разложением его левой части
на множители:
cos f(x)(b sin f(x) + c cos f(x)) = 0.
5. Решение систем тригонометрических уравнений
1°. При решении систем тригонометрических уравнений послед-
ние сводят либо к одному уравнению с одним неизвестным, либо
к системе уравнений относительно самих аргументов или функций
этих аргументов.
2°. Рассмотрим лишь некоторые типы систем тригонометриче-
ских уравнений и наиболее употребляемые методы их решения.
3°. Решим систему вида
J sin х sin у = а,
5 ь (1)
I COS X cos у = b. ' ’
а) Складывая и вычитая уравнения системы (1), получаем рав-
носильную систему
f cos (х - у) = а + Ъ,
| cos (х + у) = b - а. ' '
б) Система (2), а значит, и система (1) имеют решения тогда
и только тогда, когда выполняются условия -1<а + й<1и-1<
< b - а < 1.
Если эти условия выполнены, то
х- у = iarccos (а + b) + 2nk,
х + у = iarccos (b - а) + 2тш, ' ’
где й и п — любые целые числа, а знаки выбираются произвольно,
в) Пусть arccos (а + b) = a, arccos (b - а) = р. Таким образом,
формулы (3) определяют четыре серии решений:
J х - у = а + 2лй,
х + у = Р + 2тт; ( '
J х - у = -а + 2лй,
х + у = Р + 2пп; ' '
J х - у = а + 2лй,
х + у = -р + 2пп; ' '
J х - у = -а + 2лй,
| х + у = -р + 2пп. ' '
197
г) Решив эти системы, находим:
х = 0,5(а + Р) + л(й + п),
у = 0,5(Р - а) + п(п - k);
' х = 0,5(Р - а) + л(й + п),
у = 0,5(а + Р) + л(п - k);
х = 0,5(а - Р) + л(й + п),
у = -0,5(а + Р) + л(п - k);
х = -0,5(а + Р) + it(k + п),
у = 0,5(а - Р) + п(п - k).
4°. Аналогично решается система вида
sin х cos у = а,
cos х sin у = b.
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях а уравнение
sin4 х + cos4 х + sin 2х + а = 0 (1)
имеет решение?
1. Преобразуем уравнение (1) следующим образом:
(sin2 х + cos2 х)2 - 2 sin2 х cos2 х + sin 2х + а = О,
или
1 - sin 2х sin 2Х + sin 2х + а = 0. (2)
2. Пусть sin 2х = у, где |z/| < 1. Тогда после этой замены уравне-
ние (2) примет вид
у2 - 2у - 2 - 2а = 0. (3)
3. Найдем корни уравнения (3):
у = 1 ± л/3 + 2а , где а > -1.
198
4. Решим совокупность двух систем неравенств:
j — 1 С 1 + 73 + 2а С 1,
а) < з откуда а =
2
J-1 < 1 - 73 +2а < 1, з г
б) < з откуда-- < а < -.
2 2
5. Ответ.-, а — | .
2. Выяснить, при каких значениях параметра а уравнение
а2 - 2а + sec2 л(а + х) = 0 (1)
имеет решения, и найти эти решения.
1. Уравнение (1) равносильно следующему:
2 * +- = 2а - а2. (2)
cosz п(а + х)
2. Для того чтобы уравнение (2) имело решение, необходимо,
чтобы выполнялось неравенство
2а - а2 > 1
(так как 0 < cos2 л(а + х) < 1).
3. Тогда
а2 - 2а + 1 < 0, или (а - I)2 < 0. (3)
4. Неравенство (3) верно только при а = 1.
5. Если а = 1, то находим
cos2 их = 1, ~х = ~k, х = k, k е Z.
6. Ответ: при а = 1; х = k, k — Z.
3. При каждом значении параметра а решить уравнение
sin2 х + 4 sin х - а = 0. (1)
1. Решим данное уравнение как квадратное относительно сину-
са, введя ограничение -1 < sin х < 1.
199
2. Уравнение (1) сводится к совокупности двух уравнений:
sin х = -2 - л/4 + а ; (2)
sin х = -2 + 74 + а . (3)
3. Уравнение (2) не имеет решений ни при каких а, так как
-2 - 74 + а < -2 (по определению арифметического корня).
4. Для уравнения (3) должна выполняться система неравенств
—1 < -2 + 74 + а < 1,
4 + а > 0. 1 '
5. Решив систему (4), находим -3 < а < 5.
6. Ответ: если а е [-3; 5], то
х = (-1)* arcsin (74 + а - 2) + nk, k1— Z:
если а & [-3; 5], то корней нет.
4. При каждом значении параметра а решить уравнение
sin2 х + a sin х - а2 + 1 = 0.
1. Решим данное уравнение как квадратное относительно сину-
са, используя ограничение -1 < sin х < 1.
2. Пусть sin х = t; тогда
. - а - 7ба2 - 4 . - а + 7ба2 - 4 11-^2
’ *2 = --~2----- ПРИ 1“1 > •
3. Уравнение sin х = имеет решение, если выполняется сис-
тема неравенств
-а - 7ба2 - 4 > -2,
-а + 7ба2 - 4 < 2.
Решением системы (1) являются значения а е
и
200
4. Уравнение sin х = t2 имеет решение, если выполняется сис-
тема неравенств
-а + J5a2 - 4 > -2,
-а + л/ба2 - 4 < 2.
(2)
Решением системы (2) являются значения а е
U И;21-
L Тб J
5. Ответ: если а е (-оо; -2) и (2; +°°), то корней нет;
если а е [-2; -1], то
/ 1 + 1 а + Тба2 - 4 .
х = 1 arcsin--------- + лп;
если а е f-1; ~-^= ] U Г -^= ; 1 , то
Тб -1 L Тб 5 * 7
, . -а ± Тба2 - 4 .
х = (-1)" arcsin---------- + лп:
если а е [1; 2], то
/1\л? а +J5 а2 4 . .— п
х = (-l)n arcsin---------- + тш, п Z.
5. При каждом значении параметра а решить уравнение
sin (х - а) - sin х = sin а.
(1)
1. Перенесем все члены уравнения (1) в левую часть и восполь-
зуемся формулой разности синусов, а также формулой синуса двой-
ного угла. Тогда получим
sin (х - а) - sin х - sin а = 0;
о а ( а] п . а а А
-2 sin - cos I х - - I - 2 sin - cos - = 0.
2. Вынесем общий множитель за скобки:
sin | (^cos | J + cos
201
откуда, применяя формулу суммы косинусов, имеем
. а х (х а А п
81П — COS — COS — — J = 0. (2)
3. Рассмотрим по отдельности каждый множитель в уравне-
нии (2):
a) sin |- = 0, т. е. а = 2тш, n -Z. В этом случае уравнение (1)
удовлетворяется при любом х е R-,
б) cos | = 0, т. е. х = л + 2лк, к г— Z (независимо от значения
параметра а);
в) cos ( | ) = 0’ т- е- х = л + а + 2лк, k — Z.
4. Ответ: если а = 2лп, п — Z, то х '~ R;
если а 2лп, п — Z, то
х = л + 2л/г и х = л + а + 2лк, k‘— Z.
6. При каждом значении параметра а решить уравнение
sin Зх - a sin х = 0. (1)
1. Выразим sin Зх через sin х, используя формулу sin Зх =
= 3 sin х - 4 sin3 х. Тогда уравнение (1) примет вид
3 sin х - 4 sin3 х - a sin х = 0,
или
sin х (4 sin2 х - (3 - а)) = 0. (2)
2. Решим уравнение (2):
a) sin х = 0, откуда х = лк, k е Z, это равенство не зависит от а,
т. е. а е R.
б) 4 sin2 х - (3 - а) = 0. С помощью формулы 2 sin2 х = 1 - cos 2х
приведем это уравнение к виду cos 2х = , более удобному для
( . ,«/3 -а А
анализа чем уравнение smx = ±-*—— J.
в) Уравнение cos 2х = а имеет решение, если -1 < ~2~
т. е. -1 < а < 3. При этом
х = ±| arccos —у— + лй, /г -Z.
202
г) Заметим, что значение а = 3 приводит уравнение 4 sin2 х -
- (3 - а) = 0 к виду sin х = 0, что совпадает с уравнением из п. а).
При записи ответа это следует учитывать.
3. Ответ: если а е (-оо; -1) и [3; +оо), то х = nk;
если а е [-1; 3), то
х = ~k и х = ±i arccos —р— + ^k, k Z.
7. При каждом значении параметра b решить уравнение
sin4 х + cos4 х = Ъ. (1)
1. Понизим степень левой части уравнения (1). Для этого вос-
пользуемся формулой
тп4 + п4 = (т2 + и2)2 - 2тп2п2, где т = sin х, п = cos х.
Тогда уравнение (1) запишется в виде
(sin2 х + cos2 х)2 - 2 sin2 х cos2 х = Ъ. (2)
2. Упростив уравнение (2), получим
1 - = ь, или cos 4х = 4& - 3. (3)
3. Уравнение (3) имеет решение при условии -1С4&-ЗС1,
т. е. 0,5 < b < 1.
4. Ответ: если b е [0,5; 1], то х = arccos (4& - 3) + , k — Z;
если b & [0,5; 1], то корней нет.
8. При каждом значении параметра с решить уравнение
sin4 х + cos4 х + sin 2х + с = 0. (1)
1. Приведем уравнение (1) к виду
1 - | sin2 2х + sin 2х + с = 0,
или
sin2 2х - 2 sin 2х - 2с - 2 = 0. (2)
2. Уравнение (2) сводится к совокупности двух уравнений:
sin 2х = 1 - 72с + 3 ; (3)
sin 2х = 1 + 72с + 3 . (4)
203
3. Уравнение (3) имеет решение при условии -1 < 1 - 72с + 3 <
< 1. Эти неравенства выполняются, если -1,5 < с < 0,5.
4. Правая часть уравнения (4) больше или равна 1. Поэтому оно
имеет решение только в случае с = -1,5. Тогда уравнение (4) при-
нимает вид sin 2х = 1 и совпадает с уравнением (3) при с = -1,5.
5. Итак, уравнение (1) имеет те же решения, что и уравнение (3).
Запишем эти решения:
х = (-1)* | arcsin (1 - 72с + 3 ) + , k r— Z.
6. Ответ: если с е [-1,5; 0,5], то
х = (-1)* | arcsin (1 - 72с + 3 )- у , /г '-Z;
если с [-1,5; 0,5], то корней нет.
9. При каждом значении параметра а решить уравнение
cos2 х - 3 cos х + а = 0. (1)
1. Решим данное уравнение как квадратное относительно коси-
нуса, используя ограничение -1 < cos х < 1.
2. Уравнение (1) сводится к совокупности двух уравнений:
3 - 79 - 4а
cos х = —; (2)
гоч х _ 3 + 79 - 4а
LOb «Ъ /
3. Уравнение (3) не имеет решений, так как + —— > 1 при
4. Для уравнения (2) должна выполняться система неравенств
I _1 3 79 - 4а 1
2 (4)
[ 9 - 4а > 0.
5. Решив систему (4), находим -4 < а < 2.
6. Ответ: если а е [-4; 2], то х = ± arccos -—+ 2лй, /г‘-2;
если а & [-4; 2], то корней нет.
204
10. При каждом значении параметра с решить уравнение
cos 2х + (2с - 1) sin х + с - 1 = 0. (1)
1. Используя формулу cos 2х = 1 - 2 sin2x, преобразуем урав-
нение (1)к виду
2 sin2 х - (2с - 1) sin х - с = 0. (2)
2. Уравнение (2) сводится к совокупности двух уравнений:
sin х = с; (3)
sinx = -|. (4)
3. Уравнение (3) имеет решение, если с е [-1; 1]. Тогда
х = (-1)* arcsin с + nk, k1— Z.
4. Уравнение (4) имеет решение
х = (-1)" + 1 + тт, nr— Z,
которое не зависит от параметра с.
5. Ответ: если с е [-1; 1], то х = (-1)га+ 1 + тт,
х = (-1)* arcsin с + nk, п, k е Z;
если с (-°°; -1) U (1; +°°), то
х = (-1)" + 1 + тт, nr— Z.
11. При каждом значении параметра а решить уравнение
cos 2х + cos 4х = 2а cos х. (1)
1. Применяя формулу суммы косинусов, преобразуем уравне-
ние (1)к виду
2 cos Зх cos х = 2а cos х. (2)
2. После упрощения уравнения (2) получим
2 cos х (cos Зх - а) = 0. (3)
3. Уравнение cos х = 0 имеет решение при всех а — 7?, а уравне-
ние cos Зх - а = 0 — только при |а| < 1.
205
4. Ответ: если а е [-1; 1], то
71 I | 1 . 2 Ilk j - га
х = - + лп, х = +- arccos а + —— , п, k е Z;
Zoo
если а е (-ОО; -1) и (1; -l-oo), ТО X = + лп, nr— Z.
1 2. При каждом значении параметра т решить уравнение
(т - 1) cos2 х - 2(т + 1) cos х + 2т -1 = 0. (1)
1. Пусть cos х = t; тогда уравнение (1) примет вид
(т - 1)г2 - 2(тп + l)t + 2т - 1 = 0. (2)
2. При т = 1 уравнение (2) имеет один корень t = i , т. е. cos х =
= | . Отсюда
х = iarccos i + 2лк, k r~ Z
4
(этот корень не зависит от параметра).
3. При т 1 уравнение (2) имеет два корня:
. _ т + 1 - л/бт - т2
------------i-----> (о)
1 т - 1
, _ т + 1 + л/бт - т2 ( .
12 W
если т е [0; 1) U (1; 5].
4. Решив неравенства
т + 1 - л/бт - т2 т + 1 + 7би- т2 1
" т~1 " ’ " т~1 " ’
можно найти ограничения на т, при которых уравнения cos х =
и cos х = t2 имеют решения.
5. Ответ: если т < 0 или т > 4, то корней нет;
если т = 1, то х = iarccos i + 2лк:
4
если т е [0; 1) U (1; 4], то
х = larccos + 2лк, k^Z.
т-1
206
13. При каждом значении параметра а решить уравнение
cos2 х - 2 sin х cos х - sin2 х = а. (1)
1. После перехода к функциям двойного аргумента уравне-
ние (1) примет вид
cos 2х - sin 2х = а. (2)
2. Упростив левую часть уравнения (2), получим
sin ( - 2x^j - sin 2х = а; л/2 sin - 2x^j = а,
или
COS f 2х + 7 = -/= . (3)
4> л/2
3. Уравнение (3) имеет решение при условии -1 < -^= < 1, т. е.
72
-л/2 < а < л/2 .
4. Итак,
2х + = iarccos + 2nk, k — Z.
4 J2
5. Ответ: если а — [-»/2 ; л/2 ], то
х = ± i arccos -^= + nk, k‘— Z;
82 72
если |а| > л/2 , то корней нет.
14. При каждом значении параметра с решить уравнение
tg 2х - tg (jx - ) = с.
(1)
1. Если использовать формулы тангенса двойного угла и тан-
генса разности двух углов, то уравнение (1) преобразуется к виду
2 tg х _ tg х - 1 = с
1 - tg2 х tg х + 1
2. Упростив уравнение (2), получим
, о С - 1
tg х = ~г
(2)
(3)
207
3. Если с = -1, то правая часть равенства (3) не определена.
Вместе с тем при с = -1 уравнение (1) имеет вид
tg 2х - tg (jx - 2 ) = -1 (и его можно решать).
4. Вернемся к уравнению (1) и преобразуем его с помощью фор-
мулы разности тангенсов; тогда при с = -1 получим
sin (х +
------------г=-1, (4)
cos 2х cos (х-
5. Решим уравнение (4).
а) Используя формулу приведения, заменим cos (jx - ) на
sin (х + =).
б) Значит, при cos (х - 0 левую часть уравнения (4) мож-
но сократить и привести его к виду —3— = -1, т. е. cos 2х = -1.
cos 2х
в) Отсюда х = | + nk, kr— Z. Такие значения х входят в ОДЗ
уравнения (4).
6. Вернемся к уравнению (3). При с > 1 и с < -1 оно сводится к
уравнению tg х = ±и, значит,
х = larctg -—1 + nk, k — Z.
A/c + 1
7. Ответ: если с e (-oo; -1) и [1; Ч-оо), то x = larctg /—— + nk;
если c = -1, to x = + nk, k — Z:
если c e (-1; 1), то корней нет.
1 5. При каждом значении параметра а решить уравнение
3 cos 2х - 8а sin 2х = -5. (1)
208
1. Используя формулы sin 2х = 2 sin х cosx, cos 2х = cos2 х -
- sin2 х, 1 = sin2 x + cos2 x, преобразуем уравнение (1) к виду
sin2 х - 8а sin х cos х + 4 cos2 х = 0. (2)
2. Почленное деление уравнения (2) на cos2 х приводит к урав-
нению
tg2 х - 8а tg х + 4 = 0. (3)
Замечания.
1. Уравнение (2) является однородным.
2. Необходимо убедиться, что деление на cos2 х не приводит к по-
тере или приобретению посторонних корней.
3. Решим уравнение (3). Находим
tg х = 4а ± 2 л/4а2 - 1 , где 4а2 - 1 > 0.
Итак:
а) при -0,5 < а < 0,5 уравнение не имеет решений;
б) при а = -0,5 получаем tg х = -2, а при а = 0,5 получаем
tg х = 2;
в) при а > 0,5 или а < -0,5 получаем tg х = 4а ± 2 л/4а2 - 1 .
4. Ответ: если а е (-0,5; 0,5), то корней нет;
если а = -0,5, то х = -arctg 2 + itk;
если а = 0,5, то х = arctg 2 + itk;
если а е (-оо; -0,5) U (0,5; +°°), то
х = arctg(4a ± 2 л/4а2 - 1) + nk, k е Z.
1 6. При каждом значении параметра а решить уравнение
3a sin 2х + (а + 1) cos 2х - 1 = 0. (1)
1. Применив формулы синуса и косинуса двойного аргумента
и основное тригонометрическое тождество, получим однородное
уравнение второй степени относительно синуса и косинуса:
За • 2 sin х cos х + (а + l)(cos2 х - sin2 х) - (cos2 х + sin2 х) = 0. (2)
2. После упрощения уравнения (2) приходим к уравнению
(а + 2) sin2 х - 6а sin х cos х - a cos2 х = 0. (3)
а) Если а = -2, то уравнение (3) примет вид
cos х (6 sin х + cos х) = 0.
209
71 1
Отсюда следует, что cos х = 0, х = - + лк, k r- Z; tg х = --,
х = -arctg | + лп, n-Z.
б) Если а = 0, то уравнение (3) примет вид sin2x = 0, т. е. х =
= лт, пг‘— Z.
в) Наконец, если а -2, а 0, то обе части уравнения (3) можно
почленно разделить на cos2 х. Имеем
(а + 2) tg2 х - 6а tg х - а = О,
откуда
, _ За ± 72а(5а+ 1)
rg Х а + 2
(4)
3. Решим уравнение (4):
\ ТТ 1 4-1
а) При а = -- получаем tg х = -- , т. е.
о
х = -arctg | + лг, г— Z.
О
б) При а(5а + 1) > 0, т. е. при а е (-оо; -2) и (-2; ) U (0; +°°),
находим
X = arctg За ± V2a(5a+1) + е z
а + 2
4. Ответ: если а (-°°; -2) U ( -2;
U (0; +°°), то
х За ± ^/2а(5а + 1) . 'z
х = arctg---------—1 + лз, s Z;
а + 2
71 1
если а = -2, то х = - + л&, х = -arctg - + лп, k, п Z;
2 6
если а
1 + 1 V
= -- , то х = -arctg - + лг, г Z;
5 3
если а
(-И.
то корней нет;
если а = 0, то х = лт, mr— Z.
17. В зависимости от значений параметра а решить уравнение
2 sin2 2х - 6а sin 2х cos 2х - 11 cos2 2х _ 2(2a+l)cos2x _ 1
a cos 2х (2 sin 2х - cos 2х) cos2x-2sin2x а’
(1)
210
1. Уравнение (1) имеет смысл при а 0; значения х должны
удовлетворять условиям cos 2х 0, tg 2х 0,5.
2. Разделив числитель и знаменатель дроби в левой части урав-
нения (1) на cos1 2 2х, а первой дроби в правой части на cos 2х, полу-
чим уравнение
2 tg2 2х - 6а tg 2х - 11 _ 2(2а+1) _ 1 .„ч
a(2tg2x-l) l-2tg2x а'
3. Пусть t = tg 2х. Тогда после упрощения уравнения (2) оно
примет вид
t2 - (За - l)t + 2а2 + а - 6 = 0.
(3)
Уравнение (3) имеет два корня = а + 2 и t2 = 2а - 3.
4. Ранее было отмечено, что значения х должны удовлетворять
условию tg 2х 0,5. Поэтому необходимо исключить те значения а,
при которых tx или t2 (или оба числа) равны 0,5. Имеем:
a) tx = а + 2 = 0,5, откуда а = -1,5; при этом t2 = -6;
б) t2 = 2а - 3 = 0,5, откуда а = 1,75; при этом tx = 3,75.
5. Ответ: если а = -1,5, то х = | arctg (-6) + , п е Z;
если а = 1,75, то х = | arctg 3,75 + , k е Z;
если а -1,5, а 1,75, а 0, то
х = | arctg (2а - 3) + , т е Z;
х = | arctg (а + 2) + у J'-Z.
18. В зависимости от значений параметра а решить уравнение
a sin х - 2 _ a cos х - 2 ,х х
а-2 cos х а-2 sin х '
1. Перейдем от дробного уравнения (1) к целому с учетом ОДЗ.
При условиях а-2 cos х 0 и а - 2 sin х 0 получим равносильное
уравнение
(sin х - cos х)(а2 - 2a(sin х + cos х) + 4) = 0. (2)
2. Уравнение (2) сводится к совокупности уравнений:
a) sin х - cos х = 0, х = ? + тт, nr— Z, независимо от а;
4
211
। a2 + 4
o) sin x + cos x = —— , или
2a
л А _ а2 + 4
4 > 9./9„
(3)
3. Рассмотрим модуль правой части уравнения (3):
а2 + 4
у = 72
У2
(так как |z + - | > 2). Поэтому уравнение (3) не имеет корней.
4. В п. 2 мы установили, что х = + пп, п— Z, — корни уравне-
ния (2) (не зависящие от параметра а). Однако из множества корней
। + тш > следует отбросить те корни, при которых а - 2 cos х = О
о п а . а
и a - 2 sin х = 0, или cos х = - , sin х = - .
5. Представим множество •! + тш > как объединение двух мно-
жеств: J - + 2~к и J — + 2~k \, k Z.
I 4 14
а) Если х = + 2nk, то cos х = и cos х = при а = J2 .
Значит, при а = J2 корни х = + 2 т: к — посторонние.
5 л а г
б) Если х = — + 2лй, то cos х = и cos х = - при а = - J2 .
г~ 5л
Значит, при а = - J2 корни х = — + 2v.k — посторонние.
6. К этим же выводам приводит и условие а - 2 sin х = 0, так
как при х = + 2тт имеем sin х = cos х.
7. Ответ: еслип^-72,тох=2 + 2л/г;
г~ 5л
если а J2 , то х = — + 2nk:
4
если п^+72,тох=^ + пп, п, k — Z.
4
212
1 9. При каких значениях параметра а уравнение
sin2 Зх - (а + 0,5) sin Зх + 0,5а = 0 (1)
имеет ровно три корня, принадлежащие отрезку ?
1. Решив уравнение (1) как квадратное относительно sin Зх,
получаем, что оно равносильно совокупности двух уравнений:
sin Зх = 0,5; (2)
sin Зх = а. (3)
2. Уравнение (2) на отрезке Г ; л! имеет два корня: хг =
L о J 1о
17л
и X) = —Г- .
2 18
3. Следовательно, значение параметра а удовлетворяет требо-
ванию задачи, если уравнение (3) на данном отрезке имеет один
корень.
4. Функция у = sin Зх на отрезке принимает все зна-
чения от 0 до 1, причем каждое из этих значений, за исключени-
ем 1, — дважды. Поэтому требование задачи будет выполнено
только при значении а = 1.
5. Ответ: а = 1.
20. При каких положительных значениях параметра а неотрица-
тельные значения х, удовлетворяющие уравнению
cos (5а - 9)х = cos (9а + 17)х (1)
и расположенные в порядке возрастания, образуют бесконечную
арифметическую прогрессию?
1. Приведем уравнение (1) к виду
sin (7а + 4)х sin (2а + 13)х = 0.
2. Так как по условию а > 0, то 1а + 4 0, 2а + 13 0 и неотри-
цательные решения исходного уравнения задаются двумя сериями:
х = , где /г'-Z, /г > 0; (2)
х = о Ттч ’ гДе п е Z, п > 0. (3)
ZtCL < J. о
213
3. Здесь каждое из соотношений (2) и (3) образует бесконечную
арифметическую прогрессию с первым членом, равным нулю, и раз-
ностями d, = „ 71 , и</, = -—соответственно.
1 7а + 4 2 2а+13
4. Эти две арифметические прогрессии образуют одну бесконеч-
ную арифметическую прогрессию при условии, что хотя бы одно из
d, d2
чисел — или — является натуральным.
5. Рассмотрим случай, когда
di 2а+ 13
— = =р, гдер — натуральное.
t а + ч
Отсюда находим а =
4р- 13
2 7р
> 0. Из этого неравенства следует,
что р - {1;2; 3}, и, значит, а е J |; А ;
It) J. л
1
19
6. Рассмотрим случай, когда
<?2
dl
7а + 4
2а + 13
= д, где q — натуральное.
Отсюда находим а = 42
> 0. Здесь также оказывается, что
</ - {1; 2; 3}и, следовательно, а
- ~ _ 1 5 9 22 ок
7. Ответ-.а^ 35
21. При каких целых отрицательных п функция
/(х) = cos 7пх sin
является периодической с периодом Т = 7л?
1. Так как по условию при любом значении х должно выпол-
няться равенство
cos 7п(х + 7л) • sin (х + 7л) = cos 7пх sin , (1)
то оно будет выполняться и при х = 0.
214
2. При х = 0 получим
cos 7п(0 + 7л) • sin (0 + 7л) = cos 49лп • sin = 0.
3. Так как cos 49лп 0 при целых отрицательных п, то должно
выполняться равенство
17 5 тт z-v /о\
sin —— = 0. (2)
4. Равенство (2) имеет место, когда
5. Поскольку нас интересуют только целые отрицательные п,
простым перебором находим, что п е {-1; -5}.
6. Подставляя значения п = -1 и п = -5 в соотношение (2),
убеждаемся, что в обоих случаях получается тождество.
7. Ответ: п е {-1; -5}.
22. В зависимости от значений параметров аиЬ решить уравнение
7tg х-2а - Jigx- 2Ь = 2.
1. Полагая и = Jtg х-2а , v = л/tg х-2b , zz > 0, t> > 0, получим
уравнение
и - v = 2. (1)
2. Кроме того, имеем
и2 - v2 = (tg х - 2а) - (tg х - 2b),
т. е.
и2 - v2 = 2(Ь - а). (2)
3. Уравнения (1) и (2) образуют систему
J и - v = 2,
I и2 - v2 = 2(Ь - а),
откуда находим v = | (Ь - а - 2); так как v 0, то Ъ а + 2.
4. Вернемся к обозначению и = Jtg х-2b . Возведя обе части
этого равенства в квадрат, получим v2 = tg х - 2b, откуда
tg х = v2 + 2b, или tg х = ( -—|+ 2b.
215
5. Ответ: если Ъ - а 2, то
х = arctg ( ( -—|) + 2&^j + nk, k r- Z;
если Ъ - a < 2, то корней нет.
23. При каких значениях параметра k уравнение
cos 2х + 2 sin х + 2/г2 - 2й - 1 = О (1)
имеет хотя бы одно решение? Найти сумму таких целых значе-
ний k.
1. Так как cos 2х = 1 - 2 sin2 х, то уравнение (1) примет вид
1-2 sin2 х + 2 sin х + 2/г2 - 2k - 1 = 0. (2)
а) Пусть sin х = t, |t| < 1; тогда уравнение (2) запишется так:
t2 - t - k2 + k = 0. (3)
б) Уравнение (3) имеет корни tx = k и t2 = 1 - k.
в) Вернемся к подстановке t = sin х; имеем t\ = k = sin х, t2 =
= 1 - k = sin x.
2. Уравнение (3) имеет хотя бы одно решение, если выполняет-
ся совокупность неравенств
—0////Л7//0---------г
-1 1 *
И<1,
\k - 1| < 1.
-ШШ-----►
0 2 «
Рис. 71
а) Из рис. 71 видно, что искомыми це-
лыми значениями k являются -1, 0, 1 и 2.
б) Сумма этих целых значений k рав-
на 2.
3. Ответ: k [-1; 2]; 2.
24. При какой зависимости между параметрами aub имеет реше-
ние уравнение sin ах sin Ъх = 1?
1. Исходное уравнение равносильно совокупности двух систем:
sin ах = 1,
sin Ъх = 1;
(1)
sin ах = -1,
sin Ъх = -1.
(2)
216
2. Для системы (1) имеем
ах = | + 2 л/г = (4/г + !),/; - Z,
Ьх = + 2лп = | (4п -г 1), п — Z,
a 4fe + 1
откуда следует, что - = ----- .
Ь 4п +1
3. Для системы (2) имеем
ах = + 2 л/г = | (4k - 1), k & Z,
Ьх = -^ + 2л п = (4п - 1), п & Z,
a 4k - 1
и, значит, - = ----- .
Ъ 4га - 1
. a 4fe + 1 a 4А-1 , _ „
4. Ответ: - = ---- или - = ------ ,k,n'-£.
Ъ 4га +1 b 4п-1
25. В зависимости от значений параметра а решить уравнение
|cos 2х| = |sin2 х - а|. (1)
1. Так как обе части уравнения (1) неотрицательны, то после
возведения в квадрат получим равносильное уравнение
cos2 2х = sin4 х + а2 - 2а sin2 х. (2)
2. Упростим уравнение (2):
cos2 2х = ( у - 2g + а2,
или
3 cos2 2х + 2(1 - 2а) cos 2х - (1 - 2а)2 = 0. (3)
3. Уравнение (3) сводится к следующей совокупности:
cos 2х = 2а - 1; (4)
cos 2х = 1 2а . (5)
О
4. Решим уравнение (4). Здесь должно выполняться условие
|2а - 1| < 1, т. е. 0 < а < 1; имеем
х = ±1 arccos (2а - 1) + лп, п — Z.
217
5. Решим уравнение (5). Здесь должно выполняться условие
1 2 CL I ч ч о
—3— ч 1, т. е. -1 ч а ч 2; имеем
I 1 1 — 2 CL I 11 .— <7
х = ±- arccos —— + л/г, k Z.
Z О
6. Ответ: если а < -1 или а > 2, то корней нет;
если -1 < а < 0 или 1 < а < 2, то
I 1 1 2d, i 1 .----- га
х = +- arccos —— + лк, k-Z:
Zt о
z-v У ч । 1 1 2 CL । 1
если Очач 1, то х = ±- arccos —-— + л/г,
Z О
х = ±| arccos (2а - 1) + лтг, /г, п Z.
26. В зависимости от значений параметра а решить уравнение
|tg х + a ctg х| = .
О
(1)
1. Допустимыми значениями переменной х являются все х ,
k е Z. При таких значениях х, полагая у = tg х, перепишем урав-
нение (1)в виде
У + 7 I = • (2)
У I &
2. Если а = 0, то у = . При а 0 уравнение (2) равносиль-
О
но совокупности уравнений
У2 - У + а = О,
О
У2 + ^у + а = о.
(3)
3. Дискриминанты обоих уравнений совокупности (3) совпада-
ют и имеют вид!) = 4 ( | - а ). Поэтому если а > | , то уравнение (1)
V о J о
не имеет решений.
4. Пусть D > 0. Тогда, решив уравнения (3), находим
273 , /4 273 , /4
У1,2= -f- ± Js~a,ys’i = ~3 ± ^з~а- (4)
218
тт 4 I 273 Т>
При а = - имеем у = ±—. В остальных случаях все корни
о о
определяются формулами (4).
5. Ответ: если а < 0 или 0 < а < |, то
О
если а = 0, то х = iarctg + nk, k‘— Z;
О
4 , , 2л/3 ,
если а = - , то х = +arctg —+ пт, т — Z;
О о
4
если а > - , то корней нет.
О
27. Определить все значения параметра а, при которых уравнение
(а - 3) sin2 х + (а - 4) cos х + 1 = О
имеет единственный корень в интервале ^0; J, и указать этот
корень.
1. Положим у = cos х, sin2 х = 1 - у2 и сведем тригонометриче-
ское уравнение к алгебраическому:
(а - 3)у2 - (а - 4)у + 2 - а = 0. (1)
2. Требуется найти те значения а, при которых уравнение (1)
имеет единственный корень в интервале (0; 1).
3. Такое требование реализуется в двух случаях:
а) уравнение (1) имеет единственный корень, который прина-
длежит интервалу (0; 1); это в свою очередь возможно либо при
а - 3 = 0, либо при D = 0;
б) уравнение (1) имеет два корня, причем один из них прина-
длежит интервалу (0; 1), а другой находится вне этого интервала.
4. Рассмотрим по отдельности эти возможности.
а) При а = 3 уравнение (1) примет вид у - 1 = 0. Тогда его корень
у = 1 (0; 1) и, значит, а = 3 не удовлетворяет указанному требо-
ванию.
Так как D = (а - 4)2 + 4(а - 3)(а - 2) = 5а2 - 28а + 40 > 0 при
любом а, т. е. случай D = 0 не имеет места.
219
б) Уравнение f(y) = 0 имеет единственный корень в интервале
(0; 1), если /(0) • /(1) < 0. В данном случае
/(у) = (а - 3)у2 - (а - 4)у + 2 - а,
т. е. /(0) = 2 - а, /(1) = (а - 3) - (а - 4) + 2 - а = 3 - а. Искомые
значения а должны удовлетворять условию (2 - а)(3 - а) < 0, отку-
да 2 < а < 3.
5. Итак, уравнение (1) имеет единственный корень в интервале
(0; 1), если а е (2; 3). Найдем этот корень. Имеем
_ а - 4 - 7ба2-28а + 40 _ а - 4 + 7ба2-28а + 40
У1 2(а-3) ’У2 2(а-3)
Так как 2 < а < 3, то у} > 1, а у2 е (0; 1).
6. Из равенства cos х = у2 найдем соответствующий корень дан-
ного уравнения.
„ т а - 4 + «/ба2 - 28а + 40
7. Ответ-, а е (2; 3); х = arccos-----------—--------
Zi — О у
28. Найти все пары чисел (а; Ъ), для каждой из которых при лю-
бом х справедливо равенство
a sin х + Ъ = sin (ах + b). (1)
1. Из условия следует, что равенство (1) должно выполняться,
в частности, при х = 0.
2. При этом значении х получим равенство b = sin b, которое
справедливо только при Ъ = 0, т. е. 0 = sin 0 = 0.
3. Подставив Ъ = 0 в равенство (1), приходим к уравнению
a sin х = sin ах,
которое имеет решение при любом х только в тех случаях, когда
ае{-1; 0; 1}.
4. Ответ: (-1; 0); (0; 0); (1; 0).
29. Найти все пары чисел (а; Ъ), для каждой из которых при всех х
справедливо равенство
a(cos х - 1) + b2 = cos (ах + &2) - 1. (1)
1. Пусть (а; Ь) — пара чисел, удовлетворяющих условию зада-
чи. Поскольку данное равенство справедливо при любом х, в част-
220
ности, оно верно при х = л и х = 2л. Поэтому числа а и & удовлетво-
ряют равенствам
-2а + b2 = cos (ла + b2) - 1, (2)
Ъ2 = cos (2ла + Ъ2) - 1. (3)
2. Так как cos (2ла + b2) < 1, то из равенства (3) следует, что
Ь2 < 0. Этому условию удовлетворяет только Ъ = 0; тогда cos 2ла =
= 1, т. е. а — целое число.
3. При Ъ = 0 равенство (2) примет вид 1 - 2а = cos ла. Но -1 <
< cos ла < 1, откуда -1 < 1 - 2а < 1, т. е. 0 < а < 1. В промежутке
0 < а < 1 имеются только два целых числа: а = 0 и а = 1.
4. Итак, условию задачи могут удовлетворять только следую-
щие пары чисел: а) а = 0, Ъ = 0; б) а = 1, Ъ = 0.
5. Если а = 0, Ъ = 0, то равенство (1), очевидно, выполняется
при всех х.
6. Если а = 1, Ъ = 0, то равенство (1) также выполняется при
всех х.
7. Следовательно, обе пары чисел а = 0, Ь = 0иа = 1,Ь = 0 удов-
летворяют условию задачи.
8. Ответ: (0; 0); (1; 0).
30. При каких значениях параметра а уравнение
(х2 + 9) cos ах = 2(х2 - Зх + 9) (1)
имеет решения? Найти эти решения.
1. Уравнение (1) равносильно уравнению
2(х2-Зх + 9)
cos ах = —--------- , (2)
х2 + 9
правая часть которого положительна при всех х и в силу неравен-
ства |cos ах| < 1 не превосходит единицы.
2. Решив неравенство
2(х2-3х + 9) i
х2 + 9 ’
заключаем, что равенство (2) возможно лишь при х = 3, т. е. когда
cos За = 1.
3. Отсюда следует, что За = 2лй, /г '-Z, т. е. а = , k е Z.
О
4. Ответ: если а = , /г— Z, то х = 3.
О
221
31. В зависимости от значений параметра а решить уравнение
х2 + 4х cos ах + 4 = 0. (1)
1. Перепишем уравнение (1) следующим образом:
(х + 2 cos ах)2 + 4(1 - cos2 ах) = 0. (2)
2. Оба слагаемых в левой части уравнения (2) неотрицательны.
Следовательно, это уравнение равносильно системе
(х + 2 cos ах = 0,
| 1 - cos2 ах = 0,
или, что то же самое, совокупности двух систем:
[ х + 2 cos ах = 0,
5 1 (3)
I cos ах = 1; ' ’
1 х + 2 cos ах = 0,
< 1 (4)
I cos ах = -1. ' ’
3. Решив систему (3), находим х = -2, а = тт, п‘— Z.
4. Решив систему (4), получим х = 2, а = + nk, k — Z.
5. Ответ: если а = + лй, k е Z, то х = 2;
если а = тт, п — Z, то х = -2;
при других а уравнение не имеет решений.
32. В зависимости от значений параметра а определить число кор-
ней уравнения
sin4 х - cos4 х = a(tg4 х - ctg4 х), (1)
принадлежащих интервалу (О; | ).
1. Перепишем уравнение (1) в виде
. л л sin8 X - COS8 X
sin4 х - cos4 x = a-------— ,
sin4 x cos4 x
или
(sin4 x - cos4 x)[sin4 x cos4 x - a(sin4 x + cos4 x)] = 0. (2)
222
2. Уравнение (2) равносильно совокупности двух уравнений:
sin4 х - cos4 х = 0, (3)
sin4 х cos4 х - a(sin4 x + cos4 x) = 0. (4)
3. Уравнение (3) при любом значении параметра а имеет на ин-
тервале (О; | ) корень х = .
4. Уравнение (4) в результате преобразований приводится к виду
sin4 2х + 8а sin2 2х - 16а = 0. (5)
Полагая у = sin2 2х, получим уравнение
у2 + 8ау - 16а = 0, (6)
которое имеет действительные корни, если его дискриминант D =
= 64(а2 + а) > 0, т. е. если а> 0 или если а < -1.
При таких значениях а корнями уравнения (6) являются
уА = 4(7а(а + 1) - а), у2 = ~4( Ja(a + 1) + а).
5. Пусть а > 0. Тогда у2 < 0 и только корень у} уравнения (6)
может дать решения уравнения (5).
6. Учитывая, что речь идет об интервале (О; | ), приходим к не-
равенству
0 < 4(7а(а + 1) - а) < 1,
откуда 0 < а < |. При таких значениях а уравнение (5) имеет на
интервале (б; | ) два корня.
7. При а = | получим у1= 1, поэтому уравнение (5) имеет на
интервале (О; ) только один корень х = 2 .
8. При а > | уравнение (5) решений не имеет.
О
9. При а = 0 на интервале (О; ) уравнение (5) также не имеет
решений.
223
10. Если а < -1, то нетрудно убедиться, что корни у} и у2 не
удовлетворяют условиям 0 < у} < 1, 0 < у2 < 1, и, следовательно,
уравнение (5) снова не имеет решений.
11. Ответ: если а е (-оо; 0] U ; +°°^), то один корень;
если а (0; | ), то три корня.
33. При каких значениях параметра а уравнения
2 sin7 х - (1 - a) sin3 х + (2а3 - 2а - 1) sin х = 0 (1)
и
2 sin6 х + cos 2х = 1 + а - 2 а3 + a cos2 х (2)
равносильны?
1. Заметим, что х = л — корень уравнения (1) при любом а. Тог-
да согласно условию это значение должно быть и корнем уравне-
ния (2).
2. Подставляя х = л в уравнение (2), получаем равенство а3 = а.
Отсюда следует, что искомые значения параметра а могут прина-
длежать только множеству {0; -1; 1}.
3. Пусть а = 0. Тогда уравнения (1) и (2) перепишутся соответ-
ственно в виде
sin x(sin2 х - 1)(2 sin4 х + 2 sin2 х + 1) = 0,
и
sin2 х (sin2 х - l)(sin2 х + 1) = 0.
Так как
2 sin4 х + 2 sin2 х + 1 / 0 и sin х + 1 0,
то при а = 0 уравнения (1) и (2) равносильны.
4. Пусть а = -1. Тогда получим уравнения
sin х (2 sin6 х - 2 sin2 х - 1) = 0 и sin2 х (2 sin4 х - 3) = 0,
которые, как и в предыдущем случае, равносильны, поскольку
2 sin6 х - 2 sin2 х - 1 = 2 sin2 х (sin4 х - 1) - 1 < 0,
2 sin4 х - 3 < 0.
224
Таким образом, и при а = -1 уравнения (1) и (2) равносильны.
5. Пусть а = 1. Тогда уравнения (1) и (2) примут соответственно
вид
sin х (2 sin6 х - 1) = 0, sin1 2 3 х (2 sin4 5 х - 1) = 0.
Следовательно, с одной стороны, sin х = , а с другой sin х =
= 4Д . Поэтому
при а = 1 уравнения (1) и (2) не равносильны.
6. Ответ: а е {0; -1}.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все значения а, при которых имеет решение данное
уравнение:
a) cos2 х + 6 sin х = 4а2 - 2;
б) 5 sin х + 2 cos х = а;
в) Ja cos х - 2 sin х = J2 + J2 - а .
2. Решить относительно х уравнение:
a) a sin2 х + cos х = 0;
б) cos х - sin х = а;
в) sin (а + х) + sin х = cos |;
г) sin (х + а) + cos (х + а) = sin (х - а) + cos (х - а);
д) sin4 х - 2 cos2 х + а2 = 0;
е) cos6 х - sin6 х = cos 2х;
О
, sin х - 1 . sin х - 2
ж) --------з + а = ---------т .
sin х - 2 sin х - 3
3. Найти корни уравнения |cos 2х| = |sin2 х - а|, удовлетворяю-
щие условию 0 < х < 2л.
тт 2 - sin2 х
4. При каких значениях а уравнение + .---- = а имеет на от-
резке [0; 2л] ровно один корень?
5. Решить систему уравнений:
[ sin х + sin у = а, [ cos х - cos у = а,
a)J „ 6)1
\ I __ ТТ \ I __ тт
х + у = - ; \ х + у = — .
\ у 2 \ 3
225
Ответы
1. а) |а| < л/2 ; б) |а| < л/29 ; в) а е [Тб - 1; 2]. 2. а) Если а 0 0, то х =
= ±arccos -—+ + 2лга; если а = 0, то х = | + пп; б) если о - [ л/2 ; л/2 ],
то х = + arccos ~^= + 2пп; если а Г л/2 ; л/2 ], тох'- 0; в) если а = л +
4 л/2
+ 2nk, то х G R; если а л + 2л/г, то х = + (-1)л | + ли; г) если а = nk,
to х ~ R; если а 0 л/г, то х = + л/г; д) если а G (-оо; J2 ) U (л/2 ; +°°), то
.г Z; если а = ± л/2 , то х = л/г; если а~ ( л/2 ; л/2 ), то х = ± arccos (3 -
- 2ТЗ - а2 ) + л/г; е) если а е (-оо; 6] U [8; +°о), тох= у + ; если а е (6; 8),
ЛП , Л лп I 1 , гг\ \ Г 1 1 1
то х, = — + - , х9 = — ± - arccos (а - 7); ж) если а~ — ; - , то х =
1 2 4 2 2 4 L12 2J
, ,, „ . ( 5 1 /, , 4 А , Г 1 1 О
= (-1)” arcsin I - - - /1 + - I + ли; если а , то корней нет.
х. 2 2 Cl J |_ ±2 2 _|
о 1 1 - 2а ,1 1-2а П 1 1-2а, л
3. - arccos —-— , л ± - arccos —-— , 2тт - - arccos —-— (где -1ч ач 2);
2 о 2 о 2 о
1 arccos (2а - 1), л ± 1 arccos (2а - 1), 2л - 1 arccos (2а - 1) (где 0 < а < 1).
4. а = 0,5. 5. а) Если а G (-оо; -л/2 ) U (л/2 ; +°°), то решений нет; если а =
aJ2 „ , л
+ arccos —т— + 2л/г, и, = -
2 ’ у1 4
aJ2 „ , л aJ2
arccos —т— - 2л/г, х9 = - - arccos —т—
2 2 4 2
+ 2л/г,
л
Уг~ 4
б) если
_ 5л
“ ~6
+ arccos —— - 2л/г;
а е (-°°; -ТЗ ) U (ТЗ ; +°°), то решений нет;
Г» 7 71
+ 2т1/г, ц = -
и 4
если а =
- 2л/г;
- 2л/г,
71
У= Q
.fe + 1
х arcsin —у
О
- 2л/г, у
6 ’ у
л/г
~2 ’
5 л
~6
л , ,. ь . a J3 л /г
= л + ( arcsin —- + — ;
о о 2
2л/г.
У
4
3
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Решение тригонометрических неравенств вида
sin х > a, sin х < а
1°. Неравенства, содержащие переменную только под зна-
ком тригонометрической функции, называют тригонометриче-
скими.
2°. При решении тригонометрических не-
равенств используют свойство монотонности
тригонометрических функций, а также про-
межутки их знакопостоянства.
3°. Для решения простейших тригономет-
рических неравенств вида sin х > a, sin х < а
используют единичную окружность или гра-
фик функции у = sin х.
4°. Важно знать, что:
sin х = 0, если х = nk, /г'-Z;
sin х = -1, если х = + 2itk, k — Z:
sin х = 1, если х = | + 2itk, k — Z:
sin x > 0, если 2nk < х < л + 2лй, k r~ Z
(рис. 72, а);
sin х < 0, если -л + 2itk < х < 2itk, k r~ Z
(рис. 72, б).
Рис. 72
227
2. Решение тригонометрических неравенств вида
cos х > a, cos х < а
1°. Для решения простейших тригонометрических неравенств
вида cos х > a, cos х < а используют единичную окружность или
график функции у = cos х.
2°. Важно знать, что:
cos х = 0, если х = + лк, к — Z;
cos х = -1, если х = л + 2itk, к — Z;
cos х = 1, если х = 2itk, к — Z;
cos х > 0, если 2лк - < х < + 2itk, к — Z (рис. 73, а);
cos х < 0, если 2 л/г + | < х < + 2лк, к — Z (рис. 73, б).
Рис. 73
3. Решение тригонометрических неравенств вида
tg х > a, tg х < а
1°. Для решения простейших тригонометрических неравенств
вида tg х > a, tg х < а используют единичную окружность или гра-
фик функции у = tg х.
2°. Важно знать, что:
tg х > 0, если лк < х < + nk, к — Z (рис. 74, а);
tg х < 0, если лк - < х < iik, к — Z (рис. 74, б);
тангенс не существует, если х = + nk, к — Z.
228
Рис. 74
Замечание. Неравенства ctg х > 0 и ctg х < О выполняются
на тех же интервалах, что и неравенства tg х > 0 и tg х < 0.
ЗАДАЧИ С РЕШЕНИЯМИ
1. Решить неравенство sin х > а, где 0 < а < 1.
I способ. 1. На единичной окружности
построим дуги АС и АС1г синус которых ра-
вен а (рис. 75).
2. Из рисунка видно, что данному нера-
венству удовлетворяют все дуги, началом ко-
торых является точка С, а концом — любая
внутренняя точка дуги СВС}, т. е.
arcsin а < х < л - arcsin а.
3. Чтобы получить все решения данного неравенства, достаточ-
но прибавить к концам этого промежутка 2лй, /г '-Z.
4. Ответ: arcsin а + 2л/г < х < л - arcsin а + 2л/г, k е Z.
II способ. 1. Построим график функции у = sin х и прямую у =
= а (рис. 76).
229
2. На рисунке отмечены несколько промежутков значений х,
удовлетворяющих данному неравенству; одним из них является
(arcsin а; л - arcsin а).
3. Используя периодичность синуса, запишем ответ.
2. Решить неравенство sin х < а, где 0 < а < 1.
1. Используя рис. 75, заключаем, что данному неравенству
удовлетворяют все дуги, началом которых является точка Сх,
а концом — любая внутренняя точка дуги СХАС, т. е.
-л - arcsin а < х < arcsin а.
2. Чтобы получить все решения данного неравенства, приба-
вим к концам этого промежутка 2лй, /г -Z.
3. Ответ: -л - arcsin а + 2л/г < х < arcsin а + 2лй, k — Z.
4. Тот же результат получится, если рассмотреть график функ-
ции у = sin х и прямую у = а (см. рис. 76), а затем отметить те про-
межутки, на которых синусоида лежит ниже прямой у = а.
3. Решить неравенство cos х > а, где -1 < а < 0.
1. На единичной окружности построим дуги АС и АСХ, косинус
которых равен а (рис. 77).
Рис. 77
2. Из рисунка видно, что данному нера-
венству удовлетворяют все дуги, началом ко-
торых является точка Сх, а концом — любая
внутренняя точка дуги СХАС, т. е.
-arccos а < х < arccos а.
3. Учитывая периодичность косинуса, за-
пишем ответ.
4. Ответ: -arccos а + 2л/г < х < arccos а +
+ 2лй, /г -Z.
4. Решить неравенство cos х < а, где -1 < а < 0.
1. Используя рис. 77, заключаем, что данному неравенству
удовлетворяют все дуги, началом которых является точка С,
а концом — любая внутренняя точка дуги СА1С1, т. е.
arccos а < х < 2л - arccos а.
2. Учитывая периодичность косинуса, запишем ответ.
3. Ответ: arccos а + 2л/г < х < 2л - arccos а + 2лй, k1— Z.
230
5. Решить неравенство tg х > а.
1. Построим единичную окружность и
проведем ось тангенсов, которая является
касательной к окружности в точке А(1; 0)
(рис. 78).
2. На оси тангенсов находим точку С, ор-
дината которой равна а.
3. Точка пересечения отрезка ОС с ок-
ружностью есть конец дуги АР, тангенс кото-
рой равен а.
4. Из рис. 78 видно, что данному неравенству удовлетворяют
все дуги, началом которых является точка Р, а концом — любая
внутренняя точка дуги РВ, т. е.
arctg а < х < |.
5. Используя периодичность тангенса, запишем ответ.
6. Ответ: arctg а + nk < х < + nk, kr— Z.
6. Решить неравенство ctg х > а.
1. Построим единичную окружность
и проведем ось котангенсов, являющую-
ся касательной к окружности в точке
5(0; 1) (рис. 79).
2. На оси котангенсов возьмем точку
С, абсцисса которой равна а.
3. Точка пересечения отрезка ОС с ок-
ружностью есть конец дуги АР, котан-
генс которой равен а.
4. Из рис. 79 видно, что данному неравенству удовлетворяют
все дуги, началом которых является точка А, а концом — любая
внутренняя точка дуги АР, т. е.
0 < х < arcctg а.
5. Учитывая периодичность котангенса, запишем ответ.
6. Ответ: nk < х < arcctg а + ~k.
Замечание. Задачи 3—6 можно также решить графиче-
ски, используя графики соответствующих тригонометрических
функций.
231
7. В зависимости от значений параметра а решить неравенство
1
sin ах ч - - .
1. На единичной окружности находим две точки, ординаты ко-
торых равны (рис. 80).
Рис. 80
2. Одна из этих точек является концом
каждой из дуг множества arcsin ( -| ) + 2л/г =
= -^ + 2лй, а другая — концом каждой из
6
дуг множества -л - arcsin + 2лй = -л +
+ £ + 2лй = -^? + 2лА, k е Z.
6 6
3. Из рис. 80 видно, что данное неравен-
ство справедливо, когда
-Ё25 + 2лй < ах < + 2лй, /г -Z.
6 6
4. а) Отсюда при а > 0 получим
- f - + 2л/г - + 2~n.k \, k r— Z.
а V 6 7 а V 6 7
б) При а < 0 находим
- + 2л/й 2л/й, k‘-l.
a v 6 7 а б 7
в) При a = 0 решений нет.
5. Ответ: если а = 0, то решений нет;
если а > 0, то - f - + 2л/г - f - £ + 2лй\
а V 6 7 а б 7
если а < 0, то - f - + 2л/г - + 2лА \
а V 6 7 а б 7
k^Z.
8. В зависимости от значений параметра а решить неравенство
sin ах < Ь, где 0 < b < 1.
232
1. Построим на единичной окружности две точки с ординатой,
равной Ъ.
2. Данное неравенство справедливо, когда
-л - arcsin Ъ + 2л/г < ах < arcsin Ъ + 2лй, /г -Z.
3. а) Отсюда при а > 0 находим
- (л(2й - 1) - arcsin b) < х < - (arcsin b + 2nk), k — Z.
б) При а < 0 находим
- (arcsin Ъ + 2лй) < х < - (л(2/г - 1) - arcsin Ъ), k — Z.
в) Если а = 0, то х — любое действительное число.
4. Ответ: если а = 0, то х е R;
если а > 0, то
- (л(2й - 1) - arcsin b) < х < - (arcsin b + 2лй);
если а < 0, то
- (arcsin Ъ + 2лй) < х < - (л(2й - 1) - arcsin Ъ),
k^-Z.
9
Решить неравенство cos ах -
л А < _л/2
4 ) " 2 ’
1. На единичной окружности найдем две точки, абсциссы кото-
72
рых равны (рис. 81).
2. Данное неравенство верно, когда
+ 2л/г < ах - у -г- + 2nk,
4 4 4
т. е.
л + 2л/г < ах < + 2лй, /r'-Z.
3. а) Отсюда при а > 0 находим
- (л + 2лй) < х < - ( + 2л/г \ k Z.
а а \ 2 7
233
б) При а < 0 находим
1 f Зп + < х < - (л + 2лй), /г- Z.
а \ 2 7 а
в) При а = 0 решений нет.
4. Ответ: если а = 0, то решений нет;
если а > 0, то - (л + 2л/г) < х < - f + 2л/г ;
а а \ 2 7
если а < 0, то - f + 2л/г < х < - (л + 2л/г), /гZ.
а \ 2 7 а
10. В зависимости от значений параметра а решить неравенство
tg(ax + 2) > 73 .
1. На оси тангенсов находим точку С, ордината которой
равна л/З (рис. 82).
Рис. 82
2. Точка пересечения отрезка ОС с окруж-
ностью является концом дуги .
О
3. Поскольку период тангенса равен л, за-
ключаем, что данное неравенство справедли-
во при
+ Tik < ах + 2 < + л/?,
о Л
или
-2 + + л/г < ах < -2 + + лй,
О Л
4. а) Отсюда при а > 0 имеем
- ( £ -2 + л/й<х<-Г^ - 2 + лА \ k & Z.
а V 3 7 а \ 2 7
б) При а < 0 получим
- f - 2 + лйЧ)<хС-Г5 - 2 + nk\,k^ Z.
а \ 2 7 а З 7
в) Если а = 0, то неравенство примет вид tg 2 > ^/З , что неверно.
Следовательно, при а = 0 оно не имеет решений.
234
5. Ответ: если а = 0, то решений нет;
если а > 0, то - f -2 + л/й<х<-Г^ - 2 + ~k
а V 3 / а V 2
если а < 0, то - f -2 + л/й<хС-Г^ - 2 + ~k
а \.2 ) а \ 3
k^Z.
11. В зависимости от значений параметра т решить неравенство
ctg (тх - 1) < 2.
1. На оси котангенсов находим точку С,
абсцисса которой равна 2 (рис. 83).
2. Точка пересечения отрезка ОС с ок-
ружностью есть конец дуги arcctg 2.
3. Так как период котангенса равен л,
то приходим к выводу, что данное нера-
венство верно при
arcctg 2 + л/г < тх - 1 < л + лй,
или
1 + arcctg 2 + л/г < тх < 1 + л + лй.
4. а) Отсюда при т > 0 находим
— (1 + arcctg 2 + л/г) < х < — (1 + л + лй), k'-2.
т т
б) При т < 0 получим
— (1 + л + лй) < х < — (1 + arcctg 2 + лй), k'-Z.
т т
в) При т = 0 неравенство примет вид ctg (-1) < 2, что верно.
Значит, при т = 0 неравенство справедливо для любых х.
5. Ответ: если т = 0, то х е R;
если т > 0, то
— (1 + arcctg 2 + лй) < х < — (1 + л + лй);
т т
если т < 0, то
— (1 + л + л/г) < х < — (1 + arcctg 2 + лй), /г -Z.
т т
235
1 2. В зависимости от значений параметра а решить неравенство
(а - 2) sin х > За + 4. (1)
1. Очевидно, что при а = 2 неравенство (1) не имеет решений.
2. Будем считать, что а - 2 0. При таких значениях парамет-
ра а рассмотрим сначала случай а - 2 < 0. В этом случае неравенст-
во (1) равносильно неравенству sin х <-— .
Тогда при выполнении условий
[ а - 2 < 0,
л За + 4 <
[ а-2 "
т. е. при < а < 2, неравенство (1) не имеет решений.
3. Если же выполняются условия
[ а - 2 < 0,
л За + 4 ч
[ а-2
т. е. если а < -3, то решением неравенства (1) является любое х.
4. Далее, если
[ а - 2 < 0,
Л _ 1 < За + 4
[ а - 2 ’
т. е. если -3 < а < , то неравенство (1) имеет следующие реше-
ния:
-arcsin + + л(2й - 1) < х < arcsin „ + 2лй,k '-2.
а-2 а-2
5. Рассмотрим теперь случай а - 2 > 0. В этом случае ——> 1,
а потому неравенство (1) не имеет решений.
6. Ответ: если а < -3, то х е R;
if _ _. 1 3а "Ь 4 . /о, i \ _- _-
если —3 ч а < -- , то -arcsm -— + л(2/г - 1) < х <
2 а-2
< arcsin + + 2nk, k & Z;
а-2
1
если а > - - , то решении нет.
236
13. При каких значениях параметра а неравенство
а(4 - sin х)4 - 3 + cos2 х + а > 0 (1)
справедливо для любых значений х?
1. Поскольку неравенство (1) должно выполняться при всех
значениях переменной х, оно должно выполняться и при х = .
При этом значении х из неравенства (1) следует, что 82а - 3 > 0.
2. Таким образом, все значения параметра а, удовлетворяющие
требованию задачи, принадлежат промежутку а > — .
82
3. Замечая теперь, что при любом значении переменной х спра-
ведливы неравенства cos2 х > 0, 4 - sin х > 3, (4 - sin х)4 > 81 и при
этом а > 0, получим
а(4 - sin х)4 - 3 + cos2 х + а > 81а - 3 + а = 82а - 3 > 0.
. тт 3
4. Итак, все значения а из промежутка а > — удовлетворяют
требованию задачи.
5. Ответ: а е ( А ; +оо ).
\ 82 7
14. При каких значениях параметра а квадратное уравнение
8х2 + 8х cos а + 1 = 0 (1)
не имеет действительных корней?
1. Найдем дискриминант уравнения (1):
D = (8 cos а)2 - 4 • 8 = 32(2 cos2 а - 1).
Если он отрицателен, т. е. если
2 cos2 а - 1 < 0, (2)
то квадратное уравнение (1) не имеет действительных корней.
2. Неравенство (2) равносильно неравенству cos 2а < 0, решив
которое получим ответ.
3. Ответ: + лй < а < + л/г, k е Z.
4 4
237
1 5. При каких значениях параметра а неравенство
а2 + 2а - sin2 х - 2а cos х > 2
справедливо для любого х?
1. Так как sin2 х = 1 - cos2 х и множество значений функции
у = cos х есть промежуток [-1; 1], то задачу можно переформулиро-
вать так: при каких значениях параметра а наименьшее значение
квадратного трехчлена
f(y) = У2 ~ 2ау + а2 + 2а - 3
(1)
на отрезке -1 < у < 1 положительно?
2. В силу того, что абсцисса вершины параболы (1) равна а, за-
ключаем, что наименьшее значение функции (1) на отрезке [-1; 1]
есть:
/(-1) = а2 + 4а - 2,
/(а) = 2а - 3,
/(1) = а2 - 2,
если а < -1;
если -1 < а < 1;
если а > 1.
3. Учитывая, что быть положительным тем неравенств: наименьшее значение функции f(y) должно , приходим к совокупности следующих сис- J а2 + 4а - 2 > 0, ]а<-1; () J 2а - 3 > 0, ]-1<а<1; К-Г0’ w \ а > 1.
4. Решение системы (2) есть промежуток < а < -2 - л/6 ,
система (3) несовместна, а решение системы (4) — промежуток
л/2 < а < +°°.
5. Ответ: а -2 - д/б ) U (л/2 ; +°°).
1 6. При каких значениях параметра k неравенство
sin4 5 6 х + cos6 х + k sin x cos x > 0
(1)
справедливо для всех значений х?
238
1. Преобразуем левую часть неравенства (1). Имеем
sin6 х + cos6 х + k sin x cos x = (sin2 x)s + (cos2 x)s + k sin x cos x =
= (sin2 x + cos2 x)((sin2 x + cos2 x)2 - 3 sin2 x cos2 x) + k sin x cos x =
= 1 - 7 sin2 2x + sin 2x. (2)
4 2
2. Используя подстановку у = sin 2x, сведем неравенство (2)
к равносильному неравенству
-|у2+ ^у + 1 >0.
3. Теперь задачу можно переформулиро-
вать так: при каких значениях параметра k
неравенство (3) справедливо для всех у из про-
межутка [-1; 1]?
4. Обозначим квадратный трехчлен в ле-
вой части неравенства (3) через f(y). Так как
ветви параболы, соответствующей этому трех-
члену, направлены вниз (рис. 84), то требова-
ние задачи выполняется, если совместна сис-
тема
J /(-1) > 0, Jl -2k >0,
|/(1)> 0, ИЛИ [ 1 + 2й > 0.
1
2 ’
т> 1 < ' г, < '
Решив последнюю систему, находим -- ч k ч
5. Ответ: k е
17. При каких значениях aub система неравенств
а + sin Ьх < 1,
х2 + ах + 1 < 0
(1)
(2)
имеет единственное решение?
1. Необходимым условием существования единственного реше-
ния данной системы является равенство нулю дискриминанта D =
= а2 - 4 квадратного трехчлена в левой части неравенства (2).
2. Таким образом, требуемыми значениями параметра а могут
быть только а = -2 и а = 2.
3. Если а = -2, то х = 1, а неравенство (1) примет вид sin b < 3
и, следовательно, b — любое число.
239
4. Если а = 2, то х = -1, а неравенство (1) примет вид sin & > 1.
Решением этого неравенства являются значения b = + 2nk, k— Z.
5. Ответ: а = -2, b r— R; а = 2, b = + 2nk, k — Z.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. В зависимости от значений параметра а решить неравенство:
a) sin х > а (-1 < а < 0);
в) sin fax -
б) cos х > a (0 < а < 1);
fl)tg(= ~ах}<^;
2. Решить неравенство:
а) sin2 + a sin2 х > |;
ч , ( 2л ; л/3
е) ctg [ах + — I > V •
v Э ' о
в) 0 < cos х < 4 - a2;
б) cos х - —-— < а:
COS X
г) sin2 х + —3^— > а.
sin2 х
3. Найти значения параметра а, при которых для всех х - й
выполняется неравенство:
а) sin 2х + (а + 1)^/2 sin f х - j < 2а;
б) sin2 х - (а + 1) sin 2х + 2а + 3 > 0;
в) cos2 х + (а + 1) sin х < 2 + За.
4. Найти все значения а, при которых неравенство
sin5 х + cos5 х - a(sin х + cos х) > а ** (sin х + cos х) sin х cos х
верно для всех х таких, что 0 < х <
л
4 ’
Ответы
1. а) arcsin а + 2 л/г < х < л - arcsin а + 2л/г; б) 2л/г - arccos а < х < 2л/г +
1 А 5 тт Л
+ arccos а; в) если а = 0, то решений нет; если а > 0, то - I 2л/г - — I < х <
- С 2л/г - 2L 'l; если а < 0, то - f 2л/г - 2L 'j < х < - f 2л/г - \ г) если
а к 12 / а v 12/ а \ 12/
240
a = 0, то х G R: если a > 0, то - ( 2nk - 'l < х < - • 2nk: если а < 0, то
а v 3 7 а
- • 2nk < х < - ( 2nk - — 'l; д) если а = 0, то х G R- если а > 0, то - f - — +
а а 7 3 7 а 7 24
+ + nk\; если а < 0, то - ( + nk] < х < - ( + nk 'l;
7 а \ 8 7 а \ 8 7 а к 24 7
е) если а = 0, то решений нет; если а> 0, то - ( nk - < х - (nk -
d \ t) / d \ 1. <Э /
если а < 0, то - f л/г - 'l < х < - f nfe - Y 2. а) Если а = 0, то +
а \ 15 7 а \ 5 7 2
+ 2nh < х < + 2nk; если а Z 0, то arccos + 16а-—- + 2nk < х <
2 4а
< -arccos + 16а-—- + 2n(k + 1); б) если а < 0, то + 2nk < х < 2nk -
4а 2
а + л/а2 + 4 а + Ja2 1 4 , л , , , л . л , „
- arccos --, arccos --------------- + 2nk < х < + 2л«; если а = 0, то х =
= л(2/г + 1), -| + 2л/г < х < | + 2nk; если а > 0, то -| + 2л/г < х < | + 2nk,
arccos -—+ 4 + 2nk < х < -arccos -—+ 4 + 2n(fe + 1); в) если |а| < ^3 ,
то -| + 2nk < х < | + 2nk; если < |а| < 2, то arccos (4 - а2) + 2nk < х <
< | + 2nk, -| + 2nk < х < 2nk - arccos (4 - а2); если |а| > 2, то решений нет;
г) если а < 0, то х G R, кроме х = nk; если 0 < а < 2, то решений нет; если
а > 2, то 2nk < х < arcsin + 2nk, л - arcsin + 2-п.к <
< х < л + 2nk. 3. а) а G (1; +<х>); б) (3 - 2 J5 ; +оо); в)а _ (5 2л/7; +оо).
4. а - [-6; 1].
т
т
Гема
п
риращение аргумента и приращение функдо к - - -
2. Определение производной Z Z Z Z
3. Производная суммы, произведения, частного' - - - -
4. Производная степенной и сложной функции " 21
ные тригонометрических функций
ние производной к нахождению промежутке
монотонности функции I I I I I I I I I | | | | | |
_1_|_ 7. Критические точки функции, ее максимумы и минимумы
“ “ 8. Общая схема исследования функции _
- -. 9. Задачи на отыскание наименьшего и наибольшей . . . .
" значений функции I I I I I I I I I I I I I I I I " 2 2 Z
- - Ш-Касательная к графику функции
1111.____________________________i I I I I I I I I I I I I
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Приращение аргумента и приращение функции
1°. Пусть у = f(x) — функция, х и х0 — два значения независи-
мой переменной из D(f); тогда разность х - х0 называют прираще-
нием независимой переменной (или приращением аргумента)
и обозначают Ах (читается: «дельта икс»). Таким образом,
\х = X - х0. (1)
2°. Из равенства(1)следует, что
х = х0 + Ах, (2)
т. е. первоначальное значение переменной получило приращение Ах.
Соответственно значение функции изменится на величину
/(х) - /(х0) = /(х0 + Ах) - /(х0). (3)
3°. Разность между новым значением функции /(х0 + Ах) и пер-
воначальным ее значением /(х0) называют приращением функции
242
в точке х0 и обозначают символом А/(х0) (читается: «дельта эф в
точке х0»), т. е.
А/(х0) = f(x0 + Ах) - /(х0). (4)
4°. Приращение функции f в дан-
ной точке х0 кратко обозначают че-
рез А/ или Ау (рис. 85).
5°. Понятия приращения функ-
ции и приращения аргумента по-
зволяют сформулировать признаки
возрастания и убывания функций.
а) Функция f(x) возрастает на
промежутке X тогда и только тогда,
когда для любых значений х0 и х0 +
+ Ах (Ах 0) из промежутка X вы-
А/(х0) . п
полняется неравенство —-— > 0.
б) Функция /(х) убывает на промежутке X тогда и только тогда,
когда для любых значений х0 и х0 + Ах (Ах 0) из промежутка X
А/(х0) . п
выполняется неравенство —-— < 0.
2. Определение производной
1°. Производной функции /(х) в точке х0 называют предел отно-
шения приращения А/ функции в точке х0 к приращению Ах аргу-
мента, когда последнее стремится к нулю. Это можно записать так:
lim
Ах —> 0 &Х
= f(x0)
(читается: «эф штрих от х0»).
2°. Из определения производной следует, что функция может
иметь производную в точке х0 только в том случае, если она опре-
делена в некоторой окрестности точки х0, включая эту точку.
Заметим, что обратное утверждение является неверным.
3°. Нахождение производной функции у = f(x) называют диф-
ференцированием этой функции.
4°. Вычисление производной функции у = f(x) производится
в соответствии с правилом дифференцирования:
а) фиксируют значение аргумента х и находят /(х);
243
б) дают аргументу х приращение Ах и находят f(x + Ах);
в) находят приращение функции А/ = /(х + Ах) - /(х);
г) делят приращение функции А/ на приращение аргумента Ах,
т. е. составляют отношение
А/ _ /(х + Ах) - /(х) .
Ах Ах ’
д) находят предел этого отношения при Ах 0:
lim ¥ = Нт Л^ + Ах)-/(х).
Найденный предел и есть производная функции у = f(x).
5°. Производная постоянной функции равна нулю: с’ = 0, где
с = const.
6°. Производная функции у = х равна 1: х' = 1.
7°. Производная функции у = Jx равна —: (Jx)' = —, х > 0.
2 л/х 2 л/х
3. Производная суммы, произведения, частного
1°. Производная суммы. Пусть миг — две функции, определен-
ные на одном и том же промежутке. Тогда производная суммы этих
функций равна сумме их производных, если они существуют, т. е.
(п(х) + t>(x))' = и'(х) + v’(x). (1)
Эта формула справедлива для любого конечного числа сла-
гаемых.
2°. Производная произведения. Производная произведения двух
функций и и v вычисляется по формуле
(uv)’ = u'v + uv' (2)
в предположении, что производные и' и v' существуют.
3°. Постоянный множитель можно выносить за знак произ-
водной:
(А/(х))' = kf(x). (3)
4°. Производная частного. Если функции миг имеют в точке х
производные и если t>(x) 0, то в этой точке существует производ-
ная их частного , которая вычисляется по формуле
С и У _ u'v - uv' Z . V
I U J J2 • >
244
5°. Частные случаи формулы (4):
1 ,
= - и ,
с
(5)
(6)
(7)
4. Производная степенной и сложной функции
1°. Производная степенной функции. Производная степенной
функции xk, где k е R, х > 0, вычисляется по формуле
(xk)' = kxk ~ 1. (1)
2°. Заметим, что если /г- Z, то формула (1) справедлива для
всех значений х е R, кроме х = 0. Если же при этом k > 1, то фор-
мула (1) справедлива для х е R.
3°. Производная сложной функции. Производная сложной функ-
ции равна произведению ее производной по промежуточному аргу-
менту на производную этого аргумента по независимой переменной:
У'х = У'и • и'х • (2)
4°. Формулы дифференцирования
При условии и = ф(х) При условии и = х
с' = 0 (3) х' = 1 (4)
(uk)' = k uk~ 1 • и', k‘— R (5) (хкУ = k • xk ~ 1, k е R (5а)
Г V"' v U / (:Н <6а)
(7) 2 Ju (аД)-= 1 (7а) 2jx
5. Производные тригонометрических функций
1°. Производные тригонометрических функций находятся по
следующим формулам:
(sin х)’ = cos х, (cos х)’ = -sin х,
(tg %У = , (ctg х)' = --Д- •
COS^ X sin4 X
245
Каждая из этих формул справедлива в любой точке области оп-
ределения соответствующей функции.
2°. Формулы дифференцирования
При условии и = <р(х) При условии и = х
(sin и)' = cos и и' (1) (sin х)’ = cos х (la)
(cos и)' = -sin и и' (2) (cos х)’ = -sin х (2a)
(tg и)' = и’ cos^ и (3) (tg х\ = -L- COS^ X (3a)
, . v 1 (ctg и)' = - —‘ W sin4 и (4) , . V 1 (ctg x)f = sin4 x (4a)
6. Применение производной к нахождению
промежутков монотонности функции
1°.Теорем а 1. Если производная функции f в точке х0
положительна, то функция возрастает в некоторой окрестнос-
ти этой точки.
Если производная функции f в точке х0 отрицательна, то
функция убывает в некоторой окрестности этой точки.
2°. На рис. 86, а и 86, б графически иллюстрируется возрас-
тание и убывание функции в зависимости от знака ее производной
в окрестности данной точки х0.
Функция, график которой изображен на рис. 86, а, возрастает
в окрестности точки х0, так как f'(x0) = tg а > 0; функция, график
которой изображен на рис. 86, б, убывает в окрестности точки х0,
поскольку f'(x0) = tg а < 0.
3°.Теорема 2 (достаточное условие возрастания (убыва-
ния) функции на интервале). Если функция f имеет положитель-
нее. 86
246
ную производную в каждой точке интервала (а; Ь), то функция
возрастает на этом интервале.
Если функция f имеет отрицательную производную в каждой
точке интервала (а; Ъ), то функция убывает на этом интервале.
4°. Следует отметить, что если функция / монотонна на интер-
вале (а; Ъ) и непрерывна в точках а и Ъ, то она монотонна и на от-
резке [а; Ь].
7. Критические точки функции, ее максимумы и минимумы
1°. Внутренние точки области определения функции, в кото-
рых производная функции равна нулю или не существует, называ-
ют критическими.
2°. Точку х0 из области определения функции f называют точ-
кой минимума этой функции, если найдется такая 8-окрестность
(х0 - 8; х0 + 8) точки х0, что для всех х х0 из этой окрестности
выполняется неравенство f(x) > f(x0).
3°. Точку х0 из области определения функции f называют точ-
кой максимума этой функции, если найдется такая 8-окрестность
(х0 - 8; х0 + 8) точки х0, что для всех х х0 из этой окрестности
выполняется неравенство f(x) < f(x0).
4°. Точки минимума и максимума называют точками экстре-
мума данной функции, а значения функции в этих точках — соот-
ветственно минимумом и максимумом функции (или экстрему-
мом функции).
5°. а) Функция у = f(x), график которой изображен на рис. 87,
в точках х1 и х3 имеет минимумы (z/min), а в точках х2 и х4 — мак-
симумы (z/max).
б) Заметим, что точки а и & не считаются точками экстремума
функции /, так как у этих точек нет окрестности, целиком входя-
щей в область определения функции.
---------\----\-----\-------\------\----\-----
О a xr х2 х3 х4 b х
Рис. 87
247
6°. Теорема Ферма (необходимое условие существова-
ния экстремума функции). Если точка х0 является точкой экс-
тремума функции f(x) и в этой точке существует производная,
то она равна нулю, т. е. f’(x0) = 0.
Например, функция f(x) = х2 - 2х + 1 в точке х = 1 имеет мини-
мум, следовательно, по теореме Ферма производная функции в этой
точке равна нулю: /'(1) = 0.
7°. Отметим, что теорема Ферма выражает лишь необходимое
условие существования экстремума: из того, что производная обра-
щается в нуль или не существует в данной точке х0, не следует, что
х0 — точка экстремума.
Например:
а) Производная функции f(x) = х3 (рис. 88, а) в точке х = 0 рав-
на нулю: f’(x) = Зх2, /'(0)= 0- Однако в этой точке функция не имеет
экстремума.
б) Производная функции f(x) = 2х + |х| (рис. 88, б) в точке х = 0
не существует. В этой точке функция не имеет экстремума.
8°. Достаточные условия существования экстремума. Пусть
функция f(x) непрерывна в точке х0 и имеет производную f’(x)
в некоторой окрестности (а; Ь) этой точки. Тогда:
а) если f'(x) < 0 на интервале (а; х0) и f'(x0) > 0 на интервале
(х0; Ь) (т. е. производная меняет знак с минуса на плюс), то х0 —
точка минимума функции /(х);
б) если f'(x) > 0 на интервале (а; х0) и f'(x0) < 0 на интервале
(х0; Ь) (т. е. производная меняет знак с плюса на минус), то х0 —
точка максимума функции /(х).
Рис. 88
248
8. Общая схема исследования функции
1°. Находят область определения функции.
2°. Проверяют, не является ли функция четной или нечетной.
3°. Находят, если это возможно, точки пересечения графика
функции с осями координат и промежутки знакопостоянства
функции.
4°. Находят производную функции и ее критические точки.
5°. Находят промежутки монотонности и экстремумы функции.
6°. Строят график функции, используя полученные результа-
ты исследования.
9. Задачи на отыскание наименьшего и наибольшего
значений функции
1°. На рис. 89 изображен график некоторой функции /, опре-
деленной на отрезке [а; &]. В точке х2 функция имеет максимум,
а в точках х} и х3 — минимумы.
Как видно из рисунка, функция достигает наименьшего значе-
ния в точке х3 — точке минимума.
Наибольшее значение функция принимает на конце отрезка
в точке Ь, в которой функция не имеет экстремума (так как справа
от точки b функция не определена).
2°. Для отыскания наименьшего и наибольшего значений функ-
ции, дифференцируемой внутри отрезка и непрерывной на его кон-
цах, следует найти все критические точки функции, лежащие вну-
три отрезка, вычислить значения функции в этих точках и на кон-
цах отрезка, а затем из всех полученных таким образом чисел
выбрать наименьшее и наибольшее.
Рис. 89
249
10. Касательная к графику функции
1°. Касательной к кривой в данной точке М называют пре-
дельное положение секущей NM, когда точка N приближается
вдоль кривой к точке М.
2°. В соответствии с определением касательной получаем
k = tg ф = lim = f’(x).
Таким образом, угловой коэффициент касательной к графику
функции равен значению производной этой функции в точке ка-
сания.
3°. Уравнение касательной к кривой у = f(x) в заданной точке
имеет вид
У - Уо = /'(*о)(* - х0),
где (х0; у0) — координаты точки касания, (х; у) — текущие коорди-
наты, т. е. координаты любой точки, принадлежащей касатель-
ной, a f'(x0) = k = tg ф — угловой коэффициент касательной.
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра а функция
/(х) = 2ах3 + 9ах2 + ЗОах + 66
убывает для всех значений х?
1. Функция /(х) убывает для всех значений х, если производная
f(x) = бах2 + 18ах + 30а = 6а(х2 + Зх + 5) < 0
для всех х.
2. Отсюда находим, что а < 0.
3. Ответ: а е (-оо; 0).
2. Определить значения а и & так, чтобы многочлен
/(х) = х5 + ах2 + Ъх + 1
имел число (-2) корнем не ниже второй кратности.
1. Число (-2) является корнем не ниже второй кратности мно-
гочлена /(х), если значения многочлена /(х) и его производной
f(x) = 5х4 + 2ах + Ъ при х = -2 равны нулю.
250
2. Приравнивая /(-2) и /'(-2) нулю, получим систему уравнений
J 4а-2& = 31,
| -4а + Ъ = -80,
129
решив которую найдем а = , b = 49.
3. Ответ: а = 32,25, b = 49.
3. Найти все значения параметра а, при которых уравнение
л/2х + а = х + 3 имеет ровно один корень. В ответе указать на-
именьшее целое значение а.
1. В данном случае полезно воспользоваться графической ил-
люстрацией (рис. 90).
2. Графиком функции у = х + 3 является прямая, пересекаю-
щая ось абсцисс в точке х0 = -3, а ось ординат — в точке у0 = 3.
3. Графиком функции у = J2x + а для различных значений а
является семейство ветвей парабол, вершины которых находятся
в точке ; О), а сами ветви расположены выше оси Ох.
4. На рис. 90 изображены три такие параболы. Видно, что при
увеличении а парабола смещается влево.
5. Парабола I не имеет с прямой у = х + 3 общих точек, парабо-
ла II имеет с этой прямой одну общую точку В (в которой прямая
касается параболы) и, наконец, парабола III пересекается с пря-
мой у = х + 3 в двух точках.
251
6. При дальнейшем увеличении а парабола у = J2x + а будет
пересекать прямую у = х + 3 только в одной точке.
7. Найдем значение параметра, соответствующее точке А. В этой
точке имеем х0 = -3 и 2х0 + а = 0, поэтому а = 6. Значит, при а > 6
данное уравнение будет иметь ровно один корень.
8. Найдем значение параметра, соответствующее точке В. Так
как в этой точке прямая у = х + 3 и парабола у = J2x + а касают-
ся, то производные рассматриваемых функций совпадают, т. е.
— 2 = 1, откуда J2x + а = 1.
2j2x + а
9. Подставив это выражение в исходное уравнение, получим
х + 3 = 1, откуда х = -2. Поэтому + а = 1, т. е. а = 5.
10. Таким образом, а е (6; +°о) и {5}.
11. Ответ: а = 5.
4. При каких значениях параметра а функция
/(х) = (а2 - За + 2)(cos2 - sin2 ) + (а - 1)х + sin 1
не имеет критических точек?
1. Так как данная функция дифференцируема на всей число-
вой прямой, то критическими точками функции f(x) являются те
точки, в которых производная f'(x) = 0.
2. В данном случае имеем
f'(x) = 1 (а - 1)(а - 2)(-sin + (а - 1).
3. Очевидно, что если а = 1, то Г(х) = 0 ПРИ любом х е R, т. е.
для заданной функции каждая точка х е R является критической.
4. Предположим, что а 1. Тогда уравнение У'(х) = 0 примет
вид
(а - 2) sin = 2. (1)
Отсюда следует, что если |а - 2| < 2, т. е. если а е (0; 1) U (1; 4),
то уравнение (1) не имеет корней и, значит, при указанных значе-
ниях а функция f(x) не имеет критических точек.
5. Ответ: а е (0; 1) U (1; 4).
252
5. При каком значении а минимум функции у = ах2 + 4ах + 7 а2 - 1
равен 2?
1. Найдем критические точки данной функции:
у’ = 2ах + 4а, у’ = 0 при х = -2.
2. В точке х = -2 функция имеет экстремум, равный 2. Таким
образом, /(-2) = 4а - 8а + 7а2 -1 = 2, откуда 7а2 - 4а - 3 = 0, т. е.
3 1
аг = --;а2 = 1.
3. Мы нашли два значения а; какое из них следует взять?
4. Так как данная функция имеет в критической точке мини-
мум, то коэффициент при х2 должен быть положительным.
5. Ответ: а = 1.
6. При каком значении а наибольшее значение функции у = 2xs -
- 6х + а на отрезке [-2; 0] равно 5?
1. Выясним, имеет ли функция у = 2xs - 6х + а на отрезке [-2; 0]
критические точки.
2. Производная данной функции у' = Ъх2 - 6 равна нулю при
х = ±1.
3. Следовательно, отрезку [-2; 0] принадлежит одна критиче-
ская точка: х = -1.
4. Найдем значения функции на концах отрезка и в критиче-
ской точке: у(~2) = а - 4; у(-1) = а + 4; у(0) = а.
5. Наибольшее из этих значений у(-1) = а + 4. Оно и равно 5.
Следовательно, 4 + а = 5, откуда а = 1.
6. Ответ: а = 1.
7. Найти значения параметра а, при которых произведение дейст-
вительных корней уравнения
х2 + 2(а - 6)х + 2а2 - 17а + 42 = 0
принимает наибольшее значение.
1. Уравнение должно иметь корни, поэтому D > 0.
2. Находим
= (а - 6)2 - (2а2 - 17а + 42) = -а2 + 5а - 6 > 0,
откуда 2 < а < 3.
253
3. Согласно теореме Виета, имеем хгх2 = 2а2 - 17а + 42. Следо-
вательно, задача сводится к отысканию наибольшего значения
функции f(a) = 2а2 - 17а + 42 на отрезке 2 < а < 3.
4. Находим критические точки функции: f(a) = 4а - 17, а =
= 4,25 £ [2; 3].
5. Значит, наибольшее значение функции /(а) следует искать
на концах отрезка [2; 3]; имеем /(2) = 16; /(3) = 9.
6. Итак, произведение корней уравнения достигает наибольше-
го значения при а = 2.
7. Ответ: а = 2.
8. В зависимости от значений параметра а найти наибольшее зна-
чение функции
1
г2 _ „4 _ о „2
С4 vV vV О С4
(1)
на отрезке [-2; 1].
1. Дискриминант квадратного (относительно х2) трехчлена
2ах2 - х4 - За2 равен (-8а2), поэтому при любом значении парамет-
ра а и любом х из области определения функции f(x) ее значения
отрицательны. Кроме того, так как f(x) = f(~x), то график этой
функции при каждом фиксированном значении а симметричен от-
носительно оси ординат.
2. Найдем производную функции /(х). Имеем
№) - „ ,,, <2)
(2ах^ - х4 - 3az)z
а) Если а < 0, то справедливо неравенство х2 - а > 0 и, значит,
f(x) = 0 только при х = 0.
б) Поэтому f(x) < 0 при х < 0 и f'(x) > 0 при х > 0.
в) Таким образом, в точке х = 0 функция /(х) имеет минимум,
а наибольшее значение она принимает на левом конце данного от-
резка, т. е. в точке х = -2 (в силу симметрии графика относительно
оси ординат и того, что |-2| > 1).
3. Находим
Д-2) = -----------.
За2-8а+16
4. Если а = 0, то данная функция примет вид Дх) = ; эта
X4
функция убывает при х < 0 и возрастает при х > 0 и, следовательно,
254
в точке х = -2 она принимает наибольшее значение, которое равно
Н)-
5. Если а > 0, то производная /Дх) имеет три критические
точки: хг = - д/a , х2 = 0, х3 = *]а . В этом случае f'(x) < 0 при х е
(-оо; -Ja ) U (0; л/а ) и f(x) > 0 при х е (- J~a ; 0) U (Ja ; +°°).
6. В точке х = 0 функция f(x) имеет локальный максимум, ко-
торый равен (- . Для того чтобы полученное значение было
наибольшим, нужно, чтобы выполнялось неравенство
1 1 > о
“< -—5 , т. е. а > 2.
За2-8а+16 За2
7. Ответ: если а е (-оо; 2), то max f(x) = /(-2) = -—5-;
[ 2. i] За2 - 8а + 16
если а е [2; +°°), то max f(x) = /(0) = --Ц .
[2; 1] За
9. В зависимости от значений параметра t 0 найти значения па-
раметра а, при которых уравнение
2х3 - 3fx2 + t = а (1)
имеет три различных корня.
1. Для того чтобы уравнение (1) имело три различных корня,
функция
f(x) = 2х3 - 3tx2 + t - а (2)
должна иметь локальный максимум и локальный минимум такие,
что /(Хтах) > 0, /(xmin) < 0, где хтах < xmin.
2. Найдем экстремумы функции (2). Для этого решим уравнение
f(x) = 6х2 - 6tx = 0.
Очевидно, что х} = 0, х2 = t.
3. Пусть t > 0. Тогда х1 < х2 и х1 — точка максимума, а х2 —
точка минимума функции /(х). В этом случае имеем
/(хД = t - а > 0, /(х2) = 2f3 - 3f3 + t- a = t-t3-a<0,
и,следовательно,t - t3 < а < t.
255
4. Пусть t < 0. Тогда х2 < х1 и теперь х2 — точка максимума,
а х1 — точка минимума функции f(x). В этом случае имеем
Дх2) = t - t3 - а > 0, /(хх) = t - а < 0
и, значит, t < а < t - t3.
5. Ответ: если t < 0, то t < а < t - t3;
если t > 0, то t - t3 < а < t.
10. В зависимости от значений параметра/, указать те значения
параметра k, при которых уравнение
x3 + 2px2+p = k (1)
имеет три различных действительных корня.
1. Для того чтобы уравнение (1) имело три действительных
корня, функция
f(x) = х3 + Зрх2 + р - k (2)
должна иметь локальный максимум и локальный минимум, при-
чем Дхтах) > 0, a /(xmin) < 0.
2. Так как коэффициент при х3 положителен, то xmax < xmin.
3. Найдем экстремумы функции (2). Имеем f’(x) = Зх2 + 4рх.
Производная обращается в нуль при = 0их2 = -у .
4. Возможны три случая.
а) Еслир > 0, то х2 < х1 и, следовательно, f(x2) = +р - k > 0,
а /(хх) = р - k < 0, откудар < k < 32р +27р .
б) Если р = 0, то хх = х2 и функция (2) экстремумов не имеет:
производная f’(x) всюду, кроме х = 0, положительна и функция мо-
нотонно возрастает. Таким образом, в этом случае нет таких значе-
ний k, при которых данное уравнение имело бы три действитель-
ных корня.
в) Если р < 0, то х1 < х2 и, значит, /(хх) = р - k > 0, а /(х2) =
З2р3 . , _ п З2р3 + 27р _ , _
= +p~k<0, откуда —- < k < р.
Z ( Zi I
256
к ,^?32р3 + 27р 0
5. Ответ: если р < 0, то к е —1—^—£. ;р J
если/, = 0, то/г‘~0;
„ , < З2р3 + 27р0
если р > О, ТО К е (^р;-£-^-£ J .
11. При каких отличных от нуля значениях параметров а и b все
экстремумы функции
f(x) = а2х3 + ах2 - х + b (1)
отрицательны и локальный максимум достигается в точке х0 = -1?
1. Так как коэффициент при х3 положителен, то максимум
должен находиться левее минимума.
2. Для отыскания экстремальных точек найдем производную
функции (1) и приравняем ее нулю. Имеем
f’(x) = За2х2 + 2ах -1 = 0,
откуда xx = -i,x2 =
u Ou-
3. Пусть а < 0; тогда -Д- < - - и, следовательно, х9 = хп = -Д-,
За а и За
т. е. -Д- = -1. Таким образом, а = .
О CL о
4. Согласно условию, все экстремумы отрицательны, поэтому
при а = имеем /(-1) = -i - + 1 + & < 0. Отсюда находим, что
о У о
КПП 1/1 1
5. Пусть а > 0; тогда -- < — , а, значит, х1 = х0 = -- , т. е.
CL О CL CL
-- = -1, откуда а = 1. При а = 1 имеем /(-1) = -1 + 1 + 1 + &<0и,
следовательно, Ъ < -1.
1 5
6. Ответ: при а = и & < - - ; ПРИ « = 1 и & < -1.
1 2. При каких значениях параметра а уравнение
. 3 2х . о х
cos х + - cos — + 3 cos - = а
Z о о
имеет решения?
257
1. Рассмотрим функцию
..z \ I 3 2 х . п х
f(x) = COS X + - cos — + 3 cos - ,
Z о о
которая является периодической с наименьшим положительным
периодом Т = 6л.
2. Очевидно, что уравнение (1) будет иметь решения тогда и
только тогда, когда min f(x) < а < max f(x) на промежутке [0; 6л].
3. Для нахождения на этом промежутке критических точек ре-
шим уравнение /'(х) = 0. Это уравнение имеет вид
sin х + sin + sin | = 0, или sin
О о
¥(2“s5+1)
= 0.
2 х х 1
Отсюда либо sin — = 0, либо cos - = -- .
о о Z
4. Из первого уравнения находим х = ,« -/. Второе урав-
нение дает х = +2л + блй, /г -Z.
5. Таким образом, промежутку [0; 6л] принадлежат следующие
критические точки функции /(х): х1 = 0, х2 = , х3 = 2л, х4 = Зл,
х5 = 4л, хв = , х7 = 6л.
6. Вычислив значения функции f(x) в этих точках, находим
/(0) = /(6л) = П, /( ) = /( ,
Li к Li У к Li У Li
/(2л) = /(4л) = -|,/(Зл) = -|.
- 5 . . 11
7. Ответ'. -- ч а ч — .
1 3. Найти множество всех чисел а, при каждом из которых функ-
ция
/(х) = sin 2х - 8(а + l)sin х + (4а1 2 + 8а - 14)х
является возрастающей на всей числовой прямой и не имеет при
этом критических точек.
1. При любом фиксированном а данная функция дифференци-
руема в каждой точке числовой прямой.
258
2. Так как функция f(x) возрастает, то в каждой точке х дол-
жно выполняться неравенство f’(x) 0.
3. Так как, кроме того, f(x) не имеет критических точек, то при
любом х должно быть выполнено неравенство f’(x) 0.
4. Таким образом, если функция удовлетворяет условию зада-
чи, то при всех х должно быть выполнено неравенство f’(x) > 0.
5. С другой стороны, если при всех х выполнено неравенство
f’(x) > 0, то функция, очевидно, не имеет критических точек и воз-
растает.
6. Найдем производную данной функции:
f'(x) = 2 cos 2х - 8(а + 1) cos х + 4а2 + 8а - 14.
Теперь задачу можно переформулировать так: найти все значе-
ния параметра а, при каждом из которых для любого х выполнено
неравенство
cos 2х - 4(а + 1) cos х + 2а2 + 4а - 7 > 0. (1)
7. Учитывая, что cos 2х = 2 cos2 х - 1, и полагая cos х = t, где
-1 < t < 1, перепишем неравенство (1) следующим образом:
2t2 - 1 - 4(а + l)t + 2а2 + 4а - 7 > 0,
или
t2 - 2(а + l)t + а2 + 2а - 4 > 0. (2)
8. Обозначив функцию в левой части неравенства (2) через <р(£),
дадим новую формулировку исходной задачи: найти все значения а,
при каждом из которых наименьшее значение функции <p(f) на от-
резке [-1; 1] положительно.
9. Производная ф'(0 = 2t - 2(а + 1) обращается в нуль при t0 =
= а + 1.
10. Наименьшее значение функции <p(f) на отрезке [-1; 1] есть:
<р(-1) = а2 + 4а - 1, если а + 1 < -1;
ф(а + 1) = -5, если -1 < а + 1 < 1;
ф(1) = а2 - 5, если а + 1 > 1.
11. Так как наименьшее значение функции ф(£) на отрезке [-1; 1]
должно быть положительно, то значения параметра а, удовлетво-
ряющие условию задачи, принадлежат двум промежуткам: а < -2
иа >0.
12. Если а < -2, то искомые значения параметра а удовлетворя-
ют неравенству а2 + 4а - 1 > 0.
259
13. Если а > 0, то искомые значения параметра а удовлетворя-
ют неравенству а2 - 5 > 0.
14. Следовательно, множество искомых значений а есть объ-
единение решений двух систем неравенств:
а < -2,
а2 + 4а - 1 > 0;
J а > 0,
1 а2 - 5 > 0.
(3)
(4)
15. Множество решений системы (3) есть промежуток < а <
< -2 - V5 , а множество решений системы (4) — промежуток а > .
16. Ответ: а (-оо; -2 - ^/5 ) U (J5 ; +°о).
14. Прямая у = 5х + 3 касается параболы у = х2 + Ъх + с в точке
А(-2; -7). Найти & и с.
1. Находим производную у’ = 2х + Ъ и ее значение у'(~2) = -4 + Ъ,
которое равно угловому коэффициенту k = 5 касательной к парабо-
ле в точке А.
2. Таким образом, -4 + Ъ = 5, откуда Ъ = 9.
3. Значение с найдем из условия, что точка А(-2; -7) лежит на
параболе. Имеем -7 = 4 + 9(-2) + с, откуда с = 7.
4. Ответ: & = 9, с = 7.
1 5. Известно, что парабола у = ах2 + Ъх + 1 касается прямой у =
= 1х - 2 в точке М(1; 5). Найти значение выражения 4а - Ъ2.
1. Найдем производную функции у = ах2 + Ъх + 1:
у' = (ах2 + Ъх + 1)' = 2 ах + Ъ.
2. Так как М(1; 5) — точка касания, то х0 = 1, у0 = 5. Следова-
тельно, 5 = а-1 + &-1 + 1и2а + &=7.
3. Составим и решим систему уравнений
5 = а + b + 1,
2а + Ъ = 7,
откуда а = 3, Ъ = 1.
4. Ответ: 11.
260
1 6. При каких значениях а прямая 4х + у - 5 = 0 является каса-
2 ________________________________^2
тельной к графику функции у =-----— ?
1. Пусть х0, у0 — координаты точки касания. Тогда
2а 1 ,, ч 4а
Уо= — -1,у(^о) = -— •
х0 ХО
2. Уравнение касательной к графику функции у = х =
х2
2а 1
= — - 1 в точке имеет вид
х2
= f -ll + \ = ,г+ 6а _1
у — 1 ~ ~ х ' 1ф
\ *^q s v x0 J х0 х0
3. Чтобы уравнение (1) совпало с уравнением у = -4х + 5, тре-
буется выполнение условий
(2)
4. Решив систему (2), находим х0 = 1, а = 1.
5. Ответ: а = 1.
17. При каком наименьшем натуральном k уравнение
х3 + Зх2 - 45х + k = О
имеет ровно один корень?
1. Построим эскиз графика функции у1 = х3 + Зх2 - 45х и опре-
делим наименьшее натуральное значение k, при котором этот гра-
фик пересекает прямую у2 = -k ровно в одной точке.
2. a)D(yl) = R;
б) у[ = Зх2 + 6х - 45;
в) у[ =0 при х1 = -5; х2 = 3;
г) y1(-5)=175;i/1(3) = -81;
261
yt -5 3 x
Рис. 91
д) изменение знаков производной у[ в интервалах -5),
(-5; 3) и (3; +°°) иллюстрирует рис. 91. На рис. 92 дано схематиче-
ское изображение графика функции уг.
3. Очевидно, что данное уравнение имеет единственное реше-
ние, если -k > 175 или -k < -81, т. е. k < -175 или k > 81. Наимень-
шее натуральное значение k равно 82.
4. Ответ: k = 82.
1 8. При каком значении параметра а минимум функции
/(х) = ах2 - бах + а2 - 9
(1)
равен 1?
1. Найдем производную данной функции:
f’(x) = (ах2 - бах + а2 - 9)' = 2ах - 6а.
2. Полагая f’(x) = 0, имеем 2ах - 6а = 0, откуда а 0, х = 3.
262
3. Найдем значение функции (1) в точке х = 3:
/(3) = 9а - 18а + а2 - 9 = 1. (2)
4. Решив уравнение (2), получим а1 = -1; а2 = 10.
5. Так как по условию требуется определить минимум функции,
то ветви параболы (1) направлены вверх, а это значит, что а2 = 10.
6. Ответ: а = 10.
1 9. При каком значении параметра а минимум функции
f(x) = -2х3 + Зх2 + 12х + 4а
равен 1?
1. f(x) = —6х2 + 6х + 12.
2. у’ = 0 при х1 = -1; х2 = 2.
3. у(2) = 20 + 4а = 1; аг = .
4. у(-1) = -7 + 4а = 1; а2 = 2.
5. Схематическое изображение гра-
фика функции (рис. 93) показывает, что
ее минимум достигается в точке х1 = -1;
поэтому нужно взять значение а2 = 2.
6. Ответ: а = 2.
20. Найти множество значений параметра k, при которых каса-
тельная к параболе
у = —х2 + (k - 2)х + k - 2 (1)
в точке х0 = 1 является также касательной к параболе
у = х2 - 6х + 5. (2)
1. Уравнение касательной в общем случае имеет вид
У = f(x0) + f(x0)(x - х0).
2. Находим
/(х0) = /(1) = -1 + (k - 2) • 1 + k - 2 = 2k - 5.
3. Имеем
f(x) = -2х + k - 2, f\x0) = /'(1) = -2>l+A-2 = A-4.
263
4. Запишем уравнение касательной к параболе (1):
у = 2k - 5 + (k - 4)(х - 1), или у = (k - 4)х + k - 1. (3)
Эта касательная должна быть также касательной к параболе (2).
5. Чтобы найти общие точки касательной (3) и параболы (2), со-
ставим уравнение
(k - 4)х + k - 1 = х2 - 6х + 5, или х2 - (k + 2)х + 6 - k = 0. (4)
6. Так как прямая (3) является касательной к кривой (2), то она
имеет единственную общую точку с этой кривой.
7. Уравнение (4) имеет единственное решение, если дискрими-
нант этого уравнения равен нулю, т. е. D = 0.
8. Из равенства D = (k + 2)2 - 4(6 - k) = 0 находим /г, = -10,
k2 = 2.
9. Ответ: k е {-10; 2}.
21 . При каком значении параметра а хорда параболы
у = -а2х2 + 5ах - 4, (1)
касающая кривой
<2)
в точке с абсциссой х0 = 2, делится этой точкой пополам?
1. Так как в точке х0 = 2 значение функции f(x) = j—Ц; равно (-1),
а значение производной f'(x) = —-—- равно 1, то уравнение каса-
О-хУ
тельной к кривой (2) в точке М(2; -1) имеет вид у = х - 3.
2. Пусть эта касательная пересекает параболу (1) в точках А
и В; тогда абсциссы этих точек являются корнями уравнения
-а2х2 + 5ах - 4 = х - 3. (3)
3. Точка М есть середина отрезка АВ, поэтому ее абсцисса рав-
на полусумме абсцисс точек А и В.
4. Перепишем уравнение (3) в виде
х2 ~ 5а 9 1 х + -Д- = 0, а 0. (4)
264
5. Согласно теореме Виета, х-, + х9 = 5а * , и, следовательно,
ал
х-.+х2 5а-1 х.+х2
—-— = -----5- . С другой стороны, —-— = 2. Таким образом,
2 2а2 2
5а 1 = 2. Отсюда получим а, = i , а? = 1.
2а2 4
6. Найдем дискриминант квадратного уравнения (4):
г. <5а-1А2 4 21а2-10а+1
~Т2 =-------------• (5)
7. Подставив значение а = 1 в выражение (5), замечаем, что
D > 0, поэтому а = 1 удовлетворяет требованию задачи.
8. Если же а = i , то D < 0, т. е. а = i требованию задачи не
удовлетворяет.
9. Ответ: а = 1.
22. При каком значении параметра а касательная к графику функ-
ции у = а - х2 отсекает от I четверти равнобедренный треугольник
„ 9 ..
с площадью, равной — I
1. Уравнение касательной к графику функции у = f(x) в точке
М(х0; у0) имеет вид у ~уй = f'(x0)(x - х0), где f'(x0) = tg а, а — угол
наклона касательной к оси абсцисс.
2. Так как по условию касательная к графику данной функции
отсекает от I четверти равнобедренный треугольник, то а = 135° и,
значит, f'(x0) = -1.
3. С другой стороны, f'(x0) = -2х0 и, следовательно, х0 = |.
4. При х(1 = | находим Уо = ) = а ~ и уравнение касатель-
ной к графику данной функции запишется так:
. . 1
у = —х + а + - .
5. Эта касательная пересекает оси координат в точках А^О; а + | 'i
иВ(а+1;0).
265
6. Согласно условию, точки А и В лежат на положительных по-
1
луосях, поэтому а > -- .
7. Для площади треугольника, о котором идет речь в задаче,
имеем следующее равенство:
Отсюда находим ау = |, а2 = -1. Учитывая, что а > -i , оконча-
1
тельно получаем а = - .
8. Ответ: а = |.
23. При каком значении параметра а прямые, проходящие через
точку М(1; 1) плоскости хОу и касающиеся двух ветвей гиперболы
у = - (а < 0) в точках А и В, образуют правильный треугольник
X
МАВ? Найти площадь S этого треугольника.
1. При некотором фиксированном значении параметра а обо-
значим через t абсциссу произвольной точки гиперболы у = - .
2. Тогда уравнение касательной к указанной гиперболе в точке
(t; y(t)) запишется в виде
т. е.
а । 2а ч
У = ~Т2Х+^~- W
3. Так как касательная, заданная уравнением (1), проходит че-
рез точку М(1; 1), то 1 = , или
t2 - 2at + а = 0. (2)
4. При а < 0 уравнение (2) имеет два корня и f2, которые яв-
ляются абсциссами точек А и В соответственно. По теореме Виета
tx + t2 = 2а, t1t2 = а.
266
5. Поскольку ветви рассматриваемой гиперболы симметричны
относительно прямой у = х, а точка М(1; 1) лежит на этой прямой,
точки А и В симметричны относительно прямой у = х.
6. Таким образом, если точка А имеет координаты (tx; f2), то точ-
ка £ будет иметь координаты (t2; tx). Отсюда следует, что МА = МВ
при любом а < 0.
7. Найдем МА2 и А_В2. С учетом полученных выше соотноше-
ний между корнями fx и t2 имеем
МА2 = (tx - I)2 + (t2 - l)2 = 4а2 - 6а + 2,
АВ2 = (t, - t9)2 + (t2 - t, )2 = 8a2 - 8a.
8. Согласно условию, треугольник MAB правильный, поэтому
МА = АВ, т. е.
4а2-6а + 2 = 8а2 - 8а.
Решив это уравнение с учетом того, что а < 0, получим а = .
9. Найдем площадь треугольника МАВ:
S = | - МА -АВ -sin 60°= | - АВ2 - .
10. Ответ: а = .
24. Найти все значения параметра а, удовлетворяющие неравенст-
вам 0 < а < , при каждом из которых минимум функции
/(х) = Зх4 + 4x3(cos а - sin а) - Зх2 sin 2а
на отрезке -sin а < х < cos а принимает наименьшее значение.
1. Обозначим через <р(а) наименьшее значение функции /(х) на
отрезке [-sin a; cos а] при фиксированном а.
2. Имеем
f(x) = 12х3 + 12x2(cos а - sin а) - 6х sin 2а.
3. Решив уравнение f'(x) = 0, находим корни производной: хх = 0,
х2 = sin а, х3 = -cos а.
267
Х1
Х1
а) ---•----•----•---•---•—* б) -----•---•----•---•---•—►
х3 -sin а 0 х2 cos аа -sin а х3 0 cos а х2 а
Рис. 94
4. Рассмотрим два случая.
а) Если 0 < а < , то sin а < cos а и по отношению к отрезку
[-sin а; cos а] корни х2, х3 расположатся так, как показано на
рис. 94, а. Изменение знаков производной иллюстрирует следую-
щая таблица:
Интервал (-sin а; 0) (0; х2) (х2; cos а)
Знак f'(x) + - +
Отсюда следует, что ф(а) = min {/(-sin a); f(x2)}. Но
f(x2) - /(-sin а) = /(sin а) - /(-sin а) = 8 sin3 a (cos а - sin а) 0.
Значит,
ф(а) = /(-sin а) =
= 3 sin4 а - 4 sin3 a (cos а - sin а) - 6 sin3 a cos а =
= 7 sin4 а - 10 sin3 a cos а.
б) Если < а < , то sin а cos а и по отношению к отрезку
[-sin а; cos а] расположение корней производной будет таким, как
показано на рис. 94, б. Изменение знаков производной иллюстри-
рует таблица:
Интервал (-sin a; xg) (х3; 0) (0; cos а)
Знак f'(x) - + -
Следовательно, ф(а) = min {/(х3); /(cos а)}. Но
/(х3) “ /(cos а) = /(-cos а) - /(cos а) = -8 cos3 a (cos а - sin а) > 0.
Значит,
<р(а) = /(cos а) =
= 3 cos4 а + 4 cos3 a (cos а - sin а) - 6 sin a cos3 а =
= 7 cos4 а - 10 sin a cos3 а.
268
5. Итак,
7 sin4 а - 10 sin3 a cos а, если а
ф(а) = <
7 cos4 а - 10 sin a cos3 а, если а
Отсюда заключаем, что ф(а) = - a j при а [О; ] , и до-
статочно найти минимум функции ф(а) = 7 sin4 а - 10 sin3 a cos а на
отрезке ^0; j .
6. Имеем
ф'(п) = 28 sin3 a cos а - 30 sin2 a cos2 а + 10 sin4 а =
= 2 sin2 a cos2 а (5 tg2 а + 14 tg а - 15).
Все корни производной ф'(а), принадлежащие промежутку 0 <
< а < , являются корнями уравнения 5 tg2 a+14tga-15 = 0.
— 7 + 2 а/31 — 7 — 2 а/31
Решив его, находим tg ал = -—-— , tg = ------—-— .
1 5 5
7. Для значений а из промежутка 0 < а < значения функции
tg а положительны и не превосходят 1; поэтому находим единст-
венный корень производной ф'(п), удовлетворяющий неравенствам
п л , 2а/31 -7
0 < а < - , а именно: = arctg 4 .
4 1 5
8. На интервале 0 < а < а1 производная ф'(п) отрицательна, на
интервале аг < а < положительна. Значит, а = аг — точка мини-
мума.
9. Из непрерывности ф(а) на промежутке 0 < а < и монотон-
ности на интервалах (0; аг) и ) следует, что наименьшее зна-
чение ф(а) на промежутке 0 < а < равно ф(ах).
269
10. Такое же значение принимается в точке - аг, принадле-
жащей промежутку < а < |.
.. . 2731-7 л . 2^31-7
11. Ответ-, а = arctg „-; а = - - arctg „--.
5 2 5
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. При каком значении а прямая у = а + х In 81 является каса-
тельной к графику функции /(х) = 9Ж + 2 • Зж + 1 - х In 81?
2. Установить, при каких значениях а прямая:
а) Зах + у = а2х + 7 параллельна касательной к кривой Зх2 +
+ — + у = 0, проведенной в точке х = 1;
б) 4а2х - у = 15ах - 9 параллельна касательной к кривой -
X3
- у + х = 0, проведенной в точке х = -1;
О X &
в) 2 - Зах = 4а2х - у параллельна касательной к кривой — -
- у + — =0, проведенной в точке х = -2.
В ответе указать наименьшее значение а.
3. Установить, при каких значениях а касательная к кривой:
а) х3 - -Ц? + у = 0, проведенная в точке х = 2, параллельна пря-
мой 8ах - 5 = а2х - у;
б) ~ У ~ 2х2 = 0, проведенная в точке х = 3, параллельна
X3
прямой 10ах + у = а2х + 6;
в) х3 + у - =0, проведенная в точке х = -1, параллельна
х4
прямой 4а2х - у = 7 - 5ах.
В ответе указать наибольшее значение а.
4. Найти значение Ь, при котором наименьшее значение функ-
ции:
а) у - х3 + 27х + ЗЪ на отрезке [2; 5] равно 1;
б) у = -4х3 + 48х - 2Ь на отрезке [-4; -1] равно (-60).
270
5. Найти значение а, при котором наибольшее значение функ-
ции:
а) у = 5х3 - 60х - а на отрезке [1; 3] равно (-50);
б) у = 2х3 - 54х + а на отрезке [1; 4] равно (-50).
6. Найти множество значений параметра/,, при которых каса-
тельная к параболе:
а) у = х2 - 5х + 6 в точке х0 = 2 является также касательной
к параболе у = х2 + рх + 3;
б) у = х2 + рх + 27 в точке х0 = 6 является также касательной
к параболе у = х2 + 2х - 8.
7. На прямой х + у = 5 найти точку Л(хА; уА), расстояние от ко-
торой до точки В(1; 2) минимально. В ответе указать сумму хА + уА.
8. Найти критические точки функции:
а) у = 1 + 2 sin a cos х + i cos Зх;
/Дл „2 3
д/ — И
б) у = | sin a tg3 х + (sin а - 1) tg х + —- .
3 о — (L
Ответы
1. 7. 2. а) 2; б) -0,25; в) -2. 3. а) 4; б) 6; в) 1. 4. а) -3; б) -2. 5. а) 5; б) 2.
6. а) {-3; 1}; б) {-12; -8}. 7. 5. 8. а) Если a G (о; U ; 4), то х = nk,
7, । 1 <1 + 2 sin а < < л 5л <
х = л/г ± - arccos -------------J ; если а ; — J , то х = nk; б) если а
£ [2; л) U (2л; 8), то х = nk ± arctg —-1 ; если а [л; 2л], то критиче-
ских точек нет.
т
Гема 15
11 Потерянные и посторонние-кошн --------------
; при решении уравнений I I |
2. Решение иррациональных уравнений, посторонние корни
; иррационального уравнения
8. Иррациональные неравенства I I I I I I I I I I I I I I I
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Потерянные и посторонние корни при решении уравнений
1°. Ранее (см. тему 3, п. 3) мы отмечали, какие действия над
уравнениями не нарушают их равносильности.
2°. Рассмотрим теперь такие операции над уравнениями, кото-
рые могут привести к новому уравнению, не равносильному исход-
ному.
3°. Пример 1. Дано уравнение Зх(х - 1) = 5(х - 1). Упростив
его, придем к квадратному уравнению Зх2 - 8х + 5 = 0. Корнями
1 5
этого уравнения являются хг = 1, х2 = - .
Если сократить обе части данного уравнения на общий мно-
житель (х - 1), то получим уравнение Зх = 5, которое не равносиль-
но исходному, так как новое уравнение имеет всего один корень
_ 5
х 3.
4°. Вывод. Сокращение обеих частей уравнения на множитель,
содержащий неизвестное, может привести к потере корней урав-
нения.
5°. Пример 2. Дано уравнение 2х - 3 = 5. Это уравнение
имеет единственный корень х = 4. Возведя обе части данного урав-
нения в квадрат, получим (2х - З)2 = 25. Решив последнее уравне-
ние, найдем два корня: х1 = -1, х2 = 4.
а) Замечаем, что новое уравнение (2х - З)2 = 25 не равносильно
исходному уравнению 2х - 3 = 5.
272
б) Корень х1 = -1 является корнем уравнения 2х - 3 = -5, кото-
рое после возведения обеих его частей в квадрат приводит к урав-
нению (2х - З)2 = 25.
6°. Посторонние корни могут появиться также при умножении
обеих частей уравнения на множитель, содержащий неизвестное,
если этот множитель при действительных значениях х обращается
в нуль.
7°. Пример 3. Если обе части уравнения 2х - 1 = 3 умножим
на х + 2, то получим новое уравнение (2х - 1)(х + 2) = 3(х + 2),
которое после упрощения примет вид (х + 2)(2х - 4) = 0, откуда х =
= -2, либо х = 2.
Корень х = -2 не удовлетворяет уравнению 2х - 1 = 3, имеюще-
му единственный корень х = 2.
8°. Вывод. При возведении обеих частей уравнения в квадрат
(вообще в четную степень), а также при умножении на множитель,
содержащий неизвестное и обращающийся в нуль при действитель-
ных значениях неизвестного, могут появиться посторонние корни.
9°. Все соображения относительно потери и появления посто-
ронних корней уравнения в одинаковой мере относятся к любым
уравнениям (алгебраическим, тригонометрическим и др.).
2. Решение иррациональных уравнений,
посторонние корни иррационального уравнения
1°. Уравнение, содержащее неизвестное под знаком радикала,
называют иррациональным; например, Jx +6 = 3, '1/1 - Зх =8 —
иррациональные уравнения.
2°. Решение иррациональных уравнений сводится к переходу
от иррационального к рациональному уравнению с помощью воз-
ведения в степень обеих частей уравнения или замены переменной.
3°. П р и м е р. Пусть дано иррациональное уравнение
Jx - 1 = 2х - 3.
а) Возведя обе его части в квадрат, получим х - 1 = 4х2 - 12х + 9.
5
Найдем корни этого уравнения: хг = - и х2 = 2.
б) Проверим, удовлетворяют ли эти корни данному уравнению.
5 /б 5 5
Если хг = - , то I- -1 2 - - 3. Корень хг = - уравнению не
273
удовлетворяет, следовательно, он является посторонним; второй
корень х2 = 2 удовлетворяет уравнению.
4°. При возведении обеих частей уравнения в четную степень
возможно появление посторонних корней.
Поэтому при использовании указанного метода следует прове-
рить все найденные корни подстановкой в исходное уравнение.
3. Иррациональные неравенства
1°. Распространенным способом решения иррациональных не-
равенств является возведение обеих частей неравенства в степень,
равную степени радикала. При этом используется следующее ут-
верждение.
Теорема. Если на некотором множестве значений X, при-
надлежащем области определения неравенства
Л(х) > /2(х), (1)
функции /х(х) > 0 и /2(х) то пРи возведении обеих частей
неравенства в целую положительную степень получится нера-
венство
f1(x)> f2(x), (2)
равносильное неравенству (1) на данном множестве X.
2°. При решении иррациональных неравенств часто использу-
ют следующие утверждения:
а) неравенство
Jf(x) <<р(х)
равносильно системе неравенств
ф(х) > 0, 0 < f(x) < (ф(х))2;
б) неравенство
Jf(x) >ф(х)
равносильно совокупности двух систем неравенств:
f(x) > О,
ф(х) < 0;
[ f(x) > 0,
J ф(х) > 0,
\f(x) > (ф(х))2.
274
(3)
(4)
(5)
(6)
(7)
ЗАДАЧИ С РЕШЕНИЯМИ
1. Решить относительно х уравнение
(3 + 2а - а2)л/г = а - 3.
1. Пусть 3 + 2а-а2 /0,т-е. -1 иа/3; тогда
Г = а-3 _ _ 1
3 + 2а - а2 а+ 1 ’
при этом > 0, откуда а < -1. Следовательно,
1 1
х = ------- , где а < -1.
(а+1)2
2. Пусть а = 3; тогда уравнение примет вид 0 • Jx =3-3. Зна-
чит, х — любое неотрицательное число.
3. Пусть а = -1; тогда уравнение примет вид 0 • Jx = -1 - 3; это
уравнение не имеет решений.
4. Ответ: если а < -1, то х = —- ;
(а+1)2
если а = 3, то х > 0;
если а е (-1; 3) U (3; +°°), то корней нет.
2. Решить относительно х уравнение
л/х2 + ах - 2а = х + 1. (1)
1. Возведя обе части уравнения (1) в квадрат, получим
х2 + ах - 2а = х2 + 2х + 1,
или
(а - 2)х = 2а + 1. (2)
2. Пусть а = 2; тогда уравнение (2) примет вид 0 • х = 5, т. е. оно
не имеет решений.
3. Пусть а 2; тогда уравнение (2) имеет решение
х = . (3)
275
4. Для проверки подставим полученное выражение (3) в левую
и правую части уравнения (1).
а) Левая часть:
1(2а+1)2 + а(2а+1) _ l(3a-I)2 _ I За- 1 I
А| (а -2)2 а-2 “ А/ (а-2)2 | а-2 Г
тт 1 <> I 3а — 1 I За - 1
При а ч - и при а > 2 имеем ---— = ---— ;
3 \ а-2 \ а-2
I За - 1 I 1 -За
при - < а < 2 имеем --— = -----— .
3 | а - 2 | а-2
б) Правая часть:
2а + 1 j _ За - 1
а-2 а - 2 ’
5. Отсюда следует, что х = является корнем уравнения (1)
при а < | и при а > 2. При | < а < 2 решений нет.
О о
6. Ответ: если а < i или а > 2, то х = ;
3 а-2
если | < а < 2, то корней нет.
О
3. Для каждого значения параметра а решить уравнение
х + Jx = а. (1)
1. Перепишем уравнение (1) следующим образом:
Jx = а - х. (2)
2. Уравнение (2) равносильно смешанной системе
J х = (а - х)2,
[ а - х О,
т. е.
/ х2 - (2а + 1)х + а2 = 0, (3)
а - х > 0. (4)
3. Найдем корни уравнения (3):
, 1 /1 4. , 1 4. I1 4.
x-, = a + - - - + a,x9 = a+- + - + a .
1 2 *J4 2 2 *J4
276
4. Корень х1 удовлетворяет условию (4), если
/1 , 1 п
а - х-. = - + а - - > 0.
1 Л/ 4 2
и /1 1 1 , 1
Неравенство /- + а > - равносильно неравенству - + а > - ,
откуда следует, что а > 0.
5. Корень х2 не удовлетворяет условию (4) ни при каком а, так
как
1 /1 4. / О
а - х9 = -- - /- + а <0.
2 2 А/4
6. Итак, решением иррационального уравнения (1) является
только корень хх квадратного уравнения (3), где а > 0.
7. Ответ: если а 0, тох = а+ R + а ;
2 А/4
если а < 0, то корней нет.
4. В зависимости от значений параметра а решить уравнение
V1 -х + ?/1 + х = а. (1)
1. Полагая у = ^/1 + х , перепишем уравнение (1) в виде
у + 3j2 - у3 = а.
2. Перенеся у в правую часть и возведя обе части полученного
уравнения в куб, придем к уравнению
Зау2 - За2у + а3 - 2 = 0. (2)
3. Решив уравнение (2), находим
_ За2 ± л/3а(8 - а3)
У1’2 6^ •
4. Значения (3) будут корнями уравнения (2), если 0 < а < 2.
5. Возвращаясь к переменной х, запишем ответ.
6. Ответ: если а е (-оо; 0] U (2; +°°), то корней нет;
если а '— (0‘ 21 то х = f За2 ± J3a(8 - а3) А _
277
5. Решить относительно х уравнение
х - Ja - х2 = 1. (1)
1. Перепишем уравнение (1) в виде
х - 1 = Ja - х2 (2)
и возведем обе части уравнения (2) в квадрат:
(х - I)2 = а - х2; 2х2 - 2х + 1 - а = О,
откуда
1 - 72а- 1 1 + 72а- 1 ( 1 А
Xi = ---------, х2 = ------- ^где а > - ) .
2. Если а < |, то решений нет.
3. Проверим, какие из найденных значений х удовлетворяют
уравнению (2).
а) Подставив значение х1 в уравнение (2), получим, что его ле-
вая часть
1 +72а-1
2
отрицательна, а правая
неотрицательна, поэтому х1 не удовлетворяет уравнению.
б) Подставим теперь значение х2 в уравнение (2). Имеем
72а- 1 -1
2
(3)
Равенство (3) верно тогда и только тогда, когда J2a - 1 - 1 > О,
т. е. а > 1.
4. Ответ: если а < 1, то корней нет;
. 1 + 72а- 1
если а 1, то х = -------.
6. В зависимости от значений параметра/, решить уравнение
J4x +р = 2х - 1. (1)
Решим уравнение тремя способами.
278
I способ.
1. Уравнение (1) равносильно системе
4х +р = (2х - I)2,
т. е.
4х2 - 8х + 1 - р = О,
2. Решив уравнение (2), находим
(2)
(3)
(4)
откуда следует, что прир = -3 уравнение (2) имеет один корень х = 1.
3. Еслир > -3, то х1 < х2; поэтому уравнение (2) будет иметь два
корня при тех значениях параметра/,, которые удовлетворяют сис-
теме
2-^/рТз > 1
/ 2 2 ’
Ь>-з,
т. е. при -3 < р < -2.
4. Уравнение (2) будет иметь только один корень х2, если х} <
1
2 ’
1
2 ’
а х2 >
В этом случае получаем систему
откуда следует, что р > -2.
5. Заметив, что прир < -3 дискриминант уравнения (2) отрица-
телен, запишем ответ.
6. Ответ: еслир < -3, то корней нет;
если р = -3, то х = 1;
о , о 2 ± Vp + 3
если —3 <р ч -2, то хг 2 = -;
если р > -2, то х =
2 + л/р + 3
2
279
II способ.
1. Возведя обе части уравнения (1) в квадрат, получим уравне-
ние (2), корни которого задаются формулами (4). Однако здесь на-
до иметь в виду, что при возведении обеих частей уравнения (1)
в квадрат могли появиться посторонние корни. Поэтому в данном
случае необходимо произвести проверку.
2. Подставив корень х1 в исходное уравнение (1), придем к со-
отношению |1 - л/р + 3 | = 1- л/р + 3 , откуда -3 + р < -2.
3. Аналогично, подставив корень х2 в уравнение (1), придем к
соотношению I л/р + 3 + 11 — л/р + 3 + 1 и, значит,/) > -3.
4. Учитывая теперь, что при р < -3 корней нет, а при р = -3
имеем х = 1, получаем тот же ответ, что и при I способе решения.
III способ.
1. Воспользуемся геометрическим смыслом квадратного трех-
члена. Рассматривая равносильную уравнению (1) систему (2),
(3), заключаем, что уравнение (1) будет иметь корни х1 и х2 в том
случае, когда корни квадратного трехчлена f(x) = 4х2 - 8х + 1 - р
1
не меньше - .
2. Аналитически соответствующие условия запишем в виде
системы
D = 16(3+р) > О,
__Ь_ = 8 1
2а 8 2 ’
/(!) = 1-4 + 1-р>0.
Решив эту систему, находим, что -3 <р < -2.
3. При х = -3 уравнение (1) имеет решение х = 1.
4. Если же | ) = -2 -р < 0, т. е. р > -2, то уравнение (1) имеет
один корень х2.
5. При/> < -3 решений нет.
Замечание. Это уравнение можно решить и графически.
7. Для каждого значения параметра а определить число корней
уравнения
а/2|л:| - х2 = а. (1)
280
1. Если а < 0, то уравнение (1) не имеет решений.
2. Если а > 0, то уравнение (1) равносильно уравнению
2|х| - х2 = а2, или |х|2 - 2|х| + а2 = 0. (2)
3. Полагая |х| = z, получим уравнение
z2 - 2z + а2 = 0, (3)
дискриминант которого D = 4(1 - а2).
4. Пусть а > 1; тогда уравнение (3), а, значит, и уравне-
ние (2) не имеет решений.
5. Пусть а = 1; тогда уравнение (3) имеет единственный корень
z = 1 и равносильно уравнению |х| = 1, имеющему два корня: х1 = -1,
х2 = 1.
6. Пусть 0 < а < 1; тогда уравнение (3) имеет корни z1 = 1 +
+ л/1 - а2 из2 = 1 - л/1 - а2 • Следовательно, уравнение (2) равно-
сильно совокупности двух уравнений:
|х| = 1 + л/1 - а2 ; (4)
|х| = 1 - л/1 - а2 • (5)
7. Так как z, и z2 неотрицательны, то уравнение (4) имеет два
корня: xs 4 = +(1 + а/1 -а2 ), а уравнение (5) также имеет два кор-
ня: х5 в = +(1 - л/1 - а2 ). При этом если а 0, т. е. 0 < а < 1, то все
эти числа различны.
Если же а = 0, то х7 = х& = 0.
8. Ответ: если а < 0 или а > 1, то корней нет;
если а = 0, то три корня: х = 0, х = -2; х = 2;
если 0 < а < 1, то четыре корня: х = +(1 + л/1 - а2 ),
х = +(1 - а/1 - а2 );
если а = 1, то два корня: х = -1, х = 1.
8. Для каждого значения параметра а найти все решения уравнения
л/|х| + 1 - л/|х| = а. (1)
1. Так как «/М + 1 _ л/W > 0 при всех значениях х, то уравне-
ние (1) не имеет решений, если а < 0. В дальнейшем будем считать,
что а > 0.
281
2. Перепишем уравнение (1) в виде
J\x\ + 1 = Vjxi + а. (2)
3. Учитывая, что при любом значении х левая и правая части
уравнения (2) положительны, можно возвести их в квадрат:
|х| + 1 = |х| + 2aJ\x\ + а2,
или
2аТЙ=1-а2. (3)
4. При любом значении х левая часть уравнения (3) неотрица-
тельна, поэтому уравнение не имеет решений, если а > 1. Будем
считать, что 0 < а < 1. Тогда уравнение (3) равносильно уравнению
4а2|х| = (1 - а2)2, т. е. |х| = ——,
4а2
। (1 -а2)2
и, следовательно, 2 = + v 2 7 .
5. Ответ: если а < 0 или а > 1, то корней нет;
п , । (1 -а2)2
если 0 < а < 1, то два корня: х, 9 = + i;
’ 4а2
если а = 1, то один корень х = 0.
9. В зависимости от значений параметра k решить уравнение
V(l+x)2 - V(l-x)2 = Vl - X2 . (1)
1. Подстановкой убеждаемся, что х = 1 не является корнем
уравнения (1).
2. Поэтому после деления обеих частей уравнения (1) на V(1 - х)2
получим равносильное уравнение
3. Полагая t = кг + х , придем к квадратному уравнению t2 -
\ 1 — X
- 1 = t, или t2 - t - 1 = 0. Отсюда
, _ 1 + 7б . 1-7б
ti > t2
282
4. Так как значение f2 отрицательно, то в случае четного пока-
зателя k это значение нужно отбросить.
5. Таким образом, при четном k имеем
т*
, 11 + X _ 1 + л/б
и, следовательно,
1 + X
1-х
6. При нечетном k уравнение (2) имеет два корня:
7. Ответ: если k — четное, то один корень: х =--------— ;
если k — нечетное, то два корня:
10. В зависимости от значений параметра а решить уравнение
л/2х + а - Jx-1 = 2. (1)
1. Положим у = Jx -1 , где у > 0. Тогда х = у2 + 1 и уравне-
ние (1) примет вид
J2y- + а + 2 = у + 2. (2)
2. Уравнение (2) равносильно системе
J у2 - 4у + а - 2 = 0,
]у>о. (3)
3. Решив уравнение этой системы, находим
уг = 2 - JQ- а , у2 = 2 + JQ- а .
283
4. Система (3) будет иметь решение в следующих трех случаях:
а) 0 < уг = у2; б) О < уг < у2; в) уг < О < у2.
5. Случай а) возможен, когда а = 6. Тогда ух = у2 = 2 и, значит,
х = 5.
6. Случай б) имеет место, когда 2 - JQ-а 0. Это неравенство
равносильно системе
f 6 - а > 0,
[ 4 > 6 - а,
из которой следует, что 2 < а < 6. При таких значениях параметра
а получаем два корня:
хг 2 = 11 - а + 4 «/6 - а .
7. Случай в) возможен, когда выполняются условия
I 2 - Jfl - а < 0,
.________ (4)
2 + л/б — а 0.
Решив систему (4), находим, что а < 2. При таких значениях а
получаем один корень:
х=11-а + 4 V6 - а .
8. Ответ: если а<2,тох=11-а + 4 JQ-а ;
если 2 < а < 6, то хх 2 = 11-а±4 J11- а ;
если а = 6, то х = 5;
если а > 6, то решений нет.
11. Решить уравнение
л/Зх - 2 + л/х + 2 = а. (1)
J Зх - 2 > 0, 2 ,
1. Здесь < । м т. е. х > - . (Это необходимое условие, ко-
..Х i Л V, о
торому должны удовлетворять корни уравнения.)
2. Так как Jx + 2 > 0, J3x - 2 > 0, то а > 0.
3. Пусть Jx + 2 = z > 0. Тогда х + 2 = z2, а х = z2 - 2, т. е. Зх -
- 2 = 3z2 - 8, и уравнение (1) примет вид
J3z2 - 8 = а - z. (2)
284
Замечание. Функции z = Jx + 2 и х = z2 - 2, где z > О, —
взаимно обратные, обе они однозначны и поэтому уравнения (1)
и (2) равносильны.
4. Вернемся к уравнению (2). Значения z должны удовлетво-
рять условиям
[ z < а,
< 3z2 - 8 > О,
[ z > 0.
5. Возведя обе части уравнения (2) в квадрат, получим урав-
нение
3z2 - 8 = (а - z)2, (3)
корень которого удовлетворяет неравенству 3z2 - 8 > 0.
6. Следовательно, достаточно проследить за тем, чтобы корни
уравнения (3) удовлетворяли неравенствам 0 < z < а.
7. Приведя уравнение (3) к виду
3z2 - 8 = а2 - 2az + z2, или 2z2 + 2az - 8 - а2 = 0,
находим
zx = i (-а - л/За2 + 16 ); z2 = | (-а + J-la2 + 16 ).
8. а) Значение zx не является корнем уравнения (2), поскольку
zx < 0.
б) Так как 0 < z2 < а, то приходим к системе неравенств
| (л/За2 + 16 - а) < а,
1(73а2 + 16 -а)> 0,
ИЛИ
л/За2 + 16 < За,
л/За2 + 16 > а,
т. е.
6а2 >16,
2а2 + 16 > 0.
285
2 а/6
9. Учитывая, что а>0и 2а2 + 16 > О, получим а . Таким
2 «/б
образом, при а уравнение (2) имеет один корень z2.
О
10. Вернемся к подстановке х = z2 - 2. Имеем
х = z2 - 2 = i (л/За2 + 16 - а)2 - 2,
т. е.
х = | (2а2 + 4 - a J3a2 + 16 )
— корень уравнения (1) при а > —.
О
2л/б
11. При а < —уравнение не имеет корней,
о
2л/б
12. Ответ: если а < —2— , то корней нет;
О
если а , то х = (2а2 + 4 - а ^За2 + 16 ).
О Л
1 2. Для каждого действительного числа а найти все решения урав-
нения
Jx2 - 1 + Jx2 - 2 = а. (1)
1. Полагая Jx2 - 1 = и, Jx2 - 2 = v, получим систему
[ и + v = а,
<а2-и2 = 1, (2)
а > 0, и > 0.
Если а = 0, то система (2) несовместна.
2. Считая а 0, перейдем к системе
286
3. Решив систему неравенств а+ i > 0, а - i >0, находим а > 1.
4. При этих значениях а получим
х2 - 1 = и2 = (а + - } , х2 = 1 + i f а + - 'j ,
4 v a J 4 к a J
I 17 1A 2
x = +/l + -a + - .
J 4k a)
5. Ответ-, если a < 1, то корней нет;
I ГТ i'',2
если а > 1, то х, 9 = + /1 + - [а + - .
iJ 4 k aJ
13. В зависимости от значений параметра а решить уравнение
л/а - Ja + х = х. (1)
1. Из уравнения (1) непосредственно следует, что если а = 0, то
и х = 0 — частичный ответ.
2. Согласно определению арифметического корня, имеем х > 0,
а - Jа + х 0.
3. Решив неравенство а - Ja + х 0, получим
х < а(а - 1). (2)
4. Так как х > 0, то с учетом сказанного ранее заключаем, что
неравенство (2) справедливо при а = 0 или при а > 1.
5. Сведем уравнение (1) к системе уравнений с помощью под-
становки t = Jа + х , где f > 0. Из уравнения (1) следует, что х =
= *Ja -1, и приходим к системе
6. Возведя в квадрат оба уравнения системы (3), имеем
I t2 = а + х, ...
5 2 / W
[ хл = а - t.
7. Вычтем второе уравнение системы (4) из первого:
t2 - х2 = х + t, т. е. (t + x)(t - х - 1) = 0. (5)
287
8. Рассмотрим уравнение (5). Так как f > 0 и х > О, то f - х - 1 = 0;
после обратной замены t на л/а + х получим уравнение Ja + х =
= х + 1. Следовательно,
а + х = (х + I)2, или х2 + х+1-а = 0. (6)
9. Решив уравнение (6), находим
1 з — 1 + з з
*1 = ---, х2 = --------------, где а > - .
10. Проверим найденные значения:
а) х1 не удовлетворяет условию х > 0;
б) неравенство х = 1 + */4а_3 q справедливо при /4а - 3 > 1,
т. е. при а > 1.
11. Ответ: если а е (-оо; 0) U (0; 1), то корней нет;
,— г , I , — 1 "Ь 7 4 л — 3
если а-[1; +°°), то х =--;
если а = 0, то х = 0.
14. В зависимости от значений параметра а решить уравнение
х +
= а.
(1)
1. Из уравнения (1) непосредственно следует, что 0 < х < а. Та-
ким образом, при а < 0 уравнение не имеет решений, а при а = 0 оно
имеет решение х = 0.
2. Пусть а > 0. Тогда, возведя в квадрат обе части уравнения
Ja + л/х = а - х, получим
а2 - (2х + 1)а + х2 - Jx = 0.
(2)
3. Решив уравнение (2) как квадратное относительно парамет-
ра а, находим
а = х + л/х + 1,
(3)
а = х - л/х .
(4)
4. Так как х > 0, то из равенства (3) следует, что а > 1. При
таких значениях параметра а рассмотрим уравнение (3) как квад-
ратное относительно л/х и решим его:
-1~74а-3
- 1 + 74а-3
2
288
5. Согласно определению арифметического корня, годится лишь
г -1 + л/4а-3
второе значение: *Jx =---, откуда
_ 2а - 1 - 74а - 3
Х 2 ’
6. Рассмотрим теперь уравнение (4). Решив его относительно Jx ,
находим
!- _ 1 - 74а + 1 Г _ 1 + 74а + 1
л/х 2 , д/X 2
7. По тем же причинам, что и ранее, годится лишь второе зна-
г~ 1 + 74а + 1
чение: 7х =-----. Отсюда получаем
х = а + + i 74а + 1 > а,
2 2
т. е. это значение х не может быть корнем исходного уравнения,
поскольку оно не удовлетворяет условию х < а.
8. Ответ-, если а е (-оо; 0) U (0; 1), то корней нет;
,— г -< । \ 2 а — 1 — 74 а — 3
если а -[1; +°°), то х =---;
если а = 0, то х = 0.
1 5. Решить уравнение
л/Зх - Ja - Зх = 1. (1)
1. Найдем ОДЗ уравнения (1): х > 0, а - Зх > 0 (а > Зх а > 0);
значит, 0ч хч - .
О
2. Чтобы освободиться от радикалов в данном уравнении, на-
до дополнительно потребовать выполнения неравенства л/Зх -
- Ja - Зх > 0, поскольку правая часть уравнения (1) — положи-
тельное число.
3. Таким образом, условие для возведения в квадрат имеет вид
Зх > а - Зх, т. е. х > .
6
289
4. Итак, должны выполняться следующие ограничения:
а
3 ’
6
5. Теперь обе части уравнения (1) возведем в квадрат:
Зх + а - Зх - 2 J3x Ja - Зх = 1,
или
2j3x(a - Зх) = а - 1, (2)
где а - 1 > 0 согласно определению арифметического корня.
6. Возведем обе части уравнения (2) в квадрат и после упроще-
ний получим
4 • (Зх)2 - 4а • (Зх) + (а - I)2 = 0. (3)
7. Решив уравнение (3), находим
Зх = а ± \ , т. е. xb 2 = а ~ V2a 1. (4)
8. Полученные значения (4) должно удовлетворять условиям
а - а ч
- < х < - при а > 1.
6 3
XX тт CL О' 1
9. Проверим значение х, = —------- подстановкой в неравен-
1 6
a a - J2a-1 а /т>--т м
ство х > - ; имеем —, откуда следует -<J2a - 1 >0, что
6 6 6
тт а - а/2л- 1
неверно. Итак, х = —----- — посторонний корень.
6
10. Проверим значение х9 = а + . Подставив его в двой-
6
а а а а + J2a- 1 - а
ное неравенство - <хч - ,т. е. - <-------- ч - , после упроще-
6 3 6 6 3
ний получим
а < а + J2a - 1 < 2а, или 0 < J2a - 1 < а
— верное неравенство при а > 1.
11. Ответ: если а < 1, то корней нет;
\ 1 а + а/2л - 1
если а 1, то х =--------.
290
1 6. Решить неравенство
(а-1)7^<0. (1)
1. Понятно, что область определения есть х > 0.
2. Понятно также, что ответ зависит от знака множителя (а - 1).
3. При а < 1, очевидно, неравенству (1) удовлетворяет любое
значение из области определения, т. е. х > 0.
4. При а - 1 > 0 левая часть неравенства (1) неотрицательна;
в данном случае х = 0 — единственное решение.
5. Ответ: если а < 1, то х > 0;
если а > 1, то х = 0.
17. В зависимости от значений параметра а решить неравенство
х + 4а > 5л/ох . (1)
1. Пусть а < 0; тогда, исходя из вида правой части неравенства,
заключаем, что х < 0. Но при таких а и х левая часть неравенст-
ва (1) отрицательна, и, значит, ни при каких отрицательных зна-
чениях а неравенство не имеет решений.
2. Пусть а = 0; тогда неравенству (1) удовлетворяет любое х > 0.
3. Пусть а > 0; тогда х > 0. Отсюда, в частности, следует, что
х = 0 является решением неравенства. Кроме того, при таких зна-
чениях а их данное неравенство равносильно неравенству
(х + 4а)2 > 25ах, т. е. х2 - 17ах + 16а2 > 0. (2)
Неравенство (2) можно записать в виде
(у - 1)(у - 16) > 0, где у = , а 0. (3)
4. Решив неравенство (3), находим, что у<1,у>16,и, значит,
0 < х < а, х > 16а.
5. Ответ: если а е (-оо; 0), то решений нет;
если а = 0, тох - (0; +°°);
если а е (0; +°°), тох'- [0; а) U (16а; +°о).
18. В зависимости от значений параметра а решить неравенство
л/а + х + Ja-x > а. (1)
1. При а < 0 неравенство (1) не имеет решений.
2. Пусть а > 0; тогда ОДЗ переменной х задается неравенствами
-а < х < а.
291
3. При таких значениях х возведем обе части неравенства (1)
в квадрат и получим неравенство
2л/а2 -х2 > а2 - 2а. (2)
4. Рассмотрим следующие три случая:
а2 - 2а < 0; а2 - 2а = 0; а2 - 2а > 0.
5. Пусть а2 - 2а < 0; тогда 0 < а < 2 и неравенство (2) справед-
ливо при всех |х| < а.
6. Пусть а2 - 2а = 0, т. е. а = 2; тогда неравенство (2) примет вид
2 л/4 - х2 > 0, откуда следует, что |х| < 2.
7. Пусть а2 - 2а > 0, т. е. а > 2. Тогда, возведя обе части нера-
венства (2) в квадрат, получим равносильное неравенство
4(а2 - х2) > а4 - 4а3 + 4а2,
или
х2 < . (3)
а) Если а > 4, то неравенство (3) не имеет решений.
б) Если 2 < а < 4, то |х| < ~ U и> как легко проверить,
aja(4 - а) д
8. Ответ: если а < 0 или а > 4, то решений нет;
если 0 < а < 2, то -а < х < а;
если а = 2, то -2 < х < 2;
о , , л aJa(4 - а) , , aJa(4 - а)
если 2 < а < 4, то ~ 2----~ < х < 2---1'
1 9. Для всех значений параметра а решить неравенство
л/х + а > х + 2.
1. Проведем геометрическое исследование неравенства (рис. 95).
Построим графики прямой у = х + 2 и «плавающей» параболы у =
= л]х + а с вершиной в точке (-а; 0).
Данное неравенство выполняется для тех значений а, при кото-
рых парабола и прямая имеют хотя бы одну общую точку.
292
2. Рассмотрим уравнение Jx + а = х + 2, т. е. х2 + Зх + 4 - а = 0.
тл 3 ± 74а-7 7 д-r 7
Имеем х =-----, где а . При а = - уравнение имеет один
корень х = . Это соответствует случаю касания параболы и прямой.
7
3. При а < - неравенство не имеет решений.
7
4. Если а > - , но а < 2, то парабола пересекает прямую в двух
точках; данное неравенство справедливо при
3 74а-7 < < ~ 3 + 74а-7
2 Х 2
5. При а > 2 парабола пересекает прямую только в одной точке
— 3 + 74а — 7 г -1
х2 =---------- и данное неравенство выполняется на отрезке [-а; х2].
6. Ответ: если а (-оо; I ) , то решений нет;
7 3
если а = - , то х = - - ;
4 2
_Г7 о! Г-3-74а-7 -3 + 74а-7 1
если а е - ; 2 J , то х е -----J ;
если а е (2; +°°), то х е Г-а; 3 + ^a—1.
293
20. При каких значениях а < 0 неравенства
2 J~ax < За - х (1)
и
<2>
имеют общие решения?
1. Так как по условию а < 0, а ах > 0, то х < 0.
2. Левая часть неравенства (1) положительна, поэтому и его
правая часть должна быть положительна, т. е. х < За.
3. Аналогично, записав неравенство (2) в виде х - - > , за-
6
ключаем, что - < х.
а
4. Решим неравенство (1):
2 Jax < За - х, т. е. х2 - 10ах + 9а2 - 0 = i - (-°°; 9а) U (а; 0).
Но мы установили, что х < За, следовательно, х е (-оо; 9а).
5. Решим неравенство (2):
1х 6 б /х о 13х . 36 ,, _
х - - > - , т. е. х - - > - , т. е. хл - + — > 0 =>
Va а а уа а
Но мы установили, что х > - , поэтому х -(-;0).
6. Чтобы неравенства (1) и (2) имели общие решения, интерва-
лы 9а) и ; о) должны иметь общие точки, т. е. - < 9а =>
__ 4-9 2 ^ .-.
=> - => ал, откуда -- ч а < 0.
7. Ответ: а — ; о).
21. Для всех значений параметра а решить неравенство
|х2 - 5х + 4| < а. (1)
1. Так как |х2 - 5х + 4| > 0 при любом х, то при а < 0 неравен-
ство (1) не имеет решений.
294
2. Пусть а > 0. Поскольку х2 - 5х + 4 = (х - 1)(х - 4), числовая
прямая (ОДЗ данного неравенства) разбивается на три промежут-
ка: х<1,1Сх<4,х>4. Решим неравенство (1) на каждом из них.
3. Если х < 1, то х2 - 5х + 4 > 0, и в этом случае неравенство (1)
равносильно системе
J х2 - 5х + 4 < а,
[ X < 1.
а) Дискриминант квадратного трехчлена х2 - 5х + (4 - а) равен
9 + 4а и, следовательно, положителен при а > 0.
б) Решив неравенство х2 - 5х + 4 - а < 0, находим
| (5 - л/9 + 4а) < х < | (5 + 79 + 4а).
в) При каждом положительном а верны неравенства
| (5 + JWWa) > 4, | (5 - JWWa) < 1.
г) Поэтому из системы (2) следует: каждое х такое, что | (5 -
- л/9 + 4а) < х < 1 при всех а > 0 есть решение неравенства (1).
4. Если 1 < х < 4, то неравенство (1) на этом множестве равно-
сильно неравенству
х2 - 5х + 4 + а > 0. (3)
а) Дискриминант квадратного трехчлена х2 - 5х + 4 + а равен
9 - 4а.
б) Таким образом, неравенство (3) выполняется при любом дей-
9 п, <' 9
ствительном х, если а > - ; если же 0 < а ч - , то решением нера-
венства (3) являются все х из промежутков < х < | (5 - 79 - 4а)
и | (5 + л/9 - 4а) < х < +°°.
в) Кроме того, при 0 < а < | справедливы неравенства
1 < | (5 - 79^4^) < | (5 + 79^4^) < 4.
295
5. Заключаем, что в случае 1 < х < 4 при а > | решением нера-
венства (1) является отрезок 1 < х < 4, при 0 < а < | множество
решений неравенства (1) состоит из двух промежутков:
1 < х < | (5 - 79 - 4а), | (5 + 79 - 4а) < х < 4.
6. Если х > 4, то неравенство (1) равносильно системе
, х > 4,
J х > 4, <=> J 1 _____ 1 _____ «
|х2-5х + 4-а<0 j 2 (5 - 79 + 4а) < х < - (5 + 79 + 4а)
«4<х< | (5 + 79 + 4а).
7. Ответ: если а < 0, то решений нет;
если 0 < а ч - , то
4
| (5 - 79 + 4а) < х < | (5 - 79 - 4а),
| (5 + 79 - 4а) < х < | (5 + 79 + 4а);
если а > |, то | (5 - 79 + 4а ) < х < | (5 + 79 + 4а).
296
Замечание. Полученный ответ геометрически иллюстри-
руется на рис. 96:
а) положение I соответствует случаю а < 0;
< ? •
" 4 ’
\ ттт ^9
в) положение III — случаю а > - .
б) положение II — случаю О
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить уравнение:
а) 41^ х - 41/} + х =2; б) Ja - 6х = х - 1;
А/& + х у а х
в) J3a - 2х + х = а; г) J3- х - J3 + х = а.
2. Решить уравнение:
a) Jx = х - а; б) Jx + Ja = Jl-(x + а) ;
в) 1 - х = Ja1 2 3 4 5 6 - х2 ; г) х + Jx2 - х = а.
3. Решить уравнение:
a) Jx2 - 2х + 1 + Jx2 + 4х + 4 = а;
б) Jx2 + 6х + 9 - Jx2 - 4х + 4 = а;
в) Jx + 2jx - 1 - Jx + 3 - 4jx - 1 = a.
4. Найти количество корней уравнения
л/4 - х2 = х + а
в зависимости от значений параметра а.
5. Решить неравенство:
a) Jx - а2 + Jx 2а; б) J2ax - х2 а - х;
в) Ja + х + Ja-x < а; г) J\ - х2 2х + а;
д) Jx + а > х + 1.
6. Найти все значения параметра а, при каждом из которых не-
равенство Jx2 + 2ах + а2 + х2 <2 имеет хотя бы одно положитель-
ное решение.
297
Ответы
. а-6(1 + л/2) а-л: л _z
1. а) х = -i—JZ 27 , где —— > 0; б) если а G (-°°; 6), то нет корней;
если а G [6; +°°), то х = -2 + 73 + а ; в) если а < 0, то нет корней; если а > 0,
то х = а - 1 - Ja + 1 ; г) если а е (-оо; - J& ) U ; +°о), то нет корней; если
а е [-76 ; л/б ], то х = -0,5а«/12 - а2.2. а) Если а < -0,25, то нет корней;
если а = -0,25, то х = 0,25; если -0,25 < а < 0, то х1 2 = 0,5(2а + 1 ± 74а + 1 );
если а > 0, то х = 0,5(2а + 1 + 74а + 1 ); б) если а G (-оо; 0) U (0,5; +°о),
то нет корней; если а G [0; 0,5], то х = 0,5(1 - а - 72а - За2 ); в) если
|а| < 0,б72 , то нет корней; если |а| = 0,5 J2 , то х = 0,5; если 0,5 J2 < |а| < 1,
то х1 2 = 0,5(1 ± 72а2 - 1 ); если |а| > 1, то х = 0,5(1 - 72а2 - 1 ); г) если а е
а2
е (-оо; 0) U (0,5; 1), то нет корней; если а G [0; 0,5) U [1; +°о), то х = --j .
3. а) Если а < 3, то нет корней; если а = 3, тох - [-2; 1); если а > 3, то
х = -0,5(а + 1), х = 0,5(а - 1); б) если а G (-оо; -5) U (5; +°°), то нет корней;
если а = -5, то.г~ (-оо; 3]; если а е (-5; 5), то х = 0,5(а - 1); если а = 5, то
х G [2; +°°); в) если а G (-оо; -1) и (3; +°о), то нет корней; если а G [-1; 3),
то х = 0,5(а + I)2 + 1; если а = 3, тох - [5; +°о). 4. Если а G (-оо; -2) U
и (2 72; +оо), то нет корней; если а G [-2; 2) U {2 72}, то один корень;
если а - [2; 2 72 ), то два корня. 5. а) Если а'' 0, тох - [а2; +°о); если а > 0,
тох'- Ц а2. +оо) ; б) если а < 0, то (1 + 0,5 J2 )а < х < 0; если а = 0, то
х = 0; если а > 0, то (1 - 0,5 72 )а < х < 2а; в) если 2 < а < 4, то -а < х <
< -0,5а74а - а2,0,5а74а - а2 < х < а; если а > 4, то -а < х < а; при осталь-
ных значениях а решений нет; г) если а < -2, то -1 < х < 1; если -2 < а <
< 2, то -1 < х < 0,2(75 - а2 - 2а); если 2 < а < Тб , то -0,4(Тб - а2 + 2а) <
<х< 0,4(Тб -а2 - 2а); если а > Тб , то решений нет; д) если а < 0,75, то ре-
шений нет; если а = 0,75, то х = -0,5; если 0,75 < а < 1, то -0,5(1 + 74а - 3 ) <
< х < 0,5(74а - 3 - 1); если а > 1, то -а < х < 0,5(74а - 3 1). 6. а -( 2,25; 2).
Показательная функция и ее свойства
Показательные уравнения _ Z Z Z Z Z Z
доказательные неравенства | | | |
Системы показательных уравнений и неравенств
*..............................................................................г
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Показательная функция и ее свойства
1°. Функцию, заданную формулой вида у = ах, где а — некото-
рое положительное число, не равное единице, называют показа-
тельной.
2°. При а > 1 функция у = ах обладает
следующими свойствами (рис. 97, а):
а) область определения — множество R
всех действительных чисел;
б) множество значений — множество R+
всех положительных чисел;
в) функция возрастает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то ах > 1;
е) если х < 0, то 0 < ах < 1.
3°. При 0 < а < 1 функция у = ах обла-
дает следующими свойствами (рис. 97, б):
а) область определения D(f) = R;
б) множество значений E(f) = R+;
в) функция убывает;
г) при х = 0 значение функции равно 1;
д) если х > 0, то 0 < ах < 1;
е) если х < 0, то ах > 1.
299
2. Показательные уравнения
1°. Уравнение, содержащее переменную в показателе степени,
называют показательным. Простейшим примером показательно-
го уравнения служит уравнение ах = 1, где а > 0, а 1.
2°. Решение показательных уравнений вида af^ = aq№, где а > О,
а/1, основано на том, что это уравнение равносильно уравнению
f(x) = ф(х).
3°. Уравнение вида Аа2х + Вах + С = 0 с помощью подстановки
ах = у сводится к квадратному уравнению Ay2 + By + С = 0.
3. Показательные неравенства
1°. Неравенство, содержащее переменную в показателе степе-
ни, называют показательным.
2°. Решение показательных неравенств вида < афОО, где
а > 0, а 1, основано на следующих утверждениях:
а) если а > 1, то неравенства af^ < а'РР) и /(х) < ф(х) равносильны;
б) если 0 < а < 1, то неравенства а^ < а'РР) и /(х) > <р(х) равно-
сильны (это следует из того, что при а > 1 показательная функция
возрастает, а при 0 < а < 1 убывает).
4. Системы показательных уравнений и неравенств
Известные способы решения систем алгебраических уравнений
применяются и к решению систем, содержащих показательные
уравнения и неравенства.
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра а уравнение
9х - (4а + 2)-3х- 5а2 + 34а - 24 = 0 (1)
имеет два различных решения?
1. Положим Зж = t > 0. Тогда уравнение (1) примет вид
t2 - 2(2а + 1)? - 5а2 + 34а - 24 = 0. (2)
2. Найдем дискриминант квадратного уравнения (2):
J = (2а + I)2 + 5а2 - 34а + 24 = (За - 5)2.
300
Следовательно, корнями уравнения (2) являются
t} = 2а + 1 - (За - 5) = 6 - a; t2 = 2а + 1 + (За - 5) = 5а - 4.
3. Для того чтобы исходное уравнение имело два различных
корня, необходимо выполнение следующих условий:
*1 * *2’ j 6 - а 5а - 4, 3
> 0, или < 6 - а > 0, т. е. •< а < 6,
> 0, 5а - 4 > О, 4
z 1 Cl > — .
л гл 5 Л . . Л 5 „А
4. Ответ: а е ; - J U ; 6 J.
2. Найти все значения параметра а, при которых уравнение
4ж-а-2ж-а + 3 = 0 (1)
имеет хотя бы одно решение.
1. Положим 2х = t > 0; тогда исходное уравнение примет вид
f2 - at - а + 3 = 0. (2)
2. Для того чтобы уравнение (1) имело хотя бы одно решение,
необходимо и достаточно, чтобы квадратный трехчлен f2 - at - а + 3
имел хотя бы один положительный корень, и, следовательно, диск-
риминант этого квадратного трехчлена должен быть неотрицателен.
3. Так как
D = а2 - 4(3 - а) = а2 + 4а - 12 = (а - 2)(а + 6),
то условие D > 0 выполняется при а < -6 и а > 2.
4. Корни tх и 12 уравнения (2) удовлетворяют системе уравнений
] txt2 = 3 - а,
| fx + t2 = а.
а) При а < -6 имеем fxf2 > 0, fx + f2 < 0; поэтому оба корня fx, f2
отрицательны, и, следовательно, уравнение (1) не имеет решений.
б) При а> 2 имеем fx + f2 > 0; значит, хотя бы один из корней
fx или f2 положителен.
5. Итак, при а> 2 уравнение (1) имеет хотя бы одно решение.
6. Ответ: а [2; +°°).
301
3. Найти множество значений а, при которых уравнение
4* - (За + 2) • 2* + 2а2 - 2а - 24 = О (1)
имеет единственное решение, большее, чем 2.
1. Пусть 2Ж = t > 0. Тогда уравнение (1) примет вид
t2 - (За + 2)t + 2а2 - 2а - 24 = 0. (2)
Найдем дискриминант этого уравнения: D = (а + 10)2.
2. По условию уравнение (1) должно иметь единственное реше-
ние х > 2. Следовательно, t = 2х должно быть больше 4.
3. Рассмотрим два возможных случая:
\D = 0, [(а+10)2 = 0, Га = -ю,
а)у1>2>4 =4 За^2 >4 =^_28>8, т.е.ае0.
б) D > 0 => (а + 10)2 > 0, т. е. а + —10. Уравнение (2) имеет два
различных корня: = а - 4 и f2 = 2а + 6.
Исходное уравнение будет иметь единственное решение, боль-
шее, чем 2, если один из корней или f2 больше 4, а другой корень
неположителен. Это приводит к следующей совокупности систем
неравенств:
1а-4 >4,
12а + 6 < 0;
г , „ ил
J а - 4 < 0,
| 2а + 6 > 4,
т. е. а — (-1; 4].
4. Ответ: а е (-1; 4].
или
а1— 0,
-1 <а<4,
4. Для каждого значения параметра а решить уравнение
9-|х- 2 _ 4.3-|x- 2| _ а = о. (1)
1. С помощью подстановки 3 т 21 = t (0 < t < 1) уравне-
ние (1) сводится к смешанной системе
J f2 - 4f - а = 0,
]0<t<l.
2. Квадратное уравнение системы (2) имеет действительные
корни 2 = 2+ Д4 + а тогда и только тогда, когда а > -4.
302
а) При этом условии корень = 2 + 74 + а > 1, и, следователь-
но, не является решением системы (2).
б) Корень t2 = 2 - 74 + а удовлетворяет условиям 0 < t < 1, т. е.
неравенствам 0 < 2 - 74 + а < 1 при -3 < а < 0.
в) Таким образом, если -3 < а < 0, то система (2) имеет решение
t = 2 - л/4 + а , которому соответствуют следующие корни исходно-
го уравнения:
х = 2 ± log3 (2 - 74 + а ).
3. Если а < -3 или а > 0, то смешанная система (2), а, значит,
и уравнение (1) не имеет решений.
4. Ответ: если а < -3 или а > 0, то корней нет;
если -3 < а < 0, то хг 2 = 2 ± log3 (2 - 74 + а )•
5. Решить уравнение
4sin ж + а • 2sin ж + а2 - 1 = 0, (1)
где а — параметр, изменяющийся на промежутке [-1; 1].
1. Воспользуемся подстановкой у = 2sin х. Тогда уравнение (1)
примет вид у2 + ay + а2 - 1 = 0, где | < у < 2, так как -1 < sin х < 1.
2. Вершина параболы
f(y) = У2 + ay + а2 - 1 (2)
имеет абсциссу у
поэтому из условия -1 < а < 1 следует, что
| |. Следовательно, при -1 < а < 1 промежутку
может принадлежать только больший корень квадратного трех-
члена (2).
3. Этот факт аналитически описывается системой неравенств
/flVl + 1а + а2_1<0
4 2 (3)
/(2) = 4 + 2а + а2 - 1 > 0.
4. Решив систему (3) при условии -1 < а < 1, находим, что она
_ г , - 1 + 713 "I
совместна, если а -1; ----.
303
5. Больший корень квадратного трехчлена (2) есть
- а + д/4 - За2
У = ------2----•
Остается решить уравнение 2sin х = а + , откуда найдем
корни исходного уравнения (1).
6. Ответ: если а |^-1; 1 ’ то
х = (-1)* arcsin log2 ( а + а/4 3а /г
при других а решений нет.
6. При каких значениях а уравнение
х2 - 7х + 12 _ р
&2х- а _ ga-х ' '
имеет единственное решение?
1. Уравнение (1) равносильно системе
!х2 - 7х + 12 = 0, (2)
[32ж~а-За~ж^0. (3)
2. Находим корни уравнения (2): х1 = 3, х2 = 4.
3. Если существует такое а, что при х = 4 условие (3) не выпол-
няется, т. е. имеет место равенство 32ж ° - 3° т = 0, то знаменатель
данной дроби (1) обращается в нуль. Последнее означает, что в точ-
ке х = 4 эта дробь не определена и поэтому х = 4 не может быть
корнем уравнения (1).
4. Таким образом, уравнение (1) имеет единственное решение
х = 3, если корнем знаменателя данной дроби является х = 4. Тогда
этот знаменатель при х = 4 должен обращаться в нуль, т. е.
З2 4 у — Зу 4 = О,
откуда а = 6.
5. Рассуждая аналогично, заключаем, что уравнение (1) имеет
единственное решение х = 4, если корнем знаменателя данной дроби
является х = 3 (в этом случае дробь при х = 3 не определена). Сле-
довательно, знаменатель при х = 3 должен обращаться в нуль, т. е.
З2'3 "-3" 3 = 0,
откуда а = 4,5.
6. Ответ: а = 6; а = 4,5.
304
7. Определить все значения параметра а, при которых уравнения
4* + 2 х + 1 = 3
и
а • 49* + |а - 7| • 7х = 7
равносильны.
1. Решим уравнение
4* + 2 • 2х - 3 = 0. (1)
Полагая 2х = у > 0, придем к квадратному уравнению у2 + 2у -
-3 = 0, имеющему корни у = 1; у = -3 (посторонний корень, так как
он не удовлетворяет условию у > 0). Значит, 2х = 1, откуда х = 0.
Следовательно, уравнение (1) имеет единственный корень х = 0.
2. Согласно условию, уравнение
а • 49* + \а - 7| • 7х - 7 = 0 (2)
также должно иметь только один корень х = 0. Подставив в урав-
нение (2) значение х = 0, получим уравнение относительно а:
а + |а - 7| - 7 = 0, или |а - 7| = 7 - а. (3)
3. В силу определения модуля решением уравнения (3) являют-
ся все значения а < 7.
4. При таких значениях а уравнение (2) примет вид
а • 72* - (а - 7) • 7* - 7 = 0. (4)
5. Положим 7* = г > 0 и получим уравнение
az2 - (а - 7)z - 7 = 0. (5)
Уравнение (5) при а = 0 имеет единственный корень z = 1, а при
а 0 — два корня z = 1 и z = -- . Чтобы уравнение (5) при а 0
имело только один корень, нужно, чтобы корень z = -- был:
7
а) либо равен 1, т. е. -- =1, откуда а = -7;
7
б) либо отрицателен, т. е. -- <0, откуда а > 0.
6. Учитывая отмеченные выше условия, при выполнении кото-
рых уравнение (2) должно иметь единственный корень, оконча-
тельно получаем: 0<а<7иа = -7.
7. Ответ: а е [0; 7] U {-7}.
305
8. При каких значениях параметра а уравнение
7Ж + 7 х - 4 = а(3|х| - 5 cos х)
имеет нечетное число корней?
1. Функции f(x) = Iх + 7 х - 4 и <р(х) = а(3|х| - 5 cos х) определе-
ны при всех .г - й и являются четными:
f(-x) = 7 х + 7+х - 4 = 7х + 7 х - 4 = f(x),
ф(-х) = а(3|-х\ - 5 cos (-х)) = а(3|х| - 5 cos х) = ф(х).
2. В силу четности графики функций у = f(x) и у = ф(х) симмет-
ричны относительно оси Оу и можно утверждать, что если х = х} —
корень исходного уравнения, то х = -хг также является корнем
этого уравнения.
3. Следовательно, данное уравнение имеет четное число кор-
ней, если х = 0 не является его корнем, и нечетное число корней,
если х = 0 — корень этого уравнения.
4. Проверим, является ли х = 0 корнем исходного уравнения.
При х = 0 получаем равенство
2
1 + 1- 4 = (0- 5 cos 0)а, или -5а = -2, откуда а = - .
2
5. Значит, при а = - исходное уравнение принимает вид 7х +
+ 7 х -4=| (3|х| - 5 cos х) и имеет единственный корень х = 0:
/(0) = -2; ф(0) = -2 (рис. 98).
2
6. Ответ: а = - .
5
306
9. При каких значениях параметра k неравенство
Jx2 + 4х + 7 < х + 3 (1)
и уравнение
2х + 2_|2х+1_А| = 2х+1 + 1 (2)
равносильны?
1. Решив неравенство (1), получим х > -1 и, значит, любое
х > -1 должно быть решением уравнения (2).
2. Тогда, подставив значение х = 0 в уравнение (2), приходим
к уравнению
4 - |2 - k\ = 3 (3)
относительно неизвестного k.
3. Решив уравнение (3), находим k = 1 и k =3.
4. Пусть k = 1. Подставим это значение в уравнение (2) и полу-
чим уравнение
|2ж + 1 - 1| = 2ж + 1 - 1,
решением которого является любое х > -1. Итак, при k = 1 нера-
венство (1) и уравнение (2) равносильны.
5. Пусть k = 3. При этом значении k уравнение (2) примет вид
|2ж + 1-3| = 2ж + 1-1. (4)
6. Решив уравнение (4), получим х = 0 и, значит, неравенство (1)
и уравнение (2) при k = 3 не равносильны.
7. Ответ: k = 1.
10. При каждом значении параметра а указать, для каких х вы-
полняется неравенство
а2 _ 9х + 1 _ 8 . Зх . а > о. (1)
1. Пусть а = 0; тогда неравенство (1) имеет вид -9Ж + 1 > 0 и не
выполняется ни для какого х.
2. Пусть а — некоторое число, отличное от нуля. Обозначив Зж
через у, перепишем неравенство (1) так:
9у2 + 8ау - а2 < 0. (2)
Квадратный трехчлен 9у2 + 8ау - а2 имеет корни у} = -а,
а
У2=Э-
307
3. Если а > 0, то у, < у2 и множество решений неравенства (2)
имеет вид -а < у < |. Это значит, что при каждом положительном
а исходное неравенство равносильно двойному неравенству -а <
< Зж < | и, следовательно, множество его решений есть промежу-
ток < х < log3 |, т. е. < х < -2 + log3 а.
4. Если а < 0, то у2 < у} и множество решений неравенства (2)
имеет вид | < у < -а. Это значит, что при каждом отрицательном
„ а „
а исходное неравенство равносильно двойному неравенству - <
< Зж < -а и, следовательно, множество его решений есть промежу-
ток < х < log3 (~а).
5. Ответ: если а = 0, то решений нет;
если а > 0, то х < -2 + log3 а;
если а < 0, то х < log3 (~а).
11. Найти все значения параметра а, при которых неравенство
4*2 + 2(2а + 1)2*2 + 4а2 - 3 > О (1)
выполняется для любых х.
1. Полагая 2*2 = t > 0, запишем неравенство (1) следующим
образом:
t2 + 2(2а + l)t + 4а2 - 3 > 0. (2)
2. Тем самым решение исходной задачи сводится к отысканию
всех значений а, при которых неравенство (2) выполняется для лю-
бых t > 0.
3. Так как
t2 + 2(2а + l)t + 4а2 - 3 =
= t2 + 2t(2a + 1) + (2а + I)2 - (2а + I)2 + 4а2 - 3 =
= (t + 2а + I)2 - 4(а+ 1),
то при а + 1 < 0 (т. е. при а < -1) неравенство (2) справедливо для
любого t, в том числе и для t > 0.
308
4. При а + 1 > 0 имеем а + 1 = (Ja + 1 )2; поэтому неравенство (2)
равносильно неравенству
(t + 2а +1 + 2 J a + 1 )(t + 2а +1-2 7а + 1) > 0. (3)
При таких а справедливо неравенство -2а - 1 - 2 Ja + 1 < -2а -
-1 + 2 Ja + 1 ; следовательно, неравенство (3) выполняется для лю-
бого t > 0, если выполняется неравенство
-2а - 1 + 27а + 1 < 0, т. е. 27а + 1 < 2а + 1. (4)
5. При -1 < а < -0,5 неравенство (4) не имеет решений. При
а > -0,5 получим систему
Ja >-0,5, Ja >-0,5,
] 4(а + 1) < 4а2 + 4а + 1 Ма2 - 3 + 0
[а >-0,5,
1 л/3
6. Итак, неравенство (2) справедливо для любого t > 0, если а
принадлежит множеству (-°°; -1) U [ ; +°с .
7. Ответ: а е (-оо; -1) и [; +°о^.
1 2. Найти все значения параметра k, при которых неравенство
4*-й-2*-й + 3<0 (1)
имеет хотя бы одно решение.
1. Пусть 2Ж = t > 0. Тогда получим квадратное неравенство, со-
держащее числовой параметр k:
t2-kt-k + 3<0. (2)
2. Для того чтобы неравенство (2) имело хотя бы одно решение,
нужно, чтобы квадратный трехчлен имел хотя бы один положи-
тельный корень.
309
3. Корни квадратного трехчлена будут действительными при
условии неотрицательности его дискриминанта:
D = k2 - 4(3 - k) > 0, или к2 + 4А - 12 > О,
откуда k < -6 или й > 2.
4. Чтобы выяснить, когда хотя бы один из корней будет поло-
жителен, воспользуемся теоремой Виета:
| + f2 = k,
| trt2 = 3 - k.
5. Если k < -6, to t1t2 = 3 - k > 0; произведение корней положи-
тельно, т. е. корни имеют одинаковые знаки. Так как сумма кор-
ней + t2 = k < 0, то оба корня отрицательны. Этот случай не под-
ходит.
6. Если й > 2, то trt2 = k > 0, т. е. сумма корней положительна.
Значит, хотя бы один из корней квадратного трехчлена положите-
лен. Итак, й > 2.
7. Ответ: k [2; +°°).
1 3. При каких значениях параметра а система
J2bsin* + (а + 1)&у2 = а2,
| (а - 1)х3 + у3 = 1
имеет решение для любого значения параметра Ь?
1. Если система (1) при каком-то значении параметра а имеет
решение для любого значения параметра Ь, то эта система имеет
решение и для Ъ = 0.
2. Подставляя значение Ъ = 0 в систему (1), получим систему
I а2 = 1, (2)
| (а - 1)х3 + у3 = 1. (3)
Из уравнения (2) следует, что а = ±1.
3. Пусть а = 1; тогда система (1) примет вид
[26sin* + 2&у2 = 1, (4)
]у3 = 1. (5)
4. Из уравнения (5) находим у = 1, а уравнение (4) запишется
в виде
26sinx = 1 _ 2b. (6)
310
5. Уравнение (6) имеет решения не для любых значений парамет-
ра Ъ, а лишь для тех, которые удовлетворяют неравенству 1 - 2Ь > О,
, 1
т.е.&<-.
6. Пусть а = -1. В этом случае система (1) примет вид
J2bsin*=l, J&sinx=0,
j у3 - 2х3 = 1, Т'е' [ у3 = 2х3 + 1.
Легко установить, что эта система имеет решение для любого
значения параметра Ь.
7. Ответ: а = -1.
14. Найти все значения а, при которых совместна система урав-
нений
J 31 - Jx + l = 5a-2 tg2 у,
| 4 tg2 у + 2 = За + 3~^ .
1. Полагая и = 3 , v = tg2 у, перепишем данную систему:
[ 3 • 3-J* + 1 = 5а - 2 tg2 у, / За + 1 = 5а - 2и,
| 4 tg2 у + 2 = За + З-J* . 1 4и + 2 - За + и.
2. Учитывая, что а — параметр, а а и v — неизвестные, запи-
шем систему (1) в виде
J За + 2v = 5а - 1,
}-а + 4и = За-2. (2)
3. Умножив второе уравнение системы (2) на 3 и сложив ре-
зультат с первым уравнением, получим
14и = 14а - 7, или v = а - | .
4. Аналогично, умножив первое уравнение системы (2) на (-2)
и сложив результат со вторым уравнением, получим
-7а = -7а, или а = а.
311
5. Вернемся к первоначальным переменным и запишем систему
tg2 у = а - |,
< (3)
3-^ = а,
равносильную системе (2).
6. Левые части уравнений системы (3) удовлетворяют следую-
щим ограничениям:
О < tg2 у, 0 < 3’^ < 1 f поскольку 3’^ = -^= .
V Зл/х /
7. Отсюда получаем систему неравенств для параметра а:
а- |,
|о<а< 1.
8. Решим эту систему:
[ 1 <
<2 ’ т. е. i < а < 1.
[0<а<1, 2
9. Ответ: а е [0,5; 1].
15. Найти все значения а, при которых совместна система урав-
нений
[ sin х - 4 = За - 21+^2,
| 2 2 + у2 - 3 = а + 3 sin х.
В ответе указать наименьшее из этих значений.
1. Пусть и = sin х, v = 2yZ . Тогда получим систему
J и + 2v = За + 4,
-Зи + 4t> = а + 3.
2. Исключив из этой системы и, имеем
Q
10t> = 10а + 15, или v = а + - .
312
3. Аналогично исключив и, получим
-5и = -5а - 5, или и = а + 1.
4. Таким образом, приходим к системе
I 2у2 = а + | ,
sin х = а + 1.
5. Учитывая, что 1 < 2^2, -1 < sin х < 1, запишем систему не-
равенств для параметра at
[ 1 3 [ 1 ,
1 ча + - , -- ч а, х
< 2 или л 2 т. е. -- <а<0.
-1<а+1<1, |-2<а<0, 2
6. Ответ: а = .
1 6. Найти множество значений а, при которых система
3 • 5у2 + 2|х| = 21 - а,
(1)
51 + у2 - 3|х| = 11а + 16
не имеет решений. Найти сумму целых значений а, не входящих
в это множество.
1. Полагая |х| = и, 5у2 = v, получим систему
2и + 3v = 21 - а,
-Зи + 5v= 16 + 11а.
2. Исключив и из системы (2), имеем
v = 5 + а.
3. Аналогично, исключив v из системы (2), получим
и = 3 - 2а.
4. Таким образом, приходим к системе
|х| = 3 - 2а, (3)
5у2 = 5 + а. (4)
313
5. Уравнение (3) не имеет решений, если 3 - 2а < 0, т. е. если
а> 1,5.
6. Уравнение (4) не имеет решений, если 5 + а < 1, т. е. если
а< -4.
7. Итак, система (1) не имеет решений, если либо а < -4, либо
а > 1,5, т. е. если а (-°°; -4) U (1,5; +°°).
8. Этому множеству не принадлежат числа из отрезка [-4; 1,5].
9. Найдем сумму целых значений а из этого отрезка:
-4 - 3 - 2 - 1 + 0 + 1 = -9.
10. Ответ: а (-оо; -4) и (1,5; +°°); -9.
17. При каких значениях параметров aub система
J ах + by = 7, (1)
32(х - у) _ 6 • 3~2х - 3~!/> 0 (2)
имеет решения?
1. Преобразуем неравенство (2) следующим образом:
а) умножив все его члены на 32*ж + у\ получим
32ж . 32х _ б . 32г/ _ 32х . Зг/ > 0. б . 32г/ + 32х + у _ 34х < Q
б) учитывая, что 6 • 32l/ = 2 • 3 • Зу • Зу, 32х + у = 3 - Зу 32х - 2 • Зу • 32ж,
имеем
(2 • Зу + 32ж)(3 • Зу - 32ж) < 0;
в) так как 2 • Зу + 32ж > 0, то приходим к равносильному нера-
венству Зу + 1 - 32ж < 0, или
у < 2х - 1. (3)
2. Система (1), (2) имеет решения, если прямая (1) имеет с об-
ластью (3) общие точки.
3. Пусть b = 0; тогда очевидно, что система (1), (2) будет иметь
решения, если а 0.
4. Пусть b 0; тогда уравнение (1) можно переписать в виде
У = -ьх+ь- (4)
5. Рассмотрим прямую
у = 2х - 1. (5)
314
6. Если угловые коэффициенты прямых (4) и (5) различны,
т. е. а / -2Ь, то система (1), (2) будет иметь решения при любом
b * 0.
7. Если же а = -2Ь, то система (1), (2) будет иметь решения тог-
да и только тогда, когда прямая (4) расположена ниже прямой (5),
т. е. когда - < -1, откуда следует, что -7 < b < 0.
8. Ответ: а 0, Ъ = 0; а -2b, Ъ 0; а = -2Ъ, -7 < Ъ < 0.
18. Найти все значения а, при которых система
(х2 + 1)“+ (Ь2 + 1)у = 2,
а + Ъху + х2у = 1
имеет хотя бы одно решение для любого значения b (а, Ъ, х, у —
действительные числа).
1. Так как система (1) должна иметь хотя бы одно решение для
любого Ъ, то она должна иметь решение и для Ъ = 0.
2. Если Ъ = 0, то система (1) примет вид
(х2 + 1)“ + 1у = 2, (2)
а + х2у = 1. (3)
3. Уравнение (2) удовлетворяется либо при а = 0 и любом х, ли-
бо при х = 0 и любом а.
4. При х = 0 из уравнения (3) следует, что а = 1.
5. Таким образом, возможны только два значения а: а = 0 иа = 1.
6. Пусть а = 0; тогда система (1) примет вид
(&2 + 1)у=1, (4)
Ъху + х2у = 1. (5)
7. Уравнение (4) имеет решение для любого Ъ только если у = 0.
Однако это значение не удовлетворяет уравнению (5).
8. Пусть а = 1; тогда система (1) примет вид
х2 + (&2 + 1)г/=1,
Ъху + х2у = 0.
9. Очевидно, что система (6) для любого значения Ъ имеет реше-
ние х = 0, у = 0.
10. Ответ: а = 1.
315
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решить при всех значениях параметра а уравнение:
а) 22* - (а + 2) • 2х + 2а = 0;
б) 52* + 1 + (5а - 1) • 5х - а = 0;
в) 32<* + х) - 9(а + 1) • 3* - За = 0.
2. Установить, при каких значениях а имеет два различных
корня уравнение:
а) 49* - (4а + 2) • 7х - 21а2 + 34а - 8 = 0;
б) 4* + 2(а - 2) • 2* - За2 + 8а - 5 = 0.
3. Найти х2 - у2, если
\ 4I + VPT3 + 2(у - 4)2 = 2а - 4,
j (у - 4)2 - 4*/* + з = 7 - 2а.
4. Найти ху, если
J (х + 2)2 + 2 • З17 2 = а-1,
’3г/ 2 ' - (х + 2)2 = 4а-9.
5. Найти у2 - х2, если
j 27x^1 + 21у - 2 = 2 -а,
j 2i + |i/-2|_ 7x_i =3а- 1.
6. При каких значениях/, уравнение
х2 - (2Р - 1)х - 3(4₽-1 - 2Р-2) = 0
имеет равные корни?
7. Найти все значения а, при которых совместна система урав-
нений
\ 2 + cos х = 4a - 6 • 2у2 ,
| 10 - 23 + у2 = а - 5 cos х.
В ответе указать наибольшее из этих значений.
8. Решить уравнение и исследовать, при каких значениях па-
раметра а оно имеет решение и при каких — нет:
a + 3 1 1
а) 3 • 4* ~ 2 + 27 = a + a • 4* ~ 2; б) 2“ + 2 • 32*<“ + 2) = 4* .
9. При каких значениях а уравнение:
а) 4* - (5a - 3) • 2х + 4a2 - За = 0 имеет единственное решение?
б) 25* - (2а + 3) • 5* - За2 + 5а + 2 = 0 имеет два различных
решения?
316
10. При каких значениях а имеет единственное решение урав-
нение:
а) *2-5* + 6 = 0; б) *2~6х + 8 = 0?
' ^бх-а_^2а-х ' ^2х-а_^а-х
11. Найти множество значений а, при которых уравнение:
а) 16ж - (За + 8) • 4Ж + 2а2 + 13а + 15 = 0 имеет единственное
решение, меньшее, чем 1;
б) 4Ж - 3(а - 5) • 2х + 2а2 - 22а + 56 = 0 имеет единственное
решение, принадлежащее отрезку [1; 2];
в) 9Ж - (За - 10) • Зж + 2а2 - 16а + 24 = 0 имеет единственное
решение, большее, чем 1.
12. Решить неравенство ах2 х < а2.
13. Найти все значения параметра, при которых для всех х е R
выполняется неравенство:
а) а 5 т - (5а + 3) • 5х + а - 1 < 0;
б) а • 9х + (1 - а) • 3х - 1,75а + 1 > 0;
в) k • 7х + (4 - 8k) • 7 * > 2k - 1.
14. При каких значениях параметра а каждое решение не-
равенства 0,4*2 + 1 > 6,25° является решением неравенства
х2 - 6х + 4 < а2?
Ответы
1. а) Если а> 0, тох = 1 их = log2 а; если а < 0, то х = 1; б) если а > 0,
то х = -1; если а < 0, то х = -1 и х = log5 (-а); в) если а > 0, то х = 1; если
а < 0, тох = 1их = log3(-a). 2. a)ae(L | 'j и Г |; | 'j; б) а е f 1; | 'j и
—4. 5. 3. 6. р = -2 ар = 0. 7. 3. 8. а) Если 3 < а < 27,
о . . а - 27
то х = 2 + log4 ——
если а < 3 или а 27, то нет решений; б) если а 0 -3,
2а - 1
а 0 -2, а 0 0,5, то х = —; если а = -3, а = -2, а = 0,5, то нет решений.
9. a)a - (0; 0,75] U {!}; б) a G (-1; 1 ) U ( 1 ; 2^. 10. а) | ; 4 ; б) {3; 6}.
11. а) а е (-5; -1,5); б) а е [5; 6]; в) де (3,5; 6]. 12. Если а> 1, тох е (-1; 2);
если 0 < а < 1, то х G (-°°; -1) U (2; +°°); если а = 1, то х G 0. 13. а) а -
|;0];б)ае
0; | ; в) /г- 0; | . 14. а - (-оо; -3) U (1; +<х>).
317
т
Гема 17
- -1. Понятие логарифма * 1 2 * * I I I I I I I---
" 2. Свойства логарифмов । । । । । । । ” Z
- - 3. Логарифмическая функция, ее свойства и график Н-т-
2 2 ^Тероемы о логарифме произведения, частного и степени
- - -^-Формула перехода к новому основанию
□""5. Логарифмирование и потенцироващ £2222222222
6. Логарифмические уравнения |-|- - -- -- -- -- -- -
7. Логарифмическиенеравенства^!222222222222
, 8. Производные логарифмической
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Понятие логарифма
1°. Логарифмом положительного числа Ъ по основанию а (где
а > 0, а 1) называют показатель степени, в которую надо возвес-
ти а, чтобы получить число Ъ.
2°. Логарифм числа Ъ по основанию а обозначают символом loga Ъ.
3°. Если а > 0, а 1, Ъ > 0, то loga Ъ по определению есть показатель
степени, в которую надо возвести число а, чтобы получить число Ъ.
4°. Поэтому равенство а1°8“/’ = Ъ есть тождество, которое на-
зывают основным логарифмическим тождеством. Например,
3log34 = 0>5log0,58 = g
5°. Для обозначения десятичных логарифмов принята специ-
альная запись: вместо log10 Ъ, где Ъ — произвольное положитель-
ное число, пишут 1g Ъ.
2. Свойства логарифмов
1°. Логарифмы существуют только для положительных чисел,
т. е. loga N (где а > 0, а 1) существует, если N > 0.
318
2°. При основании а > 1 логарифмы чисел N > 1 положитель-
ны, а логарифмы чисел 0 < N < 1 отрицательны.
Например, log2 5 > 0, log2 | < 0.
О
3°. При основании 0 < а < 1 логарифмы чисел N > 1 отрицатель-
ны, а логарифмы чисел 0 < N < 1 положительны.
Например, logx 5 < 0, log2 | > 0.
_ о
2
4°. Равным положительным числам соответствуют и равные
логарифмы, т. е. если ДГХ = N2, то loga = loga N2.
5°. Если а > 1, то большему числу соответствует и больший ло-
гарифм, т. е. если ЛГХ > N2, то loga > loga N2.
Например, log2 7 > log2 5.
6°. Если 0 < а < 1, то большему числу соответствует меньший
логарифм, т. е. если ЛГХ > N2, то loga < loga N2.
Например, logx 9 < logx 3.
з з
7°. Логарифм единицы по любому основанию (а > 0, а / 1) ра-
вен нулю, т. е. loga 1 = 0.
8°. Логарифм самого основания равен 1, т. е. loga а = 1.
3. Логарифмическая функция, ее свойства и график
1°. Показательная и логарифмическая функции при одном и том
же основании являются взаимно обратными функциями.
2°. На рис. 99, а изображен график функции у = logoxnpHa> 1,
а на рис. 99, б — график функции у = loga х при 0 < а < 1.
319
3°. Свойства функции у = loga х при а > 1:
a)D(/) = 7?+;
б) E(f) = 7?;
в) функция возрастает;
г) если х = 1, то loga х = 0;
д) если 0 < х < 1, то loga х < 0;
е) если х > 1, то loga х > 0.
4°. Свойства функции у = loga х при 0 < а < 1:
a)D(/) = 7?+;
б) £(/) = R;
в) функция убывает;
г) если х = 1, то loga х = 0;
д) если 0 < х < 1, то loga х > 0;
е) если х > 1, то loga х < 0.
4. Теоремы о логарифме произведения, частного и степени.
Формула перехода к новому основанию
1°. Логарифм произведения двух или нескольких положитель-
ных чисел равен сумме логарифмов сомножителей, т. е.
loga ... Nk) = loga + loga N2 + ... + loga Nh,
где a > 0, a 1, Nt > 0.
2°. Логарифм частного положительных чисел равен разности
логарифмов делимого и делителя, т. е.
10g“ = log« “ 10g“
где а > 0, а 1, ДГХ > 0, N2 > 0.
3°. Логарифм степени равен произведению показателя степени
на логарифм ее основания, т. е.
loga Nc = с loga N, где N > 0, а > 0, а 1.
Замечание. Если N < 0, а с — четное число, то справедлива
формула
loga Nc = с loga |ДГ|,
где а > 0, а / 1.
320
4°. Формула перехода от логарифма по основанию b к логариф-
му по основанию а имеет вид
log N
log,, N = -j—2-— , где N > 0, a>0, а^1,&>0, & ^1.
loga b
5°. Если a = N, то формула перехода примет вид
, 1
log& а = 1,
loga Ь
где а> 0, а 5* 1, & > 0, & 1.
6°. Если основание логарифма и число, находящееся под зна-
ком логарифма, возвести в одну и ту же степень, отличную от нуля,
то значение логарифма не изменится, т. е.
loga N = logflC Nc,
где N > 0, а > 0, а 1.
5. Логарифмированием потенцирование
1°. Логарифмирование — это преобразование, при котором
логарифм выражения с переменными приводится к сумме или раз-
ности логарифмов переменных.
2°. Необходимо четко различать сумму логарифмов 1g а +
+ 1g Ъ и логарифм суммы 1g (а + Ь). Сумма логарифмов равна лога-
рифму произведения, т. е. 1g а + 1g Ъ = lg(a&), а для логарифма сум-
мы 1g (а + Ь) формулы нет.
3°. Потенцирование — это преобразование, обратное лога-
рифмированию.
6. Логарифмические уравнения
1°. Уравнение, содержащее переменную под знаком логариф-
ма, называют логарифмическим.
2°. Решение логарифмического уравнения вида loga f(x) =
= loga ф(х) основано на том, что такое уравнение равносильно урав-
нению f(x) = ф(х) при дополнительных условиях f(x) > 0, ф(х) > 0.
3°. Переход от уравнения loga f(x) = loga ф(х) к уравнению f(x) =
= ф(х) иногда приводит к появлению посторонних корней. Такие
корни можно выявить либо с помощью подстановки найденных
значений в исходное логарифмическое уравнение, либо с помощью
нахождения области определения исходного уравнения (эта область
задается системой неравенств f(x) > 0, ф(х) > 0).
4°. При решении логарифмических уравнений часто бывает по-
лезен метод введения новой переменной.
321
5°. При решении уравнений, содержащих переменную и в ос-
новании, и в показателе степени, используется метод логарифми-
рования. Если при этом в показателе степени содержится лога-
рифм, то обе части уравнения надо прологарифмировать по основа-
нию этого логарифма.
7. Логарифмические неравенства
1°. Неравенство, содержащее переменную только под знаком
логарифма, называют логарифмическим. Например, неравенства
loga f(x) > loga <p(x), loga f(x) < loga ф(х) при a > 0, a / 1 являются
логарифмическими.
2°. Неравенство loga f(x) > loga ф(х) равносильно системе f(x) >
> ф(х) > 0 при а > 1 и системе 0 < /(х) < ф(х) при 0 < а < 1.
3°. При решении логарифмических неравенств следует учиты-
вать общие свойства неравенств, свойство монотонности логариф-
мической функции и область ее определения.
Замечание. Известные способы решения систем алгебраи-
ческих уравнений и неравенств применяются и к решению систем,
содержащих логарифмические уравнения и неравенства.
8. Производные логарифмической
и показательной функций. Число е
1°. Приближенное значение числа е таково: е ~ 2,7.
2°. Показательная функция у = ех в точке х = 0 имеет производ-
ную, равную 1.
3°. Показательная функция ех дифференцируема в каждой точ-
ке, причем (еж)' = ех.
4°. Логарифм по основанию е называется натуральным лога-
рифмом и обозначается символом In.
5°. Формулы дифференцирования
При условии и = ф(х) Номер формулы При условии и = X Номер формулы
(In и)' = - • и' (1) (In х)' = - X (1а)
,, v 1 (loga и) = —=— • иг а и • In а (2) ,, А- 1 (loga х)' = —j а х In а (2а)
(а11)' = a11 In а и' (3) (ах)' = ах • In а (За)
(е“)' = е“ • и' (4) (еж)' = ех (4а)
322
ЗАДАЧИ С РЕШЕНИЯМИ
1. Найти все значения а, при которых уравнение
log9 _а(х2 + 4) = log9 _ а (ах - Зх)
имеет два решения. В ответе указать наибольшее целое значение а.
1. Уравнение имеет смысл, если 9 - а > О, 9 - а 1, т. е. если
а е (-оо; 8) U (8; 9).
2. Из равенства логарифмов следует, что
х2 + 4 = ах - Зх, или х2 - (а - 3)х + 4 = 0.
3. Полученное квадратное уравнение имеет два решения, если
D > 0, т. е. (а - З)2 - 16 > 0, откуда а е (-оо; -1) и (7; +оо).
4. С учетом ОДЗ находим, что данное уравнение имеет два ре-
шения, если а е (-оо; -1) и (7; 8) U (8; 9).
5. Ответ: -2.
2. Решить относительно х уравнение
ах + 1 = bs ~ х. (1)
1. Уравнение (1) имеет смысл при а > 0 и Ъ > 0.
2. Если а = & = 1, то х — любое действительное число.
3. Если а=1и&+1,тох = 3; если &=1иа+1,тох = -1.
4. Пусть теперь а + 1 и Ъ + 1; тогда
х + 1 = (3 - х) loga b, или (1 + loga b)x = 3 loga b - 1. (2)
а) Если 1 + loga Ъ = 0, т. е. Ъ = - , то правая часть уравнения (2)
равна (-4), следовательно, при Ъ = - + 1 решений нет.
1 3 log. b - 1
б) Если Ъ + - , то х = ——;-— .
а 1 + loga Ь
5. Ответ: если а = 1, Ъ = 1, то х е R;
если а = 1,& + 1,тох = 3;
если а + 1, b = 1, то х = -1;
если а = i + 1, то корней нет;
1 3 log Ь - 1
если а + - , то х = —— -— .
b 1 + loga Ь
323
3. Найти все значения а, при которых уравнение
1g ах = 2 lg (х + 1) (1)
имеет единственный корень.
1. Ясно, что ОДЗ данного уравнения определяется системой не-
равенств ах > 0, х + 1 > 0.
2. Следовательно, уравнение (1) имеет единственный корень
тогда и только тогда, когда система
\ ах = (х + I)2,
5 ах > 0, (2)
[ х + 1 > 0
имеет единственное решение.
3. Записав уравнение ах = (х + I)2 в виде
х2 + (2 - а)х + 1 = 0, (3)
заключаем, что оно имеет решение, если D = (2 - а)2 - 4 > 0, т. е.
если а < 0 или а > 4. При выполнении этих условий уравнение (3)
имеет два корня:
а-2 +Да2-4а а - 2 - Ja2 - 4а
х, = ----------- и х9 = ------------.
1 2 2 2
а) При а = 0 не выполняется неравенство ах > 0.
б) При а < 0 из системы
ххх2 = 1,
х1 + х2 = а - 2 < 0,
следует, что оба корня уравнения (3) отрицательны.
в) Для корней х1 и х2 выполняются следующие неравенства:
х1 + 1 = | > 0 и х}а > 0;
х9 + 1 = < 0 и х9а < 0;
z 2 2 z
поэтому при а < 0 система (2), а, значит, и уравнение (1) имеют
единственное решение х1.
324
4. При а = 4 система (2) имеет только одно решение х = 1.
5. При а > 4 из системы
I ххх2 = 1,
| хг + х2 = а - 2 > 2,
следует, что оба корня уравнения (3) положительны, т. е. система (2),
а с ней и уравнение (1) имеют два решения.
6. Итак, уравнение (1) имеет единственное решение, если а < О
или а = 4.
7. Ответ: а (-°°; 0) U {4}.
4. Решить относительно х уравнение
log„x2 + 2 loga (х + 2) = 1. (1)
1. Уравнение (1) имеет смысл при а> 0, 1, -2 < х < 0, 0 < х <
< +оо — это область определения данного уравнения.
2. В этой области уравнение (1) равносильно следующему:
2 loga |х| + 2 loga (х + 2) = 1, или loga |х|(х + 2) = |. (2)
3. Пользуясь определением логарифма, от уравнения (2) перей-
дем к равносильному уравнению
|х|(х + 2) = л/а . (3)
4. Рассмотрим два случая: а) -2 < х < 0; б) х > 0.
а) Пусть -2 < х < 0; тогда уравнение (3) примет вид
-х(х + 2) = Ja , или х2 + 2х + Ja =0,
откуда хг = -1 - л/1 - >/а , х2 = -1 + Ja , где 1 - Ja > 0, т. е.
0 < а < 1. Замечаем, что оба полученных корня удовлетворяют ус-
ловию -2 < х < 0.
б) Пусть х > 0; тогда уравнение (3) примет вид
х(х + 2) = Ja , или х2 + 2х - Ja =0,
откуда х3 = -1 - л/1 + л/а , х4 = -1 + л/1 + л/а • При этом корень х3 не
удовлетворяет условию х > 0, а х4 > 0 при а > 0.
325
5. Ответ: если 0 < а < 1, то три корня: х = -1 - л/1 - Ja ,
х = -1 + Ja , х = -1 + Vi + Ja ;
если а > 1, то один корень х = -1 + Jl + J~a .
5. Решить относительно х уравнение
lg (х - а) - 1g 2 = 0,5 1g (х - b).
(1)
1. Областью определения уравнения (1) служит решение систе-
\ х > а
мы < > ь В этой области уравнение (1) равносильно уравнению
1g Х 2 а = 1& ~ ’ или х - а = 2 Jx - Ъ . (2)
2. Пусть а = Ь; тогда уравнение (2) примет вид
х - а = 2 Jx - а , или Jx - а (Jx - а - 2) = 0. (3)
3. Так как Jx-а 0 (в силу неравенства х - а > 0), то от урав-
нения (3) перейдем к уравнению Jx - а = 2, откуда х = а + 4.
4. Пусть а Ъ. Тогда, возведя в квадрат обе части уравнения (2),
получим
х2 - 2ах + а2 = 4(х - Ъ), или х2 - 2(а + 2)х + а2 + 4& = 0. (4)
5. Дискриминант уравнения (4) равен D = 16(а - Ъ + 1).
а) Если D < 0, т. е. а < Ъ - 1, то уравнение (4) не имеет корней.
б) Если D = 0, т. е. а = Ъ - 1, то х1 = х2 = а + 2.
в) Если D > 0, т. е. а > Ъ - 1, то уравнение (4) имеет два различ-
ных корня:
хх = а + 2 - 2 Ja -b + 1 ; х2 = а + 2 + 2 Ja -b + 1 .
6. Теперь найдем те значения а и Ъ, при которых корни х1 и х2
удовлетворяют условию х > а (условие х > Ъ выполняется, так как
х1 и х2 — корни уравнения (х - а)2 = 4(х - &)).
7. Введем обозначение
f(x) = х2 - 2(а + 2)х + а2 + 4&
326
и вычислим
f(a) = а2 - 2(а + 2)а + а2+ 4Ь= 4(Ь - а).
а) Если Ь-1<а<Ь,тоа<Ь<х1< х2, следовательно, х1 и х2 —
корни уравнения (1).
б) Если а > Ъ, то /(а) < 0, следовательно, Ъ < х1 < а < х2, т. е.
условию х > а удовлетворяет только х2.
9. Ответ: если а = Ъ, то х = а + 4;
если b - 1 а < Ь, тохх 2 = а + 2 ± 2 Ja -b + 1 ;
если a>b, то х = а + 2 + 2 J a - b + 1 ;
если а < Ъ - 1, то корней нет.
6. Определить, при каких значениях а уравнение
log3 (9х + 9а3) = х (1)
имеет ровно два решения.
1. Пусть а — некоторое фиксированное число; ОДЗ данного
уравнения состоит из всех чисел х, удовлетворяющих неравенству
9х + 9а3 > 0.
2. Значит, если а > 0, то ОДЗ совпадает с множеством действи-
тельных чисел; если а < 0, то ОДЗ есть множество х > log9 (-9а3).
3. На ОДЗ уравнение (1) равносильно уравнению 9х + 9а3 = Зж.
4. Обозначив Зж через t, получим квадратное уравнение
t2 - t + 9а3 = 0. (2)
5. Дискриминант уравнения (2) равен 1 - 36а3. Поэтому если
1 - 36а3 < 0, т. е. если а > —, то уравнение (2), а, значит, и урав-
V36
пение (1) не имеет корней.
6. Если а = —, то уравнение (2) имеет единственный корень
3736
t = 0,5. Таким образом, исходное уравнение на своей ОДЗ равно-
сильно уравнению Зж = 0,5, которое имеет единственный корень
х = log3 0,5. Не проверяя, входит ли этот корень в ОДЗ уравнения
(1), заключаем, что при а = —уравнение (1) имеет не более одно-
3736
го корня.
327
7. Если а < —, то уравнение (2) имеет два корня: 2 =
V36
1 ± Vi - 36а3 г>
=----. Значит, в этом случае исходное уравнение равно-
сильно совокупности двух уравнений:
~ Vl ~ 36а3 # (g)
3х = 1 + ~ 36а3
о тт г\ 1 1 — 36а3 г\
8. При а ч 0 выполняется неравенство ------ ч 0 и урав-
нение (3) не имеет решений. Тогда исходное уравнение равносиль-
но на своей ОДЗ уравнению (4), которое имеет единственное реше-
, 1 + 71 - 36а3 „ п
ние х = log3-. Следовательно, при а ч 0 исходное урав-
нение имеет не более одного решения.
9. Если а удовлетворяет неравенствам 0 < а < —, то совокуп-
37зб
ность уравнений (3), (4) имеет корни
, 1 - 71 -36а3 , 1 + 71 -36а3
*1 = log3 —, х2 = log3 ---------.
В этом случае ОДЗ исходного уравнения совпадает с множест-
вом всех действительных чисел и, значит, уравнение имеет в точ-
ности два корня х, и х2.
10. Ответ: а е ( 0; —) .
V З7367
7. Найти все значения х, удовлетворяющие уравнению
log2 (а2х3 - 5а2х2 + J&-x ) = log2 + а2 (3 - Jx-1 ) (1)
при любых значениях параметра а.
1. Так как уравнение (1) должно иметь решения при любых
значениях параметра а, то оно будет иметь решение и при а = 0.
328
2. При таком значении а уравнение (1) примет вид
log2 а/6 - х = log2 (3 - ). (2)
3. Уравнение (2) имеет смысл, если выполняется условие 1 <
< х < 6. При этом условии имеем
а/6 -х = 3 - л/х - 1 . (3)
4. Упростив уравнение (3), приходим к уравнению
х2 - 7х + 10 = 0, (4)
корнями которого являются значения х = 2 и х = 5.
5. Эти два значения х дают необходимые условия существова-
ния решений уравнения (1) при всех значениях параметра а.
6. Подставив значение х = 2 в уравнение (1), приходим к со-
отношению log2 (2 - 12а2) = log2 + a2 2, которое имеет смысл, если
2 - 12а2 > 0, т. е. если < а < . Таким образом, в данном
6 6
случае уравнение (1) удовлетворяется не при любых значениях а,
что противоречит требованию задачи.
7. Если же х = 5, то уравнение (1) становится истинным равен-
ством: log2 1 = log2 + a2 1.
8. Ответ: х = 5.
8. Найти все значения а, при которых уравнение
| log3 4х2 + log3 (4 - х) - log3 2“ = 0
имеет единственное решение.
1. В области допустимых значений, т. е. при условиях
J х 0,
[ 4 - х > 0,
исходное уравнение равносильно следующему:
log3 |2х| + log3 (4 - х) = log3 2а,
или
|2х|(4 - х) = 2“. (1)
329
2. Построим графики функ-
ций уг = |2х|(4 - х) и у2 = 2°
(рис. 100).
а) Функцию у^(х) = |2х|(4 - х)
можно записать в виде
У1(х) =
2х2 - 8х, если х < 0;
-2х2 + 8х, если х (0; 4).
б) Так как 2“ > 0 для любого
а -й, то график функции у2(х) =
= 2° представляет собой прямую,
параллельную оси Ох и располо-
женную выше этой оси.
3. Уравнение (1) имеет един-
ственное решение при тех значе-
ниях параметра а, когда графики функций уг(х) и у2(х) пересека-
ются только в одной точке.
4. Очевидно, что это имеет место при у2(х) > 8, т. е. при 2° > 8.
Следовательно, а е (3; +оо).
5. Ответ: а е (3; +оо).
9. В зависимости от значений параметра а решить уравнение
2 log7 (ах - 2) = log^ (~х2 - 9х - 18). (1)
1. Уравнение (1) равносильно уравнению
log7 (ах - 2) = log7 (—х2 - 9х - 18),
которое в свою очередь равносильно системе
J ах - 2 = —х2 - 9х - 18,
—х2 - 9х - 18 > 0,
или
J х2 + (а + 9)х + 16 = 0,
]-6<х<-3.
330
2. Корни уравнения системы (2), если они существуют, задают-
ся формулами
_ - а - 9 - 7(а + 1)(а + 17) _ - а - 9 + J(a + 1)(а + 17)
Х1 2 ’ 2 •
3. Рассмотрим возможные случаи расположения корней хг и х2
в интервале (-6; -3).
4. Предположим сначала, что дискриминант уравнения систе-
мы (2) равен нулю, т. е. что а = -1 или а = -17. Проверка показы-
вает, что только в случае а = -1 корень уравнения х = -4 принадле-
жит интервалу (-6; -3).
5. Теперь рассмотрим случай, когда а е (-оо; -17) U (-1; +оо),
а) Если оба корня хх и х2 лежат в интервале (-6; -3), то должна
[х1 > -6,
быть совместна система < Решив эту систему, находим,
О»
1 2
что -1 < а < -- .
о
б) В том случае, когда только больший корень х2 принадлежит
интервалу (-6; -3), должны выполняться неравенства
-6 < х2 < -3,
хх < -6,
откуда следует, что « - 0.
в) Наконец, если только меньший корень х1 принадлежит ин-
тервалу (-6; -3), то имеем систему
-6 < х1 < -3,
-3 < х2,
2,1
решив которую находим, что -- ч а < -- .
О о
6. Ответ: если а < -1 или а > - | , то корней нет;
О
если а = -1, то х = -4;
1 2 а + 9 ± 7(а+ 1)(а+ 17)
если -1 < а < -- , то х, 9 = -——-----------;
3 2
2 ,,1 а + 9 + 7(а+ 1)(а+ 17)
если - - ча<--,тох = -------- v ——-------.
о о Z
331
10. Решить относительно х уравнение
1 1 а2-4 1
iog^a-iog^ — =1.
1. Так как Jx и а2 являются основаниями логарифмов, то х 1,
а 1; неизвестное х входит в выражение Jx , поэтому х > 0; так как
логарифмы берутся только от положительных чисел, то а > 0; кро-
д2 _ 4
ме того, 0 < т-- < +°° и, следовательно, а 2, х 2а, причем
2а - х
х > 2а, если 0 < а < 2, и х < 2а, если а > 2.
2. При указанных условиях имеем
1 2 , а2 - 4 п к , а2- 4
log г а = ----, log 2 --- =0,5 log,, --.
loga х а 2а-х а2а-х
Тогда данное уравнение можно записать в виде
х----- = log„ х х---- = х => х2 - 2ах + а2 - 4 = 0,
а 2а- х “ 2а-х
откуда х = а ± 2.
3. Так как при а е (0; 1) U (1; 2) имеем х > 2а, то из двух най-
денных решений этому неравенству удовлетворяет только х = а + 2.
4. При а > 2 имеем х < 2а и, следовательно, этому неравенству
удовлетворяют оба решения, кроме значения а = 3. Действительно,
в этом случае х = а - 2 = 1, что исключено из значений х; поэтому
при а = 3 получаем для х лишь одно решение: х = а + 2 = 5.
5. Ответ: если а е (-оо; 0) U {1; 2}, to.y‘-0;
если а е (0; 1) U (1; 2) U {3}, то х = а + 2;
если а е (2; 3) U (3; +°°), тохх 2 = а ± 2.
11. При каких значениях параметра а из интервала (2; 5) уравнение
log2 (3 - |sin ах|) = cos (лх - )
имеет хотя бы одно решение х такое, что 2 < х < 3?
1. Так как |sin ах| < 1, то 3 - |sin ах| > 2 и, следовательно,
log2 (3 - |sin ах|) > 1.
332
2. С другой стороны, учитывая, что cos ^лх - J < 1, получим
систему
[ sin ах = ±1,
| cos (их - = 1,
откуда находим
ах = + л/г, kr— Z, (1)
х = | + 2п, п — Z. (2)
3. Согласно условию, 2 < х < 3, поэтому в равенстве (2) дол-
жно быть п = 1 , откуда х = . Тогда из равенства (1) следует, что
13 __ Л . у у /— гр __ 3 Л . 6 Л h у — п
а — = - + л/г, /г - Z, или а = — +
62 13 13
4. Теперь воспользуемся условием 2 < а < 5; отсюда заключаем,
у г-, 9л 15л
что /г‘- !1;2}и, значит, а^= — , а2 = —— .
1 О J. о
г 9л 15л
5. Ответ: ал = — , а9 = —— .
1 13 13
1 2. Для каждого положительного числа а (а 1) решить уравнение
2
loga sin х + loga sin x - a = 0. (1)
1. Полагая t = loga sin x и учитывая, что всюду в области опре-
деления уравнения (1) выполняются неравенства
loga sin х > 0 при 0 < а < 1, loga sin х < 0 при а > 1,
получаем две смешанные системы:
/2 + /- а = 0, / >0 при 0 < а < 1; (2)
/2 + /- а = 0, / <0 при а > 1 (3)
(если t = 0, то а = 0, что невозможно).
2. Если 0 < а < 1, то квадратное уравнение
/2 + t - а = 0
333
имеет два различных действительных корня:
, _ _ 71 + 4а +1 , _ 71 + 4а - 1
Ч- j ’2 2 ’
причем <0, t2> 0.
3. Значит, при 0 < а < 1 система (2) имеет решение t = t2, откуда
находим
1 71 4 4а — 1 /л\
loga sin X = . (4)
При а > 1 система (3) имеет решение t = и, следовательно,
1 71 "* 4а +1
loga sin х = - *----. (5)
4. Таким образом, уравнение (1) равносильно совокупности
уравнений (4) и (5), решив которые получим ответ.
71 + 4а - 1
5. Ответ: если 0<а<1,тох = (-1)* arcsin а 2 + Ttk;
71 + 4а + 1
если а > 1, то х = (-1)* arcsin а 2 + -n.k,k‘—Z.
13. Найти все значения параметра а, при которых в область опре-
деления функции у = 1g (аах 2 - ах) входят числа 13, 15, 17, но не
входят числа 3, 5, 7.
1. По определению логарифма х е D(y) в том и только в том
случае, если аах ~ 2 > ах_ При а = 1 область определения пуста.
2. Рассмотрим два случая: а)0<а<1;б)а>1.
а) Пусть 0 < а < 1. Тогда показательная функция с основанием а
убывает, поэтому из неравенства аах 2 > ах следует, что ах - 2 < х,
т. е. (1 - а)х > -2. Учитывая, что 0 < а <1, имеем 1 - а > 0. Значит,
D(y) = 2 ! +°°^). Но в этот промежуток входят все положитель-
ные числа и, в частности, числа 3, 5, 7. Следовательно, такие зна-
чения а не удовлетворяют условию.
б) Пусть а > 1. Тогда показательная функция с основанием а
возрастает, поэтому из неравенства аах 2> ах следует, что ах - 2 >
> х, т. е. (а - 1)х > 2. Так как а > 1, то а - 1 > 0. Значит, D(y) =
= ( > +°°)- Числа 13, 15, 17 входят в этот промежуток только
334
тогда, когда его левый конец меньше 13. Для того же, чтобы этот
промежуток не содержал чисел 3, 5, 7, нужно, чтобы его левый ко-
нец был не меньше 7.
3. Итак, получаем следующее двойное неравенство для пара-
метра а > 1:
7 < < 13, 7(а - 1) < 2 < 13(а - 1), А < а - 1 < ? .
. ( 15 9 1
4. Ответ: а е ; - .
7ж + 3
1 4. В области определения функции у = logg I а т 3 - аа \ взяли
все целые положительные числа и сложили их. Найти все значе-
ния а, при которых такая сумма больше 9, но меньше 16.
7 х + 3 24
1. Графиком дробно-линейной функции z = ----— = 7 + -----
X — о X — о
является гипербола.
2. По условию х > 0. Если 0 < х < 3, то z < 0. При неограничен-
«24 ,
ном возрастании х дробь---- монотонно убывает и стремится к ну-
ге - 3
лю, а значения функции z убывают и приближаются к 7 (рис. 101).
3. По определению логарифма область определения D(z/) состо-
7ж + 3
ит из решений неравенства а т 3 > аа.
а) При а = 1 получаем неравенство, которое не имеет решений.
б) При 0 < а < 1 показательная функция с основанием а убыва-
7ж + 3
г _ я . „ 7 х + 3 ,
ет и неравенство а х ' > аа равносильно неравенству -----— < а.
т-, о 7х + 3 о 7 х + 3
Если х > 3, то --— > 7 > а, т. е. при х > 3 неравенство -— < а
х — 3 х — 3
не выполняется. Если же х < 3, то в интервале (0; 3) имеются всего
два целых положительных числа: 1 и 2. Поскольку их сумма мень-
ше 9, рассматриваемые значения а не удовлетворяют условию.
в) При а > 1 показательная функция с основанием а возрастает
7ж + 3
и неравенство а т 3 > аа равносильно неравенству---— > а. Ес-
X о
ли а < 7, то любое число, большее 3, является его решением и ука-
335
занную сумму найти нельзя.
Если же а > 7, то множество его
положительных решений — это
интервал (3; х0), где а = г(х0)
(рис. 101).
г) Найдем суммы последова-
тельных натуральных чисел, на-
чиная с 4: 4; 4 + 5 = 9; 4 + 5 + 6 =
= 15; 4 + 5 + 6 + 7 = 22; ... . Зна-
чит, указанная сумма будет боль-
ше 9 и меньше 16, если число 6
принадлежит интервалу (3; х0),
а число 7 этому интервалу не при-
надлежит, т. е. 6 < х0 < 7. Так
, 7х + 3 я
как функция 2 = --— убывает
X — о
на [6; 7], то 2(7) < z(x0) < z(6), или
7-7 + 3 , 7 • 6 + 3
7-3 " а 6 3 ’
4. Ответ: а е [13; 15).
15. Для каждого действительного значения параметра а решить
уравнение log|sin ж| 2 • logsin2 х 3 = а.
1. Левая часть уравнения представляет собой произведение
двух отрицательных множителей (так как |sin х| < 1 и sin2 х < 1, то
log|sin ж| 2 < 0, logsin2 х 3 < 0). Следовательно, а > 0.
2. Переходя к основанию логарифмов, равному 2, и учитывая,
что sin2 х = |sin х|2, получаем систему
[ log2 |sin х| = , (1)
| 0 < |sin х\ < 1, (2)
где последнее условие задает область определения исходного урав-
нения.
3. На множестве (2) уравнение (1) равносильно уравнению
|log2 |sin х|| = ,
336
или, учитывая, что |log2 |sin х|| = -log2 |sin х|, уравнению
log2 | sin x| =
4. Отсюда находим
|sin х| = 2
5. Ответ: если а < 0, то уравнение не имеет корней;
если а > 0, то х = л/г + (-1)* arcsin + 2
k^Z.
1 6. Найти все значения параметра а, при которых система урав-
нений
y=log41 + H)’
(х - а)2 + (у ~ а)2 = 1
(1)
имеет единственное решение.
1. Функция у = log2
определена только при х > 0, при
этом у = log2 (1 + 1) = 1.
2. Подставив у = 1 во второе уравнение системы (1), получим
квадратное уравнение
х2 - 2ах + 2а2 - 2а = 0.
(2)
3. Заданная система (1) имеет единственное решение тогда и толь-
ко тогда, когда уравнение (2) имеет один положительный корень.
4. Квадратное уравнение (2) может иметь один положительный
корень в трех случаях.
а) Если дискриминант уравнения равен нулю и при этом ко-
рень уравнения положителен, т. е. если
= 2а - а2 = 0,
4
а > 0,
откуда а = 2.
337
б) Если корни квадратного уравнения имеют разные знаки,
т. е. если 2а2 - 2а = 2а(а - 1) < 0, откуда 0 < а < 1.
в) Если один из корней равен нулю, а другой положителен.
Имеем 2а2 - 2а = 0, т. е. а = 0 или а = 1; тогда один корень уравне-
ния равен нулю. При а = 0 второй корень также равен нулю; при
а = 1 второй корень положителен. Значит, а = 1.
5. Объединяя найденные в пп. а)—в) значения, получим
а —(0; 1] U {2}.
6. При каждом из этих значений а система имеет единственное
решение х = а + ^2а- а2 , у = 1.
7. Ответ: а е (0; 1] U {2}.
17. При каких значениях параметра а система
| sin [3(а - у)] + 3 sin х = 0, (1)
[ 2 log4 (а - у) + 2 log4 (2 Jy) = log2 Jy + 3 log8 (2x) (2)
имеет четное число решений?
1. Здесь ОДЗ переменных х и у задается системой
[ а - у > 0,
? х > 0,
[у > о.
2. Поэтому от уравнения (2) можно перейти к уравнению
2(а - y)Jy = Zxjy
и, значит, х = а - у. Подставив это выражение в уравнение (1), име-
ем sin Зх + 3sin х = 0, или, после преобразований,
sin х (3 - 2 sin2 х) = 0.
3. Итак, получим уравнение sin х = 0, откуда х = пп, п •— N.
С другой стороны, х = а - у. Таким образом, с учетом ОДЗ прихо-
дим к системе
у = а - пп,
J X = Tin,
х > 0,
У > о,
338
из которой следует, что х = тт меньше а. Поэтому исходная систе-
ма имеет четное число решений в том случае, когда
2nk < а < л(2й + 1), /г- N.
4. Ответ: 2nk < а < л(27г + 1), 7г ' N.
18. Найти область определения функции у = loga loga loga х.
1. Область определения находим как решение неравенства
loga loga х > 0. (1)
2. При а > 1 неравенство (1) равносильно неравенству loga х > 1,
откуда получим а < х < +°°.
3. При 0 < а < 1 неравенство (1) равносильно неравенству 0 <
< loga х < 1, откуда следует, что а < х < 1.
4. Ответ: если а>1,тоа<х< +°°;
если 0<а<1,тоа<х<1.
1 9. Для каждого положительного а 1 решить неравенство
х1оё“ж + 1 > а^х. (1)
1. Пусть а > 1; тогда, логарифмируя по основанию а обе части
неравенства (1), получим
(loga х + 1) loga х > loga х + 2, или log„ х > 2. (2)
Решив неравенство (2), получим два интервала < loga х <
< - J2 и 72 < loga х < +оо, откуда находим
0 < х < а и < х < +°°.
2. Пусть 0 < а < 1; тогда аналогично получим
(loga х + l)loga х < loga х + 2, или log„ х < 2. (3)
Из неравенства (3) следует, что - J2 < loga х < J2 , откуда
< х < a-j2 .
3. Ответ: если а > 1, то 0 < х < а < х < +°°;
если 0<а<1,тоа^2 < х < а .
339
20. При каких значениях параметра а неравенство
log^ (х2 + 2) > 1 (1)
а + 1
выполняется для любого значения х?
1. Так как х2 + 2 > 2, то для того чтобы левая часть неравенства (1)
была положительной, нужно, чтобы выполнялось неравенство
откуда следует, что а < -1.
2. Перепишем неравенство (1) в виде
1Qg а (*2 + 2) > log а •
а+1 а+1
Это неравенство с учетом (2) равносильно неравенству
х2 + 2 > ,
а+1
которое будет выполняться для любого значения х, если & < 2,
т. е. если а < -2, а > -1. Из этих значений а только значения а < -2
удовлетворяют неравенству (2).
3. Ответ: а е (-оо; -2).
21. В зависимости от значений параметра а решить неравенство
10&2х + з “ 2) < 1- (1)
1. Неравенство имеет смысл при а > 2. Значения х должны
удовлетворять условиям 2х + 3 > 0, 2х + 3 1, т. е. х > -1,5, х -1.
2. Переписав неравенство (1) в виде
^°&2ж+з “ 2) < log2jt. +з (2х + 3), (2)
заметим, что если 2х + 3 > 1, т. е. если х > -1, то неравенство (2)
равносильно неравенству а - 2 < 2х + 3, откуда х > •
q __ Еу
3. Для выбора решения сравним числа и (-1), т. е. рассмот-
рим разность а - (-1) = • Имеем:
а) —р— 0 при 2 < а < 3; б) > 0 при а > 3.
340
a _
4. Отсюда при 2 < a < 3 получим < -1 и решением системы
а - 5 I х> — , х > -1
служит х > -1.
££ _ fj
5. При а > 3 получим > -1 и решением системы
а - 5 1 х> — , х > -1
а - 5
служит х > .
6. Найдем теперь те решения неравенства (1), которые удовлет-
воряют условию 0 < 2х + 3 < 1, т. е. -1,5 < х < -1. При этом условии
неравенство (1) равносильно неравенству
а-2 । о .а — 5 > 2х + 3, т. е. х < .
7. Так как при 2 < а - а - 5 , 5 3 имеем —%— ч -1, то приходим к системе [ а - 5 1 х< — , -1,5 < х < -1,
££ _ fj ££ _ fj
откуда-1,5 < х < (легко проверить, что -1,5 < при а > 2).
££ _ fj
8. При а > 3 получим > -1, следовательно, при этих зна-
чениях а система [ а - 5 1 х< — , | -1,5 < х < -1
имеет решение -1,5 < х < -1.
££ _ fj
9. Ответ: если 2 < а < 3, то -1,5 < х < ; -1 < х < +°°;
если а > 3, то -1,5 < х < -1, а < х < +°°.
341
22. При каких значениях а значение выражения
(1 - ixD^n-W)-1»-11 (1)
больше значения выражения
q,24 °2 log2s(1A’2 2т) (2)
для всех допустимых значений х‘1
1. Перейдем к одному и тому же основанию степени в выраже-
ниях (1) и (2):
а) (1 - x|)log'|(1 ° 1 = 5loSs С1 -1^1) logg (i - И) - |а - 1 . (2)
б) о,24 °2 |оЙ2'|(1а’2 2т) = (5 1 )4 °21ogs2 (1 т ,2 =
= g"2 4 2'2log'|(1 = glog5(l-Ы) + а2-4 .
2. Введем новую переменную t = log5 (1 - |х|). Тогда:
а) ее наибольшее значение равно нулю, а при стремлении х к 1
эта переменная стремится к (-°°);
б) в силу непрерывности функции t заключаем, что E(t) = (-°°; 0].
3. Сравнивая выражения (3) и (4), получаем неравенство
t(t - |а - 1|) > t + а2 - 4, t < 0,
или
f2 - (|а - 1| + l)t + 4 - а2 > 0, t < 0. (5)
4. Абсцисса вершины параболы положительна, ветви направ-
лены вверх. Значит, неравенство (5) верно при всех неположитель-
ных t в том и только в том случае, когда свободный член положи-
телен, т. е. а2 - 4 < 0.
5. Ответ: а е (-2; 2).
23. Найти все значения а, при которых неравенство
1 + log5 (х2 + 1) > log5 (ах2 + 4х + а)
выполняется для любого значения х.
1. Неравенство (1) равносильно неравенству
log5 5(х2 + 1) > log5 (ах2 + 4х + а),
которое в свою очередь равносильно системе
J 5(х2 + 1) > ах2 + 4х + а,
I ах2 + 4х + а > 0.
(1)
342
2. Таким образом, требуется найти все значения а, при кото-
рых системе неравенств
(а - 5)х2 + 4х + (а - 5) < О,
ах2 + 4х + а > О
(2)
(3)
удовлетворяет любое значение х.
а) При а = 5 неравенство (2) примет вид 4х < 0; оно не выполня-
ется, например, для х = 1.
б) При а = 0 неравенство (3) примет вид 4х > 0; оно не выполня-
ется, например, для х = -1.
в) Пусть а > 5. Рассмотрим неравенство (2). Если х = 0, то оно
примет вид а - 5 < 0. Это означает, что при любом а > 5 значение
х = 0 не является решением системы (2), (3), а следовательно, и ис-
ходного неравенства (1).
г) Пусть а < 0. Рассмотрим неравенство (3). Если х = 0, то оно
примет вид а > 0, что противоречит неравенству а < 0. Поэтому при
а < 0 значение х = 0 не является решением системы (2), (3), а сле-
довательно, и исходного неравенства.
д) Пусть 0 < а < 5. Тогда квадратный трехчлен (а - 5)х2 + 4х +
+ (а - 5) неположителен для любого х, если его дискриминант Dy =
= 16 - 4(а - 5)2 неположителен. Квадратный трехчлен ах2 + 4х + а
положителен для любого х, если его дискриминант D2 = 16 - 4а2
отрицателен.
4. Таким образом, задача сводится к решению системы
Г 0 < а < 5,
16 - 4(а - 5)2 < 0,
[ 16 - 4а2 < 0.
Так как
Г 0 < а < 5, Г 0 < а < 5,
J -4 + (а - 5)2 > 0, « Ла - 7)(а - 3) > 0, «
[а2 - 4 > 0 \(а~ 2)(а + 2) > 0
f 0 < а < 5,
«<Л-3<0, «2<а<3,
I а - 2 > 0
то исходное неравенство справедливо для всех х при значениях а
из промежутка 2 < а < 3.
5. Ответ: а — (2: 3].
343
24. При каких значениях параметра а каждое решение неравенства
logons х2 > log0 5 (х + 2) (1)
является решением неравенства
49х2 - 4а4 < 0? (2)
1. Неравенство (1) равносильно системе
х2 < х + 2,
< х О,
х + 2 > О,
решив которую находим, что
-1 < х < 0, 0 < х < 2. (3)
2. Неравенство (2) равносильно неравенству
(х- ^а2)(х + 1а2) < О,
2 9 / / 2 9
решениями которого являются все х такие, что -- аг ч х ч - а\
3. Решения (3) неравенства (1) являются решениями неравен-
ства (2), когда совместна система
-^2<-1,
2< 1а2,
т. е. когда а^ - J7 и а > л/7 .
4. Ответ: а е (-оо; - ^7 ] и [ J7 ; +оо),
25. При каких значениях параметра а неравенство
1°ёх-ах2<2 (1)
имеет по крайней мере одно решение из интервала |х| < 0,01?
1. Здесь ОДЗ переменной х определяется системой
f х - а > 0,
< х - а 1,
| х 5* 0,
причем, как это следует из вида неравенства (1), оно может иметь
решение только при а 0.
344
2. Перепишем неравенство (1) в виде
10Sx - а X2 < 10^х - а (Х ~ а)2 (2)
и рассмотрим два случая: а) 0 < х - а < 1; б) х - а > 1.
3. Пусть 0<х-а<1,т. е. а < х < а + 1; тогда неравенст-
во (2) равносильно неравенству х2 > (х - а)2 и приходим к системе
Ja<x<a + 1,
] а(а - 2х) < О, W
которая при а < 0 равносильна системе
j а < х < а + 1,
4. Тогда с учетом условий задачи получаем, что
а < О,
\а + 1 > -0,01,
I >-0,01,
откуда -0,02 < а < 0.
5. При а > 0 система (3) равносильна системе
| а < х < а + 1,
и тогда
а > 0,
L<0,01,
| <0,01,
откуда 0 < а < 0,01.
6. Пусть теперь х - а > 1, или а + 1 < х. В этом случае приходим
к системе
а + 1 < х,
а(а - 2х) > 0,
(4)
которая при а < 0 равносильна системе
а + 1 <
х,
345
С учетом условий задачи отсюда следует, что
а < О,
\а + 1 < 0,01,
I <0,01,
т. е. а < -0,99.
7. Если же а > 0, то система (4) равносильна системе
а + 1 < х < - ,
которая является несовместной.
8. Ответ: а < -0,99; -0,02 < а < 0; 0 < а < 0,01.
26. В зависимости от значений параметра а решить неравенство
log2 х + logT 2 + 2 cos а < 0. (1)
1. Допустимыми значениями переменной х являются положи-
тельные х, отличные от 1.
2. Перепишем неравенство (1) в виде
logo х + =—-— + 2 cos а < 0.
log2x
3. Заметим, что
z + | > 2 при z > 0, (2)
z + - < -2 при z < 0. (3)
z
Поэтому в случае, когда 0 < х < 1, получим неравенство
logo х + -—-— < -2,
log2 х
которое вместе с неравенствами
-2 < 2 cos а < 2 (4)
означает, что исходное неравенство будет иметь решения при любом
значении параметра а. Такими решениями являются все х е (0; 1).
4. Пусть теперь х > 1. В этом случае log2 х > 0 и тогда из нера-
венств (2) и (4) следует, что неравенство (1) будет иметь только одно
решение х = 2, когда cos а = -1, т. е. когда а = л(2й + 1), /г- Z.
5. Ответ: если а — любое, то 0 < х < 1;
кроме того, если а = л(2й + 1),/г-Z, то.г = 2.
346
27. При каких значениях параметра а неравенство
log5 [a cos 2х + (1 + 5а2 - sin2 х) cos х + 4 + а] < 1 (1)
справедливо для всех значений х?
1. Неравенство (1) равносильно двойному неравенству
О < а(2 cos2 х - 1) + (5а2 + cos2 х) cos х + 4 + а < 5.
2. Полагая у = cos х, приходим к неравенству
-4 < ys + 2ау2 + 5а2у< 1. (2)
3. Тогда задачу можно переформулировать так: найти значе-
ния а, при которых неравенство (2) выполняется для любых -1 <
< У < 1-
4. Рассмотрим функцию f(y) = ys + 2ау2 + 5а2у. Так как
f'(y) = Зу2 + 4ау + 5а2 > О
при всех а, то функция f(y) строго возрастает; поэтому требования
задачи будут выполнены, если
J /(-1) > -4, J-1 + 2а + 5а2 > -4,
}/(1)<1, Т,е’ |1 + 2а + 5а2<1.
Решив эту систему, находим, что -0,4 < а < 0.
5. Ответ: а е [-0,4; 0].
28. Решить неравенство
log2 х - 2b loga х + 2|loga x - b\ + 2 < 0, (1)
где 0 < a 1 и b — действительные параметры.
1. С помощью подстановки
t = |bga х - b\ (t > 0) (2)
данное неравенство приводится к следующей системе неравенств:
It2 + 2t + 2 - b2 < 0, (3)
\t > 0. (4)
2. Квадратный трехчлен в левой части неравенства (3) при |&| > 1
имеет два действительных различных корня = - Jb2 - 1 - 1 и 12 =
= Jb2 - 1 - 1, причем tx < 0, tx < f2. Следовательно, решением не-
равенства (3) является интервал < t < f2, а система (3), (4) может
347
иметь решение в том случае, когда больший корень положителен,
т. е. когда Jb2 - 1 - 1 > 0.
3. Последнее неравенство выполняется при |&| > 72 . При этих
значениях параметра b система (3), (4) имеет решение
ОС t < Jb2-1 - 1.
4. Воспользовавшись подстановкой (2), имеем
0 < |loga х - b\ < Jb2 - 1 - 1 (|&| > л/2 ),
откуда
b - Jb2-1 + 1 < loga х < b + Jb2-1 - 1 (|&| >72). (5)
5. Система неравенств (5) равносильна исходному неравенству (1).
Решив ее, получим ответ.
6. Ответ: если |&| > 72 , то
аь + л/ь2 -1 + 1 < х < аь ~ 'Jb2 -1 +1 при 0 < а < 1,
аъ- № -1 + 1 < х < аъ + л/ь2 -1 +1 при а > 1;
если |&| < 72 , то решений нет.
29. При каких значениях параметра а система неравенств
/ logo,5 (х - За) > -3, (1)
] |х - 2а| > 9 (2)
не имеет решений?
1. Найдем множество решений неравенства (1):
logo 5 Iх “ 3“) _3, или
х - За > 0,
х - За < 8,
откуда х е (За; За + 8].
2. Найдем множество решений неравенства (2):
\х - 2а\ 9, или
х - 2а 9,
х - 2а < -9;
откуда х е (-оо; 2а - 9] U [2а + 9; +°°).
348
3. Исходная система неравенств не имеет решений, если полу-
ченные множества не пересекаются. Это условие можно записать
в виде системы
J За + 8 < 2а + 9,
\3а > 2а- 9.
4. Решив систему (3), получим -9 < а < 1.
5. Ответ: а е [-9; 1).
30. Найти все значения х, для которых 0,5 < х < 2,5 и которые
удовлетворяют неравенству
10^Зх-х2 “ аХ^ < 1 О
при всех значениях параметра а из интервала 0 < а < 2.
1. Исходя из ограничения на х, заданного в условии (0,5 < х < 2,5),
оценим основание логарифма в неравенстве (1). Имеем
о 2 ( 3;2 , 9. 7 5 ЗА2 . 9 5 ч
Зх - х2 = -\ х - - \ +-=->1.
V 27 4 V 2 2 7 4 4
2. Итак, Зх - х2 > 1 при 0,5 < х < 2,5. Поэтому неравенство (1)
равносильно следующему:
0 < За - ах < Зх - х2. (2)
3. Теперь задача сводится к нахождению тех значений х из ин-
тервала 0,5 < х < 2,5, которые удовлетворяют двойному неравенст-
ву (2) при любых значениях а из интервала 0 < а < 2.
4. Найдем сначала решения неравенства (2), принадлежащие
интервалу (0,5; 2,5). Имеем
[ а(3 - х) > 0, f а(3 - х) > 0,
< х2 - (а + 3)х + За < 0, или < (а - х)(3 - х) < 0,
[0,5<х<2,5, [0,5<х<2,5,
т. е.
U > а,
^0,5<х<2,5. w
При последнем переходе мы воспользовались тем, что 3 - х > 0
при х < 2,5.
349
0 0,5 а
2 2,5
ЖЯ х
а
2
О
Рис. 102
5. Перейдем теперь к наибо-
лее логически трудной части ре-
шения задачи (именно здесь до-
пускаются ошибки): из решений
системы (3) нужно отобрать те,
которые справедливы при всех а
из интервала (0; 2). Этот интер-
вал в сопоставлении с интерва-
лами из системы (3) изображен
на рис. 102.
6. Замечаем, что для х, удовлетворяющих неравенству 2 < х < 2,5,
и только для этих х все условия задачи будут выполнены, т. е. сис-
тема (3) будет удовлетворяться при любых а из интервала 0 < а < 2.
7. Ответ: х [2; 2,5).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все значения Ь, при которых не имеет решений урав-
нение:
a) log& + 6 (Ьх + 2х) = log& + 6 (х1 2 3 4 5 6 * + 3);
б) log& + 7 (Ъх + х) = log& + 7 (х2 + 5).
2. Найти все значения а, при которых имеет два различных ре-
шения уравнение:
a) log7 _ а (х2 + 9) = log7 _ а (2ах - 4х);
б) 10&15 - а (*2 + !) = log15 - а (аХ ~ 8х)’
3. При каких целых значениях а неравенство
2 log0 5 а - 3 + 2х log0 5 а - х2 < 0
выполняется в любой точке оси 0x2
4. Решить уравнение
71ogat/^ + logxt/^ + Jlog„ 4^ + log, 4^1 = а.
5. Для каждого действительного числа а решить уравнение:
а) 4* - 4а 2х + 2а + 2 = 0;
б) 144* - 2 • 12М + а = 0.
6. Найти значения а, при которых уравнение:
a) log2 2х + log2 |х — 3| — log2 log2 а = 0 имеет два корня;
350
б) | log2 9x2 + log2 (6 - x) - log2 3“ = 0 имеет три корня;
в) 1g f + 1g \x - 10| - lglog2 a = 0 имеет единственный корень;
г) log3 4х + log3 |х — 2| — log3 log2 а = 0 имеет три корня.
7. При каких значениях а имеет единственное решение система
неравенств:
Jlog2 (а + х) < 1, Jlog3 (а - х) < 1,
а) ] |а - х\ < 1; б) ] |3а - х\ < 5?
8. При каких значениях а не имеет решений система неравенств:
J logo,5 (х ~ 4а) > ~3’ J bg6 (х - а) < 1,
а) [ |х - За| >7; 6Ц \х - 2а| > 12?
В ответе указать наименьшее значение а.
9. Найти все значения у, при которых неравенство
*2(2 - bg2 ) + 2х(1 + log2 ) - 2(1 + log2 ) > О
выполняется для любых х.
10. В зависимости от значений параметра а решить уравнение
log3 (31 - х2 - 6х + 5|) = а.
11. При каких значениях параметра а сумма квадратов корней
уравнения
2 log4 (2х2 - х + 2а - 4а2) + log0 5 (х2 + ах - 2а2) = 0
больше 1?
12. При каких значениях параметра а для любого значения па-
раметра b существуют решения уравнения
log2 (1 - х - х2) = Ъ + logx _х_х2 2,
удовлетворяющие условию 0 < х < 0,5?
13. Найти все значения х, удовлетворяющие уравнению
log 2 (а2х + 2) = 21og7 + 2г (5 - j6-2x)
при любом значении параметра а.
14. При каких значениях параметра а уравнение
1g (х2 + 2ах) - 1g (8х - 6а - 3) = 0
имеет единственное решение?
351
15. В зависимости от значений параметра а решить неравен-
ство
loga (1 - 8а-ж) > 2(1 - х).
Ответы
1. а) (-оо; 3) U (7; 23]; б) [-10; -1) U (2; +оо). 2. а) (-оо; и ( Z ; ];
1
б) ; I ) и (5; +°°)- 3. 1, 2, 3, 7. 4. х1 = аа2 и х2 = а"2 , где а > 1.
5. а) Если а < -1, то х = log2 (2а + J4,a2 -2а-2 ); если а = 1, то х = 1; если
а > 1, то х1 2 = log2 (2а ± tj^a2 -2а-2 ); при остальных а корней нет;
б) если а < 1, то х1 2 = ±log2 (1 + >Jl-a ); если а = 1, то х = 0; если а > 1, то
корней нет. 6. а) а = 16^/2; б) а ~ (-оо; 3); в) а ~ (31; +°о); г) а е (1; 16).
7. а) 1,5; б) -4. 8. а) -7; б) -4. 9. у G (-оо; -1) и (1; +оо). Ю. Если а < 3, то
Х1 2 = 3 ± л/35 - За ; если а = 3, то х1 2 = 3 ± 2 J2 , х3 = 3; если 3 < а <
< log3 31, то Xj 2 = 3 ± л/35 - 3“ , х3 4 = 3 ± л/За - 27 ; если а = log3 31, то
х1 = 1, х2 = 5; если а > log3 31, то корней нет. 11. а G (-1; 0) U (0,4; 0,5).
12. а е (0; 4]. 13. х = 1. 14. а е (-Z ; -ZL ( и {1}. 15. Если а < 0 или а = 1,
то решений нет; если 0 < а < 1, то loga (4 + 716 + а2 ) < х < loga 8; если а > 1,
тох ? loga(4 + 716 + а2 ).
- - Рпонятие первообразной функции...J- -
1Г2. Основное свойство первообразной функций 2
ВЗмриволинейная трапеция и ее площадь I | -
Г Формула Ньютона—Лейбница । । | | | 2
- - 5. Основные правила интегрирования
"6. Вычисление площадей с помощью интеграла
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Понятие первообразной функции
1°. Под дифференцированием функции /(х) мы понимаем на-
хождение производной f’(x).
Например, если f(x) = cos 2х, то f’(x) = -sin 2х (2х)’ = -2 sin 2х
для всех х е R.
2°. Нахождение функции f(x) по заданной ее производной f'(x)
называют операцией интегрирования.
3°. Таким образом, операция интегрирования обратна операции
дифференцирования. Следовательно, операция интегрирования со-
стоит в том, что по заданной производной f’(x) находят (восстанав-
ливают) функцию f(x).
4°. Например, пусть f’(x) = 4х3. Следует найти f(x). Опираясь
на правило дифференцирования, нетрудно установить, что f(x) = х4.
Легко догадаться, что /(х) находится неоднозначно.
5°. В качестве /(х) можно взять и такие функции, как /(х) =
= х4 + 2, /(х) = х4 - 5, /(х) = х4 + л/б и др., поскольку производная
каждой из данных функций равна 4х3. Все эти функции отличают-
ся друг от друга только постоянным слагаемым.
6°. Общее решение задачи можно записать в виде /(х) = х4 + С,
где С — произвольное действительное число. Любую из найденных
функций /(х) называют первообразной для функции f’(x) = 4х3.
7°. Функцию F называют первообразной для функции f на за-
данном промежутке, если для всех х из этого промежутка F’(x) = f(x).
353
Так, функция F(x) = х4 есть первообразная для функции f(x) =
= 4х3 на промежутке (-°°; +°°), поскольку при всех х е R справед-
ливо равенство F’(x) = (х4)' = 4xs.
8°. Множество всех первообразных для функции f(x) можно
представить в виде F(x) + С, где С — R.
2. Основное свойство первообразной функции
1°.Теорем а. Если функция F есть первообразная для функ-
ции f на промежутке X, то при любой постоянной С функция
F(x) + С (1)
также является первообразной для функции f на промежутке X.
Любую первообразную функции f на промежутке X можно запи-
сать в виде F(x) + С.
2°. Какую бы постоянную в выражении (1) ни подставить вме-
сто С, получится первообразная для функции f. Выражение F(x) + С
называют общим видом первообразных для
функции f.
3°. Какую бы первообразную для функции
f ни взять, ее можно получить из выражения (1)
при соответствующем подборе постоянной С.
4°. Геометрически основное свойство пер-
вообразных можно интерпретировать так: гра-
фики всех первообразных данной функции f(x)
получаются с помощью параллельного пере-
носа любого из этих графиков вдоль оси Оу
(рис. 103).
5°. Таблица первообразных некоторых функций
Рис. 103
Функция Общий вид первообразных Функция Общий вид первообразных
k (постоянная) kx + С 1 COS2 X tg х + С
х“ (а е R, а 5й - 1) vCt + 1 + с а+1 1 sin2 х -ctg х + С
1 Jx %Jx+C 1 X In |х\ + С
sin х -cos х + С ех ех +С
COS X sin х + С ах, а > 0, а 1 + с In а
354
3. Криволинейная трапеция и ее площадь
1°. Криволинейной трапецией называют
фигуру, ограниченную графиком неотрица-
тельной и непрерывной на отрезке [а; Ь] функ-
ции f, осью Ох и прямыми х = а и х = Ъ.
2°. Т е о р е м а. Пусть f — непрерывная
и неотрицательная на отрезке [а; Ь] функ-
ция, aS — площадь соответствующей кри-
волинейной трапеции (рис. 104). Тогда если
F есть первообразная для f на интервале, со-
держащем отрезок [а; Ь], то S = F(b) - F(a).
4. Формула Ньютона—Лейбница
1°. Интегралом от а до Ъ функции f называют приращение
первообразной F этой функции, т. е. F(b) - F(a) (очевидно, что это
приращение не зависит от выбора первообразной).
ь
2°. Интеграл от а до & функции / обозначается так: j f(x) dx (чи-
а
тается: «интеграл от а до & эф от икс дэ икс»). Числа аиЬ называют
пределами интегрирования, а — нижним, Ъ — верхним преде-
лом. Знак j называют знаком интеграла, функцию / — подын-
тегральной функцией, х — переменной интегрирования. Отре-
зок с концами aub называют отрезком интегрирования.
3°. Заметим, что верхний предел интегрирования необязатель-
но больше нижнего предела; может быть а > Ъ, а = Ъ.
4°. По определению интеграла: если F' = f, то
ь
J f(x) dx = F(b) - F(a). (1)
a
Это равенство называют формулой Ньютона—Лейбница.
5°. Для удобства записи приращение первообразной F(b) - F(a)
сокращенно обозначают так: F(x) \Ьа , т. е. F(b) - F(a) = F(x) \ba .
6°. Формулу для вычисления площади криволинейной трапеции
(см. п. 3) с помощью интеграла можно записать таким образом:
ь
S = J /(x)dx = F(b) - F(a). (2)
а
355
Формула (2) верна для любой функции f, непрерывной на от-
резке [а; Ь].
7°. Интеграл вида j /(f)df называют интегралом с перемен-
а
ным верхним пределом. Этот интеграл есть такая первообразная
функции f, которая в точке х = а обращается в нуль, и, следова-
тельно, справедлива формула
j /(f) dt j = f'(x).
а '
5. Основные правила интегрирования
1°. Постоянный множитель можно вынести за знак интеграла:
ь ь
j kf(x) dx = k j f(x) dx, где k — постоянная. (1)
a a
2°. Интеграл от суммы равен сумме интегралов:
ь ь ь
j (/(х) + ф(х)) dx = j /(х) dx + j <p(x) dx. (2)
а а а
3°. Справедлива следующая формула замены переменной:
ь kb+p
j f(kx + р) dx = | j f(t) df, (3)
a ka + p
где t = kx + p,hup — постоянные, причем новые пределы интегри-
рования получаются из формулы t = kx + р заменой х на а и на Ъ.
6. Вычисление площадей с помощью интеграла
1°. Пусть функция /(х) непрерывна и неотрицательна на отрез-
ке [а; Ь]. Тогда, как известно, площадь соответствующей криволи-
нейной трапеции (рис. 105, а) находится на формуле
ь
j /(х) dx = F(x) \ba = F(b) - F(a).
a
356
2°. В том случае, когда непрерывная функция f(x) неположи-
тельна на отрезке [а; Ь], для вычисления площади соответствую-
щей криволинейной трапеции (рис. 105, б) следует использовать
формулу
ь
S = - j f(x) dx.
а
3°. Пусть функция f(x) непрерывна на отрезке [а; Ь] и принима-
ет на этом отрезке как положительные, так и отрицательные зна-
чения. Тогда нужно разбить отрезок [а; Ь] на такие части, в каждой
из которых функция не изменяет свой знак, затем вычислить по
приведенным выше формулам соответствующие этим частям пло-
щади и эти площади сложить.
Например, площадь фигуры, изображенной на рис. 106, нахо-
дится по формуле
с Ь
S = - j f(x) dx + j f(x) dx.
357
4°. Площадь фигуры, ограниченной графиками двух непре-
рывных функций /х(х) и /2(х) и ДВУМЯ прямыми х = а и х = Ъ, где
/х(х) > f2(x) на отрезке [а; Ь] (рис. 107), находится по формуле
ь ь
S = j /х(х) dx - j f2(x) dx.
a a
ЗАДАЧИ С РЕШЕНИЯМИ
1. Найти все числа а (а > 0), для каждого из которых выполняется
неравенство
а
j (2 - 4х + 3x2)dx < а.
о
1. Преобразуем левую часть данного неравенства. Согласно фор-
муле Ньютона—Лейбница, имеем
j (2 - 4х + Зх2) dx = (2х - 2х2 + х3) |“ = 2а - 2а2 + а3.
о
2. Поэтому исходное неравенство можно переписать так:
2а - 2а2 + а3 < а, или а(а - I)2 < 0.
3. Учитывая условие а > 0, получаем, что а = 1.
4. Ответ: а = 1.
2. Найти все решения уравнения
а
j cos (х + a2) dx = sin а,
о
принадлежащие отрезку [2; 3].
1. Найдем интеграл в левой части уравнения:
а
j cos (х + a2) dx = sin (х + а2) |“ = sin (а + а2) - sin а2.
о
2. Тогда исходное уравнение можно переписать в виде
sin (а + а2) - sin а2 = sin а.
358
3. Применяя известные формулы, получим
о . а (а , ? с, . а а
2 sin - cos I - +(Г = 2 sin - cos - ;
sin
+ a2^j - cos | ) = 0;
n . a .a2 a2 + a „
-2 sin - • sin — sin —-— = 0
4. Поэтому исходное уравнение равносильно следующей сово-
купности уравнений:
sin |=0; (1)
„2
sin = 0; (2)
sin 5^ = 0. (3)
5. Уравнение (1) имеет решения а = 2nk, k — Z.
Уравнение (2) имеет решения а = ± J2~n , п = 0, 1, 2, ... .
Уравнение (3) равносильно бесконечной совокупности уравнений
а2 + а - 21п = 0,1 е Z. (4)
6. а) Дискриминант каждого из уравнений (4) равен 1 + 8/л, и
значит, при целых отрицательных I соответствующие уравнения
не имеют решений.
б) Если же I есть одно из чисел 0, 1,2, ... , то уравнение (4) име-
-1 ± 78Zn + 1
ет два корня: ах 2 =---------.
в) Итак, уравнение (3) имеет решения
а = -1 ± J8ln + 1 = 0, j, 2, ... .
7. Теперь в найденных множествах решений совокупности урав-
нений (1)—(3) выберем числа, принадлежащие отрезку [2; 3].
8. Очевидно, что ни одно из решений уравнения (1) не прина-
длежит отрезку [2; 3], а из решений уравнения (2) только одно при-
надлежит этому отрезку: а = 72л .
9. Рассмотрим решения уравнения (3). Все числа вида а =
= ——+ 1 отрицательны и потому лежат вне отрезка [2; 3]. Из
359
— 1 + J8ln + 1 го от
чисел вида а =---------- отрезку [2; 3] принадлежат те и только
те, которые удовлетворяют двойному неравенству
2 < 1 + л/SZn + 1 з, или g ^/8/л + 1 < 7, или - < I < - .
2 л л
10. Ясно, что только число I = 1 удовлетворяет этому неравен-
ству. Соответствующее ему решение данного уравнения имеет вид
_______ — 1 + л/8л + 1
а 2 ’
11. Ответ: Jiv.; + ^8л_чЩ .
3. Найти все значения параметра а (а 1), при каждом из которых
площадь фигуры, лежащей в полуплоскости х > 0 и ограниченной
прямыми у = 1, у = 2 и кривыми у = ах2, у = | ах2, будет наиболь-
шей. Найти эту площадь S.
1. На рис. 108 изображены данные кривые при фиксированном
значении а и прямые у = 1, у = 2.
360
2. Нужно определить значения параметра а (а > 1), при каж-
дом из которых площадь заштрихованной фигуры ABCD будет
наибольшей.
3. Координаты точек А и D являются соответственно решения-
ми систем уравнений
у = ах2,
У=1
I 1 2
У = Оах
и X z
\У = 1-
4. Координаты точек В иС являются соответственно решения-
ми систем уравнений
у = ах2,
У = 2
1 о
У = -ахл,
и < z
У =2.
5. Учитывая, что абсциссы точек А, В, С, D по условию должны
быть неотрицательными, находим А^ -±= ; 1), ; 1), В^ ; 2 ),
6. Точки В и D имеют одинаковые абсциссы, поэтому заштри-
хованная фигура состоит из двух частей:
а) фигуры, лежащей под кривой у = ах2 и над прямой у = 1 на
промежутке от
б) фигуры, лежащей над кривой у = | ах2 и под прямой у = 2 на
/2 2
промежутке от - до — .
Ча Ja
7. Найдем площадь заштрихованной фигуры:
72/ а 2/л/а
S = j (ах2 - 1) dx + j ^2- | ах2
1/Ja
ах‘‘
“Г
1/л/Й
2/7^ г
,--- а
361
8. Функция i ( - 2 л/2 в области а > 1 монотонно убывает.
Поэтому ее наибольшее значение в этой области достигается при
а = 1 и равно - 2 л/2 .
О
9. Ответ: а = 1; S = - 2 л/2 .
О
4. Найти все значения параметра Ъ (Ь > 0), для каждого из которых
площадь фигуры, ограниченной кривыми у = 1-х2иу = Ьх2, рав-
на числу с. При каких с задача имеет решение?
1. Пусть b — некоторое фиксированное положительное значе-
ние параметра. Для этого значения b найдем абсциссы точек пере-
сечения графиков функций у(х) = Ьх2 и у(х) = 1 - х2 (рис. 109). Они
будут корнями уравнения Ьх2 = 1 - х2.
2. Решив это уравнение, получим
Рис. 109 = - • —j— . (1)
3 л/Ь + 1
4. Так как выражение (1) по условию должно быть равно числу с,
4 1 ,
то получаем соотношение - • _ = с, откуда следует, что Ъ =
3 7& + 1
= 2£ -1.
9с2
5. Задача имеет решение тогда и только тогда, когда число с
удовлетворяет системе неравенств
362
(первое неравенство должно выполняться, так как по условию b > О,
а второе неравенство есть следствие того, что площадь фигуры долж-
на быть положительна).
5. Решением системы (2) является интервал 0 < с < |; искомое
О
, 16 1
значение Ъ равно —3 - 1.
9с2
6. Ответ: Ъ = - 1; 0 < с < .
9с2 3
5. Найти все значения параметра а (а > 0), при каждом из кото-
, „ , „ х2 + 2ах + За2
рых площадь фигуры, ограниченной параболой у = ---------- и
1 + а4
прямой у = + а* , является наибольшей.
1. Пусть а — фиксированное положительное число. Координа-
ты точек пересечения параболы и прямой удовлетворяют системе
уравнений
х2 + 2ах + За2
2. Приравнивая правые части уравнений, приходим к равенст-
ву х2 + Зах + 2d2, = 0, откуда хх = -а, х2 = -2а. Тогда у} = 4
За2 ух я
и у2 = 1 + 4 . Итак, прямая пересекает параболу в двух точках:
£(-»;ггл)“с(-2»;гй 110’-
3. Вычислим площадь фигуры СтВп.
Имеем
х2 + 2ах + За2
1+а4
-а
—5— I" (х2 + Зах + 2а2) dx =
1
1 + а4
+ 3^ +
а3
6(1 + а4) ’
363
4. Нужно найти значение а, при котором функция S(a) прини-
мает наибольшее значение на множестве а > 0.
5. Функция S(a) дифференцируема в каждой точке, причем
or/ 1 За2(1 + а4) - 4а3-а3 _
(а) 6 ’ (1+а4)2
= 1 . а2(3 - а4)
6 (1 + а4)2
Уравнение S’(a) = 0 имеет в области а > 0 единственный корень
а = 473.
6. В промежутке 0 < а < \[3 производная S'(a) положительна,
а в промежутке t/З < а < +°° она отрицательна. Следовательно,
функция Я(а) возрастает на промежутке 0 < а < \[3 и убывает на
промежутке t/З < а < +°°.
7. Так как функция S(d) непрерывна в точке а = \[3 , то в этой
точке она принимает наибольшее значение, т. е. при а = \[3 дан-
ная фигура имеет наибольшую площадь.
8. Ответ: а = \[3 .
6. Найти все значения параметра а (а > 0), при каждом из которых
площадь фигуры, ограниченной параболой
у = х2 - 2х з/ а „ + 3
' >Jl + a2
и прямой у = -Зх з—^—5 + 3 является наибольшей. Найти эту наи-
1 + а2
большую площадь.
1. Пусть а > 0 — некоторое фиксированное число. Координаты
точек пересечения указанных линий удовлетворяют системе урав-
нений
у = х2 - 2х з/ а , + 3, (1)
' 6/1 + а2
< ___________
у = -Зх зМ-2 +3. (2)
364
2. Приравнивая правые части этих уравнений, приходим к
квадратному уравнению
ках с абсциссами х1 = —2
х2 + х з—= О,
1 + а2
откуда следует, что парабола (1) и прямая (2) пересекаются в точ-
и х2 = 0, причем х} < х2.
3. Нетрудно установить, что фигура, площадь которой требует-
ся определить, находится ниже прямой (2) и выше параболы (1) на
промежутке [хх; х2].
4. Вычислим искомую площадь:
о
S(a) = J
dx =
а
6(1 + а2) ’
5. Чтобы найти значение а > 0, при котором функция S(a) при-
нимает наибольшее значение, исследуем эту функцию.
6. В каждой точке области 0 < а < функция S(a) имеет про-
изводную
,_1 + а2-а-2а_ 1 - а2
W 6(1 + а2)2 6(1 + а2)2 ’
(3)
7. Из выражения (3) следует, что на промежутке 0 < а < 1 про-
изводная S'(a) > 0, а на промежутке 1 < а < +°° производная S'(a) < 0.
Значит, функция S(a) возрастает на промежутке 0 < а < 1 и убыва-
ет на промежутке 1 < а < +°°.
8. Поскольку функция S(a) непрерывна в точке а = 1, ее наи-
большее значение достигается при а = 1.
9. Итак, при а = 1 данная фигура имеет наибольшую площадь;
эта площадь есть S(l) = .
10. Ответ: а = 1; S = .
365
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все числа а, для каждого из которых выполняется не-
равенство:
2
a) j (а2 + (4 - 4а)х + 4х3) dx < 12;
1
а
б) j (а - 4х) dx > 6 - 5а.
1
а
2. Найти все решения уравнения j cos (х + 2а2 - a) dx = -sin 2а,
-а
принадлежащие отрезку [-1,5; -0,5].
2₽
3. Найти все решения уравнения j sin (х - Р2) dx = sin 2р, при-
о
надлежащие отрезку [2; 3].
4. Найти критические точки функции j (sin2 2t - 2 cos2 2t + a)dt.
о
5. Найти все значения а, принадлежащие отрезку [0; 2л] и
а
удовлетворяющие уравнению j sin х dx = sin 2а.
л/2
6. Найти значения параметра а, при которых площадь фигуры,
ограниченной линиями:
а) у = Зх3 + 2х, х = а, у = 0, равна 1;
б) у = 8х2 - х5, х = 1, х = а, у = 0, равна ;
\ 4 1 9
в) у = — , х = 1, у = а, равна ;
г) у = sin 6х, х = а, х = , равна |.
7. Найти все значения параметра/, (р > 0), при каждом из кото-
рых площадь фигуры, ограниченной параболой у = х2 + хз/—+ 1
А/1 +
и прямой у = 2хз—+ 1, является наибольшей.
А/1 +р2
366
8. Найти все значения параметра а (а > 0), при каждом из кото-
рых площадь фигуры, ограниченной параболой у = -(1 + а2)2х2 + а
и прямой у = 0, является наибольшей.
Ответы
1. а)3;б)2. 2. ; 1 ^ + 2я . з. ^.4. Еслиа&[-1; 2], то х = ±
। 1 2 CL — 1 г-ini х 7 3
± - arccos —з— ; если а [-1; 2], то критических точек нет. 5. - ; — ; — ;
115.6. а) ± J ; б) -1; ; в) 1; ; г) - А 5.7. 1. 8. 7з .
ff--------1
T ГГло же ние 1
Текстовые задачи на составление 1
уравнений и неравенств с параметрами
г..............11111111111 Г| П
ЗАДАЧИ С РЕШЕНИЯМИ
1. Две точки начинают одновременно равномерное движение от
вершины прямого угла вдоль его сторон. С какой скоростью долж-
на двигаться первая из них, чтобы через t с после начала движения
расстояние между ними было не менее 10 м, если известно, что ско-
рость второй точки на 2 м/с больше скорости первой?
1. Пусть х м/с — скорость движения первой точки; тогда
(х + 2) м/с — скорость движения второй точки.
2. За t с точки пройдут соответственно tx м и t(x + 2) м. При
этом расстояние между ними составит .
3. Задача сводится к решению неравенства
Jt2x2 + t2(x + 2)2 >10,
которое равносильно неравенству
Zt2x2 + 4г2х + 4г2 - 100 > 0. (1)
4. Пусть D — дискриминант квадратного трехчлена
Дх) = Zt2x2 + 4г2х + 4г2 - 100. (2)
Находим = 4г4 - 8г4 + 200г2 = -4г4 + 200г2 = 4г2(50 - г2).
По смыслу задачи г > 0 и х > 0.
5. Имеем D < 0 при 50 - г2 < 0, т. е. при г > 5 л/2 . Тогда неравен-
ство (1) справедливо при любом х > 0.
6. Имеем D = 0 при г = 5 л/2 . Тогда неравенство (1) примет вид
100(х + I)2 > 0 и, значит, оно также справедливо при х > 0.
368
7. Рассмотрим теперь случай D > 0, т. е. О < f < 5л/2 . Тогда
квадратный трехчлен (2) имеет два действительных корня:
-1 - «/б О -t2 - t + л/бО -t2
х, = -------2; х9 =--------------2---------
1 t 2 t
8. Очевидно, что х1 < 0 при любых значениях t. Поэтому оста-
ется решить систему неравенств
[ х О,
| X > - * +Уб°-*2 (3)
[х t
9. а) Мы установили, что корень х1 квадратного трехчлена (2) от-
рицателен. В силу теоремы Виета если при этом 4f2 - 100 < 0, т. е.
0 < t < 5, то корень х2 неотрицателен и решение системы (3) есть
> -1 + 7бо -t2
t
б) Если же 4f2 - 100 > 0, т. е. 5 < t < 5 л/2 , то х2 < 0 и решением
системы (3) служит любое х > 0.
10. Ответ: если f > 5, то х > 0;
п , . к + л/бО - t2
если 0 < t ч 5, то х >-------.
2. Из пункта А в пункт В, расстояние между которыми равно s,
вышли одновременно два пешехода; в тот же момент из пункта В
в пунктА выехал велосипедист. Проехав путь | (от В кА), велоси-
2
педист встретил первого пешехода, а затем, проехав - всего пути,
О
он встретил второго пешехода. На каком расстоянии I от них в мо-
мент встречи находился первый пешеход?
1. Пусть v — скорость первого пешехода, w — скорость велоси-
педиста.
2. Тогда согласно условию задачи в момент их встречи выпол-
няется равенство
3
= л.
V kw ’
откуда следует, что v = (k - l)w.
369
3. Далее, время, которое затратил велосипедист на прохожде-
ние пути от момента встречи с первым пешеходом до момента
встречи со вторым пешеходом, определяется равенством
i = -f- “Л-
w \ 3 kJ
4. За это время t первый пешеход прошел от момента встречи
с велосипедистом путь
= s(fe-l)(2fe-3)
3fe
5. Таким образом, расстояние I, на котором находился первый
пешеход в момент встречи велосипедиста со вторым пешеходом,
равно
s(k- 1)(2А-3) <2 _ 1 Л _s(2fe-3)
3fe 1з kJS 3
з
Заметим, что из условия задачи вытекает, что й > - , причем
, 3
если к = - , то пешеходы могут идти с одинаковыми скоростями.
Кроме того, I < , т. е. первый пешеход далее пункта £ не движет-
О
ся. Тогда, решив неравенство
s(2fe - 3) < 2s
3 " "3 ’
, 5
находим, что к ч - .
с 3 , , 5 . s(2k - 3)
6. Ответ: если - ч к < - , то I = ——5;
Z Z О
, . 5 7 2s
если я > - , то Z = — .
Z О
3. Расстояние между пунктами А и В равно s. Из пункта А в пункт В
вылетел вертолет, а через время t в том же направлении вылетел
самолет, который догнал вертолет на расстоянии г от пункта А, за-
тем долетел до пункта В и сразу повернул обратно. На расстоянии г
от пункта В самолет встретил вертолет и вернулся в пункт А по-
зднее, чем вертолет прибыл в пункт В. На сколько раньше вертолет
прибыл в пункт В, чем самолет вернулся в пунктА?
370
1. Пусть х — скорость самолета, а у — скорость вертолета.
2. Тогда до первой встречи самолета с вертолетом первый из
них затратил время - , а второй — время - .
X у
3. Так как самолет вылетел на время t позже вертолета, то по-
лучаем уравнение
4. К моменту второй встречи вертолет находился на расстоя-
нии г от пункта В и пробыл в полете время -—-, а самолет преодо-
лел расстояние s + г и пробыл в полете время .
X
5. Составим второе уравнение:
— = s+r + Л (2)
У X
6. Далее, в соответствии с условием задачи и принятыми обо-
значениями имеем:
а) вертолет прибыл в пункт В через время - после вылета;
б) самолет вернулся в пунктА через время t + — после того как
X
вертолет вылетел из пункта А. Отсюда следует, что
t + — - - (3)
X у
— это та разница во времени, на которую вертолет прибыл в пункт В
раньше, чем самолет вернулся в пунктА.
7. Чтобы найти время (3), вернемся к уравнениям (1) и (2). Умно-
жив обе части уравнения (1) на г - s, а уравнения (2) — наги сложив
полученные соотношения, имеем
r(s + r) . r(r - s) . , ч. . , n
—------ + —----- + (г - s)t + rt = О,
X X
или
371
8. Учитывая теперь, что из соотношений (1) и (4) следует равен-
ство
1 _ 1 t _ st
у х г 2 г2 ’
получим
t + - s- = t + ^<s~ 4r>. (51
9. При этом исходя из смысла задачи должно выполняться не-
равенство s - 2г > 0 и, кроме того, положительной должна быть
и правая часть равенства (5). С учетом неравенства s - 2г > 0 по-
следнее условие будет выполняться при s > (2 + J2 )r.
10. Ответ: t + ts^s , где s > (2 + J2 )r.
2r2
4. Один сплав состоит из двух металлов, входящих в него в отно-
шении 1 : 2, а другой сплав содержит те же металлы в отношении
2:3. Из скольких частей каждого сплава можно получить новый
сплав, содержащий те же металлы в отношении а : Ь?
1. Пусть новый сплав содержит х частей первого сплава и у час-
тей второго сплава.
2. Тогда в новом сплаве будет содержаться частей пер-
3 5
вого металла и — + Т частей второго металла. Таким образом,
3 5
х + 2у
3 5 _ а 5х + бу _ а
2х + Зу Ь ’ ИЛИ 10х + 9у Ь '
Т б
(1)
3. Исходя из физических соображений будем считать, что х > О,
у > 0. Разделив числитель и знаменатель уравнения (1) на у, полу-
чим уравнение
^ + 6
У____ = а
10х+g Ь’
У
равносильное следующему:
5(b - 2а)? = 3(3а - 2Ь).
(2)
372
4. При b = 2а уравнение (2) не имеет решений.
5. Пусть b 2а. Тогда - = 3J3a и, следовательно, - > О,
у 5(Ь-2а) у
если
3(3а -26) 0 /о\
5(6-2а) > °'
6. Неравенство (3) равносильно совокупности двух систем:
J За - 2Ь > 0; J За - 2Ь < 0,
а) \b - 2а > 0; б) \b - 2а < 0.
7. Решив систему а), получаем противоречивые неравенства
2а < Ь < 1,5а.
8. Решив систему б), находим, что 1,5а <Ь < 2а.
9. Ответ: новый сплав можно получить из 3(26 - За) частей
первого сплава и 5(2а - Ь) частей второго сплава, где
а > 0, b > 0, 1,5а < b < 2а.
5. В двух сосудах вместимостью по 5 л содержится раствор некото-
рого вещества. В первом из них — 3 л раствора с объемной долей
вещества, равной а, во втором — 4 л раствора с объемной долей,
равной 2а. Сколько раствора надо перелить из второго сосуда в пер-
вый, чтобы объемная доля вещества в первом сосуде стала рав-
ной 0,1?
1. Согласно условию, в первом сосуде содержится За л вещества.
2. Если из второго сосуда перелить в первый х л раствора, то
в этом количестве раствора будет содержаться 2ах л вещества.
3. Составим уравнение
За + 2ах _ 1
х + 3 10 *
откуда находим х = —---- .
20а -1
4. Учитывая теперь, что вместимость каждого из сосудов со-
ставляет 5 л, приходим к неравенствам
л z 3- 30а п
U " 20а-1 " ’
1 1
решив которые получим, что — ч а ч — .
к 3-30а СГ1 11
5. Ответ: х = , где а Ц - ; - j .
373
6. Имеются два куска сплава серебра с медью. Один из кусков со-
держит а% меди, а другой — Ь% меди. В каком отношении нужно
взять сплавы первого и второго кусков, чтобы получить новый
сплав, содержащий с% меди?
При каких соотношениях между а, Ь, с решение задачи воз-
можно и какую максимальную массу нового сплава можно полу-
чить, если масса первого куска составляет Р г, а второго Q г?
1. Пусть отношение масс сплавляемых кусков равно т : п.
2. Тогда, согласно условию, получаем уравнение
та + пЬ
100 100 = с
т + п 100 ’
т с-Ь
Отсюда следует, что — =---.
п а - с
3. Решение задачи возможно, если а > с > Ъ или а < с < Ъ.
4. Чтобы найти максимальную массу нового сплава, рассмот-
Р Q
рим отношения ।---и , которые с учетом полученных ре-
зультатов позволяют записать полный ответ.
5. Ответ: — = -—- , где а > с > Ъ или а < с < Ь;
п а - с
Р Q
если ,--, , то
|с - Ь\ \а -с|
а-b г, а-b у-,
максимальная масса равна —- Р = ----Q;
с-Ь а-с
Р Q
если ,--, , то
|с - Ь\ |а-с|
а - Ь п
максимальная масса равна —- Р;
с-Ь
P Q
если ,--, , то
|с - Ь\ |а-с|
а - b z-,
максимальная масса равна----Q.
а- с
7. Цена бриллианта пропорциональна квадрату его массы. Брил-
лиант массой вр карат был разбит на две части, после чего его сто-
имость уменьшилась в k раз (1 карат = 0,2 г). Найти массы частей,
на которые был разбит бриллиант.
374
1. Пусть одна часть имеет массу х карат, тогда другая имеет
массу р - х карат.
2. Цены этих частей соответственно равны 1х1 2 и 1(р - х)2, где
I — коэффициент пропорциональности.
3. Так как цена целого бриллианта была равна 1р2, то получим
уравнение
1р2 = k(lx2 + 1(р - х)2),
которое после упрощений примет вид
2kx2 - 2kpx + p2(k - 1) = О,
откуда
*1, 2 = ± Jkp2(2-k) ].
4. Проведем исследование.
а) По смыслу задачи k > 1, р > 0. Следовательно, подкоренное
выражение будет неотрицательным, если k < 2, т. е. 1 < k < 2.
б) Так как *]1гр2(2 - k) = ,Jk2p2 - 2kp2(k - 1) < kp (в силу того,
что k > 1), то оба значения х неотрицательны.
в) Легко проверить, что р - х1 = х2.
5. Ответ: 1р( 1 - /| - 1 ); 1р( 1 + /| - 1 ), где 1 < k < 2.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Из одного и того же пункта одновременно в одном направле-
нии по прямолинейному участку шоссе с постоянными, но различ-
ными скоростями вышли два пешехода. Через 2 ч расстояние меж-
ду ними было s км. После этого пешеходы стали идти быстрее и за-
трачивать на каждый километр пути на 10 мин меньше. Еще через
2 ч расстояние между ними стало равным 3s км. Найти расстоя-
ния, пройденные пешеходами за первые два часа движения.
2. Два поезда выходят одновременно из пунктов А и В навстре-
чу друг другу и встречаются на расстоянии/) км от В. Через t ч пос-
ле их встречи второй поезд, миновав пунктА, находился в q км от
него, а первый в это время, миновав пункт В, находился от второго
поезда на расстоянии вдвое большем, чем расстояние между А и В.
Найти скорости поездов и расстояние между А и В, считая, что по-
езда нигде не останавливались, а их скорости были постоянными.
375
3. Куплено несколько килограммов товара двух сортов: I сорта
на 4500 р. и II сорта на 2000 р., причем I сорта куплено на 1 кг
больше. Стоимость 1 кг товара I сорта на 100а р. больше стоимости
1 кг товара II сорта. Сколько килограммов товара каждого сорта
было куплено? Определить количество решений в зависимости от
различных значений а.
4. В один из двух сосудов, каждый вместимостью по 6 л налито
4 л 70%-ного раствора кислоты, а во второй — 3 л 90%-ного рас-
твора кислоты (в процентах по объему). Сколько раствора нужно
перелить из второго сосуда в первый, чтобы в нем получился рас-
твор концентрации а% ?
5. Сосуд, содержащийр% -ный раствор кислоты, долили довер-
ху д% -ным раствором кислоты и после перемешивания отлили то
же количество. Проделав эту операцию k раз, получили г%-ный
раствор. Какую часть объема занимал первоначальный раствор?
6. Для технических целей смешали 5 л спирта I сорта и 7 л
спирта II сорта и получили спирт крепостью в 65°. Если бы взяли
20 л спирта I сорта и 4 л спирта II сорта, то получилась бы смесь
крепостью в р°. Определить крепость спирта каждого сорта.
7. Имеются два сплава никеля и железа. Первый из них содер-
жит а% железа, а второй — 2а% никеля (по массе). Сколько кило-
граммов каждого сплава нужно взять для получения 3 кг третьего
сплава, в котором содержание железа в 1,5 раза больше, чем никеля?
8. Ракета должна пролететь расстояние, равное h, начиная дви-
жение с постоянной скоростью V. В любой момент времени может
включиться ее дополнительный двигатель, работающий до конца
пути и дающий постоянное ускорение а > 0. На участке пути с по-
стоянной скоростью расход топлива пропорционален времени дви-
жения с коэффициентом пропорциональности кл > 0, а на участке
пути с включенным дополнительным двигателем расход топлива
пропорционален квадрату времени с коэффициентом пропорцио-
нальности /г2 > 0. Найти время, в течение которого ракета должна
лететь с включенным дополнительным двигателем, чтобы общий рас-
ход топлива был наименьшим.
Ответы
1.0,5(24 + s - 7s2 + 288s) и 0,5(24 - s - 7s2 + 288s) км; s < 6.
2. —— и км/ч; Зр - q км, где 0 < q < 2р, р > 0, t > 0. 3. 25 + ° + и
376
25-a + jD 25 + a-jD 25-a-jD 2 1 on । сок
---к—-— кг или к—— и ------к—-— кг, где D = а - 130а + 625, при-
za-----------------------------2а 2а
чем если а > 5, то нет решений, если 0 < а < 5 — два решения, если а = 5 —
ЛО о \ Л 280-4а -то- 230 е , lr- q ,
одно решение (3 и 2 кг). 4. -л, где 70 < а < —- . 5. к—, где либо
а -90 3 Ч Р <7
г > q, р > q, либо г < q, р < q. 6. Крепость спирта I сорта (в градусах) есть
7р 130 крепость спирта II сорта есть 130 - р, где 30 < р < 90. 7.
t) ой — J. UU
И кг, где 0 < а < 20. 8. , где 2vk2 - ah1 > 0 и ”kl <
, - v + Jv2 + 2ah -v + Jv2 + 2ah n 7 7 Л n 7 7 Л
ч ------------; -------------, где 2vk9 - ak-, ч 0 или 2vk9 - ak-, > 0 и
а а л i
vkl > - v + Jv2 + 2ah
2r/?2-a^l a
ЗАДАЧИ С РЕШЕНИЯМИ
1. При каких значениях параметра а уравнение
cos2 ах + cos х = 2(cos ах + cos х - 1) (1)
имеет единственное решение?
1. Так как косинус — четная функция, то если некоторое число
х является решением уравнения (1), то и (-х) также есть решение
уравнения (1). Поэтому необходимым условием существования
единственного решения уравнения (1) является равенство х = 0.
Это значение х, как показывает проверка, при любом а действи-
тельно удовлетворяет уравнению (1).
2. Таким образом, задача сводится к тому, чтобы указать такие
значения параметра а, при которых исходное уравнение имеет
единственное решение х = 0.
3. Перепишем уравнение (1) в виде
cos2 ах - 2 cos ах - cos х + 2 = 0 (2)
и рассмотрим уравнение (2) как квадратное относительно cos ах.
Так как его дискриминант D = 4(cos х - 1), то заключаем, что это
уравнение будет иметь решения только при условии cos х = 1, т. е.
х = 2nk, k — Z. При таких значениях х из уравнения (2) получаем,
что и cos ах = 1, и, значит, ах = 2тгп, п — Z.
4. Так как значение а = 0 не удовлетворяет требованию задачи
(при этом значении а исходное уравнение имеет бесконечное мно-
жество решений х = 2лй), то будем считать, что а / 0.
5. При отличных от нуля значениях а из уравнения ах = 2пп
2 ли -г-,
находим х =----. Если теперь предположить, что значения а при-
надлежат множеству Q рациональных чисел, то исходное уравнение
снова будет иметь бесконечное множество решений вида х = 2nk.
378
6. Предполагая же, что а — иррациональное, приходим к вы-
воду, что равенство 2л/г = выполняется только при k = п = О,
а, значит, при таких значениях кип мы получим единственное ре-
шение х = 0.
7. Ответ: а — иррациональное число.
2. Найти все значения параметра Ь, при которых система
f cos (у - Ъ) - 2 cos х = 0, (1)
[ log2 (by -у2) = 2 log4 (-х) - log0 5 3У (2)
имеет нечетное количество решений.
1. Прежде всего отметим, что допустимые значения х и у долж-
ны удовлетворять условиям х < 0, у > 0. Тогда уравнение (2) мож-
но преобразовать к виду
log2 (by - у2) = log2 (-Зху),
ИЛИ
by-у2 = -Зху. (3)
2. Очевидно, что все допустимые значения х и у, удовлетворяю-
щие уравнению (3), удовлетворяют также и условию by - у2 > 0.
3. Упростим уравнение (3), разделив обе его части на у (у > 0):
b - у = -Зх. (4)
Подставив это выражение в уравнение (1), получим
cos Зх = 2 cos х. (5)
4. Используя формулу косинуса тройного аргумента, придем к
уравнению
4cos3 х - 3 cos х = 2 cos х, т. е. cos3 х = cos х.
4
a) cos х = 0, х = + пп, п — Z.
б) cos2 х = — решений нет.
в) Учитывая, что х < 0, имеем п < 0, т. е. п = -1, -2, -3, ... .
5. Подставим найденные значения х в выражение (4):
у = Ь + + Зпп. (6)
379
Так как у > 0, то при целых п < 0 равенство (6) возможно толь-
ко в том случае, когда Ъ > 0.
6. Подберем теперь значения Ъ так, чтобы система уравнений
(1), (2) имела нечетное количество решений.
21л -Ъ 15л
2 2
9л ~Ъ Зл
2 2
Рис. 111
Зл
На рис. 111 изображены числа — + Зтгп, где п = -1, -2, ... .
Если положительные значения параметра Ъ выбирать согласно од-
ному из условий
Зл , 9л 15л , 21л 27л , 33л
- < Ъ < - , или — < Ъ < — , или — < Ъ < — ,
вообще,
+ блпг < b < + блпг, где m е Zo,
то в каждом случае найдется только нечетное количество целых от-
рицательных чисел п, при которых у > 0, т. е. система будет иметь
нечетное количество решений.
7. Ответ: + 6л m < b < + блпг, где т е Z(l.
3. Для каждого действительного числа 0 < а 1 решить уравнение
log2 sin х + р loga sin х + q = 0 (p2 - 4g > 0, q * 0). (1)
1. В области определения уравнения имеем sin х > 0.
2. Сначала рассмотрим случай а > 1. С помощью подстановки
t = loga sin х (t < 0), (2)
уравнение (1) сводится к смешанной системе
t2 + pt + q = 0, (3)
t < 0. (4)
3. Пусть tr и f2 — действительные корни уравнения (3), причем
tr < f2. Так как q 0, то ни один из этих корней не равен нулю.
4. Если оба корня положительны, то система (3), (4) не имеет
решений, а следовательно, не имеет корней и уравнение (1).
380
5. Пусть уравнение (3) имеет отрицательные корни t} < 0 и t2 < 0.
Согласно теореме Виета, это имеет место тогда и только тогда, ког-
дар > 0 и q > 0.
6. Значит, прир > 0 и q >0 уравнение (1) равносильно совокуп-
ности уравнений loga sin х = 2, где 2 — отрицательные корни
уравнения (3). Тогда получим
х = (-1)* arcsin а*1’2 + nk, kr— Z.
7. Пусть < t2 и больший корень положителен, а меньший от-
рицателен. В этом случае число 0 расположено между корнями
и t2. Необходимым и достаточным условием этого является выпол-
нение неравенства q < 0.
8. Таким образом, при q < 0 и любомр уравнение (1) равносиль-
но уравнению loga sin х = tx, где — отрицательный корень урав-
нения (3). Отсюда находим
х = (-1)" arcsin а*1 + пп, п Z.
9. Аналогично рассматривается случай 0< а < 1. Полагая
loga sin х = t и учитывая, что loga sin х > 0, получим смешанную
систему
t2 + pt + q = 0,
t >0.
10. Дальнейшее исследование проводится так же, как и в пер-
вом случае.
11. Ответ: 1) а > 1. Если q > 0, то прир > 0
х = (-1)* arcsin а*1’2 + nk, k — Z,
где 2 — отрицательные корни уравнения (3),
а прир < 0 уравнение (1) корней не имеет;
если q < 0, то при любом р
х = (-1)" arcsin а*1 + пп, п — Z,
где — отрицательный корень уравнения (3).
2) 0 < а < 1. Если q > 0, то прир < 0
х = (-1)* arcsin а*1’2 + nk, k — Z,
где 2 — положительные корни уравнения (3),
а прир > 0 уравнение (1) корней не имеет;
если q < 0, то при любом р
х = (-1)" arcsin а*2 + пп, п — Z,
где t2 — положительный корень уравнения (3).
381
с, 2пп
cos 2х = cos —— =
О
cos 4х = cos =
о
4. Определить, при каких значениях параметра а уравнение
a cos 2х + |а| cos 4х + cos 6х = 1 (1)
равносильно уравнению
sin х cos 2х = sin 2х cos Зх - 0,5 sin 5х. (2)
1. В уравнении (2) преобразуем произведения в разности синусов:
sin х - sin Зх = sin 5х - sin х - sin 5х,
• о 7Т YI
откуда sin Зх = 0, х = — .
о
2. Отсюда находим:
1 при п = 3k,
при п 3k',
1 при п = 3k,
при п 3k',
„ 6пП
cos 6х = cos —— = 1.
о
3. Подставив значения cos 2х, cos 4х и cos 6х в уравнение (1),
как при п = 3k, так и при п 3k получим соотношение а + |а| = 0,
из которого устанавливаем необходимое условие равносильности
данных уравнений: а < 0.
4. Проверим достаточность условия а < 0.
а) При этом условии уравнение (1) примет вид
a cos 2х - a cos 4х = 1 - cos 6х,
или
2а sin Зх sin х = 2 sin2 Зх. (3)
б) Уравнение (3) распадается на три уравнения:
• о А 7Т 7Z
sin Зх = 0, откуда х = — ,
о
sin х = 0, откуда х = nk,
а = 3 - 4 sin2 х. (4)
5. Для того чтобы уравнение (1) было равносильно уравнению (2),
необходимо, чтобы уравнение (4) не имело других решений, кроме
пп
х ~ Т
а) Если а > 1 или а < 0, откуда в силу условия а < 0 по-
лучаем а < -1, то уравнение (4) не имеет решений.
382
1 3
б) Если же левая часть уравнения (4) равна 0; ; 1, то реше-
ния этого уравнения входят в множество х = .
, тт 3 — ci г\ 3 — ci 1 3 — ci 3 3 — ci
в) Из соотношении —— = 0; —— = - ; —— = - ; —— = 1 нахо-
4 4 4 4 4 4
дим а = 3; а = 2; а = Оиа = -1 соответственно.
г) Учитывая условие а < 0, получаем а = 0 и а = -1.
6. Легко проверить, что условия а = 0 и а < -1 являются доста-
точными и уравнения (1) и (2) при этих условиях равносильны, а
их общее решение есть i = ^ , n -Z.
О
7. Ответ: а (-°°; -1] U {0}.
5. Для всех значений параметра а решить неравенство
1. Левая часть неравенства (1) неотрицательна на ОДЗ, поэто-
му а - 1 > 0, т. е. а > 1. Найдем ОДЗ данного неравенства. Имеем
Зх + а . м а ,
> 0, откуда получаем два промежутка: < х ч ; а <
х — а---------------------------------------------3
< X < +°°.
2. Возведя обе части неравенства (1) в квадрат, получим
< (а - I)2,
х - а
т. е.
х(2 + 2а - а2) + а(а2 - 2а + 2)
х - а
3. Это неравенство с учетом ОДЗ и условия а > 1 равносильно
совокупности двух систем:
а > 1,
о
х(2 + 2а - а2) + а(а2 - 2а + 2) > 0;
Г а > 1,
7 х > а,
х(2 + 2а - а2) + а(а2 - 2а + 2) < 0,
383
т. е. совокупности
а > 1,
(2)
О
х(а2 - 2а - 2) < а(а2 - 2а + 2);
Г а > 1,
7 х > а, (3)
[ х(а2 - 2а - 2) > а(а2 - 2а + 2).
3. Так как
а2 - 2а - 2 = (а - (1 + ТЗ ))(а - (1 - ТЗ )),
то а2 - 2а - 2 < 0 при 1 — л/3 < а < 1 + J3 ; а2 - 2а - 2 = 0 при аг =
= 1 + л/3,а2 = 1- л/3 и а2 - 2а - 2 > О при а > 1 + »/3 , а < 1 - л/З
4. При а = 1 + д/З система (3) не имеет решений, а системе (2)
— 1 — л/3
удовлетворяют все х из промежутка < х < —.
5. При 1 < а < 1 + д/З совокупность систем (2), (3) равносильна
соответственно совокупности систем
1 < а < 1 + ТЗ ,
а
х ч — - ,
5 3 <4)
а(а2 - 2а + 2) .
Х а2-2а-2 ’
1 <а< 1 + ТЗ,
< (5)
а(а2 - 2а + 2)
Х а2-2а-2
и справедливы неравенства
а(а2-2а + 2) < а а(а2-2а + 2) <
а2-2а-2 3 ’ а2-2а-2 а’
поэтому решениями системы (4) являются все х из промежутка
а(а2-2а + 2) „ а
—Ц,--------- < х ч -- , а система (5) решении не имеет.
а2 -2а-2 3
384
6. При а > 1 + д/З совокупность систем (2), (3) равносильна со-
ответственно совокупности систем
а > 1 + 73 >
- а
х ч — - ,
5 3 (6)
а(а2 - 2а + 2) .
Х а2-2а-2 ’
а > 1 + д/3 ,
х > а,
5 (7)
а(а2 - 2а + 2)
Х а2-2а-2
и справедливы неравенства
а(а2-2а + 2) > а а(а2-2а + 2) >
а2-2а-2 3 ’ а2-2а-2 а’
поэтому решениями системы (6) являются все х из промежутка
-оо < х < , а решениями системы (7) — все х из промежутка
О
а(а2-2а + 2) , , .
-Цг-------< х < +оо.
а2-2а-2
7. Ответ: если а < 1, то решений нет;
, , /о а(а2 - 2а + 2) „ а
если 1 < а < 1 + л/3 , то —Ц----- < х ч - - ;
а2-2а-2 3’
[— — 1 — а/З
если а = 1 + л/3 , то < х < -;
О
если а > 1 + д/З , то < х < - ,
О
а(а2-2а + 2) , , .
-Цг-------< х < +оо.
а2-2а-2
6. Определить, при каких значениях параметра а уравнение
2 sin7 х = (1 + sin 7ta)sin х + a sin3 х (1)
равносильно уравнению
(а - 1)(1 + cos2 х) + 2 sin6 х = 2 sin2 х + 2(а - I)3. (2)
385
1. Так как уравнение (1) имеет решение х = тт, при котором
sin х = 0, то для равносильности уравнений (1) и (2) необходимо,
чтобы значения х = тт удовлетворяли уравнению (2).
2. Подставляя значения х = тт в уравнение (2), получаем
2(а - 1) = 2(а - I)3, откуда = 1, а2 = 0, а3 = 2.
3. Проверим достаточность этих условий.
а) Пусть а = 1. Тогда уравнение (1) примет вид
2 sin7 х = sin х + sin3 х. (3)
Используя разложение на множители, получаем
sin х (sin2 х - 1)(2 sin4 х + 2 sin2 х + 1) = О,
откуда
sin х = 0, (4)
sin2 х = 1. (5)
Уравнение 2 sin4 х + 2 sin2 х + 1 = 0 не имеет решений, так как
дискриминант уравнения 2z2 + 2z + 1 = 0 (где z = sin2 х) отрицате-
лен. Объединяя решения х = лп и х = + nk уравнений (4) и (5),
пт
получаем х = — .
Уравнение (2) при а = 1 примет вид
2 sin6 х = 2 sin2 х, (6)
откуда sin х = 0 и sin2 х = 1, т. е. решение уравнения (6) также
имеет вид х = . Следовательно, при а = 1 уравнения (1) и (2)
равносильны.
б) Пусть а = 0. Тогда уравнение (1) примет вид 2 sin7 х = sin х,
откуда sin х = 0 и sin х =
Уравнение (2) при а = 0 имеет вид
-1 - cos2 х + 2 sin6 х = 2 sin2 х - 2, или 2 sin6 х = sin2 х,
— 4J|. °™но>
откуда sin х = 0 и sin х =
что при а = 0 множества
решений уравнений (1) и (2) не совпадают, т. е. эти уравнения не
равносильны.
в) Пусть а = 2. Тогда уравнение (1) примет вид
2 sin7 х = sin х + 2 sin3 х;
(7)
386
уравнение (7) распадается на два уравнения: sin х = 0, откуда
х = пп, и
2 sin6 х - 2 sin2 х = 1. (8)
Полагая z = sin2 х (0 < z < 1), рассмотрим функцию
/(z) = 2z3 - 2z = 2z(z + l)(z - 1).
Так как 0 < z < 1, то /(z) < 0 и, следовательно, уравнение /(z) =
= 1 не имеет решений при 0 < z < 1, т. е. не имеет решений и урав-
нение (8).
Множеством решений уравнения (7) являются значения х = пп.
Уравнение (2) при а = 2 имеет вид
1 + cos2 х + 2 sin6 х = 2 sin2 х + 2,
или
2 sin6 х = 3 sin2 х. (9)
Уравнение (9) распадается на два уравнения: sin х = 0, откуда
х = пп, и 2 sin4 х = 3, которое не имеет решений.
4. Итак, при а = 2 множества решений уравнений (1) и (2) сов-
падают (х = пп) и, следовательно, эти уравнения равносильны.
5. Ответ: а = 1 и а = 2.
7. Найти все значения а, при каждом из которых неравенство
л/9 - (х - а)2 > |х| (1)
имеет хотя бы одно положительное решение.
1. Рассмотрим функции ух(х) = ^9 - (х - а)2 и z/2(x) = М-
2. Неравенство (1) будет иметь хотя бы одно положительное ре-
шение, если z/x(x) > у2(х) при х > 0.
3. График функции ух(х) = ^9 - (х - а)2 есть полуокружность
с радиусом г = 3 и центром в точке С(а; 0), расположенная выше
оси Ох.
4. Действительно, уравнение ух(х) = »/9 - (х - а)2 равносильно
системе
| ух(х) > 0, [ ух(х) > 0,
z/x (х) — 9 — (х — а)2, (х - а)2 + ух (х) = 9. (2)
387
а < 0
а > 0
С(а; 0) О
С(а; 0)
Рис. 112
Уравнение (2) является уравнением
окружности с радиусом г = 3 и цент-
ром в точке С(а; 0). Условие у1(х) 0
соответствует части окружности, распо-
ложенной выше оси Ох.
5. График рассматриваемой функ-
ции при а < 0 и а > 0 изображен на
рис. 112.
6. Рассмотрим два возможных случая.
а) Пусть а > 0. Графики функций ух(х) и у2(х) имеют одну об-
щую точку А, если а = аг = Зл/2 (рис. 113, а). В этой точке выпол-
няется условие у^(х) = у2(х). Очевидно, что исходное неравенство
имеет положительные решения (выполняется условие у^(х) > у2(х)
при X > 0), если а-[0;372) (рис. 113, б).
б) Пусть а < 0. Графики функций ух(х) и у2(х) имеют одну об-
щую точку В, если а = а2 = -Зл/2 (рис. 114, а). В этой точке выпол-
няется условие z/x(x) = у2(х). Очевидно, что исходное неравенство
имеет отрицательные решения (выполняется условие z/x(x) > у2(х)
при х < 0), если а (-3^/2 ; -3) (рис. 114, б), и имеет положитель-
ные решения (выполняется условие ух(х) > у2(х) при х > 0), если
а (-3; 0) (рис. 114, в).
7. Объединяя полученные частные решения, делаем вывод:
неравенство (1) имеет хотя бы одно положительное решение, если
Яе(-3; Зл/2).
8. Ответ: а е (-3; 3^2).
388
8. В зависимости от значений параметра а решить неравенство
-2а<а2 + 1. (1)
х — 1
1. После упрощения неравенство (1) преобразуется к виду
ах2 - (а + 1)2х + (а + I)2 n
< °’
2. Пусть а 0; тогда корнями квадратного уравнения ах2 -
- (а + 1)2х + (а + I)2 = 0 являются х} = а + 1 и х2 = а + .
3. Таким образом, неравенство (2) можно переписать следую-
щим образом:
а(х - (а + 1))(х - а ) < 0. (3)
4. Ясно, что в зависимости от расположения корней будем по-
лучать разные решения.
I случай: 1 < —< а + 1 (рис. 115, а). Тогда
а + 1 . .ч г
— <а+1, (а+1)(а-1) >р
< т. е. < а
>1, \ а > 0,
а------------------I.
т. е. а > 1 (рис. 115, б).
389
1 а + 1
Я) 77777777+-------+//////+----
а + 1
а
Рис. 115
Возвращаясь к неравенству (3), заключаем, что если а > 1, то
х е (-оо; 1) и + 1 ; а + 1) (см. рис. 115, а).
II случай: < 1 < а + 1 (рис. 116). Тогда
Рис. 116 „
Этот случаи невозможен.
III случай: а + < а + 1 < 1 (рис. 117, а). Тогда
а+1 < а + j (а+ 1)(а- 1) > 0,
7 а т.е.л а
а + 1 < 1, I а < О,
т. е. -1 < а < 0 (рис. 117, б).
Возвращаясь к неравенству (3), находим, что если -1 < а < 0, то
х <= (^^11; а + 1) U (1 ; +оо) (см. рис. 117, а).
а)
— а+1 1
а
________^/////// >
х
Рис. 117
IV случай: 1 < а + 1 < а + (рис. 118, а). Тогда
Г1 < а + 1, f а > О
] а + 1 < а+ 1 , Т- е- ) (а - 1)(а+ 1) < о
а ’ а
т. е. О < а < 1 (рис. 118, б).
390
a
а) ///////Р
б)
О
а
а
О
Рис. 118
Возвращаясь к неравенству (3), получим, что если 0 < а < 1, то
(-оо; 1) и (а + 1; а + ) (см. рис. 118, а).
V случай: а + 1
1 < (рис. 119). Тогда
а + 1 < 1,
1 < а+ 1 т’
а ’
е.
а < О,
а > 0.
Этот случай невозможен.
VI случай: а + 1 < а + <
Рис. 119
1 (рис. 120, а). Тогда
. , ,а + 1
а + 1 < ---
а
а + 1 < 1
а ’
т. е.
(а+1)(а-1) < 0,
а
а < О,
а +1
а
т. е. а < -1 (рис. 120, б).
Возвращаясь к неравенству (3), находим, что если а < -1, то
xe^fl+1; Д + 1 ) U (1; +°о) (см. рис. 120, а).
VII случай: а + 1 = а + . Тогда
----------- а
а)
а2 - 1 = О,
а О,
т. е.
а = 1,
а = -1.
6)
Рис. 120
а
0
0
а
а
391
////////л
О 1
Рис. 121
Рис. 122
а) Если а=1,тоа+1 = а + = 2. Поэтому неравенство (3) вы-
полняется при X е (-ОО; 1) (рис. 121).
б) Если а = -1, то а + 1 = а + = 0. Поэтому неравенство (3)
выполняется при х е (1; +оо) (рис. 122).
VIII случай: а = 0. Тогда неравенство (1) примет вид х х < 1,
т. е. оно выполняется при х е (-оо; 1) и (1; +оо).
5. Ответ: если а ''-1.то.1"- (а + 1; а + ) и (1; +°°);
если а = -1, то.г'-(1; +°°);
если -1 < а < 0, то х е ( а + ; а + 1) U (1; +°°);
если а = 0,тох - (-°°; 1) U (1; +°°);
если 0ха''1,тох - (-о°; 1) U (а + 1; а +
если а = 1,тох- (-°°; 1);
если а ,'1,тох - (-о°; 1) U Г а + 1 • а + 1\
9. Исследовать и решить неравенство
(р-2)х2 + (р + 3)х+р + 6 0 ц)
«/4 - х2
1. Находим ОДЗ переменной х в данном неравенстве: 4 - х2 > 0,
т. е. х (-2; 2).
2. Пусть р 2; тогда!) = -Зр2 - 10р + 57.
3. Если D = 0, торх = , р2 = 3. Если D 0, то
О
r _ -Cp + 3)-Vd _ -(p + 3) + Vd
1 2(р-2) ’ 2 2(р-2)
— корни квадратного трехчлена
f(p) = (р ~ 2)х2 + (р + 3)х + р + 6. (2)
392
4. Рассмотрим возможные случаи расположения чисел хг, х2,
-2 и 2.
I случай: -2 < 2 < хг < х2 (рис. 123, а). Тогда из неравенства
2 < хг < х2 следует:
D>0,
-Д >2’
2а
af(2) > О
-Зр2 - 10р + 57 > О,
_ р + 3 > о
2(р-2)
(р - 2)[4(р - 2) + 2(р + 3) +р + 6] > О
19 „
-у <Р<3,
=* 5 5(Р- 1)
2(р-2) °’
(р - 2)(7р + 4) > 0.
Эта система не имеет решений (рис. 123, б).
19
3
-2 2 ж, х,
а) -----о----о-----о----о----►
►
12 Р
45-------
1 2 Р
7 Z
Рис.
123
II случай: -2
-2 < х1 < х2, х1 <
< х1 < 2 < х2 (рис. 124, а). Тогда от неравенств
2 < х2 переходим к системе
D>0,
_Ь_ >
/ 2а
af(-2) > О,
af(2) < О
-2,
-Зр2 - 10р + 57 > О,
- р + 3 -2,
< 2(р-2)
(р - 2)[4(р - 2) - 2(р + 3) +р + 6] > О,
(р - 2)[4(р - 2) + 2(р + 3) +р + 6] < О
<9
3
р
19 „
-у <Р<3,
Зр И >0
2(р-2)
(р - 2)(3р - 8) > О,
(р - 2)(7р + 4) < О,
393
-2 хг 2 х2
а) -----=----о-----о----о----.
19 о
т 3
<Э
о
р
Рис. 124
откуда <р < 2 (рис. 124, б). При этих значениях/, должны од-
новременно выполняться неравенства х} < х < х2 и -2 < х < 2, от-
куда хг < х < 2. Итак, еслир е ; 2 ), то х [хх; 2).
III случай: -2 < х1 < х2 < 2 (рис. 125, а). Так как (хх; х2) <= (-2; 2),
то получаем систему
D > О,
-2 < - А <
/ 2а
af(-2) > О,
af(2) > О
-Зр2 - Юр + 57 > О,
_ Р + 3 > _9
2(р-2)
_ Р + 3 о
2(р-2)
(р - 2)[4(р - 2) - 2(р + 3) +р + 6] > О,
(р - 2)[4(р - 2) + 2(р + 3) +р + 6] > О
Зр-И >0
htp-2)
I 5tP-i) >0
2(р-2)
(р - 2)(3р - 8) > 0,
(р - 2)(7р + 4) > 0,
(рис. 125, б). Таким образом, если р е
19 4
откуда -у < р < --
( 19 4. _ г т
СТ ’ -7 J’ Т0Х txl; Х^'
394
-2 х1 х2 2
а)
х1 -2 х2 2
х
19 о
р
19 о
р
1 2
Рис. 126
Рис. 125
IV случай: х1 < -2 < х2 < 2 (рис. 126, а). Тогда от неравенств
х1 < -2 < х2 и х1 < х2 < 2 переходим к системе
D > О,
-Д <2’
2а
af(-2) < О,
af(2) > О
„ ,8
откуда 2 < р < -
О
-Зр2 - 10р + 57 > О,
_ Р + 3 < 9
< 2(р-2)
(р - 2)[4(р - 2) -2(р + 3) + р + 6] < О,
(р - 2)[4(р - 2) + 2(р + 3) + р + 6] > О
5 (р-1) >п
2 (р-2)
(р - 2)(3р - 8) < О,
(р - 2)(7р + 4) > О,
(рис. 126, б). При этих значенияхр должны одно-
временно выполняться неравенства -2 < х < 2 и
х2< х <2. Значит, еслир е ( 2;
- j, то х е [х2; 2).
О
X < хг,
откуда
•А- •Л' С) у
395
a)
хг х2 -2 2
х
<9
19 о
“Т 3
_____^//////////////////////^___
1 3
-------------------------------►
......................*1.......р
//////////////////////////^ tf/////// »
р
Рис. 127
V случай: хг < х2 < -2 < 2 (рис. 127, а). Тогда от неравенства
; х2 < -2 перейдем к системе
D>0,
~тг < -2,
2а
af(-2) > 0
-Зр2 - 10р + 57 > 0,
_ Р + 3 < — 2
2(р-2)
(р - 2)[4(р - 2) - 2(р + 3) + р + 6] > 0
19 „
з <р<3’
11 < д
2(р-2)
(р - 2)(3р - 8) > О,
g
откуда - <р < 3 (рис. 127, б). При этих значениях/, неравенству (1)
О
могут удовлетворять только значения х, принадлежащие ОДЗ это-
го неравенства. Поэтому если^
| а > 0, IР ~ 2 > 0,
VI случай: < D < т. е. < _3^2 _ Юр + 57 < 0 ^рис’ 128>’ Если
р > 3, то неравенство f(p) > 0 верно при х е R, поэтому неравенство (1)
выполняется при х е (-2; 2).
f а < 0, [р ~ 2 < 0,
VII случай: < D < т. е. < _3^2 _ Юр + 57 < 0 ^рис’ 129>’ Если
т. е.
т. е.
р < , то неравенство f(p) < 0 справедливо при х е R, поэтому
О
неравенство (1) не имеет решений, так как л/4 - х2 > 0.
396
2 2
_____________________Д-/////////» //////////////////////////А,
р р
19 о 19 о
3 3 3 3
//zzzztf________________(у//////> zzzzzz^z_______________zzzzzzzz*
р р
Рис. 128 Рис. 129
-19 + 3
VIII случай:р = -. Тогда D = 0, хг = х2 = J7 + 3 = 3
( Р) 2(2 + ^)
-4-ОДЗ.
IX случай: р = 3. Тогда D = 0, хг = х2 = + 3 = -3 ОДЗ.
2(2 -р)
Значит, неравенство (1) выполняется при х е (-2; 2).
X случай: р = - ^ . Тогда неравенство f(p) 0 примет вид
- 2^)х2 + + 3^)х - + 6 > О, или 18х2 - 17х - 38 > О,
19 о
откуда находим корни х-. = и х2 = 2 соответствующего квад-
18
ратного уравнения. Поэтому неравенство (1) выполняется при
XI случай: р = 2. Тогда неравенство f(p) 0 примет вид 5х + 8 > О,
откуда с учетом ОДЗ заключаем, что х е [-1,6; 2).
g
XII случай: р = - . Тогда неравенство f(p) 0 примет вид
О
- 2^)х2 + + 3^)х + | + 6 > 0, или 2х2 + 17х + 26 > О,
откуда находим корни х} = -6,5 и х2 = -2 соответствующего квад-
ратного уравнения. Так как хг и х2 не принадлежат ОДЗ неравен-
ства (1), тох'- (-2; 2).
5. Ответ: еслир е (-00; j, то х 0;
19 1
если р = -— , то х = - - ;
О Э
397
19 4) _ r t
если p —,toxE[x1;x2];
V о (J
4 _ ( o 19 “I
если j? = -- , to x i-2; -— J ;
если/, c ^-^;2j,Toi - [xt; 2);
если/, = 2,тох - [-1,6; 2);
еслиp r- ( 2; | j, to x c_ [x2; 2);
если/, e [ |; +oo), toi - (-2; 2).
10. Определить все значения а, при каждом из которых неравенство
25у2 + jig > х - аху + у - 25х2 (1)
выполняется для любых пар (х; у) чисел таких, что |х| = |у|.
1. Пусть а — некоторое число, удовлетворяющее условию зада-
чи. Это значит, что если в неравенстве (1) заменить всюду у на х
или всюду у на -х, то полученное относительно х неравенство (1)
будет выполняться при любом х.
2. Итак, при любом х должны быть справедливы неравенства
(а + 50)х2 - 2х + -L >0, (2)
(50 - а)х2 + > 0. (3)
3. Неравенство (2) выполняется для всех х при условии — = 1 -
- (а + 50) < 0, т. е. | <0, откуда а > 50.
4. Неравенство (3) выполняется для всех х при условии 50 -
- а 0, т. е. а < 50.
5. Поэтому единственным числом, удовлетворяющим требова-
нию задачи, является а = 50.
6. При а = 50 исходное неравенство (1) примет вид
25у2 + —х ~ 50ху + у - 25х2,
398
или
(5х + 5у)2 - 2(5х + 5у) • > О,
ИЛИ
(бх + 5у- >0,
т. е. значение а = 50 есть решение задачи.
7. Ответ: а = 50.
11. Расположить в порядке возрастания числа 1; 4 и корни
уравнения
х2 - 2рх + 2р2 - 4р + 3 = 0.
1. Пусть х1 и х2 (х1 < х2) — корни данного уравнения. Решение
задачи сводится к исследованию следующих шести случаев:
1) х1 < х2 < 1; 2) х1 < 1 < х2 < 4; 3) х1 < 1, х2 > 4;
4) 1 < х1 < х2 < 4; 5) 1 < х1 < 4 < х2, 6) 4 < х1 < х2.
2. Для квадратного трехчлена f(x) = ах2 + Ъх + с эти случаи опи-
сываются соответственно условиями:
D > 0,
-А < 1,
2а
af(l) > 0;
(1)
«/(1) < 0,
«/(4) > 0;
(2)
«/(1) < 0,
«/(4) < 0;
(3)
«/(1) > 0,
«/(4) > 0;
(4)
«/(1) > 0,
«/(4) < 0;
D > 0,
-- >4,
2а
af(4) > 0.
(6)
D > 0,
3. Условия (1) в данном случае имеют вид
[ _4(р2 _ 4р + 3) > о,
/р< 1,
[ 2(р2 - Зр + 2) > 0,
откуда следует, что р е 0.
4. К тому же результату мы придем и при рассмотрении усло-
вий (3), (5) и (6).
399
5. Условия (2) запишутся так:
2(р2 - Зр + 2) < О,
2р2 - 12р + 19 > О,
откуда находим, что/, [1;2].
6. Наконец, условия (4) приводят к системе
-4(р2 - 4р + 3) > О,
1 <р < 4,
2(р2 - Зр + 2) > О,
2р2 - 12р + 19 > О,
откуда находим, что р‘-(2; 3].
7. Ответ: еслир е (-оо; 1] U (3; +°°), то решений нет;
если р = 1, ТО 1 = Х1 = Х2 - < 4;
если р (1; 2), то х1 < 1 < :х2 < ; 4;
если р = 2, то х1 = 1 <Х2< < 4;
если р (2; 3), то 1 • < Х1 < :х2 < ; 4;
если р = 3, то 1 < х1 = Х2 - < 4.
1 2. При каких значениях параметра а число решений уравнения
Зх2 + (9а2 - 2)х + За2 - 1 = О (1)
не превосходит числа решений уравнения
Зх3 + х + (За - 2)2 • 3* = (8а - 4) log3 (за - |(2)
1. Задача имеет смысл при условии 3“ > |.
2. Рассмотрим сначала уравнение (2). При любом фиксирован-
ном значении параметра а правая часть этого уравнения (с учетом
ОДЗ) является постоянной.
3. Левая часть уравнения (2) есть строго возрастающая функ-
ция, поскольку ее производная положительна:
9х2 + 1 + (За - 2)2 • 3* • In 3 > 0.
4. Так как множеством значений указанной функции является
интервал (-°°; +°°), то уравнение (2) при любом допустимом значе-
нии параметра а имеет единственное решение.
400
5. Согласно требованию задачи, уравнение (1) должно иметь не
более одного решения. Это будет выполнено при условии, когда
дискриминант уравнения (1) неположителен, т. е. когда
D = (9а2 - 2)2 - 12(3а2 - 1) = (9а2 - 4)2 < 0.
6. Отсюда находим, что ах = , а2 = |. Однако значение ах =
О о
2 Г) о
--не подходит, так как 3 J
о
1 < 1
V9 2‘
2
7. Ответ: а = - .
О
13. Функция f(x) = ——----- определена на отрезке [5; 7]. При
хл-4х + а
каких значениях параметра а наибольшее на этом отрезке значе-
ние функции /(х) не превосходит ?
1. Функция /(х) определена на отрезке [5; 7] тогда и только тог-
да, когда квадратный трехчлен <р(х) = х2 - 4х + а не имеет корней
на этом отрезке.
2. Графиком квадратного трехчлена <р(х) при каждом фиксиро-
ванном а является парабола, вершина которой имеет абсциссу х = 2.
3. Указанный трехчлен <р(х) не будет иметь корней на отрезке
[5; 7], если выполняется неравенство <р(5) • <р(7) > 0, т. е.
(5 + а)(21 + а) > 0.
Решив это неравенство, находим
-оо<а<-21, -5 < а < +°°. (1)
4. Так как функция <р(х) на отрезке [5; 7] строго возрастает, то
функция /(х) на этом же отрезке строго убывает.
5. Поэтому требование задачи будет выполнено, если справед-
ливо неравенство /(5) < , т. е. —— < . Решив это неравенство,
10 5 + а 10
находим
-оо<а<-5, 5<а<+°о. (2)
6. Учитывая неравенства (1) и (2), получаем ответ.
7. Ответ: а (-°°; -21) U [5; +°°).
401
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти все значения параметров а и Ь, при которых корни х1
и х2уравнения:
а) х2 - (а2 + За+1)х + 2а + & + 3 = 0 удовлетворяют системе
[ 3х1 - 2х2 = 5,
| 2хх + х2 = 8;
б) х2 + (2а - 7)х + Ъ2 - 8Ь + За + 18 = 0 удовлетворяют системе
[ 4хх - х2 = 5,
"1 2хх + Зх2 = 13.
2. Найти все значения параметра а, при которых совместна сис-
тема уравнений:
1 + 2 cos х = 4а - 21 + , 31 + л/*+1 = 5а-2 tg2 у,
аК г б) < г
2-2^ = За - 4 cos х; 4 tg2 у + 2 = За + 3^
(в ответе указать наименьшее из этих значений);
2 + cos х = 4а - 6 • 2vz, j 3х + *2 - 2 = 4а - sin2 у,
в) J г\ J v
| 10 - 23 + у2 = а - 5 cos х; | —6 — 4 sin2 у = 5а - З2 + *2
(в ответе указать наибольшее из этих значений).
3. При каких значениях параметра а система уравнений
j 6 • 2xZ + 2 = 4а - sin у,
| 5 sin у + 10 = а + 23 + *2
несовместна?
4. При каких значениях параметра т имеет хотя бы одно реше-
ние система:
Г х2 - 2тх + т2 - 1 = 0, J х2 - 2(т + 2) + т2 + 4m + 3 = 0,
аЦ|х + 1|<2; бЦ|х-2|<1?
5. Найти значение k, при котором касательная к указанной
кривой у в точке с заданной абсциссой х(1 является одновременно
и касательной к заданной параболе ф(х), если:
а) у = Зх2 + 5х + 4, <р(х) = 5х2 - 7х + k, х0 = 0;
б) у = 3 + 2х - х3, <р(х) = х2 - 6х + k, х0 = -2.
402
6. При каких значениях параметра а корни уравнения
(а2 + 1)х2 - 2ах = 3
удовлетворяют неравенствам 0 < х} < 1, |х2| < хх(1 - х2)?
, 5 х + 2 . -0,5
7. В области определения функции у=\аа-ах + 2 1 взяли
все целые положительные числа и сложили их. Найти все значе-
ния а, при которых такая сумма будет больше 5, но меньше 10.
8. При каких значениях параметра а график функции f(x) =
= х4 + 2axs - 2х2 - бах имеет вертикальную ось симметрии?
9. При каких значениях параметра а уравнение ах2 + Зх +
+ 2а2 -3 = 0 имеет только целочисленные корни?
10. В зависимости от значений параметра а решить неравенст-
во а - х > |1 - |х||.
11. Исследовать и решить неравенство:
х 2 - ах - х2 , „
б) (а2 + а - 2)х2 + (2а2 + а + 3)х + а2 - 1 > 0;
в) 3(а + 1)х2 - 6(а2 + а + 1)х + 7(а3 - 1) < 0.
12. Решить уравнение |2х + а| + |х - 2а| = 20.
13. При каких значениях параметра а имеет единственное ре-
шение система уравнений:
аху + х - у + 1,5 = 0,
х + 2у + ху + 1 = 0;
ах2 + 2ах + у + За - 3 = 0,
ау2 + х - бау + 11а + 1 = 0?
14. Найти все значения параметра а, при каждом из которых
неравенство:
а) 5 - (х - а)2 > |х| имеет хотя бы одно положительное решение;
б) 3 - х2 > |х - а| имеет хотя бы одно отрицательное решение;
в) sin х > \х - а\ имеет хотя бы одно решение на интервале ; л);
а)
б)
г) \х - а\ < 716 - х2 имеет хотя бы одно отрицательное решение.
15. При каких значениях а сумма loga (1 + cos2 х) + loga (5 + cos2 х)
будет равна 1 хотя бы для одного значения х?
3 _|_ 2х% 5 + 4х2
16. При каких значениях а сумма loga-----g- + loga-----g- бу-
дет больше 1 для всех значений х?
403
17. Найти наибольшее значение параметра а, при котором урав-
нение х3 + 5х2 + ах + Ъ = 0 с целыми коэффициентами имеет три
различных корня, причем один из них равен (-2).
18. Установить, при каких значениях параметра а для всех до-
пустимых значений х выполняется неравенство:
a) (sin xyg(sinx)-a2 > 10log1oo(1~oos2*) + log7a ;
б) (COSx)IOg'i(<:OSA' > 31ой'<, (1 siT2 ) I «(« 2)
19. Найти все значения параметра а, при которых:
а) функция у = 5л]бх2 - Зах + 1 - а имеет минимум в точке
х0= _2,5;
б) функция у = 6х2 + (а + 3)х + 5 - а имеет максимум в точ-
1
ке х0 = - .
и 6
20. Указать все значения параметра а, при которых уравнение
loga х + log^ а\а + loga х\ = a log* а
имеет решения, и найти соответствующие решения.
Ответы
1. a) щ = -4, Ь1 = 11; а2 = 1, b2 = 1; б) а1 = 1, Ь1 = 3; а2 = 1, Ь2 = 5. 2. а) 1;
б) 0,5; в) 3; г) 1. 3. a G (-оо; 2) U (3; +оо). 4. а) т G [-4; 2]; б) т G [-2; 2].
5. a) k = 11,2; б) k = 17. 6. a G (-1,5; 1 - л/З ) U (1 + ^3 ; +°о). 7. a G ( ) .
8. а - {-2; 0; 2}. 9. а - {-0,5; 0; 1,5}. 10. Если а < -1, то.г'-й; если -1 <
< а < 1, то х < 0,5(а - 1); если а > 1, то х < 0,5(а + 1). 11. а) Если а < -1, то
, 3 — d — f\/D 3 — d л/D тл / н\! I 1 \ 1 1
х <--- , х >------ , где D = (а - 7)(а + 1); если а = -1, то -ос < х < - ,
о о 2
| < х < Н-оо; если -1 < а < 1, то х £ й; если а = 7, то -оо < х < -i , -i <
, , . „ -г , 3 - а - JT) 3 a I Jd „ ,
< х < +°о; если а > 7, то х < ——— , х > ——-— ; б) если а < -2, то х <
О о
, 1 - а all л . 1 л , , 1 а + 1 ,
< ---т- , х > --; если а = -2, то х > - - ; если -2 < а < - - , то -- < х <
а + 2 1-а 3 5 1-а
, 1 - а 1 _ 1 , , d 1-а,, а + 1
< ---- ; если а = -- , то х fc 0; если -- < а < 1, то -- < х < ------; если
а + 2 5 5 а + 2 1-а
1 п 1 , а + 1 , 1 - а , ,5
а = 1, то х > 0; если а > 1, то х < --, х > -- ; в) если а < -- , то.г-К;
1-а а + 2 ' 4
404
5 ^ ,21 21 .
если а = -- , то < х < -— , -— < х < +°о; если -- < а < -1, то х <
4 4 4 4
< 3(а2з(^++11))+лУ^ , х > 3(а2 ’ где D = 3(а2 + а + !)(4а + 5)(2 “ а>'’
. 7 , , , ~~ 1 „ 3(а2 + а + 1) - JD , ,
если а = -1, то -- < х < +°о; если -1 < а < 2, то —ь——------4—-— < х <
3 3(а + 1)
< ’ если а-г2,то.г:-2. 12. Если а G (-оо; -8) U (8; +°°), то
х 0; если а = -8 или а = 8, то х = 4; если а Е (-8; -4), то х = -За - 20,
а + 20 г г л л . а + 20 а - 20 гл о.
х = —з— ; если а G [-4; 4), то х = —-— , х = —-— ; если а G [4; 8), то х =
= -За + 20,х = . 13. а)а -{0,5( 7-4^2 );-0,5; 1};б)а -{0; ±0,25^2 }.
14. а) а - (-^5 ; 5,25); б) а - (-3,25; 3); в) а е (| - 1; л); г) а - (-4^2 ; 4).
15. а [5; 12]. 16. а (1; 8]. 17. 7. 18. а) а е (0; 1]; б) а е (0; 2). 19. а) а =
= -10; б) а = -1. 20. Если 0 < а < 1, то уравнение имеет два корня: Xj =
= a^i “ 1 и х2 = a1 + За ; при остальных значениях а корней нет.
СПИСОК ОБОЗНАЧЕНИЙ
N — множество натуральных чисел
Z — множество целых чисел
ZQ — множество целых неотрицательных чисел
Q — множество рациональных чисел
R — множество действительных чисел
R+ — множество действительных неотрицательных чисел
[а; Ь] — замкнутый промежуток (отрезок) с началом а и концом Ъ
а < Ъ
(а; Ь) — открытый промежуток (интервал)
(а; Ь], [а; Ь) — полуинтервалы
(а; +°°), [а; +°°), (-°°; Ь), (-°°; Ь] — бесконечные промежутки
(-оо; +оо) — числовая прямая
=> — знак следования
<=> — знак равносильности (эквивалентности)
е — знак принадлежности
<= — знак включения
U — знак объединения множеств
А — знак пересечения множеств
0 — пустое множество
f(x) — функция
f(x0) — значение функции в точке х0
D(f) — область определения функции f
E(f) — множество значений функции f
ОДЗ — область допустимых значений
|х| — модуль (абсолютная величина) числа х
{х} — число х есть элемент множества
{ — знак системы
[ — знак совокупности
(хп) — числовая последовательность
4- — арифметическая прогрессия
406
-н- — геометрическая прогрессия
Ах, Ау — приращение аргумента, приращение функции
f'(x) — производная функции f(x)
l/min — минимум функции
Утах — максимум функции
min f(x) — наименьшее значение функции на отрезке [а; Ь]
[а; Ъ]
max f(x) — наибольшее значение функции на отрезке [а; Ь]
[а; Ь]
loga Ъ — логарифм числа Ъ по основанию а
1g & — десятичный логарифм
In & — натуральный логарифм
е — основание натуральных логарифмов (е ~ 2,7)
ь
j f(x) dx — интеграл от а до & функции /(х)
а
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Александров Б. И., Моденов П. С. Пособие по математике для
подготовительных курсов МГУ. М., 1967.
2. Александров Б. И., Лурье М. В., Максимов В. М. Пособие для
подготовки к письменному экзамену по математике в МГУ. М., 1972.
3. Александров Б. И., Лурье М. В., Максимов В. М. Экзаменацион-
ные задачи по математике. М., 1969.
4. Александров Б. И., Максимов В. М., Лурье М. В., Колесничен-
ко А. В. Пособие по математике для поступающих в вузы. М.,1972.
5. Амелькин В. В., Рабцевич В. Л. Задачи с параметрами. Мн.,
1996.
6. Андреянов П. А. , Гладких И. М., Сагитов Р. Ф. Варианты зада-
ний по математике на вступительных экзаменах в РЭА им. Г. В. Пле-
ханова в 1999—2004. М., 2005.
7. Анисимова Н. Т. Математика (справочник для абитуриентов
МБП). М., 2002.
8. Бабайцев В. А., Васенкова Е. К. и др. Под ред. Бабайцева В. А. и
Рылова А. А. Методическое пособие по математике для поступающих
в Финансовую академию. М., 2003.
9. Вавилов В. В., Мельников И. И., Олехник С. Н., Пасиченко П. И.
Задачи по математике. Уравнения и неравенства. М., 1987.
10. Баховский Е. Б., Рывкин А. А. Задачи по элементарной матема-
тике. М., 2004.
11. Высоцкий И. Р., Звавич Л. И., Пигарев Б. П. и др. Под ред.
Шестакова С. А. Алгебра и начала анализа. Сборник задач для подго-
товки и проведения итоговой аттестации за курс средней школы. М.,
2005.
12. Говоров В. М., Дыбов П. Т., Мирошин Н. В., Смирнова С. Ф.
Сборник конкурсных задач по математике. М., 2006.
13. Денищева Л. О. и др. Под ред. Ковалевой Г. С. Единый государ-
ственный экзамен. М., 2002.
14. Денищева Л. О., Глазков Ю. А., Краснявская К. А., Рязанов-
ский А. Р., Семенов П. В. Единый государственный экзамен по матема-
тике. М., 2004.
15. Дорофеев Г. В., Потапов М. К., Розов Н. X. Пособие по мате-
матике для поступающих в вузы. М., 1976.
408
16. Дыбов П. Т., Забоев А. И., Калиниченко Д. Ф. Сборник задач по
математике. М., 1972.
17. Дыбов П. Т., Осколков В. А. Задачи по математике для посту-
пающих в вузы (с указаниями и решениями). М., 2006.
18. Камалова Р. А., Паршев Л. П., Струков Ю. А. Типовые задания
конкурсных экзаменов по математике. М., 1996.
19. Крамор В. С. Повторяем и систематизируем школьный курс ал-
гебры и начал анализа. М., 2005.
20. Крамор В. С. Примеры с параметрами и их решения. М., 2001.
21. Крамор В. С., Лунгу К. Н. Повторяем и систематизируем
школьный курс тригонометрии. М., 2001.
22. Крамор В. С., Лунгу К. Н., Лунгу А. К. Математика. Типовые
варианты. Примеры на вступительных экзаменах. М., 2000.
23. Кутасов А. Д., Пиголкина Т. С., Чехлов В. И., Яковлева Т. X.
Под ред. Яковлева Г. Н. Пособие по математике для поступающих в ву-
зы. М., 2002.
24. Кущенко В. С. Сборник конкурсных задач по математике с ре-
шениями. Л., 1968.
25. Лидский В. Б., Овсянников Л. В., Тулайков А. Н., Шабунин М. И.
Задачи по элементарной математике. М., 1969.
26. Литвиненко В. Н., Мордкович А. Г. Задачник-практикум по
математике. М., 2005.
27. Локоть В. В. Задачи с параметрами. М., 2003.
28. Ляпин С. Е., Баранова И. В., Борчугова 3. Г. Сборник задач по
элементарной алгебре. М., 1973.
29. Максимов В. М. Пособие по математике для поступающих в МГУ.
М., 1972.
30. Моденов В. П. Математика. Пособие для поступающих в вузы.
М., 2002.
31. Мордкович А. Г. Алгебра и начала анализа. М., 2002.
32. Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи всту-
пительных экзаменов по математике. М., 1980.
33. Солодовников А. С., Родина М. А. Задачник-практикум по ал-
гебре. М., 1985.
34. Шахмейстер А. X. Уравнения и неравенства с параметрами.
СПб., М., 2004.
35. Ястребинецкий Г. А. Уравнения и неравенства, содержащие
параметры. М., 1972.
СОДЕРЖАНИЕ
Предисловие............................................. 3
Тема 1.................................................. 6
Справочный материал.................................. 6
1. Натуральные числа............................. 6
2. Простые и составные числа..................... 6
3. Обыкновенные дроби. Правильные и неправильные
дроби............................................. 7
4. Множество целых чисел, множество рациональных
чисел............................................. 7
5. Модуль числа.................................. 7
6. Возведение рациональных чисел в степень
с натуральным показателем....................... 8
7. Свойства степени с натуральным показателем... 8
8. Числовые выражения. Выражения с переменными.
Тождественно равные выражения..................... 9
9. Одночлены. Многочлены......................... 9
10. Формулы сокращенного умножения................ 9
Задачи с решениями.................................. 10
Задачи для самостоятельного решения................. 12
Ответы........................................... 12
Тема 2................................................. 13
Справочный материал................................. 13
1. Дробь........................................ 13
2. Целые и дробные выражения.................... 13
3. Понятие об иррациональном числе.............. 14
4. Числовые промежутки.......................... 14
5. Корень /г-й степени из действительного числа. 14
6. Преобразования арифметических корней......... 15
7. Степень с целым и дробным показателем........ 16
410
Задачи с решениями................................. 16
Задачи для самостоятельного решения................ 19
Ответы........................................... 20
Тема 3................................................ 21
Справочный материал................................ 21
1. Уравнения с одной переменной................ 21
2. Понятие о равносильности уравнений.......... 21
3. Свойства числовых равенств и теоремы
о равносильности уравнений..................... 22
4. Линейное уравнение с одной переменной, содержащее
параметр....................................... 22
Задачи с решениями................................. 23
Задачи для самостоятельного решения................ 32
Ответы........................................... 33
Тема 4................................................ 34
Справочный материал................................ 34
1. Понятие функции............................. 34
2. Монотонность функции........................ 34
3. Четные и нечетные функции................... 35
4. Линейная функция и ее график................ 36
5. Квадратичная функция и ее график............ 36
k
6. Функция у = - и ее график................... 37
X
Задачи с решениями................................. 38
Задачи для самостоятельного решения................ 40
Ответы........................................... 41
Тема 5................................................ 42
Справочный материал................................ 42
1. Квадратные уравнения........................ 42
2. Теорема Виета............................... 43
3. Уравнения с несколькими переменными......... 43
4. Системы уравнений........................... 43
Задачи с решениями................................. 45
Задачи для самостоятельного решения................ 77
Ответы........................................... 79
411
Тема 6................................................ 81
Справочный материал................................ 81
1. Неравенства................................. 81
2. Основные свойства неравенств................ 81
3. Действия с неравенствами.................... 82
4. Решение линейных и квадратных неравенств.... 83
Задачи с решениями................................. 84
Задачи для самостоятельного решения................. 113
Ответы........................................... 114
Тема 7................................................. 115
Справочный материал................................. 115
1. Системы и совокупности неравенств............ 115
2. Решение рациональных неравенств методом
промежутков...................................... 116
Задачи с решениями.................................. 117
Задачи для самостоятельного решения................. 144
Ответы........................................... 146
Тема 8................................................. 147
Справочный материал................................. 147
1. Применение теоремы Виета к определению знаков
корней квадратного трехчлена.................. 147
2. Расположение корней квадратного трехчлена.. 148
Задачи с решениями.................................. 152
Задачи для самостоятельного решения................. 167
Ответы........................................... 168
Тема 9................................................. 169
Справочный материал................................. 169
1. Числовая последовательность................ 169
2. Арифметическая прогрессия.................. 169
3. Геометрическая прогрессия.................. 170
4. Сумма бесконечной геометрической прогрессии
при |</| < 1................................... 171
Задачи с решениями................................ 172
Задачи для самостоятельного решения............... 174
Ответы......................................... 175
412
Тема 10............................................... 176
Справочный материал................................ 176
1. Градусное и радианное измерение угловых величин . . 176
2. Тригонометрические функции числового аргумента . . 177
3. Основные тригонометрические тождества....... 179
4. Формулы приведения.......................... 179
5. Формулы сложения............................ 180
6. Формулы двойного аргумента.................. 181
7. Преобразование произведения тригонометрических
функций в сумму................................ 181
8. Формулы суммы и разности одноименных
тригонометрических функций..................... 182
9. Тригонометрические функции половинного
аргумента...................................... 182
10. Выражение тригонометрических функций через
тангенс половинного аргумента................... 183
Тема 11............................................... 184
Справочный материал................................ 184
1. Функция у = sin х........................... 184
2. Функция у = cos х........................... 185
3. Функция у = tg х............................ 186
4. Функция у = ctg х........................... 186
5. Нахождение периодов тригонометрических функций. 187
6. Обратная функция............................ 187
7. Функция у = arcsin х........................ 189
8. Функция у = arccos х........................ 190
9. Функция у = arctg х......................... 191
10. Функция у = arcctg х........................ 192
11. Некоторые соотношения для обратных
тригонометрических функций...................... 193
Тема 12............................................... 195
Справочный материал................................ 195
1. Решение тригонометрических уравнений вида
sin х = а...................................... 195
2. Решение тригонометрических уравнений вида
cos х = а...................................... 195
3. Решение тригонометрических уравнений вида
tg х = а....................................... 196
4. Решение однородных тригонометрических
уравнений...................................... 196
5. Решение систем тригонометрических уравнений .... 197
413
Задачи с решениями................................. 198
Задачи для самостоятельного решения................ 225
Ответы.......................................... 226
Тема 13............................................... 227
Справочный материал................................ 227
1. Решение тригонометрических неравенств вида
sin х > a, sin х < а............................ 227
2. Решение тригонометрических неравенств вида
cos х > a, cos х < а............................ 228
3. Решение тригонометрических неравенств вида
tg х > a, tg х < а.............................. 228
Задачи с решениями................................. 229
Задачи для самостоятельного решения................ 240
Ответы.......................................... 240
Тема 14............................................... 242
Справочный материал................................ 242
1. Приращение аргумента и приращение функции... 242
2. Определение производной..................... 243
3. Производная суммы, произведения, частного... 244
4. Производная степенной и сложной функции..... 245
5. Производные тригонометрических функций...... 245
6. Применение производной к нахождению
промежутков монотонности функции............... 246
7. Критические точки функции, ее максимумы
и минимумы..................................... 247
8. Общая схема исследования функции............ 249
9. Задачи на отыскание наименьшего и наибольшего
значений функции............................... 249
10. Касательная к графику функции............... 250
Задачи с решениями................................. 250
Задачи для самостоятельного решения................ 270
Ответы.......................................... 271
Тема 15............................................... 272
Справочный материал................................ 272
1. Потерянные и посторонние корни при решении
уравнений...................................... 272
2. Решение иррациональных уравнений, посторонние
корни иррационального уравнения................ 273
3. Иррациональные неравенства.................. 274
414
Задачи с решениями................................ 275
Задачи для самостоятельного решения............... 297
Ответы......................................... 298
Тема 16.............................................. 299
Справочный материал............................... 299
1. Показательная функция и ее свойства........ 299
2. Показательные уравнения.................... 300
3. Показательные неравенства.................. 300
4. Системы показательных уравнений и неравенств .... 300
Задачи с решениями................................ 300
Задачи для самостоятельного решения............... 316
Ответы......................................... 317
Тема 17.............................................. 318
Справочный материал............................... 318
1. Понятие логарифма.......................... 318
2. Свойства логарифмов........................ 318
3. Логарифмическая функция, ее свойства и график . . . 319
4. Теоремы о логарифме произведения, частного
и степени. Формула перехода к новому основанию . . . 320
5. Логарифмирование и потенцирование.......... 321
6. Логарифмические уравнения.................. 321
7. Логарифмические неравенства................ 322
8. Производные логарифмической и показательной
функций. Число е.............................. 322
Задачи с решениями................................ 323
Задачи для самостоятельного решения............... 350
Ответы......................................... 352
Тема 18.............................................. 353
Справочный материал............................... 353
1. Понятие первообразной функции.............. 353
2. Основное свойство первообразной функции.... 354
3. Криволинейная трапеция и ее площадь........ 355
4. Формула Ньютона—Лейбница................... 355
5. Основные правила интегрирования............ 356
6. Вычисление площадей с помощью интеграла.... 356
Задачи с решениями................................ 358
Задачи для самостоятельного решения............... 366
Ответы......................................... 367
415
Приложение 1
Текстовые задачи на составление уравнений и неравенств
с параметрами....................................... 368
Задачи с решениями............................... 368
Задачи для самостоятельного решения.............. 375
Ответы......................................... 376
Приложение 2
Разные задачи....................................... 378
Задачи с решениями............................... 378
Задачи для самостоятельного решения.............. 402
Ответы......................................... 404
Список обозначений.................................. 406
Использованная литература........................... 408