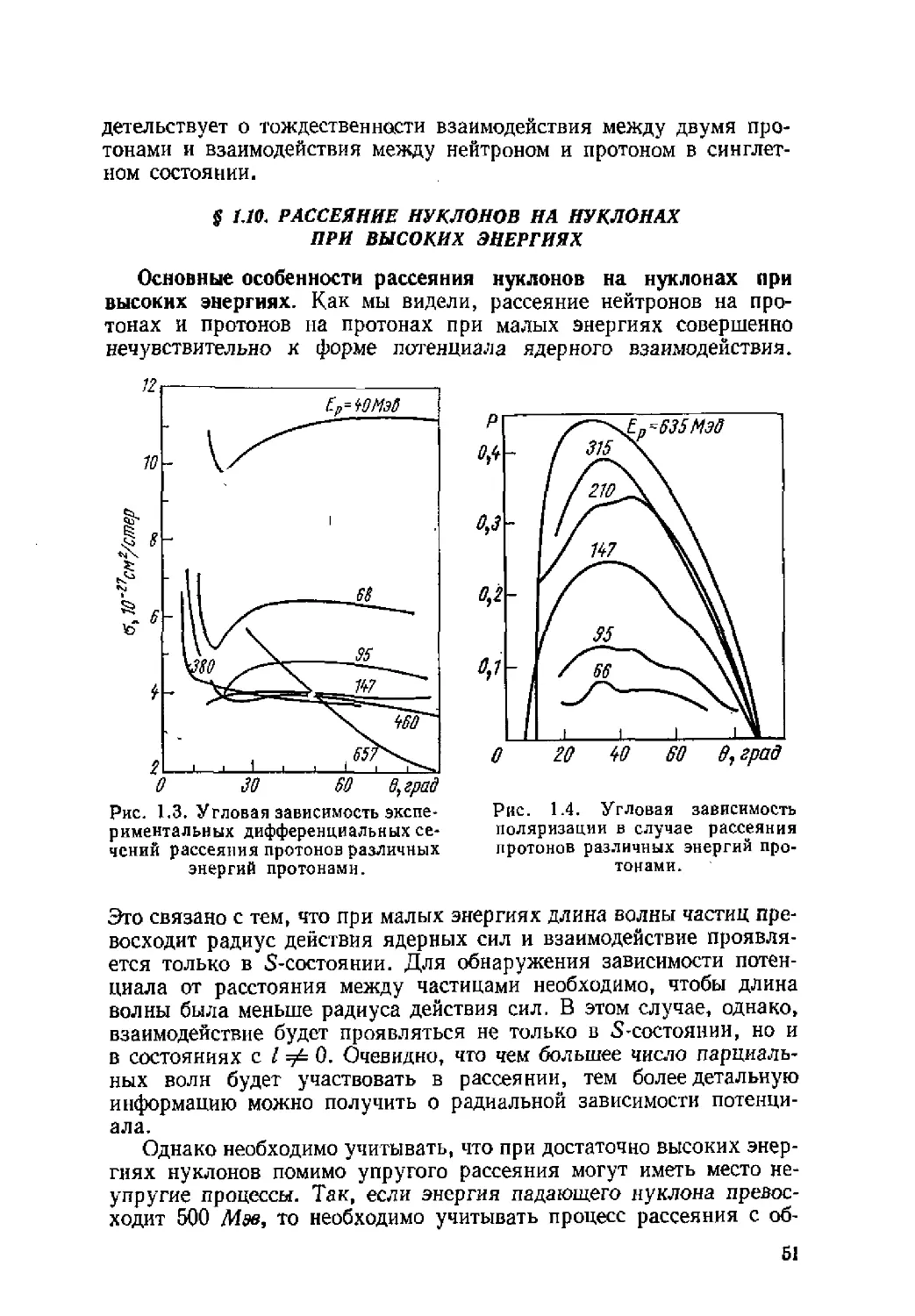
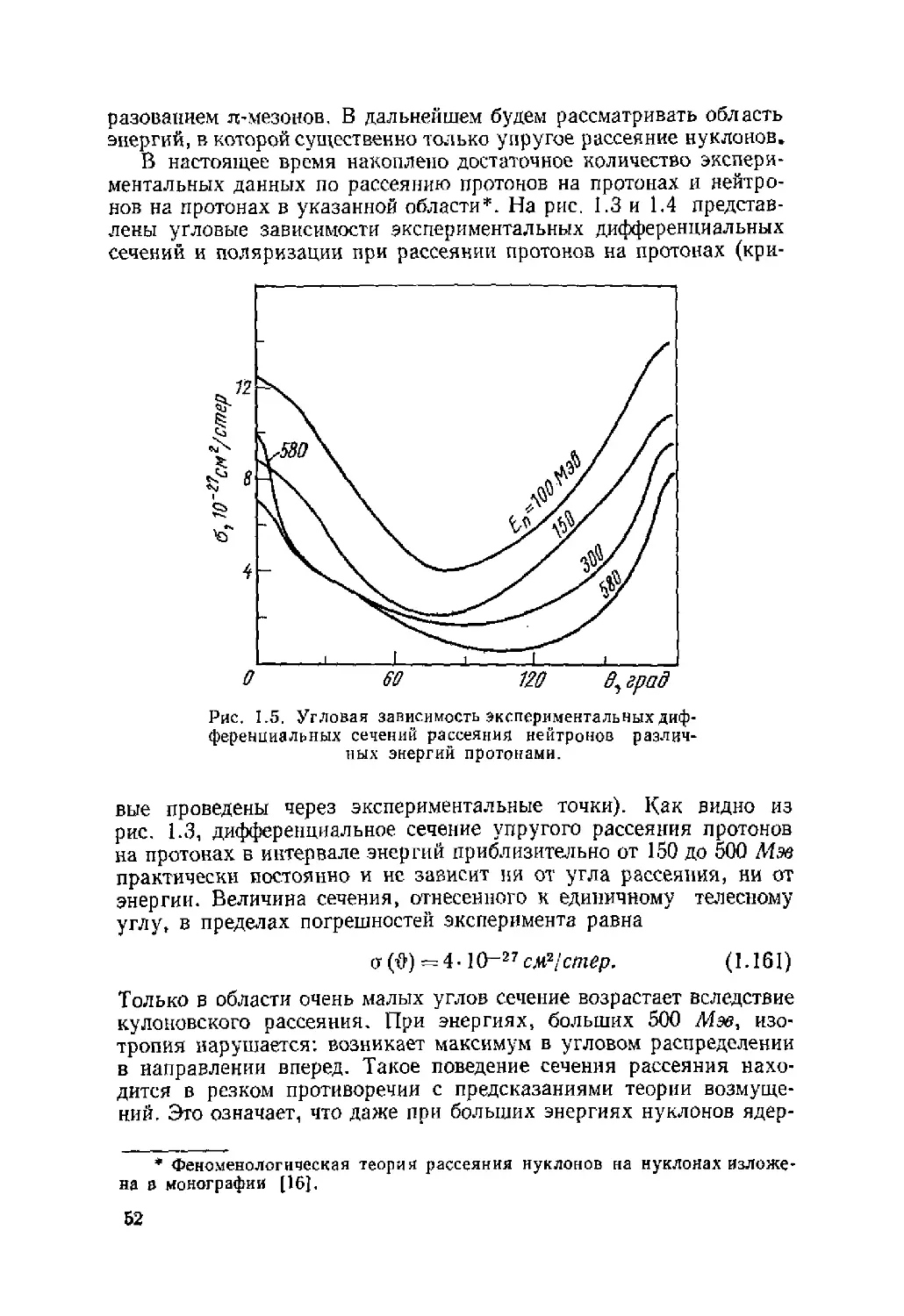
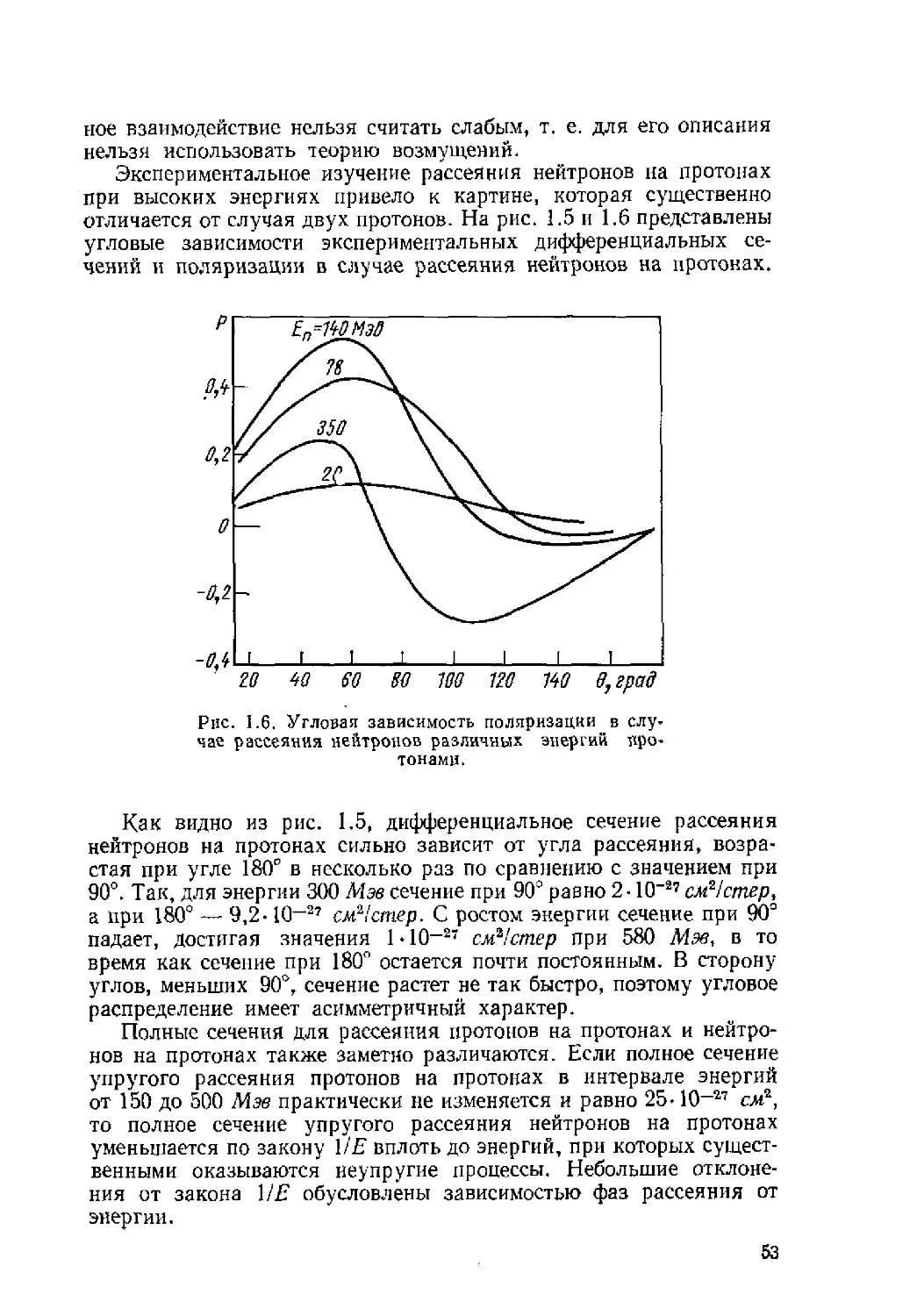
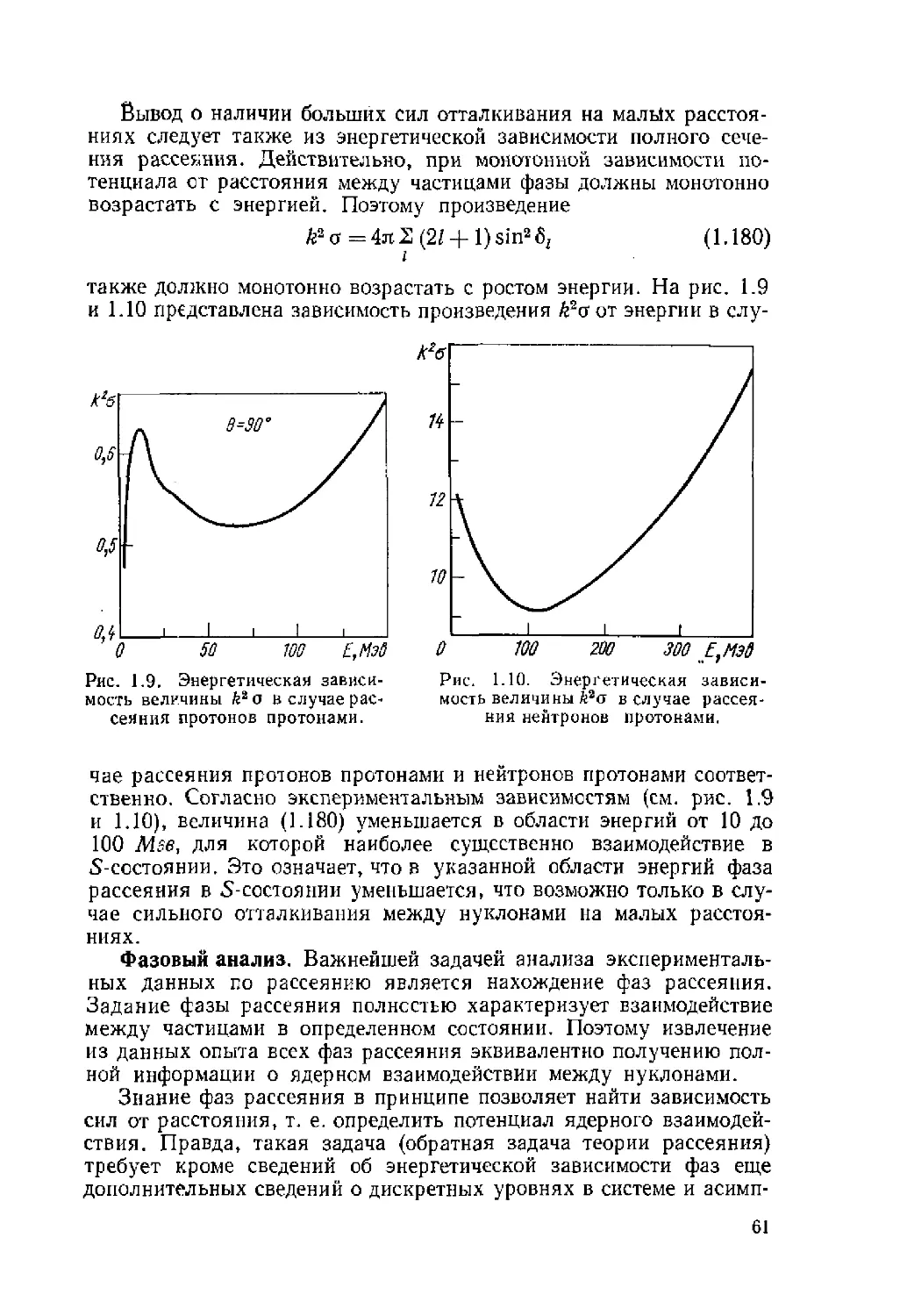
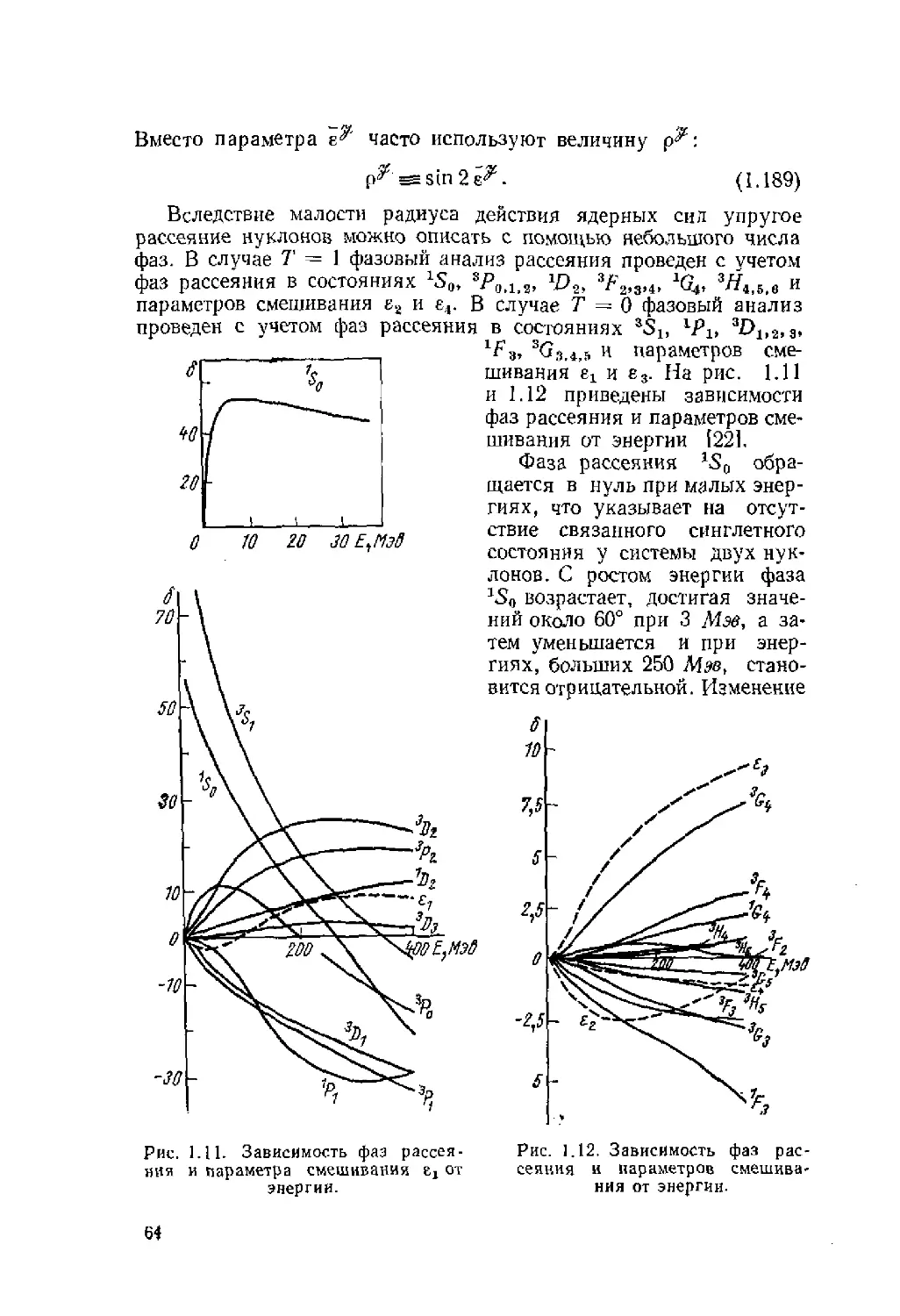
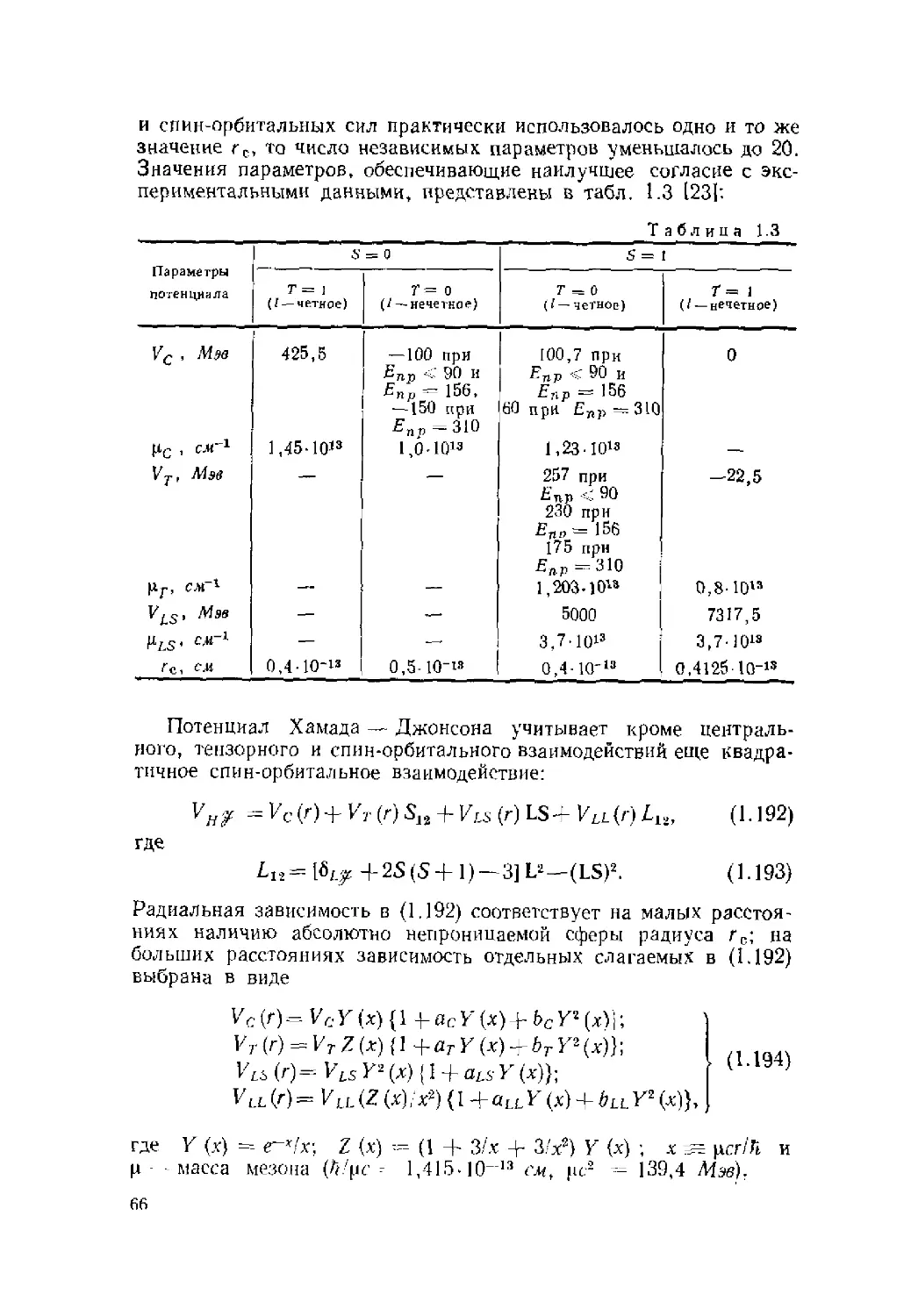
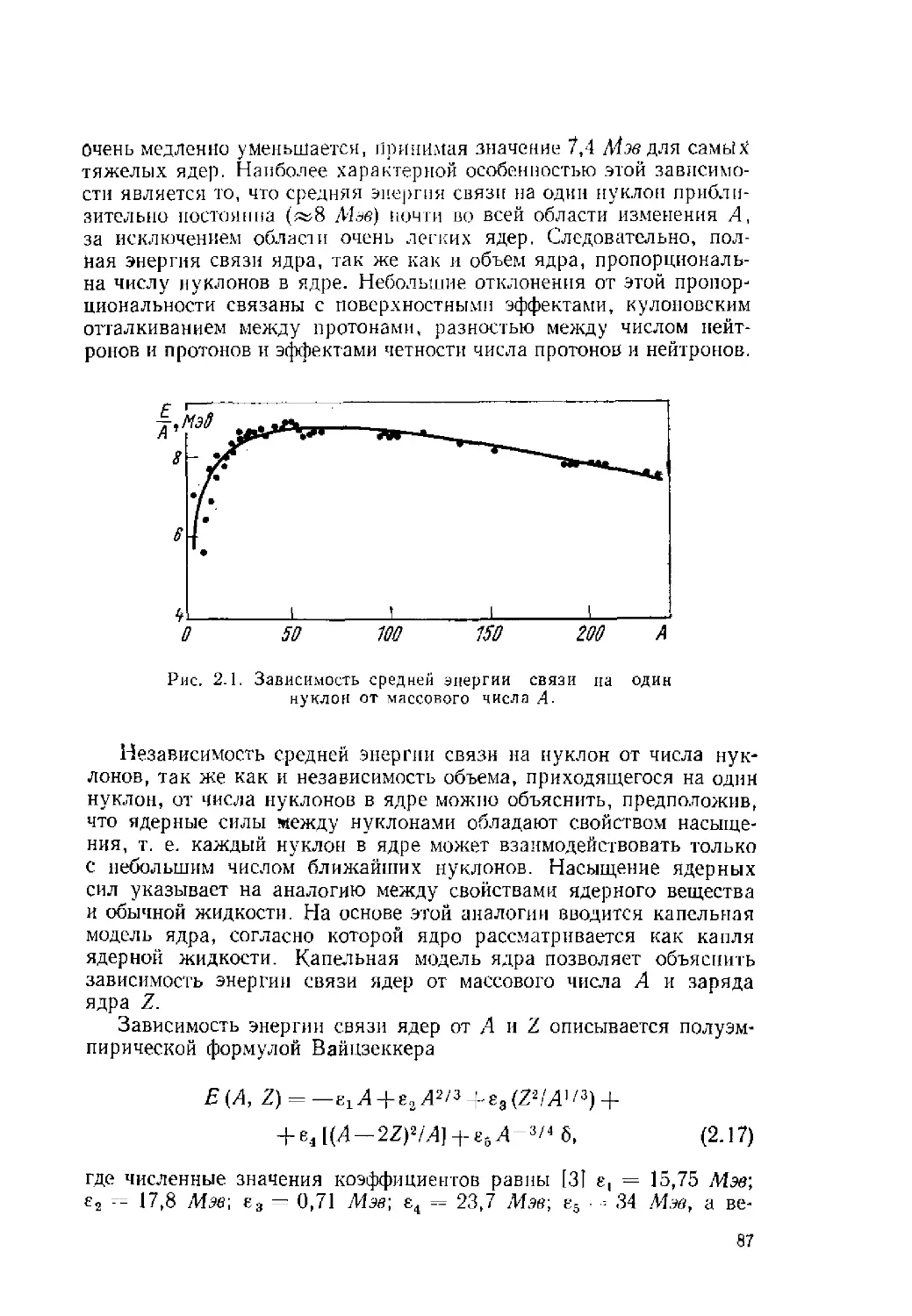
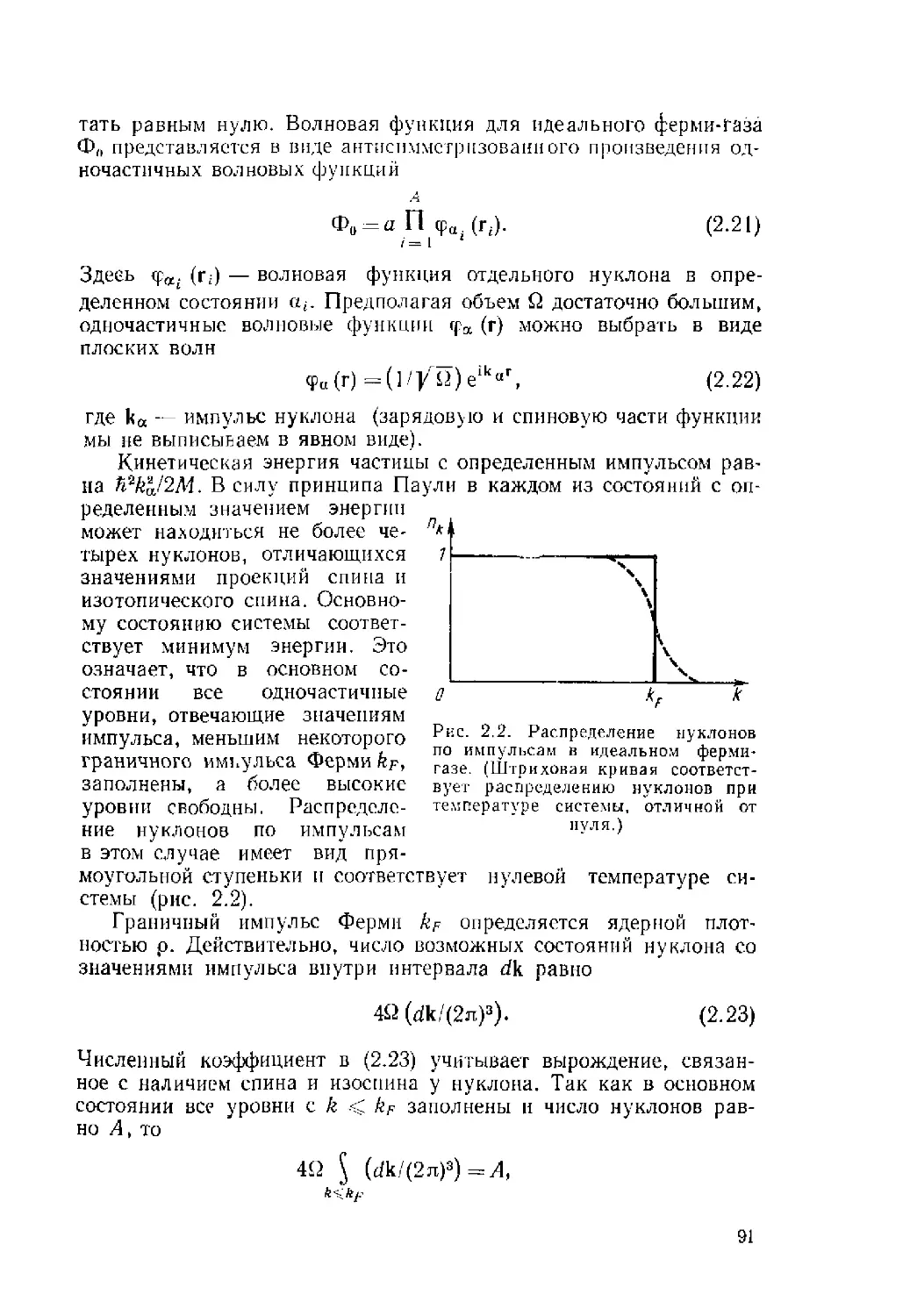
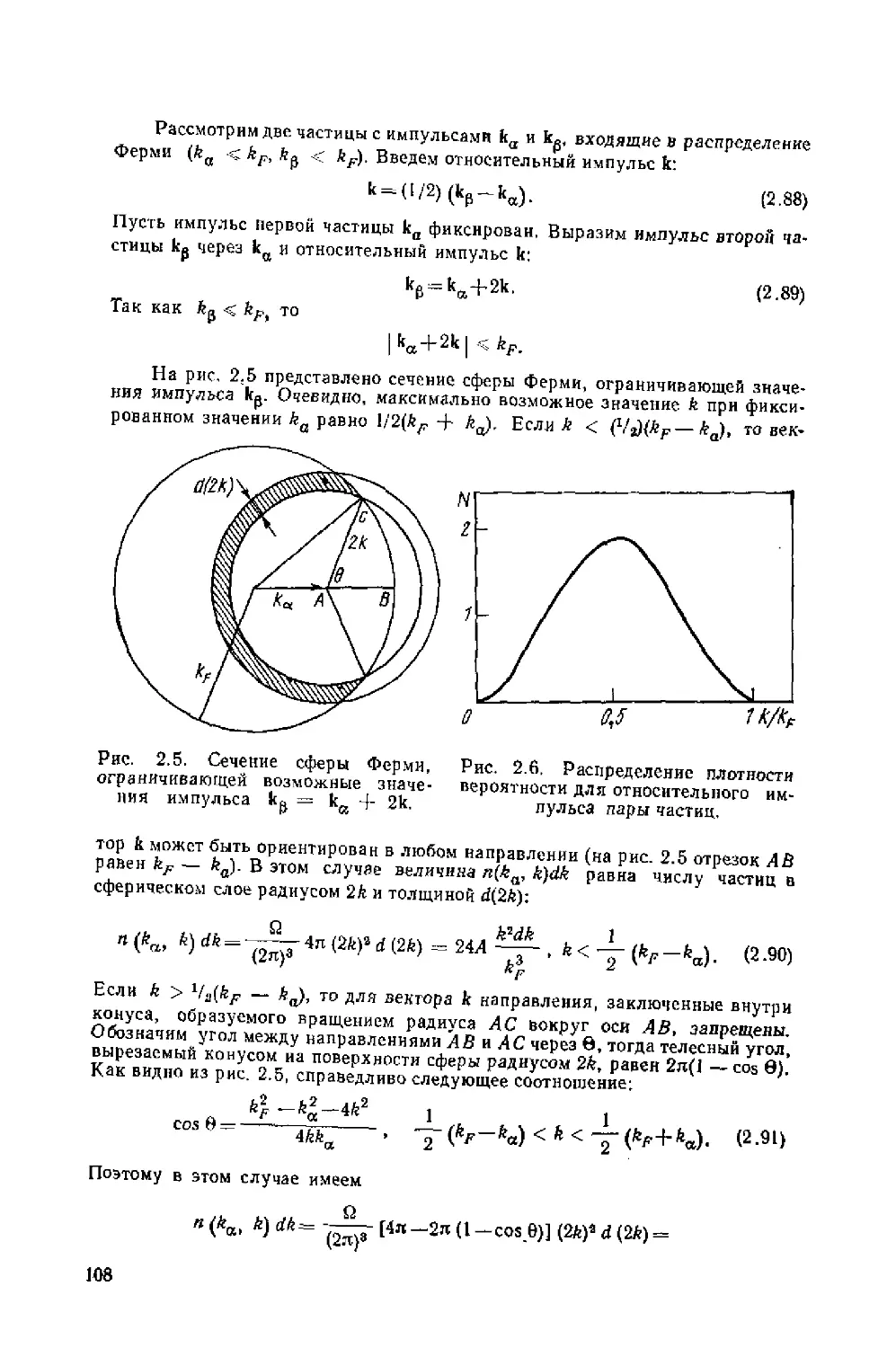
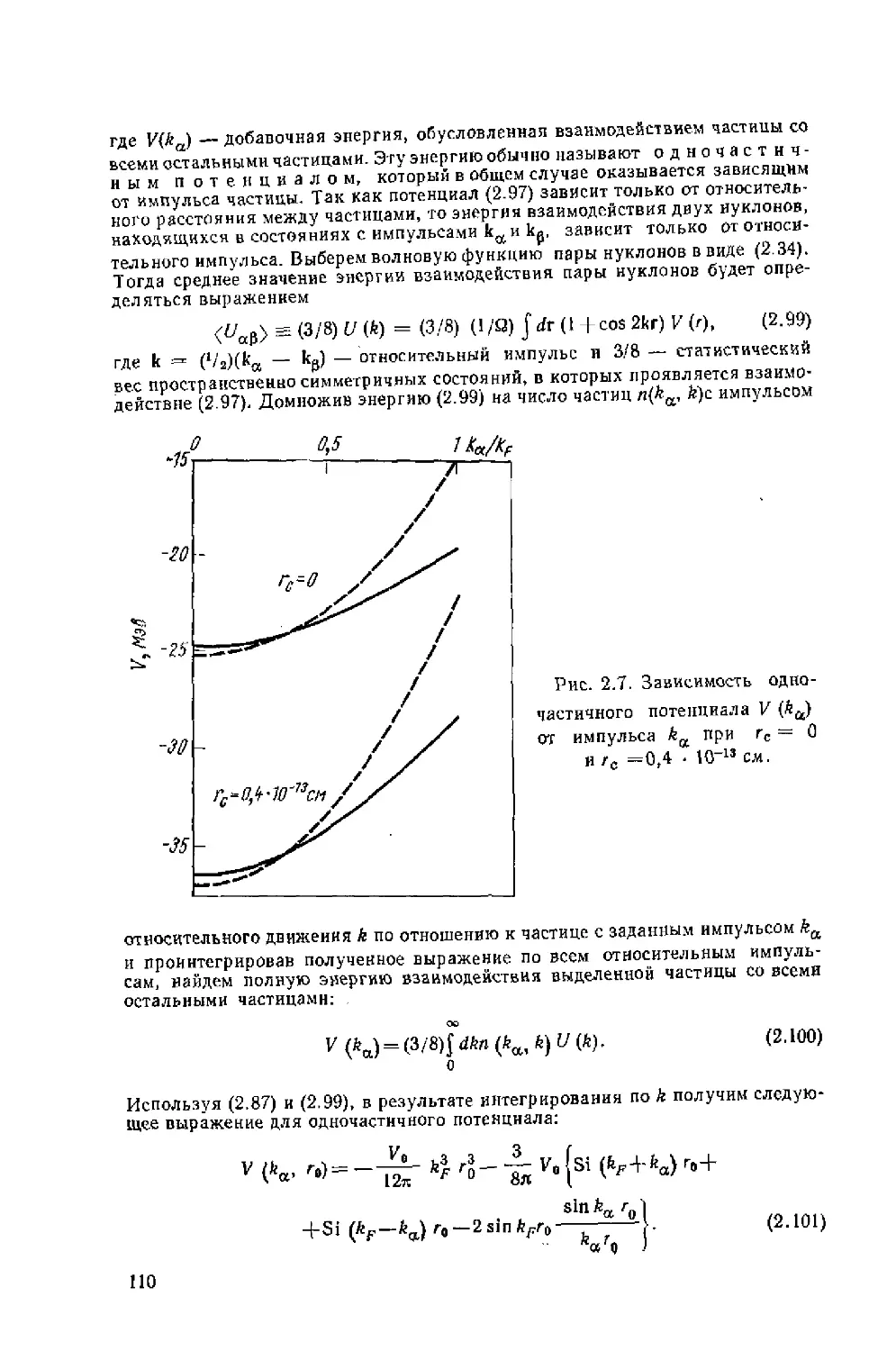
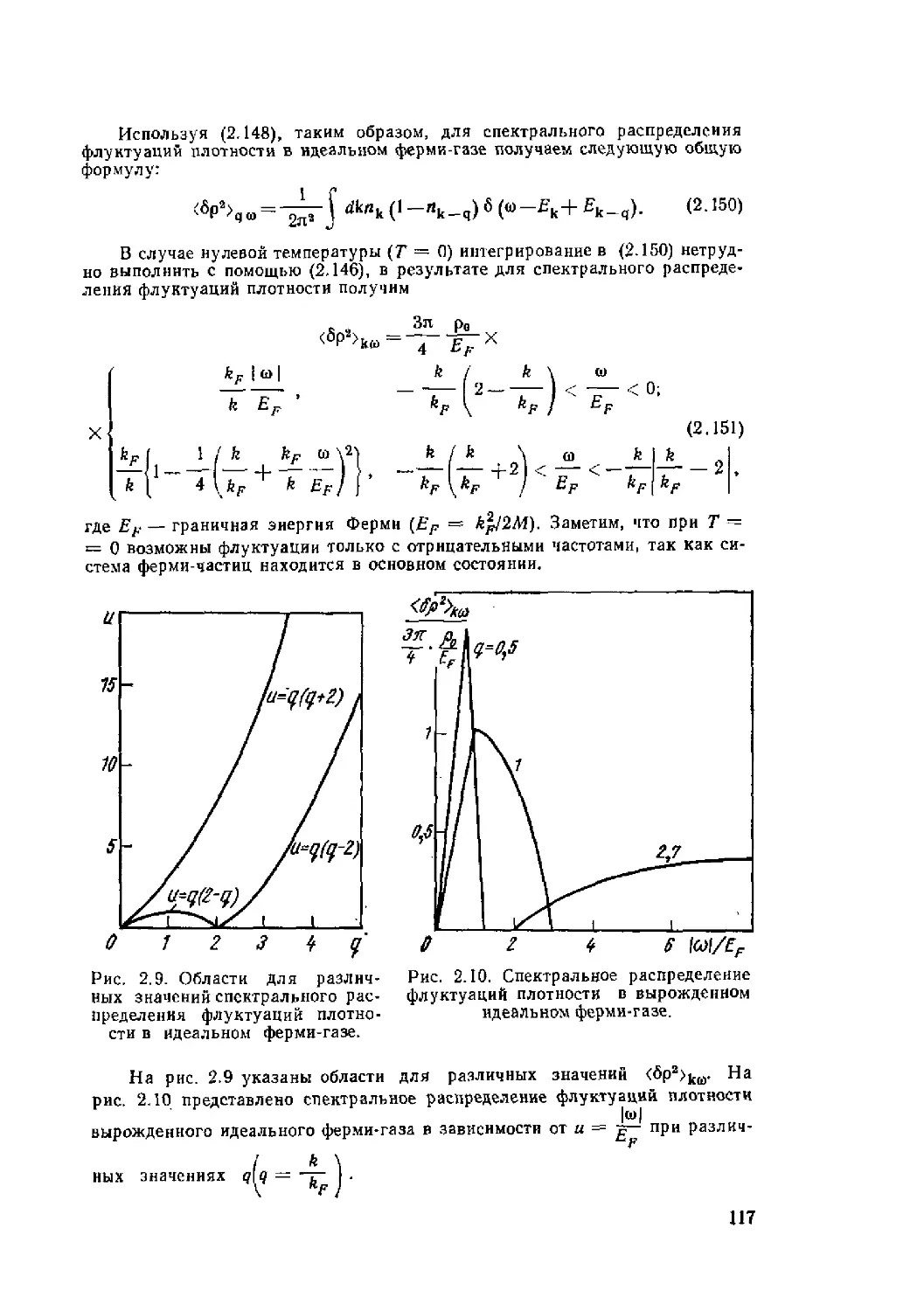
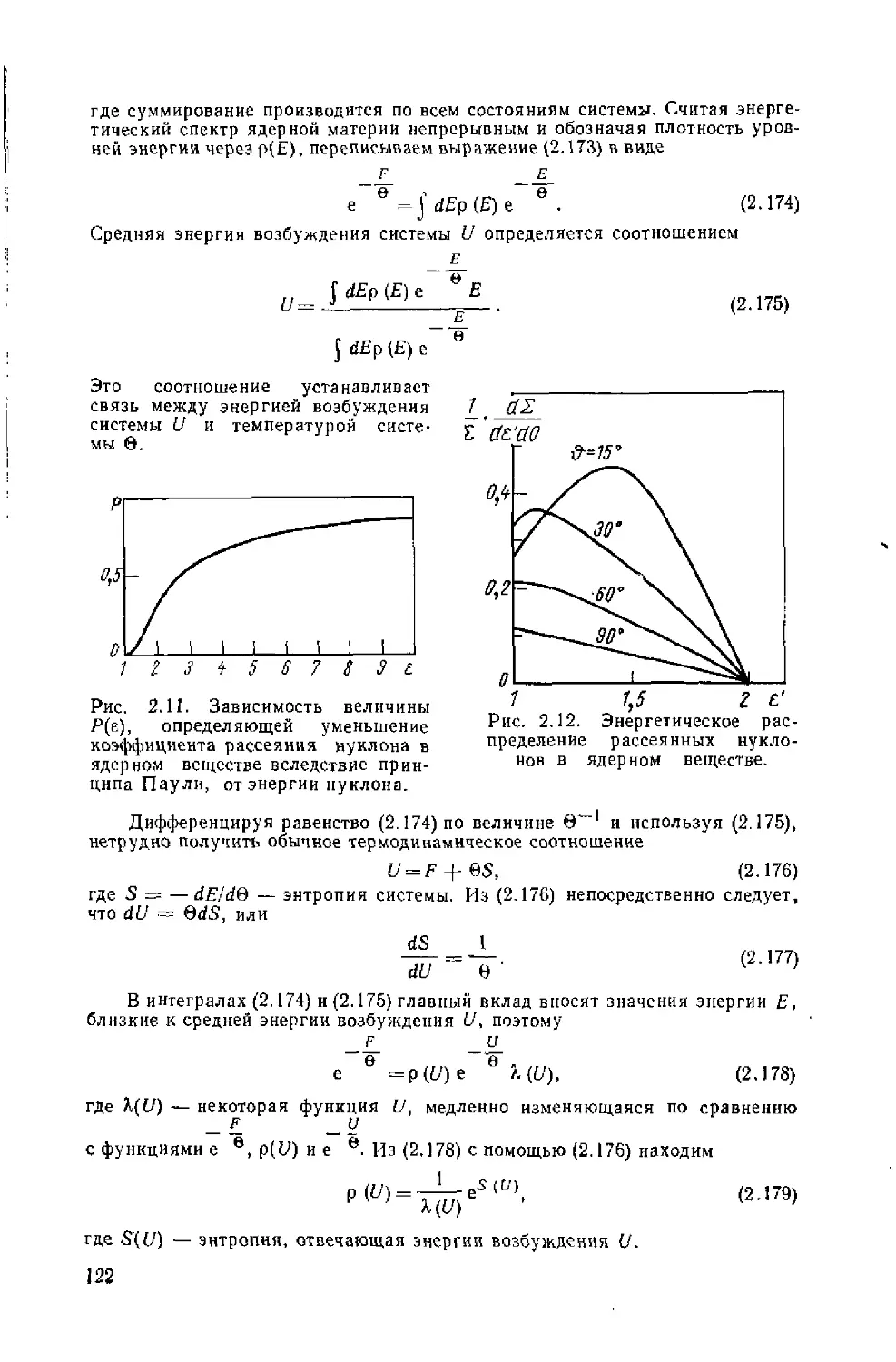
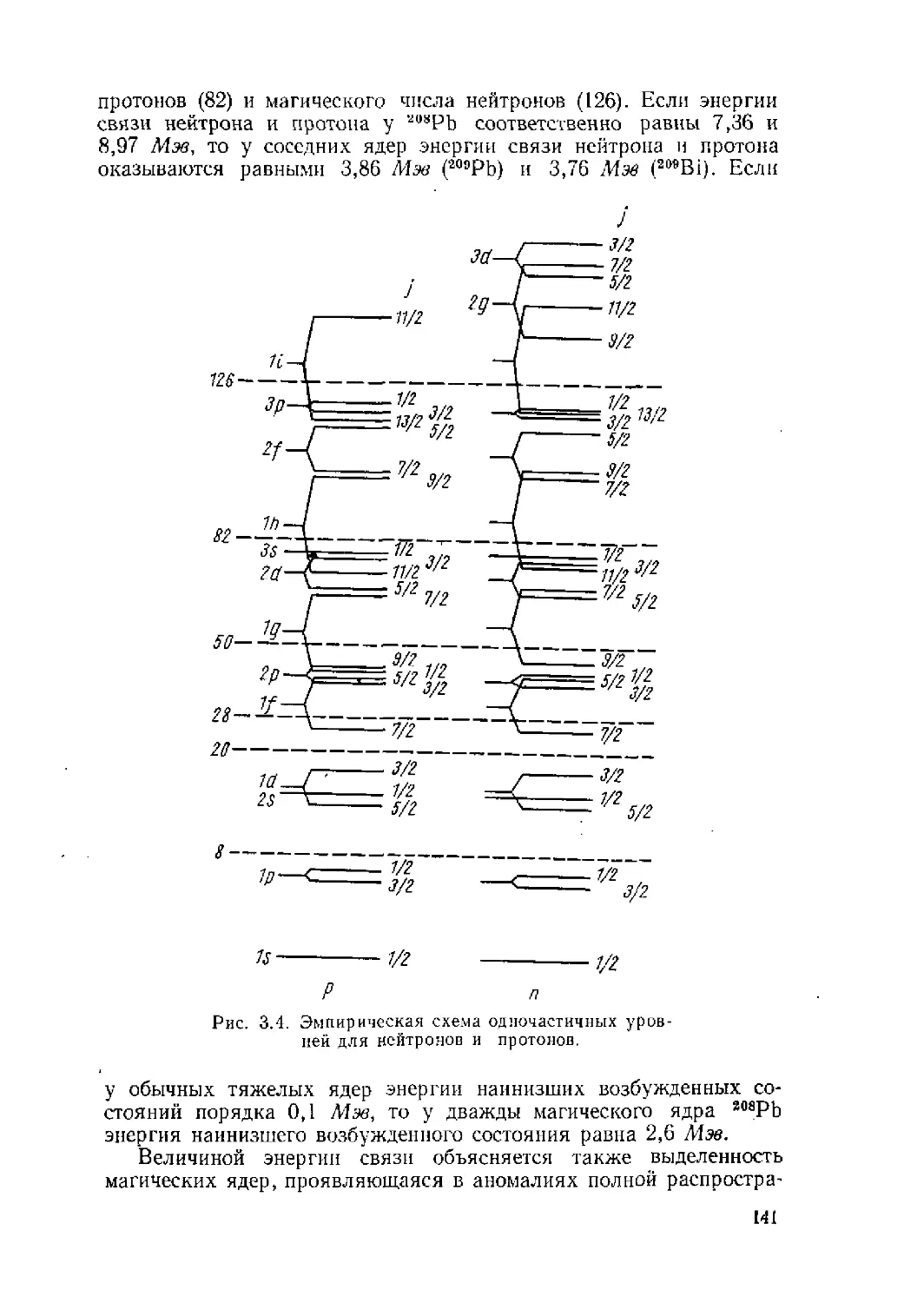
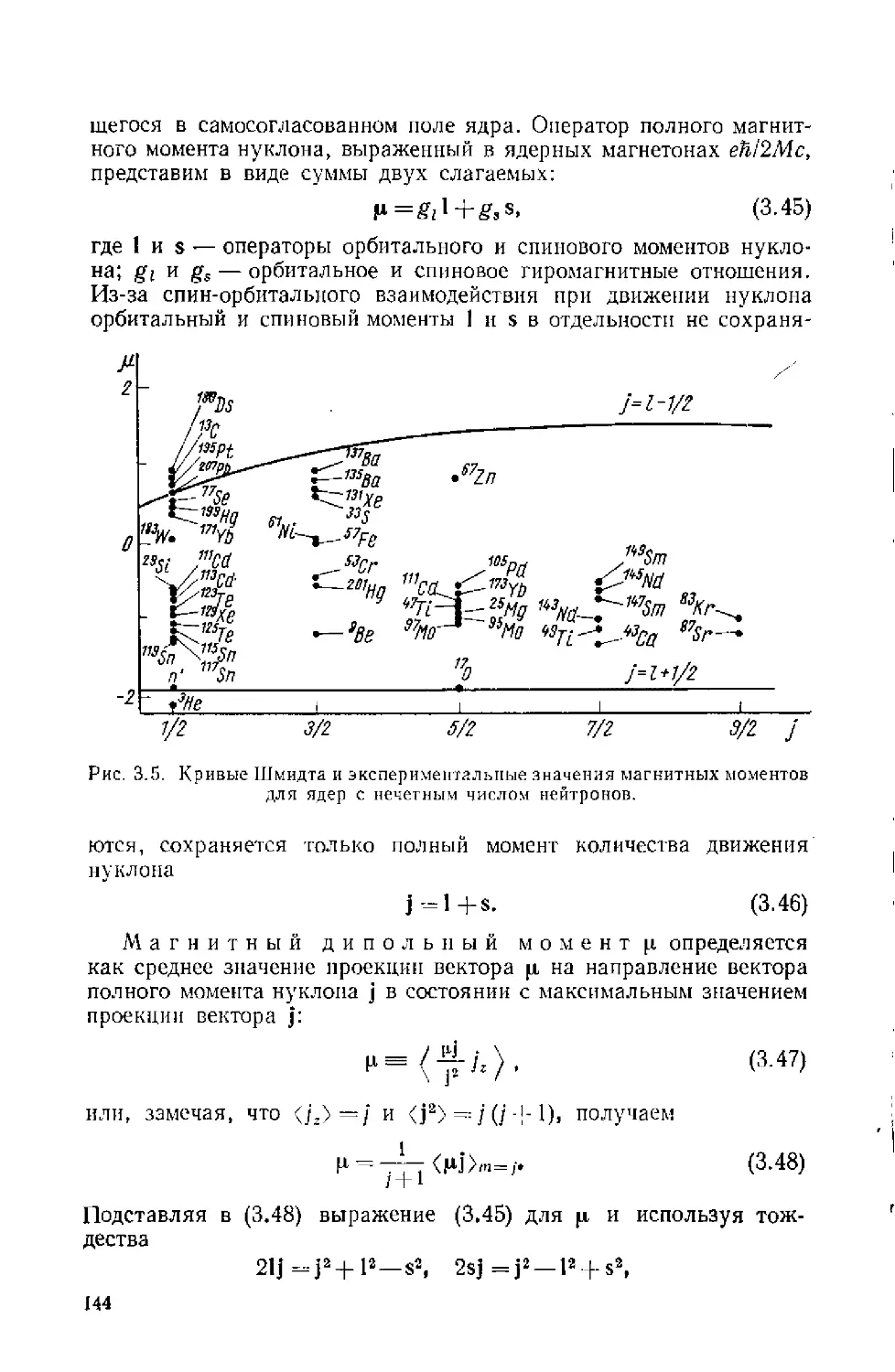
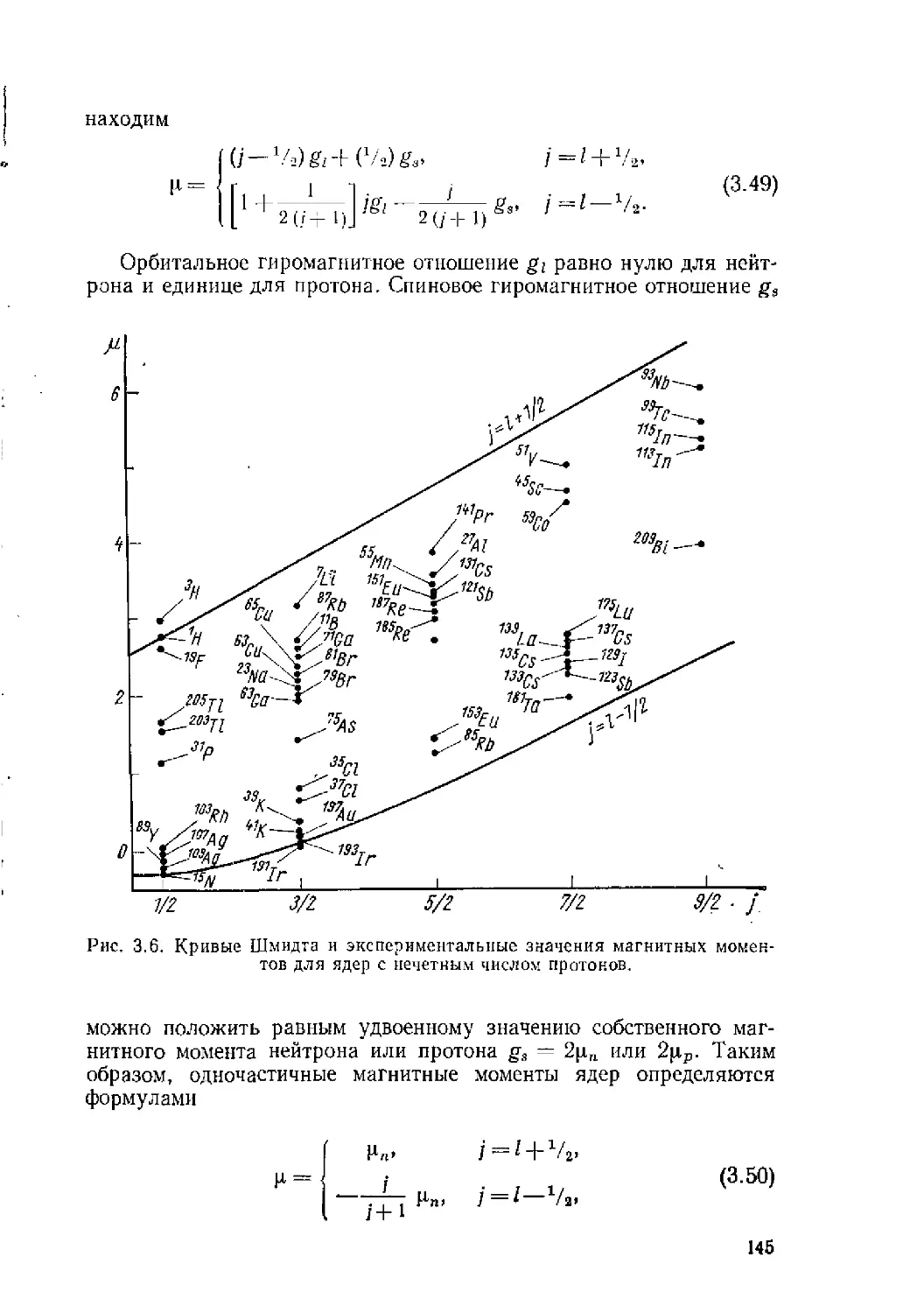
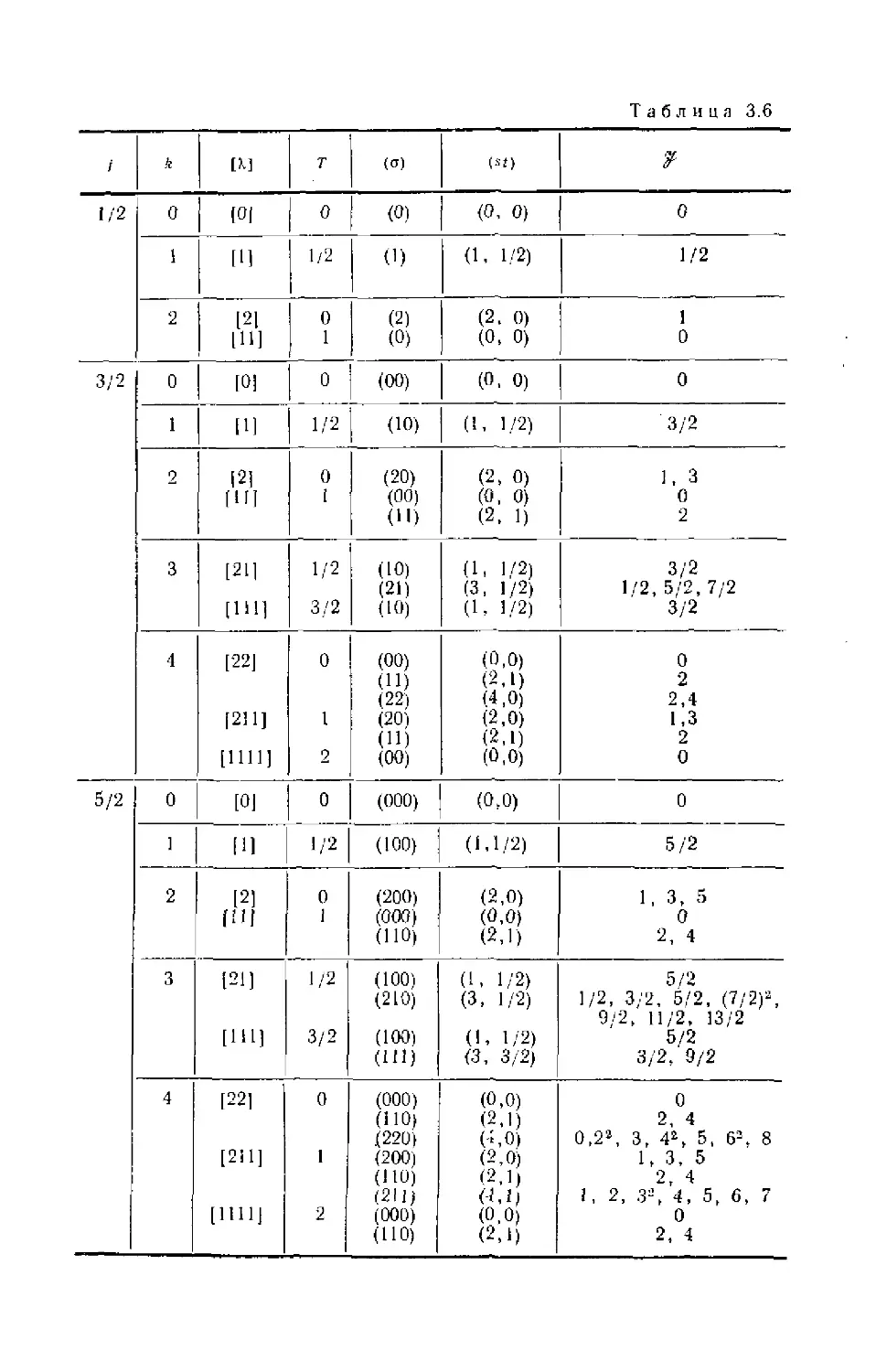
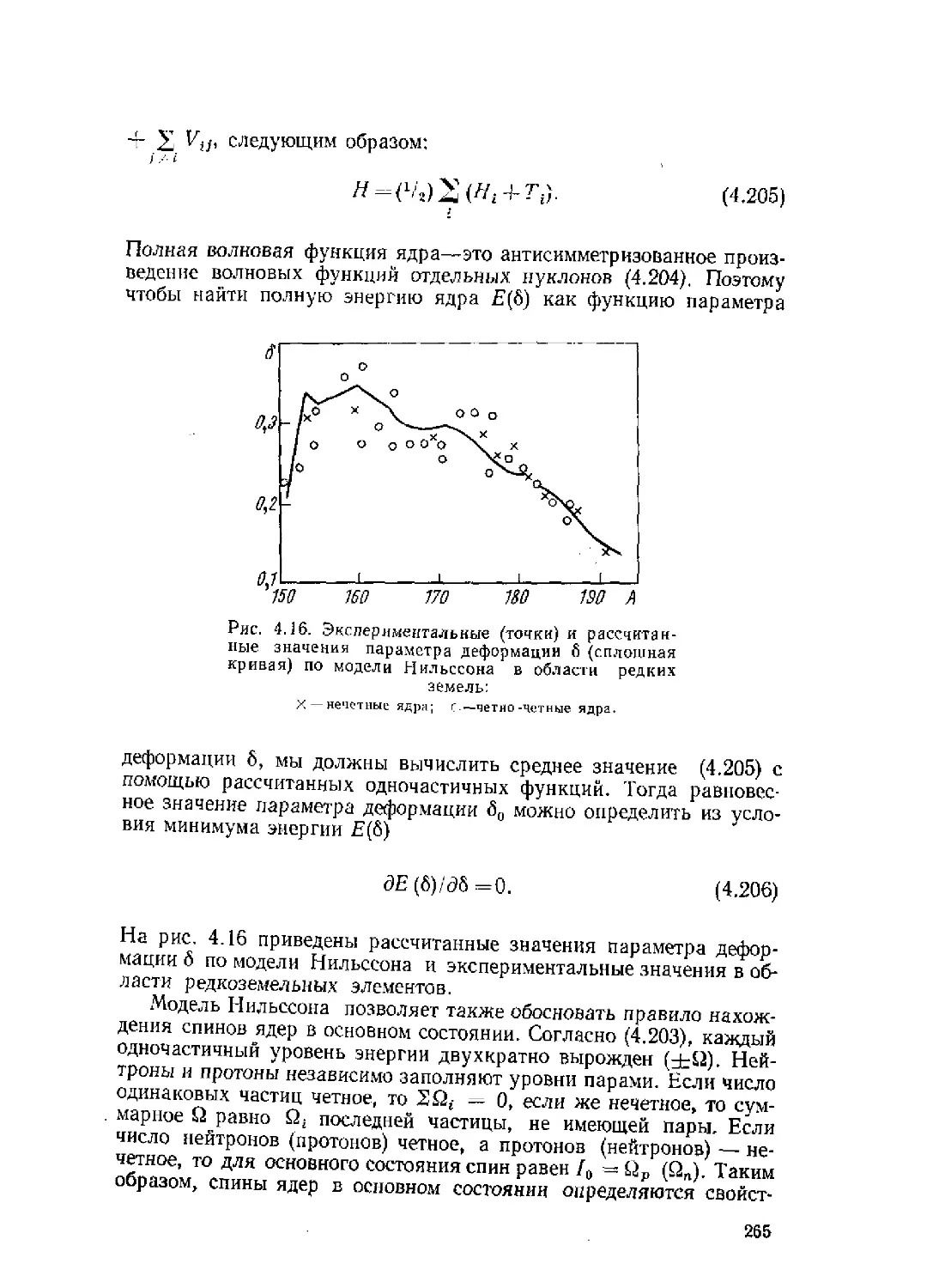
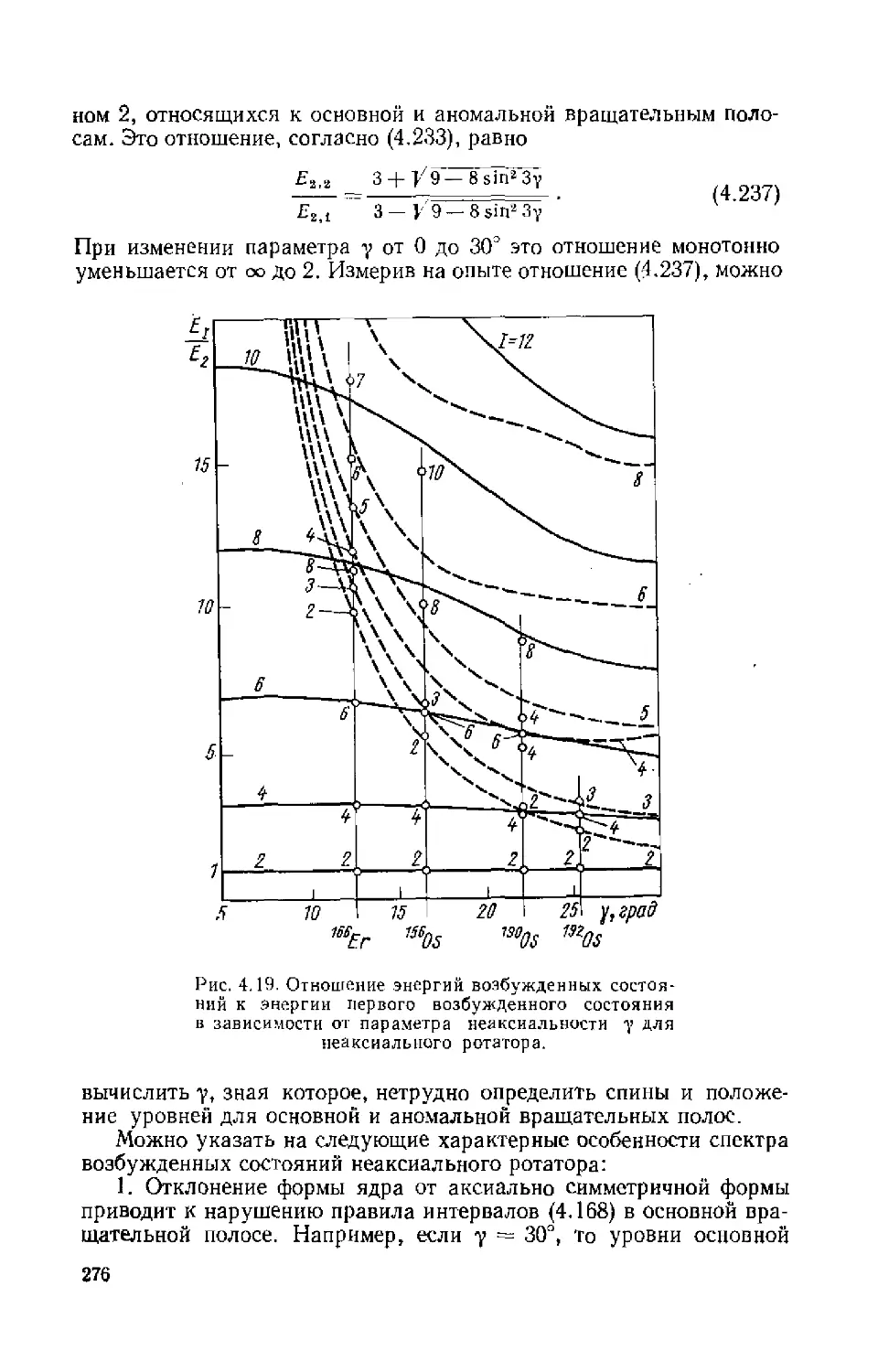
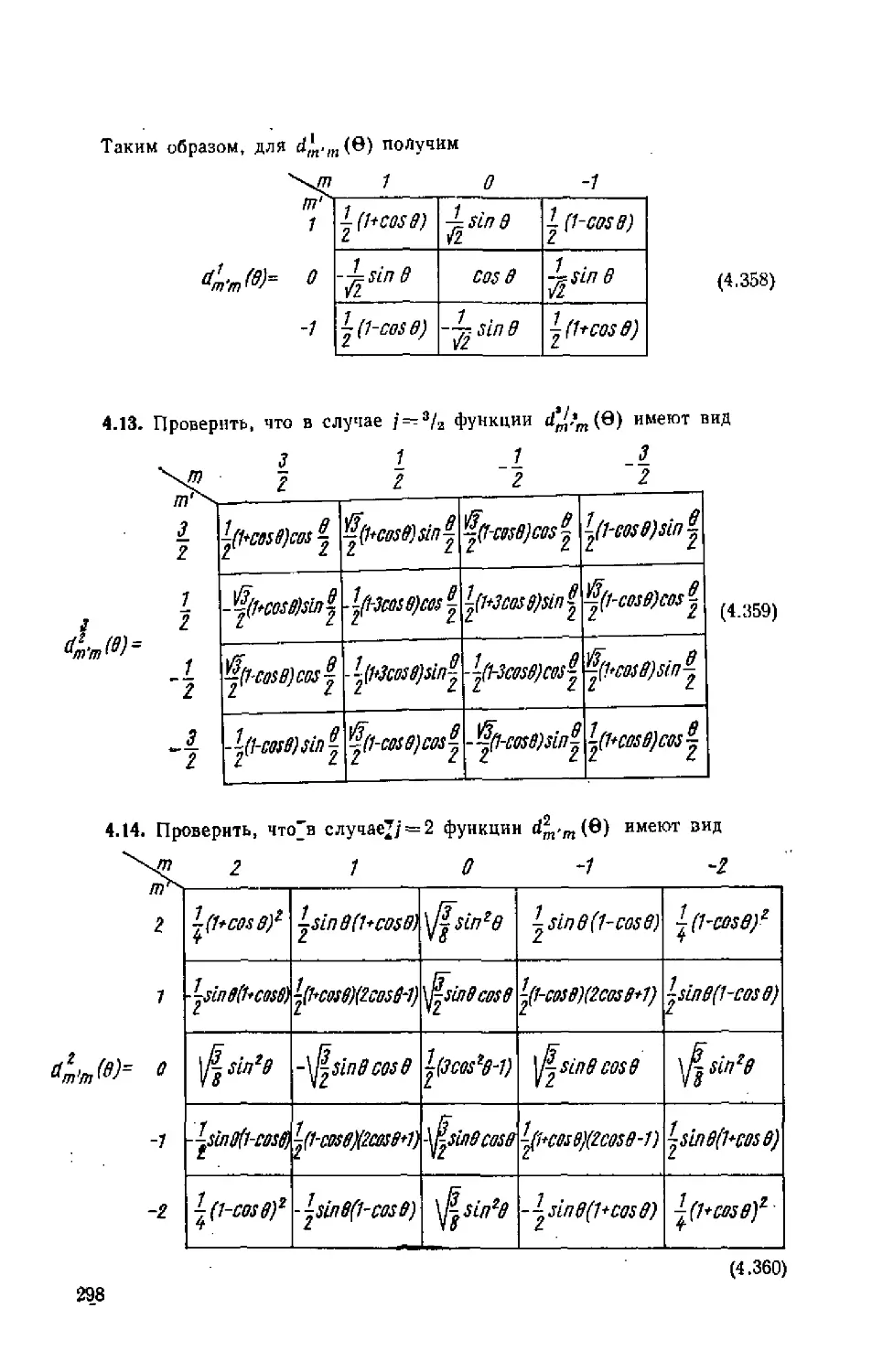
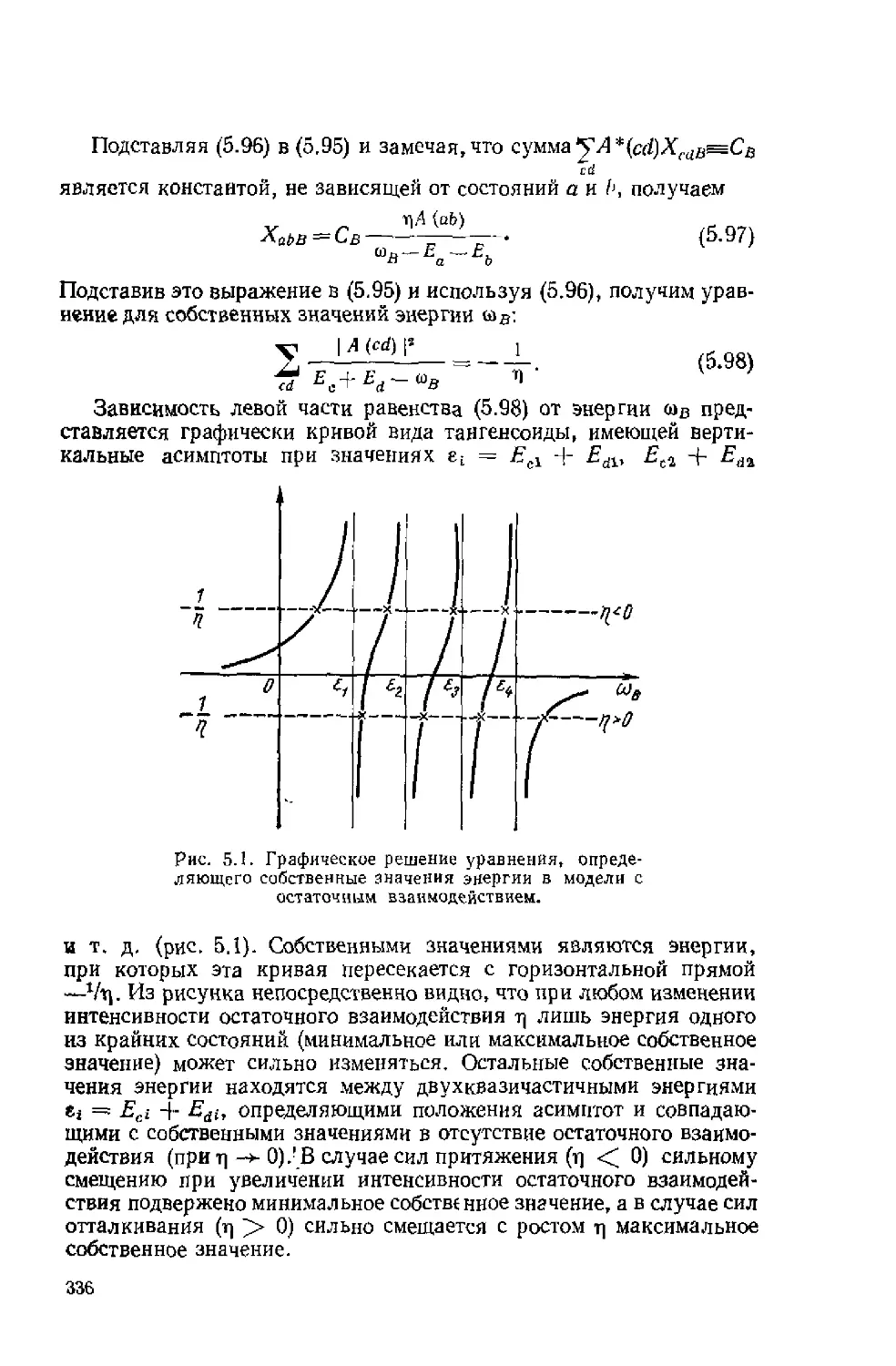
Автор: Ситенко А.Г. Tартаковский В.К.
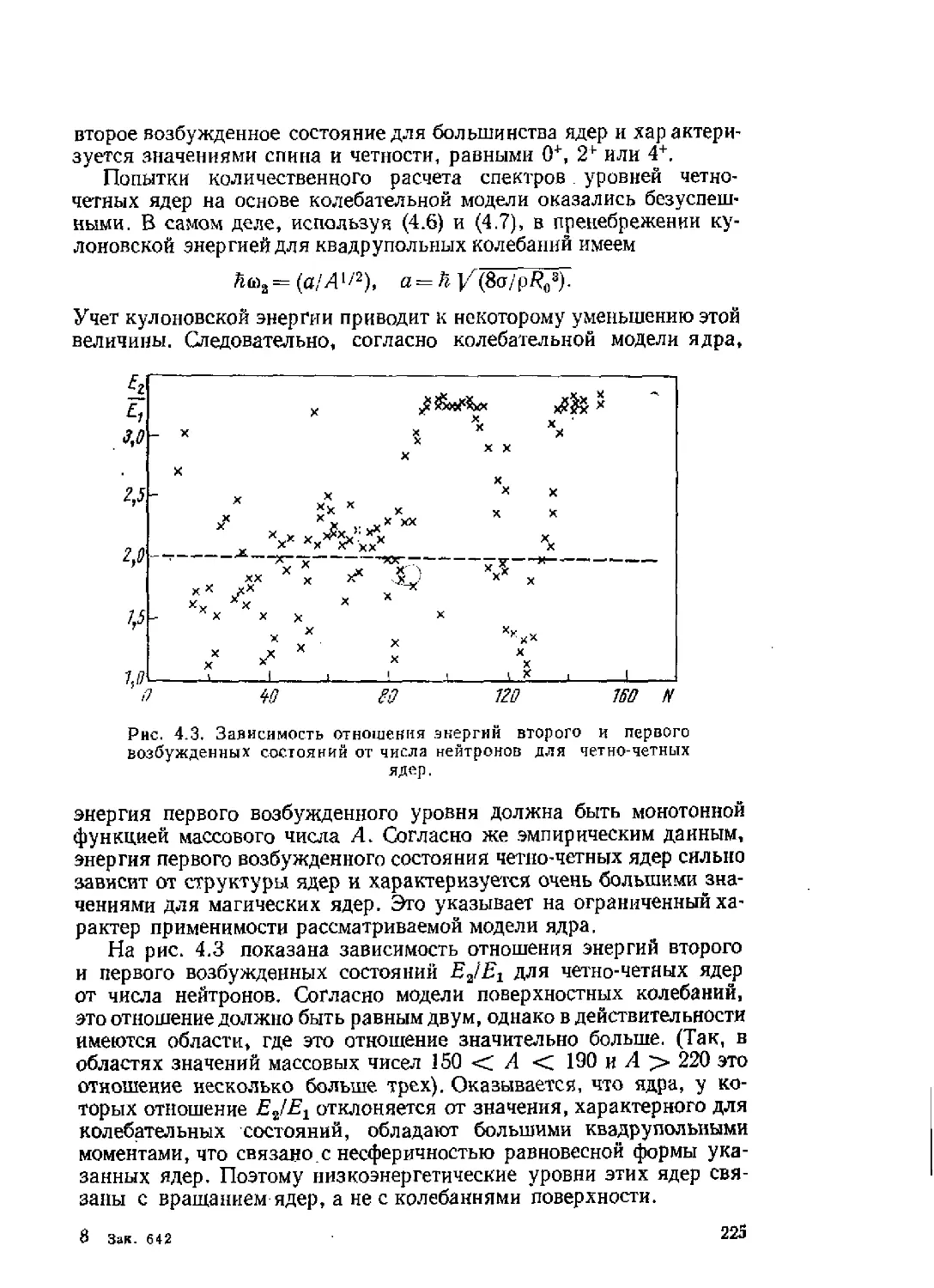
Теги: ядерная, атомная и молекулярная физика физика ядерная физика
Год: 1972
Текст
А. Г. СИТЕЧКО, В. К. ТАРТАКОВСКИЙ
ЛЕКЦИИ
ПО ТЕОРИИ
ЯДРА
Допущено Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия для студентов
высших учебных заведений
МОСКВА АТОМИЗДАТ 1972
УДК 539.1
Сите н ко А. Г., Тартаковский В. К
Лекции по теории ядра. Учебное пособие для вузов.
М., Атомиздат, 1972, 352 с.
Книга представляет собой курс лекций по теории
ядра, читаемый авторами на протяжении ряда лет в
Киевском государственном университете. В лекциях
изложены основы современных представлений о строе-
нии атомного ядра. Подробно рассмотрены различные
ядерные модели и взаимосвязь между ними. Хотя глав-
ное внимание в книге уделено изложению основ тео-
рии ядра, тем не менее в ней нашли достаточно пол-
ное отражение и новейшие достижения. Ряд изло-
женных вопросов пока лишь освещался в оригиналь-
ных работах и не излагался в учебной литературе.
Таблиц 16. Рисунков 56. Библиографий 107.
2—3—7
' 9-72
ПРЕДИСЛОВИЕ
Настоящая книга представляет собой расширенное изложение
<урса лекций по теории ядра, читаемого авторами на протяжении
)яда лет в Киевском государственном университете. В лекциях из-
южены основы современных представлений о строении атомного
ядра.
Как известно, важнейшей задачей ядерной физики является
изучение структуры ядер и объяснение их свойств на основе ядер-
ного взаимодействия между нуклонами — простейшими составляю-
щими частями ядер. Трудности современной теории ядра связаны
как с недостаточным знанием природы ядерного взаимодействия,
так и с многочастичным характером ядерных систем. Имеющиеся
в настоящее время экспериментальные данные по ядерному взаимо-
действию не противоречат допущению о двухчастичном характере
ядерных сил. Однако отсутствие строгих методов расчета много-
частичных систем с сильным взаимодействием заставляет ограни-
чиваться рассмотрением феноменологических моделей ядра, вводи-
мых для описания определенных свойств ядер. Развитие моделей
ядра происходило по различным направлениям, а сами модели мо-
дифицировались и усложнялись. Несмотря на кажущуюся про-
тиворечивость, различные модели ядра в значительной степени до-
полняют друг друга. В результате развития модельных представле-
ний удалось достичь значительного прогресса в понимании струк-
туры атомных ядер. В лекциях подробно рассмотрены различные
модели ядра, а также обсуждается взаимосвязь между ними.
Книга содержит пять глав. Гл. 1 — «Ядерные силы»; гл. 2 —
«Ядерная материя»; гл. 3 — «Оболочечная структура ядер»; гл. 4 —
«Вращение и колебания ядер» и гл. 5 — «Парные корреляции в яд-
рах». Хотя главное внимание в книге уделено изложению основ.
3
тем не менее авторы пытались отразить и некоторые новейшие до-
стижения по теории ядра. Ряд вопросов, изложенных в книге, пока
освещался только в оригинальных работах и не излагался в учеб-
ной литературе. Поскольку книга задумана как учебное пособие,
то авторы ограничились ссылками (за небольшим исключением)
только на широко доступную литературу. В конце книги приведен
список имеющихся на русском языке книг по теории ядра [1—8],
в которых читатель сможет найти более подробное изложение ряда
вопросов, а также ссылки на оригинальные работы. Для чтения
книги необходимо знакомство с квантовой механикой в объеме уни-
верситетского курса [9—11].
В заключение авторы считают своим долгом выразить искреннюю
признательность А. И. Ахиезеру, в результате совместной работы
с которым и возникла идея написания предлагаемого курса лекций.
Выражаем также искреннюю благодарность П. В. Скоробогатову
за существенную помощь при написании четвертой главы.
ГЛАВА 1
ЯДЕРНЫЕ СИЛЫ
§ 1.1. СОСТАВ ЯДЕР И СВОЙСТВА НУКЛОНОВ
Основные характеристики ядер. Атомные ядра характеризуются
определенными электрическими зарядами и массами. Заряд атом-
ного ядра q по абсолютной величине кратен и по знаку противопо-
ложен заряду электрона —е:
q = Ze.
Целое число Z определяет положение атома в периодической систе-
ме и называется атомным номером. Ядра с одинаковым
зарядом, но с различными массами называются изотопами.
Если массу наиболее распространенного изотопа углерода при-
нять равной 12, то массы всех ядер будут близки к пелым числам.
Ближайшее к значению массы целое число А называют массо-
вым числом ядра.
Согласно современным представлениям атомные ядра состоят
из протонов и нейтронов — элементарных частиц с примерно рав-
ными массами. Между этими частицами в ядрах действуют ядерные
силы. Протон имеет положительный электрический заряд, равный
по величине заряду электрона, а нейтрон электрически нейтрален.
Несмотря на различие в электрических свойствах, протоны и нейт-
роны в ядерных взаимодействиях ведут себя одинаково, и поэтому
их часто объединяют общим названием — нуклоны.
Атомное ядро с зарядом q = Ze и массовым числом А состоит
из Z протонов и N—A —Z нейтронов. Массовое число А опре-
деляет полное число нуклонов в ядре. Изотопы — это ядра
с одинаковыми числами протонов Z, но различными числами нейтро-
нов А. Ядра с одинаковыми числами нейтронов А, но различными
числами протонов Z называются изотонами. Ядра, состоящие
из одинакового числа нуклонов (одинаковое массовое число А),
называются изобарами.
Свойства нейтронов и протонов. Свойства отдельных нуклонов
хорошо изучены. Масса протона равна 1836,12 электронных масс,
или 1,007276 атомных единиц массы (а. е. лт.); масса нейтрона при-
мерно на 2,5 электронной массы больше массы протона (масса
нейтрона равна 1,008665 а. е. лт.). Протон и нейтрон имеют одина-
ковый по величине спин, равный 1/2, и подчиняются статистике
Ферми —Дирака. Магнитные моменты протона и нейтрона (выра-
5
женные в ядерных магнетонах) равны соответственно
рр =2,7927, рп= —1,9131. (1.1)
Эти значения сущее: сопло отличаются от значений 1 и 0, предска-
зываемых уравнением Дирака для частиц со спином 1/2. Аномаль-
ные значения магнитных моментов (1.1) указывают на неполноту
дираковского описания для нуклонов.
Свободный нейтрон нестабилен и распадается на протон, элект-
рон и антинейтрино: п -> р + е~ + v. При распаде нейтрона из-
быточная масса, эквивалентная примерно 1,3 Л1эе, расходуется
на образование электрона (0,5 АЪе) и на кинетическую энергию
образовавшихся частиц (0,8 Л1эв). Среднее время жизни нейтрона
составляет около 12 мин. Хотя в свободном состоянии нейтроны
нестабильны, вместе с протонами они могут образовывать стабиль-
ные ядра. Наоборот, протон в свободном состоянии — стабильная
частица, однако в связанном состоянии внутри ядра протон может
распадаться на нейтрон, позитрон и нейтрино: р п + е+ + v.
Ядра стабильны только при определенных соотношениях между
числом нейтронов и протонов. Если эти соотношения нарушаются,
то в ядре возможен распад нейтронов или протонов, происходящий
до тех пор, пока ядро не становится стабильным.
Малое различие в массах, совпадение спинов и некоторых дру-
гих свойств, а также возможность взаимного превращения позво-
ляют рассматривать нейтрон и протон как два различных состоя-
ния одной и той же частицы — нуклона. При этом нуклону
помимо пространственных и спиновой координат приписывается
еще дополнительная внутренняя степень свободы — так называе-
мая зарядовая, или изоспиновая координата.
В области нерелятивистских энергий нейтроны и протоны можно
считать точечными частицами, однако при достаточно высоких энер-
гиях необходимо учитывать пространственную структуру нуклонов.
Последняя проявляется, например, в опытах по рассеянию при до-
статочно высоких энергиях. Пространственная структура нукло-
нов, так же как и аномальные магнитные моменты последних, коли-
чественно может быть рассмотрена только в рамках полевой теории.
§ 1.2. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ МЕЖДУ НУКЛОНАМИ
Короткодействующий характер ядерных сил. Между нейтронами
и протонами, составными частями атомных ядер, действуют специ-
фические ядерные силы. Эти силы ие сводятся к электромаг-
нитным силам, так как они проявляются независимо от того, обла-
дают ли ядерные частицы электрическим зарядом или же являются
нейтральными.
Наиболее детальные сведения о природе ядерных сил можно
получить, исследуя систему двух нуклонов, так как задача двух
тел наиболее проста и допускает точное решение. Ядерные силы
6
в системе двух нуклонов обусловливают рассеяние частиц друг на
друге, а также приводят к образованию сложной частицы — дейт-
рона, состоящего из взаимосвязанных нейтрона и протона. Су-
ществование связанного состояния у системы нейтрон — протон
указывает, что ядерное взаимодействие между нейтроном и прото-
ном отвечает притяжению между частицами.
Наиболее характерным свойством ядериого взаимодействия яв-
ляется то, что ядерные силы характеризуются чрезвычайно малым
радиусом действия и очень большой величиной в пределах радиуса
действия. Допущение о короткодействующем характере ядерных
сил впервые было сделано Вигнером. На основе анализа малой
величины энергии связи дейтрона (2,23 и большой величины
энергии связи ядра 4Не (28 Мэв) им было показано, что радиус дей-
ствия ядерных сил должен быть порядка 2-10~13 см. Если охарак-
теризовать ядерное взаимодействие между нейтроном и протоном
некоторой потенциальной ямой шириной 2-10-13 см, то вследствие
малости энергии связи дейтрона эффективная глубина ямы при-
ближенно окажется равной 30 Мэе. Для сравнения укажем, что
энергия кулоновского взаимодействия между друмя протонами,
находящимися на расстоянии 2-10~13 см, по порядку величины
составляет всего 0,7 Мэв.
Другие особенности ядерных сил. В нерелятивистском пределе,
когда скорости частиц значительно меньше скорости света, ядер-
ное взаимодействие не зависит от скоростей взаимодействующих
частиц и может быть описано потенциалом. Отличительная осо-
бенность ядерных сил состоит в том, что потенциал ядерного взаи-
модействия зависит не только от расстояния между частицами, но
и от взаимной ориентации спинов взаимодействующих частиц.
Зависимость ядерного взаимодействия от спина непосредственно
вытекает из опытов по рассеянию медленных нейтронов на молеку-
лярном водороде. Наличие электрического квадрупольного момента
у дейтрона указывает, что ядерное взаимодействие является нецент-
ральным, т. е. оно зависит от взаимной ориентации суммарного
спина и относительного радиуса-вектора взаимодействующих ча-
стиц. Наконец, возникновение поляризации частиц при рассеянии
указывает на то, что в ядерном взаимодействии существенную роль
играют спин-орбитальные силы.
Из существования стабильных ядер следует, что ядерное взаи-
модействие между нуклонами в существенной своей части отвечает
силам притяжения. Однако имеющиеся в настоящее время экспе-
риментальные данные по рассеянию нуклонов при достаточно вы-
соких энергиях указывают на то, что на очень малых расстояниях
(меньших 0,4* 10-13 см) ядерные силы притяжения переходят в силы
отталкивания. Из данных по рассеянию нуклонов при высоких энер-
гиях следует также, что ядерные силы имеют частично обменный
характер, т. е. нуклоны при взаимодействии могут обмениваться
определенными свойствами (пространственными координатами,
спинами или зарядами).
7
Из свойств зеркальных ядер (зеркальными называ-
ются ядра, у которых нейтроны заменены протонами, а протоны
нейтронами) следует, что силы, действующие между двумя прото-
нами, эквивалентны силам, действующим между двумя нейтронами
(если исключить из рассмотрения кулоновское взаимодействие).
Это свойство получило название зарядовой симметрии
ядерных с и л. В дальнейшем оказалось, что зарядовая сим-
метрия ядериых сил — это. проявление более глубокой симметрии
ядерного взаимодействия, получившей название зарядовой
и л и изотопической инвариантности ядер-
н ы х~ сил.'Изотопическая инвариантность ядериых сил означает,
что взаимодействие в любых двух парах нуклонов одинаково, если
эти пары нуклонов находятся в одинаковых состояниях. Все имею-
щиеся в настоящее время экспериментальные данные о взаимодей-
ствии нуклонов (как при малых, так и при высоких энергиях)
согласуются с допущением об изотопической инвариантности ядер-
ных сил.
Еще в 1935 г. Юкава, основываясь на короткодействующей
природе ядерного взаимодействия, предложил полевую теорию ядер-
ных сил, предсказавшую существование частиц с промежуточной
массой — мезонов, впоследствии открытых экспериментально.
Однако мезонная теория до настоящего времени не смогла удовлет-
ворительно объяснить все характерные свойства ядерного взаимо-
действия. Отсутствие последовательной теории ядерных сил пре-
пятствует построению систематизированной теории ядра и ядерных
процессов. Поэтому наше дальнейшее изложение будет феноменоло-
гическим, т. е. будет существенно основываться на свойствах ядер-
ного взаимодействия, непосредственно извлекаемых из опытных
данных.
$ ГЛ. ОСНОВНОЕ СОСТОЯНИЕ ДЕЙТРОНА
Основные характеристики дейтрона. Как мы уже отмечали,
система, состоящая из нейтрона и протона, может находиться
в связанном состоянии. Связанное состояние системы нейтрон —
протон, называемое дейтроном,-— это простейшее составное
атомное ядро. Несмотря на то, что одна из частиц, входящих в со-
став дейтрона, — нейтрон — нестабильна, дейтрон характери-
зуется бесконечным временем жизни, т. е. является стабильной
системой.
Важнейшая характеристика дейтрона — энергия с в я-
з и, которая определяется разностью масс дейтрона и образующих
его частиц. Энергию связи дейтрона можно измерить по порогу
реакции фоторасщепления. Найденное таким путем значение энер-
гии связи дейтрона равно
е 2,226 ± 0,003 Мэв. (1.2)
8
Другими важными характеристиками дейтрона являются
спин, магнитный момент и электрический
квадрупольный момент. Спин дейтрона равен 1. Ве-
личину спина дейтрона можно определить по интенсивности полос
спектра молекулярного дейтерия.
Магнитный момент дейтрона близок к сумме магнитных момен-
тов нейтрона и протона. Величина магнитного момента дейтрона,
выраженного в ядерных магнетонах, равна
pd =0,8574. (1.3)
Наиболее точно магнитный момент дейтрона измерен в эксперимен-
тах по отклонению молекулярного пучка в неоднородном магнит-
ном поле.
Электрический квадрупольный момент дейтрона равен
Q = 2,82-10-27 см1, (1.4)
Эта величина была найдена по тонкой структуре в радиочастотном
спектре магнитного резонанса дейтерия. Укажем на относитель-
ную малость величины электрического квадрупольного момента
дейтрона. Действительно, величину электрического квадруполь-
ного момента необходимо сравнивать с поперечными размерами
системы. Если предположить, что размеры дейтрона совпадают
с радиусом действия ядерных сил, то даже в этом случае квадру-
польный момент примерно в 50 раз меньше площади поперечного
сечения дейтрона. Малость величины квадрупольного момента дейт-
рона и приближенная аддитивность магнитных моментов нейтрона
и протона в дейтроне означают, что основное состояние дейтрона
почти сферически симметрично. Основное состояние системы харак-
теризуется сферической симметрией в том случае, если взаимодей-
ствие центрально. Поэтому из сферической симметрии основного
состояния дейтрона следует, что ядерное взаимодействие между
нейтроном и протоном также почти центрально.
Основное состояние дейтрона в случае центральных сил *. Рас-
смотрим свойства основного состояния дейтрона, предполагая, что
ядерное взаимодействие между нейтроном и протоном описывается
потенциалом V(r), где г — абсолютная величина расстояния между
частицами. Уравнение Шредингера для волновой функции ф(г),
описывающей относительное движение нейтрона и протона, имеет
вид
А + Е(г)-£|ф(г)=°, (1-5)
где р = (1/2)Л4 — приведенная масса (для простоты предполагается,
что массы нейтрона и протона одинаковы и равны М) и Е — энер-
гия относительного движения. Для основного состояния системы
* Взаимодействие двух нуклонов при малых энергиях детально рассмот-
рено в обзоре [I], где содержится подробная библиография.
9
энергия Е отрицательна и по абсолютной величине равна Энергии
связи Е — —г. Волновая функция ф(г) должна обращаться в нуль
на бесконечности и быть конечной при г — 0.
В случае центрального взаимодействия основное состояние
системы характеризуется нулевым значением относительного ор-
битального момента I — 0 (S-состояние). Волновая функция для
такого состояния сферически симметрична и может быть записана
в виде
ф(г)=и(г)/г, (1.6)
где «(г) зависит только от абсолютной величины расстояния между
частицами. Подставляя (1.6) в (1.5), для определения функции
и(г) получаем следующее уравнение:
и" — (М/Й2)[7(г)+е]ц=0, (1.7)
причем функция и (г) должна удовлетворять граничным условиям
и (0) = ы (оо) — 0. Ядерное взаимодействие характеризуется ко-
нечным радиусом действия г0, поэтому вне области действия ядер-
ных сил уравнение (1.7) упрощается:
и" — аги=0, г>г0. (1.8)
Здесь введено следующее обозначение: а2 = Л4е/Й2.
Решение уравнения (1.8), обращающееся в нуль на бесконеч-
ности, имеет вид
и = Се~ог, г > гй, (1.9)
где С — нормировочная постоянная. Так как волновая функция и
ее производная должны быть непрерывны, то решение уравнения
(1.8) во внешней области (г г0) должно быть сшито с решением
уравнения (1.7) во внутренней области (г г0), что означает ра-
венство логарифмических производных от функций и (г) для внеш-
ней и внутренней областей при г = г0. Из выражения (1.9) следует,
что логарифмическая производная от функции и (г) во внешней
области (г Гц) не зависит от г и равна —а:
и'/и = --а.
Такое же значение должна принимать и логарифмическая произ-
водная от функции и (г) во внутренней области (г г0) при г = г0:
а. (1.10)
ивнутр r=rQ
Величина логарифмической производной от внутренней функции
при г — г0 определяется потенциальной энергией V (г) и является
основным параметром, характеризующим свойства системы нейт-
рон — протон. (Впервые такой подход к описанию системы нейт-
рон — протон был предложен Бете и Пайерлсом [21.)
10
Согласно соотношению (1.9), волновая функция дейтрона вне
области действия ядерных сил убывает с ростом расстояния по экс-
поненциальному закону, поэтому величину 1/а можно рассматри-
вать как параметр, характеризующий прост-
ранственные размеры дейтрона (радиус
дейтрона). Величина 1/а заметно превосходит величину ра-
диуса действия ядерных сил г0, а это означает, что дейтрон — это
слабо связанная система, в которой нейтрон и протон значитель-
ную часть времени проводят вне области действия ядерных сил.
Заметим, что радиальная зависимость волновой функции основ-
ного состояния дейтрона вне области действия ядерных сил пол-
ностью определяется заданием энергии связи. Это обстоятельство
позволяет в пределе нулевого радиуса действия ядерных сил по-
строить совершенно независимо от вида ядерного потенциала при-
ближенную волновую функцию дейтрона:
Фо(П =/а/2я-(е-“''/г) (г0—э-0), (1.11)
где нормировочная постоянная определена из условия
рг^(г) = 1. (1.12)
Формулой (1.11) можно пользоваться в тех случаях, когда сущест-
венно поведение волновой функции на расстояниях, превосходя-
щих радиус действия ядерных сил.
Соотношение между шириной и глубиной потенциальной ямы.
Если предположить, что ядерный потенциал имеет форму прямо-
угольной ямы радиусом г0 и глубиной Уо, то внутренняя функция
и (г), являющаяся решением (1.7), будет иметь вид
и —С sinKor, r<r0, (1.13)
где С — нормировочная постоянная, а
К0 = (1/Л)/М(70-^’. (1.14)
Подставляя (1.13) в выражение для логарифмической производ-
ной (1.10), можно получить соотношение, связывающее величины
гп и Vo. Более наглядно, однако, соотношение между шириной и
глубиной потенциальной ямы можно получить на основе следую-
щих соображений. Так как в основном состоянии функция и (г)
не имеет нулей (за исключением точки г = 0), то во внутренней
области (г < г0) может укладываться не более половины длины
волны: rft< (1/2).(2я/К0). С другой стороны, для возможности
сшивки решения (1.13) с экспоненциально убывающим решением
(1.9) необходимо, чтобы во внутренней области укладывалось не
менее четверти длины волны. Следовательно, должны выполняться
неравенства
(1/4)(2лАК0)<г0<(1/2)(2л/Ка). (1.15)
11
Используя (1.14) и пренебрегая энергией связи дейтрона по срав-
нению с глубиной ямы, из (1.15) нетрудно определить пределы,
в которых заключена глубина потенциальной ямы:
(л2/4) (Йа/Л1) Г'о г02 < л2 (1.16)
Полагая г0 ~ 1,7-10~1:1 см, получим для нижнего предела глу-
бины потенциальной ямы Vo величину порядка 35 Мэв, которая
значительно превосходит энергию связи дейтрона.
Отсутствие возбужденных состояний у дейтрона. Нетрудно
показать, что в предположении центрального характера ядерных
сил у дейтрона отсутствуют возбужденные связанные состояния.
Действительно, для возможности существования возбужденного
связанного состояния с нулевым орбитальным моментом необхо-
димо, чтобы радиальная функция и (г) во внутренней области имела
добавочный нуль, т. е. во внутренней области укладывалось больше
трех четвертей длины волны. Пренебрегая энергией связи возбуж-
денного состояния, это условие можно записать в виде
гй>(3/4). (2л7г/]ЛЙ¥0), откуда И0г02 (9/4) л2 (Д2/Л4).
Но это условие противоречит неравенству (1.16). У дейтрона не
может быть возбужденных связанных состояний, соответствующих
значениям относительного орбитального момента, отличным от
нуля.
Отсутствие возбужденных связанных состояний со значения-
ми орбитального момента I 0 объясняется тем, что уровни
с /=/= 0 лежат значительно выше уровня с I = 0, так как в состоя-
ниях с отличным от нуля орбитальным моментом добавляется центро-
бежная энергия. Среднее значение этой энергии, равной
КЧ, (I ф- 1)/Л1г3, можно оценить, если вместо г подставить величину
порядка эффективных размеров дейтрона, т. е. 1/а. При I = 1
получим для центробежной энергии величину, равную 2е, т. е. уже
P-состояние должно лежать в области непрерывного спектра.
Отметим, что при доказательстве отсутствия возбужденных
связанных S-состояний мы пренебрегли спиновой зависимостью
ядерных сил. В действительности даже при центральном характере
ядерных сил последние могут зависеть от взаимной ориентации спи-
нов нейтрона и протона. Поэтому в принципе возможно существо-
вание двух связанных S-состояний системы нейтрон — протон
с параллельной ориентацией спинов частиц (триплетное состояние,
суммарный спин частиц равен единице) и антипараллельной ориен-
тацией спинов частиц (синглетное состояние, суммарный спин
частиц равен нулю). Однако из экспериментальных данных по
рассеянию медленных нейтронов в молекулярном водороде следует,
что в системе нейтрон — протон синглетное связанное состояние не
осуществляется.
12
s 1.4. РАССЕЯНИЕ МЕДЛЕННЫХ НЕЙТРОНОВ ПРОТОНАМИ
Амплитуда и фазы рассеяния. Наряду с изучением связанного
состояния системы нейтрон — протон изучение рассеяния нейтро-
нов протонами — это второй важнейший источник получения све-
дений о ядерном взаимодействии между нейтронами и протонами.
В отличие от связанного состояния системы нейтрон — протон,
когда энергия отрицательна, в случае рассеяния нейтрона про-
гоном энергия относительного движения частиц положительна.
Волновая функция ф (г), описывающая рассеяние нейтрона про-
тоном, определяется решением уравнения Шредингера (1.5) при
положительном значении энергии Е. В этом случае на больших
расстояниях волновая функция ф(г) должна иметь вид суммы
падающей плоской волны и сферически расходящейся рассеянной
волны:
ф (r)^-eiAi! + f (ft)-(efA,7r), (I.I7)
где k = (у MEIK) — волновой вектор относительного движения
частиц, а ось z выбрана вдоль направления падающего пучка нейт-
ронов. Коэффициент при расходящейся волне f (ft), зависящий от
угла ft между направлениями движения падающих и рассеянных
частиц, называется амплитудой рассеяния, а угол ft —
углом рассеяния.
В случае центрального взаимодействия амплитуда рассеяния
непосредственно выражается через фазы рассеяния 6/:
f (ft) = (i/2A)S(2/ + l)(l— e2ift;) (cosft). (1.18)
i
Фазы бг характеризуют рассеяние частицы с различными значе-
ниями орбитального момента I и зависят от энергии частицы и вида
потенциала V (г).
Сечение рассеяния связано с амплитудой рассеяния соотноше-
нием
da — о (ft) d о = | f (ft) |2 do, (1-19)
где do - элемент телесного угла, определяющий направление
движения рассеянной частицы. Подставляя (1.18) в (1.19) и инте-
грируя (1.19) по полному телесному углу, нетрудно найти ин-
тегральное сечение рассеяния:
о (4n/fe2) (2/ + 1) sin2 6г. (1.20)
i
S-Рассеяние. Зависимость фазы рассеяния от энергии. Рассмот-
рим рассеяние медленных - нейтронов протонами в случае, когда
длина волны относительного движения X = k-1 больше радиуса
действия ядерных сил г0. Условие X > г0 выполняется, если энер-
гия относительного движения нейтрона и протона не превосходит
10 Мэв. (В лабораторной системе, в которой до рассеяния протон
покоится, энергия налетающего нейтрона меньше 20 Мэв.) Так как
13
эффективный прицельный параметр столкновения двух частиц
с относительным моментом I равен /X, то при X > г0 взаимодействие
частиц возможно только в S-состоянии (I = 0). При этом все фазы
рассеяния (за исключением фазы в S-состоянии 60 = 5) равны
нулю, и амплитуда рассеяния принимает вид
( — (1/Л) е‘в sin б. (1.21)
В этом случае рассеяние сферически симметрично. Интегральное
сечение рассеяния равно
o=-(4n/^)sin26. (1.22)
Найдем зависимость фазы рассеяния 6 от энергии в предельном
случае бесконечно малого радиуса действия ядерных сил (го->-0).
Для I — 0 радиальная функция и вне области действия ядерных сил
определяется уравнением
и" -ф k? и = 0, г > г0,
решение которого имеет вид
u = Csin(£r+ 6), г > г0. (1-23)
Фазу 6 можно найти из условия равенства логарифмических произ-
водных от волновой функции во внешней области (1.23) и волновой
функции во внутренней области при г — г0:
fectg(*r0 + 6)=^ . (1.24)
Ивнутр г~г„
Если энергия относительного движения частиц мала по сравнению
с глубиной потенциальной ямы, то волновая функция во внутрен-
ней области для задачи рассеяния практически не будет отличаться
от волновой функции во внутренней области для задачи о связан-
ном состоянии. Поэтому правую часть равенства (1.24) заменим
выражением (1.10) и таким образом получим следующее соотно-
шение:
Actg(£r0 + 6) = — а, (1.25)
или в предельном случае нулевого радиуса действия ядерных сил
Jfectg6 = —а. (1.26)
Подчеркнем, что возможность введениг одного и того же пара-
метра а для описания рассеяния и асимптотики волновой функции
связанного состояния является прямым следствием' малости энер-
гии связи дейтрона и энергии относительного движения нейтрона
и протона по сравнению с эффективной потенциальной энергией
взаимодействия нейтрона и протона.
Используя (1.26), сечение рассеяния нейтрона протоном в пред-
положении нулевого радиуса действия ядерных сил можно запи-
сать в виде
о = 4л/(а2 +^2), г0->-0.
(1.27)
14
Спиновая зависимость ядерных сил. Согласно (1.27), сечение
рассеяния в предельном случае нулевой энергии относительного
движения полностью определяется величиной энергии связи дейт-
рона
а=4л/а2, А->0. (1.28)
Если воспользоваться численным значением энергии связи дейтро-
на (1.2), то для сечения рассеяния, согласно (1.28), получим значе-
ние 2,33- IO-24 cut®. Экспериментальное значение сечения рассея-
ния нейтрона протоном при нулевой энергии оказывается значи-
тельно большим и равно
сгэкса = (20,44 ± 0,02) 10-24 см2. (1.29)
Столь значительное различие между экспериментальным значе-
нием сечения рассеяния и выражением (1.28) непосредственно ука-
зывает на существенную зависимость ядерного взаимодействия от
спинового состояния системы.
Система нейтрон — протон может находиться в двух различных
спиновых состояниях: триплетном (суммарный спин равен едини-
це) и синглетном (суммарный спин равен нулю). Так как полный
момент (спин) дейтрона равен единице и основное состояние дейт-
рона — четное, то в дейтроне осуществляется триплетное спиновое
состояние. В случае рассеяния неполяризованного нейтрона на
неполяризованном протоне система может находиться как в три-
плетном состоянии (с весом 3/4), так и в синглетном состоянии
(с весом 1/4). Если ядерное взаимодействие существенно зависит
от спинового состояния, то для описания взаимодействия между
нейтроном и протоном необходимо ввести два параметра а( и аа,
различные для триплетного и синглетного спиновых состояний.
Фазы рассеяния б; и 6,, соответствующие триплетному и синглет-
ному состояниям, связаны с а( и а, при г0 -* 0 соотношениями
k ctg fi4 = — af, k ctg 63 = —as. (1.30)
Величина а4 непосредственно связана с энергией связи дейтрона
6 = Й®а?/Л1. (1.31)
Сечения рассеяния нейтронов протонами в триплетном и синглет-
ном состояниях, согласно соотношениям (1.30) и (1.22), равны
0f = 4nl(a* + А2), о3 = 4л/(аЦ-А2), г0->0. (1.32)
В случае рассеяния неполяризованных нейтронов на неполяризо-
ванных протонах сечение рассеяния определяется формулой
a = (3/4)a( + (l/4)os, (1.33)
где коэффициенты 3/4 и 1/4 — статистические веса триплетного
и синглетного спиновых состояний соответственно. Используя экс-
периментальное значение усредненного сечения рассеяния нейт-
15
рона протоном при нулевой энергии (1.29) и зная энергию связи
дейтрона, можно определить величину а? или формально сопо-
ставляемую ей энергию:
е'=й*а1/Л4 = 0,072 (1.34)
Эту энергию называют иногда виртуальным уровнем
дейтрона. (Но следует иметь в виду, что связанного состоя-
ния системы нейтрон — протон с энергией —е' не существует.)
Длины рассеяния. Рассмотрим теперь рассеяние нейтронов
протонами в предельном случае нулевой энергии нейтронов, считая
радиус действия ядерных сил отличным от нуля. Уравнение для
радиальной функции вне области действия ядерных сил в случае
нулевой энергии имеет вид
п"=0, г>г0, (1.35)
откуда
и =С' (г—а), г>г0, (1.36)
где С' и а—постоянные. Решение (1.36) является уравнением пря-
мой, пересекающей ось г в точке а. Величина а называется дли-
ной рассеяния.
Длину рассеяния а легко связать с фазой рассеяния 5. Действи-
тельно, решение (1.36) должно совпадать с функцией и, определяе-
мой (1.23), при fe->0. Сравнение обеих формул показывает, что
а =— lim(tg6/fc), (1.37)
fe-kU
т. е. при малых k, когда выполнено неравенство krQ < 1, фаза рас-
сеяния 6 может быть выбрана в виде
6 = /гл — ak, kr0 < 1, (1.38)
где п — произвольное целое число*. Отсюда на основании фор-
мулы (1.22) следует, что сечение рассеяния в предельном случае
нулевой энергии нейтронов равно
о —4ла2, (1.39)
Длина рассеяния зависит от спинового состояния системы,
поэтому следует различать длины рассеяния at и as в триплетном и
синглетном состояниях. Измерение сечения рассеяния при ну-
левой энергии позволяет определить только абсолютную величину
длины рассеяния, но не ее знак. Длина рассеяния может быть как
положительной, так и отрицательной. Зависимость волновой
функции от г при нулевой энергии для положительной и отрица-
тельной длин рассеяния схематически изображена на рис. 1.1. По-
* Если потребовать, чтобы фаза рассеяния обращалась в нуль при
то из теоремы Левинсона следует «=1.
16
ведение волновой функции в области действия ядерных сил (г < г0)
почти не зависит от энергии, поэтому оно такое же и для связанных
состояний, если энергия связи не очень велика. Из рис. 1.1 видим,
что при положительной длине рассеяния волновую функцию для
внутренней области можно сшить с экспоненциально убывающим
решением во внешней области, соответствующим связанному со-
стоянию. При отрицательной длине рассеяния волновая функция
во внутренней области ведет себя так, что ее невозможно сшить
с экспоненциально убывающим решением во внешней области, т. е.
в этом случае связанное состояние системы невозможно. Итак,
если а > 0, то у системы возможно существование связанного
состояния; если же а < 0, то связанное состояние невозможно.
Эффективный радиус ядерного взаимодействия. Формулы (1.32),
определяющие сечение рассеяния медленных нейтронов протонами
при k #= 0, выведены в предположении, что радиус действия ядер-
ных сил равен нулю (г0->0). Покажем теперь, как можно сфор-
мулировать задачу о рассеянии, чтобы независимо от формы потен-
циала последовательно учитывать конечность радиуса действия
сил [3]. Запишем точное уравнение для радиальной функции и (г),
описывающей движение в поле V (г) и соответствующей значению
энергии относительного движения £:
ц,г — (М/Г?)У(г)ы = — k2u- (1.40)
Радиальную функцию, соответствующую нулевому значению энер-
гии, обозначим и0 (г). Эта функция удовлетворяет уравнению
4 —(М/Йг) У(г)цо = О. (1.41)
17
Умножай уравнение (1.40) на и0, а (1.41) на и и вычитая первое ра-
венство из второго, получаем следующее соотношение:
(и0'ы— иои') = k2 иои. (1-42)
dr
Введем вспомогательные функции v (г) и г0 (г), удовлетворяющие
уравнениям для свободного движения: v” = —k2v, v0" = 0, причем
определим эти функции таким образом, чтобы при г > г0 они совпа-
дали с и и и0. Очевидно, для функций о и имеет место соотношение,
аналогичное (1.42):
— (а0' V — va vr) = k2vav. (1-43)
dr
Вычитая из (1-43) соотношение (1.42), интегрируя найденное равен-
ство по г от 0 до бесконечности и замечая, что и (0) = м0 (0) = О,
получаем
(0) V' (0) — п0' (0) о (0) = k2 f dr (у9 и—и0 и). (1.44)
О
Выберем далее нормировку функций и и п0 таким образом, чтобы
функции v и п0 обращались в единицу при г = 0. Очевидно, при та-
кой нормировке функции v и о0 имеют следующий вид:
v (г) -= sin 6, oo(r)=l—г/а, (1-45)
где б и а определены ранее.
Подставляя соотношения (1.45) в (1.44), получаем общее выра-
жение
k ctg 6 = -1 /а + (1 /2) k2 г (0, Е), (1.46)
связывающее фазу рассеяния 6 с длиной рассеяния а и эффектив-
ным радиусом
г (0,£)^2§ dr^v—иои). (1.47)
о
Для связанного состояния получим соотношение, аналогичное
(1.46), заменив в последнем k2 на —а2 и fectg 6 на —а. В результате
замены имеем
а = 1/а + (1/2)а2г(0,—б), (1.48)
где
г (0,—е) = 2 dr (уоп-Е—«ои-е)« (1-49)
о
Так как функции о0 и v вне области действия ядерных сил сов-
падают с и0 и и, то в формулах, определяющих г (0, Ё) и г (0, —е),
интегрирование производится только по области ядерного взаимо-
18
действия. Заметим, что соотношения (1.46) и (1.48) совершенно не
зависят от формы ядерного потенциала, если под эффективными
радиусами понимать величины (1.47) и (1.49). (Понятие эффектив-
ного радиуса было введено Швингером [41.)
Для энергий Е, малых по сравнению с эффективной глубиной
потенциальной ямы, функции и и о в области ядерного взаимодейст-
вия практически не отличаются от функций «0 и у0, и величины
г (0, £) и г (0, —е) в первом приближении можно считать не зави-
сящими от энергии. Эти приближенные значения г (О, Е) и г (0, —е)
обычно обозначают ru:
со
r0 = 2$ dr (ng-- но)- (1.50)
'о
Величина г0, имеющая размерность длины, определяется характе-
ром ядерного взаимодействия и может быть названа эффектив-
ным радиусом действия ядерных сил. Дейст-
вительно, подынтегральное выражение в (1.50) отлично от нуля
только внутри области действия ядерных сил и по порядку вели-
чины равно единице. Поэтому интеграл (1.50) характеризует рас-
стояние, на котором происходит ядерное взаимодействие.
Длины и эффективные радиусы для триплетного и синглетного
состояний. В области малых энергий соотношение (1.46) предста-
вим в виде
ftctg 6 = —1/«4-(1/2) &аг0- (1-51)
Эффективный радиус действия ядерных сил, так же как и фаза и
длина рассеяния, зависит от спинового состояния системы нейтрон—
протон. Обозначая эффективные радиусы в триплетном и синглет-
ном состояниях через rot и rast можно написать следующие соотно-
шения :
Actg6z = — 1/а( + (1/2)А2гог, Actg6s =— l/as + (l/2)A2 rOs. (1.52)
Отметим, что для триплетного состояния имеет место дополнитель-
ное соотношение, связывающее длину рассеяния at и эффективный
радиус rot-
\lat = at~(№)a*rw (1.53)
Правая часть в формулах (1.52) представляет собой два первых
члена разложения Actg б в ряд по степеням А2. Видно, что с точ-
ностью до членов порядка А® величина Actg б определяется только
двумя параметрами (для каждого спинового состояния) и не зави-
сит от конкретной формы ядерного потенциала. Используя форму-
лы (1.52), нетрудно получить следующие выражения для сечений
рассеяния медленных нейтронов протонами в триплетном и синг-
летном состояниях:
4тг
/ 1 1 V
+‘
1 V
(1-54)
19
Усредненное сечение рассеяния цеполяризованных медленных
нейтронов свободными неполяризованными протонами определяет-
ся формулой
i 1 1 , V /1 1 \2 ' ’
Как видно, рассеяние нейтронов протонами в области малых энер-
гий падающих нейтронов характеризуется четырьмя параметрами
+, <*s, г0( и rOs и не зависит от формы потенциала, т. е. сечение рас-
сеяния одинаково для различных потенциалов V (г), приводящих
к одинаковым значениям длин рассеяния и эффективных радиусов.
Используя экспериментальное значение для усредненного се-
чения рассеяния нейтронов свободными протонами при нулевой
энергии, а также данные по рассеянию нейтронов при нулевой
энергии на параводороде, найдем длины рассеяния at и щ:
at = (5,42+0,01)10 ^l3u«; os = ^(23,71+0,01)-10~13cm. (1.56)
Заметим, что отрицательный знак длины рассеяния as указывает
на отсутствие связанного синглетного состояния у системы нейт-
рон — протон. Зная длину рассеяния в триплетном состоянии at
и энергию связи дейтрона, можно с учетом равенства (1.53) с высо-
кой степенью точности определить эффективный радиус в триплет-
ном состоянии:
г0/= (1,76±0,01) • 1(Г13с.и. (1.57)
Используя экспериментальную зависимость усредненного сече-
ния рассеяния медленных нейтронов свободными протонами от
энергии нейтрона, находим эффективный радиус в синглетном со-
стоянии:
rOs = (2,70+0,09) 10-|;1сЯ. (1.58)
При определении rgs погрешность оказывается значительно больше
погрешности определения гм.
Параметр формы. Как мы уже отмечали, соотношение (1.51)
представляет собой два первых члена разложения fectgS в ряд по
степеням А2, причем коэффициенты этого разложения не зависят
от детальной формы ядерного потенциала- Следующие члены раз-
ложения k ctg 6 по степеням ft3 зависят от формы потенциала, по-
этому, сравнивая экспериментальные данные по рассеянию мед-
ленных нейтронов протонами с теоретической формулой для се-
чения рассеяния, в которой учитываются следующие члены разло-
жения в (1.46), можно получить сведения о форме потенциала.
Разложение k ctg 6 с учетом членов, пропорциональных А4, имеет
вид
fcctg6 = —1/а + (1/2)й2г0 —Pfc4rS+..., (1.59)
20
где
Безразмерная величина Р называется параметром ф о р -
м ы, так как она связана с формой ядерного потенциала V (г).
Для характеристики потенциалов различной формы обычно
вводят параметр глубины потенциала s и характеристический ра-
диус Ь\ с помощью этих параметров сравнивают потенциалы раз-
личной формы. Параметр глубины потенциала s
определяется как число, на которое следует разделить потенциал
V (г), чтобы уменьшить энергию связи основного состояния системы
до нуля. Если параметр глубины s > 1, то потенциал V (г) допус-
кает связанное состояние, если же s < 1, то потенциал V (г) не
приводит к связанному состоянию. Характеристичес-
кий радиус потенциала £> определяется как эффектиг•
ный радиус приведенного потенциала V (г)/$ (соответствующего
нулевой энергии связи), т. е.
6 = limr0, (1.61)
s 1
где г0 определяется выражением (1.50). Для прямоугольной ямы
характеристический радиус совпадает с обычным радиусом ямы
1 а 4 „
Ъ = г0, а параметр глубины определяется выражением s = ^-Х
,, МУа
А '0-
£ /.5. РАССЕЯНИЕ МЕДЛЕННЫХ НЕЙТРОНОВ
В МОЛЕКУЛЯРНОМ ВОДОРОДЕ
Псевдопотенциал. Амплитуда рассеяния медленного нейтрона
протоном зависит от спинового состояния системы нейтрон — про-
тон. Так как в сечение упругого рассеяния нейтрона свободным
протоном входят квадраты длин рассеяния at и as, то из опытов
по рассеянию нейтронов свободными протонами можно найти
только абсолютные значения величин at и а,,. На практике обычно
приходится иметь дело с рассеянием нейтронов в веществах, содер-
жащих водород. Очевидно, протоны можно считать свободными
только в том случае, если энергия нейтронов значительно превос-
ходит энергию связи протонов в молекулах вещества. Если же энер-
гия нейтронов сравнима с энергией связи протонов или меньше ее,
то на рассеянии будет существенно сказываться химическая связь
протонов.
Знак длины рассеяния в синглетном состоянии as можно опре-
делить, изучая рассеяние медленных нейтронов в молекулярном
водороде 15]. Если длина волны нейтрона сравнима с расстоянием
между протонами, образующими молекулу, или велика по сравне-
21
нию с этим расстоянием, то при рассеянии нейтрона обоими прото-
нами имеют место интерференционные явления, исследование ко-
торых позволяет определить как абсолютные значения, так и знаки
длин рассеяния.
Рассеяние медленных нейтронов свободными протонами
сферически симметрично и определяется при k 0 постоянной
длиной рассеяния а. Эти свойства рассеяния медленных нейтронов
протонами можно формально описать с помощью своеобразной
теории возмущений, если ввести некоторый фиктивный потенциал,
приводящий при использовании теории возмущений к правильному
значению амплитуды рассеяния.
В случае достаточно медленных нейтронов (когда X г0) можно
воспользоваться приближением нулевого радиуса действия, т. е.
считать, что взаимодействие между нейтроном и протоном сущест-
вует только при совпадении их координат (контактное взаимодей-
ствие). Такое приближение соответствует выбору потенциала
в виде дельта-функции [61:
V (г) = (2лЛ3/р) а6 (г), г =гп —rp, (1.62)
где гп и гр — радиусы-векторы нейтрона и протона, а коэффициент
при дельта-функции найден из требования, чтобы амплитуда рас-
сеяния в первом приближении теории возмущений по (1.62) с точ-
ностью до знака совпадала с длиной рассеяния / = —а (р — при-
веденная масса нейтрона и протона). Различным приближениям
теории возмущений по (1.62) при учете эффектов химической связи
соответствуют различные степени отношения длины рассеяния а
к молекулярным размерам d или к длине волны нейтрона X. По-
этому условие применимости (1.62) запишем в виде а d и а X.
Кроме того, чтобы не учитывать конечный рациус действия ядерных
сил, должно выполняться следующее условие: r0 С d и r0 X.
Рассеяние медленных нейтронов в молекулярном водороде
можно исследовать с помощью псевдопотенциала (1.62), если пред-
варительно учесть в нем зависимость а от спинового состояния
взаимодействующих частиц. Введем для описания спинов нейтрона
и протона матрицы Паули <гп и <гр. Суммарный спин системы нейт-
рон — протон равен
S=(l/2)K + <rp).
Как нетрудно проверить, собственные значения оператора
в триплетном и синглетном состояниях соответственно равны
1 и —3. Поэтому величины
л, = (1/4)(3 + опоД яа=(1/4)(1-ц„ор) (1.63)
можно рассматривать как проекционные операторы, выделяющие
триплетное и синглетное состояния. Действительно, собственные
значения этих операторов равны
fl, S = 1, fО, S = 1,
[0, 5=0; И 1, 5 = 0.
22
Длину рассеяния, учитывающую спиновую зависимость ядерных
сил, можно представить с помощью проекционных операторов
в виде
a =atat-[-aant =
= (1 /4) (За, + ав) + (1 /4) (а, - а,) ап 0р. (1.64)
Если рассматривать рассеяние медленных нейтронов системой про-
тонов, то в качестве потенциала следует брать сумму выражений
типа (1.62)
1/-2(2лА2/[х)а^6(гп—г,), (1.65)
i
где г, — радиус-вектор г-го протона и — длина рассеяния нейт-
рона i-м протоном. Эта величина зависит от спинового состояния
рассеиваемого нейтрона и t-ro протона. В случае рассеяния медлен-
ных нейтронов в молекулярном водороде энергию взаимодействия
нейтрона с молекулой можно записать в виде
V = (лй2/2р) [За, + аа + (а,—ав) <rn oj 6 (rn—rt) +
+ (лй2/2р) [За, + as + (а,—as) <тп оs[ 6 (гп—ге), (1.66)
где индексы 1 и 2 соответствуют двум протонам молекулы.
Упругое рассеяние медленных нейтронов в пара- и ортоводороде.
Введем суммарный спин молекулы S = (1/2)(<тг + о2). Квантовое
число квадрата спинового момента молекулы 5 может принимать
два значения 5 = 0 и 5 = 1. Если 5 = 0, то соответствующее
состояние называется пар аводородом; при 5 = 1 состоя-
ние называется ортоводородом. Выделим в энергии взаимо-
действия нейтрона с молекулой (1.66) симметричную и антисиммет-
ричную части V = Кс + Ка, где
Vc = (л62/2р) [За, 4- as 4- (at—afi) а„ S] [6 (rn — г,) 4- & (rn—ra>],
Уа = (яй2/4р) (а,—aj an (<rx—a2) [6 [r„ — rx)—S (rn — r2)[. (1.67)
Очевидно, симметричная часть энергии взаимодействия Vc от-
ветственна за переходы, при которых спиновая симметрия молеку-
лы не изменяется, иными словами, Кс обусловливает переходы па-
раводорода в параводород и ортоводорода в ортоводород. Антисим-
метричная часть Ка вызывает переходы с изменением симметрии
молекулы, т. е. переходы ортоводорода в параводород и обратно.
Рассмотрим рассеяние медленных нейтронов в предельном слу-
чае, когда длина волны нейтрона X значительно больше среднего
расстояния между протонами в молекуле d. (Среднее расстояние меж-
ду протонами молекулы водорода в состоянии равновесия порядка
0,75-Ю-8 см.) В этом случае можно пренебречь различием в поло-
жениях обоих протонов и считать их находящимися в одной точке.
Поэтому при X d антисимметричная часть энергии взаимодейст-
вия Уа обращается в нуль и остается только симметричная часть
Vc. В этом случае, очевидно, возможно только упругое рассеяние
23
нейтронов, так как I-',. не зависит от относительных координат про-
тонов, и матричные элементы 7С, соответствующие неупругим про-
цессам, в силу ортогональности волновых функций молекулы будут
равны нулю.
Сравнивая соотношение (1.67) с (1.62), нетрудно установить,
что амплитуда упругого рассеяния медленного нейтрона молеку-
лой водорода при X 3> d равна
А (1 / 2) [За(+ а, -}- (а, - as) а„ S]. (1.68)
В этом случае сечение рассеяния медленных нейтронов молекулой
водорода определяется формулой
о = 4л (р/р)21А |2, (1.69)
где р — 2Л4/3 — приведенная масса нейтрона и молекулы водо-
рода; р = 44/2 — приведенная масса нейтрона и протона; черта
над квадратом модуля амплитуды рассеяния означает усреднение
по ориентациям спина рассеиваемого нейтрона.
Замечая, что а (о,, S)'z--S (S (-1). находим
ИР =41/4) {(За, +as)2 фЗ (S ф 1) (а, -а,)2}.
Следовательно, сечение упругого рассеяния медленного нейтрона
равно
о = (16/9) п {(За, + щ)2 + S (S ф1) (а, - а,)*}. (1.70)
Полагая в этой формуле S = 0 и S = 1, получаем значения сече-
ний упругого рассеяния медленных нейтронов в пара- и ортоводо-
роде:
<*пара = (16/9) л (За,фая)2,
tfop.ro = (16/9) л {(За, ф щф ф 2 (fl/ -фф}.
Сечение упругого рассеяния в параводороде <тпара содержит
комбинацию (3ctt Ф as)2, в сечение Ф,рт0 помимо этой величины
входит еще и величина (а, — а3)2. Из опытов по рассеянию медлен-
ных нейтронов в пара- и ортоводороде можно, следовательно, оп-
ределить величины |Зй, ф о5| и |а, — as|, т. е. определить абсо-
лютные значения at и й8 и знак отношения а,/а8.
Основное состояние молекулы водорода — это парасостояние.
Изучая рассеяние нейтронов нулевой энергии на молекулах пара-
водорода, можно определить, согласно соотношению (1.71), вели-
чину |3а, + аф Используя экспериментальное значение усреднен-
ного сечения рассеяния нейтронов нулевой энергии на свободных
протонах и тот факт, что связанное состояние системы нейтрон —
протон — это триплетное состояние, нетрудно найти значения для
а, и а. (см. § 1.4).
(1-71)
24
$ 1.6. РАССЕЯНИЕ ПРОТОНОВ ПРОТОНАМИ
Кулоновское рассеяние. Важные данные о характере ядерных
сил дает изучение рассеяния протонов протонами. Так как протоны
обладают электрическим зарядом, то при рассмотрении рассеяния
протонов протонами кроме ядерного взаимодействия необходимо
учитывать также кулоновское взаимодействие между протонами.
Волновая функция ф (г), описывающая относительное движение
двух протонов, удовлетворяет уравнению Шредингера
| — (Й2/Л4) А (е2.'г) 4 И (г) —£} ф (г) = О, (1.72)
где (е2/г) — энергия кулоновского взаимодействия; V (г) — потен-
циал ядерного взаимодействия; Е — энергия относительного дви-
жения протонов (£>0). В случае рассеяния задача заключается
в нахождении асимптотического вида функции ф (г) при больших
значениях г. Раскладывая волновую функцию ф (г) по полиномам
Лежандра Pi (cos (ft — угол между волновым вектором падаю-
щего протона к и радиусом-вектором г)
ф(г)=2^^(со5^- о-73)
г
для нахождения радиальной функции ц, (г), отвечающей моменту
относительного движения I, получаем следующее уравнение:
"I V «р=0, (1.74)
г2 г № J
где £ = e2/tlv — так называемый кулоновский пара-
метр (а — скорость относительного движения протонов). Если
бы ядерное взаимодействие протонов отсутствовало, т. е. V (г) = О,
то асимптотика решения уравнения (1.74) имела бы вид
е”1/ /
— sin kr—Е, In 2kr—
k \
r->- oo , (1.75)
гДе т]; —кулоновская фаза рассеяния, определяемая ра-
венством
егщ; =
ГG4-1 — ф '
Используя соотношение (1.75), можно показать, что волновая
функция ф (г) в пренебрежении ядерным взаимодействием при
г -> оо имеет вид
фс(г) —>-e'*z+‘£In k 4-fc (&) ---, г—> оо, (1.76)
г
где fc("&)—кулоновская амплитуда рассеяния,
fc W 2(2/ + 1 *(1 ~ e2I’1') Pl (COS =
25
e e-l£ In sin> (Ф/2)+2‘Ч.+!я (1.77)
Mu2 sin2 (Э/2)
(ft—угол рассеяния в системе центра инерции протонов).
Выражение для амплитуды рассеяния (1.77) не учитывает тож-
дественность протонов. Так как протоны обладают спином, равным
1/2, то в силу принципа Паули полная волновая функция системы
двух протонов должна быть антисимметричной. Пространственная
часть полной волновой функции при суммарном спине протонов
S = 0 связана с функцией ф (г), которая определяется разложе-
нием (1.73), соотношением фс (г) = Ф (г) + Ф (~r). S = 0 и при
суммарном спине S = 1 соотношением фа (г) = ф (г) — ф (—г),
5 = 1. Так как замена г ——г соответствует замене ft —>- л — ft,
то амплитуды рассеяния в синглетном (S — 0) и триплетном (5 =
= 1) состояниях связаны с амплитудой / (ft), вычисленной без уче-
та принципа Паули, соотношениями
m=fW+f(«-fl). = &-&). (1.78)
Усредненное дифференциальное сечение рассеяния протона про-
тоном в этом случае определяется формулой
о (ft) = (1 /4) | (ft) Р + (3/4) ] ft (ft) (1.79)
где коэффициенты 1/4 и 3/4 характеризуют вес синглетного и
триплетного состояний.
Используя формулу (1.77) для амплитуды f (ft) и учитывая
(1.78) и (1.79), получаем следующее выражение для дифференци-
ального сечения рассеяния . протона протоном в пренебрежении
ядерным взаимодействием:
„ ,в) = /^_у(_±__ + _!-----------------. (L80)
V Alt? / (sin4 (П/2) cos4 (-0/2) sin2 (Э/2) cos2 (ft/2) J
Первое слагаемое в (1.80) определяет число протонов, рассеянных
на угол ft; второе определяет число протонов отдачи, движущихся
под углом ft к первоначальному пучку; последнее слагаемое описы-
вает квантовомеханический эффект обмена сталкивающихся про-
тонов.
Опыты по рассеянию протонов протонами показали, что фор-
мула (1.80) неправильно описывает рассеяние протонов. Наблюдае-
мое на опыте число протонов, рассеянных под углом 90° при энер-
гиях порядка 1 Мэе, в несколько раз превосходит их число, опре-
деляемое по формуле (1.80). Следовательно, между протонами
кроме кулоновских сил действуют еще дополнительные ядерные,
причем их величина значительно превосходит силы электричес-
кого взаимодействия.
Рассеяние протонов протонами с учетом ядерного взаимодейст-
вия. Предположим, что ядерные силы, действующие между про-
тонами, так же как и силы, действующие между нейтронами и про-
тонами, характеризуются очень малым радиусом действия. В этом
26
случае ядерное взаимодействие проявляется только в состояниях
с малыми значениями относительного момента I. Если длина волны
превосходит радиус действия ядерных сил, то ядерное взаимодейст-
вие имеет место только в S-состоянии (Z = 0).
Амплитуда рассеяния протона протоном при наличии ядерного
взаимодействия определяется формулой (без учета принципа Пау-
ли)
f(^)=(i/2fe)2(2Z + l) {1—е21(п'+в')}Л(соз^), (1.81)
i
где бг- добавочная фаза рассеяния в состоянии с моментом I,
обусловленная ядерным взаимодействием протонов. Используя для
амплитуды кулоновского рассеяния fc (&) выражение (1.77), пере-
пишем формулу (1.81) в виде
f (fl) =fc (fl) + (i/2Jfe) 2 (2/ + I) e2il|; (1 — e2i®0 P, (cos fl). (1.82)
i
Если энергия падающего протона меньше 10 Мэв, то все фазы 6г,
кроме б0, можно считать равными нулю. В этом случае амплитуда
рассеяния, учитывающая ядерное взаимодействие только в S-со-
стоянии, определяется формулой
f (fl) = (fl) + (1 /*) sin 6eie+2ifi« (1.83)
(в дальнейшем будем опускать индекс 0 при б).
Соотношения (1.78), очевидно, справедливы как при чисто ку-
лоновском рассеянии, так и при рассеянии с учетом ядерного взаи-
модействия. В соответствии с (1.78) нетрудно получить следующие
выражения для амплитуды рассеяния протонов в синглетном и
триплетном состояниях:
е2 СР—is In sin* (0/2) р—i£ In cos* (0/2)
fs (fl) =---- 5----------------------P e----------------
sin2 (»/2) cos3 (8/2)
—— sin 6eift] e2it,"+iJ',
E J
e2 fp—In sin* (0/2) — i| in cos’ (0/2))
ft (fl) = — c-------------------------!------------------ e2 ith-нл.
Aly2) sin2 (8/2) cos3 (9/2) J
(1.84)
Как видно, ядерное взаимодействие при малых энергиях протонов
проявляется только в синглетном состоянии.
Усредненное по спиновым состояниям сечение рассеяния про-
тона протоном с учетом ядерного взаимодействия в S-состоянии
имеет вид
а (О) = (' V f 1 i 1 cos Е In tg3 (&/2)
V ’ {Mu* ' (sin4 (9/2) 'cos* (8/2) sin3 (8/2) cos3 (8/2)
___?_ sjn g Г cos [6 + ^ in sin3 (8/2)] cos IncoS3 (»/2)H 4 . a
5 [ sin3 (8/2j cos3 (8/2) J "Г Г’ J ’
(1.85)
27
В это выражение входит интерференционное слагаемое, пропор-
циональное sin 6. Поэтому сравнение экспериментальных данных
по рассеянию протонов протонами с теоретической формулой (1.85)
позволяет определить не только величину, но и знак фазы рассея-
ния 6. Положительный знак фазы рассеяния соответствует силам
притяжения, а отрицательный — силам отталкивания. Результаты
опыта показывают, что фаза 6 положительна, т. е. между протонами
в S-состоянии (I = 0) действуют ядерные силы притяжения.
Дифференциальное сечение рассеяния протона протоном (1.85)
симметрично относительно угла 90э в системе центра инерции.
В области малых углов преобладает кулоновское рассеяние. Интер-
ференция между ядерным и кулоновским рассеянием носит отри-
цательный характер, так как ядерные силы — это силы притяжения,
а кулоновские — силы отталкивания. Поэтому в области углов,
где начинает проявляться ядерное рассеяние, возникает характер-
ный интерференционный минимум. При больших углах преобла-
дает ядерное рассеяние.
Длина рассеяния и эффективный радиус. Так же, как и в случае
рассеяния нейтрона на протоне, в случае рассеяния протона на
протоне можно определить длину рассеяния и эффективный ра-
диус. Запишем уравнение для радиальной функции двух протонов
и и0 с учетом ядерного и кулоновского взаимодействий:
—(2U/r) и V (г) и = —k*u. (1.86)
Наряду с функцией и введем в рассмотрение функцию и, асимпто-
тически совпадающую при больших г с и и являющуюся решением
уравнения
и'1 — №,klr)v=i— &v. (1.87)
Уравнение (1.87) имеет два линейно независимых решения:
одно регулярное (обращающееся в нуль при г = 0) и другое нере-
гулярное в точке г — 0. Обозначим эти решения через F и G; на
больших расстояниях г оо они имеют следующий вид:
F (г) sin (kr—J; In 2kr -j-1)0), 1
G (r)-> —cos (kr — I in 2kr + i]0). |
При малых значениях г справедливы разложения
F (г) w Ckr,
G (г) ^-(1/С) (1 -Н[In (г/р) +h ф + 2у- 1]1,
I Р I
(1.89)
где
2-Ч ft2
С2 =------s; р =----------•
Me"
In Е—у;
у = 0,57722 — постоянная Эйлера.
28
Найдем решение уравнения (1.87), имеющее при больших г
такую же асимптотику, как и функция и, являющаяся решением
уравнения (1.86), т. е. v ~ sin (kr — S In 2kr + 1]O + 6), где 5 —
фаза, обусловленная ядерным взаимодействием. При этом норми-
руем функции и и и таким образом, чтобы и(0) = 1. Нетрудно по-
казать, что искомое решение v можно выразить через функции F и
G следующим образом:
o(r)=C{ctg6F(r) — G(r)|. (1.90)
Поступая далее так же, как и при выводе (1.44), получаем ана-
логичное соотношение
[v' (г) — (r)b->o j dr (vov— uou), . (1.91)
0
где функции u0 и r>0 соответствуют нулевой энергии.
Согласно соотношениям (1.90) и (1.89), при малых значениях г
имеем
V1 (г) = (1/р){1п(г/р) + 2у-!-К(Л)}, (1.92)
где введено обозначение
K(£)snctg6/(e2^-l)+A (Е). (1.93)
Величина (1/р)К (k) в случае взаимодействия двух протонов
играет такую же роль, как и k ctg 6 в случае взаимодействия нейтро-
на с протоном. Эта величина имеет простой физический смысл. Пер-
вое слагаемое, входящее в функцию (l/p)K (k), представляет
собой величину k ctg б, умноженную на проницаемость кулонов-
ского барьера С1. Второе слагаемое, входящее в (l/p)/f (k), учиты-
вает бесконечный радиус кулоновского взаимодействия.
Используя (1.92), представим соотношение (1.91) в виде
(1/р)К(£) = - (1/ар) + (1/2)Л2г(0, £), (1.94)
где
-(1/а ) = (l/p)]jm/<(&), (1.95)
г(0, £) = 2 | dr (ц0 v—иои). (1-96)
о
Величину ар, не зависящую от энергии протонов, можно наз-
вать длиной рассеяния протона протоном.
Величина г (0, Е) учитывает конечность радиуса действия ядер-
ных сил между двумя протонами и вводится точно так же, как и
в случае взаимодействия нейтрона и протона. Значение г (0, Е)
при нулевой энергии протонов обычно называют эффектив-
29
и ы м радиусом действия ядерных сили обозна-
чают гор:
со
гор = 2 J dr (о* — ц3). (1.97)
о
Заменяя в случае малых энергий в формуле (1.94) г (0, £) на гйр,
получаем соотношение (7]
(1/р)К(Аг) =—(1/ар) + (1/2)А?®/-0₽, (1.98)
определяющее зависимость фазы 6 от энергии протонов в прибли-
жении, не зависящем от формы потенциала. [Функция Д (k) свя-
зана с фазой рассеяния § соотношением (1.93).! Из формулы (1.98)
Рис. 1.2. Экспериментальная зависимость значе-
ний (1/р)Д («) от энергии протонов. Прямая ли-
ния соответствует приближению, не зависящему
от формы потенциала.
следует, что если построить зависимость функции K(k) от энергии
или k\ то получится прямая линия, определяющая два параметра:
длину рассеяния ар и эффективный радиус действия гор. Эти пара-
метры, характеризующие ядерное взаимодействие протонов в об-
ласти малых энергий, можно найти из экспериментальных данных
о фазе 6 как функции энергии.
Сечение рассеяния протонов протонами измерялось в широком
интервале энергий. На рис. 1.2 представлены экспериментально
полученные значения величины (1/р)Д (k) в зависимости от энергии
протонов. Видим, что в области малых энергий действительно имеет
место линейная зависимость Д (А) от энергии в соответствии с фор-
мулой (1.98). Сравнение экспериментальных данных с формулой
(1.98) приводит к следующим значениям для длины рассеяния ар
и эффективного радиуса гар:
ар = (—-7,83 ± 0,01) -10-13 щи, гйр = (2,79 ± 0,02) 10~13 см. (1.99)
30
ч
Отрицательный знак длины рассеяния протона протоном ар озна-
чает, что связанное состояние системы двух протонов невозможно.
Интересно сравнить параметры гор и ар, характеризующие
ядерное взаимодействие двух протонов, с параметрами rOs и ав,
характеризующими ядерное взаимодействие между нейтроном и
протоном в синглетном состоянии. Значения эффективных радиу-
сов действия ядерных сил между двумя протонами и нейтроном и
протоном в синглетном состоянии гор и rOs совпадают в пределах
погрешностей эксперимента.
Длину рассеяния протона протоном ар и длину рассеяния нейт-
рона протоном в синглетном состоянии а3 непосредственно сравни-
вать нельзя. Для возможности их сравнения необходимо исключить
влияние кулоновского взаимодействия на длину рассеяния ар.
Так как в области действия ядерных сил кулоновские силы пред-
ставляют собой малое возмущение, то можно получить 18] прибли-
женное соотношение между длиной рассеяния протона протоном
ар и эквивалентной длиной рассеяния протона протоном при от-
сутствии кулоновских сил ар':
(1/й;) = (1/ар)+(1/р)[1п(р/гОр)-(1/3)].
Подставив экспериментальные значения величин ар и гор, найдем
= ( —17,2 ± 0,1) • 10-13 см. (1.100)
Эта величина в пределах экспериментальных погрешностей нахо-
дится в соответствии с длиной рассеяния нейтрона протоном в синг-
летном состоянии (1.56). Поэтому можно считать, что ядерное взаи-
модействие между нейтроном и протоном в синглетном состоянии
такое же, как и между двумя протонами.
§ 13. НЕЦЕНТРАЛЬНЫЕ ЯДЕРНЫЕ СИЛЫ
Потенциал нецентральных сил. Наше предыдущее рассмотре-
ние основывалось на допущении о центральном характере ядер-
ных сил, что позволило объяснить некоторые свойства системы
двух нуклонов, в частности энергию связи дейтрона и рассеяние
нейтронов и протонов при малых энергиях. Наличие электричес-
кого квадрупольного момента и неаддитивность магнитных момен-
тов нейтрона и протона в дейтроне, однако, указывают на прибли-
женный характер такого допущения. Действительно, в случае
центральных сил основным состоянием дейтрона должно быть
S-состояние, описываемое сферически симметричной волновой
функцией. Присутствие электрического квадрупольного момента
и неаддитивность магнитных моментов частиц в дейтроне означают,
что основное состояние дейтрона не является чистым 3-состоянием,
а представляет собой суперпозицию S-состояния и состояний с от-
личными от нуля моментами, приводящими к нарушению сфери-
ческой симметрии в распределении заряда и к появлению добавоч-
ного магнитного момента. Такое сложное основное состояние воз-
31
можно только в том случае, если взаимодействие между частицами
не является чисто центральным. Это означает, что ядерное взаи-
модействие между нейтроном и протоном должно описываться по-
тенциалом, зависящим не только от расстояния между частицами,
но и от ориентации спинов частиц по отношению к относительному
радиусу-вектору. Учет таких нецентральных или тензорных сил
позволяет объяснить существование электрического квадруполь-
ного момента и добавочного магнитного момента в дейтроне.
Выясним прежде всего, какой вид имеет потенциал ядерного
взаимодействия при наличии нецентральных сил. В случае малых
скоростей нуклонов, рассмотрением которого мы здесь ограни-
чимся, потенциал ядерного взаимодействия двух нуклонов зависит,
очевидно, от вектора относительного расстояния между нуклонами
г и двух векторов спинов нуклонов <гх и Потенциал ядерного
взаимодействия V инвариантен относительно вращений и отраже-
ний пространства, поэтому в потенциал V могут входить только
инвариантные комбинации, которые можно образовать из величин
г, о, и tf2. Так как матрицы Паули а удовлетворяют соотношениям
= 6г/ -г ky* <Ъ, (i’ i> k = x, у, z), (1.101)
то указанные инвариантные комбинации линейны относительно
Oj и <т2. При этом величины (naj и (па2), где п — единичный век-
тор в направлении г, не могут входить в выражение для потен-
циала в отдельности, так как а — псевдовектор, и поэтому произ-
ведения (nOi) и (псг2) не являются инвариантами и изменяют свой
знак при отражении координат. Отсюда следует, что в потенциал
V могут входить, и притом только линейно, следующие величины:
(oyoj и (tiOj) (nof2). Вместо (noj (по2) удобно ввести величину
S]2 =3 (ntfj (пст2) — («т^з), (1.102)
усредненное значение которой по направлениям вектора п равно
нулю.
Таким образом, потенциал ядерного взаимодействия между
двумя нуклонами можно представить в виде [9]
V = (И + У г (И (ffi «М + (г) S12, (1.103)
где И, (г), Уг (г) и (г) — некоторые функции, зависящие от
расстояния между частицами. Выражение (1.103) — наиболее об-
щее, если не учитывать обменный характер ядерных сил. Первое
слагаемое в формуле (1.103) описывает центральные силы, не зави-
сящие от спинов, второе слагаемое — центральные силы, завися-
щие от спинов, и третье слагаемое — тензорные силы.
Классификация состояний системы нейтрон — протон. Рас-
смотрим вопрос о классификации состоянии системы нейтрон —
протон, если взаимодействие между нейтроном и протоном описы-
вается потенциалом (1.103). Заметим, что потенциальная энергия
взаимодействия нейтрона и протона, определяемая формулой (1.103),
инвариантна по отношению к преобразованиям вращения и отра-
32
жения пространства, а также по отношению к перестановке спинов
обеих частиц.
С инвариантностью энергии взаимодействия по отношению
к вращениям связано сохранение полного момента количества дви-
жения всей системы, складывающегося из орбитального и спинового
моментов. Поэтому систему нейтрон — протон можно характеризо-
вать квантовыми числами и Л4, определяющими квадрат
полного момента и проекцию полного мо-
мента соответственно. Заметим, что орбитальный и спиновый
моменты в отдельности в общем случае не сохраняются, и поэтому
возможность классификации состояний системы по значениям орби-
тального момента отпадает.
С инвариантностью энергии взаимодействия по отношению к пре-
образованию отражения связано сохранение четности системы нейт-
рон — протон w.
Инвариантность энергии взаимодействия по отношению к пере-
становке спинов частиц позволяет разделить состояния системы
нейтрон — протон на симметричные и антисимметричные относи-
тельно спиновых переменных. Симметричные состояния являются
триплетными и соответствуют значению спина системы 5=1.
Антисимметричные состояния являются синглетными и соответст-
вуют значению спина 5 = 0. Следовательно, в системе нейтрон —
протон, описываемой потенциалом (1,103), сохраняется квадрат
суммарного спина частиц. В этом можно также убедиться, непосред-
ственно пгщверив, что оператор квадрата спина S2 коммутирует
с операторам^ (<Т1<г2) и 512. Для этого следует лишь заметить, что
операторы (<т, <т2) и 512 можно представить в виде
a1ff2=2Sa—3; 1
S12 = 6(nS)2—2Sa, J (L104)
где S — суммарный спин системы: S = 1/2 (<rx + <r2). Отметим,
однако, что проекция суммарного спина на ось z не является ин-
тегралом движения.
Итак, видим, что систему, состоящую из нейтрона и протона,
можно характеризовать заданием квантовых чисел 5, w и М.
Из (1.104) следует, что в синглетном состоянии 512 = 0; это
означает, что при 5 = 0 ядерные силы являются центральными.
Поэтому в синглетном состоянии сохраняется орбитальный момент
количества движения I и состояния с 5 = 0 можно классифициро-
вать по величине I. Триплетное состояние, характеризуемое опре-
деленным значением полного момента %, представляет собой супер-
позицию состояний со значениями Z, определяемыми правилами
сложения моментов. Например, триплетное состояние с = 1 —
это суперпозиция состояний 3SX, 3РХ и 3DX. Четность состояния
связана со значением орбитального момента соотношением w =
= (—1)'. Поэтому состояния с четными значениями I 35г и 3Dx и
2 Зак. 642
33
Т аблица 1.1
3е Синглеты Триплеты
четные нечетные четные [ нечетные
0 ^0 ^0
1 35j + aDi 8Р1
2 ^2 8Ра + Зг2
состояние с нечетным I *РХ характеризуются противоположной чет-
ностью.
В табл. 1.1 приведена классификация нескольких первых состоя-
ний системы нейтрон — протон.
Основное состояние дейтрона с учетом нецентральных сил-
Рассмотрим вопрос об основном состоянии дейтрона с учетом не-
центрального характера ядерных сил. Как следует из экспери-
ментальных данных, полный момент дейтрона fy = 1. С другой
стороны, в основном состояния безусловно присутствует S-состоя-
ние, так как квадрупольный момент сравнительно мал и, следова-
тельно, асимметрия в распределении заряда невелика. Поэтому ос-
новным состоянием дейтрона является триплетное состояние 8SX +
+ 3D1 (см. табл. 1.1). Четность этого состояния равна единице.
Таким образом, основное состояние дейтрона характеризуется
квантовыми числами $ — 1, S = l, w = 1 и представляет собой
суперпозицию S- и О-состояний.
Волновую функцию основного состояния дейтрона можно пред-
ставить в виде
V0=Vs4-Vn, (1.105)
где Vs и Vo описывают S- и D-состояния и являются произведения-
ми радиальных функций и функций, зависящих от угловых и спи-
новых переменных.
Волновую функцию которая зависит от угловых и спиновых
переменных и описывает состояние системы с полным моментом
и проекцией момента Л1, можно выразить через собственные функ-
ции орбитального и спинового моментов и Хзц:
= 2 (1.106)
где I и S—квантовые числа квадратов орбитального и спинового
моментов; т и ц—их проекции; (ZrnSp | #-7И)—коэффициент Клеб-
ша—Гордона. Поэтому функции Vs и Vd можно представить
в виде
Vs ^оиль Vo=^^2IIm, (1-107)
34
Где и и ti)—радиальные функций $- и ^-состояний. Функций
^опм и ^211м имеют вид
^011М=Уоо%1.М;
Уп.м=1/(з+'и;‘2+д,,г^1х.-.-
_ /НЩГаЬ1+
I/ а *0
+ ]Л-^(3--Л1)Пл-Хц.
I/ 4-5
(1.108}
(1.110)
Так как —это ортонормированные функции, то из условия
нормировки волновой функции основного состояния дейтрона
Jdr[4r0|B = l (1.109)
оо оо
вытекает соотношение J dr(ua4-w4) = 1. Величины ps —^druz и
' о о
оо
pD = J drw2 можно, очевидно, трактовать как вероятности нахож-
о
дения дейтрона в S- и D-состояниях (р5-|-рд = 1). Непосредствен-
ной проверкой нетрудно убедиться, что имеют место соотношения
512 0^01 1М = У8 ^211ЛП
512^2им = 1^8 ^онм — 2^2им,
поэтому волновую функцию дейтрона можно записать в виде (функ-
ция Рариты и Швингера)
w _ 1 (“О'), I ш(г)<г L, л пп
ч-----г “Tin • OxalXiAft
У 4л (Г У 8 г I
где XiM — спиновая функция системы с проекцией спина, совпадаю-
щей с проекцией полного момента дейтрона ЛГ.
Уравнение Шредингера для системы нейтрон — протон, нахо-
дящейся в триплетном состоянии с энергией £, имеет вид
{— <№!М) А + Vc + VT 512 — Е] Т = 0, (1.112)
где центральная Ус и тензорная Уг части потенциала, согласно
(1.103), равны Vc — Vi + V2> Vj- — Уз- Подставляя в уравнение
Шредингера (1.112) функцию Т в виде (1.105) и используя соотно-
2* 35
тения (1.116), нетрудно получить следующую систему связанных
дифференциальных уравнений для радиальных функций и и w:
М ar*
h2 (d^w 6 \ OT. ,, (1.113)
__—----------w I + Vc —2Vt w—Ew— —у 8 VTu.
M. \ dr2 r2 !
В уравнения (1.113) входят два потенциала, Vc (г) и V? (г), для
характеристики которых в области малых энергий необходимо за-
дать четыре параметра (эффективную глубину центрального по’
тенциала Vc, эффективную глубину тензорного потенциала V?
и радиусы действия этих потенциалов г0 и гт). Однако даже в про-
стейшем случае выбора потенциалов в виде прямоугольных ям ре-
шение системы (1.113) не удается найти в явном виде.
Вне области действия ядерных сил уравнения для радиальных
функций и и w разделяются. В этом случае для связанного состоя-
ния нейтрон — протон (£ = —е) решения имеют вид
и=Се~аг,
А _|-----L-.j е-аг,
аг (аг)® J
(1-114)
где а — 'р'/Ие/А, a С и С' — нормировочные коэффициенты.
Асимптотическое выражение для радиальной функции S-со-
стояния и справедливо на расстояниях г, превосходящих радиусы
действия как центральных, так и тензорных сил; асимптотическое
выражение для радиальной функции D-состояния w справедливо
при г > гт. Действительно, в первом уравнении можно отбросить
члены Vcu и Vrw только при г > г0 и г?. Во втором уравнении
членом Vcw можно пренебречь уже при г >> zy, так как он мал по
сравнению с центробежной энергией. При малых г радиальные
функции и и w ведут себя как и ~ г, w ~ г3, г -> 0. Функция ю
имеет резкий максимум при г г?, так как выражение (1.114)
для w убывает как 1/г2 при rT <z г <. 1/а. Поэтому в интеграл,
Сю
определяющий вес D-состояния, рд = fdrtw2 главный вклад вно-
о
сят расстояния г ~ г?.
Магнитный момент дейтрона. Наличие О-волны в основном
состоянии дейтрона приводит к существованию квадрупольного
момента дейтрона и отклонению магнитного момента дейтрона от
суммы магнитных моментов нейтрона и протона. Действительно,
из-за присутствия О-волны в основном состоянии нарушается сфе-
рическая симметрия в распределении заряда, что и приводит к по-
явлению квадрупольного момента. С орбитальным моментом дви-
жения связан магнитный момент, который и обусловливает откло-
нение магнитного момента дейтрона от суммы магнитных моментов
нейтрона и протона.
36
Оператор магнитного момента дейтрона ц (в ядерных магнето-
нах) можно представить в виде
Д =Hn«Tn + lxI,ffp + 1/3l> (1.115)
где рп и рр — магнитные моменты нейтрона и протона, 1 — момент
относительного движения. (Множитель 1/2 перед 1 учитывает тот
факт, что зарядом обладает только протон.) Введя суммарный
спин системы S, перепишем магнитный момент дейтрона р, в виде
Н (11» + НР) S + V2 (р;1 — рр) (оп — <Тр) + Ч21.
Замечая, что среднее значение оператора оп — о;> в основном со-
стоянии равно нулю, для эффективного значения р получаем сле-
дующее выражение:
—(Ип+Нр —^г)!. (1.116)
где J = 1 + S — оператор полного момента системы.
Так как орбитальный момент 1 не сохраняется, то для опре-
деления магнитного момента дейтрона, находящегося в состоянии
с определенным значением J, следует в формуле (1.116) заменить
вектор 1 его составляющей вдоль направления полного момента J:
, , (U) J= J2+P-S2 j
J2 2Г
В результате получим следующее выражение для составляющей
магнитного момента дейтрона вдоль полного момента J:
f ( . 1 \ J2 +I2- S2) , „ 117.
М=|ип + |*р — (^п + Нр—(1-П7)
Это выражение усредним по основному состоянию дейтрона. Так
как J2 и S2 являются интегралами движения, то
<s2> =S(S+1).
Учитывая, что основное состояние дейтрона представляет собой
суперпозицию S- и D-волн, веса которых равны ps и р&, для сред-
него значения квадрата орбитального момента 1® находим
<12)=0./д.+2-Зрр=6рп.
Проектируя вектор (1.117) на ось г и определяя среднее значение
этой величины для основного состояния дейтрона (3f- = S = 1)
при Л4 = #• = 1, получаем магнитный момент дейт-
рона
Ид = Нп + Ь — З4(к + Нр — 1/г)Ро- (1.118)
Формула (1.118) позволяет по экспериментальным значениям
магнитных моментов р„, рр и pd определить вес D-волны в основ-
37
йоМ состоянии дейтрона. Используя соотношения (1.1) и (1.3), для
веса D-волны в основном состоянии дейтрона получаем значение
рп==0,04. (1,119)
При выводе формулы (1.118) не учитывались релятивистские эффек'
ты, а также эффекты, связанные с обменными токами. Учет этих
поправок может изменить вес D-волны ро на величину порядка 0,02.
Квадрупольный момент дейтрона. В заключение рассмотрим
электрический квадрупольный момент дейтрона. Тензор квадру-
польного момента системы одинаковых зарядов определяется фор-
мулой
(1.120)
где г — радиус-вектор заряда; суммирование производится по
всем зарядам. Квадрупольный момент системы Q определяется как
среднее значение составляющей тензора Qtz в состоянии
где — полный момент системы. В случае дейтрона составляющая
квадрупольного момента равна
= 4. (Зга - г2) = г2 У2О(<0 (1-121)
множитель 1/4 связан с тем, что радиус-вектор протона гр равен
1/2 относительного радиуса-вектора г). Квадрупольный момент
дейтрона Q определяется как среднее значение (1.121) в основном
состоянии дейтрона (1.105):
Q = CF5, Q„¥s) + 2(Ts, (2гЛо) + (^, «Л-
Замечая, что первое слагаемое в этом выражении обращается
в нуль из-за сферической симметрии функции и пренебрегая
третьим слагаемым вследствие малого веса D-волны, для квадру-
польного момента дейтрона получаем выражение
Q»(/2/10)|drratfti). (1.122)
о
Т ак как под знаком интеграла в (1.122) содержится множител
г2, то область малых значений г вносит малый вклад в интеграль
и поэтому при оценке величины Q можно для радиальных функ,
ций воспользоваться асимптотическими выражениями (1.114), спра--
ведливыми вне области действия ядерных сил.
Следовательно,
Оо
q~¥1CC' + ± + (1.123)
10 J \ «г («')’/ 1/8 <х3 v ’
о г
Учитывая малость веса D-волны, нормировочный множитель
S-волны можно считать таким же, как и в случае центральных сил
С = у 4лС да; 2а. Воспользовавшись этим значением С, норми
38
ровочный множитель D-волны можно связать с величиной квад-
рупольного момента дейтрона:
С'^2а6'Ч>. (1.124)
Зная вес D-волны pD и величину квадрупольного момента Q,
оценим величину радиуса действия тензорных сил, Действитель-
сю
но, в интеграл pc = j drw2, определяющий вес D-волны, глав-
о
ный вклад вносят значения г вблизи гт. Считая вклады внутренней
и внешней областей одинаковыми, с помощью асимптотического вы-
ражения (1.114) для w нетрудно оценить величину pD при rra<g;i:
pD^2C'2Jdrfl+— + -^-Ve-2“^24^. (1.125)
J ar (ar)2 J г?
Подставляя в это соотношение pD = 0,04 и Q = 2,82-10_27 см2,
для радиуса действия тензорных ядерных сил получаем
гт~ 3-10-13 см. (1.126)
Согласно (1.125), малый вес D-волны при заданном значении квад-
рупольного момента Q несовместим с очень малым значением радиу-
са действия тензорных сил гг.
§ 1.8. ОБМЕННЫЕ СИЛЫ
Рассеяние нейтронов протонами при высоких энергиях и обмен-
ный характер ядерных сил. При рассмотрении рассеяния медлен-
ных нейтронов протонами мы предполагали, что ядерные силы опи-
сываются потенциалом, зависящим от вектора расстояния между
частицами и спинов частиц. Основываясь на таком предположении,
можно полностью объяснить основные закономерности рассеяния
нейтронов протонами в области малых энергий. Оказалось, что если
длина волны частиц порядка или больше радиуса действия ядер-
ных сил, то рассеяние совершенно нечувствительно к зависимости
взаимодействия от расстояния. Можно было ожидать, что с увели-
чением энергии взаимодействующих частиц удастся получить бо-
лее детальную информацию о радиальной зависимости ядерного
потенциала. В действительности же с помощью потенциала вида
(1.103) вообще невозможно объяснить угловую зависимость рассея-
ния нейтронов на протонах при высоких энергиях.
Действительно, если бы между нейтроном и протоном действо-
вали только силы, описываемые потенциалом (1.103), то при доста-
точно высоких энергиях в системе центра инерции большее число
нейтронов рассеивалось бы на малые углы, а протоны отдачи дви-
гадись бы в противоположном направлении (в лабораторной систе-
39
ме координат протоны двигались бы главным образом под прямым
углом к падающему пучку нейтронов). Между тем опыты по рас-
сеянию нейтронов протонами с энергиями, большими нескольких
десятков мегаэлектронвольт, показывают, что дифференциальное
сечение рассеяния нейтронов протонами в системе центра инерции
имеет максимум как в области малых углов рассеяния, так и в об-
ласти углов, близких к 180°. Для того чтобы объяснить такой
характер рассеяния, нужно предположить, что помимо сил, опи-
сываемых потенциалом (1.103), между нейтроном и протоном дейст-
вуют еще добавочные силы, которые связаны с обменом частиц. Эти
силы можно назвать обменными, в отличие от обычных необ-
менных сил. Покажем, что введением обменных сил можно объяс-
нить рост сечения рассеяния при высоких энергиях в области боль-
ших углов. Если энергия нейтрона превосходит эффективную энер-
гию ядерного взаимодействия нейтрона с протоном, то дифферен-
циальное сечение рассеяния нейтрона протоном в системе центра
инерции можно определить с помощью теории возмущений
(1Л27)
где ф (г) = е1кг и ф' (г) = е!к'г — волновые функции относитель-
ного движения до и после рассеяния (кик' — волновые векторы);
V — потенциал ядерного взаимодействия между частицами; do —
элемент телесного угла, внутри которого лежит волновой вектор
после рассеяния.
В случае обычных сил потенциал V является функцией радиу-
са-вектора г, поэтому дифференциальное сечение рассеяния имеет
вид
de = (Л4г/16лаЙ4)|рге5(к-к'5т V(r)j do. (1.128)
Интеграл, входящий в это выражение, заметно отличается от нуля,
если |к — к'| г0~= 2fein (Ф72)г0 < 2л, где О — угол рассеяния, г0 —
радиус действия ядерных сил. Таким образом, в случае обычных
сил рассеяние происходит в основном на углы "& < Л/г0, где X =
= 2n/fe— длина волны относительного движения. Для достаточно
высоких энергий X г0, поэтому < 1.
Рассмотрим теперь рассеяние в случае обменных сил. Потен-
циал V для обменных сил представим в виде
У = Р(Г)РГ, (1.129)
где Рг — оператор обмена частиц. Действие этого оператора на
функцию ф (г) сводится к замене г на —г:
Ргф(г)=ф(—г). (1.130)
Поэтому дифференциальное сечение рассеяния, которое обуслов-
лено обменными силами, характеризуемыми потенциалом (1.129),
определяется формулой
do =(Л42/16л2 Й4) | pre-1 <k + k'> rV (г) pdo. (1.131)
40
Это выражение существенно отлично от нуля, если |к + к'| < 2л.
Следовательно, в случае рассеяния под действием обменных сил
главную роль играют углы рассеяния, для которых величина
|к + к'] мала, т. е. углы рассеяния близки к 180°. Этот результат
легко понять, если считать, что и в случае обменных сил падающая
частица отклоняется на небольшой угол, но в процессе рассеяния
изменяется природа сталкивающихся частиц, т. е. нейтрон превра-
щается в протон, а протон — в нейтрон. Следовательно, распреде-
ление нейтронов при обменном рассеянии должно совпадать с рас-
пределением протонов отдачи при обычном рассеянии, и наоборот.
В общем случае рассеяния под действием обычных и обменных
сил дифференциальное сечение имеет два максимума, соответствую-
щие направлениям вперед и назад, относительная величина кото-
рых определяется весами обычных и обменных сил во взаимодей-
ствии между частицами. Экспериментальные данные по рассеянию
нейтронов протонами при энергиях в несколько десятков мегаэлект-
ронвольт показывают, что веса обычных и обменных сил примерно
одинаковы.
Согласно формулам (1.128) и (1.131), полученным с учетом тео-
рии возмущений, полное сечение рассеяния нейтрона протоном при
высоких энергиях должно быть обратно пропорциональным энер-
гии, независимо от характера ядерных сил.
Обменные операторы. В общем случае потенциал, характери-
зующий обменное взаимодействие двух частиц, представляется
в виде произведения некоторой функции, зависящей от координат
частиц, на обменный оператор, переставляющий координаты взаи-
модействующих частиц. Так как нейтроны и протоны кроме прост-
ранственных координат характеризуются еще и спиновыми коор-
динатами, то существуют различные возможности обмена, соответ-
ствующие различным видам обменных сил. Наряду с силами, при-
водящими к полному обмену координат взаимодействующих частиц,
могут существовать силы, связанные с обменом пространственных
или спиновых координат в отдельности. Обычно различные обмен-
ные силы называют по именам исследователей, которые их впервые
рассмотрели [11—13].
Пусть ф (гх, су; га, сг2) — волновая функция системы двух ча
стиц, зависящая от пространственных и спиновых координат ча-
стиц г1( оу и г2, о3. Очевидно, можно ввести три различных обмен-
ных оператора Рг, Р<, и Рг<}, действие которых на волновую функ-
цию сведется к перестановке пространственных координат, пере-
становке спиновых координат и одновременной перестановке прост-
ранственных и спиновых координат:
Л-Ф(П- *6 г2, о2)=ф(г2, оу; гп ст2); ’
ЛтфОл, оу; г2, С2)=ф(г1( оу; г2, С!);
Л-афОг, сх; Г2, <т2)=ф(г2, о2; гп oj. ,
(1.132)
41
Оператор Рг, переставляющий пространственные координаты ча-
стиц, обычно называют обменным оператором Майо-
рана; оператор Ра, переставляющий спиновые координаты ча-
стиц, называют обменным оператором Бартлет-
та и оператор Ргв, переставляющий как пространственные, так и
спиновые координаты частиц, называют обменным опера-
тором Гейзенберга. Очевидно, что
Рга=РгР^ (1.133)
pf=p2g=pfo^ 1. (1.134)
Согласно (1.134), обменные операторы Рг, Ро и Ргв имеют только
собственные значения ±1- Перестановка координат гх и г2 экви-
валентна перемене знака относительной координаты г = п — г2.
Поэтому для системы, состоящей из двух частиц, оператор Рг сов-
падает с оператором пространственной инверсии, и, следовательно,
собственные значения оператора Рг определяются величиной от-
носительного момента количества движения Z:
Л = (-1)г. (1.135)
Собственные значения оператора Ра определяются симметрией спи-
новой части волновой функции. Так как система двух нуклонов
может находиться либо в триплетном состоянии (5 = 1), которому
отвечает симметричная спиновая функция, либо в синглетном со-
стоянии (S = 0), которому отвечает антисимметричная спиновая
функция, то собственные значения Ра можно связать с величиной
суммарного спина системы 5:
Ря = (-l)s+i. (1.136)
Собственные значения оператора РгП определяются величинами I и S:
/>,„ = (-l)H-s+i. (1Д37)
Потенциал ядерного взаимодействия с учетом обменных сил.
С помощью введенных обменных операторов Рт, Ра и Рга нетрудно
найти общее выражение для потенциала ядерного взаимодействия
с учетом обменных сил. Согласно (1.103), потенциал ядерного взаи-
модействия в общем случае состоит из двух частей, описывающих
центральные и нецентральные силы. Потенциалы для центральных
обменных сил представляются в виде произведений операторов Рг,
Ро и Рга на некоторые функции, зависящие от расстояния между
частицами. Соответствующие обменные силы обычно называются
силами Майорана, Бартлетта и Гейзенберга. Необменные ядерные
силы, описываемые обычным центральным потенциалом, часто
называют силами Вигнера.
Нецентральные ядерные силы могут быть обменными и необ-
менными. Так как тензорный оператор S12 в синглетном состоянии
42
равен нулю, а оператор Р, в триплетном состоянии равен -Н,то
(1.138)
Поэтому возможен только один вид обменных тензорных сил—
тензорные силы Майорана. (Тензорные силы Гейзенберга, вслед-
ствие (1.138), сводятся к тензорным силам Майорана.)
Таким образом, потенциал ядерного взаимодействия между
двумя нуклонами с учетом обменного и нецентрального характе-
ра ядерных сил в самом общем случае можно записать в виде
У = V]F (г) + Vju (г) Рт + У в (г) Ро + Ун (г) Рга +
+ Vrw (г) -Т Утм (г) Six Рг, (1.139)
где V«z(r), Vai (г), Ув (г), Ун (г), Ут^г) и УТм (г)—функции,
зависящие от расстояния между частицами. Эти функции могут
различаться как по величине, так и по характеру зависимости
от расстояния. Заметим, что отдельно вводить в соотношение
(1.139) слагаемое, учитывающее спиновую зависимость цент-
ральных сил, нет необхидмости, так как такая зависимость
учитывается обменными слагаемыми.
Выражение для потенциала (1.139), полученное в соответ-
ствии с требованиями инвариантности относительно простран-
ственных вращений и отражений и симметрии относительно пе-
рестановки частиц, в общем случае содержит шесть функций V(r),
вид которых можно определить только из данных опыта. Однако
практически вопрос о нахождении вида функций V(r) до настоя-
щего времени остается открытым. Это в значительной степени
связано с тем обстоятельством, что ядерные явления в области
малых энергий очень слабо зависят от формы ядерного взаимо-
действия. Первоначальные надежды на возможность определе-
ния вида V(r) из опытов по рассеянию двух нуклонов в обла-
сти больших энергий также не увенчались успехом, посколько
само выражение (1.139) получено в статическом пределе.
Потенциал Сервера. Одним из простейших потенциалов, ко-
торый часто используется в расчетах, является так называемый
потенциал Сербера, включающий смесь сил Вигнера и Майора-
на с одинаковыми весами:
Vs-Vs (r)(l+Pr)/2. (1.140)
Так как в состояниях с нечетными значениями I величина Рг
равна —1, то взаимодействие, описываемое потенциалом (1.140),
проявляется только в четных состояниях. В силу этого потенци-
ал Сербера приводит к рассеянию, симметричному относительно
угла 90°. В действительности угловое распределение при рассея-
нии нейтронов протонами в области энергий порядка сотни ме-
гаэлектронвольт имеет асимметричный характ^п, что указывает
на взаимодействие и в нечетных состояниях. Однако это взаи-
модействие значительно слабее взаимодействия в четных со-
стояниях.
43
$ 1.9. ИЗОТОПИЧЕСКИЙ СПИН И ЗАРЯДОВАЯ НЕЗАВИСИМОСТЬ
ЯДЕРНОГО ВЗАИМОДЕЙСТВИЯ
Изотопический спин нуклона. Как мы уже отмечали, несмотря
на наличие электрического заряда у протона и отсутствие заряда
у нейтрона, нейтроны и протоны обладают очень сходными физи-
ческими свойствами. Это сходство проявляется уже в близости масс
нейтрона и протона; кроме того, нейтроны и протоны имеют оди-
наковый спин 1/2, подчиняются одинаковой статистике (статисти-
ке Ферми — Дирака); нейтрон и протон могут превращаться друг
в друга, поглощая мезон; нейтроны и протоны превращаются друг
в друга при p-распаде и т. д. Однако наиболее ярким проявлением
физического сходства между нейтроном и протоном является заря-
довая независимость их ядерного взаимодействия. Зарядовая неза-
висимость, или, как ее чаще называют, изотопическая
инвариантность, проявляется в том, что ядерное взаимо-
действие между любой парой частиц — нейтронов или протонов —
не зависит от природы частиц и определяется только состоянием,
в котором находится система.
Сходство физических свойств нейтрона и протона позволяет
рассматривать их как два различных состояния одной и той же ча-
стицы — нуклона. (Эти состояния различаются по величине за-
ряда.) Нуклон кроме пространственных и спиновой координат
характеризуется еще дополнительной степенью свободы — за-
рядовой координатой. Так как зарядовая координата
(различающая нейтронное и протонное состояния нуклона) при-
нимает .всего лишь два значения, то ей удобно сопоставить в неко-
тором фиктивном пространстве вектор t, по своим свойствам подоб-
ный вектору обычного спина 1/2. Вектор t называют изотопи-
ческим спином, или изоспином [II]. Введение
изотопического спина позволяет очень просто описать изотопиче-
скую инвариантность ядерного взаимодействия.
Абсолютная величина вектора изотопического спина t для ну-
клона равна 1/2, поэтому компоненты вектора t можно непосред-
ственно выразить через матрицы Паули т:
а именно
t = (l/2)r. (1.142)
Проекция изотопического спина нуклона на ось г может при-
нимать только два значения: v = ±1/2. Значение +1/2 условно
приписывается протону, а значение —1/2 — нейтрону. Обозначим
зарядовую или изоспиновую функцию нуклона £ (т), где т — за-
рядовая или изоспнновая координата. В качестве зарядовой коор-
динаты т можно выбрать значение проекции изоспина на ось г.
Волновые функции для состояний с определенными значениями
44
проекции изоспина в таком представлении имеют диагональный вид
t,v (т) = 6vt. Обычно изоспийовые функции, отвечающие протон-
ному и нейтронному состояниям, представляются в следующем виде:
С./2 = ( о), 1 )• (1-143)
Так как пространственные, спиновая и изоспиновая координаты
независимы, то для свободного нуклона полную волновую функ-
цию ф можно представить в виде произведения пространственной
<р, спиновой % и изоспиновой функций £:
ф(г,<г,т) = ф(г)%(сг)£(т). (1.144)
Введем проекционные операторы для нейтронного и протонного
состояний:
An = i/a(l-b), Лр = 73(1 + ^- (1-145)
Оператор Л„ оставляет неизменной нейтронную функцию и обра-
щает в нуль протонную функцию, действие оператора Ар противо-
положно действию Лп, С помощью проекционных операторов (1.145)
нетрудно построить операторы заряда, массы и магнитного момен-
та нуклона:
<7= Vs (1 + тг)е;
М - (1 —гг) Мп + */а (1 + тг) Мр-
И = Va (1 —Ъ) Н™ + Va (1 + +) Нр-
(1.146)
Операторы возникновения и исчезновения заряда т^. и т_ имеют вид
, . /о 1 X . , /О О X 1
т. = т„ + i-r, = I , т_ =тж—1т ?= ( , (1-147)
'“д \0 0 / z \1 0 /
причем оператор т_|_ переводит нейтрон в протон, а оператор т_—
протон в нейтрон.
Изотопический спин системы нуклонов. Изотопический спин
системы нуклонов складывается из изотопических спинов отдель-
ных частиц по правилам векторного сложения моментов. Оператор
изотопического спина системы А нуклонов равен
(1-148)
i=t
где tj — оператор изотопического спина отдельного нуклона. Соб-
ственные значения квадрата изотопического спина (1.148) равны
Т (Т + 1), где Т — полный изотопический спин
системы. Если А — четное, то Т может принимать значения
в интервале от 0 до Д/2; если А — нечетное, то Т принимает зна-
чения в интервале от 1/2 до А/2. Для каждого Т существует 27 + 1
собственных значений Tz, представляющих собой целые или полу-
целые числа в интервале — Т < Tz < Т.
45
Для ядра с атомным номером Z и массовым числом А, содержа-
щим Z протонов и W - Л —2 нейтрснов, проекция полного изо-
топического спина равна
Tz = i/t(Z^N)=Z~A/2. (1.149)
Абсолютная величина полного изотопического спина системы Т
в этом случае может быть равна одному из значений в интервале
iT'zl < Т < А/2. При заданном числе нуклонов Л величина Tz,
согласно (1.149), определяет полный заряд ядра. Так как заряд
сохраняется, то имеет место закон сохранения проекции изотопи-
ческого спина системы Тг.
Состояния системы из А нуклонов, отвечающие одному и тому
же значению изотопического спина Т, образуют изотопичес-
кий мультиплет. При заданном значении Т изотопический
мультиплет содержит 2Т + 1 составляющих. Эти составляющие раз-
личаются значениями проекции изотопического спина Тг, т. е.
соответствуют различным зарядам системы Z. Очевидно, пре-
дельные значения заряда для составляющих мультиплета равны
А/2 ± Т. В пренебрежении электромагнитным взаимодействием
составляющие мультиплета имеют одинаковую структуру и ха-
рактеризуются одинаковой энергией связи.
Так как нуклоны обладают спином, равным 1/2, то они подчи-
няются принципу Паули. Запишем полную волновую функцию
системы А нуклонов в виде
¥ (гх, oi, Tj; г2, оа, та;... ; Гд.сТд, тл),
где Г;, о; и т; — пространственная, спиновая и зарядовая коорди-
наты г-го нуклона соответственно. Тогда принцип Паули для ну-
клонов можно сформулировать следующим образом: волновая функ-
ция системы нуклонов должна быть антисимметричной по отноше-
нию к перестановке пространственных, спиновых и изоспиновых
координат любой пары нуклонов. Вследствие независимости изо-
спиновых координат нуклонов полную волновую функцию системы
нуклонов У всегда можно представить в виде произведения прост-
ранственно-спиновой функции Ф на изоспиновую функцию Z:
= Ф (rlt о,; г2, о3;... ;гд,од)2(-г1,т2,... ,тд). (1.150)
лимметрия изоспиновой функции Z однозначно определяется ве-
личиной изотопического спина системы Т. В силу принципа Паули
солная волновая функция V антисимметрична относительно пере-
становок координат любой пары нуклонов, поэтому функции Z
и Ф должны обладать противоположной (дуальной) симметрией.
Классификация состояний системы двух нуклонов. Рассмотрим
систему, состоящую из двух нуклонов. Так как изотопический
спин каждого нуклона равен 1/2, то полный изотопический спин
системы может принимать два значения: Т ₽= 1 и Т = 0. Поэтому
все состояния системы можно разделить на две группы: одна отве-
чает изотопическому спину Т ~ 1, другая — Т = 0.
46
В случае 7 = 1 возмойшы три различных значения проекции
изоспина; Тг = 1, 0 и —1. соответствующие состояния характе-
ризуются значениями заряда 2\е и 0 и отвечают системам, состоя-
щим из двух протонов, нейтрона\протона и двух нейтронов. Вол-
новые функции, описывающие указанные состояния, симметричны
и выражаются через изоспиновые одй^нуклонные функции (1.143):
^1,1 (т1> тг) — 51/2 Сч) 5i/a (^г);
Z1.O (Ti, т2) = (1//2 ){£1/2 (Tx)S_1/2 (т2) + е_1>2 (Т1) £ 1/2 (т3)}:
21,-1 (Т1, та)= S-1/2(b) S-l/2 (Ts).
(1.151)
Функции (1.151) нормированы на единицу.
В случае Т = 0 проекция изоспина = 0, Соответствующее
синглетное состояние описывается антисимметричной изоспиновой
функцией:
200(т1,т2)= (1//2 ){£1/2 (тхК-^-е-./г^) £i/2 (т2)}. (1.152)
Антисимметричное состояние (1.152) может осуществляться только
в системе, состоящей из нейтрона и протона. Функция (1.152) орто-
гональна функциям (1.151).
Полную волновую функцию системы двух нуклонов можно
представить в виде произведения пространственно-спиновой функ-
ции на изоспиновую:
wSTMTMT ~ (Г1» а1> Г2» °а) %ТМТ (Т1’ Т2)‘ U’ ^3)
Итак, состояние системы определено, если задан полный набор
квантовых чисел: четность ла, суммарный спин S, полный момент fy,
проекция полного момента М, полный изоспин Т и проекция изо-
спина Мт- В силу принципа Паули полная волновая функция
(1.153) должна быть антисимметричной относительно перестановки
нуклонов, т. е. относительно одновременной перестановки прост-
ранственных, спиновых и изоспиновых координат нуклонов. Сим-
метрия волновой функции Ф по отношению к перестановке прост-
ранственных координат определяется четностью состояния ли, а
симметрия по отношению к перестановке спиновых координат —
величиной спина S; симметрия изоспиновой функции Z по отноше-
нию к перестановке изоспиновых координат определяется величи-
ной изотопического спина системы Т. Поэтому в системе из двух
нуклонов четные синглетные и нечетные триплетные состояния
всегда симметричны относительно изоспиновых переменных
(Т = 1), а нечетные синглетные и четные триплетные состояния
всегда антисимметричны относительно изоспиновых переменных
(Т = 0). Отсюда следует, что в системах из двух одинаковых ну-
клонов могут реализоваться только четные синглетные и нечетные
триплетные состояния (поскольку изоспиновая функция должна
быть симметричной), в то время как в системах из двух различных
нуклонов могут реализоваться состояния любой четности и спина.
47
В табл. 1.2 приведена классификация состояний системы двух
нуклонов для jf = 0, 1,2,3, 4 и 5.
Таблица 1.2
д S = 0 S= 1
1 — четное 1 — нечетное 1 — четное l — нечетное
Т = 1 Т = 0 т = 0 Т - I
0 ^0 3Л>
1
2 *Рг + ’Г2
3 SD3 + 3G3 3?з
4 1О4 + 8Н 4
5 3g5 + 3/6 3/Л
Явный вид обменных операторов. Введенные при рассмотрении
обменных ядерных сил обменные операторы Майорана, Бартлетта
и Гейзенберга Рт, Ра и Рта можно просто выразить через опера-
торы спинов и изоспинов частиц. Оператор <т1<т2 характеризуется
собственными значениями +1 и —3 для триплетного (5 = 1) и
синглетного (S = 0) состояний. Поэтому оператор перестановки
спиновых координат двух нуклонов Ра можно представить в виде
?0 = (1/2)(l+<r1ff2). (1.154)
Действительно, оператор (1.154) характеризуется собственными
значениями +1 и —1 для триплетного и синглетного состояний,
поэтому (оу, — X (ff2, °i)- Формула (1.154) дает удобное
представление для обменного оператора Бартлетта.
Аналогично можно ввести оператор перестановки изоспиновых
координат двух нуклонов
Pt = V2 (1 + ti т2). (1.155)
Оператор Рх действует на изоспиновую функцию нуклонов
PXZ (т1? т2) = Z (т2, тх). Так как полная волновая функция систе-
мы двух нуклонов антисимметрична относительно перестановки
нуклонов, сводящейся к перестановке пространственных, спино-
вых и изоспиновых координат нуклонов, то
РгРаРх==_ 1. (1.156)
Используя это равенство и замечая, что Рх = 1, нетрудно полу-
чить следующее представление для обменного оператора Майорана:
Рг= — 1/а<1Н-<г1<га)(1 (1.157)
48
Вспоминая определение обменного оператора Гейзенберга
(1.133), нетрудно найти, что
Рг0 = -1/г(1 + т1т2), (1.158)
т. е. обменный оператор Гейзенберга Рта совпадает с точностью до
знака с оператором перестановки зарядовых координат частиц Рх.
Изотопическая инвариантность ядерного взаимодействия.
Формализм изотопического спина очень удобен для описания заря-
довой независимости или, как чаще говорят, изотопической инва-
риантности ядерного взаимодействия [14, 15]. Сформулируем по-
нятие изотопической инвариантности взаимодействия, используя
понятие изотопического спина частиц.
Согласно определению, изотопический спин является вектором
в некотором фиктивном пространстве. Абсолютная величина изо-
топического спина нуклона равна 1/2. Состояние с проекцией изо-
спина + 1/2 соответствует протону, состояние с проекцией изоспина
—1/2 — нейтрону. Переход от протона к нейтрону означает изме-
нение проекции изоспина (у +1/2 до —1/2. Поэтому такой переход
по аналогии с поворотами в обычном пространстве можно рассмат-
ривать как поворот в изотопическом пространстве на угол я вокруг
оси, перпендикулярной оси квантования. Если система состоит из
нескольких нуклонов, то их изотопические спины складываются
по правилам векторного сложения в полный изотопический спин
системы. В этом случае состояния системы, отвечающие определен-
ному значению полного изотопического спина, но различным зна-
чениям проекции изоспина, можно сопоставить с поворотами в изо-
топическом пространстве. Например, система, состоящая из двух
протонов, отличается от системы, состоящей из протона и нейт-
рона при Т = 1, поворотом в изотопическом пространстве на угол
л/2; система, состоящая из двух протонов, отличается от системы,
состоящей из двух нейтронов, поворотом в изотопическом прост-
ранстве на угол л и т. д. Очевидно, при таком подходе изотопичес-
кую инвариантность ядерного взаимодействия можно рассматри-
вать как свойство инвариантности относительно поворотов системы
в изотопическом пространстве.
Отметим, что зарядовую симметрию ядерного взаимодействия
(инвариантность относительно замены всех нейтронов протонами
и наоборот), являющуюся частным случаем изотопической инва-
риантности, можно рассматривать как инвариантность относитель-
но поворота в изотопическом пространстве на угол л вокруг оси,
перпендикулярной оси квантования.
Таким образом, изотопическая инвариантность ядерного взаи-
модействия означает, что взаимодействие не должно зависеть от
ориентации вектора изотопического спина системы Т. Следователь-
но, изотопическое пространство должно быть изотропным относи-
тельно ядерного взаимодействия.
Изотопическая инвариантность не имеет места для электромаг-
нитного взаимодействия. Действительно, электрический заряд и
49
магнитный момент системы определяются проекцией изотопическо-
го спина, поэтому электромагнитное взаимодействие также зави-
сит от проекции изотопического спина, которая не сохраняется при
поворотах в изотопическом пространстве.
Так как изотопический спин обладает свойствами, подобными
свойствам обычного момента количества движения, то из изотро-
пии изотопического пространства по отношению к ядерным взаи-
модействиям следует сохранение изотопического спина Т. Закон
сохранения изотопического спина системы Т в отличие от закона
сохранения проекции изотопического спина Т г, выражающего
закон сохранения заряда системы, является приближенным, так
как он справедлив только в пренебрежении электромагнитным
взаимодействием.
Покажем теперь, что найденный ранее из соображений инва-
риантности относительно пространственных вращений и прост-
ранственной инверсии потенциал, учитывающий нецентральный и
обменный характер ядерного взаимодействия, обладает свойством
изотопической инвариантности. Действительно, используя для об-
менных операторов выражения (1.154), (1.157) и (1.158), потен-
циал ядерного взаимодействия двух нуклонов (1.139) можно пред-
ставить в виде
V = Vc (г) + V, (г) (^ <та) + Vt (г) (тх т2) + (г) (а, <га) (тх т3) +
+ Ут (г) S12 + Vrt (г) Sn (Т1 та), (1.159)
где
Vc — Vif + Vs Vb—V» Vh—Vm‘,
Va = 1/aVB-1/iVM;
vt= -^Ун-1/^-,
Уо-^-^Ум-,
Ут = Vtw—1/a Vtm',
V’74 = —1/аУтм-
Выражение (1.159) инвариантно относительно поворотов в изо-
топическом пространстве. Следовательно, ядерное взаимодействие,
описываемое потенциалом (1.159), характеризуется свойством изо-
топической инвариантности, что означает сохранение величины изо-
топического спина системы Т. Согласно (1.159), ядерное взаимо-
действие зависит от квантовых чисел S и Т, т. е. от состояния, в ко-
тором находится система. Независимость (1.159) от величины про-
екции изоспина системы означает независимость взаимодействия
от природы нуклонов (т. е. от того, являются ли они протонами или
нейтронами).
Допущение об изотопической инвариантности ядерного взаи*
модействия согласуется с результатами опытов по рассеянию нук-
лонов на нуклонах при малых энергиях. Совпадение длин рассея-
ния и эффективных радиусов в случае рассеяния протона на про-
тоне и рассеяния нейтрона на протоне в синглетном состоянии сви-
50
детельствует о тождествен пости взаимодействия между двумя про-
тонами и взаимодействия между нейтроном и протоном в синглет-
ном состоянии.
£ 1.10. РАССЕЯНИЕ НУКЛОНОВ НА НУКЛОНАХ
ПРИ ВЫСОКИХ ЭНЕРГИЯХ
Основные особенности рассеяния нуклонов на нуклонах при
высоких энергиях. Как мы видели, рассеяние нейтронов на про-
тонах и протонов на протонах при малых энергиях совершенно
нечувствительно к форме потенциала ядерного взаимодействия.
Рис. 1.4. Угловая зависимость
поляризации в случае рассеяния
протонов различных энергий про-
тонами.
Рис. 1.3. Угловая зависимость экспе-
риментальных дифференциальных се-
чений рассеяния протонов различных
энергий протонами.
Это связано с тем, что при малых энергиях длина волны частиц пре-
восходит радиус действия ядерных сил и взаимодействие проявля-
ется только в S-состоянии. Для обнаружения зависимости потен-
циала от расстояния между частицами необходимо, чтобы длина
волны была меньше радиуса действия сил. В этом случае, однако,
взаимодействие будет проявляться не только в S-состоянии, но и
в состояниях с I Ф 0. Очевидно, что чем большее число парциаль-
ных волн будет участвовать в рассеянии, тем более детальную
информацию можно получить о радиальной зависимости потенци-
ала.
Однако необходимо учитывать, что при достаточно высоких энер-
гиях нуклонов помимо упругого рассеяния могут иметь место не-
упругие процессы. Так, если энергия падающего нуклона превос-
ходит 500 /Изе, то необходимо учитывать процесс рассеяния с об-
51
разованием л-мезонов. В дальнейшем будем рассматривать область
энергий, в которой существенно только упругое рассеяние нуклонов.
В настоящее время накоплено достаточное количество экспери-
ментальных данных по рассеянию протонов на протонах и нейтро-
нов на протонах в указанной области*. На рис. 1.3 и 1.4 представ-
лены угловые зависимости экспериментальных дифференциальных
сечений и поляризации при рассеянии протонов на протонах (кри-
Рис, 1.5, Угловая зависимость экспериментальных диф-
ференциальных сечений рассеяния нейтронов различ-
ных энергий протонами.
вые проведены через экспериментальные точки). Как видно из
рис. 1.3, дифференциальное сечение упругого рассеяния протонов
на протонах в интервале энергий приблизительно от 150 до 500 Мэв
практически постоянно и не зависит ни от угла рассеяния, ни от
энергии. Величина сечения, отнесенного к единичному телесному
углу, в пределах погрешностей эксперимента равна
о (&)—4-10~27см2/опер. (1.161)
Только в области очень малых углов сечение возрастает вследствие
кулоновского рассеяния. При энергиях, больших 500 Мэв, изо-
тропия нарушается: возникает максимум в угловом распределении
в направлении вперед. Такое поведение сечения рассеяния нахо-
дится в резком противоречии с предсказаниями теории возмуще-
ний. Это означает, что даже при больших энергиях нуклонов ядер-
* Феноменологическая теория рассеяния нуклонов на нуклонах изложе-
на в монографии [16].
52
ное взаимодействие нельзя считать слабым, т. е. для его описания
нельзя использовать теорию возмущений.
Экспериментальное изучение рассеяния нейтронов на протонах
при высоких энергиях привело к картине, которая существенно
отличается от случая двух протонов. На рис. 1.5 и 1.6 представлены
угловые зависимости экспериментальных дифференциальных се-
чений и поляризации в случае рассеяния нейтронов на протонах.
Рис. 1.6, Угловая зависимость поляризации в слу-
чае рассеяния нейтронов различных энергий про-
тонами.
Как видно из рис. 1.5, дифференциальное сечение рассеяния
нейтронов на протонах сильно зависит от угла рассеяния, возра-
стая при угле 180° в несколько раз по сравнению с значением при
90°. Так, для энергии 300 Мэв сечение при 90° равно 2-10-27 смЧстер,
а при 180° — 9,2-10-27 смЧстер. С ростом энергии сечение при 90°
падает, достигая значения 1 • 10-27 смЧстер при 580 Мэв, в то
время как сечение при 180° остается почти постоянным, В сторону
углов, меньших 90°, сечение растет не так быстро, поэтому угловое
распределение имеет асимметричный характер.
Полные сечения для рассеяния протонов на протонах и нейтро-
нов на протонах также заметно различаются. Если полное сечение
упругого рассеяния протонов на протонах в интервале энергий
от 150 до 500 Мэв практически не изменяется и равно 25-10~27 ел2,
то полное сечение упругого рассеяния нейтронов на протонах
уменьшается по закону 1/Е вплоть до энергий, при которых сущест-
венными оказываются неупругие процессы. Небольшие отклоне-
ния от закона 1/Е обусловлены зависимостью фаз рассеяния от
энергии.
53
Неупругое рассеяние нуклонов. При столкновениях нуклонов
с энергиями, большими 500 Мэв, существенную роль играет н е-
упругое рассеяние, сопровождающееся рождением
л-мезонов. Учет этого эффекта приводит к росту полного сечения.
Полное сечение взаимодействия двух протонов
(сумма сечения упругого рассеяния, обусловленного ядерным взаи-
модействием, и сечения рождения л-мезонов) при энергии 800 Мэв
примерно равно 50 мбарн, и затем остается почти постоянным до
энергии 3000 Мэв. Сечение
Рис, 1.7. Зависимость полного сечения
взаимодействия Gfot Двух протонов, се-
чения упругого рассеяния сге; протонов
на протонах и сечения неупругого рас-
сеяния Двух протонов от энергии.
упругого рассеяния практи-
чески не зависит от энергии
и равно 25 мбарн. Таким
образом, в интервале энер-
гий от 500 до 3000 Мэв сече-
ния упругого и неупругого
рассеяния двух протонов
оказываются практически
равными друг другу и по-
стоянными (рис. 1.7). Угло-
вая зависимость сечения уп-
ругого рассеяния характери-
зуется резкой направленно-
стью вперед. Такими свой-
ствами характеризуется диф-
ракционное рассеяние частиц
при наличии абсолютно пог-
лощающей сферы. Сечение
поглощения и сечение упру-
гого рассеяния в этом слу-
чае равны л7?2, где 7? —-
радиус сферы. Если с помощью такой дифракционной модели опи-
сать взаимодействие двух протонов, то, положив 7? равным сумме
радиусов двух протонов, найдем величину радиуса протона 7?р:
— 0,45 - 1Q—13 см.
(1.162)
Отметим, что результаты опытов по рассеянию электронов прото-
нами находятся в соответствии с этой оценкой.
Рассеяние нуклонов при высоких энергиях и изотопическая
инвариантность. Несмотря на столь различное поведение сечений
рассеяния в системах протон — протон и нейтрон — протон, дан-
ные по рассеянию при высоких энергиях не противоречат допуще-
нию об изотопической инвариантности ядерного взаимодействия.
Если справедлива изотопическая инвариантность, то силы, дейст-
вующие между двумя протонами, действуют также между нейтро-
ном и протоном в состоянии Т = 1. Более сложное поведение се-
чения рассеяния нейтрона протоном обусловлено взаимодействием
в состоянии Т = 0, исключенном для системы двух протонов.
54
Нетрудно установить простой критерий, которому Должны
удовлетворять сечения, если взаимодействие между нуклонами изо-
топически инвариантно. Действительно, при рассеянии на угол
90° состояния с нечетными значениями I не дают вклада в сечения,
так как при нечетных значениях I Pi (90°) = 0. При четных зна-
чениях I система двух протонов (Т = 1) может находиться только
в синглетном спиновом состоянии, а система нейтрон — протон
может находиться как в синглетном (при Т = 1), так и в триплет-
ном (при Т = 0) спиновых состояниях. Поэтому если взаимодей-
ствие изотопически инвариантно, то дифференциальные сечения
рассеяния в указанных случаях можно записать в виде
<ДР (90°) = ог=1 (90°); )
опр (90°) = от=1 (90°) + з/4 ог=о (90°) J
где 1/4 и 3/4 — веса ^инглетного и триплетного спиновых состоя-
ний соответственно. Из выражений (1.163) непосредственно сле-
дует, что если взаимодействие изотопически инвариантно, то при
любой энергии должно выполняться неравенство
апр (90°) >V4opp (90°). (1.164)
Как мы уже отмечали, сечение рассеяния нейтрона протоном
быстро уменьшается с ростом энергии, в то же время сечение рас-
сеяния протона протоном практически не изменяется. Поэтому ус-
ловие (1.164) оказывается наиболее критичным в области высоких
энергий, Все имеющиеся экспериментальные данные по сечениям
рассеяния согласуются с условием (1.164).
Из сравнения формул (1.163) следует, что в случае достаточно
больших энергий сечение рассеяния на угол 90° при Т = 0 значи-
тельно меньше сечения рассеяния на угол 90° при Т = 1. В то же
время дифференциальное сечение рассеяния нейтрона протоном
на угол 180° значительно больше сечения рассеяния протона про-
тоном. Это различие, очевидно, связано с взаимодействием при
Т = 0. Таким образом, в случае Т — 0 в отличие от случая Т — 1
рассеяние очень сильно зависит от угла.
Используя экспериментальные значения для сечений орр (ft)
и стпр (ft), нетрудно найти сечения рассеяния в состояниях с Т = I
и Т = 0. Очевидно, сечение рассеяния протона протоном и есть
сечение рассеяния в состоянии Т = 1:
сгг=1 (ft) =<rpp(ft). (1.165)
Для нахождения сечения рассеяния в состоянии Т = 0 заметим’
что изоспиновое состояние системы нейтрон — протон является
суперпозицией состояний Т = 1 и Т = 0. Согласно соотношениям
(1.151) и (1.152), имеем
£|/2 (1) £_1/2 (2) = (1/ /2) {Zlo (1,2) Zoo (1,2)}.
55
Поэтому амплитуду рассеяния нейтрона протоном можно выразить
через амплитуды рассеяния в случае Т = 1 и Т = 0 аналогич-
ным образом:
(1.166)
Сечение рассеяния нейтрона протоном определяется квадратом мо-
дуля (1.166):
^PW=1/af<7r=i(#)+^=o(^ + 2Re^=1 (О)/7=о(^)}- (1.167)
В силу принципа Паули амплитуды /у=1 (6) и /г=0 (0) при задан-
ном значении спина S характеризуются противоположной четно*
стью. Поэтому в выражение опр (я — 6) для сечения рассеяния
Рис. 1.8. Угловая зависимость сечений рассея-
ния нуклонов в состояниях с различными изос-
пинами.
на угол п — 6 интерференционное слагаемое войдет с противопо-
ложным знаком [см. формулу (1.167)1, и сумма сечений оу,р (6) и
ап?> (л — <lj будет равна сумме сечений рассеяния в состояниях
с Т = 1 и Т = 0:
пр W + <ЛгР (л — "&Н <гу=1 (#) + <7т=о (Ф) - (1 -168)
Полученное выражение имеет простой физический смысл: оно оп-
ределяет суммарное число нейтронов и протонов, рассеянных под
определенным углом О'.
Используя соотношения (1.168) и (1.165), найдем сечение рас-
сеяния нуклонов в состоянии Т = 0:
Ог=о(й) =0^(0) + опр (я— $) — орр (€). (1.169)
56
Отметим, что полученное сечение стг=0(-&) всегда оказывается поло-
жительным, что экспериментально подтверждает допущение об
изотопической инвариантности ядерного взаимодействия.
На рис. 1.8схематически представлены сечения o^i^) и аг=о(#)
при энергии нуклонов порядка 400 Мэв. Как видно из рисунка,
угловая зависимость рассеяния в случае Т = 1 и Т = 0 совершен-
но различна. Если при Т = 1 рассеяние изотропно, то в случае
Т = 0 угловое распределение рассеяния характеризуется макси-
мумами в направлениях вперед и назад. Такой характер угловой
зависимости рассеяния указывает на возможность описания взаи-
модействия между нуклонами в состоянии Т = 0 с помощью тео-
рии возмущений.
Определение амплитуды рассеяния нуклона на нуклоне из дан-
ных опыта. Если бы отсутствовала спиновая зависимость ядерных
сил, то из опытов но рассеянию нуклонов на нуклонах можно
было бы определить при фиксированном значении энергии только
одну величину — дифференциальное сечение рассеяния о (Ф). Диф-
ференциальное сечение ст (1Т) и амплитуда рассеяния f (fl) связаны
соотношением ст (й) — (й)|2. Так как в отсутствие спиновой
зависимости амплитуда рассеяния f (й) — величина скалярная,
то, зная дифференциальное сечение рассеяния при всех углах и
используя оптическую теорему, в принципе можно было бы пол-
ностью восстановить амплитуду рассеяния.
Вследствие спиновой зависимости ядерного взаимодействия
между нуклонами из опытов по рассеянию кроме дифференциаль-
ного сечения рассеяния можно определять также поляризацию рас-
сеиваемого нуклона и поляризацию нуклона отдачи, а также кор-
реляцию между направлениями поляризации нуклонов. Если взаи-
модействие инвариантно относительно вращений в пространстве
и инверсии пространства и времени, то амплитуду рассеяния двух
частиц, имеющих спин 1/2, в самом общем случае [17] можно пред-
ставить в виде
f (к, к') = а ф- fJnoj • пст2 4- iyn (ст, 4- <т2) 4-
4- iy' и (оу—ста) — бгпоутст., -j-slor (1.170)
где кик' — импульс относительного движения частиц до и после
рассеяния; CTj и ст2 — матрицы Паули, отвечающие спинам взаимо-
действующих частиц; n, 1 и m — система трех единичных взаимно
ортогональных векторов:
п = кхк' , 1= к + к' , tn = к~к' . (1.171)
|кхк'| |к + к'| | к—к'|
Коэффициенты а, р,у, у', б и е— комплексные функции, завися-
щие от угла и энергии. Если учесть зарядовую инвариантность
ядерного взаимодействия между нуклонами, то коэффициент у'
в (1.170) следует положить равным пулю:
у' = 0. (1.172)
57
Таким образом, для описания упругого рассеяния двух нукло-
нов необходимо при заданной энергии найти пять комплексных
функций угла рассеяния а, р, у, б и е. Задача несколько упроща-
ется, если учесть условие унитарности амплитуды рассеяния (1.170)
(обобщенную оптическую теорему). Из этого условия вытекают
пять различных интегральных соотношений между комплексными
функциями а, р, у, б и е. Поэтому для полного определения ампли-
туды рассеяния (1,170) необходимо измерить угловую зависимость
при заданной энергии пяти независимых величин. Очевидно, тре-
буемую информацию можно получить только из поляризационных
экспериментов.
Если нуклоны первоначально не поляризованы, то из опытов
по рассеянию можно определить только угловую зависимость диф-
ференциального сечения о (ft). Опыты по двукратному рассеянию
позволяют измерить угловую зависимость поляризации Р (ft).
(Поляризация Р (ft) измеряется по асимметрии рассеяния на вторам
рассеивателе в случае компланарного двукратного рассеяния.)
Опыты по трехкратному рассеянию позволяют измерить угловую
зависимость трех других величин, в качестве которых обычно
выбирают: деполяризацию D (ft), вызываемую вторым рассеивате-
лем в случае трехкратного компланарного рассеяния; вращение
вектора поляризации на втором рассеивателе R (ft) в случае трех-
кратного рассеяния в следующих под прямым углом одна за дру-
гой плоскостях и продольную поляризацию А (ft), осуществляемую
при повороте спина рассеиваемой частицы с помощью магнитного
поля перед вторым рассеивателем.
Измеряемые величины о (ft), Р (ft), D (ft), 7? (ft) и А (ft) выра-
жаются через коэффициенты а, Р, у, 6 и е, определяющие ампли-
туду рассеяния следующим образом [18J:
<7(#Ж«12 + 101г + 2Ы2+|й|2Ч- |е|а;
<т (ft) Р (О) = 21m (а + Р)* у;
о (ft) {1~D (ft)} = 2| б )2 + 2 | е |2;
о (ft) R (ft) = (j а}2—| p |»+ Re (6 + 6)* (8- e)} cos ft/2 -
— 2Re (a—p)* у sin ft/2;
a (ft) A (ft) = — {[ a|2~-|p|2 + Re (6 + e)* (6—-e)} sin ft/2 —
^2Re(a — p)*ycos ft/2.
(1.173)
Соотношения (1.173) с учетом соотношений унитарности в прин-
ципе позволяют найти величины a, Р, у, б и е, т. е. полностью опре-
делить амплитуду рассеяния (1.170). Однако практическое осущест-
вление этой задачи чрезвычайно трудно, и поэтому обычно экспе-
риментальные данные анализируются на основе представления
амплитуды рассеяния через фазы.
Изотропный характер рассеяния протонов протонами и взаи-
модействие в состояниях с / #= 0. Основную особенность ядерного
рассеяния протонов протонами — независимость селения от угла
58
рассеяния — Можно было бы объяснить, предположив, что вплоть
до энергий порядка 500 Мэв протоны взаимодействуют только
в S-состоянии. Однако максимально допустимая величина сече
ния рассеяния в S-состоянии (равная X2) при энергии 500 Мэв ока-
зывается примерно в два раза меньше наблюдаемого сечения (1.161).
Поэтому необходимо учитывать взаимодействие протонов в состоя-
ниях с I ф 0, что подтверждается также большой величиной наблю-
даемой на опыте поляризации, возникающей при рассеянии прото-
нов на протонах. Отметим, что поляризация возможна только при
значении спина системы S = 1, которому отвечают состояния с не-
четными I. Поэтому большая величина поляризации при рассеянии
означает, что состояниям с нечетными I, в частности Р-состояниям,
соответствует сильное взаимодействие.
Взаимодействие в состоянии 3Р0 так же, как и в 150-состоянии,
приводит к изотропному рассеянию, при этом максимально допу-
стимая величина сечения также равна V. Поэтому учет взаимодей-
ствия протонов в 1S0 и 3Ро-состояниях в принципе позволяет полу-
чить величину изотропного сечения, согласующуюся с эксперимен-
тальной величиной (1.161). При этом, однако, необходимо считать,
что фазы рассеяния в других состояниях с I — 1 (3РХ и 3Р2) малы,
так как в противном случае сечение зависит от угла. Значительное
различие между фазами 3Р0, 3Р1 и 3Р2 указывает на существен-
ную роль нецентрального или же спин-орбитального взаимодей-
ствия .
Изотропный характер рассеяния можно также объяснить, пред-
положив, что взаимодействие происходит в S- и £>-состояниях,
но соответствующие фазы имеют противоположный знак. Действи-
тельно, если взаимодействие имеет место только в состояниях
с I — 0 и I = 2, то амплитуду рассеяния можно записать так:
f (#) = 1/£{е!6» sin 60 -}-5е,й* sin62 Р2 (cos О)}, (1,174)
где 60 и S2 — фазы рассеяния в состояниях и Ч)2. (Так как Т =
— 1 и четность положительна, то для рассматриваемых состояний
S = 0.)
Дифференциальное сечение рассеяния равно
<т (#) = 1 /k2 {sin2 So + 25 sin2 62 P22(cos ^) +
4-10sin 60sinS2cos (60 —62) Рг (cos#}. (1.175)
Угловая зависимость сечения определяется вторым и третьим сла-
гаемыми в соотношении (1.175). Второе слагаемое при угле рассея-
ния 90° в четыре раза меньше, чем при угле 0°. Знак третьего (ин-
терференционного) слагаемого определяется относительным зна-
ком фаз 60 и 62 и значением угла #. Так как величина Р2 (cos #)
при # = 90° отрицательна, то учет интерференции может привести
к увеличению сечения при 90°, а следовательно, и к сглаживанию
угловой зависимости сечения только в том случае, если фазы и 62
имеют противоположные знаки.
59
Отталкивание между нуклонами на малых расстояниях. Изме-
нение знака фазы рассеяния при переходе от 5- к D-состоянию мож-
но получить, предположив, что на малых расстояниях между нук-
лонами действуют большие силы отталкивания в отличие от сил
притяжения, проявляющихся на больших расстояниях [19]. При
достаточно высоких энергиях фаза рассеяния в S-состоянии опре-
деляется этим отталкиванием, в то время как фазы рассеяния в со-
стояниях с I •=£ 0 вследствие действия центробежных сил опреде-
ляются более дальнодействующими силами притяжения.
Фазу рассеяния 60 в S-состоянии нетрудно найти в предельном
случае бесконечных сил отталкивания (модель непроницаемой сфе-
ры или отталкивающей сердцевины), проявляющихся на расстоя-
ниях, меньших некоторого расстояния гс, называемого радиу-
сом отталкивающей сердцевины:
б9 = -йгс. (1.176)
Ядерные силы притяжения, проявляющиеся на расстояниях, ббль-
ших гс, приводят к положительной добавке в правой части уравне-
ния (1.176). Если ядерный потенциал выбрать в виде отталкиваю-
щей сердцевины, окруженной прямоугольной потенциальной ямой,
1 + оо, г<гс;
V(r)= -Vo, r0<r<r0; (1.177)
[ 0, г0<г,
то фаза 60 будет определяться выражением
йй = -Агс + А, (1-178)
где
Д ==(arctg^7?0)tg/e0(r0—гс) — к(гй—rc), /й2 + (2рЕ0/^).
(1.179)
Нетрудно проверить, что фаза А, определяемая равенством (1.179),
всегда положительна. Для этого нужно воспользоваться только
тем, что k < k0 и что atg х > tg ах при любом значении х (0 < х <
< л/2), если a < 1.
При малых энергиях (krc -> 0) главную роль играют силы при-
тяжения, и отрицательным слагаемым в (1.178) можно пренебречь.
С увеличением энергии положительное слагаемое в (1.178) быстро
убывает, вто время как фаза, обусловленная силами отталкивания,
возрастает по абсолютной величине, поэтому знак фазы рассеяния
60 будет изменяться от положительного значения при малых энер-
гиях к отрицательному при энергиях, больших некоторой крити-
ческой энергии, величина которой определяется параметрами по-
тенциала. Для того чтобы изменение знака фазы произошло при
энергии около 250 Мэв, следует выбрать rc » 0,4-10~13 см. Вели-
чина гс, вообще говоря, зависит от формы потенциала притяжения.
60
Вывод о наличии больших сил отталкивания на маль!х расстоя-
ниях следует также из энергетической зависимости полного сече-
ния рассеяния. Действительно, при монотонной зависимости по-
тенциала от расстояния между частицами фазы должны монотонно
возрастать с энергией. Поэтому произведение
A2o=4nS(2/ + l)sin2Sz (1.180)
i
также должно монотонно возрастать с ростом энергии. На рис. 1.9
и 1.10 представлена зависимость произведения А2о от энергии в слу-
Рис. 1.9. Энергетическая зависи-
мость величины в случае рас-
сеяния протонов протонами.
Рис. 1.10. Энергетическая зависи-
мость величины k2o в случае рассея-
ния нейтронов протонами.
чае рассеяния протонов протонами и нейтронов протонами соответ-
ственно. Согласно экспериментальным зависимостям (см. рис. 1,9
и 1.10), величина (1.180) уменьшается в области энергий от 10 до
100 Мэв, для которой наиболее существенно взаимодействие в
5-ссстоянии. Это означает, что в указанной области энергий фаза
рассеяния в S-состоянии уменьшается, что возможно только в слу-
чае сильного отталкивания между нуклонами на малых расстоя-
ниях.
Фазовый анализ. Важнейшей задачей анализа эксперименталь-
ных данных по рассеянию является нахождение фаз рассеяния.
Задание фазы рассеяния полностью характеризует взаимодействие
между частицами в определенном состоянии. Поэтому извлечение
из данных опыта всех фаз рассеяния эквивалентно получению пол-
ной информации о ядернсм взаимодействии между нуклонами.
Знание фаз рассеяния в принципе позволяет найти зависимость
сил от расстояния, т. е. определить потенциал ядерного взаимодей-
ствия. Правда, такая задача (обратная задача теории рассеяния)
требует кроме сведений об энергетической зависимости фаз еще
дополнительных сведений о дискретных уровнях в системе и асимп-
61
тотийах волновых функций, отвечающих этим уровням. Вследствие
этого подобную задачу в настоящее время еще не удалось решить
до конца. Отметим, что определение фаз из экспериментальных дан-
ных по угловым зависимостям сечения, поляризации и т. д. —
задача трудоемкая, требующая для своего решения привлечения
вычислительной техники.
Энергетическую зависимость фаз рассеяния можно найти, ис-
пользуя экспериментальные данные по рассеянию при различных
энергиях. Очевидно, фазы рассеяния вещественны только в том
случае, когда неупругими процессами можно пренебречь. Поэтому
фазовый анализ имеет смысл вплоть до энергий 500 Мэв.
Фазовый анализ рассеяния нейтронов протонами более сложен
по сравнению с фазовым анализом рассеяния протонов протонами,
так как система нейтрон — протон может находиться в изоспино-
вых состояниях Т = 1 и Т = 0, а система двух протонов может
находиться только в состоянии Т = 1. В предположении изотопи-
ческой инвариантности ядерного взаимодействия фазы рассеяния,
отвечающие Т = 1, должны быть одинаковыми для системы двух
протонов и системы нейтрон — протон. Поэтому фазы рассеяния,
отвечающие Т = 1, можно найти из данных по рассеянию протонов
на протонах, а из анализа рассеяния нейтронов на протонах необ-
ходимо определить только фазы, отвечающие Т = 0.
Воспользуемся классификацией состояний системы двух нукло-
нов (см. § 1.9) и охарактеризуем различные состояния квантовыми
числами изоспина Т, полного момента спина 8 и четности w.
Если 8 = 0 (синглетное спиновое состояние), то полный момент
совпадает с орбитальным моментом I, а амплитуда рассеяния имеет
вид
fs=o(a)=(W2(2/+ 1) (1-5,)^ (cos ^), (1.181)
где 5/ — унитарная матрица рассеяния, связанная с фазой рассея-
ния 2£+l bf обычным соотношением
S1==e2i‘6^. (1.182)
Если 8 = 1 (триплетное спиновое состояние), то орбитальный
момент не сохраняется, и амплитуду рассеяния можно представить
в виде трехрядной матрицы
(0, Ф) =('/2)^ Т К4л(2/ + 1)Г<<. (Ф, Ф) (/01р | X
и'Р
X(l'p-H'lp'^p). |6ri-S^}( (1.183)
где р. и р' — проекции спина системы в начальном и конечном
состояниях на некоторое направление; ф — угол между плоско-
стью, определяемой этим направлением и направлением движения
падающей частицы, и плоскостью рассеяния; Sf-r— матрица рас-
сеяния. Так как I не сохраняется, то матрица sf-i, вообще говоря,
62
имеет недиагональный вид. При фиксированном значении величи-
ны I и Г могут принимать значения $— 1, У- и У + 1. Если I = у,
то из-за сохранения четности I' = у. Учитывая унитарность мат-
рицы рассеяния, в этом случае можно записать
S^=e2i’e?, l=l' = y. (1.184)
Если I равно У + 1 или у — 1, то возможные значения Г также
Ж
равны 4- 1 или у — 1. Поэтому S^i—двухрядная матрица.
А так как матрица рассеяния — унитарная симметричная матрица,
то ее можно диагонализовать с помощью ортогональной матрицы
. _ ( cos sin
С/ — I ж ж
\ — sin 8^ cos
(1.185)
где — некоторый вещественный параметр. Таким образом, в слу-
чае /, I' — У ± 1 матрицу рассеяния можно представить в виде
(2РЙ® \
е 0 | / COS 8^ sin 8^ \
0 е2!’67-1 I V—Sin8^cos8^/
(1.186)
(представление Блатта—Биденхарна [20]). Согласно (1.186), матри-
ца рассеяния определяется тремя вещественными парамет-
рами: двумя собственными фазами рассеяния 3о^+1 и
в состояниях с I =у ф-1 и 1—У — 1и параметром смешивания е^.
Иногда пользуются другим представлением для матрицы рас-
сеяния (представление Стаппа [2Ц): S * * * * * * * * *
S‘’1 =
_|е^+* 0 |/cos2 i sin2e^ \/е‘0 |
I I\isin2 8^cos2e^ /I .т? Г
\ 0 е 1 \ 0 е /
(1.187)
Приведем соотношения, связывающие фазы рассеяния и пара-
метры смешивания для указанных представлений:
sin (6^4.1— 6/-1) =sin2e^/sin2e^;
sin(6>+i — 6/_i) — tg2e^/tg 2e^;
i= ^+< И- ®7-i‘
(1.188)
63
Вместо параметра часто используют величину р^:
p^'=£sin2e^. (1.189)
Вследствие малости радиуса действия ядерных сил упругое
рассеяние нуклонов можно описать с помощью небольшого числа
фаз. В случае Т = 1 фазовый анализ рассеяния проведен с учетом
фаз рассеяния в состояниях 3P0il>3, 1Р2, 3F2,s,it 1(?4, 3//4,5>в и
параметров смешивания е2 и е4. В случае Т = 0 фазовый анализ
проведен с учетом фаз рассеяния в состояниях ®Si, 1Р1, 3О1,а>3,
Рис. 1.11. Зависимость фаз рассея-
ния и параметра смешивания я, от
энергии.
F3, G3,4,ft и параметров сме-
шивания 61 и е3. На рис. 1.11
и 1.12 приведены зависимости
фаз рассеяния и параметров сме-
шивания от энергии [221.
Фаза рассеяния г80 обра-
щается в нуль при малых энер-
гиях, что указывает на отсут-
ствие связанного синглетного
состояния у системы двух нук-
лонов. С ростом энергии фаза
]80 возрастает, достигая значе-
ний около 60° при 3 Мэв, а за-
тем уменьшается и при энер-
гиях, больших 250 Мэв, стано-
вится отрицательной. Изменение
Рис. 1.12. Зависимость фаз рас-
сеяния и параметров смешива-
ния от энергии.
64
знака фазы ‘So, как мы уже отмечали, указывает на наличие силь-
ного отталкивания между нуклонами на малых расстояниях. Фаза
рассеяния 3Sr при нулевой энергии равна 180°, что непосредственно
связано с наличием связанного триплетного состояния у системы
двух нуклонов — дейтрона. При энергии 325 Мэв фаза 3Зх обра-
щается в нуль, а затем принимает отрицательные значения. Фазы
рассеяния в состояниях 3Р911,2 значительно различаются, что ука-
зывает на наличие сильного нецентрального или спин-орбитального
взаимодействия между нуклонами. Отметим, что фазы рассеяния
в состояниях S, Р и D — величины одного порядка. Фазы рассея-
ния в состояниях F, G и И не превышают нескольких градусов.
Феноменологические потенциалы. До тех пор пока неупругие
процессы не играют существенной роли, взаимодействие между
нуклонами можно описывать с помощью потенциала. Определение
вида потенциала ядерного взаимодействия между нуклонами из
данных по рассеянию — важнейшая задача нерелятивистской тео-
рии. Из данных по рассеянию нуклонов на нуклонах при высоких
энергиях следует, что ядерный потенциал должен описывать (по-
мимо сил притяжения) обменное взаимодействие, сильное отталки-
вание на малых расстояниях, значительное тензорное и спин-ор-
битальное взаимодействия. Многочисленные попытки вывода по-
тенциала нуклон-нуклонного взаимодействия из полевой мезонной
теории не привели к желаемому результату. Поэтому в настоящее
время для описания взаимодействия между нуклонами широко
используются потенциалы, феноменологически подбираемые так,
чтобы наилучшим образом объяснить совокупность эксперимен-
тальных данных по рассеянию. Было предложено несколько ва-
риантов потенциалов, хорошо описывающих данные по рассеянию
в области энергий от нуля до 400 Мэв. В качестве иллюстрации мы
приведем выражения для потенциалов Гаммеля — Талера и Хама-
да— Джонсона, наиболее часто используемых в приложениях.
Потенциал Гаммеля — Талера включает центральное, тензор-
ное и спин-орбитальное взаимодействия:
VG.r = V'c(r) + Vr(r)S12 + VrsLS. (1.190)
Радиальная зависимость всех слагаемых в (1.190) выбирается в виде
абсолютно непроницаемой сферы радиуса гс и потенциала типа
Юкавы:
Р(г)= ’
<гс'-
г >гс.
(1.191)
Параметры V, ц и гс подбирались для каждого состояния не-
зависимо, т. е. определенные значения выбирались для синглетных
четных состояний, триплетных четных состояний (отдельно для
Центральных, тензорных и спин-орбитальных сил) и аналогично
Для нечетных состояний. В общем случае потенциал (1.190) харак-
теризуется 24 параметрами. Так как для центральных, тензорных
3 Зак. 642
65
и спин-орбитальных сил практически использовалось одно и то же
значение гс, то число независимых параметров уменьшалось до 20.
Значения параметров, обеспечивающие наилучщее согласие с экс-
периментальными данными, представлены в табл. 1.3 (23Г-
Таблица 1.3
Параметры потенциала 5 = 0 S = I
Т = 1 (/ — четкое) Т = 0 (/ — нечетное) Т = 0 (/ — четное) Т= 1 (/ — нечетное)
vc, Мэв 425,5 — 100 при Епр < 90 и ЕПр = 156, —150 при £„? -310 100,7 При Епр < 90 И Епр == 156 60 при £пр -..ЗЮ 0
рс , СМ'1 1,45-10*» 1,0-Ю13 1,23-Ю13 —
VT, Мэв 257 при £пР < 90 230 при £пп= 156 175 при Епр =310 —22,5
Pj., САГ1 — — 1,203-lOW 0,8-Ю'3
, Мэв — — 5000 7317,5
HLS, см~1 — 3,7-1013 3,7-1018
Гс, СМ 0,4-10-1® 0,5-10-1» 0,4-10'13 0,412б -10-1»
Потенциал Хамада — Джонсона учитывает кроме централь-
ного, тензорного и спин-орбитального взаимодействий еще квадра-
тичное спин-орбитальное взаимодействие:
=^(r)+V7-(r)S18 + Vbs(r)LS+yLt(r)Z-12, (1.192)
где
4-25(5 + 1)-3] L2—(LS)2. (1.193)
Радиальная зависимость в (1,192) соответствует на малых расстоя-
ниях наличию абсолютно непроницаемой сферы радиуса гс; на
больших расстояниях зависимость отдельных слагаемых в (1.192)
выбрана в виде
Vc (г) = Vc Y (х) {1 + ас Y (х) + Ьс Г» (х));
VT (г) = VT Z (х) {1 + ат Y (х) + Ьт У2 (х)};
Vm (r)=l+s Y*(x) (1 +аиУ(х)};
V cl (г) - VLL (Z (x),'+) {I + aLL Y (x) + «
где Y (x) -- r"+x; Z (x) — (1 + 3/x + 3/№) Y (x) ; x pcr/й и
p -масса мезона (+pc 1,415-10 1:< сз/, pc2 = 139,4 Мэв).
66
Потенциалы Ус (г) и VT (г) выбраны так, чтобы на больших рас-
стояниях они совпадали с потенциалами мезонной теории, учиты-
вающими однопионный обмен:
Ус = 0,08 (цс3/3) (25 (5 + 1) - 3] 12Т (Т + 1) - 3];
VT = 0,08 (рс2/3) [2Т (Т + 1) — 3].
Значения параметров Ус, Ут, Vls, Vll, а и b приведены
в табл. 1.4(24],
Таблица 1.4
Параметры потенциала S =0 S = 1
T 1 (/ — четное) T = 0 (I — нечетное) Т — 0 (/ — четное) Т = 1 (1 — нечетное)
Vc, Мэв —11,2 33,5 — 11,2 3,71
«с 8,7 —8,0 6,0 -9,07
ьс 10,6 12,0 — 1,0 3,48
VT, Мэв — -11,2 +3,71
Лу , ... — -0,5 —1,29
т — — 0,2 0,55
VL.s, Мэв ....... — — 10,4 27,4
aLS •— '— -0,1 —7,12
Vll> Мэв 0,124 0,371 0,371 —0,124
aLL 0,2 2,0 1,8 —7,26
bLL —0,2 6,0 -0,4 6,92
Тензорное спин-орбитальное взаимодействие наиболее сущест-
венно в триплетном и синглетном спиновых состояниях с = L.
Потенциал Хамада — Джонсона (1.192) хорошо согласуется с дан-
ными по взаимодействию двух нуклонов при малых энергиях
(энергия связи дейтрона, длины рассеяния, эффективные радиусы
и т. д.), и хорошо воспроизводит энергетическую зависимость фаз
рассеяния вплоть до энергий порядка 400 Мэв.
Отметим следующие особенности взаимодействия, характерные
как для потенциала Гаммеля — Талера, так и для потенциала Ха-
мада — Джонсона. Во всех состояниях на малых расстояниях меж-
ду нуклонами действуют большие силы отталкивания, которые опи-
сываются сердцевиной радиуса 0,4-10—13 см. Вне области сердце-
вины потенциал для четных состояний соответствует силам притя-
жения. В нечетных состояниях взаимодействие значительно слабее
по сравнению с взаимодействием в четных состояниях. В синглет-
ных нечетных состояниях взаимодействие отталкивающее. На боль-
ших расстояниях существенный вклад во взаимодействие вносят
тензорные силы. Тензорные силы являются притягивающими
в 35г и ^-состояниях.
3*
67
Нерелятивистская теория ядра. Главная задача нерелятивист-
ской теории ядра —это объяснение свойств ядер—сложных систем,
состоящих из нуклонов, на основе сведений о свойствах нуклонов
и характере взаимодействия между ними. Свойства свободных
нуклонов и характер взаимодействия между ними в нерелятивист-
ской области энергий в настоящее время достаточно хорошо изуче-
ны как экспериментально, так и теоретически.
Нерелятивистская теория ядра основывается на допущении,
что между простейшими составляющими частями ядер — нукло-
нами — действуют только двухчастичные силы. В нерелятивист-
ской теории ядра предполагается также, что свойства самих нукло-
нов (масса, заряд, магнитный момент и т. п.) внутри ядер не изме-
няются, несмотря на наличие сильного взаимодействия между
нуклонами. Поэтому гамильтониан ядра, состоящего из А нукло-
нов, можно представить в виде
/У = 2[-(№/2Л1)Аг1+ 2 Уи, (1.195)
j i<i
где —(h2/2M)Ai — оператор кинетической энергии отдельного нук-
лона и Vtj — потенциал двухчастичного взаимодействия между
нуклонами i и /.
В отличие от систем заряженных частиц с кулоновским взаи-
модействием, для которых полная энергия складывается из энер-
гий взаимодействия отдельных пар частиц и такая аддитивность
является следствием линейности уравнений электродинамики,
в случае ядерных систем нет прямых доказательств того, что ядер-
нсе взаимодействие также аддитивно, т. е. что взаимодействие
двух нуклонов не зависит от присутствия третьего нуклона. Поэтому
основанием для допущения о двухчастичном характере ядерных
сил между нуклонами в ядрах в настоящее время может служить
только отсутствие эффектов, которые указывали бы на нарушение
такого допущения.
Согласно гамильтониану (1.195), взаимодействие между нукло-
нами в нерелятивистской теории описывается потенциалом. Одна-
ко при достаточно высоких энергиях существенными становятся
иеупругие процессы, связанные с образованием мезонов, поэтому
возможность описания взаимодействия между нуклонами с по-
мощью потенциала ограничена со стороны высоких энергий. Такое
ограничение по энергии означает, что однозначное определение
потенциала на малых расстояниях вообще невозможно. Однако
так как в ядрах максимально допустимые значения импульсов нук-
лонов соответствуют энергиям, меньшим 150 Мэв, то можно на-
деяться, что при рассмотрении структуры ядер релятивистскими
эффектами можно пренебречь.
Изучение свойств ядер, содержащих больше двух нуклонов,
может служить добавочным источником информации о взаимодей-
ствии между нуклонами. Например, свойства системы двух нукло-
нов при энергиях, близких к нулю, можно объяснить силами с ну-
68
Левым радиусом действия. Однако в случае сил нулевого радиуса
действия энергия связи системы трех нуклонов оказывается беско-
нечно большой. Поэтому сам факт существования ядер 3Н и 3Не
указывает на то, что ядерные силы характеризуются конечным
радиусом действия. Данные по рассеянию нуклонов на нуклонах
при малых энергиях (< 10 Мэе) позволяют определить только
эффективные параметры /"характеризующие величину и радиус по-
тенциала взаимодействия. Эти данные, как мы видели, недостаточ-
ны для определения формы потенциала. В отличие от задачи двух
нуклонов задача о движении системы, состоящей из трех или боль-
шего числа нуклонов, оказывается более чувствительной к форме
двухнуклонного потенциала. Это связано с тем, что рассеяние двух
нуклонов полностью определяется матрицей рассеяния на энерге-
тической поверхности, в то время как свойства систем, состоящих
из большего числа нуклонов, зависят от матрицы рассеяния и вне
энергетической поверхности. Поэтому неоднозначности потенциа-
ла, определяемого из опытов по рассеянию двух нуклонов, в прин-
ципе можно исключить, если учесть свойства более сложных ядер.
Задачи
1.1. Показать, что волновая функция основного состояния системы нейт-
рон — протон <р0(г) и функции непрерывного спектра <рк (г) образуют полную
систему.
Энергетический спектр системы нейтрон — протон состоит из дискрет-
ного уровня, отвечающего связанному состоянию системы, и непрерывного
спектра положительных значений энергии, отвечающих несвязанным состоя-
ниям. В приближении нулевого радиуса действия ядерных сил функции
Фо(г) и фк (г) имеют вид
Фо (О , Фк(г)=е’кг—-L-- .^1. (1.196)
F 2л г a-j-ife г
Функции ф0(г) и Фк (г) отвечают значениям энергии системы Еал —h~a‘2/M
н Ek — №&1М. В приближении нулевого радиуса действия ядерных сил вза-
имодействие характеризуется единственным параметром а, определяющим
как энергию связанного состояния системы, так и амплитуду рассеяния в не-
связанных состояниях.
Функции Фк(г) и <рк, (г), соответствующие различным значениям волновых
векторов к и к', ортогональны друг другу:
J dr фк (г) фк, (г) = (2л)3 6 (к —к'). (1.197)
Функции фк (г) ортогональны также функции ф0(г), описывающей связанные
состояния системы,
J <7г<рь (г) <рв (г)-0. (1.198)
Непосредственной проверкой легко убедиться, что система функций (1.196)
удовлетворяет условию полноты
С dk
Фо (г) ЧРо <'') +J Фк <г) Фк <г') <г— г') (1-199)
69
В качестве примера системы функций, учитывающих конечность радиуса
действия ядерных сил, можно привести функции для потенциала Хюльтена:
, , а(а+3)₽ е-"-'-
(r) V 2л (0-а)2
<Pk (r) = eikr4-/:(fc)
(1.200)
где
) Г 2р 2(а-|-р)!р + fe/ ’
Р — параметр, значение которого обычно выбирается равным р — 7а. функ-
ции (1.200) удовлетворяют условиям (1.197) —(1.199).
1.2. Найти нормировочный множитель для волновой функции основного
состояния дейтрона с учетом конечности радиуса действия ядерных сил [25].
Формула (1.11) для волновой функции основного состояния дейтрона дает
правильную зависимость от г вне области действия ядерных сил. Для многих
задач необходимо знать волновую функцию дейтрона именно в этой области.
Однако нормировочный коэффициент в (1.11) получен в предположении ну-
левого радиуса действия ядерных сил. Покажем, как следует изменить норми-
ровочный коэффициент в (1.11) для того, чтобы учесть конечность радиуса
действия ядерных сил.
Обозначим точную волновую функцию основного состояния дейтрона че-
рез <po(r) == ц(г)/г. Эта функция должна быть нормирована согласно условию
У dr фо2 (г) = 1.
(1.201)
Радиальная функция и удовлетворяет уравнению
Будем рассматривать вэтом уравнении а2 как некоторый параметр. Дифферен-
цируя уравнение (1.202) по этому параметру, находим
д М д д
С'203)
да,2 It2 да.1 да2
Умножая уравнение (1.202) на д/(да2')а, а равенство (1.203) на и и вычитая
из первого равенства второе, получаем
ди" „ ди д Iд и' \
U2 ~ и -— и ------ ------ ц*----------
das da2 dr \ da3 и }
откуда
°° д ' f ' 00
°-204’
О о
Введем приближенную волновую функцию дейтрона ф0(г).
, " (г)
Фо (г)==----,
г
где ц(г) — приближенная радиальная функция, совпадающая вне области
действия ядерных сил (г > г0) с точной функцией и{г):
о(г) = и(г), r>ra.
70
Для приближенной функции ц(г) можно написать соотношение, аналогичное
(1.204);
ОО
dry- -v-
о
д
да2
(1.205)
Вычитая из соотношения (1.204) соотношение (1.205) и учитывая, что н(0) = 0,
а вне области действия ядерных сил функции « и » совпадают, находим
о о
Воспользуемся теперь соотношением теории
из которого следует, что отношение у'(0)/о(0)
v’ (01 1 1
(1,207)
(1.208)
Г 7 д ! и' (0) \
\dru2 — <fro2 = o2(0)-( —“ . (1.206)
) J ’ да2 \ v (0) I
эффективного радиуса (1.48),
равно
T(or = ^T-TaV°’
и поэтому
а / у' (0) \ 1
да2 \ v(0) J — 2 Га'
Приближенная радиальная функция о(г) имеет вид
V (г) —Се~аг-
Подставляя у(г) в (1.206) и используя соотношение (1.207), получаем
» 1
dr и2 — Сг f drc’2ar = —~-C2r0.
J 2
о о
Используя условие нормировки точной волновой функции (1.201), для нор-
мировочной постоянной в соотношении (1.208) находим следующее значение:
С-1/ ---------------- (1,209)
V 2л(1—аг0)
Таким образом, приближенная волновая функция основного состояния дейт-
рона, соответствующая условию нормировки точной волновой функции
(1.201), имеет вид
/ а ₽“аг
Фо(П = 1/ ------*-------Л------ (1.210)
У 2л (1 аг о) Г
При rt -* 0 эта формула переходит в (1.11).
1.3. Найти вероятность переворачивания спинов при рассеянии медлен-
ного нейтрона на протоне [26].
Так как ядерное взаимодействие между нейтроном и протоном зависит от
их спинов, то при рассеянии возможно изменение ориентации спинов, при
этом,однако, суммарный спин системы сохраняется.
Обозначим спиновые волновые функции нейтрона и протона Хц(л) и Ху.(р),
где р —проекция спина на ось г(ц = ± 1/г). Спиновая волновая функция
системы нейтрон — протон представляет собой произведение волновых функ-
71
ций Xyfn) и Хр,(Р)-Д° рассеяния система нейтрон — протон может находить-
ся в одном из следующих спиновых состояний;
X (п, р) =
Х1/2 <") Х1/2 (р);
x-i/2^) 1/2(р);
Z1/2 (п)х-1/2(р);
X—1/2 (Л) X|/S (₽).
(1.211)
Рассмотрим собственные функции оператора квадрата суммарного спина
системы. Суммарному спину, равному единице (триплетное состояние), соот-
ветствуют спиновые функции:
xi, 1 («. р) = Xi/2 Wxi/2(р);
Х1,0 <"> 1^2) {%!/2 («) Х—1/2 (Р) + х_1/2 (*) Х|/2(Р)};
р)1/2 (п) х._т/2 (Р).
(1.212)
(1.214)
Суммарному спину, равному нулю (синглетное состояние), соответствует спи-
новая функций
Хо,о(Л. Р) = (1//2) {Х1/2 («) X—l/г <Р>—X—1/2 («) Х1/2 (Р)}- (1-213)
Первые две функции (1.211) Ху/п) Х<//р) и Х_у,(«) Х_%(р) совпадают
с собственными функциями триплетного состояния Хы(л, р) и Х1.-1(^> р), а
третья и четвертая функции (1.211) представляют собой суперпозиции трип-
летного и синглетного состояний Xi,0(п, р) и Хо,о(я, р)-
Х1/2 («) %_ 1/2 (P) = (l//2) {X! ,0 (я, Р) + Хо,о(«- Р)>
Х-1/2 (") Xi/s (P) = (l//2){Xi,o(n’ Р> —Хоо(«< Р)}.
Если нейтрон и протон находятся в спиновом состоянии %уг (п) Х%(р) или
Х_уа (n) X—уа(р), то изменение ориентации спинов, очевидно, не происхо-
дит. При этом сечение рассеяния равно
о|2 —4ла®. (1.215)
Рассмотрим теперь рассеяние нейтрона протоном в спиновом состоянии
7.уг (/О Х_у2(р)- Так как длины рассеяния в триплетном и синглетном состоя-
ниях различны, то коэффициент при расходящейся сферической волне в вол-
новой функции системы нейтрон — протон в рассматриваемом случае имеет
вид
1/У2 X, ,о (л> Р)+'аЛо,о(л- P)) = ((af+aJ/2) Xi /а («) X-i/2 (Р) +
Первое слагаемое справа в этом выражении соответствует рассеянию без
изменения ориентации спина, а второе—рассеянию с изменением ориентации
спина. Мы видим, что этим двум процессам отвечают длины рассеяния
«»)/2) и ((а; — а3)/2) соответственно. Поэтому сечение рассеяния без
изменения ориентации спина в случае спинового состояния %yt(n) 7._у(р)
равно
а3 = л: (a, + as)3- (1.216)
Сечение рассеяния нейтрона с изменением ориентации спина, если до рассея-
ния система находилась в состоянии Х%(п) X равно
о3' = л (at — а„)*. (1.217)
72
Рассеяние в спиновом состоянии х_у2(”) Ху„(р), так нее как и в состоянии
Ху (и) Х_у2 (₽)> может происходить как без изменения, так и с изменением
ориентации спинов. Соответствующие сечения равны
ст4 = л (а,+as)2,
О4'=-л (а;—ой)2.
В случае рассеяния неполяризованных нейтронов протонами все четыре
спиновых состояния (1.211) обладают одинаковым весом. Поэтому средняя
вероятность изменения ориентации спина нейтрона в этом случае равна
(а,—а,)2
(1.218)
(1.219)
u? —--------------------------
4a(8 + (at + as)2 + (at — asy>
Подставляя в уравнение (1.219) значения длин рассеяния, получаем w =
= 0,65.
1.4. Показать, что сечение рассеяния очень медленного нейтрона на про-
тоне, входящем в состав тяжелой молекулы, в четыре раза больше сечения
рассеяния нейтрона свободным протоном [27].
При рассмотрении рассеяния медленных нейтронов в веществе, содер-
жащем водород, пренебрегать химической связью протонов, т. е. считать про-
тоны свободными, можно только в том случае, если энергия нейтронов значи-
тельно превосходит энергию связи протонов в молекулах вещества. Энергия
связи по порядку величины равна йы, где w — частота колебаний протона
в молекуле вещества. Например, для парафина величина энергии связи равна
около 0,4 эв. При энергиях нейтронов, меньших энергии связи протонов few
или такого же порядка, учет химической связи протонов оказывается весьма
существенным.
Используя определение псевдопотенциала (1.62), нетрудно получить об-
щую формулу для сечения рассеяния нейтронов, учитывающую связь про-
тонов в молекулах. Обозначим волновые функции протона в начальном и ко-
нечном состояниях через ф0(гр) и ф/(гр). Волновые функции нейтрона выберем
в виде плоских волн. Таким образом, начальную и конечную функции системы
нейтрон — протон можно представить в виде
Ф(, = е‘кГп фо (гр),
Ф/ = е'к '"ф^Гр),
где кик' — начальный и конечный волновые векторы относительного дви-
жения нейтрона и молекулы. Сечение рассеяния, согласно теории возмущений,
определяется формулой
(1.220)
ц2 k’
(1.221)
~ Л4тИМол
где ц= .. , ---— приведенная масса для относительного движения неит-
Л1-)-/Имс1л
рона и молекулы; Ify— матричный элемент псевдопотенциала (1.62). В этом
случае имеет место закон сохранения энергии
Е=Е'4-Еу; E = fesfe2/2p; Е'=fesfe'a/2p. (1.222)
Здесь Ef — энергия возбуждения молекулы. (Предполагается, что до рассея-
ния молекула находится в основном состоянии.) Интегрируя матричный эле-
мент Voy по гп с помощью дельта-функции, получаем
/ ~ \ 2 Ъ>
dae/= JL — а21 <r0/|arfo,
\ ц 1 к
(1.223)
73
где -J о?— форм-фактор, определяемый интегралом
.7af =-. j с/ге1 < k~k' >г <р/ (г) фо (г) (1.224)
(ц — приведенная масса системы нейтрон — протон)- Если длина волны нейт-
рона велика по сравнению с размерами молекулы, то множитель е ** л
~ 1. В этом случае имеет место только упругое рассеяние нейтронов, при ко-
тором состояние протона в молекуле не изменяется. Сечение упругого рассея-
ния равно
da00^ (ц/р)2 a2- do. (1.225)
Рассеяние характеризуется сферической симметрией в системе центра инер-
ции нейтрона и молекулы. Полное сечение упругого рассеяния нейтрона свя-
занным протоном равно
Ооо= (р/н)2 ^о- (1.226)
где о0 — полное сечение рассеяния нейтронов свободными протонами. В пре-
дельном случае тяжелых молекул (Л1Ы0Я>> М) отношение р/ц — 2 и, следо-
вательно,
Ооо — 4о0, (1.227)
т. е. из-за эффекта химической связи протона сечение рассеяния очень медлен-
ного нейтрона в четыре раза больше сечения рассеяния нейтрона свободным
протоном.
1.5. Вычислить сечение неупругого рассеяния нейтрона с возбуждением
вибрационного уровня молекулы [28].
Если энергия нейтрона превосходит энергию возбуждения молекулы, то
рассеяние нейтрона на связанном протоне может сопровождаться возбужде-
нием молекулы. Для нахождения сечения такого процесса необходимо знать
волновые функции протона в возбужденных состояниях молекулы. Восполь-
зуемся для описания колебаний протона в молекуле моделью гармонического
осциллятора. В этом случае волновая функция протона удовлетворяет урав-
нению
{ - (й2/2М) Др +V (Гр)- Ef} q> (гР) = 0, (1.228)
в котором потенциальная энергия протона равна
г (гР)--~Л1<а2 г2
(ш — частота колебаний протона в молекуле).
Волновую функцию протона можно представить в виде произведения трех
волновых функций линейного осциллятора:
Ч> (Гр) - U) ипу (л) Un2 (£). (1.229)
□--л* t I i / <. _ / 2Л4оз
Здесь 6=1, ——х, 1) = 1/ —— У и £ = I/ ----------------- г — безразмерные
координаты: пх, пу и пг—вибрационные квантовые числа осциллятора.
Функции иПх(£) удовлетворяют уравнению
( d2 1 ]
(1-230)
74
и выражаЕотся через полином Эрмита
.п
X гг
da х
а=о
следующим образом:
(1.231)
Эти функции нормированы согласно условию
—ОО
Матричный элемент, входящий в сечение (1,223), разбивается на произ-
ведение трех интегралов типа
” . . Л
^on;e = (2n)-1/2(nj)-1/2 f d^'"^--------— e(-l/2)(S-a>* , (1,232)
Л s a=o
где
q==|/ — (k-k').
у 2Ма
^Предполагается, что до рассеяния протон находился в основном состоянии).
Интегрируя (1.232) по частям, находим
(-1/2)^
Увпх = (Чх)Пх(пх'.) 1/2 е
Поэтому сечение рассеяния нейтрона с возбуждением n-го вибрационного уров-
ня молекулы с энергией
Ef En = nh<i) (л = Пх + л!(4-н£) (1.233)
определяется формулой
nJ "у! пг!
е do,
где суммирование производится по всем значениям квантовых чисел пх, Пу
и пг, удовлетворяющих условию пх + n,j пг = п. В результате сумми-
рования получим
й' Qzn
do0n =4a3 —- е " do.
k п!
(1.234)
Замечая, что do-- 2л —т=- do2 и
2-У ЕЕ' 4
переписываем эту формулу в виде
Е
вводя безразмерную энергию е=----,
а<>
dUyy =
е
-----с 1,2 dq2.
nl
(1.235)
Используя закон сохранения энергии Е Е' +- nhu>, видим, что q заключено
в пределах
?мин—к в — п, <?макс——п-
75
Интегрируя и этих пределах выражение (1.235), получаем следующую фор-
мулу для полного сечения рассеяния нейтрона с возбуждением n-го вибра-
ционного уровня молекулы:
(1.236)
где
/ X хп \
Л.(*) = 1+ — +...+--
\ 1! п! /
В случае упругого рассеяния формула (1.236) приобретает вид
ом = (о0/е)(1 — е-^). (1.237)
В предельном случае е < 1 получаем из соотношения (1.237) известный уже
результат
0(Ю==4<То, е<\ 1. (1.238)
При 6 = 1 сечение упругого рассеяния равно ст„0 О,98ио. При е > 1 сечение
упругого рассеяния определяется выражением
^оо = ^о/в, е»1. (1.239)
Для больших значений е при любом п, не слишком близком к е, второе
слагаемое в соотношении (1.236) очень мало, а первое мало отличается от еди-
ницы. Поэтому сечение рассеяния с возбуждением любого разрешенного уров-
ня будет определяться в этом случае таким же выражением, как и сечение
упругого рассеяния;
®лп-°о/г\ е» 1. (1.240)
Максимальное значение п, согласно закону сохранения энергии, равно с,
поэтому полное сечение при больших & будет равно о0, т. е. при больших энер-
гиях нейтрона связь протона оказывается несущественной.
На рис. 1.13 представлена зависимость сечений а0(1, ow, оог и полного се-
чения рассеяния <т = 2^оп от энергии нейтрона в. Если энергия нейтрона
п
меньше энергии колебательного кванта Асо, то oil не может возбудить колеба-
ния в молекуле; в этом случае возможно только упругое рассеяние. При зна-
чениях энергии нейтрона, кратных Лы, происходит резкое увеличение сечения
рассеяния, обусловленное возможностью передачи энергии нейтрона колеба-
тельному движению протонов. Если энергия нейтрона велика по сравнению
с энергией химической связи, протоны можно считать свободными. Молекуле
передается небольшая доля энергии нейтрона, затрачиваемая на разрыв хи-
мической связи протона в молекуле. Рассеяние в этой области энергий прак-
тически упругое и характеризуется сферической симметрией в системе центра
инерции нейтрона и протона.
1.6. Если длина волны падающего нейтрона X сравнима с расстоянием
между протонами в молекуле водорода,то возможно как упругое рассеяние
нейтрона, так и неупругое, сопровождающееся изменением состояния моле-
кулы. Определить сечение упругого рассеяния нейтрона в молекуле водорода
с учетом эффектов запаздывания, а также сечения неупругих процессов рас-
сеяния, сопровождающихся возбуждением молекулы водорода [5].
Рассмотрим столкновение нейтрона, волновой вектор которого равен к,
с молекулой водорода, находящейся в состоянии, характеризуемом вибра-
ционным квантовым числом и, ротационным квантовым числом $ и спином 5.
Определим вероятность процесса, в результате которого иейтрон приобретает
волновой вектор к', а молекула переходит в состояние, характеризуемое
квантовыми числами о', У' и S',
76
Волновую функцию начального состояния нейтрона и молекулы выберем
в виде
(1.241)
i кг
где е‘кги — волновая функция относительного движения нейтрона и моле-
кулы; — волновая функция, описывающая движение протонов
в молекуле в состоянии, характеризуемом квантовыми числами v, у и
—спиновая функция нейтрона (р, — проекция спина нейтрона на ось г);
Рис. 1.13. Зависимость сече-
ний о0о, о01, <J02 и полного се-
чения рассеяния а от безраз-
мерной энергии нейтрона е —
наконец, — спиновая функция протонов в состоянии с результирующим
спином S (проекция спина на ось z равна ps). Аналогичным образом волновую
функцию конечного состояния выберем в виде
i к'г
Ф' = е (1.242)
& сГ о
Дифференциальное сечение рассеяния, усредненное по начальным и про-
суммированное по конечным магнитным квантовым числам, определяется
общей формулой
16 k' 1
dtJi f -------— —----------------------> >
9 k 2 (2S-J-1) (2^ +1)
и
Ф/.
2лй2
2
do.
(1.243)
7Ф;
где V — потенциал взаимодействия нейтрона с молекулой, определяемый
выражением (.1.66); do — элемент телесного угла, в котором лежит волновой
вектор рассеянного нейтрона. При рассеянии выполняется закон сохранения
энергии
Л-А2 hi ь'2
~W+E^=^+E^" (1-244)
Л2 k2
молекулы в состоянии Ф.,жм ; —~—энергия отно-
J -y. 2р
2
сительною движения нейтрона и молекулы р =—М — приведенная
масса).
где Е —энергия
77
Следует различать рассеяние нейтронов без изменения спинового состоя-
ния молекулы водорода (S -> S' == 5) и переходы, при которых спиновое
состояние молекулы изменяется (S->S’ — I—S). Переходы без изменения
спина обусловлены энергией взаимодействия Vc, а переходы с изменением
спина — энергией взаимодействия Va. Замечая, что
I За/ + as + («/—я8) = (За/ + as)2 + 5 (S +1) (at — й5)2,
нетрудно получить следующее выражение для сечения рассеяния нейтронов
без изменения спина молекулы:
4 k'
d<3Sv^-,Sv-^' l(3aj + ^2 + s<s+lH<4— «g)4x
1 f 1 I2
X-------- X \ cos--(k—k') гФ’ , (г) do. (1.245)
2^ + 1 J 2 \
В этом выражении и 3' должны быть числами одинаковой четности. Дейст-
вительно, так как протоны подчиняются статистике Ферми — Дирака, то
полная волновая функция молекулы водорода должна быть антисимметрич-
ной. Поэтому в случае параводорода, когда спиновая функция молекулы ан-
тисимметрична, пространственная функция должна быть симметричной, а
следовательно, ротационное квантовое число#- —четным. В случае ортово-
дорода ротационное квантовое число 3 является нечетным.
Чтобы найти сечение рассеяния нейтрона с изменением спина молекулы,
вычислим среднее значение величины |an(?i — ®г)12 по спиновым состоя-
ниям:
I (’1—’a) |2 = (з1~в2)2 = 4[3 — S (S + D1-
Поэтому сечение рассеяния нейтронов с изменением спина молекулы опре-
деляется формулой
4 к'
Tl3-S(S + 1)HO/-fls)2X
1 "V I C 1 2
X 2^ + 1 J drain — (k — k') гФ* (г) do. (1.246)
МуМу 3 г
Пара-ортопереходы и орто-парапереходы связаны с изменением четности ро-
тационного квантового числа 3-
Минимальная энергия нейтрона, необходимая для возможности перехода
молекулы из состояния п, 3 в состояние v', 3', равна
_ ЗЛ2 ,2 р
£мин = (к2 — k' )
3
Начальный импульс нейтрона в лабораторной системе к равен к, поэ-
тому минимальная энергия нейтрона в лабораторной системе координат
равна
3
Емин= g j- (1.247)
При малых значениях квантовых чисел и и 3 энергия возбуждения молекулы
водорода определяется выражением
/г2
Е„у = Пы>+~ 3W 3 П. (1-248)
78
РДе hio ~ 0,533 эв, а 6,615 за. Непосредственкый подсчёт показывает;
что нейтрон должен обладать энергией р 0,045 зв для того, чтобы перевести
молекулу из состояния v — 0, .1 в состояние vr 0, ' -- 2. Для перехода
из состояния v — 0, / — 0 в состояние v1 — 0, if' =- 1 необходима энергия
0,023 зв. Поэтому если энергия нейтрона меньше 0,045 зв, то возможны только
следующие ротационные переходы: 0 -> 0, 01, 1 0 и 1 —1.
Чтобы найти вероятности переходов для молекулы водорода, восполь-
зуемся моделью твердого ротатора. Волновую функцию молекулы в этом слу-
чае можно записать в виде
фожм (г)М1/<Иб(г~<Р)]1/2 (11г, <рг), (1,249)
/ У
где d — расстояние между протонами молекулы в состоянии равновесия
(d ж0,75-10-9 си); и фг— углы, определяющие ориентацию вектора г.
Используя (1,245) и (1.249), нетрудно получить следующее выражение для
дифференциального сечения упругого рассеяния (0 -> 0):
4
^о-О=7Г (Зо/ + os)2
У
11
Е sin —
2
2
2 л sin Wil,
(1.250)
где I = kd, & — угол рассеяния в системе центра инерции. Интегральное
сечение равно
ff(i-0= ^“л-(3а' : ’“2 j dx—~ =
о
16
= -~-л(За,+<»<№! [in 2g —ci 2g + 0,5772), (1.251)
У
где
С cosi
ci x ~— I dt-----.
.) t
Аналогичным образом нетрудно получить следующие выражения длд сечений
переходов 0-э-1, I -» 0 и 1 -> 1:
, ( sinx cosx—1 1 1 I ILI S '
<т0-.1=32л<А-<МгГ2--------h-----j-- l Vln*’ Tdxil ’ <L252)
( X X X X I |t_E
32 , „ (sinx cosx—1 1 . 1 ) !e-i-£+
°i-o=v л (-ai~ * ------+—;—+vlnx-тci* v <1 -253)
d (X Xй 2 2 J |£_£Т
16 1 sin2 E 3 / sin E V
, = — * I(3af + at)> + 2 (a,-as)2] Г2 (-cos |) +
+ ln 2g —ci 2g—0,4228}, (1.254)
где
При рассеянии очень медленных нейтронов в молекулярном водороде
существенным оказывается учет теплового движения молекул. Если v — ско-
79
рость падающего нейтрона, а и— тепловая скорость молекулы, то волновой
вектор к относительного движения, входящий в сечения, следует считать рав-
ным k— (p/fe)(v—н). Эффективные значения сечений рассеяния можно
найти, усреднив выражения ((.251)—(1.254) но тепловому движению молекул
o = f du | v —и | о (v — u) N (u),
v J
(1.255)
где N(u) — функция распределения молекул по скоростям.
Для примера приведем результаты вычислений сечений в случае рассея-
ния нейтрона с энергией 0,001723 зв (эта энергия соответствует температуре
20° К):
ао.,о'7“6’444 (3«/ |-аЛ.)2;
<4 _0-1,753 (д1—
О[., j —6,450 ^(3a(- + as)24-2 (at—аД2}.
Экспериментально можно измерить следующие величины:
ffnapa — ^0 .(Р Порто — а1-от"а1 >!•
(1.256)
(1.257)
Экспериментальные значения указанных величин при температуре 20° К
равны
Опара = 3-97.10-24 ™z, сорто = 124-Ю-84 см2. (1.258)
Используя формулы (1.256) и (1.257), по значениям (1.258) можно определить
с высокой степенью точности значения длин рассеяния ai и as.
1.7. Проверить, что коэффициенты а, р, у, б и е, входящие в амплитуду
рассеяния нуклона на нуклоне (1.170), выражаются через фазы рассеяния
•Ж
16) и 36; и параметры смешивания следующим образом:
a=4? 2 l(Z+2) a'+1+<2/+о1) <
K 1=0
+ ! + (27-1- 1) c'J Pt (cos II);
5^+' 4-/8'-'- (2/+ 1) 4] Р1 (“s э)
7+1 a‘
1=2 L 1
a‘ ‘1 Pl (cosft) ;
i “f- I J 1
af+'
2/+1 , 7—1
—------а* —-----
1U + 1) ' I
р) (cos &);
ф____________
4k cos Я
<*+(2/+!)«;+(i-М
7 =
X (cos 9— 1) (7 -j- 1) b‘+} -f- - (27 4 1) c{ cos 11 X
(1.259)
80
X(1 +cos &) P'2t (cos fl)| ;
е==4Г^Г& [2[Ъ(/ + 2)4+1 4 (2'+1Н + ('-1)«Пх
X(1 +cos 4)) — (i -\-1) 1 —(2/-j -1) C; cos P; (cos &) +
+T 2 [ж fl'+’ ~ тйТГ <+/И fcos»-') p^os»>}
где введены обозначения-.
i36^
/='^‘7
a^=H-i L. cos2 e<^ 4-p^ sin2 k^' (
+ 11/
2 V Г + 1
^-l-1. [ = a^ cos2 e^5 sin2 —
~,~l = sin2 -}-[}? cos2£^ +
1 / % I 1 (1.260)
+ 1|/
1 ^v.'^' sin2 e^4‘fl^ cosS —
-71/
2 V ^ + 1
,-зй7
a^ = sin36^ .e *;
7-1 ’
i36^
fi^sin’^e^-1;
c?=!-= sin1 6^ e11^-
1.8. Вывести интегральные соотношения унитарности для амплитуды
упругого рассеяния двух нуклонов [18].
81
Если предположить, что в систем^ двух нуклонов возможно толкко упру;
гое рассеяние, то из условия унитарности 5-матрицы нетрудно получить сле-
дующее интегральное соотношение для матричной амплитуды рассеяния
i ь г*
/(к, кг)-/+(к', к) = — do"f(k, к")/+(к', к"), (1.261)
где интегрирование производится по направлениям вектора к".
Воспользуемся для амплитуды упругого рассеяния двух нуклонов фор;
мулой Вольфенштейна (1.170). Умножая левую и правую части равенства
(1.261) последовательно на матрицы 1; п(о х-ф <j2); msj - и
l«i . 1а2, а затем вычисляя шпуры в левых частях равенств, получим пять
интегральных соотношений унитарности для коэффициентов а, р, у, 6 и е:
(4rt/k) Im а (11) — (1/4) do" Sp (k, k") f+ (k', k"));
Im ₽(&)= (1/4)^ do"Sp { nat • па2 f (k, k") f+ (k't k"));
(4n/fe) Im 7(0)= (1/81) do" Sp {n (sj + Sa) f (k, k’)f+(k', k")};
(4n/fe) lin 6 (Я) = (1/4) do" Sp mifm52 f (k, k") f + k', k")};
(4л/А) Im s(D)-(1/4) Jjdo’Sp {kj • kJ (k, k") f+(k', k")},
(1.262)
где f). — угол между векторами k' и k. Вычисление щпуров в правых частях
равенств (1.262) элементарно, но приводит к громоздким выражениям, кото-
рые мы не даем.
ГЛАВА 2
ЯДЕРНАЯ МА ТЕРИЯ
§ 2.1. НАСЫЩЕНИЕ ЯДЕРНОГО ВЗАИМОДЕЙСТВИЯ
Размеры ядер и распределение плотности внутри ядер. Про-
странственная структура атомных ядер —
сложных частиц, состоящих из более простых частиц — нейтронов
и протонов, определяется пространственной структурой послед-
них и характером взаимодействия между ними. Отличительной осо-
бенностью ядер является наличие у них резко выраженной грани-
цы. Опыт показывает, что ядерная плотность почти постоянна внут-
ри ядра и резко спадает до нуля в области, линейные размеры ко-
торой малы по сравнению с размерами ядра. Если предположить,
что ядро обладает сферической симметрией, то размеры ядра будут
характеризоваться единственным параметром — радиусом ядра.
Так как ядерное взаимодействие между нуклонами значительно
интенсивнее кулоновского, то размеры ядер и распределение нук-
лонов внутри них определяются в основном ядерными силами.
Вследствие зарядовой независимости ядерных сил пространствен-
ное распределение нейтронов и протонов внутри ядер почти одина-
ково. Некоторое увеличение занимаемого протонами объема, обус-
ловленное кулоновским отталкиванием, компенсируется примерно
таким же увеличением объема, занимаемого нейтронами, вслед-
ствие увеличения числа избыточных нейтронов с ростом заряда
ядра. Поэтому обычно предполагается, что размеры ядра с очень
хорошей точностью задаются распределением плотности заряда.
Наиболее точно радиусы ядер и распределение плотности внутри
ядер определяются из опытов по рассеянию на ядрах электронов
высоких энергий. Соотношения, характеризующие влияние прост-
ранственной структуры ядер на рассеяние, можно получить в про-
стом виде, если применимо борновское приближение. Для кулонов-
ского рассеяния ультрарелятивистских электронов борновское
приближение справедливо при выполнении условия
(Ze2/fic)< 1, (2.1)
где Z — заряд ядра; с — скорость света. Это условие хорошо вы-
полняется для не очень тяжелых ядер.
Сечение упругого рассеяния электронов высокой энергии в ку-
лоновском поле точечного заряда Z при выполнении условия (2.1)
83
определяется формулой Мотта
о0 (0) = (Ze3/2£)3 (cos"-»/2/sin4 V2), (2.2)
гдей1 — угол рассеяния; Е — энергия электронов. В случае рассея-
ния электронов на ядре с зарядом 2, характеризуемым пространст-
венным распределением p(Z> (г), сечение определяется выражением
<y(ft)=o0(W(<. (2.3)
где F (<?) — форм-фактор распределения заряда;
F(q) = (l/Z) $ dre1qfp<z> (г). (2.4)
Здесь q — импульс, передаваемый электроном ядру; для ультра-
релятивистских электронов (£ > тс2, т — масса электрона)
/у = (2£/7гс) sin 0/2. (2.5)
Формулы (2.2) и (2.3) записаны в системе центра инерции электрона
и ядра.
Сравнивая (2.3) с (2.2), видим, что отклонение закона рассеяния
электронов на ядре от закона рассеяния для точечного заряда
непосредственно связано с пространственным распределением за-
ряда в ядре. Согласно (2.4), форм-фактор F (у) — это просто пре-
образование Фурье от распределения заряда в ядре; поэтому, зная
F (q), с помощью обратного преобразования Фурье нетрудно найти
р2 (г):
pz(r) —Z §(t/q/(2n)3) e“icir £(<?). (2.6)
Так как распределение заряда совпадает с распределением нукло-
нов в ядре, то зависимостью вида (2.6) будет определяться также
распределение плотности нуклонов в ядре р (г):
p(r)=(A/Z)p^(r). (2.7)
Если длина волны электронов велика по сравнению с разме-
рами ядра, то в формуле (2.4) экспоненту можно разложить в ряд
по степеням qr, при этом найдем
£(q) = l-(l/6)q27?3 + ...(q/?<l), (2.8)
где Л* — среднеквадратический радиус ядра;
R2 — § dr • г3 р (г) / dtp (г). (2.9)
Очевидно, для возможности обнаружения эффектов, связанных
с конечными размерами ядра, необходимо, чтобы длина волны
электронов была меньше или по крайней мере сравнима с размерами
ядра. С уменьшением длины волны (т. е. с увеличением энергии)
электронов можно более детально исследовать пространственную
структуру ядра.
84
В случае тяжелых ядер борновское приближение неприменимо.
Для получения сведений о пространственной структуре таких
ядер из данных по рассеянию электронов необходимо использовать
численные методы.
Анализ многочисленных экспериментальных данных показывает
[1, 2], что наилучшим образом пространственное распределение
плотности нуклонов в ядрах с массовыми числами А > 20 описы-
вается фермиевской функцией *
р(г) =----(2.10)
1 е а
где величина R' пропорциональна А|/3:
R’ = R0' А1/3. (2.11)
Если R' а, то распределение, описываемое функцией (2.10),
характеризуется почти однородной плотностью р se р„ во всей
области ядра, кроме поверхностного слоя толщиной порядка а,
в котором плотность быстро спадает до нуля. Величина р0 опре-
деляет плотность нуклонов в центре ядра и R' соответствует рас-
стоянию от центра, на котором плотность уменьшается вдвое по
сравнению с максимальным значением. Величину а, характеризую-
щую толщину поверхностного слоя, в котором происходит быстрое
уменьшение плотности, обычно называют диффузностью
края ядра. Если а-»- 0, то распределение, описываемое фер-
миевской функцией (2.10), переходит в однородное распределение
с радиусом R'. Так как
JJdrp(r) =А,
то величины р0, а и Ro', входящие в (2.10), связаны между собой
соотношением
= (2.12)
\ К /
Численные значения величин р0, а и Rn' в пределах точности экс-
перимента одинаковы для всех ядер (А > 20) и, согласно данным
Хофштадтера, равны
р0 = 1,68-1038 сл<-3; а = 0,57-10 ' 13 см; Ro'= 1,10-10~13 см. (2.13)
Под радиусом ядра R обычно подразумевают среднеквадрати-
ческий радиус, определяемый выражением (2.9). Так же, как и R',
радиус ядра R представим в виде
R-R0A'-’\ (2.14)
* В случае очень легких ядер при нахождении распределения плотности
нуклонов из данных по рассеянию электронов существен учет внутренней
структуры нуклонов.
85
где величина медленно уменьшается с ростом А от значения
R„ = 1,3-10-'“ см для легких ядер до значения £0 = 1.2-1013 см
для более тяжелых. Для большинства ядер приближенно можно
положить
7?о = 1,2-1О-13 см- (2.15)
Однородное распределение, характеризуемое тем же значением
среднеквадратического радиуса R, что и истинное распределение,
обычно называют эквивалентным однородным
распределением. Радиус такого распределения ,^кв,
очевидно, связан с радиусом R соотношением
Яэкв-КбЖ.
Эквивалентное однородное распределение приводит к тому же
рассеянию при низких энергиях, что и действительное распределе-
ние.
Если ядро представить в виде сферы с однородным распреде-
лением плотности, то величина Ra будет пропорциональна корню
кубическому из объема, приходящегося на один нуклон. Постоян-
ство этой величины для всех ядер указывает на постоянство плот-
ности. Небольшое уменьшение R„ (примерно на 12%) означает, что
эквивалентная однородная плотность медленно увеличивается
с ростом А.
Величина Ro', определяющая фермиевское распределение (2.10),
практически постоянна для всех ядер (с точностью до 2%). Со-
гласно (2.12) это означает, что для всех ядер с А » 1 плотность
нуклонов в центральной части ядра (за исключением тонкого по-
верхностного слоя) практически одинакова. Поэтому если пре-
небречь поверхностными эффектами, то объемы ядер действительно
оказываются пропорциональными числу нуклонов А. Это свойство
несжимаемости ядерного вещества лежит в основе так называемой
капельной модели ядра.
Энергия связи ядер. Масса стабильного ядра, на-
ходящегося в основном состоянии, всегда меньше суммы масс про-
тонов и нейтронов, входящих в состав ядра. Запишем энергию яд-
ра в основном состоянии:
£(А, Z)^(M(A, Z)~ZMp — (A—Z)Mn)cs, (2.16)
где М (A, Z) — масса ядра; МР и Мп — массы протона и нейтрона.
Величину £ (A, Z), взятую с обратным знаком, называют энер-
гией связи. Очевидно, энергия связи — это работа, которую
необходимо затратить, чтобы разделить ядро на составные частицы.
Характеристикой устойчивости ядра является энергия связи,
приходящаяся на один нуклон. На рис. 2.1 представлена зависи-
мость средней энергии связи па один нуклон от массового числа А
для различных ядер. Энергия связи на нуклон с ростом А сначала
быстро растет, достигая значения 8 Мэв уже при А —• 16, затем
очень медленно возрастает до значения 8,8 Мэв при А ян 60, а потом
86
очень медленно уменьшается, принимая значение 7,4 Мэв для самых
тяжелых ядер. Наиболее характерной особенностью этой зависимо-
сти является то, что средняя энергия связи на один нуклон прибли-
зительно постоянна (»8 Мэв) почти во всей области изменения А,
за исключением области очень легких ядер. Следовательно, пол-
ная энергия связи ядра, так же как и объем ядра, пропорциональ-
на числу нуклонов в ядре. Небольшие отклонения от этой пропор-
циональности связаны с поверхностными эффектами, кулоновским
отталкиванием между протонами, разностью между числом нейт-
ронов и протонов и эффектами четности числа протонов и нейтронов.
Рис. 2.1. Зависимость средней энергии связи на один
нуклон от массового числа А.
Независимость средней энергии связи на нуклон от числа нук-
лонов, так же как и независимость объема, приходящегося на один
нуклон, от числа нуклонов в ядре можно объяснить, предположив,
что ядерные силы между нуклонами обладают свойством насыще-
ния, т. е. каждый нуклон в ядре может взаимодействовать только
с небольшим числом ближайших нуклонов. Насыщение ядерных
сил указывает на аналогию между свойствами ядерного вещества
и обычной жидкости. На основе этой аналогии вводится капельная
модель ядра, согласно которой ядро рассматривается как капля
ядерной жидкости. Капельная модель ядра позволяет объяснить
зависимость энергии связи ядер от массового числа А и заряда
ядра Z.
Зависимость энергии связи ядер от Л и Z описывается полуэм-
пирической формулой Вайцзеккера
Е (Л, Z) = —ед. А + М2/3 4-e3(Z2M'/3) +
+ e4[(4~2Z)2MH-e5-4~3/4 б, (2.17)
где численные значения коэффициентов равны [31 е, = 15,75 Мэв;
с2 17,8 Мэв; е3 = 0,71 Мэв; е4 = 23,7 Мэв; е5 •= 34 Мэв, а ве-
87
личина S в зависимости от четности чисел нейтронов и протонов
равна
'—1 А — четное, Z—четное;
О Л-— нечетное;
.-!-1 Д —четное, Z —нечетное.
Первые три слагаемых в формуле (2.17), представляющие собой
объемную, поверхностную и кулоновскую энергии, предсказыва-
ются капельной моделью ядра. Объемная энергия, учитывающая
пропорциональность энергии связи ядра полному числу нуклонов,
соответствует полному насыщению ядерного взаимодействия между
нуклонами в ядре. Наличие поверхности приводит к уменьшению
энергии связи, так как нуклоны на поверхности взаимодействуют
с меньшим числом соседей по сравнению с нуклонами, находя-
щимися внутри ядра. Кулоновская энергия — это энергия электро-
статического отталкивания в ядре, рассматриваемого как капля
однородно заряженной жидкости, Четвертое и пятое слагаемые
в (2.17) характеризуют энергию, связанную с симметрией сил
между нейтронами и протонами и с эффектом спаривания между нейт-
ронами и протонами.
Капельная модель позволяет объяснить не только эксперимен-
тальную зависимость энергии связи ядер от А и Z, но также и неко-
торые другие свойства ядер. Представление о ядре как жидкой
капле согласуется с наличием у ядер сравнительно резкой границы.
Капельная модель ядра позволяет объяснить явление деления ядер,
а также наличие у ядер возбужденных состояний, связанных с де-
формацией поверхности ядер.
§ 2.2. ГАЗОВАЯ МОДЕЛЬ ЯДРА
Насыщение ядерного взаимодействия и независимость движе-
ния отдельных нуклонов в ядре. Рассмотрим несколько подробнее
свойства ядерного вещества. Как мы видели, из анализа много-
численных экспериментальных данных о свойствах ядер следует,
что плотность ядерного вещества и средняя энергия связи на нуклон
примерно одинаковы для всех ядер, за исключением области самых
легких ядер. Постоянство плотности и энергии связи на нуклон
связано с насыщением ядерных сил, которое качественно можно
объяснить, рассматривая ядерное вещество как несжимаемую жид-
кость. Кроме того, ядра обладают некоторыми свойствами, кото-
рые удается объяснить, предположив, что нуклоны в ядрах дви-
жутся независимо, т, е. рассматривая ядра как системы независи-
мых частиц. Действительно, зная плотность ядерного вещества,
нетрудно определить среднее расстояние между нуклонами в ядре:
оно составляет около 1,8 • 10~13 см. В то же время пространствен-
ные размеры нуклонов равны 0,45 • 10-’13 см- Следовательно, нук-
лоны заполняют только около 1/50 части всего объема ядра. По-
88
этому, несмотря на насыщение ядерного взаимодействия, нуклоны
в ядре сохраняют свои индивидуальные свойства, которые, в свою
очередь, проявляются в свойствах ядер. Наличие особо стабиль-
ных ядер, содержащих определенные так называемые магичес-
кие числа нуклонов, указывает наТсуществование нук-
лонных оболочек в ядрах. Значения спинов, магнитных моментов и
некоторые другие характеристики ядер удается объяснить, рассмат-
ривая ядро как систему независимых нуклонов, находящихся в не-
котором самосогласованном поле и распределенных в силу прин-
ципа Паули по определенным оболочкам.
Итак, ядерное вещество можно рассматривать, с одной стороны,
как систему сильно взаимодействующих частиц, находящуюся
в конденсированном жидкообразном состоянии, с другой стороны —
как систему почти невзаимодействующих частиц со свойствами,
характерными для газообразного состояния. Указанная двойст-
венность — это характерное свойство ядерного вещества, которое
не связано с индивидуальными особенностями ядер.
Чтобы исключить при рассмотрении свойств ядерного вещест-
ва эффекты, связанные с индивидуальными особенностями ядер,
введем понятие я дерной материи. Под ядерной материей
будем подразумевать вещество гипотетического ядра, состоящего
из одинакового числа нейтронов и протонов, в котором отсутствует
кулоновское отталкивание между протонами и которое настолько
велико, что можно пренебречь поверхностными эффектами.
В действительности кулоновские эффекты растут пропорцио-
нально Z2 и становятся существенными раньше, чем массовое число
А достигает такой величины, чтобы можно было пренебрегать по-
верхностными эффектами. В частности, кулоновское отталкивание
приводит к тому, что не существуют ядра с массовыми числами
А значительно большими 200.
Наиболее характерное свойство ядерной материи связано с на-
сыщением ядерного взаимодействия и проявляется в том, что
плотность нуклонов р и энергия е, приходящаяся на один нуклон,
не зависят от Л. В соответствии с соотношениями (2.10), (2.12) и
(2.17) значения р и е для ядерной материи (Д 1) выберем равными
р^---------- — 1,8-1038 см-3, е = —15,75 Мэв, (2.18)
(4л/3)
т. е. будем предполагать, что р совпадает со значением ядерной плот-
ности в центре ядер (А 1), а энергия е связана только с объемным
слагаемым в формуле Вайцзеккера.
Другим, не менее важным свойством ядерной материи является
то, что динамически ядерную материю можно рассматривать как
систему независимых частиц. Так как плотность частиц фиксиро-
вана, то при заданном числе частиц система имеет вполне опре-
деленный объем. В дальнейшем для определенности под ядер-
ной материей будем понимать систему, состоящую из А нук-
89
лонов (из них Л/2 нейтронов и А!2 протонов), занимающих объем
Q, при этом А будем считать достаточно большим, чтобы можно
было пренебрегать поверхностными эффектами.
Предполагая, что между нуклонами действуют только двухча-
стичные силы, гамильтониан системы можно записать в виде
tf = S[_(Zi2/2Af)4.]+2 Vi}, (2.19)
i i < i
где 2Л1 — кинетическая энергия отдельного нуклона; Vtj —
потенциал двухчастичного взаимодействия между нуклонами t и j.
Очевидно, полная энергия ядерной материи равна
Е = <Ф | V -(ЛД/2Л1) + Е Vi} | Ф), (2.20)
/ I i<Zi
где Ф — волновая функция основного состояния системы.
Основная задача теории состоит в том, чтобы объяснить свой-
ства ядерной материи на основе сил, действующих между нуклона-
ми. Существование стабильных ядер означает, что между нуклонами
в ядрах действуют в основном силы притяжения. Однако если бы
между нуклонами действовали только силы притяжения, то это
привело бы к стягиванию ядер, т. е. линейные размеры ядер совпа-
ли бы с радиусом действия ядерных сил. В этом случае плотность
была бы пропорциональна полному числу частиц в ядре. В дейст-
вительности плотность р не зависит от А (насыщение ядерных сил),
а это означает, что силы, действующие между нуклонами, должны
быть частично отталкивающими. Как мы знаем, ядерные силы дейст-
вительно являются отталкивающими на очень малых расстояниях.
Кроме того, ядерные силы имеют частично обменный характер и,
следовательно, будут силами притяжения или отталкивания в за-
висимости от состояния взаимодействующих частиц.
Ядерные силы характеризуются чрезвычайно малым радиусом
действия и очень большой интенсивностью. Эта особенность ядер-
ных сил, на первый взгляд, несовместима с представлением о ядер-
ной материи как о системе независимых частиц. В действитель-
ности, однако, в силу принципа Паули взаимодействие между
нуклонами существенно ослабляется, и этим объясняется, почему
для описания ядерной материи применима модель независимых
частиц.
Свойства идеального ферми-газа. Некоторые свойства ядерной
материи можно удовлетворительно описать с помощью модели
ферми-газа, в которой вообще пренебрегается взаимодействием
между частицами [4]. Согласно этой простейшей модели, ядерная
материя представляется в виде идеального нуклонного газа, зани-
мающего определенный объем £2. Очевидно, полная энергия в слу-
чае идеального ферми-газа описывается общим выражением (2.20),
в котором, однако, взаимодействие между нуклонами следует счи-
90
тать равным нулю. Волновая функция для идеального ферми-Газа
Ф„ представляется в виде антисиммстризованиого произведения од-
ночастичных волновых функций
А
Фи = аП(р (rj. (2.21)
/= 1 ‘
Здесь <ра. (г,) — волновая функция отдельного нуклона в опре-
деленном состоянии аг. Предполагая объем Q достаточно большим,
одночастичные волновые функции сра (г) можно выбрать в виде
плоских волн
<P«(r) =(1//Q) eik“r, (2.22)
где ka — импульс нуклона (зарядовую и спиновую части функции
мы не выписываем в явном виде).
Кинетическая энергия частицы с определенным импульсом рав-
на Й2й„/2Л1. В силу принципа Паули в каждом из состояний с оп-
ределенным значением энергии
может находиться не более че-
тырех нуклонов, отличающихся
значениями проекций спина и
изотопического спина. Основно-
му состоянию системы соответ-
ствует минимум энергии. Это
означает, что в основном со-
стоянии все одночастичные
уровни, отвечающие значениям
импульса, меньшим некоторого
граничного импульса Ферми kF,
заполнены, а более высокие
уровни свободны. Распределе-
ние нуклонов по импульсам
Рис. 2.2. Распределение нуклонов
по импульсам в идеальном ферми-
газе. (Штриховая кривая соответст-
вует распределению нуклонов при
температуре системы, отличной от
нуля.)
в этом случае имеет вид пря-
моугольной ступеньки и соответствует нулевой температуре си-
стемы (рис. 2.2).
Граничный импульс Ферми kF определяется ядерной плот-
ностью р. Действительно, число возможных состояний нуклона со
значениями импульса внутри интервала dk равно
4Q (Л/(2л)3).
(2.23)
Численный коэффициент в (2.23) учитывает вырождение, связан-
ное с наличием спина и изоспина у нуклона. Так как в основном
состоянии все уровни с k < kF заполнены и число нуклонов рав-
но А, то
4Q J (Дс/(2л)3)=Д
k<kF
91
откуда следует, Что
А/-=((3'г) р = (Л/Й).
Далее, так как р = (3/4л/?03), то
kF = у (9H78)-(1//?o9-
(2.24)
(2.25)
Замечая, что /?0' — 1,10 • 10~13 сл!, имеем kp — 1,38 • 1013 см
откуда для граничной энергии Ферми Ер находим
Ep = (ji2 kp/2M)^39 Мэв. (2.26)
Полная энергия всей системы равна
£=V(/-Z2^/2A1),
а
(2.27)
где суммирование распространяется по всем заполненным одно-
частичным уровням. Если система находится в основном состоя-
нии, то
2ЙЗ М f dk ЬЧ- 3
== 1 ---“ • —---м .
b 2M--------------------------------J (2л)3 2M 5 2M
k^kp ' '
(2.28)
Таким образом, средняя энергия, приходящаяся на один нуклон,
в случае идеального ферми-газа равна
=Ci/5)\h2 kp/2M). (2.29)
А
Используя численное значение р (2.18), находим
Ео/А 24 Мэв.
(2.30)
Положительный знак величины Elt/A указывает на неудовлетвори-
тельность модели идеального ферми-газа, поскольку эта модель,
объясняя однородность ядерной материи и пропорциональность
полной энергии объему системы, не объясняет существование свя-
занного состояния ядерной материи.
Модель идеального ферми-газа можно несколько улучшить, а
именно связанное состояние ядерной материи можно объяснить,
рассматривая ее как газ невзаимодействующих нуклонов, движу-
щихся в некоторой потенциальной яме, занимающей объем Q. Глу-
бина ямы должна быть подобрана таким образом, чтобы энергия
отрыва отдельного нуклона совпадала с экспериментальным значе-
нием. Согласно экспериментальным данным, энергия отрыва от-
дельного нуклона S в среднем одинакова для всех ядер и равна при-
мерно 8 Мэв. Поскольку наименее связанными являются нуклоны
с энергиями, близкими к граничной энергии Ер, то глубину ямы
следует считать равной
v0^ef+s.
(2-31)
92
Согласно (2.26), величина Vo составляет около 47 Л4эв.
Модель ферми-газа в потенциальной яме для ядерной материи
подобна модели свободных электронов в теории металлов. Так же,
как и последняя, она хорошо описывает свойства ядер, связанные
с распределением нуклонов по импульсам, но не значения энергий
или пространственное распределение нуклонов в ядрах. Основным
недостатком указанной модели является необходимость введения
внешнего потенциального поля.
Стягивание ядер под действием сил притяжения между нукло-
нами. Учтем теперь взаимодействие между нуклонами, ограни-
чившись первым приближением теории возмущений. В этом приб-
лижении волновая функция Ф сохраняет вид (2.21), а полную
энергию системы можно представить в виде
Е=Е.+ 2 (2-32)
где Ua& — энергия взаимодействия пары нуклонов, находящихся
в состояниях аир:
иар | v IW (2.33)
(Фа₽ — антисимметризованная волновая функция двух нуклонов),
и суммирование в (2.32) распространяется по всем заполненным
состояниям.
Вводя координаты центра инерции и относительные координа-
ты для двух нуклонов R = (l/2) (ri + Г2) и г = п — г2, пространст-
венную часть волновой функции q?np можно представить в виде
произведения волновой функции движения центра инерции двух
нуклонов на волновую функцию относительного движения:
<РЙр(гт, гг)=(1/КГ2)е"<>£(г), K=ka + k₽, k=(l/2)(ka-kp). (2.34)
Хотя полная волновая функция (включающая зарядовую и
спиновую части) в силу принципа Паули должна быть антисиммет-
ричной относительно перестановки двух нуклонов, волновая функ-
ция относительного движения <р£ (г) может быть как симметрич-
ной, так и антисимметричной:
<₽£(±) (г) = (1//2Q) (eikr±e-ikr). (2.35)
Если число нейтронов и протонов в системе одинаково, причем
как среди нейтронов, так и среди протонов числа нуклонов с про-
тивоположными спинами равны между собой, то статистические
веса симметричного и антисимметричного состояний ср<+> и <р(_)
соответственно равны 3/8 и 5/8. Действительно, учитывая веса синг-
летных и триплетных состояний по изоспину и обычному спину,
имеем
— 1<Р(+)|2
4 ( 4 Г !s=
1 4 | k )S=O
93
= -|-l ф(+> 12+#|ф(-Ча-
о о
Поэтому энергия взаимодействия двух нуклонов (2,33), усреднен-
ная по зарядовым и спиновым состояниям нуклонов, равна
= (I/£2) {1 —(1/4) cos 2kr) V (г). (2.36)
Полную потенциальную энергию системы найдем, просумми-
ровав (2.36) по всем парам нуклонов. Если плотность нуклонов
достаточно велика (й??г9фф 1), то членом с cos 2кг в соотношении
(2.36) можно пренебречь. Поэтому энергия двухнуклонного взаимо-
действия будет одинакова для всех пар нуклонов. Всего имеется
(1/2)Л (А —• 1) пар. Используя (2.29) и (2.32), получаем следую-
щее выражение для энергии, приходящейся на один нуклон:
CdrV(r)M>> 1). (2.37)
А 10 М Зл2 J V / х z / к )
Если взаимодействие между нуклонами соответствует силам
притяжения на всех расстояниях (V (г) <; 0), то, согласно (2.37),
энергия будет уменьшаться с увеличением плотности р= /2/Зл2)/гЛ3,
и, следовательно, должно происходить стягивание ядра [5]. Этот
вывод не связан с использованием первого приближения теории
возмущений. Действительно, первое приближение теории возму-
щений дает для энергии основного состояния любой системы значе-
ние, большее истинного значения или же равное ему. Поэтому
истинная энергия ядра будет даже меньше, чем значение, получен-
ное согласно (2.37), и, следовательно, насыщения не может быть.
Очевидно, при наличии только сил притяжения стягивание
ядра происходит до тех пор, пока все нуклоны не заполнят область
с линейными размерами, равными радиусу действия ядерных сил.
В этом случае все нуклоны взаимодействуют друг с другом и пол-
ная энергия ядра пропорциональна числу взаимодействующих
пар (1/2)Л (А — 1). Все это справедливо для очень легких ядер.
Например, энергия связи ядер 2Н, аНе и 4Не соответственно равна
2,2; 7,6 и 28,1 /Изе. Несколько более быстрый рост энергии связи
по сравнению с числом взаимодействующих пар (которое для ука-
занных ядер соответственно равно 1, 3 и 6) обусловлен тем, что
в 4Не нуклоны проводят в области действия ядерных сил большую
часть времени, чем в аН и 3Не. Однако в ядрах, следующих за 4Не,
значительного увеличения энергии, приходящейся на один нуклон,
не наблюдается. Это означает, что в ядрах тяжелее 4Не каждый
нуклон взаимодействует только с ограниченным числом соседей,
т. е. имеет место насыщение ядерного взаимодействия.
Условие насыщения в случае обменных ядерных сил. Насыще-
ние ядерных сил можно попытаться объяснить, сделав допущение
94
об обменном характере ядерного взаимодействия между нукло-
нами [61.
Предположим, что кроме обычных сил, характеризуемых потен-
циалом V (г), между нуклонами действуют еще обменные силы,
характеризуемые потенциалом V (г) Рг, где V (г) <0, и Рг —
оператор перестановки пространственных координат. Собствен-
ные значения оператора Рт для состояний <р(+)(г) и ф<-> (г) соответ-
ственно равны +1. Таким образом, в случае обменного взаимодей-
ствия силы будут притягивающими в пространственно симметрич-
ных и отталкивающими (но той же самой величины) в пространст-
венно антисимметричных состояниях.
Энергия обменного взаимодействия двух нуклонов, усредненная
по различным зарядовым и спиновым состояниям нуклонов, равна
= 1/S2 $ dr | — l/4 + cos2kr] V (г). (2.38)
Просуммировав (2.38) по всем парам нуклонов и сложив с (2.37),
в случае большой плотности получим следующее выражение для
энергии, приходящейся на один нуклон:
Е 3 К1 kp* 1 - ,f ( 1 ~ 1 ,
т^ттг+^'Н^-тМ (23э>
Если V (г) и V (г) не изменяют свой знак как функции расстоя-
ния, то насыщение возможно только в том случае, когда обменное
взаимодействие по своей величине более чем в четыре раза превы-
шает необменное взаимодействие и имеет тот же знак.
Из анализа экспериментальных данных по рассеянию нукло-
нов на нуклонах следует, что интенсивности обычных и обменных
сил почти равны. В частности, к хорошему согласию с эксперимен-
тальными данными по рассеянию нуклонов на нуклонах приводит
потенциал Сервера (1.140). Поскольку условие V > 4V для реаль-
ного потенциала (1.140) не выполняется, то учет только обменного
характера ядерных сил не приводит к объяснению насыщения.
f 2.3. МОДЕЛЬ НЕЗАВИСИМЫХ ПАР
Отталкивание нуклонов на малых расстояниях. Для объясне-
ния насыщения ядерных сил предположим, что ядерное взаимодей-
ствие является отталкивающим на очень малых расстояниях между
нуклонами. О наличии сил отталкивания между нуклонами на ма-
лых расстояниях свидетельствуют опыты по рассеянию нуклонов
на нуклонах при высоких энергиях. Данные по рассеянию нуклонов
на нуклонах при высоких энергиях согласуются с предположением
о том, что у нуклонов существует сильно отталкивающая сердце-
вина, не позволяющая им сближаться на расстояния, меньшие ра-
диуса сердцевины rc as 0,4 • 10~13 см.
В случае бесконечных сил отталкивания на малых расстояниях
между нуклонами модель независимых частиц вообще непримеии-
ма и в качестве волновой функции основного состояния ядерной
материи нельзя использовать антисимметризованное произведение
одночастичных волновых функций (2,21). Действительно, оттал-
кивание на малых расстояниях не позволяет сближаться двум нук-
лонам на расстояния меньше радиуса сердцевины гс, в то время
как волновая функция (2.21) учитывает только корреляцию между
нуклонами, обусловленную влиянием принципа Паули.
Наличие сильной корреляции между нуклонами, связанной с
отталкиванием на малых расстояниях, учитывается в так назы-
ваемой модели независимых п а р [7, 8]. В этой модели
взаимодействие между любой парой нуклонов рассматривается как
можно более точно, но при этом пренебрегается взаимодействием
всех остальных нуклонов друг с другом и с данной парой.
Выбирая одночастичные состояния так же, как для свободного
ферми-газа, энергию системы можно записать в виде
Е=Е0-\- 2 UafSt (2.40)
а>₽
где (/ар — поправка к энергии, обусловленная взаимодействием
пары нуклонов в состояниях а и ₽, а суммирование распростра-
няется по всем заполненным состояниям. Величина t/ap вычисля-
ется в предположении, что взаимодействие имеет место только
между парой нуклонов в состояниях аир. При этом волновая
функция пары нуклонов <рар вследствие взаимодействия между
ними не является произведением одночастичных волновых функ-
ций нуклонов. Все остальные частицы в состояниях у а и р
предполагаются совершенно не взаимодействующими, и их волно-
вые функции выбираются в виде плоских волн. Хотя, согласно
предположению, все остальные нуклоны с выделенной парой не
взаимодействуют, тем не менее они оказывают существенное влия-
ние на взаимодействие пары вследствие принципа Паули. Для на-
хождения волновой функции (ряр и энергетической поправки Ua$
установим прежде всего уравнение, описывающее движение взаи-
модействующей пары нуклонов, входящих в распределение Ферми.
Уравнение Бете — Голдстоуна. Рассмотрим вначале уравне-
ние Шредингера, описывающее рассеяние изолированной пары
частиц:
{-(^/2М) (Дх + ДЛ- V (гг—гг)-(И. гг)=0, (2.41)
где Е%$ = (fi2/2M) (Аа3 + Ар2)—энергия; ка и кр—волновые век-
торы сталкивающихся на бесконечности частиц. Найдя решение
этого уравнения, можно определить сечение рассеяния, в резуль-
тате которого частицы переходят из состояния с волновыми векто-
рами к0 и кр в состояние с волновыми векторами kv и кв. Как
нетрудно убедиться, сечение рассеяния определяется квадратом
96
модуля фурье-компоненты второго слагаемого в уравнении (2.41)
относительно конечных значений волновых векторов к? и kfl:
а(ка, ке; кт, k6) =(М2/4л2^)|5^1^г2е-‘(^г1+каЧ) х
xV(rx—г2) (гр г2) |3. (2.42)
Если пара взаимодействующих частиц входит в распределение
Ферми, уравнение (2.41) несправедливо. Очевидно, процессы рас-
сеяния, при которых пара взаимодействующих частиц переходит
в уже занятые состояния, должны быть исключены. Для этого во
втором слагаемом уравнения (2.41) необходимо исключить фурье-
компоненты, соответствующие состояниям, занятым другими ча-
стицами .
Введем проекционный оператор Qap> исключающий все фурье-
компоненты в области внутри сферы Ферми, за исключением фурье-
компоненты, соответствующей выделенным состояниям аир. Если
Ф — произвольная функция, то, очевидно,
Фарфор Га) = 2 фу (h) Фд (ra) (?5 I Ф) +
*у.
+ фа (h) фр (г2) (а(?|Ф), (2.43)
где
(уб|Ф) = $ dr, dr2 qpv* (гт) Фа* (г2) Ф (гп г2)
(суммирование в (2.43) распространяется только по состояниям
вне сферы Ферми).
Таким образом, можно получить следующее уравнение, назы-
ваемое обычно уравнением Бете — Голдстоуна и
описывающее движение двух взаимодействующих частиц, входя-
щих в распределение Ферми [91:
(W/2M) (А, + A2) + Qo₽ V(rx-г2) —адфар(гь Га)=0, (2.44)
где Еар — собственное значение энергии пары частиц с учетом
взаимодействия и принципа Паули. Так как второе слагаемое
не имеет фурье-компонент, соответствующих энергетически раз-
решенным при рассеянии состояниям, кроме начального состояния,
то сечение рассеяния обращается в нуль. Это позволяет найти
асимптотику решения уравнения (2.44) на больших расстояниях.
Действительно, если рассеянной волны нет, то волновая функ-
ция фар (Гц г2) на больших расстояниях (|г±—r21kp > 1) сов-
падает с невозгущенной волновой функцией, представляющей собой
антисимметризованное произведение одночастичных функций
Фар (И, г2)1^з^00афа(г1)фр(г2). (2.45)
Однако на малых расстояниях принцип Паули не препятствует
искажению волновой функции из-за взаимодействия. Действи-
4 Зак. 642
97
тельно, малым расстояниям соответствуют импульсы, лежащие
значительно выше граничного импульса Ферми, поэтому на очень
малых расстояниях (| гх — гг|&р<£ 1) учет принципа Паули не-
существен, и волновая функция (рар будет совпадать с волновой
функцией для изолированной пары фор.
Вводя координаты центра инерции и относительные координаты
и учитывая сохранение суммарного волнового вектора К = ко +
+ кр, из (2.44) нетрудно получить следующее уравнение для вол-
новой функции относительного движения двух частиц срк (г):
A + (/i2/4Al)K2 + Qap V{r)-£aP} фк (г) =0. (2.46)
Это уравнение с учетом условия на бесконечности (2.45) при по-
мощи преобразования Фурье можно свести к интегральному урав-
нению
Фк (г) = (1//Й) eikr + 5 dr' G (г—г') V (г') <рк (г'), (2.47)
где
С dk' ik'(r-r')
G(r—г')= ----------------------7---(2.48)
' , J . (2л)з £aB-(W/4Al)-(^fe'2/M)
Если интегрирование в (2.48) no dk' распространить по всему
пространству (предварительно задав правила обхода полюса по-
дынтегрального выражения), то получим обычную функцию Грина
для свободных частиц. Очевидно, функцию G (г — г'), определяе-
мую выражением (2.48), можно рассматривать как функцию Грина
для частиц, входящих в распределение Ферми. Так как состоянию
а[3 отвечают импульсы ka и кр, заключенные внутри сферы Ферми,
а интегрирование в (2.48) производится вне сферы Ферми, то в от-
личие от случая свободных частиц подынтегральное выражение
в (2.48) не имеет особенностей внутри области интегрирования.
Полную функцию <рар найдем, домножив (2.47) на волновую
функцию движения центра инерции двух частиц:
Фае (Г1,гг) = (1/У Й) е‘к«фк (г). (2.49)
Так как второе слагаемое в правой части (2.47) содержит только
компоненты Фурье вне сферы Ферми, то функция срор удовлетво-
ряет условию нормировки
(ф2₽, Фа₽) = 1. (2-50)
Пределы интегрирования в выражении для функции Грина
(2.48) зависят от импульса движения центра инерции К, поэтому
волновая функция <рк (г) относительного движения частиц, входя-
щих в распределение Ферми, также в общем случае зависит от К-
Мы в дальнейшем ограничимся рассмотрением простого случая
98
К = 0. Тогда интегрирование по zZk' в (2.48) следует производить
вне сферы Ферми (k' > kr), и функция Грина принимает вид
ОО
„ . м 1 Г k' slnfe'lt-— г' I .nr..
G <r-г > = 2^ dk.---------------------, - (2.51)
2n J e—(ft»fe'a/Af) 1Óà I
Kr
где e = K4?iM — энергия относительного движения.
Если К — 0, то относительный момент количества движения
является интегралом движения, и функцию ерь (г) можно разло-
жить по парциальным волнам, отвечающим определенным значе-
ниям относительного момента:
<Pk(r) = ^<Pz(Wcostf). (2.52)
Наибольший интерес представляет исследование движения частиц
в S-состоянии (Z — 0). Из (2.47) для волновой функции S-состояния
ф (г) получим
оо
Ф(г)=-^ + 4л {dr'r'2g(r, г') V (r’)q(r'), (2.53)
fcr J
где
/ М 1 Г ,, , sin k' г sin k' г' .„г,.
g (' г ) -—у • — dk-------------------. (2.54)
Соответствующее дифференциальное уравнение для ср (г) имеет
вид
оо
{77(774- - .^-)+е]ф(г)=7(г)ф(г)—fdr' r'2x(r. г') V (г') ф (г'),
I М Xdr* г dr ) ) ,)
о
. ,, 1 fsinfeF(r—г') sin kF U + r') 1
X (г, г') = —- ------------- (2.55)
лгг | kF(r— Г ) kF (r-j-r ) J
Отметим, что последнее слагаемое в правой части (2.55) — след-
ствие учета принципа Паули.
Рассмотрим решение уравнения (2.53) или (2.55) в простейшем
случае, когда потенциал V (г) представляет собой только оттал-
кивающую сердцевину радиуса гс:
V(r)=J°°’ г<^’ (2.56)
(О г>гс.
Очевидно ф (г) = 0 при г <Z гс. Так как V (г) обращается в бес-
конечность внутри сердцевины, то произведение V (г) при
г •< гс неопределенно. Введем обозначение w (г) = V (г)ср (г). Во
внешней области г >> rc w (г) = 0. Для нахождения w (г) во внут-
4* 99
ренней области г С гс рассмотрим уравнение (2,55) при г <ZC. г
функция ф (г) непрерывна во всей области, однако производная
<р' (г) испытывает разрыв в точке г == гс, поэтому вторая произ-
водная ср" (г) в точке г — гс имеет дельтаобразную особенность.
Пусть ~ Л, тогда уравнение (2.55) при г < гс можно
dr r = rc
записать в виде
СО
(№/М) |Хб(г—rc)-b(2/r)<p' (г)} =чу(г)—dr'r'^x (г, г') to (/"').
о
Так как интеграл в правой части является непрерывной функцией,
то
ш(г)-(Йг/Л4)Х6(г—rJ + toHr), (2.57)
где функция Шх (г) не имеет особенностей. Подставляя соотношение
(2.57) в (2.53) и пренебрегая вкладом wlt который оказывается
порядка (kFre)3, находим
, , 1 sin kr . 4лД2 12/
Константа 1 определяется из условия ср (гс) — 0. Таким образом,
решение уравнения Бете — Голдстоуна для S-состояния получим
в виде
1
ФЮ
sin krc . g(r, re) 'I >
*rc g (rc, rc) / ’
(2.58)
где g (r, rc) определяется выражением (2.54).
Отметим, что функция g (г, гс) с ростом г быстро падает. Если
Г > то
g(r> 0) — )cosfer[si(fe^—k)r + si(kF + k)r] +
4л2П£ r
4-sin kr [ci (kF—k) r—ci (Af + k) r]}• (2.59)
где si хи cix—интегральные синус и косинус:
Ор ОС
six= — dt (sin tit), cix^ —dt (cos tit).
x X
Поэтому решение уравнения Бете — Голдстоуна (2.58) на больших
расстояниях (kFr > 1) переходит в невозмущенное решение, соот-
ветствующее отсутствию взаимодействия между частицами:
Фе (г) =»(1 //Q) • (sin krlkr).
(2.60)
100
Ё случае изолированной пары частиц, не входящих в распреде-
ление Ферми, функция Грина имеет вид
gw (г, И =
(2.61)
sin kr cos kr'
M- I г г'
4лй2 k cos kr sinkr’
а соответствующее решение уравнения Шредингера для частнц при
наличии отталкивающей сердцевины между ними равно
,,, . . 1 sin k (r—rc)
ф(') (г) = —=.------------—
kr cos krc
r>rc.
(2.62)
На рис. 2.3 для сравнения представлена зависимость функций
ф (г), ф(‘>(г) и фо (г) от г. Решение уравнения Бете — Голдстоуна
Ф (г) отлично от нуля, начиная с г = гс, так же как и решение урав-
Рис. 2.3. Зависимость функций <р, <р(,) и <pft от kpt.
нения Шредингера ф(‘>(г). Затем, однако, ф (г) идет ближе к невоз-
мущенному решению ф0 (г) и после нескольких небольших колеба-
ний практически совпадает с невозмущенным решением. В то
время как для изолированной пары изменение волновой функции,
обусловленное взаимодействием, сохраняется вплоть до бесконеч-
ных расстояний в виде сдвига фазы, в случае пары частиц, входя-
щих в распределение Ферми, эти изменения быстро стираются и
функция достигает невозмущенной формы уже на расстояниях
порядка l/kF.
Если помимо отталкивающей сердцевины имеется еще и потен-
циал притяжения Va (г) при г > гс, то интегральное уравнение
101
для функции <ро (г) можно представить в виде
Фа(/') = ф(П+4л(^'л’а{^(Л Г’) — g (Г’ М 8 ('С| Г ) | Va (/) ФО(Г),
< I g (Ге, ГС) J (2 б3)
где ср (г) определяется выражением (2.58). При г = гс выражение,
стоящее в фигурных скобках, обращается в нуль. Поэтому при
значениях г, мало отличающихся от гс, функция <ро (г) мало отли-
чается от <р (г). С увеличением г вследствие быстрого спада g (г, гс)
добавка в (2.63) для конечных значений Va (г) также невелика.
Таким образом, и при наличии сил притяжения волновая функ-
ция почти такая же, как для задачи с твердой сердцевиной, и почти
совпадает с волновой функцией свободных частиц, за исключением
области, непосредственно прилегающей к отталкивающей серд-
цевине. Следует оговориться, что последний вывод основан на от-
носительной слабости сил притяжения. Если бы силы притяжения
были значительно интенсивнее, они могли бы заметно модулировать
волновую функцию двух частиц и при наличии других частиц,
входящих в распределение Ферми.
Определение ядерной плотности и энергии связи. Зная решение
уравнения Бете — Голдстоуна, можно непосредственно вычислить
ядерную энергию связи. Действительно, используя уравнение
Бете — Голдстоуна (2.44) и условие нормировки волновой функ-
ции <рар (2.50), нетрудно показать, что добавочная энергия Ua$,
связанная с взаимодействием пары нуклонов, равна
^₽-(ф«р I Г(Г1-г2) | Фа₽). (2.64)
Предполагая, что каждая пара нуклонов взаимодействует незави-
симо от остальных, запишем полную энергию ядерной материи
в этом случае в виде
£=£0+1/г2 ^аР- (2-65)
. О
Полная энергия Е является функцией граничного импульса Ферми
и, следовательно, функцией плотности. Из условия минимума энер-
гии можно найти равновесное значение плотности, которое и будет
характеризовать плотность ядерной материи.
При вычислении t/ap предположим, что между нуклонами дей-
ствуют обменные силы Сербера (1.140). Эти силы отличны от нуля
только в состояниях с четными значениями относительного орби-
тального момента. Будем пренебрегать тензорными силами, а также
спиновой зависимостью ядерных сил, и выберем потенциал цент-
ральных сил V (г) в виде притягивающей прямоугольной ямы
с сердцевиной, соответствующей бесконечным силам отталкивания
на малых расстояниях:
V(r) =7c(r) + l/o(r), (2.66)
102
где
оо,
о,
г < гс;
г>гс;
Va(r)^
О, г < гс;
— 1'о, гс<-"<гв;
О, г0<г.
(2.67)
Радиус сердцевины гс, а также радиус действия и величину потен-
циала притяжения г0 и Уо следует выбрать так, чтобы правильно
описывались свойства системы двух нуклонов при малых энергиях
и в то же время воспроизводились данные по рассеянию при высо-
ких энергиях.
Используя обменный характер потенциала Сервера (1.140), для
энергии взаимодействия пары нуклонов в состояниях аир находим
t/ap = W+) (г) IV (г) 1 <р<|> (Г)), (2.68)
где <р° (+’ (г) и <р(+> (г) —симметризованные волновые функции:
Ф<+> (г) s (1//2) (<р (г) + Ф (-г)). (2.69)
Так как потенциал V (г) зависит только от относительного расстоя-
ния, то величина (2.68) будет зависеть только от относительного
импульса нуклонов к:
Uafi = U(k), к=!/2(ка-М- (2-70)
Усреднение (2.68) по зарядовым и спиновым состояниям нуклонов
сводится к умножению выражения (2.68) на статистический вес
симметричного состояния 3/8:
<t4₽>=(3/8) £/(£) (2-71)
Полную энергию взаимодействия всех пар ДЕ найдем, умножив
(2.71) на число пар нуклонов п (А) с относительным импульсом k
п(й) = 12Л(Л-1)(1~|.А + 4.4\4 (2.72)
\ 2 kF 2 fep / fep
\ Г J г
и проинтегрировав полученное выражение по возможным значениям
относительного импульса А:
kF
ДЕ = 3/3$ dA/i(A)(7(A). (2.73)
о
В соответствии с (2.66) полная энергия взаимодействия также пред-
ставляется в виде суммы
ДЕ = ДЕс + ДЕа. (2.74)
При вычислении ДЕС воспользуемся тем, что волновая функция <р
на малых расстояниях практически совпадает с волновой функ-
юз
цией (2.58), соответствующей наличию только отталкивающей серд-
цевины. Согласно (2.57), имеем
Vc (г) Ф (г) & (Ш) М (г—гс), (2.75)
где
__. 1 . Форс)
Л3 4лгс® g(rc, гс)
и, следовательно,
Uc (А) = —2 . (2.76)
S(rC> Гс}
Так как радиус отталкивающей сердцевины мал, то энергия
(2.76) очень слабо зависит от относительного импульса А, и поэто-
му можно ограничиться вычислением энергии при А = 0. Запишем
функцию Грина g (гс, гс) для этого случая:
м
2лай»гс2 J
kF
Заменив переменную k' гс на х, получим
glr" j Л
, sin2 k’ rK
sin3 x
X3
(2.77)
g (гс, гс) =
При kFrc < 1 этот интеграл удобно представить в виде ряда по
степеням Аргс. Перепишем интеграл следующим образом:
, ' Л»
g (rt, rc) — 2^3
со г с . „ \
Г
J X3 J * (
о о J
(2.78)
Первое слагаемое в скобках после интегрирования дает л/2, а во
втором слагаемом при малых значениях kPrc можно sin2 х/х2 заме-
нить единицей. Таким образом, функция Грина (2.78) принимает вид
,2-79>
Используя это выражение и учитывая, что <р0* (гс) & 1/Н при
k ->• 0, из (2.76) получаем
ycW=ye(0)=^.5^(i+^fri + ...).
Подставляя далее это выражение в формулу вида (2.73) и замечая»
что полное число взаимодействующих пар при равно (1/2)Л2>
получаем следующую приближенную формулу для полной энергии
...V ferre«l. (2.80)
Л Л Л1 v л /
Ю4
Заметим, что величина Д£с — это часть кинетической энергии (так
как потенциал (г) обращается в нуль при г > гс, где волновая
функция отлична от нуля) и обусловлена отличием волновой функ-
ции Бете — Голдстоуна от волновой функции свободных частиц.
Выражение (2.80), полученное на основе модели независимых
пар, вообще говоря, справедливо только при достаточно малых
плотностях. В общем случае энергия Д£с в виде разложения по
степеням А/.-гс была точно вычислена Янгом и Ли [10]:
АР.» 1 Й г л
-V=—• М1 1 -2ln 2)’ +
А л М I 35л
. (2.81)
Вычислим теперь энергию Д£а, связанную с потенциалом при-
тяжения Va (г). Поскольку в области, где потенциал Va отличен
от нуля, волновая функция ф (г) почти совпадает с волновой функ-
цией свободных частиц tp0 (г), то при вычислении Ua (А) можно
воспользоваться борновским приближением. Поэтому
Ua (*) = (<р1+) (г) I va (г) 5 (г)) = ± j dr (1 + cos 2kr) Va (г). (2.82)
Отметим, что применимость борновского приближения для
оценки Ua (k) обязана исключительно действию принципа Паули.
Подставляя (2.82) в формулу (2.73) и выполняя интегрирование,
находим
ДЕаМ - -(У0/л)(Арг0)-^ (^гс)], (2.83)
где функция (х) определяется выражением
f (х) = х3/6 + (3/2) Si (2х) + (3/2ха) sin 2х -J-
+ (3/4х)(1 4-l/xa)cos2x—-(9/4х)—(3/4х3), (2.84)
Si (х) =si (х) + л/2.
Таким образом, полная энергия, приходящаяся на один нук-
лон, равна
А 10
h2 kp i h2 kp r fi
^AFrc 1+А(ц_21п2)А^е +
m л Al |_ 35л
+ 0,41Ajr® + ...l—A [,f (M —F(Af/-c)].
J ft
(2.85)
Энергия Д£а/Д, связанная с силами притяжения, с увеличе-
нием плотности быстро возрастает по абсолютной величине про-
порционально р и может превысить кинетическую энергию
EJA р2*3, а тем самым вызвать стягивание ядра, если бы не су-
ществовало отталкивание на малых расстояниях. В действитель-
ности добавочная кинетическая энергия Д£СМ, обусловленная
уменьшением объема за счет отталкивающей сердцевины, растет
с увеличением плотности пропорционально р4*3 и предотвращает
стягивание.
105
Полная энергия Е/А как функция плотности р имеет минимум,
который и определяет как равновесную плотность ядра, так и
энергию связи. Из-за относительной слабости потенциала притя-
жения равновесие наступает при довольно низкой плотности, для
которой среднее расстояние между частицами d ж р—велико
по сравнению с радиусом сердцевины « 4^.
На рис. 2.4 представлена зависимость энергии Е/А от вели-
чины kF, рассчитанная по формуле (2.85). При расчетах, использо-
вались следующие значения параметров двухнуклонного потен-
циала:
гс=0,4-10-13 см- г0=2,3 10-13 сл; Г0=(л2/4)йг/Л1 (г0-ге)2. (2.86)
Рис. 2.4. Зависимость энергии Е/А от
величины
водят к значениям средней
(Глубина потенциальной ямы
выбрана так, чтобы энергия
связи двух нуклонов рав-
нялась нулю.) Кроме того,
в‘выражении для Л£с вме-
сто М использовалась эффек-
тивная масса нуклона М * =
= 0,68714. При выбранных
значениях параметров энер-
гия Е/А имеет минимум при
kF = 1,35-1013 с.и-1, которо-
му отвечает равновесная
плотность ядерного вещества
р = 1,65- Ю38 с/Г3.
Расчеты, выполненные с
использованием более реали-
стических потенциалов, при-
и связи на один нуклон и
равновесной плотности, которые согласуются с результатами
эксперимента (2.18).
Применимость модели независимых частиц. Исследование по-
ведения волновой функции Бете — Голдстоуна на больших расстоя-
ниях позволяет ответить на вопрос о причинах применимости мо-
дели независимых частиц при описании ядер. Мы видели, что
вследствие принципа Паули взаимодействие между частицами, вхо-
дящими в распределение Ферми, проявляется только на расстоя-
ниях, меньших kp1, и совершенно несущественно на расстояниях,
больших kFl. Поэтому волновая функция Бете — Голдстоуна от-
личается от волновой функции свободных частиц только на малых
расстояниях А71- Эти расстояния оказываются значительно мень-
ше среднего расстояния между нуклонами в ядрах d ж Вол-
новая функция Бете — Голдстоуна на расстояниях порядка сред-
него расстояния между нуклонами в ядрах существенно не отли-
чается от волновой функции свободных частиц. Из сказанного ясно,
106
почему модель независимых пар является таким хорошим прибли-
жением. Если одна из частиц пары сталкивается с какой-либо
третьей частицей, расстояние между исходной парой частиц в сред-
нем порядка d. Но на таком расстоянии вследствие действия прин-
ципа Паули волновая функция относительного движения практи-
чески совпадает с волновой функцией свободных частиц. Таким
образом, столкновение одной из частиц пары с третьей частицей
происходит в условиях, как если бы взаимодействие вообще от-
сутствовало между частицами в исходной паре.
Из указанного свойства волновых функций Бете — Голдстоуна
вытекает также обоснование применимости модели независимых ча-
стиц. Действительно, несмотря на ядерное взаимодействие, вол-
новые функции почти совпадают с волновыми функциями свобод-
ных частиц, за исключением тех областей конфигурационного про-
странства, в которых частицы сближаются на расстояния, много
меньшие среднего расстояния между частицами. Поэтому нуклоны
в ядре с достаточной точностью можно представлять волновыми
функциями свободных частиц, за исключением тех случаев,
когда существенную роль играет тесное соприкосновение двух
нуклонов.
Мы ограничились рассмотрением только симметричной части
(/ = 0) волновой функции Бете — Голдстоуна. Нетрудно убедить-
ся, что более высокие значения орбитального момента не играют
существенной роли. Волновая функция P-состояния не испытывает
влияния потенциала, так как мы предположили, что в нечетных
состояниях взаимодействие вообще отсутствует. В £)-состоянии
экранирующий эффект центробежных сил настолько велик, что
влиянием ядерных сил на волновую функцию можно пренебречь
даже без учета действия принципа Паули.
Задачи
2.1. Показать, что число частиц n(ka, k) с заданным импульсом k по от-
ношению к частице с определенным импульсом ka в вырожденном ферми-
газе А одинаковых частиц равно
fe2
n(k№, k)=24A~r(ka, k), (2.87)
kF
где
/ k2F-k2—4k2'\
ft)= (1/2)^ +-------------j, (l/2)(^--fea)<*<(l/2)(*f-^a);
| 0, (1/2) (WM <k.
(Граничный импульс Ферми kpсвязан с полным числом частиц А иобъемомЯ,
занимаемым
газом, соотношением
Q 4л. ,
(2л)? ' Д
.107
Рассмотрим две частицы с импульсами ка и к^, входящие в распределение
Ферми (fea < kp, ftp < kp). Введем относительный импульс к:
к = (1/2) (кр-ка). (2.88)
Пусть импульс первой частицы ка фиксирован. Выразим импульс второй ча-
стицы кр через ка и относительный импульс к:
кр = ка+2к. (2.89)
Так как kg < kPt то
I fta+2,£ | < kp.
На рис. 2.5 представлено сечение сферы Ферми, ограничивающей значе-
ния импульса kp. Очевидно, максимально возможное значение k при фикси-
рованном значении ka равно l/2(kF + k^. Если k < (4^(kp— ka), то век-
Рис. 2.5. Сечение сферы Ферми,
ограничивающей возможные значе-
ния импульса kp = кд + 2к.
Рис. 2.6. Распределение плотности
вероятности для относительного им-
пульса пары частиц.
тор к может быть ориентирован в любом направлении (на рис. 2.5 отрезок ЛВ
равен kp — fca). В этом случае величина n(ka, k)dk равна числу частиц в
сферическом слое радиусом 2k и толщиной d(2k);
□ k^dk 1
л (*a, k) dk = — 4л (2k)» d (2fe) = 24.4 — , k < — {kp - fea). (2.90)
Если k > 1/2(кд' — ka), то для вектора k направления, заключенные внутри
конуса, образуемого вращением радиуса АС вокруг оси АВ, запрещены.
Обозначим угол между направлениями АВ и АС через в, тогда телесный угол,
вырезаемый конусом иа поверхности сферы радиусом 2k, равен 2л(1 —cos 0).
Как видно из рис. 2.5, справедливо следующее соотношение;
kp ^fea~4fe2 1 1
cos 6 =------------' ___ (kF-ka) < k < — (kp+kJ. (2.91)
Поэтому в этом случае имеем
Q
п (ka> kj dk-= - * [4л—2л (1 —cos 6)] (2k)» d (2k) =
108
1 1
= 12Л(1+соз0) , — (kp-ka)<k< ~(kF+ka). (2.92)
kF z
Если k > + to n (fte, fc)=0- Таким образом, мы доказали спра-
ведливость соотношения (2.87).
Отметим, что формула (2.87) справедлива и для системы нуклонов (ча-
стиц, обладающих спином и изоспином), одиако под граничным импульсом
в этом случае следует подразумевать величину
, / Зп2 А \1/з
F \ 2 ‘ Q }
2.2. Показать, что число пар частиц с заданным относительным импуль-
сом k в вырожденном ферми-газе А одинаковых частиц равно
(3 ь 1 ft? \ k1
1-V‘^ + v 1з~<2-93)
2 kp 2 "f I kp
Число пар частиц с заданным относительным импульсом n(k) найдем,
просуммировав n(ka, k) по всем заполненным состояниям йа:
P й
"<*)= J n^k)-^-Tdka. <2’94)
Используя (2.87), получаем (2.93).
Проинтегрировав (2.93) по dk, находим полное число пар в системе
Jn(fe)dft = (l/2)4(4-l). (2.95)
Отношение (2.93) и (2.95) определяет нормированное распределение плотности
вероятности для определенного значения относительного импульса пары
частиц
(3 k 1 Ь8 V hi
1- — — +— - (2-96)
2 2 k* ft? v ’
Распределение JV(ft) показано иа рис. 2.6. Средняя величина относительного
импульса оказывается порядка 0,5 ftp, что отвечает при ядерной плотности
(2.13) относительной энергии 25 Мэв. В системе центра инерции ядра такая
энергия соответствует рассеянию нуклона с энергией 50 Мэв покоящимся ну-
клоном, а максимальная величина относительного импульса отвечает рассея-
нию нуклона с энергией около 160 Мэв.
2.3. Найти зависимость энергии нуклона от импульса в ядерной материи
в предположении, что между нуклонами действуют двухчастичные силы, опи-
сываемые потенциалом
У=Ц^П'), Пг)={-п” Г^Г0’ <2'97)
4 1^ U, Г > Гф,
Если система однородна, то даже при наличии сильного взаимодействия
между частицами одночастичные волновые функции можно выбрать в виде
плоских волн, однако одночастичная энергия в этом случае не сводится к ки-
нетической энергии частицы, а равна
Й2 ft2
£«=-^Г+у(М. <298)
109
где V(£a) — добавочная энергия, обусловленная взаимодействием частицы со
всеми остальными частицами. Эту энергию обычно называют одночаст н ч -
иым потенциалом, который в общем случае оказывается зависящим
от импульса частицы. Так как потенциал (2.97) зависит только от относитель-
ного расстояния между частицами, то энергия взаимодействия двух нуклонов,
находящихся в состояниях с импульсами ка и kg, зависит только от относи-
тельного импульса. Выберем волновую функцию пары нуклонов в виде (2.34).
Тогда среднее значение энергии взаимодействия пары нуклонов будет опре-
деляться выражением
<i/ap> == (3/8) U (k) = (3/8) (1/Q) J dr (I +cos 2kr) V (r)t (2.99)
где k = (VaXk^ — kg) — относительный импульс и 3/8 — статистический
вес пространственно симметричных состояний, в которых проявляется взаимо-
действие (2.97). Домножив энергию (2.99) на число частиц n(ka, k)c импульсом
Рис. 2.7. Зависимость одно-
частичного потенциала V
от импульса йа при гс = О
и гс =0Л • Ю-13 со-
относительного движения k по отношению к частице с заданным импульсом ka
и проинтегрировав полученное выражение по всем относительным импуль-
сам, найдем полную энергию взаимодействия выделенной частицы со всеми
остальными частицами:
ОО
1/(йа) = (3/8)рЬ(^, k)U(k).
о
(2.100)
Используя (2.87) и (2.99), в результате интегрирования по k получим следую-
щее выражение для одночастичного потенциала:
у 3 С
v v« Si ММ г»+
1 QJv (
sin k г 1
+Si (*F—йд) г0— 2з|'п/гЛг0— -----к (2.101)
Wo 1
110
На рис. 2.7 представлена зависимость одночастичного потенциала V(^a)
от импульса kg/kf прн kF = 1,38-1013 см^1. (Использовались следующие
л3 Д3
значения параметров потенциала: Уо -= ^г2 ; гс — 0; га — 2,3 X
X 1СГ'13 см). Потенциал V(ka) изменяется приблизительно по квадратичному
закону, поэтому хорошим представлением для потенциала является аппро-
ксимация в виде
У (^а) —+
k2
(2.102)
V!
где Ио ~ —25,2 Мэв, Vx = 10,2 Мэв. Выражение (2.102) можно рассматри-
вать как разложение потенциала V(£a) в ряд по степеням k&. На рис. 2.7 вы-
ражению (2.102) соответствует штриховая кривая.
Приведенная аппроксимация для потенциала позволяет записать
одночастичную энергию в виде
*2
(2,103)
где М* — так называемая эффективная масса
1/Л4*=1/Л4 + (2/й2) (Vj/^). (2.104)
Воспользовавшись численным значением для эффективной массы нук-
лона в ядерной материи, найдем М* ж 0,8 М. Таким образом, взаимодей-
ствие между нуклонами, приводящее к изменению зависимости энергии от
импульса, формально можно учесть, введя эффективную массу нуклона.
Отметим, что введенная эффективная масса (2.104) учитывает только силы при-
тяжения между нуклонами.
Если предположить, что силы притяжения проявляются только на рассто-
яниях, больших радиуса отталкивающей сердцевины гс, то одночастичный
потенциал V(ka, г0, гс), обусловленный силами притяжения, будет определять-
ся разностью выражений типа (2.101):
V(k«> ro> rJ = V(kv ro)-V^ 'с). (2.105)
На рис. 2.7 приведена также зависимость потенциала (2.105) от k при г ~
_ л2 h1
= 0,4-10 13 см; г0 = 2,3-10 1^сл и Vo= -j ^(Го _ Гд)2- Аппроксимируя
потенциал (2.105) параболой, можно найти Ve = —37,0 Мэв, 1'\ = 15,2 Мэв.
Соответствующее значение эффективной массы в этом случае равно Л4* =
= 0,7 М.
2.4. Рассмотреть корреляционные свойства идеального ферми-газа.
Волновую функцию системы А одинаковых частиц, подчиняющихся
принципу Паули, можно представить в виде детерминанта Слэтера
ф(г1’г*...........r^=W-
| Фа, (г1) <МГ2) • • •'₽а1(г4)
<МГ1) Фаг(г2) -'Фа2(гл)
4>ад(г1) Фад(г2)---(₽ал(гл)1
(2.106)
111
где <ра(г) — одночастичная волновая функция.
Вероятность нахождения какой-либо частицы в определенной точке про-
странства определяется квадратом модуля волновой функции (2.106), проин-
тегрированным по координатам всех остальных частиц:
te(rt)= jdradr3 ... drA )Ф{гг г2 , .... гл) |2 . (2.107)
Подставляя в (2.107) волновую функцию Ф(г1} r0J , гл) н виде (2.106)
находим
» (г) = (1/4) 2 I Фа (Г) I®, (2.108)
а
где суммирование производится по всем заполненным одночастичным состоя-
ниям. Домножив (2.108) на полное число частиц 4, найдем плотность распре-
деления частиц:
Р (г) = 2 I I2- (2-109)
a
Вероятность нахождения какой-либо частицы в точке гь а другой части-
цывточкег2 определяется квадратом модуля волновой функции 5>(rj, г2, ...
Гд), проинтегрированным по координатам остальных (4 — 2) частиц:
w (г1. rg) = fdr3 ... d ГЛ | Ф (гр г2, г3, ... , Гд)р. (2.110)
Используя (2.106), нетрудно получить
г'>Т7Т~7г2 |Фа(г)Фр<г')-<Рр(г)Фа(г')|з, (2.111)
А — i/ а. р
Домиожив (2.111) на полное число независимых пар частиц */а4(4 — 1), най-
дем плотность распределения пар частиц:
Р(г. г') = (1/2) 2 | Фа (г) Фр <г')— фр(г)фа(г')|в. (2.112)
а. 6
Величина р(г, г') не равна произведению р(г) на р(г'). Действительно, исполь-
зуя (2.112), нетрудно показать, что
Р(г, г') = р(г) р(г')—р'(г, г'), (2.113)
где
Р'(г, г')= 2|'Мг)ф«<г')12- <2-114)
a
Различие между р(г, г') и р(г)р(г') связана с корреляцией между тождествен-
ными частицами, обусловленной принципом Паули.
Если система однородна, то одночастичные волновые функции фа(г) мож-
но выбрать в виде плоских волн
Фа(г) = (1//ЁГ)е’к®г . (2.115)
Как н следовало ожидать, плотность частиц в этом случае постоянна:
р(г) = р0=4/Й, (2.Ц6)
а плотность распределения пар частиц можно представить в виде
р(г, т') = р? (14-g (г'—г)}, (2.117)
112
где функция g(r' — г), зависящая от разности координат г' — г, называется
корреляционной функцией. Согласно формулам (2.113) и
(2.117), имеем
‘Чт f
k < kp
откуда [11]
9 j sin ftp г \г
8 (г) = — .4 4 I ~7-—cos ftp г . (2.119)
kp Г \ kF г /
При малых значениях ftfr разложение корреляционной функции g(r)
имеет вид
ft2 г2 3
g(r)=-l+“4------— ^г4 + .... (2.120)
О I/O
Таким образом, если г' совпадает с г, то плотность распределения пар
частиц р(г, г') обращается в нуль. Это естественное следствие принципа Паули,
который запрещает тождественным частицам приближаться друг к Другу.
Рис. 2.8. Зависимость корреляционной
функции g (г) от kFr.
На рис. 2.8 представлена зависимость корреляционной функции g(r) от
Как видно из рис. 2.8, характерная длина корреляции гр определяется гра-
ничным импульсом Ферми rp ~ k~^1.
Если между частицами действуют двухчастичные силы, характеризуемые
потенциалом У(г), зависящим от относительного расстояния между части-
цами, то полная энергия взаимодействия системы Д£ непосредственно вы-
ражается в первом приближении теории возмущений через плотность рас-
пределения пар р(г, г'):
Д£= jdrdr'p(r, r')V(r—г')-
(2.121)
Выбирая потенциал V(r) в виде прямоугольной ямы (2.97), в случае одно-
родной системы с помощью (2.121) нетрудно получить для полной энергии
взаимодействия Д£ выражение, совпадающее с полученным ранее выраже-
нием (2.83) при гс = 0.
2.5. Установить связь между парной корреляционной функцией и флук-
туациями плотности частиц.
113
Парная корреляционная функция g(r — г') описывает статистические
свойства системы и связана со случайными флуктуациями плотности частиц.
Определим оператор плотности частиц следующим соотношением:
р(г) = 2б(г~Г|), (2.122)
i
где г; — радиус-вектор отдельной частицы; суммирование производится по
всем частицам в единице объема. Среднее значение плотности частиц обозна-
чим р (г):
р(г) = (р(г)>, (2.123)
где скобки <...> обозначают усреднение по квантовомеханнческому состоянию
системы:
<...>=рг14га...с(гл...|Ф(гг Га, ..., гл)|2. (2.124)
В общем случае при вычислении средних значений следует производить также
усреднение по статистическому распределению различных квантовомехани-
ческих состояний системы.
Оператор плотности распределения пар частиц определяется двойной
суммой от произведения дельта-функций
р(г, г')= 2 6 (г-гг) 6(г'—гД (2.125)
i+i
а среднее значение плотности распределения пар частиц равно
р(г, г') = < 2 6 (г—Г|) б (г' —-Tj)>. (2.126)
i * i
В дальнейшем ограничимся для простоты рассмотрением однородных си-
стем. В этом случае среднее значение плотности равно постоянной величине
р(г)=р0, (2.127)
а среднее значение плотности распределения пар зависит только от относи-
тельного расстояния между точками г — г' и равно
р (г, r')-pQ (1+^(г'— г)), (2.128)
где g(r' — г) — парная корреляционная функция.
Рассмотрим случайные флуктуации плотности частиц, которые будем
характеризовать величиной отклонения плотности р от среднего значения р0:
6р(г) = р(г) — ро- (2.129)
Очевидно, среднее значение отклонения плотности равно нулю
<6р (г)> = 0.
Определим корреляционную функцию флуктуаций плотности частиц
<др2>Г'_г кнк среднее значение произведения флуктуаций плотности в двух
различных точках пространства г и г';
<бР%._ г = <бр (г) 6р (г')>. (2.130)
В силу однородности пространства корреляционная функция флуктуаций
плотности частиц (2.130) зависит только от разности координат точек г' — г.
Подставляя в соотношение (2.130) отклонения 6р в виде (2.129) и используя
(2.122) и (2.126), находим
<бра>г-_г =р06(г—г') + р(г, г')—Pq. (2.131)
114
Используя далее (2.128), окончательно получаем соотношение
<6ps>r = Po6(r) + p2g(r), (2.132)
связывающее корреляционную функцию флуктуаций плотности < 6ра > г
с парной корреляционной функцией g(r).
2.6. Определить пространственно временную корреляционную функцию
для флуктуаций плотности частиц.
Пространственная корреляционная функция <6рг)г-_г = < бр(г) бр(г')>
характеризует корреляцию между флуктуациями плотности частиц в раз-
личных точках пространства в один и тот же момент времени и описывает
статистические свойства системы. Для описания динамических свойств си-
стемы можно ввести пространственно-временную корреляционную функцию
<6p(r, 0fip(r', Г)>, (2.133)
определяемую как среднее значение произведения флуктуаций плотности
частиц в различных точках пространства г и г' в различные моменты времени t
и t'. Усреднение в (2.133) производится как по квантовомеханическому состоя-
нию системы, так и по статистическому распределению различных квантово-
механических состояний системы. Если система пространственно однородна
и рассматриваются стационарные состояния системы, то пространственно-
временная корреляционная функция (2.133) будет зависеть только от относи-
тельного расстояния и абсолютного значения отрезка времени между точками,
в которых рассматриваются флуктуации:
< 6р(г, Обр(г', «')> = <бр*>г--г. t'-t- (2.134)
Спектральное распределение флуктуаций будет характеризоваться спект-
ральной корреляционной функцией, которую определим следующим равен-
ством:
< брз>чш = J dr dt + <6p2>r (2.135)
Аналогично
< fip«>q=J dre-iqr <fip2>r. (2.136)
Нетрудно проверить, что
f dm
< 6P2>q = J ^<6Р%». (2.137)
Вместо <6ps>qm в литературе часто используется динамический форм-фак-
тор S(q, <о), введенный в работе [12]:
S(q, (2.138)
2.7. Найти пространственно-временную корреляционную функцию для
флуктуаций плотности в идеальном ферми-газе.
Флуктуации плотности частиц в идеальном ферми-газе проще всего мож-
но рассмотреть, используя метод вторичного квантования. Определим опера-
тор плотности числа частиц при помощи соотношения
р(г, 0= 2 (с о. (2.139)
где функции ф0 и ф+ имеют вид
%(г- 0= °,
115
^(r’ . (2.140)
F “ к
Здесь ajtcr и — операторы поглощения и рождения частицы в состоянии
с импульсом к и проекцией спина о соответственно; £'к — энергия частицы с
Я2
импульсом к (предполагается квадратический закон дисперсии £к =
М ~ масса частицы, Я — 1). Подставляя (2.140) в (2.139), получаем
Р(г, 0=4- S akloak,ae--|(k-k')r + i<£k'-^k'H (2,М1)
ы кк' о
Диагональные члены (к = к') оператора р определяют среднюю плотность
частиц р0. Разность между р и средним значением р0 можно рассматривать
как оператор флуктуаций плотности
6р(г, 1} = р(г, 0—Ро- (2,142)
Корреляционная функция для флуктуаций плотности определяется выра^
жением
<бр2>г-_г, ;'_(=<6р(г, /)6р(г', /')>. (2,143)
Перемножив операторы бр(г, t) и 6р(г’, /’), получим сумму слагаемых,
содержащих различные произведения операторов ak(T и а^"а, взятых по че-
тыре. Среднее значение произведения четырех фермионных операторов а
можно выразить через средние значения произведений тех же операторов по
два;
<ах «а a3 а4> — <ях аг) <а3 at> — <0! а3> <а8 а4> + (nt а4> <ааа3>. (2.144)
Среднее значение произведения двух операторов аг и йг отлично от нуля толь-
ко в том случае, если эти операторы эрмитово сопряженные.
Пусть nk — среднее значение произведения a£6, ak6, определяющее
среднее число частиц в состоянии с заданными значениями к и о:
(2.U5)
Вследствие изотропии пространства это число не зависит от значения проек-
ции спина <т. В случае абсолютно вырожденного ферми-газа при температуре
Т = 0 функция распределения «к равна
{1, Я Яр -
О, Я > kF
Здесь kp—граничный импульс Ферми.
Непосредственной проверкой нетрудно убедиться, что
\(lkj <т4 akt' di ак"г а, ак/ а./ ~ nki (1 ’—лк,) ®к> к2 к, аг
и
<6P2>rf = 4l 2 «к,(1-Лка) еИкх-кЛг-ИЕк.-Ек,)*
Ьь Kj kg
В идеальном ферми-газе корреляция обусловлена принципом Паули, поэтому
она имеет место только между частицами с одинаково направленными спина-
ми. Считая объем Л достаточно большим, суммирование в (2.148) можно за-
менить интегрированием:
? <2149>
(2.146)
(2.147)
(2.148)
116
Используя (2.148), таким образом, для спектрального распределения
флуктуаций плотности в идеальном ферми-газе получаем следующую общую
формулу:
<V>qo)=-^rj (1 - «к_ч) « (<•>- £k+ Ек-<,). (2-150)
В случае нулевой температуры (Т = 0) интегрирование в (2.150) нетруд-
но выполнить с помощью (2.146), в результате для спектрального распреде-
ления флуктуаций плотности получим
„ .. Зл рп
<SP >kw =
kF I <о|
k EF
kp I 1 / k kp to \2
—h — —— +----------
k ( 4 k EP /
k / k \ to
~r- 2-T" < 7“<0;
(2.151)
k / k \ a k k
— — +2 < — <———- — 2 ,
kp \&F / Eft kp kp
где Ef — граничная энергия Ферми (Ер = kpl2M). Заметим, что при Т =
= 0 возможны флуктуации только с отрицательными частотами, так как си-
стема ферми-частиц находится в основном состоянии.
Рис. 2.9. Области для различ-
ных значений спектрального рас-
пределения флуктуаций плотно-
сти в идеальном ферми-газе.
Рис. 2.10. Спектральное распределение
флуктуаций плотности в вырожденном
идеальном ферми-газе.
для различных значений <бр2>к(В. На
На рис. 2.9 указаны области
рис. 2.10 представлено спектральное распределение флуктуаций плотности
|<о|
вырожденного идеального ферми-газа в зависимости от и = g— при различ-
ных значениях q
117
Интегрируя (2.151) по частотам, нетрудно получить следующее выраже-
ние для корреляционной функции одновременных флуктуаций в идеальном
ферми-газе при Т = 0:
J_
<6p«>k = po 4
k / 1 fe2 \ L
----| я — —«—1, k < 2k F
kF \ 4 kr J (2,152)
1, k > 2k,-.
Отличие <6р2>к от ро при k < 2k F обусловлено влиянием принципа Паули,
2.8. Определить оптический потенциал, описывающий взаимодействие
нуклона с ядерным веществом, считая, что преломление и поглощение нуклон-
ной волны в ядерном веществе обусловлены процессами многократного рассе-
яния на отдельных нуклонах [13].
Рассмотрим движение нуклона в системе, состоящей из хаотически рас-
пределенных рассеивателей. Обозначив волновую функцию нуклона 'И, за-
пишем уравнение Шредингера в виде
Л2 V* )
^-Д+Л (2.153)
где Vi — потенциал взаимодействия нуклона с отдельным нуклоном ядерного
вещества, (Заметим, что волновая функция Ф, вообще говоря, зависит как
от координат рассеиваемого нуклона, так и от координат рассеивающих нук-
лонов.)
Предположим, что волновая функция нуклона в отсутствие рассеивателей
имеет вид плоской волны с волновым вектором к. При наличии одного рассе-
ивающего нуклона возникает рассеянная волна, имеющая на больших расстоя-
ниях от рассеивателя вид сферически расходящейся волны с амплитудой:
/(k. П = —7^Tpre-lk'rV(r)tk(r). (2.154)
где к' - волновой вектор нуклона после рассеяния и фк(г) — точная волно-
вая функция нуклона при наличии одного рассеивателя, расположенного
в начале системы координат. Применяя к (2.154) преобразование Фурье по от-
ношению к к' и вводя новую переменную интегрирования q = к' — к, полу-
чаем
V (Г) фк (г) = — Т-ГГ7 \ d q е! qr f (к, к -f-q) ф° (г), (2.155)
где фк (г) — неискаженная волновая функция. Если рассеивающий нуклон
находится в точке г,, то рассеивающий потенциал зависит от разности г —
— гь н равенство (2.155) следует переписать в виде
Г
1/(r-ri) %(*)= dq е 4 (г-г*) f(k, k+q)^(r). (2.156)
При наличии большого числа рассеивающих нуклонов выражение
(2.156) следует просуммировать по всем рассеивающим нуклонам:
2v(r-r.) Vb=-~^-2jdqe“’(r-n)/(k1 k+q)^0»1'. (2.157)
В левую часть полученного равенства входит точная волновая функция
Чгк, учитывающая действие всех рассеивателей и описывающая рассеяние
падающего нуклона в ядерном веществе, В правую часть равенства входит
118
волновая функция не учитывающая действие отдельного рассеива-
теля i (эффективная падающая волна по отношению к рассеивателю I), но
учитывающая действие всех остальных рассеивателей. Если число рассеива-
ющих нуклонов достаточно велико (Д > 1), то влиянием одного нуклона на
волновую функцию можно пренебречь. Поэтому неискаженную отдельным
нуклоном волновую функцию 4^°)' в правой части равенства (2.157) можно
заменить полной волновой функцией Ч,к:
Ч0’1 - Ч, А » ь
Замечая далее, что рассеивающие нуклоны не занимают определенного
положения, а хаотически распределены в пространстве, волновую функцию
следует усреднить по всевозможным расположениям рассеивателей. Усред-
ненная таким образом волновая функция будет зависеть только от координат
рассеиваемого нуклона (г).
Если пренебречь зависимостью волновой функции от координат рассеи-
вающих нуклонов, то сумма в правой части равенства (2.157) сведется к пре-
образованию Фурье от плотности нуклонов в ядерной материи:
2,е lqri = р (<?).
i
Таким образом, получим
2V(r-r;)Yk (0 = ^(0^ (г),
I
где
W)=“2^M Jd4el4rpU)f(k’ k + q)-
(2. 158)
(2.159)
(2.160)
Подстановкой соотношения (2.159) в (2.153) уравнение Шредингера, описы-
вающее движение нуклона в ядерном веществе, сводится к одночастичному:
( )
д + Г(г)-£} Ч(0=о.
(2.161)
Величину ^(г) обычно называют оптическим потенциалом.
Согласно (2.160), оптический потенциал выражается через амплитуду рассея-
ния нуклона на нуклоне f(k, k + q) и плотность распределения нуклонов
р(4). Так как амплитуда рассеяния нуклона на нуклоне, вообще говоря, ком-
плексна, то оптический потенциал также комплексен. Вещественная часть
оптического потенциала описывает преломление нуклонной волны в ядерном
веществе, мнимая часть характеризует поглощение волны.
В случае однородного распределения ядерного вещества р(г) = р0 =
= const из (2.160) для оптического потенциала получим выражение
4лЛа
’»= — М Р° f
(2.162)
где /(0) — амплитуда упругого рассеяния на нулевой угол. Волновая функ"
ция, описывающая движение нуклона в ядерном веществе с определенным
импульсом, в этом случае имеет вид плоской волны;
i kr- Т- Et SB ка
Vk = e h , £ = + (2,163)
119
Записывая потенциал (2.162) в виде ^в= —(l’o + i для потенциала пре-
ломления Vo и потенциала поглощения Wo имеем
, 4лЛ4 „ „ 4лй2
Vo = ~^-pttRef(O), ТГ0 = ——poJmftO). (2.164)
2. 9. Определить длину свободного пробега нуклона в ядер ном веществе
рассмотрим движение нуклона внутри ядра, считая ядро достаточно
большим (.4 > 1) и пренебрегая поверхностными эффектами. Предполагая
также распределение ядерного вещества однородным р(г) ~ р0> длину сво-
бодного пробега нуклона в ядериом веществе Л можно найти, рассмотрев
рассеяние нуклонной волны на случайных флуктуациях плотности ядерного
вещества (14]. Действительно, в неограниченной однородной среде любая
волна распространяется без рассеяния, однако любое нарушение однород-
ности свойств приводит к возникновению рассеяния. Поэтому рассеяние ну-
клона при движении в ядерном веществе можно связать с рассеянием нуклон-
ной волны на случайных флуктуациях плотности ядерного вещества. Ука-
занный эффект рассеяния нуклонной волны можно учесть, подставив в выра-
жение для оптического потенциала (2.160) плотность р в виде
Р = Ро+бР, (2.165)
где 6р — случайные флуктуации плотности, зависящие как от координат,
так и от времени.
Считая, что |бр| < сечение рассеяния нуклонов на флуктуациях плот-
ности нетрудно вычислить, воспользовавшись теорией возмущений. Проводя
статистическое усреднение по флуктуациям, окончательно можно получить
следующее выражение для дифференциального сечения рассеяния нуклонов
(дифференциального коэффициента рассеяния), отнесенного к единице объе-
ма ядерного вещества
2
= 1 f (k’ и ,2 < брг>«® d k'’ <2-,66)
где к' и Е‘ — импульс и энергия нуклона после рассеяния; q = к' — к;
<о — Е' — Е, <бр®>?(0 — спектральное распределение флуктуаций плот-
ности ядерного вещества. (Энергия нуклона отсчитывается от центра сферы
Ферми). Интегрируя (2.166) по dk', можно определить полный коэффициент
рассеяния нуклона в ядерном веществе S. Очевидно, величина, обратная
коэффициенту 2, и определяет длину свободного пробега нуклона в ядерном
веществе
Л=1/Х- (2.167)
Предполагая для простоты, что амплитуда рассеяния нуклона на нуклоне
постоянна (f (к, к') == f0), полный коэффициент рассеяния S можно предста-
вить в виде
2 = 4лр0 ] /„]*/>,
(2.168)
где Р — безразмерный коэффициент, характеризующий флуктуационные
свойства ядерного вещества;
—f
d я
(2.169)
120
Замечая, что g>— (q2-|-2kq)/2A1, интегрирование по dq можно свести к ин-
тегрированию по dq и du:
О -|-2Л4ю
Зя г Г
р=------rv da dtK <6Р\И. (2.170)
9М bd J J 4
F k2 — kp 4—
2M
Используя спектральное распределение (2.151), для вырожденного фермн-
газа при нулевой температуре получаем
1-Л +Л (2^6)572, 8 <2,
5е 5е
(2.171)
5в
где е — отношение энергии падающего нуклона к граничной энергии Ферми
/ Е \
18= -g- . Выражение (2.171) характеризует уменьшение коэффициента рас-
сеяния нуклона в ядерном веществе 3 (или увеличение длины свободного про-
бега нуклона в ядерном веществе Л), обусловленное влиянием принципа
Паули. На рис. 2.11 представлена зависимость величины Р(е) от энергии нук-
лона е = Е!Ер.
Дифференциальное сечение рассеяния нуклона в ядерном веществе оп-
ределяется формулой
1 dZ
3 de' do
3
4лр (е)
ф (е', О) - —; =--
2 У Л (в,в')
е—е',
В(е', в)
Л (е, s')
А (в, в') > В (в, е');
В (в, в') >Л(в, е')>В(е', в);
(2.172)
А (в, в') = е-|-в' — 2 У ее' cos 0; В (в, e') = e(VB — J e'cos/})2,
где 0 — угол рассеяния нуклона, в' = £'/Ер ,
На рис. 2.12 представлено энергетическое распределение рассеянных
нуклонов при различных значениях угла рассеяния для энергии падающих
нуклонов е = 2-
Формулы (2.171) и (2.172) можно также получить на основе микроскопи-
ческого рассмотрения последовательных соударений налетающего нуклона
с распределенными по Фермн внутриядерными нуклонами [15].
2.10. Найти распределение уровней энергии возбужденных состояний
в ядерной материи.
Ядерная материя представляет собой систему с большим числом степеней
свободы, которая может возбуждаться множеством различных способов,
поэтому для описания ее свойств удобно использовать статистический под-
ход [16, 17]. Будем характеризовать ядерную материю температурой 0, а
также рассмотрим следующие термодинамические функции: энтропию S,
энергию возбуждения У и свободную энергию F. Если известен энергетичес-
кий спектр системы, то свободная энергия F определяется соотношением
__£.
е в =2е °”, (2.173)
121
где суммирование производится по всем состояниям системы. Считая энерге-
тический спектр ядерной материи непрерывным и обозначая плотность уров-
ней энергии через р(Е), переписываем выражение (2.173) в виде
_ Е
е в рЕр(Е)е в. (2.174)
Средняя энергия возбуждения системы U определяется соотношением
Е
н-
Г,- / (2.17S)
J d£p (Е) е
Это соотношение устанавливает
связь между энергией возбуждения
системы U и температурой систе-
мы в.
Рис. 2.12. Энергетическое рас-
Рис. 2.11. Зависимость величины
Р(е), определяющей уменьшение
коэффициента рассеяния нуклона в
ядерном веществе вследствие прин-
ципа Паули, от энергии нуклона.
пределение рассеянных нукло-
нов в ядерном веществе.
Дифференцируя равенство (2.174) по величине в 1 и используя (2.175),
нетрудно получить обычное термодинамическое соотношение
U = F + ®S, (2.176)
где S -= —dE/dQ — энтропия системы. Из (2.176) непосредственно следует,
что dU ~ &dS, или
dS_____1_
du " е
В интегралах (2.174) и (2.175) главный вклад вносят значения энергии Е,
близкие к средней энергии возбуждения U, поэтому
_F_ _SL
е 6 =p(Lf)e в Х(Е7), (2.178)
где %(У) — некоторая функция U, медленно изменяющаяся по сравнению
_ F _и
с функциями е в, р(17) ие е. Из (2.178) с помощью (2.176) находим
р ({/) = —!—es <с/)
к ’ Х(С7)
где S(U) — энтропия, отвечающая энергии возбуждения {/.
(2.177)
(2.179)
122
Для того чтобы найти K(U}, подставим р(£) в виде (2.179) в соотношение
(2.174) и вынесем медленно изменяющуюся функцию Л(Е) за знак интеграла
в точке U, тогда получим
S(E}-^- s (£)_s
X(17) = jdEe = JdEe . (2.180)
Разлагая в экспоненте под знаком интеграла (2.180) энтропию S(E) в ряд по
степеням Е — U » ограничиваясь учетом квадратических членов разложения,
получаем
UU)---$ с1Е е . (2,181)
Так как U — монотонно возрастающая функция 0, то величина
d2S
——— < 0. Согласно (2.177), имеем
du1
d2S 1 dQ
dU2 е* dU '
(2.182)
Распространив пределы интегрирования в (2.181) от — оо до + оо, находим
/~dU
de
(2.183)
Таким образом, окончательно получим следующую формулу для плотности
уровней возбужденных состояний:
р(£/)= ’ JL1/eS(t/).
]/2л е V du
(2.184)
Среднее расстояние между уровнями ядерной материи с энергией возбуждения
U определяется выражением
D (U) - У 2л 0
]/”
V d0
e~s<y).
(2.185)
Эта формула приобретает определенный смысл, если задана связь между эн-
тропией S(U) и энергией возбуждения, или, что то же самое, между энергией U
и температурой 6.
Будем считать энергию и температуру для основного состояния ядерной
материи равными нулю. Возбужденным состояниям ядерной материи с энер-
гиями возбуждения, малым по сравнению с полной энергией связи, соответ-
ствуют низкие температуры. При низких температурах энергия возбуждения
ядерной материи, так же как и для макроскопических тел, будет определяться
степенной зависимостью от температуры
U = ahn,
где а ил — некоторые постоянные. Используя (2.177), находим
5= —— аеп"‘.
п — 1
(2.186)
(2.187)
123
Согласно теореме Нернста, при в = 0 энтропия системы должна обращаться
в нуль, поэтому п > 1. Используя (2.184) и (2.187), находим
I п— 1
, , , А П п ,, п
1 ( a W ---------га и
е • <2Л88:
Формула (2.188) объясняет характерные особенности энергетического спектр;
ядерной материи, а именно увеличение плотности уровней с ростом энергиг
возбуждения. Заметим, что формула (2.188) неприменима при очень малы;
энергиях возбуждения, когда нельзя делать допущение о непрерывности энер
гетического спектра системы.
Наиболее простой закон распределения плотности уровней найдем, по-
лагая Л(77) = const. В этом случае и---2, и распределение плотности уровне}
определяется формулой
p(U) = Се2 (2,189
Постоянные а и С можно подобрать таким образом, чтобы воспроизводились
эмпирические данные о плотности уровней ядер [5]. Из данных по захвату
медленных нейтронов ядрами с нечетными А следует, что в области массовые
чисел 100 < А < 200 постоянные а и С имеют следующие значения; а «
Д .
~ у? Мэв, С 0,01 Мэв . Таким образом, для тяжелых ядер А ~ 200 при
энергиях возбуждения U ~ 10 Мэв температура 6 оказывается порядкг
1 Мэв, т. е. ядро действительно можно считать холодным, что и предполага-
лось раньше.
Заметим, что распределение (2.189) соответствует случаю вырожденной
идеального ферми-газа. Однако модель идеального ферми-газа приводит 1
д
завышенному значению постоянной а (аид ~ g-g Мэв), не согласующемуся
с эмпирическими данными.
ГЛАВА 3=
ОБОЛОЧЕЧНАЯ СТРУКТУРА
ЯДЕР
§ 3.1. ДВИЖЕНИЕ НУКЛОНА В САМОСОГЛАСОВАННОМ ПОЛЕ ЯДРА
Независимость движения нуклонов в ядре и самосогласован-
ный потенциал. В основе оболочечной модели ядра лежит пред-
положение о том, что нуклоны в ядре движутся почти независимо
друг от друга, несмотря на наличие сильного взаимодействия меж-
ду свободными нуклонами. Независимость движения отдельных
нуклонов в ядре означает, что средняя длина свободного пробега
нуклона в ядерном веществе велика по сравнению с размерами яд-
ра. Взаимодействие нуклонов друг с другом в оболочечной модели
сводится к взаимодействию отдельных нуклонов с самосогласован-
ным полем. Вообще говоря, каждый нуклон движется в поле, соз-
даваемом другими нуклонами. В оболочечной модели предполагает-
ся, что это поле одинаково для всех нуклонов. Потенциал такого
самосогласованного поля считается статическим и сферически
симметричным.
Введение в оболочечной модели самосогласованного поля, за-
висящего от расстояния до центра ядра, существенно улучшает
представление о ядрах по сравнению с моделью ферми-газа. Из-за
короткодействующего характера ядерных сил потенциал самосогла-
сованного поля изменяется почти так же, как и ядерная плотность:
является постоянным внутри ядра и обращается в нуль вне ядра.
В результате одночастичные волновые функции оказываются не
плоскими волнами, а более сложными функциями, которые за-
висят от расстояния до центра ядра и обращаются в нуль вне ядра.
Возможность введения самосогласованного поля и независи-
мого рассмотрения движения отдельных нуклонов в таком поле
обусловлена в значительной степени принципом Паули, которому
подчиняются нуклоны. В результате действия этого принципа эф-
фективное взаимодействие между нуклонами оказывается сущест-
венно ослабленным.
Выбрав потенциал самосогласованного поля, можно рассчи-
тать спектр энергетических уровней, соответствующих различным
состояниям отдельного нуклона. В зависимости от формы потен-
циала одночастичный спектр разобьется на группы близко рас-
положенных уровней, разделенных большими энергетическими
интервалами. Так как принцип Паули запрещает двум нуклонам
находиться в одном и том же состоянии, то основному состоянию
125
ядра, характеризуемому наименьшей энергией, соответствует кон-
фигурация, в которой нуклоны занимают самые низшие одночастич-
ные уровни. Наиболее устойчивая конфигурация (заполненная
оболочка) получится в том случае, когда между самым высоким
занятым уровнем и самым низким свободным имеется большая
энергетическая щель. В общем случае ядро состоит из определен-
ного числа заполненных оболочек и нескольких внешних нуклонов,
находящихся в незаполненной оболочке*.
Существуют различные варианты оболочечной модели ядра.
В простейшем из этих вариантов — в одночастичной оболочечной
модели, используемой для описания ядер с нечетными значениями
массового числа А, предполагается, что все парные нуклоны (вклю-
чая нуклоны в незаполненной внешней оболочке) образуют инерт-
ный остов с нулевым спином, и свойства ядра полностью опреде-
ляются состоянием последнего нечетного нуклона. В многочастич-
ной оболочечной модели свойства ядра определяются всеми нукло-
нами, находящимися как в незаполненной оболочке, так и в за-
полненных оболочках.
Уравнение движения нуклона в самосогласованном поле ядра.
Изучение оболочечной модели ядра начнем с рассмотрения про-
стейшей одночастичной модели. Будем считать, что потенциал
самосогласованного поля V (г) характеризуется сферической сим-
метрией. Рассмотрим движение отдельного нуклона в таком поле.
Волновая функция ф (г), описывающая движение нуклона, удов-
летворяет уравнению Шредингера
(^(Йа/2М) А + У(г)—Е]ф(г)=0, (3.1)
где А — оператор Лапласа и Е — энергия нуклона. Вследствие
сферической симметрии потенциала V (г) момент количества дви-
жения нуклона является интегралом движения, и волновую функ-
цию ф (г) можно представить в виде произведения радиальной
функции на угловую:
ф)- (3.2)
Угловая функция Y!т (О', ф)—это собственная функция состоя-
ния, в котором момент количества движения I и его проекция т
имеют определенные значения. Радиальная функция фпг(г) удов-
летворяет уравнению
dr2 Ф г dr "Г Д3 2М
-^Р- Фпг=« (3.3)
г3
* Впервые допущение о наличии оболочечной структуры у ядер было
высказано В. Эльзассером в 1934 г. [1]. Современная теория ядерных оболочек
основывается на работах М. Гепперт-Майер [2] и О. Хакселя, И. Йенсена и
X. Сьюесса [3], предположивших существованне сильного спин-орбитального
взаимодействия между нуклонами в ядрах. Детальному изложению теории
ядерных оболочек посвящены монографии [4—6], а также обзор [7], в которых
содержится подробная библиография.
126
и граничным условиям: функция tpn!(r) конечна в точке г = 0
и обращается в нуль на бесконечности (при г—> оо). Из условия
обращения радиальной функции <рп( (г) в нуль на бесконечности
определяются собственные значения энергии связанных состояний
нуклона Еп1 < 0. Здесь п — главное квантовое ч и с-
л о, характеризующее собственное значение энергии нуклона Епг
и равное числу узлов радиальной функции <рп; (г) плюс единица.
Так как собственные значения энергии Eni не зависят от кван-
тового числа т, то каждый уровень характеризуется (2/ + 1)-
кратным вырождением. Кроме того, каждый уровень двукратно
вырожден по спину и, если пренебречь кулоновским взаимодейст-
вием, еще двукратно вырожден по заряду. Таким образом, сред-
нее расстояние между вырожденными уровнями оказывается значи-
тельно больше расстояния, предсказываемого статистической тео-
рией.
Радиальные функции (г), так же как и последовательность
одночастичных уровней Еп1, зависят от формы потенциала V (г).
Сведения о форме потенциала можно получить из опытов по рас-
сеянию нуклонов на ядрах. Из этих опытов следует, что глубина
потенциальной ямы V (г) почти постоянна внутри ядра и быстро
уменьшается до нуля вблизи его поверхности.
Задачу о движении нуклона в самосогласованном поле V (г)
можно решить в явном виде, аппроксимируя действительный по-
тенциал V (г) осцилляторной или же прямоугольной потенциаль-
ной ямой. При этом результаты для истинного потенциала можно
получить интерполяцией результатов, полученных для этих идеа-
лизированных потенциалов.
Свойства радиальных волновых функций. Рассмотрим некото-
рые общие свойства радиальных волновых функций нуклона, дви-
жущегося в центральном самосогласованном поле.
Представляя радиальную волновую функцию <pni (г) в виде
^ni(r)=uni(r)/r, (3.4)
для функции ин! (г) из (3.3) получаем дифференциальное уравнение
^ + ^\Еп1-У(г)-^-.^±Щип1 = 0, (3.5)
dr2 A2 L 2Л1 г2 J
не содержащее первой производной. Функция nni (г) обращается
в нуль при г — 0 и для связанных состояний должна обращаться
в нуль на бесконечности.
Отметим следующее интересное обстоятельство. Если уравнение
(3.5) переписать в виде
<з-б>
2Л4 цп( (г) г2
то становится очевидным, что значения функции unI (г) при каком-
то значении I достаточно для определения потенциала с точностью
до аддитивной постоянной.
127
Предположим, что потенциал V (г), отвечающий силам притя-
жения V (г) 0, монотонно изменяется с расстоянием
|^(г1)|>|И(г2)[ при Г1<гг, (3.7)
обращаясь в нуль на бесконечности V (оо) = 0. Кроме того, будем
считать, что
limr2V(r)— 0, (3.8)
поэтому основное состояние будет характеризоваться конечным
значением энергии. Введем эффективный потенциал
V{ (г) =V (г) + (&/2М). Z(Z + l)/ra. (3.9)
При I = 0 эффективный потенциал (3.9) совпадает с V (г), а
при / Ф 0 зависимость эффективного потенциала Vi (г) от расстоя-
ния г подобна зависимости потенциала взаимодействия двух ато-
мов газа, которому на малых расстояниях соответствует отталки-
вание (рис. 3.1). Для определенной энергии Eni<0 при 1 — Q
имеется одна точка поворота г0 (Еп{ = Кг (г0)), а при I Ф 0 имеются
две точки поворота г0 и г0' (г0' < г0). Очевидно, что
Enl—К,(г)>0 для г0'<г<г0,
Enl—Vt(r)<0 для г>г0.
(3.10)
В первом случае (3.10) функция (г) искривлена по направле-
нию к оси г, а во втором случае — в противоположном направле-
нии. Поэтому в области r0' <Z г < г0 зависимость функции uni (г)
от г носит колебательный характер, а в области г > г0 функция
uni О') с ростом г уменьшается по абсолютной величине. Это озна-
чает, что узлы функции Ип( (г)
могут лежать только в обла-
сти г < г0, т. е. в пределах
области действия притягиваю-
щего потенциала. Вне области
действия потенциала функция
uni (г) экспоненциально убы-
вает с ростом г, при этом ха-
рактеристическая длина равна
Рис. 3.1. Зависимость эффективного
потенциала V} (г), учитывающего
центробежную энергию, от расстоя-
ния г.
У^/2М\Еп1\.
Если существуют два свя-
занных состояния с одним и
тем же орбитальным моментом
/, но различными значениями
nt И (п2 > «1)> ТО ЕП11 >
>ЕП1ь поэтому состояние с боль-
шим числом узлов оказывается
менее связанным. Действитель-
но, с ростом числа узлов ра-
диальной функции (распреде-
128
ляющихся в области действия потенциала) уменьшается длина
волны частицы, а это соответствует увеличению кинетической
энергии частицы, что и приводит к увеличению полной энергии
Еп1 с ростом п.
Если имеются два состояния с одинаковым числом узлов п
в радиальных функциях, но с различными орбитальными моментами
4, /2 и 1г > 1±, то энергия Enit > Епц, т. е. состоянию с меньшим
значением орбитального момента соответствует меньшее значение
энергии. (Наименьшей энергией обладает S-состояние.) В спра-
ведливости высказанного утверждения нетрудно убедиться, если
заметить, что с ростом орбитального момента I увеличивается цент-
робежная энергия z — ———4 . Гак как потенциальная энер-
\2Л1 гг /
гия в случаях /г и /3 практически одинакова, то отсюда следует,
что при /2 > 4 справедливо неравенство Еп1г > Еп[1.
Спин-орбитальное взаимодействие. Наличие спина у нуклона
при движении последнего в самосогласованном поле ядра приво-
дит к возникновению добавочного взаимодействия. Энергия этого
взаимодействия должна зависеть не только от векторов s и г, но
и от скорости нуклона V, так как из векторов s и г, имеющих раз-
личную природу (s — аксиальный вектор, г — истинный вектор),
нельзя составить скалярного выражения. Из трех векторов s, г и
v скалярное выражение можно составить следующим образом:
/(r)[rv]S, (3.11)
где f (г) — некоторая скалярная функция координат. Так как
векторное произведение [rv] пропорционально орбитальному мо-
менту нуклона 1, то (3.11) можно рассматривать как спин-орбиталь-
ное взаимодействие. Это взаимодействие носит релятивистский ха-
рактер (при v 0 оно исчезает) и оказывается значительно сла-
бее взаимодействия нуклона с самосогласованным полем.
Для нахождения явного вида энергии спин-орбитального взаи-
модействия воспользуемся аналогией с электродинамикой 15].
Рассмотрим взаимодействие частицы, движущейся с импульсом р
и обладающей магнитным моментом р, = ^s, с электростатиче-
ским полем Е~ — у grad V. В системе отсчета, связанной с дви-
жущейся частицей, напряженность магнитного поля равна Н =
1 Г Р г- I
----— Е , и, следовательно, энергия магнитного взаимодеист-
с [М J
вия определяется выражением
U = — РН = — —[pgrad ]/]s. (3.12)
АР
Замечая, что для сферически симметричного потенциала grad V =
" ~ и что Ггр] Til, энергию (3.12) можно представить в виде
U = (TilMcy (1/г). (dV/dr) (Is). (3.13)
5 Зак. 642 129
В случае нуклона, движущегося в самосогласованном поле яд-
ра V (г), спин-орбитальиое взаимодействие можно выбрать по ана-
логии с (3.13), введя, однако, в (3.13) дополнительный безразмер-
ный множитель — X, характеризующий величину спин-орбиталь-
ной связи:
U = —X(/z/Mc)2(l/r).(oV7dr) (Is). (3.14)
(Из анализа экспериментальных данных следует, что константа
спин-орбиталыюй связи X л? 10.)
Вследствие спин-орбитального взаимодействия орбитальный и
спиновый моменты нуклона 1 и s в отдельности нс' сохраняются,
сохраняется только полный момент количества движения нуклона
j = 1 + s. Замечая, что 21s ~ / (/ 1) — / (/ + 1) — s (s + 1),
энергию спин-орбитального взаимодействия нуклона в состоянии
с определенным значением полного момента можно представить
в виде
U-- (a/r)-(dV/дг), (3.15)
где
a-(Z/2)(/t/Mc)2[ l’ W + V2; (3.16)
U-(H-l). j = ( —1/2.
Уравнение Шредингера, описывающее движение нуклона в са-
мосогласованном поле V (г) при наличии спин-орбитального взаи-
модействия, имеет вид
{—(/га/2Л1) Д 4- V (г) — (а/г) • (dV (r)/dr)—£} гр = 0. (3.17)
Волновую функцию — решение уравнения (3.17) можно пред-
ставить в виде произведения радиальной и спин-угловой функций:
;1.ш. (3.18)
Спин-угловая функция
3W= S (lmlsms\jm)Yl (Ф, <р)%SJIls (3.19)
т £ 4- ov =
является собственной функцией состояния, в котором полный мо-
мент количества движения / и его проекция т имеют определенные
значения. В этом состоянии определенные значения имеют также
квадраты орбитального и спинового моментов, характеризуемые
квантовыми числами I и s.
Радиальная функция <рпг (г) при наличии спин-орбитального
взаимодействия удовлетворяет уравнению
42фпг t 2 dfpni I
dr2 ' r dr '
T
Ю + 1)1
j
dV (r) 1i"
'~сГг 2M
<p,u = 0. (3.20)
!30
Так как коэффициент ац зависит от значения полного момента j,
то при наличии спин-орбитального взаимодействия вырождение
уровней энергии по j снимается. Уровни энергии нуклона Enij
зависят от трех квантовых чисел п, I и /.
£ 3.2. ОДНОЧАСТИЧНЫЕ СОСТОЯНИЯ
Изотропный осцилляторный потенциал. В случае легких ядер
хорошим приближением для ядерного потенциала во внутренней
области ядра является трехмерный изотропный осцилляторный
потенциал
V(r) = — У0 + (1/2)Л1ы2г3, (3.21)
где Vo — глубина потенциальной ямы в центре ядра; М — масса
нуклона; и — величина, имеющая размерность частоты. В об-
ласти вне ядра потенциал V (г) следовало бы положить равным
нулю, однако для связанных состояний волновые функции с таким
потенциалом практически не отличаются от волновых функций,
соответствующих потенциалу (3.21).
Будем вначале пренебрегать спин-орбитальпым взаимодейст-
вием. Подставим формулу (3.21) в (3.3), заменим переменную г без-
размерной переменной g = — г, тогда уравнение для радиальной
функции запишем в виде
s dl2 ' 2 di 1 2 L 2 - 2g
где 8 =(£ + V0)/'iW-
Для нахождения решения этого уравнения исследуем асимпто-
тическое поведение функции ср при больших и малых значениях
При достаточно больших значениях Е. оставляя в уравнении (3.22)
только члены, пропорциональные Е, имеем cftp/dE2 — (1/4)<р = О,
откуда следует, что ср ~ е’1'2®, Е—> оо.
При малых значениях Е, оставляя в квадратных скобках урав-
нения (3.22) только член с наинизшей степенью Е, имеем
। 3 d<p <(/+1) 0
dt? 2g ‘ rfg 4g2 Т
Решение полученного уравнения ищем в виде ср — Е\ в этом слу-
чае для s получаем квадратное уравнение
s(s— l)+(3/2)s— -Н£±1>=0.
4
Так как ср должно быть конечным при Е = 0, то следует взять по-
ложительный корень квадратного уравнения s - (1/2)I.
Итак, решение уравнения (3.22) можно представить в виде
-.L i 1. i
<р- е 2 Е2 №(Е), (3.23)
5‘
131
где w (В) — полином, конечный при Е — 0. Подставляя (3.23)
в (3.22), для w получаем уравнение
+ (I -f 3/2 - ?) W +i /, (к - / - 3/2) ш = 0.
Решением этого уравнения является вырожденная гипергеометрп-
ческая функция, и, следовательно,
/ + я/2> И- (3-24)
Вырожденная гипергеометрическая функция F (а, у, Е) определя-
ется рядом
F (a у Е) = 1 1 а_-__I- а (я~1~ г а 7 (g + 2) V ..t.
' ' ? 1! У (Y+1) 21 ‘ Т (y I 1) (Y -2) 3!
обрывающимся при условии, что аргумент а есть целое отрица-
тельное число или нуль. Таким образом, решение (3.24) будет
полиномом только в том случае, если
— (1/в)е + (1/2)^Ч-3/4 — — 1)> « = 1,2,3,..., (3.25)
где (п — 1) — целое число, определяющее степень полинома.
Условие (3.25) определяет собственные значения энергии ча-
стицы в осцилляторной яме. Вводя обозначение 2(п — 1) + Z = /V,
имеем
En = ~ Vo ч-(Лг+:72)А<в, W =0,1,2,..., (3.26)
т. е. энергия зависит только от целого числа N, называемого
главным квантовым числом.
Согласно (3.26), энергетический спектр частицы в осциллятор-
ной яме состоит из ряда равноотстоящих уровней, отделенных друг
от друга интервалом h и. Каждому уровню EN соответствует не-
сколько состояний с различными значениями I, причем числа I
и N всегда одинаковой четности и I /V. Кратность вырождения
отдельных уровней, как нетрудно убедиться, равна S(2Z 4* 1) =
= (1/2)^ + l)(tf + 2).
Различные состояния обычно обозначаются с помощью пары
чисел (nl), при этом используется спектроскопический способ обо-
значения: Is, Ip; 2s, Id; 2p, 1/; 3s, 2d, 1g; ... (число n означает, что
данное значение I появляется в последовательности n-й раз),
Нормированная радиальная волновая функция, отвечающая
состоянию (n, Z), имеет вид
q>n((r)=Cn;e-(>/2>«!'V'F(l— п, Z + 3/a, а2 г2),
(3.27)
где
nt
1
Г(/Ч-3/г)
/2Г(/-п-Ы/а)
Г(п)
а1 + 3/2,
Л7ы V/2
В табл, 3.1 для нескольких первых уровней энергии, характе-
ризуемых числами N, указаны возможные состояния, а также
приведены значения максимального числа частиц (нейтронов или
132
Таблица 3.1
Состояния (/1. /) zN = («+1) nv+2) - SA
0 1s 2 2
1 1р 6 8
2 2s, Id 12 20
3 2р, If 20 40
4 3s, 2d, 1g 30 70
5 3p, 2f, 42 112
6 4s, 3d, 2g, 11 56 168
аи - (Х/2) (Л/Мс)2
протонов), допускаемого принципом Паули, па каждом уровне
N 1
Zjv — (jV + 1)(JV + 2) и полного числа частиц ^ZN = — (Л/ + 1 )(ЛГ 4*
о d
+ 2)(N + 3). Согласно табл. 3.1, заполненные оболочки в случае
осцилляторного потенциала получаются при числах нейтронов и
протонов, равных 2, 8, 20, 40, 70, 112, ... Однако магические числа,
обнаруживаемые на опыте, совпадают только с первыми четырьмя
значениями (А/3) (в табл. 3.1 они обведены). Для получения
значений остальных магических чисел необходим учет спин-ор-
битального взаимодействия. В случае осцилляторного потенциала
(3.21) учет спин-орбитального взаимодействия приводит к посто-
янной добавке к энергии — (air) • I —) — —аМоЕ. Так как вели-
ко/
чина а зависит от орбитального и полного моментов частицы I и /
I, }=l + 4z,
-(/-1-1),
то вырождение осцилляторных уровней EN частично снимается,
и каждый уровень Е^ распадается на ряд подуровней:
ENlj = — С04-(А/ ~г3/3) а/}Мм2. (3.28)
Величина спин-орбитального смещения зависит от Z и увели-
чивается с ростом I. Вследствие этого при больших значениях AZ
спин-орбитальное расщепление может существенно изменить по-
рядок заполнения оболочек, задаваемый только числом N. Дейст-
вительно, подуровень, соответствующий максимальному значе-
нию полного момента частицы /макс = /макс + 1/2 = А/ + ха-
рактеризуется наибольшим смещением в сторону меньших зна-
чений Поэтому если состояние с /макс причислять к У — 1-обо-
лочке, то, учитывая кратность вырождения этих состояний, равную
2 (N 1), для числа частиц Zn' в ААоболочке получаем Z^' =
= ZN — 2 (N + 1) + 2 (А/ 4- 2), N >0.
В табл. 3.2 приведены значения Z^’ и ZZn' для конкретных зна-
чений N (магические числа обведены). Сравнивая опытные значе-
ния магических чисел с последовательностями чисел и ZZ^,
133
Таблица 3.2
1 д,г | Состояния »(/)/ ZN
0 lsl/2 6 6
1 'Р1/2' *Рз/2 ‘ 8 . 14
2 2Sj/2* 1^3/2’ 1^5/2 ' ' ' * • 14 28
3 2Р]/2. 2р.з/г. 1/7/2 22 50
4 3S|y2, 2J3/2, ... 32 82
5 3Р[/2’ 3Рз/2’ ^5/2- 2^7/2’ 1Л9/2> 1ЛИ/2 • 44 126
6 4si/2. 3d3j,2, 3d5/2,2g7j,2,2£g/2, lill/2> 1'13/2 58 184
видим, что порядок заполнения оболочек определяется при малых
числах частиц (7V сД 40) порядком осцилляторных уровней, а при
больших 28) — влиянием спин-орбитальной связи.
Определение абсолютных значений расстояний между уров-
нями. Используя найденные одночастичные волновые функции,
можно непосредственно рассчитать пространственное распределе-
ние плотности нуклонов в ядре. Очевидно, плотность определяется
выражением р (г) — (г)ф„гут (г), где суммирование произ-
водится по всем занятым состояниям. В случае заполненных ос-
цилляторных оболочек суммирование по j и т можно выполнить,
воспользовавшись полнотой спиновых и угловых функций:
I \ 'ST 2/ |- 1 2 , .
МП- У чМ')-
п
N — 1
+ 1.
«.Д'
(3.29)
Для примера приведем пространственное распределение плот-
ности нуклонов для ядер |Не, ^6О и £°Са с заполненными нейтрон-
ными и протонными оболочками:
Ро(И~4т*
Л-
Р1 0 ) — ^72 ^(Н-2^^)е-2^;
рДг) = а:'(5 + 4а*г4) е—а'г*.
(3.30)
Плотность максимальна в центре ядра и уменьшается по гауссов-
скому закону с удалением от центра.
Зная распределение ядерной плотности (3.29), абсолютные зна-
чения расстояний между осцилляторными уровнями можно найти,
если сравнить вычисленные размеры ядер с экспериментальными
134
значениями ядерных радиусов. Например, вычислив с помощью
(3.30) среднеквадратические радиусы для гНе, 1 |О и аоСа и сравнив
их с экспериментальными значениями среднеквадратических ра-
диусов /?не — 1,61 • 10"13 см; R„ = 2,65 10"13 см; Rea ~ 3,52 X
X 10~13 СМ, получим ЙСОне = 24 Мэв] Лы0 13,3 Мэв; Й(Оса =
= 10,1 Мэв.
В случае ядер с достаточно большим массовым числом А можно
установить зависимость ha от А в общем виде. Для этого восполь-
зуемся тем, что в осциллятор ной яме средняя кинетическая энер-
гия и средняя потенциальная энергия нуклона, отсчитываемые от
дна ямы, равны. Поэтому сумму энергий (отсчитываемых от дна
ямы) всех нуклонов в ядре можно выразить через значение сред-
неквадратического радиуса 'I' ^о) ~ АМа2(г2).
i
Если ядро находится в основном состоянии, то заняты все ниж-
ние уровни, и, следовательно,
2 + vo) = 2 2 (N + 1) A + 2) + 3/2) ha,
i о
N
А~ 22^ + 1> (^ + 2).
о
Считая распределение плотности однородным (что оправдано при
больших А), положим <г2> = (3/5)7?2 (7? = 7?ОАИЗ — эксперимен-
тальное значение радиуса ядра). В результате получаем
ha=— 2(-У+1)(^+2)(^-Н3/3)
3 MR2 ' 2(ЛЧ -1) (JV + 2)
и, ограничиваясь при суммировании только членами наиболее вы-
сокого порядка, приближенно имеем
ha ।Af3. А -‘/з.
Полагая Ra = 1,2-10~13 см, для расстояния между уровнями
в осцилляторном потенциале окончательно получаем следующее
выражение:
Йсо а; 41 А-1/3 Мэв. (3.31)
Постоянную спин-орбитального взаимодействия X можно опре-
делить, используя экспериментальные данные по смещению ос-
цилляторных уровней вследствие спин-орбитального взаимодей-
ствия. Согласно (3.28), добавочная энергия, обусловленная спин-
орбитальным взаимодействием, равна
\Е —
— I,
/+1,
(3.32)
135
где безразмерная постоянная р = Наилучшее согласие
с опытными данными получается при |3 1/20. Так как т
~ 10 Мэв, находим, что постоянная спин-орбитальной связи
л х 10.
Прямоугольная потенциальная яма. Рассмотрим одночастич-
ную модель, выбрав в качестве ядерного потенциала прямоуголь-
ную яму конечной глубины:
V(r) = ( V°’
I О,
г<Р;
r>R,
(3.33)
где R — радиус ядра. Прямоугольная потенциальная яма, характе-
ризующаяся постоянной глубиной внутри ядра с резким измене-
нием на его поверхности, оказывается хорошим приближением для
самосогласованного потенциала тяжелых ядер.
Запишем уравнение для радиальной функции
+ +
dr2 г dr [ й2 ( г
dV (г) 1
dr
±+1>)ф = 0. (3.34)
г2 J
Рассмотрим связанные состояния нуклона, которым отвечает от-
рицательная энергия, по абсолютной величине меньше глубины
потенциала Е < 0, j Е | < Уо.
Вследствие скачкообразного изменения потенциала (3.33) при
г = R спин-орбитальные силы действуют на нуклон только на по-
верхности ядра:
(a/r) (dV/dr) ~ (a/R) Va8(r~R). (3.35)
Уравнение (3.34) существенно упростится, если отдельно рас-
смотреть область внутри ядра
_±Pj_±.dl + ^2 — ±<£±.221 ф = о, k2=—(V0 + E), r<R>
dr2 г dr { г2 ) й-
и область вне ядра
d’cp 2 dtp
:2 = — |Е|, г >R.
/г
В этом случае решения во внутренней и внешней областях должны
переходить друг в друга в точке г — R, так как волновая функция
является непрерывной величиной:
ср(Е—0) = ф(7? + 0). (3.36)
Однако производная от волновой функции при г = R будет испы-
тывать скачок из-за дельтаобразного члена (3.35) в исходном урав-
нении (3.34). Оставляя вблизи точки г = R в уравнении (3.34)
главные члены
Ф" -|- (2/И/Л2) (а/r) 6 (r-Е) ф -• -О
136
и интегрируя вдоль малого отрезка, содержащего точку г = 7?, на-
ходим
Ф' (7? - 0) - ф' (7? + 0) (ц/7?) • (2Л4/Йа) |70 ф (7?). (3.37)
Полученное соотношение представляет собой граничное условие,
определяющее скачок производной волновой функции на поверх-
ности ядра, обусловленный действием спин-орбитальных сил. Ре-
шение во внутренней области, удовлетворяющее условию конеч-
ности в точке г — 0, имеет вид
<p(r) = Q'l(fer), г</?,
(3.38)
где jt (х) — сферическая функция Бесселя, Соответственно реше-
ние во внешней области, обращающееся в нуль на бесконечности,
выражается через сферическую функцию Макдональда*: <р (г) ~
~ kt (иг), r>R. Коэффициент пропорциональности находим, ис-
пользуя условие непрерывности волновой функции на поверх-
ности ядра (3.36):
= г>/?. (3.39)
ki (xR)
ао
Постоянная С определяется условием нормировки J drr2 ср2 (г) — 1:
о
с (^)-h-i (kR)j!+l (W?) . (3.40)
#3/2 ( kis(xR)- J
Подставляя решения (3.38) и (3.39) в граничное условие (3.37),
получаем уравнение для нахождения собственных значений энер-
гии нуклона в прямоугольной потенциальной яме:
/е i'* 1 _ х . kt' (xR) я 2/V!
il (kR) k; (xR) R h2
(3.41)
* Определим сферические функции j; (х) и fe;(x): /z(.vj= |/ -Я J j (x),
kt (x) — К ] (x). Функции /, ix) и k, (x) можно выразить через три-
тонометрические и экспоненциальную функции; Д(х)=т(—1)' х' --------------х
(xdx)z
I sinx \ я (/-)-«)!
X ------- ; fe, (х) = — е 7 ------------------. Б частном случае 7 = 0
V х ) 1 2х п! (/— л)! (2х)« '
(о (х) — sin х/х, k0 (x) = (n/2).(e_J-7x). Функции j;(x) и fc;(x) удовлетворяют
следующим рекуррентным соотношениям: ji’= —ttl j;; kt’ =—kii —
/+1 , , x
— ----- kf, Ji = —ji+i + (7/x) /Г, fei =—feiw + (i/x} kt. Приведем также
значенйя интегралов от квадратов функций и J drr2 /;2 (аг) = (гв/2)Х
Х[/;а (“И—/;_,(аг)/;+1(аг)); idrr2kt2 (₽г) = (rs/2) {kt2 (рг) — /г;_1(₽г)^+1(Р'')) •
137
Ограничимся нахождением решения уравнения (3.41) в простей-
шем случае S-состояния (I = 0). Если Z = 0, то спин-орбитальное
взаимодействие отсутствует (а = 0), и уравнение (3.41) упрощается:
ActgW?=— х. (3.42)
Замечая далее, что k2-\-x2=~ Уо, уравнение (3.42) можно
представить в виде
|sinx[ =---~. x = kR. (3.43)
Это уравнение нетрудно решить графически, что и представлено
на рис. 3.2. Так как k и х положительны, то в силу (3.42) должно
быть ctg х <Z 0, и, следовательно, корни х должны лежать во вто-
0 5 10 X
Рис. 3.2. Графи (еское решение
уравнения для собственных зна-
чений энергии нуклона в прямо-
угольной яме при I = 0. По оси
ординат отложены значения двух
функций в левой и правой частях
равенства (3.43).
ром, четвертом, шестом и т. д. квадрантах. Полагая = 43 Мэв,
7?0 = 1.2-10"13 см и А = 125, получаем следующие значения для
корней: Xi = 2,9; х2 = 5,6; = 8,2, Соответствующие уровни
энергии, определяемые формулой £; = —Xf2’ * =
2, ..., равны Et = —38,2 Мда; £2 — —25,1 Мда; Es = —4,4 Мда.
При I Ф 0 решение уравнения (3.41), необходимое для нахож-
дения возможных уровней энергии, значительно усложняется.
Однако качественные результаты о распределении уровней можно
получить, рассматривая бесконечную прямоугольную яму (Ео^-
оо). Это связано с тем, что при переходе от ямы конечной глу-
бины к бесконечной яме порядок уровней остается неизменным,
меняются только относительные расстояния между уровнями.
В случае бесконечной ямы граничное условие (3.41) принимает
вид
/г(А/?)=0, (3.44)
и, следовательно, уровни энергии однозначно определяются кор-
нями функции ji (х).
В табл. 3.3 приведена последовательность уровней для беско-
нечной прямоугольной ямы, корни функции Бесселя, соответствую-
щие состояниям (п, /), число частиц в каждом состоянии 2 (2/ + 1)
и полное число частиц ^2 (21 -f- 1).
138
Таблица 3.3
Состояния (П/) Корень it (•>> 2(2/ 4-1) 22(24-1) п! Состояния (ПО Корень it М 2(2/-р 1) 2 2(2/+1) ill
1s 3,142 2 2 2d 9,095 10 68
1р 4,493 6 8 3s 9,425 2 70
14 5,763 10 18 1А 9,356 22 92
2s 6,283 2 20 2f 10,417 14 106
1/ 6,988 14 34 Зр 10,904 6 112
2р 7,725 6 40 и 10,513 26 138
1g 8,183 18 58 2g 11,705 18 156
Основное отличие одночастичного спектра в случае прямо-
угольной ямы от спектра в случае осцилляторного потенциала
заключается в снятии вырождения уровней по значениям орбиталь-
ного момента I, причем уровень, соответствующий наибольшему
значению /, опускается ниже всего. Это связано с тем, что с уве-
личением I центробежные силы вытесняют частицу к краю потен-
циальной ямы, который оказывается для прямоугольной ямы
значительно ниже, чем для осцилляторного потенциала. Учет спин-
орбитального взаимодействия в случае прямоугольной ямы, так же
как и в случае осцилляторного потенциала, приводит к добавоч-
ному расщеплению уровней по значениям полного момента части-
цы j.
Отдельные уровни в прямоугольной яме удобно характеризо-
вать наряду со значениями I и / теми значениями N, которые отве-
чают данному уровню, если адиабатическим путем перейти от
прямоугольной ямы к осцилляторному потенциалу. Таким обра-
зом, каждый уровень будет однозначно определяться квантовыми
числами 7V, / и /.
Магические числа. На рис. 3.3 представлена схема уровней для
изотропного гармонического осциллятора (слева) и прямоугольной
ямы (справа). Уровни, соответствующие друг другу, соединены пря-
мыми линиями, которые дают интерполяцию между обоими пре-
дельными случаями. В промежуточном случае уровни разбиваются
на отдельные группы, разделенные большими энергетическими
интервалами. Спин-орбитальное взаимодействие приводит к появ-
лению в данной группе уровней уровня из следующей осциллятор-
ной полосы, имеющего противоположную четность и более высо-
кий полный момент.
Магические числа (на рис. 3.2 они обведены) определяются
максимальным числом состояний, отвечающих данной группе уров-
ней. Как видно из рисунка, такими магическими числами явля-
ются 2, 8, 20 , 28, 40 , 50, 82, 126, из которых три первых и пятое
обусловлены осцилляторным характером потенциала, а остальные —
влиянием спин-орбитального взаимодействия.
Для тяжелых ядер вследствие кулоновского взаимодействия
последовательность одночастичных уровней для протонов будет
139
несколько отличаться от соответствующей последовательности для
нейтронов. На рис. 3.4 представлена эмпирическая схема распо-
ложения одночастичных уровней для нейтронов и протонов [8].
Ядра, в состав которых входит магическое число нейтронов
или протонов, резко отличаются по своим свойствам от остальных
Рис. 3.3. Схема уровней для изотропного гармонического осцил-
лятора (слева) и прямоугольной ямы (справа). Пунктирная
линия соответствует эмпирической последовательности одночас-
тичных уровней.
ядер. Действительно, магические числа связаны с образованием
заполненных оболочек, поэтому ядра, содержащие магическое чис-
ло нуклонов, характеризуются большой энергией связи. Энергии
возбужденных состояний относительно основного состояния у та-
ких ядер очень велики. Соседние ядра, у которых начинается за-
полнение следующих оболочек, характеризуются значительно
меньшими энергиями связи. Б качестве примера можно указать
на дважды магическое ядро 28®РЬ, состоящее из магического числа
140
протонов (82) и магического числа нейтронов (126). Если энергии
связи нейтрона и протона у 203РЬ соответственно равны 7,36 и
8,97 Мэв, то у соседних ядер энергии связи нейтрона и протона
оказываются равными 3,86 Мэв (20эРЬ) и 3,76 Мэв (20eBi). Если
j
If,____С — ?/<? >__________. м
р з/г —С / д/2
7J-----------1/2 -----------//2
Р п
Рис. 3.4. Эмпирическая схема одночастичных уров-
ней для нейтронов и протонов.
у обычных тяжелых ядер энергии наинизших возбужденных со-
стояний порядка 0,1 Мэв, то у дважды магического ядра г08РЬ
энергия наинизшего возбужденного состояния равна 2,6 Мэв.
Величиной энергии связи объясняется также выделенность
магических ядер, проявляющаяся в аномалиях полной распростра-
141
ценности элементов, а также относительной распространенности
отдельных изотонов и изотонов. Так, наибольшими оказываются
числа стабильных изотопов у элементов с Z = 20, 28, 50 и 82.
(Максимальным числом стабильных изотопов, равным 10, облада-
ет элемент 50Zn.) Аналогично наибольшие числа стабильных изо-
топов отвечают N = 20, 28, 50, 82 и 126.
Большая величина энергии связи магических ядер непосред-
ственно связана с малой плотностью уровней энергии, что приво-
дит к наблюдаемым на опыте очень малым значениям сечений за-
хвата медленных нейтронов магическими ядрами.
$ 3.3. ОДНОЧАСТИЧНАЯ ОБОЛОЧЕЧНАЯ МОДЕЛЬ ЯДЕР
Спины и четности основных состояний ядер. Одночастичная
оболочечная модель позволяет не только объяснить особую устой-
чивость магических ядер, но также и правильно предсказать спи-
ны и четности основных состояний большинства ядер с нечетными
массовыми числами А. Согласно одночастичной оболочечной моде-
ли, все парные нуклоны образуют остов с нулевым спином (это на-
ходится в соответствии с тем экспериментальным фактом, что
спин четно-четных ядер всегда равен нулю), поэтому спин и чет-
ность ядра определяются состоянием последнего непарного нук-
лона. Очевидно, такая модель может описывать только свойства
нечетных ядер. О применимости одночастичной модели свидетель-
ствует тот факт, что почти во всех случаях спины и четности ос-
новных состояний нечетных ядер, найденные экспериментально,
совпадают со значениями, предсказываемыми моделью для послед-
него непарного нуклона.
Более совершенной является модель, в которой ядро представ-
ляется состоящим из некоторого числа заполненных оболочек и
внешних несвязанных нейтронов и протонов в незаполненных обо-
лочках. В этом случае свойства ядра определяются этими внеш-
ними нуклонами. Так как, однако, для системы одинаковых частиц
можно указать несколько различных независимых состояний, от-
личающихся симметрией, а следовательно, и суммарным моментом,
то спин ядра оказывается неоднозначным. Эта неоднозначность
устраняется учетом остаточного взаимодействия между нуклонами,
приводящего к снятию вырождения состояний. Если радиус взаи-
модействия мал ио сравнению с размерами ядра, то спин основ-
ного состояния группы одинаковых частиц (нейтронов или прото-
нов) в /-оболочке оказывается равным 0 для четного и / для нечет-
ного числа частиц. Это находится в соответствии с результатами
более простой одночастичной модели.
Таким образом, зная схему одночастичных уровней, опреде-
ляющую порядок заполнения оболочек, можно непосредственно
определить спины и четности основных состояний нечетных ядер.
В табл. 3.4 приведены значения спинов и четностей для основных
состояний ряда ядер, полученные на основе схемы уровней
142
Т а б л и’ц а’3.4
Ядро (Z нечетное) Ядро (M нечетное)
Теория Экс иернмент Теория Эксперимент
'Li 3; 32 94Ве 3- •L’
2 2 2 2
"в JT 3 13Г 6^ Г r
2 2 2 2
r Г 17О 5+ 5+
2 2 2 2
l7F 91 5+ E? “Mg 5r 5
2 2 2 2
27А1 5+ 5+ 1- 7^
2 2 2 2
^С1 3+ 3+ 28Ni 5- 3
2 2 2 2
25Mn 7^ 1_ toZn £
2 2 2 2
75Д< 5“ 3 4 J Mo 5r 5+
2 2 2 2
79Br 5; 3 5b 5+
2 2 2 2
209n; 83Bl 9^ 9" 3+ 3+
2 2 2 2
(см. рис. 3.2), а также соответствующие экспериментальные
значения.
Отступления от указанного правила имеют место для ядер,
у которых начинается, заполнение следующей оболочки с большим
спином. Так как энергия спаривания двух нуклонов с большим
спином больше энергии спаривания нуклонов с меньшим спином,
то наблюдается инверсия в последовательности заполнения обо-
лочек, причем заполнение вышележащей оболочки осуществляется
парами нуклонов. (Например, в результате заполнения оболочки
fs/2, следующей за оболочкой рз!2, спин ядер в области 28 < Л'
или Z < 38 оказывается равным 3/2.) В случае инверсии состоя-
ние, отвечающее нормальному порядку заполнения оболочек, ока-
зывается низколежащим метастабильным состоянием, так как спин
его сильно отличается от основного состояния. Отклонения от об-
щего правила наблюдаются также для тяжелых ядер, что связано
с нарушением сферической симметрии ядер.
Магнитные дипольные моменты ядер. Магнитный дипольный
момент нечетного ядра, согласно одночастичной модели, определя-
ется магнитным дипольным моментом последнего непарного нук-
лона*. Вычислим магнитный момент отдельного нуклона, движу-
* Теория магнитных моментов ядер детально изложена в обзоре [9].
143
щегося в самосогласованном поле ядра. Оператор полного магнит-
ного момента нуклона, выраженный в ядерных магнетонах eh/2Mc,
представим в виде суммы двух слагаемых:
H=^l+g'3s, (3.45)
где I и s — операторы орбитального и спинового моментов нукло-
на; gi и gs— орбитальное и спиновое гиромагнитные отношения.
Из-за спин-орбитального взаимодействия при движении нуклона
орбитальный и спиновый моменты 1 и s в отдельности не сохраня-
Рис. 3.5. Кривые Шмидта и экспериментальные значения магнитных моментов
для ядер с нечетным числом нейтронов.
ются, сохраняется только полный момент количества движения
нуклона
j-1+s. (3.46)
Магнитный дипольный момент ц определяется
как среднее значение проекции вектора р на направление вектора
полного момента нуклона j в состоянии с максимальным значением
проекции вектора j:
(3-47)
или, замечая, что <jz> —j и <j2> = j (j1), получаем
И ——~ \pj//n = j« (3.48)
Подставляя в (3.48) выражение (3,45) для р и используя тож-
дества
21j-j2+I2—s2, 2sj = j2 — l2 4-sa,
144
находим
[О — ]=1 + г/^
Орбитальное гиромагнитное отношение gi равно нулю для нейт-
рона и единице для протона. Спиновое гиромагнитное отношение ga
Рис, 3.6. Кривые Шмидта и экспериментальные значения магнитных момен-
тов для ядер с нечетным числом протонов.
можно положить равным удвоенному значению собственного маг-
нитного момента нейтрона или протона gs — 2рГ1 или 2рр. Таким
образом, одночастичные магнитные моменты ядер определяются
формулами
145
если непарная частица — нейтрон, и
если непарная частица — протон. Формулы (3.50) и (3.51) при-
водят как в случае непарного нейтрона, так и в случае непарного
протона к двум кривым для зависимости магнитного момента ядра
р от спина / (кривые Шмидта). На рис. 3.5 и 3.6 представлены кри-
вые Шмидта и экспериментальные значения магнитных моментов
для нечетных ядер. Экспериментальные значения магнитных мо-
ментов ядер в основном не лежат на кривых Шмидта (что свиде-
тельствует о приближенном характере одночастнчной модели),
но всегда (за небольшими исключениями, например для 3Н, 3Не,
15N и 13С) оказываются между двумя кривыми, причем в большин-
стве случаев вблизи одной из них. Это позволяет выбирать правиль-
ное значение спина ядра в соответствии с экспериментальным зна-
чением магнитного момента.
В заключение отметим, что наличие спин-орбитального взаимо-
действия приводит к появлению у протонов в ядре некоторого
дополнительного магнитного момента. Действительно, перепишем
энергию спин-орбитального взаимодействия (3.11) в виде
!/ = }/(')№ (3.52)
выделив явно зависимость от импульса р. При наличии внешнего
электромагнитного поля, характеризуемого векторным потенциа-
лом А, импульс частицы в (3.52) необходимо заменить на р — (е/с)А,
где е — заряд частицы. Следовательно, в гамильтониане, описы-
вающем движение протона в электромагнитном поле, содержится
добавочное слагаемое
t/' = --^/(r)[rA]s. (3.53)
В случае однородного магнитного поля векторный потенциал
А непосредственно выражается через напряженность магнитного
поля Н: А = (1/2)[Нг], поэтому добавочную энергию взаимодей-
ствия (3.53) можно переписать в виде V = —р.'Н, где ц' — опе-
ратор добавочного магнитного момента протона, обусловленного
спин-орбитальным взаимодействием:
р' = (1/Л)/(г) [r[sr]]. (3.54)
Магнитный момент р/ выражен в ядерных магнетонах. Среднее
значение добавочного магнитного момента протона в состоянии с оп-
146
ределенным полным моментом / определяется аналогично (3.47)
и равно
±^4т-4<г3^г)>^ <3-55>
4 (/ + 1) 7<
где знак «плюс» соответствует значению / = I г 1/2 п знак «минус»
соответствует значению j = I — 1/2.
Так как функция f (г) существенно отлична от нуля только на
поверхности ядра, то множитель г'1 под знаком усреднения можно
заменить квадратом радиуса ядра R~. Среднее значение функции
f (г) в этом случае непосредственно выражается через спин-орби-
тальное расщепление уровня:
\f (ГУ/п1 = ~Г (Elllj = i+ 1/2 = /-1/2)-
h 21 + 1
Используя (3.32) и замечая, что R~ да ~ , находим р/ да [3,
|3 да 1/20, Следовательно, добавочный магнитный момент (3.55)
оказывается малым по сравнению с (3.51),
Электрические квадрупольные моменты ядер. Рассмотрим те-
перь на основе одночастичной оболочечной модели электрические
квадрупольные моменты ядер. Тензор электрического квадруполь-
ного момента системы одинаковых зарядов определяется формулой
= (3.56)
где г — радиус-вектор отдельного заряда, и суммирование произ-
водится по всем зарядам.
Для состояния системы, характеризуемого определенным пол-
ным моментом количества движения J, тензор квадрупольного мо-
мента системы Qij может быть непосредственно связан с вектором
J. Тензор Qu симметричен, и сумма его диагональных элементов
равна нулю, поэтому Qu однозначно выражается через : Qu =
2
— Д ($$} + — jJa5;-j), где A — некоторая постоянная.
Собственно квадрупольный момент системы Q определяется
как среднее значение составляющей тензора Qtz в состоянии, ког-
да проекция момента системы J на ось г максимальна. Полагая
<7г=$ и Ja = (У + 1), имеем
2
Q=~A%- (2^ — 1). (3.57)
О
Из этой формулы следует, что квадрупольный момент системы обра-
щается в нуль при = 0 и ЗН- 1/2, Выразив постоянную А с по-
мощью (3.57) через Q, тензор квадрупольного момента системы
можно представить в виде
<3-58>
147
В одночастичном приближении квадрупольный момент ядра
определяется квадрупольным моментом последнего непарного про-
тона. Запишем составляющую тензора квадрупольного момента
QZ2 в сферической системе координат:
/(ТВДг2У.20(О). (3.59)
Выбирая одночастичную волновую функцию в виде
= Фщ (г) У (1т' V И I /т 1 Yыг X1 -
для квадрупольного момента в состоянии с т = j получаем сле-
дующее выражение:
Q = ]/(16л/5) (r2>„z ( 1т-±- р| Ц У <Jm\У20| 1т>, (3.60)
где (г2>„;—среднеквадратический радиус (r2>ni = j dr г* <р2( (г),
о
Замечая далее, что матричный элемент от сферической функции
равен
<1т|г!0|;т> = /А-т(&а=32Г. (3.61)
в (3.60) нетрудно выполнить суммирование, воспользовавшись зна-
чениями коэффициентов Клебша — Гордана:
Таким образом, для
тона получим формулу
квадрупольного момента непарного про-
<зю>
Из этой формулы следует, что одночастичные квадрупольные мо-
менты всегда отрицательны.
Вследствие отдачи остова ядра непарный нейтрон также обла-
дает некоторым эффективным квадрупольным моментом. Величина
эффективного квадрупольного момента нейтрона составляет
Z/Л2 от величины квадрупольного момента протона.
Электрические квадрупольные моменты, рассчитанные по одно-
частичной модели, согласуются с экспериментальными значениями
148
квадрупольных моментов только для ядер, содержащих один нук-
лон сверх заполненной оболочки. Квадрупольные моменты почти
всех других ядер отличаются от одночастичных как по знаку (при-
нимают положительные значения), так и по абсолютной величине
(абсолютные значения квадрупольных моментов оказываются во
много раз больше значений, вычисленных по одночастичной мо-
дели). Наибольшие значения квадрупольных моментов наблюда-
ются у ядер с наполовину заполненными оболочками.
Рис. 3.7. Экспериментальные значения квадрупольных моментов нечетных
ядер как функции числа нейтронов или протонов;
-j- — зависимость от Z; О — от N.
На рис. 3.7 представлены экспериментальные значения элект-
рических квадрупольных моментов нечетных ядер в зависимости
от числа нейтронов или протонов. Периодическая зависимость
квадрупольных моментов ядер от числа нуклонов хотя и свидетель-
ствует об оболочечной структуре ядер, тем не менее одночастичная
модель оказывается совершенно непригодной для нахождения
величин квадрупольных моментов ядер.
Магнитные октупольные моменты ядер. Помимо дипольного
магнитного момента для некоторых ядер определены значения ок-
тупольного магнитного момента.
Оператор магнитного мультипольного момента является
сферическим тензором, ранг которого определяется мультиполь-
ностью момента X, и в одночастичной модели ядра определяется
выражением
(3.64)
\ А 1 /
149
Если К = 1, то (3.64) непосредственно переходит в выражение для
оператора дипольного момента (3.45). Так же, как и дипольный
магнитный момент, мультипольный момент (3.64) выражен в ядер-
ных магнетонах.
Мультипольный момент, соответствующий значению X = 3,
называется магнитным о к т у п о л ь н ы м моментом.
Магнитный октупольный момент является сферическим тензором
третьего ранга.
Под магнитным октупольным моментом ядра Q обычно подра-
зумевают среднее значение компоненты тензора Л430 в состоянии
с максимально возможным значением проекции полного момента
нуклона т — j:
Q = —]/(4л/7) </т = /1 Al301 (3.65)
(Множитель — |/г(4л/7) введен для удобства.) Согласно (3.64) и
(3.65), магнитный октупольный момент ядра, так же как и его
магнитный дипольный момент, связан с орбитальным и спиновым
моментами нуклона 1 и s.
Для нахождения Q воспользуемся явным видом сферической
функции
(п) = У(7/16л) (5cosa fl — 3) cos fl. (3.66)
Подстановка (3.66) в (3.64) и (3.65) с учетом того, что rl —О,
дает
Й = gtlz + У 5itgzn20(n) (z+gss2 +
4-2yA3ngs(ns)y10(n)4-2V/’5ng4iy2e(n)szj. = (3.67)
в этом случае тригонометрические функции, возникшие в резуль-
тате дифференцирования Узв (п), снова сведены в сферические.
Дальнейшие вычисления в (3.67) проведем, используя одночастич-
ную функцию (3.18):
М’П//т = фПг('-)^, £ .
' 2
Заметим, что результат действия оператора (ns) на функцию
1 можно найти, учитывая, что 5/ > и (ns)';/ > —собст-
‘o’ i »- > i у /т
венные функции оператора (si) = 2- (j1 2 — I2 — s2).
(S1) Lim = 1) - - ,m-
* у z L 4 J t у
1 г чт (3.68)
(sl)(ns)^4/m=-- / (/+!)-/(( +1) +2] (ns) .
z L 4 J t у
150
В справедливости последнего равенства нетрудно убедиться на
основе следующих равенств:
(ns) (si) (ns) (si-1-1), (ns)2 = -p
Сравнивая равенства (3.68), видим, что
W(_/TL L L 1т- <3-69)
Таким образом, интегрирование по углам в (3.67) можно выпол-
нить в явном виде, при этом в (3.67) будут встречаться инте-
гралы от произведения не более трех сферических функций:
Ja!Oy;m(n)r/lffll (п) У/г„12 (п) =
= / ° । I. т,21 /т). (3.70)
Далее используем соотношения для сферических проекций век-
тора 1 (и аналогичные соотношения для спинового вектора s)
lv)!tn) = ( — !)"’)//(/ + J) + — v|/w)| Zw + v>, v = 0, ± I.
(3-71)
Получающиеся суммы от произведений трех коэффициентов
Клебша—Гордана найдем с помощью формулы Рака:
У, (/jffl! lz ms ] -Tm3) (Z3 т1 -\-tn2lt tn—tn1 — m2 j Im) x
iTlj
X(/2m2Z4 tn— mt — — m1) =
= VW+ I) (2ZS -f-1) (Zx mx Z5 m —mx I Zm) (Zx ZaZZ4; Z3 Z5). (3.72)
Взяв из таблиц значения встречающихся коэффициентов Клебша —
Гордана и коэффициентов Рака, найдем следующие значения для
средних:
</'/ I По (ns) | /7> =
<//1 Г20зг | jj) =
<Н\ уы I //>! = —
1 j / 3
8 (/+ I) Г Л ’
2j —1 1/У
16 (j+n V Л ’
2j2H-/ + 3 1/~T
16 (Z + 1) (/ + 2) V Л
1
V’
i
2 (i + i) ’
Jz'-i i/T,
8 (/ + 1) Г л '
(3.73)
151
Собирая вычисленные средние значения, окончательно получаем
следующее выражение для магнитного октупольного момента ядра
в одночастичном приближении [10]:
8
2/—1
1
7Тг[(/+
Как и в случае дипольного магнитного момента, учет спин-ор-
битального взаимодействия приводит к незначительным поправкам
для £2. На рис. 3.8 представлены зависимость магнитных окту-
Рис. 3.8. Кривые Шварца и экспериментальные
значения магнитных октупольных моментов.
польных моментов ядер от спина и экспериментальные значения
магнитных октупольных моментов для некоторых ядер. Подобно
дипольным магнитным моментам экспериментальные значения
октупольных моментов также заключены между линиями, рассчи-
танными на основе одночастичной модели.
£ 3.4. ВОЛНОВЫЕ ФУНКЦИИ МНОГОЧАСТИЧНЫХ ОБОЛОЧЕК
Детерминанты Слэтера. В оболочечной модели ядра предпо-
лагается, что взаимодействие между отдельными нуклонами можно
свести к взаимодействию нуклонов с самосогласованным полем
ядра, в этом случае нуклоны могут рассматриваться как незави-
симые частицы, движущиеся в заданном поле. Согласно такой уп-
рощенной модели, называемой иногда моделью независи-
мых частиц, гамильтониан ядра Но представляется в виде
суммы гамильтонианов отдельных нуклонов:
#o = S ( — (й2/2М) At + V£], (3.75)
152
где •— (Л2/2Д4)Д, — кинетическая энергия и Vi — энергия взаи-
модействия отдельного нуклона с самосогласованным полем.
Собственные состояния системы независимых частиц обычно
называются конфигурациями системы. Каждой кон-
фигурации системы соответствует определенная волновая функ-
ция. Очевидно, волновые функции ядра, описываемого гамильто-
нианом (3.75), можно представить в виде антисимметризованных
произведений одночастичных волновых функций.
Если спин-орбитальное взаимодействие несущественно, то вол-
новая функция отдельного нуклона в самосогласованном поле
представляется в виде произведения пространственной, спиновой
и изоспиновой функций:
Фа (0 = (Г,) Хн (°т) Sv (Т(), (3.76)
где т — проекция орбитального момента; ц — проекция спина;
v — проекция изоспина (а — сокращенное обозначение набора
квантовых чисел tiling и -v). При наличии спин-орбитального взаи-
модействия одночастичные волновые функции представляются
в виде произведения спин-пространственной функции на изоспи-
новую функцию:
Фа (i) = (г;, crz) (тt), (3.77)
где т, — проекция полного момента (а — набор квантовых
чисел nljmj и т). Функции (3.77), так же как и (3.76), образуют
полный набор одночастичных функций. Будем считать, что каждая
система функций (3.76) и (3.77) ортонормирована, согласно усло-
вию
5 ^ФаФа' = 6аа'. (3.78)
Волновую функцию системы А нуклонов можно представить
в виде произведения А одночастичных волновых функций (3.76)
или (3.77), которое, однако, следует антисимметризовать относи-
тельно перестановок любой пары нуклонов. Такая антисимметри-
зация будет автоматически обеспечена, если волновую функцию си-
стемы А нуклонов записать в виде детерминанта Стэтера:
Фа. (1) Фа, (2) ... Фа, (Л)
=(1/ИА!)
Фа. О) Фа. (2) ... Фа. (Л)
(3.79)
Фад U) Фал (2) ... Фал М)
где (а) обозначает совокупность квантовых чисел занятых одно-
частичных состояний. Очевидно, — это антисимметризован-
ная собственная функция гамильтониана /70.
Детерминанты Слэтера Чг(а] при различных значениях {а]
образуют полный набор ортонормированных функций. Собствен-
на
ные функции оператора полного момента системы можно по-
строить с помощью линейной комбинации детерминантов Слэтера
(«}
где С^' —соответствующие геометрические коэффициенты.
Из детерминанта (3.79) непосредственно следует принцип Паули
для нуклонов, согласно которому в определенном одночастичном
состоянии не может находиться больше одной частицы. Вследствие
принципа Паули основному состоянию ядра соответствует конфи-
гурация, состоящая из нескольких заполненных внутренних обо-
лочек и одной внешней незаполненной. В общем случае свойства
ядра (например, размеры, распределение плотности, полная энер-
гия связи и т. д.) определяются состоянием всех нуклонов, в том
числе и находящихся в заполненных оболочках. Однако некоторые
свойства ядра (например, симметрия, спин, четность, изотопиче-
ский спин и другие характеристики основного состояния, а также
возбужденных состояний, связанных с переходами в незаполненной
оболочке) определяются состоянием нуклонов, находящихся толь-
ко во внешней незаполненной оболочке. Поэтому если мы будем ин-
тересоваться такими свойствами ядер, то можно ограничиться рас-
смотрением только нуклонов, находящихся во внешней незапол-
ненной оболочке. Тем не менее даже в этом случае использование
детерминантов Слэтера для построения состояний, отвечающих оп-
ределенным значениям интегралов движения, является чрезвы-
чайно громоздкой процедурой, поэтому обычно антисммметрйзован-
ные многочастичные волновые функции строятся иначе.
Схемы построения многочастичных волновых функций. В мо-
дели независимых частиц используются две схемы построения мно-
гочастичных волновых функций: схемы LS- и //'-связи. В случае
легких ядер, когда сиин-орбиталыюе взаимодействие несущест-
венно, применима схема LS-связи. В этом случае орбитальные
моменты отдельных нуклонов складываются в полный орбиталь-
ный момент системы L; аналогично спиновые моменты нуклонов
складываются в полный спиновый момент системы S; моменты L
и S затем складываются в суммарный момент системы J, обычно
называемый спином я д р а. В этой схеме связи L и S являются
интегралами движения, т. е. соответствующие операторы комму-
тируют с гамильтонианом системы Но.
Если спин-орбитальное взаимодействие существенно, то спин
и орбитальный момент отдельного нуклона складываются в полный
момент j = 1 + s, который и является интегралом движения.
Векторы j отдельных нуклонов затем складываются в суммарный
момент ядра J. Такая схема носит название схемы //-связи. Ин-
тегралом движения в этом случае будет и квадрат орбитального
момента нуклона (определяемый квантовым числом /), но не его
проекция. Так как для каждого (>0 в схеме //-связи возможны
154
два значения / — I ± 1/2, то вместо одной (nl) оболочки при LS-
связи в случае //-связи будем иметь две оболочки, которые харак-
теризуются квантовыми числами и//'.
Нуклоны, находящиеся в определенной оболочке ядра, обычно
называются эквивалентными нуклонами. Мак-
симальное число нуклонов, которые могут находиться на оболочке
nl, совпадает с кратностью вырождения уровня и равно 4(2/ + 1).
Аналогично максимальное число нуклонов для оболочки nlj равно
2(2/ + 1). Ограничимся в дальнейшем рассмотрением многочастич-
ных волновых функций для системы k нуклонов, находящихся во
внешней незаполненной оболочке, характеризуемой квантовыми
числами nl или nlj. Так как состояния частицы и дырки в оболочке
эквивалентны, то имеет смысл рассматривать число эквивалентных
нуклонов в оболочке, не превосходящее половины максимально
возможного числа, т. с, k < 2(2/ + 1) или А -С 2j 4- I.
При построении полностью антисимметричных многочастичных
волновых функций в схеме ZS-связи отдельно рассматривают набо-
ры пространственных и спин-изоспиновых функций, обладающих
всеми возможными свойствами симметрии относительно переста-
новок частиц. Аналогично в схеме //-связи рассматриваются наборы
спин-пространственных и изоспиновых функций. Полные антисим-
метричные функции всей системы в этом случае представляются
в виде линейных комбинаций произведений указанных функций.
Если А — 2, то построение тривиально, так как в этом случае
пространственные и спин-изоспиновые (или же спин-пространст-
венные и изоспиновые) функции могут быть либо симметричными,
либо антисимметричными (если мы считаем, что они характеризу-
ются определенными моментами), поэтому полный набор антисим-
.метричных волновых функций двух частиц будет' состоять только
из произведений пространственной и спин-изоспиновой (или же
спин-пространственной и изоспиновой) функций противоположной
симметрии. Если k > 2, построение полных антисимметричных
волновых функций значительно сложнее, в этом случае в наборы
пространственных и спин-изоспиновых (или же спин-пространст-
веш-тых и изоспиновых) функций входят не только симметричные
и антисимметричные функции, но и функции промежуточной сим-
метрии.
Рассмотрим совокупность (2/ I)4 произведений одночастич-
ных пространственных функций, описывающих k нуклонов в nl-
оболочке:
Фт, т2 ... (П, гз> '\) =фт, (Г^ <рпг, (Го) ... (Гй) (3.81)
(для сокращения записи опущены индексы nl). Совокупность (3.81)
образует полный набор функций. При произвольнцй перестановке
координат гь г2, ..., гй любая функция Фт,, т,... mk из этого набора
переходит в общем случае в другую функцию, принадлежащую
этому же набору.
155
Совокупность 4ft произведений одночастичных спин-изоспино-
вых функций
Цц V,. ц, v2, ... Uft Vk (°l Tj, O2 T,, ... <)J. Tj =
= Xu, (<b) Sv, (Tj) X(1! (CT2) Cva (T2) ... Хщ, (oh) (тй) (3.82)
также образует полный набор спин-изоспиновых функций. Анало-
гичным образом можно построить в случае //-связи полные наборы
спин-простраНственных и изоспиновых функций.
Любой полный набор функций можно классифицировать по не-
приводимым представлениям групп преобразований, относительно
которых свойства системы инвариантны. Так как гамильтониан
(3.75) инвариантен относительно перестановок нуклонов, то на-
боры функций (3.81) и (3.82) удобно классифицировать по непри-
водимым представлениям группы перестановок.
Неприводимые представления группы перестановок. Напомним
некоторые основные свойства группы/перестановок применительно
к нашей задаче [11, 12]. Занумеруем k эквивалентных нуклонов,
находящихся на внешней незаполненной оболочке, целыми чис-
лами 1, 2, k, под которыми можно подразумевать пространствен-
ные, спиновые или изоспиновые координаты нуклонов. Очевидно,
из этих чисел можно составить fe! перестановок. Переход от основ-
ной перестановки 1, 2, ..., k к любой другой р1} р2, ..., pk — осу-
ществляется заменой 1 на plt 2 на р.> и т, д. Эту операцию можно
изобразить так:
Р 2 3 k\=P. (3.83)
\Pi Pi Ра Ph1
Совокупность всех k\ перестановок Р образует группу. Группа
перестановок называется еще симметрической груп-
пой и обозначается llft или Sk.
Функции (3.81) и (3.82) соответственно образуют базисы (21 +
-Г 1)А-и 4*-мерного представлений группы перестановок S*. Оба
эти представления группы перестановок являются приво-
димыми.
Неприводимые представления группы пере-
становок осуществляются функциями с определенной симметрией
относительно перестановок частиц. Для нахождения функций с раз-
личными типами такой симметрии разобьем совокупность пере-
менных 1, 2, ..., k на 21 + 1 подсовокупностей. Это разбиение обо-
значим
W = [*!, К..... k+i], (3-84)
где Kj > ... > 0, Xj + %3 ... -|- Х2/_[_] = k. Указанное раз-
биение можно наглядно изобразить с помощью схемы Юнга, в ко-
торой каждое слагаемое л, представлено строкой из X, клеток, при-
1Б6
чем строки располагаются одна под другой в порядке их укороче-
ния. Каждой клетке схемы сопоставляется одна из переменных
1, 2, .... k. Например, если k — 5, то одна из возможных схем Юнга
имеет вид
[3,2] =
(3.85)
Симметризуя функцию Ф (I, 2, k), являющуюся произ-
ведением k одночастичных функций, по переменным, входящим в
состав каждой из строк, и антисимметризуя по переменным каждого
столбца схемы Юнга, получаем функцию с определенным типом
симметрии, которую обозначим Ф (lk IAJ). Так как при заданном
значении I имеется только 21 + 1 различных одночастичных функ-
ций (различающихся значениями т), то число строк в схеме [X]
не может превышать 2/ + 1. В частности, если схема Юнга состоит
только из одной строки, получим полностью симметричную функ-
цию, а если же из одного столбца, то полностью антисимметрич-
ную функцию.
Распределяя k переменных различным образом по клеткам схе-
мы Юнга [X], получаем ряд функций Ф (/ft [А.]), которые при про-
извольной перестановке переменных преобразуются друг через
друга. Эти функции и осуществляют неприводимое представление
£)[М группы перестановок 8Ь, отвечающее определенной схеме Юн-
га [Л1. Число независимых функций характеризующее размер-
ность представления, определяется числом распределений, при
которых переменные 1, 2, ..., k оказываются размещенными по
строкам (слева направо) и столбцам (сверху вниз) в нормальном
порядке, а сами распределения соответствуют базисным функциям
неприводимого представления.
Действительно, базисные функции некоторого неприводимого
представления какой-либо группы будут однозначно определены,
если указано, по каким неприводимым представлениям подгрупп,
последовательно содержащихся друг в друге, преобразуются эти
функции. Группа i является подгруппой группы S;,, Sk—2—
подгруппа Sfe— 1 и т, д. Если мы имеем некоторое неприводимое
представление группы Sft, отвечающее определенной схеме Юнга
из k клеток, то оно одновременно является представлением и под-
группы S'a-i, но уже в общем случае приводимым. С помощью
подобного преобразования это представление можно привести и
получить неприводимое представление подгруппы Sk-i- Подоб-
ное преобразование соответствует составлению из исходных базис-
ных функций определенных линейных комбинаций, которые пре-
образуются по неприводимым представлениям St— i. При этом
неприводимое представление группы распадается на те непри-
водимые представления группы 8^_], которые соответствуют
схемам Юнга из k — 1 клеток, получаемых из исходной при удале-
нии одной клетки.
157
Например, неприводимое представление группы 85, соответ-
ствующее схеме^Юпга (3.85), распадается на два неприводимых
представления группы 84, соответствующих схемам:
Этот процесс можно продолжить до тех пор, пока не получим три-
виальные представления группы S4, соответствующее схеме Юнга
из одной клетки:
- Ш - □, w
Ш— ЕМ)
- -*□/•?) (3.86)
Ш- □,»)
' 0 □ .ь>
Таким образом, каждую базисную функцию неприводимого
представления группы Sft можно характеризовать теми неприво-
димыми представлениями подгрупп 8/,_j, 8*_2 82 и 8Х,
по которым эта функция преобразуется на каждом этапе при-
ведения.
Для обозначения этих функций можно использовать схему Юнга
с размещением по клеткам строк и столбцов переменных в нормаль-
ном порядке. Последовательно вычеркивая клетку с последней
переменной, получаем цепочки схем Юнга, однозначно определяю-
щие указанные функции. Так, например, базисные функции непри-
водимого представления группы 85, характеризуемого схемой Юнга
(3.85), определяются цепочками (3.86), их можно обозначить сле-
дующим образом:
1 2
4 5
7 2
5
158
Существует другой, более удобный способ обозначения базис-
ных функций с помощью символов Я м а н у ч и. Символ
Яманучи г — это совокупность k чисел г = (rk, rk^lt rm,/у),
указывающих принадлежность переменной т к определенной строке
rm схемы Юнга [Х[. Например,
1 3
2 4
У
Так как переменные по строкам и столбцам схемы Юнга для базис-
ных функций размещены в нормальном порядке, то в любом месте
символа Яманучи число единиц справа не меньше числа двоек
и т. д. Символ Яманучи г записывается в виде индекса у функции и
определяет принадлежность функции Фг (lk [X]) к определенным
неприводимым представлениям групп перестановок Sfe, Sk-i,
Очевидно, число различных символов Яманучи, отвечающих
заданной схеме Юнга [X], равно размерности представления п\.
Например, размерность неприводимого представления группы S5,
характеризуемого схемой Юнга (3.85), равна пяти [опа совпадает
с числом цепочек (3.86)]; базисные функции этого представления
характеризуются следующими символами Яманучи:
(22111), (21211), (21121), (12211) и (12121). (3.88)
Схеме Юнга, состоящей только из одной строки или из одного
столбца, соответствует один символ Яманучи, поэтому соответст-
вующие неприводимые представления одномерны. Это значит, что
соответствующие базисные функции симметричны или антисиммет-
ричны относительно перестановки любых двух частиц.
В общем случае каждой схеме Юнга [X] соответствует п», неза-
висимых функций с определенной симметрией
Фг (I* М). (3.89)
образующих базис неприводимого представления DIM группы пере-
становок Sh. Число характеризующее размерность представле-
ния, определяется числом различных значений символа Яманучи
г. Функции Фг (lk [X]), отвечающие различным символам Яманучи,
образуют ортогональную систему функций.
Производя разбиение совокупности k переменных всеми воз-
можными способами, т. е, строя всевозможные схемы Юнга, нахо-
дим все неприводимые представления группы перестановок Sft.
Для примера приведем наборы базисных функций всех неприводи-
мых представлений группы S4:
159
(3211),
‘t) DC*"J:
(132 J);
5)
(W1).
Представления 1 и 5 — одномерны, представления 2 и 4 — трех-
мерны и представление 3 — двухмерно.
Различают внутренние и внешние произведения неприводимых
представлений групп перестановок. Произведение неприводимых
представлений одной и той же группы перестановок называется
внутренним произведением и обозначается знаком х. Сумма не-
приводимых представлений, на которые разлагается внутреннее
произведение, называется, как и в случае группы вращений, р я-
дом Клебша — Гордана.
Произведение неприводимых представлений двух различных
групп перестановок называется внешним произведе-
ние м и обозначается знаком Внешнее произведение неприво-
димых представлений двух различных групп перестановок 5^ и
5а, является приводимым представлением группы перестановок
5а,4-а,. Правило Литтлвуда позволяет определить, какие непри-
водимые представления группы 5а1+а, и в каком количестве
v?_ появляются при разложении внешнего произведения неприво-
димых представлений £Л4] и групп 5^, и 5^,:
(3.90)
14
Для нахождения возможных схем Юнга fZ] из kx + клеток
при заданных парциальных схемах (XJ из kx клеток и Щ] из k%
клеток нужно:
160
1) написать в каждой клетке первой строки схемы Юнга [Х21
букву с индексом, характеризующим номер столбца схемы ап а2,
во второй строке схемы [К2] другую букву с индексом
₽2, ... и т. д.;
2) добавить к схеме Юнга [XJ всеми возможными способами
клетку с Ср чтобы получилась разрешенная схема Юнга; затем
таким же образом добавить и другие клетки первой строки схемы
[Х21, но так, чтобы в одном столбце не стояло двух букв из одной
строки схемы [Х2] и буква с большим индексом не стояла в более
высокой строке по сравнению с буквой с любым меньшим по вели-
чине индексом;
3) подобным образом прибавить к полученным схемам клетки
второй строки схемы [Х2] с буквой [3, но так, чтобы индекс буквы
второй строки [%2] появлялся в более низкой строке, чем тот же
индекс первой строки, и т. д.
Например, перемножим [AJ [1!] и [Л2] [211:
ЛЮ Ли]
В ~
*
«2
А
Добавим к [XJ клетку а, всеми возможными способами:
Добавим далее клетку а3:
Согласно правилу Литтлвуда, схемы 2, 4 и 5 должны быть от-
брошены. Добавим теперь к оставшимся схемам I и 3 клетку Рр
6 Зак. 642
161
Схемы а и г должны быть отброшены. Таким образом, получим окон-
чательно
или
Подобным образом можно показать:
D[2W,] = 0[3M2,];
D[2J®z)f2]^Df4] + ^3I]+»f22];
D[2l®D[,1]=Dl3ll + Dl21,];
Dl"l®D[>4=D^+D[2ii] + D[iiii];
£)[21] ®D[21] = D[42] 4- D[41114-D[33]4-2E>[321] +
+ £)[311] + С([222] + е,[2211]_
Из последнего примера видно, что неприводимое представление
в разложении может появляться больше одного раза. Заметим так-
же, что внешнее произведение не зависит от порядка перемножае-
мых представлений.
Построение антисимметризованных волновых функций. Рас-
смотрим систему (2Z + l)ft пространственных функций (3.81),
описывающих k эквивалентных нуклонов во внешней незаполнен-
ной оболочке nl. В общем случае эти функции преобразуются по
приводимому представлению группы перестановок Sfe. Симметри-
зация и антисимметризация этих функций по определенным про-
странственным переменным в соответствии с определенной схемой
Юнга IX] означают, что мы составляем линейные комбинации
этих функций, которые преобразуются по неприводимому пред-
ставлению, отвечающему [X]. Выбирая всевозможные разбиения
[X], получаем новую систему (2/ + 1)* линейно независимых функ-
ций, которая разбивается на отдельные совокупности, преобразую-
щиеся при перестановках по одному из неприводимых представ-
лений группы Sh.
Волновые функции одной из таких совокупностей, характери-
зуемой схемой Юнга [X], можно записать в виде
ФД1*[Х]|), (3.91)
где г — символ Яманучи, принимающий все возможные значения
для данной схемы [Xi. Функции данной совокупности [X] отли-
162
чаются символами Яманучи. Схема Юнга [X] и символ Яманучи г
входят в набор квантовых чисел, характеризующих состояние.
Если [X] и г не образуют полного набора, то для задания состояния
необходимо ввести еще дополнительные квантовые числа £. Вве-
дение дополнительных квантовых чисел g оказывается необхо-
димым в том случае, если при приведении (3.81) неприводимое
представление [X] появляется несколько раз.
Функции (3.91) при перестановках преобразуются согласно
соотношению
Фг (lk [X] Ю = Z W (P)*r-(lk [X] I), (3.92)
где — матрица представления [X], размерность которой равна
числу базисных функций этого представления щ..
Аналогичным образом, составляя линейные комбинации спин-
изоспиновых функций (3.82), можно получить совокупность функ-
ций
(3.93)
преобразующихся по неприводимому представлению группы
Sh, где [X'] — схема Юнга из k клеток, имеющая не более четырех
строк; т' — символ Яманучи; т] — дополнительные квантовые
числа. (Для нуклонов s = 1/2 и t — 1/2.) Очевидно, полная волно-
вая функция системы k нуклонов Т должна представляться в виде
линейной суперпозиции произведений пространственных и спин-
изоспиновых функций (3.91) и (3.93). [4 (2/ + 1)]* таких произве-
дений со всеми возможными схемами Юнга образуют полную си-
стему волновых функций конфигурации 1к. Вследствие принципа
Паули полная волновая функция Т системы k нуклонов должна
быть антисимметричной относительно перестановок любой пары
нуклонов, поэтому спин-изоспиновые функции (3.93) должны
описываться схемой Юнга [Х'[, сопряженной схеме Юнга [X] для
пространственных функций (3.91). (Сопряженными называются
схемы Юнга, получаемые друг из друга заменой строк столбцами и
обратно. Схему Юнга, сопряженную данной схеме IX], обозначают
IX], а соответствующий символ Яманучи г. Размерности представ-
лений [XI и [X], очевидно, одинаковы.) Таким образом, в (3.93) сле-
дует положить IX'] — IX] и г' = г.
Поскольку функции Фг — базисные функции неприводимого
представления [XJ группы перестановок, то при перестановках ча-
стиц они преобразуются друг через друга. Аналогично функции
Нл преобразуются по сопряженному неприводимому представлению
IX]. Поэтому полную волновую функцию системы k нуклонов Т,
антисимметричную относительно перестановок любой пары нукло-
нов, можно выразить через функции Фг и Q-следующим образом:
Т (/* [X] ^)= -U 2 Фг (I*1Х] £) £2~((s/)* [X] л), (3.94)
ГА г
6*
163
где суммирование производится по всем символам Яманучи, свя-
занным со схемой [Л]. При таком выборе волновая функция V нор-
мирована на единицу, если Фг и Q- нормированы соответствующим
образом. Требование антисимметричности функции Т (Р 1Л1£л)
приводит к тому, что схема Юнга [X], определяющая симметрию
пространственной функцииФг (lk 1Х]£), описывает также симметрию
спин-изоспиновой функции Р~(Ыу;' [Л]т]) и, что особенно важно,
характеризует полную антисимметричную функцию всей системы
Y (1к 1ВД.
Так как в полной антисимметричной функции (3.94) схемы Юнга
для пространственной и спин-изоспиновой функций взаимно со-
пряжены, то число столбцов в схеме Юнга для пространственной
функции не может превышать четырех, а число столбцов в схеме
Юнга для спин-изоспиновой функции не превышает (21 + 1). От-
сюда, в частности, следует, что максимальное число нуклонов в обо-
лочке с орбитальным моментом I равно 4 (21 + 1).
Неприводимые представления группы унитарных преобразова-
ний. Структура функций (3.91) и (3.93) такова, что они не только
образуют базис неприводимого представления группы перестано-
вок, но одновременно являются базисными функциями неприво-
димого представления группы унитарных преобразований.
Рассмотрим группу линейных унитарных преобразований
в (21 + 1)-мерном пространстве функций которую обозначим
U21 + 1. Одночастичные волновые функции q>n!m при таких преобра-
зованиях преобразуются друг через друга:
(г) — Um'm (6^2f_.|_ j) (1*)* (3.95)
т'
(Указанные преобразования сохраняют ортогональность набора
функций <рп;п1.) Группа i содержит в качестве подгруппы
унимодулярную группу i, которая включает в себя все уни-
тарные преобразования в (21 + 1)-мерном пространстве, для кото-
рых определители матриц равны +1. Очевидно, группа вращений
в трехмерном пространстве Rs содержится в унитарной унимодуляр-
ной группе + i в качестве подгруппы.
Как показал Вейль 113], базисные функции неприводимого
представления группы перестановок Ф7 (Р [А]|) являются одно-
временно базисными функциями неприводимого представления
группы Sf72i+|, характеризуемого так же, как и неприводимое
представление группы перестановок схемой Юнга UJ. Размер-
ность неприводимого представления группы St/2; + i будет опре-
деляться числом возможных значений добавочных квантовых чисел
I- В дальнейшем это число будем обозначать через Таким об-
разом, под действием операции из группы SU21 + i пространствен-
ные функции (3.91) преобразуются по закону
Фг (lk [X] Ю = 2 (SU2l+ 1) Ф,. (lk [X] V). (3.96)
164
Из (3.92) и (3.96) видно, что число появления представления DtX]
при приведении (3.81) равно размерности ЛД представления М?-1,
и наоборот. Совокупность функций Фг (/* lAJg), различающихся
значениями квантовых чисел г и £, но относящихся к одной и той
же схеме Юнга [М, удобно представить в виде прямоугольной таб-
лицы, строки которой обозначаются с помощью символов Яманучи
г, а столбцы — с помощью квантовых чисел £
Под действием перестановок функции, находящиеся в одном и том
же столбце, преобразуются по неприводимому представлению ПЮ
группы Sft, а под действием операции из группы SU(2i+iy функ-
ции, находящиеся в одной и той же строке, преобразуются по пред-
ставлению (/14 группы SZ72/_|.i. _
Спин-изоспиновые функции ((s/)4 LAJr]) под действием опера-
ции из группы St/4 преобразуются по неприводимому представле-
нию этой группы. Заметим, что размерность этого представ-
ления TVp вообще говоря, отличается от размерности )V Совокуп-
ность функций Q~(($0[A1 (Йл) также удобно представить в виде
прямоугольной таблицы, строки и столбцы которой обозначаются
с помощью квантовых чисел г и ц
----н
Под действием перестановок функции одного и того же столбца
преобразуются по неприводимому представлению £>1?4 группы Sh,
а под действием операции из группы 5t/4 функции одной и той же
строки преобразуются по неприводимому представлению C’d
группы SU4.
Согласно (3.94), полные волновые функции системы k нуклонов,
антисимметризованные относительно перестановок любой пары
нуклонов, характеризуются определенными схемами Юнга. При
этом функции ¥ (lk [XJ£t]), соответствующие определенной схеме
Юнга [X] и различающиеся значениями дополнительных квантовых
чисел £ и т), преобразуются по неприводимым представлениям
групп SU^i+j и St/4. Дальнейшую классификацию состояний си-
стемы k нуклонов (3.94) можно производить, рассматривая неприво-
димые представления подгрупп группы SU2i+\ и группы SUit
например неприводимые представления группы вращения R3 и т. д.
165
g 3.5. классификация многочастичных состоянии
Классификация состояний в схеме £5-связи. Составляя линей-
ные комбинации функций (3.91) с фиксированными значениями [X),
г и различными значениями £, можно получить такие совокупности
функций, которые являются базисными функциями неприводимых
представлений DL группы вращений 7?3, т. е. являются собствен-
ными функциями суммарного орбитального момента системы L и
его проекции М. Эти функции, образующие базис неприводимого
представления DL, обозначим следующим образом;
Ф,. (/* [A] aLM), (3,97)
где а — дополнительное квантовое число, необходимое в случае
неоднократного появления представления DL при приведении
Возможные значения орбитального момента L определяются не-
посредственным разложением неприводимого представления [А]
группы SU2i+ j по неприводимым представлениям группы враще-
ния /?3.
Для примера рассмотрим простейший случай системы из двух
эквивалентных нуклонов. Пространственную функцию в этом слу-
чае можно представить в виде
Ф (I- [A] LM) = 2 (^i 1тг1LM) <р ОД ф (г2). (3.98)
Функция (3.98) симметрична для схемы Юнга [2] и антисиммет-
рична для схемы [11]. (Символ Яманучи в случае двух частиц
принимает одно-единственное значение, а дополнительное кванто-
вое число а отсутствует.) Подействуем оператором перестановки
Рг на (3,98). Используя свойства симметрии коэффициентов
Клебша—Гордана
(l/tti lnt21 LM) -^ (— 1)2/-L (lm2 | LM)
и замечая, что I — целое число, получаем
РГФ(12[А]£М) = ( —1)L Ф(12[А]£М), (3.99)
т. е. симметричным волновым функциям должны отвечать четные
значения L, а антисимметричным — нечетные значения L. Таким
образом, при приведении представления 1Л21 могут появиться пред-
ставления DL с четными L, а при приведении И11] — с нечетными
L (О -С L 2Z). Например, в случае р-оболочки (/ = 1) имеем
[2] ^£ = 0,2
[11]->£ = 1.
При рассмотрении оболочек, содержащих большее число нук-
лонов, подобные приведения значительно усложняются. Однако
возможные значения L при заданной схеме [А1 всегда можно найти
векторным сложением моментов отдельных нуклонов. Так, воз-
166
(3.100)
(3.101)
для четы-
можные схемы Юнга для трех нуклонов найдем, добавляя к схе-
мам (3.100) по одной клетке:
[2]®[1]= [3J+ [2Ц,
[111 ®[1] = [21]+[1111.
В случае р-оболочки [2] -> D° + D2, [111 D1 и [1J -> D1, поэтому
[3] + [21 ] -> (D° + Z+) ® D1 = 2D1 + D2 + D3;
[ 21 ] + [ 111 ]-> D1 (x) D1 = LX* + D1 + £>a,
откуда находим:
[3]->L = l, 3; ’
[21]-^£ = 1, 2;
[lll]->-L=0. j
Приведем еще возможные схемы Юнга и значения L
рех нуклонов в р-оболочке (fe = 4, I = 1):
[4]->L =0, 2, 4;
[31]-+L = 1, 2, 3;
[22] -+L = 0,2;
[211]->L=1.
Схемы Юнга с четырьмя строками при I = 1 запрещены, так как
максимальное число строк в схеме Юнга, характеризующей анти-
симметричную функцию (3.94), равно 2/ + 1.
Аналогичным образом можно построить совокупности спин-
изоспиновых функций:
Q? М* Ш pSTMs Мт), (3.103)
(3.102)
преобразующиеся не только по неприводимому представлению
группы SUit но также и по неприводимым представлениям ее под-
групп. Эти представления характеризуются квантовыми числами
суммарного спина S и суммарного изотопического спина Т (Ms и
Мт — их проекции). Дополнительное квантовое число р вводится
тогда, когда пара чисел (S, Т) появляется для данной схемы Юнга
[X] больше одного раза.
Полные антисимметричные волновые функции, описывающие
состояния системы k нуклонов, характеризуемые определенной
пространственной симметрией [X] и определенными значениями ор-
битального момента L, спина S, изотопического спина Г и их про-
екций М, Ms и Мт, можно записать в виде
Ч' (/* [Л] apLSTMMs Мт) =
= У Фг(/*Ш <*LM) Й? ((st)* [X] ₽STMsMr). (3.104)
г
167
В табл. 3.5 приведен полный набор состояний в схеме LS-связи
для системы k нуклонов, находящихся в р-оболочке (1 = 1) 114].
В строках табл. 3.5 каждому значению L соответствует пара зна-
чений S и Т. Например, при k = 2 и схеме Юнга [2] возможны
следующие состояния: 13S[2], 31S[2], 13£>[2] и 31D[2L Из табл. 3.5
видно, что в общем случае при определенной симметрии состояния,
описываемой схемой Юнга [X], существует несколько значений
пары чисел (Т, S). Совокупность этих вырожденных значений (Т,
S) при данной схеме [Л] называют с упермультиплетом
Вигнера. С другой стороны, одни и те же значения Т и S могут
соответствовать различным схемам Юнга, т. е. состояниям с раз-
личной симметрией.
Таблиц а 3.5
k [%] L (2Г + 1, 2S + 1)
0 [0] 0 (H)
1 HI 1 (22)
2 (2] [MJ 0,2 1 (13), (31) (H), (33)
3 [3] [211 [П1[ 1,3 1,2 0 (22) (22), (24), (42) (22), (44)
4 [4] [31] [22] [2H| 0, 2, 4 1, 2, 3 0, 2 1 (И) (13), (31), (33) (11), (15), (51), (33) (13), (31), (33), (35), (53)
5 [411 [32] [311] [221] 1, 2, 3, 4 1, 2, 3 0, 2 1 (22) (22), (24), (42) (22), (24), (42), (44) (22), (24), (42), (26), (62), (44)
6 [42] [4HJ [33] [321] [222] 0, 2\ 3, 4 1, 3 1, 3 1, 2 0 (13), (31) . (H), (33) (11), (33) (13), (31), (33)2, (15), (51), (35), (53) (13), (31), (35), (53), (17), (71)1
Квантовые числа [A], L, S и Т однозначно описывают состояния
системы, за исключением случая шести нуклонов, когда наборам
квантовых чисел 13О[42], 31£> [421, 33Р [321] и 33D [3211 отвечают
по два состояния (см. табл. 3.5). Для полного описания состояний
в этом случае необходимы дополнительные квантовые числа аир.
Если (>1, то пространственные состояния в большинстве
случаев однозначно не определяются заданием [X] и L. Для клас-
168
сификации таких состояний можно ввести некоторую группу, кото-
рая содержит 7?3 как свою подгруппу и является одновременно под-
группой группы SU21+1. В качестве такой группы удобно рас-
смотреть группу вращений в пространстве (2/ + 1) измерений
.Raz + i, оставляющую инвариантной симметричную билинейную
форму, составленную из пространственных функций двух частиц:
2 (I —mini 100) <рл;_т (гг) ср,!/т (г.,) ~
т
~ 2 1)т Ф(fj) фЩт (Г2). (3.105)
т
Группа 7?2/4-i называется (2/ + 1)-мерной ортогональной группой.
Подобно неприводимому представлению DL группы R3, которое
однозначно характеризуется целым положительным числом L (так
как I —целое), неприводимое представление группы Z?2/+1 характе-
ризуется набором неотрицательных целых чисел (coj, <о2, ..., ом),
выбираемых так, чтобы ^ ... > <о;. Этот набор чисел и
соответствует введенному ранее дополнительному числу а.
С увеличением I оказывается необходимым вводить новые груп-
пы, содержащиеся в R21 +1 и имеющие в качестве своей подгруппы
R3. Благодаря этому оказывается возможным проводить дальней-
шую классификацию состояний по неприводимым представлениям
этих групп. Таким образом, пространственные функции систем k
нуклонов в определенной оболочке nl можно полностью и однознач-
но охарактеризовать набором квантовых чисел, которые указывают
на те неприводимые представления цепочки групп
SU21+ 1 3 R21+1 } ••• (3.106)
II II
[М a L М
по которым преобразуются эти функции. Подобную задачу класси-
фикации состояний с помощью неприводимых представлений це-
почки групп мы уже рассматривали, когда строили функции не-
приводимых представлений групп перестановок (5Й, Sk-i, ... ,
S2, Sx).
Аналогичным образом можно рассмотреть спин-изоспиновые
функции £2 и выяснить смысл квантовых чисел р. Зная Ф и Q, для
конфигурации 1к нетрудно построить полный ортогональный набор
антисимметричных волновых функций Т, согласно (3.104).
Классификация состояний в схеме //-связи. Рассмотрим теперь
классификацию состояний системы k эквивалентных нуклонов во
внешней незаполненной оболочке при наличии спин-орбитального
взаимодействия [15]. В этом случае оболочка будет характеризо-
ваться квантовыми числами nlj, а одночастичные волновые функции
будут представляться в виде произведений спин-пространствен-
ных и изоспиновых функций (3.77).
169
Вместо функций (3.81) и (3.82) рассмотрим теперь произведения
k одночастичных спин-пространственных и изоспиновых функций:
фт,т!... Гасг2; ...; rh nJ = cpm, (гх<т,) X
Хфт,(г2<Гг) ... (3.107)
. vfe (Ti T2’ > Tfc) — ?V1 (^1) £v: (Ts) SvA (rk)- (3.108)
Подобно (3.91) и (3.93), составим далее из (3.107) и (3.108) с по-
мощью схем Юнга линейные комбинации, преобразующиеся по
неприводимым представлениям DPI и DPI группы перестановок
(/* 1Л1|), 2~(^ [Х]т]). Здесь £ и т] — дополнительные квантовые
числа. Спин-пространственные функции Фг (j* [Х]£) одновременно
будут базисными функциями неприводимых представлений
группы SU214-i всех унитарных унимодулярных преобразований
в (2j + 1)-мерном пространстве функций (го). Подобно случаю
LS-связи, представления С/Pl, рассматриваемые как представления
группы вращений 7?3, являющейся подгруппой SUzj+i, могут быть
приведены и разложены по неприводимым представлениям DL
группы вращений 7?3. Единственное отличие рассматриваемого слу-
чая от случая LS-связи обусловлено полуцелым характером числа j.
Итак, спин-пространственные и изоспиновые функции системы
k эквивалентных нуклонов можно выбрать в виде
<М/*[МсфИ), (3.109)
Z7(tk[b]TMT), (3.110)
где ty — полный момент оболочки; М — проекция полного момента;
а — дополнительные квантовые числа, характеризующие спин-
пространственное состояние; Т — полный изотопический спин и
Мт — проекция изотопического спина (для задания изоспинового
состояния дополнительные квантовые числа излишни).
Рассмотрим простейший случай двух нуклонов. В этом случае
спин-пространственная функция
Ф {/2IX] %М) = X (/mi IW) (ri. ^1) ф/тг (г2- о2) (3.111)
может быть либо симметричной (для схемы Юнга 12]), либо анти-
симметричной (для схемы Юнга [111). Воспользовавшись симмет-
рией коэффициентов Клебша — Горда и а
(jmi jm21 %М) =
можно написать
РФ (/2 [А] $М) = (— 1 +1 Ф (J2 М) (3.112)
(при этом мы учли, что 2/ — нечетное число). Таким образом, ан-
тисимметричные функции соответствуют четным значениям а
симметричные — нечетным значениям #. Поэтому (Л1 Ч разлагается
на представления D°, D®, ..., D2'~l, а 1Л21—-на представления
170
D1, D2, .... D->. Подобные разложения можно провести и для си-
стем с числом частиц k > 2. Например, в случае двух нуклонов
(fe = 2), находящихся в оболочке / = 3/2, имеем
[2]^ = 1. 3;
[11]^=0, 2.
(3.113)
Аналогично для трех нуклонов (k = 3), находящихся в оболочке
/ = 3/2, можно получить
[21]->$=1/2, 3/2, 5/2, 7/2; )
[111]->^ = 3/2 |
(3.114)
и Т. д.
Полные антисимметричные волновые функции системы k экви-
валентных нуклонов имеют вид
мг) =
= Лг У фг (lk [A] ajW^) (/* [X] ТМт). (3.115)
/«х г
Так как число возможных значений проекции полного момента од-
ного нуклона равно (2/ + I), а проекция изотопического спина нук-
лона принимает лишь два значения, то схема Юнга [X] может иметь
не более (2/ 1) строк и двух столбцов. Поскольку сопряженная
схема Юнга [XI, характеризующая изоспиновую функцию системы,
может иметь только две строки (и 2/ -ф 1 столбец), то сущест-
вует однозначное соответствие между схемой Юнга [А] и вели-
чиной изотопического спина системы Т. Действительно, так как
изоспиновая функция симметрична по координатам частиц, нахо-
дящимся в строках, и антисимметрична по координатам, нахо-
дящимся в столбцах схемы [X), то суммарный изотопический спин
системы Т будет равен половине разности числа клеток в двух
строках схемы [А]. (Изотопические спины частиц, координаты ко-
торых размещены по выступающим клеткам первой строки, под
которыми отсутствуют клетки второй строки, можно считать ори-
ентированными одинаковым образом, т, е. они дают максимальную
проекцию суммарного изотопического спина Т.) Очевидно, числа
клеток в двух строках схемы [А] (в двух столбцах схемы [А)) рав-
ны k -4- Т.
(3.16)
Можно сделать и обратное утверждение, а именно, ч+о при
заданном числе частиц k изотопический спин Т однозначно опреде-
ляет схему [AJ, т. е. изотопическую перестановочную симметрию,
171
а следовательно, и спин-пространственную перестановочную сим-
метрию, характеризуемую схемой [1].
Схема Юнга [Л] характеризует также полную антисимметрич-
ную функцию системы (3.115). Очевидно, одно из квантовых чисел
IA,] или Т в (3.115) лишнее, однако обычно при классификации со-
стояний в схеме jy-связи приводятся оба эти числа. Здесь имеет место
ситуация, подобная встречающейся при классификации электрон-
ных состояний в атомах, где полный спин оболочки S однозначно
определяет перестановочную симметрию волновой функции.
Сеньорити и приведенный изотопический спин. Если /' 3/2
и число эквивалентных нуклонов k превышает 3, то при определен-
ных значениях полного спина и изоспина, характеризуемых кван-
товыми числами $, Л1^, Т и Мт, возможно несколько различных
состояний. Для их разделения вводятся два дополнительных кван-
товых числа: сеньорити s и приведенный изото-
пический спин t, характеризующие поведение волновой
функции при симплектических преобразованиях.
Симплектические преобразования, оставляющие инвариантной
антисимметричную билинейную форму
£ (j—mjm 100) <р (г,, о,) ср (г2, о2) ~
тп
(Гр (Г,) фр„(Г2, <Т2), (3.1 17)
образуют симплектическую группу Sp2,+ i в пространстве (2/ + 1)
измерений. Симплектическая группа Sp2/+ i является подгруппой
по отношению к унитарной группе Uij+i, в свою очередь, Sps/^i
содержит в качестве подгруппы группу вращений R3. Симплекти-
ческая группа Sp2/-i-1 играет такую же роль в случае //-связи, ка-
кую группа играет в случае £5-связи.
Неприводимые представления симплектической группы харак-
теризуются схемами Юнга [X], из которых удалены клетки, отвечаю-
щие парам нуклонов с противоположными проекциями моментов
и изоспином, равным единице. Обозначим эти схемы через (<т):
(а) =(€4, а2> .... av), (3.118)
Очевидно, с7г > о, > ... > щ, 0, (Ц 2, где целое число v
определяется из условия 2v = 2/ + 1.
Так как (о) содержит только два столбца, то для определения
(о) достаточно задать числа клеток в этих столбцах, которые по ана-
логии с (3.116) обозначим (l/2)s ± t. Число s определяет полное
число элементов в (о) и называется сеньорити, число t пред-
ставляет собой полуразность длин столбцов (о) и называется при-
веденным изотопическим спином. Очевидно, име-
ют место соотношения s О k и t < Т.
Числа s и t однозначно определяют неприводимые представления
(а) симплектической группы Sp2/-i-i- Базисные функции неприво-
димых представлений обозначим так:
ФД?1М(с)Ж). (3.119)
172
Различные базисные функции определенного неприводимого пред-
ставления (а) различаются значениями и М. Обозначим число ба-
зисных функций, определяющее размерность представления (а),
па. Очевидно, по = S (2^ + 1), где суммирование производится
по всем значениям )/, входящим в (о). •
Вместо задания (а) в (3.119) можно задать значения s и t. Сеньо-
рита s состояния Ф определяет то наименьшее число частиц, при
котором еще возможно состояние, обладающее такими же транс-
формационными свойствами, как и Ф. Аналогично приведенный
изотопический спин t состояния Ф можно интерпретировать как
значение изотопического спина Т состояния с наименьшим числом
частиц s, имеющего те же трансформационные свойства, что и Ф.
Итак, в схеме //-связи спин-пространственные волновые функции
k эквивалентных нуклонов классифицируются по неприводимым
представлениям цепочки групп
SL72/+i )Sp2/+O7?3)7?2. (3.120)
Если указанных в (3.119) квантовых чисел недостаточно для пол-
ного описания состояния, то необходимо вводить дополнительные
квантовые числа а'.
Полную антисимметричную волновую функцию системы /г нук-
лонов можно записать в виде
Ч’’ (/* [X] a' styTMp Му) —
=- (1 2<₽г (/* [X] а' z7 (/* [X] ТМт). (3.121)
Г
Напомним, что задание [%] однозначно определяет изотопический
спин системы Т, поэтому квантовое число Т можно вообще не пи-
сать.
В табл. 3.6 приведена полная классификация состояний систе-
мы k нуклонов для оболочек / = 1/2, 3/2, 5/2 и 7/2. В таблице ука-
заны допустимые значения для каждого типа симметрии, опре-
деляемого схемами [Z] и (о). Степень числа $ указывает, сколько
раз встречается данное значение в соответствующем состоянии.
Для заданной конфигурации /А состояния размещены в порядке
возрастания Т. При заданном Т состояния размещены в порядке
возрастания s, и при заданном s — в порядке возрастания Z. Такое
размещение состояний соответствует порядку следования уровней
энергии системы, если предположить, что между нуклонами дейст-
вуют остаточные короткодействующие силы Вигнера или Гейзен-
берга. Указанные силы приводят к следующим значениям спинов
для основных состояний ядер:
А и У — четные, s =- 0, t = 0, = 0;
А — нечетное, s ~ 1, Z = 1/2, #• = /;
А — четное, N — нечетное, s = 2, t = 1, ~ 1, 3, ..., 2/.
Дополнительные квантовые числа. Введение промежуточных
групп, ортогональной группы /?2/+j в случае LS-связи и симплек-
173
Таблица 3.6
J k IM T (a) (S/) %
1/2 0 (01 0 <0) (0, 0) 0
1 [1] 1/2 (1) (1- 1/2) 1/2
2 i 121 | |H] 0 1 (2) (0) (2. 0) (0, 0) 1 0
3/2 0 [0] 0 (00) (0, 0) 0
1 14 1/2 (W) (1. 1/2) 3/2
2 12] ]H] 0 I (20) (00) (Ч) (2, 0) (0, 0) (2. 1) 1, 3 0 2
3 [21] [Hl] 1/2 3/2 (10) (21) (10) (1, 1/2) (3, 1/2) (1, 1/2) 3/2 1/2, 5/2, 7/2 3/2
4 [22] [2H] [Uli] 0 1 2 (00) (H) (22) (20) (H) (00) (0,0) (2,1) (4,0) (2,0) (2,1) (0,0) 0 2 2,4 1,3 2 0
5/2 0 [0] 0 (000) (0,0) 0
1 [11 1/2 (100) (1,1/2) 5/2
2 [2] (HI 0 1 (200) (000) (110) (2,0) (0,0) (2,1) 1, 3, 5 0 2, 4
3 [21] [Hl] 1/2 3/2 (100) (210) (100) (Hl) (1, 1/2) (3, 1/2) (1, 1/2) (3, 3/2) 5/2 1/2, 3/2, 5/2, (7/2)a, 9/2, 11/2, 13/2 5/2 3/2, 9/2
4 [22] [2И] [HUI 0 1 2 (000) (110) (220) (200) (HO) (2H) (000) (110) (0,0) (2,1) (4,0) (2,0) (2,1) (4,1) (0,0) (2,1) 0 2, 4 0,22, 3, 42, 5, 6a, 8 1, 3, 5 2, 4 1, 2, 32, 4, 5, 6, 7 0 2, 4
Продолжение табл. 3.6
i k 1М т (О) (‘0
5/? 5 [221] 1/2 (100) (1-1/2) 5/2
(210) (3,1/2) 1/2, 3/2, 5/2, (7/2)2,
9/2, 11/2, 13/2
(HI) (3,3/2) 3/2, 9/2
(221) (5,1/2) 1/2, 3/2, (5/2)2, (7/2)2, (9/2)2, (11/2)2, 13/2, 15/2, 17/2
[21И] 3/2 (ЮО) (1,1/2) 5/2
(210) (3,1/2) 1/2, 3/2, 5/2, (7/2)2,
9/2, 11/2, 13/2
(Н1) (3,3/2) 3/2, 9/2
[ШИ] 5/2 (100) (1,1/2) 5/2
А ]222] 0 (200) (2,0) 1, 3, 5
(2Н) (4,1) 1 , 2, 3®, 4, 5, 6, 7
(222) (6,0) 1, З2, 4, 5, 6, 7, 9
[2211] 1 (000) (0,0) 0
(НО)2 (2,1)2 22, 42
(220) (4,0) 0,22, 3, 4а, 5, 62, 8
(211) (4,1) 1, 2, З2, 4, 5, 6, 7
[21111] 2 (200) (2,0) 1, 3, 5
(40) (2,1) 2, 4
[НИН] 3 (000) (0,0) 0
тической группы Зрг/ц-1 в случае //-связи является удобным спо-
собом проведения с помощью неприводимых представлений этих
групп дальнейшей классификации состояний системы эквивалент-
ных нуклонов. Кроме названных иногда можно ввести и другие
промежуточные группы, однако часто возникает ситуация (как в слу-
чае LS-связи, так и в случае //-связи), когда дополнительные про-
межуточные группы преобразований отсутствуют, хотя классифи-
кация еще и не доведена до конца. В схеме LS-связи такая ситуация
возникает уже при классификации состояний в р-оболочке (/ = 1).
Здесь ортогональная группа Rzi+i при I = 1 фактически совпа-
дает с группой обычных трехмерных вращений так как непри-
водимые представления ортогональной группы при I = 1 харак-
теризуются всего лишь одним параметром <иг, как и неприводимые
представления группы вращения. В то же время, как мы знаем, для
конфигурации р6 имеются два D-состояния со схемой Юнга [42],
поэтому необходимо ввести дополнительные квантовые числа.
В таких случаях для определения полного набора квантовомеха-
нических величин необходимо найти такие характеризующие си-
стему частиц операторы Q, которые коммутировали бы с операто-
рами, соответствующими уже введенным физическим величинам,
а также между собой. В настоящее время пока не разработан об-
щий метод нахождения таких операторов и соответствующих им
физических величин, образующих полный набор, поэтому их ищут
для каждой конкретной системы отдельно. Естественно, что най-
175
денные таким образом добавочные квантовые характеристики си-
стемы далеко не всегда имеют наглядный физический смысл.
При классификации состояний d-оболочки (/ = 2) в схеме LS-
связи между унитарной унимодулярной группой 31УБ и группой
вращений /?3 можно вставить только ортогональную группу
неприводимые представления которой характеризуются двумя
числами (Oj, о)2. Но уже для конфигурации cP имеется по два со-
стояния [31] (3,1)// и [31] (3,1)/. В случае /-оболочки (Z = 3) кроме
ортогональной группы Т?7, неприводимые представления которой
характеризуются тремя числами (ых, со2, со3), существует еще груп-
па, которая содержит группу R3 в качестве своей подгруппы, а са-
ма является подгруппой /?7. Эту группу обозначают через С2.
В некоторых случаях классификация по неприводимым представ-
лениям этих групп имеет определенный физический смысл (напри-
мер, в случае короткодействующих сил между нуклонами).
В схеме //-связи набор квантовых чисел, включающий полный
момент количества движения изотопический спин 71 (или схему
Юнга [X]), сеньорити s и приведенный изотопический спин t, явля-
ется достаточным для описания отдельных состояний лишь в обо-
лочках с / = 1/2 и /' = 3/2. В оболочке с / = 5/2 уже для трех
эквивалентных нуклонов нужно вводить дополнительные кван-
товые числа. Например (см. табл. 3.6), состояния (5/3)3 [21] (s = 3,
1/2) (^==7/2), (5/2)* [211] (4,1) 3, (5/2)e [222] (6,0) 3 встречаются
дважды. С ростом j и числа эквивалентных нуклонов приходится
вводить все большее число дополнительных квантовых чисел.
Дополнительная классификация миогочастичных состояний
в случае осцилляторного оболочечного потенциала. Мы рассмотрели
общую классификацию многочастичных состояний, не зависящую
от явного вида оболочечного потенциала. В случае осцилляторного
оболочечного потенциала имеется дополнительная возможность
классификации, основанная на свойствах симметрии осциллятор-
ного гамильтониана по отношению к преобразованиям группы SU3.
Такая классификация была предложена Эллиоттом [16].
Рассмотрим частицу в трехмерной изотропной осцилляторной
яме. Гамильтониан в представлении вторичного квантования можно
представить в виде
//„-(а" а+3/2)Йсо, (3.122)
где а+ и а — операторы рождения и уничтожения, связанные с коор-
динатой и импульсом частицы соотношениями
+ 1 / . р \ 1 । , • р \ / 1 / Afwl
а =—— аг—i — ; а = —| аг +1~ а = 1/ — .(3.123)
1 2 ( ha) 1 2 \ На / \ V h )
В (3.122) входит скалярное произведение векторов а и а+, инвари-
антное относительно унитарных преобразований в трехмерном
пространстве; иными словами, гамильтониан (3.122) инвариантен от-
носительноунитарных преобразований группы U3 в трехмерном про-
176
странстве векторов а. Гамильтониан инвариантен также относи-
тельно преобразований из подгрупп группы U 3, а именно отно-
сительно преобразований унитарной унимодулярной группы SUa
и трехмерной группы вращений R3.
Собственные значения энергии изотропного гармонического ос-
циллятора определяются единственным квантовым числом N:
En = (N + 3/2)/гы, N = 0, 1, 2 ... Каждый уровень энергии вы-
рожден, и кратность вырождения равна few = (N + !)(# + 2)/2,
т. е. определяется тем же числом N. Поэтому каждому уровню энер-
гии осциллятора можно сопоставить набор из ku линейно незави-
симых функций, которые преобразуются друг через друга при пре-
образованиях, оставляющих неизменным гамильтониан (3.122).
Этот набор из функций образует базис неприводимого представ-
ления унитарной группы U 3. Само представление однозначно оп-
ределяется квантовым числом N, и его размерность равна kx. Не-
приводимое представление D{N> группы U3 является также непри-
водимым представлением группы SU3. Однако по отношению
к группе вращений Rs это представление будет приводимым и рас-
падается на неприводимые представления D1 группы 7?3, причем
/ = jV, N — 2; N — 4, ... до I = 1 или 0 в зависимости от четности
N, и каждое из представлений D1 с указанными значениями I
встречается один раз. Итак, состояния частицы в осцилляториой
яме (состояния осциллятора) можно характеризовать функциями
<Рл7ш (т — проекция орбитального момента /), квантовые числа
которых N, 1м. т определяют неприводимые представления цепочки
группы U3{SU3) => 7?3 о Т?2.
Неприводимые представления групп U3 и SU 3 можно характе-
ризовать также схемами Юнга. Как мы знаем, схема Юнга опреде-
ляет также неприводимое представление группы перестановок.
В случае движения частицы в осцилляториой яме следует иметь
в виду перестановки осцилляторных квантов. В состоянии (p.vim
имеется N таких квантов. Возможная схема Юнга из N клеток бу-
дет характеризовать свойства симметрии волновой функции срло™
относительно перестановок осцилляторных квантов, т. е. характе-
ризовать соответствующее неприводимое представление группы
перестановок. Схема Юнга будет характеризовать и свойства функ-
ции флгпп относительно преобразований из группы SU3(U3), т. е.
будет определять и^неприводимое представление группы SU3 (U3)-
Если мы имеем "несколько нуклонов в осцилляториой яме, то
свойства симметрии полной волновой функции относительно пере-
становок нуклонов характеризуются схемой Юнга [X]. Полный
гамильтониан системы будет, вообще говоря, инвариантным относи-
тельно преобразований более широкого класса по сравнению с груп-
пами U3 и SU3, хотя он сохранит инвариантность и относительно
преобразований групп Ua и SU3. Классификацию состояний не-
скольких нуклонов, движущихся в осцилляторном потенциале, мож-
но провести, основываясь как раз на симметрии полного гамиль-
тониана относительно группы SUa.
177
Неприводимые представления группы SU3 в (отличие от не-
приводимых представлений группы t/3) можно характеризовать
так называемыми усеченными схемами Юнга, которые получаются
из схем Юнга при удалении заполненных столбцов. В случае груп-
пы SU3 заполненный столбец имеет длину в три клетки. Если пред-
ставление группы U3 характеризуется схемой [X] = [Хь Х2, Х3],
то представление группы SUs можно характеризовать схемой
IX'] — [Х/Х./1, т. е. всего двумя числами X/ — — Х3 и Х2'
-_Х., — Х3'. Представления и группы SU3 эквивалентны.
Эллиотт взамен пары чисел X/ и X./ ввел другую эквивалентную
пару чисел для обозначения неприводимого представления группы
SU3.
(X, р) = (Хх— X,, Х2 —Х3). (3.124)
Мы будем пользоваться обозначениями Эллиотта.
В случае одного нуклона функцию в представлении чисел
заполнения можно получить из функции основного состояния ср000
действием на последнюю оператором рождения кванта в степени N.
Так как эти операторы коммутируют друг с другом, функция
симметрична относительно перестановок квантов. Поэтому функции
ffNim отвечает схема Юнга с одной строкой, число клеток в которой
равно числу квантов N, а сама функция является базисной функцией
неприводимого представления группы перестановок. Усеченная
схема Юнга имеет такой же вид. Поэтому неприводимое представ-
ление группы SC/3 будет описываться двумя числами Эллиотта
X = N и р. = 0, или сокращенно (/V, 0). Как и следовало ожидать,
это представление зависит только от осцилляторного квантового
числа N так же, как энергия и кратность вырождения уровня.
Назовем осцилляторной оболочкой совокуп-
ность нуклонов, волновые функции которых преобразуются по
одному и тому же неприводимому представлению (X, р.) = (Д/, 0)
группы SU3. При наличии k таких нуклонов будем говорить, что
они образуют конфигурацию или осцилляторную оболочку (У, 0)*.
Очевидно, осцилляторная оболочка содержит в общем случае не-
сколько обычных /-оболочек, с которыми мы имели дело раньше
и в каждой из которых все нуклоны имели одинаковое орбитальное
число. Только осцилляторные оболочки с А' ~ 0 и .V - 1 совпа-
дают соответственно с обычными s- и р-оболочками, где I — 0 и 1.
Классификацию состояний осцилляторной оболочки (N, 0)k
можно провести следующим образом. Задаем схему Юнга [X], т. е.
неприводимое представление D[X1 группы перестановок k нуклонов,
по которому преобразуется пространственная часть волновой функ-
ции; задаем символ (X, р.) для всех k нуклонов, характеризующий
неприводимое представление группы SU3, по которому преобра-
зуется полная волновая функция; задаем полные моменты L, S,
Г и их проекции Ml, Ms и Мт. Очевидно, указанные квантовые ха-
178
рактеристики должны быть совместимыми друг с другом. Итак,
осцилляторная конфигурация описывается волновой функцией
V ((7V0)* [X] (X, р) LSTMl Ms М7). (3.125)
Символ (X, р) для заполненной оболочки будет равен (0, 0).
Укажем теперь, как можно найти возможные значения полных
символов (Л, р), если известны символы состояний отдельных нукло-
нов (Хг, р;). Для этого от символов (Л,, р;) необходимо перейти к со-
ответствующим усеченным схемам Юнга [X/ ] — [Хх — Х3, Х2 — Х3] =
— [Хг р;, pf], перемножить их по правилу Литтлвуда и от каждой
из полученных схем Юнга опять перейти к символам (X, р) =
= (Хх — Х2, Х2 — Х3). Например, найдем возможные числа (X, р)
для конфигурации (Х;, р,-)*^ (1,0)я- В этом случае нужно разложить
произведение D(I-°) xD(1>°) хЬ(1'°* на неприводимые представления
D1-'* и) группы SU3. Так как р; — 0, то усеченная схема Юнга, соот-
ветствующая символу (1,0), имеет простой вид [11. Перемножаем,
согласно правилу Литтлвуда:
D[,] ®Dll] = (О[2] + ® П[|] =
= /?г:,5 + 2Д[211-г Д11”1.
Далее переходим к символам (X, р): [3] -> (3,0), [211->(1,1) и
[1111-> (0,0). Итак, окончательно имеем
Д(1’0)®П(,-0)®Д(1'0,=-П(3-0) + 2Д<1'1) + О(0'01.
Метод Эллиотта позволяет быстро разложить любое неприво-
димое представление D(>- и» унимодулярной группы SU3 [характе-
ризующееся схемой Юнга с числом строк, не превышающим трех,
и числом столбцов, не превышающим четырех, или соответствую-
щим символом (X, р) из двух чисел] на неприводимые представления
DL трехмерной группы вращений /?3. Метод заключается в том, что
при заданном символе (X, р) орбитальный момент L может прини-
мать следующие значения:
L = A, А+1, А+2, A + Q, (3,126)
где А — min {X, р}; min (X, р) — 2; min {X, р} —4, ..., 1 или 0, £2 =
— max {X, р}, за исключением случая min{X, р] --0, когда
L=£2, £2-2, £2—4, ..., 1 или 0. (3.127)
Используя это правило, легко воспроизвести все значения L (см.
табл. 3.5). В случае схемы Юнга [42] [соответствующий символ
(X, р) =(2,2)] получается, как и должно быть, два состояния с одним
и тем же значением L = 2.
179
Правило Эллиотта оказывается особенно полезным при класси-
фикации состояний в осцилляторной модели оболочек (классифика-
ция в схеме SU3 Эллиотта), позволяя быстро находить все воз-
можные значения суммарного орбитального момента L, совмести-
мые с квантовым символом (X, р), который характеризует непри-
водимое представление группы SUs.
§ 3.6. ДВИЖЕНИЕ ЦЕНТРА ИНЕРЦИИ ЯДРА
В ОБОЛОЧЕЧНОЙ МОДЕЛИ
Гамильтониан ядра в осцилляторной оболочечной модели и ко-
ординаты Якоби. При рассмотрении многочастичных оболочек
в ядрах наиболее широкое применение получила оболочечная мо-
дель с осцилляторным потенциалом, что связано как с относитель-
ной простотой проведения расчетов в такой модели, так и с воз-
можностью выделения в ней движения центра инерции системы от
внутреннего движения. Рассмотрим детальнее некоторые особен-
ности осцилляторной оболочечной модели.
Выберем одночастичный оболочечный потенциал в виде трех-
мерной осцилляторной ямы
V (г) = V’u + (1/2) Мы2 г'
(3.128)
Рассматривая ядро как систему А независимых нуклонов, находя-
щихся в поле одного и того же осцилляторного потенциала (3.128),
гамильтониан можно записать в виде
2 Hi = 2 {- (Аг2/2Л1} A; + (1/.J г?\. (3.129)
Существенной особенностью гамильтониана (3.129) является то,
что в нем можно выделить часть связанную с движением центра
инерции ядра, а также часть Но', связанную с внутренним движе-
нием в ядре:
2/W 2 Л
(3.130)
Так как все нуклоны движутся в поле одного и того же по-
тенциала, то аналогичным образом можно выделить в Hfj часть,
связанную с движением центра инерции группы нуклонов с любым
числом частиц k А:
ISO
Rh~\-+ 2 Hi',
R i=A+l
k
R* = T2 n;
k
2 |-^(Vi-Vy)s-2Vo + lMo)4n-r/H.
к t <2 J ' " )
(3.131)
Из (3.131) видно, что центр инерции любого числа нуклонов k < Л
в осцилляториой оболочечной модели движется в такой же осцил-
ляторной яме, как и отдельные нуклоны.
Система А нуклонов характеризуется совокупностью ЗА неза-
висимых пространственных переменных, из которых 3 переменные
характеризуют движение центра инерции ядра, а ЗА — 3 перемен-
ных характеризуют внутреннее движение в ядре. Волновую функ-
цию ядра в осцилляториой модели в силу разделения переменных
можно записать в виде произведения функции ср (R), описывающей
движение центра инерции ядра, и функции Ф' (ЗЛ — 3), описы-
вающей внутреннее движение в ядре:
Ф(г:, г2, ..., гл)=ф(И)Ф'(ЗЛ-3). (3.132)
В качестве ЗЛ — 3 переменных, характеризующих внутреннее
движение в ядре, удобно использовать так называемые коорди-
наты Якоби. Определим координаты Якоби как совокупность
векторов
Xft = (lM) 2 П-Г4+1, 6=1, 2, 3, Л —1. (3.133)
I = 1
Вектор Xfe определяет относительное расстояние между (k + 1)-й
частицей и центром инерции системы k частиц. В случае двух ча-
стиц (А = 2) имеется всего один такой вектор X = гх — г2, совпа-
дающий с относительным расстоянием между частицами.
Гамильтониан внутреннего движения Яо' в координатах Яко-
би имеет вид
Но' = S {- (W2pJ Aft- Vo +
k = 1
+ (l/2)pft<^}, (3.134)
k+1
т. e. распадается на сумму A — 1 одночастичных трехмерных ос-
цилляторных гамильтонианов, каждый из которых связан только
с одним из векторов Хк. Таким образом, в координатах Якоби
внутреннюю функцию Ф' можно представить в виде линейной ком-
бинации произведений А — 1 одночастичных осцилляторных функ-
ций <рл / ,,, (Хй), зависящих от параметров ай = Т/ (А=1,
2, ..., А — 1).
18$
Заметим, что координаты Якоби Х17 Х2, Хд_1( характери-
зующие внутреннее движение в ядре, можно определить и другим
способом. Например, эквивалентный набор координат Якоби
получится, если в (3.133) сделать некоторую перестановку номе-
ров частиц. Можно также взамен векторов Xft ввести такие векто-
ры: разбив всю совокупность нуклонов любым способом на две
группы, вводим относительный радиус-вектор, соединяющий цент-
ры инерции этих групп; затем, разбив каждую из полученных двух
групп нуклонов на две части, вводим относительные радиусы-век-
торы центров инерции соответствующих частей и т, д., пока не дой-
дем до отдельных нуклонов. Полученные таким образом А — 1 век-
торы также называют координатами Якоби, в которых
гамильтониан внутреннего движения также разделяется.
Преобразование Талми. Рассмотрим подробнее случай двух нук-
лонов, находящихся в осцилляторном потенциале. Волновую функ-
цию двух нуклонов можно представить либо в виде произведения
одночастичных функций
фП1 ц (аг,) (р,12 it (аг.2), а =-- /(М(о)/Й, (3.135)
либо в виде произведения функции движения центра инерции, за-
висящей от радиуса-вектора центра инерции R = (1/2) (гт + г2), и
функции относительного движения, зависящей от относительного
радиуса г = гт — г2:
aR) аг). (3.136)
Последние две функции являются собственными функциями гамиль-
тонианов Нр>г и Н02', входящих в (3.131) при k = 2.
Функции (3.135) и (3.136) можно выразить друг через друга,
так как они представляют два полных набора функций. Разложим,
например, произведение (3.135) по функциям (3.136):
Ф , (аг.) ф
“п, , т, \ I/ ^пг
/ ,11 ^1 1п1
NLMtllin - - *
NLM х
nlm /
Tjvlai
Цп1в(аг2) =
(/2aR) ф,Д-^-аг)
(3.137)
Это преобразование называется преобразованием Тал-
/ пЛхтх I NLM\ , ,
м и, а величины п[т у — коэффициентами
Талми. При небольших численных значениях осцилляторных
квантовых чисел коэффициенты Талми можно найти непосредст-
венно из (3.137), так как явный вид входящих сюда осциллятор-
ных функций известен. Преобразование (3.137) может оказаться
полезным при вычислении матричных элементов операторов, зави-
сящих только от относительного радиуса-вектора г, например
оператора двухчастичного взаимодействия V (г):
пъЦт2\У (r)\nl' lt' т/; пг' /2' т.г'> =
182
2/П] Zxffll
____\ /j, m.,
N LMnlmnlm
NLM^ /п/ Z/ m/
nlm / ^n,' /2' m2'
NLM\
nlm /
{nlm | V (r) | nfrn).
(3.138)
В (3.138) мы воспользовались ортонормировкой волновых функций
движения центра инерции, от координат которого оператор V (г)
не зависит.
Состояния, описываемые волновыми функциями (3.135) и (3.136),
не характеризуются определенными моментами количества движе-
ния. Состояния с определенными моментами нетрудно получить
из (3.135) и (3.136) с помощью коэффициентов Клебша — Гордана.
В результате вместо (3.137) получим
(11 т1 ^2 т2 I ^1*) Фni h (аГ1) Ф«! /г "г2 (аГз) —
тг
= Z ц2/3]х| [Af£, X
NLnl
<P,vtM (K2aR) (p , 7—^ar), (3.139)
Mm -I2 /
где К = lj + 12 = L + 1 — суммарный угловой момент, ар —
его проекция. Коэффициенты преобразования, входящие в (3.139),
также называются коэффициентами Талми. Они не зависят от
проекций моментов и ими удобно пользоваться при расчетах. Эти
коэффициенты связаны с введенными ранее коэффициентами Талми
соотношением
n2l^\[NL, nl]Ky =
2 (Л mi h т21 ^И) (LMlm | Хр) / П1 т>
пг, тг Мт П3 /2
NLM
Коэффициенты преобразования, входящие в (3.139), частично про-
табулированы в работе [6].
При рассмотрении ядерных процессов, в которых участвуют
как целое некоторые совокупности (кластеры)
нуклонов (дейтроны, а-частицы и т. д.), удобно пользоваться так
называемыми обобщенными коэффициентами
Талми. Они являются коэффициентами преобразований, подоб-
ных (3.137) или (3.139), между функциями, описывающими движе-
ние в осцилляторном потенциале двух частиц или кластеров с раз»
ными массами. Обобщенные коэффициенты Талми зависят от от-
ношения масс этих двух частиц. Для этих коэффициентов нетрудно
получить общие формулы, которые, однако, весьма громоздки.
Выделение движения центра инерции ядра в осцилляторной
оболочечной модели и трансляционно инвариантная модель обо-
лочек. Оболочечная модель обладает тем существенным недостат-
ком, что в ней волновая функция ядра представляется в виде про-
изведения (или должным образом симметризованной суммы произ-
183
ведений) волновых функций отдельных частиц, и поэтому такая
функция не обеспечивает неподвижности центра инерции ядра.
Особенно наглядно это видно на примере осцилляториой оболочеч-
ной модели, согласно которой центр инерции ядра не находится
в покое или в состоянии равномерного прямолинейного движения
(как должно было бы быть при отсутствии внешних воздействий),
а совершает колебательные движения. Волновая функция, описы-
вающая такое движение, является собственной функцией гамиль-
тониана Hr (3.130), т. е. осцилляториой функцией.
Указанное обстоятельство — это прямое следствие того, что
в оболочечной модели рассматривается независимо движение всех
ЗЛ степеней свободы ядра, в то время как при фиксированном
центре инерции ядра только ЗЛ — 3 координаты, описывающие
внутреннее движение, являются независимыми. Поэтому волновые
функции модели оболочек, отражающие след не существующего
на самом деле движения центра инерции ядра (привнесенного самой
моделью), могут, особенно при малых Л, приводить к результатам,
лишенным физического смысла.
Запишем волновую функцию ядра в осцилляториой оболочеч-
ной модели в виде произведения функции движения центра инер-
ции ф^£5й(УЛа/?) и функции Ф' (Хх, Х2, ..., Хд-i), описывающей
внутреннее движение в ядре:
Ф(ь. Ь..... Гд)..............................хл_,). (3.141)
Согласно (3.141), каждому внутреннему состоянию ядра могут от-
вечать различные состояния движения центра инерции с кванто-
выми числамиL и М. Число этих состояний определяется пол-
ной энергией и другими характеристиками ядра, зависящими от
указанных квантовых чисел. Очевидно, свойства ядра полностью
определяются волновыми функциями внутреннего движения Ф'
и не должны зависеть от движения центра инерции. В простейшем
случае, когда волновая функция ядра представлена в виде (3.141),
вычисление матричных элементов от операторов, действующих
на внутренние координаты, приводит к правильному результату,
не зависящему от состояния движения центра инерции только в том
случае, если в начальном и конечном состояниях квантовые числа
L и М одинаковы. Так как полные оболочечные функции ядра,
являющиеся (с учетом спинов и изоспинов нуклонов) антисиммет-
ризованными произведениями одночастичных функций, представ-
ляются в общем случае линейными комбинациями функций (3.141)
с различными квантовыми числами Ж, L и М, то при вычислении
матричных элементов результаты оказываются зависящими от
статистических весов различных состояний движения центра инер-
ции и, следовательно, не имеют физического смысла.
Чтобы устранить получение нефизических результатов, можно
указать два пути. Если оставаться в рамках обычной оболочечной
184
модели, то необходимо в разложении оболочечных функций по
функциям (3.141) оставить только одно слагаемое с определенными
квантовыми числами Ж, LnM (например, слагаемое с ср
а остальные слагаемые опустить. Оставшееся слагаемое часто
называют волновой функцией чистого состоя-
ния, а отброшенные слагаемые — функциями ложных
состояний. Обычно в качестве чистого состояния выбирают
состояние, соответствующее нулевым колебаниям центра инерции
ядра:
Ф (гр г2, ..., гл) =<рj^=0 у=0 й = о (V^aR) Ф (Хр Х2, ..., Хл_,).
(3.142)
Можно выбрать и другой путь, а именно, можно рассматривать
движение нуклонов в ядре относительно фиксированного центра
инерции, а не центра поля, как в модели оболочек. Такую модель
обычно называют трансляционно инвариантной
моделью оболочек (хотя это уже не модель оболочек в обычном по-
нимании), так как гамильтониан и волновые функции в этой мо-
дели обладают свойством инвариантности при трансляциях в про-
странстве. Гамильтониан в трансляционно инвариантной модели
оболочек получается из оболочечного гамильтониана при замене
в последнем части гамильтониана HR, связанной с движением цент-
ра инерции, на оператор кинетической энергии движения свобод-
ного ядра:
Н = — (КЧ2АМ) Дл + Но'. (3.143)
Волновая функция в трансляционно инвариантной модели оболо-
чек имеет вид
~ — PR
Ч>(г,.Ч........ГД=‘" (3144)
а не (3.142). В формуле (3.144) Р — импульс всего ядра.
Выделение чистых и ложных состояний в осцилляториой обо-
лочечной модели. Остановимся подробнее на вопросе об исключе-
нии ложных состояний из оболочечных волновых функций. Оче-
видно, задача сводится к представлению оболочечных волновых
функций в виде суперпозиции функций вида (3.141), которые при
Ж — 0 отвечают чистым состояниям, а при Л” О соответствуют
ложным состояниям:
V (^, [К] (X, р) LSTMl Ms Мт) =
= 2 (УЛхИ)х
,#И.' MlML'
(Г'.и')
Ж, [M(v, р') L'STMi MsMt), (3.145)
185
где Ж — полное осцилляторное квантовое число, определяющее
з
полную энергию ядра = (Ж + —Л)йш. Полная энергия Е^
• — 3
равна сумме внутренней энергии Е = [Ж— Ж + -^-(А — 1)]Й w
и энергии движения центра инерции Е-р = Очевидно,
основное состояние ядра (Ж = ^/'мин) и некоторые низколежащие
возбужденные состояния, соответствующие Ж = 0, являются чи-
стыми состояниями (теорема Бете — Роуза — Эллиотта — Скир-
ма [17, 18[).
Волновая функция движения центра инерции (1 XaR),
входящая в (3.145), не зависит от спиновых и нзоспиновых перемен-
ных и симметрична по пространственным переменным всех нукло-
нов. Поэтому полная функция Т (Ж, [Х](Х, \i)LSTMiMsMt) будет
характеризоваться той же схемой Юнга [X] и теми же числами
STMsMT, что и внутренняя функция Т'. Отсюда следует, что
ложное состояние с данным Ж =+ О будет иметь те же квантовые
числа WSTAfsAfr, что и чистое состояние Ж = 0, если внутрен-
нее состояние в обоих случаях одно и то же. Суммарный орбиталь-
ный момент L может принимать значения от |Л — Z.'| до L + L'
(L = Ж, Ж —2... 1 или 0), Ml = М-£ + M'L,, а возможные значе-
ния символа (X, р) находятся с помощью правила Литтлвуда путем
умножения представлений и
Для примера рассмотрим классификацию состояний системы
с определенным числом нуклонов (не обязательно эквивалентных),
движущихся в осцилляторном потенциале. Рассмотрим все возмож-
ные одноквантовые возбужденные состояния системы из пяти нук-
лонов и определим, какие из этих состояний являются чистыми,
какие ложными и какие смесью чистых и ложных.
Основное состояние, согласно осцилляторной модели оболочек
(в схеме SUa Эллиотта), будет иметь конфигурацию (0, О)4 (1.0)1,
в которой одна из двух осцилляторных оболочек с N = 0 пол-
ностью заполнена, а вторая с = 1 содержит один нуклон. На-
помним, что осцилляторная оболочка определяется одним осцил-
ляторным (главным) квантовым числом N, и максимальное число
нуклонов в этой оболочке равно (2s -j- 1) (2f + 1), где
s = 1/2 и t = 1/2 — значения спина и изоспина нуклона. Осцил-
ляторную оболочку с квантовым числом W иногда обозначают ука-
занием всех возможных значений орбитального момента: (Д/, 0)ft =
= (N,1 — N, 1 — N — 2, I = N — 4, ..., 1 или 0). В рассматривае-
мом случае (0, О)4 (l.O)1^^)4 (Ip)1. Полная энергия определяется
числом Ж = ^Nk. В основном состоянии для нашего случая
N
Жмин = 0 4+1 • 1 1. Согласно теореме Бете- - Роуза — Эллиот-
та — Скирма, основное состояние является чистым.
186
_ Запишем, прежде всего, квантовые характеристики [X], L и
(Л, р,) для каждой из двух оболочек. Для ^(^-конфигурации имеем:
IX] = [4], так как длина столбцов схемы Юнга не должна превышать
числа (21 + !);£ = О, так как все нуклоны в этой оболочке имеют
1 = 0; символах, р) = (0, 0), так как £)<о.°> 0 DM £)(о,о) для
конфигурации (Ip)1 имеем: [XI = [1], L = 1, (А, р) = (1, 0), так
как в оболочке имеется только один нуклон.
Квантовые числа всей совокупности пяти нуклонов с минималь-
ной энергией (,-Г = 1) будут такими:
IX] =[41], (X,й)=(1,0), £= 1, S = V2, Т='/2. (3.146)
Состояние [X] = [51 исключается, так как схема Юнга не может со-
держать более четырех столбцов. Проекции моментов мы не ука-
зывали. Состояние (3.146) соответствует Л" — 0, т. е. является
чистым.
Одноквантовые возбужденные состояния определяются полным
осцилляторным квантовым числом = Жмин -ф 1 = 2 и соответ-
ствуют уровню энергии £ = Йсо рТ + — У М = Йи[2 + - • 5^ =
\ 2 ы ' ' 2 ;
19
= 2- Й®. С такой осцилляторной энергией возможны две конфигу-
рации для системы из пяти нуклонов: (0s)3 (1р)2 и (Os)4 (2d, 2s)1.
В первой из них один нуклон из осцилляторной оболочки с N — 0
перешел в оболочку с N = 1, а во второй единственный нуклон обо-
лочки с N = 1 перешел в оболочку с N = 2.
Найдем все возможные квантовые числа указанных конфигу-
раций. Для конфигурации (0s)3 ss (0, О)3 имеем
[Х]=[3], £ = 0, (X, н) =(0,0);
аналогично для (Ip)2 == (1, О)2 имеем
(A]=[2J, Х=0или2, (А,р) = (2,0),
[Х]=[11], £ = 1, (X, р)=(0,1).
Значения орбитального момента, совместимые с данным символом
(А, р), определены ио методу Эллиотта. Согласно правилу Литтл-
вуда,
£)[3],^О[2]= _р£)[321? £)[3]^ £)[l I ] =£)[41] _|_£)[311];
£>(0,0)(g) £)(2,0) =£)(2,0); £)(O.O)0£}(O.l) = £)(O.l)t
поэтому возможными квантовыми состояниями конфигурации
(0s)3(lp)2 будут:
[X]-[41], (А, р) =(2,0), £=0,2, (3.147)
[А] = [32], (А, р)—(2,0), £ = 0,2, ST- — —; (3.148)
2 2 2 2 2 2
187
IM =(411, (X,p'l =(0,1) b = l, ST= 11; (3.149)
IM =[ЗП1, (Мй) =(0,1), L = l, ST = 11,11 ,11, 11. (3.150)
z z z z z z zz
Аналогично можно показать, что квантовые числа для конфигура-
ции (Os)4 s= (0, О)4 равны [X] = [4], L = 0, (X, р) = (0, 0) и для кон-
фигурации (2d, 2s)1 = (2,0)1 равны [X] = [l], L = 0,1, (X, р) = (2,0).
Отсюда получим, что состояние всей конфигурации (Os)4 (2d, 2s)1
определяется следующими квантовыми числами:
[X] = [41], (X, й) = (2,0), £ = 0,2, ST =-!-!-. (3.151)
Значения суммарного спина S и суммарного изотопического спина Т
взяты из табл. 3.5. Напомним, что эти значения зависят только
от схемы Юнга [X].
Так как возбуждение центра инерции не может привести к из-
менению схемы Юнга (а также значений S и Т) и так как мы огра-
ничились рассмотрением только одноквантовых возбуждений, то
состояния (3.148) и (3.150), характеризуемые схемами Юнга ([32]
и [311], являются чистыми состояниями, поскольку их схемы Юнга
отличаются от схемы Юнга [41] основного состояния (3.146). Следо-
вательно, в состояниях (3.148) и (3.150) возбуждены только внут-
ренние степени свободы ядра; центр инерции совершает только
нулевые колебания, как и в основном состоянии (Ж = 0).
Определим квантовые числа ложных состояний при однокван-
товых возбуждениях системы пяти нуклонов. В этом случае (Ж = 1)
символ (Х*, р ) состояния внутреннего движения совпадает с пол-
ным символом (X, р) — (10) основного состояния (3.146), так как
этот символ для состояния движения центра инерции в основном
состоянии (Ж = 0) будет (0, 0) и 0 ТЮ-о) = Ввиду
того, что D&' й') ® °’ = ТИ'.о) ® = Dt2-0'* + D<°-1 >,
ложные состояния (Ж = 1) будут характеризоваться следующими
квантовыми числами:
[Х]=[41], (X, й)= (2,0), L=0,2, ST = 11; (3.152)
[Х]= [41], (Х,й) =(0,1), £=1, ST=11. (3.153)
Вычитая полученные ложные состояния (3.152) и (3.153) из всех
состояний (3.147)—(3.151), получаем квантовые характеристики
всех чистых (Ж = 0) одноквантовых (Ж = 1) возбужденных со-
стояний:
[X] =[32], (X, й) =(2,0), £=0,2, ST = 11,11,11; (3.154)
Z Z Z Z Z Z
188
[Л]= (311], I, II) =(0,1), L = 1, ST = 11, A A, 11,11;
1 't v/ 22 2222 22
(3.155)
[л] ~I41], II, Д = (2,0), L =0,2, ST = 1 (3.156)
Такие же состояния имеют место в трансляционно-инвариантной
модели оболочек. То, что состояния (3.154) и (3.155) являются чи-
стыми, мы уже показали. Все эти состояния совпадают с состоя-
ниями (3.148) и (3.150). На примере состояний (3.152) и (3.156)
мы видим, чтсгчистые и ложные состояния могут характеризовать-
ся одними и теми же квантовыми числами (кроме Л'). Эти одина-
ковые состояния, встречающиеся в данном случае дважды, свя-
заны с разными конфигурациями (0$)я(1р)2 и (Os)4 (2d, s)1, и половина
из них — ложные состояния (3.152), а половина — чистые состоя-
ния (3.156). Поэтому состояния (3.147) и (3.151) являются суперпо-
зицией ложных состояний (3.152) с Ж = 1 и чистых состояний
(3.156) сЛ"-0. (Дальнейшая задача состоит в определении коэф-
фициентов этой суперпозиции.) Мы видим, что среди всех возмож-
ных чистых состояний (3.154) — (3.156) отсутствует набор кван-
товых чисел, подобный набору в (3.153). Поэтому состояния
(3.149) — это целиком ложные состояния с .4'= 1.
В заключение на простом примере покажем, как в принципе
можно определять вклад чистых и ложных состояний в состоя-
ниях осцилляторной модели оболочек, или, что то же самое, как
находить коэффициенты обратного преобра-
зования, т. е. коэффициенты разложения чистых и ложных
состояний по оболочечным конфигурациям. Например, выясним,
как можно найти эти коэффициенты при разложении функций од-
ного из чистых состояний (3.156) с L = 0 и одного из ложных
состояний (3.152) также с I. = 0 по функциям конфигура-
ции (0s)3(lp)s и конфигурации (0s)4 (2d, 2s)1 с L = 0 (3.147) и (3.151):
4\„CT([41](2,0)L=0, S=T = 1/3)= '
= аг ^((Os)3 (1р)2 [41 ] (2,0) L = 0,3 = Т = i/2) +
+а2 ((Os)4 (2d, 2s)1 [41 ] (2,0) L = 0,3 = T = 4/2), (3.157)
Тл,.кн ([41] (2,0) L = 0.S = T =i/2) =
= Ьг ((Os)3(Ip)2 [41] (2,0) L =0,S=T= ’/,) +
4- T, ((Os)4 (2d, 2s)1 [4] ] (2,0) L = 0,S = T = V2). (3.158)
Функции Тчист и ’1ГЛОЖП — это собственные функции гамиль-
тониана движения центра инерции Hr, отвечающие соответствен-
но собственным значениям энергии Ео = (3/2)Йсо и = (5/2)йш:
НдЧг,1ИСТ = (3/г)Йы¥чист, (3.159)
Эти условия в совокупности с условиями нормировки функций
ai*Qi + «2*^2 = 1, &1*&1 + b2*b2 = 1 определяют коэффициенты
189
On ft2, blt b2. Конкретные вычисления удобно провести в представ-
лении вторичного квантования. Затем с помощью обратного преоб-
разования можно выразить функции и Ya в (3.157) и (3.158) через
Чгчист и Ч/Л0Н!Н, т. е. определить вклад чистых и ложных состояний
в состояниях с определенной конфигурацией. Заметим, что волно-
вые функции чистых состояний нельзя описать в общем случае оп-
ределенной конфигурацией модели оболочек. Они являются супер-
позицией функций с различными конфигурациями, но с одной и
той же осцилляторной энергией.
Построение волновых функций чистых состояний из функций
различных оболочечных конфигураций можно проводить и другим
образом. Например, сначала можно построить все ложные состоя-
ния с какой-либо определенной осцилляторной энергией, а затем
сконструировать ортогональные к ним функции, которые будут,
очевидно, функциями чистых состояний.
§ 3.7. КОЭФФИЦИЕНТЫ РОДСТВА
Вычисление матричных элементов с помощью многочастичных
функций и коэффициенты родства. В предыдущем параграфе мы
рассмотрели классификацию состояний, описываемых полностью
антисимметризованными волновыми функциями k нуклонов во внеш-
ней оболочке, основанную на трансформационных свойствах этих
функций по отношению к определенным группам преобразований.
Полученные выражения для волновых функций можно использо-
вать при вычислении матричных элементов от различных опера-
торов, характеризующих систему. В общем случае многочастичных
систем необходимо вычислять матричные элементы от многочас-
тичных операторов с помощью многочастичных функций. В дейст-
вительности, однако, для систем с двухчастичным взаимодействием
приходится иметь дело только с матричными элементами от одно-
частичных или двухчастичных (т. е. действующих на координаты
двух частиц) операторов. Так, согласно (1.195), гамильтониан ядра
представляется в виде суммы
Я=ХЛ+ VVfj, (3.160)
1 i<(
где Тi -- —— кинетическая энергия отдельного нукло-
на, Vij — энергия двухнуклонного взаимодействия. Вычисление
матричных элементов от операторов в (3.160) с помощью много-
частичных функций можно существенно упростить, вводя так на-
зываемые коэффициенты родства*, позволяющие
свести волновую функцию системы k частиц к волновым функциям
системы k — 1 частиц и т. д. С помощью коэффициентов родства
вычисление матричных элементов от указанных операторов прак-
* В литературе часто вместо термина «коэффициент родства» исполь-
зуется неудачный термин «генеалогический коэффициент».
190
тически сводится к вычислению одно- и двухчастичных матричных
элементов. Поэтому явный вид многочастичных волновых функ-
ций практически очень редко используется, и для нахождения мат-
ричных элементов от физических величин достаточно знать коэф-
фициенты родства.
При вычислении матричных элементов от одночастичных опе-
раторов (например, оператора кинетической энергии Т}) удобно
использовать так называемые одночастичные коэф-
фициенты родства. Их введение основано на том, что
полная антисимметричная волновая функция Т системы k ча-
стиц антисимметрична по отношению к перестановкам в любой
подсистеме из k' частиц (й' < k) и, в частности, по отношению к пе-
рестановкам (fi — 1) частицы. Поэтому волновую функцию Y
можно представить в виде линейной комбинации произведений
антисимметричных волновых функций (k — 1) частиц и волновых
функций одной частицы, причем коэффициенты этого разложения
и являются, по определению, одночастичными коэффициентами
родства. При вычислении матричных элементов от двухчастичных
операторов в полной волновой функции 'F необходимо выделить со-
стояния (k — 2) частиц и двух частиц, при этом аналогичным об-
разом можно определить двухчастичные коэффициенты родства.
В качестве примера рассмотрим вычисление матричного элемен-
та от гамильтониана (3.160). Воспользовавшись видом оператора
Н и антисимметричностью полной функции Т, найдем
(Т | НIV) = k (¥' | Th | V) + [£ (k-1)/2] (¥' j V*_i, | T). (3.161)
Следующий шаг заключается в сведении (¥' | 7\]Т) и (Т' j Vk-1, | T)
к суммам соответственно одночастичных и двухчастичных мат-
ричных элементов путем соответствующих разложений функций Т
с использованием коэффициентов родства. Опишем кратко один
из способов составления таких разложений функций Т и опреде-
ления самих коэффициентов родства на примере схемы /.З^связи.
Одночастичные коэффициенты родства. Выше приведено опре-
деление полных одночастичных коэффициентов родства. Наиболее
простой путь нахождения их явного вида заключается в разложе-
нии этих коэффициентов на множители, соответствующие простран-
ственной н спин-изоспиновой частям волновых функций.
Рассмотрим вначале пространственные функции Ф и поставим
следующую задачу. Пусть нам известна полная система функций
Фг< (/*—1 [X']а'£'Л4') для конфигурации lk~l. Построим подобную
полную систему функций для конфигурации /А, содержащей на ча-
стицу больше. Отметим, что произведения Фг- (7*~![Х/]а'£'ЛГ)
(&), гДе (^) — волновая функция отдельной й-й частицы с
орбитальным моментом I и его проекцией т, образуют полную си-
стему функций, описывающих систему k эквивалентных нуклонов.
Поэтому пространственные функции k частиц с определенной сим-
метрией Фг {lk [XJaLM) можно выразить через эти произведения.
Так как функция Фг (lk [Х]аТЛ1) характеризуется определенными
191
значениями полного орбитального момента L и его проекции М,
то ее следует представлять в виде некоторой линейной комбина-
ции выражений
2(Х'Л1-(/й~‘ [X'] a' L' М — т) ф(т (k), (3.162)
преобразующихся по неприводимому представлению DL группы
вращений. Очевидно, коэффициенты этой линейной комбинации
не должны зависеть от М. (Если бы коэффициенты зависели от М,
то введенная таким путем функция не преобразовывалась бы нуж-
ным образом при вращениях и, следовательно, не соответствовала
бы определенному значению Л4.)
Функция Фг (/* 1Х]а£Л4) под действием перестановок из груп-
пы Sft—i преобразуется по неприводимому представлению
отвечающему схеме Юнга [X'], которая получается из [X] при уда-
лении одной клетки с максимальным числом. Поэтому функция
Фг (1к 1Х]аХЛ4) должна быть составлена из таких выражений
(3.162), в которые входят функции для (k— 1) частицы, преобра-
зующиеся по одному и тому же неприводимому представлению груп-
пы Sft_ 1, причем коэффициенты линейной комбинации не должны
зависеть от символа Яманучи г' (аналогично тому, что они не за-
висят от Л1). Таким образом, окончательно разложение про-
странственной функции для конфигурации 1к можно представить
в следующем виде:
Фг (1к [%] aLM) = 2 G*-1 [X'] a' L'; /1 ] lk [X] aL) X
x 'ZIL' M—т1т\ЬМ)ФГ' (/*-’ [X']a'L'M—m)(fe), (3.163)
tn
где коэффициенты разложения (lk~([X']a'L'; 11 }lk IXlaL) и назы-
ваются одночастичными орбитальными ко-
эффициентами родства. Эти коэффициенты определя-
ются из условия, чтобы функция (3.163) преобразовывалась по не-
приводимому представлению группы Sk. Вид схемы [Х'1 и сим-
вола г' в правой части (3.163) задается символом Яманучи г.
Введенные коэффициенты родства вещественны и удовлетворяют
следующему условию ортонормировки:
2 (/*“* [Х']а'Г; /1}[X] aL) X
а'Ь'
X (/й-ЧХ']а'L';Z|)/* [Х]а£) =6W[x]Saa- (3.164)
Аналогичное разложение с выделением состояния одной частицы
можно проделать и для спин-изоспиновой функции:
Q7((s/)*[X]pSTMs Мг)~
= у ((s/)*-i [X~]₽'S'r;sZ|}(s^fx]pSr)x
р'5'Г'
X у (S' Ms—psp I SMs)(T' Mt — vtv | TMr) x
xQ/'fW1 [rjp'S'T'Ms-jiMT-vH^)^). (3-165)
192
где по определению ((«0*-11л'1 P'S'T'; s/| | (st)k ЕНРЗГ) — одно-
частичный спип-изоспиновый коэффициент родства (s = 1/2, t =
= 1/2), Подстановка (3,163) и (3.165) в (3.104) приводит к сле-
дующему выражению для разложения полной антисимметричной
функции (так как сумма по г сводится к сумме по [V] и г' при фик-
сированной схеме Юнга 11]):
Т (lk [X] ар LSTMMs Мт) =
= X (/^‘ (I'la'B'L'S'T'; /sm/^lJaBLSTIX
[i']a'P'L’5'T-
X 2j (L'M—mlm\LM)\S! Ms — рД|л ISMsjxAfr—vi-v|TM^X
X^(1‘-1 [X']a’p’L'Sr 7”A'l —p/Wr—v) i])im;tv(^), (3.166
где суммирование производится по всем возможным схемам Юнга
[!'], получающимся из схемы [XI при удалении одной клетки. Ко-
эффициенты разложения в (3.166) и есть одночастичные полные
коэффициенты родства, которые выражаются через орбитальные
и спин-изоспиновые коэффициенты родства следующим образом:
(lk~l [V] a' Р' L' S' Г; 1st |} I* [1] apLST)-
= 1 (/*~] [!'] a' L'; 11} lk [1] aL) X
V «х
X ((S/)*-1 [X'] Р' S' Т'\st (} (st)k [X] pST*). (3.167)
Функции вида (3.166) и используются в конкретных задачах при вы-
числении одночастичных матричных элементов. Полные коэффици-
енты родства также вещественны и удовлетворяют условию орто-
нормировки
2 (lk~' [1'1 a' Р' L' S' T'-.lst 1} lk (I] afiLST) x
[V]a'P'
L'S'T’
X (I"-' [!'] a' p' L' S' T'\ 1st |} /* [1] a p LST) = [X] 6aa 6 Гр.
(3.168)
Для одночастичных коэффициентов родства составлены таблицы*.
В случае необходимости подобным образом можно определить
двухчастичные коэффициенты родства; в этом случае в волновых
функциях выделяются состояния двух частиц. Этими коэффициен-
тами удобно пользоваться при вычислении матричных элементов
от двухчастичных операторов. Двухчастичные коэффициенты род-
ства можно выразить через одночастичные коэффициенты родства.
* Коэффициенты родства для р- и d-оболочек вычислены в работе 119],
Коэффициенты родства для оболочек с / = 3/2, 5/2 и 7/2 вычислены в работе
120]. Подробные таблицы коэффициентов родства приведены в монографии
7 Зак. 642
193
Рекуррентное соотношение для коэффициентов родства. Одно-
частичные коэффициенты родства можно вычислить с помощью ре-
куррентных соотношений, связывающих коэффициенты родства для
конфигураций с различающимся числом частиц. Для примера рас-
смотрим рекуррентное соотношение, связывающее орбитальные
коэффициенты родства (lk~1 ]Х']£'; l\}lk 1Х]£) с коэффициентами
родства (lk~2[K"]L"; 1Х']£'), отвечающими системе с числом
частиц, уменьшенным на единицу.
Введем прежде всего проекционный оператор Юнга для систе-
мы k эквивалентных частиц:
С[Х] «х у <f. । р । syM Pi (3. 169)
р
где <r|P |s>lM = £>[Д](Р) — матрица неприводимого представления
[X] группы перестановок — размерность представления [X]
и суммирование проводится по всем перестановкам Р группы Sft.
Используя условие ортогональности матриц неприводимых пред-
ставлений
/г Г
J <Г | р | S> W </1 Р | и>[и1 = — 6[М 6ri 6sU, (3.170)
р
нетрудно показать, что
6s1 Ф( (Р [ц]) = 6Мц] 6S( Фг [X]), (3.171)
т. е. оператор Юнга С[А], действуя на произвольную функцию
1ц]), выделяет из нее компоненту Ф5 (1к IX]), которую затем
преобразует в функцию Фг (/ft [X]). Символ Яманучи г, характери-
зующий систему k частиц, одновременно определяет схему Юнга
IX'] и символ Яманучи г' системы (k— 1) частиц, а также номер
столбца pft, в котором находится последняя (A-я) частица {г = IX'],
г' и pft). Таким образом,
С[У = С[М , . (3.172)
гг [Л ] г Pkt Ц J г pfe ' '
Разобьем №. перестановок Р группы Sh на две совокупности
Р’ и PihP', где Р'— перестановки группы S^-i и Pik—оператор
перестановки двух частиц, из которых частица I относится
к системе {k—1) частиц. Замечая, что Pik = Pi, *_i Рь-\,k Pt. *-i,
перестановки групп Sft, не входящие в группу S*_j, можно
представить в виде Р; /г_., P/; l i/г Р'. В этом случае оператор
Юнга с помощью указанного разбиения представляется в виде
С"=ц]?<г'|Р'1 'W +
+ У У <г’ I Р»-1 I S')'1’’ <IVJ s'p» J ₽*_.,* JIX'J I’ P»>14 X
plkp‘ s'1’
x</'|P'k (3.173)
194
(Напомним, что Р^-^ь не вхоДит в группу S*_t, а |Л'1 и [A/j ха-
рактеризуют представления этой группы, поэтому матричный
элемент от перестановки Pk—t.ts не диагоналей по схеме Юнга
из k — 1 клеток.) Суммирование по элементам совокупности
PihP' эквивалентно суммированию по элементам совокупности
Р' при фиксированном значении i с последующим суммированием
по всевозможным значениям i: У, ... —> У .... Используя
PikP’ Р'
определение (3.169), суммы по элементам Р' в правой части (3.173)
можно свестиц операторам Юнга для системы (4—1) частиц:
+2 £ [V]>Wx
's' =Ц’К₽Ы
(3.174)
При написании этой и последующих формул мы используем то об-
стоятельство, что матричный элемент от перестановки двух по-
следних частиц Pk-i, h не зависит от символа Яманучи для пер-
вых (А — 2) частиц; кроме того, числа pft, р* . t, pft и i одно-
значно определяются заданием соответствующих пар схем Юнга
[A'1(V1, [ХЦХ'1 и [X'llV], поэтому они опущены в матричных
элементах от перестановок.
Одночастичные орбитальные коэффициенты родства определе-
ны соотношением (3.125). Обратное соотношение имеет вид
2(Ь'Л1—т1т\ЬМ)ФГ' (Z*-1 —tn) ф;т(й) =
т
= £(/*-’ [А']Ь';/П [Z1 Л) Фг (7^ [Л] 2.Л1) .. (3.175)
[X] <'
и непосредственно следует из (3.163) при использовании условия
ортонормировки коэффициентов родства:
£(/*- [K]L’-l |}НМ W"1 [ИГ;(|р[ад=^'Г- (3.176)
[М
(Подобно коэффициентам Клебша — Гордана коэффициенты род-
ства определяют унитарное преобразование между функциями.)
Используя определение проекционного оператора (3.171) и
(3.175), нетрудно получить
2(7/Л1— М—т lm[LM) х
X <Ф,'(/*-* [V] L'M-m) <pfn#) I | ф?(/й'! [Г] L 2И-т)Фй(Л)> =
= U*~l HWU*’1 [Ь] Ь'; I j }lk [X] L). (3.177)
7*
195
Подставим в левую часть полученного равенства представле-
ние (3.174) оператора Просуммируем далее левую и правую
части равенства (3.177) по символам Яманучи г' с последующим
делением обеих частей равенства на (размерность представле-
ния [X']). Так как правая часть равенства (3.177) от символов Яма-
нучи вообще не зависит, то она не изменится, а левая часть равен-
ства значительно упростится, если воспользоваться свойством ор-
тонормировки матриц неприводимого представления группы пере-
становок г
2 <г' [ Pit а_, I s' >[*'] <r' \Pi, А_, | s' > I*' J - 6S< Г- (3.178)
Г ’
В этом случае зависимость от i выпадает и сумму по i можно учесть,
введя множитель (й — 1). Так как остаются только матричные
элементы от перестановки Р^-],^ сумму по символу Яманучи г"
для (k — 2) частиц можно заменить множителем п^, равным раз-
мерности представления IX"]. Таким образом, получим следующее
равенство:
± У (фг,(р-1 [X']L'M-(й)|С^ Ф/ (/*-• [Х']Г М-т)х
%' г'
X ,— (й)) =----— 1бга ,, г,—j — 6. ,т' 6 —
' г Ml1" [ [Л ] [Л. I 'fe р;( L L тт
+ (Й-1)У ^<[Х'ПХ"]|Ра-1,а|[х'] [Х"]>^Х
[Л"] пк,
X [X'] L' М— tri) | PA-i,’*’| X
Ь М-т) <р ^(й)>}. (3.179)
Здесь подробно расписаны символы Яманучи в функциях (й — 1)
частиц, которые могут отличаться только номером столбца (й — 1)-й
частицы. Символ г", от которого не зависит матричный элемент,
произволен.
При вычислении матричного элемента от оператора Pk-i.k
волновые функции системы (й — 1) частиц выразим с помощью ко-
эффициентов родства через волновые функции системы (й — 2) ча-
стиц:
Фг- (/*-> [X'J L' М') = S (Р-2 [X''] Г; 11} [X'] L') х
L"
X Х(£" ЛГ — mlm | L' М') Ф,„ (lk~2 [X"] L" М' — m) <pZm (й— 1). (3.180)
Таким образом, найдем
<ФГ- (P~i [X'J L'M') <р1т (й) ] Pa-i. k | Ф7'( Р-1 [X'] Гм') <р ^(й)>
= (р-2 [X"] L"; 11} [X'] L') (lk~2 [X"] Г; Z | } Р-1 [X'J L') х
L"
X (L" М' — tn lm \ L' Л1') (L' М'— mlm [ L'M'). (3.181)
196
(В рассматриваемом случае г" = г".) Подставив (3.179) и (3.181)
в (3.177) и выполнив суммирование по магнитным квантовым чис-
лам, рекуррентное соотношение окончательно получим в следую-
щем виде:
(/*-< [X'] L'; /1 ] lk [X] L) (/*-' [х] LI1) lk [х] £)=
Z _ 1 /А XI
k nvn>.']lVl6L'L' +
4- Цх'](Х"]>1му(-1)£+т"-/-'-гх
[X"l njv' L"
X V(2L' + 1)(2L' + 1) W (lL" LI- L’L’) (lk~2 [X"] L”-l\} /*-i [X'] L') x
X G4-2 [X”] L”; I [} l*-i [X ] L), (3.182)
где W (lL”Ll-t L'L’) — коэффициент Рака. Эта формула позволяет
находить одночастичные коэффициенты родства для системы k
частиц, если известны коэффициенты родства для системы (k — 1)
частиц.
Полагая в (3.182) [X'] = [X'] и L' = L', получаем более простую
формулу, которая, однако, позволяет находить коэффициенты род-
ства только с точностью до знака;
(Iй-1 [Х']Г;/( | ZA[X]L)2 =
= 4 -^(l + tfe-1) У У~ <[X'][X"]|Pfe_1,,|(X'HX"])Wx
К "X' 1 [X"] L" Пк,
X ( — 1)L+L“ (2L‘ +1) 47 (IL" LI;L’ L’) (l^ [X”] 11} [X’] L')2).
(3.183)
Формула (3.182), в отличие от (3.183), позволяет находить и отно-
сительный знак коэффициентов родства. Замечая, что коэффициент
(1; /|) I2 [Х]Р) =1, с помощью рекуррентного соотношения (3.182)
можно, постепенно увеличивая число частиц k на единицу, соста-
вить полную таблицу одночастичных коэффициентов родства для
данного I.
Для примера рассмотрим случай А=3 и [X]—[21]. Пусть
[X'] = [Х ] — 2, L'=0 и L —2. Тогда для коэффициентов родства
(р2 [2] 0; 1 [} р3 [21] 1) и (р2[2[2; 1 (] р3[21] 1) из (3.182) находим:
(р2 [2] 0; 1 (} р3 [21] I)2 = (2/3) {1 + 2 <Р23> W(1111; 00)};
(р2 [2] 2; 1 j} р3 [21] I)2 = (2/3) {1 4- 2 <Р23> 547 (1111; 22)};
(р2 [2] 0; 1 (] р3 [21] 1) (р2J2] 2; 1 ! J р3 [21] I) =
= (4/3) (Ргз>/5 47(1111; 02),
где
(P29>s<[2) [1] | Р83) [2] 11]>Ё2И =((211) | Р23[ (211)>.
157
Замечая, что < (211) | Р231 (211) > =—(1/2), 00) —
=117(1111; 02) — (1/3) и W7 (1111; 22) = 1/30, окончательно получаем
(р* 12] 0; 1 |} р3121) 1) = 2/3, (р*12] 2; 1 |} р3 J21 ] 1) = - /(W
В соответствии с условиями нормировки (3.164) сумма квадратов
найденных коэффициентов родства равна единице.
Двухчастичные коэффициенты родства. В оболочечной модели
наряду с одночастичными коэффициентами родства используются
также двухчастичные. Для того чтобы определить двухчастичные
коэффициенты родства, выделим с помощью одночастичных коэф-
фициентов родства из волновой функции k нуклонов сначала нук-
лон с номером k, а затем нуклон с номером k — 1:
Т(/А [Х]сф157ЖЛД Л4Г) =
£ (Д-Ч^]а'|3'£'5'Г;/1}/ЧМс!.0£5Г)х
[>.'] a'P'L'S'T'
X X a" fi" L" S" Т""; I \) 1*-‘ [Г] a'p'L'ST) X
X П 1Г] а" Р" L" S" Т") ф; (1г - 1)]Ь'5'Г'
(3.184)
Для сокращения записи здесь введено следующее обозначение
для векторной связки функций:
[ V (/*-* [Г] а' р' L' S1 Г) ф;
= [ L' Ml Im | LMl 'l I S' Ms' — Ц | x
\ 2 !
X [гм/ у v\TMt^(1^1 [V]a' P' L' S' T' ML Ms Mr')ifim|1v (k)
(3.185)
и т. д. Переставляя в (3.184) порядок векторного сложения с по-
мощью коэффициентов Рака и связывая вместе волновые функции
нуклонов с номерами k и k — 1, получаем
¥ (1к [М a$LSTMLMs Мт) =
= У (ZA-2[X"la"p"L"S"r";/2£ST|}/ft(X]apLS7’)x
[>.''] a"P;_L"S"T"
LST
х ПК (Z*-2 [X"la"p"L''S"T")Y(/2LST)]MLMS.Mr, (3-186)
где
(lk~2 [Г] a" P"L" S" T"; r1 LS T |} /* [X] ctfLST) =
У V (2L' x 1)(2Z+ 1)(2S' Д 1)(2S+ 1)(2T'+ ПСЗТ-П X
U'Ja'P' L'S-T'
X № (L" ILl; L'T) W(S"~S--, S'S W ( T" - T - ; Т'Т\ X
v ’ \ 2 2 1(22’ /
198
X (/*~2 [Г] а" 0" L" S" [X'] а' 0' L' S' Г) X
х (Z*-1 [Г]а'Р'£'5'Г;/) ) lk \K]a$LST). (3.187)
Коэффициенты, входящие в разложение (3.186), и называются
двухчастичными коэффициентами родства.
Формула (3/187) выражает двухчастичные коэффициенты через
одночастичные коэффициенты родства.
В заключение приведем определение многочастичных коэффи-
циентов родства. Подобно случаю отделения одной и двух частиц
многочастичные коэффициенты родства
определяются как коэффициенты разложения волновой функции
У (1к |л1<7.р/.5ТЛ1/,А'1лЛ1г), характеризующей состояние k экви-
валентных нуклонов, по векторно связанным волновым функциям
h (/г < k) и k — h нуклонов:
Т(НМ а0Л57ЖЛ1зМт) =
= (lk~h 1М «1 ₽1 Si Л; ЛИ* lfeI*]a₽LST) X
[A.s]a2psL2S2T2
X [Т (/*-ЧМ аа₽2ЬгЗгГ2)]^5мг. (3.188)
Коэффициенты родства будут равны нулю, если в разложении
внешнего произведения ® не встретится неприводимое
представление DW. Это есть правило отбора по схеме Юнга, ос-
нованное на условии Литтлвуда.
Подобно (3.187) можно установить связь между коэффициентами
родства для отделения трех, четырех и т. д. частиц и коэффициен-
тами родства для отделения любого меньшего числа частиц,
§ 3.8. ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ ЛЕГКИХ ЯДЕР
Приближение промежуточной связи. Приведенная классифи-
кация многонуклонных состояний применима как для описания
основных состояний ядер, так и для описания слабо возбужденных
состояний, отвечающих низкоэнергетической части спектра ядер.
Рассмотрим конфигурацию, состоящую из полностью заполненной
нуклонной оболочки и k нуклонов сверх заполненной оболочки.
Если ядро описывать гамильтонианом оболочечной модели
Я0 = 2(Л- + Ег), (3.189)
i
т. е, считать, что нуклоны движутся в поле самосогласованного
потенциала V без взаимодействия друг с другом, то все состояния
определенной конфигурации (п/)* будут вырожденными. В дейст-
вительности гамильтониан ядра
(3.190)
199
отличается от модельного гамильтониана (3.189). Различие между
ними обусловлено наличием остаточного взаимодействия между
нуклонами, не учитываемого в оболочечной модели. Очевидно,
энергия остаточного взаимодействия определяется разностью
Vu-yyt. (3.191)
<</ i
Учет остаточного взаимодействия между нуклонами приводит к сня-
тию вырождения уровней, имеющего место в оболочечной модели.
Таким образом, для возможности расчета спектров слабовозбуж-
денных состояний ядер необходимо знать энергию остаточного
взаимодействия (3.191).
Обычно энергетические уровни ядра £ и соответствующие вол-
новые функции ¥ находят непосредственно, решая уравнения
Шредингера:
ЯТ=£Т. (3.192)
Для этого волновую функцию ¥ представляют в виде разложения
по полному набору состояний данной конфигурации опре-
деляемому оболочечной моделью:
(3.193)
{«}
Учитывая, что гамильтониан Н представляется в виде суммы одно-
частичных и двухчастичных операторов, и выделяя с помощью
коэффициентов) родства в состояния одной и двух частиц,
матричный элемент гамильтониана Н можно свести к одночастич-
ным и двухчастичным матричным элементам. Диагонализуя вы-
численную матрицу И, можно определить энергетический спектр
£(*> и коэффициенты С!а} в разложении (3.193), т. е. волновые
функции для соответствующих состояний.
Если известно, что какое-либо оболочечное квантовое число
является хорошим квантовым числом, то состояния, характеризую-
щиеся различными его значениями, связаны слабо. В данном слу-
чае уравнение (3.192) можно решать с помощью теории возмуще-
ний, однако для этого недиагональные матричные элементы долж-
ны быть малыми по сравнению с разностью соответствующих диа-
гональных элементов.
Обычно в расчетах используется гамильтониан И, включающий
центральное двухчастичное взаимодействие и одночастичное спин-
орбитальное взаимодействие:
Я=2(-(^/2М)Дг)+ miiVo'+gShSi- (3-194)
t i
Появление одночастичного спин-орбитального слагаемого в
(3.194) обусловлено усредненным двухчастичным взаимодействием
внешних нуклонов с нуклонами в заполненной оболочке. [Суммиро-
вание в (3.194) проводится только по нуклонам во внешней неза-
200
полненной оболочке. 1 Энергия взаимодействия в (3.194) выбирается
в форме, удобной для численной диагонализации гамильтониана.
Использование гамильтониана с центральным двухчастичным
и спин-орбитальным одночастмчным взаимодействием соответствует
так называемому приближению промежуточной
связи. Такое название связано с тем, что при наличии только
центрального двухчастичного взаимодействия применима схема
LS-связи, в то время как при наличии сильного спин-орбитального
взаимодействия имеет место схема jj'-связи. Состояния ядра в при-
ближении промежуточной связи находят путем диагонализации
(3.194).
Двухчастичные потенциалы, использованные в расчетах по про*
межуточной связи [22, 23], не совпадают с потенциалом, описываю-
щим взаимодействие свободных нуклонов. Так, в расчетах работы
[23] использован двухнуклонный потенциал в виде
V./=y(rj-r,)(p..+ 1РО), V(r)=-Voe-Vr*( (3.195)
где Рг и Ра — обменные операторы. Параметр у, определяющий
радиус действия сил, выбран равным у № (0,9—1,0)а. Относи-
тельные веса сил Майорана и Бартлета выбраны из условий пол-
ного насыщения [24]. Авторы работы [23] использовали модель про-
межуточной связи с взаимодействием (3.194) и (3.195) для объяс-
нения энергетических спектров легких ядер, в которых заполняется
р-оболочка. Несмотря на качественный характер расчетов, резуль-
таты оказались в хорошем согласии с экспериментальными дан-
ными, особенно для уровней, энергия возбуждения которых не пре-
восходит 6 Мэв.
Оказывается, что для 1р-оболочки в случае обменного потен-
циала (3.195) результаты зависят всего лишь от трех параметров
L и К, где i — константа спин-орбитального взаимодействия, а
L н К выражаются через так называемые интегралы Слэтера F1:
L = F° + (4/25)F2, К=(3/25)Р. (3.196)
Интегралы Слэтера определяются коэффициентами разложения
функции V (гг — Tj), характеризующей радиальную зависимость
двухчастичного потенциала, по полиномам Лежандра:
V (Г; — г,) = J Vi (Гр о) Pt (Нг пД, п=г/т (3.197)
г=о
А именно, они равны
F^ е= F1 । fij /j i 1ц /a) =
«0 00
= $ dr\ dr’ (r') Vi(r,r')<pntll(r)<fn2h(r'),
о 0
(3.198)
где q>ni(r) — радиальные одночастичные волновые функции, нор-
мированные на единицу. Исследовалась зависимость уровней энер-
201
гйй от параметров L и К, при этом явный вид радиальной функ-
ции <рп! (г) оказывался несущественным. Если параметр К выбрать
в качестве единицы шкалы энергии, то положение уровней зависит
только от двух величин, отношений L/К и УК- Как показали рас-
четы, положение уровней слабо зависит от величины UK, опреде-
ляемой центральным потенциалом, но существенно зависит от от-
ношения УК- При разумном выборе радиуса действия сил и раз-
меров ядер отношение Li К
Рис. 3.9. Зависимость энергетического
спектра в приближении промежуточной
связи для случая /1— 7 от величины у/(.
оказывается равным при-
мерно 6—7. В расчетах
для всех легких ядер ис-
пользовалось одно и то же
значение для величины
L!K- Из сравнения рассчи-
танного спектра уровней с
экспериментальным мож-
но найти величину пара-
метра £, который увели-
чивается с ростом массо-
вого числа А.
Энергетические спектры
ядер с А = 7. Для примера
рассмотрим результаты
расчетов энергетического
спектра ядер с массовым
числом А — 7 [23] и срав-
ним их с эксперименталь-
ными данными. На рис, 3.9
представлена рассчитанная
зависимость энергетичес-
кого спектра от величины УК при L/K = 6,8, а также показаны
уровни для УК = 2,0 и LIК = 8,5. Энергия Е выражена в еди-
ницах К- Из рис, 3.9 видно, что расстояния между уровнями су-
щественно зависят от величины УК и слабо от L/К. На рис. 3.10
приведены экспериментальные уровни зеркальных ядер 7Li и 7Ве
и рассчитанные уровни (L/K = 6,8, УК = 1,0 и К = —1,2 Мэв).
Для определенности будем обсуждать спектр уровней ядра 7Li.
Основное состояние 7Li в схеме LS-связи описывается схемой
Юнга [3], отвечающей наибольшей орбитальной симметрии. Со-
гласно табл. 3.5, схеме Юнга [3] сопоставляется супермультиплет,
состоящий из дублетов 22Р [3] и 22Р [3], причем энергия Р-состояния
меньше энергии Р-состояния. Если учесть спин-орбитальное взаи-
модействие как возмущение, оба дублета расщепятся, причем со-
стояние с большим полным моментом $ в каждом дублете будет
характеризоваться меньшей энергией. Так как основное состояние
принадлежит супермультиплету [3], то состояния 22Ру. [31 и 22Р^
[3] являются низшими энергетическими состояниями ядра 7Li.
202
Очевидно, основным состоянием можно считать 22Рз- [31-состояние,
тогда первым возбужденным состоянием ядра ’Li будет состояние
22Р[- [31, т. е. второе состояние дублета 2гР [3]. Выше находятся со-
~Т
ответственно уровни 22F7- [3] и 22Рц- [3]. Четность всех указанных
5Г з~
состояний, в том числе и основного, отрицательна, так как она
SEi
равна л = (—1) ‘ ,Еа три нуклона находятся в оболочке с / = 1.
Состояния, четность которых совпадает с четностью основного
состояния, называют состояниями нормальной
четности.
2iP 5/2'-------[21]
22./\5/2'------
]7/2~------
Е,ИЭ$
ytfl 5/2 5/2'
6.5$ т¥М^1/2\3/2 3/21
5.7—m
ф------7/2-
------7/2~
0/P7S 1/2~
0-------3/2'
7Ll
______1/2-
------3/2'
7ве.
Рис. 3.10. Схема уровней в приближении промежу-
точной связи для А — 7 (слева) и эксперименталь-
ные уровни для зеркальных ядер ’Li и ’Be (справа).
Таким образом, рассмотренные четыре состояния ядра ’Li опи-
сываются конфигурацией (Is)4 (1р)3 и являются состояниями нор-
мальной четности. Экспериментальные значения спинов и четно-
стей основного и первого возбужденного состояния ядра ’Li со-
гласуются с допущением, что эти два состояния соответствуют
дублету 22Р [31. Следующему возбужденному уровню можно со-
поставить состояние 22F--. Если учесть спин-орбитальное взаимо-
2~
действие в первом порядке теории возмущений, то разность энергий
уровней в дублете 22F [31 должна относиться к соответствующей раз-
ности в дублете 22Р [31 как 7 : 3. Отсюда находим, что уровень
22Л5- должен характеризоваться значением энергии от 5 до 6 Мэв.
2~
На рис. 3.10 соответствующий уровень изображен штриховой ли-
нией. Расстояние между уровнями в обоих дублетах 22Р и 22F
значительно меньше энергетической щели между двумя дублетами,
составляющей около 4 Мэв. Это подтверждает правильность допу-
щения о малости спин-орбитального взаимодействия и оправдывает
учет его по теории возмущений.
203
Выше рассмотренных уровней расположены состояния поло-
жительной четности с У = 1/2 и 3/2. Состояния с четностью, про-
тивоположной четности основного состояния, называют состоя-
ниями с аномальной или противоположной
четностью. Эти состояния соответствуют определенным од-
ночастичным возбуждениям с переходом нуклона в другую оболоч-
ку. Так, состояния 7Li противоположной четности (1/2)+ и (3/2)+
с энергией 6,54 Мэв можно описать конфигурациями (Is)1 (1р)3
(Id)1 или (ls)4(lp)2(2s)1, которым соответствует измененное значение
орбитального момента I одного из нуклонов на единицу.
Далее теоретически предсказывается состо'яние нормальной
четности (5/2)“ при 12,5 Мэв. Экспериментально уровень (5/2)"
обнаружен, но при энергии 7,47 Мэв. Согласно схеме LS-связи,
это состояние должно принадлежать другому супермультиплету,
описываемому схемой Юнга [21], и является P-состоянием. По
правилу сложения моментов суммарный спин указанного состояния
S не может быть меньше у (S = — L), поэтому в соответствии
с табл. 3.5 этим состоянием является [21].
Большое различие экспериментального и теоретического зна-
чений энергии для этого состояния можно объяснить, если учесть,
что при высоких энергиях возбуждения (^5 Мэв) в легких ядрах
большую роль начинает играть так называемое смешивание
конфигураций. Мы рассматривали чистые состояния нукло-
нов, когда одночастичные состояния описывались определенными
квантовыми числами nl (или nlj). Смешивание конфигураций соот-
ветствует случаю, когда приходится рассматривать суперпозицию
одночастичных состояний nl (или nlj), энергии которых близки.
При этом следует иметь в виду, что состояния противоположной
четности не смешиваются друг с другом. Например, в случае лег-
ких ядер состояния Id и 2s очень близки по энергиям, поэтому их
рассматривают вместе, представляя соответствующую волновую
функцию в виде линейной комбинации двух состояний. Учет при-
меси других конфигураций обычно приводит к понижению уровня
энергии по сравнению со случаем чистой конфигурации. Поэтому
возбужденное состояние 7Li с энергией 7,47 Мэе можно предста-
вить как смесь основной конфигурации (5/2)" при 12,5 Мэе с дру-
гими конфигурациями.
Задачи
3.1. Найти связь между волновыми функциями трех частиц с различными
схемами векторной связи угловых моментов.
Рассмотрим систему из трех частиц, характеризуемых моментами коли-
чества движения /х, /2 и /3. Эта система может находиться в состоянии, в ко-
тором определенные значения имеют полный момент количества движения
трех частиц проекция полного момента М, суммарный момент первых двух
частиц ^1а. Обозначим волновую функцию этого состояния [(/Ца)^12 .
204
С помощью коэффициентов Клебша — Гордана эту функцию, характеризую-
щуюся набором квантовых чисел Д, /2, /3, ^1а, и Л4, представим в виде
[(il/г)^121'з]м ~ 12М12/3/Н3 |^Л1) f । (Дя11Дя»а | УщЛДг) X
(3.199)
Если задан суммарный момент второй и третьей частиц У23 при тех же значе-
ниях полного момента трех частиц и его проекции М, то это будет другое
состояние системы трех частиц, с другой схемой связи угловых моментов.
Это состояние характеризуется набором квантовых чисел Д, /2, /3, ^аз, 5е и
М, и его волновую функцию можно представить в виде
[/1 (Л 1з)^гз ] м = S ?М) ф - X
т, Л1„
х[2 (Ммз^з 1 ^2зЛ123) Ф,- -1П1 ф,- от1. (3,200)
Функции в обеих схемах связи представляют полные наборы функций, и од-
ни из них можно выразить через другие. Например,
[/1 (/2/3/вз]м = 2 /(2^13+i)(2^33+ 1) JF ^1а 7зз) X
/12
X [(/1/а/1г/3]£. (3.201)
Коэффициенты преобразования WfJij^ja, /12, ?аз), входящие в (3.201),
называются коэффициентами Рака. Их можно выразить через коэффициенты
Клебша — Гордана. Для этого достаточно совершить обратное преобразова-
ние и выразить произведение трех одночастичных функций ф, mi, и
sr jc 1
Ф/>та, например, через функции [(Д/а) 12 /3]д/, а затем подставить получен-
ное выражение в правую часть равенства (3.200). В результате получим
pWla+l)(2/23 + 1) 1F (ДД/Д; Jla /23) =
== 2 (11«г1/2тз I /12^1 —т2) (У 12mt+msisM — 1 /Л1) X
X (Д/Па/зМ—mi —1 У23,М- mJ (/pni/23M — mi | ?М). (3.202)
Вместо коэффициентов Рака часто вводят так называемые 6/-символы
Вигнера, характеризующиеся более высокой симметрией при перестановках
моментов:
I h?/isi /п/зз)- (З.203)
'/з/.-ХгЗ '
6/-Символы Вигнера инвариантны относительно любой перестановки столб-
цов, а также относительно перестановок любых двух моментов первой
строки с соответствующими моментами второй строки.
3.2. Найти коэффициенты преобразования между волновыми функциями
в схемах LS- и //-связи.
Так как ’F((A[X]apLSTAfLAfsA-fT) и TO^A.Ja'st/T’MMj.) представляют
собой полные наборы функций соответственно в схемах LS- и //-связи, то каж-
дую из этих функций в одной схеме связи можно однозначно представить в
виде линейной комбинации волновых функций в другой схеме связи. Осо-
бенно просто коэффициенты такого преобразования находятся в случае двух
частиц. Рассмотрение можно обобщить на случай неэквивалентных нуклонов
205
с различными орбитальными моментами а также на случай частиц с произ-
вольными спинами в;.
Коэффициенты преобразования между волновыми функциями двух ча-
стиц В схемах LS- и //-связи, которые соответственно обозначим через
[W (/2s2)/e1^ и I(Zi/2)£-(sis2)s]^ .легко найдем, осуществив ряд последова-
тельных перестановок порядков векторного сложения четырех угловых мо-
ментов, от которых зависят волновые функции. Таким образом, задача сво-
дится к нахождению связи между волновыми функциями четырех частиц с
различными схемами векторной связи их угловых моментов.
Используя формулу преобразования, в которой волновая функция с
тремя угловыми моментами а, Ь и с, векторно связанными в одном порядке,
выражается через волновые функции с теми же моментами, но связанными
в другом порядке:
= + Г е£/) [(^ XflL (3.204)
е
можно последовательно написать:
[(Л S1)/' (l2ssy^ =
_ V у (2л 4-1) (2/s+"l) W s2; а/й)[(Sj)71 Zs)a s2] + =
a
= 2 (-])2'*+'*~u+;‘-L /(2a“+ 1) (21 + J) (2Л 4-1) (2/г4-1)
a, L
X W (hl^s2, ah') w (lihasx, L)\) [((Zt Z2)L sI)as2]/ =
Z1 Sjl ji'
</2s2/4 {(Zi /2)^ (siS2)
IS/
= 5/(2/i+1)(2j2+1)(2L+1)(2S+ 1)
LS
(3.205)
и, таким образом, получить искомый ответ. При написании последнего ра-
венства мы воспользовались так называемыми 9 /-символами Вигнера, кото-
рые связаны с коэффициентами Рака следующим образом:
(Zi Si/i j
Z2 з2/2 =2(-1)'‘42'!^/1-^Я(2«+1)Х
as/) п
XW аа; aj2) М/(Z2Ziasi; L/4) W (LS1/s2; aS). (3.206)
(<i si /i )
9/-Символы Вигнера </а s2 /2} инвариантны при отражениях относитель-
a S /J
но двух их диагоналей и при любой нечетной перестановке строк или столб-
цов они приобретают лишь множитель (—1)°, где о есть сумма всех девяти
моментов, входящих в 9/-символ. Если полуживую формулу преобразования
(Zi Si /1’
Z2 s21г
L'S’?,
пользоваться ортонормировкой 9/-символов
, просуммировать no /i и /2 и вос-
2 (2/1 + !) (2/2 + О
id.
ti Si /1
Z2 s2 j2
LS?
A Mi
Z2 s2 j2
A'S'/,
6. , ,
-----—““-----------, (3.20?)
(2L+ 1) (2S4- 1)
206
пб^учиМ обратйое преобразование
К'лЛ (^)5]£ -
Л1
pi ’
= 2^"(^ + I) ^ii + О (2/а + 1) 1si ss S
hi‘ liiia.
[(/iSi)'* (Ш!'г]%- (3.208)
Чаще всего используются формулы преобразования для двух частиц.
В случае большего числа частиц соотношения значительно усложняются,
гак как при классификации состояний необходимо использовать дополнитель*
иые квантовые числа, от которых будут зависеть И коэффициенты преобразо-
вания от одной схемы связи к другой.
3.3. Выразить многочастичный матричный элемент от суммы одночастич-
ных сферических тензорных операторов через приведенные одночастичные
матричные элементы.
Сферическим тензором ранга I, или неприводимым
тензорным оператором ранга I, называется совокупность (27 +
+ 1) операторов V1М, где М = —I, —7 + 1, ..., 7 — I, I, которые преобразу-
ются при вращениях по неприводимому представлению D1 группы вращения
^1М ~ м W Ъм' ’ (3.209)
м-
т. е. преобразуются таким же образом, как и волновые функции с угло-
вым моментом 1. Любой оператор можно представить в виде линейной
суперпозиции неприводимых тензорных операторов. Основное свойство сфе-
рических тензоров определяется теоремой Вигнера — Эккарта, согласно
которой матричный элемент от сферического тензорного оператора по волно-
вым функциям с определенными угловыми моментами всегда можно предста-
вить в виде произведения двух множителей, один из которых содержит в
явном виде всю зависимость матричного элемента от магнитных квантовых
чисел:
| VlM j а /гп) =
(-1)2'
Ф'2(“Г
(а'/' || (falM | /'/«'),
(3.210)
где а и а' —дополнительные до полного набора квантовые числа в началь»
ном и конечном состояниях. Здесь <а'/' ||«;> —так называемый при-
веденный матричный элемент, который можно найти из
(3.210), вычисляя левую часть равенства (3.210) при каком-либо одном возмож-
ном наборе магнитных квантовых чисел т, tn' иМ.
Рассмотрим сферический тензорный оператор ранга т, действующий на
пространственные координаты одного i-го нуклона l/xv (t). Вычислим матрич-
k
ный элемент от суммы тензорных одночастичных операторов 2 V\v (i) по обо-
[=1
лочечным волновым функциям k эквивалентных нуклонов. Выделяя с помо-
щью полных одночастичных коэффициентов родства состояние одного нукло-
на, матричный элемент можно представить в виде
(V (1* [X] o$LSTMlMsMt)
k I _________ _
2 VTV (i) 4(1* [i^LST^ Ms MT)y =
= fc 2 (z*“‘ M [XjapLST) X
207
X (lk~ 1 [X']a'p'£'S'7"; /s/|} /‘W ap£ST)x
X У j IML) (L'ML/m | LMl) X
Mk mm
Л -i 6 ~ . (3.211)
' ** о о i J M$M$ MtMt
Используя свойства сферического тензорного оператора, можно в одночастич-
ном.матричном элементе выделить зависимость от магнитных квантовых чисел
(теорема Вигнера — Эккарта):
(nlm | Vtv | nlm) —
(-1)т
/21+1
(3.212)
где (ni||Vt|| nl) — приведенный матричный элемент. Выражая сумму по маг-
нитным квантовым числам от произведения трех коэффициентов Клебша —
Гордана через коэффициенты Рака
2 [L'Ml LM^) (L'M'Llm | ~LMl) (rv/m| Im) —
= ( —l)TK(2i+l)(2i. + l)(£AlL-VTv|£AfI) ТГ (т/££'; IL),
окончательно получаем для матричного элемента выражение
। k
(1к [X] ap£SrMLMs А/) 2 /v (О
| i = 1
V (f* [X] a P £ S TML Ms A/)) =
= k 2 (‘ a'P'£'ST'; 1st | } ik [X] ap£ST) x
[V]a'₽'
L’S‘T'
X (lk~ 1 [X'J a'P'rST'; 1st ( } I* [XJ afiLST) X
X VlT+ 1 (£ ML- wv | £Ml) U7 (ilLL'; il) X
' U 111 J SS TT Mг Л1 у
(3.213)
3.4. Выразить матричные элементы от двух частичного центрального по-
тенциала через интегралы Слэтера F1.
Вычислим матричный элемент от двухнуклонного потенциала V(q — г2)
с помощью двухиуклонных волновых функций с определенным суммарным
орбитальным моментом:
<«!< <Z'£'M'| =
sprjdrj 2 (l\m\G m2 | LM) ("Л У//та' ("2)1 X
Lmi' J
x <₽„/,' (n) <Pn ' i ' (гг) V (п—Гг) Г 2 | LM) x
11 2 2
X Yti (ni) Г,>т! (n,)] (rx) <pMe (rs) 8ll, 6^,. (3. 214)
Подобные матричные элементы встречаются при диагонализации матрицы
гамильтониана в приближении промежуточной связи. Используя разложение
208
двухиуклонного потенциала по полиномам Лежандра (3.197) и теорему сло-
жения сферических функций
Pl (П1 П2) = /ЙТГ 2~ т 100) r'm (П1) Y‘-m
нетрудно выполнить интегрирование по углам векторов пх и па. Суммы по маг-
нитным квантовым числам от произведений коэффициентов Клебша — Гор-
дана можно свести к коэффициентам Рака. Введя, согласно определению
(3.198), интегралы Слэтера F1, получим следующую формулу для матрич-
ного элемента:
(nj/; n'2l'2L’ Mr I V (гх — rs) I n1liniltLM') =
= (^l)'i' Ha-L/(2/1 + l)(2/2 +
x 2 f'B7 (/?2M2; ь/)(/хо/о|/Jo) (z2oro| /'o). (3.215)
1=0
В частности, если оба нуклона находятся в 1 р-оболочке (п^ = п% = пх' =
=л8' = 1, /j — 1а = 1/ = la' = 1), то сумма по I содержит только два сла-
гаемых I = 0 и I = 2, поэтому матричный элемент будет выражаться через
два интеграла Слэтера F° и F®, (Напомним, что коэффициент (10/0|10) отли-
чен от нуля только для I = 0 и I — 2).
3.5. Определить одночастичные коэффициенты родства в случае сме-
шанных конфигураций.
Рассмотрим нуклонов в оболочке с орбитальным моментом и ka нук-
лонов в другой оболочке с моментом Используя схему LS-связи, состояние
системы fej -ф- k2 нуклонов можно описать функцией
[Ф (/** aALAT,) Y (ф [М aa₽sLsS2r2)]^5 мТ • (3.216)
которая является связкой функций для Отдельных оболочек, соответствующих
чистым конфигурациям. Указанные в (3.216) квантовые числа характеризуют
состояние всей группы -ф- й3 нуклонов. Однако состояние рассматриваемой
смешанной конфигурации можно задать и другим способом, а именно можно
задать схему Юнга [X] всех -ф- йа нуклонов, при этом соответствующая вол-
новая функция представится в виде суммы состояний (3.216). Полная схема
Юнга [А] может принимать лишь такие значения, которые появляются в раз-
ложении согласно правилу Литтлвуда.
Введенные волновые функции должны быть антисимметризованы отно-
сительно перестановок всех нуклонов. Внутри каждой оболочки функции ан-
тисимметричны, поэтому антисимметризация должна быть проведена по от-
ношению к перестановкам нуклонов из разных оболочек. Введем оператор
антисимметрнзации
4=^(-1)₽Р, (3.217)
где суммирование проводится лишь по перестановкам Р нуклонов между раз-
личными оболочками. Пусть (—1)^ = 1, если Р— четная перестановка,
и (—1)^ = —1, если Р — нечетная перестановка, причем номера нуклонов
в каждой оболочке после перестановки должны быть поставлены в возраста-
„ (fei + Аа)!
ющем порядке. Полное число таких перестановок равно-. , , ,—.
209
Полностью антисимметричная нормированная волновая функция перво*
го типа имеет вид
мт (^* [М] «iPxbiS 1Т1, [к2] a2p2£2S2T2) =
- |/(fe^ , л [Г (/** [Ad aAWx) Т (/*• [Ad a2|₽2W2)]^fs
(3.218)
Эта формула устанавливает связь между волновыми функциями смешанных Ф
и чистых конфигураций ЧЛ
Введем теперь коэффициенты родства для смешанных конфигураций.
При отделении состояния одной частицы в функции первого типа нужно ввести
два одночастичных коэффициента родства для отделения нуклона сначала от
одной оболочки, а затем от другой:
^f^Ms [Ail alPiAiSiT’i, /*г [Aj] a2Pa^SaT’j) =
=“ У ([^‘ 1 [Aj otj Pj L( Sj Tp /2S [Azl ot2 P2I-zS2T2]i' 5 T , X
L'S'T'
X G I ) pl1 [Ad «1 PAS!?!, [A2]aap2L2S2T2]LSr) X
x^l-s'T'^.-1 ф[a2]y2
+ ([ г1‘ [Ail ai Pi A* Sj Тг12г 1 [A2]a2 p2Ls S2 T2]l s r , X
14] a2 ₽2L2S2 Г2
L'S'T'
X l2 I } [Ф [Ad «1 PiLiSiTn ф [A21 a2p2L2S2T2]LSr) x
X ((‘чМ^МЛ. ф~1 [A;]a2₽'L's2T') <p/s]^$JVfr.
(3.219)
Сюда входят связки функции Ч'^" 5 !' для kr + k2 — 1 частиц и <р!1 или ф(‘
для одной частицы, причем структура функции s г подобна структуре
полной волновой функции смешанной конфигурации ^LST для kr + k2
частиц.
ч3.6. Установить связь между коэффициентами родства смешанных и чи-
стых конфигураций.
Эту связь можно установить, используя связь между волновыми функ-
циями смешанных и чистых конфигураций. Рассмотрим смешанную конфигу-
рацию из двух оболочек и для определенности вычислим одночастичиый коэф-
фициент родства для отделения одного нуклона из второй оболочки, т. е.
коэффициент, стоящий во второй сумме выражения (3.219). Умножая скал яр-
ко связку, стоящую во второй сумме (3.219), на все выражение для волновой
функции (3.219), получаем
([Ф l?‘i] ai Pi A| Sj Т।, l2‘ 1 [A2] a2 p2 L2S2T2 l s t , /2 | ] X
X p*1 [Ax] a1pi£1S17’1, /2‘ [A2] a2 ₽2L2S2T2 J =
- (/*‘ [AJ MAVi, l2~l [Ai] x
X [Ad Z^[A2]a2p2£2S2T2)>, (3.220)
210
где в правой части мы опустили у связки н функции магнитные кван-
товые числа, от которых все выражение уже не будет зависеть.
Используя (3.218) и (3.217) и выделяя во второй оболочке функции yLSr
с помощью одночастичных коэффициентов родства состояние одного нуклона,
функцию 4fLS7' для k} + k2 частиц можно представить в следующем виде:
S(-lf-P 2 (/2s"'1(^2]«2p2iaS27'2;
(fei + fe2)l P
< [k2] a2 p2 La S2 T2) [T ( if* [XJ ax px Lr Sr 7\) X
X [V ( ф ~ 1 [Xsl a2 P2 Г2 S2 Ts ) qA]L’5! LST.
(3.221)
Связав моменты с помощью коэффициентов Рака в другом порядке,
функцию удобно записать следующим образом:
2<-1)₽РХ
Р
X Ог’ ЧХа1 а2 р2 L2 S2 Т2, /2 [ } ^2![Х2] а2 р2 L2 S2 X
(XgJ CSa фа Т'а
Х_ 2_ /(2 р + 1) (2L2+ 1) (2 S' + 1) (237нЛ)“(2 г + 1) (2Т2 + 1) X
L' S' Т'
XV^U,; T'LjW S'S2 j W ( 7\ Т'г T-j- ; Т'Тг^ x
X [[T (if* [M at p2 Lt Sx Л) T (if* - 1 [X21 a2 p2 L2 S2 T8)]L’s'T' <₽'*]LST .
(3.222)
Функцию для 61 + ^2 — • частицы, которая входит в (3.220),
также выразим через функции чистых конфигураций:
YL-S'T’ = 1/ -kjfe —1)!
V (й1 + *2-1)! Л
x£(_lfP' [4r(/f‘M«1P1L1S1T1)x
P'
XV(/f=-][X'] a2f2L2S2 T2)]l'S't'. (3.223)
Здесь перестановки P' затрагивают во второй оболочке только k2 — 1 частиц.
После подстановки (3.222) и (3.223) в правую часть равенства (3.220) мы
будем иметь под знаком суммы скалярные произведения однотипных связок
трех функций соответственно частиц, k2 — 1 частиц и одной частицы. Ис-
пользуя орто нормировку этих связок, после уже несложных преобразований
и суммирований из-за символов Кронекера получим следующее выражение
одночастичного коэффициента родства смешанной конфигурации через одно-
частичный коэффициент родства чистой конфигурации:
([**’ lAl] “1 12г 1 [^2] а2 5 Г ’ 12 | } х
X [if- [М] «I ₽1 L1 Si Л, Ip [М а2 р2 Ц S2 T2]LSr) =
= 1/ (2L' + ’) (2La +1) (2S' + 1 )(2S2 + 1) (2Г +1) (2Т2 + 1) х
Г *1 + «а
211
L'/JW'^Sy; S' S2) V T2' T; T'T.jx
х('2!^' [Хг] a2P2L2S2r2; ^>1 ПЧМагМзЗзЛ). (3.224)
Подобным образом можно выразить миогочастичный коэффициент род-
ства смешанной конфигурации в общем случае для одновременного отделения
нуклонов из нескольких оболочек (чистых конфигураций) через коэффициенты
родства чистых конфигураций. Если мы имеем смешивание двух конфигура-
ций, то при выводе соотношения, подобного (3.224), можно будет в общем
случае пересвязывать четыре момента, и вместо коэффициентов Рака (6 /-
символов Вигнера) в окончательной формуле будут стоять 9 /-символы Виг-
нера и, кроме того, будет не один (как в нашем случае), а два коэффициен-
та родства чистых конфигураций для отделения нуклонов из каждой (из
двух) оболочки.
3.7. Определить магнитный момент ядра, содержащего k нуклонов во
внешней незаполненной оболочке.
Магнитный момент ядра в основном состоянии р определяется средним
значением оператора проекции на ось z суммарного магнитного момента k
эквивалентных нуклонов, находящихся во внешней незаполненной оболочке:
2 4,’) + g{i) 4°), (3.225)
i= I
где
^') = (1-т^))Рп+(Ч'Ч*))ир, (1+т*0)-
Выберем волновую функцию основного состояния в виде
То [X] apLS^TMMr) = (lml SMs | ?м) т И a$LSTML Ms Мт)
mlms
и определим среднее значение (3.225) в состоянии, в котором проекция полного
момента М на ось г равна максимально возможному значению 7-
Так как pz есть одночастичный оператор, симметричный относительно
перестановок нуклонов, удобно в волновой функции k частиц выделить с по-
мощью одночастичных коэффициентов родства волновую функцию одного
нуклона. Одночастичная функция является собственной функцией операторов
тг, sz и /г и соответствует собственным значениям v, р и т. Следовательно,
М- — I Р-i I ~
=k 2 a'p'L'S'T'; /sd] Z*[X1 ар£ ST)2x 2 (LMlSMs\^^)2x
[X.']a'p'£'S'T' MLMS
х 2 (^Xyv|™J2X 2 (s'Ms|p!SAfsy
X {[(I —2v) pn+(l+2v) Pp] p + у d + 2v) m}. (3.226)
Используем соотношение
V ' < ' Ч«||Л| A< + *) + /'(/’ + •)“"/(/ + 1)
S.” --------х
хд (/7'7) Д (771) Л (/'/' 1),
212
которое нетрудно доказать, заменив множитель т' в левой части равенства
на — (10j'm'| j'm') + 1). Множитель Д(//'£9 равен по определению еди-
нице, если три момента j, j’ и У удовлетворяют соотношению треугольника
(|/ —. у'| < у < j -|- )'), и нулю в противном случае.
Таким образом, для магнитного момента ядра, рассматриваемого по обо-
лочечной модели с LS-связью, получим следующую формулу:
2 [V] а'р'£'5'Г;
+ 1 [Г]а'3'£.'5'Г
[Ь] ар LST)!
ХД(7Т1)
п 3
S(S4-1)-S' ($' + !) + -
--------------------[^(7 + D + S(S+l)-£(£+I)]A(SSl)+
» (5+1)
Г 3 -|
t Т(Т+1)-Т' (Г + 1) + -
+ [_7 + Л4т--------------------А(ТТ1) X
2Г(Т+1)
L (£+1) + / (/ +1) — £' (L' + 1)
Х 2£(£+1)
\У (^ + 1) + £(£ + 1)-
— S (S + 1)] Д (££1) А (//1)
(3.227)
Согласно (3.227), для нахождения магнитного момента необходимо знать
некоторые квантовые характеристики ядра. В табл. 3.7 приводятся численные
значения магнитных моментов ряДа легких ядер с заполняющейся 1 p-оболоч-
кой (I = 1), вычисленные по этой формуле. Там же указаны состояния нук-
лонов в 1 р-оболочке ядра (p*[A,]2T+l’2S+l
3.8. Определить собственные волновые функции и собственные значения
энергии для нуклона, движущегося в поле трехмерного анизотропного осцил-
ляторного потенциала. Сделать переход к осцилляторному потенциалу с ак-
сиальной и сферической симметриями.
Гамильтониан частицы, находящейся в поле трехмерного анизотропного
осцилляторного потенциала с различными частотами ®1( ш2 и <о3
да М
Н = “ТТГ Д - V«++’ (°!2 г2), (3.228)
2М 2
неинвариантен относительно вращений, так как потенциал не обладает цент
ральной симметрией. Состояние частицы в таком поле не характеризуется
определенным орбитальным моментом. Так как гамильтониан (3.228) разде-
ляется в декартовых координатах, то решение уравнения Шредингера
Яф(г) = £ф(г) (3.229)
следует находить в виде произведения
ф (г) = ф(" (х) ф*2) (у) ф(3* (г)- (3.230)
При подстановке (3.230) в (3.229) для каждой из функций получаем
уравнение, например
аз М i
-Ц- + — ф(1> (х)=0 (3.231)
2М dx2 2 1 у и
213
Таблица 3,7
Ядро Состояние 1 р-оболочки Магнитный момент JX
fHe P1 [ip* j° 3- Pn=-l,91
3Li P1 [l]22^ 3- 2 pp+1=3,79
®Li p*[2]13Si + Hn + Pp = 0,88
'Li P3 [3]22 P 3- 2 Цр + т" =3,12
4 Be P3[3p2P3_ 2 2 Pn + 7 = —1,24 О
P5 [41122 P 3_ 2 1 Pn + —= —1,58 О
‘«В Pe [42]13Dg+ Bn + Hp +1 = 1,88
’sB p7 [43]23 p 2 2 Bp ‘ T =3,46 •
13r 6^ p9 [441]22 P r 2 1 4 -3 Pn+9 —1,08
>?N psI441]22P 1 2 -TBp+ ^- = —0,71 О У
p1(,[442]13D]+ 1 , , 3 — 2 (Вп + Вр) + ~ =0,31
>®N pll[443]S2P r 2 1 2 — q Bp+ , =—0,26 «5 о
и аналогично для 1|/2^ (#) и (z). Отметим, что физический смысл имеет
лишь полная энергия:
з
£=-V04-Sei- Обозначим
f=i
5“=ег: (3-232>
214
й введем функций
—
Я(£)=е4 ф(1>, (3.233)
тогда для //(;) из (3.231) получим следующее уравнение:
+ (3.234)
3g а& \ 2 J
Решениями полученного уравнения являются полиномы Чебышева — Эр-
мита:
II _1L
HniU) = (-l)n‘e2 2, (3.235)
где ₽i — ’/2 = «1, «1 — целое неотрицательное число. Полиномы Чебышева —
Эрмита обладают свойством ортогональности:
°° _ V. _
f dge 2 WAU)Hi(6)=/2nftl6fei.
Таким образом, ортонормированные собственные функции гамильтони-
ана (3.228) можно представить в виде
К 4,4, W = <l? W 'С (У) (?)=
/а,2 а,2 а32\'Г/ , , п—Г “V (а12^+а,2г/г+а32г2) и / л
- I 4 (Пх! Ла1 П31) 2е 2'1 a Ял1(/2а1х)х
\ лэ /
ХЯл,<Г)2а2г/)Я„,(/2а3г), (3.236)
при этом собственные значения энергии равны
^nin2nj ~ — Vo-j-fitOj (nx+1/2) (га2 +1 /2) -ф-h w3 («з+ 1/2), (3.237)
где пг, п3 и п3 — неотрицательные целые числа. Из (3.236) и (3.237) видно,
что в случае анизотропного осцилляторного потенциала различным наборам
квантовых чисел пх, п2 и п3, определяющих состояние, соответствуют, вообще
говоря, различные энергии. Вырождение при различных частотах со; может
иметь место только при определенных соотношениях между частотами, на-
пример, когда одна из частот кратна другой и, в частности, когда две или все
три частоты равны друг другу.
Если ых = ы3 = <а', то гамильтониан (3.228) инвариантен относительно
вращений вокруг оси z (аксиальная симметрия), поэтому состояния нуклона
в таком потенциале можно характеризовать проекцией орбитального момента
на ось z и решение ф(г) уравнения (3.229) следует находить в виде произ-
ведения
ф(г)=Ф(ср)х(р)ф<3)(г), (3-238)
1
где Ф(<р) =
e?m<p уравнение (3.229) в этом случае разделяется в пере-
менных <р, р = у х2 4- у2, z, т. е. в цилиндрических координатах. Функции
(3.238) с заданным главным квантовым числом N — + п2 + н3 являются
„ / М со'
линеиными комбинациями функций (3.236) с cq = а2 — 1 / ___ , Для ха-
V Л
рактеристики состояния, описываемого такой функцией, можно выбрать три
квантовых числа: N, п3 и гп, или п± -_2 N — п3, п3 и т. Здесь т — собствен-
215
ное значение проекции орбитального момента нуклона на ось симметрии пола,
принимающее значения: ±(/V — л3), ± (N — п3 — 2), ±1 или 0- При
этих значениях т функции (3.238) и (3.236) при заданном N преобразуются
одинаковым образом при преобразовании инверсии г -»• — г (при этом
Ф л + <р). Итак, в случае осцилляторного поля с аксиальной симметрией
собственные функции имеют вид
1 1 4/ а,4_—а г2®
Ч”<Р)/5Г И Vе 1 ».»)
ГДе ^rt±'n (Р) удовлетворяет двумерному волновому уравнению с осцилля-
торным потенциалом. В случае аксиальной симметрии собственные значения
энергии не зависят от т:
в. V° + Гги>' (л±4-1)-1"Й®з («з + 1/2). (3.240)
Кратность вырождения в случае аксиальной симметрии равна дх+ 1 = rij +
+ п2 + 1 = N — n3 + 1,
В случае изотропного осциллятор нога потенциала, когда <ах = <в2 =
= ы3 = о (сферическая симметрия), собственные значения энергии (3.237)
зависят лишь от суммы квантовых чисел: лх + пг + п3 = Д', т. е. мы прихо-
дим к выражению (3.26). Уровню энергии EN соответствует (,V 4* 1)(W Т 2)/2
состояний, каждое из которых описывается волновой функцией (3.236) с
одним из возможных наборов трех квантовых чисел «j. na, п3, удовлетворя-
ющих условию пх + п2 + п3 = JV:
® __L _Да2г3
[ «2 X 4 2 2
= ) («11 ns0 е Я„Д/2ах)х
хЯЯ!(1/МяПз(У2аг), а-j/ (3.241)
Полученные функции не соответствуют определенным значениям орбиталь-
ного момента. Однако, выбирая определенные линейные комбинации из по-
лученных функций, можно построить набор (/V + 1) (JV + 2)/2 новых функ-
ций, соответствующих определенным значениям орбитального момента. Со-
гласно табл. 3.1, определенным значениям главного квантового числа А' в
общем случае соответствует несколько значений орбитального момента I.
При небольших значениях N все возможные значения I можно найти,
используя свойства функций
//;1|(—^)—(— 1)"'y/ri£ a), nm(-n)r=(-i)‘ylm(n)
и то, что I < N. Например, при N = 3 функции Ф„1ПгПJr) При отражении
меняют знак, поэтому из них можно составить линейные комбинации, отвеча-
ющие нечетным орбитальным моментам. В данном случае возможны значения
I ~ 1 и 3, так как полное число независимых функций 2(21 + 1)= 10 должно
равняться кратности вырождения V2 (Л1 + 1) (ЛГ + 2), что согласуется с дан-
ными табл. 3.1. В общем случае при заданном N возможны все значения I <
-< отличающиеся друг от друга на две единицы, т. е. удовлетворяющие
условию (—1)Л/~^1.
ГЛАВА 4
ВРАЩЕНИЕ И КОЛЕБАНИЯ
ЯДЕР
§ 4.1. КОЛЕБАНИЯ СФЕРИЧЕСКИХ ЯДЕР
Деформации поверхности ядер. Рассмотрим состояния, свя-
занные с возбуждением коллективных степеней свободы ядер.
Оболочечная модель ядра основана на упрощающем предположении
о независимости движения отдельных нуклонов, взаимодействие
между которыми описывается самосогласованным полем. Капель-
ная модель ядра была основана на предположении о наличии силь-
ной связи между нуклонами, в результате которой длина свободно-
го пробега нуклона в ядерном веществе оказывалась малой величи-
ной по сравнению с размерами ядра. Если в оболочечной модели
ядра рассматриваются одночастичные возбуждения, связанные с
изменением состояний отдельных нуклонов, то в капельной модели
ядра учитываются коллективные возбуждения, связанные с одно-
временным изменением состояний многих нуклонов. В основе так
называемой обобщенной модели ядра, являющейся
синтезом оболочечной модели и капельной модели, лежит предполо-
жение о независимости движения отдельных нуклонов в медленно
изменяющемся самосогласованном поле. В этой модели, так же как
и в оболочечной, учитываются степени свободы, связанные с дви-
жением одного или нескольких слабо связанных нуклонов в само-
согласованном поле. В обобщенной модели, так же как и в капель-
ной, учитываются коллективные степени свободы, связанные с из-
менением формы и ориентации ядра в пространстве. Обычно в обоб-
щенной модели предполагается, что внутреннее и коллективное дви-
жения разделяются, поэтому они рассматриваются независимо*.
Так как ядерное вещество характеризуется малой сжимаемостью,
то коллективное движение нуклонов в ядрах сводится в основном
к деформациям формы ядер без изменения их объема. В случае сфе-
рических ядер коллективные возбуждения соответствуют колеба-
ниям поверхности ядра относительно равновесной формы. В несфе-
рических ядрах коллективные возбуждения могут быть связаны с
колебаниями поверхности ядра и его вращением в пространстве.
Рассмотрим произвольную деформацию поверхности ядра, оп-
ределяемую в сферической системе координат функцией ср).
* Обобщенная модель ядра была предложена Бором и Моттельсоном
[1, 2]. Детальная теория коллективных возбужденных состояний ядер изло-
жена в монографии [3].
217
Величина 7?(ft, <р) представляет собой расстояние от центра ядра
до его поверхности в направлении полярных углов О и <р, отсчитыва-
емых в лабораторной системе координат. Разложим эту функцию
в ряд по сферическим функциям Kxy.fft, <р);
Я(ft. ф)-П-| У «лц П.ц (№, <р)1 R, (4.1)
I хн 1
где 7? — радиус равновеликой сферы; а?.^ — параметры дефор-
мации, характеризующие форму деформированного ядра. Так как
/?(ft, ф) вещественно, то параметры деформации ctj^ должны удов-
летворять условию
«гщ =(— 1)ца^-ц. (4.2)
Рассмотрим малые отклонения от сферической формы ядер.
В случае небольших отклонений от сферической формы параметры
деформации — малые величины. Если ядерное вещество несжи-
маемо, то из условия сохранения объема вытекает равенство
«00 = — (IMrOUaud2, (4.3)
из которого следует, что параметр а00 является величиной второго
порядка малости. Параметры а1]Л можно считать равными нулю,
так как деформация (4.1) при К = 1 соответствует смещению ядра
как целого в пространстве. Заметим, что возможные значения X
ограничены сверху (X < А1/3), поскольку линейные размеры эле-
мента поверхности ядра должны быть больше среднего расстояния
между нуклонами. Таким образом, поверхностные деформации ядра
характеризуются конечным числом параметров деформации а?|Х.
Наибольший интерес представляют эллипсоидальные деформации
поверхности ядер, отвечающие значению Л = 2.
Кинетическая Т и потенциальная V энергии поверхностных ко-
лебаний ядра в случае малых деформаций определяются следую-
щими общими формулами;
7,= (l/2)SBx|«xJ2; (4.4)
V =(1/2) (4.5)
Mi
где коэффициенты В-,, и Q зависят от конкретных предположений
о свойствах ядерного вещества.
Рассматривая ядро как каплю идеальной несжимаемой заряжен-
ной жидкости, можно показать, что в случае безвихревого движения
этой жидкости массовый коэффициент В;. равен
BX=(P/W. (4-6)
где р — плотность ядерного вещества. Коэффициент деформируе-
мости С\, в случае равномерного распределения заряда ядра по объ-
ему определяется выражением
Сх= (X-1) (X + 2) оВ2—(3/2л) [(X- 1)/(2Х + 1)] -(Z2 е2/Я), (4.7)
2}8
где о — коэффициент поверхностного натяжения, связанный с ко-
эффициентом е2 в формуле Вайцзеккера (2.17) соотношением
4лаЯйа = ег, /? = 7?0Л|/3.
Потенциальная энергия ядра (4.5) является суммой поверхност-
ной и кулоновской энергий. Поверхностная энергия минимальна
для сферы и увеличивается по мере отклонения от сферической сим-
метрии. В результате сил кулоновского отталкивания ядро, рассмат-
риваемое как капля заряженной жидкости, стремится принять асим-
метричную форму. Согласно (4.5), ядро в равновесии имеет сфери-
ческую форму, устойчивую относительно деформаций, если коэффи-
циент деформируемости 7> 0. Используя (4.7), получаем условие
устойчивости ядра по отношению к малым деформациям:
(A. + 2)a/?2>(3/2n)-(Z2e2/(2X+ 1) R). (4.8)
Полагая л = 2 и используя значения параметров (2.17), имеем
(Z2M) < 48. Это условие выполняется для всех известных ядер.
(Например, для элементов конца периодической системы отношение
Z?IA равно 35,6 для 928U; 36,5 для 942Ри; 37,8 для дв4Ст; 39,0
для 986Cf; 40,3 для pjoFm и 41,0 для ?q?Mv.)
Поверхностные колебания сферических ядер. Рассмотрим ма-
лые колебания поверхности сферического ядра. Динамическими
переменными в этом случае явлйются параметры деформации
которые можно рассматривать в качестве обобщенных координат.
Энергия колебаний поверхности
£=1 ^{Bz|czztl|--G.|^r2} (4.9)
зависит от обобщенных координат и обобщенных скоростей
«Mi- Переход от классической энергии Е к квантовому оператору
Гамильтона Н можно осуществить, вводя обобщенные импульсы
я^^дЕ/да^ --Вк a*KVL, (4-Ю)
канонически сопряженные с координатами и постулируя пере'
становочные соотношения между величинами a>.Jt и л^, которые
следует считать операторами:
1 — (^ Д)1 (4 11)
аХ'ц'] — [Дмо Л'Х'ц' I = 0J
Полученный таким путем гамильтониан поверхностных колебаний
ядра
Д=(1/2) 2{(1/Вх)|лхи|2 + Сх{ахи12} (4.12)
Ар.
имеет вид суммы гамильтонианов для несвязанных гармонических
осцилляторов с собственными частотами:
= У(Ск/Вк). (4.13)
219
Собственные значения энергии поверхностных колебаний ядра,
согласно (4.12), представляются в виде суммы энергий отдельных
осцилляторов:
Е (нхд+ 1/2)7шх, (4.14)
где пхц — целые положительные числа. При переходе ядра из од-
ного состояния в другое энергия изменяется на величину, равную
сумме величин, кратных Очевидно, величины пьц определяют
числа элементарных возбуждений определенного типа Ар., харак-
теризуемых энергией При заданном значении А величина р
принимает 2А + 1 различных значений (—А <2 р А), поэтому
возбужденные состояния с фиксированным значением А характе-
ризуются (2А -ф 1)-кратным вырождением.
Элементарные возбуждения поверхностных колебаний ядра
можно рассматривать как квазичастицы — фон отгы. Задавая
числа фононов каждого типа, мы тем самым определим возбужден-
ное состояние ядра, обусловленное поверхностными колебаниями.
При рассмотрении возбужденных состояний ядер, связанных с по-
верхностными колебаниями, удобно использовать представление
чисел заполнения. Для этого вместо операторов и ллц введем
новые операторы Ь^:
ЛХд= i [^-(- 1)И \
(4.15)
Используя (4.11), нетрудно получить перестановочные соотношения:
(’j/p.'] бщх'* 1 /д ifi’i
из которых непосредственно следует, что операторы и
представляются в виде матриц:
/0 / 0 /1 0 0 ... 0 0 ... \ /27.0 0 ... \ '0 0 0 ...0 0... 1 /Т00...0 о... .
0 0 0 ...00 ... 0/20...0 0... (4.17)
. 0 0 о ... о/ЛГц... I 00 0 ...0 0...
\0 0 0 ... 0 0 ... / 1 0 0 0.../пхц0 /
Подставляя выражения (4.15) в (4.12), получаем гамильтониан си-
стемы в виде
(4.18)
\ 2 /
220
Волновая функция в представлении чисел заполнения (в случае
фононов) зависит от числа фононов в каждом состоянии Ар,
и ее можно записать в виде
• "An ' ^>40 • • ) =
.••Ки1 nA2ll3... | (4.19)
где Пхц—квантовые индексы состояния, a — индексы пред-
ставления, т. е. аргументы волновой функции.
Операторы и btp, действуют на переменные , причем
описывает исчезновение одного фонона типа Ар, а —
рождение одного фонона типа Ар:
| пай> = УХц. I п>.ц — 1 >, + 1 | пКи + 1 >
(4.20)
Здесь опущены переменные волновых функций, а также квантовые
числа всех состояний, кроме состояния Ар. Согласно (4.20), волно-
вую функцию однофононного возбужденного состояния типа Ар
можно представить в виде
|U>=^|O>, (4.21)
а функцию состояния с фононами — в виде
I Пхц> = W)-1/2 (Ф i о>, (4.22)
т. е. выразить через функцию основного состояния 10>, в котором
отсутствуют фононы.
Аналогию элементарных возбуждений с частицами можно про-
должить, если учесть, что оператор (как и операторы а>.р, и л\ц),
относящийся к возбуждению типа Ар, является сферическим тен-
зорным оператором ранга X. Поэтому каждое элементарное возбуж-
дение (фонон) типа Ар имеет определенный угловой момент (спин)
А с проекцией р на выделенное направление и определенную чет-
ность (—1)\ подобно тому как сферическая функция Ylm (0, <р) —
тензорный оператор ранга I — описывает частицу с угловым момен-
том I, проекцией момента т и четностью (—1);. Так как в каждом
состоянии Ар может быть сколько угодно фононов и спины их цело-
численны, то фононы являются бозонами. Поэтому волновая функ-
ция (4.19) должна быть симметричной относительно перестановок
фоионов любого типа.
Непосредственно из (4.17) следует, что оператор имеет
диагональный вид в представлении чисел заполнения, причем по
диагонали стоят возможные числа фононов типа Ар:
221
/ООО 0...00... I
/0 1 0 0...00... \
4- 0 0 2 0 ...00...
0 0 0 3 ... 00... <4'23)
^0 0 0 0,..n^0... I
Поэтому оператор
bKll (4.24)
является оператором числа фононов определенного типа Хр, который
естественно диагоналей в своем собственном представлении (пред-
ставлении чисел заполнения): 1 п-/,ц > = | п?.ц >. Из (4.16),
а также и из (4.17) следует, что
bkixbt^ = пхц.4~ 1- (4.25)
Гамильтониан системы (4.18) с помощью оператора числа фононов
(4.24) можно переписать в виде
Я (п>.ц+ 1/2)Гшх, (4.26)
Z|i
откуда непосредственно видно, что возбуждения типа Хр дают вклад
в энергию коллективных движений ядра, равный
£^ = (/1^+1/2)/г<щ, (4-27)
а полная энергия Е равна сумме выражений типа (4.27). Оператор
проекции полного углового момента системы на ось квантования z
связан с оператором числа фононов (4.24) соотношением
(4.28)
Ли.
Собственные значения (4,28) в состояниях [ пЛ|Л > равны
| Ег [(4.29)
Остановимся кратко на классификации состояний системы не-
скольких фононов. Двухфононные волновые функции 1
описывают состояния с определенной энергией Й(сщ, + сщ-), оп-
ределенной четностью (—1)Л+Х' и определенным значением проекции
полного углового момента Л4 = р + р'. (При этом квадрат полного
момента не имеет определенного значения.) Волновую функцию
с определенным угловым моментом Л, заключенным в пределах
| к—X' | Л % 4- X', можно построить с помощью линейной ком-
бинации двухчастичных функций:
| ЛМ> = 2 р' I AM) btp bi'»' I о>. (4.30)
цц'
222
В случае фононов одного типа (X = Л') из симметрии волновой функ-
ции | ЛЛ4 >• относительно перестановки фононов и свойства симмет-
рии коэффициента Клебша—Гордана (ХрХр,'| ЛЛ4) = (—1)П-Л X
х(Хр'Хр|ЛЛ4) следует, что возможными значениями Л являются
только четные числа: Л = 0,2, ..., 2Х. Например, при X — 2 воз-
можны три значения полного углового момента системы двух
фононов: Л = 0,2 и 4. Если имеется система трех фононов с X = 2,
требование симметрии волновой функции приводит к следующим
значениям полного углового момента: Л = 0, 2, 3, 4 и 6. С увели-
чением числа фононов одинако-
вого типа классификацию со-
стояний удобно проводить с
использованием групповых ме-
тодов, подобно тому как это про-
водились при классификации со-
стояний систем эквивалентных
нуклонов. Необходимость прив-
лекать групповые методы свя-
зана с тем, что задания энергии,
углового момента, его проекции
и четности уже недостаточно для
полного описания системы не-
скольких однотипных коллек-
тивных возбуждений, И поэтому Рис. 4.1. Зависимость энергии от
нужно ВВОДИТЬ дополнительные параметра деформации ядра,
квантовые числа, как, например,
при рассмотрении квадрупольных возбуждений (X = 2), если чис-
ло фононов больше трех.
Колебательные спектры ядер. Четно-четные ядра в основном
состоянии всегда имеют спин = 0. Если спин системы равен нулю,
то равновесному состоянию с наинизшей энергией отвечает сфе-
рически симметричное распределение плотности. Однако, хотя сфе-
рически симметричному распределению и соответствует условие рав-
новесия, последнее не всегда оказывается устойчивым.
Действительно, если изобразить энергию основного состояния
ядра в зависимости от параметра деформации е (например, от эк-
сцентриситета ядра в случае, если ядро имеет форму эллипсоида
вращения), то производная от энергии по параметру деформации
равна нулю при значении параметра, равном нулю. В случае устой-
чивого равновесия сферической формы кривая зависимости энергии
имеет минимум при е = 0. Сферическую форму в основном состоя-
нии имеют дважды магические и близкие к ним ядра (схематически
зависимость энергии от параметра деформации для указанных ядер
изображена кривыми 1 и 2 на рис. 4.1). Однако по мере увеличения
числа нуклонов во внешней незаполненной оболочке поляризацион-
ное действие последних приведет к нарушению сферической симмет-
рии. В этом случае на кривой зависимости энергии от параметра
деформации возникает минимум при е О (см. рис. 4.1, кривая 3),
?23
который увеличивается и смещается в сторону больших деформаций е
с увеличением числа нуклонов во внешней незаполненной оболочке.
В случае сферических ядер коллективные возбуждения соответ-
ствуют колебаниям поверхности ядра относительно равновесной
формы. Согласно (4.13), квадрат частоты поверхностных колебаний
<о?, определяется отношением коэффициентов С-г, и В^. В соответст-
вии с (4.6) и (4.7) энергия поверхностных колебаний/кох монотон-
но растет с увеличением X. Поэтому можно ожидать, что первые кол-
лективные возбуждения в низкоэнергетических спектрах сфери-
Ел кэВ
2 fat)
----------(О*) 1860
owr
2* 1363
/ Л.0* 1308
~-6+ 1286
02 0 ---------- 2* 1200
1150
----------- у------------------5Sg
-----------О* ------------------- 0*
Рис. 4.2. Энергетический спектр квадрупольных
колебаний сферических четно-четных ядер.
ческих ядер соответствуют квадрупольным колебаниям X = 2.
В качестве набора квантовых чисел, определяющих возбужденные
состояния, удобно выбрать число фононов п и момент количества
движения Л. Для п = 1 спин и четность в случае квадрупольных
колебаний равны 2+, для п = 2 имеется вырожденный триплет
четных состояний со значениями спина 0+, 2+ и 4+; для п = 3
имеется пять вырожденных четных состояний: 0+, 2+, 3+,
4+ и 6+ и т. д. (рис. 4.2).
Действительно, для большинства четно-четных ядер первое воз-
бужденное состояние и'меет спин и четность 2+. У некоторых чет-
но-четных ядер (Vs Pd, ‘^Cd и др.) обнаружены также предска-
зываемые колебательной моделью триплеты почти вырожденных
состояний 0+, 2+ и 4+. Для иллюстрации на рис. 4.2 приведена схема
наблюдаемых уровней ядра WCd. Однако у большинства ядер ожи-
даемые триплеты возбужденных состояний не наблюдаются, хотя
224
второе возбужденное состояние для большинства ядер и характери-
зуется значениями спина и четности, равными 0+, 2+ или 4+.
Попытки количественного расчета спектров. уровней четно-
четных ядер на основе колебательной модели оказались безуспеш-
ными. В самом деле, используя (4.6) и (4.7), в пренебрежении ку-
лоновской энергией для квадрупольных колебаний имеем
Ййоа = (а!А1!2), а = К j/(8o/p/?e3).
Учет кулоновской энергии приводит к некоторому уменьшению этой
величины. Следовательно, согласно колебательной модели ядра,
Рис. 4.3. Зависимость отношения энергий второго и первого
возбужденных состояний от числа нейтронов для четно-четных
ядер.
энергия первого возбужденного уровня должна быть монотонной
функцией массового числа А. Согласно же эмпирическим данным,
энергия первого возбужденного состояния четно-четных ядер сильно
зависит от структуры ядер и характеризуется очень большими зна-
чениями для магических ядер. Это указывает на ограниченный ха-
рактер применимости рассматриваемой модели ядра.
На рис. 4.3 показана зависимость отношения энергий второго
и первого возбужденных состояний E2iEt для четно-четных ядер
от числа нейтронов. Согласно модели поверхностных колебаний,
это отношение должно быть равным двум, однако в действительности
имеются области, где это отношение значительно больше. (Так, в
областях значений массовых чисел 150 < А < 190 и Л > 220 это
отношение несколько больше трех). Оказывается, что ядра, у ко-
торых отношение Ei!El отклоняется от значения, характерного для
колебательных состояний, обладают большими квадрупольными
моментами, что связано.с несферичностью равновесной формы ука-
занных ядер. Поэтому низкоэнергетические уровни этих ядер свя-
заны с вращением ядер, а не с колебаниями поверхности.
3 Зак. 642 225
Введенные в (4.1) величины «j.,, описывают изменение формы
ядра относительно фиксированной в пространстве системы коор-
динат. В случае несферической равновесной формы ориентацию
ядра в пространстве удобно описывать углами Эйлера, определя-
ющими положение главных осей ядра относительно неподвижной
системы координат. При вращении ядра параметры фиксиру-
ющие форму ядра в неподвижной системе координат, изменяются
со временем, хотя форма ядра и остается неизменной. Поэтому для
описания поверхностных деформаций необходимо ввести новые па-
раметры, определяющие форму ядра в собственной системе коор-
динат, связанной с ядром.
£ 4.2. ВРАЩЕНИЕ СИСТЕМЫ КООРДИНАТ
Повороты системы координат. Рассмотрим некоторую фиксиро-
ванную точку Р в трехмерном пространстве. Обозначим координаты
этой точки в неподвижной системе координат К. через г = (х, у, г).
Соответственно координаты этой точки в подвижной системе коор-
динат /С' обозначим через г' = (х', у', г'), Ориентацию подвижной
системы координат К' по отношению к неподвижной системе коро-
динат /< (начала обеих систем совпадают) будем описывать тремя
углами Эйлера Ф, 0 и ф, из которых Ф и 0 — это полярные углы
оси z' в координатной системе К, а ф — угол между линией узлов
(линией пересечения плоскостей ху и х'у') и осью у'*,
Переход от системы координат К к системе координат /С' можно
осуществить с помощью трех последовательных поворотов (рис. 4.4):
1. Поворота на угол Ф(0 < Ф < 2л) вокруг оси ог в направ-
лении от оси ох к оси оу, в результате которого ось оу совпадает с
линией узлов оу^. При этом система координат К переходит в систе-
му координат Klt в которой точка Р будет иметь координаты г, =
= (хъ t/i, zj, связанные с координатами той же точки в системе К
соотношениями
(созф зшФ 0\
—sin® cos Ф О].
О 0 1 )
(4.31)
2. Поворота на угол 0(0 «С 0 < л) вокруг линии узлов oylt
в результате которого ось oz совпадает с осью ог'. При этом система
координат переходит в систему координат /<2, в которой точка Р
будет иметь координаты г2 = (х2, у->, г2), связанные с координатами
в системе /<2 соотношениями
(cos 0
О
sin 0
г2 = aUi (0) п,
О —sin 0
1 О
0 cos 0
(4.32)
* В книге Вигнера 14] использовано другое обозначение углов Эйлера:
(Ф, 0, ф)=(у, Р, а).
226
3. Поворота на угол 4(0 < 4 < 2л) вокруг оси ог', при этом
система координат К2 переходит в систему координат Д', в которой
точка Р будет иметь координаты г' = (%', у', г'), связанные с коор-
динатами в системе Да соотношениями
Рис. 4.4. Переход от системы координат Д к системе
координат Д'.
Используя (4.31) и (4.32), координаты точки Р в системе коор-
динат Д' можно непосредственно выразить через координаты точ-
ки Р в системе координат Д:
г'=а(Ф, 0,4) г, (4.34)
где коэффициенты линейного преобразования а(Ф, 0, 4) равны
а(Ф,8,1)!)эаг' (ф)а»> (0)аг(Ф). (4.35)
Обращая равенство (4.34), координаты точки Р в системе коор-
инат Д мо жно выразить через координаты той же точки в системе
координат Д':
г = а~! (Ф, 0,4) г', (4.36)
где а- 1 (Ф, 0, ф) — линейное преобразование, обратное (4.35):
д-t (ф, 0, 4) =az~l (Ф)ау~1 (0) аг"' (4). (4.37)
8* 227
Оператор конечных поворотов. Рассмотрим произвольное ска-
лярное поле, характеризуемое в системе координат К в каждой точ-
ке г некоторой функцией /(г). Это же поле в системе координат /С'
характеризуется, вообще говоря, другой функцией /'(г'), зависящей
от координат точки в новой системе координат. Очевидно, значения
поля в одной и той же точке пространства Р, вычисленные в различ-
ных системах координат, должны совпадать. Поэтому должно вы-
полняться равенство
Г(гЭ=Нг), (4.38)
если г' и г связаны соотношением (4.34).
Введем оператор конечных поворотов О(Ф, 0, ф), определяющий
функцию скалярного поля /'(г) в повернутой системе координат К',
если эта функция /(г) задана в неподвижной системе координат Д’:
f'(г)= О(Ф, 0, ф)/(г). (4.39)
Используя равенство (4.38), нетрудно получить соотношение, поз-
воляющее найти явное выражение для оператора конечных пово-
ротов:
D (Ф, 0, ф) f (г) = / (а-1 (Ф, 0, ф) г), (4.40)
где а~х (Ф, 0, ф) — линейное преобразование, определяемое фор-
мулой (4,37). Обращая равенство (4.40), получаем
j)-1 (ф( 0, ф) / (г) = / (а (ф, 0, ф)г). (4.41)
Это соотношение удобно для нахождения явного вида обратного
оператора /?(Ф, 0, Ф) = £)_1(Ф, 0, ф).
Найдем явное выражение для оператора конечного поворота
системы координат на угол ср вокруг оси, направление которой за-
дано единичным вектором п. Для этого рассмотрим сначала беско-
нечно малый поворот системы координат на угол бср вокруг оси п.
При бесконечно малом повороте г -> г' = аг = г + 6г, где 6г —
=—6ф(п х г). Функция скалярного поля f(r) при таком повороте
переходит в функцию
Г (г) = f (а-1г) = f (г—6г) = [I + бери (г х у)] [ (г).
Воспользовавшись определением оператора орбитального момента
системы 1 = —i(r X v), полученное равенство можно переписать
в виде
f'(r) = (i+i6<pnl)f.(r). (4.42)
Выражение, стоящее в скобках правой части (4.42), можно рассмат-
ривать как оператор бесконечно малого поворота системы коорди-
нат. на угол бср. Поворот на конечный угол ср вокруг оси, направле-
ние которой задано вектором и, можно представить как бесконечную
228
Последовательность поворотов на бесконечно малые углы 6<р -
при k -> оо :
D"(q))f(r)=lim('l + i^nl Vf(r) = eitpnlf(r). (4.43)
Таким образом, оператор конечного поворота системы координат на
угол <р вокруг оси, направление которой задано единичным векто-
ром п, в случае скалярного поля имеет вид
Dn (ф) = е1ч,п1. (4.44)
В общем случае, если физическая система обладает внутренним мо-
ментом (спином) и функции поля характеризуются определенными
трансформационными свойствами, оператор конечного поворота
системы координат £>п(ф) выражается через оператор полного мо-
мента системы J:
Р”(ф)=^е<ч>^, (4.45)
где j есть сумма орбитального и спинового моментов системы
j.Ql + s. (4.46)
Найдем теперь явный вид оператора конечных поворотов
D (Ф, 0, ф), осуществляющего переход от неподвижной системы
координат К. к повернутой системе К'. Подставляя (4.37) в (4.40)
и используя определение оператора поворота вокруг определенной
оси, получаем
D (Ф, в, ф) / (г) = / (а2-1 (Ф) av -1 (0) (Ф) а2”1 (ф) г) =
= О2(Ф)|(а^-1(0)а2’-1 (ф)г) -О2(Ф)О^(0)Паг'-1(Ф)г) =
= О2 (Ф) Dy* (0) D2' (ф) f (г). (4.47)
В правую часть равенства (4.47) входят операторы поворотов вокруг
отдельных осей в различных системах координат.
Согласно тождеству (4.41), значение функции от координат точ-
ки в повернутой системе выражается через значение функции от
координат той же точки в неподвижной системе с помощью опера-
тора D-1 (Ф, 0, ф):
f(r')=D-'f(r), (4.48)
где г' =аг. Очевидно, при переходе от /(г) к /(г') произвольный
оператор 0 преобразуется по закону 0 —О'- О-10D. Поэтому
при переходе -> /Сй, характеризуемом оператором поворота
(0), имеем Dz' (ф)=Dy*~' (0) D* (ф) D«i (0).
Аналогично при переходе К -* Ki, характеризуемом оператором
поворота 1)г(Ф), имеем
(0) = D*~1 (Ф) Dy (0) D2 (Ф).
229
Замечая далее, что D- (Ф)Ог (ip) = D? (чр)Ог(Ф), оператор
£)(Ф, 9, ip), осуществляющий переход от системы координат 7< к
системе ТС, получаем в следующем виде:
ЩФ, 0,гр)-Г>г(1р)£^(0)Ог(Ф). (4.49)
Используя явное представление (4.45) для операторов поворотов
вокруг отдельных осей, окончательно получаем для оператора ко-
нечных поворотов следующее выражение:
D (Ф, 0, -ф) = е^'* ею0 ei4>\ (4.50)
Оператор конечных поворотов (4.50) унитарен, что непосред-
ственно следует из эрмитовости оператора момента системы:
D-1 (Ф, 0, тр) = О+(Ф, О, ip). (4.51)
Используя явный вид оператора конечных поворотов (4.50),
нетрудно получить следующие выражения для производных по уг-
лам Эйлера от оператора Е>(Ф, 0, ip):
~~ в = iDjz — jx sin 0 cos ip 4-/y sin 0 sin ip 4-/4 cos 0) D;
— D = iD(— jx sin Ф + /у cos Ф) — i (jx sin ip +/у cos ip)£>, (4.52)
— D = iD (jx cos Ф sin 0 4- j sin Ф sin 0 + / cos 0) = i/z D.
<hp
Так как /г- = jxcosO sin0 + sinO sin 0 4-/zcos 0, то из послед-
него равенства следует соотношение
LD = D^. (4.53)
Введем вектор угловой скорости
(4.54)
где вектор Ф направлен вдоль оси ог в системе координат К, вектор
0 — вдоль линии узлов оуг и вектор ip — вдоль оси ог' в системе
координат К,'. Проектируя вектор г» на неподвижные и подвижные
оси, находим
(щ. = —0sin®4-ipcos®sin 0; <0у = 0 cos Ф -|- ip sin Ф sin 0; со, = Ф4-1р COS0 (4.55)
и =—Ф sin 0 cosip 4-0 sin ip; i cOy-=Фsin ©sin ip 4-0 cos ip; сог- =Фсок0 4-тр. 1 (4.56)
230
Используя соотношения (4.52) и определение вектора угловой
скорости (4.54), нетрудно найти следующее выражение для произ-
водной по времени от оператора конечных поворотов:
D = i£> (/ж ах + а>у + /г юг) = i (<ох- jx + jy + ы2- /г) D. (4.57)
Обобщенные сферические функции. Рассмотрим совокупность
собственных функций операторов квадрата и проекции полного мо-
мента системы ф;-т(0, <р). Так как оператор конечных поворотов
О(Ф, 0, ф) содержит только операторы jy и ]г, то функцию ф>т (&', <р')
получающуюся в результате действия оператора D'1 (Ф, 0, ф)
на функцию ф;т(#, ф), можно разложить по полному набору функ-
ций ф/т'(^, ф). Учитывая унитарность оператора б(Ф, 6, ф), это
разложение можно записать в виде
ф') = (Ф, ©, ф)ф;т(^ cp)=D+ (Ф, 0, ф) ф^ (#, Ф) =
= D1^' (Ф, 0, ф) ф/т< (б’, ф), (4.58)
т'
где £>m-m (Ф, 0, ф)—матричные элементы оператора конечных
поворотов, образующие унитарную матрицу конечных пово-
ротов:
D'm'm (Ф, 0, Ф) = <]т' ID (ф, 0, ф) I jtn) =
= </щ'|е1*;ге|%е,ф^| ут). (4.59)
Используя унитарность матрицы D'm’m (Ф, 0, ф), нетрудно по-
лучить соотношение, обратное (4.58):
Ф;т (Л ф) = 2 D'm-m (Ф, 0, ф) ф/т, <р'). (4.60)
т'
Согласно (4.60), значение собственной функции операторов квадра-
та и проекции момента в определенной точке в неподвижной си-
стеме координат Д’ выражается через линейную комбинацию зна-
чений собственных функций операторов квадрата и проекции
момента, взятых в той же точке в повернутой системе координат К,'.
Элементы матрицы конечных поворотов (Ф, 0, ф) совер-
шенно не зависят от выбора системы координат, в которой опреде-
лены функции ф/П1(^, ф), и при фиксированном значении / явля-
ются определенными функциями углов Ф, 0 и ф. Если j — цело-
численное (j s= /) и один из индексов т или т' обращается в нуль,
то функции (Ф, 0, ф) сводятся к обычным сферическим функ-
циям:
о^(ф,0, Ф)
Рш- о (Ф, 0, Ф) = (-1)"1' У Уу Ylm- (0, Ф).
(4.61)
231
В частном случае т=т' — Q имеем
Doo (Ф, <9, if) = Pt (cos 0). (4.62)
Поэтому функции Dm'm(O, 0, ф) обычно называют обобщен-
ными сферическими функциями или D-ф у н к-
циями Вигнер а*.
Обобщенные сферические функции удовлетворяют следующему
условию ортонормировки:
У г/Ф 5 d& sin 0 5 ^Ф^Й* т, (Ф, О, Ф) (Ф, 0, Ф) =
0 0 о
= ^7бл,-2ЧтЛ-(.т1'. (4.63)
Интегралы от произведений трех обобщенных сферических функций
легко вычисляются с помощью формулы сложения, которая спра-
ведлива для обобщенных сферических функций:
Dmt' mi &ms' ms — S (h m[ /2 | /m') (jiMt | jtri) D'm-n. (4.64)
J
Заметим, что обобщенные сферические функции (Ф, 0, ф)
образуют неприводимое унитарное представление трехмерной груп-
пы вращений.
Используя определение (4.59), в функциях D’m-m (Ф, 0, ф) можно
явно выделить зависимость от углов Фиф. Так как ]/т> и j jm')
являются собственными функциями оператора проекции момента
то
DLm (Ф, ©, Ф) =e,m' * d'm-m (0) е1тф, (4.65)
где d{n'm(®) — вещественная функция, определяемая равенством
d'm-т (0) s (jtn' | ei6'w | jm>. (4.66)
В вещественности функции dm’m(0) нетрудно убедиться, исполь-
зуя разложение
е'в/» = 2 (0©!У)п/пI)
п = 0
и замечая» что матричные элементы оператора^ — чисто мнимые
<Х1/В| М> =-^-(K(/ + m)(/—rn + l)6m-.m_i —
— V(j — (/ + m-[-l)6m.>m + 1].,
* Детально свойства обобщенных сферических функций рассмотрены
в работах [4,5).
?32
Из вещественности и унитарности матриц следует их
ортогональность:
47m(©)=4m-(0). (4.67)
откуда вытекает следующее свойство симметрии:
din' т (в) = ( — ©)• (4.68)
Воспользовавшись соотношением
<М' | /в | /т> = —</—т' | jy | j—tn),
нетрудно проверить также следующее свойство симметрии:
dim-m(e)=dLm. _m-(0). (4.69)
Наконец, используя операторное тождество
=э^’я/* е~!%е'(ЯЧ
нетрудно получить соотношение
dbm (0) -(- l)m'-m 4m' (6). (4.70)
Функции 4'm(0) при любом значении угла 0 можно выра-
зить через значения функций 4’т(6) при Q =л/2:
dm'm (0) =е' 2 4'm’ (v) e'm"e (4‘71)
m" \ * / \ 1
При выводе этого соотношения следует воспользоваться опера-
торным тождеством
, Л • , Я . «Л. , Л .
е‘% = е 2“/г е T^eie^e“ е- г.
Отметим еще следующие полезные соотношения для
функций:
4'т(л)= (—1)( 6m',—mJ
din'n, (л~0) =(-l)'-m' 4. -m(0);
4m (Л +6) = (-I/-'"' dL„-, m (0).
4- ™ (0V
m tn \^j
—
(4-72)
В заключение приведем еще явные выражения для производ-
ной по времени от матрицы конечных поворотов D^m (Ф, 0, ф):
^-Dln-m=i S “л2£,т-т’<//П''|/л|/Щ> =
at k = x,y,x tn”
= i 2 ^k-^i<im’\ik'\!tn"') Din-m. (4.73)
k'=x',y', z' m”
233
Эти Соотношения непосредственно вытекают из операторных соот-
ношений (4,57}.
Оператор вращения R. Введем оператор бесконечно малого по-
ворота R подвижной системы координат К' Для этого выберем в
качестве динамических переменных углы Эйлера Ф, 6 и ip и рассмот-
рим произвольную скалярную функцию от них ДФ, 0, ф). Очевид-
но, при поворотах подвижной системы координат Д', ориентация
которой задается углами Эйлера, эта функция будет изменяться
так же, как функция скалярного поля при повороте физической
системы. (Поворот физической системы на бесконечно малый угол
эквивалентен повороту системы координат на такой же угол в про-
тивоположном направлении.) Поэтому при бесконечно малом по-
вороте подвижной системы координат Д' вокруг оси, направление
которой задано единичным вектором п (в результате которого углы Ф,
0 и ф переходят вФ' = Ф + 6Ф, 0' = 0 + 60 и ф' = ф + 6ф),
изменение функции равно
6/(Ф, 0, ф) sf (Ф-|-6Ф,0 - б0,ф [ 6Ф)—/(Ф, 0, ф) =
= ificp nR/(Ф, 0, ф), (4.74)
где 6<р — бесконечно малый угол поворота, a R — эрмитов опера-
тор Вращения:
nR = -iA (4.75)
Зф
Единичные векторы, направленные вдоль координатных осей
о2, оу± и oz', обозначим соответственно п®, п© и п^. Тогда проек-
ции вектора R на соответствующие направления непосредственно
выражаются через производные по углам Эйлера:
n®R~—i-~, nftR— i —, пфИ==— i — • (4.76)
ЗФ 39 Зф
Выражая скалярные произведения векторов, стоящие в левых
частях равенств, через проекции векторов в неподвижной или по-
движной системе координат, из (4.76) нетрудно найти явный вид
оператора вращения R в неподвижной и подвижной системах ко-
ординат.
Проекции оператора вращения R на оси неподвижной системы
координат определяются выражениями:
n : I .г, + ci д - 3 , cos Ф 3 )
= —1 ( — cos Ф ctg 0-----sin Ф--------------S:
I зф ад sine Зфу
Sin®ctg0 — + созФ — + ^--^1;
у I ЗФ 30 cos 0 Зф)
Kz = —i —.
ЗФ
234
Проекции оператора вращения R на оси подвижной системы ко-
ординат равны
n . ( cos ф д , . . д , , л ,51
/?,- = —1-----— — 4-sin ib--kctg ©cos ф —);
i sin0 dO 56 5i|i J
r, . 1 sincb 5 , . d , , 5 1
R»'= ~'»+cos*« ~ct8es'"M:
оф
Так как квадрат вектора есть инвариантная величина, то для опе-
ратора R2 в обеих системах координат находим
д о с. 52 , <?’
------------2 cos © ------
sin20[c!4>a-5Ф 5ф 6ф2
н——
sin в
(4.78)
Б?3 = — ( 1
(4-79)
Используя явный вид проекций оператора вращения (4.77),
нетрудно показать, что в неподвижной системе координат они удов-
летворяют обычным перестановочным соотношениям для проек-
ций момента количества движения:
— PyPx=iPz. (4.80)
Таким образом, R можно рассматривать как оператор момента
количества движения, обусловленного вращением физической си-
стемы, жестко связанной с координатной системой /('. В подвижной
системе координат /С' проекции оператора вращения удовлетворяют
перестановочным соотношениям, отличающимся от (4.80) знаком
в правой части:
Рг Ry —RyRx- = —1Рг-. (4.81)
Проекции оператора вращения как в подвижной, так и в неподвиж-
ной системе координат коммутируют с оператором R2;
R2J 0. (4.82)
Рассмотрим теперь квантовомеханическую систему, характери-
зуемую оператором полного момента количества движения
Волновую функцию системы, отнесенную к R, обозначим ф(0, ф),
соответственно волновую функцию системы в R' обозначим ф^', ф').
Согласно (4.60), функции ф(<9, ф) и ф ($', ф') связаны соотношением
(О, Ф) (Ф, ©, ф) ф^, (О', ф'). (4.83)
Очевидно, оператор R будет действовать только на функцию
ф(О', <р'), поскольку поворот системы координат R' не может ска-
зываться на значении функции ф (й, ср) в неподвижной системе коор-
динат R, т. е.
РФ (О, ф) =0.
(4.84)
235
Так как функции фСб1', <р') зависят от углов Эйлера Ф, 9 и ф,
то при бесконечно малом повороте системы координат /С на угол
6<р вокруг произвольного направления п изменение этой функции,
согласно (4.74), равно
6ф (О', ср') = i6<pnRTp (О', ср'). (4.85)
Кроме того, это изменение можно выразить через оператор пол-
ного момента системы Согласно (4.45) и (4.48), это изменение
равно
6ф(О',<р')=—!6фпЛф(О', <р'). (4.86)
Приравнивая правые части равенств (4.85) и (4.86), получаем
(И + Л)ф(0',ф')=0. (4.87)
Используя (4.83), равенство (4.84) можно представить в виде .
Мл-°- 'l’) <₽')-
М'
= 2 {(R0& д, (Ф, 0. Ф» + D?, м (Ф, 0, ф) R} ф^,(О', ф') = 0, (4.88)
м'
где (RD^,^ (Ф, 0, ф)) обозначает результат действия оператора
R на ©,ф) и представляет собой некоторую функцию
углов. Учитывая (4.87), можно переписать (4.88) в виде
2 {№?м (Ф, ©, ф)- D$.M (Ф, 0, ф) J ) ф^м, («', ф') =0. (4.89)
М'
Спроектировав равенство (4.89) на ось oz’ и замечая, что
А' Уум- (#'> Ч2 * * 5') = Ф')> имеем
2 ((/?г О^,м (Ф, 0, ф))- ЛГ D?u (Ф, 0, ф)} (О', ф') = 0.
лг
Так как функции ф^м' (О'>ф') при различных значениях М' линейно
независимы, то для выполнения этого равенства необходимо, чтобы
все коэффициенты тождественно обращались в нуль, т. е.
DL м (ф> 6»Л) = М' D? м (Ф, 0, ф). (4.90)
Аналогично можно получить
(7?х'± i/M П^.Л((Ф,0,ф) =
= /(bWTAI'+l)^T1,M (Ф,вл). (4-91)
Используя (4.90) и (4.91), нетрудно показать, что
Ra (ф> ® Л) = W + О D?,M (Ф, 0, ф). (4.92)
236
Для нахождения собственного значения проекции R в неподвиж-
ной системе координат /< выполним во втором слагаемом (4.89)
суммирование поЛГ:
—Ф) = О. (4.93)
М'
Спроектировав это равенство на ось oz и воспользовавшись соот-
ношением JztyyM (^, ф) (ft, <р), найдем
2 5 (rz < м (Ф, ©, ф)) - md?.u (ф, ©, ф)) (&', <₽') = о,
М'
откуда
Д2 D?, м (Ф, 0, ф) м (Ф, 0, ф). (4.94)
Аналогично можно показать, что
(Rx±\Ry)D?M(Q), 9,ф) =
= У&^М) (^±М + 1) О£ м ± ^Ф, 0, ф). (4.95)
Нетрудно проверить, что из (4.94) и (4.95) также следует равенство
(4.92).
Таким образом, мы показали, что обобщенные сферические функ-
ции Д^<Л((Ф, 0, ф) одновременно являются собственными функция-
ми операторов R2, R? и Rz- и отвечают собственным значениям по-
следних, равным соответственно + 1), М 'и М'.
§ 4.3. ВРАЩЕНИЕ ДЕФОРМИРОВАННЫХ ЯДЕР И КОЛЕБАНИЯ
ИХ ПОВЕРХНОСТИ
Эллипсоидальные деформации ядер. При небольших деформа-
циях ядер можно ограничиться учетом только деформаций второго
порядка. В этом случае поверхность деформированного ядра пред-
ставляет собой эллипсоид, произвольным образом ориентированный
в пространстве:
/?(Й,Ф)= {1+1ХУ2(1(<},<р)}Я (4.96)
(для упрощения записи будем опускать индекс % — 2). Вместо пяти
параметров «,г, описывающих деформации, можно ввести три угла,
определяющих ориентацию эллипсоида, и два внутренних пара-
метра, определяющих его форму. (В результате сохранения объема
ядра сумма трех главных осей эллипсоида остается постоянной при
деформациях.)
Введем собственную систему координат К', оси которой совпа-
дают с главными осями эллипсоида. Ориентация системы /(' отно-
сительно неподвижной системы К определяется эйлеровыми угла-
237
ми Ф, 6 и ip. Запишем уравнение поверхности в собственной системе
координат:
Я(й'Л') = {1 +Sa/y2v(#', (f')J (4-97)
V
где a'v — параметры деформации в собственной системе координат
А". Используя формулу преобразования сферических функций при
переходе от /С к /С (4.60), нетрудно получить следующее соотноше-
ние между параметрами сщ и
«и = 2 (Ф- ф) «V- (4.98)
V
Вследствие симметрии эллипсоида относительно главных пло-
скостей в собственной системе координат имеем
«i — a_i= 0, а2=а^2. (4.99)
Действительно, при отражении относительно плоскости г' —
= 0(1&', <р' -> я — ср') сферические функции Ум и У2±2 остаются
неизменными, а функции У2±1 меняют знак. Отсюда следует, что
а\ = a'_i = 0. При отражении относительно плоскости х' —
= 0 (О', <р' —> й', я — <р') сферические функции У2±2 переходят
в У2Т2, откуда следует а_2' = а2'. Таким образом, в собственной
системе деформации поверхности характеризуются только двумя
вещественными параметрами <*о и а2. Вместо ай' и а2' удобно вве-
сти два новых параметра Риус помощью соотношений
pcosy, a2 = (р/]Л2) sin у. (4.100)
В силу унитарности Dllv имеем
2 |«ul2 = ®oS + 2a^ = P2- (4.101)
р-
Следовательно, параметр р определяет общую деформацию ядра.
Параметр у характеризует отклонение формы ядра от аксиально
симметричной формы.
Как нетрудно проверить, главные полуоси ядра выражаются
через р и у следующим образом:
= {1 + Р cos (у — k'R,k' = 1, 2,3sx', у', z'. (4.102)
Если у = 0 и р > 0, то ядро представляет собой вытянутый эллип-
соид вращения
Если у = л и р > 0, то имеем сплюснутый эллипсоид вращения
= (|+фо₽1«- r,._(1--/jp)r.
238
Если у = зт/З или 2л/3, то осью симметрии будет ось оу' или ось
ох'.
Таким образом, взамен пяти параметров деформации ан мы вве-
ли пять новых координат: три угла Эйлера Ф, 0 и ф, определя-
ющих ориентацию в пространстве главных осей эллипсоида, и два
внутренних параметра (J и у, определяющих форму эллипсоида.
Физический смысл введения новых координат заключается в воз-
можности независимого рассмотрения вращения ядра как целого
и колебаний, связанных с изменением формы ядра.
Колебательная энергия и энергия вращения. В случае эллипсо-
идальных деформаций ядра кинетическая энергия определяется
общим выражением
T = (B/2)2|aJ2. (4.103)
1, в
Переход к новым координатам ац Ф, 6, ф, Р и у позволяет раз-
делить полную кинетическую энергию поверхностных деформаций
(4.103) на вращательную и колебательную энергии.
Для нахождения вида кинетической энергии в собственной си-
стеме координат продифференцируем равенство (4,98) по времени:
= S (*Ч ®v -j- D-чц <Xv)
V
Производная по времени от Z)uv непосредственно выражается через
производные по времени от углов Эйлера и функции 7),1V, согласно
(4,73). Подставляя выражение для а(1 в (4.103), кинетическую энер-
гию можно представить в виде суммы трех слагаемых;
Т = (В/2) 2 (Ov|x ц otv ccv'4-2Re OV|i ^v'ц ®v'
gvv'
+ Dvji DV' av tZv')1 (4.104)
Первое слагаемое в (4.104), квадратичное по av> определяет кине-
тическую энергию колебаний, изменяющих форму эллипсоида,
но сохраняющих его ориентацию в пространстве:
TD=B/2 S D*vtl DV’ц a'v .
gw'
Используя свойство унитарности функций D^, колебательную
энергию нетрудно привести к виду
7\={B/2) (Р2 + Р2?)- (4-105)
Второе слагаемое в (4.104), содержащее перекрестные члены,
обращается в нуль, в чем нетрудно убедиться, воспользовавшись
явным видом О^:
Re S Dv-ti а(, tzv. = Re i S 2 <v'! A' Iv) «v «(>'
|1W' tv' k'
239
Так как v и v' принимают только значения —2, 0 и 2< то вклад мо-
жет давать только слагаемое k' = г', и, таким образом,
Re 2j Dv> ц tty oty' = Re i ^2 vcty ctyr 0,
HVV' v
Третье слагаемое в (4.104), квадратичное по£)Иу, определяет ки-
нетическую энергию вращения эллипсоида без изменения его формы:
Tr = (B/2)2
HVv'
Используя явный вид производных D)lv и свойство унитарности
функций Dpy, находим
тг = (В/2) 2 2 <v' | /р jk, | v> a; a;. (4.106)
VV' k’k'
Так как v и v' принимают только четные значения, то вклад в
(4.106) дают только матричные элементы (у' | jk, | v> при А' =
= А'. Действительно, если одно из А' или А' равно г', а второе —
х' или у', то матричный элемент < v' |/r/V| v > обращается в нуль,
так как/г- диагонально, а у j*' или /у- отличны от нуля только мат-
ричные элементы для состояний с числами v и -v', различающимися
на единицу. Если же одно из А' или А' равно х', а второе — у', то
соответствующие матричные элементы будут чисто мнимыми и их
сумма в (4.106) будет равна нулю. Поэтому кинетическую энергию
вращения (4.106) можно записать в виде
Тг = (1/2)2 4-^', (4.107)
где Ja- — момент инерции ядра относительно главной оси А':
^'=^2 (v'l/A'I v>avOv-'
VV'
Используя явные выражения матричных элементов от операто-
ров квадратов проекции момента, окончательно получаем следу-
ющую формулу для трех моментов инерции ядра:
JA-=4B[iasin2 —~ А'), А'= 1,2,3. (4.108)
Моменты инерции пропорциональны квадрату параметра дефор-
мации ядра р. В случае аксиально симметричного ядра 7 = 0, или
7 = л, моменты инерции равны
JV=X,.=3BP2, Х'=0. (4.109)
Момент количества движения ядра относительно главной оси
А' связан с угловой скоростью и моментом инерции ядра соотноше-
нием
Ук‘- (4.110)
240
Поэтому энергию вращения ядра можно представить в виде
тг = . (4.111)
k'
Потенциальная энергия в случае малых отклонений формы ядра
от сферической, согласно (4.5) и (4.101), выражается только через
параметр деформации 0:
К = (1/2)С02. (4.112)
Поэтому коллективный гамильтониан ядра в случае малых дефор-
маций Н представляется в виде двух частей Н„ и Нг, связанных с
колебаниями поверхности ядра и вращением ядра как целого
Hk=4B^2+P2V2) + vC^- (4.113)
2 Zk‘ k’
т. е. в случае малых деформаций колебания поверхности ядра и вра-
щение ядра полностью разделяются.
Потенциальная энергия колебаний несферических ядер. Рас-
смотрим колебания поверхности вращающегося ядра, равновесная
форма которого отличается от сферической. Обозначим равновесные
значения параметров деформации через и введем отклонения
параметров деформации от равновесных значений:
а°ц- (4.114)
Под ахц, (они могут быть и немалыми) по-прежнему будем понимать
коэффициенты разложения по сферическим функциям расстояния
от центра ядра До точки на его поверхности:
я (<►. ф) - {1 + 2 («^+(а, ф)} я. (4.115)
Равновесные параметры а°м, определенные в неподвижной системе
координат /С, описывают и вращение ядра, поэтому они зависят от
времени. Во вращающейся системе координат К' параметры
определяют только форму ядра, поэтому они постоянны.
Кинетическая энергия, связанная с коллективными степенями
свободы ядра, является квадратичной функцией обобщенных ско-
ростей однако она может зависеть и от обобщенных координат
«хц. Кинетическая энергия связана как с вращением ядра, так и с
колебаниями его поверхности. Потенциальная энергия несфери-
ческого ядра будет выражаться только через отклонения парамет-
ров (Ххц от равновесных значений и не зависит от вращения
ядра.
Величины ахц, так же как и , преобразуются при вра-
щениях системы координат по неприводимым представлениям груп-
пы вращений
ахи = 5 оСц (Ф, 0, ф)a’Kv (4.116)
241
И являются сферическими тенЗорйымй операторами ранга X, удов-
летворяющими соотношениям эрмитовости й*ц, = (—I)!1 йх,-ц> вы-
текающим из вещественности (4.115). Так как потенциальная энер-
гия ядра является скалярной величиной, она должна выражаться
через инвариантные комбинации компонент тензорных величин
ахц, не зависящие от вращения системы координат; иными словами,
потенциальная энергия должна быть тензором нулевого ранга,
составленным из компонент а^. Простейшим таким инвариантом
является квадратичный инвариант (квадратичное инвариантное
выражение из компонент а^):
S2(X) = 2 (ЛрХр,' | 00)амахц- = - У | аьц. I3- (4-117)
it? УП +1 Т
Инвариант, содержащий компоненты в третьей степени, имеет
вид
S3 (X,) — ^4*21 (^М^Мз I 00) (4-11®)
Hi Hi Из
При заданном X других Инвариантов второй и третьей степени из
компонент ахц составить нельзя.
Вычислить инварианты легче всего в собственной системе коор-
динат К', жестко связанной с ядром. При X = 2, выбирая оси коор-
динатной системы вдоль главных осей эллипсоида, введем, как и в
случае равновесной сферической формы, новые параметры дефор-
мации (ag = сщ — аи°):
ao=pcosy; <z2 — сс_2 — (р/] 2) sin у; a±1=0;
a0 = p0cosy0; а2 =а_2 = (р0/у 2) sinyB; а±] = 0.
(4.119)
Используя эти определения для инвариантов S2(2) и S3(2), получаем
следующие выражения:
S2 (2) - -±=г ((Р - Ро)2 + 4ррв sin® ; (4.120)
г О \ Z J
s3 (2) (pcosy —p0cosy0){3(Psiny—pBsinyB)® —
— (р cosy — рв cos Yo)s}. (4.121)
Рассмотрим малые колебания поверхности вращающегося ядра.
В этом случае массовые коэффициенты входящие в выражение
для кинетической энергии, являются постоянными:
7" = (1/2) 2 Вх| ak!112. (4.122)
Хц.
Потенциальная энергия в этом же приближении выражается только
через инварианты S2(X):
У = (1/2)2СХ|ОХИ|®. (4.123)
Лр.
242
В случае квадрупольных (X = 2) малых колебаний, как и в
случае равновесной сферической формы (р0 = 0), можно отделить
в кинетической энергии (4.122) энергию вращения ядра от энергии
колебаний ядерной поверхности. В результате для кинетической
энергии при л = 2 получим сумму колебательной и вращательной
энергий Т = Tv 4- Tf, определяемых выражениями (4.105), (4.107)
и (4.108), в которых, однако, в общем случае f}e =£= 0 и у0 =£= 0,
так как малыми являются лишь разности |3 — р0 и Т — То> а сами
Р и у (как ро и у0) могут быть немалыми. При р0 = 0 будем иметь
сферическое ядро, в этом случае зависимость от у0 автоматически
выпадает.
Потенциальная энергия малых квадрупольных колебаний, со-
гласно (4.120), имеет вид
V (р, у) = (С/2) {(р - р0)3 + рр0 (у -у0)2} «
« (С/2) {(р—р0)2 + р02(у —у0)2}. (4.124)
Таким образом, в случае сфероидальных ядер, имеющих несфе-
рическую равновесную форму, возможны колебания поверхности
двух типов, обычно называемые р- и у-колебаниями.
В случае сферических ядер (р0 = 0) потенциальная энергия
в квадратичном приближении не зависит от параметра у. Если же
учесть ангармоничность колебаний, то и для сферического ядра,
согласно (4.121), потенциальная энергия будет зависеть от параметра
поперечных деформаций у:
V (р, у)-(1/2) Ср2 | С'р3 (3-4 cos2 у) cos у, (4.125)
где С — некоторая константа.
§ 4.4. ВРАЩЕНИЕ АКСИАЛЬНО СИММЕТРИЧНЫХ ЯДЕР
Вращательная модель. Простейшим вариантом обобщенной мо-
дели ядра является так называемая вращательная мо-
дель, в которой форма ядра предполагается фиксированной. Во
вращательной модели наряду с вращением ядра как целого учиты-
ваются также возбуждения, связанные с внутренними степенями
свободы ядра*. Вращательная модель хорошо объясняет спектры
уровней и другие характеристики деформированных ядер в областях
массовых чисел 150 <Л < 190 и А > 220. В случае деформирован-
ных четно-четных ядер почти все слабо возбужденные уровни яв-
ляются вращательными. В случае деформированных ядер с нечет-
ным А встречаются также низкорасположенные уровни, связанные
с возбуждением отдельных нуклонов. Каждому такому уровню от-
вечает отдельная вращательная полоса.
Обозначим систему координат, связанную с деформированным
ядром, через /С'. Углы Эйлера Ф, 0 иф, определяющие ориентацию
* Теория вращения аксиально симметричных ядер развита в работах
Бора и Моттельсона {1, 2].
243
К' по отношению к неподвижной системе координат К, можно рас-
сматривать как динамические переменные, описывающие вращение
ядра как целого. Координаты, характеризующие внутренние сте-
пени свободы ядра, обозначим г'.
Полный гамильтониан ядра запишем в виде
Н = Н0(г")+Нг + Н', (4.126)
где Яо(г') описывает движение внутренних степеней свободы, Нг
характеризует вращение ядра и Н' учитывает связь между враще-
нием и внутренним движением.
Дальнейшее наше рассмотрение будет основано на предположе-
нии об адиабатичности движения, т. е. на предположении о том, что
волновую функцию ядра можно записать в виде произведения
Ф^П(0)х(г'), (4.127)
где 0(0) — вращательная волновая функция, описывающая кол-
лективное движение ядра (под 0 будем подразумевать совокупность
углов Эйлера Ф, 0 и ф); %(г') — волновая функция, описывающая
движение внутренних степеней свободы.
Допущение об адиабатичности движения означает, что величи-
ной И’ можно пренебречь по сравнению с Н0(г') и Нт. Однако пре-
небрежение Н’ еще не означает полного разделения коллективного
и внутреннего движений, связь между которыми содержится
также в Нт. Поэтому вращательная функция 0(0), вообще говоря,
не является собственной функцией оператора Нт.
Пусть J — момент количества движения ядра, связанный с внут-
ренними степенями свободы, a R — соответственно момент вра-
щения ядра как целого. Полный момент количества движения яд-
ра I равен сумме моментов R и J:
I- R+J. (4.128)
Очевидно, полная волновая функция ядра (4.127) должна быть соб-
ственной функцией квадрата полного момента I® и проекции пол-
ного момента Iz.
Схема сложения моментов и волновая функция ядра. Опреде-
лим волновую функцию ядра (4.127), учитывая, что она является
собственной функцией операторов квадрата 1® и проекции полного
момента Iг. Так как потенциал деформированного ядра не обладает
сферической симметрией, то внутренний момент ядра J не является
интегралом движения. Опыт показывает, однако, что большинство
деформированных ядер характеризуется аксиальной симметрией.
Для аксиально симметричного ядра будет сохраняться проекция
внутреннего момента J на ось симметрии ядра. Поэтому внутренняя
волновая функция будет отвечать определенному значению 7г-,
которое обозначим Q:
<Л->=Й. (4.129)
244
Обозначая т все другие квантовые числа, характеризующие внут-
реннее состояние ядра, внутреннюю волновую функцию можно за-
писать в виде
(4.130)
(Волновая функция хаг(г') предполагается нормированной на еди-
ницу.)
Так как оператор полного момента I = R + J представляет
собой оператор одновременного вращения собственной системы ко-
ординат К' и физической системы, описываемой функцией ха’г(г'),
то
Щ(г'Н0- (4-131)
Следовательно, оператор полного момента 1 действует только на
вращательную функцию D(&), в то время как оператор внутреннего
момента J действует на Хп(г')-
Приведем для полноты изложения перестановочные соотноше-
ния для моментов Ли!. Оператор внутреннего момента J дей-
ствует только на внутренние координаты в собственной системе К',
поэтому компоненты J относительно осей собственной системы ко-
ординат К' удовлетворяют обычным перестановочным соотношениям
= (4.132)
Оператор полного момента I действует только на углы Ф, 0 и Y,
определяющие ориентацию ядра в неподвижной системе координат
К- Поэтому компоненты I относительно осей неподвижной системы
удовлетворяют тем же соотношениям:
1*1^1*= И,- (4-133)
Компоненты полного момента I относительно осей собственной си-
стемы координат /С' удовлетворяют перестановочным соотношениям
= (4.134)
Знак минус в правой части (4.134) связан с тем, что при произволь-
ном вращении собственной системы координат К' функция 0(0),
на которую действует I, преобразуется так же, как и при вращении
лабораторной системы координат К вокруг той же оси на тот же
угол, но в противоположном направлении. Отметим, что операторы
J и I коммутируют друг с другом.
Выберем вращательную функцию D(Q) таким образом, чтобы она
одновременно являлась собственной функцией операторов I2, Ц
и /г-. Поскольку оператор J не действует на 0(0), то это означает,
что функция 0(0) одновременно должна быть собственной функцией
245-
операторов R2, R2 и Такими свойствами, согласно (4.90),
(4.92) и (4.94), обладает функция (Ф, ф), поэтому
Р D‘KM (Ф, в, ф) = 1 (/+1) (Ф, 0, ф);
I, Dk (Ф, 0, ф) = MDlKM (Ф, в, ф);
L'D‘KM (Ф, ©, ф) (Ф, 6, ф).
(4.135)
М и К — проекции полного момента ядра на ось ог в неподвижной
системе координат К. и ось ог' в системе координат К', связанной
с ядром.
Рис. 4.5. Схема сложения мо-
ментов во вращательной модели
ядра.
Рис. 4.6. Схема сложения мо-
ментов в случае аксиально сим-
метричного ядра.
Используя (4.63), нормированную волновую функцию ядра в
предположении об адиабатичности движения можно записать в
виде
V = 1/ 2J~~ D'™ (Ф, 0, ф) Щг'). (4-136)
, оЛ“
На рис. 4.5 представлена схема сложения моментов во вращатель-
ной модели ядра.
Симметрия волновой функции. Приведенная волновая функция
(4.136), однако, еще не удовлетворяет требованиям симметрии, вы-
текающим из симметрии формы ядра. Чтобы удовлетворить этим
требованиям, волновую функцию (4.136) следует несколько видо-
изменить.
246
а. Аксиальная симметрия ядра. Вследствие
аксиальной симметрии ядра волновая функция Т не должна изме-
няться при повороте системы координат, связанной с ядром, вокруг
оси симметрии ядра:
7?г-Ч'=0. (4.137)
Замечая, что R — J —J, это условие можно переписать
(h' L)'KM (Ф, ©, ф)) х£ (г') = D!KM (Ф, 0, ф) (^г- xS (г'))-
Следовательно, требование инвариантности волновой функции от-
носительно поворота вокруг оси симметрии ядра эквивалентно ус-
ловию
К = £2. (4.138)
Это условие означает, что момент вращения Я:для аксиально симмет-
ричного ядра перпендикулярен оси симметрии.
Таким образом, для аксиально симметричного ядра волновая
функция должна иметь вид
= у '2-^Я™(Ф. *M)XR'). (4.139)
На рис. 4.6 представлена схема сложения моментов для акси*
ально симметричного ядра.
б. Симметрия ядра относительно плоско-
сти г' = 0. Если ядро представляет собой эллипсоид вращения,
то при отражении относительно главной плоскости, перпендикуляр-
ной оси симметрии, оно совмещается само с собой. Операция отра-
жения р относительно плоскости г' = 0 для аксиально симметрич-
ного ядра эквивалентна повороту Ry (л) на 180° вокруг оси у'.
При повороте Ry (л) вращательная функция (Ф, 0, 4Q преоб-
разуется согласно (4.58):
₽9-(л)П^ = ^О^л(0,л, 0)D^. (4.140)
К'
Замечая, что D^-K(0, л, 0) = (—1)/_у<5к',-к> имеем
Ry(n)D^ = (-\)l-KDLKM- (4.141)
Аналогично для внутренней волновой функции Хд- получим
Ry (л)Х^-(- 1И~ХХЪе (4-142)
где (— 1)^ следует рассматривать как оператор. Если Х/<~
= ^^Х^х, то ( —1)^Х£ =£<>(—1)^ Х^- Замечая, что
(Л/ + ^-2/<=(-1)/-^ + 2^-^ =(—1/"^, имеем
Ry(n)4IKM = (4.143)
247
Если К =/-- 0, то требование инвариантности при повороте
Ry- (л) означает, что волновая функция должна быть линейной ком-
бинацией (4.139) и (4.143). . Нормированная волновая функция
имеет вид
¥(IRM) = У (172) + (-1/-^ Т/-КМ j- (4.144)
Если К = 0, то уже функция (4.139) удовлетворяет требуемому
свойству инвариантности, при этом, однако, необходимо, чтобы /
и были одинаковой четности (в противном случае функция обра-
щается в нуль):
(^1)/-^1. (4.145)
в. Четность волновой функции. Оператор пол-
ной инверсии Р включает в себя инверсию р' внутренних коорди-
нат относительно осей (х', у', z') и инверсию р коллективных коор-
динат (осей х', у', 2) Р = р'р. Обозначим четность внутренней вол-
новой функции хк через л:
/Од-==+*£. (4.146)
Так как для аксиально симметричного ядра р = Ry- (л), то для
состояний У, инвариантных при отражении относительно плоско-
сти z' — 0, имеем
Р(Т) = л(х). (4.147)
Таким образом, четность волновой функции Т определяется чет-
ностью внутренней волновой функции %.
Если К = 0, то четность внутренней волновой функции можно
непосредственно связать со значением полного момента /. Дейст-
вительно, при К = 0 функция хк=о инвариантна относительно вра-
щений вокруг оси г', поэтому р' = Ry’ (л). Используя (4.142) и
(4.145), находим
я(х)^(-1^ = (-1/. (4.148)
г. Волновые функции. Приведем явные выражения
для волновых функций вращающегося аксиально симметричного
ядра в состояниях с определенными моментами и четностью.
Если К Ф 0, то волновая функция имеет вид
т (/КМ) = 1/2~±^ (Ф, 0. Ф) Х£ (И +
+ (-l)'-^DLKM(<D, 0, ф)%1к(г')}. (4.149)
Четность функции ¥ совпадает с четностью внутренней функции х.
Совокупность состояний (4.149), отвечающих одной внутренней
функции хк, но различным значениям полного момента /, обра-
зует вращательную полосу
/ = К, К + 1, Д + 2,... (4.150)
248
Если К = 0, то волновая функция имеет вид
т (ЮМ)=1/ D'om (Ф, 0, ф) XS (/•'). (4.151)
или
Т (ЛШ) = (1 //2л) Ъл, (0, Ф) XJ (г').
(4,152)
В этом случае возможны две вращательные полосы соответственно
для четных и нечетных состояний:
/ = 0+, 2+, 4+,... л= + 1, 1
1= 1- з- 5“,... л = — 1. J
(4.153)
Вращательные спектры ядер. Используя допущение об адиаба-
тичности движения, гамильтониан вращающегося ядра запишем
в виде
Н=Н0(г')+ЯЛ. (4.154)
Согласно (4.111), вращательная часть гамильтониана определяется
выражением
Hr=-*—J& + -*—R2y+-*—Rl, (4.155)
г 2?х. т 2^, * 2.72, * !
где Оу и О г' — моменты инерции относительно главных осей,
рассматриваемые как эмпирические параметры.
Считая ядро аксиально симметричным и выбирая ось г' в
направлении оси симметрии ядра, полагаем Оу ~ Оу> -=0. Заме-
чая, что R-=I—J, переписываем (4.155) в виде
= {F + r^2IJ}+ (4.156)
В случае аксиально симметричного ядра проекции /г- и ^2- на ось
симметрии ядра равны, поэтому гамильтониан ядра (4.154) окон-
чательно можно представить в виде
Н = Н0(г') + — J3+ — I2 — — IJ.
04 ' 1 2 J' 2.7 7
(4.157)
Первые два слагаемых в (4.157) характеризуют движение внут-
ренних степеней свободы ядра. Внутреннюю функцию хк можно счи-
тать собственной функцией этой части гамильтониана. Вращатель-
ная функция £>кл/ (Ф, 0, ф) является собственной функцией треть-
его слагаемого в (4.157). Если пренебречь четвертым слагаемым в
(4.157), получим следующую простую формулу для уровней энергии
249
вращательной полосы:
Е«(Г) = Ек+^Ц1+1), (4.158)
где Ек—внутренняя энергия, не зависящая от 1.
^2
Слагаемое—j IJ в (4.157) учитывает связь между вращатель-
ным и внутренним движениями в ядре. Для оценки вклада этого
слагаемого в энергию представим скалярное произведение момен-
тов I и J в виде
и = /г.^ + |(/+^_ + /_^+), (4.159)
где
7±-7х-±1Ъ-Л± = ^'±>^'- (4-160)
Так как функция 1¥(1КМ) (4.149) является собственной функ-
цией оператора Iz- и отвечает собственному значению №, то
учет этого слагаемого в (4.159) приводит только к смещению уровней
вращательной полосы (4.158) без изменения их относительного рас-
положения.
Два других слагаемых 1/2(/ /-?/+) в (4.159) недиагональны
в представлении (4.149), если только К. Ф V2. Нетрудно проверить,
используя перестановочные соотношения (4.132) и (4.134), что у
операторов /± и $-± отличны от нуля только матричные элементы
(Кт 11/±|К) = /(/±Ю(/Т7(+~П;
(К т 11 I К) = Г(У±юЖтУ+ТГ
Поэтому
(Ф, О, Ф)Х^(Г') =
=/(ТШ(/-к+Т)(мю(>-л+1)^-1.м(ф, 0, ф)%^-_|(г').
(4.161)
Таким образом, учет /+$_и /_^+ должен приводить к смешива-
нию состояний с различными значениями /С. Если, однако, разность
между внутренними энергиями для различных вращательных полос
велика по сравнению с эффективным значением энергии связи
^2
— -у IJ, то смешиванием состояний с различными значениями Д’
можно пренебречь. В этом случае уровни энергии в отдельной вра-
щательной полосе определяются формулой (4. 158).
Если /С = 1/а, то слагаемое —у IJ имеет диагональную часть,
зависящую от I, которую необходимо учитывать в (4.158) и которая
в некоторых случаях может изменить порядок уровней во вращатель-
ной полосе. Обозначим добавочную энергию в случае К = 1/3 че-
250
рез Д£. Учитывая симметрию функции (4.149), имеем
ДЕ
— f 1-М\КУ = 1-М\1+у-_\1-М\
2J \ 2 + 1 2 ! [ 2 |+с/|2 /
Для вычисления Д£ заметим, что
(4.162)
+ (слагаемое с К= —3/2)^.
Рис. 4.7. Отношение вращательных энергий сильно
деформированных ядер в области редких земель и
тяжелых а-активных ядер:
х-£4/Е2; О-Е«/£»; Д-£,/£1.
Используя ортонормировку функций Dkm и %£, таким образом
получаем
(/l/2Aij/+3(_|71/2M) =
= (1/2) (/ + 1/2)2 j Ср |3 (- (^+ 1/2). (4.163)
Учитывая, что при /( = 1/2 число (2J + 1) четное, выражение
для энергии (4.162) представим в виде
Д£= Л-а( —1/+,/2(/+1/2), (4.164)
* 2сХ
где a — так называемый параметр связи. Величина пара-
метра связи а зависит от внутреннего состояния нечетного нуклона
251
(4.165)
й ойреДелйеТся выражением
а = (^+ 1/2).
Объединяя (4.158) и (4.165), для уровней энергии вращательной
полосы окончательно получаем следующую формулу:
£х(/)=£^ + ^[/(/+1)+а(-1/+1/2(7+1/2)бк. 1/2], (4.166)
пригодную как в случае Д =)= 14> так и в случае К =
Сравнение с экспериментом. Вращательная модель хорошо опи-
сывает вращательные спектры сильно деформированных ядер—в
области редких земель 150<Л-<190, в области тяжелых «-активных
ядер А > 220 и в области легких ядер 20 < A <Z 30 (рис. 4.7).
Ч е т н о-ч етные ядра. В случае четно-четных ядер наи-
более низкой является вращательная полоса К = 0+, которой от-
8f
S'
5
z
O'
Ет,кэ11
1085,3 (1198) 8* 5;, КЭв 515 (530,5)
551,8 (553,1) 6* — 303,5 (309,5)
308,8 (311) 5+ — 155,8 (157,3)
93,3 Г 0* — 55,2 0
0
23SPU
3^u
Рис. 4.9. Схема уровней ядра
S38PU.
7Z4
Рис. 4.8. Схема уровней ядра
вечает последовательность спинов I — 0,2,4,... Обозначим через £7
энергию возбуждения, отсчитываемую от основного состояния ядра
'('+!)• (4.167)
Согласно (4.167), должно выполняться следующее правило интерва-
лов для уровней вращательной полосы
£2:£4:£в:£8 ... = 1 :10/3:7: 12... (4.168)
Это правило хорошо подтверждается в энергетических спектрах
сильно деформированных ядер в трех указанных областях.
Для примера на рис. 4.8 приведен вращательный спектр редко-
земельного элемента 7820 Hf. Возле каждого уровня указана энергия
возбуждения. Используя формулу (4.167), по положению первого
252
вращательного уровня можно определить момент инерции. Найден-
ный таким образом момент инерции для ядра 782°Hf равен 3 =
= 2,23-10~47 г-см2. В скобках (см. рис. 4.8) приведены значения
энергии, вычисленные по формуле (4.167). Как видно, расхожде-
ние между значениями составляет примерно 1%.
На рис. 4.9 приведен вращательный спектр тяжелого «-актив-
ного ядра g348Pu. Момент инерции ядра 2938Ри равен .7 = 4,70х
X Ю~47 г см2. Это значение почти в два раза превышает момент
инерции более легкого ядра 7820Hf.
На рис. 4.10 приведен также вращательный спектр легкого ядра
22Mg. В этом случае момент инерции равен J-0,152- 10~47 х
X г см2.
Нечетные ядра. У деформированных ядер с нечетным
А также наблюдаются вращательные спектры. Для отдельных уров-
4+
Г
0t
ЕцКЗО
6122 (6560)
1368 -
0
Рис. 4.10. Схема уровней ядра
?2«g-
L7
z
з
2
7+
2
136,2
0
Ет,кэ0
303 (302,2)
ts,Ta
731и
Рис. 4.11. Схема уровней ядра
1 8 1 Та
73 ia'
ней вращательной полосы значения спинов равны 10(=К), /0 +
+ 1, /0 + 2, ... Если 7< =/= V2, то для отношения энергий возбуж-
дения имеем
-. (4.169)
*/.+i '0 + 1
Точное измерение этого отношения позволяет определить спин ос-
новного состояния /0. На рис. 4.11 приведен вращательный спектр
т^Та. Наблюдаемое отношение т/"+2 « 2,23, следовательно,
/о+1
10 = 7/2. По положению первого вращательного уровня момент
инерции Д = 2,32 10-47 г см2, т. е. имеет тот же порядок величины,
как и у 78г°Ш.
Вращательный спектр при К = V2- При К. =
спектр уровней может существенно отличаться от простого враща-
тельного спектра. Это обусловлено связью между внутренним дви-
жением и вращением, которая учитывается слагаемым с а в фор-
муле (4.166). Уровни энергии в этом случае зависят от двух пара-
253
Метров а и j. На рис. 4.12 представлена схема уровней энергии
при Д' = Va в зависимости от параметра связи а.
Так как для вращательных спектров тяжелых ядер с /< — 1/2
—1 < а < 1, то учет связи для тяжелых ядер не приводит к изме-
нению порядка уровней. На рис. 4.13, например, приведен враща-
тельный спектр !7VW. Эмпирические значения параметров а и У,
определенные по положению дву^ первых возбужденных уровней,
равны я = 0,19 и .7 — 2,67 10-47 г см2. Используя эти значения,
Рис. 4.12. Зависимость энергий вращательных уровней
£^(7) пРи К = l/g от параметра связи а.
согласно формуле (4.166) можно рассчитать энергии возбуждения
вышележащих уровней. Однако для легких ядер параметр связи а
может принимать большие значения (например, для 2|А1 а ——3,2),
У'1 303,0 (302,^
г
г 2 — 207,0 (207,5)
Г
2 99,7 -
Г 2 ———— М,5 ~
Г 0
2 /Л
Рис. 4.13. Схема уровней
ядра )®3W.
что может привести к изменению поряд-
ка уровней.
Магнитные моменты деформирован-
ных ядер. Оператор дипольного маг-
нитного момента вращающего ядра, вы-
раженный в ядерных магнетонах, опре-
деляется выражением
n=g*R + H', (4-170)
где gn — гиромагнитный множитель,
связанный с вращением ядра как це-
лого; р/ — внутренний магнитный мо-
мент, равный сумме магнитных момен-
тов отдельных нуклонов:
М'=2 s') (4.171)
(отметим, что S(l' + s') — J). Выражая момент вращения через
полный момент ядра R — I -— J, перепишем соотношение (4. 170)
254
в виде
н=^1 + (ц'-М’ (4.172)
Магнитный момент ядра р определяется как среднее значение
проекции оператора р на неподвижную ось oz в состоянии М = 1.
При вычислении среднего, однако, вектор (р' — gRJ), характери-
зующий внутреннее движение, удобнее относить к собственной си-
стеме координат К/, связанной с вращающимся ядром.
Введя сферические составляющие какого-либо вектора L при по-
мощи соотношений
Lo L±1 = Т У(I/2jL±, (4.173)
связь между компонентами вектора в неподвижной и подвижной
системах координат Д' и ТС запишем в виде
= (4.174)
я'
Таким образом, для оператора проекции магнитного момента
рг получим выражение
Pz = gRh + 2 ^.0(Ф, 0, ф)(р' -^J) . (4.175)
?'=о, ±1 4
Используя формулу (4.149) для функции ЧГ(7ДЛ4), определим
среднее от р. в состоянии М = 7. В выражение для среднего зна-
чения от второго слагаемого в (4.175) войдут интегралы от произ-
ведения трех D-функций. Эти интегралы легко вычислить с помощью
соотношения (4.64):
(d;.0D'±m (1МЮI /М) у ± KW1I ± К). (4.176)
J zl г 1
Разные знаки при Д отвечают перекрестным членам от произведе-
ния различных слагаемых функции (4.149).
Коэффициент (/ ± Д1(?' | 7 ± К) отличен от нуля только при вы-
полнении условия
±K = q'±K. (4.177)
Поэтому если К ф Чг, отличный от нуля вклад в (4.175) дает толь-
ко слагаемое q' = 0. Таким образом, при Д J/2 имеем
р -^7 + (7ЛПО | IM) (IK\O] IK) (хЛ 1| Хд)- И-178)
[Состояния хк и х-к дают одинаковый вклад в (4.178).! Вводя внут-
ренний гиромагнитный множитель g%
(Хл-КМ^л* (4.179)
и замечая, что (IД101IK) = у JL= , получаем следующую фор-
мулу:
^=gRl+(gK-gR)~Y
(4.180)
255
Если К = 1/2> то условие (4.177) выполняется также при q' =
= ±1. В этом случае отличными от нуля будут матричные элемен-
ты, перекрестные по состояниям хк и Х-к- Поэтому в (4.178) необ-
ходимо учесть и слагаемое
и комплексно сопряженное слагаемое. Вводя обозначение
Re/Xj ,\= -L(-1)-'+1/2й,
\ т У 2
добавку к (4,178) в случае К — 1/2 получим в виде
(4181)
п / г 1 111 r IX 1 2/4-1
При этом использовали, что I----11/— =-------= • —. .
I 2 ( 2/ V8 V 1(1+1}
Объединяя формулы (4.180) и (4.181), окончательно получаем
для магнитного момента вращающегося ядра следующее выра-
жение:
P = gR7+-^^{№+^(-l)'“1/2(2/+l)66K]/2J. (4. !82)
Для основного состояния ядра в (4.182) следует считать I = Д.
В общем случае выражение для магнитного момента (4.182)
содержит три параметра gR, g% и b, для вычисления которых необ-
ходима более детальная теория. Экспериментальное определение
магнитного момента дает одно независимое соотношение между
этими параметрами. Одновременное измерение вероятностей пере-
ходов между вращательными состояниями позволяет найти для
некоторых случаев эмпирические значения параметров gR, gK и Ь.
Определим для иллюстрации с помощью (4.182) магнитный мо-
мент деформированного ядра с нечетным/!. Предположив, что рас-
пределение заряда однородно, положим g% да (Z/Д). Считая также,
что внутренний момент р.' обусловлен последним нечетным нуклоном,
который находится в состоянии с определенным можно поло-
жить gK да gy, где gy — гиромагнитное отношение для нечетного
нуклона, полученное из оболочечной модели. Таким образом, при
I > ’/2 имеем
И— . (4-183)
Для примера приведем экспериментальные значения магнитных
моментов и значения, рассчитанные по формуле (4.183), для ряда
ядер со спином I = 5/2 (табл. 4.1).
256
Таблица 4.1
Ядро I'ai.cii ! Ядро
3,61 3,77 —0,86 —0,67
3,36 3,73 —0,91 —0,81
3/8 3,73 !i l04^ -0,6 -0,81
!^Re 3,20 3,71 ii 'Ucd —0,7 —0,81
Согласно оболочечной модели, магнитный момент должен рав-
няться 4,79 пли —1,91 в зависимости от того, является ли нечетная
частица протоном или нейтроном. Следовательно, учет добавочного
магнитного момента, связанного с деформированным остовом ядра,
значительно улучшает согласие с опытом.
Квадрупольные моменты деформированных ядер! Оператор
электрического квадрупольного момента ядра определяется выра-
жением
Q,-]/-^Sr2F.27(^q), (4.184)
где суммирование распространяется по всем протонам. Переходя
в систему координат, связанную с ядром, согласно (4.60), имеем
6, (4,185)
ч'
Электрический квадрупольный момент ядра Q определяется как
среднее значение оператора Qs0 в состоянии М = I:
Q^(Q,=O\W=/. (4.186)
Используя выражение (4.149) для волновой функции ЧГ(/КЛ4),
таким образом, находим
Q = (//20j//)(/№0|//()<?0, (4.187)
где Qo — внутренний квадрупольный момент ядра, определяемый
выражением
й=ЫУ,,.»|вд. <4188>
(Отметим, что при К = С3 или 1 в (4.185) необходимо учитывать
также слагаемые q' Ф 0, матричные элементы которых, однако,
для состояний хк и Х-х обращаются в нуль.) Замечая, что
(И201 П) (1К20 ПК) - ,
9 Зак. 642
257
получаем следующее выражение для квадрупольного момента;
Q . Q (4. i89)
(/+1) (2/4-3) °
Если / достаточно велико /(/ + 1) >• 3№, то квадрупольный мо-
мент Q противоположен по знаку внутреннему квадрупольному
моменту.
Для основного состояния вращательной полосы / = К имеем
—Q (4.190)
(/-j-1) (2/4-3)
Коэффициент при Qo обычно называют проектирующим
множителем. Наличие этого множителя приводит к сильному
уменьшению измеряемого квадрупольного момента Q по сравнению
с Qo- Если I = 0 или 1/2, то квадрупольный момент ядра Q обращает-
ся в Нуль, хотя внутренний квадрупольный момент Qo при этом мо-
жет быть отличным от нуля. При I = 1 множитель равен 1/10, при
/ = \ равен г/6, при дальнейшем увеличении / множитель медлен-
но стремится к единице.
Внутренний квадрупольный момент ядра можно вычислить,
предполагая распределение заряда однородным:
Q0^(2Z/V) $dr(a2-^)^-(2Z/5)(^-^.). (4.19])
v
Используя выражение (4.102) для главных осей эллипсоида,
таким образом, получим
Qo=-1-Wpl 1+у]/ Ъ), (4.192)
где р — параметр деформации ядра.
Экспериментально Qo можно определить, измеряя вероятности
у-переходов ядра из одного вращательного состояния в другое.
В табл, 4.2 приведены значения Qo и соответствующие значения па-
раметра деформации р для ряда четно-четных ядер, найденные по
вероятностям £2-переходов.
Таблица 4.2
Ядро Qo, IO-24 <.и» Ядро Qo. 10~24 ₽
‘eoNd 4,8 0,25 : *72™ 8,1 0,31
152о 62'-ТП 5,7 0,28 I 6,5 0,24
154<j 62^m 6,7 0,33 ! ««Os 5,1 0,18
i60r 10 0,46 '
258
Таблица 4.3
Ядро 1 Qu (спектро- скопические измерения) (£2- переход) Ядро / (спектро- скопические измерения) <2Й (Е2- переход)
'iisu 6/3 7,0 7,7 1751 11 71т 12 8,2
'б5^ 5,5 8,0 б/2 7,8 5,4
5,0 7,7 1
У ядер с нечетным А квадрупольный момент можно также опре-
делить из спектроскопических измерений сверхтонкой структуры
спектральных линий (/ > */2). В табл. 4.3 приведены значения внут-
ренних квадрупольных моментов Qo для ряда нечетных ядер, най-
денные по спектроскопическим изме-
рениям и измерениям вероятностей
£2-переходов.
На рис. 4.14 представлены значе-
ния квадрупольных моментов для
сильно деформированных ядер в
области i массовых чисел 150 <
А < 193.
Одночастичные состояния в дефор-
мированных ядрах. Рассматривая
оболочечную модель, мы предполага-
ли, что самосогласованный потенциал
ядра, в котором движутся нуклоны,
обладает сферической симметрией.
Определяемая таким потенциалом
форма ядра также характеризовалась
сферической симметрией. Действи-
тельно, в области заполненных оболо-
Рис. 4,14. Значения квадру-
польных моментов сильно де-
формированных ядер в области
редких земель.
чек равновесной формой реальных
ядер является сферически симметричная форма. Однако ядра, у кото-
рых последняя оболочка заполнена примерно наполовину,характери-
зуются значительными деформациями. Для объяснения свойств
деформированных ядер помимо изучения коллективных движений
в них необходимо также рассмотреть одночастичные состояния нук-
лонов, движущихся в несферическом потенциале. В адиабатическом
приближении одночастичные и коллективные движения в ядре раз-
деляются, поэтому полную волновую функцию ядра можно пред-
ставить в виде произведения двух функций, каждая из которых опи-
сывает соответственно движение ядра как целого, т. е. вращение
ядра и колебания его поверхности, и внутреннее движение в несфе-
рическом ядре.
Рассматривая внутреннее движение в ядре, будем предполагать,
что отдельные нуклоны движутся независимо в некотором фикси-
259
рованном несферическом поле ядра. Гамильтониан внутреннего
движения тогда представится, как и в обычной модели оболочек
(без учета остаточного взаимодействия), в виде суммы одночастич-
ных гамильтонианов. Таким образом, задача сводится к решению
уравнения Шредингера для одной частицы с одночастичным потен-
циалом, который нужно выбрать так, чтобы он отражал основные
особенности движения нуклонов в несферических ядрах и в то же
время имел по возможности простой вид. Подобная задача решалась
для нескольких потенциалов разными авторами. Наиболее простой
вид имеет так называемый потенциал Нильссона [61, который хо-
рошо применим в случае средних и тяжелых ядер.
Потенциал Нильссона выбирается в виде суммы
V = (Л1/2) (сщ2 х2 + со,2 у2 -ф <я32 г2) Cis 4-ОГ2, (4.193)
где первое слагаемое есть потенциал анизотропного осциллятора,
учитывающего несферичность потенциальной ямы и размытость ее
края; второе слагаемое описывает спин-орбитальное взаимодейст-
вие; третье слагаемое, пропорциональное 1а, вводится для пониже-
ния энергии одночастичного состояния при больших значениях
орбитального момента /. Так как большинство несферических ядер
имеет форму, близкую к эллипсоиду вращения, будем считать, что
поле ядра характеризуется аксиальной симметрией и ы, = ш2
#= (о3. Как мы знаем, в этом случае форму ядра при постоянном его
объеме можно описать, введя всего лишь один параметр деформации.
В потенциале Нильссона этот параметр, обозначаемый 6, опреде-
ляется следующим образом:
Из условия постоянства объема ядра, обратно пропорционального
произведению частот <о1г со2 и со3, следует, что величина со не являет-
ся постоянной и зависит от параметра деформации 6 следующим
образом:
со = со (6) - со (0) — (4.195)
В случае малых деформаций величина 6 связана с введенным ра-
нее параметром деформации [1 соотношением
(4.196)
Полный гамильтониан нуклона Н найдем, добавляя к (4.193)
оператор кинетической энергии — ?м Д. Выделив в гамильтониане
сферически симметричную часть
(4.197)
260
(4.198)
(4.199)
одночастичный гамильтониан представим в виде
где
Нь = - 41/ М& Ьг* У20 (п).
Of О
Отметим, что с оператором Н не коммутируют операторы квад-
цата полного момента нуклона j2, квадрата орбитального момента
I2 и проекций орбитального и спинового моментов на ось z (ось
симметрии поля) /z и s2. Заметим, что сферически симметричная часть
Но также не коммутирует с полным гамильтонианом Н. Однако опе-
ратор проекции полного момента на ось симметрии jz = lz + sz
коммутирует с Н, поэтому состояния нуклона в поле (4.193) харак-
теризуются определенными значениями проекции полного момен-
та Й.
Следующим шагом является диагонализация , одночастичного
гамильтониана Н. Для этого нужно выбрать удобное представление
и записать матрицу гамильтониана И в этом представлении. Обычно
выбирается представление, в котором симметричный гамильтониан
Но диагоналей. Иными словами, в качестве базисных функций, по
которым будем раскладывать функции нуклона, движущегося в
потенциале Нильссона, и с помощью которых определяется матрица
гамильтониана Н, будем использовать функции гармонического
изотропного осциллятора определяемые уравнением
= + (4.200)
где Ли 2 — проекции орбитального и спинового моментов нукло-
на на ось симметрии ядра. Хотя матрица полного одночастич-
ного гамильтониана, вычисленная с помощью этих функций
<jV7'A'S'|Н\NIAZ), не диагональна ни по одному из квантовых
чисел N, I, Л и X, вычисление ее в указанном представлении прово-
дится довольно просто. В самом деле, два слагаемых в полном га-
мильтониане, Но и D12, диагональны в выбранном представлении.
Матричные элементы оператора 1s (не равные нулю) можно записать
следующим образом:
<А' Г Л' S' [ls|A/AX>=-l^'^6''i х
X { f(/TA)(l±A+l) 6Л'Л± 1 -х ± Л6л- л г} . (4.201)
.Более громоздко вычисляется матричный элемент от /76. Матричный
элемент от угловой части оператора (/'Д'| У201 ZA> вычисляет-
ся согласно (3.70). Для вычисления радиальных матричных элемен-
тов <A7'|t2|jV/> можно воспользоваться явным видом радиальной
261
волновой функции частицы в поле изотропного осцилляторного по-
тенциала (3.27). Приведем результат вычисления более общего мат-
ричного элемента с помощью функций (3.27):
После того как матрица <ATTA'S' |/71 Л7Л2> вычислена, за-
дача сводится к ее диагонализации. Диагонализация проводилась
с помощью электронно-вычислительных машин для нескольких
значений параметра деформации 6 и ряда фиксированных значений
квантовых чисел N и £2. При этом численные значения С и D выби-
рались таким образом, чтобы при 6 = 0 воспроизводилась последо-
вательность уровней оболочечной модели. (В расчетах при 6 = 0
величину а выбирали в соответствии с (3.31), а С = —0,1 Йсо.)
Отношение р, — ‘2D! С считали равным 0 при N = 0,1 и 2; 0,35 при
jV == 3; 0,45 при N = 4,5 и 6; 0,40 при N = 7. Обозначим собст-
венные значения части гамильтониана Н — Но через—(С/2)Гцй, где
индекс а нумерует эти собственные значения. Тогда собственные
значения одночастичного гамильтониана (4.198) с учетом (4.200)
представятся в виде
£аЯ(6)= ^+|^оДб)-(С/2)г"й(6). (4.203)
Собственную функцию гамильтониана Н, соответствующую кванто-
вым числам N, £2 и а, обозначим через Хца. Эта функция яв-
ляется суперпозицией функций
(4.204)
/л
где 2 = £2 — Л. Коэффициенты суперпозиции (6), норми-
рованные так, что 2 | а(л“(б),2 = 1, определяются одновремен-
1Л
но с собственными значениями энергии при численной диагона-
лизации матрицы гамильтониана. Составлены таблицы для коэф-
262
фициентов разложения а^д (6) и получены кривые зависимости
одночастичных энергий как функций параметра деформации
6 [6].
Из соотношения (4.202) видно, что матрица гамильтониана не-
диагональна по квантовому числу ЛГ, причем N’ отличается от N
на четное число. Однако недиагональные матричные элементы по
числу N в большинстве случаев значительно меньше по модулю бли-
жайших диагональных по N матричных элементов, поэтому связью
между состояниями с различными N можно пренебречь, за исклю-
чением некоторых особых случаев. Таким образом, одночастичные
состояния в потенциале Нильссона можно характеризовать наряду
с проекцией полного момента £2 также и квантовым числом JV. В слу-
чае достаточно малых деформаций, когда слагаемым в гамиль-
тониане Н можно пренебречь, операторы I2 и ja коммутируют с Н,
и поэтому при б 0 одночастичные состояния можно характери-
зовать набором квантовых чисел N, I, / и £2. При малых б слагаемое
Яб можно учесть по теории возмущений. С увеличением деформа-
ции квантовые числа I и j теряют смысл. При достаточно больших
деформациях, когда в гамильтониане можно пренебречь членами
с 1s и I2 по сравнению с Н6, в пределе получим гамильтониан анизо-
тропного осциллятора с аксиальной симметрией. В этом случае
одночастичные состояния можно описывать наборами квантовых
чисел N, п3, Лий (при этом S также имеет определенное значение:
2 = £2 — Л). Члены, содержащие 1s и I2, можно при больших де-
формациях б учесть по теории возмущений. Заметим также, что в
суперпозицию (4.204) входят слагаемые с I, отличающиеся друг от
друга и от числа N на четное число, поэтому однбчастичные состоя-
ния характеризуются определенной четностью л.
Для иллюстрации на рис. 4.15 приведена схема уровней в зави-
симости от параметра деформации б для области 50 < N < 82,
в которой находятся многие несферические ядра. При б > 0 ядро
вытянуто вдоль оси симметрии, а при б<0 ядро сплюснуто. Каждой
кривой на рис. 4.15 сопоставлены квантовые числа/у | £2 Iя (Яп3^Л|),
из которых независимо от величины деформации хорошие квантовые
числа — это проекция полного момента £2 (по знаку £2 имеется вы-
рождение) и четность л; почти хорошим в указанном выше смысле
является энергетическое осцилляторное квантовое число Я; кван-
товые числа I и / являются хорошими лишь при б —0, а па и Л,
наоборот, хорошие квантовые числа при больших деформациях
(асимптотические квантовые числа). Например, одна из кривых
(см. рис. 4.15) отмечена следующим образом: gj Б/3(402), что озна-
2~
чает: I = 4, / = ’/2 при б = 0; | £2 | = 5/2, л = + 1; N = 4, п3 =
= 0, - |Л| — 2. (Последние два числа имеют указанные значения
при больших деформациях б). Заметим, что так как параметры,вхо-
дящие в одночастичный потенциал Н, для протона и нейтрона не-
сколько отличаются, то и схемы уровней, а также наборы коэф-
фициентов суперпозиции в (4.204) будут различными.
263
На основе рассмотренной модели можно рассчитать полную
энергию и равновесную деформацию ядер. Если предположить,
что между нуклонами действуют только двухчастичные силы, то
V*-------1--------1--------1-------1--------1_________।_______।
'V -0,2 -0,1 -о 0,1 0,2 0,3 6
Рис. 4.15. Схема уровней энергии в зависимости от параметра деформации
5 для области ядер 50 <Л'< 82, согласно модели Нильссона.
полный гамильтониан ядра Н = У 7\ + (V,) У непосредственно
i ‘ i j
выражается через гамильтониан отдельного нуклона IIL = Ti +
264
+ У К-p следующим образом:
i /• i
(4.205)
Полная волновая функция ядра—это антисимметризованное произ-
ведение волновых функций отдельных нуклонов (4.204), Поэтому
чтобы найти полную энергию ядра £(6) как функцию параметра
Рис. 4.16. Экспериментальные (точки) и рассчитан-
ные значения параметра деформации 6 (сплошная
кривая) по модели Нильссона в области редких
земель:
X — нечетные ядра; с —четно-четные ядра.
деформации 6, мы должны вычислить среднее значение (4.205) с
помощью рассчитанных одночастичных функций. Тогда равновес-
ное значение параметра деформации <50 можно определить из усло-
вия минимума энергии £(6)
дЕ(6)/д6=О. (4.206)
На рис. 4.16 приведены рассчитанные значения параметра дефор-
мации 6 по модели Нильссона и экспериментальные значения в об-
ласти редкоземельных элементов.
Модель Нильссона позволяет также обосновать правило нахож-
дения спинов ядер в основном состоянии. Согласно (4.203), каждый
одночастичный уровень энергии двухкратно вырожден (±й). Ней-
троны и протоны независимо заполняют уровни парами. Если число
одинаковых частиц четное, то 2£2(- = 0, если же нечетное, то сум-
марное £2 равно £2г последней частицы, не имеющей пары. Если
число нейтронов (протонов) четное, а протонов (нейтронов) — не-
четное, то для основного состояния спин равен /0 = Q;> (Qn). Таким
образом, спины ядер в основном состоянии определяются свойст-
265
вами последнего нечетного нуклона и равны /0 = £2 — К, за ис-
ключением случая £2 = l/2. Если £2 '/2, то спин основного со-
стояния /0 определяется величиной параметра связи а (табл. 4.4).
Таблица 4.4
Пределы изменения Спин основного состояния /0 Пределы изменения параметра связи а Спин основного состояния
параметра связи а
— 14 < а . —10 и/3 4 < а < 8 5/2
— 10 < а < —6 7/2 8 < а <. 12 й/2
—6 < а < —1 3/2 12 < а <- 16 13/2
—1 < а < 4 ’Л
(4.208)
Параметр связи а, определяемый соотношением (4.165), выра-
жается непосредственно через коэффициенты а1А, входящие в фор-
мулу (4.204):
a = 2(-!)'G4+2' И)а|воа). (4.207)
i
Аналогичным образом можно найти гиромагнитное отношение g%
и коэффициент Ь, входящий в выражение для магнитного момента
ядра (4.182) в случае /0 = К = х/2:
8к = g, + (1 Ж) (gs-gj к_ i /2 - 4 к+1/2);
i
-gR)b= (gs -gt) ^ (-1 )4o + (£/-£«)a-
t
Рассчитанные значения магнитных моментов для деформированных
нечетных ядер хорошо согласуются с экспериментальными данными.
Моменты инерции ядер. Важнейшим свойством, отличающим
несферические ядра от сферических, является наличие у несфери-
ческих ядер вращательных уровней энергии. В то время как общие
закономерности вращательных спектров (например, отношение энер-
гий, значения спинов и четности, симметрия состояний и т. д.)
полностью определяются вращательной природой уровней, абсо-
лютные значения вращательных энергий (т. е. величины моментов
инерции) существенно зависят от внутренней структуры ядер.
Предположим, что аксиально симметричное ядро медленно вра-
щается с определенной частотой о> вокруг оси, перпендикулярной
оси симметрии ядра. Момент количества движения, связанный с
вращением ядра, равен
где .7 — момент инерции. Для нахождения момента инерции J не-
обходимо воспользоваться определенными представлениями о внут-
ренней структуре ядра.
266
В качестве предельных случаев вращательной модели ядра мож-
но рассмотреть вращение твердого тела и потенциальное движение
идеальной жидкости во вращающейся оболочке. Различие между
указанными предельными случаями наглядно проявляется на при-
мере вращения тела сферической формы. В случае модели твердого
тела момент инерции при переходе к сферически симметричному слу-
чаю стремится к конечной величине — моменту инерции.сферически
симметричного тела (шара). В случае гидродинамической модели
при вращении сферической оболочки скорость каждой точки поверх-
ности направлена по касательной, а нормальная составляющая ско-
рости равна нулю. Поэтому уравнениям движения идеальной гидро-
динамики в таком сосуде будет удовлетворять только покоящаяся
жидкость (так как v = 0 удовлетворяет как уравнениям движения,
так и граничным условиям), и, следовательно, момент инерции си-
стемы будет равен нулю. Если оболочка имеет несферическую фор-
му, то нормальная составляющая скорости на поверхности отлична
от нуля и жидкость будет увлекаться при вращении оболочки. При
этом энергия вращения для заданной угловой скорости будет тем
больше, чем больше форма оболочки отличается от сферы.
Представим ядро в виде эллипсоида вращения, длины полуосей
которого равны J.
£₽)*• <4-2М>
Здесь р — параметр деформации. Если ядро рассматривать как твер-
дое тело, то момент инерции будет равен
-^(^+«?)=4^2 H i-4 <4-210>
5 5 \ 2 14л 32 л/
где т — масса ядра.
Определим теперь момент инерции при потенциальном движе-
нии жидкости в эллипсоидальном сосуде, имеющем форму ядра.
Потенциальное движение жидкости описывается потенциалом ср,
удовлетворяющим уравнению Лапласа:
Аср =0.
Скорость движения жидкости v определяется градиентом потен-
циала
v =§габф.
В случае идеальной жидкости граничные условия сводятся к требо-
ванию, чтобы нормальная составляющая скорости жидкости на по-
верхности совпадала с нормальной составляющей скорости стенки
сосуда.
Скорость точки с радиусом-вектором г на поверхности вращаю-
щегося сосуда равна [сог]. Замечая, что нормаль к поверхности эл-
липсоида характеризуется составляющими
N = (х/ЯД у//?/, г/R^)
267
(если ось симметрии направлена вдоль оси oz), условие равенства
нормальных составляющих скоростей v и (юг] на поверхности за-
писываем в виде
х / dq>
coz') 4
У д<р
/?? ’ ду
Это условие будет удовлетворено, если в качестве решения уравне-
ния Лапласа выберем
<p = Axz, (4.212)
где А —некоторая постоянная. Подставляя (4.212) в (4.211), на-
ходим значение этой постоянной:
со.
Вычислим кинетическую энергию жидкости при вращении обо-
лочки. Эта энергия равна
(4.213)
Тт = (р/2) drva = (р/2) Л2 dr (х2 + za),
где р — плотность жидкости, и интегрирование производится по
объему эллипсоида. Подставляя (4.213) и выполняя интегрирование,
находим
7 =Л
г 5 ' R22 + RA ' 2
(4.214)
где m — масса жидкости. Коэффициент в (4.214) при соа/2 и следует
считать моментом инерции в гидродинамической модели ядра:
m (R^-Rf)2
5 ‘ RJ + Ri2
(4.215)
Используя выражения (4.209) для /?г и /?2, момент инерции в гидро-
динамической модели можно переписать в виде
(4.216)
Отношение моментов инерции (4.216) и (4.210) в случае малых де-
формаций равно
= (4.217)
16 л '
На рис. 4.17 изображено поле скоростей при вращении твердого
тела и при потенциальном движении идеальной жидкости во вра-
щающейся жесткой оболочке. Если в случае твердого тела вся си-
268
стема вращается как целое, то при вращении жесткой оболочки,
заполненной идеальной жидкостью, последняя увлекается стенка-
ми только вблизи поверхности оболочки.
На рис. 4.18 приведена зависимость моментов инерции от вели-
чины параметра деформации для четно-четных редкоземельных
ядер. Как видно из рис. 4.18, при малых деформациях [} наблюда-
емые на опыте моменты инерции значительно меньше значений,
предсказываемых твердотельной моделью. Кроме того, они значи-
тельно больше значений, предсказываемых гидродинамической мо-
делью.
Рис. 4.17. Поле скоростей при вра-
щении твердого тела (а) и при потен-
циальном движении идеальной жид-
кости во вращающейся жесткой
оболочке (б).
Более последовательно момент инерции ядра можно рассчитать
на основе так называемой модели принудительного вращения,
предложенной в работе [8]. Для этого рассмотрим движение системы
частиц, находящихся в медленно вращающейся (вокруг оси, не сов-
падающей с осью симметрии) несферической потенциальной яме.
Уравнение Шредингера, описывающее движение системы, имеет
ВИД ;
— —(4.218)
где
//(/) -T-j-1'(г, /)
[Г — кинетическая энергия; V(r, t) — потенциал, медленно изме-
няющийся со временем в неподвижной системе координат). Если
вращение происходит медленно по сравнению с внутренним движе-
нием, то можно говорить об энергии вращения системы при неизмен-
ном внутреннем состоянии.
Введем вращающуюся систему координат, жестко связанную
с ядром. Выберем ось ог в направлении оси симметрии ядра, и пусть
вращение происходит вокруг оси ох. Тогда при переходе во враща-
ющуюся систему координат функция ф ~ ф (г) переходит в функ-
цию ф' н= ф (г'), которая, согласно (4.48), связана с ф соотноше-
нием
ф' — е 10Jx ф,
(4.219)
269
где 9 = cot Соответственно гамильтониан системы Н перехо-
дит в Н':
Heieix-
Так как Н' — это гамильтониан внутреннего движения в собствен-
ной системе координат, то он не зависит от времени. Обозначим соб-
Рис. 4.18. Зависимость моментов инерции .//.Т",, от
величины параметра деформации для четно-четных
редкоземельных ядер, полученная на основе сверхте-
кучей модели (сплошная кривая) и на основе
гидродинамической модели (штриховая кривая).
ственные значения И’ и собственные функции Е. и причем
Я'Х^ЕД,. (4,220)
Найдем уравнение, определяющее функцию ф', заданную во
вращающейся системе координат. Для этого выразим функцию ф
через ф' и подставим в (4.218). В результате получим
—(Й/с) (дф'/df) =Нф\ (4,221)
где
H = H'+hajx. (4.222)
Введем обозначение
ф'=Хе-О/Л)^. (4,223)
Считая частоту со достаточно малой, величину Е и функцию х мож-
но вычислить с помощью теории возмущений. Так как диагональ-
ный матричный элемент от /ж равен нулю, то
Е = £ — да ц)2 V BJJ /*1122 •
1 X £,-Ее
270
Зная функцию (4.223), нетрудно вычислить энергию системы в не-
подвижной системе координат:
ОЬ W) = (ФЛ Н' ф/) = (X;, (н-г^х) хг)
Et + П2 to® V iLLLkLflll. (4.225)
Et—Ei
Очевидно, добавка к внутренней энергии Ei и должна рассматри-
ваться как энергия вращения, при этом момент инерции можно оп-
ределить как удвоенный коэффициент при о2. Таким образом, по-
лучим следующую формулу:
J = 2й2 (4.226)
! -А 1 ]
Если в качестве внутренних волновых функций использовать
оболочечные функции независимых частиц, движущихся в несфери-
ческой яме (например, в анизотропной осцилляторной яме), то
получается момент инерции такой же, как и при Вращении твер-
дого тела. Это связано с тем, что при медленном адиабатическом
вращении потенциальной ямы одночастичные состояния независи-
мых (нескоррелированных) частиц не изменяются, и, следователь-
но, коллективное вращение всей системы осуществляется так же,
как и в случае твердого тела. Отклонения наблюдаемых значений
моментов инерции ядер от твердотельных значений обусловлены
наличием корреляции между нуклонами. Остаточное взаимодей-
ствие между нуклонами (которым пренебрегается в модели неза-
висимых частиц) приводит к корреляции между нуклонами, стремя-
щейся замедлить коллективное вращение и уменьшить момент инер-
ции системы. Если взаимодействие между нуклонами было бы на-
столько сильным, что средняя длина свободного пробега оказалась
бы малой по сравнению с размерами ядра, то применима была бы
гидродинамическая модель и коллективное движение стало бы по-
тенциальным. Корреляция между нуклонами, обусловленная си-
лами спаривания, учитывается в сверхтекучей модели ядра. По-
следовательный метод расчета моментов инерции ядер на основе
сверхтекучей модели развит Мигдалом [9].
$ 4.5. ВРАЩЕНИЕ НЕЛКСИАЛ ЬНЫХ ЯДЕР
Модель неаксиального ротатора. Детальное сравнение наблю-
даемых спектров возбуждения деформированных ядер с предска-
заниями вращательной модели, согласно которой ядро рассматри-
вается как аксиально симметричный ротатор, показало, что хотя
для многих ядер вращательная модель и хорошо воспроизводит осо-
бенности вращательных спектров, тем не менее для некоторых ядер
имеет место несоответствие между наблюдаемой картиной и пред-
сказаниями простой вращательной модели. Попытки объяснить
271
несоответствие учетом поправок на неадиабатичность вращения ус-
пеха не имели. А. С. Давыдов и Г. Ф. Филиппов показали, что труд-
ности можно устранить, если отказаться от допущения об аксиаль-
ной симметрии деформированных ядер. Они развили теорию неак-
сиальных ядер [10], в основе которой лежит допущение о том, что
деформированное ядро — это трехосный эллипсоид, вращение ко-
торого и определяет спектр коллективных возбуждений ядра.
Данная теория позволила описать основные закономерности спект-
ров возбужденных состояний большинства четно-четных ядер.
В адиабатическом приближении, когда вращательное движение
можно отделить от колебаний ядерной поверхности и от одночастич-
ного движения, форму ядра можно считать фиксированной; при этом
гамильтониан, описывающий вращение четно-четного ядра, можно
записать в виде
где Ih' — проекции оператора полного момента на главные оси
эллипсоида и У к' — моменты инерции относительно главных осей:
3~ 4В[32 sin2 I у--— k' 'l
(все три момента инерции ядра предполагаются различными). Опе-
ратор вращательной энергии (4.227) действует лишь на углы Эй-
лера и представляет собой оператор Гамильтона жесткого неакси-
ального ротатора (асимметричного волчка). Прежде чем находить
решения уравнения Шредингера для асимметричного волчка, со-
ответствующие определенным значениям полного момента количе-
ства движения / и его проекции Л4 на ось oz
(Hr — Ei~) Ф,м (Ф, 0, ф) =0 (4.228)
(т—дополнительные квантовые числа), выясним, какие условия,
вытекающие из свойств симметрии гамильтониана Нт, должны на-
кладываться на волновые функции неаксиального ротатора
Ф/\ (Ф, 0, ф).
Оператор Нг и перестановочные соотношения (4.134) для про-
екций полного момента /;/ на главные оси инвариантны относи-
тельно преобразований группы О2, включающей три поворота на
угол 180' вокруг осейх', у' и z'\ Rr (л) — и тождественный эле-
мент е. Инвариантность легко проверить, если воспользоваться со-
отношениями
Rr (л) 4- (л) = (26rt-- 1) Ik’ (4;229)
[при каждом повороте Rr (л) два из трех операторов (j'=l, 2, 3)
изменяют свой знак], откуда сразу следует, что гамильтониан ком-
мутирует со всеми операциями из группы D2. Так как каждый эле-
272
мент группы D3 представляет собой класс группы, а число классов
группы равно числу неприводимых представлений, то всего имеется
четыре одномерных неприводимых представления группы D2, ко-
торые обозначим буквами A, Bt, В2, В3. Укажем их характеры
(совпадающие в данном случае с одномерными матрицами неприво-
димых представлений), используемые при нахождении собственных
функций оператора Нг (табл. 4.5).
Таблица 4.5
D, е (я) Иг (Я) И, (л) Ds е Я1 (Л) (Я) Яз'(я)
А Bi 1 1 1 -1 1 — 1 1 ! Оз Св 1 1 — 1 1 1 —1 —1 — I
Известно, что между собственными функцией стационарных
состояний и неприводимыми представлениями группы преобразо-
ваний, коммутирующих с гамильтонианом, имеется тесная связь.
Энергетические состояния системы можно классифицировать по не-
приводимым представлениям, которые соответствуют указанным
состояниям. Ясно, что кратность вырождения энергетического уров-
ня совпадает с размерностью представления, т. е. с числом базис-
ных функций представления. Все эти функции относятся к одному
л тому же значению энергии. Таким образом, зная, по каким непри-
водимым представлениям группы симметрии преобразуются волно-
вые функции стационарных состояний, мы, не решая уравнение
Шредингера, сможем найти некоторые свойства указанных функций.
В рассматриваемом случае все неприводимые представления
группы одномерны, поэтому энергетические состояния соответ-
ствующей физической системы не вырождены. Так как имеется всего
четыре неприводимых представления, то по свойствам симметрии
волновые функции стационарных состояний делятся на четыре
типа. Те состояния, которые относятся к неприводимому представ-
лению А, согласно приведенной выше табл. 4.5 характеров, не из-
меняются при действии на них любых операций из группы D2. Эти
состояния называют полносимметричными состо-
яниями, а соответствующее им представление А — полно-
симметричным представлением. Обычно к такому
представлению относится и основное состояние системы.
Волновые функции коллективных движений в четно-четных яд-
рах зависят только от пространственных координат нуклонов.
Так как спины двух тождественных нуклонов, находящихся в оди-
наковом одночастичном (орбитальном) состоянии, противоположны
по направлению, координатная волновая функция будет симметрич-
ной. Поскольку при операциях В/ (л) переставляются пространст-
венные координаты нуклонов, волновая функция, описывающая
273
вращение ядра, должна относиться к полносимметричному пред-
ставлению А группы Ds, так как только в этом случае при любых
операциях из группы Г>2 волновая функция коллективных движе-
ний будет переходить сама в себя с тем же знаком.
Легко проверить, что функции (4.149) для жесткого симметрич-
ного волчка (с четным К) инвариантны относительно поворотов
R/ (л), если учесть, что на обобщенные сферические функции
£>ДА-(Ф, 0, ф) операторы Rj>(n) действуют следующим образом:
Ri (л) Цмк = (—1)К Кг (я) =(—1/~х Е*м,—к!
/?3 (л) Dmk = (—1/ к-
[Заметим, что при любом Д преобразованная функция симметрич-
ного волчка ^'(IRM) будет отличаться от (4.149) лишь заменой мно-
жителя (—I)1 во втором слагаемом на множитель (—1)’+к, поэтому
функции Т(/ДЛ1)с нечетным К не обладают указанной инвариант-
ностью). Учитывая это обстоятельство, решения уравнения (4.228),
относящиеся Гк полносимметричному представлению А группы D2,
можно представить в виде
Ф/м(Ф.0.Ф)= S giK^tlKM). (4.230)
четные К > О
Подставляя (4.230) в уравнение (4.228), получаем систему линей-
ных однородных уравнений для определения коэффициентов g^‘.
2 {<!KM\Hr\IK'M)-ElbKK-}gl^=0. (4.231)
к • ?• о
Число этих уравнений совпадает с возможным числом различных
(но четных!) значений Д и равно (//2) ф- 1 при четном / и (I — 1/2)
при нечетном I. Из равенства нулю детерминанта системы урав-
нений находим собственные значения энергии Е1х.
Для примера рассмотрим состояния с угловым моментом (спи-
ном) 1 = 2. Возможные значения К = 0 и 2, поэтому система (4.231)
будет состоять из двух уравнений. Используя соотношения (4.90)
и (4.91), нетрудно определить матричные элементы оператора Га-
мильтона </ДМ | НГ\IK'M}, которые могут быть отличными от
нуля лишь при К' = К и Д' = К ± 2. Итак, в случае /= 2 по-
лучим систему
[4 («1 +аг)— + («1—az)gv> =0;
J L J 2 (4.232)
где
h*
a., =----------------------------•
k Wk,
274
Из условия обращения в нуль детерминанта находим два значе-
ния энергии’
— (аг + fl2 + йз) +
+ (— 1Г У (ai + а2 + «з)г — 3 (ах оа + ог а3 4- ах а3)
(т=1,2),
р __ 4В02 3 [3 + (—1)х ^9 - 8 sin33yl
£2 2 т——"-- ---------------------------
Я2 sin2 Зу
(4.233)
Коэффициенты g]K, ортонормированные условиями
2 gixgixJPjglxgiK' = ^kk’i (4.234)
К > О т
будут для / = 2, согласно (4.232) и (4,233), равны
„т= 1 _ Т / 1± ,_ПТ sin у sin Зу + 3 cos у cos 3?
2 + t И 2/9 - 8 sin2 3^
(4.235)
2 - К
=(-!) 2 SW-К, К=0, 2.
При 1 = 3 возможно лишь значение К = 2, поэтому
и Фз^’(0J =Т(3,2Л4). Значение энергии равно
£з..=<3,2Л(|//г|3,2Л4> = 2(а1+.о2+а3)=^.^- (4.236)
ft2 sin23y
[Состояние с / — 3 и К — 0 отсутствует, так как V(3, О, М) - 01
Основные особенности вращательных спектров неаксиальных
ядер. Спектр вращательных энергий аксиально симметричных ядер
(у = 0 или л/3) связан с вращением ядра вокруг оси, перпендику-
лярной оси симметрии ядра. В неаксиальных же ядрах вращения
более разнообразны, поэтому соответствующий спектр энергий
более сложен. При у О или у -+ п/3 некоторые уровни неакси-
ального ядра остаются конечными и переходят в уровни аксиально
симметричного ядра. Такие уровни неаксиального ядра образуют
основную вращательную полосу в спектре вращательных энергий.
Остальные вращательные уровни неаксиального ядра при у -> О
или’у -> я/3 стремятся к бесконечности. Эти уровни образуют ано-
мальные] вращательные полосы.
Отношение любых двух вращательных энергий неаксиального
ядра зависит только от одного параметра у, который можно опре-
делить для данного ядра из отношения наблюдаемых энергий двух
наиболее низко расположенных возбужденных состояний. Зная у,
можно предсказать положения остальных энергетических уровней
вращательного спектра неаксиальных ядер.
Параметр у можно найти, воспользовавшись отношением экспе-
риментальных значений энергии для первых двух уровней со спи-
275
ном 2, относящихся к основной и аномальной вращательным поло-
сам. Это отношение, согласно (4.233), равно
Е2 2 3 + У9— 8sina3y
. (4.237
Егл 3—1'9 —8sin23y
При изменении параметра у от 0 до 30° это отношение монотонно
уменьшается от оо до 2. Измерив на опыте отношение (4.237), можно
Рис. 4.19. Отношение энергий возбужденных состоя-
ний к энергии первого возбужденного состояния
в зависимости от параметра неаксиальности у для
неаксиального ротатора.
вычислить у, зная которое, нетрудно определить спины и положе-
ние уровней для основной и аномальной вращательных полос.
Можно указать на следующие характерные особенности спектра
возбужденных состояний неаксиального ротатора:
1. Отклонение формы ядра от аксиально симметричной формы
приводит к нарушению правила интервалов (4.168) в основной вра-
щательной полосе. Например, если у = 30°, то уровни основной
276
вращательной полосы будут удовлетворять следующему правилу
интервалов:
£г:£4:Е„:£8... = 1 : 2,67 : 5 : 8:..., (4.238)
которое существенно отличается от (4.168).
2. Кроме изменения правила интервалов для уровней основной
вращательной полосы наличие неаксиальности ядер приводит к
появлению новых аномальных вращательных полос. Первая ано-
мальная полоса состоит из уровней со спинами 2, 3, 4, 5..., вторая—
из уровней со спинами 4, 5, 6, 7, ... и т. д. Если у > 23°, то первый
уровень аномальной полосы со спином 2 лежит ниже уровня со спи-
ном 4 в основной вращательной полосе. Уровень со спином 3 всегда
находится выше уровня со спином 4 в основной вращательной по-
лосе. Для модели жесткого неаксиального ротатора аномальные
полосы связаны с вращением, хотя в действительности (при неадиа-
батическом рассмотрении) они соответствуют возбуждениям вра-
щательно-колебательной природы.
Для иллюстрации на рис. 4.19 изображено отношение энергии
возбужденных состояний к энергии первого возбужденного состоя-
ния в зависимости от параметра неаксиальности у для неаксиаль-
ного ротатора. Сплошные кривые соответствуют основной враща-
тельной полосе, пунктирные — первой аномальной полосе. Круж-
ками указаны экспериментальные отношения энергий для ядер
б8бЕг, 7G60s, 76°Os и 7g20s- Около кружков указаны экспери-
ментальные значения спинов. Если, например, для ядра 76°Os у=
= 22°, то рассчитанные отношения энергий в основной вращатель-
ной полосе
1 : 3, 01 : 5, 76 : 9,24
будут очень близки к экспериментально наблюдаемым отношениям:
1 : 2,99 : 5,61 : 8, 90.
Значение у = 22° объясняет также положение второго уровня со
спином 2 и уровня со спином 3 при у = 25,5°, относящихся к ано-
мальной полосе.
Модель неаксиального ротатора наряду с энергиями возбужден-
ных состояний позволяет определять также и волновые функции.
В общем случае волновые функции для неаксиального ротатора
(4.230) представляются в виде суперпозиции состояний (4.149),
соответствующих определенным значениям проекции полного мо-
мента на ось oz. Коэффициенты g/к, определяющие вклады состоя-
ний с различными К, зависят от параметра неаксиальности у и
определяются системой алгебраических уравнений (4.231). Если
у < 15°, то в сумме (4.230) основной вклад вносит только одно сла-
гаемое, и, следовательно, /С является приближенным интегралом
движения. Основной вращательной полосе в таком приближении
соответствует значение К =0, поэтому вращение происходит вокруг
оси, перпендикулярной oz'. Первой аномальной полосе при у <15°
277
соответствует одно К = 2. Нижайший уровень этой полосы / — 2
соответствует вращению ядра вокруг оси oz'. При больших зна-
чениях спина на вращение вокруг оси oz' накладывается вращение
вокруг оси, перпендикулярной oz'. Если у>15°, то число К теряет
смысл интеграла движения. Волновая функция в этом случае яв-
ляется суперпозицией состояний с различными значениями К-
§ 4.6. ВРАЩАТЕЛЬНО-КОЛЕБАТЕЛЬНЫЕ ВОЗБУЖДЕНИЯ ЯДЕР
Общий вид волнового уравнения в случае квадрупольных де-
формаций. В адиабатической теории коллективных возбуждений,
рассмотренной раньше, пренебрегалось связью между вращением
ядра и колебаниями его поверхности. Такое пренебрежение не
всегда оправданно, так как во многих случаях энергии вращатель-
ных и колебательных возбуждений оказываются одного порядка.
Рассмотрим неадиабатическую теорию вращательно-колебательных
возбуждений в ядрах*.
При учете деформаций только второго порядка (X = 2) коллек-
тивные движения в ядре характеризуются пятью степенями свобо-
ды. В качестве обобщенных координат удобно выбрать три угла
Эйлера Ф, ® и ф, задающих ориентацию деформированного ядра,
и два внутренних параметра 0 и -у, определяющих его форму. Чтобы
написать волновое уравнение в этих переменных, необходимо перей-
ти от классической энергии коллективных движений к квантовому
оператору Гамильтона, действующему в пространстве пяти пере-
менных: Ф, 0, ф, р и у.
Оператор потенциальной энергии V (0, у), зависящий только от
координат 0 и у, и в квантовом случае сохраняет свой прежний вид.
Часть гамильтониана, связанная с вращением, квантуется элемен-
тарно, так как проекции момента количества движения на оси коор-
динат, связанные с ядром, и соответствующие углы поворота —это
обычные канонически сопряженные операторы. Поэтому квантовый
гамильтониан вращения Нт получается из классической энергии
вращения (4.111) простой заменой проекций момента количест-
ва движения на операторы составляющих момента количест-
ва движения относительно главных осей эллипсоида:
^'=4Bp*sin2(y—— И . (4.239)
k’ k‘ \ 3
В случае вращения четно-четных ядер, для которых внутренний
момент = 0, момент вращения R совпадает с полным моментом
количества движения системы I:
R-I.
* Неадиабатическая теория коллективных возбуждений в ядрах развита
в работах А. С. Давыдова [3, 11, 12].
278
Переход к квантовому описанию кинетической энергии (4.105) по-
верхностных колебаний ядер значительно сложнее.
Полная кинетическая энергия системы, выраженная через обоб-
щенные координаты q, (индекс i нумерует все степени свободы си-
стемы), обычно записывается в виде
T^{Bi2)^gi}qiq}, (4.240)
О'
где В — масса системы, a gtj — симметричные коэффициенты, ко-
торые могут быть произвольными функциями координат. Введем
квадрат дифференциала длины в пространстве обобщенных коор-
динат:
(4.241)
П
тогда кинетическую энергию можно представить в виде
Т = (B/2).(ris/d/)2. (4.242)
Если квадрат дифференциала длины известен, то оператор Лапла-
са v2> действующий в пространстве обобщенных координат, опре-
деляется следующим образом П3|:
(4 243>
где g— определитель матрицы^;, gTj1—матрица, обратная мат-
рице gij. При этом оператор кинетической энергии выражается че-
рез оператор Лапласа следующим образом:
Т~ — (7г2/2В) V2. (4.244)
Согласно (4.105) и (4.107), полную кинетическую энергию ядра,
связанную с квадрупольными деформациями, запишем в виде
7'т; + 7\ = (В/2) (ds/d/)2;
ds3 = 2 (•?*' IB) d^k, + rip2 + p2 riy2, (4.245)
k'
где ri(pft< = Wfe-riZ — углы поворота вокруг главных осей эллипсо-
ида ох', оу' и oz' за интервал времени dt. В общем случае р0 Ф 0
и УоТ^О. Если выразить через производные от углов Эйлера,
согласно (4.56), то ds3 будет квадратом дифференциала длины
в 5-мерном пространстве'переменных Ф,0, ф, р и у. Однако проще
получить явный вид оператора Лапласа непосредственно в прост-
ранстве переменных дц., <p^', <рг-, р и у. Действительно, в этом
случае матрица g^, определяющая квадрат дифференциала длины
(4.245), имеет диагональный вид. Обозначим <pt-, <p^-, <рг-, р и у
соответственно через ц,, где i — 1,2, 3, 4 и 5. Согласно (4.245), имеем
(4-246)
где £(»=(Д^/В), £3=(^JB); ^<з>=(Д2,/В), £<<)=1, £<5>=р2.
279
Поэтому обратная матрица g/f 1 также диагональна:
g^=g^~'^ (4-247)
Определитель матрицы (4.246), как нетрудно проверить, равен
£=4088ШгЗу. (4.248)
Таким образом, оператор Лапласа в 5-мерном пространстве коор-
динат срх-, (ру-, сргг, 0 и у, в соответствии с (4.243), принимает вид
V — 7---------г Ч------Р-----------------sin Зу — . (4.249)
Ук, дср£, р4 tip dp Р2 sin Зу ду ду
Так как производные по углам <р^- непосредственно определяют со-
ставляющие оператора момента количества движения R в собст-
венной системе координат, то (4.249) можно переписать в виде
= A pi A +J-------!—Lsin3YA. (4.250)
Лл Jk, pi ар 1 ар рг sin Зу ду а?
Первые три слагаемых в правой части (4.250) характеризуют вра-
щательную часть оператора Лапласа, а последние два — колеба-
тельную часть.
Используя (4.244), оператор полной кинетической энергии по-
лучаем в виде
т V1 fl2 D2 Г 1 5 Ц1 д 1 1 д . n ') ' _
Т = > _—Rk'~— -----------Р--------------------sin3y — . (4.251)
2В [ р4 ар ар Р2 sin Зу ду ду 1
Таким образом, квантовый оператор Гамильтона для коллектив-
ных движений ядра с учетом деформаций второго порядка имеет
Вид
н V1 л'2 т2 Г 1 д а 1 1 в . д ,. /й .
Н == > — 1к--------------В4----------------sin Зу -ч- 4- V (0, у).
2в L р4 ар ар р2 sin Зу ду т ду] 4 г/
, (4.252)
Здесь составляющие оператора R заменены на составляющие опе-
ратора I. Запишем соответствующее волновое уравнение для ста-
ционарных состояний:
Я¥(Ф, 0, ф, 0, у)=£Т(Ф, 0, ф, 0, у). (4.253)
Собственные функции Т (Ф, 0, ф, 0, у) оператора Н рассматривают-
ся в пространстве пяти переменных Ф, 0, ф, 0 и у, изменяющихся
в пределах 0 45 Ф 45 2л; 0 0 л; 0 <5 ф <5 2л; 0 0 <; оо;
0 < у 2л. (Иногда, например, для сферического ядра и малых
колебаний его поверхности выбирают более узкий интервал: 0 <5
<ус-4л/3.) Функции ^(Ф, 0, Y, 0, у) нормированы согласно условию
Jr/TT*Y= 1, (4.254)
280
где элемент объема di, пропорциональный равен
dr =04 j sin Зу | sin Qd ФЛ ©dipdfWy,
(4.255)
Выражение (4.252) справедливо в случае малых колебаний ядер-
ной поверхности около равновесных значений параметров 0 = 0В
и Y = То (так называемые 0- и у-колебания). В общем случае урав-
нение Шредингера (4.253) с оператором Гамильтона (4.252) не ре-
шено. В дальнейшем рассмотрим решения этого уравнения в отдель-
ных частных случаях с некоторыми упрощающими предположе-
ниями.
Мы записали оператор Гамильтона и соответствующее ему вол-
новое уравнение лишь для коллективных движений ядра, не учи-
тывая одночастичные движения отдельных нуклонов. Однако эти
движения связаны, и, вообще говоря, отделить коллективные дви-
жения в ядре от одночастичных не всегда можно. Разделение коллек-
тивных и одночастичных возбуждений, например, хорошо выпол-
няется для четно-четных ядер, в которых минимальная энергия одно-
частичных возбуждений значительно превосходит энергии коллек-
тивных возбуждений. В дальнейшем будем предполагать, что кол-
лективные и одночастичные движения разделяются, т. е. будем поль-
зоваться адиабатическим приближением. В адиабатическом прибли-
жении полный гамильтониан ядра представляется в виде суммы
двух слагаемых, относящихся соответственно к коллективным и
однонуклонным движениям. Волновая функция в адиабатическом
приближении записывается в виде произведения волновой функции,
зависящей от коллективных переменных, и волновой функции,
зависящей от одночастичных переменных. Используя эту функцию,
можно учесть по теории возмущений и связь между коллективным
и одночастичным движениями в ядре, если считать эту связь малой
поправкой к гамильтониану.
Решение волнового уравнения для сферического ядра. Если рав-
новесная форма ядра — сферическая, то 0о = О, и при малых коле-
баниях ядерной поверхности потенциальная энергия равна V —
= (1/2)С02. В этом случае решение уравнения Шредингера (4.253)
с оператором (4.252) удобно выбрать в виде произведения двух функ-
ций, выделив зависимость функции от переменной 0:
¥(Ф, 0, ф, 0 у)=Н0)Ф(в;, у), (4.256)
где 0; — три угла Эйлера. Подставляя (4.256) в (4.253), получаем
два уравнения:
+ (4'257)
I, р ор ор л2 р2 A2 J
1
sin Зу
д . „ д
— sin Зу----------N
<Эу 1 ду
,Ф(М) = 0,(4.258)
где N — параметр разделения, зависящий от /.
281
Рассмотрим вначале уравнение для функции /(Р). Введем новую
функцию
фФ)-П(Р) (4.259)
и новую переменную
*=(№)’. $с = Укчвс.
Функция Ф (х) будет тогда удовлетворять уравнению
[ d2.ld х zV-|-2 , Е 'i . . „
! х----Р----------------1------J ер (x) = 0 (4.260)
\ dx* 2 dx 4 4x ' 2.TO i
и граничным условиям
ср (0) = 0, lim х~2 ф> (х) =0.
Jf —► СЮ
При малых х это уравнение имеет решение
q>(x)=xs, х->0; (4.261)
а при больших х
ф(х)^е. 2 , х-э-оо. (4.262)
Поэтому во всей области переменной х решение уравнения (4.260)
удобно представить в виде
Ф>(х) =xse-V2P(x). (4.263)
Функция Р(х) удовлетворяет уравнению
{х (tP/dx2) + (2s + х) (d/dx) ф-n} P (x) -0, (4.264)
где
n = (ЕШ®) —s —V4 = (£’/2M — /НЖ (4.265)
Функция P(x), согласно (4.261) и (4.262), при х->0 должна стре-
миться к конечной постоянной, отличной от нуля, а при х -> оо
вести себя как полином. Такие решения уравнения (4.264) возмож-
ны при целых положительных значениях п и выражаются через вы-
рожденную гипергеометрическую функцию
Р(х) =-£( — /;; 2s + V2; х). (4.266)
Окончательно для функции ф> (р), нормированной согласно уело-
оо
вию f dp ф>2 (р) = 1, получим выражение
m /ВТО Г2Г 6; + 2^ + 1/2) I1/2! Р \2sp(—1/2) (Р/РсР v
- [mi P(2S + 1/2)| Uc ' Х
хГ 2s+v; (4’267)
282
Соответствующие значения энергии, согласно (4.265), будут
£na = 2/z<o(n + s-p/4) (4.268)
и зависят через s (или Л/) от полного спина ядра !.
Рассмотрим теперь решения уравнения (4.258). Так как полный
момент количества движения I и его проекция М на ось z в лабора-
торной системе координат £ сохраняются, функцию Ф, (6,, у)
представим в виде
Ф)м(0Р у) = 1/2-^- £ £Ik(t)Dkm(9.), (4-269)
I А'= —i
где DJow (6j) —обобщенные сферические функции, а значок т обо-
значает квантовые числа, необходимые для полной характеристики
состояния. Прежде чем переходить к нахождению функций gj^ (у),
выясним, каким условиям симметрии они удовлетворяют.
При переходе от переменных а2Ц к переменным 9г-,р, у только па-
раметр деформации р однозначно определяется переменными ааи,
в то время как четыре переменных Ф, в, ф и у зависят от обозначения
осей х', у', г' и от выбора направления отсчета по каждой из них.
Функция Ф/.и, зависящая от этих четырех переменных, должна быть
инвариантной относительно указанных преобразований координат-
ных осей. Это приводит к определенным ограничениям, наклады-
ваемым на функции g/к- В частности, используя свойства функций
Окм(Ог) относительно преобразований осей, можно показать, что
требование инвариантности функций Ф/м приводит к следующим
условиям, которым должны удовлетворять функции §7л'(у):
K(V); (4,270)
^(у)=е.Я<к/2)^к(_7); (4.271)
ёх1к (y) =ej nKg]K (у); (4.272)
£/к(у) (0. л/2, n/2)g/K-(у—2л/3). (4.273)
К'
Из (4.272) следует, что
£}к(у)=0 при К нечетном, (4.274)
а из (4.270) получаем
^к(у)=(-1)'^. -к(у). (4.275)
Используя эти условия, функцию Фхм (0it у) представим в виде
Ф/м(9;, у)= 2 £/к(у)Ф(ЖЛ1), (4.276)
четные
283
где
WO) I/ 2i?2л К (б,)}. (4.277)
Г 16лг(14-о0к)
есть нормированные функции жесткого симметричного волчка, ин-
вариантные относительно отражения в плоскости г' = 0 (с четны-
ми /<).
Рассмотрим состояния с нулевым спином (/ = М = К, = 0).
В этом случае функция goo (? ) g(y) удовлетворяет уравнению
(вращение ядра отсутствует)
(---J—Asjn3y — No}g(y) = O, (4.278)
• \ sin Зу ду ду /
решениями которого с учетом условий (4.271) и (4.273) будут поли-
номы Лежандра
(V) = ]/ /’.(cos Зу), (4.279)
если
V0 = 9/n(m+l), т—0, 1, 2,;.. (4.280)
Из (4.261) получаем связь между s и т:
s = l+:!/2m, (4.281)
так что для значений энергии возбужденных состояний нулевого
спина имеем
£„то —/но (2/i 4 3m ! т =0, 1, 2,..., (4.282)
т, е. энергетический спектр будет эквидистантным.
Отметим, что состояния со спином I — 1 отсутствуют, так как
в этом случае единственно возможное значение К — это К = 0,
а из условия (4.275) получаем g?0 (?) = —gio (у) = О-
Рассмотрение ядер с / > 1 приводит, как и в случае нулевого
спина, к эквидистантному энергетическому спектру для коллектив-
ных возбуждений. Как и следовало ожидать, эти результаты пол-
ностью совпадают с результатами теории поверхностных колебаний
сферических ядер (в которой не выделялись внутренние параметры
деформации и углы Эйлера, см. § 4.1),
Сферическую равновесную форму имеют дважды магические,
а также близкие к ним ядра. Экспериментально наблюдаемый спектр
энергий этих ядер отличается от спектра, предсказываемого теори-
ей квадрупольных (X = 2) колебаний. Возможно, это различие свя-
зано с пренебрежением ангармоничностью колебаний, а также вза-
имодействием колебаний ядерной поверхности с движением отдель-
ных нуклонов.
Вращательно-колебательные возбуждения неаксиальных ядер.
Модель жесткого неаксиального ротатора, в которой полностью
284
пренебрегаете^ взаимодействием между деформациями формы ядра
и вращением ядра, является довольно грубым приближением к
действительной картине коллективных возбуждений в ядрах. На
самом деле ядра при вращении могут испытывать растяжение, по-
этому в общем случае необходимо учитывать связь вращения ядра
с деформациями его поверхности.
Ограничиваясь деформациями второго порядка (Л — 2), рассмот-
рим частный случай волнового уравнения, описывающего коллек-
тивные движения в ядре, закрепив переменную поперечных коле-
баний у (заменив ее некоторым эффективным значением Г), но оста-
вив переменную продольных колебаний 0 свободной. Такой неадиа-
батический подход при рассмотрении вращательно-колебательных
возбуждений в ядрах был предложен в работе [14]. Коллективные
движения в ядре в этом случае характеризуются четырьмя степе-
нями свободы, соответствующими трем углам Эйлера 6г(Ф, Ф)
и переменной р. Классическая энергия коллективных движений
в этом случае имеет следующий вид:
з
£=2 2B|32siti2(r — (2л/3)А/)с4. + (В/2) р2, (4.283)
k'= 1
а квантовый оператор Гамильтона для коллективных движений
будет отличаться от выражения (4.252). Матрица gij, определяющая
квадрат дифференциала длины, теперь будет четвертого порядка.
Зная матрицу легко записать выражение для оператора Лап-
ласа, согласно (4.243), для случая четырех рассматриваемых пере-
менных, а также оператор Гамильтона
<4284>
Волновые функции Y (6£, р), удовлетворяющие уравнению
(НГ-£)Т(О;, р)=0, (4.285)
нормированы условием
^тЧ”=(Ог, (3) ¥(0г, р) = 1; | (4 286)
dT = t/0cf0dl|?rfPsin6|33. j
В рассматриваемом приближении возможно отделение перемен-
ной р от углов Эйлера Волновую функцию выберем в виде
Т(6;, р) = р-3/2 ф (Р) Ф (0;), (4.287)
подстановка которой в уравнение (4.285) с гамильтонианом (4.284)
приводит к двум уравнениям:
( 3 Л2 Z2 1
2 (4.288)
1 «
285
Ь£-^+^+к<р)-г,Н)=0' e-=e~e- <4289>
Уравнение (4.288) для функции Ф (0() совпадает с уравнением
Шредингера для жесткого неаксиального ротатора (см. § 5).
Уравнение (4.289), описывающее 0-колебания, можно решить
приближенно, если заметить, что два слагаемых в этом уравнении
У (0) = (3.W8B02) + V (0) (4.290)
играют роль эффективной потенциальной энергии. Разлагая ее в
ряд по отклонениям величины 0 от ее равновесного значения 0/
и ограничиваясь учетом квадратичных членов разложения, полу-
V (₽) = Vi + е/2)С, (0-Р/)2, (4.291)
где Cf — коэффициент упругости. Уравнение (4.289) тогда пере-
ходит в уравнение
{“£-• + -тг<0-₽')г- (ф (₽) =°- (4.292)
Введем следующие обозначения:
“'“Ит- и-Т1/вё!; (4-293)
= vJjfXj—L,
r Y Cj P, I Па, 2
а также новую переменную
(4.294)
и новую функцию ф (z)
Ф (0) — ф(г)е. -2’/2. (4.295)
Функция ф (г) удовлетворяет уравнению
[^-а-2г4+Чф(г)=0 (4.296)
\ dz* dz /
и граничным условиям
(р \
— — 1=0, Ншф (г) е-г’/2 =0.
rV У z-юо
Решением уравнения (4.296) является функция Эрмита первого
рода
"’(2)<22>*г <4-297>
286
где v—корни уравнения Hv( — — 0. Собственные значения
энергии, согласно (4.293), равны
(4298’
е;= 4В^2Е1/г1\
Так как собственные значения Е1 уравнения (4.288) зависят от Г,
энергии Eiv также будут зависеть от параметра Г. Величина Pi оп-
ределяется при решении уравнения
(4.299)
вытекающего из (4.293).
Используя волновую функцию основного состояния, можно по-
казать, что среднее значение квадрата отклонений £ от равновесно-
го значения (50 в этом состоянии равно (Й/2)]/ ВС0. Тогда, согласно
(4.293), параметр р. пропорционален отношению амплитуды нулевых
колебаний поверхности ядра к величине равновесного значения рй.
Значение р, — 0 отвечает абсолютно жесткому ядру и соответствует
полному разделению возбуждений на вращательные и колебатель-
ные (адиабатическое приближение). С увеличением р. увеличива-
ются поправки к адиабатическому приближению. Параметр р по-
этому можно назвать параметром неадиабатич по-
сти ядра.
В связи с этим ядра с р < V8 называют жесткими, а ядра с
р > 1/3 — мягкими ядрами. В жестких ядрах возможно
приближенное разделение коллективных возбужденных состояний
на вращательные и колебательные; для мягких ядер такое разде-
ление условно. В мягких ядрах коллективные возбужденные со-
стояния представляют сложную смесь вращательных и колебатель-
ных движений. Спектр энергий для мягких ядер даже в основной
вращательной полосе может резко отличаться от спектра адиаба-
тической теории. В частности, может случиться, что спектр энергий
мягких ядер будет почти эквидистантным при некоторых значениях
параметров, хотя равновесная форма будет значительно отличаться
от сферической.
Зная экспериментальные отношения энергий для трех уровней,
можно определить параметры ядра р. и Г, используя которые, мож-
но найти отношения энергий других ядерных состояний. К мягким
ядрам, как показывает сравнение теории с экспериментом, отно-
сятся, например, ядра *°Fe, g2Ge, “8Pd, и др. Для них
параметр р^0,5. К жестким ядрам, у которых р-<0,3, можно отнес-
ти ядра J*®Gd, ав’Ег, J®®Os, )«8Os, ”2Os, 280Th, *8®U, =’aPu.
Вращательные состояния у таких ядер хорошо выделены. Имею-
287
щиеся опытные данные для некоторых ядер подтверждают наличие
большой связи вращательных движений этих ядер с колебаниями
их поверхности, а также находятся в хорошем согласии с численны-
ми теоретическими результатами [3].
Задачи
4.1. Найти закон преобразования спинорного поля при поворотах си-
стемы координат.
Пусть xsll — собственная функция оператора квадрата спинового момента
и его проекции на выделенное направление, характеризуемое единичным век-
тором N:
s2 7-sii-s (s + 1) XS(l; 1
(Ns)XSM = PXsu. J
(4.300)
Функция зависит от пространственных координат частицы г и от спиновой
переменной
xstl(r> °)-
Рассмотрим поворот системы координат на некоторый угол tp вокруг
оси, направление которой задано единичным вектором п. При повороте со-
ставляющие любого вектора в повернутой системе координат К' и первона-
чальной системе координат К связаны линейным соотношением
г'-йг. (4.301)
Если частица находится в начале системы координат, то при повороте системы
координат ее координаты останутся неизменными. Изменение функции ](s(t
в этом случае будет определяться только зависимостью от спиновой перемен-
ной а.
Определяя закон преобразования функций % при поворотах системы
координат, будем исходить из требования инвариантности уравнений вида
(4.300) в различных системах координат. В системе координат К’ вместо вто-
рого уравнения (4.300) имеем
(N's)Z;il=PXsu- (4-302)
(Вид спиновых матриц S одинаков в любой системе координат.) Функции
и xS(l должны быть связаны некоторым унитарным преобразованием
7sp. (4.303)
вид которого нетрудно найти из требования эквивалентности (4.302) и втсГ
рого уравнения (4.300). Подставляя (4.303) в (4.302), находим
aijNJDM siD^7^r-^-
Это уравнение эквивалентно второму уравнению (4. 300), если
D(s) = s>
ИЛИ
(4.304)
поскольку матрица ортогональна.
288
В случае поворота на бесконечно малый угол 6<р вокруг оси, вдоль ко-
торой направлен единичный вектор п, матрица аг-у имеет вид
— tyt'ijk nk> (4,305)
где
D,.
(s)
—полностью антисимметричный
(0) — 1, то унитарный оператор D (6
единичный тензор. Так
ср) можно искать в виде
как
®(s) ~ 1 “Ь^фпА,
где А — некоторый оператор, подлежащий определению.
Рассмотрим случай спина, равного половине s = 1/й. Оператор спина s
в этом случае выражается через матрицы Паули
s = (l/2)?,
а функция xS|1 является двухкомпонентным спинором. При бесконечно ма-
лом повороте уравнение (4.304) принимает вид
(1 — 6<pnA) о, (1 +6фпА) = (бу -)-бфбу/пА) оу,
ИЛИ
0^7—= 0J. (4.306)
Используя перестановочные соотношения для матриц Паули, легко видеть,
что решением уравнения (4.306) является А = {(72) ст. Таким образом, опера-
тор поворота на бесконечно малый угол имеет вид
Dj,s)(6T)-l+^-6<pn9. (4.307)
Оператор поворота на конечный угол ср вокруг оси, направление которой
задано вектором п, можно представить как бесконечную последовательность
поворотов на бесконечно малые углы:
„ / ( <р ~Г 4>па
D(")(CP)=lim Н+тт"0 =е (4-308)
' £^ск>\ £ R, J
Если учесть теперь зависимость компонент спинора от пространствен-
ных координат, то
XSJX (Г'’ °) = D(5) Xsp. (Г-®).
ИЛИ
&ц(< (4.309)
Определяя далее унитарный оператор D с помощью равенства
о)
и используя (4.309), имеем
^ш(г,о) = /)(,)х41Л(й-1г, ст).
Откуда окончательно получим следующее выражение:
i4>n(1+T’) (4.310)
Dn (<р) --= е 2 '.
Оператор D" (ф) и определяет закон преобразования двухкомпонентпого спи-
нора при поворотах системы координат.
4.2. Найти закон преобразования векторного поля при поворотах систе-
мы координат.
10 Зак. 642
289
При повороте системы координат, задаваемом линейным преобразованием
г'=аг, (4.311)
векторное поле А (г) преобразуется согласно закону
А'(г') = аА (г),
или
Ai {r'k) -=aiiAi <4-312>
Определим оператор конечных поворотов D с помощью равенства
A'(r) = DA(r). (4.313)
Используя (4.312), получаем следующее уравнение для нахождения D:
РЛ.^^ЛДо^г,). (4.314)
В случае поворота на бесконечно малый угол Sip вокруг осн п матрица
aij определяется выражением (4.305). При этом из (4.314) находим
D" (6<р) At (rk) = (Sy + 6<peym nm)( 14- 6<рейпг nn ц Aj{rk). (4.315)
\ uffc /
Определим теперь три матрицы s; (i = 1, 2, 3) с помощью соотношения
(Si)/A= (4.316)
и введем оператор орбитального момента
k= — (4.317)
ось
Сохраняя линейные члены по 5<р в (4.315), находим
£>" (6q>) A(r) = [l+»n (1 + s)] А (г). (4.318)
В случае поворота на конечный угол имеем
D" (<р) =е'фп<!+5)- (4.319)
Легко проверить, что векторная величина (4.316) удовлетворяет переста-
новочным соотношениям
(аг5^ = 1ег-д sft, (4.320)
и собственное значение квадрата величины з равно
s3 = s (s+ 1) = 2.
Таким образом, векторному полю А (г) можно сопоставить спин, равный
единице ($ 1). Отметим, что оператор I, входящий в (4.319), характеризует
изменение функции векторного поля, обусловленное координатной зависи-
мостью последней, а оператор s характеризует изменение функции, обуслов-
ленное’векторной природой поля.
Если рассмотреть векторное поле, значение которого в каждой точке про-
порционально радиусу-вектору точки
А (г)=Аг
(Л —скалярная постоянная величина), то изменение функции поля при по-
воротах системы координат будет равно нулю. В этом нетрудно убедиться,
если проверить соотношение
n(I + s)r—0, (4.321)
где 1 и s определены равенствами (4.316) и (4.317).
290
4.3. Показать, что проекции оператора R на ось ог в неподвижной, си-
стеме координат и ось oz' в подвижной системе координат коммутирую^ Друг
с другом:
[Яг,, /?г] = 0. (4.322)
Согласно (4.77) и (4.78), проекции и Иг, непосредственно выражаются
через производные от углов Эйлера Фиф:
„ . & „ . д
Rz~- —( тт ; /?г.=—I—.
дФ дф
Используя (4.77), оператор R*. можно выразить через проекции опера-
тора R на оси в неподвижной системе координат:
Rz. = cos Osin ©Rj.-1-sin Ф sin 07?„-|-cos 07?г.
Замечая, что
[cos Osin BRX, /?г] = — i (sin Osin в/?х +cos Osin в/?и);
[sin О sin &Ry, /?г] = i (sin Ф sin 0/?x + cos О sin 0/?у);
[cos0/?z, «z] = 0,
убеждаемся в справедливости соотношения (4.322).
4.4. Доказать операторное соотношение
~ 1-тУ1 ,
е хЬ аетЬ = >--------— [6, [t>,... [&, а[...]]—а— т[6, в] +
/г!
+-£ IМь, в]][£, [&, [S, <Г]1] +..., (4.323)
2! о!
где а и b—произвольные операторы.
Представим операторное выражение, стоящее в левой части (4.323); в
виде ряда по степеням параметра т:
е~^ Нех? = 2 тл fn (&, а), (4.324)
п=0
где fn(b, а) —некоторая функция от операторов а и ?• Дифференцируя
равенство (4.324) по т, находим
е“a] exS = 2 ят"-1 fn(S, Й).
п=0
Дифференцируя равенство (4.324) последовательно k раз по т, имеем
Л_________________________*_________ Л °° .
( — 1)* е~[ 6,[6, ...[6, a]...]] exS = V —— tn~k fn (b, а).
Полагая в этом равенстве т — 0, находим
(-l)*[S,[ft,...[S, aj...]]=fcl/ft(&, а).
Подставляя найденное таким путем fn (i>, а) в (4.324), получаем соотношение
(4.323).
4.5. Доказать операторное соотношение
е ,*/;/fte,'t’^ = cos®;\ + sin®ejWjz (i^=fe), (4.325)
291
О*
где ji — проекции оператора момента, удовлетворяющие перестановочным
соотношениям [ji, j’J
Используя соотношение (4.323) и выделяя в правой части четные и нечет-
ные степени параметра Ф, находим
<к ____,а«____
ке"''’' -//,1 V Г//. [/;, ... [/t. Ml - Jl-I-
n=l * ’
00 /__(ф\2п-1-1
+ 2 ~(2^Н)Г C/i’ f/i’ (4-326)
Так как |/;, [ц, [j(> /h]]| = [fb /ft), то
2п
[/ь [it..... [ji>/л]---11 = Д /=М.
2п+1
[ii, [/;. l/i. jftl -ll = [/i. /д].
Подставляя эти равенства в (4.326), получаем соотношение (4.325).
4.6. Доказать операторное соотношение
е~1Ф)'г ei0'\ е/ф// = е'0 5C°S */j,+sin , (4,327)
где ji — проекции оператора момента.
Используя соотношение (4.325), имеем
е-14/‘ Ш)" е1Ф/г = (cos ФД Д-sin jt)n.
Домножая это равенство на и суммируя левую и правую части по п от О
п!
до ро, получаем соотношение (4.327).
4.7. Показать, что
Dlom (Ф, 6, ф) = [ / -11- Ylm (6, Ф). (4,328)
Воспользуемся соотношением (4.60), определяющим закон преобразо-
вания сферических функций при поворотах системы координат:
Ylm («, Ф) = £ D‘m,m (Ф, 0, ф) Y 1т. (Г, Ф'). (4.329)
т'
Выберем -ft' = 0, т. е. рассмотрим направление вдоль оси oz' в повернутой си-
стеме координат, тогда
2±!-v.
В неподвижной системе координат направление оси ог‘ характеризуется уг-
лами & = 0 и <р = Ф, поэтому
Ylm О, Ф) = 1 / D'm (Ф, 0, ф),
4л
откуда и следует соотношение (4.328).
4.8. Получить формулу сложения для сферических функций, восполь-
зовавшись законом преобразования сферических функций при поворотах си-
стемы координат.
292
Выберем произвольную точку Р на единичной сфере с полярными коор-
динатами иф в первоначальной системе координат и координатами ф'иф'
в повернутой системе координат. Полярные координаты оси ог' в первоначаль-
ной системе координат равны 0 и Ф. Положив в формуле, обратной (4.329),
Пт (»', <₽') = 2 (ф, 0, ф) Ytm, (», ф),
т'
величину т равной нулю (т = 0) и подставив Dl0*m, (Ф, 6, ф) в виде (4.328),
получим формулу сложения для сферических функций:
1/ 2*±1у(о(&',ф')-= £ШР;(со5й')=Уг;т(е1 ф) Г,т(9,ф). (4.330)
4л 4л т
4.9. Найти правила связи для D-функций при сложении моментов.
Пусть Ф/]П11 (ri) и фдт1(гг) — волновые функции для двух систем с оп-
ределенными значениями квадрата момента и проекции момента на ось ог.
Эти функции при поворотах системы координат преобразуются по закону
*/, т. ('J = 2 D^' m. (Ф‘ % тг (Г1');
Г??! *
т, (ге) = 2Dk,' т2 (ф- ®- W т,- (г2')-
т2'
(4.331)
Согласно правилам сложения моментов, имеем
*/х т> (г1) %. гч2 (гг) = 2 ( Il mi к т21 >т) tm (гг ч). (4.3Э2)
/т
где ф>т(г1, г.2) — волновая функция всей системы в состоянии, характеризуе-
мом определенными значениями квадрата момента и его проекции. Функции
ф/т (гг, г2) при поворотах системы координат преобразуются, аналогично
(4.331):
*лп(гР гг)=2^'т(ф. Ш/тЧП', Г2). (4.333)
т'
Правило сложения моментов (4.332) справедливо также в повернутой системе
координат, поэтому
Ф/т, ('/> Ч') = 2 0'1 т1' 4 тг ! im’) m,< С1') */, т/ (г3'). (4-334)
/и/™/
и, следовательно,
Ч>/, т, (Г2) =
= 2 </imi (iitni 12т2' [ jm')X
!тт'
х О^т(Ф, 0, ф)ф/1ОТ1, (г/) фЛ т/ (г/).
Подставляя (4.331) в левую часть полученного равенства и учитывая,
что Ф;- m > (г/) и Ф/гГП{- (гг') линейно независимы, находим
0,Ф)О^И1(Ф, 0, ф)==
= 2(/1m1 (2m2|J2m^jm')D^.m(O, 6, ф). (4.335)
тт'
293
Воспользовавшись ортогональностью коэффициентов Клебша — Гордана,
окончательно получим следующую формулу связи для D-функций при сло-
жении моментов:
D^, m (Ф, О, ф) = X (Л «1 Ъ та I М) X
/ns ^а'
* е’ Ф) т, (ф- е. Ф). (4.ззб)
4, 10. Вычислить матричный элемент
4-т<0) •= <-lm' I (4.337)
воспользовавшись связью между оператором момента и операторами рож-
дения и поглощения для двух несвязанных гармонических осцилляторов.
Рассмотрим два независимых гармонических осциллятора, которые бу-
дем характеризовать индексами 1 и 2. В представлении чисел заполнения
каждому из осцилляторов можно сопоставить операторы поглощения и рож-
дения квантов возбуждения at и a~f\i — I и 2), удовлетворяющие следующим
перестановочным соотношениям:
[аг, aj+] = 6(j, [a; а,] = [Oi+. a/j = O. (4.338)
Из указанных операторов можно построить четыре независимых квадратич-
ных оператора:
П1+а1. Оа+а2> °1+«г и а2+0д. (4.339)
В представлении чисел заполнения первые два оператора имеют диагональ-
ный вид и определяют числа квантов возбуждения (бозонов) первого или вто-
рого типа. Два других оператора а+ а2 и a’^ui имеют отличные от нуля мат-
ричные элементы при переходах, для которых числа квантов возбуждения
изменяются на единицу. Поэтому с операторами (4.339) можно сопоставить
операторы проекций момента, если числа квантов возбуждения пх и п2 свя-
зать с квантовыми числами квадрата и проекции момента.
Непосредственной проверкой можно убедиться, что операторы jx, jy
и jz, определяемые с помощью равенств:
/х+ * jy— <*1+ a2t
ix—i iu = ai+ai>
(4.340)
/г —(1/2) («/«!—a2+a2),
удовлетворяют обычным перестановочным соотношениям для составляющих
момента количества движения. Соотношения (4.340) можно компактно за-
писать, если формально определить двухкомпонентные спинорные операторы
а+=(Я1+, яа+), «=(£*)
и ввести двухрядные матрицы Паули
/0 П /0 — i \ /1 0\
0J; i ..-0.1 ; °г“ to J’
Тогда оператор вектора момента J запишется в виде
j =1/20+10. (4.341)
Если вместо а в (4.341) подставить единичную матрицу, то получим скаляр-
ный оператор
/ = (1/2) о+ а. (4.342)
294
Нетрудно проверить, что
P=j(j + 1). (4.343)
Величины j и j являются операторами в представлении чисел заполнения.
Собственные значения операторов j и /г, которые обозначим j и т, выражаются
через числа квантов возбуждения лг и л2:
/=(1/2) (И1 + л2), гл = 1/2(л1—л2). (3.344)
Следовательно, квантовые числа и л2 полностью определяют значения квад-
рата момента и проекции момента на выделенное направление.
Обозначим волновую функцию основного состояния системы двух осцил-
ляторов (л2 = л2 = 0, вакуумное состояние) через |0>. Очевидно, этому со-
стоянию отвечают значения
/=т = 0.
С помощью операторов рождения а у и ая+ нетрудно построить волновую
функцию для состояния с определенными значениями квадрата и проекции
момента / и пг. Эта функция, нормированная на единицу, имеет вид
+ ..
|/т> = Г _ ~ 10>.
/(/ + т)! (J —т) I
С помощью (4.323) можно доказать следующие соотношения для опера-
торов ас
e"ie>i е1 0 О = cos -у 4 -1 sin у а+
e-i 6 !i ak е1 0 !i = cos у ak + i sin у o',. af
Нам потребуются два частных случая (i — у, k = 1,2):
(4.345)
(4.346)
e10^a+ -iOj 0 , . 0 + e “ = cos — 4 — sin4a2
-! e A, 0 + . . 6 + e y _ cos — aT + sin— aT, 2 2 2 1
(4.347)
Вычислим результат действия оператора ei0Jy иа функцию (4.345), ис-
пользуя соотношение (4.347). Так как
e’0/J'|O> = O>,
то
!©/,,, 1 / в г в
е -7 jm> = — ~ cos — aT —sin аТ X
Г(/ + ш)! (/-«)! V 2 ‘ 2 2 ’
/ [0 , 0 , Ч-
X I cos — 4 + sin — ay I | 0> =
\ 2 2 J
_______________ /+m /—ni ci a
== V(/+m)l (/—m)! 2 2 (-l)'+m-'1sin2/-fc-''4-cosfe + "-^x
n=0 к -П * 2
(аУ)'~т-*+" (а,У + m + k- n
X ' 1 --------- X J ’ | Q\
n! (j + m—n)t k! (}—m—fc)l
295
Если произвести замену в индексах суммирования
k — j—m*—х, n=j-ym—и ( —/ < т' < j),
то
I
i е7„ . . V V, пИ [(j + fft)! (/—m)i O' + m')! (j-ffl')l]2
6 /fft «'«-у х х!(/ + /п—х)! (/—m'—х)1 (x+m'—/п)1
/ 0 \2X —m + m' I 0 + — 2x
ХГ‘ПТ/ (cos — 1 (4.348)
Окончательно получим следующее представление для функции
(в) И]:
у , _пи [<7+т)1 (!—ту. (j-j- m')l (/—m')!] 2
х! (/ + m —x)t(/—m'+х)! (x + m'—m)l
0 \2x—m4-m' / 0 \2/ + nt —/n'—2x
xlsinyl (cos —) , (4.349)
где сумма берется по всем и > 0.
4.11. Найти явный вид функций dlm,m (0) в случае / = 1/з-
Воспользуемся определением
= |е1в/гЧ7т> (4.350)
и заметим, что в случае / = 1/2 имеем
1у=е/2)ву, (4,351)
где сгу — матрица Паули. Разложим экспоненту в (4.350) в ряд по степеням 0
и выделим четные и нечетные слагаемые:
'Г1 / i 6 X 2«+1 1 1 \
\ 2 (2л-М)1 Т т/ '
Так как $у2= 1, то
— /li f 0 \ 2rt 1
гс= 0
хд . п / в Vrt+1 1 1 \
+ 1 ст,, 7 (— 1) — 1 - п-------- — т > ,
„““о \ 2 (2г1+‘)' 2 /
ИЛИ
= cos у 6mm- + i sin у (CTy)m,m.
(4.352)
296
В представлении, в котором матрица о2 диагоналъна, матрица Паули
(ojm'm имеет вид
• /° "1 \
1 I । 0 J
1
Таким образом, для (0) окончательно получим
2
2
«к®-
m'4'
2
2
_2
2
cos^'
-sinj
sinj
cos^
(4.353)
1
Функции d^m,m (9) для любого j могут быть получены из d£,m (0)
с помощью последовательного применения правил связи (4.336) для D-функ-
ций. Положив в (4.336) ф = ф = 0, получим
dm'm(0)= У (/i«i /«) (йт/jam0'|/т')Х
гП|т>'
Х^/т1(в)^г.т1(0). (4.354)
Это соотношение позволяет находить d!m,m (0) при любом j из (4.353).
4.12. Найти явный вид функций dJm,m (0) в случае /=1.
Поступим так же, как и в предыдущем случае:
30
4.m(0)=<lrn'|l+ 2
п= О
(i 0/g)2n+1
(2n-f-l)t
(i0/j,)2n+?
(2» + 2)l |lm >
+ 2
n = 0
Так как для момента, равного единице,
/И/У-1)=0, (4.355)
то
j2n+!= - ,-2л+2_,-2
‘у ‘У> ‘у ~ ‘у-
Таким образом, получим
“ 02л
4'm(e)=<lm' 11+ isine/p+ /2 У (_1)"(—|lm>,
ИЛИ
(0) = <lzn' J1 + j Sin 0/р + (cos 0-1) /211 m>. (4.356)
В представлении, в котором матрица ]г диагоналъна, матрица jy для/=1
имеет вид
Z о —i О X / —1 О 1 \
/=— i 0 -i , j2=-— 0 -2 0 . (4.357)
" ко I о/ 2 к 1 0-1/
297
Таким образом, для (6) получим
‘т
1 0 -1
t(i+cose) -L Sin 8 ft Z (1-COS8)
— sin 8 C0S8 -% sin 8 ft
jp-cose) -~sln8 tfircose)
(4.358)
4.13. Проверить, что в случае /— 3/2 функции ?т (0) имеют вид
3 I _1 Л
^COSB)COS^ ^(hcosBJsiOj ^-css6)cas~ ~z(Hos8)sinj
-^C0SB)sln^ -l(t-3cose)cos^ j(h3C0S8)Sin^ ^(1-COS8)COS^
^(l-COSS)COsj -1-(83ct№8)sin^ -j(i-3COS8)COS^ ^C0S8)Sinj
-l(1-WS8)Sin? ^(1-№Se)COS^ ^cosejcosj
4.14. Проверить, что^в случае7/ = 2 функции (0) имеют вид
2 1 0 ~1 ~2
~(1+cos8)z T jSln8(1+cosB) \[jsin!e t sin 8(1-cos 8) ^(1-cos8)z
—sinSfrttSB) -^cos8)(Zcos8-1) ^sinews# ^(1-C0S8)(2C0S8^1) ^sin8(1-cos8)
\^с1пг8 -\ljsin8cos8 yecas^V \^sin8cos8 \fgsinz8
-~slnO(l-cosff) 1^l-f№8)(2C№8^) -\^sio8cose -^COS8)(2COS8-1} 1-sin8(bcos8)
~(1-cos8)z -^Sin8(i-cos8) \]?зй1г8 --^sin8(1+cosd) j(hC0S8)z
(4.360)
298
4.15. Ориентация осей подвижной системы координат вдоль главных осей
инерции физической системы возможна 24 различными способами (в случае
использования только правых систем координат). Действительно, ориента-
цию оси ог' можно выбрать шестью различными способами по трем взаимно
перпендикулярным направлениям в пространстве, и при каждом фиксирован-
ном направлении оси ог' можно четырьмя различными способами ориентиро-
вать ось ох’ (ось оу' при этом будет занимать в правой системе координат
вполне определенное положение).
Физический смысл имеют только те решения уравнения Шредингера,
которые инвариантны относительно преобразований, соответствующих пере-
ходу от одной ориентации системы координат к другой. Переходы от одной
системы координат к другой можно описывать с помощью трех операторов
Di, D8, D3 и их степеней.
Оператор Dr изменяет направления отсчета вдоль осей ог' и оу' и соот-
ветствует повороту системы координат на угол л вокруг оси ох' (Оха = 1).
Оператор П2 соответствует повороту системы координат вокруг оси ог' на
л/2(О24 = 1). Оператор D3 соответствует циклической перестановке осей
(£>.г- о.
Оператор можно представить как совокупность поворотов на углы
Эйлера Ф = 0, в — j£ и ф= л. Оператор Da можно представить как поворот
на угол Эйлера ф = л/2. Оператор D3 можно представить как совокупность
поворотов на углы Эйлера ф = 0, 0 = п/2 и ф = л/2.
При любом преобразовании Одфункция ф(г) переходит в преобразован-
ную функцию
ф (г') = ₽ьф(г),
гдеСогласно соотношениям (4.58), при поворотах системы коор-
динат преобразованная функция выражается через функции в неподвижной
системе координат:
Wr') = Мл»(')=£л£г (Ф(4). 6(*>, ф(4)) Ф/т- (И. (4.361)
Вычислить результат действия операторов 7?3 и на D-функцин -
«ЛЛ- е, Ф) = 2 ^V(o- ". ")^-«(ф. в. Ф)-
т"
Так как
^т'т" (О’ ". я) = е 1 m Я(") = ( 0
ТО
R1 °^-т(Ф. ©. Ф)=(-1Г'’^,т(Ф. 6. Ф)- (4.362)
В соответствии с (4.361) имеем
< , л
*2 (Ф> 6, ф) = е 2 &т,т (Ф, 0, ф); (4.363)
*3 (Ф. е. Ф) = 2 Dm'm" (о. V ’ V ) (ф’ (4-364)
т" \ х z /
Вычислить результат действия операторов /?х, Р2 и /?3 на переменные Р
и у. Используя формулы преобразования (4.58), находим
*1 аЭц= 2 (°- Л- а2ц- = а2,-ц-
ц/
299
Так как
«20=PcosY И «2,2= а2,—2 = у% £1Пу,
Я1!т}=Ы- (4.365)
Далее
. л
-1|1у ,
^2 а2ц =е а2ц>
или
/? 2 ® д о а2О’ 0*22“ ^22*
Таким образом,
Я2 (?} = {-?}. (4.366)
Наконец,
*з ^<л/2> p*0(n/2)a'0 + (d£2 (n/2) + d£_2 (л/2)) а'ц].
Используя явный вид функций (л/2), находим
/?3cos у = (]/"3 /2) sin у—(1/2) cos у = cos (у — 2л/3);
^з sin у = —(1/2) sin у — (pz3 / 2) cos у и sin (у — 2л/3),
или
Д3(у} = {у-2л/3}. (4.367)
4.16. Показать, что трехфононные квадрупольные возбуждения харак"
теризуются значениями полного момента Л — 0, 2. 3, 4. 6 и имеют положитель-
ную четность.
Полный момент трехфононного возбуждения Л равен сумме моментов
•отдельных возбуждений:
A = A1-f-X3-f- Х3.
Соответственно проекция полного момента Лг на ось ог в лабораторной системе
координат равна
-{- А,аг X.3z.
Однофононное квадрупольное возбуждение характеризуется моментом,
равным двум, и проекцией р, соответствующая функция |0>, где —
оператор рождения фонона — удовлетворяет уравнениям
12б+ |0> = 2(2+l)b+ | 0>, 1г&+ |0>=р&+ 10>.
Полный набор трехфононных функций можно выбрать в виде
С1! |°>, (4.368)
где р2 и р3 пробегают все возможные значения. Очевидно, имеется 125
различных независимых функций (4.368). Из них требуется построить пол-
ностью симметричные линейные комбинации, которые должны быть собствен-
ными функциями операторов Л2 и Лг:
ЛгФлм = Л(Л+1) ФЛЛ(; (4.369)
ЛгЧ’ллт=лл1’лл<-
300
Правила векторного сложения моментов допускают, вообще говоря,
следующие значения моментов Л: 0, 1, 2, 3, 4, 5 и 6. Однако в системе из трех
фононов не все указанные значения полного момента разрешены, так как вол-
новая функция должна быть полностью симметричной относительно переста-
новок фононов. Выясним, сколько линейно независимых функций, удовлет-
воряющих требуемым условиям симметрии, можно построить для каждого
значения М.
Если М = 6 или 5, то можно построить только по одной полностью сим-
метричной функции:
М = 6; ^2(1)^2<2)£,22(3>1°>-
М = 5; Ь22<г> btl<3> 1°>-
Если Af = 4, можно построить две функции;
М=4; &+<!)&+<2^+<3)|0>, й+/Пф2)&+£)|0>.
Если М = 3, то можно построить три функции:
М = 3;
£,+ <’’*+<2> <3>|0>-
Если М = 2 или I, то можно построить по четыре функции:
М = 2; &+<2> 1°>. *22<П&2-1(2> । °> ’
} б+< 2> й+/3) I 0>, б+ < > Ь^2> й+(3> I о>;
M=l; b+2( 11 &+(2) &+£3] | 0>,
&+(,^+(2>413)|0>,
И, наконец, если М— 0, то можно построить пять функций:
м=0; 6+<‘>&+j:2’&+<3)|0>, &+<,,&t22i,4_<?'|0>.
&+/!'б+<2)б+Л>|0>,
h+ (1) h+ (2) h+ (3) in,
°20 °20 °20
Каждое из произведений после симметризации дает линейно независимую
функцию с определенным значением М. То, что при переходе от М = 6 к
М = 5 и от М = 2 к М = 1 не появляется дополнительной линейно незави-
симой комбинации, говорит о том, что значения Л = 5 и 1 запрещены.
Положительная четность каждого из состояний следует из того, что функ-
ции этих состояний построены из квадрупольных однофононных функций.
Подобное же элементарное рассмотрение показывает, что двухфоионные
квадрупольные возбуждения могут иметь только три значения квадрата мо-
мента Л — 0,2 и 4.
4.17. Показать, что четырехфоноиные квадрупольные возбуждения име-
ют положительную четность и характеризуются следующими значениями пол-
ного момента Л: 0, 2, 4, 5, 6 и 8; значения Л= 2 и 4 встречаются дважды, для
их классификации вводят дополнительное квантовое число—с еньоритй.
Решение задачи аналогично решению предыдущей задачи.
4.18. Показать, что трехфоноиные октупольные (А. = 3) возбуждения
имеют отрицательную четность и следующие значения полного момента Л:
0, 3, 4, 5, 6, 7 и 9, причем значение Л = 3 встречается дважды (уже при трех
301
фононах необходимо вводить дополнительное квантовое число — сеньорити
для полной классификации состояний).
Решение задачи аналогично решениям предыдущих задач.
4.19. Проквантовать кинетическую энергию, связанную с вращением и
деформациями поверхности ядра, выбрав в качестве независимых переменных
углы Эйлера Ф, 6 и ф и параметры деформации [J и у.
Классическое выражение для кинетической энергии, связанной с вра-
щением и деформациями поверхности ядра, имеет вид
Г = (1/2)2 У^ + (В/2) (&2 + ₽2 ? ). (4.370)
ft'
где составляющие угловой скорости на оси подвижной системы координат
выражаются через производные от углов Эйлера:
Oj.. =— sin в cos ф Ф + sin ф 0;
юу. = sin 0 sin ф ф + cos ф 0;
сог, = cos 0 Ф + ф.
В качестве обобщенных координат (/( выберем величины
<71 = Ф, </s = 9, ?з = ф, <7« = ₽ и <7s = Y-
Тогда кинетическую энергию (4.370) можно представить в виде
В ( ds V
т= — — ,
2 \ Л J
где ds2 — квадрат дифференциала длины
ds2=gij dqi dq}.
Симметричная матрица gtj в этом случае имеет вид
£1з £1з 0 0 \
£зз 0 0 0 \
О £зз О О I,
о о £« о I
О 0 0 £й5 /
где отличные от нуля матричные элементы равны:
<7. У3
gn-=~ sin2 0 cos2 ф — —g- sin3 6 sin2 Ф + ~ cos30;
/£п
/ £21
St j — I £si
I 0
\ 0
Уз
cos0;
D
§22 = ^ sin3 ф + cos2 ф;
0 D
Уз .
£зз- B ,
£« 1;
£m = ₽2-
(4.371)
(4.372)
(4.373)
(4.374)
(4.375)
302
Используя (4.375), нетрудно найти определитель матрицы (4.374):
g = I gij I = 171 дз"- Рг sin* в. (4.376
Найдем цалее по правилам линейной алгебры матрицу обратную (4.374):
8ik 8hj = 6(;.
Эта матрица имеет внд
1 8Г11 812 813 0 0
/ — 1 S22 82З 0 0
1 1 £31* 832 —‘1 833 0 0
=
\ ° 0 0 Й44 0
\ 0 0 0 0 гГз1
где
(4.377)
sll I /V.
sin -ф cos ф '
sin 6 ’
cos2 ф sin2ф \
+ #2 )
ctg0;
, „ ( sin3 ib cos3 ф \
^'“в(^г+-эг);
(4.378)
S23=B ctg в sin ф cos ф;
w 1 а 7
। „ / cos2 ф . sin3 ф \ „ В
^, г8 вч ^
-I -1 1
^44 Ь £55 ps '
Лапласиан в пятимерном пространстве определяется общим выражением
. 1 д I „г- й \
Подставляя в эту формулу значения определителя (4.376) и матричных эле-
ментов обратной матрицы (4.377), получаем
__у в п2 , 1 д . Г. 1 8 / д X
' к'+ р* ‘ 8₽ Р + Р3 * sin3y ' 0? tS‘n ? й? )’
(4.379)
303
гд< — составляющие момента вращения на подвижные осн:
/ cos ф д д д \
Rх> = —i - l ^'rip -' -ctg 9 cos ф — ;
х \ sin 0 ЭФ d0 dip}
i sin ip д д d \
— i тг + созф —-ctgOsinxp — ; (4.380)
y \ sin 9 дФ d9 cn|) J
d
Rz' ~ dip
Оператор кинетической энергии, связанной с вращением и деформациями
поверхности ядра, имеет вид
Я» V 9 У ( 1 д „ д
Т= “2BV ^'~2в{₽1 д₽Р\р+
1 1 д / д \ 1
+-------------— sin Зу — I. (4.381)
р2 sinЗу dy \ * <5у /)
Эта формула, как и следовало ожидать, совпадает с формулой, полученной
ранее (4.251).
4.20. В неадиабатическом приближении рассмотреть коллективные
движения ядра, связанные с аксиально симметричными деформациями.
Если ограничиться учетом только аксиально симметричных деформаций
(т, е, положить у = 0), то
ZTz,=O, cojl ~H(^,=sin2O<i>2 + 02,
и кинетическая энергия коллективных движений принимает вид
Т = у{3₽2(з1п26Ф2 + О2)+0а}- (4.382)
Так как в случае аксиальной симметрии ядро может вращаться только вокруг
направлений, перпендикулярных оси симметрии, то движение характеризует-
ся только тремя степенями свободы: = Ф, q2 ~ 0, Чз =: Р- Вводя квадрат
дифференциала длины dsa = g,j dqtdqj и замечая, что матрица диаго-
иальна
/3p2sin2 0 0 0\
яИ ° зра ° •
\ о 0 у
согласно общим правилам, получаем трехмерный лапласиан
, 1 в д 1/1 д . „ д 1 д2 X
V “ р2 dp Р dp + 3p2(,sin9 d0Sln9 d0~ sin20d<D2 J ' (4‘383)
Учитывая, что потенциальная энергия в случае малых деформаций про-
порциональна квадрату параметра деформации р, гамильтониан системы за-
пишем в виде
Л2 f 1 д д 1 Г 1 д д
2В[р2 dp₽ dp + 3p2[sin0 <39 51П0 d0 +
1 <3*11 1'
+ <4-384)
304
Заметим, что угловая зависимость гамильтониана (4.384) совпадает с уг-
ловой зависимостью обычного оператора Лапласа, поэтому уравнение Шредин-
гера
(4.385)
(4.386)
Яф = £Чг
можно решить методом разделения переменных.
Выберем функцию Т (Ф, 6, р) в виде
^(ф,е,Р)=/(Р) пт(в,Ф),
тогда функция /(£) будет определяться уравнением
„ . Ара JL_ + — ср2/(f)=E/(0), (4.387)
2ВI р2 ар ар зр2 | ' р/ 2 р
Введем новые переменные:
Р=М; Ро=Г—
|_ВС.
с
4 :
(4.388)
При этом
Исследуем поведение решения при 0. Полагая /(£)* |я>
чаем характеристическое уравнение а2 + $——/(/-[-1) = 0,
3
"I /” 1 1
= — ~± I/ ^-+-g + Так как f (|) должно быть конечным
при | = 0, то выбираем первое решение. Из двух асимптотических решений
(4.389)
для s полу-
откуда s =
(4.390)
при Е,->-оо выбираем /(£)-*-е 2 , и решение уравнения (4.389) ищем в виде
_V
/® = Г«е 2’
где и- полином, удовлетворяющий уравнению
u1
£ ц' — (2s+3— %)u = 0.
(4.391)
£
Решен ием этого уравнения
. 1 i 3
функция и = F I ~ I s + —
которая обращается в полином, если
1 , 3 Z \
— s +—— — = —п,
2 \ 2 2
является вырожденная гипергеометрическая
X \ 3 \
, s+-, £2 -
(4.392)
где п — неотрицательное целое число (п = 0, 1,2, ...). В этом случае вырож-
денная гипергеометрическая функция сводится к полиному Лагерра
р(~п, в + -у, = П'
L 2(&2), а условие (4.392) определяет
п
305
возможные значения энергии. Окончательно уровни энергия системы
и соответствующие им волновые функции можно представить в виде
/3 \
Епг~ [ —+ 2п + s ) few; (4.393)
' Ч^т(Ф,6,₽) = Л^/‘Гг (5!)е 2 Угт(9,Ф), (4.394)
1 / --4------\ <. Р
где $ = — —1+1/1+-г-/(/‘Н , ь = "X" и N—нормировочная посте-
2 \ Г 3 } ро
янная:
/• Г (П +1) 4
\Ро3 Г (n + s+ 1) /
Из требования симметрии волновой функции относительно плоскости’
перпендикулярной к оси симметрии ядра и проходящей через центр ядра,
следует, что возможны только четные значения I.
На рис. 4.20 изображена схема уровней энергии, рассчитанных по фор-
муле (4.393). Справа на рис. 4.20 отложены уровни энергии для ядер Zr,
JJJZr и 62°^m- Величина ha для каждого из ядер определялась по положению
первого наблюдаемого возбужденного уровня. Рассмотренная модель позво-
ляет объяснить наличие близко расположенных друг к другу уровней 0+ и
4+ Отношение энергий близких уровней 4+ и 0+, вычисленное по формуле
(4.393), равно 1,06, в то время как отношения экспериментальных значений
уровней для трех указанных ядер равны 1,08 (®gZr), 1,12 (^Zr) и 1,05 (g^Sm).
4.21. Предполагая, что самосогласованный потенциал ядра мало отли-
чается от сферически симметричного, определить по теории возмущений по-
правку к одночастичной энергии, обусловленную деформацией ядра.
В отличие от случая больших деформаций ядер в случае малых деформаций
одночастичные уровни энергии и волновые функции нуклонов, движущихся
в слабо деформированном поле ядра, можно найти в явном виде, используя
теорию возмущений. В качестве возмущения V' будем брать разность несфе-
рического потенциала, зависящего от параметров деформаций, и сферическо-
го (оболочечного) потенциала. Для нахождения первой поправки ДЕ к энер-
гии нужно вычислить диагональный матричный элемент от возмущения V'
с помощью волновых функций оболочечной модели
1 , (4.395)
где j — спин-угловая функция. Выбирая для простоты потенциал
в виде прямоугольной ямы с глубиной Ve, поправку к энергии ДЕ представ-
ляем в виде
( Я(О,ч>)
2 рОГ' -Vo J ^'г'3[Х^| 2 +
спины I °
я 1
+М^|$|г ! *
О J спины I— 1Q
I df Т 1 Rnl )1 а’ (4.396)
306
Рассматривая только эллипсоидальные деформации и учитывая малость от-
клонения величины £(&, <р) ==(! + ^(О, <р)) R от радиуса равновеликой
сферы поправку ЛЕ после суммирования по спиновым переменным полу-
чаем в виде
Д£= - Vo R3 | Rni (R) | 2S av'(/2 | F2v | /«>. (4.397)
v
Если бы мы использовали не прямоугольный потенциал V, то в возмущении
V', которое для прямоугольного потенциала имело вид
V' = - VG RS (,'_R) S а ' y2v (11, ф),
V
с
нужно заменить V0Z?o(r — 7?) на величину г Замечая, что
</я I y2v I /Q) = -1 VА ААЖА 6VO,
х ' 4 г 4л 1 (/-j-1)
для поправки к одночастичной энергии окончательно получаем выражение
1 /"V
bE = Cj [ЗЙ4—j (j+l)]a0', cJ = Tj/3±-V0(?3|/?nI^)|2//(/+ i)( (4.398)
или, так как а0'= р cos у, то (у <15°)
ДЕ = ДЕяО.п = с;-[ЗЙ2 — /(/+1)] pcosy. (4.399)
При малых деформациях (Р < I) состояние нуклона в ядре можно при-
ближенно характеризовать квантовым числом полного момента /. Из (4.399)
следует, что при j = 1/2 первая поправка по теории возмущений ЛЕ равна
нулю. По знаку проекции полного момента £2 имеется вырождение.
Если мы имеем несколько нуклонов в оболочке nlj, то соответствующая
поправка к энергии будет равна сумме отдельных поправок (4.399) для каж-
дого из нуклонов. Если оболочка nlj полностью заполнена, т. е. в ней на-
ходится 2/ + 1 нуклонов с различными проекциями £2, то суммарная поправ-
ка к энергии равна нулю, так как 2[3£22 — /(/ + 1)] = 0.
0=-/
4.22. Определить равновесную деформацию и порядок заполнеиня одно-
частичных состояний во внешней оболочке слабо деформированного ядра.
Ядро с полностью заполненной внешней оболочкой имеет сферическую
форму. Если к такому ядру присоединить один нуклон, то новее ядро будет
уже несколько отличаться от сферы, причем равновесная деформация будет
определяться взаимодействием внешнего нуклона с остовом ядра, образуе-
мого заполненными оболочками. Вследствие этого взаимодействия остов по-
ляризуется, деформируется; в результате поле, в котором движется внешний
нуклон, не будет обладать сферической симметрией. Остов как бы сопротивля-
ется деформациям; напротив, внешний нуклон стремится увеличить дефор-
мацию .Равновесная деформация будет, таким образом, зависеть от упругих
свойств остова и состояния внешнего нуклона в деформированном поле остова.
Зависимость потенциальной энергии остова от деформации при малых
деформациях определяется квадратическим законом
Е' (₽)=Е' (0)4-(1/2) Ср2. (4.400)
3 ависимость потенциальной энергии всего ядра с одним внешним нуклоном
от.деформации определяется выражением (у <15°)
Е (Р) = Е (0) + с; [ЗЙ2-(/ + 1)] Р cos у+ (1 /2) Ср2. (4.401)
307
Рассмотрим деформированные ядра с аксиальной симметрией, т. е. положим
7 - 0. Тогда равновесное значение параметра рл получим из условия
ag(P) 1
д₽ I ₽=р.
(4.402)
Подставляя сюда £(р) из (4.401), получаем для величины равновесной дефор-
мации значение
ро(й) = —— [ЗЙ2—/(/+1)]. (4.403)
Рис, 4.20. Схема вращательно-колебательных уровней для аксиально симмет-
ричных деформаций. Приведена также схема наблюдаемых уровней ядер-
®gZr, 9JZr, и 62°®П1' Для которых параметр йы равен соответственно 932, 920
и 334 кэв.
Энергию ядра в равновесном состоянии получим, подставив (4.403) в (4.401)
при у — 0:
С;2
£{₽„(Й)) =Е(0)--------J- [ЗЙ2- /(J+1)]2-
(4.404)
Отсюда видно, что для одного внешнего нуклона энергия в равновесии бу-
дет минимальной, если взять возможно большее значение |Q|, т. е. если поло-
жить £2 = ±/. При этом р0 < 0, т. е. ядро будет сплюснутым вдоль оси сим-
метрии и с отрицательным квадрупольный моментом.
Если в оболочке nlj имеется несколько нуклонов, то так как мы считаем
их не взаимодействующими друг с другом, результаты легко обобщить, за-
менив в формулах величину [ЗЙ2 — j(j 4~ 1)I на сумму по нуклонам
аЗ£12г-/0’+ 1)1-
Принцип Паули позволяет иметь одинаковую величину Й? только двум
одинаковым нуклонам. Если оболочка полностью заполнена, то, как и должно
быть, равновесная деформация равна нулю:
₽о=-4,- 2 [3£2;2-/(/+1)]=0.
с аг=-/
308
Если в оболочке будет два нуклона, то энергия будет минимальна; если
проекции их моментов по абсолютной величине будут равны, а по знаку
противоположны: £2Х = -ф/ и Q2 ——/, то суммарная проекция будет
равна нулю. Если добавить к двум нуклонам третий, то он будет иметь
®з — j — 1 или ' —/ + 1 и т. д. Суммарная проекция полного момента
будет равна нулю, если число нуклонов в незаполненной оболочке чет-
i
но; в противном случае она равна проекции момента последнего нечетного
нуклона.
Когда оболочка заполнена более чем наполовину, энергетически выгод-
но, чтобы занимались нуклонами состояния с минимальными проекциями пол-
ного момента: Й112 = ±’/г, Й3,4 = ±’/s, .... Это хорошо видно из
общего выражения для энергии ядра в равновесном состоянии:
Е jS =Е (O'j -SL {2(ЗЙ?-Н/ + 1)]Р. (4.405)
i ZL i
Допустим, например, что до заполнения оболочки не хватает одного нуклона.
Из (4.392) видно, что энергия будет минимальна, если не заполнено состояние
с [Q;| = /. В самом деле, в этом случае имеем для квадрата суммы в правой
части равенства (4.405)
( 1 I2
(S[3£V-/(/+l)]}3 = 2 [3£V-j(/+l)]-[3)2-/(j+l)] =
1 {ai=—i
= [3ja-j (/+!)]’,
что является максимальным значением из всех величин [3£2f — /(/ + I)]2
при j > 3/2, Равновесная деформация при этом равна
Si,(Q.) = -7-2[3Qf-j(/+l)]-.- -^-[ЗР—j (/4-1)1,
i G i G
t. e. является величиной положительной, что соответствует вытянутому вдоль
оси симметрии ядру и положительному квадрупольному моменту.
Таким образом, можно сделать следующее общее заключение. Если чис-
ло нуклонов в оболочке не превышает половины максимально возможного
числа в данной оболочке, то энергетически выгодно, чтобы были заполнены
все состояния с |Q,| — j, j — 1, j — 2 и т. д. до некоторого |Qf] > V2(j + Va).
В этом случае равновесная деформация отрицательна, что соответствует сплюс-
нутому ядру, имеющему отрицательный квадрупольный момент. Если же в
оболочке находится больше половины возможного числа нуклонов, то запол-
няются состояния с —- 1/2, 3/2, ... ит. д. до некоторого значения |Й;|,
которое также превосходит или равно 1/2(/ + 1/2). При этом ядро вытянуто
(равновесная деформация положительна) и квадрупольный. момент его поло-
жителен. Ясно, что максимальная равновесная деформация будет достигну-
та, если оболочка заполнена ровно наполовину.
Описанная простая модель помогает качественно понять механизм воз-
никновения деформации ядер. Однако она не объясняет количественно вели-
чину квадрупольных моментов и спинов ядер. Лишь для некоторых ядер,
близких к магическим, эта модель правильно предсказывает спины основных
состояний ядер. Вдали же от магических ядер, где деформации уже нельзя
считать малыми, квантовое число полного момента нуклона / даже прибли-
зительно нельзя считать хорошим. Кроме того, в разложении энергии ядра
по степеням параметра деформации нужно учитывать более высокие степени
разложения.
Если изобразить энергию ядра (4.405) в зависимости от числа тождествен-
ных частиц в оболочке, то получим симметричную зависимость относительно
середины оболочки, где энергия будет иметь минимум. Как мы видели на при-
мере потенциала Нильссона, одночастичные уровни, изображенные как фуик»
309
ции параметра деформации, с ростом энергии возбуждения и величины де-
формации все чаще и чаще пересекаются. Если мы зафиксируем число нукло-
нов и будем строить функцию их энергии от величины деформации, то в этой
зависимости будут наблюдаться изломы, которые связаны с тем, что отдель-
ные нуклоны будут переходить из одних состояний в другие, которые энерге-
тически более выгодны. Смена состояния будет происходить как раз на пере-
сечении кривых одночастичных энергий. Такая кривая с изломами, изобра-
жающая энергию нескольких нуклонов в зависимости от деформации, имеет
обычно несколько минимумов, причем может случиться, что величина энер-
гии в некоторых минимумах почти одна и та же. В этом случае небольшое
изменение потенциала может сильно изменить порядок уровней.
ГЛАВА 5
ПАРНЫЕ КОРРЕЛЯЦИИ
В ЯДРАХ
§ 5.1. СВЕРХТЕКУЧИЕ СОСТОЯНИЯ ЯДЕР
’ Короткодействующие силы спаривания и дальнодействующие
мультипольные силы. Рассмотренные в предыдущих главах оболо-
чечная и обобщенная модели позволили объяснить многие свойства
ядер, а также установить общие закономерности в зависимости от
зарядов и массовых чисел ядер. Имеется, однако, несколько особен-
ностей, которые не удается объяснить в рамках оболочечной и обоб-
щенной моделей, что указывает на необходимость привлечения
иного подхода для описания свойств основных и возбужденных, со-
стояний ядер.
Среди таких свойств и закономерностей укажем прежде всего
на следующие: различие в массах четных и нечетных ядер; нали-
чие энергетической щели в спектрах возбужденных состояний
четно-четных ядер и отсутствие такой щели в спектрах нечетных и
нечетно-нечетных ядер; плотность одночастичных уровней; равно-
весные деформации ядер и их зависимость от массового числа; зна-
чения инерциальных параметров ядер в случае коллективных дви-
жений и др.
В новой, так называемой сверхтекучей модели ядра
так же, как и в многочастичной оболочечной модели, предполагает-
ся, что нуклоны в ядре движутся так, как предсказывает оцночастич-
ная оболочечная модель, и учитывается остаточное взаимодействие,
т. е. корреляции между нуклонами. Однако учет остаточного вза-
имодействия в сверхтекучей модели производится совсем другими,
более совершенными способами. Вспомним, как учитывалось оста-
точное взаимодействие в многочастичной модели оболочек. Там за-
дача о нахождении собственных функций и собственных значений
гамильтониана ядра сводилась к трудоемкой численной диагона-
лизации гамильтониана по конфигурациям с помощью вычислитель-
ных машин. При этом даже не ставилась задача о вьщелении остаточ-
ного взаимодействия из двухчастичных взаимодействий нуклонов
У, Vjy. Как уже говорилось, помимо вычислительных трудностей
></
такой подход не позволяет понять как следует физику явлений,
так как при этом почти невозможно выделить наиболее существен-
ные черты основных физических эффектов. (Забегая вперед, ука-
жем, что в новой модели задача выделения этих существенных черт
в значительной мере решается введением сил спаривания.) Это как
311
раз и мешает в рамках оболочечной модели объяснить те особенно-
сти, которые частично перечислены выше. Эти недостатки оболочеч-
ной модели смогла устранить сверхтекучая модель, в которой ис-
пользованы новые методы рассмотрения остаточных взаимодейст-
вий, с помощью которых значительно легче исследовать свойства
систем многих частиц.
Как будет показано ниже, из остаточного взаимодействия мож-
но выделить специфическое короткодействующее взаимодействие
спаривания, играющее особо важную роль в объяснении свойств
ядер. Некоторые опытные данные (например, энергия связи послед-
него нейтрона в легких ядрах, равенство нулю спинов четно-четных
ядер в основных состояниях и др.) указывают на то, что сильная кор-
реляция между двумя нуклонами осуществляется лищь тогда,
когда эти нуклоны находятся в состояниях с одинаковой энергией
и одинаковыми квантовыми числами, за исключением проекций их
полных моментов.
Природа остаточных короткодействующих сил такова, что она
приводит к значительно более сильному взаимодействию пары ну-
клонов в состояниях, в которых их суммарный момент равен нулю
(эффект спаривания).
В сверхтекучей модели ядра предполагается, что отдельные
нуклоны в ядре характеризуются такими же одночастичными со-
стояниями, как и в модели независимых частиц. Поэтому спарива-
ние нуклонов можно описать с помощью квантовых чисел моде-
ли независимых частиц. Например, если один нуклон описывает-
ся набором квантовых чисел п, I, j и т, то спаренный нуклон
должен описываться набором квантовых чисел п, I, j л — т.
Чтобы разделить пару нуклонов, необходима определенная энер-
гия (парное взаимодействие есть взаимодействие притяжения),
что и приводит к возникновению энергетической щели между ос-
новным и первым возбужденным состояниями в четно-четных яд-
рах, где все нуклоны спарены (а потому и суммарный момент ядра
равен нулю).
Аналогичная энергетическая щель возникает и в энергетических
спектрах систем других фермионов, например электронов в метал-
лах. В связи с наличием щели в спектре возникает определенная
устойчивость системы к внешним воздействиям, приводящая к яв-
лению сверхпроводимости. Эго явление связано со свойством сверх-
текучести систем, состоящих из одинаковых бозонов, так как при оп-
ределенных условиях электроны в металлах, как и нуклоны в ядре,
объединяются в пары, совокупность которых можно рассматривать
как некоторый бозе-газ, поскольку каждая пара обладает целочис-
ленным спином. Этот бозе-газ при низких температурах может об-
ладать свойством сверхтекучести. Таким путем на основе представ-
ления о парах была построена теория явления сверхпроводимости
электронов в металлах [1—3]. Подобное свойство в случае ядер обыч-
но называют явлением сверхтекучести, а не сверхпроводимости.
Впервые на свойство сверхтекучести ядерной материи указал
312
Н. Н. Боголюбов [4], основываясь на сходстве свойств ядерной
материи со свойствами электронов в металлах*.
Свойство сверхтекучести ядер обусловлено парными корреляция-
ми между нуклонами, являющимися, в свою очередь, проявлением
остаточного взаимодействия между ними. Поэтому эти корреляции
называют часто парными корреляциями сверх-
проводящего типа. В этом случае энергия основного со-
стояния будет заметно ниже энергии состояния, не учитывающего
корреляций. Это состояние с уменьшенной энергией называют
сверхтекучим.
В основе метода рассмотрения сверхтекучего состояния лежит
формализм вторичного квантования. Любая волновая функция си-
стемы фермионов в этом формализме будет автоматически антисим-
метричной. В то время как в обычном представлении функция за-
писывается в неудобном для расчетов виде (детерминант Слэтера),
в новом представлении она имеет очень простой вид и удобна при вы-
числениях. Операторы рождения и уничтожения, входящие в гамиль-
тониан и волновые функции, соответственно увеличивают или умень-
шают на единицу число нуклонов в каком-либо состоянии. Путем
линейного канонического преобразования этих операторов рожде-
ния и уничтожения вводятся новые операторы, которые в общем
случае ответственны за рождение и уничтожение не отдельных
нуклонов, а определенного сорта квазичастиц, являющихся
суперпозициями нуклонных и дырочных состояний^ -Выраженный
через новые операторы* рождения ^ уничтожения (квазичастиц)
оператор Гамильтона будет зависеть также рт коэффициентов ка-
нонического преобразования. _Эти коэффициенты можно найти из
условия минимума э'нёргии систсмЫ В основном состоянии с помощью
вариационного принципа. При этом полный гамильтониан систем
приближенно представляется в виде суммы гамильтонианов невзаи-
модействующих квазичастиц.
Мы видели, что в рамках оболочечной модели учет остаточного
взаимодействия между нуклонами, т. е. учет корреляции между
ними, является очень трудоемкой задачей. Поэтому обычно в обо-
лочечной модели корреляции не принимают во внимание, т. е. счи-
тают, что нуклоны движутся в самосогласованном поле независимо.
Хотя самосогласованное поле и включает значительную часть двух-
частичного взаимодействия между нуклонами, тем не менее оно не
учитывает силы спаривания, которые существенно сказываются
на некоторых свойствах ядер. Переход к квазичастицам в сверхтеку-
чей модели даже в случае пренебрежения взаимодействием между
квазичастицами позволяет учесть значительную часть корреля-
ционных эффектов**.
* На сходство спектров возбуждения ядер со спектрами сверхпроводя-
щих металлов обратили внимание Бор, Моттельсон и Пайне [5].
** Теория сверхтекучих состояний ядер разработана С. Т. Беляевым [6 J и
В. Г. Соловьевым [7, 8].
313
Перейдем теперь к общему рассмотрению остаточного взаимо-
действия. Считая, как и раньше, оператор потенциальной энергии
ядра U равным сумме двухчастичных потенциалов
l/=2Vih (5.1)
*</
выясним, как в произвольном двухчастичном потенциале Уц =
= У(гг — Г;) можно выделить часть, дающую вклад в самосогласо-
ванный потенциал модели независимых частиц , а также часть,
характеризующую остаточное взаимодействие: силы спаривания
и мультипольные силы. Выясним смысл и природу возникновения
сил спаривания и мультипольных сил*.
Выбрав начало координат в центре инерции ядра, разложим двух-
частичный потенциал в ряд по полиномам Лежандра:
V (П-П) = S V, rz)Px (COS0/Z), (5.2)
х=о
где — угол между векторами гг и rz. Если ядро сферическое»
то главный вклад в самосогласованное поле ядра дает первый член,
содержащий изотропную часть двухчастичного потенциала У0(гг, О)>
а все другие слагаемые с X 0 представляют остаточное взаимодей-
ствие. Если же ядро деформировано, то в самосогласованный потен-
циал будет давать также вклад и квадрупольное слагаемое с X — 2.
Слагаемые с 1 > 2 и в этом случае не вносят вклада в самосогласо-
ванный потенциал.
Остаточное взаимодействие можно разделить на две части: ко-
роткодействующую и дальнодействующую. Посмотрим, как это
можно сделать. При изменении угла 0,; функция /\(cos©iZ) резко
убывает от своего максимального значения Рх Icos (0Z/ = 0)] = 1
на угловом интервале порядка VX. Так как расстояние |г{ — rz|
между двумя нуклонами приблизительно равно где /? есть
среднее значение величин гг и rz, ясно, что компонента X потенциа-
ла Р(гг — rz) будет давать вклад во взаимодействие частиц i и /
только тогда, когда |г,- — rzl < R/k. Таким образом, с увеличением
X радиус действия сил убывает. Вклад слагаемых с большими X
будет расти с уменьшением области действия сил. В пределе б-
образных сил с нулевым радиусом действия имеем
У(Г; — Г;) = А6(Гг— Tj) =
= У А6 (rt-r}) л (cos 0iZ). (5.3)
хТо 4nrz
Здесь Vx (г;, г^)=Аб(гг—rz) (2Х + 1)/4лг® растет с увеличением
X. А для сил с радиусом действия, превосходящим размеры ядра,
основной вклад будет давать член с X = 0.
* Вопрос о силах спаривания и мультипольных силах хорошо изложен
в книге Лейна 19].
314
Итак, можно сказать, что слагаемые с малыми X ответственны
за ту часть двухчастичного взаимодействия, которая имеет большой
радиус действия. Эти слагаемые связаны с дальнодейст-
вующими мультнпольными силами (корре-
ляциями дальнего порядка). Они приводят к возник-
новению самосогласованного поля (Х=0), удерживающего нуклоны
в ядре, а также к коллективным движениям в ядрах. Так, слагаемое
с X - 2 ответственно главным образом за возникновение коллек-
тивных квадрупольных колебаний. Сумма же всех слагаемых с боль-
шими X представляет короткодействующую часть двухчастичного
потенциала, которая приводит к силам спаривания.
Таким образом, сверхтекучая модель ядра основывается на сред-
нем самосогласованном поле модели независимых частиц, но в ней
учитывается также короткодействующая часть нуклон- нуклонных
взаимодействий, приводящая к парным корреляциям сверхпрово-
дящего типа. Сверхтекучая модель дает микроскопическое описание
структуры ядра, однако в ней используются феноменологические
параметры. В сверхтекучей модели учитываются также мультиполь-
ные силы (X 2), которые своим происхождением, как и среднее
самосогласованное поле, обязаны дальнодействующему взаимодей-
ствию. В настоящем параграфе для простоты не учитываются муль-
типольные силы, ответственные за коллективные эффекты. Это даль-
нодействующее остаточное взаимодействие мы учтем при рассмот-
рении одного наиболее общего и эффективного приближенного ме-
тода по изучению структуры ядра в конце этой главы.
Итак, учет парных корреляций сверхпроводящего типа позво-
лил объяснить некоторые важные свойства ядер и привел к созда-
нию сверхтекучей модели ядра. Рассмотрим теперь более последо-
вательно сверхтекучую модель ядра.
Гамильтониан сверхтекучей модели. Рассмотрим систему нукло-
нов, находящихся в аксиально симметричном самосогласованном
поле. Пусть гамильтониан отдельного нуклона в этом поле Но.
Собственные волновые функции в этом случае можно выбрать так,
чтобы они отвечали определенным значениям проекции момента
нуклона Й на ось симметрии ядра. Обозначим собственные значения
Но через ev и соответствующие волновые функции через |v > (v
характеризует определенное значение проекции момента и допол-
нительные квантовые числа, необходимые для полного описания
состояния нуклона). Функцию |v > можно разложить по собствен-
ным функциям момента нуклона:
|v>=sc;xL (5.4)
!
Если система инвариантна относительно обращения времени, то
уровни ev двукратно вырождены. В случае аксиальной симметрии
вырожденные состояния отличаются знаком проекции момента Й
и —Й. Введем оператор отражения времени Т. Тогда состояние
|—v>, сопряженное состоянию |v>, можно определить как |—v> =
= T|v>.
315
Перейдем к представлению вторичного квантования, используя
в качестве базисных функций одночастичные функции. Формализм
вторичного квантования позволяет автоматически учесть принцип
Паули, которому подчиняются нуклоны. Введем операторы рожде-
ния и уничтожения нуклона в состоянии v: й+ и «v- Эти операторы
удовлетворяют соотношениям антикоммутации:
ciy' -|- cty’ ciy —7 6v, v' (5.5)
Волновую функцию вакуума нуклонов |0 определим из условия
av|0)=0. (5.6)
Тогда одночастичные волновые функции |v> можно выразить че-
рез волновую функцию вакуума |0> и операторы рождения а+ сле-
дующим образом:
|v)=a+|0). (5.7)
Используя операторы av и оф, гамильтониан системы взаимо-
действующих нуклонов представим в виде
// бу ($v П — v Ц — v) 1
„ v, . , , (5.8)
|-Jj <V1 V2|
viv2v’iv2 1 2
где ev — энергия отдельного нуклона в самосогласованном поле,
a (v1'v2' |V| v2V! >—матричный элемент остаточного парного вза-
имодействия между нуклонами. Сумма у включает также суммиро-
вание по сопряженным состояниям.
Гамильтониан (5.8) описывает систему с определенным числом
частиц п, где п — собственное значение оператора:
п— S(atnv4-fl--uH-v)- (5-9)
V
Так как решение задачи упрощается при переходе к системе с не-
сохраняющимся числом частиц (используемое в дальнейшем кано-
ническое преобразование не сохраняет числа частиц), то удобно
ввести вспомогательный гамильтониан
(5.10)
в котором множитель X можно рассматривать как химический по-
тенциал (X характеризует энергию последнего нуклона). Потенциал
X определяется из условия
<T|/7|V>-n, (5.11)
где Т — собственная функция (5.10). Результаты, полученные на
основе гамильтониана (5.10), будут описывать только усредненные
316
свойства ядер. Усреднение следует проводить по небольшому (неоп-
ределенность п мала) числу соседних либо четных, либо нечетных
ядер.
Взаимодействие между нуклонами, остающееся после выделения
самосогласованного поля, не является слабым, поэтому систему,
характеризуемую гамильтонианом (5.8) или (5.10), нельзя исследо-
вать при помощи теории возмущений. Однако если предположить
(по аналогии с явлением сверхпроводимости в металлах) наличие
сильной корреляции между нуклонами в сопряженных состояниях
(с противоположно направленными моментами), то при помощи
канонического преобразования (аналогичного введенному в теории
сверхпроводимости Н, Н. Боголюбовым) можно перейти от систе-
мы взаимодействующих нуклонов к системе квазичастиц, взаимо-
действием между которыми можно пренебречь (системе независи-
мых элементарных возбуждений).
Предположим, что остаточное парное взаимодействие проявляет-
ся только между нуклонами, находящимися в состояниях с суммар-
ным моментом, равным нулю. Это означает, что в (5.8) состояния
и v2 (v/ и v/) должны быть взаимно сопряженными. Следователь-
но, в дальнейшем будем исходить из гамильтониана
Н =2 (ev — av4~ atva_v) +
V
+ 2 <У' —v' I УI — vv> Д-v' av a—-v- (5.12)
VV'
Матричный элемент <v' — v'|V| — w> антисимметричен от-
носительно начальных и конечных состояний нуклонов. Кроме
того, из определения сопряженных состояний следует, что
< v'jv/l — ( — v/ — v2'| V| — v2 — Vj)*. Поэтому матричный
элемент <v' - v'|V| — vv> симметричен относительно индексов v
и v'. Отметим также, что в результате выделения самосогласован-
ного поля диагональная часть V равна нулю.
Каноническое преобразование Боголюбова. Введем взамен опе-
раторов av к a-v новые операторы
cty — Ну Пд, а—yj Пу а—у -f- vv av, (5.13)
где uv и uv—вещественные числа, связанные соотношением
«v + = 1. (5.14)
Нетрудно проверить, что операторы av (|3V) и at (pt) удовлетво-
ряют таким же перестановочным соотношениям, как и операторы
av и at, поэтому преобразование (5.13) является каноническим.
Преобразование (5.13) — это обобщение обычного преобразова-
ния, при помощи которого переходят от частиц вне поверхности
Ферми и дырок внутри этой поверхности к элементарным возбужде-
ниям. Действительно, если положим
fl f 0 ev > С,
uv = , vv = {
(О (I ev<;,
317
то получим
Gy (Л — у
Следовательно, av — это оператор уничтожения элементарного воз-
буждения (вне поверхности Ферми—частицы в состоянии v, внутри—
дырки в состоянии— v), соответственно а£ — это оператор рожде-
ния элементарного возбуждения. Состояние, отвечающее полностью
заполненной поверхности Ферми, при таком преобразовании пере-
ходит в состояние вакуума элементарных возбуждений. В общем
случае, когда (uv, vv) (0,1), новые квазичастицы (элементарные
возбуждения) av и pv представляют собой суперпозицию частиц и
дырок, при этом вакуум элементарных возбуждений соответствует
поверхности Ферми с размытым краем.
Преобразование, обратное (5.15), имеет вид
£1у — Il v Gt у Оу р+; а у — t/y ру Оу Ct у .
(5.15)
Подставляя (5.15) в (5.12) и приводя произведения операторов a
ирк нормальной форме (операторы рождения должны стоять слева
от операторов поглощения), гамильтониан системы представляем
в следующем виде:
{5.16)
Здесь U — постоянная величина, не зависящая от операторов ква.
зичастиц аир:
где
i(^y —X) 2Пу2 —Ду«у Пу),
(5.17)
Ду = v' 1 V|—w>uv- Vy'.
(5.18)
Слагаемые Яи и //зо представляют собой квадратичные выражения
от операторов аир. Причем зависит только от операторов чисел
квазичастиц atav и ptPv, а Н20 зависит от операторов либо рожде-
ния, либо поглощения двух квазичастиц: atp^ и pv av
Ни — S Uev— X) (tty—Пу)+2 Ду «у fy) (a^av+p^pvf, (5.19)
Н20 = 2 {(ev— Л,)2«у vv — Ду («у—Пу)| (ay pt+PvOtv)- (5.20)
Последнее слагаемое в (5.16) Н' содержит произведения четырех
операторов а или р и описывает взаимодействие между квазичасти-
цами. Это слагаемое можно записать в виде
Я'=Я40 + Я31 + Я2г,
(5.21)
318
где
Hi0 = — 2<Х—v| V| —vv> UyUv(at pj' ayPy-)-avpv ay pv-);
vv'
#31 == ~ 2 <V'~v' I V I — VV> (uy — t>v) Uy Vv- X
vv*
X |ffv pv (ay ay' -)- py Py) -(ay ay' —|- Pypy) avPy),
= — 2(v'-v'| У)—w> {(t/yUy 4-УуИу) &v Pv«v'Pv' +
W'
“4"Uy vу uy Чу* (av ay' ay ay' '( pv py py Pv' -j- 2ay py' ay Pv') j
Индексы возле отдельных слагаемых указывают числа операторов
рождения или поглощения, входящие в соответствующие произ-
ведения. Так, Hi0 описывает процесс рождения четырех квазичастиц
из вакуума или обратный процесс и т. д. Ограничимся в дальнейшем
рассмотрением модели независимых квазичастиц, т. е. в (5.16) пре-
небрежем остаточным взаимодействием между квазичастицами Н'.
Выберем коэффициенты канонического преобразования uv и vv
таким образом, чтобы слагаемое H2Q в (5.16) обращалось в нуль.
Тогда в принятом приближении (пренебрежение Н') гамильтониан
(5.16) будет описывать систему независимых квазичастиц
Н — U Т"#ц = U -р 2 {(®v—(щ>— fv) Н_ 2Ду Uy Оу} х
X (ay"ay + Pv). (5.22)
Очевидно, U имеет смысл энергии вакуума квазичастиц. Из
условия Hw ~ 0 получим следующее уравнение для нахождения
Uv и ov:
(еу—A)2uyOv—Ду («у—Оу)=0. (5.23)
Нетрудно убедиться, что условие обращения в нуль Я20 (5.23)
эквивалентно условию минимума энергии вакуума U, Поэтому ос-
новным состоянием системы в терминах квазичастиц является ва-
куумное состояние. Возбужденные состояния характеризуются оп-
ределенным числом квазичастиц.
Уравнение (5.23) удобно представить в другой форме. Для этого,
используя (5.23) и (5.14), выразим uv и щ. через Ду
ц2 - J-/1 4- —
s I Г(ву~^ + д2
2 1 (, еу —
Чу =- 1---7===
И /(еу-ма+д^
Подставляя uv и ov из (5.24) в (5.18), получаем вместо (5.23) следу-
ющее уравнение для нахождения Av:
<v' —у' j V | — w>
Av = “ т* к(ву--^)2+Ду'”
(5.25)
319
Для выяснения физического смысла величины Av определим
энергию квазичастицы Ev. Из (5.22) и (5.24) следует
Ev = ]/(ev —2.)2+Д?. (5.26)
Таким образом, в случае непрерывного спектра частиц величи-
на Av характеризует щель в спектре квазичастиц.
Уравнение (5.25) имеет тривиальное решение
Av=0 или wvnv = 0, (5.27)
которое соответствует резкой поверхности Ферми. Действительно,
если положить в этом случае
«V — {
о;
[О ev> X
j 1 ev< А.,
то квазичастицы аир будут соответствовать старым частицам вне
поверхности Ферми и дыркам внутри этой поверхности. В случае
достаточно слабого остаточного взаимодействия между частицами
уравнение (5.25) допускает только тривиальное решение (5.27).
Однако если выполнено неравенство
<v'— v' | V |—vv>
(5.28)
V' I ev'
то существует нетривиальное решение уравнения (5.25), соответ-
ствующее размытой поверхности Ферми. Согласно (5.28), такое ре-
шение возможно, если парное взаимодействие носит когерентный
характер, т. е. для большинства состояний v и v' матричный эле-
мент <v'— v'| V| — vv> имеет один и тот же знак.
Оператор полного числа частиц (5.9), выраженный через опе-
раторы рождения и поглощения квазичастиц, имеет вид
tl = 2 2l?v -|- 2 (^V- ^v) (®v" H" Pv” Pv) 'l“
V V
+ 2 Vv (a* f'v + Pv «v) • (5.29)
V
Среднее число частиц в основном состоянии системы (состоянии
вакуума квазичастиц) определяется, очевидно, постоянным слага-
емым в (5.29). Используя выражение (5.24) для Vy, имеем
(5.30)
Это уравнение позволяет найти химический потенциал Л при задан-
ном числе частиц системы п. Уравнения (5.25) и (5.30) полностью
определяют Av и X для системы в основном состоянии, если известны
одночастичные уровни энергии ev.
320
Волновые функции и энергетический спектр. Волновая функция
вакуума квазичастиц 4% определяется из условий
av4fo=pv4fo=0. (5.31)
Используя равенства (5.13), условия (5.31) можно переписать в
виде
(ич av— pv atv) 4% = 0; (uv a-v 4- ov at) Ч^ ~ 0.
Непосредственной проверкой легко убедиться, что этим условиям
удовлетворяет следующая функция:
Фо = П (uv +ovciv) [ 0>. (5.32)
V
Волновая функция вакуума квазичастиц согласно (5.32),
представляет собой суперпозицию состояний с различным числом
реальных частиц (нуклонов в самосогласованном поле). При этом
учитываются только состояния с четным числом нуклонов, так как
в (5.32) все нуклоны распределены по парам (у и —v).
Из (5.32) нетрудно установить следующий физический смысл
коэффициентов uv и uv, входящих в каноническое преобразование
(5.13): vv2 — вероятность того, что в состоянии Ч^, соответствую-
щему вакууму квазичастиц, имеется пара нуклонов v и —v; uva —
вероятность того, что парное состояние (v, —-v) не занято.
Волновые функции возбужденных состояний системы можно
найти, действуя на волновую функцию квазичастичного вакуума
(5.32) операторами рождения квазичастиц at и pt- Так, волновая
функция возбужденного состояния системы, соответствующего на-
личию одной квазичастицы, имеет вид
Ч\,=а+%. (5.33)
Используя (5.13), нетрудно получить
% = at П (uv- 4- vv> at' a±v.) 10). (5.34)
v' 4 V
В отличие от Чг0 волновая функция 4*4, согласно (5.34), предстаг
ляет собой суперпозицию состояний с нечетным числом частиц.
Волновая функция возбужденного состояния системы, соответ-
ствующего двум квазичастицам, определяется выражениями:
(5-35)
или
4fv,_v-= at atv' П («v-aiv")|0>- (5.36)
V*^vt V'
Функция 4*4,-v, также как и Фо, является суперпозицией состояний
с четным числом частиц. Параметры A„ и X, для основного состояния
системы определяются из уравнений (5.25) и (5.30). В возбужденном
П Зак. 642
321
состоянии среднее число частиц, вообще говоря, отличается от
(5.30). Например, в случае возбужденного состояния при наличии
двух квазичастиц имеем
„ - в.,—Ъ
<Ч\.. - v I ПI Tv. _v> - <4% I п I Yo> = 2
Однако этой разностью можно пренебречь при небольших возбуж-
дениях, когда X bv. Поэтому для низколежащих возбужденных
состояний можно пользоваться теми же значениями Av и А, что и
для основного состояния.
Волновые функции, отвечающие состояниям с четным и нечет-
ным числами квазичастиц, описывают различные физические си-
стемы. Первые соответствуют системам, состоящим из четного числа
частиц, вторые — из нечетного числа частиц.
В случае ядра с четным А основное состояние описывается
волновой функцией квазичастичного вакуума (5.32). Энергия
основного состояния равна
Л «v-Ч ^1
•V I 1 — - I •- I
\ / 2Ej
Eu^U'-ln~
V
(5.37)
Возбужденные состояния ядра с четным А характеризуются четным
числом квазичастиц. Наинизшее возбужденное состояние (в случае
двух квазичастиц) описывается функцией (5.35). Энергия возбуж-
денного состояния при наличии двух квазичастиц равна
£(v,-V-) ^Ео -|-£v +£V'- (5.38)
В энергетическом спектре ядер с четным .4, согласно (5.38), имеется
щель, отделяющая первое возбужденное состояние от основного,
ширина которой превосходит величину 2AV : А£ > 2AV.
В случае ядра с нечетным А основным состоянием является на-
инизшее состояние с одной квазичастицей (5.33). Возбужденными
являются состояния с одной, тремя и т. д. квазичастицами. Энер-
гия основного состояния и энергии низколежащих возбужденных
состояний (отвечающих одной квазичастице) для ядра с нечетным А
определяются выражением
£(v)=£o+£v. (5.39)
Так как для ядра с определенным А существует несколько
типов квазичастиц v, то в энергетическом спектре ядер с нечетным А
щель отсутствует. Таким образом, энергетические спектры воз-
буждения ядер с четными и нечетными А совершенно различны. В то
же время энергии основных состояний отличаются несущественно,
так как энергией нечетной частицы можно пренебречь по сравне-
нию с вакуумной энергией.
Модель когерентного парного взаимодействия. Рассмотрим при-
мер простейшей модели парного взаимодействия, когда условие
(5.28) выполнено, и уравнение (5.25) допускает нетривиальное ре-
шение [6]. Для получения этого решения в явном виде приходится,
3?2
однако, сделать упрощающие предположения не только относитель-
но характера взаимодействия, но и относительно характера одно-
частичного спектра ev.
В случае сферических ядер уровни ev разделены на группы,
соответствующие отдельным оболочкам. Пренебрежем взаимодей-
ствием между нуклонами, находящимися в различных оболочках.
(Можно показать, что влияние других оболочек приводит к увеличе-
нию эффективного взаимодействия между частицами.) Предполо-
жим далее, что матричный элемент, входящий в (5.25), одинаков
для переходов между любыми уровнями внутри оболочки:
(V'—v'lyj—vv> = —(1/2)G. (5.40)
Тогда уравнение (5.25) для Л, которое, согласно (5.18), не зависит
от v, принимает вид
1=—б у ..... 1 ....
2 V / (>\-*)2 + Да
(5-41)
В наиболее интересном случае, когда Д значительно больше рас-
стояния между уровнями, суммирование в (5.41) можно заменить
интегрированием
1=ур(>)
Де
/ еа+ Да ’
(5.42)
где а — е' — X, b — е" — Хи е', е" характеризуют границы оболоч-
ки. Определяя среднее значение плотности уровней с помощью
соотношения
из (5.42) получаем
Д=—!—[йа + аа—2ai>ch2np, (5,43)
sh 2г)
где введена безразмерная величина
r] = (pG)-1. (5-44)
Рассмотрим случай, когда b = —а = (VJeo > 0. Тогда будем
иметь Д = E0(chT]/sh2iq). Считая т) > 1, получаем
Д х еое-11 — еас_ 1/?g. (5.45)
(Как и должно быть, величина Д стремится к нулю при G + 0.)
Отсюда непосредственно видно, что выражение для Д нельзя найти
по теории возмущений. В самом деле, теория возмущений должна
" давать поправки к энергии, содержащие параметр парного взаимо-
действия G в какой-нибудь целой степени, а ехр (—VpG) нельзя раз-
11*
323
ложить по степеням G, если даже предположить, что парное взаимо-
действие между нуклонами мало.
Химический потенциал можно исключить из (5.43), воспользо-
вавшись соотношением (5.30):
ь
п = С / 1---—------') Р (8) de. (5.46)
JI /е2 -р А2 /
Предположим, что плотность уровней р (е) зависит линейно от е:
р(8) = р0[1- ^+-2Lel (5.47)
где
p0-VIp(i,)+pfa)]’
2 р(&) + р(а)
Средняя плотность р0 связана с полным числом парных состоя-
ний в оболочке £2 соотношением
р0(е"—е') = Q. (5.48)
Выполняя интегрирование в (5.46) и используя (5.43), имеем
41-------Mcthi) +
Q b — a 2 ( sh2r| у 11
+ 1|НИ2/'1---------2jOthT) = 0. (5.49)
‘ 2 — аМ sh 2ц / 1 1 1
—. й i 1_ о
Введем величину Хд = ^ _ Q *пт|, через которую химическим
потенциал выражается следующим образом:
. е'' + е' 8"- е' ,, .с сп.
^ = —--------— x„cthT]. (5.50)
Из (5.49) для хп имеем
где y(T])=cthTj(l—2r]/sh2T]).
Так как |£| С 1 и 0 < у < 1, то, согласно (5.51), |xn| < 1.
Предельные значения ±1 достигаются на границах оболочки
(п = 0 и п = 2 £2):
1 п=0,
Хп= 0 п = 1- (1/2) |у,
— 1 n = 2Q.
324
Величина Хп характеризует степей заполнения оболочки. В случае
однородного распределения уровней (| = 0)
— nlQ. (5.52)
Исключая А из (5.43), находим ширину щели:
Д = (1-(5.53)
Этот результат получен в предположении, что А превосходит сред-
нее расстояние между уровнями (Ар0 > i). Используя (5.48) и
(5.53), условие применимости (5.53) и (5.50) можно записать в виде
(1-х;)‘/2>1. (5-54)
Энергия основного состояния определяется выражением
ь
Еи — С ( 1------- 6 'j р (е) ede — ~ + Ап.
J V /еа + А2 / G
Выполнив интегрирование, получим
Ео= -^-[е" + е' + -|-(е"— е')1 п---J- (в" —е') (1— %na) х
• z L j
х [ctgT] + JLXn(i— Зу (л)cthл)—у т(л)
(5.55)
В случае сильно деформированных ядер (когда оболочечными
эффектами можно пренебречь) распределение уровней почти одно-
родно. Матричный элемент (5.40) при этом следует считать отлич-
ным от нуля для группы уровней, симметричной относительно гра-
ницы Ферми. Поэтому в (5.42) и дальше следует положить а = —5.
(Для сферического ядра область взаимодействия совпадает с обо-
лочкой, а положение границы Ферми определяется числом частиц
в оболочке. Очевидно, деформированное ядро будет эквивалентно
сферическому ядру с оболочкой, заполненной наполовину, когда
а — ~Ь.)
§ 5.2. ОСТАТОЧНОЕ ВЗАИМОДЕЙСТВИЕ И КОЛЛЕКТИВНЫЕ
ЭФФЕКТЫ В ЯДРАХ
Инвариантная запись гамильтониана с остаточным взаимодей-
ствием. В предыдущем параграфе, рассматривая сверхтекучие со-
стояния ядер, мы ограничились учетом только остаточных сил спа-
ривания, а мультипольными силами, ответственными за коллектив-
ные эффекты, пренебрегли. Осуществив переход с помощью кано-
нического преобразования к квазичастицам, мы пренебрегли также
Взаимодействием между квазичастицами, т. е. рассмотрели модель
независимых квазичастиц. Такой подход позволил объяснить на-
325
личие энергетической щели в спектре четно-четных ядер. Однако
для объяснения некоторых других особенностей спектров ядер учет
влияния только сил спаривания недостаточен. Рассмотрим теперь
мультипольные силы, причем остаточное взаимодействие вообще не
будем разделять на две части, соответствующие силам спаривания
и мультипольным силам, так как такое разделение является доволь-
но условным. Покажем, что с таким общим гамильтонианом взаимо-
действия можно записать уравнения движения так, что они будут
описывать одновременно как одночастичные возбуждения, которые
мы рассматривали в модели независимых частиц, так и коллектив-
ные возбуждения в ядрах. Это позволит также рассматривать ча-
стично коллективизированные состояния, которые другими мето-
дами описать невозможно*.
Так как метод применяется и к тяжелым ядрам, будем использо-
вать //-связь и считать протоны и нейтроны различными частицами.
(Обычно также предполагается, что взаимодействие между одинако-
выми нуклонами значительно сильнее взаимодействия нейтронов
с протонами, которым пренебрегают.) Одночастмчные состояния
оболочечной модели, характеризуемые совокупностью квантовых чи-
сел п, /, /, т (проекция /±) и q (заряд), обозначим греческими-бук-
вами а, р, у 6, ... . Совокупности всех указанных квантовых чисел
без магнитного квантового числа т обозначим соответствующими ла-
тинскими буквами a, b, с, d...Сопряженные состояния а и —а
будут отличаться только знаком магнитных квантовых чисел
а ~ (а, т) и —а = (а, —т).
Исходный гамильтониан, представленный через операторы рож-
дения и уничтожения нуклонов и аи, запишем так, чтобы прояв-
лялась его инвариантность при вращениях и отражениях:
Я= 2еавайа+ at°eaV (5.56)
к аРуб
Очевидно, преобразованию подвергнется лишь вторая сумма в
(5.56), описывающая остаточное взаимодействие. Представим для
этого состояние двух частиц а и £ в виде
| а) [ р> = (ата) | Ьт$) = 2 (/а та | | аЬуМ)
и аналогично поступим для пары частиц в состояниях у и 6. Матрич-
ный элемент остаточного взаимодействия в этом случае будет равен
<а0 | 7(у6> =
= X S (/ama/pmp|^M)(/Tmv/4mfl|^'M')<ab^Al| V
WM'
* Более детально теория ядерных моделей с учетом остаточного взаимо-
действия между нуклонами изложена в лекциях Беранже [ 10} и Жилле [11],
а также в монографии Брауна [12]. Теория конечных систем ферми-частиц с
сильным взаимодействием, основанная на использовании метода функций
Грина, развита в монографии Мигдала [13].
326
Так как оператор V инвариантен относительно вращений
(коммутирует с оператором поворота), то матричный элемент
(abtyM | V | cdty'М'у, согласно теореме Вигнера — Эккарта, можно
записать в виде
(altyM\V \cdy М'> = 1 <aby\Wioty>,
откуда следует, что отличны от нуля лишь матричные элементы
при fy'=ty и М'=Л4. Вводя обозначение
G(abaty) =------ <at>#||V||W>, (5.57)
/2^+1
окончательно записываем
<а₽ | V | уб> = -(1/2) SG (abaty) (ja та | %М) х
X (/vmv jeme |#Л4). (5.58)
Если связывать состояния а и у и подобным образом (i и 6
(или а с 6, а р с у), это приведет к другой, отличной от G,
функции F:
<«Р| V |уб> =
= (-1/2)2
X (/в fo-mp | У-М) =(1/2) 2 F[adcby) (-1)^”^ х
X (iatn^jn—тй\ум) (— т^\У-М). (5.59)
Функции F и G связаны с помощью коэффициентов Рака следу-
ющим образом:
F [acdtty’) = -2 (2^ + 1) W (jaibjcid-f т G (booty). (5.60)
Функции G и F вещественны и обладают некоторыми свойствами
симметрии, которые следуют из эрмитовости V и свойств симмет-
рии матричных элементов <сф |V| -рб>:
G (aboty) = G (cdabfr) = — (— 1)'° +G [booty) =
= — (— l)J'c+/<f+^ G[abdty)\ (5.61)
F (acdb fy) = F (dbaty) = ( -1) WV'd f (cabd#).
В случае чистых сил спаривания имеем
G(aboty)=bab8cd8^gac. (5.62)
327
Введем теперь с помощью преобразования Н. Н. Боголюбова
операторы рождения и уничтожения квазичастиц Ьа и 5а:
— иааа ( а> 1 (5 63)
bt = uaa+~(- l)^m-vaa^a, )
где иа и va — вещественные коэффициенты, связанные соотно-
шением
(5.64)
Множитель (—i^a-ma вводнтся в (5.63) для того, чтобы опе-
раторы и Ьа обладали определенными трансформационными свой-
ствами при вращениях координат, а именно были бы неприводимы-
ми тензорными операторами. В частности, оператор Ь~}т при таком
определении является тензорным оператором ранга j, а т опреде-
ляет компоненту этого тензора (—j т < /). С учетом (5.64) опе-
раторы Ьа и bt удовлетворяют таким же антикоммутационным свя-
зям, как и операторы аа и а^. Кфазичастичное вакуумное состоя-
ние |0 > определяется из условия
5К|0)=0 или <0 j b„ =0. (5.65)
Подобно тому как это делалось ранее, введем химические потен-
циалы и (отдельно для нейтронов и протонов) и операторы
числа нейтронов пп и протонов
/?„ = 2 Оа аа, Пр= 2 аа «а, (5.66)
а(п) а(р)
где суммирование проводится соответственно по нейтронным а(п)-
или протонным а(р)-состояниям, и рассмотрим оператор
Н = Н-кппп-Кр'пр (5.67)
вместо оператора Гамильтона Н. Чтобы выразить Н через квази-
частичные операторы рождения и уничтожения, используем пре-
образования, обратные (5.63):
aa=M«+(-i)/rtM±«; | (5б8)
а£ = и<Х+(— 1)/«~т«Уо6_а.|
Вводя обозначения
ди = .. -1 У V2jc 4- 1 ис vc G (аасс 0); (5.69)
У 2/'а+ 1 с
На = —------У + 1) vfc (ababty) =
У + 1
328
= , у V2jb + 1 vlF (aabbO); (5.70)
V2ia+ i
Па = еа — (5-71)
оператор H можно представить в виде:
H = U+Hll+H,l)+Hl-
U = 2^(Па + (1/2)на)-(1/2)иаУоДа]; (5-72)
а
Ни - Z [(u«— v«) ’]« +2ыа va Да] b+ Ьа;
а
н2о= 2(- 1)'а“т“ кvaПа+(1/2)к-«а) да] (b+b±« + b_aba);
а
Н' = 2 I VW N (а£ а0+ ав ат).
а|3?6
Если основное состояние системы совпадает с квазичастичным
вакуумным состоянием |0>, то U является энергией этого основного
состояния, так как U = <0 \Н\ ’0). Величины иа и va выбираются
таким образом, чтобы Н20 обращалось в нуль. При этом U прини-
мает минимальное значение, а Нп становится равным
Ни = ь+ Ьа, Еа = У t]a + Aa- (5-73)
a
(Такой же результат можно получить, если использовать вариацион-
ный принцип.) При этом получаем еще соотношения 2 wava == Да/£о,
ч-а—Va = na/£a, которые вместе с приведенными ранее соотношения-
ми (5.69)—(5.71) определяют величины А 0, ро и Хо в случае самого об-
щего остаточного ядерного потенциала G. Задача значительно упро-
щается при учете только сил спаривания, когда можно пренебречь
величиной ра. Из выражения (5.73) видно, что£а имеет смысл энергии
квазичастицы, а До — половины энергетической щели. Последнее
слагаемое в (5.72)—Н‘ представляет собой остаточное взаимодействие
между квазичастицами. Оно выражается через нормальные произ-
ведения квазичастичных операторов и Ьа. Остаточное взаимодей-
ствие между квазичастицами необходимо учитывать, если рассмат-
риваются коллективные эффекты в ядрах, которые обязаны мульти-
польным силам в двухчастичном взаимодействии нуклонов.
Приближение хаотических фаз. Известно, что для вычисления
различного рода наблюдаемых физических величин нужно знать
лишь матричные элементы от определенных операторов; знание же
волновых функций, с помощью которых определяются эти матрич-
ные элементы, часто не является необходимым. Поэтому в некоторых
случаях можно с самого начала поставить задачу о нахождении со-
ответствующих матричных элементов, или амплитуд из уравнений
движения, не интересуясь явным видом волновых функций системы.
329
Такой подход оправдывается тем, что нахождение волновых функ-
ций является в общем случае более сложной задачей.
Определим операторы рождения и уничтожения пары квази-
частиц, находящихся в состоянии с полным моментом^ и его проек-
цией М на ось г:
А+ (ab#M) = 5 (/«>па J₽ | #М) b% bf;
mamp
A (ab#M) = 2 (/а ie тр | #М) Ь$ Ьа.
та тр
(5-74)
Пусть То будет точной волновой функцией основного состояния
системы частиц, которое, вообще говоря, не является квазичастич-
ным вакуумным состоянием |0>, а лишь близко к нему по энергии.
Волновые функции возбужденных состояний системы частиц с мо-
ментом # и проекцией М обозначим Твлт, где В есть набор всех (кро-
ме М) квантовых чисел состояния, включая Определим теперь
две амплитуды:
фоЬВ = (Т0|Д(а5»1 ТВЛ1>; 1
„ „ , } (5.75)
фа6в (-<¥01 л+ (ab#M) j 4W ,1
которые, согласно определению операторов А+, А и Ьа, не зави-
сят от М.
Уравнения для амплитуд фоЬВ и tpabB можно получить, если
взять матричные элементы с помощью волновых функций 'If0 и Ч^ч
от квантовых уравнений движения для операторов А и А+.
Матричный элемент от левой части уравнения А = [Н, AJ равен
icos<Т0|Д |Твлг>, где сов есть энергия возбужденного состояния
с волновой функцией отсчитываемая от энергии основного
состояния. Итак, мы можем написать уравнение
(Ф'о | [Д, И] ) 'Fm) = а)в (Yq | А | = совфя^в- (5.76)
Отметим, что Wo и Тдл/ являются собственными функциями га-
мильтониана Н. Аналогичное уравнение можно получить и с опе-
ратором Д+. Используя явный вид гамильтониана (5.72) с Т/20 =
0, вычисляем коммутаторы [А, Н] и [А+, Н]:
[Д (ab#M), Н] = 2 Р (abed#) A (cd#M) 4-
cd
4-2 Р (abed#) (- 1)? д+ (cd# — M) +OH 4- (5.77)
cd
= — 2 Р (abed#) (-1)^"" д+ (cd#—М) —
cd
— 2 R (abed#) A (cd#M) + Оз+) 4- О(4+) • (5.78)
cd
330
Функции Р (abed/) и R(abcd/) выражаются через функции
G(abcd'/) и F(abcdy-), характеризующие остаточное ядерное взаимо-
действие между нуклонами. Слагаемые содержат произведения
двух квазичастичных операторов Ь^Ь#, а слагаемые включают
в себя произведения четырех квазичастичных операторов.
Приближение хаотических фаз заключается в том, что в комму-
таторах (5.77) и (5.78) пренебрегают вкладом слагаемых 0^±> и О^±>.
При этом из уравнения (5.76) и аналогичного уравнения для опера-
тора А+ получается система линейных однородных уравнений для
нахождения амплитуд фД(>в и <раЬв‘-
«в фа&в = 2 {Р (abed/) i|wB + R (abed/-) (5.79)
cd
— Ив qus (flbcdty) ycdB + R (abed/-) фС(/л).
cd
Приближение хаотических фаз иногда называют еще методом
линеаризации уравнений движения. Можно
привести ряд аргументов в пользу справедливости приближения
хаотических фаз, однако строго обосновать его в общем случае, как
и установить пределы его применимости, трудно. Можно ожидать,
что опущенные слагаемые Ог^ и О**’ в (5.77) и (5.78) будут приводить
к малым поправкам для матричных элементов, так как в пределе
независимых квазичастиц (Я'->0) коммутаторы (5.77) и (5.78) вооб-
ще не содержат слагаемых и Само название метода (прибли-
жения) хаотических фаз связано со следующими обстоятельства-
ми. Матричный элемент от оператора представляется в ваде сум-
мы произведений двух матричных элементов от произведений двух
квазичастичных операторов, согласно обычному правилу нахож-
дения матричного элемента от произведения операторов. Далее
утверждается, что эта сумма мала, поскольку слагаемые из-за хао-
тичности фаз гасят друг друга. (Такое объяснение, конечно, не впол-
не убедительно.)
Основные уравнения метода хаотических фаз (5.79) представ-
ляют иногда в другом, более удобном виде. Определим две новые ам-
плитуды:
/абВ = фабВ 4“ фа&В> gabB ~tyabB файВ- (5.80)
Подставляя их в (5.79), получаем для них уравнения
«в fabB = (Еа +ЕЬ) gabB—'Zi Щ- (abedty) gcdB’, '
С</ у
®В gabB = (£в +£Ь) fabB-'Z t/_ (abed/) fcdB-
cd
(5.81)
Здесь новые функции (J+ и t/_ выражаются через функции
G и F следующим образом:
(abcd'J) = (u„ ub ± va vb) (uc ttd ± vc vd) G (abed/) |-
+ (ua vb т Va ub) (a, vl( T Vc Ult) x
331
X [F (abed#) ± ( — i)fe+'d+^ F(abcdy-)], (5.82)
а с функциями P и R они связаны так:
P (abcdy) ± R (abcdy) = (Ea + Eb) bae&bd-U± {abebf}. (5.83)
Позднее увидим, что решения уравнений (5.81), а значит, и
(5.79), наряду с одночастичными описывают также и некоторые
коллективные эффекты в ядерных системах.
Если взаимодействие между квазичастицами мало (Д' -> 0),
функция R(abcdy-) в (5.77) и (5.78) значительно меньше P(abcd У),
a f/_|_ и U— мало отличаются друг от друга по величине. В этом
случае амплитуды fat>B и §аьв примерно одинаковы, так как при
U+ = U— они симметрично входят в систему уравнений (5.81).
Это означает, что |фа(,в| <$. |файв|- Если мы пренебрежем <paj,B
в уравнениях (5.79), то получим следующие уравнения для ампли-
туд фа&д:
«в фаыз = 2 р (abcdy) (5.84)
Эти уравнения соответствуют так называемому методу Тамма —
Данкова — частному приближенному случаю метода хаотических
фаз, в котором волновую функцию основного состояния системы
полагают равной волновой функции квазичастичного вакуума |0>.
Действительно, если = |0>, то, согласно определению (5.75),
амплитуда файВ обращается в нуль, так как <0|Д+ = [Д|0>]+ = О,
а Фоба = (0|Л(а£$Л1)|Ч'вм >• В приближении Тамма — Данкова
корреляции между частицами учитываются только в возбужденных
состояниях, а основное состояние здесь такое же, как и в оболо-
чечной модели независимых частиц .
Как уже отмечалось, при изучении коллективных движений в
ядрах необходимо учитывать взаимодействия между квазичастицами.
Учет коллективных эффектов приводит к увеличению вероятностей
переходов в ядрах. В методе Тамма—Данкова весь эффект коллек-
тивности связан со структурой возбужденного состояния. Этого,
однако, оказалось недостаточно для согласования с опытными дан-
ными; чтобы усилить переходы, необходимо учесть корреляции ча-
стиц и в основном состоянии. Этот недостаток метода Тамма — Дан-
кова устраняет метод хаотических фаз, в котором учитываются кор-
реляции как в основном, так и в возбужденных состояниях системы.
Волновую функцию основного состояния в методе хаотических
фаз можно представить в виде суперпозиции
То = [Хо + 2 Хг (ap) f’a ftp +
ар
+ 2 Х4 (аРУ«) b+ b$ b+ bt + -\\&>, (5.85)
что наглядно показывает наличие квазичастиц в основном состоя-
нии То, в то время как волновая функция |0>, по определению,
332
соответствует вакууму квазичастиц. Однако состояния с волновыми
функциями 4% и |0> близки друг другу, так что коэффициент Хо в
(5.85) близок к единице, а все остальные коэффициенты %г>г малы
по величине.
Метод приближенного вторичного квантования. Чтобы лучше
понять, каким образом возникают коллективные состояния системы
нуклонов, а также структуру этих состояний, выведем уравнения
приближения хаотических фаз (5.79) несколько иным путем и при-
ведем другую интерпретацию амплитуд фабв и <ра&в.
Найдем операторы QBM, Qcm и т. д., которые бы удовлетворяли
следующим свойствам:
[Qbm, Н] — wbQbm;
[<2вм, Я] =—
(5.86)
Будем искать эти операторы в виде линейной комбинации опе-
раторов Ди А+ с вещественными коэффициентами:
Qbm = 2 ХаЬВ Д (abfM) -2 YabB (- 1)^ Д+ (abfr-M);
(5.87)
SYabBA (abtyM).
Если подставим эти выражения в уравнения (5.86), а в комму-
таторах и Qbm с. гамильтонианом Н пренебрежем, как и в (5.77)
и (5.78), членами иО^, для коэффициентов ХаЬВ и YabB полу-
чим такие же уравнения, как и для амплитуд фоьв и (ра&а в прибли-
жении хаотических фаз (5.79). Следовательно, коэффициенты ХаЬВ
и YabB пропорциональны соответственно амплитудам и (ра*д.
Операторы QBM и QBm, таким образом, можно считать определен-
ными в приближении хаотических фаз. Эти операторы, согласно
уравнениям (5.86), ответственны за рождение или уничтожение
одного кванта возбуждения колебаний гармонического осциллятора.
Оператор Qbm — это оператор рождения колебательного кванта
или фонона с энергией мв, a Qbm — оператор уничтожения такого
кванта.
Волновую функцию основного состояния системы Yq можно оп-
ределить из системы уравнений
— О*
(5.88)
Она соответствует отсутствию фононов (но не квазичастиц). Возбуж-
денные состояния системы с энергией определяются как одно-
фононные с волновой функцией
'ЕвмЧ'о-
(5.89)
333
Возбужденные состояния с волновыми функциями (Qbjw)2 Vo,
Qbm^cm' и т. д., которым отвечают энергии 2<£>в, ©в 4- «с
и т. д., в принятом приближении существенно отличаются от дей-
ствительных состояний (по сравнению с однофононными) и здесь
рассматриваться не будут.
Из определения операторов А и Л+ следуют точные соотношения
коммутации:
м (abfyM), Д+ (а' Ь' Л4')] =
= [Л+ (аЬУМ), А+ (a', b' Cf' М')] = 0. (5.90)
Чтобы эти операторы обладали всеми свойствами операторов бо-
зонов, необходимо выполнение еще и коммутационного условия:
[A(ab$M, А+(а', b'0-’М1)] а-ь-м>. (5.91)
Однако прямое вычисление коммутатора в (5.91) дает в правой
части равенства (5.91) дополнительные слагаемые, содержащие опе-
раторы bab$. Среднее значение от этих операторов по квазичастич-
ному вакууму |0>, однако, равно нулю, а число квазичастиц,
появившихся в результате учета корреляций между нуклонами в
основном состоянии Vo, как уже отмечалось, невелико. Если это
число квазичастиц значительно меньше полного числа возможных
одночастичных состояний, которые они могут занимать, т. е. состоя-
ние То близко к вакуумному состоянию |0 > (что обычно и имеет
место), то можно пренебречь указанными дополнительными слага-
емыми в коммутаторе [Л, Л+). Тогда будет выполняться и соотно-
шение (5.91). Таким образом, мы приходим к квазибозонному при-
ближению, или к методу приближенного вторичного квантования.
В этом приближении операторы Q и Q+ приближенно удовлетво-
ряют коммутационным соотношениям
[Qbm, Qcm'] = Qcm'] —0;
Г + 1 (p.yz;
|Qbm, ,Qcm'J =бвсбмм',
т.е. они являются операторами бозонного типа. Заметим, что квази-
бозонное приближение — это по существу другая формулировка
метода хаотических фаз.
Из (5.91) и (5.92) следует, что в квазибозонном приближении
имеется некоторое нарушение принципа Паули. Простота формули-
ровки рассматриваемого приближения как раз и достигается вслед-
ствие нарушений этого принципа. Можно сказать, что условие при-
менимости квазибозонного приближения, или метода приближенного
вторичного квантования, сводится к тому, что нарушением принципа
Паули в указанном выше смысле можно пренебречь.
Коллективные состояния ядер в модели с остаточным взаимодей-
ствием. Основные уравнения метода хаотических фаз описывают
как одночастичные, так и коллективные возбуждения в ядрах, что
является одним из достоинств этого метода. Используя соотноше-
334
ния (5.86) и (5.92), оператор Гамильтона системы нуклонов можно
при вести к виду
Н = const. (5.93)
вм
Полученный гамильтониан описывает систему частиц Бозе, которые
могут находиться в различных осцилляторных потенциалах, зави-
сящих от индекса В. Оказывается, что из всех возможных состояний
В, по которым происходит суммирование в выражении (5.93), лишь
одно соответствует коллективному состоянию, которое имеет энер-
гию а>в= <околл, значительно отличающуюся от энергий всех осталь-
ных возможных состояний. Соответствующее слагаемое в (5.93) бу-
дет коллективным гамильтонианом:
Дцолл = ®но.1л Фколл Фкол.т (5.94)
Если это выражение отождествить с феноменологическим коллек-
тивным гамильтонианом, то можно установить связь коллективной
координаты с операторами <9К0ЛП и <2кОлл. В приближении коле-
баний гармонического осциллятора это будет линейная зависимость.
Согласно (5.74), (5.87) и (5,89), волновая функция коллективного
возбужденного состояния Чгколл = <?колл является суперпози-
цией функций двухквазичастичных состояний.
Появление коллективного состояния сравнительно просто объ-
ясняется в приближении Тамма — Данкова в случае, если оста-
точное взаимодействие можно записать в сепарабельной форме
(в виде произведений нескольких множителей, зависящих от раз-
личных координат). Этот случай обычно называют моделью
Брауна и Болстерли [14]. В принятых обозначениях
уравнения в приближении Тамма — Данкова • (когда взаимодейст-
вие между квазичастицами учитывается только в возбужденных
состояниях) можно записать, согласно формулам (5,81)—(5.84),
в следующем виде (фоЬВ = const • ХаЪВ, YabB = 0):
(®в—Еа—Еь)Хаьв = —J&U (flbcdfy) Хсйв (5-95)
rd
(в принятом приближении tAj. = U— = U.) Сделаем теперь основ-
ное предположение относительно взаимодействия, которое сводится
к тому, что функцию Uiabcd#) можно представить в виде следующего
произведения:
U (abcdfy) = — T\A(ab)A*(cd). (5.96)
Здесь т] — вещественная постоянная, характеризующая интенсив-
ность остаточного взаимодействия. Знак этой постоянной совпадает
со знаком взаимодействия, так что т) < 0 будет соответствовать си-
лам притяжения, а т) > 0 — силам отталкивания. Из свойства сим-
метрии U(abcd$) = U(cdabty) следует вещественность функции
U(abcd^).
335
(5.97)
Подставляя (5.96) в (5.95) и замечая, что сумма t^'A*(cd')X(.aB^CB
cd
является константой, не зависящей от состояний а и !>, получаем
v „ 'И (оЬ)
Aat>B = Св —------~
— £ —Е.
В а Ь
Подставив это выражение в (5.95) и используя (5.96), получим урав-
нение для собственных значений энергии ай;
у I A (cd] j
Ec+Ed-^B
Зависимость левой части равенства (5.98) от энергии (ов пред-
ставляется графически кривой вида тангенсоиды, имеющей верти-
кальные асимптоты при значениях е; = Ес1 £dl, £са -Ь £da
(5.98)
Рис. 5.1. Графическое решение уравнения, опреде-
ляющего собственные значения энергии в модели с
остаточным взаимодействием.
и т. д, (рис. 5.1). Собственными значениями являются энергии,
при которых эта кривая пересекается с горизонтальной прямой
—Чч\. Из рисунка непосредственно видно, что при любом изменении
интенсивности остаточного взаимодействия ц лишь энергия одного
из крайних состояний (минимальное или максимальное собственное
значение) может сильно изменяться. Остальные собственные зна-
чения энергии находятся между двухквазичастичными энергиями
в; == Eci 4- Edi, определяющими положения асимптот и совпадаю-
щими с собственными значениями в отсутствие остаточного взаимо-
действия (при р-> 0).'В случае сил притяжения (р < 0) сильному
смещению при увеличении интенсивности остаточного взаимодей-
ствия подвержено минимальное собствг иное значение, а в случае сил
отталкивания (к] > 0) сильно смещается с ростом т] максимальное
собственное значение.
336
Ясно, что энергия коллективного состояния должна быть более
чувствительной к различным изменениям остаточного взаимодей-
ствия, чем энергии одночастичных состояний. Это происходит по-
тому, что корреляционные эффекты, обязанные остаточному взаимо-
действию, приводят, как уже говорилось, к коллективным движе-
ниям в ядрах. Поэтому состояние, энергия которого испытывает
большое изменение с включением остаточного взаимодействия, и
является коллективным. Это состояние обычно отделено от других
состояний значительным энергетическим интервалом, и ввиду на-
личия остаточного взаимодействия во всех ядрах может регулярно
встречаться приблизительно с одной и той же энергией в спектрах
многих соседних по массам ядер. (Это является одним из признаков
того, что подобные наблюдаемые состояния по природе коллектив-
ные.)
Выясним теперь причину большой величины вероятности элект-
ромагнитных переходов с возбуждением коллективных состояний
ядер. Интенсивность перехода пропорциональна выражению
SI 1 Ли I Лм >г - К'ЛII nil ’П) I2- (5.99)
Одночастичный тензорный оператор запишем в представле-
нии вторичного квантования
ЛЦ = 2 | Пц | Р) =
ct (3
= 2^2 <а/ата|Лц|&/ртр>д+ае= (5.100)
ab
= 2 2 t"1* (io.ma.ifi— mfj| ?.р) <ajП||6>а^а&.
ab ma m/j 1' 2^ -p 1
В последнем выражении, как и в (5.99), мы воспользовались тео-
ремой Вигнера — Эккарта. Рассматривая только частично дырочные
возбуждения, когда состояния аир находятся соответственно выше
и ниже поверхности Ферми, т. е. когда иа и va в (5.68) равны или
единице, или нулю, а также удерживая в (5.100) то слагаемое, ко-
торое дает вклад в матричный элемент (5,99) в приближении Тамма —
Данкова, получим
*5? /2Х-Н
(5.101)
Подставляя соотношение в (5.99), видим, что
2 <а||ПИ> Ха);В
ab
(5.102)
В случае электрического перехода знаки числителей вёех слагаемых
под знаком модуля в последнем выражении одинаковы.
337
Из (5.102) непосредственно видно, что если <вв равно одному из
крайних собственных значений, то все слагаемые в сумме (5.102)
имеют одинаковый знак и складываются когерентно для максималь-
ного собственного значения при ц>0 и для минимального собствен-
ного значения при т] < 0. Это приводит к резкому увеличению
вероятности перехода в указанные крайние состояния, которые по
своей природе и будут коллективными. Заметим в связи с этим, что
одним из основных критериев коллективности состояния является
увеличение вероятности электромагнитного перехода по сравнению
со значением, которое получается при одночастнчном переходе, по
крайней мере в несколько раз. Для переходов же во все остальные
(некогерентные) состояния, для которых <ов заключены между ег =
— Eai + Ebi, в сумме (5.102) встретятся слагаемые с противополож-
ными знаками, которые будут частично гасить друг друга (т. е.
складываться некогерентно). В этом случае вероятность перехода
будет малой.
Коллективная природа указанного когерентного состояния, энёр*
гия которого испытывает сильное смещение при изменении интен-
сивности остаточного взаимодействия, обусловлена когерентной
суперпозицией элементарных двухквазичастичных состояний.
В случае сил притяжения (ц < 0) мы имеем низколежащее коллектив-
ное состояние, которое, как показывает опыт, является колебатель-
ным. В случае отталкивающих сил (ц > 0) будем иметь высоколе-
жащее коллективное состояние, называемое обычно гигант-
ским резонансом.
В предельном случае вырождения, когда все энергии е; =
= Ей1 + Еь1 одинаковы и равны е, легко найти энергетический
сдвиг коллективного состояния относительно некогерентных со-
стояний, так как в этом случае из формулы (5.98) имеем
ов= И(й/)|®. (5.103)
В приближении хаотических фаз рассмотрение значительно слож-
нее и отличия от выводов в приближении Тамма — Данкова сводят-
ся, в частности, к тому, что вместо формулы (5,103) в случае ег —
= е имеем
<вв = 1/е«+2т]82|Л(с4)|®, (5.104)
Г cd
а вероятность перехода будет содержать дополнительный множитель
е/сов. Таким образом, в приближении хаотических фаз вероятность
перехода в состояния, сдвинутые вниз относительно е(т| <Г 0), воз-
растает, так как тогда а>в < в, а в состояния, сдвинутые вверх
(П > 0), — уменьшается.
ЛИТЕРАТУРА
К предисловию
1. Ахиезер А. И., П о м е р а н ч у к И. Я- Некоторые вопросы
теории ядра. М., Госте хтеор изд ат, 1950. .
2. Давыдов А. С. Теория атомного ядра. М., Физматгиз, 1958.
3. Л а и д а у Л. Д., Смородинский Я- А. Лекции по теории
атомного ядра. М., Гостехтеориздат, 1955.
4. Б е т е Г., Моррисон Ф. Элементарная теория ядра. Перев. с
англ. М., Изд-во иностр, лит., 1958.
5. Блатт Дж., Вайскопф В. Теоретическая ядерная физика. Перев.
с англ. М., Изд-во иностр, лит., 1954.
6. Престон М. Физика ядра. Перев. с англ, М., «Мир», 1964.
7. Де Бенедетти С. -Ядерное взаимодействие. Перев. с англ. М.,
Атомиздат, 1968.
8. Айзенбуд Л., Вигнер Е. Структура ядра. Перев. с англ. М.,
Изд-во иностр, лит., 1959.
9. Ландау Л. Д-, Лифшиц Е. М. Квантовая механика. М., Физ-
матгиз, 1963.
10. Давыдов А. С. Квантовая механика. М., Физматгиз, 1963.
11. Ситенко А. Г. Лекции по теории рассеяния. Киев. «Высшая школа»,
1971,
К главе 1
1. Хюльтен Л., Сугавара М. Проблема взаимодействия двух
нуклонов. В сб. «Строение атомного ядра». Перев. с англ. М., Изд-во
иностр, лит., 1959.
2. Bethe Н., Peierls R. Proc. Roy. Soc., A148, 146 (1935).
3. Bethe H, Phys. Rev., 76, 38 (1949).
4. Schwinger J. Phys. Rev., 72, 742 (1947).
5. Schwinger J., Teller E. Phys. Rev., 52, 286 (1937).
6. Breit G. Phys. Rev., 72, 215 (1947).
7. Ландау Л. Д., Смородинский Я- А. «Ж. эксперим.
и теор. физ.», 14, 269 (1944).
8. Jackson J., Blatt J. Rev. Mod. Phys. 22, 77 (1950).
9. Wigner E. Proc. Nat. Acad. Sci. U. S. A., 27, 281 (1941).
10. R а г i t a W., Schwinger J. Phys. Rev., 59, 436 (1941).
11. Heisenberg W. Z. Phys., 77, 1 (1932).
12. M a j о г а п a E. Z. Phys., 82, 137 (1933).
13. В a r t 1 e t t J. Phys. Rev., 49, 102 (1936).
14. Breit G. et al. Phys. Rev., 50, 825 (1936).
15- Cassen B., Condon E. Phys. Rev., 50, 846 (1936).
16. В и льсон P. Нуклон-нуклонные взаимодействия. Перев. с англ.
М., «Мир», 1965.
17. Вол ьфенштейн Л. «Усп. физ. наук», 62, 71 (1957).
18. П у з и к о в Л. и др. «Ж- эксперим. и теор. физ.», 32, 592 (1957),
339
19. J astr ow R. Phys. Rev., 81, 165 (1951).
20. Blatt J. Biedenharn L. Phys. Rev., 86, 399 (1952).
21. S t a p p H. et al. Phys. Rev., 105, 302 (1957).
22. M a c G г e g о г M. et al. Phys. Rev., 169, 1128 (1968); 173, 1272 (1968).
23. Gammel J., Thaler R. Phys. Rev., 107, 291 (1957); 107, 1337
(1959).
24. Hamada T., Johnston I. Nucl. Phys., 34, 382 (1962).
25. Л а н д а у Л. Д., Спор од и нс к и й Я- А. Лекции по теории
атомного ядра. М., Гостехтеориздат, 1955.
26. Ферми Э. Ядерная физика. Перев. с англ. М., Изд-во иностр, лит.,
1951.
27. Ferm i Е. Ricerca scient., 7, 13 (1936).
28, Б е т е Г. Физика ядра. Ч. 2. Перев. с англ. М., Гостехтеориздат, 1948.
К главе 2
1. Хофштадтер Р. Электромагнитная структура ядер и нуклонов.
Перев. с англ., М., Изд-во иностр, лит., 1958.
2. Э л т о н Л. Размеры ядер. Перев. с англ. М., Изд-во иностр, лит.,
1962.
3. Green A. Nucl. Phys. N. Y. 1955.
4. Б e т e Г., Вечер Р. Физика ядра. Перев. с англ. Харьков, 1938.
ОНТИ НКТП ГНТИУ.
5. Блатт Дж., Вайскопф В. Теоретическая ядерная физика.
Перев. с англ. М., Изд-во иностр, лиг., 1954.
6. Heisenberg W. Z. Phys., 77, 1 (1932).
7. Бракнер К- Теория ядерной материн. Перев. с англ. М., «Мир»,
1964.
8. Г о м е с Л. и др. «Проблемы современной физики», 4, 56 (1958).
9. Be the Н., Goldstone J. Proc. Roy. Soc., 238A, 551 (1957).
10. Yang C„ Lee T. Phys. Rev., 105, 1119 (1957).
11. Wigner E., Seitz F. Phys. Rev., 43, 804 (1933).
12. V a n Hove L. Phys. Rev., 95, 249 (1954).
13. Lax M. Rev. Mod. Phys., 23, 287 (1951).
14. С и т e и к о А. Г. «Ж- эксперим. и теор. физ.», 43, 319 (1952).
15. Н ayakawa S. et al.' Prog. Theor. Phys., 13, 415 (1955).
16. Ландау Л. Д. эксперим. и теор. физ.», 7, 819 (1937).
17. Бете Г. Физика ядра. Ч. 2. Перев. с англ. М., Гостехтеориздат, 1948.
К главе 3
1. Е 1 s a s s е г W. J. Phys, et radium, 5, 625 (1934).
2. Goeppert Mayer M. Phys. Rev., 75, 1969 (1949); 78, 16 (1950)
3. H a x e 1 O. et al. Phys. Rev., 75, 1766 (1949); Z. Phys., 128, 295(1950).
4. Г e п п e p т-М а й e p M., Йенсен И. Элементарная теория ядер-
ных оболочек. Перев. с англ. М., Изд-во иностр, лит,, 1958.
5. Гайзенберг В. Теория атомного ядра. Перев. с нем. М., Изд-во
иностр, лит., 1953.
6. de-S h а 1 i t А., Т а 1 m i I. Nuclear Shell Theory. N. Y., Academic
Press, 1963.
7. Эллиотт Дж., Лейн А. Модель ядерных оболочек. Веб. «Строение
атомного ядра. Перев. с англ. М., Изд-во иностр, лит., 1959.
8. Klinkenberg Р. Rev. Mod. Phys., 26, 63 (1952).
9. Blin-Stoyle R. Rev. Mod. Phys., 28, 75 (1956).
10. S c h w a r z C. Phys. Rev., 97, 380 (1955).
11. Вигнер E. Теория групп. Перев. с англ. М., Изд-во иностр, лит.,
1961.
12. Бейман Б. Лекции по применению теории групп в ядерной спектро-
скопии. Перев. с англ. М-, Физматгиз, 1961.
340
13. В е й л ь Г. Классические группы. Перев. с аглн. М., Изд-во иностр,
лит., 1947.
14. J a h n Н. Proc. Roy. Soc., А201, 516 (1950).
15. Flowers В. Proc. Rov. Soc., A212, 248 (1952).
16. E 1 1 i о t t J. Proc. Roy. Soc., A245, 128 (1958); A245, 562 (1958).
17. Bethe H., Rose M. Phys. Rev., 51, 283 (1937).
18. Elliott J., Skyr me T. Proc. Roy. Soc., A232, 561 (1955).
19. J a h п H. Proc. Roy. Soc., A209. 502 (1951).
20. Edmonds A., Elowers B. Proc. Roy. Soc., A214, 515 (1952).
21. H e у д а ч и и В. Г., Смирнов Ю. Ф. Нуклонные ассоциации
в легких ядрах. М. «Наука», 1969.
22. Inglis D. Rev. Mod. Phys., 25, 390 (1953).
23. К u r a t h D. Phys. Rev., 101, 216 (1956).
К главе 4
1. Бор О. Пробл. соврем, физ. Сб. перев. и обз. ин. период, лит., 9, 9 (1955).
2. Бор О., Моттельсон Б. Пробл. соврем, физ. Сб. перев. и обз.
ии. период, лит., 9, 34 (1955).
3. Д а в ы д о в А. С. Возбужденные состояния атомных ядер,
М., Атомиздат, 1967.
4. Вигнер Е. Теория групп. Перев. с англ. М., Изд-во иностр, лит., 1961.
5. Edmonds A. Angular Momentum in Quantum Mechanics. Princeton
University Press, 1960.
6. Нильссон С. Связанные состояния индивидуальных нуклонов в
сильно деформированных ядрах. В сб. «Деформация атомных ядер».
Перев. с англ. М., Изд-во иностр, лит., 1958.
7. Мошковский С. Модели ядра. В сб. «Строение атомного ядра»,
Перев. с англ. М., Изд-во иностр, лит., 1959.
8. Inglis D. Phys. Rev., 96, 1059 (1954); 103, 1786 (1956),
9, М и г д а л А. Б. «Ж. эксперим. и теор. физ.»., 37, 249 (1959).
10. Давыдов А. С., Филиппов Г. Ф. «Ж. эксперим. и теор. физ.»,
35, 440 (1958).
11. Давыдов А. С. «Изв. АН СССР. Сер. физ.», 23, 792 (1959).
12. Давыдов А. С. «Изв. АН СССР. Сер. физ.», 24, 820 (1960).
13. Паули В. Общие принципы волновой механики. Перев. с нем. М,,
Гостехтеориздат, 1947.
14. Davydov A., Chaban A. Nucl. Phys., 20, 499 (1960).
К главе 5
1. Bardeen J. ct al. Phys. Rev., 108, 1175 (1957).
2. Боголюбов H. H. «Ж- эксперим. и теор. физ.», 34, 58 (1958); 34,
73 (1958).
3. Боголюбов Н. Н. и др. Новый метод в теории сверхпроводимости.
М., Изд-во АН СССР, 1958.
4. Боголюбов Н. Н. «Докл. АН СССР», 119, 52 (1958).
5. В о h г A. et al. Phys. Rev., ПО, 936 (1958).
6. Belyaev S. Kgl. Danske vid. selskab. Mat.-fys. Medd., 31, No. 11 (1959).
7. С о л о в ь e в В. Г. «Ж. эксперим. и теор. физ.»., 35, 823 (1958); 36,
1869 (1959).
8. С о л о в ь е в В. Г. Влияние парных корреляций сверхпроводящего
типа на свойства атомных ядер. М., Госатомиздат, 1963.
9, Лейн А. Теория ядра. Перев. с аигл. М., Атомиздат, 1967.
10. В aranger М. Theory of Finite Nuclei. Cargese Lectures. N. Y., 1962.
11. Ж и л л e В. Приближенные методы в теории структуры ядер. Допол-
нение к книге: Н а т а ф Р. Модели ядер и ядерная спектроскопия.
Перев. с франц. М., «Мир», 1968.
12, Браун Дж. Единая теория ядерных моделей и сил. Перев. с англ.
М. Атомиздат, 1970.
13. М и гд а л А. Б. Теория конечных ферми-систем и свойства атомных
ядер. М., «Наука», 1965.
14. В г own G., В о 1 s t е г 1 i М. Phys. Rev. Lett., 3, 472 (1959).
341
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатичность движения 244, 259
Адиабатическое приближение 259,
272, 281, 287
Аксиально симметричное ядро 240,
243, 247
Амплитуда рассеяния 13, 25, 57
-----нуклона на нуклоне 57, 80
Анизотропный осцилляторный по-
тенциал 213, 260
Аномальные вращательные полосы
275, 277
Асимметричный волчок 272
Асимптотические квантовые числа 263
Атомная единица массы 5
Атомный номер 5
Бозоны 231, 312, 334
Вакуум квазичастиц 318, 319, 321,
328
Вероятность электромагнитных пе-
реходов с возбуждением коллек-
тивных состояний ядер 337
Вес D-волны в основном состоянии
дейтрона 35, 37, 38
Виртуальный уровень дейтрона 16
Внешнее произведение неприводи-
мых представлений групп пере-
становок 160
Внутреннее произведение неприво-
димых представлений группы пе-
рестановок 160
Внутренний квадрупольный момент
ядра 257, 258
Возбуждение коллективных степе-
ней свободы ядер 217
Волновая функция вакуума квази-
частиц 321
— — вакуума нуклонов 316
— — возбужденного состояния си-
стемы, соответствующего наличию
одной и двух квазичастиц 321
342
— — в трансляционно инвариант-
ной модели оболочек 185
— — чистого состояния 185, 189
Волновые функции вращающегося
аксиально симметричного ядра
244, 246, 248
-----многочастнчных оболочек 152
Вращательная модель 243
— полоса 243, 248, 249
Вращательно-колебательные воз-
буждения иеаксиальных ядер 284
—-------ядер 278
Вращательные спектры неаксиаль-
иых ядер 275
-----ядер 249, 252, 253
Вращение аксиально симметричных
ядер 243
— деформированных ядер 237
— неаксиальных ядер 271
— системы координат 226
— ядер 217, 237, 240, 244
Выделение движения центра инер-
ции ядра в осцилляторной обо-
лочечной модели 183, 184, 185
— чистых и ложных состояний в ос-
цилляторной оболочечной модели
185
Высоколежащее коллективное со-
стояние 338
Вычисление матричных элементов
с помощью многочастичных функ-
ций 190
Газовая модель ядра 88
Гамильтониан в представлении вто-
ричного квантования 176, 316,
317, 318, 326, 329
— поверхностных колебаний ядра
219, 220, 222
— сверхтекучей модели 315
- ядра 68, 90, 152, 180, 190, 199,
200, 219, 265, 316
— — й оболочечной модели 199
— — в осцилляторной оболочечной
модели 180
Гигантский резонанс 338
Гидродинамическая модель 267,
269, 270
Главное квантовое число 127, 132,
186
Глубина потенциальной ямы 7, 11, 12
Граничный импульс Ферми 91
Группа вращений в трехмерном про-
странстве 164, 166
— линейных унитарных преобразо-
ваний 164
Дальнодействующие мультиполь-
иые силы 311, 315
Движение центра инерции ядра
в оболочечной модели 180
Двухчастичные коэффициенты род-
ства 193, 198, 199
Дейтрон 7, 8
Детерминант Слэтера 111, 152
Деформации поверхвости ядер 217
Диффузность края ядра 85
Длина свободного пробега нуклона
в ядерном веществе 120, 217
— рассеяния 16, 19, 28, 29
Дополнительные квантовые числа
166, 167, 168, 169, 173, 176, 223, 301
D-фуикции Вигнера 232
Жесткие ядра 287
Зависимость фазы рассеяния от энер-
гии 13
Заряд атомного ядра 5
Зарядная или изотопическая инва-
риантность ядерных сил 8
— координата 6, 44
— симметрия ядерных сил 8
Зеркальные ядра 8
Идеальный ферми-газ 90
Изобары 5
Изоспииовая координата 6, 44
— функция 44, 45, 153, 170
Изотопы 5
Изотопическая инвариантность
ядерного взаимодействия 44, 49,
54
Изотопический мультиплет 46
— спин нуклонов 44
— — системы нуклонов 45
Изотопы 5
Изотропный осцилляторный по-
тенциал 131, 176, 180, 216
— характер рассеяния протонов
протонами и взаимодействие в со-
стояниях с / #= 0 58 ‘
Инвариантная запись гамильтониа-
на с остаточным взаимодействием
325
Интегральное сечение рассеяния 13
Интегралы Слэтера 201, 208
Каноническое преобразование Бого-
любова 317, 328
Капельная модель ядра 87, 217
Квадрупольные колебания 224,
225, 243, 284, 315
— моменты деформированных ядер
257
Квадрупольный момент дейтрона 38
Кназибозонное приближение 334
Кпазичастицы 220, 313, 318
Кинетическая энергия вращения
ядра 240
— — колебаний ядра 239
— — поверхностных колебаний
ядра 218
Классификация в схеме SC7, Эл-
лиотта 176, 180, 186
— многочастичных состояний 166
— состояний в схеме //-связи 169
— — — LS-связи 166
-----системы двух нуклонов 46
— — — нейтрон — протон 32
— — — нескольких фононов 222,
300, 301
Кластеры 183
Колебания сферических ядер 217
— ядер 217, 219, 237
Колебательная модель 224, 225
— энергия ядер 239
Колебательные спектры ядер 223,
224
Коллективные возбуждения в ядрах
217
— состояния ядер в модели с оста-
точным взаимодействием 334
Коллективные степени свободы ядер
217
Коллективный гамильтониан ядра
241
Контактное взаимодействие 22
Конфигурации системы 153, 200
Координаты Якоби 180, 181, 182
Короткодействующие силы спари-
вания 311, 313, 315, 327
Короткодействующий характер ядер-
иых сил 6
Корреляции дальнего порядка 315
Корреляционная функция 113, 115
Коэффициент деформируемости 218
— поверхностного натяжения 219
Коэффициенты родства 190, 209
— — для смешанных конфигура-
ций 209, 210
— Талми 182
343
Кулоновская амплитуда рассеяния
25
— фаза рассеяния 25
Кулоновский параметр 25
Кулоновское рассеяние 25
Ложные состояния 185, 186, 189
Магические числа нуклонов 89, 133,
139
Магнитные дипольные моменты ядер
143
— моменты деформированных ядер
254
— октупольные моменты ядер 149
Магнитный дипольный момент 144
— октупольный момент 150
— момент дейтрона 9, 36, 37
— — нейтрона 6
— — протона 6
---ядра 212, 213, 254
— — — рассматриваемого по обо-
лочечной модели с LS-связью 213,
214
Масса стабильного ядра 86
Массовое число ядра 5
Массовый коэффициент 218
Матрица рассеяния 62, 63
Мезоны 8
Метод линеаризации уравнений дви-
жения 331
— приближенного вторичного кван-
тования 333, 334
— Тамма — Данкова 332, 337
— Эллиотта по разложению неприво-
димого представления группы SU3
179
Многочастичные коэффициенты род-
ства 199
Модель Брауна и Болстерли 335
— идеального ферми-газа 92
— когерентного парного взаимодей-
ствия 322
— неаксиального ротатора 271
— независимых квазичастиц 319,
328
— — пар 95, 96
— — частиц 152
— принудительного вращения 269
Момент инерции в гидродинамичес-
кой модели ядра 268
— количества движения ядра от-
носительно главной оси 240
Моменты инерции ядер 240, 266, 272
— — — в сверхтекучей модели
270, 271
Мягкие ядра 287
Набор квантовых чисел 153, 176,
224
344
Насыщение ядерного взаимодейст-
вия 83, 87, 88, 90, 94
Неадиабатическая теория враща-
тельно-колебательных возбуж-
дений в ядрах 278, 281, 285, 304
Независимость движения отдельных
нуклонов в ядре 88, 125, 152, 217
Нейтрон 5
Неприводимые представления груп-
пы вращений 166, 232
— — — перестановок 156
--------Sl/3 178
Нерелятивистская теория ядра 68
Неупругое рассеяние нуклонов 54
Нецентральные ядерные сиды 31
Низколежащее коллективное со-
стояние 338
Нуклоны 5, 6, 44
Обменные операторы 41, 48
— силы 39, 40
— оператор Бартлетта 42, 48
— — Гейзенберга 42, 49
— — Майорана 42, 48
Обобщенная модель ядра 217
Обобщенные импульсы 219
— координаты 219, 278, 279, 302
— коэффициенты Талми 183
— скорости 219
— сферические функции 231, 232,
237
Оболочечная модель ядра 89, 125,
152, 217
Общий вид волнового управления
в случае квадрупольных дефор-
маций 278
Одночастичные возбуждения в ядрах
217
— коэффициенты родства 191
— орбитальные коэффициенты род-
ства 192
— состояния 131, 133, 134, 139,
140, 141, 142, 263
— — в деформированных ядрах
259, 263
— спин-изоспиновые коэффициен-
ты родства 193
Одночастнчный потенциал 110, 131,
136, 260
Оператор антисимметризации 209
— бесконечно малого поворота 234
— вращения R 234
— конечных поворотов 228, 229, 230
— отражения времени 315
— полного числа частиц 316, 320
— рождения квазичастицы 318, 328
---частицы 176, 221, 313, 316
— уничтожения квазичастицы 318
— — частицы 176, 221, 313, 316
— числа нейтронов 328
— — протонов 328
— — фононов 222
Определение амплитуды рассеяния
нуклона на нуклоне из данных
опыта 57
Оптический потенциал 119
Ортоводород 23
Ортогональная (21 + 1)-мерная груп-
па 169
Основная вращательная полоса 275,
277
Основное состояние дейтрона в слу-
чае центральных сил 9
— — — с учетом нецентральных
сил 34
Основные уравнения метода хаоти-
ческих фаз 331, 333
Остаточное взаимодействие и кол-
, лективиые эффекты в ядрах 325,
329, 332
— — между квазичастицами 319, 329
— — — нуклонами в ядре 200,
271, 311, 313, 325
Осцилляторная оболочка 178
— оболочечная модель 176, 180
— функция 132, 184, 215
Осцилляторный оболочечный потен-
циал 131, 176, 180
Отсутствие возбужденных состояний
у дейтрона 12
Отталкивание нуклонов на малых
расстояниях 60, 95, 102
Отталкивающая сердцевина 60, 99,
103
Параводород 23
Параметр неадиабатичиости 287
— глубины потенциала 21
— у отклонения формы ядра от ак-
сиально симметричной формы 238
— смешивания 63
— общей деформации ядра р 238
— связи 251, 253, 254, 266
— формы 20, 21
Параметры деформации ядра 218
Парные корреляции в ядрах 311,
313, 315, 317
— — сверхпроводящего типа 313
Плотность распределения пар ча-
стиц 112
Поверхностные колебания сферичес-
ких ядер 219
Повороты » изотопическом прост-
ранстве’49
Полная волновая функция системы
эквивалентных нуклонов 163,
167к 171
Полное сечение взаимодействия 54
Полносимметричное представление
273
Полноси.мметричные состояния 273
Полный изотопический спин си-
стемы 45
Поправка к одночастичной энергии,
обусловленная деформацией ядра
306, 307
Порядок заполнения одночастичиых
состояний во внешней оболочке
слабо деформированного ядра 307,
308, 309
Построение антисимметризованных
волновых функций 162
Потенциал Гаммеля — Талера 65
— нецентральных сил 31
— Нильссона 260
— Сервера 43, 103
— Хамада — Джонсона 65, 66
Потенциальная энергия колебаний
несферических ядер 241
— — поверхностных колебаний
ядра 218
Правило интервалов для уровней
вращательной полосы 252, 277
— Литтлвуда 160
Представление Блатта-Биденхарна
63
— вторичного квантования 176, 220,
316
— Стаппа 63
— чисел заполнения 220
Преобразование векторного поля
при поворотах 289
— спинорного поля при поворотах
288
— Талми 182
Приближение нулевого радиуса
действия ядерных сил 11, 22, 69
— промежуточной связи 199, 201
— хаотических фаз 329, 331, 333
Приведенный изотопический спин
172
— матричный элемент 207, 208
Применимость модели независимых
частиц 106
Принцип Паули 46, 89, 154
Проектирующий множитель 258
Проекционный оператор Юнга 194
Пространственная структура атом-
ных ядер 83
— функция эквивалентных нукло-
нов 155, 162, 166
Пространственно-временная корре-
ляционная функция 115
Пространственное распределение
плотности нуклонов в ядрах 85,
134
Пространственные размеры дейтро-
на 11
Протон 5
345
Прямоугольная потенциальная яма
136
Псевдопотенциал 21
Равновесная деформация слабо де-
формированного ядра 307, 308, 309
— плотность ядерного вещества 106
Равновесные значения параметров
деформации 241, 265
Радиус действия тензорных сил 39
— — ядерных сил 7, 12, 19
— дейтрона 11
— отталкивающей сердцевины 60,
95, 99, 103
Разложение неприводимого пред-
ставления группы по непроводи-
мым представлениям подгруппы 166
Распределение уровней энергии воз-
бужденных состояний в ядерной
материи 121
Рассеяние медленных нейтронов в
молекулярном водороде 21, 23
— — — протонами 13
— нейтронов протонами при высо-
ких энергиях 39
— нуклонов на нуклонах при высо-
ких энергиях 51, 54
— протонов протонами 25
Расстояние между уровнями 134
Рекуррентное соотношение для ко-
эффициентов родства 194
Ряд Клебша — Гордана 160
Самосогласованное поле ядра 89,
125, 126, 152, 217, 313, 315
Самосогласованный потенциал 125,
199
Сверхтекучая модель ядра 311
Сверхтекучее, состояние ядер 311,
313
Свойства радиальных волновых
функций 127
Связь между волновыми функциями
смешанных и чистых конфигура-
ций 210
— — коэффициентами родства сме-
шанных и чистых конфигураций
210
Сеньорити 172, 301
Сечение рассеяния 13
Силы Бартлетта 42
— Вигнера- 42
— Гейзенберга 42
— Майорана 42
— отталкивания 7
Символ Яманучи 159
Симметрическая группа 156
Симплектическая группа 172
Синглетное спиновое состояние 15
Смешанная конфигурация 209, 210
346
Смешивание конфигураций 204
Собственные значения энергии ядер
в модели с остаточным взаимодей-
ствием 336
Соотношение между шириной и глу-
биной потенциальной ямы 11
— треугольника для трех моментов
213
Сопряженнные состояния 315, 326
— схемы Юнга 163
Состояния нормальной четности 203
Состояния с аномальной или проти-
воположной четностью 204
Спектральная корреляционная функ-
ция 115
Спектральное распределение флук-
туаций плотности 117
Спин дейтрона 9
Спни-изоспииовая функция 156, 163
Спиновая зависимость ядерных сил
15
Спин-орбитальное взаимодействие
129, 153
Спин-пространствеиная функция
153, 170
Спины основных состояний ядер 142
Спин ядра 142, 154, 224, 265
Среднее расстояние между уровнями
ядерной материи 123
Среднеквадратичный радиус ядра 84
Статистика Ферми — Дирака 5
Статистические веса спиновых со-
стояний 15
Стягивание ядер 93
Супермультиплет Вигнера 168
Сферические функции Бесселя и
Макдональда 137
Сферический тензор илн неприводи-
мый тензорный оператор 207
Схема jj-связн 154, 169, 205
— LS-связи 154, 166, 202, 205
— построения многочастичных вол-
новых функций 154
— Юнга 156
Твердотельная модель 267, 269
Теорема Бете — Роуза — Эллиот-
та— Скирма 186
— Вейдя 164
— Вигнера — Эккарта 207, 208, 327
Трансляционно инвариантная мо-
дель оболочек 183, 185
Триплетное спиновое состояние 15
Углы Эйлера 226
Угол рассеяния 13, 84
Унимодулярная группа 164
Унитарная матрица рассеяния 62,
63
Уравнение Бете — Голдстоуна 96,97
Усеченная схема Юнга 178
Условие насыщения в случае обмен-
ных ядериых сил 94
— устойчивости ядра по отношению
к малым деформациям 219
Фазовый анализ 61
Фазы рассеяния 13, 63
Феноменологические потенциалы 65
Флуктуации плотности частиц 114,
115, 120
Фононы 220, 221, 333
Формула Вейцзеккера 87
— Вольфенштейна 57, 82
— Мотта 84
Форм-фактор распределения заря-
да 84
Функции ложных состояний 185,
189
Функция Грина 98, 99, 101, 104
Характеристический радиус потен-
циала 21
Химический потенциал 316, 328
Центральное самосогласованное по-
ле 127, 128
Частота поверхностных колебаний
ядра 219, 224
Четности основных состояний ядер
142, 248
Четность состояния 33, 203, 224, 248
Числа (символы) Эллиотта 178
Чистая конфигурация 209, 210, 212
Чистые состояния 185, 186, 189
Эквивалентное однородное распре-
-деленне 86
Эквивалентные нуклоны 155
Электрические квадрупольные мо-
менты ядер 147
Электрический квадрупольный мо-
мент дейтрона 9
Элементарные возбуждения 220, 221
Эллипсоидальные деформации по-
верхности ядер 218, 237
Энергетическая щель 311, 312, 320,
323, 329
Энергетические спектры возбужде-
ния ядер с мечетным Л 322
-----------с четным А 322
— — легких ядер 199, 202
Энергия вращения ядер 239, 240, 241
— квазичастицы 320, 329
— кулоновского взаимодействия
между двумя протонами 7
— поверхностных колебаний ядра
218, 219
— связи дейтрона 8
— — ядер 7, 86
Эффективная масса 106, 111
Эффективный радиус действия ядер-
ных снл 17, 19, 28, 29
----ядерного взаимодействия 17,
19, 29
Эффект обмена 26
— спаривания 88
Ядерная материя 83, 89
Ядерные силы 5, 6, 7, 8, 12, 15, 19,
26, 31, 39, 49, 60, 65, 90, 94, 95
ОГЛАВЛЕНИЕ
Стр.
Предисловие ................................................... 3
Глава 1. Ядерные силы........................................... 5
§ 1.1. Состав ядер и свойства нуклонов...................... 5
Основные характеристики ядер.............................. 5
Свойства нейтронов и протонов............................. 5
§ 1.2. Ядерное взаимодействие между нуклонами............... 6
Короткодействующий характер ядерных сил................. 6
Другие особенности ядерных сил............................ 7
§ 1.3. Основное состояние дейтрона.......................... 8
Основные характеристики дейтрона.......................... 8
Основное состояние дейтрона в случае центральных сил ... 9
Соотношение между шириной и глубиной потенциальной ямы И
Отсутствие возбужденных состояний у дейтрона..............12
§ 1.4. Рассеяние медленных нейтронов протонами............. 13
Амплитуда и фазы рассеяния.........1......................13
S-рассеяние. Зависимость фазы рассеяния от энергии........13
Спиновая зависимость ядерных сил..........................15
Длины рассеяния.......................................... 16
Эффективный радиус ядерного взаимодействия................17
Длины и эффективные радиусы для триплетного и синглетного
состояний.................................................19
Параметр формы............................................20
§ 1.5. Рассеяние медленных нейтронов в молекулярном водороде 21
Псевдопотенциал...........................................21
Упругое рассеяние медленных нейтронов в пара- и ортоводороде 23
§ 1.6. Рассеяние протонов протонами.........................25
Кулоновское рассеяние.....................................25
Рассеяние протонов протонами с учетом ядерного взаимодейст-
вия ......................................................26
Длина рассеяния и эффективный радиус......................28
§ 1.7. Нецентральные ядерные силы...........................31
Потенциал нецентральных сил...............................31
Классификация состояний системы нейтрон- -протон..........32
Основное состояние дейтрона с учетом нецентральных сил ... 34
Магнитный момент дейтрона ............................... 36
Квадрупольный момент дейтрона.............................38
§ 1.8. Обменные силы........................................39
Рассеяние нейтронов протонами при высоких энергиях и обмен-
ный характер ядерных сил..................................39
Обменные операторы........................................41
Потенциал ядерного взаимодействия с учетом обменных сил . . 42
Потенциал Сервера.........................................43
§ 1.9. Изотопический спин и зарядовая независимость ядерного
взаимодействия........................................ ... 44
348
Сер.
Изотопический спин нуклона...............................44
Изотопический спин системы нуклонов......................45
Классификация состояний системы двух нуклонов............46
Явный вид обменных операторов............................48
Изотопическая инвариантность ядерного взаимодействия . . 49
§ 1.10. Рассеяние нуклонов на нуклонах при высоких энергиях , 51
Основные особенности рассеяния нуклонов на нуклонах при
высоких энергиях ......................................... 51
Неупругое рассеяние нуклонов.............................54
Рассеяние нуклонов при высоких энергиях и изотопическая ин-
вариантность ............................................54
Определение амплитуды рассеяния нуклона на нуклоне из дан-
ных опыта................................................57
Изотропный характер рассеяния протонов протонами и взаимо-
действие в состояниях с I =£ 0...........................58
Отталкивание между нуклонами на малых расстояниях . ... 60
Фазовый анализ...........................................61
Феноменологические потенциалы............................65
Нерелятивистская теория ядра.............................68
Задачи.........................................................69
Глава 2. Ядерная материя.......................................83
§2.1 . Насыщение ядерного взаимодействия...................83
Размеры ядер и распределение плотности внутри ядер.......83
Энергия связи ядер.......................................86
§2.2 . Газовая модель ядра................................88
Насыщение ядерного взаимодействия и независимость движения
отдельных нуклонов в ядре................................88
Свойства идеального ферми-газа...........................90
Стягивание ядер под действием сил притяжения между нуклона-
ми ......................................................93
Условие насыщения в случае обменных ядерных сил..........94
§2,3. Модель независимых пар...............................95
Отталкивание между нуклонами на малых расстояниях .... 95
Уравнение Бете—Голдстоуна................................96
Определение ядерной плотности и энергии связи............102
Применимость модели независимых частиц...................106
Задачи.........................................................107
Глава 3. Оболочечная структура ядер........................... 125
§3.1 . Движение нуклона в самосогласованном поле ядра .... 125
Независимость движения нуклонов в ядре к самосогласованный
потенциал.................................................125
Уравнение движения нуклона в самосогласованном поле ядра 126
Свойства радиальных волновых функций....................127
Спин-орбитальное взаимодействие.........................129
§ 3,2. Одночастичные состояния..........................131
Изотропный осцилляторный потенциал......................131
Определение абсолютных значений расстояний между уровнями 134
Прямоугольная потенциальная яма.........................136
Магические числа........................................139
§ 3.3. Одночастичная оболочечная модель ядер............142
Спины и четности основных состояний ядер................142
Магнитные дипольные моменты ядер........................143
Электрические квадрупольные моменты ядер................147
Магнитные октупольные моменты ядер......................149
§ 3.4. Волновые функции многочастичных оболочек.........152
Детерминанты Слэтера....................................152
349
Схемы построения многочастичных волновых функций........154
Неприводимые представления группы перестановок...........156
Построение антисимметризованных волновых функций . . . .162
Неприводимые представления группы унитарных преобразований 164
§3.5 . Классификация многочастичных состояний.............166
Классификация состояний в схеме LS-связи.................166
Классификация состояний в схеме //-связи.................169
Сеньорнти и приведенный изотопический спин...............172
Дополнительные квантовые числа...........................173
Дополнительная классификация многочастичных состояний в слу-
чае осцилляторного оболочечного потенциала...............176
§3.6 . Движение центра инерции ядра в оболочечной модели . . . 180
Гамильтониан ядра в осцилляторной оболочечной модели и
координаты Якоби ........................................ 180
Преобразование Талми.....................................182
Выделение движения центра инерции ядра в осцилляторной обо-
лочечной модели и трансляционно инвариантная модель оболочек 183
Выделение чистых и ложных состояний в осцилляторной оболо-
чечной модели............................................185
§3.7 . Коэффициенты родства..............................190
Вычисление матричных элементов с помощью многочастичных
функций и коэффициенты родства...........................190
Одночастичные коэффициенты родства......................191
Рекуррентное соотношение для коэффициентов родства . . . 194
Двухчастичные коэффициенты родства......................198
§ 3.8. Энергетические спектры легких ядер.............199
Приближение промежуточной связи.........................199
Энергетические спектры ядер с А — 7......................202
Задачи.......................................................204
Глава 4. Вращение и колебания ядер............................217
§4.1. Колебания сферических ядер........................217
Деформации поверхности ядер ... ....................... 217
Поверхностные колебания сферических ядер...............219
Колебательные спектры ядер..............................223
§ 4.2. Вращение системы координат.........................226
Повороты системы координат..............................226
Оператор конечных поворотов.............................228
Обобщенные сферические функции..........................231
Оператор вращения R.....................................234
§ 4.3. Вращение деформированных ядер и колебания их поверх-
ности ...................................................237
Эллипсоидальные деформации ядер.........................237
Колебательная энергия и энергия вращения................239
Потенциальная энергия колебаний несферических ядер.....241
§ 4.4. Вращение аксиально симметричных ядер...............243
Вращательная модель.....................................243
Схема сложения моментов и волновая функция ядра.........244
Симметрия волновой функции ............................. 246
Вращательные спектры ядер...............................249
Сравнение с экспериментом ............................. 252
Магнитные моменты деформированных ядер..................254
Квадрупольные моменты деформированных ядер............ 257
Одночастичные состояния в деформированных ядрах.........259
Моменты инерции ядер....................................266
§ 4.5. Вращение иеаксиальных ядер......................... . 271
Модель неаксиального ротатора...........................271
Основные особенности вращательных спектров неаксиальиых
ядер....................................................275
§ 4,6. Вращательно-колебательные возбуждения ядер..........278
350
Стр
Общий вид волнового уравнения в случае квадрупольных дефор-
маций .................................................278
Решение волнового уравнения для сферического ядра......281
Вращательно-колебательные возбуждения неаксиальаных ядер 284
Задачи......................................................288
Глава 5. Парные корреляции в ядрах..........................311
§5.1 . Сверхтекучие состояния ядер.....................311
Короткодействующие силы спаривания и дальнодействующие
мультипольные силы ....................................311
Гамильтониан сверхтекучей модели.......................315
Каноническое преобразование Боголюбова.................317
Волновые функции и энергетический спектр...............321
Модель когерентного парного взаимодействия.............322
§ 5.2. Остаточное взаимодействие и коллективные эффекты в ядрах 325
Инвариантная запись гамильтониана с остаточным взаимодейст-
вием ....................................................325
Приближение хаотических фаз............................329
Метод приближенного вторичного квантования.............333
Коллективные состояния ядер в модели с остаточным взаимо-
действием .............................................334
Литература..................................................339
Предметный указатель...................................342