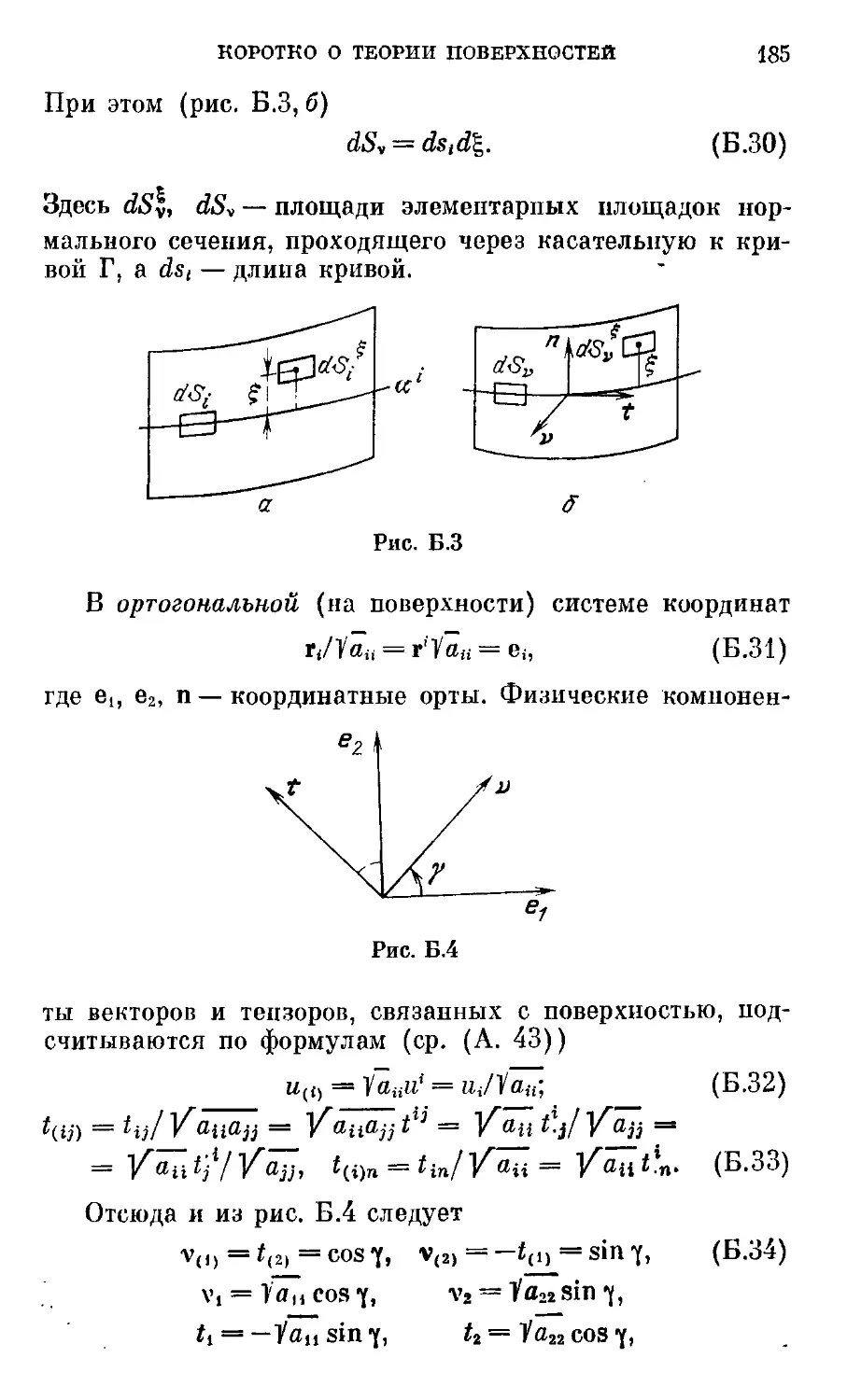
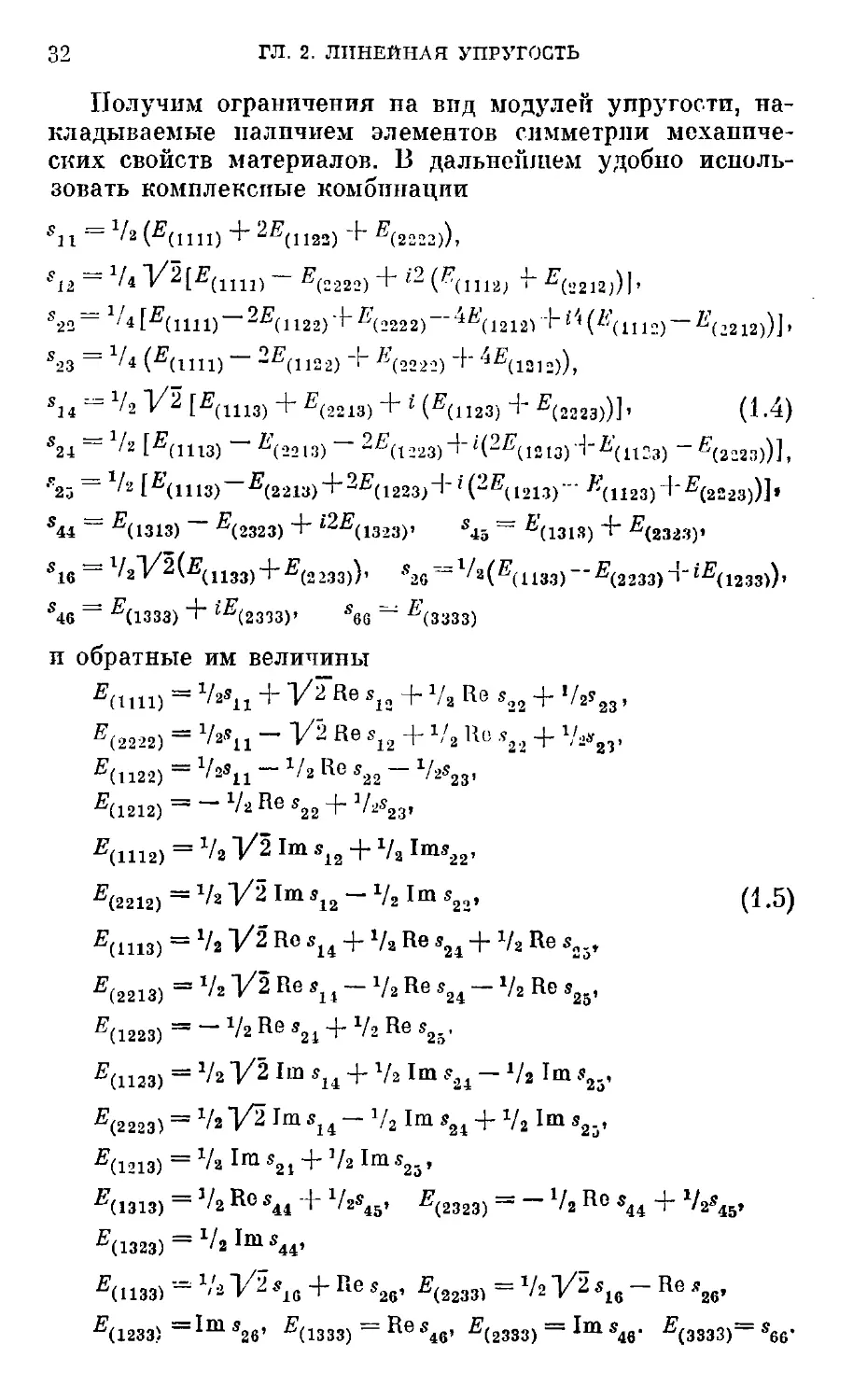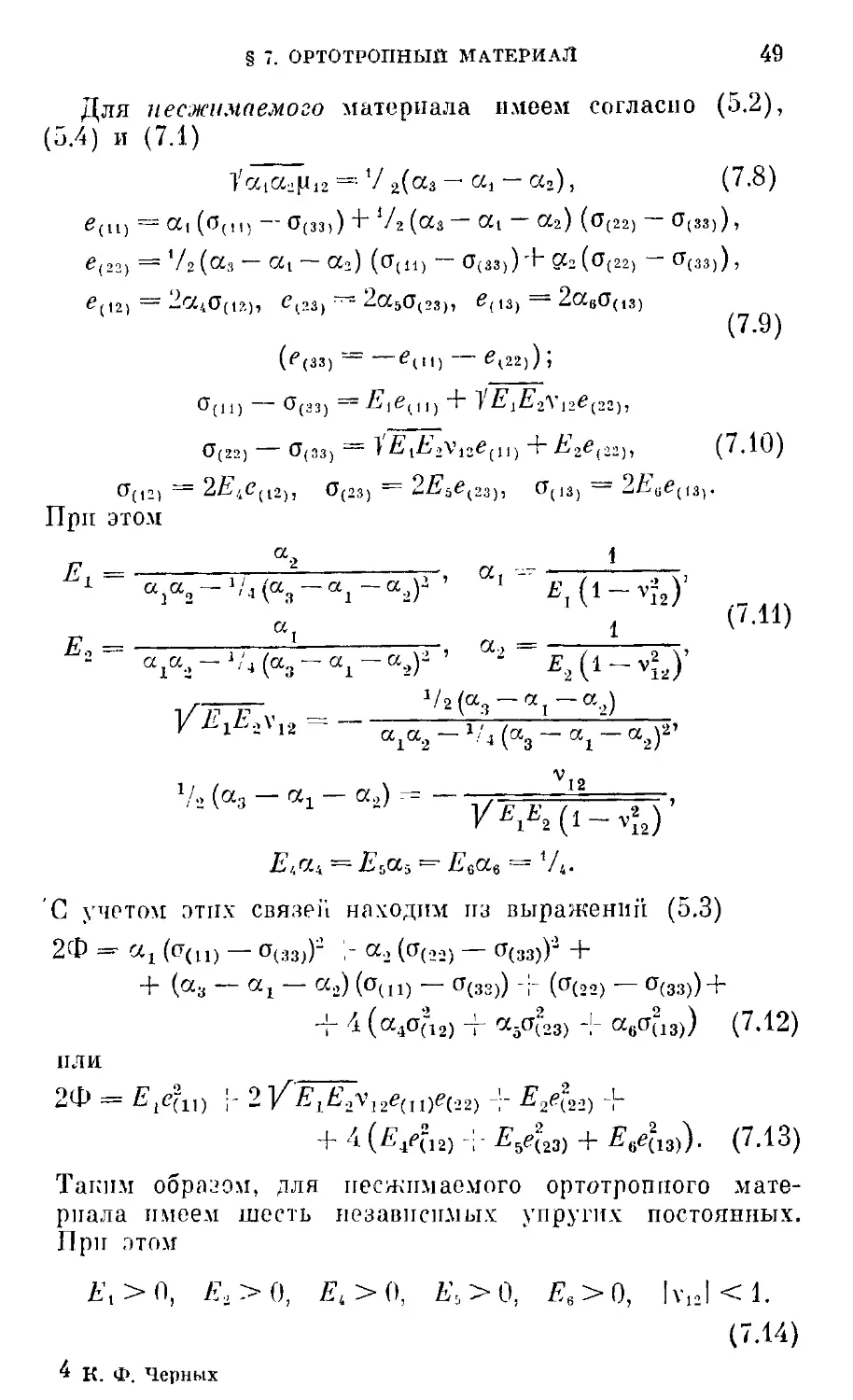Автор: Черных К.Ф.
Теги: механика деформируемых тел упругость деформация механика материаловедение
ISBN: 5-02-013807-Х
Год: 1988
Текст
К.Ф. ЧЕРНЫХ
ВВЕДЕНИЕ
В АНИЗОТРОПНУЮ
УПРУГОСТЬ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1988
ОГЛАВЛЕНИЕ
К читателю 5
Предисловие автора 6
Глава 1. Соображения симметрии 9
§ 1. Симметрия конечных фигур 9
§ 2. Понятие группы симметрии 12
§ 3. Точечные группы симметрии 13
§ 4. Кристаллические классы 22
§ 5. Симметрия физических свойств кристаллов. Принцип
Неймапа 29
§ 6. Криволинейная анизотропия 29
Глава 2. Линейная упругость 31
§ 1. Структура закона Гука 31
§ 2. Главные оси анизотропии 37
§ 3. Пределы изменяемости компонент положительно-оп-
положительно-определенной симметричной матрицы 39
§ 4. Пределы изменяемости упругих постоянных. Объем-
Объемные и сдвиговые деформации 42
§ 5. Несжимаемый материал 44
§ 6. Плоское напряженное состояние 46
§ 7. Ортотропный материал 47
§ 8. Трапсверсально-изотропный материал .... 51
§ 9. Изотропный материал 54
§ 10. Ортотроппый цшшпдр под давлением .... 56
Глава 3. Нелинейная упругость 59
§ 1. Основпые зависимости нелинейной теории упругости 59
§ 2. Закон упругости 64
§ 3. Плоское напряженное состояние 67
§ 4. Ортотропный материал 68
§ 5. Трансверсально-изотропиый материал 73
§ 6. Изотропный материал 78
§ 7. О выборе упругого потенциала 81
§ 8. Полый цилиндр из несжимаемого материала . . 85
Глава 4. Деформационная анизотропия 94
§ 1. Возмущение равновесной конфигурации тела . . 94
§ 2. Деформационная анизотропия первоначально изо-
изотропного материала 97
§ 3. Армированные волокнами эластомеры .... 99
4 ОГЛАВЛЕНИЕ
Глава 5. Тонкие анизотропные оболочки при больших де-
деформациях Ю*
§ 1. Деформация оболочки 101
§ 2. Усилия и моменты. Силовые граничные величины Ю-t
§ 3. Уравнения двпжения 1уд
§ 4. Закон упругости . НО
§ 5. Изотропный несжимаемый материал JJ*
$ И. Армирование нерастяжимымп волокнами . . . 117
§ 7. Растяжепие цилипдрпческой пластины . . . . 11°
§ 8. Осегимметричная деформация оболочки вращения 121
§ !). Армированная цилиндрическая оболочка . . . 124
§ 10. Армированный конический тонкостенный амортиза-
амортизатор 126
Глава 6. Некоторые вопросы теории 130
§ 1. Групповой тензорный базис 130
§ 2. Полусимметричпый тензор четвертого ранга . . . 135
§ 3. Ассоциированный базис 140
§ 4. Тензорный репер 145
§ 5. Одна общая ось 148
§ 6. Соосные тензоры 149
§ 7. Тензорные функции векторного типа .... 150
§ 8. Шестимерное пространство 155
§ 9. Сопряженные (энергетические) пары. Объективные
скорости изменения напряжений 156
§ 10. Устойчивость анизотропного материала .... 159
§ 11. Устойчивость изотропного материала .... 168
Приложение А. Криволинейные координаты . . . 173
При ложе ипе Г>. Коротко о теории поверхностен . . 181
Список литературы 187
К ЧИТАТЕЛЮ
Нужно иметь немалое мужество, чтобы взяться за из-
изложение анизотропной теории упругости в самой общей
ее (нелинейной) форме. Ведь очевидно, что при этом
неизбежна встреча с выкладками и формулами, которым
практически невозможно придать обозримость, и нелег-
нелегко убедить читателя в их прикладной ценности. Однако
сильная сторона К. Ф. Черных состоит в умении прео-
преодолевать трудности именно такого рода. В рассматривае-
рассматриваемой книге можно найти удачную, во многом оригиналь-
оригинальную, систематизацию формул линейной теории упругости
анизотропных тел и обстоятельное изложение нелиней-
нелинейной теории, вплоть до предложений конкретных по-
потенциалов для практически наиболее важных видов
анизотропии. Подробно рассмотрены проблемы больших
деформаций тонких анизотропных оболочек. Поскольку
анизотропные и конструктивно анизотропные (т. е. ком-
композитные) материалы находят все более и более широкое
применение, небольшая, но содержательная монография
об их упругих свойствах песомпенно найдет своего чи-
читателя.
Академик В. В. Новожилов
ПРЕДИСЛОВИЕ АВТОРА
Невозможно даже просто перечислить многочислен-
многочисленные публикации, и которых рассматриваются всевозмож-
всевозможные задачи расчета изделий и конструкций из изотроп-
изотропного упругого материала. Здесь следует прежде всего упо-
упомянуть основополагающие работы С. Г. Лехиицкого и
Н. Г. Ченцова. Вместе с тем имеется поразительно мало
работ, посвященных собственно анизотропии упругих
свойств. Среди них отметим публикации [4—6, 24, 34, 35,
41, 53-57, 60, 62, 63, 68-71, 77, 78].
Непосредственным поводом к написанию книги послу-
послужил доклад Я. Рыхлевского, в котором методами функ-
функционального анализа рассматривалась проблема приве-
приведения матрицы упругих модулей к диагональному виду.
Предлагаемая читателю книга была задумана как крат-
краткое систематическое изложение круга вопросов, связан-
связанных с законами упругости анизотропных материалов.
При этом осповное внимание было уделено вопросам,
сравнительно редко рассматриваемым в литературе и
имеющим четкую прикладную направленность (плоское
напряженное состояние, деформационная анизотропия,
несжимаемый и армированный материал, геометрическая
и физическая нелинейности, нелинейная теория оболо-
оболочек) . После написания первых пяти глав возникла мысль
изложить тесно примыкающие к основному содержанию
книги работы автора, развивающие основополагающие
исследования В. В. Новожилова [36—38, 40, 43] и школы
Л. И. Седова [53, 54, 29]. Так появилась шестая глава.
Наиболее полными до настоящего времени остаются
исследования П. Бехтерева [G], содержащие всесторон-
всестороннее исследование закона Гука для линейно анизотроп-
анизотропного материала. Решение поставленной там проблемы
нахождения наитеснейших интервалов изменения упру-
упругих постоянных (§ 3 гл. 2) было дано автором в статье
[68]. Стимулом для дальнейших исследований автора в
ПРЕДИСЛОВИЕ АВТОРА 7
этом направлении послужило появление исследования
В. В. Новожилова [41] о главных осях анизотропии и
числе существенно различных упругих постоянных (§2
гл. 2).
В гл. 1 дается краткое, но систематическое изложе-
изложение используемых в механике твердого деформируемого
тела соображений симметрии. Разъясняется понятие
группы симметрии конечной фигуры. Выявляются огра-
ограничения на возможные виды симметрии, связанные с
наличием у среды пространственной кристаллической ре-
решетки. Перечисляются кристаллические классы и тек-
текстуры. Формулируется принцип Неймана.
В гл. 2 выявляется структура закона Гука для ани-
анизотропного материала. Нетрадиционный подход позволя-
позволяет ввести симметричные коэффициенты Пуассона раз-
различных порядков. Это дает возможность установить наи-
наитеснейшие (неулучшаемые) интервалы изменяемости уп-
упругих постоянных, обеспечивающие положительпость
выражений для энергии деформации. Рассматриваются
несжимаемый материал и плоское напряженное состоя-
состояние. Основное внимание (как и в последующих главах)
уделяется наиболее часто используемым материалам: ор-
тотрошюму, трансверсально изотропному и изотропному.
В гл. 3 рассматриваются нелинейно-упругие анизот-
анизотропные материалы. Приводятся основные зависимости
нелинейной теории упругости. Изучается структура уп-
упругих потенциалов, отвечающих различным анизотроп-
анизотропным материалам. Рассматриваются несжимаемый мате-
материал и плоское напряженное состояние. Выписываются
условия перехода при малых деформациях законов упру-
упругости в закон Гука.
В гл. 4 изучается возникающая при больших дефор-
деформациях изотропного материала деформационная анизот-
анизотропия. Рассматривается несжимаемый изотропный мате-
материал, армированный семействами нерастяжимых волокон
(нитей).
Гл. 5 посвящена приложению полученпых результа-
результатов к оболочкам из эластомеров (резиноподобпых мате-
материалов), работающих при больших деформациях. Крат-
Кратко излагается предложенная автором «рабочая» общая
нелинейная теория упругих оболочек. Рассматриваются
оболочки из анизотроппого материала, а также со сре-
срединной поверхностью, армированной двумя семействами
волокон.
8 ПРЕДИСЛОВИЕ АВТОРА
В гл. 6, последней, рассматривается ряд теоретиче-
теоретических вопросов, примыкающих к изложенному в преды-
предыдущих главах. Излагаемый материал был в разное вре-
время опубликован в ряде статей автора [67, 69—72] и,
как уже было сказано выше, является дальнейшим раз-
развитием фундаментальных работ В. В. Новожилова и шко-
школы Л. И. Седова. Появляющиеся время от времени пуб-
публикации на эту тему свидетельствуют о неослабеваю-
неослабевающем интересе к проблемам структуры и свойств опреде-
определяющих уравнений механики сплошных сред.
Заключают книгу приложения А и Б. В них для
удобства читателя приведены необходимые для чтения
книги сведения по криволинейным координатам, кривым
и поверхностям.
ГЛАВА 1
СООБРАЖЕНИЯ СИММЕТРИИ
Трудно найти область человеческих знаний, где в той
или иной степени не использовались бы соображения
симметрии. Широко они используются и в теории упру-
упругости при рассмотрении как естественных (кристаллы),
так и искусственных (композиты) материалов.
Механические свойства сред во многом определяются
наличием у структур материалов отдельных элементов
симметрии конечных тел. Поэтому в начале этой гла-
главы дается краткое, элементарное, но систематическое рас-
рассмотрение всех возможных групп симметрии конечного
тела. Далее выявляются ограничения на вид симметрии,
налагаемые наличием у среды пространственной (кри-
(кристаллической) решетки. Перечисляются кристаллические
классы и текстуры.
Читателю, желающему более основательно познако-
познакомиться с налагаемыми (классическими) вопросами сим-
симметрии, а также с расширенным ее толкованием, реко-
рекомендуем руководство [78].
§ 1. Симметрия конечных фигур
Рассмотрим какую-нибудь трехмерную фигуру. Речь
об ее симметрии может идти только в случае, если фи-
фигура может быть разбита на несколько одинаковых ча-
частей, расположенных в некотором правильном порядке.
Законы правильности определяются преобразованиями
симметрии, переводящими одинаковые части фигуры друг
в друга. Если при этом не делать различия между оди-
одинаковыми частями фигуры, то можно сказать, что пре-
преобразования симметрии совмещают фигуру саму с собой.
Несложные геометрические построения показывают
[78], что преобразованиями симметрии могут быть отра-
отражения в плоскостях, повороты вокруг осей симметрии
и зеркальные повороты.
На рис. 1.1.1 показана фигура, состоящая из двух
тетраэдров с основаниями, лежащими в плоскости рисун-
10
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
ка. Отражение в плоскости симметрии, проходящей че-
через общее ребро тетраэдров перпендикулярно плоскости
рисунка, переводит части фигуры друг в друга.
На рис. 1.1.2 показаны фигуры, имеющие оси сим-
симметрии, проходящие через точки соприкосновения тет-
тетраэдров перпендикулярно пло-
плоскости рисуггка. Ось поворота
называют осью симметрии п-го
порядка, если при полном по-
повороте фигуры она п раз сов-
совмещается сама с собой. На
рис. 1.1.2 показаны оси симмет-
симметрии 2-го, 3-го ц 4-го порядков.
Р11С- 1-1-1 Если при повороте вокруг
оси, перпендикулярной пло-
плоскости, на угол 2п/п и последующем отражении в
плоскости фигура самосовмещается, то ось называют
зеркальной осью п-го порядка. На рис. 1.1.3 показаны
зеркальные оси 2-го, 4-го и 6-го порядков.
Простые геометрические соображения показывают
[78], что в конечном теле все преобразования симметрии
должны оставлять неподвижной по крайней мере одну
точку. Отсюда следует, что при наличии у фигуры не-
нескольких элементов симметрии (осей и плоскостей) все
они проходят через одну неподвижную точку, называе-
называемую особенной. Последняя может находиться и вне фи-
фигуры (например, центр шестерни с отверстием).
Кроме перечисленных преобразований симметрии,
в теории рассматривают еще инверсию, при которой точ-
точки фигуры переходят в симметричные относительно не-
некоторой точки (центра симметрии — рис. 1.1.4), и пере-
§ ). СИММЕТРИЯ КОНЕЧНЫХ ФИГУР
11
ворачивание, при котором точки фигуры переходят в
симметричные относительно данной прямой (рис. 1.1.5).
Преобразования симметрии называют эквивалентны-
эквивалентными, если в результате каждого из них происходит одно
и то же самосовмещение фигуры. Из рис. 1.1.4 видно,
что инверсия эквивалентна зеркальному повороту 2-го
порядка, а переворачивание — повороту 2-го порядка.
Ниже будет показано, что зеркальный поворот нечетного
порядка можно получить комбинированием соответству-
соответствующего поворота с отражением в плоскости, перпенди-
перпендикулярной оси.
Рис. 1.1.4
Рис. 1.1.5
Наибольший интерес представляет выявление всех
неэквивалентных преобразований симметрии. Поэтому
мы не рассматриваем преобразование переворачивания.
Преобразование же инверсии, хотя и не самостоятельное,
все же удобно использовать. Заметим, наконец, что от-
отражение в плоскости эквивалентно повороту вокруг оси,
перпендикулярной плоскости, с последующей инверсией
относительно точки пересечения плоскости и оси.
12 ГЛ. i. СООБРАЖЕНИЯ СИММЕТРИИ
§ 2. Понятие группы симметрии
Совокупность всех неэквивалентных преобразований,
которыми симметричная фигура совмещается сама с со-
собой, образует группу симметрии. Так, группа симметрии
фигуры с одной плоскостью симметрии (рис. 1.1.1) вклю-
включает в себя дна преобразования: отождествление (при
котором все равные части продолжают занимать свои
исходные места) и отражение в плоскости. Группа сим-
симметрии фигуры, показанной на рис. 1.1.2, б, содержит
три преобразования (элемента группы): отождествление
и, например, повороты влево на углы 1 • 2п/п = 120°,
2 • 2л/п — 240". Фигуре 1.1.3, в отвечает группа, состоя-
состоящая из шести преобразований: зеркальных поворотов на
углы 1 • 2я/б, 2 • 2я/6, ..., 6 • 2я/б (последний поворот
является преобразованием отождествления).
Число преобразований, образующих группу симмет-
симметрии, называют ее порядком. Очевидно, что порядок груп-
группы симметрии равен максимальному числу правильно
расположенных частей фигуры. В рассмотренных трех
примерах порядок группы равняется соответственно 2, 3
и 6. Фигуру, имеющую лишь тривиальное преобразова-
преобразование симметрии — отождествление, называют асиммет-
асимметричной.
Обсудим некоторые основные свойства групп симмет-
симметрии. Пусть А и В — преобразования из рассматриваемой
группы симметрии. Под произведением этих преобразо-
преобразований АВ = С понимают результат последовательного
осуществления предшествующего преобразования В и
последующего — А. Поскольку каждое преобразование
совмещает фигуру саму с собой, результирующее пре-
преобразование обладает тем же свойством. Тем самым и
оно является преобразованием группы. Следует отметить,
что в общем случае преобразования А и В некоммута-
некоммутативны (непереставимы), т. е. АВФВА. В этом проще
всего убедиться на примере, показанном на рис. 1.2.1.
Здесь А — преобразование поворота на угол 90° вокруг
оси 1, а В — такой же поворот вокруг оси 3.
Обозначим / преобразование отождествления. Очевид-
Очевидно, что для любого преобразования А. справедливо IA =
= А1 = А. Пусть А — преобразование, переводящее ка-
каким-нибудь определенным способом друг в друга оди-
одинаковые части фигуры. Назовем обратным преобразова-
преобразованием (обозначая его А~') преобразование, возвращаю-
§ 3. ТОЧЕЧНЫЕ ГРУППЫ СИММЕТРИИ
13
щее одинаковые части на их исходные места. Очевидно
ЛА~* = А~1А = /.
Рассмотренные выше примеры убеждают нас и п
свойстве ассоциативности (сочетательности) произведе-
произведении преобразований группы симметрии, т. е. в справед-
справедливости равенств вида (АВ)С — Л (ВС).
Рис. 1.2.1
Названные свойства совокупности преобразований
симметрии показывают, что эта совокупность удовлетво-
удовлетворяет аксиомам, определяющим алгебраическую структу-
структуру — группу [14, 78]. Тем самым оправдано использова-
использование термина — группа симметрии.
Группы симметрии, состоящие из преобразовании
симметрии, оставляющих неподвижной хотя бы одну
точку фигуры, называют точечными. В следующем пара-
параграфе будут рассмотрены все возможные точечные
группы.
§ 3. Точечные группы, симметрии
Точечные группы симметрии наглядно изображаются
[78] прозрачным шаром, на который паклеиваются ма-
маленькие несимметричные треугольники с двумя сторо-
сторонами: белой и черной. Если мы видпм треугольник бе-
белым, то он расположен па обращенной к нам половине
шара. Если — черным, то треугольник наклеен на зад-
заднюю половину. Центр шара располагается в одной из
неподвижных точек фигуры, п частности, в центре со'
симметрии. Зачерненными значками (двуугольник, тре-
треугольник, четырехугольник, ...) показываются место вы-
выхода оси симметрии и ее порядок B-й, 3-й, 4-й, .,.)'.
14
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
Рассмотрение начнем с группы, определяемой осью
симметрии п-го порядка и обозначаемой п. На рис. 1.3.1
показаны группы 1, 2, 3, 4. Группа 1 состоит нз одного
элемента — преобразования отождествления. Группа п
содержит п различных элементов вида
л лг Дп— т
где А — преобразование поворота на угол 2я/га.
Предельной для групп 1, 2, 3, ...является группа °°,
включающая в себя все повороты вокруг рассматривае-
рассматриваемой оси (поворот на произвольный угол можно рассмат-
рассматривать как бесконечное число последовательных поворо-
поворотов на бесконечно малые углы). Группы такого рода
называют непрерывными.
Преобразование отражения в плоскости обозначают
символом тп. Очевидно, что повторное отражение в той
же плоскости приводит части фигуры в их первоначаль-
первоначальные местоположения. Поэтому группа симметрии состо-
состоит из двух элементов: m и mz = /
Рис. 1.3.2
Соответствующие зеркальным поворотам четного по-
порядка фпгуры показаны па рис. 1.3.2. Группы симмет-
симметрии обозначают символами 2, 4, б,... При этом группа
2га состоит из 2га элементов
А,А\А\ .... Л2"-/,
§ 3. ТОЧЕЧНЫЕ ГРУППЫ СИММЕТРИИ
15
гдо А — зеркальный поворот на угол 2я/Bга). Как видно
из рис. 1.3.2, преобразования
А\ А\ ..., А2п = /
эквивалентны поворотам на удвоенные углы 2 • 2л/Bга),
4-2л/Bп), ..., 2п ¦2л/Bп) — I. Это -я показывают на
рис. 1.3.2 двойные значки. Нетрудно видеть, что послед-
последние преобразования образуют группу п, являющуюся
подгруппой [14, 78] группы 2п. Из рис. 1.3.2 видно также,
что для осей, порядок которых не кратен четырем, име-
имеет место преобразование инверсии.
Повороты с поперечной (перпендикулярной оси пово-
поворота) плоскостью симметрии определяют группы сим-
симметрии, обозначаемые 1 : тп, 2 : тп, ..., п : тп. Первые че-
четыре из них показаны на рис. 1.3.3. При этом точка
Г.т
2'.т З'.т
Рис. 1.3.3
4'.т
означает, что в проделанное в верхнем белом треуголь-
треугольнике отверстие как бы виден расположенный под ним
черпый нижний. По числу треугольников на рисунке
видно, что каждая из рассматриваемых групп симметрии
содержит 2п элементов:
А, А\ ..., Ая = 1 и АВ, А2В, ..., АпВ = В,
где А — преобразование поворота па угол 2л/п, а В —
отражение в поперечной плоскости. Отметим, что 1 : т =
= т. Далее, при п нечетном операции (АВ), (АВJ, ...
..., (АВJп = 1 являются зеркальными поворотами вок-
вокруг оси нечетного порядка. Операции (АВJ, (АВI, . . .
суть повороты на удвоенные углы. При всех четных п
имеет место (см. рис. 1.3.3) инверсия.
Предельной для групп п и п : т является непрерыв-
непрерывная группа, изображаемая символом °° : т.
Группы, определяемые поворотом и отражением в
продольной (проходящей через ось поворота) плоскости.
1С
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
Рассмотрим, например, группу 4 с расположением тре-
треугольников, показанным на рис. 1.3.4, а, и добавим к
ней одно отражение в плоскости, проходящей через ось.
При этом число треугольников удвоится (рис. 1.3.4,6)
и появится еще три плоскости симметрии (рис. 1.3.4, в).
Аналогично находим, что для оси 7г-го порядка число
плоскостей симметрии равно п (рис. 1.3.5). Группы рас-
рассматриваемого вида обозначают символами п ¦ т A •т —
— т). Они содержат 2га элементов: (считаемая п раз)
ось /г-го порядка и п продольных плоскостей.
2-т
3 -т
Рдс. 1.3.5
Предельной для рассматриваемых групп является не-
непрерывная группа <*> • т, имеющая ось бесконечного по-
порядка и бесчисленное множество продольных плоскостей.
Группы, определяемые поворотом и отражениями в
поперечной и продольной плоскостях, (рпс. 1.3.6). До-
Дополнительно к элементам симметрии предыдущего слу-
случая добавим поперечную плоскость. Согласно рис. 1.3.4,6
и 1.3.6, б количество треугольников после отражения в
поиеречной плоскости удваивается. Для оси 4-го поряд-
порядка появляются четыре дополнительные оси 2-го порядка
(рпс. 1.3.0, в), перпендикулярные основной оси.
На рнс. 1.3.7 видно, что для оси 7?-го порядка груп-
группа, которую будем обозначать m • п т, имеет порядок in.
§ 3. ТОЧЕЧНЫЕ ГРУППЫ СИММЕТРИИ
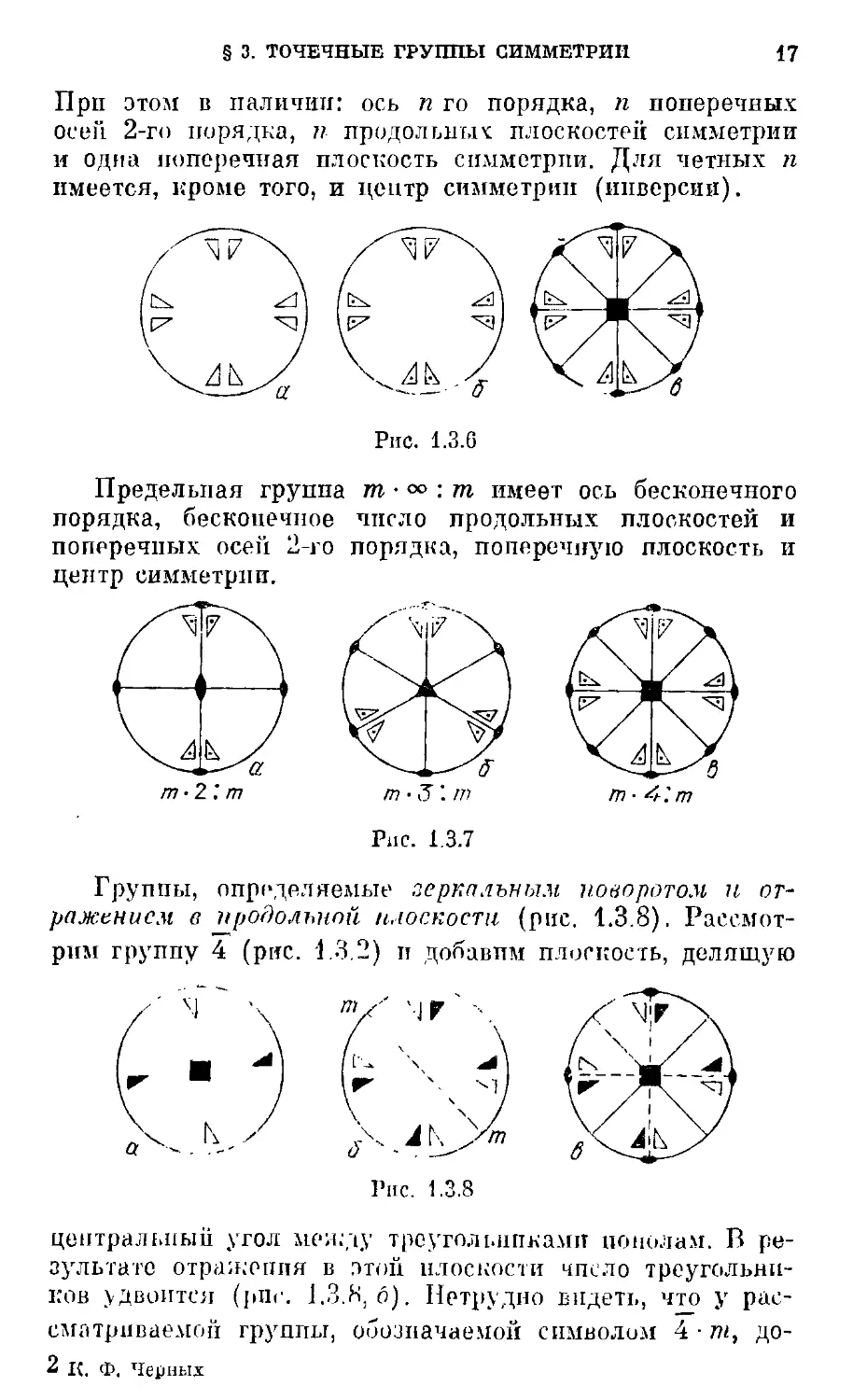
17
При этол! в наличии: ось п го порядка, п поперечных
осек 2-го порядка, п продольных плоскостей симметрии
и одма поперечная плоскость симметрии. Для четных п
имеется, кроме того, и центр симметрии (инверсии).
Рис. 1.3.6
Предельная группа т • °° : т имеет ось бесконечного
порядка, бесконечное число продольных плоскостей и
поперечных осей 2-го порядка, поперечную плоскость и
центр симметрии.
т • 2 .' т
Группы, определяемые зеркальным поворотом, и от-
отражением в продольной плоскости (рис. 1.3.8). Рассмот-
Рассмотрим группу 4 (ряс. 1.3.2) и добавим плоскость, делящую
Рис. 1.3.8
центральный угол между треугольниками пополам. В ре-
результате отражения в этой плоскости чпсло треугольни-
треугольников удвоится (рис. 1.3.8,6). Нетрудно видеть, что у рас-
рассматриваемой группы, обозначаемой символом 4 • т, до-
2 К. Ф. Черных
18
ГЛ. i. СООБРАЖЕНИЯ СИММЕТРИИ
полнптелыю появляется еще одна плоскость симметрии
и две поперечных оси второго порядка.
В общем случае зеркальной оси 2га (рис. 1.3.9) груп-
группа имеет зеркальную ось 2га-го порядка, га поперечных
осей второго порядка и га делящих углы между ними
¦4-т
6-т
Рис. 1.3.9
пополам продольных плоскостей. Таким образом, поря-
порядок группы 4га. Как уже говорилось выше, зеркальная
ось 2га является одновременно и осью га-го порядка. При
га, не кратном четырем, имеется и центр симметрии.
Предельной для введенных групп является рассмот-
рассмотренная выше непрерывная группа т • °° : т.
Группы, определяемые поворотом вокруг основной оси
и поворотом вокруг поперечной оси 2-го порядка. Рас-
Рассмотрим, например, ось поворота 3-го порядка (рис. 1.3.1
и 1.3.10, а). Добавим к ней поперечную ось 2-го поряд-
порядка. Последняя удваивает число треугольников
(рис. 1.3.10,6). Из рис. 1.3.10, в видно, что имеются
еще две поперечные оси. В результате имеем группу,
обозначаемую символом 3:2. В общем случае
(рис. 1.3.11) группа п: 2 имеет порядок 2га, включая
в себя: ось га-го порядка, п поперечных осей 2-го по-
порядка. Предельная группа °° : 2 имеет ось симметрии
бесконечного порядка и бесчисленное множество попе-
поперечных осей 2-го порядка.
§ 3. ТОЧЕЧНЫЕ ГРУППЫ СИММКТ1ЧШ
19
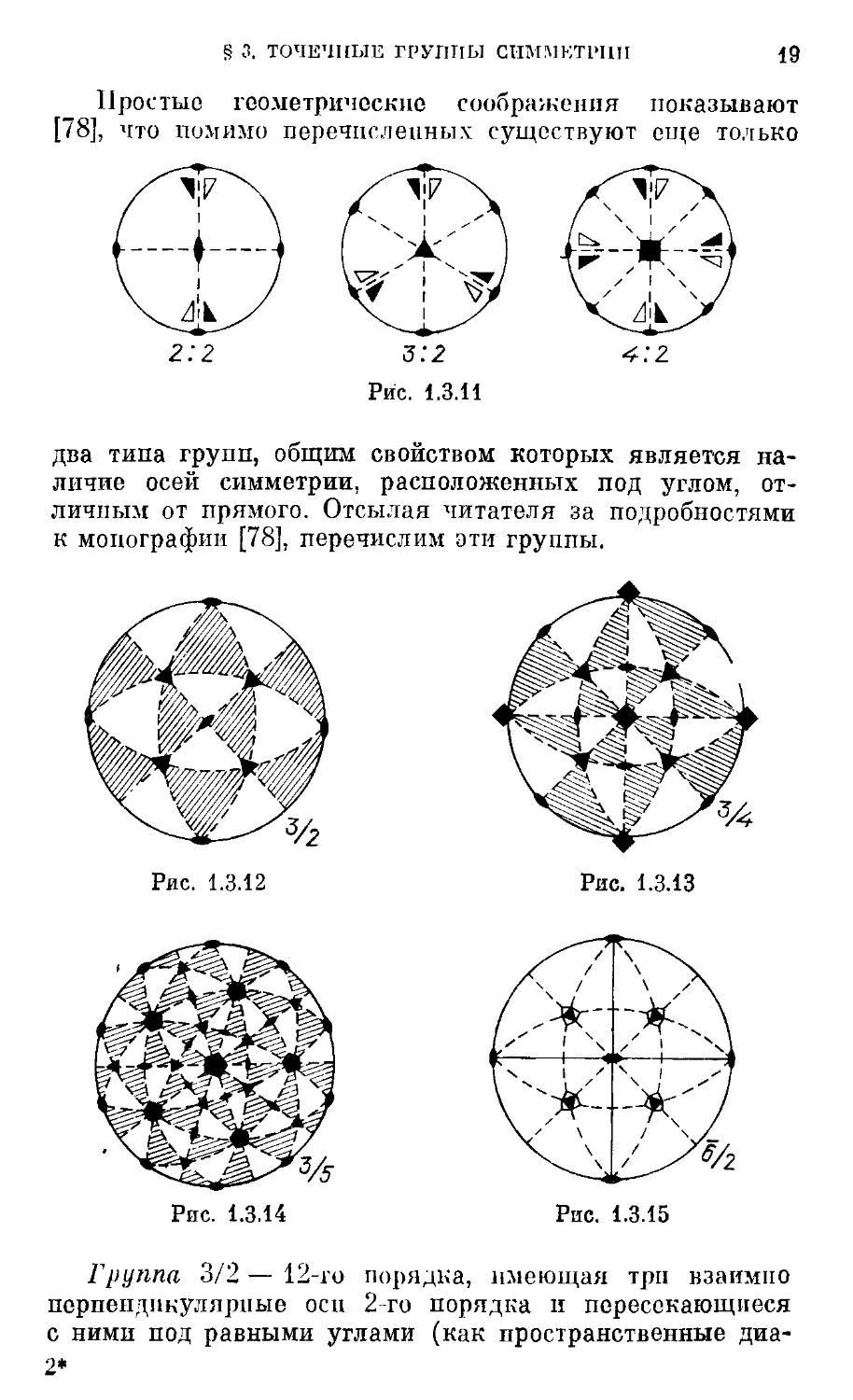
Простые геометрические соображения показывают
[78], что помимо перечисленных существуют еще только
Z:2
два типа групп, общим свойством которых является на-
наличие осей симметрии, расположенных под углом, от-
отличным от прямого. Отсылая читателя за подробностями
к монографии [78], перечислим эти группы.
Рис. 1.3.12
Рис. 1.3.13
Рис. 1.3.14
6/2
Рис. 1.3.15
Группа 3/2 — 12-го порядка, имеющая три взаимно
перпендикулярные осп 2-го порядка и пересекающиеся
с ними под равными углами (как пространственные диа-
2*
20
ГЛ. i. СООБРАЖЕНИЯ СИММЕТРИИ
гонали куба) четыре осп 3-го порядка. На рис. 1.3.12
показаны точки пересечения указанных осей с обращен-
обращенной к нам половиной сферы.
Группа ,'!/4 — 24-го порядка, имеющая: три оси 4-го
порядка, четыре осп 3-го порядка и шесть осей 2-го по-
порядка. Расположенно осей на по-
полусфере показано на рис. 1.3.13.
Группа 3/5 - - 60-го порядка,
содержащая в себе: шесть осей
5-го порядка, десять осей 3-го
порядка и пятнадцать осей 2-го
порядка. Расположение их пока-
показано на рис. 1.3.14.
Продельная группа °°/°° со-
состоит из бесчисленного множества
осей бесконечного порядка, нап-
направленных во все стороны. Суще-
Существенно, что эта непрерывная
группа не имеет плоскостей симметрии.
Последний тип групп отличается от только что опи-
описанного наличием дополнительной плоскости симметрии.
Группа 6/2 — 24-го порядка, содержащая: три оси
2-го порядка, четыре оси 3-го порядка (они же зеркаль-
пые оси 6-го порядка), три плоскости симметрии и центр
симметрии. Расположение осей показано на рис. 1.3.15.
Рис. 1.3.16
Рис. 1.3.17
Рис. 1.3.18
Группа 3/4—также 24-го порядка, содержащая: три
зеркальных оси 4-го порядка, четыре оси 3-го порядка
и шесть плоскостей симметрии. Расноложеиие осей по-
показано на рис. 1.3.10.
Группа 6/4 — 48-го порядка, содержащая: четыре
зеркальных оси 6-го иорядка, три оси 4-го порядка,
§ 3. ТОЧЕЧНЫЕ ГРУППЫ СИММЕТРИИ
21
шесть осей 2-го порядка, девять плоскостей симметрии
и центр симметрии. Расположение осей показано на
рис. 1.3.17. _
Группа 3/10 — 120-го порядка. Дополнительно к эле-
элементам группы 3/5 в нее входят пятнадцать плоскостей
симметрии и центр симметрии. Расположение осей пока-
показано па рис. 1.3.18.
Предельной является общая ортогональная группа
оо/оо • т, содержащая все повороты и отражепия в пло-
плоскостях.
Все перечисленные шестнадцать групп сведены в
табл. 1. При этом в ней приведены лишь порождающие
элементы симметрии, комбинируя которые можно полу-
получить все элементы группы симметрии.
Таблица 1
Точечные группы симметрия трехмерных фигур
I
1
3
5
7
II
2
4
6
8
ОО
IX
2: 2
4:2
0:2
8: 2
X
1 : 2
3:2
5:2
7 : 2
оо : 2
III
0
10
14
IV
1
8-
12
16
V
1 : m
3 : m
5 : m
7: m
оо ; m
XI
m-2 : m
/ге-4 : m
m-Q : m
m-8 : m
XII
m-1 : m
m-3 : m
m-5 : m
m-7 : m
VI
2 : m
4 : m
6 : m
8 : m
VII
2-/re
i-m
6-m
8-m
VIII
1-m
3-m
5-m
1-m
oo-m
XIII
4-m
T-m
12-m
16-m
XIV
I'm
T-m
10 -m
14-ra
m-oo : m
XV
3/2
3/4
3/5
oo/oo
XVI
6/2
3/4
6/4
3/10
oo/oo • m
22
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
§ 4. Кристаллические классы
Симметрия кристаллов и анизотропия их физических
свойств тесно связаны с наличием кристаллической ре-
решетки, в узлах которой располагаются атомы, ионы или
молекулы. Тройная периодичность (бесконечной, иде-
идеальной) решетки дает возможность бесконечным числом
трансляций (поступательных смещений) совмещать ре-
решетку саму с собой. При этом всегда можно выбрать
Рис. 1.4.1
такие не лежащие в одной плоскости векторы а,, а-., а3
(рис. 1.4.1), что любая трансляция может быть пред-
представлена в виде
+ 1
где Si, s2, s3 — целые числа (положительные, отрицатель-
отрицательные, либо нули). Векторы а„ а2, а3 называют основными
периодами (векторами), а построенный на них паралле-
параллелепипед — элементарной ячейкой кристаллической ре-
решетки.
Если одинаковые атомы располагаются только в уг-
углах элементарной ячейки, кристаллическую решетку на-
называют простой. Поскольку у ячейки восемь вершин и
в каждой вершине сходятся восемь ячеек, в простой
решетке на элементарную ячейку приходится по одному
атому (иону, молекуле). Если же в элементарную ячей-
ячейку попадает у. (ц>1) атомов, одинаковых или различ-
различных, решетку называют сложной, а совокупность ато-
атомов, приходящихся на элементарную ячейку,— базисом
кристаллической решетки. Элементарная ячейка, ^повто-
^повторяясь, заполняет всю решетку. При этом каждый атом
базиса повторяется с периодами ai, a2, а3.
Совокупность всех узлов, которые могут быть совме-
совмещены друг с другом посредством трансляций на целое
§ 4. КРИСТАЛЛИЧЕСКИЕ КЛАССЫ
23
число основных периодов кристаллической решетки, на-
называют решеткой Бравэ кристалла. Таким образом, каж-
каждый атом базиса определяет свою решетку Бравэ, а вся
сложная кристаллическая решетка как бы состоит из
вдвинутых друг в друга ц, простых решеток Бравэ.
Отметим, что выбор основных периодов, а стало быть,
и элементарной ячейки кристаллической решетки, неод-
неоднозначен. Для простоты покажем это па двумерной пло-
плоской решетке (сетке), изображенной на рис. 1.4.2. Не-
Нетрудно видеть, что сетку можно заполнить элементар-
пыми ячейками а,, а2; аь а2; ai, a2. Ячейки же ах, а2
О
аг
о"
а'г/
/
О
/Г
о а;
О а]
Рис. 1.4.2
и ах, а2 не являются таковыми, нескольку узлы, по-
помеченные крестиками, пе могут быть достигнуты из точ-
точки О трансляциями, кратными отвечающим этим ячей-
ячейкам периодам.
Та же ситуация имеет место и для трехмерной ре-
решетки: элементарные решетки не могут содержать узлов
внутри себя и на гранях. Каждая элементарная ячейка
объединяет восемь расположенных в ее вершинах узлов.
Поэтому при любом выборе элементарной ячейки мак-
макрообъем V разбивается на N равных частей, и объем
элементарной ячейки равен Vo = V/N. В приложениях
используют как элементарные, так и пеэлементарные
ячейки.
- Решетка Бравэ полностью определяется заданием три-
триэдра основных периодов (векторов) а,, а2, а3. С послед-
последними связана так называемая кристаллическая система
координат (рис. 1.4.3), оси которой направлены вдоль ос-
основных векторов а,, а2, а3. При этом в качестве мас-
масштабных (осевых) единиц принимают величины a=|aj,
24
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
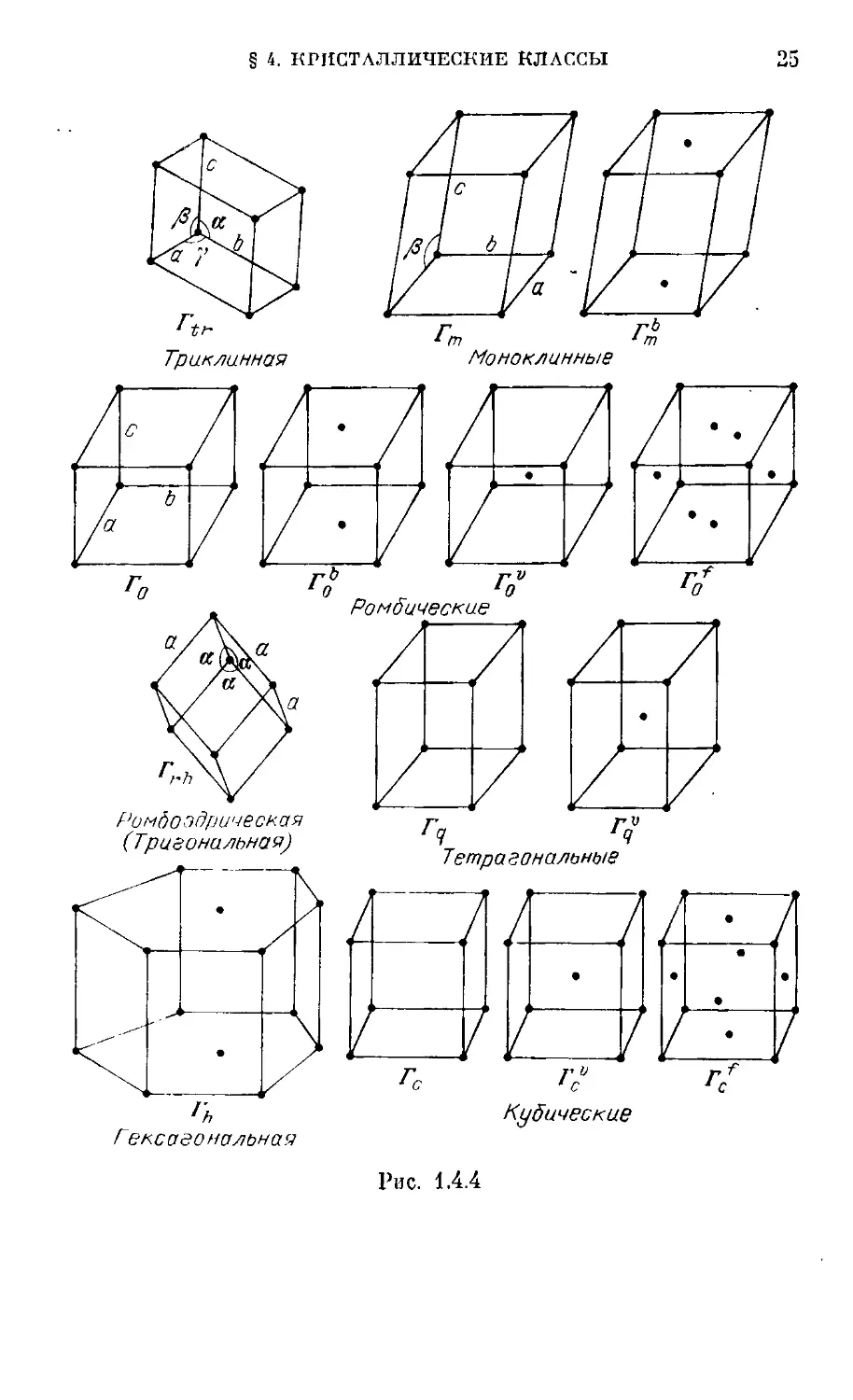
6 = ]а21, с= 1а31. Углы а, $, f пазывают осевыми. Бра-
вэ показал [78], что все названные впоследствии его име-
именем решетки могут быть разбиты на 14 типов, отнесен-
отнесенных к семи кристаллографиче-
кристаллографическим системам — сипгониям
(табл. 2 и рис. 1.4.4).
Для триклинной сингонии
(Г(Г) узлы решетки Бравэ распо-
располагаются в вершипах параллеле-
параллелепипеда с произвольными сторона-
сторонами и углами.
Моноклинной сингонии отвеча-
отвечают два типа решеток. Для перво-
первого (Гт) узлы располагаются в
вершинах прямого (в направлении Ь) параллелепипеда
с произвольным основанием. Для второго (решетка с
основанием — Г™) имеются дополни-
дополницентрах противоположных граней па-
паРис. 1.4.3
центрированным
тельные узлы в
раллелепипедов.
Кристаллографические системы
Таблица 2
(сингонии)
1
2
3
4
5
С
7
Кристаллографи-
Кристаллографическая система
Триклинная
Моноклинная
Ромбическая
Тетрагональная
Ромбоэдрическая
(тригональная)
Гексагональная
Кубическая
Осевые единицы
а ФЪ, Ъ Ф с, афс
афЪ,Ъ фс, афс
а ФЬ, b Фс, афс
а—Ьфс
а = Ь = с
а—Ьфс
а= Ь = с
а
а
а
а
а
а
У
а
Осевые углы
— R —
= Р =
— R —
= 120°
= Р =
Фу,афу
90° ф$
у = 90°
Y=90°
Y^=90°
90°,
у= 90°
К ромбической сингонии относятся четыре типа ре-
решеток. В простой ромбической решетке (Го) узлы рас-
располагаются в вершинах прямоугольных параллелепипе-
параллелепипедов. В решетках с центрированными основаниями (Го)
имеются также узлы в центрах двух противоположных
граней. В объемоцентрированной решетке (Г?), помимо
вершип, узлы находятся в центрах параллелепипедов.
§ 4. КРИСТАЛЛИЧЕСКИЕ КЛАССЫ
Триклинная
/
/¦
с
ь
/
/
Моноклинные
/
/
•
/
/
Ромбические
г"
'о
•
/
•
/
Римдоодрическая
(Григональная)
Га
Tempo гональные
71
71
Гексагональная
Кубические
Рис. 1.4.4
26 ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
Наконец, в гранецентрированной решетке (Го) узлы
находятся в вершинах параллелепипеда и центрах его
граней.
Для тетрагональной сингонии имеет место либо про-
простая решетка (Г,) с узлами в вершинах призмы с квад-
квадратным основанием, либо объемоцеитрпрованная (Гд)
с дополнительным узлом в центре призмы.
В ромбоэдрической (тригоналъной) сипгонии (ГгЛ)
узлы расположены в вершинах ромбоэдра (фигуры, по-
полученной путем растяжения — сжатия куба вдоль его
пространственной диагонали).
В кристаллах гексагональной сипгонии (Г\) узлы рас-
располагаются в вершинах правильных шестигранных призм
и центрах их оснований.
Кубической сингонии отвечают три типа решеток:
простая кубическая (Гс), объемоцентрическая (Г") и
гранецентрическая (Гс).
В соответствии со сказанным выше, объемоцентри-
рованные, гранецентрированные и решетки с центриро-
центрированными основаниями за-
^А даны па рис. 1.4.4 своими
неэлементарными решет-
решетками. Сделано это для
удобства выявления эле-
элементов симметрии кри-
кристаллов.
Наличие периодической
решетки у кристаллов су-
существенно сужает мпожество допустимых точечных групп
симметрии. Покажем, например, что не каждая ось сим-
симметрии допустима. Пусть через узел А (рис. 1.4.5) про-
проходит перпендикулярно плоскости рисунка ось симмет-
симметрии п-то порядка. Через каждый узел решетки Бравэ и,
в частности, через В проходит ось того же порядка.
Совершая поворот вокруг узла А на угол ср„ = 2л/п, мы
должны совместить решетку саму с собой. При этом
узел В переходит в некоторый узел В'. Аналогично, при
повороте на тот же угол, но в противоположном направ-
направлении, вокруг В, узел А переходит в узел А'. Отсюда
следует, что отрезок В'А' кратен периоду решетки а,
т. е.
а -\- 2а sin (q>n - л/2)
- = 1 — 2 cos cpn = р, ¦
§ 4. КРИСТАЛЛИЧЕСКИЕ КЛАССЫ
27
где р — целое число. Отсюда следует cos ср„ = д/2, где
q = 1 — р — также целое число. Поскольку Icos <р„| =S 1,
из этого неравенства следует, что имеется лишь пять
значений (отвечающих q = О, ±1, ±2): 0°, 180°, 120°,
Таблица 3
Кристаллические классы
Кристаллографи-
Кристаллографическая система
Триклинная
Моноклинная
Ромбическая
Тетрагональ-
Тетрагональная
Ромбоэдриче-
Ромбоэдрическая (трпто-
нальная)
Гексагонал ьная
Кубическая
Номер
класса по
Гроту
1
2
3
4
5
С
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Класс по номенклатуре Фе-
Федоровского института
Примитивный
Центральный
Аксиальный
Планальный
Планаксиальный
Аксиальный
Планальный
Планаксиальный
Гироидо-примитпвный
Примитивный
Гироидо-планальный
Аксиальный
Центральный
Планальный
Планаксиальный
Примитивный
Центральный
Аксиальный
Планальный
Планаксиальный
Гироидо-примитнвныи
Гироидо-илапальный
Примитивный
Аксиальный
Центральный
Планальный
П ланаксиал ьны й
Примитивный
Аксиальный
Центральный
Планальный
Планакспалыгый
Порождающие
элементы (
рм
1
2
2
т.
2 : т
2:2
2-т
m-2 : m
4
4
A-m
4: 2
4 : m
4'm
m-4 : m
3
6
3:2
3-m
6-m
3: m
m-3 : m
6
6 : 2
6 : in
6 • /71
m-& : in
3/2
3/4
6/2
3/4
6/4
;иммет-
1
1
2
2
2
2: 2
2
2
2
2
4
4
4
4
4
4
4
3
3
3
3
3
6
6
6
6
6
6
6
2
2
2
2
2
2
2
2
0
2
2
3/2
3/4
3/2
3/4
3/4
90° и 60°. Таким образом, в кристаллах возможны оси
симметрии лишь 1, 2, 3, 4 и 6-го порядков.
Можно показать [78], что число точечных групп сим-
симметрии, совместимых с наличием кристаллической решет-
28
ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
ки, равно 32. Эти группы называют кристаллическими
классами. Все они сведены в табл. 3, в четвертом столб-
столбце которой помещены порождающие элементы симмет-
симметрии, позволяющие восстановить всю группу. В пятом
столбце помещены порождающие элементы симметрии
кристаллических классов, которые с дополнительным
преобразованием инверсии (§ 1) позволяют восстановить
всю группу. Это нетрудно проверить с помощью введен-
введенных выше шаров и треугольников. Для тензоров четных
рангов преобразование инверсии, очевидно, не меняет
значения компонент. Поэтому для них следует исполь-
использовать столбец 5.
В табл. 4 приведены семь классов — текстур — сред,
точечными группами которых являются рассмотренные
Таблица 4
Тек-
Текстуры
[S
go
1
oo
2
oo : m
oo
3
oo -m
4
in • oo : m
5
oo : 2
oo : 2
о
oo/oo
7
oo/oo -m
oo/oo
в § 1 непрерывные (предельные) группы (см. последнюю
строку табл. 4).
Как видно из табл. 3, кристаллические классы 4, 15,
7, 11, 13, 14, 19, 20, 21, 25 и 26 имеют среди своих
элементов симметрии одну плоскость симметрии. Помимо
текстур (табл. 4) °° : пг, °° ¦ тп, оо/оо . щ, ее имеют и мно-
многие искусственные анизотропные среды.
Ортотропными называют материалы, включающие в
свои группы симметрии три взаимно ортогональные пло-
плоскости симметрии (простое геометрическое построение
показывает, что наличие двух плоскостей влечет и
третью). Ортотропными являются кристаллические клас-
классы 8, 15, 22, 27 ромбической сингошш (табл. 3) и тек-
текстура m-oo-.m (табл. 4). Ортотропными являются также
многие искусственные материалы: фанера, бумага, ком-
композиты регулярного строения.
Транееерсалъная анизотропия материала характери-
характеризуется наличием в его группе симметрии поворотной осп
бесконечного порядка. Как видно из табл. 4, трансвер-
сальной анизотропией обладают все текстуры.
§ В. КРИВОЛИНЕЙНАЯ АНИЗОТРОПИЯ 29
Изотропными называют среды с полной ортогональ-
ортогональной группой симметрии (содержащей в качестве элемен-
элементов симметрии всевозможные повороты и отражения).
Можно показать [78], что отвечающие текстуре 7 (табл. 4)
порождающие элементы °°/оо . щ и определяют полную
ортогональную группу симметрии. Текстуру °°/°° назы-
называют гиротропным материалом.
§ 5. Симметрия физических свойств кристаллов.
Принцип Неймана
Наличие в тело кристаллической решетки приводит,
грубо говоря, к тому, что тело в различных направле-
направлениях неодинаково «насыщено» частицами, образующими
решетку. Это приводит к различию физических, в том
числе и механических, свойств кристаллов в различных
направлениях — к так называемой анизотропии.
Свойства симметрии кристаллов приводят к появле-
появлению эквивалентных направлений, неразличимых в отно-
отношении тех или иных физических свойств. Связь между
симметрией кристалла и симметрией его физических
свойств устанавливает фундаментальный принцип
Неймана: элементы симметрии любого физического
свойства кристалла должны включать элементы симмет-
симметрии точечной группы симметрии кристалла.
Сформулированный принцип утверждает, таким обра-
образом, что симметрия рассматриваемого физического свой-
свойства пе может быть ниже симметрии кристалла, в кото-
котором оно проявляется. Физическое свойство может обла-
обладать и более высокой симметрией, чем точечпая группа
симметрии кристалла. Так, например, кубические кри-
кристаллы в отношении свойств, описываемых тензорами
второго ранга (в частности, оптических), ведут себя как
изотропные тела. Далее, свойства, описываемые тензо-
тензорами четных рангов (например, упругость), инвариантны
относительно преобразования инверсии. Сказанное отно-
относится также к текстурам и другим средам с соответству-
соответствующими группами симметрии.
§ 6. Криволинейная анизотропия
Пусть в теле имеется криволинейная ортогопальная
система координат. Пусть, далее, в каждой точке тела
имеющиеся три координатные оси являются осями по-
30 ГЛ. 1. СООБРАЖЕНИЯ СИММЕТРИИ
ворота (зеркального поворота) того или иного типа, а ка-
касательные к координатным поверхностям плоскости —
плоскостями симметрии. В этом случае можно говорить
о криволинейной анизотропии. Криволинейная анизотро-
анизотропия, очевидно, носит локальный характер, поскольку при
переходе от точки к точке координатпые оси и поверх-
поверхности поворачиваются.
Со сделанной оговоркой сказанное выше справедливо
и для криволинейной анизотропии. Криволинейная ани-
анизотропия более характерна для искусственных материа-
материалов.
ГЛАВА 2
ЛИНЕЙНАЯ УПРУГОСТЬ
В этой главе рассматриваются вопросы, связанные с
выявлением структуры закона Гука для анизотропного
материала. Используются нетрадиционные более удобные
упругие постоянные, связапные с введением симметрич-
симметричных коэффициентов Пуассона. Для упругих постоянных
устанавливаются наитеснейгаие, пеулучшаемые пределы
изменяемости, автоматически обеспечивающие положи-
положительность выражения для энергии деформации. Рассмат-
Рассматриваются несжимаемый материал и плоское напряжен-
напряженное состояние. Особое внимание уделяется ортотропному,
трапсверсалыю-изотроппому и изотропному материалам.
§ 1. Структура закона Гука
Как известно [41, 25], для анизотропного материала
в ортогональных координатах физические компоненты
тензора напряжепий и тензора деформации связаны за-
законом Гука *) (г, /, к, 1,а,$ = 1, 2, 3)
A.1)
При этом физические компоненты тензора модулей упру-
упругости обладают, в силу симметрии тензоров напряжений
и деформации и наличия упругого потенциала, следую-
следующими свойствами симметрии:
E^jhi) — E(jW) = E{ijih) = E^i-ii). A-2)
При переходе к другой, также ортогональной, системе
координат модули упругости преобразуются по формулам
A-3)
где <7ц — косинусы углов поворота, подсчитываемые по
формулам (А.45) (формулы D5) Приложения А).
') Здесь и ниже по повторяющимся греческим индексам
производится суммирование от 1 до 3.
32 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
Получим ограничения на вид модулей упругости, на-
накладываемые наличием элементов симметрии механиче-
механических свойств материалов. В дальнейшем удобно исполь-
использовать комплексные комбинации
»14 = V. УЩиП) - ?(=222)
?(
B213) + г (Я(И23) + Е1гш))], A.4)
BEA2l3)- Л'A123)
^B323)
^B333)' *66 ~
и обратные им величины
yj + V,
^B222) = V2.'n - У2 Re ,12 + V2 Ho .?2, + V,v23,
?(H23) = V» /2 Im »14 + 1/2 Im »„ - V2
?B223) = Va У2 Im *u - Va Im »„ + Vi Im »8.,
?A213) = Va Im »21 + V»Im«a3,
= V8 Re *44 + Vi««, ?B32з) = - V. Re
= V» У2 Im s12 + V,
?B2i2) = Vi 1/2 Im »la - V, Im *2a, A.5)
= V2 У'2 Re *u + Va Re »„ + Vi Re *„.,
V» T/2 Re ,14 - V, Re su - V2 Re ,25,
?(U33) "-= V* V2 *ie + Re *26, ?B233) = У2 /2 ,u - Re v
?A233) =ImS26' ?A333) = ReS46' ?B333) = ImS46' ?C333)= S66"
СКОРМА
J.,
§ 1. СТРУКТУРА ЗАКОНА ГУКА
33
Рассмотрим поворот вокруг третьей координатной оси
на угол о. При атом, согласно (А.45),
«з = «>> «J = ю2 = О, Q - | qi} | =-
cos ы -- sin ы ll
sin (й cos ы (I
0 0 l|
Отсюда и из выражений A.3), A.4) находим
Н\
г
S23
¦%в
г
S16
f
«и
"S45
S16
S06
S14
Я4С
S25
S14
= S46
S25
2
12
26
44
,—i2(o
с —
22 —
Для оси 2-го порядка B)
A.G)
A.7)
Отсюда п из выражений A.7) следует, что требование
инвариантности величин sl7 относительно рассмотренного
поворота приводится к требованиям, сведенным в первую
строку следующей таблицы:
= S25 = S12 = S26 = S44 = S21 =
6: «14 = S46 = S25 = S12 = S26 = S44 *= ^22 = *24 = 0"
A.8)
Остальные ограничения A.8) выявляются аналогично.
Согласно выражениям A.5) отсюда следуют ограниче-
ограничения на модули упругости:
~" ?(.4313) — ?A-223) ~ ?
A213)
1:
~ ?
{2213)
"C313)— ^A223)"
?A213) ~ ?
C312)
?B222) = ?A111)' ?B212) = "~ ?A112)' ?A313) = ?B323)'
3 К. Ф. Черных
34 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
= ^C312) = ^C323) =
^B222)
^B213)
A212)
A112)
A113)
^B222)
¦БA212)
= ^A111)
= ~Е(П
= 1/*(ЯA
= ^B212)
= ^B213)
= ^A111)
= 1h (^(i
' ^B233) ~ ^
13) — ^A223)'
111) ~ A122
= -^C312) =
= ^A223) =
' ^B233) =
.111)— %122
A133)'
¦ ^A313)
^C323) =
?A123) =
^A133)'
))•
" ^B223) - 1
= ^B323)'
= ^C313) = '
= ^B223) =
¦^A313) =
v(ll23) ~ ¦ОA213)
A.9
БB313) =
ЯA213>=0'
^B323)'
Рассмотрим поперечную поворотную ось 2-го поряд-
порядка (:2), считая ее совпадающей с первой координатной
осью (&)! = я, &J = а)з = 0). Нетрудно видеть, что огра-
ограничения для этого случая можно получить из ограниче-
ограничений для 2 в A.9) путем циклической перестановки ин-
индексов 3->-1, 1->-2, 2 -*¦ 3. С учетом соотношений A.2)
имеем
:2 ^A112) = ^A11!) = ^B212) = ^B213) = ^C312) = ^C313) =
= -ЕA223) = ?B313) = 0- A.10)
Рассмотрим, наконец, равнонаклоненную к координат-
координатным осям ось симметрии третьего порядка (/3). Нетруд-
Нетрудно видеть, что поворот вокруг этой оси на угол 2я/3 =
¦= 120° переводит первую координатную ось во вторую,
вторую — в третью и третью — в первую. При этом не-
неизменность модулей упругости имеет место при
= ^B222) = ^C333)' ^A122) = ^B233) = ^A133)'
= ^B223) = ^C313)' ^B212) = ^C323) =
= -^A123) = ^B213)' ^A212) = ^B323) =
^A213) = ^B312) = ^A323)- A.11)
Соотношения A.9) — A.11) и пятый столбец табл. 3 по-
позволяют получить ограничения па вид упругих модулей
для всех кристаллических классов. Учитывая условия
симметрии A.2) и руководствуясь следующими правила-
правилами замены индексов:
A1)^A), B2)*= B), C3)^C), A 12
A2) ±* D), B3) ±* E), A3) ±р F),
§ 1. СТРУКТУРА ЗАКОНА ГУНА 35
можно собрать существенно различные модули упругости
в симметричные матрицы для спнготшй (кристаллографи-
(кристаллографических систем) и кристаллических классов:
?A111) ?A122) ?A133) ?A112) ЕО12Э) ?A113)
?B222) ?B233) ?B212) ?B223) ?B213)
?C333) ?C312) ?C323) ?C313)
пгриклинная Я Е
?A111) ?A122) ?A133)
?B222) ?B233)
?C333)
моноклинная
?A111) ?A122) ?A133)
B222) B233)
?C333)
ромбическая
?AШ) ?(U22) ?(пзз)
?(Ш1) Е(пзз) -
C333)
тетрагональная
(классы: 9; 10; 13)
?A111) ?A122) ?A133)
A111) ?A133)
?C333)
тетрагональная
(классы: И, 12, 14, 15)
?A112)
г»
B212)
?C312)
?A212)
0
0
0
?A212)
?A112)
- я(т2)
0
?A212)
0
0
0
?A212)
?B323)
0
0
0
0
?B323)
0
0
0
0
?B323)
0
0
0
0
?B323)
0
0
0
0
?B323)
?B313)
?A313)
0
0
0
0
?B313)
?A313)
0
0
0
0
0
?A313)
0
0
0
0
0
?B323)
0
0
0
0
0
?B323)
A.13)
36
ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
p
(III!)
р
A12-1)
?(uii)
тригоналышя
(классы: 16, 17)
?(iiii)
?(п22)
?Aш)
m ригоналъшя
(классы:
?(im
18, 19,
) ?A12,
?A133)
?um;
?C333)
?A133)
?A133)
?C333)
^2(?(iin
20)
A111) ?A133)
гексагональная
сю, сю: т,
т • сю: т
, оо -т
со: 2
C333)
'-( (П.
0
0
0
—
0
0
0
) ~
Ю'
?A122))
-?A122))
0
0
0
~?(П22>)
?A123)
~ ?A123)
0
' ?(П13)
B323)
?(П2
0
0
3)
3)
?B323)
0
0
0
0
?B323)
0
0
п
0
0
V
?Aпз)
" (IU3)
0
?A123)
0
?B323)
0
0
0
?A123)
0
?B323)
B323)
?A111) ?(Н22) ^'A122)
БA122)
кубическая
0
0
0
?B323)
0
0
0
0
Е
0
0
1)
0
... 0
B323)
"B323)
Из соотношений A.5), (!•") и матрицы гексагональ-
гексагональной спнгопии устанавливается, что в последней «уце-
«уцелели» лишь модули, инвариантные относительно произ-
произвольного попорота вокруг третьей координатной осп. По-
Поэтому текстура с продольной группой °° в отношении
упругих свойств ведет себя как кристаллы гексагональ-
гексагональной сингонин. Как нетрудно показать, это и;е относится
н к остальным четырем текстурам, указанным возле
матрицы гексагональной еннгонии.
0
0-
0
0
ЧП22))
0
0
0
0
0
S -. ГЛАВНЫЕ ОСП АНИЗОТРОПИИ 37
Гнротроппая (оо/оо) и изотропная (оо/оо ¦ т) среды
должны, очевидно, обладать симметрией как гексагональ-
гексагональной, так и кубической сипгошш. Сопоставление их мат-
матриц приводит к матрице
^A122) ^A122) °
0
О
~^A122))
гиротропняя (оо/оо), изотропная (оо/оо-ш) i/'-(J^(mn—¦
A.14)
удовлетворяющей элементам симметрии обеих сингоппй.
Можно показать, что они удовлетворяют также всем эле-
элементам симметрии щротрогшой и изотропной сред.
§ 2. Главные оси анизотропии
Следуя В. В. Новожилову [41, с. 149], введем главные
оси анизотропии. Для этого рассмотрим деформацию из-
изменения объема
e(ij) = leOij/6,
где /,. = е(И, + еB2) + еC3) — относительное изменение объ-
объема. Деформации изменения объема отвечает тензор на-
напряжений
0 (. — /s ..,хA g / /з — Е jaa I /3
Величины
К — F 19 1 \
* (О) — (ij*Aa) \ /
можно рассматривать как компоненты тензора объемных
модулей. В силу равенств A.2) — это симметричный тен-
тензор второго ранга. Его главные оси уместно называть
главными осями анизотропии. Из выражении B.1) сле-
следует, что is главных осях анизотропии
ЛA2) = 0'. ?A211) ~Г ?A222) Т -С>A233) == О,
ft оз _ 0; Е -зц + ? ->3- +?2333 =0, B.2)
Вернемся к таблице модулей A.13).
,'!S ГЛ. 2. ЛТТПЕПНАЯ УПРУГОСТЬ
Для триклишшй сингопии в главных осях анизотро-
анизотропии, в силу связей B.2), имеется 18 существенно раз-
различных модулей упругости.
Для моноклинной сингонии из условий B.2) остается
лишь первое, так что существенно различных модулей —
12. Нетрудно при этом непосредственно отыскать глав-
главные оси анизотропии. Аналогично тому, как это дела-
делалось в предыдущем параграфе, находим с учетом A.6)
= V
V2 (^B2<ха) — ^(паа)) Sin 2а + E(Uaa) COS 2ш.
Приравнивая нулю эту величину, приходим к соотно-
соотношению
2Е
^2ы=Е1аа-7ггаа' <2-3)
определяющему поворот вокруг третьей координатной оси,
переводящий координатные оси в главные оси анизотро-
анизотропии.
С учетом соотношений B.2) из таблицы A.13) ус-
усматривается, что остальные сингопии отнесены к глав-
главным осям анизотропии. Далее, аналогично B.3) нахо-
находим, что для тетрагональной сипгонии поворот, опреде-
определяемый соотношением
tg4co== 4^(Ш2) ,, , дает E[ini) = 0, B.4)
i4(lUl)~i4A122) ^A212)
а для тригоиалъной —
tg3M = — Я(шз)/Я(п2я). Даот Е'(шз) = 0. B.5)
При этом в двух последних спнгониях матрицы модулей
уже унифицированы внутри сингошш. Таким образом,
в тригональной и тетрагональной сннгониях по шесть
существенно различных модулей. Наконец, пз A.13) и
A.14) усматривается: в ромбической сингопии девять,
в гексагональной — пять, в кубической — три, а в изо-
изотропной среде — два существенно различных модуля.
Заметим, что сказанное в § 1—2 целиком относится
и к коэффициентам податливости a(mt), вводимым соот-
соотношениями
е(И) ~ Ot(«<»P>0(aP> B.6)
и удовлетворяющим условиям симметрии
§ 3. ПРЕДЕЛЫ ИЗМЕНЯЕМОСТИ КОМПОПЕПТ МАТРИЦЫ 39
§ 3. Пределы изменяемости компонент
положительно-определенной симметричной матрицы
Рассмотрим квадратную симметричную матрицу ше-
шестого порядка ?* = II ^{j Hi- Согласно известному критерию
Сильвестра [14] необходимым условием положительной
определенности симметричной матрицы является поло-
положительность всех главных миноров ее определителя.
В частности, tn > 0, ..., ?вв > 0. Используя эти неравен-
неравенства, введем обозначения
у» = ^1Ыи (v« = l), C.1)
при помощи которых матрице Т можпо придать вид
'll V1 VQ7 /у7 VUT У /^
12
V35
V45
22 66
V56 V 'м'вв
C.2)
Наряду с Т7 рассмотрим вспомогательную матрицу
26
V35 V36 C.3)
V V '
45 46
Используем обычную [14] сокращенную запись
(t,...,t + m-i \
для минора, полученного из определителя матрицы C.3)
вычеркиванием первых i — 1 строк, / — 1 столбцов и по-
последних п — (i + m—1) строк, п — (у + m—1) столбцов.
При указанном вычеркивании образуется мпиор т-го
порядка с элементом vo+m-^a+m-i) в правом верхнем уг-
/;, <-;- m — I \
лу. Если мерез Dt (у,..., j _;. ,п _ [ I обозначить анало-
аналогичный минор для матрицы Т, то нетрудно убедиться в
40
гл. 2. линейная упругость
справедливости следующего тождества:
-|- т — 1
-\-m — l
•m-l)(ifm-l)
m-n Z)
/, .... i-^m —
C.4)
Будем последовательно рассматривать элементы, рас-
расположенные на первой над диагонали (vi:, ..., vr.o), на
второй (vi3, ..., л*4в) и т. д., предполагая на каждом ша-
шагу, что элементы предыдущих паддиагоналей известны.
Используем положительность главных миноров. При
этом из выражения C.4) и положительности tu следует,
что можно ограничиться рассмотрением вспомогательной
матрицы C.3). Прежде всего
i,...,H-w--l
1 t(i4 m—1)^
+W!;::::!t;i1i),
+
где
;, ..., i-\-m — i
I 1 v
vi(i+m-2) ^
Требование положительности минора C.5) приводит
к следующему выражению для элементов (т— 1)-й над-
днагоиалн:
§ 3. ПРЕДЕЛЫ ИЗМЕНЯЕМОСТИ КОМПОНЕНТ МАТРИЦЫ 41
г, ..., I -\- т — 2
\
v , ,,..., l\-m-2 у
i, ...,
Подставляя выражения C.G) в C.5), приходим к сле-
следующему рекуррентному выражению для главного мпно-
мпнора иг-го порядка:
U\i l-\-m~i)
f COS
i- 1, ..., i-y m —
r-l,..., i-\-m —
Используемьп! критернГг Сильвестра является, как
jf3BecTiio, и достаточным. Так что изменение \is в naii-
денных для каждого из них пределах гарантирует поло-
положительную определенность матрицы.
Отыскание возможно более тесных границ изменения
элементов положительно-определенной .матрицы было
предметом многих работ. По-видимому, наиболее пол-
полным и интересным является исследование П. Бехтерева
[6]. Но его терминологии, найденные выше интервалы
изменения элементов — наитеснейшие [6, ч. 1, с. 81].
Элементы первых двух надднагоналей имеют следую-
следующие компактные трцгопометрпчоскпе представления:
vi(i+i) = sin p(+),
C.7)
v,-(,-+2) = sin ф,(,-.ц, sin ф(,-+|)A+2) +
+ cos ф1A+1) cos ф,,-.,.,и,-+2) sin ф,-(,Ч2) (—л/2 < фд < л/2).
Отсюда, как впрочем и из C.6), усматривается, что
при нагнем подходе интервалы изменения элементов,
принадлежащих рассматриваемой наддиагоналп, зависят
от «заполненности» интервалов, установленных для эле-
элементов предшествующих наддиагоналеи.
42 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
§ 4. Пределы изменяемости упругих постоянных.
Объемные и сдвиговые деформации
Закону Гука в прямой A.1) и обращенной B.G)
формах записи отвечает упругий потенциал
ij\f — '-'(ар)С' (сер) ¦*-' (Тбсср)С' (Тб)^ (йр) |-лGбсср)и (Тб) и (сер) • \ /
Используя замены индексов A.12) и вводя величины
?(П) = ?A)э ?B2) ~ ^B)? ^C3) == ^C)?,
^^A2) == ^D)» ^?B3) ^E)) "^A3) ^(б)?
' _ D.2)
О(Ц) 0A), 0B2) 0B), 0C3) 0C),
*^0A2) === 0D), *^ОB3) 0E), ^0A3) 0F),
имеем
2Ф = F р р = г/ а п fn « = 1 fit C4 Я^
Из положительной определенности выписанных квадра-
квадратичных форм (плотности энергии деформации) следует
положительная определенность матриц Ш^И, llajl. По-
Поэтому к упругим постоянным применимо сказанное в
§ 3. Так,
ti (v« = l), D.4)
ц (ц« = 1). D.5)
При этом
?„ ..., ?6>0; аи ..., сс6>0, D.6)
а величины Vy, цы изменяются в пределах, определен-
определенных для них в § 3. Величины Ei можно рассматривать
как обобщенные модули Юнга, а \ц = \ц — как симмет-
симметричные коэффициенты Пуассона различных порядков.
При этом под порядком понимается величина I/ — i\.
Тензор деформации можно представить в виде суммы
ЧИ) = ebi) + eW)- D.7)
Первое слагаемое — шаровая часть —
е№ = 1/зГе8ц (Те = 6(?v) = е(ц) + 6(.22) + еC3)) D.8)
определяет деформацию изменения объема, а вторая —
девиаторная часть
4) = е<У> - Va^Sii (efw) = 0) D.9)
§ i. ПГЕДИЛЫ 1Ш1КНЯГОЮСТ1] УПРУГИХ ПОСТОЯННЫХ 43
характеризует деформацию формоизменения при сохра-
сохранении объема.
Подстановка сумм D.7) в закон Гука A.1) приводит
к соответствующему разбиению тензора напряжения
где
V3 ( УЕгЕ2\12 -|- E2 + VE2E3v23)fe,
При деформации всестороннего сжатия имеем для ве-
величины среднего нормального давления
е. D.13)
Отсюда и из соотношений D.1), A.12) и D.4) находим
2Ф = i/,/;/e. D.14)
Из полученного выражения для (положительного) уп-
упругого потенциала следует, что деформации всесторонне-
всестороннего сжатия (/„ < 0) отвечает отрицательное среднее нор-
мальпое напряжение.
Для анизотропного материала полученный результат
не совпадает, вообще говоря, с утверждением, что все-
всестороннее нормальное давление уменьшает объем. Для
доказательства последнего рассмотрим всестороннее нор-
нормальное давление, при котором
аЬз) = V3^o6{j (Л* = C(w) = °m) + 0B2) + О(зз))- D.15)
Аналогично проделанному выше находим
2Ф = i/Л^, D.16)
где
К = Vs [«1 + К2 + «3 +
44 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
¦— отвечающее всестороннему обжатию изменение объе-
объема. Отсюда н следует, что всестороннее нормальное дав-
давление (/„ < 0) уменьшает объем (/е<0).
§ 5. Несжимаемы» материал
В механике твердого деформируемого тела часто пред-
предполагают материал несжимаемым. Это позволяет в ряде
случаев упростить решение задач. Применительно к ли-
линейно-упругому материалу используем выражения B.6)
и D.5), подставляя их в условие несжимаемости еПТ) =
= 0. Требуя, чтобы последнее выполнялось при произ-
произвольных напряжениях, получаем условия несжимаемости
материала в виде
Из них находим
2 /5^ц12 = *.,-«,-а,. /у,4-=- /«>и- /V2l.
2 УЧаЛз = а2 - аз - «1. /аз^о = - УаЛе - /«2^с-
E.1)
В силу использованпоп связи еGТ) = 0, из шести вы-
выражении B.G) линейно независимых лишь пять. Опу-
Опуская поэтому третье и подставляя выражения E.1),
D.5) в оставшиеся, получаем
б(п) = с, (а(п) — аC3)) + х/2 (а.ч — °Ч — а2) (Оо2 — аC3)) +
+ 2 /а^(/а4|х14аA2) + /cc5u]soB3) + /авц,ваA8)),
еB-з) = V2 (а.ч — ее, — а.а) (а(п) — аC3)) + сс2 (аB2) — аC3)) + .
+ 2 /l(/l(]2); /^45B3)! /Зд4в
E.2)
6B3) /^[ / (f О /Г ( )] +
f 2 /а ( /a#CT + Vatf т
2 /а,
s :•. несжимаемый материал 45
— oC3)) \- V сс^.,,,^,^
С уютом соотношении 0-2). A.3), (/i.-r)) н E.t) подсчи-
подсчитываем
2Ф -, а, (аA|)— а,,.))-• -4 а2 (о-C2) — аC3))- -|-
¦ 1-(а3 — «! — ос2) (а(п) — а(яя)) (оB2) — а(яч)) |-
I- 7i /a, (o^o, — uC3)) ( Vа.АЦц
-I- 2 /ai^i^Od^CTf.,,) + cts0(fl3) v 2 /а4
; 2 /a^ja^aj^^daj f a0a;213)). E.3)
Как известно из курса алгебры, из положительной
определенности квадратичном формы (•">.3) (плотности
энергии деформации) следует разрешимость системы
B.6), так что
i2e(U)
E.1)
0A3) = VX [ /^V'lGfOl) +
Формулы, связывающие упругие постоянные Eit Vi, и аь,
нЛ', не ныппсыцаем из-за п.\ громоздкости.
\\л иос.чеднп.х cooTiioiiieiinii ппдпо, что нормальные
напряжения определяются с точностью до произвольной
функции типа всестороннею давления р. Пользуясь
этим, можно придать выражениям E/i) (и притом не-
едпнетвеиньш способом) симметричную относительно
оA() форму. Форма же записи E.4) удобна, когда в
46 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
рассматриваемой проблеме имеется предпочтительное
(третье) направление. Из E.3) также усматривается,
что в общем случае несжимаемому материалу отвечают
15 независимых упругих постоянных.
§ 6. Плоское напряженное состояние
Плоское напряженное состояние определяется равен-
равенствами
о(зз) = 0, e(i3) = еB3) = 0. F.1)
С учетом этого находим из соотношений A.1), A.2) и
D.4) для сжимаемого материала
где
(v« = V« = 1). F.4)
Для несжимаемого же материала имеем с учетом со-
соотношений F.1) и E.2)
26^50 - ЦявМи) + 2 V^^eH-se - |J.45)aA2)], F.5)
I ^"i^^ - Hie)
- И2б) %2) + 2 /^
§ 7. ОРТОТРОПНЫЙ МАТЕРИАЛ 47
У 2 к ai
а2аB2) + 2 к a
где
(и-is = 'А (а3 — «1 — а2), ц« = 1).
§ 7. Ортотропный материал
Как уже отмечалось в § 4, ортотропный материал в
отношении упругих свойств «ведет себя» как кристаллы
ромбической сингонии. Поэтому из третьей матрицы в
A.13) при замене индексов A.12) имеем с учетом выра-
выражений D.4) и D.5)
Vu = Vis = V16 = V24 = V25 = V2e = V34 = V35 = V3e =
= viS = v4e = v5e = 0,
yw-' G.1)
ЦН = H-15 = file = Ц24 = |^25 = Ц26 = М34 = H-35 =
= Цзв= |i<5 = |i46 = Ц56 = 0.
Отсюда и из соотношений A.1) и B.6) имеем для сжи-
сжимаемого материала
+ V ¦?'l
V ElE
+ у E
У ^i-^3vi3e(ii) + к E
G.2)
= 2a4a(i2),
48 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
B3) ¦= 2а5аB3),
G.3)
При этом сопоставление выписанных выражении приво-
приводит к следующей связи меж/iy упругими постоянными:
1 (l — ц12), A
A = 1 -Ь 2ц,2И2зИ13 — (м'Г-2 + fiaa -;- His),
G.4)
Согласно соотношениям D.1) выражениям G.2) и
G.3) отвечает ynpyrnii потенциал
2Ф - #!<??„
+ 2
+ 4 [Еле12) + Ebef23)
a3ofm) + 2[ /с^а^,,
4 [a4aB12) + abo\iS) -\- cc0aB13)]. G.5)
Согласно соотношениям C.7) положительность упругого
потенциала обеспечивается соотношениями
v,2 = sin ф,п, v.a = sin rr,3, G.6)
Vis = sin фц sin ((.3 + cos ф,; cos cp23 sin cpl3
(-7гл<Фо<72я).
Последние иавнсн.мостн можно заменить неравенствами
G.7)
§ 7. ОРТОТРОПНЫЙ МАТЕРИАЛ 49
Для несжимаемого материала имеем согласно E.2),
E.4) и G.1)
Со(и12 =¦¦ 72(а3- а, —аг), G.8)
(ц) = а,(а(п) — а(зз>) + 72(а3 — at — а2) (аB2) — а(зз)),
,22) = 72(а3 — oti — а2) (а(И) — о(з3)) + а2(оB2) — о133)),
.П) = 2с44о(|?0, с.23) — 2а5аB3), е(,3) = 2а6аA3)
G.9)
C3) *-J 1^A1) ' ' *-J J *~J 2* 12^B2);
g зз = }:Е{Ел\-е и + E2e v, G 10)
U(I2) '-(ij'lt'A2) 5 OB3)
При этом
X Г/ Г/ - 1 I %П
к.
G.11)
'/о (ос3 — rx1 — a2) ^
?4a4 = ?sa3 =¦ /?6а6 = 74.
С учетом этих связей находим из выражении E.3)
2Ф =• <хх (a(ll) — oC3J)- ;- a, (a(,2) — aC3)J +
+ (a3 — ot1 — cx2) (o(u) — aC3)) -¦- (aB2) — oC3)) +
-f 4 (a4aC12) -f a5af23) -\- a,of13)) G.12)
ИЛИ
2Ф = ?I<?f10 p 2 /Ж^12вA1)е(,2) -!- ?2<??22) +
. G.13)
4
Таким образом, для несжимаемого ортотроппого мате-
материала имеем шесть независимых упругих постоянных.
При этом
?\>П, Е,>0, Е,Х), Е.а>0, Ев>0, |v12Kl.
G.14)
4 К. Ф. Черных
50 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
Нетрудно проверить, что закону Гука G.10) можно
придать и симметричную форму
сгB2) — /> = Tf4e(H) + Tf2eB2) + if5eC3), оB3) = 2?seB3), G.15)
°(зз) — Р = Tf«e(«i) + Tse<22) + Тзе<зз) 2#
где /) — произвольная функция,
G.16)
а коэффициенты "fi, Тг> Тз могут быть фиксированы про-
произвольным образом.
Для сжимаемого материала в плоском напряженном
состоянии имеем из соотношений G.1), F.2) — F.4)
G.17)
G.18)
(стаз) = стB3) = 0);
2Ф = IVBn) -|- 2 VEiEavlftivell2y+
lf 2); G.19)
V23
В соотношения G.18) —G.19) входят четыре упругие
постоянные. При этом положительность упругого потен-
потенциала обеспечивается неравенствами
1,>0, Ё2>0, ?4>0, |v,,l<l. G.21)
Для определения же е(зз> необходимо дополнительно
знать еще три упругие постоянные.
Для несжимаемого материала в плоском напряжен-
напряженном состоянии имеем с учетом соотношений F.6)
и F.7)
' EiE2
0ГB2) = /ад.Уивй,, + ^2^B2), G.22)
§ 8. ТРЛНСВЕРСЛЛЫЮ-И30ТР01ШЫЦ МАТЕРИАЛ 51
o(i2) — 2?[4еО2) (°(i3) = 0B3) = О)!
I- г a^
е(П) =
^ a2aB2), G.23)
еA2) = 2а4оA2)
а1 — аг)> ai = ai» а2 = а2,
а4 = а4, ^4а4 = V*. G.24)
= аГЧ?- и,), ^2 =«2 'A - Й)"Л
При этом положительность упругого потенциала
2Ф = c^ofu)
= ЁАи> + 2 /Ij^v12eai)eB2) + S2ef22) + 4?3eB]2) G.25)
обеспечивается неравенствами
ai>0, a2>0, a3>0, I7i12l<l. G.26)
Как видно из выражения G.17), при поперечном мо-
модуле Ez, являющемся величиной того же порядка, что и
Ei, E2, поперечное относительное удлинение еCз) является
малой того же порядка, что и еA1), еB2). Пренебрежение
им по существу устраняет различие между сжимаемым и
несжимаемым материалами в плоском напряженном со-
состоянии. Если же модуль Е3 мал (как, например, в пла-
пластине с мягким заполнителем), пренебрегать еC3) уже
нельзя.
§ 8. Трансверсально-изотропный материал
Трансверсально-изотропный материал в отношении
упругих свойств идентичен (см. гл. 1) кристаллам гекса-
гексагональной сингонии. Сопоставление же предпоследней
матрицы в A.13) с третьей, которая отвечает ортотропно-
му материалу, показывает с учетом A.12), что трансвер-
трансверсально-изотропный материал можно рассматривать как
частный случай ортотропнОго при
Ег = Еи v,,-vu, Я4-'/,?, A - v,s),Я, = Я5;
(8.1)
a* = a,, Hii = fiMf а4-=7аа,A-ци),ав = а(.
4*
52 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
С учетом этого получаем из соотношении предыдущего
параграфа для сжимаемого материала
0,11, = А'|(е(П) Н- Vi2CB2)) + УЕ,1?3х13еоз„
о,,;., =-?,A -v,:)e,i;:),
о(=2) = ?1i(v1,e(,,) + e(c:)) +- У ?',?>,,с(П),
<T(aj) = 2?5e(;a), (8.2)
еB2) =ai(Hi2<T(i!) + °B2,)
еB3) =- 2а;,оBз), (8.3)
—
1;, - a,"J
Выписанным соотношениям отвечает упругий потенциал
2Ф = Ех [efu) + 2v]2e(U) eB2) -j eB2i)+ 2A — vJ2) efl2)] +
+ 2 /^ЯдЛ^з (<?(ю -г e{i2)) em -f ¦ ^efos) + 4?3 Dз) + ''аз)),
(8.5)
положительность которого обеспечивается неравенствами
(см. G.7))
Е, > О, Е3 > 0, ?5 > О,
(8.6)
Для несжимаемого материала имеем
aiMi: = 'Aa-j —a,; (8.7)
2cx3-ai) (о(:2) - oC3)),
C3,) + a,(OB2)- OC3)),
(8.8)
§ 8. ТРЛНСВЕРСЛЛЬНО-ИЗОТРОПНЫП МАТЕРИАЛ 53
), еA2) =Bai —
6B3) = -0^5^B3M 6A3) =
0A1) — 0,33) =?'1FA1) + V( 12NB2)),
ОB2) — 0C3) = ?l(V]2e(ll) + 6,22)),
(8.9)
o,i2) —Ei A — v12)e(l2), oB3) = 2?0e,23), o(i3) = 2?5eA3),
где
" 4 '
(8.10)
Положительность упругого потенциала (см. G.12), G.13))
2Ф = at (оШ) — aC3)J -Ьсц (aB2) — aC3)J +
-h(oc3 — 2ai) (a(]1) — aC3)) (aB2) — aC3)) + D^ — a3)aB12) +
-!- /(аз (ffB23) — o213)) = El (e(u) •¦!- 2v12e(n)eB2) + eB22)) +
+ 2?, A - v12) 6?2 -f AEb (eB23) + eB13)) (8.11)
обеспечивается неравенствами
0<а3<4а„ 0<а5. (8.12)
Для сжимаемого материала в плоском напряженном
состоянии имеем (см. G.17) — G.21))
(8.13)
(8.14)
0,22, = Ei (е,22) + Vi2e(n,) (о(гз) = 0A3) = 0);
2Ф = ?, (efn) + 2v12e(ll)eB2) + ef22)) + 4?4ef12); (8.15)
v1 V»JTI'3
12 - JTVI '
(8Л6)
E,>0, Es>0, lv,2l<l.
Для несжимаемого материала в плоском, напряженном
54 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
состоянии (см. G.22) —G.26))
ст(М, =Е1(е(И) + v12eB2)), aB2) = /^(e^j +
2Я4еA2); (8.17)
(еB2) + Ци^И)),
(8.18)
^ = «Г1 A- fii'J, Ы
При этом положительность упругого потенциала
2Ф = «х (crfii) + 2jx12o-Ai)O-B2) + of22)) + 4а40B12) =
= Ei (efu) + 2viaeA1)e(aa) + e(fM)) + 4f4eJu) (8.20)
обеспечивается неравенствами
сё,>0, а4>0, 1ц„|<1. (8.21)
§ 9. Изотропный материал
Сопоставление отвечающей трансверсально-изотропно-
му материалу предпоследней в A.13) матрицы модулей
с матрицей A.14) показывает, с учетом A.12), что изо-
изотропный материал можно рассматривать как частный слу-
случай трансверсально-изотропного материала при
,
(9.1)
-
Вводя обычпые для изотропного материала обозначения
упругих постоянных (Е — модуль Юнга, v — коэффици-
коэффициент Пуассона) а, = Е~\ yLi2 = —v, находим из выражений
(8.4) и (9.1) для сжимаемого материала
«1 = а3 == Е~\ аъ = A -f v) Е~\ ц12 = ц13 = — v,
(9.2)
Е -Е - Еи~ч) Р Е v -у - v
1 3 (l + v)(l-2v)' 5~2(l + v)' 12 13 1 —v'
а из соотношений (8.2) — (8.6)
)A j2v) [(I - v)eA1) -,L v(eB2) + eC3))],
E
§ э. изотропный Материал 55
v) A _ 2v) [A - v) eB2) + v
e). (9-3)
°(зз) = A + v)A_2v) [A - v) em + v(eA1j + бB2))],
Е
6A1) = "g- [°A1) — V (<^B2) + °C3))], ^A2) = —?— СГA2),
1 1 + V
[О( V(°( + °())] 6( =
Положительность упругого потенциала
2Ф = A + )^2у) (g(ll)
6B13))] (9.5)
обеспечивается неравенствами
?'>0, -Kv<72. (9.6)
Для несжимаемого материала имеем с учетом соотно-
соотношений (9.1), (9.2), (8.7) —(8.12)
и = —ЧгЕ~\ а5 = УцЕ~\
(9.7)
i/E l
е^2) =
=(ОB2) — 0C3))— V2(O(ll) — 0C3)), EeB3)=3/2<J{23), (9.8)
> =-'/2[@(„,- 0C3)) + @B2, — 0C3))], ?<?(,3) = 3/2О(,3);
) ())
(9.9)
0B2) — 0C3) = 4/з#(<?B2) + 'Ае(,,,),
0A2) == /3-^6A2), 0B3) == '3^6B3), 0(K) = /зС'6(K).
Положительность упругого потенциала
2Ф = 4/зй(бB11) + 6A1)еB2) + 6B2) + <?B12) + 6B3) + 6B13))
(9.10)
обеспечивается единственным неравенством
?>0. (9.11)
56 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
Для сжимаемого материала в плоском напряженном
состоянии согласно зависимостям (9.2) и (8.13) —(8.16)
инеем
<*B2)
2Ф -
e
E
1 — v2 V l"
l-v2^1'
(за, !_>„
) + Ve(ll))i (a(-23)
) + 2ve(n)e(i2) + e
E>0, -Kv
E
1 + v-l
¦B2)+ 2A
<72.
0);
(9
(9
У; (9
(9.
.12)
.13)
.14)
15)
Для несжимаемого материала в плоском напряженном
состоянии находим из соотношений (9.7) — (9.11) и (fi.l)
,; (9.16)
§ 10. Ортотропный цилиндр под давлением
Рассмотрим полый цилиндр (рис. 2.10.1), нагружен-
нагруженный наружным и внутренним давлением со стесненным
(нулевым) осевым растяжением. Для него
3
Согласно соотношениям G.2) для ортотропного материа-
материала имеем
СТ(гг) — Cjr^(rr) + ' ^i^eVreC(ee),
a,ee) = y^?"ev,ee(rr) + Яве(вв„ A0.2)
Имеет место единственное уравнение равновесия
—тг1 = ^сое)- A0.3)
10. ОРТОТРОППЫП. ЦИЛИНДР ПОД ДАВЛЕНИЕМ
57
Подстановка выражений A0.1), A0.2) в уравнение
равновесия A0.3) приводит к уравнению
"(г)
idif
с общим решением
где
dr Er r*
X = УЕо/Ег > 0.
Отсюда и из соотношений A0.1), A0.2) находим
A0.4)
A0.5)
A0.6)
Ё3 = С, (Vro + Ves) Г7-'1 + С2 (-Vr3 + Тез) Г'*'1.
Удовлетворяя граничным условиям (рис. 2.10.1)
(T(")(ri) = —?i, a(rr)(r2)=-g2, A0.7)
получаем
г _ 1 угх~' +угх~'
" A0.8)
«X 1„ — А — 1 _|_ „ — А— 1«Л 1
Г1 Л2 "I" Г1 '2
Рассмотрим снлошно1г цилиндр, принимая г4 = 0, г2 =
= /•„., q-i = q. Согласно соотношениям A0.4) и A0.5) ко-
конечность смещений оси цилиндра (г = 0) обеспечивается
Рис. 2.10.1
58 ГЛ. 2. ЛИНЕЙНАЯ УПРУГОСТЬ
при Сг = 0. При этом из A0.8) следует
г _ ч 1_
1 т/"п 77 ,м I . \ У — 1
п согласно A0.4), A0.6)
17 ' ' > • A0.9)
Х-1
Е,-
Отметим, что прп % = 1, т. е. при Е6 — Ег, напряжен-
напряженное состояние не зависит от г. При % > 1 (Ее > Ет) на-
напряжения убывают при приближении к оси цилиндра,
обращаясь на ней в нуль. И наоборот, при % < 1 (Ее <
<ЕГ) по мере приближения к оси напряжения неогра-
неограниченно возрастают. Нетрудно дать этому физически
правдоподобное объяснение. Цилиндр можно представить
как бы состоящим из множества вложенных друг в друга
тонкостенных цилиндров. При большей кольцевой жест-
жесткости (.Ее > Ег) сжимающая внешняя сила давления вос-
воспринимается в основном кольцевым распором внешних
цилиндров, и напряжения падают при переходе от одпого
цилиндра к другому, меньшего радиуса. Наоборот, при
меньшей кольцевой жесткости (Е6<ЕГ) распор невелик,
и внешняя сила давления, мало убывая, передается на
внутренние цилиндры. Поскольку последние все умень-
уменьшаются в диаметре, напряжения растут по мере прибли-
приближения к оси.
При ортотропии, обусловленной армированием мате-
материала, случай Е6 < Ег может служить наглядным приме-
примером неудачного армирования.
ГЛЛБЛ 3
НЕЛИНЕЙНАЯ УПРУГОСТЬ
В главе рассматриваются нелинейно-упругие материа-
материалы. Приводятся основные соотношения нелинейной тео-
теории упругости. Выявляется структура упругих потенциа-
потенциалов, отвечающих различным типам анизотропных мате-
материалов. Выписываются условия перехода при малых де-
деформациях упругих законов в соответствующие законы
Гука. Рассматривается плоское напряженное состояние.
Особое внимание уделяется ортотронному, трансверсаль-
но-изотропному и изотропному материалам.
§ 1. Основные зависимости
нелинейной теории упругости
Приведем основные зависимости нелинейной теории
упругости в криволинейных координатах общего вида
[73, 53]. Пусть уравнения движения материальной точки
в пространстве, отнесенном к прямоугольным декартовым
координатам хи х2, х3, имеют вид
xt = x,(al, a2, a3; t) (t = l, 2,3). A.1)
Здесь а1, а2, а3 — криволинейные материальные коорди-
координаты, индивидуализирующие материальную точку рас-
рассматриваемой материальной частицы.
При рассмотрении материальной криволинейной си-
системы координат будем использовать соотношения При-
Приложения А. Следует, однако, различать две конфигура-
конфигурации тела: недеформированную (исходную, отвечающую,
например, в соотношениях A.1) значению t = t0) с коор-
координатными векторами
Rlt R2, R3; R\ W, R3; A.2k
компонентами метрического тензора
60 M. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
и деформированную (текущую) с координатными век-
векторами
R,, R2, R3; R1, R2, R3; A.3),
компонентами метрического тензора
Ri-Rj-gii, R'-R'-^', Я1-К] = ё} = 6]. A.3),
Введенные координатные векторы связаны соотноше-
соотношениями
Rj = FRi, R; = F -Rj, „^
R'^F^R', RJ' = F*-R'.
Здесь
F = RPRP = ?apRaRp, F* = RVRV = ?vR>v,
A.5)
— градиент движения и отвечающие ему: обратный (-1) и
сопряженный '*' тензоры. Здесь и ниже по повторяю-
повторяющимся греческим индексам производится суммирование
от 1 до 3.
Градиент движения F характеризует как деформацию,
так и поворот материальной частицы. Имеют место так
называемые полярные разложения
F = Q Л,
A.6)
F* = A-Q*, F^-A^-Q*, F^'-F* = Q-A~\
о
Здесь А—тензор кратностей удлинений, в своих главных
осях имеющий вид
А = Aaeaea, A.7)
о о о о
где eve2, еЛ— орты главных направлений тензора А.
Своим названием тензор обязап тому, что
Xt = dst/dsi, A.8)
О
где dst, dsi — длины элемента (следующего главному на-
направлению) материального волокна до и после деформа-
§ 1. ОСНОВНЫЕ ЗАВИСИМОСТИ 61
цпи; Q — ортогональный тензор поворота материальной
частицы. При этом
Q* = Q'; Q*.Q = Q.Q* = 1. A.9)
Наряду с тензором кратностей удлинений широко ис-
используются: тензор деформации Коши — Лагранжа
С8 = Л2 = F* • F = Я^ёаеа A.10)
и тензор деформации Грина — Лагранжа
Е = V* (Л2 - 1) = V2 (F*-F - 1) = V2 О« - 1) ё«ёа. A.И)
Из соотношений A.10), A.11), A.2J. A.3J п A-5) сле-
следует (LpRaRfl = 1)
С = ce(,R°Rp = F* • F = fopR'R^, A 12)
Ё = pal1RaRp = V, (F* ¦ F - 1) = V4 &*р - lap) RaRP.
т. е.
ct) = ?y, ey = x/2 (ft; - i«)- A -13)
Кратность изменения объема материальной частицы
при ее деформации иодсчптывается по формулам
/ = dV/dV = Я^Дз = Vg/g. A.14)
Пусть dSn и rfiS,, — площади материальной элементар-
о
hoi'i площадки до и после деформации, а п, п — единич-
единичные векторы нормалей к ним. Имеет место соотношение
ndSn = n-J?-4Sn. A.15)
Вектор смещения материальной точки и связан с ее
радиусами-векторами до и после деформации соотноше-
соотношением
u = R-R. A.16)
Отметим, что в нелинейной теории упругости вектор сме-
смещения часто просто не используется, поскольку в качест-
качестве искомой величины удобнее рассматривать непосред-
непосредственно R.
Напряженное состояние описывает тензор истинных
напряжений Коши
2 = а*(ВД, (о" = о"). A.17)
62 ГЛ. 3. НЕЛШПЗПНАЯ УПРУГОСТЬ
При рассмотрении больших деформаций наряду с векто-
вектором напряжений
0-. = п-2 A.18)
вводят в рассмотрение вектор напряжений в расчете на
единицу площади до деформации
о. = ап (dSn/d°Sn), A.19)
для которого
=n-{F-1./S). A.20)
п
Здесь {F • /2} — номинальный тензор напряжений. Для
него согласно соотношениям A.17) и A.4) имеет место
представление
{F-1 • m = /oaPRaRP. A.21)
Тензор второго ранга, индексы которого отнесены к раз-
разным базисам, называют двойным [73, 83]. Таким образом,
в записи A.21) тензор номинальных напряжений пред-
представлен как двойной тензор напряжений. О преимущест-
преимуществах последнего подробно сказано в [73].
В недеформированиой конфигурации имеют место:
уравнения равновесия (V = RWdaT)
f>f = 0 A.22)
и статические граничные условия
i-lF-'-./Sl-a-fa*). A.23)
о
В приведенных соотношениях р — плотность материала
до деформации, f—вектор массовых сил, о о — заданный
вектор напряжений.
Подстановка выражения A.21) в A.22) —A.23) при-
приводит к первым двум из следующих зависимостей крае-
краевой задачи:
R^.A(/a^RaRp) + pf = 0 (аье=У),
оса,'
n-(/aapRaRp) = (To(afe) (afe €=?„), A.24)
u = u(ccft) (R = R(cc&)) {ak<=Su).
§ 1. ОСНОВНЫЕ ЗАВИСИМОСТИ 63
При формулировке краевой задачи было принято, что
S =Sa+ Su, где Sa и Su—части недеформированной гра-
граничной поверхности, на которых заданы соответственно
напряжения и смещения (деформированная конфигура-
конфигурация). Используя соотношения (А.31), (А.38) для вели-
величин с °, приводим задачу к компонентной (скалярной)
форме записи (/=]/ g/°g)
^(ah) (а1е5„), A.25)
и'" = и''(а*) (а1е1).
В случае, если поверхностной нагрузкой является нор-
нормальное давление an = —qn, то согласно соотношениям
A.15), A.19) и A.4)
о о
Go = (dSjdSn) On = — qJn^'Rr,
,-. a," A-26)
B
Закон упругости имеет следующий вид: для сжимае-
сжимаемого материала
Л"-2^, A.27)
а для несжимаемого
„«-2^ +ре*. A-28)
Здесь р — произвольная функция типа всестороннего дав-
лепия, определяемая из статических соображений.
Для изотропного материала
Ф = Ф(/С, IIс, ///с), A.29)
где главные инварианты подсчптываются по формулам
= gIg. A.30)
При переходе к физическим компопентам векторов п
тензоров необходимо точно указывать, по отношению к
04 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
какой материальной метрике (недеформированной или
деформированной) это делается. В дальнейшем, сохраняя
символ ( ) для физических компонент в деформирован-
деформированном материальном базисе, введем < > для недеформпро-
ванного.
Итак, в недеформированном материальном (ортого-
(ортогональном) базисе имеем согласно формулам (А.41),
(А.43), (А.40) и A.30)
ij = g<u> V gag», оl] - o\ J V gngjj-,
A.32)
A.33)
С учетом выражении A.32) соотношениям упругого
закона A.27) — A.28) можно придать вид: для сжимае-
сжимаемого материала
A.34)
A.35)
а для несжимаемого (J = IIIс = 1)
§ 2. Закон упругости
Запишем упругий потенциал (плотность энергии де-
деформации) в виде
Ф = Ф[^,(?(Ы>), ..., Чп(Вю)], B-1)
где х? i — инварианты рассматриваемого анизотропного
материала. Согласно соотношениям A.34) в главных осях
§ 2. ЗАКОН УПРУГОСТИ 65
анизотропии для сжимаемого материала
Ja<-v> = 2W-arL G = 1,..., га). B.2)
В частности, для тензора деформации Грина — Лагранжа
A.13) можно ввести упругий потенциал (ср. B.4.2) —
B.4.4))
2Ф = УЕаЕц vaCe<a>e<(i> (vti = 1)
°оОоооо о /о О\
(e<i> = eai>, e<2> = F<22>, е<з> = *?<зз>, %> = 2е<|3>, ^ • '
О О О О
Е<5> = 2е<2з>, е<6> = 2е<13>),
которому отвечает сжимаемый стандартный анизотроп-
анизотропный материал
/а<0 = ВД^вда (I, р = 1, ..., 6). B.4)
Закон упругости для несжимаемого материала имеет,
с учетом соотношений A.28), B.1), следующий вид:
ЭФ
По аналогии с законом B.4) можно ввести в рассмотре-
рассмотрение несжимаемый стандартный анизотропный материал,
о
заменяя в соотношениях B.5.4) е<«> па е^:
В ортогональной системе координат с координатными
осями, не являющимися главными осями анизотропии,
имеем согласно соотношениям B.2) и (А.48)
Jm= V
V
Вернемся к закону упругости B.2), потребовав, что-
чтобы при малых деформациях он переходил в закон Гука
B.1.1). Прежде всего согласно A.13J при малых дефор-
деформациях имеют место переходы
(
Здесь и ппже индексом 0 помечаются величппы, подсчи-
подсчитанные при е(ц) = 0, т. е. при отсутствии деформации.
«J К. Ф. Черных
66 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
С учетом выписанных соотношений находим, что выра-
выражения B.2) при малых деформациях переходят в зави-
зависимости _
2A- баре(аР)) Ф?, + 4ФЬ.а№*»), B.8)
где использованы обозначения (?, /, к, 1 = 1, 2, 3; ^ —
= 1, ...,»)
B-9)
^v io
Сопоставление выражения B.8) с B.1.1) приводит к
условиям перехода при малых деформациях закона упру-
упругости для сжимаемого материала в закон Гука:
Ф?,- = о, Ф°Ш1 + ФЬ,ш = ЧЛту B.Ю)
Переходя к несжимаемому материалу, исключим из
уравнений B.5) с помощью третьего из них величину р:
ЭШС 0Шс о оф 1дЩс дУу 0Шс дУ
Используя соотношения B.7) и легко проверяемые при
помощи A.33) равенства
дТПс I 01IIЛ I д2Шс \
fiip6ja) e(ali), B.11)
бюбщ + бгабгр = бор — бзобзр,
получаем, исключая из правой части е(зз> (= — е(I) — еB2)),
2 (Ф?; - 6{jO^3) + 4 (Ф?;,«р - буФ3Оз,ар -
Сопоставление получеппого выражепия с B.fi.'5), B.1.12)
приводит к условиям перехода при малых деформациях
закона упругости для несжимаемого материала в закон
§ Я. ПЛОСКОЕ ТТЛТТРЯГШГ.ППОГ. СОСТОЯНИЕ 07
Гука
Ф9, ^ буФзз,
B 12)
V (о? + OS) V/ (Ф^ + Ф?мя) -
= 1UE№iv
§ 3. Плоское напряженное состояние
Обобщая определение B.6.1) на случай больших де-
деформаций, будем называть нелинейным плоским напря-
напряженным состоянием такое, при котором
0<зз> = О, g(.3> = ?<23> = 0. C.1)
При этом для сжимаемого материала имеет место согласно
соотношению B.2) уравнение
е/Лз, =) -|jr- S1- = ° (V = 1, •¦¦,»), C-2)
из которого gC3> определяется через остальные искомые
величины. Далее,
/, У = 1, 2;
i
где ?<1з> = ?<2з> = 0, a gC3> заменено его выражением из
уравнения C.2) и согласно C.1) и A.33)
/^C=(g(il>?<22>-?<12>gB1>)^<33). C.4)
Для несжимаемого материала из условия несжимае-
несжимаемости Шс == 1 и C.4) находим
?<зз> = (?<u>?<22> - g<12>g<21>) -1. C.5)
Далее из соотношений C.1), C.4) и B.5) следует
= 2 'дФ дУу
5*
68
ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Из полученных выражений и C.4) получаем
_ о ЭФ
9 дФ
UB2) = ^~Ш~
У
. C.6)
5Ф V
5?-^--, aB3, =
ЭФ
Преобразованиями, аналогичными проведенным в
предыдущем параграфе, получаем условия перехода при
малых деформациях уравнений упругости сжимаемого
материала C.3) в закон Гуна B.6.3)
Ф3°3 =
33
где
^^ V
^B222) = -^2>
¦#
B212)
К -
Для несжимаемого же материала условия перехода
имеют тот же вид B.12), но при г, ;, к, 1 = 1, 2.
§ 4. Ортотропный материал
Ортотропный материал имеет три ортогональные
между собой плоскости симметрии. Согласно формулам
(A/i9) при отражении в первой координатной плоскости
= ?B2I
/ /
?A2) — ~~ ?(i2)r ?(i3) = —
" ?(зз)>
?B3) = ?B3)-
Отсюда видно, что упругий потенциал не меняет своего
вида при рассматриваемом преобразовании, коль скоро
§ 4. 0РТ0ТР01ШЫЙ МАТЕРИАЛ С9
ого аргументами являются величины
g #
8A1), 8B2), gC3)!
Совершеппо апалогнчпо обнаруживаем, что при отраже-
отражении п оставшихся координатных плоскостях вид потен-
потенциала сохраняется соответственно при аргументах
8A1), ?B2)» ?C3)! ?A3), 8B3I gfl2h 8B3)8A2)', D.1K
8A1), gB2)> 8C3)', 8A2), 8A3), 5B3)» gA8)gB3)' D.1K
Аргументами упругого потенциала являются общие
для трех вьшисанных наборов инвариантные комбинации
8(и), 8B2), 8C3), 8A2), 8B3), 8A3), 8{12)8Bз)8из)- D-2)
Но согласно третьему из выражений A.33)
= 2g(l2)gB3)gA3) + g(U)gB2)gC3) —
2
Отсюда видно, что в аргументах D.2) подчеркнутый член
можно заменить на П1С, так что в симметричном по ин-
индексам виде
D.3)
и согласно выражениям B.2) для сжимаемого материала
= 2U^ h d/// (gC3)g(ll) —
= 2 \
= 2 Ig25_ + ^^- (gAi)gB2) — |fi«))J, D.4)
-Щ g(i2) + JJJj-(8A3)8B3)— 8A2)8C3)) \,
2
70 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Согласно зависимостям D.3) и B.9) для ортотронного
материала (г, /, к — 1, 2, 3; ^)
фп =( д2Ф \ . ( д2Ф \
д2
л ЧШ+A-«&1, («>
Отсюда и из соотношений B.10) следуют условия пере-
перехода при малых деформациях закона упругости D.4) в
закон Гука B.7.2)
Щ.) + U*L\ = о
(г, Л = 1, 2, 3; i^ft),
/ эЧ \ ( д*ф \ ( <?Ф
?Ф_\ _ /_аф_\ _ 1 г-
«*(.J. I a///cio ~ 2 4'
эф \ = j_ г,
h 2 в>
ЭФ
С учетом зависимостей B.7.2) и A.13) можно ввести
ортотропный сжимаемый стандартный материал
, /^ ?ч
О
Ja{23) = 2^БеB3>,
§ 4, ОРТОТРОПНЫЙ МАТЕРИАЛ 71
Для несжимаемого материала имеем согласно форму-
формулам B.5) и A.33)
а1п) = 2 j-- -1- р (g{22)g{S3) — g%3)),
а<22) = 2 rj^- -f р (g{33)g(u) — g{i3)X D-8)
°Ь B2)
а(;,;,) = 2 — h /J (g(Li}g{22) — ?A2)).
"& C3)
= 2
g{23) -{- Pig^g{12)
Условия перехода при малых деформациях выписан-
выписанного закона упругости в закон Гука B.7.10) находим из
соотношений B.12), D.5), B.1.12), учитывая при этом
независимость для несжимаемого материала упругого
потенциала от Н1С, равного 1:
_?Ф_\ /Эф \ _ (_дФ_
/ аФ \ / аФ \
/ вФ % 1 „
V од(зз' У о 4
! д2Ф \
[(дЛ*)
f'b/OUft /1Q\ / n
72
ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
С учетом зависимостей B.7.10) и A.13) можно ввести
ортотропный несжимаемый стандартный материал (/ = 1)
— "(зз) = -^ie(ii> + У ЕХЕ% v12eBa>,
= У~Ё\Ёг v12eA1> + Е2в{22), D.10)
2?14еA2>1 "B3) = 2?seB3>,
Согласно соотношениям C.1) и D.4) имеем для сжи-
сжимаемого материала в плоском напряженном состоянии
D.11)
jQ(\r> = 2 (т,
дф
При этом g<33> определяется из уравнения
дф , дф /
Из соотношений C.7), C.8) и D.5) приходим к следую-
следующим условиям перехода при малых деформациях закона
упругости D.11) в закон Гука B.7.18):
РФ
/ дФ
E
Ф33,33
33.33
11 |ма v it«it v i * ч w it ??m&tt *¦ t / ^^^ #,t *T\ U J.T
Г5 =Tt/ ?l^2 V12' Ф12.21 = — A4-
^ЗЗ.ЗЗ
D.13)
Для несжимаемого материала в плоском напряжен-
напряженном состоянии имеем с учетом соотношений C.6), D.3)
и C.5)
дФ ?(я2> ОФ
"(И) = 2
дф
дФ
D.14)
§ 5. ТРАПСВЕГСАЛЬПО-ИЗОТРОППЫЙ МАТЕРИАЛ То
— 9
1 г
J ^
(<т<13> = o<23> = 0);
в ^-Ле e — г2 V1 D 1Г))
ЬC3) ^Ь{ПГB2) bil2)' " * \ ;
Закон упругости D.14) при малых деформациях пере-
переходит в закон Гука B.7.21) — B.7.23) при выполнении
условий D.9), из которых исключены последние два.
§ 5. Трансверсально-изотроппый материал
Переходя к рассмотрению нелинейно-упругого транс-
версально-изотропного материала, напомним (§ 4 гл. 1),
что последний дополнительно к элементам симметрии
ортотропного материала содержит поворотную ось (пусть
она будет третьей) бесконечного порядка. Поэтому для
него необходимо сформировать из аргументов упругого
потенциала D.3) комбинации, ипвариантные относи-
относительно поворота бесконечного порядка (т. е. произволь-
пого оборота) вокруг третьей оси. Согласно формулам
B.1.6) и (А.47) имеем
/У('п, = cos2 Щ{ц) + 2 sin со cos o>gll2) + sin2 atg^2)t
glsi) = sin2 (i>g{n) — 2 sin m cos cogA2) + cos2 (agii2),
' = sin со cos co(gB2) — gun) + (cos2 со — sin2(o) gil2),
cos(x>g{l3) + sinci)gB3), g'i23) = — sinco?A3) + cos(ogB;i).
Из выписанных выражений, как нетрудно проверить,
следует инвариантность следующих трех комбинаций:
Инвариантами, очевидно, являются и величины 1НС, ^зз>.
Таким образом, имеем пять «базовых» инвариантов
Ч\ = I'c, 4f2 = П'с, Ч'3 = IIIc, Vt = IVC, ?5 = Vc, E.1)
где
IVС = ffA3)ffC1) + ?183)?C2). VC — g{33)-
При этом согласно A.33)
Ic = l'c + VCl IIC = II'C + I'CVC-IVC, E.3)
74
ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Сопоставление выражений E.1) и D.3) показывает,
что соотношения для трансверсалшо-изотрогшого мате-
материала можно получить из аналогичных зависимостей для
ортотропного материала путем замен
РФ
РФ дФ
7 Г ятт'
olc dllc
РФ
дФ дФ
дФ
дФ
дФ
дФ
дФ
дФ
дФ
5Ф
Так, из соотношений D.4) имеем для сжимаемого ма-
материала
77
дФ
а \1
— ею)) U
ЗФ
(gB3)gA3> —
r(a3) = 2 -^р—
L ^
B3) = 2 bjf
E.5)
+
J
— SB3)S{U)) »
— g{ia)g{22))U
г= 2
Добавляя к соотношениям E.4) следующие из них со-
соотношения
й2ф а2Ф
а2
"Г
о'Ф
(i^/; J,/=*i2),
с>2Ф
с>2Ф
§ 5, ТРАНСВЕРСАЛЬНО-ИЗОТРОПНЫЙ МАТЕРИАЛ 75
з2ф , д** E 6)
(<ЗД2 (dVcf
находим из выражений D.5) п B.7) (? = 1, 2)
п,п (щ j0
я2.т,
'О
2(—^^
^ + ( )
\ / Э2Ф
l + {
+
[апу>ш0 H + { wr&cl + {{9iiicfH
хз.3!
Отсюда н из соотношений B.10) и B.1.12) следуют ус-
условия перехода при малых деформациях закона упру-
упругости E.5) в закон Гука B.8.2):
,
<0-S)
ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Замены E.4) дают возможность получить из D.8)
закон упругости для несжимаемого материала
„ /' дФ , дФ \ , ( 2 \
ОЩ) = 2 —Г + —p-gB2) + P \8{22)SC3) ~~ g{23)),
\дГс дПс )
дФ дФ \ , / #2 \
Гр Г < ё(И> I + /^ V6(ll!b<33) — 5A3),/»
С С 1
дФ i ч
Ь Р (?B3)?A3) — ?A2!#<33)).
2 Я^~ + Р (g(U)g{22) — ^B12))»
+ P(§B3)g(l2) —
Из соотношений B.12) и E.7) следуют условия пере-
перехода при малых деформациях выписанного закона упру-
упругости в закон Гуна B.8.9) —B.8.10)
дФ \ ( дФ \ / дФ \ ¦
дф
E.10)
§ 5. ТРАНСВЕРСАЛЬНО-ПЗОТРОПИЬТЙ МАТЕРИАЛ 77
С учетом замен B.8.1) получаем из равенств D.7) и
D.10) для трансверсалъно-изотропного сжимаемого стан-
стандартного материала
Jow = Ех (еA1, + v12e<22)) + %
о о -..— — - о
/(ТB2, = Ег (8B2) + Vl28A1)) + V ЕХЕЪ V138C3),
Мзз, = VE~jf3 v13 (eA1) + eB2)) + ?е;ззь E.11)
О О О
J*J(i2) = El(l — v12)eA2;, /аB3, = 2Ь'5еBз>, Jo{l3) = 2^5e{13,
и для трансверсально-изотропного несжимаемого стан-
стандартного материала
°*(п) — °*{зз) = EL (e(u)
о о
^1 (sB2) + v12eB2)),
E.12)
Согласно равенствам E.5) и C.1) для сжимаемого
материала в плоском напряженном состоянии
дФ Л ( дФ I П дФ
шт
г __о/-^-4- дф \ ( —
Ш) [дП'с <33>WC/ A2) <23>
При этом величина ?<3з> определяется из уравнения
w + шг
с с
Условия перехода при малых деформациях выписанного
закона упругости в закон Гука B.8.14) имеют вид C.7)
при гшачопиях E.7) входящих в пих величин.
Из соотношений E.9), C.5) и C.1) получаем для
несжимаемого материала в плоском напряженном
78 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
состоянии
о Г оф л ( дф \оф
- 2 +
—? Гдф (дф - —
E.15)
дФ 1 дф\
@Г<|1> = О{23> = 0) .
Условия перехода этого закона при малых деформациях
в закон Гука B.8.17) имеют вид E.10) при опущенном
в них последнем соотношении.
§ 6. Изотропный материал
Изотропный материал обладает полной ортогональной
группой симметрии, содержащей всевозможные повороты
и отражения в плоскостях. Поэтому аргументами упру-
упругого потенциала являются «абсолютные» — главные ин-
инварианты
Ф=Ф(/С, Пс, Шс). (G.1)
При этом согласно соотношениям E.2)
дФ дФ дф дф дф
дф дф дФ дФ . дФ п ( '
+ 1
divc з//с' dvc dic • a//cv-b
Пользуясь этими соотношениями, можно получить со-
* отношения для изотропного материала из зависимостей
предыдущего параграфа. Так, для сжимаемого материала
находим из формул E.5)
Тс 9 Г/ дФ Л. Т дФ
{11> = [(Щ + °Щ
дФ
а///с
дФ , т дф\ дФ
дФ
'С,1 дПС
— ?A3)) U
§ 6. ЙЛОТРОПНЫЙ МАТЕРИАЛ 79
т ЭФ \ ЭФ
+ 7 ) g +
о 17 ОФ
^2; = 2 —
1Щ g«» +
дФ
+ д1и
С С
2 I — -щ^ g{23) + ЛЩ (&13>?<12) — gB3)g{U)) I F.3)
— gjj- ?<i3) + dIII (^,23,^A2)— g.wg&i)) •
2
С учетом формул F.2) выражения E.7) принимают вид
(г, к, j = 1,2,3;**=/)
о
+
Согласно формулам B.10), B.1.12) и B.9.2) условия
перехода при малых деформациях закона упругости
(().3) в закон Гука B.9.3) припимают вид
-0
/ Э2Ф \ , / Э2Ф \ , / Э2Ф \
\ д!<?Пс )• 1 E^сJ Jo I'7V^/^c )n +
о2ф
4 A + v) A — 2v) '
+ I тт~ i i — 4(j 4-"v)"-
F.5)
80 гл. з. нелинейная упругость
Замены @.2) в выражениях E.9) приводят к закону
упругости для несжимаемого материала
„ Г/ дФ , т 0Ф \ 0Ф
„ г/ дф . т яф \ эф
= + J
ЭФ \ 9Ф
J
@.6)
12> = 2 f — ^JJ- ?<12) J
2 (—^77^
= 2 Г —
При dtom согласно соотпошешшм B.12), F.4), B.9.7)
условия перехода при малых деформациях выписанного
закона в закон Гуна B.9.9) сводятся к выполнению един-
единственного условия {дФ/дШс = 0)
дФ
Согласно соотношениям F.3), C.1) и C.5) имеем
для сжимаемого материала в плоском напряженном со-
состоянии
г„ о Г/аф > г #Ф \ ЭФ , дФ 1
(П> = [^ *ВД ~ ^^ ^U)
о Г/аф . г дф \
22)= 2 [(7^ + СШ~С) ~
о
F.8)
СГB3> — 0) .
При отом ^<33> определяется из уравнения
/ 9Ф1 т дф\ дф дф (
[ + 1 ) & + U
(G.9)
§ 7. О ВЫПОГЕ УПГУГОГО ПОТЕНЦИАЛА
81
Из соотношений F.G), C.1) и C.5) имеем для не-
несжимаемого материала в плоском напряженном состоянии
дф
°*B2> =
дФ_
dic
Оф
эф
en,
1-
дф
с
1 —
Е> т дФ
, F.10)
1}
Jl
§ 7. О выборе упругого потенциала
Напомним инварианты для сжимаемых ортотропного,
трансверсально-изотроппого и изотропного материалов
(см. § 4—6 гл. 3): ортотропный материал
G.1)
грансверсально-илотропный материал
= ?A1»?B2) - ?<12)?B1)
= ?B3)?<82) + ?а8)?C1)
К, Ф, Черных
G.2)
82 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
изотропный материал
Ic=l'c+Vc = Vl + W2 + W3,
IIс = П'с + I'cVc - TVC = VXV2 - W4 +
Для несжимаемого материала в приведенных соотноше-
соотношениях следует положить
///с = V, = 0. G.4)
Начнем рассмотрение с наиболее изученного изотрон-
пого материала. В главных осях деформации имеем
(см. A.10), A.12), A.32))
*(«) = Ч, вм =0 (/,/=1,2, 3; / ф /). G.5)
Часто упругий материал задается упругим потепциалом,
рассматриваемым как функция главных кратностей удли-
удлинений
Ф = Ф(Х„ 12, 13). G.6)
Так, для песжимаемого изотропного д^атериала хорошо
зарекомендовали себя [77] трехконстаитный потенциал
3Л, — 0)\ (I. I)
и более простой двухконстантный (A = 1) потенциал
Здесь ц, п, $ — константы материала. Зпачоиию п = 2
отвечает материал My ни, значениям A = 1, и = 2 — ноогу-
ковский, значениям J3 =• 1, га = 1 — материал Бартенева —
Хазановича.
В главных осях деформации
= Я^|. G.9)
§ 7. О ВЫБОРЕ УПРУГОГО ПОТЕНЦИАЛА 83
Отсюда находим
"с , д11С
1
01c 01Ic
Обращение этих соотношений дает
dlllc
ох\
!)ШС
0Шс
С
1ПС
Ч
шс
ох\
G.10)
oxl х\
дПс
oxl
оис
ох\
А
Шс
д
шс
ох\
отс
oxl
дШс
oxl
I2 J
д
12 1,2
Л3 Aj
" Д
I2 12
д
д (л.; — %\) {К - II) {II - II); G.11)
<ЭФ
G.12)
0Ф 0X1 ОФ 0X1 Аф , 0Х3 ОФ
оф
Соотношения G.11) —G.13), при условии, что уравнении
G.9) разрешены относительно %i, %г, л3, позволяют (с уче-
учетом зависимостей G.1) — G.3)) использовать упругие
потенциалы вида G.6) в произвольных (пе обязательно
главных) координатах.
Перейдем к трансверсалъно-изотропному материалу.
Согласно соотношениям G.2) и G.5) в главных осях
деформации
G.14)
6*
84 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Отсюда следует
*| = Vc. G.15)
Особенностью траисверсалыю-изотропного материала по
сравнению с изотропным является то обстоятельство, что
в главных осях не представлен инвариапт IVс = ?<2з>?<зг> +
+ ?аз>?<з1>. Поэтому разумно искать упругий потенциал
в виде
Ф = Фу (Х„ К kt) + /(?wff(»»> + ff<u>ff(«>), G.16)
где А,,- заменены выражениями G.15).
Рассмотрим, наконец, ортотропный материал. С уче-
учетом соотношений G.1), G.5) и G.8) примем для не-
несжимаемого материала упругий потенциал в виде
Ф - А [п? {gndS - О + «Г1 (gX -О^ЧЙ2 -О] +
+ вз ЫиЯ&1) + (g№g№i)T'] (mi > 1). G.17)
Его характерной особенностью является независимость
вклада каждого инварианта в упругий потенциал. Не-
Нетрудно пидеть, что в главных осях деформации при Пу =
= п2 = щ = п, Л = 2\ап~1 принятый потенциал переходит
в двухконстантный G.8). Подстановка потенциала в со-
соотношения D.9) приводит к условиям перехода при ма-
малых деформациях отвечающего ему закона упругости в
закон Гука
G.18)
2В, + А = Eit 252 + А = Еь, 2В3+А= Е6.
По аналогии с G.17) для несжимаемого трансеерсаль-
но-изотропного материала можно принять G.16)
Ф = А [«Г1 (Й? + S$ - 2) + гтг (Й2 - 1)] +
(^>1).
G.19)
§ 8. ПОЛЫЙ ЦИЛИНДР ИЗ НЕСЖИМАЕМОГО МАТЕРИАЛА 85
§ 8. Полый цилиндр из несжимаемого материала
Рассмотрим полый цилиндр. В цилиндрической (не-
деформированной материальной) системе координат
(рис. 3.8.1)
a1 = r, a2 = 9, a3
(8.1)
Пусть после деформации цилиндрические координаты
материальной точки принимают значения
г = г Q(r), G = 0 + v (г) + Цх3, x = %x3 + w (r). (8.2)
о о о
Искомые функции Q(r), w(r), v{r) и постоянные к, if
Рис. 3.8.1
l9, %
Vac. 3.8.2
описывают одновременные деформации полого цилиндра:
раздувание, продольный и поперечный сдвиги, растяже-
растяжение и кручение. Из выражений (8.2), (А.З), рис. 3.8.2
и очевидных равенств
gr = cos 0 ¦ gi + sin 0 ¦ g2) g9 == -sin 0 • gi + cos 0 ¦ g2 (8.3)
о
находим (r = d/dr)
R2 = (rQ) ge«
ge +
(8.4)
86 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Отсюда и из выражений (А.11) следует
'\ gaa =
fti = W2 "I' (rQfv* + w'\ gaa
g33-^(rQJ + W, (8.5)
fta = (rQY V, ft,
)'}*• (8-6)
Соответствующие величины для недеформированной кон-
конфигурации находим, полагая в утих выражениях
<? = Л = 1, у == ш = -ф = 0; (8.7)
fti = ?зз = 1, g22 == г2, g12 = g13 = |23 = 0; g= r2.
(8.8)
11з_условия несжимаемости материала (A.14)) / ==
= У gig = ^<? (г<?)' = 1 следует
(/•(?)' = K-'Q-1, Q' = г' -1 (ЯГ'СГ1 - ()), ^ = 'g = И.
(8.9)
Интегрирование второго уравнения дает
<? = *,-' +с.г-2. (8.10)
С учетом первого из соотношении (8.9) и (8.7) выраже-
выражения (8.4) и (8.5) можно записать в виде
Ri = ^(ГЫт + rQv'go + w'g»
R2 - rQg0, R3 = pQg» -|- %,, .(8.11)
их = gr, Л2 = rg9, R3 = g3;
fti = ^~2<?~2 + (^<?J v* + «Л fta = W,
Согласпп гоотиппюппям (Л.1П) полпчипн g1'-1 — прпподон-
ные (т. о. делеппые па g — у нас g = г2) мппоры элемен-
элементов gu определителя \gi}\. Подсчитывая их, получаем с
5 8. ПЛЛЫП ЦИЛИНДР ПЗ НЕСЖИМАЕМОГО МАТЕРИАЛА 87
учетом раиенсть (8.9K и (8.12)
g" = -k2ty - \\iQ2w'2 + KQ^ip', (8.13)
а с учетом соотношений (8.7)
#u = ?3 = 1, g22 = У\ к1* = ^18 = k* = 0. (8.1/,)
По формулам (Л.32), (8.12) и (8.13) подсчитываем
G\x = V-^l - k~1Q-2)
= г
- К1) \\-u/
= X^V^ + r^y' (Xy' - i|w'), (8.15)
= rQ2v'w', G]3=C
^ - ifip'), G233 = ifr ^u>', G^2 = - XrQ2,
G222 = r Q2 {h>' - три;'), G», = г (?2ш', Gj3 = -ЩРг Q2,
Git = ^2r Q' (h/ - yw'), О3ЗЯ = ^rQ°-w'.
По формулам A.32), (8.8) и (8.12) находим
^-^<?2 + ^, (8.16)
Отсюда и ил соотнопюниГ! D.8) следует
n — 9
ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
я/и *"'' - to% (8.17)
"&{12>*>B1)
С учетом того, что входящие в уравнения равновесия
величины зависят в нашем случае лишь от координаты
о
а1 = г, получаем при отсутствии массовых сил согласно
соотношепиям A.25), A.32) и (8.8)
+ 2 (G{2rV* + Gi3 m" + GU га2Я) = 0 (/ = 1, 2, 3), (8.18)
a22 = r~2aB2), a33 = amh
(8.19)
Подстановка выражений (8.17), (8.15) и (8.19) в
уратшгния рашювгсия (8.18) дает с учетом формул (8.9)
р'^У^У^У*, (8.20)
где
У
/
§ 8. ПОЛЫЙ ЦИЛИНДР ИЗ НЕСЖИМАЕМОГО МАТЕРИАЛА 89
ЧГ2 - 1) V + °rv" - k-^rw" -
Г V*
V* - 1) w' + °rW2 (W - ibw')
') + * ^{kv' ^w/) Г
+ 2 [Я~У rV + ij)<?-"V +
о о
+
, (8.21)
X2'
+ [К'1 (k-iQ-2 -l)w' + r^v'W + k-^
[ф г2 (<?2 + 2Я) у' + p-3Q2v" +l(w' + rw")
дФ
Подстановка этих выражений в следующие из равенств
(8.20) соотношения Yi = ^?3 и Wi — ^?z последовательно
дает (с учетом соотношений C.9)) две квадратуры
w j- V к ($r2Q2v + kw )
(8-22)
Здесь упругий иотепциал Ф является функцией аргумен-
аргументов (см. (8.16))
+ k\ gwgw =>0V»,
(8.23)
90 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
Рассматривая упругий потенциал как сложную функцию
величин i/, w', ty, X, находим при помощи последних
выражений
дФ „ г , дФ , л , , ,°гл» , , 1 м дФ
7 == 2\w -гг- V X[i|)(/-(?)V + %и>\
дш
, (8.24)
ho']
Отметим, что при подсчете последней величины мы не
учитывали параметр X, входящий через равенство (8.10),
и, следовательно, первое слагаемое в g(u) (происхождение
о
которого связано с величиной (rQ)').
Если воспользоваться первыми двумя из полученных
равенств, а также (8.10), и ввести новые постоянные
цс3 = 2(^,~'г|зс1са + с3), цсл — 2сг, то система двух нелиней-
нелинейных алгебраических уравнений (8.22) запишется особен-
особенно компактно:
дФ
В дальнейшем удобно использовать обозначения (см.
(8.2), (8.10))
гi = г (г,) = °riQu Q\ = <? (г,) = Г1 + с°г7\
(8.26)
Pi = Р (п), w\ = w' (rj), v'i = у' (/ч) (i = 1, 2).
Для постановки краевых условий на лицевых поверх-
поверхностях цилиндра учтем, что на них
n = g,: И] = 1, п2 = и3 = 0 (г = га);
п = — gr: rei = — l, n2 = щ = 0 (г = гх).
§ S. ПОЛЫЙ ЦИЛИНДР ИЗ ПЕСЖНМЛЕМОГО МАТЕРИАЛА 91
Согласно же соотношениям A.2В), A.15), A.19), A.20),
.A.5), (8.17), (8.11), (8.15), (8.19), (8.21), (8.20) и (8.27)
вектор напряжения (в расчете на единицу площади де-
деформированной лицевой поверхности) и его проекции
соответственно на радиальное, окружное и осевое на-
направления равны
ап = о о
= an.g, = A. Qi a \°rj>Ti-
+ pu (8.28)
'{id
= >Ггг; (r'o11 + a12 + i|xt13);
+ гЬ (iLt2<?V + Ь'')
,-1 n-2'W
= an.g3 = X^QT1 (w'on
Выясним статический смысл постоянных с2 и с3. Под-
Подсчитывая для этого осевую силу и моменты относительно
оси приложенных к лицевым поверхностям напряжении
о о
и обозначая / и 1 = Х1 длииы цилиндра до и после
92 ГЛ. 3. НЕЛИНЕЙНАЯ УПРУГОСТЬ
деформации, находим (рис. 3.8.2)
= 2nlh-iQiam |. „ = (— l)'2n?{i<r,, (8.29)
=_= = (- 1I2я/цс,. (8.30)
Г—fj
Отсюда и усматривается статический смысл постоянных
с2, с3: с точностью до постоянных они являются соответ-
соответственно осевой силой и осевым моментом напряжений,
приложенных к лицевым поверхностям цилиндра.
Если на лицевой поверхности задано нормальное дав-
давление (—</,), то из равенства о„ = — qn и соотношений
(8.27) и (8.28) получаем граничное условие
+*--*• С8-3*)
Если же лицевая поверхность опирается на упругое ос-
о о
нование, то onr — f[r — rt] = f[rt(Qt — 1)], и согласно со-
соотношению (8.28) 1
„ +Pi = (-l)V[n(<?i-1)b (8-32)
В случае, если упругое основание линейно,
f[ri(Qt-l)] = kri(Qi-i), (8.33)
где к — так называемый коэффициент постели (упругого
отпора).
На поперечном сечении цилиндра со стороны поло-
о о о о о
жителыюго направления оси xs n = g3: nl = п2 — 0, щ — i
о
и Оо = «aCr^PRp = a3PRp. Отсюда и из соотношений (8.11),
(8.17), (8.19) и (8.24) находим для осевой и кольцевой
составляющих вектора напряжений:
art О Ш' '-'- "^° ' • * - ¦ ' v w4^
о .Д, = ? \W
о g3 2[м/ (i|!r(?V + ho)rr+ ЬРЛ
g +
§ 8. ПОЛЫЙ ЦИЛИНДР ИЗ НЕСЖИМАЕМОГО МАТЕРИАЛА 93
эф
Поскольку dSn = rd9dr, а плечо силы равно г = rQ, осе-
осевая сила и крутящий момент, приложенные к попереч-
поперечному сечению, равны
(8.34)
(8.35)
В получеппые выше соотпотепия входит функция р,
определяемая согласно равепствам (8.20) квадратурой
(8.3G)
При этом в качестве Ч' можно взять любое из выраже-
выражений (8.21), равных между собой при v' и и/, найденных
из нелинейной системы алгебраических уравнений (8.25).
Полученное решение дает возможность провести экс-
эксперименты по определению упругих свойств ортотропных,
трансверсальио-изотропиых и изотропных эластомерных
материалов. При использовании приведенных в § 7 упру-
упругих потенциалов можно определить входящие в них кон-
константы. В частности, можно найти усредненные по тол-
толщине стенки упругие характеристики кровеносных сосу-
сосудов, рассматриваемых как ортотропные цилиндры.
ГЛАВА 4
ДЕФОРМАЦИОННАЯ АНИЗОТРОПИЯ
При больших деформациях первоначально изотроп-
изотропный материал может приобрести заметную анизотропию
упругих свойств. Это явление — называемое деформаци-
деформационной анизотропией — и рассматривается в этой главе.
Другим, тесно примыкающим к первому, является вопрос
о деформации материала, армированного семействами не-
нерастяжимых либо малорастяжимых волокон. Армирован-
Армированный материал является первоначально анизотропным.
Вместе с тем он прн большой деформации получает ха-
характерную деформационную анизотропию.
§ 1. Возмущение равновесной конфигурации тела
Вернемся к приведенным в § 1 гл. 3 зависимостям
нелинейно-упругого тела. Наряду с величинами
u, Rj, JaV, 0^, f, ...,
определяющими рассматриваемую деформированную кон-
конфигурацию тела, рассмотрим величипы
u + u, Rj + Ri, JcV + Jav, 0o+0o, f + f, ...
n n
возмущенной _равновеснон конфигурации. При этом воз-
возмущения u. R,, ... будем считать малыми, связанными
между собой линейными соотношениями вида
A1)
Кроме того, необходимо помнить, что относящиеся к не-
деформированной конфигурации величины возмущению
§ 1. ВОЗМУЩЕНИЕ РАВНОВЕСНОЙ КОНФИГУРАЦИИ ТЕЛА 95
но подлежат. Так из равенств C.1.3), C.1.13), (А.37)
и (А.9) следует
A-2)
Далее, возмущая соотношение (А.16), находим
lia.^1 + 8i^F> = б] = 0.
Умножая это равенство на g'h и суммируя но i = Y, по-
получаем с учетом того же соотношения (А.16)
?**== - gneai!va= - Whga~eya = - gyl'Hai (Vvua + Vauv).
A.3)
Согласно же формулам (А.40), AЛ) и A.2)
Отсюда и из выражений C.1.14) находим
7 = Jg^'eat = Jga^aufi. A.4.)
Возмущение первого из соотношении C.1.25) дает
?-O. A.5)
Подсчитаем с учетом формул A.2), (А.31) и (А.34)
В силу симметричности по индексам f и v, (A.38) и A.2)
Подстановка этого выражения в A.5) приводит к перво-
96 ГЛ. 4. ДЕФОРМАЦИОННАЯ АНИЗОТРОПИЯ
му из следующих (выводимых аналогично) равенств:
A.6)
(a"e= ?„),
Hi = п4 (a'') (ah <= ?u).
Из этих и следующих ниже выражений для напряжений
усматривается, что линеаризованные уравнения равпове-
сия и статические граничные условия пе содержат воз-
возмущений углов поворота, коль скоро их не содержат j'
и оЛ, т. е. если
п
Рассмотрим второе условие. Прежде всего согласно
C.1.26), A.2) и A.3) для следящей нагрузки — нормаль-
нормального давления
^q +q[geji"iV-(g
A.8)
и условие A.7J выполняется. Иначе при мертвой (не
зависящей от возмущепия смещений) поверхностной па-
грузке, для которой согласно формулам A.2) и (А.12)
о
т. е.
о = ape RB = const, о о = (ар= + gvPa'i Vuuv) Rp = О,
n n p n \ n ° n * J v
A.9)
и условие A-7J, вообще говоря, пе выполняется. Ана-
Аналогично для мертвой массовой силы
? = -Г/"^, A.10)
и условие A.7) i также, вообще говоря, не выполняется.
Несколько обобщая определение, данное В. В. Боло-
тиным [7], назовем следящей массовую силу, в каждой
§ 2. ПЕРВОНАЧАЛЬНО ИЗОТРОПНЫЙ МАТЕРИАЛ 97
точке тела направленную в процессе деформации вдоль
определенного материального волокна. Если направление
последнего определялось до деформации вектором к =
= k7R7, то согласно равенствам C.1.4) его положение
о о
после деформации определяет вектор "k = F • к = /c7Rv.
Таким образом, следящая массовая сила имеет вид
f = /k = /°^RVi A.11)
где / — скалярный множитель — интенсивность силы.
Отсюда с учетом формул A.2) следует
и условие A.7)! выполняется. Заметим, что сказанное
полностью относится и к материальным волокнам по-
поверхности тела.
Из сказанного следует особая роль следящих нагру-
нагрузок: для них линеаризованные уравнения равновесия и
статические граничные условия не содержат возмуще-
возмущений углов поворота, а записываются через компоненты
линеаризованного тензора деформации ёц.
§ 2. Деформационная анизотропия
первоначально изотропного материала
Вернемся к законам упругости C.1.27), C.1.28). Воз-
Возмущая их, получаем, используя соотношения § 1 и обо-
обозначения
для сжимаемого изотропного материала
(Фи + 'сФ23 + ШСФЮ)
+ [gijghl - V8 (gihg}l + gilgik)}
(JEm = Em = Em = Emi), B.2)
7 К. Ф. Черны*
98 ГЛ. 4. ДЕФОРМАЦИОННАЯ АНИЗОТРОПИЯ
для несжимаемого изотропного материала
0« =, [fi*v _ (gbg* + g'Yv) /»] ёЙУ + g'% B.3)
%Яи" = gi}?1 (Фц + 2/сФ12 + /?Ф22) -
¦'* = ?гз'*г = ?«'* = Ет).
Переходя в полученных соотношениях к физическим
компонентам, получаем с учетом соотношений C.1.31),
C.1.32),
Ет1) = Ет Vguhkkkgu B-4)
т1)
для сжимаемого изотропного материала
вубы (Фп + 2/сФ12 + /^Ф22) + B.5)
а///с diпЛ дшгдш
+ в е (ф + ^Ф) 2 ^
Фаз -
¦ [6<A* — V2 (SihSji + &u&jh)] Фг -г
. lamcaiiic diiicainc
для несжимаемого изотропного материала
Г !dlliconic aillcdlllc\ 1-
OIIIC-
1/77 * fi {лу +¦ 2/сФ12 + /сФ22) -
§ 3. ЛРМИРОВЛПНЫЕ ВОЛОКНАМИ ЭЛАСТОМЕРЫ 99
Полученные формулы дают возможность при задан-
заданном упругом потенциале и достигнутой деформации под-
подсчитать мгновенные упругие модули и в соответствии
с изложенным в гл. 2 классифицировать полученную
упругим телом деформационную анизотропию.
§ 3. Армированные волокнами эластомеры
Рассмотрим эластомер (резиноподобный материал
[16, 77]), армированный семейством нерастяжимых воло-
волокон, определяемых в недеформированиой конфигурации
единичным вектором
\ = Ца\<#, a3)=°/aRa. C.1)
Будем считать, что волокна (нити) абсолютно гибки,
расположены настолько часто, что можно пренебречь
неравномерностью деформации между ними, и, кроме
того, прочно соединены с материалом — изотропным эла-
эластомером.
о о
Элемент недеформированного волокна 1 ds после де-
деформации переходит в (см. C.1.4) i) Y-\ds. Отсюда
следует, что условие нерастяжимости волокна имеет вид
(F-I)-(F-l) = 1-1. C.2)
Согласпо же формулам (А.50) и C.1.12)
п условие перастяжимости материала вдоль волокна за-
записывается в виде (см. C.1.12))
(йГаэ — Яар)/в^Э =- 0 или еарКгр = О. C.3)
Определяющий направление нерастяжимого волокна век-
вектор C.1) переходит после деформации в вектор (см.
C.1.4)) l = ZaRa = F-i=>(F-Ra) = }aRa. Отсюда
следует
Z'-f (i=l, 2, 3). C.4)
100 ГЛ. 4. ДЕФОРМАЩТОПНАЯ АНИЗОТРОПИЯ
Яакопьт упругости C.1.27) н (Л.1.28) переходят [10,
73] в следующие: для сжимаемого материала
Ja4-2^ + qW C.5)
и для несжимаемого
a« = 2^ + ^« + 7VV. C.G)
Здесь q — произвольная, определяемая из соображении
статики функция.
В физических компонентах (отнесенных к ортого-
ортогональной педеформировапной материальной системе коор-
координат) имеем согласно соотношениям C.1.32): для сжи-
сжимаемого материала
3d) о о
J°m = 2 si""
а для несжимаемого
й ^ C-8)
Последние два соотношения при заданном армировании
позволяют определить характер анизотропии армирован-
армированного эластомера.
Если материал армирован несколькими семействами
волокон, необходимо просуммировать приведенные доба-
добавочные члены.
ГЛАВА 5
ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
ПРИ БОЛЬШИХ ДЕФОРМАЦИЯХ
В главе дается краткое изложение предложенной ав-
автором [74, 75] общей нелинейной теории тонких упругих
оболочек, предназначенной, главным образом, для расче-
расчета оболочек из эластомеров (резипоподобных материа-
материалов). Отметим три характерные особенности предложен-
предложенного варианта теории. Прежде всего используется уточ-
уточненная геометрическая гипотеза Кирхгофа, позволяющая,
без повышения порядка разрешающей системы уравне-
уравнений, учесть существенное для оболочек из эластомеров
деформационное утонение оболочки. Далее, применение
двойного тензора напряжений позволяет одновременно
использовать преимущества материальных координат как
в недеформированной, так и в деформированной конфи-
конфигурациях оболочки. Наконец, принятие линейного закона
распределения напряжений по толщине позволило зна-
значительно упростить связь между усилиями — моментами
и компонентами деформации срединпой поверхности
оболочки.
Необходимые для понимания изложенного сведения
из теории поверхностей приведены в приложении Б.
§ 1. Деформация оболочки
Радиусы-векторы одной и той же материальной точки
оболочки до и после деформации представим выраже-
выражениями (рис. 5.1.1)
R (а1, а2; I) = г (а1, а2) + Ы (а\ а2), A.1)
Н(а\ а2;!) = г(а\а2) +
+ h(al, а2)[| + 72Гх|(а\ «2)]п(а\ а2).
о
Здесь г, г — радиусы-векторы проекции материальной
точки на срединную (до деформации) материальную
о
поверхность; n, n—единичные векторы нормалей к по-
последней. Как выяснится ниже, А.$ и щ характеризуют
102
ГЛ. 5. ТОПКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
растяжение нормального к срединной поверхности ма-
материального волокна.
Используя формулы (А.З), (А.9), (А.11), (Б.5), под-
подсчитываем, удерживая лишь члены, линейные по %:
Ri = Гг — ЪЬ*Та, R3 = П,
Ri = П + g [- а,еЬ?гв
A.2)
Эа1)п], RW + ЗДЛ
A.3)
о о о о о
Рот А ,*
^7, A.5)
Соотиошения A.1) являются математической записью
уточненной геометрической гипотезы Кирхгофа: мате-
материальное волокно, нормальное к материальной срединной
Рис. 5.1.1
поверхности до деформации, остается нормальным к ней
и после деформации, удлиняясь по линейному закону.
Последняя часть утверждения следует из выражения
для #зз в A.5). Связь параметров Я,6, хь с основными
компонентами деформации будет установлена ниже.
Используя соотношения C.1.30), A.4), A.5), нахо-
находим следующие шлражоння для главных инвариантов
§ 1. ДЕФОРМАЦИЯ ОБОЛОЧКИ 103
деформации:
ГС= "Лар + Ч + 12 (- V«V + аа^ + Х|хе),
A.6)
IIIс = i [ P Н
Введем симметричные величины
Ху = — ЦЪ^ -|- V2 (а^,Ь? + aiv?/) = Xjj. A.7)
С их помощью и учетом соотношений (Б.17) запишем
выражения A.6) в виде
/с = aapaap + 4 + 12 (aapxap + Я|хе),
IIclIUc = aapaaP + Ч2 + & (aapaa7apvx7v + Xf 2x?).
A.8)
= (e/e) XI [1 + |2 (aapxap + xe)].
Из последнего выражения следует, в частности, что ус-
условие несжимаемости материала ///с = /2 = 1 записыва-
записывается в виде
X.=(e/e)-1/f, xE = -aaPxaP. A.9)
Выясним геометрический смысл величин A.7). Сог-
Согласно A.4), A.5) и A.7)
ij — gij = (aU —
— Уг [(aiv — fliv) frj И- (Д,у — Ojv) bV[).
Согласно соотношениям (Б.6) для тонких оболочек под-
подчеркнутые члены малы но сравнению с аналогичными,
входящими в первую скобку правой части. Опуская н\,
о
видим, что члены («,., — «,,;) определяют деформацию
срединной поверхности [тангенциальную деформацию),
а ху — деформацию, меняющуюся линейно по толщине
(изгибную деформацию). Таким образом, величины
A.7) — (коварнантные) компоненты тензора пзгибной
деформации.
104
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
С учетом тоикостеииости оболочки примем выраже-
выражения A.4) —A.5) в следующем упрощенном виде:
О О п
gij = aih gij — aij + ?2>tij, g33 = ?l| A + ?2и&),
A.10)
Нетрудно проверить, что последние не изменяют глав-
главных инвариантов деформации
A.8) и, стало быть, правильно опи-
описывают деформацию оболочки.
Существенно, что в выражения
A.10) не входят величины gi3>
g'3, так что можно считать
Рис. 5.1.2 Согласно выражению A.1)
нормаль к срединной поверхности
пересекает лицевые поверхности (| — ±1/гк) в точках
(рис. 5.1.2)
Отсюда следует, что толщина деформированной оболочки
/i=|R+ — R~| связана с толщиной не деформированной h
соотношением
h —
A.12)
§ 2. Усилия и моменты. Силовые
граничные величины
Подсчитаем главный вектор и главный момент на-
напряжений, действующих на элемент нормального сече-
сечения деформированной оболочки. Пусть (рис. 5.2.1) dS%
d$\ — и.чощядн элементарных площадок нормального
сечения оболочки до и после деформации; v = v7n ,
t о
v —единичные векторы нормалей к ним, v—орт тан-
тангенциальной нормали па срединной линии нормального
о
сечения. За n, n сохраним обозначения единичных век-
§ 2. УСИЛИЯ II МОМЕНТЫ
105
торов пормали к срединной поверхности. При этом
(рис. 5.2.1)
Tvdst = J" avdSl, Mvdst = J (R — r) X avdS\. B.1)
Здесь Tv, Mv — погонные (в расчете "на единицу длины
срединной линии недеформированного нормального сече-
сечения) векторы усилий и моментов.
С учетом произведенных измепений в обозначениях
имеем согласно формулам C.1.18), C.1.15) и C.1.21)
+ /aa3RaR3 + /a33R3R3)
= v|(/aapRs + Joa3R3) dSl B.2)
Согласно же формулам (Б.28) —
(Б-3°)
_
= *S\IVgu = Vha'dZ, -_
¦|/"оо о /| / о .• "i/ooo о "I /~
= V g/a dSij V ail = К g/a \idSv = V
Рис. 5.2.1
о о о о
g/a
Подстановка этого выражения в B.2) и полученного п
B.1) дает с учетом A.1), A.3) и (Б.19)
М1 = п X
V;
-ft/а
ft/2
B.3)
B.4)
B.5)^,3
-ft/2
Л/2
j"
ap) Ja^\ V g/a d\.
о
-ft/2
Из зависимостей B.3) и B.4) следует
= v-M,
106 ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
Отсюда видно, что Т"— (контравариантные) компоненты
двойного (§ 1 гл. 3) тензора усилий, а Ми — двойного
тензора моментов, Т]п — так называемые перерезываю-
перерезывающие усилия.
Для тонких оболочек подчеркнутые в B.5)i, 2 члены
могут быть согласно (Б.6) опущены. При этом для мо-
моментов (теперь уже симметричных величин) имеем
л/а
Л/У = ЯЕ J Jo%di = M}\ B.7)
о
-ft/2
Используя же симметричные усилия Новожилова
Sij = J Joij d\ = Sj\ B.8)
о
-Л/2
получаем из выражений B.5) i и B.7)
Г« = ?« _ Ь*м*т. B.9)
Пусть
/a« = (/o")<o, + &(/o")<i,. B.10)
Подставляя зти представления в B.7) — B.8), находим
?" = й(/о")(о„ ДГ" = 7„к5(/ом)<1„ B.11)
и по B.10)
Л«,^+^^4; + -^- = . B.12)
А А/2Я5Л А А/2 ЦА2
Особенностью теории тонких оболочек является то
обстоятельство, что физические компоненты тензоров и
векторов вводятся в недеформированной и деформирован-
деформированной метриках срединной поверхности, так что, например,
at} = о-(у)/ Vaudji = Q{ij)l V auajj, ^ ^
) = °№ V anajil
Согласно же выражениям B.6) 3>t тензоры усилий п мо-
моментов являются двойными (§ 1 гл. 3). Поэтому при
переходе к их физическим компонентам следует учиты-
§ 3. УРАВНЕНИЯ ДВИЖЕНИЯ 107
вать, что ио первому индексу их компоненты отнесены
к недеформированной, а по второму — к деформирован-
деформированной метрикам срединной поверхности. Поэтому физиче-
физические компоненты вводятся соотношениями
(ij) = Л1 у ацпу). (Z.14)
Пренебрегая в зависимостях A.8K изгибными слагаемы-
—— о
ми, имеем / = У///с — (а/а) i/zk%. С учетом этого, а также
равенств A.12), B.13) — B.14) находим
м ... т ... I % \ 6Л/,...
B.15)
§ 3. Уравнения движения
Рассмотрим условия равновесия элемента деформиро-
деформированной срединной поверхности, ограниченного коорди-
координатными линиями а', а' + da1 и а2, а2 + da2. Для этого
——\ -I дссг
Рис. 5.3.1
подсчитаем главный вектор и главный момент прило-
приложенных к нему усилий, моментов и внешних сил. На-
Напомним, что введенные усилия и моменты отнесены к
единице длины недеформированного контура.
При dtom согласно форл1улам (Б.18), (Б.26) и (Б.27)
о о -в Г о о а
на линии а1 = const: da1 = 0, vxdst = V a da?, \\dst — П.
Поэтому с учетом равенств B.3), B.4) на пару сторон
108 ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
а1 — const, a1 + da1 = const действуют силы (рис. 5.3.1)
{(Т1 + 7*,n) Vadat+^r [(Т1 + Т]пп) VIda?} йаА -
Т]пп) VI d*
осе
Добавим сюда аналогичные величины для другой пары
сторон и поверхностную силу qVa da'da2, где q — интен-
интенсивность поверхностной нагрузки в расчете на единицу
площади деформированной срединной поверхности. В ре-
результате получаем, приравнивая нулю полученный глав-
главный вектор,
Подсчитывая главный момент, получаем прежде все-
всего аналогичные слагаемые
da2.
К ним следует добавить момент, создаваемый парами
сил (рис. 5.3.1)
tjda1 X (Т1 + Т]пп) Va da2 + r2da2 x(T2 + Т%п) Vada1.
Приравнивая нулю сумму выписанных слагаемых, при-
приходим к условию равенства нулю главного момента
V" М1 д У а М2
L 9a1 дат
+ r2xV°a (Т2 + T*nn) 1 da1 da? = 0. C.2)
В это уравнение следовало бы включить и поверхностный
момент miada^a2. Обычно он мал, и мы его опускаем.
После сокращения в соотношениях C.1) и C.2)
множителя da1 da2 приходим к векторным уравнениям
§ 3. УРАВНЕНИЯ ДВИЖЕНИЯ 109
равновесия (движения)
С помощью соотношений B.4) и (Б.23) получаем отсю-
отсюда систему пяти уравнений движения (равновесия)
(/, ч, р = 1, 2)
+ ^ VI Т^ - К VI Т\ + j Va = 0,
+ by, Va Г* + qn Va = 0, C.4)
да?
д
Заметим, что при выводе двух последних уравнений бы-
было использовано полученное с учетом (Б.18) и (Б.24)
равенство
Шестое уравнение равновесия имеет вид
(Г12 + ЫМа1) - (Т*\+ h\Mai) = 0
и в силу выражений B.7) — B.9) удовлетворяется тож-
тождественно.
Практически наиболее важным видом поверхностной
нагрузки является нормальное давление
q=gn: (/4 = (/2 = 0, qn = q. C.5)
Рассмотрим силы инерции. Имеет место закон сохра-
сохранения массы в элементарном материальном объеме
(dm-=) pdV = pdV. C.6)
о
Здесь р, р — плотность материала в деформированной и
недеформированной конфигурациях тела. Отсюда с уче-
110 ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
том равенства (А.27) сила инерции в элементарном
объеме деформированного тела равна ( = d/dt)
— R"pdV = _ R"pdV = — R "p Vg da4a4l.
В расчете на единицу площади деформированной средин-
срединной поверхности (dS = Уй daldaz)
Л/2 , г
С •• ° 1 / ° 1/°°
q = - J R р У а/а V g/a dg.
-Л°/2
Для тонкой оболочки, как и выше, подчеркнутый член
можно заменить на 1. Пренебрегая также изменяемостью
о
по толщине р, получаем с учетом A.1) упрощенное вы-
выражение для сил инерции
/V. C.7)
§ 4. Закон упругости
В § 1 была установлена возможность принятия пер-
первых двух из следующих приближенных равенств:
gi* = 'gi, = O, gt» = g» = O; o33 = 0. D.1)
Последнее равенство является математической записью
статической гипотезы Кирхгофа, согласно которой
С( 11), СГB2)) ^A2) -** 0C3)!
т. е. основные напряжения в нормальных сечениях обо-
оболочки значительно превосходят нормальные напряжения
на параллельных поверхностях (? = const) оболочки.
Принятие соотношений D.1) означает, что в оболочке
имеет место плоское напряженное состояние (§ 3 гл. 3).
Для сжимаемого материала имеет место закон упру-
упругости (C.1.27), A.11)) (г,/ = 1,2)
Разлагая с учетом выражения A.11) производные упру-
упругого потенцдала а ряд цо {-. и сохраняя лишь линейные
§ i. ЗАКОН УПРУГОСТИ HI
члены, получаем, используя последнее из равенств D.1),
/o«_2{(^|+62
Tn™ — 2 —
I \ J-' 'о
д-ф
+
й-ф
= 0.
D.2)
Здесь ноликами помечены величины, отнесенные к сре-
срединной поверхности (при |и= 0).
Обозначим выражением (см. A.11))
значение упругого потенциала на срединной поверхно-
поверхности. Нетрудно видеть, что
(дФ_\
D.4)
Используя эти равенства и представления B.10), полу-
получаем из D.2)
й- = °; D-5)
D.6)
D.7)
Из соотношений D.6), D.7) п B.11) находим выраже-
выражения для усилий и моментов:
дФ°
D.8)
D.9)
Ц2 ГЛ. В. ТОПКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
\ daadaki daijdaih)
~
Величины Е"ы являются текущими (касательными) из-
гибными модулями. Входящая в выписанные выражения
величина Кг определяется из уравнения D.5).
Для несжимаемого материала имеем согласно соот-
соотношениям C.1.28) и A.11)
?ij ' 9#зз
Исключая отсюда р, находим
Повторяя проделанное выше для сжимаемого материала,
получаем отсюда с учетом формул A.9), A.10) и A.11):
DЛ1)
12
4-)^[«««ы + -ИЛ" + «V*)] D.12)
= Е"м = Ет = ЕШз)
В ортогональной (недеформированной материальной)
системе координат имеем с учетом формул (Б.ЗЗ),
C.1.31) и B.14)
° а ° —1 ее в
а = аи , а12 = а12 = 0, а
( }
S 4. Закон упругости И
Si} = SmIVa(jj)auajh Mi} = Л/<У) /Vа^анаи; (АЛА)
да~) =
д2Ф°
В выписанных соотношениях Y? — значения на
срединной поверхности инвариантов рассматриваемого
анизотропного материала. Согласно формулам C.4.3),
C.5.1), A.8), A.11) имеем для ортотропного несжимае-
несжимаемого материала
^ = а<и), ^°2 = «<22), ?2 = А|, 41 = W<21); D.16)
для трапсверсальпо-изотропного несжимаемого материала
^ ^ + fl<22). 4*2
D.17)
Y» = Vc = XJ.
Для несжимаемого ортотропного материала можно
принять
Ф° = А [п? (аП(? - 1) + п? {аП? - l) +
+ «з (^("з/2) - 1)] + В [а<12)а<21> + (а<Г2>«<21))т]. (т > 1).
D.18)
При этом согласно C.4.9)
A(ni + n2) = 2Ei, А(п2 + щ) = 2Е2,
D.19)
Ап3 = -1/EiEzv12, 2
8 I{. Ф. Черных
114 гл. 5. тонкие лттипотропные оволопки
С помощью соотношений D.15) подсчитываем для вве-
введенного упругого потенциала отличные от нуля произ-
производные от Ф° из числа входящих в D.11) — D.12):
8ФР___А_ ("i/^) 0Ф° _ дф° __ В /. 2(m-i)\
даП 2ап ' davz "Й2, у ;^
0Ф° A ,(",-i) <?2Ф° A(nt ~2) ,('Ч-«
(Wj — 2)
11 22
-г-1)
§ 5. Изотропный несжимаемый материал
Полученные в предыдущем параграфе соотношения
D.11) — D.12) справедливы для произвольного несжи-
несжимаемого анизотропного материала. Для изотропного же
материала их можно подвергнуть дальнейшим преобразо-
преобразованиям, введя в рассмотрение инварианты
А = аа?'аа?п В = а/а = {аиа22 — а12а21)/'а. E.1)
Используя эти выражения, а также (Б.18), находим
дА = ° ц дв_ = да1} Фа = q
ik 31 ij kl il jk /г л\
с = a a — ua. [y-^i
daHdahi
Рассматривая теперь Ф" как функцию инвариантов
Л, В и Я|, получаем с учетом выражений E.2) из соот-
соотношений D.11) — D.12) для несжимаемого материала
мц = 4i
§ 5. ИЗОТРОПНЫЙ НЕСЖИМАЕМЫЙ МАТЕРИАЛ Ц5
ава\\
+ В'1 —2 Га«а*' + -L (a*W + a"a»)l. E.4)
В частности, для неогуковского материала
5y = |ife(ay-fi-VJ), E.5)
М =
Часто упругий потенциал задают в виде
Ф° = Ф°(?ч,и Xs).
В этом случае также можно использовать соотношения
E.3), E,4). Прежде всего в главных осях деформации
А = %1 + %1 В = %1%1 (ац = Ь\аи). E.6)
Отсюда находим (Xi > Я2)
а - 2
= \ [УА + 2 /5 - /Л-2/5);
д_2 Г.4 ЙФ огг,2 ^Ф 4 5Ф ]
= [ Ч"^!У2" 12^4 2K?J
д3
я.»
8*
д2Ф°
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
= .-а Г aW _ 2 aV аУ I _2 /0фЦ_ мЛ
[{dxiy дКдК №2J д31^2 дЧ У
э2ф°
д = %1 _ х«. E.9)
Для трехконстантного потенциала C.7.7)
J
0Ч< }" Г/л . п\ /f\ f\ \ — Jl-J-2 /A O\ /'i ^
Щ-51<1 + Р><*Л> -(!~P)(V
- Р)
§ 6. АРМИРОВАНИЕ НЕРАСТЯЖИМЫМИ ВОЛОКНАМИ Ц7
§ 6. Армирование нерастяжимыми волокнами
Рассмотрим оболочку, срединная поверхность которой
армирована двумя семействами нерастяжимых нитей
(волокон). Материал оболочки считаем изотропным и
несжимаемым. В отличие от изложенного в § 3 гл. 4,
армируется лишь срединная поверхность. Поэтому
М = °Гк(а\ a2), qh = qh(<x\a*) (i, ft = 1,2), F.1)
а соотношения D.3.3) необходимо заменить на следую-
следующие из них при | = 0 (см. A.10)):
(я<хр - аар) "it Ч = 0 или гсф°1%°1% =0 (ft, а, Р = 1, 2).
F-2)!,,
Здесь уже
ё« = т(а«-"«) F-3)
— компоненты тензора тангенциальной деформации.
Запишем условия нерастяжимости
F.2) 2 в физических компонентах,
отнесенных к ортогональным матери-
материальным координатам на недеформи-
рованной срединной поверхности (см.
D.13)):
e<o|»>?<a>iJ<p>fc = 0. F.4) Рис. 5.6.1
О
При этом согласно рис. 5.6.1 для единичных векторов ]к
= cosa2, lBJ =sina2.
F.5)
Теперь условия F.4) можно записать в виде следующей
системы двух уравнений:
cos2 ax e<u> + sin2 axE<22> = — sin 2ax
в о о о о о
cos2 a3 e<n> + sin2 a2 e<22> = — sin 2a2 e<12>
с определителем
Л = cos2 ai — cos2 a2 = -т Vcos ^ai — cos 2a2J. F.7)
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
Возможны два случая:
а) А =И=0; при этом пз системы F.6) следует
[sin 2( а1 — аг) — (sin 2 aj — sin 2аЛ 1 „
е<> = ! '- е<>
<2>,
cos2ai-cos2a2
sin 2 I ах — a I + sin 2а1 — sin 2а2) „
е<22> = " 'т-1 5 [ ЧпУ,
cos 2a1 — cos 2 а2
б) А = 0; в этом случае из системы F.6) находим
о о о в о о о о
at = — a2 = a, e<]2> = 0, cos2 ae<n> + sin2 ae<22> = 0.
F.9),_3
Таким образом, случаю б) отвечает равнонаклоненность
семейств армирующих волокон и совпадение координат-
координатных осей с главными осями тангенциальной деформации.
Рассмотрим подробнее более интересный случай б)
равнонаклоненных волокон. Согласно равенству F.9J
материальные координаты ортогональны и на деформи-
деформированной срединной поверхности. Из рисунка, аналогич-
аналогичного рис. 5.6.1, имеем
ZAI = coscd, ZB)i = sinai; /AJ == cosa2, ZBJ = sina2.
F.10)
Здесь и в F.5)
1@ = il V^u ku> = I1 Wn (б.нь.2)
— физические компоненты по отношению к деформиро-
деформированной и недеформированной материальной системе коор-
координат на срединной (также материальной) поверхности.
Из соотношений F.11) (ср. C.18)) следует
а по равенствам F.5), F.10) имеем (at = — cc2 = a)
« cos a . sin a la «o-
Aj = , Л2 = -. ^O.lOj
cos a sin a
Напомним, что Xu k2 — главные кратности удлинений
(реализующиеся в рассматриваемом случае вдоль коор-
координатных линий).
Согласно соотношениям @.1) входящие в выражения
для напряжении D.3.5) — D.3.6) дополнительные, обус-
§ 7. РАСТЯЖЕНИЕ ЦИЛИНДРИЧЕСКОЙ ПЛАСТИНЫ Ц9
ловленные армированием срединной поверхности слагае-
слагаемые зависят только от координат срединной поверхности.
Поэтому добавочные слагаемые войдут лишь в выраже-
выражения для усилий. При этом согласно B.11), D.3.5),
D..'!.6), F.5) и (fi.ll)o учет двух равнонаклоненпых се-
семейств нерастяжимых волокон сводится-к заменам
Su-+Sn — hcoH2a{ql + q2)/an,
?22 _^ ?22 _ °h sin2 °a (?i _j_ q2)/a22, F.14)
?12 _^ ?12 _}b sin „ cos a (^ _
и принятию соотношений F.13). Можно показать, что
последние эквивалентны условию нерастяжимости F.9K.
Для этого следует подставить выражение F.13) в F.9K
и учесть, что согласно F.3) и C.1.11) e^..s, = 1/2 (Xf—l).
С учетом соотношений D.14) и E.6K зависимости
F.14) можно заменить на следующие:
¦ S<n) - h cos2 a (?i + Яг) %v
о о
5<22) ~ k Sifl2 "^l + ?2) ^2»
о о о (E 15)
^<12) — h sin a cos a{q1 — q2) X2,
о о о
cos a (gx — g2) Яг
§ 7. Растяжение цилиндрической пластины
Рассмотрим цилиндрическую пластину (рис. 5.7.1),
растягиваемую равномерно распределенными усилиями
S(u), приводящимися к растягивающим силам Р. Рассмот-
Рассмотрим эту задачу, относя недефор-
мированную срединную поверх-
поверхность к прямоугольным декарто-
декартовым координатам, в которых
G.1)
Координатные оси будут, очевид-
очевидно, п главными осями тангенциальпой деформации (из-
гибная деформация отсутствует).
Пусть армирование произведено равнонаклоненными
перастяжимыми нитями (волокнами), а связующий ма-
120
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОЕОЛОЧКИ
териал является неогуковским. Тогда согласно формулам
F.15), E.5), D.14) и (Б.12) имеем
S<u) =
<22) = I* °h (X2 - K*K') + °h si
о о о
(n\ = Л sin a cos a (gx — q2) X2,
00 о
^ ч = fcsin a cos a (^ — q2) ^
q2) klf
Яг) Я-а,
G.2)
Исключая из первых двух выражений вторые слагаемые,
находим
=ь ctg2 ^
G.3)
Из очевидных граничных условий на сторонах пластины
?<22) = 0, 5<21)=0, 5A2) = О
следует, что, в силу однородности напряженно-деформи-
напряженно-деформированного состояния, эти соотно-
соотношения выполняются во всей пла-
пластине. Поскольку у нас усилия
по первому индексу отнесены
к недеформированному контуру
(§ 2), Р =.&$<„,.
Подстановка выписанпых ве-
величин в выражение G.3) приво-
приводит к зависимости
Р-Р/С/л dh)
20
72
/ ~ 1.1 1.2 73 А,
Рис. 5.7.2
-ctga^-V1^4)- М
Добавляя сюда равенства F.13)
n cos a л sin a ,7 гч
cos a
sin a
приходим к зависимости безразмерной растягивающей
о о
силы P/(\ibh) от «ведущего» параметра а —текущего
угла наклона нерастяжимого волокна к образующей пла-
о
стины. В эти зависимости входит параметр a — началь-
начальный угол наклона.
§ 8. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
121
На рис. 5.7.2 показана зависимость безразмерной рас-
растягивающей силы от кратности продольного удлине-
удлинения A-i.
§ 8. Осесимметричная деформация оболочки вращения
При осесимметричной деформации оболочка вращения
переходит опять же в оболочку вращения. В качестве
материальных координат примем длину дуги меридиана
-dx-
Рис. 5.8.1
Рис. 5.8.2
s и угол 9 недеформированной срединной поверхности
(рис. 5.8.1), так что
а1 = s, а2-
9.
(8.1)
8 силу предположенной осесимметричности деформации
9 = 9 и
хг = r(s) cos 9, x2 = r (s) sin 9, x3=x3(s),
xx = r (s) cosЭ, x2 = r(s)sin9, a:3=-xa(s).
о
Из рис. 5.8.2 усматривается (' = d/ds)
о о о, о
г' = cos ф, а'з = — sin ф.
(8.2)
(8.3)
Пусть As(=Ai), А.е(=Я2)—главные кратности удлинений
вдоль меридионального и окружного направлений, явля-
являющихся главными линиями деформации. Из рис. 5.8.1,
5.8.2 следует
К = ds/ds, Xe = г/г. (8.4)
Из этих зависимостей и аналогичного рис. 5.8.2 рисунка
122 ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
для деформированной конфигурации следует по анало-
аналогии с (8.3)
г' = Xs cos ф, х3 = — Xs siiKp. (8.5)
С учетом полученных зависимостей подсчитываем по
формулам (Б.35) —(Б.38), (Б.22) и A.7)
о о о в о о о о о о
ап = 1, а12 = 0, а22 = г2, а = г2, я11 = 1, а12 = 0, а22 = г~2;
(8.6)
6l= —J', ь5= —г^втф, ь" — Ьа = 0;
о о
ап = Xs, а12 = 0, а22 = г2А.§, а =
п
о
— Х8ф', Ь12 — 0, Ь22 = — гК sin ф,
= —ХГУ, 6l = -rVsin(p, Ь2=Ьг2 = 0;
rix = ^Г1^ И2 = г-хХ, V1 cos Ф, (8.7)
Г22 = — rXJ Кв cos ф, Г2! = Г12 = Г23 = 0;
9, х12 = 0;
Примем более употребительные обозначения D.14)
= S<n) = ^", 59 = *<22) = ^-, (8-8)
<71 rp ml
•* sn — •* <[])« — •* •«•
При этом согласно B.9) и (8.6)
Ss = Ts — К\'М„ Se--=T0— r'%1 sin фЛ/и. (8.9)
При необходимости можно считать
S.*T., Se^Te. (8.10)
Положительные направления нормальных усилии Ts, Те
изгибающих моментов М„ Me и перерезывающего усилия
§ 8. ОСЕСИММЕТРПЧНАЯ ДЕФОРМАЦИЯ 123
Tsn показаны на рис. 5.8.3. Переобозначая физические
компоненты напряжении
/О Л Л \
Os —0A1). Яе=ЯB2), (8.11)
имеем согласно формулам B.15) и (8.6)
3.12)
где
Л = к5. (8.13)
С учетом соотношений (8.6), (8.8) уравнения равно-
равновесия (движения) для осеснмметричной деформации
C.4) принимают вид
(гТ.у - cos фГв + r<f'Tsn + к Ms = О,
(rTsn)' - sin фГ9 - гфТ, + ЛМп = 0, (8.14)
(гЛ/,)' - cos ц>Мв — г\,Тт = 0.
Из первых двух уравнений следует квадратура
г (sin (fTs — cos rp Tsn) =
fan cos ф - qs sin ф) (Xer) (X,d»), (8.15)
являющаяся условием равенства нулю осевой составля-
составляющей главпого вектора всех сил, дей-
действующих на пояс sfs деформировап-
пой срединной поверхности оболочки. MS
Постоянная QisA—вертикальная сила
о о
па круге s = s1.
Для равномерного нормальпого дав-
давления
qn = q = const, qs = 0 (8.16)
и с учетом соотношений (8.4), (8.5) квадратура (8.15)
принимает вид
о
r(sin(pfs — cos(pfsn) = !f1' -j- ~ q (r3 — r2 (sj). (8.17)
124
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
Вернемся к формулам (8.3) — (8.5). С их помощью
получаем
о / о
r%Q -\- COS фХд — COS wK. = 0, . . о.
, (о. 18)
г = гХе, х3 -)- Xs sin ф = 0.
Для изотропного несжимаемого трехкопстантного ма-
материала имеем согласпо соотношениям (8.8), E.3), E.4),
E.9), E.10) и (8.0) после некоторых упрощений [75]
S, = цШГ'К1 [A + Р) + A - Р) *е ] (А,? - ЯГПЯБ"ЭТ),
5е = иЛ»^1 [A -I- Р) -I- A ~ Р) X?] (XS - ХГХ"), (8.Ю)
V[(i + P)X7n^n +
^r' [(I + Р) ХГПЛГ +
+ A + Р) Ое] (хв + V.X.).
Согласно A.9) и (8.6) для несжимаемого материала
h = К1**1. (8.20)
§ 9. Армированная цилиндрическая оболочка
Рассмотрим осесимметрично деформируемую цилинд-
цилиндрическую оболочку из неогуковского материала ([J = 1,
п = 2), армированную двумя семействами нерастяжи-
нерастяжимых волокон, равнонаклоненных к координатным осям
Рис. 5.9.1
(рис. 5.9.1). Рассматривая эту задачу, С. А. Кабриц свел
соотношения § 6, 8 к следующей разрешающей системе
О О О
уравнений (ф = л/2, ' = d/dst O^s^Z):
о о
(г — г)' = — ^s sin (ф — ф),
5 9. АРМИРОВАННАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА $25
(х3 — х3)' = — ks cos (ф — ср) + 1,
(ф-°ср)' = ^Аэх*, (9.1)
M's = — Мвг ~г sin (ф — ф) + ksTsn,
T'sn = TsJ-1 соз(Ф - й -f 2давх« ~ ^Лз.
7^ = — Уег" sin (Ф — ф) — Г.пМЛох,;
fs = u/1 (Xs - Я.Г3Я.5-2) + h cos2 a (9l + g2) Xs,
TQ = (i? (A,e ~ ^~2^e~3) + /I sin2 a ((jfj + ?1) ко,
Ms = V8H**^ V (x, + V,xe), (9<2)
Л/в = '/.^^rVVxe + 'Ли,);
Яе = 1 + (г-г)г-1,
Xl cos2 a + X| sin2 a = 1, (9.3)
xe = r-1 IV1 V соэ(ф — ф) — l].
Выражая из уравпений (9.2) — (9.3) неизвестные
о о
функции к„ к*, Те, xs, Же через г —г, ф^ф, Ms, Ts и
подставляя их в (9.1), приходим к разрешающей систе-
системе обыкновенных дифференциальных уравнений для
о о о
функций г— г, х3 — х3, ф — ф, М„ Т,п, Т..
Пусть цилиндрическая оболочка (обечайка), растяги-
о
ваемая осевой силой Р, заделана на краю s = 0 и имеет
о
скользящую заделку на краю s = 1, т. е.
о о о о
s = 0: г — г = 0, ф — ф = 0, ж3 — ^з = О*
s = l: г —г = 0, ф — q) = Oj Ta = P/Bnr).
Здесь, в отличие от случая гладкой (неармированной)
о
оболочки, из краевого условия г — г = 0 (кв = 1) и урав-
уравнения (9.3J следует к.~ 1, т. е. на самом краю оболочки
тангенциальная деформация полностью отсутствует.
На рис. 5.9.2 показаны диаграммы равновесных со-
состояний. По оси ординат отложены значения безразмер-
0 0
ной осевой силы Р — P/(\ihr), j по оси абсцисс — без-
безразмерное сокращение оболочки А =
126
ГЛ. 5. ТОНКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
На рис. 5.9.3 представлены^ профили меридиана де-
деформированной оболочки при Р = 9. На обоих рисунках
кривые 1, 2, 3 отвечают соответственно l/r=l, 2, 10.
Из рис. 5.9.2 видно, что с увеличением растяжения
оболочки резко возрастает ее жесткость на растяжение.
15
10 —
5 -
I
1
и
/
0,5
ff 0,05 0,10
0,7
г/г
Рис. 5.9.2
Рис. 5.9.3
Объясняется это тем, что при растяжении армирующие
волокна поворачиваются к образующим цилиндра, «пре-
«препятствуя» дальнейшему растяжению.
Рассмотренная нелинейная двухточечная краевая за-
задача решалась численно на основе сочетания методов
продолжения по параметру, квазилинеаризации Ньюто-
Ньютона — Канторовича и ортогопальпой прогонки.
§ 10. Армированный конический тонкостенный
амортизатор
Рассмотрим осесимметричио деформируемую кониче-
коническую оболочку из материала Бартенева — Хазановича
(Р = 1, п={), армированную по срединной поверхности
двумя семействами нерастяжимых волокон, равнонакло-
ненных к координатным осям (рис. 5.10.1). Рассматривая
эту задачу, С. С. Прасникова свела соотношения § 6—8
к следующей разрешающей системе уравнений .(' = d/dst
§ 10. АРМИРОВАННЫЙ КОНИЧЕСКИЙ АМОРТИЗАТОР
127
COS ф
г
ка sin
XsXexl
COS ф
r
sin ф
о
r
COS ф
r
1
Ф.
si
T
1 a
T
1 e
Mo
COS ф
r
о
COS ф
о
г
о
COS ф
о
г
о
COS ф
г
х3 ф
о
cosjp coscp ,т
s ф ¦* sm
sn -г ф ^ s —
а + hal
Ts = 2\ih A - Х7 V1) + h cos2 a [qt + qt)
A0.1)
Л/, =
л/в =
V.xe),
(хв
= г
(Х72^
in Ф — sin ф).
= гг~\ "к\ cos2 а + К sin2 а = 1.
э' A0.2)
A0.3)
За основные неизвестные функции примем кв, Ф, Хз, Т„
Tsn, Ms. Выражая с помощью
A0.2), A0.3) через них остальпые 1^
величины и подставляя эти вели-
величины в A0.1), приходим к разре-
разрешающей системе обыкновенных
дифференциальных уравнений.
Рассмотрим случай, когда ко-
коническая оболочка находится под
действием сжимающей осевой си-
силы Р и внутреннего давления р.
При этом будем считать, что
о о
нижнее основание (*' = s.2) задола-
ь g_ ^ "
I
Рис. 5.10.1
но, а на верхнем (s = Sj) — скользящий шарнир, т. е.
(*°i) = 1. -Ч (*,) = .т3 (я,) - Л,
= 0;
О О О
(S2) = 1, Х3 (S2) = Х3
О OQ
ф (S2) = ф (Sjj),
V * /
128
ГЛ. 5. ТОПКИЕ АНИЗОТРОПНЫЕ ОБОЛОЧКИ
где А — осадка верхнего основания. Отмстим, что из ус-
условий Х9 (s,) = Хв (s2) = 1 и последнего в A0.3) ра-
равенства следует A.s(Sj) = Xs(s2) = 1. Таким образом,
в силу армирования и принятых граничных условий, на
краях оболочки отсутствует тангенциальная деформация,
а значит, и тангенциальные напряжения.
Рис. 5.10.2
На рис. 5.10.2 приведены зависимости безразмер-
ной вертикальной силы F — F/(EhH) от безразмерной
осадки верхнего основания А = А/Я для амортизатора
с параметрами Ф = 60°; h/H = 0,217; R/H = 0,875, под-
подверженного и внутреннему давлению р/Е = 0,01. Сплош-
Сплошные линии отвечают амортизаторам с различными зна-
о
чениями угла армирования а; линии с кружками — не-
армированному амортизатору. Напомним, что, в силу на-
наличия внутреннего давления, вертикальная сила F не
совпадает со сжимающей Р.
На рис. 5.10.3 показано изменение диаграммы F— Л
в зависимости от угла конусности (<р = 60°; <р = 70°) при
§ 10. АРМИРОВАННЫЙ КОНИЧЕСКИЙ АМОРТИЗАТОР
129
фиксированном значении угла армирования а = 45". Здесь
также сплошные линии отвечают армированным амор-
амортизаторам, а линии с кружками—нсармировашшм.
Рассмотренная нелинейная двухточечная краевая задача
сводилась к последовательности задач Коши, которые ре-
решались методом «стрельб».
9 К. Ф. Черных
ГЛАВА 6
НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
В этой главе рассматриваются некоторые теоретиче-
теоретические вопросы, примыкающие к изложенному в предыду-
предыдущих главах. Излагаемый материал был в разное время
опубликован в статьях автора [67, 69—72] и является,
по существу, дальнейшим развитием фундаментальных
работ В. В. Новожилова. Появляющиеся время от вре-
времени публикации на эту тему свидетельствуют о неосла-
неослабевающем внимании к вопросам о структуре и свойствах
определяющих уравнений механики сплошных сред и
убеждают автора, что изложенное ниже отнюдь не
устарело.
§ 1. Групповой тензорный базис
Если ввести тензорный базис
Hj = ete,, H4 = (eje2 + e2e,) /У 2,
Н2 = е2е2, Н5 = (е2е3 + е3е2)/У2, A.1)
Н3 = е3е3, Н9 = (е3е, + е^з) /У 2,
где е( — орты:
A при i = /,
р..р. _ ft... _ ) г ' м о\
e.-e^-Oy-JQ при 1ф^ A.Z)
то симметричный тензор
А = а„реаеэ (а, 0 = 1, 2, 3) A.3)
можно представить разложением
А = атНт (f = l, ..., 6). (l/i)
Здесь
а, = У2 а„. A.5)
§ 1. ГРУППОВОЙ ТЕНЗОРНЫЙ БАЗИС 131
Введем еще один тензорный базис, который по сооб-
соображениям, изложенным ниже, будем называть тригоно-
тригонометрическим:
Gl = W(Hl + Нг + Нз) = WFl<!l + е'2в2 + езвз)'
G2 = -L- BH3 - П, - H2) = -L. Be3e3 - e^ - e2e2),
G = —(H _H) = -L(ee —ее)
. A.6)
\Jfc Л К ~~ - ' (CnUo "T" 60G9 )•
Gtt 1 / 1 \
6- 6 — y^ v 3 1-1 1 зу-
Компоненты разложения тензора в тригонометрическом
базисе
A = aTGT (if — 1 6) A.7)
связаны с таковыми в разложении A.4) очевидными
соотношениями
1 - 1 - 1 - - 1
й2
ая
а.
1 -
1 ~
= а,, аъ
1 -
2 -
уёЙ2'
/7 ft
1 ""
f уГаз'
= а6-
1
Й2 ~ уъ
1
пз~У2
Используя операцию свертки (двойного скалярного
произведения) тензора A.3) и В = Ь^е^
А : В = aapb(tv(ep • е„) (еа • е,) = йарЬ^брмбау = aap6pa, A.9)
нетрудно убедиться в ортонормированности введенных
тензорных базисов:
H,:Hj = G<:GJ = 6«. A.10)
Пусть используемые координатные линии являются
главными для тензора А, т. е. в них ak = аь = at = 0.
9»
132 1"Л. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Обратимся к широко использованным В. В. Новожиловым
тригонометрическим представлениям главных значений
[Н]
ccs ^а "" Оа sin"
ст^а+»аЗт^а\ A.11)
где
A1 = a1 + ai + a3 A.12)
— первый главный инвариант тензора А,
0а = ^ /К"- a2f + («8 - a3f+ (a3 - a,f A.13)
— интенсивность тензора, а -фа — ого угол вида. Согласно
соотношениям A.7), A.8) и A.11) в своих главных осях
тензор представим разложением
^iG1 + i^cos^aG, + dasint|;aG3. A-14)
Полученное представление и оправдывает принятое
для тензорного базиса A.6) название — тригонометриче-
тригонометрический. Тригонометрический базис обладает еще одним
примечательным свойством. Сохранение в представлении
A.7), A.14) первого слагаемого выделяет из тензора его
шаровую часть. Сохранение двух слагаемых означает со-
согласно A.14) и A.11) я|\, ~ 0 и а[ = я2. Таким образом,
при атом А становится осесимметричпым тензором с осью
вращения, направленной вдоль третьей координатной
огп. Сохрапение трех членов выделяет часть A.14) с ко-
координатными осями в качестве главных. Добавление чет-
четвертого слагаемого не отражается на направлении
третьей главной осп. Наконец, добавление оставшихся
двух слагаемых приводит к симметричному тензору об-
общего вида. Тензорные базисы такой структуры Ю. И. Си-
Сиротин предложил называть групповыми [57].
Аналогичный формализм можно развить и примепи-
тельно к несимметричному тензору. Так, добавляя в
3 г групттонлй ТГСПППРТП.ТЙ г.ллш:
133
базисы A.1) и A.6) еще по три компоненты
Н8 = G8 = -д- (е2е3 — е^), A.15)
Н9 = GS> = yg" (еЗе1 ~ е1ез).
представим несимметричный тензор разложениями
А = 0,^ = 5,0,
где, в отличие от A.5),
= 1, .... 9),
A.16)
а, = а,
а, =
1 — U/11' w 2
1 / . х 1 /
«4 = " («12 + «2l)> пЪ = (Я23
11
— J («12 — a2i). «8 = зг(«23 —
1
«6= j
A.17)
1
J з «э = ^ (а31 — «is)-
Пополненные базисы ортонормированы в смысле
где
при
Н//Н,- \-1 при / = 7,8,9.
A.18)
A.19)
В другой, также прямоугольной декартовой системе
координат [53]
G^Q-Gi-Q*, A.20)
где
Q = gapeacp A.21)
— ортогональный тензор поворота, компоненты которого
связаны с компонентами вектора поворота ю = ш,ет мат-
матричным соотношением (А.45)
?21
II ООП
0 1 0 +
0 0 1 1
, 1 — cos со
sin со
со
0 — со со
О Z
О -
о
со
Ш1Ш3 Ш2Шв Ш3
. A.22
134 ГЛ. 0. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Подставляя в соотношение A.20) выражения A.21),
A.6) и перераскладывая правую часть полученного ра-
равенства в тригонометрическом базисе A.6), находим
G'i = miaGa (i, a = l, ...,6), A.23)
где
ти = гпц = 6ц, т22 =1 (Зд33 — 1), m23 = ^-(qls—q\a),
m33= j(q2i2 — q212 — q2n — q2n),
'4=
«i25 = /3 ^33<723, m52 --- /3 ry33^,
62 = /3
31 = G22?12 —
-22713, Щь^ЧпЧзХ + 7и7з2, me4 = 72l7l3 + 711723,
22q33, rni6
A.24)
Если при переходе к новой системе координат ис-
используется преобразование отражения в плоскости с еди-
единичной нормалью п(а, р, -у), то в соотношении A.23)
игу — компоненты следующей симметричной матрицы:
/Иц = 1, 7И12 = ТПи = 7Пц = TOi5 = 7И1в = 0,
т24 = 4 УЗ apf, ш;з = -2V3
mse=»-2V3af(l-2f2),
m33 = 2(p2-a2J-(l-2f), A.25)
т34 = 4ap № ~ a2), m35 - 2[JT [I - 2 (ji2 - a2) ],
m44 = 2y2 + 8a2^2 - 1, m45 = - (
m46 = -2?y A - 4a2), m55 = 2a2 + 8p2f - 1,
m56 = -2ap A - Af), mee = 2^2 + 8а2^'2 - 1.
Проводя преобразования A.23) — A.24) для порождаю-
G,
G,
G1:
G,,
G,
инвариантные
, G2,
, G2,
, G2,
G2
G3,
G3,
G3
G4, G5,
G4
тензоры
G6
A.26)
§ 2. ПОЛУСИММЕТРИЧНЫЙ ТЕНЗОР ЧЕТВЕРТОГО РАНГА 135
щих элементов симметрии пятого столбца табл. 3, полу-
получаем следующие инвариантные тензоры:
сингонии и текстуры
триклинная
моноклинная
ромбическая
тетрагональная, тригоналъная, гек-
гексагональная оо, оо : т, оо • т,
т • оо ; т, оо • 2
кубическая оо/оо, оо/оо • т
Составляя различные комбинации ш приведенных
тензоров, получаем все тензоры, инвариантные относи-
относительно преобразований симметрии той или иной спнго-
нии, текстуры.
§ 2. Полусимметричный тензор четвертого ранга
Пусть два симметричных тензора второго ранга А и
В связаны полу симметричным тензором четвертого ран-
ранга S, для которого выполняются условия симметрии
sijhl ~ sjihl == Sfj/fc = shlij- B-1)
Компонентная запись
Ъц = simaafi, B.2)
согласно A.5), аналогичной зависимости для тензора В
и соотношений (i, ) — 1, 2, 3)
^45 ^^1223) ^46 ^^1213, ^дб == ^^2313
дюжет быть представлена в виде
fti = siTflT (s« = Sj(, i, 1 = 1, ..., 6) B.4)
или, наконец, в прямой тензорной записи
B = S:A; B.5)
S = sapGa(i, G(J = V2(G(GJ + G,G,) = Gj1-. B.6)
В соответствии с темой книги один из тензоров А и В
будем рассматривать как тензор деформации, а другой —
как тензор напряжении. При этом S — тензор упругих
постоянных. Величины G,-j можно рассматривать как
компоненты тензорного базиса для полусимметричных
136 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
тензоров четвертого ранга, нормированных согласно B.6)
и A.18) соотношениями
«:.ЬЫ= /2 (bikOji + Ojh0a). (/.7)
При переходе к другим, также прямоугольным декарто-
декартовым координатам имеем согласно формулам B.6) и A.23)
B.8)
где по-прежнему mti — величины A.25) или A.24). Так,
например, при повороте координатных осей вокруг
третьей оси на угол о
10 0 0
0 10 0
|, || 0 0 cos 2<в — sin 2<в
II УII ДО sin 2<в cos 2<в
0 0 0 0
0 0 0 0
0
0
0
0
COS О)
sin о
0
0
0
0
— sin О)
COS О)
B.9)
Пользуясь формулами B.8), A.26), A.22) и табл. 3,
выявляем инвариантные комбинации тензоров:
инвариантные комбинации
G;j кроме (Gm, G15, Gie)
Gu, G12, G13, G22, G23, G24, G33, G34,
G44, G55, G56, G66
Gn, Gi2, G13, G22, G23, G33, G44, G55, G66
Gu, G12, G22, G33, G4j, G55 + G66
Gu, Gi2, G22, G33 + G44, G55 + G6e,
G35 — G46
(VI) гексагональная
oo, 00 : те, 00 • те,
те • oo ; m, 00 : 2
(VII) кубическая
(VIII) гиротропная
(/)
сингонии и текстуры
(I) триклинная
(II) моноклинная
(III) ромбическая
(IV) тетрагональная
(V) тригональная
u, G12, G22, G33 -|- G44, G55 + G6g
u, G22 + G33, G44 + G55 + G66
(оо/оо), изотроп-
изотропная (оо/оо • щ)
«Hi 2+ «33 "Г ««4 + «55 + lx6,
B.10)
Здесь в качестве основной поворотной оси принята
третья координатная, а в качестве боковой — вторая. Все
оси здесь — главные оси анизотропии (§ 2 гл. 2). При
этом для унификации внутри сингонии использованы по-
повороты типа B.2.3) —B.2.5).
Предложенный подход удобен и при сравнении ани-
анизотропных материалов с ближайшими к пил (в смысле
наименьшего квадратичного отклонения) изотропными
([60], с. 189). У нас при этом дело сводится к подсчету
§ 2. ПОЛУСИММЕТРИЧНЫЙ ТЕНЗОР ЧЕТВЕРТОГО РАНГА 137
двух инвариантных величин:
а = sn, bb = s22 + s33
see.
B.11)
Из группы (VIII) таблицы B.10) и соотношений B.6) —
B.7) усматривается, что эти величины получаются в ре-
результате операций свертывания тензора S с инвариант-
инвариантными комбинациями тензоров изотропной среды. Анало-
Аналогично можно получить и ближайшие материалы других
сингоний. Так, для трансверсально-изотропного материа-
материала (ведущего себя в отношении упругих свойств как
гексагональный материал (VI)), ближайшего к материа-
материалам более низких сингоний, следует принять
b = siz,
а = siu
с = szz, d =
su, e
Таблица B.10) приводит к следующим, унифицирован-
унифицированным внутри каждой сингоний каноническим симметрич-
симметричным матрицам упругих модулей
триклиннпя
11
(I)
0
'u '12 '18 °
S22 S23
S33
35
S45
33 31
66
ромбическая
моноклинная
0 0
0 0
0 0
(П) *44 О О
S55 S56
тетрагональная
S12 '18
S22
(III)
°33
0
0
о
11 12
S22
(IV)
о
о
B.11)
тригоналъная
0 0 0 0
55
гексагональная аз; оо: т\
со -т; т-оо : т; с» : 2
12
*22 °
зз
0 0
0 s.
зз
(V)
35
0 —
S55 '
22
О
О
(VI)
О
О
о
'ss
О
о
о
о
'55
55
5
138 гл. 6. некоторые вопросы теории
кубическая
) 0 0
,2 о и
*i« °
S44
S
0
0
0
0
44
0
0
0
0
0
гиротропная
изотропная (
slt 0 0 0
s 0 0
S22 0
(VIII) s2,
(оо/со),
оо/сс
0
0
0
г 0
| -т)
о
0
0
0
0
(VII)
Существенно, что все координатные оси являются
здесь главными осями анизотропии. При этом во всех
сингониях, кроме первых двух, это условие выполняется
автоматически. Сопоставление полученных матриц с мат-
матрицами B.1.13) показывает, что здесь матрицы средних
сингоний по своей структуре проще обычно используе-
используемых B.1.13). Для кубической же сингоний и изотропной
среды матрицы и вообще диагональные. Кроме первых
двух (самых низких) сингоний, все остальные не имеют
элементов выше второй наддиагонали. Поэтому к ним
применимы формулы B.3.7), гарантирующие положи-
положительность квадратичной формы (плотности энергии де-
деформации).
Соотношение B.5) показывает, что тензор S можно
рассматривать как оператор, переводящий произвольный
симметричный тензор второго ранга А в некоторый тен-
тензор В того же типа. В общем случае этот оператор иска-
искажает вид тензора, переводя, например, шаровой тензор
в нешаровой и т. д. Характер указанного искажения мо-
может служить внутренней характеристикой сингоний и
текстур. Несложный анализ с использованием соотноше-
соотношений B.4), A.26) и сказанного в § 1 о групповом базисе
приводит к следующему результату:
сингоний
и текстуры инвариантные свойства
триклинная
моноклинная сохраняется главная ось (третья)
ромбическая сохраняются все главные оси
тетрагональная сохраняются: а) ось вращения (тре-
(третья) и б) две другие главные оси
тригопальная сохраняются: а) отношение я4/"з при
я5 = ае = 0 и б) боковая главная ось
(вторая)
гексагональная сохраняются: а) отношения а$/а6,
оо, оо : тп, оо • m, /i4/a3 н б) все главные осп (третья —
m ¦ оо : пг, оо : 2 ось вращения)
§ 2. ПОЛУСИММЕТРИЧНЫН ТЕНЗОР ЧЕТВЕРТОГО РАНГА 139
кубическая сохраняются: а) все главные оси,
которые к тому же б) равноправны
изотропная не искажается приведенный (при
¦О = 1) девиатор
Поясним приведепную таблицу. Прежде всего соглас-
согласно формулам A.7) (при опущенной черте), A.5) и A.10)
а{ = а : G{ = пуШ^ (Gv : Ga) = avmia8ya = nija^a. Отсюда и
из матрицы B.9) следует а^ = sin 2соаая + cos 2coaa4. При-
Приравнивая нулю это выражение, получим первое из выво-
выводимых аналогично выражений
aja, = -tg 2coa, 6/6,==-tg2(o». B.13)
Равенства a5 = a6 = 0 означают, что третья координатная
ось является главной для тензора А. Отсюда видно, что
а>а — угол поворота вокруг третьей оси, переводящего
остальные две координатные оси в главные для тензо-
тензора А. При этом равенство bjb3 = aja3 означает coa = <х>ъ,
т. е. пара волокон, между которыми отсутствует сдвиг
(а4 = 0), не испытывает дополнительного поворота во-
вокруг третьей координатной осп (ие являющейся, конеч-
конечно, главной для тензора В). Аналогично показывается,
что сохранение отношения aja6 = a23/at3 означает не-
неискажение отношения остальных двух сдвигов.
Формулы A.26), B.12) позволяют установить следу-
следующее: преобразование B.4) (B.2), B.5)) переводит
тензоры, допускающие преобразования симметрии той
или иной сингонии (текстуры), в таковые же.
Отметим, что все сказанное в гл. 2 относительно
упругих постоянных относится и к компонентам тензо-
тензора S. Так, симметричные коэффициенты Пуассона вво-
вводятся соотношениями
s^VyVsjSj (v« = vj(, vh = 1). B.14)
Для них, в частности, справедливы тригонометрические
представления B.3.7).
Для изотропного материала имеем согласно формулам
B.12), B.4), B.3) и A.5)
а<п) = '/3Eц + 2s22)e(I1) + 72(«н - s22) (e(I1) + eB2)),
0A2) ~ ^226A2), ¦ • .
Сопоставление полученных выражений с традиционной
140 гл- 6. некоторые вопросы теории
записью закона Гука B.9.3) приводит к соотношениям
Поскольку 0<sn, s22<+°°, отсюда следуют хорошо из-
известные неравенства Е>0, — 1 < v < 1/2. По-видимому,
для всех реальных материалов v > 0. Это условие соглас-
согласно B.15) можно записать в виде
*«<«н, B.16)
т. е. модуль искажения формы (sa2) для реальных ма-
материалов меньше модуля изменения объема («и). Кри-
Критерий B.16), в котором sn и s22 заменены на а и b
B.11) или какие-нибудь другие усредненные величины,
может выявить «неиспользуемые» интервалы изменения
модулей (аналоги интервала — l<v<0 для изотропных
материалов).
§ 3. Ассоциированный базис
В. В. Новожилов показал [43] возможность построе-
построения шестичленного тензорного базиса из двух разноос-
ных (не имеющих пи одной общей оси) тензоров. Ниже
приводится фактическое построение такого базиса [67].
Прежде всего составим с помощью соотношений A.6)
таблицу симметризованного скалярного умножения
GG G GG+GG G5'
11 1
<VG2 = yf Gl + y^ G,' G2-GG+G6'G2 = yf G6'
G5'
C.1)
G+G^ « GG + GG G
G+GG GG+GG
G2-G3 = G3-G2 = - yf G3' G4-G6"'iG6"G4= yf G5'
S 3. АССОЦИИРОВАННЫЙ БАЗИГ. 141
В качестве первого опорного тензора примем приве-
приведенный девиатор тензора А (см. A.Н))
Ai)i)> ^ G (:¦'..2)
С шшощыо таблицы умножения 0>.1) Подсчитываем
Sa - -% G: = ~ (cos 2i>nGa - sin 2tf«G3). C.3)
Из приведенных соотношений видно, что более иысо-
кис стеиепи Sa не могут дать составляющих по G,, G5, Gr.
Для получения последних введем прпведенпый девиатор
тензора В, не имеющего с Л нтт одной общей главной оси,
Sb = (в -~ И.И'Л П' -- с.« i|)bGa I- sin iI^G; (ИЛ)
Здесь штрихами помечены компоненты тензорного бази-
базиса, отвечающего главным осям тензора В. Считая, что
формулы A.23) отвечают переходу от главных осей тен-
тензора Л к таконым для В, имеем
в
Уь =^' 2 ЪьЛЪаО,м ftb^bi = COS Л\Ь1П21 f Sill tybl'hi. C.5)
a -2
В качестве второго опорного тензора примем
Si' = 8ь - OJT1 Шя + ЬЩ3) = Ьь * (blGt + b"bG3 + №),
(У.О)
являющийся частью S6, «выходящего» из «плоскости»
G:®G3.
Рассмотрим специально подобранные выражения
Q4 = ЛГ^^, Q5 = AA^Sa-S^ SbA-Sa -A3Ar2S,A), C.7)
Q6 = Bsm^aA2)~
COS 3ta (SbA2 • Sa f S? • Sa • S? ) H-
j St2 + A4 (SS - ~ Gaj + AbSa
142 гл. 6. некоторые вопросы теории
тде
л, = чУь? + Ы* + ь?,
Л» = i $Г* [4 Sin2 Х^ЫХ* + (Sin фа - /3 COS фа)
Л3 = -i=r ^Г2 [- 2 cos i|job;* + (cos г[)а + /3 sin фв) Ь?2 +
уб
+ (cos ij)a — /3 sin г|;„) С
+:+
(i^V3|J 5 +(j4 + y34)8
e) (e
Г Ьа2
1
6а2
+
Используя соотношения C.1) —C.3) и C.6), приво-
приводим зависимости C.7) к виду
Qi = Gi, Q2 = cos t|:aG2 + sin t|:aG3, Q3 = — sin i[-aG2 + cos \j)<,Gs,
Q4 = X.G4 + x& + XsGe, Q6 = ^(G4 + tiA + ri3G6,
Qs = (ЛзХз - ЛзХз) G4 + (TlsJCi - life) Gi + (Л* - ЛгХ<) G6,
C.9)
где
/X C.10)
С помощью этих выражений и C.8) убеждаемся, что
Xi + Xi + Хз = Ч\ + Ла + Пз = 1, Х1Л1 + Х2Л2 + ХзПз = 0.
C.11)
§ 3. АССОЦИИРОВАННЫЙ БАЗИС 143
т. е. на величины у_{, т], можно смотреть как на компо-
компоненты ортогональных между собой единичных векторов
(Oi t1A1j)- Если ввести шестимерные векторы
q(Ql! ..., Q.) и g(G,, .... G6), C.12)
то их компоненты связаны соотношениями
Q« = p»Ge, C.13)
где р,
1
0
0
0
0
0
i, — компоненты
0
cosx|)a
— sin i|>o
0
0
0
0
sini|)a
cosi|)a
0
0
0
матрицы
0
0
0
xx
t)
0
0
0
0
0
0
^3
^з V2-V1
^3
C.14)
При помощи соотношений C.11) нетрудно подсчи-
подсчитать, что \рц\ = 1, т. е. C.14) является ортогональной
матрицей поворота, так что
Pio-Pja. = PaiPaj = бц, (/)"') у = (р* ) ц = Рц,
C-15)
При этом переход от g к q происходит как бы путем
двух поворотов: в «плоскости» G2 ® G3 (Q2 ® Q3) на угол
вида ifa; в «пространстве» G4 ® G5 ® G6, причем «косину-
«косинусы углов поворота» определяются ортами х> X X t), t].
В силу соотношений A.10) и ортогональности матри-
матрицы C.14) имеем
Qi : Qj = i'ia/'* (Ga : Gp) = piap№bati = /)tai?ja = Stf. C.16)
Из этих соотношений и C.7) следует, что на величины
Q< можно смотреть как на компоненты ортонормировап-
ного, ассоциированного с парой тензоров А и В тензор-
тензорного базиса.
Аналогично тому, как были получены выражения
C.4) — C.5), находим разложение произвольного симмет-
симметричного тензора С в постоянном и ассоциированном
144 гл. 6. некоторые вопросы теории
базпсах (см. C.15))
с"
С = ^4f-c1G1 + ^ cSGa, с" = ^c(cosi|icm2j -\- sin\pemsi);
C.17)
p. C.18)
Здесь т*;, ???.,; — компоненты матрицы A.26), отвечающие
переходу от главных осей тензора А к главным осям
тензора С.
В работах Рпвлина было показано (см., например, [16], с. 386),
что при построении симметричного тензорного базиса из двух раз-
нооспых симметричных тензоров А и В можно ограничиться рас-
рассмотрением следующих девяти комбинаций (назовем их тензора-
тензорами Рпвлина):
Р, = 1, Р2 = А, Р3 = А2, Р4 = В, Р5 = В2,
Р6 = А • В + В • А, Р7 = А2 В + В • А2, Р8 = А • В2 + В2 • А,
Р„=А2ВЧ-В2- А2.
Сформулированное утверждение есть следствие полученпого Рив-
шшом обобщением па случай двух тепзоров тождества Гамильто-
Гамильтона — Коли.
Естественно возникает вопрос о связи результата Ривлина с
изложенным выше и, в частности, насколько «волевым» был выбор
комбинаций при построении ассоциированного базиса C.7). По-вп-
дпмому, не вызывает сомнения вопрос о целесообразности выбора
компонент Pi, Р2, Рз, Р* В. В. Новожиловым было показано ([43],
с. 796), что шестой компонент ортонормированного базиса опреде-
ляетси через заданные пить. Поэтому «волевым», по существу,
является лишь решение использовать комбинацию А • В + В • А.
Проделанная автором работа показала, что сделапный выбор при-
приводит к соотношениям простейшего вида.
Далее, естественным являетси предположение, что девятичлен-
пый тензорный базис Рпвлина «шире» предложенного шестичлен-
пого ассоциировапого базиса, т. е. что использование тензоров Рив-
Ривлина позволяет рассмотреть случаи, когда ассоциированный базис
перестает быть полным. Покажем, что это пе так.
Прежде всего, как будет показано ниже, в случае, если тензо-
тензоры А и В имеют одпу общую ось, ассоциированный базис стано-
становится четырехчленным. При трех общих осях — трехчленным.
Пусть, далее, один из опорных тензоров (например В) являетси
осеецмметршшым. Нетрудно проследить, что в рассматриваемом
случае базис остается полным. Если оба тензора осесимметрпчпые,
то они имеют [\Щ одну общую ось — случай уже рассмотренный.
Для шарового тензора все направления главные. Таким образом,
ассоциированный базнс полон, коль скоро порождающие его тен-
тензоры А п В не пмрют общих главных осей.
При помощи таблицы умножения C.1) можно проверить, что
и тензоры Ривлина в случае совпадения главных осей дают соот-
§ 4. ТЕНЗОРНЫЙ РЕПЕР 145
ветственно четырех- и трохчлснпые базисы. Из сказанного следует,
что совокупность тензоров Рпвлина «пе шире» предложенного
шестнчленного ортонормированпого ассоциированного базиса.
§ 4. Тензорный репер
Пусть
е,@, с, @, е3@ D.1)
— зависящий от времени t ортонормированныи вектор-
векторный базис, a t0 — некоторый фиксированный момент вре-
времени. Тогда
е,(*) = М*о) «МО, D-2)
где qtj — косинусы углов поворота A.22). Введем в рас-
рассмотрение величины
det(t) da}(t)
-±
являющиеся соответственно мгновенными скоростями
компонент векторного базиса и углов поворота. Прн этом
повороты рассматриваются относительно неподвижных
осей, вдоль которых в рассматриваемый момент времени
t = U направлены оси вращающегося векторного бази-
базиса D.1).
Дифференцируя по времени выражения D.2), A.22)
п осуществляя предельный переход (полагая в получен-
полученных формулах (Oft(i0):=0), получаем, опуская для крат-
краткости записи аргумент ta,
с[ = ще2 — а'2е3, е2' = (л[е3 '
Дифференцируя с учетом полученных выражений три-
тригонометрический тензорный базис A.6), находим
Gi = miaGa, D.3J
где m,j
рицы:
Ю к. Ф.
—
0
0
0
0
0
0
компоненты следующем
0
0
0
О
-I/Job
Черных
0
0
0
-ы;
0
0
0
@2
~a'l
кососимм
0
-уг»;
0
гетр:
0
уз"
«2
ю1
а
0
D.4)
146 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Пусть компоненты симметричного тензора зависят от
некоторого скалярпого параметра, т. е. afi = atj(t). Сле-
Следуя статье [43], назовем телзор J A(l)dt симметричной
тензорной кривой. При построении ассоциированного с
ней тензорного базиса — репера — примем в качестве
второго опорного тензора величину (см. C.2))
Sa = Sa — (— simj)aG2 -f cos^aG3)i|J — cos^aGj+sin^oGa,
D.5)
определяющую часть скорости изменения приведенного
девиатора, обусловливаемую поворотом главных осей тен-
тензора А. Из выражений D.3) —D.5), C.6), C.8) и C.10)
следует, что при S^ = Sj
Ъъ1^ = sin г|заг|)а = — (cos г|?а)\
^ь^Ьз = — cosif>tt^a = — (sin 1|за)",
Ъ~ь1К = — 2 sin г|5асоз; ®ь1Ъ1 = (sin г|за — / cos i|)o) col,
¦OiT1b? = (sini|)a+ /3 cos^a)o^,
li д ' ™2 T ' V4-0^
7 "«
(sinfa + V3"cos^a)u)^ _ 0K со \
Ъ д- , Лз д~>
/ о
Л7 = [4sin2^a(Oa2 + (sinrfa— 1^3 cosi^J щ2 +
+ (sin г|5а + /3 cos i[vJ щ2]112%
Л8 22 22
Тензорный же базис C.7), который теперь уместно
называть ассоциированным с тензорной кривой репером,
принимает вид
•»•-?
4. ТЕНЗОРНЫЙ РЕПЕР 147
Q6 = B /2 sin23i|v\8)-1[3(Sa-Sl + Sl-SaY -
-V2 /6 cos ^„(Sj'-Sa + Sr-Sa-Sl) +
S-^G^ + A11Sa+A12G1], D.7)
где
+ cos % (и>[* + ©22 — 2(Оз2) + /3 sin i|ja (w[2 — co22)], D.8)
Alo = sin Зг|за [2 sin г|за(о32 + (sin if>a — V^3 cos гра) «i2 +
+ (sin l|5tt + /3 COS I|?a) COJ2],
+ (sin2i|?e+
A12 = B//3) sin2 Зг|)а (coi2 + co^2 + <o32).
Совершенно аналогично для тензора
A(*) = aT(*)H7(*) (f = l, .... 6) D.9)
находим с учетом соотношений D.3)
А' = [а[ + /2 (aeoJ — аАщ)] Иг +
+ [а\ + /2 (а4соз — аьа>[)] Н2 +
+ [а'3 + У2 {аъ(й[ — ав<Ог)] Нз +
+ [a'i + V2 (а1 — а2) щ + abw'2 — «e^i] H4 +
+ [а'ь + V2 (а2 — а3) щ + а^з — а&'2] Hs +
(а3 — аг) щ + aiw1 — аъщ] Н6. D.10)
Ортонормированный тензорный репер может быть вы-
выбран произвольным образом. Особенно важен случай,
когда во все время движения он остается главным для
симметричной тензорной кривой A(t). В этом случае аи
#2, о-г — главные значения тензора А, я4 = <Ь = а6 = 0 и
А' = a^Hj + а2Н2 + а'3П3 +
+ V2 {{ау — а2)ЮзН4 + {аг — а3) щЩ + (a3 — a^oojH,,}.
D.11)
10*
148 ГЛ. 0. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Представим тензор А" разложением
А' ^(А')УЩ G = 1, ...,6),
U-Ji-UOai), (Л-J^(Л%2),(Л-):, = И-)(,31, DЛ2)
в неподвижном базисе, мгновенно (н рассматриваемый
момент времени) совпадающем с главным базисом тен-
тензора А. Сопоставление разложений D.11) и D.12) при-
приводит (при некратных главных значениях) к лыражепиям
D.13)
для скоростей изменения главных значений и углов по-
поворота главных осей через физические компоненты тен-
тензора А в неподвижном базисе, мгновенно совпадающем
с главным базисом тензора А.
§ 5. Одна общая ось
Обратимся к важному для приложений случаю, когда
рассматриваемые тензоры имеют одну общую ось (пло-
(плоское напряженное состояние, плоская и антиплоская де-
деформации и т. п.). Будем считать, что эта общая ось
является третьей координатой. При этом матрица коси
нусов угла поворота A.24) принимает вид B.9). А тогда
согласно выражениям C.5) имеем
¦б^Ь" = cos -фь, ftiT'cJ — cos \|>c,'
¦б^Ьз = sin о|)ь cos 2 (соь — ч>а), ^Г'сз = sin i|ic cos 2 (сое—©»),
ф^1^ =—sin г|)Ь sin2(cob—<»„), ft^ci =— sin^csin2(u)c—cpa),
"Ы-bS-O; cf = ^=O; E.1)
где со», «i, coc —углы поворота от. первой координатной
оси до первой главной оси соответствующего тензора.
Согласно формулам E.1)
Sc = cos февг + sinific[cos2(cuc— a)n)G3 — sin2(coc— Q)a)Gi],
S6 = cos ipbG2 + sin i|?b [cos 2 (а>ь — coa) G3 — sin 2 (a>b — a>a) G4].
§ 6. СООСНЫЕ ТЕНЗОРЫ
149
Исключая отсюда G4 и используя следующие из выра-
выражений C.2) — C.3) соотношения
sin
sin
E.2)
приходим к представлению девиатора тензора C(DC =
= 'OcSc) в тензорном базисе, образованном тензорами
Л и В:
Dc— С
1/6 dc (sin фа cos %\ . tg tc sin 2 (coc — coa)
Л2 I sin3i|>. tg\b. sin2(coh —©„)
cos i|)a cos ^c cos 2 (coc — coa) Г tg 2 (coc — coa)
sin 3i|>a I tg2 (cob — coa)
tg ^e sin 2 (coe—coa)
sin3>J)a"~ | " "~tg%sin2(cob—coa)
cos 2\|)a sin фс cos 2 (cdc — coa) Г tg 2 (coc — coa)
sin 3i|Ja I tg 2 (wb — coa)
Напомним, что тензоры А, В, С имеют общую главную
ось.
§ 6. Соосиые тензоры
Наиболее важным для приложений является случай
соосных тензоров. В общих главных осях тензоров
Аи С
Dc = С — -i= C1G1 = ftc cos
уз
sin
Заменяя здесь тензоры G2 и G3 их выражениями E.2),
приходим к полученной В. В. Новожиловым связи двух
сооспьтх симметричных тензоров
.F.1)
150 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Отметим, что полученное соотношение отражает лишь
одну сторону связи между тензорами А и С — их соос-
соосность. Для установления полной фундаментальной связи
необходимо задать зависимости между инвариантами тен-
тензоров. Так, В. В. Новожилов, рассматривая в качестве
первого тензора (А) тензор малой деформации Е, а в ка-
качестве второго (С)—тензор напряжений 2, ввел (в на-
наших обозначениях) три инвариантные характеристики:
К = т-тг — обобщенный модуль объемного расширения,
G = -z ¦? — обобщенный модуль сдвига и F-2)
" е
ю = tya — г|)е — фаза подобия девиаторов.
Существование упругого потенциала обеспечивается
следующими связями между введенными величинами,
рассматриваемыми как функции инвариантов тензора де-
деформации:
?i 0К_ _ 9 д (G cos со)
Ъе дЪе ~г дЕх '
V дК _ oft2 g(GsinC0> /й Q\
— ^lg^-^e Щ . (Ь.6)
д (G cos со) _i_ 9 (ftffi sin со)
При этом для изотропного материала (не обязательно
упругого) было показано, что приращения работ измене-
изменения объема и изменения формы положительны соответ-
соответственно при выполнении условий
Б,>0, cos со ЬЬ - де sin ю б\|зе > 0. F.4)
§ 7. Тензорные функции векторного типа
Пусть Ф(а*;') — некий инвариант тензора А. Рассмот-
Рассмотрим величины дФ/да1.]. Смешанные компоненты тензора
в старом и новом координатных базисах Связаны соотно-
соотношением (см. (А.43), (А.47), (А.48)) a4i=a%~~.
Поэтому по правилу дифференцирования сложной
§ 7. ТЕНЗОРНЫЕ ФУНКЦИИ ВЕКТОРНОГО ТИПА 151
функции
дф дФ да\ дф даУ да'' ,rj j.
да1'., да"*, да1'., да"*, да1' да6'
Отсюда видно, что величины дФ/da.j являются смешан-
смешанными компонентами тензора, который будем называть
градиентом инварианта Ф по тензору А и обозначать
так:
6.Ф
В главных осях тензора (см. (А. 41), А. 43)) А
a-i = Vgjj/gu fl(ij) = tya»
где а, — главные значения тензора и (см. A.1))
ЛФ дФ „ 9Ф„ , зФхт
-77 = ^— -П., + — И, + -— Н„.
dA да, 1 дао 2 да„ 3
JL — «i
Отсюда и из соотношений A.6), A.11) находим
Подставляя в полученные выражения вместо Ф последо-
последовательно инварианты аи а2, а3, ЛЛЗ, Фа cos ^V Oasinijja,
находим
da da^ da^
Hj = i, H2 = ?, H3 = —;
''A' a dA] ft G.5)
1 dA ' 2 rfA
Упомянутые инварианты, определяющие базисные тен-
тензоры, уместно называть базисными инвариантами.
Для соосного с А тензора С имеем
С = с ,Н, + с2Н2 + с3Н3 = _
= C.G Л 3 + ftc cos t|?cG3 + Ос sin f CG3. G.6)
Все входящие сюда величины являются инвариантными
(относительно выбора системы координат в трехмерном
физическом пространстве). Уместно ввести в рассмотре-
рассмотрение трехмерное векторное пространство, в котором (со-
152 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
осные симметричные) тензоры трактуются как векторы.
Это пространство будем называть пространством инва-
инвариантов.
Обозначая отвечающие тензорам векторы соответст-
соответствующими маленькими буквами, имеем отвечающие тен-
тензорным представлениям G.6)—векторные:
С = c,h1 + c2h2 + c3h3 =
= C,gjn + flc cos 4)cg2 + 6-e sin ^cg3. G.7)
Пространству инвариантов можно приписать радиус-век-
радиус-вектор
г = а = ajii + a2h2 + a3h3 =
= A &J1Z + Оа cos i|>ng2 + ft, sin i|3ag3. G.8)
Отсюда и из A.6) следует
2* 11
hg ll +
G.9)
При этом орт gt равнонаклонен к hj, h2, h3, a g(, g2 ле-
лежат в так называемой девиаторной плоскости.
Для того чтобы тензор С был функцией тензора А,
необходимо и достаточно, чтобы коэффициенты в разло-
разложениях G.7) были определенными функциями инвари-
инвариантов тензора С = С(а):
ci = ci(a1, й2, а3) (i = l, 2, 3) G.10)
или
c c {^Л ®а cos ^a' ^a sin
¦Ос cos \|зс = dc cos i(H{...}, 0c sin i|)c = do sin i()o{.. J.
Примем условия регулярности функции, понимая под
ними выполнение равенств
Ci = C] при a( = aj. G-И)
Следуя [83], можно показать, что при выполнении усло-
условий регулярности функция С = С (А) будет полиномиаль-
полиномиальной, а значит, и изотропной. Таким образом, рассматри-
рассматриваются симметричные полиномиальные (изотропные) тен-
тензорные функции общего вида.
§ 7. ТЕНЗОРНЫЕ ФУНКЦИИ ВЕКТОРНОГО ТИПА 153
Установленная связь соосных симметричных тензоров
п вектор-функций позволяет использовать хорошо изве-
известные свойства последних. Так, в векторном анализе
показывается, что любой трехмерный вектор можно пред-
представить в виде [22]
c = gradoq> + rotai|>, ' G.12)
где
дф д<р
5) gl + д(К™*%) g2 д(Ъят
,
Соответствующее разбиение тензорной функции на гра-
диентальиую и роторную части имеет вид
С = gradA ф + roU if, G.14)
где
\ да да !
154 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Известно ([9], [22], с. 192), что любая вектор-функ-
вектор-функция с = с(а) представима в виде
Отсюда и из установленного свойства двойственности
следует, что любая симметричная полиномиальная функ-
функция симметричного тензора второго ранга представима
в виде
или
В силу условия регулярности G.11) при а{ = а^Ф а3
(согласно A.11) при этом ij)o = 0) имеем
1
' G.20)
Наконец, при а^ — аг = аъ (в„ = 0) оба тензора шаровые
и тензорная связь вырождается в скалярную:
С-1 :==z- Сл = Со :==
Условия регулярности G.11), очевидно, выполняются,
коль скоро ф; — симметричные по oh функции.
В классической теории аналитических функций от
тензора (матрицы) скалярным функциям комплексной
переменной /(z) сопоставляются соответствующие функ-
§ S. ПГЕГ.Т1ШЕРН0Е ПРОСТРАНСТВО 155
ции тензора /(А). В случае, когда А — симметричный
тензор,
/(А) = /(аОН, + /(«2)Н2 + / (а,)Н,. G.22)
Отсюда видно, что последние функции являются весьма
частными случаями тензорных функций векторного типа
G.19), отвечающими равенствам
Фг = Фз = 0. Ф1 = J / К) dat + j / (а2) da2 + J / (а3) da3.
В силу симметрии ф! по ak функции G.22) удовлетво-
удовлетворяют условиям регулярности и являются, следовательно,
также полиномиальными. Поэтому их уместно называть
симметричными полиномиальными (изотропными) тензор-
тензорными функциями скалярного типа или просто [69] клас-
классическими тензорными функциями.
Из сказанного выше следует, что регулярная симмет-
симметричная изотропная тензорная функция может быть пред-
представлена в виде G.19).
§ 8. Шестимерное пространство
При рассмотрении анизотропных тензорных функций
вида С = С(А), где А и С — симметричные тензоры, не-
необходимо уже вводить шестимерное векторное простран-
пространство, в котором тензоры рассматриваются как шестимер-
шестимерные векторы
г = а(а„ ..., а6), с = с(с,, ..., с»). (8.1)
Здесь аиск — компоненты тензоров в некоторой фиксиро-
фиксированной системе координат физического пространства.
При этом использована замена индексов B.1.12). Кроме
того, первый тензор в (8.1) рассматривается как радиус-
вектор введенного векторного пространства.
В векторных терминах связь между тензорами А и
С следует рассматривать как вектор-функцию
с = с(а): с; = с,(а„ ..., а6) (г=1, ..., 6). (8.2)
Вектор-функцию, а вслед за ней и тензорную, будем на-
называть регуляр)юй (ср. G.11)), если для нее
ui^aj влечет с( ^ ch Q „.
at = as влечет с* = с}.
456 гл. в. некоторые вопгосы теории
Как известно [9], в общем случае
.-*?+*?+*?• <«¦*>
где
Ф* = ф*(я1, • • -, ве). (8.5)
Соответственно и тензорную функцию можно предста-
представить в виде
или
В качестве упомянутой фиксированной системы ко-
координат в физическом пространстве удобно принимать
такие, чтобы координатные оси были главными осями
анизотропии рассматриваемого материала.
§ 9. Сопряженные (энергетические) пары.
Объективные скорости изменения напряжений
Мощность напряжений можно записать в виде [53, 64]
о Я Э
о
Здесь р — плотность материала в отсчетной (недеформи-
3 Э
рованной) конфигурации, 25 -<-»¦ Е — сопряженная (по
Хиллу [64]) пара тензоров (играющая в механике дефор-
деформируемого тела роль «обобщенное перемещение — об-
обобщенная сила»). Для упругого материала упомянутые
пары могут быть названы энергетическими.
Рассмотрим следующие пары:
9 Э
2 а Е
(I) F-^S-F-1* 1/2C = У2\* пли Е = У2 (Л.2 - 1)
(II) F*-y2-F — i/2C-i = _ i/8A~2 пли 6 = V2(l — ЛГ2)
(III) Q*-y2Q f (9.2)
(IV) J/2(P--/2:-Q + Q*-./2:-F~:1*) А или А —1
(V) V2(F*-^2:-Q + Q*-/2-F) —А или 1 —Л.
Тензор F~l-yS-F* называют в зарубежной литера-
литературе симметричным (вторым) тензором Пиала — Кирхго-
§ 9. СОПРЯЖЕННЫЕ (ЭНЕРГЕТИЧЕСКИЕ) ПАРЫ 157
фа, а 1/,(?-1 • J2- Q+ Q* ¦ JZ •?-**)- симметричным тен-
О о
сором Био, С — тензор деформации Коши, Е — тензор
о
деформации Грина, 0 — тензор деформации Альманси.
о
Тензор деформации Т вводится соотношением
1" =1/2(Л-Л~1 + Л-!"). (9.3)
о о #
В случаях, когда тензор Л соосен тензору Л либо
Q* • /2 • Q, т. е. при мгновенном отсутствии поворота
главных осей деформации либо при изотропном материа-
о
ле, тензор Т можно заменить на 1дЛ.
Систематический вывод первых четырех пар дан
Р. Хиллом [64]. Пятая и, uo-видимому, последняя пара
была получена автором в [71].
С учетом соотношений (А. 41) — (А. 43) имеем в ор-
ортогональной системе координат, связанной с главными
осями анизотропии (§ 2, гл. 2):
е°; = R4/ Vgn - R* Vgn, с; = Q-еь
о о о о о . о . а о
Л = Л цу euev, Л = (Л~ Лцло^ву,
кУ Т (^jl (9.4)
aapR R = сГ(ар)еаер,
„Q U О 1 / О О
та0Л .. .А.. у „а „
Используя эти выражения, а также C.1.4), C.1.6), по-
получаем из (9.2)
F* • /S • F -= /aapRaRP = A(ai,)/0((iV)AAf,eaep, (9.5)
V2
Q*-/S-F) = ЧА
158 ГЛ. 6, НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Существенно, что все выписанные величины представля-
представляют собой тензоры, заданные в базисах, связанных с от-
счетной (недеформнроваиной) конфигурацией.
В механике сплошных сред часто приходится рас-
рассматривать скорости изменения напряжений. Для их
описания тензор 25* мало подходит. Действительно, пусть,
например, балка, растянутая в направлении оси, повора-
поворачивается при фиксированной растягивающей силе, т. е.
2 = о(зз)е3е3, о(зз) = const.
Поскольку при иовороте е3 = е3 (?), 25' Ф 0 при жестком
повороте, не изменяющем напряженного состояния.
От этого недостатка, очевидно, свободны скорости из-
изменения сопряженных (энергетических) тензоров напря-
напряжения (9.5), поскольку последние при жестком повороте
О О . О О
(т. е. при Л == Л =1) равны аC3)е3е3 = const. Их про-
производные по времени называют объективными скоростя-
скоростями изменения напряжений:
контравариантная конвективная скорость
ковариантная конвективная скорость (скорость по
Коттреллу)
(F*./25-F)- =(/аар)" RaRp = {°A,atl)Jo(ilv)\^})' ёаёр,
скорость по Яуману (со по во ротная)
(Q*-/2.Q)!=/a;aWee?p, (9.6)
скорость по Био (контравариантно-соповоротная)
ковариантно-соповоротная (предложена автором)
о в
еаер.
§ 10. УСТОЙЧИВОСТЬ АНИЗОТРОПНОГО МАТЕРИАЛА 159
Выявим физический смысл рассмотренных скоростей.
Так, с учетом соотношений C.1.4)
Отсюда видно, что отвечающий контравариантной кон-
конвективной скорости тензор F • (F • /2 • F"*)' • F* являет-
является скоростью изменения напряжения внутри (движуще-
(движущегося и деформирующегося) основного материального ба-
базиса. Аналогично ковариантная конвективная скорость
характеризует скорость изменения напряжений внутри
взаимного материального базиса, скорость по Яуману —
скорость изменения напряжении в жестком ортонорми-
рованном базисе, вращающемся со скоростью вращения
материальной частицы. Скорость по Био является проме-
промежуточной между контравариантной конвективной и ско-
скоростью по Яуману. Наконец, ковариантно-соповоротная
промежуточна между ковариантной конвективной и ско-
скоростью по Яуману.
Шестую пару сопряженных (энергетических) тензо-
тензоров
з э
* Е (9.7)
VI F-./!; F
составляют тензор номинальных напряжений (сопряжен-
(сопряженный с несимметричным тензором напряжений Пиала)
и градиент движения (деформации). В отличие от пер-
первых пяти эта пара зависит не только от деформации, но
и от углов поворота.
Отметим, что применительно к изотропным материа-
материалам вопрос о сопряженных парах тензоров рассматривал-
рассматривался еще в работе В. В. Новожилова [37, 38].
§ 10. Устойчивость анизотропного материала
Имея в виду читателя, не знакомого с тонкостями
терминологии, несколько уточним понятие упругого ма-
материала. Согласно [83] простым называют материал, для
которого
I @ = Г {е (т)}, (ЮЛ)
т. е. значение тензора напряжения в рассматриваемый
момент времени t определяется историей деформации,
160 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
т. с. значениями последней во все предшествующие мо-
моменты времени т. В правой части выписанного соотно-
соотношения стоит тензорнозпачный функционал истории де-
деформации.
Для квазиупругого материала (за рубежом его назы-
называют упругим по Коши либо просто упругим) значение
тензора напряжений в рассматриваемый момент времени
t зависит от значения тепзора деформации в этот же
момент времени, т. е. не зависит от истории деформации:
A0.2)
Для квазиупругого материала работа напряжений при
переходе из конфигурации A) в конфигурацию B) цод-
считывается по формуле (см. (9.1), (8.6))
<2) B) B)
fo п я э г-
pbW = \ 25 : <Ж = \ (фх^ф2 + Фз^ф« + Фб^фе) (Ю.З)
О) 11) A)
и зависит, вообще говоря, от пути деформирования.
Материал, для которого ра-
работа напряжений пе зависит
Ж_ от пути деформирования, назы-
Ш вают упругим (за рубежом —
упругим по Грину, гиперупру-
гиперупругим). Формально упругий ма-
материал можно рассматривать
как частный случай квазиупру-
¦ -т_ гого, отвечающий
РИС. 6.10.1 3 4 6
где ф _ упругий потенциал (плотность энергии дефор-
деформации).
Для малых деформаций Друкер сформулировал [18]
постулат устойчивости материала
2*: Е-=а;ар)е(ар)>0. A0.4)
Его механический смысл усматривается из примера од-
одноосного растяжения стержня (рис. 6.10.1). Выполнение
критерия устойчивости
>0
означает в этом случае только возрастание напряжения
§ Ю. УСТОЙЧИВОСТЬ АНИЗОТРОПНОГО МАТЕРИАЛА 161
при увеличении деформации (участок /). В этом смысле
участок /// отвечает «неустойчивому материалу», & II—
«безразличному».
Постулат A0.4) естественно обобщить на случай боль-
больших деформаций неравенствами:
2": Е'>0. " A0.5)
Напомним, что входящие сюда величины нечувствитель-
нечувствительны к жестким смещениям. В компонентном виде выпи-
выписанные неравенства записываются в виде
<%>0 (y = 1, ..., 6). A0.6)
Для квазиупругого материала определяющее уравне-
уравнение имеет вид (см. (8.2))
2 = S UEJ: en = 0i ^ ej. A0.7)
Подстановка последних выражении в A0.6) дает
э
да э. э.
—Г еаер > 0.
Первые сомножители заменим их разбиениями
С учетом того, что свертка кососимметричной части с сим-
э.э.
матричным образованием е*е7- равна нулю [66], прихо-
приходим к следующей положительно-определенной квадратич-
квадратичной форме
(W.8)
деа
которой отвечает положительно-определенная матрица
э
||4|if.+S.||>0. A0.9)
К. Ф. Черных
102 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Напомним, что согласно известному критерию Сильвест-
Сильвестра положительная определенность матрицы (символиче-
(символически показанная знаком неравенства) связывается с поло-
положительностью главных миноров матрицы A0.9).
Для выяснения механического смысла условия A0.8)
з /э э \
назовем величину 8^, ...,ей) вектором деформации
и будем рассматривать ее как радиус-вектор введенного
в § 8 шестимерного векторного пространства, в котором
в / а в \
определим также вектор напряжений o\av ..., ае).
Пусть t(ti, ..., te) — единичный постоянный вектор
некоторого направления во введенном пространстве. Обо-
Обозначим через
8 Э Э 9 8 0
8j = t «8 = tyEy, Oi = t'O = taOaf
dzt dep
э э
проекции векторов о, е на это направление и произ-
производную в этом направлении. Тогда
э э э / э в \
det dep дЕ|3 \5ер дга)
Согласно A0.9) квадратичная форма в правой части iio-
ложительна, а значит, и
A0.11)
det
т. е. производная в любом направлении от проекции век-
вектора напряжений на это направление всегда положи-
положительна. Если направить t по г-й координатной линии, то
A0.11) примет вид
э
dCt
dzi
— перавепство, следующее непосредственно п из поло-
положительной определенности матрицы A0.9). Поскольку
§ 10. УСТОЙЧИВОСТЬ АНИЗОТРОПНОГО МАТЕРИАЛА
1ГД
doJOti представляет собой «нормальный» i й модуль
упругости, величину dot/det можно рассматривать как
нормальный модуль упругости (квазиупругостн) в на-
направлении, определяемом вектором t. С учетом сказанно-
сказанного неравенство A0.11) означает, что нормальный модуль
упругости (квазиупругости) любого
направления положителен. Квадра-
Квадратичным формам A0.8) и A0.10) —
A0.11) отвечает одна и та же мат-
матрица. Поэтому оба неравенства вы-
выполняются одновременно, и установ-
установленную положительность нормально-
нормального модуля можно рассматривать как
физический (механический) смысл
неравенства A0.8) и, тем самым,
положительной определенности мат-
матрицы A0.9).
Пусть ъ и еB) — радиусы-векторы двух точек рас-
рассматриваемого пространства, at — единичный вектор пря-
прямой, соединяющей эти точки (рис. 6.10.2). По теореме о
среднем
Рис. 6.10.2
4
й--
где ггР =
t • aB)— величины, отвечающие еA) и
— зпачепие величины dot/det,
тайное в некоторой точке промежутка
равенства A0.11) следует неравенство
Й»-4»)(еУ-3»)>0 при
По смыслу вектора t (рис. 6.10.2)
еB) - е(
- ei1}) t,
- eV>
подсчи-
Из не-
A0.13)
Отсюда п из неравенства A0.13) следует так называемое
И*
164 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
э э /э\
условие монотонности функции а = a\Ej:
(>>->).[№-&>)> О,
которое можно записать в тензорном виде
A0.14)
A0.15)
Рассмотрим два вектора деформации
е :
э, . э
В силу условий регулярности (8.3) отсюда следует
Подставляя выписанные векторы в неравенство A0.14),
приходим к условию упорядоченности компонент векто-
векторов деформации и напряжений
(at - о,) (et - е;) > 0 (г, / = 1, .. ., 0). (Ю.16)
Если ввести в рассмотрение функцию
A0.17)
то
-J Л Э a л Э яG_ Э Э Э 3
— -е = —ер = -— Еае0 + ааеа.
Согласно неравенству A0.9)
э э
и из предыдущего равенства следует еще одна форма за-
записи критерия устойчивости
или Ц-
йг
§ 10. УСТОЙЧИВОСТЬ АНИЗОТРОПНОГО МАТЕРИАЛА 165
В случае yiipyiwo материала
i-^Ь, о-<*Д аг = д-ф. A0,19)
dE de дег
Неравенства A0.14) —A0.15) переходят л условие гло-
глобальной выпуклости упругого потенциала
W2) dB^J A0.20)
0.
Из A0.9) следует положительная определенность матрицы
52Ф
>0- A0.21)
Наконец, зависимости A0.11) приводят к условию ло~
калькой выпуклости упругого потенциала
**ф --О
>и- A0.22)
Вернемся к соотношениям A0.7). Для устойчивого
материала они обратимы:
ЭЗЭ Э ЗЭ Э ЗЭ -
в = в(о), е| = е,(ал), Е = ЕB). (Ю.23)
Дойствительпо, для обратимости необходимо, чтобы было
I 3 / э I
да А дв- \ф 0, — условие, которое выполняется. Допустим против-
( э / М
нос. Тогда система уравнений \^ail^ea) flp = 0 (i,p==l, ...,G)
имеет нетривиальное решение oi, ..., ое- Умножая уравнения си-
системы на at и суммируя по i = а, приходим к равенству
э / о я
/
противоречащему положительной определенности матрицы A0.9),
а значит, и положительности любой ассоциированной с ней квад-
квадратичной формы.
Для упругого материала имеем из A0.19) и A0.17)
j'a = (а«ея)" — аа1'а - (Л — Ф)" (а = 1, ..., 6). A0.2-1)
ICC
ГЛ. G. ПЕКОТОРЫЕ ВОПРОСЫ ТЕОРПП
Отсюда следует (А — Ф
э dV
ч
х?)
A0.25)
(/с, U 1, ..., 6). (Ю.26)
Выявим механический смысл величин А и Ч1". Для этого
изобразим (рис. 6.10.3) символически
кривой процесс деформирования эле-
элемента от педеформировашюй конфи-
конфигурации до текущей. Текущему зна-
Э
чению деформации 8 статически отвеча-
8
ет напряжение о. Из рис. 6.10.3 впд-
3 Э
но, что А = а-е —работа на данной
Рис. fi.10.3 деформации статически отвечающего
ей напряжения. Часть со, располо-
расположенная пгоке «кривой деформировапия» и равная
D ==Ф, представляет работу, сопровождающую
деформацию. Часть, расположенная выше кривой, равна
э в
о о
г-da = J dx? = W и дополняет Ф до А. Поэтому упру-
0 О
гий потенциал Ч*" и называют плотностью дополнитель-
дополнительной энергии (работы).
В случае линейно-упругого материала кривая пере-
переходит в прямую, и из рисунка усматривается теорема
Клапейрона
Ф = Цг = г/ъА. A0.27)
Для несжимаемого материала / = ХДгЯ3 = 1, ив энер-
энергетических (сопряженных) напряжениях следует [16]
заменить /2 на S.+ pl, где р — произвольное, определяе-
определяемое при решении задач слагаемое типа, всестороннего
давления. Из сказанного следует, что к энергетическим
(сопряженным) тензорам напряжений следует добавить
слагаемые (см. (9.2))
(I) pF~1'F-]*=pA-2
(II) pF*-F =M2
(III) pQ*-Q =pi .
§ 10. УСТОЙЧИВОСТЬ АНИЗОТРОПНОГО МАТЕРИАЛА 167
(IV) pVi(F-Q
(V) pVi(**-Q+<*••*) =-Д
обусловливающие появление в левых частях неравенств
A0.5) слагаемых
(I) р-А-.1: A'-f V«p(A-»)*: (A2)*
(II) р-А-1: A*-V,p(A-»)-:(A»)-
(III) p-A: А"
(IV) /г A: X+piX.-1)': X
(V) р-А: А -^(А-1) : А
о о
В главных осях тепзороь Л, Л~ имеем согласно
о о и о о о о
Л = Xlc1e1 f Я2е2е2 + Я3е3е3,
0_ _ о о о о о о
Л = Хх е^! + Х2 е2е2 + Я,3 е3е3,
° , .оо %оо тоо
Л = Ке^г + Я,2е2е2 + Я,3е3е3 +
-I- (К — М «г (c3ei -I • ехе3) -(- (^ — ^) Юз (е^а + еге,) f
+ (К - К) % (вЛ + е3е2).
Отсюда находим (/ = 1)
Л: А' = Х/\ + X'JK + KIK - (In /)' - 0.
Таким образом, для третьей энергетической пары сла-
слагаемое с р' выпадает, а остальные пары имеют дополни-
дополнительные слагаемые:
. (I) V«p(A-«)*: (A2)*
(II) -Vtf(A-2)': (А2)' A029)
(IV) piX-1)': A*
(V) -СЧ'Л'
накладывающие условия на величину /л
.Показано, таким образом, что для несжимаемого ма-
материала постулат устойчивости материала нечувствите-
нечувствителен к р лппн, для моры деформации Т (9.3), заменяемой
для изотропного материала на In А. Что касается послед-
168 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
ней пары (9.7), то согласно C.1.5), C.1.21) и C.1.2J
F = RVRV, {F-1. /2} = /0apRaRg,
= (Ra.Rv) [(Jo**)' Rp + (Jaaf) RP].R; -
= [(/a0*)' Щ + (/aap) Rp]-R;. A0.30)
Имеют место формулы [53]
где v' — ковариантные компоненты вектора скорости ма-
материальной точки v = i/Re. С помощью первого из этих
выражений и A0.30) постулат устойчивости A0.5) при-
принимает вид
(/0ap)" Vave + (Jaa&) ffViiVe^Vpi7v> 0. A0.31)
Любое из полученных выше неравенств представляет
собой, по существу, пять (а точнее — шесть) критериев
устойчивости, в зависимости от того, какая из энергети-
энергетических пар выбрана. Пока, кроме замечания об удобстве
использования третьей энергетической пары при рас-
рассмотрении несжимаемого материала, ничего по этому
поводу не было сказано. Кроме того, остались неясными
отдельные названия, использованные для различных
форм критерия устойчивости. Для того чтобы получить
необходимые пояснения, рассмотрим изотропный ма-
материал.
§ 11. Устойчивость изотропного материала
Для изотропного материала в общих для тензоров де-
деформации и напряжений главных осях имеем с учетом
соотношений (9.2)
(I) (*ЛЬ8)ЬГЧ Vi*f ^)
(ii) (^y^vh - Vi^r2 «ли Vi (i - я-г')
(III) {\jkfa) o{ ln^ A1.1)
(IV) (Я.,*„*,,) ЬГ'о, А,, или а,,-1
(V) (X^^j) Ji^ - ЯГ1 или 1 - ЯГ1
§11. УСТОЙЧИВОСТЬ ИЗОТРОПНОГО МАТЕРИАЛА 169
Для всех пяти пар (/ = Xi^s\3)
Нетрудно проверить, что для пар пелпчип
э _ э . . „
а4 = Jdi [/' (^i) ^{] ¦*-*¦ ej = / (hi) К1 l-d)
имеет место соотношение A1.2). Таким образом, для
изотропного материала существует целое семейство энер-
энергетических пар тензоров A1.3), в которое, очевидно, вхо-
входят и рассмотренные для анизотропных материалов пары
A1.1).
Для упругого материала имеем (см. C.1.27), C.1.13),
C.1.10))
л дФ
JOi = h-^ A1.4)
и согласно A1.2)
а = Ф". A1.5)
С этим, собственно, и связан термин — энергетическая
пара.
Шестимерное пространство заменяется трехмерным
пространством инвариантов, в котором
ээээ ээээ' ... „
r = E(El, ?2,e3), а(аиая,ая), ("-о)
э э э э .
at = t-o
ЗГ-'Р-Г («, P, Т - 1, 2, 3).
Сохраняется неравенство A0.11) и его физический
смысл. То же относится к неравенствам A0.13), A0.14).
Условие упорядоченности компонент A0.16) переходит
в условия упорядоченности главных значений. Соотно-
Соотношения A0.20) —A0.22) сохраняют свою форму.
Поясним геометрический смысл неравенства A0.22).
/э э э \
В рассматриваемом случае Ф \Ej, e2, e3j = const — поверх-
ность уровня упругого потенциала (плотности энергии
деформации). Как известно, компоненты единичного
вектора нормали к поверхности уровня определяются
170 ГЛ. G. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
выражениями
«Iя-5-/l/ ^" + Hr +f^T
«"ii
1/G") +f^T+fyT* о1-8)
» v7ei/ \5е2; ^r3;
Пусть t — единичный вектор касательной в точке в к
проходящей через нее поверхности уровня. Радиус кри-
кривизны поверхности (Rt) в направлении t определяется
формулой [42, 66]
8
an дп$ dea
9
Подсчитывая входящие сюда величины dni/d?j по фор-
формулам A1.8), получаем с учетом того, что t-n = 0,
Отсюда и из A0.22) следует, что критерий локальной
выпуклости при произвольном касательном к поверх-
поверхности уровня векторе t сводится к утверждению о поло-
положительности гауссовой кривизны (т. е. выпуклости) по-
поверхности уровпя энергии деформации.
Переходя к рассмотрению несжимаемого материала,
подсчитаем с учетом соотношений D.11) входящие в
A0.29) величины
': (Х«)* = - 4 [(КМ + (К/КУ
- 2 [(^л2 - h/Kf «i2 + (К/К - K/hJ «i2 +
(Л)' :А" - - [{К/КУ + (К/КУ + (W1"
-2
Отсюда и из A0.20), A1.1) и D.11) находим, напри-
например, для четвертой энергетической пары условие устой-
устойчивости материала (У = 1)
ЧУК)
§ 11. УСТОЙЧИВОСТЬ ИЗОТРОПНОГО МАТЕРИАЛА 171
- 2р (К - h)/(hh)] (К - К) «з2 + КА2 - <*зА3 -
- 2р (Х2 - Ь3)/( W1 {К - *з) »12 + КАз - <*iAi -
- 2Р (К - KyihK)] (К - М «г2] > о.
В силу произвольности величин o>i отсюда следует
положительность последних трех слагаемых, т. е.
(o,Ai - аЛг) (Xi - Х2)> 2p(Xi - hV/iW,
2-Хз)>2р(Х2-Х3O(ХД3), A1.10)
- >.1)>2р{\3 - K,J/(hh).
Что касается остальных слагаемых, то здесь ничего нель-
нельзя сказать, поскольку в силу условия несжимаемости
(/= АДгХ.1 = 1) величины Я{ не являются независимы-
независимыми, будучи связанными вторым из соотношений
Исключая из оставшейся части Х3 и Хз, получаем
A1.12)
''7("аМа) , Ч/К)\ 1
( ]
172 ГЛ. 6. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ
Поскольку в полученной квадратичной форме ^ и Х2
независимы, можно использовать критерий Сильвестра,
согласно которому
А>0, О О, ААС-В2>0. A1.14)
Для изотропного упругого материла в полученных нера-
неравенствах следует провести замену A1.4) при / = 1.
В заключение изложим некоторые соображения по
выбору критерия устойчивости, т. е. энергетической пары
в неравенстве A0.5), (A0.6)). Если задаться целью
выбрать единственную наиболее предпочтительную пару,
то она, очевидно, должна быть пригодна и для анизотроп-
анизотропных материалов. А тогда выбор невелик — пять пар
A1.1)!
В одной из бесед с автором В. В. Новожилов отме-
отметил, что выбор той или иной пары должен связываться
не только с типом материала, но и с условиями его ра-
работы. С этих позиций наиболее предпочтительной явля-
является четвертая пара, в которой «обобщенной силой»
является условное напряжение, т. е. сила в расчете на
единицу площади первоначальной недеформированной
площадки, а «обобщенным перемещением» — кратность
удлинений %i.
Инженерная практика давно уже выявила преиму-
преимущества использования условных напряжений перед
истинными при исследовании механических свойств ма-
материалов. Так, известная величина — временное сопро-
сопротивление — на условной диаграмме растяжения является
одной из основных характеристик конструкционного ма-
материала (входящей в его технический паспорт).
Более того, в конструкции материал ведет себя обыч-
обычно, как на условной диаграмме, поскольку на практике
фиксированными оказываются не напряжения, а силы,
действующие па конструктивные элементы (исключе-
(исключением является нормальное давление). Кроме того, воз-
возникающие в местах заделки реактивные истинные на-
напряжения совпадают с условными, при неизменной пло-
площадке заделки. Сказанное свидетельствует об известных
преимуществах четвертой пары: условное напря-
напряжение— кратпость удлинения.
ПРИЛОЖЕНИЕ А
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
Пусть (рис. А.1)
R = ar
— радиус-вектор точки физического пространства.
Xi — прямоугольные декартовы координаты точки,
координатные орты. По
повторяющимся греческим
индексам здесь и пиже
производится суммирова-
суммирование от 1 до 3.
Криволинейные коор-
координаты а1, а2, а3 введем
соотпошепиями
Xi = Xi(a\ а2, а3)
(i =1,2, 3). (А.2)
Равенство а* = а0 = const
определяет i-ю координат-
координатную поверхность, а соотно-
соотношения ссг= c*oi а3 == ао —
/f-ю координатную линию
{кФ1Ф)Фк). Векторы
яп дх,
(А.1)
Здесь
а й< —
Рис. А.1
за1
касательпы (рис. А.1) к координатпым а'-линиям
ют длины — так называемые параметры Ламе
Очевидно, что величины
= 37=J^-g« (* = 1,2,3)
(А.З)
и име-
(А.4)
(А.5)
174
ПРИЛОЖЕНИЕ А
— единичные координатные векторы, в общем случае не-
неортогональные.
Из системы равенств (А.5) находим
gft = (Hft/V)es, (A.0)
где
3^,
А Аи - дХ* д*3 - ^ дХ>
1 ЛгЛ Я~2 я„1«
За* да* да' да
да2 да3
да
2'
да3 да1 да1 За3*
За1 за2
За
l
1'
дХ1
,332
з
1 2Цзз~аа1^~^За1'
\\А*
в 9 2
да да да
дХ1 дх2 дхз
да3 да3 да3
Наряду с основными координатными векторами
да1 да1 да1
1
]2 дХ3
(А.7)
(А.8)-,-,
используются и взаимные координатные векторы
R3XR1
(A.8L_,
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 175
связанные с основными условиями взаимности
Ri-R'-eJ-jJ; \^Jj\ (A.9)
Нетрудно проверить, что
Величины
связывают основные и взаимные лекторы
Н, = **«Н", # = Л. (A. 12)
Векторы и тензоры представляются разложениями в
координатных базисах:
u = uaRa = waR«,
Т = tafJRaRp = <?PRaRp - tfRaRp = ^PRaRp, (A. 13)
w = ^ap:::^RaRP..
Величины RiRj, RjRJ, R^Rj, R'Rj называют коорди-
координатными диадами, а R,-Rj... RftR! — координатными по-
лиадами. В соответствии с соотношениями (А.9) и (А.11)
введенные формальные образования наделяются свой-
свойствами
RiRj.Rft = ^R,, Rft¦ RiRj = 6?Rjt {A щ
RiRj ¦ RftR, = 6*RiR/, RiR3 RfeR' = ^RiR', ...
. .., RjR, . .. R'Rtt-RjR, = ^-RiRj ... R'R,, .. .
Коэффициенты разложений в (А. 13) с верхпими ин-
индексами называют контравариантными, с нижними —
ковариантными, с теми и другими — смешанными компо-
компонентами. В смешанных компонентах точки указывают по-
порядок следования индексов. В случае симметричных тен-
тензоров порядок следования индексов несуществен, и точки
опускаются.
С помощью соотношений (А.14) устанавливаются сня-
зи между компонентами разного типа одного и того же
17В ПРИЛОЖЕНИЕ Л
тензора (вектора):
Щ = giaU*, U3 =-- ?&Щ,
Скалярпо умножая первое из соотношений (А.12) па R1,
получаем с учетом (А.9)
Тензор
1 = ga^W = R*Ra = RaRa = gatRaR, = G (A.17)
называют единичным, поскольку согласно (А,14) для лю-
любого тензора
Его пазывают и метрическим, так как, зная его компонен-
компоненты, можно совершать различные метрические операции.
Так длина элемента дуги подсчитывается по формуле
В частности, для элемента дуги i-й координатной литши
dsf = Vi«da* = Atda{. (А.20)
Угол между элементами касательных к пересекающимся
кривым dR(da\ da2, da3) и 6RFa', 6a2, 6a3) подсчиты-
подсчитывается по формуле
- ( }
В частности, угол между г-й и у-й координатными ли-
линиями определяется формулой
). (А.22)
Дискриминантный тензор определяется его ко- и
контравариантными компонентами:
гт = R,- • (R, X КО, eiik = R< ¦ (R1 X R"). (A.23).
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 177
При ЭТОМ 0ТЛНЧ1Ш ОТ 11уЛЯ ЛиШЬ KOMUOlieilTbl (g=\gi]\)
Е123 — Е231 == Ё312 = Ei32 = Ез21 =а —Ё213 = V gi
JA.24)
е«» = еИ1 = е»« = _Е»2 = _ем, = _е2,3 = {/1g_
Далее,
R.XRj-e^R", R'' X R' = e'7aRa. (Л.25)
Площадь i-ii координатной площадки определяется по
формуле
AФ]ФкФг). (А.26)
Элемент объема равен
dV = Ygda,id<x2da3. (A.27)
Наконец, единичный вектор
нормали п к скошенной гра- з
пи (рис. А.2) определяется
соотношением
n dSn = -5= dSa, (A.28)
щ = -1—-**—. (А.29) Рис. Л.2
При дифферепцировапии коордппатпых ортов исполь-
луют формулы
^ = G§R«, (A.30)
где
4 = 4-1% + —3-^)^ (А.32)
; ^ \ да1 да1 да?) в К '
— символы Кристоффеля первого рода.
При рассмотрении общих вопросов теории упругости
часто используют ковариаптные производные компонент
векторов и тензоров. Так, величины
j = Ь _ Gluv, V,u> = d-f. + GW; (A.33)
12 к. Ф, Черных
17S приложение л
^ G^ (A.34)
v / . - dt" rv * . rv t
•fell —" ^^"^*TT* ^^l/t Л57 " ' \JT ъ \Л/ \jvk
являются ковариантными производными компонент раз-
различного типа вектора и тензора второго ранга (ранг тен-
тензора определяется числом индексов у его компонент).
Ковариантное дифференцирование добавляет в компо-
компонентах тензора ковариантный (нижний) индекс, делая
их компонентами тензора, имеющего ранг па единицу
больший,— так называемого градиента тензора (см.
(А.13)):
VT = (VT«eA) R4VRI1 = (V") l№aRe = ... (Л.35)
Ковариантная производная обладает рядом примеча-
примечательных свойств:
j = 0, Vftgy-0, (Л.36)
Таким образом, координатные векторы, компоненты мет-
метрического и дискриминантного тензоров при ковариант-
ном дифференцировании можно считать постоянными.
Отмстим, что операция ковариаитпого дифференциро-
дифференцирования введена для компонент лектора и тензоров. Сама
же тензоры (векторы) являются инвариантными (не за-
зависящими от выбора системы координат) величинами (без
индексов). Для них ковариантная производная совпадает
с обычной частной производной. Поэтому
—{= ViU = Vi (uvRv) = (VfUv) Rv =
¦ dec
(V{«V)RV, (Л.37)
RaRp - ...
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ 179
Порядок ковариантиого дифференцирования можно ме-
менять (в евклидовом пространстве).
Имеют место следующие полезные соотношения:
(А.38)
^^ ); (A.39)
<"-т&,- (A-40)
В приложениях большей частью используются орто-
ортогональные координаты, для которых единичные векторы
ef (A.5) являются ортами, т. е.
е, • е, = е2 • е2 = е3 • е3 = 1, е, • е2 = е2 • е3 = е3 • et — 0;
= е„ е3Хе, = е2;
eu Rj = е^ = е,
u
Кодшоиенты векторов и тензоров в представлениях
и == и(а)еа, Т == ?(ае)Саец,
(А.42)
W = и?(аР... uv)eaep... сЙе,
называют физическими. Сопоставление этих представле-
представлений с (А. 13) дает с учетом соотношении (А.41)
(A.43)
Наряду с исходной рассмотрим новую (штрихованную)
систему координат, также ортогональную. Имеем
ej = ea<7aj, eh = 7лрСр, (А.44)
где g,j — косинусы углов поворота, связанные с компопеп-
12*
180
ПРИЛОЖЕНИЕ А
тами вектора поворота « = (оаеа матричным соотношением
I'll '12
721 '22
'33
110 01]
0 1 0 +
ll
si it to I
CO
110 0 1|
0 - ш3 Si
со„ О — со.
1 — COS CO
I— «о..
01.
0
(О
.2
(со -
(А.45)
Имеют место обратные соотношения
cos со = 72(?n + g22 + gj3 — 1),
^ = Ь2'- Чз %_ = У13-?31| Шз = 121~я12 (А.46)
со 2 sin со ' со 2 sin со ' со 2 sin со
Из зависимости (А.44) и (А.42) следуют связи между
физическими компонентами векторов и тензоров в старой
и новой системах ортогональных координат
aU)
(A.47)
Если переход от одной ортогональной системы коор-
координат к другой отвечает преобразованию координат
а"=а"(ос\ а2, а3) (г = 1, 2, 3),
то
(A.48)
Пусть преобразование координат сводится к отраже-
отражению в пг-й координатной плоскости (касательной к коор-
координатной поверхности). В этом случае
' / Л \Р j' j. / Л \Р
/I,.. /I/I. f __ 1 I Г/.-, т—= Г,. ¦. I _^ 1 1
",i ' (A.49)
(А.50)
где jw — число индексов компоненты, равных т.
В заключение приведем соотношения
Т • а == а • Т*, Т* • а = а • Т,
связывающие произвольные вектор а, тензор Т и сопря-
сопряженный с ним тензор Т*.
ПРИЛОЖЕНИЕ Б
КОРОТКО О ТЕОРИИ ПОВЕРХНОСТЕЙ
Приведем необходимые для понимания гл. 5 сведения
из теории поверхностей. Для более обстоятельного зна-
знакомства с последней рекомендуем руководство [66].
Пусть поверхность описывается уравнением
г = г(а|, а2), (Б.1)
где а\ а2 — криволинейные координаты. Пусть далее
п(а\ а2) —единичный вектор
нормали к поверхности
(рис. Б.1). Радиус-вектор про-
произвольной точки окрестности
поверхности запишем в виде
R(a', a2; g) = r(a\ a2) +
+ !n(al,a*), (Б.2)
где % — расстояние по пормали
от точки до поверхности. Такую
систему координат называют
нормально связанной с поверх- Рис. Б.1
ностью. Все зависимости во
введенной системе координат можно получить из соот-
соотношений приложения А, полагая в последних a3 = \ и
заменяя R выражением (Б.2).
Так, из формул (Б.2) имеем
R, = г, + gn,, R2 = r2 + gn2, R3 = n
(Б.З)
(i\ = dtlda1, п( = dn/da').
В этом и последующих соотношениях буквенные индексы
принимают значения 1, 2. Из выражений (Б.З) и (А.11)
находим
Еи = ан-\2Ъц + \гпг-п1л gl3 = g23 = 0, gM = l, (Б.4)
где (г( • п = 0)
7 ОТ т /Г* Г\
Ьц = — Г{ • rij = П '
182
ПРИЛОЖЕНИЕ Б
Излагаемое в этом приложении используется в гл. 5
для тонких оболочек, в которых рассматриваемая поверх-
поверхность является срединной (равноудаленной от верхней н
нижней лицевых поверхностей). Поэтому рассматривает-
рассматривается лишь ближайшая окрестность поверхности, так что
«1.
Ниже будет показано, что это означает малость толщины
оболочки по сравнению с радиусами кривизны срединной
поверхности. С этим связано и то, что все рассматривае-
рассматриваемые величины приближенно продставимы в виде
W Сга1 п2- М = Ч"') Со-4 г/2\4- two („i n2\ (i\ ел
т. е. зависимость от \ принимается линейной.
Отсюда и из (Б.4) прежде всего следует
gti^Oa-Vbth *в = 0, gr33 = l (Б.7)
и усматривается, что fl« = 5yU=o •— компоненты симметрич-
симметричного метрического тензора срединной поверхности.
Из соотношения (A.1G) следует, что g" — приведенные
миноры элементов gy в определителе g = \ga\, принимаю-
принимающем согласно (Б.7) вид
, е„ о
0
*22 0
О 1
12
Стало быть,
gn = gJg,
-gJg, g22 = gJg
- (B.8)
(Б.9)
Согласно же соотношениям (Л.19), (A.2G), (Б.7) и (Б.9)
dSt =
(i Ф j),
(Б.11)
Полагая в формулах (Б.8) — (Б.9) g = 0, получаем с уче-
учетом (Б.7) на срединной поверхности
П —~"z?J") «* — tt ==: —«jo/ft, Я = м 11/f/, ^1Э, 1Z )
л л
11 12 /Ti < O\
u- _ u'llu'22- ]2 21' ^u.if^
КОРОТКО О ТЕОРИИ ПОВЕРХНОСТЕН 183
Далее из формул (Б. 10) — (Б. 13) и (Л.22) находим
dsj = fa~,daJ = faa/'da^ (i Ф j, I, j =1,2), (Б.14)
tJS = dS31?„„ =Уа rfoAfa8, (Б. 15)
Здесь dsj — длина элемента дуги у'-й координатной линии
срединной поверхности, dS — площадь элемента средин-
срединной поверхности, % — координатный угол.
Зависимости (А.9), (А.11), (А.15) принимают на сре-
срединной поверхности следующий вид:
ri-Tj = aij, rrr=bj, r-r=a\
ut = aiaua, и' —
(Б.17)
Поверхностны]! дискримипантный тспяор вводится за-
зависимостями (см. (А.23) — (А.25))
U (),
(Б.18)
С]2 = — С2{ = Уй, ¦ Си = С22 == 0,
г,- X i-j = Сцп, п X i-j = cjor°,
YXf^&'n, пХг! = с'ага.
Из соотношений (Б.12) и (Б.18) усматривается
, (B.20)
ip j Р = 2. (Б.21)
Приступим к дифференцированию коордипатпых век-
векторов. Так, согласно формулам (А.32) и (А.31)
116=о = %- Gf3 l|=o = haa«h = ftj, (Б.22)
184
ПРИЛОЖЕНИЕ Т,
Из соотношений (Б.22) и (Б.12) следует также
2а daJ
(Б.24)
Пусть Г — некоторая линия срединной поверхности
(рис. Б.2). С пей связывают тройку
ортов: t — орт касательной к кри-
кривой, п — орт нормали к поверхности,
v — орт тангенциальной нормали
(нормали к кривой, лежащей в ка-
касательной плоскости). Введенные ор-
орты связаны зависимостями
tXn = v, nXv = t, vXt = n,
t ¦ t = n -n = v • v = 1,
t.n = n-v = vt = 0. (Б.25)
Кроме того, имеет место соотношение
Рис. Б.2
dt _ Or cfap _
rfa
dst P'
т. е.
At»
Согласно же формулам (Б.25) и (Б.19)
v = tXn = tara X n = c^t
т. е.
Vi = Cnf.
(Б.26)
(Б.27)
Запишем соотношения (Б.11J в виде первого из сле-
следующих двух:
dS\ = V"jjgu dasdl, dS{ = Yalfi ddd\ (t Ф ]). (Б.28)
Здесь рассматривается нормальное сечение оболочки. При
этом индексом \ помечена величина площади площадки,
отстоящей от срединной поверхности па \ (рис. Б.З,а).
Аналогично, заменяя п на v, имеем из (А.29)
/?
КОРОТКО О ТЕОРИИ ПОВЕРХНОСТЕЙ
При этом (рис. Б.З, б)
185
(Б.ЗО)
Здесь dSl, dSv — площади элементарных площадок нор-
нормального сечения, проходящего через касательную к кри-
кривой Г, a dst — длина кривой.
¦ а1
Рис. Б.З
В ортогональной (на поверхности) системе координат
ti/Уаи = г'пи = еи (Б.31)
где еь е2, п — координатные орты. Физические комнонен-
Рис. Б.4
ты векторов и тензоров, связанных с поверхностью, нод-
считываются по формулам (ср. (А. 43))
hi) =
, (Б.32)
^i= Van «*„. (Б.ЗЗ)
Отсюда и из рис. Б.4 следует
v()) = *B)=cosif, vB) =-f<ir= sin т, (Б.34)
\'i = Тип cos f, v2 = Vfl22 sin if,
186 ПРИЛОЖЕНИЕ В
v1 = cos у/Уяц, v3 = sin 1/Уя2з,
t' = — sin-y/Уя,,, t2 = cos 7/Уа^.
Пусть в пространственной прямоугольной декартовой
системе координат с ортами gi, g2i g3
г (а1, а2) = .г,(а\ a2)gi + ж2(а\ «2)g2 + ж3(а\ a2)g3. .
Прежде всего
дх дх Ох
и по формулам (Б.5)
х дх2дх 2Эхядх3
i + S?S? + te«5S' (Ь>35)
^
11 V 2
где
. г дх„ !)х„ дх„ дхл
(Б-37)
дхо
sin x = V^u.j3 + Иаз + Им,
а х — координатный угол. Согласно же выражениям
(Б.5) и (Б.36)
д2х д2х
sin
дх дх дх,
ц13 —^-. + Ц2з —^~- + Ичэ —^- (Б.38)
СПИСОК ЛИТЕГЛТУРЫ
1. Лмбарцумян С. А. Теория анизотропных оболочек.— М.: Фпз-
матгиз, 1961.
2. Лрутюнян II. X. Некоторые вопросы теории ползучести.-- М.;
Л.: Гостехиздат, 1952.
3. Арутюнян Н. X., Колмановскнй В. Б. Теория ползучести неод-
неоднородных тел,— М.: Наука, 1983.
4. Ашкенаш Е, 1С, Ганов Э. В. Анизотропия конструкционных ма-
материалов: Справочник.— Л.: Машиностроение, 1980.
5. Берт Т. Расчет оболочек Ц Fipayuuran JT., Крок Р. Композици-
Композиционные материалы, Т. 7, ч. 1.--М.: Машиностроение, 1978.
6. Бехтерев П. Аналитическое исследование обобщенного закона
Гука: В 2 ч.— Л.: Литограф, изд. автора, 1925.
7. Болотин В. В. Основные уравнения теории армированных
сред I/ Механика полимеров.— 1966.— № 1.
8. Болотин В. В., Новичков Ю, II, Механика многослойных конст-
конструкции.— М.: Машиностроение, 1980.
П. Бондарь Б. Д. Об одном представлении тензорной функции //
Докл. АН СССР.—191U.—Т. 141, № 1.
10. Пан Фо Фы (Uaiiuu) /'. А, Теория армированных материалов.—
Киев: Наукова думка, 197).
И. Панин Г. А., Семенюк II, П., Емельянов Р. Ф. Устойчивость обо-
лопек из армированных материалов.—Киев: Наукова думка,
1978.
12. Ворович И. М., Александров В. М., Бабешко В. А. Неклассиче-
екпо сметанные задачи теории упругости.—М.: Наука, 1974.
13. Галимов К. 3. Нелинейная теория тонких оболочек типа Тимо-
Тимошенко / Исследование по теории пластин и оболочек. Вып. 9,—
Казань, 1975.—С. 92.
14. Гаптмахер Ф. Р. Теория матриц.— М.: Гостехиздат, 1953.
15. Годунов С. К. Элементы механики сплошной среды,—М.: Нау^
ка, 1978.
10. Грин А., Адкинс Дж. Большие упругие деформации и пелипей-
ная механика сплошной среды.— М.: Мир, 1965.
М. Г узь А. Н. Устойчивость упругих тел при конечных деформа-
деформациях.— Киев: Наукова думка, 1973.
18. Друккер Д. О постулате устойчивости материала в механике
сплошной среды Ц Механика (сб. переводов).—1964,—№ 3.
19. Ильюшин А. А. Механика сплошных сред.—М.: Изд-во МГУ,
1978.
20. Ильюшин А. А., Победря Б. Е. Основы математической теории
термовнзкоупругости.— М.: Наука, 1970.
21. Королев В. И. Слоистые анизотропные пластинкя и оболочки
из армированных пластмасс— М.: Машиностроение, 1971..
188 Список литературы
22. Ночкн //. Е. Векторное нечисленно и начало тензорного исчис-
исчисления,—М.: Изд-во АН ССР, 1951.
23. Кристенсен Р. Введение в механику композитов,—М.: Мир,
1982.
24. Ландау Л. Д., Лифшиц Е, М, Механика сплошных сред.— М.:
Госте хиздат, 1953.
25. Лехницкий С. Г, Теория упругости анизотропного тела.— М.:
Гостехиздат, 1950.
26. Лехницкий С. Г. Анизотропные пластинки,— М.: Гостехиздат,
1947.
27. Лехницкий С. Г. Теория упругости анизотропного тела.— М.:
Наука, 1977.
28. Ломакин В. А. Теория упругости неоднородных тел.—М.: Изд-
во МГУ, 1976.
29. .Лохин В. В., Седов Л. И. Нелинейные тензорные функции от
нескольких тензорных аргументов // ПММ.—1963.—Т. 27, № 3.
30. Лурье А. И, Нелинейная теория упругости.—М.: Наука, 1980.
31. Ляв А. Математическая теория упругости.— М.; Л.: ОНТИ, 1935.
32. Малиник Н. И. Расчеты па ползучесть машиностроительных
конструкций.— М.: Машиностроение, 1981.
33. Малмейстер А. К., Тому ж Я. П., Тетере Г. А. Сопротивление
полимерных и композитных материалов.— Рига: Зинатие, 1980.
34. Малолетник Г. Н., Фомин В. Л. Тензорные базисы в кристалло-
кристаллофизике.— Л.: Изд-во ЛГУ, 1972.
35. Микляев П. Г., Фридман Я. Б, Анизотропия механических
свойств материалов.— М.: Металлургия, 1969.
3fi. Новожилов В. В. Основы нелинейной теории упругости.— М •
Л.: Гостехнздат, 1948.
37. Новожилов В. В. О связи между напряжениями и деформация-
деформациями в нелинейно ynpyroii среде // ПММ.—1951,—Т. 15, вып. 2.
38. Новожилов В. В. О принципах обработки результатов стати-
статических испытании изотропных материалов / ПММ.—1951 —
Т. 15, вып. 6.
39. Новожилов В. В. О физическом смысле инвариантов напря-
напряжения, используемых и теории пластичности // ПММ —1952 —
Т. 16, вып. 5.
40. Новожилов В. В, О классе сложных нагружепий, который ха-
характеризуется сохранением направлений главных осей Ц
ПММ.— 1954,— Т. 18, вып. 4.
41. Новожилов В. В. Теория упругости.—Л.: Судпромгиз, 1958.
42. Новожилов В. В. Теория тонких оболочек.— Л.: Судостроение,
1962.
43. Новожилов В. В. О формах связи между напряжениями и де-
деформациями в первоначально изотропных иеупругих телах (ге-
(геометрическая сторона вопроса) Ц ПММ.— 1963.— Т. 27, вып. 5.
44. Образцов И. Ф,, Васильев В. В., Бунаков В. А. Оптимальное
армирование оболочек вращения из композиционных матери-
материалов.— М.: Машиностроение, 1977.
45. Образцов И. Ф., Васильев В. В. Нелинейные феноменологиче-
феноменологические модели деформирования волокнистых композитных мате-
материалов И Механика композитных материалов.—1982,— № 3.
46 Огибалов П. М., Колтунов М А. Оболочки и пластины.— М.:
Изд-во МГУ. 1969.
47. Огибалов П. М., Суворова Ю. В. Механика армированных плас-
пластиков.— М.: Изд-во МГУ, 1965.
СПИСОК ЛИТЕРАТУРЫ 189
48. Очан М. 10. Программированная намотка изделии из компози-
композитов, нелинешю-уцругих в поперечном направлении // Механи-
Механика полимеров.— 1977.— № 6.
49. Лотураев В. Н., Дырда В. И., Круш И. М. Прикладная меха-
механика резины.— Киев: Наукова думка, 1980.
50. Рабинович А. Л. Введение в механику армированных поли-
полимеров.— М.: Наука, 1970.
51. Работное Ю. Н. Ползучесть элементов конструкций.— М.: На-
Наука, 1966.
52. Саркисян В. С. Некоторые задачи теории упругости анизотроп-
анизотропного тела.—Ереван: Изд-во Ереванского ун-та, 1970.
53. Седов Л. И. Введение в механику сплошной среды.— М.: Физ-
матгиз, 1962.
54. Седов Л. И. Механика сплошной среды. Т. 1.— М.: Наука,
1970.
55. Сендецки Дж. Упругие свойства композитов // Браутмап Л.,
•Крок Р. Композиционные материалы. Т. 2, Мир, 1978.
5G. Сендецки Дж. Некоторые вопросы теории упругости анизот-
анизотропного тела I/ Браушмап Л., Крок Р. Композиционные мате-
материалы. Т. 7, ч. 1.— М.: Машиностроение. 1978.
57. Сиротин Ю. И. Групповые тензорные пространства Ц Кристал-
Кристаллография.— I960.— Т. 5, вып. 2.
58. Смирнов А. Ф. Сопротивление материалов.— М.: Высшая шко-
школа, 1975.
59. Тимошенко С. П., Гудъер Дж. Теория упругости.— М.: Наука,
1975.
СО. Федоров Ф. И. Теория упругих воли в кристаллах.— М.: Нау-
Наука, 19G5.
G1. Феодосъев В. И. Десять лекций-бесед по сопротивлению мате-
материалов.— М.: Наука, 1969.
С2. Хантингтон Г. Упругие постоянные кристаллов.— УФН.—
1961.— Т. 74, а) вып. 2, б) вып. 3.
СЗ. Хаткевич А. Г. Об упругих константах кристаллов / Кристал-
Кристаллография.— 1961.—Т. 6, вып. 5.
64. Хилл Р. Об определяющих неравенствах для простых мате-
материалов. 1 а Механика (сб. переводов).— 1969.— № 4A10).
65. Циглер Г. Экстремальные признаки термодинамики необ-
необратимых процессов и механика сплошной среды.— М.: Мир,
1966.
66. Черных К. Ф. Линейная теория оболочек. Ч. 2 — Л • Изд-во
ЛГУ, 1964.
07. Черных К. Ф. О формах связи между симметричными тензо-
тензорами в механике сплошных сред / МТТ.— 1967.— № 3.
08. Черных К. Ф. Симметричные функции симметричных тоизо-
ров в анизотропной теории упругости Ц МТТ.— 1970.— № 3.
69. Черных К. Ф. О функциональных связях между сооспыми сим-
симметричными тензорами второго ранга / Проблемы механики
твердого деформированного тела (к 60-летию академика
В. В. Новожилова).— Л.: Судостроение, 1970.
70. Черных К. Ф. Определяющие неравенства упругих тел / Ме-
Механика сплошной среды и родственные проблемы анализа (к
80-летию академика Н. И. Мусхелишвили).—М.: Наука, 1972.
71. Черных К. Ф. О постулате устойчивости анизотропного мате-
материала II Избранные проблемы прикладной механики (к 60-ле-
60-летию академика В. Н. Челомея).—М.: Наука, 1974,
190 СПИСОК ЛИТЕРАТУРЫ
72. Черных К. Ф. Большие деформации упругого тела // Мехапн-
иа деформируемых icji и конструкции (к tiU-лешш академики
Ю. 11. 1'аботноьа). — М.: Машиностроении, 1975.
73. Черных К. Ф. Нелинейная теория упругости в машинострои-
машиностроительных расчетах.— Л.: Машиностроение, 1980.
74. Черных 1С. Ф. Нелинейная теория изотропных упругих тонких
оболочек I/ МТТ.— 1980.— № 2.
75. Черных К. Ф. Теория тонких оболочек из эластомеров (рези-
ноподобных материалов) // Успехи механики.—1983.— Т. 6,
вып. 1/2.
70. Черных К. Ф,, Милякова Л. В. Тонкие резино-металлическяо
элементы / Вестник ЛГУ.—1981.—№ 19.
77. Черных К. Ф., Шубина И. П. Законы упругости для изотроп-
изотропных несжимаемых материалов (феноменологический подход) //
Механика эластомероп. Научные труды.— Краснодар: Изд-во
КПИ, 1978, т. 2, вып. 268.
78. Шубников Л. В. Симметрия и аптисимметрия конечных фи-
фигур.— М.: Изд-во АН СССР, 1951.
79. Coleman В., Noll W. Material symmetry and thermostatic ine-
inequalities in finite elastic deformations // Arch. Ration. Mech. and
Anal- 1901— V. 15, № 2.
80. Green Л. E., Zerna W. Theoretical elasticity.— Oxford: Clarendon
Press, 1008.
81. Hcannon R. F. S. An Introduction to applied anisotropic. elasti-
elasticity.— London; New York: Oxford Univ. Press, 19G1.
82 Sokolnikoff I, S. Mathematical theory of elasticity.—New York:
McGraw-Hill, 1956.
83. Traesdell C, Noll W. The non-linear field theories of mechanics.—
Handbuch dor Physik. 13d. II1/3; Springer-Verlag, 1965.
84. Hill R. Constitutive inequalities for isotropic elastic solids un-
under finite strain / Proc, Roy. Soc, London,— 1070.— A314. 1519.
85. Drncker D. С Some implication of work hardening and ideal
plasticity /I Quart. Appl. Math.— 1950.— V. 7, № 4.