Автор: Козлов Б.А. Ушаков И.А.
Теги: электротехника автоматика радиоэлектронные аппараты справочник
Год: 1975
Текст
Б. А. КОЗЛОВ, И. А. УШАКОВ
СПРАВОЧНИК
ПО РАСЧЕТУ НАДЕЖНОСТИ
АППАРАТУРЫ
РАДИОЭЛЕКТРОНИКИ
И АВТОМАТИКИ
МОСКВА
«СОВЕТСКОЕ РАДИО»
1975
6Ф2.1
К59
УДК 621.3.019 (031)
Козлов Б. А., Ушаков И. А. Справочник по расчету надеж-
ности аппаратуры радиоэлектроники и автоматики. М., «Советское
радио», 1975, 472 с.
Предлагаемое издание является переработанным н сущестад-нно
расширенным по сравнению с «Кратким справочником по рариету
надежности», выпущенным в 1966 г.
В справочнике рассматриваются вопросы расчета надежности
на различных этапах разработки и эксплуатации, определения
оптимальных режимов эксплуатации и устранения неисправностей,
нахождения оптимального числа запасных или резервных элементов
при наличии экономических ограничений, а также производится
оценка надежности по результатам испытаний и эксплуатации.
Весь материал представлен в виде таблиц, удобных для практи«
ческого использования. Существенно увеличено количество число-
вых таблиц, необходимых для расчетов. Приводится аннотиро-
ванная библиография книг по проблеме надежности, вышедших
на русском языке.
Справочник будет полезен инженерам и математикам-приклад-
никам, занятым созданием современных сложных систем и обеспе-
чением надежности их функционирования, а также преподавателям
и студентам вузов, специализирующимся в технической кибер»
нетике, системотехнике и исследовании операций.
Рис. 126. Табл. 175. Библ. назв. 166.
Редакция радиотехнической литературы
30405-022
К 046(01)-75
86-74
© Издательство «Советское радио», 1975 г.
Предисловие
Со времени выхода в свет первого издания «Краткого справочника
по расчету надежности» Б. А. Козлова и И. А. Ушакова прошло уже
около восьми лет, и за этот срок он сделался библиографической ред-
костью. В настоящее время вопросы надежности прочно вошли в ин-
женерную практику. Именно по этой причине не может быть сомнений
в необходимости справочных изданий такого рода. Авторы проделали
огромную работу, они явились «первопроходцами» в области отбора
и систематизации накопленных в теории надежности и практике ее
использования задач и методов их решения. Именно поэтому первому
изданию справочника можно было предъявить многочисленные пре-
тензии — и недостаточно полный охват материала, и чрезмерную при-
вязанность к экспоненциальному распределению и многое другое.
Однако их труд нашел и заслуженную положительную оценку. За это
говорит хотя бы тот факт, что уже в 1970 г., т. е. через три с половиной-
четыре года после выхода в свет в Советском Союзе, книга была переве-
дена на английский язык и издана в США.
Если учесть время, которое было потрачено авторами на подготов-
ку первого издания справочника и его публикацию, то нужно признать,
что содержащийся в нем материал относится приблизительно к 1965 го-
ду. Последующие результаты и постановки задач по естественным при-
чинам в него войти не могли. Вот почему можно считать, что необходи-
мость нового издания Справочника по расчету надежности назрела и
назрела давно.
Думаю, что специалисты оценят тот труд, который авторы допол-
нительно вложили в подготовку этого издания. Достаточно сказать, что
теперь справочник содержит 13 глав, вместо 9 глав в первом издании.
Одно это показывает, что в книге появился значительный новый мате-
риал. Но этого мало, поскольку сделано больше — коре'нным образом
переработаны все главы, начиная с первой.
Основная идея второго издания сохранилась прежней: дать опреде-
ление основных понятий, привести расчетные формулы, указать на ос-
новную монографическую и журнальную литературу, на примерах
показать приемы расчетов. На мой взгляд, эти примеры имеют особую
ценность, поскольку они вводят читателя в типичные ситуации и учат
использованию приведенных в книге формул.
Само собой разумеется, что при составлении справочника возник
ряд затруднений. Одно из них состоит в том, как из безбрежногб моря
журнальной и монографической литературы отобрать действительно
необходимое, не пропустить что-либо важное и перспективное, но пока
еще непривычное. В вопросах отбора материала с авторами можно со-
3
глашаться и in ге соглашаться, поскольку каждый читатель и каждый
автор исходят из своих профессиональных интересов, имеют свои точ-
ки зрения. К содержанию предлагаемого издания также могут быть вы-
сказаны многие и при том серьезные претензии. Так, для примера,
в книге явно не хватает рекомендаций по прогнозу неисправностей,
очень сужена часть, посвященная испытаниям на надежность, прак-
тически нет данных о том, как повышает надежность использова-
ние метода понижения нагрузок. Этот список можно продолжить
и дальше. Далее, мне кажется, что вопросам резервирования авторы
и в этом издании уделили несколько большее внимание, чем это следо-
вало бы делать (я имею в виду не абсолютный объем сведений, а относи-
тельный, по сравнению со всеми задачами и методами теории надежно-
сти).
Я прекрасно понимаю, что в работах других всегда легче найти не-
достатки, чем самому сделать что-то положительное и полезное. Имен-
но поэтому мои замечания носят не слишком категорический характер.
Я достаточно хорошо понимаю, что, скажем, теория прогноза отказов
находится еще в зачаточном состоянии и имеющиеся в ней предположе-
ния заслуживают еще длительного обсуждения и экспериментальной
проверки.
Мне известно также, что многие задачи теории резервирования
удается решить лишь в предположениях весьма узких, когда по меньшей
мере одно распределение является экспоненциальным. Точно так же
ускоренные испытания нуждаются в систематической и длительной ис-
следовательской работе, прежде чем их теория позволит охватить бо-
лее или менее широкий круг практически важных ситуаций.
Для меня нет сомнений в том, что справочник в предлагаемом виде
принесет пользу. Но это совсем не означает, что работа над ним закон-
чена. Хотелось бы надеяться, что читатели сообщат авторам свои по-
желания на будущее, а также источники полезных сведений, которые
оказались вне поля зрения авторов. Доброжелательная критика помо-
жет не только уточнить объем сведений, необходимых для читателей,
но и улучшить систему изложения и форму преподнесения накоплен-
ных сведений.
Академии АН УССР Б. В. Гнеденко
От авторов
В 1966 г. издательство «Советское радио» выпустило наш «Краткий
справочник по расчету надежности» радиоэлектронной аппаратуры.
С момента выхода в свет этого издания прошло около восьми лет. За
это время явно обозначилась тенденция утилитарного использования
научных и методологических результатов теории надежности на всех
этапах проектирования, производства и эксплуатации современных тех-
нических систем, что, в свою очередь, привело к постановке новых за-
дач и разработке методов их решения.
В течение 1968—1970 гг. на русский язык был переведен и издан
3-томный американский «Справочник по надежности» (издательство
«Мир»), который, на наш взгляд, представляет собой не справочник
в общепринятом смысле этого слова, а скорее тематически скомпоно-
ванный сборник восемнадцати больших по объему статей разных авто-
ров.
Примерно в этот же период издательство «Советское радио» выпу-
стило в «Библиотеке инженера по надежности» около двух десятков,
книг прикладного характера по отдельным узким темам. Тематика этих
книг существенно перекрывает круг вопросов, затронутых в американ-
ском справочнике.
По нашему мнению, наличие такого рода изданий все же не снимает
с повестки дня необходимости появления издания действительно спра-
вочного характера. По сути дела, справочник должен представлять со-
бой такую книгу, пользование которой доступно любому специалисту,
понимающему проблему в целом, способному сформулировать в доста-
точно четкой форме стоящую перед ним задачу и умеющего применить
приведенные в справочнике результаты для ее решения. Очевидно,
пользование справочником не должно предполагать того, что человек,
применяющий приведенные результаты, должен понимать, как эти ре-
зультаты получены. Однако требуется, чтобы он привел в соответствие
свою реальную техническую задачу имеющейся в справочнике матема-
тической модели и понял те ограничения, при которых эта модель спра-
ведлива.
Как известно, теория надежности—молодая наука, ей нет еще двад-
цати лет. Принадлежа к инженерным дисциплинам, она тесно связана
с современной прикладной математикой, широко использует разно-
образные ее методы как для решения своих задач, так и для точной фор-
мулировки основных своих понятий. Сами определения и содержание
понятия надежность обусловливают то, что для теории надежности тео-
рия вероятностей и математическая статистика служат основными мето-
5
дами.Само собой разумеется, что объем и глубина использования мате-
матического аппарата в теории надежности не превращает ее в ветвь
прикладной математики; она остается инженерной дисциплиной, по-
скольку основными для нее являются те реальные задачи, которые вы-
двигаются практикой, а не те методы, которые к ним применяются.
Одним из самых сложных (и до сих пор удовлетворительно нере-
шенных) вопросов в теории надежности является задание целесообраз-
ных или хотя бы оправданных количественных требований по надеж-
ности на аппаратуру и системы различного назначения.
В настоящее время задание количественных требований по надеж-
ности (включая различные характеристики безотказности, долговеч-
ности, ремонтопригодности и др.) является необходимым моментом
в процессе создания любой технической системы или отдельного устрой-
ства. Без этого невозможно обоснованно проектировать технические
системы, причем ответственность и важность функций, выполняемых
аппаратурой, не только не ставят под сомнение вопрос о целесообразно-
сти задания количественных требований по надежности, но, напротив,
приводят к обязательности их задания.
До настоящего времени попытки формулировать эту задачу для
математически обоснованного ее решения приводили лишь к тому, что
произвол в назначении количественных требований более или менее
правдоподобно камуфлировался различными математикообразными по-
строениями, создаваясь определенная иллюзия обоснованности реше-
ния. Видимо, норму надежности можно считать обоснованной, если она
целесообразна, т. е. в определенном смысле оптимальна. Повышение
надежности разумно спроектированных систем, как и улучшение прочих
технических характеристик, связано тем или иным образом с увеличе-
нием затрат на производство этих систем. (Говоря о разумно спроектиро-
ванных системах, мы имеем в виду такие системы, которые нельзя суще-
ственно улучшить, изменив, например, принципиальную схему, умень-
шив число используемых деталей или упростив алгоритм их функциони-
рования; предполагается, что в системе нет бесполезных и тем более
вредных составных частей.) Таким образом, обоснованное задание тре-
бований по надежности подразумевает оптимальное (или хотя бы рацио-
нальное) распределение средств между системами.
Не менее серьезным и важным вопросом, чем выбор норм надежно-
сти, является вопрос о выборе наиболее подходящего и наиболее полно
характеризующего надежность системы показателя. На выбор типа ос-
новного показателя надежности (или некоторой системы таких пока-
зателей) влияют различные факторы, например: назначение системы;
характер процесса ее функционирования (или использования) и опре-
деленные требования к самому показателю (простота физического
смысла, возможность априорного расчета и опытной проверки или хотя
бы подтверждения и пр.).
Усложнение современных технических систем неизбежно привело
к тому, что для описания качества их функционирования пришлось
применять новые, более полные и сложные показатели. Зачастую нао
уже не устраивает ответ, работает система или не работает: нам необхо-
димо еще знать, как она работает. Иначе говоря, Ёозникает вопрос о
6
задании требований на эффективность функционирования системы с
учетом надежности.
Для сложных систем надежность функционирования не является
исчерпывающей или самодавлеющей характеристикой. Более того, для
многих систем вообще нельзя определить, что такое надежность, по-
скольку многие состояния системы не могут в процессе эксплуатации
быть четко отнесены к состояниям отказа или работоспособности. Обы-
чно Для сложных систем можно говорить лишь о состояниях работоспо-
собности или отказа для отдельных устройств, подсистем и т. д. Эти по-
казатели надежности отдельных частей системы должны учитываться
определенным образом при анализе и оценке других более естествен-
ных характеристик качества и эффективности функционирования всей
системы в целом.
На ранних этапах проектирования систем основной задачей являет-
ся построение структуры и определение алгоритмов функционирова-
ния. Обе эти задачи первоначально решаются конструкторами систем
на основании интуиции и большого опыта практической работы. Одна-
ко, как правило, при проектировании сложных систем не удается найти
однозначного решения. Всегда существует несколько альтернативных
вариантов построения системы, причем каждый из вариантов допускает
возможность существенных модификаций. Таким образом, факти-
чески производится анализ оптимальной системы путем перебора и по-
следовательного сравнения различных вариантов (правильнее говорить
о рациональной системе, поскольку исходные данные и представление
о системе не всегда бывают настолько точны, чтобы можно было гово-
рить об оптимальной системе в точном смысле слова).
На этом этапе очень важной задачей является создание достаточно
простой, но в то же время и достаточно точной математической модели
реальной системы. Необходимая точность математической модели,
конечно, определяется частично точностью и достоверностью исходных
данных. Однако недостоверность исходных статистических и других
Данных ни в коем случае не может служить основанием для отказа от
проведения оценок различных показателей надежности и эффектив-
ности функционирования систем, поскольку большинство расчетов и
оценок на ранних этапах проектирования носит характер относитель
кого сравнения нескольких конкурентоспособных вариантов. При этом,
как правило, неточность исходных данных приводит к отклонению
результатов для всех сравниваемых вариантов в одну и ту же сторону.
(Конечно, возможны отклонения и иного вида, однако ошибку при
выборе варианта можно сделать лишь в том случае, когда абсо-
лютные значения оцениваемых показателей достаточно близки, т. е.
даже при ошибке будет выбран вариант если и неоптимальный, то
Достаточно близкий к оптимальному). Во многих случаях достаточно
проведения даже чисто параметрических расчетов, где некоторые пара-
метры, входящие в выражения окончательных показателей надежности
и эффективности функционирования систем, совершенно неизвестны,
и все расчеты проводятся для целой области возможных значений.
В процессе проектирования сложных технических систем одним из
основных условий принятия целесообразных решений является систем-
7
нии подход при рассмотрении различных характеристик, включая и
характеристики надежности. Это связано с тем, что требования, предъ-
являемые к системе при проектировании, зачастую являются противо-
речивыми. (Типичным примером таких противоречивых требований яв-
ляется требование высокой надежности и одновременно требование сни-
жения затрат на проектирование и производство системы.) Наличие
таких противоречий ведет к тому, что конструктор системы вынужден
искать компромиссы, поскольку изолированное, выхваченное из общих
взаимосвязей решение отдельных проблем не может быть удовлетво-
рительным во всех смыслах. В процессе составления математической
модели для системы в целом приходится постоянно анализировать вза-
имосвязь отдельных параметров системы, взаимодействие отдельных ее
агрегатов, последовательность и взаимозависимость различных про-
цессов, составляющих общий процесс функционирования. Процесс
постановки задачи фактически осуществляется на всем этапе предвари-
тельного проектирования, хотя многие отношения, существующие
в системе, обнаруживаются в процессе исследования грубых первона-
чальных математических моделей.
Основная задача теории надежности иа этапе технического проек-
тирования — помочь разработчику принять обоснованные решения,
касающиеся выбора структуры системы, необходимости использования
и мощности вводимой избыточности, построения оптимальной системы
контроля и т. д. Более строго, теория надежности призвана здесь участ-
вовать в решении следующей двойственной задачи, которая (явно
или, что чаще, неявно) всегда стоит перед создателями устройств и
систем:
— при заданных характеристиках системы (в том числе и надеж-
ности) создать систему с минимальной «стоимостью»;
— при заданной «стоимости» системы добиться наилучших (макси-
мальных) технических показателей (опять-таки в том числе и надеж-
ности).
Под «стоимостью» здесь может пониматься собственно стоимость
системы, либо ее вес, габариты или какой-либо другой дисципли-
нирующий показатель или показатели.
Весьма важным вопросом, который прорабатывается на этапе тех-
нического проектирования и в котором теория надежности может
оказать разработчику существенную помощь, является проблема
разработки рациональной системы контроля и поиска неисправностей.
Известно, что из общего времени ремонта примерно 70% составляет
время отыскания и локализации неисправности с точностью до смен-
ного элемента и установление характера неисправности. Поэтому за
счет применения рациональных систем контроля и поиска неисправно-
стей следует искать возможность увеличения надежности восстанавли-
ваемой аппаратуры. Методами теории надежности можно рассчитать
необходимую для достижения заданной надежности полноту и глубину
контроля, установить приоритетную последовательность проверки эле-
ментов при отказе системы, выдать рекомендации по целесообразно-
сти применения и соотношению контроля встроенного и выносного,
автоматического и полуавтоматического и т. д.
в
Основная задача теории надежности па этапе «опытных образ-
цов» — всестороннее рассмотрение вопросов будущей эксплуатации
системы: определение частоты и глубины профилактических и регла-
ментных проверок; обоснование комплектации запасными элементами
и приборами (ЗИП), предварительная проработка вопросов рациональ-
ной организации самой системы снабжения ЗИП; оценка целесообраз-
ности различных режимов технического использования системы и т. д.
На этапе «опытных образцов» специалисты по теории надежности мо-
гут оценить целесообразность и эффективность использования разра-
ботанной системы для решения различных тактических задач, исследо-
вать влияние режимов работы системы (частоты включений, допустимо-
сти перерывов функционирования и т. д.).
На этапах—от испытаний опытных образцов до изготовления уста-
новочной партии на заводах-изготовителях, очень важных в процес-
се создания высоконадежной аппаратуры, использование методов
теории надежности и статистики также весьма эффективно. Действи-
тельно, здесь теория надежности занимается планированием испы-
таний, оценкой результатов испытаний систем и устройств, оценкой
надежности сложного комплекса по результатам испытаний его компо-
нентов, разработкой экономичных планов контроля надежности и т. д.
Очень важная проблема, обращенная в значительной своей части
в будущее техники, состоит в прогнозе отказов и управлении режимом
эксплуатации, для получения максимального экономического эффекта
на протяжении всей жизни изделия. Как менять режим эксплуатации
изделий, чтобы отсрочить или с большей вероятностью избежать явле-
ния отказа в заданный период? Решение этих задач связано с новым
разделом математической статистики — теорией управляемых слу-
чайных процессов.
Появление новых методов проектирования и исследования совре-
менных технических систем и обилие новых конструктивных резуль-
татов, полученных в теории надежности (оценка эффективности, надеж-
ности и живучести сетей связи, методы учета влияния контроля, ре-
гламентных проверок и профилактики, оценка надежности «старею-
щих» элементов и систем из «стареющих» элементов, методы оценки на-
дежности восстанавливаемых систем при неэкспоненциальных распре-
делениях и т. д.) — все это привело нас к мысли о необходимости заме-
ны прежнего Краткого справочника новым Справочником по расчету
надежности.
Предлагаемый справочник, как и старый, рассчитан на специа-
листов, работающих в области надежности, и предназначен в качестве
практического руководства для проведения повседневных работ по
обеспечению надежности радиоэлектронной аппаратуры и различных
сложных систем. Хотя почти все изложение материала справочника
носит сугубо рецептурный характер, авторы хотели бы предостеречь
читателя от ошибочных заключений о простоте и бездумности исполь-
зования предлагаемых результатов. Предполагаются у читателя и
определенные знания по теории надежности. Читатель должен уметь
правильно формулировать свою задачу, а затем уже находить соответ-
ствующую ей математическую модель, рассмотренную в Справочнике.
S
При написании справочника авторы стремились к тому, чтобы опре-
деленными главами и параграфами можно было пользоваться авто-
номно. Однако читателям при первом знакомстве со справочником ре-
комендуется просмотреть его, хотя бы бегло, целиком.
Авторы считали необходимым изложить весь материал с единых по-
зиций и по единому плану, поэтому нам пришлось большинство резуль-
татов получить заново, причем многие из них являются оригинальны-
ми. Кроме того, представляют интерес для практики приближенные ме-
тоды вычисления показателей надежности и оценка погрешностей вы-
числений.
Многочисленные отзывы и пожелания, полученные в период подго-
товки нового справочника, а также собственный опыт работы авторов
в промышленности, помогли нам выработать критерий отбора материа-
ла и построения книги. В интересах читателей в предлагаемом
справочнике сохранен предложенный Б. В. Гнеденко основной прин-
цип представления материала в виде компактных таблиц, несмотря на
высокую (ддя авторов) трудоемкость такого рода изложения.
В гл. 1 Справочника основные термины и понятия надежности,
используемые в книге, приводятся в соответствии с ГОСТом
13377—75, утвержденном в 1975 г. Кроме того, в главе определяет-
ся несколько новых терминов и понятий, связанных в основном с та-
кими величинами, как суммарная наработка восстанавливаемого
устройства за время /, вероятность появления участка работоспособно-
сти длительностью больше заданной за время t и т. д. Как показывает
практика, подобные показатели надежности оказываются весьма по-
лезными и конструктивными при анализе вычислительных и инфор-
мационных систем.
В гл. 2 рассматриваются основные показатели надежности элемента.
Приводятся математические определения общепринятых и вновь
введенных (в гл. 1) показателей. Здесь же приведены показатели надеж-
ности элементов (систем) с различного рода характером функциони-
рования: с переменными режимами работы, с допустимыми кратко-
временными перерывами в работе и т. д. Приводятся для широкого ди-
апазона изменения параметров числовые таблицы значений тех пока-
зателей, для которых не удается выписать аналитических выражений
в явной форме.
В гл. 3 даны показатели надежности типовых резервированных не-
восстанавливаемых систем. Излагается также ряд общих принципи-
альных вопросов резервирования.
В гл. 4, посвященной восстанавливаемым резервированным систе-
мам, наряду с экспоненциальными моделями имеется также и материал,
касающийся систем с так называемым быстрым восстановлением и сис-
тем, время работы и восстановления элементов которых подчиняются
произвольным законам.
Содержание гл. 5 касается ряда специальных задач резервирования.
В гл. 6 оценивается надежность различных моделей последователь-
ных систем, в том числе систем, состоящих из «стареющих» элементов.
Вопросы оценки влияния контроля на надежность резервирован-
ных восстанавливаемых систем рассматриваются в гл. 7.
10
Гл. 8 посвящена опенке специальных показателей надел ностн ряда
типовых систем со сложной структурой.
В гл. 9 содержатся результаты по оценке эффективности сетей связи
и управления, оценке эффективности ветвящихся систем и некоторые
другие.
Гл. 10 посвящена задачам оптимального резервирования. Здесь рас-
смотрено также несколько типовых схем построения оптимальных сис-
тем обслуживания сложных комплексов.
В гл. 11 рассматривается ряд типовых задач по выбору рациональ-
ной периодичности профилактики и замён. Приводятся числовые таб-
лицы.
Гл. 12 посвящена построению типовых алгоритмов оптимального
обнаружения неисправностей.
В гл. 13 излагаются простейшие методы статистической обработки
данных по надежности.
Вопросы общетеоретического и методического характера отнесены
в вспомогательную часть Справочника (Приложения 1—8) с целью
придания книге чисто справочного характера, удобного для практиче-
ского пользования специалистами различных профилей и уровней под-
готовки. На наш взгляд, это позволяет читателю (скорее «спрашива-
телю»), не нашедшему в основном тексте Справочника ответа на свой
конкретный вопрос, обратиться к вспомогательной его части, где в крат-
кой форме изложены те математические методы, использование
которых может позволить ему получить нужные результаты.
В Справочнике содержится большое количество числовых таблиц,
необходимых для проведения непосредственных расчетов, а также ма-
тематических сведений общего характера, специфических для задач на-
дежности. Это дает возможность автономно использовать Справочник
без обращения к другим источникам.
Приводится аннотированный библиографическцй указатель книг
по проблеме надежности, вышедших на русском языке, а также для
ряда глав списки основных статей по нестандартным вопросам, что,
по мнению авторов, должно существенно облегчить читателям про-
цесс ознакомления с работами по интересующим их вопросам.
При подготовке справочника авторы получили болЬшую помощь
от коллег и товарищей по работе. В первую очередь нам хотелось бы
выразить глубокую благодарность основоположникам советской школы
математической теории надежности—профессорам МГУ Борису Вла-
димировичу Гнеденко, Юрию Константиновичу Беляеву и Александру
Дмитриевичу Соловьеву, которым мы обязаны едва ли не всеми досто-
инствами нашей книги. Их строгая, но доброжелательная критика
позволила нам существенным образом улучшить подготовленную ру-
копись. Мы с глубокой благодарностью вспоминаем также много-
численные беседы с профессором Яковом Борисовичем Шором, сове-
ты которого всегда помогали нам находить удобную для читателя
форму изложения материала.
Три раздела справочника—гл. 8, посвященная оценке вероятност-
ных характеристик систем со сложной структурой, § 10.6, посвящен-
ный управлению запасами, и гл. 13, освещающая методы статистической
11
обработки данных, основаны на материалах, предоставленных
В. А. Гадасиным, Г. Б. Рубальским и Ю. А. Васильевым. В процессе
работы над книгой полезным оказалось содействие Е. М. Воловика
и Г. С. Пашковского. Для гл. 11 были использованы результаты
Е. Ю. Барзиловича и В. Н. Каштанова.
Ряд вычислительных работ выполнен М. В. Топольским и
А. Н. Даценко-Чигориным.
Незаметную, но совершенно необходимую работу по оформле-
нию рукописи проделали М. В. Барсукова, Н. А. Дьяконова.
В. А. Гаврилина и Н. С. Еремеева.
Как и первое издание, новый Справочник по надежности редакти-
ровала А. А. Александрова, бесконечному терпению и требователь-
ности которой мы обязаны тем, что книга увидит свет без многочислен-
ных авторских ляпсусов.
Мы считаем необходимым отметить в заключение, что на подго-
товку этого Справочника большое влияние оказали две прекрасные
книги по теории надежности: Б. В. Гнеденко, Ю. К. Беляев и
А. Д. Соловьев «Математические методы в теории надежности» и
Р. Барлоу и Ф. Прошан «Математическая теория надежности».
Поскольку вся ответственность за достоинства книги переложена
на плечи коллег и помощников, авторы с благодарностью примут все
критические замечания и пожелания в свой адрес (Москва, Главпо-
чтамт, а/я 693), ибо уступить права на допущенные ошибки нам
некому.
Б. Козлов
И. Ушаков
Основные условные обозначения
F(t) — функция распределения времени работы до первого отказа.
f(t) — плотность распределения F (/).
Ht(t) — i-e состояние системы в момент времени t.
k — коэффициент простоя.
К — коэффициент готовности.
k(t) — нестационарный коэффициент простоя.
К(0 — нестационарный коэффициент готовности.
/<*(£) — нестационарный средний коэффициент готовности.
М{А} — математическое ожидание случайной величины А.
&{А) — вероятность события А.
Р(у) — вероятность безотказной работы в интервале времени [0, г/].
Р(х,у) — вероятность безотказной работы в интервале времени 1х, у].
Q(y) — вероятность отказа в интервале времени [0, у\.
R(t0) — коэффициент оперативной готовности для интервала вре-
мени длительности t0.
R(x,y) — нестационарный коэффициент оперативной готовности для
интервала времени [х, у].
tn—время переключения.
t0 — заданное время непрерывной работы.
Т — среднее время безотказной работы.
г — обозначение статистической оценки для соответствующего
вероятностного показателя г.
Д — абсолютная погрешность показателя надежности.
О — случайная наработка между отказами.
0Х — случайная наработка до первого отказа.
Z(f) — интенсивность отказов.
р(0 — интенсивность восстановления.
i — случайное время восстановления (простоя).
т — среднее время восстановления.
1
ТЕРМИНЫ И ПОНЯТИЯ НАДЕЖНОСТИ.
ПОКАЗАТЕЛИ НАДЕЖНОСТИ
1.1. Основные используемые термины
и понятия надежности
1.1.0. Предварительные замечания. В параграфе приводятся ос-
новные термины и понятия, используемые в данном справочнике.
В основу данного перечня положен Государственный стандарт
Союза ССР 13377 — 75 «Надежность в технике. Термины и опре-
деления» (Москва, 1975), цель которого — сформулировать приме-
няемые в науке и технике термины и определения в области надеж-
ности. Однако не все термины, используемые в данном справочнике,
охватываются указанным ГОСТом, что привело к необходимости вве-
дения дополнительных терминов. Эти новые термины с соответству-
ющими определениями отмечены звездочкой. Все приводимые термины
расположены в тематическом порядке, необходимые примечания и по-
яснения даны петитом.
Основные термины и понятия теории вероятностей и математиче-
ской статистики, используемые в справочнике, приведены в приложе-
нии 1.
1.1.1. Общие понятия.
Объект. — предмет определенного целевого назначения, рассма-
триваемый в периоды проектирования, производства, эксплуатации,
изучения, исследования и испытаний на надежность.
Объектами могут быть системы и их элементы, в частности! сооружения,
установки, технические изделия, устройства, машины, аппараты, приборы и их
части, агрегаты и отдельные детали.
Надежность — свойство объекта, заключающееся в его способно-
сти выполнять определенные задачи в определенных условиях эк-
сплуатации.
В зависимости от назначения объекта и условий его эксплуатации надеж-
ность может включать безотказность, долговечность, ремонтопригодность, со-
храняемость или сочетание этих свойств объекта.
Под качеством продукции понимается совокупность ее свойств, обусловли-
вающих пригодность продукции для удовлетворения определенных потреб-
ностей в соответствии с ее назначением. Одним из свойств этой совокупности
является надежность. Надежность — сложное свойство, включающее, в свою
очередь, такие свойства, как безотказность, долговечность, ремонтопригодность
и сохраняемость.
Для конкретных объектов и условий их эксплуатации эти свойства могут
иметь различную относительную значимость.
Количественно надежность объекта оценивается с помощью показателей,
которые выбираются с учетом особенностей объекта, режимов и условий ёго эк-
сплуатации и последствий отказов.
14
Значения показателей надежности объекта могут изменяться на различных
стадиях его создания и существования — в процессах проектирования, произ-
водства и эксплуатации, что связано с уровнем качества этих процессов, подго-
товки персонала и т. п.
Система* — объект, представляющий собой совокупность эле-
ментов, взаимодействующих в процессе выполнения определенного
круга задач и взаимосвязанных функционально.
Элемент (системы)* — объект, представляющий собой простей-
шую часть системы, отдельные части которого не представляют само-
стоятельного интереса в рамках конкретйого рассмотрения.
Понятия система и элемент выражены друг через друга, поскольку одно из
них следовало бы принять в качестве исходного, постулировать. Понятия эти
относительны: объект, считавшийся системой в одном исследовании, может рас-
сматриваться как элемент, если изучается объект большего масштаба. Кроме того,
само деление системы на элементы зависит от характера рассмотрения (функцио-
нальные, конструктивные, схемные или оперативные элементы), от требуемой
точности проводимого исследования, от уровня наших представлений, от объек-
та в целом и, наконец, даже от технических и научных «вкусов» исследователя.
Безотказность — свойство объекта непрерывно сохранять работо-
способность.
Долговечность — свойство объекта сохранять работоспособность
до наступления предельного состояния с необходимыми перерывами
для технического обслуживания и ремонтов.
Ремонтопригодность — свойство объекта, заключающееся в при-
способленности к выполнению его ремонтов и технического обслужи-
вания.
Сохраняемость — свойство объекта непрерывно сохранять зна-
чения установленных показателей его качества в заданных пределах
в течение и после хранения и (или) транспортирования.
Исправность — состояние объекта, при котором он соответствует
всем требованиям, установленным нормативно-технической докумен-
тацией.
Неисправность — состояние объекта, при котором он не соответ-
ствует хотя бы одному из требований, установленных нормативно-
технической документацией.
Работоспособность — состояние объекта, при котором он способен
выполнять заданные функции, сохраняя значения основных парамет-
ров в пределах, установленных нормативно-технической документа-
цией.
Основные параметры характеризуют функционирование объекта при вы-
полнении поставленных задач и устанавливаются в нормативно-технической до-
кументации.
Неработоспособность — состояние объекта, при котором он не
способен нормально выполнять хотя бы одну из заданных функций.
Понятие «исправность» шире, чем понятие «работоспособность». Работоспо-
собный объект в отличие от исправного удовлетворяет лишь тем требованиям нор-
мативно-технической документации, которые обеспечивают его нормальное функ-
ционирование при выполнении поставленных задач. При этом он может не удов-
летворять, например, требованиям, относящимся только к внешнему виду. Рабо-
тоспособный объект может быть неисправным, однако его повреждения при этом
15
не настолько существенны, чтобы препятствовать нормальному функционирова-
нию объекта.
Предельное состояние — состояние объекта, соответствующее тех-
нической невозможности или нецелесообразности его дальнейшей эк-
сплуатации, обусловленное требованиями безопасности или неустрани-
мым снижением эффективности.
Невосстанавливаемый объект достигает предельного состояния при воз-
никновении отказа или при достижении заранее установленного предельно допу-
стимого значения срока службы или суммарной наработки.
Предельно допустимые значения срока службы и наработки устанавлива-
ются из соображений безопасности эксплуатации, в связи с необратимым сниже-
нием эффективности использования ниже допустимой или в связи с увеличением
интенсивности отказов, закономерным для объектов данного типа после установ-
ленного периода эксплуатации.
Для восстанавливаемых объектов переход в предельное состояние опреде-
ляется наступлением момента, когда дальнейшая эксплуатация невозможна или
нецелесообразна вследствие следующих причин:
— становится невозможным поддержание его безопасности, безотказности
или эффективности на минимально допустимом уровне;
— в результате изнашивания и (или) старения объект пришел в такое сос-
тояние, при котором ремонт требует недопустимо больших затрат или не обеспе-
чивает необходимой степени восстановления исправности или ресурса.
Для некоторых восстанавливаемых объектов предельным состоянием счи-
тается такое, когда необходимое восстановление исправности может быть осуще-
ствлено только при помощи капитального ремонта.
Повреждение — событие, заключающееся в нарушении исправ-
ности объекта.
Отказ — событие, заключающееся в нарушении работоспособно-
сти объекта.
Повреждение может быть незначительным или значительным. Первое озна-
чает нарушение исправности при сохранении работоспособности, второе означает
отказ. Однако некоторые незначительные повреждения со временем могут пере-
ходить в категорию значительных и тем самым приводить к отказу объекта. На-
пример, царапина на металлическом корпусе высоковольтного трансформатора
может иа первых порах не нарушать его работоспособности, но через некоторое
достаточно длительное время коррозия корпуса в этом месте может явиться при-
чиной отказа. Некоторые отказы объектов не связаны с их повреждениями. На-
пример, ошибочная установка оператором органов управления объектом может
привести к несрабатыванию в нужный момент определенных устройств (эксплу'
атационный отказ), но прн этом объект каких-либо повреждений не имеет.
Восстановление* — процесс обнаружения и устранения отказа
(повреждения) с целью восстановления его работоспособности (ис-1
правности).
Восстанавливаемый объект — объект, работоспособность которого
в случае возникновения отказа, подлежит восстановлению в рассматри-
ваемой ситуации.
Невосстанавливаемый объект — объект, работоспособность которо-
го в случае возникновения отказа не подлежит восстановлению в рас-
сматриваемой ситуации.
При анализе надежности, особенно при выборе показателей надежности
объекта, существенное значение имеет решение, которое должно быть принято
в случае отказа объекта. Если в рассматриваемой ситуации восстановление рабо-
18
тоспособности данного объекта в случае его отказа по каким-либо причинам
признается нецелесообразным ли неосуществимым (например, из-за невозмож-
ности прерывания выполняемой функции), то такой объект в данной ситуации
является невосстанавливаемым. Таким образом, один и тот же объект в зависимо-
сти от особенностей или этапов эксплуатации может считаться восстанавлива-
емым или невосстанавливаемым.
Например, аппаратура метеоспутника на этапе хранения относится к вос-
станавливаемой, а во время полета в космосе, естественно, является невосстанав-
ливаемой. Более того, даже совершенно один и тот же объект может быть отнесен
к тому или иному типу в зависимости от назначения: ЭВМ, используемая для
неоперативных вычислений, является объектом восстанавливаемым, так как
в случае отказа любая операция может быть повторена, а та же ЭВМ, исполь-
зуемая для управления сложным технологическим процессом в металлургии
нли химии, является невосстанавливаемым объектом, так как отказ или сбой
приводит к непоправимым последствиям.
Показатели надежности — количественная характеристика од-
ного или нескольких свойств, определяющих надежность объекта.
Наработка — продолжительность или объем работы, выполненный
объектом.
Объект может работать непрерывно или с перерывами. Во втором случае
учитывается суммарная наработка. Наработка может измеряться в единицах вре-
мени, циклах, единицах выработки (гектарах, кубометрах), и других единицах.
В процессе эксплуатации или испытаний различают «суточную наработку», «ме-
сячную наработку», «наработку до первого отказа», «наработку между отказами»,
«заданную наработку» и т. д.
Если объект эксплуатируется в различных режимах нагрузки, то, напри-
мер, наработка в облегченном режиме может быть выделена и учитываться
отдельно от наработки при номинальной нагрузке.
Ресурс — наработка объекта от определенного момента времени до
наступления предельного состояния.
Срок службы — календарная продолжительность эксплуатации
объекта от определенного момента времени до предельного состояния.
Под «определенным моментом» в двух последних определениях понимается
начало эксплуатации или ее возобновление после капитального ремонта.
Срок сохраняемости — продолжительность хранения объекта в
определенных условиях, в течение которой сохраняются установлен-
ные показатели его качества.
1.1.2. Характеристики отказов (табл. 1.1.1.).
Внезапный отказ — отказ, характеризующийся скачкообразным
изменением значений одного или нескольких основных параметров
объекта.
Постепенный отказ — отказ, характеризующийся постепенным
изменением значений одного или нескольких основных параметров
объекта.
Независимый отказ элемента — отказ элемента объекта, не обус-
ловленный повреждениями и отказами других элементов объекта.
Зависимый отказ элемента — отказ элемента объекта, обусловлен-
ный повреждениями или отказами других элементов объекта.
По тный отказ — отказ, после возникновения которого использо-
вание объекта по назначению невозможно до восстановления его ра-
ботоспособности
17
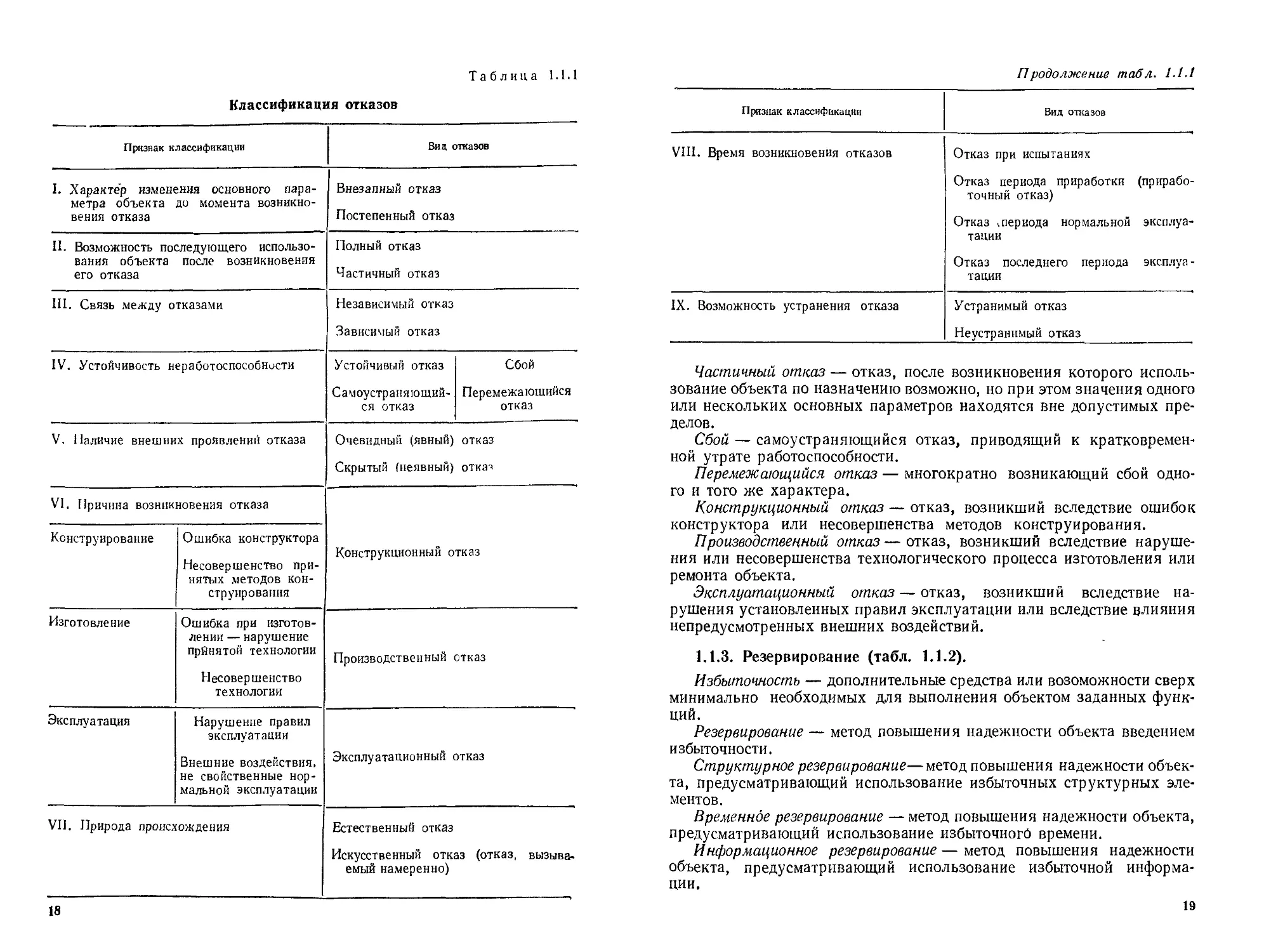
Таблица 1.1.1
Классификация отказов
Признак классификации Вид отказов
I. Характер изменения основного пара- метра объекта до момента возникно- вения отказа Внезапный отказ Постепенный отказ
II. Возможность последующего использо- вания объекта после возникновения его отказа Полный отказ Частичный отказ
III. Связь между отказами Независимый отказ Зависимый отказ
IV, Устойчивость неработоспособности Устойчивый отказ Самоустраняющий- ся отказ Сбой Перемежающийся отказ
V. Наличие внешних проявлений отказа Очевидный (явный) отказ Скрытый (неявный) откат
VI. Причина возникновения отказа
Конструкционный отказ
Конструирование Ошибка конструктора Несовершенство при- нятых методов кон- струирования
Изготовление Ошибка при изготов- лении — нарушение прйнятой технологии Несовершенство технологии Производственный отказ
Эксплуатация Нарушение правил эксплуатации Внешние воздействия, не свойственные нор- мальной эксплуатации Эксплуатационный отказ
VII. Природа происхождения Естественный отказ Искусственный отказ (отказ, вызыва. емый намеренно)
18
Продолжение табл. 1-1.1
Признак классификации Вид отказов
VIII. Время возникновения отказов Отказ при испытаниях Отказ периода приработки (прирабо- точный отказ) Отказ ^периода нормальной эксплуа- тации Отказ последнего периода эксплуа- тации
IX. Возможность устранения отказа Устранимый отказ Неустранимый отказ
Частичный отказ — отказ, после возникновения которого исполь-
зование объекта по назначению возможно, но при этом значения одного
или нескольких основных параметров находятся вне допустимых пре-
делов.
Сбой — самоустраняющийся отказ, приводящий к кратковремен-
ной утрате работоспособности.
Перемежающийся отказ — многократно возникающий сбой одно-
го и того же характера.
Конструкционный отказ — отказ, возникший вследствие ошибок
конструктора или несовершенства методов конструирования.
Производственный отказ — отказ, возникший вследствие наруше-
ния или несовершенства технологического процесса изготовления или
ремонта объекта.
Эксплуатационный отказ — отказ, возникший вследствие на-
рушения установленных правил эксплуатации или вследствие влияния
непредусмотренных внешних воздействий.
1.1.3. Резервирование (табл. 1.1.2).
Избыточность — дополнительные средства или возоможности сверх
минимально необходимых для выполнения объектом заданных функ-
ций.
Резервирование — метод повышения надежности объекта введением
избыточности.
Структурное резервирование—метод повышения надежности объек-
та, предусматривающий использование избыточных структурных эле-
ментов.
Временное резервирование — метод повышения надежности объекта,
предусматривающий использование избыточного времени.
Информационное резервирование — метод повышения надежности
объекта, предусматривающий использование избыточной информа-
ции.
19
Таблица 1 12
Классификация резервирования
Признак классификации Вид резервирования и резерв?
Способ включения резерва Постоянное резервирование Резервирование замещением
Кратность резервирования Однократное резервирование Многократное резервирование
Схема включения резерва Общее резервирование Раздельное резервирование
Состояние резерва Ненагруженнын резерв Облегченный резерв Нагруженный резерв
Характеристика резерва Восстанавливаемый резерв Невосстанавливаемый резерв
Фиксация резерва Фиксированное резервирование Скользящее резервирование
Однородность резервирования Однородное резервирование Смешанное резервирование
Функциональное резервирование — метод повышения надежности
объекта, предусматривающий использование способности элементов
выполнять дополнительные функции.
Нагрузочное резервирование — метод повышения надежности объек-
та, предусматривающий использование избыточности по его способ-
ности к восприятию нагрузок.
Основной элемент. — элемент структуры объекта, минимально не-
обходимой для обеспечения его работоспособности.
Резервный элемент — элемент, предназначенный для обеспечения
работоспособности объекта в случае отказа основного элемента.
Общее резервирование — резервирование, при котором резерв пре-
дусматривается на случай отказа объекта в целом.
Раздельное резервирование — резервирование, при котором резерв
предусматривается на случай отказов отдельных элементов объекта
или их групп.
Смешанное резервирование — резервирование, при котором имеет
место совмещение различных видов резервирования в одном объекте.
2)
Однородное резервирование* — резервирование, при котором в одном
объекте используется лишь один вид резервирования.
Постоянное резервирование—резервирование, при котором резерв-
ные элементы участвуют в функционировании объекта наравне с ос-
новными.
Резервирование замещением — резервирование, при котором функ-
ции основного элемента передаются резерву только после отказа ос-
новного элемента.
Скользящее резервирование—резервирование замещением, при ко-
тором группа основных элементов объекта резервируется одним или
несколькими резервными элементами, каждый из которых может за-
менить любой отказавший основной элемент в данной группе.
Фиксированное резервирование* — резервирование, при котором
место подключения каждого резервного элемента строго определено
заранее.
Нагруженный резерв — резервный элемент, находящийся в том же
рабочем режиме, что и основной элемент.
Облегченный резерв — резервный элемент, находящийся в менее
нагруженном рабочем режиме, чем основной.
Непогруженный резерв — резервный элемент, практически ие не-
сущий нагрузок.
Восстанавливаемый резерв — резервный элемент, работоспособ-
ность которого в случае отказа подлежит восстановлению.
Невосстанавливаемый резерв — резервный элемент, работоспособ-
ность которого в случае отказа не подлежит восстановлению.
Кратность резервирования — отношение числа резервных эле-
ментов к числу резервируемых элементов объекта.
Однократное резервирование (дублирование) — резервирование,
кратность которого равна единице.
Многократное резервирование — резервирование, кратность кото-
рого выражается числом, большим единицы.
Резервирование с восстановлением — резервирование, при котором
работоспособность любого основного и резервного элементов объекта
в случаях возникновения их отказов подлежит восстановлению.
Резервирование без восстановления — резервирование, при котором
работоспособность любого основного и резервного элементов объекта
в случаях возникновения их отказов восстановлению не подлежит.
1.1.4. Показатели безотказности и ремонтопригодности (табл. 1.1.3).
Вероятность безотказной работы — вероятность того, что в пре-
делах заданной наработки отказ объекта не возникает.
Для режимов хранения и транспортирования может применяться аналогич-
но определяемый термин «вероятность невозникиовения отказа».
Эффективность (техническая) функционирования* — мера каче-
ства собственно функционирования объекта или целесообразности ис-
пользования объекта для выполнения заданных функций.
Техническая эффективность функционирования объекта определяется ко-
личественно как математическое ожидание выходного эффекта объекта, т. е. в за-
висимости от назначения системы принимает конкретное выражение. Часто эф-
21
Таблица 1.1.3
Основные показатели надежности
Свойстве Показатель
Безотказность Вероятность безотказной работы Средняя наработка до отказа Средняя наработка между отказами Интенсивность отказов Ведущая функция потока отказов Параметр потока отказов
Ремонтопригодность Вероятность восстановления Среднее время простоя Среднее время восстановления Интенсивность восстановления
Безотказность и ремонтопригод- ность Коэффициент готовности Коэффициент простоя Коэффициент технического использования Коэффициент оперативной готовнос'ги
Долговечность Гамма-процентный ресурс Средний ресурс Средний суммарный ресурс Гамма-процентный срок службы Средний срок службы Средний срок службы до списания Средний межремонтный ресурс Медианный ресурс Медианный срок службы Средний межремонтный срок службы
Сохраняемость Средний срок сохраняемости Интенсивность отказов при хранении Параметр потока отказов при хранении Гамма-процентный срок сохраняемости Медианный срок сохраняемости
фективность функционирования определяется как полная вероятность выполне-
ния объектом задачи с учетом возможного снижения качества его работы из-за
возникновения частичных отказов.
Средняя наработка до отказа — математическое ожидание наработ-
ки объекта до первого отказа.
Средняя наработка между отказами — математическое ожидание
наработки объекта между отказами для установившегося процесса
эксплуатации.
В принципе, если объект представляет србой систему из нескольких эле-
ментов, каждый из которых независимо от других восстанавливается после отка-
за, то средняя наработка зависит от номера предыдущего отказа. Однако с ростом
номера отказа (т. е. с увеличением длительности эксплуатации) эта величина стре-
мится к некоторой постоянной или, как говорят, к своему стационарному зна-
чению.
22
Средняя наработка на отказ — отношение наработки объекта к
математическому ожиданию числа отказов в течение этой наработки.
Этим термином можно назвать кратко среднюю наработку до отказа и сред-
нюю наработку между отказами, когда оба показателя равны. Для равенства
последних необходимо, чтобы после каждого Отказа объект восстанавливался до
первоначалЬйого состояний.
Случайная наработка* — случайная продолжительность или объем
работы, выполненной объектом, до наступлеНйй некоторого события
или момента времени.
Заданная наработка* — наработка, в течение которой объект
должен безотказно работать для выполненйя своих функций.
Наработка между отказами* — случайное значение наработки
объекта между отказами.
Если наработка выражена в единицах времени, то применяются соответ*
ствующие термины: «заданное врекя (безотказной) работы», «йрёмя работы до от-
каза», «время работы между отказами!»
Заданное время (безотказной) работы*— см., «заданная наработка».
Время работы до отказа* — см. «наработка до отказа».
Время работы между отказами* —см. «наработка между отказами»
Время простоя* — случайное время вынужденного нерегламенти-
рованного пребывания объекта в состоянии неработоспособности, опре-
деляемое длительностью обнаружения отказа, длительностью ожида-
ния начала ремонта и длительностью собственно ремонта объекта.
Время восстановления* — случайное время собственно ремонта,
т.е. время отыскания и устранения одного отказа.
Если наработка выражена в единицах времени, то применяются со-
ответственно термины: «среднее время работы до отказа», «среднее
время работы между отказами» и «среднее время безотказной работы».
Среднее время работы до отказа* — см. «средняя наработка до
первого отказа» с учетом примечания.
Среднее время работы между отказами* — см. «средняя наработ-
ка между отказами» с учетом примечания.
Среднее время безотказной работы*— см. «средняя наработка на
отказ» с учетом примечания.
Среднее время простоя — математическое ожидание времени выну-
жденного нерегламентированного пребывания объекта в состоянии
неработоспособности.
Среднее время восстановления — математическое ожидание времени
восстановления работоспособности (собственно ремонта).
Вероятность восстановления — вероятность того, что фактическая
продолжительность работ по восстановлению работоспособности
объекта не превысит заданной.
Нестационарный коэффициент готовности*— вероятность того,
что объект окажется работоспособным в заданный момент времени, от-
считываемый от начала работы (или от другого строго определенного
момента времени).
Средний коэффициент готовности* — усредненное на заданном
интервале времени значение нестационарного коэффициента готовно-
сти.
23
Коэффициент готовности — вероятность того, что объект ока-
жется работоспособным в произвольно выбранный момент времени в
установившемся (стационарном) процессе эксплуатации.
Коэффициент готовности может быть определен и как доля време-
ни, в течение которого объект находится в работоспособном состоянии -
в установившемся (стационарном) процессе эксплуатации.
Коэффициент готовности (стационарный) является предельным зна-
чением, к которому стремятся и нестационарный и средний коэффи-
циенты готовности с ростом рассматриваемого интервала времени.
Часто используются показатели, характеризующие простой объекта, —
так называемые коэффициенты простоя соответствующего типа. Каждому коэф-
фициенту готовности можно поставить в соответствие определенный коэффици-
ент простоя, численно равный дополнению соответствующего коэффициента
готовности до единицы, В соответствующих определениях работоспособность
следует заменить на неработоспособность
Нестационарный коэффициент простоя — см. «нестационарный ко-
эффициент готовности» с учетом последнего примечания.
Средний коэффициент простоя — см. «средний коэффициент готов-
ности» с учетом последнего примечания.
Коэффициент простоя — см. «коэффициент готовности» с учетом
последнего примечания.
Коэффициент оперативной готовности — вероятность того, что
объект, находясь в режиме ожидания, окажется работоспособным в
произвольный момент времени в установившемся (стационарном)
процессе эксплуатации, и, начиная с этого момента времени, будет
работать безотказно в течение заданного интервала времени.
Предполагается, что рассматривается установившийся (стационарный)
процесс эксплуатации
Нестационарный коэффициент оперативной готовности* —
вероятность того, что объект, находясь в режиме ожидания, окажется
работоспособным в заданный момент времени, отсчитываемый от на-
чала работы (или от другого строго определенного момента времени),
и, начиная с этого момента времени, будет работать безотказно в те-
чение заданного интервала времени.
Коэффициент технического использования — отношение средней
наработки объекта в единицах времени за некоторый период эксплуа-
тации к сумме средних значений наработки, времени простоя, обуслов-
ленного техническим обслуживанием, и времени ремонтов за тот же
период эксплуатаци!.
Интенсивность отказов — плотность распределения наработки
объекта до отказа, определяемая при условии, что до рассматриваемого
момента отказ не возник.
Для режимов хранения и транспортирования может применяться ана-
логично определяемый термин «интенсивность отказов при хранении (транс-
портировании)»
Ведущая функция потока отказов—математическое ожидание числа
отказов восстанавливаемого объекта в течение заданной наработки.
Параметр потока отказа — первая производная ведущей функ-
ции потока отказов.
24
Интенсивность восстановления" — плотность вероятности момента
окончания восстановления объекта, определяемая при условии, что
дэ данного момента восстановление не завершено.
1.1.5. Показатели долговечности и сохраняемости (см. табл. 1.1.З.).
Гамма-процентный ресурс — наработка, в течение которой объект
не достигает предельного состояния с заданной вероятностью у.
Средний ресурс — математическое ожидание ресурса.
Назначенный ресурс — суммарная наработка объекта, при дости-
жении которой эксплуатация должна быть прекращена независимо от
его состояния.
Средний ремонтный ресурс — средний ресурс между смежными
капитальными ремонтами объекта.
Средний суммарный ресурс — средний ресурс объекта от начала
эксплуатации до его списания.
Средний ресурс до капитального ремонта — средний ресурс от
начала эксплуатации объекта до его первого капитального ремонта.
Гамма-процентный срок службы — срок службы, в течение кото-
рого объект не достигает предельного состояния с вероятностью у.
Средний срок службы — математическое ожидание срока службы.
Средний межремонтный срок службы — средний срок службы ме-
жду смежными капитальными ремонтами объекта.
Средний срок службы до капитального ремонта — средний срок
службы от начала эксплуатации объекта до его первого капитального
ремонта.
Средний срок службы до списания — средний срок службы от нача-
ла эксплуатации объекта до его списания.
Гамма-процентный срок сохраняемости — продолжительность хра-
нения, в течение которой у объекта сохраняются установленные пока-
затели с заданной вероятностью у.
Средний срок сохраняемости — математическое ожидание срока
сохраняемости.
1.2. Математическое определение основных
показателей надежности невосстанавливаемых объектов
1.2.0. Предварительные замечания. Под невосстанавливаемым объек-
том понимается такой объект, работа которого после отказа считается
полностью невозможной или нецелесообразной. Типичными примера-
ми объекта, которые вообще не могут быть отремонтированы, служат
электровакуумные и полупроводниковые приборы, аппаратура различ-
ных устройств однократного действия (метеорологические ракеты или
управляемые снаряды военного назначения).
Однако к невосстанавливаемым объектам можно отнести не только
те, которые принципиально не могут ремонтироваться. Само понятие
«невосстанавливаемый объект» в первую очередь характеризуется не
видом данной аппаратуры, а ее специфическим назначением.
В основном под невосстанавливаемыми объектами на практике при-
ходится понимать такие объекты, отказ которых в процессе функцио-
25
нирования приводит к непоправимым последствиям, иначе говоря,
восстановление которых не приводит к ликвидации последствий отка-
за. В этом смысле, например, электронные вычислительные маши-
ны, используемые для управления сложным химическим комплексом,
для которого любые перерывы в нормальном технологическом процес-
се приводят к срыву всей работы, могут рассматриваться как объекты,
невосстанавливаемые при анализе надежности этого технологического
процесса. (В то же время ясно, что сама ЭВМ после появления отказа
ремонтируется и становится вновь годной для дальнейшего использо-
вания.)
При рассмотрении статистических показателей надежности невос-
станавливаемых объектов будем рассматривать такую схему испыта-
ний или эксплуатации этих объектов, когда у нас несколько образцов
этих объектов работают до полного отказа. В этом случае статистичес-
кие показатели в пределе с рбстом числа испытываемых объектов будут
сходиться (по вероятности) к аналогичным вероятностным показате-
лям, которые являются в определенном смысле математической абстрак-
цией. Однако многие показатели надежности понятнее определяются
в вероятностных терминах, а не в статистических, что делает их очень
полезными в инженерной практике. Кроме того, все априорные рас-
четы надежности на стадии проектирования радиоэлектронной и другой
аппаратуры и систем приходится делать в виде вероятностных рас-
четов.
1.2.1. Основные показатели надежности.
1. Вероятность безотказной работы объекта в интервале времени
от 0 до t0.
а) Вероятностное определение
Р (/„) == Р (0; Q = {0^4} = 1-/ч (Q, (1.2.1)
где 0Х—случайное время работы (наработка) объекта до отказа; F^t)—
функция распределения случайной величины 0Р
Р (t0)—вероятность того, что объект проработает безотказно в те-
чение заданного времени работы t0, начав работать в момент времени
t =0, или вероятность того, что время работы объекта до отказа окажет-
ся больше заданйого времени работы /0.
б) Статистическое определение
Р («о) = N (0) = 1-я O7V (0), (1.2 2)
где N (t0) — число исправных объектов в момент времени /0; N (0) —
число исправных объектов в начальный момент времени / = 0; п (4) —
число отказавших объектов за время t0.
Р — отношение числа объектов, безотказно проработавших до
момента времени /0, к числу объектов, исправных в начальный мо-
мент времени t — 0, или частость события, состоящего в том, что реа-
лизация времени работы объекта до отказа окажется больше задан-
ного времени работы /0 (рис. 1.2.1.).
Примечание. Иногда сама выполняемая объектом задача имеет слу-
айную длительность £, характеризующуюся функцией распределения IF (/)
= &U.Z, < 0 с плотностью w (t). В этом случае «вероятность Ра безотказной
26
работы объекта» (вероятность выполнения задачи) запишется в виде полной ве-
роятности:
P# = j P(t)dW (/)=J P(t)w(t)dt.
о о
2. Вероятность безотказной работы объекта в интервале времени
от t до t + t<.
а) Вероятностное определение
Р V, t + Q = ^{0! > t + t0) |0! >/} Р (0, t + /0)|Р (0,0 «
= />(/ + /0)|Р (0.
Р (t, t + t0) — вероятность того, что объект проработает безотказно
в течение заданного времени работы /0, начинающегося с момента вре-
мени t, или условная вероятность того, что случайное время работы
объекта до отказа окажется больше величины t + t0 при условии, что
объект уже проработал безотказно до момента времени t.
где (V (0 — число объектов, исправных к моменту времени I.
Р (t,t + /0) — отношение числа объектов, проработавших до мо-
мента времени t + t0, к числу объектов, исправных к моменту вре-
мени t, или частость события, состоящего в том, что реализация вре-
мени работы объекта до отказа окажется больше величины / Ч~
при условии, что эта реализация больше величины t (рис. 1.2.2).
3. Вероятность отказа объекта в интервале времени от 0 до t0.
а) Вероятностное определение
Q (to) = Q (0, 4) = ^{0! < to) = Р (U-
Q (t0) — вероятность того, что объект откажет в течение заданного
времени работы t0, начав работать в начальный момент времени t — 0,
или вероятность того, что случайное время работы объекта до отка-
за окажется меньше заданного времени работы /0.
27
Очевидно, что
Q (4) = !-/’( ^о).
б) Статистическое определение
Q «о) = п (l»)/N (0),
где W (0) — число исправных объектов в начальный момент времени
/ ® 0; п (/(,) — число отказавших объектов к моменту времени t0.
Q fy>) — отношение числа объектов, отказавших к моменту времени t0,
к числу объектов, исправных в начальный момент времени t = 0,
или частость события, состоящего в том, что реализация време-
окажется меньше заданного t0 (см.
Очевидно, что
Рис 122 Временная диаграмма, пояс-
няющая статистическое определение по-
нятий Р (t, t + t0) , Q (/, /-Но), f (0
а !(/)-
Реализации № /—7 составляют Af(O) объектов,
реализации X? 2, 5 составляют nit); реализа-
ции № 2. 4, 5, 7 составляют п(/4-го), реализа-
ции № /. 3, 4. 6. 7 составляют N(t). реализа-
ции № !, 3, 6 составляют объектов.
Q (U = 1-р (U-
4. Вероятность отказа объекта в интервале времени от t до t A- t0.
а) Вероятностное определение
Q (t, t + t0) = 1-Р (/, t 4- I—/7 + Q!P (!)
Q (t, t + t0) — вероятность того, что объект откажет в течение задан-
ного времени работы t0, начинающегося с момента времени t, или услов-
ная вероятность того, что случайное время работы объекта до отказа
окажется меньше величины t + tQ при условии, что объект уже прора-
ботал безотказно до момента времени t.
б) Статистическое определение
л/# / । м + М—п (0 , W(l-l-fo) An(t, 1о)
V (/, / 4- /о) - — = 1-----
где N (f) — число объектов, исправных к моменту времени /; п (!) -~
число объектов, отказавших к моменту времени Ап (/, /0) —
число объектов, отказавших именно в интервале времени (/ ,t 4- 6,1
(на практике An (t, t0) должно быть достаточно велико).
Q (t, t +t0) — отношение числа объектов, отказавших именно
в интервале [t, t 4- tol, к числу объектов, исправных к моменту t,
28
пли частость события, состоящего в том, что реализация времени
работы объекта до отказа окажется меньше величины t -J- to при усло-
вии, что эта реализация больше величины t (см. рис. 1.2.2).
5. Плотность распределения отказов объекта.
а) Вероятностное определение
/ W = ~ F (t) = ~ Q (/) = - 4 р {t).
at dt dt
f (/) — плотность вероятности того, чтр время работы объекта до
отказа окажется меньше t, или плотность вероятности отказа к
моменту времени t.
б) Статистическое определение
/= »(< + AQ—»(0 == ЛГ(<4-ДО—!#(<) _ Ап(О А/)
М ' Д' (0) Ы Л/(0)Д/ ~ Л/(О)Д/ ’
где п (t) — число объектов, отказавших к моменту времени Р, N (0) —
число исправных объектов в начальный момент времени t = 0; Ап (/,
АО — число объектов, отказавших именно в интервале времени [?, t +
Ч-АН (на практике, с одной стороны, А/ должно быть достаточно мало,
а с другой стороны, An (t, At) достаточно велико).
/ (/) — частость отказов в интервале времени [/, /Ч~ЛП, или отно-
шение числа отказов в интервале времени [/, t Ч- А/] к произведению
числа исправных объектов в начальный момент времени t = 0 на дли-
тельность интервала времени А/ (см. рис. 1.2.2 с заменой t0 на А/).
6. Интенсивность отказов объекта в момент времени t.
а) Вероятностное определение
Х(/) =----*------ F(/)=
v 1— F (l) dt ' P(t)
X (t) — плотность вероятности отказа объекта к моменту времени
t при условии, что до этого момента отказ изделия не произошел.
б) Статистическое определение
X(,) = » U 4-ДО—«(О = N(J + bt)—N(t) = An (Г, А/)
' N(t)&d ЛЦ/)Д/ Л/(ОД/ ’
где N (0 — число объектов, исправных к моменту времени п (/) —
число объектов, отказавших к моменту времени Р, An (t, At) — число
объектов, отказавших именно в интервале времени U, t + АН (на
практике, с одной стороны, А^ должно быть достаточно мало, а с дру-
гой стороны, Ап (/, At) достаточно велико).
Х(/)—отношение числа отказов в интервале времени li, f-J-AH к про-
изведению числа исправных объектов в момент времени t на длитель-
ность интервала времени At (см. рис. 1.2.2 с заменой /0 на At).
2»
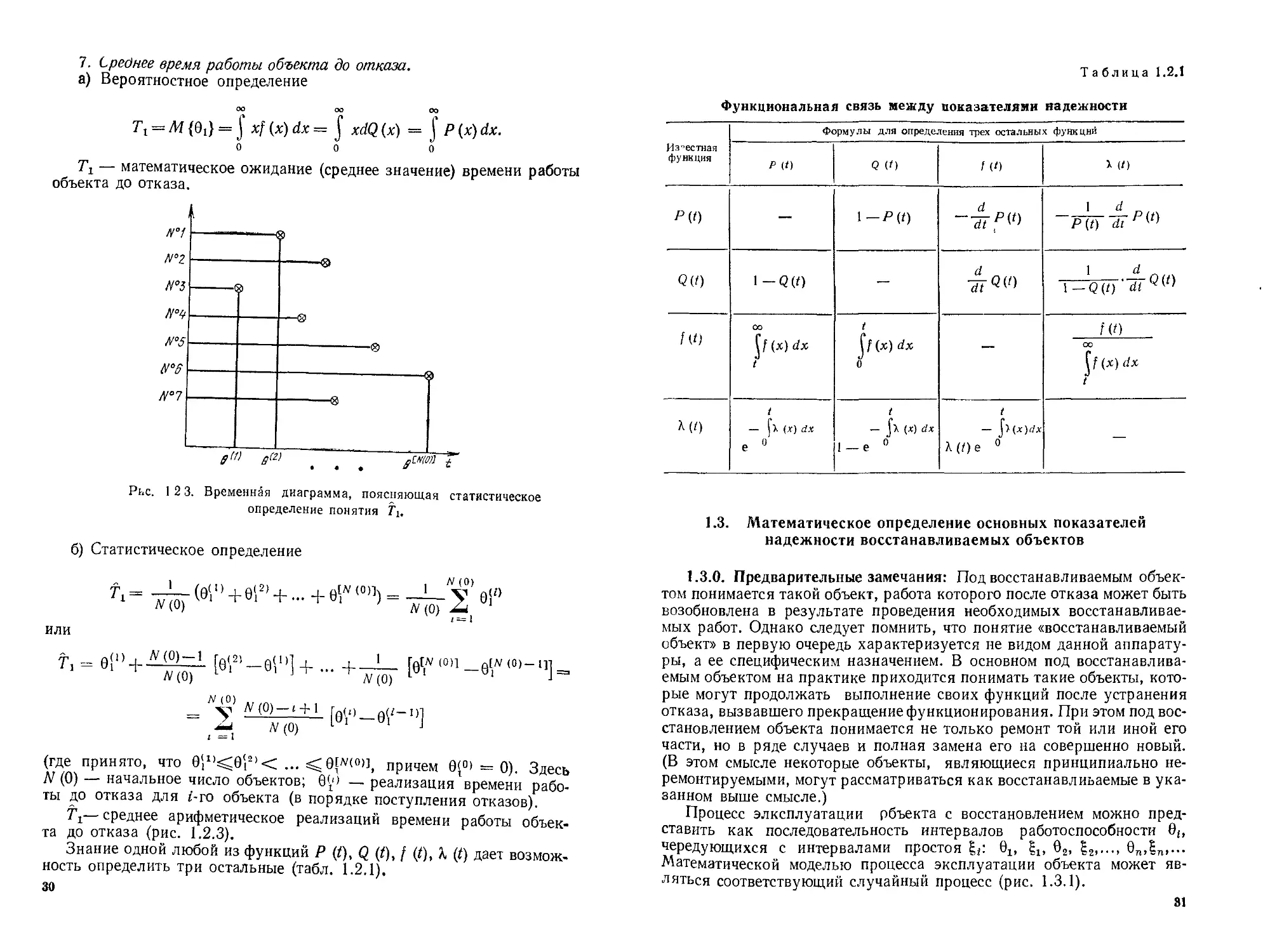
7. Среднее время работы объекта до отказа.
а) Вероятностное определение
1\ = М {01} = J xf (х) dx = J xdQ (х) = J Р (х) dx.
ООО
Тг — математическое ожидание (среднее значение) времени работы
объекта до отказа.
Рис. 1 2 3. Временная диаграмма, поясняющая статистическое
определение понятия Л.
б) Статистическое определение
. . W(0)
ft= —!—(0<1>+912, + ..- +е[1Л/(0)1) = —— у
1 N (0) ' N (0)
I --- 1
или
71 = !. [е<2>_eV»] + ...
Л/(0) L J
1
7V(0)
[gtW (0)1 _0[(V (0)-О]_,
Лу 1У(0)-Ц-1
'V(O)
[eV’-0'Г1’]
(где принято, что G^sgJG'i^C ... 0W°>], причем 0<°> — 0). Здесь
N (0) — начальное число объектов; G^) — реализация времени рабо-
ты до отказа для г-го объекта (в порядке поступления отказов),
7\—среднее арифметическое реализаций времени работы объек-
та до отказа (рис. 1.2.3).
Знание одной любой из функций Р (/), Q (/), f (t), К (t) дает возмож-
ность определить три остальные (табл, 1.2.1),
30
Таблица 1.2.1
Функциональная связь между показателями надежности
Известная функция Формулы для определения трех остальных функций
р (/) Q (0 f (0 X (0
Р(0 — 1-P(o d —dtPV P(t) dt
<2(0 1 — <2(0 — 1 d
НО t t ^f(x) dx 0 — HO p(x) dx t
МО t — (x) dx e 0 t — Jx (x) dx 1 —e 0 t — J) (x)dx 0 —
1.3. Математическое определение основных показателей
надежности восстанавливаемых объектов
1.3.0. Предварительные замечания: Под восстанавливаемым объек-
том понимается такой объект, работа которого после отказа может быть
возобновлена в результате проведения необходимых восстанавливае-
мых работ. Однако следует помнить, что понятие «восстанавливаемый
объект» в первую очередь характеризуется не видом данной аппарату-
ры, а ее специфическим назначением. В основном под восстанавлива-
емым объектом на практике приходится понимать такие объекты, кото-
рые могут продолжать выполнение своих функций после устранения
отказа, вызвавшего прекращение функционирования. При этом под вос-
становлением объекта понимается не только ремонт той или иной его
части, но в ряде случаев и полная замена его на совершенно новый.
(В этом смысле некоторые объекты, являющиеся принципиально пе-
ремонтируемыми, могут рассматриваться как восстанавливаемые в ука-
занном выше смысле.)
Процесс элксплуатации объекта с восстановлением можно пред-
ставить как последовательность интервалов работоспособности 0г,
чередующихся с интервалами простоя 6Х, £х, 02> 6пЛп,-”
Математической моделью процесса эксплуатации объекта может яв-
ляться соответствующий случайный процесс (рис. 1.3.1).
31
Для объектов с восстановлением характерен специфический вид
случайного процесса, описывающего функционирование их во время
эксплуатации. Основная особенность этого случайного процесса за-
ключается в том, что в общем случае распределения F1 (t), F2 (/),
F3 (t),... соответствующих случайных величин 6Ь 62, 63, ... отличны
I
„ ^2
J 8f .1^^.
t
Рис. 1.3.1. Случайный процесс, соответствующий последовательности череду-
ющихся интервалов работоспособности и простоя устройства.
друг от друга. Это объясняется тем, что в момент времени t — 0 объект
характеризуется вполне определенным начальным состоянием.
Например, если рассматриваемая система, состоящая из двух дуб-
лирующих друг друга независимых восстанавливаемых элементов, то
начальным ее состоянием Нй (0) обычно считается такое состояние, ког-
да оба элемента исправны, В то же время после первого же отказа
Нг
Но
Hz
Hf
Но
Рис. 1.3 2. Временные диаграммы возможных переходов системы из двух дубли-
рованных элементов.
такой системы состоянием, с которого начинается второй участок без-
отказной работы 62, является состояние Нх (9lt 4- |х), когда всего
лишь один из элементов системы работоспособен, а второй еще находит-
ся в состоянии отказа. (Предполагается, что вероятность того, что при
независимом восстановлении элементов оба они будут восстановле-
ны в один и тот же момент, практически равна нулю.) Временная ди-
аграмма возможной реализации переходов такой системы из состоя-
ния в состояние с течением времени приведена на рис. 1.3.2, а.
Правда, можно представить себе такую схему ремонта, что очередной
32
участок работы системы начинается всегда только с такого состояния,
когда оба элемента системы работоспособны (см. Но (fij + на
рис. 1.3.2, б).
Вообще говоря, в самом общем случае исходные состояния могут
быть различными перед каждым очередным участком нормальной рабо-
ты. Однако ниже будут рассматриваться в основном такие объекты, у
которых начальные состояния перед вторым, третьим и т. д. участками
безотказной работы одинаковы, а следовательно, все случайные вели-
чины 62, 63 и т. д. имеют одинаковое распределение. Более того, в ряде
случаев вообще все случайные величины 6lt Q2,... являются эквивалент-
ными. Такие случаи представляют наибольший практический интерес.
Кроме того, для рассматриваемых объектов также будем предпола-
гать, что все длительности восстановления ••• имеют одинаковые
распределения. (Такой случайный процесс носит название альтерни-
рующего процесса восстановления.)
1.3.1. Основные показатели надежности*.
1. Вероятность безотказной работы объекта в интервале времени от
О до to (см. § 1.2.2).
2. Вероятность безотказной работы объекта в течение заданного
времени работы to, начиная с момента окончания (/г—1)-го восстановле-
ния.
а) Вероятностное определение
( k—। Ik—i ]
Ph (t0) = sp z + to < 2 (0/ 4Л) + eJ 2 (0,- + U = z0 -
I r — 1 I I — I J
= ^{0ft>z0}=l— Fk(to).
Ph (t0) — вероятность того, что объект проработает безотказно в те-
чение заданного интервала времени Zo при условии, что начало этого
интервала совпадает с моментом окончания (k — 1)-го восстановления
объекта (рис. 1.3.3).
б) Статистическое определение
Pk(to)
NkW
Nk (0)
1
№ (0)’
где (0) — число исправных объектов в момент Z' — 0; (Zo) —
число объектов, не отказавших ни разу к моменту Z'= Zo; nk (Zo) —
число объектов, отказавших хотя бы раз к моменту Z' = Zo.
Примечание. Здесь для удобства пояснения введен новый отсчет вре-
мени. Для каждого объекта он начинается с момента окончания (k — 1)-го вос-
k— 1
становления, т. е. для каждого объекта f = 0 в момент времени t = S (0/ +
, . «=1
+ Si). Пояснение этой процедуры дается на рис. 1.3.4.
(Zo) — отношение числа объектов, у которых время работы от
момента окончания (k—1)-го восстановления до момента наступления
* Для восстанавливаемых объектов приводятся показатели, специфиче-
ские только для них. Все показатели для невосстанавливаемых объектов, кото-
рые применимы и для характеристики восстанавливаемых объектов, повторно
не приводятся, иа них даются лишь ссылки.
2 Зак 943 33
fe-ro отказа больше заданного времени работы t0, к общему числу
объектов (рис. 1.3.4).
3. Нестационарный коэффициент оперативной готовности, или
вероятность безотказной работы объекта в интервале времени от i до
t + ^0*
Tiz/7 благоприятного события
1-й тип неблагоприятного события
2-й тип неблагоприятного события
3-й тип неблагоприятного события
Рис. 1.3.3. Временные диаграммы, поясняющие вероятностные определения поня-
тий Pk (to) и Qk (to).
Примечание. Этот показатель для восстанавливаемых объектов опре-
деляется совершенно иначе, нежели вероятность безотказной работы в интервале
времени от I до t + t0 для невосстанавливаемых объектов.
Рис. 1.3.4. Временная диаграмма, поясняющая статистическое определение поня-
тий Pk (to) и Qk (to), для случая k=3.
Реализации № /—7 составляют А'з(О) объектов, реализации № Д 2, 5, 6 составляю;
реализации № 3, 4, 7 составляют объектов. *-------------------------
а) Вероятностное определение
се / k
R(t,t+t0)^ s W 5 (6г+^) </</+/«<
л=1 U = o '
k ос
<eA+i+ 2 (е;-^) = 2 +
<=1 J *=1
34
R (t, t 4- t0) — вероятность того, что объект проработает безотказно
в течение заданного времени работы t0, начиная с момента времени t,
или вероятность того, что интервал времени [/, t + £0] целиком попа-
дает внутрь одного из интервалов 6fe, k = 1, 2, ... (рис. 1.3.5).
б) Статистическое определение
У(0)
где п (t, I + /0) — число объектов, неисправных в момент I или отка-
завших хотя бы один раз в интервале от^ not + ^0; N (t, t + t0) —
’ Тип благоприятного события
Типы неблагоприятных событий
t+ta
бТ/л
}.....
t+t0
t+tg
Рис. 1.3.5. Временные диаграммы, поясняющие вероятностное определение
понятия R (t, to).
число объектов, исправных в момент t и не отказавших ни разу в интер-
вале времени от t до t + ta\ N (0) — общее число объектов.
R (t, t + t0) — отношение числа объектов, исправных в момент вре-
мени t и проработавших безотказно до момента времени t + tn, к об-
щему числу объектов в момент времени t (рис. 1.3.6).
4. Коэффициент оперативной готовности, или стационарная веро-
ятность безотказной работы объекта в течение заданного времени ра-
боты t0.
а) Вероятностное определение
R (i0) = Um R (/, f+t0)-
R (Q — вероятность того, что объект проработает безотказно в те-
чение заданного времени работы ta, начиная с произвольного «доста-
точно удаленного» момента времени t.
Примечание. Для любых распределевий времени работы между отка-
зами и времени восстановления, имеющих конечные средние значения Т и т со-
ответственно, всегда можно записать:
Я«о) =
1
т-н
ос
рос (*)<«.
t.
где PecU) = HmP*(0 = l-F0o(/),
оо
где Т* (f)—функция распределения времени работы от (k — 1)-го восстановления
до fe-ro отказа при безграничном увеличении номера k, т. е. распределение вре-
мени работы между отказами.
Рис. 1.3.6 Временная диаграмма, поясняющая статистическое определение поня-
тия R (/, to).
Реализации Ns 7 составляют N(ty объектов, реализации Ns 2, 4t 7 составляют
объектов.
б) Статистическое определение
Я(/о)
0 N (0)
где N (0) — общее число объектов; N 4- t0) — число объектов,
исправных в произвольный «достаточно удаленный» момент времени tx
и проработавших затем безотказно в течение заданного времени /0.
R (/о) — отношение числа объектов, исправных в произвольный
«достаточно удаленный» момент времени и проработавших затем безот-
казно в течение заданного времени работы /0, к общему числу объектов
(рис. 1.3.7.).
5. Вероятность отказа объекта в интервале времени от 0 до t0
(см. § 1.2.2).
36
6. Вероятность отказа объекта в течение заданного времени работы
t9, начиная с момента окончания (k—1)-го восстановления.
а) Вероятностное определение
Qh (Q = {0h< М = Fb (Q= 1-Pft (Q.
Qh (Q — вероятность того, что объект откажет в течение заданного
времени работы t*0 при условии, что начало этого интервала времени
совпадает с моментом (k—1)-го восстановления объекта (см. рис. 1.3.3).
- •
Н°2 —•
№3 - •
№4 -> •
№6 - •
№7
ис. 1.3.7. Временная диаграмма, поясняющая статистическое определение поня-
тия R (ta).
еализации № 1—7 составляют М(0) объектов, реализации № 2, б, 6 составляют
объектов.
б) Статистическое определение
ft \ nh (^о) 1 Nh(lo)
4i o) Nh(0) A/ft(0)’
ie (0) — число исправных объектов в момент t' = 0; Nb (t0) —
пело объектов, не отказавших ни разу к моменту nk (Q— число
эъектов, отказавших хотя бы раз к моменту t' = t0.
Примечание. Здесь для удобства пояснения введен новый отсчет
земени. Для каждого объекта он начинается с момента окончания (k — 1)-го
установления, т. е. для каждого объекта f = 0 в момент времени
k-1
i=l
Пояснение этой процедуры дается на рис. 1.3.4.
k (Q — отношение числа объектов, у которых время работы от мо-
ента окончания (fe—1)-го восстановления до момента наступления
37
ft-го отказа меньше заданного времени работы /0, к общему числу объек-
тов (см. рис. 1.3.4).
7. Плотность распределения отказов объекта (см. § 1.2.2).
8. Интенсивность отказов объекта в момент времени t (см. §.1.2.2).
9. Среднее время работы объекта до отказа (см. § 1.2.2).
10. Среднее время безотказной работы объекта от момента окон-
чания (ft—1)-го восстановления до k-го отказа.
а) Вероятностное определение
ОО <30 оо
Th = M {0ft) = j tfh (t) dt — tdQh (t) = f (/) dt.
ООО
Th — математическое ожидание (среднее значение) времени безотказ-
ной работы объекта от момента окончания (ft—1)-го восстановления до
момента наступления ft-го отказа.
б) Статистическое определение
или
ф = е^> . №>_oVЧ +... + -1- W<0)]-о^<°>-
h ~ Л/(0) 1 J У(0) 1
N (0)
где принято, что б*1’ < 6V’ ...< 6^(0)1, причем 0»°’ = 0. Здесь
N (0) — общее число объектов, начавших работать после (ft—1)-го вос-
становления; 6V1 — реализация времени работы после (ft—1)-го вос-
становления до ft-го отказа для Pro изделия (в порядке поступления от-
казов).
Тв — среднее арифметическое реализаций времени безотказной
работы объектов от момента окончания (ft—1)-го восстановления до
ft-го отказа (рис. 1.3.8).
Примечание к пп. 10 и 11. Как указано в § 1.1, в дальнейшем будем
пользоваться также понятием среднего времени безотказной работы для случаев,
когда среднее время работы до отказа и среднее время работы между отказами
полностью эквивалентны.
11. Интенсивность восстановления объекта в момент времени t,
отсчитываемый от момента начала восстановления.
а) Вероятностное определение
И(/) =—!-------L fв(/)= -/в(0 ,
1-FB(/) dt l-Fvti)
где FB (t) = t} — функция распределения времени восста-
новления; /в (0 — плотность распределения FB(Z).
38
p, (i) — условная плотность вероятности восстановления объекта к мо-
менту времени t, отсчитываемого от момента начала восстановления,
при условии, что до момента времени t восстановления объекта не про-
изошло.
б) Статистическое определение
Д / а _ Лв U ~F AQ лв (/) __ Л7В (/ -р AZ)— Л7В (О AnB А/)
. NB(t) &t “ NB(t)&t ’
где NB (0 — число объектов, не восстановленных за время t; пй (t) —
число объектов, для которых восстановление закончилось к моменту
Рис. 1.3.8. Временная диаграмма, поясняющая- статистическое определение по-
нятия Tk для случая А = 3.
времени t (отсчет времени ведется от момента начала восстановления);
Дпв (/, Д/) — число объектов, восстановленных именно в интервале
времени [I, t + Д/1.
Примечание. На практике, с одной стороны, А/ должно быть доста-
точно мало, а с другой стороны, Дпв (/, А/) достаточно велико.
p(Z) — отношение числа восстановлений в интервале времени [t,t +
+ ДИ к произведению числа объектов, еще не восстановленных к мо-
менту t, на длительность интервала времени Д/ (рис. 1.3.9).
13. Среднее время восстановления объекта.
а) Вероятностное определение
ОО ОО 00
< = У tfB(t)dt = f tdFB(t)= У (1-FB(t)]dt,
ООО
т — математическое ожидание (среднее значение) времени восстанов-
ления объекта.
39
б) Статистическое определение
. . W(0)
’-Tk,E"’+v"+-+‘l''<’")=»k 2*"
или
... + -7—-^ (0)J-^,0)-,]l
Л (0)
N.S.91____L+l [р(о________su-in
/V (0)
где принято, что £<2) ... QN <0)1, причем £(0) = 0.
Рис 139 Временная диаграмма, поясняющая статистическое определение поня-
тия |Л (Q.
Реализации № 2, б составляют лв объектов, реализации № 1. 3, 4, 5, 7 составляют Л/в(О»
реализации № 1, 2, 5, 6 составляют лв(/ + Д/), реализации К» 3, 4, 7 составляют ЛМ/ + Д0
объектов
Здесь N (0) — общее число объектов (или число наблюдений за
одним и тем же объектом); £<‘> — реализация времени восстановления
для /-го объекта (или /-я реализация одного и того же объекта).
т — среднее арифметическое реализаций времени восстановления
объектов или среднее арифметическое реализаций времени восста-
новления одного и того же объекта (рис. 1.3.10).
14. Нестационарный коэффициент готовности объекта.
а) Вероятностное определение
2 (2 (0д + k)<t< 2 (0д + и + 0.+1
U»=0 k = 0
или
= /о = 0).
Л (/) — вероятность того, что в момент времени t объект находится
в состоянии работоспособности.
40
б) Статистическое определение
/<(/) = N (t)/N (0) = 1—n (t)JN (0),
где /V (0) — общее число объектов; N (/) — число объектов, исправ-
ных в момент времени t; п (t) — число объектов, находящихся в мо-
мент времени t в состоянии отказа.
К (!) — отношение числа объектов, находящихся в момент времени
I в состоянии работоспособности, к общему числу объектов (рис. 1.3.11).
Рис. 1.3.10. Временная диаграмма, поясняющая статистическое опре-
деление понятия т.
15. Нестационарный средний коэффициент готовности объекта.
а) Вероятностное определение
/<* (/) = % wdx-
о
/С* (() — математическое ожидание доли времени, в течение кото-
рого объект находится в состоянии работоспособности в интервале
времени [0, /1.
б) Статистическое определение
, N (0)
К*(/)=4- 2S'^-
Z=I
где N (0) — общее число объектов; St(t) — суммарная наработка /-го
объекта за время /.
— среднее арифметическое суммарных наработок объектов
за время t
16. Коэффициент готовности объекта.
а) Вероятностное определение
/< = lim/<(/) = lim/<*(/) или К = R (t0 = 0).
/-too /-»ао
41
К — вероятность нахождения объекта в состоянии работоспособ-
ности для стационарного случайного процесса (т. е. в произвольный
«достаточно удаленный» момент времени), или математическое ожида-
ние доли времени, в течение которого объект находится в исправном
состоянии.
Примечание. Для любых распределений времени работы между отка-
зами и времени восстановления, имеющих конечные средние значения Т и т со-
ответственно, всегда можно записать
К = т! (Т 4- т).
Рис. 1.3.11. Временная диаграмма,
поясняющая статистическое опреде-
ление понятий К (0 и k (/).
Реализации № /—7 составляют Л/(0) объ-
ектов, реализации № /, 2, 5, 6 составляют
N(i) объектов, реализации № 3, 7 со-
ставляют n(i) объектов.
б) Статистическое определение
K_'V(Z°o) -1 ff(Zcc)
N (0) W(0) ’
где N (0) — общее число объектов; N (tx) — число объектов, находя-
щихся в состоянии работоспособности в произвольный «достаточно
удаленный» момент времени; п (tx) — число объектов, находящихся
в состоянии отказа в произвольный «достаточно удаленный» момент
времени.
Л — отношение числа объектов, находящихся в состоянии работо-
способности в произвольный «достаточно удаленный» момент времени,
к общему числу объектов (рис. 1.3.12).
17. Нестационарный коэффициент простоя объекта.
а) Вероятностное определение
^(/)= i His\oft+^)|-
1 = 0 (4 = 0 6 = 0 J
k (/)—вероятность того, что в момент времени t объект находится
в состоянии отказа (восстановления).
Очевидно, что
k (0 = 1-Л (/).
42
б) Статистическое определение
k (I) = п (t)/N (0),
где N (0) — общее число объектов; п (t) — число объектов, находящих-
ся в момент времени t в состоянии отказа.
k (t) — отношение числа объектов, находящихся в момент време-
ни t в состоянии отказа, к общему числу объектов (см. рис. 1.3.10).
Л/о? . . -
ы.л Z3I V77 A . ,
. Рта
№4 • • • Л/ОС . . —• • • fVAU , ,
г >7777) А . . .
• • • V777*
N°7 , . . Р7771 . .
t
Рис. 1 3 12 Временная диаграмма, поясняющая статистическое определение поня-
тий Кий.
Реализации № 1—7 составляют Л'(О) объектов, реализации № 1, 3, 4, 6, 7 составляют
реализации № 2, S составляют Па> объектов,
18. Коэффициент простоя объекта.
а) Вероятностное определение
k = lim k (/).
k — вероятность нахождения объекта в состоянии отказа для ста-
ционарного случайного процесса (т. е. в произвольный «достаточно
удаленный» момент времени).
Очевидно, что
k = 1-К.
б) Статистическое определение
£ = и (Q/AT(0),
где N (0) —общее число объектов; п (/«>) — число объектов, нахо-
дящихся в произвольный «достаточно удаленный» момент време-
ни в состоянии отказа.
k — отношение числа объектов, находящихся в произвольный
43
«достаточно удаленный» момент времени в состоянии отказа,
к общему числу объектов (см. рис. 1.3.11).
1.3.3. Специальные показатели. В последнее время, в особенности
в связи с появлением современных сложных систем, использующих вы-
числительные средства, для многих практических расчетов надежно-
сти стал использоваться ряд специальных показателей, основными из
которых являются:
— вероятность заданной суммарной наработки за фиксированное
календарное время t;
— вероятность наличия не менее чем заданного интервала безотказ-
ной работы за фиксированную суммарную наработку i;
— вероятность наличия не менее чем заданного интервала безот-
казной работы за фиксированное календарное время г,
— вероятность отсутствия интервала простоя, большего допусти-
мой величины, за фиксированное суммарное время простоя t;
— вероятность отсутствия интервала простоя, большего допусти-
мой величины, за фиксированное календарное время t.
Первый показатель оказывается важным для тех систем, которые
допускают перерывы в работе и могут продолжать выполнение своих
функций, начиная с любого момента. Эти системы имеют своеобразный
временной резерв: для них важно, чтобы за требуемое время суммарная
наработка системы составила бы не менее заданной величины (или ины-
ми словами, чтобы суммарное время простоя не превысило определен-
ной величины). К подобного рода системам можно отнести системы,
выпускающие какую-либо массовую однородную продукцию, когда
объем выпуска зависит только лишь от длительности суммарной нара-
ботки.
Третий показатель используется для оценки надежности систем, ко-
торые имеют возможность повторных попыток выполнения задачи.
Эти системы также характеризуются определенной временной избы-
точностью; необходимо, чтобы система за требуемое время t прорабо-
тала непрерывно хотя бы один раз в течение интервала времени, до-
статочного для выполнения задачи.
Второй показатель является частным случаем третьего. Он полу-
чается из третьего в предположении пренебрежимой малости суммар-
ного времени простоя по сравнению с периодом t. Для математических
моделей в этом случае делается предположение о мгновенном восстанов-
лении объекта после отказа.
Эти два показателя можно использовать для оценки ЭВМ, в кото-
рых после сбоя или отказа возможно повторное выполнение прежней
программы.
Второй показатель полезен для описания систем, которым свойствен-
на своеобразная «инерционность» в процессе функционирования: эти
системы не чувствительны к достаточно кратковременным перерывам.
Примерами таких систем могут служить средства обработки траекторий
управляемых объектов, у которых допускается экстраполяция коорди-
нат при пропадании ограниченного количества данных.
1. Вероятность заданной суммарной наработки а за фиксированное
время t.
44
а) Вероятностное определение
Л (a, 0 = 9й {s (0 > а},
где а — заданный уровень суммарной наработки; s (0 — суммарная
наработка за время t.
А (а, 0 — вероятность того, что суммарная наработка объекта за
время t превысит заданную величину /0.
Sf % 63 \
О . .
••e-------->-i
Рис 1.3.13. Временная диаграмма, поясняющая вероятностное определение поня-
тия В* (6, /). (После появления первого такого интервала работоспособности,
что 0j^6, длительности остальных интервалов не имеют значения.)
б) Статистическое определение
. N (0)
' /= 1
где N (0) — общее число объектов; 8г(0 — суммарная наработка £-го
объекта за время I.
Запись [зг (0JU означает следующее:
мои-}!’ кл"
(0, если st(t)<a.
Рис. 1.3.14. Временная диаграмма, поясняющая ситуацию, когда часть незавер-
шенного последнего интервала, попадающая в заданный интервал суммарной
наработки [0, 0, больше заданного значения Ь.
А (а, 0 — отношение числа объектов, суммарная наработка которых
за время t превысила величину а, к общему числу объектов.
2. Вероятность наличия интервала безотказной работы, большего
заданной величины Ь, за фиксированную суммарную наработку t.
а) Вероятностное определение
В* (b, t) = SB {имеется 0г >- b]s (0 = t},
где 0г — любой интервал безотказной работы, включая часть незавер-
шенного последнего интервала 0Х*.
В* (b, I) — вероятность того, что за суммарную наработку t по-
явится хотя бы один интервал безотказной работы 0г, включая часть
незавершенного последнего интервала 0г*, больший заданной вели-
чины b (рис. 1.3.13 и 1.3.14).
45
б) Статистическое определение
М(0)
«•(‘’•о- w 2 |(9!1Ь
' ' I г=1
где У (0) — общее число объектов; {0}; — реализация последова-
тельности интервалов безотказной работы для i-ro объекта за время
t* при условии, что восстановление отказов мгновенно.
Запись [{9}tlb означает следующее:
1, если за суммарную наработку t в {9},- существует хотя
1 = бы один интервал 0, (включая часть незавершенного no-
li Jib следнего), больший Ь,
О в противном случае.
Рис. 1.315. Временная диаграмма, поясняющая вероятностное определение
понятия В (b, t). (После появления первого такого интервала работоспособно-
сти, что 0,>6, длительности остальных интервалов не имеют значения.)
В* (b, I) — доля объектов, у которых в реализации процесса функ-
ционирования за суммарную наработку t окажется хотя бы один ин-
тервал безотказной работы 9г (включая часть незавершенного послед-
него интервала 9г*), больший заданной величины Ь.
3. Вероятность наличия интервала безотказной работы, боль-
шего заданной величины Ь, за фиксированное календарное время t.
а) Вероятностное определение (рис. 1.3.15)
В (b, t) = З5 {на (0, /] имеется 8t > b},
где 9г — любой интервал безотказной работы внутри интервала вре-
мени 10, t], включая часть незавершенного последнего интервала 9*г),
если [0, t] обрывается на интервале безотказной работы (рис. 1.3.16).
В f) — вероятность того, что за наработку t появится хотя бы один
интервал безотказной работы 0;, включая возможную часть незавер-
шенного последнего интервала 9*г, больший заданной величины Ь.
б) Статистическое определение
N(0)
8,'«'>=ж2 к0^'1-
где N (0) — общее число объектов; {9, £}г— реализация последова-
тельности интервалов безотказной работы и простоя для t-го объекта
за время t.
46
Запись I{0, £};]й означает следующее:
' 1, если за время I в {0, |}г существует хотя бы один
tmtii интервал 0; (включая часть незавершенного послед-
11 него), больший Ь,
0 в .противном случае.
В (b, t) — доля объектов, у которых в реализации процесса функ-
ционирования за время t окажется хотя бы один интервал безотказной
работы 0;-, включая возможную часть незавершенного последнего ин-
тервала 0*j (см. рис. 1.3.15 и 1.3.16), больший заданной величины Ь.
Рис. 1.3.16. Временная диаграмма, поясняющая ситуацию, когда часть незавер-
шенного последнего интервала, попадающая в заданный интервал -времени [0, /],
больше заданного значения Ь.
4. Вероятность отсутствия интервала простоя, большего допусти-
мой величины с, за фиксированное суммарное время простоя t.
а) Вероятностное определение
С* (/0, 0 = & {& < c|sB (0 = о.
где — любой интервал простоя, включая часть незавершенного
последнего интервала; sB (/) — суммарное время простоя.
С* (с, t)—вероятность того, что за суммарное время простоя не
.появится ни одного интервала простоя включая часть незавер-
шенного последнего интервала £*г (по аналогии с рис. 1.3.13 и 1.3.14),
большего заданной величины с.
б) Статистическое определение
М(0)
i 1
где N (0) — общее число объектов; {£}; — реализация последова-
тельности интервалов простоя для i-ro объекта за время t при условии,
что периоды работоспособности исключены; 1{£}г]с означает:
II, если за время t в {|}г не существует ни одного ин-
тервала (включая часть незавершенного последнего),
большего с,
0 в противном случае.
С* (с, f) — доля объектов, у которых в реализации времени простоя
за суммарное время простоя t не окажется ни одного интервала про-
стоя g (включая часть незавершенного последнего интервала), боль-
шего заданной величины с.
5. Вероятность отсутствия интервала простоя, большего допусти-
мой величины с, за фиксированное календарное время t.
47
1{0,
а) Вероятностное определение
С (с, t) — Ф {на [О, Л все < с},
где В» — любой интервал простоя внутри интервала времени [О, Л,
включая часть незавершенного последнего интервала, если [О, Л
обрывается на интервале простоя.
С (с, f) — вероятность того, что за время t не появится ни одно-
го интервала простоя (включая возможную часть незавершенного
последнего), большего с.
б) Статистическое определение
АГ (0)
где (0) — общее число объектов; {0, £}г — реализация последова-
тельности интервалов безотказной работы и простоя для /-го изделия
за время t.
Запись [{0, £}г1с означает следующее:
1, если за время t в {0, £}г не существует ни одно-
го интервала | (включая возможную часть неза-
вершенного последнего), большего с,
0 в противном случае.
С (с, I) —для объектов, у которых в реализации процесса функцио-
нирования за время t не окажется ни одного интервала простоя (вклю-
чая возможную часть незавершенного последнего), большего с.
Список литературы
1. Б р у е в и ч Н. Г. Вопросы надежности и точности электронных устройств
в машиностроении и приборостроении. — «Известия АН СССР, ОТН. Энерге-
тика и автоматика», 1961, № 1.
2. Г н е д е н к о Б. В., Козлов Б. А., Ушаков И. А. О роли и
месте теории надежности в процессе создания сложных систем. — В кн.:
Теория надежности и массовое обслуживание. Под ред. Б. В. Гнеденко М.,
«Наука,» 1969.
3. Дружинин Г. В. О методах расчета надежности систем. — В кн.:
Надежность рад1 электронной аппаратуры, 1958.
4. Л е в и н Б. Р. О некоторых вопросах теории надежности радиоэлектрон-
ного оборудования. — «Радиотехника», 1960, № 2.
5. Л е в и н Б. Р., Ушаков И. А. Некоторые аспекты современного со-
стояния проблемы надежности. — «Радиотехника», 1965, т. 20, № 4.
6. Майоров А. В. К теории резервирования в системах автоматики. —
«Известия АН СССР, ОТН», 1956, № 9.
7. С и н и ц а М. А. К вопросам резервирования радиоэлектронных уст-
ройств. — В кн.: Надежность радиоэлектронной аппаратуры, 1958.
8. У ш а к о в И. А. Основные принципы и методы теории надежности. —
«Вопросы философии», 1967, № 6.
9. Ф и ш б е й н Ф. И. Об отказах, не имеющих отношения к свойству «на-
дежность». — «Надежность и контроль качества», 1971, № 1.
10. Ш и ш о н о к Н. А., Неледва В. А. Ряды показателей восстанавли-
ваемости и обобщенных показателей. — «Надежность и контроль качества»,
1971, Ns 9.
2.
НАДЕЖНОСТЬ ЭЛЕМЕНТА
2.0. Предварительные замечания
Элемент и система являются очень тесно связанными понятиями,
взаимоотношения между которыми эквивалентны взаимоотношениям
между целым и его частью. Обычно в теории надежности под элемен-
том системы понимается достаточно самостоятельная и четко выде-
ляемая (конструктивно, схемно или функционально) ее часть, даль-
нейшая детализация которой не представляет существенного интереса
в пределах проводимого анализа.
Понятие элемент поэтому является весьма относительным, зави-
сящим от объекта исследования в целом. Так, при анализе надежности
сложных радиоэлектронных комплексов элементом может считаться
целая радиолокационная станция, система передачи данных, элект-
ронно-вычислительная машина, энергосистема и т. д. При анализе
надежности радиолокационной станции элементом можно считать
отдельный ее канал, блок или стойку аппаратуры. При анализе на-
дежности какого-либо блока элементом могут считаться отдельные
модули, ячейки, радиодетали, электровакуумные приборы, тран-
зисторы и т. д.
2.1. Невосстанавливаемый элемент
2.1.1. Произвольное распределение. Предполагается, что извес-
тен закон распределения времени работы элемента до отказа F (/) =
= SP {0^0- Показатели надежности элемента выражаются через
известный закон распределения или его основные параметры.
В табл. 2.1.1 приведены основные показатели надежности для
произвольного закона распределения времени до отказа. Пояснение
основных формул этой таблицы дается на рис. 2.1.1—2.1.4
Если F (t) задана в виде ступенчатой функции, формула для Т
может быть записана в виде (см. для пояснения рис. 2.1.5)
оо
Т=2Ж;+1)-ЖЖ (2.1.1)
7 = 0
или в виде (см. для пояснения рис. 2.1.6)
оо
<2.1.2)
/=о
49
Таблица 2.1.1
Невосстанавливаемый элемент. Произвольный закон распределения
времени работы до отказа F(t)
Показатель Точное значение Показатель Точное значение
Непрерь 1вная функция Диск* иетная функция k(t«i
Р«„) 1 - Л /о) P(h) 1- 3 f(A.) = i—1
Q(tt) N == 3 f(A4) i=k (/0) + 1 * (<o)
P(t. t+t') Qd.t + t,,) Q(t») i=l N 2 нл,) (£ + ^o)"Ы
F(t + t,)-F(t} l-F(t) P (t>t + /о)
N 2 k (< + Q
T 00 00 J* HO d/=jp(n dt Q(t, t + 0) 2 i—k (0 + 1
0 0 fit) f(t) N 2 i=A (0 + 1 N
P(t) l-F(t) T 2w i=i
Рис. 2 1.2. Пояснение формул для
Р (/, /+4) и Q (I, t+t0).
50
Для X (0 при ti t < tl+1 для дискретного распределения
X (/) = F М+1) — F (О)
(ti+i h) F (it)
Пример 2.1.1. Пусть при испытаниях N => 35 элементов после каждого часа
фиксировалось число произошедших отказов, и результаты этих испытаний све-
дены в таблицу!
Момент времени tt
123456789 10
Число отказов n(tt)
0335876210
Рис. 2.1.3. Пояснение принципа инте-
00
грирования по формуле Т— j" tdF (t).
Рис. 2.1.4. Пояснение принципа инте-
оо
грирования по формуле Т— \ Р (t)dt.
О
Требуется построить эмпирическую функцию распределения и вычислить основ-
ные показатели надежности элемента, приняв эмпирическую функцию в качестве
истинной.
Решение. 1. Для этого случая эмпирическую функцию распределения
можно вычислить по формуле
1 "V
F п
k= 1
и записать в виде следующей таблицы:
tt 123456789 10
F Vt)
О 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00 1,00
2. Вероятность безотказной работы для t0 = 4 ч: Р (4) = 1 — F (4) = 1—
— 0,314 = 0,686.
3. Вероятность отказа за время /0 = 4 ч:
Q (4) = F (4) = 0,314.
51
4.Вероятность безотказной работы в интервале времени от / “=> 2 я до I +
-|- t0 =• 6 ч при условии, что элемент проработал безотказно 2 ч:
1 —F(6) 1 — 0,743
В (2; 6)= (2) - i-o oge
«0,28.
5. Вероятность отказа в интервале времени от / = 2 ч до / + = 6 ч
при условии, что элемент проработал безотказно 2 ч:
Q (2; 6) = 1 — Р (2,6) = 1 — 0,28 0,72.
Рис. 2.1.5. Пояснение формулы
(2.1 1)
1,... А — площадь, равная сумме от I
до А-го слагаемого в формуле (2 1.1),
6. Среднее время работы до отказа находим по формулам (2.1.2) и (2.1.1)
соответственно:
ю
Т = Д< 2 Р (И) = 14-0,9144-0,828 4-0,786 + 0,457 +
1=1
+0,257 + 0,086 + 0,029 = 4,357 ч,
10 '
Т= 3 (F(/i+1)-F(/,)]G=2.0,086 +3(0,172 - 0,086)+4(0,314 - 0,172) +
<=1
+ 5(0,543—0,314)+6 (0,743—0,543)+7 (0,914 —0,743) +
+8(0,971 —0,914)+9 (1—0,971) «4,357 ч.
7. Интенсивность отказов (как функцию времени) удобнее всего вычислять
в этом случае непосредственно из данных испытаний по формуле
где t0 = 0.
Результаты вычислений сведены в следующую таблицу:
+4 1 2 3 4 5 6 7 8 9
Л(Г,), 1/ч 0 3/35= =0,086 3/32= =0,095 5/29= =0,172 8/21= =0,333 7/16= =0,437 6/9= =0,667 2/3 = =0,667 1,00
62
Пример 2.1.2. Пусть закон распределения времени работы элемента до
отказа является нормальным со средним значением Т *=• 100 ч и дисперсией
а2 — 1000 ч2. Требуется вычислить основные показатели надежности элемента.
Решение. 1. Вероятность безотказной работы за время t0 = 70 ч и t0 =•
= 130 ч:
г . (Q—T
Р(/О)=^{0>(0|7', = —
где Ф (у) — нормированная функция нормального распределения.
Рис. 2.1.6. Пояснение формулы
(2.1.2).
1. .... k — площадь, численно равная сум-
ме от 1 до fe-ro слагаемого в формуле
(2.1.2),
По табл. П.8.4 Приложения находим
/ 70—100 \
Р(70) = 1 —Ф ———— =1 — Ф(—0,95)= Ф (0,95) =0,829,
\ 31,6 )
/130—100 \
Р (130) = 1 — Ф —1=1 —Ф (0,95) =0,171.
\ 31,6 /
2. Вероятность отказа за время ta = 70 ч и ta = 130 ч>
Q (70) = 1 — 0,829 - 0,171, Q (130) = 1 — 0,171 = 0,829.
3. Вероятность безотказной работы в интервале времени от t = 70 ч до
t + ta = 90 ч:
, Л / 90—100 \
1 — Ф ---------
V 31,6 / Ф(0,32)
Р (70; 90 =------------1---— =------v •
1_ф/ 70~ 100 Ф(0,95)
\ 31,6 J
По табл. П.8.4 находим Ф (0,32) = 0,626*, тогда Р (70; 90) •= 0,626 : 0,829 ~
« 0,755.
4. Вероятность отказа в интервале времени от t = 70 ч до t + /0 = 90 ч:
Q (70; 90) = 1 — Р (70; 90) = 0,245.
5. Среднее время работы до отказа задано в условии задачи: Т = 100 ч.
* Значение получено линейной интерполяцией.
53
6. Интенсивность отказа для / •= 70 я и 130 ч. Предварительно по
табл. П.8.3 Приложения находим значения плотности нормального распределения
тогда
1 П(П_ ф(°’95) - - °’254 -о 30R
> 1-Ф( —0,95) Ф(0,95) 0,829 °’306,
-,1чт «Р 0,254 . _
х (130) - ~фф,95) =1 -485-
2.1.2. Экспоненциальное распределение. В табл. 2.1.2 приведены
основные показатели надежности элемента для экспоненциального
распределения времени до отказа. Пояснение основных формул этой
таблицы дается на рис. 2.1.7.
Таблица 2.1.2
Невосстанавливаемый элемент. Экспоненциальный закон
распределения времени до отказа F (/) = 1 — е~ х/
Показатель Точное значение Приближенное значение Погрешность
Р(?о) e— 1 - AZ0 ®+< 2
Q(M 1 — e~ x/° Mt » , (AM2 a_< 2
Р (t. t + to) e~ x/° 1 — Mo 3+< 2
Q (t, t + to) 1 _ e- Mq » (AM2 a_ -
T 1
X
A (0 A — —
Приближенные значения приводятся для условия Х/о<1.
Практически приближенные значения показателей можно использовать, если Х(о < Од
Пример 2.1.8. Пусть элемент имеет экспоненциальное распределение вре-
мени работы до отказа с параметром распределения
А = 2,5 • 10-6 1/ч.
Требуется вычислить основные показатели надежности элемента.
Решение. 1. Вероятность безотказной] работы за время = 2000 ч
Р (2000) ==е—2'5,10~6'2000 =е-°.06 =0,9512,
54
Приближенное значение
Р (2000) » 1 =2,5 10-9-2000 = 0,95
2. Вероятность отказа за время tg = 2000 ч
Q (2000) = 1 — 0,9512 = 0,0488,
Приближенное значение
Q (2000) =2,5-10-5-2000 = 0,05.
3. Вероятность безотказной работы в интервале времени от / = 500 ч до
+ /0 «= 2500 ч при условии, что элемент проработал безотказно 500 ч
Р (500; 2500) =е~ 2,5'10—5’2000 =е~° 05 =0,9512.
Приближенное значение
Р (500; 2500) = 1-2,5-10-5-2000 = 0,95.
4. Вероятность отказа в интервале
времени от 1° 500 ч до i + /0 = 2500 ч
при условии, что элемент проработал без-
отказно 500 ч
Q (500 ; 2500) =» 0,9512 «= 0,0488.
Приближенное значение
Q (500; 2500) = 2,5 • 10~5 2000 «= 0.05.
5. Среднее время работы до отказа
Т = 1 ; (2,5 IO-3) = 40 000 ч.
2.1.3. Вероятность безотказной
работы при случайной длительности
выполнения задачи. Если требуемое
время работы элемента, или время выполнения элементом задачи t0
являет.ся само случайной величиной, то вероятность безотказной
работы элемента можно записать в виде
ОО ОО
Р= $P(t)dG(t) = $P(t)g(t)dt,
о о
где Р (/) — вероятность безотказной работы элемента за время t (ве-
роятность выполнения задачи длительности t}\ G (t) — вероятность то-
го, что длительность задачи не превысит величины t (распределение
длительности задачи); g (t) — плотность распределения G (t).
Выражения для Р для основных случаев приведены в табл. 2.1.3.
Пример 2.1.4. Электронно-вычислительная машина, характеризующаяся
пуассоновским потоком сбоев с интенсивностью Х = 0,1 1/ч, предназначена для
решения задач, длительность которых является случайной величиной, рас-
пределенной по нормальному закону со средним /0 = 3 ч и среднеквадратиче-
скнм а = 0,5 ч. Требуется найти вероятность того, что сбой не появится при ре-
шении произвольно выбранной задачи.
Решение. По формуле, приведенной в табл. 2.1.3 для нормального рас-
пределения, находим
0,01 (9 + 0,25)
р = 1-0,3 + —’—' 2 ; =0,74625» 0,75.
Заметим, что если бы длительность решения задачи была постоянной, то
Р = е~ °-1 ' 3 = 0,7408 » 0,74.
55
Таблица 2.1.3
Невосстанавливаемый элемент. Вероятность безотказной работы при случайной длительности выполнения задачи
Примечание m* — k-й начальный мо- мент распределения G (t) mf = t, ^3 = + 3> i
Погрешность V + «о , М Г 1 8+ <— р9 +"б“] при We 1 i + E Й ~ A « g|^ s
Приближенное выражение •ч + G®+°7)sY СЧ 1- + "tv — [ It® +^(sY
Точное выражение °Л — 1 ,. ( «*'* -u0+< — e — 00 VI s
Вид распределения G (t) Экспоненциальное рас- пределение Нормальное распреде- ление , (to-1)’ 1 tPZ ' Y,*' и Й ад Произвольное распре- деление G(/)
66
отказов или может убывать
время жизни ит.
сходные признаки
строго говоря, и
в математическом
Рис. 2.1.8. Характер верхней и ниж-
ней границ для «стареющего» рас-
пределения при известном среднем
значении.
2.1.4. «Стареющее» распределение. На практике часто приходит-
ся сталкиваться с различными изделиями, обладающими одним очень
естественным свойством: изделие, проработавшее некоторое время,
обладает в среднем худшими вероятностными характеристиками по
сравнению с изделием совершенно новым или проработавшим мень-
ший срок. Такое ухудшение вероятностных характеристик может
проявляться различным образом: например/с течением времени у из-
делия может возрастать интенсивность
(в среднем) так называемое остаточное
быть и другие
старения, хотя,
различающиеся
смысле).
Оказывается, информация о том,
что элемент имеет «стареющее» рас-
пределение, позволяет существенно
улучшить классические оценки для
квантилей распределения, полу-
ченные на основании известных
значений математического ожида-
ния и дисперсии. (Кстати, для не-
равенства Чебышева знание дис-
персии является необходимым.)
В табл. 2.1.4 приведены формулы для нахождения верхней и ниж-
ней границ (гарантированных) вероятности безотказной работы и
квантили Вр при известном математическом ожидании распределения,
которое имеет возрастающую интенсивность отказов X (/). Общий
характер верхней и нижней границ Р (/) для этого случая иллюстри-
руется на рис. 2.1.8. Для удобства практических оценок верхняя
граница табулирована (табл. 2.1.5).
п. (Могут
Таблица 2.1.4
Верхняя и нижняя границы вероятности безотказной работы
и квантили для „стареющих" распределений
Показатель Нижняя граница Верхняя грани ца Интервал, для которого справед- лива оценка Примечание
/> (О t / е 0 I —to t е * OsS/ <Г зависит от i н опреде- ляется из уравнения . - —<O.t 1—ss е t
е~“' е~а( определяется из уравнения р (Ер) = Р In (1-р)
— In (1 — р) т 1 _ 1п (| ~ т р _ 1п ~ р> 7 Р 1 — е-' р> 1— е"'
5?
Таблица 2.1.3
Верхние границы для P(t) = 1— F(t), где F(t) есть „стареющее"
распределение с известным математическим ожиданием Т — 1
//г 00 02 04 06 08
1.0 1,000 0,961 0,924 0,889 0,856
1.1 0,824 0,794 0,765 0,738 0,711
1.2 0,686 0,662 0,640 0,618 0,597
1.3 0,577 0,558 0,540 0,522 0,505
1.4 0,489 0,474 0,459 0,444 0,430
1,5 0,417 0,404 0,392 0,380 0,369
1.6 0,358 0,348 0,337 0,328 0,318
1.7 0,309 0,300 0,292 0,283 0,275
1.8 0,268 0,260 0,253 0,246 0,239
1,9 0,233 0,226 0,220 0,214 0,209
2,0 0,203 0,198 Р, 193 0,188 0,183
Если кроме математического ожидания известна и дисперсия рас-
с^актьоласут быть с^щестьедтта сажены.. В табл. 2Л .6
приведены численные значения верхних границ, а в табл. 2.1.7 —
нижних границ для случая возрастающей интенсивности отказов.
Таблица 2.16
Верхние границы для Р(/) = 1— F (t), где F(t) есть „стареющее"
распределение с известным математическим ожиданием Г = 1
и дисперсией о2
t/r
0,10 0,20 0,30 0,40 0.50
0,30 1,000 1,000 1,000 1,000 0,993*
0,33 1,000 1,000 1,000 1,000 0,964
0,36 1,000 1,000 1,000 1,000 0,936
0,39 1,000 1,000 1,000 0,978* 0,909
0,42 1,000 1,000 1,000 0,951 0,883
0,45 1,000 1,000 1,000 0,924 0,857
0,48 1,000 1,000 0,974* 0,897 0,833
0,51 1,000 1,000 0,947 0,872 0,809
0,54 1,000 1,000 0,921 0,847 0,785
0,57 1,000 0,985* 0,896 0,823 0,763
0,60 1,000 0,959 0,871 0,800 0,741
0,63 1,000 0,933 0,847 0,777 0,719
0,66 1,000 0,909 0,824 0,755 0,699
0,69 0,995* 0,885 0,801 0,734 0,678
0,72 0,972 0,862 0,779 0,713 0,659
0,75 0,949 0,840 0,758 0,693 0,640
0,78 0,927 0,819 0,737 0,674 0,622
0,81 0,906 0,798 0,718 0,655 0,604
0,84 0,887 0,778 0,698 0,636 0,587
0,87 0,868 0,758 0,680 0,619 0,570
0,90 0,850 0,740 0,661 0,601 0,554
58
Продолжение табл. 2.1.6
ЦТ а“/Г!
0,10 0,20 0.30 0,40 0,60
1,00 0,796 0,682 0,608 0,548 0,503
1,05 0,774 0,656 0,579 0,523 0,479
1,10 0,756 0,632 0,554 0,499 0,457
1,15 0,742 0,609 0,531 0,476 0,435
1,20 0,633 0,588 0,509 0,455 0,415
1,25 0,514 0,570 0,488 0,435 0,396
1,30 0,411 0,554 0,469 0,416 0,377
1,35 0,326 0,519 0,451 0,397 0,360
1,40 0,258 0,444 0,434 0,380 0,343
1,50 0,163 0,321 0,405 0,348 0,313
а/Р
ЦТ o,t>o | 0,71 0,80 I 0.90 1.00
h.W л/т i./m Q.,%U
0,10 1,000 1,000 1,000 0,952* 0,905
0 15 1,000 1,000 0,957* 0,906 0,861
0,20 1,000 0,964* 0,910 0,862 0,819
0,25 0,976s 0,917 0,866 0,820 0,779
0,30 0,930 0,873 0,824 0,780 0,741
0,35 0,884 0,831 0,784 0,742 0,705
0,40 0,842 0,790 0,746 0,706 0,670
0,45 0,801 0,752 0,709 0,671 0,638
О', 50 0,762 0,716 0,675 0,639 0,606
0,55 0,726 0,681 0,642 0,608 0,577
0,60 0,691 0,648 0,611 0,578 0,549
0,65 0,658 0,616 0,581 0,550 0,522
0^70 0,626 0,587 0,553 0,523 0,497
0,75 0,596 0,558 0,526 0,497 0,472
0,80 0,567 0,531 0,500 0,473 0,450
0^85 0,540 0,506 0,476 0,450 0,427
0,90 0»514 0,481 0,453 0,428 0,407
0,95 0,490 0,458 0,431 0,407 0,387
LOO 0^67 0,436 0,410 0,388 0,368
1,05 0,444 0,415 0,390 0,369 0,350
1,10 0,423 0,395 0,371 0,351 0,333
1,15 0,402 0,376 0,353 0,334 0,317
1,20 0,383 0,358 0,336 0,317 0,301
1,25 0,365 0,340 0,320 0,302 0,286
1,30 0,348 0,324 0,304 0,287 0,272
1,35 0'331 0,308 0,289 0,273 0,259
1 40 0,316 0,293 0,275 0,260 0,247
1,45 0,300 0,279 0,262 0,247 0,235
1,50 0»286 0,266 0,249 0,235 0,223
59
Таблица 2.1.7
Нижние границы для Р(0 = 1—F(t), где F(t) есть „стареющее"
распределение с известным математическим ожиданием 7=1
и дисперсией а2
ЧТ а»/га
0,10 0,20 0,30 0.40 0,50
0,05 0,987 0,978 0,970 0,965 0,961
0,10 0,974 0,956 0,941 0,931 0,923
0,15 0,962 0,934 0,913 0,893 0,886
0,20 0,949 0,913 0,886 0,866 0,851
0,25 0,937 0,892 0,860 0,836 0,818
0,30 0,925 0,872 0,834 0,806 0,686
0,35 0,913 0,853 0,810 0,778 0,755
0,40 0,901 0,834 0,786 0,751 0,725
0,45 0,886 0,813 0,762 0,724 0,696
0,50 0,868 0,790 0,737 0,698 0,669
0,55 0,847 0,763 0,709 0,671 0,642
0,60 0,819 0,731 0,677 0,639 0,613
0,65 0,787 0,695 0,643 0,608 0,583
0,70 0,747 0,655 0,605 0,574 0,551
0,75 0,699 0,609 0,567 0,538 0,518
0,80 0,640 0,562 0,524 0,502 0,486
0,85 0,569 0,510 0,482 0,466 0,454
0,90 0,502 0,460 0,411 0,431 0,424
0,95 0,452 0,412 0,403 0,399 0,395
1,00 0,368 0,368 0,368 0,368 0,368
1.05 0,315 0,329 0,336 0,340 0,342
1,10 0,270 0,292 0,305 0,312 0,318
1,15 0,230 0,264 0,280 0,290 0,298
1,20 0* 0,236 0,256 0,268 0,277
1,25 0 0,211 0,233 0,248 0,258
1,30 0 0,188 0,213 0,229 0,241
1,35 0 0* 0,194 0,212 0,224
1,40 0 0 0,177 0,196 0,209
1,45 0 0 0,162 0,181 0,195
1,50 0 0 0,146 0,167 0,182
//7 а3/7 *
0.60 0.70 0,80 0,90 1,00
0,05 0,957 0,955 0,953 0,952 0,951
0,10 0,917 0,912 0,909 0,906 0,905
0,15 0,878 0,871 0,866 0,863 0,861
0,20 0,840 0,832 0,826 0,821 0,819
0,25 0,804 0,794 0,787 0,782 0,779
0,30 0,770 0,758 0,750 0,744 0,741
0,35 0,737 0.724 0,715 0,708 0,705
0,40 0,706 0,692 0,682 0,674 0,670
0,45 0,676 0,660 0,650 0,642 0,638
0,50 0,647 0,631 1,619 0,611 0,606
60
Продолжение табл 2.1.7
I/T а=/73
0,60 i 0,70 | 0.8« | С,90 1,00
0,55 0,619 0,602 0,590 0,582 0,577
0,60 0,592 0,575 0,563 0,554 0,549
0,65 0,564 0,548 0,536 0,527 0,522
0,70 0,534 0,521 0,511 0,502 0,497
0,75 0,505 0,494 0,485 0,478 0,472
0,80 0,475 0,466 0,460 0,454 0,449
0,85 0,446 0,440 0,435 0,431 0,427
0,90 0,419 0,415 0,411 0,409 0,407
0,95 0,392 0,390 0,389 0,388 0,387
1,00 0,368 0,368 0,368 0,368 0,368
1,05 0,345 0,347 0,348 0,349 0,350
1,10 0,324 0,326 0,329 0,331 0,333
1.15 0,303 0,308 0,311 0,314 0,317
1,20 0,284 0,290 0,294 0,298 0,301
1,25 0,266 0,273 0,278 0,283 0,286
1,30 0,250 0,257 0,263 0,268 0,272
1,35 0,234 0,242 0,249 0,254 0,259
1.40 0,220 0,228 0,235 0,241 0,247
1,45 0,206 0,215 0,222 0,229 0,235
1,50 0,193 0,202 0,210 0,217 0,223
Пример 2.1.5. Пусть элемент имеет «стареющее» распределение времени ра-
боты до отказа со средним Т = 100 ч. Требуется вычислить границы вероятно-
сти безотказной работы для /0 = 70 ч и /0 =• 130 ч.
Решение По табл. П8.1 экспоненциального распределения находим
нижнюю границу для tB •= 70 ч:
0,4966 = е-".’ < Р (70) < 1.
По табл. 2.1.4 находим верхнюю границу для /0 — 130 ч:
0 < Р (130) < 0,5770.
Пример 2.1.6. Пусть элемент имеет «стареющее» распределение времени ра-
боты до отказа со средним Т = 100 ч и дисперсией о2 = 1000 ч2. Требуется вычис-
лить границы вероятности безотказной работы для (0"= 70 ч и (0«= 130 ч.
Решение. По табл. 2.1.7 находим нижние границы, а по табл. 2.1.6 —
верхние границы для /= tJT. равного 0,7 и 1,3:
0,7470 < Р (0,7) < 0,9875*,
0 < Р (1,3) < 0,411.
Примечание. В примере 2.1.2 было известно, что распределение вре-
мени работы до отказа является нормальным, которое относится к классу «ста-
реющих». Напомним, что в упомянутом примере Р (0,7) = 0,829 и Р (1,3) »
= 0,171
* Значение получено линейной интерполяцией, так как в таблице есть зна-
чения 0,9950 для t = 0,69 и 0,9715 для t = 0,72.
61.
2.2. Восстанавливаемый элемент
2.2.0. Предварительные замечания. Процесс функционирования
восстанавливаемого элемента можно описать как последовательность
чередующихся интервалов работоспособности и простоя (рис. 2.2.1):
01, Il 02, |2> •••
В данном параграфе будет рассмотрен случай, когда все 0г имеют
одно и то же распределение F (t) = SP {0 t), а все — одно и то же
распределение FB (t) = З5 {£ i), причем все величины 0г и сг взаи-
монезависимы. (Такой случайный процесс называется альтерниру-
„Т Г~Ы~1 I нг\
V_____ у
Рис. 2.2.1. Случайный процесс, соответству-
ющий последовательности чередующихся интер-
валов работоспособности и простоя элемен-
та с восстановлением.
лТ
Hi
Рис. 2 2 2. Граф переходов эле-
мента с восстановлением из
одного состояния в другое. z
ющим процессом восстановления.) Этот же процесс функционирова-
ния восстанавливаемого элемента удобно описать (рис. 2.2.2) графом
переходов из состояния работоспособности Нй в состояние отказа Нг.
2.2.1. Произвольные распределения времени безотказной работы и
времени восстановления. В табл. 2.2.1 приведены основные показа-
тели надежности для произвольных законов распределения времени
безотказной работы F (/) и времени восстановления FB (t).
Примечание. Используемое иногда как точное выражение для коэф-
фициента оперативной готовности
R (ta) = КР (ta) (2.2 1)
является в общем случае неверным. Эта формула справедлива только для экспо-
ненциального распределения времени безотказной работы элемента, т. е. при
Р (t0) = e~w°.
Если известно, что распределение времени работы между отказа-
ми является «стареющим», то коэффициент оперативной готовности
R (<0) имеет следующие верхнюю и нижнюю границы:
(2.2.2)
62
Табли'ца 2.2.1
Восстанавливаемый элемент. Произвольный закон распределения
времени между отказами F (t) и произвольный закон
распределения времени восстановления F„ (t)
Показатель Точное значение Приближенное значение Погрешность
со со
Г $xf (х) dx — (х) =
0 0
ОС
= Гр (х) dx •
0
00 со
ч, jxfB (х) dx = JxdPB (х) =
0 0
ОС
= J[i — Рв(х)] dx
0
1-P(Q — —
Q(M F (to) — —
К T _ 1 I -Y. *+ <Ya
Г+т 1+y
т у Y < y2
Г+t 1+Y
00
К I' — F (x)] dx—
R U.) ^0 00 1 c См. примечание в тексте к форму-
лам (2.2.2) и
'J' | t I (X) »X (2.2 3)
to
Для случая /0« Гит « Т можно записать приближенное вы-
ражение
/?(/„)« 1—(2.2.3)
с погрешностью 8+ < 2,5 |\max^0> т),
Пример 2.2.1. Пусть F (t) распределение времени работы элементов до отка-
Ва задано в виде следующей таблицы:
tt 1 2 3 4 5 6 7 8 9
Г(/.) 0 0,086 0,172 0,314 0,543 0,743 0,914 0,971 1,00
83
Считаем, что время работы между отказами имеет такое же распределение.
Время восстановления является случайной величиной, принимающей значение
0,1 ч с вероятностью /Д == 0,6, значение 0,2 ч с вероятностью р2 = 0,3 и значе-
ние 1,5 ч с вероятностью р3 = 0,1. Требуется вычислить основные показатели
надежности элемента.
Решение. Поскольку Fit) элемента совпадает с элементом из примера
2.1.1, то можно из этого примера воспользоваться готовыми значениями; Р (4) =
= 0,686, Q (4) = 0,314, Р (2; 6) = 0,28, Q (2; 6) «= 0,72, Т = 4,357 ч « 4,36 ч.
Перейдем к вычислению показателей надежности характерных для восстанавли-
ваемых элементов.
1. Среднее время восстановления. В данном случае формула для т может _
быть записана в виде следующей суммы:
п
Т = 2) ^Pi
Г=1
или в условиях данного конкретного примера
Т = 51Р1 + £2Р2 + 1зРз = 0.1 • 0,6 + 0,2 • 0,3 + 0.15 • 0,1 = 0,27.
2. Коэффициент готовности
К = 4,36 : (4,36 + 0,27) = 0,942.
Приближенное значение
К - 1 — 0,27 : 4,36 = 0,938
3. Коэффициент простоя
k = 0,27 : (4,36 + 0,27) = 0,058.
Приближенное значение
'fe = 0,27 : 4,36 = 0,062.
4. Коэффициент оперативной готовности для = 2 ч.
Для случая заданного в примере дискретного распределения выражение
для коэффициента оперативной готовности имеет вид
1 "
R(t0) = K-^~ V P((i)(ti+l-tt),
1 = 3
т. е.
R (2) = 0,942 • (0,828 + 0,786 + 0,457 + 0,257 + 0,086 + 0,029) > 4,36 =
= 0,525.
Примечание. При использовании формулы (2 2.1) был бы получен
неверный результат, причем существенно отличающийся от истинного
R (2) = КР (2) = 0,942 • 0,914 « 0,861.
(Здесь взято значение Р (2) = 1— F (2) = 0,914 нз таблицы к условиям данного
примера.)
2.2.2. Экспоненциальные распределения F (/) и (/). В табл. 2.2.2
приведены основные показатели надежности элемента для экспонен-
циальных законов распределения времени безотказной работы F (/) =
= 1 — и времени восстановления FB (/) — 1 — e~ll/.
Приближенные значения Р (t0) и Q (t0) приведены для условия
Мо« 1, а для остальных показателей — для условия у = Х/р. « I.
Коэффициенты К (0 и k (t) соответствуют тому случаю, когда в мо-
мент времени t — 0 элемент находится в состоянии работоспособно-
сти, коэффициенты № (I) и k° (/) — случаю, когда в момент времени
t = 0 элемент находится в состоянии отказа. Формулы для коэффици-
ентов готовности и простоя поясняются на рис. 2.2.3 и 2.2.4.
64
Восстанавливаемый элемент. Экспоненциальный закон распределения времени
между отказами —ew и экспоненциальный закон распределения
времени восстановления Г, (0=1 — е—ц,г
3
Зак. 943
6S
Формула для нестационарного коэффициента оперативной готов-
ности для случая, когда в начальный момент времени элемент нахо-
дится в состоянии отказа, не приводится, так как практическое ев
использование весьма ограничено.
Пример 2.2.2. Пусть элемент имеет экспоненциальные законы распределе-
ния времени работы до отказа и времени восстановления с параметрами соответ-
ственно X =» 0,04 1/ч и ц = 2 1/ч. Требуется вычислить основные показатели.
Решение. 1. Вероятность безотказной работы для =• 2 я;
Р (2) = е—0,04-2 Q 0 923,
Приближенное значение
Р (2) = I — 0,04 • 2 = 0,92.
Рис. 2.2.3. Пояснение формул для Рис. 2 2.4. Пояснение формул для
коэффициента готовности. коэффициента простоя,
2. Вероятность отказа за время t0 =• 2 ч
Q (2) => 1 — 0,923 = 0,077.
Приближенное значение
Q (2) = 0,04 • 2 « 0,08.
3. Среднее время безотказной работы
7я 1 I 0,04 = 25 ч.
4. Среднее время восстановления
t •* 1 : 2 =• 0,5 ч.
5. Коэффициент готовности
К => 2 I (2 4- 0,04) = 0,9804
Приближенное значение
К - 1 — 0,04 I 2 = 0,98.
6. Коэффициент простоя
k = 0,04 1 (2 4- 0,04) = 0,0196,
Приближенное значение
k =• 0,04 : 2 = 0,02.
7. Нестационарный коэффициент готовности для t 2 ч для случая, когда
момент t = 0 элемент находится в состоянии работоспособности!
/C(2)=0,9804 4-0,0196-e_<2 + 0'04,,2 = 0,9808,
3*
67
66
Приближенное значение
/С(2)=1 —0,04 : 2(1 —е“ 2'2) = 0,9804.
8. Нестационарный коэффициент простоя для того же случая
k (2)=0,019б(1—е_(2+0-04>’2) = 0,0192.
Приближенное значение
'А(2) = (0,04 । 2) (1 — е“2,2) = 0,0196.
9. Коэффициент оперативной готовности для /0 = 2 ч:
R (2) = (2 > (2+0,04)) е“ °-04 ’2 = 0,9146.
Приближенное значение
R (2) = 1 — (0,5 + 2) I 2,5 = 0,9.
10. Нестационарный коэффициент оперативной готовности для интервала
времени от t = 1 ч до t + /0 = 3 ч:
R (1; 3)=(0,9804 + 0,0196е-<0’04 + 2)'1)е-°'04-2 = 0,906.
Приближенное значение
R (1 ; 3) = 1 —0,04.(2 + 1) = 0,88.
2.3. Специальные показатели для восстанавливаемого
элемента
2.3.1. Вероятность заданной суммарной наработки за фиксиро-
ванное календарное время. На практике часто отказы, возникающие
в системе (элементе), не приводят к полному отказу, а лишь вносят
определенную задержку в выполнение требуемой задачи. Эта за-
держка может объясняться как прямым простоем системы, связан-
ным с проведением восстановительных работ, так и с другими прояв-
лениями последствий отказов. (Например, кратковременный отказ
или сбой в ЭВМ может привести к необходимости повторения части
программы, что эквивалентно с точки зрения времени решения всей
задачи непроизводительному простою в течение этого времени.)
Математически эта задача может быть сформулирована следу-
ющим образом.
Имеется альтернирующий процесс восстановления, образован-
ный чередующимися последовательно случайными величинами вре-
мени безотказной работы и времени восстановления:
11> ®2> ^2> •••> ®п> £п» •••
Этот процесс рассматривается на интервале времени [0, Л. В этот
интервал может попасть некоторое случайное число k интервалов
безотказной работы, причем если в момент i система оказывается
в состоянии работоспособности, то рассматриваться будет не весь
последний интервал 0h, а лишь его часть O'h, принадлежащая интер-
валу [0, Л.
68
Требуется найти вероятность A (t0, t) того, что за фиксированное
время t суммарная наработка системы S (/) — 0t 4- 0» + ••• 4*
+ Ofe-i + 0\ достигнет заданной величины ta, т. е.
A (t9, t) - ff> {S (0 < м.
1. Произвольные распределения
Для произвольных распределений времени безотказной работы
и времени восстановления
F (0 = {0 < t}, FB (t) = З5 а < О
можно записать
эо
ЛСг'о, /)= 2 [F^(^-Q-F:(&+,)(^f0)]F^(Q.
k—0
где верхний индекс *п означает я-кратную свертку, т. е.
X
Z*n(x) = ^Z*(n~,>(x—y)dZ{y),
о
причем F*° (х) = F*| (х) =s 1.
По приведенной формуле значения A (t0, t) для относительно боль-
ших t вычисляются довольно громоздким путем. Однако в этом слу-
чае можно использовать следующую асимптотическую формулу1
А(/о, 0«Ф
где
/ MS (t) \
\ (О / '
Здесь Т — среднее время безотказной работы системы; оа — диспер-
сия распределения времени безотказной работы; т — среднее время
восстановления системы и о2в — дисперсия распределения времени
восстановления, а Ф (х) — функция нормального распределения,
численные значения которой приведены в табл. П8.3 Приложения.
2. Экспоненциальные распределения
В случае экспоненциальных распределений F (/) = 1 — e~w и
Fв (0=1 — е-^ принципиально формула для вычисления
A (ta, t) не упрощается, а лишь принимает конкретный вид
00 оо
А о = 2 l|,('~WI>- 2 —
fe=l ft! / = fe
Непосредственные вычисления по этой формуле также затруд-
нительны, поэтому в табл. 2.3.1 приведены численные значения
1—4 (/„,/) для наиболее важного с практической точки зрения диапа-
зона—значений t0/t, W и Vp.
69
о
Таблица 2.3.
Вероятность 1 — Л(Х/р., X/, ta't) того, что у элемента с интенсивностями отказов X и восстановления р на
интервале (О, XZ) суммарная наработка t0 будет меньше чем 0,81 (т. е. /о//=О,8)
If Х/р.
0,01 | 0,02 | 0.03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,1 | 0,2 0,3 0,4 0,5
0,1 0,843 0,603 0,460 0,370 0,309 0,265 0,232 0,206 0,186 0,169 0,088 0,060 0,045 0,036
0,2 0,969 0,821 0,682 0,576 0,496 0,435 0,386 0,348 0,316 0,289 0,157 0,107 0,082 0,066
0,3 0,993 0,912 0,800 0,699 0,616 0,549 0,494 0,449 0,411 0,378 0,211 0,146 0,112 0,090
0,4 0,998 0,955 0,869 0,779 0,698 0,630 0,572 0,523 0,482 0,446 0,254 0,177 0,136 0,110
0,5 — 0,976 0,911 0,833 0,757 0,690 0,631 0,581 0,537 0,499 0,289 0,202 0,155 0,126
0,6 — 0,987 0,939 0,871 0,801 0,736 0,678 0,626 0,581 0,542 0,317 0,223 0,172 0,139
0,7 — 0,993 0,957 0,900 0,835 0,773 0,715 0,664 0,618 0,577 0,341 0,240 0,185 0,150
0,8 — 0,996 0,970 0,921 0,862 0,803 0,746 0,695 0,648 0,606 0,360 0,254 0,195 0,159
0,9 — 0,998 0,978 0,937 0,884 0,828 0,773 0,721 0,674 0,632 0,377 0,265 0,204 0,166
1 — 0,999 0,984 0,950 0,902 0,849 0,795 0,744 0,697 0,654 0,391 0 275 0,211 0,171
1,5 — — 0,997 0,983 0,955 0,917 0,873 0,826 0,781 0,737 0,441 0,305 0,231 0,185
2 — 0,999 0,994 0,979 0,952 0,917 0,877 0,834 0,791 0,473 0,319 0,237 0,187
2,5 — — — 0,998 0,989 0,972 0,945 0,911 0,872 0,831 0,496 0,326 0,236 0,183
3 — — 0,999 0,995 0,983 0,963 0,934 0,900 0,862 0,514 0,330 0,233 0,176
4 0,999 0,994 0,982 0,964 0,937 0,905 0,543 0,332 0,224 0,162
5 ___ — —- 0,998 0,992 0,979 0,960 0,934 0,565 0,331 0,213 0,148
6 —- 0,999 0,996 0,988 0,974 0,953 0,583 0,329 0,202 0,135
7 — — 0,998 0,993 0,983 0,966 0,599 0,326 0,192 0,123
8 ___ . 0,999 0,996 0,989 0,975 0,614 0,323 0,182 0,112
9 . — 0,999 0,998 0,992 0,982 0,626 0,319 0,172 0,102
10 — — — — — — — 0,999 0,925 0,987 0,638 0,315 0,164 0,093
Продолжение табл. 2.3.1
^=0,85
х* Ын
0,01 1 0,02 0.03 | 0.04 0,05 0.06 0.07 0,08 0,09 °,1 [ 0,2 0.3 I 0,4 [ 0,5
о,1 0,749 0,498 0,368 0,292 0,241 0,205 0,179 0,158 0,142 0,129 0,067 0,045 0,034 0,027
0,2 0,924 0,721 0,572 0,471 0,398 0,345 0,304 0,272 0,246 0,224 0,119 0,081 0,061 0,049
0,3 0,974 0,833 0,694 0,587 0,506 0,444 0,395 0,356 0,323 0,296 0,160 0,110 0,084 0,067
0,4 0,991 0,896 0,773 0,668 0,584 0,517 0,463 0,419 0,383 0,352 0,194 0,133 0,102 0,082
0,5 0,997 0,933 0,827 0,727 0,643 0,573 0,516 0,469 0,429 0,396 0,220 0,152 0,116 0,094
0,6 0,999 0,955 0,866 0,772 0,688 0,618 0,559 0,509 0,467 0,431 0,242 0,167 0,128 0,103
0,7 — 0,970 0,895 0,807 0,725 0,654 0,594 0,542 0,498 0,461 0,259 0,179 0,137 0,111
0,8 — 0,980 0,915 0,835 0,756 0,685 0,623 0,570 0,525 0,485 0,273 0,189 0,144 0,117
0,9 — 0,986 0,933 0,858 0,781 0,711 0,648 0,594 0,547 0,507 0,285 0,197 0,150 0,121
1 — 0,991 0,946 0,878 0,803 0,733 0,671 0,615 0,567 0,525 0,295 0,203 0,155 0,125
1,5 — 0,999 0,981 0,938 0,879 0,815 0,752 0,694 0,641 0,594 0,326 0,219 0,164 0,131
2 — — 0,993 0,967 0,922 0,866 0,806 0,747 0,692 0,641 0,341 0,222 0,162 0,127
2,5 — — 0,997 0,982 0,949 0,901 0,845 0,787 0,731 0,677 0,349 0,219 0,156 0,119
3 — — 0,999 0,990 0,966 0,926 0,875 0,819 0,762 0,707 0,354 0,214 0,148 0,111
4 — — — 0,997 0,984 0,957 0,916 0,866 0,810 0,754 0,359 0,202 0,131 0,094
5 — — — 0,999 0,993 0,975 0,943 0,898 0,846 0,790 0,360 0,189 0,116 0,079
6 — — — * — 0,996 0,985 0,960 0,922 0,874 0,819 0,360 0,177 0,102 0,066
7 — — — — 0,998 0,991 0,972 0,940 0,896 0,843 0,359 0,165 0,090 0,056
8 — — — — 0,999 0,994 0,980 0,953 0,913 0,863 0,357 0,155 0,080 0,047
9 — — — — — 0,997 0,986 0,964 0,927 0,880 0,355 0,145 0,071 0,040
10 — — — — — 0,998 0,990 0,971 0,939 0,894 0,353 0,135 0,062 0,033
Продолжение табл. 2.3.1
«О
£,//=0,9
Х/р,
It 0.01 | 0,02 1 0,03 0.04 1 0,05 0.06 1 0.07 j 0.08 0.09 j ОЛ 0.2 j о.з 1 0,4 О, а
0,1 0,600 0,367 0,263 0,204 0,167 0,141 0,122 0,108 0,097 0,087 0,045 0,030 0,023 0,018
0,2 0,816 0,569 0,429 0,342 0,285 0,244 0,213 0,189 0,170 0,154 0,080 0,054 0,041 0,033
0,3 0,907 0,690 0,539 0,440 0,370 0,319 0,281 0,250 0,226 0,206 0,108 0,074 0,056 0,045
0,4 0,951 0,768 0,618 0,511 0,434 0,377 0,333 0,298 0,269 0,246 0,131 0,089 0,068 0,054
0,5 0,973 0,822 0,676 0,566 0,484 0,422 0,374 0,335 0,304 0,278 0,149 0,102 0,077 0,062
0,6 0,985 0,861 0,721 0,609 0,524 0,459 0,407 0,366 0,332 0,303 0,163 0,111 0,084 0,068
0,7 0,991 0,890 0,757 0,645 0,557 0,489 0,434 0,390 0,354 0,324 0,174 <0,119 0,090 0,073
0,8 0,995 0,912 0,786 0,674 0,585 0,514 (0,457 0,411 0,373 0,341 0,183 0,125 0,095 0,076
0,9 0,997 0,929 0,811 0,700 0,609 0,536 0,477 0,429 0,389 0,356 0,190 0,129 0,098 0,079
1 0,998 0,942 0,832 0,722 0,630 0,555 0,494 0,444 0,402 0,368 0,195 0,132 0,100 0,080
1,5 0,979 0,903 0,803 0,708 0,625 0,556 0,498 0,450 0,409 0,208 0,137 0,102 0,081
2 0,992 0,941 0,855 0,761 0,674 0,598 0,534 0,480 0,433 0,208 0,132 0,096 0,075
2,5 0,997 0,963 0,891 0,801 0,712 0,631 0,561 0,502 0,451 0,203 0,124 0,088 0,067
3 0,999 0,977 0,916 0,832 0,742 0,658 0,584 0,519 0,464 0,197 0,115 0,079 0,059
4 —— 0,991 0,950 0,878 0,790 0,701 0,619 0,547 0,484 0,182 0,097 0,062 0,044
5 0,996 0,969 0,909 0,826 0,735 0,648 0,568 0,499 0,168 0,082 0,049 0,033
6 0,998 0,981 0,932 0,854 0,763 0,672 0,587 0,511 0,155 0,069 0,039 0,025
7 0,999 0,988 0,948 0,877 0,787 0,692 0,602 0,521 0,142 0,058 0,030 0,019
8 0,992 0,960 0,895 0,807 0,711 0,616 0,530 0,131 0,049 0,024 0,014
9 0,995 0,969 0,911 0,825 0,727 0,629 0,538 0,121 0,041 0,019 0,010
10 — — —- 0,997 0,976 0,924 0,841 0,742 0,640 0,545 0,112 0,035 0,015 0,008
. . Продолжение табл 2.3.1
z/,//=0,95 К
лг 0,01 | 0,02 1 0,03 | 0,04 0,85 0,06 0.07 | 0,08 | 0,09 | 0,1 0,2 | о.з | 0,4 | 0,5
0,1 0,366 0,203 0,141 0,107 0,087 0,073 0,063 0,055 0,049 0,044 0,022 0,015 0,011 0,009
0,2 0,565 0,340 0,242 0,187 0,153 0,129 0,112 0,098 0,088 0,079 0,041 0.027 0,020 0,016
0,3 0,685 0,435 0,316 0,247 0,203 0,172 0,149 0,132 0,118 0,107 0,055 0,037 0,028 0,022
0,4 0,763 0,505 0,372 0,293 0,242 0,206 0,179 0,158 0,142 0,129 0,066 0,045 0,034 0,027
0,5 0,816 0,558 0,415 0,329 0,272 0,232 0,202 0,17.9 0,161 0,146 0,075 0,051 0,038 0,031
0,6 0,855 0,601 0,450 0,358 0,297 0,253 0,220 0,195 0,175 0,159 0,082 0,055 0,042 0,033
0,7 0,884 0,635 0,479 0,382 0,316 0,270 0,235 0,208 0,187 0,169 0,087 0,059 0,044 0,036
0,8 0,907 0,664 0,503 0,401 0,332 0,283 0,246 0,218 0,196 0,177 0,091 0,061 0,046 0,037
0,9 0,925 0,689 0,524 0,418 0,345 0,294 0,256 0,226 0,202 0,183 0,094 0,063 0,047 0,038
1 0,938 0,711 0,542 0,432 0,357 0,303 0,263 0,232 0,208 0,188 0,096 0,064 0,048 0,039
1,5 0,977 0,791 0,610 0,482 0,394 0,330 0,284 0,248 0,220 0,197 0,096 0,063 0,047 0,037
2 0,991 0,843 0,656 0,515 0,415 0,343 0,290 0,251 0,220 0,195 0,089 0,056 0,041 0,032
2,5 0,996 0,880 0,693 0,540 0,429 0,350 0,292 0,248 0,215 0,189 0,080 0,049 0,035 0,027
3 0,998 0,907 0,722 0,560 в,440 0,354 0,291 0,244 0,209 0,181 0,070 0,041 0,029 0,022
4 — 0,942 0,769 0,592 0,456 0,357 0,286 0,233 0,194 0,164 0,054 0,029 0,019 0,014
5 — 0,963 0,805 0,618 0,467 0,357 0,278 0,222 0,180 0,149 0,042 0,020 0,013 0,009
6 — 0,976 0,833 0,639 0,476 0,356 0,271 0,210 0,167 0,135 0,032 0,014 0,008 0,005
7 — 0,985 0,856 0,658 0,483 0,354 0,263 0,200 0,155 0,122 0,024 0,010 0,005 0,003
8 0,990 0,876 0,675 0,489 0,351 0,255 0,189 0,143 0,111 0,019 0,007 0,004 0,002
9 — 0,993 0,892 0,689 0,495 0,349 0,248 0,180 0,133 0,101 0,015 0,005 0,002 0,001
10 — 0,996 0,906 0,703 0,500 0,346 0,241 0,171 0,123 0,091 0,011 0,003 0,002 0,001
Продолжение табл. 2.3.7
Для относительно больших / в этом случае также целесообразно
использовать асимптотическую формулу
7о—
(О
74
где
Ms (/) ^
Л +ц
°S(/) ~
2Лц. ,
(Л 4- ц)3
Здесь Ф (х) — функция нормального распределения, численные зна-
чения которой приведены в табл. П8.3.
2.3.2. Вероятность наличия не менее чем заданного интервала
безотказной работы за фиксированную суммарную наработку. Во
многих случаях хотя отказ системы (элемента) и приводит к невыпол-
нению задачи за время t0, но при этом в течение некоторого отведен-
ного заранее фиксированного времени t возможно повторить решение
этой же задачи, начиная с момента этого отказа. Часто такой режим
работы называют временном резервированием.
В простейшем случае можно рассмотреть ситуацию, когда собст-
венно простои системы из-за отказов пренебрежимо малы, т. е. когда
рассматриваемый процесс является обычным процессом восстанов-
ления. На практике этому случаю соответствует, например, процесс
кратковременных самоустраняющихся отказов и сбоев в ЭВМ при
выполнении неквантованной программы.
Если в качестве начального состояния в момент времени t = 0 мы
имеем совершенно новую систему, то интересующий нас показатель
надежности запишется в виде
(6)1 0 — {6; 6> ИЛИ Q'k й? to
ь-1 k
3 ej,
г=1 (=1
где 6/ — часть 0h, принадлежащая интервалу [0, /].
1. Произвольное распределение
В случае произвольного распределения для В (t0, t) можно запи-
сать следующее интегральное уравнение:
^0
в* (to, t) = 11 —F (70)J 6(z) + J Д* (t—x) 6 (t—x) dF (x),
о
где F (x) — функция распределения случайной величины 0г, 6 (/)—
единичная функция
б(Д = /1’
[0, если t < /0.
Для произвольного распределения F (/) решение для В* (tn, f)
можно найти лишь численными методами.
Если t > t0 и F (t0) достаточно близко к единице, т. е. Р (to) <1,
то можно записать асимптотическую формулу вида
75
—-PW I 1 r
B*(/e,/)^l—e r* , где 7*=[F(/e)J J xdF(x),
T* — математическое ожидание усеченной случайной величины
0 (при 0<7о); при сделанных допущениях практически Т*жТ. (Зна-
чения функции е~~х даны в табл. П8.1.)
2. Экспоненциальное распределение
Для случая экспоненциального распределения времени безотказ-
ной работы F (0 = 1 — е-1-! для записанного ранее интегрального
уравнения может быть получено решение в виде ряда
о° . и fe4-1
в* (/о, ^=е-/
k = 0 ' / = 0 '
(fe+i)4> V
t )+
где оператор (х)+ означает
, . (х, если х> О,
(х).={
(О, если х С 0.
Вычисление В* (t0, 7) в виде указанного ряда также может вызвать
определенные затруднения вычислительного характера, поэтому чис-
ленные значения функции В* ((й, t) для важного в практическом отно-
шении диапазона значений параметров приведены в табл. 2.3.2.
Таблица 2.3.2
Значения t) для приведенного времени М
xt
hit 0.1 0,2 0,3 0,4 0.5 o.e 0,7 0,8 0.9
0,1 I 1 I 1 1 1 1 1 1
0.2 1 1 1 1 0,9’88 0,9’70 0,9’32 0,9’87 0,9’75
0,3 0,9586 0,9*88 0,9’57 0,9’89 0,9’79 0,9’62 0,9’38 0,9’05 0,9’86
0.4 0,9’79 0,9’12 0,9’80 0,9’62 0,9’40 0,9’11 0,988 0,984 0,979
0,5 0,9’88 0,9’53 0,9’00 0,982 0,974 0,963 0,951 0,938 0,925
0,6 0,979 0,958 0,936 0,912 0,889 0,865 0,841 0,817 0,793
0,7 0,960 0,922 0,884 0,846 0,810 0,775 0,741 0,708 0,676
0,8 0,942 0,886 0,834 0,784 0,737 0,693 0,651 0,612 0,574
0,9 0,923 0,852 0,786 0,726 0,670 0,618 0,570 0,526 0,485
XI
1 2 3 4 5 8 8 9 10
0,05 1 1 1 1 1 1 1 1 1 1
0,10 1 1 1 1 1 0,9’45 0,9’73 0,9*89 0,9*67 0,9*09
0,15 1 0,9’28 0,9*87 0,9*05 0,9’58 0,9’87 0,9’66 0,9’27 0,986 0,976
0,20 0,9’56 0,9’84 0,9’87 0,9’50 0,987, 0,971 0,947 0,914 0,873 0,824
0,25 0,9’81 0,9’70 0,987 0,963 0,925 0,873 0,808 0,736 0,660 0,583
0,30 0,9’81 0,983 0,946 0,886 0,807 0,716 0,622 0,531 0,445 0,369
0,35 0,9’14 0,950 0,873 0,771 0,659 0,549 0,447 0,357 0,282 0,220
0,40 0,974 0,892 0,773 0,641 0,514 0,402 0,307 0,231 0,172 0,127
0,45 0,946 0,817 0,664 0,516 0,388 0,285 0,206 0,147 0,103 0,072
0,50 0,910 0,736 0,558 0,406 0,287 0,199 0,136 0,092 0,061 0,040
П
Если t tn и величина ?Л0 достаточно велика, то можно записать
асимптотическую формулу вида
В* (/0, t)& 1 _
Численные значения функции е~Л приведены в табл. П8.1.
2.3.3. Вероятность наличия не менее чем заданного интервала
безотказной работы за фиксированное календарное время. Этот по-
казатель является синтезированным из двух предыдущих специаль-
ных показателей A (t0, t) и В (t0, t).
Выражение для вероятности наличия не менее чем заданного ин-
тервала безотказной работы за фиксированное календарное время
t имеет в общем случае вид
В(/о, O = y)d{\—A(y, /)].
ъ
Для нахождения В (/0, t) могут быть использованы лишь числен-
ные методы.
Для практических целей интегрирование может быть заменен©
суммированием:
B(t0,t)& 2 В* к 0-А(ум, 01-
.<yn=t \ 2 )
В случае если / i0 и при этом Р (t0) 1, то можно исполь-
зовать следующую асимптотическую формулу
— - Р О0)
Д(/0,/)^1-е г’+т
где Т* и т — математическое ожидание усеченной случайной ве-
личины 0 и среднее время восстановления (практически Т*л$Т).
Численные значения функции е~х приведены в табл. П8.1.
2.3.4. Вероятность отсутствия интервала простоя, большего до-
пустимой величины, за фиксированное суммарное время простоя. Рас-
смотрим последовательность интервалов простоя системы (элемента):
и...
Нахождение вероятности Ь* (т0, /) отсутствия интервала простоя
Вг, большего допустимой величины т0, за фиксированное суммарное
время простоя t является задачей (с точностью до обозначений), экви-
валентной нахождению вероятности наличия хотя бы одного интер-
вала безотказной работы, большего заданной величины.
Обозначим через Ь* (т0, t) вероятность того, что за суммарное
время простоя t появится хотя бы один интервал простоя ё;, больший т0.
Величина Ь* (т0, t) определяется так же, как и величина В* {t0, t)
заменой обозначений i0 на т0 и функции распределения времени бе-
зотказной работы F (0 на функцию распределения времени восста-
новления FB (f). Искомая вероятность равна
Ь* (т0, I) - 1 -£*~(т0, /) = 1-Д(т0П.
77
1. Произвольное распределение
Для произвольного распределения FB (f) решение для Ь* (т0, 0
можно найти лишь численными методами.
Если t т0 и Ев (т0) достаточно близко к единице, то можно
записать асимптотическую формулу вида
. [*-fb <*•>]
6*(Ъ.0«е
где т* — математическое ожидание усеченной случайной величины
§ (при £<т0); при сделанных допущениях практически т*»т.
Численные значения функции е~Л приведены в табл. П8.1.
2. Экспоненциальное распределение
Пусть распределение времени восстановления является экспо-
ненциальным: FB (0 = 1 — e-v1.
В этом случае с учетом отмеченного выше можно воспользоваться
численной табл. 2.3.2, где приведены значения функции В* (т0, 0 =
= 1 — Ь* (т0, 0 для важного в практическом отношении диапазона
значений параметров.
Если t > т0 и величина цт0 достаточно велика, то можно запи-
сать асимптотическую формулу вида
6*(т0, 0« 1 — e-Ще-м. s
Численные значения функции е~х приведены в табл. П8.1.
2.3.5. Вероятность отсутствия интервала простоя, большего до-
пустимой величины, за фиксированное календарное время. Рассмот-
рим процесс функционирования системы (элемента), описываемый
альтернирующим процессом восстановления, который представля-
ет собой чередующуюся последовательность интервалов безотказной
работы и интервалов восстановления:
®1> £1> ^2, •••> Qfe, •••
Нас интересует вероятность b (т0, 0 того, что за время I в рассмат-
риваемом процессе ни разу не появится случайная величина |г, боль-
шая допустимого значения т0. Подобный показатель надежности ока-
зывается полезным при оценке качества функционирования систем,
обладающих своеобразной «временной инерционностью». Такие си-
стемы могут быть достаточно нечувствительными к кратковремен-
ным перерывам в работе.
Для практических целей имеет смысл рассматривать лишь случай,
когда среднее время безотказной работы существенно больше средне-
го времени восстановления, т. е. Т > т. В этом случае для оценки
искомой вероятности b (т0, 0 с успехо.м может быть использована асим-
птотическая формула
-----Н-Р (Т„)1
&(то,0~е г+г*1
Численные значения функции е~х приведены в табл. П8.1.
78
Список литературы
1. Акулиничев Н. М., Козлов Б. А. Об асимптотическом распре-
делении суммарного времени работы резервированной системы — «Надеж-
ность н контроль качества», 1970, № 7.
2. Коваленко И. Н. Некоторые вопросы теории надежности сложных
систем. — В кнл Кибернетику — на службу коммунизму. Под ред.
А. И. Берга, Н. Р. Бруевича, Б. В. Гнеденко. Т. II, М., «Энергия», 1964.
3. Колегаев Р. Н. О показателях для оценки надежности машин. —
«Стандарты и качество», 1968, № 2.
4. С о л о в ь е в А. Д. Математическое обоснование теории надежности.
«Радиоэлектронная промышленность», 1958, № 4.
5. У л и н и ч Р. Б. К вопросу о методе выбора критериев надежности. —
«Стандарты и качество», 1966, № 1.
6. Ч е р к а с о в Р. Н. Оценка надежности систем е временной избыточно-
стью. — В кн.: Основные вопросы теории и практики надежности. М., «Сов,
радио», 1971.
3
РЕЗЕРВИРОВАНИЕ НЕВОССТАНАВЛИВАЕМЫХ
СИСТЕМ
3.0. Предварительные замечания
В данной главе оцениваются основные показатели надежности
таких резервированных систем, которые либо действительно явля-
ются невосстанавливаемыми как, например, системы однократного
действия, либо таких восстанавливаемых систем, восстановление
которых по каким-либо причинам невозможно непосредственно в
рассматриваемый период. Предполагается, что все элементы, состав-
ляющие резервированную систему, отказывают независимо друг от
друга.
3.1. Произвольный закон распределения времени работы
до отказа
В данном параграфе предполагается что время переключения
резервного элемента на место отказавшего рабочего мало и им можно
пренебречь, а сам переключатель считается практически абсолютно
надежным. Кроме того, делается еще допущение о том, что индикация
отказов отдельных элементов в системе является мгновенной.
Именно для этой модели резервированных систем приводятся
основные характеристики надежности.
3.1.1. Резервирование одного элемента п резервными элементами
(рис. 3.1.1), работающими в нагруженном режиме.
1. Вероятность безотказной работы системы в случае независимо-
го функционирования всех п+1 ее элементов определяется по фор-
муле
Р(и=1- п'п-МШ (3.1-1)
«=1
где (/0) — вероятность безотказной работы Z-го элемента.
2. Средняя наработка до отказа системы находится по формуле
T = ^P(t)dt, (3.1.2)
о
где Р (0 определяется из (3.1.1).
В случае экспоненциального закона
ri(ta) = e-Ki\ l^i^n+1, (3.1.3)
so
для вероятности безотказной работы Р (fa) системы справедлива еле»
дующая оценка Р (/0) снизу:
_ п+1
п (3-1.4)
(=1
Ошибка 6 (Zo) в формуле (3.1.4) не превосходит величины
/*4-2 *4-1 *4-1
. P(/o)-P(/o) = S(/o)<-^- (3.1.5)
i=i i=i
Средняя наработка до отказа в этом случае определяется по формуле
п+1 a—/n—(i—t)
т-2 2 2-
1 = 1 t^ll^'+l I.
п+1 1
^1 + 1Ч+Ч+”'+Ч
/о = О. (3.1.6)
Рис. 3.1 1. Структурная схема систе-
мы из одного рабочего и п резерв-
ных элементов.
При экспоненциальном законе и равнонадежных элементах (см.
также § 3.2)
G(^o) = r(4) = e-W% (3.1.7)
для вероятности безотказной работы Р (tQ) системы справедлива
следующая оценка Р (Q снизу:
?(^)=1-(Ч)п + ‘- (3-1.8)
Ошибка 6 (/0) в формуле (3.1.8) не превосходит величины
6(/o)<-^(4)ft+2- (3-1.9)
Средняя наработка до отказа определяется по формуле
Если п + 1 велико, то среднюю наработку до отказа можно вычислить
приближенно по формуле
7 = A[0l58 + ta(«+1) + 5^]. (3.1.11)
81
В случае закона Гнеденко—Вейбулла и равнонадежных элементов
(3.1.12)
1 + 1,
средняя наработка до отказа системы определяется формулой
С'п +1 i~1 /“ « Р^+-21]1 /а. (3.1.13)
L
В случае степенного закона и равнонадежных элементов
i п 4-1, р > 1
(3.1.14)
Рис, 3.1 2. Структурная схема
системы из k рабочих и п ре-
зервных элементов.
средняя наработка до отказа системы определяется формулой
Если система состоит из равнонадежных «стареющих» элементов
с функцией г (t) выпуклой вниз, т. е. когда
0<г"(/)<г'2 (ОШ
(3.1.16)
для средней наработки Т до отказа системы справедлива следующая
(грубая) оценка:
0,56
л 4-2
п+2
(3.1.17)
Неравенство (3.1.17) показывает, что оценку снизу для средней
наработки до отказа системы можно получить из приближенной
формулы
r(t0 = Т)
п+2
(3.1.18)
Приближенные значения для Т в формулах (3.1.13) и (3.1.15)
получены из (3.1.18).
В системе из k рабочих и п резервных элементов (рис. 3.1.2) отказ
резервной системы наступает в тот момент, когда происходит п 4- 1-й
отказ.
82
Для определения вероятности безотказной работы этой системы
в случае, когда все элементы различны, удобно рассмотреть произво-
дящий многочлен вида
я(х) = (rx х + <7i) (г2 х + <72)... (гк *4-7w) = Вы xN
4- Дл-i xN~x + • •• 4-В(хг4-• 4-Вох°,
где
r( = G qi = ql(t0)=1 — r(t0);
N = k 4- n — общее число элементов в системе.
Очевидно, коэффициент = Вг (/) при х{ есть вероятность того,
что к моменту времени / из W элементов останутся неотказавшими
ровно i элементов. Тогда:
1. Вероятность безотказной работы системы определяется по фор-
муле
Р(/о)= (3.1.19)
i=k
Если все элементы равнонадежны, то
W , я
/>(/»)= 2 c*kU)]'li-r(/o)Jv-'-' (3.1.20)
t=k
2. Средняя наработка до отказа системы определяется по формуле
T=^P(()dt, (3.1.21)
о
где Р (t) задается формулами (3.1.19) и (3.1.20) для соответствующих
случаев.
Например, для системы из двух рабочих и двух резервных элемен-
тов, работающих в нагруженном режиме, вероятность безотказной
работы определяется формулой
р (/о) = i Bt (t0) = в2 (Zo) + (/о) + Оо) =*
1 = 2
= (ri г2 <7з Qi + rir3 Qi Qi + ri ri Qi Qs + r2 rs Qi Qi + ri Qi Qs + rs rt qt q2) 4-
4- (fl r2 r3 qi 4- r2 rt q3 4- r3 rt д2 + г2г3Г1 qj 4- r2 r3 rt.
Специально рассмотрим случай резервированной системы с нагру-
женным режимом работы элементов, в которых могут происходить
отказы двух типов: «короткое замыкание» и «обрыв». Для исключения
влияния на систему отказа элемента типа «короткое замыкание»
элементы должны быть соединены последовательно, а для отказа типа
«обрыв» — параллельно. Для того чтобы одновременно исключить
влияние обоих типов отказов, необходимо применить параллельно-
последовательное соединение элементов (рис. 3.1.3).
83
Пусть в каждой последовательной цепочке — k элементов, а та-
ких цепочек п + 1 штук. Предположим, что короткие замыкания и
обрывы не изменяют надежности тех элементов, которые про-
должают работать, и что, если произошло короткое замыкание в дан-
ном элементе, то обрыва в нем произойти уже не может, и наоборот.
Тогда вероятность безотказной работы рассматриваемой системы
определяется по формуле
Р (/о) = [1—^3 (/0)Р+1 - (1 - [1 - ^06 (/о)Пп+ *, (3-1-22)
где ркз (/0) — вероятность отказа элемента по причине короткого за-
мыкания; <уоб (/0) — вероятность отказа элемента по причине обрыва.
Рис. 3.1 3. Структурная схема си-
стемы с параллельно-последова-
тельным соединением элементов.
Средняя наработка до отказа находится по формуле
T = ^P(t)dt,
о
(3.1.23)
где Р (t) определяется из (3.1.22).
Для того чтобы применение параллельно-последовательного со-
единения было оправдано в смысле надежности, очевидно, необходимо
выполнение условия
1FUO, k,n+l) =
P(ta, k, л + D
P (te, k = l, n-H = 1)
> 1
или, используя (3.1.22),
M ОЧГ ’ >0 -<70б) + [ 1 -(1 ~qo5}k]n+1 - (3.1.24)
3.1.2. Резервирование одного элемента п резервными элементами,
работающими в облегченном режиме. При облегченном режиме работы
резервных элементов каждый резервный элемент включается в тот
момент, когда откажет последний из предыдущих элементов (последний
по времени, а не по номеру).
1. Вероятность отказа системы определяется следующим рекур-
рентным соотношением:
(/о) = $ 11 1 (9) 4РЛ (9, /о)] dQn (9),
о «
Q(1)U) =!-/?> (0,10)^1-г<₽Ц10), (3.1.25)
84
где r«+i (9) — вероятность безотказной работы п 4- 1-го элемента
в облегченном режиме; (9, /0) — условная вероятность того,
что п 4- 1-й элемент не откажет, находясь в рабочем состояний на
участке времени (9, t0) при условии, что он не отказал на участке
(9, 9), находясь в облегченном режиме (9 — момент перехода элемен-
та в рабочее состояние); Qn (9) — вероятность отказа системы, состоя-
щей из одного основного и п — 1 резервных элементов, находящихся
в облегченном режиме.
2. Средняя наработка T(„+i) до отказа системы находится по
формуле
<30
^(п+1) —/Q(n+l)(O At,
о
(3.1.26)
где Q(n+i) (0 определяется из (3.1.25).
Рассмотрим частный случай описанной системы, когда вероятность
безотказной работы элементов в рабочем и в нерабочем состоянии под-
чиняется экспоненциальным законам (и, следовательно, вероятность
безотказной работы элемента в рабочем состоянии не зависит от вре-
мени пребывания его в нерабочем состоянии). Пусть при этом, —
интенсивность отказа й-го элемента в рабочем состоянии, a — ин-
тенсивность отказа й-го элемента в нерабочем состоянии. Для ко-
эффициента нагрузки vk, естественно, предположить, что
Vi = 1, 9<vft<l, 2<fe<n+l.
Таким образом, в нашем случае
4°) (9) = e~Vft 9;
4₽) (9, /0) = е“к* (<0“9).
Используя (3.1.25) и (3.1.26),
ДЛЯ Р(2) (t0) = 1 — Q(2)(U И ^(2)
например, при п + 1 = 2, можно
получить следующие выражения:
Л2)(и = е-Х‘/’ 4
е-Л, t, [ J__(1 -v,)] t, I
A.1—A-2 (1 — V2)
'P 1 1 A.i
^2(M4*v2 • ^2)
(3.1.27)
При малых интенсивностях отказов для вероятности безотказной
работы системы справедлива следующая приближенная формула:
~ /п+1 п+*
Лп+1)(6>)=1~-rVrr П XH14-(i-l)v.l. (3.1.28)
(«4-1)1 Z = 1
В отличие от нагруженного и йена гр уженного режима работы
резервных элементов, при облегченном режиме существует оптималь-
ный порядок подключения резервных элементов, а именно из (3.1.28)
следует, что вероятность безотказной работы системы будет наиболь-
85
1у£Й в том случае, если элементы подключаются в следующей последо-
вательности:
v2>v3> ... > vn+1, (3.1.29)
т. е. раньше нужно использовать те элементы, для которых коэффи-
циент нагруженности больше.
Пример 3.1.1. Рассмотрим дублированную систему идентичных элементов о
интенсивностью отказов каждого элемента Хр в рабочем состоянии и Ххр в нера-
бочем состоянии (при хранении), при этом Хр>Ххр.
Рис. 3 1.4. Режим (/у, Zjp).
Система на объекте за промежуток времени 10 должна непрерывно находить-
ся в течение времени /р в рабочем состоянии и в течение времени /хр (также
непрерывно) в нерабочем (храниться), при этом, естественно,
*o = fP+/xp = 6tp-HP-
Для нормального функционирования системы безразлично, будет ли она в тече-
ние времени t0 сначала работать, а потом храниться, или наоборот. Требуетси из
двух возможных режимов функционирования системы {(<р, ^хр), (£хр, (!р)1 вы-
брать, в смысле надежности, наилучший, т. е. такой, который бы обеспечил
через время 10 наибольшую вероятность готовности системы к возобновлению
функционирования.
Решение. В этой задаче применить непосредственно соотношение (3.1.29)
не удается и поэтому ее решение, вообще говоря, неочевидно.
В соответствии*с рис. 3.1.4, 3.1.5 для искомой вероятности, безотказной
работы системы имеем,
для режима (tp, /хр)
/’(^р + ^хР)=е-(ХР 'р+ХхР (р> [1 - (1 -е"1х” 'хрГ] +
/р
+/ (Хр4-Ххр)е-<ЛР + ЛхР^е-ХР('Р Ъе->1₽'ХР..
О
86
= е“(лР 'р + ^хр (р ) 'хр)а] | Д-р+^хр х
Ххр
Хе'^'Ре"^ '₽);
для режима (/хр, <р)
Р('хр+/р) = е“2Чр '’‘Р [e-Kp‘P+fPlpe“^P+4P)' e~xP ('₽—'> rf/l-f.
о J
* хр
+ J 2Лкре- хР ' е-?’х₽ ('xP-')d/e“?‘P'р =
о
—। -растает
злемеит ^-^рл-хрммся
ив -втлЫл
Рис. 3.1.5. Режим (Gp> /Р).
Теперь, составляя разность
получаем
₽ = /’(^p+/xp)-P(«xp + fp).
д^Лр—^хр с-хр
Кхр
Р е — Ххр <хр G_e~’''Хр *р) G _е—*хр *хр'
Поскольку Лр>Лхр, то Р>0 при (/р=£0=£/хр).
Таким образом, если в процессе функционирования системе предстоит
храниться и работать, то, в смысле надежности, лучше сначала работать,
а потом храниться, а не наоборот.
3.1.3, Резервирование одного элемента п резервными элемента-
ми, находящимися в ненагруженном режиме.
87
1. Вероятность Qn+i (Q отказа системы определяется следующим
рекуррентным соотношением:
to
Q(n+i) (А>)= § <7п+1(А> (6);
о
Q(i) (6>)= (А>)> (3.1.30)
где q(rt+i) (0) — вероятность отказа (п + 1)-го элемента;
Qn (0) — вероятность отказа системы, состоящей из одного основ-
ного и (п — I) резервных элементов, находящихся в ненагруженном
режиме-
2. Средняя наработка /’(п+о до отказа системы определяется по
формуле
п+ 1
7’(п+1)= 2 (зл.зо
i=l
где Tt — средняя наработка до отказа z-ro элемента.
В отличие от средней наработки Т’(П+1) до отказа системы, ко-
торая определяется едеяъ просто, вероятность отказа системйл
Ф(л-М) (^о) в большинстве случаев в конечном виде не вычисляется.
Поэтому известный интерес приобретают различные приближенные
формулы и оценки, которые представлены в табл. 3.1.1.
В случае экспоненциального закона
<?г(/о)=1—+ (3.1.32)
средняя наработка до отказа определяется формулой
п+1 .
r<n+D=2v’ (3J-33)
Точные и приближенные значения для вероятности отказа системы
приведены в табл. 3.1.2.
В случае нормального закона
(x-о/)'
оо — *----
1-<Ш) =------7=-fe 20/2 + (3.1.34)
Oi у 2л J
to
вероятность отказа рассматриваемой системы при
о>/й| « 1, 1 < i < п + 1, (3.1.35)
определяется следующей приближенной формулой:
, / п+1 \ 2 Рв - »- s °1 ) 1 е / п+ • 9 / 2.0' ' dx. (3.1.36)
88
Таблица 3.1.1
Оценки для вероятности отказа
системы из одного рабочего и п
резервных элементов.
Ненагруженный резерв
S1 + S1+.. +Sn+1=s
Г (х) — (полная) гамма-функция
№ п/п £,+> ('»> <?я + 1 (М Условия, наложенные В8 вероятности (/0) отказов и интенсивности отказов (/о) элементов, состав- ляющих систему
1 /И + 1 П + 1 с^угП Ъ 7=1 /п +1 п + 1 (^тгП 7=1 t (4) 1 1 п + 1
п+1 00 Zn+S + 1 П ЪЗ < (п+а+1), /=| 5=0 п + 1 00 /n + s+l П ( l) Л«(П+5 + 1)1 /=1 5=0 2г ('°)
е — 7=1 1^1<л +1
п + 1 2% 4"’ "Й , П 2sr(“i+1> /=i п +1 Е-< '=' п + 1 _ <0 f] Xjr(«i + 1) 7=1
3 / п + 1 \ г (1 + S “* \ 1=1 ) / п+1 \ г( I + S “г \ *=1 / 1 £= 1 п + 1
— п + 1 S “< п + 1 4=* 7=1 (п + 1)1
*- й^г п'ь»« /=1 0 (Л>)>0. t0>0; ls;i!gn + I
— п Г to -|« 1 -3 4г Нх <9) di х i=0 Lo J to _f > (Ю<7в X е Х< (!„)==> (Q. 1' (U>0. 'е>0. IsSisgn + 1
89
Вероятность отказа системы из одного рабочего и п
резервных элементов. Ненагруженный резерв.
Экспоненциальный закон
Точное значение Приближенное значение
п+1 п +1 _д ? /=1 *=• A, fl (Xt—Л4) 1=1 1^1 Я+1 £ пх# 2j а> («+«+!)( j=l s=o ‘ "+1 2L jn+s+i П Xj Zj (~1) A* (« + s+ 1)! /=1 s=0
sri+l *0 tt («4-1)1 LJ /=i
n+l _JS+' (n 4- 1)! П X'e 1=1
Ф i
/ n + l
90
Таблица 3.1.2
«(/.) = Q(/,)-1 [3(Л.)-<Ж)];
4= 3 W- Л«№-
si+s2+...4-sn+ t=s
Условие приближения
Погрешность
Xt/0 — в среднем малы,
rt + l
S < л+ 2 Л‘
1=1
«+1
пХ ”(п + 1)а У} (Xizo)2=°.
i-0
At^0 — конечны, 1 < i п + 1;
п — велико
л+1
8<м-2Ипр£ (W
1=1
9!
Если вероятности отказов всех элементов равны
„ it X — nlt .
— ?vo)— г, . >
1 Vх/
(3.1.37)
1
где
м,
у(«, %/«) = 5г“-1 e~zdz — неполная гамма-функция, тогда вероят-
о
ность отказа рассматриваемой системы определяется формулой:
Q(n+i> (Q = Y [(п + 1) а, Ц.1/Г [(и + 1) а]. (3.1.38)
Наконец, отметим, что почти во всех случаях величина
1 п+1
-П
рг+1)! /=1
(3.1.39)
либо является хорошим приближением для вероятности отказа системы
Q(n+t> (^о)> либо дает для нее оценку сверху.
3.2. Экспоненциальный закон распределения времени
работы до отказа: «схема гибели»
Частным случаем, широко распространенным в инженерных при-
ложениях, резервированной системы с распределением времени рабо-
ты отдельных элементов, подчиняющимся экспоненциальному закону,
является система, поведение которой во времени описывается так на-
зываемой «схемой гибели». В этой «схеме» в теории надежности обычно
рассматривается система, состоящая из k рабочих и п резервных
элементов. Все N = k 4- п элементов могут отказывать, при этом воз-
никающий поток отказов подчиняется следующим условиям:
1. Если к моменту времени t произошел/-Й отказ, то независимо от
момента возникновения всех предыдущих отказов вероятность того,
что на бесконечно малом участке (/, t 4- Д/) произойдет один отказ,
равна Л,Д< 4* о (А/), а вероятность того, что на этом участке не прои-
зойдет отказа, равна 1 — Л;А/ 4- о (А/).
2. После того, как происходит п 4- 1-й отказ, невосстанавливае-
мая система попадает в состояние отказа и никаких изменений в си-
стеме в дальнейшем не происходит, а поэтому A„_|_i = 0.
Если к моменту t произошел /-й отказ, то предполагается, что си-
стема переходит в состояние Hj. Другими словами, система может по-
пасть в конечное число состояний, соответствующих числу отказав-
ших элементов Но, Нъ .... H!t ..., Нп, Нп-\-\, причем последнее
состояние Hn+i, по условию 2, является состоянием отказа («по-
глощающим»), Состояние Нj есть такое состояние системы, в котором
у нее есть / отказавших элементов.
92
Граф переходов рассматриваемой системы представлен на рис. 3.2.1,
в соответствии с которым получаем систему дифференциальных урав-
нений следующего вида:
р/(О = Л7_1р7_1(/)-ЛурД/),
(3.2.1)
+ 1, л_х = лп+1 = о.
Здесь р} (/) есть вероятность того, что система в момент времени t
находится в состоянии Н}. Пусть эти вероятности удовлетворяют
начальным условиям вида:
Ро (0) = 1; Pi (0) = 0;
(3.2.2)
1 j п + 1,
т. е. система в момент времени t является полностью исправной.
• -Ло Л, Aj-i Л/ Ajt-f А»
" а Hi ‘ ‘‘ Нп
Рис. 3.2.1. Граф переходов из одного состояния в другое системы из k рабочих
и п резервных элементов.
Соответствующие выражения для вероятности безотказной работы
системы Р (t0) представлены в табл. 3.2.1
Средняя наработка Т до отказа системы определяется формулой
Т=2Н/А(. (3.2.3)
1=0
Приведем еще одно, удобное особенно в случае машинного счета,
представление для вероятности безотказной работы системы:
п 14 \ ._ е_л»' е~Л1/ • е—Anz Ло Aj • Лп Ag Л? • Л* AS Л? . Л;' /3 о дх
* Оьэ О > . > > - н* • • • • • > • > > “ за дм»
Если рассматриваемая система состоит из идентичных элементов,
то в случае нагруженного, облегченного и ненагруженного режимов
работы резервных элементов имеем:
93
Вероятность безотказной работы системы, поведение
которой во времени описывается <схемой гибели»
Точно® значение Приближенное значение
" д. -А/. па-Ё—— /=° ,=0 Л4 П (Л, — At) 1=0 п 21 ^n+s+1 1 - П Л* ’) л* (И + s + 1)! 1=0 s=0
tn + i п 1 (п + 1)! П Aj
/п+1 " А‘ , 'О Па + 1=0 1 (л + 1)! П Л,е /=Э
1 -Ф ———’— 'Mi •*? •—
84
Таблица В .2.1
.... P(t,)-P(tB)-.
о (/о) =---—--------> t
P(t0)
А,= 2 AjX...A„4 st>0
s0+s, + .. +sn=s
Условие приближения Погрешность
Л4/о — в среднем малы, —
0 -С i < п /П+2 « n 8 (fo) (n -f- 2) 1 П Лу Л< /=0 >=0
£<ЛЛ>‘-0. i=0 At/0—конечны, п — велико 8(/o) («4-1)1 2(n + I)8 * хПл,{ ft=° , /=0
п Sxr Ilm ( п П"4'00 1 V 1 | \Jua* 1 x 1=0 ' i=0 <* CO. )/Sj n — велико —
95
нагруженный
Ay = kk + (re — /) A, — (N — j) к, 0 n,
где A. — интенсивность отказов одного элемента; W = fe + re;
облегченный
Л; = kk + (re — /) vk, 0 < / < re,
где vk — интенсивность отказов одного резервного элемента;
О < V < 1, v — коэффициент нагруженности резерва; ненагруженный
Лу = kk, < re.
В табл. 3.2.2 даются точные значения показателей надежности
системы с п резервными элементами; в табл. 3.2.3 приведены прибли-
женные значения вероятности безотказной работы системы из одного
рабочего и п резервных элементов, находящихся в различных режи-
мах.
Пример 3.2.1. Пусть имеется система, состоящая из k =• 2 рабочих и п == 2
резервных элементов, из которых первый элемент находится в нагруженном, а
второй в ненагруженном режиме. После отказа любого из трех работающих эле-
ментов (двух рабочих и одного нагруженного резервного) находящийся в неза-
груженном режиме резервный элемент переводится в нагруженный. Элементы
идентичные, характеризуются интенсивностью отказов А. Требуется определить
точное и приближенное значения вероятности безотказной работы системы.
Решение. Для рассматриваемой системы имеем;
Ло = Лу = Л «= ЗА; Л2 «=• 2А.
Используя табл 3.2.1, находим:
1. Точное значение вероятности безотказной работы определяется формулой
2 2 —Л(Ц
Р (М = П Лу 2 ------е--------- -
»=° '=° Л, П(Лу-Лу)
/=о
1 *1
___Лу Л2 (Лу —Л2) е~л '° —Др Л2 (Ло —Д2) е~л< До Лу е~л- f* ,
(Ло — Лу) (До — Л2) (Лу — Л2) (Ло — Л2) (Лу—Л2)
В нашем случае
Лв = Лу = Л,
а поэтому первое слагаемое полученного выражения представляет собой неопре-
деленность, раскрывая которую по правилу Лопиталя, имеем:
Лу Л2 (Лу-Л2) е~л* (>-Л0 Л2 (Ло —Л2) е~л‘ _
(Лв—Лу) (Лв—Л3) (Лу—Л2)
Л2 е-л<» [(2Л- л2) + Л (Л-Л2) („]
(Л —Л2)а
Таким образом,
р п = A*e~A»f> _ Л2 [(2Л-Л2) + Л (Л -Л2) М .
(Л-Л2Р (Л-Л2)8 -
99
ео
ео
со
ТО
Я
S
ч
хо
то
н
.истема с п резервными элементами, находящимися в различных режимах
Ненагруженный режим со * 1 + с /=о
Облегченней режим «. + I 1 . Y & -1 + -й* qt •« u » *—4 F + лг f Л,о 4Ил 1 vN~k(N— fell ^4 k + vi »=*o e — M+»i)
। Нагруженный режим 1 + % 1 Л k(k+l) (i+?) — э%~~ ат—э 1 A j /з==0 1 X л t л К г? ъ* х 5 ।
Показатель 1 h, (°lid S. 0,
Система k рабочих элемен- тов и 1 резервный k рабочих эле- ментов и п резервных. N — k-i-n
4 Зак 943
97
Таблица 3.2.3
Приближенное значение вероятности безотказной работы системы
из одного рабочего и п резервных элементов, находящихся
в различных режимах
Режим Приближенное значение ?(t0) Условие приближения Погрешность
Нагруженный 1 — (А/о n+I А/о 1 п 4-1 g—-\ta
Облегченный 1 <xz°)n+1 гт„ , ч 1- („+!)> И (1 + v;) t=0 Мо< 1 а (/о) < f 1 , п \ < ( ту -г 44 v 1
Ненагруженный (kt0)n+Ie-u° (п 4- Х/о-^1 ° !р(п+ 1)
Подставляя в это выражение значения Ло = Aj = Л = ЗА и Л2 = 2А, получаем:
Р = 9е" 2W° — 2 (4 4- ЗА/0) е ~ зи«.
2. Приближенное значение для вероятности безотказной работы системы при
I = 1 запишем-
2 2 /3 | s
?(/») = !- П Л, 2 (~ l)s As-b------= 1-Л0Л1Л2Х
; = 0 s—0 (3-f-s) !
Aa= 2 Ло° AS1‘ AV=1;
s« + s, + s2 = O
/lj= 2 Л0° A^1 As2 =A04-Aj 4-A2;
$o4" S14"S8= 1
л2= 2 Aso»As1‘AV=Aj+AHAHAoA1+A()A2+A1A2.’
so4“ + Sa = 2
Тогда
P(^o) = l—Ao Aj Л2 —(Ao + Ax-f-Aa)~4-
L O Z4
+ (Aq 4-A| 4-A| 4-A0 Ax 4-Ao A2 4-Ai Л2)
Подставляя в это выражение значения Ло, Ат и Л2, получаем
?(/0) = 1-3(А/0)з [1-2А/«4-^|- (U>)2 1-
98
3.3. Некоторые общие положения относительно
резервирования невосстанавливаемых систем
1. Чем мельче масштаб резервирования, тем выше надежность
системы.
Уровень (масштаб резервирования), на котором производится ре-
зервирование, может быть различным: резервировать можно отдель-
ные элементы, модули, блоки, панели, стойки, наконец, всю систему
в целом. Будем говорить, что масштаб резервирования тем мельче,
чем меньшая часть системы резервируется как единое целое.
Проиллюстрируем влияние масштаба резервирования на надеж-
ность системы на примере дублированной системы, состоящей из
двух устройств, находящихся в нагруженном режиме. Если устрой-
ство дублируется целиком, то вероятность Р(1)(/о) безотказной рабо-
ты системы на интервале (О, <0) равна:
(/о) = 1 _ [1 _ г (QP,
где г (to) = Го — вероятность безотказной работы одного устройства
на том же интервале времени (О, <0) при 0 < r0 < 1. Если произво-
дится раздельное дублирование (для простоты выкладок предполагает-
ся k равнонадежных частей устройства, т. е. вероятность безотказной
работы каждой части составляет г0), то вероятность Р№ (t0) безот-
казной работы такой дублированной системы будет равна:
Р(^0)==[1-(1-/г0УТ-
Нетрудно убедиться в том, что вероятность Pw (t0) с увеличением k
растет, при этом:
• (1—го)г
lira PW (/0) ~ lime к =1. (3.3.1)
k-*oo 1(->Х
Поскольку последнее соотношение выполняется для случая нагру-
женного (самого тяжелого) режима работы системы, то оно тем более
справедливо для облегченного и ненагруженного режимов.
Отметим, что как (3.3.1), так и все сказанное ранее справедливо
только в случае весьма высоконадежных контрольно-переключающих
устройств в резервированных системах. Если же это не имеет место и,
например, надежность контрольно-переключающего устройства умень-
шается с уменьшением масштаба резервирования (из-за усложнения
контрольно-переключающего устройства), то
lim P<*)(Q=^1,
fe->oo
при этом существует
шах (ta) = Р<Ы (/0),
k
где k0 — оптимальный масштаб резервирования.
4 е 99
На практике k0 — невелико, так как контрольно-переключающее
устройство с уменьшением масштаба дублирования быстро услож-
няется. Отметим также, что практически редко удается дублируемое
устройство «разбить» на равнонадежные части, однако именно к это-
му надо стремиться, поскольку при дублировании равнонадежных
частей выигрыш получается наибольшим.
2. Объединения резервов групп системы увеличивает ее надежность.
Рассмотрим систему, состоящую из k рабочих равнонадежных
(для простоты выкладок) блоков. Пусть имеем еще k дополнительных
блоков, предназначенных для ненагруженного резервирования си-
стемы, которое производится двумя способами:
— все k рабочих блоков системы имеют индивидуальный резерв;
— все k рабочих блоков имеют объединенный резерв.
Нетрудно показать, что средняя наработка до отказа для этих двух
модификаций системы равна:
тр)=— г(2)^(3.3.2)
Л /г* /I X k
где ‘к const — интенсивность отказов одного блока.
Из (3.3.2) следует, что
= (3.3.3)
k bi
i = 0 н
Используя (3.3.3), легко получаем:
№1=1,00; W2 « 1,20; W8 « 1,38; №4 « 1,55;
W5 1,71 и т. д.
Из (3.3.3) следует, что
lim ~ lim
k-*<x> у 2 л
т. е. выигрыш от объединения групп с увеличением числа групп не-
ограниченно возрастет.
3. Вклады резервных устройств, «.вносимые» в среднюю наработку
до отказа системы, в «лучшем случае» суммируются.
Выигрыш, получаемый от применения резервирования без восста-
новления, относительно невелик (даже без учета оганиченной надеж-
ности контрольно-переключающих устройств) и по средней наработ-
ке до отказа растет, в лучшем случае, как линейная функция числа
резервных устройств. Действительно, для самого легкого режима
использования резервных устройств, ненагруженного режима, из
(3.1.31) имеем:
М-i _
2Л<Г(п+1), (3.3.4)
_ 1=1
где Т = max Tt.
(MCb-f-I
100
Если вероятности безотказной работы устройств, составляющих
систему, подчиняются экспоненциальному закону, то, используя
(3.1.10), (3.1.11) и (3.1.33), соответственно получаем:
П-|-1 | I
XT|v=i= 2 — ~ С + In (п 4- 1) + ——-;> (3.3.5)
i 2(«+1)
КТ |v=o — и Ф 1»
где С—постоянная Эйлера; С = 0,577 ...
Из (3.3.5) следует, что при больших п величина КТ (при любом v)
с увеличением п, для рассматриваемого случая, растет не медленнее
логарифмической функции и не быстрее линейной (рис. 3.3.1).
Рис. 3 3 1. Характер роста сред-
ней наработки до отказа системы
при увеличении числа резервных
элементов.
4. Резервированная система, поведение которой описывается схе-
мой «.гибели и размножения'», является системой «строго стареющей».
«Строго, стареющей» называют систему, у которой интенсивность
отказов К (0 есть функция возрастающая во времени, т. е.
К' (/) >0, t > 0.
(3.3.6)
Если поведение системы описывается «схемой гибели и размно-
жения» (§ 3.1, случай экспоненциального закона, и § 3.2), то такая
система является системой «строго стареющей», т. е. для ее интенсив-
ности отказов К (I) выполняется условие (3.3.6).
5. При применении раздельного дублирования п частей си-
стемы вместо общего дублирования выигрыш в среднем времени безот-
1
казной работы порядка ТУ п. Пусть для повышения надежности
Функционирования устройства предполагается дублирование, которое
может быть реализовано двумя способами:
— устройство дублируется целиком (рис. 3.3.2),
101
— устройство дублируется раздельно (предполагается равнонадеж-
ное разбиение) (рис. 3.3.3)*. >
Предположим, что вероятность безотказной работы дублируемого
устройства подчиняется экспоненциальному закону, при этом интен-
сивность отказов устройства в рабочем режиме равна А, в резервном
Тогда оценка Т\П) снизу для средней наработки до отказа системы
с раздельным дублированием (рис. 3.3.3) определяется как
КТМ = ]/ —
- V 2(i+v)
(3.3.7)
Поскольку в рассматриваемом случае общего дублирования (см.
рис. 3.3.2) точное значение средней наработки Т до отказа равно
(3.3.8)
АТ = v
1 -[-V ’
Рис. 3 3 3. Раздельное дублирование устройства из п элементов.
то отсюда имеем следующую оценку снизу выигрыша полу-
чаемого в случае применения раздельного дублирования
(3.3.9)
* Случай «разбиения» устройства при раздельном дублировании на равно-
надежные части (реально трудновыполнимый) рассматривается здесь потому, что
именно в этом случае получается наибольший выигрыш от применения раздель-
ного дублирования и именно к «равнонадежному» разбиению нужно стремиться
на практике.
102
Поскольку 0 < v < 1, то из (3.3.9) следует, что
(3.3.10)
Так, поэлементное дублирование в устройстве, состоящем из
п = 2000 идентичных элементов (например, микросхем), может
привести к выигрышу
TOoo)>T^2000 ^22-
Список литературы
1. Васильев Ю. А., К о з л о в Б. А. Резервированная система — си-
стема стареющая. — В кн..’ Теория надежности и массовое обслуживание.
М., «Наука», 1969.
2. Л е в и н Б. Р. О повышении надежности систем путем резервирова-
ния. — «Электросвязь», 1957, № 11.
3. С и и и ц а М. А. Методы резервирования радиоаппаратуры. — «Электро-
связь», 1958, № 7.
4. Соловьев А. Д. О резервировании без восстановления. — В кнл
Кибернетику — на службу коммунизму. Под ред. А. И. Берга, Н. Г. Бруе-
вича, Б. В. Гнеденко. М., «Энергия», 1964.
4
РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ
4.0. Предварительные замечания
По расчету надежности резервированных восстанавливаемых си-
стем, состоящих из идентичных элементов, имеется обширная библио-
графия-*, относящаяся в большинстве своем к так называемым
экспоненциальным моделям, т. е. таким системам, времена работы и
восстановления элементов которых подчиняются экспоненциаль-
ным законам. Работ по расчету надежности неэкспоненциальных
моделей систем сравнительно мало. Они посвящены, как правило,
достаточно частным случаям, в основном так называемым полумар-
ковским моделям. Поэтому систематическое изложение имеющихся
здесь результатов предварительно требует классификации резер-
вированных восстанавливаемых систем. В основе такой классификации,
в интересах читателя, по нашему мнению, должно лежать подразде-
ление систем по структурным признакам и моделям отказов и восста-
новлений, а не по математическим методам получения показателей
надежности этих систем.
Предлагаемая ниже классификация (впрочем, как и любая другая),
конечно, условна, имеет пределы применимости и удобна лишь для
определенного круга задач. По этой классификации резервированная
восстанавливаемая система описывается пятеркой чисел k, nlt п2,
п3, I и тремя функциями F (t), Fv (t), G (t) (табл. 4.0.1), при этом
предполагается, что m-параметрические законы распределения вре-
мени работы до отказа элементов, находящихся соответственно в ра-
бочем и облегченном режимах (функции F (/; а1( а2, ат) и (Z;
а^, <4V), ..., ««’)), принадлежат к одному и тому же параметри-
ческому классу законов и могут отличаться между собой лишь зна-
чениями параметров: (а1( а2, ..., ат) и (aiv), а^, а№). Например,
в случае экспоненциального закона
F(/) = E(/)=1—е-*',
Fv (0 = Ev (/) = 1 —
закона Гнеденко—Вейбулла
где отличны параметры, по крайней мере, в одной из пар: X, Xv; a, av.
* Библиография упомянутых работ, более чем 200 наименований, приведена
в книге. Б. А. Козлов. Резервирование с восстановлением. ?)., «Сов.
радио», 1969.
104
Таблица 4.0.1
Законы распределения Число ра- бочих эле- ментов k Число эле- ментов на- груженного резерва th Число эле- ментов об- легченного резерва «а Число элементов ненагружел- ного ре- зерва п8 Число ре- монтных органов 1
Законы распределения времени работы F (t), Fv(t), времени восстанов- ления G (/) элементов F(t) F(t) т,(0 0* 6(0
* Функция распределения Ф(?) времени работы до отказа элемента ненагруженного резерва,
по определению, предполагается равной
Табл. 4.0.1 сокращенно можно представить в виде:
k tli «2 «з I
F F F, 0 Q
Порядок замены отказавшего на любой позиции элемента исправ-
ным, очевидно, должен специально оговариваться в каждом конкрет-
ном случае, хотя общая идея замены остается во всех случаях одной
и той же и иллюстрируется рис. 4.0.1.
----А
v I__________________________"П
Рис. 4 0 1. Схема замены отказавшего элемента исправным.
В табл. 4.0.2 представлены, на наш взгляд, наиболее интересные
для приложений частные случаи классификационной табл. 4.0.1.
В табл. 4.0.2 под Е (/) понимается экспоненциальное распределение,
а под G* (/) — функция распределения «быстрого» восстановления
(см. § 4.2).
Таблица 4.0 2
1 . «2 «3 1 Т (/) ^,(0 6(0
0 1 0 1 0 1 1 и=п1+п2+ "Нгз"Н £(/) £,(0 £(/) G*(0
Если теперь выписать частные случаи классификационной табл.
4.0.1 в виде «дерева» моделей, используя в качестве таблицы—ключа
табл. 4.0.2, то «сплошь увешанной плодами» (результатами решенных
задач) у этого дерева будет только одна ветвь — модель
k «1 п, п* /
Е Е 0 Е
105
На остальных же ветвях-моделях этого классификационного де-
рева плодов-результатов будет немного и «висеть» они будут доста-
точно высоко, т. е. решены по нашей классификации только весьма
частные случаи.
В соответствии с этим, при дальнейшем изложении мы прежде все-
го подробно рассмотрим ветвь — модель
k п, nt п} I
Е Е Е, О Е
а затем остальные случаи (см. § 4.2).
4.1. Экспоненциальные законы распределения времени
работы до отказа и времени восстановления:
«схема гибели и размножения»
В соответствии с введенной классификацией в данном параграфе
рассматривается модель системы
k nt nt п3 I
Е Е Е„ О Е
т. е. рассматривается система (рис. 4.1.1), состоящая из k рабочих
и п = + п3 + пз резервных элементов, из которых пг элементов
находится в нагруженном, п2 — в облегченном и п3 — в ненагружен-
ном режимах. (Под элементами здесь, по-прежнему, может пони-
маться отдельная деталь, узел, блок, стойка, в некоторых случаях
целая система и т. д). В любой момент времени рассматриваемая
система считается работоспособной, если не менее чем k ее элементов
из общего числа N = k + п работоспособны.
Предполагается, что момент отказа любого рабочего элемента сразу
же обнаруживается, причем он мгновенно заменяется на исправный
из числа резервных элементов. Исправность самих резервных эле-
ментов постоянно контролируется. Эти допущения соответствуют
практически тому случаю, когда в аппаратуре с резервированием
имеется стопроцентный безошибочный контроль работоспособности
всех элементов, а все переключающие устройства, используемые для
подключения резервных элементов, характеризуются весьма малым
временем переключения и высокой надежностью*.
Пусть в любой момент времени одновременно в системе может вос-
станавливаться I отказавших, элементов, где 1^ I п + 1.
Будем различать три режима восстановления отказавших элемен-
тов в системе:
I =» 1 — полностью ограниченное восстановление,
1 <* I < п -j- 1 — ограниченное восстановление,
Z =» n + 1 — неограниченное восстановление.
* Случаи моделей, отличных от описанной (см. гл. 5)
100
Таким образом, полностью ограниченное восстановление — тако!
режим восстановления, когда в любой момент времени не может вос-
станавливаться более одного отказавшего элемента, т. е. предпола-
гается, что имеется ровно один ремонтирующий орган. Ограниченное
восстановление — такой режим восстановления, когда в любой мо-
мент времени не может восстанавливаться более I отказавших элемен-
тов, 1 < I < п -г 1. Неограниченное восстановление — такой режим
Рис. 4.1.1. Структурная схема системы
k щ п2 п3 I.
Е Е Ev О Е
восстановления, когда любой отказавший элемент сразу же поступает
на ремонт, т. е. предполагается, что число ремонтирующих органов
достаточно для одновременного восстановления всех отказавших
элементов системы. Заметим, что более п + 1 отказавших элементов
в системе, по предположению, быть не может, поскольку, если
в системе нет необходимого числа k исправных рабочих элементов,
то система не работает и ресурс оставшихся исправными k — 1 »ле-
ментов не расходуется.
Поведение рассматриваемой нами системы во времени характе-
ризуется следующими условиями. Если в момент времени I система
107
находится в состоянии Н} (где через Н, обозначено состояние, в ко-
тором система имеет j отказавших элементов), то за последующий про-
межуток времени Д/ она с вероятностью Л7Д^ -f- о (Д/) может перейти
в состояние Z//+I (т. е. в системе откажет еще один из исправных
элементов), с вероятностью MjM + о (Д/) — в состояние
(т. е. будет восстановлен один из / ранее отказавших элементов) и
с вероятностью 1 — Л^Д/— М}М 4~ о (Д/) может остаться в со-
стояние Hj. Все Ду, М} — величины^постоянные, имеющие простой
физический смысл. Так, например, в случае системы, состоящей из
k рабочих, Их нагруженных резервных, м2 облегченных резервных
(с коэффициентом нагруженности v, 0 < v < 1), м3 ненагруженных
резервных элементов, и при восстановлении отказавших элементов
системы I ремонтными органами, имеем:
— для интенсивностей переходов (отказов) Aj, 0^/^/г = nx -f- д- п3
Ло = kk + мх X 4- rt2 vX
Лх = 1гк 4- nx X /г2 vX = Ло
А«3 = Ад
A/ij-p 1 — kK 4- nx X 4- (м2 — 1) vA>
Л„з+2 = ХХ4-ПхХ4-(па—2) vX
— XX 4~ мх X
ЛПз+„!+1 = XX 4- («х— 1) X,
= XX 4" (М2— 1 ) X,
Ana+»s+ni — XX;
— для интенсивностей переходов (восстановлений) М} 1 п,
Мх = р, Л12 = 2р, ...,
Mi = /р, М1+1 = /р, ..., Мп — /р.
Очевидно, в рассматриваемом случае система, имеющая п. -резерв-
ных элементов, может находиться в конечном числе состояний соот-
ветственно числу отказавших элементов:
fiit Нц •••> Нjt ..., Нп,
Состояние Нп+1, в котором система содержит п 4- 1 отказав-
ших элементов (т. е. отказавшими являются все п резервные и еще
один из рабочих элементов), есть состояние отказа системы. Для
данной системы будут рассмотрены две модели, соответствующие
задачам, в которых состояние отказа системы является поглоща-
ющим и отражающим.
108
В первом случае рассматривается процесс «жизни» системы толь-
ко до ее отказа, т. е. предполагается, что система, попав в состояние
Hn+i, уже из него больше не выходит.
Во втором случае система, оказавшись в состоянии Нп+1, мо-
жет перейти затем в состояние Нп и т. д. (Как уже указывалось,
в системе не может быть более п, -f- 1 отказавших элементов.)
В теории надежности первая модель соответствует задачам оты-
скания вероятности безотказной работы системы, средней наработ-
ки до отказа и т. д.; вторая модель — задачам отыскания нестацио-
нарного коэффициента готовности и коэффициента готовности, простоя
и т. п.
Mf Ла Mz Aj Mj Aj-t M,+t Aj An.f An
% -к .. . > »-.., -« — *- • •. —s
Рис. 4 1 2 Граф переходов из одного состояния в другое системы, содержащей п
резервных элементов.
Граф переходов системы (для обоих случаев) приведен на рис. 4.1.2,
где обозначено:
Н] — состояние системы, в котором среди всех ее N = k + п.
элементов имеется / отказавших, 0 п + 1;
А} — интенсивность перехода системы (отказа одного из ее ис-
правных элементов) из состояния, в котором в системе было / отказав-
ших элементов, в состояние, в котором в системе будет на один отказав-
ший элемент больше, т. е. / + 1 элемент, 0 м;
Mj—интенсивность перехода системы (восстановления одного
из ее отказавших элементов) из состояния, в котором в системе было /
отказавших элементов, в состояние, в котором в системе будет на один
отказавший элемент меньше, т. е. / — 1 элемент, 1 п + 1.
Поведение системы, у ‘которой состояние Нп+1 является погло-
щающим, описывается системой дифференциальных уравнений сле-
дующего вида:
Р' (0 — pj-i (0—(Aj ф- Му) pj (i) -f- Му+1 р;+1 (0;
О и + 1»== Лп+1 = Мо = Мп+1 = Мп+2 = 0, (4.1.1)
где pj (/) есть вероятность того, что система в момент времени t нахо-
дится в состоянии Hj, при этом
п+1
2рД/)=1. (4.1.2)
/=о
Поведение системы, у которой состояние Нп+1 является отра-
жающим, описывается системой дифференциальных уравнений (4.1.1)
109
и (4.1.2), за исключением двух последних уравнений, которые здесь
имеют вид:
Рп (О = Лп_! рп_1 (0—(Л„ + М„) рп (0 + Мп+1 рп+1 (/);
p^+1(0 = A„pn(/) — Mn+1pn+1(/), Мп+174=0. (4.1 3)
В табл. 4.1.1 сведены точные значения основных показателей на-
дежности системы (из k рабочих и п резервных элементов), получен-
ные решением приведенных выше дифференциальных уравнений.
В таблице обозначено:
п
1) ^)=Sp>(Q=l~Pn + lW
1=0
— вероятность безотказной работы системы, начавшей свою работу
при произвольных начальных условиях (0), 0 j sC п -f- 1;
2) P^(t0) — вероятность безотказной работы системы, начавшей
свою работу, будучи полностью исправной, т. е. при начальных усло-
виях (0) = 1, р}- (0) = 0, 1 п 4- 1;
3) — вероятность безотказной работы системы, начав-
шей свою работу, только что «выйдя» из состояния отказа, т. е. при
начальных условиях рп (0) = 1, (0) = 0, 0 j п — 1, п -f- 1;
к °°
4) /?(4) = -~Г)$ P^(e)de
/а
— коэффициент оперативной готовности;
5) Т, Tw, Т^, T!'R'1 — средние наработки, соответствующие
пп. 1—4.
В табл. 4.1.2 приведены приближенные значения этих показателей.
При выводе приближенных оценок использовалось следующее основ-
ное предположение:
р= min Mj»nmax Л; = пЛ. (4.1.4)
!</<«+! 0 < /< п
Дополнительно к табл. 4.1.2 в табл. 4.1.3 приведены грубые
оценки для интервальных показателей надежности системы.
Замечание, рели имеется не одно (п + 1)-е состояние отказа, но и так-
же состояния с номерами п + 2, п + 3, .... N—1, что соответствует случаю,
когда отказавшая система «не выключается», то легко понять, что коэффициент
готовности и среднее время восстановления будут равны (см. табл. 4.1,1);
п N
s=0 s=0
НО
Таблица 4.1.1
111
Продолжение табл. 4.1.1
to
Показатель Точное значение
Z3'01 (/о) П п + 1 —х(« + 1) ta Па. У /=о ,=! X(»+Djj (х^ + О—%(«+*)) s—1 s^l
Р1п> (/о) ^.1 П (хг",+1,-4'1,)П(1Г)-х!М”) . п V Л" - »=1 ₽=« -X^+lh0 jU x|n + 1) г—1 м + 1 е i=l П (*r+l)-*r+,)) П (х?+1)-%Г+1)) 7=1 г=1+1
R Ро) /—1 п П+1 П (xjra+1)-я?*) П (*3n)-*r+1))< ®n yi ( V e=l 3 -x(n + l)f0 «+> Zj Ix<n+ij ) *-“ n+i e 2 0r»=i4 7 Ц (x<"+l>-xf+1>) JI (xf+,,-xp+1>) r=0 7=1 !=i + l
продолжение табл. 4.1 I
1
"J (0) = 3 Р>
s = 0
J Показа гель Точное значение
Т i п "1 (°) 3 0г V — г=0 4J Ai®J ;=0
тт Ф1, ф* о **
7-(") е Ф е ф
Т’СЛ) © *- .® > it М" Ф О Лч «7 Ф •i
Pi 1 п+1 &i 2 ** 1
к / In \ ”|—) 1 + 0я+1 / 3 ®‘ \ 1 1=0 /
т l/^Wn + l
Таблица 4.1.2
Система с п резервными элементами. Общий случай
п
SI „ AoAj ... Л„_,
А1, ’ в«- 11,11г ... M„ 1
7 = 1
значения Л°), Л”), Т, К приведены в
табл. 4.1.1. Погрешность б (/0) для соответст-
вующего показателя S (?0) определяется как
3 (Q |« (U-S (Ml •
Показатель Приближенное значение Погрешность (порядок)
P(tJ /о Т г(0) Л«) е
А») (/„) — е М) 3
Pm (М — Т(п) г(0) Л^е
R(to) — Т(0) Ке
Погрешность 3 для соответ-
ствующего показателя М
определяется как 8 ~М — М
Показатель Приближенное значение Погрешность (порядок)
т "л (0) Л„0„ - Л 0 п "л-1 (0) + дя111 "л (0) 1
Л °) 1 л„ея 1 + ЛлМ, ^п- 1®я-1
Л”) 1 ЛПНЛ Ло Ля1110„
114
Продолжение табл. 4.1.2
y(R) 1 . t ЛОМП 1 + ДА Еп-^П-1
Pi 0}(1 —0,) -0J (0г - 0f)
к 1 ®п + 1 <№+>
Таблица 4.1.3
Система с п резервными элементами. Общий случай
Л = max At;
р. = min Mt
+1
Показатель Грубая оценка Погрешность (порядок)
Pf.it) А Н-
PW (М
А") (/.)
Л (/о) (1 - 0я+1) е~Л"е"/о
Пример 4.1.1. Рассмотрим в качестве примера
системы
k nt п2 п3 I
F Р F, О G
систему
3 1 112
Е Е Е, О Е
т. е. рассмотрим систему, состоящую из!
k = 3 рабочих элементов; nj= 1 резервного элемента, находящегося в нагружен-
ном режиме; п2 — 1 резервного элемента, находящегося в облегченном режима
с коэффициентом нагруженности V = 0,5; п3 = 1 резервного элемента, находя-
щегося в ненагруженном режиме.
Предположим, что восстановление в системе является ограниченным (Z = 2),
а элементы характеризуются интенсивностью отказов А = 0,1 1/ч и интенсив-
ностью восстановления ц = 1 1/ч.
Будем также считать, что в случае отказа рабочего элемента, его функции
принимает на себя нагруженный резервный элемент, при этом элемент, ранее
находившийся в облегченном режиме, переводится в нагруженный режим, а
элемент, ранее находившийся в ненагруженном режиме, — в облегченный. В слу-
чае отказа нагруженного резервного элемента его функции принимает на себя
элемент, ранее находившийся в облегченном режиме, при этом его режим заме-
няется на нагруженный, а элемент, ранее находившийся в ненагруженном режи-
115
ме, переводится в облегченный. В случае отказа облегченного резервного элемен-
та его функции принимает на себя элемент, ранее находившийся в ненагружен-
ном режиме, при этом его режим Заменяется на облегченный. Этот же алгоритм
работает н в том случае, когда в системе имеется более одного отказавшего
элемента. В соответствии с этим граф переходов рассматриваемой системы
имеет следующий вид:
В нашем случае:
Лй = Л1 = ЗХ + X + 0,5 X = 4,5 X = 0,45 1/ч,
Л2 = ЗА + X = 4Х = 0,4 1/ч, Л3 = ЗХ = 0,3 1/ч,
М4 = р. = 1 1/ч, М2 == М3 = М4 = 2р = 2 1/ч;
п “ П1 + «а + п3 == 3.
Структурная схема системы представлена на рис. 4.1.3. Требуется определить
основные показатели надежности системы.
Решение. Для рассматриваемой системы условие (4.1,4), как легко ви.
деть, не выполняется:
u= min Mj = Mi = 1 1/ч,
1 4
п шах Л# = пЛ0 = 1,35 1/ч.
о < / < з J
Поэтому точные значения показателей
1. Вероятность безотказной работы:
з 3 4
найдем при помощи табл. 4.1.1
,(4>
S
(О_„(4)
р ('о) = 2j Pi W П ЛА
1^0 —,
*=.’ 44) П (Ч41-*?1)
г— 1
r^s
lie
Как следует из приведенной формулы, для отыскания вероятности безотказной
работы системы необходимо знать величины:
хр->, х[2}, х’з2’, х(10), х(23>, xi4’> х21'- xs4)> х44)>
которые имеют размерность 1/ч (далее размерность опускается). Из табл. 4.1,1
последовательно имеем*:
1) Дх (К) = - (Ло + х) = - (0,45 + х),
откуда х?’ = 0,45;
2) Д2 (х) = -(Aj + Мх + х)Дх (х) — ЛОМХДО (х) « х3 + 1,9х + 0,2025,
откуда xi21 = 0,113340, х22’ = 1,786660;
3) Дд (х) = — (Л2 + М2 + х) Д2 (х) — Л1 М2 Дх (х) 1=1 — (х3 + 4,3х2 +
+ 3,8625х + 0,081),
откуда x't3> = 0,021482, х^3> = 1,241573, х^3> = 3,036945;
4) Д4 (х) = —(Ад + Ms + х) Д3 (х) — Л2 Мд Д2 (х) => и* + 6,63х 4-
+ 12 9525х2 + 7,44475х + 0,0243,
откуда xi4> = 0,003283; х<2*> = 1,025771; x^> = 2,048906; х'^’=3,522040.
Пусть начальные условия работы системы заданы следующим образом:
Ро(°)=4"; Р2(0)=4-| Рз(0)=-^-«
и О *т 12
Тогда, подставляя найденные значения корней в выражение для вероятности
безотказной работы, получаем**:
р (/0) = 0,982 e“°‘003Zo4-0,013e~1,Q26Zo Ц-О.ООбе”2,049^ — 0,001е“ 3>522/» .
2. Вероятность безотказной работы системы, начавшей свою работу, будучи
полностью исправной, т. е. при начальном условии р0 (0) = 1,
3 4 _ x$l} t„
Р(О,(/о) = П Л; 2 -------------------------
1 = 0 <=1 ri
Х<1) 11 (х«4» —Хр))
Подставляя в данное выражение числовые значения. Находим
Р<0> (/0) = 1,006“ 0'003;о— 0,009е“ 1,026;° 4-0,004е“ 2,049;° — 0,001е — 3*522/».
3. Вероятность безотказной работы системы, начавшей свою работу, только
что «выйдя» из состояния отказа, т. е. при начальном условии ра (0) = 1,
4 -Л^Ч.
1 = 1
1-1 3
П (Ч4,-Ч3>) П (43)—*j4’)
а = 1__________6 — 1___________
1-1 4
П (^’-Ч4*) П (44,-*i4))
v=1 e=Z+l
* Отметим, что процедура отыскания корней довольно проста, поскольку
все корни —х<т\ l<s < т, 0<m< n 4~ 1, Действительные, различные,
отрицательные и корни соседних (по т) многочленов Дт (х) перемежаются.
** Неприятной спецификой определения точных значений интервальных по-
казателей надежности является необходимость проведения расчетов с точностью,
на несколько порядков большей точности конечного результата. Так, в частности,
в данном примере, получение значений показателей с точностью 10~8 потребова-
ло проведения расчетов (и знания корней х£т)) с точностью 10-в.
117
Подставляя в это выражение числовые значения, получаем:
(/о)=0,849е-0'003‘“ + 0,049е~ 1*026/<’-|-0,076е“2 *'049;“+0,026е-3'522\
4. Коэффицвент оперативной готовности 2? (/0) рассматриваемой системы
1—1 з
4 п (4‘>-4s>) п
D... 08 V I Л-1 I «=> P=Z X
R Ы =—--------Z ( 7Z1----------------1------------- х
3 ©г /=1 П (44>-44)) П
(сО V=1 6 = 1+1
— r(4> t
Xe xi Ч
Вычислим предварительно:
<д1 = Aq/Mj = 0,45,
02 = Л0Л1/М1М2 = 0,10125,
08 = Лв Л^/М^Мз = 0,02025,
04 = Л0Л1Л2Л8/М1М2М3М4 = 0,003038,
08/2 0г = 0,012061.
г=0
Подставляя полученные значения и значения корней, находим
R (/о)==О,998 е_0'003/“-!-Со,
где с0 10-8.
5. Средний наработка системы
I
з nj (0) 2
„ -Ч.1 г = 0
I
Поскольку (0)= 2 Ps Т01
s = 0
По (О) = Ро(О) = _~ ,
&
2
П1 (0) = Ро (0) + Pi (0) =— ,
□
па (О)=Ро (0)+Р1(0)+р2(0) = -^-,
Яз (0) = Ро (0) + Р1 (0) +Рг (0) +Рз (0) = Е
Используй значения величин, полученные в п. 4 настоящего примера, &а-
кодим
Т = 299 ч,
118
6. Средняя наработка системы до отказа
з
J’(O) _ V1 г=0
Л.-0, ’
1=о 3 3
Подставляя сюда числовые значения, получаем!
= зоб ч.
7. Средняя наработка системы между отказами
з
2^
Т(3) =Г=_2— = 259 ч.'
Л303
8. Средняя стационарная наработка системы
откуда
Г(^'=304 ч.'
9. Стационарные вероятности pj пребывания системы в состоянии Hf,
0 < / < 4, определяются как
0 j &]
Pj = ~ = 1,574538 '
1 = 0
Тогда:
р0 — 0,635, Pj = 0,286; р2 = 0,065, р3 = 0,012, р4 =» 0,002.
10. Коэффициент готовности
11. Среднее время восстановления
<г=-~— = 0,5 ч.
В конце настоящего параграфа приведены табл. 4.1.4—4.1.29,
в которых даны показатели надежности для нескольких, на наш
взгляд, наиболее распространенных в инженерной практике, част-
ных случаев рассмотренной в § 4.1 системы.
119
Таблица 4.1.4
Дублированная система
элементов.
Нагруженный резерв.
Неограниченное восстановление
110 0 2
Е Е 0 0 Е
х1л = "2^" (1 + Зу+ V ч-буч-у2);
е1,г — (1 + У) (3 + 1)1
Уг . X
Yo = 1 + 2у’ Y = "iT’
Показатель Точное значение Приближенное значение Погрешность
Л») - 1 1_±3у к 2у 1 1 Л 2у ’+=2Т
лч 1 1 + 2у X 2у 1 1 X 2у
1 2р. — —
А») У*) г _v (х^~х‘*° — хге~Х11°) л 1 Л2 е-ГТз^»» 6 2у2
K(t) 2Х2 Г 1 1 1 — Че-'**— ®1®2 [_ ®1 — ег ' 1 1 — уг £] _ ^2 — \ т -е 1 /е 1 J 6 'х. 8у3
К 1 1 + Ус 1-Уг 6+ - 2у3
R(Q хе (к—xs) е~*1<0—х, (X—xQ е~хЛ р.(%1 — хг) (1 +у)2 _! е 1 + 37 х‘% I +Ус е 5 ~ 2у2
120
Таблица 4.1.5
Дублированная система
элементов.
Нагруженный резерв.
Полностью ограниченное
восстановление
110 0 1
Е Е 0 0 Е
*1.г =-§7 [(1+37)±/1+бу+№1;
Ча =-^7 [(2 + з-г) ±/фГПЧ;
2у2 . X
Yc== 1 + 2-г’ [л •
Показатель Точное значение Прибтиженное значение Погрешность
тт 1 14-Зу Л 2/ 1 1 Л 2/ 1
лч _2_1+Л К 2у~ 1 J_ X 2-f 8+="Г
т 1 Р- — —
А») (/„) х,-х2 (х^°- хге~^) ГТз7и° е «•ч, 2-7
K(t) 2V Г 1 1 — 1 (е.е-'3' — ®1®2 L е1 — «2 ' - М~е1<) ] 1— 2у2 р — (1 + + ~ / 1 8 -v 8у*
К 1 1 + %' 1 — 2уа 8+ -v 4f3
R%) Х2 (X—Xi) e~Xit°— х, (К—Xj) е~*л —J е 1+ЗтН“ 1 +Го 8 -v 2-7
Р- (х> — х2) (1 4- 2у + 2у2)
121
Таблица 4.1.6
Дублированная
система элементов.
Облегченный резерв.
Неограниченное
восстановление
10 10 2
Е 0 0 Е
*>,г = -^-{[1 + (2 + *)т]±
± ri + 2(2 + v)t + vY };
•).! = -^-{[3+(2+v)y1±’
±/1 +2(2 —v)y + v2y2};
„ - (l + V ._______________L
Ye- 2[1 +(1+v)y]’ ’
Показатель Точное значение Приближенное значение Погрешность
T(°> 1 1 + (2 + v) y A (I + v) Т 1 1 A (l + v)Y 3+ = _2+v 1 l+*‘ X
TV) 1 1 + (1 + v) Y X (I+v)Y 1 1 A (1 + v) Y 1 3+ = Y
T 1 2р. — —
А») (t9) ' ' (х^~к^ — хге~Х1'°) Л] — AJg 1+ U + v) T u° e З-41+v) Ya
K(0 1. J1 + v)xa Г1 _ ele2 L e — e (®>e M — ®2e 6l/) 1 el —®2 J 1 (1 ~'~V) 2 Г1 1- 2 Y p — / -LA - (p-e T JX Xe 1 ] 8-v(l+v)3 y3
к 1 1 + Yc i * ~b v г 1 2 Y2 3 + ^ (l+v)2 , - 2 Y’
R(ta) 2 [хг (X—x2) e~Xlt° — p.(*i — xs) [2 + 2(l + v) y + —X, (A — xt) e— * +(!+,) (H-H 1 ,, 1 l + (2 + v)T to 1+Yoe a^O+v) y2
122
Таблица 4.1.7
Дублированная
система элементов.
Облегченный резерв.
Полностью ограничен-
ное восстановление
10 10 1
Е 0 Ev 0 £
*1,г = V1 (2 + v) yJ di
r±/1 + 2 (2 + v) Y + vY };
e 1,2 = {[2 + (2 + v) Y] di
+ K4y + vy} ;
_ (1 + v) Y2 . _2L
Yo - 1 + (1 + v)Y. Y- p.-
Показатель Точное значение Приближенное значение Погрешность
7\°> l 1 + (2 4- v) y X (1 + v) y 1 1 X (l + v)Y з+=4-х 2+ v
7V) 1 1 -4- (1 + у) у X (1 + *)y 1 1 X (1 + v) y 5+ = -r
T 1 P- —. —
Pm (f o) Xj — Xg l + (2-h>)7 0 e 3-ч.(1+Ч Y2
1-(1 + /)Y2 [1- > t -(‘+T')'1 ] 1-(1+’')Y2[1 - ( »Л 'i 5M1+*)’Y3
K. 1 1 + Yo 1 — (1 + V) Y2 3+a. (1 + v)s Y3
R(t0) хг (Х-хг)е~Х1<°- p. (*i — x2) [1 + (1-H) Y+ "* —x, (X —Xj) e—*“4 "* +d+v)Y2] __o+xu_x. 1 1+(2 + v)y “° e i+y« S'- (Id-*) Ys
123
Таблица 4.1.8
Дублированная
система элементов.
Ненагруженный
резерв.
Неограниченное
восстановление
10 0 12
Е 0 0 0 Е
= +2у) + И +4у];
=1.г = 1(3 + 27) + ГГ+ТП;
№ . х
Y‘~ 2(1 + у) ; Y = р. •
Показатель Точное значение Приближенное значение Погрешность
тт А + •--'j х \ Y J 1 Ху J+_A
И') 1 / 1 X “V + Tj 1 Ху а+=4-
г 1 2р. — -—
„ г (х.е-^ — х2е~х^) *1 ’ Л2 1 е 3 -vy3
K(t) X2 г 1 — 1 — е1е2 [ (e,e~eaZ — e2e“s,z) 1 Ч — е2 v 1 2 7 !-^-р-^2- -е т Je 7 ] уЗ
К 1 1 + т. 1_.д 1 2 й Y’ 8+
R(tQ) 2 [х2 (X — х2) е-^о_ Iх (xi — х2) X —х, (Л — Xi) X (2 + 2у + у2) — • j— м0 1 + Y« 8 -х. у2
124
Таблица 4.1.9
Дублированная система эле-
ментов.
Ненагруженный резерв.
Полностью ограниченное
восстановление
‘10 0 11
Е 0 0 0 Е
xilS = ^1(1 + 2y)±/1+4yJ;
ei.s = 71(1 + y) ± Ky];
Y2 X
Y‘ = T+P Y = iT-
Показатель Точное значение Приближенное значение Погреш- ность
TV) X \ ' Y / 1 + II NO
TV) 1 / 1 \ X +Y ) 1 Xy -.4
T 1 Р- — —
P(°) Go) (х1б х,‘° — х2е *>'«) Aj “ Л2 ' 1 . X/q 8 y2
K(t) '-тИ 1“Т=Г е1Е2 1_ Б1 В2 Г / х \-т*1 1-Y2 1+7 Не 7 3 -ч, y’
к 1 1 + Y« 1 —Y2 3+-Y*
Я Go) х2 (X — х2) е~Л1<0 — Xi (X — ж,) е~~*а<0 JX (хх — х2) (1 + Y + Y2) Ц-и, 1 2+~ — е 1 1 + Хс 3 ~Ya
125
Таблица 4.1.10
Система из k рабочих
и одного резервного
элемента.
Нагруженный резерв.
Неограниченное вое*
становление
k 1 0 0 2
ЕЕ 0 0 Е
^..=^{[l + (2*+l)Y]±/l+2(2^+l)Y+Y2};
®i.s=§7<[3+ 26+1)y]±/1+2(26-1)y+y«};
ft(ft+l)Y* . Л
Ъ-2[1-Н£+1)у]’ Y-p.*
Показатель Точное значение Приближенное значение Погрешность
л») 1 l + (2fe+l)r kt. (ft-(-l)Y 1 1 k\ (ft + 1)y a+ = _ 1 1 + 2ft ft\ft+ 1
/ЧО) 1 l + (^+l)Y kK (ft+l)Y 1 1 ftft (ft + 1)y d+==ftX
•Е 1 2р. —
Р'п‘ (to) (х,е-*'° - xte~x't°) Л-i Л2 1 + (2й+1)т e a-vft(ft+i)Ya
KV) ft(ft+ 1)Ха „ Sl£2 X [1 - Г-Ц- - е2е-е*')1 L г1 — г2 J ft (ft + 1) 1 2 t [*- _(2-e T Je 1 3-^(ft+l)3Y3
к 1 1 + Ге ft(ft+l) I-" 2 V’ 3+^. fe(ft+D2 , - 2 f
R(to) 2 [х2 (k\ — х,,) e~Xlt° р. (X! — х2) [2 + —X] (Н —х1)е~~*,М + 2(fe+ 1) t + k(k+ 1)Тг] (ft+l)T 1 1 + (2* + 1)y 1+Ye 6 3~ft(ft4-l)Y’
126
Таблица 4.1.11
Система из k рабочих
и одног.о резервного
элемента.
Нагруженный резерв.
Полностью ограничен-
ное восстановление
k 1 0 0 1
ЕЕ О О Е
^.2=^{[1 + (2^+1)y]±K14-2(2A+1)y+^};
*1.2 = {[2 + (2ft + 1) у] ± /4AY+ п:
+ 1) Y2 . _£
Yc — 1 + {k + 1) y’ p.'
Показатель Точное значение Приближенное значение Погренностъ
Л»' £ 1 + (26 + 1) y k\ (k + 1) y 1 1 kK (k + 1) Y 3+ = _1 2fe + 1 kXk+ 1
Л1) 1 1 +(^+ 1)Y kk (k + 1)Y £ 1 k\ (k+ 1) Y 8+ ^kk
т £ P- — —
Р(°)а») (x,e хЛ — хге Xlta) Л 1~~~ л2 (fe+DT и, l+(2*+l)7 0 e 6^^4-1)y«
K(t) , M& + 1)*2 .. *1*2 X‘ e-'a'-*2e-’*')] l-k(k+ 1) y“X Г f * \-Ы X ’-(j+fje J 3-(ft+l)’Y‘
к 1 1 + Y. l_£(fc+l)Y* ^^(^+1)«Y‘
Rih) x 2 (ftX—x2 )e—x‘ta—x i (k\—x,) e—Za(° p.(%i-x2) [l+(fe+l)Y+^+l)Y2] 4 (A+1)T .. 1 1 + (2й + 1)т’ 0 f 1 6 1 + Ye 3^ft(^4-l)Ya
127
Таблица 4.1.12
Система из k рабочих
и одного резервного
элемента.
Облегченный резерв.
Неограниченное вос-
становление
k 0 1 0 2
E 0£v0 E
^,2=^{[l+(2ft+^)Y]±l/l+2(2ife+v)Y+^};
^,2=^{[3+(2fe4-v)'f]±/l+2(2fe-.)f+^^2} I
k (k + v)y2 t A
lf« = 2[l+(HvM ’’
Показатель Точное значение Приближенное значение Погрешность
Л °) 1 1 + (2A + v) Y kk (k 4- v) у 1 1 ЙХ (й + v) Y a+ = _ 2fe + v feX (k 4- y)
лч 1 1 + (fe + v) Y k\ (fe + v) Y 1 1 kK (k + v) y ®+ = feX
t 1 2;л —
Pm (to) -Д x,e~x‘,:r) _ _±L2±L_ ax, e l+(2ft + v)T ° 3 •x.fe(^4-y)Y’
K(f) (fe 4- v) X2 ’ “' X xf 1 -(Sie'6i< - sae-8'Z)l [ ®1— «2 J 1 k (k + V> 2 Г 1 1 2 t Г -Ъ] Д2-е 7 Л 1 J 5^(/г+у)зхз
к 1 1 + Yc 1 № + у) , 1 2 Ya &+^. fe(fe+v)* , 2 7
R(to) 2[хг (kX—Хг) e—x‘ to—xt (k\—xt) e~~x‘ (fe+y)T .. 1 1+(2A + »)T 5 ~^(/;4-v)Y2
H(^—x,)[2+2(fe4-y)Y4-fe(ft+v)Y2] l+Y.e
128
I a ii j: и u d 4 1.13
Система из k рабочих и од-
ного резервного элемента.
Облегченный резерв.
Полностью ограниченное
восстановление
k 0 1 0 ]
Е О Е, О Е
х,, = -^-{|1 4- (2k + v) 71 +
± К1 + 2 (2fe + v) Y + v2yt};
е.,г = ^Г <J2 -f- <2/г + v) yj-t
± /W 4-*V};
k(k + у) у8 , _X_
~ 1 4- (k 4- v) у ’ — f*.
Показа* гель Точное эдачение Приближенное значение “ Погрешность
r<*> 1 1 4- (2A- ч- V) Y kX tk v| y 1 1 kk (£4-4')’ 3 2k+v + ~kX (k 4- V)
7(’> 1 1 + I* + *)Y kX (&4-v)y 1 1 kX ik 4- v) Y 5+ =='kk
г 1 H- —- —
- r {ХуГ~Хг‘°— хге x,t°) Xj Xj l + (2/t+»)T ° e 8 •x. k (fc4-'1) Y*
K(O 1 Г, 1 eles [ el —es X X (e.e"'1' — ese—') j l— k (M-v)Y8 [l ~ ( K \ “T4 -(1+vOe ) S -к. (k 4- v)’y’
к 1 l — k (k 4- v) v8 8 + -s-fe <fc4-42 y*
W.) x2 (k\ — x,) e~*|(° — у. (x, — xs) [ 1 + (k + v) Y + "* — x, (a — x<) e~*,<0 -J- k (k 4- v) y8| 14-Yc X Xe 8 -4, k (k 4- V) Y*
5 Зак 943
129
Таблица 4 1.14
Система из k рабочих иодного
резервного элемента.
Нена груженный резерв.
Неограниченное восстанов-
ление
k 0 0 1 2
£ 0 0 0 £
*>.« = ^-[(1 +2*Г)±
± И 4-4^];
е,., = 1(3 + ±'
± К1 + 4fef];
/г2у2 , X
Y.== 2(1 4-fef) ’ Y“ и *
Показа течь Точное значаще Приближенное значение Погрешность
Л»> 1 f J X ЛА ^2 kf J 1 1 йЛ йу я 1 6+ ~
лч 1 / IX ах V + М 1 1 feX ky 1 S+ = АХ
г 1 2р. — —
Я»' (/„) • _ -(jqe x*to~ хге~х'‘°) Л | — —Т! j &Х/о 2 +тг е а -х. ay
К(0 /г!Х2 Г I 1—гг —гХ е1®3 |_ е1 е2 Х^1е-‘*,-еге—>') ] — — t \ — — 11 Т 1 а 7 —с ] е 1 а -ч, A’f3
к 1 1 4" Тс k2 1- —т2 s--r^3
2 [х2 (kK — х2) e~Xlt« — М* (xi — хъ) [2 4~ — Xi (kk — х:) е~***°] 4- 2*т 4- k^2] L— k\t0 1 2 + ~ —-— е *Т ( 4- .Yc а ч. k2t2
1?Э
Таблица 4.1.15
Система из k рабочих и одного
резервного элемента.
Ненагруженный резерв.
Полностью ограниченное
восстановление
k 0 0 1 1
£ 0 0 0 £
х.,г=-^г((1+2йг)±
± К1 + 4Лу];
г.2 = ~-[(1 ± V^V,
___А.
= 1 4- kf' ~~ и
Показа- тель Точное значение Приближенное значение Погрешность
ДО, а V + J J |_ Л - 2 3+ _ k\
те» 1 / 1 \ а ( +~Wj 1 1 5+==1к
т 1 Iх — —
р>’| (С.) х,-х2 <х‘е хЛ-х1е-х‘/«) 1—. а;, 2 + ~- е в -ч, к1у3
кю , Г. 1 1 1 х ®1®2 L 81 —'2 X j 1 — fe2Y3 [1 ~ + XX -у '] + — Су е ’ J 3 -ч, й’ч’
к 1 1 + Y. 1 — б2?2 а+ •х. кз-(з
R (С») х2 (а — хг) e~Xlt° — Iх (*i — х2) (1 -J- — х, (feX— х,) е-^» +^r + AY) — _ Ц- ftXZ0 _L-e 2 + хГ 1 4- г. S -Ч, кггг
5*
131
Таблица 4.1.13
система с одним резервным
элементом. Общий случай
k п = 1 I
ЕЕЕ,йЕ
______I
*1.»=4" кло+л1+м>> ±
± /(A^+Aj + М,)’—4Л.Л,),
ei,t — ~2~ I(Ло + Л] + Ml + j;
d” V (Л„ -f- Л] + Л11 + М2)2
— 4 (A0Ai -f~ Л|>Ма .lljilj) ];
ЛрЛ J
f« = M2 (Л. + М,)'
Показатель Точное значение Приближенное значение Погрешность
7(’) At 4~ At М, AqA] М, ЛвЛ/ „ Ло+Л, 8+ АцЛ,
7(4 Ар + Mt A0Aj. М, AqA] з+ = 4;
1 М2 — —
fw (ta) 1 х -х* X XU1 л2 е-лА) AqAj Л0+Л1+М, ° е Л.Л, д'-йГ
‘-тгф-ггггХ е1®2 L *! ®2 Х(®1 е-'>'-е,е—*') J Л0Л, Г 1 1 Mjiu, [* м2 —м, X Х(М2 е~м>' -М> е-м*')]; если М, = №г = М, то 1-з£Ч1-(1 +Ж)е-М/]
к 1 1 + Y. ЛсА, 1 М1М2 з Л"Л1 м?м.
K(ta) М2 [х2 (Л] — хг) — . A»Ai t * Д0+Д1 + М1 ® 1 + Y.e
(Xi — х2) (AqA, 4- — х, (Л, — х,) е~
+ Л,М2 + М,М2)
132
Таблица 4.1.17
Система из одного рабочего и п
резервных элементов.
Нагруженный резерв.
Неограниченное восстановление
р. ’ — г] (/п—г)! >
I п 0 0 п + I
Е Е О О Е
Пока- затель Точное значение Приближенное значение Погрешность
Л») $ , " SC«+iYl 1 УЧ 1=0 (1+л)хДг с« , 1 (i Ч-n) Ay" 14-n(n4-l) + 'ч'А(л4-1) л?п~*
Л») п (1 + il) Tj ^n + lf* i (1 +«)XYn ®+
т 1 (1 +«)|A — —
«•)(/,) См. табл. 4.1.1 exp (1 4- n) Af<, n a^(«+i)Y"+’^7 /^i
s n SCn+lYl У1 4=0 В C^‘
к 1 I + Y. 1 y«+i «+ ~ (n + l)Yn+’
«(О См. табл. 4.1.1 Xexp 1 + Y«X (l+n)A/0 ч 6Mn4-l)Yn+’X 4 т /=1
*da о a +
^4 C^Y« s=0 n 1
133
Таблица 4.1.18
Система из одного рабочего и п резервных
элементов.
Нагруженный резерв.
Полностью ограниченное восстановление
гг т’
'“т rl (т — г)1
X
1
П + 1
1=1
1 п 0 0 1
Е Е О О Е
Пока- затель Точное значение Приближенное значение Погрешность
г (°) п S х S 2 (i + l)'C‘ + 1 , л1 s—0 1=0 л—S-H4-I J 1 1_ п+1 + ~ X 1«—+
7(п) п 1 1 х ZJ (i + D’f 1=0 1 1 * «'fis+D1 6 ' ‘ 4- X п1л-1
т 1 * н — —
p<.°)(tc> См табл. 4.1.1 ехр Х/р ЕЁ^Н s=) 1=0ХСя_5 + ; +)7 5~Тя + | («4-1)1 п
к 1 + 1 — l"4-1 (Л + 1)1 5+~1« + 2(л4-1 (л 4-1)1
R (<о) См. табл 4*1.) хехр '+1. * ' ЕЁ^.'гг, s=0 1=0х л—^ + / + 1* (Л + 1)1 П
134
I а блица 1 1.19
Система из одного рабочего и п
резервных элементов.
Облегченный резерв.
Неограниченное восстановление
10л 0 л-|-1
Е 0 £, 0 £
—
J21L П [!+(«+!-г>4
<,+'"’ г=|
,е = _------.---------------.
24г П11+(п+1~г)’)
1=0 г=1
X 0
т = —: П11 + (п + 1-г) >1-1.
Г = 1
Пока 1 затель 1 Точное значение | Приближенное значение Погрешность
п *'2^г-п il+(rt+ 1 п> 1 s ~_L12_rl>Lx + * 7"-i л
у(0) 1 VI ‘-( Г = 1 . S=O 17 (1 + (П + г=1 + !—') »1 * + 1 - г) ,) | X п + ] п u+(n+i—о»1 Г=1 л + 1 + л*» х П + 1 Ц (l + pl + l-r) »/ г=»1
П 1 2 т‘ п П+ («+'-'•>»] 1 п' i-O '=[ I п 1 j ’ _Л_х + А -1 1 + flsv
к п-Н fJ[l + («+l-r) ¥]
т(п> X п+1 П 11+(« + !—О »1 Г=1 Г=1 Я + 1 П I' + l" + 1 -Г) »| т=|
* 1 (л + 1) V — —
P(’'(W См. табл. 4,1.1 , tq_ е Г<°> .~ll+nv]Vn+,2TX (=1 х ^7 |'+ vl 1=1
к 1 1 («4-1)1 Х л + 1 X П U+ (л + 1-O’I г=1 ,«+2 " + п- * я + 1 X П U+ (л+1-r) »| Г«1
Ом. табл. 4.1.1 —— е" Т(а> 1 + 1, 5~.(1+л>1 1Я+’2 т * /=1 х п 11 i=i
135
Таблица 4.1.20
Система из одного рабочего
и л резервных элементов.
Облегченный резерв.
Полностью ограниченное
восстановление
я + 1
7П+‘ П (1+ (л +1—г) V)
г—1
п I
2 П
1 0 п 0 1
Е 0 0 Е
0
I — PJ l + w + Ud»=‘
г=1
Показа тель Точное значение Приближенное значение Погрешность
г(0) я S ;‘П U+lfl + l-r)»] 1 V i-=o Г-1 1 1 X «4-1 7пП '+ 'Гх '4- Hv
X ZJ S + 1 s=0 т* П г> *1 Г = 1 Х я+1 ^Л-’П l+n + l—l-)v) г=|
у(л) У ?П 1>+(л+1—О’) । 1=0 г=1 1_ 1 с+~г х } -г«»
л +1 J7 il+(n + l— Г)*] Г=1 X я + 1 т" П ll+(« + l—г) Vi '=1 х П 4- I т"-1 П 3+ « + '—г Г=1
т i — -
р(0)(/о) См табл. 4 1.1 е ’**” ь~тп+'х п X П 11+1»—•)»] 1=0
л ) 1 + 1. 1-7п+,Х н + 1 х П и») г=1 6+ ~ 1п+г (!+»») X л + 1 X П |1+1« + 1—'’)«) Г=1
л (*о) См Талл 4 1 1 _ *0 1 t Т(о> 1 +т0 г+~»1я+1х п х п 1+<«—0*1
136
Таблица 4.1.21
Система из одного рабочего и п
резервных элементов.
Ненагруженный резерв.
Неограниченное восстановление
1 0 0 п п+1
£ 0 0 0 £
1
Т«= п+Л '
Sc‘!+,v
1=1
__Л_. Cr ml
~~ у. ’ т г! (т—r)i'
Показа тель Точное значение Приближенное значение Погрешность
л») + + — е и Л «+-4-х z (1 + п)' X л^п-1
Тт н- О 1 п< Л 7“ й J п' д+ ~ х 7"-*
1 (1 + п) р. — ——
«•) (G) См. табл. 4.1.1 i ^0 ехР п 1 1 X cJi! £ / 1=0 уп + 1 п хХ-7- 1=1
К 1 1 4-Те уП + 1 1 (п+В! уП + 2 (п +1)!
Я(М См. табл. 4.1.1 1 ( Л/. А 1+1.СХР ’« “ ГС<+1Л ( Zj S+i 1* J 1=0 тп + 1 ] ni 2L / ,=1
।
137
138
Таблица 4 1 23
Система из k рабочих и п
резервных элементов.
Нагруженный резерв.
Неограниченное
восстановление
k п 0 0 л-}-}
£ Е О О Е
<V = fi+n С'щ -
Пока зателъ Точное значение Приближенное значение Погрешность
7(0) 51- iTM“ 1 V о “ 35* 1 АХСд? тп V/z 8 1+~ + (*+i))4+i з"-1
Т(я> 1=0 1 МСн 1п 6+ Л-1 )Су_1 7
-S 1 (n + l) ц — —
— См табл. 4.1.1 Sxp £ »[аН! "у • 1 . 1п+' 2 т 7=1
л — 1 +3. , „« + > ,п+1 - SV 3 5 + ~<т" + 2
См табл. 4.1Д i 1 м= - °" а ” Ъ-^kCN т"+1 2 Г /=1
139
Таблица 4.1.24
Система из k рабочих и п
резервных элементов.
Нагруженный резерв.
Полностью ограниченное
восстановление
.. «Г
М=Л+я; Сг = ; 1 1 t
т г*
к 1
*=iT: •>. = ;------
k п 0 0 1
Е Е О О Е
Пока- затель Точное значение Приближенное значение Погрешность
Г (°) я $ ' у V 1 1 1 l ч~ > * х c«+i
(1 + 1)1 С'+1 . .? s=0 (=0 N—s + l l”(n + l)lC« + '
r(«> п Х 3 (i + lp C' + 'y* <=0 *+' 1 1 X 1п (Л1 + 1)1 с”+1 б+~4-х Х ’"-1”
т I м> — —
pW (/о) См. табл. 4.1.1 ехр п S 1 2 3 (/+1>1С‘+| л*! >=Si=0 /V-s + i1 j J ~ (n + IV X X пС« + |1я+‘ /V
к 1 1 + ’« 1 —(п + 1)1С" + '-("+‘ а+~ (« + i)i х X NCnv+,tn + 2
См. табл. 4.1.1 X ехр ч-т. х X t, П л 2 3 (/+!)> с' + ' ,т‘ s=0 i=0 N—s+l 8 + IV т? X пС« + 11п + ‘ N
140
Г а б 1 и ' । а 4 1.25
Система из k рабочих и п
резервных элементов.
Облегченный резерв.
Неограниченное восстанозление
ft 0 п 0 п 4- 1
£ 0 £, О Е
О +-! ’•-т-гг* 2 4“ ПI* + <п +1 - г> ’] 1=0 Г=1 0 ,_L. П I» + (п + • — о»1 = с И ’ Г=1
Пока затель Точное значение Приближенное значение Погрешность
Tf) s < ‘ п «' 2 IT II tA+(n + l—г)»] L ’V <=о '=1 * S + 1 s=0 7s п [* + (» + 1— ') ») г=1 1 п1 к т»х х —j—! п + 1 П |*+(п + 1—Г)») >•=1 , 1 (п-1)1 ’+ ' Г —« V X т X Я — I V п2,+ (я + 1) * х rt + l 1*+ (П +1— г) у] Г=|
Г(п) 2 H-J] !*+(«+l-П ») 1 П> *=«> г=| k т” п+1 П 1* + Iя + 1 — О »J Г=1 L Пх х ;»х Хп + 1 ’ П [* + (« + ! — г) »] г=1 . 1 п< 5+ ~ г ргп х v b+ nv х л + 1 1“[ (*+(«+ 1—Г) у) r=J
1 (п+1 )1* -
₽(•)и») См табл. 4.1.1 В Г<°> S [Л + «у] тп + ’ х я я /=| <=|
к 1 1 + т. Я + 1 ' (1+п)! X п + 1 х П [*+(«4-1—Г) »j Г=| »Я + 2 г+ ~(1+«)! ‘*+"’!Х Я + 1 П [* + (п + 1 - Г} у] Г=]
См. табл. 4.1.1 tp ' е Г«” 1 + 1. ь — [fe + nvj yn+1 X я я xSzLn^^’ ,=1 1=1
141
Таблица 4 1.26
Система из к рабочих и л резерв-
ных элементов.
Облегченный резерв.
Полностью ограниченное восста-
новление
7п+1 П W+ 1 — r)v!
k 0 п 0 1
Е 0 О Е
X? ni* + (п + 1 — г)»|
г=1
ч О
т=—"• П [* + (п + 1 — О ’1 = 1 •
г=1
Пока затель Точное значение Приближенное значение Погрешность
г(°) з 1 п S 7< П (*+<« + '— о»! t 1=0 r= 1 1 5+~Г * ‘>н + Г? » х п +1 Гп' * fl (*+(»+>— Г = 1
X /1 3 + 1 T* П I* r=l X ., + 1 in П r^i r=l
Т<«> n r t 2 Г* -П /*+(«+ 1 Z=9 r=l 1 6+~г* £+«»
X n + 1 ln П !*+(«+ r=| X n+ i In П l*+ (^+ 1— r=l п+1 1п~ 1 Л+ rt+L—rjvl r=i
1_ — —
рС>)(М См 1абл 4 1 1 e r(°’ 8~njn + 1X п хП Z=0
К 1 1 +1. n + 1 1—Tn+1 J} [* + (« + !—r)»l r=l s + — Jn+![fc+nv]x n + 1 x П (*+(«+ '-H’l r=l
RIV См табл. 4 1.1 — 1 T(0) S~nin + ,X n xfl [*+("— 0’1 i=0
142
Таблица 41 27
Система из k рабочих и п резерв-
ных элементов.
Ненагруженный резерв.
Неограниченное восстановление
k 0 0 п п+1
£ 0 0 0 £
1
Тс = н + 1 >
C«+l (W-
i=i
_L- rr т'
7 р ’ r'(m — г)1'
Показатель Точное значение Приближенное значение Погрешность
Т(») LVc‘+1 — п+' (Ат)’ 1 п kt. (/{•(')“ 1 (1 + я)| б+^АХ п(Ат)"-1
Л") 5|- <?> 1 п' АА (АТ)” 1 п' 5+~ а (л-т)”-*
1 (1 + /г) р —
Pm См. табл. 4.1.1 ехр - г- а <?> а + + о £ 1 ? *О !
к 1 1 + Y. 1 №У+' 1 (1 + п)\ » (feY)n+i й + " (1 +п)1
К(*о) См. табл. 4.1.1 1 / йА/о т ’ + ^eXPj ' ,1 J 1 J] Cn + 1 I о» ? "'I-
143
Таблица 4.1.28
Система из k рабо Ненагр Полностью огр чих и п ре (уженный аниченное k 0 0 п 1 Е 0 0 0 Е зервных элементов, эе^ерв, восстановление (fo)"+l (1 — feY) . Ye “ 1 — (kt)n+' ' X 1 Y ~ p. < K.
Показатель Точное значение Приближенное значение Погрешность
Tt*) 1 l-(fe7)"+1|l + ('i+ kk W(l—*Y)a J 1_ kx (Ay)” . 2 + kk(kt}n~l
T(”> I I —(feY)”*1 kX (*y)”(1—*Y) i i_ kk (kt)n
T 1_ P- — —“
P(01 (1„) См табл. 4 1.1 / —k^kktj, I exp| l-(*Y)n+1[l+(«+l)(l-AY)|( S n (AY)n+I
к 1 1+ Y. 1 — (^Y)n+1 г+ - (*y)«+»
См. табл 4.1.1 f (feY)" (1 — feY)8 feXt„ 1 exp( 1-(£y)',+‘|1+<«-H>(1-£yH f г n (£y)"+1
1 + Y<>
Показатель Система
Точное значение О os
k п—п 1 Е Е Е^ОЕ резервными элементами. 5щий случай
Приближенное значение
Погрешность
з 0 3 • М = ? i ф + ~ Ф 1? > Ф
4.2. Системы с «быстрым» восстановлением
и некоторые другие частные случаи
В настоящем параграфе приводятся показатели надежности для
некоторых частных случаев систем с «быстрым» G* (/) и произволь-
ным G (I) законом восстановления*.
Точная формулировка «быстрого» восстановления и соответствую-
щих условий приближения (в виде некоторых ограничений на функцио-
налы от функций распределения времени работы F (/) и времени вос-
становления G* (/) элементов системы) сложна и громоздка. Смысл
этой формулировки, грубо говоря, заключается в требовании, чтобы
вероятность отказа (одного) элемента системы за время восстанов-
ления (другого) элемента была бы мала.
В этом случае справедливо (подробнее, в том числе и об условиях
приближения, см. работу А. Д. Соловьева. Резервирование с быст-
рым восстановлением, «Известия Академии наук СССР», Техническая
кибернетика, 1970, № 1) асимптотическое представление для вероят-
ности безотказной работы и средней наработки системы до отказа
(табл. 4.2.1).
Система
k 0 1 0 1 (2)
Е 0 0 G
с произвольным восстановленьем Q (t)
Точное значение вероятности безотказной работы системы имеет вид:
Р°’(/о)== 2 (4.2.1)
Здесь
^0
Bi (Q = 5 Вi-1 (to~x) В (х) dx;
о
о
Во (/0) = Q—(k+v) е—х e-vU [1 —G —x)J dx;
о
to
В (/0) = е~ш» (k + v) 1. g (t0—z) dz;
о
g(0 = G'(0. (4.2.2)
* К моменту сдачи рукописи в набор авторы не располагали кроме приве-
денной в этом параграфе никакой другой информацией, касающейся систем с
«быстрым» восстановлением, и будут признательны тем читателям, которые со-
общат свои или просто известные им новые результаты.
146
Таблица 4.2.1
Система с ^быстрым" восстановлением
00 00
T=\tdF(t), mk= J thdG (Q;
о о
Л = (0)Гд~^; X
*—i
S/ 1 \n.+s+l
C|_I(n>+s + l)'”^— ) X
s=0
Г ! -1Л-.-1 >
X у - F' (°) I
система
Р (Q
7<»>
k ni 0 пг I
F F О О G*
Атп,+п, *1
0~ («i + Ла)1
-Ь
Атп^п,
k nt 0 п, nt + п,
F F 0 0 G*
S. 1
е (я.+яз)1
(п, + л,)!
Ат^+п‘
I О О Л I
F О О О G*
IF’ (0)1" t0
nl Т
е
m„[F' (0)]»
I О 0 п п
F О ООО*
[m,F' (0)|я ta
nl Г
е
ImtF’ (0)]»
Если время t0 мало по сравнению со средней длительностью цикла
(средней длительностью между соседними моментами восстановле-
ний), т. е. если
тг + г,
«Л
147
ГАС
т = ^tdG (/),
о
то ряд (4.2.1) и (4.2.2) можно эффективно использовать для вычисления
вероятности Р(0) (t0), так как он быстро сходится и первые два-гр:!
слагаемых дают достаточно точно сумму ряда.
Точное значение средней наработки до отказа, а также прибли-
женные значения вероятности безотказной работы и средней наработ-
ки до отказа при условии, что вероятность а отказа системы на
одном цикле
а = $ (1—e-*A‘)<iG (/)
о
мала, представлены в табл. 4.2.2.
Таблица 4.22
А: 0 1 0 1
Е 0 Еу О G
Система
а = J (1 — dO (t),
О
со
I = | tdG
о
: = j/ j (/ - т)г dG (/).
Показлель Точное значение Приближенное значение Условия приближения Погрешность
Г(«) ±+ 1 — XX ~ (Х+v) а 1 (k + v) аХ а 1 1 8+ = XX
А»/ (/.) 1 *0 е г(«| а 1 й О (а2)
е- (£+v) й х. О (а)
е— (* + ») а 1, / а2\ ХХт 1 -|- J 1 —
Ha практике часто бывает известна не сама функция распределения
времени восстановления G (0, а лишь только п, несколько ее первых
моментов, например начальных: mlt т2, ...» тп. (Обычно при испыта-
ниях устойчиво наблюдаются первые четыре момента.) В этом случае
148
для величины Т<°> могут быть получены следующие оценки снизу
Т(0> и сверху Г<°> (табл. 4.2.3).
Таблица 4.2.3
Оценки Т1‘) и ТС» для средней наработки до отказа
системы
*0101
Е 0 Е, 0 G
п
г(«>
г(®)
[X (* + v) (1 — е~
со
mt, m2
(* + *)(! -е-^)]-’
т\
I mi /
йС+ ^Гх(&+у)\1-е
тг
niv tn2,
-^-+ [К (fe+v) (1—р<,3) е Шо *
,ч. — feXip)
-рре 1 )]-’
/и2
— X.
1 ,ni /
^X(fe+v)(1-e
krrii
fnit m2 tnlt
m.
^4- [Л (k+v) (1—р^ е ’
,3> —ш<3)
—ТГ’е 1
-jgj- + [Л (£-}-*) (1 — Р^
,4) -Ш<4> «) _-ЛН<4'
— p<ve । —/?у' е 2 )
В табл. 4.2.3 обозначено:
К ’ 2 2 У4а| + Щ
«з_тКМ+«!.;<
2аг
= [2 (mt tn3—/и!)]-1 [^1 m4—m2 m3=F
4= V(/Щ т^—тг тзУ—$ m3—ml) (т2 ;
aa —m2 — m\\ a.x — tn3—‘imimx + 2m’\.
Если величина X мала, то вместо табл. 4.2.3 можно пользоваться
табл. 4.2.4.
149
Таблица 4.2.4
Оценки 7у>) и Г(«> при Л-»0 для средней наработки до отказа
системы
k 0 1 0 1
Е 0 £, О G
m2 = ; X —» 0;
т2
т3 —----;
—13 т,
т3— 2тЗтгт3 Ц- /Пд 1
т4 =-------------2-----.
— тг — т\
-0;-+ |Ы,А (k + v) Л]-1
т,, тг
kk
-у^-+ p/HjX (k + v) Л ^1 —
й/я2 \1“’
2/П, ) J
1 , Г. ( km,
lr+p/n1X(^+v)x(l-g^-X+
k2m3 \ 1 ”*
+^A2)J
m3, п1г,
m3, tnt
-^+Г^Л(^)хЛ-^-Л+
~+ pm.X (k+v) к (1 - Л +
, fes'»3 ,2 k^nu \1 -1
+ bm-i 24m,
Для моментов реальных функций распределения часто выпол'
няетсЯ условие так называемого квазистарения n-го порядка:
а1 а2 Ok > On
°0 °1 аА-1 °п-1
где ak = ; а0 = 1. В этом случае справедливы следующие оценки,
приведенные в табл. 4.2.5, в которой обозначено:
а2
150
где
2)
п0,1
1 + mi
2 ~ 2Va|+mf
т'1* 4,2 — [2 (r/Zj т3 — ml)] 1 ]Шу т4 — т2т3+
=F- —m2 mJ2—4 (m^Zg—ml) (т2т4—т3)Ь
По4’ = 1 — Л1!1'—лУ1’, Л^2 = =р
ОТ2 —
’1*Л (’г4' —’141)’
tnt = 4m1 т3.
Таблица 4 2.5
Оценки для _Г<’> и Т(’> для средней наработки до отказа „стареющей"
системы
k 0 1 0 1
е О £, О G*
т(»>
£x+[<ft+v>x (4—
--Le-^)]”
-^ + [(* + *) Mi-42>е **“ х-
_пре-ЪРХ)]-’
1 Г/п1 /
wc+[^7 {k+'>} Ч1~
1 <3>
+ [(*+») * >е 0
mb тг, mt
_^(3) е”«/3)Х)]-«
+ v) (1 — по**
(4) -*Т<4)Х (4) -Ц4>Х
-пре 1 —we 2 )] ’
Если величина X мала, то вместо табл. 4.2.5 можно пользоваться
табл. 4.2.6.
Показатели для еще двух резервированных систем в случае про-
извольных законов отказов и восстановлений F (0 и G (0 приведены
в табл. 4.2.7 и 4.2.8.
151
Таблица 4.2.6
Оценки при л.-»и для Г(о) и Г(0'
«стареющей> системы
А 0 1 0 1
Е 0 О G*
т, — /Пр X -» 0;
т2
т| — 2zzz, z?z2zn а + f^2
mt = ’
О
т2 —
тп = пгпхт
п L$ Гс)
Wj 1 Г ( —I-1 km,\ (k + v) (1 — km, XT — 1 2m, ХЛ —h £й/п.Х (й 4- v) X ^1 — kmt \1~‘ 2m, J 1
mtl т2 —h £й/п,Х (k + v) X — kmi k'm, \]_| 2m, X + Sm, Х‘Л jX (k + v) A — km2 k*m3 \l—l 2m, X+ 6m, X J]
nil, ni2, 1 Г f —I- 1 km ,X (k + v) X 1 1 — km, k'm, k*mt XT —1 о X 4" а. X8 ла X* ) I 2m, 'but, 24m, J} ^+[йт,Х (*+v)x(l-^-X + , k*m, k*mt , \1~1 1 6zn, X “ 24m, X Л
Таблица 4 2.7
Система 10 0 11 F 0 0 0 G ^=^F{t)dG (I); 0 00 T = j tdF (t). 0
Показатель Точное значение Приближенное" значение Условие приближения Погрешность
TV) 1 "Ь a ~ —— T a T a a 1 «+ = 7
PC'(/.) __ a/® e~“ —
152
Таблица 4.2.8
Система
I п О О п 4- 1
F F О О G
Т = ^tdF (О;
О
1 = j tdG (/).
о
Показа тель
ToiHoe значение
Приближенное
значение
Условие
приближения
Погрешность
. Список литературы
1. Васильев Ю. А., Козлов Б. А. О влиянии вида закона распреде-
ления времени восстановления на надежность дублированной системы. —
В кн.: «Теория надежности и массовое обслуживание». Под ред. Б. В. Гне-
денко. М., «Наука», 1969.
2. Васильев Ю. А., К о з л о в Б. А. Резервированная система — си-
стема «стареющая». — В ки.: Теория надежности и массовое обслуживание.
Под ред. Б. В. Гнеденко. М., «Наука», 1969.
3. Гнеденко Б. В. О дублировании с восстановлением. — «Известия АН
СССР. Техническая кибернетика», 1964, №5.
4. Гнеденко Б. В. О ненагруженном дублировании. — «Известия АН
СССР. Техническая кибернетика», 1964, Xs 4.
6 Гнеденко Б. В., Наср Ю. О ненагруженном резервировании с вос-
становлением. — «Автоматика и телемеханика», 1968, №7.
6. Г н е д е н к о Б. В. Об эффективности восстановления резервированных
устройств. — В кн.: Предельные теоремы и статистические выводы. АН
УзССР. Институт математики им. В. И. Романовского. Под ред. С. X. Сираж-
динова. Ташкент, «Фан», 1966.
7. К л я м к о Э. И. Надежность систем с восстанавливаемым резервом. —
«Известия АН СССР, ОТН, Энергия и автоматика», 1961, № 3.
8. К о в а л е и к о И. Н. Об условии независимости вероятности состояний
системы от вида распределения времени обслуживания. — «Проблемы пере-
дачи информации», 1962, вып. И.
9. Козлов Б А. Об определении математического ожидания времени по-
падания системы в поглощающее состояние. —«Известия АН СССР. Техни-
ческая кибернетика», 1966, № 4.
10. Марьянович Т. П. Надежность системы при наличии резерва. —
«Доклады АН УССР», 1961, Xs 7.
Н. Марьянович Т. П. Некоторые вопросы надежности резервированных
систем. — «Украинский математический журнал», 1963, т. XV, Xs 2.
153
12. Соловьев А. Д. Асимптотическое поведение больших отклонений
в процессе гибели и размножения. — В кн: Кибернетику — на службу ком-
мунизму. Под ред. А. И. Берга, Н. Г. Бруевича, Б. В. Гнеденко. Т. 11. М.,
«Энергия», 1964.
13. С о л о в ь е в А. Д. Асимптотическое поведение момента первого наступ-
ления редкого события в регенерирующем процессе. — «Известия АН СССР
Техническая кибернетика», 1971, № 6.
14. С о л о в ь е в А. Д. Надежность систем с восстановлением. — В кн.; Ки-
бернетику — на службу коммунизму. Под ред. А. И. Берга, Н. Г. Бруеви-
ча, Б. В. Гнеденко. Т. II. М., «Энергия», 1964.
15. С о л о в ь е в А. Д. Об определении резервов для систем многократного
действия. — «Известия АН СССР, ОТН. Энергетика и автоматика» 1962,
№ 2.
16. С о л о в ь е в А. Д. Одно комбинаторное тождество и его применение к за-
даче о первом наступлении редкого события. — «Теория вероятностей и ее
применения», 1966, т. XI, вып. 2.
17. С о л о в ь е в А. Д. Предельные теоремы для процесса гибели и размно-
жения. — «Теория вероятностей и ее применения», 1969, № 4.
18. С о л о в ь е в А. Д. Резервирование с быстрым восстановлением. — «Из-
вестия АН СССР. Техническая кибернетика», 1970, № 1.
19. С о л о в ь е в А. Д. Эвристический вывод характеристик надежности
резервных систем с быстрым восстановлением М., «Знание», 1968
20. У ш а ко в И. А. Об оценке одного показателя надежности системы с вос-
становлением. — В кн.: Прикладные задачи технической кибернетики. Под
ред. Л. С. Гурина, И. А. Ушакова, Б. С. Флейшмана. М., «Сов радио», 1966
5
НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОССТАНАВЛИВАЕМЫЕ
РЕЗЕРВИРОВАННЫЕ СИСТЕМЫ
5.0. Предварительные замечания
В настоящей главе проводится оценка показателей надежности
некоторых специальных резервированных систем в предположении
экспоненциального распределения времени работы и времени восста-
новления каждого элемента системы.
Подробное описание моделей рассматриваемых систем приводится
в соответствующих параграфах.
5.1. Восстанавливаемая резервированная система,
состоящая из п + 1 элементов с разными
показателями надежности *
Рассматривается резервированная система, состоящая из п + 1
элементов с разными показателями надежности, характеризующими-
ся интенсивностями отказов и интенсивностями восстановления
щ; Х2, р2; ...; Х;, рг; ...; Xn+I, рп+1 соответственно. Резервирован-
ная система функционирует непрерывно, при этом контроль работо-
способности элементов предполагается полным и безошибочным.
Кроме того, делается допущение о том, что переключающее устрой-
ство в системе характеризуется высокой надежностью и весьма ма-
лым временем переключения.
Система считается отказавшей в некоторый момент времени t,
если в этот момент все «4-1 ее элементов неисправны и находятся
в режиме восстановления (рис. 5.1.1).
Оценки сверху и снизу для всех показателей надежности рас-
сматриваемой системы легко получаются при введении в рассмотрение
«верхней» и «нижней» систем.
«Верхняя» система —это система, состоящая из п. 4- 1 идентичных
элементов с параметрами К, р, определяемыми как
X = min hit
р — шах рг-;7 = Х/р.
!</<«+1
* В данной главе элементы с разными показателями надежноств будем на-
вивать для краткости разными элементами.
155
«Нижняя» система — это система, состоящая из п + 1 идентич-
ных элементов с параметрами X, р определяемыми как
X = max Х;,
р = min рг;у = Х/р.
l-i.n-f-l —
Для случая неограниченного (полностью
ограниченного) восстановления оценки свер-
ху и снизу для всех показателей надежности
рассматриваемой системы- легко получаются
из табл. 4.1.17 (соответственно 4.1.18), где
вместо величин X, р, у надо взять:
X, р, у — для оценок сверху,
X, р, у — для оценок снизу.
Рис. 6.1.1. Структурная схема резервированной си-
стемы нз п+1 элементов с разными показателями
надежности.
Для случая неограниченного восстановления в рассматриваемой
системе некоторые показатели надежности приведены также в
табл. 5.1.1, в которой уг — Хг/рг.
Таблица 5.1.1
Резервированная система из л 4- 1 разных элементов
Неограниченное восстановление
Пока затель Точное значение Приближенное значение Погрешность
Т(») — 1 n+l п+1 2 'Х‘П Yi <=1 /=1 п + 1 2 Y< 8+ П 4-1 п + 1 2 П Yi i=i i=i
тт 1 п+\ 1=1 ” rt + l ~~ П (1 +ь) ' 1=1 1 п + 1 п + 1 2 П Yi <=i 1=1 >= да! >1! £ г
1 и + 1 2 р,£ — —
к п + 1 •-П t=1 и + 1 ’-П * 'л+1 П+1 г+ ~ 2 Y< П YJ 1 = 1 /=|
156
5.2. Восстанавливаемая резервированная система,
состоящая из зависимых элементов с разными
показателями надежности
Для повышения надежности наиболее сложных или особо ответ-
ственных устройств нередко приходится применять так называемое
функциональное резервирование, заключающееся в том, что основ-
ное (рабочее) устройство резервируется устройствами, не'аналогич-
ными ему по своей структуре и зачастую основанными даже совсем
на других принципах. Так, например, электронное устройство может
резервироваться механической или оптической системой и т. п.
Такие устройства, резервирующие рабочее устройство только по
его функциональному назначению, характеризуются весьма сильно
Л л lf> // //!f}
. Л2-Лг»/^>Л
Рис 5 2 1 Структурная схема дуб-
лированной системы из элементов
с разными показателями надежно-
сти.
Рис 52 2 Граф переходов из одного со-
стояния в другое дублированной системы
из зависимых элементов с разными пока-
зателями надежности
отличающимися интенсивностями отказов и восстановления и часто
являются зависимыми по нагрузке (входным параметрам), которая
в случае отказа одного из устройств перераспределяется на устройст-
ва, оставшиеся исправными.
В данном параграфе рассматривается только два частных случая
системы с функциональным резервированием, а именно: оцениваются
показатели надежности дублированной системы и системы из трех
элементов, в которой отказ двух любых элементов приводит к ее отказу
(система типа простейшего мажоритарного элемента).
5.2.1. Дублированная система. Для данной системы (рис. 5.2.1)
обозначим:
Xi2’ (Хр') — интенсивность отказов первого (второго) элемента
при условии, что второй (первый) уже отказал;
|Х12,(ц г1’)— интенсивность восстановления первого (второго) эле-
мента при условии, что второй (первый) элемент также
уже восстанавливается.
Граф переходов дублированной системы из одного состояния в дру-
гое представлен на рис. 5.2.2, где обозначено: Но — состояние систе-
мы, в котором отказавших элементов нет; Н± (Й2) — состояние си-
157
стемы, в котором отказавшим является первый (второй) элемент; Я1|2—
состояние отказа системы, в котором отказавшими являются оба
элемента.
В табл. 5.2.1 приводятся точные и приближенные формулы для ос-
новных показателей надежности дублированной системы.
Таблица 5.2.1
Дублированная система из
разных зависимых элементов.
Неограниченное
восстановление.
4” Л<2>
ai~4'’+<
A, *2
?. = X(D ’
Ф1 = (1 — я2) (1 -f-
4~ a2^2 (1 -j- a i г , Ф2 “ (1 я i) (1 +
\ Л2 /
4~ я2^2) -|- a>?i f 1 4- a2 )•
Пока- затель Точное значение Приближенное значение Погрешность
Г(») 1 + а1?1 + Р-1|Х2
«Л1 + а+а Х,Х|(2)Н.1 4- МрРч
Г(*) Н -f- р-2 фа ((Ар 4- 14”) («Л 4- а,К.) Р-1Р-2 А^Р’р., 4-МрН2 3+""Г
' т (Н(2> 4-^”)-* — —
к (1 । я1^< 4~ я2х2 1 V л+14%; 1 (42> + p-2I,i 8+ - 2?
Приближенные формулы, приведенные в табл. 5.2.1, справедливы
при выполнении условия
. (5.2.1)
где
1 = шах (A.J, Л2, М2)> А.?1 ’);
н = н(Л1Л.
158
Нижние (грубые) оценки для вероятности..безотказной работы и
коэффициента оперативной готовности системы имеют вид:
P(/0) = e-2v х/„/(1+зу), (5.2.2)
(5.2.3)
где значения величин аъ а2, и ф2 приведены в табл. 5.2.1.
5.2.2. Система, состоящая из трех разных зависимых элементов.
Для данной системы (рис. 5.2.3) будем пользоваться двухиндексны-
ми обозначениями для интенсивностей отказов и восстановления,
например:
Рис. 5 2.3. Структурная
схема системы из трех эле-
ментов с разными показа-
телями надежности.
Рис. 5 2.4. Граф переходов из одного состояния
в другое системы из трех зависимых элементов
с разными показателями надежности, отказ двух
любых из которых приводит к отказу системы.
А.!,1’ — интенсивность отказов третьего элемента при условии,
что первый элемент уже отказал;
р'12’ — интенсивность восстановления первого элемента при усло-
вии, что второй элемент уже восстанавливается и т. д.
(см. § 5.2.1).
Отказом системы считается отказ двух любых ее элементов, при
этом отдельно эксплуатация оставшегося исправным (третьего) эле-
мента не производится.
Граф переходов системы из одного состояния в другое представ-
лен на рис. 5.2.4, где обозначено:
Но — состояние системы, в котором отказавших элементов нет;
Д2 — состояние системы, в котором отказавшим является второй
элемент;
Hi з—одно из трех состояний отказа системы, в-котором отка-
завшими элементами являются первый и третий и т. д.
Средняя наработка до отказа рассматриваемой системы задается
выражением
j'(O) __ t>! bz 63 4-X) b3 4-X2 bj Z>3 4-A.3 b1 (5 2 41
М(1)Мз+Ы<2)Мз + ^(3>М2‘ ' ’ ' ’
159
где
1<” «1< ”4-ЦП; 1<г) = 1(2) + Ц2). >.(3) = х(з) + цз). (5 2 5)
£t = W> + f4; ^а = Х<2> + Иа; 68 = Л<3> + нз.
При выполнении условия
y = V|i<l/3, (5.2.6)
где
1 = тах (\, 12,1„,1<2>, Ц3>, 1<»>, 1<3>, 1<”, Ц2>):
!! -mln и,, |*„. иГ. Р$”, н4”. rf’. hS”)
может быть получена следующая приближенная формула:
° 1) _______________М-i Ц2 н __________ (5 2 7)
Xj V1' ц,2 ц,з + Аг л? щ U3 + A3 А111 Ц1
при этом абсолютная ошибка формулы (5.2.7) имеет соответственно
порядок:
6+~ 5/61 для Т(0); (5 2 8)
6+~ 1/21 для 74”. (5.2.9)
Оценка сверху для среднего времени восстановления системы имеет
вид
т = 1 /р. (5.2.10)
В табл. 5.2.2 приводятся нижние грубые оцен«и для основных
показателей надежности системы.
Таблица 5.2.2
Восстанавливаемая система из трех разных зависимых
элементов, отказ двух любых из которых приводит
к отказу системы
Показатель Нижняя грубая оценка
Р (/о) 6? Г t0 е ,+5~
к 1 + 3? 1 + з-г + 3Т‘
R(tJ _ “to 1 + зт 1 + з7+ 3Ve
160
5.3. Восстанавливаемая система и «канальная»
надежность
5.3 1. Постановка задачи. В практике часто встречаются случаи
использования скользящего резерва для повышения надежности
системы. Оценка показателей надежности системы из k последова-
тельно соединенных (рабочих) элементов со скользящим резервом
из п элементов в случае обычного критерия отказа системы (отказ
любых п + 1 элементов есть отказ системы) была произведена нами
в гл. 4. Здесь рассматривается та же система из k рабочих и п резерв
ных элементов, но задача ставится уже по-другому.
Пусть имеется k равноправных рабочих «мест», для обеспечения
функционирования которых предназначено N = k + п элементов
(рис. 5.3.1). Взаимосвязь элементов, стоящих на рабочих местах,
Рис 5 3 1 Структурная схема си-
стемы из N—k+n элементов с %
выделенными равноправными под-
системами.
осуществляется только через общий резерв и восстанавливающий
орган; в остальном же каждый из них выполняет свои собственные
задачи, возможно функционально совершенно различные. Нас будет
интересовать надежность одного, произвольно фиксированного, ра-
бочего «места» системы, т. е. мы хотим установить, что же дает сколь-
зящий резерв и восстановление именно для выбранного нами рабочего
места, «нашего» места, выделенной подсистемы системы.
Подобная задача часто встречается при организации связи (или
управления) по k направлениям, «каналам». В этом случае имеем k
изолированных каналов связи (возможно разнесенных территориаль-
но). Для повышения надежности всей системы и каждого из k каналов
можем применить еще п (обходных) каналов в качестве резервных.
Задачу оценки надежности одного из k произвольно фиксированных
каналов при условии, что резервные каналы предназначаются для
замены любого отказавшего рабочего канала, будем называть задачей
оценки «канальной» надежности. Данный параграф целиком посвящен
именно этой задаче.
5.3.2. Средняя наработка до отказа выделенной подсистемы си-
стемы, состоящей из N идентичных элементов. Рассмотрим два вида
восстановления в системе:
б Зак 913 161
1) полностью ограниченное восстановление (когда при любом
числе отказавших элементов в системе одновременно может восста-
навливаться не более одного из них);
2) неограниченное восстановление (когда число одновременно вос-
станавливаемых элементов равно числу отказавших).
1. Полностью ограниченное восстановление. Рассмотрим сначала
систему, состоящую из N — k 4* 1 (т. е. с одним резервным эле-
Рис 532 Структурная схема си-
стемы из N=k+l элементов с k
выделенными равноправными под-
системами
ментом) идентичных элементов, предназначенных для функциониро-
вания на k рабочих местах (рис. 5.3.2). Пусть каждый элемент харак-
теризуется интенсивностью отказов X и интенсивностью восстановле-
ния р. Граф переходов системы из одного состояния в другое для
задачи отыскания средней наработки выделенной подсистемы до отка-
за (любой в это'м случае в силу предположения об идентичности эле-
ментов) представлен на рис. 5.3.3, где обозначено: Но — состояние,
при котором в системе отказавших элементов нет; Нг — состояние,
и (к+1)Л. и (к-1) Л и. (к-2)Л р. 2к и. Л
Нд-*--------//, —-----»- HZ ---------------------------------* 4
Рис 53 3 Граф переходов из одного состояния в другое системы из N=A+1
элементов с k выделенными равноправными подсистемами для задачи отыскания
средней наработки до отказа произвольно фиксированной подсистемы при пол-
ностью ограниченном восстановлении.
при котором в системе имеется один отказавший элемент, любой из N
элементов, Н2 — состояние, при котором в системе есть два отказав-
ших элемента, но на выделенном рабочем месте стоит исправный эле-
мент; ...; Hh — состояние, при котором в системе есть k отказавших
элементов, но на выделенном рабочем месте стоит исправный эле-
мент; Н0ТК — состояние отказа выделенной подсистемы, т. е. таксе
состояние системы, при котором на выделенном рабочем месте исправ-
ного элемента нет.
(62
Для среднего времени работы выделенной подсистемы до отказа
имеем:
(5.3.1)
Если выполняется условие (k + 1) 1, то из (5.3.1) прибли-
женно получаем
?Д0) _ 1 1 +3у
% <* +1) V
Абсолютная погрешность формулы (5.3.2) имеет порядок
1 2V( — 2fe2 4-5fe—3)
% k + 1
(5.3.2)
(5.3.3)
Рассмотрим систему из N = k + п элементов (и — резервных),
предназначенных для функционирования на k рабочих местах
/I НЯ. /z р {к^К р !М)Я р (к-1)Я р (к-2)Я, р Л
Рис. 534. Граф переходов из одного состояния в другое системы из
элементов с k выделенными равноправными подсистемами для задачи отыска-
ния средней наработки до отказа произвольно фиксированной подсистемы при
полностью ограниченном восстановлении.
(см. рис. 5.3.1) при полностью ограниченном восстановлении
(рис. 5.3.4). Для этого случая
(5 3 4)
Если выполняется условие Л^у« 1 (где по-прежнему у = %/р),
то из (5.3 4) можно получить следующую оценку:
T<0)==TF^u + (rt+2)T1’ (5-3-5)
6*
(63
Абсолютная погрешность формулы (5.3.5) имеет порядок:
— при п = 1 она определяется формулой (5.3.3);
— при п = 2
б 1 — 3fe2+l7fe+3 .
~ A (fe 4-1) (*4-2) ’
— при п>2
б_____1 fe! [n2+n (fe-4-l) — 4fe2 + 12fe—5[
~ \ Д?1?П-2
2. Неограниченное восстановление. Рассмотрим теперь случай не-
ограниченного восстановления системы из N == k 4- п идентичных
элементов, предназначенных для функционирования на k равноправ-
ных рабочих местах. Граф переходов системы для задачи отыскания
р NA, 2jl [N-рЛ lk+2fr njj. pvfyi (к-1)Л [H-tyl &
Рис 535 Граф переходов из одного состояния в другое системы из М=*+л
элементов с k выделенными равноправными подсистемами для задачи отыска-
ния средней наработки до отказа произвольно фиксированной подсистемы при
неограниченном восстановлении.
средней наработки выделенной подсистемы до отказа приведен на
рис. 5.3.5. Система дифференциальных уравнений,отвечающих этому
графу, имеет вид:
Ро (0 = — NKp0 (/) + рР1 (/);
pi (0 = NKp. (/) - [(Д/_ 1) А + р] Р1 (0 + 2рр2 (0;
р'п (t) = (k + 1) Арп_х (0—(М + пр) рп (/) + (п 4-1) р Рп+1 (/),
P«+i(0 = — 1)^Рп (0—[(^— 1)А4"(п4"1)н1 Рп+1 (04- (п-Ь 2)ррп+2(/);
Pn-z (0 = 2Xpw_3 (()—(2k 4- (N—2) p) px—2 (04- (A — l)ppw-i (0'»
Pn-i (0 = ^Pw-2 (0 — P-4-VV—UNPn-i (/)>
Л-1
2 p<(04-Potk(0==i.
1=0
Средняя наработка выделенной подсистемы до отказа определяется
в этом случае по формуле
jxoj ____L
р Gn
(64
где определитель Fn имеет все строки, кроме первой,, те же, что и опре-
делитель Gw, все элементы первой строки определителя Fw — единицы,
а определитель Gw задан формулой:
— A'Y A'y 1 0 0
0 0 -vi-Hv)
Gw = 0 0 (Л—1)Y
0 0 0
0 0 0
0 0 0
0 0 0
n + 1 0 0
-> —[(n-M)-l-(fe—1)T1 «4-2 0 (5.3 6)
(fc —2) у _[(n+2)->(fe-2)y] • 0
0 0
5.3.3. Стационарные показатели надежности выделенной подси-
стемы. Для рассматриваемой задачи возможны следующие случаи
восстановления в системе:
1) одновременно в системе могут восстанавливаться не более
I (1 п) отказавших элементов, т. е число одновременно восстанав-
ливаемых элементов в системе не больше числа резервных;
2) одновременно в системе могут восстанавливаться не более
I (п I N) отказавших элементов, т. е. число одновременно вос-
станавливаемых элементов в системе не меньше числа резервных.
Рассмотрим последовательно эти два случая:
1. Число одновременно восстанавливаемых элементов в системе
I (1 I п). Граф переходов системы из одного состояния в другое
приведен на рис. 5.3.6, где Нл — состояние, при котором в системе
есть i 4- 1 отказавший элемент, причем на выделенном рабочем месте
исправного элемента нет.
Составляя систему уравнений, отвечающих этому графу, нетруд-
но получить следующее ее решение:
I , , N' I1 ра ,
VI ll + ' Ра
—1;
165
РП + i Л I
Nl Z; (t, + l)m'i+z+1 po
(k—/—1)1/1 k
0
(5.3.7)
Ml
Hl
(N- /МТ
Рис. 5 3.6. Граф переходов из одно-
го состояния в другое системы из
N=k+n элементов с k выделенными
равноправными подсистемами при
восстановлении с I, ремонт-
ными органами
6V-Z+2M'
Hi-i
Z/г,
[N-l+DK ’’
Hi
МЧМ V
(Ic+Z'iK "
^-1
1ик
/Л+Г/Л! Lu М-/М Zzt
z?
А 1к-1)К Л’ з1/1 !к-2',К к 1Р л
Нп,Г* ~^*~Нп-ил
Вероятность р0 определяется из условия нормировки и равна
166
2. Число одновременно восстанавливаемых элементов в системе
I (п I < N). Граф переходов системы из одного состояния в другое
Nk Zjt W-fM (rt-fy (ЫЦ nil (к+^Л pl+flp Л
Hq * Ht ••• Hn< J (ntl)p n r П
(n+2)p 7+7" J-A '(k-f)K u-1,1
'(к-г) л?
Рис. 5.3.7. Граф переходов из од-
ного состояния в другое системы из
элементов с k выделенными
равноправными подсистемами при
восстановлении с / ремонт-
' ними органами
а-ир
1-П J
/jh+w
-Lip
1-п
. v(N-l+1)K
л
1-П+1 '
1/4
Л к1^ к U
приведен на рис. 5.3.7. Составляя систему уравнений, отвечающих
этому графу, нетрудно получить:
Pn+i
1 I I — IV,
Pn+i,i = ?"+'+' Ро, 0^l<l-tv, (5 3.9)
= N> lt(i>l+iP»
P1+i л (Д'— l—i—1)| k ’
1 1;
Pl+i,l=
N\ ll(l—n+l + l)(dl+l+lpe .
/_ ijtfe ’
—1-\.
167
Вероятность р0 определяется из условия нормировки и равна
/ — п
1 + 2 1 + т) +
< = 1
+ Ф + ?)l CnN+‘+l /+' +
— 2 П +(/—«+ l)ffi + «co]------------------—--------- . (5.3.10)
Полученные стационарные вероятности (5.3.7), (5.3.8) и (5.3.9),
(5.3.10) позволяют определить коэффициент готовности Л, среднюю
наработку между отказами и среднее время восстановления т
выделенной подсистемы. Точные и приближенные (при AZw <£ 1)
выражения для этих показателей сведены в табл. 5.3.1.
Таблица 5.3 1
Стационарные показатели надежности выделенной подсистемы
Г Пока затель То шое значение Приближенное зна 1ение Погрешность
с V V/ к О» + е~1 ’11 + + 013 Л"/'шп + 1 ' 441 / k-1\ Л/>7п + -" 1 V —2—— 1 j < 5 L k4'ln—]
L + Ль х ь13 и । + , rv (V - 1) „ 4-1 k- 11 ' d + + J
>/'Л ш"
г Ха,2 у [1 + (k — 1) <») t + ~ (fe“- tt + 3)
у V/ е к Оц + Оы + ’а 4 1” + ' «-Cjv а, . . c^n + 2 8< o, 1 "J
Г(п) 1 gai X Хф^я 1 + N (N — 1) fe — 1 /fe — 1 л> fe J - 2 + ul ' al 4 /
-<п
1 Хсаа ч+'5-‘+~У’] (4- 1)7Д ( 3 (4 - 2) k 1 _ + "* Ха. 1 b. c. 2 i 1 i I ЗЙ - 41
В табл. 5.3.1 используются следующие обозначения:
(п + 1, если />п,
а, = {
‘ ( /, если I = п;
1в8
| /г + 2,
bi = 1
I alt
(tt + 3,
и
( 2,
M i,
если
если
если
если
если
если
/>п + 1,
/<п + 1;
I п 2,
/<п + 2;
/>2,
/=1;
2«?'+
/ =о *!
и— 1
у_________,
i=Tt 1(^-0!
со*
/<п-
3 C'N у1,
/=0
S Ск у>,
/ = 0
1 = п—
к— 1
№ I1 у юл+/ ,
ЛА (А-/-1)1 ’
№ I1 у (/ 4-1) Юп+, + 1 .
life ;^0 (fe-j-ni ’
п— 1
о21= 5 cw?';
1=0
Г1— п
N\ у yn+f
k [/=0 (A-<-l)!(/> + i)l
(Л?—/—/-
1)1
'1—п— 1 , I .
_ _ ЛИ у (Z + l)Vn+,+ 1
23 4 < = 0 (А-1-1)!(п + 1+01
\ N — I — 1 Т
, Д у (Z + I —п + 1)<0
и < = 0 (Л/-1-/-1)! J’
Для случая п — 1, 1^1
Г1")=^[1 + (Л/-^7±)Т1’
Му L \ Li J J
где погрешность имеет порядок
Оц =
1 — п—
б П V / А —1
Mh k h
А—2
ё1
/г = гшп{2,/}; £г = пип{/г, 3}.
Здесь
169
Рассмотрим систему из элементов с разными показателями надеж-
ности, законы распределения времени работы и восстановления ко-
торых произвольны. Пусть система состоит из N элементов. Пред-
положим, что:
а) для каждого а-го элемента (1 а ДГ) соответствующие имен-
но этому элементу времена его работы между последовательными от-
казами 0ai, 6а2, •••» 9а,х-1, 9ах. ... (где Вах есть время работы
а-го элемента между х — 1 и х-м отказами) являются независимыми и
одинаково распределенными случайными величинами со средним зна-
чением
Та, 1 С а С ЛГ.
Длительности восстановления этого а-го элемента
Bal> ?a2> • ••> £a, х— li £ax>
(где %ax есть длительность восстановления a-го элемента после его
х-го отказа) также являются независимыми и одинаково распреде-
ленными случайными величинами со средним значением та, 1=^а^М;
б) для любых элементов аи₽(а, ₽ = 1, 2, N) величины 9аь
0а2, 0а,*-ь 9ах, ••• не зависят как от
?al> ?а2» •••> ?а, х— Ь ?ах» •••«
так И ОТ
0pi, 0р2, 9р. х-Ь 9рх, ...
И
Ь1> ^2> •••» х-l, —
— соответствующих величин элемента с номером |3;
в) все рассматриваемые случайные величины имеют распределе-
ния, которые не являются «решетчатыми», т. е. не существуют такие
числа a, h, при которых все возможные значения случайной величины
могут быть представлены в виде а + mh, где параметр пг может при-
нимать любые целые значения.
При сформулированных выше условиях для всех k рабочих под-
систем коэффициент готовности и все другие стационарные характе-
ристики будут одинаковыми. Наша задача заключается в отыска-
нии коэффициента готовности К, средней наработки между отказами
Т и среднего времени восстановления т выделенной (произвольно
фиксированной) подсистемы.
Воспользуемся результатами, приведенными в Приложении 5;
Т = KJA, (5.3.11)
т=(1 — К)/А, (5.3.12)
= 2 Ptfh), (5.3.13)
* • • . | отказовым |
‘с (состояниям/
2 (5-3.14)
* • • . _ (предотказовым) *1
• ( состояниям I
17®
где в нашем случае под предотказовым состоянием выделенной под-
системы понимается такое ее состояние, из которого она может попасть
в отказовое уже на следующем шаге, т. е. если при отсутствии резерв-
ных элементов откажет тот элемент, который стоит на выделенном ра-
бочем месте; при этом величина Ti есть средняя наработка между
отказами этого элемента.
Определим Л — частоту переходов выделенной подсистемы из
предотказовых состояний в отказовые. Предотказовые состояния вы-
деленной подсистемы, очевидно, могут реализоваться при числе исп-
равных элементов в системе, равном i — 1, 2, k.
При произвольном i слагаемое р (Hi) в сумме формулы (3.5.14),
очевидно, равно
N — (l— 1) N— (I — 2) N
| 2 2-2 (f+f+•+?-)—!—•
а,—1 a2=a,-H aj = aj-i+ 1 '1 a‘ 1 ‘ < Va, Ya, ••• Та;
где
Последнее слагаемое будет при i = k. Таким образом,
Аналогичным образом находится и величина А—коэффициент го-
товности выделенной (произвольно фиксированной) подсистемы
/<= 1-
2 p(Hi) = \-®-x
Низошли 1 **
* б (состояниям
х *+£(*_,) 2 2-2 <5.з.1б)
1 Уаг Va2 ••• Va;
at = l Qt — Qi 1
Итак, мы определили величины Л и К 1см. формулы (5.3.15) и
(5.3.16)1, при помощи которых, используя формулы (5.3.11) и (5.3.12),
можно найти среднюю наработку выделенной подсистемы между от-
казами Т и среднее время ее восстановления т.
171
Заметим, что для идентичных элементов, т, е., если все Та == Т
и та = т, из (5.3.16) и (5.3.15) можно получить
Д — у' Сл'-|
Tk(\- + y)N у‘
(5.3 17)
(5.3.18)
где по-прежнему у ~ т/Т.
Пример 5.3.1. Имеется система из Л'= 5 разных элементов. Из них в систе-
ме fe=4 рабочих, один резервный. Интенсивности отказов и восстановления эле-
ментов'системы равны
А{, Ш» Ag, Ugl A3, Usi ^4» Ра» А5, Ш*
Необходимо выписать формулы для К и Л.
Решение. 1. По формуле (5.3.16) имеем
5
4 5
«=>-т
3 4 5 ,
S 22“^
1=1 »>m n
где
5
Ч Va
=А-
* * 1 + Уа
а = 1
2. Величина Л, определяемая формулой (5.3.15), равна
4 5 т, j . 3 4 5. . . , _
V у г 1 у у у Ат+Ау+ Xf
И а™ У1У1 УтУ.У!
= 1 i>l U m=l 1>т 1>/ I™ U ы
5
Q
Л-Т
Ya
у у у у + + +
и — I m>n 1>/ Уч Ут У] У(
3. Зная К и Л, по формулам (5.3.11), и (5.3.12) легко можно вычислить сред-
нюю наработку системы между отказами Т и среднее время ее восстановле-
ния т.
Заметим, что кратные суммы, входящие в выражение для К и Л, раскры-
ваются обычным порядком. Например:
у, + у, Ag+Xt у, Aa+^i yt Аз + А; у, Xj-рх,-
-1 Vl Yi Y; Y2 yt + Ys yt + Ya Ya
Уз У1
А1-|-А.2 | Ад-рХз -р А4 + А-5 \ / Х2 + К3 + Х4 А2 ~|~ Xs
Y1Y2 Y1Y3 + YiVa YiYs Y2Y3 Ya Ya + YaYs
_j_ f ^3+^4 1 \ Xg Х5
' \ Ya Ya Ya Ya / Ya Ya
172
5.4. Восстанавливаемая система с невосстанавливаемым
резервом
Рассматривается система из п + 1 идентичных элементов, из кото-
рых один является рабочим, а остальные п — ненагруженными ре-
зервными. Система функционирует таким образом, что после отказа
рабочего элемента производится его замена (восстановление системы)
одним из резервных элементов, при этом восстановление (ремонт) от-
казавшего элемента ни сразу, ни потом не производится и в дальней-
шей работе системы он участия не принимает. Система функциони-
рует до тех пор, пока не откажет последний п + 1 элемент. Смысл
такого рода резервирования заключается в том, что хотя каждый отказ
элемента, стоящего на рабочем месте как отказ системы фиксируется, но
Рис. 5.4.1. Граф переходов из одного состояния в другое восстанавливаемой
резервированной системы с невосстанавливаемым резервом.
быстрая замена отказавшего элемента позволяет форсированно пере-
вести систему в состояние работоспособности, поддерживая тем самым
высокую ее готовность к функционированию.
Начав работать, система последовательно попадает из состояния
работоспособности в состояние отказа, затем опять в состояние работо-
способности и т. д., причем, очевидно, за время функционирования
система может побывать только в конечном числе состояний: Но, Нъ
Н2, ..... Н2п, Н2п+\. Будем считать, что система находится в состоя-'
нии работоспособности, если она находится в состояниях: Нй, Н2,
..., H2j, ..., Н2п и, напротив, система находится в состоянии отказа,
если она находится в состояниях: Hlt На................Н2п+1. Таким
способом введенная индексация состояний соответствует тому, что:
H2j — состояние работоспособности, в которое система приходит
после j-го отказа и соответственно /-Й замены (/-го восстановления);
— состояние отказа, в которое система приходит после j-й за-
мены и соответственно / + 1-го отказа.
Граф переходов описанной системы представлен на рис. 5.4.1.
На этом графе все нижние (нечетные) состояния — состояния отказа
системы, верхние состояния — состояния работоспособности. Если
ввести обозначения
N = 2п + 1; Xj = и2у, Pj — 0 < / n; = О,
то граф переходов можно представить в другом виде (рис. 5.4.2). Этот
граф уже полностью совпадает с графом переходов системы для так
называемой «схемы гибели» (см. гл. 3).
173
Решая систему дифференциальных уравнений (отвечающих графу
рис. 5.4.2) для вероятностей pk (t) того, что система в момент вре-
мени t находится в состоянии Hh, при (очевидных) начальных условиях
Ро (0); ph (0) = 0; 1 k N
для случая, когда все а>г различны, получим
ph(t)= п W; 2
1 = о о
—-------------, 1; (5.4.1)
П (СО; —Иг)
1=0
N-l N-l _Q.t
p„(o=i- П », 2—si------------------------<5-4-2>
/ — 0 i= 0 т
(О; И (О)( — О)г)
1 = 0
l=ri
и, a>zj-t г °f-t
Рис. 5 4 2. Преобразованный граф переходов — «схема гибели».
Если замена отказавшего элемента на резервный производится с од-
ной и той же интенсивностью р независимо от номера отказа системы,
а интенсивности последовательных отказов также равны друг другу
(не зависят от номера отказа) и равны величине к, т. е.
w2/+i ~ Iх! О / ; (о2у = X, 0 < / ,
то в этом случае (по-виднмому, наиболее типичном для практики) по-
лучаем
Л-£
/ Л. _ Д|
V 2 /•
2Г? ((H-W
2L-I-1 i ь \ •
=о 2^ / 2L ,• 1 и
I 2
(5.4.3)
174
если k — четное, О С k N — 1;
£__1 fi__I
2
X Ck— 1
1=0 2 + '
»+!
фе"^.(—1) 2 х
[(н —?.)/] 2
(5.4.4)
1Ф-Х)/] 2
если k— нечетное
+ (-!)"+1
(5.4.5)
Используя формулы (5.4 1) — (5.4.5), для соответствующих слу-
чаев легко определить вероятность пребывания системы в момент
времени t в одном из состояний работоспособности К (t):
N-l
K(i)= 5 Pk(t).
k = 0
{no k четным}
(5.4.6)
Очевидно, в условиях рассматриваемой модели значение коэффи-
циента готовности равно
Я = lim К (0 = 0. (5.4.7)
t ->оо
Среднее время Т,у функционирования системы до ее окончательного
отказа (попадания в состояние Hn) и среднее время пребывания
системы в состояниях работоспособности определяются из очевидных
соображений
N — 1
tn= 2 —; (5.4.8)
(= 0
N-l
2-
;=0
{по I четным}
(5.4.9)
175
Вероятность того, что система в интервале времени 10; t] еще функ-
ционирует (либо работает, либо производится замена отказавшего эле-
мента), т. е. вероятность того, что она за этот интервал времени еще не
попадет в последнее состояние Hn, определяется по формуле
5Л, (0 = 1- pN (0,
(5.4.10)
где вероятности рц (/) для соответствующих случаев определяются
по формулам (5.4.2) и (5.4.5).
Пример 5.4.1. Пусть имеется система из одного основного аппарата и одного
резервного аппарата, находящегося в ненагружеином режиме. Интенсивность
отказов работающего аппарата равна X = 0,02 1/ч, интенсивность подключения
резервного аппарата на место отказавшего рабочего (интенсивность восстанов-
ления, равна р = 2 1/ч.
Требуется определить вероятность того, что в момент времени t = 24 ч
система будет работоспособной.
Решение. Система может находиться в четырех состояниях: /Уо, Н, —
состояния работоспособности; Hi, Н3 — состояния отказа, причем Нй — со-
стояние системы, характеризующееся тем, что основной аппарат работает безот-
казно; Н± — состояние системы, в котором основной аппарат отказал и началось
подключение резервного аппарата (восстановление системы); Н2 — состояние
системы, в котором произошло подключение резервного аппарата и он продол-
жает работать безотказно; Н3 — состояние окончательного отказа системы, когда
произошел отказ резервного аппарата, стоящего на рабочем месте.
Так как в нашем случае п = 1, N = 2п + 1 = 3, то, воспользовавшись фор-
мулами (5.4.3) — (5.4.5), для вероятностей pft (f) того, что в момент времени t
система находится в состоянии Hh(k — 0, 1, 2, 3), получим:
р0 (/)=e-lz,
Pi(O = —Ц(е V
ц — Л. -
е-^),
(р —Л)-
р3 Ю=1—Ц-
ц —А.
Л
р~ А
_АЛ_
р—А.
ре”и ( 1 +М
Вероятность того, что система в момент времени t будет работоспособной в
соответствии с формулой (5.4.6), равна
К (О=Ро (О + Рг (l) = e-xz + —-Ц—-{e-w 1(Ц- X) t— l]+e-u/}.
({Л — Л»)
В момент времени t = 24 ч эта вероятность составляет
К (i = 24 ч) » 0,91.
Вероятность того, что система в момент времени t —
стояние окончательного отказа (в состояние Я3) равна
24 ч уже попала в со-
1 Г /1 А \ А2 4
PW(0 = P3 (* = 24 ч)=1------ ре~ w -( и--------- 4-----е^' ^0,08.
р — л[_ \ р—А,/ р—л J
176
5.5. Система массового обслуживания с потерями заявок
в случае ограниченной надежности обслуживающих
приборов
5.5.1. Система массового обслуживания, состоящая из п приборов,
выходящих из строя независимо друг от друга. На систему массового
обслуживания, состоящую из п приборов, поступает поток заявок от
у абонентов. Случайные длительности ц занятия обслуживаемых зая-
вок независимы и имеют функцию распределения Н (х). Приборы в
моменты обслуживания заявок могут выходить из строя. Если заявка
в некоторый момент занимает прибор, то случайная длительность ис-
правного состояния прибора 0, отсчитываемая от этого момента, имеет
функцию распределения А (х) при условии занятости прибора.
Отказавший прибор восстанавливается. Случайное время восста-
новления | имеет функцию распределения G (х). Рассматриваются два
вида восстановления: полностью ограниченное и неограниченное. Мате-
матические ожидания случайных величин ц, 0, I предполагаются ко-
нечными.
Рассматривается система с потерями, т. е. очередная заявка не при-
нимается на обслуживание и считается потерянной, если застает си-
стему в одной из следующих ситуаций: все п приборов заняты обслу-
живанием заявок, один прибор отказал, а остальные п — 1 приборов
заняты обслуживанием, два прибора отказали, а остальные обслужи-
вают заявки и т. д. Заявки, у которых приборы отказали во время
обслуживания, тоже считаются потерянными.
Указанную систему массового обслуживания будем характеризо-
вать следующими величинами: К. — коэффициент готовности системы
обслуживания, т. е. вероятность того, что в системе имеется хотя бы
один исправный и свободный от обслуживания прибор; Т — среднее
время между двумя соседними моментами попадания системы в со-
стояние потери заявок; т — среднее время пребывания системы в
состоянии потери заявок.
Далее приводятся нижние и верхние оценки показателей эффек-
тивности системы. Нижнюю оценку получаем при условии, что суммар-
ный поток заявок от абонентов является пуассоновским с постоянным
параметром Л = УЛ0, который не зависит от числа уже обслуживаю-
щихся заявок в системе. Эта оценка тем точнее, чем больше число N
всех абонентов. Верхнюю оценку находим из условия, что параметр
суммарного потока заявок от абонентов в момент времени, когда в си-
стеме обслуживаются k заявок и I приборов отказали, равен ==
=(У —k — Г)Л.О, где Ло— параметр потока заявок от одного абонента.
Эта оценка тем лучше, чем сильнее неравенство N > п.
Для общего случая приводится лишь нижняя оценка величины К
при условии неограниченного восстановления приборов. В предполо-
жении, что функции распределения величин г], 0, £ имеют вид:
Н(х) = 1—е—Мх, Л(х) = 1—e~x*, G (х) = 1 — e~i‘x,
приводятся верхние и нижние оценки для неограниченного и полностью
ограниченного восстановления.
177
В табл. 5.5.1—5.5.3 приведены указанные выше оценки для основ-
ных показателей эффективности системы.
Таблица 5.6.1
Система массового обслуживания с потерями
заявок при ограниченной надежности
обслуживающих приборов.
Общий случай. Неограниченное восстановление
00
а — J (1—// (х)) (1—А (х)) dx
о
00
b = у (1 — Н (х)) dA (х)
о
00
с — JVA.O J (1 — G (х)) dx
о
Показате ть
Нижняя оценка
(а + 6с)71
п'
1 _ ~~п
V (а + be I1
Таблица 5.5.2
Система массового обслуживания с потерями заявок при ограниченной
надежности обслуживающих приборов. Экспоненциальный случай.
Неограниченное восстановление
X Л Y - |Х ’ Р - V + Л -1=V (ур)< V р* ^00 Zj (i k' 1=0 й=0 А . Ao Y p. ’ p - M + X n n—l ^'=2 (YP)’S t=0 ft=o
Показа те пь Hi жняя оценка Верхняя оценка
т 1 — (1 + Т)” Poo A (z! 1)1 0 + Y) Poo i-c^g + Yrpoo (AC— л_|_ 1) AoQ- * 1 p" - ’ (1 +1 ’Poo
т P (1 + Y) /?Л p (1 4~ y) «Л»
к 1 — U + Y)n Poo 1-C^ P"(1+y)"p„o
178
Таблица 5.5.3
Система массового обслуживания с потерями заявок при ограниченной
надежности обслуживающих приборов. Экспоненциальный случай.
Полностью ограниченное восстановление
X . A
Y- p. > P - M+X
-i^VlP* l-(YP)n~,t+1
А» /j k\
1 —YP
X . A„
Y “ I* ’ P ~ M + *
n n—l
pm = 2 (w Sc*+^+zp*
;=o *=o
Показа-
тель
Нижняя оценка
Верхняя оценка
т
т
к
п
1—(YP)”POO J] -fcfpr
6=0
' п—_1
Mrp)"-’/’.. Jj
____________fe=o_______
?[i+ («!y»2 if)
n
1 - (YP)nAo J]
*-o
n
1 — n'.C^ (YP)nAo^
*=0
n—1
(У—л+1)Л„(л—1)!C"-1(yp)»-,^00
YP
Л,
(n — 1 \ ”* 1
6=0'
n
l (X?)" Pho
ft—0
5.5.2. Система массового обслуживания, состоящая из п приборов,
выходящих из строя одновременно. На многоканальную систему из
п приборов поступает поток заявок от N абонентов. Все п каналов по-
Рис 5 5 1. Граф переходов из одного состояния в другое системы массового
обслуживания, состоящей из п приборов.
стоянно включены и из строя выходят одновременно с интенсивностью
X. Система восстанавливается с интенсивностью р. Интенсивность об-
служивания заявок равна М. Заявки, во время обслуживания которых
происходит отказ системы, покидают систему обслуживания. Рассмат-
179
ривается система с потерями, т. е, очередная заявка не принимается
на обслуживание, если застает систему в одной из следующих ситуаций:
либо все п приборов заняты обслуживанием заявок, либо система на-
ходится в состоянии отказа. Граф переходов описанной системы при-
веден на рис. 5.5.1.
Коэффициент готовности системы обслуживания Л в этом случае
подсчитывается по формуле
К — [/ j\n-j-1 Л"N {N—1) . (ТУ—п-}-1) (5511
где
/?п = - (1 + пМ) (?„_! - пМЛ0 (ЛГ - n + 1) Q„_2,
Qn = - (А + Ло (N - n) + nM) Qn_x - пМЛ0 (N - п + 1) Qn_2, (5.5.2)
Qo=-(A + Aon п=1, 2, ...
Список литературы
1 Козлов Б. А. О канальной надежности. — В кн.: О надежности слож-
ных технических систем. М., «Сов. радио», 1966.
2 . К о з л о в Б. А. Надежность выделенных подсистем в резервированной
системе с восстановлением. — «Известия АН СССР. Техническая киберне-
тика», 1966, № 4.
6
СИСТЕМА ИЗ ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ
ЭЛЕМЕНТОВ
6.0. Предварительные замечания
Последовательным соединением при расчетах надежности называет-
ся такое соединение элементов, при котором отказ хотя бы одного из
них приводит к отказу всего соединения в целом. Блок-схема расчета
надежности для последовательного соединения приведена на рис.6.0.1.
Последовательное соединение в указанном выше смысле не всегда
совпадает с физическим последовательным соединением элементов. Так,
если мы рассматриваем электрическую
схему группы параллельно включен- —11
ных конденсаторов (рис. 6.0.2), то по
отношению к отказу типа «короткое ' 11 '
Рис 6 0 1. Структурная схема последе»
вательного соединения элементов.
Рис. 6 0 2. Группа параллельно вклю-
ченных конденсаторов (электрическое
соединение).
замыкание» подобное соединение будет иметь блок-схему расчета
надежности, эквивалентную изображенной на рис. 6.0.1, так как
замыкание любого из них приводит к общему замыканию. В то же
время последовательное соединение в смысле надежности совпадает
с физическим последовательным соединением для отказов типа «обрыв».
В дальнейшем, если особо не оговаривается обратное, отказы эле-
ментов предполагаются независимыми, т. е. отказ любой группы эле-
ментов никак не влияет на вероятностные характеристики остальных
элементов.
Напомним, что под элементом здесь понимается в широком смысле
слова — один из самостоятельных участков последовательного соеди-
нения. (Сам по себе такой участок системы может представлять собой,
например, резервное соединение.)
6.1. Система из последовательно соединенных
невосстанавливаемых элементов
6.1.1. Произвольное распределение времени работы до отказа.
Время работы до отказа системы из т. последовательно соединенных
181
невосстанавливаемых элементов определяется минимальным значе-
нием времени безотказной работы ее элементов (рис. 6.1.1), т. е.
О'1’ = min 0)u,
1<КШ
где 0(1) — время работы до отказа системы; 0,<п — время работы до
отказа i-ro элемента.
Предполагается, что известны выражения для вероятности безот-
казной работы отдельных элементов Pt (f) или оценки для этих функ-
ций.
Кроме того, предполагается, что все элементы системы взаимно неза-
висимы, т. е. отказ любого элемента никак не зависит от состояния лю-
бых других элементов системы.
Рис. 611. Временная диаграмма, поясняющая понятие времени
безотказной работы системы из т последовательно соединенных не-
восстаиавливаемых элементов.
В табл. 6.1.1 приведены основные показатели надежности для си-
стемы из последовательно соединенных невосстанавливаемых элемен-
тов при произвольных распределениях времени работы до отказа, т. е.
при произвольных функциях /’,(/)• Приближенные выражения для по-
казателей надежности даны при условии, что max Qt (/0) <
Пример 6.1.1. Имеется система из двух элементов, структурная схема кото-
рой представлена на рис. 6.1.2. Первый элемент, в свою очередь состоит из двух
последовательно соединенных компонент и одной скользящей резервной компо-
ненты, работающей в нагруженном режиме, а второй элемент представляет со-
бой дублированное соединение, причем резервная компонента находится в нена-
груженном режиме. Все компоненты (составные части элементов) одинаковые и
имеют экспоненциальное распределение времени работы до отказа с параметром
А. =0,005 1/ч. Требуется определить основные показатели надежности системы.
Решение 1. Вероятность безотказной работы системы за время =
= 50 ч;
Р (h) = Pi {Ч)Р2 (/0).
182
Таблица 611
Система из последовательно соединенных невосстанавливаемых элементов.
Произвольный закон распределения времени работы отдельных элементов
до отказа
Показатель Точное значение Приближенное значение Погрешность
P(to) m П р( ы 1=1 tn tn j=1 m i+<— [max Q, (t„)P
<2(<о) 1 - П Pt <'»> :=1 П pt (<' + « = 1=1 m S ((a> 1=1 a_<-2“ [max Q (/0)? /
Р (t. t + t0) П pt <* + '•» _ :=i _ р (t+to'i m ' Р (/) П pt^ 1=1 m i — ГГ Pt (t, t + m= I — Q (t + fo) + Q(O «+ <<? (0 IQ (O-Qtt+toH
Q (t, f+M :=i , p (< + <°> -> - oo Q (t + to) - Q (t) »_ «2 (0 [<2 (t)-<2 (t + to)l
Т J 0 —
Выражения для Pt (0 н Р2 (0 находятся по формулам табл. 3.2.2:
ру (/0) = е~’ 4- Зе~2w 0 (I — е—ь< ’) = Зе~2 •—2e~3W|1,
P2(W = e“w» +
Отсюда получаем
Pt (50) =3е_'г'°’°05'50 — 2е"3’° •°05’50 = 0,8743,
Рг (50) =е-о.оо5.5о (1 +0>005-50) = 0,9735.
Тогда
Р (50) = 0,8743 • 0,9735 = 0,8511.
Приближенное значение
Р (50) = 1 - [Qi (50) 4- Q2 (50)].
Величины Qi (50) и Q2 (50) определяются как
Qi (50) = 1 — Pt (50) = 1 — 0,8743 = 0,1257,
Q2 (50) = 1 — Р, (50) = 1 — 0,9735 = 0,0265.
18*
Отсюда находим
Р (50) = 1 — (0,1257 + 0,0265) = 0,8478.
2. Вероятность отказа системы за время /0 = 50 ч.
Воспользуемся предыдущими результатами!
Q (50) = 1 — Р (50) =* 1 — 0,8511 = 0,1489.
Приближенное значение
Q (50) = Qi (50) + Q2 (50) = 0,1257 + 0,0255 = 0,1522.
3, Вероятность безотказной работы системы в интервале времени от t» 25 ч
до t + tf) 50 ч при условии, что система проработала безотказно 25 ч.
Предварительно вычислим значение Р (25), для чего найдем
Pi (25) = 3е—2’0,005'25-—2е~3'°-°05’25 = 0,9618,
Р2 (25)= е~0,°05’25 (l-f-0,005-25)= 0,9934.
Рис. 6.1 2. Структурная схема систе-
мы аз двух элементов для првмера
0,9618 • 0,9934 = 0,9552.
1-й. злемент
Отсюда получаем
Р (25) = Р, (25) • Р2 (25) ₽=
Искомое значение находим по формуле
Р (25; 50) = 0,8511 : 0,9552 = 0,8893.
Приближенное значение
Р (25; 50) = 0,8511 (1 + 0,0448) = 0,8892.
4. Вероятность отказа системы в интервале времени от t = 25 ч до t + /0 =
= 50 ч при условии, что система проработала безотказно 25 ч.
Воспользуемся предыдущими вычислениями
Q (25; 50) = 1 — Р ( 25; 50) = 1 - 0,8893 = 0,1107.
Приближенное значение
3 (25; 50) = Q (50) — Q (25) *= 0,1489 — 0,0448 “ 0,1041.
5. Среднее время работы системы до отказа.
Для Нахождения Т выразим сначала в удобной форме Р (/);
Р («) = (Зе'”2Х/—2е—зх')е-х' (14-Х/) = Зе~зх' — 2е— 4-ЗМе~ЗКг —2XZe~ш.
Далее, используя формулу для Т> -
dt,
о
получаем
ОО 00 ОО ор
T = 3fe-3Vd/_2f e'^'d/^SXf /e"3Wd/-2Xj 1е~4М dt,
0 0 0 0
184
откуда- воспользовавшись таблицей интегралов (см. Приложение П7.6),
нахОДим
J________1_ 1 __ 1_________17
X 2Х, + ЗХ 8Х ~ 24Х,*
Подставив численное значение Л « 0,005 1/ч, имеем
Т = 17 : (24 . 0,005) « 144 ч.
Пример 6.1.2. Имеется система из трех независимых последовательно соеди-
ненных элементов, каждый из которых характеризуется нормальным распреде-
лением времени работы до отказа со следующими характеристиками:
Т\ = 100 ч, 01=1 ч;
Т2 = 100 ч, а2 = 5 ч;
Тз 120 ч, а3 = 10 ч.
Требуется определить основные показатели надежности.
Решение. Данный пример допускает только численное решение. Пред-
варительно запишем в табл. 6.1.2 значения Pt (/), Р2 (/) и Р3 (/), а также резуль-
тирующую величину Р (/), используя табл. П8. 4 Приложения.
Значения Р (/0) для любых t0 находятся непосредственно из табл. 6.1.2.
Налример, Р (95) = 0,835.
Р (94; 95) =» 0,835 : 0,881 = 0,949.
Таблица 6.1.2
Таблица значений вероятности безотказной работН элементов
и системы для примера 6.1.2
». Р (О t
83 85 90 91 92 93 94 95
Р, (0 — 1,0 •v] -vl ^1 u ~1 •vl
Рг(1) — 1,0 0,9987 0,977 0,964 0,945 0,919 0,885 0,841
Л (б -1,0 0,9998 0,9987 0,9981 0,9974 0,9965 0,9953 0,9938
Р(П •vl 0,9985 0,976 0,962 0,941 0,916 0,881 1. 0,835 1
Продолэкение табл. 6.1.2
p (O t
96 97 98 99 100 101 105
0,9998 0,9987 0,977 0,841 0,5 0,159 •K.0
Л 0 0,788 0,724 0,655 0,579 0,5 0,421 0,159
P3 (0 0,9918 0,981 0,986 0,982 0,977 0,971 0,933
P(t) 0,780 0,714 0.633 0,478 0,245 0,067 <v0
Значение среднего времени работы до отказа определяете^ путем численного
интегрирования функции Р (0. Примем для простоты, что длД всех t < 90 ч ве-
личина Р (/) sk 1, тогда
Тх 1,89 + 0,976 + 0,962 + 0,941 + 0,916 + 0,8^1 +
4- 0,835 + 0,780 + 0,714 + 0,633 + 0,478 + 0,245 + 0,06? = 97,332 ч.
6.1.2. Экспоненциальное распределение. В табл. 6.1.3 приведены
основные показатели надежности для системы из последовательно
185
соединенных невосстанавливаемых элементов, когда каждый из эле-
ментов имеет экспоненциальный закон распределения времени работы
до отказа, т.е.
pt (/) = е~^‘.
Таблица 6.1.3
Система из последовательно соединенных
невосстанавливаемых элементов. Экспонен-
циальный закон распределения времени
работы отдельных элементов до отказа
т
А =2
i=l
Показатель Точное значение Приближенное значение Погрешность
1 <u II о 7 о II <и S 1 ! ~Й 1 -л/„ (ЛМ2 2
Q(O) 1-е~Л/‘ Л«„ а — < (Л/р)2 2
P(t. t + е-Л/0 1 ~ма <Л70)г 2
QU; t + t.) 1 — е~л<< М, а — < (А/0)г 2
Г 1_ Л —
Приближенные выражения для показателей надежности даны при
условии, что
т
^0 = ^0 2 \ 1 •
Пример 6.1.3. Имеется система нз пяти независимых последовательно соеди-
ненных элементов. Каждый элемент имеет экспоненциальное распределение вре-
мени работы до отказа с параметрами: X* = 0,05 1 /ч; «= 0,02 1/ч; — 0,01 1/ч;
= 0,01 1/ч; = 0,08 1/ч. Требуется определить основные показатели надеж-
ности системы.
Решение. Предварительно находим значение А:
А = 0,05 -I- 0,02 0,01 + 0,01 4- 0,08 = 0,17 1/ч:
1. Вероятность безотказной работы системы за время ta =» 0,5 ч;
Р(0,5) =е—0,17-0»Б = е~0’085 = 0,9187.
Приближенное значение
Р (0,5) = 1—0,085 = 0,915.
186
2.Вероятность отказа системы за время t0 = 0,5 Ч!
Q (0,5) = 1 — 0,9187 •= 0,0813.
Приближенное значение
Q (0,5) = 0,17 . 0,5 = 0,085.
3. Среднее время работы до отказа
Т = 1 : 0,17 = 5,9 ч.
6.1.3. «Стареющее» распределение. В табл. 6.1.4 приведены нижняя
и верхняя оценки для некоторых показателей надежности системы,
представляющей собой последовательное соединение элементов, имею-
щих «стареющее» распределение времени работы до отказа, причем
предполагается, что известны значения среднего времени работы до
отказа каждого элемента Т[.
-С1)Д
Примечание. Значения е 1 протабулированы и приведет!
в табл. 2.1.5.
Таблица 6.1.4
Нижняя и верхняя границы системы из последовательно соединенных
„стареющих" элементов
Показа тель Нижняя граница Верхняя граница Интервал, для ко торого справед лива граница Примечание
P(t) m 1^1 1 t min Tt cop зависит от t и оп- ределяется из уравнения -«.Olt 1—ioJ1* min Tt~ e ‘ ; k — число элементов, у которых среднее время работы до отказа совпа- дает с минимальным зна- чением Тг.
0 е * t min Tt
Более iочное значение е —[aid) е m е '=> Y Y : v/ V/ V/ • S-ч bs. 1\<Тй<Т3<... <тт зависит от t и опре- деляется из уравнения . —cod)/ 1— с0(/)г5 = е 1
т 1 m (=1 min Tt
187
Если дополнительно известны дисперсии о,? для каждого элемента,
то верхняя и нижняя границы вероятности безотказной работы после-
довательной системы Р (t) могут быть найдены как произведения соот-
ветствующих численных верхних и нижних границ элементов, приве-
денных в табл. 2.1.6 и 2.1.7.
Численные значения границ для среднего времени работы до отказа
Т могут быть получены путем численного интегрирования соответствую-
щих границ вероятности безотказной работы.
Пример 6.1.4. Имеется система их трех независимых последовательно соеди-
ненных элементов. Каждый элемент имеет «стареющее» распределение времени
работы до отказа со значениями среднего времени безотказной работы;
1\ = 100 ч; Тг = 100 ч и 73 = 120 ч.
Требуется оценить основные показатели надежности.
Решение 1. Нижняя оценка вероятности безотказной работы системы
для /0 = 95 ч;
В табл. П8.1 Приложения находим, что даже е-2 = 0,135, т. е. Р (95) <
<0,135. (Точное значение е~2,8 х 0,06.)
2. Нижняя оценка для среднего времени до отказа
1 ’ ( 100 + 100 + 120 ) ~35 Ч"
Верхняя оценка для среднего времени работы до отказа
7= min (ЮО, 100, 120) = 100 ч.
(Ср. с результатом примера 6.1.2.)
6.2. Система из последовательно соединенных
восстанавливаемых элементов
6.2.0. Предварительные замечания. Показатели надежности систе-
мы из последовательно соединенных восстанавливаемых элементов
зависят от различных факторов, часть которых приводится ниже.
1. Зависимость показателей надежности от распределения времени
работы элементов системы до отказа. Если отдельные элементы систе-
мы имеют произвольное распределение времени работы до отказа, а при
отказе системы восстанавливается только отказавший элемент, то время
работы системы до первого отказа будет отличаться от времени работы
между первым и вторым отказом и т. д. При этом будут отличаться не
только средние значения интервалов безотказной работы, но и законы
распределения соответствующих случайных величин.
Проиллюстрируем это на примере для случая, когда восстановление
отказавших элементов в системе производится мгновенно. Рассмотрим
систему, состоящую для простоты всего из трех элементов. Допустим,
что все элементы идентичны и имеют нормальное распределение времени
работы до отказа с относительно малой дисперсией (иными словами,
188
каждый элемент работает до отказа почти постоянное время с неболь-
шим разбросом вокруг среднего значения). Понятно, что впервые си-
стема откажет, проработав время, близкое к среднему времени работы
до отказа одного элемента. Затем в течение относительно короткого
интервала времени откажут и два остальных элемента системы
(рис. 6.2.1). После этого в течение времени, близкого к среднему вре-
мени работы до отказа одного элемента, опять не возникнет ни одного
отказа, а затем опять достаточно близко друг к другу появятся снова
три отказа. Заметим, что с течением времени отказы системы будут все
Рис. 6.2.1. Пояснение механизма
образования отказов в системе из ,
трех последовательно соединен-
ных восстанавливаемых элементов
(с1 мгновенным восстановлением).
более равномерно «размазываться» по временной оси, однако если дис-
персия распределения мала, то это ’будет происходить медленно.
Таким образом, видно, что случайные величины 0и> имеют суще-
ственно различные распределения.
Рассмотрение произвольных законов распределения случайных
интервалов безотказной- работы и интервалов простоя отдельных эле-
ментов приводит к громоздким результатам, по существу, неприемле-
мым для практических расчетов. В дальнейшем основное внимание
будет уделено рассмотрению случая, когда все элементы имеют экспо-
ненциальные законы распределения времени работы и времени вос-
становления:
Л (О = Зэ{0г<О = 1 — е-М»
где Х; и — параметры соответствующих распределений, называемые
интенсивностью отказов и интенсивностью восстановления.
2. Зависимость показателей надежности от характера восстанов-
ления системы. Показатели надежности зависят от того, в каком ре-
жиме находятся исправные элементы системы при восстановлении от-
казавшего элемента.
Можно рассмотреть два следующих основных режима работы си-
стемы:
— при отказе любого одного из элементов остальные элементы
системы выключаются, т. е. интенсивности отказов исправных эле-
ментов (!) на это время считаются равными нулю (рис. 6.2.2).
189
Это означает, что при восстановлении одного из элементов ни один из
остальных элементов системы не может отказать. В этом случае для
восстановления системы достаточно наличия всего одной-единствен-
ной ремонтной бригады;
Рис. 6 2 2. Временная диаграмма для режима работы системы, когда при отка-
зе одного из элементов остальные элементы выключаются.
X — момент отказа элемента; О — момент отключения элемента на время ремонта отказав-
шего, fcW—4-й интервал восстановления i-го элемента; — fe-ft интервал восстановления
системы.
Рис. 6 2 3. Временная диаграмма для режима работы системы, когда при отказе
одного из элементов остальные элементы остаются в рабочем состоянии. (Ус-
ловные обозначения те же, что и на рис. 6.2.2)
190
— при отказе любого одного из элементов остальные элементы си-
стемы остаются в рабочем режиме, т. е. характеристики надежности
каждого из элементов не зависят от состояния других элементов
(рис. 6.2.3.).
6.2.1. Экспоненциальные распределения времени работы и вре-
мени восстановления элементов. В табл. 6.2.1 и 6.2.2 приведены по-
Рис. 62.4. Граф переходов систе-
мы для табл. 6.2.1:
Но — состояние исправности системы; Hi —
состояние отказа системы по вине i-ro эле-
мента
казатели надежности последовательной системы, состоящей из п раз-
личных элементов, интенсивности отказов и восстановления каждого
из которых равны соответственно Яг- и цг. В табл. 6.2.1 показатели
надежности приведены для случая, когда при отказе любого элемен-
Рпс. 6.2.5. Граф переходов системы для табл 62 2:
Ло — состояние исправности системы; s — состояние отказа системы, когда восста-
навливаются именно элементы /, ...» fe.
та система выключается (граф переходов системы см. на рис. 6.2.4), —
а табл. 6.2.2 — для случая, когда исправные элементы системы про-
должают работать при восстановлении любых отказавших элементов,
причем восстановление предполагается неограниченным' (граф пере-
ходов системы см. на рис. 6.2.5). Для случая ограниченного восста-
191
Таблица 6.2.1
Последовательная система из п различных восстанавливаемых элементов с интенсивно-
стями отказов At и восстановления р.г (экспоненциальные распределения). При отказе
система выключается.
Пока* затель Точное значение Приближенное значение Условие Погрешность
т II — — —
п 1-1 — — —
р (to) е-л'о 1 — дг0 А/о<1 , (А/о)2
к / п \ —* H+S ь \ 1=1 J iiM* - 1 max Y- — i *г п б+ < пг (max у£)2 1
К(() —t (д + —) 1—ДтС—е Ат<1 г -в 5+ (Ат)2\ 1 — е /
R (t0) Ке~к‘° 1 — Л (т А1о<1. Ат<<1 3+ < 2,5 [A max (ta, -t)]2
Т а б л и ц а 6.2.2
Зак. 943
Последовательная система из п различных восстанавливаемых элементов с интенсивностя-
ми отказов и восстановления iJ-t (экспоненциальные распределения). Восстановление
неограниченное. При отказе система не выключается.
Пока Затель Точное значение Приближенное значение Условие Погрешность
т 1 >1“ II 1Мг — — —
т* / П \ t ( П <’ +YJ — 1 ) \х = 1 / _к । 1 maxv, <g — t 11 п » п2 8 _ < (max yJ2
/’(М 1 —до А/о< 1 (А/о)2 а + < 2
К* П (1 + y,)-1 'Wi । 1 max Yi <С — л2 б + < 2~ (max уг)2
K(t) Точное значение не приводится 1— Ат* С— е Ат* 1 й+ -ч. (Ат*)2 (1 — е-'л*)
К* е“Аг° 1 -А(т* + /0) А/о<1, Ат*<1 8 + < 2,5 [A max (10, тл)]2
новления возникает вопрос о выборе приоритета восстановления тех
или иных отказавших элементов, но и в случае выбранной дисципли-
ны обслуживания расчет показателей надежности в общем случае при-
/ л
7?Я
Рис. 6 2 6. Граф переходов системы для
табл. 6.2.3:
Но =* состояние исправности системы, состоя-
ние отказа системы,
водит к очень громоздким результатам, чаще всего в виде преобра-
зований Лапласа, обращение которых возможно лишь численными
методами.
В табл. 6.2.3 и 6.2.4 приведены показатели надежности для анало-
гичных систем: с выключением системы при отказе элементов (граф
Рис. 6 2.7. Граф переходов системы для табл. 6.2.4:
Но — состояние исправности системы; //(Л) — состояние отказа системы, когда ровно k эле-
ментов системы восстанавливается.
переходов системы см. на рис. 6.2.6) и без выключения системы при
неограниченном восстановлении, но уже для случая одинаковых эле-
ментов (граф переходов системы см. на рис. 6.2.7).
Л
Рис. 6.2.8. Граф переходов системы для табл. 6.2.5:
Но — состояние исправности системы; Нцу — состояние отказа системы, когда ровно I эле-
ментов системы восстанавливаются, k — число ремонтных бригад.
В табл. 6.2.5 приведены показатели надежности для случая пол-
ностью ограниченного восстановления без выключения системы при
отказе для случая одинаковых элементов (см. граф переходов системы
на рис. 6.2.8).
194
Таблица 6.2.3
Последовательная система из п одинаковых восста-
навливаемых элементов с интенсивностями отказов
X и восстановления р. (экспоненциальные распреде-
ления). При отказе система выключается.
Y = X/p.
Пока- затель Точное значение Приближенное значение Условие Погрешность
т 1 нХ — — —
т 1 Р- — — —
р (М е— пМ„ 1 — пМл nXf0 1 (пХ/0)г 3 + < 2
к (1 + ну)-1 1 —пу 8 + < (ну)2
МП —Мх+ — 1 К+(1-/С)е ' 1 > / _£\ 1—/гХт\1—е / пХт 1 8+ ^(нХт)2(1-е''л)
ММ Ke~nU° 1 — /гХ (г + /0) zzXZ 0 << 1, пХт<^ 1 8 + <2,5Х XfnXmax г)]2
Т аблица 6.2.4
Последовательная система из п одинаковых восста-
навливаемых элементов с интенсивностями отказов
X и восстановления р. (экспоненциальные распреде-
ления). Восстановление неограниченное. При отка-
зе система не выключается.
Y= Х/р.
Пока затель Точное значение Приближенное значение Условие Погрешность
т 1 пК — — —
т* 1 р- 1 п — 1 V 5 + <-— 1 + 2 р
е—пМ0 1 — /гХ/0 /гХ/0 1 (nXZ0)2 S + < 2
К* (1+у)-" 1 — /гу 1 п (п — 1) а + < 2 У2
МО Точное значение не приводится 1 — пХт* X Х\1-е 7 пХт* < 1 а + < («Хт*)2 х ХО-е-^’)
ММ /С*е— 1 — пХ(т*-р0) nXl0 1, пХт* <<; 1 а + <2,5х х JrtX max (/„ г1-)]2
7*
195
Таблица G.2.5
Последовательная система из п одинаковых восста-
навливаемых элементов с интенсивностями отказов
X и восстановления р. (экспоненциальные распреде-
ления). Восстановление ограниченное. При отказе
система не выключается.
Пока- затель Точное значение Приближенное значение Условие приближения Погреп нисть
т 1//гЛ — — —
т -li = И.. 1 <)! 1_ р- («- 1)1 j («-1)1 3+- м.’
/’(/о) е—пУ10 1 — nkt0 <С 1 8+ < j («Х/о)г
к < 1 т с —1 1 — n't ну 1 8+<«12
₽Чо) Ке-'г’ f° 1 — fi (kt о + Y) «:Ху/0<5 1 о+ ~ «2ЛуО
Пример 6.2.1. Имеется система из трех независимых последовательно со-
единенных элементов. Каждый из элементов имеет экспоненциальное распреде-
ление как времени безотказной работы, так и времени восстановления. Соответ-
ствующие интенсивности отказов и восстановлений элементов равны
Xj = 0,05 1/ч; щ = 1 1/ч; Л2 = 0,02; р2 = 0,5; Х8 = 0,01;
Мз= 1-
Требуется найти основные показатели надежности системы для работы в тече-
ние ta = 0,5 ч, коэффициент готовности для режима работы, когда при отказе
одного из элементов система выключается, и средние значения времени безотказ-
ной работы и времени восстановления (для того же режима).
Решение. Предварительно определяем значения:
'Л = X, + Х2 + Х8 = 0,05 + 0,02 + 0,01 = 0,08 1/ч,
7, =, Л,/м, = 0,05, у2 = Х2/р2 = 0,04, у3 = Х8/р8 = 0,01.
1. Среднее время безотказной работы
Т = 1/Л =- 1/0,08 = 12.5 ч.
2. Среднее время восстановления
т=^-(Т1+у2 + ?з)= (°’05+°’04 + 0,01) = 1'25 ч-
3. Вероятное^ безотказной работы системы за время /0 = 0,5 ч:
р (/О)=е-л/“ = е-0>08'0'5 = 0,&62.
196
Приближенное значение
Р (/0)=1 — Л/0=1—0,08-0,5 = 0,96.
4. Коэффициент готовности системы
К =----------------=--------—5—--------=0,909.
1 + Yi “Ь Ys “Ь Vs 1 + 0,05 + 0,04+0,01
Приближенное значение коэффициента готовности
К=4 —(Yi + y2 + y3) =1—(0,05 +0,04+0,01) = 0,9.
Примечание. Если предварительно вычислены значения Л и Т, то
часто удобнее бывает находить коэффициент готовности по формуле
К = 1/(1 + Лт) ж 1 — Лт
(приближение справедливо при Лт 1).
5. Коэффициент оперативной готовности системы для /0 => 0,5 ч:
R (t0) = Ке “Af» = КР (t0) = 0,909 • 0,962 = 0,874.
Приближенное значение коэффициента оперативной готовности
R (t0) = 1 —Л (т + /0) = 1 —0,08 (1,25 + 0,5) = 0,86.
Пример 6.2.2. Имеется система из 100 независимых последовательно соеди-
ненных элементов. Все элементы идентичны, причем каждый из них имеет эк-
споненциальные распределения времени безотказной работы и времени восста-
новления с параметрами
к = 1 . 10“’ 1/ч и |х = 0,2 1/ч.
Требуется найти основные показатели надежности системы для работы в тече-
ние 10 => 10 ч, коэффициент готовности для режима, когда при отказе одного из
элементов остальные элементы системы продолжают находиться в рабочем режи-
ме, и среднее значение времени безотказной работы и времени восстановления
(для того же режима).
Решение. Предварительно определяем значение у = 1 10“® /0,2 =
= 5 10-§.
1. Среднее
время безотказной работы
1 1
Г = — =----------г = 1 000 ч.
пк 100.10“®
я восстановления
2. Среднее
т* = 4-[(1+у)'1—1] =----!---[(I+5-Ю-6)100— 11 = 5,01 ч.
пк v 100-10-2 3 4 5 1
Приближенное значение
Г* = 1/11 = 1/0,2 = 5 ч.
3. Вероятность безотказной работы системы за время fn = 10 ч:
P(/0) = e-'1?’z» = e-100-10’5-,0 = e-0’01 =0,9901.
Приближенное значение
Р (/О) = 1—Шо= 1-100-10“6 * *.10 = 0,99.
4. Коэффициент готовности системы
К * =---5---=-----------— =0,99503.
(1 + Y)n (1+5-10-5)10»
Приближенное значение коэффициента готовности
К* = 1_Пу = 1 — 100-5-IO-5 = 0,995.
197
Примечание. Если предварительно вычислено значение т*, то часто
удобнее бывает находить коэффициент готовности по формуле
К = 1/(1 + нХт*) « 1 — гАт*
(приближение справедливо при гАх* < 1).
5. Коэффициент оперативной готовности системы для /0 = 10 ч:
R*(t0) = K* e~nKt = К*Р(/о) = О,9950-0,9901 =0,9851.
Приближенное значение
Й*(/о)=1-^(т+/о) = 1— Ю0-10-5(б+ 10) = 0,985.
6.3. Последовательное соединение зависимых
элементов
Предположение о независимости элементов систем на практике
часто оказывается неверным. Например, такая зависимость может
проявляться следующим образом:
1) на все элементы одновременно оказывает влияние один и тот же
внешний воздействующий фактор (температура, вибрация, радиация
и т.п.), поэтому все элементы одновременно становятся более надеж-
ными;
2) производится расчет системы, в которую входят однотипные эле-
менты, причем в качестве исходных данных для расчета используются
одни и те же статистические данные, что приводит либо к одновремен-
ному завышению, либо к одновременному занижению показателей на-
дежности всех однотипных элементов.
Таким образом, на практике чаще всего элементы являются не не-
зависимыми, а зависимыми — с положительной корреляцией. Для
двух зависимых случайных событий А и В имеет место выражение
Р (АВ) = Р (А)Р (В) + р (А, В),
где р (А, В) — коэффициент корреляции.
Для последовательного соединения зависимых элементов можно
записать оценку
т
P(tu)> п р.(1)
1=1
(т т \
п Ki, R(t0)^ П Rt(t0) ,
г=1 г=т /
т. е. истинная вероятность безотказной работы (коэффициент готов-
ности, коэффициент интервальной готовности) последовательной си-
стемы из зависимых элементов выше, чем значение вероятности, вы-
численное в предположении независимости.
Аналогичным образом,
оо со т
Tv = $ Р(0^> $ П Pt(t)dt,
о о 1= 1
198
т. е, истинное среднее время работы до отказа для последовательной
системы из зависимых элементов выше, чем значение среднего времени,
вычисленное в предположении независимости.
Пример 6.3.1. Система состоит из /п=10 последовательно соединенных иден-
тичных элементов, каждый из которых имеет экспоненциальное распределение
времени работы до отказа. Система предназначена для использования в режиме
с переменной нагрузкой, интенсивность которой меняется случайным образом.
Нагрузка а имеет экспоненциальное распределение со средним значением а0,
т. е.
3J {а > х} = е—х/а».
Предполагается, что интенсивность отказов пропорциональна интенсивности на-
грузки, причем при а = ай значение Хо = 10-3 1/ч. Это означает, что 3‘ {X >
е—Требуется найти вероятность безотказной работы системы за вре-
мя t = 10 ч и среднее время работы до отказа.
Решение. Вероятность безотказной работы одного элемента равна
Р1(Ю) = е-10"3-10 = е-10"2.
Нижняя оценка для вероятности безотказной работы последовательной системы
находится как
Р (10) > (е~ 10"2)1') = 0,905.
Нижняя оценка для среднего времени работы до отказа равна
Т = 1//иЛ0 = 100 ч.
Истинное значение вероятности безотказной работы определяется следу-
ющим образом:
Р (/„) = | е — еdz= - 1 -------------,
v An 1 “j-An tn tn
0
откуда
P (10) =-------!------=---------= 0,909.
1 + 10-10.10-3 1 + 0,1
Точное значение среднего времени работы до отказа находится как
оо оо
т=[р(С d/ = f —
J J 1 + mW
0 Г
Последний интеграл является расходящимся, т. е. истинное значение вели-
чины Т неограничено.
Список литературы
1- Д р у ж и н и н Г. В. Метод расчета надежности работы аппаратуры. —
«Автоматика и телемеханика», 1967, № 12.
2. С и н и ц а М. А. Расчет среднего времени безотказной работы аппарату-
ры. — «Радиотехника», 1960, № 3.
3. С и ф о р о в В. И. О методах расчета надежности работы систем, содержа-
щих большое число элементов, — «Известия АН СССР, ОТН», 1954, № 6.
4- Соловьев А. Д., Ушаков И. А. Некоторые оценки для систем из
«стареющих» элементов.—«Автоматика и вычислительная техника», 1967,№ 6.
5. Щербаков О. В. К оценке надежности последовательных систем
с восстановлением. — «Известия АН СССР, Техническая кибернетика»,
1966, № 1.
199
7.
УЧЕТ влияния КОНТРОЛЬНЫХ
И ПЕРЕКЛЮЧАЮЩИХ УСТРОЙСТВ
НА НАДЕЖНОСТЬ
7.0. Вводные замечания
Часто априорные расчеты надежности различных систем, в осо-
бенности резервированных систем, дают значения показателей надеж-
ности, существенно завышенные по отношению к получаемым при
эксплуатации или путем специальных испытаний. Это в первую оче-
редь объясняется тем, что используемые для расчетов формулы не
учитывают некоторых характеристик таких, казалось бы, второстепен-
ных устройств, как переключатели и контрольные устройства, кото-
рые в результате оказывают весьма существенное влияние на надеж-
ность.
В данной главе будут рассмотрены только дублированные системы,
поскольку они являются наиболее частым случаем резервирования.
Даже дублирование порождает огромное число частных схем, пред-
ставляющих собой различные случаи для расчета. В рамках данной
главы рассмотрены лишь основные из них. Заполнение справочника,
используемого для практических расчетов, формулами для вычисле-
ния показателей надежности многочисленных экзотических, но редко
встречающихся схем не представляется разумным (это же относится
и к случаям систем с большим числом резервных элементов).
Все расчетные формулы (за единственным исключением) получены
при помощи эвристического метода (см. приложение 6), т. е. справед-
ливы лишь при оговоренных соотношениях соответствующих пара-
метров, причем не приводится оценка не только для величины погреш-
ности, но даже и для ее знака. Это же относится и к приводимым верх-
ним и нижним оценкам.
7.1. Дублированная система с конечным временем
переключения
Рассмотрим дублированную систему с абсолютно надежным пе-
реключателем, но при условии, .что при отказе основного элемента
переключение происходит за конечное время /п. Для всех показате-
лей надежности приведены приближенные формулы, справедливые
для условия, если среднее время безотказной работы элементов (7)
много больше среднего времени простоя (т) и времени переключения
(tn), т. е. Т > т и Т > ta. Ограничений для соотношения т и Zn не де-
лается.
200
Таблица 711
Нагруженный резерв. Неограниченное восстановление у = И/ и у = т/ Т; Yo = tc Т или Го = Wo; или Ги=Т/п.
Показатель Экспоненциальное рас пре де чаше Произвольное распредетеьле Р (1}
нижняя оценке верхняя оценка
Ц 1 Л г т
% 1п + тх 1п + о,5ут Ц + гх
Ра ((о) 1 — 2Го е-'
К > — (Тп + №) 1 — 2 (f + 0,5№) 1 — ttn + г)
R Uo) П — (Тп+ Г2)] е-1” [1 -(2у„+ ,2)-(1 -То)2 (1 — (Тп + Г2)]?'1’
Таблица 712
Нагруженный резерв. Ограниченное восстановление Г — Лл или у — х Т; Го = 1о/7 или г»— Гп = tjl или у„ —
Показа гель Экс поненциальное распределение ।Троизво 1ыкх распределение Р (/)
ннжняя оценка верхпч 1 о 1енка
Т 1 0 1 Л 0,5Г г
<П + 2гх 1а + 0,5ут Ц + 2г
Uo) g“* То 1-2у0 е-7с
к 1 - (Гп + 2г!) 1 ~ (2уп + Г2) 1 — (Гп + 2т2)
R(io) [1 — (Гп+2г2)1 е—То [1- (2Гп+у2)] (1 “Го)2 [1 “(Гп + 2т2)]е-То
201
Таблица 7.1.3
Ненагруженный резерв.
Неограниченное восстановление
у = Xt или у = t/T',
Yo = to'T или Yo = X/o:
Yn= *п'т или Yn = XTO.
Показатель Экспоненциальное Произвояьное распределение Р (О
распределение нижняя оценка верхняя оценка
Та 1 Л Т Т
хо tn 4- °,5Yx tn + 0,5yt tu + 0,5yt
Ра (to) е-То P(to) Р (/о)
к 1 — (Тп + 0,5у2) 1 - (Тп + O.&r2) 1 — (Yn + 0,5y2 i
R(te) [1 — (Тп + °>5Т2)] е~Ь [1 — (Тп + 0,5y2)] X Х(1 - То) fl — (Тп 4- 0,5y2)] е~ь
Таблица 7.1.4
Ненагруженный резерв.
Ограниченное восстановление
Y = Хт или Y = х/^’>
Yo = ta/T или Yo = Мо
Tn = tn'1 или Ya — Мп-
Показатель Экспоненцнапыюе распределение Произвольное распределение Р (О
нижняя оценка | верхняя оценка
Те 1 X Т Г
'п + Тх /о + 0,5уч +
Ра (to) е~Ъ P(to) P(to)
к 1 — (Тп + Y2) 1 — (Ta 4- 0,5у-2) 1 — (Та4-Т2)
R(t«) [1 — (Тп + Т8)]^ [ 1 —(Тп4-0.5у2)] [1—Yo] fl -(Тп+ Y2)! е-''
202
Заметим, что, по существу, любой отказ основного элемента
приводит к отказу системы и что наличие работоспособного резерва
в это время позволяет лишь сократить время восстановления работо-
способности системы.
Формулы для показателей надежности дублированной системы
при различных режимах работы и восстановления приведены в
табл. 7.1.1—7.1.4. Распеделение P(t) предполагается «стареющим».
7.2. Дублированная система С ненадежным переключателем
Рассматривается дублированная система, состоящая из двух иден-
тичных элементов. При отказе основного элемента переключение на
резерв происходит при помощи переключателя, который в свою оче-
редь может отказать. Природа отказов переключателей может быть
следующая:
— переключатель отказывает с течением времени (вероятность
безотказной работы переключателя Рп (/));
— переключатель отказывает только в процессе переключения
с вероятностью q.
В случае, когда переключатель отказывает с течением времени,
можно рассмотреть две существенно различные схемы:
— отказ переключателя обнаруживается немедленно после его
возникновения;
— отказ переключателя обнаруживается только непосредственно
в момент переключения, т. е. при отказе основного элемента.
В последнем случае отказ переключателя неизбежно приводит
к отказу системы в целом, так как даже при наличии исправного ре-
зервного элемента, его нельзя подключить для выполнения основных
функций.
Все формулы расчета показателей надежности, приведенные в
табл. 7.2.1—7.2.3, получены эвристическим методом, поэтому оценки
погрешностей не приводятся. Эти формулы справедливы для следую-
щих условий:
— среднее время безотказной работы каждого из двух элементов
системы (Т) или переключателя (Тп) много больше среднего времени
восстановления этих устройств т и тп соответственно, т. е. Т Э1 т
и гп » тп,
— все произвольные распределения Р (/) и предполагаются
«стареющими».
7.3. Частично контролируемый восстанавливаемый
элемент
Рассматривается элемент, часть которого (составляющая а-100%
от общего объема) контролируется лишь периодически. После обна-
ружения отказа элемент начинает восстанавливаться, причем собст-
венно восстановление длится в среднем время т. Если отказ происхо-
203
Таблица 7.2.1
Дублированная система с ненадежным переключателем,
отказывающим с течением времени
(обнаружение отказа мгновенное)
Т=т/7’ или
Tn=V7u ИЛИ
7П=\1/Г или~п=Хтп:
То=(о/Г и-™ То=ХТо
или 7*=>т*
Показатель Нагруженный резерв Ненагруженныи резерв
Р («). Ра (О -хт -М е , е р | e-U. e~V
Т Q нижняя ©цепка верхняя оцерка / 2f + 7Л 1 X (27 + 7П) т Q СО + 7П 1 X (т + тв)
тс ннжняя оценка С 7 + 0,5тпуи 1’7 + 0.5tnx“ VQ СО + 0.5хпТп т*7 + 0,5гптп
27 + 7п 27 + ТЛ О (т) + 7П 7 + 7П
верхняя оценка + У° 27 4 7Л +^П I" 27 + 7П СО + tn7n О (х) + 7П т<7 + У° 7 + 7И
е-То (Т + Тп)
нижняя оценка 1 — 7о (-'7 + l“> е—То (27+7п) е-7о (Q СО + Тп|
верхняя оценка е“То <2Т +т“)
К нижняя оценка 1 — (77* + ~П7П) 1 — (77* +~П7П) IT*Q со + Ти ТП1 1 — (Т*Т +~П7П)
верхняя фценка 1 — (77« + О.^П7П) 1 — (ТТ* + 0,57п 7п) 1 - [7*0 (О +0,5 ГПТП| 1 — (Т*7 + 0,57п7п)
Л (То) нижняя оценка U—То (2у + 7П)]Х X [1—(ТТ*+ТП 7П)1 [1—(TT’+'i”!0)] е—1с1 <27 +Т > {1—17*0 (О + т“ тл1 }х Xe-To!Q С) + ТП| [1 —(Т*Т +~П7П)1 X хе-То(Т + ТП1
верхняя оценке 11—(71* + 0.5тптп)J X хе—То (2Т + Тп) |1— (ТТ* + 0.57П7П) 1 X Хе-То (27 + ТП) {1-(7*<2СО +057птп[}Х ye-To\Q (0+7“, |1—(Т*Т + О.5ТПТП)1 X Хе-То (Т +7П)
Т а б л и ц а 7.2.2
Дублированная система с ненадежным переключателем, отка-
зывающим с течением времени (обнаружение отказа
в момент переключения)
у = т/Т или у = \z,
уп = тп/Гп или уп = хптп
Уп = 'сп/7' или у" = ?л„
Уо = ta/T или у0 = и„,
у* = t*/T или у* = Хт*
Показ цель Погруженный речорв {
Р(>), р„ (Т) е-Ч 1
нижняя опенка Гв=С-е ‘)т„ I + 2уЛ
верхняя оценка ТТ 7.-7- + 2уГп
нижняя оценка Я - 27 '-Г \ тв = mm И 1 — е j т* 4- т 4-tB е ТТ ) 7-+2>я<Т” + 2уу*)’ 2уу* + уп 2уЛ + Хп
верхняя оценка // -2Т^\ тв = max | 1 — е j Vs + 1 ~2t -S 1 т + хп е > r + 2-k ап + 2уу*)|
Неп°гружен’ыи резерв
р (Т), Рп (Т) | е—7(
т'а =- 6 — ' ) Т V / и 1 7-п + Y^
ГТ 7 в ~ 1 + Y4
'•я = т!пП1 — е j г* + -Т^ + Тп е т ТТ„ ) T+^7<Yn + YY*)} уу* + yb YT. + Ап
Я -’Т) т в = Шах — е у т* + т —т — 1 т + тп е 77„ ) Г + у7п + П*) f
g Продолжение табл 7 2 2 <з>
Показатель Нагруженный резерв Ненагруженный резерв
Рп(» I e-^,e-M
Ра (to) нижняя оценка ( 1(1 1 Ри = < е “ при t0 < Т„, (.0 при ta > Та —fo (ХП+27М e u f 6} Ph (to) = < e ‘ при to < Ta, 10 при to Ta g — to (^ц + Т21)
верхняя оценка ПрИ to <.Ти. Ро ={ _ Ц. 2 (.е в при to > Гп Г e—По при to<,Ta, Ph (to) = { _ to. 1 г [e в при to Эг
к нижняя оценка ( х* Дн = I — max < т—г ( 1 а Т (^Т- Г1, I -J- Yn \е — 1J + 2ff* | 1—C(n + 2n*) / 1 T* Kn — 1 — max < 7—h Vй T / 7 Vх 1 f * 7 1 \ —1 J , уп-Ьп*| i — Crn + tt*)
верхняя оценка ( х* Кл — 1 — min < 7—г u т ' t У, 1 + Yn — 1J Yn + 2n*j , (t* KB — 1 — min { 7—b Г" T (t-т X\ 1 + Tn \e — 1 J № + W*|
R (/о) нижняя оценка КцРh (M [l-(Yn+ + 2П*)]Х •Хе~‘° <xn+22X) КнРь (tQ) [1-(1п + н’)| X xe~'° (X»+X)
верхняя оценка KoPo do) К ъРВ (t o)
Таблица 723
Дублированная система с ненадежным переключателем, отказывающим при переключении с вероятностью q.
Показатель Нагруженный резерв Ненагруженный резерв
р (0 e—xz Pit) e—M
To Нижняя оценка т 2 (7 +7) T 2f + q T Q w + q r 7 + Q
верхняя оценка т 27 + q
xe нижняя оценка ( Т«* + Qt„ 2ft* + qt 1 min - — . — J!-}’ 1 7 + q If + q ) 2ft* + qxn t*Q (x) + tn<? + 7 + <7
верхняя •ценк 1 ( ft* + qt 2ft* + qt 1 max s — , — —f l 7 + q 2f + q j 2f + q Q (t) + q
po (to) нижняя оценка e—27o (7 + q) e-7o (27 + <?) Pu (to) = min {P (70), e—7o IQ (’) + « } (/0) 1= max {P (t0)t e To [Q (*) + <7] J, —7o (7 + <?)
верхняя оценка e-7o (27 + q)
к нижняя оценка 1 — 2 iff* + 77n) 1 - (277* + qfn) , (t*Q (X) ~„\ 1 ~ У^7— + n I 1— (77* + <77n)
верхняя оценит I — (277* +<7~n)
о нижняя оценка (1—2 (tf* + <?7n)] e—2lo (7 4- g) (1 — (277* + <nn)]X X e—7o (27 + q) p _ p,<?r(T> + «fnyj e~to lQ (T) + 71 11 — (77* + «7n)l* Xe~7o (7 + q)
вер хняя оценка [1 — 4- e—lo + q)
2С8
нижняя оценка (' То)[1 (“Т, + Т)] (]—у0) [ 1 — (ау„ + y)j (1—f0) (1 — (“Tv + f)i
7
о
+
>
Й
1Л
о
дит в неконтролируемой части, то с этого момента до момента проверки
элемент находится в состоянии необнаруженного отказа.
Приближенные выражения для показателей надежности, полу-
ченные с использованием эвристического метода (см. приложение 6)
приведены в табл. 7.3.1. Формулы справедливы лишь при выполнении
условий у 1.
В головках табл. 7.3.1 символы Р (t) и е~к< обозначают вероятность
безотказной работы для произвольного и экспоненциального распре-
делений соответственно; ty — постоянный.период проверок неконтро-
лируемой части, a v — интенсивность этих проверок в предположении,
что они образуют пуассоновский поток.
7.4. Дублированные системы с частичным контролем
7
о
+
>
Й
ю
о
Во многих практических случаях при дублировании не удается
осуществлять одинаковый контроль основного и резервного элемен-
тов. Например, иногда возможен контроль только основного элемен-
та за счет использования функциональных тестов в процессе выпол-
нения рабочих операций, а иногда аппаратный контроль возможен
только лишь элемента, находящегося в резерве, т. е. не выполняющего
рабочих функций. Оказывается, что весьма существенным является,
какой из элементов контролируется полностью, а какой частично (так,
очень важно осуществлять как можно более полный непрерывный
контроль основного элемента), а также характер резерва и вид восста-
новления (см. табл. 7.4.1).
Таблица 7.4.1
Й
Приближенные значения г*
е>Ким восстановления Harp} жеяный резерв Незагруженный резерв
Произвольное распре- деление времени вое* ста ювтешя СКСПОНеН- ЦИаЛЬКОе распреде- ление вре мени вое становле ния Произвольное распре деление времени вое становления Экспонен- циал ькое распреде- ление вре- мени вос- становле НИЯ
Ограниченное восста- новление Т т 0,5т т
Неограниченное вос- становление Нижняя оценка Верхняя оценка 0,5т Нижняя оценка Верхняя оценка 0,5т
'0,5 т т 0,5 т т
Для пояснения режима контроля элементов системы в табл. 7.4.2—
7.4,8 приводятся условные схемы, на которых затемненная часть эле-
мента обозначает долю, не контролируемую непрерывно (т. е. конт-
ролируемую только периодически). Всюду предполагается, что переход
с Отказавшего основного элемента на резервный происходит только
209
Таблица 7 4.2
Полностью неконтролируемые элементы с одно-
временными периодическими проверками
Ь = /о/Т; Г = г*/Г;
Y, = tJT или 7„ =
Показатель Pit). t„ P(0- v —\t e , tv —It e , v
T 1 с нижняя оценка 0,5Г 0,57 1 X 1 X
верхняя оценка т T
нижняя оценка 0.5rv(l + 2Y*) +Y*) 0,5rv (1 4- 2y*) + Y*)
верхняя оценка M’+Y*) Mi + y*)
ра V') нижняя оценка 1 — Yo 1 — Yo e—io e-ь
верхняя оценка e-To е~ь
к нижняя оценка 1-Y, (1 + Y*) 1-Y,(1 +Y*) 1 ~Y, (1 + Y*) 1 — Y, (1 + Y*)
верхняя оценка 1 —0,5yv(1 + 2Y*) 1 — 0,5Yv (1 + 2у-*)
R(t„) нижняя оценка (1 - Yo)2[1 “ Y,(l + Y*)l (1 — Yo)[l — Y,<1 +Y*)| |1 — Y, (1 + Y*)l e"1" |1 — Y, (1 + rile"1’
верхняя оценка [1 — 0,5yv(l + 2у*)]е~7» [1 — Y, О +13е“1. [1 —0,5yJ] 4- 2у*)]е~1п
Таблица 743
Полностью неконтролируемые элементы
с независимыми периодическими провер-
ками
т X
у = у- или у — — или у = Ат,
Yo " t0/f; у* = т*/Т;
Y, = tv/I или yv =^y--
211
Показатель Pit). 1, Pit), , —xt , e . tv —xt e , v
Ta нижняя оценка 0.5Т 0,5/ 1, X 1 X
верхняя оценка т Г
ъ нижняя оценка 0.5ГД1 + 0,5y„ +Y*) M1 +Y, + Y*) 0,5«,(l + 0,5yv + y*) M1+y, + y*)
верхняя оценка Mi + y, + y*> \(1 +yv + y*)
Pit,) нижняя оценка 1 — Yo 1 — Yo e—T° « e-To
верхняя опенка e~To e—To
к нижняя оценка 1~2y„(1 +Y» + Y*) 1 — 2yv (1 + y, + y*) 1-Y, (1 +Y,+Y*) i-y,(1+y, + y*)
верхняя оценка 1-0,5yv(I +0,5Yv+y*) 1 — Y, (1 + Yv + Y*> 1—0,5y,(1 + 0,5Yv+y*)
Rd,) нижняя оценка (1-Yo)2X X[1 — 2yv(1 +Y, + Y*)1 (1 _ 7o) f 1 — 27v X X(1 +y, + y*)1 [1—Y,(l + Y,+ Y*)le_b [1—Y,(l +Y,+ Y*)]e“'[o
верхняя опенка |1-0.5y,X X (1 + 0.M+ Y*)]e—10 |1 — YVX X (1 +Y, + Y*)1 e~b [1 — 0,5YvX Х(1+0М,+ Y*)] e" 1“
Таблица 7 4.4
to
to
Полностью неконтролируемый резервный элемент
с периодическими проверками
Y = t/T или у — Лт и III
У = X/jt, у* = т*/Г
1, -= tJT. y0= t^T
Показатель р («). г. P (0 v e—U, t. e . v
те нижняя опенка 7 T Yv+ Y 1 1
Y, + Y т (yv+y)
верхняя оценка Т T X(YV bY)
0,5yv + y >’.5Y,+ Y
ч т* T* г’ T*
ра (М нижняя оценка шах {Р (/„), е-То + 7>} max{P(/0), e~ 1’n’ +v)} -Wv + I) e —To(b +M e
верхняя оценка тах{Р(/0),е-Ь,°’5^+П}
—Io (0,"nv + V) e
К Rito'l нижняя оценка i—y*(y, + y) 1 — Y* (Y, + Y) 1— y*(y, + y) ' 1 — Y* (Y, + Y)
верхняя оценка 1 — Y* (0,5y, + Y)
1 —Y“ (0.5у, + y)
нижняя опенка [1 — Y*(YV+ Y)J [1 — — Yo (Y, + Y)] [1-y*(yv + y)1 [1- — Yo (Y, + Y)J [1 — Y* (Y,+ + Y)e-b<^> (l-Y’(Yv + . . , -Ъ Gv + + Y)]e
верхняя оценка |1-Y* (°.5yv + + T)]e-7o(0.57, + 7) il-Y*(Yv + + Y)]e-I’(lf’ + n [1 — Y* (0.5yv + Y>j <0’51!v + v)
Полностью неконтролируемый основной
элемент с периодическими проверками
Таблица 7 4.5
Y = т/Т или Y = Хт или у = Х/р.
Yo = te/T\ y* = tr/T,
Y, =- t^/T или yv — 1/мТ
Q9
Показатель Р (0.«, /»(«).» e-Xf, e , v
To нижняя оценка 0.5Г 0,5T 1 X 1 X s
верхняя оценка т T
нижняя опенка 0.5Y.4- yt* f,+ Y’* 0.5', 4-Yt* \ + Yx*
верхняя оценка + YT* <, + Yx*
Pc (t0) нижняя оценка 1 — Yo 1 — Yo e-Yo
верхняя оценка е—Y° e—To
к нижняя оценка 1 —2yv —2yy* 1 -2y,-2yy* 1 -Y,-YY* 1 — Y„— YY*
верхняя оценка 1- 0.5yv- YY* 1 —Yv~YY* 1 — 0.->y,— yy*
Rtto) нижняя оценка (1-Y»)2(1-2yv-2yy*) (1—Yo) (1 —2y,—2YY*) (1 — Ya — YY*) e-7“ (1 — Yv~ YY*) e-1°
верхняя оценка (I — 0,5yv—YY*le-b (1 — Yv —YY*) e“To (1—0 5(, — YY*) e-b
Таблица 7.4.6
Частично контролируемый резервный элемент
с периодической проверкой
у - - ~ 7' или у — Лт или у = Л/р;
у* = т*/Л; у0 = t0/T-
У, = tv/T или yv = 1/мГ;
А-- 2у + ayv; Ав— 2у + 0,5ayv.
Показатель р (0. ч Р It). V е~и, to е v
т ' 2 с нижняя оценка т А Т А 1 ллн 1 ЛА
верхняя оценка т А 1 fA„
% нижняя оценка 2ут* + 0,5a/vyv Ав 2ут* + afyv г* + О,5«7„у, ** + «г, to
верхняя оценка 2yt* + a/vYv А А т* + 47,
Л (to) нижняя оценка max {Р (to), е~т<А} тах{Р(/0), е То/1н} е~ьА —т<и е н ,
верхняя оценка max {Р (t0), е~7'А } ‘ е~1°Ао
к ннжняя оценка 1 — (2уу* + ayj) 1 — (2уу* + ау*„) 1 — (2уу* + а7,) 1 — (2уу* + ау^)
верхняя оценка 1-(2уу* + 0,5ау‘) 1 — (2уу* + 0,5ау^)
R(t<>) нижняя оценка [1 —(2уу* + + “Yv)] О — УоА) [1-(2уу* + + «Yv)] (1 — 7оА) [1~(2уу* + + “Yv>] U — 7оА) [1 - (2уу* + + «/„)] е н
верхняя оценка [1 — (2уу* + + 0,бау2)] е-7оД- [1-(2уу* + + ау*)]е [1 — (2уу* + + °,5ау2)] е 1<И"
Частично контролируемый основной элемент
с периодической проверкой
Y а б лица 7.4.7
у = т/7 или у = Л/р;
у*=т*/7; уо=<о/7';
у, = /,'? или y„ = 1/vT;
А—а + у (2—«) (1—«)
Показатель Р (t). to Р (t). V е-И, to е , к
Т 1 о точная оценка т ~А Т ~А 1 КА 1 КА
нижняя оценка J0,5a^ + -t*y (2 + + «(1 — а)| Jj-[a/v + t*y (2 — -а) (1 - а)] -!г[0.5а/¥ + г*у (2- — а) (1 —а)] -Ь[А + т*у (2- — а) (1 — а)|
Ja/v+t*y (2—а) (1—«)]
верхняя оценка ~д [4+т*7 (2—а) (1—а) J
Ре (^о) точная оценка max {Л5 (to). е~'1оА} max {P(to). е -1 <А е-ТоЛ
1 —[«7о + 77*(2 — — а) (1 — а)] 1 — I«Yv + 77* 12 — — а) (1 — «)1
к нижняя оценка 1 —[“/, + 77*<2 — — а) (1 — а)] 1 — I“Yv + 77* (2— — а) (1 — а)]
верхняя оценка 1 — [О.бау, + уу* (2 — — а) (1 — а)] 1 — [0,5ayv+ уу* (2 — — а) (1 — а)]
{1 — И, + 77 " (2— -а) (1 — а)]> е—
нижняя оценка {1 —[“Yv + YY* (2 — — а) (1 —а)]} (1—У«И) {1 — I«7v + 77* (2- —а) (1— а)|} (1—То-4) (1 — |ау0 + 77* (2— -а) (1 -а)]} е-4»-4
верхняя оценка {1 — [0,5ayv+ уу* (2 — — а) (1 — а)]} е '"л {1 — Hv + 77* (2 — -а) (1 - с- ’»4 {1-[0,5ау„+уу*Х Х(2-«) (1 -«)]} е-7«Л
Таблица 7.4.8
го
Частично контролируемые идентичные элементы
с одновременными периодическими проверками
X = ади у — Дуу.
Т’=т”/7 Х, = /,/Г Yo^/o/T,
Лн = О + (J — Я) (2-fv + X);
Л, = » + (1 - а) (xv 4- х).
_______-___________________________I
Показатель Р (t). » tv V
Т’с нижняя оценка Т т лв 1 мв 1 м,
верхняя оценка Т А,
1 АЛ,
ч нижняя оценка XtJa’ Iя + (1 -а)Х X Х,1 (1—«)Т* (Х,+Х)} ft,l“+2 (1— а)х,1 + + (!—“) т* (2х, + X)} 4- 14-1“+ (1-“) X,J+ Пв 1 2 + (1 — т* (X, 4- X)} Т7<М“+2(1~Я)Х,] + + (1 — а) -с* (2уу + у)}
верхняя оценка 1 ( [“ +2(1 — а)Х ХХ,]+(1—“) t*(2xv+Y)}
^{М«4-2(1-а)Х,]Х + (1 - “) X* (2х„ 4- X)}
Продолисение табл 71 8
Показатель р to, Р <0, ’ е~Ч
Pc (0 нижняя опенка max {Р (Хо), е 7°Ди} max [Р (/0) е"1"’’} —1оИ (1~а) (2l v + П) £ е~То [а+(1 -а) (27, + 7)]
верхняя оценка max {Р ((„). е °} —То1а+ (1 — а) (Tv + 1)1 £
К нижняя опенка верхняя опенка 1—{х, {“4-2 (I—«)х,!+ + (1 -а)х* (2x,4-х)} 1 — {0,5уу [а + (1 — -а) Х,] + (1 -«)Х*Х Х(Х,4-Х)} 1—ft, [“ + 2(1 — — “)Х,1 + (1 X Х(2х, 4-Х)} ^4-2Л'—X 7,? А + (1 -*)х* (2x,4-х)} 1 — {°.5х, [« + (1 - — а) X ,1 + (1 — — «)Х* (X, 4-Х)} 1 - {х, [“ + 2(1 - — “) х,] + 0 -“) 7* X X (2х, +х)}
R(t„y нижняя оценка (1 -{X,h4-2(1 - - ») Х,14-(1-“) X* (2х,4~ 4-х)}) (1 — ХоА) (1 — ft,l“ + 2 a — - я) Х,1 4- 0 - “)Т’Х X (2х„4-г)}Н!—ГоА.) (1-{Х, ,'а+2(1-«)Х,]+ + (!—“) Х*(2Х,+Х)})Х —г„ <=: + (!—«; (2i, + гу де (1 - ft, [“ + 2(1 - — “) х,14- (1 — “) х* X Х(2х, + х)})Х -Ыа+ (l-“) (21!» + 7» X е
верхняя оценка (1 — {О+х, [а + (1 — — “)х,1 4- (1 — “) х* X X (X, 4- X)}) c~Mb (1-ft, [а+ 2(1- -а) Y,j + (1 -“)Y*X Х(Ч + х)})е~ьЛв (1-{0.5х,1»+ (1- — а) Т,] 4- (1 -»)Х*Х X а, + х)}) X ч, -То 1»+ (1-«> (Т» + Т)) 2^
с помощью переключателя, т. ё. осуществляется резервирование за-
мещением, а не постоянное резервирование (переключатель пред-
полагается абсолютно надежным). Отказ в неконтролируемой части
основного элемента всегда приводит к отказу системы, так как она
остается в состоянии необнаруженного отказа до момента очередной
периодической проверки.
В головках таблиц 7.4.2—7.4.8 приняты следующие обозначения:
Р (/) — вероятность безотказной работы отдельного элемента для
произвольного распределения времени работы до отказа; —та же
вероятность для экспоненциального распределения; tv — постоянное
значение периода проверок неконтролируемой части; v — интенсив-
ность случайных проверок неконтролируемой части (предполагается,
что проверки производятся через экспоненциально распределенные
случайные интервалы времени).
Все формулы являются приближенными и справедливы лишь в
предположении, что 1, ?(>« 1, L Yv < 1. Они получены
при использовании эвристического метода (см. приложение 6), поэто-
му оценки погрешностей не приводятся. Среднее время безотказной
работы (Тс) и вероятность безотказной работы (Рс (/)) приведены для
стационарного режима.
Нижние и верхние оценки приводятся для случаев, когда те или
иные распределения предполагаются «стареющими».
Для всех случаев дублирования с неполным контролем в таблицах
для обозначения среднего времени восстановления системы исполь-
зуется символ т*. Выражение для т* зависит от характера резерва,
вида распределения времени восстановления отдельного элемента
и от характера восстановления (ограниченное или неограниченное).
Если рассматриваются системы, состоящие из высоконадежных эле-
ментов, т. е. если т/Т 1, то выражение для приближенных значе-
ний т* можно найти из табл. 7.4.1.
Список литературы
1. Веселов В. Н. Оценка показателей надежности дублированной сис-
темы с неполным контролем при учете периодических проверок. — «На-
дежность и контроль качества», 1969, № 8.
2. Е п и ш и н Ю. Г. Зависимость надежности от полноты контроля резер-
ва. — В кн.: Кибернетику — на службу коммунизму. Под ред. А. И. Берга,
Н. Г. Бруевича, Б. В. Гнеденко, М., «Энергия», 1964.
3. Иванцов В. М. Об одной модели оптимизации контроля при наличии
ошибок. — «Надежность и контроль качества», 1971, №5.
4. И в н и ц к и й В. А. Об одной задаче резервирования с переключени-
ем. — В кн.: Кибернетику — на службу коммунизму. Под ред. А. И Берга,
Н. Г. Бруевича, Б. 5- Гнеденко. М., «Энергия», 1964.
5. И в н и ц к и й В. А., Данилов К- П. Учет контроля в задаче надеж-
ности. — В кн.: Теория надежности и массовое обслуживание. Под ред.
В. В. Гнеденко. М., «Наука», 1969.
8.
СИСТЕМА СО СЛОЖНОЙ СТРУКТУРОЙ
8.0. Предварительные замечания
Очень многие реальные системы имеют такую структуру соеди-
нения (или взаимодействия) элементов, которая не может быть сведе-
на ни к параллельно-последовательно, ни к последовательно-парал-
лельной схеме (рис. 8.0.1).
Наиболее простой пример подобных систем (так называемая мости-
ковая схема) показана на рис. 8.0.2. В общем случае такие системы
Рис. 8.0.1. Пример системы со сложной струк-
турой
Рис. 8.0 2. Мостиковая
схема.
могут представлять собой сети очень сложной конфигурации. На
практике к подобным системам можно отнести различные системы свя-
зи, информационные системы, системы управления территориально
разнесенными объектами и т. п.
Методы оценки различных показателей надежности со сложной
системой весьма специфичны.
8.1. Метод прямого перебора
Произвольная система, состоящая из п элементов*, может на-
ходиться в 2п различных состояниях:
Но — все п элементов работоспособны;
Нг — отказал i-й элемент, остальные работоспособны;
И if — отказали i-й и /-й элементы, остальные работоспособны;
... ,п — отказали все элементы.
* Каждый элемент может находиться в состоянии работоспособности и
в состоянии отказа.
Если каким-либо образом определен критерий отказа системы, то,
применив его к каждому из состояний, все множество состояний мож-
но разделить на два подмножества: подмножество состояний работо-
способности системы «Г и подмножество состояний отказа системы
Тогда, если для каждого состояния На вычислить вероятность его по-
явления Рп, то вероятность состояния работоспособности системы
в целом можно записать как
SP {а € = 2 Ра-
а 6 &
Если система состоит из взаимно независимых элементов, то
п п
Л = п Ph==
г=1 ’ t=i Pi
кФ I
п
Pi,j~9t4j П =
k= i
k^-t, j
Р\,Ъ..n — P« П уг= П
1=1 1=1
где pt — вероятность состояния работоспособности Его элемента
системы; qt — верояпюсть состояния неработоспособности i-ro эле-
мента,
yt = qJpi-
Обычно системы обладают своеобразным свойством монотонности,
которое заключается в том, что, если На — состояние отказа системы
(т. е. « f $), то и На* — также состояние отказа, когда а* эа (т. е.
в индекс а* входят обязательно все индексы элементов, входящих в
а и еще какие-нибудь индексы). Это существенно облегчает разделе-
нию множества состояний па два подмножества 3F и
Если pt — вероятность работы до отказа для Его элемента, т. е.
Pt W ~ >• О, где — случайное время работы до отказа Его
элемента, то формула для Р позволяет вычислять вероятность безот-
казной работы системы до отказа, т. ё. Р (t) ~ {Е > О, где ? —
случайное время работы до отказа системы.
В этом случае можно вычислять и среднее время работы системы
до отказа по общей формуле
со
Т = $ P(t)dt.
о
Если pi — коэффициент готовности (нестационарный коэффици-
ент готовности, коэффициент оперативной готовности или нестацио-
нарный коэффициент оперативной готовности) Его элемента, то ве-
роятность Р является коэффициентом готовности (нестационарным
220
коэффициентом готовности, коэффициентом оперативной готовности
или нестационарным коэффициентом оперативной готовности) системы
в целом.
Пример 8.1.1. Мостиковая схема (рис. 8.0.2) состоит из идентичных эле-
ментов, каждый из которых характеризуется вероятностью безотказной работы
р (/) = с параметром X = 0,01 1/ч. Требуется найти вероятность безотказ-
ной работы схемы за t = 10 ч и среднее время работы до отказа.
Решение. Составляем таблицу возможных состояний (табл. 8.1.1) и
по рис. 8.0.2 непосредственно определяем, к какому подмножеству относится
то или иное состояние.
неисправен.
ы
состоянии орались в соответствии с правилом.
три индекса возрастают.
Заметим, что при составлении таблицы нами использовалось свойство моно-
тонности: при комплектовании комбинаций из трех индексов не использовалось
сочетание «1, 2» (заведомо отказовое), а для построения комбинаций из четырех
индексов использовалось лишь сочетание «1, 3, 4» (единственное состояние рабо-
тоспособности, индекс которого можно наращивать, добавляя элементы с боль-
шими номерами). В то же время комбинации из трех индексов, содержащие со-
четание «4, 5» (например, «1, 4, 5» или «2, 4, 5»), относились к подмножеству
сразу, без обращения к рис. 8.0.2, так как уже а = (4, 5) принадлежало подмно-
жеству .9.
Таким образом,
Р (0 = Р’ (0 + 5<? (0 р’ (/) + Чф (0 р3 (0 ± 293 (/)р2 (/).
(8.1 1)
221
Иногда при расчете Р (I) для малых значений t удобнее сделать замену р = 1—q
и выразить в функции от q:
р5=1—5g+10g2 —10g3 + 5g4 — д5
5qpi= 5q—20g2 + 30g®—20g4 + 5g5
8g2p3 = 8g2—24g®+24g4—8g® (8.1 2)
2g3p2 = 2g3— 4g4 4-2g5
P = 1 — 2g2—2g3 + 5g4—2g5
При g (t = 10) = 1 — e~0,1 « 0,1 нмеем P (t = 10) = 1-2-0,01 — 2 • 0,001+
+ ... ~ 0,978
В то же время для вычисления среднего времени работы до отказа удобнее
представить Р (t) в функции от р, так как в этом случае легко находитсн требуе-
мый интеграл.
В окончательном виде имеем
Р (0 = 2р® (0 — 5р4 (0 + 2р3 (/) + 2р2 (/). (8.1.3)
Интегрируя Р {t) с учетом того, что pk (f) = е~k,'‘, получаем
С „ 2Т 5? 2Т 2Т
—г+-г+—-
о
24—75+40 + 60 49
-----т-—--Т=— 7 ss 0,82 Т = 82 ч
60 60
8.2. Метод разложения относительно особого элемента
В редких случаях удается воспользоваться известной из матема-
тической логики теоремой о разложении функции логики по любому
аргументу. Применительно к задачам надежности эта теорема мо-
жет быть сформулирована следующим образом:
Р = ptP (х( = 1) + qtP (Xi = 0),
где Р (xt = 1) — вероятность состояния работоспособности системы
при условии, что i-й элемент абсолютно надежен, а Р (х, = 0) — та же
вероятность при условии, что i-й элемент заведомо отказал.
Можно использовать подобное разложение функции Р относитель-
но нескольких элементов, однако в этом случае процедура будет сво-
диться к своеобразному перебору. Например, для случая разложения
по двум элементам:
р = PiPjP (Xi = 1, Xj = 1) + ptqjP (Xi = 1, Xj = 0) +
+ q.pjP (x, = 0, Xj = 1) + qtqjP (xt = 0, X/ = 0).
Заметим, что каких-либо четких рекомендаций по выбору элемента,
относительно которого производится разложение функции Р (i), сде-
лать в общем случае не удается.
Пример 8.2.1. Рассмотрим ту же мостиковую схему, что и в предыдущем
примере, и найдем выражение для вероятности безотказной работы. В качестве
элемента, относительно которого производится разложение, возьмем х8.
222
При х3 — I мостиковая схема превращается в параллельно-последователь-
ное соединение (рис. 8.2.1), где перемычка вместо элемента х3 означает, что эго
соединение присутствует всегда, т. е. элемент х3 абсолютно надежен. Для этого
случ_ая
Р (хз = 1) = (1 QiQi)(1 — <7з?«)-
При х3 = 0 мостиковая схема превращается в последовательно-параллельное
соединение (рис. 8.2.2), где отсутствие элемента х3 эквивалентно тому, что этот
элемент постоянно находится в состоянии отказа. Для этого случая
Р (х, = 0) = 1 — (1 — рщ4)(1 — р2р5).
Рис. 8 2.2. Представление мостиковой
схемы в виде последовательно-парал-
лельного соединения для случая до-
стоверно отказавшего диагонального
элемента (х3=0).
Рис. 8 2 1 Представление мостиковой
схемы в виде параллельно-последова-
тельного соединения для случая до-
стоверно исправного диагонального
элемента (х3=1).
Окончательно находим
р = Рз (1 — ЯхЯяМЛ — + <7з П — (1 — Р1Р«)( 1 — РгРоЖ
что при идентичных элементах дает
Р = Р(1 + ~(1 -р2)Ч.
Нетрудно убедиться, что эта запись эквивалентна (8.1.1) — (8.1.З.).
8.3. Метод минимальных путей и минимальных сечений
Введем два необходимых понятия:
1. Минимальный путь в структуре произвольного ти-
па — такой минимальный набор работоспособных элементов, исклю-
чение любого из которых (т. е. отказ) переводит систему из состояния
работоспособности в состояние отказа.
2. Минимальное сечение в структуре произвольного
типа — такой минимальный набор отказавших элементов, восстанов-
ление любого из которых переводит систему из состояния отказа в
состояние работоспособности.
У систем с произвольной структурой может быть несколько мини-
мальных путей и минимальных сечений. Последовательное соедине-
ние из п элементов имеет п минимальных сечений, проходящих через
каждый элемент, и всего один минимальный путь. Параллельное сое-
динение из п элементов имеет п минимальных путей, проходящих че-
рез каждый элемент, и всего одно минимальное сечение.
Обозначим j-й минимальный путь (j = 1, 2...па) через и7-, a k-e
минимальное сечение (k = 1, 2, .... пр) системы с произвольной струк-
турой — через рй. Тогда можно записать следующие верхнюю и ниж-
223
нюю оценки для вероятности Р, выраженной через характеристики
элементов, входящих в минимальные пути и минимальные сечения:
«р «а
п {I- П (I_Р1)] I_ П (I- П ?,).
k = l I 6 /=1 I еа;
Если pt — вероятность работы до отказа т-го элемента является
экспоненциальной функцией рг (/) = е_\', то, проинтегрировав
правую часть этого неравенства, можно получить верхнюю оценку
для среднего времени работы до отказа системы в целом:
Т
</<па 1 «
_____1______
, Ла + Ла. +Ла,
at « 1
у __________
< k < Пг.
па
—1)"“
i Ла
: ' < "а
где Та =—---------•—среднее время работы до отказа /-го пути;
} 2
iGa,
л„=1/та.
7 7
Пример 8.3.1 Рассмотрим мостиковую схему, представленную на рис. 8 0.2.
Все элементы этой схемы характеризуются вероятностью безотказной работы
р (/) = е~к1 с параметром X =» 0,01 1/ч Требуется дать оценку вероятности без-
отказной работы схемы за /0 = 10 ч и верхнюю оценку среднего времени работы
до отказа.
Решение. Для этой схемы минимальными путями будут: 1) лд, х4;
2) х^хзхь, 3) 4) *2*3X4, а минимальными сечениями: 1) xtx2, 2) xix3x5;
3) 4) х2х3х4. Обозначим р (I = 10) — е—=> р и q = 1 — р и за-
пишем верхнюю и нижнюю оценки в развернутом виде для данного случая:
(1 - </2 )2 (1 - р8)2 < Р < 1 — (1 - р2)2 (1 - р3)2.
Подставив численное значение q ~ 0,1, получим
0,978 < Р < 0,9976
(напомним, что истинное значение 0,978 было вычислено в примере 8.1.1).
Для верхней оценки среднего времени работы до отказа вычислим предвари-
тельно интесивности отказов для каждого из минимальных путей:
1) At = 0,02 1/ч, 2) Л2 = 0,03 1/ч, 3) Л, = 0,02 1/ч 4) Л4 = 0,03 1/ч.
В итоге находим
Т < 50 4- 50 -I- 33,3 + 33,3 — 20 — 25—20—20—16, 7 — 20 + 14,1 4- 12,5 +
4- 14,1 + 12,5—10 = 97,2 ч
(напомним, что истинное значение 82 ч было вычислено в примере 8.1.1).
8.4. Аналитико-статистический метод
8 4.1. Общее описание метода. При исследовании сложных сетей
связи, где количество элементов и линий связи между ними очень ве-
лико, ни один из указанных методов не оказывается достаточно эффек-
тивным. Если линии связи между элементами достаточно надежны,
224
а сеть обладает определенной избыточностью, то прямое использова-
ние метода статистических испытаний также оказывается мало эффек-
тивным, так как многие реализации оказываются неинформативными
(очень часто появляются реализации, когда не отказала ни одна ли-
ния связи, либо возник ровно один отказ, что обычно не сказывается
на работоспособность сети в целом).
В этом случае для изотропных сетей, у которых все линии связи
равнонадежны, можно использовать смешанный способ оценки:
1) аналитически вычислять вероятности различных типов состоя-
ний сети, включающей п линий связи между элементами:
/7(0) — работоспособность всех линий связи в сети,
/7(1) — отказ ровно одной линии связи в сети;
..., H(k) — отказ ровно k линий связи в сети.
Вероятность события H(k) равна
n Л Ь Л1 — k
где р — вероятность состояния работоспособности линии связи меж-
ду элементами сети, q — 1 — р ),
2) методом статистических испытаний оценивать условные вероят-
ности Фк того, что сеть, находящаяся в состоянии На-), работоспо-
собна по выбранному критерию,
3) вычислять полную вероятность работоспособности сети по фор-
му ле
k= 1
Примечание. Если сеть построена таким образом, что отказ j любых
линий связи не приводит к отказу сети в целом, го
При этом, чем больше /, тем более эффективен смешанный аналитико-статистиче-
ский метод оценки
Обычно в качестве критерия работоспособности сети выбирается
наличие связи (включая транзитные) между всеми элементами, т. е.
так называемая связность сети. В этом случае Фй есть условная ве-
роятность связности сети при отказе ровно k линий связи, которая
находится следующим образом.
При помощи метода статистических испытаний осуществляется
конкретная реализация ровно k отказов тех или иных линий связи.
(Например, выбираются k различных случайных целых чисел, равно-
мерно распределенных в интервале (1, п].) Далее, эта конкретная
реализация сети проверяется на связность. Если данная реализация
удовлетворяет критерию, т. е. сеть’связна, то в счетчик числа успеш-
& Зак 943 225
них исходов к имеющемуся там числу прибавляется единица. Услов-
ная вероятность Фь вычисляется как
Фд = (Nh)/Nk,
где Nk — полное число реализаций при k отказавших линиях связи;
vk (AM — число успешных исходов из общего числа Л\ реализаций.
Алгоритм проверки связности сети с конкретно реализованной
структурой приведем ниже.
Пример 8.4.1. Рассмотрим опять мостиковую схему (см. рис. 8.0.2) с теми
же характеристиками, что и в предыдущем примере. Мостиковая схема допуска-
ет отказ любого одного элемента без нарушения работоспособности. Это означает,
что Фо = Ф1 = 1. Отказ любых четырех элементов приводит к обязательному
отказу схемы (так как нет ни одного пути, состоящего из единственного элемен-
та), т. е. Фа = 0. Естественно, что Ф5 = 0.
Величины Ф2 и Ф3 найдем, используя таблицу случайных чисел
(табл. П8.18). Будем сч’итать, что появление цифр 0 и 1 соответствует отказу
элемента xlt цифр 2 и 3 — отказу элемента х2, цифр 4 и 5 — отказу элемента
х3, цифр 6 и 7 — отказу элемента х4, и, наконец, цифр 8 и 9 — отказу элемен-
та х5.
Возьмем подряд все числа первого столбца: 218155512 и т. д. и перекоди-
руем в последовательность «отказавших» элементов:
x2xlxix1x3x3x3x1 х2 и т. д. Разобьем последнюю последовательность на пары,
наблюдая при этом, чтобы в каждой паре не было двух одинаковых элементов
(запрещенная комбинация). Двадцать реализаций незапрещенных комбинаций
таких пар поместим в табл. 8.4.1 и для каждой из них поставим в соответствие
единицу, если отказ данной пары элементов не приводит к отказу схемы, и нуль —
в противном случае. Далее возьмем второй столбец таблицы случайных чисел
(табл. П8.18) и каждой тройке чисел приведем в соответствие свою последова-
тельность «отказавших» элементов по тому же правилу, исключая из анализа
те тройки, в которых попадаются хотя бы два одинаковых элемента (запрещен-
ная комбинация).
Двадцать реализаций незапрещенных комбинаций таких троек поместим в ту
же табл. 8.4.1, поставив в соответствие каждой из них единицу или нуль по тому
же правилу (столбец 4 табл. 8.4.1). (В этой же таблице приведены и примеры
запрещенных комбинаций.) Проверку связности для этого простого случая осу-
ществляем простым анализом рис. 8.0.2.
Таким образом, табл. 8,4.1 позволяет вычислить статистические оценки
для Ф2 и Ф3:
Ф2 = 13 :20=0,65 и Ф3 = 3:20 = 0,15.
Вероятности равны
Р(0) = 0,95 = 0,5905, Р(1) = 5 . 0,1 • 0.94 = 0,3281,
Р,9, = 10 0,12 • 0,93 = 0,0729, Р,,, = 5 . 0,13 0,92 = 0,041.
(2) (о)
Отсюда окончательно находим
Р = 0,5905 + 0,3281 + 0,65 • 0,0729 + 0,15 • 0,0041 = 0,9722.
(Напомним, что истинное значение было вычислено в примере 8,1.1 и равнялось
0,978. Ошибка в данном случае вызвана малой достоверностью значений Ф2 и
Фз.)
226
Таблица 841
Номер незап решенной комбинации Реачизация двух етгказавщих элементов Индикатор работоспо- собности схемы Номер не зап решенной комбинации Реа тизация трех отказавших элементов Индикатор рамное ю СОЛ1ОСТИ схемы
1 X2Xj 0 Х,Х4Х4 —
2 Х5Х1 1 ХзХ3Хз —
X3X3 — 1 ^3X5X1 0
3 X3X1 1 Х2Х3Х2 —
4 Х2Х4 1 Х3Х3Х5 —
5 Х2Х3 1 2 X2X4Xi 0
Х2Х2 —- Х4Х4Х3 —
6 X jXg 0 3 Х^Х2Хз 0
7 Х]Х3 1 4 х4х2х5 0
8 Х4Х3 0 5 Х2Х3Х5 1
9 Х2Х5 1 6 X3X2X5 1
10 XgXi 0 7 XjX4X5 0
11 X4Xi 1 8 Х2Х3Х5 1
X3X3 — 9 ^4X3X5 0
12 X4X3 1 10 X5XjX3 0
13 xdx2 1 11 х3х4х5 0
14 X3X4 1 12 х5х2х4 0
15 XjX2 0 13 X5XjX2 0
16 X1X2 0 14 X2XJXi 0
17 XjXj 1 15 Х.Х1Х4 0
18 x,x3 1 16 0
19 X 3 X2 1 17 Х3Х4Х2 0
18 х4х5х2 0
19 Х3Х)Х5 0
20 Х2Х0Х! 0
8.5. Вводные замечания о системах
с рекуррентной структурой
На рассматриваемые классы так называемых рекуррентных струк-
тур накладывается ряд ограничений, связанных в основном с опреде-
ленной однородностью структуры (рекуррентность) и равенством
вероятностных параметров идентичных по назначению элементов си-
стемы (изотропность). Подробнее это будет пояснено несколько ниже.
Предполагается, что отказы элементов системы (объектов и каналов
связи) есть взаимонезависимые события, вероятности которых заданы,
и что взаимодействие между любыми двумя объектами системы дости-
гается использованием остальных объектов системы в качестве ре-
трансляторов по примыкающим каналам связи. При этом отказ объек-
та приводит к невозможности его использования для ретрансляции
и тем самым к невозможности использования всех примыкающих
к нему каналов связи.
Задачи расчета надежности таких структур возникают в процес-.
се проектирования и эксплуатации сложных- систем сбора и передачи
информации, систем связи, автоматизированных систем управления.
Приведем основные используемые определения и обозначения.
8
227
Система задается и изображается на рисунках в виде совокупности
элементов: узлов и линий их соединяющих. Узлы соответствуют
объектам системы, линии со стрелкой — ориентированным (симплекс-
ным) каналам связи, линии без стрелки — неориентированным (дуп-
лексным) каналам связи. Объекты системы нумеруются арабскими или
римскими цифрами, способ нумерации ясен из графического изобра-
жения структуры.
Для описания размера системы вводится понятие-ранга системы.
Связь между рангом системы и числом элементом ее задается, в целях
Рис. 85 1 Замкнутая рекуррент-
ная радиально-кольцевая система
компактности, графически: изоб-
ражение структуры и' нумерация
объектов приводятся для системы
н-го ранга таким образом, чтобы
структура и нумерация объектов
системы (н + 1)-го ранга были
очевидны.
Рассмотренные классы струк-
тур удовлетворяют условию рекур-
рентности построения: в терминах,
не зависящих от конкретного зна-
чения ранга п системы, может быть
сформулировано правило полу-
чения системы н-го ранга посред-
ством преобразования системы
(п — 1)-го ранга введением «новых»
элементов и удалением «старых».
Пример 8.5.1. Для системы, представленной на рис. 8.5.1 условие рекуррент-
ности есть: вводится дополнительно один объект (номер п) и каналы связи, сое-
диняющие его с объектом, введенным на предыдущем шаге [номер (п—1)], и объек-
тами I, II, 1; удаляется канал связи между объектом 1 и объектом, введенным
на предыдущем шаге [номер (п — 1)].
Ввиду очевидности получения условия рекуррентности из изобра-
жения структуры, в целях компактности, в дальнейшем это условие
не приводится.
Обозначим через [а, р] канал связи между объектами а и |5 систе-
мы; если канал связи ориентированный, то считается, что он исходит
из объекта а и входит в объект р.
Вероятностью связи между объектами а и р системы называется
вероятность события: «Объекты а и Р исправны сами и существует
хотя бы один путь связи (последовательность исправных объектов
а1( а2, ..., ah и исправных каналов связи [a, aj, [alt а2].
aj, [ah, J3], соединяющих эти объекты)».
Если в число каналов связи [а, а^], [аь а2], ..., laft_1, ah], [ah, pl
входит хотя бы один ориентированный канал, то используется
также понятие вероятности существования пути из объекта а в
объект р.
Вероятностью сильной связи между объектами аир называется
вероятнссть события: «Существует одновременно путь из объекта at
в объект р и наоборот, — путь из объекта р в объект а».
228
Вероятностью связности подмножества А объектов системы назы-
вается вероятность события: «С данным объектом подмножества свя-
заны (сильно связаны) все остальные объекты подмножества». Оче-
видно, что если в системе все каналы связи неориентированные, то это
есть вероятность связи между любыми двумя объектами этого подмно-
жества.
Вероятностью безотказной работы системы называется вероятность
связности всего множества объектов ее.
Система называется изотропной, если вероятности отказа идентич-
ных по назначению элементов системы равны между собой.
В дальнейших разделах приводятся соотношения для вычисления
характеристик связности (вероятностей связности того или иного под-
множества объектов) изотропных систем с рекуррентной структурой.
8.6. Показатели надежности изотропных систем
с* рекуррентной структурой
Для записи итоговых выражений используются в основном сле-
дующие обозначения:
Q{a} — вероятность отказа объекта а;
Q{[a, (31} — вероятность отказа канала связи [а, (?) между объек-
тами аир (для ориентированного канала считается, что он исходит
из объекта а и входит в объект р);
s=l — г, 8=1 — г — обозначения, используемые для вероят-
ности отказа объекта;
р=1—- р, q = 1 — р, г = 1 — у, о=1 — л,
ст = 1 — п — обозначения, используемые для вероятностей отказа
каналов связи;
Рп {«, р}, Рп {а, р, у} — вероятность существования связи (пути)
между объектами аир (а и р, а и у, р и у) в системе n-го ранга;
Рп{а, Pl Р, — вероятность сильной связи между объектами a
и р в ориентированной системе п-го ранга;
Рп {а, т 4- k} — вероятность существования связи (пути) между
объектом а системы и объектами tn, tn + 1, ..., k— 1, /г;
Пп — вероятность безотказной работы системы п-го ранга;
Рх {а, р} — асимптотическое значение вероятности связи между
объектами а и р в системе бесконечного ранга;
Д-оо.оо {а, 1} — асимптотическое значение вероятности связи
между объектом I и объектом а, равноудаленным от «краев» системы
бесконечного ранга;
Ф^ (0 — производящая функция числа объектов, с которыми
объект а связан (прямой или транзитной связью) в системе п-го ран-
га:
ОО
ф£”(0 = 2 /’(?„ = *} Л
229
где Р {£n — k} — вероятности события: «С объектом а связано (пря-
мой или транзитной связью) ровно k объектов системы n-го ранга»;
Ф|,а) (т)—значение производящей функции в точке т; Mna\(D(na))—мате-
матическое ожидание (дисперсия) числа объектов, с которыми объект
а связан (прямой или транзитной связью) в системе п-го ранга.
8.7. Вероятностные характеристики систем
с сетевой структурой
8.7.1. Изотропная система с разомкнутой радиально-кольцевой
структурой (рис. 8.7.1). Вероятности отказа элементов системы:
Q {1} = 0, Q {/} =s = 1 - г, Q {II, И) = q = 1 - р,
Q{1; — 1, /1} = о = 1 — л; I — 1, i g 1, п.
Рис. 8 7 1. Изотропная система
С разомкнутой радиально-кольцевой структурой.
Характеристики системы (см. § 8.6):
рп{1> =
1 — гя.7
Рп {1, т} = Рт{\, \} + л(г-Рт{\, \})Рл,т{], 1};
Р-оо, 00{1, 1} = г-г<?^~<^-;
(1 — ГЛ?)2
1 лл(1) „ (1 — ГЛ)2 о .. . 1—(то}п
— Мп —г — rq ------------2r р (1 — гл)---5——------
п (1 — гл?)2 п(\ — ГЛ?)3
— 2г2 яр W'-;
(1 - гл?)2
lira — О',1’ = rPq (1 ~ЛП)2 [ 1 + Зглу (1 — гл) — г3л V] 4-
О-.00 п (1—гл?)2
~ГШ7И1 — Г2л27)4-4ГЛ7(1 — гл)];
Р1— ц2
230
где
Hi. 2 = -у (? + 2пр ± Vр2 + 4лор</);
если 4n<jq^p, то г (1 — <j2q), р,2 » rn2q,
з
Фп’(0= 2 (1г| I”1 1(^~mqt)2 — r2n2pqt(\ —
г — I \ 0Л- JX= %. J
где Хг — корни уравнения f (X) = О
f (X) = X3 — (1 — гр + г pl + 2лл^/)Х2 4-
+ rnqt (2 — глр + гл/)Х — r2n2qt (qt + spt — sp).
8.7.2. Изотропная система с замкнутой радиально-кольцевой
структурой (рис. 8.7.2). Вероятности отказа элементов системы;
Q {1} = О, Q {[I, i]}^q=\-p, ___
Q {[i — 1, г'1) = Q {In, 11} = о = 1 — л; i — 1, if 1, п.
Рис. 8 7 2. Изотропная система с замкнутой
радиально-кольцевой структурой.
Характеристики системы (см. § 8.6):
Рп {1, т) = ± = r—rq
п (1 — гл<?)3
2 zn r.¥L (t-nqy _(п _ 1) грп {rnqyi-1.
(1— mq)2 l — rxq
nn = Hi + H? —2(гл7)п,
где
Hi, 2 = ~ (р + 2пр ± ]/‘р2 + 4лор<?);
если 4ло<7 < р, то pt « г (1 — o2q), р2 « rn2q,
Ф„ (0 = Xt + Х2 + Х3 - 2 (rqty,
где Хг — корни уравнения f (X) = О
f (X) = X3 — (1 — гр + rpt + 2гл<?0^2 + rnqt (2 — rnp + rnt)K —
— r2n2qt (qt + spt — sp).
Асимптотическое значение дисперсии, lim-ОФ, совпадает с при-
П->оо И
веденным в §8.7.1.
231
8.7.3 Изотропная система с разомкнутой симметрической ради-
ально-кольцевой структурой (рис. 8.7.3) Вероятности отказа элемен-
тов системы:
Q{I}=0, Q {<} = s = 1 — г, Q {(I, 11} = Q{lt, !)}=£_= 1—р>
Q {It — 1, (1} = Q {It, i — 11} = о = 1 — л; i, i — 1 £ 1, п.
Характеристика системы (см. §8.6):
р„{1, 1} = РП{1. [} = гр1~т^’
Рп{1, т} = Рп{т> 1}=Рт{1, О-Нг + Ли!, 1})лР„_т{1, 1};
Рис. 8 7 3. Изотропная системы
с разомкнутой симметрической пади-
ально-кольцевой структурен.
р )[ р 1 П гр2 О + гл?) 2гр2 (гпд)"
" ’ ’ (1 —— r2n2q2) (1 — rnq} (1 — nq)
гр2 (I +л<?) (m2q2)n
(1 —rn2q2)(l—nq) ’
Рп {1, т; т,
|2 (1 — m2q2) (1—г2л2</2)2 .
(1 — rnqP (1 — гл2д2У
-----2мягР^-----1_о [(гпо\т~11 + О |(г ш/)"-'”];
(l-mqp(l-m2q2)--4
Яп = гпр* S (г 'j (н« —
W р=рг /
где pf — корни уравнения <р(р) = О
Ф(р.) =ц3 — |рл(1+<?л) + (1— <?о)2]ц24-<?л|л2(1 + д2 + дп)—ро(р0
— 2<?л2)] р, — д3 л5.
8.7.4. Изотропная система с разомкнутой радиально-кольцевой
структурой с двумя центрами (рис. 8.7.4) Вероятности отказа эле-
ментов системы:
Q{I} = Q{I1} = 0; Q{i} = s = 1 — Г; Q {[I, fl} = q = 1 - p-
Q{UI, tl} -’= г = 1 — у, Q {[t — 1, r]} = о = 1 — л; t — 1, i £ 1 n.
Характеристики системы (см. § 8.6):
Pn{h И}= 1— V [^-1 'j [(Л.г — гл^г)’— i2n2qp?y] К",
232
где X; — корни уравнения f (А.) = О
I (Л) — л°—(1 —гру + 2rnqz) Х2 + rn.qz(2—rnp-}-rnz) 7.—
— r'ljt2qz(qz — spy)-,
Hl — Ms
5 ,g j
— У ( уЧ ) 1(ЯУ+рг)у-1 — nqz\p + y)]y"
, = 3 X 'н=иг/
Рис. 8 7 4 Изотропная система с разомкну-
той радиально-кольцевой структурой с дву-
мя центрами.
где щ, г = -|- [1— qz + 2nqz± 4naqz(l—qz)+ (\—qz)2
Цз> р4, Ps — корни уравнения <р (ц) = О
<p(pt) = |Л3 — (ду + рг + Зл<?г)р,2 + nqz (л + nq + nz + op + otj)y —
— n3q2z2.
8.7.5. Изотропная система с замкнутой радиально-кольцевой струк-
турой с двумя центрами (рис. 8.7.5). Вероятности отказа элементов
системы: - *
Q {I} = Q{II} = 0; Q{t) =s= 1 - г; Q {[1, /]} = q = 1 - p-
Q {[Ц, Л) = г = 1 — у, Q {It — 1,
i — 1, i g 1, n.
Рис 875 Изотропная система с замк-
нутой радиально-кольцевой структурой
с двумя центрами.
»]} = Q {!«> 11} = о = 1 — щ
Характеристики системы (см. §8.6):
Рп{1,
233 '
где Аг — корни уравнения / (А) = О
/:(А) = А3—(1—гру -\-2гядг) А2 4-
4- rnqz (2 — гяр 4- /"лг) X—г2я2дг (qz—spy)',
п„ = р? + Р? — Р з — Р"—И? + (rnqz)",
где
Pi, 2 = -j- [1 ~дг + 2пдг ± ]/4myqz(l — qz)-)-(l — qz)2],
р3, р4, р5 — корни уравнения гр (р) = О,
Ф (р) = р3 — г (qy + рг + Зядг)р2 + r2nqz (л + яд + яг + ар +
4* ш/)р — rsn3q2z2-,
Vm±M^^r~rgzl{-r^ ,
п -ж п (1 — глдгр
8.7.6. Изотропная система с разомкнутой радиально-кольцевой
структурой шахматного типа с двумя центрами (рис. 8.7.6). Вероят-
ности отказа элементов системы:
Q {1} = Q {11} = 0; Q(i) = s=l-r; Q {[1, i]} = q = 1 -p-
Q{i} — s—\—r\ Q {[II, Г|} = г=1— у;
Q{[t, Л} = С{[^> i+l]} = o=l —n; i, i+ 1 £ 1, n.
Рис. 8 76 Изотропная система с разомкну-
той радиально-кольцевой структурой шах-
матного типа.
Характеристики системы (см. §8.6):
лль п}= i
;= I ( ok luij /
+ г2яру (оА; — г2я2дг)] X",
где — корни уравнения f (А) = 0
f (А) = А3— (14- 2г2я2дг — г2яру — г2яору) А2 4~
4- г2л2 [qz (2 4- г2л2qz — 2г2яру) 4- ру (1 — гр) (1 — гу)] А — г4л«^г2,
Р-оо.ооП, 1} = Р_СО, =с{1, II, 1} = Г-Г711~ГЛ)2(1+ГЛг)2 ;
' (1 —Г2л2<?г)2
lim г й (‘ ~2 и' + гяг)2 + г (! +'Л<7)2];
234
5
Пп = г2плру 2 Г д (фд Ф2) I-1 (И._n2qz) 4.
— 1 L И I Ц — . J
+ Wi (Hi — лsqz 4- л2о(?г)] р'*,
где ръ р2 — корни уравнения <рх (р) = О
<рг (р) = р2 — (л + ло + 2ла^г + n2qz + о2ру)р + л4</г;
р3, Рз> Из — корни уравнения <р2 (р) = О
<Рг (И) = р3—[л2 (i? + г) + 2ло (pz + qy) 4- л2<?г + а2ру] р2 —
— n2qz [ла + л2 (fl + z) 4- 2ла (р 4- у) 4- а2ру\ р + n6q2z2 = 0.
8.7.7. Изотропная система с замкнутой радиально-кольцевой
структурой шахматного типа с двумя центрами (рис.8.7.7). Вероят-
ности отказа элементов системы:
Q {1} = Q {11} = 0; Q{i} = Q{i} = s=l-r, Q {[I, 1]} = 7 = 1 -p;
Q{|11, П} = г=1 — у, Q{|i, f]} = Q{[t, i + l]} = o=l —л;
Рис. 8 7 7. Изотропная система с замкнутой
радиально-кольцевой структурой шахмат-
ного типа.
t» l + 1 € Ь n; Q {['i,
Характеристики системы (см. §8.6):
Рп {I, 11} = 1 — Х«— Х«—+ 2 (г2л2рг)«,
где Хг — корни уравнения f (X) = 0
/ (X) = X3— (1 4- 2г2л2дг—г2пру—г2лару) X2 4-
+ г2 л2 [qz (2 4- г2 л2 qz — 2г2пру) 4- ру (1 — гр) (1 — г у)] X—г4л4<?2г2;
Пп = г2п [р? 4- р« 4- p«-p«-pg 4- (л2рг)«|,
где р1( р2 — корни уравнения срг (р) = 0
<рг (р) = р2 — (л2 4- ла 4- 2ла<?г 4- n2qz 4- ару) р 4- л4дг;
Нз> Pi, р5 —корни уравнения <р2(р) = 0
tp2 (р) = р3 — [ л2 (7 4- г) 4- 2ло (рг 4- qy) 4- n2qz 4- а2ру] р2 —
•—n2qz |л24~ л2(р4~2)4~ 2ло (р4~ У) + о2ру] р4~ ^ql'z2.
235
Асимптотические характеристики Р_х,х {I, 1}, lim— Мп} сов-
п ->ос П
падают с приведенными в § 8.7.6 для соответствующей разомкнутой
системы.
8.7.8. Изотропная система со структурой параллельно-лестнич-
ного типа (рис. 8.7.8). Вероятности отказа элементов системы:
Q{i}=s=l — г; Q{z} = s=l— г; Q {[i, /]} = <? = 1—р\
Q {[i — l, i]} = о = 1 — л; Q {[г—1, Г]} = о = 1 — л, i g 1, п, i £ 1, п.
Рис. 87 8 Изотропная система со струк-
турой параллельно-лестничного типа.
Характеристики системы (см. §8.6):
- 11П —ип
Пп = гп Г^р t
Hl —Р2
где 2 = -Т(р+ 2nnq— оор ± V (р4-2ллр —оор)2— 4п2 л2);
+ гг‘г л л2 (р2 — sp)]
рп {Т «} = ггр У \ 1 (Хг —1 4-гл + г л —гл'лрр?,
I ЗА |х = ь. /
где А,; — корни уравнения f (X) = О
f (А.) = А,3— (гл 4-г л — ггля 4- 2гг ллр) А2 4-
4-гглл(1 4^ ^л<72 4~ z" л<?2—ггр2 — rsnp2—
— гзлр2) А, — г2г2 л2л2 (72—ssp2).
Если 1 < п, то с погрешностью порядка
{ггллр)т‘п{к- П-,П)Т
3
df
л —-
дХ |х = х-
ггл2г лд \2
А.* /
— г л (1 — гл — 2mq) А.г 4-г2г2лл2 (д2 — sp)] А,1 ;
236
Х(Хг—l+гл+гл — глглр)Х™ k+i
8.7.9. Изотропная система со структурой диагонально-лестничного
типа (рис. 8.7.9). Вероятности отказа элементов системы:
Q{i} = s = 1 — г; Q {[г — 1, г]} = q — 1 — р; Q{li — 2, zl} = о =*
= 1 — п;
i — 2, i — 1, i g 1, n.
Рис. 8 7.9. Изотропная система co струк-
турой диагонально-лестничного типа
(два варианта начертания).
Характеристики системы (см. §8.6):
Ц1 —Ц2
где pi, 2 = -j- (р + 2л<? ± V p2 + 4nopq)-,
Рп{1, п} = г У /-J- ‘ (М — rJiqXi + r2n2pq)^,
11= )
гдеХг — корни уравнения / (X) = О
/ (X) = X4 — г (1 — ро)Х3 — гл (1 — гр — rnpqYk2 + r2n2q (1 — rp}k—
— rssn3pq.
8.7.10. Изотропная система с ориентированной полной структурой
(рис. 8.7.10) (для наглядности изображена структура пятого ранга).
Вероятности отказа элементов системы:
Q{I} = 0; Q {i} = s = 1 — г,
Q{U, z]) = Q{[/, tl} = q = 1 — p; j <i\ j, i g
Характеристики системы с абсолютно надежными объектами:
Ф*11 (/1 s = 0) = +1 (1 -- <Г) Ф^1 (/18 = 0), ф<о1)(/|э = 0) = 1;
Ф,'11 (/18 = 0) = qn + 2 tnqn-k(\— qn)(l ... (1 — q^+i)-
237
Pn{\, m]s = O} = Pm{I, m] s=O}=p+(g —дт)Рт^{\, m—l|s=O);
РД1, 0|s = 0} = 0;
M„!) (s = 0) = (1—<7П) +(1M‘^^0), M^(s = O) = O;
D<n (s = 0) = (1 -qn) П21 (S = 0) + qn (1 + M<!lt (s = 0))],
Mn(s = 0) = 0.
Рис. 8 7 10 Изотропная система с ориентированной полной структурой (два
варианта начертания).
Оценки характеристик системы л-го ранга с абсолютно надежными
объектами (s = 0):
Рп {1, п Is = 0} = 1 — nqn— (1 —qn—nqn~l p);
P2
Ф^’((|8 = 0); P„{I, /i|s = 0}; M<n(s = 0)
— обозначения характеристик системы с абсолютно надежными объек-
тами (s = 0), соответствующие принятым в § 8.6 для системы с нена-
дежными объектами (s 0);
M'1’(8 = 0)«П p2^ + ql-4^-qWP-q^)
Р3(1+9)
(I-?3) (1-^+4 .
q ^ — q)n
p2
Ф'1’
tq
__1_
р(1-Н) Р2(1+<?)а
0)~ <п+1-?п+1
t—q
.. W/ 2 At'^t-q^ + q'^^-q^-q^t^-q^}.
P(t — q) (t — q2)
Характеристики системы с ненадежными объектами (s±0):
<’= i. C^rAs"-ftO<I,(s-0);
6 = 0
238
М^ = 2 Ckrk s"-‘mV)(s = O);
k = 0
Pn{l, m} = Pm{l, m} = r—rq®ml-i (t = q) =
m
= r 2 Ck—\ гк~1 sm~k Pk{l, k\s = O}.
k=\
8.7.11. Изотропная система с неориентированной полной струк-
турой (рис. 8.7.11) (для наглядности изображена структура пятого
ранга). Вероятности отказа элементов системы:
Q{I} = 0; Q{i} = s=l-r; Q{H, Л} = <? = 1-А
Q{[/, z]}==a = 1 — Л, i, j 6 1. п.
Рис. 8 7,11, Изотропная система с неориентированной полной структурой (три
варианта начертания).
Характеристики системы (см. § 8.6):
Пп = г"-“S Cknak{n-k\rq}n~kX\h> По=1;
k=Q
oV’(/)= 2 ф0= 1;
k = 0
2 CkZ\(s + rqaky-knh^nPn{I,mY,
k= i
ЧЧЧГЧ =fi m+l) 2 Ck-^(s + rqok)n-knh=.
dtm k=m
— H (rt — 1)... (n — tn -|- 1) Pn {I -|- иг),
239
где Рп{1 + tn} — вероятность связи с объектом I заданных т объек-
тов системы n-го ранга,
№ = 2 C*zKs + r<7a/',)'!-*nft +
k=2
+ п s'
k= 1
n„ « rn exp [ — (/i + 1) <7an] + O (n~!).
8.8. Краткое описание метода анализа систем
с сетевой структурой
Два объекта системы называются смежными, если имеется канал связи, их
соединяющий.
Под элементами п системы n-го ранга подразумеваются элементы, введенные
при получении системы n-го ранга из системы (п — 1)-го ранга.
Обозначим: Хп— множество всех объектов системы^ n-го ранга; хп =
00
= Xn\Xn_j — множество объектов п; и = р| Хп — постоянное для всех п мно-
п= 1
жество объектов; Хп — множество объектов п и смежных им объектов системы
n-го ранга.
Условия существования рекуррентной сетевой системы:
— число объектов, вводймое вновь, постоянно, т. е. |xn | = const;
— объекты, смежные объектам п в системе n-го ранга, являются или объек-
тами п — 1 или входят в постоянное множество объектов х, т. е. {Xn\xn) С
G {хп-1 U
— структура подсистемы, образованной множеством объектов Хп, постоян-
на при всех п;
— структура подсистемы, образованной множеством объектов {Xn\xn} U z
(которое, очевидно, м ложено в X^-j), при переходе от системы (п—1)-го ранга
к системе n-го ранга не изменяется.
Идея метода вычисления вероятностных характеристик системы с сетевой
структурой заключается в сведении анализа системы n-го ранга к изучению ха-
рактеристик систем меньшего ранга. Рассмотрим основные этапы анализа.
1. Находятся все возможные состояния системы n-го ранга, обусловленные
отказом и (или) исправностью элементов п. В силу независимости отказов эле-
ментов вероятности найденных состояний определяются как произведения со-
ответствующих характеристик надежности элементов п.
2. Каждое из найденных состояний анализируется с точки зрения возмож-
ности образования путей ретрансляции между объектами системы (п—1)-го ран-
га, входящими в множество Хп\^п- Если такой путь образуется некоторой после-
довательностью исправных элементов п, то он заменяется одним каналом связи,
соединяющим соответствующие объекты системы (п—1)-го ранга, вероятность
отказа этого канала связи полагается равной нулю. Если некоторые элементы
п не могут участвовать в создании ни одного пути ретрансляции (например, изо-
лированный объект), то они отбрасываются. Если дополнительный путь соеди-
няет объекты из множества Хп\хп, которые уже связаны каналом связи, то счи-
тается, что указанные объекты соединяются одним абсолютно надежным каналом
связи.
В приведенных рассуждениях и ниже предполагается, что элементы п вхо-
дят в множество объектов Y, вероятность свя ности которого необходимо уста-
новить. В противном случае (например, вычисление вероятности безотказной
работы) метод в общих чертах сохраняется, но требуется учитывать зависимость
связи объектов п с остальными объектами множества Y от наличия (или отсут-
240
ствия) связи соответствующих объектов п—1 с объектами множества Y. Ввиду
непринципиальности отличий и требований компактности изложения этот вопрос
не рассматривается.
3. Таким образом, для каждого состояния множества элементов п анализ
системы м-го ранга сводится к изучению некоторой деформированной системы
(п — 1) -го ранга. Характер деформации определяется наличием дополнитель-
ных и (или) абсолютно надежных каналов связи.
В соответствии с формулой полной вероятности записывается соотношение
для искомой характеристики системы n-го ранга. Формула состоит из слагаемых,
являющихся произведением двух сомножителей:
— вероятности конкретного состояния элементов п;
— одноименной характеристики соответствующей деформированной систе-
мы (п — 1)-го ранга.
4. Для каждого типа деформированной системы (п—1)-го ранга строится ана-
логично деформированная система n-го ранга. Такое построение оказывается воз-
можным в силу рекуррентности исходной системы. Затем проводится анализ
полученных систем n-го ранга согласно пп. 1—4. Исследование проводится до
тех пор, пока новые типы деформированных систем образовываться не будут.
5. Полученные в соответствии с п. 3 соотношения для исходной и деформи-
рованной систем n-го ранга записываются в матричном виде. В итоге получается
выражение типа
Pl. п — (An ] Pi, n-i=..-=(An][An_1] ... [ Ат+11 Pi, m, (8.8.1)
где Pi, n — вектор-столбец одноименных характеристик исходной и деформиро-
ванной систем n-го ранга (далее, если это специально не ограничивается,
предполагается, что искомая характеристика — первая координата вектора),
[Ап1—матрица, элементы которой есть полиномы первой степени от парамет-
ров элементов п. —
6. Анализ согласно пп. 1—5 возможен, обычно, только если значение ранга
п системы не ниже некоторого значения т. Если т > 1, то, в ряде случаев, воз-
можно проведение аналогичного исследования с другого «края» системы, вплоть
до значения k < т. В результате получается общее соотношение
[Pi,n] = [AJ!A„_i]...|Am+1]|Pn,m][A*T_1] [а*’_2] ... [AfT], (8.8.2)
где [Pi, nl — квадратная матрица одноименных характеристик деформирован-
ных (с обоих «краев») систем н-го ранга. Далее, если это специально не огова-
ривается, предполагается, что искомая характеристика является левым верхним
членом матрицы; [А;], (А* ] — некоторые квадратные матрицы из полиномов
первой степени от параметров надежности элементов i, i + 1
Нахождение начальной матрицы характеристик [Ра,ml возможно либо не-
посредственно, если | т—fe| мало, либо аналогичным методом, но учитывая, что
объекты могут входить в состав множества, вероятность связности которого
необходимо вычислить.
Характеристики изотропных систем вычисляются проще. Вероятности отказа
элементов п не зависят от значения п, поэтому матрицы [А,] и [A/J в формулах
(8.8.1) и (8.8.2) постоянны и тогда эти соотношения переписываются в виде
Р„ = [Af-"1 Р"‘, (8.8.3)
[Р„]=[А]п-т [Рт-А+11 [А*тр-’, (8.8.4)
где [А]г, [А*т]г —i-я степень матриц [А], [А т] соответственно.
Для решения уравнений (8.8.3) и (8.8.4) необходимо найти характеристи-
ческие числа Ль Л* матриц [А], [А*]. По определению Л, есть корни уравнения
А (Л) =ЦЛ] —Л [Е] |, (8.8.5)
241
где [Е] — единичная матрица; |[-]| — определитель матрицы [ • ]. Тогда харак-
теристика Рп представляется в виде линейной комбинации степеней характе-
ристических чисел;
pn=2 Wm2c* Kk~l-
> i
(8.8.6)
Коэффициенты Ct, С; вычисляются из значений начальной матрицы характе-
ристик
Пример 8.8.1. Дана система n-го ранга, представленная на рис. 8.7.1, Веро-
ятности отказа элементов системы;
= Q{i} = Si = l— rt, Q{[1, = = РА
Q{(r—1, ij} = nj = l— лг| i—1, <0, n.
Найти Plt n {I, — вероятность связи между объектами I и т.
Решение. Проведем анализ согласно изложенному методу по этапам;
1. Возможные состояния:
а — отказал хотя бы один из элементов (объект п, каналы связи [1, /г], [л — 1, л]),
вероятность состояния 1—гпрпяп; б — объект п, каналы связи [/, п], [п — 1, п]
исправны, вероятность состояния 'прп^п'
2. В состоянии а дополнительные пути ретрансляции не образуются, в сос-
тоянии б имеется дополнительный путь между объектами I и п—1. Полагаем ве-
роятность отказа канала связи [I, п—1] в деформированной системе
i-о’ равН0Й НУЛ10, Характеристики деформированной системы
^n-lU„_I=0 буДеМ обозначать как Р1,п-1(Л т|?„_1=ор
3- Р1, п {I, т} = (1—гп РпЯп\ Pl, П-1 {l> m}+rn Рп яп Pl, n-l [I, ,n|?n_J = 01,
4. Множество возможных состояний деформированной системы .*0 | дп_0
разбивается на два подмножества и соотношение для харатктеристики дефор-
мированной системы записывается как:
^*1. п JI» q = о ] = (1 гплп)^1, п-1 {I» ~t~ rn Рп X
X Лп Р-ц п-1 |1 > г — 0| *
5. Pl, п 0 ) т} = | Р1, п 0 » т} t Pl, n j 1 > q^ — о j |T >
, . ,_ Г 1 ГТ1 Рп^П Гп рп Л п "|
lAnJ — | .
L 1 гп Лп Гп Jtn J
6. ГАЙ] = ГАП]
IP п „11 = |п Р' т} р1.п{1, mlqn=0} I
11 П ' ' I Pi. п {1, т | 91 = 0} Pi п {/, m|?1 = ?n = 0}
г» < > > I rm Pm rm J
Рт, т{1, 0 =
I гт Гт I
7. Характеристический многочлен и его корни:
А (X) = V — (1 + ГЛ9)Х + глд; Л, = 1; Х2 = гп<1-
8. Для изотропной системы n-го порядка получим окончательный ответ:
рп{1, ”0 = . "7ЯО I1 —(тЯ)п] + т [1— р -~(ГЯ1?) ] = [—Г— [1-(гл?)«-"г]
1—гл? [ 1—гл? J [1— mq J
242
8.9. Системы с иерархической структурой
8.9.0. Предварительные замечания. Отличительной чертой иерар-
хических систем является наличие явно выраженного основного уп-
равляющего элемента и направленной системы управления исполни-
тельными элементами. Качество функционирования таких систем
определяется числом нормально функционирующих исполнительных
элементов, причем под нормальным функционированием понимается
исправность самого исполнительного элемента и наличие исправной
связи его с основным управляющим элементом.
Для удобства дальнейшего изложения введем следующие обозна-
чения: <р (%) — производящая функция или моментная производя-
щая функция (в зависимости от контекста) распределения числа нор-
мально функционирующих выходных элементов системы; М — мате-
матическое ожидание числа нормально функционирующих выходных
элементов; D — дисперсия этой же величины; A1W—начальный мо-
мент k-ro порядка этой же величины.
8.9.1. Одноярусная иерархическая система.
Простая одноярусная система. Структура подсистемы представле-
на на рис. 8.9.1.
Рис. 8 9 1. Структура простой
одноярусной системы
Вероятность отказа элементов подсистемы:
Q{I} = 0, Q{i} = s = 1 — г, Q {[I, z]} = q = I — р, i £ 1, т
(р (х) = (1 — гр + rpx)m; М - mrp\ D = mrp (1 — гр).
Замкнутая радиально-кольцевая одноярусная система. Структура
подсистемы представлена на рис. 8.9.2. Вероятности отказа элементов
подсистемы;
Рис. 8.9.2. Замкнутая радиально-
кольцевая одноярусная система,
<?{!} = 0, Q{0 = s = 1 - г, Q{[I, Л} = <7= 1-р,
243
Q{Ii — 1, г]} = Q{lm, 11} = a = 1 — я, i — 1, i g' 1, tn,
ip (x) = Z"! + zV« -{- AZ” — 2 (rm/x)"1,
где Хг — корни уравнения f (А) = О
I (X) = X3 — (1 — гр + г pt + 2гл<^)А2 + rnqt (2 — тр + mt)K —
— rWqt (qt 4- spt — sp)
[(1—m)2 2 —гл— mq .
r—rq±-----7— rP ~7\-
(1 — mq)2 (l—rnq)2
— (m— 1) rpn s + fqq (rnq)^1
1 —mq
Одноярусная система с неориентированной полной структурой.
Структура подсистемы представлена на рис. 8.9.3.
Рис. 8.9 3. Одноярусная система
с неориентированной полной
структурой.
Вероятности отказа элементов подсистемы:
Q{I} = 0, Q{z) = s=l— г, Q{[I, /]} = q = 1— р,
Q{[i. ]]} = а=\—л, i, j el,m,
m
ФП(Х)= 2 C'm(s4-r9O*)m-An/i,
k = 0
tn
M = m 2 C^-11(s + r7oA)m-Anft,
Л«=1
где
k~ 1
Щ = 2 C^V<A-V)(^-Vnv, По = 1.
v=0
8.9.2. Иерархическая система с ветвящейся структурой с простым
подчинением. Характер структуры системы представлен на рис.8.9.4,
где для примера приведена структура с двумя ярусами подчинения.
Будем систему с п ярусами подчинения называть системой n-го по-
рядка. Система предполагается изотропной тогда, когда:
— показатели надежности всех элементов одного яруса одинаковы,
— все элементы одного и того же яруса управляют одним и тем же
числом элементов (равенство коэффициентов разветвления).
244
Рекуррентность построения структуры системы состоит в том, что
каждый элемент системы (исключая элементы 0-го и и-го ярусов) под-
чинен одному элементу предыдущего яруса и является управляющим
по отношению к определенной группе элементов последующего яруса.
Обозначим через аг число элементов i + 1-го яруса, подчиненных
одному элементу i-го яруса (коэффициент разветвления i-ro яруса).
Используем прежние обозначения:
Q{i} = sb ri=l—Sj,
Q{i, i + И = Qi, pt = l—qt
и введем дополнительно rt — rtpt, s; = 1 —
Рис 8 9 4. Система с ветвящейся структурой с простым подчинением.
Кроме того, обозначим через полное число элементов i-ro яруса,
т. е.
i
Ni= П
/=о
Если через Рт {г) обозначить вероятность того, что на m-м ярусе
нормально функционирует ровно г элементов, то тогда моментная
производящая функция может быть записана в виде
Nm
Фт(*) = 2 Рт(г)е«;
2 = 0
для этой моментной производящей функции в нашем случае нетрудно
получить следующее рекуррентное соотношение:
(*) = Фп-1 U*)»
где х* = гп е* 4- sn,
которое позволяет вычислять моменты распределения числа нормаль-
но функционирующих элементов нужного яруса. (Обычно представ-
ляет' интерес п-й ярус, содержащий выходные, или исполнительные
элементы системы).
Приведем выражения для первых трех начальных моментов ука-
занного распределения для п-ro яруса:
п
MV> = mV! 1 ап гп = г0 п аг г,,
1
245
М<2) = M<22 1 (a„7„)2 4- M<,21 7nsn an =>
==r0 П aJi ( П at 7t + П s, П ah7&),
i—i m = 1 z=l k=-f-l /
причем £)n = M^2)—(M^1’)2,
M<3) = M<32. (an7„)3 + 3M<.22, (an7„)2 ~sn + 2M<,'2, a~rn I2 =
/ n \ 3, n
= r0 П a.7, I 4-3 2 M^22(_1 (a„_,7„_()2s„_( x
\< = i / i=i
X П a„__A 7„_ft + 2 П «г 7г S s2 П ak rh .
V=o / <=i i=0 \*=I+i /
Выражения для моментов более высоких порядков значительно
сложнее по виду, но само их нахождение не вызывает принципиальной
трудности.
Вероятность нормального функционирования данного элемента
т-го яруса вычисляется по формуле
т
P(I, m) = r0 П 7г
i= ।
а вероятность нормального функционирования всех элементов т-го
яруса равна
пг
п (гА
t~ 1
Примечание. Иногда рассматриваются иерархические системы с вет-
вящейся структурой с простым подчинением, исполнительные элементы которых
являются резервными, т. е. достаточно нормальное функционирование хотя бы
одного из них. В этом случае вероятность нормального функционирования систе-
мы в целом (вероятность выполнения ею своей задачи) может быть вычислена
при помощи выражения для производящей функции с соответствующей подста-
новкой
P = l—<pn(ev = O)
или в развернутом виде
Р — 1 — (н> (rl...(rn_iSnn-f-Sn_i) п~1 ... + S1)°’ + So).
8.9.3. Иерархическая система с ветвящейся структурой со сложным подчи-
нением. Характер структуры системы представлен на рис. 8.9 5, где для примера
приведена структура с тремя ярусами подчинения
Сложность подчинения заключается в том, что все элементы (кроме элемен-
тов 0-го и 1-го ярусов) имеют двойное подчинение: соответствующему элементу
предыдущего и предпредыдущего ярусов. Систему с п ярусами подчинения будем
называть системой n-го порядка. Система предполагается полностью изотропной
в том смысле, что все элементы системы имеют одинаковые показатели на-
дежности, все короткие линии связи обладают одинаковыми показателями надеж-
246
ности, все длинные линии связи также обладают одинаковыми показателями
надежности, а коэффициент разветвления постоянен для всех ярусов и равен а.
Свойство изотропности позволяет получить относительно простые рекуррент-
ные соотношения для моментов распределения числа нормально функциониру-
ющих элементов на выбранном ярусе системы. (В данном случае также обычно
представляет интерес п-й ярус, содержащий выходное элементы системы).
Используем прежние обозначения.
Q {О = s, г = 1 — s,
Q {I, i + 1} = q, р = 1 — q,
Q a, i + 2} = о, л =» 1 — о.
и введем дополнительно
Pt = Hl — ?о). Р2 = Рг, Рз = яг,
причем qt = 1 — pt.
Производящая
функционирующих
соотношения вида
моментная функция для распределения числа нормально
элементов п го яруса записывается в виде рекуррентного
ф,7; (*) = [р<2 <Рп-1 W + ?2 Фп- 1 МЛ
где в свою очередь
Фп « = [pi ф“- 1 W + ?! Фп- 1 W]“.
Фп (*) = [РзФл-1 (х) + ?з]Я>
причем
Фо W = Фо = Фо (х) =1.
Рекуррентное выражение для вычисления первого начального момента рас-
пределения числа нормально функционирующих элементов n-го яруса имеет вид
^п = я (Рг «п-1 +?2 а’п-?!),
где в свою очередь
«п = «(Р1 «п-1 + 91 и'п-т).
wn=ap3vn-lf
247
причем
а0 = v, «= 1 tt>o — 0.
Рекуррентное выражение для вычисления второго начального момента этого
же распределения можно записать
а— 1
(Аг + */2 ^n-i) + ~
где в свою очередь
Un = a (р, Un_i +71ГП_,)+ и®,
1РП = ар3 V п _ х 4-- wflt
причем UQ => Ро => 1, W'o = 0.
Список литературы
1 Гадасин В А. Вероятностные характеристики полных систем с нена-
правленными связями. — «Автоматика и вычислительная техника», 1970,
№ 3
2 . Гадасин В А. Вероятностные характеристики систем с радиально-
кольцевой структурой (замкнутые системы) — В кн.: Теория надежности и
массовое обслуживание Под ред Б. В Гнеденко М., «Наука», 1969
3 . Гадасин В А Вероятность связи в сложных радиально-кольцевых
системах. — «Известия АН СССР. Техническая кибернетика», 1970, № 4.
4 . Г а д а с и н В А. Надежность связи в сложных системах ретрансля-
ции — «Проблемы передачи информации», 1972, вып. II.
6 Гадасин В А., Ушаков И. А Вероятностные характеристики
систем с радиально-кольцевой структурой (разомкнутые системы) — В кн :
Теория надежности и массовое обслуживание Под ред. Б. В. Гнеденко М.,
«Наука», 1969
6 . К е л ь м а н с А. К. Некоторые вопросы анализа надежности сетей —
«Автоматика и телемеханика», 1965, т. 26, № 3
7 . КельмансА К Об оценке вероятностных характеристик случайных
графов — «Автоматика и телемеханика», 1970, № 11.
8 Кельманс А. К О связности вероятностных сетей. — «Автоматика
и телемеханика», 1967, № 3.
9 Кельманс А. К. Оценка надежности систем передачи информации
произвольной структуры. — «Автоматика и телемеханика», 1963, т. 24, Ks 9.
10 Кельманс А. К. Оценка надежности структуры связи и вопросы по-
строения надежных систем. — В кн.: Теория и применение автомати-
ческих систем. М., «Наука», 1964.
11 . О статистическом моделировании функционирования информационных се-
тей.— В кн.: Прикладные задачи технической кибернетики. Под ред.
И А Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966 Авт.: А. М Виш-
невская, Р. И Герасимова, И. А. Ушаков, Г. А Фомин.
12 . С т е п а н о в В Е. Комбинаторная алгебра и случайные графы —
«Теория вероятностей и ее применение», 1969, т. XIV, № 3.
13 . Степанов В Е. О вероятности связности случайного графа. —«Теория
вероятностей и ее применение», 1970, т. XV, № 1.
14 . У и а к о в И А Об оценке надежности функционирования иерархиче-
ской ветвящейся системы с неравноценными исполнительными элементами —
«Известия АН СССР. Техническая кибернетика» 1967, № 5.
248
15 Ушаков И А О надежности информационной системы с кольцевыми
трактами передачи сообщений — В кн : Адаптивные системы Большие
системы. Под ред. В. С. Пугачева. М., «Наука», 1970.
16 Ушаков И А., Коненков Ю. К. Одна задача резервирования
в системах с ветвящейся структурой. — «Известия АН СССР. Техниче-
ская кибернетика», 1965, № 3.
17 У ш а к о в И. А., ’К о н е н к о в Ю. К. Оценка эффективности функцио-
нирования систем с ветвящейся структурой — В кн : Кибернетику — на
службу коммунизму. Под ред. А. И. Берга, Н Г. Бруевича, Б В. Гнеденко.
М., «Энергия», 1964.
18 Ушаков И А Инженерные методы расчета надежности. М., «Знание»,
1970.
19 . Э з а р и Д ж., П р о ш а н Ф. Надежность связанных систем/— В кнл
Л1етоды введения избыточности для вычислительных систем Под ред.
В. С. Пугачева. М., «Сов. радио», 1966.
20 Соловьев А Д Методы расчета эффективности ветвящихся систем —
«Вопросы радиоэлектроники», 1964, сер. XII, вып. 31
21 Соловьев А Д. Некоторые нестандартные задачи из теории резерви-
рования. — «Вопросы радиоэлектроники», 1964, сер. XII, вып. 7.
9.
ОЦЕНКА ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ
СИСТЕМ
9.0. Предварительные замечания
Наличие определенной функциональной! избыточности в структу-
ре большинства сложных систем приводит к тому, что появление от-
казов отдельных элементов или значительные изменения тех или иных
рабочих параметров могут привести не к полному выходу системы из
строя, а лишь к некоторому ухудшению качества функционирования
и снижению эффективности системы в целом. Для оценки качества
функционирования таких систем целесообразно ввести количествен-
ный показатель эффективности функционирования, учитывающий
влияние таких частичных отказов.
Выбор соответствующего показателя эффективности функциони-
рования в каждом конкретном случае определяется типом системы,
ее назначением, видом выполняемой задачи, характером различных
внешних условий и другими факторами.
Оценку эффективности функционирования системы можно прово-
дить для двух типов систем:
1) системы длительного действия;
2) системы кратковременного действия.
Система длительного действия выполняет некоторую требуемую
от нее задачу в течение интервала времени длительностью 10, начиная
с некоторого t. Эффективность функционирования такой системы за-
висит от конкретной реализации процесса изменения состояний си-
стемы в течение этого периода.
Система кратковременного действия выполняет задачи, продолжи-
тельность решения которых /0 такова, что за это время система навер-
няка остается в одном и том же состоянии. Практически можно счи-
тать, что величина /0 равна нулю. Системы кратковременного действия
являются частным случаем систем длительного действия.
В некоторый произвольный момент времени каждый из элементов
системы может находиться в определенном состоянии, например
в состоянии работоспособности или в состоянии отказа. Совокупность
состояний элементов системы однозначно определяет состояние си-
стемы в целом.
Каждое состояние системы кратковременного действия может быть
охарактеризовано вполне определенным условным показателем эф-
фективности функционирования. Этот показатель количественно ха-
рактеризует качество выполнения системой своих функций при усло-
вии, что она при этом находится именно в данном состоянии.
250
С течением времени система претерпевает изменение своих состоя-
ний из-за изменения состояний входящих в ее состав элементов (отка-
зы элементов, их восстановление и пр.). Каждая реализация процес-
са переходов системы длительного действия из состояния в состояние
может быть охарактеризована вполне определенным условным показа-
телем эффективности функционирования. Этот показатель количест-
венно характеризует качество выполнения системой своих функций
при условии, что система при этом во время решения задачи имела
именно данную реализацию процесса переходов из одного состояния
в другое.
9.1. Общая схема оценки эффективности
функционирования систем кратковременного действия
Если обозначить через hs (f) вероятность того, что система кратко-
временного действия в момент времени t находится в s-м состоянии,
и через Ф8 — условный показатель эффективности функционирова-
ния системы и в s-м состоянии, то показатель эффективности функцио-
нирования системы кратковременного действия может быть опреде-
лен по формуле
^(0=2Л8(ПФ8. (9.1.1)
где суммирование производится по всем состояниям системы.
Для системы, состоящей из п взаимно независимых элементов,
каждый из которых может находиться лишь в двух состояниях (рабо-
тоспособности и отказа), вероятности hs (t) легко выражаются через
показатели надежности элементов системы:
— вероятность того, что все элементы системы работоспособны,
М)=М0М0-.'п(0 = П (9.1.2)
1=\
— вероятность того, что в состоянии отказа находится только
ьй элемент системы,
п
— П (9.1.3)
— вероятность того, что в состоянии отказа находится только г-й
и /-й элементы системы,
/г . (/) = -SiW. р rk (t) (9.i.4)
13 ri(t) rt(t)
и т. д.
Здесь через rt (!) обозначена вероятность состояния работоспособ-
ности г-го элемента системы в момент времени t, a qt (/) = 1 — rt (t).
251
В случае, если имеет место условие
max 9; (t) < Un,
(9 1 5)
оценка эффективности функционирования системы может быть про-
изведена по приближенной формуле
Ё (0 «Фо
1- 2 Яг (0(1- ФГ)
I — 1
(9 16)
где
ФГ = Фг/Ф0.
Формула (9.1.6) дает заниженную оценку по сравнению с истин-
ным значением.
Погрешность приближенной оценки эффективности по формуле
(9 1 6) имеет порядок (грубая оценка)
8^ [max О)12 Фо- (9-17)
Пример 9.1.1. Радиоэлектронная система гражданского аэропорта, предна-
значенная для просмотра пространства в пределах 180°, обслуживается двумя
одинаковыми станциями а и Ь. Станция а перекрывает пространство в пределах
сектора 0—110°, а станция b — в пределах сектора 70—180°. Среднее время без-
отказной работы для каждой станции примем равным 95 ч, а среднее время про-
стоя — 5 ч. Тогда коэффициент готовности отдельной станции равен Х = 0,95
Вероятность обнаружения объекта в зоне действия одной станции равна р =>
= 0, 9, а в зоне действия одновременно двух станций (в зоне перекрытия)
& = 1 — (1 — р)а = 0,99.
Требуется найти вероятность обнаружения на заданной дальности подлета-
ющего самолета, появляющегося в произвольный момент времени с равной веро-
ятностью на любом азимутальном направлении в пределах сектора 0—180°
Решение. Рассмотрим состояние So Вероятность того, что система в не-
который момент времени будет в этом состоянии, равна hr) = № = 0,9025.
При этом в пределах сектора от 70 до 110°, т. е. в пределах 40°, действуют сразу
две станции, а в пределах оставшегося сектора 0—70° и 110—180°, т. е в пределах
140°, — по одной станции. Таким образом, условный показатель эффективности
состояния So, определяемый как средневзвешенное значение, равен
40° 140°
ф“=^-°’99+7^-0’9=0’92-
• 0 = 0,55.
Перемножив значения hn и Фо, получим Л0Ф0 = 0,828.
Вероятность состояния Sa равна
ha = K(\-К) = 0,0495.
В этом состоянии в пределах сектора 0—110° действует одна станция, а в
пределах сектора 110—180° — ни одной, т е
110° 70°
а 180° 180°
Значения ИаФа, следовательно, равно
ha Фо = 0,028.
Так как состояния Sa и Sb абсолютно идентичны, можно записать
hb фь = 0,028.
В результате имеем
Е = /(о Фо +2й0 Фо = 0,828 + 0,056 = 0,883.
252
9.2. Общая схема оценки эффективности систем
длительного действия
Если обозначить через dhn (t, t + t0) элемент вероятности того,
что система длительного действия в интервале [t, t + /01 имела л-ю
реализацию процесса перехода из одного состояния в другое, и через
Фл — условный показатель эффективности функционирования си-
стемы для этой реализации процесса, то показатель эффективности
функционирования системы длительного действия может быть опре-
делен по- формуле
Е (t, t -|- /0) == Фл dhn (t, t -f- to), (9.2 1)
^л
где интегрирование производится по пространству всех возможных
реализаций процесса перехода системы из одного состояния в другое
в интервале времени [/, t + ;0].
Для системы, состоящей из п независимых невосстанавливаемых
элементов, каждый из которых может находиться лишь в двух состоя-
ниях (работоспособности и отказа), формула (9 2.1) может быть за-
писана в виде
п /4“
£(м+/0)= ФА+2 л* S
<=1 t
Z4- z0 t4" z©
+ h*4 \ fAxx)dxi 5 ф!7 (X„ X,) fj (Xj) dx, +
1<j< z t
Z4-x Z4- /0 z 4" z©
+ ,l*ik 5 fAxi)dx> 5 fl(xl)dx] $ (xlt X}, Xk) x
l^i<l<k^n t t t
Xfh(xk)dxh+..., (9 2 2)
где fi (хг)—плотность вероятности отказа z-го элемента в момент вре-
мени х(, h0 — вероятность того, что ни один из элементов системы не
откажет в течение интервала [£ t + ;01
Ло = П г, (t, t + t0Y, (9 2 3)
<= i
hf — вероятность того, что все элементы, не включая z-й, не от-
кажут в течение интервала [Z, t + /01
hl = f]rh (t, t + t0) - - 1 До; (9 2 4)
. , G (t, t +/0)
k^l
2J3
h*/ — вероятность того, что элементы, не включая i-й и /-й, не от-
кажут в течение интервала [i, i + (01
1
(9.2 5)
И}, =---------------------ha',
r,(t, t + tol-rjtf, t + t0)
" Фо — условный показатель эффективности функционирования
системы при условии, что ни один из элементов не отказал в интерва-
ле tt, t + £0]; Ф, (х,) — условный показатель эффективности функцио-
нирования системы при условии, что отказал только i-й элемент, при-
чем отказ его произошел в момент времени xt (t<Z xt <Z t + i0);
(*;, xj) — условный показатель эффективности функционирования
системы при условии, что отказали только i-й и /-й элементы, причем
отказы их произошли в моменты времени xt и х} соответственно (i <
< xt <L t i0, i< х} < t + i0)-
В случае, если выполняется условие
i +
max qt (t, t + i0) = max § ft (x() dx, < i/n,
возможна приближенная оценка
t 4- to
qdt.t+Q- J ФЖ)ШЖ
i
(9 2.6)
(9 2 7)
где Ф: (х,) = Ф, (х,)/Ф0.
Погрешность оценки не превышает величины
6 _ (n~-^ max [q, (t, t +Z0)]2 Фо. (9 2 8)
2. 1<Z n
Пример 9.2.1. Рассматривается система накопления информации, состоящая
из двух одинаковых приемников а и & В случае работоспособности обоих при-
емников пропускная способность системы оценивается некоторой величиной А.
Пусть в случае отказа одного из приемников пропускная способность системы па-
дает, например, до величины В = 0,ЗЛ При отказе двух приемников сбор инфор-
мации прекращается. Вероятность безотказной работы каждого приемника рас-
пределяется по экспоненциальному закону и характеризуется интенсивностью
отказов X, т. е г = е~м. Длительность выполнения задачи определяется как
t— 0,1/А.. Отказы приемников предполагаются независимыми. Для различных
реализаций процесса перехода системы из одного состояния в другое приняты
следующие условные показатели эффективности:
Ф0 = Л/,
Ф( (xt) = Bt -f- (Л — В) х, (i=a, b),
x]) = BxJ + (A — B) х( (х;>х,; i, ] = а, Ь).
Иначе говоря, показатель эффективности системы для каждой траектории опре-
деляется как объем накопленной информации (произведение пропускной способ-
ности на время функционирования).
Требуется определить показатель эффективности системы,
254
Решение. Оценка эффективности проводится по формуле (9.2.2). Для
данного случая эта формула примет вид
t
E = r2At+2r^[Bt + (A — B)x]'ke-udx +
О
t х
4-2ре-Лл: [5гн-(Д — В) у]Ке~^ dy.
о о
Вычислив интегралы, получим
Е = сь At+2r[Btq + (A— В) [1— г(1 +%/)]) +
( Л у
(в г з 1 1
+ + 2М) +
( л L 4 4 J
1 Г 1 / 3 1 \ Ъ
+<Л-в>т[т-''+(т+тх,)г’])-
После подстановки численных значений, например г = 0,905 и ( — 0,1/Х,
имеем
Е = (0,819 + 0,109 + 0,004) Л/ = 0.932Л/.
9.3. Оценка эффективности систем с аддитивным
показателем эффективности
Ряд систем характеризуется очень простым видом условного по-
казателя эффективности функционирования: каждый элемент такой
системы вносит свою определенную и независимую долю в общий вы-
ходной эффект. Такого типа условные показатели эффективности ха-
рактерны для систем, представляющих собой совокупность, напри-
мер, транспортных средств.
Если некоторый i-й элемент такой системы вносит в общий выход-
ной эффект некоторую долю <рг, то можно записать:
Фг = Ф0 —(рг, Фо = Фо — (ф, + Ф;). (9.3.1)
Для систем кратковременного действия такого типа в момент вре-
мени t имеем
Д=2ф,гг(/), (9 3 2)
г=1
где г, (i) — вероятность состояния работоспособности i-ro элемента
в момент времени t.
255
Для систем длительного действия, у которых i-й элемент дает
«вклад» ф, (/г) в общий выходной эффект системы в случае отказа
в момент + t0, выражение для эффективности можно запи-
сать:
i — 1
£(М-Н0) =
G [t, t +4) Фо; + $ Ф/ (*i) dxt •
t
где ф0!- — «вклад» i-го элемента в общий выходной эффект системы
в случае безотказной работы в интервале времени [Z, t -j- /0].
Пример 9.3.1. Система, предназначенная для накопления информации, со-
стоит из трех элементов, пропускная способность каждого из которых равна
ф1 = ЮО бит/с, <р2 = 200 бит/с и <р3 = 250 бит/с (бит — двоичная единица ин-
формации), а интенсивности отказов этих элементов равны = 0,01 1/ч, Х2 =
= 0,03 1 /ч и Х3 = 0,04 1/ч. Вероятность безотказной работы каждого элемента
распределяется по экспоненциальному закону. Требуется определить с учетом
отказов среднюю пропускную способность системы в момент времени i — 10 ч
и количество собранной информации системой при непрерывной работе с полной
нагрузкой в течение tQ = 50 ч.
Решение. Средняя пропускная способность системы для произвольного
момента времени t будет иметь вид
£(/)= 2 /
г = 1
или после подстановки численных значений для I = 10 ч
£ (10)== 100 е~°-1 + 200 е-0,3 + 250 е—0,4 =405,5 бит/с.
В данной задаче фог = Ф1^, а Ф/(^) = ф(//.
Тогда
£(0, i) = 2 (е — *1<° Фг + f Ф1 *е~*г =
I = 1 \ о /
3 t 13
= 2 (e-V4/[l-e-^'» (1 +А/М] = 2 7L(l-e~V°).
, = 1 l X/ J i=i X/
Заметим, что если функция ф/ (ti) линейна, то количество собранной инфор-
мации к моменту времени Г можно определить и более простым образом:
' ‘ 3 —Л
Е (0, t) — [ Е (х) dx = J 2 Ф1 е dx =
" о 0 1=1
3 f 3
= 2J фге'^хДх= 3 ^(1-e’V).
/= 10 /=1
После приведения ф и X к одинаковым единицам времени и подстановки числен-»
ных значений получаем
/ 100 200 250 \
£(0,50) = 1 -уу- • 0,39+ -уу • 0,78+ уу 0,86 3600-5,2-10’ бит.
256
9.4. Оценка эффективности систем с резервированием
функций
Имеется целый ряд систем кратковременного действия, в которых
выполнение одной и той же задачи может осуществляться, например,
несколькими самостоятельными исполнительными элементами. Вы-
полнение задачи хотя бы одним из элементов является достаточным,
чтобы система в целом выполнила свою задачу. Пусть вероятность
выполнения задачи одним элементом равна cps при условии, что си-
стема находится в s-м состоянии. Требуется определить вероятность
выполнения задачи хотя бы одним из N исполнительных элементов.
Такая задача может быть решена для двух основных случаев.
1. Исполнительные элементы системы выполняют задачу одно-
временно и независимо, т. е. для всех элементов вероятность выпол-
нения задачи равна одинаковой величине <ps.
Для этого случая можно записать формулу оценки эффективности
функционирования
£= S#s[l-(l-q)8)wl. (9.4.1)
где Hs — вероятность того, что система находится в s-м состоянии;
1 — (1 — ф^) — условная вероятность выполнения системой задачи
при ЛГ-кратном резервировании функции при условии, что система
находится в s-м состоянии.
Пример 9.4.1. Пусть по некоторой цели можно сделать залп из двух выстре-
лов. Если в момент залпа устройство точной наводки исправно, то вероятность
попадания с одного выстрела будет равна <pj = 0,85, а если это устройство отка-
зало, то вероятность попадания с одного выстрела будет равна <р2 = 0,58. Пусть
вероятность безотказной работы устройства точной наводки равна г = 0,7.
(Предполагается независимость попаданий с каждого выстрела.) Требуется опре-
делить полную вероятность попадания.
Решение. Полная вероятность попадания будет равна
Е = г [1 - (1 - ф1)2] + q [1 - (1 - <р2)2]
или после подстановки численных значений
Е = 0,7 (1 — 0,152) + 0,3(1 — 0,42г) = 0,931.
2. Исполнительные элементы выполняют задачу в различные мо-
менты времени, т. е. для каждого элемента вероятность выполнения
задачи равна величине ф5, соответствующей состоянию системы в мо-
мент выполнения задачи данным элементом.
В этом случае формула оценки эффективности будет
£=1- Л -£Яв<рЛ". (9.4.2)
\ S /
Пример 9.4.2. Изменим несколько условия предыдущего примера. Пусть
по цели производятся теперь два независимых выстрела (это может быть, в част-
ности, в том случае, если стреляют в один и тот же момент две независимые
артиллерийские системы).
Требуется определить полную вероятность попадания.
9 Зак. 943 2^7
Решение. Для этого случая полная вероятность попадания равна
Е = 1 — [1 — (/•<{>! + <?<ра)]2
или после подстановки тех же численных значений, что и в предыдущем примере
Е = 1 — [1 — (0,7 • 0,85 + 0,3 • 0,58)]2 = 0,947.
9.5. Оценка эффективности многофункциональных
систем
Многофункциональной системой будем называть такую систему,
которая может выполнять одну и ту же задачу различными способами,
характеризующимися различными показателями эффективности, при-
чем при любом состоянии системы всегда выбирается тот способ, ко-
торый для данного состояния является наиболее эффективным.
Рассмотрим систему, состоящую из п элементов. Пусть некоторая
задача может выполняться т различными способами, причем при вы-
полнении задачи /-м способом условный показатель технической эф-
фективности системы равен Фг Положим для определенности Фх >
®2 ••• Ф>П'
Разобьем систему на т подсистем Glt G2, Gm таким образом,
чтобы в каждую из подсистем входили те элементы, которые обеспе-
чивают выполнение задачи /-м способом (отдельные элементы могут
в общем случае входить в состав нескольких подсистем), т. е. могут
участвовать в выполнении одной и той же задачи различными спосо-
бами.
Для двух частных случаев могут быть записаны сравнительно
простые выражения для оценки эффективности функционирования.
1. Каждый элемент может входить в состав только одной подсисте-
мы. В этом случае вероятность того, что задача будет выполняться
/-м способом, равна
Н,= Р} п Qh, (9 5 1)
ь= i
где Pj — вероятность безотказной работы /-й подсистемы, Q, — ве-
роятность отказа /-й подсистемы.
Формула для оценки эффективности функционирования системы
имеет вид
т j—1
£ = 2 Ф,Р} П (9.5.2)
/=1 4=1
2. Подсистемы G, «вкладываются друг в друга», т. е. для выполне-
ния задачи первым способом требуется, чтобы все элементы были ра-
ботоспособны; для выполнения задачи вторым способом — не все
элементы, а лишь часть; для выполнения третьим способом — еще
меньше элементов и т. д. Иначе говоря, Gx :z> G2 п ... Gm.
Обозначим через G*_i множество элементов системы, принадле-
жащих подсистеме G;_i и в то же время не принадлежащих подсисте-
ме Gj.
258
По принципу работы рассматриваемой системы задача будет вы-
полняться именно /-м способом при условии, если все элементы под-
системы Gj работоспособны, а в подсистеме G*_i есть хотя бы один
отказавший элемент (при этом уже неважно, будут ли отказавшие
элементы среди элементов О*_2, б*-з и т. д).
Для этого случая вероятность выполнения системой задачи /-м
способом будет равна
н, = л-Л-ь
Формула для оценки эффективности функционирования запишется
как
т
£= 2 ФДЛ-Л-х). (9.5.3)
?=i
Пример 9.5.1. Рассматривается система, от которой требуется последова
тельное выполнение трех этапов поиск, обнаружение и сопровождение некоторо
го объекта На каждом этапе выполнение функций может быть осуществлено не-
сколькими способами. Возможные комбинации способов выполнения каждого
отдельного этапа, обеспечивающие решение системой своей задачи, и соответ
ствующие этим комбинациям показатели технической эффективности приведены
в табл 9 5 1. Кроме того, для выполнения задачи любым способом необходимо,
чтобы пульт управления был исправным. Значения вероятностей безотказной
работы отдельных элементов системы для некоторого момента времени (индексы
элементов взяты в соответствии с рис. 9.5 1) равны:
/у = 0,80, гг — 0,99, г3 — 0,80, = 0,95; г6 = 0,90, г6 = 0,95
Требуется вычислить полную вероятность выполнения системой задачи
Таблица 951
Показатели технической эффективности для различных
способов выполнения задачи
Номер способа вы пол нения Этап Показатель технической эффектив ности
поиска обнаружения сопровождения
1 Локатор поиска Индикатор Локатор сопровож- дения 1 00
2 Локатор сопро- вождения Индикатор Локатор сопровож- дения 0,60
3 Локатор поиска Индикатор Оптическое уст- ройство и вычис- литель 0,30
4 Оптическое уст- ройство Оптическое уст- ройство Оптическое уст- ройство и вычис- литель 0,15
5 Оптическое уст- ройство Оптическое уст- ройство Оптическое уст- ройство 0,10
Решение. Выполнение задачи первым способом будет производиться с
вероятностью
й, = Г1Г2г3г4ггг9 х 0,52
(работает или не работает оптическое устройство, в этом случае не играет роли)
9* 259
Выполнение задачи вторым способом будет производиться только в том
случае, если произошел отказ локатора поиска, т. е. вероятностью
й2 “ qirtrtrbrt ~ 0,13.
Выполнение задачи третьим способом будет производиться только в том
случае, если произошел отказ локатора сопровождения, т. е. с вероятностью
hs — ЦзГгГцГьГъ де 0,13.
Выполнение задачи четвертым способом будет производиться только в том
случае, если произошли отказы либо:
— индикатора;
— индикатора и локатора поиска;
— индикатора и локатора сопровождения;
индикатора, локатора поиска и локатора сопровождения;
— локатора поиска и локатора сопровождения.
Рис. 9 5.1. Структурная схема многофунк-
циональной системы:
/ — локатор поиска; 2 — оптическое устройство;
3 — локатор сопровождения; 4 — индикатор; 5 —
выключатель, 6 — пульт управления.
Во всех этих случаях оптическое устройство и вычислитель предполагаются
исправными.
Вероятность этого события равна
+ а<Мз) де 0,08.
И, наконец, выполнение задачи пятым способом производится только в
случае, если дополнительно еще отказало вычислительное устройство, т. е. с
вероятностью
Л» = r2q&r6 де 0,01.
Окончательное значение полной вероятности выполнения задачи равняется
Е = 0,52 - 1 + 0,13 . 0,6 + 0,13 • 0,3 + 0,08 • 0,15 +
+ 0,01 0,1 = 0,66.
Расчет же вероятности того, что в такой системе не произойдет ни одного
отказа, дает значение, равное лишь 0,51.
9.6. Оценка эффективности систем при известных
моментах распределения числа исправных
исполнительных элементов
Многие системы имеют сложную внутреннюю структуру, но
в смысле эффективности функционирования состоят из двух частей:
управляющей части и совокупности исполнительных элементов.
Будем говорить, что исполнительный элемент системы нормально
функционирует, если он сам работоспособен и работоспособны все
элементы, необходимые для управления им.
Если условный показатель эффективности такой системы зависит
только от г — числа нормально функционирующих выходных эле-
260
ментов, и задается в виде функции Ф (г), то для оценки эффектив-
ности достаточно знать начальные моменты распределения.
Эффективность функционирования подобной системы может быть
определена по формуле
„ ak ф
Л dzk
(9.6.1)
г = 0
где — £-й начальный момент распределения числа нормально
функционирующих исполнительных элементов; d — k-я
dzk г=о
Рис. 9 6.1. Различные варианты ветвящейся структуры второго порядка с шестью
выходными элементами.
производная Ф (г) по г с последующей подстановкой г = 0 (при усло-
вии, что аппроксимирующая функция Ф (г) дифференцируема).
Обычно функция Ф (г) может быть достаточно хорошо аппрокси-
мирована полиномом невысокой степени.
Пример 9.6.1. Рассмотрим различные варианты ветвящихся систем второго
порядка, имеющих шесть выходных элементов (рис. 9.6.1). Допустим сначала,
что функция Ф (г) имеет вид
Ф (г) = Ct г,
т. е. эффективность функционирования системы пропорциональна количеству
нормально функционирующих выходных элементов, К таким системам могут
быть отнесены транспортные системы, системы связи и т. п.
Тогда эффективность системы с учетом выражения для Л1'1) (см. § 8.9.2)
равна
п
Е — kM< 1 ’ = Ci го П a, ri.
i = 1
п
Учитывая, что П at = Nn есть число всех исполнительных (выходных) эле-
<=1
ментов, имеем
Е = с^п П rt.
/=1
261
Из этой формулы можно сделать интересный вывод, что все системы, изображен-
ные на рис. 9.6.1, при данном выбранном показателе Ф (г)м эквивалентны неэф-
фективности
Допустим теперь, что функция Ф (г) имеет вид
Ф (г) = с2г2,
т. е. эффективность функционирования пропорциональна квадрату числа нор-
мально функционирующих выходных элементов. Это имеет место, например,
при некоторых игровых ситуациях. Для такого случая эффективность функцио-
нирования равна
Е <= с2Л1*2\
Для системы с ветвящейся структурой выражение Л4(2) приведено в § 8.9.2.
Для высоких значений вероятностей состояния работоспособности элементов
(т. е. qi < 1/Nn) формулу начального момента второго порядка приближенно
можно записать в виде
Л1(2)«4Л'п 1 —
Полагая для простоты q0 = qt =» q2 = q, получим
Ea « 2c2 № (1 — 0,83g), E6x 2c2 № (1 — 1 ,33g),
Eg » 2c2 № (1 — 1,5q), Ег 2c2 № (1 — 1,67g).
Следовательно, в этом случае предпочтительнее система, у которой наиболь-
шей является величина a2/ap
Список литературы
1. Варжапетян А. Г. Техническая эффективность и ее исследование
методом статистических испытаний. В кнл Адаптивные системы. Большие
системы. Труды 1-го всесоюзного симпозиума по статистическим проблемам
технической кибернетики. М., «Наука», 1971.
2. В а с и л ь е в Б. В. Прогнозирование надежности и эффективности дина-
мических систем. В кнл О надежности сложных технических систем. М.,
«Сов. радио», 1966.
3. Вертлиб В. А., Вишневский В. М. Эффективность иерархи-
ческих систем с учетом надежности. — «Автоматика и телемеханика» 1970,
№ 11.
4. Москатов Г. К. К вопросу об эффективности и инвариантности много-
функциональных управляющих систем. В кн.: Кибернетику — на службу
коммунизму. Под ред. А. И. Берга, Н. Г. Бруевича, Б. В. Гнеденко, Т. II,
М., «Энергия», 1964.
5. Ушаков И. А., К о н е н к о в Ю. К- Оценка эффективности функцио-
нирования сложных ветвящихся систем с учетом надежности. В ки.: Кибер-
нетику — на службу коммунизму. Под ред. А. И. Берга, Н. Г. Бруевича,
Б. В. Гнеденко, Т. II., Ма, «Энергия», 1964.
6. У ш а к о в И. А. Оценка надежности функционирования иерархической
ветвящейся системы с неравноценными исполнительными элементами. —
«Известия АН СССР. Техническая кибернетика», 1967, № 5.
7. У ш а к о в И. А. Оценка эффективности сложных систем. В кнл Надеж-
ность радиоэлектронной аппаратуры. М., «Сов. радио», 1960.
8. У ш а ко в И. А. Эффективность систем с показателями качества функ-
ционирования, зависящими от длительности непрерывной работы. — «Радио-
техника», 1967, т. 22, № 6.
9. У ш а к о в И. А. Эффективность функционирования сложных систем.
В кнл О надежности сложных технических систем. М., «Сов. радио», 1966.
10. Ш а с т о в а Г. А. Критерий средних потерь для оценки надежности си-
стем управления. — «Автоматика и телемеханика», 1962, № 6.
262
10.
ЗАДАЧИ ОПТИМАЛЬНОГО РЕЗЕРВИРОВАНИЯ
10.0. Предварительные замечания
10.0.1. Постановка задачи. При использовании резервирования для
повышения надежности различных систем возникает задача не только
обеспечить заданные показатели надежности, но и произвести это
как можно более экономично, с наименьшими суммарными затратами
на резервные элементы для системы в целом, т. е. оптимальным об-
разом.
На практике в качестве подобных затрат могут быть рассмотрены
различные характеристики системы, такие, как ее стоимость, вес или
габариты. Выбор характеристики определяется конкретным видом
системы и ее назначением. Обычно удается выделить одну наиболее
важную характеристику, которую для краткости назовем «весом»
вне зависимости от ее физической сущности.
Рассмотрим систему, представляющую собой последовательное
соединение взаимонезависимых участков. Участком системы в данном
случае будем называть такую часть системы, для резервирования ко-
торой могут быть использованы однотипные компоненты. Таким об-
разом, участок системы — это не обязательно конструктивно оформлен-
ная часть системы. Например, в задачах обеспечения системы ЗИПом
к одному участку системы могут быть отнесены условно все однотип-
ные компоненты, если даже они конструктивно разнесены и схемно
не связаны между собой.
В качестве основных показателей надежности системы, которые
требуется улучшить путем использования резервирования, взяты
вероятность безотказной работы системы за время t0, коэффициент го-
товности или коэффициент надежности, т. е. такие показатели на-
дежности системы, которые могут быть выражены в виде произведе-
ния соответствующих показателей надежности отдельных участков
системы. (При этом для восстанавливаемых систем предполагается
неограниченное обслуживание, т. е. количество ремонтных бригад
в системе ровно количеству последовательно соединенных участков
системы, что является необходимым для взаимонезависимости эле-
ментов системы в процессе восстановления.)
Приближенные методы решения задачи оптимального резервиро-
вания имеются и в случае, когда в качестве показателя надежности
системы выбрано среднее время работы до отказа.
Часто на практике возникаю? так&е ситуаций, в которых требует-
ся оптимизировать надежность при нескольких ограничениях, напри-
мер; на стоимость, вес, габариты и т. п. одновременно, либо когда
необходимо минимизировать затраты на избыточные элементы в слу-
263
чае задания различных требований по надежности на различные под-
системы. Близкими к задачам оптимального резервирования по ха-
рактеру являются определенные задачи управления запасами эле-
ментов.
10.0.2. Путеводитель по главе 10. Для удобства поиска и исполь-
зования материала, изложенного в гл. 10, на рис. 10.0.1 изображена
схема, поясняющая смысловую связь отдельных разделов этой главы
и одновременно указывающая их расположение в «Справочнике».
Рис. 10 0 1. Путеводитель по гл. 10.
10.0.3. Дополнительные обозначения к главе 10.
а — параметр пуассоновского распределения;
gt (*;) — отиосительное приращение показателя надежности Pro участка систе-
мы на единицу затрат;
£0 =—log/?o,
L- • •» ^m)= log R (Xj, ...» Хт) t
Lt (х,) = — log Rt (xt);
nt — начальное число элементов Pro участка (начальное число элементов
Pro типа);
Pt Cl xt) — вероятность безотказной работы f-го участка системы за время
I при условии, что на нем имеется xi резервных элементов;
264
Рл (о) — 'вероятность появления равно k событий для пуассоновского рас-
пределения с параметром а
а11
PkW = ~kr е~°»
(а) — вероятность появления не менее k событий для пуассоновского
распределения с параметром а
рл(“)= 5 = 2 "ve~0;
Qo = l-/?o,
Q(Xj, • ••, Xm)- 1 —R (Xj, • Xm)i
Qt (xi) = 1 — Ri (*/)!
Ro —заданное значение показателя надежности R;
R (-4... xm) — показатель надежности (типа Р (/„); R (Zo) или К] систе-
мы при условии, что на /м участке имеется xt резервных элементов;
RiM — показатель надежности (типа Р (t0,), R (10) или Л) /-го участка
системы при условии, что на нем имеется xt резервных элементов;
Т (xi...хт) — среднее время работы системы до отказа при условии, что
на i-м участке имеется xt резервных элементов;
Та — заданное значение среднего времени работы системы до отказа;
wt — «вес» одного элемента /-го участка системы;
wij — затраты /-го типа, связанные с одним элементом /-го участка системы;
Ц7(о> — начальный »вес» системы (без резервных элементов»);
Wo — заданное (допустимое) значение «веса» системы;
W'o — заданное (допустимое) значение /-го типа затрат на систему;
W (xj...хт) — «вес» системы при условии, что на /-м участке имеется xt
резервных элементов;
W! (xt, .... хт) — затраты /-го типа на систему прн условии, что на /-м
участке имеется xt резервных элементов;
Wt(xt) — «вес» /-го участка системы при условии, что на нем имеется xj
резервных элементов;
xt — число резервных элементов на /-м участке системы;
А, — нитенснвиость отказов одного элемента /-го участка;
Pi — неотрицательные весовые коэффициенты: 2 pj = 1;
i
<р(х) — плотность нормального распределения;
Ф (х) — функция нормального распределения.
10.1. Формулировка задач оптимального
резервирования
10.1.1. Формулировка задачи для случая одного ограничения и
показателя надежности типа вероятности безотказной работы (коэф-
фициента готовности, коэффициента оперативной готовности). Харак-
терной особенностью этих задач является то, что показатель надеж-
ности системы выражается в виде произведения соответствующих по-
казателей надежности отдельных участков этой системы:
7? (Xj, хт) = П (Х;),
»=i
265
где R (х1( хт) — показатель надежности системы при условии,
что на 1-м участке имеется хх резервных элементов..........на т-м
участке — хт резервных элементов, Rt (xt) — показатель надеж-
ности i-го участка системы при условии, что на нем имеется хг резерв-
ных элементов, т — общее число участков системы (i = I, 2, т).
Заметим, что, если в этом случае рассмотреть логарифмы указан-
ных величин L (хъ ..., хт) = —log R (xlt хт) и L{ (хг) =
= —log Ri (xt), то показатель надежности может быть записан в ви-
де
т
Л (Хр • Хт) ^2 (Xf)<
Кроме того, если показатель надежности системы близок к едини-
це, т. е.
1 — R (х^, Хщ) ~ Q (xj, хт) 1,
то можно приближенно записать
т
Q (х1( ..., хга) Qi (Xf),
z=i
где Qi(x,) = l— Ri(xt).
При наличии одного ограничивающего фактора возможна поста-
новка двух следующих задач оптимального резервирования.
Обычно в задачах оптимального резервирования предполагаемся,
что «вес» системы в целом W (хъ .... хт) определяется как
tn
W{xlt .... xm) = 2 WtiXi),
Z=1
где Wt (x;) — «вес» i-ro участка системы при условии, что на нем
имеется хг резервных элементов.
Кроме того, сам «вес» i-ro участка системы обычно определяется
как
Г/ (х,) = ищ,
где wt — «вес» одного резервного элемента, используемого на i-м
участке системы
При наличии одного ограничивающего фактора возможна поста-
новка двух следующих задач оптимального резервирования.
1. Путем раздельного резервирования системы, состоящей из т
участков, добиться того, чтобы показатель надежности был не менее
заданного Ro (или не более заданного показателя Qo или Lo) при ми-
нимально возможном «весе» системы в целом.
Используя введенные обозначения, эту задачу можно записать
в виде
найти min W (Xj.....xm)
при условии R (х1( ..., хт) > Ro
(или Q (хь ..., хт) < Qo или L (х1( ..., xm) Ln).
266
2. Путем раздельного резервирования системы, состоящей из т
участков, добиться того, чтобы при максимально возможном показа-
теле надежности системы Л? (или при минимально возможных показа-
телях L или Q) «вес» всей системы не превысил заданного значения Wo.
Используя введенные обозначения, эту задачу можно записать
в виде
найти max /? (хъ хт)
(или min Q (лу, .... xm) или min L(xt, xm)) при условии IV (xlt ...,
.... xm) < №o-
В дальнейшем будем пользоваться терминами вероятностей без-
отказной работы для невосстанавливаемых систем. Однако простой
заменой приведенных величин на соответствующие им коэффициенты
готовности (или на коэффициенты оперативной готовности) может быть
решена оптимальная задача и для восстанавливаемых систем.
10.1.2. Формулировка задачи для случая одного ограничения и
показателя надежности типа среднего времени работы до отказа.
В этом случае показатель надежности систем равен
00
Т (Л\, ..., xm) = J Р (/1 ..., xm) dt,
о
где Р (/| х1г хт) — вероятность безотказной работы системы за
время t при условии, что на 1-м участке имеется х^ резервных эле-
ментов, ..., на т-м участке — хт резервных элементов, или
<» т
Т(хъ ..., хт) = ( П (f\Xi)dt,
о Z = 1
где Pt (t | xt) — вероятность безотказной работы t-ro участка системы
за время t при условии, что на нем имеется Xi резервных элементов.
В данном случае могут быть сформулированы две следующие оп-
тимальные задачи.
1. Путем раздельного резервирования системы, состоящей из т
участков, добиться того, чтобы среднее время работы до отказа Го
было не менее заданного при минимально возможном «весе» системы
в целом. Используя введенные обозначения, эту задачу можно запи-
сать в форме
найти min W (лу....хт)
при условии Т (xt....хт) > То.
2. Путем раздельного резервирования системы, состоящей из т
участков, добиться того, чтобы при максимально возможном среднем
времени работы до отказа То «вес» системы не превысил заданного зна-
чения Жо.
231
Используя введенные обозначения, эту задачу можно записать
в форме
найти max Т (хх...xm)
при условии W (лу, хт) №0.
10.1 3 Формулировка задачи для случая нескольких ограниче-
ний и показателя надежности типа вероятности безотказной работы
(коэффициента готовности, коэффициента оперативной готовности).
Пусть имеется М ограничений, например: на стоимость, вес, габариты
системы ит. п., которые должны быть выполнены одновременно. Обо-
значим через W1 (хх, ..., хт) затраты /-го типа на систему в целом при
условии, что на 1-м участке имеется резервных элементов, ..., па
т-м участке имеется хт резервных элементов, а через W £ заданные
ограничения на /-й тип затрат.
Используя введенные обозначения, можно сформулировать сле-
дующую задачу:
найти max 7? (xlt ..., хт)
(или min Q (Хх..хт) или min L (хи ..., хт)) при условиях:
..., хт)^П
Г'(хъ .... xm)C ЯП.
Здесь
m
F(xi,...,xra) = s Wji xlt
z=l
где Wjt — затраты /-го типа, связанные с одним элементом г-го участка
системы.
10.1.4. Формулировка задачи для случая минимизации стоимости
многофункциональной системы, когда имеется несколько ограничений
в виде заданных показателей надежности выполнения каждой из
функций. На практике часто встречаются многофункциональные си-
стемы, для которых задаются требования по надежности в виде набора
значений вероятности выполнения каждой из этих функций. (Значения
этих вероятностей зависят от важности и ответственности соответст-
вующих функций.) Выполнение каждой функции зависит от работо-
способности определенных элементов системы, причем в общем слу-
чае подмножества элементов, необходимые для реализации различных
функций, различны, хотя могут иметь и общие части (пересекаться).
В этом случае может быть сформулирована следующая задача:
добиться заданных значений вероятности выполнения каждой функции
при условии минимизации суммарных затрат, связанных с введением
резервных элементов, или в математических терминах: найти
268
т
min У, Wj xt
t= i
при условиях
П Rt (Xi) > Rlf
/to,
П Ri (xt) > R,,
i^Gj
П Ri(Xi)^Rh,
i€Gh
где tn — общее число участков системы (типов элементов);
Gj — подмножество элементов, работоспособность которых необ-
ходима для выполнения j-й функции (у = 1, 2, fe); — стоимость
одного элемента i-ro типа (i = 1, 2, /п); xt — число резервных эле-
ментов на t-м участке системы; Rt (xt) — вероятность безотказной ра-
боты t-го участка системы при условии, что на нем содержатся ре-
зервных элементов;/?;—требуемое значение вероятности выполне-
ния у-й функции.
10.2. Определение оптимального количества резервных
элементов для случая одного ограничения и показателя
надежности типа вероятности безотказной работы
(коэффициента готовности, коэффициента оперативной
готовности)
10.2.1. Методика с использованием модифицированного метода
динамического программирования. В ряде практических случаев бы-
вают сравнительно хорошо известны статистические характеристики
надежности отдельных элементов системы и характер зависимости по-
казателей надежности от увеличения количества резервных элементов.
В подобной ситуации, если только не возникает чрезмерных вычисли-
тельных трудностей из-за необходимого объема вычислений, целесо-
образно использовать методику точного определения оптимального
количества резервных элементов, основанную на модифицированном
методе динамического программирования. Методика состоит в следую-
щем:
1. Для каждого i-ro участка резервирования системы при некотором
фиксированном интервале времени /0 и при различном числе резервных
элементов xt вычисляются значения вероятностей безотказной работы,
которые мы обозначим через Rt (х^), где xt = 0, 1, 2...
2. Для удобства составляется сводная таблица значений Д, (х,)
при различных хг (табл. 10.2.1).
26Э
Таблица 10.2.1
Сводная таблица значений Rt (xt)
Ri(Xi) Ra(Xa) ... Rt(xt) ...
0 1 2 «.(0) Я.О) «.(2) /?г(0) /?г(2) Rt(0) Яг(1) Kt(2) . . . /?т(0) Ят(1) Rm(2)
X Rd'x) 7?г(х) Rd*) ... Rm(x)
3. Для двух участков системы, например для m-го и (т — 1)-го,
составляется таблица следующего вида (табл. 10.2.2).
Т а б л и на 10.2.2
Композиция (т — 1)-го и m-го участков
•Sn-l
0 1 2 ...
0 K*m-l(0,0) t4)*m_1(0,0) ^т-ДО,!) К*т-Д0.2) ^*т-Д0.2) ...
1 К*т-Д1,0) <.-1(1,0) (1, 1) ’ Л*т-Д1.2) w*m-l(l>2) ...
2 К*т-,(2.0) ^*m-i (2.0) ^m-i(2,l) ге-’т-Дг,!) Л*т-Д2,2) ^*«-1(2,2) ...
. •. ...
В клетке на пересечении хт-го столбца и хт_гй строки записыва-
ются значения
Rm— 1 (Лт-1, = 7?m-i Rm (хт), (10.2.1)
— 1 (-^m-l, хт) = Хт-1 +®т хт +^т— I + (10.2.2)
где 1И — начальный вес i-ro участка.
4. Значения Rm-\ хт) и соответствующие им значения
Wm-i (xm_i, хт) располагаются в табл. 10.2.3 в порядке возраста-
ния величин W*m-1 (Х/n-l, хт).
5. Из табл. 10.2.3 исключаются все столбцы, содержащие значения
Rm-i, не превосходящие соседних с ними слева.
270
Таблица 10.2 3
Упорядоченные пары
1> %”). ..
р* К т-1 (0.0) Я’т-Дх’т-П х'т) /?* М1 у11')
6. Оставшаяся в результате указанной процедуры последователь-
ность, называемая доминирующей, заносится в новую табл. 10.2.4.
Таблица 10.2.4
(т—1)*-я доминирующая последовательность
Ут-1 1 2 • • .
т—1* (*Li- х2т) . . .
1) ^пг— l(^m—1 ’ %т) 5Q 5 » it 3 1. X 3_У • . .
Здесь ут_\ — номер члена доминирующей последовательности.
При ут_\ — 1 в системе имеется xA-i резервных элементов на
(т — 1)-м участке и Хт — на /n-м, при ут-\ — 2 в системе имеется
Хт-\ резервных элементов на (т — 1)-м участке и хА — на т-м
п т. д. Иначе говоря, z/OT_j = k есть вектор с компонентами Xm-t
k
И Хт.
Таким образом, в результате соединения двух участков в один
в рассматриваемой системе стало т — 1 участков, а не т, как было
сначала, причем последний участок является эквивалентным, объе-
диняющим m-й и (т — 1)-й.
7. Полученные значения RA-i (Ут-i) заносятся в табл. 10.2.5,
аналогичную табл. 10.2.2.
Таблица 10.2.5
Композиция эквивалентного (т—1)-го и (т—2)-го участков системы
^т-1
т-2 > 2 3
0 Л*т-г(0,1) ^*т-г(0,1) К*т-г(0,2) Я*т-2(0,3) Ш*т-г(°>3)
1 Я*т-г(1,1) /?*т-2(1.2) 2G »3) >3)
2 /?*т-г(2,1) ^*т-2(2,1) R*m-2(2,2) ®*т-!(2.2) е(2,3)
• . . > . . . . .
271
Здесь в клетке на пересечении ут-\- го столбца и хт-2-й строки
записываются значения
Rm— 2 (-^тп—2» Ут-1) ~ Rm-2 (•''т-2) Rm — I (.Ут-1)
И
даД_ 2 (хто_2, ут-г) = wm_2 хт_2 + -1 (г/^0 + 2,
где WZm_2 — начальный вес (т — 2)-го участка.
8. Как описано в пп. 4—6, строится новая доминирующая последо-
вательность, которая заносится в табл. 10.2.6.
Таблица 10 26
(т—2)*-я доминирующая последовательность
Ут - 2 1 2 . . .
О’*т-2(Дт-2) ^*т_2(х}т_2, ylm_s) 2’ У tn— l) • . .
Я*т-2(Дт-2) -S с. 1 - £ сч 1 » Е сц 1 см S Ci 1 Ci S Ci 1 . . .
Здесь опять ут—2 — номер члена данной доминирующей последо-
вательности и уш_2= k означает, что на (т — 2)-м участке системы
имеется х‘п_2 резервных элементов, а на эквивалентном (т — 1)-м
участке используется &-й член доминирующей последовательности
(*/«— i)
9. Указанная процедура продолжается до тех пор, пока через
т — 1 шаг, наконец, не будет построена окончательная доминирующая
последовательность (у-^ и соответствующих им величин w* (yt).
10. В окончательной доминирующей последовательности отыски-
вается решение х*, такое, чго для первой задачи оптимального резер-
вирования
/?;«-1) </?</?;«) (ю.2.3)
или же для второй задачи
(xj) с «ч-i). (Ю.2 4)
11. Найденное х| содержит в себе все неизвестные оптимальные зна-
чения х(, которые могут быть определены следующим образом:
Xj = (Xj, xz),
т. е. на основании хТ можно найти хг и х2. Далее
X* = (х2, X*) и т. д.
Примечания.
1. Если задача рассчитывается вручную, то обычно с вычислительной точки
зрения удобнее сначала произвести попарную композицию всех т участков
системы, затем попарную композицию полученных, участков и т. д., т. е. способ
композиции по схеме рис. 10.2.1, а может оказаться менее предпочтителен способа
композиции по схеме рис. 10 2.1, б. Если задача рассчитывается на ЭВМ, то прак-
тически применима только схема рис. 10.2.1, а.
272
2. При решении первой задачи оптимального резервирования построение
доминирующей последовательности для каждого t-ro участка системы следует на-
чинать со значений xt, определяемых из условия
Rt (х,— 1) < Ro < Rt (xt),
так как в любом случае показатель надежности любой подсистемы должен быть
выше требуемого показателя для всей системы.
3 При расчетах следует иметь в виду, что табл. 10.2.1 — 10.2.5 можно за-
полнять постепенно по мере развития процесса решения.
4. При проведении практических расчетов часто оказывается полезным в це-
лях сокращения объема последующих вычислений исключать из рассмотрения
некоторые члены доминирующих последовательностей. Если, например, два со-
седних члена назиачительно отличаются друг от друга по весу, то можно прене-
Рис. 10 2 1. Два возможных способа композиции участков системы в модифици-
рованном методе динамического программирования.
бречь тем из них, который характеризуется меньшим показателем надежности.
Аналогично, если наблюдается незначительное различие в показателях надеж-
ности двух соседних членов доминирующей последовательности, то можно прене-
бречь тем из них, у которого больше вес.
Пример 10.2.1. Пусть система состоит из элементов с разными показателями
надежности, причем для повышения надежности применяются различные спосо
бы резервирования на различных участках (рис. 10 2.2).
Требуется определить оптимальный резерв на каждом участке для двух слу-
чаев'
а) общая стоимость системы должна быть не более 50 стоимостных единиц;
б) вероятность безотказной работы должна быть не менее 0,45.
Решение. В табл. 10.2.7 представлены значения Rt (xt) для различ-
ных xt.
Для 1-го и 3-го участков (при i = 1 и 3) расчет Rt (х() производится по фор-
муле
Я,(хг) = 1-<,+ 1;
для 2-го и 4-го участков (при i = 2 и 4) — по формуле
/?Н-Ч)=е ‘ >, ----;—
J=o
273
Таблица 10.2.7
Значения для различных участков
Число резервных элементов на >частке
1=1 <=2 1=3 <=4 1=5
0 0,2000 0,2000 0,9000 0,9000 0,1250
1 0,3600 0,5219 0,9900 0,9948 0,3125
2 0,4880 0,7809 0,9990 0,9998 0,5000
3 0,5904 0,9199 0,9999 1 0,6563
4 0,6723 0,9758 1 — 0,7734
5 0,7379 0,9938 — — 0,8555
6 0,7903 0,9986 — 0,9102
7 0,8322 0,9997 — — 0,9453
8 0,8658 0,9999 — — 0,9673
9 0,8926 1 0,9807
10 0,9141 — — — 0,9888
и для 5-го участка (при п = 3) — по формуле
п+л
R6(X6)= 2 С’п+Хв r'5 q^->.
}=п
Численные значения равны: <71 = 0,8; <?з = 0,1; е—^=0,2; е— ^ = 0,9 и
г6 = 0,5
Поэлементный резерв
Скользящий резерв
Непогру-
женный
т\=0,9
Нагру-
женный
rcOt2
Непогру-
женный
wz=Z
rz^O,2
Нагру-
женный
ш3 = 1
rs = D,9
’ Нагруженный
ws=5
г5=О,в
(для каждого элемента)
Рис. 10 2 2. Структурная схема
системы в примере 10 2 1.
В табл. 10.2.8 и 10.2.9 приведена композиция 5-го с 4-м и 2-го с 3-м участков
соответственно. В каждой клетке таблицы приведены значения вероятности
безотказной работы и стоимости. Цифры в правых нижних углах указывают
порядковый номер данного числа в доминирующей последовательности.
Табл. 10.2.10 дает композицию двух вновь образованных участков, а в
табл. 10.2.11 приводится окончательная доминирующая последовательность.
Обозначим условно для нашего примера
Т/i = (х4, х5), (/2 = (х2. *з), Уз = (И> Уз) и Уа = (ль Уз)-
Таким образом, номера в правых углах табл. 10.2.8 есть уг, табл. 10.2.9 —•
у2, табл. 10.2.10 — уз и табл. 10.2.11 — yt.
274
Таблица 10.2.8
Композиция 4-го и 5-го участков системы
Xi *5
0 1 2 3 4 5 6
0 0» 1125 16 № 1 0,2812 21 № 6 0,4500 26 № 11 0,5906 31 № 16 0,6961 36 Ns 21 0,7699 41 0,8191 46
1 0,1244 17 № 2 0,3100 22 № 7 0,4974 27 № 12 0,6529 32 № 17 0,7694 37 № 22 0,8510 42 № 27 0,9054 47 N« 32
2 0.1250 18 № 3 0,3124 23 № 8 0,4999 28 № 13 0,6561 33 Ns 18 0,7733 38 № 23 0,8553 43 Xs 28 0,9100 48
3 0,1250 19 № 4 0,3125 24 № 9 0,5000 29 № 14 0,6562 34 Ns 19 0,7734 39 № 24 0,8555 44 Xs 29 0,9102 49
4 0.1250 20 № 5 0,3125 25 № 10 0,5000 30 № 15 0,6562 35 Ns 20 0,7734 40 № 25 0,8555 45 Xs 30 0,9102 50
5 0,1250 21 0,3125 26 0,5000 31 0,6562 36 0,7734 41 № 26 0,8555 46 Ns 31 0,9102 51
6 0,1250 22 0,3125 27 0,5000 32 0,6562 37 0,7734 42 0,8555 47 0,9102 52
Примечание. Для удобства контроля процесса вычислений
в табл. 10.2.10 и 10.2.11 приведены не только номера yi, у2 и Уз< но и соответст-
вующие им значения вероятности безотказной работы и стоимости.
По табл. 10.2.11 находим, что решением для первой задачи (стоимость си-
стемы не должна превышать 50 единиц) является у4 = 5, т. е. хг — 3 И у3 = 8.
Затем по табл. 10.2.8 находим значение у3 = 8 и сразу определяем у± = 12 и
у2 = 9. Взяв ух = 12, по табл. 10.2.8 имеем xs = 1 и х6 = 2, а взяв у2 = 9, по
табл. 10.2.9 находим х2 = 3 и х3 = 2. При этом вероятность безотказной работы
системы составляет 0,2699.
Аналогичным образом по табл, 9.2.11 определяем, что решением для второй
задачи (вероятность безотказной работы должна быть не ниже 0,45) является
У,= 17. Также последовательно находим, что yt = 17 соответствуют значения
xi 4, = 3, = 1, xt = 1 и х5 = 4. При этом стоимость системы составляет
62 единицы.
10.2.2. Методика с использованием метода наискорейшего спуска.
Если неизвестны точные статистические характеристики отдельных
элементов или же составленная математическая модель является весьма
грубым приближением к реальной системе,то использовать для расчетов
точные методы для определения количества резервных элементов не
имеет смысла, так как неточность метода не играет в этом случае суще-
ственной роли.
Метод наискорейшего спуска, вообще говоря, позволяет получить
не все возможные варианты оптимального распределения резервных
элементов, однако получаемые с его помощью решения являются оп-
тимальными. Этот метод удобен тем, что требует значительно меньше-
275
Таблица 10.2.9
Композиция 2-го и 3-го участков системы
Xj *3
0 1 2 3 4
0 0,1800 3 № 1 0,1980 4 №2 0,1998 5 0,2000 6 0,2000 7
1 0,4697 5 № 3 0,5166 6 № 4 0,5214 7 0,5218 8 0,5219 9
2 0,7028 7 № 5 0,7731 8 Я° 6 0,7801 9 0,7808 10 0,7809 11
3 0,8279 9 № 7 0,9107 10 № 8 0,9190 11 № 9 0,9198 12 0,9199 13
4 0,8782 11 0,9660 12 № 10 0,9748 13 № 11 0,9757 14 0,9758 15
5 0,8944 13 0,9839 14 № 12 0,9928 15 № 13 0,9937 16 № 14 0,9938 17
6 08988 15 0,9886 16 0,9976 17 № 15 0,9985 18 № 16 0,9986 19 № 17
7 0,8998 17 0,9897 18 0,9987 19 0,9996 20 0,9997 21
8 0,9000 19 0,9899 20 6,9990 21 0,9999 22 0,9999 23
го объема вычислений, чем метод динамического программирования и
состоит в следующем:
1. Для каждого i-ro участка резервирования системы в некоторый
фиксированный интервал времени t0 при различном числе резервных
элементов xt вычисляются значения вероятностей безотказной работы
R, (х>), где xt = 0, 1, 2, ...
2. Составляется сводная таблица значений* Lt (х,) при различных
xt (табл. 10.2.12).
3. На основании табл. 10.2.12 и известных значений весов элементов
Wi составляется таблица значений g, (xt), рассчитанных по формуле
gi (х^ = (Lt (xt) - Li (xt - 1)1/зу4 (10.2.5)
для всех i и различных значений xt (табл. 10.2.13),
* Логарифм может браться по любому удобному основанию, например Ю
или е.
276
, Таблица 10.2.10 Композиция двух вновь образованных участков системы 14 ! 0,4937 16 0,4472 42 0,4942 43 0,4968 1 44 Я 698S‘0 0,6488 48 0,6520 49 0,6917 52 0,7646 53 g О ю 0,8456 58
13 0,9428 15 0,4468 41 0,4938 42 0,4963 1 43 0,5863 46 0,6481 47 0,6482 48 СП со ою 0,7639 52 0,7677 53 0,8449 57
12 0,9839 14 0,4428 40 0,4894 41 0,4919 42 0,5811 45 0,6424 46 № 16 0,6455 47 0,6849 50 0,7570 0,7608 52 0,8373 56
11 0,9748 1 13 0,4387 39 0,4849 40 | 0,4873 । 41 0,5757 44 0,6364 45 Я» 15 0,6396 46 0,6786 49 0,7500 50 Я» 20 0,7539 51 0,8296 55
10 0,9660 12 0,4347 38 0,4805 39 №9 0,4829 40 0,5705 43 0,6307 44 Я° 14 0,6338 45 0,6724 48 0,7432 49 Я» 19 0,7470 50 О сч см ОО о" LQ
9 0,9190 11 0,4136 37 ОС ю • оо о со 0,4594 1 39 1 0,5428 42 0,6001 43 №13 0,6029 44 0,6397 47 0,7071 48 №18 0,7107 49 0,7821 53
8 0,9107 10 0,4098 36 0,4530 37 №7 0,3553 38 0,5379 41 0,5946 42 № 12 0,5975 . 43 0,6339 46 0,7007 47 Я° 17 0,7042 48 О ю ою
7 0,8279 9 0,7326 35 №5 0,4118 36 №6 0,4139 37 0,4890 40 0,5405 41 Яз 11 0,5432 42 0,5763 45 0,6370 46 0,6402 47 0,7045 51
6 0,7731 8 0,3479 34 ю со СО • ю О со 0,3845 36 0,4566 39 0,5048 40 Я» 10 СЧ о LO о" 0,5382 44 0,5948 45 0,5978 46 сл ю СО •О о ю
5 0,7028 7 0,3163 33 Я°3 СО еО1 сп СО о со 0,3513 35 0,4151 38 0,4589 39 0,4611 40 0,4892 I 43 О', 5407 44 0,5435 45 0,5981 49
4 0,5166 6 0,2320 32 0,2570 33 СМ ОО ю СМ о" СО ю о СО о со СО со • со О со 0,3389 39 0,3596 42 0,3975 43 0,3995 44 0,4396 48
3 0,4697 5 0,2114 | 31 № 1 0,2336 32 №2 0,2348 33 см • о О СО ю о со о со 0,3081 38 0,3270 41 0,3613 42 0,3632 43 0,3997 47
£ 11 0,4500 26 12 0,4974 27 13 0,4999 28 16 0,5906 31 СП см ю сч СО СО о 18 0,6561 33 СО СП со со со o' см 22 0,7694 37 23 0,7733 38 27 0,8510 42
277
Окончательная доминирующая последовательность
17 | 0,7007 0,3419 56 0,4137 0,4711 62 № 17 0,5170 65 0,5538 68
16 в,6424 46 0,3135 55 ' 0,3793 0,4319 61 I 0,4740 1 0,5077 67
4 15 0,6364 45 0,3106 54 0,3757 57 0,4279 60 0,4636 63 0,5029 66
14 0,6307 44 0,3078 53 '' 1 0,3724 56 № 11 ' 0,4240 59 № 14 I 0,4654 : 1 62 0,4984 65 i
13 0,6001 43 0,2028 52 0.3543 55 № 10 0,4034 58 № 13 0,4428 61 № 16 0,4742 64
0,^46 42 0,2902 51 № 6 0,3511 54 Лй 9 0,3997 57 № 12 0,4388 60 № 15 1 0,4699 63
11 0,5405 41 0,2637 50 1 0,3191 53 № 8 0,3634 56 0 3988 59 0,4272 62
10 0,5048 40 со С£5 О 0,2980 52 № 7 0,3394 55 0,3725 58 0,3998 61
9 0,4805 39 0,2345 48 № 3 0,2837 51 0,3230 54 0,3546 57 0,3797 60
8 0,4571 38 0,2230 47 № 2 S 5Я 09 6695‘0 0,3073 53 0,3373 56 1 0,3612 59 1
7 0,4530 37 0,2211 46 Ла 1 0,2674 49 № 4 0,3046 52 0,3343 55 0,3580 ' 58
М* 1Л
278
Таблица 10.2. 12
Сводная таблица значений £((xt)
д UM W ...
0 y?i Ьг (0) (0) M(0)
1 £2(1) tjl) МП
2 £,(2) £2(2) М2) М2)
X £4 (х) Ц (x) Д (x) Lm W
Таблица 10.2.13
Значения (хг)
xl gd^i) gs(^) ... ... ^т^Хт)
0
1 g> (1) gi (О gi(l) gm0)
2 gi(2) Ы2) ... gi(2) gm(2)
X gi(x) gi (x) gi (x)
Примечание. Для значений Lt (xt), близких к единице, вычисление
величин gt (хг) можно вести по приближенной формуле
gi (xt) ж [Q; (Xi—l)~Q(xt)]/wt. (10.2 6)
4. Все значения gt (хг) в табл. 10.2.13 перенумеровываются в по-
рядке убывания.
5. Далее осуществляется многошаговый процесс.
Первый шаг:
— выбирается g11' = g'i1} — максимальная из величин gt (1),
— по табл. 10.2.12 отыскивается соответствующая величина L} (1),
— вычисляется значение
L(1) = L10’— (0) + Ly (1), (10.2.7)
где Z,<0) = 27,г(0) — начальное значение логарифма вероятности без-
i=i
отказной работы системы,
— вычисляется значение
ц/d) = ^(о) +ау/> (10.2.8)
где Ц7(о> — начальный вес системы.
Второй шаг:
— выбирается g(a> — максимальная среди оставшихся gt (1) для
i ф j или gj (2),
2 79
— по табл. 10.2.12 отыскивается соответствующая величина (1)
(или Lj (2), если номер 2 имеет g} (2)]
— вычисляется значение
L<2> = Л<1> _ L. (0) _|_ ц (]) (10.2.9)
[или Ll2) = Lll) — L} (1) + Lj(2)l,
— вычисляется значение
г<2> = г<1> _|_ Wi
(10.2.10)
[или U712’ = + Wj, если номер 2 имеет gj (2)1.
т
Процесс прекращается на таком шаге N (N = S Xt), когда для пер-
вой задачи оптимального резервирования выполняется условие
L(w-D<L0<L(W) (10.2.11)
или же для второй задачи выполняется условие
<r0<W + '). (10.2.12)
ЮДЛ. Рассмотри ту жг састшу, тк> » а арамгрг W.1A. Tpt€yvscs
определить оптимальный резерв на каждом участке для двух случаев:
а) общая стоимость системы не более 50 стоимостных единиц:
б) вероятность безотказной работы не менее 0,45 (т. е. чтобы логарифм етой
вероятности был не менее — 0,8).
Решение. В табл. 10.2.14 представлены значения £; (х;) при различ-
ных xt, для вычисления которых можно непосредственно использовать
табл. 10.2.5.
На основании табл. 10.2.14 составляем табл. 10.2.15 значений gi (xt).
Далее в этой таблице нумеруем в порядке убывания все gi (х/), начиная с на-
ибольшей (соответствующие номера поставлены в скобках).
Таблица 10.2.14
Значения для различных участков
Число резервных элементов на участке х/ Д((х4)=1п Я4(л4)
1=1 /=2 1=3 (=5
0 — 1,6094 —1,6094 —0,1054 —0,1054 —2,0794
1 — 1,0217 —0,6503 —0,0100 —0,0052 —1,1632
2 —0.7174 —0,2473 —0,0010 —0,0002 —0,6931
3 —0,5270 —0,0835 —0,0001 ~ 0 —0,4212
4 —0,3970 —0,0245 <4.0 — —0,2569
5 —0,3040 —0,0062 — — —0,1561
6 —0,2354 —0,0014 — —0,0941
7 —0,1836 —0,0003 — — —0,0562
8 —0,1441 ~0 — — —0,0333
9 —0,1139 — — —0,0195
10 —0,0898 — — —0,0113
280
Таблица 10.2.15
Таблица значений gi(xt) для различных участков
Х1 g.(Xs) giW
0
1 0,1959 (3) 0,4796(1) 0,0953(7) 0,1000(6) 0,1833(4)
2 0,1014(5) 0,2015(2) 0,0090 (23) 0,0050 0,0940 (8)
3 0,0635(10) 0,0819(9) 0,0009 0,0002 0,0544(11)
4 0,0433(12) 0,0295(15) -vO ~0 0,0329(13)
5 0,0310(14) 0,0091 (22) — 0,0202(17)
6 0,0229(16) 0,0024 —— 0,0124 (20)
7 0,0172(18) 0,0006 0,0076
8 0,0132(19) 0,0001 0,0046
9 0,0102(21) ~0 0,0028
10 0,0079(24) — — — 0,0016
Для нахождения окончательного решения поставленных задач составим
табл. 10.2 16, куда занесем результаты пошагового процесса решения.
Табл. 10.2.16 заполняется следующим образом: по табл. 10.2.15 находим наи-
большее из всех gt (xt), которое Р нашем примере принадлежит индексу i = 2;
число резервных компонентов, стоящих во втором столбце, увеличиваем на
т
единицу, т. е. в данном случае заменяем 0 на 1; в сумме Lt0) = S Z-j(O) за-
i=l
меняем член L2 (0) = — 1,6094 на L2 (1) =» —0,6503 и вычисляем новое значение
7-<1>=/,(о)—(pj _|_ 0), которое заносим в столбец значений в сум-
т
ме = 2 wt (0) заменяем член а>2 (0) иа ш2 (1) и вычисляем новое значение
z=i
ц/(1> = ц/(о> — Ш2 (pj _|_ (j), которое заносим в столбец значений W^.
Решение задач при помощи тара. 10.2.16 крайне простое. Для первой задачи
находим наибольшее из значений реса системы, еще не превышающее 50 ед. (в на-
шем случае это 49 ед.), и в этой же строке считываем остальные интересующие нас
результаты: = —1,3188 или, что то же самое, = 0,267, при этом xt =
“ х2 = 3, хя =» х} = 1, хв = 2.
Для второй задачи находим первое значение lAN\ больше 0,45 (в нашем слу-
чае это значение £(13> = —0,752р), и в этой же строке считываем другие интере-
сующие нас данные: 8> 62, при этом хя =» 4, х2 = 3, ха •= = 1, х5 = 4.
10.2.3. Методика с использованием метода наискорейшего спуска
(нестрогий алгоритм). При строгом алгоритме, основанном на методе
наискорейшего спуска, применяют в качестве целевой функции
т т
2 ц (*<) = s In Ri (Xi).
1=1 « = >
Если используется нагруженное или ненагруженное резервирова-
ние элементов, то для расчетов могут применяться табулированные
гамма-и бета-функции (соответственно пуассоновское и биномиальное
Распределения). В этом случае дополнительная операция логарифми-
рования бывает нежелательна.
281
Таблица 10.2 16
Итоговая таблица значений W и L в зависимости от N
Номер шага N Число резервных элементов на участках Итоговый вес U7(^) Итоговое зна :&ше г(ЛГ)
1 2 3 4 5
0 0 0 0 0 0 22 —5,5090
1 0 1 0 0 0 24 —4,5499
2 0 2 0 0 0 26 —4,1469
3 1 2 0 0 0 29 —3,5592
4 1 2 0 0 1 34 —2,6430
5 2 2 0 0 1 37 —2,3387
6 2 2 0 1 1 38 —2,2385
7 2 2 1 1 1 39 —2,1431
8 2 2 1 1 2 44 — 1,6730
9 2 3 1 1 2 46 —1,5092
10 3 3 1 1 2 49 — 1,3188
11 3 3 1 1 3 54 — 1,0469
12 4 3 1 1 3 57 —0,9169
13 4 3 1 1 4 62 —0,7526
14 5 3 1 1 4 65 —0,6596
15 5 4 1 1 4 67 —0,6006
16 6 4 1 1 4 70 —0,5320
17 6 4 1 1 5 75 —0,4312
18 7 4 1 1 5 78 —0,3794
19 8 4 1 1 5 81 —0,3399
20 8 4 1 1 6 86 —0,2779
21 9 4 1 1 6 89 —0,2477
22 9 5 1 1 6 91 —0,2294
23 9 5 2 1 6 92 —0,2204
24 10 5 2 1 6 95 —0,1963
При нестрогом алгоритме наискорейшего спуска используют в ка-
честве целевой функции
т
R(xlt .... хп) = П R^xt),
z=i
т. е. не требуется дополнительного логарифмирования.
Методика состоит в следующем:
1. Для каждого i-ro участка резервированной системы для некото-
рого фиксированного интервала времени t0 при различном числе резерв-
282
ных элементов х; вычисляются значения вероятности безотказной ра-
боты Ri (хс), где хг = 0, 1, 2,...
2. Составляется сводная таблица значений (х,) при различных
х, (табл. 10.2.17).
Таблица 10.2.17
Значения Rt (xt)
/?,(Л1) /?2(Х2) . . . R(fx<) . . .
0 (0) Л2 (0) Rt (0) Rm(0)
1 Л.(1) ЯД1) g«(i) Rm(l)
2 । /?ж(2) ЯД2) ЯД2) Rm (2)
Z /?>(/)' gj/j guo
• » , • « . . » . . . . • . •
3. На основании табл. 10.2.17 и известных значений «весов» эле-
ментов wt составляется таблица значений gt (хг), рассчитанных по фор-
муле
gt (xt) =
Rj (Xj) — Rj (Xj — 1)
Ri (X<—1)
(10.2.13)
для всех i и различных значений xt (табл. 10.2.18).
Значения gt(xt)
Таблица 10.2.18
g2(x2> . . . w . . .
0 1 2 / gxO) gx (2) gx(O* g2(l) g2(2) g2 (0 • . . gjl) gx(2) gi Ь) ♦ • * • • • gm(!) gm (2) gm(l)
Примечание. Для значений Ri (х,), близких единице, вычисление ве-
личин gi (xt) можнр вести по приближенной формуле
gi(xi)^lQi(xi-l)-~Q(xi)]/wi. (10.2.14)
В этом случае строгий и нестрогий алгоритмы, использующие метод наи-
скорейшего спуска, полностью совпадают.
4. Все значения gt (xt) в табл. 10.2.18 перенумеровываются в поряд-
ке убывания g*1’, g<2) ...g(W) ,...
5. Далее рассматривается многошаговый процесс.
Первый шаг:
— выбирается gll) = g)1’ — максимальная из величин gt (1),
283
— по табл. 10.2.17 отыскивается соответствующая величина Rj(l),
— вычисляется значение
P(i) Pj(1).R(Q> (10.2.15)
Я,(0)
т
где R<°> = П Rh (0) — начальное значение вероятности безотказной
*=| работы системы,
— вычисляется значение
Ц7(1) = Ц7(°> 4-й»,, (10.2.16)
где W7'0’ — начальный вес системы.
Второй шаг:
— выбирается gl2) — максимальная среди оставшихся gt, (1) для
k^=j или g>(2);
— по табл. 10.2.17 отыскивается соответствующая величина Rh (1)
[или R} (2), если номер 2 имеет gt (2)1,
— вычисляется значение
=<4 Rd) (10.2.17)
№
или R<2) = —-— R^'), если номер 2 имеет g;(2) ,
— вычисляется значение
W4) = W<" +wk. 10.2.18)
[или IF12’ = W7'1’ + wj, если номер 2 имеет g, (2)].
т
Процесс прекращается на таком шаге М (W = S xt), когда для пер-
1=1
вой задачи оптимального резервирования выполняется условие
R(W->)<RO (10.2.19)
или же для второй задачи выполняется условие
•>. (10.2.20)
Пример 10.2.3. Рассмотрим ту же систему, что и в примере 10.2.1. Требуется
определить оптимальный резерв на каждом участке для двух случаев:
а) общая стоимость системы не более 50 стоимостных единиц,
б) вероятность безотказной работы не менее 0,45.
Решение. Для решения воспользуемся значениями g; (х,), записанными
в табл. 10.2.5.
На основании табл. 10.2.5 составлена табл. 10.2.19, в которую сведены зна-
чения gi (xt), рассчитанные по формуле (10.2.13).
284
Таблица 10.2.19
Значения gf(Xj) для различных участков
Число резервных элементов на участке xt gtU,)
1=1 1=2 (=3 1=4 >=5
0
1 0,2667(3) 0,8047(1) 0,1000(8) 0,1054(7) 0,3000(2)
2 0,1185 (6) 0,2482 (4) 0,0091 (23) 0,0050 0,1200(5)
3 0,0699(10) 0,0890(9) 0,0009 0,0002 0,0625(11)
4 0,0463(12) 0,0304(15) — — 0,0357(13)
5 0,0325(14) 0,0092(12) —— 0,0212(17)
6 0,0239(16) 0,0024 — 0,0128 (20)
7 0,0177(18) 0,0006 — — 0,0077
8 0,0134(19) 0,0001 — 0,0046
9 0,0103(21) — — 0,0028
10 0,0080(24) — — — 0,0016
Окончательные результаты расчета приведены в табл. 10.2.20, которая по-
зволяет решать как прямую, так и обратную задачу оптимального резервирова-
ния. Из этой таблицы видно, что:
а) процесс нужно закончить на 10-м шаге. При этом вероятность безотказной
работы системы равна 0,267, а соответствующие значения xi равны: Xj =» х2 =
= 3, х3 = х4 = 1, х5 = 2;
б) процесс нужно оборвать на 13-м шаге, затратив на систему 62 ед. веса.
Значения xi будут равны: xt = 4, хг <=• 3, х3 = xt 1, х5 = 4.
Замечание.
В ряде практических задач может возникнуть следующая ситуация: (У —
1)-й шаг еще не дает требуемого решения (например, еще не израсходован весь
«вес» или еще не достигнуто требуемое значение вероятности безотказной работы),
а У-й шаг оптимального процесса требует введения элемента с очень большим
«весом».
Так, при решении первой задачи введение оптимального элемента дает зна-
чение показателя надежности системы (например, вероятности безотказной ра-
боты), заведомо больше требуемого. В то же время резервирование других
(не оптимальных на данном шаге) участков системы обеспечивает требуемое зна-
чение вероятности безотказной работы при меиьших затратах.
При возникновении подобных ситуаций при решении первой задачи можно
рекомендовать применение следующих методов распределения остатка ресурсов.
1. Если некоторый У-й шаг оптимального процесса приводит к сущест-
венному перерасходу «веса» (или к достижению излишне высокого значения R),
то на /V-м шаге исключается из рассмотрения один участок, имеющий макси-
мальное значение Если и в этом случае имеет место существенный перерас-
ход «веса» или достигается излишне высокое значение R, то процедуру следует
продолжить в том же направлении, т. е. на ZV-м шаге исключается из рас-
смотрения два участка, имеющие самые большие значения g^N\ и т. д.
2. Если некоторый iV-ii шаг оптимального процесса приводит к существен-
ному перерасходу «веса» (или к достижению излишне высокого значения R),
то следует «снять» резервный элемент, прибавленный на (N — 1)-м шаге опти-
мального процесса.
Затем после (У—2)-го шага продолжить процесс, исключив из рассмотрения
одни участок, имеющий максимальное значение g^W—1 \ Если и в этом случае име-
ет место существенный перерасход «веса» или достигается излишне высокое зна-
чение R, то процедуру следует продолжать в том же направлении, т. е. после
(N — 2)-го шага исключается из рассмотрения два участка, имеющих самые
большие значения g^-’’ и т. д.
285
Таблица 10.2.20
Результирующая таблица для примера 10.2.3
Но ер шага V Число резервных элементов на участках х* Вероятность безот- казной работы системы Вес системы V W
1 » 3 4 5
0 0 0 0 0 0 0,004 22
1 0 1 0 0 0 0,011 24
2 0 1 0 0 1 0,026 29
3 1 1 0 0 1 0,048 32
4 1 2 0 0 1 0,714 34
5 1 2 0 0 2 0,114 39
6 2 2 0 0 2 0,154 42
7 2 2 0 1 2 0,170 43
8 2 2 1 1 2 0,188 44
9 2 3 1 1 2 0,221 46
10 3 3 1 1 2 0,267 49
11 3 3 1 1 3 0,350 54
12 4 3 1 1 3 0,398 57
13 4 3 1 1 4 0,472 62
14 5 3 1 1 4 0,516 65
15 5 4 1 1 4 0,549 67
16 6 4 1 1 4 0,588 70
17 6 4 1 1 5 0,650 75
18 7 4 1 1 5 0,684 78
19 8 4 1 1 5 0,712 81
20 8 4 1 1 6 0,757 86
21 9 4 1 1 6 0,780 89
22 9 5 1 1 6 0,795 91
23 9 5 2 1 6 0,802 92
24 10 5 2 1 6 0,820 95
10.2.4. Упрощенная методика приближенного решения. Если в ре-
зультате резервирования требуется добиться высокого значения ве-
роятности безотказной работы системы, т. е.
1 - Ro = Qo « 1, (10.2.21)
то можно применять два вида методики оптимального резервирования,
основанной на приближенном решении задачи.
1. Определение оптимального резерва для достижения требуемого
значения вероятности безотказной работы системы Ro (или допустимого
значения вероятности отказа системы Qo):
286
1) находится величина g:
/т
2 (10.2.22)
i «в J
2) определяется величина сг:
Wt
Ci — Wtg — ----Qo; (10.2.23)
2 wi
i =1
3) из уравнения
Qt (x,) = Ct (10.2.24)
находим значение хг.
Примечание. Обычно значение xt получается дробным. В этом случае
при практических расчетах можно округлять найденное значение до ближай-
шего целого числа.
В случаях, когда дробные части полученных точных величин х; близки к 0,5,
можно рекомендовать меньшие из величин xt‘, округлять в сторону увеличения,
а большие — в сторону уменьшения.
В ряде случаев при ориентировочных расчетах удобнее округлять все полу-
ченные значения до ближайшего большего целого числа.
2. Определение оптимального резерва при заданном «весе» системы:
1) определяется начальное значение g(1) следующим образом:
— вычисляется
Х(1> = (Го- 1Г°>) / 2 Wt,
/ 4=1
— вычисляется
т
Qm = S Qi(x<'’),
i= I
— определяется
/ tn
g(n / 2 Wt-,
I 4=1
2) для найденного значения g(1), используя формулы (10.2.22) —
(10.2.24), вычисляется х)1’, хг1’, ...» х^1’;
3) производится контроль полученного «веса» системы по формуле
Ц7<» =Ц7<0) + 2 х^’шр (10.2.25)
/= I
Если ЦИ1’ > IV0, то выбирается новое значение g<2) > g(1> и для
него, как и раньше, определяются xi2), Хг2) ..х^’. Если же Ц/(1) <
< Wo, то выбирается такое новое значение g<2), что g(2) <gtl), и
для него аналогичным образом находятся х!2>, хр*, ..., Хт\
Указанный процесс продолжается до тех пор, пока на М-м шаге про-
цесса не будет найдена величина практически совпадающая с ве-
личиной Wo.
281
Примечание. Практически процесс поиска решения может быть
прекращен в пределах 3—5 шагов, если для отыскания очередного значения
использовать метод линейной интерполяции, когда
(10.2.26)
или
(10.2.27)
и линейной экстраполяции, когда
UZ(*-1)<U70, U7<fe> <U70 (10.2.28)
или
ц7(*-1)>П70, r(fe)> IFO. (10.2,29)
Иначе говоря, в случае, когда выполняются условия (10.2.26) или (10.2.28),
очередное значение g'*+]' следует выбирать на основании выражения
^+l) = g(^+(g(^l)_gW)^r-^r) (10.2.30)
и когда выполняются условия (10.2.27) или (10.2.29) — на основании выражения
8»+1)=е.>-1)+(г«>_г1»-П) . <10.2.31>
10.2.5. Практическая методика определения оптимального числа
запасных невосстанавливаемых компонент. Предполагается, что запас-
ные компоненты’ находятся в режиме ненагруженного резерва, а в ра-
бочем режиме время работы до отказа распределяется по экспонен-
циальному закону. Отказавшая компонента может быть заменена только
на исправную, а сама быть отремонтирована не может.
Для определенного периода эксплуатации t требуется обеспечить
систему оптимальным количеством запасных компонент.
Порядок расчета сводится к следующему:
1. Определяется общее количество компонент i’-го типа в системе п,.
2. Находится суммарная интенсивность отказов компонент i-ro
типа
Аг — иДг-.
3. Вычисляется математическое ожидание числа отказов компонент
i-ro типа за время t0:
4. Для каждого i-ro типа компонентов составляются таблицы зна-
чений g,k) для различных k = 1, 2, ... по формуле
_(&) _ Pk
wtlX-PM]'
где ph (at) находится по табл. П 8.7, a Ph (а() — по табл. П 8.8.
Далее повторяется процедура', описанная в § 10.2.3.
Примечание. В табл.П 8.7 и П 8.8 приводятся значения лишь
для величины параметра а, лежащего в пределах от 0,1 до 20. В-то же
время иногда на практике возникает задача определения величин
k °° 5
рИа)=тГе-'’,- Pk(a) = V е-
к! $1
s—k
288
fl я значений параметра а < 0,1 и а > 20. В обоих случаях вычисление
южет вестись по приближенным формулам.
Случай а <0,1.
л*
kl
Значения ft! для k 10:
k 1 2 3 4 5 6 7 8 9 10
k\ I 2 6 24 1,2.10s 7,2.10s 5,0- 10»j 4,0-10* 3,6-10» 3,6.10»
Для k> 10 значения ft! могут быть приближенно подсчитаны по
формуле Стирлинга (см. приложение П7).
а*
2)
При этом, если ft > 1, то при расчетах оптимального количества
необходимых запасных элементов практически для любых а <0,1
можно считать, что
1 - Ph (а) « 1.
Случай а > 20.
В этом случае распределение Пуассона может быть с успехом ап-
проксимировано нормальным распределением со средним а и средним
квадратическим отклонением о = У а.
1)
\ Va ) .
где ф (н) — плотность нормального распределения, значения которой
приведены в табл. П8.4;
2) 1-
\ /
где Ф (и) — функция нормального распределения, значения которой
приведены в табл. П8.3.
При этом для >> 24-2,5 можно считать, что^Р^а) л; 0.
г а
Пример 10.2.4. Пусть система укомплектована из пяти типов элементов.
Элементов первого типа в системе содержится 2000 шт., второго—250 шт., третье-
го—400 шт., четвертого—300 шт. и пятого — 100 шт. Интенсивности отказов
различных типов элементов равны:
A1 = l,5.10-« 1/4, Х2 = 610-5 1/ч, Х3= 1-10-51/ч,
X4 = 1.10-‘1/4, Л,5 = 1.10-« 1/4.
Стоимость одного элемента каждого типа:
= 0,1 руб., = 1 руб., ws = 0,5 руб., => 1 руб., = 5 руб.
10 Зак 943 289
Требуется обеспечить систему оптимальным количеством запасных элементов
на период эксплуатации 1000 ч для следующих случаев:
а) при максимально возможной вероятности того, что запасных элементов
будет достаточно при условии, что суммарные затраты на них не превысят
100 руб.;
б) при минимальных затратах вероятности того, что запасных элементов
будет достаточно, равной 0,995.
Решение. Определяем для каждого типа элементов величины
01 = 2000-1,5-10-" • 1000 = 3,
аа = 250 • 6 - 10"5 • 1000 = 15,
а3 = 400 - 1 • 10-2 • 1000 = 4,
а, = 300 • 1 • 10-4 • 1000 = 30,
а5 = 100 • 1 • IO-4 • 1000 = 10.
Используя табл. П8.7 и П8. 8, вычисляем значения g^, которые сводим в
табл. 10.2.21.
По табл. 10.2.21 делаем ориентировочные оценки некоторых уровней, за-
метив, что оптимальному процессу решения соответствуют для любого jV-го шага
некоторые близкие значения g^ при всех i = 1, 2, ..., п. Результаты ори-
ентировочной оценки сводим в табл. 10.2.22.
Таблица 10.2.21
Значения gt
Номер шага N ез М 65
1 3,0-10 1 2,1 2,5 2
2 1,1-10 8,7-Ю"1 1,6 2,5 9,1-10-’
3 5,2 8,1-Ю-1 1,2 2,5 5,5-10-’
4 2,6 7,5-10-1 9,1-10-’ 2,5 3,7-10-’
5 1,2 6,9-10-’ 6,2-10-’ 2,5 2,5-10-’
6 5,5-Ю*1 6,3-Ю-1 3,9-10-’ 2,5 1,9-10-’
7 2,2-Ю*1 5,5-10-’ 2,4-10-’ 2,5 1,4-10-’
8 8,М0-а 5,1-10-’ 1,3-10-’ 2,5 1,0-10-’
9 2,7-10-’ 4,6-10-’ 6,0-10-’ 2,5 7,6-10-’
10 8,1-10-’ 4,0-10-’ 2,6-10-’ 2,1 5,4-10-’
11 2,2-10-’ 3,5-10-’ 1,0-10-’ 1,9 3,9-10*’
12 5,5-10-4 3,2-10-’ 3,8.10-’ 1,6 2,7-10-’
13 1,3- IO-* 2,6-10-4 1,2-10-4 1,4 1,8-10-’
14 3,0.10-4 2,1-10-’ 4,0-10-* 1,3 1,2-10-’
15 1,0-10-4 1,7-10-’ 1,2-10-‘ 1,1 7,6-10-4
16 1,4-10-» 3,0-10-4 9,9-10-’ 4,6 IO-’
17 1,3-10-’ 8.0-10-» 8,8-10-’ 2,6 ID'»
18 1,2-10-’ 2,0-10-’ 7,8-10-’ 1,4 IO-’
19 6,6-10-’ 6,9-10-’ 7,4 IO*4
20 4,8-10-’ 5,9-10-’ 3,7 10-*
21 3,3-10-’ 5,4-10*’ 1,8-10-4
290
Продолжение табл 10.2.21
Номер шага N е2 *3 e(V)
22 23 24 2,1.10*’ 1,3-10-’ 8,3-10-’ 4,8-10-' 4,2-10-' 3,8-10“ 8,0-10-’ 3,6-10-’ 1,5-10-’
£855 5,0-10-’ 2,9-10-’ 1,6-10-’ 3,2- 10“ 2,8-10-' 2,4-10-' 5,8-10-’ 2,2-10-’ 8,0-10-’
28 29 30 8,6-10“ 4,4-10“ 2,2-10-* 2,1-10“ 1,8-10-* 1,5-10-* 2,0-10-’
31 32 33 1,1-10-* 5,0-10-5 2,3-10-’ 1,3-10-* 1,1-10-' 8,7-10-’
34 35 36 4-10-» 2-10“ 1-10-’ 7,1-10-’ 5,6-10“ 4,5- 10-’
37 38 39 3,5-10-’ 2,6-10-’ 2,0-10-’
40 41 42 1,5-10-’ 1,0-10-* 1,3-10-’
43 44 45 5,1-10-* 3,5-10“ 2,3-10-’
46 47 48 1,6-10-’ 9,6-10-* 6,0-10-*
49 50 51 3,7-10-* 2,2-10-* 1,3-10-*
52 53 54 7,5-10-’ 4,2-10“ 2,4-10-’
55 56 57 5 1,3-10“ 7,0-10-’ 4,0-10-’
58 59 2,0-10-’ 1,0-10“
10*
291
Таблица 10.2.22
Ориентировочная оценка значений xt, и
gM Jfl xt *8 х4 х* UZW, ру0.
ыо-’ 7 18 8 32 8 0,093 94,7
ыо-> 9 23 11 41 14 0,80 140,4
ыо-’ 11 27 13 46 18 0,978 170,6
ыо-* 13 31 15 51 21 0,999 195,8
ЫО” 15 33 16 55 24 0,99981 217,5
Для первого случая поставленной задачи по табл. 10.2.22 находим, что
при g = blO*1 цена дополнительных элементов будет составлять 94,7 руб.,
причем оптимальное решение дают значения хг «=> 7, хг <=> 18, х3 = 8 х4 = 32
и х5= 8 (т. е. соответствует уже 73-му шагу оптимального процесса). Исполь-
зуя табл. 10.2.21, составим сводную таблицу, начиная с 74-го шага процесса, в ко-
торой приведены окончательные результаты (табл. 10.2.23).
Таблица 10.2.23
Результирующая таблица
Номер шага .V Хъ Х4 X.
74 7 18 8 33 8 95,7
75 8 18 8 33 8 95,8
76 8 18 8 33 9 0,160 105,8
Для второго случая по табл. 10.2.22 находим, что при g~10~4 искомая ве-
роятность равна 0,999, причем оптимальное решение дают значения х4 •=> 13,
х2 = 31, 15, х4«= 51 и х6 = 21 (т. е. это соответствует 131-му шагу опти-
мального процесса). Поскольку полученное на этом шаге значение вероят-
ности превышает требуемое, необходимо процесс с этого уровня вести в обратную
сторону, т. е. отнимать элементы на тех участках, для которых значения g^N~^
оказываются наименьшими. Составим сводную таблицу, начиная с 131-го шага
процесса в обратную сторону, из которой и видны окончательные результаты
(табл. 10.2.24).
Таблица 10.2.24
Номер шага N *1 Xt Хъ Xi rW
131 13 31 15 51 21 0,99788
130 13 30 15 51 21 0,99776 ——
129 13 30 14 51 21 0,99760
128 12 30 14 51 21 0,99755 —-.
127 12 30 14 50 21 0,99733 ЧВ
126 12 30 14 50 20 0,99546
125 12 30 14 49 20 0,99509 186,7
124 12 30 13 49 * 20 0,99489 186,2
Примечание. Очевидно, что в этом случае контрольные значения
Й7(Л,) подсчитывать нет необходимости.
292
10.3. Приближенный метод определения оптимального
количества резервных элементов для случая одного
ограничения и показателя надежности типа среднего
времени работы системы до отказа
Строгое решение этого метода может быть получено лишь путем пря-
мого перебора. Однако, для случая ненагруженного резерва можно
найти грубое решение, используя тот факт, что распределение времени
работы до отказа i-ro участка при достаточно большом числе х, имеет
приближенно нормальное распределение. В этом случае можно для
среднего времени работы системы до отказа записать достаточно оче-
видные верхнюю (Гв) и нижнюю (Тв) оценки
Тв — min (xt Tt — bna, min xt Tt — TR,
1-SiCn
где Tt — среднее время работы до отказа одной i-й компоненты;
а, — среднее квадратическое отклонение распределения времени ра-
боты до отказа i-й компоненты;
X; — число компонентов i-ro типа, включая и основной; Ьп— коэф-
фициент, зависящий от числа типов элементов системы и определяе-
мый из уравнения
00
Ф(6П) = —Ur —
п’ У2л J ’
ьп
где Ф (х) — нормированная функция нормального распределения
(численные значения см. в табл. П8.3).
Можно отметить два основных случая, когда истинное среднее время
работы системы до отказа близко к одной из своих границ:
1. Если все величины (или большинство из них)
Tf(x,) = х,Тг — 6паг/х1
приблизительно равны между собой, то истинное значение ближе
к нижней границе.
2. Если среди величин 7\(хг) одна (или очень небольшое число) су-
щественно меньше величин Тг (хг) для остальных компонент, то истин-
ное значение ближе к верхней границе.
Эти рекомендации носят весьма качественный характер, но более
Удачные оценки истинного значения Т можно получить лишь путем
непосредственного вычисления.
Примечание. При рассмотрении данной задачи оптимального резерви-
рования однотипные компоненты, стоящие на различных схемных позициях,
не объединяются в один условный участок резервирования, как это было в слу-
чае оптимального резервирования по критерию вероятности безотказной работы
(или коэффициента готовности)
293
Методика оптимального резервирования в этом случае выглядит
следующим образом:
1. По табл. П8.5 находим значение коэффициента Ьп из условия
2. Вычисляются значения
Т,(хР’)₽хИ’
длях}1) = 1,2, ... и 1—1,2,...»пи результаты заносятся в табл. 10.3.1.
Таблица 10.3.1
Значения Tt (х)
X Г1М . . > Гг<х) . . . тп ™
1 Г, (1) • • • Ti (1) • • . Тп(Ц
2 Л (2) • • • Ti (2) • • « Тп (2)
3 Т, (3) • • • 7\(3) . . . Тп (3)
3. На первом шаге процесса решения среди величин Т, (xi1*) нахо-
дится наименьшая (пусть ее номер j):
7<«) = min ТДхр’) = ТДх)1’).
4. В табл. 10.3.2 заносятся итоговые значения х/1* для всех
1 = 1, 2, «, C(l) s= S CiXw, а также Т, (х/’).
i-i
Таблица 10.3.2
Итоговая таблица значений x'(N\ С<Л7) и T(W)
Нейлер шага /V « • • .(ЛО *1 л С(«) г(«)
1 1 • « • 1 • * • 1 Й1 JI ST min Tt (xj11)
2 1 • • • 2 • • « 1 СЫ=С^+с} min Tt (x!2>)
294
5. Находятся некие значения xi2> по правилу
если I =/=
1Л если I —
6. Вычисляются
Л(х?>) = хР>Гг-6паг/^
для всех i = 1, 2, ..., п и процедура продолжается с п. 3.
Пр имечание. Естественно, что все Tt (х/) для «=/= / равны соответст-
вующим Ti (xz1’).
Пример 10.3.1. Рассмотрим систему, представляющую собой последователь-
ное соединение десяти элементов, характеристики которых приведены ниже.
Показатель Номер элемента
1 2 3 4 5 6 7 8 9 10
Tt 10 10 10 10 30 30 30 30 30 30
1 1 3 3 1 1 3 3 10 10
Ct 1 5 1 5 1 5 1 5 1 5
Требуется найти такой оптимальный состав резервных элементов для систе-
мы, чтобы средняя наработка системы между отказами была не менее 100 ч.
Решение. Из условия I — */0,5, используя табл. П8. 5, пред-
варительно получаем, что 1,5.
В данном случае начинать пошаговый процесс со значений xt = I нецеле-
сообразно, так как ясно, что для элементов с Tt= 10 ч необходимо не менее
10 запасных элементов, а для элементов с Tt “ 30 ч — не менее четырех. При-
няв во внимание это соображение, запишем:
xl = x2=10, T'f=rf=IOO—1,5-1 /ГО»95;
х1 = х2=11, Tf = 7-?= 110—1,5-1 УП~ 10,5;
х3 = х4=Ю, T|=Tf=10O— 1,5-3/16» 86;
X3=Xi = Ht Tf=Tf=llO— 1,5-3/П»95;
^3=x4 = 12, = = 120—1,5-3/12» 104;
x5=xe=4, T* = rf=120—1.5-1У4» 117;
x7 = x8 = 4, T, =T8 = 120—1,5-3/4 » 111;
x9 = xie = 4, ^ = 7^ = 120—1,5-10 У4» 90.
x9 = xt0 = 5, Tj =Tfe = 150—1,5-10 У§ » 116.
Итак, решением нашей задачи является набор следующих значений: х< ==
= х2 = 11, х9 = х4 = 12, х6 = хв = х7 = х8 = 4, х9 = хю = 5.
Заметим, что в большинстве практических задач оптимального резервиро-
вания при целевой функции в виде среднего времени работы между отказами ре-
шение в первую очередь зависит от Ti и о/ и в значительно меньшей степени —
от показателя затрат с/.
295
10.4. Определение оптимального количества резервных
элементов для случая нескольких ограничений
и показателя надежности типа вероятности безотказной
работы (коэффициента готовности, коэффициента
оперативной готовности)
Данная задача может быть решена теми же способами, которые опи-
саны в § 10.2, при сведении многомерной задачи к одномерной путем
введения «приведенных» затрат.
Рассмотрим для простоты случай двух ограничений (М — 2). Для
образования «приведенных» затрат используем неотрицательные весо-
вые коэффициенты pi и р2, такие, что pi + р2 == 1. Выберем, далее, оп-
ределенный шаг изменения весовых коэффициентов, например 1/k,
и запишем все возможные пары весовых коэффициентов;
' pV>==0, рИ>=1,
р<2> = 1/6, р^)=1_1/й;
р<3> = 2/6, р<3> = 1 — 2/6;
р<*+»=], p(*+D = 0
Теперь составим k 4- 1 различных «приведенных» затрат для каждого
типа компонент, т, е.
u»)1’=u»np(i' +ьуа(р21),
для всех I — 1, 2, .... т.
Для каждого набора «приведенных» затрат ..., (/ = 0,
1, ..., 6+1) решим задачу оптимального резервирования как при
одном ограничении, считая точкой остановки процесса первое наруше-
ние хотя бы одного из заданных ограничений (117' или ,W2 в данном
случае). Для каждого вида «приведенных» затрат находим получив-
шееся значение показателя надежности и затем среди них отыскиваем
наибольшее, например, для /-й пары весовых коэффициентов р<'> и
р<+ Это решение и принимается в качестве приближенного оптималь-
ного решения, а соответствующий набор полученных значений числа
резервных компонент х*0, х^’, ...t х„} считается искомым.
Точность решения определяется выбранным значением шага 1/й.
Однако следует заметить, что в силу дискретного характера получае-
мых решений хр>, ..., х„} после некоторого определенного уровня
уменьшение шага не приводит к повышению точности (значение этого
уровня зависит от конкпетной задачи}.
В случае нескольких ограничений существо решения не меняется:
м
выбираются весовые коэффициенты рп ..., рм, такие, что 2 р; = 1,
/=1
и составляются возможные наборы этих коэффициентов, с учетом ко-
торых вычисляются «приведенные» затраты. По существу, задача ос-
23»
тается той же, что и в двумерном случае (М = 2), увеличивается лишь
объем вычислительных работ.
Пример 10.4.1. Рассматривается та же система, что и в примере 10.2.1. Как
уже указывалось в этом примере, стоимости компонент на различных участках
системы равны в условных единицах соответственно:
= 3, ю12 = 2, ю18 = 1, ц>14 = 1, и>15 = 5.
Пусть дополнительно известны значения веса (также в некоторых условных еди-
ницах) этих компонент:
Щ21 => 1, ю22 =» 3, ю28 = 5, wu •=• 5, ю25 «= 1.
Требуется определить оптимальный резерв на каждом участке системы для трех
случаев:
а) допустимая стоимость системы 65 усл. ед., а допустимый вес системы
45 усл. ед.;
.6) допустимая стоимость системы 65 усл. ед., а допустимый вес системы
40 усл. ед.;
в) допустимая стоимость системы 55 усл. ед., а допустимый вес системы
30 усл. ед.
Решение. Решение проведем только о использованием строгого метода .
иаискорейшего спуска. (Это объясняется лишь соображениями простоты изло-
жения, поскольку другие методы приводят к большим промежуточным вычис-
лениям и громоздкому изложению).
Выберем для коэффициентов рх и р2 шаг изменения, равный 0,25, т. е. =
«= 0, = 0,25, ..., р^1> = 1,00. В этом случае «приведенные» затраты для
каждого из типов элементов будут равны:
ц,;1>=з, aV>=2, ®81> = 1. ^> = 1, и^1> = 5;
да<12>=2,5, w<22>=2,25, <®^»=2, ш^>=2, в^> = 4
лу)31 =2, Ц8>=2,5, о43)=3, ®48) =3, ^’>=3;
СО|4)= 1,5, Ц*>=2,75, =4, к/<4> = 4, «4*>=2;
to((5 > = 1, ^5>=3, =5, СО(46> =5, ю‘8> = 1.
Для случая р^> = 0 задача сводится к одномерной и можно, не вычисляя
специально значений gj1’ (xj), воспользоваться табл. 10.2.15. Для остальных
р<0 составлены специальные таблицы значений (xt) (табл. 10.4.1 —
10.4.4). На этих таблицах, как и ранее, в скобках после соответствующих зна-
чений gj;) (х;) поставлены нЪмера шагов процесса оптимального решении.
Таблица 10.4.1
Таблица значений gf}(xt) для различных участков при р^2) = 0,25
С,2) (X1I 42) <*»> ез2) 42) 42) w
0 —
1 0,2351(2) 0,4230(1) 0,0474(12) 0,0500(11) 0,2290(3)
2 0,1288(5) 0,1790(4) 0,0045 0,0025 0,1175(6)
3 0,0762(7) 0,0727 (8) 0,0005 0,0001 0,0679 (9)
4 0,0527(10) 0,0262(16) 0 0 0,0412(13)
5 0,0372(14) 0,0081 —— 0,0252(17)
6 0,0275(15) 0,0021 —— 0,0155 (20)
7 0,0206(18) 0,0005 — — 0,0095 (22)
8 0,0158(19) 0,0001 —— 0,0058
9 0,0123(21) 0 0,0035
10 0,0095(23) — — — 0,0020
2ОТ
Таблица 10.4.2
Таблица значений g^fx^ для различных участков пр» = 0,50
g(® W
0
1 0,2940(4) 0,3818(1) 0,0318(16) 0,3333(2} 0,3060 (3)
2 0,1520 (7) 0,1622 (.5) 0,0032 0,0017 0,1568(6)
3 0,0953(8) 0,0655(10) 0,0003 0,0001 1 0,0910(9)
4 . 0,0650(11) 0,0236(18) 0 0 0,0548(12)
5 0,0465(13) 0,0073 — —W 0,0357(14)
6 0,0344(15) 0,0019 — — 0,0207(19)
7 0,0258(17) 0,0005 — 0,0127(22)
8 0,0198(20) 0,0001 —— —• 0,0077
9 0,0153(21) 0 — — 0,0047
10 0,0118(23) — — — 0,0027
Таблица 10.4.3
Таблица значений g^4’(xt) для различных участков при р^4) = 0,75
gV’(Xi) <-е«> Да> (*з) eV’ (х‘> gV’w
0
1 0,3918(2) 0,3490 (3) 0,0240(19) 0,0250(18) 0,4580(1)
2 0,2028(5) 0,1475(6) 0,0022 0,0013 0,2350 (4)
3 0,1270(8) 0,0595(12) 0,0002 0,0001 0,1358(7)
4 0,0866(9) 0,0214(20) 0 0 0,0820(10)
5 0,0620(11) 0,0066 —— — 0,0508(13)
6 0,0458(14) 0,0017 — —• 0,0310(16)
7 0,0344(15) 0,0004 —<• —— 0,0190 (22)
& 0,0264(17) 0,0001 I 1^ 0,0115
9 0,0204 (21) 0 —- 0,0070
10 0,0158(23) — — — 0,0040
Таблица 10.4.4
Таблица значений gf\xt) для различных участков при р*25) = 1,00
g(t5)W eV* (*) £3* (*s) Д(45’ <х‘> ₽<5>W
0
1 0,5870(2) 0,3200(4) 0,0191 0,0200 0,9150(1)
2 0,3042(5) 0,1350 (9) 0,0018 0,0010 0,4700 (3)
3 0,1900(7) 0,0547(15) 0,0002 0 0,2720(6)
4 0,1300(10) 0,0197 О —- 0,1645(8)
5 0,0930(12) 0,0061 — 1^ 0,1010(11)
6 0,0687(13) 0,0016 — 1^ 0,0620(14)
7 0,0516(16) 0,0004 — — 0,0380(18)
8 0,0396(17) 0 ___ 0,0230(21)
9 0,0306(19) — — 0,0140
10 0,0237 (20) — — — 0,0080
298
Результирующая табл. 10.4.5 составлена в компактной форме:
на основании табл. 10.2.15 и 10.4.1—10.4.4 и заданных величину и
w2i для каждого значения р<Д приводятся величины W1 и W"2 (стоимо-
сти и веса) на каждом шаге. По этой таблице можно определить для
любого р|п номер шага, на котором произошло нарушение одного из
заданных ограничений W[ или W%, а затем по соответствующей таблице
значений gP* (хг) определяются величины х}'\
Т а б л ид а 10.4.5
Пошаговые изменения стоимости и веса системы
для различных случаев «приведенной" стоимости
Номер шага N f<»=0 pJ,2)=0.25 0(3)_ P2 - 0,50 P^Uq.75 p^l.OJ
Ц71 W1 W’1 w? W' W1 IV’’ W
0 22 17 22 17 22 17 22 17 22 17
1 24 20 24 20 24 20 27 18 27 18
2 26 23 27 21 25 25 30 19 30 19
3 29 24 32 22 30 26 32 22 35 20
4 34 25 34 25 33 27 37 23 37 23
5 37 26 37 26 35 30 40 24 40 24
6 38 31 42 27 40 31 42 27 45 25
7 39 36 45 28 43 32 47 28 48 26
8 44 37 47 31 46 33 50 29 53 27
9 46 40 52 32 51 34 53 30 55 30
10 49 41 55 33 53 37 58 31 58 31
11 54 42 56 38 56 38 61 32 63 32
12 57 43 57 43 61 39 63 35 66 33
13 62 44 62 44 64 40 68 36 69 34
14 65 45 65 45 69 41 71 37 74 35
15 67 48 68 46 72 42 74 38 76 38
16 70 49 70 49 73 47 79 39 79 39
17 75 50 75 50 76 48 82 40 82 40
18 78 51 78 51 78 51 83 45 87 41
19 81 52 81 52 83 52 84 50 90 42
20 86 53 86 53 86 53 86 53 93 43
Для случая а из табл. 10.4.5 находим, что ограничение по весу не
является критическим, так как даже при рг1’ = 0 впервые ограниче-
ние нарушается по т. е. по тому виду ресурса, который расходо-
вался оптимальным образом. Нарушение ограничения по стоимости
происходит на 12-м шаге (см. табл. 10.4.5). Из табл. 10.2.16 находим,
что за 11 шагов процесса решения система будет иметь;
, х^ == 3, х2 == 3, == 1, х4 1, Хд 3.
Для случая а из табл. 10.4.5 находим, что ограничение по стоимо-
сти не является критическим, так как даже при рз6) — 1,0 впервые
ограничение нарушается повесу (1^7), т. е. опять потому виду ресурса,
который расходуется оптимальным образом. Решение для этого случая
293
находим из табл. 10.4.4. Нарушение ограничения происходит на 10-м
шаге, т. е. за 9 шагов процесса решения система будет иметь:
хг = 3, х2 = 2, х3 — 0, xt = 0, х& = 4.
Наиболее сложный случай—случай б, для которого по табл. 10.4.5
находим условные оптимальные решения для всех значений р!Д и
сравниваем их.
Далее, составим итоговую табл. 10.4.6, в которой запишем для раз-
личных значений р<'> номера шагов остановки процесса, израсходо-
ванные к этому шагу ресурсы и найденные из табл. 10.2.15 и 10.4.1—
10.4.4 условно оптимальные значения хР.
Таблица 10.4.6
Итоговая таблица значений xt и L
р</> Номер шага остановки процесса Xj А х3 X. L
0 9 2 3 1 1 2 1,509
0.25 10 4 3 0 0 3 1,112
0,50 10 3 3 0 1 3 1,142
0,75 9 4 2 0 0 3 1,275
1,0 9 3 2 0 0 4 1,241
По значениям хр из табл. 10.2.14 нетрудно для каждого условно
$
оптимального решения вычислять величину L = 2 In (х{), которая
!=l
заносится в последний столбец табл. 10.4.6.
По результатам сравнения величин L в последнем столбце следует
выбрать в качестве решения
хх = 4, х2 = 3, х3 = 0, х4 = 0, х5 = 3.
Вообще говоря, это решение может и не быть истинно оптимальным,
так как выбранная серия значений рР достаточно груба. Для уточ-
нения решения можно взять значения р2 = 0,20 и р2 = 0,30. Однако
следует иметь в виду, что небольшие изменения р2 могут привести
к прежнему решению, так как величины xt имеют дискретную природу.
10.5. Определение оптимального количества резервных
элементов для многофункциональной системы для случая
одного ограничения и показателя надежности типа
вероятности безотказной работы (коэффициента готовности,
коэффициента оперативной готовности)
Для решения этой задачи может быть предложен алгоритм приближенного
решения. Этот алгоритм дает точные результаты в двух предельных случаях:
а) когда каждая из функций выполняется при работоспособности всех т элемен-
тов системы; б) когда для выполнения каждой функции требуется работоспособ-
ность совершенно различных (иепересекающихся) подмножеств элементов. Для
пре межуточных случаев точность алгоритма оценить не удается.
300
С использованием введенных в § 10.1.4 обозначений алгоритм решения этой
вадачи можно записать в следующем виде:
а) решается k задач вида:
min У, wt XI
lf:G. ~
при условии П R;(xi) > R, для всех /=1,2,..., k.
Находятся соответствующие оптимальные значения х{, х'п для каждой
/-й задачи любым из методов, описанных в § 10.2;
б) для каждого i-ro элемента находятся наибольшие значения, т. е.
Xi = max х{',
в) для каждого подмножества элементов Gy находится часть (обозначим ее
через Gj ), которая нужна только для выполнения именно /-й функции. Через
G* обозначим оставшуюся часть подмножества Gf,
г) для каждого подмножества G/ находится значение
П ri(xt) = Rl.
itc*
Примечание. Если в подмножество G* не входит ни один элемент,
т. е. если /-я функция выполняется при помощи независимой группы элементов,
то положим R; = 1;
д) для каждого множества 6? вычисляется значение
R** = Rt/R*,
которое представляет собой требование к вероятности безотказной работы эле-
ментов, принадлежащих подмножеству Gf,
е) решается дополнительно k задач вида:
найти
min У WiXt
ito**
при условии
П Ri(xi)>R** для всех /=l,2,...,fe.
iCG**
Найденные значения оставшихся Xi* принимаются в качестве решения.
Таким образом, в качестве решения принимаются значения х/*, найденные
и п. б, и значения х/*, найденные в п. е.
Пример 10.5.1. Система состоит из пяти элементов рис. 10.5.1 со следующими
показателями надежности и стоимости:
и = 0,85, 1;
rt = 0,90, сг *= 2;
r3 = 0,97, c8 = 1
rt = 0,95, 5 j
r6 = 0,99, C5 = 3.
Система выполняет три функции, для каждой из которых требуется работо-
способность следующих элементов:
Gj = {4, 5}, Ga = {1, 2, 41, Gs = {1, 3, 5},
801
причем требуемые вероятности безотказного выполнения этих функций (показа-
тели надежности соответствующих подсистем) равны Rt > 0,9999, Rt > 0,9975
и R3 > 0,9995 соответственно. Допускается повышение надежности каждого
элемента системы путем нагруженного резервирования.
Требуется найти оптимальное число запасных элементов, обеспечивающих
заданные требования по надежности при минимальных затратах.
Рас. 10.5.1. Структурная схема си-
стемы в примере 10.5.1.
Решение. Используя модифицированный алгоритм динамического про-
граммирования, находим:
для первой подсистемы х| = 4, xj=3;
для второй xf=3, х|=3, *4=3.
и для третьей xf — 5 х|=3, х|=2.
Далее определяем!
rf = max(xf, xf)=5,
х*2 =max (x|)=3,
*^ = max(x|) = 3,
X4=max (xj, xl) = 4,
xg=max (x|, x|)=3.
Проверим, можно ля уменьшать кратность резерва элементов 2 и 3, которые
нужны только для выполнения соответственно второй и третьей функций.
Вычислим
0,995
R** =-------------1-----------ж 0,99501
2 [1—(0,15)5] [1 —(0,05)4]
0,9995 „ „
3 “ (I — (0,15)4(1— (0,01)4 ~ *9 Э58,
Для обеспечения R2* > 0,99501 необходимо иметь х2 = 3, а для R|* >
> 0,99958 иметь Ха = 3, т. е. решение, полученное в данном случае, неулуч-
шаемое.
10.6. Управление запасами элементов при случайном
потоке запросов
10.6.1. Предварительные замечания. Создание запасов элементов сопряжено
с двумя противоположными факторами: с одной стороны, избыточный запас тре-
бует затрат на приобретение и хранение, с другой стороны, недостаточный уро*
вень запаса создает частый дефицит, что сопряжено с простоями и связанными
с ними издержками.
302
Расход элементов (спрос на элементы) задается в виде случайного процесса
потока заявок. Чаще всего предполагается, что интенсивность этого потока ие
зависит от состояния запасов на складе. Одной из простейших форм зависимости
между расходом элементов и наличием их в запасе является прерывание пото-
ка заявок при опустошении склада. (Например, недостача элементов приводит
к отказу и выключению объекта и, следовательно, к приостановлению расхода
этих элементов).
Правило -выполнения заказа указывает момент заказа партии, задержку
в поставке заказанной партии и размер этой партии.
10.6.2. Одноменклатурный запас элементов.
Обозначим:
Zi — случайные независимые и одинаково распределенные интервалы между
моментами поступления требований на один элемент;
F (х) — функция распределения случайной величины Е;;
F*k (х) — fe-кратная свертка F (х); а — среднее значение распределения
F (х);
г (/) — уровень запаса в момент t (отрицательные значения соответствуют
длине очереди);
г — стационарный средний уровень запаса; k = FP{z >0} — коэффициент
готовности склада (вероятность того, что в «достаточно удаленный» момент вре-
мени на складе нет дефицита запасных элементов, или доля времени, в течение
которого нет такого дефицита); т—случайное время доставки заказанной партии;
G (х) — функция распределения случайной величины т; т| — случайное время
до первого опустошения склада; Р (f) = £Р (п > t) — вероятность бесперебой-
ного функционирования.
Будем считать, что первый заказ размера п подается при снижении г (() до
т (т — точка заказа). Всё последующие заказы имеют размер п и подаются по
получении п очередных требований.
Такое правило заказа для краткости назовем (т, п)-правилом.
Рассмотрим два случая:
1) модель с прерыванием входного потока требований (при п > т)>
2) модель без прерывания входного потока требований.
Соответствующие формулы для этих случаев приведены в табл. 10.6.1.
10.6.3. Централизованные системы снабжения элементами. Рассмотрим два
случая.
1. Центральный склад располагает N элементами, чтобы снабжать k низовых
складов в течение фиксированного времени t0. Время безотказной работы эле-
мента § с функцией распределения F (х). Время доставки с центрального склада
на объекты постоянно и равно /д. На каждом низовом складе используется (т,
п)-правило заказа (при п > т). Пусть Р (/0) — вероятность того, что ни на одном
низовом складе не произойдет перебоя в снабжении элементами й центральный
склад будет своевременно отправлять заказанные партии. Тогда
/ \
I а 1
F*m (/Д)Ф ------.............. , (10.6.1)
I т/ оЦ/р \
где М = у (п + 1) (fe — 1), D = -у (k — 1)( н2 — 1); Ф (х) — нормированная
функция нормального распределения Формула (10.5.1) дает хорошее прибли-
жение, когда:
1) F*m Цд) I, т. е. за время доставки заказанной партии вероятность по-
явления более т требований мала,
2) суммарное число требований, поступивших за время t0 от всех k низовых
складов, достаточно велико (что позволяет использовать нормальную аппрокси-
мацию для распределения числа поступивших требований).
2. С центрального склада имеется возможность посылать заказы на пополне-
ние, причем они доставляются за фиксированное время Тд. Центральный склад
зад
Ц Таблица 10.6.1 Показатели бесперебойной работы одиночного склада I Схема с прерыванием входящего потока 1 Схема без прерывания входящего потока Показа- тель общий случай пуассоновский лоток и постоянное время пуассоновский поток и постоянное враля Примечание доставки доставки е е е । 1 8^И •V а ? 1 е, т 2",» —UT -ЦТ -UT Выражение г (ч е Ч1 е Ч1 е—Ч1 справедливо при 7 « 1 а оо m+n+1 m+n—2 m 1 t k—m__ k—m + i k=m k—0 _______ n (m + 0 1 -я|а 1 + E .N O1 + s* H *S 8 N И •ae — Is 1 + E N + e *< 3 c •s _ > ? + F + e , *><—-*o 8^'jq -H Is 1 ** Условные обозначения: oo 7 — вероятность того, что наступит более m — 1 заявки за время доставки заказа /д: т =j [1 — G (х)] dF*"1 (х), 0 00 аа — средняя продолжительность простоя в ояшдании доставки заказа: “° = J I1 ~ G (х)1 F*m W dx, вероятность поступления ровно k требований пуассоновского потока за Ликсиоованное воамя доставки f : п. = — е~
использует (М, АО-правило заказа, а низовые склады (т, направило, причем
„ > m, N > М. Поскольку в центральный склад поступают требования сразу
на п элементов, удобно перейти к приведенным параметрам М' = М/п, N' =
= N/n, считая нх целыми. Вероятность бесперебойного снабжения Р (!) за время
i можно вычислить в предположении k > 1, что позволяет использовать пу-
ассоновскую аппроксимацию для описания суммарного потока заказов с низовых
складов в центральный склад. Параметр этого аппроксимирующего потока Л'
вычисляется по формуле А' = k/na, где а' х а [1 + m/nF*m(t^)] (предполагает-
ся, что F*m (7д) < 1). Если дополнительно предположить, что
1=0 jl
то искомая функция Р (() хорошо приближается экспоненциальной функцией
—Xvi 1
Р(/)з:е с параметром Л2, равным
k К'
Ч F*m (/д + w7’ Лл,'~1 (Л'Гд)-
! Список литературы
1. АврамченкоР. Ф. Выбор оптимального расписания включений за-
пасных элементов в нагруженный режим. — «Известия АН СССР. Техни-
. ческая кибернетика», 1970, № 3.
2. А л е к с е е в О. Г. Об одной задаче оптимального резервирования. —
i «Известия АН СССР. Техническая кибернетика», 1967, № 1.
3. АлексеевО. Г. Оптимизация надежности сложных систем при несколь-
ких ограничениях. — «Автоматика и телемеханика», 1967, № 12.
4. Ал е кс ее в О. Г., Я к у ше в В. И. Комбинированный метод расчета
оптимального резервирования. —«Изв. высш, учебн. заведений. Приборо-
строение», 1964, т. 7, № 4.
5. Г а г а н о в П. Г., И в л е в В. В. Определение оптимального объема за-
пасных элементов для сложных технических систем. — «Автоматика и теле-
механика», 1969, № 3.
6. Г е р ц б а х И. Б. Динамическое резервирование. Оптимальное управле-
, ние включением резервных элементов. — «Автоматика и вычислительная тех-
, ника», 1970, № 1.
7. И с а е в Л. К., Мамед-Заде Н. А. Об оптимизации надежности ре-
зервированной системы. — «Известия АН СССР. Техническая кибернетика»,
1967, № 1.
’ 8. Карштедт И. М., Коган Л. М. Задача оптимального резервиро-
вания с выбором вариантов исполнения. — «Известия АН СССР. Техниче-
ская кибернетика», 1971, № 2,
, 9. Карштедт И. М., Коган Л. М. Оптимальное нагруженное резер-
вирование элементов многофункциональной системы.—«Известия АН СССР.
Техническая кибернетика», 1972, № 4.
10. К о г а н Л. М., Цейтлин В. А. Алгоритмический подход к рацио-
нальному резервированию информационной системы. — «Автоматика и теле-
механика», 1970, № 1.
11. Корман А. Г. Об оптимальном резервировании аппаратуры.—«Из-
вестия АН СССР. Техническая кибернетика», 1964, № 4.
12. К у з и е ц о в И. Н. Алгоритм решения задачи нанлучшего резервнрова-
, ння. — В кн.: Прикладные задачи технической кибернетики. Под ред.
И. А. Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966.
е 13. К у л а к о в Н. Н., Загоруйко А. С. Метод определения оптнмаль-
’ ного распределения надежности между отдельными элементами системы. —
«Известия АН СССР. Техническая кибернетика», 1966, №6. ’
303
14 .Потоцкий В. А., Райкин А. Л., Савицкий Ю. П. Опти-
мальная структура эксплуатации систем с резервными элементами. —«Ав-
томатика и телемеханика», 1968, № 4.
15. Райкин А. Л. Оптимизация избыточности при наличии ограничений. —,
«Автоматика и телемеханика», 1965, № 2.
16. Р а й к и н А. Л. Определение оптимального резерва. — «Автоматика и те-
лемеханика», 1962, № 11.
17. Ран кин А. Л. Определение оптимального резерва системы с учетом
повреждения в резервном режиме. — «Автоматика и телемеханика», 1962,
№ 11.
18 Р у б а л ь с к и й Г. Б., У ш а к о в И. А. Приближенная формула для
вероятности бесперебойного снабжения в централизованной системе уп-
равления запасами.—«Автоматика и вычислительная техника», 1971, № 6.
19. Рыжи ков Ю. И. Оптимальное планирование запасов резервных ячеек
и элементов ЭВМ для вычислительных центров. — В кн.: Прикладные за-
дачи технической кибернетики. Под ред. И. А. Ушакова, Б. С. Фленшмана.
М., «Сов. радио», 1966.
20. С м о л и ц к и й X. Л., Чукреев П. А. К вопросу об оптимальном
резервировании аппаратуры. — «Энергетика и автоматика», 1959, № 8.
21. Т о п о л ь с к и й М. В. Об одном алгоритме решения задачи оптимального
резервирования. — «Надежность и контроль качества», 1969, № 5.
22. Ушаков И. А. О задаче оптимального резервирования с немультипли-
кативной целевой функцией. — «Автоматика и вычислительная техника»,
1967, № 3.
23. У ш а к о в И. А. Оптимальные задачи надежности. — «Надежность и
контроль качества», 1969, № 1.
24. Ушаков И. А. Оптимизация надежности сложных систем методом наи-
скорейшего спуска. — В кн.: Прикладные задачи технической кибернетики.
Под ред. И. А. Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966.
25. У ш а к о в И. А. Приближенный алгоритм для построения оптимально
надежных систем с произвольной структурой. — «Известия АН СССР. Тех-
ническая кибернетика», 1965, № 2.
26 Ушаков И. А. Приближенное решение задачи об оптимизации сред-
него времени безотказной работы системы. — «Надежность и контроль ка-
чества», 1971, № 11.
27. Ушаков И. А. Приближенное решение задачи оптимального резервиро-
вания. — «Радиотехника», 1965, т. 20, № 12.
28. Ушаков И. А. Расчет оптимального количества запасных элементов. —
«Стандарты и качество», 1967, № 2.
29. У так о в И. А. Эвристический метод оптимизации резервирования много-
Тункциональных систем. — «Известия АН СССР. Техническая кибернетика»,
972, Ms 4.
30. У таков И. А., Топольский М. В, Оптимизация среднего
времени безотказной работы системы. — «Надежность и контроль качества»,
1974, № 3.
и
ЗАДАЧИ ОПТИМАЛЬНОЙ ПРОФИЛАКТИКИ
11.0. Предварительные замечания
11.0.1. Постановка задачи. В процессе эксплуатации под воздейст-
вием различных случайных факторов происходит разрегулировка па-
раметров, стареют или отказывают отдельные компоненты системы,
что снижает качество ее функционирования. Система из состояния, ха-
рактеризующегося номинальными значениями параметра, переходит
в процессе эксплуатации последовательно в состояния с худшими ка-
чественными характеристиками, в результате чего снижается произво-
дительность, ухудшается качество выполнения системой своих функ-
ций и т. д.
Своевременные и целесообразные по глубине и объему профилакти-
ческие работы позволяют не только повышать технические характерис-
тики эксплуатируемых систем и улучшать показатели их надежности,
но и сокращать эксплуатационные расходы. В ряде случаев можно
добиться требуемых показателей надежности вообще лишь соответст-
вующей организацией оптимальных профилактических работ.
Подрегулировки, замены отказавших элементов и т. п. связаны
с вполне определенными затратами не только из-за ухудшения качества
функционирования системы, но и из-за проведения собственно профи-
лактических и ремонтных работ. Кроме того, отказы, появляющиеся
в достаточно сложных системах, часто носят скрытый характер, так
что для их выявления требуется специальная проверка, что опять-таки
приводит к дополнительным затратам.
Таким образом, обслуживающий технические системы персонал
оказывается перед дилеммой: либо продолжать использовать систему,
если эффективность ее функционирования снизилась до некоторого
уровня (или возникло подозрение, что подобное снижение могло про-
изойти), либо проводить специальные профилактические мероприятия.
На практике в большинстве случаев существует возможность принять
такой метод проведения профилактических мероприятий, который по-
зволяет минимизировать суммарные потери, учитывающие затраты на
собственно профилактику и потери в результате’ ухудшения эффектив-
ности функционирования системы. Возможны и другие целевые функ-
ции, оптимизация которых достигается соответствующим регламентом
профилактических работ, например показатели надежности.
Обычно предполагается, что возможно проводить два типа про-
филактических работ: плановую профилактику, назначаемую заранее
к моменту достижения системой заданной наработки, и внеплановый
аварийный ремонт, назначаемый в момент выявления отказа. Выявле-
ние отказа в системе может осуществляться мгновенно в случае непре-
307
рывного контроля, либо через некоторое время после возникновения
в случае периодического контроля. Возможны ситуации, когда вы-
явить отказ бывает практически невозможно без демонтажа системы.
Тогда в системе можно проводить лишь плановые предупредительные
профилактики, во время которых в случае отказа и производится
ремонт.
Обычно предполагается, что проведение профилактики или ремонта
полностью обновляет тот объект, по отношению к которому они при-
меняются.
Выбрав соответствующим образом период проведения плановой про-
филактики, можно добиться максимально возможных значений выбран-
ных показателей качества функционирования системы. В качестве
основных показателей качества функционирования системы берутся
два основных показателя надежности: коэффициент готовности и коэф-
фициент оперативной готовности, а также два экономических показа-
теля: средняя удельная прибыль от системы в единицу времени и сред-
ние суммарные издержки, отнесенные к единице времени работы. Пер-
вый из экономических показателей оказывается удобным, когда и вы-
ходной эффект от системы и затраты на ее эксплуатацию измеряются
в одних и тех же единицах.
В главе рассмотрены пять основных моделей профилактики. Пер-
вые три из них касаются проведения профилактик для элементов (про-
стых систем), а две последние — для последовательных систем.
11.0.2. Путеводитель по гл. 11. Для удобства поиска и использо-
вания материала, изложенного в гл. 11, на рис. 11.0.1 изображена схе-
ма, поясняющая смысловую с-вязь отдельных разделов и одновре-
менно указывающая расположение соответствующих разделов в Спра-
вочнике.
Рис 110 1. Путеводитель к гл. 11.
Условные обозначения. АПР — аварийно профилактический ремонт; ЛП =- плановая профи-
лактика.
308
11.0.3. Дополнительные обозначения к главе 11.
С — средняя удельная прибыль от системы за единицу календарного вре-
мени;
С* — средние суммарные потери и затраты на систему, отнесенные к единице
полезного времени;
са — потери за единицу времени при проведении в системе аварийного ре-
монта;
с0 — прибыль, получаемая за единицу времени безотказной работы си-
стемы;
сп — потерн за единицу времени при проведении плановой профилактики;
с0 — потери за единицу времени при наличии в системе скрытого отказа;
F (0 — функция распределения времени работы системы до отказа;
Hi (0 — функция восстановления i-го элемента;
Ц—средняя длительность аварийного ремонта f-го элемента при его
отказе;
/0 — оперативное время работы, необходимое для выполнения задачи;
tc — среднее время выявления скрытого отказа;
Т — среднее время работы системы до отказа;
Та — средняя длительность аварийного ремонта системы;
Тап — средняя длительность внепланового аварийно-профилактического
ремонта;
Та — средняя длительность плановой профилактики;
Л (7) — интенсивность отказов системы;
т0 — оптимальный период плановой профилактики.
11.1. Формулировка задач оптимальной профилактики
Модель 1. Аварийные ремонты, обеспечивающие полное восста-
новление системы, производятся только после самостоятельного прояв-
ления отказа.
Модель 2. Плановые профилактики и аварийные ремонты пол-
ностью восстанавливают систему, причем последние начинаются сразу
же после возникновения отказа.
Модель 3. Производятся только плановые профилактики, пол-
ностью восстанавливающие систему, причем при обнаружении отказа
производится аварийный ремонт системы.
Модель 4. В последовательной системе производятся аварийные
ремонты после самостоятельного проявления отказов элементов.
Модель 5. В последовательной системе производятся аварийные
ремонты отказавших элементов, а также плановые профилактики всей
системы в моменты, когда наработка системы достигает заданной вели-
чины (в результате профилактики система полностью обновляется).
Более подробное описание процессов функционирования, соответ-
ствующих каждой из упомянутых моделей, приведено в соответст-
вующих параграфах данной главы.
11.2. Аварийные ремонты
11.2.1. Описание процесса функционирования. Рассматривается
система, в которой возможно проведение только аварийных ремонтов.
Предполагается, что индикация отказа происходит в среднем через
309
время Тп (время проявления отказа) после возникновения. В течение
этого времени система простаивает в неработоспособном состоянии
(наличие скрытого отказа). В случайный момент индикации отказа
(проявления) начинается аварийный ремонт, который длится в среднем
в течение времени Тя. После этого ремонта система полностью обнов-
ляется. По окончании ремонта весь процесс функционирования систе-
мы и ее обслуживания повторяется.
11.2.2. Исходные данные и результаты. Необходимые исходные дан-
ные для расчета:
— функция распределения времени работы системы до отказа
— среднее время работы системы для отказа г; .
— среднее время проявления отказа /п;
— средняя длительность аварийного ремонта Тя,
— потери за единицу времени при наличии в системе скрытого от-
каза сс;
— потери за единицу времени при проведении в системе аварийно-
го ремонта са;
— прибыль, получаемая за единицу времени безотказной работы
системы, с0;
— оперативное время работы системы, необходимое для выпол-
нения задачи, t0.
Формулы для расчета показателей качества функционирования
системы приведены в табл. 11.2.1.
Т аблица 11 2.1
Основные показатели качества функционирования для случая
аварийных ремонтов
Показатель Формула для расчета Показатель Формула для расчете
к т т + h + 4 с* Сс4 + Са4 т
•'б Т — J [1 — Г (хП dx 0 1 + 4 + 4 с к (с, - С*) = 4+4 + 4
11.2.3. Примечания.
а) В системе, эксплуатируемой согласно данному правилу, прово-
дятся только внеплановые восстановительные работы, связанные с про-
явлением отказов, поэтому задача ограничивается только получением
численных значений показателей качества.
б) Если возникший в системе отказ проявляется мгновенно, то не-
обходимо положить 4 = 0.
в) Если возникший в системе отказ самостоятельно проявиться не
может (4 — оо ), то такую систему эксплуатировать согласно сформу-
810
лированному правилу нельзя, так как в этом случае К — R ((») = О,
С = О, С* = оо .
Пример 11.2.1. Система имеет следующие исходные характеристики:
P(t) Т, ч г.-4 ч (г с,. еД/ч са> еДУч_ с» ел/ч to, ч
, 10 1 1 1 2 2 2
Требуется иайти показатели- качества функционирования системы.
Решение. Вычислим показатели качества функционирования!
1) Коэффициент готовности
„ 10 10
К=-^Т+Г = 7Г=°>8333-
2) Коэффициент оперативной готовности
Я(2) =
J е—0,I*dx
)Л ------=4те—0,2 =0,6822.
10 + 1 + 1 И
3) Средние удельные затраты
с* = = 0,3000.
10
4) Среднюю удельную прибыль
10 17
С = ~(2-0,3) = —= 1,415.
11.3. Плановые профилактики при внеплановых аварийных
ремонтах
11.3.1. Описание процесса функционирования. Предполагается,
что в системе возможно проведение плановых предупредительных про-
филактик и аварийных ремонтов. Индикация появившегося отказа про-
исходит мгновенно.
Восстановительные работы проводятся в следующей очередности.
В момент начала работы планируется проведение профилактики.
Если система не отказала к назначенному моменту, то проводится пла-
новая профилактика, средняя длительность которой равна Та. Если
же отказ системы произошел ранее, то в момент отказа начинается ава-
рийный ремонт, который длится в среднем время Т&. После проведения
любой из возможных восстановительных работ система полностью
обновляется. В момент окончания восстановительных работ последую-
щая профилактика перепланируется, и далее весь процесс обслужи-
вания повторяется. Предполагается, что во время проведения про-
филактики и ремонта система неработоспособна.
311
11.3.2. Исходные данные и результаты. Необходимые исходные дан-
ные для расчета:
— функция распределения времени работы системы до отказа
F (0;
— среднее время работы системы до отказа Т;
— интенсивность отказов системы к (/);
— средняя длительность плановой профилактики Тп;
— средняя длительность аварийного ремонта Та;
— потери за единицу времени при проведении плановой профилак-
тики сп;
— потери за единицу времени при проведении аварийного ре-
монта са;
— прибыль, получаемая за единицу времени безотказной работы
системы, с0;
— оперативное время работы системы, необходимое для выполне-
ния задачи, t0.
Формулы для расчета оптимальных величин показателей качества
функционирования и оптимальных периодов профилактик приведены
ь табл. 11.3.1.
11.3.3. Примечания
а) Рассматриваемое правило может быть использовано только для
систем, а которых происходит мгновенная индикация возникающего
отказа.
б) Для определения оптимальных периодов проведения плановых
профилактик рекомендуется приведенные в табл. 11.3.1 уравнения ре-
шать графическим методом. С этой целью уравнения выписаны в виде,
удобном для графического решения: справа стоит функция от времени
(периода профилактики), слева — постоянная величина.
в) Если время безотказной работы системы подчиняется экспо-
ненциальному закону, то проведение плановых профилактик для дан-
ного случая нецелесообразно.
Пример 11.3.1. Система имеет следующие характеристики:
/>(О МО. 1/ч Г, ч гв.’ ад/ч са. ед/ч с0. ед/ч 'о- 4
-0.00025М 0,0005/ 56,05 5 30 1 2 2 1,0
Требуется определить оптимальные периоды проведения профилактических
работ для системы.
Решение. Вычислим оптимальные показатели качества функциониро-
вания:
1) Коэффициент готовности.
Подставляем исходные данные, взятые из приведенной таблицы, в уравне-
ние для нахождения оптимального периода профилактики ти для К из
табл. 11.3.1 и получаем
<р (т) =-I +е-0.00025т’ + 010005т f е-0.°002бх’ dx = -1-=0,2.
Й оО— о
312
313
Приведенное уравнение имеет единственный корень. Этот корень опреде-
ляется по графику функции ф (т), стоящей в правой части уравнения (график
функции <р (т) приведен на рис. 11.3.1). В нашем случае т0 « 29 ч.
Определяем оптимальную величину коэффициента готовности
1 1
К (т0) 1+(Га_Гп)х,(ть):= 1 +(30 — 5)0,0005.29 °’734’
Для сравнения приведем величину коэффициента готовности для случая,
когда плановые профилактики не проводятся:
Т 56,05
К(оо) = К =---------=--------:-----=0,650.
k } Г+Га 56,05 + 30
Заметим, что выигрыш тем значительнее, чем меньше среднее время проведения
плановой профилактики. Например, при Т'п==2 ч имеем т0 = 17 ч К (17) =
«=* 0,810.
Рис. 11.3.1. График <р(т) для опре-
деления оптимальных периодов про
филактик для примера 11,31.
2) Коэффициент оперативной готовности.
Из таблицы исходных данных видно, что < Т. Поэтому воспользуемся
приближенным уравнением из табл, 11.3.1. для определения оптимального
периода проведения плановых профилактик, при котором R (ta) достигает абсо-
лютного максимума. Подставляя исходные данные в это уравнение, получаем
или
5
30—5 + 1
= -1+е-°-00025г,+0,0005т j е-о.ооо25^ dx_
о
5-1
—, 0,0005т
30—5 + 1
0,192 = <р (т) — 0,0001т.
График функции ф (т) — 0,0001т в интересующем нас диапазоне изменения
т практически совпадает с графиком функции <р (т) (вторым членом можно пре-
небречь).
Следовательно, в этом случае корень уравнения т0 можно определить по
графику ф (т), приведенному на рис. 11.3.1. Оптимальный период получается рав-
ным т„ = 28,5 ч, а максимальная величина коэффициента оперативной готов-
ности
28,5
у е-0,00025 (х+1)’^
4(1) = 28?5--------2----------------------------------=0’730-
f e-°-00026^dx+5 + 25(l-e-0-0002 5 ‘2b-5^)
о
314
Для сравнения приведем величину вероятности выполнения задачи, если
в системе не проводятся плановые профилактика
T—‘fp(x)dx 56,05—je-0-00025*’^
/?„((«)= ---°--------=---------5-------------
56,05 + 30,0
г+та
55,048 „
= ’ =0,640.
86,05
Заметим также, что из-за малости ta оптимальное значение вероятности вы<
полнения задачи близко к оптимальному значению коэффициента готовности;
причем близки и периоды, при которых достигается оптимум.
3) Средние удельные затраты.
Подставляя исходные данные в уравнение для нахождения То для С* из
табл. 11.3.1, получаем
1-5
2-30— 1-5
.-0,00025V +0>0005т J е -0,00055л’ dx
о
или 0,091 = sp (т), если использовать обозначения, принятые выше.
В силу монотонности интенсивности отказов приведенное уравнение имеет
один корень, который определяется по графику функции <р (т) (см. рис. 11.3.1).
Период, минимизирующий средние удельные затраты, равен т0 = 19 ч.
Определяем минимальную величину затрат:
min С* (т) = С* (То) = (са Га — сп Гп) X (т0) =
= (2.30—1-5).0,0005-19 = 0,5225.
Для сравнения приведем величину средних удельных затрат для случая
когда в системе не проводятся плановые профилактики:
саГа 2-30
а = •--------= 1,07.1
Г 56,05 1
С*
4) Сре’днюю удельную прибыль.
Подставляя исходные данные в уравнение для нахождения То для С из
табл. 11.2.1, получаем
0,143 = — 1 + е~° •0002 5V + 0,0005т § е ~° •000 25x2 dx +0,000715т
е
или 0,143 = <р (т)4-0,000715т.
График функции ф (т) + 0,000715 т в интересующем нас диапазоне изменения
т практически совпадает с графиком функции <р(т) (вторым членом в уравнении
можно пренебречь). Следовательно, в рассматриваемом случае Корень уравнения
т0 может быть определен по графику функции <р (т), приведенному на рис. 11.3.1.
Получаем оптимальный период т0 = 24,5 ч, а максимальная средняя
ная прибыль равна
удель-
„ , , . Со—(саГа—спГп)Х(То)
““ = ----1+(г.-гп)Мх.) ’
_ 2-(2.30-1.5)-0,0005-24,5 _ } '
“ 1-Н30 — 5)-0,0005-24,5 - "
315
Для сравнения приведем величину средней удельной прибыли, если в систе-
ме не проводятся плановые профилактики:
1 ' т+та 56,05 + 30 86.05
11.4. Плановые профилактики
11.4.1. Описание процесса функционирования. Существуют систе-
мы, в которых невозможно обнаружить отказ без проведения специаль-
ных проверок.
Для предупреждения, обнаружения и устранения отказов в системе
предусматривается проведение только плановых профилактик, во вре-
мя которых производится и аварийный ремонт, если система к этому
моменту отказала. Средние длительности профилактики и аварийного
ремонта соответственно равны Тп и Тя.
Устанавливается следующая очередность проведения восстанови-
тельных работ. В начальный момент назначается проведение плановых
восстановительных работ через определенное время. Если к назна-
ченному моменту система не отказала, то проводится плановая про-
филактика. Если же к назначенному моменту система отказала, то вмес-
то профилактики проводится аварийный ремонт. От момента появления
отказа до начала планового аварийно-профилактического ремонта си-
стема простаивает в неработоспособном состоянии. После окончания
восстановительных работ планируется новый момент для проведения
плановых восстановительных работ наследующем периоде эксплуата-
ции системы, и весь процесс обслуживания повторяется.
11.4.2. Исходные данные и результаты. Необходимые исходные
данные для расчета:
— функция распределения времени работы системы до отказа
f (0;
— плотность распределения времени работы системы до отказа
/ (0 = F' (0;
— интенсивность отказов системы X (/);
— средняя длительность плановой профилактики Тп;
— средняя длительность аварийного ремонта Тя>
— потери за единицу времени при проведении плановой профилак-
тики сп;
— потери за единицу времени при проведении аварийного ремон-
та са;
— потери за единицу времени при наличии в системе скрытого
отказа сс;
— прибыль, получаемая за единицу времени безотказной работы
системы, с0;
— оперативное время работы системы, необходимое для выпол-
нения задачи, t0.
Формулы для расчета оптимальных величин показателей качества
и оптимальных периодов проведения плановых восстановительных
работ проведены в табл. 11.4.1.
316
Основные показатели качества функционирования для случая плановых профилактик
ГС
И
S
ч
о
ГС
317
11.4.3. Примечания.
а) Рассматриваемое правило может быть использовано для систем,
в которых нет самостоятельной индикации появившихся отказов. Ис-
тинное состояние такой системы становится известным только через
некоторое время после начала профилактики.
б) Для определения сроков проведения восстановительных работ
приведенные выше уравнения удобно решать графически. Основная
трудность здесь будет заключаться в построении графиков функций,
стоящих в правых частях уравнений.
в) Для рассматриваемого случая плановые восстановительные ра-
боты должны проводиться через конечное время.
Пример 11.4.1. Система имеет следующие характеристики:
Р(О Х(0. 1/4 КП Лг 4 V ед/ч ед/ч со ед/ч ед/ч 'о’4
е-о.оы 0,01 О,О1е_°’ои 20 30 1 2 2 3 10
Рис. 11.4.1. График <р(Лт) для
определения оптимальных пе-
риодов профилактик для при-
мера 11.4.1.
Требуется определить оптимальные пе-
риоды проведения восстановительных работ
в системе.
Решение. Определим оптимальные
показатели качества функционирования.
1) Коэффициент готовности.
При подстановке экспоненциальной функ-
ции распределения F (/) = 1 — e~U в урав-
нение для нахождения т0 для R(t0) из табл.
11.4.1 при /0—О получаем, что первые два
слагаемых правой части уравнения тождест-
венно равны нулю и данное уравнение пре-
образуется к виду
т
J xdF (х)
Тп о_________________
Та—Тп (Т а—Тп)Р(т)
или
1 А А
Тп = \ xdF = ew \ xd (1 — е_u) =
Р (т) J J
о о
= -^-(еХт —1)—т,
Л
ХРП = (еХт — 1)—Хт = <р (Хт).
Корень этого уравнения легко определить, если построить график функции
<р (Хт), стоящей в правой части (рис. 11.4.1). При Та = 20 ч и X = 0,01 1/ч из
графика функции <р (Хт) получаем Хт0 = 0,575. Отсюда оптимальный период про-
ведения плановых восстановительных работ равен
0,575 0,575 „ _
T# = ~ = W = 57’54-
318
Определяем величину максимального коэффициента готовности, соответ-
ствующего выбранному периоду профилактики:
.________Р(т0)________________е~0,575__________п
Т° l+(Ta-Ta)ffrQ) 1-НЗО—20). 10~2е—0,575 ’ '
2) Коэффициент оперативной готовности.
В рассматриваемом случае, когда система имеет экспоненциальное распреде-
ление времени безотказной работы, период, при котором коэффициент оператив-
ной готовности достигает максимума, совпадает с периодом, максимизирующим
коэффициент готовности: т0 => 57,5 ч. Подставляя т0 в выражение для R (/0) из
табл. 11.4.1, определяем максимальное значение искомой вероятности
„—0,575 „—0,100
1+(30 - 20).0,0^7575- = К е—0,1оо = 0,530-0,9048 = 0,480.
3) Средние удельные затраты.
Подставляя функцию распределения F (/) — 1 — e~w в уравнение для нахож-
дения т0 для С* из табл. 11.4.1, после простых преобразований получаем
или
сп т
с п~
сс
j xd F (х) +[l-e“u]
° - B =~ (ev — 1)—и
Л
Р(т>)
е-и
-—2- X Тп = (е!л — 1) —?.т = <р (Хт).
сс
(График функции ф (Лт) приведен иа рис. 11.4.1.) При Гп = 20 ч, сп = 1 ед./ч,
сс — 2 ед/ч и Z = 0,01 l/ч имеем
— ЛГП=О,1.
се
Из графика функции ф (Лт) находим Л т0 = 0,420. Отсюда оптимальный период,
минимизирующий средние удельные затраты, равен
0,420 0,420
а величина минимальных затрат в соответствии с формулой для С* определяется
из табл. 11.4.1:
т0 =
F(42) , 1—е-°*420
С*(42) = 7777? +(Са Га~с“ Г«^ = 2 ~ Р-0.420- +
г\^) с
+(2.30- 1-20)-0,01=2-0,522 +0,400 =1,444.
4) Среднюю удельную прибыль.
Подставляем заданную функцию распределения Г(/) = 1 — e~w в уравнен и.
для нахождения т0 для С из табл. 11.4.1 и после преобразований получаем
(со + сП) Гп — Сп) lv ।
— = (е — 1) — ат -р
, (са — Сп)+7’я(Сс—<п) ,,, , „
-f-Лт-----------------------, (11.4.1)
Ср +Сс , ™ .
о + ^а(Сс— св)
319
Гели коэффициент
Га (са—+ (сс —сп)
^^+Та(с0-сп)
X
то последним слагаемым в правой части уравнения (11.4.1) можно пренебречь.
Тогда получим уравнение вида
(^+са)Т„^ТаТа(ся-с^ = 1)_Хт==ф
-±Cq ¥(св-са)Тл
(11.4.2)
к
В рассматриваемом примере
Та(са-сд) + Тп (сс-сп) = 30 (2-1)+20 (2-1) = 50 =
Со+Сс 3 + 2 530 ’ ’
^Т^ + Т’а^с-Сп) -^-+30(2-1)
Поэтому решаем приближенное уравнение (11.4.2):
„ 4.20-0,01-20.30.1 74 „
Ф (2л) =---------------= — = 0,140.
44 ’ 100-5 + 30.1 530
Далее по графику функции ф (Хт) определяем корень этого уравнения:
Хт0 = 0,490.
Отсюда оптимальный период проведения плановых восстановительных работ,
максимизирующий среднюю удельную прибыль С, равен
0,490 0,49
—Ж”49’-
Величина максимальной средней удельной прибыли определяется по формуле
для С из табл. 11.4.1. В нашем примере
З.е~0,49—2 (1 —е~°’49) —(2-30—1.20) 0,01е~0,49
С(49) =------------ -1а п.-„-0.49 -----------------= 0.771.
1+(30 — 20) 0,01е—0,49
11.5. Аварийные ремонты отказавших элементов
(подсистем) последовательной системы
11.5.1. Описание процесса фукционирования. Рассматривается
система, состоящая из tn последовательно соединенных элементов, при
отказе одного из которых наступает отказ всей системы. Будем пред-
полагать, что появившийся отказ проявляется не мгновенно, а в сред-
нем через время Та независимо от номера отказавшего элемента. При
обнаружении отказа i-ro элемента проводится внеплановый аварий-
ный ремонт (замена этого элемента на новый), средняя длительность
которого равна t{ (i — 1, ..., tn). Процесс функционирования и вос-
становления системы можно описать следующим образом.
Система (новая в нулевой момент времени) работает до отказа, далее
от момента возникновения отказа до момента его выявления она на-
320
ходится в неработоспособном состоянии. В случайный момент выявле-
ния отказа начинается аварийный ремонт (замена) отказавшего элемен-
та. После восстановления работоспособности система Вновь функциони-
рует до отказа, и весь процесс обслуживания повторяется. Предпола-
гается, что при простое системы и замене отказавшего элемента работо-
способные элементы отключаются, т. е. не ухудшают своих характери-
стик безотказности.
Отметим одну существенную особенность рассматриваемого прави-
ла обслуживания: в системе не предусматривается проведение восстано-
вительных работ, полностью ее обновляющих.
11.5.2. Исходные данные и результаты. Необходимые исходные дан-
ные для расчета:
— среднее время работы до отказа г-го элемента Tt (i — 1, ..., m);
— средняя длительность проведения аварийного ремонта (замены)
г-го элемента tt (г = 1, ..., т);
— среднее время простоя системы при скрытом отказе ic;
— потери за единицу времени при скрытом отказе сс;
— потери за единицу времени при замене г-го элемента после от-
каза сг;
— прибыль, получаемая за единицу времени безотказной работы
системы, с0.
Формулы для расчета показателей качества функционирования
приведены в табл. 11.5.1.
Таблица 11.5.1
Основные показатели качества функционирования для
случая аварийных ремонтов отказавших элементов
(подсистем) последовательной системы
Показатель
Формула для расчета
И Зак 943
321
11.5.3. Примечания.
а) В системе для данного случая не проводятся предупредительные
восстановительные работы, поэтому задача ограничивается только по-
лучением численных значений показателей качества функциониро-
вания.
б) Если возникший в системе отказ выявляется мгновенно, то необ-
ходимо положить /с — 0.
в) Если возникший в системе отказ самостоятельно выявиться не
может (tc = оо ), то такую систему эксплуатировать согласно данному
правилу нельзя, так как в этом случае К. = 0, С ~ 0, С* = оо.
Пример 11.5.1. Система имеет следующие исходные характеристики:
Tv ч 'с-’ ct, ед/ч се, ед/ч %, ед/ч
1 15 2 1 0,5 1,5 2
10 1 1 1,0 1,5 2
3 8 1 1 0,8 1,5 2
t 5 1 1 0,3 1,5 2
Требуется определить показатели качества системы.
Решение. Вычислим показатели качества функционирования.
1) Коэффициент готовности
1+2 1 + 1 1 + 1 1+1 37
+ —— + —!-р —1--—
^15 10 8 5
2) Средние удельные затраты
0,5-2 + 1,5-1 1-1 + 1,5-1
С* =~ -1!—!----------+
15 10 т
0,8-1 + 1,5-1 ,
8 +
0,3-1 + 1,5-1 2,5 2,5 2,3 1,8
-=—+—+—+—=,06 ед/ч.
15 10 8 5
5
3) Среднюю прибыль
С = (2 — 1,06) - 0,541 = 0,509 ед/ч.
11.6. Аварийные ремонты отказавших элементов
(подсистем) и плановая профилактика всей последовательной
системы
11.6.1. Описание процесса функционирования. Рассматривается
последовательная система, состоящая из т элементов (подсистем).
Как и ранее, под элементом будем понимать некоторую часть системы,
которая при ремонте может быть заменена как единое целое.
Предположим, что в системе возможно проведение плановых про-
филактик, полностью обновляющих систему, и внеплановых аварийных
ремонтов элементов (замена отказавшего элемента на новый), причем
индикация появившегося отказа происходит мгновенно.
Устанавливается следующий порядок проведения восстановитель-
ных работ. В начальный момент назначается проведение профилактики
322
по достижении определенной заданной заранее наработки. (При экс-
плуатации системы, хотя и известна величина наработки, при которой
должна проводиться профилактика, заранее неизвестен календарный
момент, когда наработка достигнет заданной величины.) Если до мо-
мента проведения плановой профилактики происходит отказ системы,
то проводится аварийный ремонт отказавшего элемента системы. Будем
предполагать, что во время проведения аварийного ремонта система
выключается, т. е. характеристики надежности элементов не ухуд-
шаются и наработка системы не увеличивается. Так поступают до
тех пор, пока наработка не достигнет заданной величины. В этот момент
начинает проводиться плановая профилактика независимо от прочих
факторов, включая число аварийных ремонтов за данный период.
В результате проведения плановой профилактики система полностью
обновляется. В момент окончания профилактики вновь назначается
величина наработки систем на следующем периоде, по достижении ко-
торой необходимо провести очередную плановую профилактику, и весь
процесс обслуживания повторяется.
11.6.2. Исходные данные и результаты. Необходимые исходные
данные для расчета:
— функция распределения времени работы до отказа i-ro элемента
(подсистемы) Ft (/), i = 1, ..., m;
— среднее время работы до отказа i-ro элемента
— средняя длительность аварийного ремонта i-ro элемента при его
отказе /г;
— средняя длительность плановой профилактики Тп;
— потери за единицу времени при проведении аварийного ремонта
i-ro элемента сг;
— потери за единицу времени при проведении плановой предупре-
дительной профилактики сп;
— прибыль, получаемая за единицу времени безотказной работы
системы, с0;
— оперативное время работы системы, необходимое для выполне-
ния задачи, t0.
Вспомогательные операции.
Для каждого i-ro элемента определяется так называемая функция
восстановления Н, (i) из интегрального уравнения
t 5
О
Это можно сделать с помощью преобразования Лапласа:
и; (х) =
Fl (х)
l-Fi(%)
где Н* (х) — преобразование Лапласа для функции (/); F* (х) —
преобразование Лапласа для функции F; (i).
Формулы для расчета показателей качества функционирования
приведены в табл. 11.6.1.
11* 323
«5
И
s
ю
Примечание 1 В случае несколь- 1 кик корней т01,.... то» оптимальное значение находится прямой под становкой каждого из них в формулу для случая единственного корня с последующим выбором наилучщего из них с учетом значения I для т0=оо
Формула для расчета пока зателя при отсутствии камчей ( 00 т J + ад dx П —— l=sl 1 т t. 1=1 т X? сДг* 2j Tt 1=1
Й u 5 Mil I SM11 +
- m 1=1
Формула для расчета показателя при единственном корне Ъ 1 - tn 1 + S <’о) 1 = 1 П Р (Чо + Q + ,=| L — 1 1 , S 3 as* 13 м 5= ? * 1 *» О ?М1 J ± С <?<—-с t as * Ml + m i=i Co-S Tici”iM 1=1 V sMl +
Уравнение, корень которого т0 является периодом оптимальной профилактики 1 т т * S w” - S <” = л, i=i SM1 + 1 tn nt i=i »=i + <? — w Y + <r 5- 5? г EM1 -b 11 ® + ?“ - ? + г L г w” 3 -- smI 5- 5 Ml E^qli 1 13 C +
0 l=fQ (/?) ’яр [Я-Xj + X) J + («; +х) ’</ £] J X Ui 1 0 |=> (Л) 'яр (/?-"; + !) ’я/ +(°;+1) ’j LI 1 J ш 1 = ! (1) ’д’; X + “г +1 IU
Показа-1 тень { 1 0$ (J
324
Пример 11.6.1. Система имеет следующие исходные характеристики:
F(0 X, 1/ч ч гп-’ са, ед/ч сп, ед/ч со. ед/ч 'о- ’
1 (1-е-х')2 10-2 Ю 1 2 1 3 2
Требуется определить оптимальные значения показателей качества функцио-
нирования.
Решение. Произведем вспомогательные операции.
Определяем
О
Рис. 116.1. График <р(х) для оп-
ределения оптимальных периодов
профилактик для примера 11 6.1.
Тогда
и
F* (х)
2V
. 2А.
Н* (х! = --------—— = --------------— —
1 — £*(х) х(х-{-ЗА.) Зх
2Х
3(х+ЗХ)
3 3
= — U -
ЗА. 3
2 2 ,,,
—— е~3Ч
9 Т 9
н' (о=4^--
о о о
1) Коэффициент готовности.
Подставляем' исходные данные в уравнение для нахождения значения тв
Для К из табл. 11.6.1 и получаем
Т7а Х(1-е-3^) - Та) [y V+T e~3W] = 7n
или
— = 1 —e~3v (1 +3W).
2Га
График правой части записанного выше уравнения, имеющего вид
<pW = Ll-(l + x)e-4,
приведен на рис. 11.6.1.
325
При
=0,45
2Та
Г,. 1 кол
*0=1,524 и то = — —---------= 50,8 ч.
ЗА 0,03
Максимальное значение коэффициента готовности достигается при т0 = 50,8 ч
и равно
ts _ _________
т“~ \-VTaH'М
0,9505.
Для сравнения приведем величину коэффициента готовности при т = <х>
(когда не проводятся плановые профилактики):
2) Коэффициент оперативной готовности.
Подставляем выражения функций И (0 и Н' (0 в уравнение для нахожде-
ния значения т0 для R (/0) из табл. 11.6.1:
6АТП(1 — 0,25е~х/«) — -у А'Га (1-е-Х/")
(14-2АТа)-(1+АТа) e~w»
, _з>т SATnd-e-^»)
-1 (1+3 т)е (1-^зАГа)—(1АГа) е—w<1”
Если в это уравнение подставить исходные численные значения параметров дан-
ного примера, то можно убедиться, что вторым членом в правой части уравнения
можно пренебречь (коэффициент при e~SXl равен примерно 0,0006). Поэтому зна-
чение корня х0 — ЗАт0 будем определять по графику рис. 11.6.1.
Для заданных значений параметров левая часть уравнения равна
6Ara(l-0,25e-w»)—— АТа (1 — е~
----------------------£----------------= 0,3502,
(14-2А7’а)-(14-А7’а)е-^о
Отсюда *о = ЗАг'о = 1,236. Следовательно, = 41,2 ч.
Соответствующая этому значению t0 оптимальная величина R(t0) подсчиты-
вается по соответствующей формуле из табл. 11.6.1 и равна
/?То (/„) = 0,973.
Для сравнения рассчитаем величину вероятности выполнения задачи,
если плановые профилактики не проводятся (формула для /?(/0) из табл. 11.6.1
при т = оо);
R (t0) = 0,925.
Заметим, что если задачу выполняет новая система, то
/?(/о) = е~Х/" =0,9802.
3) Средние удельные потери.
326
Подставляем исходные данные в уравнение для нахождения значения
То для С* из табл. 11.6 1 и получаем
9 сп Та
V —~ =1-е~Пт(1+ЗХт).
z са » а
„ 9 спТп
При 2 саГа и 0.225 определяем по графику рис. 11.6.1 Хо “ ЗХт0 ™ 0,888 или
0,888
то = ------= 29,6 ч.
0,03
Тогда проводить предупредительные профилактики необходимо после наработ-
ки, равной 29,6 ч и С* (29,6) = 0,0786 ед/ч Если не проводить предупредитель-
ных профилактик (т = со), то средние потери составят
с.(«)_^_^»А=0,,333 ед,ч.
4) Среднюю удельную прибыль.
Подставляем исходные данные в уравнение для нахождения значения т0 для
С из табл. 11.6.1 и после соответствующих преобразований получаем
0,354= 1— (1+0,0064-3-10-2 т) е—3'10-2 х-
Корень этого уравнения А,т0 = х = 1,248, поэтому
1,248
То=ГТ^=41’64
(Этот корень приближенно определяется графически по рис. 11.6.1, так как
графики функции, стоящей в правой части исследуемого уравнения, и функции
ф (х), изображенной'на рисунке, практически совпадают).
В рассматриваемом случае проводить предупредительные профилактики
необходимо через 41,6 ч наработки и
Со-"Са Та Н' (То)
max С(т)=С (41,6)=-° * * =2,78 ед/ч.
т 1 + /ап (То)
Для сравнения приведем величину средней удельной прибыли, для случая,
когда не проводятся предупредительные профилактики (т == оо);
10
3__2 —
С(оо) =_____1Ё9 = 152 = 2,68 ед/ч.
, . >0 160
1+ ТГо
Список литературы
1. Барзилович Е. Ю. Определение оптимальных сроков профилакти-
ческих работ на автоматических системах. — «Известия АН СССР Техни-
ческая кибернетика», 1964, № 3.
2 Барзилович Е Ю. Оптимизация периодичности контроля систем,
недоступных непрерывным проверкам. — «Автоматика и телемеханика»,
1969, № 8.
3. Барзилович Е. Ю., Воскобоев В. Ф. Организация профилак-
тики технических комплексов с учетом ограничений на средства обслужива-
ния. — В кн.: Теория надежности и массовое обслуживание. Под ред.
Б. В. Гнеденко. М., «Наука», 1969.
327
4. Барзилович E. Ю., Воскобоев В. Ф., Симаков В. Г.
Об оптимальной профилактике с неполным восстановлением. — В кн.: Тео-
рия надежности и массовое обслуживание. Под ред. Б. В. Гнеденко. М.,
«Наука», 1969.
5. Барзилович Е. Ю., Каштанов В. А., Коваленко И. Н.
О минимаксных критериях в задачах надежности. — «Известия АН СССР.
Техническая кибернетика», 1971, № 3.
6. Г е р ц б а х И. Б. О выборе оптимального режима обслуживания группы
однотипных элементов в автоматической системе. — «Автоматика и телеме-
ханика», 1964, № 9.
7. Г е р ц б а х И. Б. Оптимальное правило обслуживания системы со многи-
ми состояниями, — «Известия АН СССР. Техническая кибернетика», 1964,
Xs 3.
8. Г е р ц б а х И. Б. О профилактике по прогнозирующему параметру. —
«Известия АН СССР. Техническая кибернетика», 1967, Xs 1.
9. Дружинин Г. В. О профилактических работах в устройствах автома-
тики. — «Автоматика и телемеханика», 1962, № 5.
10. Д у х о в н ы й И. М. Об оптимальных профилактиках в однолинейных
системах массового обслуживания с ожиданием. В кн.: Теория надежности
и массовое обслуживание. Под ред. Б. В. Гнеденко. М., «Наука», 1969.
11. Ко пеле вич Б. М. Задача оптимизации профилактики наконечном
времени. —«Автоматика и вычислительная техника», 1967, Xs 6.
12. Л е о н т ь е в Л. П. Оценка критериев выбора оптимальных характери-
стик профилактики. — «Автоматика и вычислительная техника», 1967, Xs3.
13. М а р н о И. Б. О цикличности оптимального управления в задачах
о профилактиках. — «Известия АН СССР. Техническая кибернетика»,
1969, Xs 5.
14. Пер роте А. И. О режиме оптимальной профилактики системы длитель-
ного использования. —«Автоматика», 1961, № 3.
15. С о л о в ь е в А. Д. Определение оптимальных профилактик для си-
стемы с резервом. — В кн.: Прикладные задачи технической кибернетики.
Под ред. И. А. Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966.
16. С к л я р е в и ч А. Н., Цветкова Э. И. Оптимальные сроки полной
профилактики системы с возможными нарушениями структуры. — «Автома-
тика и вычислительная техника», 1967, № 4
17. У ш а к о в И. А. Оптимальные задачи надежности. — «Надежность и
контроль качества», 1969, Xs 1.
12.
ОПТИМАЛЬНЫЙ ПОИСК НЕИСПРАВНОСТЕЙ
12.0. Постановка задачи
Система, рассматриваемая как объект контроля, представляет сово-
купность п составляющих ее элементов (множество G), соединенных
между собой функциональными связями. Каждый из элементов систе-
мы может находиться водном из двух возможных состояний: исправно-
сти или отказа. Вероятность исправного состояния г-го элемента обо-
значается рь а вероятность отказа — qt (qt = 1 — pt). Предполагается,
что отказы отдельных элементов системы взаимно независимы.
Контроль системы заключается в последовательном применении
специальных тестов, каждый из которых проверяет исправность впол-
не определенного подмножества элементов.
Проверка производится для следующих целей:
— проверить исправность системы (обнаружение любой имеющейся
неисправности),
— отыскать неисправность (локализация всех отказавших
элементов).
В первом случае достаточно применить тест, проверяющий всю си-
стему (так называемый глобальный тест). Однако иногда проведение та-
кого теста бывает принципиально невозможно либо нецелесообразно,
так как он требует весьма существенных затрат времени и (или)
средств, поэтому оказывается выгоднее использовать последователь-
ность нескольких простых тестов.
Исход теста Tt назовем успешным, если в проверяемом им подмно-
жестве элементов Gt не обнаружено неисправных элементов. Если не-
исправные элементы обнаружены, исход теста назовем неуспешным,
причем в этом случае среди проверяемых элементов имеется по крайней
мере один неисправный элемент.
В общем случае подмножестваG/, проверяемые различными тестами
Т'[, могут пересекаться.
Совокупность тестов, достаточную для выполнения требуемой про-
цедуры контроля, удобно задавать в виде таблицы, строки которой со-
ответствуют имеющимся тестам, а столбцы — элементам, причем знак
« + » на пересечении означает, что данный элемент может быть прове-
рен данным тестом (см. табл. 12.2.1).
Задача заключается в построении такой процедуры проверки, что-
бы цель этой проверки достигалась при минимальных в среднем за-
тратах на ее проведение.
Составление программы контроля заключается в выборе из всей со-
вокупности тестов {Т} необходимой группы тестов и определения по-
рядка их применения так, чтобы процесс проверки был оптимальным
относительно принятого критерия.
329
12.1. Общее описание процедуры проверки
Порядок применения тестов представляет собой рекуррентную про-
цедуру следующего вида: в соответствии с некоторым правилом опреде-
ляется оптимальная условная последовательность проверок для исход-
ного множества элементов G. Первый этап процедуры проверки про-
должается до тех пор, пока очередной тест не окажется неуспешным.
При проверке исправности системы процесс проверки на этом завер-
шается.
При отыскании неисправностей осуществляется переход к следую-
щему этапу. Все множество элементов проверяемой системы в этом слу-
чае оказывается разделенным на три следующие подмножества:
G' — подмножество еще не проверявшихся элементов,
G* — подмножество элементов, охваченных данным неуспешным
тестом, за вычетом тех элементов этого подмножества, которые были
до того проверены успешными тестами,
G(0)—прдмножество элементов, исправность которых подтвержде-
на предыдущими успешными тестами.
На втором этапе роль исходного подмножества играет G*. Для
всех тестов совокупности {Т} производится переоценка вероятностей
успешной реализации, исходя из условия применения их к упомяну-
тому подмножеству G*. После локализации всех неисправных элемен-
тов в подмножестве G* процесс поиска неисправностей продолжается
в подмножестве G'. Опять для всех тестов совокупности {Т} производит-
ся соответствующая переоценка вероятностей и осуществляется отыс-
кание неисправностей с использованием описанной выше рекуррент-
ной процедуры.
12.2. Отыскание единственного неисправного элемента
Проверяемая система состоит из п элементов. До начала проверки
известно, что в ней отказал ровно один элемент. (Такая ситуация может
возникать, если отказ любого одного элемента системы приводит к бло-
кировке и отключению всей системы.) Требуется отыскать неисправный
элемент при минимальных средних затратах.
12.2.1. Приближенный алгоритм при произвольных пересекающих-
ся тестах. Пусть к началу некоторого /И-го шага процесса проверки
проведена последовательность тестов ст<0) — {71!, ..., Дм-i} и задача
сводится к отысканию неисправного элемента в подмножестве G(0). (Пе-
ред самым началом процесса проверки системы G<0 — G, т. е. включает
в себя все элементы системы, а о(0) не включает в себя ни одного теста )
Алгоритм отыскания единственного неисправного элемента состоит
в следующем.
1. Определяются величины ?)0) — условные вероятности отказа
именно г-го элемента, если в проверяемом множестве G<0’ ровно один
отказавший элемент
330
Примечание. В принципе при используемой далее процедуре достаточ-
но вычислять лишь величины
Чг — <7г
так как ниже в п. 5 имеют существенное значение лишь относительные, а не аб-
солютные величины qt на каждом шаге. Это существенно сокращает вычисления
поскольку не нужно производить пересчет этих величин после каждого шага про-
цесса.
2. Для каждого теста Т, вычисляется вероятность неуспешного ис-
хода в проверяемом подмножестве G<0)
<2/0) = 2 ?i0).
16С7ПО(<”
3. Для каждого теста Т} находят связанные с ним затраты т)0>
с учетом того, что уже проведена последовательность тестов о<0>. (В об-
щем случае затраты на проведение теста Tf могут как убывать, так и
возрастать при условии проведения других тестов. Например, могут
быть уже подключены при предыдущих проверках необходимые для
данного теста приборы либо наоборот проведение предыдущих прове-
рок привело к затруднению в доступе к нужной части системы.)
4. Для каждого теста Т, определяется величина
5. Выбирается такой тест Th, для которого gh минимальна:
g-ft = min gt.
6. Применяется тест Th:
а) если тест Th завершается успешно, то задача сводится к поиску
отказавшего элемента в подмножестве G*1* = G<0)\Gh;
б) если тест Th заканчивается неуспешно, то задача сводится к поис-
ку отказавшего элемента в подмножестве G*1’ = Gh f) G<0>.
Примечание. Если в случае а или б подмножество б*1' состоит из
единственного элемента, то задача отыскания неисправного элемента на этом за-
канчивается.
7. Фиксируется новая последовательность примененных тестов
о(1), включающая в себя предыдущую последовательность o<Q) и послед-
ний примененный тест Th
о(1> = {сг<0\ 7\},
8. К подмножеству G(1> применяется процедура проверки, начиная
сп. 1, с соответствующей заменой верхнего индекса (0) на индекс (1).
Процедура проверки продолжается до тех пор, пока в п. 6 на некото-
ром шаге k не сформируется такое подмножество G(/i), которое состоит
из единственного элемента.
Описанную процедуру можно реализовать по мере развития про-
цесса проверки в особенности, если для целей текущих расчетов и вы-
боре очередного теста использовать ЭВМ с заранее занесенным в ее
память массивом исходных данных (вероятности отказов, длительно-
сти проверок, характеристики тестов) и необходимым программным
обеспечением.
331
Эту же процедуру можно провести заранее и составить инструкцию
по очередности применения тестов в зависимости от результатов преды-
дущих, например, «если тест успешный, то далее провести тест Ть
если же тест 7* неуспешный, то далее провести тест Т(рис. 12.2.1).
Рис. 12.2.1. Пример инструкции для проверки системы.
Пример 12.2.1. Система состоит из 8 элементов и может быть проверена 6
тестами, описание которых приводится в табл. 12.2.1. Известны затраты, связан-
ные с проведением каждого теста:
т, => 1, т2 = 2, та = 1,2, т4 = 1,5, т5 => 2,5, тв = 1,
причем предполагается, что величины Т; не зависят от порядка применения
тестов.
Таблица 12.2.1
Тесты и проверяемые ими элементы системы
Номер элемента Тест
т, г. т, т, г,
1 + 4- 4-
2 + 4-
3 4- 4-
4 4- 4-
5 4- 4- 4- 4-
6 4- 4- 4-
7 4- 4-
8 4- 4-
S32
Априорные вероятности отказа элементов также известны и равны
91 = 0,1, </2 = 0,1, 9з = 0,2, 94 "= 0,3,
9s — 0,1, 96 = 0,05, 9, = 0,05, qs = 0,2.
Известно, что в системе имеется ровно один отказавший элемент.
Требуется найти этот элемент при минимальных средних затратах иа про-
ведение необходимых для этого тестов.
Решение. Находим величины qt для каждого элемента.
91=0,11, 92 = 0,11, % = 0,25, '94 = 0,43,
9s = 0,11, 7в = 0,053, 9,-0,053, ~qs — 0,25.
Вычисляем величины для каждого теста!
Ci0’ = 9х + 92 + 95 + 9« = 0,383, <?< °> = 92 + 9а + 9, = 0,593,
<2(з0)=9з + 95+ 9в = 0,413, + ^=0,413,
= 914- 9з+ 9а 4-95 = 0,9, — 9s 4 9? 4-98== 0,413.
Далее, для каждого теста находим величины gfi
g(i0) = 1/0,383^2,61, g<20) = 2/0,593 »3,38,
g'°> = 1,2/0,413 г» 2,90, g<0) = 1,5/0,413» 3,62,
g<0) = 2,5/0,9»2,78, g(e0) = 1/0,413» 2,41.
Видно, что первым тестом должен быть так как gt наименьшая из всех.
* Проведение теста Т6 может быть успешным и неуспешным. Рассмотрим пер-
вый исход, т. е. неисправный элемент находится средн тех, которые не были охва-
чены тестом Т8.
Осталось подмножество элементов G(I> = {1, 2, 3, 4, 6}. Вычислим величины
У/ для каждого из оставшихся тестой.
С(1’ ’ = 914-92 + 93 = 0,273, 1 > = 92 4-91 = 0,54,
Q(3’} = 9з + 9в = 0,303, Q<1 > = 9в = 0,053,
^5*'= 914-9з 4-91 = 0,79,
а затем величины gp
gV} = 1/0,273 = 3.66, g< ° = 2/0,54 = 3,70,
g<3’ > = 1,2/0,303 = 3,96, g<1 > = 1,5/0,053 = 38,3,
g<1) = 2,5/0,79 = 3,17.
Таким образом, после успешного теста Т6 следует проводить тест Тв. Само
по себе проведение этого теста может быть в свою очередь успешным и неуспеш-
ным. Рассмотрим и а этот раз вторую возможность: неисправный элемент находит-
ся в подмножестве, которое проверяется тестом Тв среди элементов G(1) = {1, 2, 3,
4, 6), т е. это один из элементов б<2> = {1, 3, 4).
Вычислим величины Qj2’ для каждого из оставшихся тестов!
(2<2) = 9=0,11, Q<22)= 91 = 0,43,
<?(,2> = = 0,413, <2<2> = 71 = 0,11,
а затем величины gf.
g<2) = l/0,ll=9, g(22) = 2/0,43 = 4,7,
g<2> = 1.2/0,413 = 2,9 g<2) = 1,5/0,11 = 13,5,
e. следует проводить тест Ts.
333
Если проведение этого теста неуспешно, то неисправность найдена — это
элемент 3. Если же тест Т3 проходит успешно, то неисправными могут быть эле-
менты 1 и 4. Здесь можно использовать тесты 1\, Т3 и Г4. Ясно, что любой из них
приводит к отысканию отказавшего элемента (либо непосредственно, либо мето-
дом исключения), поэтому следует выбрать тот из них, который просто характе-
ризуется минимальными затратами, т. е. Т4.
Рис. 12 2.2. Первый фрагмент инструкции проверки (для примера 12.2.1).
В кружочках помещены номера отказавших элементов, выявленных данной проверкой.
Если нам нужно составить инструкцию с описанием последовательности про-
верок, то следует прежде всего зафиксировать полученную в данном решении
последовательность (рис. 12.2.2) и вернуться к моменту, когда проводился тест
Ts, но теперь положить, что он оказался успешным, т. е. искать отказавший эле-
мент среди подмножества элементов G(2) = 2,6.
Рис. 12.2.3. Второй фрагмент инструкции проверки (для примера
122.1).
Из табл. 12.2.1 нетрудно видеть, что для разделения элементов 2 и 6 мож-
но использовать тесты Т2, Т3 и Т4, причем наименьших затрат требует Т3, т. е.
его и надо проводить. Если Т3 неуспешен, то отказавшим является элемент 6,
а если успешен, то — элемент 2 (методом исключения). В результате получен еще
один фрагмент требуемой инструкции (рис. 12.2.3).
Затем нужно вернуться к моменту, когда проводился тест Тв, но теперь пред-
положить, что он проходит неуспешно, т. е. G(1> = {5, 7, 8}. Для разделения этих
элементов можно воспользоваться, как это видно из табл. 12.2.1, тестами Г4, Т3,
Т3 и Т4, каждый из которых локализует отказ с точностью до элемента. Легко
найти, что наиболее целесообразным является применение теста Г4. Если он не-
334
успешен, то это означает, что отказавшим является элемент 8. Если он успешен,
то отказавшим может быть либо элемент 5, либо элемент 7. В этом случае следует
проводить тест с наименьшими затратами 7\. Если он успешен, то отказал эле-
мент 7, а если неуспешен — элемент 5.
В результате определен последний требуемый фрагмент данной инструк-
ции (рис. 12.2.4). Сшивая все эти фрагменты в единое целое, окончательно полу-
чаем инструкцию для проверки системы (рис. 12.2.5).
12.2.2. Поэлементная проверка системы. Если имеется возмож-
ность проверять каждым тестом только один из элементов системы, то
наилучший порядок проверки элементов для отыскания неисправности
соответствует нумерации их в порядке возрастания величин
Si =
Рис. 12 2.4. Третий фрагмент инструкции проверки (для примера
12.2.1).
Пример 12.2.2. Рассмотрим систему, состоящую из пяти элементов, характе-
ризующихся следующими показателями!
t\ = 0,2, Tt = 10 мин; г2 = 0,3, т2 = 20 мин;
г3 = 0,4, т3 =» 10 мин; г4 “ 0,5, т4 = 5 мин;
г8 =• 0,6, т6 = 10 мин.
Требуется определить, в каком порядке следует проверять элементы для
отыскания среди них всех неисправных.
Решение. Вычисляем величины gfl
6,“м'10’2'5’ й-йу20-8’6’
8.-g.5 = S.0. 8.-^- Ю= 'М-
Из расчета следует, что для минимизации среднего времени отыскания не-
исправных элементов следует всегда проверять элементы данной системы в сле-
дующем порядке! 1, 4, 3, 2, и 5.
12.2.3. Проведение любых тестов при равных затратах. Если имеет-
ся возможность проверять любые комбинации элементов, причем за-
335
траты на проведение любого тестр равны между собой, то оптимальную
процедуру проверки производят в следующем порядке:
1) элементы располагаются в порядке'невозрастания величин qt\
2) два последних элемента группируются в один условный элемент,
у которого q = qn + 'qn-T,
3) полученный элемент устанавливается на соответствующее место
в исходной последовательности в соответствии с величиной q\
4) процесс продолжается до тех пор, пока все элементы не будут
сгруппированы в один исходный элемент;
5) оптимальной программой проверки системы с целью отыска-
ния отказавшего элемента будет такая, которая позволит произвести
разбиение полученного условного элемента в порядке, обратном тому,
которым он был получен.
Пример 12.2.3. Пусть устройство состоит из семи элементов, для каждого
из которых известны значения:
71=0,3, </2 = 0,3, </*=0,1, </1 = 0,1,
</5=0,1, </в=0,05 и </* = 0,05.
336
Требуется найти систему контрольных проверок, позволяющих в кратчай-
шее время отыскать неисправный элемент.
Решение. Согласно описанной выше методике составим диаграмму про-
цесса оптимальных проверок (рис. 12.2.6). Из этой диаграммы видно, что первая
проверка Tj должна позволить разделить всю совокупность элементов на две.
1 и 2, с одной стороны, ис 3 по 7, с другой стороны. Если неисправным является
1 или 2 элемент, то необходимо применить проверку Т2. Если же неисправным
является один из элементов с 3 по 7, то следующая проверка (Г3) должна позво-
лить отделить 3 и 4 элементы от 5, 6 и 7 и т. д.
Рис. 12 2 6. Диаграмма процесса
оптимальных проверок для при-
мера 12.2.3.
12.2.4. «Информационный» метод (приближенное решение). Этот
приближенный метод предлагается использовать в тех случаях, когда
различные проверки имеют различную длительность (тг), а также в тех
случаях, когда имеющаяся система проверок не является достаточно
гибкой и не позволяет выполнить процедуру, описанную в § 12.2.3.
Для оптимального отыскания единственного неисправного элемен-
та предлагается следующий алгоритм.
1. Рассматривается исходная совокупность из п элементов, входя-
щих в состав устройства. Для каждой возможной z-й проверки, кото-
рая охватывает некоторую совокупность At из всех элементов устрой-
ства, вычисляется величина
gt =
Здесь Д//г = [Рг 1пРг + Q; InQj, где, в свою очередь, Q; — вероят-
ность того, что отказавший элемент находится среди элементов совокуп-
ности Ait a Pt =5 1 — Qj.
2. Выбирается в качестве первой та проверка, у которой значение
gt является максимальным.
3. С оставшейся совокупностью элементов устройства (и с самой
совокупностью Аг) повторяется та же процедура, что и с исходной со-
вокупностью из п элементов.
Пример 12.2.4. Имеется то же устройство, что и в примере 8.2.3. Однако мож-
но провести лишь следующие проверки:
— разделение элементов 1,5 от элементов 2, 3, 4, 6, 7;
Тг — разделение элементов 1, 2, 4 от элементов 3, 5, 6, 7;
Т % — разделение элементов 6, 7 от элементов 1, 2, 3, 4;
Tt — разделение элементов 2, 7 от элементов 1, 3, 4, 5, 6;
— разделение элементов 2, 3, 5 от элементов 1, 4, 6, 7,
причем = 3 мин, т2 = 1,5 мин, т3 = 1 мин, т4 = 2 мин, т5 = 3 мин.
Требуется найти систему оптимальных проверок.
337
Ре ш е н и е. Определяем величины gt для первого шага процесса Поиска
неисправного элемента (используем десятичные логарифмы):
(0,4.0,398 + 0,6-0,222) = 0,098,
3
g<,)=A (0,7.0,155 + 0,3-0,523)= 0,177,
1,5
gO> = 1.(0,1.1+0,9.0,056)= 0,150,
g^1 > =-^- (0,35- 0,456 + 0,65- 0,187) = 0,142,
g<1) = 4- (0,5-0,301+0,5-0,301) = 0,100,
О
Выбираем в качестве первой проверки Т2.
Пусть неисправный элемент оказался среди группы элементов 1, 2 и 4. В этом
случае проверка позволяет разделить элемент 1 от элементов 2 и 4; Т3 не по-
зволяет произвести дальнейшей локализации отказавшего элемента; 7\ и Т8
разделяют элемент 2 от элементов 1 и 4.
Итак, предварительно вычислим значения q*, q2 и ql при условии, что
отказавший элемент находится среди этих элементов:
• 0,3 3 „
?1= --------------7 = ~г_ = 0,43,
0,3 + 0,3+0,1 7
« 0,3 3 п
= ----------------=-— = 0,43,
0,3 + 0,3+0,1 7
* 0,3 1
о, =-------------- = —- = 0,14.
0,3 + 0,3+0,1 7
В этом случае
g(11>=-^- (0,43-0,366 + 0,57-0,244) = 0,099,
g(21>==0>
g(s1) = 0,
g(*1)=“ (0,43-0,366 + 0,57-0,244) =0,148,
g<)1) = — (0,43-0,366 + 0,57-0,244) = 0,099.
3
Видно, что для проверки на втором шаге процесса поиска неисправ-
ленного элемента следует применить тест Ё4.
Если исправным элементом оказывается элемент 2, то на этом про-
цедура заканчивается. Если же неисправным элементом является либо
элемент 1, либо элемент 4, процесс продолжается, причем, как нетрудно
заметить, для проверки на третьем шаге можно использовать лишь 7\.
338
12.3. Отыскание неизвестного числа неисправных
элементов
Проверяемая система состоит из п элементов. До начала проверки
известно, что в ней могут быть отказавшие элементы, но сколько их,
заранее неизвестно. При отыскании отказавшего элемента его заменяют
на исправный и продолжают процедуру отыскания остальных эле-
ментов.
Требуется отыскать все имеющиеся неисправные элементы при ми-
нимальных средних затратах.
Примечание. В общем случае при неизвестном числе отказавших
элементов для выявления их необходимо иметь возможность проверять каждый
элемент отдельно. Поэтому в § 12.3.2 приводится лишь точный алгоритм отыска-
ния неисправностей с помощью поэлементной проверки.
12.3.1. Приближенный алгоритм при произвольных пересекаю-
щихся тестах. Пусть к началу некоторого /И-го шага процесса проверки
проведена последовательность тестов а<0) = {Tlt ..., Тм-Д, и задача
сводится к отысканию неисправных элементов в подмножестве О<0>.
(Перед самым началом процесса проверки системы G<0> = G, т. е.
исходное множество включает в себя все элементы системы, а <у<0) не
включает в себя ни одного теста.)
Алгоритм отыскания неисправных элементов состоит в следующем.
1. Проводится (если это возможно) глобальный тест для опреде-
ления того, есть ли в непроверенном еще подмножестве G<0) хотя бы
один неисправный элемент. Если глобальный тест проходит успешно,
то на этом процедура проверки прекращается, если же тест проходит
неуспешно, то начинается основная процедура, приводимая ниже.
Примечание. Строго говоря, применение глобального теста не всегда
оправдано, так как он может потребовать больших затрат, чем проведение ло-
кализации всех возможных (или имеющихся) отказов в проверяемом подмноже-
стве элементов G<0>. Однако для практической методики, чтобы упростить приме-
няемую процедуру отыскания неисправных элементов, мы не будем учитывать
такой возможности, тем более, что обычно затраты на глобальный тест в силу его
неспециализированности не столь существенны.
, 2. Если глобальный тест проходит неуспешно, то для каждого теста
7^ вычисляется вероятность неуспешного исхода в проверяемом под-
множестве G<0!.
1— П pt
i- п Pi
Z6G(I”
при условии, что уже проведена последовательность тестов
Примечание. В принципе при используемой далее процедуре доста-
точно вычислить лишь величины
Q<°> = 1- П Pif
1 (ео;.по(0>
Поскольку в п. 5 наибольшее значение имеют лишь относительные, а не абсолют-
ные величины Q)o>.
ззэ
3. Для каждого теста Т} находят связанные с ним затраты т)в) при
условии, что уже проведена последовательность тестов о<0).
Примечание. Перед началом процесса проверки т)в> » т^.
4. Для каждого теста Т; определяется величина
5. Выбирается такой тест Th, для которого gh минимальна:
gh = min gj.
6. Применяется тест Th, причем
а) если тест Th завершается успешно, то процесс поиска отказав-
ших элементов продолжается для оставшегося подмножества G(ly —
= G<0>\Gfe;
б) если тест Тк заканчивается неуспешно, то задача разбивается на
две части:
— последовательное отыскание всех имеющихся отказавших
элементов в подмножестве G(1> = G<0,\Qh.
— после этого процесс поиска отказавших элементов продолжает-
ся для нового оставшегося подмножества G’1’ = G(0>\Gk.
7. Фиксируется новая последовательность о’п примененных тестов,
включающая в себя предыдущую последовательность о10’ и последний
примененный тест 7\:
о'*, = {ст<о)( Thy
8. К подмножеству GU), указанному в п. 6, вновь применяется
процедура проверки, начиная с п. 1, если последняя проверка Th была
неуспешной, и, начиная с п. 2, если она была успешной, с соответству-
ющей заменой верхнего индекса (0) на индекс (1).
Процесс проверки продолжается до тех пор, пока не будут найдены
все неисправные элементы системы.
Примечание. Описанную процедуру, как и приведенную ранее
процедуру отыскания единственного неисправного элемента, можно также реали-
зовывать по мере развития процесса проверки либо провести заранее и составить
инструкцию по последовательности применения тестов. Однако в этом случае
подобная инструкция может оказаться крайне громоздкой.
Пример 12.3.1. Рассматривается система, аналогичная той, которая приве-
дена в примере 12.2.1. Тесты, при помощи которых проверяются элементы
системы, приведены в табл. 12.2.1.
Количество отказавших элементов в системе заранее неизвестно. Для кон-
кретности будем считать, что неисправны элементы 1, 3 и 6, но тому, кто произ-
водит проверку, это неизвестно.
Требуется найти все отказавшие элементы при минимальных средних затра-
тах на проведение необходимых для этого тестов.
Решение
Вычисляем величины Qj0) по формуле
<?<»>=1- пр< ,
340
находим, что
Q(°) = 0,31, Q(2°> = 0,40, Q<0> = 0,315
Q<°> = 0,315, Q<°> = 0,545, Q(6o) = O,315.
Затем для каждого теста находим величины g/0>i
g[0> = 1/0,31 = 3,24, g<2°> = 2/0,4 = 5,0,
g(30) = 1,2/0,315 = 3,52? g<4°> = 1,5/0,315 = 4,77,
g£0) = 2,5/0,545 = 4,6, g<0)= 1/0,316 = 3,18.
Видно, что первым тестом должен быть Тв, так как g^°> наименьшая из веек.
Тест должен пройти успешно, так как мы в условиях задачи определили элемен-
ты 1 и 3 как отказавшие. В связи с этим задача сводится к обнаружению отка-
завших элементов в оставшемся подмножестве элементов G(1> = {1, 2, 3, 4, 6}.
Найдем величины Q)1’ по формуле
Q<”=1- П Pj.
Они равняются соответственно
QV> = 0,23, QV^O.S?, QV’^0.24,
Q<1) = 0,145, Q<’> = 0,495.
Затем вычисляем новые величины gJ<1>.
gV’= 1/0,23 = 4,35, & > = 2/0,37 = 5,4, gP^ 1,2/0,24 = 5,0,
g[i} = 1,5/0,145 =10,05, g<*> = 2,5/0,495 = 5,05
Минимальное значение g/1’ имеет тест 7\, проверяющий элементы 1, 2 и 6.
По принятым условиям примера этот тест оказывается неуспешным. На этом про-
цедура проверки в данном случае завершается.
В наихудшем случае с точки зрения общей длительности проверки пришлось
бы проверять все элементы системы. Тогда, если бы и тест Т\ оказался успеш-
ным, то осталось бы проверить лишь оставшиеся непроверенными элементы 3 и 4.
Для этой цели можно использовать последовательно тесты Т2 и Т3 либо тест 7'5.
Вычислим соответствующие величины g}-2>-
g<2> =--------15--------= 2А = 89.
1-(1-7з)(1-<74) 0,28
Таким образом, следует провести тест Т 3. В качестве последнего теста сле-
дует взять любой тест, проверяющий элемент 4 с минимальными затратами. В на-
шем случае это будет Т2. На этом проверка заканчивается.
Заметим, что при малых вероятностях отказа элементов подобная проце-
дура последовательного применения тестов Т3 и Т2 может оказаться невыгод-
ной по сравнению с применением теста Т3, сразу отвечающего на поставленный
вопрос. Например, в нашем случае с вероятностью 0,8 элемент 3, проверяемый
тестом Т3, окажется исправным и проверку придется продолжить. Это означает,
что в среднем при выбранной процедуруе будет затрачено
0,8 (1,2 + 2) + 0,2-1,2 = 2,6 ед.
Таким образом, в среднем выбранная процедура оказывается худшей по
сравнению с прямым применением теста Т-а.
341
Подобные же погрешности возникают при данном приближенном алгорит-
ме и на других шагах процесса, однако для практических целей этот алгоритм
дает приемлемые результаты.
12.3.2. Метод последовательных проверок для отыскания неисправ-
ных элементов. Предполагается, что в некоторой системе, например
в процессе эксплуатации без постоянного наблюдения, может произой-
ти несколько отказов. Имеется возможность провести полную проверку
системы за некоторое время и проверку отдельных ее элементов (за
время тг каждого i-го элемента).
Процесс проверки протекает следующим образом: проводится пол-
ная проверка, и если система оказывается неисправной, то последова-
тельная проверка продолжается до тех пор, пока не будет найден неис-
правный элемент; обнаруженный элемент восстанавливается (ремонти-
руется, заменяется на новый) и снова проводится полная проверка;
если система продолжает оставаться неисправной, т. е. в ней есть еще
хотя бы один неисправный элемент, то процедура продолжается.
Требуется найти такой порядок проверки элементов системы, чтобы
процесс отыскания всех неисправных элементов протекал в среднем ми-
нимальное время.
Предлагается следующий алгоритм.
1. Вычисляются для каждого элемента значения
gt = т/Лй-
2. Элементы нумеруются в порядке возрастания величин gt. Полу-
ченный порядок и есть порядок оптимальных проверок.
Пример 12.3.2. Рассмотрим систему, состоящую из пяти элементов, харак-
теризующихся следующими показателями:
П = 0,2, т, = 10 мин; г2 = 0,3, т2 = 20 мин;
га = 0,4, т3 = 10 мин; г4 = 0,5, г4 = 5 мин;
г5 = 0,6, тБ = 10 мин.
Требуется определить, в каком порядке следует проверять элементы для
отыскания среди них всех неисправных.
Решение. Вычисляем величины g,:
_Щ2 0,3
10 = 2,5, g2 = —-20 = 8,6,
0,4 0,5
йз~0,б' 10 = 6,7, g4=— -5 = 5,0, U,о
0,6
4 • 10= 15,0.
Из расчета видно, что для минимизации среднего времени отыскания неис-
правных элементов необходимо всегда проверять элементы данной системы
в следующем порядке: 1, 4, 3, 2 и 5.
12.4. Обнаружение неисправного элемента
Проверяемая система состоит из п элементов. Цель проверки со-
стоит в том, чтобы удостовериться, исправна ли система или нет, при-
чем если она неисправна, то требуется обнаружить это в среднем за
342
минимальное время. (При обнаружении первой же неисправности про-
верка прекращается.)
Предполагается, что глобальный тест провести нельзя, либо его при-
менение нецелесообразно (связано с большими затратами).
12.4.1. Приближенный алгоритм при произвольных пересекающих-
ся тестах. Пусть к началу некоторого Л4-го шага процесса проверки
проведена последовательность тестов о<0) = {Tj, ..., Тм— 1} и задача
сводится к обнаружению хотя бы одной неисправности в оставшемся
подмножестве G<0). (Перед самым началом процесса проверки системы
G<0) = G, т. е. исходное множество включает в себя все элементы си-
стемы, а о<0) не включает в себя ни одного теста.)
Алгоритм обнаружения неисправности состоит в следующем.
1. Для каждого теста Т} вычисляется вероятность неуспешного
исхода в проверяемом подмножестве GU)
0»>=1_П р(
;tg^.qg(i,)
при условии, что уже проведена последовательность тестов G<e).
2. Для каждого теста Т} находят связанные с ,ним затраты т)0’ при
условии, что уже проведена последовательность тестов о<в>,
3. Для каждого теста Т} определяется величина
gt =
4. Выбирается такой тест Th, для которого^ минимальна:
gh =₽ min gj.
КМ
5. Применяется тест Th:
а) если тест Th завершается успешно, то процесс обнаружения не-
исправности продолжается в оставшемся подмножестве
G(1) = G(0>\Gfe;
б) если тест Th завершается неуспешно, то процесс прекращается,
поскольку подмножество элементов Gh содержит в себе по меньшей
мере один неисправный элемент.
6. Фиксируется новая последовательность <т(1> примененных тестов,
включающая в себя предыдущую последовательность а<(П и последний
примененный тест Тк.
о'1* = {<т(0>, Тк}.
7. К подмножеству G!1>, указанному в п. 5, вновь применяется про-
цедура проверки, начиная с п. 1, с соответствующей заменой верхнего
индекса (0) на индекс (1).
Процесс проверки продолжается до обнаружения хотя бы одной не-
исправности или до полной проверки работоспособности системы.
Примечание. Описанную процедуру можно реализовать по мере
развития процесса проверки, особенно если для текущих расчетов и выбора оче-
редного теста использовать ЭВМ с заранее занесенным в ее память массивом
исходных данных (вероятность отказов, длительности проверок, характеристики
тестов) и необходимым программным обеспечением.
343
Эту же процедуру можно провести заранее и составить инструкцию
по очередности применения тестов в зависимости от предыдущих ре-
зультатов.
В данном случае процедура обнаружения отказавшего элемента
практически совпадает с приближенной процедурой отыскания неиз-
вестного числа неисправных элементов, поэтому численный пример
не приводится.
12.4.2. Проверка системы непересекающимися тестами. Если имеет-
ся возможность использовать только непересекающиеся тесты, т. е.
каждый из элементов системы может быть проверен только каким-
нибудь одним тестом, то наилучший порядок проверки системы с целью
обнаружения неисправности соответствует нумерации их в порядке
возрастания величин:
gt = itlqt-
Пример 12.4.1. Рассмотрим систему, описанную в примере 12.3.2.
Требуется определить, в каком порядке следует проверять элементы с целью
проверки исправности системы.
Решение. Вычисляем величины g;:
10= 12,5, £2 = ^ 20= 28,6, g3=^10=16,7,
£« = “: 5= 10,0, £6 = Л 10 = 25,0.
0,5 0,4
Из расчета видно, что для минимизации среднего времени проверки исправ-
ности системы требуется всегда проверять элементы данной системы в следую-
щем порядке: 4, 1, 3, 5 и 2.
Список литературы
1. Б е л я е в Ю. К., Ушаков И. А. Математические модели для задач
обнаружения и локализации неисправностей. В кн.: «Кибернетику —
на службу коммунизму». Под ред. А. И. Берга, Н. Г. Бруевича, Б. В. Гне-
денко. Т. 2. «Энергия», 1964.
2. КарибскийВ. В. Анализ систем для контроля работоспособности
и диагностики неисправностей. — «Автоматика и телемеханика», 1965,
т. 26, № 2.
3. Карибский В. В., Пархоменко П. П., Сотом о-
н я н Е. С. Вопросы контроля работоспособности и поиска неисправ-
ностей в конечных автоматах. —«ДАН СССР», 1965, т. 161, № 1.
4. К и н ш т Н. В. О критериях оптимизации процесса поиска неисправно-
стей. — «Известия СО АН СССР. Сер. техн, наук», 1965, № 10.
5. Кузнецов П. И., Пчелинцев Л. А., Гайденко В. С.
О статистических задачах контроля работоспособности и поиска неисправно-
стей (обзор). — В кн.: Теория надежности и массовое обслуживание. Под
ред. Б. В. Гнеденко. М., «Наука», 1969.
6. Линковский Г. Б., Крапивин В. В. О поиске неисправности
в сложных системах. — «Энергетика», 1962, № 3.
7. Линковский Г. Б. Элементарное обоснование принципа Беллмана
для поиска неисправности в системе блоков с разными вероятностями от-
каза и временами поиска. — «Известия вузов, Энергетика», 1961, № 3
8. Линковский Г. Б., Крапивин В. Ф. Среднее время поиска не-
исправности в системе электрических блоков. —«Известия вузов. Электро-
механика», 1962, № 9.
344
9, Л юб а то в Ю. В. Оптимальная процедура локализации неисправности
в модуляризованной радиоэлектронной системе. — «Известия АН СССР.
Техническая кибернетика», 1964, № 4.
10. Л ю б а т о в Ю. В. Некоторые оптимальные методы поиска неисправно-
стей в технических системах. — В кн.: О надежности сложных технических
систем. М., «Сов радио», 1966.
11. Любатов Ю. В. О рациональном планировании операций поиска. —
«Известия АН СССР. Техническая кибернетика», 1964, № 1.
12. Пашковский Г. С. Методы оптимизации программ последовательно-
го поиска неисправностей. «Известия АН СССР. Техническая кибернетика»,
№ 2, 1971.
13 Пчелинцев Л. А. Поиск неисправностей как поглощающая марков-
ская цепь. — «Известия АН СССР. Техническая кибернетика», 1964, № 6.
14. Р у д е р м а н С. Ю. Вопросы надежности и поиска неисправностей в си-
стемах с учетом вероятностного режима использования элементов.—«Извес-
тия АН СССР. Техническая кибернетика», 1963, № 6.
15. С и н д е е в И. М. К вопросу о синтезе логических схем для поиска неис-
правностей и контроля состояния сложных систем. — «Известия АН СССР.
Техническая кибернетяка», 1963, № 2.
16. С о г о м о н я н Е. С. Контроль работоспособности и поиск неисправно-
стей в функционально связанных системах. — «Автоматика и телемеханика»,
1964, т. 26, № 6.
17 Т и м о н е н Л. С. О построении оптимальных программ контроля работо-
способности. — «Автометрия», 1966, № 1.
18 Ушаков И. А. Оптимальные задачи надежности. М., «Знание», 1971.
13
МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ МЕТОДЫ
ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
ПО НАДЕЖНОСТИ
13.1. Форма учета отказов и простейшие методы
обработки результатов испытаний
13.1,1. Основные формы учета работы и регистрации отказов. Ос-
новным исходным материалом для анализа надежности аппаратуры
служит аппаратный журнал, ведомость отказов в котором может иметь
вид табл. 13.1.1.
Таблица J3JJ
Пример сводной ведомости для комплекта № 1 аппаратуры
Дат;*
Характеристика отказа
Внешняя причина отказа
Принятые
меры
1 5.1.73 г<
2 10.1.73 г.
3 7.11,73 г.
4 13,11,7^ г
5 22.П.73 г>
01 Выходное напряжение не
соответствует ТУ
02 Не срабатывает реле Р-1
01 Периодическое пропада- 65
ние выходного сигнала
03 Отсутствует АРУ 83
Упал коэффициент уси-
ления
В ИМС 1УТ221 пробой
базового элемента
Пробит транзистор
Переметный контакт вну-
три ИМС 1ИР141А
Сгорело сопротивление
МЛТ
Пробит конденсатор
К-53-1
ИМС заменена
Транзистор
заменен
ИМС заменена
Сопротивление
заменено
Конденсатор
заменен
По данным сводной ведомости для каждого комплекта аппаратуры
составляется временная диаграмма потока отказов в зависимости от
наработки (рис. 13.1.1). График показывает наработку аппаратов
в часах в момент наступления отказа и интервал времени между двумя
последовательными отказами. Результаты обработки графика потока
отказов или непосредственно сводной ведомости отказов приведены
в табл. 13.1.2 и 13.1.3.
13.1.2. Построение эмпирической функции плотности распределе-
ния наработки на отказ. На основании данных табл. 13.1.3 строится
гистограмма распределения наработки на отказ (эмпирическая функ-
ция плотности). Для этого временная ось (рис. 13.1.2) делится на интер-
валы [0, Z1), [z1; z2), [z2, z8), ... (интервалы равной длины А/= 10 ч)
и подсчитывается число наработок на отказ, попавших в каждый интер-
346
Рис 13.1.1. Временная диаграмма
потока отказов для пяти комп-
лектов аппаратуры.
Таблица 13.1.2
Наработка на отказ для пяти различных комплектов аппаратуры
Номер отказа Наработка, ч
Ло 1 № 2 д« 3 № 4 № 5
1 21 1 1 18 19
2 31 63 13 18 12
3 13 45 22 15 16
4 18 11 37 5 1
Г» 15 13 15 66 15
6 5 25 3 3 5
7 12 25 51 16 10
8 74 64 26 30 1
9 27 3 42 27 46
10 7 24 21 21 7
11 10 55 5 1 33
12 3 48 84 27 25
13 8 72 30 5 4
14 86 18 17 1 9
15 16 8 50 21 1
16 32 45 36 I 10
17 20 18 21
18 12 И 9
19 31 2 16
20 62 6 21
21 1 7 23
22 3 16 9
23 104 27 8
24 15 11
25 6 9
26 31 10
27 24 1
28 18
29 6
30 6
31 5
32 27
33 5
347
Таблица 13.1.3
Вариационные ряды значений наработки для пяти
различных комплектов аппаратуры
№ п/п Наработка ч
№ 1 № 2 № 3 № 4 № 5
1 1 1 1 1 1
2 3 3 2 1 1
3 3 3 3 1 1
4 5 11 5 1 4
5 7 12 5 3 5
6 8 18 5 5 7
7 10 24 6 5 9
8 12 25 6 8 10
9 12 25 6 9 10
10 13 45 6 9 12
11 15 45 7 9 15
12 16 48 11 10 16
13 18 55 13 11 19
14 20 63 15 15 25
15 21 64 15 16 33
16 27 72 16 16 46
17 31 17 18
18 31 18 18
19 32 18 21
20 62 21 21
21 74 22 21
22 86 24 21
23 104 26 23
24 27 27
25 27 27
26 30 30
27 31 66
28 36
29 37
30 42
31 50
32 51
33 84
вал. Если N — общее число отказов, nh — число отказов, попавших
вй-й интервал [гд._1( zfe) (k = 1, 2, ...), то эмпирическая функция плот-
ности имеет вид
f (z) = nhIN (zk — zk-i) для г < гк.
13.1.3. Построение эмпирической функции распределения наработ-
ки на отказ. На основании данных табл. 13.1.3 могут быть построены
и эмпирическая функция распределения на отказ Fn (г) и эмпири-
ческая функция вероятности безотказной работы Pn (г). Если N —
общее число отказов, то »
Fn (г) = п (z)/N, PN (г) = 1 — [n (z)/N],
348
где п (г) — число значений наработок на отказ, попавших в интервал
[О, г). На рис. 13.1.3 приведена эмпирическая функция распределения
наработки на отказ на основе данных табл. 13.1.3.
13.1.4. Определение зависимости интенсивности отказов от времени.
На основании данных рис. 13.1.1 или табл. 13.1.1 может быть
Рис. 13 1 2. Эмпирическая функ-
ция плотности распределения на-
работки на отказ, соответству-
ющая табл. 13.1 3.
построена эмпирическая зависимость интенсивности отказов от време-
ни. По виду этой функции можно получить информацию, например,
о времени приработки аппаратуры, начале периода старения и т. п.
Для построения эмпирической функции интенсивности отказов К (г)
Рис. 13 13 Эмпирическая
функция распределения нара-
ботки на отказ, соответству-
ющая табл 13 1 3.
временная ось [0, оо) на рис. 13.1.4 делится на интервалы (равной
длины Аг = 50 ч) 10, zj, [гь г2), [г2, г3), ... и подсчитывается число
отказов, происшедших в интервалах времени [z^—i, zft).
Тогда
Z(z) = nfe/M(z)(zft—г^), для zf[_1Cz<zh,
349
где М (z) — число аппаратов, находящихся на испытании в момент
г. Для вычисления эмпирической функции интенсивности отказов
£ (г) на основе данных рис. 13.1.1 и табл. 13.1.1 может быть составлена
Рис. 13 1.4. Эмпирическая функция
интенсивности отказов, соответст-
вующая табл. 13.1.3.
таблица времени отказов аппаратуры. Например, табл. 13.1.1 соот-
ствует табл. 13.1.4.
Таблица 13.1.4
Таблица времен отказов пяти комплектов аппаратуры
Номер отказа Время отказа, ч
№ 1 № 2 № 3 № 4 № 5
1 21 1 1 18 19
2 52 64 14 36 31
3 65 109 36 51 47
4 83 120 73 56 48
5 98 132 88 122 63
6 103 157 91 125 68
7 115 182 142 141 78
8 189 246 168 171 79
9 216 249 210 198 125
10 223 273 231 219 132
11 233 328 236 220 165
12 236 376 320 247 190
13 244 448 350 252 194
14 330 466 367 253 203
15 346 469 417 274 204
16 378 514 453 275 214
17 398 471 296
18 410 482 305
19 .441 484 321
20 503 490 342
21 504 497 365
22 507 513 374
23 611 540 382
24 555 393
25 561 402
26 592 412
27 616 413
28 634
29 640
30 646
31 651
32 678
33 683
350
13.2. Выборочные распределения, связанные
с испытаниями на надежность
13.2.1. Выборочные распределения, связанные с нормальным рас-
пределением. Предположим, «то последовательно и независимо произ-
водится п испытаний. Результат i-ro испытания есть случайная вели-
чина xt, имеющая нормальное распределение с параметрами (а, о).
Тогда выборочная функция (эмпирическое среднее)
имеет нормальное распределение с параметрами (а, o/j/и). Выборочная
функция
= £=£ У ,г (13.2.2)
имеет нормальное распределение с параметрами (0, 1). Значения функ-
ции Ф (х) иормалъиото распределения параметрами (ОД) см. в. прило-
жении 8 (табл. П8.3).
Выборочная функция
(13.2.3)
имеет плотность распределения
М—1 \(п 1)/2)ж[(п-1)/2]-1
------—---------------------- е-(/г-1) л/2аа прИ Х>О,
(13-2Л>
V 2 J
при х^О,
Ms2 = о2, Ds2 = 2а4/ (п — I)2.
Выборочная функция
X2 == (п — 1) s2/a2 (13.2.5)
имеет Х2-распределение с (и — 1) степенями свободы. Функция плот-
ности Х2-распределения с (ц — 1) степенями свободы запишется в виде
при х^О
f(*) =
---------!-------- х(п-3)/2 е—х/2( ПрИ
х>0
(13.2 6)
М (н— 1) s2/o2 = п— 1,
O(n-l)s2/o2=2(«-l).
351
В табл. П8.12 приведены значения X2 (г, Q), определяемые равен-
ством
оо
£ = 7{х2>Х2<Л <2)}=* . $ f(x)dx, (13.2.7)
X1(r.Q)
(f (x) — функция плотности ^-распределения с г степенями свободы)
для различных значений Q и степеней свободы г.
(Более подробно см. Л. Н. Большее и Н. В. Смирнов.
Таблицы математической статистики, М., ВЦ АН СССР, 1968)
Выборочная функция
/ = (13.2.8)
S
имеет /-распределение (распределение Стьюдента) с (и — 1) степенями
свободы. Функция плотности /-распределения с п степенями свобо-
ды запишется в виде
гР-±1) _2±1
/(х)=-к--'-Цч1+—) 2,
/ля р \ п / (13.2.9)
М/ = 0, Dt = —^—.
' п — 2
Таблицы /-распределения с различным числом степеней свободы
можно найти там же, где и таблицы Х2-распределения.
В табл. П8.13 приведены значения / (п, Q), определяемые равенст-
вом
/ W — функция плотности /-распределения с п степенями свободы)
для различных значений Q и степеней свободы п.
13.2.2. Выборочные распределения, связанные с экспоненциальным
распределением. Испытания на надежность могут быть организованы
эазличными способами. Ограничимся только планами типа [А, В, 7],
N, В, г] [А, В, (г, Т)], [А, Б, Т], [А, Б, г], [А, Б, (г, 7)1, [А, Б, 7J.
3 начальный момент испытанию подвергаются А устройств. Буквой
В обозначаются планы, для которых каждое устройство при его отказе
мгновенно заменяется новым идентичным устройством (испытания
с восстановлением). Буквой Б обозначаются планы, при которых от-
казавшие во время испытаний устройства новыми не заменяются (без
восстановления). Предполагается, что наблюдения за отказами устрой-
ства производятся непрерывно, в результате чего отказы сразу же об-
наруживаются.
352
Планы различаются способами задания моментов окончания испы-
таний:
— планы, при которых испытания ведутся в течение времени Т;
— планы, при которых испытания ведутся до момента появления
r-го отказа;
— планы, при которых испытания ведутся до момента tr появле-
ния r-го отказа, если tr<Z Т, либо до истечения времени Т\
— планы, при которых испытания ведутся до достижения суммар-
ной наработки Т%.
Во всех планах предполагается, что функция распределения отка-
зов каждого устройства экспоненциальна (F (/) =1 — е~и).
Введем следующие обозначения:
d — число отказов, имевших место за время испытаний;
tr — время наступления r-го отказа при испытаниях;
S — суммарная наработка к моменту окончания испытаний.
Рассмотрим последовательно перечисленные выше планы испытаний.
1. [2V, В, Т]. Случайная величина diNT имеет дискретное распре-
деление
р — п I d — 1 = p—KNT
к P\NT NT) k\ ’ (13.2.11)
Md = X, Dd = ШТ.
2. [Л/, В, г]. Случайная величина tr (время окончания испытаний)
имеет плотность распределения
f(O = x№^-e-^r,
(г-1)! (13.2.12)
Mtr^rlNK, Dtr = r/(NW.
3. [2V, В, (г, T)J. Случайная величина d имеет дискретное распре-
деление
P{d — k} =
для k = Q 1,..., Г—1,
fe!
1 — 2 —e~KNr, для k = г.
k = 0 k\
(13.2.13)
4. [А/, Б, Т]. Случайная величина d имеет дискретное распреде-
ление
P{d = k] =Cw(l — e-^)fte-Mw-fe) т для fe = 0, 1,..., N;
Md = N([—e->-r), Dd = N (1 — е~~кг) е~кг. (13.2.14)
5. [N, Б, г]. Случайная величина S (суммарная наработка в момент
г-го отказа) имеет плотность распределения
f (0 = X — е-«;
Р-1)!
DS = r/№.
(13.2.15)
12 Зак 943
353
6. [Д\ Б, (г, 71)]. Случайная величина d имеет дискретное рас-
пределение
CkNa— e-^ke-K(N-k)T для /е = 0, 1,..., г—1,
г— 1
1— 2 Слг(1— e-^T)ke-X(N-k)T для
k = 0
7. [Л7, Б, Т$. Случайная величина d имеет дискретное распре-
деление
P{d = k} =
дЛЯ fe=0, 1,..., лг_1,
fe!
для,=„.
k=o fe!
(13.2.17)
13.3. Проверка гипотез о характере закона
распределения отказов
По статистическому материалу об отказах устройств можно попы-
таться отнести функцию распределения отказов к какому-нибудь из-
вестному закону: нормальному, экспоненциальному, гамма-распреде-
лению и т. п. Проверка соответствия опытных данных принятой гипоте-
зе чаще всего осуществляется с помощью критерия х2.
13.3.1. Критерий X2. Пусть имеется ряд наработок 0!, 02, .... 0„
устройства. Требуется проверить гипотезу о том, что функция распре-
деления наработки устройства есть F (t) = Р {0^£}— некоторая
полностью определенная функция распределения. Разбиваем ось
[О, оо ) на А/ интервалов [0, ^), 1^, /2), ..., Uw_2, 6/-i), U/V-i, оо).
Рассчитываем теоретическую вероятность pt попадания в i-й интервал
при одном опыте (при полностью определенной теоретической функции
это всегда возможно). Подсчитываем число наработок, попавших
в i-й интервал. Если гипотеза верна, то по К. Пирсону при больших
значениях п величина
N
х2= 2
(•= 1
(т,- —пр,)2
npi
(13.3.1)
имеет Х2-распределение с (У — 1) степенями свободы. По заданному
уровню значимости е (обычно из набора 0,1; 0,05; 0,01; 0,001) по
табл. П8.12 находим такое значение X2 (А/ — 1, е), что
Р {Х2> X2 (А/ — 1, е)} = е.
Если сумма X2 > X2 (N — 1, е), то считаем, что эксплуатационные
данные не соответствуют гипотезе. Если сумма X2 X2 (А/— 1, е),
то считаем, что эксплуатационные данные не противоречат гипотезе.
354
Если проверяется гипотеза о том, что функция распределения нара-
ботки на отказ устройства зависит от некоторого числа неизвестных
параметров, например распределена ' по экспоненциальному закону
F (t) = 1 — е~м (неизвестен параметр X), нормальному закону
F(0 =
1
а У'2л
е—(х—а)!/2аг dx
—ОО
(неизвестны среднее а и дисперсия о2) и т. п., то проверка осуществ-
ляется следующим образом. Пусть проверяется гипотеза о том, что
функция распределения наработки на отказ устройства есть F (аъ
а2, ...» а8) (а1> ••» as неизвестны). Вся прямая разбивается на N интер-
валов [О, ix) [ix, t2),...» Un— ь о°). Обозначим теоретическую вероят-
ность попадания в i-й интервал [i(-_i, tt) через (ax, a2,as), которая,
естественно, зависит от значения неизвестных параметров ах, а2, ..., as.
Подсчитываем число mt наработок, фактически попавших в i-й интер-
вал. Составляем сумму
X2 («1» -
N
i= I
[mj — npiiat,..., <х5)]3
(ai,..., as)
(13.3.2)
значение которой опять же зависит от значений неизвестных парамет-
ров ах, .... as. Находим такие значения а*, а?, ..., а« параметров
ах....as, при которых X2 принимает наименьшее значение. Тогда по
Фишеру величина
[mj — npt (at, ... , al)]2
ai, ... , as)
N
- У
fvmin —
асимптотически при n->oo имеет х2-распределение c (N— S—1)
степенями свободы.
Если Xm/n X2 (N — S — 1, e), то считаем, что эксплуатацион-
ные данные не противоречат гипотезе. Если Х^„>Х2 (N— S — 1, е),
то считаем, что эксплуатационные данные не соответствуют гипотезе
(е — уровень значимости критерия). Здесь
00
%2(AZ—S —1, е)= f(x)dx,
(W-S-1, е)
(13.3.3)
где / (х) — функция плотности Х2-распределения с (N — S — 1) степе-
нями свободы. Значения X2 (Л/ — S— 1, е) находятся с помощью
табл. П8.12.
Отыскание значений параметров а*...at, при которых X2 в (13.3.2)
принимает наименьшее значение, представляет собой, как правило,
трудоемкую задачу, требующую большого объема вычислений. При
ориентировочных расчетах рекомендуется следующий критерий. Оце-
12* 355
ниваются более простыми методами значения параметров ах.......аь по
имеющейся выборке 61( 02, ...» 6П;
аг = аг (0!, 02, .... 0n), i = 1, 2....s. (13.3.4)
Рассчитываются значения pt (cq......as) и определяется
(7 = 2 . (13 3.5)
npi (an ..., <£s)
Если U -С X2 (N — 1, е), то считаем, что эксплуатационные данные
не расходятся с гипотезой о виде распределения, если U> X2 (N — 1, е),
то эксплуатационные данные не соответствуют гипотезе. Следует иметь
в виду, что (7 в формуле (13.3.5), вообще говоря, уже не имеет асимп-
тотически Х2-распределение ни с (У — 1), ни с (У — S — 1) степенями
свободы. Предложенный критерий (см. Ван дер Варден. Мате-
матическая статистика. М., ИЛ, 1960) имеет уровень значимости меньше
е и меньшую мощность.
13.3.2. Критерий Колмогорова. Проверка гипотезы, что функция
распределения наработки на отказ есть F (t) — некоторая полностью
определенная непрерывная функция распределения, может быть осу-
ществлена с помощью критерия Колмогорова.
По имеющимся значениям наработок 01, 02, ..., 0П строится эмпири-
ческая функция распределения Fn (t). Тогда величина
Dn = sup | Fn (0 - F (01
O^fcoo
имеет распределение, не зависящее от проверяемой функции F(t).
При ц 50 по заданному уровню значимости е с помощью
табл. П8.14 (е выбирается из набора 0,1; 0,05; 0,02; 0,01) находится
такое значение А (п, е), что P{Dn > А (п, е)} = е.
Если опытное значение Dn 'С А (п, е), то считаем, что эксплуата-
ционные данные не противоречат гипотезе. Если Dn> А (п, е),"то счи-
таем, что эксплуатационные данные не соответствуют гипотезе. При
п > 50 используется предельная теорема Колмогорова.
Если гипотеза справедлива, то
lim Р {у[п Dn > у] = 1 —К (у),
п -+ ОО
где К (у) — функция распределения Колмогорова (табл. П8.15). По
заданному уровню значимости е из табл. П8.15 находится такое At,
что К (Л8) = 1 — е. Если опытное значение Dn < AdY п, то считаем, что
эксплуатационные данные не противоречат гипотезе. ЕслиЕ>п> Ае/У~п,
то считаем, что эксплуатационные данные не соответствуют гипотезе.
Пример 13.3.1. Пусть в результате наблюдения над некоторым устройством
получено 42 значения наработки на отказ в часах: 15; 24, 28; 37; 49; 54- 60,
75; 87; 92; 93; 111; 114; 121; 127; 130; 134; 138; 140; 144; 147, 149; 155; 168; 170;
173; 189; Г92; 197; 198; 201; 204; 225; 231; 243; 248; 249; 256; 265; 274; 281; 297.
Требуется проверить гипотезу об экспоненциальности распределения вре-
мени наработки на отказ. Уровень значимости критерия принять равным ь =
= 0,01.
356
Разбиваем ось [0, оо] на б интервалов; [0, 50), [50, 100), [100, 150), [150, 200),
[200, 250), [250, оо).
Оценивается Л, до формуле
п—1
1=1
41
= ^ = 0-0063 1/1.
Рассчитываются mt и pi (Л). Результаты сводятся в таблицу
Номер интервала PjCfi [т(—npt(£)P
1 5 0,27 11,34 3,51
2 6 0,20 8,40 0,62
3 11 0,15 6,30 3,86
4 8 0,11 4,62 2,16
5 7 0,07 2,94 5,41
6 5 0,20 8,40 1,43
Подсчитывается
[mt—npt (X,)]2
npi (X)
= 17,04
в
( = 1
По заданному уровню значимости 6 = 0,01 по табл. П8.12 находим X2 (<V —
__ 1( е) = х2 (5; 0,01) = 15,09, откуда маловероятно, чтобы наработка на отказ
была распределена по экспоненциальному закону.
Пример 13.3.2. В условиях примера 13.3.1 проверить гипотезу об усечен-
ном нормальном законе распределения наработки на отказ. Уровень значимо-
сти критерия положить равным 0,01.
Функция распределения F (/) усеченного нормального закона имеет вид
Р (О =
j т/а
Ф(т/о) = —— С е~и^2 du.
"|/ 2л J
Оцениваем т и о2 по формулам
т= — V 01 = 154 ч}
П £
1 " 1 42
52= П 2 (0'~ 2 (91-!54)2=5791 ч2, 0 = 76,1 ч.
Подсчитываем pi (т, о)
1 Г / 7,-—Л / ti-i—m
---\ ~ - Ф —~— I — Ф I--------
ф(т/о) \ о / \ о
357
значения Ф (х) берутся из табл. П8.3. Результаты расчетов сводятся в таблицу
интервала Ft(m. npt(in, о) [mt—npt(m, a)]3
npt(m, a)
1 5 0,066 2,77 1,76
2 6 0,156 6,59 0,05
3 11 0,245 10,29 0,05
4 8 0,253 10,63 0,65
5 7 0,172 7,22 0,01
6 5 0,108 4,54 0,04
Находим
V npi
i^\ nPi o)
Имеем
(7 = 2, 6 < /2 (У — 1, e) = x2 (5; 0,01) = 15,09.
Делаем вывод, что эксплуатационные данные не противоречат гипотезе об
усеченном нормальном распределении времени наработки на отказ.
Пример 13.3.3. В условиях примера 13.3.1 проверить по критерию Кол-
могорова гипотезу о том, что распределение наработки на отказ равномерное
в интервале [0,300]. Уровень значимости е принять равным 0,01. Тогда (см.
табл. П8.14)
А (п, е) = А (42; 0,01) = 0,246.
Имеем
max 1 F42 (^)—“Z} =0>07 < 0,246.
0<t<30Q\ 3001
Таким образом, эксплуатационные данные не противоречат гипотезе о рав-
номерном распределении в интервале [0,300].
13.4. Оценки показателей надежности устройства
по результатам испытаний для экспоненциального
распределения времени работы до отказа
В табл- 13.4.1 приведены рекомендуемые оценки для интенсивности
отказов и средней наработки на отказ для различных планов испыта-
ний. Все оценки асимптотически несмещенны, состоятельны и асимп-
тотически эффективны при увеличении длительности испытания;
NT —> оо
г —> оо
min (г, Т)-+<х>
min (N,
min (N, г)->оо
min (N, г, Т)-^<х>
min (N, Т£) ->оо
в плане [N, В, Т],
в плане [N, В, г],
в плане [N, В, (г, Т)],
в плане IN, Б, 71,
в плане [jV, Б, г],
в плане [N, Б, (г, 7)],
в плане [N, Б, Т21.
358
Таблица 13 4.1
Опенка показателей надежности устройства прй экспоненциальном
законе распределения времени работы до отказа
План испытаний Оценки интенсивности отказов Оценки средней наработки на отказ
[N, В, Г] Оценка несмещенная и эффективная 7сР = NT/d
[ЛВ В, г] Г=(г-1)ЖГ Оценка несмещенная для г> 1 = Ntr/r Оценка несмещенная и эффективная
[N. В, (г. ГЦ I d/NT, если tr>T I.V—1)ЖЦ. если /г si Г Оценка несмещенная для г> 1 ~ ( NT/d, если/г> Т ^sp если
(.V. Б, Г] T = d S ' Gs= S/d
[ЛЦ Б, г] £^(r-ns . Опенка несмещенная для г > 1 t<X) — S/r Оценка несмещенная
[N. Б, (г, У)] _ | d/S, если tr~>T | (/-—1),S, если 1г<Г <S/d, если tr^T оР lS/r, если
[Л/. Б. 7Д / <рТ\, если d < N 1 (N — 1 )/S, если d = Л-' lTs/d если d < N lS/ЛГ, если d = N
Здесь d~~ число отказов, имевшее место за время испытаний; S —суммарная наработка за вре-
мя испытаний, t — момент наступления ' го отказа; Ту — заданная суммарная наработка. Если
^«0, ю при оценке средней наработки на отказ рекомендуется принимать d=l
Для вероятности безотказной работы устройства за время t рекомен-
дуется применять оценку
P(r) = e-4
где X — оценка для интенсивности отказов X.
Оценка Р (/) асимптотически несмещенна, состоятельна и асимп-
тотически эффективна при увеличении длительности испытаний.
Пример 13.4.1. План [N, В, Т]. Пусть за время испытаний по плану
12V = 500, В, Т = 100 ч] зафиксировано 5 отказов. Требуется оценить X, /ср.
359
Решение-
NT 500-100
1/4J
NT
?cP= d
50000
5
= 10000 ч.
Пример 13.4.2. План [АГ, В, г]. Испытания при г = 15 и N » 500 закон-
чились на 1211 ч. Оценить X, fCp, Р (100)
Решение.
Ntr
14
500.121Г “°’000023 Ьч:
ГСр = —~ = 40000 ч; Р(Ю0) = е-х,100= 0,998.
Пример 13.4.3. План [N, Б, Т]. Пои Д' =. 500 и Т а inn „ „„л
5 отказов на 15, 31, 47, 62 и 96 ч. Оценить к, /РР и Р (100)° зафиксиР°вано
Решение. р '*
= 3 15+31 +47+ 72-4-96-4-100-495 49761 10l,l°-e J/45
- S 49 761 Л j
1OD=—-—= —:— = 9950 ч; Р(100) =е_v 100 =0,9899.
а о
Пример 13.4.4. План [N, Б, г] Прн N = 150, г = 5 суммарная наработ-
ка к концу испытаний составила 13 202 ч. Оценить А, /ср н Р (100).
Решение.
г (г—1) 4
S
(Ср = — = 13202 I 5 = 3600 ч;
г
Р(100) = е~ ^'1оо = О,97.
Пример 13.4.5.
План [АГ, В, (г, 74L При N — 50, г = 5, Т = 100 ч испытания были пре-
кращены на 40 часу после возникновения пятого отказа. Оценить X, Zcp и Р( 100).
Решение.
(А-1)
4
50-40
= 2-10-3
1/ч;
7 Ntr
'ср —
50-40
5
= 400 ч;
Р(100) = е-Х' 10° = 0,82.
360
13.5. Доверительные интервалы
13.5.1. Доверительные интервалы для параметра биномиального
распределения. По заданному значению доверительной вероятности
1 — а, количеству устройств N, поставленных на испытание в течение
времени t, и числу п устройств, отказавших за время испытания,
строится доверительный интервал для неизвестного значения /’-вероят-
ности отказа устройства за время i. Границы доверительного интервала
(Р, Р) находятся из системы двух уравнений
k = Q 2
2 ckN(i—p)k(P)N~k = .
k=n — — 2
Значения P и P табулированы для различных значений N, п и довери-
тельной вероятности 1 — а (см. табл. П8.7).
13.5.2. Доверительные интервалы для параметра распределения
Пуассона. По заданному значению доверительной вероятности 1 — а,
числу и происшедших событий строится доверительный интервал для
параметра А, распределения Пуассона
Границы доверительного интервала (X, Л) находятся из системы двух
уравнений
у ... « у
2d fei 2 ’ .2d *| 2
Искомыми значениями А и А являются
А = 4х2(2(п+1), -±-а
21 2п, 1-------
\ 2
а I ,
где х2 (2 (« + 1), а/2), х2 (2п, 1 — а/2) — квантили х2-распределения
с 2(п + 1) и 2 и степенями свободы, соответственно.
Значения А и А, табулированы для различных п и доверительной ве-
роятности 1 — а (см. табл. П8.11).
13.5.3. Доверительные интервалы для параметров нормального
распределения. По заданному значению доверительной вероятности
1 — сс и результатам испытаний 62,..., 9П при известной дисперсии
°2 доверительный интервал для среднего значения tcp имеет вид
t—и
361
— 1 п
где t = — у, 9;, и 1 —квантиль нормального- распределения,
" < = 1 2 “ определяемый по формуле
-4г f е-^/2^х = ф (и ! \ = 1-------------
/2л J I 1-Т“ 2
—ОО \ “ /
При заданном значении доверительной вероятности 1 — а и резуль-
татах испытаний 91, 92, 9П и при неизвестной дисперсии довери-
тельный интервал для среднего значения имеет вид
t----—— а)</ор<7ч------—— t (п~ 1. а),
/п-1 /п-1
где 52 = -Ц (0.-OL
п—1 /=1
t (п — 1, а) — квантиль распределения Стыодента (/-распределения)
с (п — 1) степенями свободы, т. е. значение, удовлетворяющее равен-
ству Р { |/| >/ (п — 1, а)} = а (см. табл. П8.13).
По заданной доверительной вероятности 1 — а и результатам испы-
таний 9Ь 92, ..., 9„ доверительный интервал для дисперсии имеет вид
nS2 D<Z
X2 (п — 1, а/2) у_2 (п — 1, 1 — а/2) ’
где X2 (п — 1, а/2), %2 (п — 1,1 — а/2) — квантили Х2-распределения
с (п— 1) степенями свободы (см. табл. П8.12).
Пример 13.5.1. Испытывалось 20 устройств в течение 100 ч. Отказало
2 устройства. Во время испытаний устройства не восстанавливались. Требуется
построить доверительный интервал для вероятности Р отказа устройства за
100 ч. Доверительная вероятность интервала должна быть 0,95.
Решение. Доверительный интервал для вероятности отказа определя-
ется по табл. П8.7.
Имеем Р = 0,012, Р = 0,317, доверительный интервал -(0,012; 0,317).
Пример 13.5.2. Суммарная наработка устройств определенного типа соста-
вила S = 105 ч. За это время наблюдалось 10 отказов устройств. Требуется по-
строить доверительный интервал для интенсивности X отказов устройства с до-
верительной вероятностью 0,95.
Решение. По табл. П8.11 определяется доверительный интервал для
Л (Л = XS). Имеем Л = 4,8 1/ч; Л = 18,39 1/ч. Отсюда X = 4,8/10? =
= 4,8-10-5 1/ч; Л = 18,4-10-5 1/ч. Тогда доверительный интервал для X с до-
верительной вероятностью 0,95 есть (4,8-10~5, 18,4-10~5 1/ч).
Пример 13.5.3. При испытаниях некоторого устройства, имеющего время
работы до отказа, распределенное по нормальному закону, получено 10 реали-
заций наработки до отказа (в часах): 120, ПО, 80, 130, 120, 140, 80, 150, 130 н
140. Требуется найти доверительные границы с доверительной вероятностью
0,9 для средней наработки на отказ и дисперсии D.
Решение. Имеем
362
-1 10 1 10
*=— 2е*=,2°ч* р= f 2 (6г~7)8=576 ч>
i = 1 < = 1
S = V b = 24 ч’,
__ s _ s
t— t(n — 1, a) — ~__: <_tC9<zt +t(n— 1, a) —- —;
]/n-l T/n-1
a) = I(9; 0,l) = l,83 (см. табл. П8 13);
/ср = 120 — 1,83-8 = 105,4 ч; = 120 + 1,83 • 8 = 134,6 ч. Отсюда для
1ср доверительный интервал (105,4; 134,6).
Доверительный интервал для дисперсии
nS2 — nS2
- х2(я—1. a/2) ’ '/2(n—1, 1 —«/2) ‘
Имеем п = 10, S2 = 576, х2 (9; 0,05) = 16,92, х2 (9; 0,95) = 3,33. Отсюда D -=>
= 340 ч, D = 1735 ч и доверительный интервал для дисперсии есть (340,
1735).
Список литературы
1 Колмогоров А. Н. Несмещенные оценки.—«Известия АН СССР.
Сер. матем.», 1950, вып. 14, с. 303—326.
2. Сираждинов С. X., Эй де л ьн ант М. И К вопросу об оценках
качества продукции по результатам выборочного контроля. — В кн.: Труды
ин-та матем. АН УзССР. Ташкент, 1961, вып. 22.
3. Мирный Р. А., Соловьев А. Д. Оценка надежности системы по
результатам испытаний ее компонент. — В кн.: Кибернетику — на службу
коммунизма. Под ред. А. И. Берга, Н. Г. Бруевича, Б. В. Гнеденко Т. II. М.,
«Энергия», 1964, с. 213—218. ~
4 Боровков А. А., Сычева Н. М. О некоторых асимптотически оп-
тимальных непараметрических критериях. — «Теория вероятностей и ее
применения» 1968, т XIII, вып. 3, с. 385—418
5. X о л е в о А. С. Об оценках коэффициентов регрессии. — «Теория вероят-
ностей и ее применения», 1969, т. XIV, вып. 1, с. 78—100.
6. Л умел ьс кий Я- П-, Сапожников П. Н. Несмещенные оцен-
ки для плотностей распределений. — «Теория вероятностей и ее примене-
ния», 1969, т. XIV, вып. 2 с. 372—380.
7. Лумельский Я- П. Доверительные границы для линейных функций
от неизвестных параметров. — «Теория вероятностей и ее применения».
1969, т. XIV, вып. 2, с. 381—384.
8 Чибисов Д. М. Некоторые критерии типа хи-квадрат для непрерыв-
ных распределений. —«Теория вероятностей и ее применения», 1971,
т. XVI, вып. 1, с. 3—20.
9. Конаков В. Д. Непараметрическая оценка плотности распределения
вероятностей. —«Теория вероятностей и ее применения», 1972, т. XVH,
вып. 2, с. 377—379.
10. X о л е в о А. С. Об оценивании функций от среднего значения. — «Тео-
рия вероятностей и ее применения», 1972, т. XVII, вып. 3, с. 572—576.
И- Чибисов Д. М. Асимптотическое разложение для одного класса оце-
нок, включающего оценки максимального правдоподобия. — «Теория веро-
ятностей и ее применения», 1973, т. XVIII, вып. 2, с. 303—311.
363
Приложение I
ОСНОВНЫЕ ПОНЯТИЯ и КРАТКИЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ
П 1.1. Случайные события и их характеристики
(термины и определения)
Случайные события — события, которые в результате произведенного опыта
могут произойти или не произойти. Обозначим случайное событие символом А.
Достоверное событие — такое событие, которое непременно должно прои-
зойти. Обозначим достоверное событие символом Е.
Невозможное событие — такое событие, которое заведомо не может прои-
зойти. Обозначим невозможное событие символом U.
Совместные (несовместные) события —такие события, появление одного из
которых не исключает (исключает) возможности появления другого события.
Зависимые (независимые) события — такие события, появление одного из
которых влияет (не влияет) на появление другого события.
Противоположное событие относительно некоторого выбранного события
А — событие, состоящее в непоявлении этого выбранного события. Обозначим
противоположное событие А (Противоположное событие называется также до-
полнительным.)
Полная группа событий — такая совокупность событий, что в результате
опыта обязательно должно произойти хотя бы одно из событий этой совокупности.
Примечание. События А и А составляют полную группу событий,
так как в результате опыта возможны только два исхода: либо событие А прои-
зойдет, либо событие А не произойдет (т. е. произойдет событие Л).
Сумма событий Л1, Л2, ..., Ап—такое событие Л, появление которого
в опыте эквивалентно появлению в том же опыте хотя бы одного любого из собы-
тий Ait Л2, .... Лп. Обозначим сумму событий как
Л = Л1 V^V... V^n= U Al,
z = i
где V — знак логического сложения событий, a U — знак логической суммы
событий.
Если события Л;, где i = 1,2, ..., п, составляют полную группу событий, то
U л=е
z = i
В частности, Л/ V At = Е.
Сумма событий называется также объединением событий. Для логической
суммы событий справедливы следующие равенства:
Л\/Л = Л;
Л\/^ = Л;
Л Х/Е — Е.
ЗМ
Произведение событий Д1э Аг, ..., Ап —такое событие А, появление кото-
рого в опыте эквивалентно появлению в том же опыте всех событий А1г Ая,
Ап одновременно. Обозначим прозведение событий как
Л=Л1ЛЛЛ ••• ЛЛП= П Л- (П1.1.1)
1 = 1
где Л — знак логического умножения событий, a f] — знак логического про-
изведения событий.
Произведение событий называется также пересечением событий. Для логи-
ческого произведения событий справедливы следующие равенства:
А Д А = А,
А/\Е — А,
A/\U = U,
Ai/\A}=U,
если А( и Aj несовместны.
П1.2. Вероятность события
Вероятность события — числовая характеристика степени возможности
реализации случайного события в определенных условиях.
Классическое определение. Рассмотрим равновозможные события Ая, А2, ....
Ат, т. е. такие события, при которых не существует никаких объективных
причин для более частого появления любого из них. (Предполагается, что все
эти события независимые и несовместные и составляют полную группу событий.)
Такие события называются элементарными. Пусть интересующее нас событие
Л может быть разделено на некоторое число k элементарных событий Аг....
Aft, т. е. появление одного любого из элементарных событий эквивалентно на-
ступлению события А. Назовем благоприятным исходом такой исход испытания,
в котором наблюдается событие А. Вероятностью события А называется отно-
шение числа k благоприятных исходов к общему числу т всех элементарных
исходов:
P(A)=k/m. (П1.2.1)
Основные свойства вероятности.
Вроятности случайных событий обладают следующими основными свойст-
вами:
Р (U) = 0;
Р (Е) = 1;
0 = Р (U) < Р (Д) < Р (Е) = 1; (П1.2.2)
Р (Д) + Р (Д) = 1.
Теорема сложения вероятностей. Если Дп Д2.... Ап — несовместные со-
бытия и А — сумма этих событий, то вероятность события А равна сумме ве-
роятностей события Ая, Д2, .... Ап, т. е.
(п \ п
J At =Р(Д1) + Р(Д2) + ... + Р(Дп)= Р(Л*)- (П1 2.3)
I = 1 / i = l
Следствие П1.2.1. Если несовместные случайные события А±, Д2... Д1г
составляют полную группу событий, то
Р | и ДИ = Р(Е) = 1. (П1 2 4)
\ i = 1 /
Следствие П1.2.2. Для любых случайных событий Аг и Д2 имеет место
Р Mi Л лг)+^(Л1ЛЛ2)=Р Ml). (П12 5)
365
Действительно,
Р (А Л А2) + Р (А Д А2) = Р (41 Л А +41 Д А2) =
= р Ml Л (42 + А2)) = Р (А2 Д £) = Р (4j) Р (£) =Р (At).
Условная вероятность события А, при наступлении события А2 — вероят-
ность события 41, вычисленная в предположении, что событие А2 наступило.
Обозначим эту условную вероятность Р (Ai | А2):
P(4i|42)=- (^2). (П1.2.6)
г Иг)
Следствие П1.2.3. Для независимых событий и
Р(41|42) = Р(41|42) = Р(41) и Р М2 14р =Р(421 41)=Р(42).
Коэффициент регрессии события At относительно события 42 характери-
зует степень зависимости этих событий и определяется как
р (А„ А2) = Р {Aj | А2}— Р {Ai | А2} = М?) Р
Р{42}Р{42}
Коэффициент корреляции событий At и 42 характеризует степень зависи-
мости этих событий и определяется как _
г(л1. Л.) - Ур(л„ Л,)р(Л„ Л,) _
УР(Л1)Р<Л,)Р(Л.) Р(Л,)
Коэффициент корреляции обладает следующими свойствами:
1) г (Aj, А2) = 0, если события независимы;
2) г (Aj, А2) = 1, если события Ai и А2 эквивалентны;
3) г(А, А)=-1;
4) г (Ai А2) =/-(++)= — г (Aj А2);
5) г (Aj, A2) = r (А1, А2).
Теорема умножения вероятностей. Вероятность совместного появления
двух событий At и А2 в данном опыте равна вероятности одного из них, умно-
женной на условную вероятность другого, вычисленную в предположении, что
первое событие появилось, т. е.
Р (Ai Л А2) = Р (Ai | А2) Р (А2). * (П1.2.7)
В общем случае теорема умножения может быть записана в виде
₽ - ..Л»п) = Р(А1|А2л...дап)х
ХР(А2|АзД ... ДАП)... Р(Ап_1|Ап)РМч). (П1 28)
Формулу (П1.2.8) можно переписать в виде следующих эквивалентных
выражений
р[ П аД= 2 Р(Аг)-2Р(Аг7А7) +
+ 2Р(4г V4;V^)- ... +(-1)п+1Р ( и А^
\ I = 1 /
или
( п 'j ( п _ )
Р П Ai =1- Р и Аг .
U = i J [г-1 )
366
В последнем случае используется обобщение известной в математической логике
теоремы де Моргана
ЛЛ4=Л V ^2
или в эквивалентной записи
4 V л2 = А V Л2.
Следствие П1.2.4. В формуле (П1.2.8), поменяв местами Лу и Аг, получим
Р (AtAA2) = Р (Л2 | Лх) Р (ЛО,
Р(А0 Р(А2 |Л)= Р (Л2) Р (Л1| Л2). (П1.2.9)
Теорема умножения вероятностей для независимых событий. Используется
следствие П1.2.3, для независимых событий теорему умножения вероятностей
можно записать в виде
р( П лЛ^р^ААА ...длп) =
\/ = 1 /
= Р(Л1)Р(Л2)...Р(ЛП)= П P(Ai). (П1 2 10)
I— 1
Следствие П1.2.5. Для несовместных случайных событий /If и Л2
Р (4j Л Л2) = Р (0 = 0. (П1.2.11)
Следствие П1.2.6. Независимые случайные события At и А2 всегда совмест-
ны, так как
P(AiA А2)> Р(А}) Р(А2)> 0 (П1.2.12)
(Р (<41) > 0, Р (Л2) > еслн -41 и Л2 не являются невозможными событиями).
Теорема сложения для совместных случайных событий. Рассмотрим два
совместных события А± и Л2. Для них можно записать
Р (At V Л2) = Р (4J + Р (Л2) - Р (Д, Д Л2). (П1.2.13)
Для п совместных случайных событий Alt А2, .... Ап формула сложения вероят-
ностей (П1.2.13) имеет вид
(п \ п п— 1 п
ил = 2рш-2 5 тлл7)+
»=! / f = l Z = l 1 = 1+1
п — 2 п~ 1 п [ п \
+ 2 2 2 +(_l)n+ip П Л (П1.2.14)
1 = 1 /=<+1 &=/+! \< —1 /
Формулу (П1.2.14) можно переписать в виде выражения
Р ( U Ai ) = 1 —Р ( П Ai ),
\i=l ) V = 1 /
полученного также на основании теоремы де Моргана.
Формула полной вероятности является обобщением формул умножения и
сложения вероятностей. Если событие Ло может осуществиться лишь при условии,
что произошло какое-нибудь событие А, из числа несовместных событий Ai,
А2, .... Ап, вероятности которых известны, и если известны условные вероят-
ности Р (A0/Ai) (для всех i = 1, 2, п), то вероятность события Р (<40) может
быть вычислена по формуле полной вероятности
Р(Ло)= 2 р(л')р(/,ом1). (П1.215)
1 = 1
367
Действительно,
Ло= U Ио Л Л,)
I = 1
На основании правила сложения вероятностей имеем
! п \ п
Р(Ло) = Р U (ЛоДЛг) = р(лоАЛ;).
м = 1 / / = 1
а на основании правила умножения вероятностей каждое из слагаемых пред-
ставляем в виде
Р(ЛоА^) = Р(^)РМоМ^
откуда окончательно получаем
Р(Ло)= 2 Р(Л,)Р(Л0|ЛД
I = 1
Формула вероятностей гипотез (формула Байеса).
Несовместные события Лр А2, .... Ап, при которых только и может насту-
пить событие Ло, называют гипотезами относительно Ло
Вероятность Р (Лг) осуществления гипотезы Аг, вычисленная безотноси-
тельно к событию Ао, называется априорной вероятностью.
Условная вероятность гипотезы Аг, вычисленная в предположении, что
событие Ао имело место, называется апостериорной вероятностью и опреде-
ляется по формуле
Р(Л;|Л0) =
Р(Л,)Р(Ло|Л;)
п
2 Р(Лг)Р(Л0|Л,)
(П1 2 16)
П1.3. Случайные величины и функции распределения
Случайная (стохастическая) величина — переменная величина, значение
которой может случайным образом меняться от опыта к опыту.
Детерминированная величина — неслучайная величина.
Дискретная случайная величина — случайная величина, которая может
принимать только конечное или счетное множество значений.
Непрерывная случайная величина — случайная величина, которая может
принимать любые значения из замкнутого или открытого (возможно, бесконеч-
ного) интервала.
Смешанная случайная величина — случайная величина, которая может
принимать любые значения из замкнутого пли открытого (возможно, беско-
нечного) интервала, причем конечное или счетное подмножество ее значений
может появляться с отличной от нуля вероятностью.
Функция (интегральная функция) распределения случайной величины £ —
вероятность события {| ч х}, где х — переменная величина:
F («) — #’{£< х} (П13 1)
Следствие П1 3.1. Из определения функции распределения следует, что
F (— оо) = 0,
F(+oo)=l, (П1 3 2)
0 < F(x) < 1.
Эвв
Следствие П1.3.2. Из определения функции распределения имеем
P{xi<Z< x2} = F(x2)-F(X1) (П1 3 3)
В частности, для непрерывной случайной величины
•3°{x<g < x+0} = F(x + 0)—F(x) = 0,
т. е. вероятность того, что непрерывная случайная величина примет конкретное
значение х, равна нулю.
Следствие П 1.3.3. Если некоторая дискретная случайная величина с ве-
роятностью Pi принимает определенное значение xt из конечного числа п воз-
можных значений xi, х2,.... хп, то функция распределения может быть записана
в виде
X < X,
х, < х < х2
Х2 < X < х3
X. < X < х4
Хп_2 < X
*П-1 < X
Х>ХП
(Ш 3 4)
Хп—1
хп
Примечание. Если число возможных значений п = 1, т. е. дискрет-
ная случайная величина может принять одно и только одно значение с, то такая
величина является детерминированной, или неслучайной. Функцию распреде-
ления ее можно записать следующим образом:
(О,
AW = (1
х < с,
X > с
(П1 3 5)
Плотность распределения случайной величины (дифференциальная функция
распределения, плотность вероятности} — предел отношения вероятности то
го, что случайная величина £ при испытании примет значение, лежащее в интер-
вале [х, х + Ах], к величине интервала Ах, когда Ах -* 0:
Дх->0 Ах
Иными словами, плотность распределения есть первая производная от ин-
тегральной функции распределения
d
t(x}=— F(x} = F'(x) (П13 7)
Плотность распределения обладает следующими очевидными свойствами:
1) f (х) > 0 для всех значений х,
4*-ОО
2) j f (х) dx = 1, так как этот интеграл означает вероятность реализации
—оо
любого (хотя бы какого-нибудь) значения случайной величины, что является до-
стоверным событием
Следствие П 1.3.4. Из определения плотности распределения (П1.3.7) сле-
дует
х
F(x) = J t(x)dx.
— оо
Отсюда и из (П1.3.3) вытекает следующее утверждение.
369
Следствие П 1.3.5.
ь
Р(а < х <fe) = f (fe) —f (а)= J l(x)dx.
а
(П1.3.8)
Условной плотностью распределения случайной величины в точке х будем
называть плотность распределения, вычисленную при условии, что случайная
величина больше, чем х — Ах, при Дх -> 0:
к (х) = Нх)/[1 - Г (х)]. (П 1.3.9)
Примечание. Могут быть определены условные плотности распре-
деления и для других условий, одиако в теории надежности именно данная ус-
ловная плотность наиболее важна.
П1.4. Числовые характеристики случайных величин
Математическое ожидание (среднее значение) случайной величины о пре де-
ляется
а) для дискретных случайных величин В
Mi(£)= W(x = хг}’ (П1.4.1)
б) для непрерывных случайных величин g
+ □0
Mx(g) = J 4(x)dx; (П1.4.2)
—• 00
в) для неотрицательных случайных величин g
A4j(g) = f [1-F(x)]dx=f P(x)dx. (П1.4.3)
О о
Удобно записывать Мг (g) в обобщенной форме
Mi(g) = Г xdF (х).
—• 00
Примечание. Математическое ожидание часто называют начальным
моментом первого порядка для распределения F (х). Начальный момент л-го
порядка для случайной величины g определяется как
Mn(g) = °f xndF(x).
— оо
Следствие П1.4.1. Из формул (П1.3.5) и (П1.4.3) имеем
ML (с) = с. (П1.4.4)
Следствие ГН.4.2. Из правила вынесения постоянной за знак интеграла
следует
Mi (eg) = сМ (g). (П1.4.5)
370
Следствие П1.4.3. Из правила об интеграле суммы сумма любых случай-
ных величин определяется
(п \ п
2 ч = 2 м®-
i=i / z=i
(П1.4.6)
Следствие П1.4.4. Из следствий П1.4.2 и П1.4.3 вытекает
М (с + g) = с + М (g).
(П1.4.7)
Следствие ГИЛЛ. Для произведения независимых случайных величин
из правила разделения независимых переменных в n-кратных интегралах сле-
дует
Ah( П
V = 1
П MHgi).
r = i
(П1 4 8)
Дисперсия случайной величины — характеристика разброса случайной ве-
личины g, определяемая по формулам
D(g)=Al1(g-Al(x))2 (П14 9)
ИЛИ
r>a)=M1(g2)-(M1(x))2; (П1.4.Ю)
а) для дискретных случайных величин g
D(g) = 2 {х = Xi} (Xi-М (х))2 (П1.4.11)
или
п / п \ 2
D(g) = 3 ^{g = x;}x?- ’ (П14 12)
0= 1 V = 1 /
б) для непрерывных случайных величин g
D(g)= f £(х) [х —М (x)]*dx (П1.4.13)
— оо
ИЛИ
D(x) = J х2[(х)с1х—( j xfi (х) dx j . (П1.4 14)
--ОО \--00 /
Удобно записывать D (х) в обобщенной форме
ОО
D(g) = J [х-М (x)]dF(x).
— оо
Примечание. Дисперсию часто называют центральным моментом
второго порядка для распределения F (х).
Центральный момент п-го порядка случайной величины определяется как
Dn(£) = J [х-Л1(х)]МГ(х).
— оо
371
Следствие П1.4.4». Из определения дисперсии и из (П1.4.4) вытекает
D (с) = 0. (П1.4.15)
Следствие П1.4.7 Из (П1.4.9) и (П1.4.5) имеей D (сх) = c2D (х). (П1.4.16)
Следствие П1.4.8. Из (П1.4.11) и (П1.4.15) следует D (с + х) = D (х). (П1.4.17)
Следствие П1.4.9. Для суммы независимых случайных величин
D ( 2 xt ) = 2 (ni 4 18)
\/ = 1 / i = I
Среднее квадратическое (стандартное) отклонение — величина, опреде-
ляемая по формуле
о =I1/d7DI-
Коэффициент вариации случайной величины — величина, определяемая по
формуле
v = о/ М (х).
Центрированная случайная величина g° — случайная величина, полученная
из исходной § как
- 5 - М (g).
Нормированная случайная величина g* — случайная величина, полученная
из исходной как
5* = g/a.
Центрирование и нормирование случайных величин очень часто использу-
ется при табулировании функций распределения.
Медиана (срединное или вероятное значение) — такое значение Me случай-
ной величины, при котором
Р (£ < Me) = Р (g > Me) = 0,5,
т е. F (Me) — 0,5.
Примечание. Для дискретных величин медиана может определяться
неоднозначно.
Мода — такое значение Мо случайной величины, для которой при непрерыв-
ном распределении плотность вероятности принимает максимальные значения.
Квантиль уровня р — такая величина gp, при которой Р (g < g„) =
= Р (Ы = ₽•
П1.5. Сводка характеристик функций распределения
В табл. П1.5.1. приведены выражения для плотностей различных непре-
рывных распределений, а также основные характеристики: математическое
ожидание, дисперсия и мода.
В табл. П1.5.2 содержатся аналогичные сведения для дискретных распре-
делений (приведены распределения, лишь наиболее часто используемые при ве-
роятностных расчетах или статистических оценках в задачах надежности).
372
Таблица П1.5.1 Основные непрерывные распределения Мода [ <3 о» О О CU у/ а — hca (при а > 1)
Дисперсия « 'о' СЧ —ц о» О е2а+’! (е” -1) / 2 \ Г 1\ Г ( 1 4-—) — Г2 1 ) \ а / \ а/ . ”/гэ
Матем атиче ское ожидание а+ Ь е“ + 3
Плотность распределения 1 (х-аУ —~=е а И (In х—ay U=r-e 2о‘ Хг К 8 ’т t о X
Область значений (а, 6) 8 (0, оо) (U, оо)
Распределение Равномерное Нормальное (Гаусса) Логарифмически нормальное Г неденко-Вейбулла оэ os ..
£
«с
s
Mo та ‘ (Г— I1 “Г (при Я> -1) 1 OJ с а + b — 2 о
Дисперсия Ч- г. , *се СЧ ah + + <3 + 04 _ 1 с |сч
| Математиче ское ожид аниь, <3 1^- — jr< Q j + О
Плотность, распределения ч со» 1 (D О X рз е «• ч . и|я 1 <и *!« 7 Д4 U, 1 X И* 1 1 d И гттп ih [в 4^ + "к X е 1 О) । »
Область значений (0. со) (0, со) 8 (0, 1) (— со, оо)
Распределение Гамма-распределение Экспоненциальное 1 ^-распределение Бе та-ра (Определение Стьюдента
Таблица П1.5Т
Основные дискретные распределения
>—.— Распределение Возможное значение Вероятность Математи- ческое ожидание Дисперсия
Биномиальное 0, 1, 2, ...,п II •% II 1 S пр прч
Гипергеометри- ческое 0, 1, ... ..., min (ДТ, п) II С) S3 С) (?) •U С М (N-МУ п (N-n) № (N-l)
Пуассона 0, 1, 2, ... р А А т! е X X
Геометрическое 7 0, 1, 2, ... Рт = pqm~' q/Р2
/ 7 /
Отрицательное биномиальное г. г+ 1, ... Р Л’Г—1 Г)ГПШ’-Г т— ^ГП—\Р ч Г/Р qr/P2
П1.6. Предельные теоремы теории вероятностей
Неравенство Чебышева. Для неотрицательной функции ш (?) случайной
величины g и любого k >> 0 выполняется неравенство
В частности,
Р & (g) > k) < М !ш (?))/fe.
Р (I Б — Мх (?) | > fea) < 1//г2,
где о — среднее квадратическое отклонение случайной величины ?, а ЛД (?) —
ее математическое ожидание.
Теорема Бернулли. Если Проводится п независимых опытов, в каждом из
которых некоторое событие осуществляется с вероятностью р, то частость
(относительная частота) появленяя события р при п -* оо сходится по вероятности
к р, т. е. при любом 8 > О
lim р / |д_д| > е|= о.
п-^оо ' '
Теорема Пуассона. Если прОВОдИТСЯ п независимых опытов и вероятность
осуществления события в i-м ог>ыте равна pi, то частость появления события р
при п -> оо сходится по вероятное™ к среднему из вероятностей о,-, т. е. при
любом 8 > О
lim Р
п -> оо
- 1 I 1
Р — --- 2 Pi > 8 =0.
п i=:1 I )
Теорема Чебышева. Если в п независимых опытах получены реализации
61. 5а... случайной величцНЬ1 g, то ПрИ п оо среднее арифметическое
375
сходится по вероятности к математическому ожиданию этой случайной величины,
т. е. при любом е > О
(I 1 « I )
НтР — 2 gi-AlU) >е =°.
П-+ОО U /в| * '
Центральная предельная теорема. Если .......In — независимые одина-
ково распределенные случайные величины, имеющие математическое ожидание
Alt и дисперсию о2, то при п оо распределение нормированной случайной
п
величины £ == S сходится к нормальному
1=1
{Ё-------ПЛ"11 1 1 р #2/0
а < -----7=- < Ь\ = • \ е * dt = Ф (Ь)— Ф (а)
о у п ) у 2л J
При определенных условиях нормированная сумма и неодинаково распре-
деленных случайных величин также имеет нормальное распределение.
Теорема Лапласа. Если проводится п независимых опытов, в каждом из ко-
торых некоторое событие осуществляется с вероятностью р, то
lim Р
п-*сх>
Уп — пр
Упр(1 — р)
< Ь } = Ф(6)—Ф (а),
а <
где Vn — число появлений интересующего события в п опытах.
Приложение 2
ОСНОВНЫЕ ПОНЯТИЯ и КРАТКИЕ СВЕДЕНИЯ
ИЗ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Статистическое описание любого физического явления обладает тем свой-
ством, что, хотя результат отдельного измерения физической величины х не
может быть предсказан с достаточной точностью, значение некоторой «подходя-
щей» функции y(xlt х2..хп) от множества результатов xlt х2... повторных
испытаний может быть предсказано с существенно лучшей точностью. Такая
«подходящая» функция называется статистикой, а указанное свойство физи-
ческого процесса — его статистической устойчивостью.
Испытание (или опыт) — осуществление на практике какого-нибудь
комплекса условий.
Реализация случайного события — событие, которое осуществилось в ре-
зультате проведения опыта.
Реализация случайной величины—величина, которая получена в результате
проведения опыта.
Генеральная совокупность — множество, включающее все однородные объек-
ты, обладающие интересующими качествами.
Случайная выборка — часть генеральной совокупности, отобранная наугад
Репрезентативная (представительная) выборка — выборка, в которой про-
порции объектов различных типов в среднем соответствуют пропорциям в гене-
ральной совокупности.
Статистические оценки — числовые характеристики <р (х1, х2, .... хп) эм-
пирического распределения, полученные в результате обработки наблюдений
случайной выборки объема п.
376
Частость (относительная частота) случайного события. Если N раз
проведен опыт, в котором возможно появление некоторого события А, и при этом
nN раз это событие фактически имело место, то частость появления указанного
события равна
WN{A) = nN!N.
Вероятность случайного события (статистическое определение). Можно
ваметить, что при увеличении числа опытов N значение WN(A) начинает все
более и более устойчиво приближаться к некоторому числу Р (А). Вероятность
случайного события может быть определена как предел WN(A) при безграничном
увеличении числа опытов N:
lim WN (4)= lim nN'/N=P (Л).
2V-+oo Л/-+ОО
Величина WN сходится по вероятности к величине Р, если для любого сколь
угодно малого е может быть выбрано такое N, что вероятность выполнения не-
равенства | WN — Р| < е будет сколь угодно близка к единице, т. е.
lim ^{|U7W-P| < е} = 1.
W—оо
Вариационный ряд п реализаций случайных величин — совокупность рас-
сматриваемых величин, расположенных в порядке возрастания (неубывания):
К Х2 Хп
Размах эмпирического распределения — величина
Х = хп —
Эмпирическая функция распределения (для п реализаций случайных вели-
чин) — функция Fn (х), определяемая равенствами
Рп М =
О для х < х^,
i
-- ДЛЯ Xi < X < Xi+i,
п
1 ДЛЯ X > хп
1 < i < п— 1J
При безграничном увеличении числа опытов максимальное отклонение эмпи-
рической функции распределения от теоретической с вероятностью единица
сходится к нулю (теорема Гливенко):
J lim max|E(x)— Fn (х) | = 0| = 1.
I /2-+0О X J
Гистограмма (для п реализаций случайных величин) —• функция fn (х),
определяемая^авенствами
fn(x)=—~~ -для ~ < х <х 0) +
п &Xi 2 2
Здесь aj — число наблюдений, удовлетворяющих неравенству
Ах, , Ах,
— —— < X < Х(,) + —— I
A*!, Axg, Ахт — длины интервалов группировки:
х“\ .... х(т) —середины интервалов группировки.
377
Группировка — некоторое разбиение интервала, содержащего все п наблю-
денных результатов xt, х2, ..., хп, на т интервалов, называемых интервалами
группировки.
Точечная оценка параметра <р — оценка <р, зависящая только от результа-
тов испытаний (xt) .....хп) и известных величин, ио не от неизвестного пара-
метра.
Несмещенная оценка <р параметра <р — такая оценка, математическое ожи-
дание которой совпадает с оцениваемым параметром независимо от числа наблю-
дений, т. е. при любом п
М {<р (xt, х2, ..., хп)} = Ф
Асимптотически несмещенная оценка —такая оценка, математическое ожи-
дание которой совпадает с оцениваемым параметром при п оо.
Состоятельная оценка <р — такая оценка, которая при неограниченном
увеличении числа опытов сходится к оцениваемому параметру ф по веро-
ятности, т. е. при любом е >• 0 имеет место соотношение
lim ^ { | ф — ф | > е} =0
П—>оо
Эффективная оценка <р — такая оценка, которая характеризуется мини-
мальным из всех возможных значением дисперсии оценки <р относительно пара-
метра ср.
Достаточная оценка (статистика) — такая оценка <р параметра ф, что
условное распределение вектора результатов испытаний (xlt х2, .... хп) при из-
вестном значении ф не зависит от параметра ф. Каждая эффективная оценка
является одновременно и достаточной.
Метод наибольшего правдоподобия — метод нахождения так называемой
оценки максимального правдоподобия. Пусть случайная величина £ имеет
плотность распределения / (х, а). Функция
п
L(xlt ......хп; а) = П f(xk, а)
k= 1
называется функцией правдоподобия. Если случайная величина дискретна и
принимает значения г1( г2, ... гп соответственно с вероятностями Pi (а), р2 (а),
.... Рп(а). гДе
п
2 Ра (а) = 1,
А=1
то функция правдоподобия берется в виде
п
Ц-Н Х2......хп', а)= П Ра, (а),
(=1
где индексы у вероятностей показывают, что наблюдались значения zftl, гд2, ...,
г/,п. Метод максимума правдоподобия состоит в том, то в качестве оценок пара-
метра а принимается то значение а, при котором функция L достигает своего
максимума. Поскольку L и In L достигают экстремума при одном и том же
значении а, то эти критические значения а определяются из уравнения прад-
доподобия
Э1пЕ „
378
Гели для параметра а существует эффективная оценка а, то уравнение правдо-
подобия имеет единственное решение а.
Метод моментов —общий метод точечной оценки неизвестных параметров
состоит в том, что моменты распределения, зависящие от неизвестных нам па-
раметров, приравниваются эмпирическим моментам. Взяв число моментов, рав-
ное числу неизвестных параметров, и составив соответствующие уравнения,
получим необходимое число уравнений.
Метод квантилей (так же чисто эмпирический как и метод моментов), сос-
тоит в том, что квантиль теоретического распределения приравнивается к эмпири-
ческой квантили (если оценке подлежат несколько параметров, то соответствую-
щие уравнения пишутся для нескольких квантилей).
Доверительный интервал — интервал, накрывающий неизвестное значение
оцениваемого параметра <р с вероятностью не меньше заданной.
Доверительные границы (верхняя и нижняя) — крайние точки довери-
тельного интервала.
Двусторонний доверительный интервал для параметра <р с коэффициентом
доверия, не меньшим а, случайный интервал (ф (х), ср (х)], концы которого
Ф (х) < ф < ф (х)
зависят только от исходов испытаний х и для любого ф > О
^®{ф(х) < Ф<Ф (х)}>а.
Верхний [—оо, <р (х)] и нимний\д> (х), +оо] односторонний интервал—слу-
чайные интервалы, для которых при любом ф > 0 соответственно
SP (ф < ф (x)}>aj
&> {ф (х) < ф} > а.
Доверительный уровень (доверительная вероятность) — вероятность Р
выхода параметра ф за доверительные границы:
Р = 1 — а,
где а — коэффициент доверия.
Средняя арифметическая реализаций случайной величины — величина
определяемая как
1 п
х = — 2 xt-
Несмещенная оценка дисперсии реализаций случайной величины — вели-
чина, которая находится по следующей формуле:
s2=~4 2
п~~ 1 /=1
Вероятность ошибки первого рода — вероятность отклонить некоторое
предположение, когда оно верно.
Вероятность ошибки второго рода — вероятность принять некоторое пред-
положение, когда оно ложно.
Уровень значимости критерия а — вероятность непринятия проверяемой ги-
потезы, когда она верна.
379
Приложение 3
ПОТОКИ
П3.1. Определения
Потоком однородных событий называется случайный процесс, образован-
ный совокупностью случайных моментов 4, t2........ /д+i, ... появления
этих событий, где t^+i > k > 1.
В теории надежности обычно исследуются потоки двух видов: поток момен-
тов отказов (устройства) и моментов окончания ремонтов (отказавшего устрой-
ства); оба эти потока могут быть охарактеризованы случайным процессом rj (I),
означающим соответственно число отказов или число произведенных ремонтов
на интервале времени (0,/). Таким образом, в общей классификации случайных
процессов (рис. ПЗ.1.1) потоки, рассматриваемые в теории надежности, отно-
сятся к дискретным случайным процессам (по типу множества значений слу-
чайной функции) с непрерывным временем (по типу множества значений аргу-
мента).
В общем случае для задания потока необходимо задать для каждого п 1
распределение случайного вектора (г1; г2, ..., гл), где
гА = <й-^_1, k>l, (о = О. (П3 11)
Если случайные величины ц, г2, .. , гп независимы в совокупности, т. е.
для любой группы гг1, zI2...г,- (Zj < :2 < ... < im) этих случайных вели-
чин имеет место равенство
{г < t , г < t ......г < t } =
i it' it im
= </Zi}^{zi2</,2) .. (ПЗ 1 2)
то соответствующий поток называется потоком с ограниченным последействием.
Для задания такого потока, очевидно, достаточно задать набор функций рас-
пределения
Fk(t) = &{zh< t). k>l. (П3.1.3)
Поток с ограниченным последействием, для которого
F2 (0 = F3 (Z) = ... = F (О, (ПЗ.1.4)
называется рекуррентным потоком с запаздыванием, определяемым функциями
распределения (/) и F (/).
Рекуррентный поток с запаздыванием, для которого
MWW, (ПЗ.1.5)
называется просто рекуррентным потоком. В этом случае F (/) — функция
распределения длины промежутка между любыми двумя последовательными
моментами наступления событий.
Рекуррентный поток, для которого
F (0 = 1-е-Ч а > О, (ПЗ 1.6)
называется пуассоновским потоком, при этом а (среднее число событий, насту-
пающих в единицу времени) есть интенсивность пуассоновского потока. Для
пуассоновского потока вероятность (/0, t), й > О, наступления ровно k со-
бытий в промежутке (/0, t0 + t) равна
pft(^0=Pft(0=^e-a< (П3 1.7)
380
и не зависит от 4. т. е- в пуассоновском потоке время ожидания наступления
нового события не зависит от того, сколько прошло времени после последнего
наступления события; это свойство называется отсутствием последействия.
В частности, если обозначить через 0(о время ожидания наступления первого
после момента /0 события, то
5° {0Zo </} = l-e“aZ. (ПЗ 1 8)
Дискретный
Не пр ерь вкуй
С дискретным временем
(случайная поолеровцтельность]
С непрерывным временем
Стационарный
Нестационарный
Со стационарными..
С Нрзависи мыми. —~2ййыприраще-
Снекоррелировачнымир ниями.
С ортогочальнь ми /
Эргодцчесчиу
Незргода чесвий
Марковский
Немарковский
Сйц^й
Специальный
Рис. ПЗ 1 1. Классификация случайных процессов.
Для пуассоновского потока математическое ожидание случайного числа г] (/)
событий, наступивших за время Л равно
СО
= 2 kph(f)=at. (П3 19)
fe = 0
Пуассоновский поток можно также определить тремя характеристически-
ми свойствами, которые, являясь в известном смысле качественными, приводят
381
к строгому определению, которое было дано выше. Эти характеристические
свойства следующие:
1) свойство стационарности, которое означает, что вероятностные характе-
ристики потока для любого интервала времени зависят только от протяжен-
ности этого интервала, но не.зависят от момента, когда он начинается;
2) свойство ординарности, которое означает, что в бесконечно малом ин-
тервале времени вероятность появления более чем одного события есть величина
большего порядка малости,чем вероятность появления ровно одного события;
3) свойство отсутствия последействия, которое означает, что вероятность
появления события в потоке, начиная с некоторого произвольного момента
времени, не зависит от всей предшествующей реализации этого потока.
Точные определения этих свойств (справедливые, естественно, для произ-
вольного потока) могут быть сформулированы следующим образом:
1) обозначим т] (/) число событий, наступивших в интервале (0, /). Поток на-
зывается стационарным, если для всякого натурального числа п > 1, всякого
набора чисел тх, т2, ..., тп, такого что
О < Tj < т2 < ... < тп,
и всякого т > 0 распределение случайного вектора
<П И + И) — П И), П (т + т2) — п (т)... т] (т + тп) — т] (т)}
не зависит от т. Из свойства аддитивности математического ожидания следует,
что для стационарного потока существует такое неотрицательное число а, что
Л1т] (/) = at. (ПЗ.1.10)
Здесь число а есть интенсивность стационарного потока}
2) поток называется ординарным, если
lim {п(т) > 1}/т = 0; (ПЗ 1 И)
т — О
3) обозначим через Л интервал (t0, t0 -f- /). Поток событий называется по-
током с отсутствием последействия, если для любого набора непересекающихся
интервалов Д1( Д2, ..., Дп случайные числа г] (Д2), г] (Д2), ..., г] (Дп) независимы.
Для того чтобы поток событий был стационарным ординарным потоком с от-
сутствием последействия, необходимо н достаточно, чтобы он был пуассоновским.
Стационарный ординарный поток с ограниченным последействием назы-
вается потоком Пальма. Поток однородных событий является потоком Пальма,
если это есть рекуррентный поток с запаздыванием, определяемым функциями
t
F2(/)= a J[l—f (u)\du и F(t), (ПЗ 1 12)
О
где а-1= J [1 — F(u)]du.
о
Примером ограниченного потока может служить поток Бернулли. Пусть
в каждом из п независимых «источников» в интервале (0, t0) обязательно проис-
ходит лишь одно событие, причем для каждого «источника» вероятность появ-
ления события в любом интервале, содержащемся в (0, t0) и имеющем длину Д,
равна Д//о. Суммарный поток, получающийся наложением этих потоков, и есть
поток Бернулли.
Пусть pk (0 — вероятность появления k событий потока Бернулли в
(О,/) С (0, /о)- Так как вероятность наступления данного события в (0, /) равна
t/t0 и события наступают независимо, то
./ t \k / t \n—k
Pk&=cn\~r] i-~ • (П3.1.13)
Альтернирующий процесс восстановления. Процесс функционирования лю-
бого устройства с точки зрения надежности может быть представлен в виде чере-
382
дующейся последовательности интервалов нормального функционирования и
интервалов простоя (ремонта) устройства 0!, ....0А, где 0й — случай-
ное время работы устройства с момента окончания предыдущего ремонта до мо-
мента наступления следующего k-ro отказа, а —случайное время простоя
(ремонта) из-за k-ro отказа.
Если все величины 0й имеют одной тоже распределение F (/), а случайные
величины имеют одно и то же распределение G (/), причем все рассматривае-
мые случайные величины взаимно независимые, то говорят, что имеет место
альтернирующий процесс восстановления.
При рассмотрении процессов функционирования высоконадежных устройств
часто сталкиваются с такими альтернирующими процессами восстановления,
у которых периоды нормального функционирования в среднем намного больше
периодов простоя. В этом случае иногда можно рассматривать процесс функцио-
нирования, состоящий из одних отрезков 0ft, считая, что отказы устройства уст-
раняются практически мгновенно. Такой процесс называют просто процессом вос-
становления; поток отказов в этом случае будет просто рекуррентным потоком.
Для многих задач надежности иногда необходимо знать распределение
R (/) остаточного времени от произвольной точки до ближайшего события в ста-
ционарном рекуррентном потоке (определяемом функцией распределения F (I)):
R (/) = < (},
где £ — случайное расстояние от произвольной точки до момента наступле-
ния ближайшего события (остаточное время). Можно показать, что
/?(0 = а J [1 — FJ(u)]du, (ПЗ.1.14)
t
где a~l=J [1 — F (u)]du.
о
П3.2. Просеивание потока
Поставим в соответствие каждому моменту наступления события k > 1,
число 6й = 6 (th), принимающее значение 0 или 1. Поток событий, наступивших
в моменты t^ для которых = 1 (т. е. fe-e событие при = 0 «теряется»,'при
6(1 = 1 остается) называется просеянным (разреженным) потоком.
Для полного определения просеянного потока нужно (кроме задания основ-
ного потока) задать для каждого п > 1 вероятности
P(5i, 62, ..., 6П) = {6 (t-d = 6Ь 6 (/2) = 62, .... 6 (/п) = 6П},
6; = 0 или 1, (=1,2,......... (П3.2.1)
Пусть исходный поток является рекуррентным, определяемым функцией
распределения F (t). Тогда рекуррентная операция просеивания задается соот-
ношениями
р(1) = а0;
р(0, 1) = ^;
р (0, 0, 1) = а2;
Р(0, о, 0. l)=aft;
k '
(ПЗ 2.2)
ОО
S ah = \.
fe = 0
383
Смысл рекуррентной операции просеивания заключается в том, что если
I — случайное число, принимающее значения 0, 1, 2, ... и 3s {I = k} = ati,
k > 0, то просеянный поток получается следующим образом: сначала случай-
ное число I событий основного потока «теряется», следующее затем событие
остается, затем снова случайное число I (имеющее тот же закон распределения)
событий «теряется», следующее событие основного потока остается и т. д. Поток
оставшихся событий и есть просеянный поток.
Функция 31 (г), определяемая как
5?(г) = 2 айг*, 31 (V) = 1, (ПЗ 2.3)
k = 0
называется функцией, задающей рекуррентную операцию просеивания.
Справедливы два следующих утверждение:
1) поток, получаемый из рекуррентного потока с помощью рекуррентной
операции просеивания, есть рекуррентный поток;
2) если поток, получаемый из рекуррентного потока путем просеивания
(разрежения), снова является рекуррентным, то существует такая рекуррент-
ная операция просеивания, с помощью которой можно получить этот же поток.
Если основной поток пуассоновский с параметром а, а операция просеи-
вания задается функцией
1 — Р
31(г)=------- = (1-р) + (1-р)рг + (1-р)рЗг2+ (ПЗ 2 4)
1 —гр
которая означает, что любое наступившее событие основного потока с вероят-
ностью р «теряется» и с дополнительной вероятностью 1 — р = q остается, то
просеянный поток будет пуассоновским с параметром qa. При просеивании
произвольного рекуррентного потока, определяемого функцией распределения
F (/), имеющей математическое ожидание
а-1— f [1 — F (w)l du,
о
просеянный поток будет снова рекуррентным. Если теперь изменить масштаб
времени просеянного потока таким образом, чтобы средняя длина интервала
между двумя последовательными моментами наступления событий просеянно-
го потока совпадала с соответствующей длиной для исходного потока, то полу-
ченный таким способом поток будет рекуррентным, определяемым некоторой
функцией распределения Е(1) (/). Продолжая эту операцию, в пределе полу-
чаем пуассоновский поток, т. е.
limFw(f) = l-e"<1'. (ПЗ 2 5)
П-юо
Если основной поток пуассоновский с параметром а, а операция просеи-
вания задается функцией
31 (г) = г*, (ПЗ.2.6)
которая означает, что первые k событий ^основного потока «теряются», (fe-f-l)-e
событие остается, затем снова k событий «теряются», следующее событие остает-
ся и т. д., то просеянный поток будет потоком Эрланга fe-ro порядка (рекур-
рентным), при этом плотность распределения fk+1 (I) интервала между сосед-
ними событиями в этом потоке имеет вид
а (а/)*
fft+i(0 = е~а<- (ПЗ 2 7)
384
Математическое ожидание Sft и дисперсия о! случайой величины, распределен-
ной по этому закону, равны соответственно
k -f-1 k +1
Sa= а 4 = (ПЗ'2'8)
ПЗ.З. Наложение потоков
Рассмотрим п «источников», порождающих события. Поток, событиями ко-
торого являются события, поступившие от всех «источников», называется суммар-
ным потоком, т. е. суммарный поток получается наложением (суперпозицией)
потоков событий, посылаемых «источниками».
Если слагаемые потоки независимы между собой и каждый представляет
собой пуассоновский поток, то суммарный поток будет также пуассоновским с ин-
тенсивностью а2, равной сумме интенсивностей слагаемых потоков, т. е.
п
а2 == 2 (ПЗ 3 1)
где а; — интенсивность (-го суммируемого пуассоновского потока; п — число
суммируемых потоков.
В теории восстановления доказывается, что суперпозиция произвольных
потоков асимптотически сходится к пуассоновскому потоку при сравнительно
слабых ограничениях на составляющие потоки. Интенсивность суммарного
потока а2 при этом равна
п .
«2 = 2 77 • (ПЗ 3 2)
1 = 1
где Ti — среднее расстояние между двумя соседними событиями в t-м сумми-
руемом потоке; п — число суммируемых потоков.
Приложение 4
АНАЛИТИЧЕСКИЕ МЕТОДЫ ОЦЕНКИ
НАДЕЖНОСТИ СИСТЕМ, ПОВЕДЕНИЕ КОТОРЫХ
ОПИСЫВАЕТСЯ ОДНОРОДНЫМ МАРКОВСКИМ
ПРОЦЕССОМ
П4.1. Общий принцип составления систем уравнений
Большое число аналитических результатов может быть получено при оцен-
ке восстанавливаемых систем для тех случаев, когда все распределения времени
работы и времени восстановления отдельных элементов являются экспоненци-
альными.
Следует заметить, что предположение об экспоненциальности распределе-
ний не всегда оправдано. Особенно это относится к распределениям времени
восстановления, поскольку предположение о постоянстве остаточной длитель-
ности ремонта является довольно неестественным. Однако если в среднем время
безотказной работы элементов значительно больше времени ремонта, то многие
13 Зак 943 385
показатели надежности не зависят от характера распределения времени ре-
монта
Если известно словесное описание принципа функционирования и восста-
новления системы, то можно определить множество всех возможных состояний
системы, причем, задав определенный критерий отказа, все состояния можно
разделить на два класса: работоспособности и отказа. Если известны интенсив-
ности отказов и восстановления отдельных элементов системы, то может быть
построен граф переходов, у которого вершинами будут возможные состояния си-
стемы, а ребрами — возможные переходы с интенсивностями, определяемыми
соответствующими характеристиками надежности и ремонтопригодности эле-
ментов Например, если известно, что система находится в некотором состоянии
Hl и для перехода ее в состояние Н} необходимо, чтобы произошло определен-
ное событие (отказ какого-либо элемента или восстановление), то от состояния
Hi к состоянию Н} проводится стрелка, у которой указывается интенсивность
реализации данного события. Заметим, что не все события (переходы) могут ока-
заться разрешенными при построении подобных графов. Так, если, например,
имеется всего одна ремонтная бригада (полностью ограниченное восстанов-
ление) и восстановление производится в порядке поступления отказавших эле-
ментов, то в случае очереди отказавших элементов не может произойти прямой
переход из данного состояния в состояние, где восстановленным окажется не
гот элемент, который находится в процессе восстановления. Следует заме-
тить, что все подобные ограничения на граф переходов в явном виде содержат-
ся в словесном описании принципа функционирования и восстановления систе-
мы. На основании построенного графа переходов легко выписать необходимую
систему уравнений, решение которой позволяет получить требуемый показа-
тель надежности.
П4.2. Получение нестационарного коэффициента
готовности
Обозначим через £ множество всех состояний работоспособности системы, а
через е — множество состояний отказа (в соответствии с выбранным критерием
отказа). Обозначим через Е (k) множество тех состояний, из которых возможен
непосредственный переход в некоторое состояние/;. Аналогично обозначим через
г {k) множество состояний, в которые возможен непосредственный переход из
тайного состояния k.
Для каждого состояния k можно записать следующее дифференциальное
уравнение:
Phi*) 2 A-Si + 2
lEe(k) l ЕЕ (1г)
где запись i £ А означает, что суммирование ведется по всем таким состояниям
i, которые относятся к множеству А. Через обозначена интенсивность пе-
рехода из состояния i в состояние j, а через pi (t) — вероятность пребывания
системы в состоянии Hi в момент времени t.
Если граф переходов содержит п различных состояний, то в результате
может быть составлено п различных дифференциальных уравнений. Для на-
хождения нестационарного коэффициента готовности необходимо взять (п — 1)
уравнение указанного вида (любых), одно дополнительное уравнение вида
п
2 Рг й-1
I = 1
и начальные условия вида pi (0) = Pt, где через pt (0) обозначена вероятность
состояния в момент времени t = 0. Если известно, что в момент времени t = 0
система находится именно в состоянии Hi, то рг- (0) = 1 и pj (0) = 0 для всех
остальных состояний / -ф i.
зав
Для нахождения искомого показателя надежности к записанной систе-
ме дифференциальных уравнений применяется преобразование Папласа, в ре*
зультате чего получается система алгебраических уравнений
(х) — ph = — ak (х) 2 Afti + 2 at (x)
i G e (k' I 6 E (k)
(для выбранных n — 1 уравнений),
n
2 ^ai (X) = 1,
Z=1
где at (x^ — преобразование Лапласа для pt (f)\
00
(x) = J Pi (i) e~Ht dt
о
Эту систему уравнений удобно записать
в упорядоченном виде
i’ll «I W +Ьца2 (х) + + i>ln ап (X) = Cj
bZi <h (х) + i22 аг (х) + + *2п ап (х) = сг
Ьщ а,, (х)+6П2аь (х) + + &пп ап (х)=сп,
где Ьц — иоэффициент при /-м члене в i-й строке, а с/ — i-й свободный член
Решить данную систему алгебраических уравнений можно, используя
правило Крамера:
at M=Dt (x)/D (х)
где D (х) — определитель системы алгебраических уравнений; a Dt (х) — тот
же определитель, в котором i-й столбец заменен на столбец свободных членов.
Далее находим преобразование Лапласа искомого показателя надежности
а (х) = 2 at = 777Д Di W
z е ь D ~
Для обращения полученного преобразования Лапласа можно пользоваться
следующей простой процедурой
1. Записываем а (х) в виде
._____До -р Дд х + Д2 ха 4- .. Ч-Am х”1
~ Bb + S, x + S2x2 + . +Sm+Ixm+1
(П4 2 1)
где Aj и Bj — известные коэффициенты
2. Находим корни полинома
В +ВХ х + В2х'2 + 4-Bm+iXm+l = 0.
Пусть эти корни равны
&1> •••
Это означает, что
т+ 1
Bo + BiX+ , + Sm+iXm+‘= П (х— £>;)
= 1
3. Далее записываем а (х) условно в виде суммы простых дробей
а(х)=-^- + -Ц- 4 ... + . (П4.22,
Х-—Ь] X— 02 X — + 1
где р, — искомые коэффициенты
13“ 387
4. Переписываем а (х) в приведенном виде
2 0, П (х-йг)
а(х) = -------------------------
(х— *0 (х —Ьг) • (х— »гац)
и далее, раскрывая все произведения и приводя подобные члены, получаем
_ а0 + х 4~«г х2+ +сстхт
(х — ^1) (х— 6-г) (х — 6т + 1)
где ссг выражены через различные и b
5. Полиномы вида а (х) и (П 4 2 1) равны тогда и только тогда, когда
До = <Хд, А± = <Xi, А% <= о^2, ..., Ащ = (Хщ*
Из этих уравнений определяются искомые коэффициенты аг
6. После нахождения а} к а (х) вида (П4.2.2) применяется обратное преоб-
разование Лапласа (см. приложение П7.7)
т-\-1 n m-f-1
«(Х)= У —О/<(0= У₽,е"‘Л
Примечание. Если (3 (и) имеет кратные корни знаменателя, т. е.
несколько равных значений 6^ то в (П4.2.2) р (х) должно быть записано в виде
Р1 0; Pm + i
х—&1 (х — Ь/)“ X — bm+l
где k — кратность корня й7.
К членам вида Р7/(х — bj)k применяется соответствующее обратное преоб-
разование Лапласа (см. приложение П7.7).
П4.3. Оценка вероятности безотказной работы
При нахождении вероятности безотказной работы необходимо в графе пе-
реходов ввести так называемые поглощающие состояния вместо всех состояний
отказа. Это в принципе означает, что следует обратить в нуль все интенсивности
переходов из любого состояния отказа. При написании дифференциальных урав-
нений можно лишь соответствующими образом изменить области суммирования
Обозначим через Е (fe) множество тех состояний работоспособности, из кото-
рых возможен непосредственный переход в некоторое состояние fe а через
е (fe)—состояния, в которые возможен переход из состояния fe.
Для каждого состояния работоспособности k можно записать следующее
дифференциальное уравнение:
P'kV'^-PkV'l 2 Ад, + 5 ЛгАр((0.
item геем
где использованы те же обозначения, что и в предыдущем пункте.
Если граф переходов содержит т различных состояний работоспособности,
то в результате может быть составлено т различных дифференциальных уравне-
ний. Все эти уравнения и начальные условия вида рг (0) => р( используются
для нахождения вероятности безотказной работы.
388
Для определения искомой характеристики надежности к записанной системе
дифференциальных уравнений применяется преобразование Лапласа, в резуль-
тате чего получается система алгебраических уравнений вида
хаА(х) — а*(х) 2 л«+ S ^kaiix) (П4.3.1)
leek lee {k)
для всех k £ Е.
Решение этой системы уравнений и нахождение интересующей характери-
стики надежности осуществляется далее в точности так же, как и в предыдущем
разделе для нестационарного коэффициента готовности.
П4.4. Оценка среднего времени работы до отказа
и среднего времени работы между отказами
Напомним, что
ОО
о
Нетрудно заметить, что если а (х) есть преобразование Лапласа для вероятно-
сти безотказной работы, то
Т= J е~м P(t)dt
.о
= |х=0.
х=о
Таким образом, чтобы найти среднее время работы до отказа (или между от-
казами), достаточно решить систему уравнений вида
—Рй = а*(0) У, Л*г+ У, A(k ai (0)
ieE(k)
для всех k С Е. (Эта система получается из (П4.3.1) путем приравнивания
х = 0).
Заметим лишь, что для получения среднего времени работы до отказа не-
обходимо взять в качестве начальных условий р, (0) = 1 и р; (0) = 0 для
/ 4= ‘г где i — исходное состояние процесса. В то же время для получения сред-
него времени безотказной стационарной работы необходимо взять в качестве
начальных условий pi (0) = pt, где pt — стационарные вероятности пребыва-
ния процесса в Z-м состоянии (/ С Е)-
П4.5. Представление показателей надежности системы
через определители
Пусть система может находиться в (п + 2) состояниях! Но, Hi, ...,
Hj.... Нп+1, причем последнее состояние Нп+х является состоянием отказа.
Возможны переходы с постоянными интенсивностями из каждого состояния
в любое другое. (Для реальных систем всегда существенная часть этих интенсив-
ностей будет равна нулю, однако здесь это для нас несущественно). Поведение
системы во времени описывается однородным марковским процессом с (п + 2)
состояниями. Здесь будут рассмотрены два случая.
П4.5.1. Состояние отказа //п+1 — поглощающее. По предположению
система, попав в состояние отказа Нп+ъ продолжает оставаться в нем неогра-
13В Зак. 943 38®
ниченно долгое время. Процесс описывается системой дифференциальных урав-
нений, следующих из уравненй Колмогорова—Чепмена
Pi (0— У| Vsi Ps (О >
s=0
п+1 п+1
2й(/) = 1, pis = 0,
t=0 s=0
(П4 5 I)
где pi (f) — вероятность пребывания системы в момент времени I в состоянии
Нй Vst — известные постоянные величины, представляющие собой алгебраиче-
ские суммы соответствующих величин интенсивностей переходов.
Составленный очевидным способом определитель
Voo Кн, ••• Vn0
Voi Vu ••• Vnl
(П4 5 2)
Von Ущ Vnn
назовем определителем системы. Тогда при произвольных начальных условиях
рг(/ = 0) = Л(0),
п+ 1
2} рг(0) = 1, (П4 5 3)
»=о
математическое ожидание Т случайного времени попадания системы всостояние
отказа (поглощающее) Hn+i равно
1 1 1 0
V0o Vlo ••• v01 vn ... Vn0 Vnl Po (0) Pi (0)
von vln ... Vnn Pn (0) (П4 5 4)
Г=Г (— 1)'’+ Voo Vlo v0I vn ••• Vno ••• Vnl
VOn Vln ••• Vnn
Докажем это утверждение; для этого применим к системе дифференциальных
уравнений (П4.5.1) при начальных условиях (П4.5.3) преобразование Лапласа
й<(х)=| р,(/)е~к‘^.
О
Так как
J р‘{ (0 е-и/ dt= — Pt (0)4-ха,(х),
о
то (П4.5.1) преобразуется к виду
У| (V^f хб^) (х) = Pi (0),
s = o
(П4 5 5)
(П4.5 6)
(П4 5 7)
390
где 6Si — символ Кронекера:
=
П,
io.
если s = f
если s=j=l, 0<< <л + 1.
По правилу Крамера из(П4.5.7) при начальных условиях (П4.5.3) получаем
«п +1 (х) = — Лп + J (х)/хР (Х), (П4 5 8)
где в соответствии о (П4.5.6)
V'oo и и1в ••• ИП0 — р0 (0)
^о! Кц—х ••• Vni —Pi (0)
Лп + i (х) — •
Von Vln ••• V nn — X —Pn(0)
Vo n+i Vi n+i ••• Vn —p„+i(0)
Voo — ••• Vno
Р(х) = Voi vu—x ••• Vnl (П4.5 9)
Von Vln ... Vnn — x
Из (П4.5.6) и (П4.5.8) следует, что математическое ожидание времени попа-
дания системы в состояние отказа равно
ОО
tp'+, (t)dt =
о
[хап+1 (х)]х=0 =
_л;+1(0)р(0)-лп+1(0)Р' (0)
~ Р2 (0)
Прибавляя к последней строке определителя ЛП4-т (0) все лежащие выше стро-
ки, с учетом (П4.5.1) получаем
Лп+1 (0) = -Р(0),
откуда
1 d 1 dD* (х) I
Здесь
где
Тогда
D* (х) = Л„+1(х)-'-Р(х) = хР<л>‘ <*),
V00 X Vlo Kno Po (0)
Koi Ktl—x ••• Kni Pi (0)
D (n)’ (x) =
Коп К[Л ••• Knn — x pn (0)
1 1 ... 1 1
l dP4x)| =J-------l_[xD^(x)| =
P(0) dx |x=o P(0) dx K=o
P<n)* (0) P(n)*
D (0) ~ P
138*
391
Но
£>(“>• (0) = (—l)"+1
1 1 ...
Voo Vw • • •
Voi Vn ...
1 0
Vno Po (0)
Vni Pi (0)
(П4.5.10)
(_!)"+1 D(n)e
Von Vln ••• Vnn Pnlfi)
откуда и получаем (П4.1.4).
При начальных условиях
Ро(О) = Ь Pi(0)=0, 1 < i < п +1 (П4.5.11)
математическое ожидание 740’ случайного времени попадания системы в со-
стояние отказа (поглощающее) Hn+i равно:
(Р<0>=_ 1 1 ... 1 Voi Vu ... Vm Voo Vio ••• Vno Voi Vu ... Vni Von Vln ... Vnn (П4.5.12)
где D — определитель системы (П4.5.2); D<0) — определитель, полученный
из D заменой всех V!0 на 1.
П4.5.2. Состояние отказа //n+i — отражающее. Через определители
можно выразить и коэффициент готовности К — стационарную вероятность пре-
бывания системы вне состояния отказа
К = 1 — lim pn+i (/). (П4.5.13)
/-►ОС
Пусть из отражающего состояния Нп+т возможны переходы в другие (для
общности, во все другие) состояния. Система уравнений имеет вид
«+1
P'i(t)= j} Vs(Ps(l), 0</<п + 1. (П4.514)
s — 0
Производя преобразование Лапласа, находим;
где
, , Bn+i (и)
Оп+1(Х) =----——-
— KDc(n)
Voo—x Vjo ••• Vn0 Vn+lt о Voi Vu—к ••• Vnl Vn+1(1
De (K) — Von VIn ••• Vnn— X Vn + i. n 1 1 ... 1 1
Voo — K Vio Voi Vu—x ••• Vn0 —Po(O) ••• Vnl -pt(O)
Bn+i (x) =
Von Vln ••• ^nn Pn (0)
Vo,n+i Vi, n+i Vn, n + l —Pn+l(0)
392
Обращение преобразования Лапласа для вероятности pn+i (0 выразит-
ся контурным интегралом (здесь —1)
Рп + 1
(0=-^— f оп+1(х) еи/ dx = —
2ш J 2 л j
L
f Дп + 1 (x)eK/dx
J — хПс(х)
где контур L охватывает все нули знаменателя подынтегральной функции.
Если уравнение Dc (х) = 0 не имеет корней, равных нулю, то
Пт рп+г (1)=1—К =
i ~>оо
Дп+1(0)
Рс(0)
Прибавляя к последней строке определителя Вп-н 00 все лежащие
выше строки, получаем
Вп+1 (0) = -П(0),
откуда К где D Тогда К = Таким образом, условно можно npei а .1 0(0) дс (°) ~ “Ьс(0)~ ос(С “v?o—vTo-“~V Vol Vu ... V Von V.n ••• V, 1 1 ... 1 1 1 ... 1 ''oo Vlo ••• Vn0 ''el Vu ... V,u Von Vln ... Vnn D(0) >) “ D no | Vn4-1T ni 1 Vn+11 .1 . . гп । Vn+i, 0 0 Vn + t,o Vn+1,1 Vn+l,n Dfl c(0)* 0 1 n (П4.5.15) еделитель системы D,
1С 1 1 1 Voo Vlo ^по V»i Vu I'm Von VIn ••• Vnn )езультаты, полученные тавить в следующем ви 1 Vn + 1,0 Vn + 1,1 Vn+l,n через onp де:
1 ... 1 0
1 i i ! D i i ц t 1 PO (0) I I _J Pn'(0)
i' р
I
393
т<0) = =
(П4.5.17)
1 . . 1 о
Г'"“-
j D i ^n+i,o
L----------! ^n + 1 n
i... i i
г........ 1
t D ! ^n+i,o
; i :
!----------! ^n+i, n
(П4.5.18)
Пример П4.5.1. Рассмотрим восстанавливаемую дублированную систему,
состоящую из разнонадежных элементов (рис. П4.5.1), интенсивности отказов и
восстановления которых соответственно
равны: Z.J, Л2, |1Ь ц2. Граф переходов
представлен на рис. П4.5.2, где Н, —
состояние системы, в котором отказав-
ших элементов нет; Hi (Я2) — состоя-
ние системы, в котором первый (вто-
рой) элемент является отказавшим,
— состояние системы, в котором
оба элемента являются отказавшими.
Рис. П4 5 1. Восстанавливаемая
дублированная система, состоя-
щая из разнонадежных элемен
тов.
Рис. П4 5 2. Граф переходов дуб'
лированной системы.
Обозначая через (/) вероятность пребывания системы и состояние Яд»
получаем следующие две системы дифференциальных уравнений, соответствую-
щих двум случаям: состояние — поглощающее и отражающее:
1) Ро (0 = — (bi+X2)Po(O+HtPi(/)+tiaPi(O;
Pi (0 = ^i Ро (0 —(^s+pi) Pi (0:
Рз (О=х2 р0 (0 — (^1+р.г) Pi (0|
Pl, г Я) = ^гPi (0+^1 Рг lf)i
394
2) Ро U) = — (^1+Х2)р0 (0+piPi(0+p2p2(0;
pi (О—^1 Рч + nJ Pi (О+g2 Pi>2(0;
Рг (О = ^2 Ро (О — (Xi + p,2) р2 (O + Pi Pi,s(Ol
Ро W+Pi (/) + р2 (О+Р1,2 (/) = !.
Отсюда, используя соотношения (П4.5.12), (П4.5.4) и (П4.5.15), запишем:
.1 1 10
—(%1 + Х2) щ ца р0 (0)
‘-(X»+Hi) 0 Pi (0)
Ъ_____________о ~(А1+цг) Рг(О)
— (Xi + X2) pi р2
А-1 —• (X2+pi) О
^•2 О' (Xj -|- Ц2)
3’<0)= —
1 1 1
— (Х2+Ц1) О
_____Хг___________0 —(А.14~ р2)
— (Xi+X2) gi р2
— (Х2 +pi) о
Х2 0 — (Xj + p2)
к=
I 1 10
— (Хх 4- Х2) р! р2 о
Xj “(X2+pj) 0 р2
Х2 0“~(^i ~1~ Рг) Pi
1 1 11
— (Xt + X2) цх р2 о
Хх —(Х2 + Ц1) 0 р2
Х2 0 “(Xi+|i2) pi
П4.6. Показатели надежности системы, поведение
которой описывается схемой «гибели и размножения»,
отказов и восстановлений
П4 6.1. Описание модели. Поведение большого числа реальных резервирован-
ных восстанавливаемых систем может быть описано с помощью следующей моде-
ли. Рассматривается система с k рабочими и п резервными элементами. Такая
система может находиться в конечном числе состояний (соответственно числу
отказавших элементов): Но, Hlt .... Нj, ..., Яп+ь где Н]— состояние, при
котором в системе имеется / отказавших элементов. Состояние Яп+i, в кото-
ром в системе имеется п + 1 отказавших элементов (т. е. отказавшими являют-
ся все п резервные и еще один из рабочих элементов), есть состояние отказа
системы.
Поведение системы характеризуется следующими условиями: если в момент
времени t система находится в состоянии Н} (в системе j отказавших элементов),
то за последующий промежуток времени А( она с вероятностью Л^А; -|- о (А/)
перейдет в состояние Hj+i (т. е. в системе откажет еще один из исправных эле-
ментов); с вероятностью МуА( + о (AZ) перейдет в состояние Н(т. е. будет
восстановлен один из / ранее отказавших элементов); с вероятностью 1 — (Лу +
+ Mj) + 9 (А() останется в состоянии Hj.
SS5
Рассмотрим два случая: состояние отказа системы Hn+i — поглощающее
и отражающее. Первый случай в теории надежности соответствует задачам оты-
скания вероятности безотказной работы системы, среднего времени работы до
отказа, среднего времени работы между отказами и т. д. Второй — задачам
отыЛания нестационарного и стационарного коэффициентов готовности, простоя,
различных стационарных характеристик и прочее.
Граф переходов описанной системы из одного состояния в другое приведен
на рис. П4.6.1, где обозначено;
Hj, 0 < j < п + 1, — состояние системы, в котором из всех N = k + п
элементов имеется / отказавших;
Лу, 0 < j < п, —интенсивность перехода системы (отказа одного из
N — j оставшихся исправными элементов) из состояния, в котором в системе
У отказавших элементов, в состояние, в котором в системе будет На один отказав-
ший элемент больше, т. е. j 4- 1;
Л) Ле К Л Н} A/.f М; ЛЛг А„., ___________________________________
— • “Zf — '~ffn
Рис. П4 6 1. Граф переходов из одного состояния в другое системы из k рабо-
чих и п резервных элементов.
Mj, 1 < / < п + 1, — интенсивность перехода системы (восстановления
одного из ранее отказавших элементов) из состояния, в котором в системе / отка-
завших элементов, в состояние, в котором в системе будет на один отказав-
ший элемент меньше, т. е / — 1.
П4.6.2. Состояние отказа //п-и — поглощающее. Поведение системы
описывается следующей системой дифференциальных уравнений:
Р/ (O = Ay_1p7_j(^—(A74-M7.)py(C + M/+1pj+1(O> 0 < /<п + 1,
п+1
2 Р;(О = 1,
1 = о
Д-1 = +’ = Мо = = = (П4.6.1)
где P'j (f) — вероятность того, что система в момент времени i находится в со-
стоянии Hj.
Пусть вероятности р} (I) удовлетворяют начальным условиям вида
р;(/ = 0) = р;-(0), 0</<п + 1. (П4.6.2)
Для нахождения закона распределения {0п+1 < 1} = ^n+i (0 =
~ pn+i (f) случайной величины 0п+1 (случайный момент времени, когда
система первый раз приходит в поглощающее состояние отказа Нп+х) приме-
ним к системе дифференциальных уравнений (П4.6.1) преобразование Лапласа.
Тогда (П4.6.1) преобразуется в систему алгебраических уравнений
A^i а;_ j (х)—(Лу- + М; + х) «у (х) +
4" My+i Qj+i (х) = —Pj (0), 0 < j < п + 1,
Л—1 = Лп+1 = Мо 1 = Мд^-2 ~ 0» (П4.6.3)
По правилу Крамера
ап+1 (и) ~Dn+l (^J/^An+i (х)> (П4.6.4)
3-96
где
—(Ао 4* и) Mt 0
Ao; —(А| 4- М, -4 х) Mg
0 Aj —(Л2 4* М2-Ни)
Дп+1(х) =
0 0 0
0 0 0
—(An-i+Mn_ 1+х) Мп
An-ii —(Лп4-Мп-^-х)
О О
О о
0 о
п+1 =(-1)л+1 п (> s= 1 +4п+1)). (П4.6.5)
—(A0-|-x) м. 0 . 0 0 —Ре (0)
Aq — (Л1-+ + М1-|-х) М2 . 0 0 —Pi (0)
0 Л> —(А2+ •f-M2-]-x) . о 0 —Рг (0)
Dn+i (х) = • •
0 0 0 • —(A«_i+ м„ —Рп~1(0)
+ Мп-1 + х)
0 0 0 • лп -~i -(Л„+ + Мп4-х) Рп (0)
0 0 0 . 0 Ап Рп+1(0)
(П4.6.6)
Легко показать, что лп+1 W — многочлен степени п имеет все корни
х(« + 1>==_х|"+1), х<л+,>>0, l<s<n + l, (П4 6.7)
различные и отрицательные н что корни соседних по п многочленов переме-
ж потея.
Раскладывая определитель £)п-н (х) по последней строке, получаем рекур-
рентное соотношение, последовательно используя которое, находим
п п
Dn+i(x)=-Pn+i(O)An+1(x) + 2 (-1)"+1-^МШи)Пл5. (П4 6 8)
1 — 0 s=t
Искомая вероятность (О = Рп+i (0 определяется обратным пре-
образованием Лапласа (здесь t = "|/—1)
If „/ 1 Г Dn+i(x)eK dx
Pn+i(0 = 7~ I an+1(x)ex/rfx = — —д (П4 6 9)
2л1 J 2т J —xAnj_j (л)
SB SB
где контур SB охватывает все нули знаменателя подынтегральной функции.
Используя (П4.6.5), имеем:
Рп+1 (0 =
п_|_ । —.zv ' Ч
1)П|. V Рл + 1(~**П+1>)е ’
д«+1(°) х^+^'п'(х^+1)-х;'1+1))
S=1
S^l
397
Прибавляя к первой строке определителя Дл+1 (0), заданного выраже-
нием (П4.6.5), все остальные строки и раскладывая его по элементам первой
строки, а затем последовательно по элементам первого столбца, находим
An+i(0) = (-ir+J П Лг. (П4.6 II)
< = о
Тогда из (П4 6.8) следует, что
а (П4.6.10) принимает вид
Dn+i (0)--&п 1-1 (0) >
((П4.6 12)
«4-1
Pn+i(0 = !-(-!)" У}
"^1
Оп+1(-^+'’)е '
(П4.6 13)
Отсюда, используя (П4.6.8), для вероятности безотказности работы системы
Р (t) = 1 — рп+1 (I), получаем
п п п +1
i = 0 j = i k=l
е т= 1
х*,+0 п (^(п+1)—4"+1))
/= 1
(П4 6 14)
где следует положить
о
П «°>-х<л+»)=1.
m = 1
Отметим два важных частных случая.
1. Если система начинает свою работу, будучи полностью исправной, т. е.
Ро(°) = 1. Р;(0) = 0, 1<<<п-|-1»
то нз (П4.6.6) и (П4.6.14) находим
Р‘0)(0=лвл1.,.лп V--------------------------
хр+1) п (xsn+I)—4п+1>)
8=1
s^i
(П4.6.15)
2., Если система начинает свою работу, только что «выйдя» из состояния от*
каза, т. е.
Ри (0) = 1, р,(0)=0, 1 = 0, 1......п-1, п-1-1,
то
^+* д ( —Х(п+Ч) е_Х/< + >z
(/) = (-!)» Л„ V ------------• (П4.6.16)
xjn + 1> П (х<л+1)—xj"+l))
8=1
398
Определим теперь при произвольных начальных условиях (П4.6.2) математиче-
ское ожидание Т времени попадания системы в поглощающее состояние отказа
Нп+1. В соответствии с (П4.5.4) н (П4.5.16), имеем:
1...1 । О
________I
I Р(0)
° I :
I Р(0)
(П4.6.17)
I D I
I______________!
где определитель D (в соответствии с (П4.2.1) имеет вид!
—Ло мх 0 ... 0 0
Ло -(Aj+Mi) М2 ... 0 0
D= 0 Лх —Vh+M2) ••• 9 0 . (Пч.6.18)
0 0 0 ••• —(An_i-{-Mn_i) Мп
0 0 0 ... &П — 1 —(Лп4-М„)
После несложных преобразований из (П4.6.17) и (П4.6.18) получим
/
п ";(О)20!
Т = У--------, (П4.6.19)
j=o 1 1
где
i »,<!». в.-,.’ «ш.6.20)
Из этой общей формулы, как частные случаи, находим соответствующие
формулы: для среднего времени работы системы до отказа Г(0) н для среднего
времени работы системы между отказами 7'(п).
Действительно, в первом частном случае при
из (П4.6.19) получаем Ро (0) = 1 (П4.6.21) л i ^0)=У-^Д-. (П4 6 22) ,=о
Во втором частном случае при Рп(0) = 1 (П4 6 23)
из (П4.6.19) имеем п s О; Т<п> = ' • (П4.6 24) Ап 0п
399
Отметим, что для принятой модели среднее время работы между i-м и
(< + 1)-м отказами (попаданиями в поглощающее состояние отказа) не зависит
от i при i > 1.
П4.6.3. Состояние отказа Яп+1 — отражающее. Рассмотрим теперь
систему, у которой состояние отказа Hn+i является отражающим. Поведение
такой системы описывается той же системой дифференциальных уравнений, что
и (П4.6.1), за исключением двух последних уравнений, которые теперь будут
иметь вид
рА(/) = Лп_1рп_1(О —(Лп + Мп)рп (04-Mn+iPn+i(0i
pA+i (0 = Лп рп Pn+i(0-
(П4 6 25)
Найдем стационарный коэффициент готовности, который по определению
равен
K=l-limpn+1(0.
t-юо
Используя (П4.5.18) и (П4.6.18), после несложных преобразований получим
(П4.6 26)
Вообще стационарные вероятности легко вычисляются следующим обра-
зом. При / ->- оо вместо системы дифференциальных уравнений (114.6.1) и
(П4.6.25) можем написать:
(Л;+М7)р7-=Л;_1ру„1Ч-Л1> + 1 Р;+ъ 0 < / < 1,
х = Мо = лп+1 = М п +2 = о.
Отсюда
Р} = <Э7Ро.
где &j — по-прежнему определяется формулой (П4.6.20).
Так как из условия нормировки следует, что
1
Ро~ п+ 1 *
2 «Ъ
(=0
то окончательно
е)
Pj=~n+1-----• 0</<п + 1. (П4.6.27)
; = 0
Определим еще стационарное среднее время безотказной работы Т, т. е.
среднее время работы до отказа системы, которая начала работать при начальных
условиях
pj (0) = lim pj (/) =pj, 0 < / < n-f-1,
t-f X
(П4.6.28)
где pj определены формулой (П4.6.27).
400
Используя (П4.6.19), (П4.6.20) и (П4.6.27), получаем
-А V
J~0 1
Л/ 6/
Г<Л) =
(П4.6.29)
П4.6.4. Система с несколькими состояниями отказа. Системой с несколько
более общим критерием отказа по сравнению с системой, рассмотренной в разде-
лах П4.6.1—П4.6.3, является система из fe рабочих и п резервных элементов,
у которой ие одно состояние отказа, а несколько: Hn+i, Нп+г, •••> HN=k+n.
Очевидно, это такая система, у которой после отказа всех резервных и одного
из fe рабочих элементов оставшиеся исправными элементы продолжают нахо-
диться во «включенном» состоянии, ожидая конца восстановления системы. Эта
AJ Лй Мг Л) Нп Лг.,____________Л .______
Но- ип Ыц, Л
Рис. П4 6 2. Граф переходов из одного состояния в другое системы из fe рабочих
и п резервных элементов, когда число отказовых состояний более одного.
ситуация характерна, в частности, для сложных систем, различного рода вы-
числительных комплексов, которые, как правило, не «останавливаются» на вре-
мя ремонта отказавших элементов.
Граф переходов данной системы из одного состояния в другое приведен на
рис. П4.6.2, где, начиная с состояния Hn+i (отказало п + 1 элементов) до
состояния HN=k_^n (отказали все W элементов системы), все состояния от-
каза.
Легко понять, что в этом случае такие показатели надежности системы,
как среднее время работы системы до отказа Т(о), среднее время работы сис-
темы между отказами 7’<n) и вероятность безотказной работы системы Р (t)
будут те же, что и у системы, рассмотренной в разделах П4.6.1—П4.6.3.
Не менее очевидно, что в этом случае
1^,(0=—---
s = 0
О < j < N,
(П4.6.30)
где &j определяется формулой (П4.6.20).
Тогда коэффициент готовности системы равен
(П4.6.31)
401
Приложение 5
ВЫЧИСЛЕНИЕ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ДЛЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ СЛУЧАЕВ
НЕМАРКОВСКИХ МОДЕЛЕЙ ВОССТАНАВЛИВАЕМЫХ
СИСТЕМ
П5.0. Предварительные замечания
На практике часто возникает необходимость вычисления среднего времени
работы между отказами Т и среднего времени простоя т системы с восстановле-
нием для стационарного процесса функционирования.
Пусть рассматриваемая нами система, состоящая из п восстанавливаемых
элементов, может находиться в
могут быть разделены на два
2” различных состояниях множества Е, которые
класса: состояния работоспособности системы
(подмножество Е+) и состояния отказа систе-
мы (подмножество £_). В процессе функцио-
нирования система, переходя из одного со-
стояния в другое, блуждает по состояниям
внутри одного класса, а затем попадает в дру-
гой класс состояний. Переход из подмно-
жества Е+ в подмножество Е_ может осу-
ществляться не из любого состояния работо-
способности, а только из граничного состоя-
ния (подмножество е^.). Аналогичным образом
Рис П5 0 1 Примеры подмножеств Е+, Е_,
е+, е_ для условного графа переходов:
О—состояние работоспособности (подмножество Е+Ц
• — состояние отказа (подмножество Е-); □ —гра-
ничное состояние работоспособности (подмножество
е<). Я — граничное состояние отказа (подмноже-
ство е_).
переход из подмножества Е_ в подмножество Е+ может осуществляться только
из состояния, принадлежащего подмножеству граничных состояний е_____(При-
меры подмножества Е+, Е-, е+, приведены на рис. П5.0.1 для условного
графа переходов.)
Рассмотренному стационарному случайному процессу блуждания по сос-
тояниям работоспособности и отказа системы можно поставить в соответствие
альтернирующий процесс {0, |), где 9 — случайное время работы между отказа-
ми, § — случайное время простоя системы. Задача заключается в нахождении
математических ожиданий величин 0 и £ для стационарного процесса.
П5.1. Произвольный стационарный процесс*
Часто восстанавливаемую систему S со структурной избыточностью можно
представить как систему, состоящую из п. подсистем Slt S2, .... Sx, .... SB, ....
S„ (например, п находящихся в какой-либо функциональной зависимости эле-
* На самом деле здесь на процесс накладываются определенные формальные
ограничения, несущественные, однако, на практике.
402
ментов). Известен набор или наборы этих подсистем, которые должны быть
исправными, чтобы обо всей системе можно было сказать, что она исправна;
короче, известен критерий отказа системы. Пусть для каждой подсистемы Sx
известны среднее время работы между отказами Тх и среднее время ее восста-
новления тх, х = 1,2, ..., п. Предположим, что
1) для каждой подсистемы Sx соответствующие ей случайные длительности
времени работы между отказами 6Х1, 6Х2, ••• являются независимыми и одина-
ково распределенными случайными величинами со средним (математическим ожи-
данием) Тх,
2) для подсистемы Зх длительности времени восстановления £г1, gx2, ...
также являются независимыми и одинаково распределенными случайными ве-
личинами со средним тж;
3) для подсистемы величины 6^!, 0Ж2, ... ие зависят как от §х1, .
так и от Offi, &у2, ... и ggl, 1у2, ... — соответствующих величин подсистемы
Sy для всех х, у;
4) распределения всех случайных величии, характеризующих поведение
рассматриваемой системы, ие являются «решетчатыми».
При этих предположениях среднее время работы между отказами Т и сред-
нее время восстановления т всей системы, а также ее коэффициент готовности К
определяются следующими выражениями;
2 п Mix
ifE+ х=\____
I V-1-
(I, nee Ty(i, п х=1
(П5 1 1)
(П5.1.2)
(П5.1.3)
Здесь
{Тх, если подсистема исправна, когда вся система S находится в со-
стоянии Hi;
тх, если подсистема Sx неисправна, когда вся система S находится
в состоянии Ну,
е — набор всех пар индексов (г, /'), отвечающих таким состояниям сис-
темы, что если система S в некоторый момент времени t является исправной и на-
ходится в состоянии Hi, то отказ простой подсистемы Sy переводит систему S
в состояние отказа Ну Е+ — набор всех индексов, отвечающих состояниям рабо-
тоспособности системы S; у (I, j) — индекс у такой подсистемы Sy /)t отказ
которой переводит систему S из состояния Hi в состояние Н}-
Выражение для среднего времени пребывания системы в каком-ни-
будь определенном состоянии Нл может быть получено из (П5.1.1) и равно
уО) _ ----------------------
п
2 «л 1)
^в== 1
(П5.1.4)
403
П5.2. Полумарковский процесс
В этом случае процесс смены индексов (номеров) состояний системы обра-
зует марковскую цепь, а время пребывания в каждом состоянии перед перехо-
дом в другое состояние является случайной величиной с произвольным распре-
делением.
Предполагается известным:
1) матрица переходных вероятностей соответствующей марковской цепи
Ри Рп Pin
Р21 Р22 ••• Ргп
....... ри •••
Рт Рп2 Рпп
где рц — вероятность перехода из состояния в состояние Н fl
2) функция Ftj (i) распределения длительности пребывания процесса
в состоянии Ht при условии перехода в состояние Hj
Можно показать, что в этом случае средняя наработка Т определяется по
формулам
Г = 2 Ргог(2 Рг 2 ptt\~l (П5.2.1)
\/бе+ /е£- /
или
?= 2 P.d 2 Pt 2 pj-1. (П5.2.2)
< 6 £4- ;6£+ )
а среднее время простоя т — по формулам
т = 2 ptut( 2 Pi 2 рМ-1 <П5-2-3>
ИЛИ
т= 2 Pich( 2 Pt 2 РоГ1’ <П5-2-4)
«6Е- \<ее- )GE+ 'J
Здесь at = S PijTij — среднее времи пребывания полумарковского процесса
/ЁЕ
п
в состоянии Нр. Pt = OjT, Dj — стационарная вероятность пребывания мар-
/=1
ковской цепи с матрицей переходных вероятностей Р в состоянии Hi, где в свою
очередь Dt — минор, получаемый вычеркиванием i-й строки и i-ro столбца
матрицы D, равной
1——р12 ... —р1п
D_ — Р21 1—Р22 ••• —Р2п
............... -РП
— Pnl —Рп2 1 — Рпп
При марковском процессе задаются интенсивности Х/у перехода про-
цесса из состояния Ht в состояние Hjn и формулы для данного случая могут
быть получены как частные случаи для полумарковского процесса.
Средняя наработка Т находится по формулам
т=к( 2 Pt 2 ЧГ1 <П5 2 5>
\iee+ 1ЁЕ—
ИЛИ
т=к (2 рг 2 ЧГ1
je£+ 'J
(П5.2.6)
404
а среднее время простоя т — по формулам
’“‘(Л<П5-27)
или
т = /г( 2 Pl 2 М-1« (П5 2.8)
\iee- 1ЕЕ+ )
где Хи k —коэффициенты готовности и простоя соответственно, определяемые
как
«- 2 ^(2-^
‘ ' 6 £+ 2- ^1] \А6Ь 2-i ™ki
6 Е 1 ' 1£Е
(П5.2.9)
.2.
П5.3. Способ введения фиктивных состояний для описания
произвольных распределений
В некоторых случаях предположения об экспоненциальное™ распределе-
ний оказываются неправомерными, причем не удается сделать и предположения
о существенной малости времени простоя по отношению к времени безотказной
работы. В этом случае может быть использован следующий искусственный прием,
вводятся дополнительные фиктивные состояния (фазы), которые позволяют с оп-
ределенными приближениими описывать неэкспоненциальные схемы.
Рис П531. Граф переходов си-
стемы из элементов, имеющих
различные распределения показа-
телей. со «стареющим» распреде-
лением времени безотказной рабо-
ты (о), с «молодеющим» распре-
делением времени восстановле-
ния (б)
Рис. П5 3 2 Граф переходов системы из элементов, имеющих различные распре-
деления показателей со «стареющим» распределением времени безотказной ра-
боты и распределением времени восстановления (а), с «молодеющим» распреде-
лением времени безотказной работы и распределением времени восстановления
(б), со «стареющим» распределением времени безотказной работы и «молоде-
ющим» распределением времени восстановления (в), с «молодеющим» распреде-
лением времени безотказной работы и «стареющим» распределением времени вос-
становления (г),
405
Суть введения фиктивных состояний заключается в том, что распределе-
ния с возрастающей интенсивностью отказов могут быть получены, если мы про-
суммируем несколько экспоненциальных случайных величин (т е «стареющее»
распределение может быть получено как свертка экспоненциальных распределе-
ний), а распределения с убывающей интенсивностью
отказов получаются, если произвести «взвешивание»
нескольких экспоненциальных распределений (Воп
рос о точности н приемлемости такой аппроксима-
ции должен рассматриваться в каждом конкретном
случае особо.)
С одной стороны, используя марковскую модель
для произвольных распределений, мы упрощаем
задачу, с другой, — вводя дополнительные состоя-
ния в граф переходов, мы ее усложняем
Приведем простейшие графы для типовых слу
чаев (одиночный элемент, дублированная система),
Рис. П5 3.3. Граф переходов дублированной системы
из элементов, имеющих «стареющие» распределе-
ния времени безотказной работы и времени вос-
становления
когда распределения времени безотказной работы и времени восстановления
имеют возрастающие или убывающие функции интенсивности (рис. П5.3.1 —
П5 3.3) На этих рисунках индекс «О» соответствует состоянию работоспособ-
ности, а индекс «1» — состоянию отказа.
Приложение 6
ЭВРИСТИЧЕСКИЙ МЕТОД ОЦЕНКИ НАДЕЖНОСТИ
ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
П6.1. Предварительные замечания
На практике при оценке показателей надежности восстанавливаемых сис-
тем часто приходится встречаться с такой ситуацией, когда элементы, образующие
систему, яеляются сравнительно надежными В данном случае имеется в виду,
что среднее время безотказной работы каждого из элементов системы намного
больше, чем среднее время восстановления. При этом обычно оказывается, что и
сама система, построенная из таких элементов, тоже является достаточно на-
дежной в том же смысле. Иначе говоря, можно сказать, что коэффициенты го-
товности отдельных элементов системы и самой системы достаточно близки к еди-
нице.
В этом случае удается получить выражение для различных показателей на-
дежности, не прибегая к составлению и решению часто весьма громоздких систем
уравнений Кроме того, в ряде случаев удается получать сравнительно хорошие
оценки и при распределении времени работы и восстановления, отличающихся
от экспоненциальных Точность получаемых решений из этих приближенных
выражений тем выше, чем надежнее в указанном смысле составляющие систему
элементы, однако оценку погрешности получить здесь не удается (как и для мно
гих других эвристических методов).
Процедура получения приближенных формул для расчета различных пока-
зателей надежности восстанавливаемых систем состоит в следующем Любые
406
два элемента системы, связанные определенным образом через структуру систе-
мы (т. е. соединенные тем или иным образом), через алгоритм функционирования
(например, нагруженный или ненагруженный характер резерва) и через алго-
ритм восстановления (возможность очереди на ремонт, приоритет в очереди,
число восстанавливающих органов и пр.), могут быть условно объединены в один
эквивалентный элемент. Этот элемент может быть охарактеризован альтерни-
рующим процессом восстановления, представляющим собой последовательность
интервалов нормальной работы с интервалом простоя. Сама система, состоявшая
из п элементов, с учетом этого эквивалентного элемента становится, таким обра-
зом, состоящей из (п — 1) элементов. Такими последовательными объединения-
ми элементов часто удается свести всю систему к одному эквивалентному элемен-
ту, для которого оказывается построенным и соответствующий приближенный
альтернирующий процесс восстановления. Иначе говоря, для такого эквивалент-
ного элемента известно среднее время работы между отказами и среднее время
восстановления, что и позволяет определить основные показатели надежности.
При условии, что время безотказной работы каждого отдельно взятого эле-
мента намного больше соответствующего времени простоя, процесс функцио-
нирования такого элемента можно представить в виде последовательности
сравнительно узких «импульсов» простоев, разделенных интервалами безотказ-
ной работы Процесс функционирования системы в целом может быть представ-
лен в виде совокупности таких потоков импульсов, над которыми в соответствии
со структурой системы совершаются операции (см приложение 3) суперпозиции
(наложения), разрежения (просеивания) и некоторые более сложные операции
(например, так называемые задержки). Ниже приведем три стандартных частных
случая объединения пары элементов системы в один им эквивалентный элемент.
П6.2. Последовательно соединенные элементы
Рассмотрим систему, состоящую из т последовательно соединенных эле-
ментов. Функционирование каждого нз элементов описывается альтернирующим
процессом восстановления, состоящим из относительно узких «импульсов»
простоя и больших «пауз» (интервалов работоспособности) между ними
(рис. П6.2.1 для т = 2).
/-« элемент
Рис П6 2 1. Пример аль-
тернирующего процесса
восстановлений для си-
стемы из двух повледо-
вательно соединенных
элементов.
2-й элемент
Система,
При рассмотрении последовательного соединения т элементов можно вос-
йользоваться правилом суперпозиции потоков.
Интенсивность отказов X* последовательной системы из т элементов равна
т
/,’Й У 1/7г,
< = 1
где — среднее время безотказной работы i го элемента.
Если элементы имеют экспоненциальные распределения времени работы
с интенсивностями Л/, то
т
2
407
Среднее время восстановления системы равно
т
2 'i/Tl
I 1
т* «----------,
т
2 1/Л
Z=1
де Tj — среднее время восстановления г-го элемента.
Для экспоненциальных распределений времени безотказной работы
'=1
В первом приближении режим восстановления (ограниченное или неограни-
ченное) роли не играет.
П6.3. Параллельно соединенные элементы
Рассмотрим два параллельно включенных элемента. Среднее время безот-
казной работы и среднее время простоя эквивалентного элемента, состоящего
из этих двух элементов, будет определяться в общем случае видом соответст-
вующих функций распределения, режимом их работы (нагруженный или йена-
груженный) и режимом восстановления (ограниченное или неограниченное).
В табл. П6.3.1 приведены приближенные значения интенсивности отказов
и среднего времени простоя эквивалентного элемента.
Таблица П6.3.1
Значения интенсивности отказов и среднего времени простоя для
резервированных систем
Режим работы резервного элемента Восстановление элементов Интенсивность отказов X Среднее время простоя т
Экспоненциаль- ное распределение Постоянное врем восстановления
Нагруженный Неограниченное ^•1^2 (Х1Н~Х2) 'Ci'Ca
т, + -tl +-t2
Ненагружзнный* Неограниченное Л2Т
Нагруженный Полностью ('ci+'t2) •cf+^2 2 L £
ограниченное Т1 -|- т2 2 (Т1 + т2)
Ненагруженный* Полностью t
ограниченное 2
* При незагруженном резерве оба элемента (основной и резервный) предполагаются идеитич
ними.
Примечание. Если известно, что время восстановления элементов
имеет «стареющее» распределение, среднее время простоя для экспоненциаль-
ного распределения дает верхнюю оценку, а для постоянного времени — нижнюю.
408
П6.4. Элемент с задержкой
Понятие элемента с задержкой поясним следующим конкретным примером.
Часто в системах встречаются элементы, которые не имеют постоянного контроля
работоспособности, а проверяются через некоторые интервалы времени Харак-
тер контроля работоспособности одиночного элемента ^влияет на время простоя
элемента (пребывание в состоянии необнаруженного отказа), но не влияет на вре-
мя безотказной работы. Эта схема соответствует тому случаю, когда событие,
образованное одним потоком, сохраняется без изменения (задерживается)
до тех пор, пока не произойдет очередное событие другого потока (соответственно
необнаруженный отказ и проверка для рассматриваемой конкретной модели).
Здесь можно выделить два следующих основных случая:
а) проверка через постоянный интервал времени. Среднее время простоя
равняется
т2=т + ^/2;
б) проверка через случайное время, распределенное экспоненциально.
Среднее время простоя равняется
т2
Пример П6.4.1. Рассмотрим дублированную систему, основной элемент
которой контролируется непрерывно не полностью, а лишь частично, причем
охват этим контролем составляет 1 — а = 0,99. Полностью этот элемент про-
Рис. П6.4.1. Эквивалентная схема рас-
чета надежности для примера П6 4 1.
верится периодически через постоянный интервал времени = 2 ч. Резервный
элемент контролируется непрерывно и полностью. При обнаружении отказа
оановного элемента происходит переключение на резервный, причем это осу-
ществляется за конечное и постоянное время /п = 0,1 ч. Для ремонта отказав-
ших элементов имеется одна ремонтная бригада, которая производит восстановле-
ние в порядке поступления отказавших элементов. Предположим, что резерв-
ный элемент работает в нагруженном режиме. Распределение времени безотказ-
ной работы экспоненциальное с параметром А=» 0,011 ч, а время восстановления
постоянное, равное т = 3 ч.Требуется найти показатели надежности системы
Решение. Заметим предварительно, что в данной дублированной сис-
теме отказ фактически наступает при каждом отказе основного элемента, по-
скольку переключение на резерв происходит за конечное время. Наличие резер-
ва по существу лишь обеспечивает очень быстрое восстановление работоспособ-
ности системы (за время переключения), но не обеспечивает бесперебойной ра-
боты системы даже при наличии полностью исправного резервного элемента.
Это позволяет сразу записать, что
XS = X = O,O1 1/ч.
Кроме того, любой отказ основного элемента всегда влечет за собой про-
стой длительностью /п. Это означает, что остается оценить среднее время простоя
системы при идеальном переключении (tn = 0), а затем прибавить к нему ве-
личину tn.
Систему можно приближенно представить в виде параллельно-последователь-
ного соединения (рис. П6.4.1), где использованы следующие обозначения:
К — непрерывно контролируемая часть основного элемента с интенсив-
ностью отказов (1 — а) А и постоянным временем восстановления т;
Р — резервный элемент с интенсивностью отказов А и постоянным временем
восстановления т;
14 Зак. 943 409
ti — неконтролируемая часть основного элемента (охват а-100%), конт-
ролируемого лишь периодически через время 1^, с интенсивностью отказов «1
и временем простоя /й/2;
П — условный элемент, заменяющий абсолютно надежный переключатель
с конечным временем переключения tn, с интенсивностью отказов Л и временем
простоя /п.
Решение проведем следующим образом?
1) объединим параллельно соединенные элементы К и Р в эквивалентный,
используя формулы табл. П6.3.1 для нагруженного резерва и полностью огра-
ниченного восстановления при постоянном времени восстановления;
М я2 (1-а)12т = 0,00059 1/ч; т? «т/2 = 1,5 ч,
2) объединим последовательно соединенные элементы: полученный эквива-
лентный элемент, элемент Н и элемент П:
X,*«X-J-2 (1 — а) X2 т+ «1 = 0,0116 1/ч;
* ж 1<п+2(1 —а) 12т(т<2}+о'1 (th/2) = Q 241 q
1 + 2(1 — а)12т + а1
Отсюда можно найти, например, что для этой системы
Р(%)^е-°'0116<з К~- , '-- = 0,9971.
1+1* т*
Приложение 7
НЕКОТОРЫЕ КОНСТАНТЫ И ФОРМУЛЫ,
ЧАСТО ВСТРЕЧАЮЩИЕСЯ ПРИ РЕШЕНИИ
ЗАДАЧ НАДЕЖНОСТИ
П7.1. Константы
1. е = 2,718 1/6 = 0,368
е2 = 7,389 1/е2 = 0,135
У?= 1,649 1/УТ = 0,607
2. л = 3,142 1/л = 0,318
2л = 6,283 1/2л = 0,159
л/2=1,571 2/л = 0,637
п2 = 9,870 1/л2 = 0,101
У л" = 1,772 1/У л =0,564
У2л = 2,507 1/У2л = 0,399
2/л= 1,128 Ул/2 = 0,886
Ул/2= 1,253 У2/л = 0,798
3. log е =0,434 1о§Уё = 0,217
4 log л = 0,497 log У л = 0,249
5. Постоянная Эйлера
/ п 1 \
С=Пп1 I У, ———In п 1=0,577.
п-»оо \ь — j /
410
П7.2. Элементарные формулы комбинаторики
6. п’ = 1.2. ... п.
7. О! = 1.
8. (—п)! = 0.
9. Формула Стирлинга
я’ я; (п/е)п 1/2лл (1 -j- 1/12л).
10. In(n') « (п+1/2) In л —п+0.92.
11 С^ =-----------.
т\(п — т)\
12. С« = п
13 С" = С« = 1.
И С^+от=0 (т>1).
15 . С^=С"-т.
16 2 С* = 2".
17 - i^crfe=C’+m.
Л = 0
18 V Сп _______сп-+-\
k = 0
19. Значения nl и 1/n!
п rt’ 1/rt’ rt rt' 1/л1
1 1 1 7 5040 0.0’2
2 2 0,5 8 40320 0.0’2
3 6 0.167 9 362880 0,0’3
4 24 0,042 10 3628800 0,0«3
5 120 0,028 11 39916800 0.0’3
6 720 0,0г1 12 479001600 0,0’2
П7.3. Конечные суммы
20. Арифметическая прогрессии
Ч 1 д д
V (a + fcr) = —- [2a + (n— 1) г] ~ — (а + /) [/ — последний член].
й=о 2 2
21. Геометрическая прогрессия
'-й-
14»
411
22.
23.
к" 1-«
Бином Ньютона
(I—?)2 ’
(а-Н)п = У С*ал-АЛ
i=0
24. £fe=^±!>.
& 2
25. 2
t=l 6
26.
У, 0,577 + 1пл+—-------------!----.
*“! * 2л 12n(n+D
П7.4. Ряды
27. Ряд Тейлора (для функции одной переменной)
(х) =/(а)+~~ f'(a) + -XJt- f {а) + ••• + '~nf+
Л А2 Ап
t(a + h) = [(a)+—f'(а)+—/" (а) + ...+~ /<л) (а)+ ...
28. (1±х)?=1±<7х+^р-)х2±...+
К1
29. (1 ± %)-«==! т qx + ^~x2^ . ..+
+(Т 1)*(?(|? + 1) + ХЛ ± .. j | х | < 1].
К'
м'
1 00
31 = У Ck„xk.
(1—-*)" £0 п
32. (1 ±х)-> = 1 т х + х2 Т х3 + х4 т ... [ |х| < 1].
33. (1 ±х)2 = 1 Т 2x + 3x2T 4xJ+5x4 Т ...[|х| < П-
34. (1 +х)’^ = 1 +— х- — х2 +— Xs— х4 + ...
2 2-4 2-4-6 2-4-6-8 г
35. (-1 -}-х)~,г — 1 — — х Н-х2 —--х3 + ...
2 2-4 2-4-6
412
36.
1“ 2fe-t
у I o4“l I ,
x 1 4=1 X2 +1
37.
2
4=0 1~?
38.
rq
2 a
4=0 ! — q (! — «)*
39.
» j
-S 7Г = е = 2,718.,
4 = 0
40.
6 = 0
(—1)* 1
= — = 0,368.
fe! e
41.
X , X2 X2
— _L.— _1_---
1! 2! 3!
42.
-X , X Xa X3
s = 1 "4~ '
1! 2! 3!
ОО Й
*=o й
43.
e'
oo у24
6 = 9 R1
44.
a = 2j
4 = 0
(x In a)k
M
45.
ft—o
—J— fa>l, x<0}
1 — a
46.
ln(l+x) = x-x2+-|-x3—^-x«+ ...=»
2 3 4
OO j-k
47.
In X= (X— 1) —“ (X— l)s+-|~ (X— I)3— . . . =
2 о
fe
=’2 (~n*+‘
*=i
48.
x-l , 1 /Х-1 V
lnx =------------
x 2 \ x /
1 /х—IV
3 \ x ,
X— 1 V 1 ]
--- x> •
X / 2 .
4|3
П7.5. Неопределенные интегралы
49. Ceoxdx = — еах.
J а
Р / X 1 \
50. I хеох dx = еох (—---------:|.
J \ a a2 J
х2 еах dx = еах
53. \Inxdx = xlnx—х.
П7.6. Определенные интегралы
54. f e"oxdx = —е—а/,(1 —е—а (/2-/,)) t, а
55 i I f е-ах _ е—°'). 0 а ~ ]
56. J е-йх dx = —. о ° h p—att
57. J xe‘azdx =—— Il-J-aZ, —е fl (1+a6)L h
58. t J f xe~ax dx~— (1 —e~e/ (I -J-uZ)/. о
59 ? 1 f xe~ax dx^= —. i a2
60 c „ , «! n! tk 6 X~ a”+i 6 k\ a"-^1
61. Jxn e-^ dx^e-^ 2 77""Lt« U = o p. 00
62. ^xne~ax dx = n! a“("+l).
63 J fei^ + l)
414
64. J q>Q>
о
где
<D*(X) = -L Се^’й.
У« J
65. fe-<?’x'dx=ii2-f а>0
Ь 2q
1-3...(2fe —1) V л
66. J x" e-**’ dx =
fl
2*+l a*+%
а — четное;
fel
2aft+‘ ’
n — нечетное.
Я7 г _________агхг л n
67. e dx =---------------,
J0 2a
a> 0.
68 [x2e-^'dx = ^> fl>0<
5 4a3
69. F Ф* (qt) e~pt dt~ — [1 — Ф* f — 1 е₽*/4Л
0 P L \ 2q }]
6 («6 В (y)
70. — C f(x, y)dx — C **’ dx-f-
dy J ’ J dy
a (y) a(y)
+0' (У) l(^(y), y} — «'(y)f{a(y), y).
П7.7. Преобразование Лапласа
Преобразование Лапласа ставит в соответствие каждой функции (оригина-
лу) р (/) действительной переменной t функцию (изображение) а (к) комплекс-
ной переменной по формуле
a(x) = f p(t) e-^'df, ОО.
0
Для изображений и их оригиналов справедливы два следующих утверж-
дения:
lim ха (х) =lim р (t)l
Х-*0 /-*>оо
lim ха (х) =р (0).
Х-юо
Приведем таблицу формулы преобразований Лапласа от основных функций,
используемых при расчетах надежности.
415
Таблица П7.7.1
Формулы преобразований Лапласа
Изображение Оригинал
(*) 4" fat (*) aPi (0 + ₽ Ps (6
— Р (0) + М (X) р' (0
а (х) _С_ ~х X t J р (х) dx + С 0
4а (4) •*>о р(Ы)
e-fc*d(x), bsO р и — Ь)
Qi (*) as (х) t j Pi (%) Pi {t — x) dx 0
<РА' ix) (-1)47(0
а (х — а) ea'p(t)
4- «=1,2,... in-l (n- 1)!
(х— Ь)" '1=1.2, r"-’ 01-1)' e
i Ха + Ь2 1 -y sin bt
хг + Ь2 cos bt
1 ха — Ь2 1 -y sh bt
X к2 — ь2 ch bt
1 х (х2 Ь2) y-(l — cos bt)
Продолжение табл. П7.7.1
Изображение Оригинал
1 x (x — b) ЯеЬ'4- К , 1 1 Л = -у, К=—у
x 4- d X (x — b) А-~^- К- А~~ b ’ К ь
1 (X — b) (x — c) ЛеЬ| 4- Вес* А^=1Г~' B = ~^~h Ь — с с — b
x4- d (X — b) (x — c) л _ в_ f + d A~~b — c' B^c — b
1 x (x — b) (x — c) + К А L_ b(b~c)' c(c — b)' 1
x 4- d x (x — b) (x — c) X2 4- gx 4- d X (X — b) (x — c) Ле"‘4- Вес| 4- /( b 4- d c 4~ d b(b — c)’ B c(c—b)' K-± K~ be
д _ fca + A~~ b(b — c) ’ R — Ci + SC + d d c (c — b) ’ be
1 (x — b) (x — c) (x — d) Леы 4. Be'» 4- Се1" A~ (b-c) (b-d)’ B - (c - b) (e - d) ’ C= ! G (d — b) (d — c)
x 4- e (x — b) (x — c) (x — dj
л_ b + e (b — c) (b — d) ’ л c + e D~ (c-b)(c-d)' r- d +g C - (d - b) (d - c) ’
xi +gx 4- e . _ b2+ bg + e A~ (b~c) (b-d) ’ c2 4- eg 4- e
(x — b) (x —c) (x — d) (e~b) (c-d)’ C = di+ ds + e (d — b) (d — c)
418
417
Приложение 8
Числовые таблицы
Таблица П8.1
Функция е**
X 0 1 2 3 4 5 6 7 8 9
0,00 1,000 0,999 0,998 0,997 0,996 0,995 0,994 0,993 0,992 0,991
0,0 1,000 0,990 0,980 0,970 0,961 0,951 0,942 0,932 0,923 0,914
0,1 0,905 0,896 0,887 0,878 0,869 0,861 0,852 0,844 0,835 0,827
0,2 0,819 0,811 0,802 0,795 0,787 0,779 0,771 0,763 0,756 0,748
0,3 0,741 0,733 0,726 0,719 0,712 0,705 0,698 0,691 0,684 0,677
0,4 0,670 0,664 0,657 0,651 0,644 0,638 0,631 0,625 0,619 0,613
0,5 0,606 0,600 0,594 0,589 0,583 0,577 0,571 0,566 0,560 0,554
0,6 0,549 0,543 0,538 0,533 0,527 0,522 0,517 0,512 0,507 0,502
0,7 0,497 0,492 0,487 0,482 0,477 0,472 0,468 0,463 0,458 0,454
0,8 0,449 0,445 0,440 0,436 0,432 0,427 0,423 0,419 0,415 0,411
0,9 0,407 0,403 0,398 0,395 0,391 0,387 0,383 0,379 0,375 0,372
1, 0,368 0,333 0,301 0,273 0,247 0,223 0,202 0,183 0,165 0,150
2, 0,135 0,122 0,111 0,100 0,091 0,082 0,074 0,067 0,061 0,055
3, 0,050 0,045 0,041 0,037 0,033 0,030 0,027 0,025 0,022 0,020
4, 0,018 0,017 0,015 0,014 0,012 0,011 0,010 0,009 0,008 0,007
5, 0,0067 0,0061 0,0055 0,0050 0,0045 0,0041 0,0037 0,0033 0,0030 0,0027
6, 0,0025 0,0022 0,0020 0,0018 0,0017 0,0015 0,0014 0,0012 0,0011 0,0010
Таблица 118.2
Функция In— (обратная е**)
X 0 1 2 3 4 5 6 7 8 9
0,999 0,0010 0,0009 0,0008 0,0007 0,0006 0,0005 0,0004 0,0003 0,0002 0,0601
0,99 0,010 0,009 0,008 0,007 0,006 0,005 0,004 0,003 0,002 0,001
0,9 0,105 0,094 0,083 0,073 0,062 0,051 0,041 0,030 0,020 0,010
0,8 0,223 0,211 0,198 0,186 0,174 0,162 0,151 0,139 0,128 0,117
0,7 0,357 0,342 0,329 0,314 0,301 0,288 0,274 0,261 0,248 0,236
0,6 0,512 0,494 0,478 0,462 0,446 0,431 0,416 0,400 0,386 0,371
0,5 0,693 0,673 0,654 0,635 0,616 0,598 0,580 0,562 0,545 0,528
0,4 0,916 0,892 0,867 0,844 0,821 0,798 0,777 0,755 0,734 0,713
0,3 1,204 1,171 1,139 1,109 1,079 1,050 1,022 0,994 0,968 0,942
0,2 1,609 1,561 1,514 1,470 1,427 1,386 1,347 1,309 1,273 1,238
0,1 2,303 2,207 2,120 2,040 1,966 1,897 1,833 1,772 1,715 1,661
0,0 СО 4,605 3,912 3,506 3,219 2,996 2,813 2,659 2,526 2,408
0,00 оо 6,908 6,215 5,809 5,521 5,298 5,116 4,962 4,828 4,711
0,000 оо 9,210 8,517 8,111 7,824 7,601 7,419 7,264 7,131 7,013
418
Таблица П8.3
Функция нормального распределения Ф(х) Се -u^-da
— _ — '—00
X 0, 1, 2, 3,
,00 0,500 0,841 0,9773 0,9=865
,05 520 853 798 886
,10 540 864 821 0,93С32
, 15 560 875 842 184
,20 573 885 861 313
,25 599 894 878 - 423
,30 618 0,9032 893 517
,35 637 115 9С6 596
,40 655 192 0,92180 663
,45 674 265 286 720
,50 692 332 379 767
,55 709 394 461 807
,60 726 452 534 841
,65 742 505 598 863
,70 758 554 653 892
,75 773 599 702 912
,80 788 641 745 0,94277
,85 802 678 781 409
,00 816 713 813 519
,95 829 744 841 609
Примечание: О,Оча; 0.9fta означают цифры 0,00. . .0a; 0,99. . .9a, соответственно. Например
0.9*277 = 0,9999277. ’ k"'
Таблица П8.4
Плотность нормального распределения
1 —х!/2
X 0, 1, 2,
,00 0,399 0,242 0,0540
,05 398 230 488
,10 397 218 440
,15 395 206 396
,20 391 194 355
,25 387 183 317
,30 381 171 283
,35 375 160 252
,40 368 150 224
,45 361 140 198
,50 352 130 175
,55 343 120 ' 155
,60 333 111 136
,65 323 102 119
,70 312 0,0941 104
,75 301 863 0,029Ю
,80 290 790 792
,85 278 721 687
,90 266 656 595
,95 254 596 514
419
Таблица П8.5
Квантили Up нормального распределения
1 г”
P=WJ = W
р VP Р
0,50 0 0,98 2,054
0,55 0,126 0,99 2,326
0,60 0,253 0,9г5 2,58
0,65 0,385 0,9’ 3,09
0,70 0,524 0,9’5 3,29
0,75 0,674 0,9» 3,72
0,80 0,842 0,9»5 3,89
0,85 1,036 0,95 4,27
0,90 1,282 0,9’5 4,42
0,91 1,341 0,9» 4,75
0,92 1,405 0,965 4,89
0,93 1,476 0,9’ 5,20
0,94 1,555 0,9’5 5,33
0,95 1,645 0,9s 5,61
0,96 1,751 0,985 5,73
0,97 1,881 0,9е 6,00
Таблица П8.6
Суммарные значения биномиального распределения
Q. = S ЛМ-*
п а р
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10
1 0,0490 0.0961 0,1413 0,1846 0,2262 0.2661 0,3043 0,3409 0,3760 0,40'15
г 2 0010 0038 0085 0148 0226 0319 0425 0544 0674 0815
3 0000 0001 0003 0006 0012 0020 0031 0045 0063 0(86
4 0000 0000 0000 0000 0000 0001 0001 0002 0003 0005
1 0,0585 0,1142 0.1G70 0,2172 0.2649 0,3101 0,3530 0.3936 0,4321 0,4586
2 0015 0057 0125 0216 0328 0459 0608 0773 0952 1143
6 3 0000 0002 0005 0012 0022 0038 0058 0085 0118 0159
4 0000 0000 0000 0000 0001 0002 0003 0005 0009 0013
5 0000 0000 0000 0000 0000 0000 0000 0000 0000 С001
1 0,0679 0,1319 0,1920 0.2486 0,3017 0.3515 0,3983 0,4422 0,4832 0,5217
2 0020 0079 0171 0294 0444 0618 0813 1026 1255 1497
7 3 0000 0003 0009 0020 0038 0063 0097 0140 0193 0257
4 0000 0000 0000 0001 0002 0004 0007 0012 0018 0027
5 0000 0000 0000 0000 0000 0000 0000 0001 0001 00112
1 0,0773 0,1492 0.2163 0,2786 0,3366 0,3904 0,4404 0,4868 0,5298 0.5695
2 0027 0103 0223 0382 0572 0792 1035 1298 1577 1869
8 3 0001 0004 0014 0031 0058 0096 0147 0211 0289 0381
4 0000 0000 0001 0002 0004 0008 0013 0022 0034 0050
5 0000 0000 0000 0000 0000 0000 0001 0002 0003 0004
1 0,0865 0,1663 0,2398 0,3075 0,3698 0,4270 0,4796 0,5278 0,5721 0.6126
2 0034 0131 0282 0478 0712 0978 1271 1583 1912 2252
9 3 0001 0006 0020 0045 0084 0138 0209 0298 0405 0530
4 0000 0000 0001 0003 0006 0013 0023 0037 0057 0083
5 0000 0000 0000 0000 0000 0001 0002 0003 0006 0009
42»
П родолжение табл 118.6
Р
п а 0,01 | 0.02 I 0,03 | 0,04 | 0,05 I 0,06 | 0,07 0,08 0,09 0,10
1 0,0956 0,1829 0,2626 0,3352 0,4013 0,4614 0,5160 0,5656 0,6106 0,6513
2 0043 0162 0345 0582 0861 1176 1517 1879 2255 26 39
10 3 0001 0009 0028 0062 0115 0188 0283 0401 0540 0702
4 0000 0000 0002 0004 0010 0020 0036 0058 0088 0128
5 0000 0000 0000 0000 0001 0002 0003 0006 0010 0016
1 0,1047 0,1993 0,2847 0,3618 0,4312 0,4937 0,5499 0,6004 0,6456 0,6862
2 0052 0195 0414 0692 1019 1382 1772 2181 2601 3026
н 3 0002 0012 0037 0083 0152 0248 0370 0519 0695 0896
4 0000 0000 0002 0007 0016 0030 0053 0085 0129 0185
5 0000 0000 0000 0000 0001 0003 0005 0010 0017 0028
1 0,1136 0,2153 0,3062 0,3873 0,4596 0,5241 0,5814 0,6323 0,6775 0,7176
2 0062 0231 0487 0809 1184 1595 2033 2487 2948 3410
12 3 0002 0015 0049 0107 0196 0316 0468 0652 0866 1109
4 0000 0001 0003 0010 0022 0043 0075 0120 0180 0256
5 0000 0000 0000 0001 0002 0004 0009 0016 0027 0043
1 0,1225 0,2310 0,3270 0,4118 0,4867 0,5526 0,6107 0,6618 0,7066 0.7458
2 0073 0270 0564 0932 1354 1814 2298 2794 3293 3787
13 3 0003 0020 0062 0135 0245 0393 0577 0799 1054 1339
4 0000 0001 0005 0014 0031 0060 0103 0163 0242 0342
5 0000 0000 0000 0001 0003 0007 0013 0024 0041 0065
1 0,1313 0,2464 0,3472 0,4353 0,5123 0,5795 0,6380 0,6888 0,7330 0,7712
0 0084 0310 0645 1059 1530 2037 2565 3100 3632 41г4
14 3 0003 0025 0077 0167 0301 0478 0698 0958 1255 1584
4 0000 0001 0006 0019 0042 0080 0136 0214 0315 0441
5 0000 0000 0000 0002 0004 0010 0020 0035 0059 0092
1 0,1399 0,2614 0,3668 0,4579 0,5367 0.6047 0,6633 0,7137 0,7570 0,7941
2 0096 0353 0730 1191 1710 2262 2832 3403 3965 4510
15 3 0004 0030 0094 0203 0362 0571 0829 ИЗО 1469 1841
4 0000 0002 0009 0025 0055 0194 0175 0273 0399 0556
5 0000 0000 0001 0002 0006 0014 0028 0050 0082 0127
Таблица П8.7
Доверительные пределы для параметра р биномиального распределения.
Коэффициент доверия 0,95
п
N—n 0 1 1 2 3 4 5 6
1 0,975 0,987 0,992 0,994 0,995 0,996 0,996
1 0,000 0,013 0,994 0,194 0,284 0,359 0,421
о 0,842 0,906 0,932 0,947 0,957 0,963 0,968
Z 0,000 0,008 0,068 0,147 0,223 0,290 0,349
о 0,708 0,806 0,853 0,882 0,901 0,915 0,925
О 0,000 0,006 0,053 0,118 0,184 0,245 0,299
А 0,602 0,716 0,777 0,816 0,843 0,863 0,878
0,000 0,005 0,043 0,099 0,157 0,212 0,262
Е 0,522 0,641 0,710 0,755 0,788 0,813 0,833
О 0,000 0,004 0,037 0,085 0,137 0,187 0,234
с 0,459 0,579 0,651 0,701 0,738 0,766 0,789
О 0,000 0,004 0,032 0,075 0,122 0,167 .0,211
421
Продолжение табл. П8.7
Продолжение табл. П8.7
• n
N—n 0 1 2 3 4 5 6
0,410 0,527 0,600 0,652 0,692 0,723 0,749
1 0,000 0,003 0,028 0,067 0,109 0,151 0,192
8 0,369 0,483 0,556 0,610 0,651 0,684 0,711
0,000 0,003 0,025 0,060 0,099 0,139 0,177
0,336 0,445 0,518 0,572 0,614 0,649 0,677
9 0,000 0,003 0,023 0,055 0,091 0,128 0,163
0,308 0,413 0,484 0,538 0,581 0,616 0,646
10 0,000 0,002 0,021 0,050 0,084 0,118 0,152
0,285 0,385 0,454 0,508 0,551 0,587 0,617
11 0,000 0,002 0,019 _ 0,047 0,078 0,110 0,142
12 0,265 0,360 0,428 0,481 0,524 0,560 0,590
0,000 0,002 0,018 0,043 0,073 0,103 0,133
1 Q 0,247 0,339 0,405 0,456 0,499 0,535 0,565
10 0,000 0,002 0,017 0,040 0,068 0,097 0,126
0,232 0,319 0,383 0,434 0,476 0,512 0,543
14 0,000 0,002 0,016 0,038 0,064 0,&91 0,119
0,218 0,302 0,364 0,414 0,456 0,491 0,522
Io 0,000 0,002 0,015 0,036 0,061 0,087 0,133
16 0,206 0,287 0,347 0,396 0,437 0,471 0,502
0,000 0,001 0,014 0,034 0,057 0,082 0,107
0,195 0,273 0,331 0,379 0,419 0,453 0,484
11 0,000 0,001 0,013 0,032 0,054 0,078 0,102
1 ft 0,185 0,260 0,317 0,363 0,403 0,436 0,467
Io 0,000 0,001 0,012 0,030 0,052 0,075 0,098
1 Q 0,176 0,249 0,304 0,349 0,388 0,421 0,451
l У O.COO 0.C01 0,012 0,029 0,050 0,071 0,094
on 0,168 0,238 0,292 0,336 0,374 0,407 0,436
ZU 0,000 0,001 0,011 0,028 0,047 0,068 0,090
01 0,161 0,228 0,280 0,324 0,360 0,393 0,423
Z i 0,000 0,001 0,010 0,027 0,045 0,066 0,086
00 0,154 0,219 0,270 0,312 0,349 0,381 0,410
zz 0,000 0,001 0,010 0,025 0,044 0,063 0,083
no 0,148 0,211 0,260 0,301 0,338 0,369 0,397
Zu 0,000 0,001 0,010 0,024 0,042 0,061 0,080
24 0,142 0,203 0,251 0,292 0,327 0,358 0,386
0,000 0,001 0,009 0,024 0,040 0,058 0,077
N—n n
0 1 2 3 4 5 6
25 0,137 0,196 0,243 0,282 0,317 0,347 0,375
0,000 0,001 0,009 0,023 0,039 0,056 0,075
26 0,132 0,190 0,235 0,274 0,307 0,337 0,364
0,000 0,001 0,009 0,022 0,030 0,055 0,072
27 0,127 0,184 0,228 0,265 0,298 0,328 0,355
0,000 0,001 0,008 0,021 0,036 0,053 0,070
28 0,123 0,178 0,221 0,257 0,290 0,319 0,345
0,000 0,001 0,008 0,020 0,035 0,051 0,068
29 0,119 0,172 0,215 0,250 0,282 0,311 0,336
0,000 0,001 0,008 0,020 0,034 0,050 0,066
30 0,116 0,167 0,208 0,243 0,275 0,303 0,328
0,000 0,001 0,008 0,019 0,033 0,048 0,064
A5 0,100 0,145 0,182 0,214 0,242 0,268 0,292
0,000 0,001 0,007 0,017 0,029 0,042 0,056
40 0,088 0,129 0,162 0,191 0,217 0,241 0,263
0,000 0,001 0,006 0,015 0,025 0,037 0,049
45 0,079 0,115 0,145 0,172 0,196 0,218 0,239
0,000 0,001 0,005 0,013 0,023 0,033 0,044
50 0,071 0,104 0,132 0,157 0,179 0,200 0,219
0,000 0,001 0,005 0,012 0,021 0,030 0,040
60 0,060 0,088 0,112 0,133 0,152 0,170 0,187
0,000 0,000 0,004 0,010 0,017 0,025 0,034
RO 0,045 0,067 0,085 0,102 0,118 0,132 0,145
0,000 0,000 0,008 0,008 0,013 0,019 0,026
1 on 0,036 0,054 0,069 0,083 0,096 0,108 0,119
0,000 0,000 0,002 0,006 0,011 0,016 0,021
0,018 0,027 0,035 0,043 0,049 0,056 0,062
zuu 0,000 0,000 0,001 0,003 0,005 0,008 0,011
0,007 0,011 0,014 0,017 0,020 0,023 0,026
DUU 0,000 0,000 0,000 0,001 0,002 0,003 0,004
Таблица П8.8
Доверительные пределы для параметра р биномиального распределения.
Коэффициент доверия 0,99
N—n n
0 1 2 3 4 5 6
1 0,995 0,000 0,997 0,003 0,998 0,041 0,999 0,111 0,999 0,185 0,999 0,254 0,999 0,315
422
423
Продолжение табл. П8.8
N—n п
0 1 2 3 4 5 6
0,929 0,959 0,971 0,977 0,981 0,984 0,986
2 0,000 0,002 0,029 0,083 0,144 0,203 0,258
0,829 0,889 0,917 0,934 0,945 0,953 0,958
3 0,000 0,001 0,023 0,066 0,118 0,170 0,219
0,734 0,815 0,856 0,882 0,900 0,913 0,923
4 0,000 0,001 0,019 0,055 0,100 0,146 0,191
0,653 0,746 0,797 0,830 0,854 0,872 0,886
5 0,000 0,001 0,016 0,047 0,087 0,128 0,169
0,586 0,685 0,742 0,781 0,809 0,831 0,848
6 0,000 0,001 0,014 0,042 0,077 0,114 0,152
0,531 0,632 0,693 0,735 0,767 0,791 0,811
7 0,000 0,001 0,012 0,037 0,069 0,103 0,138
0,484 0,585 0,648 0,693 0,728 0,755 0,777
8 0,000 0,001 0,011 0,033 0,062 0,094 0,127
0,445 0,544 0,608 0,655 0,691 0,720 0,744
9 0,000 0,001 0,010 0,030 0,057 0,087 0,117
0,411 0,509 0,573 0,621 0,658 0,688 0,714
10 0,000 0,000 0,009 0,028 0,053 0,080 0,109
11 0,382 0,477 0,541 0,589 0,627 0,658 0,685
0,000 0,000 0,008 0,026 0,049 0,075 0,101
0,357 0,449 0,512 0,561 0,599 0,631 0,658
12 0,000 0,000 0,008 0,024 0,045 0,070 0,095
0,335 0,424 0,486 0,534 0,573 0,605 0,633
1о 0,000 0,000 0,007 0,022 0,043 0,065 0,090
0,315 0,402 0,463 0,510 0,549 0,582 0,610
14 0,000 0,000 0,007 0,021 0,040 0,062 0,085
0,298 0,381 0,441 0,488 0,527 0,560 0,588
1£> 0,000 0,000 0,006 0,020 0,038 0,058 0,080
0,282 0,363 0,422 0,468 0,507 0,539 0,567
1b 0,000 0,000 0,006 0,019 0,036 0,055 0,076
0,268 0,346 0,404 0,449 0,488 0,520 0,548
1 / 0,000 0,000 0,006 0,018 0,034 0,053 0,073
0,255 0,331 0,387 0,432 0,470 0,502 0,531
1о 0,000 0,000 0,005 0,017 0,032 0,050 0,069
1 Q 0,243 0,317 0,372 0,416 0,453 0,485 0,514
1У 0,000 0,000 0,005 0,016 0,031 0,048 0,066
ол 0,233 0,304 0,358 0,401 0,438 0,470 0,498
2U 0,000 0,000 0,005 0,015 0,029 0,046 0,064
О1 0,223 0,292 0,345 0,387 0,423 0,455 0,483
Z1 0,000 0,000 0,005 0,015 0,028 0,044 0,061
22 0,214 0,000 0,281 0,000 0,332 0,004 0,374 0,014 0,410 0,027 0,441 0,042 0,469 0,059
0,206 0,271 0,321 0,362 0,397 0,428 0,455
28 0,000 0,000 0,004 0,013 0,026 0,041 0,056
424
П родолжение табл. П8 3
п
N—п 0 1 2 3 4 5 6
24 0.198 0,262 0,310 0,351 0,385 0,416 0,443
0,000 0,000 0,004 0,013 0,025 0,039 0,054
25 0,191 0,253 0,300 0,340 0,374 0,404 0,431
0,000 0,000 0,004 0,012 0,024 0,038 0,053
26 0,184 0,245 0,291 0,330 0,363 0,393 0,420
0,000 0,000 0,004 0,012 0,023 0,037 0,051
97 0,178 0,237 0,282 0,320 0,353 0,382 0,409
0,000 0,000 0,004 0,012 0,023 0,035 0,049
9Q 0,172 0,230 0,274 0,311 0,344 0,373 0,398
ZO 0,000 0,000 0,004 0,011 0,022 0,034 0,048
9G 0,167 0,223 0,266 •0,303 0,335 0,363 0,389
0,000 0,000 0,003 0,011 0,021 0,033 0,046
ЧП 0,162 0,216 0,259 0,295 0,326 0,354 0,379
oU 0,000 0,000 0,003 0,011 0,020 0,032 0,045
0,140 0,189 0,227 0,260 0,289 0,315 0,339
OU 0,000 0,000 0,003 9,009 0,018 0,028 0,039
A A 0,124 0,168 0,203 0,233 0,260 0,284 0,306
4U 0,000 0,000 0,002 0,008 0,016 0,025 0,035
A 'X 0,111 0,151 0,183 0,210 0,235 0,258 0,279
4Э 0,000 0,000 0,002 0,007 0,014 0,022 0,031
ЕЛ 0,101 0,137 0,166 0,192 0,215 0,237 0,257
ьи 0,000 0,000 0,002 0,006 0,013 0,020 0,028
cn 0,085 0,116 0,141 0,164 0,184 0,203 0,229
W 0,000 0,000 0,002 0,005 0,011 0,017 0,024
0,064 0,088 0,108 0,126 0,143 0,158 0,173
80 0,000 0,000 0,001 0,004 0,008 0,013 0,018
0,052 0,071 0,088 0,103 0,116 0,129 0,142
100 0,000 0,000 0,001 0,003 0,007 0,010 0,015
0,026 0,036 0,045 0,053 0,061 0,068 0,075
200 0,000 0,000 0,001 0,002 0,003 0,005 0,008
0,011 0,015 0,018 0,022 0,025 0,028 0,031
500 0,000 0,000 0,001 0,001 0,001 0,002 0,003
Таблица Г18.9
ак
Распределение Пуассона рк — -^й~а =0, ...
k a
0.001 0,002 0,003 0,004 0,005 0,006 0,007
0 9990 9980 9970 9960 9950 9940 9930
1 0’999 0’200 0’299 0’398 0’498 0’596 0’695
2 0’1 0’200 0’449 0’797 0*124 0479 0’243
425
Продолжение табл. П8.9
k 0,008 0,009 0,010 0,020 0,030 0,040 0,050
о 0920 9910 9900 9802 9704 9608 9512
1 0’794 0’892 0’990 0196 0291 0384 0476
2 0*317 0*401 0*495 0’196 0’437 0’769 02119
3 — —- —. 0’131 0’437 0*102 0*198
—' а
к 0,06 0,07 | 0,08 0,09 | 0,10 0,20 0,30
о 0418 9324 9231 9139 9048 8187 7408
] 0565 0653 0738 0823 0905 1637 2222
2 О2170 0’228 0’295 0’370 0’452 0164 0333
з 0*339 0*533 0*788 0’111 0’151 О2109 02333
4 Pl 0’93 0’158 0’250 0’377 0*546 0’250
5 — — — 0’218 0*150
1 .<
— а
k 0.4 0,5 0,6 0,7 0,8 0,9 1,0
о 6703 6065 5488 4966 4493 4066 3679
1 2681 3033 3293 3476 3595 3659 3679
2 0536 0758 0988 1217 1438 1647 1839
з 0’715 0126 0198 0284 0383 0494 0613
4 0’715 О2158 0’296 0’497 0’767 0111 0153
5 0*572 0’158 0’356 0’696 О2123 0’200 0’307
6 0’381 0*132 0*356 0*811 0’164 0’300 0’511
7 0’1 0’305 0’811 0*187 0*386 0*730
8 — 0’1 0’187 0’434 0’912
9 — — — — — .— 0’101
k а
2 3 4 5 6 7 8 9 10
о 135с* 0498 0183 0’674 0’248 0’912 0’335 0’123 0*454
1 2707 1494 0733 0337 0149 О2 638 0’268 0’111 0’454
2 2707 2240 1465 0842 0446 0223 0107 0’500 0’227
з 1804 2240 1954 1404 0892 0521 0286 0150 0’757
4 090z 1680 1954 1755 1339 0912 0573 0337 0189
5 0361 1008 1563 1755 1606 1277 0916 0607 0378
6 012С1 0504 1042 1462 1606 1490 1221 0911 0631
7 О’ 34 4 0216 0595 1044 1377 1490 1396 1171 0901
8 0’85® 0’810 0298 0653 1033 1304 1396 1313 1126
9 0’19' 0’270 0132 0363 0688 1014 1241 1318 1251
10 0*382 0’810 0’529 0181 0413 0710 0993 1186 1251
И 0’694 0’221 0’192 0’824 0225 0452 0722 09ТО 1137
12 0’11® 0*524 0’642 0’343 0113 0263 0481 0728 0948
13 0*127 0’197 0’132 0’520 0142 0296 0504 0729
14 — 0’273 0*564 0’472 0’223 0’709 0169 0324 0521
426
Продолжение табл. П8.9
k a
2 3 4 5 6 7 8 9 10
15 - 0’1 0*150 0’157 0’891 0’331 0’903 0194 0347
16 — 0*376 01491 0’334 0’145 0’451 0109 0217
17 05l 04(44 0’118 0’596 0’212 0’579 0128
18 .— 0*401 0*393 0’232 0’944 0’289 0’709
19 — —- — 0*106 0*124 0*854 0’397 0’137 0’373
20 y— 0’373 0*299 0’159 0’617 0’187
21 _ 0’106 0’997 0*606 1’264 0’889
22 — x— — 0’317 0*220 0’108 0’404
23 —— y— — 0’1 0’766 0*423 0’176
24 — — — S~ — — 0’255 0*159 0*732
25 y— — 0’1 0’571 0*293
26 —— y— —. — — 0’198 0*113
27 — v — — — 0’1 0’417
2& — — r- 1 — , 1 — 1 — । Wil
Таблица П8.10
00
Пуассона Qd = S -rre-“ = О,
k=d
Суммарные значения распрёДеления
d a
0,001 0,002 0,003 0,004 0,005 0,006 0,007
1 0’999 0’200 0’300 0’399 0’499 0’598 0’698
2 0’10 0’200 0’449 0’798 0*125 0*179 0*244
d a
0.008 0,009 0,010 0,020 0,030 0,040 0,050
1 0’797 0’896 p’995 0198 0296 0392 0488
2 0*318 0*403 p*497 0’197 0’441 0’779 0’121
3 — 0’131 0’440 0*104 0*201
d a
0.06 0,07 0,08 0,09 0,10 0,20 0,30
1 0582 0676 P769 0861 0952 1813 2592
2 0’173 0’234 (9’303 0’382 0’468 0175 0369
3 0*344 0*542 P*804 0’114 0’155 0’115 0’360
4 0’1 0’1 P’160 0’254 0’385 0*568 0’266
5 III" —. — 0’226 0*158
6 — — — — —I 0’1
427
Продолжение табл П8.16
d а
0,4 0,5 0.6 0,7 0,8 0,9 1.0
1 3297 3935 4512 5034 5507 5934 6321
2 0616 0902 1219 1558 1912 2275 2642
3 0’793 0144 0231 0341 0474 0629 0803
4 0’776 0’175 0’336 0’575 0’908 0135 0190
5 0*612 0’172 0’394 < 0’786 0’141 0’234 0’366
6 0’404 0*142 0*388 0*900 0’184 0’343 0’594
7 0’100 0’329 0’888 0*207 0’434 0’832
8 04 0’205 0’482 0*102
9 — 1 I — — — 0’113
Продолжение табл. П8.10
d а
2 3 4 5 6 7 8 9 1Э
1 8647 9502 9817 9933 9975 9991 9997 9999
2 5940 8009 9084 9596 9826 9927 9970 9988 9995
3 3233 5768 7619 8753 9380 9704 9862 9938 9972
4 1429 3528 5665 7350 8488 9182 9576 9788 9897
5 0527 1847 3712 5595 7149 8270 9004 9450 9707
6 0166 0839 2149 3840 5543 6993 8088 8843 9329
7 0’453 0335 1107 2378 3937 5503 6866 7932 8699
8 О’НО 0119 0511 1334 2560 4013 5470 6761 7798
9 0’237 0’380 0214 0681 1528 2709 4075 5443 6672
10 0’465 0’110 0’813 0318 0839 1695 2834 4126 5421
11 0’831 0’292 0’284 0137 0426 0985 1841 2940 4170
12 0’136 0’714 0’915 0’545 0201 0533 1119 1970 3032
13 0*162 0’274 0’202 0’883 0270 0638 1242 2084
14 0’340 0*763 0’698 0’363 0128 0342 0739 1355
15 —- 0’1 0’199 0’226 0’140 0’572 0173 0415 0835
16 0’489 0*690 0’509 0’241 0’823 0220 0487
17 0’113 0’199 0’175 0’958 0’372 0111 0270
18 0’542 0*569 0’362 0’159 0’532 0143
19 0’140 0*176 0’130 0’650 0’243 0’719
20 — — — 0’518 0’444 0’253 0’106 0’345
21 0’146 0’145 0*940 0’439 0’159
22 . 0’453 0’334 0’175 0’700
23 — 0’135 0*114 0’668 0’296
24 — 0’373 0*245 0’120
25 — — — — — — 0’117 0’865 0’470
428
Продолжение табл. 118 10
а
d 2 3 1 4 5 6 7 8 9 10
26 __ 05294 0*177
27 — — — . — __ 04 05642
28 — — — — — — — 05225
29 — — — — — — — — 04
Таблица П8.11
Доверительные пределы для параметра X распределения Пуассона
Колн- чеегва отказов п Коэффициент доверия
0,999 0,99 0,95 0,90
0 7,60 0,0000 5,30 0,0000 3,69 0,0000 3,00 0,0000
1 10,00 0,0005 7,43 0,0050 5,57 0,0253 4,74 0,0513
2 12,05 0,0320 9,27 0,103 7,22 0,242 6,30 0,355
3 13,93, 0,149 10,98 0,338 8,77 0,619 7.75 0,818
4 15,71 0,355 12,59 0,672 10,24 1,09 9,15 1,37
5 17,41 0,63 14,15 1,08 11,67 1,62 10,51 1,97
6 19,05 0,97 15,66 1,54 13,06 2,20 11,84 2,61
7 20,67, 1,35 17,13 2,04 14,42 2,81 13,15 3,29
8 22, ?2 1,77 18,58 2,57 15,76 3,45 14,43 3,98
9 23,75 2,22 20,00 3,13 17,08 4,12 15,71 4,70
10 25,26 2,70 21,40 3,72 18,39 4,80 16,96 5,43
11 26,74 3,20 22,78 4,32 19,68 5,49 18,21 6,17
12 28,20 3,73 24,14 4,94 20,96 6,20 19,44 6,92
13 29,65 4,27 25,50 5,58 22,23 6,92 20,67 7,69
14 31,08 4,83 26,84 6,23 23,49 7,65 21,89 8,46
15 32,50 5,40 28,16 6,89 24,74 8,40 23,10 9,25
16 33,90 5,99 29,48 7,57 25,98 9,15 24,30 10,04
17 35,29 6,59 30,79 8,25 27,22 9,90 25,50 10,83
18 36,68 7,20 32,09 8,94 28,45 10,67 26,69 11,63
19 38,05 7,82 33,38 9,64 29,67 11,44 27,88 12,44
20 39,41 8,45 34,67 10,35 30,89 12,22 29,06 13,25
21 40,76 9,09 35,95 11,07 32,10 13,00 30,24 14,07
22 42,11 9,74 37,22 11,79 33,31 13,79 31,42 14,89
23 43,45 10,40 38,48 12,52 34,51 14,58 32,59 15,72
24 44,78 11,06 39,74 13,25 35,71 15,38 33,75 16,55
25 46,11 11,73 41,00 14,00 36,90 16,18 34,92 17,38
26 47,42 12,41 42,25 14,74 38,10 16,98 36,08 18,22
27 48,74 13,09 43,50 15,49 39,28 17,79 37,23 19,06
28 50,05 13,78 44,74 16'24 40,47 18,61 38,39 19,90
29 51,35 14,47 45,98 17,00 41,65 19,42 39,54 20,75
30 52,64 15,17 47,21 17,77 42,83 20,24 40,69 21,59
42»
Таблица П8.12
Критические значения Х2(г, (?) распределения X2.
2
<7 =
е 2 dx
х2(с. ч)
Ч
Г 0.99 0,98 0,95 0,90 0.8J 0,70 0,50 0,30 0,20 0,10 0,05 0,02 0,01 0,001
1 0,000 0,001 0,004 0,016 '0,064 '0,148 0,455 1,074 1,642 2.7! 3,84 5,41 6,63 10,83
2 0.020 0,040 0,103 0,211 0,446 0,713 1,386 2,41 3,22 4,60 5,99 7,82 9,21 13,82
3 0,115 0,185 0,352 0,584 1,005 1,424 2,37 3,66 4,64 6,25 7,81 9,84 11,34 16,27
4 0,297 0,429 0,711 1,064 1,649 2,20 3,36 4,88 5,99 7,78 9,49 11,67 13,28 18,46
0,554 0,752 1,145 1.610 2,34 3,00 4,35 6,06 7,29 9,24 11,07 13,39 15,09 20,5
6 0,872 1,134 1,635 2,20 3,07 3,83 5,35 7,23 8,53 10.64 12,59 15,03 16,81 22,5
7 1,239 1,564 2,17 2,83 3,82 4,67 6,35 8,38 9,80 12,02 14,07 16,62 18,48 24,3
8 1,646 2,03 2,73 3,49 4,59 5,53 7,34 9,52, 11,03 13,36 15,51 18,17 20,1 26,1
9 2,09 2,53 3,33 4.17 5,38 6,39 8.34 10,66 12,24 14,68 16,92 19,68 21.7 27,9
10 2.56 3,06 3,94 4.86 6,18 7,27 9.34 11,78 13,44 15,99 18,31 21.2 23,2 29,6
II 3,05 3,61 4,58 5,58 6,99 8,15 10,34 12,90 14,63 17,28 19,68 22,6 24,7 31,3
12 3,57 4,18 5,23 6,30 7,81 9,03 11,34 14,01 15,81 18,55 21.0 24,1 26,2 32,9
13 4,11 4,76 5,89 7,04 8,63 9,93 12,34 15,12 16,98 19,81 22,4 25,5 27,7 34,6
14 4,66 5,37 6.57 7,79 9,47 10,82 13,34 16,22 18,15 21,1 23,7 26,9 29,1 36,1
15 5,23 5,98 7,26 8.55 10,31 11,72 14,34 17,32 19,31 22,3 25,0 28,3 30,6 37,7
16 5,81 6,61 7,96 9,31 11,15 12,62 15,34 18,42 20,5 23,5 26,3 29,6 32,0 39,3
17 6,41 7,26 8,67 10,08 12,00 13,53 16,34 19,51 21.6 24,8 27,6 31,0 33,4 40,8
18 7,01 7,91 9,39 10,86 12,86 14,44 17,34 20,6 22,8 26,0 28,9 32,3 34,8 42,3
19 7,63 8,57 10.11 11.65 13,72 15,35 18,34 21,7 23,9 27,2 30,1 33,7 36,2 43,8
20 8,26 9,24 10,85 12,44 14,58 16,27 19.34 22,8 25,0 28,4 31,4 35,0 37,6 45»3
21 8,90 9,92 11,59 13,24 15,44 17,18 20,3 23,9 26.2 29,6 32,7 36,3 38,9 46,8
22 9,54 10,60 12,34 14,04 16,31 18,10 21,3 24,9 27,3 30,8 33,9 37,7 40,3 48,3
23 10,20 11,29 13,09 14,85 17,19 19,02 22.3 26,0 28,4 32,0 35.2 39,0 41,6 49,7
24 10,86 11,99 13.85 15,66 18,06 19,94 23,3 27,1 29,6 33.2 36,4 40.3 43,0 51,2
25 11,52 12,70 14,61 16,47 18,94 20,9 24,3 28,2 30,7 34,4 37.7 41.7 44,3 52,6
26 12,20 13,41 15,38 17,29 19,82 21,8 25,3 29,2 31,8 35,6 38,9 42,9 45,6 54,1
27 12,88 14,12 16,15 18,11 20,7 22,7 26,3 30,3 32,9 36,7 40,1 44.1 47,0 55,5
23 13,56 14.85 16,93 18,94 21,6 23,6 27,3 31.4 34,0 37,9 41,3 45,4 48,3 56,9
29 14,26 15,57 17.71 19,77 22.5 24,6 28,3 32,5 35,1 39,1 42.6 46,6 49,6 ъ8,3
30 14,95 16,31 18,49 20,6 23,4 25,5 29.3 33,5 36,2 40,3 43,8 48,0 50,9 59.7
Таблица П8 13
Критические значения t(n, q) распределения Стьюдента
п я
0,80 0,40 0,20 0.10 0,05 0,02 0,01 0,001
1 0,325 1,376 3,078 6,314 12,706 31,821 63,657 636,619
2 0,289 1,061 1,886 2,920 4,303 6,965 9,925 31,598
3 0,277 0,978 1,638 2,353 3,182 4,541 5,841 12,941
4 0,271 0,941 1,533 2,132 2 776 3,747 4,604 8,610
5 0,267 0,920 1,476 2,015 2,571 3,365 4,032 6,859
6 0,265 0,906 1,440 1,943 2,447 3,143 3,707 5,959
7 0,263 0,896 1,415 1,895 2,365 2,998 3,499 5,405
8 0,262 0,889 1,397 1,860 2,306 2,896 3,355 5,041
9 0,261 0,883 1,383 1,833 2,262 2,821 3,250 4,781
10 0,260 0,879 1,372 1,812 2,228 2,764 3,169 5,587
430
Продолжение табл. П8.13
п ч
0,80 0,40 0,20 0,10 0,05 0,02 0,01 0,001
11 0,260 0,876 1,363 1,796 2,201 2,718 3,106 4,437
12 0,259 0,873 1,356 1,782 2,179 2,681 3,054 4,318
13 0,259 0,870 1,350 1,771 2,160 2,650 3,012 4,221
14 0,258 0,868 1,345 1,761 2,145 2,624 2,977 4,140
15 0,258 0,866 1,341 1,753 2,131 2,602 2,947 4,073
16 0,258 0,865 1,337 1,746 2,120 2,583 2,921 4,015
17 0,257 0,863 1,333 1,740 2,110 2,567 2,898 3,965
18 0,257 0,862 1,330 1,734 2,101 2,552 2,878 3,922
19 0,257 0,861 1,328 1,729 2,093 2,539 2,861 3,883
20 0,257 0,860 1,325 1,725 2,086 2,528 2,845 3,850
21 0,257 0,859 1,323 1,721 2,080 2,518 2,831 3,819
22 0,256 0,858 1,321 1,717 2,074 2,508 2,819 3,792
23 0,256 0,858 1,319 1,714 2,069 2,500 2,807 3,767
24 0,256 0,857 1,318 1,711 2,064 2,492 2,797 3,745
25 0,256 0,856 1,316 1,708 2,060 2,485 2,787 3,725
26 0,256 0,856 1,315 1,706 2,056 2,479 2,779 3,707
27 0,256 0,855 1,314 1,703 2,052 2,473 2,771 3,690
28 0,256 0,855 1,313 1,701 2,048 2,467 2,763 3,674
29 0,256 0,854 1,311 1,699 2,045 2,462 2,-756 3,659
30 0,256 0,854 1,310 1,697 2,042 2,457 2,750 3,646
40 0,255 0,851 1,303 1,684 2,021 2,423 2,704 3,551
60 0,254 0,848 1,296 1,671 2,000 2,390 2,660 3,460
120 0,254 0,845 1,289 1,658 1,980 2,358 2,617 3,373
0,253 0,842 1,282 1,645 1,960 2,326 2,576 3,291
Таблица П8. И
Критические значения Л(п, (?) для наибольшего отклонения
эмпирического распределения от теоретического (критерий
Колмогорова)
^{suPlfnW— F(x)\>A(n. q)} = q
п Q п Q
0,1 0,05 0,01 0,1 0,05 0.01
1 0,950 0,975 0,995 26' 0,233 0,259 0,311
2 776 842 929 27 229 254 305
3 636 708 829 28 225 250 300
4 565 624 734 29 221 246 295
5 509 563 668 30 218 242 290
6 468 519 617 31 214 238 285
7 436 483 576 32 211 234 281
8 410 454 542 33 208 231 277
9 387 430 513 34 205 227 273
10 369 409 489 35 202 224 269
И 352 391 468 36 199 221 265
12 338 375 449 37 196 218 262
13 325 361 432 38 194 215 258
14 314 349 418 39 191 213 255
15 304 338 404 40 189 210 252
431
Продолжение табл. П8.14
п Q п Q
0,1 0,05 0,01 0.1 0.05 0,01
16 295 327 392 41 187 208 249
17 286 318 381 42 185 205 246
18 279 309 371 43 183 203 243
19 271 301 361 44 181 201 241
20 265 294 352 45 179 198 238
21 259 287 344 46 177 196 235
22 253 281 337 47 175 194 233
23 247 275 330 48 173 192 231
24 242 269 323 49 171 190 228
25 238 264 317 50 170 188 226
Таблица П8.15
Критические значения kq функции распределения Колмогорова
К(М = 1 - q
Q 0,50 0,40 0,30 0,20 0,10 0,05 0,02 0,01 0,001
0,828 0,895 0,974 1,073 1,224 1,358 1,520 1,627 1,950
Таблица Г18.16
Распределение Гнеденко— Вейбулла
А0 = еХр[-^У]
Цо ь
0,1 0,3 0,5 0,7 0.9 1.1
0,1 0,452 0,606 0,729 0,819 0,882 0,924
0,2 0,427 0,540 0,639 0,723 0,791 0,843
0,3 0,412 0,498 0,578 0,650 0,713 0,766
0,4 0,402 0,468 0,531 0,591 0,645 0,694
0,5 0,393 0,444 0,493 0,540 0,585 0,627
0,6 0,387 0,424 0,461 0,497 0,532 0,566
0,7 0,381 0,407 0,433 0,459 0,484 0,509
0,8 0,376 0,392 0,409 0,425 0,441 0,457
0,9 0,372 0,380 0,387 0,395 0,403 0,410
1,0 0,368 0,368 0,368 0,368 0,368 0,368
1,5 0,353 0,323 0,294 0,265 0,237 0,210
2,0 0,342 0,292 0,243 0,197 0,155 0,117
2,5 0,334 0,268 0,206 0,150 0,102 0,065
Продолжение табл. П8.16
t /а Ъ
1.3 1.5 1.7 2,0 3,0 4,0
0,1 0,951 0,969 0,980 0,990 0,999 1,000
0,2 0,884 0,914 0,937 0,961 0,992 0,998
0,3 0,811 0,848 0,879 0,914 0,973 0,992
432
Продолжение табл. П8.16
Ча ь «г
1,3 1,5 1.7 2,0 3,0 4,0
0,4 0,738 0,776 0,810 0,852 0,938 0,975
0,5 0,666 0,702 0,735 0,779 0,882 0,939
0,6 0,598 0,628 0,657 0,698 0,806 0,878
0,7 0,533 0,557 0,580 0,613 0,710 0,786
0,8 0,473 0,489 0,504 0,527 0,599 0,664
0,9 0,418 0,426 0,433 0,445 0,482 0,519
1,0 0,368 0,368 0,368 0,368 0,368 0,368
1,5 0,184 0,159 0,136 0,105 0,034 0,006
2,0 0,085 0,059 0,039 0,018 0,000 —
2,5 0,037 0,019 0,009 0,002 — —
Таблица П8.17
Функция распределения Релея f(x) = 1—ехр(—хг/2а2)
х/о F(x) Fix) х/8 Fix)
0 0,000 1,5 0,675 3,0 0,9889
0,1 005 1.6 722 3,1 9918
0,2 020 1,7 764 3,2 9940
0,3 044 1.8 802 3,3 9957
0,4 077 1.9 836 3,4 9969
0,5 117 2,0 865 3,5 9978
0,6 165 2,1 890 3,6 9985
0,7 217 2,2 911 3,7 9990
0,8 274 2,3 929 3,8 9993
0,9 333 2.4 944 3,9 9995
1,0 393 2,5 956 4,0 9997
1,1 454 2,6 966 4,01 99978
1,2 513 2,7 974 4,02 99985
1,3 570 2,8 980 4,04 99994
1,4 0,625 2,9 0,985 4,06 0,99998
Таблица П8.18
Случайные числа (равномерное распределение)
218 167 737 498 237
155 844 335 308 003
512 480 704 201 345
635 342 658 752 481
331 485 402 864 398
205 360 181 402 657
682 674 459 904 295
831 304 043 132 766
705 767 185 517 215
564 532 937 594 319
433
Продолжение табл П8 13
825 354 514 505 152
613 739 043 284 528
131 485 232 356 453
515 248 325 786 176
424 429 930 479 394
340 716 108 056 839
654 958 790 703 499
805 154 202 368 925
337 376 471 473 701
931 069 322 301 595
217 258 688 308 632
684 352 164 744 611
148 723 383 913 102
634 633 136 102 389
048 758 603 204 857
360 914 378 194 260
674 579 436 939 724
304 936 506 651 677
767 672 239 422 936
532 797 366 819 204
354 813 648 347 392
739 345 692 352 142
207 334 851 934 837
512 290 316 645 283
406 054 726 965 031
008 877 841 295 475
561 917 428 279 133
707 354 381 848 370
475 090 376 637 997
109 831 031 151 018
982 472 819 659 881
569 793 888 980 052
094 880 615 538 288
217 508 912 020 713
670 290 636 701 612
321 425 136 884 677
989 102 242 634 606
121 192 026 719 760
323 707 189 490 653
597 307 656 992 197
АННОТИРОВАННЫЙ БИБЛИОГРАФИЧЕСКИЙ
СПРАВОЧНИК КНИГ ПО НАДЕЖНОСТИ
Б.О. Руководство к пользованию
Аннотированный библиографический справочник охватывает книги
по надежности (монографии, сборники статей и т. п.), вышедшие на
русском языке по 1971 г. включительно.
Справочник для удобства пользования состоит из нескольких раз-
делов.
В разделе Б.1 приводятся краткие аннотации книг, которые рас-
положены по годам их выхода в свет, по алфавиту внутри каждого года.
Такое размещение представляется целесообразным для освещения со-
временного состояния литературы по надежности, а также характера
развития проблемы надежности, имеющего, по мнению автора, наи-
больший интерес для читателя.
В разделе Б.2 перечислены основные книги по проблеме надежности
в целом.
В разделе Б.З работы расположены по тематике, причем некоторые
отнесены одновременно к нескольким рубрикам (Книги, указанные
в первом разделе, не помещены во втором, так как они, как правило,
являются достаточно многоплановыми и их пришлось бы помещать во
все рубрики второго раздела.)
В разделах Б.2 — Б.З приводятся лишь наименования книг. Но-
мер, стоящий перед названием книги, указывает на номер аннотации,
помещенной в разд. Б.1.
В разделе Б.4 дается алфавитный список авторов и редакторов сбор-
ников статей и переводных книг с указанием номеров аннотаций, при-
веденных в предыдущем разделе.
Б.1. Аннотации книг по надежности по годам выпуска
1954 г.
1. Малогабаритная радиоаппаратура. (Вопросы конструирования, произ-
водства и эксплуатации.) Пер. с англ, под ред. В. И. Сифорова. М., ИЛ, 1954.
Первая книга, посвященная проблемам надежности, опубликованная на
русском языке. Основное внимание уделено вопросам технологии производства
и конструирования надежной радиоаппаратуры.
435
1956 г.
2, Автоматы. Сб. статей под ред. К. Э. Шеннона и Дж. Маккарти.
Пер. с англ. Под ред. А. А. Ляпунова. М., ИЛ, 1966.
В сборнике напечатана статья Дж. фон Неймана «Вероятностная логика
и синтез надежных организмов из ненадежных компонент».
1957 г.
3. Надежность наземного радиоэлектронного оборудования. Пер. с англ.
Под ред. Н. М. Шулейкина. М., «Сов. радио», 1957.
Первая книга на русском языке, в которой систематически излагаются
проблемы теории и практики надежности, в том числе влияние внешней среды
на надежность. Рассмотрены также основные вопросы инженерной психологии.
1958 V.
4. А ф о н и н Н. С. Надежность электроснабжения промышленных
предприятий. М., Госэнергоиздат, 1958.
Основное внимание уделено изучению ущерба, наносимого промышленным
предприятиям различных отраслей промышленности вследствие перерывов
в электроснабжении. Приводятся соображения по увеличению надежности
систем электроснабжения.
5. М е с я ц е в П. П Применение теории вероятностей и математической
статистики при конструировании и производстве радиоаппаратуры. М., Оборон-
гиз, 1958.
Приведена интересная тематическая подборка примеров, относящихся
к процессу проектирования и производства радиоэлектронной аппаратуры.
Их решение базируется на простых вероятностных и статистических методах.
6. Надежность радиоэлектронной аппаратуры. Сб. статей. М., «Сов. радио»,
1958.
Первый монографический сборник статей советских авторов, посвященный
вопросам надежности радиоэлектронной аппаратуры.
1959 г.
7. А с т а ф ь е в А. В. Окружающая среда и надежность радиотехни-
ческой аппаратуры. М., Госэнергоиздат, 1959.
Описываются вопросы надежности радиотехнической аппаратуры в зави-
симости от влияния окружающей среды. Рассматриваются климатические
условия, в которых может работать аппаратура. Приведен анализ типичных
повреждений радиодеталей и радиоматериалов. Излагаются общие вопросы
конструирования радиоаппаратуры с учетом влияния окружающей среды.
8. Вопросы надежности радиоэлектронной аппаратуры. Сб. статей. Пер.
с англ. Под ред. И И Морозова. М., «Сов. радио», 1959.
Сокращенный перевод статей, представленных на 4-м симпозиуме по надеж-
ности и контролю качества в радиоэлектронике (США), проходившем в 1958 г.
9. Организация контроля качества в промышленности США. Пер. с англ.
Под ред. В. В. Головинского. М., ИЛ, 1959.
Отчет группы английских специалистов, изучавших организацию контроля
качества в промышленности США.
10. Основы теории и надежности. М., Изд-во Судпромгиз промышленности,
1959. Авт.: И. М. Маликов, А. М. П о л о в к о, И. А. Романов,
П. А. Ч у к р е е в.
В популярной форме излагаются основные понятия теории надежности и
приводятся простейшие методы расчета. Это — одна из первых в нашей стране
систематических работ по надежности.
11 Щукин А. Н. Теория вероятностей и экспериментальное опрсдс*
ление характеристик сложных объектов. М., Госэнергоиздат, 1959.
436
Кратко изложенц оценки качества, надежности и эффективности различ-
ных приборов и сложных устройств, например управляемых объектов. Решение
задач показано на ряде примеров.
1960 г.
12. Л е в и н Б. Р. Теория сучайных процессов и ее применение в радио-
технике. М., «Сов радио», 1960.
Несколько разделов книги посвящено решению задач теории надежности.
13. Надежность радиоэлектронной аппаратуры. Сб. статей. М., «Сов.
радио», 1960.
Монографический сборник статей по вопросам априорного расчета надеж-
ности и эффективности сложных радиоэлектронных систем и устройств.
14. Основы теории и расчета надежности Изд 2-е. М., Изд-во судостроитель-
ной промышленности, 1960. Авт.: И. М. Маликов, А М. П о л о в к о,
Н. А. Романов, П. А. Ч у к р е е в.
Книга представляет собой незначительную переработку вышедшей ранее
работы тех же авторов. Добавлена глава, в которой приведены основные спо-
собы повышения надежности систем, включая оптимальное резервирование.
15. Проблемы надежности радиоэлектронной аппаратуры. Пер. с англ.
По ред. Б. Е. Бердичевского. М., Оборонгиз, 1960.
Сборник переводов докладов, представленных в 1959 г. на 5-м националь-
ном симпозиуме США по надежности и контролю качества радиоэлектронной ап-
паратуры, а также на Национальной конференции института радиоинженеров.
В первой части рассмотрены различные математические модели, во второй —
ряд практических работ, содержащих интересные результаты испытаний.
16. X и н н е й К., Уолш К- Радиодетали и проблема их надежности.
Пер. с англ. Под ред. Б. М Тареева. М., «Сов. радио», 1960.
Приведен обширный материал по деталям радиоэлектронной аппаратуры и
проблеме их надежности, даются технические и эксплуатационные требова-
ния к радиодеталям. Содержится классификация и общие данные о сопротивле-
ниях всех типов, дан анализ работы конденсаторов и применяемых материалов
и приведена классификация основных видов конденсаторов, описываются реле и
различные переключающие устройства; даются технические условия и рекомен-
дации по выбору реле для радиоэлектронной аппаратуры.
1961 г.
17. Б е л о в М. И., Соловейчик Ф. С. Вопросы надежности ра-
диоэлектронной аппаратуры. М., Госэнергоиздат, 1961.
Приводится реферативное изложение докладов, представленных на 6-м
симпозиуме по надежности и контролю качества в радиоэлектронике (США),
проходившем в 1960 г. Даны краткие сведения о предыдущих симпозиумах.
18 Болотин В. В. Статистические методы в строительной механике.
М., Гос. издательство литературы по строительству, архитектуре и строительным
материалам, 1961.
Рассматриваются различные модели разрушения материалов и вероятност-
ные методы оценки. Исследуется вопрос колебаний конструкций под воздействи-
ем случайных сил, а также накопление повреждений при случайных перегруз-
ках. Указывается, что многие из изложенных методов могут быть использованы
три анализе надежности механических конструкций. Представлена библиогра-
фия, насчитывающая более 150 наименований.
19. Л е б е д е в А. В Надежность и долговечность. М., Профиздат, 1961.
Дается популярное изложение проблемы надежности и долговечности тех-
нических изделий.
20 Месяцев П. П. Введение в теорию проектирования и производ-
ства радиоаппаратуры. М., «Высшая школа», 1961.
Изложены элементарные вопросы теории надежности. Основное внимание
уделено анализу связи точностных характеристик аппаратуры и надежности.
Рассмотрена взаимозависимость надежности и экономических вопросов.
437
21. С о р и н Я- М. Надежность радиоэлектронной аппаратуры (Мас-
совая радиобиблиотека). 'flL,' Госэнергоиздат, 1961.
Популярно излагается проблема надежности радиоэлектронной аппарату-
ры, показывается ее значение для народного хозяйства и оборонной техники.
1962 г.
22. Башаринов А. Е., Флейшман Б. С. Методы статисти-
ческого последовательного анализа и их приложения. М., «Сов. радио», 1962.
Глава 7 книги посвящена вопросам оптимального статистического контро-
ля качества и испытания надежности.
23. Вопросы точности и надежности в машиностроении. Под ред. Н. Г. Бруе-
вича. М., изд-во АН СССР, 1962.
В сборнике приводится анализ надежности различных устройств с учетом
постепенных отказов. Рассмотрены некоторые вопросы контроля на автомати-
ческих линиях машиностроения, исследованы корреляционные и функциональ-
ные зависнмостн между погрешностями размеров изделий при автоматическом
производстве.
24 Мамонтов О. В. Методы кибернетики в теории электронных
защит. М., Госэнергоиздат, 1962.
Одна из глав книги посвящена вопросам надежности работы устройств за
щиты.
25. С о р и н Я М., Лебедев А. В. Главное мерило качества (про-
блема надежности). М., «Знание», 1962.
Популярно излагается проблема надежности технических устройств.
26. Руководство для инженеров по решению задач теории вероятностей.
М., Судпромгиз, 1962. Авт i А. А. Свешников, Б. Г. Володин,
М. П. Ганин, И. Я Д и и е р, Л. Б Комаров, К. Б. Старо-
бин.
Многие задачи в книге касаются вопросов надежности и контроля качества
продукции.
27. Шор Я. Б. Статистические методы анализа и контроля качества и
надежности. М., «Сов. радио», 1962. 4
Рассматриваются вопросы анализа и контроля качества и надежности. При-
водятся общие сведения из теории вероятностей и математической статистики,
методы обработки опытных данных в случае стабильных и нестабильных усло-
вий испытаний, методы статистического контроля качества, методы анализа и
контроля надежности, математическое дополнение: некоторые специальные
функции, свертки и преобразование Лапласа.
1963 г.
28. А с р а т я и Э. А., Симонов П. В. Надежность мозга. М.,
Изд-во АН СССР, 1963.
Брошюра посвящена актуальным вопросам современной нейрофизиологии,
имеющим отношение к проблеме восстановления нарушенных функций цент-
ральной нервной системы. Анализируются основные принципы деятельности
головного мозга.
29. Берг А. И. Кибернетика и надежность. М., «Знание», 1963.
Рассматриваются проблемы надежности с позиций кибернетики.
30. 3 и з е м с к и й Е. И. Надежность радиоэлектронной аппаратуры.
М., Судпромгиз, 1963.
Изложены элементарные понятия надежности в объеме, достаточном для
учащихся радиотехнических техникумов.
31. К о л е г а е в Р. Н. Определение наивыгоднейших сроков службы
машин. М., Экоиомиздат, 1963.
Рассматриваются методы определения экономически оптимальных сроков
службы машин, а также связанные с этой проблемой вопросы: эффективность
капитального ремонта, оптимальные межремонтные сроки, остаточная стой-
438
мость машин перед капитальным ремонтом или ликвидацией. Исследуется влия-
ние морального износа на сроки службы машин.
32. Кордонский X. Б. Приложения теории вероятностей в инже-
нерном деле. М., Физматгиз, 1963.
Приведены модели надежности (§ 2, 7, 8, 16), а также некоторые задачи,
связанные с приемочным контролем и контролем качества.
33. Л е о н т ь е в Л. П. Введение в теорию надежности радиоэлектронно-
ной аппаратуры. Рига, изд-во АН Латв. ССР, 1963.
Основное внимание уделяется методам расчета надежности при постепен-
ных отказах.
34. Л у цк и й В. А. Расчет надежности и эффективности радиоэлектрон-
ной аппаратуры. Киев, изд-во АН УССР, 1963.
Обзор некоторых методов расчета надежности радиоэлектронной аппара-
туры.
35. Месяцев П. П. Надежность производства электронно-вычисли-
тельных машин. М., Машгиз, 1963.
Книга — дополненное и переработанное издание предыдущей работы того
же автора, выпущенной в 1961 г.
36. Надежность полупроводниковых устройств. Пер. с англ. Под ред.
А А. Маслова. М., ИЛ, 1963.
Освещена проблема надежности полупроводниковых устройств, а также
физика протекания процессов. Приведено большое количество фактических
данных.
37. Н е ч и п о р е н к о В. И. Функционально надежные электронные
схемы. Киев, Гостехиздат УССР, 1963.
Рассмотрены вопросы повышения надежности неконтактных релейных и
релейно-контактных схем.
38. Ш е н н о н К. Работы по теории информации и кибернетике. Пер.
с англ. Под ред. Р. Л. Добрушина и А. Н. Лупанова, М., ИЛ, 1963.
В книге напечатана статья Э. Мура и К. Шеннона «Надежные схемы из
ненадежных реле»
1964 г.
39. Б у с л е н к о Н. П. Математическое моделирование производст-
венных процессов на цифровых вычислительных машинах М , «Наука», 1964.
Излагается материал, полезный при моделировании многих задач по на-
дежности. Гл. 9 посвящена формализации некоторых видов нарушений нор-
мального течения производственного процесса (учет отказов, износа и периоди-
ческой наладки оборудования).
40. В е н т ц е л ь Е. С. Введение в исследование операций. М., «Сов.
радио», 1964.
Гл. 10 книги посвящена методам учета надежности технических устройств
при анализе систем вооружения и оценке их эффективности.
41. Д р у ж и н и н Г. В. Надежность устройств автоматики. М., «Энер-
гия», 1964.
Приводятся методы исследования надежности элементов и систем по данным
об их отказах: характеристики надежности элементов и систем, распределение
времени безотказной работы, расчет надежности проектируемых систем, эксп-
луатационные характеристики систем. Рассматриваются основные пути повы-
шения надежности систем автоматики: уменьшение опасных нагрузок, повы-
шение надежности при проектировании, изготовлении и эксплуатации систем
автоматики; методы проверки, отыскания причин неисправностей и предска-
зания работопособности систем. Затрагиваются вопросы резервирования без
восстановления. Приведена библиография из 120 наименований.
42. Е п и ф а н о в А. Д. Надежность автоматических систем. М., «Ма-
шиностроение», 1964.
Систематически излагаются вопросы теории надежности автоматических
систем с использованием как вероятностного математического аппарата, так
и методов теории автоматического управления. Даются общие сведения о на-
дежности автоматических систем, приведены основные временные характе-
439
ристики безотказности систем и элементов, дан анализ влияния условий эксп-
луатации и режимов работы. Затронуты методы расчета невосстанавливаемых
систем, включая резервирование с применением логических схем и восстанав-
ливаемых резервированных систем. Описаны методы экспериментального
определения надежности элементов и систем.
43. Л е б е д е в А. В., Сорин Я М. Беседы о надежности. М.,
«Знание», 1964.
Популярно излагаются основные проблемы надежности и пути ее повы-
шения.
44. Л л о й д Д. К., Липов М. Надежность: организация исследова-
ния, методы, математический аппарат. Пер. с англ. Под ред. Н. П. Бусленко.
М., «Сов. радио», 1964.
Фундаментальная работа, посвященная различным аспектам проблемы на-
дежности. Во введении анализируются причины ненадежности и возможности
ее предупреждения. Первый раздел состоит из трех глав, в нем рассматриваются
вопросы организации работ по надежности, задачи и деятельность при плани-
ровании и выполнении программы исследования надежности, организация си-
стемы сбора, обобщения и анализа информации о надежности. Второй раздел
(10 глав) посвящен математическому аппарату надежности. Первые три главы
касаются неформального описания моделей надежности и основных сведений
из теории вероятностей и математической статистики, включая описание основ-
ных дискретных и непрерывных распределений. В гл. 7 и 8 проведены методы
оценки надежности: свойства оценок (несмещенность, состоятельность, эффектив-
ность и т. д.), точечные и интервальные оценки для различных распределений.
В гл. 9 описываются интересные структурные модели надежности, в том числе
задачи определения доверительных оценок для систем по данным для подси-
стем, модель «слабейшего звена», некоторые задачи резервирования, нахожде-
ния допусков и пр. В гл. 10 разбираются различные планы испытаний на на-
дежность (выборочные планы, планы по методу Вальда, усеченные и цензури-
рованные испытания и пр.); в гл. 11 приведены основные модели повышения
надежности; в гл. 12 — планы экспериментирования и специальных испыта-
ний (граничных, на долговечность, на влияние окружающей среды и пр.);
в гл. 13—статистические планы для исследования надежности. В третьем
разделе приводятся примеры программ оценки надежности и ее подтверждения
для мощного ракетного двигателя, турбогенератора, мощного жидкостного ра-
кетного двигателя.
45. Обеспечение надежности полупроводниковых устройств. Пер. с англ.
Под ред. А. С. Савиной, М., «Мир», 1964.
В сборнике приводятся материалы конференции по проблеме обеспечения на-
дежности полупроводниковых приборов, которая состоялась в США в 1961 г.
Основные разделы книги: методы анализа данных, способы уменьшения интен-
сивности отказов, инженерный подход к оценке требований на полупроводни-
вые приборы, методы выборочного контроля, обеспечение надежности в новых
технических условиях.
46. П а р о л ь Н. В. Надежность приемно-усилительных ламп. М.,
«Сов. радио», 1964.
Дается краткое описание основных физических -процессов, определяющих
надежность работы ламп. Описывается влияние режимов использования и внеш-
них условий на показатели надежности ламп.
47. П о л о в к о А. М. Основы теории надежности. М., «Наука», 1964.
Систематически излагаются методы вероятностных расчетов надежности:
даются основные поня'тия теории надежности и количественные характеристики
надежности, расчет надежности при последовательном соединении элементов,
расчет надежности резервированных систем без восстановления: общее резер-
вирование, поэлементное (раздельное) резервирование и резервирование с дроб-
ной кратностью. Рассматриваются некоторые методы повышения надежности
сложных систем.
48. Ремонтопригодность радиоэлектронной аппаратуры. Пер. с англ. Под
ред. О. Ф. Пославского. М., «Сов. радио», 1964.
В сборнике приводятся доклады 3-й конференции по ремонтопригодности
радиоэлектронной аппаратуры, состоявшейся в 1960 г. в США. Кроме общетеоре-
449
тических вопросов, рассматриваются также вопросы автоматизации контроля,
обеспечения запасными частями и пр.
49. Самоорганизующиеся системы. Пер. с англ. Под ред. Т. Н. Соколова
М., «Мир», 1964.
Доклады на конференции, состоявшейся в 1959 г. в США. В сборнике по-
мещена статья У. Мак-Коллока «Надежность биологических систем».
50. Сапожников Р. А., Бессонов А. А., [По лом и ц-
к и й А. Г. Надежность автоматических управляющих систем. М., «Высшая
школа», 1964.
Даются некоторые сведения об испытаниях по оценке надежности, о на-
дежности отдельных элементов рассматриваемых систем (сопротивлений, конден-
саторов, реле, полупроводниковых приборов), приводятся простейшие методы
расчета резервируемых невосстанавливаемых систем, излагаются вопросы
обеспечения надежности при проектирования, производстве и эксплуатации.
51. Теория надежности и теория массового обслуживания. Сб. статей под
ред. А. И. Берга, Н. Г. Бруевича, Б. В. Гнеденко. Т. 2 «Кибернетику — иа
службу коммунизму». М., «Энергия», 1964.
Приведен материал по различным вопросам надежности; эффективность
многофункциональных управляющих систем, методы повышения надежности,
резервирование с восстановлением и-без восстановления, анализ зависимости
надежности от полноты контроля, профилактическое обслуживание, обнаруже-
ние и локализация неисправностей, методы аналитической оценки различных
систем со сложной структурой.
52. Т р е й е р В. Н. Теория долговечности и надежности машин. Минск.
«Наука и техника», 1964.
Освещаются проблемы долговечности и надежности машин, испытания изна-
шивающихся деталей машин на долговечность и надежность, технико-экономи-
ческие вопросы. Приводятся методы проектирования, а также примеры расчета.
53. III и ш о н о к Н. А., Репкин В. Ф., Барвинский Л. Л.
Основы теории надежности и эксплуатации радиоэлектронной техники. М.,
«Сов. радио», 1964.
На доступном уровне систематически изложены вопросы теории надеж-
ности. Рассматриваются количественные показатели надежности, методы их
инженерного расчета и статистической оценки; методика обоснования требова-
ний к надежности; способы повышения надежности путем резервирования и
рациональных методов эксплуатации аппаратуры; влияние на надежность про-
филактик и восстановительных работ; влияние систем контроля параметров на
надежность; вопросы оценки оперативной эффективности сложных систем; методы
оптимального резервирования при наличии ограничений; методы моделирова-
ния процессов функционирования с учетом надежности. Некоторые из этих
вопросов рассмотрены впервые.
1965 г.
54. А с т а ф ь е в А. В. Окружающая среда и надежность радиотехни-
ческой аппаратуры. Изд. 2-е. М., «Энергия», 1965.
В книге незначительно переработан материал первого варианта того же
наименования.
55. Б а з о в с к и й И. Надежность: теория и практика. Пер. с англ.
Под ред. Левина Б. Р. М., «Мир», 1965.
Сделана одна из первых попыток в зарубежной литературе систематически
изложить вопросы теории надежности радиоэлектронной аппаратуры. Первые
две главы посвящены количественному и качественному определению основных
понятий надежности. Гл. 3—9 и 15 содержат подробное физическое и математи-
ческое описание отказов (гл. 3—5, 9 — внезапные отказы, подчиняющиеся
экспоненциальному закону, гл. 6 — постепенные отказы, подчиняющиеся нор-
мальному закону), исследование влияния режима использования элемента и
окружающей среды иа интенсивность этих отказов (гл. 15), анализ совместного
действия внезапных и постепенных отказов (гл. 7) и анализ надежности с учетом
приработочных, внезапных и износовых отказов. В гл. 10—14 приведены
краткие сведения из теории расчета надежности резервированных систем.
15 Зак. 943
441
В гл. 17 и 20 затрагиваются вопросы профилактического обслуживания.
В гл. 1-8, 19 и 25 рассматриваются проблемы учета надежности при проектиро-
вании, примеры анализа конструкций, обеспечения надежности. В гл. 21—24
излагаются методы экспериментальной оценки надежности (обработка ста-
тистики, точечные и доверительные оценки, метод последовательных испыта-
ний). В дополнении к книге содержатся замечания к отдельным главам, а также
специальное приложение, посвященное вопросам оценки резервированных си-
стем с восстановлением.
56. Б р а у д о С. И. Сохранение надежности радиолокационной аппара-
туры (настройка, контроль параметров, предупреждение и диагностика отказов).
М., «Сов. радио», 1965.
Книга состоит из двух частей: подход к сохранению и поддержанию на-
дежности РЛС (настройка аппаратуры, импульсных и транзисторных схем,
контроль узловых параметров, предупреждение отказов аппаратуры, диагно-
стика и поиск неисправностей); настройка и контроль параметров некоторых
устройств РЛС (подробно рассматриваются приемное и передающее устройства).
57. Вольпин А. Г. Основные понятия и расчет надежности радио-
передатчика. М., «Связь», 1965.
Излагаются элементарные сведения- о расчете надежности простейшей схе-
мы, которые иллюстрируются примерами.
58. Г н е д е н к о Б. В. Курс теории вероятностей. Изд. 4-е переработ.
М., «Наука», 1965.
Один из разделов книги посвящен элементам теории резервирования: в нем
приводится несколько теорем, касающихся восстанавливаемых и невосстанав-
ливаемых систем.
59. Г н е д е н к о Б. В., Беляев Ю. К., Соловьев А. Д.
Математические методы в теории надежности. М., «Наука», 1965.
В фундаментальной работе излагаются современные математические методы
теории надежности. В гл. 1 приводятся строгое описание элементов теории ве-
роятностей и математической статистики, сведения из преобразований Лапласа.
Гл. 2 посвящена характеристикам надежности элементов и систем. В гл. 3
приводятся методы оценки показателей надежности по результатам испытаний;
основное внимание уделяется экспоненциальному распределению. В гл. 4
описываются методы проверки гипотез о надежности: проверка гипотезы об
экспоненциальности распределения, критерии проверки гипотез о значениях
параметра экспоненциального распределения, критерии типа последователь-
ного анализа и непараметрические методы оценки однородности статистического
материала. В гл. 5 рассматриваются различные схемы резервирования без
восстановления, изучаемые в основном с использованием схемы гибели, в гл. 6 —
схемы резервирования с восстановлением, изучаемые с помощью процессов
гибели и размножения; здесь же сообщаются некоторые результаты изучения
нестационарйого периода. Последняя глава посвящена статистическим методам
контроля качества и надежности массовой продукции: планы приемочного конт-
роля, экономичные планы контроля, последующие оценки качества по результа-
там контроля, некоторые сведения о текущем контроле. В приложении приво-
дятся таблицы, в том числе таблицы Колумбийского стандарта для однократной,
двукратной и последовательной выборок. Библиография насчитывает около
120 наименований.
60. Даммер А., Гриффин Б. Испытание радиоэлектронной аппа-
ратуры и материалов на воздействие климатических и механических условий.
Пер. с англ. Под ред. Б. Е. Бердичевского. М., «Энергия», 1965.
Показано влияние на надежность воздействий окружающей среды: повы-
шенной влажности, электрохимической коррозии, высокой и низкой темпера-
тур, механических воздействий, условий транспортирования и хранения, вы-
сотных и космических условий, воздействий ядерной радиации, акустического
шума. Даются отдельные рекомендации по защите от влияния внешних воздей-
ствий.
61. К с е н з С. П. Поиск неисправностей в радиоэлектронных системах
методом функциональных проб. М., «Сов. радио», 1965.
Рассматриваются пути создания комплексной методики обнаружения
причин отказов радиоэлектронного оборудования средней и большой сложности,
442
Приводятся примеры построения схем функциональных проб для различных
систем.
62. К у з н е ц о в В. А. Основные вопросы надежности радиоэлектрон-
ной аппаратуры. М., «Энергия», 1965.
Популярно излагаются различные вопросы надежности аппаратуры.
63. Основы исследования операций в военной технике. М., «Сов. радио»,
1965. Авт.: Ю. В. Чуев, П. М. Мельников, С. И. Петухов, Я. Б. Шор.
Приведены критерии надежности элементов восстанавливаемых и невосста-
навливаемых изделий и сложных комплексов (гл. 1), рассмотрены некоторые
оптимальные задачи надежности: обоснование оптимальных режимов профилак-
тических работ, требований к надежности, длительности тренировки, выбор
оптимального резервирования (гл. 6).
64. С а а т и Т. Л. Элементы теории массового обслуживания и ее при-
ложения. Пер. с англ. Под ред. И. Н. Коваленко и Р. Д. Когана. М., «Сов.
радио», 1965.
В гл. 14 два раздела посвящены вопросам обеспечения запасными частями
и управления запасами. Многие модели массового обслуживания прн незначи-
тельной переформулировке могут быть использованы в задачах надежности.
65. Сборник задач по теории вероятностей, математической статистике и
теории случайных функций. М., «Наука», 1965. Авт.: Б. Г. Володин, М. П. Га-
нин, И. Я. Динер, Л. Б. Комаров, А. А. Свешников, К. Б. Старобин.
Существенно дополненное издание первой книги тех же авторов.
66. Сед я к » н Н. М. Элементы теории случайных импульсных пото-
ков. М., «Сов. радио», 1965.
Одна из глав книги (гл. 9) посвящена исследованию некоторых задач на-
дежности, связанных с оценкой восстанавливаемых систем.
67. С о л о м о н о в П. А. Вопросы надежности авиационной техники.
Воениздат, 1965.
Излагаются элементарные вопросы расчета надежности, рассматриваются
некоторые характерные неисправности авиационной техники.
68. Теория конечных и вероятностных автоматов. М., «Наука», 1965.
В сборнике имеется ряд статей по вопросам надежности.
69. Ш и р о к о в А. М. Основы надежности и эксплуатации электронной
аппаратуры. Минск, «Наука н техника», 1965.
Книга посвящена элементарным сведениям по расчету надежности и оценке
ее по результатам эксплуатации, основным методам повышения надежности и
описанию методов испытания на надежность и долговечность; рассмотрены
вопросы технического обслуживания аппаратуры.
1966 г.
70. Бердичевский Б. Е. Оценка надежности аппаратуры автома-
тики (методы оценки надежности в процессе разработки). М-, «Машинострое-
ние», 1966.
Изложен метод оценки надежности с помощью системы характеристических
критериев, посредством которых можно оценить соответствие структуры и прин-
ципиальной схемы, конструкции, основных технических характеристик ряду
специфических требований. Подробно разъясняются характеристические Крите--
рии оценки надежности, обусловленной техническими параметрами, характе-
ристиками и схемами аппаратур, качеством работы элементов, конструкцией
аппаратуры, а также критерии для оценки эксплуатационной надежности.
71. Герцбах И. Б., Кордоиский X. Б. Модели отказов.
(Библиотека инженера по надежности.) М., «Сов. радио», 1966.
Рассматриваются различные математические модели отказов: мгновенные и
накапливающиеся повреждения, случаи одновременного действия нескольких
причин. Для указанных моделей получены законы распределения времени бе-
зотказной работы, приведены способы оценки их параметров путем обработки
опытных данных с помощью методов моментов и разделяющих разбиений.
72. Г н е д е н к о Б. В., Коваленко И. Н. Введение в теорию
массового обслуживания. М., «Наука», 1966.
15* 443
В гл. 4 дается анализ однолинейной системы с ожиданием при учете возмож-
ности выхода обслуживающего прибора из строя и восстановления его.
73. И ы у д у К. А. Оптимизация устройств автоматики по критерию на-
дежности. М., «Энергия», 1966.
Сообщается о методах нахождения совокупности значений параметров
устройства, обспечивающих максимальную (потенциальную) его надежность
при заданных условиях работы и при заданной схеме.
74. К а л а б р о С. Р. Принципы и практические вопросы надежности.
Пер. с англ. Под ред. Д. Ю. Панова. М., «Машиностроение», 1966.
В популярной форме излагается широкий круг вопросов надежности: рас-
чет последовательных и параллельных соединений, сведения из теории вероят-
ностей (включая описание основных распределений вероятностей, нормального,
биномиального, пуассоновского), вопросы сбора и анализа данных по надеж-
ности, вопросы ремонтопригодности, методы выборочного и приемочного конт-
роля, различные организационные аспекты.
75. К л и м о в Г. М. Стохастические системы обслуживания. М., «Нау-
ка», 1966.
Подробно рассматриваются вопросы обслуживания ненадежными прибора-
ми. Приводится также случай обслуживания дублирующими приборами.
76. Козлов Б. А., Ушаков И. А. Краткий справочник по расче-
ту надежности радиоэлектронной аппаратуры. Л-1 , «Сов. радио», 1966.
Справочник рекомендуется для специалистов, работающих в области на-
дежности, и предназначен в качестве практического руководства для расчетов,
оценки и обеспечения надежности радиоэлектронной аппаратуры и различных
сложных систем. В гл. 1 приводятся основные понятия надежности и объясня-
ются показатели надежности восстанавливаемых и невосстанавливаемых уст-
ройств. В гл. 2 расматриваются главные показатели надежности элемента, по-
нимаемого как часть более общей системы В гл. 3 дан вывод формул для расчета
типовых невосстанавливаемых систем. В гл. 5 рассмотрены некоторые специ-
альные задачи резервирования В гл. 6 описываются методы расчета последо-
вательных систем, отдельными элементами которых могут быть как избыточ-
ные, так и неизбыточные элементы. Большинство приведенных результатов по-
лучено в предположении экспоненциальности распределений времени безотказ-
ной работы и времени восстановления отдельных элементов системы. В гл 7
излагаются общие методы оценки эффективности (оперативной эффективности)
Таких сложных систем, в которых отказ отдельных элементов приводит не
к полному отказу системы, а лишь к некоторому ухудшению качества функ-
ционирования В гл. 8 рассматриваются методы решения основных оптимальных
задач надежности, в первую очередь задач оптимального резервирования и
обеспечения запасными элементами. В гл. 9 сообщается о некоторых простей-
ших методах обработки статистических данных, получаемых в процессе эксп-
луатации и специальных испытаний аппаратуры.
77. К о ф м а н А. Методы и модели исследования операций. Пер. с франц.
Под ред. Д. Б. Юдина. М., «Мир», 1966.
Отдельные главы книги (гл. 4, 5, 9, 10) посвящены вопросам управления
запасами, а также задачам, связанным с износом и заменой оборудования.
78. К о ф м а н А., Фор Р. Займемся исследованием операций. Пер.
с франц. Под ред. А. А. Корбута. М., «Мир», 1966.
В гл. 8 книги приведена задача замены оборудования, подверженного
износу.
79. К у л и к о в В. А. Обеспечение надежности сложной радиоэлект-
ронной аппаратуры при мелкосерийном производстве. (Библиотека инженера
по надежности.) М., «Сов. радио», 1966.
Излагаются вопросы связи надежности с конструкцией изделия и техно-
логией производства; рассматриваются задачи контроля качества и надежности,
некоторые аспекты ремонтопригодности, связи надежности с экономическими
затратами на ее обеспечение.
80. Л у ц к и й В. А. Расчет надежности и эффективности радиоэлект-
ронной аппаратуры (справочник). Изд. 2-е, Киев, «Наукова думка», 1966.
Незначительно переработанный вариант первого издания.
444
81. Математическая теория надежности информационно-логических управ-
ляющих устройств. Под ред. В. И. Зубова. Л., Изд-во ЛГУ им. А. А. Жданова,
1966.
Излагаются математические методы анализа процессов, протекающих при
функционировании приборов с отказами.
82. Методы введения избыточности для вычислительных систем. Пер.
с англ. Под ред. В. С. Пугачева. М., «Сов. радио», 1966.
В сборник вошли доклады, прочитанные на симпозиуме, по надежности вы-
числительных машин и управляющих систем, состоявшемся в 1962 р. в США.
Описываются различные методы использования информационной и структур-
ной избыточности с целью повышения надежности вычислительных устройств,
дается анализ надежности всевозможных типов мажоритарной логики, кодов
с обнаружением и исправлением ошибок, схем с применением принципов адап-
тивности при голосовании и усреднении выходных сигналов.
83. О надежности сложных технических систем (Сборник трудов семинара
секции надежности научного совета по комплексной проблеме «Кибернетика»
при Президиуме АН СССР). М., «Сов. радио», 1966.
Помещены работы по общим вопросам теории надежности сложных систем
(взаимосвязь надежности, долговечности и точности; эффективность функциони-
рования сложных систем; оптимальные методы управления случайными про-
цессами), приводятся методы расчета сложных систем (оптимальные методы по-
иска неисправностей, оценка «канальной» надежности, автоматизированные пред-
рабочие проверки, оптимальные границы для контрольных допусков, асимпто-
тический метод оценки надежности сложных систем, оценка надежности мето-
дами статистического моделирования, построение нижней доверительной границы
для вероятности безотказной работы системы по результатам испытаний ее ком-
понент), расмотрены также вопросы физики отказов и ускоренных испытаний.
84. П а в л о в Б. В. Кибернетические методы технического диагноза.
М., «Машиностроение», 1966.
Рассматриваются математический аппарат и общая теория технического
диагноза, приводятся методы акустической диагностики.
85. Прикладные задачи технической кибернетики. Под ред. Л. G. Гурина,
И. А. Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966.
В сборник вошли материалы конференции по технической кибернетике, со-
стоявшейся в 1964 г. в Ереване. Одна из трех частей сборника (ч. 2) посвящена
вопросам надежности сложных систем: исследование методом Монте-Карло вос-
станавливаемых систем, а также информационных сетей; оптимальное профи-
лактическое обслуживание и задача циклического обслуживания; несколько
работ, связанных с оптимальным резервированием и обеспечением запасными
элементами; оценка эффективности функционирования устройств с мажоритар-
ной логикой и устройств, подверженных отказам и сбоям.
86. С а н д л е р Дж. Техника надежности систем. Пер. с англ. А. Л. Рай-
кина. М., «Наука», 1966.
Систематически излагаются вопросы теории надежности технических си-
стем. В первых трех главах даются общие понятия надежности и некоторые све-
дения из теории марковских цепей. В гл. 4 описываются модели необслуживаемых
систем (последовательные и параллельные соединения, специальные случаи).
В гл. 5 — модели обслуживаемых систем. В гл. 6 рассматриваются модели на-
дежности, описываемые марковскими процессами с доходами. В гл. 7 — методы
оптимального резервирования в обслуживаемых и необслуживаемых системах.
В гл. 8 приведены задачи профилактического обслуживания (контроль, провер-
ка и профилактика). Последняя глава посвящена распределению интенсивно-
стей отказов и ремонтов на основе конфигурации системы, в частности при нали-
чии ограниченных возможностей. В заключение дана обширная библиография.
87. Ткаченко Л. Г. Надежность радиоэлектронной аппаратуры.
М., «Знание», 1966.
В популярной форме излагаются основные понятия и задачи надежности.
88. Т у р к е л ь т а у б Р. М. Методы исследования точности и надежно-
сти схем аппаратуры. М., «Энергия», 1966.
Излагаются методы анализа точности аппаратуры и надежности при внезап-
ных и параметрических отказах. Приводятся методы моделирования и статисти-
'!'!5
ческих испытаний для исследования схем, задачи синтеза схем по заданному
критерию точности и надежности.
89. X е в и л е н д Р. Инженерная надежность и расчет на долговечность.
Пер. с англ. Под ред. Г. Н. Баласанова. М., «Энергия», 1966.
Излагаются вопросы надежности с использованием минимума математи-
веского аппарата. Анализируются статистические и функциональные факторы,
влияющие на надежность. Рассматриваются понятия прочности, нагрузки и от-
каза, вопросы влияния старения на долговечность, изучается взаимосвязь
прочности и долговечности объектов различной сложности.
90. Ш и ф р и н-К рыжаловский Ю. А., Митин В. С. Тепло-
вая устойчивость транзисторов и надежность радиоэлектронной аппаратуры.
М , «Сов радио», 1966.
Исследованы вопросы воздействия повышенной температуры на надежноть
радиоаппаратуры. Приводятся конкретные данные по тепловой устойчивости
транзисторов.
1967 г.
91. Б у к а н Д ж., Кенигсберг Э. Научное управление запасами.
М., «Наука», 1967.
Многие из изложенных в книге задач имеют непосредственное приложение
к вопросам обеспечения систем с целью достижения требуемой надежности.
92. Голубе в-Н овожилов Ю С. Многомашинные комплексы вы-
числительных средств. М., «Сов. радио», 1967.
Третий раздел книги посвящен интересным задачам оценки влияния харак-
теристик эксплуатационной надежности ЭВМ на время выполнения вычислений.
Рассмотрено несколько типовых моделей процесса вычислений (пересчет в слу-
чае отказов или сбоев или частичный пересчет при одних типах неисправностей
и полный при других и т. п.).
93. Г у т ч и н И. Б., К у з и ч е в А. С. Бионика и надежность. Эле-
менты теории формальных нейронов. М., «Наука», 1967.
Приводится основной аппарат описания функционирования формальных
нейронов в смысле Мак-Коллока, методы синтеза таких нейронов и надежных
сетей из них. Даются некоторые технические приложения для синтеза вычисли-
тельных систем.
94. Д р у ж и н и н Г. В. Надежность систем автоматики Изд. 2-е, М.,
«Энергия», 1967.
Существенно переработанный вариант первого издания книги. Добавлены
две новые части: исследование надежности элементов и систем по данным о при-
ближении к отказам (процессы, предшествующие появлению отказов; моделирова-
ние процессов появления отказов); исследование надежности работ по обслужи-
вание устройств автоматики (распределение времени проведения отдельных
рабо|, Исследование выполнения отдельных работ).
95. Зиземский Е. И. Надежность радиоэлектронной аппаратуры.
Изд. 2-е. М., «Судостроение», 1967.
Незначительно переработанный вариант ранее вышедший книги.
96. К е м п и н с к и й М. М , Н е в е л ь с о н М. С., Старо-
б и н К- Б. Надежность автоматических средств обработки и контроля в маши-
ностроении. М., «Машиностроение», 1967.
Даются общие понятия надежности и основные параметры автоматических
станков и приборов для контроля размеров, а также методы испытания их на на-
дежность, и определения показателей точности и надежности по результатам
испытаний.
97. Кибернетику — на службу коммунизму. Т. 4, 5. Сб. статей. Под ред.
А. И. Берга. М., «Энергия», 1967.
В т. 4 помещены статьи по теории резервирования и управления запасами.
98. Кибернетику — на службу коммунизму. Т. 5. Сб. статей под ред.
А. И. Берга. М., «Энергия», 1967.
В т. 5 приведена статья «Надежность и долговечность (теория, эксперимент,
практика)».
99. Кокс Д. Р., С м и т В. Л. Теория восстановления. Пер. с англ Под
ред. Ю К. Беляева. М., «Сов. радио», 1967.
446
Одна из глав книги посвящена вероятностным моделям отказов.
100. Колегаев Р. Н. Определение оптимальной долговечности тех-
нических систем. (Библиотека инженера по надежности.) М., «Сов. радио», 1967.
Освещаются вопросы оптимальной долговечности технических систем в за-
висимости от материального и морального износа.
101. Маликов И. М. Надежность судовой электронной аппаратуры и
систем автоматического управления. М., «Судостроение», 1967.
Даются элементарные методы расчета последовательных и резервных соеди-
нений при невосстанавливаемых элементах и простейшие методы эксперименталь-
ной оценки показателей надежности.
102. Молоканов Г. Ф. Точность и надежность навигации летательных
аппаратов. М., «Машиностроение», 1967.
Приводятся краткие сведения из математического аппарата теории надеж-
ности и примеры решения отдельных навигационных задач.
103. Надежность электроснабжения. Под ред. И. А. Сыромятникова.
М., «Энергия», 1967.
В сборнике излагается методика определения ущерба от перерывов в элект-
роснабжении и технико-экономическое обоснование уровней надежности электро-
снабжения, а также влияние этих уровней на основные .параметры электрических
сетей.
104. Пампуро В. И. Анализ радиоцепей и их схемной надежности.
Киев, «Техника», 1967.
Рассматриваются аналитический (функциональный) и вероятностный методы
анализа схем и систем с учетом постепенных отказов.
105. Р а й к и и А. Л. Элементы теории надежности для проектирования
технических систем. М., «Сов. радио», 1967.
В первых двух главах даются основные понятия и определения, форму-
лируются проблемы надежности при проектировании технических систем. Гл. 3
посвящена анализу необслуживаемых систем, гл. 4 — обслуживаемых. Решен
ряд оригинальных задач. В ключевой главе излагается проблема оптимального
снабжения систем резервными н запасными элементами при наличии ограничений
по стоимости, весу и пр. В последней главе рассматриваются вопросы планиро-
вания эксплуатационного обслуживания, применения к этим задачам марковских
процессов с доходами.
106. Решение задач надежности и эксплуатации на универсальных ЭЦВМ.
М., «Сов. радио», 1967. Авт.: Б. П. Креденцер, М. М. Ластовчеико, С. А. Сенец-
кий, Н. А. Шишонок.
На конкретных примерах излагается методика применения ЭЦВМ для реше-
ния задач надежности и эксплуатации, основанная на статистическом моделиро-
вании. Решения доведены до конкретных программ в системе команд ЭВМ
«Урал-2».
107. Рябинин И. А. Основы теории и расчета надежности судовых
электроэнергетических систем. М., «Судостроение», 1967.
Излагаются вопросы надежности: методы статистической оценки по резуль-
татам испытаний, методы проверки различных гипотез о надежности судового
электрооборудования, аналитические методы расчета невосстанавливаемых и
восстанавливаемых устройств, методы исследования надежности восстанавлива-
емых устройств указанного класса статистическим моделированием на ЭЦВМ.
108. Спорыш И. П. Надежность механизмов систем автоматического
регулирования. М., «Машиностроение», 1967.
Изложены вопросы надежности механических связей систем автоматического
регулирования (на примерах из области парового турбостроения).
109. Старосельский А. А., Гаркунов Д. Н. Долговечность
трущихся деталей машин. М., «Машиностроение», 1967.
Даются основы прочности поверхностного слоя деталей машин, рассмотрены
конструктивные и технологические способы повышения долговечности и надеж-
ности работы трущихся деталей. Гл. 4 посвящена вопросам эксплуатации машин
с точки зрения их долговечности и надежности.
110. Федосенко Р. Я. Надежность электроснабжения и электриче-
ские нагрузки. М., «Энергия», 1967.
447
Изложены методы и результаты исследования электропотребления и электр и-
ческих нагрузок в зоне современной жилищно-общественной застройки и о не и-
ки надежности работы городских электросетей.
1968 г.
111. Б у еле н ко Н. П. Моделирование сложных систем. М., «Наука»
1968.
В одной из глав рассматривается система массового обслуживания с йена»
дежными элементами.
112. Введение в техническую диагностику. М., «Энергия», 1968. Авт.1
Г. Ф. Верзаков, Н. В. Киншт, В. И. Рабинович, Л. С. Тимонен.
Показано современное состояние научных исследований в области техниче-
ской диагностики. Приведено описание диагностических тестов и построение
оптимальных программ поиска отказов, контроля работоспособности и восста-
новления сложных технических систем.
113. Гнеденко Б. В. Беседы о математической статистике. М., «Зна-
ние», 1968.
Рассмотрены вопросы испытаний изделий на качество и надежность и ста-
тистические методы приемочного контроля.
114. Гольдберг О Д. Качество н надежность асинхронных двигате-
лей. М., «Энергия», 1968.
Анализируется качество асинхронных двигателей по результатам их конт-
рольных испытаний; рассматриваются проблемы повышения надежности этих
двигателей.
115. Гуревич А. С., Курбатов Н. Д. Надежность кабелей свя-
зи. М., «Связь», 1968.
Рассмотрены основные факторы, влияющие на надежность кабельных ли-
ний связи, анализируется эксплуатационная надежность этих линий.
116. Инженерные методы исследования надежности радиоэлектронных си-
стем. Пер. с англ. Под ред. А. М. Половко, А. Г. Варжапетяна. М., «Сов. радио»,
1968.
Дается в виде подборки статей изложение основных вопросов надежности.
117. К у гель Р. В. Ускоренные ресурсные испытания в машинострое-
нии. М., «Знание», 1968.
Излагаются основные сведения о ресурсных испытаниях в машиностроении,
вопросы их организации в режимы испытаний, приведены критерии предель-
ного состояния.
118. Математические основы современной радиоэлектроники. М., «Сов.
радио», 1968. Авт.: И. А. Большаков, Л. С. Гуткин, Б. Р. Левин, Р. Л. Страто-
нович.
Гл. 7 посвящена основным вопросам теории надежности.
119. Надежность в эффективность дискретных систем. Рига, «Зиватне»,
1968.
В сборнике излагаются теоретические вопросы надежности функцво; .ро-
вания дискретных систем.
120. Нечипоренко В. И. Структурный анализ и методы построения
надежных систем. М., «Сов. радио», 1968.
Приводятся основы структурного анализа систем, дается сравнительный ана-
лиз различных способов и методов резервирования, рассмотрены вопросы синтеза
надежных систем.
121. Оптимальные задачи надежности. Под ред. И. А. Ушакова Изд-во Ко-
митета стандартов, мер и измерительных приборов при СМ СССР, 1968.
Даны переводы статен зарубежных авторов и редакторских дополнений,
посвященных трем основным классам оптимальных задач надежности: оптималь-
ному резервированию при наличии ограничений, оптимальным диагностическим
процедурам для локализации неисправностей, оптимальным профилактическим
работам. В каждом разделе приводится обширная библиография насчитываю-
щая более 120 наименований.
122. Основы эксплуатации радиоэлектронной аппаратуры М , «Высшая
школа», 1968. Авт.: А. К. Быкадоров, Л. И. Кульбак, В. Ю. Лавриненко,
И. Н Рысейкви, В. Л. Тихомиров.
448
Приводятся основные вопросы теории и практики надежности в элементар-
ном изложении.
123. Перроте А. И., Карташов Г. Д., Цветаев К. Н.
Основы ускоренных испытаний радиоэлементов на надежность. М., «Сов. ра-
дио», 1968.
Излагаются основные положения ускоренных испытаний на надежность,
позволяющих получать информацию о надежности изделий за время, меньшее
гарантийной долговечности. Объясняется разработанный авторами принцип «на-
следственности» в теории надежности. Рассмотрены форсированные и ускорен-
ные испытания. Получены инженерные формулы для планирования пред-
варительных исследований н ускоренных испытаний.
124. Пирс У. Построение надежных вычислительных машин. Пер. с англ.
Б. Л. Овсиевича и Л. Я. Розенблюма. М., «Мир», 1968.
Даны основы теории надежности специфического типа аппаратуры (электрон-
ных вычислительных машин), указываются методы построения надежных си-
стем из ненадежных элементов, приводятся некоторые предельные теоремы, не-
обходимые длн анализа избыточных схем, изучается пороговый элемент, орган
юлосования, излагаются методы кодирования в проектировании надежных вы-
числительных машин.
125. Сорин Я- М., Лебедев А. В. Беседы о надежности. Изд. 2-е.
М., «Знание», 1968.
Второе переработанное и дополненное издание вышедшей ранее книги тех
же авторов.
126. Точность и надежность автоматических станков и приборов активного
контроля. Сб. статей под ред. М. С. Невельсона. М., «Машиностроение», 1968,
В сборнике излагаются новые методы анализа и расчета надежности и точ-
ности систем автоподналадки станков, приборов, контроля размеров и пр.
127. X о л п и н Дж Бездефектность (Новый подход к проблеме обеспе-
чения качества). Пер. с англ. Под ред. Я. М. Сорина. М., «Мир», 1968.
Излагаются различные аспекты системы бездефектного производства. Рас-
смотрены основные предпосылки бездефектного труда, различные фазы орга-
низаторской и воспитательной работы по внедрению программ бездефектности,
в том числе в области умственного труда.
128. Шор Я. Б., Кузьмин Ф. И. Таблицы для анализа и контроля
надежности. (Библиотека инженера по надежности.) М., «Сов. радио», 1968.
Приведены статистические и математические таблицы, необходимые при рас-
чете, анализе н контроле надежности. В первых семи разделах содержатся таб-
лицы наиболее часто встречающихся распределений вероятностей: нормального,
экспоненциального, Вейбулла, гамма, логарифмически-нормального, биноми-
ального, Пуассона. Далее приведены таблицы дли решения некоторых типовых
задач: определение доверительных границ, статистический контроль надежно-
сти, расчет норм запасных деталей, построение вероятностных шкал и другие.
Последний раздел содержит некоторые вспомогательные таблицы. Приводятся
многочисленные примеры использования этих таблиц для решения разнообраз-
ных инженерных практических задач.
129. ЯстребенецкийМ. А., Соляник Б. Л. Определение на-
дежности аппаратуры промышленной автоматики в условиях эксплуатации. М.,
«Энергия», 1968.
Излагаются некоторые вопросы сбора и обработки информации о надежно-
сти, приводятся методы расчета основных показателей надежности. Исследу-
ются вопросы проверки качества и возможности объединения информации об
отказах.
1969 г.
130. Барлоу Р., Прошаи Ф. Математическая теория надежности.
Пер. с англ. Под ред. Б. В. Гнеденко. М., «Сов. радио», 1969.
Основное внимание уделяется исследованию так называемых «стареющих»
систем и систем из «стареющих» элементов. С этой позиции рассмотрено большое
число вероятностных моделей, имеющих важное практическое значение. В гл. 1
дается исторический обзор математической теории надежности и вводятся основ-
449
ные определения надежности. В гл. 2 излагаются основные распределения вре-
мени безотказной работы, причем главное внимание уделяется экспоненциаль-
ному распределению и распределениям с монотонной функцией интенсивности,
приводятся основные неравенства отказа, являющиеся существенными улучше-
ниями чебышевских неравенств, полученных без учета монотонности функции
интенсивности. В гл. 3 рассматриваются основные характеристики правил об-
служивания (предупредительные замены, основанные на наработке, групповые
замены), приводятся также необходимые сведения из теории восстановления.
В гл. 4 описываются оптимальные правила предупредительных замен и инспек-
ционных проверок. В гл. 5 излагаются вопросы изучения вероятностных моделей
сложных систем (в основном марковские и полумарковские модели). Гл. 6 посвя-
щена задачам оптимального резервирования при наличии одного ограничения,
где приводится модификация метода динамического программирования. Здесь
же дается задача оптимального резервирования при двух типах отказов: отказы
типа «короткое замыкание» и отказы типа «обрыв». В гл. 7 затрагивает некоторые
количественные соотношения для сложных систем, продолжающие работы Мура
и Шеннона. Наиболее интересно здесь соотношение между интенсивностью отка-
зов системы и составляющих ее элементов.
В специальное дополнение вынесено шесть статей тех же авторов в соавтор-
стве с Э. Шойером, А. Маршаллом и Т. Бреем.
Приведена библиография более 200 наименований.
131. Варжапетян А. Г. Техническая эффективность и надежность
судовых систем управления. Л., «Судостроение», 1969.
Приведены методы аналитической оценки и моделирования надежности сис-
тем управления. Большое внимание уделено вопросам расчета при частичных
отказах.
132. Волчкевич Л. И. Надежность автоматических линий. М., «Ма-
шиностроение», 1969.
Рассмотрены вопросы производительности и надежности однопоточных
и многопоточных автоматических линий и пути их повышения.
133. Г е р ц б а х И. Б. Модели профилактики (теоретические основы пла-
нирования профилактических работ). (Библиотека инженера по надежности.)
М., «Сов. радио», 1969.
Рассматривается построение вероятностных моделей функционирования
систем, на основании которых решается ряд задач о нахождении оптимального
правила проведения профилактических работ, представляющих собой со-
вокупность мероприятий, направленных на улучшение рабочих свойств
систем и их элементов (замены элементов, частично отработавших свой ресурс,
регулировки, подналадки и т. п.). Оптимизация достигается варьированием сро-
ков и объемов профилактических работ. Профилактики заключаются в принуди-
тельной замене элементов, возраст которых достиг определенной величины, при-
чем сроки замены назначаются на основании априорной информации о распреде-
лении времени безотказной работы элементов системы. Описываются системы,
у которых можно выделить ряд промежуточных состояний, позволяющих
судить о степени «приближения» системы к отказу. Для таких систем профилак-
тика проводится по достижении системой некоторого критического состояния.
134. ГолинкевичТ. А. Оценка надежности радиоэлектронной аппа-
ратуры. (Библиотека инженера по надежности.) М., «Сов. радио», 1969.
Разъясняются понятия оценки и контроля надежности, приводится перечень
возможных методов оценки надежности и видов испытаний, рекомендации по
оценке эффективности контроля.
135. Груничев А. С., Кузнецов В. А., Шипов Е. В. Испы-
тания радиоэлектронной аппаратуры на надежность. М., «Сов. радио», 1969.
Приводятся общие методы контроля надежности и обработки результатов
испытаний.
136. Диксон Дж. Проектирование систем: изобретательство, анализ
и принятие решений. Пер. с англ. Е. Г. Коваленко. М., «Мир», 1969.
Одна глава посвящена изложению элементарных вопросов надежности.
137. Ефимов И. Е., Кальман И. Г..Мартынов В. И. Надеж-
ность интегральных полупроводниковых схем. М. Изд-во Комитета стандартов,
мер и измерительных приборов при СМ СССР, 1969.
450
Рассматриваются назначение и классификация интегральных схем, основные
виды и причины отказов,
138, Козлов Б. А, Резервирование с восстановлением. (Библиотека ин-
женера по надежности.) М., «Сов. радио», 1969.
Рассмотрены методы расчета восстанавливаемых резервированных систем.
Большинство задач формулируется для так называемых экспоненциальных
моделей, т. е. для случаев, когда распределения времени работы и времени вос-
становления отдельных элементов системы являются экспоненциальными. В гл. 1
изучается надежность резервированных систем, поведение которых описывается
однородным марковским процессом: дается представление показателей надежно-
сти через определители, приводятся приближенные оценки, их погрешности,
схема «гибели и размножения». Гл. 2 касается специальных задач дублирова-
ния (влияние вида закона распределения времени восстановления на надежность
системы, влияние зависимости элементов, характера контроля и ограниченной на-
дежности переключающих устройств на характеристики системы). Гл. 3 посвя-
щена рассмотрению одного важного класса систем, в которых существенным по-
казателем надежности является работоспособность некоторой определенным
образом выделенной подсистемы. Для таких систем ряд показателей получен для
произвольных распределений времени работы и времени восстановления. В книге
приводится обширная библиография (более 200 наименований).
139. Кузинец Л. М., Романов Е. А. Надежность телевизионных
приемников. (Библиотека инженера по надежности.) М., «Сов. радио», 1969.
Сообщается о методах расчетов надежности и обработки опытных данных.
Описаны технологические процессы производства, обследования и испытаний
телевизоров, сбора и анализа статистических данных.
140. Кузнецов А. С. Надежность радиолюбительской аппаратуры.
М., «Энергия», 1969.
Приводятся элементарные сведения из теории надежности.
141. Кузнецов П. И., Пчелинцев Л. А., Гайденко В. С-
Контроль и поиск неисправностей в сложных системах. М., «Сов. радио», 1969-
Излагаются методы статистической оптимизации процессов поиска неисправ-
ностей и контроля работоспособности сложных электротехнических и радио-
электронных систем. Используется аппарат марковских процессов и математи-
ческого программирования. Приводятся не только точные методы нахождения
оптимальных решений, но и приближенные.
142. Кулаков Н. Н., Загоруйко А. С. Методы оценки повы-
шения надежности технических изделий по технико-экономическим показателям.
Новосибирск, «Наука», Сибирское отделение АН СССР, 1969.
Описываются экономические вопросы повышения надежности технических
изделий. Выводятся основные зависимости между надежностными и экономиче-
скими критериями изделий при повышении их надежности.
143. Левин В. И. Вероятностный анализ ненадежных автоматов. Рига
«Зинатне», 1969.
Рассматриваются вопросы анализа ненадежных конечных автоматов. Изу-
чаются автоматы без памяти и с памятью, описываемые в первом случае линейным
стационарным преобразователем распределения вероятностей входных сигналов,
а во втором — простой цепью Маркова. В основу анализа положено предположе-
ние о малости вероятности ошибки автомата за один такт.
144. Математические методы контроля качества и надежности (Труды Все-
союзного коллоквиума). Ташкент. «Фан», 1969.
В сборник включены тексты обзорных докладов по основным направлениям
современных математических методов в теории надежности и контроля качества.
145. Новиков О. А., Петухов С. И. Прикладные вопросы теории
массового обслуживания. Под ред. Б. В. Гнеденко. М., «Сов. радио», 1969.
Гл. 5 книги посвящена количественным методам опенки систем массового
обслуживания с учетом надежности работы обслуживающих приборов.
146. Овчаров Л. А. Прикладные задачи теории массового обслужи-
вания. М., «Машиностроение», 1969.
В гл. 4 рассматривается модель с недостоверным обслуживанием, которая
может найти применение при анализе надежности систем.
451
147. Организация производства на промышленных предприятиях США.
Пер. с англ. Под ред. С. А. Хеймана. М., «Прогресс», 1969.
Сокращенный перевод американского справочника инженера по организа-
ции производства. Гл. 3 посвящена принципам управления запасами, гл. 6 —•
непосредственно вопросам надежности.
148. Проников А. С. Основы надежности и долговечности машин.
М., Изд-во Комитета стандартов, мер и измерительных приборов при СМ СССР,
1969.
Приводятся основные понятия и положения теории надежности и долговеч-
ности машин, вопросы износостойкости изделий (износ и его закономерности,
установление предельных износов и сроков службы).
149. Рахвальский В. М. Надежность кибернетических систем. М.,
«Знание», 1969.
В популярной форме излагаются основные сведения из теории надежности.
150. Рыжиков Ю. И. Управление запасами. М., «Наука», 1969.
Систематически излагается теория управления запасами, которая может быть
непосредственно приложена к задачам обеспечения надежности сложных систем.
Рассмотрены задачи управления запасами однородного продукта на изолиро-
ванном складе при фиксированной задержке поставок, при случайной задержке,
а также управление многономенклатурными запасами. Описываются некоторые
специальные модели управления запасами. Приведена обширная библиография
(около 450 наименований).
151. Сорин Я- М. Физическая сущность надежности. М., Изд-во Ко-
митета стандартов, мер и измерительных приборов при СМ СССР, 1969.
В популярной форме рассматривается физическая сущность надежности,
от правильного понимания которой в значительной мере зависит ее практическое
обеспечение.
152. Справочник по надежности (Т. 1). Пер. с англ. Под ред. Б. Р. Левина.
М., «Мир», 1969.
Справочник представляет собой тематический сборник статей, в которых
рассматриваются вопросы анализа эффективности системы, построения моделей
долговечности, планирования испытаний на надежность и приемочных испыта-
ний. Приводится краткое изложение теории вероятностей и математической ста-
тистики. Дается достаточное число математико-статистических таблиц.
153. Теория надежности и массовое обслуживание. Сб. статей под ред.
Б. В. Гнеденко. М., «Наука», 1969.
Сборник состоит из четырех разделов. В первом сообщается о новых резуль-
татах исследований резервированных систем. Второй раздел посвящен контролю
и профилактике технических систем. В третьем разделе рассматриваются новые
задачи теории надежности: некоторые вопросы вибронадежности, анализ сис-
тем с радиально-кольцевой структурой и т. д. Последний раздел касается задач
массового обслуживания.
154. Ушаков И. А. Методы решения простейших задач оптимального
резервирования при наличии ограничений. (Библиотека инженера по надежно-
сти.) М., «Сов. радио», 1969.
Систематически излагаются задачи оптимального резервирования и основ-
ные методы их решения: метод перебора, метод множителей Лагранжа, градиент-
ный метод (метод наискорейшего спуска), метод динамического программирова-
ния. Рассмотрены задачи оптимального резервирования при нескольких ограни-
чениях и некоторые эвристические методы их решения. В специальном приложе-
нии даны программы решения задач оптимизации надежности различными мето-
дами, изложенные на универсальном языке АЛГОЛ-60 и языке ЭВМ «Мир». Ма-
териал книги иллюстрируется числовыми примерами.
155. Ушакова Г. Н. Аппаратный контроль и надежность специализи-
рованных ЭВМ. М., «Сов. радио», 1969.
Рассматриваются вопросы оценки влияния системы контроля на характерис-
тики надежности ЭВМ. Описаны методы и способы контроля и показан общий
принцип проектирования рациональной системы аппаратного контроля ЭВМ.
156. Хедли Д ж., У а й т и н Т. Анализ систем управления запасами.
Пер. с англ. Под ред. А. Л. Райкина. М., «Наука», 1969.
452
Излагаются вопросы управления запасами в системах с одним пунктом хра-
нения. Рассмотрены математические модели для случаев, когда имеется опе-
ративная информация о состоянии запасов и периодическая информация, полу-
чаемая при специальных проверках.
1970 г.
157. Броди С. Н., Власенко О. Н., Марченко Б. Г. Расчет
и планирование испытаний систем на надежность. Киев, «Наукова думка», 1970.
Книга состоит из двух основных частей: в первой части (гл. 1) приведены
методы расчета надежности систем с помощью математического аппарата полу-
марковских процессов, во второй (гл. 2 и 3) рассмотрены вопросы планирования
испытаний технических систем на надежность, причем большое внимание уделен-
лено разработке различных вспомогательных средств (номограмм, таблиц и т. п.).
158. Васильев Б. В. Прогнозирование надежности и эффективности
радиоэлектронных устройств. М., «Сов. радио», 1970.
Излагаются методы прогнозирования надежности и эффективности систем на
основе получаемой при контроле информации о состоянии данного экземпляра
системы в прошлом. Рассматривается физическое (граничные и матричные испы-
тания) и математическое моделирование методом Монте-Карло применительно
к исследованию надежности и эффективности систем.
159. Горский Л. К. Статистические алгоритмы исследования надеж-
ности. М., «Наука», 1970.
Приводикя методика построения алгоритмов статистического моделирова-
ния для исследования надежности восстанавливаемых и невосстанавливаемых
систем при произвольных распределениях времени безотказной работы н времени
восстановления. Для каждого рассмотренного алгоритма дана его запись на
алгоритмическом языке АЛГОЛ-60.
160. Гук Ю. Е. Теория и расчет надежности систем электроснабжения.
Под ред. Р. Я. Федосеенко. М., «Энергия», 1970.
Книга посвящена вопросам применения вероятностных методов расчета на-
дежности энергетических установок систем электроснабжения. Излагаются ме-
тоды оценки ущерба от перерывов в электроснабжении.
161. Гуревич А. М., Нейштадт И. С. Надежность логических
систем управления. М., «Энергия», 1970.
Приводится краткое описание структуры логических систем управления
различных типов, произведен выбор критериев надежности, предложены ме-
тоды расчета их надежности для различных способов непрерывного и периоди-
ческого контроля работоспособности.
162. Доманицкий С. М. Надежность устройств дискретного типа.
М., «Энергия», 1970.
Рассмотрены вопросы теории и практики построения надежных систем авто-
матического управления, осуществляющих логическую обработку информации.
Приведены методы расчета надежности неизбыточных и избыточных логических
элементов, устройств и систем управления. Большое внимание уделено практи-
ческим рекомендациям по использованию избыточных структур, выбору схем
восстанавливающих органов и пр.
163. Дулин В. А. Методы исследования надежности низковольтных
аппаратов. М., «Энергия», 1970.
Излагаются основные методы исследования надежности низковольтных эле-
ктрических аппаратов в зависимости от условий эксплуатации, свойств применен-
ных материалов и конструкции, а также от уровня и стабильности производства.
164. Защита радиоэлектронной аппаратуры от влияния климатических
условий. Пер. с немец. Л. С. Богуславского. М., «Энергия», 1970.
Описаны методы защиты и повышения стойкости радиоэлектронной аппара-
туры по отношению к климатическим воздействиям.
165. Интегральные схемы. Основы проектирования и технологии. Пер.
с англ. Под ред. Н. М. Мартющова. М., «Сов радио», 1970.
Рассматриваются вопросы проектирования и технологии интегральных схем
и их надежности. Приводятся методы испытания на надежность, анализ отказов.
453
166. Использование избыточности в информационных системах. Под ред.
Н. А. Железнова. Л., «Наука», 1970.
В сборнике трудов второго симпозиума по использованию избыточности в ин-
формационных системах имеется ряд статей по надежности вычислительных
систем и систем автоматизированного управления.
167. К о с т ы р к и н А. И. Логический контроль релейно-контактных
схем. М., «Связь», 1970.
Книга знакомит читателя с вопросами контроля и поиска неисправностей и
автоматизации этих процессов.
168. Кульбак Л. И, Основы расчета обеспечения электронной аппара-
туры запасными элементами. (Библиотека инженера по надежности.) М., «Сов.
радио», 1970.
Освещаются вопросы комплектования радиоэлектронной аппаратуры опти-
мальным количеством запасных элементов. В основном предлагаются методы рас-
чета с использованием универсальных ЭВМ, приводятся подробные алгоритмы
счета.
169. Малинский В. Д. Контроль и испытания радиоаппаратуры.
М., «Энергия», 1970.
Рассматриваются общие вопросы испытаний радиоэлектронной аппаратуры,
ускоренные, граничные, матричные испытания, методика составления программы
испытаний, основные сведения о климатических и механических воздействую-
щих факторах. Излагаются понятия теории надежности и факторы, определяю-
щие надежность РЭА. Предлагаются методы испытаний на различные клима-
тические и механические воздействия, а также — описание применяемого испы-
тательного оборудования.
170. Меламедов И. М. Физические основы надежности. Л., «Энер-
гия», 1970.
Освещаются физические основы процессов разрушения и возникновения
отказов; описываются как общие физические модели отказов, так и модели отка-
зов отдельных (типовых) элементов и технических устройств. Приводится клас-
сификация отказов и процессов их возникновения, даны вероятностные представ-
ления свойств и характеристик элементов. Даются методы количественной оцен-
ки надежности элементов и устройств.
171. Михайлов А. В. Эксплуатационные допуски и надежность в ра-
диоэлектронной аппаратуре. (Библиотека инженера по надежности.) М., «Сов.
радио», 1970.
Излагаются способы оценки и установления допусков на параметры радио-
электронной аппаратуы для обеспечения эксплуатационной надежности, а так-
же способы выбора точностных характеристик контрольно-измерительной аппа-
ратуры.
172. Сотсков Б. С. Основы теории и расчета надежности элементов
и устройств автоматики и вычислительной техники. М., «Высшая школа», 1970.
Книга является учебным пособием для вузов. Основное внимание уделено
физике отказов, определяющей необходимые конструктивные, технологические
t эксплуатационные мероприятия по повышению и сохранению надежности уст-
ройств и элементов, входящих в системы. Приводятся элементарные сведения
о расчете надежности невосстанавливаемых систем и об оценке их по результатам
испытаний.
173. Справочник по надежности (Т. 2). Пер. с англ. Под ред. Б. Е. Берди-
чевского. М., «Мир», 1970.
Справочник представляет собой тематический сборник статей, в которых
рассматриваются вопросы оценки надежности, накопления и систематизации
статистических данных, организации системы сбора данных по надежности, ана-
лиза неисправностей и отказов.
174. Справочник по надежности (Т. 3). Пер. с англ. Под ред. Б. Е. Бердиче-
вского. М., «Мир», 1970.
Справочник представляет собой тематический сборник статей, в которых рас-
сматриваются основные принципы конструирования и ведения разработки, обес-
печивающие получение надежных систем (учет требований к обслуживаемости,
роль факторов инженерной психологии, обеспечение надежности в процессе про-
454
изводства, учет требований по надежности в контрактах, организованные и эко-
номические аспекты программы обеспечения надежности и качества).
175. Теория и практика эксплуатации радиолокационных систем. Под ред.
С. М. Латинского. М., «Сов. радио», 1970. Авт.: С. М. Латинский, В. И. Шарапов,
С. П. Ксенз, С. С. Афанасьев.
Излагаются вопросы поддержания надежности при возникновении отка-
зов (гл. 4), оптимальных программ диагностики состояния системы (гл. 5) и кон-
троля работоспособности радиолокационных систем (гл. 6).
176. Точность и надежность кибернетических систем. Киев, «Науковя дум-
ка», 1970.
В сборнике приведены математические методы анализа точности систем и
алгоритмов и вопросы проектирования и оценки надежности сложных систем.
177. Фокин Ю. Г. Надежность при эксплуатации технических средств.
М., Воениздат, 1970.
Излагаются элементарные вопросы теории надежности технических средств
с учетом специфики эксплуатации и использования их в войсках.
178. Фролов А. Д. Теоретические основы конструирования к надеж-
ности радиоэлектронной аппаратуры М., «Высшая школа», 1970.
Рассматриваются требования, предъявляемые к конструкции радиоэлект-
ронных аппаратов в зависимости от условий их эксплуатации и различных воз-
действий (температура, влага, электрические и магнитные поля, вибрации и уда-
ры). Излагаются различные способы защиты от этих воздействий.
179. Чуев Ю. В. Исследование операций в военном деле. М., Воениз-
дат, 1970.
Последняя глава книги посвящена задачам замены оборудования.
1971 г.
180. Адаптивные системы. Большие системы (Труды I Всесоюзного симпо-
зиума по статистическим проблемам в технической кибернетике). М., «Наука»,
1971.
Разделы 3 и 4 сборника посвящены вопросам аналитической оценки надеж-
ности, статистического моделирования сложных систем и статистического конт-
роля качества.
181. А к о ф ф Р., С а с и е и и М. Основы исследования операций. Пер.
е англ. Под ред. И. А. Ушакова. М., «Мир», 1971.
Две главы посвящены задачам управления запасами, замены, ремонта и оп-
ределения надежности оборудования.
182. Барзилович Е. Ю., Каштанов В. А. Некоторые матема-
тические вопросы теории обслуживания сложных систем. М., «Сов. радио», 1971.
Рассматриваются вопросы построения оптимальных программ профилакти-
ческого обслуживания сложных систем в зависимости от наличия информации
о наработке элементов или об их состоянии в заданные моменты контроля. Боль-
шинство приведенных математических моделей завершаются краткой методикой,
удобной для проведения практических расчетов.
183. Г е р м е й е р Ю. Б. Введение в теорию исследования операций. М.,
«Наука», 1971.
Один параграф в гл. 2 посвящен гарантированным оценкам надежности,
когда известны лишь некоторые характеристики распределения времени безот-
казной работы.
184. Доманицкий С. М. Построение надежных логических уст-
ройств. М., «Энергия», 1971.
Освещаются вопросы построения надежных устройств автоматического уп-
равления, осуществляющих логическую обработку информации. Рассматривают-
ся как неизбыточные, так и избыточные логические элементы и устройства. Ис-
следуется надежность адаптивных избыточных структур с изменением порога.
Даются практические рекомендации.
185. Карпушин Б. В. Вибрации и удары в радиоаппаратуре. М.,
«Сов. радио», 1971.
Изложены некоторые результаты исследований действия вибраций и ударов
на надежность радиоэлектронной аппаратуры, а также вопросы испытания аппа-
455
ратуры и ее элементов на вибрации, удары и акустические шумы. Приведены
справочные таблицы.
186. Краснове к ий А. А., Ткаченко Л Г. Этажи надежности.
М., «Машиностроение», 1971.
Основные вопросы надежности излагаются в популярной форме, полезной
для первого знакомства с этой проблемой.
187. Основные вопросы теории и практики надежностя. М., «Сов. радио»,
1971.
Сборник докладов семинара по надежности Научного совета по комплекс-
ной проблеме «Кибернетика» при Президиуме АН СССР.
188. О ш е р Ф. Н., Малинский В. Д., Теплицкий Л. Я.
Регулировка и испытания радиоаппаратуры. М., «Энергия», 1971.
Рассматриваются вопросы регулировки и испытаний радиоаппаратуры. Из-
лагаются принципы устройства установок для электрических, механических и
климатичеекях испытаний.
189. Павленко К- И. Надежность радиоэлектронной аппаратуры при
циклическом и непрерывном режимах использования. (Библиотека инженера по
надежности.) М., «Сов. радио», 1971.
Приводятся методы расчета и экспериментальной оценки надежности радио-
электронной аппаратуры, работающей в циклическом и непрерывном режимах
работы. Рассматриваются влияние включений и приведены некоторые рекомен-
дации по защите от влияния переходных процессов в устройствах. Излагаются
вопросы физики отказов радиоэлектронной аппаратуры.
190. П о л л я к Ю. Г. Вероятностное моделирование на электронных вы-
числительных машинах. М., «Сов. радио», 1971.
Систематически изучаются вопросы статистического моделирования для
исследования технических систем. Приводится много примеров из области на-
дежности.
191. Пушкин В. Г. Проблема надежности. М., «Наука», 1971.
Философский очерк, в котором затрагиваются различные аспекты проблемы
надежности: место ее в современной кибернетике и бионике, природа надеж-
ности и философский смысл категории надежности, социальные аспекты пробле-
мы надежности.
192. Райкин А. Л. Вероятностные модели функционирования резер-
вированных устройств. М., «Наука», 1971.
Рассмотрен широкий круг вопросов, связанных с резервированием техни-
ческих систем: модели проведения аварийных замен при резервировании замеще-
нием (гл. 1), модели резервирования с восстановлением отказавших элементов
(гл. 2), задачи оптимального резервирования и обеспечения запасным оборудова-
нием при наличии ограничений на затраты (гл. 3), модели оптимального подклю-
чения резервных элементов (гл. 4), задачи планирования проверок исправности
систем, необходимых для подключения резерва (гл. 5), методы прогнозирования
потребностей в запчастях и материалах (гл. 6).
193. Райкин А. Л., Кравцов О. С., Пении В. С. Таблицы
расчета надежности и оптимального резерва (Библиотека инженера по надежно-
сти.) М., «Сов. радио», 1971.
Приводятся подробные таблицы приращения логарифма вероятности безот-
казной работы для случая обобщенного биномиального распределения, позво-
ляющего охватить не только нагруженный и ненагруженный режимы работы,
но и облегченный (коэффициент нагрузки меняется от 0 до 1 через 0,1). Таблицы
составлены для систем, в которых в каждой группе однотипных рабочих элемен-
тов содержится не более 10 элементов, и к ней придается резервная группа не
более 10 элементов. Допустимые значения среднего числа отказов рабочих
элементов за рассматриваемый период лежат в диапазоне от 0,05 до 2.
194. Раков А. И. Надежность радиорелейных систем связя. М.. «Связь»,
1971.
Выбираются показатели для оценки надежности наземных и космических
радиорелейных систем связи, формулируются различные варианты задания тре-
бований к их надежности, дается классификация отказов. Приводится методика
расчета надежности проектируемых и реконструируемых систем связи, анализи-
руются методы повышения их надежности.
456
195. С и и ь ч у г о в Ф. И. Расчет надежности схем электрических сое-
динений. М., «Энергия», 1971.
Излагаются методики расчета надежности и сбора и обработки статистиче-
ских данных, схем электрических соединений, энергетических и электромехани-
ческих установок, электростанций, подстанций и участков электрических сетей.
196. Цветков А. Г. Принципы количественной оценки эффективности
радиоэлектронных средств. Под ред. С. Ф. Матвеевского. М., «Сов. радио», 1971.
Рассматриваются основные показатели, используемые при оценке эффектив-
ности радиоэлектронных средств. Приводятся методы оценки эффективности
радиоэлектронных средств с учетом их реальной надежности и возможного про-
тиводействия.
197. Чуев Ю. В., Спехова Г. П. Технические задачи исследования
операций. М., «Сов. радио», 1971.
Одна глава книги посвящена изложению методов определения оптимальной
надежности (прочности) технических устройств и рациональным путям ее обес-
печения.
198. Я м а и о в С. А. Новые электроизоляционные материалы и проб-
лема надежности. М., «Энергия», 1971.
Приводятся статистические данные и анализ причин выхода из строя элект-
рических машин, аппаратов, радиоаппаратуры, работающих в тяжелых условиях
эксплуатации. Показывается роль электротехнических материалов в повышении
надежности электрооборудования.
Б.2. Основные монографии по проблеме надежности
55. Б а з о в с к и й И. Надежность: теория и практика. Пер. с англ. Под
ред. Б. Р. Левина. М., «Мир», 1965.
130. Барлоу Р., Прошан Ф. Математическая теория надежности.
Пер. с англ. Под ред. Б. В. Гнеденко. М., «Сов. радио», 1969.
70. Бердичевский Б. Е. Оценка надежности аппаратуры автома-
тики (методы оценки надежности в процессе разработки). М., «Машиностроение»,
1966.
158. Васильев Б. В. Прогнозирование надежности и эффективности
радиоэлектронных устройств. М., «Сов. радио», 1970.
60. Гнеденко Б. В., Беляев Ю. К-, Соловьев А. Д. Ма-
тематические методы в теории надежности. М., «Наука», 1965.
94. Дружинин Г. В. Надежность систем автоматики. Изд. 2-е. М.,
«Энергия», 1967.
42. Епифанов А. Д. Надежность автоматических систем. М., «Маши-
ностроение», 1964.
118. Инженерные методы исследования надежности радиоэлектронных сис-
тем Пер. с англ. Под ред. А. М. Половко, А. Г. Варжапетяна. М., «Сов. радио»,
1968.
74. К а л а б р о С. Р. Принципы и практические вопросы надежности.
Пер. с англ. Под ред. Д. Ю. Панова. М., «Машиностроение», 1966.
51. Кибернетику — на службу коммунизму. Сб. статей под ред. А. И. Берга,
Н. Г. Бруевича, Б. В. Гнеденко, т. 2, М., «Энергия», 1964.
76. К о з л о в Б. А., У ш а к о в И. А. Краткий справочрик по расчету
надежности радиоэлектронной аппаратуры. М., «Сов. радио», 1966.
44. Л л о й д Д. К-, Липов М. Надежность: организация исследова-
ния, методы, математический аппарат. Пер. с англ. Под ред. Н. П. Бусленко.
М., «Сов. радио», 1964
3. Надежность наземного радиоэлектронного оборудования. Пер. с англ.
Под ред. Н. М. Шулейкина, М., «Сов. радио», 1957.
83. О надежности сложных технических систем. (Сб. трудов семинара секции
надежности Научного совета по комплексной проблеме «Кибернетика» при Пре-
зидиуме АН СССР). М., «Сов. радио», 1966.
124. Пирс У. Построение надежных вычислительных машин. Пер. с англ.
Б. Л. Овсиевича и Л. Я. Розенблюма. М., «Мир», 1966.
457
47. Неловко А. М. Основы теории надежности. М,, «Наука», 1964.
85. Прикладные задачи технической кибернетики. Под ред. Л. С. Гурина,
И. А. Ушакова, Б. С. Флейшмана. М., «Сов. радио», 1966.
105. Райкин А. Л. Элементы теории надежности для проектирования
технических систем. М., «Сов. радио», 1967.
64. Решение задач надежности и эксплуатации на универсальных ЭЦВМ.
М., «Сов. радио», 1967, Авт.: Б. П. Креденцер, М. М. Ластовченко, С. А. Сенец-
кий, Н. А. Шишонок.
86. С а н д л е р Дж. Техника надежности систем. Пер. с англ. А. Л. Рай-
кина, М., «Наука», 1966.
152. Справочник по надежности (Т. 1). Пер. с англ. Под ред. Б. Р. Левина.
М., «Мир», 1969.
173. Справочник по надежности (Т. 2). Пер. с англ. Под ред. Б. Е. Берди-
чевского. М., «Мир», 1970.
174. Справочник по надежности (Т. 3). Пер. с англ. Под ред. Б. Е. Берди-
чевского. М., «Мир», 1970.
153. Теория надежности и массовое обслуживание. Сб. статей под ред.
Б. В. Гнеденко, М., «Наука», 1969.
53. Ш и ш о н о к Н. А., Репкин В. Ф., Барвинский Л. Л.
Основы теории надежности и эксплуатации радиоэлектронной техники. М., «Сов.
рад..о», 1964.
27. Шор Я- Б. Статистические методы анализа и контроля качества и на-
дежности. М., «Сов. радио», 1962.
Б.З. Тематическая подборка книг по надежности
Б.3.1. Методы испытаний и опытная оценка
1. Методы испытаний на надежность
134. Голинкевич Т. А. Оценка надежности радиоэлектронной ап-
паратуры. М., «Сов. радио», 1969.
135. Груничев А. С., Кузнецов В. А., Шипов Е. В. Ис-
пытания радиоэлектронной аппаратуры на надежность. М., «Сов. радие», 1969.
60. й а м м е р А., Гриффин Б. Испытание радиоэлектронной аппара-
туры и материалов на воздействие климатических и механических условий. Пер.
с англ. Под. ред. Б. Е. Бердичевского. М., «Энергия», 1965.
117. К у гель Р. В. Ускоренные ресурсные испытания в машинострое-
нии. М., «Знание», 1968.
169. Малинский В. Д. Контроль и испытания радиоаппаратуры. М.,
«Энергия», 1970.
188. О ш е р Ф. Н., Малинский В. Д., Т е п л и ц к и й Л. Я.
Регулировка и испытания радиоаппаратуры. М., «Энергия», 1971.
123. Перроте А. И., Карташев Г. Д., Цветаев К. Н. Ос-
новы ускоренных испытаний радиоэлементов на надежность. М., «Сов. радио»,
1968.
2. Оценка надежности по результатам испытаний
22. Б а ш а р и н о в А. Е., Ф л ей шма н Б. С. Методы статистиче-
ского последовательного анализа и их приложения. М., «Сов. радио», 1962.
157. Броди С. Н., Власенко О. Н., Марченко Б. Г. Расчет
и планирование испытаний систем на надежность. Киев, «Наукова думка»,
1970.
71. Г е р ц б а х И. Б., Кордовский X. Б. Модели отказов. (Биб-
лиотека инженера по надежности). М., «Сов. радио», 1966.
115. Г н е д е н к о Б. В. Беседы о математической статистике. М., «Зна-
ние», 1968.
458
134. Голинкевич Т. А. Оценка надежности радиоэлектронной аппа-
ратуры (Библиотека инженера по надежности). М., «Сов. радио», 1969.
128. Шор Я. Б., Кузьмин Ф. И. Таблицы для анализа и контроля
надежности. (Библиотека инженера по надежности.) М., «Сов. радио», 1968.
129. Ястребенецкий М. А., Со л я н и к Б. Л. Определение на-
дежности аппаратуры промышленной автоматики в условиях эксплуатации. М.,
«Энергия», 1968.
3. Влияние внешних воздействий на надежность
54. А с т а ф ь е в А. В. Окружающая среда и надежность радиотехни-
ческой аппаратуры. Изд. 2-е. М., «Энергия», 1965.
60. Д а м м е р А., Гриффин Б. Испытание радиоэлектронной аппара-
туры и материалов на воздействие климатических и механических условий. Пер.
с англ. Под. ред. Б. Е. Бердичевского. М., «Энергия», 1965.
164. Защита радиоэлектронной аппаратуры от влияния климатических ус-
ловий. Пер. с немец. Л. С. Богуславского. М., «Энергия», 1970.
185. Карпушин Б. В. Вибрации и удары в радиоаппаратуре. М.,
«Сов. радио», 1971.
90. Ш и ф р и н-К р ы ж а л о в с к и й Ю. А., Митин В. С. Тепло-
вая устойчивость транзисторов и надежность радиоэлектронной аппаратур.ы.
М., «Сов. радио», 1966.
4. Надежность элементов и деталей
137. Ефимов И. Е., Кальман И. Г., Мартынов В. И. На-
дежность интегральных полупроводниковых схем. М., Изд-во Комитета стандар-
тов, мер и измерительных приборов при СМ СССР, 1969.
165. Интегральные схемы. Основы проектирования и технологии. Пер.
с англ. Под ред. Н. М. Мартюшова. М., «Сов. радио», 1970.
36. Надежность полупроводниковых устройств. Пер. с англ. Под ред.
А. А. Маслова. М., ИЛ, 1963.
45. Обеспечение надежности полупроводниковых устройств. Пер. с аигл.
Под ред. А. С. Савиной. М., «Мир», 1964.
46. П а р о л ь Н. В. Надежность приемно-усилительных ламп. М., «Сов.
радио», 1964.
195: Синьчугов Ф. И. Расчет надежности схем электрических сое-
динений. М., «Энергия», 1971.
172. Сотсков Б. С. Основы теории н расчета надежности элементов и
устройств автоматики и вычислительной техники. М., «Высшая школа», 1970.
16. X и н н е й К., Уолш К. Радиодетали и проблема их надежности.
Пер. с англ. Под ред. Б. М. Тареева. М., «Сов. радио», 1960.
198. Я м а н о в С. А. Новые электроизоляционные материалы и пробле-
ма надежности. М., «Энергия», 1971.
Б.3.2. Методы расчета
5- Расчет систем с резервированием
59. Г н е д е н к о Б. В. Курс теории вероятностей. Изд. 4-е, переработан-
ное. М., «Наука», 1965.
72. Гнеденко Б. В., Коваленко И. Н. Введение в теорию мас-
сового обслуживания. М., «Наука», 1966.
75. Климов Г. П. Стохастические системы обслуживания. М., «Наука»,
1966.
138. Козлов Б. А. Резервирование с восстановлением. (Библиотека
инженера по надежности.) М., «Сов. радио», 1969.
99. К о к с Д. Р., Смит В. Л. Теория восстановления. Пер. с англ.
Под ред. Ю. К. Беляева. М., «Сов. радио», 1967.
12. Л е в и и Б. Р. Теория случайных процессов и ее применение в радио-
технике. М., «Сов. радио», I960.
459
81. Математическая теория надежности информационно-логических управ-
ляющих устройств. Под ред. В. М. Зубова. Л. Изд-во ЛГУ им. А. А. Ждано-
ва, 1966.
82. Методы введения избыточности для вычислительных систем. Пер. с англ.
Под ред. В. С. Пугачева. М., «Сов. радио», 1966.
15. Проблемы надежности радиоэлектронной аппаратуры. Пер. с англ.
Под ред. Б. Е. Бердичевского. М., Оборонгиз, 1960.
66. С е д я к и н Н. М. Элементы теории случайных импульсных потоков.
М., «Сов. радио», 1965.
6. Учет контроля при оценке надежности
56. Б р а у д о С. И. Сохранение надежности радиолокационной аппара-
туры (настройка, контроль параметров, предупреждение и диагностика отказов).
М., «Сов. радио», 1965.
112. Введение в техническую диагностику. М., «Энергия», 1968,
Авт.: Г. Ф. Верзаков, Н. В. Киншт, В. И. Рабинович, Л. С. Тимонен.
92. Голубе в-Н о в о ж и л о в Ю. С. Многомашинные комплексы вы-
числительных средств. М., «Сов. радио», 1967.
167. К о с т ы р к и н А. И. Логический контроль релейно-контактных
схем. М., «Связь», 1970.
171. Михайлов А. В. Эксплуатационные допуски и надежность в ра-
диоэлектронной аппаратуре. (Библиотека инженера по надежности.) М., «Сов.
радио», 1970.
155. Ушакова Г. Н. Аппаратный контроль и надежность специали-
зированных ЭВМ. М., «Сов. радио», 1969.
7. Оценка надежности и эффективности сложных систем и структур
2. Автоматы. Сб. статей под ред. К. Э. Шеннона и Дж. Маккарти. Пер.
с англ. Под. ред. А. А. Ляпунова. М., ИЛ, 1956.
131. Варжапетян А. Г. Техническая эффективность и надежность
судовых систем управления. Л., «Судостроение», 1969.
40. В е н т ц е л ь Е. С. Введение в исследование операций. М., «Сов. ра-
дио», 1964.
93. Г у т ч и н И. Б., Кузичев А. С. Бионика и надежность. Элемен-
ты теории формальных нейронов. М., «Наука», 1967.
143. Левин В. И. Вероятностный анализ ненадежных автоматов. Рига,
«Зинатне», 1969.
82. Методы введения избыточности для вычислительных систем. Пер. с англ.
Под ред. В. С. Пугачева. М., «Сов. радио», 1966.
13. Надежность радиоэлектронной аппаратуры (Сб. статей). М., «Сов.
радио», 1960.
120. Нечипоренко В. И. Структурный анализ и методы построения
надежных систем. М., «Сов. радио», 1968.
15. Проблемы надежности радиоэлектронной аппаратуры. Пер. с англ.
Под ред. Б. Е. Бердичевского. М., Оборонгиз, 1960.
49. Самоорганизующиеся системы. Пер. с англ. Под ред. Т. Н. Соколова.
М., «Мнр», 1964.
196. Цветков А. Г. Принципы количественной оценки эффективности
радиоэлектронных средств. Под ред. С. Ф. Матвеевского. М., «Сов. радио», 1971.
38. Ш е н н о н К. Работы по теории информации и кабернетике. Пер.
с англ. Под ред. Р. Л. Добрушина и А. Н. Лупанова М., ИЛ, 1963.
8. Статистическое моделирование в расчетах надежности
39. Б у с л е н к о Н. П. Математическое моделирование производствен-
ных процессов на цифровых вычислительных машинах. М., «Наука», 1964.
ШбвШ" БУсленК0 Н. П. Моделирование сложных систем. М., «Наука»,
460
159. Горский Л. К. Статистические алгоритмы исследования надеж-
ности. М., «Наука», 1970.
106. Решение задач надежности и эксплуатации на универсальных ЭЦВМ.
М., «Сов. радио», 1967. Авт.: Б. П. Креденцер, М. М. Ластовченко, С. А. Сенец-
кий, Н. А. Шишонок.
190. П о л л я к Ю. Г. Вероятностное моделирование на электронных вы-
числительных машинах. М., «Сов. радио», 1971.
9. Исследование постепенных отказов
23. Вопросы точности и надежности в машиностроении. Сб статей под ред.
Н. Г. Бруевича. М. Изд-во АН СССР, 1962.
71. Герцбах И. Б., Кордонский X. Б. Модели отказов. (Биб-
лиотека инженера по надежности.) М., «Сов. радио», 1966.
73. И ы у д у К- А. Оптимизация устройств автоматики по критерию на-
дежности. М., «Энергия», 1966.
34. Леонтьев Л. И. Введение в теорию надежности радиоэлектронной
аппаратуры. Рига. Изд-во АН Латв. ССР, 1963.
170. Меламедов И. М. Физические основы надежности. Л., «Энер-
гия», 1970.
104. П а м п у р о В. И. Анализ радиоцепей и их схемной надежности.
Киев, «Техника», 1967.
126. Точность и надежность автоматических станков и приборов активного
контроля. Под ред. М. С. Невельсона. М., «Машиностроение», 1968.
88. Т у р к е л ь т а у б Р. М. Методы исследования точности и надежности
схем аппаратуры. М., «Энергия», 1966.
10 Надежность механических систем.
18. Б о л о т и н В. В. Статистические методы в строительной механике.
М., Гос. изд-во литературы по строительству, архитектуре и строительным ма-
териалам, 1961.
23. Вопросы точности и надежности в машиностроении. Сб. статей под ред.
Н. Г. Бруевича. М., изд-во АН СССР, 1962.
108. Спорыш И. П. Надежность механизмов систем автоматического
регулирования. М., «Машиностроение», 1967.
109. Старосельский А. А., Гаркунов Д. Н. Долговеч-
ность трущихся деталей машин. М., «Машиностроение», 1967.
126. Точность и надежность автоматических станков и приборов активного
контроля. Под ред. М. С. Невельсона. М., «Машиностроение», 1968.
51. Т р е й е р В. Н. Теория долговечности и надежности машин. Минск,
«Наука и техника», 1964.
11. Вопросы долговечности
31. Колегаев Р. Н. Определение наивыгоднейших сроков службы
машин. М., Экономиздат, 1963.
100. Колегаев Р. Н. Определение оптимальной долговечности техни-
ческих систем. (Библиотека инженера по надежности.) М., «Сов. радио», 1967.
51. Т р е й е р В. Н. Теория долговечности и надежности машин, Минск,
«Наука и техника», 1964.
89. X е в и л е н д Р. Инженерная надежность и расчет на долговечность.
Пер. с англ. Под ред. Г. Н. Баласанова. М., «Энергия», 1966.
Б.3.3. Оптимальные задачи надежности
12. Оптимальное обнаружение и поиск отказов.
Вопросы ремонтопригодности
112. Введение в техническую диагностику. М., «Энергия», 1968. Автл
Г. Ф. Верзаков, Н. В. Киншт, В. И. Рабинович, Л. С. Тимонеи.
<61
61. Ксенз С. П. Поиск неисправностей в радиоэлектронных системах
методом функциональных проб. М., «Сов. радио», 1965.
121. Оптимальные задачи надежности. Под ред. И А. Ушакова. М., Изд-во
Комитета стандартов, мер и измерительных приборов при СМ СССР, 1968.
63. Основы исследования операций в военной технике. М., «Сов. радио»,
1965. Авт.: Ю. В. Чуев, П. М. Мельников, С. И. Петухов, Я. Б. Шор.
13 Оптимальная профилактика и управление процессом эксплуатации
182. Барзилович Е. Ю., Каштанов В. А. Некоторые матема-
тические вопросы теории обслуживания сложных систем. М., «Сов. радио», 1971.
133. Герцбах И. Б. Модели профилактики (теоретические основы пла-
нирования профилактических работ). (Библиотека инженера по надежности.)
М., «Сов. радио», 1969.
78. К о ф м а и А., Фор Р. Займемся исследованием операций. Пер,
с франц. Под ред. А. А. Корбута. М., «Мир», 1966.
121. Оптимальные задачи надежности. Пер. с англ. Под ррд. И. А. Ушакова.
М., Изд-во Комитета стандартов, мер и измерительных приборов при СМ СССР,
1968.
63. Основы исследования операций в военной технике. М., «Сов. радио»,
1965. Авт.: Ю. В. Чуев, П. М. Мельников, С. И. Петухов, Я. Б. Шор.
14. Оптимальное резервирование
142. Кулаков Н. Н., Загоруйко А. С. Методы оценки повыше-
ния надежности технических изделий по технико-экономическим показателям.
Новосибирск, «Наука», Сибирское отделение АН СССР, 1969.
168. Ку л ьб а к Л. И. Основы расчета обеспечения электронной аппара-
туры запасными элементами. (Библиотека инженера по надежности.) М., «Сов.
радио», 1970.
121. Оптимальные задачи надежности. Под ред. И. А. Ушакова. М. Изд-во
Комитета стандартов, мер и измерительных приборов при СМ СССР, 1968.
63. Основы исследования операций в военной технике. М., «Сов. радио»,
1965. Авт.: Ю. В. Чуев, П. М. Мельников, С. И. Петухов, Я. Б. Шор.
192. Райкин А. Л. Вероятностные модели функционирования резерви-
рованных устройств. М., «Наука», 1971.
193. Райкин А. Л., Кравцов О. С., Пенин В. С. Таблицы
расчета надежности и оптимального резерва. (Библиотека инженера по надеж-
ности.) М., «Сов. радио», 1971.
154. Ушаков И. А. Методы решения простейших задач оптимального
резервирования при наличии ограничений. (Библиотека инженера по надежно-
сти.) М., «Сов. радио», 1969.
15. Управление запасами применительно к задачам надежности
91. Бу кап Дж., Кенигсберг Э. Научное управление запасами.
М., «Наука», 1967.
77. К о ф м а н А. Методы и модели исследования операций. Пер. с франц.
Под ред. Д. Б. Юдина. М., «Мир», I960.
150. Рыжиков Ю. И. Управление запасами. М., «Наука», 1969
156. Хедли Дж., У а и т и н Т. Анализ систем управления запасами.
Пер. с англ. Под ред. А. Л. Райкина. «Наука», 1969.
Б.3.4. Общие вопросы
16. Организационные вопросы
9. Организация контроля н качества в промышленности США. Пер. с аигл.
Под. ред. В. В. Головинского. М., ИЛ, 1959.
462
147. Организация производства на промышленных предприятиях США.
Пер. с англ. Под ред. С. А. Хаймана. М., «Прогресс», 1969.
127. X о л п н'н Дж. Бездефектность. Пер. с англ. Под ред. Я. М. Сорина.
М., «Мир», 1968.
17. Сборники статей, обзоры, сборники задач и пр.
180. Адаптивные системы. Большие системы. (Труды I Всесоюзного симпо-
зиума по статистическим проблемам в технической кибернетике). М., «Наука»,
1971.
17. Белов М. И., Соловейчик Ф. С. Вопросы надежности радио-
электронной аппаратуры. М., Госэнергоиздат, 1961.
8. Вопросы надежности радиоэлектронной аппаратуры (Сб. статей). Пер.
с англ. Под ред. И. И. Морозова. М., «Сов. радио», 1959.
166. Использование избыточности в информационных системах. Под ред.
Н. А. Железнова. Л., «Наука», 1970.
97. Кибернетику — на службу коммунизму, т. 4. Сб. статей. Под ред.
А. И. Берга. М., «Энергия», 1967.
98. Кибернетику — на службу коммунизму, т. 5. Сб. статей. Под ред.
А. И. Берга. М., «Энергия», 1967.
1. Малогабаритная радиоаппаратура. (Вопросы конструирования, производ-
ства и эксплуатации.) Сб. переводов под ред. В. И. Сифорова. М., ИЛ, 1954.
5. М е с я ц е в П. П. Применение теории вероятностей и математической
статистики при конструировании и производстве радиоаппаратуры. М., Оборон-
гиз, 1958.
82. Методы введения избыточности для вычислительных систем. Пер. с англ.
Под ред. В. С. Пугачева. М., «Сов. радио», 1966.
119 Надежность и эффективность дискретных систем Рига, «Зинатне», 1968.
6. Надежность радиоэлектронной аппаратуры. (Сб. статей). М., «Сов. радио»,
1958.
14. Надежность радиоэлектронной аппаратуры (Сб. статей). М., «Сов. радио»,
1960.
103. Надежность электроснабжения. Сб. статей. Под. ред. А. А. Сыромят-
никова. М., «Энергия», 1967.
45. Обеспечение надежности полупроводниковых устройств. Пер. с англ.
Под ред. А. С. Савиной. М., «Мир», 1964.
121. Оптимальные задачи надежностя. Под ред. И. А. Ушакова. М. Изд-во
Комитета стандартов, мер и измерительных приборов при СМ СССР, 1968.
187. Основные вопросы теории и практики надежности. М., «Сов. радио»,
1971.
15. Проблемы надежности радиоэлектронной аппаратуры. Пер. с англ. Под
ред. Б. Е. Бердичевского. М., Оборонгиз, 1960.
194. Раков А. И. Надежность радиорелейных систем связи. М., «Связь»,
1971.
49. Самоорганизующиеся системы. Пер. с англ. Под ред. Т. Н. Соколова.
М., «Мир», 1964.
65. Сборник задач по теории вероятностей, математической статистике и тео-
рии случайных функций. М., «Наука», 1965. Авт.: Б. Г. Володин. М. П. Ганин,
И. Я. Динер, Л. Б. Комаров, А. А. Свешников, К- Б. Старобин.
68. Теория конечных и вероятностных автоматов. М., «Наука», 1965.
176. Точность н надежность кибернетических систем. Киев, «Наукова дум-
ка», 1970.
11. Щукин 'А. Н. Теория вероятностей и экспериментальное определе-
ние характеристик сложных объектов. М., Госэнергоиздат, 1959.
18. Различные дополнительные вопросы
181. Акофф Р., Сасиени М. Основы исследования операций. Пер.
с англ. Под ред. И. А. Ушакова. М., «Мир», 1971.
463
28. Асратян Э. А. Симонов П. В. Надежность мозга. М., Изд-во
АН СССР, 1963.
4. А ф о н и н Н. С. Надежность электроснабжения промышленных пред*
приятии. М., Госэнергоиздат, 1958.
133. Волчкевич Л. И. Надежность автоматических линий. М., «Ма*
шиностроение», 1969.
183. Гермейер Ю. Б. Введение в теорию исследования операций. М.,
«Наука», 1971.
114. Гольдберг О. Д. Качество и надежность асинхронных двига*
телей. М., «Энергия», 1968.
160. Гук Ю. Б. Теория и расчет надежности систем электроснабжения.
Под ред. Р. Я. Федосеенко. М. «Энергия», 1970.
161. Гуревич А. М. Нейштадт И. G. Надежность логических
систем управления. М., «Энергия», 1970.
115. Гуревич А. С., Курбатов Н. Д. Надежность кабелей связи.
М., «Связь», 1968.
162. Доманицкий С. М. Надежность устройств дискретного типа.
М., «Энергия», 1970.
184. Доманицкий С. М. Построение надежных логических уст*
ройств. М., «Энергия», 1971.
163. Дулин В. А. Методы исследования надежности низковольтных
аппаратов. М., «Энергия», 1970.
96. Кемпинский М. М., Невельсон М. С., Старо-
бин К. Б. Надежность автоматических средств обработки и контроля в маши*
построении. М., «Машиностроение», 1967.
24. М а м о н т о в О. В. Методы кибернетики в теории электронных за-
щит. М., Госэнергоиздат, 1962.
102. Молоканов Г. Ф. Точность и надежность навигации летательных
аппаратов. М., «Машиностроение», 1967.
103. Надежность электроснабжения. Сб. статей. Под ред. И. А. Сыромятни-
кова. «Энергия», 1967.
145. Новиков О. А., Петухов С. И. Прикладные вопросы теории
массового обслуживания. Под ред. Б. В. Гнеденко. М., «Сов. радио», 1969.
146. Овчаров Л. А. Прикладные задачи теории массового обслужи-
вания. М., «Машиностроение», 1969.
189. Павленко К- И. Надежность радиоэлектронной аппаратуры при
циклическом и непрерывном режимах использования. М., «Сов. радио», 1971.
64. С а а т и Т. Л. Элементы теории массового обслуживания и ее прило-
жения. Пер. с англ. Под ред. И. Н. Коваленко и Р. Д. Когана. М., «Сов. радио»
1965.
191. Пушкин В. Г. Проблема надежности. М., «Наука», 1971.
67. С о л о м о н о в П. А. Вопросы надежности авиационной техники.
М., Воениздат МО СССР, 1965.
108. Спорыш И. П. Надежность механизмов систем автоматического
регулирования. М., «Машиностроение», 1967.
175. Теория и практика эксплуатации радиолокационных систем. Под ред
С. М. Латинского. М., «Сов. радио», 1970. Авт.: С. М. Латинский, В. И. Шарапов,
С. П. Ксенз, С. С. Афанасьев.
ПО. Федосенко Р. Я. Надежность электроснабжения и электриче-
ские нагрузки. М., «Энергия», 1967.
179. Чуев Ю. В. Исследование операций в военном деле. М., Военнз
дат, 1970.
197. Ч у е в Ю. В., С п е х о в а Г. П. Технические задачи исследования
операций. М.. «Сов. радио», 1971.
19. Популярные книги и брошюры
29. Б е р г А. И. Кибернетика и надежность. М , «Знание», 1963
186. Красновский А. А., Ткаченко Л. Г. Этажи надежности.
М., «Машиностроение», 1971.
464
139 Кузинец Л. М., Р ы м а н о в Е. А. Надежность телевизионных
приемников. (Библиотека инженера по надежности.) М., «Сов. радио», 1969.
62. Кузнецов В. А. Основные вопросы надежности радиоэлектронной
аппаратуры. М., «Энергия», 1965.
79. К у л и к о в В А. Обеспечение надежности сложной радиоэлектрон-
ной аппаратуры при мелкосерийном производстве. (Библиотека инженера по на-
дежности.) М., «Сов. радио», 1966.
19. Л е б е д е в А. В. Надежность и долговечность. М., Профиздат, 1961.
44. Лебедев А В., G о р и и Я. М Беседы о надежности. М., «Зна-
ние», 1964.
80. Л у ц к и й В. А. Расчет надежности и эффективности радиоэлектрон-
ной аппаратуры (справочник). Изд 2-е, доп. и переработ. Киев. «Наукова дум-
ка», 1966.
101. Маликов И. М Надежность судовой электронной аппаратуры и
систем автоматического управления. М., «Судостроение», 1967.
118. Математические основы современной радиоэлектроники. М., «Сов. ра-
дио», 1968. Авт.: И. А. Большаков, Л С. Гуткин, Б. Р. Левин, Р. Л. Стратоиович.
20. М е с я ц е в П. П. Введение в теорию проектирования и производства
радиоаппаратуры. М., «Высшая школа», 1961.
35. М е с я ц е в П. П. Надежность производства электронно-вычисли-
тельных машин. М., Машгиз, 1963
122. Основы эксплуатации радиоэлектронной аппаратуры. М., «Высшая
школа», 1968. Авт.: А. К- Быкадоров, Л. И Кульбак, В. Ю. Лавриненко.
И Н. Рысейкин, В. Л. Тихомиров.
148. Проников А. С. Основы надежности и долговечности машин.
М., Изд-во Комитета стандартов, мер и измерительных приборов при СМ СССР,
1969.
149. Рахвальский В. М. Надежность кибернетических систем. М.,
«Знание»,' 1969.
107. Рябинин И. А. Основы теории и расчета надежности судовых
электроэнергетических систем. М., «Судостроение», 1967.
52. Сапожников Р. А., Бессонов А. А., Шоломиц-
к и й А. Г. Надежность автоматических управляющих систем. М., «Высшая
школа», 1964.
21. Сорин Я- М. Надежность радиоэлектронной аппаратуры. (Массо-
вая радиобиблиотека.) М., Госэнергоиздат, 1961.
151. Сорин Я- М. Физическая сущность надежности. М., Изд-во Комите*
та стандартов, мер и измерительных приборов при СМ СССР, 1969.
127. Сорин Я- М., Лебедев А. В. Беседы о надежности. М., «Зна-
ние», 1968.
25. С о р и н Я- М„ Лебедев А. В. Главное мерило качества (проб-
лема надежности). М., «Знание», 1962.
87. Т к а ч е н к о Л. Г. Надежность радиоэлектронной аппаратуры. М.,
«Знание», 1966.
177. Ф о к и и Ю. Г. Надежность при эксплуатации технических средств.
М., Воениздат, 1970.
178. Фролов А. Д. Теоретические основы конструирования и надеж-
ности радиоэлектронной аппаратуры. М., «Высшая школа», 1970.
69. Ш и р о к о в А. М. Основы надежности и эксплуатации электронной
аппаратуры. Минск, «Наука и техника», 1965.
20. Элементарные сведения
136. Диксон Дж. Проектирование систем: изобретательство, анализ н
принятие решений. Пер. с англ. Под ред. Е. Г. Коваленко. М., «Мир», 1969.
95. 3 и з е м с к и й Е. И. Надежность радиоэлектронной аппаратуры.
Изд. 2-е, доп. и переработ. М., «Судостроение», 1967.
140. Кузнецов А. С. Надежность радиолюбительской аппаратуры.
М., «Энергия», 1969.
465
Алфавитный указатель авторов и редакторов книг
по надежности и смежным вопросам с номерами аннотаций
Акофф Р. — 181
Асратян Э. А. — 28
Астафьев Д. в< — 7, 54
Афанасьев С. С. — 175
Афонин Н. С. — 4
Базовский И. — 55
Баласаноц Г. Н. — 89
Барвинский Л. Л. — 53
Барзиловт1Ч Е. Ю. — 182
Барлоу Е>. -- 130
Башарннов А. Е. — 22
Белов М. И, — 17
Беляев Kj. к. — 59, 99
Берг А. И, — 29, 51, 97, 98
Бердичевский Б. Е. — 15, 60, 70,
173
Бессонов А. А. __ 50
Богусловскнй Л. С. — 164
Болотин В. В. — 18
Большаков И. А. — 118
Браудо С. И. — 56
Броди С. Н. — 157
Бруевич Н. Г. — 23, 51
Букан Дж. — 91
Бусленко н. П. — 39, 44, 111
Быкадоров А. К. — 122
Варжапетян А. Г. — 116, 131
Васильев Б. В. — 87, 158
Вентцел ь Е. С. — 40
Верзаков Г. Ф. — 112
Власенко О. Н. — 157
Володин Б. Г. — 26, 65
Волчкевич Л. И. — 132
Вольпин А. Г. — 57
Гайденко В. С. — 141
Ганин М. П. — 26, 65
Гаркунов д. н. — 109
Гермейер Ю. Б. — 183
Герцбах И. Б. — 71, 133
Гнеденко Б. В. — 51, 58, 59, 72, 91,
113, 130, 153
Голинкевнч Т. А. — 134
Головинский В. В. — 9
Голубев-Новожилов Ю. С. — 92
Гольдберг О. Д. — 114
Горский Л. К- — 159
Гриффин Б. — 60
Груничев А. С. — 135
Гук Ю. Б. — 160
Гуревич А. м. — 161
Гуревич А. С. — 115
Гурин Л. С. — 85
Гуткин Л. С.— 118
Гутчин И. Б. — 93
Даммер А. — 60
Диксон Дж, _ 136
466
Дннер И. Я. — 26, 65
Добрушин Р. Л. — 38
Доманицкий С. М. — 162, 184
Дружинин Г. В. — 41, 94
Дулин В. А. — 163
Епифанов А. Д. — 42
Ефимов И. Е. — 137
Железнов Н. А. — 166
Загоруйко А. С. — 142
Зиземский Е. И. — 30, 95
Зубов В. И. — 81
Иыуду К. А. — 73
Калабро С. Р, — 74
Кальман И. Г. — 137
Карпушин Б. В. — 185
Карташев Г. Д. — 123
Каштанов В. А. — 182
Уеминискии М. М. — 96
Кенигсберг Э. — 91
Киншт Н. В, — 112
Климов Г. П. — 75
Коваленко Е. Г. — 136
Коваленко И. Н. —72
Козлов Б, А. — 76, 138
Кокс Д. Р. — 99
Колегаев Р. Н. — 31, 100
Комаров Л. Б. — 26, 65
Корбут А. А. —77
Кордонский X. Б. — 32, 71
Костыркин А. И. — 167
Кофман А. — 77, 78
Кравцов О. С. — 193
Красновский А. А. — 186
Креденцер Б. П. — 106
Ксенз С. П. — 61, 175
Кугель Р. В. — 117
Кузинец Л. М. — 139
Кузичев А. С. — 93
Кузнецов А. С. — 140
Кузнецов В. А. — 62, 135
Кузнецов П. И. — 141
Кузьмин Ф, И. — 128
Кулаков Н. Н. — 142
Куликов В. А. — 79
Кульбак Л. И — 122, 168
Курбатов Н. Д, — 115
Лавриненко В. Ю. — 122
Ластовченко М. М. — 106
Латинский С. М. — 175
Лебедев А. В. — 19, 25, 43, 125
Левин Б. Р. — 12, 55, 118, 152
Левин В. И. — 143
Леонтьев Л. П, — 33
Липов М. — 44
Ллойд Д. К. — 44
Лупа нов А Н. — 38
Луцкий В. А. — 34, 80
Ляпунов А. А, — 2
Маккарти Дж. — 2
Маликов И. М. — 10, 14, 101
Малинский В. Д. — 169, 188
Мамонтов О. В. — 24
Мартынов В. И. — 137
Мартюшов Н. М. — 165
Марченко Б. Г. — 157
Маслов А. А. — 36
Меламедов И. М. — 170
Мельников П. М. — 63
Месяцев П. П. — 5, 20, 35
Митин В. G. — 90
Михайлов А. В. — 171
М>локанов Г. Ф. — 102
Морозов И. И. — 8
Невельсон М. С> — 96, 126
Нейштадт И. С. — 161
Нечипоренко В. И. — 37, 120
Новиков О. А. — 145
Овсиевич Б. Л. — 124
Овчаров Л. А, — 146
Отер Ф. Н. — 188
Павленко К. И. — 189
Павлов Б. В. — 84
Пампуро В. И. — 104
Панов Д. Ю. — 74
Пароль Н. В. — 46
Перроте А, И. — 123
Петухов G. И. — 63, 145
Пирс У. — 124
Полляк Ю. Г. — 190
Половко А. М. — 10, 14, 7, 116
Пославский О. Ф. — 48
Проников А. С. — 148
Прошан Ф. — 130
Пу гачев В. С. — 82
Пушкин В. Г. — 191
Пчелинцев Л. А. — 141
Рабинович В. И. — 112
Райкин А. Л. — 86, 105, 156, 192,
193
Раков А. И. — 194
Раквальскин В. М. — 149
Репкин В. Ф. — 53
Розенблгсм Л. Я. — 124
Романов Н. А. — 10, 14
Рыжиков Ю. И. — 150
Рыманов Е. А. — 139
Рысейкнн И. Н. — 122
Рябинин И. А. — 107
Саати Т. Л. — 64
Савина А. С. — 45
Сандлер Дж. — 86
Сапожников Р. А. — 51
Сасиени М. — 181
Свешников А. А. — 26, 65
Седякин Н. М. — 66
Сенецкий С. А. — 106
Симонов П. В. — 28
Снньчугов Ф. И. — 195
Сифоров В. И. — I
Смит В. Л. — 99
Соколов Т. Н. — 50
Соловейчик Ф. G. — 17
Соловьев А. Д. — 59
Соломонов П. А. — 67
Соляник Б. Л. — 129
Сорин Я. М. — 25, 43, 125, 127, 151
Сотсков Б. С. — 172
Спехова Г. П. — 197
Спорыш И П. — 108
Старобин К. Б. — 26, 65, 96
Старосельский А. А. — 109
Стратонович Р. Л. — 118
Сыромятников И. А. — 103
Тареев Б. М. — 16
Теплнцкий Л. Я. — 188
Тимонен Л. С. — 112
Тихомиров В. Л. — 122
Ткаченко Л. Г. — 87, 186
Трейер В. Н.—52
Туркельтауб Р. М, — 88
Уайтин Т. — 156
Уолш К — 16
Ушаков И. А. — 76, 85, 121, 154, 181
Ушакова Г. Н. — 155
Федосенко Р. Я. — 110, 160
Флейшмаи Б. С. — 22, 85
Фокин Ю. Г. — 177
Фор Р. — 78
Фролов А. Д. — 178
Хевнленд Р. — 89
Хедли Дж. — 156
Хейман С. А. — 147
Хинней К- — 16
Холпин Дж. — 127
Цветаев К. Н. — 123
Цветков А. Г. — 196
Ч\ев Ю. В. — 63, 179 197
Чукреев П. А. — 10, 14
Шарапов В. И. — 175
Шеннон К- — 2, 38
Шипов Е. В. — 135
Широков А. М. — 69
Шифрин-Крыжаловский Ю. А. —90
Шншонок Н. А. — 53, 106
Шоломицкий А. Г. — 50
Шор Я. Б. — 27, 63, 128
Шулейкин Н. М. — 3
Щукин А. И. — Н
Юдин Д. Б. — 77
Аманов С. А. — 198
Ястребенецкнй М. А. — 129
467
Оглавление
Предисловие.................................................. 3
От автора..................................................... 5
Основные условные обозначен!.я................................ 13
I. ТЕРМИНЫ И ПОНЯТИЯ НАДЕЖНОСТИ. ПОКАЗАТЕЛИ НАДЕЖНОСТИ
1.1. Основные используемые термины и понятия надежности ... 14
1.2. Математическое определение основных показателей надежно-
сти невосстанавливаемых объектов.........................25
1.3. Математическое определение основных показателей надежно-
сти восстанавливаемых объектов . ........................31
Список литературы ............................................48
2. НАДЕЖНОСТЬ ЭЛЕМЕНТА
2.0. Предварительные замечания...........................49
2.1. Невосстанавливаемый элемент.........................49
2.2. Восстанавливаемый элемент...........................62
2.3. Специальные показатели для восстанавливаемого элемента 68
Список литературы.............................................79
3 РЕЗЕРВИРОВАНИЕ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ
3.0. Предварительные замечания.......................... 80
3.1. Произвольный закон распределения времени работы до отказа 80
3.2. Экспоненциальный закон распределения времени работы до от-
каза: «схема гибели».....................................92
3.3. Некоторые общие положения относительно резервирования
невосстанавливаемых систем...............................99
Список литературы ............................................103
4. РЕЗЕРВИРОВАНИЕ С ВОССТАНОВЛЕНИЕМ
4.0. Предварительные замечания...........................104
4.1. Экспоненциальные законы распределения времени работы до от-
каза и времени восстановления: «схема гибели и размножения» . . 106
4.2. Системы с «быстрым» восстановлением и некоторые другие част-
ные случаи..............................................146
Список литературы............................................153
б. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ВОССТАНАВЛИВАЕМЫЕ РЕЗЕРВИРОВАННЫЕ
СИСТЕМЫ
5.0. Предварительные замечания......................... 155
5.1. Восстанавливаемая резервированная система, состоящая из
п + 1 элементов с разными показателями надежности.......155
5.2. Восстанавливаемая резервированная система, состоящая из
зависимых элементов с разными показателями надежности...157
5.3. Восстанавливаемая система и «канальная» надежность .... 161
5.4. Восстанавливаемая система с невосстанавливаемым резервом 173
5.5. Система массового обслуживания с потерями заявок в случае
ограниченной надежности обслуживающих приборов..........177
Список литературы...................................... . . . 180
488
6. СИСТЕМА ИЗ ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ЭЛЕМЕНТОВ
6.0. Предварительные замечания............................181
6.1. Система из последовательно соединенных невосстанавливаемых
элементов.................................................181
6.2. Система из последовательно соединенных восстанавливаемых
элементов . . . 188
6.3. Последовательное соединение зависимых элементов......198
Список литературы.............................................199
7. УЧЕТ ВЛИЯНИЯ КОНТРОЛЬНЫХ И ПЕРЕКЛЮЧАЮЩИХ УСТРОЙСТВ
НА НАДЕЖНОСТЬ
7.0. Вводные замечания....................................200
7.1. Дублированная система с конечным временем переключения 200
7.2. Дублированная система с ненадежным переключателем .... 203
7.3. Частично контролируемый восстанавливаемый элемент . . . 203
7.4. Дублированные системы с частичным контролем..........209
Список литературы ............................................218
8. система со сложной структурой
8.0. Предварительные замечания.......................... 219
8.1. Метод прямого перебора...............................219
8.2. Метод разложения относительно особого элемента.......222
8.3. Метод минимальных путей и минимальных сечений........223
8.4. Аналитико-статистический метод.......................224
8.5. Вводные замечания о системах с рекуррентной структурой . . 227
8.6. Показатели надежности изотропных систем с рекуррентной
структурой ............................................_ . . 229
8.7. Вероятностные характеристики систем с сетевой структурой . 230
8.8. Краткое описание метода анализа систем с сетевой структурой 240
8.9. Системы с иерархической структурой...................243
Список литературы.............................................248
9. ОЦЕНКА ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ СИСТЕМ
9.0. Предварительные замечания............................250
9.1. Общая схема оценки эффективности функционирования систем
кратковременного действия ............................... 261
9.2. Общая схема оценки эффективности систем длительного действия 253
9.3. Оценка эффективности систем с аддитивным показателем эф-
фективности ..............................................255
9.4. Оценка эффективности систем с резервированием функций . . 257
9.5. Оценка эффективности многофункциональных систем .... 258
9.6. Оценка эффективности систем при известных моментах рас-
пределения числа исправных исполнительных элементов .... 260
Список литературы.............................................262
10. ЗАДАЧИ ОПТИМАЛЬНОГО РЕЗЕРВИРОВАНИЯ
10.0. Предварительные замечания...........................263
10.1. Формулировка задач оптимального резервирования .... 265
10.2. Определение оптимального количества резервных элементов
для случая одного ограничения и показателя надежности типа ве-
роятности безотказной работы (коэффициента готовности, коэффи-
циента оперативной готовности) .......................... 269
10.3. Приближенный метод определения оптимального количества
резервных элементов для случая одного ограничения и показателя
надежности типа среднего времени работы системы до отказа . . 293
10.4. Определение оптимального количества резервных элементов
для случая нескольких ограничений и показателя надежности типа
вероятности безотказной работы (коэффициента готовности, коэффи-
фициента оперативной готовности) ......... . ............ 296
10.5. Определение оптимального количества резервных элементов
для многофункциональной системы для случая одного ограничения
469
и показателя надежности типа вероятности безотказной работы (ко-
эффициента готовности, коэффициента оперативной готовности) . . 300
10.6. Управление запасами элементов при случайном потоке за-
просов ...................................................302
Список литературы.............................................305
11. ЗАДАЧИ ОПТИМАЛЬНОЙ ПРОФИЛАКТИКИ
11.0. Предварительные замечания...........................307
11.1. Формулировка задач оптимальной профилактики ..... 309
11.2. Аварийные ремонты...................................309
11.3. Плановые профилактики при внеплановых аварийных ре-
монтах ...................................................311
11.4. Плановые профилактики...............................316
11.5. Аварийные ремонты отказавших элементов (подсистем) по-
следовательной системы ................................. 320
11.6. Аварийные ремонты отказавших элементов (подсистем) и
плановая профилактика всей последовательной системы.......322
Список литературы........................................... 327
12. ОПТИМАЛЬНЫЙ поиск неисправностей
12.0. Постановка задачи................................. 329
12.1. Общее описание процедуры проверки...................330
12.2. Отыскание единственного неисправного элемента.......330
12.3. Отыскание неизвестного числа неисправных элементов . . , 339
12.4. Обнаружение неисправного элемента...................342
Список литературы.............................................344
13. МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПО НАДЕЖНОСТИ
13.1. Форма учета отказов и простейшие методы обработки резуль-
татов испытаний...........................................346
13.2. Выборочные распределения, связанные с испытаниями на
надежность................................................351
13.3. Проверка гипотез о характере закона распределения отказов 354
13.4. Оценки показателей надежности устройства по результатам
испытаний для экспоненциального распределения времени работы
до отказа.................................................358
13.5. Доверительные интервалы ..........................361
Список литературы.............................................363
Приложение 1. Основные понятия и краткие сведения из теории вероят-
ностей ...................................................364
П1.1. Случайные события и нх характеристики (термины и опре-
деления) .................................................364
П1.2. Вероятность события.................................365
П1.3. Случайные величины и функции распределения.......368
П1.4. Числовые характеристики случайных величин.........370
П1.5. Сводка характеристик функций распределения-.......372
П1.6. Предельные теоремы теории вероятностей............375
Приложение 2. Основные понятия и краткие сведения из математической
статистики...............................................376
Приложение 3. Потоки..........................................380
П3.1. Определения.......................................380
П3.2. Просеивание потока................................383
ПЗ.З. Наложение потоков.................................385
Приложение 4. Аналитические методы оценки надежности систем, пове-
дение которых описывается однородным марковским процессом . . 385
П4.1. Общий принцип составления систем уравнений........385
470
П4.2. Получение нестационарного коэффициента готовности 386
П4.3. Оценка вероятности безотказной работы готовности • • оВЬ
П4.4. Оценка среднего времени работы до отказа' й 'синего
времени работы между отказами......................... среднею
П4.5. Представление показателей надежности 'системы' через’ он-
ределители................................................... 1 „„„
П4.6. Показатели надежности системы, поведение которой описы-
вается схемой «гибели и размножения», отказов и восстановлений 395
Приложение 5. Вычисление показателей надежности для некоторых спе-
циальных случаев немарковских моделей восстанавливаемых систем 402
П5.0. Предварительные замечания.............................402
П5.1. Произвольный стационарный процесс.....................402
П5.2. Полумарковский процесс................................404
П5.3. Способ введения фиктивных состояний для описания произ-
вольных распределений.......................................405
Приложение 6. Эвристический метод оценки надежности восстанавлива-
- мых систем...................................................406
П6.1. Предварительные замечания..............................406
П6.2. Последовательно соединенные элементы...................407
П6.3. Параллельно соединенные элементы.......................408
П6.4. Элемент с задержкой....................................409
Приложение 7. Некоторые константы и формулы, часто встречающиеся
при решении задач надежности.................................410
П7.1. Константы.............................................410
П7.2. Элементарные формулы комбинаторики....................411
П7.3. Конечные суммы........................................411
П7.4. Ряды..................................................412
П7.5. Неопределенные интегралы..............................414
П7.6. Определенные интегралы................................414
П7.7. Преобразование Лапласа................................415
Приложение 8. Числовые таблицы...................................418
Аннотированный библиографический справочник книг по надежности 435
Б.0. Руководство к пользованию..............................435
Б.1. Аннотации книг по надежности по годам выпуска..........435
Б.2. Основные монографии по проблеме надежности.............457
Б.З. Тематическая подборка книг по надежности...............458
Б.4. Алфавитный указатель авторов и редакторов книг по надеж-
ности и смежным вопросам с номерами аннотаций...............466
Козлов Б. А., Ушаков И. А.
К 59 Справочник по расчету надежности аппаратуры
радиоэлектроники и автоматики. М. «Сов. радио»,
1975 г.
472 с. с ил.
Рассматриваются вопросы расчета надежности на различных эта-
пах разработки и эксплуатации, определения оптимальных режимов
эксплуатации и устранения неисправностей нахо/кдения оптимального
числа запасных или резервных элементов при наличии экономических
ограничений, а также производится оценка надежности. Приводится
аннотированная библиография книг по проблеме надежности.
Справочник будет полезен инженерам и математикам прикладни-
кам, занятым созданием сложных систем н обеспечением надежности
их функционирования, а также преподавателям и студентам вузов.
к _3<^-022 86-71
046(01)-75
6Ф2.1
БОРИС АНАТОЛЬЕВИЧ КОЗЛОВ
ИГОРЬ АЛЕКСЕЕВИЧ УШАКОВ
СПРАВОЧНИК ПО РАСЧЕТУ НАДЕЖНОСТИ
АППАРАТУРЫ РАДИОЭЛЕКТРОНИКИ
И АВТОМАТИКИ
Редактор А. А. Александрова
Художественный редактор 3. Е. Вендрова
Обложка художника В. В. Волкова
Технические редакторы: А. А. Белоус, Г. А. Мешкова
Корректор 3. Г. Галушкина
Сдано в набор 12/П-1974 г. Подписано к печати 25/XI-1974 р.
Т-18636. Формат 60х90/18 Бумага типографская № 2
Объем 29,5 усл. п. л. 32,512 уч-изд. л.
Тираж 37 500 Зак. 943 Цена 1 р. 79 к.
Издательство <Советское радио», Москва, Главпочтамт, a/я G93
Московская типография № 4 Союзполиграфпрома
при Государственном Комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
Москва И-41» Б, Переяславская, 46