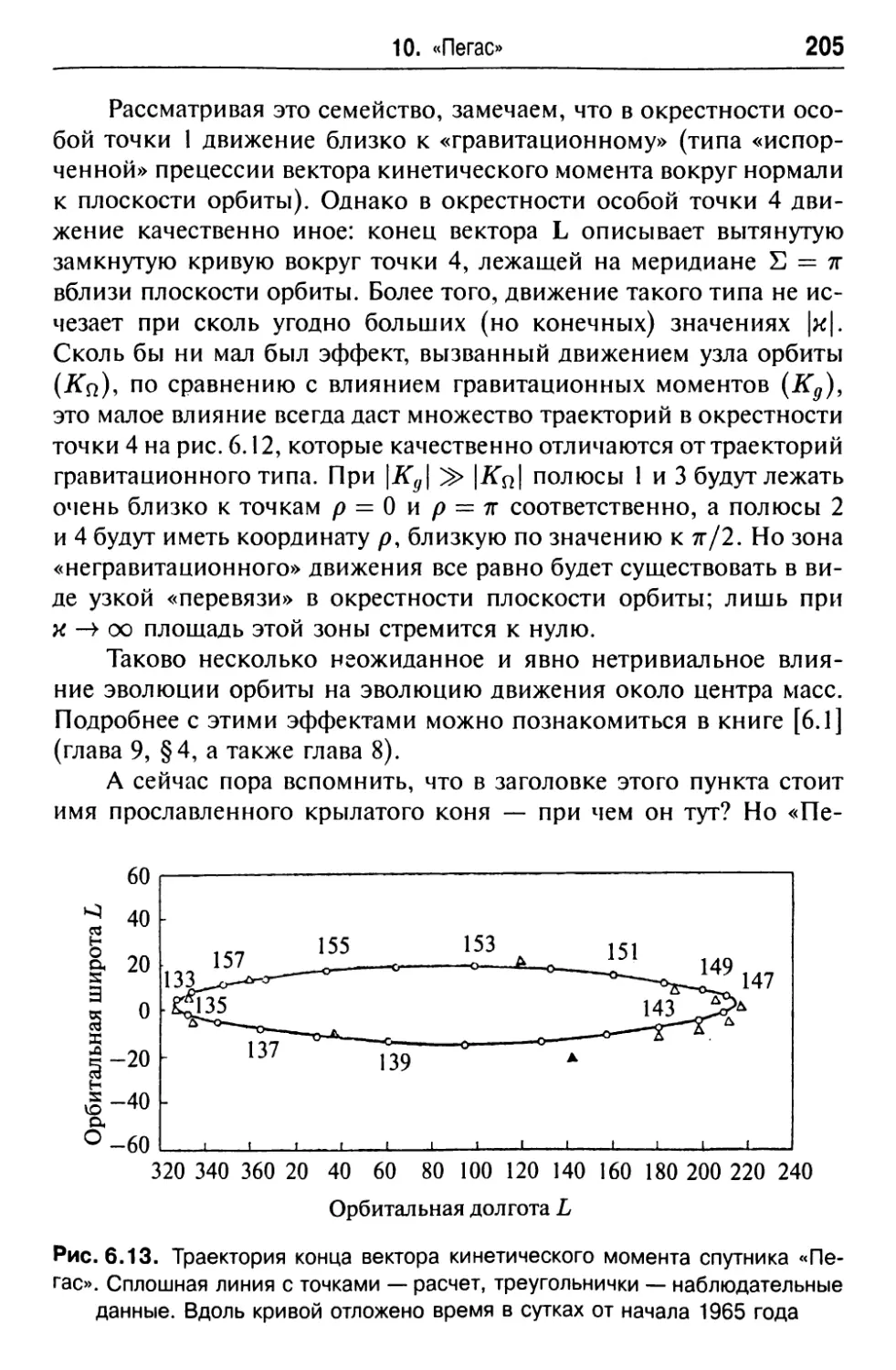
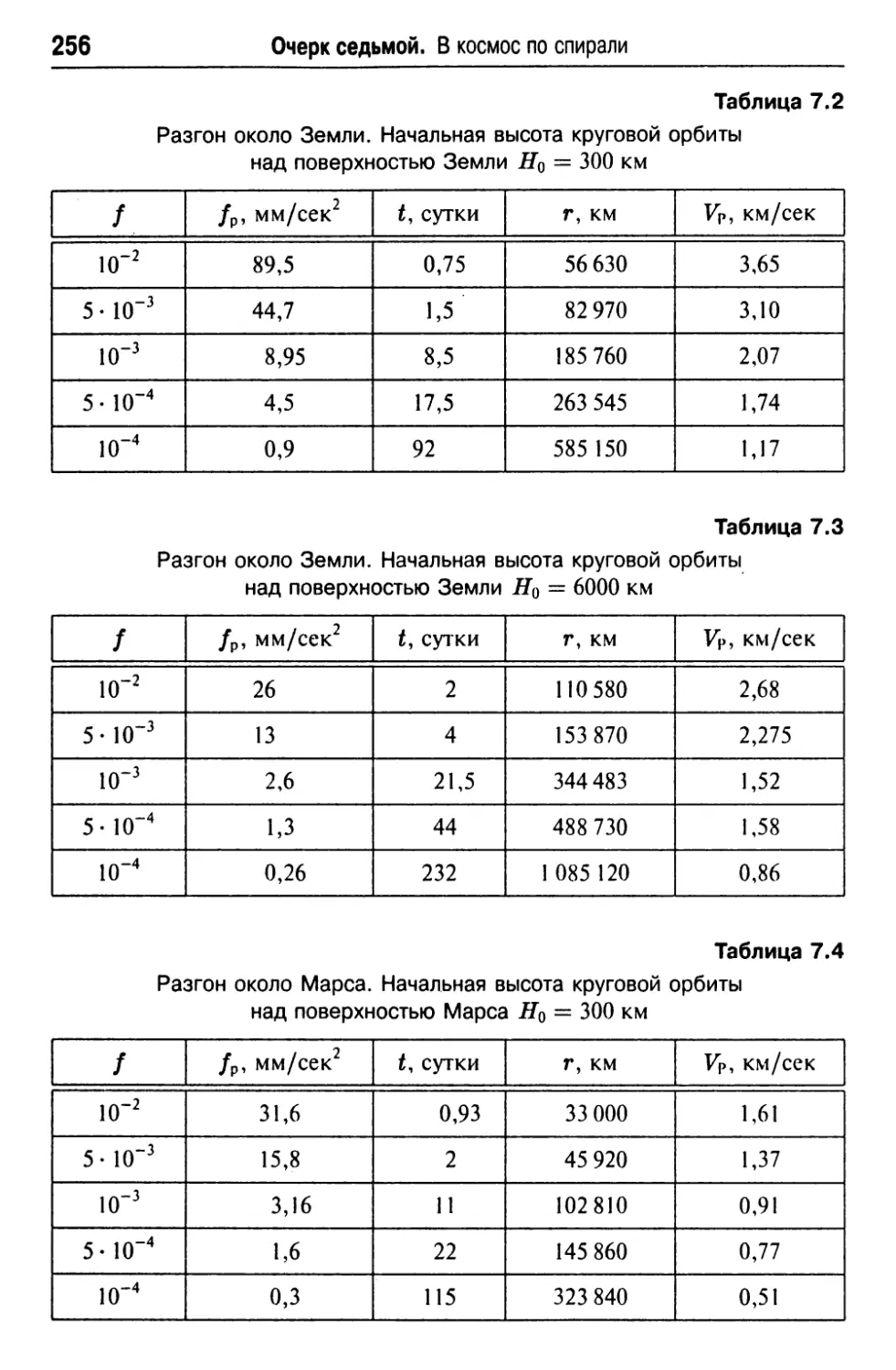
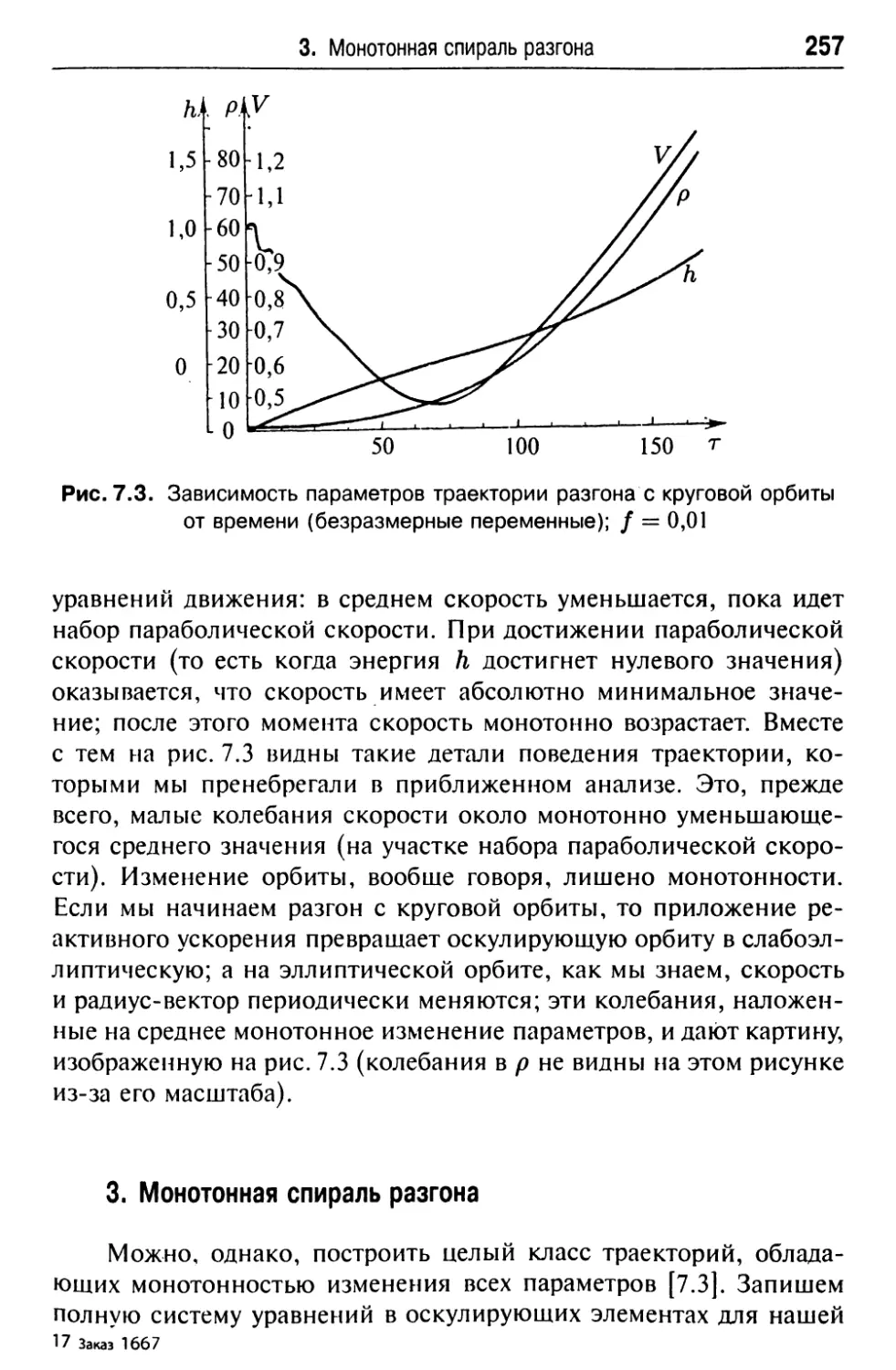
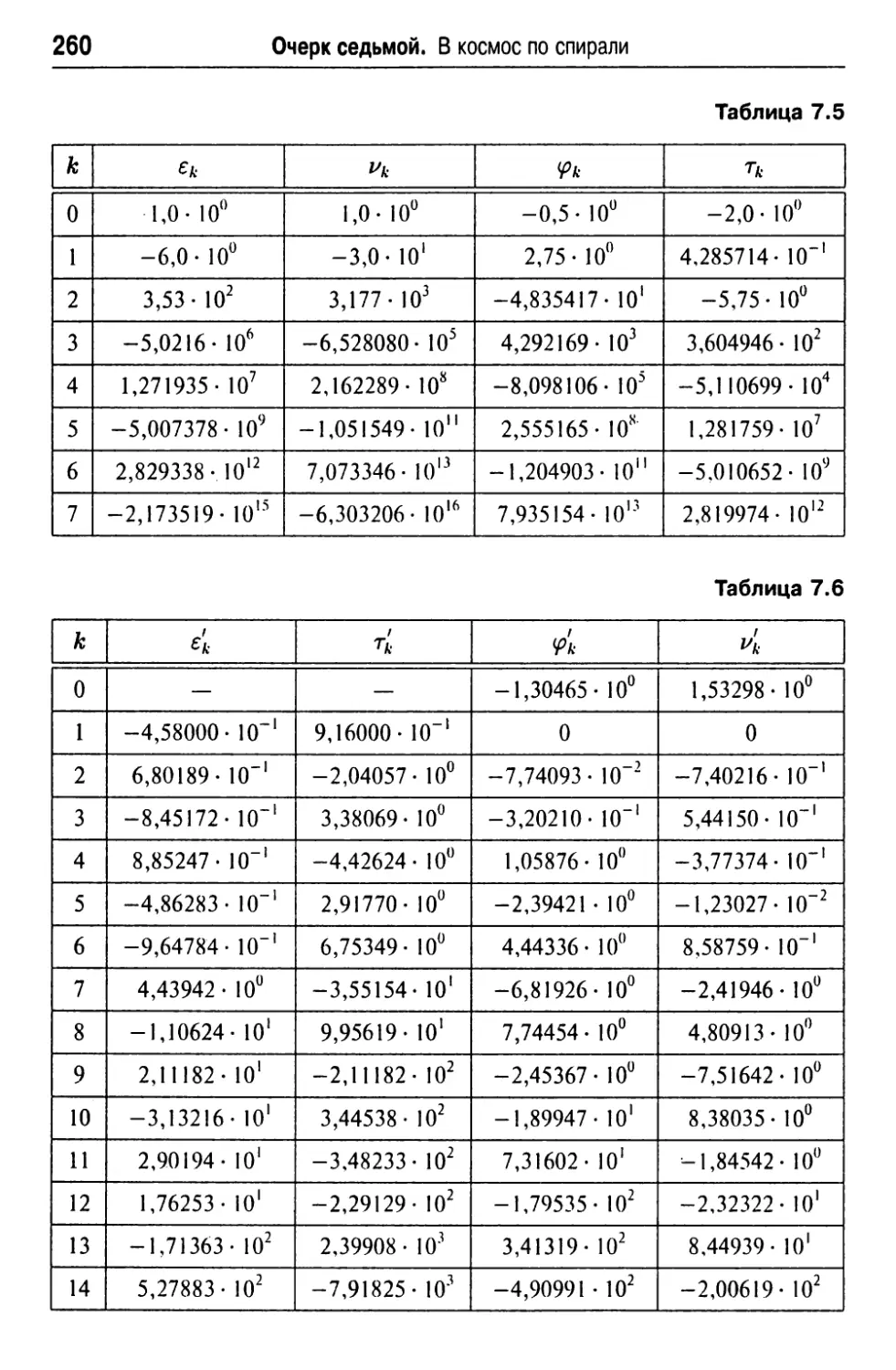
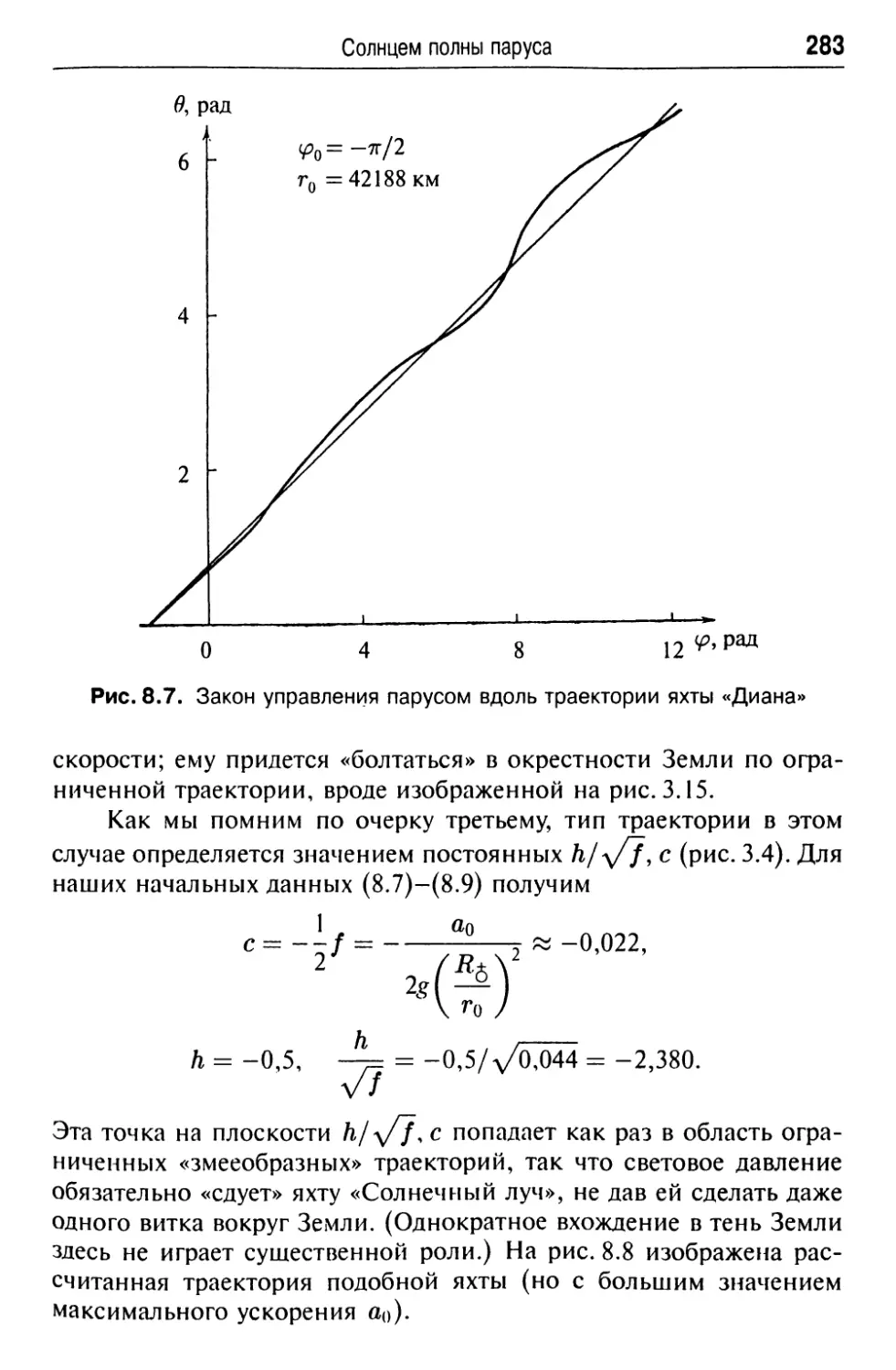
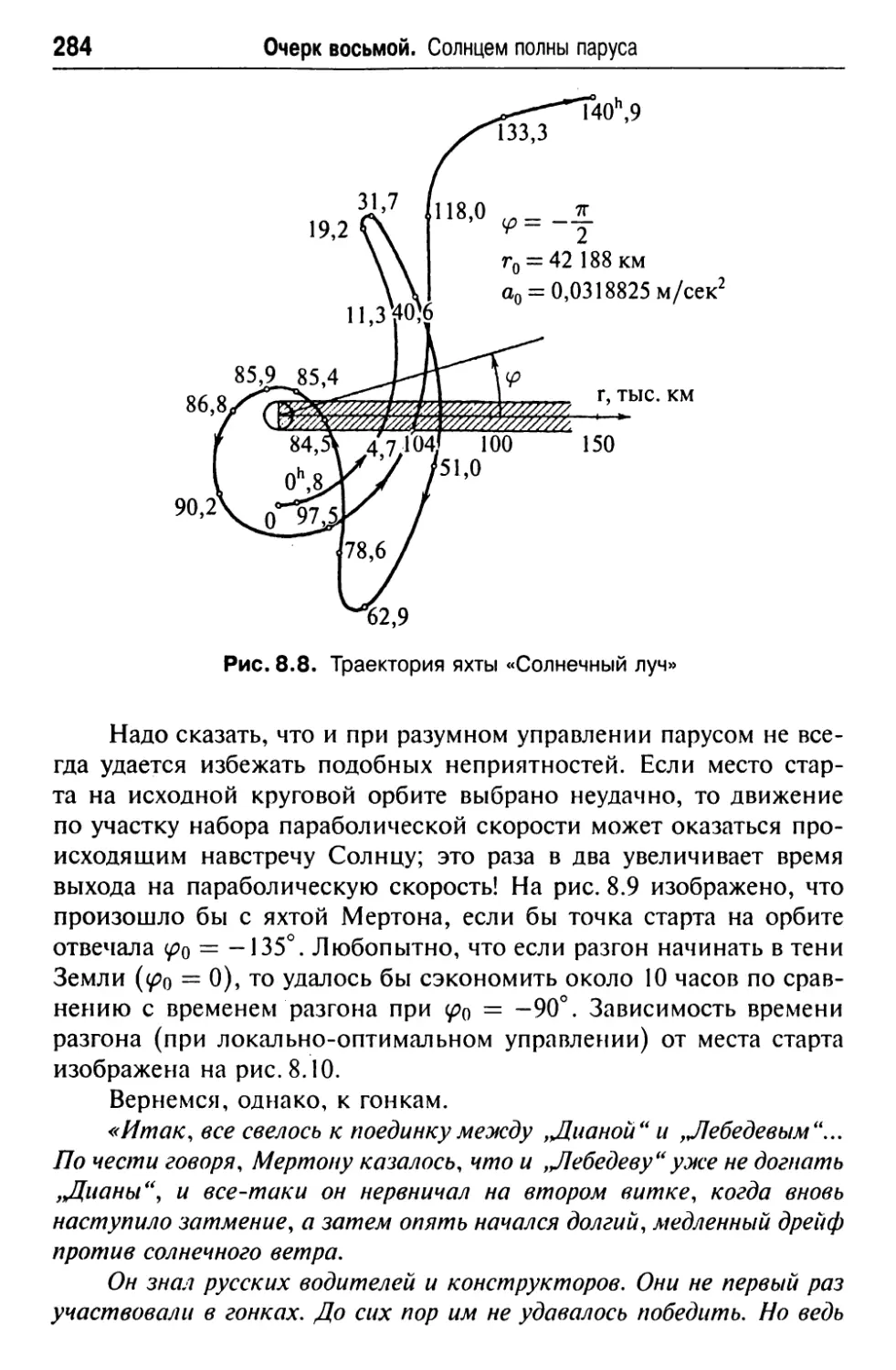
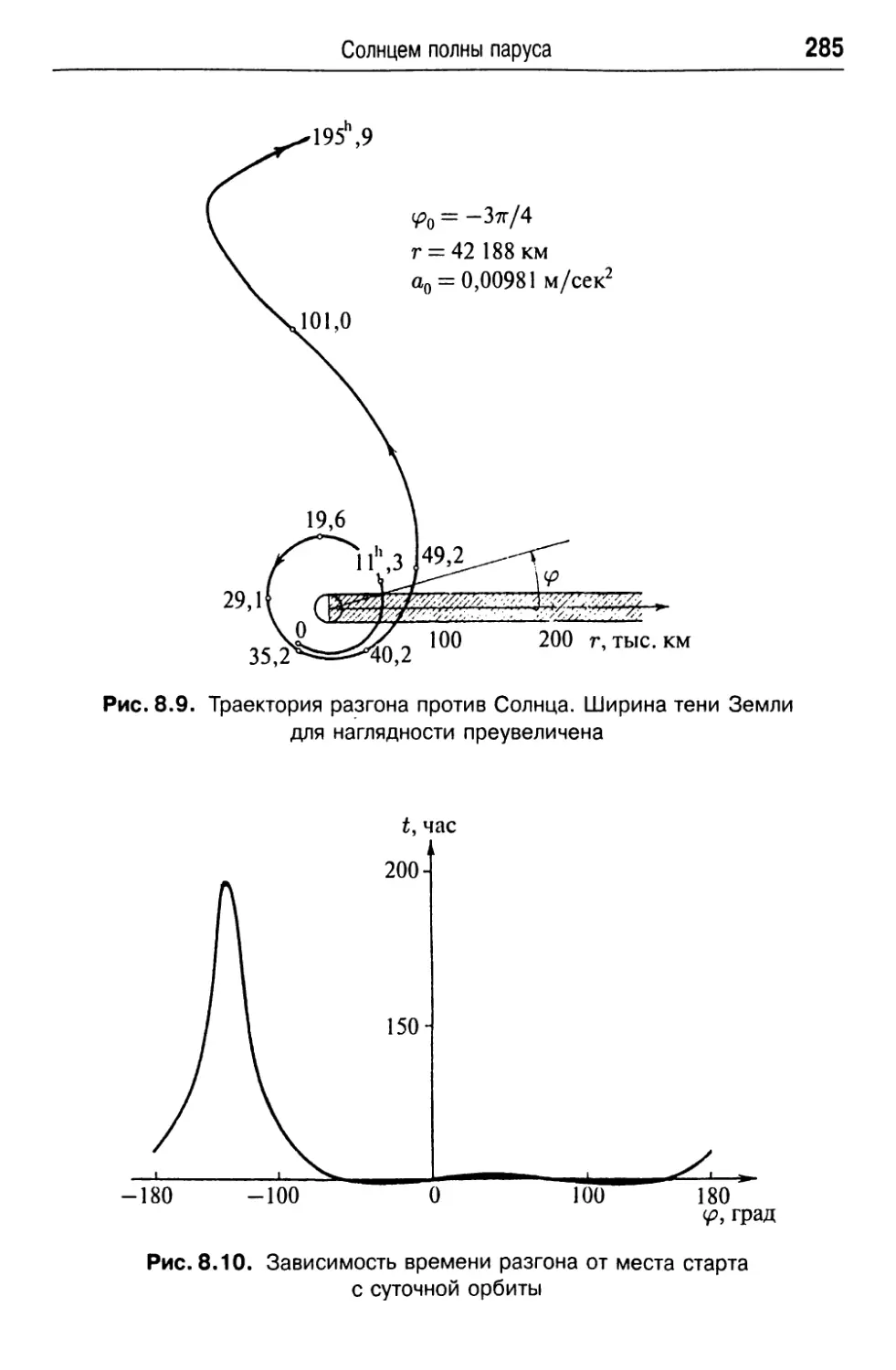
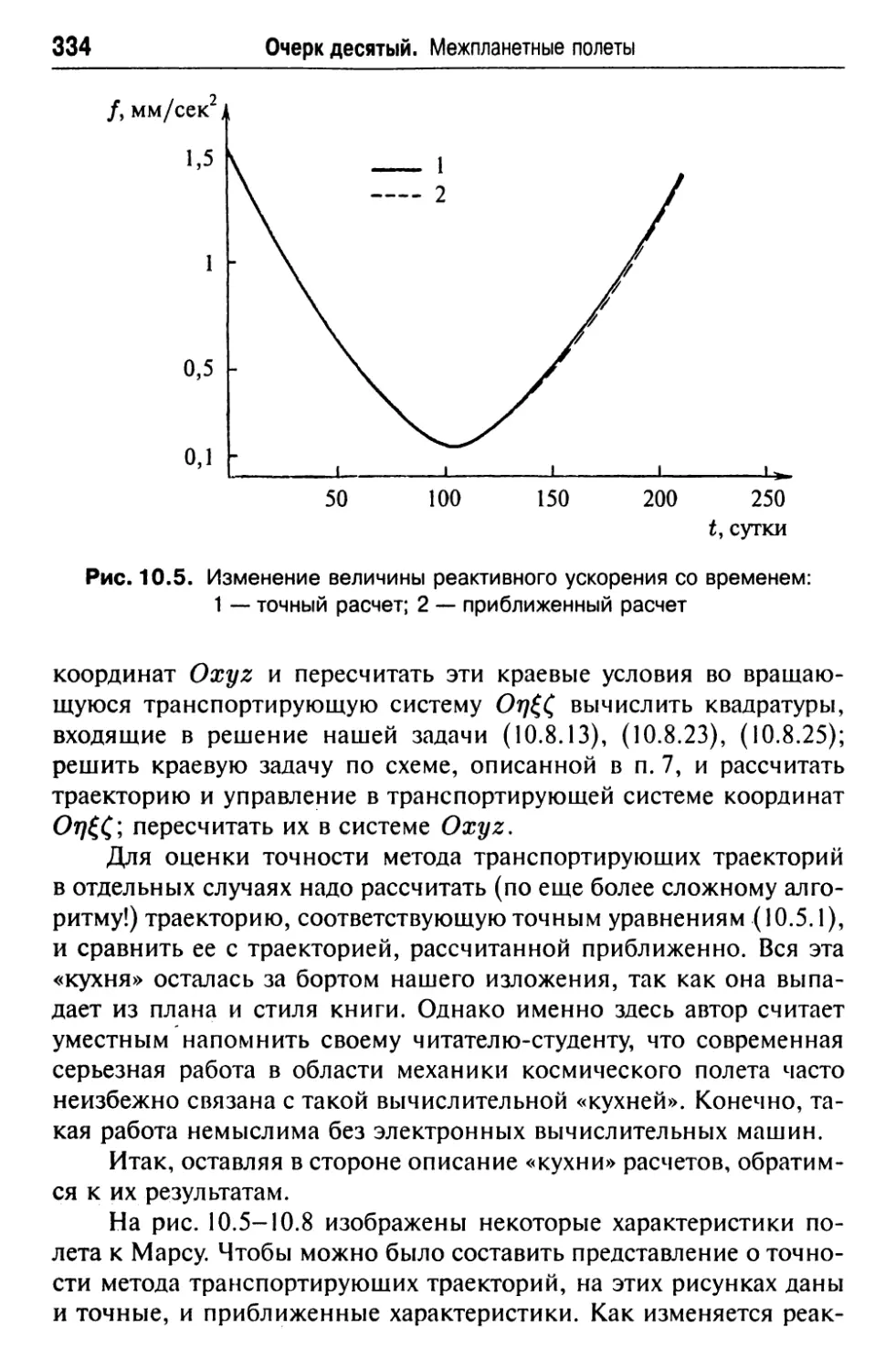
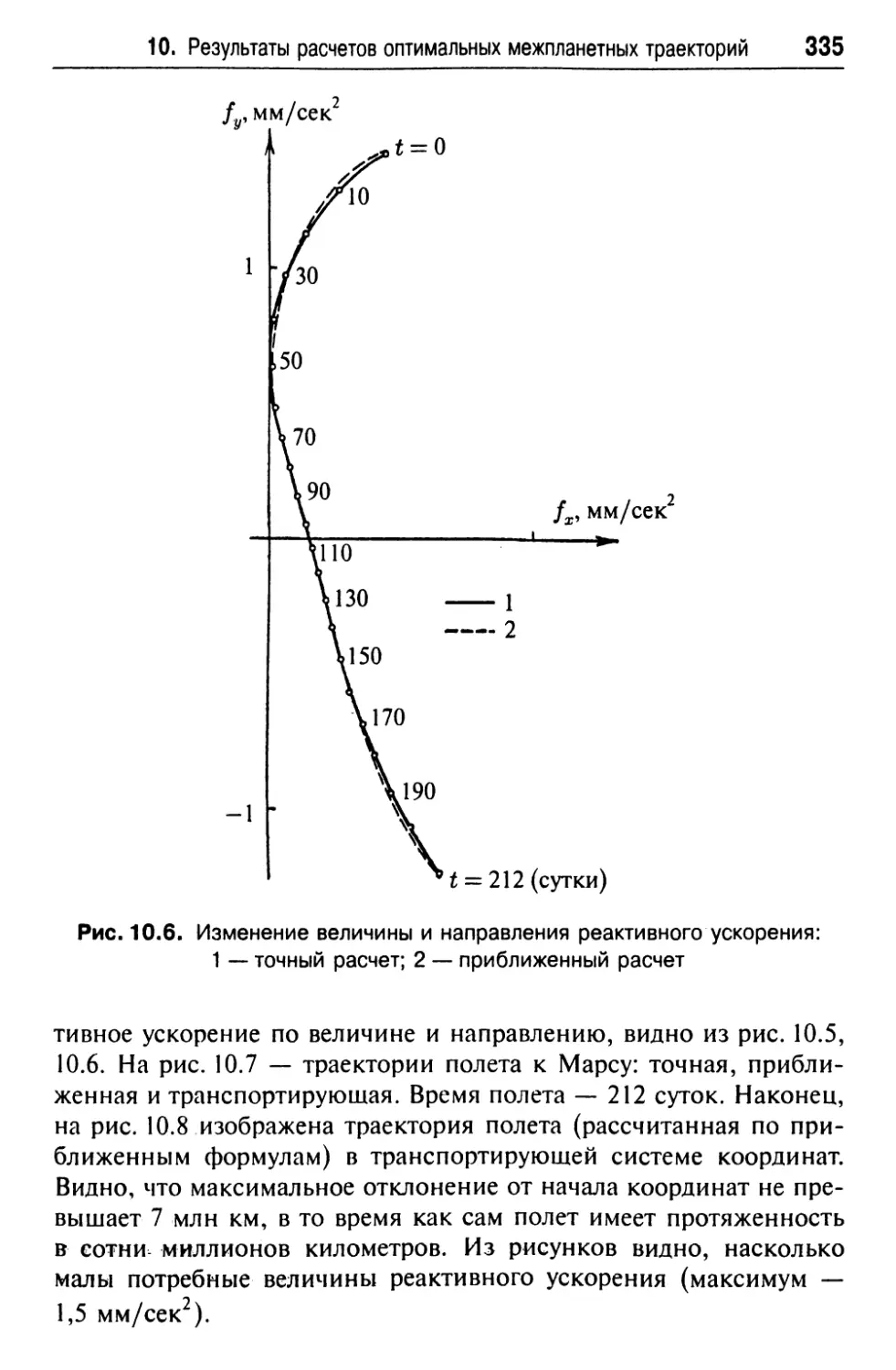
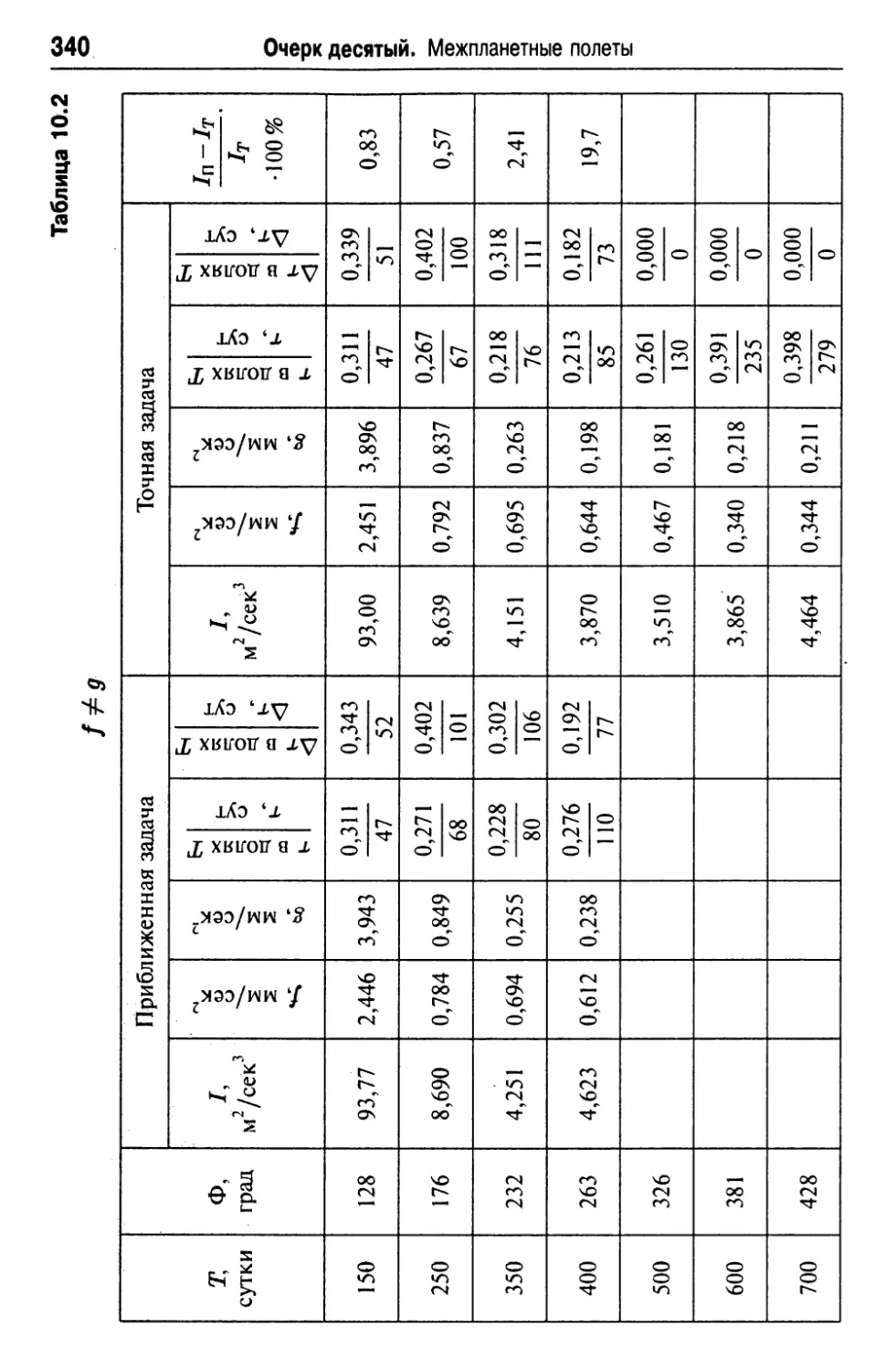
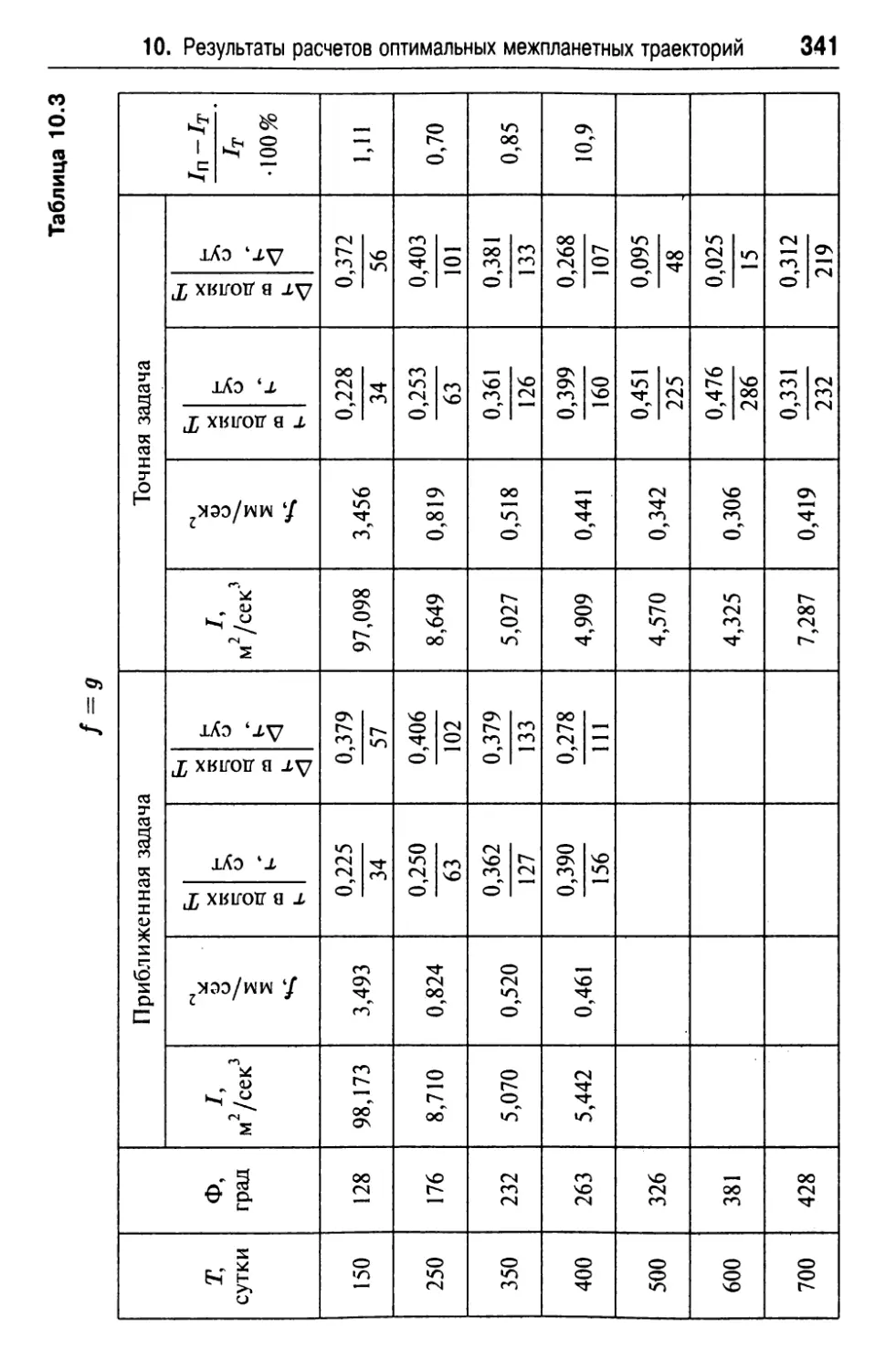
Текст
(
I
В. В. Белецкий
ОЧЕРКИ
О ДВИЖЕНИИ
КОСМИЧЕСКИХ
тел : _
URSS
В. В. Белецкий
ОЧЕРКИ
О ДВИЖЕНИИ
КОСМИЧЕСКИХ
ТЕЛ
Издание третье,
исправленное и дополненное
URSS
МОСКВА
ББК 22.21 22.622.8 39.6
+
Настоящее издание осуществлено при финансовой поддержке
И Российского фонда фундаментальных исследований
(проект № 07-01-07085-д)
Белецкий Владимир Васильевич
Очерки о движении космических тел. Изд. 3-е, испр. и доп.
М.: Издательство ЛКИ, 2009. — 432 с.
Настоящая книга содержит серию очерков об интересных задачах механики
космического полета и небесной механики. В них рассматриваются различные
траекторные задачи механики космического полета, эволюция орбит искусствен¬
ных и естественных небесных тел, встречающиеся резонансные явления; описаны
оригинальные задачи динамики относительного движения на орбите и многие
другие проблемы. Дается параллельное изложение необходимого математическо¬
го аппарата, однако упор делается на выявление механической сути задач.
Книга предназначена всем, кто интересуется или занимается механикой кос¬
мического полета, особенно молодым специалистам в этой области и студентам
соответствующих специальностей.
Второе издание этой книги было в 1999 году удостоено
премии им. Ф. А. Цандера Российской академии наук
Рисунки доктора физико-математических наук И. В. Новожилова
Издательство ЛКИ. 117312, Москва, пр-т Шестидесятилетия Октября, 9.
Формат 60x90/16. Печ. л. 27. Зак. № 1667
Отпечатано с готовых диапозитивов в ООО «Полиграфический комбинат «Зауралье».
640022, Курган, ул. К. Маркса, 106.
ISBN 978-5-382-00982-7 © Издательство ЛКИ, 2008
НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
URSS
E-mail: URSS@URSS.ru
Каталог изданий в Интернете:
http://URSS.ru
Тел./факс: 7 (499) 135-42-16
I Тел./факс: 7 (499) 135-42-46
4652 Ю 50797
785382
9827
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или
передана в какой бы то ни было форме и какими бы то ни было средствами, будь то элек¬
тронные или механические, включая фотокопирование и запись на магнитный носитель,
а также размещение в Интернете, если на то нет письменного
Оглавление
Начало нового стиля в научной литературе (из рецензии
В. И. Арнольда и Я. Б. Зельдовича на первое издание
«Очерков» В. В. Белецкого) 7
Посвящение 9
От автора 10
Слово прощания 15
Очерк первый. О невозмущенном и возмущенном движении
спутника с отступлением об асимптотических методах
нелинейной механики 16
1. Нам повезло . . . . 16
2. Кеплеровское движение 21
3. Возмущенное движение. Оскулирующие элементы .... 26
4. Оскулирующая орбита экваториального спутника 27
5. Уравнения в оскулирующих элементах.
Элементы Делоне 33
6. Отступление об асимптотических методах нелинейной
механики. Колебания спутника около центра масс.
Осреднение канонических уравнений 37
7. Спутник в поле тяготения Земли 56
Очерк второй. О втором рождении старой задачи, или что
получится, если две массы поместить на чисто
мнимое расстояние друг от друга 63
1. От Эйлера до наших дней 63
2. Связь двух задач 66
3. Интегрирование. Система координат 71
4. Метод Гамильтона—Якоби 73
5. Интегрирование 74
6. Область движения спутника 77
4
Оглавление
7. Эллиптические функции Якоби 80
8. Движение полярного спутника Земли 83
Очерк третий. Еще одна старая задача,
возвращенная к новой жизни 87
1. Что за задача? 87
2. Коротко об уравнениях движения
и их интегрировании 89
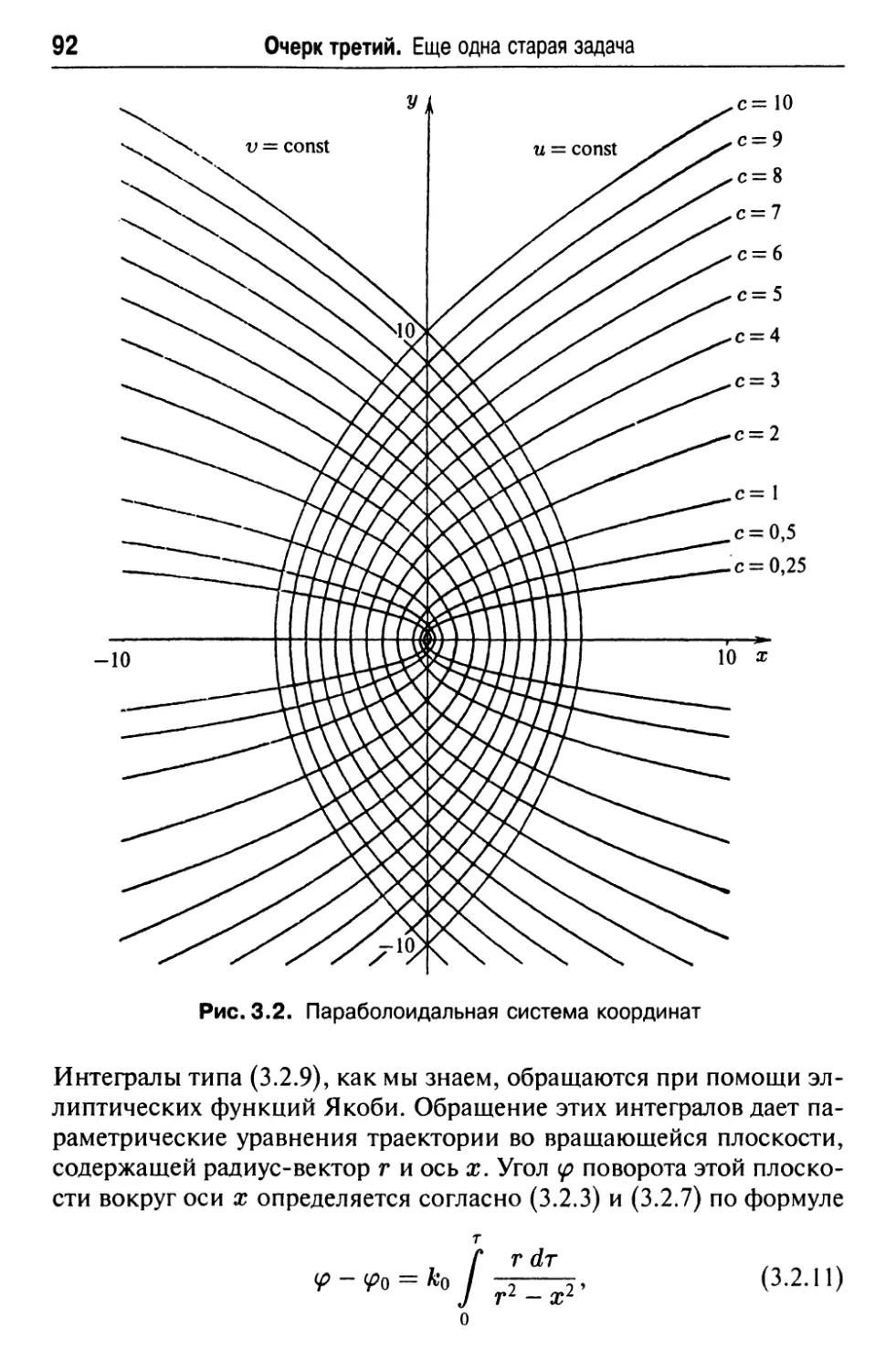
3. Плоское движение 93
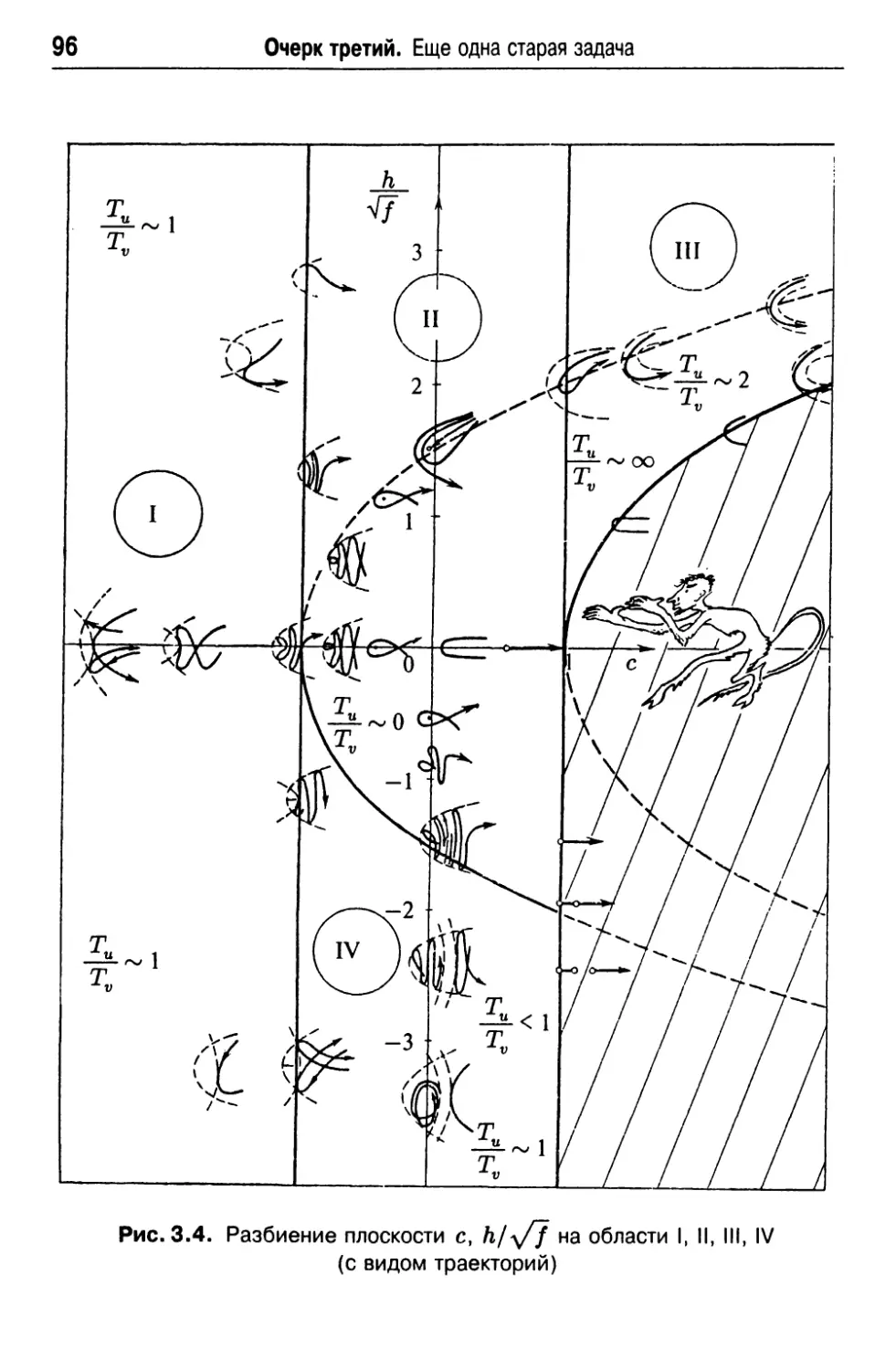
4. Описание траекторий плоского движения 95
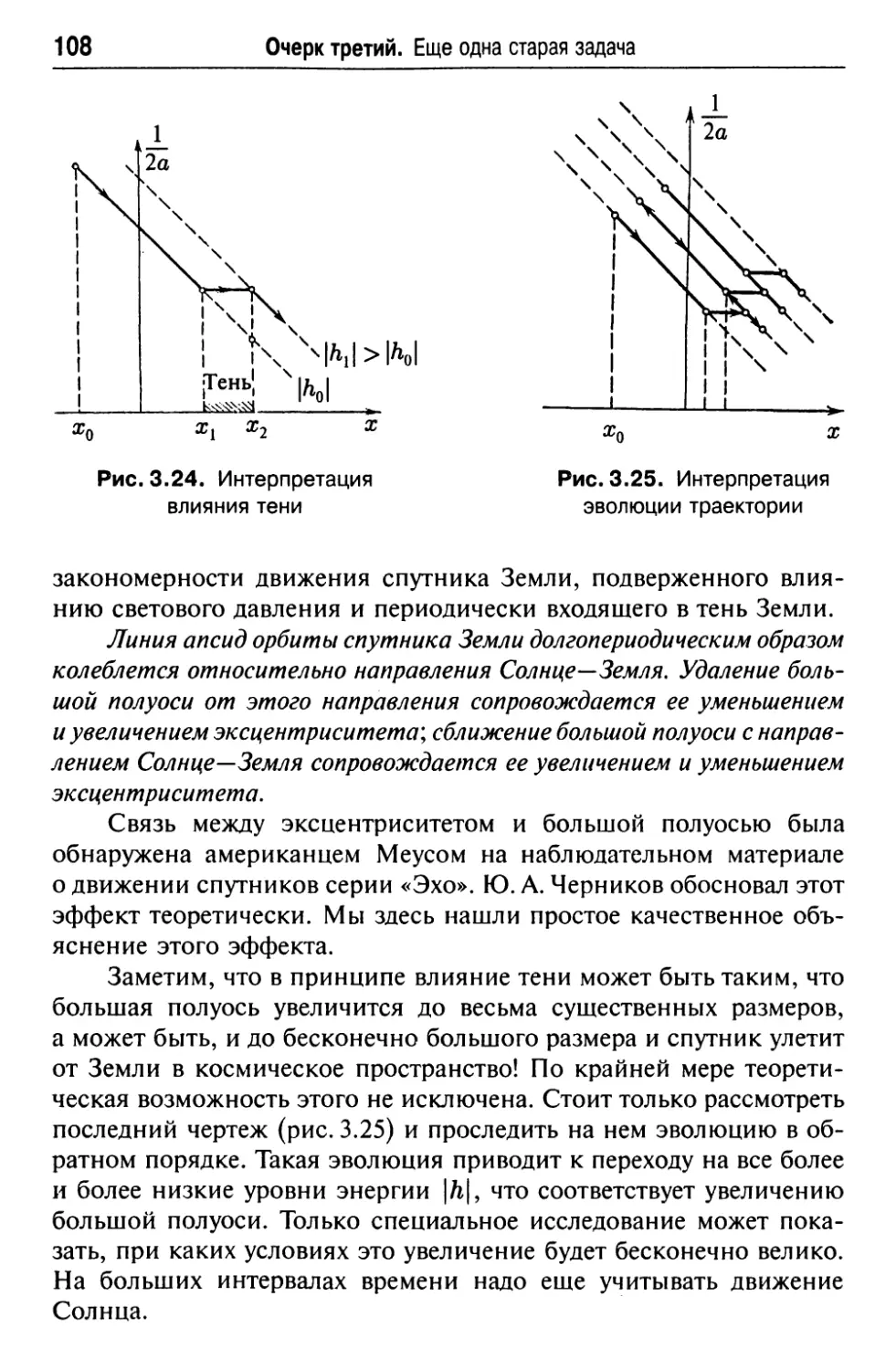
5. Немного о влиянии светового давления
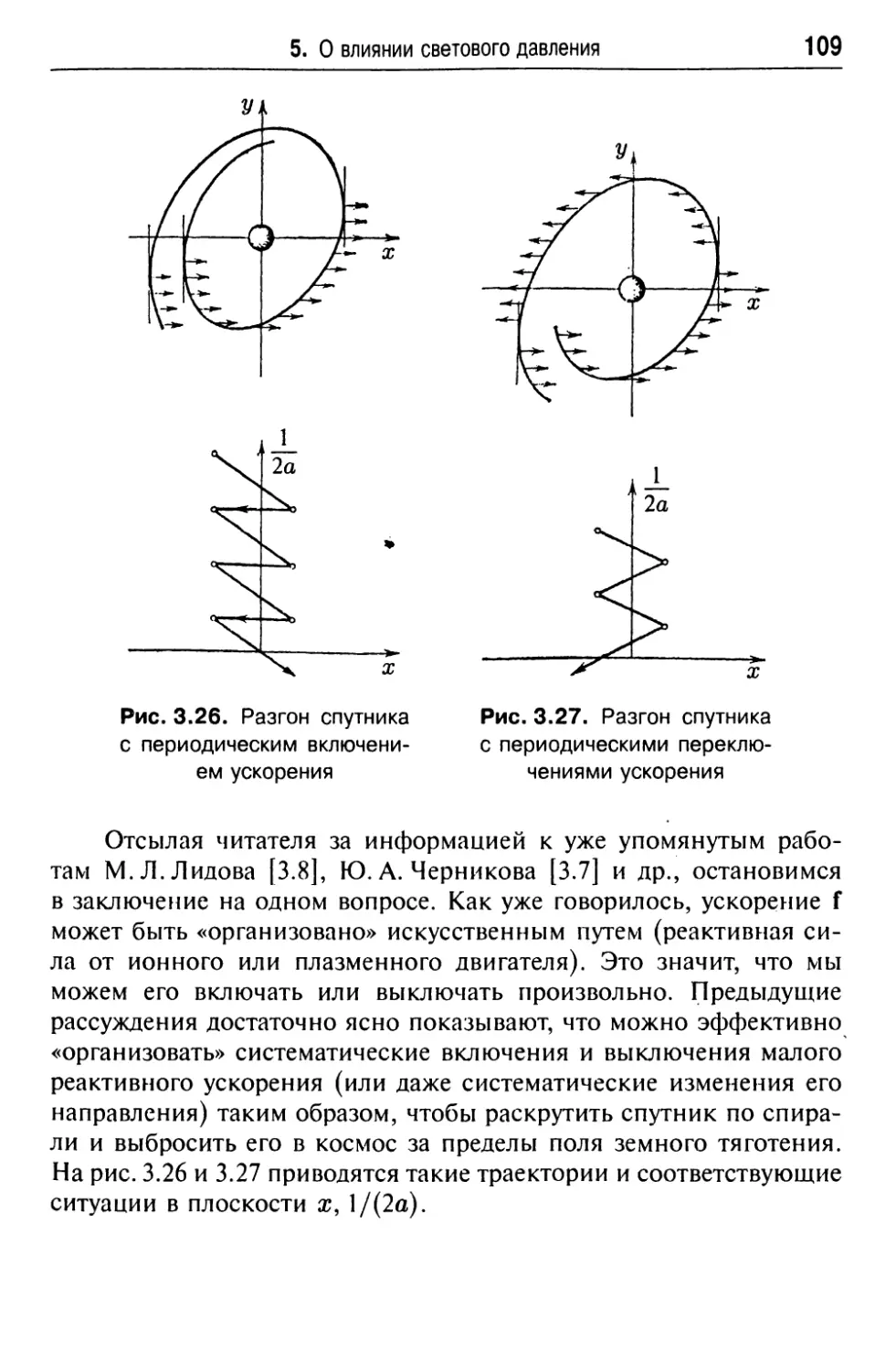
на движение спутников Земли 105
Очерк четвертый. Движение миров 110
1. Еще раз о «теореме Лапласа»
и других Серьезных Вещах ; . . . . 110
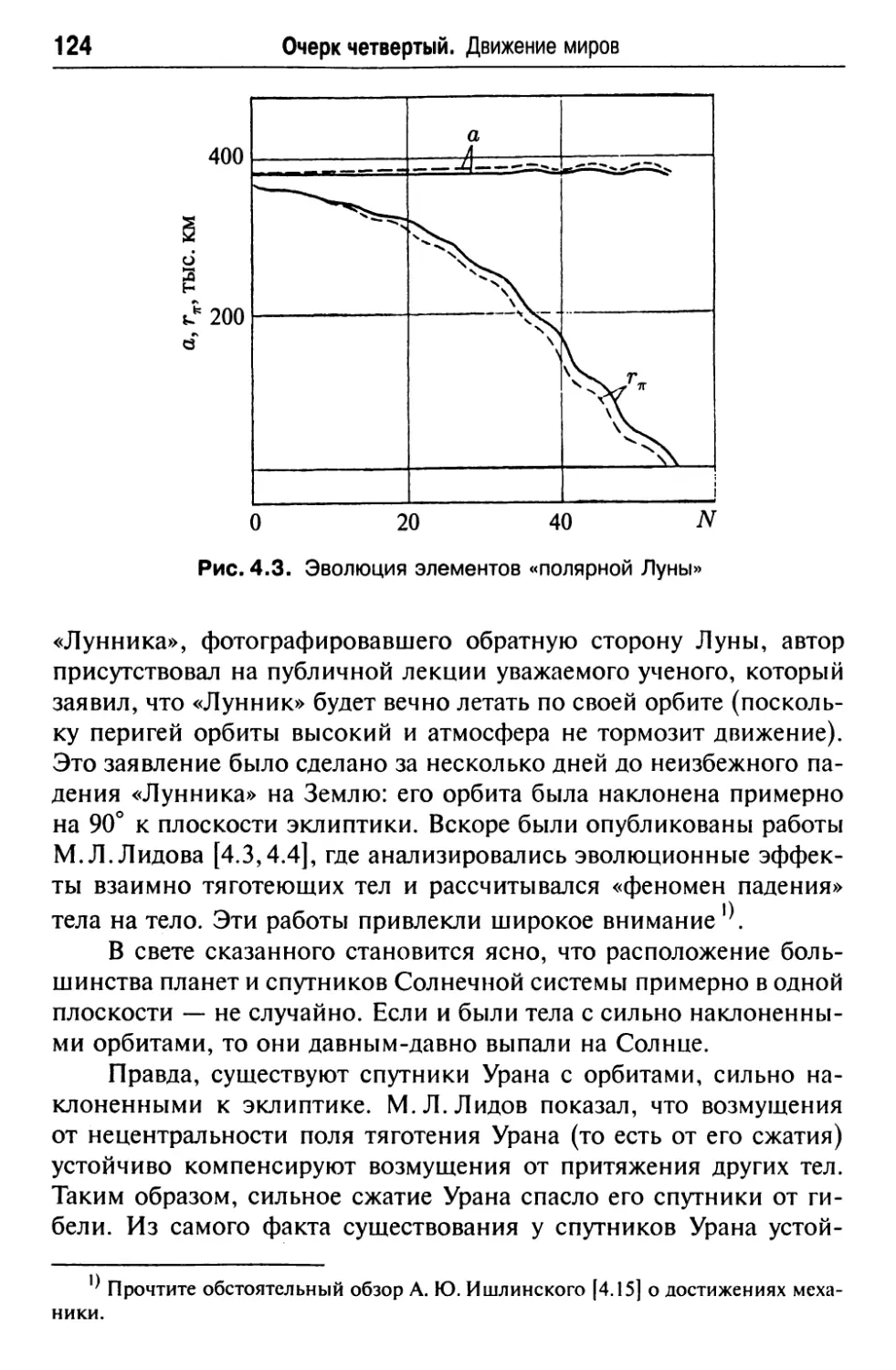
2. Не хотите ли Луну уронить на Землю? 118
3. Область маловозмущенного движения 125
4. Устойчивость Солнечной системы 130
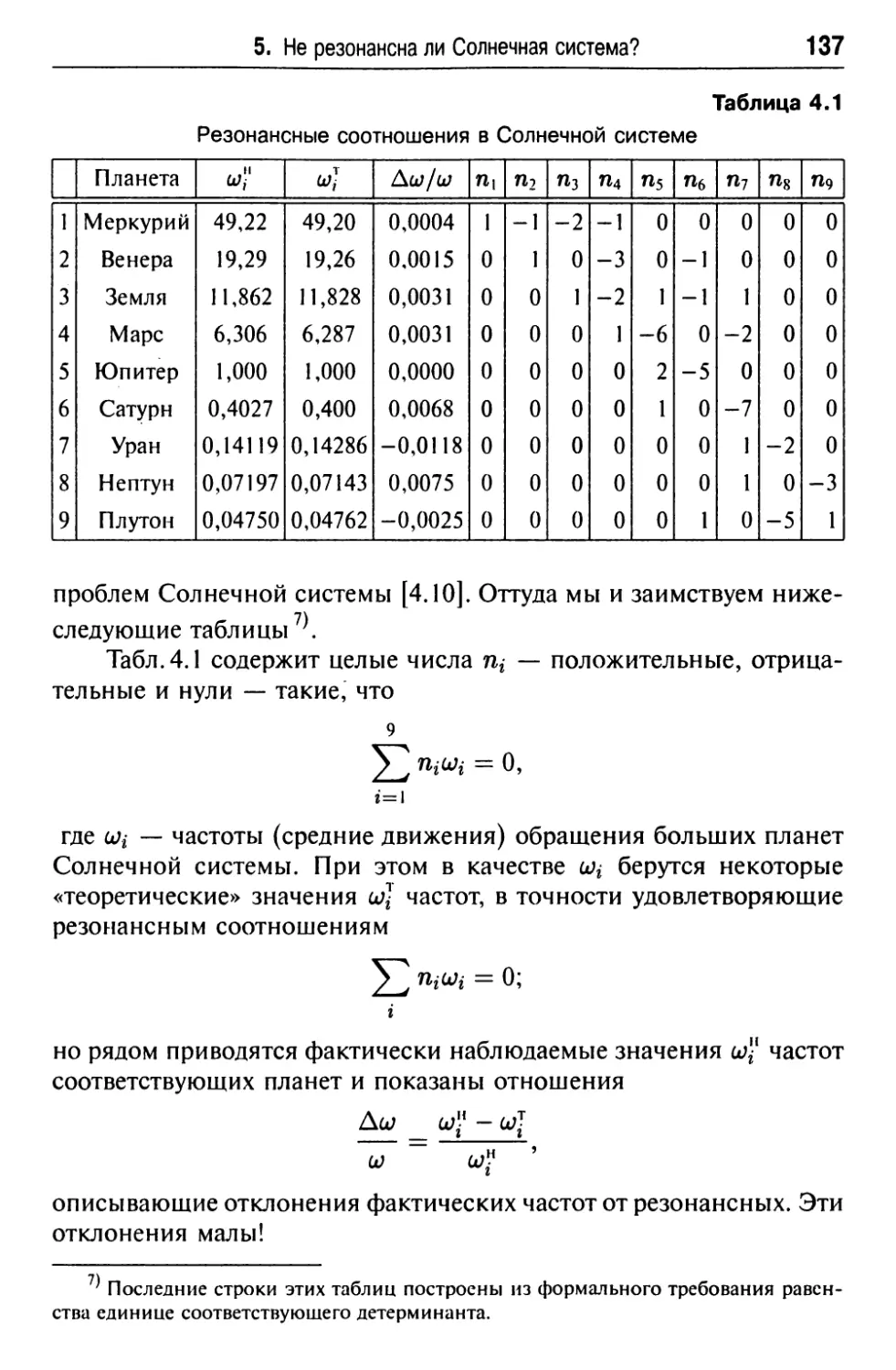
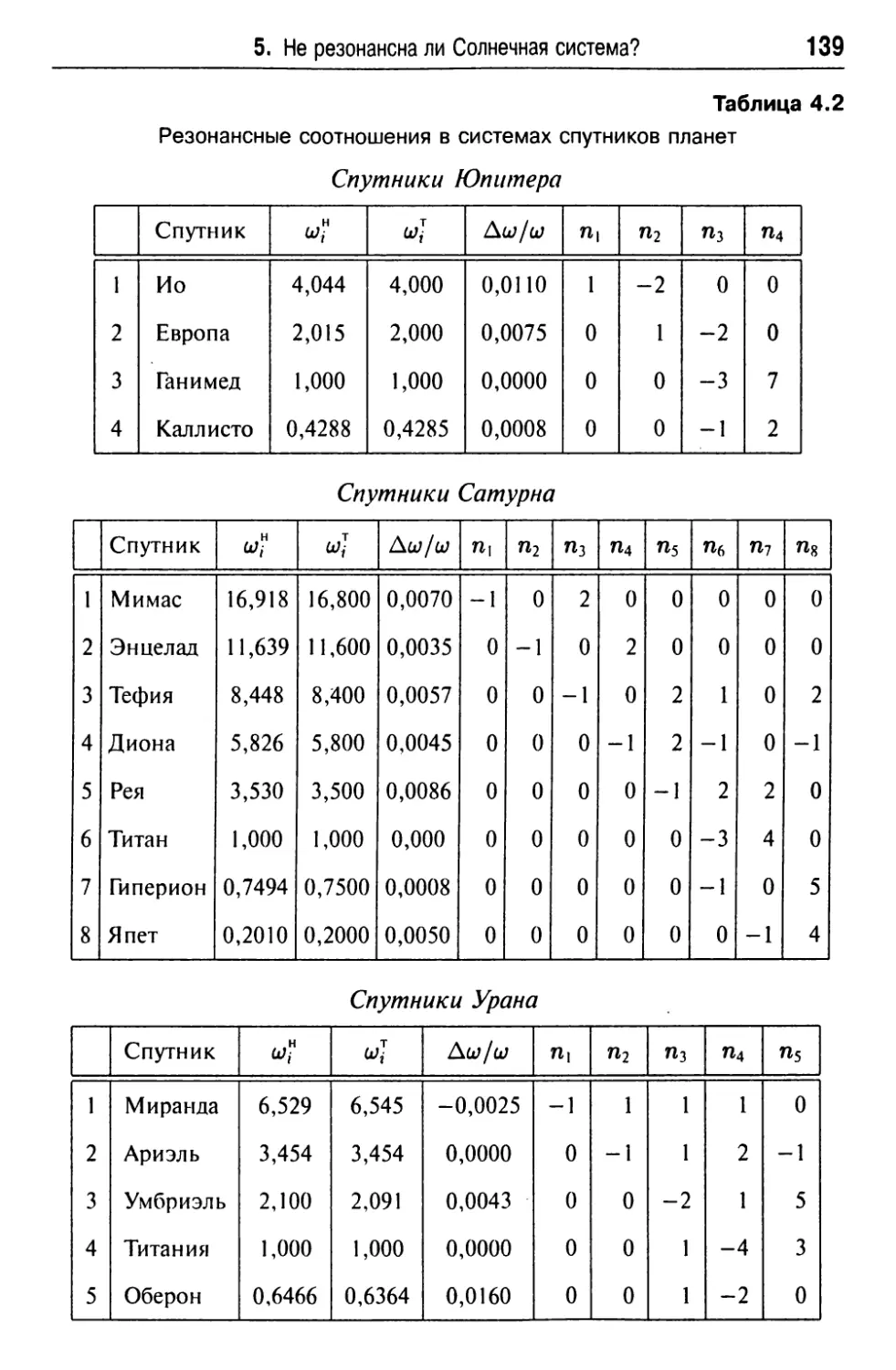
5. Не резонансна ли Солнечная система? 136
Очерк пятый. Ограниченная задача трех тел,
полет к Луне и эволюция галактик 147
1. Поверхности Хилла 147
2. Отступление о точках либрации 153
3. Траектории сближения и метод их исследования 155
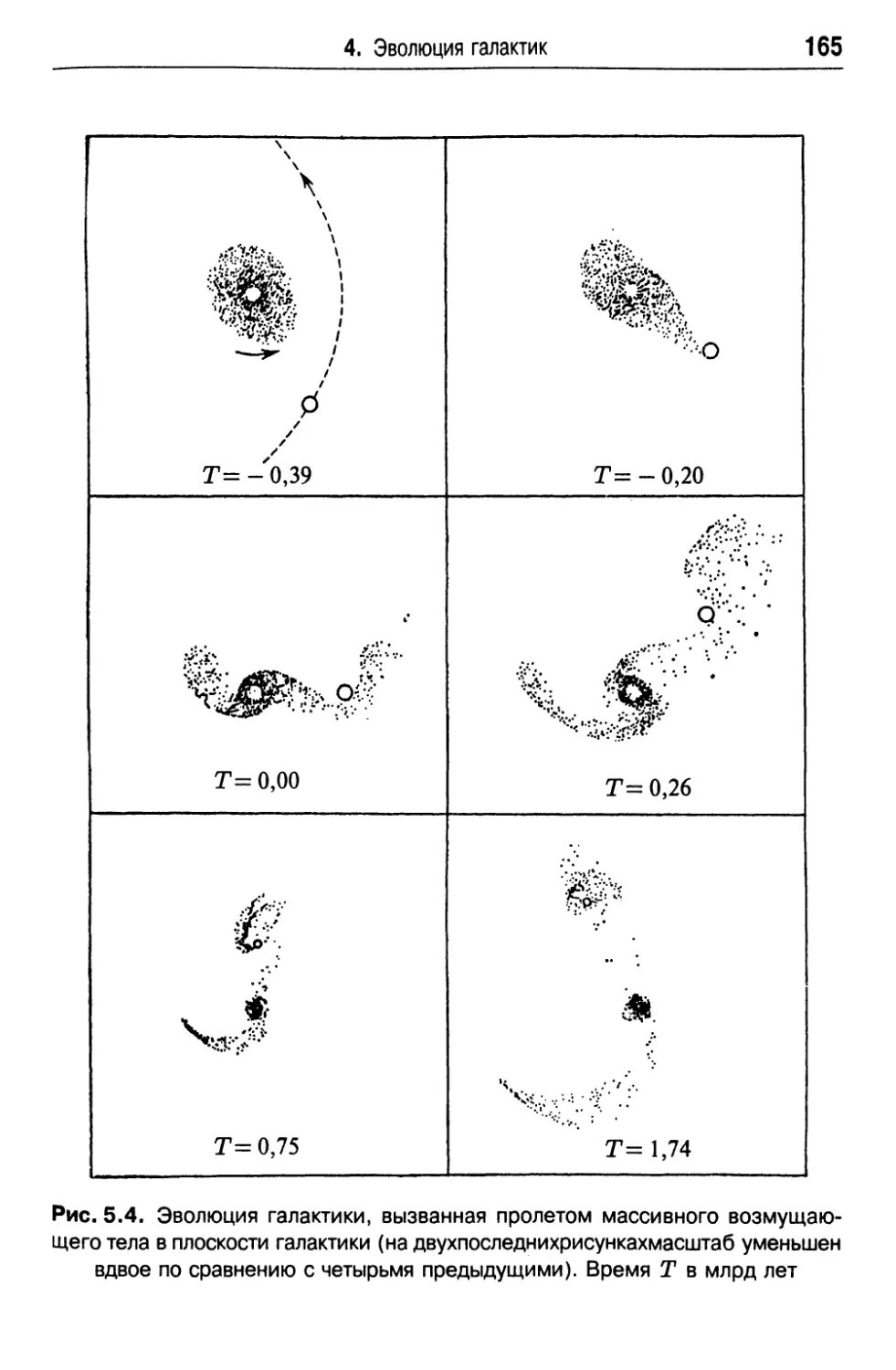
4. Эволюция галактик 159
Очерк шестой. Они вальсируют на орбитах 167
1. Гравитационный потенциал 167
2. О вращении Луны. Сведения из теории устойчивости . . 170
3. Устойчивость относительного равновесия
в гравитационном поле 177
4. Ринограденция на орбите 180
5. О пассивной стабилизации искусственных спутников .. 183
6. Нелинейные колебания 184
7. Быстрые вращения 191
8. Автор слегка припугнет читателя 196
9. Возмущенное движение в явном виде 199
Оглавление
5
10. «Пегас» 200
11. Луна, Меркурий, резонансы 206
12. Скиапарелли и другие 211
13. Резонансные вращения небесных тел и обобщенные
законы Кассини 214
14. Тенденция к синхронизации вращательного движения
в сложных гравитационных полях. Лунно-солнечная
прецессия и нутация земной оси 229
15. Модель приливных явлений и захват в резонансное
вращение 231
16. Магнитная и магнитно-гравитационная стабилизация . . 234
Очерк седьмой. В космос по спирали 246
1. Малая тяга 246
2. Параметры и парадоксы разгона 247
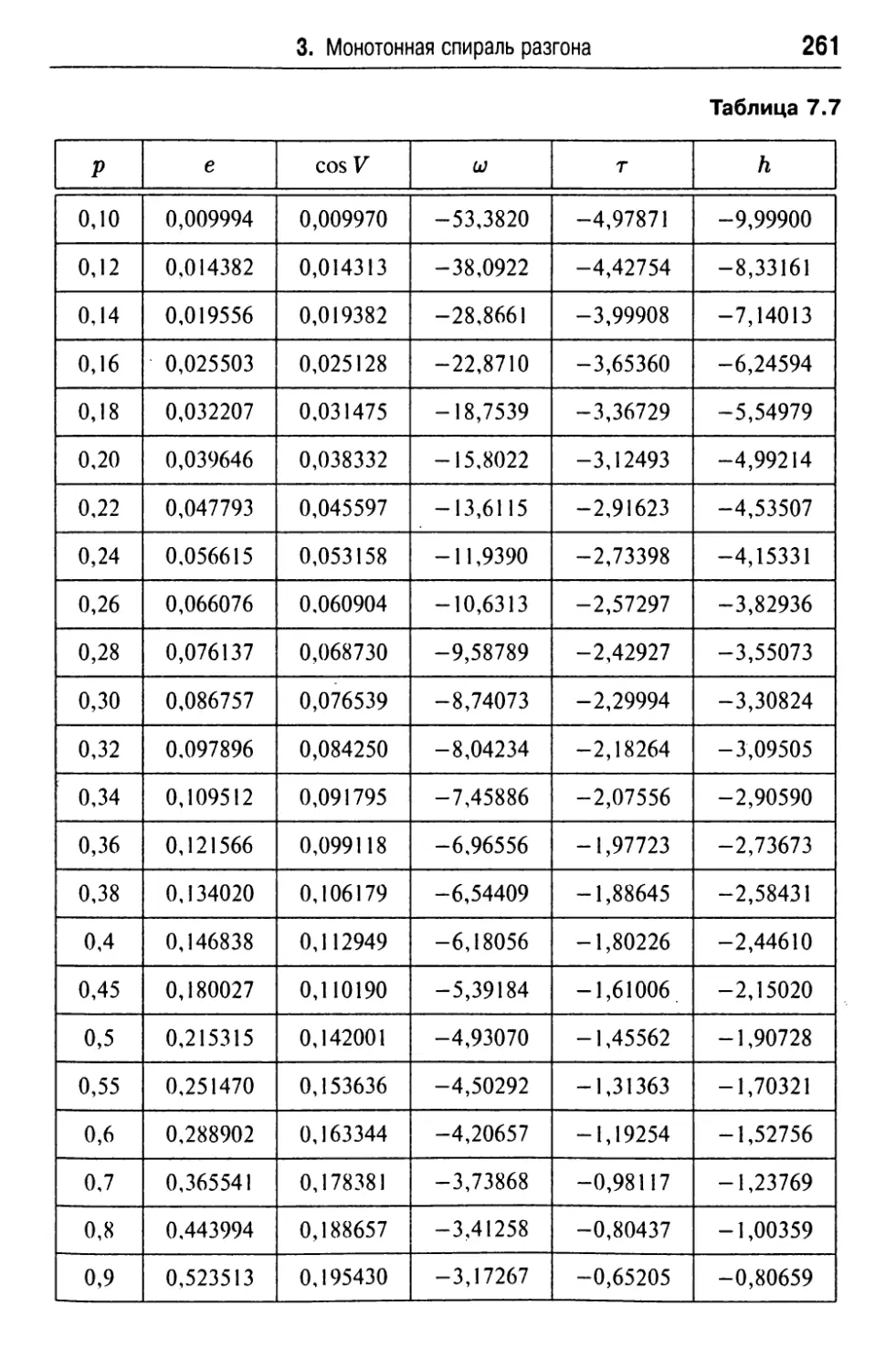
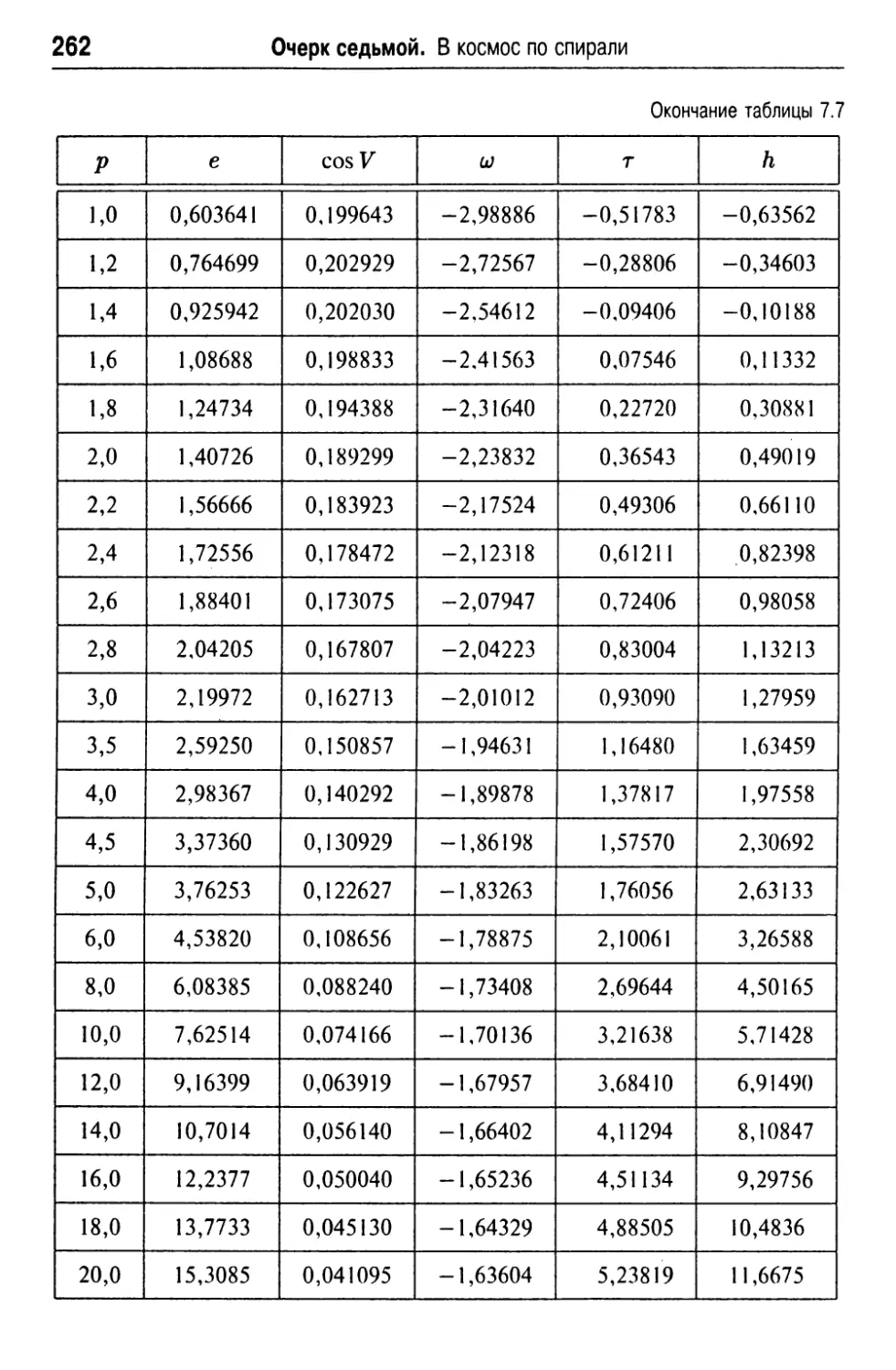
3. Монотонная спираль разгона 257
4. Произвольные траектории
с малыми эксцентриситетами 265
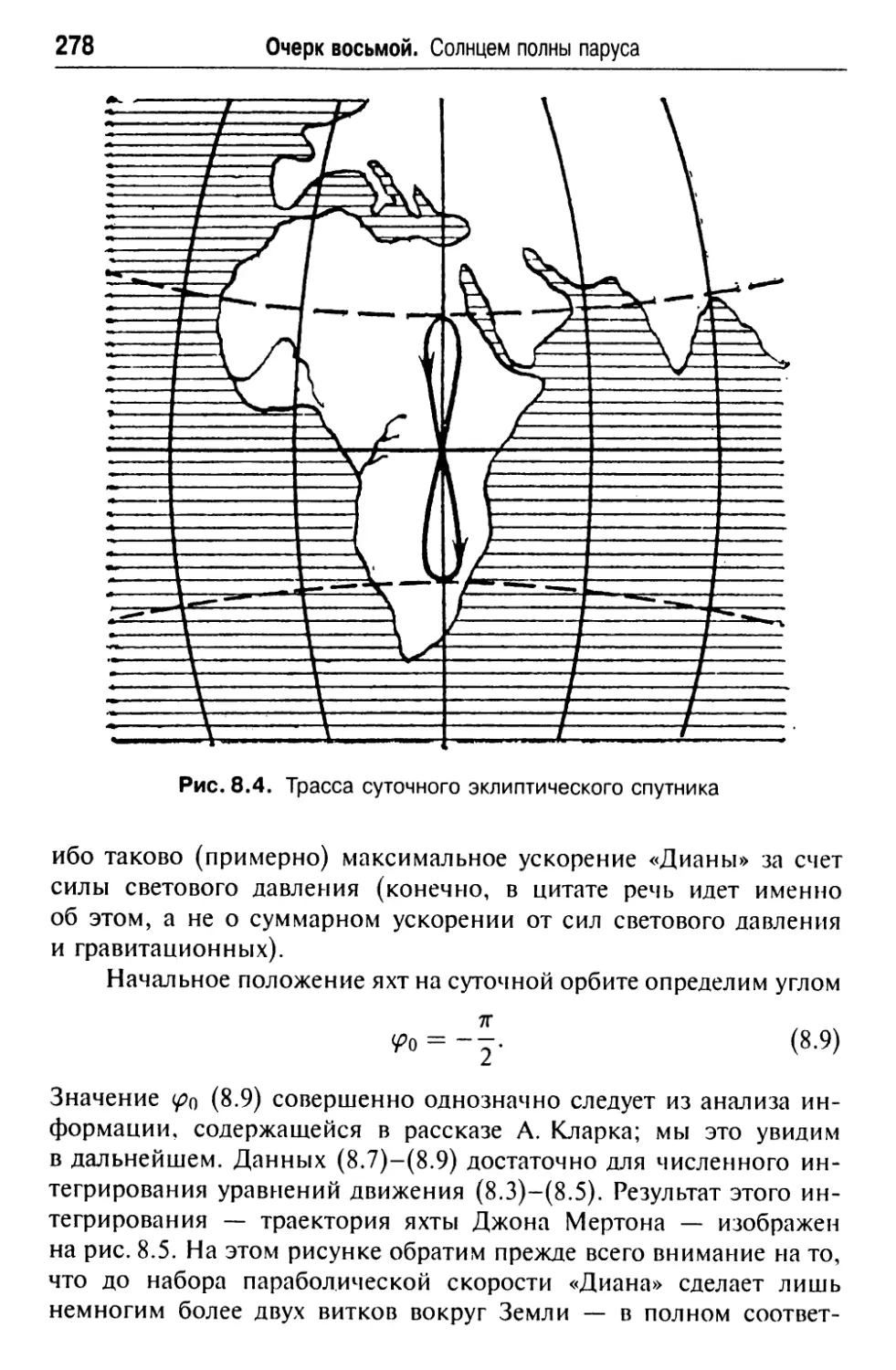
Очерк восьмой. Солнцем полны паруса 270
Очерк девятый. Г^авилет 288
1. Притяжение тела конечных размеров 288
2. Пульсирующий космический корабль 290
3. Отстал от спутника — плыви брассом! 295
4. Гравилет и читатели 299
5. Гравилет как резонансное явление 301
6. Гравилет и писатели 305
Очерк десятый. Межпланетные полеты —
малые тяги для больших целей 310
1. Вступление 310
2. Побольше полезного груза, поменьше топлива 311
3. Принцип максимума Понтрягина 314
4. Уравнение оптимального полета 316
5. Откажемся от ограничений 319
6. Метод транспортирующей траектории 320
7. Схема решения краевой задачи 322
8. Интегрирование 324
6
Оглавление
9. О задачах относительного движения 331
10. Результаты расчетов оптимальных межпланетных
траекторий 333
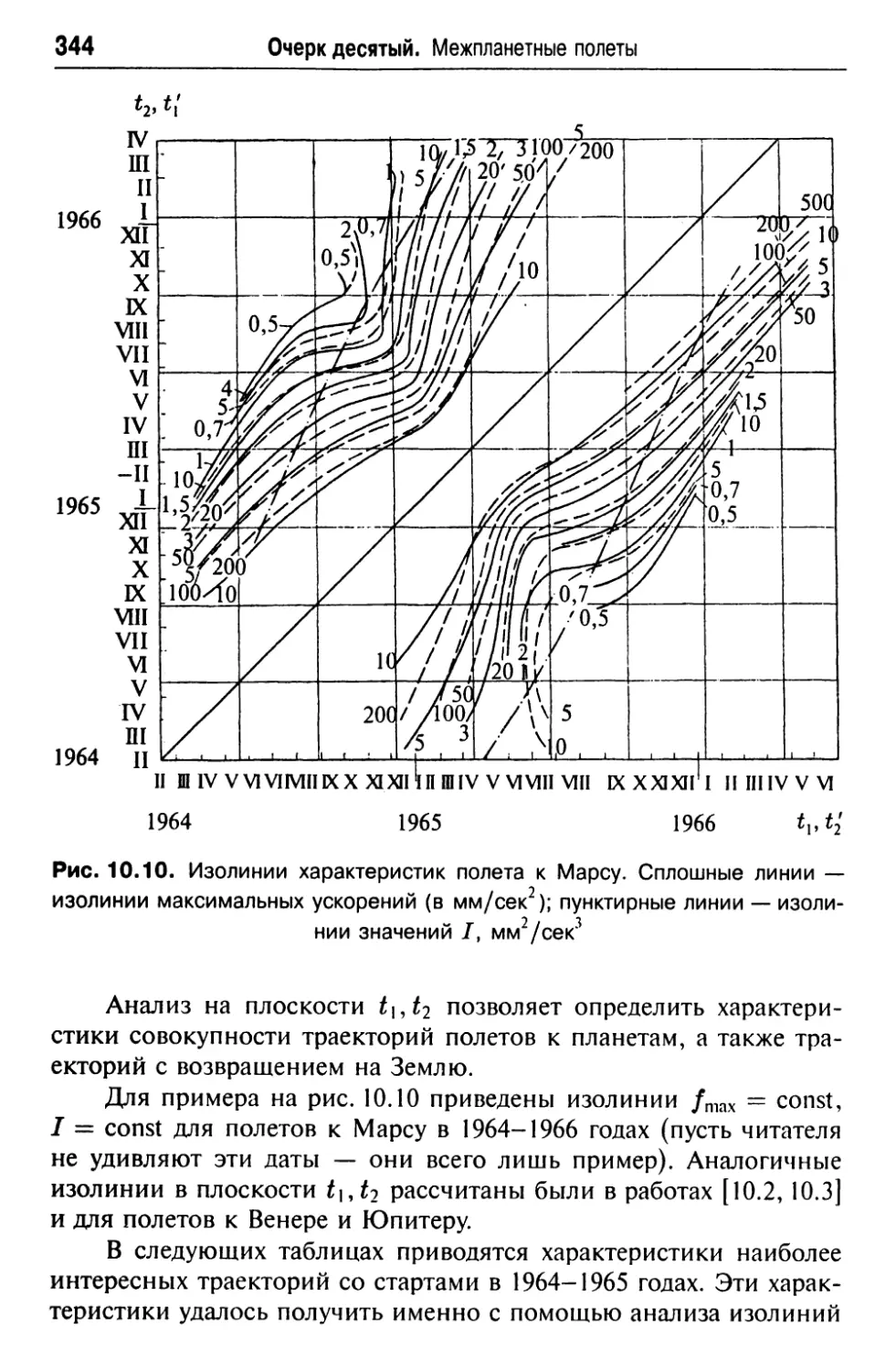
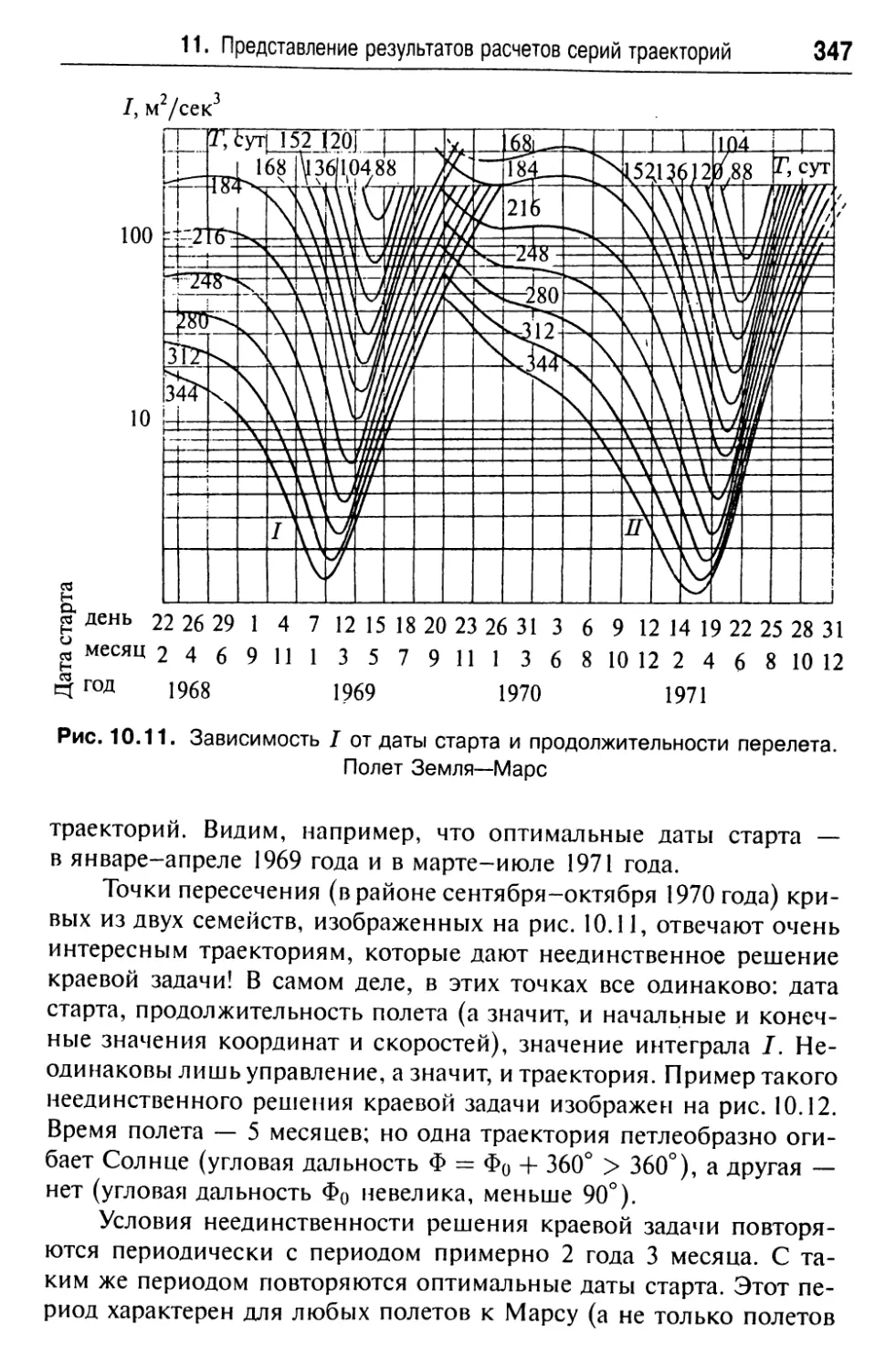
11. Представление результатов расчетов серий траекторий . . 343
12. Коррекция межпланетных траекторий 348
Очерк одиннадцатый. Относительное
движение орбитальных тел 351
1. На орбитах — два спутника 351
2. Уравнения относительного движения 356
3. Свободное движение космонавта
относительно спутника 357
4. Леонов и заглушка 360
5. Космический зонд 363
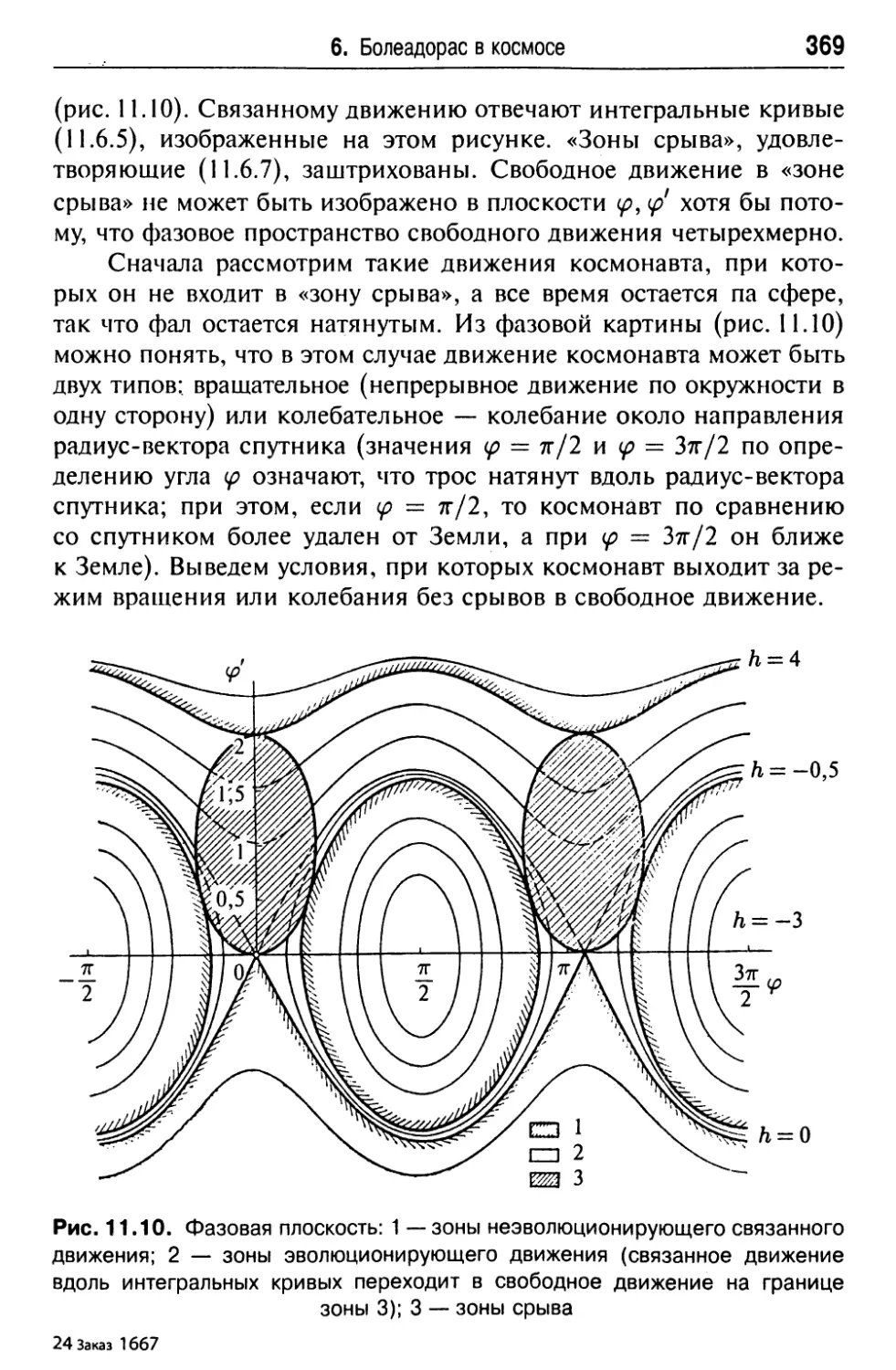
6. Болеадорас в космосе 365
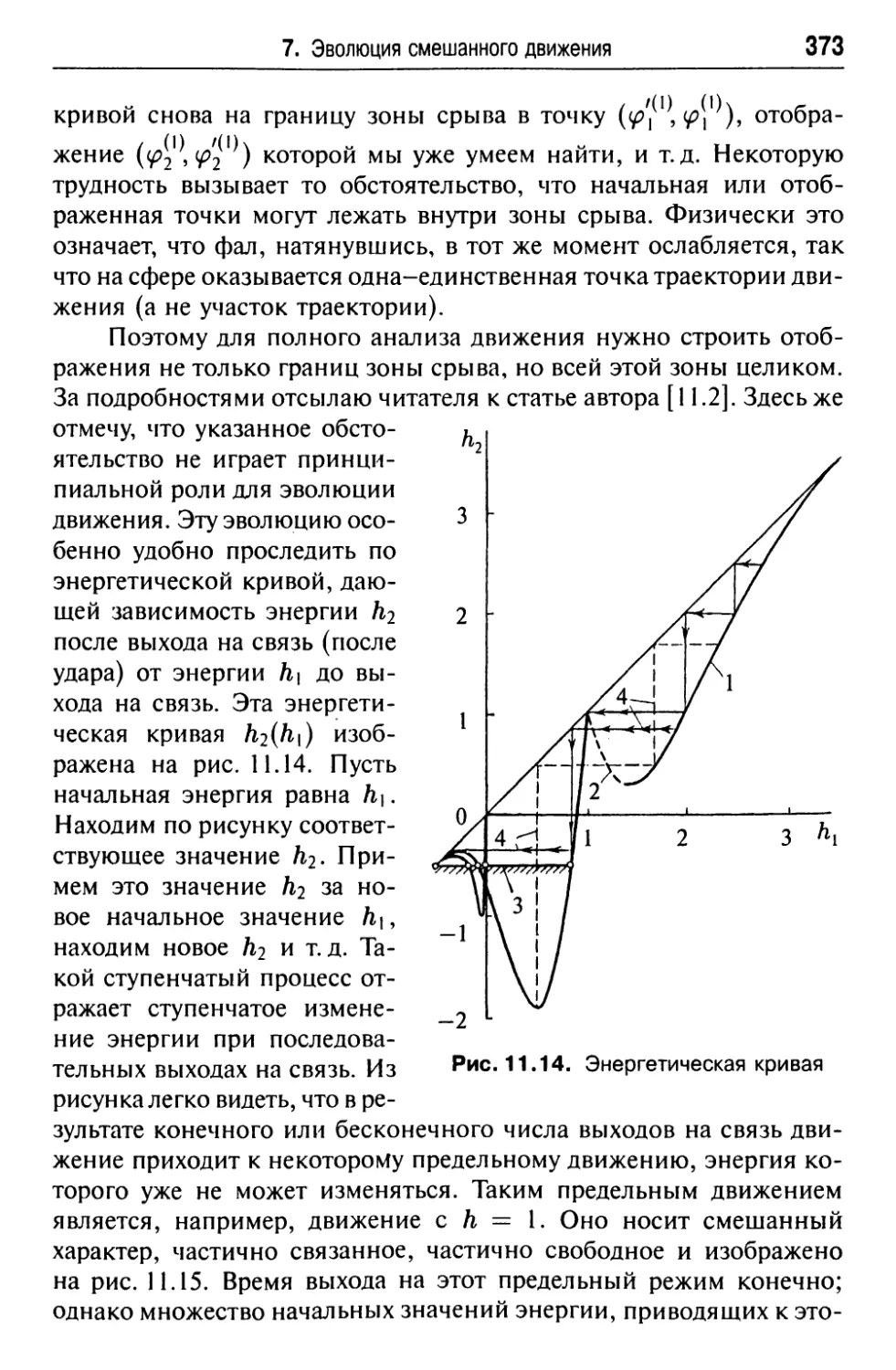
7. Эволюция смешанного движения 371
8. Пространственная связка тел 378,
9. Орбитальное облако частиц
и теорема Пуанкаре о возвращении 379
Очерк двенадцатый. Космическая вертушка 389
1. Спутники «Протон» 389
2. Как это было обнаружено 390
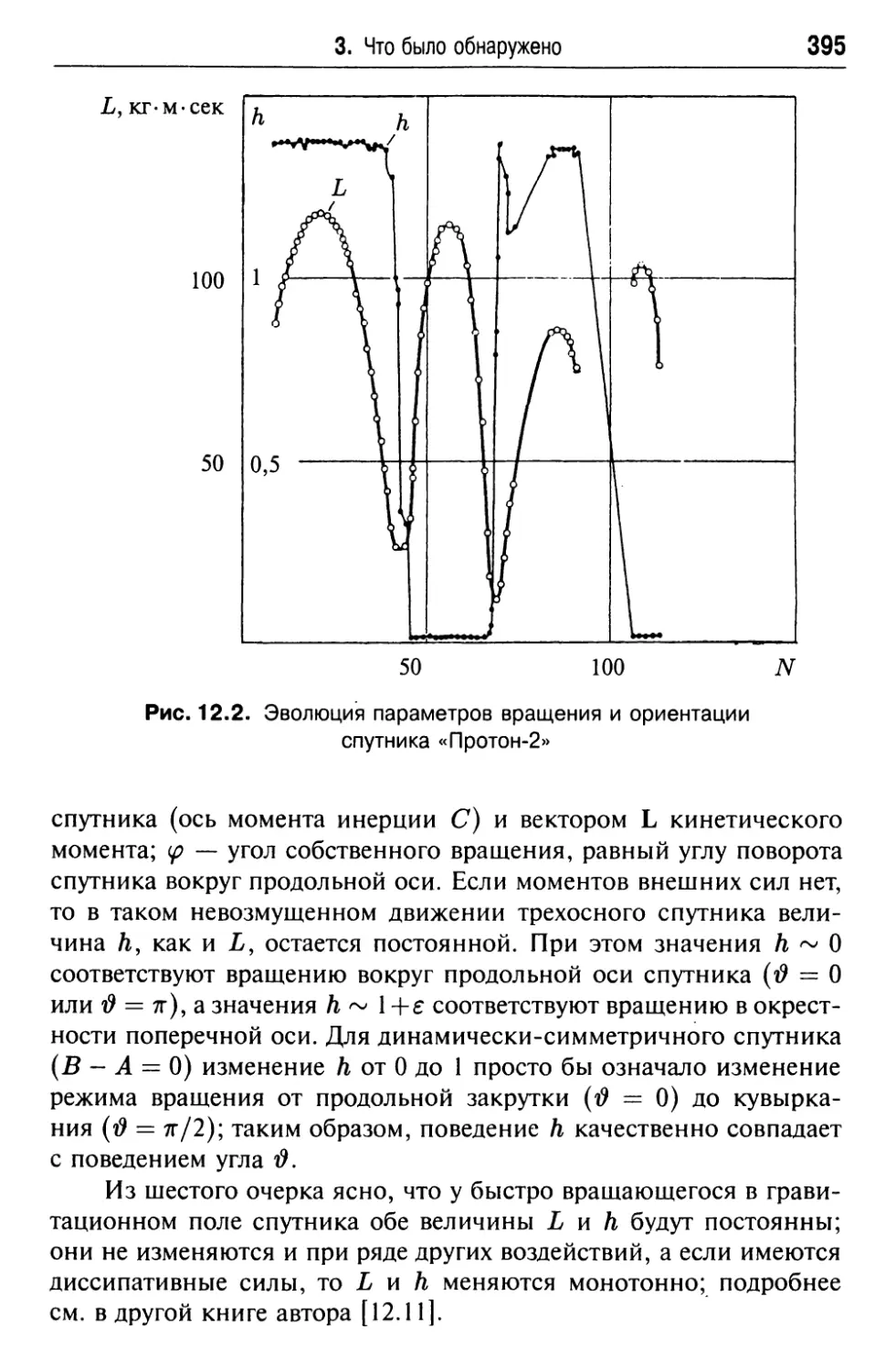
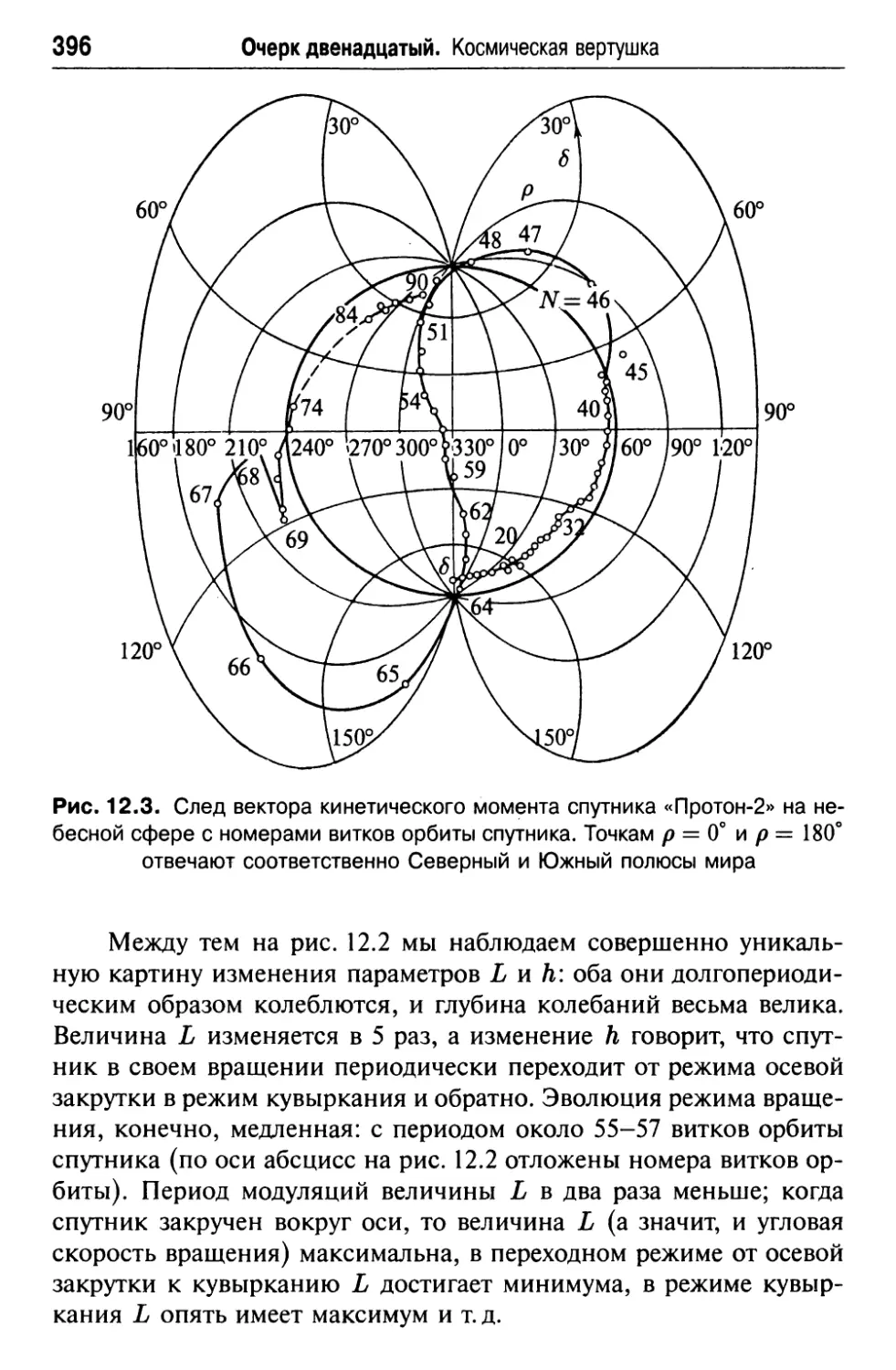
3. Что было обнаружено 394
4. Как это объяснить 397
Литература 406
Комментарии к рисункам И. В. Новожилова 418
Именной указатель 420
Предметный указатель 422
Начало нового стиля
в научной литературе
(из рецензии В. И. Арнольда и Я. Б. Зельдовича
на первое издание «Очерков» В. Б. Белецкого)*
«Однако мы заговорились, дорогой Фагот, а публика начинает
скучать. Покажи для начала что-нибудь простенькое», — именно
такой эпиграф взят из «Мастера и Маргариты» М. Булгакова для
первого очерка рецензируемой книги. Читатель не обманется —
она рассказывает о некоторых хорошо известных, и по этой причи¬
не простых, классических результатах. Благодаря стилю изложения,
весьма необычному для научной литературы, с самых первых стра¬
ниц (точнее, с блестящего посвящения Ферри Брену, частному лицу,
солдату Австро-Венгерской армии, позже бойцу Интернациональ¬
ного красногвардейского полка) читатель будет исподволь захва¬
чен неожиданной новизной результатов. И, перевернув последнюю
страницу, он, конечно, согласится с рецензентами в том, что на¬
личие таких книг и таких писателей есть отражение удивительного
возрождения небесной механики, переживаемого ею в ответ на тре¬
бования, которые предъявляет теория космических полетов.
Казалось бы, задача о движении тела в поле тяготения Земли
или в Солнечной системе настолько проста и настолько подроб¬
но изучена, что трудно искать в этой проблеме что-либо новое.
Однако здесь действует правило, не раз повторенное в других обла¬
стях науки: практические применения делают необходимым более
детальное, более точное знание, ставят задачу разработки опти¬
мальных способов действия. Поначалу возникают только ослож¬
нения в задаче, теряется ясность и красота упрощенных теорий,
но на следующем этапе появляются и новые точки зрения, и тео¬
рии, описывающие результаты более детальных расчетов, и новая
красота. Именно этот этап отражен в книге В. В. Белецкого.
* Природа. 1973. № 10. С. 115-117; Успехи физических наук. 1974. Т. 112. Вып. 3.
С. 541-542.
8
Начало нового стиля в научной литературе
Как справедливо отмечает автор книги, имена специалистов,
работающих в прикладных областях, успехи которых в создании
космической техники и освоении космического пространства сти¬
мулировали прогресс во многих точных науках, не часто появляются
на страницах научных журналов; эти люди, как правило, не пишут
книг и лишь изредка защищают диссертации. Но без их усилий
был бы немыслимым отраженный во многих диссертациях про¬
гресс механики, остались бы ненаписанными многие книги и среди
них данные «Очерки о движении космических тел». Посему из уст
автора, известного специалиста по механике космического полета,
обычные слова: «Эта книга — скромная попытка отдать дань моим
учителям, друзьям и коллегам» — звучат с особой значимостью.
...Для солидной научной монографии стиль книги В. В. Белец¬
кого необычен во многих отношениях. Без преувеличения можно
сказать, что она знаменует утверждение нового стиля в научной ли¬
тературе. Автор откровенно и подробно объясняет побудительные
причины каждого расчета, его трудности, всякий раз подчеркивает
психологическую сторону исследования. В книге нет и следа напы¬
щенной важности, стремления дать результаты, спрятав методы...
Книгу украшают и оживляют юмористические рисунки докто¬
ра физико-математических наук И. В. Новожилова и неожиданные,
но уместные эпиграфы, от Рождественского до Булгакова, в стихах
и в прозе. Не скучная лекция, а разговор с блестящим, знающим
и остроумным собеседником — таково общее впечатление от книги.
Даже человек, далекий от космических проблем, с удовольствием
пробежит книгу, пропуская, быть может, выкладки.
Знаменитый француз XIX века Камилл Фламмарион издал по¬
следовательно «Астрономию», «Астрономию для всех» и «Астроно¬
мию для дам». Не следует ли автору книги В. В. Белецкому, а вместе
с ним и издательству, последовать его примеру и издать новые ва¬
рианты «Очерков»?
Посвящение
Ферры Брен, рядовой австро-венгерской армии, окончательно вы¬
бился из сил. Была глубокая ночь, когда он вышел из лесу на проселочную
дорогу. По дороге шел обоз. Силуэты редких возничих едва угадыва¬
лись в темноте; хлюпала грязь под копытами лошадей. Ферри Брен,
не колеблясь, завалился в идущую без возничего подводу, накрылся бре¬
зентом и заснул.
Его разбудили на рассвете толчком кулака в бок. Вокруг стояли
возничие, солдаты российской армии. Незлобно поругиваясь, похоха¬
тывая и потыкивая кулаками, они отняли у Брена оружие и ра¬
нец. Словенский немец Ферри Брен, слегка испуганный, слез с подводы
на осеннюю, грязную землю — землю России. Не зная еще, э/яо —
навсегда. Что впереди — в составе интернационального крас¬
ногвардейского полка. И полвека жизни и труда на новой Родине.
И большая приемная семья, которую он вскормит и взрастит своим
редким ремеслом театрального портного. И далекая могила на тихом
Иркутском кладбище...
И что впереди — эта книга, посвященная его светлой памяти,
Федора Иосифовича Брена, л*оего дедя.
В. Б.
От автора
Бесконечно дышит вселенная,
Мчат ракеты, /ся/с сгустки солнца.
Это — ваши мечты и прозрения.
Ваши знания. Ваши бессонницы.
Р. Рождественский
В этой книге рассказано о некоторых интересных теорети¬
ческих исследованиях в механике космического полета, то есть
в теории движения космических аппаратов. Отражены и некото¬
рые новые задачи небесной механики.
Эта книга — не учебное пособие, и автор не стремится дать
стройный обзор или систематическое изложение механики косми¬
ческого полета. Более того, многие интересные и первостепенной
важности результаты останутся вне нашего поля зрения. Цель книги
иная. В процессе своего бурного развития механика космическо¬
го полета дала жизнь целому ряду задач, пленяющих своеобразной
красотой и новизной. Мне хочется дать представление о тех лю¬
бопытных и порой неожиданных достижениях, которые позволили
взглянуть по-новому на ряд старых задач механики; показать связи
классических задач с новыми результатами механики космическо¬
го полета; рассказать о некоторых новых постановках и решениях,
возникших в динамике космического полета.
Вместе с тем рассказ о задачах механики космического поле¬
та — это одновременно рассказ и о методах исследования. Меха¬
ника космического полета использует методы и результаты теоре¬
тической механики, небесной механики, технических наук, многих
разделов математики. Как модно сейчас говорить, механика кос¬
мического полета родилась на стыке этих наук.
Задачи, которые будут описаны в книге, различны по значимо¬
сти. Решения некоторых из них уже легли в основу всем известных
достижений (полеты спутников и лунных станций), решения других
найдут свое практическое применение в не столь далеком будущем
От автора
11
(космические полеты с двигателями малой тяги); возможно, неко¬
торые вопросы, затронутые в книге, вообще лишены сиюминутной
важности. Но все рассмотренные задачи объединяет одно нема¬
ловажное обстоятельство: они интересны. Во всяком случае, автор
постарается доказать это тем читателям, на которых он рассчитыва¬
ет прежде всего, — студентам, специализирующимся по механике
и начинающим задумываться над вопросом о более узкой специа¬
лизации. Автор хочет помочь им сделать выбор!
Если эта книга хотя бы в малой степени поможет почувство¬
вать, какой это удивительный и богатый событиями мир — ме¬
ханика космического полета, то автор будет считать свою задачу
выполненной.
В книге такого характера не всегда удается избежать длинных
выкладок, но при этом автор старается показать, где возможно,
красоту самого процесса исследования, приводящего к тому или
иному результату. Упор делается на анализ результатов, который
доводится до графиков и чертежей, а иногда — до чисел. Там, где
это возможно, исследование проводится максимально наглядно,
изящными геометрическими приемами. Типичный прием — анализ
первых интегралов уравнений движения.
В «отступлениях» приводятся некоторые сведения из механи¬
ки и математики, необходимые для чтения книги, но этот материал
не должен утяжелять задуманного легкого стиля очерков. Автор
не может отказать себе в удовольствии иногда, по ходу дела, высту¬
пить с несерьезным предложением или с неожиданной аналогией,
взяв на вооружение приемы научно-популярной литературы. Од¬
нако основной математический аппарат книги — системы обык¬
новенных дифференциальных уравнений, в силу чего изложение
нельзя считать общедоступным.
Основной материал в книге доступен пониманию студентов
третьего, четвертого (а возможно, и второго) курсов механико-ма¬
тематических, физико-математических и технических факультетов,
а отдельные пункты может разобрать дотошный школьник. Если же
некоторые места покажутся попервоначалу трудными и непонят¬
ными, то отчаиваться ни в коем случае не нужно. Их следует про¬
работать с карандашом в руках. Однако автор стремился по мере
сил к легкости рассказа и упорно избегал «академической» сухости
изложения. Там, где это не удалось, читатель будет снисходителен,
понимая, что порой традиции сильнее желаний.
Автор надеется, что книга доставит несколько минут удоволь¬
ствия и другим ее читателям: студентам старших курсов и аспи¬
12
От автора
рантам, преподавателям теоретической механики, инженерам и на¬
учным сотрудникам в области механики космического полета и
смежных специальностей. Содержание и стиль предлагаемых очер¬
ков уже опробованы автором на этих категориях слушателей при
чтении обзорных лекций в университетах страны.
В книге использованы публикации современных ученых — ме¬
хаников и математиков. Но значительное место занимают также
собственные исследования автора.
В целом в книге отражена лишь малая часть проблем и задач
современной механики космического полета и небесной механи¬
ки. В решении некоторых задач, описанных в книге, существен¬
ные успехи достигнуты лишь в самые последние годы. Но любой
наш успех недостаточно велик перед лицом природы. Нерешенных
(и даже еще не поставленных) задач всегда было и будет больше,
чем решенных. Исаак Ньютон говорил:
«Я не знаю, что скажет мир о том, что мне удалось сделать.
Сам себе я всегда казался маленьким мальчиком, который, играя
на берегу моря, находит то разноцветный камушек, то перелива¬
ющуюся раковину, в то время как необозримый океан истины без
конца и без края простирается передо мной».
Автору посчастливилось в течение многих лет учиться у вы¬
дающихся ученых-педагогов ]\ сидеть на одной студенческой ска¬
мье с ныне известными исследователями и сотрудничать по работе
с превосходными специалистами. Эта книга — скромная попытка
отдать дань благодарности моим учителям, друзьям и коллегам.
Автор выражает благодарность Дмитрию Евгеньевичу Охоцим-
скому за поддержку идеи этой книги; Владимиру Григорьевичу Де¬
мину — за тяжкий труд редактирования; Наталье Самуиловне Ко-
никовой и Евгении Алексеевне Степановой — за труды по оформ¬
лению рукописи; Николаю Алексеевичу Парусникову и Георгию
Рафаиловичу Сазыкину — за солидарность и энтузиазм.
Эта книга не могла бы появиться без неустанной заботы Нины
Александровны Белецкой. Автор признателен Тимуру Магомето¬
вичу Энееву, добрые советы которого использованы в работе над
рукописью.
Особую благодарность автор выражает доктору физико-мате¬
матических наук Игорю Васильевичу Новожилову — за прекрасные
рисунки к этой книге.
^ Назову прежде всего Владимира Васильевича Голубева, Николая Гурьевича
Четаева, Аркадия Александровича Космодемьянского.
От автора
13
Автор хотел бы отметить также роль специалистов-практиков,
чьи успехи в развитии космической техники и освоении космиче¬
ского пространства стимулировали прогресс многих точных наук.
Имена этих специалистов не примелькались на страницах журна¬
лов; они, как правило, не пишут книг и редко защищают диссер¬
тации. Но без их трудов немыслимо было бы развитие механики,
отраженное во многих диссертациях, и не были бы написаны мно¬
гие книги. В том числе и эта.
Первое издание «Очерков» встретило благосклонность чита¬
телей; ряд журналов («Земля и Вселенная», «Природа», «Успехи
физических наук», польский журнал «Urania») откликнулись доб¬
рожелательными рецензиями.
Автор благодарен рецензентам — В. И. Арнольду, Я. Б. Зельдо¬
вичу, К. Зиолковскому, А. Л. Куницыну — за анализ и замечания.
Эти замечания по мере возможности учтены в настоящем издании.
Исправлены обнаруженные неточности и опечатки. В целом кни¬
га сохраняет план и стиль изложения первого издания, материал
которого подвергнут лишь минимальной переработке. Однако чита¬
тель, знакомый с первым изданием, обнаружит добавления: о резо¬
нансных вращениях небесных тел и обобщенных законах Кассини;
об эволюции галактик и теореме Пуанкаре о возвращении; о новой
точке зрения на явление лунно-солнечной прецессии оси Земли
и о магнитной стабилизации спутников; о развитии идеи грави¬
лета в научной, научно-популярной и художественной литературе;
наконец, о «чуде замкнутых орбит» в ньютоновском центральном
поле тяготения.
И. В. Новожилов добавил новые иллюстрации к тексту.
В издательстве Birkhauser Verlag в 2001 году вышел англоязыч¬
ный вариант книги (переводчик Andrei Iacob), в который автор
книги и переводчик внесли некоторые дополнения и комментарии,
публикуемые в настоящем, третьем, издании на рурском языке.
В. Белецкий
Слово прощания
Игорь Васильевич Новожилов, доктор физико-математических
наук, профессор, выдающийся ученый, всесторонне талантливый че¬
ловек, поэт и писатель — автор уникальных художественных книг,
добродушно-ироничный художник, скончался 15 января 2006 годя. Нас
со студенческих времен — более полувека — связывала дружба.
Прощай, фуг.
5. Белецкий
Очерк первый
О невозмущенном и возмущенном
движении спутника с отступлением
об асимптотических методах
нелинейной механики
...Любезный Фагот, покажи нам
для начала что-нибудь простенькое.
М. Булгаков
«Мастер и Маргарита»
1. Нам повезло
Рассказ начнем с описания некоторых классических результа¬
тов, слишком хорошо известных, чтобы быть интригующе интерес¬
ными, но совершенно необходимых для дальнейшего изложения.
Фундамент, на котором построена небесная механика и меха¬
ника космического полета, — это ньютоновский закон тяготения:
две материальные точки, обладающие массами т и М, тяготеют
друг к другу с силой
где г — расстояние между точками, а / — универсальная посто¬
янная тяготения, одна и та же для всей Вселенной (/ = 6,67 • Ю-8
см3/г • сек2).
Если рассматривать движение одной из этих точек (га) отно¬
сительно другой (М), считая, что можно пренебречь всеми силами,
кроме силы (1.1.1), то дифференциальные уравнения движения по¬
1. Нам повезло
17
лучат вид [1.1] ^
* + ? = о, у+™= о, * + ^=0, (1.1.2)
где // = f(M + m), x,y,z — координаты точки т в поступа¬
тельно перемещающейся системе координат с началом в точке М;
г = л/х2 + у2 + z2. Эти уравнения легко интегрируются в эле¬
ментарных функциях. Это обстоятельство столь значительно, что
требует добавочного обсуждения. В самом деле, мы пренебрегли
«посторонними» силами, действующими на нашу точку т. Но эти
силы существуют, и с их учетом уравнения движения имеют вид
Х + = y + -pr = f»> z + ^J = f*’ О-1-3)
где Д, fy, Д — компоненты добавочных ускорений. Уравнения
(1.1.3), вообще говоря, уже не интегрируются. Почти все задачи ме¬
ханики, к сожалению, описываются неинтегрируемыми уравнени¬
ями. И лишь очень немногие задачи относятся к интегрируемым,
как, например, задача о движении двух материальных точек под
действием силы (1.1.1) взаимного тяготения.
Судьба распорядилась так, что человечество возникло и разви¬
лось на планете, входящей в систему одиночной звезды — Солнца,
причем в эту систему входят планеты, находящиеся друг от друга
достаточно далеко и имеющие массы, намного меньшие массы цен¬
трального светила — Солнца. При этих условиях в исследовании
движения каждой планеты можно с большой точностью обойтись
уравнениями (1.1.2), учитывающими только притяжение Солнцем
данной планеты. В самом деле, «точные» уравнения типа (1.1.3)
будут содержать добавки Д, Д, Д, при указанных условиях очень
малые:
у/fl + fy + fz < ^2-
Поэтому в уравнениях (1.1.3) можно пренебречь правыми частями,
то есть получить уравнения (1.1.2). А эти уравнения обладают двумя
важнейшими свойствами:
1. Они интегрируются.
2. В результате их интегрирования оказывается, что движение
весьма простое (периодическое).
^ Библиографический список см. в конце книги.
2 Заказ 1667
18 Очерк первый. О невозмущенном и возмущенном движении спутника
1. Нам повезло
19
Иначе говоря, в конструкции Солнечной системы кроется при¬
чина того, что, во-первых, движение каждой планеты сравнитель¬
но простое; во-вторых, это движение может быть описано инте¬
грируемыми дифференциальными уравнениями. Это в свою оче¬
редь способствовало тому, что человечеству за сравнительно корот¬
кий срок2) удалось, во-первых, постичь законы движения планет
(Кеплер) и, во-вторых, объяснить их (Ньютон).
Надо сказать, что большое количество звезд в Галактике пред¬
ставляет собой кратные звезды — двойные, тройные, а не оди¬
ночные, как наше Солнце. При условии существования в системе
кратных звезд планет с устойчивыми орбитами (а такие орбиты
могут быть) на какой-либо планете с такой орбитой могла возник¬
нуть раса разумных существ [1.2]. Разумные существа, появившиеся
на планете в системе двойной звезды, поставлены природой в худ¬
шие условия для познания ее законов, чем земное человечество.
Действительно, движение планеты в системе двойной звезды будет
описываться уравнениями (1.1.3) с непренебрежимыми правыми
частями (влияние обеих звезд на планету сравнимо по величине).
Поэтому траектория планеты будет очень сложной; для выявле¬
ния ее закономерностей понадобится сравнительно большое вре¬
мя, и уж совсем трудно будет понять, что эти закономерности обу¬
словлены простым законом (1.1.1) притяжения планеты к каждой
из звезд. Так что тамошним Кеплерам и Ньютонам приходится ту¬
го. Проверкой справедливости закона (1.1.1) является однозначное
сопоставление решения уравнений (1.1.3) с наблюдаемыми законо¬
мерностями; но уравнения (1.1.3) неинтегрируемы.
Путь познания у такой гипотетической разумной расы будет бо¬
лее тяжек и медлен (достаточно только представить себе эпициклы
Птолемея системы кратной звезды!). А так как темпы развития ци¬
вилизации зависят от суммы накопленных знаний, то можно, с не¬
которым риском для автора, формулировать следующее положение:
Развитие цивилизации в системах кратных звезд при прочих рав¬
ных условиях3^ происходит медленнее, чем в системах одиночных звезд.
Поэтому можно считать, что нам повезло.
Несколько тысячелетий существования цивилизации составляют менее одного
процента времени существования вида homo sapiens.
Автор не исключает возможности более быстрого пути познания, не использу¬
ющего такого, в сущности, несовершенного аппарата, как дифференциальные урав¬
нения, или даже существования качественно несопоставимых цивилизаций. В этом
смысл оговорки «при прочих равных условиях».
2*
20 Очерк первый. О невозмущенном и возмущенном движении спутника
2. Кеплеровское движение
21
2. Кеплеровское движение
Так как масса планеты по сравнению с массой Солнца (или мас¬
са искусственного спутника по сравнению с массой Земли) прене¬
брежимо мала, то можно считать, что центр масс рассматриваемой
системы совпадает с центром масс большего тела. В дальнейшем,
если не оговорено другое, будем понимать под центральным телом
Землю, а под телом с пренебрежимой массой — искусственный
спутник Земли.
Спутник обладает ускорением ньютоновской силы тяготения
направленным к центру Земли. В формуле (1.2.1) ег — единич¬
ный вектор по направлению от центра Земли к спутнику (который
считаем материальной точкой). Этому ускорению соответствует си¬
ловая функция ньютоновского центрального поля сил
так что компоненты ускорения по осям х, у, z неподвижной си¬
стемы координат, начало которой совпадает с центром Земли, будут
равны
а уравнения движения (1.1.2) интегрируемы. Орбиты, удовлетворя¬
ющие этим уравнениям, назовем кеплеровыми.
Нас интересовал сам факт интегрируемости уравнений (1.1.2),
а не процесс интегрирования. Этот процесс излагается во всех кур¬
сах теоретической и небесной механики (см., например, [1.1,1.3]),
и нет надобности излагать его еще раз. Поэтому опишем лишь
конечные результаты интегрирования. Оказывается, что спутник
движется по эллиптической, параболической или гиперболической
орбите, такой, что с центром Земли совпадает фокус эллипса, па¬
раболы или гиперболы.
Нас будет интересовать в основном случай эллиптических ор¬
бит. На рис. 1.1 изображена такая орбита. В полярных координа¬
тах г, v уравнение эллипса имеет вид
(1.2.1)
(1.2.2)
. _dU___yx t _dV___W . /п^
U~ дх~ г3’ h~ ду~ г3’ lz~ dz~ г3’ КХ-1'5)
Р
(1.2.4)
1 + е cos v ’
22 Очерк первый. О невозмущенном и возмущенном движении спутника
причем угол v отсчитывается от
направления гп из центра Земли
к ближайшей точке орбиты — пе¬
ригею. Наибольшее удаление гп
спутника от Земли достигается
в апогее — наиболее удаленной
от Земли точке орбиты — при
значении v = 180°. В уравнении
(1.2.4) величины р и е постоян¬
ны; р называется фокальным па¬
раметром орбиты, и его геомет¬
рический смысл ясен из рис. 1.1;
эта величина характеризует раз¬
мер орбиты; вторая величина —
эксцентриситет орбиты е — характеризует ее сжатие, вытянутость.
При е = 0 орбита круговая, а при е —> 1 орбита стремится к пара¬
болической. Величины р и е можно выразить через апогейное (гп)
и перигейное (tv) расстояния:
Рис. 1.1. Кеплерова
эллиптическая орбита
*-• а17г га гтт /. ^
р = , е = . (1.2.5)
Га +Г* Га+ 7V
Наибольший размер эллипса характеризуется его большой полуосью
а, при этом
а =
а между р, е, а существует связь
Га + Г,г
р = а( 1 - е2).
(1.2.6)
(1.2.7)
Угол v в формуле (1.2.4) называется истинной аномалией.
Зависимость v(t) от времени дает закон движения спутника
по орбите. В теории кеплеровых орбит наиболее трудное место —
отыскание явного выражения v через время t. Угловая скорость
dvjdt движения по орбите удовлетворяет так называемому инте¬
гралу (или закону) площадей:
о dv
Т dt = ^ ^'2'8^
Если сюда подставить выражение r{v) из (1.2.4) и вычислить
соответствующую квадратуру, то получим явное выражение вре¬
мени через у. t — t(u). Задача состоит в решении этого транс¬
цендентного уравнения относительно и. Для этого вводится новая
2. Кеплеровское движение
23
переменная Е, называемая эксцентрической аномалией (смысл ее
виден на том же рис. 1.1) и связанная с v соотношениями
cos Е - е sin Е /
cosu=- sinI/ = v 1 - е2, (1.2.9)
1 - е cos Е 1 - е cos Е
причем
г = а(\ - ecosE). (1.2.10)
Эксцентрическая аномалия Е связана со временем t уравнением
Кеплера:
Е - е sin Е = n(t - т*), (1.2.11)
где п = vVo3 — так называемое среднее движение', постоянная т*
обозначает момент прохождения через перигей орбиты. Из (1.2.11)
легко следует, что период обращения спутника по орбите
Г- 2^. 0.2.12)
Если решить уравнение Кеплера (1.2.11) относительно Е, то есть
определить E(t), то тем самым определится по (1.2.9) как явная
функция времени и и = v(t), а также г = r(t). О методах и резуль¬
татах решения уравнения Кеплера можно почитать в уже упомяну¬
той книге Г. Н.Дубошина [1.1].
Наконец, модуль скорости V движения по орбите удовлетво¬
ряет соотношению
V = yJ^V 1+e2 + 2ecost/, (1.2.13)
причем ее радиальная и трансверсальная проекции соответственно
равны
Vr = ^~~е sin v, VT = yJ^( 1 + ecosi/), (1.2.13')
так что в перигее (и = 0) скорость максимальна, а в апогее (^ = тг) —
минимальна. Так как движение происходит в консервативном поле
сил (1.2.2), то, естественно, имеет место закон сохранения энергии
(или интеграл энергии):
V2 и
== h = const, (1.2.14)
2 г
24 Очерк первый. О невозмущенном и возмущенном движении спутника
причем, подставляя сюда (1.2.13) и (1.2.4) и учитывая (1.2.7), можно
обнаружить, что
(1.2.15)
Отметим еще, что вместо интеграла площадей (1.2.8) можно напи¬
сать векторный интеграл площадей
где г — радиус-вектор, У
оказывается, вектор
г х V = с, (1.2.16)
- вектор скорости спутника. Тогда, как
1 = —г +V х с
г
(1.2.17)
является постоянным {вектор Лапласа), то есть 1 — интеграл урав¬
нений движения. Этот вектор направлен вдоль большой полуоси
по направлению в перигей орбиты, а его модуль
\\ — ре.
(1.2.18)
Таковы основные закономерности кеплеровского движения по эл¬
липтической орбите. Однако мы рассматривали движение в плос¬
кости орбиты, а чтобы полностью определить движение в про¬
странстве, надо еще знать пространственное положение орбиты.
Это положение фиксируют следующим образом (рис. 1.2). Спроек¬
тируем плоскость орбиты на небесную сферу и рассмотрим систему
координат XYZ такую, что ось Z направлена на Северный полюс
мира (это вполне определенная точка на небесной сфере вблизи По¬
лярной звезды), ось X — на точ¬
ку весеннего равноденствия (тоже
вполне определенная точка: в на¬
шу эпоху находится в созвездии
Рыб); начало координат совпада¬
ет с центром Земли, а плоскость
XY — с плоскостью земного эк¬
ватора. Линию пересечения плос¬
костей орбиты и экватора назо¬
вем линией узлов, а ее следы на не¬
бесной сфере — узлами орбиты.
При этом назовем восходящим уз¬
лом орбиты ту точку на небесной
сфере, в которой спутник пере¬
секает экватор в своем движении
Рис. 1.2. Положение орбиты
в пространстве
2. Кеплеровское движение
25
из южного полушария в северное; противоположный узел называ¬
ется нисходящим.
Положение плоскости орбиты полностью определяется двумя
постоянными углами: углом между направлениями на точку весен¬
него равноденствия и на восходящий узел — этот угол обозначим Q,
и назовем долготой восходящего узла\ углом между экваториальной
плоскостью и плоскостью орбиты — этот угол обозначим г и назо¬
вем наклонением. Далее, перигей 7г орбиты находится на постоян¬
ном угловом расстоянии ш от линии узлов, угол ш отсчитывается
от этой линии в плоскости орбиты до направления на перигей ор¬
биты. Назовем угол и) аргументом перигея. Часто вместо истинной
аномалии v вводят в рассмотрение другой переменный полярный
угол и = ш + и, называемый аргументом широты. Это угол, отсчи¬
тываемый в плоскости орбиты от линии узлов до текущего радиус-
вектора орбиты.
Подведем итоги. Орбита спутника характеризуется двумя не¬
зависимыми постоянными параметрами: р (или а) и е\ положение
орбиты в пространстве определяется тремя независимыми углами:
П, о;, г; положение спутника на орбите в каждый момент време¬
ни определяется параметром г*. Итак, имеем шесть независимых
постоянных параметров, полностью определяющих движение спут¬
ника в пространстве (его координаты и скорость в каждый момент
времени), например:
а, е, П, и), *, т*. (1.2.19)
Параметры (1.2.19) называются элементами орбиты спутника 4\
Обратим теперь внимание на следующее обстоятельство. Ис¬
ходная система (1.1.2) дифференциальных уравнений движения яв¬
ляется системой шестого порядка (три уравнения второго порядка);
следовательно, решение системы (1.1.2) должно содержать шесть
произвольных постоянных интегрирования. Как только значения
этих постоянных будут определены через начальные (или краевые)
условия, будет полностью определено данное конкретное движение.
Так вот, элементы (1.2.19) как раз и являются такими произвольны¬
ми постоянными интегрирования (их шесть, и они независимы).
Начальные данные придают элементам конкретные числовые зна¬
чения и определяют конкретное движение.
Элементы орбиты могут быть определены по-разному. Например, положение
плоскости орбиты можно отсчитывать не от плоскости экватора, а от плоскости
эклиптики; вместо е и и рассмотреть две независимые их комбинации и т. п.
26 Очерк первый. О невозмущенном и возмущенном движении спутника
3. Возмущенное движение. Оскулирующие элементы
Кеплеровское движение, рассмотренное в предыдущем пункте
(и удовлетворяющее уравнениям (1.1.2)), называют еще невозмущен¬
ным движением спутника. На самом же деле истинное движение
спутника удовлетворяет некоторым уравнениям типа (1.1.3), так
как на спутник, кроме ньютоновской силы притяжения, вызываю¬
щей ускорение (1.2.3), действует еще большое количество разнооб¬
разных сил: сопротивление атмосферы, отличие силы притяжения
Земли от ньютоновской силы, притяжения Луны и Солнца и т.д.
Все перечисленные силы (и многие другие), как правило, весьма
малы по сравнению с силой ньютоновского тяготения, то есть удо¬
влетворяют условию
Поэтому учет этих сил дает лишь некоторые малые добавки в урав¬
нениях движения, а именно компоненты fx, fy, fz в правых частях
уравнений (1.1.3).
Движение спутника, происходящее под одновременным дей¬
ствием силы ньютоновского притяжения к центру Земли и доба¬
вочных сил, называется возмущенным движением', уравнениями воз¬
мущенного движения являются уравнения (1.1.3). Конкретный вид
компонент fx, fy, fz возмущающего ускорения зависит от характе¬
ра учитываемых возмущающих сил (или сопротивление атмосферы,
или гравитационные возмущения, или световое давление и т.д., а то
и все вместе в зависимости от характера задачи).
Уравнения (1.1.3) неинтегрируемы, и поэтому остро встает во¬
прос о способе исследования возмущенного движения. Здесь по¬
могает следующее рассуждение. Так как возмущающие силы малы
по сравнению с основной силой ньютоновского тяготения, то сле¬
дует ожидать, что возмущенное движение в каком-то смысле мало
отличается от невозмущенного кеплеровского движения. Значит,
решение уравнений (1.1.3) надо искать в виде, близком к реше¬
нию уравнений (1.1.2). А именно, будем считать, что возмущенное
движение происходит по какой-то «эллиптической» орбите с эле¬
ментами (1.2.19), но они уже не являются постоянными, а меняются
со временем:
Задача сводится тогда к отысканию явных зависимостей (1.3.1)
от времени (в силу уравнений (1.1.3) возмущенного движения).
a(t), e(t), Q(t), w(t), i(t), T*{t).
(1.3.1)
4. (Эмулирующая орбита экваториального спутника
27
«Эллипс» с переменными элементами (1.3.1) называется оску-
лирующим эллипсом, а сами переменные элементы — оскулирующи-
ми элементами. Это назва-ние отражает некую тесную (как говорил
Н.Д. Моисеев5^ «интимную») близость возмущенной и невозму¬
щенной орбит6^. Если неожиданно зафиксировать в некоторый мо¬
мент t* значения параметров (1.3.1), то движение пойдет по кепле-
ровскому эллипсу и будет в некоторой окрестности времени t*
весьма близким к движению (в этой же временной окрестности)
с нефиксированными параметрами (1.3.1).
Чтобы составить дифференциальные уравнения для оскулирую-
щих элементов (1.3.1), надо перейти от переменных х,у, z,x,y, z
к переменным (1.3.1), подставить их в уравнения (1.1.3) и разрешить
их относительно производных
dp de dQ, du di dr*
~dV dt9 ~dt ’ ~dt ’ ~dV ~dt
оскулирующих элементов. Нетрудно понять, что метод оскулиру-
ющих элементов является методом вариаций произвольных посто¬
янных невозмущенного движения в силу уравнений возмущенного
движения. Отметим основное правило оскулирующего движения:
координаты x,y,z и компоненты скорости х, г/, z выражаются че¬
рез элементы одинаковым образом как в возмущенном, так и в не¬
возмущенном движениях; только, повторим, в невозмущенном дви¬
жении элементы постоянны, а в возмущенном — функции времени.
4. Оскулирующая орбита экваториального спутника
Рассмотрим сравнительно простой пример, на котором можно
проследить ряд эффектов возмущенного движения.
Пусть спутник движется в экваториальной плоскости Земли
[1.16, 1.17]. Земля несколько сжата к своему экватору, поэтому си¬
ла, действующая на спутник, будет несколько отличаться от нью¬
тоновской. Однако при движении спутника в плоскости экватора
Профессор Николай Дмитриевич Моисеев (1902-1955) — основатель москов¬
ской школы небесной механики, многочисленные труды и педагогическая деятель¬
ность которого оказали существенное влияние на современное поколение небесных
механиков.
Оскулирующие элементы придуманы великим французом Лагранжем. Oskula-
tio (лат.) — поцелуй (см.: Латинско-русский словарь. М.: Гос. изд-во иностр. и нац.
словарей, 1952. С. 480).
28 Очерк первый. О невозмущенном и возмущенном движении спутника
эта сила остается центральной, постоянно направленной к центру
Земли. Выражение для центрального ускорения /, сообщаемого
спутнику этой силой, имеет вид
Здесь первый член — обычное ньютоновское центральное ускоре¬
ние, а второй член — возмущающее ускорение, вызванное сжатием
Земли. При этом г — расстояние от спутника до центра Земли,
Ro — экваториальный радиус Земли, е — постоянная (безразмерная
величина, зависящая от степени сплюснутости Земли; для Земли
можно принять е = 0,0016. Ускорению /(г) соответствует силовая
функция
Так как движение обладает силовой функцией J7(r), не за¬
висящей явно от времени, то, как известно из механики, полная
энергия движения будет сохраняться:
Атак как действующая сила — центральная, то уравнения движения
должны допускать еще один первый интеграл — интеграл площадей
(имеющий место при любых центральных силах)
Здесь ip — полярный угол в полярной системе координат г, ip.
Попробуем теперь получить уравнения в оскулирующих эле¬
ментах для нашей задачи. В невозмущенном движении интеграл
площадей имеет вид (1.2.8). В возмущенном и невозмущенном
движении левая часть интеграла площадей может быть записана
как rVn, где Vn — трансверсальная проекция скорости спутника.
Но по основному правилу оскулирующего движения координаты
(г) и скорости (Vn) выражаются через элементы одинаково как
в возмущенном, так и в невозмущенном движении. Значит, по¬
стоянная с в интеграле площадей (1.4.3) нашего возмущенного
движения будет записываться так же, как и правая часть (1.2.8).
Следовательно, с = у/рр, откуда р = const или, если угодно,
4. Оскулирующая орбита экваториального спутника
29
Это и есть первое из уравнений в оскулирующих элементах для на¬
шего движения. Фокальный параметр оскулируюшей орбиты оста¬
ется постоянным.
Далее, учитывая выражения (1.2.14), (1.2.15) и (1.2.7), можем
записать интеграл энергии (1.4.2) возмущенного движения в виде
(,.4.20
Дифференцируя по времени, получим
de pRl
е— = -е—т-г.
dt г4
Но, опять вспоминая основное правило оскулирующего движе¬
ния, выражение для радиальной скорости г = Vr следует записать
в том же виде (1.2.13'), что и в невозмущенном движении. Тогда
последнее уравнение принимает окончательный вид:
^ = _£vMpi sini/ (14 5)
— - _ VEER«
dt £ г4
Разумеется, здесь г выражается формулой (1.2.4). Обратимся снова
к интегралу площадей (1.4.3). Заметим, что (р = v + о;, откуда
интеграл площадей может быть записан в форме
dw = ^p_du_
dt г2 dt' v ' ’ '
Следовательно, чтобы написать дифференциальное уравнение для
третьего оскулирующего элемента а;, нужно получить выражение
dvjdt в возмущенном движении.
Возьмем из (1.2.13/) выражение для радиальной скорости и за¬
пишем его в виде
Гр
es\nu = \ —Vr.
V И
Дифференцируем по времени это выражение, учитывая, что в оску-
лирующем движении р = const. Получим
de dv Гр .
— sin v + — ecosv = х — Vr.
dt dt \ p
Но из кинематики известно, что Vr = г = (fr + гф2), где /г —
полное радиальное ускорение. Оно задается формулой (1.4.1). С по¬
мощью интеграла площадей (1.4.3) выразим ф через г и подставим
30 Очерк первый. О невозмущенном и возмущенном движении спутника
в Vr. Получим
т> Fp_\/pU(p .\_eVppRо
ГУ fl г2 \г ) • г4 •
Учитывая, что р/г - 1 = ecosu, и используя явное выражение
(1.4.5) для de/dt, окончательно находим
= (|47)
<й г2 ег"
Теперь немедленно из (1.4.5) следует
du е s/JIpRl
Л=е-^-СХ''' ('А8)
и система дифференциальных уравнений (1.4.4), (1.4.5), (1.4.7),
(1.4.8) замкнута относительно р, е, Строго говоря, надо бы¬
ло бы добавить уравнение для г*, но этого можно не делать, так
как выписанных уравнений достаточно для анализа движения.
Прежде всего, обратим внимание, что при отсутствии сжатия
Земли (г = 0) немедленно получаем, кроме р = Ро, еще и е = ео,
и) = щ (как и должно быть в кеплеровском движении). Однако при
€ Ф 0 эксцентриситет е и долгота перигея и) будут функциями вре¬
мени — и именно это определяет отличие возмущенного движения
от невозмущенного.
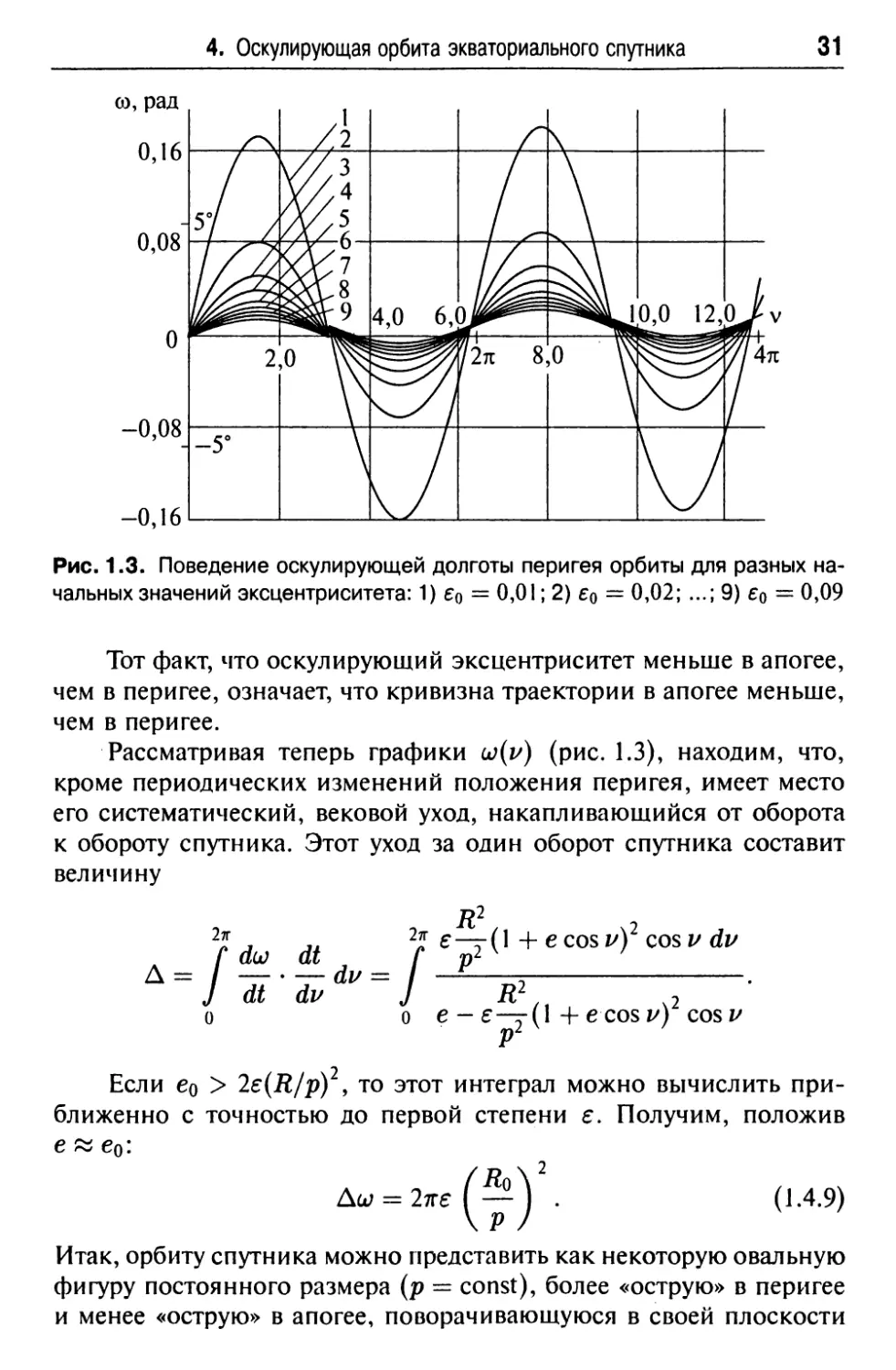
На рис. 1.3 представлены зависимости w(v), а на рис. 1.4 — за¬
висимости e(t) в оскулирующем движении для разных начальных
данных. Эти зависимости получены численным интегрированием
уравнений (1.4.4), (1.4.5), (1.4.7), (1.4.8). Видим, что эксцентриситет
орбиты периодически меняется со временем с малой амплитудой
и не имеет систематических (как принято говорить, вековых) изме¬
нений, которые с течением времени могли бы привести к сущест¬
венному отличию эксцентриситета от первоначального. Амплитуду
колебаний эксцентриситета можно оценить, записав интеграл энер¬
гии (1.4.2) в виде
г(е2 - el) = [(1 + ecost/)3 - (1 +е0)3].
2
Отсюда следует, что в оскулирующем перигее (и = 0) е = е1ШХ = во.
В оскулирующем апогее v — тг; приближенно решая кубическое от¬
носительное е уравнение, получим с точностью до первой степени е
о /М2 л /До\2
е = ет|П ~ во — 2ег ( — } , если только en > 2е I — ) .
V Р ) V Р )
4. Оскулирующая орбита экваториального спутника
31
Рис. 1.3. Поведение оскулирующей долготы перигея орбиты для разных на¬
чальных значений эксцентриситета: 1) е<> = 0,01; 2) ео = 0,02; ...; 9) ео — 0,09
Тот факт, что оскулирующий эксцентриситет меньше в апогее,
чем в перигее, означает, что кривизна траектории в апогее меньше,
чем в перигее.
Рассматривая теперь графики ш{и) (рис. 1.3), находим, что,
кроме периодических изменений положения перигея, имеет место
его систематический, вековой уход, накапливающийся от оборота
к обороту спутника. Этот уход за один оборот спутника составит
величину
R?
2п 2* £—j(\ + ecosv)2 cosv dv
= i*,= f —В.
J dt dv J
R2
e - r(l + e cos i/) cos и
VL
Если во > 2e(R/p)2, то этот интеграл можно вычислить при¬
ближенно с точностью до первой степени £. Получим, положив
е & е0:
Au = 2ne\^-yj . (J.4.9)
Итак, орбиту спутника можно представить как некоторую овальную
фигуру постоянного размера (р = const), более «острую» в перигее
и менее «острую» в апогее, поворачивающуюся в своей плоскости
32 Очерк первый. О невозмущенном и возмущенном движении спутника
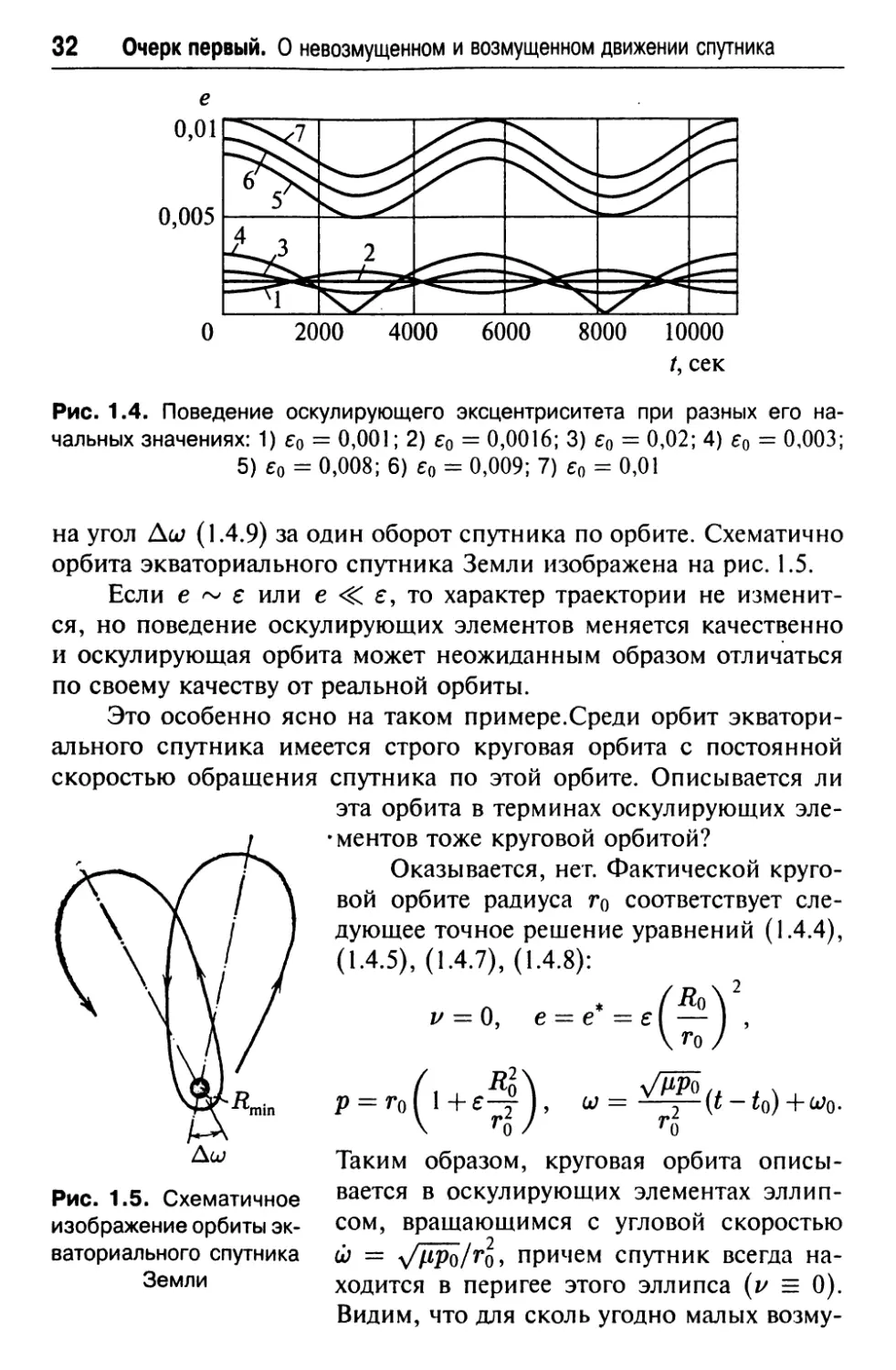
/, сек
Рис. 1.4. Поведение оскулирующего эксцентриситета при разных его на¬
чальных значениях: 1) е0 = 0,001; 2) е0 = 0,0016; 3) е0 = 0,02; 4) е0 = 0,003;
5) е0 = 0,008; 6) е0 = 0,009; 7) е0 = 0,01
на угол Аш (1.4.9) за один оборот спутника по орбите. Схематично
орбита экваториального спутника Земли изображена на рис. 1.5.
Если е ~ е или е <С е, то характер траектории не изменит¬
ся, но поведение оскулирующих элементов меняется качественно
и оскулирующая орбита может неожиданным образом отличаться
по своему качеству от реальной орбиты.
Это особенно ясно на таком примере.Среди орбит экватори¬
ального спутника имеется строго круговая орбита с постоянной
скоростью обращения спутника по этой орбите. Описывается ли
эта орбита в терминах оскулирующих эле-
• ментов тоже круговой орбитой?
Оказывается, нет. Фактической круго¬
вой орбите радиуса Го соответствует сле¬
дующее точное решение уравнений (1.4.4),
(1.4.5), (1.4.7), (1.4.8):
v = 0,
Р = Го(
Rl
. (Ro Г
e=e=£UJ’
\ vm
)' w
(t — to) + U)q.
Рис. 1.5. Схематичное
изображение орбиты эк¬
ваториального спутника
Земли
Таким образом, круговая орбита описы¬
вается в оскулирующих элементах эллип¬
сом, вращающимся с угловой скоростью
и = у/Щ/го, причем спутник всегда на¬
ходится в перигее этого эллипса (и = 0).
Видим, что для сколь угодно малых возму-
5. Уравнения в оскулирующих элементах. Элементы Делоне
33
тений (е Ф 0) в возмущенном движении может быть dvjdt = 0,
чего не бывает в невозмушенном движении.
Мы кончаем рассмотрение нашего примера — оскулирующе-
го движения экваториального спутника. Из проведенного анализа
видны основные свойства оскулирующего движения. Перечислим
их. Оскулируюший эллипс, как правило (но не всегда), качественно
отражает свойства реального движения; возмущения в оскулирую¬
щих элементах могут носить периодический и вековой характер.
Наиболее существенны вековые возмущения, описывающие эво¬
люцию движения; их следует выделять в первую очередь.
5. Уравнения в оскулирующих элементах.
Элементы Делоне
Все сказанное в конце п. 4 верно и для более сложных слу¬
чаев — произвольных (но малых) возмущающих сил и простран-
ственности движения. Естественно, что вид уравнений в оскулиру¬
ющих элементах для общего случая более сложен. Подробнее о по¬
лучении этих уравнений можно прочитать в курсах небесной меха¬
ники (например, в курсе Г. Н. Дубошина) [1.1]. Изящный и краткий
вывод уравнений в оскулирующих элементах принадлежит А. И. Лу¬
рье [1.4].
В нашу задачу не входит повторение этих выкладок; однако
для справок дадим полную сводку уравнений в оскулирующих эле¬
ментах, отсылая за подробностями к цитированным выше работам.
Уравнения имеют вид:
34 Очерк первый. О невозмущенном и возмущенном движении спутника
Здесь
V
р2 Г cos vdv
N = 2-r / — -г, u = v + w.
г2 J (1 + е cos иу
о
Вместо уравнения для фокального параметра р можно пользо¬
ваться уравнением для большой полуоси а:
da 2а?е sin v ~ 2а? ~ ,
м = ^ S + ~VT■ 0-5.2)
at р г
Тогда, соответственно, в правых частях уравнений надо выразить р
через а и е согласно (1.2.7). Здесь обозначено:
s = Д*. г = Дг, w = x[^w,
у р \ р у р
где S,T,W — соответственно радиальное, трансверсальное и нор¬
мальное возмущающие ускорения (рис. 1.6). Вместо г подразуме¬
вается выражение (1.2.4). Предполагается, что известен явный вид
зависимости S, Т, W от оскулирующих элементов и времени. Часто
оказывается, что S, Т\ W зависят от времени не явно, а только че¬
рез истинную аномалию v или аргумент широты и, которые входят
в S, Г, W явным образом.
Закон площадей (1.2.8) в возмущенном движении не имеет ме¬
ста. Аналогичная формула в возмущенном движении имеет вид
2 dv Гр
rTt =^+Vp
sin v ( r\
COS V л sin. . . .
S 1 + - Г
(1.5.3)
e
Уравнения (1.5.1) в оскулирующих элементах имеют вид ничуть
не более простой, чем уравнения (1.1.3) в координатах. Уравнения
(1.1.3) в координатах даже «красивее» — симметричны и коротки.
Если неинтегрируемы уравнения (1.1.3), то неинтегрируемы и урав¬
нения (1.5.1) в оскулирующих элементах. Однако уравнения (1.5.1)
имеют следующее преимущество: они сразу помогают понять отли¬
чие возмущенной траектории от невозмущенной. Действительно,
правые части этих уравнений содержат возмущающие ускорения
и обращаются в нуль/ как только возмущающие ускорения исчеза¬
ют. В этом последнем случае уравнения (1.5.1) сразу дают решение:
р = const, е = const, ш = const,
i = const, Q = const, r* = const,
то есть кеплеровскую траекторию.
5. Уравнения в оскулирующих элементах. Элементы Делоне
35
Если же S, Т, W не равны нулю, то, как это обычно бывает,
они являются малыми величинами. Естественно ожидать, что то¬
гда оскулирующие элементы в каком-то смысле мало отличаются
от своих начальных значений. В этом случае к уравнениям (1.5.1)
можно применить хорошо разработанные методы приближенного
решения дифференциальных уравнений, содержащих малый пара¬
метр. Применение этих методов к уравнениям (1.5.1) дает богатые
результаты. Особенно эффективны при исследовании таких задач
асимптотические методы нелинейной механики.
Понятие об асимптотиче¬
ских методах будет дано ниже.
Эти методы позволяют неинте-
грируемую задачу заменить та¬
кой интегрируемой задачей, ре¬
шение которой приближенно,
но с высокой степенью точно¬
сти совпадает с неизвестным
решением исходной неинтегри-
руемой задачи 7\
Мы ввели оскулирующие
элементы, исходя из того, что
возмущенное движение мало от¬
личается от невозмущенного в
силу малости возмущающих ускорений. Однако малые возмуще¬
ния могут накапливаться с течением времени. Возмущенное дви¬
жение близко к невозмущенному на небольшом интервале време¬
ни, но по прошествии достаточно (большого промежутка време¬
ни накопившиеся малые возмущения могут существенно исказить
движение. И если теперь зафиксировать оскулирующие элементы
на достигнутых значениях, то получим кеплерово движение по эл¬
липсу, весьма далекому от первоначального. Эти долговременные
изменения движения, или, как говорят, эволюция движения, пред¬
ставляют собой наиболее важный объект в исследовании возму¬
щенного движения. На рис. 1.7 дана схема изменения какого-либо
Разработки этих методов фактически начаты классиками небесной механики,
и в знаменитом трактате А. Пуанкаре [1.5] подобный метод уже достаточно широ¬
ко используется для исследования движения. Дальнейшая разработка, обоснование
и широкое внедрение асимптотических методов в теорию колебаний принадлежат
Н. М. Крылову, Н. Н. Боголюбову, Ю. А. Митропольскому, В. М. Волосову и другим
советским ученым 11.6— 1.81.
3*
Земля
Рис. 1.6. Компоненты
возмущающего ускорения
36 Очерк первый. О невозмущенном и возмущенном движении спутника
э
2
t
Рис. 1.7. График изменения оскулирующего элемента со временем: 1 — не¬
возмущенное движение, 2 — возмущенное движение, 3 — эволюция движения
оскулирующего элемента э со временем, она иллюстрирует введен¬
ные понятия.
Асимптотические методы позволяют на основе точных урав¬
нений (1.5.1) в оскулирующих элементах получить уравнения при¬
ближенные, описывающие лишь эволюцию движения (кривая 3
на рис. 1.7); это описание будет достаточно точным на весьма боль¬
шом (но, вообще говоря, конечном) интервале времени. Важно,
что такие приближенные эволюционные уравнения часто оказыва¬
ются интегрируемыми, что позволяет подробно исследовать ка¬
чественную и количественную картину эволюции движения. При
желании асимптотические методы позволяют построить и более
высокие приближения к возмущенному движению, описывающие
даже и мелкие вариации кривой 2 на рис. 1.7.
В небесной механике, а также в механике космического поле¬
та вместо классических оскулируюших элементов иногда выгодно
употреблять некоторые их комбинации. Если возмущающие силы
имеют силовую функцию U, то уравнения возмущенного движе¬
ния имеют особенно симметричный вид, если их записать в так
называемых элементах Делоне:
Эти элементы вводятся через оскулирующие элементы (1.3.1) сле¬
дующим образом:
Zr, G, Н, /, д, h.
(1.5.4)
I = n(t - т*),
(1.5.5)
6. Асимптотические методы нелинейной механики
37
Предполагается, что силовая функция U выражена явно через эле¬
менты Делоне, и вводится гамильтонова функция
F=^~2+U(L,G,HJ,g,h). (1.5.6)
Тогда уравнения возмущенного движения принимают канониче¬
ский вид:
dL
OF
dl
dF '
~dt =
= In’
dt ~
~dL’
dG
OF
dg _
OF
~dt =
= ¥’
dt ~
~0G’
dH
of
dh
dF
~dt “
= ~dh'
It ~
~Hh: ■>
Такой вид уравнений особенно удобен для применения асимптоти¬
ческих методов, как будет показано несколько ниже8\
Отметим следующее важное обстоятельство. В невозмущенном
движении элементы L, G, Н,д, h постоянны; при наличии малых
возмущений эти элементы медленно эволюционируют. Их так и на¬
зовем медленными переменными. Элемент I в невозмущенном движе¬
нии не постоянен, он меняется линейно со временем со скоростью
i = п = у/р,/а?\ в возмущенном движении элемент I сохранит
примерно эту же быструю скорость своего изменения, лишь не¬
сколько искаженную за счет действия малых возмущений. Поэтому
переменную I назовем быстрой переменной. Разделение перемен¬
ных на медленные и быстрые является характерной особенностью
задач, для анализа которых удобно применять асимптотические ме¬
тоды исследования.
6. Отступление об асимптотических методах нелинейной
механики. Колебания спутника около центра масс.
Осреднение канонических уравнений
Описание асимптотических методов удобно начать с какого-
либо характерного примера, а уж потом переходить к изложению
более общих алгоритмов. Поэтому рассмотрим частную задачу о ко¬
лебаниях спутника около центра масс.
Вывод уравнений в элементах Делоне дается, например, в книге Г. Н. Дубо-
шина [1.1].
38 Очерк первый. О невозмущенном и возмущенном движении спутника
На спутник, центр масс которого движется по орбите, действу¬
ет момент гравитационных сил, стабилизирующий спутник относи¬
тельно его радиус-вектора. Об этом подробнее будет сказано в од¬
ном из следующих очерков. А здесь, имея в виду иллюстрировать
асимптотические методы теории колебаний, рассмотрим уравнение
плоских колебаний спутника на эллиптической орбите [1.17, 1.18]:
(1 + е cos v)8" - 2е sin v • S' + n2 sin 8 = 4e sin v,
. ЛЛ 2 A-С (1.6.1)
d = 20, n2 = 3 .
Здесь (рис. 1.8) v — истинная аномалия, е — эксцентриситет
орбиты, 9 — угол между осью спутника, находящейся все время
в плоскости орбиты, и его текущим радиус-вектором; А, В, С —
главные центральные моменты инерции спутника. Для определен¬
ности В > А > С, причем, ось, которой соответствует момент
инерции Б, направлена нормально к плоскости орбиты. Штрихи
в (1.6.1) означают производные по v.
Если бы орбита была круговая (е — 0), то уравнение (1.6.1)
имело бы решение 8 = 0, отвечающее относительному равнове¬
сию спутника (ось момента инерции С все время совпадает с ра¬
6. Асимптотические методы нелинейной механики
39
диус-вектором спутника). При е Ф 0 относительного равновесия
не будет — спутник совершает колебания около направления ра¬
диус-вектора. Эти колебания исследовать затруднительно, так как
уравнение (1.6.1) неинтегрируемо. Однако можно ожидать, что при
малых эксцентриситетах е существуют малые колебания, описыва¬
емые линейным уравнением, которое получится из (1.6.1) заменой
sin 5 ~ 8. С этого уравнения малых колебаний и начнем анализ.
Заменой 8/2 = в = z/( 1 + ecosv) переходим к новому урав¬
нению:
!"+(
п2 + е cos v
z — 2е sin v,
1 + е cos v
которое, являясь линейным, все-таки неинтегрируемо из-за пере¬
менности своих коэффициентов. Так как эксцентриситет орбиты е
по предположению мал, то с точностью до первой степени е по¬
следнее уравнение можно записать так:
, /„2
z” + п2z = е [2 sin v + (п2 - 1 )z cos v].
(1.6.2)
Обратим внимание, что при е = 0 уравнение (1.6.2) имеет
решение
z = acosip, z' = -ans\nip9 (1.6.3)
в котором
гр = пи + V;o-
Если (1.6.3) рассматривать просто как замену переменных (введение
новых переменных а,гр вместо z,z) в уравнении (1.6.2), то это
уравнение окажется эквивалентно системе
da 1 ^
— = —f(u, a cos ip) sin гр,
dv п
где
dip 1
— = п f(i/, a cos гр) cos ip,
dv па
dv
dv
f(v, z) — e[2 sin v + (ft2 - I)z cos v].
(1.6.4)
Так как / мало вместе с е, то отсюда следует, что система (1.6.4)
имеет одну медленную переменную и две быстрые (ip, v). При е = О
имеем / = 0 и из системы (1.6.4) получаем решение а = а0,
40 Очерк первый. О невозмущенном и возмущенном движении спутника
'ф = пи + 'фо, описывающее в силу (1.6.3) малые колебания на кру¬
говой орбите. При е ф 0 будем искать решение системы (1.6.4)
в виде _
а = а + еа\(ф, а, и) 4- е1а2{'ф, а,и) + ...,
■ф = ф + е(}\(ф, a, v) + е2р2{ф, а,и) +... .
Здесь функции а(и), ф(и), oti(ip,a,v), /3i(ip,a,v) подлежат опре¬
делению, примем функции а и ф должны удовлетворять системе
da ~ _ 2 ~ '
— = evl|(a) + е А2(а) + ...,
- > (1.6.6)
dib v ;
—— = 71 + вВ\ (а) + е В2(а) -4-...,
dv >
где А{(а), Bi(d) — также подлежащие определению функции только
медленной переменной а. Решение исходной системы уравнений
(1.6.4) в виде разложений (1.6.5), (1.6.6) по малому параметру е
будем называть асимптотическим решением в том смысле, что при
е —> 0 оно стремится к точному решению исходной системы, если
в ней положить е = 0 (определяемые функции а,-,/?* для этого
должны быть ограничены). Точность асимптотического решения
зависит от количества взятых приближений. Можно утверждать,
что если ап — решение n-го приближения в асимптотическом
смысле, то |а - ап| ~ еп на интервале времени t ~ 1/е. Иначе
говоря, асимптотический метод дает достаточно точное решение
на ограниченном, вообще говоря, интервале времени (а иногда —
на бесконечном).
Заметим, что уже исходное дифференциальное уравнение (1.6.2)
нашей задачи записано с точностью лишь до первых степеней е, по¬
этому в (1.6.5) и (1.6.6) имеет смысл оставить лишь члены не выше
первого порядка по е. Смысл замены переменных (1.6.5), (1.6.6)
в том, что система (1.6.6) гораздо проще исходной системы (1.6.4)
(и интегрируема в нашем случае), а функции а*, А находятся с по¬
мощью простых выкладок. Таким образом, можно просто найти при¬
ближенное решение системы, точное решение которой не известно.
Вместо решения (1.6.5)—(1.6.6) системы (1.6.4) мы можем ис¬
кать решение эквивалентной задачи прямо для исходного уравне¬
ния (1.6.2). С точностью до первых степеней е эта задача форму¬
лируется так:
найти решение уравнения (1.6.2) в виде
2 = a cos гр 4- еи\а, и), (1.6.7)
(1.6.5)
б. Асимптотические методы нелинейной механики
41
где щ ограничена, а а и if) удовлетворяют уравнениям
<^ = еА\(а), = п + еВ\(а), (1.6.8)
аи
причем А\ и В\ подлежат определению.
Подставляя (1.6.7) в (1.6.2) с учетом (1.6.8) и собирая члены
не выше чем первого порядка малости, получим после преобразо¬
вания
- 2еп(у1| sin^ + В\a cos -ф) +
(д2и\ д7и\ д2щ \ 2
+ e{Wn' + 2^n+~^)+neu' =
= е^2 sin v + а^П ^—— [ cos (v + ф) + cos (v - ф)] |. (1.6.9)
На е обе части уравнения можно разделить. В правую часть не вхо¬
дят гармоники sin -0 и cosфч поэтому А\ = 0, = 0. Отсюда
<1ф
а = ао, = п. (1.6.10)
av
Заметим, что тот же результат получится, если осреднить пра¬
вые части системы (1.6.4) независимо по быстрым фазам v и ф.
Далее, при выполнении условий А\ = В\ = 0 уравнение в частных
производных (1.6.9) имеет решение
п2 - 1
U\ = — sin V +
-» l 1
1 1 .
cos (у - ф) cos (v 4- ф)
2n - 1 2n + 1
(1.6.11)
Формулами (1.6.10), (1.6.11) искомое решение (1.6.7) уравнения
(1.6.2) полностью определено. В первом приближении малые ко¬
лебания на эллиптической орбите почти не отличаются от малых
колебаний на круговой орбите, и можно ограничиться приближен¬
ным решением
z = ао cos (пф + фо).
Однако это решение теряет смысл, когда наступает резонанс между
частотой п собственных колебаний и частотой «1» орбитального
движения: при п —> 1 согласнр.ДХб. 11) колебания неограниченно
42 Очерк первый. О невозмущенном и возмущенном движении спутника
возрастают — наступает резонанс. (Другой резонанс, так называ¬
емый параметрический, наступает при п = 1/2). Но неограничен¬
ность колебаний несовместима с постановкой задачи (линейное
уравнение (1.6.2) описывает лишь малые колебания). Поэтому в ок¬
рестности резонанса необходимо исследовать нелинейное уравнение.
С этой целью исходное уравнение (1.6.1) запишем в виде
д" + п26 = f(v,6,6',d”), (1.6.12)
где
/ = е[4 sin v + 2S' sin v - 6" cos v] + n2(S - sin 6),
и будем считать величину / малой, что неизбежно предполагает
одновременно малость эксцентриситета е и малое отличие sin 6
от д. Кроме того, п2 близко к 1 по условию (окрестность резонанса).
При / = 0 решение имеет вид (1.6.3), где при резонансе следует
еще положить я = 1. Будем искать и решение уравнения (1.6.12)
в виде
б = а cosip, ip = v + x, (1.6.13)
где а и х — новые переменные. Как и в нерезонансном случае,
уравнение (1.6.12) эквивалентно системе типа (1.6.4), только запи¬
санной теперь в виде
da I ,
— = —f(ip - х, a cos ip, —an sin ip, an cos ip) sin ip,
dv n
du 1 2
— = n — 1 f(ip - x, a cos ip, -an sin ip, an cos ip) cos ip,
dv na
dip dx
1Г = T~’
dv dv
(1.6.14)
В силу малости / и близости я к единице наша система имеет уже
две медленные переменные (а и к) и одну быструю (ip). Принципи¬
альной разницы между системами (1.6.4) и (1.6.14) нет, и решение
системы (1.6.14) тоже можно искать в виде, аналогичном (1.6.5)-
(1.6.6), причем в первом приближении должно быть
6 = acosip, ip = v + x,
da dx .
— = A\(a,x), — = n - \ + B\(a, x).
Как и в рассмотренном выше случае, функции j4|(o,к), я — I +
В\(а,х) от медленных переменных а,х получаются в процессе
6. Асимптотические методы нелинейной механики
43
исполнения алгоритма как средние по быстрой переменной гр правые
части уравнений (1.6.14) для медленных переменных:
Здесь Jo(a) и J\(a) — функции Бесселя соответственно нулевого
который дает «амплитудно-фазовые» траектории (зависимость ам¬
плитуды а от фазы х околорезонансных траекторий). Пример та¬
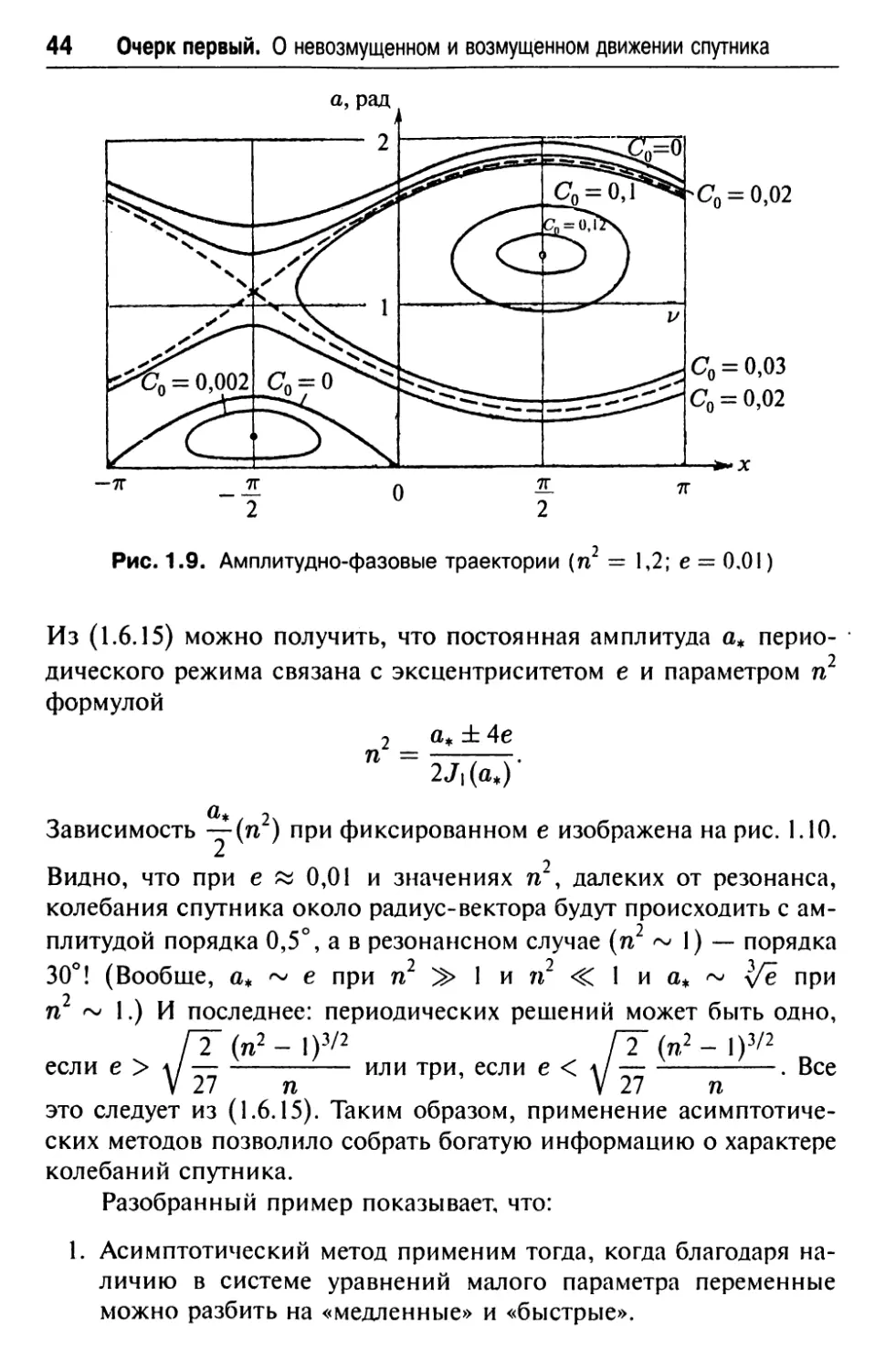
ких траекторий изображен на рис. 1.9 для разных значений Со.
Когда а(и) и х(и) меняются (медленно) с изменением и, изоб¬
ражающая точка на плоскости а, х обегает одну из интегральных
кривых (рис. 1.9).
Неподвижные точки на этом рисунке (х = ±7г/2, а = а*) от¬
вечают периодическим колебаниям (с периодом 2п по v и посто¬
янной амплитудой); в любых других случаях амплитуда медленно
колеблется между своими наибольшим и наименьшим значениями.
27Г
0
и аналогично В\. Тогда в явном виде [1.17]:
da 4е 1 дФ
— = cos х = —,
Л. ,
dv п+1 а ох
1 дФ
а дя ’
п + 1 4
2 )
и первого порядков9^. Дифференцируя Ф по и, в силу уравнений
(1.6.15) обнаружим, что
11Ф дФ da дФ dx _
dv да dv дя dv ~
Значит, уравнения (1.6.15) имеют первый интеграл
Ф(а, я) — Со = const,
^ Из спойстн функций Бесселя нам достаточно знать, что первые члены их
разложений в ряд по аргументу имеют вид
44 Очерк первый. О невозмущенном и возмущенном движении спутника
-7Г
2L
2
2L
2
7Г
Рис. 1.9. Амплитудно-фазовые траектории (п = 1,2; е = 0.01)
Из (1.6.15) можно получить, что постоянная амплитуда а* перио¬
дического режима связана с эксцентриситетом е и параметром п2
формулой
2 а* ± 4е
п =
2«7| (а*)
2
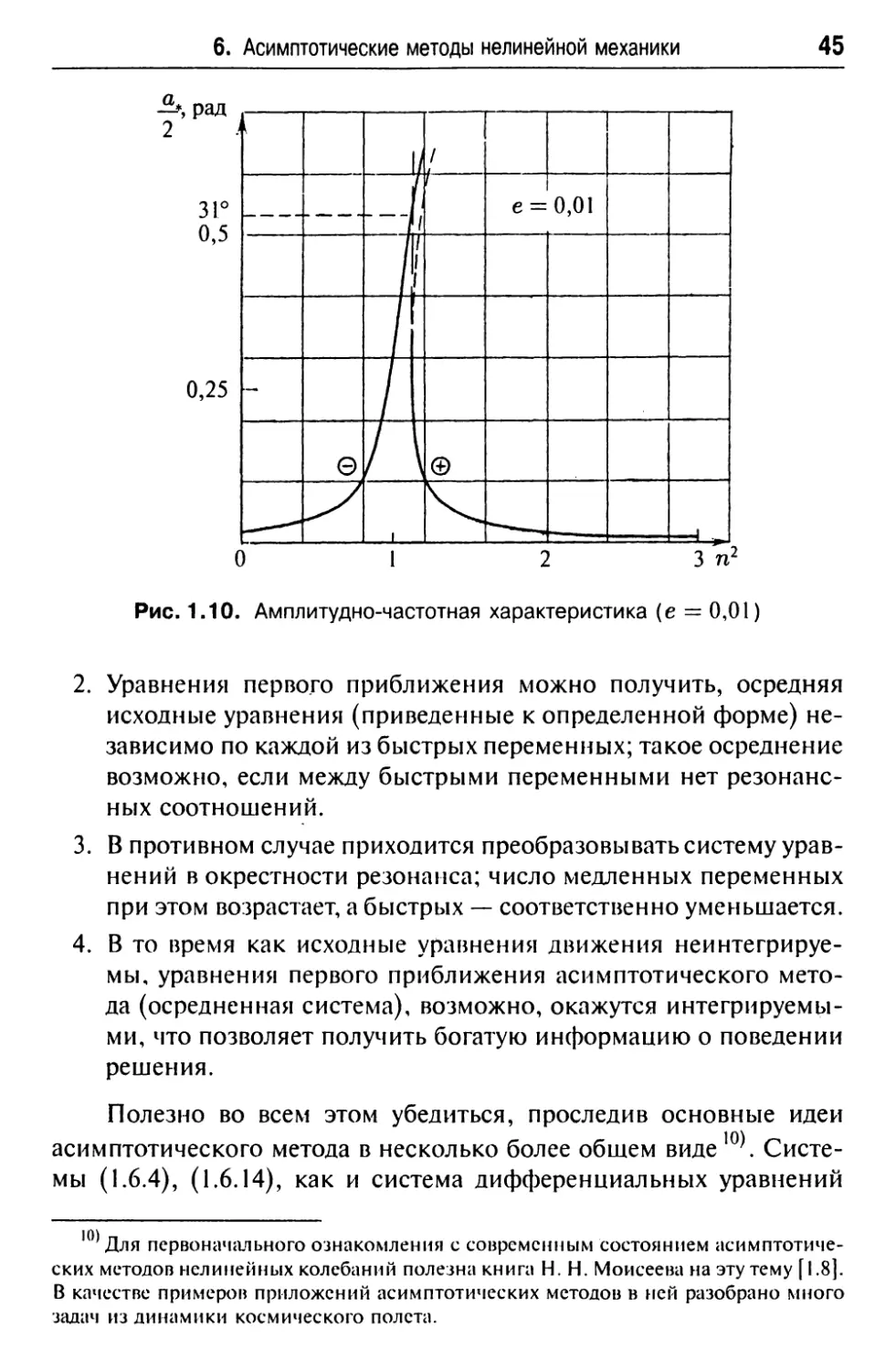
Зависимость — (п ) при фиксированном е изображена на рис. 1.10.
Видно, что при е « 0,01 и значениях п2, далеких от резонанса,
колебания спутника около радиус-вектора будут происходить с ам¬
плитудой порядка 0,5°, а в резонансном случае (n2 ~ 1) — порядка
30°! (Вообще, а* ~ е при п2 » 1 и п2 « 1 и а* ~ 1/е при
п2 ~ 1.) И последнее: периодических решений может быть одно,
2 (п2 — I)3/2 _ ^ [~2 (п2 — I)3/2 ^
если е > \1 —
или три, если е < \/ —
п V 11 п
это следует из (1.6.15). Таким образом, применение асимптотиче¬
ских методов позволило собрать богатую информацию о характере
колебаний спутника.
Разобранный пример показывает, что:
1. Асимптотический метод применим тогда, когда благодаря на¬
личию в системе уравнений малого параметра переменные
можно разбить на «медленные» и «быстрые».
6. Асимптотические методы нелинейной механики
45
2. Уравнения первого приближения можно получить, осредняя
исходные уравнения (приведенные к определенной форме) не¬
зависимо по каждой из быстрых переменных; такое осреднение
возможно, если между быстрыми переменными нет резонанс¬
ных соотношений.
3. В противном случае приходится преобразовывать систему урав¬
нений в окрестности резонанса; число медленных переменных
при этом возрастает, а быстрых — соответственно уменьшается.
4. В то время как исходные уравнения движения неинтегрируе-
мы, уравнения первого приближения асимптотического мето¬
да (осредненная система), возможно, окажутся интегрируемы¬
ми, что позволяет получить богатую информацию о поведении
решения.
Полезно во всем этом убедиться, проследив основные идеи
асимптотического метода в несколько более общем виде 10\ Систе¬
мы (1.6.4), (1.6.14), как и система дифференциальных уравнений
|0* Для первоначального ознакомления с современным состоянием асимптотиче¬
ских методов нелинейных колебаний полезна книга Н. Н. Моисеева на эту тему [1.8].
В качестве примеров приложений асимптотических методов в ней разобрано много
задач из динамики космического полета.
46 Очерк первый. О невозмущенном и возмущенном движении спутника
возмущенного движения (1.5.7), имеют такую структуру:
х = еХ(х, у,е), Л
у = u(x) + eY(x,y,e)J
}
(1.6.16)
где х — вектор медленных переменных, а у — вектор быстрых
переменных, е — малый параметр. Конкретно в уравнениях (1.5.7)
имеется всего одна быстрая переменная I, но их может быть, во¬
обще говоря, и больше; это обобщение мы и имеем в виду. То, что
возмущенное движение подвержено малым возмущениям, мы под¬
черкнули введением явно написанного малого параметра е « 1.
Если е = 0, то х = const = хо, у = u)(xo)t + уо. Будем считать,
что X и Y периодичны по быстрым переменным у с периодом 2п.
Будем искать решение системы (1.6.16) в виде
где х, у — новые переменные, а подлежат определению и
должны быть выбраны так, чтобы переменные х, у удовлетворяли
новой системе дифференциальных уравнений
Взяв то или иное количество членов в (1.6.17), получаем реше¬
ние с той или иной степенью точности. Ясно, что система (1.6.18)
гораздо проще исходной системы (1.6.16), так как быстрые и мед¬
ленные переменные разделены. В таком разделении — суть асимп¬
тотических методов.
Потребуем ограниченности функций щ, Vi (только в этом слу¬
чае каждый последующий член в (1.6.17) будет мал по сравнению
с предыдущим). Подставим (1.6.17) в (1.6.16) с учетом (1.6.18) и со¬
берем члены при одинаковых степенях е. Получим системы урав¬
нений в частных производных с известными правыми частями:
(1.6.17)
х = еА|(х) + е2А2(х) + ...,
ij = ш(х) + еВ\(х) + £2В2(х) + ...
(1.6.18)
6. Асимптотические методы нелинейной механики
47
к ди
Е
—Wi(x) =gn-An,
tr д*
Е = hn~Bn •
г=1
Здесь первые два уравнения соответствуют членам при £, а по¬
следние два — при еп\ Uj,Vj,Aj,Bj — искомые вектор-функции;
к — число быстрых переменных (и размерность векторов Vj, Bj, о;г ,
Y); m — число медленных переменных (и размерность векто¬
ров Uj, X); и® — «а-компонента» вектора и\; функции gn,hn,
Ап, Вп явно выражаются через функции, найденные в предыдущих
приближениях. Так как все уравнения в частных производных одно¬
типны, то достаточно решить первое из этих уравнений, остальные
решаются по аналогии.
Вектор-функция X по определению периодична по каждой
из переменных у и, значит, разлагается в ряд Фурье
^ П У' + • •
П\,...,Пк
Это позволяет искать и\(х,у) в виде
щ(х,у)= 6П| Пк(х)е1{п'у'+--+пш) + Y^Ci{x)yi. (1.6.19)
711 . . ,71к i'= 1
Подставляя это значение и\ в первое из написанных выше уравне¬
ний в частных производных, получим
аТ1\ пк (х)
*’ ; i(n\U\ + ... + ЩШк)
к
Ci{x)wi{x) = а0 ’ 0(х) - 4, (ж).
i= 1
(1.6.20)
В первой из этих формул хоть одно из щ отлично от нуля. По усло¬
вию ограниченности и\ все сг должны быть равны нулю (иначе и\,
как видно из (1.6.19), неограниченно растет вместе с у). Но если
все С{ — 0, то из (1.6.20) немедленно следует А\(х) = ао 0(®)-
Но «нулевой» член ряда Фурье равен среднему значению разлагае¬
48 Очерк первый. О невозмущенном и возмущенном движении спутника
мой функции. Итак,
2тг 27Г
Л|(Ж)=(2^ / "'/ dy' •■•йУк = Х,
... _ °п' ПкJ(nlyl+...+nkyk) , .(я) /_ч
+"»"*) +V-..OW.
(1.6.21)
Функция &о о(#) произвольна и может быть определена из других
соображений. Аналогично
e=i ОХа
I >
в у' ап1.,пк(х) Hn^+...+пф) + и т д
Однако все эти выкладки имеют смысл в том и только том
случае, когда в системе нет никаких резонансов, то есть
П\Ш\ + 712072 + • . . + Ф 0.
каков бы ни был набор целых чисел щ. Иначе функции и\ и v\
не определены (бесконечно велики).
Если условие нерезонансности выполнено, то, обрывая ряды
(1.6.17) на членах еп~ \ получим на интервале времени t ~ 1/е точ¬
ность определения медленных переменных порядка еп и быстрых
переменных порядка еп~ \ так что
|ж-ж|~£ГП, |у - у| ~
Стало быть, члены выше порядка еп~{ в быстрых переменных и учи-
тывать не стоит. В частности, первое приближение дает вместо
уравнений (1.6.16) новые уравнения:
х = х, у = у,
dx л t-\ dy <-\ ^ (1.6.22)
й=еМх)’ м=ф}'
где А\{х) определяется формулой (1.6.21).
6. Асимптотические методы нелинейной механики
49
Таким образом, асимптотический метод в первом приближе¬
нии есть метод осреднения. Решение этих последних уравнений
на t ~ \/е дает точность \х - х\ ~ е, \у - у\ ~ \. Так как параметр е
обычно мал в силу малости возмущений, то интервал времени,
на котором справедливо первое приближение, достаточно велик,
чтобы можно было понять тенденции эволюции системы.
Быстрые переменные определяются с меньшей точностью, но
это неважно, так как весь интерес обычно заключен в эволюции
медленных переменных, а они асимптотически (по е при е -э 0)
близки к своим точным значениям (как уже отмечалось, в этом
смысл названия «асимптотические методы»).
Замечательно, что уравнения первого приближения определя¬
ются так просто — независимым осреднением по каждой из быст¬
рых переменных. Однако это имеет место лишь в нерезонансном
случае. Если же найдется такой набор чисел щ, что сумма
то есть имеется соизмеримость между частотами, то в окрестности
этого резонанса величина
пУ = щу\ + ... + П°кук
будет меняться медленно, так как ее производная
к
мало отличается от нуля. Поэтому проводить независимое осредне¬
ние по каждой из Уг уже нельзя — осреднится медленная перемен¬
ная #! Но 'в можно рассматривать как новую независимую пере¬
менную. Вектор быстрых переменных обозначим z = (yj,..., Jfe),
и систему (I.6.16) можно теперь привести к виду
Эта система имеет ту же структуру, что и (1.6.16), только содержит
на одну медленную переменную больше и на одну быструю пере¬
менную меньше. Задача свелась к предыдущей, так как число быст¬
рых и медленных переменных не принципиально. Мы рассмотрим
к
i= I
х = еХ*(х, #, z, е),
А = ев*(х, 1?, 2, е),
z = ш(х) + eZ*(x, , z, е).
4 Заказ 1667
50 Очерк первый. О невозмущенном и возмущенном движении спутника
далее алгоритмы осреднения в резонансном и нерезонансном дви¬
жениях для специально интересующего нас случая канонических
уравнений возмущенного движения.
Осреднение канонических уравнений. Итак, дифференциальные урав¬
нения первого приближения асимптотического метода получаются
осреднением правых частей уравнений для медленных переменных
по быстрым переменным, причем при осреднении подставляются
невозмущенные значения переменных. Посмотрим, как будет вы¬
глядеть процесс осреднения для канонического (типа (1.5.7)) вида
уравнений. Пусть эг- — медленная переменная, удовлетворяющая
уравнению
d3{ dF
-37 = ±тг-, 0.6.23
dt 03j
а гамильтонова функция F зависит периодическим образом от быст¬
рой переменной. В нашем случае быстрая переменная — одна
(их может быть в общем случае и больше), а именно Z; обычно
в задачах механики космического полета функция F зависит явно
от истинной аномалии и(1), а не от /; поэтому можно записать
F = F(v(l)). (1.6.24)
Быстрый период в нашем случае — период Т = 2п/п обра¬
щения спутника по орбите, и осреднение правой части уравнения
(1.6.23) будет выглядеть так:
2тг 2тг
1 Г 3F д 1 Г д ~
±3“ / Т" Л1 = ±1ГТ- / Fdl = ±—F. 1.6.25
27Г J 03j - 03j Z7T J 03j
0 * * 0
Здесь символ = 5k означает, что осреднение происходит при
фиксированных значениях параметров э^.
Выпишем выражение F несколько подробнее:
2тг 2тг 27Г
~ 1 Г . dl , 1 rdldtj 1 Г г, dt
F=— F(y)— dv = — / F——dv = — / Fn—dv.
2n J dv 2n J dt dv 2ж J dv
ooo
(1.6.26)
Здесь надо выразить dt/dv явно через v и элементы. Таким об¬
разом, осреднение функции F по быстрой переменной I эквива¬
лентно осреднению той же функции F по явно входящей истин¬
ной аномалии v, производимому с весом п dt/dv. Удобно ввести
6. Асимптотические методы нелинейной механики
51
безразмерное время т = nt и новое среднее значение F — F/n
функции F. Тогда окончательно:
d3i OF
d^ = ±
I Г dt
F = — / F— dv.
2n J dv
2ж
(1.6.27)
0
Эволюционные уравнения (1.6.27) обладают следующими за¬
мечательными свойствами:
1. Осреднение исходных точных уравнений движения эквива¬
лентно осреднению силовой функции. Это значит, что для
получения эволюционной системы не надо предварительно вы¬
писывать полную систему уравнений, а достаточно выписать
характеристическую функцию F, осреднить ее и, зная F, пи¬
сать сразу эволюционные уравнения.
2. Правые части системы (1.6.27) не зависят от v (по v мы осред-
нили), а значит, и от /, то есть dF/dl = 0. Тогда из первого же
уравнения Делоне следует
Таким образом, если возмущающая движение спутника сила кон¬
сервативна,, то большая полуось орбиты спутника не эволюцио¬
нирует, сохраняя в среднем постоянное значение. Это имеет
место и для случая зависимости F от нескольких быстрых пере¬
менных l\, I2,. * •, Z&. Этот факт является отражением известной
в небесной механике так называемой «теоремы Лапласа» о том,
что большие полуоси планет не имеют вековых (то есть накап¬
ливающихся с течением времени) изменений (более подробно
об этом можно прочитать в книге Г. Н. Дубошина [1.1]). Факти¬
чески «теорема Лапласа» строго была доказана лишь в недавнее
время В. И. Арнольдом, после чего стала ясна и область при¬
менимости этой теоремы и^.
L = L о
(1.6.28)
или, иначе,
а = clq.
(1.6.29)
См. работы В. И. Арнольда [1.9, 1.10], а также очерк об устойчивости Солнеч¬
ной системы в настоящей книге и отличную популяризацию В. Г. Демина [1.11].
52 Очерк первый. О невозмущенном и возмущенном движении спутника
3. Так как быстрая переменная I в первом приближении в возму¬
щенном движении меняется так же, как в невозмущенном,
а медленная переменная L не эволюционирует, то вместо
шести уравнений движения эволюционная система содержит
лишь четыре уравнения:
4. Функция F не зависит от г, значит, эволюционные уравнения
(1.6.30) имеют первый интеграл
Таким образом, полная система уравнений в эволюционном дви¬
жении имеет два первых интеграла движения: (1.6.28) и (1.6.31).
Мы до сих пор считали, что в наших уравнениях быстрая пе¬
ременная — одна, а именно переменная I. Однако те же уравнения
в элементах Делоне (1.5.7) могут содержать в выражении F дру¬
гие быстрые переменные. Например, при исследовании влияния
на спутник Луны и Солнца в F неизбежно войдут координаты Лу¬
ны и Солнца, которые при определенных условиях можно считать
тоже быстро меняющимися.
Но и в этом случае все выводы 1-4 останутся справедливыми,
только под средним значением F надо понимать соответствующее
значение F, осредненное по всем быстрым переменным, причем
по каждой из них — независимо. Однако в этом случае (несколько
быстрых переменных) может возникнуть качественно новая ситуа¬
ция: соизмеримость частот быстрых переменных, или, как говорят,
резонанс. Независимое осреднение по быстрым переменным (и,
значит, все предыдущие выводы об эволюционном движении) дей¬
ствительно лишь при отсутствии резонанса. Если же имеет место
резонанс, то исследование надо проводить особо и эволюционные
уравнения принимают иной вид. Чтобы понять качественные осо¬
бенности резонансных случаев, достаточно разобрать случай двух
быстрых переменных.
Итак, пусть в уравнениях в элементах Делоне
(1.6.30)
F = const.
(1.6.31)
F = F(3i,l,l,),
где э — медленные, а 1,1] — быстрые переменные.
(1.6.32)
6. Асимптотические методы нелинейной механики
53
В невозмущенном движении положим, несколько изменив обо¬
значения,
dl
— = и; = const, (1.6.33)
at
Л1\
— = и)\ = const. (1.6.34)
at
Здесь будет удобнее считать, что F явно зависит от I и 1\ (а не
от каких-либо функций этих аргументов). Последнее соотношение
(1.6.34) сохраняется и в возмущенном движении (что, впрочем,
не принципиально),
Пусть можно указать такие произвольные целые (положитель¬
ные или отрицательные) числа щ, то, что оказывается справедли¬
вым равенство
щи) + m0u) | = 0. (1.6.35)
Тогда говорят, что имеет место резонанс. Сумма
\щ\ + |ш0| (1.6.36)
называется порядком резонанса. Если же при любых целых, поло¬
жительных или отрицательных, щ, то будет
щи) + m0u)\ Ф 0, (1.6.37)
то имеем нерезонансный случай. Практически резонанс (1.6.35)
надо рассматривать вместе с некоторой малой его окрестностью,
так что щи) + m0o;i = е, где е — малая величина. Если движение
нерезонансно, то введение
27Г 27Г
// nih)dldh (1.6.38)
о о
сводит эволюционные уравнения для медленных переменных эг к виду
1} = ±т~■ (|-6-39)
dt dsj
Здесь время t — размерное. Но для только что написанных уравне¬
ний (1.6.39) действительны все свойства 1-4 эволюционных урав¬
нений, в частности и «теорема Лапласа» об отсутствии эволюции
большой полуоси орбиты. И эти свойства обобщаются на любое
конечное число быстрых переменных, лишь бы между частотами
54 Очерк первый. О невозмущенном и возмущенном движении спутника
быстрых переменных не выполнялось никакое резонансное соот¬
ношение.
Обратимся теперь к резонансному случаю. Так как F(l, 1\) пе¬
риодична по /, 1\ то она может быть разложена в ряд Фурье
Здесь F дается формулой (1.6.38), а коэффициенты Фурье апт,
Ьпш, как известно, легко вычисляются. Так как мы рассматриваем
окрестность резонанса (1.6.35), то переменные кпт = nl + ml\ все
быстрые, если только п Ф кщ одновременно (к = 1,2,...), и по¬
этому соответствующие члены могут быть осреднены, причем их
средние значения суть нули. В формуле (1.6.40), кроме члена F,
следует оставить лишь члены, отвечающие одновременному при¬
своению значений п = щ, т = то- Переменная к = п01 + rn0l\
медленная, так как в окрестности резонанса (1.6.35) имеем
то есть к меняется медленно. Поэтому вместо F можно записать
следующие эволюционные члены:
Здесь под 3i подразумеваются пять медленных переменных: L, G, Н,
g, h. Составим эволюционное уравнение для новой переменной к:
00 00
F(l, /,) = F + ^2 {апт sin (nl + ml\) + Ьпт cos (nl + mi,)}.
n=1 m— 1
(1.6.40)
dx.
— = щш + m0k> i = £,
dt
00
F(ai, I, i,) = F + sin kx + bk coskx),
k= I
27Г 27Г
(1.6.41)
0 0
O'к = ®fcno,fcmo(5i)> = Ькпо,кто(эг)-
dx dl dF
dF
Введем
Ф(эг-, x) - n0F - m0W\L.
(1.6.42)
Тогда
dx 8Ф dL OF dF дФ
6. Асимптотические методы нелинейной механики
55
А полная эволюционная система имеет вид
dL дФ dx дФ '
И = ~дк' ~dt ~ ~~дЬ’>
dG _ \ дФ dg _ 1 дФ
dt щ dg' dt щ 0G ’
dff _1_дФ dh_ 1 дФ
dt щ dh ’ dt п0 дН ,
(1.6.43)
В выписанной системе все переменные медленные,
Ф = Ф (L,G,H9x,g9h)
не зависит явно от t; поэтому, как легко проверить, существует
первый интеграл Ф = const, или в развернутом виде
+ bk(L, G, Д <7, h) cos kx] >no - rri{)(jj\L = const. (1.6.44)
Сказанного достаточно, чтобы понять, насколько глубоко ре¬
зонансный случай отличается от нерезонансного. В функции F,
кроме члена F, существующего в нерезонансном случае, необхо¬
димо рассматривать добавку
зависящую от новой медленной переменной и вызванную исключи¬
тельно резонансностью явления. Эта добавка в свою очередь ведет
к тому, что эволюционная система будет содержать 6 уравнений,
а не 4, как в нерезонансном случае. Исследование эволюционной
резонансной системы поэтому представляет большие трудности,
чем исследование нерезонансной системы.
В резонансном случае не имеет места «теорема Лапласа» о со¬
хранении величины большой полуоси орбиты. Большая полуось эво¬
люционирует. В резонансном случае эволюционная система имеет,
как и в нерезонансном, первый интеграл, отражающий постоянство
новой гамильтоновой функции. Однако структура этого интеграла
существенно сложнее структуры аналогичного интеграла в нерезо¬
нансном движении.
00
56 Очерк первый. О невозмущенном и возмущенном движении спутника
7. Спутник в поле тяготения Земли
Анализ его движения может быть проведен только что изло¬
женным методом осреднения.
Сила ньютоновского притяжения (1.2.1) и соответствующая
силовая функция (1.2.2) лишь приближенно описывают силу при¬
тяжения, действующую на спутник со стороны реальной Земли.
Если бы Земля была совершенно шарообразна и однородна или же
состояла бы из однородных концентрических слоев, то формулы
(1.2.1) и (1.2.5) были бы верны. На самом деле этого нет. Земля не¬
сколько «сплюснута» в направлении полюсов (в очень малой степе¬
ни также и «с боков»), не совсем симметрична, неоднородна, в ре¬
зультате чего поле сил, создаваемое Землей, имеет довольно слож¬
ную структуру. В качестве более хорошего, чем (1.2.2), приближения
к реальному полю сил берут силовую функцию в следующем виде:
u = »=fM. (ил)
Здесь М — масса Земли, / — универсальная постоянная тяготения,
R — экваториальный радиус Земли, р — географическая широта
точки (отстоящей от центра Земли на расстоянии г). Коэффици¬
енты Д имеют фиксированные безразмерные значения. Функции
Pk представляют собой полиномы Лежандра, определяемые следу¬
ющим образом:
Ро(х)= 1,
Р\(х) = X,
Р2(х) = -{Ъх2 - 1),
Р3{х) = ^(5ж3 - Ъх),
Рп(х) =
1
dn
(х2 - 1)".
(1.7.2)
2п • п\ dxn
Таким образом, силовая функция (1.7.1) зависит не только от рас¬
стояния до центра притяжения, как силовая функция (1.2.5), но еще
и от широты места. Силовая функция (1.7.1) предполагает, что поле
сил осесимметрично (относительно оси, проходящей через полю¬
сы Земли). Более точное выражение для U учитывает и «боковую
7. Спутник в поле тяготения Земли
57
сплюснутость» поля сил, его несимметрию. Тогда U будет зависеть
еще и от долготы места; однако для нас достаточно ограничиться
выражением (1.7.1). Видим, что (1.7.1) представляет собой сумму
ньютоновского потенциала (1.2.5) и добавочных членов, которые,
по определению возмущений, должны быть малы по сравнению
с основным (первым) членом. Действительно, по последним дан¬
ным, коэффициенты Д в (1.7.1) имеют такие значения:
/2 = -1082,2 ,п~6 4
/З = 2,3 --6
-6
10“
Д = 2,1
10“
10“
(1.7.3)
так что даже самый большой из этих коэффициентов 12 дает добав¬
ку порядка десятой доли процента, а остальные коэффициенты —
еще на несколько порядков
меньше. Коэффициент /2 ха¬
рактеризует наиболее суще¬
ственное отличие поля тя¬
готения реальной Земли от
«Земли» идеальной шаровой.
Это отличие вызвано замет¬
ным сжатием Земли в поляр¬
ном направлении.
Рассмотрим влияние ос¬
новного возмущения на дви¬
жение спутника в поле тяго¬
тения Земли, пользуясь из¬
ложенными выше сведения¬
ми об асимптотических ме¬
тодах. Задача о движении спутника в поле тяготения «сжатой» Зем¬
ли доставляет прекрасную иллюстрацию к асимптотическим мето¬
дам нелинейной механики. Вместе с тем эта задача является одной
из основных задач во всей теории движения искусственных спут¬
ников. Итак, возмущающая силовая функция
// /R\2 \ . 2
Рис. 1.11. Орбита спутника
в экваториальной системе координат
(1.7.4)
Вспоминая определение аргумента широты и — и v и на-,
клонения г орбиты к экватору, можем, пользуясь вспомогательным
58 Очерк первый. О невозмущенном и возмущенном движении спутника
чертежом (рис. 1.11), написать
siтр — sin г sin и. (1.7.5)
Гамильтонова функция F отличается от U слагаемым, зависящим
только от одной переменной L, а эта переменная, как показано в
«Отступлении об асимптотических методах», не эволюционирует.
Поэтому вместо среднего значения F в четырех эволюционных
уравнениях (1.6.30) достаточно рассмотреть среднее значение U.
Это значение согласно формулам (1.7.4), (1.7.5), (1.6.27) опреде¬
лится так:
27Г
U — -?--2 f [3 sin2(o; + v) sin2 i - l] —dv. (1.7.6)
2 2тг У L V y/JIp
0
V
Подставляя r = , и производя необходимые действия,
1 + е cos v
получим
f7=ip?<|-3cosIi>- С'7'7»
или, подставляя вместо оскулируюших элементов их выражения
через элементы Делоне (что можно получить из формул (1.5.5)),
_ 1 n2I2R2 ( Н2\ ,
Видим, что U не содержит элементов g, h. Поэтому, кроме инте¬
грала
L = Lo,
уравнения движения имеют интегралы
G = Go, Н = Н0.
В обычных оскулирующих элементах это значит, что
а = const, е = const, i = const. (1-7.9)
Конечно, тогда и р = а(1 - е2) = const. Итак, сжатие Земли не ме¬
няет форму орбиты и ее наклонение к экватору (уместно напомнить,
что речь идет об основных эффектах движения, описываемых осред-
ненными эволюционными уравнениями). Весь эффект эволюции
оказывается заключенным в изменении элементов g и ft, то есть
в изменении долготы восходящего узла П и аргумента перигея со.
7. Спутник в поле тяготения Земли
59
Эти изменения легко определяются подстановкой силовой функ¬
ции (1.7.8) (вместо F) в оставшиеся эволюционные уравнения для g
и Л и обратным переходом от Н, G к оскулирующим элементам.
Результат таков:
Итак, под влиянием сжатия Земли плоскость орбиты прецес-
^ирует со скоростью (1.7.10), а сама орбита, не меняя своей формы,
прецессирует в своей плоскости со скоростью (1.7.11). Движение
плоскости орбиты — попятное (Ij < 0, cos г > 0) (рис. 1.12). Для
многих советских искусственных спутников наклон орбиты к плос¬
кости экватора г ^ 65°. При этом величина 1 - 5 cos2 г мала и дви¬
жение перигея орбиты происходит очень медленно по сравнению
с движением узла орбиты. Типичная скорость движения узла ~ 3
градуса в сутки, скорость движения перигея ~ 0,5 градуса в сутки.
Формулы (1.7.10), (1.7.11) опубликованы, например, в статье
Д. Е. Охоцимского, Т. М. Энеева, Г. П. Таратыновой в № 1а журна¬
ла «Успехи физических наук» за 1957 год [1.12] 12\ В этой статье
речь идет также о возмущениях в движении спутника, вызывае¬
мых действием верхней атмосферы. Ведь на тех высотах, где летает
спутник, атмосфера хотя и очень разрежена, но все-таки достаточно
существенна, чтобы затормозить движение спутника. Он понемногу
из-за этого приближается к Земле (и в конце концов падает на Зем¬
лю). В настоящей книге не будет рассматриваться влияние атмосфе¬
ры на орбиту; интересующийся этими вопросами читатель может
найти подробный анализ невозмущенного и возмущенного движе¬
ния спутника в книгах Д. Е. Охоцимского [1.13] и П. Е. Эльясбер-
га [1.14]. Отличный материал о проблемах механики космического
полета изложен в книге М. Б. Балка [1.15], в которой, в частности,
обращает на себя внимание читателя пункт «Парадокс спутника»
(с. 287). Этот парадокс в книге М. Б. Балка сформулирован так:
«Вследствие торможения атмосферой линейная скорость спутника,
|2* В этом номере журнала и преддверии запуска 1-го советского искусственного
спутника (4 октября 1957 года) группа ученых-механиков опубликовала свои уже
законченные работы по динамике искусственных спутников Земли и траекториям
лунных перелетов.
(1.7.10)
60 Очерк первый. О невозмущенном и возмущенном движении спутника
Рис. 1.12. Возмущенная орбита спутника в гравитационном поле Земли:
а — движение в плоскости орбиты; б — движение плоскости орбиты
движущегося по орбите, близкой к круговой, возрастает; ускоре¬
ние в направлении движения оказывается таким же, каким бы оно
было, если бы сила лобового сопротивления изменила свое направ¬
ление и толкала бы спутник вперед» (! — В. Б.).
Если читатель (с карандашом и бумагой в руках) не сможет сам
догадаться, почему получается этот парадокс, то стоит прочитать
об этом в книге М. Б. Балка (см. также очерк седьмой).
Ряд эффектов динамики искусственных спутников, особен¬
но аэродинамические эффекты, обсуждаются в обзорной статье
Л. И. Седова [1.19].
Дополнительные комментарии к этому изданию. Уравнение (1.6.1)
плоских колебаний (и вращений) спутника на эллиптической орби¬
те, опубликованное автором в 1959 г. [1.18] (см. также [1.17]), оказа¬
лось благодатной ареной как для изучения динамических эффектов
проблемы, так и для приложения новых методов анализа. В яв¬
ном виде это уравнение впервые появилось в 1956 г. во внутреннем
7. Спутник в поле тяготения Земли
61
отчете организации, известной сейчас как Институт прикладной
математики им. М. В. Келдыша Российской Академии Наук (ИПМ
РАН им. М. В. Келдыша).
С того момента — более полувека прошло! — это уравнение
продолжает привлекать неослабевающее внимание ученых. Пер¬
вые исследования, выполненные аналитическими и численными
методами, были опубликованы в [ 1.18’], [ 1.20]—[ 1.22], и объеди¬
нены в монографии автора [1.17] и частично в настоящей книге
(очерк шестой). Обзор В. А. Сарычева [1.23] содержит результаты
этих и других исследований уравнения (1.6.1) вплоть до 1978 г.
В статьях [ 1.24]—[ 1.26] В. А. Сарычев и его коллеги продолжили
начатые ими в [1.21] исследования периодических вращений и ко¬
лебаний спутника на эллиптической орбите и устойчивости таких
движений.
Надо отметить, что фазовые траектории, изучавшиеся в на¬
званных выше работах, имели регулярный (периодический и иног¬
да квазипериодический) характер. В начале 1980-х анализ плоских
движений спутника на эллиптической орбите вышел на качествен¬
но новый уровень. К этому времени теория динамических систем
и техника вычислений были настолько разработаны, что позволили
изучать не только изолированные траектории системы, но и пол¬
ную структуру ее фазового пространства. Оказалось, что, несмотря
на детерминированность начальных условий, типичной ситуаци¬
ей являются почти хаотические траектории, которые заполняют
фазовое пространство наподобие «моря»; в этом хаотическом «мо¬
ре» есть «острова» периодических и квазипериодических движений.
Подобная структура фазового пространства тесно связана с неин-
тегрируемостью динамической системы.
В этих разработках использовались и движения, описываемые
уравнением (1.6.1). С начала 1980-х во многих странах было опубли¬
ковано множество работ по исследованию уравнения (1.6.1) имен¬
но с указанной выше точки зрения. Результаты этих исследований
представлены в [ 1.27]—[ 1.33]. В случае е = 0 (круговая орбита)
уравнение (1.6.1) интегрируемо и его фазовое пространство запол¬
нено регулярными траекториями. Для малых величин е появляются
тонкие хаотические области — слои, которые делят фазовое про¬
странство и сливаются, образуя хаотическое море, когда величина
эксцентриситета орбиты возрастает (время от времени при этом
наблюдаются удивительно красивые фазовые портреты).
Следует упомянуть, что первые вычисления фрагментов фа¬
зовых портретов для уравнения (1.6.1), проникнутые описанными
62 Очерк первый. О невозмущенном и возмущенном движении спутника
выше идеями, были опубликованы в более ранних статьях [1.21]
и [1.41]. В последние годы в работах А. Д. Брюно и его сотрудни¬
ков [ 1.34]—[ 1.40] достигнут еше более глубокий уровень изучения
уравнения (1.6.1). Эти исследования основаны на новом конструк¬
тивном методе анализа сильно нелинейных задач, разработанном
А. Д. Брюно [1.34]. Как пишут авторы в [1.37]: «Для начала мы
решили применить этот метод к конкретной задаче, не слишком
простой, но и не слишком сложной. В качестве такой задачи мы
взяли задачу о колебаниях спутника в плоскости эллиптической ор¬
биты». В частности, метод, разработанный А. Д. Брюно, позволяет
обойти трудности, связанные с тем, что уравнение (1.6.1) сингу¬
лярно для значений е, близких к 1 (для е = 1 коэффициент при
старшей производной обращается в 0 в точке v — 7г). Были изу¬
чены семейства периодических решений в общем случае — для
произвольных величин параметра п2 (в задачах механики \п2\ < 3)
и для всех величин эксцентриситета в интервале 0 < е < 1. Ис¬
следованы также устойчивость и асимптотики этих семейств для
малых и больших величин п2 и правила, определяющие их струк^
туру. Построены пределы этих семейств при е —> 1; одно из таких
предельных семейств сворачивается во фрактальную спираль.
Очерк второй
О втором рождении старой задачи,
или что получится, если две массы
поместить на чисто мнимое расстояние
друг от друга
... И чем больше он смотрел на шнурок
колокольчика, тем больше он чувствовал,
что он где-то видел что-то очень похо¬
жее... Где-то совсем в другом месте, ко¬
гда-то раньше...
А. А. Милн
«Винни-Пух и все, все, все»
— А потом?
— Тогда мы все скажем «АГА».
— Все трое?
-Да.
А. А. Милн
«Винни-Пух и все, все, все»
1. От Эйлера до наших дней
В первом очерке уже рассказывалось о движении спутни¬
ка в поле тяготения земного сфероида. Мы видели, что хоро¬
шо разработанные аппараты уравнений в оскулирующих элемен¬
тах и асимптотических методов нелинейной механики позволяют
весьма просто установить основные возмущения в орбите спут¬
ника, вызванные сжатием Земли. Полученные формулы дают на¬
глядную геометрическую картину движения спутника, выявляю¬
щую качественные и количественные закономерности движения.
64
Очерк второй. Второе рождение старой задачи
Но этого, конечно, недостаточно для точного расчета орбит. Точ¬
ное решение задачи о движении спутника в поле тяготения, опи¬
сываемом силовой функцией (1.7.1), невозможно в силу неинте-
грируемости уравнений движения. Но если заняться глубже во¬
просом интегрируемости (что мы и намерены сделать), то выяв¬
ляются удивительные вещи, замечательные с неожиданной точки
зрения.
Обнаружилось, что эта задача в известном смысле эквивалент¬
на старой классической проблеме движения точки в поле тяготения
двух неподвижных притягивающих ньютоновских центров. Эта по¬
следняя проблема, как известно, была поставлена и сведена к квад¬
ратурам Леонардом Эйлером. С тех пор в течение двух столетий
эта задача занимала многих ученых, прельщенных как академиче¬
ской красотой ее, так и призрачным ее сходством со знаменитой
«задачейтрех тел», имеющей столь огромное значение для небес¬
ной механики и механики космического полета. Действительно, так
называемая «ограниченная задача трех тел» рассматривает движе¬
ние непритягивающей материальной точки в поле тяготения двух
свободных ньютоновских центров (которые, стало быть, движутся
относительно друг друга по кеплеровским законам). Решение огра¬
ниченной задачи трех тел позволило бы, например, непосредствен¬
но исследовать движение космического корабля от Земли к Луне.
Задача о движении в поле двух неподвижных центров отличается
от ограниченной задачи трех тел «всего лишь» тем, что притят
гивающие центры закреплены. Не удивительно, что имели место
многочисленные попытки применить известное решение эйлеро¬
вой задачи к поиску неизвестного решения ограниченной задачи
трех тел. Но эти попытки зримыми успехами не увенчались. «Зада¬
ча двух неподвижных центров» не нашла конкретного применения
в небесной механике, и наиболее интересные ее исследования но¬
сили до последнего времени абстрактно-математический характер.
Появление искусственных спутников стимулировало бурный
прогресс механики и привело, в частности, к открытию глубокой
и неожиданной аналогии между задачей двух центров и задачей
о движении спутника в поле тяготения Земли. Таким образом, ста¬
рая задача получила новое и очень важное конкретное приложение
к теории движения искусственных спутников Земли. Первая публи¬
кация [2.1], устанавливающая эту аналогию, появилась в 1961 году
и принадлежала троим соавторам — молодым (тогда) советским
ученым Е. П. Аксенову, Е. А. Гребеникову, В. Г Демину. В последу-
1. От Эйлера до наших дней
65
5 Заказ 1667
66
Очерк второй. Второе рождение старой задачи
ющих публикациях они подробно исследовали движение спутника
в поле тяготения Земли на основе открытой аналогии
Перейдем к рассмотрению этой аналогии вплотную.
2. Связь двух задач
Пусть в двух неподвижных центрах расположены материаль¬
ные точки с массами гп\ и т2 соответственно. Построим систему
координат Oxyz так, чтобы ось Oz проходила через точки тп\ и
m2 (рис. 2.1). Расстояние от О до
массы тп\ обозначим с\, а от О
до 7712 — через С2. Пусть в сум¬
марном поле сил ньютоновского
притяжения к каждой из точек
тп\, 7П2 находится точка с массой
771, движение которой изучается.
Ее движение определяется сило¬
вой функцией
<->
представляющей собой сумму си¬
ловых функций тяготения двух
ньютоновских центров (на что и
указывает индекс (2) в левой ча¬
сти формулы (2.2.1)). Здесь / — универсальная постоянная тяготе¬
ния, Г\, Г2 — расстояния от rri\, 77i2 соответственно до движущейся
ТОЧКИ 777!
Г, = ^Jx2 + у1 + (z - С|)2,
г2 = yjx2 + у2 + (z - с2)2.
^ В книге Д. Брауэра и Дж. Клеменса [2.2], изданной в 1961 году, также со¬
держится краткое упоминание о такой аналогии двух задач. Подробное изложение
рассматриваемых вопросов можно найти в монографии В. Г. Демина [2.3] и в книге
Г. Н.Дубошина [2.4]. Идея замены задачи движения спутника в реальном грави¬
тационном поле какой-то близкой интегрируемой задачей впервые, по-видимому,
была предложена и осуществлена М. Д. Кисликом в 1958-1959 годах [2.5]. В США
аналогичный подход осуществлен в работах Дж. Винти [2.6].
2. Связь двух задач
67
Рассмотрим для примера выражение \jr^
1111
Гг yj V2 — 2 c2z + с\
(2.2.2)
где г = л/х2 + у2 + z2 — расстояние движущейся точки от начала
координат. Обозначив z/r = sin <р (<р — широта движущейся точки,
отсчитанная от плоскости Оху), а = Cj/r, используем известное
в теории полиномов Лежандра разложение
1 00
=f = Z a"p"(sin *)■ (2-2J)
у/1 - lasmifi + а2 ^
Учитывая (2.2.2) и (2.2.3), можно написать
~ = (jJPnisinip). (2.2.4)
Г2 г г/
Здесь Рп — многочлен Лежандра n-го порядка.
Аналогично можно записать и выражение для т\/г\. Тогда
силовая функция (2.2.1) задачи двух центров запишется в виде
*« = 4^{1 + Ё$А(<«4 (2-2.5)
где определяется из равенства
(mi + m2)7fc = т\Ск\ + т2с\. (2.2.6)
И тут невольно напрашивается сравнение силовой функции U(i)
(2.2.5) с уже известной нам силовой функцией U земного сфе¬
роида (см. формулу (1.7.1)). Вид у обеих силовых функций почти
тождествен; они были бы полностью одинаковыми, если бы равны
были постоянные коэффициенты в соответствующих членах разло¬
жений; и так как задача с силовой функцией (2.2.5) интегрируема,
то была бы интегрируема и задача о движении спутника. На самом
деле это, конечно, не так. Ведь разложение (2.2.5) содержит всего
четыре свободных параметра: 7П\, mi, С\, Ci и, значит, можно отож¬
дествить лишь четыре члена разложения (1.7.1) с четырьмя членами
разложения (2.2.5). Естественно такое отождествление провести для
68
Очерк второй. Второе рождение старой задачи
первых членов разложений, то есть потребовать, чтобы
1) тп\ + тп2 = М,
2) тп\С\ + гп2с2 = О,
3) гп\с] + m2cl = MI2R2,
4) Ш|С| + m2cl = М/3Д3.
Более далекие члены разложений U и U(2) при этом совпасть не мо¬
гут, но это не столь важно, так как хорошо известны лишь первые
из констант Д., а другие Д очень малы и их значения все равно
известны плохо.
Таким образом, если выбрать параметры т\,т2,С\,с2 зада¬
чи двух неподвижных центров так, чтобы выполнялись равенства
(2.2.7), то силовая функция U(2), оставаясь силовой функцией этой
задачи, вместе с тем в главных своих членах будет совпадать с си¬
ловой функцией U поля тяготения Земли. Иначе говоря, если по¬
тенциал земного поля тяготения немного «испортить», переделав
ему «хвостик» (заменяя весьма малые коэффициенты при членах
разложения с индексами к ^ 4 тоже весьма малыми, но другими
коэффициентами), то задача о движении спутника в поле тяготения
Земли (или какой-либо иной планеты) становится интегрируемой.
При этом движение точки под действием такого «испорченного»
потенциала будет весьма близко к движению под действием перво¬
начального потенциала, так как действие главных членов потенци¬
ала учитывается точно. А в силу интегрируемости задачи получа¬
ющиеся после интегрирования точные формулы должны отразить
все эффекты влияния главных членов силовой функции поля тяго¬
тения Земли (а не только эволюционные эффекты, рассмотренные
нами выше).
Итак, интегрируемая задача двух неподвижных центров с вы¬
сокой точностью совпадает с задачей о движении точки в поле
тяготения земного сфероида, если параметры задачи двух центров
выбраны специальным образом, а именно удовлетворяющими урав¬
нениям (2.2.7). Алгебраическая система (2.2.7) без труда разреша¬
ется. Из первых двух уравнений (2.2.7) получаем
Мс2 Мс\
Ш\ = , тп2 = .
С\ - С2 С\ - с2
Подставляя (2.2.8) во вторые два уравнения (2.2.7), получим
С|С2 = -I2R2, С|С2(с2 + С|) = -I3R3,
(2.2.8)
(2.2.7)
2. Связь двух задач
69
70
Очерк второй. Второе рождение старой задачи
или
I R
С\С2 = -I2R2, С2 + С\ — (2.2.9)
h
Отсюда видно, что С\ и С2 являются корнями следующего квадрат¬
ного относительно с уравнения:
с2 -^c-I2R2 = 0. (2.2.10)
h
Решая это уравнение, получим
Подставляя теперь (2.2.11) в (2.2.8), полностью определим
параметры Ш|,Ш2,С|,С2. Вспоминая численные значения вели¬
чин /2Д3 {h ~ — 10—3, /3 ~ 1СГ5), обнаружим удивительное обсто¬
ятельство: расстояния Ci и С2 и массы mi и m2 необходимой нам
задачи двух центров оказываются комплексными! Тем самым мы
получили обобщение классической задачи на комплексные массы
и расстояния. Пугаться этого не следует — ведь силовая функция
остается действительной, а вместе с ней — и движение.
Коэффициент /2 характеризует сжатие Земли, а /3 — ее асим¬
метрию относительно плоскости экватора. Эта асимметрия весьма
мала (IJ3/J2I ~ КГ2), и ею можно пренебречь. Если учитывать толь¬
ко сжатие Земли, положив /3 = 0, то получим
Го, = т2 = у, с, = iRy/\h\, с2 = -iRyfihl (2.2.12)
.Итак, движение спутника в поле тяготения сжатой, симмет¬
ричной относительно экватора Земли можно интерпретировать за¬
дачей (интегрируемой) о движении точки в поле двух неподвижных
центров, имеющих одинаковые массы и расположенных на чисто
мнимом (!) расстоянии друг от друга. (Расстояние было бы дей¬
ствительным для вытянутой, а не сжатой Земли.) Найденная Аксе¬
новым, Гребениковым и Деминым аналогия двух задач позволила
рассмотреть движение спутника в поле тяготения Земли в замкну¬
том виде — в эллиптических функциях (см. ниже). Надо сказать,
(2.2.11)
3. Интегрирование. Система координат
71
что классическая задача рассматривалась в основном в плоском
случае, а траектории спутника — существенно пространственные,
что само по себе стимулировало дальнейшее исследование пробле¬
мы двух неподвижных центров.
Важно отметить, что открытие аналогии двух задач далось не
сразу. К нему исподволь подбирались в течение нескольких лет
ученые разных стран. Дж. Винти [2.6] в США, М. Д. Кислик [2.5]
в СССР и другие ученые приводили задачу о движении спутника
в земном поле тяготения к интегрируемому виду с помощью так
или иначе «подпорченного» потенциала. Но только рассмотрение
проблемы Аксеновым, Гребениковым, Деминым в указанном выше
виде внесло полную ясность в постановку, место и характер зада¬
чи. Ранее рассмотренные случаи получаются отсюда как частные.
Сейчас задачу с двумя неподвижными центрами, расположенны¬
ми на некоем комплексном расстоянии друг от друга и обладаю¬
щими комплексными массами, называют обобщенной задачей двух
неподвижных центров. В таком виде задача продолжает привлекать
внимание исследователей (В. М. Алексеев [2.7] и др.).
3. Интегрирование. Система координат
Теперь можно приступить к интегрированию задачи. Будем рас¬
сматривать случай (2.2.12). Введем обозначение с = Ry/\l/\; тогда
Не всякая система координат хороша для интегрирования за¬
дач. Обычно каждая конкретная задача требует разумного выбора
системы переменных, в которых анализ проходит наиболее удоб¬
ным образом; выбор такой системы переменных не всегда прост;
над этим стоит поломать голову, так как это предопределяет успех
(или неудачу) исследования. В нашей задаче вместо декартовых ко¬
ординат ж, у, z введем криволинейную систему координат А, р, w
так, что
у/х2 + у2 + (z + гс)2 у/х2 + у2 + (z - гс)
(2.3.1)
(2.3.2)
72
Очерк второй. Второе рождение старой задачи
Разберем смысл новых переменных. Из (2.3.2) можно получить
_2
X2 + у2
с2(1 + А2)
ж2 + у2
с2(1 -/X2)
+
с2Х2
= 1,
Z2
= 1,
с2»2
X
— =
tg W.
У
(2.3.3)
Отсюда видно, что геометрическое место точек А = const (0 ^ А < +оо)
есть сжатый эллипсоид вращения с осью симметрии, направленной
по оси z старой системы координат. Малая полуось эллипсоида
имеет величину сА, большая полуось — величину c\J 1+А2 (рис. 2.2).
Геометрическое место точек /х = const есть однополостный гипер¬
болоид вращения (с той же осью симметрии z). (При этом гипербо¬
лоиды заполняют все пространство при прохождении у2 от 0 до 1.)
Наконец, w = const (-00 < w < +оо) — плоскость, содержащая
ось z (меридиональная плоскость). В этих переменных
Г| = yjx2 + у2 + (z + ic)2 = с(А + г/х),
г2
= yjx2 + у2 + (z - ic)2 = с(А - г»,
а поэтому
U( 2) = /М-
(2.3.4)
с(А2 + /х2)
Так как U(i) > 0 всегда, то область определения А такова: 0 < А < оо.
Рис. 2.2. Эллиптическая система координат
4. Метод Гамильтона—Якоби
73
Выписывая в силу (2.3.2) выражения производных по време¬
ни х, у, z через производные можно получить выражение
кинетической энергии Т = -(х2 + у2 + i2) через А, р, w, A, /i, w.
Оказывается тогда, что
т = + т^2 + 0+а2)(| " ^2}- (215)
Полная энергия движения будет
Н = Т-17(2). (2.3.6)
4. Метод Гамильтона-Якоби
Здесь и в дальнейшем нам понадобится метод Якоби интегри¬
рования уравнений динамики. Изложим его без вывода и в том
простейшем виде, в каком он будет употребляться в этой книге,
отсылая за подробностями к любому курсу аналитической или не¬
бесной механики (см., например, [2.8,2.9]).
Пусть кинетическая энергия зависит от обобщенных (криволи¬
нейных) координат gi, 9з и соответствующих скоростей q\, q^, qy
Т = T(quq2,q3,q],q2,q3). (2.4.1)
Тогда частные производные
дТ дТ дТ ,
Р1 = Pi = Pi = (2.4.2)
dq\ dq2 dq3
называются обобщенными импульсами. Выразим из формул (2.4.2)
скорости gi,?2>?3 через обобщенные импульсы Р\,Р2,Рз (пред¬
полагая, что это возможно) и подставим их в выражение (2.4.1)
кинетической энергии. Получим ее преобразованное выражение
т = T{q\,q2,q2,p\,p2,p3).
Пусть U(q\,q2,q2) — силовая функция поля сил, в котором про-
исходит движение. U не зависит явно от времени. Тогда полная
энергия движения
Н = т-и
будет постоянна:
H{q\,q2,q2,P\,p2,Pi) = h. (2.4.3)
Функция H(q\, <72, Яз,Р\,Р2,Рз) называется функцией Гамильтона.
74
Очерк второй. Второе рождение старой задачи
Уравнения движения в этом случае имеют следующий канони¬
ческий вид'.
<“♦>
и называются уравнениями Гамильтона.
Составим уравнение в частных производных, заменив в (2.4.3)
dW dW dW
P\,P2,Pi на —, ——, ——:
6q, dq2 dq3
/ dW dW dW\ u /ЛЛС,
H — — — j= H. (2.4.5)
Это уравнение называется уравнением Гамильтона—Якоби. Функ¬
ция W в этом уравнении подлежит определению. А именно, нужно
найти такое решение уравнения (2.4.5) Гамильтона—Якоби
J^(/l, ^2? Я.\ч 0.2) 9з)?
чтобы оно зависело от трех постоянных: от Л и еще двух произволь¬
ных постоянных а2, аз. Если такую функцию W удалось найти, то
общий интеграл системы (2.4.4) канонических уравнений движения
записывается в виде
dW dW dW
Ж=1 + (!" а^=А'
dW dW dW
о Pi9 "о Р2> Р^9
dq\ dq2 dq}
(2.4.6)
Здесь /3|, /32, /?з — новые произвольные постоянные. Формулы (2.4.6)
дают связь координат q\, q2, q2 и импульсов P\,P2,Pi со временем t
и шестью произвольными постоянными h, а2,а2, (3\, /32, (32. Сле¬
довательно, эти формулы полностью решают динамическую задачу.
(Для завершения исследования нужно из системы уравнений (2.4.6)
получить явные зависимости координат и импульсов от времени
и произвольных постоянных. Это обычно нелегкая работа.)
5. Интегрирование
Итак, следуя методу Гамильтона—Якоби, выпишем обобщен¬
ные импульсы для нашей задачи:
5. Интегрирование
75
дТ 2 А2 + /t2 •
Рх~ дх~с 1 + А2 ’
дТ 1Х2 + ц2
P/t = ЖТ = С г-/Х,
ofi \ ~ Р
дТ
Ри, = 7Г7 = С2( 1 +А2)(1 -n2)w.
aw
Выражая отсюда скорости через импульсы и подставляя в выраже¬
ние (2.3.5) для Г, получим преобразованную кинетическую энергию
в виде
— 1 Г 1 + А2 2 1 — //2 2 Pw 1 / \
т = 2? { + VT^P,‘ + (1 + А2)(1 - ц2) } (15-2)
и функцию Гамильтона в виде
H = T-U, (2.5.3)
где С/(//, А) дается формулой (2.3.4). Теперь можно сразу соста¬
вить уравнение Гамильтона—Якоби, принимающее после умноже-
(2.5.1)
ния на 2с2(А2 + ц2) вид
2 JdW\2 . 2 JdWX2
( '(ж) +(|-',>(ж)+
1 1 \fdw\
2
* 1 - р2 1 + А2) У dw )
= IfMcX + 2hc2(X2 + ц2). (2.5.4)
Будем искать нужное нам решение этого уравнения в виде
W = W, (А) + W2(p) + W3(w) (2.5.5)
и положим
dW?,
—— = аз = const (И^з = азтд). (2.5.6)
dw
Тогда уравнение (2.5.4) Гамильтона—Якоби будет удовлетворено,
если
(1 + А2) ( ^ ) = —'—+ 2/МсА + 2hc2X2 + 2а2, (2.5.7)
/dtfiV = _
1 V dX ) 1 + А2'
(1-/г2)(^) =-T^—1a\ + 2hc1ii1-2et7, (2.5.8)
1 -Р2
76
Очерк второй. Второе рождение старой задачи
где «2 — новая постоянная. Из этих выражений JV|(A) и W2(p)
легко вычисляются квадратурами; тем самым определяется и W,
имеющая вид
ш=1Шлх+!
(2.5.9)
где
1
(2.5.10)
L(X) = а\ + 2(1 + X2)(hc2X2 + fMcX + а2),
М(ц) = -а] + 2(1 - fi2)(hc2fi2 - а2).
Теперь можно завершить сведение задачи к квадратурам, об¬
ращаясь к формулам (2.4.6). Однако получающиеся после этого
уравнения непосредственно необратимы (то есть невозможно их
разрешить относительно координат). Поэтому несколько отойдем
от традиционного метода Гамильтона—Якоби. А именно, восполь¬
зуемся одновременно соотношениями (2.4.6) и (2.5.1) для импуль¬
сов; получим
dW %/Z
Рх
Р» =
Pw
дх
т_
дц
0W
dw
1 + А2
л/М
= сг^±£л,
1 +А2
, А2 + fi2
1-//2 1-Ц2^
= «з = с2(1 + А2)(1 - fi2)w.
(2.5.11)
Введем теперь новую независимую переменную г, связанную
со старой t соотношением
dt = с2(А2 + fi2)dr;
(2.5.12)
тогда только что написанные уравнения дают
dfi
dr
dw
dr
= у/Щр),
X 2 + ц2
«3-
(2.5.13)
(1 + A2)(l — p2)
Первые два уравнения немедленно приводят к квадратурам:
d\ Г dn
/
л/Щ)
— Т + fix,
/
Vм (р)
= Т + Рц,
(2.5.14)
6. Область движения спутника
77
где (3\, /3/х — новые произвольные постоянные. Если эти квадрату¬
ры удается обратить, то есть получить явные выражения А(т), //(т),
то правая часть третьего из уравнений (2.5.13) будет являться явной
функцией от т, и тогда
Г А2 + //2
W = 0C3J (1+A2)(I -/*2) dr + /3»’ (2-5Л5)
что вместе с /г(т) и А(т) дает параметрическое (параметр т) уравне¬
ние траекторий (Дш — последняя произвольная постоянная). Нако¬
нец, из (2.5.12) получим и явную зависимость времени t от этого же
параметра:
t = c2 J{\2 + fi2)dT, (2.5.16)
и задача будет полностью разрешена.
б. Область движения спутника
Итак, дело требует прежде всего обращения квадратур (2.5.14).
Это не очень простая задача. Так как подрадикальные полиномы
имеют четвертый порядок, то обращение может быть проведено
в эллиптических функциях Якоби, но, в зависимости от значений
корней полиномов, каждый раз по-разному. Имеются трудности
также и с вычислением корней полиномов четвертого порядка че¬
рез коэффициенты полиномов, хотя при качественном анализе тра¬
екторий этого вычисления можно избежать.
Из определения криволинейной системы координат следует,
что переменные определены в области
-00 < W < +00, ^
О ^ А < +оо, I (2.6.1)
— 1 ^ ц ^ +1, J
и поэтому при анализе движения во внимание нужно принимать
лишь те значения А, /г, w, которые попадают в область (2.6.1)
определения движения. Учитывая это, рассмотрим качественно ти¬
пичную «спутниковую» ситуацию.
Пусть значение постоянной энергии h < 0. Тогда М([л) -+ +оо
при ц -» ±оо и M(fi) < 0 при fi = ±1 (что легко видеть из формулы
(2.5.10) для полинома Так как в действительном движении
обязательно должно быть М(ц) > 0, как и L(А) > 0 (иначе получа¬
ются мнимые значения для координат и скоростей), то на интервале
78
Очерк второй. Второе рождение старой задачи
-1 < // < +1 определения // должно
быть два действительных корня //ь //2 •
Полином М(/л) биквадратный, по¬
этому всякому положительному кор¬
ню сопутствует такой же по модулю
отрицательный. В результате M(fi)
имеет вид, указанный на рис. 2.3.
В реальном движении -1 ^//j ^
2^1? М\ = -Ц2, значения \i-\i\
и ц = Ц2 отвечают одному и тому же гиперболоиду; отрицательное
значение // соответствует движению в области z < 0 (южном полу¬
шарии), положительное — в области z > 0 (северном полушарии).
Таким образом, в рассматриваемом движении Ц2 ^ ц] = li\> что
соответствует движению «вне» гиперболоида /х2 = /xf = \.
Обратимся теперь к полиному L(А) (2.5.10). Распишем его
подробно:
L(А) = 2hc2X4 + 2/МсЛ3 + (2he2 + 2а2)А2 + 2/МсЛ + а\ + 2а2. .
При том же условии h < 0, L -¥ -со при А -»• ±оо.
Далее, из анализа полинома
М(ц) ясно, что
М{0) = -а\ - 2а2 > 0,
в полиноме L(А) все коэффици¬
енты при четных степенях А от¬
рицательны (в том числе и сво¬
бодный член), а коэффициенты
при нечетных степенях А поло¬
жительны. Значит, при А ^ 0
L( А) < 0. Все действительные
корни лежат на полуоси А > 0.
Этих (действительных) корней
либо два, либо четыре. По тео¬
реме Виета произведение всех
четырех корней равно свобод¬
ному члену, деленному на ко¬
эффициент при старшем члене:
Рис. 2.4. Полином L(А) (случай
двух действительных корней)
Рис. 2.5. Полином L(А) (случай
четырех действительных корней)
А1А2А3А4 =
<*з + 2а2
2 he2
>0,
6. Область движения спутника
79
Рис. 2.6. Область движения
спутника
Рис. 2.7. Область эволюционного
движения спутника
и, стало быть, действительных положительных корней может быть
два или четыре. Если действительных корней два (пусть Aj и А2),
то полином L(А) имеет вид, изображенный на рис. 2.4. Итак,
в действительном движении L(А) > 0, что возможно лишь при
Ai ^ А ^ А2, то есть движение заключено между двумя эллип¬
соидами А = Aj и А = А2. Если действительных корней четыре
(рис. 2.5), то А во все время движения все равно заключено между
двумя значениями корней (пусть между Ai и А2). Подведем итог.
При единственном условии h < 0 движение всегда происходит вне
гиперболоида = pi (-//* ^ р ^ //*) и внутри полости, заключен¬
ной между двумя эллипсоидами А = А| и А = А2 (0 < А| ^ А ^ А2),
так что движение происходит в эллипсоидальном кольце, изобра¬
женном на рис. 2.6.
Этот результат можно лучше прочувствовать, используя полу¬
ченную ранее приближенную (эволюционную) картину движения.
Вспомним, что в плоскости орбиты оскулирующий эллипс медлен¬
но прецессирует, не меняя своей формы, так что расстояние спутни¬
ка от центра Земли никогда не меньше гп и не больше га. Но сама
плоскость орбиты медленно прецессирует вокруг оси Земли, так
что кольцо г = гж заметает пояс на сфере радиуса г = гп, угловая
ширина пояса равна 2г (где г — угол наклона орбиты к экватору).
Аналогично, кольцо г = га заметает на сфере радиуса г = га по¬
яс той же угловой ширины. В результате эволюционное движение
происходит в сфероидальном кольце, изображенном на рис. 2.7.
Это кольцо очень похоже на описанное выше эллипсоидальное
кольцо точной области определения движения, но все же отлича¬
ется от него. Отличие это чрезвычайно мало. В самом деле, экс-
80
Очерк второй. Второе рождение старой задачи
центриситет внутреннего, например, эллипсоида €\ = + А^).
Но из (2.3.2) можно получить г2 = с2(1 + А2), где гэ — расстояние
спутника до центра Земли в момент прохождения спутником эква¬
ториальной плоскости. Поэтому
Следовательно, эллипсоидальное кольцо мало отличается от сфе¬
роидального.
При подробном разборе возможных случаев ограниченного
движения (h < 0) выявляются не только спутниковые траекто¬
рии, лежащие целиком вне поверхности Земли, но и баллистиче¬
ские траектории, лишь частично лежащие над поверхностью Земли
(для таких траекторий внутренний граничный эллипсоид А = Ai
лежит под поверхностью Земли). Может оказаться, что траектория
целиком лежит на одном эллипсоиде (а не в пространстве между
двумя эллипсоидами); это соответствует наличию кратных корней
в полиноме L{\) (например, А| = А2).
Отсылая за подробностями к первоисточнику [2.1], разберем
лишь частный случай. Он поможет нам понять, как анализ инте¬
грируемых задач доводится до «почти» последнего этапа — явных
формул, дающих, например, в рассматриваемой задаче зависимости
А(г), ц(т). Если такие явные формулы есть, то они позволяют про¬
вести подробный анализ свойств траекторий и (вот он, «последний
этап») довести этот анализ до числовых результатов.
Для этих целей нам понадобятся сведения об эллиптических
функциях Якоби.
7. Эллиптические функции Якоби
f dx
Интеграл типа / — - , где G(x) — полином третьего или
J у/G(x)
четвертого порядка, может быть приведен к интегралу следующего
вида:
~ Ю“3.
Z
F(k, <р) = j
dtp
/
о
у/\ — k2 sin2 (р
о
(2.7.1)
7. Эллиптические функции Якоби
81
Этот интеграл называется нормальным эллиптическим интегралом
Лежандра первого рода; при этом 0 ^ k ^ I; число к называется
модулем эллиптического интеграла. Определенный интеграл
называется полным интегралом первого рода. Интеграл К (к) — моно¬
тонно возрастающая функция своего аргумента, причем K(0) = ir/2,
if(]) z= оо. Функция К (к) затабулирована; при небольших значе¬
ниях к удобно пользоваться разложением
Здесь двойной факториал, как обычно, означает произведение всех
нечетных (четных) чисел от единицы до 2п — 1 (до 2п) включи¬
тельно.
Обозначим
Зависимость и от <р при некоторых значениях к указана на рис. 2.8.
Задача обращения эллиптического интеграла F(k, (р) означает рас¬
смотрение обратной зависимости р от и вместо известной зави¬
симости и от (р. Величина р, задаваемая как функция от и и к
соотношением (2.7.4), называется амплитудой и и обозначается
(2.7.2)
fc4 + ...+
(2.7.3)
u = F(k, <р).
(2.7.4)
р = am и.
(2.7.5)
U)
8
6
4
2
4К(к)
к = 0,86
7Г
2
7Г
37Г 27Г (р
2
6 Заказ 1667
Рис. 2.8. График функции и(р)
82
Очерк второй. Второе рождение старой задачи
Эллиптическим синусом (sn и) называется синус амплитуды, то есть
sn и = sin (am и). (2.7.6)
Аналогично определяется эллиптический косинус:
сп и — cos (am и). (2.7.7)
Кроме того, вводится функция
dn и = у/ \ - k2 sn2 и, (2.7.8)
называемая дельтой амплитуды. Функции sn и, сп и, dn и носят
название эллиптических функций Якоби.
Ряд задач механики, начиная с задачи о движении маятника,
решается в этих функциях. Задачи динамики космического поле¬
та, рассматриваемые в этом и следующем очерках, тоже приводят
к эллиптическим функциям Якоби. Свойства эллиптических синуса
и косинуса отчасти напоминают свойства тригонометрических си¬
нуса и косинуса. Надо, однако, помнить, что эллиптическая функ¬
ция есть функция двух аргументов и, к. Обозначение аргумента к
обычно опускается, но функции от него зависят! Функции sn и
и сп и периодические с периодом 4К(к), функция dnw — пе¬
риодическая с периодом 2 К (к); sn и и сп w принимают значения
на отрезке [—1,+1], dn и — на отрезке [у/1 - к2, +1].
В следующей табличке приведены некоторые значения эллип¬
тических функций.
и
0
К
2 К
ЪК
4К
sn и
0
1
0
-1
0
СП и
1
0
-1
0
1
dn и
1
х/i -к2
1
у/\ - к2
1
На рис. 2.9 изображены графики функций sn и, сп и, dn и для
некоторых значений к. Величина К (к) играет ту же роль для эллип¬
тических функций, что и величина п/2 для тригонометрических.
Однако, как уже говорилось, К может принять любые числовые
значения на интервале 7г/2 ^ К < оо в зависимости от значения
модуля к. Поэтому период эллиптических синуса и косинуса может
8. Движение полярного спутника Земли
83
О 0,5 К К и
Рис. 2.9. Графики функций snu, спи, dn и
принять любое значение от 2тг до оо. При к = 0 эллиптические
функции вырождаются в тригонометрические с периодом 27г:
к = 0, snu = s\nu, спи = cos и, dnu=\.
При к = 1 эллиптические функции выражаются через непериоди¬
ческие, а именно гиперболические функции:
к— 1, snti = thw, спи = (chu)~\ dnu = (chu)~].
Полезно отметить следующие свойства эллиптических функ¬
ций Якоби:
sn(-w) = - snu, sn(2K — u) = snu, sn2u + cn2u= 1,
cn(-u) = cnu, cn(2 К -u) — - спи, dn2 u + k2sn2u = 1,
dn(-tz) = dnw, dn(2K -u) = dnu, dn2u-k2cn2u = 1 -k2.t
(2.7.9)
Формулы дифференцирования:
d
— sn и = cn и dn и,
du
d
— спи — - snudnu, (2.7.10)
du
d A b?
— dnu ——к snu спи.
du
Теперь мы можем изучить один интересный частный случай
движения спутника.
8. Движение полярного спутника Земли
Рассмотрим формулы (2.5.13) и (2.5.10). Если с*з = 0, то
dw/dr = 0, w = Wo, то есть движение происходит в неподвиж-
6*
84
Очерк второй. Второе рождение старой задачи
ной меридиональной плоскости. При этом
/М
\h\c
L( А) = -2|Л|с2(1 + А2)
ЛГ(^) = -2|Л|с2<1 -^2) (#*2 - ^|х|) •
Имеем из (2.5.14)
02
h
(2.8.1)
(2.8.2)
dfi
О ^21021(1 - /Л2) (l- с2
Обозначив и = ^2Ы(г + /Зд) и с2 |/г/о2| = kj, получим
А
о2
!)
. = [
/ Л/(1 - /*2)(1
^(1-^)0-^)'
Анализируя полином М(^) в общем виде, можно заключить
(рис. 2.3), что из четырех его действительных корней два меньше
или равны единице по модулю, а два строго больше единицы. По¬
этому
1
02
h
> 1 и кр < 1.
Более того, к^ имеет порядок квадрата сжатия Земли: к^ ~ l\.
Действительно,
lh\~v\ Ы~(%) ~{^}.
откуда
h
а2
с4
R4
с т2
~ 17Т = ±2 *
Но если к < 1, то последний интеграл есть уже эллиптический
интеграл первого рода в нормальной форме Лежандра, а потому
тотчас же можно написать
11 = «а[у/2\а2\(т + ^)].
(2.8.3)
8. Движение полярного спутника Земли
85
Период по т координаты /t будет
4 К%)
Т„ =
лДы
Теперь рассмотрим координату А(т). Действительные корни
полинома L(А) (2.8.1):
1М
Лг“2№ +
ш
MFi
-L
h
02
h
и исследуемый интеграл можно представить в виде
А
= v7 2с2|Л|(т + Да).
/
dX
у/(А2 + 1)(А2 - А)(А - А|)
(2.8.4)
Этот интеграл приводится к нормальной форме более сложным
путем. Опуская выкладки, напишем окончательный результат:
А + В сп <т(т + Да)
А =
С + D сп (т(т + Да) ’
(2.8.5)
где
А = Х2 - А,
С = 1 -
f Aj + 1
А?+Г
/а? + 1
В — А2 + А|
1X1 + 1
А? + 1 ’
1 +
'А2 + 1
, A? + l’ V А? + 1 ’
<г=у/2с2|Л|у/(А2 + 1)(А2+1).
Отсюда период по т функции А(г) равен
4ЛГ(*а)
Га =
причем
*5 = i
1 (А2 - АД2 - {yjХ\ + 1 - у^А? + 1 )
\/ (^2 + 1)(А? + О
86
Очерк второй. Второе рождение старой задачи
Так как Т\ Ф Т^, то движение непериодично. Когда А достигает
исходного значения, // несколько «сдвигается». В результате траек¬
тория имеет вид «розетки» (рис. 2.10). Раз¬
ность Т\ - Tfl характеризует скорость дви¬
жения «большой полуоси оскулирующего
эллипса» орбиты.
Отметим наличие почти круговых («ква-
зикруговых») орбит А = const, отвечающих
равенству Ai = А2.
Сказанного, пожалуй, достаточно для
первого знакомства с задачей; заинтересо¬
вавшийся читатель обратится за подробно¬
стями к первоисточникам, полная библиография которых имеется
в книге В. Г. Демина [2.3].
Рис. 2.10. Траектория
полярного спутника
Очерк третий
Еще одна старая задача,
возвращенная к новой жизни
Культурный человек только слегка
обгрызает кости, а потом бросает
их под стол.
Фафик
(Из «Мыслей людей великих,
средних и песика Фафика»)
1. Что за задача?
В этом очерке речь пойдет о такой задаче. Пусть материальная
точка движется в поле тяготения ньютоновского притягивающего
центра, и пусть еще на материальную точку действует «возмущаю¬
щее» ускорение, постоянное по величине и направлению (рис. 3.1).
Эта задача рассматривалась еще Лагранжем, в XIX веке француз¬
скими математиками Селерье, Сен-Жерменом, а также И. В. Ме¬
щерским. Они показали интегрируемость в квадратурах этой зада¬
чи, однако не довели решение до конца, так как полученные ими
квадратуры имели неудобную для обращения форму. В дальнейшем
указанная задача была заброшена под стол и не получила, по-ви-
димому, развития.
Эту интегрируемую, но полузабытую задачу возродили к новой
жизни шестидесятые годы двадцатого века. Для космических по¬
летов недалекого будущего проектируются и разрабатываются так
называемые «двигатели малой тяги» (ионные, плазменные и т.п.),
^ Фафик — пес из породы терьеров, сотрудник польского журнала «Пшекруй».
88
Очерк третий. Еще одна старая задача
которые должны придавать космическому аппарату небольшое ре¬
активное ускорение в течение очень большого промежутка времени
(подробнее см. в следующих очерках). Можно представить ситу¬
ацию, когда двигатель дает ускорение, постоянное по величине
и направлению. Тогда движение космического корабля может быть
описано в рамках указанной классической задачи Селерье и Сен-
Жермена.
Важное приложение этой задачи — исследование влияния све¬
тового давления на траекторию спутника. Как известно, солнечное
излучение создает малое, но заметное давление на освещенные ча¬
сти тел; существуют спутники, для которых сила светового давления
является главной возмущающей силой. Например, американские
спутники типа «Эхо» представляют собой огромные (до 30-40 мет¬
ров в диаметре) надувные балло¬
ны. Из-за малой массы и боль¬
шой поверхности этих спутни¬
ков возмущения в их движениях,
вызванные световым давлением,
будут очень существенны. На не¬
большом (сравнительно) интер¬
вале времени, пока Солнце не
сместилось заметным образом в
своем годовом движении по не¬
бесной сфере, можно считать, что
сила светового давления дает по¬
стоянное по величине и направ¬
лению («от Солнца») ускорение.
Тогда опять приходим к модели
движения, описываемой нашей
классической задачей.
Не удивительно, что в последние годы задача о движении
в ньютоновском поле сил при наличии еще и постоянного век¬
тора добавочного ускорения была извлечена из сундуков забвения
и очищена от пыли веков [3.1—3.6, 3.9]
Ссылка [3.9] является шуткой автора. Здесь обыгрывается стихотворение Мар¬
шака «Сундук»: Шел дурак по трясине, Нашел сундук на осине. И говорит: «Вот
удача! Буду всех теперь я богаче: Я нашел сундук с деньгами, С изумрудами и жем¬
чугами!»... и т.д. Нашелся же в сундуке только поросячий хвостик.
2. Коротко об уравнениях движения и их интегрировании
89
2. Коротко об уравнениях движения и их интегрировании
Свяжем с ньютоновским центром О декартову систему коорди¬
нат Oxyz (рис. 3.1) и введем безразмерные переменные формулами
W = M, M = -pL < = ^==. ш = ^.
Г0 \TTogO V Го/go So
где go = v/rl, а остальные обозначения таковы: {г}, {v}, {/}, t —
соответственно безразмерные координаты, компоненты скорости,
компоненты реактивного ускорения и время; {r^}, {Vr}, {fit}, —
аналогичные размерные величины; Го — фиксированное (напри¬
мер, начальное) расстояние от центра притяжения; go — ускорение
силы тяготения на расстоянии Го от притягивающего центра.
Направим ось х неподвижной системы координат вдоль по¬
стоянного вектора f реактивного ускорения. Тогда уравнения дви¬
жения принимают вид
* , * - У z
ж = -^ + /’ У = --^ 2==-^’
Г = \Ле2 + у2 + Z1.
Если бы в правой части первого из этих уравнений не было ве¬
личины /, то мы имели бы просто дифференциальные уравнения
кеплеровского движения. Наличие параметра /, как будет видно
из дальнейшего, влечет за собой обильное разнообразие движений.
Уравнения (3.2.1) имеют следующие первые интегралы:
интеграл энергии
^ (ж2 + у1 + i2) - - - fx = h, (3.2.2)
2 г
интеграл площадей (относительно оси х — направления ускорения f)
zy -yz = -к0 (3.2.3)
и третий интеграл, обобщающий так называемый «интеграл Лапла¬
са» кеплеровского движения,
х 3 т 1 9
xrr -fx - -fr -2hx — c. (3.2.4)
г 2 2
Эти интегралы нам пригодятся в дальнейшем. А сейчас от¬
метим только, что существование достаточного количества первых
90 Очерк третий. Еще одна старая задача
2. Коротко об уравнениях движения и их интегрировании
91
интегралов уравнений движения (в данном случае трех) являет¬
ся условием интегрируемости этих уравнений. Поэтому, начиная
интегрирование какой-либо системы уравнений, полезно найти,
по возможности, все ее независимые (не следующие друг из друга)
первые интегралы. Наличие трех первых интегралов (3.2.2)-(3.2.4)
позволяет свести задачу к квадратурам.
Конечно, как и в задаче двух неподвижных центров, инте¬
грирование можно было бы провести методом Гамильтона—Якоби,
выбрав подходящую систему криволинейных координат. Однако,
зная систему трех первых интегралов (3.2.2)-(3.2.4), можно пы¬
таться провести интегрирование непосредственно, преобразуя эти
интегралы к должному виду. А именно, введем новые переменные
u — r-x, v = r + x, (3.2.5)
так что
r=]-{u + v), x=l-{u-v), (3.2.6)
и третью переменную у?, определяемую соотношениями
cos р — —, sin<^=—, г\ = л/у2 + z2. (3.2.7)
г I ГI
Подставим вместо х, у, z в первые интегралы (3.2.2)-(3.2.4)
новые переменные и, v, р согласно (3.2.5)—(3.2.7) и введем вместо
времени t параметр т, монотонно увеличивающийся вместе со вре¬
менем так, что
dr = —. (3.2.8)
г
Тогда интегралы (3.2.2)—(3.2.4) легко разрешаются относительно
производных du/dr, dv/dr, dip/dr и последующей квадратурой ин¬
тегрирование заканчивается. Опуская «кухню» интегрирования, при¬
ведем лишь окончательные результаты. Оказывается, что движение
подчиняется следующим квадратурам:
Г dv Г du
J y/Viv) -Т + Сь / т/Щй) ~Т + С2’
где
V(v) = fv> + 2hv7 + 2(\+c)v-kl |
U (и) = -fu3 + 2 hu2 + 2(1 -c)u-klj
Рис. 3.2. Параболоидальная система координат
Интегралы типа (3.2.9), как мы знаем, обращаются при помощи эл¬
липтических функций Якоби. Обращение этих интегралов дает па¬
раметрические уравнения траектории во вращающейся плоскости,
содержащей радиус-вектор г и ось х. Угол <р поворота этой плоско¬
сти вокруг оси х определяется согласно (3.2.3) и (3.2.7) по формуле
т
lP-<Po = к0 J r2 l'x2 ’ (3.2.11)
О
3. Плоское движение
93
где, конечно, г их считаются уже известными функциями т (в силу
(3.2.6) и обращенных интегралов (3.2.9)). Видим, что <р меняется
монотонно по т. Из (3.2.8) получим
и задача полностью сведена к квадратурам.
Отметим, что выбранная нами для интегрирования система
криволинейных координат u, v, <р является параболоидальной. Ко¬
ординатные по верхности и = const, v = const суть параболоиды вра¬
щения с общей осью, совпадающей с осью х декартовой системы
координат. В плоскости (р = const координатная сетка задается се¬
мейством парабол и = const, v = const, как это изображено на рис. 3.2.
Можно заранее сказать, что параболоидальная система коор¬
динат наиболее естественна для рассматриваемой задачи. В самом
деле, на достаточно большом расстоянии от центра притяжения
/ > 1 /г2 (так как f постоянно, а 1 /г2 может быть сколь угодно
мало). Значит, движение будет близко в этом случае к движению
лишь под действием вектора f постоянного ускорения (ньютонов¬
ское ускорение 1 /г2 будет мало). А движение в однородном поле
сил (то есть в таком поле, где f = const), как известно, происходит
по параболической траектории (и ось параболической траектории
имеет направление f).
3. Плоское движение
Всюду в дальнейшем мы ограничимся случаем плоского дви¬
жения (в плоскости ж, у). Тогда ко = 0 и (р = <ро. Полиномы
(3.2.10) представимы в виде
т
(3.2.12)
о
V = fv(v - v2){v - v2), 3
U = -fu(u - и2)(и - Из),/
}
(3.3.1)
причем корни полиномов (3.3.1) имеют значения
V\ =0,
Hi = 0,
г>2 =
-h + y/h2-2f(\ + с)
/
и2 =
h + y/h2 + 2/(1 - с)
7
Vi =
-h- y/h2 -2/(1 + с)
/
Из =
h — y/h2 + 2/(1 — с)
7
94
Очерк третий. Еще одна старая задача
Плоская задача имеет, таким образом, то несомненное до¬
стоинство, что все корни полиномов (3.3.1) (а значит, и модули
эллиптических функций и другие параметры, описывающие дви¬
жение) легко выражаются в явном виде через начальные условия
(через значения констант h, с). Поэтому удобно провести класси¬
фикацию движений в плоскости Л, с при фиксированном значении
f Ф 0. Это делается без особого труда, так как, повторяю, име¬
ются явные зависимости координат и, v от т и постоянных Л, с:
u(r,h,c); v(r,h, с). Однако эти зависимости, даваемые эллипти¬
ческими функциями Якоби, различны в различных случаях (кото¬
рых довольно много). Мы не будем выписывать эти зависимости,
а расскажем лишь о результатах анализа. Детали читатель может
посмотреть в работах [3.1, 3.2]. Важен для характеристик траекто¬
рий лишь тот факт, что траектории определяются комбинациями
таких зависимостей и(т) и v(r), которые схематично изображены
на рис. 3.3. Различие типов этих зависимостей объясняется тем, что
при разных Лис корни и, v полиномов (3.3.1) имеют разные знаки
и комплексность. Заметим еще, что если v(r) —» оо при т —> т*,
то и реальное время t -> оо при т т*, так что бесконечное значе¬
ние v может достигаться лишь на бесконечном интервале времени.
Имеются две качественно различные возможности для зависи¬
мости и(т) и три — для зависимости v(r) (рис. 3.3). Характер тра¬
ектории полностью определяется следующими двумя факторами:
и
и
о
т
о
т
V
-0- и т т
v
Рис. 3.3. Возможные типы зависимостей и(т), v(t)
4. Описание траекторий плоского движения
95
1) какая именно комбинация функций и(т), v(r) из шести логи¬
чески возможных (рис. 3.3) имеет место для данной траектории;
2) каково значение отношения Tu/Tv периодов функций и(т), v(r).
Ввиду того, что для и(т), v(t) имеются явные выражения
(через функции Якоби), то ответы на вопросы 1) и 2) всегда можно
получить.
4. Описание траекторий плоского движения
Эти траектории принадлежат к четырем основным типам:
I. Неограниченные, самопересекающиеся, не огибающие центра
притяжения. Область значений параметров для траекторий ти¬
па I:
с < -1.
II. Неограниченные, самопересекающиеся, огибающие центр при¬
тяжения. Область значений параметров для этих траекторий:
— 1<с<+1, —jj > — у^2(1 + с).
III. Неограниченные, без самопересечений. Для них область зна¬
чений параметров:
с > I, -J= > у/-2(1 -с).
IV. Ограниченные. Такие траектории существуют при
— 1<с<+1, -—у < — + с).
В этой области, однако, могут существовать и траектории типа L
В оставшейся части плоскости с, h/y/f (а именно при с > 1,
h/Vf ^ ^ ^(1 Р^^льных движении нет. Разбиение плоско¬
сти с, h/y/f на области I, II, III, IV дано на рис. 3.4. На этом же
рисунке схематично изображены траектории разных типов (а имен¬
но такие типы траекторий, которые характерны для данной части
плоскости с, h/y/f). Перейдем к рассмотрению свойств траекто¬
рий внутри областей I—IV и на их границах. Будем останавливать
внимание лишь на самых интересных траекториях.
96
Очерк третий. Еще одна старая задача
Рис. 3.4. Разбиение плоскости с, h/л/] на области I, II, III, IV
(с видом траекторий)
4. Описание траекторий плоского движения
97
Траектории типа I — неограниченные и при t —> оо стремятся
к какой-либо параболе и = и*; эти траектории не огибают центра
притяжения и довольно «плавные»; при больших значениях с они
носят характер дуг произвольной ширины (в том числе и очень
узких). Очень интересно, что существуют «самовозвращающиеся»
траектории, приводящие в некоторую точку щ, с нулевой скоро¬
стью; равновесия в точке щ, Vu нет (силы не нулевые), и движение
пойдет дальше по той же самой траектории, но в обратном на¬
правлении! Ситуация получается такая, как если бы мы долго шли
по тропинке, которая вдруг окончилась тупиком, так что мы вы¬
нуждены сделать «поворот кругом, назад шагом марш!» по той же
самой тропинке. Два космических корабля, запущенные в разные
моменты времени по такой траектории, через некоторое время не¬
избежно столкнутся друг с другом! (Пример чисто математической
ситуации. В реальных условиях капитаны кораблей вовремя изме¬
нят величину или направление тяги f и благополучно разойдутся;
но это уже другая задача). На рис. 3.5 изображены только что опи¬
санные траектории. Если величина с не очень велика, то траектории
могут самопересекаться (рис. 3.6) и носить даже змееобразный ха¬
рактер (рис. 3.7).
Траектории типа II отличаются от траекторий предыдущего
вида лишь способностью огибать центр притяжения (тем самым
исключаются «самовозвращающиеся» траектории). На рис. 3.8-3.11
изображены некоторые из траекторий этого типа.
Рис. 3.5. Траектории типа I
7 Заказ 1667
Рис. 3.6. Траектория типа I
с самопересечениями
98
Очерк третий. Еще одна старая задача
Рис. 3.7. Змееобразная
траектория типа I
Рис. 3.9. Петлеобразная
траектория типа II
Рис. 3.8. Траектория типа II
с самопересечениями
Траектории типа III очень «плавно», без самопересечений
(рис. 3.12, 3.13), огибают центр притяжения. Среди траекторий это¬
го вида есть чисто параболические траектории, в частности радиаль¬
ные (движение происходит вдоль направления f).
Вернемся к змееобразной траектории типа II (рис. 3.11). Она
имеет заметное «сгущение» петель в «средней», так сказать, своей
4. Описание траекторий плоского движения
99
части. Интересно проследить, что делается с подобной траекторией
при переходе из области II в область IV (ограниченных движений).
На этой границе происходит следующее расщепление нашей тра¬
ектории на три новых (рис. 3.14). Прежде всего, на месте сгущения
появляется периодическая траектория v = const = v^. Движение
материальной точки происходит по ограниченной дуге этой парабо¬
лы, а именно по участку, заключенному внутри некоторой параболы
и = и2. Материальная точка, колеблясь, движется туда и обратно
по дуге v = V} между двумя точками с координатами и = v,2,v = v^.
Слева к этой траектории асимптотически стремится при t -э оо
змееобразная ограниченная траектория. При приближении к v = V3
петли змееобразной траектории все теснее и теснее приближаются
друг к другу. Полностью характер этой змееобразной траектории
такой: она, колеблясь, удаляется от параболы v = v3, один раз
огибает центр притяжения, а затем, как было уже сказано, асимп¬
тотически при t -> оо колеблющимся образом приближается к дуге
параболы v = v3. Хотя траектория и ограничена, но фактически она
не поддается удобному описанию в терминах оскулирующих эле¬
ментов: слишком велики возмущения от добавочного ускорения f,
и траектория, как видим, не имеет ничего общего с «оскулирующим
эллипсом».
Наконец, справа от дуги v = V3 уходит еще одна траектория,
сначала змеевидно колеблющаяся, а затем, при t -э оо, стремя¬
щаяся к некоторой параболе и — и {и вместе с ней уходящая
в бесконечность, рис. 3.14).
Рассмотрим теперь траектории в области ограниченных дви¬
жений (в этой области, как уже упоминалось, могут существовать
и неограниченные траектории).
Траектории типа IV. При малом «соскальзывании» с границы
между областями II и IV внутрь области IV плоскости с, h/yfj по¬
лучим траектории, изображенные на рис. 3.15. Ограниченная траек¬
тория заметно змееобразна из-за существенного влияния не малого
добавочного ускорения f. Характер траектории таков: обогнув центр
притяжения, материальная точка, колеблясь между ветвями пара¬
болы и = щ, движется в сторону увеличения значения и вплоть
до v = V3; достигнув этой границы, точка в «попятном» (по v)
движении снова по змеевидной траектории приблизится к центру
притяжения, обогнет его и т.д.
Наряду с ограниченными траекториями в этой области суще¬
ствуют и неограниченные траектории (см. рис. 3.15). Их неогра-
7*
100 Очерк третий. Еще одна старая задача
траектория типа II
Рис. 3.13. Траектория типа III
Рис. 3.14. Траектории на границе
областей II и IV
4. Описание траекторий плоского движения
101
ниченность вызвана значительным удалением центра притяжения
(вследствие чего влияние добавочного постоянного ускорения f су¬
щественней, чем влияние ньютоновского притяжения).
С увеличением значения |Л|/\/7 ограниченные траектории су¬
щественно изменяют свою форму, приобретая квазиэллиптический
вид. Это вызвано малостью влияния f по сравнению с силой нью¬
тоновского притяжения к центру. Траектория такого типа на зна¬
чительном ее участке может быть описана в терминах медленно
(в среднем) меняющихся оскулирующих элементов. Вид этой тра¬
ектории изображен на рис. 3.16.
В терминах оскулирующих элементов можно говорить, что
большая полуось орбиты по величине примерно сохраняется, а на¬
правление линии апсид меняется. Причем удаление линии апсид
от направления f (от оси х) сопровождается увеличением эксцен¬
триситета, траектория эволюционирует в сторону все большего ее
сжатия. Точка касания траектории с границей v = V3 на рис. 3.16
перемещается вдоль v = v3 в сторону пересечения параболы v = V3
с граничной параболой и = щ. Если в процессе движения мате¬
риальная точка попала в указанную критическую точку v = 03,
и — из, то скорость материальной точки здесь будет равна нулю
и дальнейшее движение будет происходить по уже пройденной тра¬
ектории, но в обратном направлении (рис. 3.17).
В общем случае траектория не пройдет через критическую точ¬
ку (вероятность этого мала), но в районе критической точки все
равно произойдет смена направления движения так, как это изоб¬
ражено на рис. 3.18, и эволюция траектории пойдет в обратном по¬
рядке. Прямому движению материальной точки сопутствует прямое
движение линии апсид оскулирующего эллипса, обратному — обратное;
удаление большой полуоси от направления f сопровождается увеличе¬
нием оскулирующего эксцентриситета, сближение направлений линии
апсид и вектора f сопровождается уменьшением эксцентриситета.
Смена направления движения создает определенные трудности
в описании движения в терминах оскулирующих элементов, так как
в этот момент оскулирующие элементы меняются скачком [3.6].
Практически движущаяся точка может «не дожить» до смены
направления движения, так как из-за большого «сжатия» траек¬
тории (увеличения эксцентриситета) траектория подойдет опасно
близко к поверхности центрального тела (скажем, Земли) и в даль¬
нейшем встретит эту поверхность на своем пути [3.6]. Для простран¬
ственных траекторий эта опасность гораздо менее существенна или
102
Очерк третий. Еще одна старая задача
Рис. 3.15. Ограниченная и неограниченная Рис. 3.16. Квазиэллиптическая
траектории в области IV траектория в области IV
Рис. 3.17. Смена направления
движения
Рис. 3.18. Смена направления
движения в общем случае
4. Описание траекторий плоского движения
103
вообще не существует, так как ограниченное движение происходит
всегда вне области, ограниченной некоторыми двумя параболоида¬
ми вращения и = и , v = v* (вся Земля может спрятаться внутрь
этой области и стать недосягаемой).
В заключение остановимся кратко на описании некоторых пе¬
риодических траекторий. Так как Tu/Tv ^ 1 во всей области IV, то
а) б)
Рис. 3.19. Периодические траектории (Tu/Tv = 1/2)
104
Очерк третий. Еще одна старая задача
это отношение может быть и рациональной дробью, что в случае
ограниченных траекторий как раз соответствует их периодичности.
Вид периодических траекторий зависит не только от отношения
Tu/Tv но и от разности начальных фаз и(т) и v(r).
Некоторые периодические траектории изображены на рис. 3.19.
Часть из них носит формальный характер, так как траектории про¬
ходят через центр притяжения. Особенно любопытны траектории,
проходящие через критическую точку, в которой скорость равна ну¬
лю. Эти траектории имеют вид незамкнутых петель, вдоль которых
и движется материальная точка попеременно в прямом и обратном
направлениях (рис. 3.19я). На рис. 3.19 изображены траектории при
Tu/Tv = 1/2. Траектории вида 3.19 а получаются при совпадении
момента достижения минимума функции v(r) с моментом дости¬
жения максимума функции и(т) (назовем такие траектории траек¬
ториями в «противофазе»). На рис. 3.19б, в — траектории с различ¬
ным сдвигом фаз, а на рис. 3.19г — траектории «в фазе»: минимум
v(t) достигается одновременно с минимумом и(т). Последняя тра¬
ектория проходит через центр притяжения.
На рис. 3.20 изображены траектории в фазе и противофазе при
Tu/Tv = 1/3, а на рис. 3.21 — траектории при Tu/Tv — 2/3: в фазе
и противофазе на рис. 3.21 а и «в 1/4 фазе» на рис. 3.21 б.
У
У
х
Рис. 3.20. Периодические
траектории (Tu/Tv = 1/3)
Рис. 3.21. Периодические траектории
(Т./Т, = 2/3)
5. О влиянии светового давления
105
Материал этого очерка хорошо иллюстрирует богатство инфор¬
мации, предоставляемой точно интегрируемыми задачами. Змее¬
образные траектории, асимптотически стремящиеся к колебаниям
по ограниченной дуге параболы; траектории «возврата», по которым
точка «вдруг» начинает двигаться в противоположном направле¬
нии; колебательные движения вдоль ограниченной дуги параболы;
скачки в оскулирующих элементах медленно эволюционирующе¬
го эллипса и смена прямого движения на попятное; возможность
падения движущейся материальной точки на центральное тело по¬
сле многих оборотов вокруг него; удивительные «усатые» перио¬
дические траектории — все эти эффекты трудно было бы ожидать
с полной очевидностью от «суперпозиции» (наложения) двух таких
простых движений, как движение в ньютоновском центральном
поле сил и движение в однородном поле сил. Но, проинтегрировав
задачу точно, мы смогли обнаружить эти эффекты, и, честно при¬
знаться, доброй половины из них мы никак не ждали.
5. Немного о влиянии светового давления
на движение спутников Земли
Если спутник летает достаточно высоко над Землей, достаточ¬
но велик по размерам, но в то же время достаточно мал по массе, то
на его движение очень сильно влияет световое давление солнечных
лучей. Таким условиям удовлетворяют, например, американские
спутники-баллоны «Эхо», представляющие собой 30-40-метровые
надувные оболочки.
Спутники серии «Эхо» за сутки делают несколько витков во¬
круг Земли, а за одну-две недели — несколько десятков витков.
Этого времени достаточно, чтобы уловить тенденции в короткопе¬
риодической эволюции орбит спутников. Но за такое время Солнце
не очень сильно смещается по небесной сфере, и поэтому направ¬
ление силы светового давления, действующей на спутник, мож¬
но считать приближенно постоянным в пространстве. Кроме того,
расстояние спутника от Солнца практически не меняется, поэтому
и величина силы светового давления практически постоянна. В ре¬
зультате задача об изучении движения такого спутника сводится
к постановке, рассматриваемой в настоящем очерке. Однако в эту
постановку следует внести существенный корректив: спутник мо¬
жет периодически проходить через тень Земли, где сила светового
давления отключается.
106
Очерк третий. Еще одна старая задача
Отмеченный факт вносит новые качественные и количествен¬
ные особенности в эволюцию движения спутника. Эти особенности
довольно подробно рассмотрены Ю. А. Черниковым [3.7], М.Л.Ли-
довым [3.8] и другими исследователями, и мы не будем повторять
их детальный анализ. Попробуем лишь, пользуясь известными нам
закономерностями, понять качественные тенденции эволюции дви¬
жения спутников, подверженных влиянию светового давления и пе¬
риодически проходящих через тень Земли. Мы используем с этой
целью сведения об эволюции ограниченных траекторий (рис. 3.16)
и интеграл энергии (3.2.2), который запишем в виде
Здесь а — оскулирующая большая полуось орбиты.
Так как величина / ускорения от светового давления очень
мала, то ограниченные траектории будут иметь квазиэллиптиче-
ский вид.
Будем считать, что тень Земли — цилиндрическая, а движе¬
ние плоское, так что всюду, кроме участка орбиты, для которого
Х\ < х < х2 (рис. 3.22), спутник подвержен возмущающему дей¬
ствию ускорения f, постоянного по величине и направленного па¬
раллельно оси х. На отрезке [х\,х2] это ускорение отключается;
здесь |f| = 0. Так как для ограниченных движений h < 0, то можно
записать
и рассмотреть интерпретацию движения на х, 1 /(2а). На рис. 3.23
изображено семейство прямых (3.5.2) для фиксированного / и раз¬
ных значений h. Мы знаем из анализа ограниченных траекторий,
что при неизменном f и фиксированном h значения х не могут
выйти из некоторого интервала —х* < х < х*. Поэтому на плоско¬
сти х, 1 /(2а) изображающая точка будет колебаться вдоль отрезка
прямой (3.5.2) внутри отрезка [-х*,х*], время от времени дости¬
гая его границ; размах колебаний на каждом цикле будет, конечно,
различным, но это не имеет особого значения для нашего анализа.
Пусть теперь движение при фиксированном h начинается в не¬
которой точке Хо, а в некоторой точке Х\ > 0 произошло «отключе¬
ние» ускорения f, то есть спутник вошел в земную в тень. С этого
момента движение в плоскости ж, 1 /(2а) будет происходить уже
по прямой 1 /(2а) = const (рис. 3.24) вплоть до значения х = х2,
где спутник выходит из тени.
(3.5.1)
(3.5.2)
5. О влиянии светового давления
107
z
X
Рис. 3.22. Прохождение через
тень Земли
Рис. 3.23. Интерпретация
движения на плоскости ж, 1/2а
Рассмотрим ситуацию, изображенную на рис. 3.22, на котором
вход в тень происходит ближе к Земле, чем выход из тени. Тогда после
входа в тень координата х продолжает увеличиваться (х > Х\) и,
как видно из рисунка на плоскости х, 1 /(2а), после выхода из тени
движение переходит на более высокий уровень энергии \h\. Это значит,
что в среднем значение большой полуоси орбиты уменьшилось. Здесь мы
наблюдаем появление нового качества, вызванного влиянием тени.
Если без «отключения» ускорения имеются лишь короткоперио¬
дические колебания величины большой полуоси, то вход и выход
спутника из тени вызывают систематические (долгопериодические)
изменения большой полуоси. Возможная цепочка переходов на все
более и более высокие уровни энергии изображена на рис. 3.25.
Теперь заметим, что вход в тень происходит ближе к Земле, чем
выход, лишь (при ситуации, изображенной на рисунке) в прямом
движении; оно, как мы знаем, сопровождается прямым движением
линии апсид, которое в данном случае соответствует удалению ли¬
нии апсид от направления ускорения f. Из анализа ограниченных
траекторий мы видели, что такое движение линии апсид сопрово¬
ждается увеличением эксцентриситета. Отсюда следует, что долгопе¬
риодическое увеличение эксцентриситета, обусловленное действием
светового давления, сопровождается долгопериодическим уменьшени¬
ем величины большой полуоси орбиты, вызванным влиянием земной
тени. Анализируя обратное движение спутника, точно так же об¬
наружим, что уменьшение эксцентриситета сопровождается увели¬
чением большой полуоси орбиты, и приходим к следующей общей
108
Очерк третий. Еще одна старая задача
Рис. 3.24. Интерпретация
влияния тени
Рис. 3.25. Интерпретация
эволюции траектории
закономерности движения спутника Земли, подверженного влия¬
нию светового давления и периодически входящего в тень Земли.
Линия апсид орбиты спутника Земли долгопериодическим образом
колеблется относительно направления Солнце—Земля. Удаление боль¬
шой полуоси от этого направления сопровождается ее уменьшением
и увеличением эксцентриситета; сближение большой полуоси с направ¬
лением Солнце—Земля сопровождается ее увеличением и уменьшением
эксцентриситета.
Связь между эксцентриситетом и большой полуосью была
обнаружена американцем Меусом на наблюдательном материале
о движении спутников серии «Эхо». Ю. А. Черников обосновал этот
эффект теоретически. Мы здесь нашли простое качественное объ¬
яснение этого эффекта.
Заметим, что в принципе влияние тени может быть таким, что
большая полуось увеличится до весьма существенных размеров,
а может быть, и до бесконечно большого размера и спутник улетит
от Земли в космическое пространство! По крайней мере теорети¬
ческая возможность этого не исключена. Стоит только рассмотреть
последний чертеж (рис. 3.25) и проследить на нем эволюцию в об¬
ратном порядке. Такая эволюция приводит к переходу на все более
и более низкие уровни энергии |Л|, что соответствует увеличению
большой полуоси. Только специальное исследование может пока¬
зать, при каких условиях это увеличение будет бесконечно велико.
На больших интервалах времени надо еще учитывать движение
Солнца.
5. О влиянии светового давления
109
Рис. 3.26. Разгон спутника Рис. 3.27. Разгон спутника
с периодическим включени- с периодическими переклю¬
ем ускорения чениями ускорения
Отсылая читателя за информацией к уже упомянутым рабо¬
там М. J1. Лилова [3.8], Ю. А. Черникова [3.7] и др., остановимся
в заключение на одном вопросе. Как уже говорилось, ускорение f
может быть «организовано» искусственным путем (реактивная си¬
ла от ионного или плазменного двигателя). Это значит, что мы
можем его включать или выключать произвольно. Предыдущие
рассуждения достаточно ясно показывают, что можно эффективно
«организовать» систематические включения и выключения малого
реактивного ускорения (или даже систематические изменения его
направления) таким образом, чтобы раскрутить спутник по спира¬
ли и выбросить его в космос за пределы поля земного тяготения.
На рис. 3.26 и 3.27 приводятся такие траектории и соответствующие
ситуации в плоскости х, 1 /(2а).
Очерк четвертый
Движение миров
Старый серый ослик Иа-Иа стоял один-одинешенек
в заросшем чертополохом уголке леса... и думал о Серьез¬
ных Вещах. Иногда он грустно думал: «Почему?», а ино¬
гда: «По какой причине?», а иногда он думал даже так:
«Какой же отсюда следует вывод?»
А. А. Милн
«Винни-Пух и все, все, все»
1. Еще раз о «теореме Лапласа»
и других Серьезных Вещах
Искусственный спутник, летающий вокруг Земли, подвержен,
помимо всего прочего, притяжению Луны и Солнца. Действие этих
возмущений на орбиту спутника оказалось несколько удивитель¬
ным, даже в некоторой степени неожиданным... Но не будем забе¬
гать вперед в нашем изложении, ведь небесная механика двести лет
только тем и занимается, что изучает движение светил под действи¬
ем взаимных притяжений. Задача о движении спутника Земли мо¬
жет рассматриваться как частный случай «задачи п тел», о которой
можно почерпнуть информацию у классиков небесной механики:
им есть что сказать по этому поводу.
Классическая небесная механика рассматривает ситуацию, ко¬
гда масса одного тела (Солнца!) существенно больше массы других
взаимно тяготеющих тел; в первом приближении поэтому можно
считать, что все тела (планеты) движутся вокруг Солнца по кепле-
ровским орбитам; вопрос состоит в том, как эволюционируют эти
орбиты в силу взаимных притяжений планет. И вопрос вопросов:
сохранится ли вечно нынешняя конфигурация Солнечной систе¬
мы? Иначе говоря, устойчива ли Солнечная система? Не могут ли
1. Еще раз о «теореме Лапласа» и других Серьезных Вещах
111
сильно измениться нынешние движения планет, не сойдут ли све¬
тила «со круги своя», не упадут ли друг на друга и на Солнце?
И не улетят ли из родной Солнечной системы в бесконечность?
При этом мы сейчас имеем в виду устойчивость (или неустой¬
чивость) под действием только сил взаимного ньютоновского тя¬
готения планет. Планеты предполагаются материальными точками
с массами, равными массам планет, как это принято в классической
постановке «задачи п тел».
Итак, пусть имеется система п + 1 взаимно притягивающих¬
ся по ньютоновскому закону точек Ms (s = 0,1, 2,..., п), каждая
из которых имеет массу ms. Будем считать, что масса то весьма
велика по сравнению со всеми остальными массами, вместе взя¬
тыми. В Солнечной системе — это масса Солнца; в системе трех
тел — Земля, Луна, искусственный спутник — это масса Земли.
В дальнейшем будем говорить для простоты о системе планеты—
Солнце (если не оговорено другое).
Сделанное предположение никак не сказывается на точности
уравнений движения, но позволяет в них выделить основную и воз¬
мущающую части.
Если за начало декартовой системы координат взять точку га0,
то уравнениями движения г-й точки (координаты которой суть
Xi,Vi,Zi) будут [4.1]
dUi out дщ
Xi = ——, Vi = -г—, zi = ——. (4.1.1)
дх{’ yt dyi’ dzi' v ’
где
TT _ /(mo + mi) t TT,
Ui — ~r Ui ,
rr* ( 1 XiXj + ViVj + ZiZj \
~ zrf \ A«7 - r] )■
(4.1.2)
Здесь штрих у знака суммы означает, что при суммировании должен
быть пропущен член, для которого
j = г\ г,- = у/xj+yj + zf
— расстояние от г-й точки до точки М0;
Aij — yj^j)2 (Уг J/jf)2 "t" (zi )2
— расстояние между г-й и j-й точками. Если бы существовали
только точки т0 и 7Щ, то движение точки тг происходило бы
112
Очерк четвертый. Движение миров
относительно точки то по кеплеровской орбите, отвечающей си¬
ловой функции
f(m0 + тщ)
и о = .
Гг
Однако наличие других точек вносит возмущения в движение точ¬
ки тг. Эти возмущения описываются возмущающей частью U*
силовой функции Ui. Имея в виду для дальнейшего выражение
(4.1.2) возмущающей функции и? перейдем, однако, к следующим
важным преобразованиям.
Чтобы уравнения возмущенного движения планет приводились
к удобному для исследования каноническому виду, приходится рас¬
сматривать специфическую систему координат для исследования
движения каждой планеты Ms [4.1] — прямоугольную декартову
систему координат xs,ys,zs с началом в центре масс Gs-\ точек
Мо, М\,..., Ms-1 и с неизменными направлениями осей. При этом
в уравнениях движения фигурируют так называемые «приведенные
массы»
_ mo + m, +... + m5_i //f ,
Tns — Trig . (4.1.3)
mo + m, | + .., + ms_| +ms
Ясно, что в предположении о преимущественной величине
S
массы то > Е mi окажется, что ms ~ ms. В Солнечной систе-
*=1
ме все точки Gs-\ находятся внутри Солнца, вблизи его центра.
Центр масс системы Луна—Земля находится внутри Земли; при
этом отношение массы Луны тпд к массе Земли Шз составляет
тл/шз ~ 1/81.
Рассмотрим полную силовую функцию U системы точек
М0,МЬ... ,МП:
U = f (4.1-4)
s<j s3
Здесь Asj суть взаимные расстояния между точками. Силовую
функцию (4.1.4) можно в новых координатах xrs,y'S9z8 преобра¬
зовать к виду
п morrij
^ = /£ = +ЕЛ (4.1.5)
где
г•
i=1 э
r'j = у/ х'} + у'2 + г'2 (г, = Д0|).
1. Еще раз о «теореме Лапласа» и других Серьезных Вещах
113
В выражении (4.1.5) возмущающая функция U1 имеет, конечно,
другой вид, нежели возмущающая функция £7* (4.1.2), из-за новой
системы координат (а также потому, что U* относится к одной
точке, a U' — ко всей системе).
Мы не будем явно выписывать выражение для U\ так как
в дальнейшем нам понадобятся лишь некоторые ее общие свойства.
Силовая функция U1 имеет второй порядок малости относительно
возмущающих масс [4.1]. Если ее отбросить в выражении (4.1.5),
то окажется, что уравнения движения точки Ms не будут зависеть
от координат любой другой точки Mj, j ф s, и точка Ms будет
двигаться по кеплеровской орбите, которую относительно системы
координат ж', j/', zs определим элементами
так что is — наклонение плоскости орбиты к плоскости xs, ys
и т.д., как определялось в первом очерке.
Но вследствие взаимодействия масс будет работать возмуща¬
ющая функция UРассматривая возмущенное движение в оску¬
лирующих элементах (4.1.6), обнаружим, что за счет U1 они будут
изменяться относительно своих постоянных невозмущенных значе¬
ний. Для анализа этих изменений удобно ввести элементы Делоне
аналогично тому, как они вводились в первом очерке:
Ls = у/ Ps^S J Is = H'sit ~~ Ts)?
Здесь n's = /(mo + ms), где ms определяется формулой (4.1.3);
(4.1.6)
>
(4.1.7)
среднее движение ns = у p,s/as^ a большая полуось
(4.1.8)
Введем функцию Гамильтона
п ,2
(4.1.9)
где, конечно, предполагается, что U1 выражено через элементы
Делоне. Тогда уравнения возмущенного движения принимают ка-
8 Заказ 1667
114
Очерк четвертый. Движение миров
ноническии вид:
W dHs 8F
dt dls ’ dt dgs' dt dhs ’
dls OF dgs OF dhs OF
~dt=~~dTg' ~dt=~dG~s' Ht = ~d¥s
(s=\,2...,n).
(4.1.10)
Это точные уравнения движения, и им отвечают некоторые
точные первые интегралы. Известно, что задача о движении систе¬
мы п тяготеющих друг к другу точек имеет 10 первых классических
интегралов. Так как силы в системе можно рассматривать как внут¬
ренние, то количество движения системы сохраняется (что дает три
первых интеграла в компонентах по осям координат); центр масс
системы движется равномерно и прямолинейно (еще три интегра¬
ла); сохраняется момент количества движения системы (еще три
интеграла в компонентах по осям координат); наконец, десятый
интеграл — интеграл энергии.
Интегралы, определяющие движение центра масс системы, ма¬
ло интересны, но из оставшихся четырех первых интегралов можно
извлечь определенную информацию о движении. В частности, ока¬
зывается, что для ограниченности движений необходимо (но не доста¬
точно!), чтобы константа энергии была отрицательна (что мы далее
и будем предполагать). Простое доказательство этого факта можно
посмотреть, например, в книге Г. Н. Дубошина [4.1], которую мы,
кстати сказать, широко используем и в настоящем очерке.
Из трех интегралов, описывающих сохранение момента коли¬
чества движения, мы выпишем (и используем для анализа) в наших
переменных один интеграл. Он имеет вид
Е
S= I
т
Wv'sPs COS ig = с. (4.1.11)
Напомним, что (4.1.11) — точный интеграл уравнений движения!
Далее, отметив, как и в первом очерке, что F является пери¬
одической функцией от 13, представим F в виде n-кратного ряда
Фурье:
F = F+ а*, kn cos (Mi + ••• + Kin) +
fc k„ (4.1.12)
+ bkl kn sin (Mi + ... + knln),
1. Еще раз о «теореме Лапласа» и других Серьезных Вещах
115
где
27Г 27Г
<41'3)
О О
а коэффициенты *п, Ьл, А;л в (4.1.12) зависят от всех элемен¬
тов (вообще говоря), кроме ls \ при этом во всех членах под знаком
суммы хотя бы один из ki не равен нулю. Пусть ни при одном
наборе целых (положительных или отрицательных) чисел
к\, &2,..., кп (4.1.14)
п
не выполняется условие резонанса Е ksns = 0. Для всех чисел (4.1.14)
5=1
П
(4.1.15)
5=1
Тогда уравнения первого приближения (в смысле асимптотических
методов) получаются осреднением правых частей уравнений (4.1.10)
или, что то же, гамильтоновой функции (4.1.12) по переменным ls,
независимо по каждой. Фактически это означает, что вместо га¬
мильтоновой функции (4.1.9) следует взять ее среднее значение
(4.1.13) и подставить в уравнения (4.1.10). Так как F не зависит
dL g
от ls (по ним осреднили), то из (4.1.10) следует, что —— = 0 (ввиду
_ dt
dF
— = 0) и тогда из определения Ls (4.1.7) следует, что большие
01$
полуоси всех орбит постоянны:
as = const. (4.1.16)
Мы пришли к так называемой теореме Лапласа о «неизменности»
(в смысле отсутствия вековых возмущений) больших полуосей пла¬
нет Солнечной системы. Этот вывод справедлив, вообще говоря,
на ограниченном интервале времени, так как только на ограничен¬
ном интервале времени «работает» первое приближение асимпто¬
тических методов. Точнее, мы можем утверждать, что \as - а50| ~ е
на t ~ \/е, где малая величина е имеет порядок возмущений, asо —
начальные значения больших полуосей.
Точные оценки сопряжены с существенными трудностями;
от этих оценок зависит и ответ на вопрос, является ли движение
8*
116
Очерк четвертый. Движение миров
рассматриваемой системы устойчивым на бесконечном интервале
времени. Мы еще вернемся к этому вопросу (ведь из-за него и пи¬
шется этот очерк). А пока посмотрим, если (4.1.16) выполнено, то
«какой же отсюда следует вывод?»
Обозначим
п
y^m's л/ц'3а$ = <р (4.1.17)
5=1
и вычтем из (4.1.17) интеграл (4.1.11). Тогда, учитывая (4.1.8), найдем
Е
5=1
rnsy/n'sas( 1 - у/\-е\ cos is) = <р - с,
или
П
I Г~, М1! *5-Г^5^ Ъз
msy/n’sas г - ip - с. (4.1.18)
Е
5=1
sin2 is + el cos2 s.
1 + yj 1 — e2 cos i8
Но если выполнено (4.1.16), то (p-с = Cq — новая постоянная,
равная значению левой части равенства (4.1.18) в начальный мо¬
мент времени. Ввиду положительности каждого члена левой суммы
в (4.1.18) имеем Со > 0 и каждый член суммы меньше, чем Со.
Отсюда — оценка
sin2 is + е2 cos2 is Cq
^ ^7=. (4.1.19)
1 + v 1 - e2 cos is m's yj^sas
To, что as не постоянно, но мало отличается от постоянной
(|as - as0| ~ s), не нарушает оценки (4.1.19) — ее можно провести
и с учетом этого обстоятельства.
Если начальные значения es0, i8о очень малы, то постоянная Со
также весьма мала, тогда из (4.1.19) следует, что и на всем рассмат¬
риваемом интервале времени величины es, is останутся малыми. От¬
сюда — «теорема Лапласа об устойчивости Солнечной системы»:
Пусть орбиты планет, обращающихся в одном и том же на¬
правлении, близки к круговым, мало наклонены друг к другу, и пусть
средние движения планет несоизмеримы. Тогда на достаточно боль¬
шом интервале времени большие полуоси орбит останутся близкими
к своим начальным значениям, а орбиты — близкими к круговым и ма¬
ло наклоненными друг к другу.
Эта теорема — замечательный результат классической небес¬
ной механики. Ведь планеты Солнечной системы движутся по по¬
чти круговым орбитам и почти в одной плоскости. Значит, по «тео¬
1. Еще раз о «теореме Лапласа» и других Серьезных Вещах
117
реме Лапласа об устойчивости», так и будет продолжаться доста¬
точно долго. Столкновений планет можно пока не опасаться.
Заметим, что если в начальный момент все орбиты круговые
и лежат в одной плоскости, то со = 0, и из (4.1.19) следует, что все
орбиты так и останутся круговыми и лежащими в одной плоскости.
Плоская круговая система не эволюционирует.
Однако слова «теорема Лапласа об устойчивости системы» взя¬
ты в кавычки не зря. Что это за устойчивость до послезавтрашнего
дня! (Или до последующего столетия — какая разница?) Нас ин¬
тересует устойчивость в классическом смысле слова, устойчивость
с точки зрения вечности! Верна ли «теорема Лапласа» на бесконеч¬
ном интервале времени? На этот вопрос дан ответ совсем недавно
трудами современных математиков, в первую очередь исследова¬
ниями советского математика В. И. Арнольда. Мы еще вернемся
к ним чуть позже. А в заключение этого пункта опишем характер
возмущенного движения планетной системы. К результатам, опи¬
санным в «теореме Лапласа», следует добавить еще такие сведения.
Пусть е* — вектор Лапласа к-й планеты (он направлен в пе¬
ригелий орбиты по большой ее оси и пропорционален по величине
эксцентриситету орбиты, а именно: |е^| = \Jт\а^ек). Тогда анализ
п
возмущенного движения показывает, что где каждый
г= I
вектор ел,- равномерно вращается с частотой vf.
Частоты у!? весьма малы. Таким образом, перигелии всех орбит
медленно, но неуклонно («вековым образом») движутся в плоско¬
стях своих орбит; их движение определяется набором п частот ,
притом так, что вектор Лапласа каждой орбиты является суммой п
равномерно вращающихся (с частотами i/f) векторов. Далее, плос¬
кость орбиты наклонена к основной координатной плоскости под
углом г*, линия пересечения этих плоскостей называется линией
узлов. Вековое изменение этих величин описывается вектором i&,
направленным вдоль линии узлов, причем |i&| = yjm\dkik- Этот
вектор тоже является суммой равномерно вращающихся с медлен¬
ными частотами vf векторов; но этих векторов уже п — 1.
Таково, приближенно, возмущенное движение системы п пла¬
нет вокруг массивного центрального тела (Солнца). Планеты дви¬
жутся по всегда малоэллиптическим и малонаклоненным орбитам,
сохраняющим величины своих больших полуосей; плоскости орбит
118
Очерк четвертый. Движение миров
и сами орбиты в своих плоскостях прецессируют вековым образом,
причем скорости прецессий определяются описанной выше супер¬
позицией равномерных вращений. Такое движение называется ла-
гранжевым движением планет.
2. Не хотите ли Луну уронить на Землю?
Самые удивительные эффекты в механике космического по¬
лета выявлены при исследовании задачи трех тел и многих тел,
взаимно тяготеющих друг к другу.
Исследования движения планет и других тел Солнечной систе¬
мы, которыми занималась классическая небесная механика, были,
как правило, несколько утилитарными — приспособленными к слу¬
чаю орбит, лежащих почти в одной плоскости и мало отличающихся
от круговых. Такой подход, конечно, был оправдан запросами аст¬
рономической практики. Теорема Лапласа — отражение этого под¬
хода. Большинство исследователей, занимавшихся классической
небесной механикой, не проявляли достаточно пристального инте¬
реса к «экзотическим орбитам» — сильно наклоненным и сильно
эллиптическим. С запуском первых космических аппаратов вспых¬
нул естественный интерес к исследованиям, не накладывающим
никаких ограничений на форму и взаимное расположение орбит.
Обратимся, например, к задаче движения искусственного спут¬
ника Земли с учетом возмущений, вызванных Луной. Иначе говоря,
рассмотрим задачу трех тел: «Земля, Луна, спутник». Ввиду крайней
малости массы спутника по сравнению с массами Земли и Луны
естественно считать, что Земля и Луна спутником совсем не при¬
тягиваются. Поэтому Земля и Луна (рассматриваемые как матери¬
альные точки) будут двигаться по невозмущенным кеплеровским
орбитам относительно общего центра масс. Вопрос только в том,
как возмущается орбита спутника при его движении относитель¬
но Земли. Такая постановка задачи называется ограниченной. Если
спутник не подходит чересчур близко к Луне, то возмущения в его
движении будут малы, и применимы рассуждения предыдущего
пункта этого очерка, из которых, в частности, следует, что большая
полуось орбиты спутника в среднем не меняется:
а = const. (4.2.1)
Рассмотрим теперь интеграл площадей (4.1.11), в котором оста¬
нется в нашем случае всего два члена суммы, содержащей только
2. Не хотите ли Луну уронить на Землю?
119
элементы орбит Луны и спутника. Но Луна движется по невозму¬
щенной орбите, значит, ее элементы рд, cos г л постоянны. Поэтому
интеграл (4.1.11) свяжет только элементы спутника:
Возводя (4.2.2) в квадрат и учитывая (4.2.1) (а также (4.1.8)), полу¬
чим
где постоянная с определяется начальными значениями ео, cosio
элементов орбиты спутника. Заметим, что здесь угол г можно рас¬
сматривать как наклонение плоскости орбиты спутника к плоско¬
сти орбиты Луны.
Кроме интеграла (4.2.3) в осредненном движении, как это ясно
из изложения, должен еще существовать интеграл
где F определено формулой (4.1.13). Этот интеграл в рассматрива¬
емом случае приводится к виду
при фиксированных значениях с и для различных значений ft0-
Возможные «портреты» этих зависимостей изображены (условно)
гопериодическим образом колеблясь вдоль нее между предельно
возможными значениями переменных. Отсюда ясно, что долго¬
та перигея о; может монотонно меняться, но может и колебать¬
ся в ограниченных пределах (обратим внимание на существова¬
ние стационарной орбиты о; = const, % = const и, следовательно,
е = const). Что касается угла г, то его величина всегда колеблется
между двумя экстремальными своими значениями.
у/p cos г = const.
(4.2.2)
(1 - е2) cos2 г = с,
(4.2.3)
F = const = h,
(4.2.4)
(4.2.5)
Интеграл (4.2.5), после исключения е2 с помощью интеграла
(4.2.3), приводится к виду
(4.2.6)
По формуле (4.2.6) нетрудно построить зависимость sin2 ш от cos2 i
на рис. 4.1а и 4.1 б. Изображающая точка на плоскости (sin2 а>,
cos2 г) полностью проходит всю данную интегральную кривую, дол-
120
Очерк четвертый. Движение миров
*
2. Не хотите ли Луну уронить на Землю?
121
Рассмотрим теперь на плоскости (1 - е2, cos2 г) картину инте¬
гральных кривых (4.2.3) при различных значениях постоянной с
(то есть при различных начальных значениях е0, го). Эта карти¬
на изображена на рис. 4.1 в. Область определения переменных: 0 ^
1 -е2 ^ 1,0^ cos2 г ^ 1. Кривые (4.2.3) представляют собой равно-
2 2
бочные гиперболы относительно переменных 1-е , cos г. В процес¬
се эволюции орбиты спутника его эксцентриситет е и наклонение г
меняются так, что на плоскости (1-е2, cos2 г) изображающая точка
колеблется по гиперболе, отвечающей значению константы
с = Со = (I - е,2,) cos2 *0.
Анализ эволюционных уравнений и интеграла (4.2.6) показывает,
что в реальном движении проходится не вся интегральная кривая
(4.2.3), а только ограниченная ее дуга; пределы колебаний изоб¬
ражающей точки на рис. 4.1 в зависят от значения постоянной h
интеграла (4.2.4); однако эти пределы могут быть достаточно ши¬
роки, так что в колебаниях изображающая точка проходит большую
часть дуги интегральной кривой (4.2.3). На рис. 4.1 в пределы коле¬
баний схематично отмечены светлыми точками, а участок реального
движения — жирной линией.
Правый верхний угол на рис. 4.1 в соответствует орбитам с ма¬
лым наклонением (г « 0) и малым эксцентриситетом (е « 0). Мы
видим, что если в начальный момент орбита близка к круговой
(е « 0) и мало наклонена к плоскости орбиты возмущающего тела
(г'о ~ 0), то колебания величин е и г будут малы; орбита устойчи¬
ва и всегда останется близкой к круговой и малонаклоненной —
в полном соответствии с теоремой Лапласа (кривая 1 на рис.4.1<?).
В частности, плоская круговая орбита (во = 0, го = 0) останется
плоской и круговой. Впрочем, для рассматриваемой задачи, как сле¬
дует из интегралов (4.2.3), (4.2.5), в плоском случае (г = 0) остается
неизменным произвольный эксцентриситет (е — ео). (В плоской
задаче многих тел это, конечно, не так.)
Совсем другая картина эволюции движения получается при
начальных наклонениях, близких к 7г/2. Тогда даже первоначаль¬
но круговая орбита стремится к очень сильно вытянутой (экс¬
центриситет стремится к величине, близкой к единице), так что
(1 - е2) -> е ~ 0. Этой ситуации отвечает кривая 2 на рис. 4.1 в.
Но при неизменной большой полуоси увеличение эксцентриситета
может означать только то, что орбита сильно сжимается. На рис. 4.2
изображены орбиты спутника Земли с неизменной полуосью, но
122 Очерк четвертый. Движение миров
Рис. 4.1. Интегральные кривые эволюционных уравнений
с разными эксцентриситетами. Нетрудно понять, что в процессе
эволюции орбита спутника может сжаться настолько, что прой¬
дет через поверхность Земли. Спутник после нескольких оборотов
(или нескольких десятков оборотов) может упасть на Землю только
за счет влияния притяжения Луны!
Хотя в классической небесной механике и более поздних ис¬
следованиях (Н. Д. Моисеев [4.2]) содержится материал, позволяю¬
щий прийти к такому выводу, однако только после запусков первых
искусственных спутников к анализу эволюции произвольных орбит
было привлечено широкое внимание.
Цикл работ в этом направлении выполнен М. Л. Лидовым, ко¬
торый, например, установил сроки существования («время жиз¬
ни») спутников на сильно наклоненных орбитах и провел деталь¬
ный анализ возмущенного движения. М.Л.Лидову принадлежит,
в частности, следующий воистину убийственный по результатам
и убедительности расчет [4.3,4.4].
2. Не хотите ли Луну уронить на Землю?
123
Рассмотрим систему трех тел: Солнце, Земля, Луна. Как из¬
вестно, орбита Луны в ее движении вокруг Земли лежит почти точ¬
но в плоскости орбиты Земли в ее движении относительно Солнца
(плоскость эклиптики). А что будет, если, ни в чем не меняя орбиту
Луны, повернуть эту орбиту на 90° так, чтобы она была нормальна
к плоскости орбиты Земли?
Читатель, конечно, уже предчувствует ответ: Луна свалится
на Землю! И довольно быстро. М.Л.Лидов провел точный расчет
(путем численного интегрирования уравнений движения на элек¬
тронной быстродействующей вычислительной машине). Результа¬
ты этого расчета изображены на рис. 4.3, где в зависимости от чис¬
ла N оборотов «Луны» вокруг Земли приведены значения величины
большой полуоси а и расстояния гж перигея орбиты до центра Зем¬
ли. Видно, что, действительно, большая полуось а примерно посто¬
янна; зато гж стремительно уменьшается, и всего за 55 оборотов гп
станет меньше радиуса Земли! Иначе говоря, на такой орбите Луна
просуществовала бы всего около четырех с половиной лет! (Пока¬
зательна оценка времени существования такой Луны, проведенная
М. Л. Лиловым по осредненной теории: 52 оборота. Сравнивая эту
оценку с точным значением времени существования, мы можем
понять, что осредненные теории дают не только верные качествен¬
ные результаты, но и правильные количественные оценки.)
Обнаружение возможности падения спутников на центральное
тело за счет действия только гравитационных сил, безусловно, од¬
но из самых интересных достижений механики. Еще несколько лет
назад широкие круги исследователей плохо чувствовали эту воз¬
можность (или не чувствовали совсем). После запуска советского
О 20 40 N
Рис. 4.3. Эволюция элементов «полярной Луны»
«Лунника», фотографировавшего обратную сторону Луны, автор
присутствовал на публичной лекции уважаемого ученого, который
заявил, что «Лунник» будет вечно летать по своей орбите (посколь¬
ку перигей орбиты высокий и атмосфера не тормозит движение).
Это заявление было сделано за несколько дней до неизбежного па¬
дения «Лунника» на Землю: его орбита была наклонена примерно
на 90° к плоскости эклиптики. Вскоре были опубликованы работы
М.Л.Лидова [4.3,4.4], где анализировались эволюционные эффек¬
ты взаимно тяготеющих тел и рассчитывался «феномен падения»
тела на тело. Эти работы привлекли широкое внимание1^.
В свете сказанного становится ясно, что расположение боль¬
шинства планет и спутников Солнечной системы примерно в одной
плоскости — не случайно. Если и были тела с сильно наклоненны¬
ми орбитами, то они давным-давно выпали на Солнце.
Правда, существуют спутники Урана с орбитами, сильно на¬
клоненными к эклиптике. М.Л.Лидов показал, что возмущения
от нецентральности поля тяготения Урана (то есть от его сжатия)
устойчиво компенсируют возмущения от притяжения других тел.
Таким образом, сильное сжатие Урана спасло его спутники от ги¬
бели. Из самого факта существования у спутников Урана устой-
^ Прочтите обстоятельный обзор А. Ю. Ишлинского [4.15] о достижениях меха¬
ники.
3. Область маловозмущенного движения
125
чивых орбит, нормальных к плоскости эклиптики, можно вывести
оценку величины сжатия Урана. Для других планет отношение воз¬
мущений от сжатия к возмущениям от внешних тел не настолько
велико, чтобы препятствовать выпадению неэклиптических спут¬
ников на центральное тело.
Читатель, убедившийся в возможности падения на Землю Луны
с «поставленной на ребро» орбиты, наверное тревожно задумался
о судьбе настоящей Луны. По-видимому, оснований для тревоги
нет — Луна будет летать вечно и достаточно спокойно. Это при¬
ближенно следует из «теоремы Лапласа» и точно — из исследо¬
ваний В. И. Арнольда, о которых речь еще впереди. Однако мы
имеем в виду только силы взаимного тяготения «точечных масс»;
в природе же действуют и иные силы. Так называемые «прилив¬
ные силы», вызванные протяженностью и нежесткостью планет,
способны убыстрить или замедлить их бег по орбитам и, как след¬
ствие, изменить эти орбиты; судьба Солнечной системы во многом
зависит от этих сил. С учетом приливных сил заключение об устой¬
чивости орбиты Луны уже не выглядит столь бесспорным. Об этом
подробно и увлекательно рассказано в книге В. Г. Демина «Судьба
Солнечной системы» [4.5]. Но для искусственных спутников Земли
приливные силы имеют меньшую значимость, и мы не будем здесь
на этом останавливаться специально.
3. Область маловозмущенного движения
Весь предыдущий анализ и заключения об эволюции справед¬
ливы, конечно, лишь при слабых возмущениях кеплеровского дви¬
жения. Если в процессе эволюции спутник Земли подлетит чересчур
близко к Луне, то возмущения от Луны будут столь сильными, что
орбита резко «сломается» и эволюционные (то есть осредненные)
уравнения перестанут работать. Поэтому все предыдущие заклю¬
чения верны при условии, что спутник не попадает в некоторую
окрестность возмущающего тела. Этому условию удовлетворяют,
например, любые «внутренние» орбиты (спутник вращается вокруг
Земли достаточно «глубоко» внутри орбиты Луны) или устойчи¬
вые «внешние» орбиты (орбита Луны — внутри орбиты спутника);
неустойчивые внешние орбиты тоже могут не привести спутник
в близкую окрестность Луны (но могут и привести). Однако для
внешних орбит более существенна роль возмущений от притяже¬
ния к Солнцу. Наличие устойчивых внешних орбит говорит в пользу
126
Очерк четвертый. Движение миров
упомянутой в первом очерке возможности существования устойчи¬
вых планетных систем у двойных звезд.
Определим несколько точнее, что имеется в виду под «окрест¬
ностью возмущающего тела», в которую не должен попадать спут¬
ник, если мы хотим, чтобы эволюционные уравнения не потеряли
смысл.
Рассмотрим систему (рис. 4.4) материальных точек с масса¬
ми 772-0 (Земля), тп\ (Луна), га2 (спутник). Тогда силовой функции
(4.1.2) соответствует основное ускорение ао точки га2, обусловлен¬
ное притяжением Земли, и возмущающее ускорение f0, вызванное
притяжением Луны:
Здесь Го — геоцентрический радиус-вектор спутника, Г| — селено¬
центрический радиус-вектор спутника, I — расстояние между Лу¬
ной и Землей. Но то же движение спутника можно рассматривать
и относительно Луны под действием основного ai и возмущающего
fi ускорений:
(4.3.1)
»i = -/ з г,,
rf
ТП\ + ш2
(4.3.2)
Рис. 4.4. Система трех точек ш0, тп\, га2
3. Область маловозмущенного движения
127
Если величина
£о = pj (4-3.3)
М
достаточно мала, то движение близко к невозмущенному кеплеров-
скому движению вокруг Земли. Наоборот, если величина
*1 = ГГ (4-3-4)
1*11
достаточно мала, то движение близко к невозмущенному кеплеров-
скому движению в окрестности Луны. Отношение
е = ^ (4.3.5)
будем принимать за меру близости движения к кеплеровскому дви¬
жению вокруг Земли. С уменьшением £о растет е\9 движение все
более близко к движению вокруг Земли и все более далеко от дви¬
жения вокруг Луны. Указанные изменения £q и е\ ведут к умень¬
шению £.
Рассмотрим теперь поверхность е = const. Эта поверхность
должна разбить пространство на области, «разрешенную» и «за¬
прещенную» для применения эволюционных уравнений; «запре¬
щенная» область должна охватывать окрестность Луны, а в «разре¬
шенной» области эволюционные уравнения описывают движение
(согласно общим принципам асимптотических методов) с точно¬
стью порядка £ на интервале времени порядка 1/е. Будем называть
такую поверхность £-поверхностью.
Возведем (4.3.5) в квадрат и, сделав некоторые простые пре¬
образования, получим (пренебрегая еще массой m2, очень малой
по сравнению с то и Ш|)
44/1 1 2 \
т'гЧн+^ - Tv?cosA; =
jjjp . 1 . 2(/r, cosA -12)\
\i* rj щ j.
(4.3.6)
где A — угол между направлениями Луна—Земля и Луна-спутник
(рис. 4.4), а
rl = l2 + r] -2r,icosA. (4.3.7)
Формулы (4.3.6), (4.3.7) дают е-поверхность Г|(А).
128
Очерк четвертый. Движение миров
Сложную формулу (4.3.6) легко упростить. Естественно ожи¬
дать, что е-поверхность ограничивает около Луны область малого
(по сравнению с расстоянием Луна—Земля) размера, так что Т\/1
мало. Приведем (4.3.6) к общему знаменателю и разложим по сте¬
пеням Г\/1. Сохраним только члены разложения с самой низкой
степенью Г\/1. Получим
p(^), = (t)'0(1+Wa)' <«-8>
Эта поверхность вращения не очень сильно отличается от сфе¬
ры. В самом деле, при cos А = О Г\ = г™ах, при cos2 А = 1 г\ = г™1П,
причем отношение максимального размера г™ах поверхности к ее
минимальному размеру r™m составляет \П ~ 1,15. Поэтому в ка¬
честве е-поверхности возьмем сферу
r'=i^Tw <4i9)
Итак, если траектория нашего спутника не попадает в процессе
своей эволюции в окрестность Луны, ограниченную сферой (4.3.9),
то наши эволюционные (осредненные) уравнения будут давать ре¬
шение, отличающееся от истинного на величину порядка е, притом
на большом интервале времени (вообще говоря, порядка 1/£2^).
При е = 1 уравнение (4.3.9) дает сферу, широко используемую
в механике космического полета и называемую сферой действия
[4.6]. Если спутник попал в сферу действия Луны, то его уже сле¬
дует рассматривать как спутник Луны (пока он не выйдет из ее
сферы действия). Вне этой сферы спутник, действительно, можно
рассматривать как спутник Земли.
Мы говорим о системе Луна—Земля для определенности. Но
можно рассматривать и другие системы, например систему Земля-
Солнце. Тогда формула (4.3.9) определит г-сферу (и сферу действия
при е=1) Земли относительно Солнца. В следующей таблице
(см. стр. 129) приводятся размеры радиуса г\ £-сфер и сфер дей¬
ствия Луны (относительно Земли) и Земли (относительно Солнца).
В этой таблице радиусы е-сферы вычислены для спутника
Земли, возмущаемого либо Луной (первая строка), либо Солнцем
Из дальнейшего будет ясно, что этот интервал времени может быть и неогра¬
ниченным при конечном е.
3. Область маловозмущенного движения
129
£ = 1
е-0,1
<У)
II
О
о
е = 0,001
Луна
66 280 км
105 050 км
166 360 км
263 790 км
Земля
924820 км
583 490 км
368460 км
232 370 км
(вторая строка). Поэтому с уменьшением е радиусы в первой стро¬
ке растут (растет запретная зона вокруг Луны), а во второй строке
уменьшаются (уменьшается разрешенная зона вокруг Земли). Для
расчета второй строки в формуле (4.3.9) надо, естественно, брать
не е, а е~]. Интересно отметить, что для е = 0,1 существует разре¬
шенная область, охватывающая и Луну и Землю, где могут суще¬
ствовать орбиты спутников Земли, одинаково «не сильно» (е ~ 0,1)
возмущаемые и Луной, и Солнцем. Для бг = 0,01 нет слабовозмуща-
емых «внешних» орбит, охватывающих и Луну, и Землю (рис. 4.5).
Необходимые для расчета предыдущей таблицы значения па¬
раметров взяты следующими:
то/т |
1
Луна (относительно Земли)
81,35
384300 км
Земля (относительно Солнца)
332400
149598 500 км
Рис. 4.5. Область слабовозмущенного движения
9 Заказ 1667
130
Очерк четвертый. Движение миров
Заметим, что в механике космического полета используются также
гравитационные сферы, определенные и из других соображений [4.7].
Понятие сферы действия нам еще понадобится для анализа
траекторий окололунных перелетов.
4. Устойчивость Солнечной системы
Все предыдущие выводы об устойчивости планетных орбит
и их эволюции были сделаны нами на основе неточных, осреднен-
ных, эволюционных уравнений и поэтому не могут дать строгого
ответа об устойчивости на бесконечном интервале времени.
Напомним, что, когда мы ставим вопрос об «устойчивости Сол¬
нечной системы», имеется в виду математическая проблемаустой-
чивости траекторий в задаче п материальных взаимно притяги¬
вающихся по ньютоновскому закону точек; масса одной из них
(Солнца) существенно больше масс других точек. Никакие другие
силы, кроме силы ньютоновского взаимного притяжения, не рас^
сматриваются.
В этой постановке задача в течение двух веков была предметом
исследований ряда выдающихся математиков, но их усилия не при¬
водили к цели.
Но в 1961 году молодой советский математик В. И. Арнольд
уже докладывал о своих фундаментальных результатах, являющих¬
ся крупнейшим шагом к решению этой проблемы. Эти результаты,
основанные на ряде идей академика А. Н. Колмогорова, носят об¬
щий характер анализа поведения решений канонических систем.
Заключения о поведении Солнечной системы вытекают отсюда как
частный случай.
Рассмотрим каноническую систему с гамильтонианом
Н(р, q) = Н0(р) + £ff, (р, q, е),
где p,q — n-мерные векторы, е мало, Н\ периодично по q с пе¬
риодом 2ж. Если е = 0, то движение определяется из уравнений
р = 0, q = w(p),
/\ дНо ( ^
где (jjyp) = —— = (u;i,... ,шп) и представимо на n-мерном торе
ар
р = const «обмоткой» q(t) этого тора.
4. Устойчивость Солнечной системы
131
Для двумерного случая ситуа¬
ция изображена на рис. 4.6. На дву¬
мерном торе («баранке») отложена
долгота #| и широта qi. Равномер¬
ное одновременное изменение q\
со скоростью и| и q2 со скоро¬
стью Ш2 дает траекторию, обматы¬
вающую тор, как можно показать,
всюду плотно3\ если из\ и 072 несо¬
измеримы. Такое движение назы¬
вают условно-периодическим. Если же Ш\/ш2 = т/п, где т и п —
целые числа, то через время t = 2itm/u)\ = 27гп/ш2 траектория за¬
мкнется. В этом случае движение периодично. Так же в п-мерном
случае при 07|fc| + ... + о)пкп = 0, где &г — целые числа и по край¬
ней мере два из них не равны нулю, траектория будет периодичной,
замкнутой на n-мерном торе, а если ш\к\ + .. .+шпкп ф 0, то движе¬
ние будет условно-периодическим, траектория qi(t) (i = 1,..., n)
всюду плотно заполняет n-мерный тор р = const.
Подключим теперь «возмущающую часть» еН\ гамильтониана
Я. Пусть е достаточно мало. Можем ли мы утверждать, что движе¬
ние останется близким к исходному условно-периодическому или
периодическому движению? Иначе говоря, сохраняются или раз¬
рушаются исходные торы невозмушенного движения?
Если исходные торы не разрушаются, а лишь «слегка деформи¬
руются», то возмущенное движение вечно близко к невозмущенно¬
му. В возмущенном движении (г Ф 0) ф const («деформирован¬
ный тор»), но pi близки к pi = const («недеформированный тор»),
отвечающим невозмущенному (е = 0) движению. Чтобы убедиться
в малом отличии траекторий возмущенного движения от траекто¬
рий невозмущенного, достаточно (всего лишь!) построить в окрест¬
ности невозмущенного движения сходящиеся при малом е ряды,
описывающие возмущенное движение. Над этим «всего лишь» и би¬
лись двести лет различные математики, но «испечь» эту баранку
(тор возмущенного движения) удалось лишь В. И. Арнольду.
Следуя идее А. И. Колмогорова, В. И. Арнольд построил после¬
довательные приближения типа «метода Ньютона» (аналог метода
касательных в нахождении корней алгебраических уравнений). Этот
Это значит, что движущаяся точка рано или поздно окажется внутри любой
сколь угодно малой области на торе.
9*
Рис. 4.6. Тор условно-периодиче¬
ского невозмущенного движения
132
Очерк четвертый. Движение миров
2 А;
метод в k-м приближении дает ошибку порядка е что при к оо
обеспечивает быструю сходимость. При практическом построении
доказательств В. И. Арнольду пришлось преодолеть ряд серьезных
трудностей. Назовем некоторые из них.
1. Резонансностъ. Если в невозмущенном движении кгщ = О,
то в возмущенном движении траектории, вообще говоря, могут
не лежать на торе. Тор разрушается. Сходящиеся ряды, описы¬
вающие возмущенное движение, если и можно построить, то не
во всем фазовом пространстве, а лишь в некоторых его «слоях».
А именно, как оказалось, в окрестностях невозмущенных торов с
условно-периодическими (но не периодическими!) движениями.
Вторая трудность, вызванная резонансностью, состоит в том,
что ряды, описывающие возмущенное движение, содержат зна¬
менатели вида Е fejo;*, которые малы, если частоты близки
к резонансным. Малость знаменателей препятствует сходимо¬
сти рядов. Эти трудности обойдены в теореме А. Н. Колмогоро¬
ва, полное доказательство которой проведено В. И. Арнольдом
9 к
[4.8]. Сходимость ньютоновского типа (е ) «забивает» зловред¬
ное влияние малых знаменателей.
Однако применение результатов анализа гамильтоновых си¬
стем к задаче устойчивости планетных орбит встречает еще
ряд трудностей, преодоленных В. И. Арнольдом в процессе до¬
казательства его теоремы, развивающей теорему А. Н. Колмо¬
горова. Отметим эти трудности.
2. Собственное вырождение. Под этим термином подразумевает¬
ся тот факт, что количество частот в возмущенном движении
может быть больше, чем в невозмущенном. Вспомним, что
«лагранжево движение планет» содержит больше частот, чем
кеплеровское движение: кроме быстрых «частот» кеплеровских
движений планет по орбитам имеются медленные «частоты»
прецессий перигелиев планет и восходящих узлов их орбит.
Путь к преодолению этой трудности —■ рассматривать в ка¬
честве невозмущенного «новое» движение (например, вместо
кеплеровского более точное лагранжево движение).
3. Предельное вырождение. Этот термин подразумевает следующее.
Среди n-мерных торов р = const невозмущенного движения
могут встретиться торы размерности к < п, например, по¬
ложение равновесия (к = 0) и одночастотное периодическое
движение (к = 1).
4. Устойчивость Солнечной системы
133
В результате большой и тяжелой работы В. И. Арнольд строго
и последовательно пришел к теореме [4.9], суть которой заключа¬
ется в следующем:
Возмущенное движение, описываемое гамильтоновой системой,
для большинства начальных данных является условно-периодическим,
вечно близким к соответствующе подобранному «невозмущенному»
условно-периодическому движению.
Существенная оговорка «для большинства начальных данных»
подразумевает, что в возмущенном движении сохраняются любые то¬
ры невозмущенного движения, кроме, может быть, торов с резонанс¬
ными частотами вместе с малой их окрестностью. Эти последние
торы в возмущенном движении, вообще говоря, разрушаются. Об¬
щая картина возмущенного движения может быть представлена
в виде условно-периодических движений по сохранившимся (слег¬
ка деформированным) торам, шели между которыми заполнены
остатками разрушенных торов.
О поведении траекторий в этих «щелях» мало что известно4^.
Если задача — с двумя степенями свободы, то интеграл энергии
Н = const дает трехмерное многообразие, которое делят торы
условно-периодических движений (рис. 4.7), и траекториям из ще¬
лей между этими торами некуда деться (пересечь торы условно-пе¬
риодических движений они не могут в силу однозначной зависимо¬
сти движений от начальных данных).
А так как ширина щели мала вместе
с е, то в системах с двумя степеня¬
ми свободы можно говорить об устой¬
чивости даже и резонансных движений.
В системах с большим числом степе¬
ней свободы размерность торов услов¬
но-периодических движений по край¬
ней мере на две единицы меньше раз- Рис. 4.7. Торы условно-пе-
мерности фазового пространства. Эти риодических возмущенных
торы не делят пространства и похо- движений
жи на сколь угодно густо растущий
сосновый лес, в котором белка, спустившаяся на землю, может
сколь угодно долго бегать меж трех сосен (устойчивость), но может
меж сосен и убежать сколь угодно далеко (неустойчивость). Дру-
Примечание переводчика. Это утверждение было, конечно, справедливо в то
время, когда была написана эта книга. См. примечания переводчика в Дополни¬
тельных комментариях к этому очерку.
134 Очерк четвертый. Движение миров
4. Устойчивость Солнечной системы
135
гая белка тем временем бегает по стволу одной и той же сосны
в условно-периодическом движении, устойчивом даже при силь¬
ном ветре5^.
Приложением теоремы Арнольда является следующий силь¬
ный результат. Пусть массы планет достаточно малы по сравнению
с массой центрального светила (Солнца). Тогда, если эксцентри¬
ситеты и наклонения орбит достаточно малы, то для большинства
начальных условий истинные движения планет условно-периодичны
и вечно близки к соответствующе подобранным лагранжевым движе¬
ниям. При этом эксцентриситеты и наклонения вечно останутся ма¬
лыми, а большие полуоси орбит вечно будут близки к своим начальным
значениям. Иначе говоря, «теорема Лапласа» верна на бесконечном
интервале времени.
Так как мы ранее получали «теорему Лапласа» методом осред¬
нения, то можем заключить, что имеются случаи (да какие!), когда
метод осреднения дает картину движения, близкую к истинной,
на всем бесконечном интервале времени.
То «большинство начальных условий», о которых говорится
выше, повторяем, исключает резонансные соотношения между ча¬
стотами движений.
Результаты В. И. Арнольда трудно переоценить. Они достигну¬
ты благодаря синтезу глубоких идей с изнурительным трудом при
их осуществлении. Только формулировки отдельных лемм и теорем
занимают целые страницы его работ. Сам Арнольд по этому по¬
воду употребляет довольно сильные выражения, например: «...Мы
будем пользоваться устрашающим формальным аппаратом дина¬
мики» ([4.9], с. 94) 6\
Решение проблем, насчитывающих двухвековую историю, ко¬
нечно, не может даться легко. Существенный вклад в это дело
внесли замечательные математики — А. Пуанкаре, Дж. Биркгоф,
А. Н. Колмогоров, К. J1. Зигель, Ю. Мозер. Теоремы Арнольда-
Колмогорова нанесли один из завершающих ударов в решении
проблемы устойчивости движений системы гравитирующих тел.
См. работу Н. Н. Нехорошева «О поведении гамильтоновых систем, близких
к интегрируемым» (Функциональный анализ, 1971, №4).
«Иа-Иа, старый серый ослик, однажды стоял на берегу ручья и понуро смотрел
в воду на свое отражение.
— Душераздирающее зрелище, — сказал он наконец. — Вот как это называется —
душераздирающее зрелище».
А. А. Милн. «Винни-Пух и все, все, все».
136
Очерк четвертый. Движение миров
Остается, однако, задача о применимости этих результатов
в каждом конкретном случае, например в случае нашей конкретной
Солнечной системы.
5. Не резонансна ли Солнечная система?
Трудности со сходимостью рядов, описывающих возмущенное
движение в небесной механике, возникли в значительной степени
потому, что среди частот есть приближенно соизмеримые. Так, на¬
пример, если среднее движение (частоту) о;юп обращения Юпитера
вокруг Солнца принять за 1, то среднее движение (частота) а;сат
обращения Сатурна будет равно 0,4027, откуда
2д>юп ~ 5&Сат — —0,0135. (4.5.1)
Видна приближенная соизмеримость (резонанс с^юп/^сат = 5/2)
движений Юпитера и Сатурна.
Удивительную гипотезу выдвинул А. М. Молчанов. В процессе
эволюции, справедливо считает он, надо учитывать малые дис¬
сипативные (то есть рассеивающие энергию) силы. В Солнечной
системе это могут быть приливные силы, тормозящие силы от меж¬
планетной пылевой материи и другие, может быть даже неизвест¬
ные нам еще, диссипативные силы.
Мы знаем, что возмущения за счет взаимодействия планет
очень малы. Диссипативные силы на порядки меньше даже этих
малых возмущений. Но, действуя миллиарды лет, диссипативные
силы систематически меняют орбиты и приводят движение планет
к каким-то стационарным орбитам — практически неизменным
в последующие миллиарды лет.
Пока мы не сказали ничего оригинального. «Все это давно
известно». Оригинальное же состоит в том, что, по гипотезе Мол¬
чанова, эти стационарные орбиты должны быть резонансны\ «Эво-
люционно зрелые колебательные системы неизбежно резонансны,
а их строение задается набором целых чисел», — пишет А. М. Мол¬
чанов. В частности, А. М. Молчанов выдвинул гипотезу полной ре-
зонансности Солнечной системы: частоты (средние движения) обра¬
щения планет ненамного отличаются от таких частот, для которых
А. М. Молчанов нашел полную систему резонансов для девяти из¬
вестных больших планет. Более того, аналогичные резонансы он
обнаружил для некоторых из спутников планет. Соответствующие
таблицы опубликованы им в «Икарусе» — международном журнале
5. Не резонансна ли Солнечная система?
137
Таблица 4.1
Резонансные соотношения в Солнечной системе
Планета
*?
Аш/ш
П|
п2
п3
п4
п5
пь
п7
п8
щ
1
Меркурий
49,22
49,20
0,0004
1
-1
-2
-1
0
0
0
0
0
2
Венера
19,29
19,26
0,0015
0
1
0
-3
0
-1
0
0
0
3
Земля
11,862
11,828
0,0031
0
0
1
-2
1
-1
1
0
0
4
Марс
6,306
6,287
0,0031
0
0
0
1
-6
0
-2
0
0
5
Юпитер
1,000
1,000
0,0000
0
0
0
0
2
-5
0
0
0
6
Сатурн
0,4027
0,400
0,0068
0
0
0
0
1
0
-7
0
0
7
Уран
0,14119
0,14286
-0,0118
0
0
0
0
0
0
1
-2
0
8
Нептун
0,07197
0,07143
0,0075
0
0
0
0
0
0
1
0
-3
9
Плутон
0,04750
0,04762
-0,0025
0
0
0
0
0
1
0
-5
1
проблем Солнечной системы [4.10]. Оттуда мы и заимствуем ниже¬
следующие таблицы 1\
Табл. 4.1 содержит целые числа щ — положительные, отрица¬
тельные и нули — такие, что
9
^2 пм=о,
*=I
где щ — частоты (средние движения) обращения больших планет
Солнечной системы. При этом в качестве щ берутся некоторые
«теоретические» значения а)} частот, в точности удовлетворяющие
резонансным соотношениям
щщ = 0;
i
но рядом приводятся фактически наблюдаемые значения ичастот
соответствующих планет и показаны отношения
Да; _ ш" - а;Т
" и"
описывающие отклонения фактических частот от резонансных. Эти
отклонения малы!
^ Последние строки этих таблиц построены из формального требования равен¬
ства единице соответствующего детерминанта.
138
Очерк четвертый. Движение миров
Аналогичные таблицы приводятся и для систем спутников
Юпитера, Сатурна, Урана (табл. 4.2).
Эти таблицы производят достаточно убедительное впечатле¬
ние. Отклонение истинных частот от резонансных не превосходит
в худшем случае 1,5 %. В резонансах друг с другом находятся, как
правило, ближайшие друг к другу планеты (или спутники планет).
Ввиду того, что частоты мы
вынуждены приближенно зада¬
вать конечными десятичными
дробями (то есть рациональны¬
ми числами), то, вообще гово¬
ря, всегда можно найти доста¬
точно большие по модулю це¬
лые числа щ обеспечивающие
резонансные соотношения для
частот. Однако таблицы Молча¬
нова содержат не большие |пг|,
а малые, что тоже говорит в пол Ьт
зу гипотезы Молчанова. На гра¬
фике рис. 4.8 приведено рас¬
пределение количества N дан¬
ных чисел \щ\ в таблицах Мол¬
чанова в зависимости от вели¬
чины \щ\. Видим, что \щ\ сосредоточены в области небольших
своих значений. Вряд ли поэтому открытые резонансные соотно¬
шения могут быть случайны.
В связи с этим для ответа на вопрос об устойчивости реальной
Солнечной системы может оказаться важным обследование устой¬
чивости как раз резонансных движений, выброшенных из рассмот¬
рения в теории Арнольда (что, к слову сказать, не умаляет выдаю¬
щегося значения этой теории). С другой стороны, гипотеза Молча¬
нова рождает больше вопросов, чем отвечает на них. Однозначна ли
система «небольших» резонансных чисел, найденных Молчановым,
или можно подобрать другую, не хуже? Ведь отличие от нуля ре¬
зонансных соотношений между наблюдаемыми (а не подобранны¬
ми) частотами может достигать заметной величины по сравнению
с наименьшими частотами Солнечной системы. Сравним, напри¬
мер, рассогласование 0,0135 в резонансе (4.5.1) с частотами 0,07197
и 0,04750 обращения Нептуна и Плутона.
Почему система «скатилась» в процессе эволюции именно к та¬
ким резонансам, а не к другим? Каков, наконец, действительный
Рис. 4.8. Распределение
резонансных чисел Солнечной
системы
5. Не резонансна ли Солнечная система?
139
Таблица 4.2
Резонансные соотношения в системах спутников планет
Спутники Юпитера
Спутник
*?
ш-
Аш/ш
72,
п2
п3
72 4
I
Но
4,044
4,000
0,0110
1
-2
0
0
2
Европа
2,015
2,000
0,0075
0
1
-2
0
3
Ган и мед
1,000
1,000
0,0000
0
0
-3
7
4
Каллисто
0,4288
0,4285
0,0008
0
0
-1
2
Спутники Сатурна
Спутник
и"
и]
Аш/ш
П\
п2
п3
724
п5
72?
72g
1
Мимас
16,918
16,800
0,0070
-1
0
2
0
0
0
0
0
2
Энцелад
11,639
11,600
0,0035
0
-1
0
2
0
0
0
0
3
Тефия
8,448
8,400
0,0057
0
0
-1
0
2
1
0
2
4
Диона
5,826
5,800
0,0045
0
0
0
-1
2
-1
0
-1
5
Рея
3,530
3,500
0,0086
0
0
0
0
-1
2
2
0
6
Титан
1,000
1,000
0,000
0
0
0
0
0
-3
4
0
7
Гиперион
0,7494
0,7500
0,0008
0
0
0
0
0
-1
0
5
8
Я пет
0,2010
0,2000
0,0050
0
0
0
0
0
0
-1
4
Спутники Урана
Спутник
ш"
ш]
Аш/ш
л,
722
723
724
п5
1
Миранда
6,529
6,545
-0,0025
-1
1
1
1
0
2
Ариэль
3,454
3,454
0,0000
0
-1
1
2
-1
3
Умбриэль
2,100
2,091
0,0043
0
0
-2
1
5
4
Титания
1,000
1,000
0,0000
0
0
1
-4
3
5
Оберон
0,6466
0,6364
0,0160
0
0
1
-2
0
140
Очерк четвертый. Движение миров
механизм «скатывания» системы в резонансный режим? Напом¬
ним, что гипотеза Молчанова пока гипотеза, поскольку не дока¬
зано строго математически, что колебательная система при каких-
то условиях (каких)? обязательно выйдет на резонансный режим
(да еще на режим полного резонанса)8^.
Хорошо известно из наблюдений, что астероиды «избегают»
двигаться по некоторым резонансным (с Юпитером) орбитам; ще¬
ли в кольцах Сатурна тоже имеют резонансную структуру. Молодой
московский математик А. Д. Брюно показал [4.11], что в канони¬
ческих системах вероятность неустойчивости периодического ре¬
жима тем больше, чем меньше порядок резонанса 9\ На рис. 4.9,
заимствованном из [4.12], показано распределение числа астерои¬
дов по средним суточным движениям п; по горизонтали отложены
значения п (в секундах дуги за сутки), по вертикали —■ число
астероидов в 5"-х интервалах средних суточных движений. Свер¬
ху указано отношение п/%, где Пю = 300;/ — среднее суточ¬
ное движение Юпитера. Порядок резонанса равен разности между
числителем и знаменателем этих отношений. А. Д. Брюно заме¬
тил, что характер наблюдаемых щелей (люков) в распределении
астероидов качественно соответствует его теории. Щель порядка
3 (п/пю = 5/2) полная, возможное периодическое движение все¬
гда неустойчиво — и таких движений нет. Щели более высоких
порядков неполные, и с ростом порядка они становятся менее за¬
метными, так как убывает вероятность неустойчивости: в зависи¬
мости от начальных условий движение может быть и устойчиво,
и — с убывающей вероятностью — неустойчиво.
Как сочетать гипотезу о резонансности Солнечной системы
с нежеланием астероидов двигаться по резонансным орбитам? Де¬
ло, видимо, в том, что резонансные движения являются «особыми
траекториями» системы и по аналогии с «особыми точками» диффе¬
ренциальных уравнений могут быть устойчивыми или неустойчи¬
выми. Поэтому система, эволюционируя, уходит от одних резонан¬
сов (неустойчивых) и скатывается в другие резонансы (устойчивые).
Богатая и интересная информация о подобных явлениях в природе и технике
и о теории этих явлений содержится в книге И. И. Блехмана «Синхронизация дина¬
мических систем» (Наука, 1971).
Пусть среднее суточное движение астероида равно п, а Юпитера — П\о • Тогда
относительная средняя угловая скорость астероида равна п — Пю • Если отношение
пю/(п — Пю) = Р/Я* гДе q>0npuq— целые взаимно простые числа, то число q>
по А. Д. Брюно [4.11], и называется порядком резонанса.
5. Не резонансна ли Солнечная система?
141
ть
Рис. 4.9. Распределение числа астероидов
Особая роль резонансов в Солнечной системе проявляется
и во вращательном движении планет вокруг своих осей. Всем из¬
вестно, что Луна обращена одной стороной к Земле — прекрасный
пример резонанса 1 : 1 между периодом обращения по орбите
и периодом вращения вокруг оси. Мы еще позже, в другом очер¬
ке, вернемся к объяснению этого эффекта. Совсем недавно, после
обработки данных радиолокации планет Меркурий и Венера, стали
известны новые факты [4.13] о вращении этих планет. Оказывает¬
ся, период вращения Тцр Меркурия относится к периоду обращения
Тобр, как 2/3! И совсем уж феноменальный характер носит резонанс
во вращении Венеры. Каждый раз, когда Земля и Венера макси¬
мально сближаются друг с другом, Венера оказывается повернутой
к Земле одной и той же стороной, то есть вращение Венеры нахо¬
дится в резонансе даже не с ее орбитальным движением, а с движе¬
нием Венеры относительно вращающейся линии Солнце — Земля!
Период вращения Венеры, по последним обработкам радиоло¬
кационных данных, составляет = 243,24 ± 0,1 суток, что в пре¬
делах точности измерений совпадает со значением 243,16 суток,
при котором Венера в каждом нижнем соединении должна быть
обращена к Земле одной и той же стороной. Период соединений
г = 583,92 суток. В результате за это время Земля в беге по своей
орбите опишет дугу
а3 = 27Г + 27Г • 0,6 = а;3т,
где а;3 — среднее суточное движение Земли.
142
Очерк четвертый. Движение миров
Аналогично, Венера в своем орбитальном движении опишет дугу
ав = 27Г • 2 + 2тг • 0,6 = а>вт;
вращаясь вокруг своей оси обратным образом (то есть в сторону,
противоположную обращению по орбите) с угловой скоростью О,
Венера повернется вокруг оси за время т на угол
/3 = -27Г • 3 4- 27Г • 6 = -0,Т.
Таким образом, за время т все три угла аз, ав, /3 примут оди-
наковые значения ^ 27Г *0,6 (с точностью до кратных 2тг). Вычитая
последнее равенство из двух предыдущих, обнаружим, что
2тг ^ 2тг
5 • — — 4" ^2, 4 • — = из3 -J-
т г
Это означает, что за время т Венера относительно собственной
орбитальной системы координат (относительно линии Солнце—
Венера) сделает 5 полных оборотов, а относительно линии Солнце-
Земля сделает 4 полных оборота. Два последних резонансных со¬
отношения (ввиду того, что 27г/т = — и;3) приводят к одному
и тому же:
= 4д^в — 5сд^з.
Данные о резонансах во вращении планет собраны в табл. 4.3.
Все сказанное свидетельствует в пользу особой и неслучайной
роли резонансов в движении миров.
Говорят, что всякая хорошая идея в процессе завоевания об¬
щественного мнения проходит три стадии:
«Этого не может быть»;
«Это может быть, но не доказано»;
«Это давно известно».
Идея А. М. Молчанова сейчас находится, по-видимому, где-то
на полпути от первой стадии ко второй 10\ Вокруг этой гипотезы
кипят споры и страсти. И хотя она не доказана, само ее суще¬
ствование стимулирует развитие исследований в этом направлении;
естественнонаучное значение этой гипотезы неоспоримо.
Идея А. М. Молчанова перекликается с более ранними идеями
Н. Г. Четаева n\ Н. Г. Четаеву принадлежит интереснейшая мысль
,0^ Это было сказано в 1972 г. За минувшее время, по-видимому, оставлена позади
и вторая стадия.
Николай Гурьевич Четаев (1902-1959) — член-корр. АН СССР, выдающийся
советский механик и математик, автор фундаментальных работ и идей в области
теории устойчивости и аналитической механики.
5. Не резонансна ли Солнечная система?
143
Таблица 4.3
Резонансы во вращении планет и их спутников
1. Луна
Период обращения вокруг Земли,
Т0 = 27,32
ср. сутки
Период вращения вокруг своей оси,
Ти = 27,32
ср. сутки
Направление вращения
прямое*
Резонанс
о
II
1
2. Меркурий
Период обращения вокруг Солнца,
То = 87,97
ср. сутки
Период вращения вокруг своей оси,
Ти = 59 ± 3
ср. сутки
Направление вращения
прямое
Резонанс
3 Ты
— - 1 « ±0,017
2 Т0
3. Венера
Период обращения Венеры вокруг
То = 224,7
Солнца, ср. сутки
Период обращения Земли вокруг
То = 365,24
Солнца, ср. сутки
Период между ближайшими положени¬
г = 583,92
ями Земли и Венеры, ср. сутки
Период вращения Венеры вокруг оси,
Тив = 243,24 ±0,1
ср. сутки
Направление вращения Венеры
обратное
Резонанс
Прямое вращение — вращение в сторону орбитального движения,
обратное — в противоположную сторону
144
Очерк четвертый. Движение миров
[4.14]: «Устойчивость, явление принципиально общее, как-то долж¬
на, по-видимому, проявляться в основных законах природы».
Последовательно развивая эту мысль, Н. Г. Четаев пришел,
в частности, к гипотезе о квантовании устойчивых орбит дина¬
мики. По Н. Г. Четаеву, устойчивыми могут быть лишь некоторые,
исключительные траектории — аналогично тому, как в квантовой
механике устойчивы лишь исключительные орбиты электронов.
В заключение осмыслим с точки зрения «принципа резонанс-
ности» некоторые хорошо известные свойства движения в цен¬
тральном поле сил.
Если материальная точка массы т движется в поле централь¬
ных сил с силовой функцией U(r), зависящей только от расстоя¬
ния г точки от начала координат, то движение точки — плоское
и полностью определяется законами сохранения энергии и момен¬
та количества движения. Введем в плоскости движения полярные
координаты г, р. Тогда интегралы энергии и площадей принимают
соответственно вид
У (г2 + гУ) - U(г) = h, (4.5.2)
г2ф — с. (4.5.3)
Исключая из (4.5.2) ф с помощью (4.5.3), приходим к задаче ис¬
следования одномерного движения:
у г2 - U*(r) = h, U* (г) = U(г) - (4.5.4)
Величина U*(r) носит название эффективной силовой функции. Обо¬
значив
Ф(г) = -(h + U*)9
т
из (4.5.4) получаем интегрируемое уравнение
г = ±у/ф(г). (4.5.5)
В действительном движении Ф(г) > 0; если при этом Г\ и гг —
два соседних корня уравнения Ф(г) = 0 и Ф(г) > 0 при г| < г < ri,
то действительное движение, начавшись в промежутке Г\ ^ г < г2,
уже не покинет его. Величина г будет, как правило, периодически
колебаться с неким периодом Тг между своими экстремальными
значениями Г\ и г^. И эта картина, вообще говоря, имеет место
5. Не резонансна ли Солнечная система?
145
при любых значениях постоянной энергии ft, взятой из некоторого
вполне определенного интервала h! ^ Л ^ h".
Далее, исключая dt из (4.5.3) с помощью (4.5.5), получаем, что за
время Тг радиус-вектор орбиты совершит поворот на угол 2А<р, где
= f _£* ,4.5.6)
J r2v/¥(r)
ГI
Если А<р = 7г, то траектория — замкнутая и замкнется за один
оборот радиус-вектора. Траектория замкнется в общем случае, если
Aip = {к/п)7Г, где к и п — целые.
Но это ниоткуда не следует! При произвольно взятых постоянных
энергии h и площадей с траектория в поле центральных сил, вообще
говоря, разомкнута и представляет собой, например, бесконечно¬
лепестковую розетку, изображенную на рис. 1.12 а в очерке первом.
Тем поразительней, что в реально существующем во Вселенной
ньютоновском поле сил с силовой функцией
U = — (4.5.7)
г
траектории — кеплеровы эллипсы! — всегда замкнуты при любых
отрицательных значениях константы энергии ft; замыкание проис¬
ходит за один оборот радиус-вектора. Это свойство никак не следует
из законов сохранения; оно является следствием специфичного ви¬
да эффективной силовой функции
е
отвечающей ньютоновскому закону тяготения. Кроме ньютонов¬
ского силового поля (4.5.7) аналогичным свойством обладает лишь
поле
U = -кг2, к = const,
обеспечивающее гармонические колебания точки.
Таким образом, ньютоновское центральное поле — уникум,
чудо природы. Поразительно, что природа избрала для себя некий
особый, уникальный способ тяготения, обеспечивающий замкну¬
тость орбит.
Но что такое замкнутая орбита? Это соизмеримость между
периодом Тг колебаний величины радиус-вектора и периодом Ту
поворота радиус-вектора на угол 27т! Кеплеровы орбиты обладают
10 Заказ 1667
146
Очерк четвертый. Движение миров
соизмеримостью Tr : = 1 : 1. Иначе говоря, «внутри» кеплерова
движения — и, следовательно, ньютоновского закона всемирного
тяготения — заложен резонанс!
«Эволюционно-зрелые системы неизбежно резонансны» — гла¬
сит принцип резонансности. Невольно задумаешься: не является ли
сам ньютоновский закон тяготения продуктом эволюции Вселен¬
ной согласно «принципу резонансности»? Эта дерзкая мысль также
принадлежит А. М. Молчанову.
Дополнительные комментарии к этому изданию. Прошло более
20 лет со времени второго издания этих «Очерков», лет, богатых
новыми исследованиями и результатами в теории динамических
систем. Совершенно типичным явлением в динамических систе¬
мах оказался «детерминированный хаос» — траектории, поведение
которых практически хаотично, несмотря на детерминированность
начальных условий и параметров системы [4.16,4.17]. Были от¬
крыты особые предельные движения, названные хаотическими или
«странными» аттракторами. Это показало, что предельные режи¬
мы динамических систем не обязательно резонансны. Таким обра¬
зом, «принцип резонансности» в общей формулировке Молчанова
(«Эволюционно-зрелые системы неизбежно резонансы») неверен.
Это, конечно, не исключает существования предельных резонансов
в динамических системах, в частности, многочисленных резонан¬
сов в Солнечной системе.
Что касается упомянутого в этом очерке вращательного движения
Венеры, см. очерк шестой и дополнительные комментарии к нему.
Примечания переводчика.
1. В последние годы поведение орбит в щелях между возмущенными
инвариантными торами в теории Колмогорова—Арнольда—Мозера,
включая явление, известное как «диффузия Арнольда», стало пред¬
метом интенсивных исследований. Поскольку трудно привести до¬
статочно полный список соответствующих ссылок, упомянем здесь
только статью P. Lochak «Arnold diffusion: a compendium of remarks and
questions» в: Hamiltonian Systems with Three or More Degrees of Free¬
dom (S’Agars, 1995). 168-183. NATO Adv. Sci. Inst. Ser. C. Math. Phys.
Sci. Dordrecht. Kluver Acad. Publ. 1999. 533, где проведен критический
анализ состояния теории к 1995 году.
2. Интересующийся читатель может обратиться также к недавно вы¬
шедшей книге: Murray С. D. and Dermott S. F. Solar System Dynamics.
Cambridge: Cambridge Univ. Press, 1999.
Очерк пятый
Ограниченная задача трех тел,
полет к Луне и эволюция галактик
Мефысто: ... Луна, тебе — мой поцелуй.
(Распростирает свой темный на красной под¬
кладке плащ, садится на него и со свистом
улетает в шумно распахнувшееся окно.)
А. В. Луначарский
«Фауст и город»
1. Поверхности Хилла
Освоение маршрута Земля—Луна—Земля, происходящее на на¬
ших глазах, началось задолго до запуска первого спутника — на бу¬
маге, в чертежах, в числах, полученных расчетами на быстродей¬
ствующих электронных машинах. Уже в 1957 году В. А. Егоров опуб¬
ликовал большую работу [5.1] с результатами анализа траекторий
полетов кЛуне. В этом маленьком очерке мы лишь вкратце остано¬
вимся на исследованиях В. А. Егорова, имея в виду показать, сколь
много можно получить самыми простыми средствами. Подробное
описание этих исследований можно найти в монографии [5.2]. По¬
пулярное, но очень глубокое изложение работ В. А. Егорова содер¬
жится также в книге В. И. Левантовского «Ракетой к Луне» [5.3].
Проблему полета к Луне можно рассматривать в рамках огра¬
ниченной задачи трех тел. Пусть гп\ — масса Земли, га2 — масса
Луны; под влиянием притяжения этих масс движется снаряд мас¬
сы то, столь малой по сравнению с Ш| и т2, что притяжением
Луны и Земли снарядом можно пренебречь. Тогда Луна и Земля
движутся по известным кеплеровым траекториям вокруг общего
центра масс. Примем эти траектории круговыми (круговая задача
трех тел). Период обращения Т по этим траекториям, деленный
ю*
148
Очерк пятый. Ограниченная задача трех тел
*
1. Поверхности Хилла
149
на 27г, примем за единицу времени, а расстояние а между центра¬
ми Луны и Земли — за единицу длины (а = 384400 км). Тогда
по третьему закону Кеплера в принятых единицах измерения
где / — универсальная постоянная тяготения.
Задача состоит в определении траектории точки то. Диффе¬
ренциальные уравнения ее движения могут быть записаны в виде
Уравнения (5.1.1) и представляют собой уравнения движения нетя¬
готеющей точки то в ограниченной круговой задаче трех тел. Коор¬
динаты х, у, z определяют положение этой точки во вращающейся
системе: ось х постоянно проходит через центры Земли и Луны;
ось у находится в плоскости орбиты Луны и проходит через центр
масс Луны и Земли Ось z дополняет систему до правой. При этом
где Х\ и Xj — постоянные координаты точек т\ и т2, расположен¬
ных на оси ж; г и р — соответственно расстояния от нетяготеющей
точки (снаряда) до Земли (mi) и Луны (шг).
Уравнения (5.1.1), играющие огромную роль в небесной меха¬
нике и механике космического полета, к сожалению, неинтегрируе-
мы. Точнее говоря, до сих пор никому не удалось проинтегрировать
эти уравнения в конечном виде. Исследование траекторий полета
Именно вращением системы координат вызваны члены 2у и — 2х в (5.1.1) и
член 1/2(ж2 + у2) в (5.1.2). Не будь этих членов, уравнения (5.1.1), (5.1.2) преврати¬
лись бы в известные уже нам интегрируемые уравнения задачи двух неподвижных
центров.
дФ
(5.1.1)
где
ф = ^(х2 + у2) +
fm\
г
Р
(5.1.2)
150
Очерк пятый. Ограниченная задача трех тел
ракеты в системе Луна—Земля приходится проводить либо каки¬
ми-то приближенными способами, либо с помощью численного
интегрирования уравнений движения.
Некоторые выводы, правда, можно сделать и на основе анализа
уравнений (5.1.1). Легко получить, что эти уравнения имеют первый
интеграл — интеграл Якоби
1г2 = Ф + Л, (5.1.3)
где V = л/х2 + у2 + z2 — скорость движения во вращающейся
системе, ft — произвольная постоянная, а Ф(ж, у, z) задается фор¬
мулой (5.1.2). Так как V2 ^ 0, то в реальном движении
Ф(x,y,z) ^ -ft. (5.1.4)
Поверхности
Ф {x,y,z) = -ft, (5.1.5)
ограничивающие область возможных движений, называются по име¬
ни первого их исследователя поверхностями Хилла. Для системы
Луна—Земля Ш\ : mi = 81,30, и в этом случае представление о по¬
верхностях Хилла дает рис. 5.1.
На этом рисунке изображены сечения поверхностей (5.1.5)
плоскостью z = 0; нарисованы несколько поверхностей, отвеча¬
ющие разным значениям постоянной энергии относительного дви¬
жения ft. При больших отрицательных значениях ft, как показывает
исследование, движение возможно лишь внутри некоторых ^со¬
прикасающихся поверхностей S' и S", близких к сферам с цен¬
трами гп\ и тп,2, да еще вне некоторой поверхности S, охватыва¬
ющей поверхности S* и S". Сечение каждой из поверхностей S*
и S" близко к кругу. Эти поверхности не изображены на рис. 5.1,
но их легко представить (небольшим сдвигом внутрь поверхностей
S\ и S\ и наружу по отношению к поверхности S\). Значит, при
таких значениях ft снаряд может быть либо спутником Земли, ли¬
бо спутником Луны (или еще может двигаться вдалеке от системы
Луна—Земля, не пересекая границы 5).
Но не может быть такого движения, чтобы снаряд сначала
двигался в близкой окрестности Земли, а с течением времени про¬
ник бы в близкую окрестность Луны; чтобы это стало возможным,
необходимо увеличить постоянную энергии ft. А именно, при не¬
котором значении ft = h\ поверхности S' и S" будут соприкасать¬
ся в общей точке L\. Обозначим такие поверхности через S\ и S”
1. Поверхности Хилла
151
Рис. 5.1. Сечение поверхностей Хилла плоскостью лунной орбиты
(рис. 5.1). Еще несколько увеличив значение Л, так, чтобы разность
h - h\ была мала, мы обнаружим, что около точки L\ на поверх¬
ности Хилла образовалась узкая горловина. Область возможных
движений снаряда теперь уже включает в себя и окрестность Земли
и окрестность Луны, которые соединены узкой горловиной. Значит,
«не запрещены» такие траектории, которые начинаются в окрестно¬
сти Земли и могут проникнуть в окрестность Луны через горловину
около точки L\. Иначе говоря, только при энергиях h > h\ стано¬
вятся возможными полеты к Луне. Так как полет начинается всегда
очень близко к Земле (допустим, с орбиты спутника Земли, нахо¬
дящейся на высоте 200 км от поверхности Земли), то вопрос увели¬
чения энергии h — это вопрос увеличения начальной скорости Vo.
Начальное положение снаряда на орбите спутника Земли прак¬
тически не влияет на величину скорости Vo, потребной, скажем, для
обеспечения значения энергии h = h\ (назовем эту скорость V^;
соответствующие численные значения будут приведены ниже).
(2)
Увеличим еще начальную скорость до такого значения У0
(энергию до значения hi > h|), что соприкоснутся поверхности Sf
и S" в некоторой точке Li (на рис. 5.1 этому случаю соответствует
единая поверхность Si). Ясно, что дальнейшее увеличение энер¬
гии приведет к появлению второй горловины около точки Li. Это
означает следующее. Если энергия ненамного превосходит hi, то
возможна такая траектория снаряда: он сначала находится в окрест¬
152
Очерк пятый. Ограниченная задача трех тел
ности Земли, затем проникает через горловину около точки L\
в окрестность Луны, а потом через горловину у точки L2 покидает
систему Земля—Луна. Сколько витков сделает снаряд вокруг Земли,
прежде чем попасть в окрестность Луны? будет ли снаряд обращать¬
ся и вокруг Луны, как ее временный спутник, прежде чем вылететь
прочь из системы Земля—Луна? — на эти вопросы ответа нет. Мы
можем только утверждать, что при h > траектории такого ти¬
па не являются запрещенными; они возможны, но существуют ли
в действительности — не ясно без добавочных исследований. Ниже
этот вопрос несколько прояснится. Пока же, рассматривая рис. 5.1,
видим, что при некотором h = Л3 запрещенной для движения обла¬
стью является в каждой полуплоскости некоторая «каплеобразная»
область, стягивающаяся в точку Ь4 (или L$) при увеличении зна¬
чения h от /&з до h4.
При h > /13 становится возможен уход снаряда в бесконечность
в окрестности точки L3 на оси ж, а при h > h4 (h4 < 0) снаряд
может уйти в бесконечность по любому направлению в плоскости
х, у. Мы рассмотрели эволюцию поверхностей Хилла в плоско¬
сти х, у. Однако в пространстве х, у, z исчезновение поверхностей
Хилла, ограничивающих движение, происходит при h = 0.
Точки L{ (г = 1,2, 3,4, 5) называются точками либрации. В
табл. 5.1 приведены результаты расчета расстояний гг и рг точек
либрации соответственно от Земли и Луны, энергий hj отвечающих
этим точкам, и скоростей V$ \ отвечающих этим энергиям. При
т Ai)
расчете К0 принималось, что начальная точка находится на высоте
200 км от поверхности Земли.
Расстояния точек L\ и L2 от Луны равны соответственно
58 ООО км и 65 ООО км, то есть обе точки лежат внутри введен-
Таблица 5.1
Точка либрации
г,
Pi
hi
к(0
к0 >
в ед. (27го)/Т
К('>
ко >
км/сек
Lx
0,8491539
0,1508461
-1,594067
10,60335
10,84890
Ьг
1,1677237
0,1677237
-1,585991
10,60411
10,84968
Ьг
0,9929263
1,9929263
-1,506062
10,61165
10,85738
и
1
1
-1,494001
10,61278
10,85854
2. Отступление о точках либрации
153
ной в предыдущем очерке сферы действия Луны близко к границе
этой сферы (ее радиус равен 66000 км).
Отметим малую разницу (~ I м/сек) между скоростями
и Vq2) (а также между VJ,(3) и vj4*). Это значит, что очень ма¬
лое изменение начальной скорости может привести к качественно¬
му изменению траектории: при V0 ~ траектория обязательно
(2)
ограничена, а при Vo ~ VJy траектория уже может стать неограни¬
ченной — сила притяжения Луны сможет выбросить снаряд (через
горловину Lj) из системы Земля—Луна.
2. Отступление о точках либрации
Точки либрации Li являются особыми точками поверхности
Ф(ж, у, z) = h, то есть координаты этих точек суть решения системы
уравнений
дФ дФ дФ ,
*=*• *“0' 9?=°- <5А1>
Важен механический смысл точек либрации: сравнивая уравнения
движения (5.1.1) и условия (5.2.1), видим, что координаты точек
либрации определяют положения относительного равновесия: если
начальная скорость снаряда (во вращающейся системе) нулевая,
то есть х = у = z = 0, а сам снаряд помещен в одну из точек
либрации, то и все последующее время снаряд будет находиться
в этой точке либрации.
Еще Лагранжем была поставлена задача об устойчивости этих
положений равновесия. Будет ли снаряд двигаться неограниченное
время в окрестности точки либрации, если его чуть-чуть отклонить
от этой точки и (или) придать ему малую скорость? Быстро выяс¬
нилось, что точки либрации L\, L2, £3 неустойчивы.
Вопрос об устойчивости точек L4 и L$ оказался более слож¬
ным (эти точки называются треугольными точками Лагранжа, так
как образуют треугольные конфигурации с притягивающими мас¬
сами тп\ и m2). Оказалось, что если линеаризовать уравнения дви¬
жения (5.1.1) в окрестности треугольных точек либрации, то реше¬
ние линейных уравнений будет ограничено тогда и только тогда,
когда отношение масс притягивающих точек к = тп\/(гп\ + m2)
(mi < т2) удовлетворяет условию
х(1-х)<^. (5.2.2)
154
Очерк пятый. Ограниченная задача трех тел
Если условие (5.2.2) не выполнено, равновесие неустойчиво. Ес¬
ли же условие (5.2.2) выполнено, то движение устойчиво в линей¬
ном приближении. Мы знаем, что этого может оказаться недоста¬
точно для устойчивости.
Почти два столетия вопрос об устойчивости треугольных точек
Лагранжа оставался открытым. Возможность прогресса в исследо¬
вании этой задачи наметилась лишь в последние годы, после того
как В. И. Арнольдом была сформулирована теорема об устойчиво¬
сти равновесия в системах Гамильтона с двумя степенями свободы.
Это дало возможность продвинуться в исследовании плоской зада¬
чи. Опираясь на результаты В. И. Арнольда, А. М. Леонтович пока¬
зал [5.4], что для всех значений отношения масс, удовлетворяющих
условию (5.2.2), движение устойчиво, кроме, может быть, некото¬
рого дискретного множества значений этого отношения. Американ¬
ские ученые Депри и Депри-Бартоломе [5.5] впоследствии указали
конкретно, что представляет собой это исключительное множество.
Завершающий удар по проблеме был нанесен в 1969 году А. П. Мар-
кеевым [5.6].
Результаты А. П.Маркеева позволяют сформулировать следу¬
ющую теорему. Треугольные точки Лагранжа устойчивы для всех
отношений масс, удовлетворяющих условию (5.2.2), кроме двух отно¬
шений:
при которых треугольные точки Лагранжа неустойчивы.
Этой теоремой закрывается имеющая двухсотлетнюю историю
проблема об устойчивости точек либрации в плоской ограниченной
круговой задаче трех тел. Пространственная задача также подробно
исследована.
Отметим, что устойчивость точек либрации существенно обус¬
ловлена влиянием так называемых «гироскопических» членов в урав¬
нениях движения. Эти члены появились потому, что рассматрива¬
ется движение во вращающейся (вместе с линией Земля-Луна)
системе координат. Равновесие сил притяжения и центробежных
сил как раз достигается в точках либрации.
В теории устойчивости доказывается, что «гироскопическая»
устойчивость разрушается силами диссипации (силы сопротивле¬
ния межпланетной материи, например). Поэтому при наличии дис¬
х =
X =
(5.2.3)
3. Траектории сближения и метод их исследования
155
сипативных сил частица, пришедшая в окрестность точки либра¬
ции, может задержаться около этой точки лишь временно, — может
быть, на очень длительное время, но не навсегда.
Тем интереснее отметить, что в 1961 году польский астроном
К. Кордылевский обнаружил в окрестности треугольных точек либ¬
рации системы Земля—Луна скопления космической пылевой ма¬
терии. Эти образования, возможно, носят нестабильный характер —
часть пылинок постепенно уходит из окрестностей точек либрации
под влиянием возмущающих сил, но на место ушедших пылинок
приходят новые из окружающего пространства.
Вернемся теперь снова к задаче о полете к Луне.
3. Траектории сближения и метод их исследования
Итак, если в окрестности Земли сообщить снаряду скорость
(во вращающейся системе) = 10,84890 км/сек (см. табл. 5.1),
то снаряд имеет шанс рано или поздно попасть в близкую окрест¬
ность Луны.
Но рано или поздно?
Ведь практически интересны быстрые полеты к Луне, а не та¬
кие, которые будут длиться... несколько столетий. Между тем чис-
т/-( I)
ленные расчеты показывают, что, получив скорость к0 , снаряд
достигнет расстояния «всего» около 260 000 км от Земли (а до Лу¬
ны-то 384 400 км!) и вернется назад к Земле, правда, на следую¬
щем обороте снаряд достигнет расстояния от Земли чуть большего,
но опять вернется к Земле и т.д. Нужны, видимо, сотни или тысячи
оборотов вокруг Земли, чтобы снаряд смог близко подойти к «гор¬
ловине» около точки либрации L\ и пролететь через нее к Луне.
Так лететь скучно и долго. Лучше обеспечить подлет к Луне на пер¬
вом же витке траекторий. Будем рассматривать такие траектории,
которые на первом своем (относительно Земли) витке пересека¬
ют сферу действия Луны. Эти траектории названы В. А. Егоровым
траекториями сближения.
Среди траекторий сближения особый интерес представляют
такие, которые обеспечивают попадание в Луну на первом обо¬
роте снаряда вокруг Земли; минимальная абсолютная скорость,
необходимая для такого попадания, по В. А. Егорову, составляет
V\ = 10,90525 км/сек. Эта скорость рассчитана без учета притя¬
жения Луны, но такой учет мало влияет на величину V\. Поэтому
156
Очерк пятый. Ограниченная задача трех тел
скорость V\ следует рассматривать как некоторую опорную, харак¬
терную скорость. Интересно составить таблицу характерных на¬
чальных скоростей полета в системе Земля—Луна (все расчеты —
для начальной высоты 200 км над поверхностью Земли; скорости
пересчитаны на невращающуюся систему координат):
V0^ = 10,86570 км/сек — в принципе возможно достижение
Луны после многих оборотов вокруг Земли;
Vq2^ = 10,86640 км/сек — возможен вылет из системы Луна-
Земля (с использованием притяжения Луны для дополнительного
разгона);
Vi = 10,90525 км/сек — минимально необходимая скорость
достижения Луны на первом витке траектории относительно Земли;
Vn = 10,99967 км/сек — параболическая скорость, обеспечи¬
вает вылет из системы Луна—Земля (независимо от действия при¬
тяжения Луны).
Выше уже говорилось о том, что задача вычисления траектории
полета к Луне очень сложна, так как даже с учетом только главных
факторов — притяжения Луны и Земли — задача не решается
в аналитическом виде.
Если бы исследовалось движение спутника Земли с учетом
притяжения Луны, то, как мы знаем по предыдущему очерку, можно
было бы использовать малость лунных возмущений для применения
асимптотических методов анализа.
В рассматриваемом здесь случае этого сделать нельзя, так как вли¬
яние Луны не только не мало, но и доминирует при подлете к Луне.
Однако именно этим можно воспользоваться для построения
приближенного алгоритма расчета траекторий полетов к Луне. Бу¬
дем рассматривать только траектории сближения. Тогда влияние
Луны мало до тех пор, пока снаряд не вошел в сферу действия
Луны. До этого момента полностью пренебрежем влиянием Луны.
Наоборот, при движении снаряда в сфере действия Луны учтем ее
притяжение, но полностью пренебрежем влиянием Земли. Тогда
задача трех тел сведется к двум задачам двух тел, а задачу двух тел
решить, как известно, нетрудно. Ее решением являются кеплеровы
траектории. Алгоритм расчета траектории полета к Луне будет те¬
перь строиться так:
1) рассчитываем геоцентрическое движение от Земли до сферы
действия Луны по законам Кеплера;
2) на границе сферы действия пересчитываем параметры геоцентри¬
ческого движения на параметры селеноцентрического движения;
3. Траектории сближения и метод их исследования
157
3) рассчитываем селеноцентрическую кеплерову траекторию;
4) если надо, расчет можно продолжить и дальше: после выхода
из сферы действия Луны рассчитать новую геоцентрическую
траекторию.
Такой метод расчета траекторий небесных тел предложен еще
Лапласом (применительно к движению естественных небесных тел).
Оказалось, что этот простой метод расчета дает отличные при¬
кидки параметров движения, мало отличающиеся от точных значе¬
ний параметров. Это было проверено сравнением приближенного
расчета с результатами численного интегрирования уравнений дви¬
жения. Указанный метод с успехом применялся для расчета орбит
лунных аппаратов в работах В. А. Егорова [5.1,5.2], работе М. Л. Ли-
дова, Д. Е. Охоцимского, Н. М.Тесленко [5.7] и других. Разберем,
следуя В. А. Егорову, несколько подробнее примерный ход постро¬
ения траекторий лунных перелетов.
Пусть снаряд стартует из точки А0 в окрестности Земли (рис. 5.2)
и движется по дуге кеплерова эллипса в направлении кЛуне, кото¬
рая в начальный момент находится в точке Ло. (На рис. 5.2 изобра¬
жена траектория для вполне конкретного случая: вдоль траектории
отложено время полета в сутках.) В точке А\ снаряд пересекает сфе¬
ру действия Луны (пунктирная окружность на рис. 5.2). Луна к это¬
му моменту времени успела переместиться вдоль своей траектории
из точки Ло в точку Л |. Геоцентрическая скорость снаряда в момент
пересечения сферы действия изображена на рис. 5.2 вектором vBX.
Согласно ранее принятой договоренности в этот момент мы
должны пересчитать движение на селеноцентрическое. Скорость
движения Луны по орбите есть уЛ| . Абсолютная величина этой
скорости |vji,| = 1,02 км/сек. Скорость снаряда относительно Луны
Чх = Vex - Vfl, (5.3.1)
вычисляется по обычной формуле: «относительная скорость равна
разности абсолютной и переносной скоростей». Переносная ско¬
рость в нашем случае — скорость Луны; отсюда — векторная фор¬
мула (5.3.1). Векторы vBX, -ул также изображены на рис. 5.2.
Итак, снаряд вошел в сферу действия Луны со скоростью увх.
В. А. Егоровым обнаружен достопримечательный факт: для лю¬
бых траекторий сближения скорость |увх| входа снаряда в сферу дей¬
ствия Луны, вычисленная относительно Луны, будет всегда больше
селеноцентрической параболической скорости на границе сферы дей¬
ствия. Эта последняя скорость Vп' км/сек обеспечивает неизбежный
Рис. 5.2. Приближенный расчет траектории облета Луны по В. А. Егорову
(цифры вдоль траектории — время полета в сутках)
выход снаряда из сферы действия Луны. Так как |v(lx| > V^, то сна¬
ряд либо попадет в Луну, либо обязательно покинет сферу действия
Луны, обогнув Луну по гиперболической траектории.
На рис. 5.2 изображена такая гиперболическая траектория, оги¬
бающая Луну внутри сферы действия. Снаряд пролетит по этой
траектории из точки А\ в точку В. Но за время движения снаряда
по дуге А\В сфера действия Луны сама переместится из поло¬
жения I в положение II. Когда снаряд пересечет сферу действия,
выходя из нее в точке В, Луна будет занимать положение Л2,
а точка В займет положение А2. В результате гиперболическая
относительно Луны траектория А\В является относительно Земли
«странной» петлеобразной траекторией А\А2. Описав эту петлю,
снаряд выйдет из сферы действия Луны, имея относительно нее
скорость упых (она по величине практически равна скорости v„x,
но имеет, конечно, другое направление). Геоцентрическая скорость
выхода УрЫХ вычисляется по формуле «абсолютная скорость равна
4. Эволюция галактик
159
сумме относительной и переносной скоростей», так что
V»,,IX =v',x + VTb. (5.3.2)
Вектор vBblx изображен на рис. 5.2, и по величине и направлению
этого вектора нетрудно построить теперь кеплерову траекторию
возвращения в окрестность Земли, как это и сделано на рис. 5.2.
Мы видим на этом примере, что метод, примененный В. А. Его¬
ровым, позволяет строить сложные траектории задачи трех тел
очень простыми средствами. Уже отмечалось, что этот метод обла¬
дает точностью достаточно высокой, чтобы быть использованным
на стадии предварительного проектирования орбит полетов к Лу¬
не. В. А. Егоровым были рассчитаны, проанализированы и опи¬
саны в [5.1,5.2] сотни траекторий лунных перелетов, составлена
полная классификация траекторий сближения и рассмотрен ряд
других интересных задач динамики полета к Луне. Об этом по¬
дробно и увлекательно рассказано в отличных научно-популярных
книгах В. И. Левантовского [5.3, 5.8], после знакомства с которы¬
ми будет не «страшна» и оригинальная книга В. А. Егорова [5.2].
Для первого знакомства с проблемой интересна обзорная статья
Л. И. Седова [5.9] об орбитах лунных ракет.
4. Эволюция галактик
Вместо одной-единственной точки т0, движение которой под¬
чиняется уравнениям (5.1.1), представим себе целое «облако» таких
точек, содержащее несколько сотен, или несколько тысяч частиц.
Иначе говоря, рассмотрим сразу, одновременно, несколько сотен
(тысяч) ограниченных задач трех тел. Такое множество задач пред¬
ставляет хорошую математическую модель взаимодействия и эво¬
люции галактик. При этом, например, точка массы тп\ играет роль
ядра интересующей нас галактики; облако нетяготеющих (но при¬
тягиваемых) точек то изображает собственно галактику (звезды,
пылевые или газовые частицы, обращающиеся первоначально во¬
круг ядра m|); наконец, масса тп2 моделирует «возмущающее тело»;
это может быть соседняя галактика или сверхмассивные невидимые
тела. При этом естественно рассматривать гиперболическую задачу
трех тел: масса m2 пролетает по гиперболической орбите относи¬
тельно массы гп\, возмущая при этом изначальное движение облака
частиц-спутников массы тп\. Задача состоит в том, чтобы просле¬
дить, как при этом меняется структура облака-галактики.
160
Очерк пятый. Ограниченная задача трех тел
4. Эволюция галактик
161
Астрономов уже давно заинтересовали удивительные особен¬
ности наблюдаемой структуры галактик. Многие галактики обла¬
дают четко выраженной спиральной структурой; на фотографиях
некоторых звездных систем видны протяженные «хвосты»; встреча¬
ются пары близких галактик с «хвостами», направленными в проти¬
воположные стороны. Иногда видны «мосты», как бы связывающие
галактики друг с другом. Подобные пары галактик названы взаимо¬
действующими. Существует «Атлас взаимодействующих галактик»,
составленный Б. А. Воронцовым-Вельяминовым2^.
После открытия взаимодействующих галактик для объяснения
наблюдаемой их структуры были предложены различные гипотезы
о различных силах взаимодействия. Однако представляется совер¬
шенно естественным прежде всего проанализировать и обсчитать
гравитационные эффекты. В чем можно быть уверенным, так это
в том, что близкие галактики гравитационно взаимодействуют. Гра¬
витационные возмущения на галактику могут оказывать и мате¬
риальные объекты, не наблюдаемые непосредственно оптическими
или радиоастрономическими инструментами: претерпевшие грави¬
тационный коллапс «мертвые» квазары и старые, потухшие галак¬
тики, звезды которых исчерпали запасы ядерной энергии. Суще¬
ствование таких объектов как раз и может быть обнаружено по воз¬
мущению структуры галактик, мимо которых прошли эти объекты.
В 1971-1972 годах в Институте прикладной математики АН
СССР Н. Н. Козлов, Р. А. Сюняев и Т. М. Энеев провели исследо¬
вание воздействия больших масс вещества на развитие галактик.
Результаты исследования были изложены авторами в ряде работ
[5.10-5.13]; здесь мы следуем в изложении их обзору [5.10]. Была
принята математическая модель галактики, описанная в начале это¬
го пункта; при этом считалось, что точки-спутники первоначально
образовывали дискообразную структуру, плотность которой падала
по мере удаления от ядра. В исходном (невозмущенном) состоянии
все спутники двигались в одном направлении по различным круго¬
вым орбитам. Процесс гравитационного взаимодействия моделиро¬
вался на цифровой вычислительной машине с последующим отоб¬
ражением на экране дисплея — устройства, которое переводит циф¬
Профессор Б. А. Воронцов-Вельяминов, между прочим, является автором за¬
мечательной научно-популярной книги «Вселенная» («Очерки о Вселенной»), вы¬
державшей большое количество изданий. Это счастливая книга. Многие научные
работники еще в школьные годы определили круг своих интересов и свою дальней¬
шую научную судьбу благодаря этой книге, — и автор данных строк в том числе.
11 Заказ 1667
162
Очерк пятый. Ограниченная задача трех тел
ровую информацию в зрительные образы. С экрана дисплея сни¬
мался на кинопленку фильм, демонстрирующий изменение струк¬
туры галактик под действием гравитационных возмущений.
Надо сказать, что чудовищный объем расчетов при модели¬
ровании эволюции галактик доступен лишь современным быстро¬
действующим машинам; в описываемой задаче приходилось одно¬
временно интегрировать 1000 систем дифференциальных уравне¬
ний шестого порядка для описания движения 1000 точек-спутни¬
ков. Именно поэтому работы такого типа появились лишь сейчас,
хотя астрономы уже много десятилетий изучают структуры галак¬
тик. Особенно впечатляющим средством познания является экран
дисплея. Он позволяет собственными глазами увидеть то, что, ка¬
залось бы, никогда не дано видеть человеческому оку: измене¬
ние формы галактики со временем, весь эволюционный процесс.
И не однократно, а при многих различных условиях. На прилага¬
емых рисунках приведены некоторые кадры фильма, иллюстри¬
рующего проделанную Т. М.Энеевым и его сотрудниками работу.
К сожалению, эти кадры лишь в малой степени отражают картину,
которая является на экране дисплея восхищенному взору исследо¬
вателя: живую, дышащую картину эволюции галактики, мерцаю¬
щей зеленоватым блеском сотен своих «звезд».
Обратимся к рис. 5.3 и 5.4. На каждом из них представлено
шесть кадров для данного варианта пролета возмущающего тела.
В действительности каждый вариант занимает несколько тысяч кад¬
ров. На первых кадрах показано направление вращения галактики
и направление движения возмущающего тела по орбите. Каждый
кадр «датирован»; время Т приводится в миллиардах лет. Момент
Т = 0,00 соответствует самому тесному сближению пролетающего
тела с галактическим ядром.
Кадры рис. 5.3 демонстрируют пролет возмущающего тела в про¬
екции на плоскость невозмущенной галактики. Тело с массой, рав¬
ной массе галактики, движется перпендикулярно ее плоскости с ги¬
перболической (в данном случае с удвоенной параболической) ско¬
ростью на расстоянии 40 кпс3^ от центра галактики. Масса галакти¬
ки составляет 1011 солнечных масс, ее радиус равен 36 кпс. Период
обращения частицы по орбите радиуса 36 кпс достигает 2 млрд лет.
Пролет массивного тела приводит, прежде всего, к образованию
двух четко выраженных спиральных рукавов у галактики. Кроме
1 килопарсек (кпс) = 3529 световых лет = 30,84 • 101л км.
4. Эволюция галактик
163
того, возмущающее воздействие тела для некоторых частиц оказы¬
вается столь сильным, что одни частицы выбрасываются из сферы
притяжения галактики, другие быстро меняют направление свое¬
го движения и обрушиваются на центральные области галактики
и даже на ее ядро. Искажается и невозмущенная плоскость дис¬
ка галактики: структура становится пространственной (в плоской
проекции рис. 5.3 этого, конечно, не видно).
На рис. 5.4 представлен эпизод фильма, соответствующий про¬
лету возмущающего тела в плоскости диска галактики в направле¬
нии ее вращения. Возмущающее тело имеет массу, в 4 раза пре¬
восходящую массу галактики, мимо которой оно пролетает. Это
тело движется с параболической скоростью и приближается к га¬
лактике на расстояние, вдвое превышающее ее радиус (72 кпс).
Оно, как оказывается, «захватывает» и уводит с собой 1/5 вещества
галактики. Таким образом, «мертвый» квазар или какой-либо дру¬
гой массивный компактный объект, пролетевший мимо галактики
и захвативший часть ее вещества, может породить новую галакти¬
ку. Захваченное вещество может оформиться в отдельное скопление
звезд и газа, связанное с галактикой перемычкой — «мостом».
Авторы излагаемой работы [5.10] заканчивают статью сле¬
дующим осторожным заявлением: «Математическое моделирова¬
ние процессов гравитационного взаимодействия галактик помогло
обнаружить эффекты, которые напоминают реальные структуры
на фотографиях галактик. Пока нельзя утверждать, что именно эти
механизмы стали причиной образования хвостов и перемычек меж¬
ду галактиками. Однако уже сейчас ясно, что гравитационное взаи¬
модействие сильно влияет на динамику развития звездных систем.
Дальнейшие исследования позволят установить истинные масшта¬
бы этого влияния и его подлинную роль в эволюции галактик».
Однако значение работы Т. М.Энеева и его сотрудников, без¬
условно, выходит за рамки этой осторожной самооценки. Вот что
пишет по этому поводу во втором издании своей книги «Судьба
Солнечной системы» [5.14] В. Г. Демин: «В астрономии господству¬
ет тенденция объяснить все неясное с позиций новых физических
законов и открытий. Но, к сожалению, это делается в условиях, ко¬
гда развитие систем небесных тел не исследовано сколько-нибудь
аккуратно даже в рамках механических схем!...
Т. М. Энеев со своими сотрудниками решил выяснить, мож¬
но ли объяснить процесс образования спиральных рукавов галактик
только механическими процессами. В отличие от других астроно¬
мических работ, никаких физических взаимодействий не предпо-
п*
N
164 Очерк пятый. Ограниченная задача трех тел
)
о
et
I
Т = 0,00 |
II
О
(
I
*
ч
II
о
о
II
О
О
.. •- ••
. Ч ■ 'ч
: • . -8Ш1 ^
;1Ш
1V. t • * ; •" V .
о
Г= 1.00
Т= 1,89
Рис. 5.3. Эволюция галактики, вызванная пролетом возмущающего тела
(маленький светлый кружок) перпендикулярно исходной плоскости галак¬
тики. Время Т в млрд лет
4. Эволюция галактик
165
Рис. 5.4. Эволюция галактики, вызванная пролетом массивного возмущаю¬
щего тела в плоскости галактики (на двухпоследнихрисункахмасштаб уменьшен
вдвое по сравнению с четырьмя предыдущими). Время Т в млрд лет
166
Очерк пятый. Ограниченная задача трех тел
лагалось. И, несмотря на это, результаты Энеева и его сотрудников
превзошли все ожидания... Из приведенных изображений эволю¬
ции галактики с большой убедительностью следует, что развитие
спиральных рукавов можно объяснить приливным эффектом».
Дополнительные комментарии к этому изданию. Классическая
ограниченная задача трех тел, одна из фундаментальных задач
небесной механики, привлекала и продолжает привлекать к себе
внимание многих исследователей. Одна из последних монографий
на эту тему — книга А. Д. Брюно [5.15]. В ней читатель найдет
обширную библиографию и обзор ранних исследований, но основ¬
ная ее ценность состоит в использовании оригинальных методов
и в результатах анализа ограниченной задачи трех тел. Главную роль
играют порождающие решения задачи при тп2 -> 0 и их анализ (диа¬
грамма Хенона для симметричных периодических орбит [5.16] и ее
интерпретация в терминах остальных параметров и т.д.). В част¬
ности, Брюно [5.17] удалось построить периодические траектории,
каждая из которых проходит как вблизи поверхности Земли, так
и вблизи поверхности Луны. Особенно удивительны устойчивые
периодические решения, проходящие вблизи Юпитера и Земли,
которые Брюно нашел в задаче Солнце — Юпитер — космический
аппарат 4\
Примечание переводчика. Другие книги на эту тему: Szebehely V. Theory of
Orbits: The Restricted Problem of Three Bodies. New York: Academic Press, 1967 (pyc.
перев.: Себехей В. Теория орбит: Ограниченная задача трех тел. М.: Наука, 1982);
Marchal Ch. The Three—Body Problem // Studies in Astronautics. 4. Amsterdam: Elsevier
Science Publishers, В. V., 1990; и Henon M. Generating Families in the Restricted Three-
Body Problem. Lecture Notes in Physics. New Series: Monographs, 52. Berlin: Springer-
Verlag, 1997.
Очерк шестой
Они вальсируют на орбитах
Это дамы, которые в небе танцуют...
Гийом Аполлинер
Земля плывет по своей орбите, величаво вращаясь вокруг оси.
Крутятся вокруг своих осей большие и малые планеты. Нелени¬
вый и любопытный читатель наблюдал, конечно, проплывающие
по ночному небу звездочки, то ярко вспыхивающие, то потухающие
подобно светлячкам: это искусственные спутники в своих коловра¬
щениях поворачиваются к наблюдателю разными сторонами, под¬
ставляя Солнцу то большой блестящий бок, то днище, отражающее
мало света.
Танцы светил сложны и разнообразны. Иные степенно пока¬
чиваются, иные медленно поворачиваются сразу вокруг нескольких
своих осей, а иные вертятся со страшной скоростью, как щенок,
догоняющий собственный хвост.
Изучению закономерностей вращений искусственных спутни¬
ков посвящен раздел механики космического полета — динами¬
ка движения искусственного спутника относительно собственного
центра масс [6.1].
О некоторых примечательных эффектах во вращении й ориен¬
тации спутников пойдет речь в предлагаемом очерке.
1. Гравитационный потенциал
Для задач, которые мы собираемся здесь рассмотреть, движе¬
ние спутника около своего центра масс будет существенно опре¬
деляться моментами гравитационных сил. В свою очередь эти мо¬
менты легко вычисляются через силовую функцию (взятая с обрат¬
ным знаком, она называется гравитационным потенциалом), опи-
168
Очерк шестой. Они вальсируют на орбитах
сывающую действие ньютоновского центрального поля сил на наш
спутник. Мы знаем, что если спутник можно рассматривать как
материальную точку с массой dm, то силовая функция dU дается
формулой
a dm
dU = - , (6.1.1)
г
где р = fM (f — универсальная постоянная тяготения, М —
масса Земли), г — расстояние от «спутника» (точки с массой dm)
до центра Земли.
Но в задачах о движении спутника относительно собственного
центра масс существенно как раз то, что спутник является протя¬
женным телом, а не материальной точкой. Тогда формула (6.1.1)
верна для каждого элемента dm объема спутника и, будучи распро¬
странена на весь этот объем V, запишется в виде
С dm
u = fij—. (6.1.2)
V
Пусть (рис. 6.1) R — расстояние от центра притяжения О*
до центра масс спутника О. Со спутником жестко свяжем систему
координат Oxyz. Расстояние р от О до текущей точки dm вычис¬
ляется тогда по формуле р2 = ха + у2 + z2, угол между векторами
Рис. 6.1. К вычислению гравитационного потенциала
1. Гравитационный потенциал
169
R и р определяется своим косинусом:
cos (R, р) = —7 + —7' + — 7".
Р Р Р
Здесь 7,7' 7;/ — направляющие косинусы вектора R в осях х\ у\ z,
так что 7 = cos(R, #'), 7' = cos(R, у'), 7'' = cos (R, z'). В этих
обозначениях в формуле (6.1.2)
г = yjR? + 2R(x'j + у' 7' + ^/7//) + х'2 + у'2 + za. (6.1.3)
Интегрирование в (6.1.2) проходит по текущим координатам х\ у\ z\
в результате чего можно получить явную зависимость
У
U = U(R, 7,7;, 77/).
(6.1.4)
Таким образом, силовая функция (6.1.2) зависит как от расстояния
спутника до притягивающего тела, так и от ориентации спутника
относительно направления «притягивающий центр — центр масс
спутника».
Как можно показать [6.1], проекции моментов гравитационных
сил записываются в виде
„аи ,ди ]
Мх' = 7 df-^dr’
dU
fry'
-7
,9U_
~fry’
dU
>dU --
M*'=7W"7«r
(6.1.5)
Конкретный вид U и моментов (6.1.5) зависит, вообще говоря,
от формы тела и распределения масс в его объеме. Это услож¬
няет анализ. Однако дело облегчается тем, что спутники имеют
малые размеры по сравнению с расстоянием R. Поэтому величины
х /И, у fR, z /R малы и выражение (6.1.3) можно разложить в ряд
по степеням этих величин. Оставляя в этом разложении лишь чис¬
ла до второго порядка малости включительно, интеграл (6.1.2) уже
просто вычислить. При этом учитывается, что
J z! dm — J У' dm = J х'd™ = О
170
Очерк шестой. Они вальсируют на орбитах
(поскольку начало системы координат Ox'yz' является центром
масс спутника) и что положение осей х, у\ z в спутнике можно
выбрать так, что
J х у dm = У х z dm = J у z dm = 0.
V V V
Выбранные таким образом оси х, у\ z являются главными цен¬
тральными осями инерции спутника. При сделанных упрощениях
вычисление U по формуле (6.1.2) приводит к формуле
u^^T + w?{a + b + c)~\b? ^ + в^ + с^"2) • (6-1 -6>
Здесь т — масса спутника, а постоянные
А = J(у2 + z2) dm, В = J{z2 + xt2) dm,
V V
С = J(х2 + у2) dm,
v
суть главные центральные моменты инерции спутника. Формулы
(6.1.5) при этом приобретают вид
mx' = i-^(c-bWW,'
МУ’ =
Mz' = ЪВ?{В ~ A)i
7'
'ъ \
(6.1.7)
2. О вращении Луны.
Сведения из теории устойчивости
С древнейших времен люди обращали внимание на неизмен¬
ность лунного лика. Луна всегда обращена к Земле одной и той же
стороной, и ее «затылка» люди не могли видеть вплоть до октября
1959 года, когда обратная сторона Луны была впервые сфотогра¬
фирована советской автоматической станцией.
Такое неизменное положение Луны относительно Земли озна¬
чает, что период осевого вращения Луны в точности совпадает с пе¬
риодом ее обращения вокруг Земли. Для простоты будем считать
лунную орбиту круговой.
2. О вращении Луны. Сведения из теории устойчивости
171
Введем орбитальную систему координат Отпг следующим об¬
разом (рис. 6.2). Начало координат О поместим в центр масс Луны,
ось г направим из центра масс вдоль геоцентрического радиус-век¬
тора R Луны, ось г — по касательной к круговой орбите и ось
п — по нормали к плоскости лунной орбиты. Таким образом, ор¬
битальная система координат — вращающаяся; оси гиг лежат
всегда в плоскости лунной орбиты и поворачиваются вокруг оси
п с угловой скоростью и) орбитального движения. (Линейная ско¬
рость движения центра масс Луны по орбите V = и)R.)
Угловая скорость осевого вращения Луны тоже равна о; и на¬
правлена по п; осевое вращение совершается в сторону орбиталь¬
ного движения. В результате этого Луна все время обращена одной
стороной к Земле и, как можно понять, неподвижна относительно
орбитальной системы координат. Иначе говорят, что Луна находится
в относительном равновесии (с точностью до малых покачиваний —
либраций).
Заметим, что вращение Луны определяется в первом прибли¬
жении законами Кассини, согласно которым ось вращения Луны
находится в относительном равновесии в системе координат, вра¬
щающейся вместе с линией узлов лунной орбиты; эта ось Луны
нормальна к линии узлов, угол между осью вращения Луны и нор¬
малью к плоскости ее орбиты составляет 6°417. Здесь мы не учиты¬
ваем движения линии узлов лунной орбиты. Это позволяет заменить
172
Очерк шестой. Они вальсируют на орбитах
законы Кассини более простым движением — относительным рав¬
новесием в орбитальной системе координат. (Подробнее о законах
Кассини см. [6.14] и ниже.)
Совпадение рассматриваемых угловых скоростей вращения и
обращения небесного тела не может быть случайным, тем более
что в Солнечной системе это, по-видимому, не единичное явле¬
ние. Астрономические наблюдения последних лет говорят в пользу
того, что спутники Юпитера Ио, Европа, Каллисто и спутники
Сатурна Тефия, Рея, Диона, Япет все время обращены одной сто¬
роной к центральной планете [6.2] (см. также: Astroph. J. 1971.
V. 165. Р. 431). По некоторым сведениям, даже спутники Марса Фо¬
бос и Деймос движутся подобным образом [6.2;] — в состоянии
относительного равновесия.
Чтобы это было возможно не случайным образом, должен сущест¬
вовать какой-то стабилизирующий фактор, удерживающий спутники
(Луну, например) в положении относительного равновесия. Этот
фактор должен влиять и на искусственные спутники Земли.
Таким стабилизирующим фактором являются гравитационные
моменты, определяемые гравитационным потенциалом (6.1.6). По¬
кажем это.
Прежде чем переходить к анализу, дадим некоторые опреде¬
ления и — без доказательства — теоремы теории устойчивости
А. М. Ляпунова. Доказательства можно найти, например, в книге
Н. Г. Четаева [6.56]. Исследование устойчивости какого-либо дви¬
жения q(t) можно заменой переменных свести к исследованию
устойчивости решения = 0 некоторой системы дифференциаль¬
ных уравнений
dx
-£=Xt(xi,t), Xt(0,t) = 0, (i,s = 1,..., n). (6.2.1)
dt
Уравнения (6.2.1) будем называть уравнениями возмущенного движе¬
ния:; частное их решение ж,- = 0 — невозмущенным движением.
На правые части уравнений (6.2.1) накладывается обычно требова¬
ние аналитичности.
#
Определение 1 (А. М. Ляпунов). Если при всяком произволь¬
но задаваемом числе А > О, как бы .мало оно ни было, может
быть выбираемо число А > 0 так, чтобы при всяких возму¬
щениях Жю,..., хпо, удовлетворяющих условию x2So < А,
S
и при всяком t ^ 0 выполнялось неравенство x2s < А, то
2. О вращении Луны. Сведения из теории устойчивости
173
174
Очерк шестой. Они вальсируют на орбитах
невозмущенное движение устойчиво, в противном случае —
неустойчиво.
Заметим, что понятие устойчивости, которым мы пользовались
при описании результатов В. И .Арнольда, является более слабым, чем
определение устойчивости по А. М. Ляпунову. Тому — две причины:
1. В. И. Арнольд требует близости возмущенной и невозмущен¬
ной траекторий, а не близости, в любой момент времени, по¬
ложений движущихся по этим траекториям точек. Если взять
какое-либо условно-периодическое движение, устойчивое по
В. И. Арнольду, то оно, вообще говоря, неустойчиво по Ляпунову.
2. По В. И. Арнольду, устойчивость доказывается не для всех на¬
чальных данных, а лишь для большинства из них. По Ляпунову,
движение неустойчиво, если найдется хоть одна возмущенная
траектория, не удовлетворяющая определению устойчивости.
В дальнейшем в этом пункте всюду подразумевается устойчи¬
вость по Ляпунову.
До А. М. Ляпунова устойчивость движения исследовалась глав¬
ным образом путем линеаризации уравнений (6.2.1) и анализа реше¬
ний соответствующих линейных уравнений. После работ А. М. Ля¬
пунова стало ясно, что линейные уравнения дают, вообще говоря,
лишь необходимые условия устойчивости («если движение устой¬
чиво, то эти условия будут выполнены»). Но на вопрос «если эти
условия выполнены, то будет ли движение устойчиво?» нельзя все¬
гда ответить утвердительно. Поиск достаточных условий устойчи¬
вости — одна из труднейших задач.
Определение 2. Пусть в области t > to, Е < Н, Н ф О,
S
определена функция V(xs,t), принимающая только значения
одного знака и нулевые значения. Тогда V называется знако¬
постоянной функцией (положительной или отрицательной).
Определение 3. Если знакопостоянная функция V не зависит
от £, а постоянная Н (в определении 2) может быть выбра¬
на достаточно малой для того, чтобы V уничтожалась толь¬
ко в начале координат (при всех xs = 0), то V называется
знакоопределенной функцией (определенно-положительной или
определенно-отрицательной).
Пример. Функция от двух переменных Х\, х2 V = х\ + х\ определенно¬
положительная, а функции V = (a?i + х2)2 и V = х] лишь знакопостоянны
2. О вращении Луны. Сведения из теории устойчивости
175
(положительны), так как обращаются в нуль, кроме начала координат, еще
на множествах Х\ = -х2 (первая) и Х\ = 0 (вторая). Функция V = х]-х\
не является знакопостоянной.
Определение 4. Функция V, зависящая от t, называется зна¬
коопределенной, если найдется не зависящая от t определенно¬
положительная функция W такая, что одно из двух выражений
V — W или -V - W есть функция положительная.
Теорема 1 (А. М. Ляпунов). Если дифференциальные уравнения
(6.2.1) возмущенного движения таковы, что возможно найти
знакоопределенную функцию V, производная которой
в силу этих уравнений есть функция знакопостоянная противо¬
положного с V знака или тождественно равна нулю, то невоз¬
мущенное движение устойчиво.
Доказательство (см. [6.56]) основано на том, что при условиях
теоремы траектория всегда остается внутри некоторой замкнутой
вокруг начала координат поверхности W(xs) ^ I.
Теорема Ляпунова дает достаточные условия устойчивости.
Функция V называется функцией Ляпунова. Существует довольно
богатый арсенал способов построения функций Ляпунова для задач
различных классов. Но, к сожалению, не известен общий алгоритм
построения функций Ляпунова для любых задач.
Теорема Ляпунова пригодится нам впоследствии в п. 3 очерка.
А здесь нам будет интересно узнать для дальнейшего, что эта теоре¬
ма позволяет в некоторых случаях решить вопрос об устойчивости,
рассматривая лишь уравнения первого приближения. Но прежде —
некоторые определения.
Функция x(t) называется ограниченной, если при любом t^to
ее модуль |х(£)| < С, где С — некоторая постоянная. Функцию, мо¬
дуль которой может делаться большим всякой данной положитель¬
ной величины, как бы она ни была велика, назовем неограниченной.
Ограниченная функция называется исчезающей, если х(£)-> 0 при
£-*оо.
Лемма 1. Если z = x(t)ext представляет функцию, исчезаю¬
щую при А = Aj и неограниченную при А = А2, где Х\ и —
вещественные постоянные, то всегда можно найти такое веще¬
ственное Ао, что функция z при X = АоН-£ будет неограниченной
176
Очерк шестой. Они вальсируют на орбитах
для всякого положительного постоянного е и исчезающей для вся¬
кого отрицательного постоянного е.
Определение 5. Число Ао называется характеристичным чис¬
лом функции x(t).
Рассмотрим теперь вместо системы (6.2.1) линеаризованную
в окрестности начала координат систему
Здесь psr — вещественные, ограниченные, непрерывные функции t.
Пусть ,xn(t) — какое-либо решение системы (6.2.2).
Под характеристичным числом этого решения будем понимать наи¬
меньшее из характеристичных чисел функций ..., хп. Как из¬
вестно, всегда найдется п независимых решений системы (6.2.2);
они будут характеризоваться набором п характеристичных чисел xs
(каждое из которых, как можно показать, конечно). Обозначим их
сумму
Лемма 2. S + р ^ 0.
Определение 6. Система (6.2.2) называется правильной, если
S + р = 0, и неправильной в противном случае.
Характеристичные числа позволяют судить о качественном по¬
ведении решений системы (6.2.2) и делать выводы об устойчивости
невозмущенного движения в первом (линейном) приближении. Это
важно, так как интегрировать систему (6.2.2) в общем случае пе¬
ременных коэффициентов psr(t) мы не умеем. А. М. Ляпуновым,
однако, доказано, что характеристичные числа уравнений первого
приближения позволяют во многих случаях судить об устойчиво¬
сти или неустойчивости невозмущенного движения в силу и полной
системы (6.2.1) дифференциальных уравнений возмущенного дви¬
жения. А именно, верны следующие теоремы.
—J- =р,\Х\ +...+ps„(x„) (в =1(6.2.2)
П
5=1
Пусть еще р есть характеристичное число функции
3. Устойчивость относительного равновесия в гравитационном поле 177
Теорема 2 (А. М. Ляпунов). Если система (6.2.2) дифференци¬
альных уравнений первого приближения есть правильная и все ее
характеристичные числа положительны, то невозмущенное дви¬
жение устойчиво.
Теорема 3. Если система (6.2.2) дифференциальных уравнений
первого приближения есть правильная и среди ее характеристич¬
ных чисел есть хотя бы одно отрицательное, то невозмущенное
движение неустойчиво.
3. Устойчивость относительного равновесия
в гравитационном поле
Задача об устойчивости относительного равновесия искусствен¬
ного спутника в гравитационном поле возникла в середине пяти¬
десятых годов нашего бурного столетия, но имеет древнюю, уходя¬
щую вглубь веков предысторию. В небесной механике исследова¬
ния устойчивости относительного равновесия Луны и ее колебаний
(либраций) восходят к Лагранжу (1780). Эти классические исследо¬
вания проводились на основе линеаризованных уравнений малых
колебаний. После трудов А. М. Ляпунова (1892) стало понятным,
что анализ линейных уравнений, вообще говоря, не дает ответа
на вопрос об устойчивости. В 1959 году автором этой книги бы¬
ло впервые опубликовано [6.3] проведенное еще в 1956-1957 годах
строгое в смысле Ляпунова и в смысле механической постанов¬
ки задачи исследование вопроса о существовании и устойчивости
относительного равновесия твердого тела в гравитационном по¬
ле. Один из основных результатов этого исследования описывается
ниже в упрощенном изложении. Более подробный анализ читатель
может найти в [6.1,6.3].
Если Луна (или искусственный спутник Земли) движется по кру¬
говой орбите, то в орбитальной системе координат на Луну (спут¬
ник) будут действовать силы: гравитационные, центробежные и ко-
риолисовы. Моменты кориолисовых сил не производят работы,
а моменты гравитационных и центробежных сил определяются по¬
тенциалами (6.1.6) для гравитационных сил и аналогичным выра¬
жением для потенциала центробежных сил
Up = V { А02 + В0'2 + С0"2} . (6.3.1)
12 Заказ 1667
178
Очерк шестой. Они вальсируют на орбитах
Здесь Р, 0, /3" — направляющие косинусы нормали п к плоскости
орбиты с осями х, у\ z, так что
Р = cos (п, х'), 0 = COS (п, у'), 0' = cos (n, z').
Приведем вывод для дотошного читателя. Компонента элементарного мо¬
мента центробежных сил, например, по оси х' будет
dMjf = у' Д- - z'fy. =
= {у'[(х'а + у'а + za")a" + (ху + у'у' + z'y")y"] -
- z'[(x'a + у'а' + z а")а + (х'у + у'у' + z'y")n"]}ui2dm.
Здесь fyi, fz> — компоненты элементарной центробежной силы по осям у,
z спутника, а, а', а" — направляющие косинусы орта т относительно осей
х, у1, z!. Интегрируя по всему объему и учитывая, что 0р" = -(а'а"+00'),
получим Мх> = -ш2(С - В)0 0'. Сравнение с аналогичными формулами
(6.1.7) для гравитационного момента, определяемого силовой функцией
(6.1.6), приводит к силовой функции (6.3.1) центробежных сил.
Так как суммарная потенциальная энергия не зависит-явно
от времени (на круговой орбите), то должен иметь место закон
сохранения механической энергии
T-U-Up = H, (6.3.2)
где Т — кинетическая энергия спутника в его относительном вра¬
щении, Н — постоянная полная энергия вращательного движе¬
ния спутника. Учитывая в (6.1.6) то, что R = const и при этом
p/R2 = ш2, можно записать закон сохранения энергии (6.3.2) в яв¬
ном виде [6.3]:
\ (Ар2 + Bq2 + Cr2) + L2 (Ay2 + By'2 + Су"2) -
1 , ‘ , <6-3'3)
- -ш2(Ар2 + Bp'2 + CP" ) = h.
Здесь p,q,r — компоненты относительной угловой скорости вра¬
щения спутника по его главным центральным осям х\ у\ z .
В относительном равновесии относительная угловая скорость
равна нулю, а направляющие косинусы могут принимать, как ока¬
зывается, либо нулевые, либо единичные по модулю значения. На¬
пример, движению
p = q = r = 0, у = у' = р = р" = 0, у" = р' = 1 (6.3.4)
соответствует такое относительное равновесие, когда ось 0 спутника
совпадает с направлением радиус-вектора (у" = cos{z', г) = 1), а ось
3. Устойчивость относительного равновесия в гравитационном поле 179
у — с направлением нормали к плоскости орбиты ((3' = cos(j/7,n)).
Ось х спутника при этом совпадает с касательной к орбите.
Движение (6.3.4) назовем невозмущенным движением, а откло¬
нения от него — возмущениями. При любых возмущениях сохра¬
няется полная энергия (6.3.3) относительного движения; выраже¬
ние (6.3.3) является первым интегралом уравнений движения (здесь
не выписанных; полные уравнения движения см. в книге [6.1]).
Учитывая известные соотношения между направляющими ко¬
синусами
У'2 = 1 - у - у2, /?'2 = I - у - /з"2, (6.3.5)
можно выражение (6.3.3) записать так:
'-(Ар2 + В? + Ст2) + \и:2{(А - С)72 + (В - С)У2} +
+ '-ш2{(В - А)(52 + (В- С)@"2} = h0.
(6.3.6)
Здесь h0 — новая постоянная. Она определяется начальными дан¬
ными р0> 9о> го, То? То? Аь Ро- Левая часть выражения (6.3.6) являет¬
ся квадратичной формой своих переменных. Потребуем, чтобы эта
квадратичная форма была определенно-положительной. Все ко¬
эффициенты этой квадратичной формы будут положительны при
выполнении условия
В > А > С. (6.3.7)
Отсюда сразу следует вывод об устойчивости относительного равно¬
весия (6.3.4). Действительно, так как сумма положительных членов
всегда больше какой-либо части этой суммы, то из (6.3.6) при усло¬
вии (6.3.7) следуют, например, такие оценки:
У < Vh < д2 у2 < < д2 '
7 " 3шЦА - С) ’ 7 " 3ш2(В - С)
.. <А2, f „ < А;.
(6.3.8)
и)2(В - А) ’ ш2(В - С)
Здесь Д2 < 1 — какое-то наперед заданное число. Из (6.3.8) следует,
что всегда можно выбрать начальные данные (Л0) так, чтобы вели¬
чины I7I, |7;|, |/3|, \f3"\ не превосходили наперед заданного сколь
угодно малого значения |Д|, то есть чтобы возмущенное движе¬
ние сколь угодно мало отличалось от невозмущенного — относи¬
тельного равновесия. А это, согласно определению устойчивости
12*
180
Очерк шестой. Они вальсируют на орбитах
по Ляпунову, как раз и доказывает устойчивость невозмущенного
движения.
Таким образом, достаточные условия устойчивости относи¬
тельного равновесия спутника на круговой орбите даются неравен¬
ствами (6.3.7). Выбор величины Ло, обеспечивающей выполнение
неравенств (6.3.8), производится следующим образом:
Ло < min |^w2(i4 - С)Д2, ^и>2(В - Л)Д2|, (6.3.9)
то есть ho должно быть меньше наименьшего из двух выражений,
стоящих в фигурных скобках в (6.3.9). Заметим, что при таком выбо¬
ре Ло, согласно (6.3.6), угловые скорости р, q, г не превзойдут вели¬
чин порядка ш. Это весьма малые величины (для орбит искусствен¬
ных спутников ш ~ 0,05-0,07 град/сек, а для Луны ш ~ 0,00015
град/сек). Иначе говоря, стабилизирующее действие гравитацион¬
ного поля может сказаться лишь при весьма малой кинетической
энергии вращения спутника относительно его центра масс.
Приведенное здесь рассуждение, показывающее устойчивость
относительного равновесия, является фактически использованием
уже известной нам теоремы А. М. Ляпунова об устойчивости. На¬
помним ее формулировку: если из переменных возмущенного дви¬
жения можно образовать определенно-положительную функцию V,
производная V от которой в силу дифференциальных уравнений
отрицательная или тождественно равна нулю, то невозмущенное
движение устойчиво. В нашем случае функция V — левая часть ра¬
венства (6.3.6); она положительно определена при условии (6.3.7).
А так как V является первым интегралом уравнений движения, то
V = 0; отсюда — устойчивость.
Эта теорема Ляпунова является сильным средством доказа¬
тельства устойчивости в тех случаях, когда в системе не происходит
рассеяние энергии и, следовательно, невозможна асимптотическая
устойчивости. Многие задачи динамики космического полета об¬
следованы на устойчивость с помощью этой теоремы или ее моди¬
фикаций. Большое количество таких задач описано В. В. Румянце¬
вым в книге [6.4].
4. Ринограденция на орбите
Из условия (6.3.7) следует, что устойчивость относительно¬
го равновесия обеспечивается прежде всего отличием спутника
Ринограденция на орбите 181
182
Очерк шестой. Они вальсируют на орбитах
(или Луны) от однородного шара. В самом деле, в случае одно¬
родного шара А = В = С и о действии гравитационных моментов
говорить не приходится.
Проанализируем условия (6.3.7) подробнее. Максимальный мо¬
мент инерции В соответствует оси у спутника, которая в отно¬
сительном равновесии, как мы помним, направлена по нормали
п к плоскости орбиты. Минимальный момент инерции С отве¬
чает оси z спутника, которая в относительном равновесии на¬
правлена вдоль радиус-вектора орбиты. Геометрия масс твердого
тела в механике характеризуется, как известно, центральным эл¬
липсоидом инерции тела, направления осей которого совпадают
с главными центральными осями инерции х\ у, z тела, а величи¬
ны полуосей а, Ь, с связаны с главными центральными моментами
инерции А, В, С соотношениями
к к к
а = 72’ 7в’ с = 7д’
где к — некоторая постоянная. Таким образом, максимальному
моменту инерции соответствует наименьшая ось эллипсоида инер¬
ции, и наоборот.
Резюмируя сказанное, мы можем сформулировать следующее
положение, полученное В. В. Белецким в 1956 году и опубликован¬
ное в 1959 году [6.3]:
Для устойчивости относительного равно¬
весия твердого тела на круговой орбите в нью¬
тоновском центральном ноле сил достаточ¬
но, чтобы в невозмущенном движении боль¬
шая ось центрального эллипсоида инерции те¬
ла была направлена по радиус-вектору орбиты,
меньшая ось — по нормали к плоскости орби¬
ты и средняя ось — по касательной к орбите
(рис. 6.3).
Можно сказать, что спутник, если мы
хотим обеспечить его гравитационную устой¬
чивость, должен быть изрядно сжат по на¬
правлению к плоскости орбиты, более вытя¬
нутым, «длинным» по направлению к Земле.
Пожалуй, хорошей в этом смысле конст¬
рукцией спутника будет конструкция, близ¬
кая к форме известного животного Rhinogra-
Рис. 6.3. Устойчивое
положение эллипсои¬
да инерции спутника
на орбите
5. О пассивной стабилизации искусственных спутников
183
dentia Otopteryx volitans, которое было открыто проф. X. Штюмпке
и описано в его монографии «Строение и жизнь ринограденций»
[6.5] (см. также более доступное издание [6.6]).
5. О пассивной стабилизации искусственных спутников
Упомянутая выше мимоходом возможность создания гравита¬
ционно-стабилизированного спутника является весьма принципи¬
альной. За счет «даровой» гравитационной энергии можно удержи¬
вать спутник сколь угодно долго в положении, ориентированном
на Землю одной стороной (подобно Луне). Нет нужды говорить,
насколько это важно для наблюдений за метеорологической об¬
становкой, фотографирования земной поверхности и выполнения
многих других задач. А. Ю. Ишлинский в своем обзоре [6.18] среди
важных достижений механики описал и указанный принцип ста¬
билизации спутника с помощью гравитационных сил.
При практическом осуществлении такой, как говорят, пас¬
сивной ^ системы стабилизации важно погасить первоначальную,
обычно довольно большую, угловую скорость спутника. Требует¬
ся ввести угловую скорость в весьма узкий диапазон, в котором
«срабатывает» гравитационный захват спутника в ориентированное
положение. Поэтому системы гравитационной стабилизации обя¬
зательно содержат механизмы демпфирования (гашения) угловых
скоростей. У естественных спутников (Луна, спутники Юпитера
и Сатурна, перечисленные в начале этого очерка) таким меха¬
низмом демпфирования являются моменты сил приливного тре¬
ния, которые в ходе тысячелетней эволюции «застопорили» враще¬
ние Луны и некоторых других небесных тел [6.2]. Демпфирование
первоначальных вращений искусственных спутников производится
с помощью введения в систему того или иного вида трения, рассеи¬
вающего кинетическую энергию вращения: употребляется упругое
демпфирование, магнитные демпферы и др.
Для создания систем пассивной стабилизации можно исполь¬
зовать не только гравитационное поле, но и стабилизирующее дей¬
ствие аэродинамики, магнитного поля Земли и даже светового дав¬
ления солнечных лучей.
В отличие от активных систем, где стабилизация обеспечивается реактивными
двигателями, маховиками и т. п. активными средствами, требующими расхода энер¬
гии, запасенной на борту спутника.
184
Очерк шестой. Они вальсируют на орбитах
Впервые система гравитационной стабилизации в СССР предло¬
жена в 1956 году Д. Е. Охоцимским [6.34]. В литературе можно найти
описание систем пассивной стабилизации ряда уже запущенных спут¬
ников [6.7,6.8]. Подробное описание динамики систем пассивной
стабилизации содержится в работах В. А. Сарычева ([6.9] и др.).
6. Нелинейные колебания
Если спутник вывести из положения относительного равнове¬
сия, он будет совершать пространственные колебания около этого
положения. Исследование этих колебаний — трудная задача. Очень
обычный способ анализа состоит в следующем. Предположим, что
угловые отклонения от положения равновесия (и угловые скорости
колебаний) весьма малы. Тогда вместо точных уравнений движе¬
ния можно рассмотреть приближенные, в которых оставлены члены
не выше первого порядка малости. Решение этих линейных урав¬
нений движения должно оставаться ограниченным в течение всего
бесконечного времени. Ведь если решение не ограничено, то тем
самым нарушается исходная предпосылка о малости колебаний.
Если же при сколь угодно малых начальных отклонениях ограни¬
ченные колебания будут тоже сколь угодно малы, то естественно,
казалось бы, заключить, что условия ограниченности линейных ко¬
лебаний являются условиями устойчивости исходного положения
равновесия.
Но с появлением работ А. М. Ляпунова стало ясно, что та¬
кие «условия устойчивости», полученные из линейных уравнений,
совсем не обязательно являются «настоящими» условиями устойчи¬
вости. По линейным уравнениям можно заключить, что исходное
невозмущенное движение (равновесие) устойчиво, а на самом деле
этого может и не быть. Прекрасной иллюстрацией к сказанному яв¬
ляется наша задача о пространственных колебаниях твердого тела
(спутника) в гравитационном поле.
Будем рассматривать колебания спутника около положения от¬
носительного равновесия на круговой орбите. Тогда условия огра¬
ниченности линейных колебаний сводятся [6.1] либо к знакомым
уже нам условиям
В> А>С, (6.6.1)
6. Нелинейные колебания
185
либо к совокупности условий
Неравенства (6.6.1), (6.6.2) являются необходимыми условиями устой¬
чивости равновесия. Если оно устойчиво, то условия (6.6.1), (6.6.2)
будут выполнены. Но если условия (6.6.1), (6.6.2) выполнены, то
движение не обязательно устойчиво. Мы выше доказали, что при
выполнении условий (6.6.1) (будем говорить: «в области I») от¬
носительное равновесие в самом деле устойчиво. Условия (6.6.1)
являются достаточными условиями устойчивости.
Про условия (6.6.2) (определяющие «область II») такого за¬
ключения сделать нельзя. Чтобы понять характер движения в этой
области (а также чтобы глубже изучить движение и в области I),
необходимо рассматривать нелинейные уравнения колебаний. Та¬
кие нелинейные эффекты изучались в работе американских ученых
Дж. Брэкуэлла и Р. Прингля [6.10]. Кратко опишем метод и резуль¬
таты их анализа.
Функция, стоящая в левой части равенства (6.3.3), является
гамильтонианом нашей задачи и после ряда преобразований может
быть сведена к следующему нормализованному виду:
Н — ±“ +(^2\V\^ + 2 (^2 +^2*?2) +
+ 2 (d + а,з??з) + (6.6.3)
Здесь T)i — угловые переменные, описывающие так называемые
нормальные колебания, а & — соответствующие им импульсы.
Выписанная явно часть Н (исключая Н^) как раз соответствует
линейным колебаниям, частоты которых суть Ш\, и»2, о>з (они выра¬
жаются через моменты инерции спутника). Верхний знак (плюс)
в (6.6.3) и ниже относится к области I (6.6.1), а нижний знак —
к области 11 (6.6.2).
В Н^ содержатся члены только третьего и более высокого
порядка малости относительно &,*/»• Если этими членами прене¬
бречь, то оставшаяся часть гамильтониана может быть использована
186
Очерк шестой. Они вальсируют на орбитах
для получения линеаризованных уравнений движения. Их решение
может быть записано в виде
y^2ct\
V\ =± sin (х ± /3|), £| = \/2а~\ cosW|(r ± /3\),
U)\
^^sin u>2(r + /32), £2 = \/2а2 cosш2(т + Р2),
0)2
^/2а~
sinw3(r + ^3), 6 = л/2^сов«з(г + А).
Т)2 =
ш2
Пг =
ш3
(6.6.4)
Здесь т — «время», а сц и /% — постоянные интегрирования.
Заметим, что о, пропорциональны квадратам амплитуд коле¬
баний. При этом »/з(т) описывает продольные колебания (в плос¬
кости орбиты), а т}\(г) и 772(7") — поперечные колебания спутника.
Будем теперь искать решение точных уравнений движения, соот¬
ветствующих полному гамильтониану (6.6.3), в том же виде (6.6.4),
где только теперь величины аг и (Зг уже не постоянные, а некото¬
рые искомые функции времени. Такой метод вариации постоянных
приводит к следующим дифференциальным уравнениям
da, flgWfa.ft.r) dfij дНЩсц,&,т)
йт д/Зг ’ dr да{ ' ( '
Здесь под Я^ подразумевается из (6.6.3), куда вместо &, щ
подставлены их выражения (6.6.4).
Эти хорошо известные в классической механике уравнения
(см., например, [6.11]) удобны для исследования: они имеют кано¬
нический вид. Если Я^ = 0, то из (6.6.5) сразу следует аг- = const,
/3,- = const, что отвечает линейным колебаниям (6.6.4). При любом
Я^ Ф 0 решение уравнений (6.6.5) сразу покажет в явном виде
отличие нелинейных колебаний от линейных.
Если колебания не очень сильно отличаются от линейных, то
Я^ мало и к исследованию уравнений (6.6.5) можно применить
асимптотический метод — метод осреднения. Оказывается тогда,
если только
что среднее значение Я^ = lim - f dr = О,
т-юо Т J
О
между частотами о?* не выполняются резонансные соотношения
3
5^ ЩШ, = О,
г= I
6. Нелинейные колебания
187
где щ — любые целые числа (одно из щ может быть равно нулю).
Иначе говоря, формулы (6.6.4) с постоянными аг и Д,- с большой
точностью описывают истинное движение вне окрестностей любых
резонансов. Однако вблизи резонансов это не так; среднее значение
Н^ не равно нулю.
Оставим в Н''У) члены только третьего порядка малости. Тогда
выявляется возможность следующих резонансов третьего порядка:
(I) СДз = 2Ш\, (II) (Дз = U?2 — Ш\, (Ш) Д>3 = ^2 "Н W|. (6.6.6)
Других резонансов третьего порядка быть не может. Движение в ок¬
рестности резонансов (6.6.6) исследовано в цитируемой работе [6.10].
Рассмотрим, например, резонанс типа (I) из (6.6.6). Пусть
в — £Дз — 2ш\ — «расстройка» резонансного соотношения (I). То¬
гда уравнения (6.6.5) в £-окрестности резонанса типа (I) из (6.6.6)
в первом приближении (в смысле метода осреднения) имеют сле¬
дующие первые интегралы:
oi2 = const, /?2 = const, (6.6.7)
Н* = а——а*\/oil cos 103 (Дз =F Д*) Т —«* = const, (6.6.8)
U)2 Сс^з
С = а] ± аз = const, (6.6.9)
где обозначено:
о;3 2wi/3| =f ет
<*i = ot] —, p | =
2a; i a;3
Постоянная а в (6.6.8) зависит только от моментов инерции. Пусть
Ф = a;3(/33 =f /3*). Тогда из (6.6.8) и (6.6.9)
h0±e0a* е тсм\\
cos Ф = ■ -ео = - • (6.6.10)
а\у/±(С-а\) 2аш\
Здесь h0 — постоянная интегрирования, пропорциональная Н*.
Уравнение (6.6.10) дает возможность построить интегральные
кривые в плоскости а|(Ф) и исследовать движение. Рассмотрим
сначала область I, отвечающую (6.6.1) (верхний знак в (6.6.10)).
На рис. 6.4 построены интегральные кривые для двух случаев: |£о| >
у/С и |е0| < у/С. В первом случае, как видим, малые колебания
«амплитуды» а* сначала остаются малыми. Это вполне естествен¬
но, так как неравенство |бГо| > у/С означает, что движение не близ¬
ко к резонансному; следовательно, оно должно мало отличаться
188
Очерк шестой. Они вальсируют на орбитах
а) б)
Рис. 6.4. Амплитудно-фазовая характеристика движения в области I (доста¬
точных условий устойчивости): а — нерезонансный случай; б — резонанс
от линейного случая (то есть от случая а* = const). Наоборот, ес¬
ли расстройка |£о| достаточно мала (|ео| < VC, движение близко
к резонансному), то первоначально малое значение а* как видно
из рис. 6.4 б, становится с течением времени существенным (если
только С и а® не очень мало).
ф„у'.рад
0;2 -
Число витков
Рис. 6.5. Поперечные колебания на круговой орбите в резонансном случае
6. Нелинейные колебания
189
Иначе говоря, в резонансном случае начальные отклонения
от положения равновесия в плоскости орбиты вызывают большие
отклонения первоначально малых углов поперечных колебаний.
В силу интеграла (6.6.9) происходит «перекачка» колебаний из плос¬
кости орбиты в поперечные, затем обратная перекачка и т.д. Этот
факт впервые выявил численным интегрированием точных уравне¬
ний движения американский ученый Т. Р. Кэйн [6.12]. (После этого
и появилась работа [6.10] Брэкуэлла и Прингля, объясняющая об¬
наруженные Кэйном эффекты.)
На рис. 6.5 и 6.6, заимствованных из [6.12], приводятся измене¬
ния со временем угла, описывающего поперечные колебания спут¬
ника. Начальные данные одинаковы для обоих рисунков, но рис. 6.5
отвечает резонансному случаю, а рис. 6.6 — нерезонансному. Ес¬
ли во втором случае амплитуда колебаний не превосходит 0,5°, то
в первом случае 20°!
фп„’>рад
Число витков
Рис. 6.6. Поперечные колебания на круговой орбите
в нерезонансном случае
а) 6)
Рис. 6.7. Амплитудно-фазовая характеристика движения в области II (не¬
обходимых условий устойчивости): а — нерезонансный случай, |бг0| > у/\С\\
б — резонансный случай, |е0| < \/|С|
Такова роль резонанса. Следует, однако, подчеркнуть, что на¬
личие рассмотренной резонансной раскачки колебаний не нару¬
шает, разумеется, ранее доказанной устойчивости по Ляпунову от¬
носительного равновесия спутника. В самом деле, как в резонанс¬
ном, так и в нерезонансном случае всегда можно выбрать в (6.3.6)
и (6.3.8) столь малое ho, что амплитуды колебаний не превзойдут
наперед заданной величины. Только в резонансном случае этот вы¬
бор гораздо более жестко обусловлен, чем в нерезонансном.
А теперь обратимся к области И выполнения необходимых
условий (6.6.2) устойчивости. В формуле (6.6.10) в этом случае на¬
до брать нижние знаки. Соответствующие «амплитудно-фазовые
портреты» движения изображены на рис. 6.7 а и б. Оказывается,
как и раньше, при достаточно больших отклонениях от резонанса
(|го| > \/С) движение может оставаться ограниченным (рис. 6.7 а).
Но при попадании в окрестность резонанса (|£о| < у/С) движение
становится неограниченным (рис. 6.7 б)\ В этом качественное от¬
личие движения при выполнении условий (6.6.2) (необходимых)
от движения при выполнении условий (6.6.1) (достаточных).
Лучше всего результаты анализа, изображенные на рис. 6.7, трак¬
товать так. Сколь бы мала ни была расстройка |£о| Ф 0 между часто¬
тами, всегда можно найти такие начальные данные
что движение будет ограниченным; таких начальных данных нель¬
зя найти только при |бг0| = 0, то есть строго на резонансе. При
строгом резонансе (|ео| = 0) движение (в области II) обязательно
не ограничено (в нашем приближении). При этом, в силу интегра¬
7. Быстрые вращения
191
ла (6.6.9), одновременно возрастают и продольные, и поперечные
колебания. Все сказанное позволяет заключить, что при выпол¬
нении лишь необходимых условий устойчивости (6.6.2) движение
действительно устойчиво, если только частоты не удовлетворяют
резонансному соотношению, но в случае резонансного соотноше¬
ния между частотами устойчивость может исчезнуть и превратиться
в неустойчивость. Этот вывод носит, конечно, приближенный ха¬
рактер (из-за приближенности анализа). Однако математические
работы последних лет [6.13,6.14] позволяют сделать аналогичное
заключение строго. Оказывается, при выполнении лишь необхо¬
димых условий устойчивости, когда старшие члены гамильтониана
(6.6.3) образуют квадратичную форму, не являющуюся определен¬
но-положительной, равновесие может быть неустойчивым, если
частоты линейных колебаний строго подчиняются резонансному
соотношению нечетного порядка.
Итак, устойчивость, обнаруженная с помощью линейных урав¬
нений, должна быть еще доказана (построением функции Ляпуно¬
ва, например). Иначе эта устойчивость может оказаться обман¬
чивой. Она может нарушиться при резонансе. Анализ колебаний
спутника около положения относительного равновесия убедитель¬
но это демонстрирует.
Заметим, что для практических задач стабилизации спутников
имеет значение лишь область I (6.6.1) достаточных условий устой¬
чивости. Введение диссипативных сил превращает здесь устойчи¬
вость в асимптотическую. А в области II (6.6.2) диссипативные силы
разрушают устойчивость и уводят спутник от положения равнове¬
сия, удовлетворяющего (6.6.2).
7. Быстрые вращения
Гравитационный «захват» спутника в режим колебаний около
положения относительного равновесия возможен, как уже объяс¬
нялось, лишь при довольно малой угловой скорости спутника из-за
сравнительной «слабости» гравитационных моментов.
Ну, а если начальная угловая скорость спутника, как это обыч¬
но и бывает, сравнительно велика? Тогда действие моментов внеш¬
них сил (гравитационных, например) настолько слабо меняет ис¬
ходное вращение спутника, что в грубом приближении можно счи¬
тать это исходное вращение неизменным, происходящим по инер¬
ции. Вращение твердого тела по инерции вокруг центра масс хоро-
192
Очерк шестой. Они вальсируют на орбитах
шо изучено в классической механике — это так называемое «дви¬
жение Эйлера—Пуансо». Однако моменты внешних сил оказывают
хотя и малое, но систематическое, постоянно действующее возму¬
щение. В результате этих возмущений малые изменения в исходном
вращении спутника, накапливаясь с течением времени, могут су¬
щественно изменить движение по сравнению с первоначальным.
Отсюда ясна задача: исследовать эволюцию движения Эйлера—
Пуансо под влиянием малых моментов возмущающих сил (подобно
тому как в теории орбит исследуется эволюция кеплеровых траек¬
торий под влиянием малых возмущающих сил). Отметим, что воз¬
мущающие силы могут иметь и не гравитационную природу.
Движение Эйлера—Пуансо (которое иногда будем называть
«невозмущенным движением») очень просто описывается для част¬
ного, но важного практически случая, когда спутник представля¬
ет собой динамически-симметричное тело. Это значит, что из трех
главных центральных моментов инерции спутника два равны меж¬
ду собой. Пусть, например, А = В Ф С. Ось момента инерции С
назовем осью динамической симметрии или продольной осью спутни¬
ка. Будем в дальнейшем опираться именно на этот простой случай.
Невозмущенное движение Эйлера—Пуансо для динамически-сим-
метричного тела, как известно из теоретической механики, является
регулярной прецессией. Опишем это движение (рис. 6.8).
7. Быстрые вращения
193
Если p,q,r — компоненты абсолютной угловой скорости спут¬
ника по главным центральным осям инерции x,y,z, то вектором
кинетического момента L будет вектор с компонентами Ар, Bq, Сг
по тем же осям. При этом продольной осью является ось z . Ока¬
зывается, что в движении Эйлера—Пуансо вектор кинетического
момента L постоянен по величине и направлению в абсолютном про¬
странстве (L = const). В регулярной прецессии компонента век¬
тора L по продольной оси спутника постоянна: Сг = Сгц. Ось
симметрии спутника обходит вектор кинетического момента на по¬
стоянном угловом расстоянии 'д с постоянной угловой скоростью гр',
одновременно спутник «кружится» вокруг своей продольной оси
с постоянной угловой скоростью ф. Спутник «вальсирует»2^ вокруг
вектора кинетического момента, подобно неутомимому танцору,
кружащемуся в зале.
Угол д назовем углом нутации, угловые скорости ф и ф —
соответственно скоростями прецессии и собственного вращения. По¬
ложение вектора кинетического момента в пространстве можно
задать двумя постоянными углами: р и сг. Тогда регулярная пре¬
цессия описывается шестью параметрами:
L, р, а, ■&, ■ф, <р, (6.7.1)
из которых четыре первых постоянны, а два последних равномерно
меняются со временем с постоянными скоростями ф,ф.
«Включим» теперь действие моментов возмущающих сил. Тогда
четыре первых параметра (6.7.1) уже не будут, вообще говоря, оста¬
ваться постоянными, зависимости (р и ф от времени будут отли¬
чаться от линейных. Задача состоит теперь в том, чтобы выяснить,
как именно меняются (эволюционируют) со временем параметры
(6.7.1) под действием возмущающих моментов. Наши параметры
(6.7.1) аналогичны оскулирующим элементам в динамике орбит,
и прежде всего для параметров (6.7.1) нужно составить дифферен¬
циальные уравнения «в оскулирующих элементах».
Рассмотрим, например, возмущения, обусловленные гравита¬
ционным потенциалом (6.1.6). Входящие в него величины 7,7' у"
надо выразить через наши новые переменные (6.7.1). Оказывается,
для случая А = В потенциал не будет зависеть от <р, так что
U = U(p, сг, #, ф, wot). (6.7.2)
Термин «вальсирует» применительно к вращению спутника несколько лет тому
назад пустил в ход Нам Тум По, бывший тогда аспирантом Ленинградского госу¬
дарственного университета.
13 Заказ 1667
194
Очерк шестой. Они вальсируют на орбитах
Явная зависимость U от времени вызвана перемещением спутни¬
ка по орбите со средней угловой скоростью cvo, а в случае не¬
круговой орбиты — также и тем, что значение текущего радиус-
вектора R, входящее в выражение (6.1.6) для Е/, тоже будет функ¬
цией (периодической) от t: R = Потенциал U является
27г-периодической функцией по каждому из своих аргументов, так
что, например, и(гр + 2тт) = и{ф), U(щt + 27т) = U(wot) и т. д.
Оказывается, что уравнения «в оскулируюших элементах» в рас¬
сматриваемом случае имеют, как было выведено В. В. Белецким
в 1962 году, следующий вид [6.1,6.15]:
Эти уравнения верны не только в случае гравитационных воз¬
мущений, но и для любых возмущений, обладающих силовой функ¬
цией типа (6.7.2). (При определенных условиях к таким возмущени¬
ям относятся аэродинамические и магнитные моменты, моменты
сил светового давления.) Уравнение для (р в (6.7.3) не выписано,
так как правые части от (р не зависят и уравнение для (р можно
интегрировать отдельно (простой квадратурой, после того как будет
проинтегрирована система (6.7.3)).
Итак, задача сводится к интегрированию системы (6.7.3) че¬
тырех дифференциальных уравнений первого порядка (с учетом
конечного соотношения (6.7.4)).
Если возмущающих моментов нет, то U = 0 и уравнения
(6.7.3) дают L = Lo (из (6.7.4) тогда следует д = 0О), р = /?0,
а = (То, ip = Lq/A = фо, что как раз отвечает невозмущенному
движению — регулярной прецессии. Будем считать, что существу¬
ют малые возмущения U; малость возмущений определим тем, что
L/A > тах|С7|/Х; тогда в уравнениях (6.7.3) переменные L,p,a
будут медленными, а переменная гр — быстрой в смысле асимп¬
тотических методов, и для исследования этих уравнений удобно
применить уже известный нам метод осреднения по быстрой пере¬
менной. Заметим, что уравнения (6.7.3) содержат вообще-то две
dL _dU da _ 1 dU
dt дф9 dt L sin р др 9
\
>
(6.7.3)
dip L 1
~dt=A~L
(6.7.4)
7. Быстрые вращения
195
быстрые переменные: фит= щЬ. Но обычно ф изменяется
со скоростью порядка I — 10 град/сек, а г — со скоростью порядка
0,05-0,07 град/сек, поэтому легко допустить, что переменные фит
не резонируют (то есть частоты фо и и несоизмеримы), и можно
провести осреднение только по ф. Пусть
2тг
и
= (6.7.5)
о
Учтем, что в силу периодической зависимости U от ф
2тг
^ 4» = ^{U(2т) - £7(0)} = 0.
Z7T
-(
2тг J
L0 1 (dU dU Д „ ч
= т-^{^с,8,,+wc'8'’} (6'7J)
й
(6.7.8)
Тогда система (6.7.3) и равенство (6.7.4) немедленно дают соотно¬
шения
L = Lo, cos 'в = cos tfo, (6.7.6)
(1ф
~dt
и каноническую систему, двух дифференциальных уравнений
dp 1 dU da 1 dU
dt Lq sin р да' dt L0 sin p dp ’
Таким образом, задача свелась к интегрированию всего двух
уравнений (6.7.8), после чего из (6.7.7) можно определить скорость
возмущенной прецессии (вместе с малой добавкой, стоящей в скоб¬
ке в (6.7.7)). Главный же вывод, который следует из (6.7.6)-(6.7.8),
таков [6.15,6.16]:
Возмущенное движение динамически-симметричного спутни¬
ка в потенциальном силовом поле (6.7.2) является квазирегулярной
(то есть почти регулярной) прецессией с измененной скоростью
прецессии (6.7.7), вращающей ось симметрии спутника на посто¬
янном угловом расстоянии #() вокруг постоянного по величине
вектора L кинетического момента. Основное влияние возмущений за¬
ключается в изменении направления вектора L в пространстве. Это
изменение описывается уравнениями (6.7.8).
Говоря проще и короче, «фигура вальсирования» спутника,
изображенная на рис. 6.8, усложняется лишь за счет медленного из¬
менения направления вектора L. На рис. 6.9 схематично изображе¬
ны обе, невозмущенная и возмущенная, «фигуры вальсирования».
13*
196
Очерк шестой. Они вальсируют на орбитах
Основные уравнения (6.7.8) возмущенного движения назовем
эволюционными уравнениями.
8. Автор слегка припугнет читателя
Автор считает эволюционные уравнения (6.7.8) весьма изыс¬
канными. Не столько даже из-за их формы, сколько из-за того,
что все возмущенное движение фактически вытекает из этих двух
простых (а потому и красивых) уравнений. Однако красота эта об¬
манчива. Ведь прежде чем пользоваться этими уравнениями, нуж¬
но в явном виде выписать формулу (6.7.2) силовой функции U.
Это вовсе не простая формула, а, наоборот, довольно громоздкая.
Механику-исследователю в своей работе приходится иметь дело
и с громоздким, и с неизящным аппаратом — увы, необходимым
для получения истины.
С исключительной целью приближения читателя к пониманию
этого факта автор выпишет здесь выражение (6.7.2) в явном виде.
Вот оно: если в (6.1.6) оставить члены, существенные для исследо-
Рис. 6.9. «Фигуры вальсирования»: а — невозмущенное движение; б —
возмущенное движение
Далёко, далёко на озере Чад
Изысканный бродит жираф.
Н. Гумилев
Точка на поверхности
спутника
8. Автор слегка припугнет читателя
197
198
Очерк шестой. Они вальсируют на орбитах
вания движения около центра масс, и положить А = В, то
U =\{\ -е2)3^1 + ecosuf(A ~СЬ"2' (6-8л)
где
•у"2 = ^ sin2 д + ^ sin2 р(3 cos2 •в — 1) +
+ ^ sin2 р(3 cos2 д - 1) cos 2(у - а) +
1 2 2
+ sin р cos р sin 1? cos •д sin ip + - sin i?sin pcos2^ +
+ ^ sin cos d sin p{ 1 + cos p) sin (ip - 2v + 2a) -
— - sin cos t? sin p( 1 - cos p) sin (tp + 2v - 2a) -
1 ~:—2 л/i , \2
— — sin i?(l+cosp) cos (2ip - 2v + 2<r) -
- ^ sin21?( 1 - cos p)2 cos (2tp + 2v - 2a);
причем истинная аномалия v связана с безразмерным временем
г = wot формулой
/1 - е v ефI - е2
т = 2 arctg \ tg - - sin v. (6.8.2)
V I + е 2 l + e cos v
В формулах (6.8.1), (6.8.2) e — эксцентриситет орбиты, Wo = p,^2a~3^2
— среднее движение по орбите с большой полуосью а. Углы р и а
выбраны здесь вполне конкретным образом: р — угол между векто¬
ром L кинетического момента и нормалью п к плоскости орбиты,
а — угол, отсчитываемый в плоскости орбиты от направления
на перицентр орбиты до проекции вектора L на плоскость орби¬
ты. Я надеюсь, что, взглянув на (6.8.1), (6.8.2), читатель «отделался
легким испугом».
Если бы я хотел припугнуть читателя посильнее, то выписал бы
в явном виде выражение U для трехосного (Аф В ф С) тела3^.
^ Быстрые нерезонансные вращения трехосного спутника в гравитационном
поле исследовал Ф.Л. Черноусько [6.17].
9. Возмущенное движение в явном виде
199
9. Возмущенное движение в явном виде
Чтобы из выражения (6.8.1) для U получить выражение U,
входящее в эволюционные уравнения (6.7.8), надо из (6.8.1) просто
«повыбрасывать» все члены, содержащие множителем тригономет¬
рические функции от г/). Ведь именно эти члены «съедаются» осред¬
нением (6.7.5). Проделав такую операцию, увидим, что U будет
уже гораздо проще выглядеть, однако остается явная зависимость
U от времени (через v)\ в силу этого досадного факта уравнения
(6.7.8) неинтегрируемы.
Из этого положения есть два выхода:
1. Частный: в случае круговой орбиты (е = 0) уравнения (6.7.8)
приводятся к интегрируемому виду подстановкой к — v — а
[6.1,6.15].
2. Общий: для любой орбиты можно считать т быстрой перемен¬
ной и снова применить к уравнениям (6.7.8) асимптотический
метод, осредняя правые части уравнений по т.
Применим второй путь исследования. Тогда в уравнения (6.7.8)
надо вместо U подставить
2п 2п 2п
° = TjUdT=(^IIUd*dr-
0 0 0
Вычислять этот интеграл удобно заменой переменной г на у: ведь
U явно зависит от v, а
dr (1 - е2)3/2
dr = —du = ~^dv.
dv (l+ecosi/)'1
Проделав такую операцию над U, из (6.8.1) получим
^ = 1(1 -е2)У2 sin2 д+\ sin2 cos2 ~ ')}• (6’9Л)
Подставляя (6.9.1) в (6.7.8) (вместо U), сразу получим [6.1,6.16]
dcr 3 (А - С)шо 2 „ /
dr = 4 L0(l - е2)3^2 C°S <6«)
Постоянство угла р следует из первого уравнения (6.7.8) пото¬
му, что U не зависит от а: члены с а в (6.8.1) все пропадут после двух
200
Очерк шестой. Они вальсируют на орбитах
осреднений. Таким образом, возмущенное движение вектора кине¬
тического момента в гравитационном поле очень простое. Вектор
кинетического момента прецессирует вокруг нормали п к плоскости
орбиты на постоянном угловом расстоянии р0 от нее и с постоянной
угловой скоростью (6.9.2). Напомним, что вокруг вектора кинети¬
ческого момента спутник «вытанцовывает» регулярную пре_цессию
(6.7.6)—(6.7.7), причем в (6.7.7) теперь U надо заменить на U\ ока¬
жется, что угловая скорость прецессии ф будет строго постоянной.
Если невозмущенное движение есть просто вращение вокруг
оси симметрии (частный случай регулярной прецессии), то #0 = 0
и L = Сг0; именно такой случай рассматривается в классической
небесной механике (прецессия земной оси под влиянием солнечно¬
го и лунного притяжений). Формулы (6.9.2) в этом частном случае
превращаются в классические формулы скорости прецессии земной
оси. Известно, что период этой прецессии ни много, ни мало —
26 ООО лет. Однако для искусственных спутников эффекты куда
более «весомы, грубы, зримы»: период прецессии вектора кинети¬
ческого момента, вычисленный по (6.9.2), составляет всего лишь,
несколько суток.
10. «Пегас»
Но за несколько суток изрядно изменится и сама орбита спут¬
ника, а мы это пока никак не учли. В самом деле, в первых очерках
было показано, что за счет сжатия Земли плоскость орбиты пово¬
рачивается (прецессирует) вокруг оси Земли со скоростью
dQ eRl .
— = г- cos г = Kq (6.10.1)
dr р2
(это скорость движения восходящего узла орбиты) и, кроме того,
орбита поворачивается в собственной плоскости со скоростью
^ = ^0(5c°s2i-\) = Kы (6.10.2)
(это скорость движения перицентра орбиты). Возмущенное дви¬
жение (6.9.2) вектора кинетического момента потому только полу¬
чилось столь простым, что мы пренебрегли эволюцией орбиты,
описываемой формулами (6.10.1), (6.10.2). А расчет по формуле,
10. «Пегас»
201
например, (6.10.1) показывает, что типичная орбита спутника по¬
вернется в пространстве на 360° за 10-12 суток 4К
Влияние эволюции орбиты на эволюцию вращения и ори¬
ентации спутника впервые рассматривалось автором этой книги
в работах [6.16,6.19]; построенная теория была затем развита им в
монографии [6.1] с учетом разнообразных моментов сил, действу¬
ющих на спутник. Изящно усовершенствовал эту теорию С. И. Тру¬
шин в своем этюде [6.20]. Исходя из перечисленных работ, за¬
пишем уравнения возмущенного движения вектора кинетического
момента в следующем виде:
dp
— = +Kq sin i sin E,
dr
dE
— = 2Ka cos p - Kq(cos i - sin i ctg p cos E).
dr y
(6.10.3)
Здесь постоянная
3 {A-C) W0 2 a 14
*' = I Lo< I-<’)>/><
a Kq — постоянная, определяемая формулой (6.10.1). Переменная р
имеет прежний смысл, а новая переменная Е связана со старой а
соотношением
7Г
Е = (г + ш* - -.
Отметим, кстати, что для трехосного спутника (А Ф В Ф С)
эволюционные уравнения имеют точно такой же вид (6.10.3), толь¬
ко постоянный коэффициент Кд вычисляется по более сложной
формуле, найденной Ф. Л. Черноусько [6.17].
Смысл уравнений (6.10.3) прост. Рассмотрим небесную сферу
(рис. 6.10), изобразив на ней небесный экватор, ее пересечение
с плоскостью орбиты и след вектора L кинетического момента.
Пусть момент гравитационных сил не действует (так же как
и никакой другой). Тогда вектор L остается неподвижным в абсо¬
лютном пространстве (в системе координат XYZ, ось X которой
направлена на точку весеннего равноденствия, а ось Z — на Север¬
ный полюс мира), но меняет свое положение относительно орбиты
^ В формулах (6.10.1) и (6.10.2) обозначено: Яэ — экваториальный радиус Земли
(6371 км), р — фокальный параметр орбиты, i — наклонение орбиты к экватору,
ё = 0,0016331 — безразмерный параметр, определяемый величиной сжатия Земли.
202
Очерк шестой. Они вальсируют на орбитах
Рис. 6.10. Относительное положение вектора кинетического момента и
орбиты: Z — направление на Северный полюс мира, X — направление
на точку весеннего равноденствия, п — направление нормали к плоскости
орбиты, L — направление вектора кинетического момента, ОП — на¬
правление радиус-вектора перигея орбиты, I — проекция L на плоскость
орбиты, — линия отсчета угла £
из-за ее эволюции. Иначе говоря, углы р и сг, определяющие поло¬
жение вектора L относительно орбиты, меняются из-за изменения
углов (]иц, описывающих положение орбиты. Из рис. 6.10 совер¬
шенно ясно, что за счет изменения угла (движение перицентра
орбиты в ее плоскости) угол р между нормалью п к плоскости
орбиты и направлением L меняться не может, а меняется лишь
угол сг, притом так, что приращению Ашп соответствует прираще¬
ние Acr = —Awjf.
Удобно поэтому вместо угла сг ввести новый угол, не завися¬
щий от движения перицентра. Таким углом является, например,
сумма (т + , определяющая угловое положение проекции 1 век¬
тора L на плоскость орбиты относительно линии узлов. Этот угол
неизменен при движении перигея. Однако еще удобнее ввести угол
£= (г + — 7г/2, производя тем самым отсчет поворота вектора
L от «наивысшей» точки орбиты (на рис. 6.10 изображен угол -£).
Итак, углы р и £ не меняются за счет движения перигея орбиты.
Однако они меняются за счет движения узла орбиты, причем, как
можно вычислить, со скоростями
= Kq sin i sin S,
i
(t)
10. «Пегас»
203
dE\
— ) = -Kn(cos i - sin i ctg p cos £)
dr )\
где Kq — ранее выписанная скорость (6.10.1) движения узла op-
биты. Но угол Е меняется еще и за счет влияния гравитационного
момента со скоростью (6.9.2). Складывая все скорости изменения
сначала угла р, затем угла Е, получим два эволюционных уравне¬
ния (6.10.3).
Эти уравнения могут быть приведены к каноническому виду с
не зависящими от времени правыми частями, из которых следует
первый интеграл уравнений (6.10.3):
Kq(cos г cos р -I- sin г sin р cos Е) - Кд cos2 р = ho. (6.10.4)
Здесь ho — постоянная интегрирования. Уравнение (6.10.4) опре¬
деляет семейство р(Е, Л0) возможных траекторий конца вектора
кинетического момента. Естественно, что при Kq = 0 это семей¬
ство является множеством малых кругов р = ро (вдоль которых
прецессирует L под влиянием гравитационных моментов), а при
Кд = 0 семейство превращается в множество малых кругов Д = До,
где Д — угол между L и направлением оси Z на полюс мира
(рис. 6.10) (ведь при отсутствии гравитационных моментов вектор
L неподвижен в пространстве и, значит, угол Д постоянен). Однако
при одновременном отличии от нуля параметров Kq и Кд семей¬
ство (6.10.4) траекторий обладает существенно более сложным ха¬
рактером. Все траектории замкнуты и симметричны относительно
большого круга Е = 0,7Г. На этих меридианах, как следует из вида
правых частей уравнений (6.10.3), лежат неподвижные точки семей¬
ства траекторий (полюсы), определяемые координатами Е = 0,7г,
р = /Этт, причем рп удовлетворяет уравнению
Неподвижных точек будет две или четыре в зависимости от зна¬
чений г и параметра к — -K(J/Kq. Так, например, при \х\ > 1
неподвижных точек всегда четыре независимо от значения г. Точ¬
нее [6.14]: неподвижных точек две, если
и четыре, если знак неравенства противоположен.
На рис. 6.11 изображена примерная зависимость рж(г), опреде¬
ляемая из (6.10.5), для фиксированного х > 1 (равного приближен¬
но 1,1). Сплошными линиями показано множество значений рп,
Кд sin 2рп - Kq sin (рж т г) = 0.
(6.10.5)
|2к|2/3 < sin2/3 г + cos2/3 г,
204
Очерк шестой. Они вальсируют на орбитах
Рис. 6.11. Зависимость положения рж полюса траекторий
от наклонения г орбиты при и > I
отвечающее устойчивым полюсам траекторий, а пунктирной лини¬
ей — неустойчивым. Рассматривая на этом рисунке вертикальное
сечение г = const, видим, что всякому фиксированному значению
г ф 0°, 90° отвечает семейство траекторий с тремя устойчивыми и
одним неустойчивым полюсом. При этом на меридиане £ = тг ле¬
жит один (устойчивый) полюс, а все остальные — на меридиане
£ = 0. Соответствующая картина семейства траекторий изображе¬
на на рис. 6.12.
Рис. 6.12. Семейство траекторий конца вектора кинетического момента
10. «Пегас»
205
Рассматривая это семейство, замечаем, что в окрестности осо¬
бой точки 1 движение близко к «гравитационному» (типа «испор¬
ченной» прецессии вектора кинетического момента вокруг нормали
к плоскости орбиты). Однако в окрестности особой точки 4 дви¬
жение качественно иное: конец вектора L описывает вытянутую
замкнутую кривую вокруг точки 4, лежащей на меридиане £ = тг
вблизи плоскости орбиты. Более того, движение такого типа не ис¬
чезает при сколь угодно больших (но конечных) значениях |и|.
Сколь бы ни мал был эффект, вызванный движением узла орбиты
(Kq), по сравнению с влиянием гравитационных моментов (Кд),
это малое влияние всегда даст множество траекторий в окрестности
точки 4 на рис. 6.12, которые качественно отличаются от траекторий
гравитационного типа. При \Кд\ 3> \Kq\ полюсы 1 и 3 будут лежать
очень близко к точкам р = 0 и р = 7г соответственно, а полюсы 2
и 4 будут иметь координату р, близкую по значению к 7г/2. Но зона
«негравитационного» движения все равно будет существовать в ви¬
де узкой «перевязи» в окрестности плоскости орбиты; лишь при
к -» оо площадь этой зоны стремится к нулю.
Таково несколько неожиданное и явно нетривиальное влия¬
ние эволюции орбиты на эволюцию движения около центра масс.
Подробнее с этими эффектами можно познакомиться в книге [6.1]
(глава 9, §4, а также глава 8).
А сейчас пора вспомнить, что в заголовке этого пункта стоит
имя прославленного крылатого коня — при чем он тут? Но «Пе-
Орбитальная долгота L
Рис. 6.13. Траектория конца вектора кинетического момента спутника «Пе¬
гас». Сплошная линия с точками — расчет, треугольнички — наблюдательные
данные. Вдоль кривой отложено время в сутках от начала 1965 года
206
Очерк шестой. Они вальсируют на орбитах
гас» — название американского спутника, эволюция движения око¬
ло центра масс которого прекрасно укладывается в только что из¬
ложенную теорию. Характер этой эволюции был определен экспе¬
риментально5) и сравнен с теорией в американской работе [6.21]
На спутник «Пегас» наибольшее влияние оказывали как раз гра¬
витационный момент и движение узла орбиты, так что эволю¬
ция его вращения должна описываться уравнениями типа (6.10.3).
На рис. 6.13, заимствованном из [6.21], изображена (сплошной ли¬
нией) рассчитанная по уравнениям (6.10.3) траектория конца век¬
тора кинетического момента спутника «Пегас» и (треугольничками)
наблюдательные данные об этой траектории. Видно, что точки ло¬
жатся как раз на экзотическую, вытянутую овально вдоль плоскости
орбиты, кривую, отвечающую движению по одной из траекторий
в окрестности точки 4 на рис. 6.12.
11. Луна, Меркурий, резонансы...
Уравнения (6.7.3) с силовой функцией (6.8.1) имеют частную
форму, отвечающую колебаниям спутника в плоскости орбиты: р = 0,
# = 90°, <т = 0о. В этом случае из (6.7.3) остаются лишь два уравнения:
dL 8U dip L „
H-W i = A• (6IU)
которые эквивалентны одному уравнению второго порядка
d2ip dU 1 „
где
3ojn -у
и ~ ЗГтО +ecos v) (А - С) cos (2ip - 2v + 2<т0). (6.11.3)
4(1 — еАу
Если раньше полагалось, что tp — быстрая переменная, то теперь
это не обязательно, зато будем считать, что разность моментов
инерции А — С мала, так что спутник близок к динамически-сфе-
рическому. Этот случай важен для естественных спутников и планет.
Если А - С = 0, то решение уравнений (6.11.1) или (6.11.2)
определяет равномерное вращение
ip = flr + ipo, г = (Jot. (6.11.4)
Что скрывается за этими словами, будет объяснено в двенадцатом очерке.
Теория, изложенная в [6.21], повторяет более ранние результаты [6.1,6.17].
11. Луна, Меркурий, резонансы.
207
При А - С Ф 0, но малых, можно искать решение уравне¬
ния (6.11.2), близкое к равномерному вращению (6.11.4), пользуясь
асимптотическими методами (малый параметр — разность момен¬
тов инерции спутника). Такое исследование провел Ф. JI. Черноусь-
ко в работе [6.22]. Будем искать решение уравнений (6.11.1) в виде
(6.11.4), где ipo — новая переменная.
Удобнее ввести вместо другую переменную 5, связанную с
гро линейно:
Чтобы получить теперь асимптотическое решение, надо осред-
нить U по т и подставить в уравнения (6.11.1). Однако при любых
не целых значениях га результат осреднения будет равен нулю:
нерезонансное вращение спутника не отличается от равномерного.
При целых значениях га U является периодической функцией от и,
и тогда
где t(v) определяется по формуле (6.8.2), а уравнение движения
(6.11.2) превращается в уравнение
Уравнение (6.11.6), как можно показать, справедливо и для трех¬
осного спутника: нужно только заменить в знаменателе момент
25 = 7г-ь2(<7-0 + ^о).
Обозначим еще Q = га/2. Тогда
(1 + е cos v)3(A - С) cos (гат - 2v + 25).
2ж
2тг
0
0
Результат осреднения оказывается таков:
о
d25 3 А-С
dr2 2 А
Фш(е) sin 25 = 0.
(6.11.6)
208
Очерк шестой. Они вальсируют на орбитах
инерции А на третий момент инерции В. Уравнение (6.11.6) весь¬
ма содержательно, и мы опишем основные свойства и результаты,
следующие из (6.11.6).
1. Это уравнение имеет вид уравнений колебаний физического
маятника.
2. Оно интегрируется. Первый интеграл — интеграл энергии —
имеет вид
Х-Ад2 + т{е){А - С) sin2 6 = h0. (6.11.7)
Эта формула дает возможность построить на плоскости д, 6 так
называемый фазовый портрет траекторий (зависимость <j(<J, ho)
при различных фиксированных значениях ho). Этот портрет
изображен на рис. 6.14 для случая, когда Фт(е)(А - С) > 0.
3. По смыслу угла 5 равенство его нулю (или 7г) при прохожде¬
нии перигея орбиты означает, что спутник здесь расположен
осью момента инерции С вдоль перигейного радиус-вектора.
Из фазового портрета рис. 6.14 можно понять, что при Фш > 0
устойчив такой режим вращения, когда в перигее спутник вы¬
тянут вдоль радиус-вектора (А > С), а при Фт < 0 — вдоль
вектора скорости (А < С).
4. Фазовая плоскость д, 6 делится на область «вращательного дви¬
жения», где угол д монотонно возрастает (убывает) со време¬
нем, и область «колебательного движения» (колебания угла <5).
11. Луна, Меркурий, резонансы.
209
Эту последнюю область назовем резонансной зоной. Ее ширина
5. Произвольные колебания <5(т) в резонансной зоне описыва¬
ются в эллиптических функциях с модулем
где К (к) — полный эллиптический интеграл первого рода.
6. Частота малых колебаний около устойчивого положения
Заметим теперь, что для круговой орбиты (е = 0) все Фш = 0 при
любом га, кроме га = 2. В последнем случае период вращения
вокруг оси в точности равен периоду обращения по орбите. Мы
уже знаем, что именно так движется по своей орбите Луна.
На круговой орбите не может быть иных устойчивых резо¬
нансных движений, кроме движения лунного типа. Интересно за¬
метить, что при е = 0 $2(0) = 1 и уравнение (6.11.6) является
точным уравнением плоских колебаний спутника около положе¬
ния относительного равновесия. В этом случае уравнение (6.11.6)
может быть получено строго, без осреднения. Угол 8 при этом
является углом между осью инерции спутника и текущим ради¬
ус-вектором его центра масс. На эллиптической орбите движение
лунного типа (га = 2), как видим, тоже может быть. Кроме то¬
го, на эллиптической орбите существует бесчисленное множество
14 Заказ 1667
так что
sin 8 = к sn (г - го) + F0,k ,
max | sin 8\ = к.
Безразмерный период колебаний
210
Очерк шестой. Они вальсируют на орбитах
резонансных устойчивых движений, отвечающих разным целочис¬
ленным значениям т. Из всех возможных резонансных движений
интересны именно движение лунного типа (т = 2) и движение
меркуриального типа (т = 3). На рис. 6.15 приведены зависимости
Фг(е) и Фз(е) [6.22,6.23]. Для малых значений е [6.2,6.22]
Ф2(е)= 1 —5у + 13^ + -.. , Фэ(е) = 7^-123^+... .
Резонансы при т > 3 играют все меньшую роль (по крайней мере
для малых эксцентриситетов) с возрастанием га, так как Фш ~ ет~2.
Устойчивые вращения лунного типа изображены на рис. 6.16.
При малых эксцентриситетах спутник проходит перигей, располага¬
ясь продольной осью вдоль радиус-вектора. Однако при е > 0,682
устойчивым будет такое вращение, когда спутник проходит пе¬
ригей, «вытянувшись» вдоль вектора скорости. Про резонансное
вращение Меркурия уже упоминалось в четвертом очерке. Угло¬
вая скорость его осевого вращения ровно в полтора раза больше
орбитальной угловой скорости (П = 3/2). У Меркурия довольно
эксцентричная орбита (е = 0,206). Для такой орбиты Фз(е) « 0,7,
в то время как Ф|(е) « 0,9. Иначе говоря, ширина резонансной
зоны для га = 3 (П = 3/2) имеет тот же порядок, что и ширина
зоны при га = 2 (Г2 = 1). В процессе эволюции, уменьшая свою
угловую скорость под влиянием приливных сил, Меркурий имел
хороший шанс угодить в резонанс т — 3, не дойдя до резонанса
с меньшей угловой скоростью (т = 2), — так оно и случилось7*.
На рис. 6.17 изображено вращение типа Меркурия. В перицентре
Удивительно интересным является факт, что характер приливных сил не позво¬
лил Меркурию «застрять» на резонансе сш>3,а вот на т = 3 — пожалуйста [6.2]!
12. Скиапарелли и другие
211
Рис. 6.16. Вращение
лунного типа (га = 2)
Рис. 6.17. Вращение типа
Меркурия (га = 3)
спутник всегда вытянут вдоль радиус-вектора (поочередно: то «но¬
сом», то «кормой» к центру притяжения), а в апоцентре вытянут
вдоль вектора скорости (то «кормой», то «носом» вперед).
Мы кратко рассмотрели плоские резонансные вращения в гра¬
витационном поле. Фактические резонансные движения осложне¬
ны пространственным характером вращения небесных тел. Так,
например, вектор кинетического момента вращательного движе¬
ния Меркурия составляет угол, возможно, около 25° с нормалью к
плоскости его орбиты [6.2,6.27]. Это уменьшает ширину резонанс¬
ной зоны по сравнению с той, какая получается в рассмотренном
здесь плоском случае. А. П.Торжевский [6.24а,6.246] и А. П. Марке -
ев [6.25] провели большую серию исследований резонансных вра¬
щений спутников.
Теперь мы можем заключить, что наличие устойчивых резо¬
нансных вращений небесных тел — не случайно; оно проистекает
из природы гравитационных сил.
12. Скиапарелли и другие
Нет нужды подчеркивать, что исследование резонансных вра¬
щений имеет равно важное значение в теории движения естествен¬
ных и искусственных небесных тел. Классический пример резонан¬
са 1 : I (период обращения равен периоду вращения) — движение
Луны; но этот же резонанс играет первостепенную роль в системах
гравитационной стабилизации искусственных спутников. Резонанс
3 : 2 не использовался (и не наблюдался) у искусственных спут¬
ников, но открытие такого резонанса в движении Меркурия столь
14*
212
Очерк шестой. Они вальсируют на орбитах
поучительно, что стоит вкратце остановиться на истории этого от-
8)
крытия \
Долгое время считалось, что вращение Меркурия вокруг своей
оси синхронно с его орбитальным движением, то есть Меркурий,
как и Луна, вращается в резонансе 1:1. Тогда Меркурий по¬
чти точно должен был быть обращенным одной стороной к Солн¬
цу. Именно так знаменитый итальянский астроном Скиапарелли9^
в 1889 году истолковал обширную серию своих наблюдений Мер¬
курия. Период обращения Меркурия вокруг Солнца, как известно,
88 суток. Скиапарелли заключил, анализируя свои наблюдения, что
и период осевого вращения Меркурия составляет 88 суток. В тече¬
ние почти столетия (до 1965 года) оптические наблюдения различ¬
ных астрономов «подтверждали» результат Скиапарелли.
Однако развитие техники (в том числе космической) со време¬
нем дало возможность организовать принципиально новые методы
наблюдения планет — радиолокационные. Радиолокационные на¬
блюдения Меркурия в 1965 году позволили американским ученым
Петтенгилу, Дайсу и Шапиро [6.27, 6.28] установить, что период
осевого вращения Меркурия составляет 59 ± 3 суток, а вовсе не 88
суток. Итальянский ученый Коломбо (долго работавший в США)
обратил внимание, что установленный радиолокационно период
вращения Меркурия близок к 2/3 от периода обращения Мер¬
курия 2/3 • 88 = 58,65 суток); Коломбо первый высказал идею
о резонансности вращения Меркурия с отношением угловой ско¬
рости вращения к угловой скорости обращения, равным 3 : 2. Вслед
за этим, конечно, снова пересмотрели данные Скиапарелли и его
последователей. Было показано, что оптические наблюдения до¬
пускают неоднозначное толкование и период вращения ~ 59 суток
прекрасно укладывается в эти наблюдения!
Таким образом, Скиапарелли рискует войти в историю науки
в несколько печальной роли исследователя, допустившего две зна¬
менитые ошибки в истолковании собственных наблюдений. Это —
открытие у Меркурия синхронного вращения, которого нет, и ка¬
налов на Марсе, которых, по-видимому, тоже нет|0\
Библиографию по этому вопросу см., например, в обзорах [6.2, 6.26].
Он прославился тем, что в 1877 году во время великого противостояния Марса
открыл на Марсе сеть темных линий, названных им «каналами».
,0) фотографии поверхности Марса, сделанные американскими космическими
зондами «Маринер-4» в июле 1965 года, «Маринер-6» в июле 1969 года и «Маринер-7» в
12. Скиапарелли и другие
213
Описывая историю установления периода вращения Мерку¬
рия, невозможно умолчать о том, как был установлен период вра¬
щения Венеры. Оптические наблюдение Венеры, ввиду мощности
ее атмосферы, в принципе позволили измерить период вращения
лишь верхних слоев атмосферы. Было получено, что атмосфера Ве¬
неры имеет обратное вращение; это дало намек (правильный, как
потом оказалось) на обратное вращение самой планеты.
Что касается периода вращения собственно Венеры, то за сто¬
летия здесь не было получено ничего, кроме укрепившегося здоро¬
вого любопытства ряда исследователей и\
Положение изменилось в 1962 году после радиолокацион¬
ных измерений в СССР (коллектив В. А. Котельникова [6.26,6.31])
и в США (Карпентер и Голдстейн [6.32,6.33]). Было получено, что
Венера вращается вокруг своей оси в обратную сторону по срав¬
нению с орбитальным движением и с периодом около 250 суток.
Наклон ее оси к нормали к плоскости орбиты составляет 1,2°.
Несколько позже период вращения был уточнен, он оказался
равным 243,24 ±0,1 суток, что с точностью до результатов изме¬
рений совпадает со значением 243,16 суток, при котором Венера
в каждом нижнем соединении ,2^ обращена одной стороной к Зем¬
ле. Гольдрейх и Пиил [6.2] были, по-видимому, первыми, кто это
понял. Таким образом, во вращении Венеры имеет место резонанс
совершенно феноменальный, связанный не только с орбитальным
движением Венеры, но и с орбитальным движением Земли. За вре¬
мя между двумя нижними соединениями (583,92 суток) Венера
сделает в своей орбитальной системе координат пять полных обо¬
ротов (в обратном вращении!), а в орбитальной системе координат
Земли — четыре полных оборота.
августе 1969 года, с потрясающей неожиданностью показали, что поверхность Марса
более похожа на поверхность Луны, чем на что-либо другое. Значительные области
Марса покрыты системой кратеров, похожих на лунные. По крайней мере некоторые
из знаменитых «каналов» удалось отождествить с цепочками таких кратеров [6.30].
1 ^ Автор этой книги сам имеет многолетний, документально установленный, стаж
такого любопытства: в 1948 году, еще будучи школьником, опубликовал (в журнале
«Физика в школе») письмо с «теоретическим» определением возможного периода
вращения Венеры — на основе только что появившейся космогонической теории
О. Ю. Шмидта.
12^ В нижнем соединении Солнце, Венера, Земля находятся на одной прямой,
причем Венера и Земля — по одну сторону от Солнца.
214
Очерк шестой. Они вальсируют на орбитах
Теория резонансных вращений Меркурия и Венеры только на¬
чинает разрабатываться [6.2] и еще ждет своих вдохновенных ис¬
следователей.
13. Резонансные вращения небесных тел
и обобщенные законы Кассини13^
Изложенные выше факты позволяют говорить о тенденции
к синхронизации вращения как об объективном законе природы.
Системы пассивной стабилизации искусственных спутников
используют эту тенденцию.
Резонансные вращения небесных тел описываются специально
построенными теориями. Эти теории действительно подтверждают
синхронизацию вращательного движения как закономерное явле¬
ние природы. Теория позволила получить обоснование эмпириче¬
ских законов вращения Луны — законов Кассини — и построить
обобщенные законы Кассини, которым подчиняется, например,
вращение Меркурия.
Обобщенные законы Кассини описывают весьма тонкую двой¬
ную синхронизацию (двойной резонанс): во-первых, между осевым
вращением небесного тела и его орбитальным движением, во-вто¬
рых, между движением оси вращения тела и возмущенной прецес¬
сией орбиты.
Луна имеет двойную синхронизацию 1 : 1 и 1 : 1, Меркурий —
двойную синхронизацию 3 : 2 и 1:1.
Двойная синхронизация, описываемая обобщенными закона¬
ми Кассини, может быть с успехом использована для пассивной
стабилизации спутников, например для двойной орбитальной ста¬
билизации орбитальных станций. Автор намерен дать обзорное
описание теории резонансных вращений небесных тел, приведшей
к теоретическому установлению «обобщенных законов Кассини»,
но не может не уделить сначала несколько строк колоритной лич¬
ности Джованни Доменико Кассини.
В момент, когда пишутся эти строки, исполняется 350 лет
со дня его рождения. Дж. Д. Кассини (8.6.1625, Перинальдо —
14.9.1712, Париж) — итальянец по рождению, член Парижской
13* До конца этого очерка изложение следует в основном обзорному докладу [6.35],
сделанному автором на симпозиуме по динамике спутников в 1974 году в г. Сан-
Пауло (Бразилия).
13. Резонансные вращения небесных тел и законы Кассини
215
Академии наук, первый директор и основатель династии дирек¬
торов Парижской обсерватории. Представители этой династии
жили долго (Джованни Доменико — 87 лет, его сын Жак —
79 лет, внук Цезарь Франсуа Кассини де Трюи — 70 лет, правнук
Жан, последний директор династии, — 97 лет), работали много
и оставили потомкам огромное количество своих трудов, откры¬
тий и... заблуждений.
Нелегко сориентироваться в изобилии материала, подпи¬
санного фамилией Кассини (был еще представитель династии —
известный ботаник, но тоже занимавшийся астрономией). Это
и привело к тому, что в последующей литературе не вЬегда резуль¬
таты Кассини правильно привязаны, так сказать, к локальному
Кассини. Бывает, что открытия Джованни Доменико приписы¬
ваются Жаку, а заблуждения Жака — Джованни Доменико. На¬
пример, во многих источниках упоминается, что Жак Кассини
ошибочно считал Землю не сжатой а вытянутой. В других ис¬
точниках эта ошибка приписывается Дж. Д. Кассини.
Безусловно, самой интересной фигурой династии был ее ос¬
нователь. По-видимому, он обладал ярким итальянским полеми¬
ческим характером. Родившись уже после установления Кепле¬
ром законов движения планет, Дж.Д. Кассини тем не менее счел
необходимым предложить счзои собственные соображения о тра¬
екториях небесных тел. С этой целью он построил некие кри¬
вые четвертого порядка. Эти кривые вошли в математику под
названием «овалов Кассини» или «кассиноид», увековечили имя
Кассини, но не имеют отношения к той задаче, для которой
они выдуманы. Будучи современником Ньютона, Дж.Д. Кассини
не признавал ньютоновского закона тяготения, а по некоторым
сведениям — трудно поверить! — даже и учения Коперника.
Но не эти ошибки прославили имя Дж.Д. Кассини. Он был
прекрасным наблюдателем, и факты, открытые им, осмыслива¬
ются теоретиками вот уже триста лет. Он открыл щель в кольце
Сатурна («щель Кассини»). Сейчас становится ясным, что эта
щель имеет резонансную природу. Он открыл основные зако¬
ны вращательного движения Луны («законы Кассини») — тон¬
кая резонансная структура этих законов осмыслена только сей¬
час. Спутники Сатурна — Рея, Тефия, Диона, Я пет — открыты
Дж.Д. Кассини. А в нашу эпоху обнаружено, что эти спутники
представляют примеры резонансных вращений. Таким образом,
имя Кассини прямо или косвенно связано с самыми современ¬
ными — резонансными — проблемами небесной механики.
Дж.Д. Кассини, будучи крупным ученым своего времени,
имел много учеников и был основателем не только «династии
директоров», но и научной школы математиков и астрономов.
Например, под руководством Дж. Д. Кассини учились четыре
216
Очерк шестой. Они вальсируют на орбитах
француза, которые позже, в 1685 году, посланы были Людови¬
ком XIV с миссионерскими целями в Китай, прижились при
дворе Цинского императора Канси и пользовали его совета¬
ми и услугами. Один из этих четырех королевских математи¬
ков и учеников Дж. Д. Кассини, Франсуа Жербийон, в качестве
советника и переводчика китайской стороны, вел переговоры
в Нерчинске с посольством Ф. А. Головина и активно содейство¬
вал заключению Нерчинского договора 1689 года.
Меня привлекает личность Джованни Доменико Касси¬
ни — эта странная, противоречивая фигура в истории науки —
с его субъективными заблуждениями и объективно прогрессив¬
ной научной ролью. Биография Дж. Д. Кассини мало изучена.
А ведь он жил в интереснейшую эпоху; был приглашен в Париж
Людовиком XIV и, возможно, блистал при дворе «короля-солн-
ца». Королевскому астроному вменялась в обязанность, меж¬
ду прочим, и научно-просветительная деятельность при дворе.
Придворные дамы находили пикантным наносить визиты в Па¬
рижскую обсерваторию для наблюдений звездного неба: «Ах,
я провела чудесную ночь с господином Кассини...»
Но вернемся к вопросу о теории резонансных вращений не¬
бесных тел. Такая теория должна обнаружить и использовать:
1) стабилизирующий фактор, устойчиво удерживающий небесное
тело в резонансном режиме;
2) диссипативный фактор, приводящий произвольное первона¬
чальное вращение тела к захвату в резонансный режим движения.
Стабилизирующим фактором являются моменты гравитацион¬
ных сил, действующие на тело со стороны других небесных тел. В
качестве диссипативного фактора рассматриваются приливные явле¬
ния в Солнечной системе и другие возможные диссипативные силы.
Опишем последовательно конструкции, приводящие к постро¬
ению теории резонансных вращательных движений небесных тел.
Будем отталкиваться от наиболее известного и исследованного слу¬
чая — вращения Луны.
В 1693 году Кассини установил следующие законы вращения
Луны [6.36, 6.37]:
1. Луна вращается равномерно вокруг оси, остающейся непо¬
движно в теле Луны, причем период вращения Луны совпадает
с периодом ее обращения по орбите вокруг Земли.
2. Плоскость экватора Луны сохраняет постоянный наклон к эк¬
липтике, равный 1°32,1/.
13. Резонансные вращения небесных тел и законы Кассини
217
3. Восходящий узел экватора Луны на эклиптике всегда совпадает
с нисходящим узлом орбиты Луны на эклиптике.
Эти законы, надо сказать, удивительны. В силу третьего закона
три плоскости — эклиптики, лунного экватора и лунной орбиты —
всегда пересекаются по одной прямой. Это тем изумительнее, что
две из этих плоскостей подвижны!
На рис. 6.18 приведена схема, иллюстрирующая законы Касси¬
ни. Так как орбита Луны наклонена к эклиптике на угол г « 5°09\то
из второго и третьего законов Кассини следует, что вектор и осевой
угловой скорости Луны нор¬
мален к линии узлов и состав¬
ляет угол р ~ 6°41/ с нормалью
п к плоскости орбиты Луны.
Начиная с Лагранжа и Ла¬
пласа, законы Кассини ложи¬
лись в основу теории либра¬
ции Луны [6.38, 6.39] — ис¬
следовались линеаризованные
уравнения движения, решение
которых дает движение, близ¬
кое к движению по Кассини.
Классическая линейная теория
базируется на эмпирическом факте малости угла между осью враще¬
ния Луны и осью эклиптики, а также малости наклонения орбиты
Луны к эклиптике.
Развитием классических работ явилась квазилинейная теория
либрации Луны, построенная Ш. Т. Хабибулиным (работа [6.40]
и др.; см. также описание этой теории в книге [6.41]). Эта тео¬
рия охватывает ряд тонких эффектов в нелинейных колебаниях
Луны относительно ее центра масс. Нас здесь будет интересовать
другой аспект проблемы: не столько колебания Луны относительно
движения «по Кассини», сколько, главным образом, возможность
получения из уравнений движения самих законов Кассини (и воз¬
можных их обобщений) как законов природы.
Законы Кассини носят эмпирический характер, точным урав¬
нениям движения не удовлетворяют и поэтому не были выведены
из точных нелинейных уравнений движения.
Сам факт существования в природе движения «по Кассини» го¬
ворит об устойчивости (в каком-то смысле) этого движения. Мож¬
но ожидать, что существуют приближенные, но достаточно близ¬
218
Очерк шестой. Они вальсируют на орбитах
кие к точным, нелинейные уравнения, содержащие в себе устой¬
чивые движения «по Кассини» в качестве стационарных движе¬
ний. Построение таких уравнений и их анализ дается в работах
В. В. Белецкого [6.14,6.42]. Исследование на эту же тему незави¬
симо провели в своей совместной работе М. J1. Лидов и А. И. Ней-
штадт [6.43]. Ранее проблема частично исследована Коломбо [6.44]
и Пиилом [6.45].
Построить нелинейные уравнения, обладающие указанными
свойствами, позволяют успехи в исследовании движения тел в гра¬
витационном поле, достигнутые в последние годы [6.246,6.1,6.3,
6.16,6.17,6.19,6.20,6.22].
Эти уравнения являются уравнениями первого приближения
в смысле асимптотических методов нелинейной механики (метод
осреднения). При конструировании этих уравнений существенно
учитываются факторы, определяющие вращательное движение Лу¬
ны: поворот плоскости орбиты Луны в пространстве (вековое дви¬
жение узла лунной орбиты вследствие возмущений со стороны
Солнца); влияние на Луну моментов гравитационных сил Земли;
резонансность явления (соизмеримость периода осевого вращения
Луны и ее орбитального периода). Применение асимптотических
методов оправдано малостью гравитационных моментов из-за бли¬
зости эллипсоида инерции Луны к шару. Аналогичные факторы
учитываются и в случае Меркурия.
Близкой нелинейной моделью законов Кассини является устой¬
чивое относительное равновесие тела на круговой невозмущаемой
(неподвижной в пространстве) орбите, описанное в пп. 2-4 насто¬
ящего очерка (рис. 6.3).
Относительное равновесие — это синхронизация 1 : 1 между
периодом осевого вращения тела и периодом орбитального движения.
В относительном равновесии одна ось тела (спутника) устой¬
чиво направлена к центру притяжения. Этот факт фундаментально
используется в системах гравитационной стабилизации искусствен¬
ных спутников Земли. При этом спутник стабилизируется в таком
положении, что одна сторона его все время обращена к Земле, —
«подобно Луне», как добавляют обычно. Эта добавка не совсем
отвечает фактическому состоянию дел. Относительное равновесие
удовлетворяет первому из трех законов Кассини. Однако два других
закона Кассини не удовлетворены.
Второй и третий законы Кассини существенно связаны с эво¬
люцией лунной орбиты под действием внешних возмущений (в ос¬
новном притяжение Солнца), а именно с эффектом поворота плос¬
13. Резонансные вращения небесных тел и законы Кассини
219
кости лунной орбиты. Этот эффект состоит в том, что нормаль
к плоскости лунной орбиты прецессирует вокруг нормали к эк¬
липтике с угловой скоростью [6.36] Kq = 1934°08/31// за 36 525
эфемеридных суток (100 лет). (Таким образом, период движения
узла ~ 18,6 года.) Второй и третий законы Кассини означают, что
при этом всегда ось вращения Луны, нормаль к эклиптике и нор¬
маль к орбите Луны лежат в одной плоскости, не совпадая друг
с другом (рис. 6.18). В этом отличие законов Кассини от «закона
относительного равновесия». В последнем — ось вращения спутни¬
ка (Луны) совпадает с нормалью к плоскости орбиты. Отклонение
оси вращения реальной Луны от нормали к плоскости орбиты со¬
ставляет весьма заметную величину: 6°41/.
Согласно второму и третьему законам Кассини плоскость, со¬
держащая ось вращения Луны и нормаль к лунной орбите, всегда
нормальна к линии узлов и, следовательно, вращается с угловой
скоростью Kq вокруг нормали к эклиптике. Таким образом, лун¬
ная ось отслеживает движение нормали к лунной орбите.
Иначе говоря, имеет место еще одна синхронизация 1:1 —
между периодом движения (прецессии) лунной оси в пространстве
и периодом прецессии лунной орбиты.
Такое движение лунной оси можно трактовать как ее непо¬
движность в системе координат, вращающейся с угловой скоростью
Kj\ вокруг нормали к эклиптике.
В 1958-1965 годах В. В. Белецкий исследовал [6.1,6.16,6.19]
быстрое движение спутника под влиянием гравитационных мо¬
ментов с учетом эволюции орбиты спутника за счет внешних воз¬
мущений. Метод исследования — получение и анализ некоторых
эволюционных уравнений движения, являющихся хорошим при¬
ближением к точным уравнениям и дающих достаточно точную
качественную и количественную картину движения. Результат ана¬
лиза кратко описан в п. 10 настоящего очерка. Было показано, что
спутник должен совершать невозмущенное движение вокруг посто¬
янного по величине вектора кинетического момента, сам же этот
вектор медленно движется в пространстве. Траектории конца век¬
тора кинетического момента замкнуты во вращающейся системе
координат, одна из осей которой коллинеарна линии узлов орби¬
ты спутника, а другая — ось вращения — совпадает с нормалью
к плоскости орбиты. Вид траекторий конца вектора кинетического
момента изображен на рис.6.12,4\
|4* В работах [6.1, 6.16, 6.19] исследовался случай динамически-симметричного
220
Очерк шестой. Они вальсируют на орбитах
Хочется подчеркнуть, что замкнутость траекторий конца век¬
тора кинетического момента во вращающейся вместе с орбитой си¬
стеме координат отражает тенденцию к синхронизации вращений
орбиты и вектора кинетического момента. В работах [6.1,6.16,6.19]
этот факт обнаружен с учетом не только гравитационных, но и маг¬
нитных и аэродинамических эффектов.
Частным случаем описанного движения является осевое вра¬
щение тела вокруг главной центральной оси инерции, совпадающей
с направлением на особую точку 3 на рис. 6.12 5 (или с направлени¬
ем на другую стационарную точку). Из характера траекторий конца
вектора кинетического момента в окрестности этого направления
(рис. 6.12 5) ясно, что это частное движение устойчиво в смысле
положения рассматриваемой оси. Кроме того, это частное движе¬
ние удовлетворяет в обобщенном смысле второму и третьему законам
Кассини, на что указал Дж. Коломбо в 1966 году [6.44]. В этой же
работе Дж. Коломбо высказал и обсудил идею о применимости
обобщенных законов Кассини к движению других, помимо Луны,
небесных тел (Меркурий, Япет).
Но по самому методу исследования указанное в [6.1,6.16,6.19]
движение не может удовлетворять первому закону Кассини. Эво¬
люционные уравнения строились исходя из факта наличия малого
параметра — отношения орбитальной угловой скорости к угловой
скорости вращения тела. Таким образом, по постановке вторая ско¬
рость существенно превосходит первую и не может быть равна ей,
как этого требует первый закон Кассини.
Однако малый параметр, потребный для построения эволюци¬
онных уравнений, можно ввести по-другому. А именно, используем
тот факт, что эллипсоид инерции Луны близок к шару, то есть мо¬
менты инерции Луны близки друг к другу. Эволюционные уравне¬
ния в этом случае (без учета эволюции орбиты) построил и иссле¬
довал в 1963 году Ф. Л. Черноусько [6.17]. Они позволяют рассмат¬
ривать любые угловые скорости (но только не резонансные) враще¬
ния спутника, в том числе близкие к орбитальной угловой скорости.
Добавляя к этим уравнениям, согласно [6.1,6.16,6.19], влияние эво¬
люции орбиты, обнаружим то же самое качество движения, какое
тела. Но результаты без труда обобщаются на случай трехосного тела, благода¬
ря работе 1963 года Ф. Л. Черноусько [6.17]. В этой работе исследованы быстрые
вращения трехосного спутника в гравитационном поле. Эволюция орбиты не учи¬
тывалась. В некоторых более поздних американских публикациях [6.44, 6.46-6.48]
эффекты, обнаруженные в [6.1,6.16,6.17,6.19], открываются повторно.
13. Резонансные вращения небесных тел и законы Кассини
221
изложено выше: спутник совершает невозмущенное (с некоторы¬
ми оговорками) движение вокруг постоянного по величине вектора
кинетического момента, а сам этот вектор описывает в простран¬
стве траектории, изображенные на рис. 6.12. Частный случай: век¬
тор кинетического момента совпадает с главной центральной осью
инерции спутника и одновременно с направлением на стационар¬
ную точку на рис. 6.12, причем угловая скорость осевого вращения
спутника в точности равна орбитальной угловой скорости. Это дви¬
жение формально удовлетворяет всем трем законам Кассини.
Однако только что указанное частное движение носит фор¬
мальный характер, так как на этом движении нарушается условие
нерезонансности, принятое в постановке. Будучи устойчивым от¬
носительно второго и третьего законов Кассини, это движение не¬
устойчиво относительно первого закона: любое изменение осевой
угловой скорости сохраняется, в результате чего Луна, хотя и мед¬
ленно может быть, но повернулась бы к Земле в конце концов
противоположной своей стороной.
Первый закон Кассини устанавливает резонансность движе¬
ния Луны: осевая и орбитальная угловые скорости Луны находятся
в отношении 1:1. Движения резонансные и близкие к резонанс¬
ным обладают своей спецификой, и эволюционные уравнения для
таких движений конструируются более сложным образом, чем для
нерезонансных движений. Предыдущие конструкции не учитывают
резонансности разбираемого явления.
Ф. Л. Черноусько в работе 1963 года [6.22], изложенной в п. 11
настоящего очерка, получил и исследовал полезное уравнение, ко¬
торое описывает плоские резонансные вращения искусственных
и естественных небесных тел с эллипсоидом инерции, близким
к шару. Затем резонансные пространственные движения спутника
в гравитационном поле — без учета эволюции орбиты — исследо¬
вал А. П. Торжевский [6.24а, 6.246] в работах 1968-1969 годов. Воз¬
мущенное движение спутника, согласно этим исследованиям, уже
не является столь простым, как в нерезонансном случае. Однако су¬
ществуют стационарные движения, в которых спутник вращается
вокруг главной центральной оси инерции (вектор кинетического
момента постоянен по величине и совпадает с этой осью инер¬
ции), а движение вектора кинетического момента относительно
неподвижной (неэволюционирующей) орбиты аналогично его дви¬
жению в нерезонансных случаях относительно такой орбиты. При
этом движение устойчиво (при определенных условиях) относи¬
тельно возмущений осевого вращения — факт, которого не хвата¬
222
Очерк шестой. Они вальсируют на орбитах
ло в предыдущих нерезонансных конструкциях. Среди устойчивых
стационарных движений, исследованных А. П. Торжевским, имеет¬
ся подходящий для нашего анализа случай резонанса 1 : 1 между
орбитальной и осевой частотами для тела с близкими моментами
инерции.
Совмещая конструкции упомянутых работ [6.24а,6.1,6.15-6.17,
6.19,6.22], естественно приходим к «движениям по Кассини», устой¬
чивым (в смысле эволюционных уравнений) относительно всех трех
законов Кассини. При этом в пределе, при стремлении скорости
прецессии орбиты к нулю, должны получиться относительное рав¬
новесие и условия устойчивости относительного равновесия, опи¬
санные в [6.3], а также в [6.1].
Отметим еще, что у орбиты Луны уход перигея существен¬
но больше ухода узла. Перигей вращается с угловой скоростью
Кц = 4069°02/03// за 36 525 эф. суток (период движения перигея
~ 8,85 года). Согласно результату С. И.Трушина [6.20] (1970), мож¬
но ожидать, что уход перигея не нарушает стационарности движе¬
ния, по крайней мере, в главных членах возмущающего потенциала.
Изложенные идеи реализованы в работах автора [6.14] и [6.42].
Не затрудняя читателя изложением формального аппарата,
опишем некоторые результаты проведенного в [6.14] и [6.42] иссле¬
дования. Подробности читатель может найти в обзорах [6.49, 6.50]
или в новой книге автора [6.51].
Эволюционные (осредненные) уравнения движения, постро¬
енные в [6.14] и [6.42], допускают, в зависимости от значений па¬
раметров, либо два, либо четыре типа стационарных движений.
В каждом из этих движений, в зависимости от значений парамет¬
ров, с восходящим узлом орбиты совпадает либо восходящий, либо
нисходящий узел экватора спутника. Все эти движения можно на¬
звать «движениями по Кассини». Различаются прямые движения,
когда угол ро между вектором кинетического момента и норма¬
лью к плоскости орбиты находится в окрестности значения ро ~ 0
(это — собственно «движение по Кассини»), обратные движения
(ро находится в окрестности значения ро ~ п) и «опрокинутые»
движения (ро — в окрестности значения ро ~ п/2). В прямом
движении осевое вращение происходит в одном направлении с ор¬
битальным, в обратном — наоборот.
Обобщенные законы Кассини. Пусть твердое тело имеет трехос¬
ный эллипсоид инерции, близкий к сферическому; центр масс тела
движется со средней угловой скоростью о;о относительно притя¬
гивающего центра по орбите, отличающейся от кеплеровой лишь
13. Резонансные вращения небесных тел и законы Кассини
223
постоянной прецессией нормали к плоскости орбиты вокруг неиз¬
менной в пространстве оси прецессии и постоянным вращением
большой полуоси орбиты в ее плоскости. На тело действуют грави¬
тационные моменты со стороны притягивающего центра.
Тогда среди возможных движений тела существуют такие дви¬
жения, которые в первом приближении (в смысле асимптотических
методов нелинейной механики) удовлетворяют следующим обоб¬
щенным законам Кассини [6.14,6.42,6.51]:
1. Тело вращается равномерно вокруг своей главной центральной
оси; угловая скорость этого вращения близка к одному из ре¬
зонансных значений: о;0 (Луна), (3/2)(д0 (Меркурий) ,5\
2. Ось углового вращения тела и нормаль к плоскости орбиты
составляют постоянный угол /90. При фиксированных значе¬
ниях параметров тела и орбиты существуют два или четыре
возможных значения угла ро.
3. Ось углового вращения тела, нормаль к плоскости орбиты и ось
прецессии орбиты лежат в одной плоскости.
Кроме того, имеет место «закон постоянной фазы».
4. При каждом прохождении перицентра орбиты одна из главных
осей инерции, нормальных к оси вращения, и радиус-вектор
перицентра имеют равные угловые расстояния от линии узлов.
Поясним эти законы несколько подробней.
Введем следующие обозначения: Л, J3, С — главные централь¬
ные моменты инерции тела, г — постоянное наклонение орбиты
небесного тела к эклиптике; Kq и Кш — соответственно посто¬
янные угловые скорости движения узла и перицентра орбиты не¬
бесного тела вследствие возмущений со стороны других небесных
тел. Пусть Lo — значение модуля вектора кинетического момента
в стационарном движении. Угловая скорость стационарного дви¬
жения тогда равна Ьц/В и определяется формулой
£() / ч 772
— = ft + Кш + Кп cos (г q= ро), О = — щ, т — 2, 3.
В 2
Это и есть первый закон Кассини (уточненный): осевая угловая
скорость равна резонансной — орбитальной в случае Луны или 3/2
орбитальной в случае Меркурия (с малой добавкой за счет движения
перицентра и узла орбиты).
Могут иметь место и другие стационарные резонансные вращения.
224
Очерк шестой. Они вальсируют на орбитах
Несколько обобщен и третий закон Кассини: совпадающие
узлы орбиты и экватора могут быть как разного, так и одинакового
наименования. Угол ро, входящий в формулировку второго обоб¬
щенного закона Кассини, определяется через параметры движения
следующим образом. Обозначим:
Р = \т^-^В - (2 + J)C] + [-В - (2 + 7)4}’
о ЬоЛп
y/sin2 г + (а + cos г)2 ’
* cos г + а * sin г
cos р = гг-.-.- , sin р —
у/sin2 г + (а + cos г)2 ’ \/sin2 г + (а + cos г)2
Здесь I = Фт(е) является только функцией эксцентриситета
(рис.6.15). Резонансу 1 : 1 (Луна) отвечает тп — 2, резонансу 3 : 2
(Меркурий) отвечает тп = 3. Тогда определяется из уравнения
cos р* q= sin р* ctg ро + х cos р0 == 0. (6.13.1)
Это уравнение рассмотрено еще в 1965 году в книге [6.1] при
изучении нерезонансного вращения искусственного спутника с уче¬
том эволюции его орбиты и ряда возмущающих факторов (гравита¬
ционных, аэродинамических и магнитных). Частным случаем явля¬
ется уравнение (6.10.5). Отметим, что этот анализ в [6.1] охватывает
ряд результатов более поздних работ [6.44,6.46-6.48].
Условию
cosvV+sin гпр'<х7Р
соответствует существование четырех решений уравнения (6.13.1);
в частности, это условие при \х\ > 2 выполнено для любых р*.
Условию
coS2V+sin2/V>XV5
соответствует существование двух решений уравнения (6.13.1); в част¬
ности, последнее условие выполнено при \х\ < 1 для любых р*.
Отметим, что в рассматриваемой здесь задаче малые значения \х\
(1x1 < 1) означают преобладание влияния эволюции орбиты над
влиянием момента гравитационных сил, а большим значениям \х\
соответствует преобладание влияния гравитационных моментов.
13. Резонансные вращения небесных тел и законы Кассини
225
Что касается четвертого закона, то он не имеет аналога в исход¬
ных законах Кассини. Однако роль этого закона принципиальна.
Он показывает, что резонансным движениям отвечают вполне опре¬
деленные фиксированные фазовые соотношения — в данном случае
между угловым движением радиус-вектора орбиты и угловым дви¬
жением главных центральных осей инерции тела. Для случая Луны
(резонанс 1:1) этот закон означает просто, что одна ось инерции
Луны в своем движении «отслеживает» радиус-вектор орбиты.
Обобщенные законы Кассини отражают двойной резонанс во
вращении небесных тел: во-первых, между осевыми и орбитальны¬
ми вращениями и, во-вторых, между прецессиями орбиты и оси
вращения тела. Луна имеет двойной резонанс 1 : 1 и 1 : 1, Мерку¬
рий — 3 : 2 и 1:1.
Пример. Луна. В случае Луны примем [6.36]: В = 0,88836978, А =
0,88800195, С = 0,88781798 (в единицах 1035 кг • м2); i = 5°08'43". Пе-
риод вращения узла орбиты Луны около 18,6 года (Kq = 1934°08,31/г, за
|^|
100 лет — 36 525 эфемеридных суток); таким образом, = 0,00398324.
Щ
Период движения перигея орбиты — около 8,85 года (К^ = 4069°02/03”
за 100 лет).
В формулах этого пункта можно считать, что Lq = Вщ. Ис¬
пользуя эти данные, вычислим
X ~ -0,218; cos р* « 0,970,
то есть с избытком выполнено условие существования только двух
стационарных движений. Можно найти, что нужное нам стацио¬
нарное движение (ро < п/2) обеспечивает совпадение нисходяще¬
го узла экватора Луны с восходящим узлом ее орбиты. Подставляя
приведенные числовые данные в коэффициенты уравнения (6.13.1)
(и считая / = 1), вычисляем корень ро этого уравнения (близ¬
кий к ро ~ 0). Оказывается ро = 6°39/42//. Отсюда для угла на¬
клона оси Луны к оси эклиптики имеем вычисленное значение
po~i = Г30'59" « 1°31'. По наблюдениям (второй закон Кассини)
этот угол равен 1°32/1//, Хорошее совпадение вычисленной и на¬
блюдаемой величин говорит о высокой точности принятой модели
движения.
Устойчивость. Уравнение (6.13.1) имеет либо два корня, отве¬
чающих устойчивым положениям оси вращения тела, либо четы¬
ре корня, из которых три отвечают устойчивым положениям оси,
а один — неустойчивому положению. Обозначим единственное
15 Заказ 1667
226
Очерк шестой. Они вальсируют на орбитах
возможное неустойчивое значение ро через ро . Приведем главные
результаты проведенного в [6.14] и [6.42] анализа устойчивости ре¬
зонансного (1:1) движения.
Необходимые, близкие к достаточным, условия устойчивости
таковы:
1. Вращение происходит вокруг наименьшей оси эллипсоида инер¬
ции тела.
2. Радиус-вектор орбиты отслеживается наибольшей осью.
3. Наклон ро оси вращения к нормали к плоскости орбиты удо¬
влетворяет неравенству (3 + 2л/б)/15 < cos ро < 1.
4. роФ ро •
Для Луны эти четыре условия выполнены. Как следует из эво¬
люционных уравнений, движение оси в окрестности ее стационарно¬
го положения условно-периодично с двумя частотами: ш\ ~ у/е и
и)2 ~ где е — принятый порядок малости коэффициентов в пра¬
вых частях уравнений движения. Таким образом, траектории, опи¬
сываемые осью тела на небесной сфере, вообще говоря, не замкнуты.
Уже отмечалось, что спутники Юпитера Ио, Европа, Каллисто
(JI, JII, JIV) и спутник Сатурна Япет (SV1I1), а также, возможно,
спутники Сатурна Рея, Тефия, Диона и спутники Марса Фобос
и Деймос вращаются подобно Луне в резонансе 1:1. Поэтому для
них тоже может быть применена построенная теория. Можно ожи¬
дать, что приливные эффекты привели эти спутники, как и Луну,
к стационарным движениям «по Кассини» (в обобщенном смысле
настоящего очерка).
В [6.14,6.42] построены также следующие достаточные усло¬
вия устойчивости резонансного движения типа движения Меркурия
(резонанс 3:2):
1. е^О.
2. Вращение происходит вокруг наименьшей оси эллипсоида инер¬
ции.
3. Четвертый закон выполняется для наибольшей оси эллипсода
инерции.
4. ро ф тг, ро ф ро-
Отметим еще такой факт. При фиксированных моментах инер¬
ции ширина резонансной зоны, то есть «области устойчивости»,
определяется величиной порядка о;0\/Ф^; очень маленькие значе¬
ния Фт означали бы, что вероятность попадания в данный резонанс
13. Резонансные вращения небесных тел и законы Кассини
227
очень мала. Оказывается, что, по крайней мере, с этой точки зре¬
ния у Меркурия шансы на резонанс 3 : 2 не малы по сравнению
с шансами Луны на резонанс 1:1. Это следует из отношения
(Атпх)м (тл\ /фГ 28 /отй
(Ащах)л \ТМ)\]Ф2 88 У 0,993 ~ ’ ’
где Дтах означают ширину резонансной зоны соответственно для
Меркурия и Луны.
Замечания о резонансе во вращении Венеры. Вопрос о теорети¬
ческом обосновании резонансного вращения Венеры, описанного
в п. 5 очерка четвертого, обсуждался в работе Гольдрейха и Пии-
ла [6.2]. Как уже говорилось, угловая скорость f1 вращения Венеры
связана с угловой скоростью о;в ее орбитального движения и уг¬
ловой скоростью ьоз орбитального движения Земли резонансным
соотношением
П = 4о;в - 5о;3. (6.13.2)
При каждом максимальном сближении с Землей Венера повернута
к Земле одной и той же стороной. В [6.2] было показано, что устой¬
чивый резонанс указанного типа действительно возможен и что
при интересующем нас резонансе (6.13.2) доминирующим является
влияние Земли, а влияние Солнца пренебрежимо мало в среднем.
Гольдрейх и Пиил в [6.2] рассмотрели лишь модель плоского враще¬
ния Венеры в поле гравитационных моментов от Солнца и Земли
и получили для описания этого вращения следующее приближен¬
ное (в смысле метода усреднения) уравнение:
н + + к2{р)] sin 2н = 0. (6.13.3)
Здесь х — угловая расстройка движения относительно строго ре¬
зонансного, А, В, С — моменты инерции Венеры, Мф — масса
Земли, Ь — большая полуось орбиты Земли, / — универсальная
константа тяготения, к j, к2 — числа, зависящие от «резонансного
числа» р, при этом к\ отражает влияние гравитационного момента
Земли, a kj — гравитационного момента Солнца. Это влияние отра¬
жается лишь в среднем на данном резонансном вращении. Так, для
резонанса (6.13.2) оказывается р = -5 (знак «минус» из-за «обрат¬
ного» вращения Венеры) и к\ = 2,513, к2 = 1,78 • 10-2. Из (6.13.3)
видно, что чисто резонансное вращение (и = 0) действительно
может быть устойчивым, притом почти исключительно за счет вли¬
яния Земли (к| » к2).
15*
228
Очерк шестой. Они вальсируют на орбитах
Но можно привести и некоторые соображения, говорящие ско¬
рее не в пользу действительного существования исследуемого ре¬
зонанса.
1. Резонанс (6.13.2) ничем не лучше многих соседних резонан¬
сов — с той же (по порядку величин) шириной резонансной
зоны. Поэтому трудно объяснить неслучайную преимуществен-
ность этого резонанса.
2. Относительная ширина резонансной зоны Дв у Венеры (по срав¬
нению с шириной резонансной зоны Дл у Луны, Дм у Мер¬
курия) ничтожно мала:
Д = « 0,225 • КГ3.
(A max) Л
3. Проведенный в [6.2] анализ оставляет чувство некоторой не¬
удовлетворенности ввиду фактического пренебрежения мощ¬
ным влиянием Солнца. В среднем влияние Солнца, действи¬
тельно, пренебрежимо мало; но амплитуда периодических (ус¬
редненных в [6.2]) возмущений от Солнца может оказаться
весьма значительной, так как максимальное значение момента
гравитационных сил от Солнца в 106 раз больше, чем от Земли.
Более подробный анализ этого вопроса [6.50] обнаруживает
следующее. Чтобы периодические солнечные возмущения не вы¬
водили движения из резонансной зоны, необходимо, чтобы отно¬
шение моментов инерции Венеры лежало в следующих пределах:
Л-С 5
—^— < 2,5 - 10"\
Значения моментов инерции Венеры неизвестны. Вспоминая, од¬
нако, что, например, для Луны аналогичное отношение примерно
равно 5 • 10-4, заключаем, что написанное требование, по-видимо¬
му, лежит на границе разумных пределов. Поэтому и с рассматри¬
ваемой точки зрения исследуемый резонанс во вращении Венеры
находится на грани возможного.
Заметим еще, что, по анализу в [6.2,6.50], приливные явления
не могут (в отличие от случаев Луны и Меркурия) объяснить захват
Венеры в резонанс (6.13.2). Венера вращается обратным образом
по отношению к своему орбитальному движению. В [6.50] показано,
что приливной момент от Солнца имеет тенденцию «опрокинуть»
Венеру, перевести ее из обратного вращения в прямое. Поэтому для
14. Тенденция к синхронизации вращательного движения
229
объяснения захвата Венеры в резонанс (6.13.2) приходится строить
другие модели диссипативных явлений. Это четвертый аргумент,
говорящий не в пользу закономерного (не случайного) существо¬
вания резонанса (6.13.2).
Таким образом, резонанс во вращении Венеры не является
столь бесспорным, как резонансы Луны и Меркурия. Если он
тем не менее существует, то все перечисленное дает полное право
назвать резонансное вращение Венеры феноменальным явлением
природы. Феноменальное, не до конца объяснимое, резонансное
вращение Венеры показывает, по-видимому, что тенденция к син¬
хронизации в природе сильнее уровня наших нынешних знаний.
14. Тенденция к синхронизации вращательного движения
в сложных гравитационных полях. Лунно-солнечная
прецессия и нутация земной оси
До сих пор мы рассматривали вращательное движение тела
при доминирующем влиянии поля тяготения одного-единственно-
го притягивающего центра. Однако в природе могут возникнуть
ситуации, требующие учета сравнимого по величине влияния боль¬
шего числа притягивающих центров. Классический пример такой
ситуации — возмущенное движение земной оси. В это движение
вносят сравнимый вклад притяжения Солнца и Луны.
Возмущенное движение Земли — лунно-солнечная прецессия
и нутация — не является резонансным в том смысле, в каком ре¬
зонансны движения Луны или Меркурия. Тем примечательнее обна¬
ружить, что и в движении Земли есть тенденция к синхронизации.
Поясним это утверждение подробнее.
Введем обозначения: С и А — продольный и поперечный мо¬
менты инерции Земли, тд и газ — массы Луны и Земли соответ¬
ственно, е — эксцентриситет орбиты Луны, ез — эксцентриситет
орбиты Земли, #о — угол между осью вращения Земли и векто¬
ром кинетического момента Земли (с высокой точностью #о — 0),
Lq — модуль вектора кинетического момента Земли, & — угловая
скорость прецессии узла лунной орбиты. Пусть еще сиз — средняя
угловая скорость движения Земли по орбите, сид — средняя угловая
скорость движения Луны по орбите. Введем постоянные параметры
3 А - С 2 q г\ тя ^л
Кс =-——(3 cos $0-1)-
8 L0 Шд + m3 (1 — е2)3/2 ’
230
Очерк шестой. Они вальсируют на орбитах
и построим функцию
Ф = -L0KC cos2 р - LqKq cos2 Д + L0Kq cos Д,
где р — угол между вектором кинетического момента и нормалью
к плоскости орбиты Луны, а Д — угол между тем же вектором
и нормалью к плоскости эклиптики (орбита Луны наклонена к эк¬
липтике на постоянный угол г). В силу эволюционных уравнений
движения [6.51] углы р и Д — переменные во времени. Но из этих
уравнений следует существование интеграла
а из (6.14.1) сразу следует такой фундаментальный факт:
все возможные траектории вектора кинетического момен¬
та замкнуты в системе координат, вращающейся вместе
с плоскостью орбиты Луны.
В классической теории лунно-солнечной прецессии и нутации
земной оси этот факт (и интеграл (6.14.1)), по-видимому, не был
установлен. Между тем этот факт как раз отражает тенденцию
к синхронизации прецессии оси Земли и прецессии орбиты Луны.
Действительно, множества замкнутых траекторий стягиваются к осо¬
бым точкам, отвечающим стационарным движениям. Эти стацио¬
нарные движения можно трактовать как дальнейшее обобщение
законов Кассини на случай влияния многих центров притяжения
(здесь двух). В процессе эволюции под действием диссипативных
факторов движение должно стянуться к такому стационарному дви¬
жению, в котором ось Земли прецессирует с той же скоростью,
с какой прецессирует плоскость лунной орбиты. Конечно, реальная
ситуация далека от описанной стационарной (период прецессии ор¬
биты Луны — 18,6 лет, а оси Земли — 26000 лет). Но нас интересует
принципиальная сторона дела. Отражением тенденции к синхрони¬
зации является реальная нутация земной оси с периодом 18,6 года.
Подробности читатель может найти в книге [6.51].
Ф = Ф19 = const,
(6.14.1)
15. Модель приливных явлений и захват в резонансное вращение 231
15. Модель приливных явлений
и захват в резонансное вращение
Было показано, что гравитационные моменты сил, действую¬
щие на небесное тело, могут обеспечить его устойчивое резонансное
движение, описываемое обобщенными законами Кассини. Однако
начальные данные движения могут лежать вне резонансной зоны;
попадание начальных данных в резонансную зону маловероятно.
Поэтому должен существовать механизм, обеспечивающий доста¬
точно высокую вероятность захвата движения — в процессе его
эволюции — в резонансную зону, если начальные данные нахо¬
дятся вне этой зоны. Таким механизмом, по-видимому, являются
приливные явления. Теория приливных явлений сложна и зависит
от многих факторов. Здесь ограничимся рассмотрением некоторых
простых моделей приливных явлений [6.50,6.51].
Рассмотрим сферическую, не вполне твердую планету, находя¬
щуюся в поле тяготения Солнца. Вследствие различия притяжений
ближайшей к Солнцу, центральной и наиболее удаленной частей
планеты на ней образуются приливные горбы. Масса этих гор¬
бов т ~ к/r3, где г — расстояние до Солнца [6.2,6.52]. За счет
вращения планеты относительно орбитальной системы координат
с относительной угловой скоростью си приливные горбы смещаются
на некоторый угол 6 относительно линии «центр масс планеты —
Солнце». (Система планета—Солнце принята условно; все рассуж¬
дения приемлемы и для пары Луна—Земля или спутник—планета.)
Немедленно возникает обычный гравитационный момент
т „ к sin 26
sin 25 = , к > 0. (6.15.1)
Обозначим: — единичный вектор по направлению относитель¬
ной угловой скорости планеты, ег — единичный вектор направле¬
ния планета—центр притяжения. Рассмотрим плоскость еш, ег. Со¬
ставляющая еш по ег не уводит приливной горб; увод горба относи¬
тельно ег осуществляется компонентой = [е^ хег] хег, нормаль¬
ной к ег и лежащей в плоскости ew, ег. Следовательно, ось прилив¬
ных горбов будет лежать в плоскости, нормальной к е]ш, и подвора¬
чиваться (гравитационным моментом) в этой плоскости по направ¬
лению к ег. Это значит, что М направлен по е^. Учитывая (6.15.1),
получаем следующую модельную формулу приливного момента:
к sin 26. , ,
М = т—[е^ х ег] х ег. (6.15.2)
232
Очерк шестой. Они вальсируют на орбитах
Формула (6.15.2) определит приливной момент, если будет известна
зависимость угла 5 от времени и параметров задачи. Эта зависи¬
мость определяется взаимодействием сил вязкого трения внутри
планеты и сил притяжения, а также угловой скоростью о; относи¬
тельно вращения планеты.
Обычно употребляются две аналитические модели 5(ш) [6.2,6.52]:
1) sin 25 ~ 25 ~ к\ш, к\ = const, (6.15.3)
2) sin 25 = sin 2rf0, <?о = const. (6.15.4)
Линейная по относительной угловой скорости модель (6.15.3)
верна на ограниченном диапазоне угловых скоростей; но, по-ви¬
димому, во всех реальных случаях можно ограничиться этим диа¬
пазоном. Сигнатурная модель (6.15.4) охватывает более широкий
диапазон, но груба в окрестности малых значений ш и 5. Опи¬
шем кратко эффекты, вызываемые приливным моментом, отсылая
за подробностями к [6.51].
Анализ эволюционных уравнений вращения планеты под дей¬
ствием приливного момента (6.15.2)—(6.15.3) показывает, что вра¬
щение стремится к осевому — вокруг главной оси инерции.
Обозначим: Q = L/(Awо) — абсолютная угловая скорость вра¬
щения планеты, отнесенная к угловой скорости сдо ее орбитально¬
го движения; р — угол между вектором кинетического момента L
и нормалью к плоскости орбиты.
Интегральные кривые П(р) схематично изображены на рис. 6.19
[6.51]. Движение в пределе стремится к единственной стационарной
точке
* 1 + Ц-е2 + ^е4 + Тье6
р = О, J7 = Q* = - * . * (6.15.5
(1 _е2)3/2 (] +Зе2 + |е4)
Таким образом, приливной момент стремится привести дви¬
жение к прямому вращению вокруг нормали к плоскости орбиты
с угловой скоростью, соответствующей (6.15.5). Видно, что прилив¬
ной момент (в отсутствие других моментов) обязательно выводит
движение из обратного (р ~ 7г) вращения — факт интересный,
например, для теории вращения Венеры. Ее обратное вращение,
по-видимому, нельзя объяснить захватом под действием прилив¬
ных моментов.
Не менее интересным является факт зависимости предельной
угловой скорости от эксцентриситета орбиты. Функция Г2*(е) изоб¬
ражена на рис. 6.20. Видим, что при е = 0 оказывается П* = 1, то
15. Модель приливных явлений и захват в резонансное вращение 233
Рис. 6.19. Эволюция парамет¬
ров вращения под действием
приливов
О 0,2 0,4 0,6 е
Рис. 6.20. Предельные значе¬
ния безразмерной угловой ско¬
рости вращения планеты в за¬
висимости от эксцентриситета
ее орбиты
есть на круговой орбите предельным является вращение в резонансе
l : I (относительное равновесие). Коломбо [6.44] и Шапиро [6.52]
исследовали с этой точки зрения плоское движение Меркурия и об¬
наружили, что именно эксцентриситетом е « 0,2 орбиты Меркурия
можно обосновать факт его захвата в резонансное вращение с резо¬
нансом 3 : 2. В модели (6.15.3) f2* = 3/2, если е « 0,28; другие мо¬
дели могут снизить потребное значение е. Например, в предполо¬
жении (6.15.4) предельное значение ft* = 3/2, если е « 0,23. И во¬
обще, спектру резонансных значений ft* соответствует спектр зна¬
чений эксцентриситетов, при которых данная величина ft* дости¬
гается в пределе под действием приливных сил [6.50] (см. табл. 6.1).
В таблице вторая строчка рассчитывается согласно формуле
(6.15.5), а третья строчка — по соответствующей формуле для мо¬
дели (6.15.4):
19 2 461 4 119703 6 ^
ft — 1 + —е + — е Н—+ • • • • (6.15.6)
Формула (6.15.6) приближенная: содержит лишь старшие чле¬
ны разложения в ряд по степеням е. Формула (6.15.5) — точная.
Если кроме приливных явлений учесть и ранее изученный
гравитационный момент, то формулы (6.15.5), (6.15.6) приобрета¬
ют несколько иной смысл. А именно, орбиты с эксцентриситетами,
234
Очерк шестой. Они вальсируют на орбитах
Таблица 6.1
п*
1
1,5
2,0
2,5
3,0
3,5
е
Модель (6.15.3)
0
0,284
0,392
0,465
0,519
0,561
е
Модель (6.15.4)
0
0,219
0,290
0,340
0,365
0,385
указанными в табл. 6.1, обеспечивают максимальную вероятность Р
захвата (Р « I) в соответствующий резонанс ,6\ Если эксцентри¬
ситет близок к значению, указанному в таблице, то вероятность за¬
хвата хотя и меньше 1, но все еще велика. В предположении (6.15.3)
расчет вероятности [6.2,6.50] захвата для Луны (е « 0,05) в резо¬
нанс 1 : 1 и для Меркурия (е « 0,2) в резонанс 3 : 2 дает: Луна —
Р « 0,6, Меркурий — е « 0,25 • 10“'. Таким образом, вероятность
захвата Луны велика, а Меркурия — не очень велика, однако конеч¬
на. Результат расчета вероятности захвата для Венеры: Р « 0,5-10-4.
Иначе говоря, вероятность захвата Венеры в резонансное вра¬
щение приливными силами ничтожна. Следует отметить еще, что
расчет вероятности захвата проводился для плоской модели дви¬
жения. Для Венеры такая оценка весьма проблематична, так как
плоское вращение, как мы видели, неустойчиво при наличии при¬
ливных сил по отношению к пространственным возмущениям.
Что касается Луны и Меркурия, то они лишены этого недо¬
статка в силу прямого вращения; другие модели приливных эффек¬
тов могут повысить оценку вероятности захвата (для Меркурия —
на порядок [6.2]).
16. Магнитная и магнитно-гравитационная стабилизация
Среди всех возможных систем пассивной стабилизации спут¬
ников неискушенному читателю покажется наиболее понятной и
«родной» магнитная система. Все мы с детства привыкли к стаби¬
лизации компасной стрелки. И действительно, «эффект компасной
стрелки» используется в практике космических полетов для стаби¬
лизации спутников по магнитному полю Земли — там, где стаби¬
лизация потребна. На иной легкий спутник достаточно поставить
16^ Вероятность захвата — отношение фазового объема начальных данных, при¬
водящих к захвату, к объему рассматриваемой области фазового пространства.
16. Магнитная и магнитно-гравитационная стабилизация
235
постоянный магнит величиной с карандаш, чтобы заставить спут¬
ник надежно «отслеживать» силовую линию магнитного поля Зем¬
ли. Такое отслеживание обеспечивается моментом магнитных сил
М = I х Н, (6.16.1)
где I — так называемый «вектор магнитного момента», характе¬
ризующий степень намагниченности спутника, а Н — вектор маг¬
нитной напряженности магнитного поля Земли. Момент (6.16.1)
стремится «подвернуть» ту ось спутника, по которой направлен
вектор I, к вектору Н, обеспечивая тем самым стабилизацию спут¬
ника по этому вектору.
Однако в деталях дело обстоит не столь просто — из-за слож¬
ной «конструкции» магнитного поля Земли. Простейшая аппрок¬
симация магнитного поля — так называемое «дипольное поле» —
описывается формулой
Н=^[3(к*ег)ег-М]. (6.16.2)
Здесь к# — единичный вектор оси магнитного диполя (еще бо¬
лее упрощая дело, полагают, что кЕ направлен по оси вращения
Земли — к Южному полюсу), ег — единичный вектор по направ¬
лению текущего радиус-вектора орбиты (величина которого есть г),
fiE — константа, величина магнитного момента диполя (для Земли
fiE « 8 • 10ь эрстед • см3). Таким образом, в силу (6.16.2) момент
(6.16.1) сложным образом зависит от положения спутника; кроме
того, вектор Н изменяется вдоль орбиты неравномерно, что также
усложняет уравнения движения.
Продемонстрируем это на примере движения на круговой по¬
лярной орбите. На такой орбите существует плоское (в плоскости
орбиты) движение спутника, и оно описывается следующим урав¬
нением [6.1]:
d2ip / — 6sin2гг I0Ue „ , ч
—- + ал/l +3sin2wsin(^= ——■ .■ — ——• (6.16.3)
du2 г (1 + 3 sin2 гг)2 Вц v 7
Здесь ip — угол между «осью намагниченности» спутника и векто¬
ром Н. Ось намагниченности — ось вектора магнитного момента
I спутника (|1| = /0 = const) — по предположению фиксирована
в спутнике и всегда расположена в плоскости орбиты; и — аргумент
широты (отсчитываемый от экватора); в безразмерную константу а
входят, кроме уже указанных величин, момент инерции В спутника
236
Очерк шестой. Они вальсируют на орбитах
Рис. 6.21. Амплитуды периодических колебаний спутника в магнитном
поле в зависимости от параметра намагниченности
относительно оси, нормальной к плоскости орбиты, и гравитаци¬
онная постоянная ц.
Уравнение (6.16.3) показывает прежде всего, что точной ориен¬
тации (<р = 0) по магнитному полю достичь нельзя: этому мешает
правая часть уравнения (возникшая из-за неравномерного изме¬
нения вектора Н вдоль орбиты). Но можно надеяться построить
периодические решения уравнения (6.16.3), описывающие перио¬
дические колебания оси спутника относительно магнитной силовой
линии (то есть относительно вектора Н). Как видно по коэффи¬
циентам уравнения (6.16.3), период этих колебании должен быть 7Г
(ибо вектор Н возвращается к исходному направлению через по¬
ловину оборота спутника по орбите).
Результаты численного определения периодических решений
изображены на рис. 6.21 (эти результаты получены автором и впер¬
вые опубликованы в статье его ученика А. А. Хентова [6.53]). Этот
рисунок представляет собой зависимость амплитуды а периоди¬
ческого решения уравнения (6.16.3) от единственного параметра
задачи — от а*. Можно назвать рис. 6.21 «амплитудно-частот¬
ной» характеристикой. Прежде всего видим, что периодическое
решение неоднозначно. Число периодических решений растет бес¬
конечно при а* —> оо. На нижних частях всех ветвей кривой
(рис. 6.21) действительно достигается магнитная стабилизация: ам¬
плитуды колебаний невелики (и, кроме того, соответствующие
движения устойчивы). Однако в окрестностях некоторых крити¬
ческих — «резонансных» — значений а* амплитуды не малы,
и если мы хотим обеспечить стабилизацию спутника, то долж¬
ны избежать этих критических характеристик. Их легко оценить
16. Магнитная и магнитно-гравитационная стабилизация
237
из следующих соображений. В области малых амплитуд sin</> ~ <р\
правая часть уравнения (6.16.3) представима в виде ряда Фурье
00
Ък sin 2ки, а коэффициент при (р в левой части — в виде ряда
к= I
а* ( ао/2 + ак cos ], причем для а^/2 в качестве хорошего
' к= I '
приближения можно принять значение у/5/2. Если искать пери¬
одическое решение линеаризованного уравнения (6.16.3) в виде
00
ч> = Х> ksin2kw, то для коэффициентов Ак в первом прибли-
к= I
жении получим Ак « Ък/(у/5/2 а* - 4&2), откуда для резонанс¬
ных (критических) значений а* имеем а* = (8/VTo) А:2 « 2,5&2,
& — 1,2,, что дает последовательность а* = 2,5; 10; 22,5; 40;
62,5; 90; 122,5; 160; 202,5; 250 и т.д. Эта последовательность хоро¬
шо «чувствуется» и на рис. 6.21 (в работе [6.53] приведены несколько
более точные значения чисел в этой последовательности). Отметим
еще, что на всех периодических решениях sin <р —> 0 при а* —> оо,
то есть амплитуда решения стремится либо к 7Г, либо к 0, что тоже
хорошо видно на рис. 6.21.
Во всех случаях спутник — в абсолютном пространстве — де¬
лает ровно два оборота вокруг своей оси за один период обращения
по орбите (резонансное 2 : 1 вращение).
Ну, а как быть, если орбита спутника не полярная? Помня о
компасной стрелке, мы можем уверенно заявить, что и здесь осуще¬
ствить стабилизацию возможно; и этой уверенности уже достаточно,
чтобы сесть и писать уравнения движения, а затем их интегрировать.
Однако автор неоднократно за свою научную жизнь убеждался,
что этап размышлений часто ценнее и плодотворней «рабочего» эта¬
па, включающего написание уравнений, их счет и т.д. Размышляя
над задачей, поворачивая ее то так, то этак, приходишь (если су¬
меешь) к простым геометрическим и механическим соображениям,
делающим задачу прозрачной, план работы — четким, а ожидаемые
эффекты — предсказуемыми. И в описании задачи о магнитной ста¬
билизации мы остановимся именно на этом этапе, не затрагивая
«рабочего» этапа с его громоздким математическим аппаратом.
С этой целью сначала рассмотрим поведение вектора Н, зада¬
ваемого формулой (6.16.2), вдоль орбиты искусственного спутника
238
Очерк шестой. Они вальсируют на орбитах
Земли. Введем кенигову систему ко¬
ординат OXYZ (рис. 6.22) с началом
в центре масс спутника и осью OZ,
коллинеарной оси вращения Земли;
направление ОХ коллинеарно на¬
правлению из центра Земли в вос¬
ходящий узел орбиты. При движе¬
нии спутника по орбите вектор Н
(6.16.2) опишет в системе координат
OXYZ коническую поверхность, за¬
мыкающуюся за половину оборота
спутника по орбите (Н-конус). Дей¬
ствительно, из (6.16.2) видно, что
Н(ег) = Н(-ег). Одна из образую¬
щих конуса совпадает с осью OZ, сам Н-конус симметричен от¬
носительно плоскости ZY (рис. 6.22). Пусть Тц — период движе¬
ния вектора Н по Н-конусу, То — орбитальный период спутника.
Введем частоты ин = (2яг)/Т#, = (27г)/Т0. Тогда ид = 2ш0.
Пусть и — аргумент широты центра масс спутника, i — наклоне¬
ние орбиты спутника к экватору Земли. Модуль вектора Н имеет
значение Я = HE/rW1+3 sin2 i sin2 и. Когда спутник находится
в восходящем узле орбиты (и = 0), модуль Н принимает мини¬
мальное (по и) значение iTmjn = //#/r3, а сам вектор Н направлен
7Г
по оси OZ. При и = — вектор Н имеет максимальную (по и) дли-
Рис. 6.22. Конус магнитной
напряженности
ну ятах = 1 + з sin2 г и максимально отклоняется от оси OZ,
г3
образуя с ней угол 2v, v ^ 7г/2, причем [6.54]
sin 2г
1 - 3 sin2 г + л/1 Н- 3
sin2 i
(6.16.4)
Отметим еще, что конец вектора Н описывает окружность, ком¬
планарную плоскости орбиты спутника. На экваториальной орбите
Н-конус вырождается в прямую, а на полярной — разворачивается
в плоскость. Таковы основные свойства Н-конуса.
Назовем осью Н-конуса ось Z', лежащую внутри Н-конуса
в плоскости ZY и образующую с направлением OZ угол и, опреде¬
ляемый формулой (6.16.4). Построим круговой конус, ось которого
совпадает с осью Н-конуса, а угол при вершине равен 2и. Ока¬
зывается, что этот круговой конус (назовем его ^-конусом) почти
16. Магнитная и магнитно-гравитационная стабилизация
239
в точности совпадает с Н-конусом. Пусть к — угловое отклонение
вектора Н от оси Н-конуса. Тогда к — v при и = 0 и и = 7г/2
и к > v при любом другом и на интервале 0 < и < 7г. Иначе
говоря, круговой v-конус лежит целиком внутри Н-конуса, имея
с ним две общие, диаметрально противоположные, образующие.
Однако разность к — v всегда мала и не превышает величины 1° 1 \'
(для % « 52°6/; на орбитах с другим наклонением i максимальное
значение н-и еще меньше [6.54]). Таким образом, Н-конус весьма
близок к круговому v-конусу.
Однако уместно напомнить, что скорость движения вектора Н по
Н-конусу непостоянна; неравномерность вращения вектора Н до¬
вольно существенна; тем не менее близость Н-конуса к круговому
позволяет предложить следующий способ построения и описания
движений спутника, стабилизированных относительно вектора Н.
Известно, что невозмущенное движение динамически-симмет-
ричного спутника около центра масс в общем случае представляет
собой регулярную прецессию: ось симметрии спутника равномер¬
но вращается вокруг неподвижного вектора кинетического момен¬
та — на постоянном угловом расстоянии от него. Пусть спутник
магнитно-нейтрален. Придадим ему регулярную прецессию такую,
чтобы ось симметрии спутника равномерно вращалась по поверх¬
ности г/-конуса с частотой о;#. Для этого вектор кинетического
момента должен быть направлен по оси ^/-конуса, а угол оси спут¬
ника с осью v-конуса должен быть равен v.
Ясно, что такая регулярная прецессия заставляет ось спутника
«отслеживать» вектор магнитной напряженности Н. Дважды за пе¬
риод прецессии ось спутника в точности совпадает с вектором Н,
а в промежутках между этими моментами отклоняется от Н, два¬
жды достигая максимальной величины отклонения. Отклонение
оси спутника от Н происходит потому, что Н вращается неравно¬
мерно, а ось спутника — равномерно.
Таким образом, ось спутника совершает относительно вектора
Н периодические колебания с периодом, равным половине пери¬
ода обращения спутника по орбите. Максимальное значение Д
амплитуды этих колебаний зависит только от наклонения г орби¬
ты. Наибольшее из возможных Д достигается на полярной орбите
(г = 90°) и составляет 19,5°. (На рис. 6.21 при а* = 0 значение
амплитуды Д как раз равно 19,5°.) На других орбитах Д меньше —
монотонно убывает до 0° с уменьшением г до 0° [6.54].
Однако указанный периодический режим отслеживания Н не¬
устойчив ввиду неустойчивости регулярной прецессии (по углу пре¬
240
Очерк шестой. Они вальсируют на орбитах
цессии) нейтрального спутника. «Включим» теперь магнитный мо¬
мент I спутника, направив его по оси симметрии. Тогда возникает
момент (6.16.1) магнитных сил. Он сделает два полезных дела: пре¬
вратит отслеживание вектора Н осью спутника в устойчивое и —
при достаточно больших значениях /о = |1| — уменьшит амплитуду
колебаний между осью спутника и вектором Н. Соответствующие
устойчивые периодические режимы можно построить, взяв в ка¬
честве порождающего решения описанную выше регулярную пре¬
цессию оси спутника по 1/-конусу с частотой прецессии, равной
a;# =
Вот теперь, вооружившись пониманием сути дела, можно бы¬
ло бы приступить и к построению уравнений движения. И действи¬
тельно, описанные идеи, предложенные автором, были доведены
его учеником А. А. Хентовым до аналитического исследования, рас¬
четных формул, графиков и чисел [6.54].
Если намагниченность спутника мала, то периодические от¬
клонения от стабилизации по Н могут не только не уменьшиться,
но увеличиться. Это видно уже из рис. 6.21 (при малых а* ампли¬
туда колебаний больше, чем при а* = 0). Правда, периодические
движения становятся устойчивыми, но что с того толку, если их
амплитуда достигает 30° или более!
Чтобы понять природу этих больших отклонений и найти спо¬
соб с ними бороться, хорошо осмыслить ситуацию с точки зрения
теории возмущений. Аппарат теории возмущений как раз приме¬
ним при малых магнитных моментах.
Возмущенное движение спутника описывается, как мы пом¬
ним, суперпозицией возмущенного движения вектора кинетиче¬
ского момента и движения спутника относительно вектора кине¬
тического момента. Среди множества таких движений существуют
стационарные резонансные режимы — вектор кинетического мо¬
мента L неподвижен и постоянен по величине, а ось спутника
вращается вокруг L с частотой ujjj — 2щ. Среди этих стационар¬
ных движений найдутся и такие, которые приближенно отражают
ранее рассмотренные периодические движения. Неприятность со¬
стоит в том, что ось стационарного направления вектора L на этих
движениях не совпадает (и сильно!) с осью iz-конуса (Н-конуса).
В результате — существенное отклонение оси спутника от Н.
Здесь наступает торжественный момент. Нельзя ли «улучшить»
стационарное направление вектора L за счет влияния иных, не маг¬
нитных сил?
16. Магнитная и магнитно-гравитационная стабилизация
241
Действительно, среди резонансных движений спутника в гра¬
витационном поле существует устойчивое движение с резонансом
2:1, когда ось спутника совершает два оборота в пространстве
за один оборот спутника по орбите. Это дает принципиальную
возможность использовать «гравитационное» резонансное движе¬
ние 2 : 1 для отслеживания осью спутника вектора магнитной
напряженности. Подключая магнитный момент, мы не испортим
резонансной прецессии оси спутника, зато улучшим стационарное
положение вектора L за счет «игры» величин магнитного и грави¬
тационного моментов.
В построенном таким образом движении будут два свободных
параметра: угол при вершине конуса прецессии и соотношение
модулей магнитного и гравитационного моментов. Выбирая подхо¬
дящим образом эти параметры, можно совместить конус прецессии
с 1/-конусом.
К тому же совместное влияние двух стабилизирующих факто¬
ров должно расширить зону устойчивости по сравнению с зоной,
обеспечиваемой одним из них.
Таким образом, обеспечивается стабилизация спутника по маг¬
нитному полю Земли за счет принципиально совместного влияния
гравитационного и магнитного моментов. Эта идея гравитационно¬
магнитной стабилизации по магнитному полю Земли предложена
и исследована в работе В. В. Белецкого и А. А. Хентова [6.55].
По-видимому, подобные эффекты могут играть определенную
роль и во вращении некоторых естественных спутников планет, ес¬
ли эти планеты и их спутники обладают собственными магнитными
полями. Мы уже привыкли к мысли, что ряд естественных спутни¬
ков (Луна, некоторые спутники Юпитера и Сатурна, оба спутника
Марса) вращаются в резонансном режиме 1:1. Меркурий враща¬
ется в резонансном режиме 3:2. Движение этих тел подчиняется
обобщенным законам Кассини, являющимся результатом воздей¬
ствия на тела гравитационных моментов и только их. Но влияние
магнитных моментов может способствовать возникновению резо¬
нанса 2 : 1 во вращательном движении естественных небесных тел!
Благоприятные условия для этого возникают у тех спутников,
которые имеют собственное магнитное поле и в то же время враща¬
ются вокруг планеты, обладающей магнитным полем. Может быть,
какие-нибудь из спутников Юпитера или Сатурна удовлетворяют
этим условиям. Пока о магнитных полях спутников планет Солнеч¬
ной системы (исключая Луну) ничего не известно, и вращательные
16 Заказ 1667
242
Очерк шестой. Они вальсируют на орбитах
движения естественных небесных тел в резонансе 2:1с орбиталь¬
ным — не открыты. Но если вы когда-нибудь услышите о таком
открытии — вспомните эту книгу!
Дополнительные комментарии к этому изданию
А. О вращении Венеры. Феноменальное вращение Венеры породи¬
ло ряд работ [6.2,6.51,6.57,6.58], посвященных построению резо¬
нансной теории этого вращения. В этих исследованиях отмечались
трудности реализации такого резонанса, в частности, малая шири¬
на резонансной зоны и малая вероятность захвата Венеры в резо¬
нанс. Объяснение обратного вращения Венеры было найдено в ее
космогонической истории [6.69], согласно космогонической тео¬
рии Т. М. Энеева и Н. Н. Козлова [6.60], во влиянии чрезвычайно
плотной атмосферы [6.61] и в других факторах. В соответствии с со¬
временными данными [6.62] период вращения Венеры составляет
243,022 ± 0,006 земных суток, а параметр (А — С)/В в уравнении
(6.13.3) равен (8,19 ±0,33) • 10_6. Такая величина инерционного
параметра удовлетворяет условию (А - С)/В < 2,5 • 10~5, при ко¬
тором движение не выходит из резонансной зоны под влиянием
солнечных возмущений (стр. 228). Но здесь оптимизму энтузиа¬
стов, поддерживающих резонансную теорию, приходит конец. Точ¬
ные вычисления (см. [6.63,6.64], впервые анонсированы в [6.65])
с помощью улучшенного численного метода при использовании
указанных значений периода вращения и инерционного парамет¬
ра показали, что вращение Венеры лежит вне резонансной зоны
и, следовательно, не резонансно. Возможность того, что вращение
Венеры не резонансно, отмечалась и раньше [6.66-6.69].
Согласно вычислениям, приведенным в [6.63-6.65], ширина
резонансной зоны крайне мала, а именно (в терминах безразмер¬
ной угловой скорости) порядка Д| и 4,35 • КГ5. В то же время
истинная угловая скорость Венеры удалена от центра резонансной
зоны на величину Д2 ~ 1,4 • КГ3, на два порядка большую, чем
полуширина резонансной зоны.
В заключение отметим, что резонансное вращение Венеры со¬
ответствовало бы резонансному числу р = -5, что означает, что
за время между двумя последовательными нижними соединениями
с Землей Венера совершает ровно 5 оборотов в своем обратном вра¬
щении по отношению к текущему радиус-вектору Солнце—Венера.
Ближайшие резонансные зоны с шириной того же порядка, что
16. Магнитная и магнитно-гравитационная стабилизация
243
и зона с р = -5, имеют резонансные числа р = -4,5 и р — -5,5.
И хотя, как оказалось, истинный период вращения Венеры лежит
вне резонансной зоны с р = — 5, он явно тяготеет к последней, так
как расположен от зон с р — -4,5 и р — -5,5 на много поряд¬
ков (точнее, в 103 раз) дальше, чем до зоны с р = -5. Возможно,
это значимое наблюдение, а может быть, и нет. Вопрос о приро¬
де и происхождении обратного вращения Венеры все еще остается
открытым. Пока, в своей новой книге [6.70], посвященной резо¬
нансному вращению небесных тел, Белецкий и Хентов поместили
в главу о вращении Венеры примерно такие разделы: «§ 4. Резо¬
нансное вращение Венеры; §5. Опровержение резонансной теории
вращения Венеры».
В. О связи между орбитальным и вращательным движениями в гра¬
витационных полях. Устойчивость относительного равновесия спут¬
ника на орбите (стр. 177, 182) и другие эффекты во вращательном
движении небесных тел рассмотрены в очерке 6 в предположении
отсутствия взаимосвязи между орбитальным и вращательным дви¬
жениями (спин-орбитального взаимодействия). Движение по ор¬
бите задается независимо от вращательного — например, законами
Кеплера. А между прочим, такая связь существует. Она описывает¬
ся, например, в [6.1], [6.11], [6.71] и становится заметной для тел
протяженных (не пренебрежимых) размеров. Она может стать суще¬
ственным фактором, например, для орбитальных тросовых систем
[6.72]. Далее, в очерке 9, мы опишем «эффект гравилета», который
основан на том, что орбита протяженного тела в ньютоновом цен¬
тральном силовом поле, строго говоря, не кеплерова.
В совместной статье автора с О. Н. Пономаревой [6.71 ] (см. так¬
же [6.64]) изучаются интересные эффекты связи между орбиталь¬
ным и вращательным движениями в гравитационном поле. Вот два
поучительных результата, полученных в этой статье.
1. Рассмотрим движение гантели, состоящей из двух одинако¬
вых масс т, соединенных невесомым стержнем длины Z, которая
движется в гравитационном поле однородного сферического тела
массы Mq. Тогда существует движение гантели, при котором орбита
ее центра масс круговая (с радиусом Д0), а сама гантель располо¬
жена вдоль его текущего радиус-вектора. В принятой выше в этом
очерке постановке «ограниченной задачи» такая орбита рассматри¬
вается как кеплерова и, согласно результату, сформулированному
на стр. 182, рис. 6.3, расположение гантели вдоль радиуса устойчиво
по отношению к возмущениям ее углового движения.
16*
244
Очерк шестой. Они вальсируют на орбитах
Однако в общем случае это не так: достаточно длинная гантель
будет неустойчивой. Как показано в [6.71], для гантели малой массы
(тп/Мо —> 0) такое движение устойчиво по отношению к возмуще¬
ниям углового и орбитального движений в плоскости орбиты, если
^ < л/з - \/2 йг 0,318,
но неустойчиво, если это неравенство не выполнено! Эта неустой¬
чивость по существу орбитальная, орбита катастрофически изменя¬
ется. (Любопытная деталь: в [6.71] вместо \/3 —\/2 авторы получили
число у/5-V24. Можете ли вы сразу сообразить, что эти два числа
равны?)
2. Рассмотрим движение сферического тела массы Мо и те¬
ла массы М, эллипсоид инерции которого близок к сфере. В этом
случае существует плоское круговое движение, при котором рассто¬
яние Ro между центрами масс тел Мо и М остается постоянным,
а главные центральные оси инерции тела М направлены по ради¬
ус-вектору тела на круговой орбите, по касательной к орбите и по
нормали к плоскости орбиты, соответственно. Обозначим момент
инерции тела М по оси, нормальной к плоскости орбиты, как В.
Тогда, если выполнено условие B/(MRl) < 3 • М0/(М + М0), то
движение устойчиво, когда эллипсоид инерции вытянут вдоль каса¬
тельной к орбите (как в результате, описанном на стр. 182, рис. 6.3).
Написанное выше условие означает, что тело М имеет ограничен¬
ные размеры (В ~ Ml2, где I — характерный размер тела М).
Если выполнено противоположное неравенство (тело М до¬
статочно большое), то движение тела М, вытянутого вдоль радиус-
вектора, неустойчиво! Но вот интересный факт: когда тело вытянуто
перпендикулярно к радиус-вектору, то появляется так называемая
«гироскопическая устойчивость»! Более естественно рассматривать
такой случай, как гироскопическую устойчивость малого спутника
(массы Мо) на суточной орбите вокруг большой планеты (Зем¬
ли) массы М, имеющей трехосный эллипсоид инерции. Суточ¬
ный спутник устойчиво (гироскопически устойчиво) располагается
на воображаемом продолжении в пространство меньшей из двух
осей эллипсоида инерции планеты, лежащих в плоскости орбиты.
Таким образом, две задачи — гравитационная устойчивость
относительного равновесия Луны (или искусственного спутника)
и гироскопическая устойчивость суточного спутника Земли — пе¬
реходят друг в друга непрерывным изменением параметров. В кон¬
16. Магнитная и магнитно-гравитационная стабилизация
245
тексте ограниченной формулировки связи между этими двумя за¬
дачами не выявлено.
С. Об устойчивости относительного равновесия в гравитационном поле
и пассивной стабилизации искусственных спутников. В статье автора
[6.3] результат, дающий достаточные условия устойчивости относи¬
тельного равновесия, был доказан не только в ограниченной форму¬
лировке, рассмотренной в пп. 3 и 4 настоящего очерка, но и в общем
случае, когда учтена взаимосвязь между поступательным и враща¬
тельным движениями спутника. На заседании президиума Акаде¬
мии наук СССР 14 сентября 1956 года Мстислав Всеволодович
Келдыш сделал доклад (тогда еще секретный). Здесь приводится
выдержка из стенограммы этого доклада ([6.73], стр. 238-239):
Надо сказать, что многие механики давно уже считают, что
в области механики твердого тела все сделано и никаких инте¬
ресных задач решить нельзя. Оказывается, в связи со спутником
решили новую интересную задачу.
Доказано, что каждое тело, свободно летящее в поле земно¬
го тяготения, имеет только три положения равновесия по отно¬
шению к радиус-вектору, проведенному из центра Земли в центр
масс тела, причем среди этих положений равновесия устойчиво
только одно. Для этого необходимо, чтобы самая большая ось
инерции тела была ориентирована по указанному радиус-векто¬
ру, т. е. вертикально к поверхности Земли, самая маленькая —
нормально к траектории, средняя — по траектории...
...Эта интересная задача механики твердого тела была ре¬
шена совсем еще молодым сотрудником В. В. Белецким в Отде¬
лении прикладной математики.
Здесь редакторы книги [6.73] сделали в сноске следующий ком¬
ментарий:
В данном случае Мстислав Всеволодович имеет в виду фун¬
даментальную теорему о равновесии твердого тела относитель¬
но своего центра масс в центральном поле тяготения, впервые
доказанную В. В. Белецким. Первая же схема гравитационной
стабилизации спутника с использованием демпфирования была
предложена Д. Е. Охоцимским еще в 1954 году, до доказательства
Белецким своей теоремы.
Сам Д. Е. Охоцимский датировал свою первую схему грави¬
тационной стабилизации 1956 годом (см. [6.34]), что согласуется
с другими источниками (например, [6.9]).
Очерк седьмой
В космос по спирали
Представьте себе ослепительную, упругую спираль,
уносящуюся в небо!..
А. Вознесенский
«Треугольная груша»
1. Малая тяга
В различных лабораториях мира проектируются и разрабатыва¬
ются реактивные двигатели, у которых реактивная струя создается
разгоном заряженных частиц в электростатическом поле (ионные
двигатели, работающие на принципе взаимодействия электрическо¬
го тока с магнитным полем, плазменные и другие двигатели [7.1]).
В отличие от реактивных двигателей, работающих на химическом
топливе, реактивная тяга получается очень малой и может сообщить
космическому кораблю ускорение всего в несколько мм/сек2. Ина¬
че говоря, реактивное ускорение составляет тысячные доли ускоре¬
ния силы тяжести па поверхности Земли (g0 = 9,81 м/сек2). Ясно,
что с таким ускорением от Земли не оторвешься. Для этого нужны
ускорения большие, чем go, что и обеспечивается ракетами на хи¬
мическом топливе.
Но если космический корабль уже выведен на околоземную
орбиту, то тут-то двигатель малой тяги может очень пригодиться.
Двигатели малой тяги могут работать непрерывно длительное вре¬
мя. Это позволяет осуществить медленную (из-за малости тяги),
но длительную эволюцию орбиты спутника. Космический корабль
может не спеша, виток за витком, раскручиваться по спирали во¬
круг Земли вплоть до того момента, когда скорость корабля станет
параболической и он сможет улететь из окрестностей Земли к даль¬
ним планетам. Такой маневр может оказаться выгодным, так как
2. Параметры и парадоксы разгона
247
потребует меньшего расхода массы, чем при полете с помощью
только химических двигателей. Можно будет отправить в межпла¬
нетное путешествие больший полезный груз.
Траекторию космического корабля, первоначально летящего
по замкнутой орбите вокруг планеты, а затем разгоняющегося до па¬
раболической скорости, называют траекторией разгона. Некоторые
свойства спиральных траекторий разгона будут рассмотрены в этом
очерке.
2. Параметры и парадоксы разгона
Ограничимся только тем частным, но важным случаем, когда
тяга реактивного двигателя направлена все время по касательной
к траектории, а ускорение fp этой тяги постоянно по величине.
Введем обозначения (рис. 7.1): г — расстояние от центра притяже¬
ния до космического корабля (массу которого, как всегда в таких
случаях, предполагаем сосредоточенной в его центре масс); Vp —
скорость корабля; вектор тяги fp по предположению коллинеарен
вектору скорости Vp; наконец, угол а является углом между на¬
правлениями векторов г и Vp. На рис. 7.1 обозначен еще полярный
угол (р. Пусть, кроме того, Го — произвольное фиксированное
расстояние корабля от центра притяжения (например, начальное
расстояние), a g — ускорение силы тяготения на этом расстоянии.
г-
а
г
Рис. 7.1. Параметры траектории
248
Очерк седьмой. В космос по спирали
Удобно ввести безразмерные переменные
д.
(7.2.1)
V Го
Здесь г — безразмерное, at — размерное текущее время.
Введем безразмерную величину реактивного ускорения
Следуя дальше работе В. В. Белецкого и В. А. Егорова [7.2], запишем
уравнения движения в переменных V, р,а в виде
Первое из этих уравнений — уравнение движения в проекции на ка¬
сательную к орбите, причем / — реактивное ускорение, а второй
член в правой части — проекция ускорения от силы ньютоновского
тяготения. Второе уравнение просто описывает радиальную компо¬
ненту скорости корабля. Третье уравнение — уравнение движения
в проекции на нормаль к траектории. В это уравнение входит ве¬
личина h — безразмерная механическая энергия движения.
Для полного определения траектории нужно еще выписать
уравнение для полярного угла <р:
Это уравнение может быть проинтегрировано квадратурой, если
известно решение системы (7.2.3).
Система (7.2.3) замкнута, и ее интегрирование вместе с (7.2.4)
дает полное описание траектории и закона движения. Интегриро¬
вание, к сожалению, не может быть проведено в замкнутом анали¬
тическом виде.
Для качественного анализа удобно выписать еще дифферен¬
циальные уравнения для оскулирующих элементов орбиты: энер¬
гии h и фокального параметра р. Эти уравнения легко получить
дифференцированием по времени тождеств h = V2/2 - \/р и
(7.2.2)
(7.2.3)
(7.2.4)
2. Параметры и парадоксы разгона
249
250
Очерк седьмой. В космос по спирали
р = p2V2 sin2 а\ подставляя в результат дифференцирования вы¬
ражения V, р, а из (7.2.3), обнаружим, что
£r=fv• !=?• <7-2'5>
Из этих двух уравнений сразу видно, что энергия h и фо¬
кальный параметр р монотонно увеличиваются. Энергия h связана
с величиной большой полуоси орбиты соотношением h = —(1 /2)а;
при этом, конечно, а > 0, следовательно, h < 0 (до тех пор, пока
не будет достигнута параболическая скорость; в этом случае h = 0).
Монотонное увеличение h означает монотонное увеличение боль¬
шой полуоси орбиты а. Одновременное увеличение параметров р
и а показывает, что орбита как бы «распухает», ее размеры увели¬
чиваются. Ясно, что при малых значениях ускорения / на одном
витке траектории она будет мало отличаться от кеплеровского эл¬
липса, который бы получился при / = 0. Но в силу da/dr > 0
и dp/dr > 0 этот эллипс от витка к витку увеличивается в разме¬
рах, в результате чего космический корабль движется вокруг Земли
по раскручивающейся спирали.
Пример такой спирали (полученной численным интегрирова¬
нием уравнений движения (7.2.3) и (7.2.4)) приведен на рис. 7.2.
Для расчета этой спиральной траектории взято довольно большое
значение / = 0,01, чтобы не очень затягивать расчет; однако тра¬
ектория, изображенная на рис. 7.2, обладает основными качествен¬
ными особенностями, свойственными и траекториям с другими,
меньшими значениями /. Предполагалось, что исходная орбита —
круговая (на круговой орбите V = 1, р = 1, h = -0,5).
Как видно из этого рисунка, космический корабль, сделав не¬
сколько оборотов вокруг Земли по развертывающейся спирали,
выходит на конечный участок — плавную дугу траектории, уже
не закручивающуюся вокруг Земли; на этом участке достигается
параболическая скорость (или, что то же, достигается h = 0). Да¬
лее корабль продолжает удаляться от Земли, набирая все большую
энергию.
Рассмотрим приближенно свойства движения, которые следу¬
ют из уравнений (7.2.3). Пусть начальная орбита — круговая, а /
очень мало. Тогда космический корабль опишет около Земли очень
много витков спирали, и каждый ее виток можно приближенно
рассматривать как круговую орбиту (по крайней мере на достаточ¬
но большом участке траектории в начале движения). В этом и будет
2. Параметры и парадоксы разгона
251
Рис. 7.2. Пример траектории разгона с круговой орбиты. Вдоль траектории
указано безразмерное время полета
состоять наше приближение (оно подтверждается численными рас¬
четами). Если каждый виток траектории является (приближенно)
кеплеровой круговой орбитой, то должно выполняться равенство
Но в этом случае,
л - — - - - •
2 р~ 2 ’
подставляя это значение h в (7.2.5) для производной ft, получим
(из первого уравнения (7.2.3) тогда следует, что cos а = 2 fp2).
Уравнение (7.2.6) замечательно тем, что с очевидностью опи¬
сывает парадоксальный, казалось бы, факт: если к спутнику при¬
ложена сила, направленная вдоль вектора его скорости в сторону
движения, то скорость спутника (в среднем) будет уменьшаться', это
уменьшение происходит так, как будто приложенная сила изменила
252
Очерк седьмой. В космос по спирали
направление на противоположное и толкает спутник назад! «Пара¬
докса», конечно, нет: все объясняется тем, что энергия движения,
а значит, и большая полуось орбиты, увеличивается, но по третье¬
му закону Кеплера увеличение большой полуоси орбиты вызывает
увеличение периода обращения спутника вокруг Земли, то есть
уменьшение в среднем скорости его движения. Что и описывается
формулой (7.2.6).
В первом очерке мы упоминали об аэродинамическом «пара¬
доксе» в движении спутника. Спутник под влиянием атмосферного
сопротивления увеличивает в среднем скорость своего движения.
Суть аэродинамического парадокса точно такая же, как и рас¬
смотренного здесь «парадокса». Сила сопротивления атмосферы
направлена по касательной к орбите спутника, только в сторону,
обратную движению. В результате энергия движения уменьшается,
вместе с ней — и большая полуось орбиты; стало быть, умень¬
шается период обращения спутника, то есть увеличивается средняя
скорость движения спутника по орбите. Это увеличение тоже может
быть описано формулой (7.2.6), где только надо положить / < 0.
Точнее, в этом случае / = -cpaTV2, где с — постоянный параметр,
Рат *— плотность атмосферы.
Вернемся к нашей задаче о разгоне космического корабля по¬
стоянным, касательным к траектории ускорением.
Уменьшение в среднем скорости движения спутника происхо¬
дит, пока его энергия h < 0. Но в силу монотонного увеличения
энергии h она обязательно достигнет нулевого значения за конеч¬
ное время и будет продолжать увеличиваться уже в области своих
положительных значений. Это следует из того, что при h = 0 V Ф 0
и, из (7.2.5), dh/dt ф 0. Однако если h > 0, то из третьего диф¬
ференциального уравнения (7.2.3) следует монотонное увеличение
cos а. При этом cos а —> 1 при т -> оо; из второго уравнения (7.2.3)
тогда р —> оо при г —» оо; а из первого получим, что dV/dr « / > О
при т -э оо, так как в этом уравнении член cos а/p2 становится
сколь угодно малым при т -э оо. Таким образом, скорость дви¬
жения по орбите можно считать в среднем монотонно уменьша¬
ющейся при h < 0 и монотонно увеличивающейся при h > 0.
Значит, в окрестности h я 0 скорость имеет абсолютный минимум
и dV/dr = 0.
Этот факт можно использовать для получения приближенных
значений параметров траектории в конце участка разгона. Ведь нас
больше всего интересует именно момент достижения параболиче¬
2. Параметры и парадоксы разгона
253
ской скорости (h = 0). На каком расстоянии от Земли это произой¬
дет? Через какое время? Какова будет при этом скорость корабля?
Условие dV/dr = 0 при h = 0 помогает ответить на поставленные
вопросы. Из этого условия, обращаясь к первому уравнению (7.2.3),
получим
/ cos а*
Р* = у—]г-’ (7-2-7)
причем звездочкой обозначено, что берутся параметры в конце
участка разгона. Значение cos а» нам пока неизвестно.
Так как параболическая скорость V* удовлетворяет условию
V* =2/pt, то из (7.2.7) следует
(7.2.8)
cos а,
Для вычисления времени т* разгона до параболической скорости
поступим так. Интегрируя первое из уравнений (7.2.5), получим
К ~ h0 = fVn, (7.2.9)
где V — среднее значение скорости на участке разгона. Можно
положить V = 0,5(Vo +V*), где Vo — начальное значение скорости,
V* — параболическая скорость. Но так как Л* = 0, ho = -0,5,
Vo = 1, a Vt определяется формулой (7.2.8), то из (7.2.9) получим
т* = \=—. (7.2.10)
/ 1 +
4 м/ \
у cos а* )
Для полного расчета параметров траектории в конце участка
разгона осталось определить угол а*. В работе [7.2] получена соот¬
ветствующая формула ]\ однако для прикидочных расчетов можно
обойтись без нее. Нам важно оценить с небольшой точностью па¬
раметры в конце участка разгона. Для этого воспользуемся тем
фактом, что при т -> оо cos а* -> 1, и в качестве приближенной
^ Вот эта формула:
1 . _ _b/L
sin а* = - (t/47 )2у/71ГТ ■
254
Очерк седьмой. В космос по спирали
величины cos а* положим его предельное значение cos а* и 1. То¬
гда формулы (7.2.7), (7.2.8), (7.2.10) упростятся:
p'~Tt’ r, = /(i + щу (7'2П)
Эти формулы, как показывает сравнение с точным расчетом (с чис¬
ленным интегрированием уравнений движения), дают ошибку в оп¬
ределении параметров разгона всего 5-15 %. Такая точность вполне
достаточна для прикидочных расчетов, предварительного выбора
орбиты и т.д. Выбрав нужный вариант траектории с помощью при¬
ближенных формул (7.2.11), мы всегда можем затем просчитать этот
вариант и близкие к нему численным интегрированием уравнений
движения.
Для перехода к размерным значениям параметров разгона нуж¬
но, вычислив р*, V*, г* по (7.2.11), воспользоваться затем формула¬
ми (7.2.1).
Отметим еще, что V = dS/dr, где S — путь (безразмерный),
пройденный космическим кораблем. Если это выражение для V
подставить в первое из уравнений (7.2.5) и проинтегрировать, то
получим точное соотношение
h-h0 = f(S-So). (7.2.12)
по которому легко узнать путь, пройденный космическим кораблем.
Так, для ускорения / = 10-4 к моменту набора параболической ско¬
рости (h = 0) корабль, стартовавший с круговой орбиты (Л0 = -1 /2),
пройдет (безразмерный) путь S = 0,5 • 104. Но S = 5р/г0, где г0 —
размерный радиус исходной орбиты, Sp — размерный путь. Если
Го = 7000 км, то получим Sp = 35 млн км.
Некоторые результаты расчетов параметров спиральных траек¬
торий разгона приведены в нижеследующих таблицах. Все данные
в таблицах относятся к моменту набора параболической скорости.
Звездочкой отмечены параметры, вычисленные по приближенным
формулам (7.2.11); те же параметры без звездочки получены точно
численным интегрированием уравнений движения.
В табл. 7.1 приводится также оценка точности счета по при¬
ближенным формулам: 6р,ду,бт — относительные ошибки сче¬
та по этим формулам (например, 5Р = |(р* - р)/р| и аналогично
для 6у, дт). В последнем столбце табл. 7.1 приводится число вит¬
ков спирали разгона, пройденных кораблем до момента набора
параболической скорости. В табл. 7.1 все параметры безразмерные,
2. Параметры и парадоксы разгона
255
Таблица 7.1
Разгон с круговой орбиты
6т
К
а
10“
69,1
75
0,078
10,00
8,839
0,118
0,447
0,473
0,072
37,5
5- 10“
145
157
0,074
14,14
12,438
0,137
0,375
0,401
0,063
36
10“
799
856
0,066
31,62
27,846
0,135
0,251
0,268
0,068
33
39
5- 10“
1651
1758
0,061
44,72
39,506
0,132
0,211
0,225
0,066
32,5
79
10“
8761
9192
0,047
100,00
87,115
0,139
0,141
0,151
0,066
31,5
398
а в табл. 7.2-7.4 приведены некоторые размерные характеристики
разгона.
Из таблиц можно заключить, что время разгона при ускорении
порядка 1 мм/сек2 составляет около 100 суток при движении вокруг
Земли и около 30 суток при движении вокруг Марса (если разгон
начинается с высоты 300 км над поверхностью планеты). Те же
времена потребуются для торможения от параболической скорости
до круговой с выходом на орбиту с высотой 300 км. Если начальная
орбита имеет высоту 6000 км, то с ускорением порядка 1 мм/сек2
достигнем параболической скорости примерно за 40 суток. (Расчеты
для больших высот исходной орбиты (порядка 6000 км) целесооб¬
разны потому, что такие орбиты лежат вне первого радиационного
пояса Земли. Энергетические затраты на вывод аппарата на такую
высоту могут окупиться уменьшением веса антирадиационной за¬
щиты.)
Отметим еще одну любопытную формулу. Из табл. 7.1 следует,
что число п витков спиральной траектории разгона (с исходной
круговой орбиты) очень хорошо представляется формулой
0,04
(7.2.13)
п =
f
Эта формула получена анализом численных результатов; аналити¬
чески ее вывести не удается.
Приведем еще (рис. 7.3) расчеты (численное интегрирование)
зависимости параметров траектории разгона от времени. Обратим
внимание на поведение скорости V со временем. Это поведение
как раз такое, какое мы и получили при качественном анализе
256
Очерк седьмой. В космос по спирали
Таблица 7.2
Разгон около Земли. Начальная высота круговой орбиты
над поверхностью Земли Н0 = 300 км
/
/р, мм/сек2
t, сутки
г, км
Vp, км/сек
10"2
89,5
0,75
56 630
3,65
5 * 10_3
44,7
1,5
82 970
3,10
1<Г3
8,95
8,5
185 760
2,07
5-10"4
4,5
17,5
263 545
1,74
1(Г4
0,9
92
585 150
1,17
Таблица 7.3
Разгон около Земли. Начальная высота круговой орбиты
над поверхностью Земли Я0 = 6000 км
/
/р, мм/сек2
t, сутки
г, км
Vp, км/сек
10"2
26
2
110 580
2,68
5- 10~3
13
4
153 870
2,275
10~3
2,6
21,5
344 483
1,52
5- 10~4
1,3
44
488 730
1,58
10"4
0,26
232
1 085 120
0,86
Таблица 7.4
Разгон около Марса. Начальная высота круговой орбиты
над поверхностью Марса Н0 = 300 км
/
/р, мм/сек2
t,сутки
г, км
Vp, км/сек
ю-2
31,6
0,93
33 000
1,61
5- 10_3
15,8
2
45 920
1,37
10_3
3,16
11
102 810
0,91
О
1
-U
1,6
22
145 860
0,77
10'4
0,3
115
323 840
0,51
3. Монотонная спираль разгона
257
Рис. 7.3. Зависимость параметров траектории разгона с круговой орбиты
от времени (безразмерные переменные); / = 0,01
уравнений движения: в среднем скорость уменьшается, пока идет
набор параболической скорости. При достижении параболической
скорости (то есть когда энергия h достигнет нулевого значения)
оказывается, что скорость имеет абсолютно минимальное значе¬
ние; после этого момента скорость монотонно возрастает. Вместе
с тем на рис. 7.3 видны такие детали поведения траектории, ко¬
торыми мы пренебрегали в приближенном анализе. Это, прежде
всего, малые колебания скорости около монотонно уменьшающе¬
гося среднего значения (на участке набора параболической скоро¬
сти). Изменение орбиты, вообще говоря, лишено монотонности.
Если мы начинаем разгон с круговой орбиты, то приложение ре¬
активного ускорения превращает оскулирующую орбиту в слабоэл¬
липтическую; а на эллиптической орбите, как мы знаем, скорость
и радиус-вектор периодически меняются; эти колебания, наложен¬
ные на среднее монотонное изменение параметров, и дают картину,
изображенную на рис. 7.3 (колебания в р не видны на этом рисунке
из-за его масштаба).
3. Монотонная спираль разгона
Можно, однако, построить целый класс траекторий, облада¬
ющих монотонностью изменения всех параметров [7.3]. Запишем
полную систему уравнений в оскулирующих элементах для нашей
17 Заказ 1667
258
Очерк седьмой. В космос по спирали
задачи:
dp 2 р de 2(е + cos v) '
(7-3.1)
Здесь, как и в первом очерке, е — оскулируюший эксцентриситет
орбиты, ш — оскулирующая долгота перигея, v — истинная ано¬
малия. Величины р и V выражаются через введенные переменные
формулами
Тогда уравнения (7.3.1), (7.3.2) относительно переменных V, р,р, т
будут иметь точно такой вид, как если бы мы в (7.3.1) положили
2/ = 1 и написали V, р, р, т вместо V, р, р, т. Поэтому, определив
какую-либо траекторию по (7.3.1) для 2/ = 1, мы согласно (7.3.3)
получаем целое множество траекторий для произвольных /.
Что касается траектории с 2/ = 1, то, следуя Д. Е. Охоцимско-
му [7.3], будем искать такое решение уравнений (7.3.1), у которого
при т —> ~оо е -» 0, р 0, а также cosi' —> 0 (в дальнейшем
в обозначениях опустим черточки над буквами). Такое решение
оказывается всего одно. Оно в определенном смысле универсаль¬
но, ибо никак не зависит от наперед заданных начальных данных,
отвечающих ненулевому расстоянию от центра притяжения. Па¬
раметры этого решения меняются монотонно вплоть до набора
параболической скорости.
Описывающий это решение оскулируюший эллипс тем ближе
к окружности, чем меньше его размеры. Любая исходная орбита,
отвечающая этому решению, будет эллиптической, с определен¬
ной малой эллиптичностью (если размеры орбиты не очень вели¬
ки). Описываемой универсальной траектории, ввиду подстановки
(7.3.3), отвечает множество траекторий, обладающих тем же свой¬
ством е —> 0, р —у 0, cos v -» 0 при т —> —оо; добавим, что решение
строится так, чтобы е = 1 при т = 0.
у
р — ,
1 + е cos v
Напомним, что наши переменные — безразмерные.
Теперь введем замену переменных
(7.3.2)
V = (2f)V, p = (2fy'/2p,
p = (2f)~ll2p, r = (2/)"3/4f.
(7.3.3)
3. Монотонная спираль разгона
259
Опишем конечные результаты расчета монотонной спирали
разгона [7.3]. Эту спираль удобно разбить на три характерных
участка: первый участок при очень малых значениях р описывается
асимптотическим решением — рядами по степеням р; второй уча¬
сток определяется численным интегрированием (начальные данные
находятся по асимптотическим формулам первого участка); третий
участок при больших значениях р описывается рядами по степе¬
ням 1/р. Параболическая скорость (е = 1) достигается на втором
участке.
Оказывается, что на первом участке решение представляется
в виде рядов по степеням величины р4:
ОС ОС' v
2 4 А; 2 4 А;
е=Р 2^екР > COS I/ = р 2_^Vkp ,
А:=0 /
ОС
ш = -3,40942 + р~2 ФкРАк 1
А:=0
А:=0
(7.3.4)
т= 1,34571 +р~1/2^т*Р4*:-
А:=0
Основой для получения этих формул служит преобразование части
уравнений (7.3.1) к виду
de dcos и
~г = /е(р* е’ C0S "Г; = Д (Р’ е>cos ^)-
dp dp
Коэффициенты i/*, <рд;, ти разложений (7.3.4) собраны в табл. 7.5.
При больших значениях р (на третьем участке траектории)
разложения имеют вид
ОС ос
е = 0,76649р + У] Сд:р~А:, cosi/ =
А: = 1 А:= I
00
w = -1,5708 + р~' 53 ’
А:=0
оо
/
г = -1,611 + 2_^ткр
к=0
(7.3.5)
Коэффициенты £*., щ, т[: содержатся в табл. 7.6. Наконец,
в табл. 7.7 приведены функции е(р), cos i/(p), о;(р), т(р) для проме¬
жуточных значений р (0,10 ^ р ^ 20,0). В той же таблице дается
17*
260
Очерк седьмой. В космос по спирали
Таблица 7.5
к
£к
<Рк
тк
0
1,0- 10°
о
О
CD
-0,5- 10°
-2,0- 10й
1
-6,0- 10°
-3,0- ю1
2,75- 10°
4,285714- 10“'
2
3,53- I02
3,177- 103
-4,835417- 10'
1
Vj
о
о
3
-5,0216- 106
-6,528080- 105
4,292169- 103
3,604946- 102
4
1,271935- 107
2,162289- 108
-8,098106- Ю5
-5,110699- 104
5
-5,007378 ■ 109
-1,051549- 10"
2,555165- 108
1,281759- 107
6
2,829338- 1012
7,073346- И)13
-1,204903- 10"
-5.010652- 109
7
-2,173519- 1015
-6,303206- 1016
7,935154- 1013
2,819974- 1012
Таблица 7.6
к
е'к
/
тк
<Рк
/
Vk
0
—
—
-1,30465-10°
1,53298- 10°
1
-4,58000- 10"'
9,16000- 10“'
0
0
2
6,80189- 10'1
-2,04057- 10°
-7,74093- 10"2
-7,40216- 10"'
3
-8,45172-10"'
3,38069- 10°
-3,20210-10"'
5,44150- 10"'
4
8,85247- 10"'
-4,42624- 10й
1,05876-10°
-3,77374-10"'
5
-4,86283- 10"'
2,91770- 10°
-2,39421 • 10°
-1,23027- 10"2
6
-9,64784- 10“'
6,75349- 10°
4,44336- 10°
8,58759- 10"'
7
4,43942- 10°
-3,55154- 10'
-6,81926- 10°
-2,41946- 10°
8
-1,10624- 10'
9,95619- 10'
7,74454- 10°
4,80913-10°
9
2,11182- 101
-2,11182- 102
-2,45367- 10°
-7,51642-10°
10
-3,13216- 10'
3,44538- 102
-1,89947- 10'
8,38035-10°
11
2,90194- Ю1
-3,48233- 102
7,31602- 10'
-1,84542- 10°
12
1,76253- 10'
-2,29129- Ю2
-1,79535- 102
-2,32322- 10'
13
-1,71363- 102
2,39908- Ю3
3,41319- 102
8,44939- 10'
14
5,27883- 102
-7,91825- 103
-4,90991 • 102
-2,00619- 102
3. Монотонная спираль разгона
261
Таблица 7.7
р
е
cos V
ш
т
h
0,10
0,009994
0,009970
-53,3820
-4,97871
-9,99900
0,12
0,014382
0,014313
-38,0922
-4,42754
-8,33161
0,14
0,019556
0,019382
-28,8661
-3,99908
-7,14013
0,16
0,025503
0,025128
-22,8710
-3,65360
-6,24594
0,18
0,032207
0,031475
-18,7539
-3,36729
-5,54979
0,20
0,039646
0,038332
-15,8022
-3,12493
-4,99214
0,22
0,047793
0,045597
-13,6115
-2,91623
-4,53507
0,24
0,056615
0,053158
-11,9390
-2,73398
-4,15331
0,26
0,066076
0,060904
-10,6313
-2,57297
-3,82936
0,28
0,076137
0,068730
-9,58789
-2,42927
-3,55073
0,30
0,086757
0,076539
-8,74073
-2,29994
-3,30824
0,32
0,097896
0,084250
-8,04234
-2,18264
—3,09505
0,34
0,109512
0,091795
-7,45886
-2,07556
-2,90590
0,36
0,121566
0,099118
-6,96556
-1,97723
-2,73673
0,38
0,134020
0,106179
-6,54409
-1,88645
-2,58431
0,4
0,146838
0,112949
-6,18056
-1,80226
-2,44610
0,45
0,180027
0,110190
-5,39184
-1,61006.
-2,15020
0,5
0,215315
0,142001
-4,93070
-1,45562
-1,90728
0,55
0,251470
0,153636
-4,50292
-1,31363
-1,70321
0,6
0,288902
0,163344
-4,20657
-1,19254
-1,52756
0,7
0,365541
0,178381
-3,73868
-0,98117
-1,23769
0,8
0,443994
0,188657
-3,41258
-0,80437
-1,00359
0,9
0,523513
0,195430
-3,17267
-0,65205
-0,80659
262
Очерк седьмой. В космос по спирали
Окончание таблицы 7.7
р
е
cosF
т
h
1,0
0,603641
0,199643
-2,98886
-0,51783
-0,63562
1,2
0,764699
0,202929
-2,72567
-0,28806
-0,34603
1,4
0,925942
0,202030
-2,54612
-0,09406
-0,10188
1,6
1,08688
0,198833
-2,41563
0,07546
0,11332
1,8
1,24734
0,194388
-2,31640
0,22720
0,30881
2,0
1,40726
0,189299
-2,23832
0,36543
0,49019
2,2
1,56666
0,183923
-2,17524
0,49306
0,66110
2,4
1,72556
0,178472
-2,12318
0,61211
0,82398
2,6
1,88401
0,173075
-2,07947
0,72406
0,98058
2,8
2,04205
0,167807
-2,04223
0,83004
1,13213
3,0
2,19972
0,162713
-2,01012
0,93090
1,27959
3,5
2,59250
0,150857
-1,94631
1,16480
1,63459
4,0
2,98367
0,140292
-1,89878
1,37817
1,97558
4,5
3,37360
0,130929
-1,86198
1,57570
2,30692
5,0
3,76253
0,122627
-1,83263
1,76056
2,63133
6,0
4,53820
0,108656
-1,78875
2,10061
3,26588
8,0
6,08385
0,088240
-1,73408
2,69644
4,50165
10,0
7,62514
0,074166
-1,70136
3,21638
5,71428
12,0
9,16399
0,063919
-1,67957
3,68410
6,91490
14,0
10,7014
0,056140
-1,66402
4,11294
8,10847
16,0
12,2377
0,050040
-1,65236
4,51134
9,29756
18,0
13,7733
0,045130
-1,64329
4,88505
10,4836
20,0
15,3085
0,041095
-1,63604
5,23819
11,6675
3. Монотонная спираль разгона
263
Рис. 7.4. Поведение оскулирующих элементов
универсальной спирали Д. Е. Охоцимского
Рис. 7.5. Зависимость от времени скорости V, энергии h,
расстояния р вдоль универсальной спирали
264
Очерк седьмой. В космос по спирали
а)
Рис. 7.6. Общий вид универсальной спирали
значение удвоенной энергии
Р
Поведение этих функций в зависимости от р показано также
на рис. 7.4. На рис. 7.5 показано, как меняются в зависимости
от времени скорость V, энергия h, расстояние р.
Наконец, на рис. 7.6 изображен общий вид описываемой спи¬
рали; вдоль траектории отложены значения параметра р, а буквой
П отмечена точка набора параболической скорости. В этой точке
V = 1,26846, р = 1,242592).
Очень интересный цикл работ о построении аналогичных, но оптимальных
траекторий разгона выполнил Г. Б. Ефимов |7.5].
4. Произвольные траектории с малыми эксцентриситетами
265
4. Произвольные траектории с малыми эксцентриситетами
Исследованные в предыдущем пункте траектории представля¬
ют собой, конечно, лишь частный класс решений уравнений (7.3.1).
В этом классе при заданном ускорении малой тяги к фиксирован¬
ному расстоянию от центра притяжения присовокупляется вполне
определенное единственное значение оскулируюшего эксцентри¬
ситета орбиты. Это решение очень удобно для расчета, например,
необходимых для разгона энергетических затрат (для множества
близких исходных орбит с одинаковыми начальными энергиями Л*
затраты на разгон будут примерно такими же, как и на рассмотрен¬
ной выше спирали, если только за начальную точку на ней выбрана
точка, отвечающая значению Л*). Однако траектория, описанная
в предыдущем пункте, «слишком гладка» — соответствующий класс
решений обладает монотонным изменением параметров. Эта тра¬
ектория, строго говоря, не типична по поведению своих оскулиру-
юших параметров.
Представляет интерес поэтому попытаться аналитическим пу¬
тем исследовать поведение произвольных траекторий разгона. Это
можно сделать, используя малость реактивного ускорения. Малость
«возмущающей силы» (реактивного ускорения) позволяет приме¬
нить для анализа асимптотические методы нелинейной механики.
Такое исследование проведено, например, Ю. Г. Евтушенко в работе
[7.4]. Мы сейчас рассмотрим только одну из задач, решенных в этой
работе. А именно предположим, что начальная орбита обладает про¬
извольным, но достаточно малым эксцентриситетом, и рассмотрим
поведение разгонной траектории до тех пор, пока эксцентриситет
еще остается достаточно малым.
Предварительно преобразуем уравнения (7.3.1). Введем ком¬
поненты вектора Лапласа
a = esino;, /3 = е cos о; (7.4.1)
в качестве новых переменных (вместо е и о>). Это дает возможность
избавиться от е в знаменателях правых частей уравнений и, таким
образом, избежать особенности при е —> 0. Далее, введем аргумент
широты
и = uj + v.
Из (7.3.1) легко видеть, что
266
Очерк седьмой. В космос по спирали
следовательно, и меняется монотонно и притом быстро (du/dr ~ 1)
по сравнению с а, (3, р. Удобно взять и в качестве независимой
переменной вместо т. После таких преобразований система (7.3.1)
примет вид
dP т/ Зр
и =2/р F-
da
du
2fp (a + sin u)F,
d/3 ,
— = 2fp (/3 + cos u)F,
du
F = (1 + /3 cos и + a sin и)-2 x
x (1 + a2 + /32 + 2/3 cos и + 2a sin и)
-1/2
(7.4.2)
или, с точностью до первых степеней эксцентриситета (то есть с
точностью до первых степеней а и /3),
dp 1
— = 2fp'(\ - 3a sin и - 3/3 cos и),
du
da 2/
~7~ — JP \~a + 2 sin и + 3a cos 2u - 3/3 sin 2и),
du
d/3
— = fp~{—/3 + 2 cos и - За sin 2и - 3/3 cos 2u).
(Jl It
(7.4.3)
К этой системе непосредственно можно применить алгоритм асимп¬
тотического метода, считая / малым параметром, а и быстрой пе¬
ременной. Осредняя по этой переменной правые части в (7.4.3),
получим
dp „ . з da -2 dP ± 2 о
Тп=21р’ di = -fpa- Tn=-<v!i-
(7.4.4)
Из (7.4.4) видим, что
rfC d О О 1 3 3 л
!+Л = -5/Л!+Л<о.
Таким образом, эксцентриситет орбиты под действием касатель¬
ного реактивного ускорения в среднем монотонно уменьшается.
Это находится в досадном несоответствии с известными уже нам
свойствами траекторий разгона. Ведь к моменту разгона скорость
достигает параболического значения, что соответствует значению
4. Произвольные траектории с малыми эксцентриситетами
267
эксцентриситета е — 1. Значит, рано или поздно эксцентриси¬
тет должен начать увеличиваться, что не «ухватывается» решением
осредненной системы (7.4.4). Объяснение этого факта может быть
одно: так как решение усредненной системы (7.4.4) отвечает ре¬
шению исходной системы (7.4.3) лишь на ограниченном интервале
«времени», то эффект увеличения эксцентриситета начинает про¬
являться только после истечения этого интервала.
Чтобы получить этот эффект, надо увеличить интервал «вре¬
мени», на котором достаточно точно аппроксимируется решение.
Проше говоря, надо взять более высокое приближение к решению
системы (7.4.3). Для этого, следуя работе [7.4], будем считать ве¬
личины /, а,/3 одного порядка малости (для определенности, е).
Тогда решение системы (7.4.3) будем искать в виде
р = р + ери а = а + еа\, /? = Д + е/?ь (7.4.5)
где р, а, Д — решение осредненной системы второго приближения,
то есть системы типа
^-= ер\ + е2р2, (7.4.6)
аи
а р\,а\,/3\ должны определиться в результате подстановки (7.4.5)
в (7.4.3) и приравнивания членов с одинаковыми степенями е.
Оказывается, что эти функции должны удовлетворять уравнениям
dp\ da| Л 2 . dP\ _ 2 „ „ч
— = 0, = 2р sm и, = 2р cos и. (7.4.7)
du du du
Но система (7.4.6) тождественно совпадает с (7.4.4). Правые части
последних двух уравнений из (7.4.4) имеют второй порядок малости,
так как по условию fa~e2, ~ е2\ в первом же уравнении (7.4.4)
содержится только член первого порядка малости, а член второго
порядка тождественно равен пулю.
Решение системы (7.4.4) легко получить ее интегрированием,
а в качестве решения системы (7.4.7) возьмем
р] = 0, а\ = -2р2 cos w, /31 = 2р2 sin и.
Подставляя эти значения в (7.4.5) (считаем, что е = /) и учитывая,
что а, /3,р — решение системы (7.4.4), получим окончательно:
268
Очерк седьмой. В космос по спирали
р = Ро(\ - 4plfu) |/2,
(7.4.8)
А 2
а — 2 fp cos и,
Vp
В ,
/3 = h 2fp sin и.
Vp
Постоянные А, В определяются условием а = а0, (3 = /3() при
« = 0. Решение (7.4.8) аппроксимирует точное решение системы
(7.4.3) с погрешностью ~ /2 на интервале и ~ /_|, если только
= \А*о+$~/-
Исследуем решение (7.4.8). Фокальный параметр р монотон¬
но возрастает, так что орбита увеличивается в размерах. Возводя
выражения а и /3 в (7.4.8) в квадрат, складывая и осредняя по и,
получим среднее по витку орбиты значение ё2 квадрата оскулиру-
ющего эксцентриситета. Это выражение имеет вид
ё2 = А +В + 4/У. (7.4.9)
Р
Если ввести начальное значение ё02 функции ё2, то
А2 + В2 = ро{ёо - 4/У )•
Функция (7.4.9) имеет минимум при
s _ s = Ро(ёр ~ 4/У)
16/2
Если р* > ро, то минимум ё2 лежит в области реальных измене¬
ний параметров (ведь р монотонно увеличивается от ро). Условие
р* > ро эквивалентно следующему (несколько огрубляя, считаем,
что yfOj = е0):
е„>2 V4fpl (7.4.10)
Итак, если начальный эксцентриситет во и безразмерное уско¬
рение тяги / связаны неравенством (7.4.10), то текущий средний
эксцентриситет оскулирующей орбиты будет сначала уменьшаться
до некоторого минимального значения, затем монотонно возрас¬
тать, так что при больших р будет е ^ 2fp2. Если неравенство
4. Произвольные траектории с малыми эксцентриситетами
269
Рис. 7.7. Годограф оскулирующего вектора Лапласа для траектории
разгона (схематическое изображение)
(7.4.10) не выполнено, эксцентриситет (в среднем) немедленно на¬
чинает возрастать.
Нетрудно видеть также, что годограф вектора Лапласа описы¬
вается уравнением окружности
переменного радиуса 2fp2 с переменными координатами А/у/р,
В/у/р ее центра. С течением времени радиус окружности монотон¬
но увеличивается, а центр монотонно (по прямой) стремится к на¬
чалу координат. В результате годограф представляет собой развер¬
тывающуюся спираль, каждый виток которой проходится за «вре¬
мя» Аи = 2п (рис. 7.7). Радиус-вектор годографа по величине равен
эксцентриситету е орбиты, а полярный угол — долготе и перигея
орбиты. Рассматривая годограф (рис. 7.7), можно понять довольно
непростое поведение обоих этих параметров.
Очерк восьмой
Солнцем полны паруса
На полярных морях и на южных,
По изгибам зеленых зыбей,
Меж базальтовых скал и жемчужных
Шелестят паруса кораблей.
Быстрокрылых ведут капитаны,
Открыватели новых земель...
Н. Гумилев
«Капитаны»
«Протянителадони к Солнцу. Что вы чувствуете? Тепло, конеч¬
но. Но кроме него есть еще давление. Правда, такое слабое, что вы
его не замечаете. На площадь ваших ладоней приходится всего около
одной миллионной унции. Но в космосе даже такая малая величина
играет важную роль, потому что она действует все время, час за ча¬
сом, день за днем. И запас энергии, в отличие от ракетного горючего,
неограничен. При желании можно ее использовать. Мы можем со¬
здать паруса, которые будут улавливать солнечное излучение».
Эта цитата взята из научно-фантастического рассказа Артура
Кларка «Солнечный ветер» [8.1]. В рассказе поэтично и научно до¬
стоверно описана гонка вокруг Земли яхт с солнечными парусами.
Нам еще не раз придется цитировать этот рассказ (цитаты выде¬
лены курсивом). Предлагаемый очерк является как бы научным
комментарием к рассказу А. Кларка.
Световое давление падающего потока солнечного излучения
на орбите Земли составляет примерно р — 4,5 х 1СГ8 Г/см2. Это
ничтожная величина. Однако если космический аппарат спабдить
парусом, достаточно легким и достаточно большого размера, то
суммарная сила светового давления на парус может сообщить кос¬
мическому кораблю ускорение, достаточное для маневрирования
Солнцем полны паруса
271
в пространстве. Например, разумно управляя парусом, можно разо¬
гнать космический корабль по спиральной траектории вокруг Зем¬
ли и, набрав параболическую скорость, улететь в открытый космос,
к планетам! Об этом можно прочитать, например, в книге Г. Л. Гро-
дзовского, Ю. Н. Иванова, В. В. Токарева [8.2], где дан обзор работ
по анализу динамики полета аппаратов с солнечным парусом.
Мыв нашем анализе будем опираться на работу А. П. Скопцо-
ва [8.3] ^). Если парус плоский и обладает идеально отражающей
зеркальной поверхностью, то результирующая сила светового дав¬
ления, на него действующая, дается формулой
и направлена по нормали п к плоскости паруса. В формуле (8.1)
обозначено: R — расстояние от Солнца до паруса, a Rg — от Солн¬
ца до Земли, S — площадь паруса, в — угол между направления¬
ми результирующей силы и солнечных лучей. В дальнейшем будут
рассматриваться лишь околоземные орбиты космических кораблей.
Для таких орбит можно положить R^/R = 1.
Однако парус не обязательно должен быть плоским. Мы по¬
ставим оптимальную задачу быстрейшего набора параболической
скорости. Чтобы достичь параболической скорости за минималь¬
ное время, нужно соответственно управлять положением паруса
в полете, но и конструкцию паруса можно выбрать так, чтобы
способствовать минимизации времени разгона. Можно наилучшим
образом управлять в полете плоским парусом, а можно наилучшим
образом управлять парусом наилучшей конструкции; время полета
во втором случае будет меньше, чем в первом.
Пусть К| — главный вектор количества движения светово¬
го потока, падающего на парус, а К2 — отраженного от пару¬
са светового потока. Результирующая сила Р светового давления
Р ~ ДК = Kj - К2. Наилучшей конструкцией паруса является та¬
кая конструкция, при которой [8.3]
2) величина |Kj| не зависит от направления К2.
При этом (рис. 8.1) |ДК| = 2|K||cos0, и тогда величина сум¬
марной силы светового давления зависит от угла в следующим
(8.1)
О |К,| = |К2|;
^ Пользуюсь случаем выразить признательность А. П. Скопцову за помощь в ана¬
лизе и расчеты, проделанные специально для этого очерка.
272
Очерк восьмой. Солнцем полны паруса
Солнцем полны паруса
273
образом:
Р = Р* cos в, —7г/2 ^ в ^ 7г/2. (8.2)
Закону (8.2) соответствует круговая диаграмма изменения силы
в зависимости от угла в (рис. 8.1). На том же рисунке (пунк¬
тирная линия) приведена диаграмма сил (8.1) для плоского па¬
руса. Диаграммы не очень, хотя и за¬
метно, отличаются. Конкретные кон¬
струкции «наилучшего паруса» неодно¬
значны. Один из возможных вариантов
описан в [8.3]2)). Если наилучший па¬
рус и плоский парус обладают одной
и той же максимальной тягой Р*, то
при любом в наилучшему парусу мож¬
но сопоставить плоский парус, распо¬
ложенный нормально к тяге Р наилуч¬
шего паруса. Тогда плоский парус будет
давать тягу в том же направлении, что
и наилучший парус (однако по величи¬
не тяга плоского паруса будет несколь¬
ко меньше).
Напишем уравнение движения в полярных координатах (р, г.
Предположим, что направление <р = О совпадает с направлением
солнечных лучей (рис. 8.2). Солнце можно считать неподвижным
в пространстве, так как наш полет продлится недолго (несколько
суток). Обозначим, как обычно, через и, v радиальную и трансвер-
сальную составляющие скорости корабля. Согласно предыдущему,
действующая на корабль тяга складывается векторно из двух сил:
Р| и Р2; сила Р| постоянна по величине и направлению (вдоль
солнечных лучей); ее радиальная и трансверсальная компоненты
соответственно равны (Р*/2) cosp ,-(Р*/2) sin ip. Сила Р2 образует
с радиальным направлением некоторый угол — пусть 7. Компо¬
ненты этой силы суть (P*/2)cos7 ,(Р*/2) sin7.
Обозначим через а(> = Р*/т максимальное ускорение, разви¬
ваемое наилучшим парусом. Уравнения движения имеют вид
2) Забавно отметить, что эта конструкция в качестве составного элемента содер¬
жит «гиперболоид инженера Гарина», описанный в одноименном фантастическом
романе А. Толстого: два софокусных параболоида, обращенных «чашами» друг к дру¬
гу и имеющих сильно различающиеся фокусные расстояния.
18 Заказ 1667
Рис. 8.1. Условия для наи¬
лучшей конструкции солнеч¬
ного паруса
274
Очерк восьмой. Солнцем полны паруса
du v2 // а0/ ... .
= 7 “ ^2 + y(cos7 + cosy?)/(r,y?),
mv а0 .
— = + —(sin 7 - sin <p)f(r, <p),
dt т 2
dr
— = u,
dt
(8.3)
dip v
dt r
Здесь \i — гравитационный параметр Земли. Уравнения (8.3) содер¬
жат существенный фактор — «функцию тени» f(r,ip). Ведь сила
светового давления может действо¬
вать на парус только вне земной
тени. Если корабль зашел в тень
Земли, то, естественно, светового
давления он испытывать не будет.
Поэтому компоненты силы свето¬
вого давления домножены на функ¬
цию /, которая равна нулю в те¬
ни Земли и единице вне тени. Тень
Земли — сложная вещь; ее граница
не определяется четко из-за нали¬
чия полутени, из-за рассеивающего
действия атмосферы Земли. Поэто¬
му в качестве функции тени / луч¬
ше взять не «релейную» функцию
типа 0—1, а какую-то непрерывную
функцию, аппроксимирующую реальные свойства тени, типа функ¬
ции, изображенной на рис. 8.3.
В работе [8.3] используется, например, функция
/(г, (р) = — arctga
7Г
(8.4)
где а — параметр, выбор которого определяет скорость возрастания
функции тени при переходе ее границы (то есть длину участка
полутени на рис. 8.3).
Уравнения (8.3) содержат свободную функцию j(t). Функцией
7(t) следует распорядиться так, чтобы разгон нашего парусника
до параболической скорости происходил за минимальное время.
В работе [8.3] рассмотрено такое оптимальное управление парусом.
Оно довольно сложно. Однако, как показано там же, результат
(время разгона) оказывается очень близким к тому, что получается
Солнцем полны паруса
275
Рис. 8.3. Функция тени
при так называемом локально-оптимальном управлении. Это такое
управление 7(£), которое в каждой точке фазового пространства
дает максимальный прирост энергии h = и2 + и1 - 2р/г.
Составим производную
&
— — ац/(и cos 7 + v sin 7 + и cos р - v sin р).
at
Максимум производной по управлению 7 достигается на управлении
cos7 = —, sin 7+—, V — л/и2 + v2. (8.5)
В этом случае сила Р2 направлена по вектору скорости корабля.
При этом
^ = a0(V + Vs), (8.6)
at
где V — модуль полной скорости корабля, a Vs — проекция вектора
скорости на направление солнечных лучей.
Так как V + Vs ^ 0, то из (8.6) следует монотонное возраста¬
ние энергии /г, что гарантирует достижение любого значения этой
энергии, в частности выход на параболическую скорость.
Назовем управление (8.5) локально-оптимальным и будем рас¬
сматривать впредь уравнения движения (8.3), (8.4) с управлением
(8.5). Получилась интересная задача динамики, являющаяся супер¬
позицией двух уже известных нам задач: движение при совместном
действии постоянного по величине и направлению в пространстве
ускорения и постоянного касательного ускорения. Абсолютные ве¬
личины этих ускорений в нашем случае одинаковы.
Во всеоружии уравнений движения (8.3)—(8.5) мы теперь мо¬
жем заняться динамическим анализом рассказа А. Кларка.
18*
276
Очерк восьмой. Солнцем полны паруса
«Снасти дрожали от натуги: межпланетный ветер уже наполнил
огромный круглый парус. До старта осталось три минуты... Зеркаль¬
ная гладь исполинского паруса блестела и искрилась на Солнце. Неве¬
сомо парящему у перископа Мертону казалось, что парус заслонил все
небо. Ничего удивительного — пятьдесят миллионов квадратных фу¬
тов соединено с его капсулой чуть не сотней миль такелажа. Если бы
сшить вместе паруса всех клиперов, какие в прошлом белыми тучками
летели над Индийским океаном, то и тогда они не сравнялись бы с па¬
русом, в который уДиана“ловила солнечный ветер. А вещества в нем
чуть больше, чем в мыльном пузыре: толщина этих двух квадратных
миль алюминированного пластика — всего лишь несколько миллионных
дюйма».
Пятьдесят миллионов квадратных футов — это 4,65 квадрат¬
ного километра, что соответствует круглому парусу с диаметром 2,4
километра! Только при таких огромных размерах солнечного пару¬
са можно надеяться получить ускорения, достаточно большие для
маневрирования в пространстве. При этом парус должен быть как
можно легче и, значит, как можно тоньше. Ведь сила давления про¬
порциональна площади паруса, а ускорение получается делением
этой силы на массу всего корабля (вместе с парусом). Поэтому ясно,
как важно уменьшить вес паруса. Создание паруса очень большой
площади и очень малой толщины — главная техническая трудность
в осуществлении полетов под солнечными парусами.
Парус «Дианы», несмотря на ничтожную толщину (порядка од¬
ной десятитысячной миллиметра), должен бы весить 700-1000 кг.
(Удельный весалюминированной пластиковой пленки 1,2-103 кг/м3.)
Мыльный пузырь, о котором говорит Кларк, естественно, дол¬
жен иметь размеры, близкие к размеру паруса... Если вес осталь¬
ной части корабля (такелаж, кабина, космонавт и т.д.) составляет
1-1,5 тонны, то ускорение, сообщаемое кораблю, может дости¬
гать ~ 10-3g. Именно яхты такого «класса» участвуют в гонках
у А. Кларка. Их семь, и гонки полны драматизма. Но здесь не место
описанию приключений на трассе гонок и судьбы мужественного
капитана «Дианы» Джона Мертона. Нас интересует механика по¬
лета, и нам достаточно проследить за движением одной-двух яхт.
«На четырех обитаемых планетах наберется от силы два де¬
сятка человек, умеющих управлять солнечной яхтой, и все они сейчас
здесь, кто на линии старта, кто на борту эскортирующих судов,
кружатся вместе по орбите в двадцати двух тысячах миль над эква¬
тором».
Солнцем полны паруса
277
Исходная орбита, по-видимому, круговая. Кроме того, она су¬
точная: период обращения спутника на суточной орбите равен пе¬
риоду вращения Земли (24 часа). На экваториальной суточной ор¬
бите спутник все время «висит» над одной и той же географической
точкой Земли. Радиус суточной круговой орбиты г о ~ 42190 км.
Если учесть, что радиус Земли Rg « 6370 км, то высота орбиты
над поверхностью Земли h = 35 820 км, или 22 260 миль — как
раз, округленно, те 22 тысячи миль, о которых говорится у Кларка.
Несколько позже в рассказе упоминается о движении именно по су¬
точной орбите. Поэтому в качестве начальных данных для интегри¬
рования уравнений движения (8.3)—(8.5) возьмем данные, отвеча¬
ющие суточной круговой орбите:
(последняя формула, как известно, определяет круговую скорость
на орбите радиуса г0). Начальный угол (р0 выберем позже.
«Семь сверкающих ножей перерезали семь тонких линий, при¬
вязывающих яхты к базам, на которых их собрали и обслуживали.
До этой секунды все в строгом строе летели вокруг Земли; теперь ях¬
ты начнут расходиться, словно влекомые ветром семена одуванчика.
Победит та, которая первой достигнет орбиты Луны.
На УМианеи как будто ничего не изменилось. Но Мертон знал,
что это не так. Хотя он не ощущал тяги, приборная доска говорила
ему, что ускорение приближается к одной тысячной g. Для ракеты
смехотворно мало, но для солнечных яхт это было рекордом. Диа¬
на" хорошо сконструирована, огромный парус оправдывает надежды,
которые он на него возлагал. При таком ускорении после двух кругов
он разовьет достаточную скорость, чтобы покинуть околоземную ор¬
биту. А затем, подгоняемый всей мощью Солнца, он пойдет курсом
на Луну».
Так как цель гонок — Луна, то естественно считать, что гонки
проходят в плоскости лунной орбиты (или, приближенно, в плос¬
кости эклиптики). Будем считать, что исходная суточная орбита
лежала в этой плоскости. Этому не противоречит упоминание о ях¬
тах, движущихся над экватором: можно полагать, что в момент
описания трасса яхт пересекала экватор. Примерный вид трассы
суточного эклиптического спутника (то есть след его радиус-векто¬
ра на поверхности Земли) изображен на рис. 8.4. Из приведенного
отрывка следует также, что в уравнениях (8.3) нужно положить
(8.7)
а0 = 0,001#,
(8.8)
278
Очерк восьмой. Солнцем полны паруса
ибо таково (примерно) максимальное ускорение «Дианы» за счет
силы светового давления (конечно, в цитате речь идет именно
об этом, а не о суммарном ускорении от сил светового давления
и гравитационных).
Начальное положение яхт на суточной орбите определим углом
¥>о = “. (8.9)
Значение <рц (8.9) совершенно однозначно следует из анализа ин¬
формации, содержащейся в рассказе А. Кларка; мы это увидим
в дальнейшем. Данных (8.7)—(8.9) достаточно для численного ин¬
тегрирования уравнений движения (8.3)—(8.5). Результат этого ин¬
тегрирования — траектория яхты Джона Мертона — изображен
на рис. 8.5. На этом рисунке обратим прежде всего внимание на то,
что до набора параболической скорости «Диана» сделает лишь
немногим более двух витков вокруг Земли — в полном соответ-
Солнцем полны паруса
279
63,1
37 100 г, тыс. км
(р0 = 7г/2
г0 = 42 188 км
Рис. 8.5. Траектория «Дианы;
ствии с утверждением А. Кларка, только что цитированным. Прав¬
да, в другом месте у А. Кларка содержится неточность:
«За два дня будет достигнута вторая космическая скорость» —
и весь рассказ построен на предположении, что разгон до парабо¬
лической скорости занимает примерно двое суток. На самом деле
у Мертона на это уйдет около 120 часов, то есть 5 суток (время поле¬
та проставлено вдоль траектории на рисунке). При этом на первый
виток уйдет около 30 часов (более суток), а все остальное полетное
время съест сильно вытянутый второй виток орбиты...
Существенно уменьшить время полета невозможно, так как наша
программа полета, как уже говорилось, очень близка к оптимальной,
обеспечивающей наибыстрейший разгон. Но простим А. Кларку
неточность хронометража: ведь «Солнечный ветер» не диссерта¬
ция, а художественный рассказ, в котором допустимы некоторые
вольности. Зато какой научной достоверностью блистают другие
детали рассказа...
«,Диана“ хорошо начала гонки; теперь можно взглянуть
и на соперников... Вот они, будто невиданные серебристые
цветки среди черных полей космоса... Присланный Марсиан¬
ской республикой „Солнечный луч “ представлял собой плоское
кольцо с полумильным отверстием; кольцо медленно враща¬
лось, и центробежная сила придавала ему устойчивость.
Идея старая, но никому еще не удавалось успешно осуще-
280
Очерк восьмой. Солнцем полны паруса
ствить ее. Мертон мог бы поклясться, что экипаж пому¬
чается с парусом, когда надо будет поворачивать.
Правда, оставалось еще шесть часов до той поры, когда ях¬
ты завершат первую четверть своего медленного, величавого
полета по суточной орбите. Сейчас, я самом начале гонок,
они идут от Солнца, так сказать, с попутным солнечным
ветром. Надо выжать все из этого галса, яокя яхт/ //в 060-
гнут Землю и Солнце не окажется впереди».
Шесть часов на первую четверть полета, если понимать под
этим изменение полярного угла <р на 90°, — почти точное число.
Если бы не было паруса, это было бы совершенно точно. Измене¬
ния орбиты на начальном участке полета за счет влияния паруса
не могут быть слишком велики (не успевают накопиться). С учетом
влияния паруса на прохождение первой четверти витка затрачива¬
ется около 6 часов 5 минут. Что касается того, чтобы «выжать все
из этого галса», то, действительно, на начальном участке ускорение
от светового давления максимально или близко к максимальному;
парус почти нормален к солнечным лучам. На рис. 8.6 изображен
годограф ускорения светового давления вдоль траектории «Дианы».
Ее плоский парус должен быть всегда нормален к вектору ускоре¬
ния, отложенному на годографе рис. 8.6.
От момента старта (<р = -90°), когда парус нормален к солнеч¬
ным лучам, а ускорение от тяги максимально (равно ао = 0,00lg),
до момента входа в земную тень (<р = -7,5°) парус повернулся
меньше чем на 40°, а ускорение тяги упало лишь на 20% (до 0,8ао).
Рис. 8.6. Годограф возмущающего ускорения «Дианы»
Солнцем полны паруса
281
«... Крохотные брашпили непрерывно вращались, то выдавая, то
выбирая фалы по команде автопилота, который держал парус под
нужным углом к Солнцу...
Земли почти не видно, остался только узенький яркий серп,
мящийся к Солнцу. Рядом с пламенной дугой тускло обрисована ночная
сторона планеты, тут и там в просветах между тучами поблескива¬
ет зарево больших городов. Темный диск уже заслонил часть Млечного
Пути, через несколько минут он начнет закрывать Солнце.
Свет угасал; по мере того как , Диана “ бесшумно погружалась
в тень Земли, парус загорался сумеречным пурпурным оттенком —
отблеском многократных закатов, удаленных на тысячи миль. Солнце
кануло за невидимый горизонт, и в несколько минут сгустилась ночь.
Мертон посмотрел назад вдоль орбиты, по которой прошел уже
четверть пути вокруг родной планеты. Одна за другой гасли яркие
звездочки остальных яхт, когда они следом за ним ныряли в быстро¬
течную ночь. Какой-нибудь час — и Солнце опять покажется из-за
огромного черного щита; до тех пор все они беспомощны, должны идти
по инерции».
Итак, до входа в тень Земли яхты прошли четверть витка —
вот оно, начальное значение (8.9): щ = -90°, взятое нами для
интегрирования уравнений движения. Точнее, надо было бы взять
<Ро = -97, 5°, чтобы до входа в тень пройти ровно четверть витка,
ибо угловое перемещение яхт поперек всей тени составит около
15°. Но не будем гнаться за скрупулезной точностью в реставрации
гонок — ведь не сказано, что яхта прошла до входа в тень точно
четверть витка; можно думать, что она прошла почти четверть вит¬
ка... существенного значения это не имеет (в чем автор убедился,
сделав все-таки расчет траектории для = -97, 5°). Заметим еще,
что время прохождения зоны тени составляет действительно около
часа, как указано в приведенном выше отрывке; через час яхта вы¬
ходит из тени...
«Отныне и на протяжении почти половины околоземной орбиты
надо держать всю эту огромную плоскость ребром к Солнцу. В бли¬
жайшие двенадцать—четырнадцать часов парус будет только поме¬
хой, ведь яхта пойдет навстречу Солнцу и его лучи могут отбросить
ее назад».
Опять обратимся к диаграмме ускорений «Дианы» на первом
витке (рис. 8.6). Действительно, на значительной части полувитка
орбиты плоскость паруса почти параллельна солнечным лучам. Так,
от ip = 48° до (р = 144° наклон плоскости паруса к направлению
светового потока не превышает 20°. На большом участке орбиты
282
Очерк восьмой. Солнцем полны паруса
(от (р = 24° до <р = 168°), где движение идет более или менее
«против Солнца», наклон плоскости паруса к потоку солнечных
лучей не превышает 35-45°. Этот участок проходится за 14 часов.
Строго ребром к Солнцу парус находится в единственной точке
(р = 96°). В этой точке тяга паруса равна нулю.
«Жаль, что нельзя совсем убрать парус, пока он не понадобится
вновь».
Неоправданные сожаления. Без паруса набор энергии тотчас
же прекратился бы. А так, хотя и медленно, но энергия монотонно
увеличивается.
Отметим, что общий характер локально-оптимального управ¬
ления парусом очень близок к такому простому управлению: парус
непрерывно вращается в ту же сторону, в какую движется корабль,
но с угловой скоростью, вдвое меньшей угловой скорости дви¬
жения корабля. Иначе, если в — угол между нормалью к парусу
и направлением солнечных лучей, то локально-оптимальное управ¬
ление близко к следующему:
7Г Ф
0=- + |. (8.10)
При этом предполагается, что обе стороны паруса облада¬
ют одинаковой отражающей способностью (иначе, вместо (8.10),
можно написать аналогичное кусочно-линейное по <р управление).
На рис. 8.7 изображена зависимость в^ для траектории яхты «Диа¬
на». Видим, что отклонения от закона (8.10) не превышают 5°.
«... Через несколько минут число участников сократилось до че¬
тырех. Мертон усомнился в конструкции „Солнечного луча как толь¬
ко увидел его, теперь сомнения оправдались.
Вращение сделало марсианскую яхту слишком устойчивой, она не
хотела лавировать. Вместо того, чтобы повернуться ребром к Солнцу,
огромное кольцо смотрело на него всей плоскостью, и яхту погнало
обратно с предельным ускорением».
Для упрощения рассуждепий примем, что парус «Солнечного
луча» из-за чрезмерной устойчивости совершенно не менял поло¬
жения в пространстве. Тогда вектор ускорения от светового дав¬
ления постоянен по величине и направлению. Но такую задачу
[8.4, 8.5] мы уже разбирали в очерке третьем и видели, что дей¬
ствительно существуют траектории, «заворачивающие обратно», —
хотя бы траектория типа изображенной на рис. 3.15. Если экипажу
«Солнечного луча» не удастся справиться с управлением парусом,
то он не сможет увеличить энергию и достигнуть параболической
Солнцем полны паруса
283
Рис. 8.7. Закон управления парусом вдоль траектории яхты «Диана»
скорости; ему придется «болтаться» в окрестности Земли по огра¬
ниченной траектории, вроде изображенной на рис. 3.15.
Как мы помним по очерку третьему, тип траектории в этом
случае определяется значением постоянных h/y/f, с (рис. 3.4). Для
наших начальных данных (8.7)—(8.9) получим
1 а0
с = —/ = г * -0,022,
2 *(*)
Л = -0,5, — = -0,5/^0,044 = -2,380.
V f
Эта точка на плоскости h/y/f, с попадает как раз в область огра-
ниченных «змееобразных» траекторий, так что световое давление
обязательно «сдует» яхту «Солнечный луч», не дав ей сделать даже
одного витка вокруг Земли. (Однократное вхождение в тень Земли
здесь не играет существенной роли.) На рис. 8.8 изображена рас¬
считанная траектория подобной яхты (но с большим значением
максимального ускорения а()).
284
Очерк восьмой. Солнцем полны паруса
Надо сказать, что и при разумном управлении парусом не все¬
гда удается избежать подобных неприятностей. Если место стар¬
та на исходной круговой орбите выбрано неудачно, то движение
по участку набора параболической скорости может оказаться про¬
исходящим навстречу Солнцу; это раза в два увеличивает время
выхода на параболическую скорость! На рис. 8.9 изображено, что
произошло бы с яхтой Мертона, если бы точка старта на орбите
отвечала = -135°. Любопытно, что если разгон начинать в тени
Земли (<ро = 0), то удалось бы сэкономить около 10 часов по срав¬
нению с временем разгона при (р0 = -90°. Зависимость времени
разгона (при локально-оптимальном управлении) от места старта
изображена на рис. 8.10.
Вернемся, однако, к гонкам.
«Итак, все свелось к поединку между Дианой" и ,Лебедевым"...
По чести говоря, Мертону казалось, что и ,,Лебедеву"уже не догнать
Дианы", и все-таки он нервничал на втором витке, когда вновь
наступило затмение, а затем опять начался долгий, медленный дрейф
против солнечного ветра.
Он знал русских водителей и конструкторов. Они не первый раз
участвовали в гонках. До сих пор им не удавалось победить. Но ведь
Солнцем полны паруса
285
Рис. 8.9. Траектория разгона против Солнца. Ширина тени Земли
для наглядности преувеличена
t, час
Рис. 8.10. Зависимость времени разгона от места старта
с суточной орбиты
286
Очерк восьмой. Солнцем полны паруса
их соотечественник Петр Николаевич Лебедев в начале двадцатого
столетия первым открыл световое давление солнечных лучей. Есте¬
ственно, что они упорствуют. Дмитрий (Марков, капитан уДебеде-
ва“ — В. Б.), наверно, задумал что-нибудь эффектное...
Если ничего не изменится, это будет последний виток для него
и для русских. Под напором солнечного ветра они поднялись по спирали
на тысячи миль. На втором витке они преодолеют земное тяготение
и устремятся в долгий путь к Луне... К счастью, самые трудные
маневры позади, отныне ,Диане“ все время идти прямо по ветру. Как
говорили в старину моряки, легко справляться с судном, когда ветер
дует тебе в спину».
Снова приходится поражаться достоверности описания траек¬
тории яхты. На рис. 8.5 видно, что в момент набора параболической
скорости вектор скорости «Дианы» составляет с направлением сол¬
нечных лучей угол около 25°, а вектор тяги и того меньше (около
15°). При дальнейшем движении по траектории ухода эти углы мо¬
гут только уменьшаться: «ветер в спину». А ведь мы знаем, что
участок выхода на параболическую скорость вовсе не обязательно,
расположен «по ветру», — может быть и наоборот, если неудачно
выбрана точка старта на исходной орбите.
«И тут на пятидесятом часу гонок, когда завершался второй
виток, Марков поднес ему сюрприз.
— Алло, Джон, — небрежно сказал он, включившись в межъях-
тенную сеть, — посмотри-ка, тебе, наверное, будет интересно.
Мертон подвинулся к перископу и включил предельное увеличение.
В поле зрения, такой неправдоподобный среди звезд, очень маленький,
но очень четкий, мальтийским крестом засверкал „Лебедев Вдруг
на глазах у него все четыре крыла отделились от квадрата в середине
и ушли в космос.
Теперь, когда Марков набрал вторую космическую скорость и не
нужно было больше терпеливо крутить по околоземной орбите, копя
кинетическую энергию, он сбросил излишнюю массу. С этой минуты
,,Лебедев “ почти неуправляем, но это неважно, все сложные маневры
позади. Все равно как если бы какой-нибудь яхтсмен прошлого наме¬
ренно освободил лодку от руля и тяжелого киля, зная, что дальше его
ждут попутный ветер и тихое море».
О неточности хронометража («на пятидесятом часу гонок»)
уже говорилось выше. Но вот вопрос: насколько эффективен эф¬
фектный маневр Маркова — сброс части паруса? (Другая часть,
квадратная, осталась.) Намек на ответ содержится в том факте, что
Солнцем полны паруса
287
«яхтсмены прошлого» сбрасывали тяжелый киль, а вовсе не движи¬
тель-парус. Надо сказать, что Марков выбросил в космос не только
излишки паруса, но и второго пилота своей яхты (сопровождаю¬
щий корабль подберет!).
«Мертон... торопливо обрабатывал новые данные. Закончив вы¬
числения, он убедился, что исход гонок далеко не решен».
Интересно было бы проделать вслед за Мертоном такие вы¬
числения. Увеличится ли ускорение яхты Маркова? Предоставляю
3)
читателю самому решить эту задачку .
^ В англоязычном издании книги и этом месте сделана сноска, текст которой,
по-видимому, написал переводчик Andrei lacob. Ниже следует перевод на русский
язык этой сноски.
Первые серьезные исследования проблемы космического полета с помощью
давления излучения от Солнца было предпринято Ф. А. Цандером (1887-1933)
в 1924-1925 гг. Результаты этих исследований были опубликованы в его книге:
Цандер Ф.А. Проблема полета при помощи реактивных аппаратов: Межпланетные
полеты. 2-е доп. изд. М.: Оборонгиз, 1961. См. также следующие книги: Clarke А. С.
eel. Project Solar Sail. New York: Penguin Books, 1990; Friedman L. Starsailing: Solar Sails
and Interstellar Travel. New York: J. Wiley, 1988; Mclnnes C. R. Solar Sailing; Technology,
Dynamics and Mission Applications. Berlin; New York; Springer Verlag, 1999; Поляхо-
ва E. H. Космический полете солнечным парусом. М.; Наука, 1986; Wright J. L. Space
Sailing. Philadelphia: Gordon and Breach, 1992. Интересующийся читатель может так¬
же посетить домашнюю страницу Solar Sail homepage (http://www.kp.dlr.de/SolarSail/)
и множество подобных сайтов.
Гравилет
Очерк девятый
... Индикатор показывал, что бак сух и топлива
не осталось ни капли... Круг несколько минут повисел
без движения, привыкая к этой мысли. Топлива нет.
Тогда как же, черт побери, он попадет на корабль?
И тут он впервые понял, что, может статься, о//
туда вовсе и не попадет...
... И тогда он совершил очередной нелогичный по¬
ступок... сделал то, что делает всякий утопающий',
поплыл. Он плыл, хотя это было крайней глупостью —
плыть в пространстве, где не от чего было оттолк¬
нуться. Он выбрасывал вперед руки и делал ногами
движения, какие делает пловец. Скваммер послушно
загребал пустоту своими широкими броневыми ладо¬
нями, шевелил тяжелыми ногами — плыл, плыл...
В. Михайлов
«Среди звезд»
1. Притяжение тела конечных размеров
Обычно нет надобности помнить, что спутник, летающий по ор¬
бите вокруг Земли, — тело, а не материальная точка. При расчетах
орбит об этом, как правило, и не вспоминают. Но факт остается
фактом: сила притяжения Земли, действующая на тело, отличается
от силы, действующей на материальную точку той же массы, что
и тело, расположенную на том же расстоянии от центра Земли,
что и центр масс тела. Из этого очевидного, но легко забываемого
факта могут следовать удивительные выводы!
Рассмотрим, например, гантелеобразный спутник (рис. 9.1) с
двумя одинаковыми шариками массы т/2 каждый; массой соеди¬
няющего стержня пренебрежем. Пусть стержень перпендикулярен
1. Притяжение тела конечных размеров
289
к направлению центр гантели — центр Земли. Пусть расстояние
от центра масс спутника (то есть от середины стержня) до центра
Земли есть г, полудлина гантели Z, R = л/Р + г2 — расстояние
от шарика до центра Земли. На каждый шарик действует ньютонов¬
ская сила, определяемая силовыми функциями {7, = U2 = //ш/2Д,
и суммарная силовая функция
и =
//777
[im
I
\/l2 + Г2
ту/Г-Н а2’
(9.1.1)
Если спутник не обладает сверхгигантскими размерами, то ве¬
личина а (и тем более а2) очень мала (сравним хотя бы I = 7 м
и г ~ 7 000 000 м). Так что силовая функция U близка к силовой
функции UH = цт/г притяжения Землей материальной точки мас¬
сы т, помещенной в центр масс нашей гантели. На каждый шарик
действует ньютоновская сила
сЮг
F; =
fim
W?
OR
(9.1.2)
Каждая из сил Fu Fj направлена к центру Земли. Суммарная сила
определяется из параллелограмма сил (рис. 9.1) и по модулю ока¬
зывается равной
F =
dU
дг
fim
I
(1 + а2)3/2 ’
(9.1.3)
Суммарная сила F в нашей схеме
направлена к центру притяжения и
почти равна «обычной» ньютонов¬
ской силе Fu = fim/r2. Почти, но не
совсем! Сила F меньше, чем сила
Fu. Иначе говоря, эффект протяжен¬
ности тела в данном случае как бы
вносит добавочную отталкивающую
радиальную силу. И хотя эта доба¬
вочная сила в случае малых спутни¬
ков практически неощутима, но она
есть! И для больших спутников мо¬
жет стать более заметной. Этот факт
и лег в основу нового и несколько
19 Заказ 1667
Рис. 9.1. Притяжение гантели
ньютоновским центром
290
Очерк девятый. Гравилет
неожиданного способа маневров в космическом пространстве, ко¬
торый был предложен автором книги и М. Е. Гиверцем [9.1,9.2].
(Близкую идею независимо высказал Шефер в работе [9.8].)
2. Пульсирующий космический корабль
Ход наших рассуждений сводится к трем пунктам.
1. Сила тяготения, действующая на тело конечных размеров, от¬
личается от силы, действующей на материальную точку той же
массы, сосредоточенной в центре масс тела.
2. Изменяя размеры и форму тела, можно менять величину дей¬
ствующей на него силы тяготения.
3. Этими изменениями размера и формы тела можно управлять
таким образом, что возникающие вариации силы тяготения
с течением времени приведут к существенному отличию тра¬
ектории тела от первоначальной.
Первое из этих утверждений очевидно. Второе является след¬
ствием первого. Третье утверждение будет доказано ниже.
В общем случае движение тела (а не материальной точки)
в ньютоновском поле сил не поддается описанию в конечном виде
и осложнено взаимосвязью движения центра масс тела с движением
около центра масс. Однако, как показано в книге [9.3], симметрич¬
ное тело может двигаться в ньютоновском центральном поле сил
так, что ось симметрии тела нормальна к плоскости орбиты. Такая
ситуация изображена на рис. 9.1. При этом действующая на те¬
ло сила оказывается центральной, зависит только от расстояния г
от центра масс тела до центра притяжения и определяется силовой
функцией U(г). Движение происходит по плоской орбите и пол¬
ностью определяется интегралами площадей и энергии:
Введем оскулирующий фокальный параметр p(t) и оскулируюший
эксцентриситет e(t) орбиты. Радиус-вектор г и скорость V оску-
лирующей орбиты представятся в виде
1 + е cos v ’
V
(9.2.3)
2. Пульсирующий космический корабль
291
Здесь v — истинная аномалия в возмущенном движении. В си¬
лу (9.2.1) оказывается, что в возмущенном движении фокальный
параметр р постоянен, — это известное свойство движений в про¬
извольном центральном поле сил.
Вычислим величину
—— - = — (1 + е2 -h 2е cos и) - — (1 + е cos v) =
2 г 2р р
= ^(е2-\). (9.2.4)
2 р
Теперь в силу (9.2.4) и постоянства р интегралы (9.2.1) и (9.2.2)
запишутся так:
V = Ро, (9.2.5)
^ - -U(г)
г т
= h, (9.2.6)
где h — новая постоянная. В нашем случае U(r) определяется
формулой (9.1.1) и интеграл (9.2.6) после преобразований может
быть записан в виде
е2 + — = К, а = ~. (9.2.7)
г 1 +а2 + VI +а2 Г
Отсюда видно, что е является функцией от г и не постоянно.
В процессе движения оскулирующий эксцентриситет e(t) и ра¬
диус-вектор r(t) изменяются так, что выполняется соотношение
(9.2.7). Поэтому можно рассмотреть движение на плоскости е2, г/р
согласно (9.2.7). Однако реальное движение может происходить
не во всей плоскости е\г (г = r/р), а только в некоторой ее ча¬
сти. В самом деле, из первого равенства в формулах (9.2.3) имеем
2 9 2
е cos“ v — (pjr - 1) , следовательно,
е2^ (^-\) =е;(г). (9.2.8)
Таким образом, на плоскости е2, г движение может происхо¬
дить только выше кривой e2(f), определяемой уравнением е2 =
(p/r - I)2. Очевидно, ei(f) -> оо при г —> 0, е2 = 0 при p/r = I
и е2 -» 1 при г —у оо. Кроме того, е2 = 1 при г/р = 1/2 (рис. 9.2).
19*
292
Очерк девятый. Гравилет
Рис. 9.2. Диаграмма движения пульсирующей гантели
Построим в области (9.2.8) реального движения кривую (9.2.7)
при фиксированных р и h (рис. 9.2). При увеличении г от 0 до оо
эксцентриситет монотонно возрастает от е2 = -оо до е2 = h. Реаль¬
ное движение определяется дугой кривой (9.2.7), лежащей в обла¬
сти, определяемой неравенством (9.2.8). Пересечение кривой (9.2.7)
страничной кривой е2 = е2(г), определяемой соотношением, сле¬
дующим из (9.2.8), дает экстремальные точки траектории: г = гт\п
(при этом е = emin) и f = rmax (при этом е = етах). Движение тела
периодично по е и г, так что в плоскости е2, г оно происходит,
например, по дуге 1—2 (рис. 9.2) от точки 1 (е = emin, г = Fmjn)
к точке 2 (е = етах, г = гтах), затем обратно от точки 2 к точке 1
и т.д. Если бы вместо тела была материальная точка той же массы
(I = 0), то, как следует из (9.2.7), эта точка двигалась бы по не¬
возмущенной кеплеровской эллиптической траектории е — const
(например, туда и обратно по отрезку 2—3 на рис. 9.2).
Итак, при движении гантели, нормальной к плоскости своей
орбиты, оказывается, что эксцентриситет периодически колеблет¬
ся между наименьшим и наибольшим своими значениями. Когда
гантель находится ближе всего к Земле, эксцентриситет минима¬
лен; в точке орбиты, наиболее удаленной от Земли, эксцентриситет
максимален. Эти колебания эксцентриситета невелики, и в целом
орбита гантели будет похожа на кеплеровский эллипс; спутник-
гантель будет двигаться в ограниченной окрестности Земли, не уда¬
ляясь от нее.
Если уметь изменять эксцентриситет орбиты заметным обра¬
зом, то первоначальную эллиптическую (е < 1) орбиту можно пре¬
вратить последовательными изменениями эксцентриситета в гипер¬
болическую (е > 1), и спутник улетит в дальний космос. Но у спут¬
2. Пульсирующий космический корабль
293
ника — материальной точки эксцентриситет орбиты неизменен;
а в только что разобранном случае спутника-гантели эксцентри¬
ситет хоть и меняется, но периодически и в небольших пределах.
Систематического изменения эксцентриситета нет.
При ограниченных размерах спутника большого изменения
эксцентриситета как будто получить нельзя.
Однако потребуем следующее (мы подошли к самому важ¬
ному пункту обсуждения). Пусть рассматриваемая гантель может
пульсировать: в нужные моменты сжиматься в точку или мгно¬
венно выпрямляться на полную длину. Возможность мгновенных
пульсаций, впрочем, не принципиальна и введена для упрощения
рассуждений. Можно рассматривать и медленные изменения дли¬
ны гантели.
Итак, пусть гантель начинает движение в ближайшей к Земле
точке и пройдет полувиток орбиты до наиболее удаленной от Земли
точки (вдоль отрезка 1—2 на рис. 9.2); в этой точке эксцентриситет,
как уже говорилось, достигнет наибольшего значения (е = emL,
г = fmах). Тут мы сложим обе части гантели, мгновенно уменьшив
ее длину «до нуля» (это значит, что длина сложенной гантели прене¬
брежимо мала по сравнению с длиной открытой гантели). С этого
момента спутник будет двигаться, как материальная точка, то есть
по дуге кеплеровского эллипса (вдоль отрезка 2—3 на рис. 9.2), со-
(|)
храняя только что полученное значение эксцентриситета е = efnax
постоянным.
Вернувшись в точку, ближайшую к Земле (это будет, конеч¬
но, точка, отличная от первой «ближайшей» точки), мы донесем
в сохранности приобретенное значение эксцентриситета. Здесь мы
мгновенно откроем гантель на полную длину! Теперь, на новом
полувитке орбиты, за счет раскрытой гантели снова будет увеличи¬
ваться значение эксцентриситета (вдоль отрезка 3—4 на рис. 9.2).
Когда во второй раз достигнем самой удаленной от Земли точки,
эксцентриситет вшах будет больше, чем при первом максимальном
удалении (втах > Стах)- Сложим гантель и понесем благоприобре¬
тенную величину эксцентриситета в сохранности до того момента,
когда снова можно будет открыть гантель, и т. д. В конце кон¬
цов, после многократных пульсаций гантели, можно добиться су¬
щественного изменения эксцентриситета орбиты и, может быть,
даже достичь гиперболического значения эксцентриситета (е > 1)
и уйти из поля тяготения Земли.
294
Очерк девятый. Гравилет
3. Отстал от спутника — плыви брассом!
295
В результате описанного процесса энергия, затраченная на
«включение» и «выключение» гантели, перекачивается в энергию
движения аппарата по орбите, что и позволяет разогнать аппарат
вплоть до ухода из поля тяготения Земли. Орбита аппарата пред¬
ставляет при этом раскручивающуюся спираль с числом витков,
равным числу пульсаций гантели. Космический аппарат, орбита
которого меняется за счет вариаций действующей на аппарат гра¬
витационной силы, назовем гравилетом.
Внутренние силы, затраченные на «включение» и «выключе¬
ние» гантели, дают заметный внешний эффект потому (и только
потому), что существует внешнее силовое поле, которое с ними
взаимодействует. При этом необходима определенная резонансная
настройка между внешними и внутренними силами. Не это ли имел
в виду в своей знаменитой истории барон Мюнхгаузен?
3. Отстал от спутника - плыви брассом!
Не правда ли, захватывающая перспектива: вместо реактивного
двигателя поставить электромотор, чтобы он вовремя сматывал или
разматывал трос, соединяющий шарики гантели, или даже... поса¬
дить для этой цели «матроса»?
Реальные оценки несколько охлаждают загорающийся энтузи¬
азм. За п циклов (включения и выключения гантели) эксцентри¬
ситет изменится примерно до значения
еп ~ е0 + п О + в1)
(от своего начального значения е0). Так что для достижения е ~ 1
необходимо п ~ (р/1)2 циклов (оборотов по орбите). Если исходная
орбита имеет р = 10 000 км, а I = 1 км, то п ~ 10х оборотов. Так
как даже у поверхности Земли один оборот спутника совершается
за полтора часа, а чем дальше от Земли, тем период обращения
больше, то такому количеству оборотов соответствует время полета
Т > 1,5 • 10х час, что равно примерно 20 000 лет! Вряд ли наш
«матрос» согласится на столь нудную работу. При этом отношение
возмушаюшего ускорения к основному ускорению силы тяготения
на исходной орбите имеет порядок / ~ (1/р)2.
Однако если при той же орбите взять гантель с длиной I =
10 км или даже I = 100 км, то соответственно получим / ~ 10_6
296 Очерк девятый. Грэвилет
*
*
3. Отстал от спутника — плыви брассом!
297
или / ~ 10-4. Эти числа дают порядок ускорений такой же, какой
обеспечивается ионными и плазменными двигателями малой тяги.
Но для этого космический аппарат должен иметь протяженность
в десятки, а то и сотни километров! Для I = 100 км число вит¬
ков, потребных для разгона до параболической скорости, снижает¬
ся до п ~ 104, а нижняя оценка времени разгона — до двух лет, что
уже по крайней мере не выглядит юмористически; но надо помнить
о сотнях километров сматываемого и разматываемого троса и свя¬
занных с этим проблемах. Если дать волю воображению и пред¬
ставить космический корабль длиной в 1000 км (в космосе места
много), то такой корабль разогнался бы до параболической скоро¬
сти всего за сотню витков, что заняло бы примерно неделю времени!
Отметим еще следующее обстоятельство. Эффективность кос¬
мического корабля тем больше, чем больше масса центрального
тела и чем ближе может находиться аппарат к центру этого тела.
Масса Солнца велика, но велик и размер его; близко к центру Солн¬
ца не подлетишь. К центру Земли можно подлететь близко; но масса
Земли сравнительно мала. Однако в безграничных просторах космо¬
са есть много звезд, словно предназначенных для маневрирования
гравилетов в окрестности этих звезд. Это так называемые «белые
карлики», размеры которых сравнимы с размерами планет, а мас¬
сы с массой Солнца. В окрестности «белых карликов» разгон
гравилета вплоть до выхода из сферы притяжения звезды может со¬
вершиться в десятки и сотни раз быстрее, чем разгон в окрестности
Земли. В табл. 9.1 даны характеристики разгона 140-километрового
Таблица 9.1
Небесное
тело
Начальное
расстояние
корабля до
центра
небесного
тела, км
'“(г)’
Количество
витков до
разгона
Время
разгона
Земля
7- I03
10~4
Ю4
не менее двух лет
Солнце
7- I05
кг"
Ю8
не менее 80 лет
Белый карлик
(Сириус-В)
2- I04
Ю'5
ю5
несколько часов
(не менее 1,5 часа)
298
Очерк девятый. Гравилет
+
4. Гравилет и читатели
299
космического корабля в окрестности Земли, Солнца и «белого кар¬
лика». Полудлина гравилета принята равной I = 70 км. Может
быть, жители планетных систем «белых карликов» пользуются для
космических путешествий не ракетами, а гравилетами?
Не обязательно понимать под пульсациями изменения формы
корабля. Может быть, с теми же результатами, удастся заставить
пульсировать внутри неизменного корабля массу жидкости [9.4].
Можно, наверное, вообще отказаться от пульсаций, если за¬
ставить корабль каким-либо способом в нужные моменты повора¬
чиваться нужным образом (с помощью маховиков, например). Ведь
сила притяжения зависит и от того, как расположен корабль по от¬
ношению к Земле. Тогда энергия, затраченная на поворот гравиле¬
та, перейдет в энергию, изменяющую орбиту корабля; сам корабль
сохраняет свою форму неизменной, что, конечно, удобнее пуль¬
сирующего гравилета. Но принцип остается тот же — изменение
орбиты гравилета за счет вариации силы тяготения, действующей
на него.
Наша цель, однако, не инженерная разработка аппарата, а до¬
казательство принципиальной возможности эволюции орбиты пуль¬
сирующего тела. Принципиально говоря, космонавт, отставший
от спутника и потерявший индивидуальный двигатель (любимая
фантастами ситуация), может догнать этот спутник, меняя свою
орбиту целенаправленными пульсациями. Пусть плывет брассом!
Тем самым приобретается шанс спастись. Но не спрашивайте меня,
сколько на это уйдет времени.
4. Гравилет и читатели
Опубликование статей [9.1, 9.2] о гравилете вызвало до¬
вольно оживленную реакцию читателей. Инженер И. Троицкий
из г. Тулы пишет в редакцию журнала «Техника — молодежи»
о статье В. Белецкого и М. Гиверца, опубликованной в журнале
«Космические исследования»: «Сообщение произвело на меня
ошеломляющее впечатление. Со школьных лет мы привыкли
к мысли, что перераспределение масс в „замкнутой системе"
(например, спутнике) не влияет на траекторию ее движения.
Оказывается, это далеко не так... Возникает вполне реальная
возможность — за счет вариации формы корабля, перекачки
жидкости внутри него, определенных маневров изменить на¬
правление полета и отправиться в далекое путешествие. „Кос¬
мические исследования“ — сугубо научный журнал с ограничен¬
ным гиражем... Было бы неплохо, если бы редакция попросила
300
Очерк девятый. Гравилет
кого-либо из авторов написать популярную статью, рассчитан¬
ную на массового читателя».
Откликаясь на эту просьбу, редакция журнала «Техника —
молодежи» опубликовала статью [9.2]. Немедленно было полу¬
чено послание от одного сердитого московского инженера:
«Уважаемые товарищи! В журнале № 3 за текущий год
опубликована статья профессора В. Белецкого „ Гравилет“... Рас¬
суждения, приводимые в статье, основаны на простом невеже¬
стве и свидетельствуют о порочной практике присвоения уче¬
ных званий лицам, не представляющим самых элементарных
вещей... Давно пора разоблачить некоторых докторов, не же¬
лающих признавать очевидные, установленные наблюдениями
закономерности; в том числе и автора ,,Гравилета“».
Вот так письмо!
Не смог «умолчать о совершенно неверных толкованиях
В. Белецкого» и читатель из Джезказгана: «Внутренние силы
космического аппарата никак не могут повлиять на величину
ньютоновской силы притяжения этого аппарата к Небесному
Телу. Поэтому „гантель“ профессора Белецкого до и после ее
раздвижения должна занимать такое положение относительно
Небесного Тела, при котором ее масса всегда будет находиться
на неизменном расстоянии от центра Небесного Тела, ибо этой
ньютоновской силой масса космического аппарата как будто бы
привязана к Небесному Телу. Поэтому хитромудрые измышления
профессора и доктора физико-математических наук В. Белецко¬
го явились результатом полного непонимания им физических
законов небесной механики, в которых, по-видимому, он „пла¬
вает брассом“».
Автор с уважением относится к мнению читателей и по¬
нимает, что «природе наши звания — ничто; перед ней человек
как голенький» Но как воодушевленные, так и негодующие
читатели явились жертвами двух недоразумений.
Первое недоразумение основано на тезисе: «внутренние си¬
лы не способны изменить движение центра масс системы». Это,
конечно, верно, но лишь при отсутствии каких бы то ни бы¬
ло внешних сил. В реальных условиях, однако, всегда найдутся
внешние к данной системе силы. И во многих случаях движение
определяется именно взаимодействием внутренних и внешних
сил. Пример: паровоз (трение колес о рельсы!). Другой пример:
гравилет.
^ Афоризм принадлежит известному сибирскому геологу, члену-корреспонденту
АН СССР В. П. Солоненко (газета «Восточно-Сибирская правда» от 18 декабря
1966 г.).
5. Гравилет как резонансное явление
301
Второе недоразумение происходит от нечеткого понимания
того, что ньютоновская гравитация действует на протяженные
тела и что поэтому их движение, строго говоря, не кеплерово.
Приведем яркий пример «гравилетного» эффекта [9.3].
Уравнения движения гантели в ньютоновском центральном
поле сил имеют следующее строгое частное решение: центр масс
гантели движется по плоской круговой орбите произвольного
постоянного радиуса iZ0, причем центр притяжения совпадает
с центром орбиты; сама гантель при этом все время расположена
вдоль текущего радиус-вектора орбиты. Скорость V центра масс
гантели определяется формулой
_ 1 4- а2 а
у- J—
(1 -оС-У Д0
где а = l/Ro, а I — полудлина гантели. Эта круговая ор¬
бита не кеплерова (для кеплеровой орбиты круговая скорость
определяется формулой V2 = fi/Ro). При а ^ 0,47 окажется
V2 ^ 2ц/Rq, т. е. V будет больше параболической скорости.
Поэтому, если гантель с таким значением а «схлопнуть» в ма¬
териальную точку, то она сорвется с круговой орбиты и улетит
в бесконечность. Для этого, однако, гантель должна иметь раз¬
меры порядка размеров орбиты! Для аппарата же умеренных
размеров можно, как мы видели, использовать этот же принцип,
заменяя однократное «схлопывание» гантели разумно организо¬
ванным многократным ее включением и выключением.
Важно подчеркнуть, что доказательство возможности осу¬
ществления гравилетного маневрирования получено не словес¬
ными рассуждениями, а путем точного решения строгих уравне¬
ний движения.
5. Гравилет как резонансное явление
Гравилет представляет собой пример удивительных закономер¬
ностей резонансных явлений. Управление гравилетом принципи¬
ально резонансно. Именно в этом состоит «разумная организа¬
ция» управления. Действительно, полный цикл пульсаций гравиле¬
та (совпадает со временем одного оборота по орбите. Иначе говоря,
имеет место резонанс 1 : 1 между двумя характерными частотами
системы. При других резонансных соотношениях между характер¬
ными частотами эволюция орбиты будет протекать, может быть,
медленней. Если бы резонанса не было, глубокой эволюции ор¬
биты получить не удалось бы, подобно тому, как беспорядочное
болтание ногами не приводит к раскачке качелей.
302
Очерк девятый. Гравилет
Резонансная сущность гравилетной идеи хорошо продемонстри-
2)
рована А. Б. Митницким, результаты которого изложены ниже \
Ограничимся плоским движением и плоской схемой грави¬
лета, динамически-симметричного относительно оси, нормальной
к плоскости орбиты.
Тогда в силовой функции (6.1.6), описывающей в высокоточ¬
ном приближении воздействие ньютоновского поля на гравилет,
надо положить С = А + В = J, j" = 1. Получим
//га 1 //
г 2 г3
Уравнения движения в полярных координатах г, р имеют вид
U = -V. (9.5.1)
“ ' т»-*
и с2 3 uj
Г=--2+~г (9,5'2)
г2ф = с. (9.5.3)
Кроме того, для угла гр между фиксированными направлени¬
ями в пространстве и в гравилете получим уравнение
С\ с ,
* = ту - -7. (9.5.4)
2 J г~
В (9.5.2)-(9.5.4) С\ и с — постоянные.
Момент инерции J является управлением — переменным
за счет пульсации гравилета. Потребуем, чтобы 0 < Jmin < J ^ «7тах,
и будем считать J = J(p) = Jo- f(p) явной функцией от полярного
угла р.
Проделаем так называемое «преобразование Бине»: введем но¬
вую зависимую переменную и = р/r, где р = с2/ц, и преобразуем
уравнение (9.5.2) к новой независимой переменной р, используя
при этом (9.5.3). Тогда получим вместо (9.5.2)
d2u я/ ч , 3J0 ,
—j +и = 1 + ef(<p) -и , е = -—(9.5.5)
dp1 vr/ 2 тр2 '
Теперь зададимся конкретной зависимостью f(p). По поста¬
новке f(p) > 0. Чтобы отразить «пульсации» гравилета, следует
считать f(p) периодической функцией своего аргумента. Примем
простейшую зависимость, удовлетворяющую поставленным требо¬
ваниям:
f(p) = 1 + S sin (ар - /3). (9.5.6)
Автор благодарит А. Б. Митницкого за предоставление этих материалов.
5. Гравилет как резонансное явление
303
Здесь постоянная д удовлетворяет условию 0 < 6 < 1, а постоян¬
ная а пока произвольна, как и постоянная /3.
Обратимся к уравнению (9.5.5). При е = 0 (Jo = 0) получаем
случай движения материальной точки в ньютоновском поле сил и,
естественно, решение уравнения (9.5.5), отвечающее кеплеровым
орбитам. Это решение записывается в виде
и = 1 + е cos (р - из), (9.5.7)
где е имеет смысл эксцентриситета орбиты, а из — долготы перигея.
Вспоминая, что г = р/и, заключаем, что р — фокальный параметр
орбиты. Параметр е очень мал. При е Ф 0 естественно искать
решение уравнения (9.5.5) в том же виде (9.5.7), считая только е
и из переменными. Задача сводится тогда к отысканию функций
е(р) и из(р). Можно сказать, что (9.5.7) является «порождающим
решением» для искомого.
Но мы несколько улучшим порождающее решение из следу¬
ющих соображений. Наше движение эквивалентно движению ма¬
териальной точки в некотором центральном, но не ньютоновском
поле сил (9.5.1). Отличие от ньютоновского поля сил обязательно
приведет к «разомкнутости» орбиты в том смысле, что перигей ор¬
биты будет иметь систематический «уход». Хорошо бы этот эффект
хотя бы частично учесть уже в порождающем решении. С этой це¬
лью положим и = 1 + q и подставим в (9.5.5) с учетом (9.5.6). Тогда
для q получим уравнение
0+А», = «*,.„). Л2 = ' - 2,, 1 (9 5 8)
Ч>) = 1 + ?2 + Sin (а<р - /3) ■ [ I + 2(7 + q2]. у
В качестве порождающего решения уравнения (9.5.8) можно
теперь взять решение этого же уравнения при F = 0:
q = е cos (\<р - ш), q = -е\ sin (А<р - и). (9-5.9)
В исходных переменных это будет отвечать траектории
V
т — .
1 -f- е cos (Atp - из)
Так как А Ф 1, то эта траектория, очевидно, представляет собой
незамкнутую розетку типа изображенной на рис. 1.12 я. Теперь ре¬
шение уравнения (9.5.8) будем искать в виде (9.5.9), считая только е
304
Очерк девятый. Гравилет
и ш переменными. Получаем уже знакомую нам ситуацию, приво¬
дящую к уравнениям типа (1.6.4):
de s
— = --F(e cos (Хр -w),p) sin (Ар - а;),
dp А
— = — F(e cos (Хр - а;), <р) cos (Хр - а;).
dp Хе
(9.5.10)
В силу конструкции (9.5.8) функции F(q, р) возможны только
следующие резонансы между частотой а пульсаций гравилета и ча¬
стотой А его орбитального движения:
а = кХ, к = 1, 2, 3.
(9.5.11)
Применяя стандартную процедуру метода осреднения к уравне¬
ниям (9.5.10), сразу получаем следующий результат: если а не близ¬
ко к А, 2А или ЗА, то орбита не эволюционирует — правые части
уравнений (9.5.10) в среднем равны нулю и е « во, ш и щ. Наобо¬
рот, при выполнении одного из условий (9.5.11) орбита подвержена
глубокой эволюции, описываемой в первом приближении метода
осреднения уравнениями
de еб ,
= ~2Х 05
dw ед к, . . /
Ир = г\ еш
(9.5.12)
где выражения J?(е), J*(e) для резонансов к = I, 2, 3 имеют соот¬
ветственно вид:
Je
j3 - 1е2
Je ~ 4е ’
J£ = к
э 1
Jl = -Ае.
(9.5.13)
Из (9.5.13) и (9.5.12) видно, что наибольшая скорость эволюции
орбиты по эксцентриситету отвечает резонансу 1 : 1. В этом случае
de
— ~ е, в то время как для резонансов 1 : 2 и 1:3 имеем соответ-
dp
de de 2
ственно — ~ ее и — ~ ее .
dp dp
6. Гравилет и писатели
305
Система (9.5.12) интегрируется в квадратурах; но это уже не столь
интересно: наша цель была убедиться в резонансной природе гра-
вилетного эффекта, и мы убедились в этом.
6. Гравилет и писатели
Идея гравилета не только получила развитие в научной ли¬
тературе [9.5-9.8], но и нашла отражение в популярных и даже
художественных произведениях. Журнал «Квант» №2 за 1974 год
откликнулся статьей И. И. Воробьева «Необычное путешествие».
Автор этой статьи так перепоставил задачу о гравилете, что ее
оказалось возможным изложить языком элементарной математи¬
ки: «гравилетная» траектория склеивается из участков чисто кепле-
ровых орбит. (В эту статью вкралась непринципиальная ошибка:
нужно вместо cos (а/2) писать cos3(a/2).) В своей научно-попу¬
лярной книге «Новая занимательная астрономия» («Наука», М.,
1972) В. Н. Комаров посвятил раздел описанию идеи гравилета. Но,
пожалуй, самый яркий отклик был помещен на страницах журнала
«Земля и Вселенная» №2 за 1972 год — в виде научно-фантастиче¬
ского рассказа В. Н. Комарова «Этюдное решение». Вот выдержки
из этого рассказа:
«Транспортный звездолет „Омикрон44 совершал очередной
рейс к Мегосу, имея на борту двенадцать человек экипажа и 360
пассажиров. Капитан Менг и штурман Гасконди молча смотрели
на табло и оба отчетливо понимали, что положение безвыход¬
ное... Ошибка произошла в момент выхода из гиперпростран-
ства. Что-то не сработало в сложном хозяйстве автоматическо¬
го управления кораблем. Ничтожное отклонение от программы,
случайная флуктуация, впрочем, ее оказалось достаточно, чтобы
звездолет оказался в пяти парсеках от расчетной точки... А здесь
его поджидал белый карлик — маленькая звездочка с огромной
плотностью и могучим тяготением.
Были включены на полную мощность все двигатели. Это
лишь спасло „Омикрон41 от падения в бездну, но было недоста¬
точно, чтобы разорвать цепи притяжения. Теперь корабль дви¬
гался вокруг карлика по замкнутой орбите на среднем расстоя¬
нии около 20 тысяч километров от центра звезды, и всей мощи
его двигателей не хватало, чтобы вырваться из плена. К тому же
расчетное время истекало и запасы энергии подходили к концу.
...Карлик был слишком близко. И хотя звездолет охраняло
защитное поле, Менг почти физически ощутил горячее дыхание
20 Заказ 1667
306
Очерк девятый. Гравилет
звезды. Пока охраняло... Но через шесть с половиной часов
энергия иссякнет, и тогда...
...За свою долгую космическую службу капитан Менг не раз
попадал в критическое положение. Но это были ситуации, из ко¬
торых существовал выход. Тогда все решали опыт и находчивость
командира, так как требовалось в считанные секунды найти оп¬
тимальное решение. И до сих пор Менг всегда его находил.
Но сейчас выхода не было, о чем неумолимо свидетель¬
ствовал несложный расчет, который мог бы произвести любой
студент.
... Нет, все равно надо бороться. Не сдаваться ни при каких
обстоятельствах. Даже, если безнадежно...
— ...Надо еще раз проверить все варианты.
— Но это же элементарный случай! — взорвался Гаскон-
ди. — Какие могут быть варианты?
Капитан Менг понимал это ничуть не хуже своего штурма¬
на. Классическая ситуация, которую исследовали вдоль и попе¬
рек еще на заре космических полетов и которой много лет уже
никто не интересовался. Новейшие средства навигации избавили
космонавтов от подобной угрозы. По крайней мере, за послед¬
ние пятьдесят лет в гравитационные ловушки не попадал ни один
корабль. И только „Омикрону" не повезло...
Но, может быть, именно в этом и заключен их единствен¬
ный шанс? В том, что теоретически этой проблемой давно не за¬
нимались. А наука ведь не стоит на месте. И если еще раз взгля¬
нуть на безвыходную ситуацию, в которой они оказались, с по¬
зиций современного знания, возможно, и отыщется вариант,
не учтенный классической навигацией.
Во всяком случае, искать надо. Но как убедить Гасконди?
...Менг встал и подошел к штурманскому креслу:
— Подумаем вместе. А что, если...
Они не заметили, как в рубку вошел Вель, и увидели его,
когда он уже стоял возле главного пульта и, близоруко щурясь,
вглядывался в табло.
Вообще-то, заходить в командную рубку пассажирам вос¬
прещалось самым строжайшим образом. Но Вель был не про¬
сто пассажиром. В основе конструкции „Омикрона" лежала со¬
зданная им физическая теория. Велю принадлежало бесчислен¬
ное множество оригинальных идей, оказавших заметное влияние
на развитие физики и астрофизики. В университете Мегоса он
собирался прочитать курс лекций по теории гиперпространства.
Но все же на „Омикроне" Вель летел как пассажир, и Менг
с тревогой подумал о том, что их бедственное положение теперь
перестало быть секретом.
6. Гравилет и писатели
307
— Любопытная ситуация, не правда ли?
В создавшемся положении эти слова прозвучали довольно
странно, да и произнесены они были с каким-то неуловимым
оттенком не то сарказма, не то непонятного удовлетворения.
Гасконди только пожал плечами.
— Не хватает мощности, да? — спросил Вель, оторвавшись,
наконец, от табло.
— Как видите, — не слишком вежливо буркнул Гасконди.
— И тепловая зашита иссякнет через несколько часов?
— Через шесть с половиной, — машинально ответил Менг.
— Так, — неопределенно протянул теоретик. — М-м, так...
В его глубоко посаженных глазах вспыхнули азартные ис¬
корки, и в этот момент он невольно напомнил Менгу охотни¬
ка, неожиданно увидевшего редкую дичь. Казалось, Веля совсем
не интересовало, что дичью-то в сложившейся ситуации был как
раз он сам...
...Вель привычным усилием воли отбросил все, кроме усло¬
вий необычной задачи, поставленной нелепым стечением об¬
стоятельств. Задачи, которая по всем существующим канонам
не имела положительного решения. Но Вель всю жизнь решал
именно такие задачи...
— Могу я воспользоваться вашим вычислителем? — спро¬
сил он, на секунду выйдя из задумчивости.
...Менг и Гасконди молча ждали. Наконец Вель оторвался
от клавишей и вздохнул не то облегченно, не то разочарованно,
но в его прищуренных серых глазах снова заблистали беззабот¬
ные искорки.
— Вы играете в шахматы? — осведомился он будничным
голосом.
— Да, — сказал Менг.
— Знаете, что такое этюдное решение? Позиция начисто
проиграна, но есть ход, казалось бы ускоренно ведущий к пора¬
жению. Но именно этот странный ход приносит победу...
Теперь Менг точно знал, что Вель нашел-таки выход.
— И что же? — спросил он, не в силах сдержать нетерпение.
— ...Необходимо включить тягу, — сказал Вель. Он быстро
набросал на листе несколько цифр и протянул бумажку Менгу.
— Но, — пробормотал смятенно Гасконди, — ведь это же
все равно ничего не даст. Разве что сделает орбиту более вытя¬
нутой.
— Вот, вот, — сказал Вель.
...Но в душе капитан Менг верил Велю. Без колебаний
протянул он руку к главному пульту и один за другим перевел
на несколько делений четыре красных рычага.
308
Очерк девятый. Гравилет
Гасконди побледнел. Послышалось характерное жужжание
двигателей, щелкнули реле противоперегрузочной защиты.
— Может быть, теперь вы объясните? — попросил Менг.
— Если я не ошибаюсь, — медленно начал Вель, — „Омик¬
рон44 состоит из двух обособленных частей?
— Да, — подтвердил Менг. — В одной — командный ком¬
плекс и двигатели, в другой — каюты и подсобные помещения.
— И эти части можно отделить и отвести друг от друга
на значительное расстояние?
— Да, такая возможность предусмотрена на случай аварии
или ремонта силовых установок. Обе части разводятся и сводятся
с помощью специального „пульсатора44.
— А каково максимальное расстояние между ними?
— Сто пятьдесят километров.
— Достаточно и ста сорока, — пробормотал Вель.
— Вы хотите избавиться от пассажирского отсека? — на¬
конец заговорил Гасконди. — Но тяги все равно не хватит.
— Нет, — энергично возразил Вель. — Это было бы слиш¬
ком просто. Карлик нас так легко не отпустит... Тут совсем
другая идея.
— Мы теряем время, — вмешался Менг. — Может быть...
— О! Времени у нас вполне достаточно, — невозмутимо
сказал Вель. — Так вот... вам, конечно, знакома идея пульсиру¬
ющего космолета? Гасконди и Менг недоуменно переглянулись.
— Да, — заметил Вель. — Это очень старая и давно забытая
идея...
— Смутно я что-то припоминаю, — медленно произнес
Менг. — Встречал в старых учебниках3*... Если не ошибаюсь,
дело в том, что космический корабль не точка, и его масса
распределена по некоторому объему.
— Вот, вот, — оживился Вель, — если разделить наш звез¬
долет на две части, то равнодействующая сил тяготения, к ним
приложенных, окажется меньше той силы, которая действует
на „Омикрон44 сейчас.
Он говорил четко и ясно, словно читал лекцию студентам.
— А это значит, — подхватил Менг, — что на растянутый
звездолет действует сила отталкивания?
— И если в апоцентре соединять обе части, а в перицен¬
тре — разъединять, то „Омикрон44 сойдет с кеплеровской орбиты
и начнет двигаться по раскручивающейся спирали.
— М-да..., — протянул Менг.
3* По случайному стечению обстоятельств журнал «Земля и Вселенная» поме¬
стил рецензию на один из таких «старых учебников» (на первое издание данных
«Очерков») сразу после цитируемого рассказа. — В. Б.
6. Гравилет и писатели
309
— Я тоже вспомнил, — неожиданно заговорил Гасконди
возбужденно. — Чудесно, превосходно, гениально!... — он нерв¬
но расхохотался. — Но, насколько я помню, чтобы преодолеть
таким способом даже земное притяжение, кораблю необходимо
несколько лет. А притяжение карлика?...
— В том-то вся и штука, —. невозмутимо произнес Вель. —
Притяжение в данном случае работает на нас. Чем массивнее
звезда или планета, тем скорее будет достигнута скорость осво¬
бождения. В том-то и парадокс!
— Сколько же часов нам потребуется? — спросил Менг.
— Думаю..., часа полтора, не больше4*.
— Вы гений, — улыбнулся капитан и занял место у пульта.
— Надо только выбрать оптимальные моменты для разде¬
ления и сближения, — предупредил Вель.
— Понимаю, — отозвался Менг, нажимая клавиши вычис¬
лителя.
— Приступаю к операции через шесть минут...
Это было невиданное зрелище. Гигантский звездолет как бы
распался на две части. Они то расходились, отделяясь друг от дру¬
га, то снова сближались, объединяясь в единое целое. И в процес¬
се этого небывалого „космического танца “ смертельная орбита,
по которой двигался „Омикрон“, стала постепенно раскручи¬
ваться.
Могучая сила тяготения, подчинившись силе человеческого
разума, уверенно уводила звездолет все дальше и дальше от угро¬
жающей звезды».
4* Увы, не меньше, чем полтора часа. Время разгона может отличаться от этой
нижней оценки на порядки. — В. Б.
Очерк десятый
Межпланетные полеты -
малые тяги для больших целей
Мы были узники на шаре скромном,
И сколько раз, в бессчетной смене лет,
Упорный взор Земли в просторе темном
Следил с тоской движения планет!
В. Брюсов
«Сын земли»
Мы должны нести другим планетам
Благовестье маленькой Земли!
В. Брюсов
«Детские упования»
1. Вступление
Достижения человечества в покорении космоса велики. За две¬
надцать лет, с 1957 по 1969 год, пройдена дистанция от запуска
первого искусственного спутника до высадки первой экспедиции
на Луну. Однако заветнейшая цель — экспедиции на другие пла¬
неты — еще впереди. Осуществление таких экспедиций — трудная
задача, которая может быть разрешена различными путями. Может
быть, сборка межпланетного корабля и заправка его химическим
горючим будет осуществлена на орбите около Земли. А может быть,
корабль стартует с такой орбиты не с помощью реактивных двига¬
телей на химическом горючем, а с помощью двигателей малой тяги.
Это, например, разрабатываемые конструкторами ионные и плаз¬
менные двигатели, о которых уже говорилось в седьмом очерке.
Максимальное ускорение, которое такие двигатели смогут сооб¬
щить межпланетному кораблю, составляет всего лишь несколько
2. Побольше полезного груза, поменьше топлива
311
мм/сек2. Однако, действуя постоянно, в течение всего полета (не¬
сколько месяцев!) даже такая малая тяга создает большие возмож¬
ности для маневрирования корабля в космосе. Можно представить,
как корабль, раскручиваясь по спиральной траектории вокруг Зем¬
ли, достигает параболической скорости и уходит в космос, курсом
на Марс. В окрестности Марса двигатели малой тяги постепенно
затормозят корабль до параболической (относительно Марса) ско¬
рости; затем корабль по спиральной траектории выйдет на окон¬
чательную орбиту относительно Марса и останется на ней, пока
«космический бот» с экспедицией опустится на поверхность пла¬
неты и вернется назад.
Спиральные траектории с малой тягой в окрестности планет
уже рассматривались в одном из предыдущих очерков этой кни¬
ги. Здесь же рассмотрим траектории полета с малой тягой между
планетами. Этот участок начинается после достижения параболи¬
ческой скорости относительно одной планеты и кончается выходом
на параболическую скорость относительно другой планеты. Поэто¬
му притяжение планет на этом участке совершенно несущественно,
и им можно пренебречь.
Движение корабля определяется притяжением Солнца и тягой
реактивных двигателей. В такой постановке и будем рассматри¬
вать задачу. Дальнейшее изложение будет следовать, в основном,
работам [10.1-10.3] автора и его коллег — В. В. Голубкова, В. А. Его¬
рова, В. Г. Ершова. Читатель, заинтересовавшийся динамикой по¬
летов с двигателями малой тяги, может получить большой объем
информации из монографии [10.4] Г. J1. Гродзовского, Ю. Н. Ива¬
нова, В. В. Токарева.
2. Побольше полезного груза,
поменьше топлива
Таково обычное требование к космическому (и не только кос¬
мическому) полету (и даже не обязательно к полету). Иначе говоря,
мы так должны управлять полетом, чтобы выполнить его задачу
с наименьшим возможным расходом массы. Управлять полетом —
это значит отыскать нужный закон изменения со временем ре¬
активного ускорения f(£). Известно (по определению реактивной
312
Очерк десятый. Межпланетные полеты
где Vr — относительная (относительно аппарата) скорость истече¬
ния продуктов сгорания (скорость движения частиц в реактивной
струе), m(t) — переменная масса ракеты, dm/dt — секундный рас¬
ход массы. Для широкого класса ракет (с химическим топливом,
например) можно положить VT = const; тогда из (10.2.1) следует
тк -I/Vrffdt
— = е " , (Ю.2.2)
Шо
где Т — время полета. Отношение конечной массы шк (полезного
груза) к начальной массе то тем больше, чем меньше величина
интеграла
= Jfdt. (10.2.3)
Управлением f(£) надо распорядиться так, чтобы осуществить
заданный полет с наименьшим значением интеграла (10.2.3).
Однако для многих двигателей малой тяги величина VT не яв¬
ляется постоянной. Зато постоянна мощность N в струе, то есть та
часть мощности бортовой двигательной установки, которая пере¬
ходит в кинетическую энергию реактивной струи. Имеем по опре¬
делению
dm V}
N=-nri- <|0'2'4)
1 dm
Тогда из (10.2.4) и (10.2.1) следует —, откуда
m1 dt 2 N
m* 1
m0 т
(10.2.5)
о
Отношение масс тем больше, чем меньше величина интеграла
г
1 = J f2dt. (10.2.6)
0
Таким образом, осуществляя заданный полете помощью двигателей
малой тяги, надо так распорядиться реактивным ускорением f(£),
чтобы минимизировать значение интеграла I (10.2.6).
2. Побольше полезного груза, поменьше топлива 313
314
Очерк десятый. Межпланетные полеты
Задачи такого кдасса называются задачами оптимального управ¬
ления.
В этом очерке в основном речь будет идти об оптимальных
полетах, минимизирующих функционал I (10.2.6). Однако в конце
очерка будет рассмотрена одна важная задача на минимизацию
функционала S (10.2.3).
3. Принцип максимума Понтрягина
Задача оптимального управления применительно к интересу¬
ющему нас случаю может быть поставлена так. Пусть уравнения
движения записаны в векторном виде:
где х — вектор с компонентами Ж|, ж2,..., хп\ f — вектор с ком¬
понентами /|,..., fn, а и — вектор с компонентами щ, щ,..., иГ.
Вектор и является вектором управления; в каждый момент времени
управления и\,... ,иг могут принимать значения, только принадле¬
жащие некоторому замкнутому множеству U. Таким образом, u £ U.
В практических задачах почти всегда имеются какие-то огра¬
ничения на управления: реактивная тяга не может превзойти своей
максимальной величины, рули не могут повернуться больше чем
на некоторый максимальный угол и т. п. Этим и объясняется зада¬
ние управлений и на замкнутом множестве, что как раз означает
ограниченность управлений: точка и = (и\,... ,иг) может находить¬
ся внутри U или на его границе. Однако в частном случае можно
рассматривать и ничем не ограниченные значения и. Допустимыми
управлениями будем называть любые кусочно-непрерывные функ¬
ции us(t) (s = 1,..., г), принадлежащие множеству U.
Пусть какое-то качество процесса управляемого движения (10.3.1)
характеризуется функционалом
где £о и t\ — начальный и конечный моменты движения, а /о(х,и) ^0
(что, впрочем, не принципиально важно). Задача оптимизации дви¬
жения (10.3.1) ставится тогда так: среди всех допустимых управлений
u = u(t), под воздействием которых фазовая точка хо = x(to) пере¬
водится уравнениями движения (10.3.1) в фазовую точку х\ = x(tj),
x = f(x, u),
(10.3.1)
(10.3.2)
3. Принцип максимума Понтрягина
315
выбрать такие управления, которые минимизируют значение функ¬
ционала (10.3.2).
Наиболее широко применяемым методом решения задач оп¬
тимального управления является принцип максимума Понтрягина.
Строгие постановки и доказательства можно найти в монографиях
[10.5, 10.6]. Здесь же нас интересует формальный аппарат решения
задач оптимального управления.
Введем в рассмотрение вспомогательный вектор
ip = (i>o,ip\,...,ipn), (ю.з.з)
где гро — постоянная величина, гро ^ 0, а ip\,..., ipn — некоторые
функции времени: ^;г- = rpi(t).
Построим из правых частей уравнений (Ю.3.1) функции /о
и вектора (Ю.З.З) функцию
п
Ж = X V’i/ifr. “)• (Ю.3.4)
г=0
Заметим, что уравнения (Ю.3.1) тогда могут быть записаны так:
дЖ /• /
жг = .Т7Т- (*=l,...,n). (10.3.5)
от
Определим теперь функции ipi(t) (г = 1 ,...,п) дифференциаль¬
ными уравнениями
dipj дЖ , ч ,
1 = -^- <i = l ">• <,0Л6>
Оказывается [10.5, 10.6], что для оптимальности (в смысле ми¬
нимума функционала (10.3.2)) процесса \(t), u(t), переводящего фа¬
зовую точку х0 в фазовую точку Х|, необходимо существование та¬
кого нетривиального решения системы (10.3.6) и такой константы
1ро ^ 0, что для любого момента т, где to ^ т ^ t\ выполнено
условие максимума
Ж{ф{т), х(т), и(т)) = max Ж{ф{т), х(т), v). (Ю.3.7)
v€U
Итак, оптимальное управление и находится из условия (Ю.3.7) —
практически через гр их; это дает возможность затем, интегрируя
совместно уравнения (10.3.6) и (10.3.5) (или, что то же, (10.3.1)), по¬
строить оптимальную траекторию. Обычно наиболее сложная часть
задачи — нахождение начальных данных для интегрирования си¬
стемы (10.3.6).
316
Очерк десятый. Межпланетные полеты
Заметим, что система (Ю.3.5)-( 10.3.6) имеет порядок 2п; ее
решение, стало быть, зависит от 2п произвольных постоянных, что
дает возможность в действительности удовлетворить 2п краевым
условиям
Xi(t0) = Xfo, Xj(f|) = Xji (г = 1,2,... ,n).
Принцип максимума Понтрягина дает лишь необходимые усло¬
вия оптимальности. Он необходимо выполняется в оптимальных
процессах. Но если принцип максимума в каком-то процессе вы¬
полнен, то, может статься, этот процесс и не оптимален. Поэто¬
му задачи, решенные с помощью принципа максимума, требуют,
вообще говоря, проверки на достаточность полученных условий
оптимальности. Часто (например, в линейных задачах) принцип
максимума дает одновременно и достаточные условия оптимально¬
сти. Но следует помнить, что не для всякой задачи это так.
4. Уравнение оптимального полета
Рассмотрим движение ракеты массы т в поле сил с потенци¬
алом U. Обозначим
U _ . , fau зи аи\]
m Ui<x'y'z)' g™dU \дх' ду’ dz)'\ (10.4.1)
r=(x,y,z), \=(u,V,w), f=(fx,fy,fz)-)
Здесь x,y,z — координаты ракеты, u,v,w — компоненты ее
скорости,fx,fy,fz — компоненты реактивного ускорения. Урав¬
нения движения в векторной форме запишутся тогда так:
V-grad*7 = f, г = V. (10.4.2)
Предположим, что двигатель ракеты обладает постоянной мощ¬
ностью реактивной струи. Тогда нужно искать траектории, обеспе¬
чивающие минимум функционала (10.2.6). Наложим еше ограни¬
чения на реактивное ускорение:
в ^ fx ^ ^ fy ^ в. О/ ^ Д ^ fl. (10.4.3)
Согласно (10.3.4) строим функцию
Ж = - (fx + fy + fz) + Фи (fx + + Фхи +
+ i>v (fy + + 4>yV + фу, (fz + + фгЬ}. (10.4.4)
4. Уравнение оптимального полета
317
Ж1
—а
X
Рис. 10.1. К построению оптимального управления
В (10.4.4) принято фо = — I; можно принять любое фо < 0, пере¬
определив соответственно величины фх, фу,... ,ipw.
Согласно принципу максимума (10.3.7) управления fx,fy,fz
оптимальны, если они максимизируют величину Ж (10.4.4). Так
как эти управления входят в Ж аналогичным образом, то доста¬
точно рассмотреть одно управление, например fx. Зависимость Ж
от fx представлена на рис. 10.1 (для фи > 0; если фи < 0, карти¬
на симметрично отразится). Видим, что максимум Ж достигается
при fx = Фи/2, если \tj}u/2\ ^ а, и при fx = а, если \фи/2\ > а.
Аналогичная ситуация имеет место для fy,fz• Итак, оптимальное
управление задается формулами вида
Аналогичные соотношения имеют место для fy,fz• Зависимость,
например, fx от фи представлена на рис. Ю.2.
При этом согласно (Ю.3.6) и (Ю.4.4') величины ф должны
удовлетворять системе уравнений
fx — * Фи/Ъ
а, если фи/2 > а,
и/2, если \фи/2\ ^ а, (Ю.4.4')
-а, если rpu/2 < -а.
(10.4.5)
Здесь точки проставлены вместо аналогичных уравнений для дру¬
гих переменных ф. В векторном виде уравнения (10.4.5) можно
318
Очерк десятый. Межпланетные полеты
представить так:
фг + Alpv = 0, ipv = -1рг,
(l 0.4.6)
d2U
д2и
д2и
дх2
дхду
дхдг
d2U
d2U
d2U
дудх
ду2
дудг
d2U
d2U
d2U
дгдх
дгду
dz2
фт — векторе компонентами фх, фу, фг; фу — векторе компонен¬
тами фи, фь, фу,. Уравнения (10.4.2), (10.4.4'), (10.4.6) представляют
собой замкнутую систему уравнений оптимального (в смысле ми¬
нимума интеграла (10.2.6)) полета ракеты с учетом ограничений
(10.4.3) на управления.
Большое достоинство принципа максимума Понтрягина со¬
стоит в том, что он при расчете оптимальных движений позволяет
просто и единообразно учитывать различные ограничения, нало¬
женные на управления. Это очень важно для современных задач
механики. На примере уравнений (10.4.2), (10.4.4'), (10.4.6) мы
продемонстрировали действенность формализма принципа макси¬
мума. В дальнейшем, однако, для простоты изложения будет рас¬
сматриваться случай, когда на управления fx, fy, fz не наложено
ограничений (а = оо). Это эквивалентно также рассмотрению лишь
таких траекторий полета, оптимальное управление вдоль которых
не требует достижения предельного значения а ф оо компонент
реактивного ускорения.
5. Откажемся от ограничений
319
5. Откажемся от ограничений
Тогда, как легко понять из (10.4.4), оптимальное управление
дается векторной формулой f = гру/2 и вместо уравнений (10.4.6)
можно написать прямо дифференциальные уравнения оптималь¬
ного управления! Вместе с (10.4.2) они дадут замкнутую систему
уравнений оптимального полета. Эту систему можно записать так:
Здесь матрица А та же самая, что и в (10.4.6).
Мы условились ранее не учитывать притяжения планет на участ¬
ке полета между ними. Тогда приближенно краевые условия для
задачи (10.5.1) совпадают с условием отлета с планеты (непритяги¬
вающей!) с какой-то начальной относительно планеты скоростью
и прилета на другую планету с какой-то скоростью относительно
этой планеты. Относительные скорости старта и финиша можно
считать нулевыми (так как они малы по сравнению с перенос¬
ной скоростью движения самих планет). Итак, в качестве краевых
условий будем брать впредь координаты и компоненты скорости
планеты старта (пусть — Земли) и планеты назначения (допустим,
Марса).
Двенадцать постоянных интегрирования системы (10.5.1) сле¬
дует определить так, чтобы удовлетворились 12 краевых условий:
где Ж дается выражением (10.4.4), в которое надо подставить вме¬
сто 'фи,'фх),'фи) соответственно 2Д,2Д,2Д, а вместо ‘фх.'фу.'фг,
соответственно -2Д, -2Д, -2Д. Если же на силовую функцию U
наложить добавочное условие, что она представляет собой силовую
функцию поля центральных сил (для нашей задачи это так и есть),
то уравнения (10.5.1) будут допускать еще три первых интеграла,
эквивалентных одному векторному интегралу:
(10.5.1)
о . .о
г = г , г = г при
г = гк, г = гк приЕстественно, система (10.5.1) допускает первый интеграл
М = Ж0ч
(10.5.2)
(10.5.3)
rxf + fxr = k.
(10.5.4)
320
Очерк десятый. Межпланетные полеты
Однако интегралов (10.5.3), (10.5.4) недостаточно для полного ин¬
тегрирования системы (10.5.1), и она, по-видимому, неинтегрируе-
ма]\ Поэтому необходимо искать приближенные методы решения
краевой задачи (10.5.1)—(10.5.2).
6. Метод транспортирующей траектории
Можно решать краевую задачу (10.5.1)—(10.5.2) численными
методами, с помощью ЭВМ. Для этого нужно знать какое-то при¬
ближенное решение задачи и использовать его в качестве первого
приближения в итерационном процессе решения краевой задачи.
Итерационный метод (метод последовательных приближений) по¬
чти всегда неизбежен в нелинейных краевых задачах. На итерации
уходит много машинного времени, что затрудняет получение обо¬
зримых результатов.
Численные методы всегда остаются в нашем распоряжении.
Однако попытаемся обойтись без них если не для любых крае¬
вых задач (10.5.1)—(10.5.2), то хотя бы для достаточно широкого
их подкласса. Если удастся получить приближенное аналитическое
решение задачи, то его, между прочим, можно использовать в каче¬
стве первого приближения для численного итерационного решения
точной краевой задачи.
Т. М. Энеев предложил использовать в динамике полета с малой
тягой метод, названный им «методом транспортирующих траекторий».
Пусть мы хотим совершить межпланетный полет, отбыв в мо¬
мент to с планеты старта и прибыв в момент t\ на планету назначе¬
ния. Найдем сначала обычную кеплеровскую траекторию, решаю¬
щую эту задачу. Это можно сделать, так как уравнения кеплеровско-
го движения, как известно, интегрируемы. Если для этого случая
краевая задача решена, то тем самым определяется некоторая эл¬
липтическая траектория, проходящая через точки старта и финиша
соответственно в моменты to и t\. Интересующая нас траектория
полета с малой тягой должна не очень сильно отличаться от только
что найденной кеплеровской траектории. Ведь если время полета
не очень велико, малое реактивное ускорение просто «не успеет»
^ Все попытки автора пробить эту стену привели лишь к нахождению частного
случая оптимального управления, удовлетворяющего системе (10.5.1): f = 2/?/(2 +
+/?£)¥, где Р — произвольная постоянная. С помошью этого управления, конечно,
можно решить не любую задачу оптимального полета, а только такую, которая
зависит всего от семи краевых условий.
6. Метод транспортирующей траектории
321
сильно отклонить траекторию полета от соответствующим образом
подобранной кеплеровской траектории. Кеплеровская траектория
как бы ведет за собой траекторию с малой тягой. Назовем такую
кеплеровскую траекторию транспортирующей траекторией. Систе¬
му координат, которая движется поступательно по транспортирую¬
щей траектории, назовем транспортирующей системой координат.
Идея состоит в том, чтобы рассматривать движение ракеты
с малой тягой в транспортирующей системе координат. Траектория
такого относительного движения, как нетрудно сообразить, не ухо¬
дит далеко от начала координат, что дает возможность линеаризо¬
вать и решить до конца краевую задачу. Это показано в работе [10.1]
В. В. Белецкого и В. А. Егорова. Следуя этой работе, предположим,
что траектория движения есть
г = г0 + р, (10.6.1)
где г0 — известная транспортирующая трактория, и величина \р\
мала по сравнению с |г0|. Вектор-функция г0(£) удовлетворяет урав¬
нению невозмущенного движения
г0 - grad Uo = 0, (10.6.2)
где U — значение силовой функции U вдоль транспортирующей
траектории г0(£)- Подставим (10.6.1) в (10.5.1), разложим U(x,y,z)
в ряд и пренебрежем малыми величинами второго и более высоких
порядков малости. При этом учтем, что по условию малы не только
величины /9,/9, но и f; это значит, что членами вида р{ и т.п.
тоже пренебрегаем. Учтем (10.6.2). Тогда вместо системы (10.5.1)
получим линеаризованную систему
p-A0p = f, (10.6.3)
f- j40f = 0. (10.6.4)
Здесь Ао — значение матрицы А вдоль транспортирующей тра¬
ектории Го(£); матрица -Ао(<) содержит известные периодические
функции времени.
Линейная система любого порядка интегрируема, если коэф¬
фициенты ее однородной части постоянны; в нашем случае этого
заведомо нет. Линейные системы с переменными коэффициентами,
вообще говоря, неинтегрируемы. Но наша система (10.6.3)—(10.6.4)
обязана интегрироваться! (В этом и состоял «тайный» замысел при
введении транспортирующей системы координат.) Действительно,
допустим на секунду, что в системе (10.6.3)—(10.6.4) f = 0. Тогда
21 Заказ 1667
322
Очерк десятый. Межпланетные полеты
оставшаяся (левая) часть векторного уравнения (10.6.3) по идее
имеет решением вариацию кеплеровского движения! Кеплеровское
движение описывается в квадратурах, значит, и его вариация — то¬
же. Далее, векторное уравнение (10.6.4) имеет в точности такой же
вид, как и уравнение (10.6.3) с нулевой правой частью. Значит,
интегрируемо и (10.6.4)! Определяя его решение f(£) и подставляя
в правую часть уравнения (10.6.3), придем к неоднородному вектор¬
ному уравнению, в котором правая часть есть известная функция
времени, а соответствующее ему однородное уравнение интегриру¬
емо. Решение уравнения такой структуры, как известно, находится
в квадратурах (например, методом вариации постоянных). Итак,
система (10.6.3)—(10.6.4) интегрируется в квадратурах.
Из этих соображений (и сообра¬
жений размерности), между прочим,
следует, что в рассматриваемом приб¬
лижении оптимальное управление век¬
тором реактивного ускорения дается
формулой
f = a|(r,.-r0), (Ю.6.5)
где To(t) определяет транспортирую¬
щую кеплерову эллиптическую орби¬
ту, г*(£) — кеплерову эллиптическую
орбиту, параметры которой определя¬
ются краевыми условиями задачи, g —
ускорение ньютоновского притяжения
на расстоянии R от центра притяжения, а ~ 1 — безразмерная
скалярная постоянная. На рис. 10.3 приведена схема управления,
отвечающая (10.6.5).
Фактическое интегрирование системы (10.6.3)—(10.6.4) прове¬
дем несколько позже.
7. Схема решения краевой задачи
Линейные уравнения (10.6.3)—(10.6.4) хороши не только своей
интегрируемостью, но и тем, что позволяют решить краевую задачу,
так сказать, одним ударом, без последовательных приближений.
Для нелинейных задач это, вообще говоря, невозможно.
Рис. 10.3. Оптимальное
управление в линейном
приближении
7. Схема решения краевой задачи
323
Краевые условия (10.5.2) ввиду (10.6.1) запишутся теперь так:
р=р0, р = р0 при t = t0A (Ю7 1)
= t |.J
Здесь
Р =Рк, р = Рк ПРИ 1
Ро = Г° - Го(<о), р0 = г° - r0{t0)
Рк = ГК - Г0(*|), рд = Г* -Г0(*|).
1
(10.7.2)
Так как транспортирующая траектория r(£),r(f) известна в любой
момент времени, то краевые условия относительного движения
(10.7.1) легко вычисляются через краевые условия (10.5.2) абсо¬
лютного движения по формулам (10.7.2).
Схема интегрирования системы (10.6.3)—(10.6.4) и решения
краевой задачи (10.7.1) может быть описана следующим образом.
Обозначим теперь через р шестимерный вектор, включающий
как координаты, так и компоненты скоростей. Решение уравне¬
ния (10.6.3) тогда можно искать в виде
р = /9* + р**, (10.7.3)
где р* — решение однородной системы (10.6.3), а р** — частное
решение неоднородной системы (10.6.3).
Пусть pi — частные линейно независимые решения однород¬
ной системы (10.6.3). Они должны быть известны, так как известна
вариация кеплеровского движения. Тогда
6
= (10.7.4)
i= I
где С{ — постоянные интегрирования. Из сказанного выше ясно,
что решение системы (10.7.5) является другой линейной комбина¬
цией тех же функций pi:
6
f = YlaiPi' (10.7.5)
*'= I
где аг — новые постоянные интегрирования. В формуле (10.7.5),
конечно, под f понимается уже шестимерный вектор, включающий
компоненты ускорения и производные по времени от них.
21*
324
Очерк десятый. Межпланетные полеты
Теперь, подставляя (10.7.5) в (10.6.3), методом вариации по¬
стоянных находим частное решение
6
Р** = '52а№’ (10.7.6)
г = I
причем выберем р.* так, чтобы р»»(£о) = 0, то есть
<Pi(to) = 0. (10.7.7)
Тогда, учитывая (10.7.4) и (10.7.3), окончательно получим
6
р = ^2(ciPi + ацрг). (10.7.8)
i= I
Произвольные постоянные с,-, а,- дают возможность удовлетворить
12 краевым условиям (10.7.1). А именно, постоянные с*, а* опреде¬
ляются из следующей системы линейных алгебраических уравнений
(напомним, что р, Pi,<fii — шестимерные векторы, причем щ удо¬
влетворяет (10.7.7)):
6
р0=^2ар{(10), (10.7.9)
г= I
6 6
Рк “ ^ ^ сг‘Рг(^|) — ^ ^ (10.7.10)
*=1 г= 1
Из системы (10.7.9) определяются с*, а затем решение системы
(10.7.10) дает а*. Выписанный алгоритм полностью решает краевую
задачу (10.6.3), (10.6.4), (10.7.1).
8. Интегрирование
Выберем такую абсолютную систему координат XYZ с нача¬
лом S в центре притяжения, чтобы плоскость транспортирующей
траектории совпадала с плоскостью XY, а ось X была направле¬
на в перицентр транспортирующей траектории. Транспортирующая
система координат Oxyz имеет оси, параллельные соответственно
осям XYZ (рис. 10.4). Уравнения движения (10.6.3) и управления
(10.6.4) будем считать записанными в безразмерных переменных.
8. Интегрирование
325
Если Д, V, Т, /р — величины размерности соответственно рассто¬
яния, скорости, времени, ускорения, то соответствующие безраз¬
мерные величины г, v, t, f определим так:
г =
R_
До’
где Д0 —начальное расстояние от центра притяжения, g = p/Ro “
ускорение силы тяготения на этом расстоянии.
При таком выборе системы координат и безразмерных пере¬
менных элементы матрицы Ао в уравнениях (10.6.3), (10.6.4) имеют
вид
77 и
и т.
= -t(3cos2 v - 1), Uyy = ~з-(3 sin2 v - 1),
1
и0 =
Vxy
уу
3 cos v sin v
U° =77° =0
UXZ — uyz —
(10.8.2)
'o 'o
ro(t) — текущий радиус транспортирующей траектории, а и —
истинная аномалия вдоль нее, связанные соотношениями кепле¬
ровского движения
Р dv у/р
1 + е cos v ’ dt rl'
ra =
(10.8.3)
В формулах (10.8.3) е означает эксцентриситет транспортиру¬
ющей траектории, ар — ее безразмерный
фокальный параметр.
Для интегрирования системы (10.6.3),
(10.6.4) удобно перейти к вращающейся
системе координат начало которой
совпадает с точкой О транспортирующей
траектории (рис. 10.4), ось у направлена
по радиус-вектору, ось £ — по трансвер-
сали (в сторону движения) к транспор¬
тирующей траектории, а ось ( совпадает
с z. Тогда
х = 7] cos v - £ sin v,'
у = 77 sin г/ -f £ cosv,
z = С
(10.8.4)
Рис. 10.4. Системы
координат
326
Очерк десятый. Межпланетные полеты
и уравнения (10.6.3) запишутся после некоторых преобразований
в следующем виде:
2 2
jj - 2ш(, - Ш 1] - з 7/ = Д,
т П
i + 2wfi - w £ + ujtj + — ( = Д,
го
€ + Лс = /с-
(10.8.5)
Здесь си = v — угловая скорость движения по транспортирующей
траектории, Д, Д, Д — проекции вектора реактивного ускорения
на оси 7?, £,С- Уравнения (10.8.5) можно было бы выписать сразу,
пользуясь общими уравнениями относительного движения.
Отметим, что коэффициенты в (10.8.5) зависят от времени
только через истинную аномалию и. Поэтому совершенно есте¬
ственно, пользуясь соотношениями (10.8.3), перейти в (10.8.5) от
независимой t к новой независимой переменной г/. Сделав такое
преобразование, получим вместо (10.8.5) систему
(10.8.6)
v" - 2%' - 2£' - (1 + 2р)г] + Ц-£= рУ/ч,
Р Р
?'-2^' + 2ч'-(\-рК-2А = Р3Р4Ь,
Р Р
С"-2^' + Х = рУ/<.
р
Здесь и в дальнейшем обозначено:
р = (1 + ecos v)~\ р = е sin 7/(1 + ecos*/)-2. (10.8.7)
Штрихи означают дифференцирование по и.
На некоторое время забудем, что компоненты Д, Д, Д удовле¬
творяют в нашей задаче дифференциальному уравнению (10.6.4),
и будем считать их произвольными, но известными функциями ис¬
тинной аномалии и.
Мы получили замкнутую систему (10.8.6) с явно выписанными
коэффициентами, периодически зависящими от новой независи¬
мой переменной v. Эта система на первый взгляд выглядит страш¬
новато. Но мы вдохновлены уверенностью в ее интегрируемости и,
не робея, приступим к делу.
8. Интегрирование
327
Третье уравнение системы (10.8.6) не зависит от предыдущих
двух, поэтому начнем с него. Прежде всего постараемся избавиться
в нем от члена с первой производной . Как известно из теории
линейных дифференциальных уравнений, это всегда можно сделать
подстановкой
где р\ — коэффициент при к — новая переменная вместо £.
В нашем случае р\ = -2р'/р и подстановка (10.8.8) имеет вид
и поэтому уравнение (10.8.10) принимает простой вид, допускаю¬
щий непосредственное интегрирование:
Однородное уравнение, соответствующее (10.8.11), имеет решение
где с$, Сб — постоянные интегрирования.
Будем, согласно методу вариаций постоянных, искать решение
неоднородного уравнения (10.8.11) в том же виде (10.8.12) для н
и только с$ и Сб уже будем считать зависящими от и. Тогда,
как известно, для производных от Cs{v) и С(,(и) получим систему
уравнений
(10.8.8)
С = хр
Подставив (10.8.9) в третье уравнение (10.8.6), получим
(10.8.9)
х" + p-l(^j +^ к=рУ/(-
(10.8.10)
Но оказывается в силу (10.8.7), что
х" + к =рУ/<-
(10.8.11)
(10.8.12)
Отсюда
dc5 з з
dC(, з з
- - р
328
Очерк десятый. Межпланетные полеты
Проинтегрируем эти равенства, подставим в (10.8.12) и вер¬
немся еще к исходной переменной £ согласно (10.8.19). Результат:
£ = Csp sin v + Сб/9 cos v+
+ Р*Р
sin»/ J f^p3 cos v dv - cos v J f^p3s\nvdv
(10.8.13)
Третье из уравнений (10.8.6) проинтегрировано. Из (10.8.13) диф¬
ференцированием легко получить и явную формулу для С!.
Нас, однако, здесь интересует скорее «технология» процесса
интегрирования системы (10.8.6), чем получение полной сводки
расчетных формул (такая сводка есть в первоисточнике [10.1], ко¬
торому мы здесь следуем). Поэтому, отсылая за явным выражением
для £(и) к [10.1], перейдем к рассмотрению первых двух уравне¬
ний (10.8.6). Решению третьего уравнения (10.8.6) очень помогла
подстановка (10.8.9). Естественно опробовать аналогичную подста¬
новку и для первых двух уравнений (10.8.6):
£ = ра, Г1 = р/3. (10.8.14)
Тогда эти уравнения принимают вид
р" -ЪРр-2а' =рУ/„ о" + 2/3,=рУд. (10.8.15)
Подстановка (10.8.14) оказалась плодотворной: немедленно мож¬
но один раз проинтегрировать второе из уравнений (10.8.15):
а' = с, - 2Р + Ц, I(=p3 j p*Udv, (10.8.16)
где С| — новая постоянная интегрирования, 1^(и0) = 0 по опреде¬
лению. Подставляя теперь выражение а из (10.8.16) в первое из
уравнений (10.8.15), получим
р" + (4 - Зр)Р = Ф(1/), (10.8.17)
где
Ф(|/) = 2с, + 21( +рУЛ- (10.8.18)
Что делать теперь с уравнением (10.8.17), не очень ясно, но
если вернуться к исходной переменной г) (подстановка (10.8.14) уже
сделала свое дело), то вместо (10.8.17) получим теперь уравнение
(1 + е cos v)p" — 2е sin vr] + (1 + Зе cos v)rj = Ф. (10.8.19)
8. Интегрирование
329
Не нужно очень долго всматриваться в это уравнение, чтобы обна¬
ружить частное решение соответствующего ему однородного урав¬
нения
т/2 = sin v. (10.8.20)
Но из теории дифференциальных линейных уравнений известно,
что уравнение
tj" + а^и)^' + a2(v)r} = 0,
имеющее частное решение 7/ = 7/2, имеет второе, линейно незави¬
симое частное решение, определяемое формулой
Vi = V2 J rf" dv.
В нашем случае
2е sin v
| 5
1 + е cos v
а 7/2 дается формулой (10.8.20). Поэтому второе частное решение
рассматриваемого однородного уравнения будет
7/3 = /* sin v, Г = [ ----- du. (10.8.21)
У sin2 v
Квадратура Т может быть вычислена в явном виде [10.1], однако
выражение I*(v) несколько громоздко. Чтобы за деревьями не поте¬
рять леса, оставим за I*(v) компактное обозначение (10.8.21). Ука¬
жем только, что на круговой орбите (е = 0, р — 1) I*{v) = - ctg v,
а с точностью до первой степени эксцентриситета
Г (и) sin v и - cos v + 2е. (10.8.22)
Итак, найдены два частных решения однородного уравнения.
Это позволяет уже знакомым нам методом вариации постоянных
получить общее решение уравнения (10.8.19). Оно имеет вид
7/ = — (/* sin v + cos v) + С2 sin v + с37* sin v+'
e
+ jP2 sin v + I*F3 sin v,
Fi=-pi / +Sf*)dv’
(10.8.23)
330
Очерк десятый. Межпланетные полеты
Осталось определить £(v). Вернемся к уравнению (10.8.16). Так
как а значит, и /3(v) = Т)/р нам теперь известны, то одной
квадратурой находим
(х = C\V — 2 J ^dv + J Д dv + c4.
Учитывая теперь (10.8.14) и (10.8.23), получим
£ = C,£| + С2& + Сз^з + C4I4 + />Ф,
/ 2 /* I* sin I/ + cos v \
b-T-'J -Р—V'
£2 = р{2 + е cos v) cos v,
(10.8.24)
(10.8.25)
Г I* sin v
J P
dv, = p,
(F2 sin v + I*F3 sin v)
dv.
(10.8.25)
Выражения для rf и £ получаются из (10.8.23), (10.8.25) диффе¬
ренцированием. Тем самым интегрирование в квадратурах системы
(10.8.6) завершено.
Квадратуры, входящие в £| и , вычисляются в конечном виде;
эти явные выражения приведены в работе [10.1], в полной сводке
расчетных формул. Выражение в явном виде квадратур Д, Fj, F3, Ф,
вообще говоря, проблематично. Это зависит от вида управлений
Д, Д, Д. При практических массовых расчетах траекторий назван¬
ные квадратуры удобней, по-видимому, находить численными ме¬
тодами; однако вполне реальны случаи, когда эти квадратуры ока¬
жется возможным выписать в явном виде.
Трудности проведенного интегрирования системы (10.8.6) свя¬
заны с переменностью ее коэффициентов, или, иными словами,
с эллиптичностью транспортирующей траектории. Поэтому мы вы¬
нуждены были решать систему (10.8.6) для произвольных значений
эксцентриситета е < 1. Зато полученные формулы могут быть упо¬
треблены (и действительно употреблялись в [10.1-10.4]) для расчета
траекторий межпланетных управляемых полетов с произвольным
реактивным ускорением (в частности, с оптимальным2*).
2)
Все квадратуры задач оптимального полета явно проинтегрированы в статье:
Суханов А. А. Оптимизация перелетов с малой тягой // Космич. исследования. 1999.
9. О задачах относительного движения
331
9. О задачах относительного движения
Однако эти формулы имеют гораздо более обшее значение.
С их помощью можно решать целый класс задач относительного
движения близких космических тел и другие задачи. Назовем не¬
которые из них.
1. Вариация кеплеровского движения и изохронные производные. Ни¬
какая заранее рассчитанная траектория не может быть реали¬
зована абсолютно точно. Этому мешают многочисленные (хоть
и малые обычно) ошибки в исполнении траектории, в допу¬
щениях, сделанных при ее расчете, и т. п. Отклонение дей¬
ствительной кеплеровской траектории межпланетного поле¬
та от расчетной (как говорят, от номинальной) можно най¬
ти по полученным формулам, положив |f| = 0. Номиналь¬
ная траектория при этом выступает в роли транспортирую¬
щей. Определяя константы интегрирования через начальные
данные и собирая члены при начальных координатах и ско¬
ростях (7/0,7/о и т.д.), получим выражения для так называемых
изохронных производных кеплеровского движения. Изохронные
производные играют большую роль в теории космических по¬
летов. Они дают возможность вычислить отклонение по каж¬
дой координате (или компоненте скорости) в каждый момент
времени. Если отклонения чересчур велики, можно дать ко¬
манду на коррекцию (исправление) траектории и рассчитать
импульс, потребный для коррекции.
2. Задана о движении тела в окрестности спутника. Например,
можно рассмотреть движение космонавта в окрестности спут¬
ника-станции как при наличии у космонавта «заплечного»
реактивного аппарата (/ Ф 0), так и при отсутствии такого
аппарата ( / = 0). Можно выявить «опасные» режимы (или ис¬
ходные положения относительно спутника), когда космонавту
грозит удаление от спутника.
3. Задана о сближении двух косминеских объектов. Предполагая,
что на предыдущем этапе один космический объект уже выве¬
ден в окрестность другого, можно рассмотреть заключительный
этап — управление реактивным ускорением /, обеспечиваю¬
щее встречу с наименьшей относительной скоростью (посадка
ракеты на спутник-станцию, монтирование спутника-станции
Т. 37. №2. С. 182— 191. Для этого использовалась другая, невращающаяся транспор¬
тирующая система координат.
332
Очерк десятый. Межпланетные полеты
и т. п.) или с произвольной скоростью. В эту последнюю зада¬
чу можно не вводить реактивное ускорение (/ = 0), а искать
импульс (то есть начальные значения компонент скорости),
обеспечивающий встречу.
4. Движение облака частиц, выброшенных со спутника, относи¬
тельно спутника.
5. Получение заданной орбиты при помощи добавочного импульса
или реактивного ускорения, то есть задача о малом изменении
исходной орбиты космического тела.
6. Кратковременное действие возмущающих факторов на орбиту.
Для многих из перечисленных задач транспортирующая траек¬
тория может быть выбрана слабоэллиптической (е мало), а иногда
и круговой. Это существенно упрощает расчетные формулы: их
можно выписать с точностью лишь до первой степени эксцентри¬
ситета е или даже положить е = 0. В этом последнем случае исход¬
ные уравнения (10.8.6) содержат лишь постоянные коэффициенты
в левых частях (р = 0, р = 1). Это принципиально упрощает их
интегрирование. Конечно, решение можно получить и предельным
переходом (е 0) из общих формул (10.8.13), (10.8.23), (10.8.25).
Для раскрытия неопределенности в первом члене в выражении
(10.8.23) для rj и, соответственно, в £| следует воспользоваться
аппроксимацией (10.8.22). В остальном предельный переход е —> 0
осуществляется просто: полагаем I* — - ctg v, р = 1, а также Р = 1.
Результат — решение уравнений (10.8.6) для случая круговой транс¬
портирующей траектории — запишется так:
rj = 2С| + Ci sin v — cj cos v +
10. Результаты расчетов оптимальных межпланетных траекторий
333
£ = Cs sin v + Сб cos v +
+ sini/ J Д cos v dv + cos v J (10.9.3)
Квадратуры, входящие в эти формулы, уже легче вычисляют¬
ся, чем в общем случае эллиптической транспортирующей траекто¬
рии. В ряде случаев (например, постоянные компоненты Д, Д, Д)
квадратуры берутся совсем просто. В формулах (10.9.1)—(10.9.3), как
и в исходных общих формулах (10.8.13), (10.8.23), (10.8.25), управле¬
ния Д, Д, Д считались произвольными функциями истинной ано¬
малии v. Однако более всего нас интересует случай, когда эти ком¬
поненты удовлетворяют уравнениям (10.6.4) оптимального управ¬
ления. Тогда, как следует из рассуждений п. 7 (см. формулу (10.7.5)),
решение уравнений оптимального управления в общем случае эл¬
липтической транспортирующей траектории запишется в виде
Д = — (J* sin v + cos v) + а,2 sin v + a^I* sin и, 1
Д = ai£i + aiii + &з£з + | (Ю.9.4)
Д = о>5р sin v + аьр cos и. )
Здесь а|,..., а6 — новые произвольные постоянные, £ь ..., £* да¬
ются формулами (10.8.25).
Подставляя (10.9.4) в формулы (10.8.23), (10.8.25) и (10.8.13),
получим полное решение в квадратурах задачи (10.6.3)—(10.6.4) оп¬
тимального перелета. По таким формулам была проведена целая се¬
рия расчетов траекторий полетов к Марсу, Венере, Юпитеру [10.1-
10.3]. Некоторые результаты этих расчетов мы сейчас рассмотрим.
10. Результаты расчетов
оптимальных межпланетных траекторий
Ценность решенной задачи механики космического полета за¬
частую определяется возможностью доведения решения «до числа».
Путь «доводки до числа», как правило, нелегок. Так, в рассматри¬
ваемом нами методе расчета оптимальных траекторий необходимо
проделать по крайней мере такую расчетную работу: определить по¬
ложения и скорости планет в моменты старта t0 и финиша t\; рас¬
считать транспортирующую траекторию; вычислить краевые усло¬
вия в поступательно-перемешаюшейся транспортирующей системе
334
Очерк десятый. Межпланетные полеты
50 100 150 200 250
t, сутки
Рис. 10.5. Изменение величины реактивного ускорения со временем:
1 — точный расчет; 2 — приближенный расчет
координат Oxyz и пересчитать эти краевые условия во вращаю¬
щуюся транспортирующую систему Otj£( вычислить квадратуры,
входящие в решение нашей задачи (10.8.13), (10.8.23), (10.8.25);
решить краевую задачу по схеме, описанной в п. 7, и рассчитать
траекторию и управление в транспортирующей системе координат
Orj((; пересчитать их в системе Oxyz.
Для оценки точности метода транспортирующих траекторий
в отдельных случаях надо рассчитать (по еще более сложному алго¬
ритму!) траекторию, соответствующую точным уравнениям (10.5.1),
и сравнить ее с траекторией, рассчитанной приближенно. Вся эта
«кухня» осталась за бортом нашего изложения, так как она выпа¬
дает из плана и стиля книги. Однако именно здесь автор считает
уместным напомнить своему читателю-студенту, что современная
серьезная работа в области механики космического полета часто
неизбежно связана с такой вычислительной «кухней». Конечно, та¬
кая работа немыслима без электронных вычислительных машин.
Итак, оставляя в стороне описание «кухни» расчетов, обратим¬
ся к их результатам.
На рис. 10.5-10.8 изображены некоторые характеристики по¬
лета к Марсу. Чтобы можно было составить представление о точно¬
сти метода транспортирующих траекторий, на этих рисунках даны
и точные, и приближенные характеристики. Как изменяется реак-
10. Результаты расчетов оптимальных межпланетных траекторий
335
Рис. 10.6. Изменение величины и направления реактивного ускорения:
1 — точный расчет; 2 — приближенный расчет
тивное ускорение по величине и направлению, видно из рис. 10.5,
10.6. На рис. 10.7 — траектории полета к Марсу: точная, прибли¬
женная и транспортирующая. Время полета — 212 суток. Наконец,
на рис. 10.8 изображена траектория полета (рассчитанная по при¬
ближенным формулам) в транспортирующей системе координат.
Видно, что максимальное отклонение от начала координат не пре¬
вышает 7 млн км, в то время как сам полет имеет протяженность
в сотни миллионов километров. Из рисунков видно, насколько
малы потребные величины реактивного ускорения (максимум —
1,5 мм/сек2).
336
Очерк десятый. Межпланетные полеты
у, млн км
х, млн км
Рис. 10.7. Траектории полета к Марсу: 1 — транспортирующий эллипс;
2 — приближенная траектория; 3 — точная траектория
Рис. 10.8. Траектория в транспортирующей системе координат. Вдоль тра¬
ектории указаны значения истинной аномалии на транспортирующем эллипсе
10. Результаты расчетов оптимальных межпланетных траекторий
337
Важной характеристикой полета является его угловая дальность
Ф, то есть угол, заметаемый радиус-вектором космического аппа¬
рата от начала координат до конца полета. Для рассматриваемого
на рис. 10.5-10.8 примера Ф ~ 150°. Именно для таких, не очень
больших угловых дальностей метод транспортирующих траекторий
оказывается достаточно точным. Ведь тогда траектория полета дей¬
ствительно не очень отличается от дуги соответственно подобран¬
ного эллипса. Если же угловые дальности велики (360°, 720° и т.д.),
так что полет представляет собой, например, участок спирали, ле¬
жащей между орбитами старта и назначения, то никакая кепле-
ровская траектория не может быть достаточно близкой к истинной
траектории полета с малой тягой, и метод транспортирующих тра¬
екторий пасует.
Но следует иметь в виду, что наиболее интересные для прак- •
тики полеты имеют небольшую угловую дальность, так как тогда
и время полета будет невелико. Поэтому метод транспортирующей
траектории хорош именно тем, что позволяет быстро и высокоточно
рассчитать множество практически наиболее интересных траекто¬
рий. Рис. 10.9 дает представление о том, насколько мы ошибемся
в вычислении основной характеристики полета — интеграла I, если
используем метод транспортирующей траектории. На этом рисунке
дано в зависимости от Ф отношение AI/I (в процентах), где I —
100%
Ф, град
Рис. 10.9. Зависимость ошибки приближенного расчета величины I
от угловой дальности Ф полета к Марсу и Венере
22 Заказ 1667
338
Очерк десятый. Межпланетные полеты
Таблица 10.1
Некоторые характеристики полетов к Марсу и Венере
Даты старта
и финиша
7,
м2/сек2
т,
сут
Ф
/к.
мм/сек2
/о,
мм/сек2
7п — 7т
100%
7т
К Марсу
28.1Х.1960
28.IV.1961
11.53
11.54
212
147,38°
1,44
1,43
1.51
1.52
0,09
15.XI.1964
11.Х. 1965
3,23
3,20
330
222,65°
0,405
0,42
0,89
0,88
0,94
К Венере
22.111.1964
21.VII.1964
26,44
26,43
121
136,35°
4,02
4,08
1,85
1,845
0,04
11.X1I.1963
18. VI 1.1964
11,975
11,385
220
234,79°
2,25
2,24
1,26
1,15
5,18
точное значение интеграла, Д7 — ошибка в его вычислении мето¬
дом транспортирующих траекторий. При полетах с угловой дально¬
стью 225-235° ошибка составляет всего 1-5%, но резко возрастает
с увеличением Ф сверх 235°. При Ф ~ 180° ошибка составляет ни¬
чтожную величину: десятые, а то и сотые доли процента. Отметим
еще, что полеты с совсем малыми угловыми дальностями (Ф < 50°)
не очень интересны, так как требуют весьма больших значений ве¬
личины реактивного ускорения.
Некоторые характеристики полетов к Марсу и Венере, вычис¬
ленные по изложенной приближенной методике, и их сравнение
с точными характеристиками даются в табл. 10.1, где Т — пол¬
ное время полета, а Ф — угловая дальность полета между сфе¬
рами действия планет, /к, /0 — конечная и начальная величины
модуля реактивного ускорения; в последней колонке указано отли¬
чие приближенного значения 7П от точного 7Т в процентах к 7Т.
В столбцах 7, /к, /0 содержатся приближенные (верхние) и точные
(нижние) значения величин.
Отметим теперь, что оптимальное управление, как видим, очень
сложно для осуществления. Реактивное ускорение сильно меняется
по величине и направлению. А ведь одним из инженерных тре¬
бований всегда является, по возможности, простота управления.
Выигрывая в массе доставляемого на другую планету груза, мы
проигрываем в простоте и, следовательно, в надежности полета.
Поэтому законен вопрос: нельзя ли аппроксимировать оптималь¬
10. Результаты расчетов оптимальных межпланетных траекторий
339
ное управление более простым по исполнению? Пусть, например,
в начале полета ускорение постоянно по величине и направле¬
нию, в середине полета реактивные двигатели вообще отключены
(пассивный участок полета), а в конце полета снова ускорение
постоянно по величине и направлению. Есть надежда, что такое
«ступенчатое» управление в какой-то степени аппроксимирует оп¬
тимальное.
В. В. Голубковым были рассмотрены [10.3] два простейших сту¬
пенчатых закона управления. Пусть
f, о ^ г ^ т,
0, т < t ^ т + Дт,
g, т Ат ^Т.
(10.10.1)
В. В. Голубковым рассматривались два случая реализации закона
(10.10.1): 1) / — д\ 2) / Ф д. Здесь f, g — реактивные ускорения со¬
ответственно на первом и третьем участках полета, представляющие
собой векторные постоянные, t — текущее время, Т — время по¬
лета, т — время работы двигателя на первом участке полета, Дг —
длительность пассивного участка полета, / = |f|, д = |g|. Таким об¬
разом, траектория содержит, вообще говоря, два активных и один
пассивный участок. Параметры закона управления используются
для удовлетворения краевым условиям и условию минимизации /.
Были проведены численные расчеты полетов Земля—Марс при
некоторой фиксированной дате старта по методу транспортирую¬
щих траекторий и в точной постановке (в точной постановке урав¬
нения движения интегрировались численно). Некоторые из резуль¬
татов расчетов приведены в табл. 10.2 и 10.3.
Из табл. 10.2 и 10.3 видно, что точность расчета ступенчатого
управления одинакова с точностью расчета оптимального управ¬
ления (рис. 10.9). Это дает право сравнить величины интеграла I
в ступенчатом и оптимальном управлении при приближенном рас¬
чете соответствующих траекторий.
Такое сравнение покажет, что мы теряем, вводя ступенчатое
управление вместо оптимального. Соответствующие данные для
полетов Земля — Марс выписаны в приведенной ниже табл. 10.4.
В ней Г0’{ — значение интеграла I для оптимального управления
в первом приближении, 1\ — значение интеграла I для ступенча¬
того управления в первом приближении, Т — время полета, Ф —
угловая дальность.
22*
Таблица 10.2
340
Очерк десятый. Межпланетные полеты
ж
I §
0,83
0,57
СЧ~
19,7
хЛэ 4л,у
04
со
сч
о
О
ОО
_
СЧ
оо
СО
о
о
о
о
о
о
X XKLTOtr я ху
со
o'
«/0
о"
гп
o'
о
С'
о^
o'
о^
о"
о
о*"
Я
аг
03
CJ
iXo ‘х
j; XKLrorr я i
0,311
Г"*
0,267
40
0,218
40
0,213
‘П
оо
0,261
130
0,391
235
0,398
279
я
го
05
Я
X
3*
лээ/ww
3,896
0,837
0,263
0,198
оо
о"
0,218
0,211
£
г>1Э0/|Л11Л1
2,451
0,792
0,695
0,644
0,467
0,340
0,344
ГП
и
„ CD
ГЧ
93,00
8,639
4,151
3,870
3,510
3,865
4,464
iXd ‘ху
СО
сч
сч
о
СЧ
о
гч
о\
Г"-
j; Х151/01Г я ху
со
о"
UO
о"
со
o'
о
o'
Я
5
3
СО
±Лэ ‘2
X ХВ1Ю1Г Я 1
0,311
г-
тг
0,271
ОО
чО
0,228
о
оо
0,276
о
я
я
X
X
4>
*
5
_>1ээ/пп '8
3,943
0,849
0,255
0,238
ё
X
о.
С
^МЭЭ/ШЛ! ‘/
2,446
0,784
0,694
0,612
m
*
с U
TN
93,77
8,690
4,251
4,623
ф,
град
128
176
232
263
326
381
428
т,
сутки
150
250
350
400
500
009
700
Таблица 10.3
10. Результаты расчетов оптимальных межпланетных траекторий
341
*4
1
с
/г
•100%
1,11
0,70
0,85
10,9
±Лэ ‘xv
гч
г-
сп
NO
СО
ГО
о
тГ
О
ОО
СО
133
ОО
NO
ГЧ
107
СП
ON
00
тГ
СП
ГЧ
О,
СП
гч
СП
ON
X ХВ1ГОТГ 9 XV
о
о"
o'
о"
©"
o'
о*
Л
т
сз •
3
Г)
К
(Л
1Ло ‘х
X ХК1Г01Г 9 X
0,228
Tj*
го
0,253
ГО
NO
0,361
126
0,399
160
0,451
225
0,476
NO
ОО
ГЧ
0,331
232
X
X
£
хээ/ww
3,456
0,819
00
СП
о"
0,441
0,342
0,306
0,419
* w
гм
2
97,098
8,649
5,027
4,909
4,570
4,325
7,287
хХэ ‘ху
ON
ГО
г-
СО
NO
О
102
ON
Г"
СП
133
ОО
Г"»
111
X ХК1ГОЕГ 9 XV
o'
о"
о"
о"
(УЗ
т
03
EJ
(Г)
05
сз
X
X
(U
iXo ‘х
X XBIfOtr 9 X
0,225
Tj-
ГО
0,250
СП
NO
0,362
127
0,390
156
S
г*
ю
X
О.
с
г>10Э/ИИ1 ‘/
3,493
0,824
0,520
0,461
*
гч
2
98,173
О
Г-
ОО
5,070
5,442
ф,
град
128
176
232
263
326
381
428
т,
сутки
150
250
350
400
500
009
700
342
Очерк десятый. Межпланетные полеты
Таблица 10.4
Оптимальный закон
II
Ф,
град
Т,
сутки
/(,)
-*opt ’
м2/сек3
м2/сек2
г _ /0)
1 нр‘ • 100%
1\
м2/сек3
о
о
— с.
1 ^
128
150
85,0
98,2
15,5
93,8
9,2
152
200
21,4
25,4
18,7
24,1
12,6
176
250
7,5
8,71
16,1
8,69
15,9
203
300
4,2
5,4
28,6
5,0
19,0
232
350
3,3
5,0
51,5
4,3
39,4
Это сравнение показывает, что по энергетике (в смысле I) оп¬
тимальный закон управления заметно отличается от ступенчатого.
Как видно из табл. Ю.4, это отличие зависит от времени полета.
При времени полета 150 суток выигрыш по энергетике оптималь¬
ного закона управления по сравнению со ступенчатым составляет
9,2% в случае f ф g и 15,5% в случае / = g. Для времени полета
350 суток этот выигрыш составляет соответственно 39,4% и 51,5%.
Ступенчатое управление в случае f ф д заметно выгоднее, чем
в случае f — g.
Анализ точного расчета полетов Земля — Марс со ступенчатым
управлением (см. табл. 10.2 и 10.3) показал, что имеется минимум I
по времени полета Т при фиксированной дате старта. Этот мини¬
мум достаточно пологий, что позволяет варьировать время полета
в довольно широких пределах (порядка 200 суток), не изменяя су¬
щественно значения I. Кроме того, как видно из табл. 10.2 и 10.3,
этот минимум достигается при достаточно большом времени поле¬
та Т (530 суток при f — д и 500 суток при / Ф д).
Отметим также, что при f — д минимум 1 может достигаться
на траекториях, не имеющих пассивного участка (см. табл. 10.2).
В случае оптимальных траекторий ситуация будет иная. Точ¬
ные расчеты оптимальных траекторий показывают, что для них нет
таких значений времен полета Т, чтобы I достигло минимума. Чем
больше время Т, тем меньше будет I (и тем больше витков спирали
вокруг Солнца опишет траектория полета). При Т -» оо, I —> 0,
11. Представление результатов расчетов серий траекторий
343
и мы могли бы сильно сэкономить на топливе, если б человеческая
жизнь не была столь коротка.
В заключение этого пункта отметим, что использование при¬
ближенного метода транспортирующей траектории позволяет со¬
кратить время счета в среднем в семь-десять раз по сравнению
со временем точного расчета. Это весьма эффективно сказывается
при массовых расчетах целых серий траекторий.
11. Представление результатов
расчетов серий траекторий
Когда траекторий рассчитывается достаточно много, важно на¬
глядно представить результаты этих расчетов так, чтобы по ним
удобно было выбирать траектории с нужными характеристиками.
В качестве основных определяющих параметров возьмем мо¬
менты начала t\ и конца t2 полета между сферами действия планет.
Во всех случаях при расчетах требовалось, чтобы скорость аппарата
относительно планеты в момент выхода из сферы ее действия рав¬
нялась нулю.
Для представления результатов используем [10.2, 10.3] плос¬
кость t\,t2 (рис. 10.10). В этой плоскости удобно рассматривать
различные семейства изолиний, в частности, линии одинаковых
реактивных ускорений или одинакового расхода топлива. Каждому
полету «туда» на этой плоскости отвечает точка (t\, t2) над биссек¬
трисой первого квадранта, поскольку t2 > t\.
Величина необходимого для данного полета реактивного уско¬
рения (или величина I) определяется изолинией, проходящей через
эту точку. Биссектриса соответствует полетам с бесконечно боль¬
шой скоростью. Если для обратных полетов на ординате отклады¬
вать время начала полета t\, а на абсциссе той же плоскости время
завершения полета t2, то обратным полетам будут отвечать точки
под биссектрисой этой плоскости, так как tf2 > t\ .
Чтобы пара точек (t\, t2), (^1, t2) могла представлять полет туда
и обратно, необходимо, чтобы было t\ ^ t2 при этом разность t\ —t2
есть время пребывания вблизи планеты назначения. Разность =
t2 - £|, равная расстоянию по горизонтали между точками (t\,t2)
и (t\,t2), очевидно, представляет собой полное время экспедиции.
На плоскости t\, t2 представим результаты расчета интеграла I
в виде линий I = const. Кроме этих линий построим изолинии
максимальных величин реактивного ускорения.
344
Очерк десятый. Межпланетные полеты
II Ш IV V VIVIIVIIIIX X XIXII1П III IV V VIVIII VIII IX ХХ1Х1ГI II III IV V VI
1964
1965
1966
М2
Рис. 10.10. Изолинии характеристик полета к Марсу. Сплошные линии —
); пунктирные линии — изоли¬
нии значений /, мм2/сек3
изолинии максимальных ускорений (в мм/сек2'
Анализ на плоскости t\,t2 позволяет определить характери¬
стики совокупности траекторий полетов к планетам, а также тра¬
екторий с возвращением на Землю.
Для примера на рис. 10.10 приведены изолинии /тах = const,
I = const для полетов к Марсу в 1964-1966 годах (пусть читателя
не удивляют эти даты — они всего лишь пример). Аналогичные
изолинии в плоскости t\,ti рассчитаны были в работах [10.2, 10.3]
и для полетов к Венере и Юпитеру.
В следующих таблицах приводятся характеристики наиболее
интересных траекторий со стартами в 1964-1965 годах. Эти харак¬
теристики удалось получить именно с помощью анализа изолиний
11. Представление результатов расчетов серий траекторий
345
Таблица 10.5
Некоторые характеристики полетов к Марсу и обратно
с минимальным суммарным временем полета
I
11
Ill
IV
V
/max, MM/сеК2
^ст
Тс, сут
/г.о» м2/сек3
/Е, м2/сек3
1
20.Х 1 1964 г.
564
13,5
18,7
2
20.Х И 1964 г.
470
37
47,4
5
3.1 1965 г.
330
170
196
10
6.11 1965 г.
236
500
550
I = const и /тах = const на плоскости В табл. 10.5-10.7 при¬
ведены характеристики полетов соответственно к Марсу, Венере
и Юпитеру с возвращением на Землю. В первом столбце таблиц
приведены значения максимального реактивного ускорения /тах
в рассматриваемом полете; во втором столбце — дата старта tCT;
в третьем столбце — полное время полета (в сутках) с уче¬
том времени, потребного на торможение в сфере действуя планеты
(до круговой орбиты с высотой h = 300 км при полете к Марсу и Ве¬
нере и с высотой пятого спутника Юпитера Амальтеи при полете
к Юпитеру) и обратный разгон; в четвертом столбце — потреб¬
ные значения интеграла / = Ij на полет между сферами действия
планет (туда и обратно); в пятом столбце — полное потребное зна¬
чение интеграла 1 = 1% с учетом затрат на торможение и обратный
разгон. Затраты на торможение около планеты и обратный разгон
легко вычислить, зная характеристики такого торможения и разго¬
на (см., например, седьмой очерк в этой книге).
Из табл. 10.5-10.7 видно, что максимальное ускорение 2-3
мм/сек2 обеспечивает приблизительно полуторагодичные полеты
к Марсу или Венере с возвращением на Землю, а также полет
к Юпитеру с возвращением на Землю в трехгодичный срок. Полу¬
торагодичный полет к Марсу возможен даже при /тах = 1 мм/сек2.
Рассматривая плоскость i|,<2, можно заметить одно свойство
оптимальных траекторий: наличие даты старта, обеспечивающей
резкий минимум в значениях I и /тах при заданном времени по¬
лета. Действительно, геометрическое место точек равных времен
полета То есть прямая, параллельная биссектрисе первого квадран-
346
Очерк десятый. Межпланетные полеты
Таблица 10.6
Некоторые характеристики полетов к Венере и обратно
с минимальным временем полета
I
II
Ill
IV
V
/max* MM/сеК2
£ст
Те, сут
Jr.o, м2/сек3
/Е, м2/сек3
3
4.V 1964 г.
490
45
84
5
1 .IX 1964 г.
340
125
185
10
9.1 1965 г.
200
350
454
Таблица 10.7
Некоторые характеристики полетов к Юпитеру и обратно
I
II
Ill
IV
V
/max, MM/сеК2
£с т
сут
1т,о, м2/сек3
/Е, м2/сек3
2
2.VII 1965 г.
1090
85
178
3
21.VII 1965 г.
1000
135
275
5
10.Х 1965 г.
890
320
562
та на плоскости t\, £2- Эта прямая пересекает некоторые изолинии
в двух точках — значит, полет со временем Т0 возможен (с данным
значением I) при двух датах старта. Одна-единственная изолиния
I = /о касается прямой £2 - t\ = То; /о как раз и есть минимально
возможное значение / для полета со временем Т0, а соответствую¬
щая дата старта оптимальна. Оптимальные даты старта приходятся
на октябрь 1964 года-январь 1965 года, как видно из рис. 10.10.
При I < /0 полет со временем Т0 невозможен (соответствую¬
щие изолинии не пересекают прямую tj-tx = Го). Зависимость ин¬
теграла I от даты старта при фиксированных продолжительностях
перелета Земля—Марс изображена на рис. 10.11, заимствованном
из работы [10.7] американских ученых Мельбурна и Зауэра. Они
численными методами решали краевую задачу для точных уравне¬
ний (10.5.1) оптимального движения. Рис. 10.11 интересен прежде
всего широтой диапазона дат старта (четыре года) для рассчитан¬
ных траекторий и выявлением на этом диапазоне двух семейств
11. Представление результатов расчетов серий траекторий
347
I, м2/сек3
| День 22 26 29 1 4 7 12 15 18 20 23 26 31 3 6 9 12 14 19 22 25 28 31
2 месяц 2469111 3579111 368 10 12 2468 10 12
«5 год 1968 1969 1970 1971
Рис. 10.11. Зависимость I от даты старта и продолжительности перелета.
Полет Земля—Марс
траекторий. Видим, например, что оптимальные даты старта —
в январе-апреле 1969 года и в марте-июле 1971 года.
Точки пересечения (в районе сентября-октября 1970 года) кри¬
вых из двух семейств, изображенных на рис. 10.11, отвечают очень
интересным траекториям, которые дают неединственное решение
краевой задачи! В самом деле, в этих точках все одинаково: дата
старта, продолжительность полета (а значит, и начальные и конеч¬
ные значения координат и скоростей), значение интеграла I. Не¬
одинаковы лишь управление, а значит, и траектория. Пример такого
неединственного решения краевой задачи изображен на рис. 10.12.
Время полета — 5 месяцев; но одна траектория петлеобразно оги¬
бает Солнце (угловая дальность Ф = Ф0 + 360° > 360°), а другая —
нет (угловая дальность Ф0 невелика, меньше 90°).
Условия неединственности решения краевой задачи повторя¬
ются периодически с периодом примерно 2 года 3 месяца. С та¬
ким же периодом повторяются оптимальные даты старта. Этот пе¬
риод характерен для любых полетов к Марсу (а не только полетов
348
Очерк десятый. Межпланетные полеты
Рис. 10.12. Пример двух различных траекторий перелета Земля — Марс,
совпадающих по датам старта и финиша и по расходу рабочего вещества
с двигателем малой тяги): примерно через такой промежуток вре¬
мени (от 2 лет 34 дней до 2 лет 80 дней) повторяются взаимные
положения Земли и Марса относительно Солнца.
Если мы знаем величину интеграла J, потребную для осуществ¬
ления заданного полета, то по формуле (10.2.5) можно вычислить
и отношение конечной массы к начальной. Для этого надо задать¬
ся величиной начальной массы то и мощностью двигателя N. Так
как мощность двигателя ограничена и зависит от веса двигательной
установки, который в свою очередь входит в то, то такой весовой
анализ полета представляет собой самостоятельную задачу. Об этом
можно прочитать в уже упоминавшейся монографии Г.Л.Гродзов-
ского, Ю. Н. Иванова и В. В. Токарева [10.4].
12. Коррекция межпланетных траекторий
На наших глазах был осуществлен целый ряд полетов авто¬
матических межпланетных станций к Венере и Марсу. Траекто¬
рии полетов этих станций были близки к кеплеровским, потому
что полеты происходили с выключенными двигателями. Однако
при запуске неизбежны какие-то ошибки выведения межпланетной
станции на траекторию перелета, поэтому в процессе полета мо¬
гут накапливаться плохо известные нам возмущения. В результате
межпланетная станция летит, как правило, не совсем по той траек¬
тории, по какой надо бы, и если ее не «подправить», то можно силь¬
но промахнуться и пролететь мимо планеты назначения. Поэтому
12. Коррекция межпланетных траекторий
349
в реально осуществляемых полетах производят такую «подправку»,
или, как говорят, коррекцию, траектории. Коррекция производится
с помощью включаемого на время реактивного двигателя. Возни¬
кает масса вопросов: когда и насколько включать двигатель? Вклю¬
чать его один раз или несколько? Как направлять включенную
реактивную тягу в пространстве? И, главное, как при этом обес¬
печить выполнение необходимой коррекции наиболее экономным
образом? Ведь запас топлива, несомый межпланетной станцией,
крайне невелик и этим запасом надо распорядиться с умом.
Если еще учесть, что ответы на поставленные вопросы зависят
от реальной траектории, параметры которой измеряются с некото¬
рыми ошибками и поэтому неизвестны точно, а включение двига¬
теля тоже производится не буквально точно, то станет понятным,
что теория коррекции межпланетных траекторий не может быть
проста. Эта теория построена и продолжает развиваться трудами
многих ученых.
Мы опишем здесь л ишь упрощенную задачу коррекции, рассмот¬
ренную в более общей постановке А. К. Платоновым в работе [10.8].
Естественно движение по фактической траектории описывать в от¬
клонениях от номинальной траектории при помощи уже известно¬
го нам линеаризованного векторного уравнения движения (10.6.3).
Мы это уравнение еще больше упростим, пренебрегая гравитацион¬
ными возмущениями траектории, то есть членом А0р. Исследова¬
ние показывает, что это вносит не очень большую ошибку в расчет,
но зато позволяет просто понять качественные особенности кор¬
ректирующих маневров. Тогда наши уравнения принимают вид
v = f, r = v, (10.12.1)
а задачу коррекции можно поставить так: в момент t — T окончания
полета координаты г и скорости v должны принять номинальные
значения гк и vK соответственно. При этом управление вектором f
должно обеспечить минимум функционала S (10.2.3). Будем счи¬
тать, что f ограничен по модулю, так что
-а ^ |f| ^ +а. (10.12.2)
Составим функцию Понтрягина для нашего случая:
Ж = -|f| + Фу • f + Фг • v, (10.12.3)
и уравнения сопряженной системы переменных Фу? Фг-
Фг = 0, Фу = -Фг.
(10.12.4)
350
Очерк десятый. Межпланетные полеты
Оптимальным будет такой закон управления, который доставляет
максимум функции Ж по управлению f. Эта функция достигает
максимума при
Формулы (10.12.5) (в которых а — произвольная постоянная ска¬
лярная величина) дают закон оптимальной коррекции. Двигатель
надо включать только тогда, когда функция |Фу(£)| > 1; ПРИ этом
величина ускорения должна быть максимальна, а его направление
должно совпадать с вектором Фу. Заметим, что уравнения (10.12.4)
легко интегрируются и дают явную зависимость
По характеру зависимости (10.12.7) сразу ясно, что величина
|Фу(*)| на замкнутом интервале [t0,T] времени полета может пре¬
взойти единицу (|Фу| > 1) не более чем на двух участках, причем
один из них находится в начале, а другой — в конце полетного
интервала. Итак, мы уже получили любопытный вывод: при нашей
постановке задачи оказалось, что оптимальная коррекция содержит
не более двух активных участков, причем один из них начинается в мо¬
мент to начала полета, а другой кончается в момент Т окончания
полета.
При благоприятных условиях один из этих участков может
исчезнуть, а при неблагоприятных (очень большие начальные от¬
клонения от номинальной траектории) оба участка сливаются и вся
траектория проходится с непрерывно работающим двигателем.
Отметим еще, что в силу (10.12.5) и (10.12.6) компоненты ре¬
активного ускорения включенного двигателя в оптимальном управ¬
лении линейно меняются со временем. Конкретный закон управ¬
ления реактивным ускорением определяется выражением векторов
Фг, Фу через краевые условия г0, гк, v0, vK нашей задачи.
Обзор работ по коррекции траекторий можно найти в [10.9].
If I = о,
|f| =а, f = аФу,
(10.12.5)
Фу (t) = -Ф °rt + ф!
г0
V»
(10.12.6)
откуда
|ФУ(£)| = у/ гпЧ2 + 2 nt + к2,
т2 = |Ф?|2, п = -Ф?.Ф&, *2 = |Фу|2.
(10.12.7)
Очерк одиннадцатый
Относительное движение
орбитальных тел
Он умер, da! Но он не мог упасть,
Войдя в круги планетного движенья.
Бездонная внизу зияла пасть,
Но были слабы силы притяженья.
Лучами был пронизан небосвод,
Божественно-холодными лучами.
Не зная тленья, о// летел вперед,
Смотрел на звезды мертвыми очами.
Н. Гумилев
«Орел»
1. На орбитах - два спутника
Каждый из них движется вокруг Земли. Мы знаем как. Но как
спутники движутся относительно друг друга? Это относительное
движение необходимо, например, знать при решении задачи о сты¬
ковке двух спутников.
Два спутника соединены тросом. Как это повлияет на относи¬
тельное движение спутников?
Космонавт отделился от корабля-спутника. Он соединен со спут¬
ником тросом (фалом). Этот фал — не простая «перестраховка»,
а совершенно необходимая мера. Иначе, в силу законов небесной
механики, космонавт неизбежно отстанет от спутника. Или обгонит
его, что безразлично для последствий (см. эпиграф). А как будет
двигаться относительно спутника космонавт, привязанный фалом?
Все перечисленные вопросы (и многие другие, им подобные)
входят в класс задач об относительном движении космических объ¬
ектов — будь то спутники, космонавты или секции орбитальных
станций, нежестко связанные друг с другом.
Мы начнем анализ относительного движения со случая свобод¬
ного движения двух материальных точек относительно друг друга.
352 Очерк одиннадцатый. Относительное движение орбитальных тел
Если угодно, можно считать, что одна из этих
материальных точек — спутник, другая — кос¬
монавт. Пока фал, соединяющий космонавта
и спутник, не натянут до отказа, движение
космонавта можно считать свободным. При
натяжении фала на спутник действует реакция
связи. Такая же, но противоположно направ¬
ленная сила действует на космонавта.
Рассмотрим сначала постановку задачи
о движении по орбитам двух материальных то¬
чек, связанных тросом, а уже потом перейдем
к анализу свободного движения точек. Анализ
движения связки двух тел (системы двух мате¬
риальных точек, соединенных гибкой невесо¬
мой нерастяжимой нитью) проведен в работах
В. В. Белецкого и Е. Т. Новиковой [11.1, 11.2].
Следуя работе [11.1], обозначим через та,
т массы материальных точек, rrt,r — их гео¬
центрические радиус-векторы. Пусть точки со¬
единены невесомой нерастяжимой гибкой нитью длины I (рис. 11.1).
Тогда во время движения должно быть выполнено условие связи
|г- га| ^ I. (11.1.1)
Иначе говоря, расстояние между точками не может превысить дли¬
ну нити. Векторные уравнения движения могут быть тогда записаны
в виде уравнений Лагранжа первого рода.
Поясним, что это такое. Пусть на систему п материальных то¬
чек с координатами жг, у*, Z{ наложены идеальные освобождающие
связи
,xn,yn,z„) < О
Уравнения движения
Рис. 11.1. Связка
двух тел на орбите
(j = 1,2,... ,m).
(а)
т„
т„
т„
d2x„
~ШГ
d2yu
dt2
d2zv
dt2
j=i
m
-x
~ v + ^X]dXv'
Wl r\ *
j=\ ozv
(6)
1. На орбитах — два спутника
353
называются уравнениями Лагранжа первого рода и описывают движе¬
ние системы материальных точек с массами ти, на каждую из ко¬
торых действует сила с компонентами XU,YU, Zv и на точки систе¬
мы наложены указанные связи. При этом множитель Лагранжа A j
не равен нулю только в том случае, если связь fj «натянута» (знак
строгого равенства); тогда обязательно Xj < 0. Если же связь fj
не «натянута» (знак строгого неравенства), то соответствующий
множитель Лагранжа A j = 0. Уравнения движения (их 3 га) вме¬
сте с га уравнениями условий связанного движения определяют
Зга + га неизвестных величин: Зга координат xv,yu,zu и га множи¬
телей Лагранжа A j.
Для задачи, рассматриваемой здесь, уравнения Лагранжа пер¬
вого рода (в векторной форме) имеют вид
В уравнениях (11.1.2) учтены силы ньютоновского притяжения каж¬
дой точки к центру Земли. Правые части этих уравнений представля¬
ют собой реакцию связи. Множитель X еще подлежит определению.
Если движение свободно, то в (11.1.1) стоит строгий знак не¬
равенства, и тогда полагают в (11.1.2) А = 0. Если движение свя¬
занное, то в (11.1.1) стоит строгий знак равенства и А Ф 0 в (11.1.2).
Нас интересует относительное движение точек га и та. Будем
рассматривать их движение относительно их общего центра масс.
Естественно, тогда нужно знать движение этого центра масс. Он,
вообще говоря, не будет двигаться по кеплеровской орбите. Это
можно понять на следующем простом «мысленном эксперименте».
Пусть две несвязанные материальные точки одинаковой мас¬
сы начинают движение из одной точки пространства: по круговой
орбите одна и по очень близкой эллиптической соприкасающейся
орбите другая. В силу весьма малой разницы в периодах обращения
через некоторое, достаточно большое количество оборотов матери¬
альные точки будут находиться почти на одинаковом расстоянии
от центра тяготения, но угловое расстояние между их радиус-век¬
торами будет близко к 180°. В этот момент, очевидно, центр масс
системы будет почти совпадать с центром тяготения, в то время
как в начальный момент он находился в точке касания двух рас¬
сматриваемых орбит. При этом радиус-вектор центра масс системы
23 Заказ 1667
а
(11.1.2)
354 Очерк одиннадцатый. Относительное движение орбитальных тел
не только существенно изменился по модулю, но и, как легко
понять, описал достаточно много оборотов вокруг центра притя¬
жения. Значит, на рассмотренном интервале времени траектория
центра масс носит спиральный характер (конечно, с локальными
модуляциями вдоль спирали). На бесконечном интервале времени
получится траектория типа пульсирующей спирали, так что мо¬
дуль радиус-вектора центра масс будет то уменьшаться до весьма
малой величины, то увеличиваться до размера, близкого к перво¬
начальному.
Однако в рассматриваемой задаче анализ существенно упро¬
щается следующим путем. Сделаем естественное предположение
о том, что I — максимально возможное расстояние между точка¬
ми — всегда мало по сравнению с расстояниями г, га от точек
до центра притяжения, то есть
Тогда с высокой точностью можно считать, что центр системы дви¬
жется по кеплеровской орбите. Покажем это. Обозначим радиус-
вектор центра масс через R. Тогда
Здесь р и ра — радиус-векторы точек га и гаа, проведенные из их
общего центра масс. Так как р ^ /, ра ^ I, то р « г, ра «га;
ПОЭТОМУ Г « Га « R И
Разложим в (11.1.4) выражение, стоящее в скобках, по сте¬
пеням малых величин (11.1.5) и сохраним лишь члены до второго
порядка малости включительно. Тогда вместо (11.1.4) получим урав¬
нение
гаг + таха
(11.1.3)
т + та
Из (11.1.2) получим, обозначив т + та = М,
(11.1.4)
(11.1.5)
(11.1.6)
1. На орбитах — два спутника
355
где
F = F| + F2,
Зц 3 /л
F, = - (тр + mapa)}R + jp(mp + тара),
-5(1й)
+ та
+
+
В силу определений (11.1.3) и (11.1.4) получим
т
(11.1.7)
Ра
т + та
тп
(га - г),
п i \
Р= —; (г~г«),
тп + тпа
т„ра + тр = 0.
(11.1.8)
(11.1.9)
Если бы в уравнении (11.1.6) не было возмущающей силы F, то
из этого уравнения для R(<) получили бы кеплеровское движение.
Наличие F «портит» кеплеровскую орбиту. Но вследствие (11.1.9)
видим, что в возмущающей силе F (11.1.7) члены первого порядка
малости тождественно равны нулю: F| = 0. Значит, главный член
в F имеет второй порядок малости относительно величин (11.1.5)
(он дается формулой (11.1.7) для F2). Следовательно, |F| чрезвы¬
чайно мала по сравнению с основным членом
рМ
R3
R
рт
~R?
в уравнении (11.1.6). И с высокой степенью точности (до эффектов
второго порядка малости) можно принять, что
R+£R = 0,
(11.1.10)
то есть центр масс системы движется по кеплеровской орбите.
23*
356 Очерк одиннадцатый. Относительное движение орбитальных тел
2. Уравнения относительного движения
Мы пришли, таким образом, к обычно употребляемой ограни¬
ченной постановке задачи: исследовать движение системы относи¬
тельно ее центра масс, который движется по заданной кеплеровской
орбите.
Так как в силу (11.1.8)
Р = -—Ра, (П.2.1)
тп
то достаточно рассмотреть движение только одной точки, например
точки тпа (космонавт); движение второй точки (спутник) опреде¬
ляется тогда из (11.2.1). Заметим, что если та/т < 1 (масса космо¬
навта существенно меньше массы спутника), то получим (в пределе
при та —> 0) \р\ ~ 0, так что движение точки та относительно
центра масс системы (та, тп) почти совпадает с движением точки
та относительно точки тп.
Поскольку на движение наложено ограничение (11.1.5), дей¬
ствующее на всем бесконечном интервале времени из-за наложения
связи (11.1.1), то при изучении относительного движения естествен¬
но рассматривать лишь уравнения в малых отклонениях от центра
масс системы.
С этой целью линеаризуем уравнения (11.1.2) относительно р
и ра. Процесс линеаризации удобно провести так. Поделив первое
уравнение (11.1.2) на тп, второе на тп„ и вычитая одно из другого,
получим
Дг ++ 2АДгГ —-I——^ =0,1
\г3 г3/ \тп та) > (11.2.2)
Дг = г - ra. J
Линеаризация этого уравнения относительно Дг с учетом соотно¬
шения Дг = -(тп + тпа)/тп ра получаемого из (11.1.8), дает
Ра + _ Д5^(^’ ^“) = (11.2.3)
Г Ша + ТП
где ла = -2А новый, подлежащий определению множи-
тптп0
тель. Теперь вместо (11.1.1) связь будет определяться неравенством
(П.2.4)
тп + тпа
и в связном движении в (11.2.3) должно быть Аа < 0.
3. Свободное движение космонавта относительно спутника 357
Векторное уравнение (11.2.3) вместе с (11.2.4) и определяет
движение точки массы та (космонавта) относительно центра масс
системы точек т и тп (спутник-космонавт). В уравнении (11.2.3)
R(t) — известная функция времени, определяющая кеплеровскую
траекторию центра инерции системы. Само уравнение (11.2.3) есть
частный случай уже известных нам линейных уравнений [11.2],
описывающих движение в транспортирующей системе координат
(см. очерк десятый).
Рассмотрим теперь свободное движение материальной точки
тп относительно центра масс системы точек га, тп. В этом случае
в (11.2.3) следует положить Аа = 0. Это значит, что возникла такая
ситуация. От корабля-спутника отделился космонавт. Он не соеди¬
нен со спутником фалом и не имеет индивидуального реактивного
двигателя. Какова дальнейшая судьба космонавта?
3. Свободное движение космонавта
относительно спутника
Для простоты анализа будем считать орбиту центра масс системы
круговой, а движение космонавта происходящим в плоскости этой
орбиты. Ввиду того, что масса космонавта намного меньше мас¬
сы корабля, в дальнейшем не будем отличать центр масс корабля
от центра масс системы корабль-космонавт. Пусть с центром масс
О спутника связана система координат 7/, £, £, оси которой направ¬
лены все время по радиус-вектору орбиты спутника т/, по трансвер-
сали £ и по нормали к плоскости орбиты £. Для круговой орбиты
спутника в случае плоского движения космонавта текущие коорди¬
наты tj, £ космонавта удовлетворяют уравнениям
Т)" - 2? - 3ri = 0, £" + 2tj' = 0. (11.3.1)
Эти уравнения как частный случай легко получаются из век¬
торного уравнения (11.2.3). Штрихи в (11,3.1) означают производ¬
ные по безразмерному времени г = , где щ — угловая скорость
движения центра масс спутника по орбите. Уравнения (11.3.1) опи¬
сывают движение космонавта только до тех пор, пока фал не натя¬
нут. Такое движение назовем свободным. Рассмотрим его. Уравне¬
ния (11.3.1) легко интегрируются. Решение такое:
г] = 2с\ + с2 sin т + Сз cos г,
£ = С4 - ЗС|Т + 2с2 cos т — 2сз sin г,
(11.3.2)
358 Очерк одиннадцатый. Относительное движение орбитальных тел
где произвольные постоянные C|,C2,c3,C4 выражаются через на¬
чальные (при т = 0) данные задачи следующим образом:
С| = 2»7о+£о> с2 = щ, с3 = -Зщ-2(о, с4 = (q-2t&. (11.3.3)
Чтобы лучше представить вид траектории, описываемой кос¬
монавтом, заметим, что координаты »?(т),£(г) и время г связаны
соотношением (его легко получить из (11.3.2))
= („.3.4)
с\ + с] 4(cj + <%)
Здесь предполагается, что хотя бы одно из сз отлично от нуля.
В противном случае, как видно из (11.3.2), космонавт будет рав¬
номерно удаляться от спутника
вдоль оси £, то есть параллельно
касательной к орбите (рис. 11.2).
^ Здесь уместно напомнить о прибли-
* *—ftp * женности наших линейных урав-
Сггутник нений (11.3.1). Строго говоря, и
Рис. 11.2. Равномерное удаление космонавт, и спутник летят по ка-
космонавта от спутника ким-то близким эллиптическим
орбитам, а уравнения (11.3.1) опи¬
сывают относительное движение лишь в малой окрестности спут¬
ника, то есть пока расстояние между космонавтом и спутником
мало по сравнению с размерами орбиты спутника.
Из (11.3.3) видно, что равномерное свободное удаление воз¬
можно лишь при отсутствии начальной скорости, направленной
вдоль радиус-вектора спутника (необходимое, но недостаточное
условие; надо еще, чтобы Сз = 0).
Возвращаясь к общей формуле (11.3.4), рассмотрим сначала
случаи периодических движений космонавта. Из (11.3.2) и (11.3.4)
видно, что такие движения имеют место лишь при С\ = 0. Пе¬
риод этих движений совпадает с периодом обращения спутника
по орбите, а сами движения происходят по эллипсу, центр кото¬
рого лежит в точке rf = 0, = С4, малая полуось направлена
параллельно оси 77 и равна У? + с], а большая полуось в два раза
больше по величине (рис. 11.3). В частности, возможно и «зависа¬
ние» космонавта в точке т/ = 0, £ = £о если в начальный момент он
находился в этой точке и не имел скорости относительно спутника.
В этом случае космонавт движется вокруг Земли по той же орбите,
3. Свободное движение космонавта относительно спутника
359
Рис.11.3. Периодическое
движение космонавта
что и спутник (но находится в дру¬
гой точке орбиты). Важно отме¬
тить, что и такое «зависание», и
вообще периодические движения
относительно спутника неустой¬
чивы. Достаточно лишь изменить
начальные данные так, чтобы
С\Ф 0 (пусть даже |с|| сколь угод¬
но мало), как периодичность раз¬
рушается и получается более об¬
щий случай движения.
В этом случае равномерное движение (рис. 11.2) и периоди¬
ческое движение (рис. 11.3) складываются и получается движение
по траектории, изображенной на рис. 11.4. Из (11.3.4) видно, что
это движение представимо движением по эллипсу с полуосями
\Jс\ + с\ и 2yjс\ + cj, вытянутому вдоль оси £, причем коорди¬
ната 7]* центра эллипса остается неизменной: rf = 2сь однако
вторая координата £* центра эллипса равномерно движется вдоль
оси £: £ = С4 - ЗС|Т. Таким образом, одновременно с прохожде¬
нием космонавтом некоторой дуги эллипса этот эллипс успевает
сместиться вдоль оси ( на некоторую величину.
Итак, только в исключительных случаях космонавт, не привя¬
занный к спутнику, может вновь вернуться на спутник. В общем же
случае космонавт, однажды покинув корабль-спутник, не сможет
вернуться никогда. Сначала космонавт будет находиться вблизи
спутника, но, понемногу удаляясь, будет все больше отставать от ко¬
рабля (или обгонять его). Через половину витка полета спутника
космонавт даже начнет сближаться с кораблем и может подойти
к нему довольно близко. Но вспыхнувшая искра надежды быстро
lcil велико
Рис. 11.4. Схема свободного движения космонавта
относительно спутника в общем случае
360 Очерк одиннадцатый. Относительное движение орбитальных тел
погаснет: коварная траектория относительного движения заставит
космонавта описать пируэт и вновь удалиться от родного корабля...
Дальнейшая судьба космонавта была бы ужасна. Он обречен
нескончаемо долго кружиться вокруг Земли по собственной орбите,
потеряв из виду покинутый корабль. Через много-много витков
космонавт может снова сблизиться с кораблем, но поздно...
Нет, давайте привяжем космонавта фалом, хорошей, доброй,
надежной веревкой!
4. Леонов и заглушка
Предыдущее рассмотрение относительного движения приме¬
нимо не только к исследованию свободного движения космонавта
относительно спутника, но и к анализу свободного движения лю¬
бого предмета относительно любого тела, движущегося по орбите.
Например, можно проследить движение относительно космонавта
любого предмета, брошенного (или потерянного) космонавтом.
Такая ситуация возникла, например, при выходе в открытый
космос А. Леонова. Вот кусок репортажа П. Беляева и А. Леонова
об их полете [11.4]:
«...Он отвинтил заглушку с киноаппарата, укрепленного сна¬
ружи корабля. Куда деть ее? Может запустить на орбиту? И кос¬
монавт, размахнувшись, швырнул ее в сторону Земли. Небольшой
предмет, поблескивая на Солнце, стал быстро удаляться и вскоре
исчез из глаз».
Поучительно разобрать, что произошло с заглушкой. Размыш¬
ления над этим вопросом неизбежно проходят через несколько
этапов.
Первый этап — бездумный: привыкнув мыслить земными ка¬
тегориями, мы не нашли бы ничего удивительного в том, что бро¬
шенный на Землю предмет будет падать именно на Землю.
Второй этап — задумчивый: мы вспоминаем, что космонавт
летит над Землей с огромной скоростью, около 8000 м/сек! С ка¬
кой скоростью бросил Леонов заглушку к Земле? Довольно силь¬
ный бросок человеческой рукой сообщает легкому камню скорость
15-20 м/сек. Примем для определенности начальную скорость за¬
глушки относительно Леонова равной 10 м/сек. При рассмотрении
движения заглушки относительно Земли мы должны геометрически
сложить скорость космонавта относительно Земли и скорость за¬
глушки относительно космонавта (рис. 11.5). Видим, что результи¬
рующая скорость заглушки по величине и направлению изменится
4. Леонов и заглушка
361
заглушки
Рис. 11.5. К задаче о движении заглушки
ничтожно мало! Это значит, что заглушка просто перешла на дру¬
гую эллиптическую орбиту относительно Земли, весьма близкую
к орбите космонавта. Согласуется ли это с утверждением о быст¬
ром удалении заглушки, брошенной в сторону Земли?
Здесь наступает третий этап размышлений — исследователь¬
ский. Мы резонно вспоминаем, что в репортаже речь идет не о том,
как движется заглушка относительно Земли, а о том, как видел это
движение Леонов! Иначе говоря, нужно рассмотреть движение за¬
глушки относительно Леонова. Что же, мы к этому готовы. Обра¬
тимся к уравнениям (11.3.2) траектории относительного движения.
Так как заглушка была брошена прямо по направлению к Земле,
то можно считать начальные данные такими: щ = £о = 0, £о —
7/о ф 0. Тогда, как видно из (11.3.3), С\ = Сз = 0, Ci = щ , с4 = -2щ.
Подставляя эти значения постоянных в (11.3.2) или в (11.3.4), об¬
наружим, что заглушка опишет периодическую траекторию отно¬
сительно Леонова! На рис. 11.6 изображена эта траектория.
Рис. 11.6. Периодическая траектория заглушки
362 Очерк одиннадцатый. Относительное движение орбитальных тел
Если бы Леонов находился в свободном полете целый виток
орбиты, то он бы дождался возвращения заглушки прямо в руки,
но с противоположной относительно Земли стороны. (Здесь, ко¬
нечно, не учитываются второстепенные факторы — отличие броска
от рассмотренного, различные возмущения, по-разному влияющие
на космонавта и заглушку в их полете, и т. п.) Взглянув на рисунок,
изображающий траекторию заглушки относительно космонавта, мы
задаемся вопросом: могли Леонов видеть, что заглушка быстро уда¬
ляется по направлению к Земле?
Здесь наступает четвертый этап размышлений — этап расчет¬
ный. Параметрическое уравнение траектории в рассматриваемом
случае дается формулами
г] = % sin г, £ = 27/q(cost - 1) = -47/о sin2 (11.4.1)
При этом |7/q | = v/V « 10 м/сек : 8000 м/сек = 0,125 • 10“2.
Здесь v — начальная скорость брошенной заглушки относитель¬
но космонавта, V — скорость космонавта относительно Земли;
Пусть Леонов наблюдал за заглушкой в течение полутора минут
(t = 1,5 минуты). Тогда т = ut = 2nt/T = 27г1,5/90, где Т — 90 ми¬
нут — период обращения по той орбите, на которой находился Лео¬
нов. В градусной мере получим т = 360 • 1,5/90 = 6°. Подставляя
в формулу (11.4.1) числовые значения щ и г, вычислим коорди¬
наты заглушки по отношению к космонавту: т/ = -0,131 • 10-3, £ =
0,0137* 10_3. Чтобы перейти к размерным величинам, надо эти числа
умножить на расстояние от центра Земли до космонавта. Примем
это расстояние равным R = 6600 км. Тогда 7/ = rjR& -865 м, £ =
t]R ^ 90 м. Но координата 7/ соответствует смещению заглушки
к Земле, а координата £ — в сторону от Земли.
Вряд ли можно проследить простым глазом полет маленького
тела — заглушки на расстояние почти 1 км. Если же это удалось,
то трудно заметить смещение заглушки в сторону от радиального
направления, так как это смещение составляет всего (примерно)
одну десятую часть от пройденного пути. Если же считать, что
Леонов потерял заглушку из виду раньше (а это гораздо вероятнее),
то доля поперечного смещения заглушки по отношению к полному
пути, пройденному ею, будет еще меньше. Отсюда вывод: пока
видит глаз, заглушка кажется летящей по направлению к Земле.
Бросив заглушку в сторону Земли, Леонов должен был наблюдать
тривиальное ее падение на Землю!
5. Космический зонд
363
5. Космический зонд
Свободное движение одного тела относительно другого мы
рассматривали, предполагая малость расстояния между телами. Это
позволяло ограничиться в анализе линеаризованными уравнениями.
Однако существуют задачи, где относительное движение тел
надо рассматривать и на больших их расстояниях друг от друга.
Такова, например, задача о зондировании околосолнечного про¬
странства. Представим себе, что с Земли запущен космический
аппарат, который должен глубоко проникнуть в космос и после
нескольких месяцев (или лет) полета вернуться снова на Землю.
Во время полета этот аппарат — автоматическая научная стан¬
ция («космический зонд») — собирает и накапливает информацию
о космическом пространстве и затем сам доставляет эту информа¬
цию на Землю. Можно ли осуществить такую траекторию полета
космического зонда? Очевидно, можно. Если зонд движется во¬
круг Солнца по эллиптической орбите с периодом, соизмеримым
с периодом обращения Земли вокруг Солнца, то зонд и Земля, есте¬
ственно, будут периодически встречаться. Например, если период
обращения зонда 1,5 года, то через три года он вернется на Землю.
Рис. 11.7. Две траектории космического зонда относительно Земли
364 Очерк одиннадцатый. Относительное движение орбитальных тел
Рис. 11.8. Две траектории космического зонда относительно Солнца
Интересно и нужно проследить движение зонда не относительно
Солнца, а относительно Земли.
В работе [ 11.5] В. А. Егоров рассмотрел такую задачу. На рис. 11.7
и 11.8, заимствованных из [11.5], приведены траектории космиче¬
ского зонда во вращающейся вместе с Землей системе координат
(рис. 11.7) и те же траектории в абсолютной системе координат
(рис. 11.8). Одна из этих траекторий имеет в движении относитель¬
но Солнца период 4/5 года и подходит к Солнцу на минимальное
расстояние 108 млн км (максимальное расстояние, очевидно, сов¬
падает с радиусом орбиты Земли и равно 149 млн км). Между двумя
встречами зонда с Землей проходит четыре года; зонд за это время
сделает пять оборотов вокруг Солнца. Другая траектория имеет пе¬
риод (в движении вокруг Солнца) полтора года, и зонд встретится
с Землей через три года. Минимальное расстояние зонда от Солнца
149 млн км, максимальное — 242 млн км.
Для различных задач зондирования пространства могут приго¬
диться траектории и с периодами другой кратности (3/4, 2/3 года
или 2, 3, ... года и т.д.).
Вернемся, однако, к нашей задаче об относительном движении
одной точки вблизи другой.
6. Болеадорас в космосе
365
6. Болеадорас в космосе
Займемся, наконец, динамикой заброшенной на орбиту связки
двух тел [11.1, 11.2]. Эта конструкция из двух масс, соединенных
«идеальной» веревкой (рис. 11.1), напоминает аргентинское «боле¬
адорас». В аргентинской пампе с помощью болеадорас отлавливают
полуодичавший скот; несколько более необычное применение бо¬
леадорас красочно описано Дж. Дарреллом.
«У всех пеонов теперь были в руках болеадорас, и я видел, как бле¬
стели шары на концах веревок, когда они раскручивали их над голова¬
ми. Нанду повернули всей стаей и побежали в нашу сторону... Тонкий
свист болеадорас внезапно усилился и замер на протяжном гудящем
звуке. Веревка с шарами пролетела по воздуху и оплеласъ вокруг шеи
и ног птицы подобно щупальцам спрута. Нанду пробежал еще пару
шагов, веревка затянулась, и он упал на землю, дергая ногами и кры¬
льями». (Дж. Даррелл. «Под пологом пьяного леса».)
Мы в дальнейшем будем говорить о космонавте и спутнике,
соединенных фалом; однако не надо забывать, что наша идеализи¬
рованная схема равным образом годится и для описания движения
других орбитальных систем, например, двухсекционного спутника,
секции которого соединены тросом.
Все сказанное ранее о движении космонавта относилось к сво¬
бодному его движению. Проведенный анализ показывает, что в об¬
щем случае космонавт неизбежно удаляется от спутника (ведь веро¬
ятность попасть на периодическую траекторию мала) и в какой-то
момент времени удалится на полную длину фала (обозначим эту
длину I). С этого момента и начинается самое интересное. Даль¬
нейшая судьба космонавта существенно зависит от упругих свойств
фала. Рассмотрим сейчас абсолютно неупругий фал. Предположе¬
ние об абсолютной неупругости очень существенно: в иных пред¬
положениях движение космонавта может носить совершенно иной
характер.
Итак, космонавт удалился от спутника на расстояние Z, рав¬
ное длине фала. Рассмотрим движение начиная с этого момента,
предполагая начальные данные для такого движения известными
(хотя бы из решения предыдущей задачи о свободном движении
космонавта). В дальнейшем можно ожидать из общих соображений
либо продолжения свободного движения космонавта, либо движе¬
ния по дуге окружности радиуса I вокруг центра масс спутника.
Второе движение назовем связанным.
366 Очерк одиннадцатый. Относительное движение орбитальных тел
6. Болеадорас в космосе
367
При каких условиях свободное движение переходит в связан¬
ное? Каков характер связанного движения? Может ли связанное
движение перейти обратно в свобод¬
ное и при каких условиях? Постара¬
емся ответить на эти вопросы.
При выходе космонавта в какую-
то точку сферы радиуса I или окруж¬
ности этого же радиуса в рассматри¬
ваемом плоском случае (будем гово¬
рить «при выходе на сферу») из-за
абсолютной неупругости фала полно¬
стью гасится составляющая скорости,
направленная вдоль фала, в сторону
от спутника. Составляющая же ско¬
рости, направленная нормально к натянутому фалу, сохраняется.
Из уравнений (11.3.1) можно легко вывести интеграл энергии в виде
г}2 + £/2 - Зт]2 = h = const. (11.6.1)
Введем полярные координаты р, <р так, чтобы (рис. 11.9)
7/ = psin<p, £ = pcos(p. (11.6.2)
В этих переменных интеграл (11.6.1) имеет вид
р'2 + рУ2 - Зр2 sin2 <p = h. (11.6.3)
В свободном движении космонавта вплоть до его выхода на сфе¬
ру энергия h сохраняется, так что в момент гк выхода на сферу
имеем
hi * — Рк + РкФк ~ ЗРк — Ро + РоФо ~ Зро s*n2 Аь (Ч -6.4)
причем рк = 1\ нуликами отмечены начальные значения перемен¬
ных, индексом «к» — значение в момент выхода на сферу. Здесь,
как было сказано, радиальная скорость р скачком падает до нуля.
Однако трансверсальная скорость ру полностью сохраняется1^).
^ Это можно доказать совершенно строго, используя теорему Карно об измене¬
нии кинетической энергии при неупругом ударе. По теореме Карно потерянная
кинетическая энергия АТ равна энергии потерянных скоростей, так что 2АТ =
(р2 + p2ip'2) | - {р2 + р2р2) 2 = (V\ - V2)2. Здесь индекс 1 соответствует моменту до
удара, индекс 2 — моменту после удара; очевидно, р\ ф 0, рг2 = 0, р\ = рг, (р\ Ф О,
Ч>2 подлежит определению, V| = р\ро + P\<P\Tq, V2 = Р2Р2Т0 = Р1Р2Т0, где ро
и то — радиальный и трансверсальный единичные векторы. Вычисляя квадрат
разности (V\ — V2)2 и подставляя в предыдущую запись теоремы Карно, убеждаемся,
что ip\ = {р2.
Рис. 11.9. Полярные
координаты
368 Очерк одиннадцатый. Относительное движение орбитальных тел
Это значит, что и энергия скачкообразно изменилась от значения
hx \ определяемого формулой (11.6.4), до значения
Лк'* = р1<Рк - ЗРк sin2 <рк, рк = I.
С этого момента движение происходит по сфере радиуса р = I.
Движение будет определено полностью, если известно значение
<р(т), а это значение определяется интегрированием уравнения
<ра - 3 sin2 V? = Ль (11.6.5)
где h1 = Лк V^2- Уравнение (11.6.5) получено из (11.6.3) при условии
р = 0, р = I и является интегралом энергии для движения типа
движения физического маятника и может быть проинтегрировано
или проанализировано.
Однако движение, описываемое уравнением (11.6.5), может
происходить только тогда, когда фал натянут, а это может иметь
место только в случае, когда производная р положительна. В са¬
мом деле, так как на сфере р — 0, то условие р > 0 означает,
что радиальная скорость стремится возрасти, то есть космонавт
имеет тенденцию уйти по радиусу р из сферы. Но фал его туда
«не пускает», гасит «на корню» эту тенденцию, сохраняя постоян¬
ным (равным нулю) значение радиальной скорости.
Пусть теперь р < 0. Фал немедленно даст «слабину»! Ведь
это условие означает, что радиальная скорость уменьшится, то есть
станет меньше нуля, но тогда космонавт сойдет со сферы внутрь
ее, не будучи ничем сдерживаемым. Поэтому ясно, сколь важно
получить значение р на сфере. Напишем это выражение. На сфере
р = 0 и р = /, используя уравнение (11.3.1) движения, найдем
= у2 - 2<рг + 3 sin2 tp.
I
Итак, если
<р'2 — 2ф + 3 sin2 (р > 0, (11.6.6)
то движение происходит согласно интегралу (11.6.5).
Если же
ц>а - 2<р' + 3 sin2 ip < 0, (11.6.7)
то происходит «срыв» движения со сферы внутрь ее. Таким об¬
разом, (11.6.7) определяет условие перехода в свободное движе¬
ние, в то время как (11.6.5), (11.6.6) определяют связанное дви¬
жение. Удобно рассмотреть движение на фазовой плоскости <£>, tpf
6. Болеадорас в космосе
369
(рис. 11.10). Связанному движению отвечают интегральные кривые
(11.6.5), изображенные на этом рисунке. «Зоны срыва», удовле¬
творяющие (11.6.7), заштрихованы. Свободное движение в «зоне
срыва» не может быть изображено в плоскости <р, р хотя бы пото¬
му, что фазовое пространство свободного движения четырехмерно.
Сначала рассмотрим такие движения космонавта, при кото¬
рых он не входит в «зону срыва», а все время остается па сфере,
так что фал остается натянутым. Из фазовой картины (рис. 11.10)
можно понять, что в этом случае движение космонавта может быть
двух типов: вращательное (непрерывное движение по окружности в
одну сторону) или колебательное — колебание около направления
радиус-вектора спутника (значения р = 7г/2 и р = 37г/2 по опре¬
делению угла р означают, что трос натянут вдоль радиус-вектора
спутника; при этом, если р = 7г/2, то космонавт по сравнению
со спутником более удален от Земли, а при р = Зп/2 он ближе
к Земле). Выведем условия, при которых космонавт выходит за ре¬
жим вращения или колебания без срывов в свободное движение.
Рис. 11.10. Фазовая плоскость: 1 — зоны неэволюционирующего связанного
движения; 2 — зоны эволюционирующего движения (связанное движение
вдоль интегральных кривых переходит в свободное движение на границе
зоны 3); 3 —* зоны срыва
24 Заказ 1667
370 Очерк одиннадцатый. Относительное движение орбитальных тел
Заметим, что, вообще говоря, колебательные и вращательные
движения разграничены кривой (сепаратрисой), проходящей через
начало координат и, следовательно, отвечающей значению h 1 = 0
в интеграле (11.6.5). При h\ > 0 получаются вращательные дви¬
жения, при h\ < 0 — колебательные (о срывах пока не говорим).
Из рассмотрения «фазового портрета» (рис. 11.10) видно, что кос¬
монавт будет вращаться в одну сторону, без срывов, в следующих
двух случаях:
1) h\ ^ 4 в области <р > 0;
2) Л, ^ 0 в области tp' < 0.
Схемы движения космонавта, соответствующие этим случаям,
изображены на рис. 11.11. Условие колебательного движения без
срывов: h\ < h*, где h* определяется из условий касания кривых
tp'2 - 3sin2 tp — h\ = 0 и tp'1 — 2<р' + 3sin2 tp = 0. Как нетрудно
определить, в точке касания фазовой кривой, отвечающей колеба¬
тельному движению, с кривой, ограничивающей зону срыва, будем
иметь: tp' = 1/2, sin<p = -1/2, соответственно Л* = -1/2.
Итак, если
3) hx ^ -1-,
то будет происходить колебательное движение космонавта относи¬
тельно направления радиус-вектора спутника, и притом без срывов
в свободное движение (рис. 11.12). Очевидно, существует предель¬
ная амплитуда колебаний, происходящих без срыва. Эта амплитуда
определяется из (11.6.5) при условиях h\ = h\ = -1/2, <р' = 0, что
дает sin2 (р = 1/6. Вспоминая определение угла tp, заключаем, что
предельная амплитуда колебаний около радиуса вектора
^шах ~ 65 55 .
1) h{ ^ 4, <р' > 0
Направление
орбитального
движения
Рис. 11.11. Схема вращения космонавта на натянутом фале
7. Эволюция смешанного движения
371
Рис. 11.12. Схема колебания на натянутом фале
«Чистые» колебания с амплитудой большей, чем атах, невозможны:
неизбежно произойдет срыв космонавта в свободное движение.
В рассмотренных случаях 1)-3) движение нашей системы ана¬
логично движению твердого гантелеобразного спутника относи¬
тельно его центра масс (см. очерк шестой).
Наконец, если
4) - Х~ < ^ <0,
то происходят колебания со срывами в свободное движение, а если
5) 0 ^ h\ ^ 4, р > 0,
то происходят вращения со срывом в свободное движение.
Области 4), 5) составляют зону незавершенного смешанного
движения. Рассмотрим его более подробно.
7. Эволюция смешанного движения
Можно поставить следующие вопросы. Если движение на сфе¬
ре проходило по фазовой кривой, отвечающей значению h\ кон¬
станты энергии в (11.6.5), а затем ушло в зону срыва, то
а) выйдет ли оно из зоны срыва снова на сферу?
6) если да, то на какую фазовую кривую?
На первый вопрос, вообще говоря, можно ответить положитель¬
но, так как по изученным выше свойствам свободного движения
мы знаем, что рано или поздно космонавт опять выйдет на сферу.
Ответ на второй вопрос более сложен. Придется проследить
все свободное движение после срыва вплоть до нового выхода
на сферу, вычислить угловую координату выхода на сферу и угловую
скорость. Это вычисление ставит в соответствие некоторую точку
фазовой плоскости другой точке (<рг*Ч>г)- Точка (<Р\9р\)
24*
372 Очерк одиннадцатый. Относительное движение орбитальных тел
лежит на границе зоны срыва; в эту точку «упирается»
интегральная кривая, по которой шло движение до срыва. Точка
{VhVi) ~ начальная точка нового участка связанного движения;
дальнейшее движение идет по интегральной кривой, на которой
лежит точка ^2) (если только Ф2) не попадает внутрь зоны
срыва). Таким образом, для понимания картины движения необ¬
ходимо построить так называемое точечное отображение участков
границы зоны срыва.
Метод исследования задач нелинейной механики, использую¬
щий такие построения, называется методом точечных отображений.
Этот метод удобен при исследовании движения, которое на раз¬
ных своих участках описывается разными системами дифферен¬
циальных уравнений. Необходимое для нас точечное отображение
строилось численными методами, с использованием быстродей¬
ствующих электронных машин. Результат вычислений изображен
на рис. 11.13. Там построено отображение только для одной зоны
срыва. Для другой — все аналогично.
Самое главное — это отображение помогает представить всю
эволюцию движения (а не только второй этап). В самом деле, ес¬
ли есть отображение (</?|, (р\) => ^2) Для любой точки (<р|, <р\)
на границе зоны срыва, то дальнейшая картина движения стано¬
вится ясной: точка (<^2^2) приводит по некоторой интегральной
Рис. 11.13. Отображение границ зоны срыва: 1 — фазовые траектории и гра¬
ницы зоны срыва; 2 — отображаемые участки границы зоны срыва; 3 — их
отображения. Участки (1,1*—7,7*) и (6,6*—10) не отображаются
7. Эволюция смешанного движения
373
кривой снова на границу зоны срыва в точку отобра¬
жение (^2^2^) которой мы уже умеем найти, и т.д. Некоторую
трудность вызывает то обстоятельство, что начальная или отоб¬
раженная точки могут лежать внутри зоны срыва. Физически это
означает, что фал, натянувшись, в тот же момент ослабляется, так
что на сфере оказывается одна-единственная точка траектории дви¬
жения (а не участок траектории).
Поэтому для полного анализа движения нужно строить отоб¬
ражения не только границ зоны срыва, но всей этой зоны целиком.
За подробностями отсылаю читателя к статье автора [11.2]. Здесь же
отмечу, что указанное обсто¬
ятельство не играет принци¬
пиальной роли для эволюции
движения. Эту эволюцию осо¬
бенно удобно проследить по
энергетической кривой, даю¬
щей зависимость энергии h2
после выхода на связь (после
удара) от энергии h\ до вы¬
хода на связь. Эта энергети¬
ческая кривая ^2(^1) изоб¬
ражена на рис. 11.14. Пусть
начальная энергия равна h\.
Находим по рисунку соответ¬
ствующее значение hi. При¬
мем это значение hi за но¬
вое начальное значение Л|,
находим новое hi и т.д. Та¬
кой ступенчатый процесс от¬
ражает ступенчатое измене¬
ние энергии при последова¬
тельных выходах на связь. Из
рисунка легко видеть, что в ре¬
зультате конечного или бесконечного числа выходов на связь дви¬
жение приходит к некоторому предельному движению, энергия ко¬
торого уже не может изменяться. Таким предельным движением
является, например, движение с h = 1. Оно носит смешанный
характер, частично связанное, частично свободное и изображено
на рис. 11.15. Время выхода на этот предельный режим конечно;
однако множество начальных значений энергии, приводящих к это¬
374 Очерк одиннадцатый. Относительное движение орбитальных тел
Рис. 11.15. Периодиче¬
ское движение при h =
Рис. 11.16. Периодические режимы
с отрицательными энергиями
му режиму, дискретно («имеет меру нуль» по отношению ко все¬
му множеству начальных значений энергий). Поэтому вероятность
попасть на такой режим мала (в строгом смысле — вероятность
равна нулю).
Аналогичный характер носит бесконечная серия периодиче¬
ских предельных режимов с малыми отрицательными значениями
энергии. Некоторые из этих режимов изображены на рис. 11.16.
Это режимы с очень большими периодами (колебания с малы¬
ми отрицательными значениями энергии происходят по участкам
фазовых кривых, близких к сепаратрисе; каждая «волна» свободно¬
го движения соответствует половине периода обращения спутника
по орбите).
Но имеются предельные режимы, к которым приводят не дис¬
кретные, а плотные множества значений энергии. Это чисто свя¬
занные движения — колебания около положения относительного
равновесия со значениями энергии -1,85 ^ h ^ -0,5. Движение
«скатывается» за конечное время к колебаниям с каким-либо фик¬
сированным значением h из указанного интервала; но может также
случиться, что движение будет бесконечно долго стремиться к коле¬
баниям со значением h = -0,5. На рис. 11.17 и в табл. 11.1 указаны
все возможные предельные движения.
Конечно, читатель отдает себе отчет, что рассмотренная эво¬
люция движения лишь условно может быть отнесена к реальной
картине движения космонавта в окрестности спутника. Прежде
всего, для анализа движения космонавта нет надобности рассмат¬
ривать очень большие интервалы времени и предельные движения.
Но эта же задача применима к любой системе двух тел, связанных
тросом и летящих в космосе; например, это может быть спутник,
состоящий из двух секций. Его относительное движение описыва-
7. Эволюция смешанного движения
375
Рис. 11.17. Предельные режимы на фазовой плоскости: 1 — множество пре¬
дельных режимов, ограниченное предельным циклом с h = -0,5; 2 — фазо¬
вые траектории и границы зоны срыва; 3 — область предельных движений
с h = -0,00825; h = -0,00095 и т.д.; 4 — предельный цикл с h = -0,5
и предельное движение с h = 1
ется точно так же. Такие двухсекционные спутники применяются,
в частности, для их ориентации по направлению к Земле с помощью
гравитационных сил (так называемые «пассивные гравитационные
системы ориентации», о которых говорилось в шестом очерке). Для
таких спутников как раз важно ответить на вопрос о предельных ре¬
жимах их движения. Желательно, чтобы в пределе спутники строго
ориентировались на Землю. (В нашей схеме видим, что если при
первом же выходе на связанное движение не получатся колеба¬
ния относительно направления на Землю с амплитудой, меньшей
48° (h = -1,85), то амплитуда меньше 48° не будет никогда.)
Гораздо большей условностью является принятая схема абсо¬
лютно неупругого выхода на связь. На самом деле, выход на связь
является частично упругим; кроме того, в процессе «свободного»
движения происходит рассеяние энергии за счет изгибов и кручения
троса, так что движение носит сложный характер. Но исследование
более строгих постановок — дело специальных работ. Наша цель
была другая — понять характер задачи, ее место среди прочих за¬
дач механики космического полета, прочувствовать возникающие
проблемы и возможные методы исследования.
Таблица 11.1
376 Очерк одиннадцатый. Относительное движение орбитальных тел
(D
X
X
<и
X
X
со
е*
+
В
05
9
00
2
оо
<L>
X
of
X
X
<D
X
X
00
п
<D
*
X
CQ
>*
о
X
X
п
S
1~
1 с
X гм
& u
X +
S d
JO rf
S 1j
Ю ,
Q« I
® V
о ^
« +
о ^
О гм"
<u D
x I
X +
Cj гм
2 ^
X О
O.
<u —
с V
V/ <N
+
<15
СЧ
СЧ |
+ £
+
04
05
X
cd
D,
00
X
о
Ou
+
2
X
X
<D
cd
cx
X
cd
X
о
X
05
X
X
<u
*
о
§
о
X
о
X
о
+ +
vy>
X
н
о
si «5
2aS&
|SSg
g х ^х
5 « 2 2
x x о 5
О х г I
о Э 5 я
й Cd 2 cd
О О, X X.
—ОСЧ
00 £
IX X
о «
ё s
2 х
X Cd
JQ ю
Р
Хчу
ID A
Do
О rn
О
A
A\
ГМ
с
’55
СП
I
о
V
o'
A\
•*2
<N
I
1П
o"
I
V/
V/
m
I
о
сн
I
X
o,
S5-
+
ГЧ
W
X
5
о
x «д.
Cl 3
с S
—, <L>
o.
■VS
+ 8.
ЧГ
CQ
x m
В о
. о I
о x
x * V/
5 a^s
_ x x
>x £ ° V/
X О О СП
2 x оо
cd Ю
Ю 05
ё §s 1
й> о ® 5
X S х g
ию ь
о, CU cd
ё§а
«* ё
s*i 5
W Л х
О- X го
и J0 г
2 5 ^ g ^2
X go Э -
оо о- 1 £* о
ЮС || Сю
rfSfN ч
и
&
о
о
X
X 2
2|
CL X
5 «
cd
В
О
X
*
>>
о,
X
о
о
£
0
1
о
о
о
S
§. На
зХ U S
х fi*s
g s«
" is
X ^ н
и 4)0
S' О rti
х
<и
a
х
X
X
и
<и
х
.§
О X
х a
3- <и
0) X •
§><
si
-04 .
Е®о
«О I
S9 и <
<и о х
о £•« £>
X OQ^.CX
a • о
I
О)
а 11 2
зХ л)
2^0
° 3
-"^81
о-с Г§
° „ Iе*
2 со СП S
S^ON 9
■с S
^ о22 о.
g, й®в«
ГТ О .—> /—«> г-
Ос
vg
I
05
00 и И U
Оо гм о 2 СГ
Хсл vyrj- S*CS^0Q
X
2
X
X
cd
СЗ
X
2
х
3
X
X
cd
е*
X
3
X
JO
О
OQ
5
<D
X
о
о
00
н
о
<D
X
О
X
S
§ §
X
cd
X
о
5S
8 8
г- Л
О D q D
« 2 « 2
S ^ S
х 2 зх
о ;
<и s; «и s;
о 2 о 2
X £ X £
н х Н X
« X « X
СХ Cd о. cd
о Ж
00*“
W
х~
х 2 —
о J0 о
сп е тГ
I ? I
n— cd ^
l<t/r> + z/v>AZ + \*°\ °9И1Г
‘О ф + °bz 09И1Г
7. Эволюция смешанного движения
377
378 Очерк одиннадцатый. Относительное движение орбитальных тел
Двухсекционный спутник, секции которого соединены доста¬
точно длинным тросом, представляет собой благодарный объект
для исследования. Самый безобидный из вопросов, которые еще
ждут ответов: может ли эта система сама завязаться узлом?
8. Пространственная связка тел
Можно вообразить себе космическую станцию, состоящую
из нескольких одинаковых секций, связанных тросами так, что
станция представляет собой пространственную конфигурацию. На¬
пример, четыре одинаковых секции, соединенные друг с другом
тросами одинаковой длины, образуют тетраэдральную связку тел
(рис. 11.18). Может ли подобная связка сохранять постоянную кон¬
фигурацию на орбите? На этот вопрос, поставленный Е. А. Девя-
ниным, дан ответ Е. Т. Новиковой. Рассмотрим эту задачу.
Аналогично (11.2.3), уравнения движения имеют вид
3 3
Pi Н" Pi — (R * A')R = У! \j{Pi ~ Pj)• (1 1-8.1)
j= I
Здесь pi — радиус-вектор г-й секции станции относительно центра
масс станции, Аг; — множитель Лагранжа за счет связи между г-й
и j-й секциями. В связанном движении (сохранение тетраэдраль¬
ной конфигурации) все Ац должны быть отрицательны. Условия
связей:
I Pi ~ Pj I ^ I-
Если конфигурация сохраняется, то станция неизбежно будет
вращаться с постоянной по величине и направлению в пространстве
угловой скоростью Г2, потому что эллипсоид инерции «затвердев¬
шей» станции — сфера (А = В = С).
dpi dp т
— = Пх pi, — = Пх (Пх р() = - р{) - р{П ,
и уравнение (11.8.1) принимает вид
Г2(12*р,-) + ^ ^ Pi ~ ^5 ^ ^ ^ij(Pi ~ Pj)• (1 1-8.2)
j= I
9. Орбитальное облако частиц и теорема Пуанкаре о возвращении 379
Умножим это уравнение скалярно на Q. Получим
- ^(R • Pi)(R • Q) = biiPi - Pjh (11.8.3)
j= I
где pf означает проекции векторов pf. на ось fi. Все эти проекции
pf постоянны в силу того, что станция, как целое, вращается вокруг
оси П. Пусть pf > 0 есть наибольшее
из pf. Тогда все р\1 - рf > 0. Ввиду
того, что Q = const, a R заметает не¬
которую плоскость (плоскость орби¬
ты), наступит момент, когда Rfi = 0.
В этот момент левая часть (11.8.3)
положительна, что возможно, если
хотя бы одно из Aij положительно
(ввиду pf - pf > 0). Но положи¬
тельность A ij означает «ослабевание»
троса между г-й и j-й секциями, то Рис> 11<18> тетраэдральная
есть сход со связи. Таким образом, связка тел
постоянное сохранение конфигура¬
ции рассматриваемой пространственной связки тел невозможно.
9. Орбитальное облако частиц
и теорема Пуанкаре о возвращении
Одной из примечательных задач динамики относительного
движения является задача об облаке частиц, выпущенных со спут¬
ника. Каково будет поведение облака с течением времени? В 1963 г.
был осуществлен американский проект «Вест Форд» запуска на ор¬
биту «облака» металлических иголок — для нужд радиосвязи. Тот же
вопрос можно задать, конечно, и по отношению к большому скоп¬
лению спутников, если бы такое скопление существовало.
Рассмотрим цепочку задач (они пронумерованы), предельно
упрощенных, но подводящих к правильному ответу на поставлен¬
ный вопрос.
Задача 1. Большое количество спутников в начальный момент распо¬
ложено по одному радиусу и имеет — каждый свою — круговые скоро¬
сти (рис. 11.19). Какова будет конфигурация этого множества спутников
по прошествии времени?
380 Очерк одиннадцатый. Относительное движение орбитальных тел
Решение. Фиксированный спутник рассматриваемого множе¬
ства движется по круговой орбите радиуса г, причем полярный
угол р меняется по закону tp = w(t—to). По третье¬
му закону Кеплера ш = л/Ji/r3^2. Следовательно,
конфигурация системы по прошествии фиксиро¬
ванного времени Г* = t - to определяется уравне¬
нием
у/U,
V ~ j.3/2 Т* ’
то есть
г +
tp
2/3 ’
= \/Wi
Рис. 11.19.
Конфигурация
множества
спутников
Это — уравнение спирали, которая также изоб¬
ражена на рис. 11.19. Чем больше время Г*, тем
больше витков спирали содержится между двумя
фиксированными значениями радиуса Г\ и г2. >
Кстати, если бы кольцо Г\ ^ г ^ г2 изна¬
чально было заполнено частицами, за исключе¬
нием некоторой радиальной «щели», то в каждый
фиксированный момент времени t Ф to щель име¬
ла бы вид спирали (11.9.1). Спиральная структу¬
ра галактик в значительной степени определяется этим простым
фактом. Имеющиеся (по каким-либо причинам) «выступы» или,
наоборот, «щели» в галактике должны с течением времени закру¬
чиваться по спирали типа (11.9.1) — это неизбежное следствие
законов Кеплера.
Задача 2. Возьмем любые два спутника из предыдущего множества.
Каково будет их относительное движение?
Ответ. Обозначим через Г\,Ш\ и r2,u;2 радиус и частоту об¬
ращения по орбите соответственно первого и второго спутников.
Относительное движение р = г2 — Г| определяется в полярных ко¬
ординатах р, р формулами
= \Jr2\+r2 - 2Г|Г2 cos (w, - w2)(t - to), (11.9.2)
tg<P
Г2 sin U)2(t — to) - Г\ sin U)\(t - to)
Г2 COSUJ2(t - to) — T\ COSU>t(i - <o)
(11.9.3)
9. Орбитальное облако частиц и теорема Пуанкаре о возвращении 381
Зависимость p(t) — периодическая функция с периодом
2тг _ Г,Г2
Ш\ — U)2 Т2 — Т\
ТР = - = (11-9.4)
Величина р изменяется периодически между максимальным
(Pmnx = i'\ +^2) и минимальным (pmjn = г2 - г j) значениями. Период
Тр весьма велик для спутников с близкими периодами Т\ и Т2.
Пусть, например, Т2 = Т\ +Т\/п, где п — большое число.
Тогда
Тр = (п + 1)Т,. (11.9.4')
Между тем скорость изменения угла р определяется часто¬
тами и)\,и)2 (а не их разностью). Поэтому траектория р(р) пред¬
ставляет собой многовитковую «медленно пульсирующую спираль».
Приблизительно за (п+ 1)/2 оборотов первого спутника по орби¬
те второй спутник отойдет от него на максимальное расстояние,
а приблизительно за п + 1 оборотов спутники вернутся в исходную
конфигурацию. >
Задача 3. Проследить эволюцию «облака спутников» на большом ин¬
тервале времени.
Постановка и решение. Мы максимально упростим структуру «об¬
лака», полагая, что частицы движутся по серии круговых орбит с пе¬
риодами Тг, которые могут быть упорядочены следующим образом:
Т, - Т0, Т2 = Т0 + -Т0,
71
Т3 = То + -То,..., Т,+ 1 - То + -Т0, (11.9.5)
тг п
где тг — достаточно большое (пусть — целое) число и к ^ п.
Каждым периодом Тг обладает группа частиц, но мы будем говорить
об одной частице с данным периодом.
Проследим эволюцию такого облака. Из задачи 1 следует, что
облако довольно быстро «размажется» по некоторой кольцевой об¬
ласти г* ^ г ^ 7*2. Действительно, за время тТо первая частица
сделает га оборотов по орбите, а (к + 1)-я частица сделает
гаТ0 га
= Г оборотов,
Тк+' 1 + -
п
382 Очерк одиннадцатый. Относительное движение орбитальных тел
так что спираль из задачи 1 будет иметь
тп тп
тп j- = -й ~ тп витков (если к > п).
1 + — т + >
71 Ь
Период близкого к Земле спутника равен примерно 1,5 часа. Это
значит, что всего за сутки частицы облака рассредоточатся по 16-
витковой спирали, засоряя практически все околоземное простран¬
ство в кольце г* ^ г ^ 7*2. Если даже к ~ п, то число витков спи¬
рали будет га/2 (то есть за сутки образуется 8-витковая спираль).
Однако посмотрим, что будет дальше.
Согласно задаче 2 (формула (11.9.4')) через время Т\ = (п+1 )Т0
повторится конфигурация первого и второго спутников. За это вре¬
мя третий спутник сделает Tj/Тз = п/(п + 2) оборотов по орбите.
За время Т2 = (п + 2)Т\ конфигурация первых двух спутников по¬
вторится (в (п + 2)-й раз), а третий спутник сделает п оборотов
по орбите и, таким образом, впервые возникнет повторение кон¬
фигурации трех спутников. Рассуждая подобным образом дальше,
убедимся, что за время
Tfi = (п + 1 ){ть + 2)... (ть + к)То (11.9.6)
повторится исходная конфигурация всех к -h 1 спутников, то есть
наше облако частиц-спутников соберется в исходное положение!
Однако время Т^ чудовищно велико. В самом деле,
Г* >2fc"'f|. (11.9.7)
Пусть время Т\ повторения конфигурации двух частиц — сут¬
ки (заниженная оценка, отвечающая п = 15). Тогда всего для 102
частиц время возвращения системы в исходную конфигурацию бу¬
дет заведомо больше, чем 2100 суток, что составляет число суток
большее, чем Ю30. Для сравнения: время существования Солнеч¬
ной системы приблизительно 1012— IО13 суток («всего»). >
Наша задача — всего лишь бледная тень замечательной тео¬
ремы динамики — «теоремы Пуанкаре о возвращении». Ее можно
сформулировать так. Пусть движение системы а) консервативно,
б) ограничено по фазовым переменным. Тогда система из большин¬
ства исходных состояний по прошествии достаточно большого вре¬
мени возвращается в положение, сколь угодно близкое к исходному.
Таким образом, факт возвращения системы в состояние, сколь
угодно близкое к исходному, доказывается теоремой Пуанкаре в
9. Орбитальное облако частиц и теорема Пуанкаре о возвращении 383
весьма общих предпосылках. Так, в рассмотренной выше задаче
этот факт совершенно не зависит от конкретного упорядочения
(11.9.5) частиц; имеет место и при учете влияния на частицы раз¬
личных возмушаюших факторов (но консервативной природы!),
консервативного взаимодействия частиц и т.д. Важна лишь именно
консервативность системы плюс естественное требование ограни¬
ченности фазового пространства, в котором совершается движение
(что улетело в бесконечность — того не вернешь).
Теорема Пуанкаре о возвращении предоставляет один из не¬
многих общих выводов о характере движения, хотя детали движения
«никому не известны» [11.6] уже в самых простых задачах (напри¬
мер, неинтегрируемых двумерных задачах).
Эта теорема имеет многочисленные, порой неожиданные кон¬
кретизации. Вот феномен из книги В. И. Арнольда [11.6]: если раз¬
городить комнату перегородкой, выкачать из одной половины воз¬
дух и сломать перегородку, то воздух сам по себе «через достаточно
большое время» соберется в одной половине комнаты. (Однако по¬
требное время сравнимо с возрастом Вселенной.)
Мы приведем формулировку и доказательство теоремы Пуан¬
каре, следуя великолепной книге В. И. Арнольда [11.6].
Рассмотрим уравнения Гамильтона (2.4.4) для общего случая
г = 1, 2,..., п.
Назовем 2п-мерное пространство с координатами рг, дг, г —
1, 2,..., п, фазовым пространством.
Определение. Фазовым потоком называется однопараметри¬
ческая группа преобразований фазового пространства
gf :(pi(0),qi(0))^(pi(t),qi(t)), (11.9.8)
где Pi(t),qi(t) — решение системы уравнений Гамильтона.
Теорема Лиувилля. Фазовый поток сохраняет объем: для любой
области D имеем {рис. 11.20)
объем glD = объем D.
Доказательство здесь опускаем; его можно найти, например в [11.6].
Теорема Пуанкаре о возвращении. Пусть g — сохраняющее
объем, непрерывное, взаимно однозначное отображение, перево¬
дящее ограниченную область D евклидова пространства в себя:
gD = D. Тогда в любой окрестности Д любой точки области D
найдется точка х Е Д, которая возвращается в область Д, то
есть gnx Е Д при некотором п > 0.
384 Очерк одиннадцатый. Относительное движение орбитальных тел
Рис. 11.20. К сохранению фазового Рис. 11.21. К доказательству
объема теоремы Пуанкаре
Доказательство. Рассмотрим образы окрестности Д (рис. 11.21):
Д, дА, д2А,..., дпА,... Все они имеют одинаковый положитель¬
ный объем. Если бы они не пересекались, объем D был бы беско¬
нечен. Поэтому при некоторых к ^ О, I ^ 0 (к > I) пересечение
дк > 0 и д1 > 0 не пусто:
/др|</д^о.
Следовательно, gklA О Д Ф 0. Пусть дк~1х = у, х € Д, у € Д.
Тогда х Е А, дпх Е А (п = к - I), что и требовалось доказать. □
Теорема Пуанкаре носит общий, абстрактно-математический
характер. Механические ее приложения следуют из того, что отоб¬
ражение g можно задавать в виде (11.9.8) (удовлетворяющем усло¬
виям теоремы Пуанкаре в силу теоремы Лиувилля). Существенным
требованием в условиях теоремы Пуанкаре является ограниченность
(и самоотображение) области D фазового пространства, в которой
происходит движение. Этому условию в одномерных системах (ма¬
тематический маятник, например) удовлетворяют области «внутри»
сепаратрис; в двумерных системах с растущим на бесконечности по¬
тенциалом V = -U — области «внутри» фиксированного уровня
энергии: Т + V ^ h и т. д.
Задача. В [11.7] и других своих работах Н. Н. Козлов, Р. А. Сюняев
и Т. М. Энеев моделируют взаимодействие галактик следующим образом.
Облако взаимно нетяготеющих частиц движется с начальными круговыми
скоростями относительно массы т0 («ядра галактики»), каждая частица
9. Орбитальное облако частиц и теорема Пуанкаре о возвращении 385
облака притягивается к т0 по закону Ньютона. По этому же закону части¬
цы облака притягиваются к некоторой массе тп\ («возмущающая масса»).
Массы га0 и тп\ взаимно тяготеют по ньютоновскому закону, и масса тп\
согласно законам Кеплера, движется по гиперболической орбите относи¬
тельно массы га0.
Удовлетворяет ли описанная система условиям теоремы Пуанкаре
о возвращении?
Ответ. Нет. D>
Этому мешает неограниченное, по условию, движение мас¬
сы гп\. Таким образом, нельзя утверждать, что галактика когда-
либо вернется к исходному состоянию движения всех частиц обла¬
ка по круговым орбитам вокруг массы га0.
Расчеты Н. Н. Козлова, Р. А. Сюняева и Т. М. Энеева показа¬
ли, что возмущающая масса га \ может «захватить» и увести с со¬
бой часть частиц; иные же частицы приобретают гиперболические
скорости относительно обеих масс (гао и raj) и «выбрасываются»
из галактики. Оставшиеся в окрестности гао частицы имеют эллип¬
тические скорости относительно гао, а само облако частиц замет¬
но трансформируется, приобретая ярко выраженную спиральную
структуру.
Теперь спиральное облако из частиц, оставшихся в окрестно¬
сти массы гао, «изолируем» от улетевшей массы т\: будем считать,
что гп\ полностью «перестала» притягивать частицы облака. Тогда
приходим к новой исходной задаче: имеется масса гао; спиральное
облако частиц в окрестности гао; частицы тяготеют к гао, но не друг
к другу; скорости частиц относительно гао — все эллиптические.
Вот такая система уже удовлетворяет условиям теоремы Пуанкаре.
Можно утверждать, что как бы ни деформировалась такая «галак¬
тика», в конце концов она снова придет к исходной спиральной
структуре!
Однако напомним, что потребное для этого время много боль¬
ше любого разумно оцененного времени физического существова¬
ния галактики.
Дополнительные комментарии к этому изданию. Автор не может
пожаловаться на отсутствие интереса к настоящей книге. Со вре¬
мени выхода в свет первого издания «Очерков» (1972 г.) они не¬
однократно рецензировались (В. И. Арнольдом и Я. Б. Зельдовичем
в российских журналах «Природа» (1973. № 10) и «Успехи физиче¬
ских наук» (1974. Т. 112, вып. 3)), переиздавались (польское издание
25 Заказ 1667
386 Очерк одиннадцатый. Относительное движение орбитальных тел
1976 г., второе русское и болгарское издания 1977 г. и французское
издание 1986 г.) и цитировались. Например В. И. Арнольд вклю¬
чил задачу «Леонов и крышка объектива», обсуждаемую в этом
очерке, в свои широко известные книги [11.6] и [11.8]. Проблемы,
рассматриваемые в этом очерке, продолжают исследоваться и раз¬
рабатываться многими авторами. Некоторые из этих работ кратко
описаны ниже.
А. Разработка теории безударного движения
В 1992 году А. П. Иванов опубликовал статью [11.9], содержа¬
щую его общую теорию систем с односторонними связями 2\
Это позволило, в частности, рассмотреть с новой стороны ди¬
намику двух связанных тел, описанную в п. 7 настоящего очер¬
ка. Согласно доказанной Ивановым теореме, мера множества на¬
чальных значений энергии, которые в процессе эволюции приво¬
дят к безударным траекториям, показанным на рис. 11.15 и 11.16,
отлична от нуля. В [11.10] Иванов и А. Б. Базиян нашли оцен¬
ки для областей притяжения безударных движений, классифици¬
рованных в табл. 11.1 и показанных на рис. 11.15 (h = ho ~ 1)
и рис. 11.16 (h = hn,n = 1,2,3...). Оказалось, что область при¬
тяжения (Д/i)о решения с h = ho существует и ее порядок 10”7;
точнее, (A/i)o < 1,810-7. Другими словами, на рис. 11.14 в точке
h\ = 1, Л2 — 1 кривая энергии касается линии h = ft2, а сама точка
«полуустойчива». Все эти детали можно было бы разглядеть, ис¬
пользуя хороший микроскоп с разрешением 10-7, если бы показан¬
ная на рис. 11.14 кривая была рассчитана с достаточной точностью.
Области притяжения (A/i)n решений с h — hn, п— 1,2,3...
удовлетворяют оценке (Дh)n < 2,5 • 10-9п-6.
Значения начальных данных и энергий в рассматриваемых
здесь смешанных безударных периодических режимах были уточ¬
нены в статьях [11.11], [11.12] и независимо в [11.10]. Например,
для двух траекторий, показанных на рис. 11.13, достаточно точные
значения таковы:
<р{0]) = 0,586, 4$ = я- + <р'0 = 1,3706;
Т = 2,9028; h = h0 = 1,0158;
См. также книгу А. П. Иванова «Динамика систем с механическими соударе¬
ниями» (М.: Международная программа образования, 1997).
9. Орбитальное облако частиц и теорема Пуанкаре о возвращении 387
здесь Т — безразмерная длительность полета по дуге (свободного)
движения. Точные значения указанных величин удовлетворяют си¬
стеме уравнений
Т <Ро Т 1 1-2^о
tg- =ctg(p0— Г, - = - Ctg v^o j?
2 2<p'0 - 3 2 3 2 - (p0
(<p'0)2 -2^o + 3 sin2 (p0 = 0, h = ((p'0)2 - 3 sin2 <p0.
Для траекторий с h = hn, n= 1,2,3..., показанных на рис. 11.16,
эти формулы приводят к приближенному решению
<р{) = (67ГП)" 1, (fo = (247Г V)"1,
hn = -(127г2п2)-1, Т = 2жп - <ро.
Это, в свою очередь, ведет к следующим уточненным значени¬
ям hn в табл. 11.1 (ив подписи к рис. 11.17)
h{) = 1,01580, h\ = -0,00844, h2 = -0,00211, h3 = -0,00094,
/*4 = -0,00053, hs = -0,00 034, hb = -0,00023, hn - -0,00017,
и так далее. В [11.10] значения этих величин были вычислены с
11 значащими цифрами.
Б. Система двух связанных тел
на орбите как динамический бильярд
В [11.11-11.13] проблема динамики системы связанных тел
рассматривалась с современных позиций в предположении абсо¬
лютной упругости ударов при достижении ограничивающего мно¬
жества. Точнее, в этих статьях изучается структура полного фазового
пространства — с хаотическим «морем», островами регулярности,
безударными движениями и т. д. Задача кусочно интегрируемая,
и движения на интервале времени между двумя ударами описы¬
ваются аналитическими формулами. Благодаря гипотезе об абсо¬
лютно упругих ударах существует интеграл энергии, постоянное
значение которого служит параметром задачи; фазовый портрет за¬
дачи зависит от величины этой константы. Как обычно, фазовый
портрет строится в дискретные моменты времени, а именно, в на¬
шей задаче в моменты соударения с ограничивающим множеством.
В «обычном» кинематическом бильярде каждая траектория явля¬
ется ломаной линией, состоящей из линейных сегментов. В дан¬
ном случае каждая ломаная траектория состоит из криволинейных
25*
388 Очерк одиннадцатый. Относительное движение орбитальных тел
сегментов, форма которых зависит от действующих сил; поэто¬
му естественно назвать такую задачу «динамическим бильярдом»
[11.14,11.15]. В статьях [11.11] и [11.12] действующей силой являет¬
ся гравитационно-градиентная сила, а в [11.13] учитывается также
сила аэродинамического давления.
Почти 40 лет прошло со времени публикации статей [11.1]
и [11.2]. Новые достижения теории динамических систем позволили
развить и обогатить старые результаты, и это очень своевременно,
так как проблемы динамики связанных систем в настоящее время
привлекают большой интерес (см., например, [11.16]).
Очерк двенадцатый
Космическая вертушка
— Помилуйте, сеньор, — возразил Санчо Панса, —
это вовсе не великаны, я ветряные мельницы.
Сервантес
«Дон Кихот»
1. Спутники «Протон»
В очерке шестом этой книги рассказывалось о достоприме¬
чательных эффектах в движении спутника около его собственного
центра масс, в эволюции вращения и ориентации спутника. Од¬
нако там речь шла о явлениях, в некотором роде общих и для
естественных, и для искусственных небесных тел; эти явления вы¬
званы воздействием гравитационного поля.
Между тем на искусственные спутники действует ряд других
сил. Например, аэродинамических. Спутник движется в верхних,
сильно разреженных слоях атмосферы Земли, где систематиче¬
ское влияние очень малых аэродинамических сил может привести
(и действительно приводит) к медленной эволюции как орбиты
спутника, так и его вращательного движения.
Так как формы спутников могут быть разнообразными и порой
весьма «экзотическими», а аэродинамические свойства существен¬
но зависят от формы спутника, то и эволюция ориентации спутника
под действием моментов аэродинамических сил оказывается порой
довольно эффектной, также «экзотической».
В 1965-1968 годах в СССР была запущена серия тяжелых (са¬
мых тяжелых из научных) спутников «Протон». Характерной осо¬
бенностью их конструкции является наличие на спутнике боль¬
ших лопастей солнечных батарей, расположенных по отношению
390
Очерк двенадцатый. Космическая вертушка
к осям спутника кососимметрично. Это
видно из рис. 12.1, на котором изобра¬
жен спутник «Протон».
При движении спутника по орбите
на него набегает поток разреженной сре¬
ды. Этот поток, попадая на лопасти бата¬
рей, раскручивает спутник подобно то¬
му, как раскручивается ветром детская
вертушка или крылья ветряной мельни¬
цы. С той только разницей, что крылья
нашей «мельницы» намертво скреплены
со спутником и заставляют его крутить¬
ся вместе с собой. Это вызывает целый ряд своеобразных явлений
в эволюции вращения и ориентации спутника «Протон».
2. Как это было обнаружено
Эти явления были обнаружены при анализе эксперименталь¬
ных данных о вращении и ориентации «Протон-2».
В шестом очерке было обещано объяснить, что это такое —
экспериментальное определение ориентации спутников. Настало
время выполнить обещание.
Дело в том, что об ориентации спутника и изменении ее со вре¬
менем заранее, как правило, ничего не известно (мы подразумева¬
ем, что на спутнике нет специальной системы ориентации). А эту
ориентацию знать нужно: без этого часто невозможно правильно
объяснить показания научных приборов на спутнике. А ведь науч¬
ные приборы измеряют физические характеристики околоземного
и космического пространства; цель запуска спутника — какой-то
новый этап в познании природы. Но какое уж тут познание, если
нельзя объяснить показания приборов? Вот и нужно знать, в какой
момент куда «смотрит» тот или иной прибор, то есть знать ориен¬
тацию спутника в пространстве. Для этого на спутнике устанавли¬
вают какие-либо «датчики ориентации». Показания этих датчиков
передаются на Землю. Солнечные датчики, например, дают инфор¬
мацию о том, освещено Солнцем окно датчика или нет; магнитные
датчики могут показать, как направлена в данный момент отно¬
сительно корпуса спутника силовая линия магнитного поля Земли
и т.д. По этим данным и требуется восстановить ориентацию спут¬
ника.
Рис. 12.1. Общий вид
спутника «Протон»
2. Как это было обнаружено
391
392
Очерк двенадцатый. Космическая вертушка
Беда в том, что, во-первых, обычно показания датчиков рас¬
средоточены так, что не на каждый момент времени есть показания
более одного датчика, а на некоторые моменты вообще нет никаких
показаний.
Беда, во-вторых, в том, что показания датчиков неизбежно
врут: всегда имеется хоть малая, но ошибка в этих показаниях (хо¬
рошо, если малая). Ведь датчик — это прибор, и существует тысяча
помех его работе, и при передаче его показаний на Землю, и при
считывании этих показаний; поэтому то, что ты держишь в ру¬
ках, — это всегда немного (хорошо, если немного) не то, что тебе
хотел сказать датчик.
Беда, в-третьих, в том, что заранее ничего не известно о дви¬
жении спутника около центра масс, хотя бы приближенно, и нам
не на что первоначально опереться в своем анализе.
Беда, в-четвертых, в том, что мы еще плохо знаем силы и мо¬
менты, действующие на спутник в космосе в каждом конкретном
случае, и во многих случаях не можем уверенно прогнозировать
эволюцию ориентации спутника.
Беда, в-пятых, в том, что существуют такие комбинации дви¬
жения спутника и показаний датчиков, когда по этим показаниям
принципиально нельзя определить это движение...
Кругом беда, а работать надо.
Естественно, что определение ориентации требует серьезной
математической обработки результатов измерений. Необходимо за¬
даться какой-то моделью движения спутника около центра масс,
чтобы иметь возможность объединить одной «траекторией» дви¬
жения разрозненные показания датчиков ориентации. Необходимо
задать статистический алгоритм обработки информации, который
позволил бы «наилучшим образом» использовать показания датчи¬
ков со всеми их случайными ошибками, «сгладить» влияние этих
ошибок и получить какую-то «среднюю» траекторию, наилучшим
образом соответствующую тому, что действительно «хотели сказать»
датчики. При этом, если необходимо, то надо распорядиться обра¬
боткой так, чтобы параллельно с ориентацией спутника определять
и возмущающие факторы (моменты сил, действующих на спутник).
Пусть, например, движение около центра масс описывается
каким-то вектором
г (а, 0, (12.2.1)
который и определяет модель движения. Будем считать, что движе¬
ние полностью известно, если известен набор постоянных парамет¬
2. Как это было обнаружено
393
ров а(аг) (г = 1,2,..., га). Например, моделью движения является
решение дифференциальных уравнений движения. Пусть моменты
сил, входящие в эти уравнения, записаны в явном виде, но содер¬
жат некоторые, неизвестные точно, постоянные параметры; тогда аг
суть начальные данные для интегрирования этих уравнений и по¬
стоянные параметры в выражениях моментов сил.
Предположим, что в моменты времени tn (га= 1,2,...,JV;ra<7V)
сделаны какие-то измерения на спутнике, дающие величину ipn,
зависимость которой от ориентации спутника может быть вычис¬
лена, так что расчетное значение грп (обозначим его ipn) будет
1рп{г(а, tn), tn}. Составим разности £п = грп - грп между вычислен¬
ным и измеренным значениями функции ip. Нужно так теперь
определить искомые параметры а, чтобы вся совокупность разно¬
стей £п былахаким-то образом минимизирована. Тогда рассматри¬
ваемая функция ip(t) будет «в среднем» отвечать измерениям грп.
В математической статистике для этого употребляется, например,
так называемый метод наименьших квадратов, когда минимизиру¬
ется по а сумма
N 1
~2il (12.2.2)
П=1 Сп
где \/<rl — некоторые весовые коэффициенты, зависящие от ха¬
рактера случайных ошибок в измерениях ip. Необходимые условия
минимума функции Ф
дФ дФ дФ ,
^ = 0' о^= в^=0 (|2-2-3)
дают га уравнений для определения га искомых параметров а\,..., ат.
Решение системы уравнений (12.2.3) относительно аг — сама
по себе трудная задача. Она решается обычно методом последова¬
тельных приближений. Для этого нужно знать начальное, нулевое
приближение к значениям параметров Это нулевое приближе¬
ние неоткуда взять, кроме как из той же информации об ориен¬
тации, которую предоставляют измерения ipn\ поэтому алгоритм
определения должен включать в себя составной частью независи¬
мый алгоритм определения нулевого приближения. Работы хвата¬
ет, и она немыслима без современных вычислительных средств —
электронных вычислительных машин.
В теории движения искусственных спутников сформировалось
целое направление [12.1]: математическая обработка траекторных
* = Е
394
Очерк двенадцатый. Космическая вертушка
измерений с целью определения фактических орбит и определе¬
ния возмущающих факторов, действующих на них. Одна из первых
работ этого направления выполнена Т. М. Энеевым, А. К. Платоно¬
вым, Р. К. Казаковой [12.10]. В многочисленных работах описыва¬
ется определение по траекторным измерениям плотности верхней
атмосферы Земли, гармоник потенциала земного тяготения, а в по¬
следнее время — и гармоник потенциала лунного тяготения по на¬
блюдениям за движением искусственного спутника Луны. Первую
работу такого рода выполнил Э. Л. Аким [12.2].
Задача определения по наблюдениям ориентации спутников
в значительной степени соответствует задаче определения орбит
и опирается на аналогичные методы; однако задача определения
ориентации имеет свою специфику и свои трудности. Первое в мире
определение ориентации спутника по данным бортовых измерений
было проведено для третьего советского искусственного спутника
[12.3]. Метод, использованный для определения ориентации спут¬
ников «Протон», и результаты такого определения описаны в [12.4],
а также в ряде статей, из которых укажем [12.5-12.9]
Остановимся на некоторых интересных динамических эффек¬
тах в эволюции ориентации спутника типа «Протон».
3. Что было обнаружено
На рис. 12.2 изображена полученная экспериментально [12.4],
[12.8] картина эволюции со временем двух параметров вращения
и ориентации спутника «Протон-2». Смысл одного из этих па¬
раметров — модуля L вектора кинетического момента — нам уже
известен (очерк шестой); другой параметр имеет следующий смысл:
h = sin2 $(1 + esin2 ф), (12.3.1)
В-A С
£~ С-В А'
Здесь А, В, С — главные центральные моменты инерции спутника
(С > В > А), д — уже известный нам угол между продольной осью
^ В процессе выполнения этих работ автору книги в течение нескольких лет
посчастливилось сотрудничать с рядом исследователей. Это — Ю. В. Зонов (опреде¬
ление ориентации третьего советского спутника) [12.3]; В. В. Голубков и И. Г. Хацке-
вич (разработка автоматизированных методов, определение ориентации спутников
серии «Протон» и других спутников) [12.3-12.8]; Э. К. Лавровский и С. И. Трушин
(определение ориентации спутников серии «Электрон») [12.5].
3. Что было обнаружено
395
Рис. 12.2. Эволюция параметров вращения и ориентации
спутника «Протон-2»
спутника (ось момента инерции С) и вектором L кинетического
момента; <р — угол собственного вращения, равный углу поворота
спутника вокруг продольной оси. Если моментов внешних сил нет,
то в таком невозмущенном движении трехосного спутника вели¬
чина ft, как и L, остается постоянной. При этом значения ft ~ О
соответствуют вращению вокруг продольной оси спутника (# = О
или # = 7г), а значения ft ~ 1 +е соответствуют вращению в окрест¬
ности поперечной оси. Для динамически-симметричного спутника
(В - А = 0) изменение ft от 0 до 1 просто бы означало изменение
режима вращения от продольной закрутки (1? = 0) до кувырка¬
ния (# = 7г/2); таким образом, поведение ft качественно совпадает
с поведением угла #.
Из шестого очерка ясно, что у быстро вращающегося в грави¬
тационном поле спутника обе величины L и ft будут постоянны;
они не изменяются и при ряде других воздействий, а если имеются
диссипативные силы, то L и ft меняются монотонно; подробнее
см. в другой книге автора [12.11].
396
Очерк двенадцатый. Космическая вертушка
Рис. 12.3. След вектора кинетического момента спутника «Протон-2» на не¬
бесной сфере с номерами витков орбиты спутника. Точкам р = 0° и р = 180°
отвечают соответственно Северный и Южный полюсы мира
Между тем на рис. 12.2 мы наблюдаем совершенно уникаль¬
ную картину изменения параметров L и Л: оба они долгопериоди¬
ческим образом колеблются, и глубина колебаний весьма велика.
Величина L изменяется в 5 раз, а изменение h говорит, что спут¬
ник в своем вращении периодически переходит от режима осевой
закрутки в режим кувыркания и обратно. Эволюция режима враще¬
ния, конечно, медленная: с периодом около 55-57 витков орбиты
спутника (по оси абсцисс на рис. 12.2 отложены номера витков ор¬
биты). Период модуляций величины L в два раза меньше; когда
спутник закручен вокруг оси, то величина L (а значит, и угловая
скорость вращения) максимальна, в переходном режиме от осевой
закрутки к кувырканию L достигает минимума, в режиме кувыр¬
кания L опять имеет максимум и т. д.
4. Как это объяснить
397
Надо сказать, что положение вектора кинетического момента
в пространстве тоже сильно меняется, колеблясь с размахом около
180°. На рис. 12.3 изображен след вектора кинетического момента
спутника «Протон-2» на небесной сфере на первых 90 витках полета
спутника; видно, что за это время он дважды прошел в окрестности
каждого из полюсов мира.
4. Как это объяснить
Все эти модуляции бывших когда-то спокойными величин объ¬
ясняются пропеллирующим эффектом — воздействием набегающе¬
го потока на кососимметрично посаженные плоскости солнечных
батарей. Нет никакой надобности строить здесь строгую теорию
эффектов, так как они настолько «грубы», что проявляются в ра¬
зумно поставленных модельных задачах. Будем считать спутник
динамически-симметричным, линии, соединяющие центры проти¬
воположных лопастей, — проходящими через центр масс спутни¬
ка, а корпус спутника, за исключением лопастей, — не дающим
никакого аэродинамического момента (например, так будет, если
корпус — шар с центром в своем центре масс).
В таких предпосылках от всего аэродинамического момента
останется лишь момент пропеллирования. Его выражение мы сей¬
час смоделируем из простых соображений (более строгие постанов¬
ки [12.4,12.9] дают то же самое качество).
Пусть продольная ось спутника совпадает с направлением ско¬
рости V центра масс спутника. Тогда за счет «крыльев мельницы»
должен создаться постоянный крутящий момент, вращающий спут¬
ник вокруг его продольной оси (дуем в лоб вертушке — крутится).
Этот момент должен, как всегда в аэродинамике, быть пропорци¬
ональным динамическому напору pV2, где р — плотность набега¬
ющего потока, V — его скорость. Итак, пропеллирующий момент
М = aopV2; постоянная ао должна иметь размерность м3 ((произ¬
ведение площади на «плечо»).
Естественно ожидать, что если отклонить ось спутника от на¬
правления потока, то величина пропеллирующего момента умень¬
шится и даже станет равной нулю, если ось спутника нормальна
вектору скорости (дуем в ребро вертушке — не крутится). Если же
ось спутника направлена против скорости, то момент должен быть
равен по величине опять a^pV2, но противоположен по знаку, так
как относительно фиксированного положительного направления
398
Очерк двенадцатый. Космическая вертушка
продольной оси спутника вращение будет идти в обратную сторо¬
ну (из состояния покоя). Весь ход этой зависимости продольной
составляющей момента от положения оси относительно вектора V
проще всего аппроксимировать формулой (которую мы и примем
на вооружение)
Mz = pV2a0a", (12.4.1)
где а — cos (z,Y) — косинус угла между продольной осью z спут¬
ника и скоростью V его центра масс. Две другие оси х и у напра¬
вим по линиям, соединяющим центры противоположных лопастей.
Но направления х и у ничем не хуже направления z — только рабо¬
тают две лопасти вместо четырех (другое а0), да лопатки повернуты
в другую сторону (другой знак момента). В результате для компо¬
нент момента по осям ж, у можно написать
Мх = -pV2a\a, Му = -pV2a]d, (12.4.2)
где а = cos (ж, У), а = cos(j/,V). Если лопатки наклонены, как
это имеет место у «Протона», под углом 45° к продольной оси, то
a j = 1/2 ао (за счет работы всего двух лопастей из четырех при
равных «эффективных площадях»2^ каждой лопасти). При других
наклонах лопатки к продольной оси соотношение между а| и ао
будет другое за счет разных «эффективных площадей», но всегда
можно считать
й\ < а0. (12.4.3)
Таким образом, поставлена следующая задача: изучить эво¬
люцию быстрого вращения динамически-симметричного спутника,
подверженного воздействию моментов (12.4.1), (12.4.2). Эволюцию
можно рассматривать в уже знакомых нам по очерку шестому пере¬
менных L, р, а (модуль вектора кинетического момента и два угла,
определяющие его положение относительно плоскости орбиты) и •&
(угол между вектором кинетического момента и продольной осью
спутника). Однако здесь вместо р, а удобнее ввести: угол в меж¬
ду вектором L кинетического момента и направлением скорости
Утг в перигее орбиты; угол А поворота L вокруг V*-, отсчитанный
от радиус-вектора перигея орбиты (рис. 12.4).
Выписывая эволюционные уравнения и проводя обычную про¬
цедуру осреднения по быстрой переменной — углу прецессии tp,
2^ Площадь проекции лопасти на плоскость, нормальную к рассматриваемой оси.
4. Как это объяснить
399
Рис. 12.4. Переменные, определяющие положение спутника
и его кинетический момент
получим следующую систему эволюционных уравнений [12.4]:
d\
dv
<Ю
du
dL
Рп у/рР
L
Pir у/ pP
a\ - (ao + oi)- sin2 d
a,\ - (ao + a\)~ sin2 d
V2
sin A
sin в ’
x (Vt sin в + V2 cos в cos A),
— = pvy/pP[-a\ +(a0 + ai)cos2#] x
x (F| cos в - V2 sin 9 cos A),
dtf _ pjrs/pP t
dv ~ J
-(ao + Gi) sin <0 cos x
(12.4.4)
x (V\ cos в - V2 sin в cos A).
В качестве независимой переменной вместо времени здесь взя¬
та истинная аномалия и. Как всегда, р, — гравитационная постоян¬
ная, Р — фокальный параметр орбиты; кроме того, рп — плотность
атмосферы в перигее орбиты. Если обозначить р = р/рп, то функ¬
ции V\9 V2 могут быть записаны в виде
vx = т
v2 = p(h)
Ре
(е -h cos и)у/\ + е2 + 2е cos v
sin
(1 + е cos и)2
vvT+'eM^ecosT'
h =
(1 + e cos v)2
1 - cos v
1 + e 1 + e cos v
Здесь e — эксцентриситет орбиты; h имеет смысл высоты спут¬
ника, отсчитанной от уровня перигея орбиты. Впрочем, явный вид
400
Очерк двенадцатый. Космическая вертушка
периодических по v функций V\ и Vi нам не понадобится. За¬
метим лишь, что правые части уравнений (12.4.4) явно зависят
от «времени» и, что, конечно, осложняет и без того не простые
уравнения. Ведь эволюционные уравнения (12.4.4), описывающие
влияние на спутник эффекта пропеллирования, существенно труд¬
нее для анализа, чем эволюционные уравнения в гравитационном
поле (очерк шестой). В самом деле, там было всего два уравнения
относительно углов ориентации вектора кинетического момента,
а здесь — четыре. Добавочные уравнения описывают изменение
модуля L вектора кинетического момента и угла # между ним и
продольной осью спутника.
Тем знаменательней, что столь непростые, с явной зависимо¬
стью от времени в правых частях, уравнения (12.4.4) имеют, ока¬
зывается, два точных первых интеграла. Это позволяет провести
эффективный качественный анализ поведения решения эволюци¬
онных уравнений. Вот эти первые интегралы:
I tg #|2а| cos #| cos2 р = ср, cos р = - sin в sin А. (12.4.6)
Угол р представляет собой угол между L и нормалью к плоскости
орбиты.
Интегральные кривые (12.4.5), (12.4.6) изображены на рис. 12.5 я,
12.5 5. В реальном движении эти кривые могут полностью и не про¬
ходиться. Так как правые части дифференциальных уравнений
(12.4.4) периодичны явно по v с периодом 27т, то и их решение
должно содержать периодическую составляющую примерно с та¬
ким же периодом. В результате в плоскостях р, cos и L, cos #
(рис. 12.5) изображающая точка колеблется вдоль интегральной
кривой (12.4.5) и, соответственно, (12.4.6) с периодом, примерно
равным периоду Т„ обращения спутника по орбите; эти колебания
происходят с весьма небольшой амплитудой, заметая за период Ти
очень маленький кусочек дуги интегральной кривой. При этом на
круговой орбите продвижение изображающей точки «вперед» по ин¬
тегральной кривой на первом полупериоде обращения спутника
по орбите компенсируется таким же отступлением «назад» по ин¬
тегральной кривой на втором полупериоде, в результате изобража¬
ющая точка колеблется около среднего неподвижного положения.
Иначе говоря, переменные L, р, D будут колебаться (с малой ампли¬
тудой) около своих начальных значений, не изменяясь в среднем.
L sin#| ctg#|a = I,
а =
4. Как это объяснить
401
а град
150
120
90
60
30
О
я)
L
6
4
2
О
б)
О, град
150
120
90
60
30
О
—6j='0;09—
'
-
Св = 0,36
"V
-
с
Сд = 0,64
/Ср=&72"
J
U
-У
I-J-
^ = 0,01
О 0,5 1 cos'd
Рис. 12.5. Интегральные кривые
Физически это легко объяснимо равноправием всех точек круго¬
вой орбиты; динамический напор набегающего потока одинаков
в любой точке, поэтому возмущения в движении компенсируются
в диаметрально противоположных точках орбиты.
26 Заказ 1667
402
Очерк двенадцатый. Космическая вертушка
Ведь вектор кинетического момента сохраняет за один ор¬
битальный период направление в пространстве и, значит, меня¬
ет направление относительно набегающего потока. Максимальное
различие между этими относительными направлениями как раз
в диаметрально противоположных точках круговой орбиты. Грубо
говоря, в одной точке орбиты «ветер дует» в одну сторону вертуш¬
ки, а в противоположной точке — в противоположную.
Много ли тут раскрутишься?
Однако на эллиптической орбите дело обстоит по-другому. Ди¬
намический напор в перигее существенно больше, чем в апогее,
поэтому возмущения движения в апогее не могут компенсировать
возмущений в перигее. В результате возмущения понемногу накап¬
ливаются. На интегральных кривых (рис. 12.5) изображающие точ¬
ки за один период Ти обращения спутника продвигаются «вперед»
больше, чем отступают «назад», в результате чего через несколько
периодов Tv обнаруживается существенная эволюция параметров
Из-за этого существенного изменения первоначальной ори¬
ентации набегающий поток в перигее меняет свое направление
относительно спутника, что приводит в конце концов к эволюции
параметров движения в обратном направлении, и т.д. В конечном
счете эволюция параметров вращения и ориентации спутника бу¬
дет носить на эллиптической орбите долгопериодический характер
(с периодом в несколько десятков периодов обращения спутника
по орбите).
На интегральных кривых рис. 12.5 в результате этого изобра¬
жающие точки заметают более или менее существенный отрезок
кривой, колеблясь вдоль этого отрезка долгопериодическим об¬
разом, причем эти долгопериодические колебания складываются
из многих, некомпенсированных полностью, короткопериодиче¬
ских (с орбитальным периодом). На рис. 12.5 выделены участки
интегральных кривых, проходимых в реальном движении.
Из рис. 12.56 видно, что величина L может долгопериодиче¬
ским образом изменяться в довольно широких пределах, что эк¬
вивалентно изменению угловой скорости собственной прецессии
спутника. Она то увеличивается, когда составляющая пропеллиру-
юшего момента по вектору L положительна в среднем, то умень¬
шается — при изменении ориентации пропеллирующего момента
относительно вектора L.
Одновременно меняется режим вращения спутника, характе¬
ризуемый величиной #. Спутник может переходить из режима ку-
4. Как это объяснить
403
выркания (# « 7г/2) в режим закрутки (t? « 0) и обратно тоже
долгопериодическим образом. При этом, как ясно из интегральных
кривых (рис. 12.5 6), режим закрутки (cost? « 1) и режим кувырка¬
ния (cos t? ~ 0) сопровождаются максимальными значениями вели¬
чины L кинетического момента, а переходный режим — минималь¬
ным значением величины L. Это полностью соответствует картине,
найденной экспериментально и изображенной на рис. 12.2.
Можно выделить эволюцию движения в чистом виде, прене¬
брегая короткопериодическими колебаниями. С этой целью эволю¬
ционные уравнения (12.4.4) следует осреднить еще раз — по быст¬
рой переменной v. Тогда
в этом приближении. Значит, вектор L не вращается вокруг на¬
правления скорости \п в перигее, а движется только в плоскости,
содержащей V*. Иначе говоря, из двух углов, определяющих поло¬
жение вектора L в пространстве, меняется лишь один, а именно в.
Учитывая (12,4.7), из (12.4.6) немедленно получаем этот первый
интеграл в новой форме:
Интегральные кривые (12.4.8) также изображены на рис. 12.5 в.
Из этих кривых видно, что если спутник периодически выходит
из режима кувыркания t? « 7г/2 в режим осевого вращения t? « 0, то
это неизбежно должно сопровождаться колебаниями (с тем же пе¬
риодом) ориентации вектора кинетического момента в диапазоне,
почти равном 180°. Но это тоже соответствует экспериментально
найденной картине пространственного движения вектора кинети¬
ческого момента спутника «Протон-2» (рис. 12.3). Как мы помним,
вектор кинетического момента «гуляет» от Северного полюса ми¬
ра до Южного и обратно, в то время как осевой режим вращения
сменяется режимом кувыркания и наоборот. Итак, качественное
соответствие экспериментальных данных и изложенной теории —
налицо.
2п
2ж
НО
о
о
откуда немедленно следует, что
А = А0 = const
(12.4.7)
| tg t?|2a| cos t?| sin2 в = Ce.
(12.4.8)
26*
404
Очерк двенадцатый. Космическая вертушка
Требовать количественного соответствия в рамках изложенного
нет смысла. Ведь мы не учли гравитационных моментов (они со¬
ставляют у «Протонов» около 5% от аэродинамических моментов),
диссипативных факторов, аэродинамики самого корпуса спутника,
возможности «затемнения» корпусом лопастей и многих, многих
других эффектов. Этими неучтенными факторами объясняется, на¬
пример, «восьмеркообразный» след вектора кинетического момента
на небесной сфере (рис. 12.3) — мы объяснили лишь 180-градусную
амплитуду этой «восьмерки».
Аккуратная постановка аэродинамической задачи должна учи¬
тывать характер взаимодействия молекул набегающего потока воз¬
духа с поверхностью спутника; более того, пользуясь эксперимен¬
тальными данными о движении спутников типа «Протон» вокруг
центра масс, можно установить, каков этот самый характер взаи¬
модействия [12.9].
Но здесь наша цель была гораздо более скромной — построить
модель обнаруженных явлений, и мы в этом преуспели.
Отметим под конец, что из интегральных кривых следует на¬
личие (в среднем по и) устойчивой стационарной точки 0* = 7г/2,
sin2 в* = 2а. Если движение угодит в эти начальные данные (или близ¬
кие), то там и останется; при этом будет неизменной (но произ¬
вольной) и величина вектора кинетического момента L = Lq. Как
Рис. 12.6. Графики функций L/Lq(v), 0(i/), fl(v)
4. Как это объяснить
405
уже упоминалось, для спутника «Протон» в нашей модели можно
взять «о = 2а |, тогда а = 1/3 и стационарное значение угла
определяется равенством
cos = -—= (0* « 54, 7°).
При начальных данных, далеких от стационарной точки, дви¬
жение будет глубокомодулированным (как мы уже знаем).
На рис. 12.6 изображены зависимости в(и), д(и), L/Lq(u) по¬
лученные численным интегрированием уравнений (12.4.4). Чтобы
подчеркнуть эффекты, было взято сильно завышенное значение для
пропеллирующего момента — при этом четко видны коротко-пе¬
риодические колебания, наложенные на додгопериодическую эво¬
люцию. Что касается этой долгопериодической эволюции, то она,
конечно, обладает всеми уже обследованными выше свойствами.
Автор нарочно для заключительного очерка выбрал задачу,
которая была бы немыслима в старой, доспутниковой, механике,
и с тем говорит читателю: до свидания.
Знаю, что смертен, что век мой не долог, и все же — когда я
Сложный исследую ход круговращения звезд,
Мнится, земли не касаюсь ногами, но гостем Зевеса
В небе амвросией я, пищей бессмертных, кормлюсь.
Птолемей
Литература
К очерку первому
1.1. Дубошин Г. Н. Небесная механика. Основные задачи и методы. М.:
Наука, 1968.
1.2. Шкловский И. С. Вселенная. Жизнь. Разум. Изд. 4-е, М.: Наука, 1976.
1.3. Березкин Е. Н. Лекции по теоретической механике. Ч. I. М.: Изд-во
МГУ, 1967.
1.4. Лурье А. И. Аналитическая механика. М.: Физматгиз, 1961.
1.5. Пуанкаре А. Новые методы небесной механики. Из бранные труды
в трех томах. Т. I. М.: Наука, 1971.
1.6. Боголюбов Н. //., Митропольский Ю. А. Асимптотические методы
в теории нелинейных колебаний. Изд. 3-е. М.: Физматгиз, 1963.
1.7. Волосов В. М. Усреднение в системах обыкновенных дифференци¬
альных уравнений // Успехи матем. наук. 1962. Т. 17. №6 (108).
1.8. Моисеев Н.Н. Асимптотические методы нелинейной механики. М.:
Наука, 1969.
1.9. Арнольд В. И. Доказательство теоремы А. Н. Колмогорова о сохране¬
нии условно-периодических движений при малом изменении функ¬
ции Гамильтона // Успехи матем. наук. 1963. Т. 18. №5 (113).
1.10. Арнольд В. И. Малые знаменатели и проблемы устойчивости движе¬
ния в классической и небесной механике // Успехи матем. наук.
1963. Т. 18. №6 (114).
1.11. Демин В. Г. Судьба Солнечной системы. М.: Наука, 1969.
1.12. Охоцимский Д. Е., Энеев Т. М., Таратынова Г. П. Определение време¬
ни существования искусственного спутника Земли и исследование
вековых возмущений его орбиты // Успехи физ. наук. 1957. Т. 63.
№ la.
1.13. Охоцимский Д. Е. Динамика космических полетов. Конспект лекций.
М.: Изд-во МГУ, 1968.
1.14. Эльясберг П. Е. Введение в теорию полета искусственных спутников
Земли. М.: Наука, 1965.
1.15. Балк М. Б. Элементы динамики космического полета. М.: Наука,
1965.
1.16. Белецкий В. В. Орбита экваториального спутника Земли // Искус¬
ственные спутники Земли. 1962. Вып. 13.
Литература
407
1.17. Белецкий В. В. Движение искусственного спутника относительно
центра масс. М.: Наука, 1965.
1.18. Белецкий В. В. О либрации спутника // Искусственные спутники
Земли. 1959. Вып.З.
1.18’. Белецкий В. В. Либрация спутников на эллиптической орбите //
Искусственные спутники земли. 1963. Вып. 16.
1.19. Седов Л. И. Динамические эффекты в движении искусственных спут¬
ников Земли // Искусственные спутники Земли. 1958. Вып. 2.
К очерку второму
2.1. Аксенов Е. Я., Гребеников Е.А., Демин В. Г. Общее решение задачи
о движении искусственного спутника в нормальном поле притяжения
Земли // Искусственные спутники Земли. 1961. Вып. 8.
2.2. Брауэр Д., Клеменс Дж. Методы небесной механики. М.: Мир, 1964.
2.3. Демин В. Г. Движение искусственного спутника в нецентральном поле
тяготения. М.: Наука, 1968.
2.4. Дубошин Г. Н. Небесная механика. Аналитические и качественные
методы. М.: Наука, 1964.
2.5. Кислик М. Д. Движение искусственного спутника в нормальном гра¬
витационном поле Земли // Искусственные спутники Земли. 1960.
Вып. 4.
2.6. Vinti J. P. Theory of an accurate intermediary orbit for satellite astronomy //
J. Res. Nat. Bur. Standards. 1959. V. 63B. №3.
2.7. Алексеев В. М. Обобщенная пространственная задача двух неподвиж¬
ных центров. Классификация движений // Бюлл. Ин-та теор. астрон.
1965. Т. 10. №4 (117).
2.8. Лурье А. И. Аналитическая механика. М.: Физматгиз, 1961.
2.9. Дубошин Г. Н. Небесная механика. Основные задачи и методы. М.:
Наука, 1968.
К очерку третьему
3.1. Белецкий В. В. О траекториях космических полетов с постоянным век¬
тором реактивного ускорения// Космич. исследования. 1964. Т. 2. № 3.
3.2. Белецкий В. В. Описание плоских траекторий космических полетов
с постоянным вектором реактивного ускорения // Труды конферен¬
ции по общим и прикладным вопросам небесной механики, Москва,
1967. М.: Наука, 1972.
3.3. Nita М. М. Uiber die Bewegung der Rakete in einen Zentralkraftfeld //
Revue de Mecanique, Applique. 1961. V.6. №2.
3.4. Демин В. Г. Об одном способе исследования движения космического
аппарата в сфере действия планеты // Труды Ун-та дружбы народов
им. Патриса Лумумбы, сер. теор. мех. 1966. Т. 17. Вып. 4.
408
Литература
3.5. Куницын А. Л. О движении ракеты в центральном поле сил с посто¬
янным вектором реактивного ускорения // Космич. исследования.
1966. Т. 4. №2.
3.6. Копнин Ю. М. Эволюция орбиты спутника под влиянием малой воз¬
мущающей силы, постоянной по величине и направлению // Инже¬
нерный журн. 1965. Т. 5. №6.
3.7. Черников Ю. А. Эволюция финитных планетоцентрических орбит ма¬
лых тел под влиянием прямого светового давления // Космич. иссле¬
дования. 1968. Т. 6. №6.
3.8. Лидов М. Л. Вековые эффекты эволюции орбит под влиянием свето¬
вого давления // Космич. исследования. 1969. Т. 7. №4.
3.9. Маршак С. Я. Сундук. Норвежская народная сказка // Собр. соч. Т. 1.
1957.
К очерку четвертому
4.1. Дубошин Г. Н. Небесная механика. Основные задачи и методы. М.:
Наука, 1968.
4.2. Моисеев Н.Д // Труды ГАИШ. 1945. Вып. 15.
4.3. Лидов М. Л. О приближенном анализе эволюции орбит искусственных
спутников // Проблемы движения искусственных небесных тел. М.:
Изд-во АН СССР, 1963.
4.4. Лидов М. Л. Эволюция орбит искусственных спутников планет под
действием гравитационных возмущений внешних сил // Искусствен¬
ные спутники Земли. 1961. Вып. 8.
4.5. Демин В. Г. Судьба Солнечной системы. М.: Наука, 1969.
4.6. Чеботарев Г. А. Аналитические и численные методы небесной меха¬
ники. М.: Наука, 1965.
4.7. Кислик М. Д. Сферы влияния больших планет и Луны // Космич.
исследования. 1964. Т. 2. №6.
4.8. Арнольд В. И. Доказательство теоремы А. Н. Колмогорова о сохране¬
нии условно-периодических движений при малом изменении функ¬
ции Гамильтона // Успехи матем. наук. 1963. Т. 18. №5 (113).
4.9. Арнольд В. И. Малые знаменатели и проблемы устойчивости движения
в классической и небесной механике // Успехи матем. наук. 1963.
Т. 18. №6 (114).
4.10. Molchanov А. М. The resonant structure of the solar system // Icarus,
Intern. J. of the Solar System. 1968. V. 8. N° 2.
4.11. Брюно А. Д. Неустойчивость в системах Гамильтона и распределение
астероидов// Математический сборник. 1970. Т. 83 (125). Вып. 2 (10).
4.12. Brower D. The problem of the Kikwood Gaps in the asteroid belt // Astron.
J. 1963. V. 68. №3.
4.13. Ржига О. H. Результаты радиолокации планет // Космич. исследова¬
ния. 1969. Т. 7. № 1.
Литература
409
4.14. Четаев Н. Г. Устойчивость движения. Работы по аналитической ме¬
ханике. М.: Изд-во АН СССР, 1962.
4.15. Ишлинский А. Ю. Механика // Октябрь и научный прогресс. Т. 1. М.:
АПН, 1967.
4.16. Lichtenberg A. J. and Lieberman М. A. Regular and Stochastic Motion. New
York; Berlin: Springer Verlag, 1983.
4.17. Thompson J. M. T. and Stewart H. B. Nonlinear Dynamics and Chaos.
Geometrical Methods for Engineers and Scientists. Chichester: John Wiley
& Sons, Ltd., 1986.
К очерку пятому
5.1. Егоров В. А. О некоторых задачах динамики полета к Луне // Успехи
физ. наук. 1957. Т. 63. Вып. 1а.
5.2. Егоров В. А. Пространственная задача достижения Луны. М.: Наука,
1965.
5.3. Левантовский В. И. Ракетой кЛуне. М.: Физматгиз, 1960.
5.4. Леонтович А. Л/. Об устойчивости лагран^кевых периодических реше¬
ний ограниченной задачи трех тел // Докл. АН СССР. 1962. Т. 142.
№3.
5.5. DepritA., Deprit-Bartholome A. Stability of the triangular Lagrangian points //
Astron. J. 1967. V. 72. №2.
5.6. Маркеев А. П. Об устойчивости треугольных точек либрации в круго¬
вой ограниченной задаче трех тел // Прикл. матем. и мех. 1969. Т. 33.
№ 1.
5.7. Лидов М. Л., Охоцимский Д. Е., Тесленко Н. М. Исследование одного
класса траекторий ограниченной задачи трех тел // Космич. иссле¬
дования. 1964. Т. 2. Nq 6.
5.8. Левантовский В. И. Механика космического полета в элементарном
изложении. М.: Наука, 1970.
5.9. Седов Л. И. Орбиты космических ракет в сторону Луны // Искус¬
ственные спутники Земли. 1960. Вып. 5.
5.10. Козлов Я. Я., Сюняев Р. А., Энеев Т. М. Приливное взаимодействие
галактик // Земля и Вселенная. 1974. №6.
5.11. Козлов Я. Я., Сюняев Р. А., Энеев Т. М. Приливное взаимодействие
галактик. Препринт №76 / Ин-т прикл. матем. АН СССР. М., 1971.
5.12. Козлов Я. Я., Сюняев Р. А., Энеев Т. М. //Докл. АН СССР. 1972. Т. 204.
№ 3. 579.
5.13. Eneev Т. Л/., Kozlov N. N., Sunjaev R. А. // Astron. and Astroph. 1973.
V. 22. No 1.
5.14. Демин В. Г. Судьба Солнечной системы. Изд. 2-е. М.: Наука, 1975.
5.15. Брюно А. Д. Ограниченная задача трех тел. Плоские периодические
орбиты. М.: Наука, 1990. 295 с.
410
Литература
5.16. Нёпоп М. Sur les orbites interplan6taires qui rencontre deus fois la terre //
Bull. Astron. Ser.3. 1968. 3. №3. 377-402.
5.17. Bruno A. D. On periodic flybys of the Moon. Celestial Mech. 1981. 24.
№3. 255-268.
К очерку шестому
6.1. Белецкий В. В. Движение искусственного спутника относительно цен¬
тра масс. М.: Наука, 1965.
6.2. Goldreich P., Peale S.J. The dynamics of planetary rotations // Annual
Review of Astronomy and Astrophysics. V. 6. Palo Alto, Calif., USA, 1968.
6.2r. Экспресс-информация «Астронавтика и ракетодинамика». 1972. № 12.
6.3. Белецкий В. В. О либрации спутника // Искусственные спутники
Земли. 1959. Вып.З.
6.4. Румянцев В. В. Об устойчивости стационарных движений спутников.
М.: ВЦ АН СССР, 1967.
6.5. Stumpke Н. Professor, Bau und Leben der Rhinogradentia mit einem Nach-
wort von Gerolf Steiner. Stuttgart: Gustav Fischer Verlag, 1967
6.6. Штюмпке X. Строение и жизнь ринограденций // Наука и жизнь.
1963. №4.
6.7. Де Бра Д. В. Принципы работы пассивных систем стабилизации и
основные направления исследований // Современное состояние ме¬
ханики космического полета / Под ред. П. Б. Ринардса; Перев. с англ.
М.: Наука, 1969.
6.8. Проблемы ориентации искусственных спутников Земли / Под ред.
С. Ф. Сингера. М.: Наука, 1966.
6.9. Сарычев В. А. Исследование динамики системы гравитационной ста¬
билизации // Искусственные спутники Земли. 1963. Вып. 16.
6.10. Breakwell J. К, Pringle Я Nonlinear resonances affecting gravity-gradient
stability // XV International Congr. IAF. Athen, 1965.
6.11. Дубошин Г. И. Небесная механика. Основные задачи и методы. М.:
Наука, 1968.
6.12. Капе ТЯ Attitude stability of Earth-pointing satellites // AIAA J. 1965.
V. 3. № 4.
6.13. Хазин Л. Г. Об устойчивости гамильтоновых систем при наличии ре¬
зонансов // Прикл. матем. и мех. 1971. Т. 35. № 3.
6.14. Белецкий В. В. О законах Кассини. Препринт №79 / Ин-т прикл.
матем. АН СССР, 1971.
6.15. Белецкий В. В. Эволюция вращения динамически симметричного спут¬
ника // Космич. исследования. 1963. Т. 1. № 3.
^ Существование литературы о ринограденциях не является достаточным усло¬
вием существования ринограденций.
Литература
411
6.16. Белецкий В. В. Движение искусственного спутника Земли относитель¬
но центра масс // Искусственные спутники Земли. 1958. Вып. 1.
6.17. Черноусько Ф. Л. О движении спутника относительно центра масс под
действием гравитационных моментов // Прикл. матем. и мех. 1963.
Т. 27. №3.
6.18. Ишлинский А. Ю. Механика // Октябрь и научный прогресс. Т. 1. М.:
Изд-во АПН, 1967.
6.19. Белецкий В. В. Классификация движений искусственного спутника
Земли около центра масс // Искусственные спутники Земли. 1961.
Вып. 6.
6.20. Трушин С. И. Об учете движения перигея орбиты в задаче о вращении
и ориентации ИСЗ // Космич. исследования. 1970. Т. 8. №4.
6.21. Holland R. L. and Sperling H.J. A first-order theory for the rotational
motion of a triaxial rigid body or biting and oblate primary // Astron. J.
1969. V. 74. №3.
6.22. Черноусько Ф. Л. Резонансные явления при движении спутника относи¬
тельно центра масс // Ж. вычисл. матем. и матем. физ. 1963. Т. 3. № 3.
6.23. Lutze F. Я, Abbitt М. W. Rotation locks for near-symmetries satellites //
Celest. Mech. 1969. № 1.
6.24a. Торжевский А. П. Быстрое вращение искусственного спутника вокруг
центра масс в резонансном режиме // Космич. исследования. 1968.
Т. 6. Вып. 1.
6.246. Торжевский А. П. Движение искусственного спутника относительно
центра масс и резонансы // Astronautica Acta. 1969. V. 14. № 3.
6.25. Маркеев А. Я. Исследование устойчивости движения в некоторых за¬
дачах небесной механики. Препринт/ Ин-т прикл. матем. АН СССР,
1970.
6.26. Ржига О. Н. Результаты радиолокации планет // Космич. исследова¬
ния. 1969. Т. 7. № 1.
6.27. Pettenglll G. Я., Dyce R. В. A radar determination of the rotation of the
planet Mercury // Nature. 1965. №206. P. 1240.
6.28. Dyce R. В., Pettenglll G. Я, Shapiro /. /. //Astron. J. 1967. V. 72. P. 351.
6.29. Colombo G. Rotational period of the planet Mercury // Nature. 1965.
№208. P. 575.
6.30. Конашенок B.H., Кондратьев К. Я. Новое о Венере и Марсе. J1.: Гид-
рометеоиздат, 1970.
6.31. Котельников В. А. и др. Радиолокационные наблюдения Венеры в Со¬
ветском Союзе в 1964 г. // Докл. АН СССР. 1965. Т. 163. Вып. 1.
6.32. Carpenter R. L. Study of Venus by cw radar — 1964 results // Astron. J.
1966. V. 71. P. 142.
6.33. Goldstein R. M. Moon and Planets. Amsterdam: North-Holland, 1967.
412
Литература
6.34. Охоцимский Д. Е., Сарычев В. А. Система гравитационной стабили¬
зации искусственных спутников // Искусственные спутники Земли.
1963. Вып. 16.
6.35. Белецкий В. В. Резонансные явления во вращательных движениях ис¬
кусственных и естественных небесных тел. Препринт № 10 / Ин-т
прикл. матем. АН СССР, 1975; Beletskii V. V. Resonance phenomena at
rotations of artifical and natural celestial bodies // Satellite Dynamics —
Symposium Sao Paulo, Brasil, June 19-21, 1974 / Editor G. E. O. Gia-
gaglia. Berlin; Heidelberg; New York: Springer-Verlag, 1975.
6.36. Справочное руководство по небесной механике и астродинамике /
Под ред. Г. Н. Дубошина. М.: Наука, 1971.
6.37. Tisserand F. Traite de mecanique celeste. Tome II. Paris, 1891.
6.38. Lagrange J. L. Oeuvres. Tome V. Paris: Ganthier-Villars, 1870.
6.39. Laplace P. S. Mecanique celeste. Paris, 1793.
6.40. Хабибулин Ш. Т. // Труды Казанской гор. астр, обсерват. № 34. Казань,
1966.
6.41. Куликов К. А., Гуревич В. Б. Основы лунной астрометрии. М.: Наука,
1972.
6.42. Beletskii V. V. Resonance rotation of celestial bodies and Cassini’s laws I I
Celestial Mechanics. 1972. V. 6. №3.
6.43. JIudoe М.Л., Нейштадт А. И. Методы канонических преобразований
в задачах о вращении небесных тел и законы Кассини. Препринт
№9/ Ин-т прикл. матем. АН СССР, 1973.
6.44. Colombo G. Cassini’s second and third laws // Astron. J. 1966. November.
№ 1344. P. 891.
6.45. Peale S. Generalized Cassini’s laws // Astron. J. 1969. April. N° 1368.
P. 483.
6.46. Holland R. L. and Sperling H. J. A first-order theory for the rotational
motion of a triaxial rigid body or biting and oblate primary // Astron. J.
1969. V. 74. №3.
6.47. Johnson D. B. Precession rate matching a space station in orbit about an
oblate planet // J. of Spacecraft and Rockets. 1973. V. 10. N° 7.
6.48. Haifa M. Effect of magnetic and gravitational torques on spunning satellite
attitude // AIAA J. 1973. V. II. № 12.
6.49. Белецкий В. В., Трушин С. И. Резонансы во вращении небесных тел
и обобщенные законы Кассини // Механика твердого тела. Вып. 6.
Киев: Наукова думка, 1974.
6.50. Белецкий В. В., Трушин С. И. Устойчивость обобщенных законов Кас¬
сини // Механика твердого тела. Вып. 6. Киев: Наукова думка, 1974.
6.51. Белецкий В. В. Движение спутника около центра масс в гравитацион¬
ном поле. М.: Изд-во МГУ, 1975.
6.52. Shapiro /. /. Radar astronomy, general relativity and celestial mechanics //
Modern questions of celestial mechanics / Ed. Cremonese. Roma, 1968.
Литература
413
6.53. Хентов А. А. Влияние магнитного и гравитационного полей Земли на
колебания спутника вокруг своего центра масс // Космич. исследо¬
вания. 1967. Т. 5. Вып. 4.
6.54. Хентов А. А. Пассивная стабилизация искусственных спутников по маг¬
нитному полю Земли // Космич. исследования. 1967. Т. 5. №4.
6.55. Белецкий В. В., Хентов А. А. Магнитно-гравитационная стабилизация
спутника // Изв. АН СССР. Механика твердого тела. 1973. №4.
6.56. Четаев Н. Г. Устойчивость движения. Работы по аналитической ме¬
ханике. М.: Изд-во АН СССР, 1962.
6.57. Белецкий В. В., Левин М. £., Погорелое Д. Ю. К вопросу о резонанс¬
ном вращении Венеры // Астрономический журнал. 1980. Т. 57. № 1.
С. 158-167.
6.58. Белецкий В. В., Левин М. Е., Погорелое Д. Ю. К вопросу о резонансном
вращении Венеры. 4.2 // Астрономический журнал. 1981. Т.58. № 1.
С. 198-207.
6.59. Beletsky V. V. Tidal evolution of inclinations and rotations of celestial
bodies // Celestial Mech. 1981. 23. № 3. 371-382.
6.60. Козлов H.H., Энеев Т. М. Численное моделирование процесса обра¬
зования планет из протопланетного облака. Препринт. № 134. М.:
ИПМ АН СССР, 1974.
6.61. Хентов А. А. Динамика вращения Венеры с учетом супервращения ее
атмосферы //Астрономический журнал. 1992. Т. 69. №3. С. 655-659.
6.62. Bills В. С., Kiefer W. S., Jones R. L. Venus gravity: a harmonic analysis //
J. Geophys. Res. 1987. 92. no. BIO. 10335-10351.
6.63. Beletsky V. K, Pivovarov M. L., and Starostin E. L. Regular and chaotic
motions in applied dynamics of a rigid body // Chaos 1996. 6. № 2.
155-166.
6.64. Beletsky V. V. Reguldre und Chaotische Bewegung Starrer Korper. Stuttgart:
Teubner Studienbucher Mechanik, B.G.Teubner, 1995.
6.65. Белецкий В. В., Пивоваров М. Л., Старостин Е. Л. Регулярные и хаоти¬
ческие движения в задаче вращения небесного тела в гравитационном
поле двух центров. Препринт. № 184. М.: ИПМ АН СССР, 1990.
6.66. Shapiro /. L., Campbell D. В., and De Campli W. M. Nonresonance rotation
of Venus
Astrophys. J. Lett. 1979. 230. №. 2.
6.67. Хентов А. А. Динамика формирования резонансных вращений есте¬
ственных небесных тел // Астрономический журнал. 1982. Т. 59. № 4.
С. 769-778.
6.68. Хентов А. А. К вопросу об интерпретации наблюдаемых вращений
Венеры // Астрономических журнал. 1989. Т. 66. № 1. С. 202-204.
6.69. Peale S.J. Some unsolved problems in the evolutionary dynamics in the
solar system // Celestial Mech. Dyn. Astron. 1989. 46. № 3. 253-275.
414
Литература
6.70. Белецкий В. В., Хентов А. А. Резонансные вращения небесных тел.
Нижегородский гуманитарный центр, 1995.
6.71. Белецкий В. В., Пономарева О. Н. Параметрический анализ устойчи¬
вости относительного равновесия в гравитационном поле // Космо¬
физические исследования. 1990. Т. 28. №5. С. 664-675.
6.72. Белецкий В. В., Левин Е. М. Динамика космических тросовых систем.
М.: Наука, 1990. 329 с.
6.73. Келдыш М. В. Избранные труды. Ракетные технологии и космонавти¬
ка. М.: Наука, 1988.
К очерку седьмому
7.1. Гродзовский Г.Л., Иванов Ю. Я, Токарев В. В. Механика космического
полета с малой тягой. М.: Наука, 1966.
7.2. Белецкий В. В., Егоров В. А. Разгон космического аппарата в сфере
действия планеты // Космич. исследования. 1964. Т. 2. №3.
7.3. Охоцимский Д. Е. Исследование движения в центральном поле под
действием постоянного касательного ускорения // Космич. исследо¬
вания. 1964. Т. 2. №6.
7.4. Евтушенко Ю. Г. Влияние касательного ускорения на движение спут¬
ника // Прикл. матем. и мех. 1966. Т. 30. N° 3.
7.5. Ефимов Г. Б. Оптимальный разгон в центральном поле до гипербо¬
лических скоростей // Космич. исследования. 1970. Т. 7. N° 1.
К очерку восьмому
8.1. Кларк А. Солнечный ветер. (Библиотека современной фантастики,
Т. 6.) М.: Молодая гвардия, 1966.
8.2. Гродзовский Г. Л., Иванов Ю. Я., Токарев В. В. Механика космического
полета. Проблемы оптимизации. М.: Наука, 1975.
8.3. Скопцов А. Я. Вариационная задача о выходе космического аппарата
с солнечным парусом из сферы притяжения планеты // Проблемы
механики управляемого движения. Вып. 1. Пермь, 1972.
8.4. Белецкий В. В. О траекториях космических полетов с постоянным век¬
тором реактивного ускорения // Космич. исследования. 1964. Т. 2. № 3.
8.5. Белецкий В. В. Описание плоских траекторий космических полетов
с постоянным вектором реактивного ускорения // Труды конферен¬
ции по общим и прикладным вопросам небесной механики. М., 1964.
К очерку девятому
9.1. Белецкий В. В., Гиверц М. Е. О движении пульсирующей системы в гра¬
витационном поле // Космич. исследования. 1967. Т. 5. №6.
9.2. Белецкий В. В. Гравилет // Техника — молодежи. 1970. N° 3.
9.3. Белецкий В. В. Движение искусственного спутника относительно цен¬
тра масс. М.: Наука, 1965.
Литература
415
9.4. Донов А. Е. Теория полета гравитолета // Космич. исследования. 1971.
Т. 9. №3.
9.5. Гиверц М. Е. Один частный случай оптимизации управления грави¬
летом // Космич. исследования. 1972. Т. 10. №2.
9.6. Марков В. Е. Парирование внешних возмущений на космический
аппарат методом изменения его геометрии масс // Изв. АН СССР.
Механика твердого тела. 1974. N° 5.
9.7. Холшевников К. В., Марков В. Б. О стабилизации высоты перицентра//
Космич. исследования. 1975. Т. 13. №2.
9.8. Schaefer J. F. Artifical satellite orbit shifting without mass expulsion utilizing
gravity gradient // 17th Int. Astr. Congr., Madrid, 1966; Proc. 4 Astrodyn.
Guidance and Control. Paris, 1967.
К очерку десятому
10.1. Белецкий В. В., Егоров В. А. Межпланетные полеты с двигателями
постоянной мощности // Космич. исследования. 1964. Т. 2. №3.
10.2. Белецкий В. В., Егоров В. А., Ершов В. Г. Анализ траекторий межпла¬
нетных полетов с двигателями постоянной мощности // Космич.
исследования. 1965. Т. 3. №4.
10.3. Белецкий В. В., Голубков В. В., Егоров В. А., Ершов В. Г. Исследова¬
ние траекторий полета с малой тягой // Второй Всесоюзный съезд
по теоретической и прикладной механике. Аннотации докладов. М.:
Изд-во АН СССР, 1964.
10.4. Гродзовский Г. Л., Иванов Ю. #., Токарев В. В. Механика космиче¬
ского полета с малой тягой. М.: Наука, 1966.
10.5. Понтрягин Л. С., Болтянский В. С, Гамкрелидзе Р. В., Мищенко Е. Ф.
Математическая теория оптимальных процессов. Изд. 2-е, М.: Наука,
1969.
10.6. Болтянский В. Г. Математические методы оптималь ного управле¬
ния. Изд. 2-е. М.: Наука, 1969.
10.7. Melbourne W.G., Sauer G.G. Optimum interplanetary rende vous with
power-limited vehicles // AIAA J. 1963. V. 1. № 1.
10.8. Платонов А. К. Оптимальные свойства корректирующих маневров
при использовании двигателя с ограниченной тягой // Космич. ис¬
следования. 1967. Т. 5. №2.
10.9. Гродзовский Г. Л., Охоцимский Д. ЕБелецкий В. В., Иванов Ю. #.,
Курьянов А. Я., Платонов А. К., Сарынев В. А., Токарев В. В., Яро-
шевский В. А. Механика космического полета // Механика в СССР
за 50 лет. Т. I. М.: Наука, 1968.
К очерку одиннадцатому
11.1. Белецкий В. В., Новикова Е. Т. Об относительном движении связки
двух тел на орбите // Космич. исследования. 1969. Т. 7. № 3.
416
Литература
11.2. Белецкий В. В. Об относительном движении связки двух тел на ор¬
бите, II // Космич. исследования. 1969. Т. 7. №6.
11.3. Белецкий В. В., Егоров В. Л. Межпланетные полеты с двигателями
постоянной мощности // Космич. исследования. 1964. Т. 2. №3.
11.4. Беляев П. Я., Леонов А. А. В открытом космосе // Правда. 1965.
14 апреля.
11.5. Егоров В. А. Некоторые вопросы оптимизации траекторий зондиро¬
вания межпланетного пространства // Автоматика и телемеханика.
1970. № 5.
11.6. Арнольд В. И. Математические методы классической механики. 5-е
изд. М.: URSS, 2003.
11.7. Eneev, Т. Л/., Kozlov N. N.., and Syunyaev R.A. Tidal interaction of galax¬
ies // Astron and Astrophys. 1973. 22. № 1. 41-60.
11.8. Арнольд В. И. Обыкновенные дифференциальные уравнения. 3-е изд.
М.: Наука, 1984.
11.9. Иванов А. П. О безударных движениях в системах с неудерживаю¬
щими связями // Прикл. Мат. Мех. 1992. Т. 1. С. 3-15.
11.10. Иванов А. Я., Базиян А. Б. Исследование асимптотических движений
связки двух тел на круговых орбитах // Космические исследования.
1995. Т. 33. №5. С. 491.
11.11. Белецкий В. В., Панкова Д. В. Связка двух тел на орбите как дина¬
мический биллиард. Препринт. № 7. М.: ИПМ им. М. В. Келдыша
РАН, 1995.
11.12. Панкова Д. В., Белецкий В. В. Связанные тела на орбите как дина¬
мический бильярд// Per. хаот. дин. 1996. 1 (1). С.87-103.
11.13. Белецкий В. В., Панкова Д. В. Влияние аэродинамики на относитель¬
ное движение орбитальной связки двух тел. Часть 2. Хаотические
и регулярные движения. Препринт. №40. М.: ИПМ им. М. В. Кел¬
дыша РАН, 1996.
11.14. Beletsky V. К, Kasatkin G. К, and Starostin Е. L. The pendulum as a dy¬
namical billiard // Chaos Solitons Fractals 1996. 7. №8. 1145-1178.
11.15. Beletsky V. V. Reguldre und Chaotische Bewegung Starrer Korper. Stuttgart:
Teubner Studienbucher Mechanik B.G.Teubner, 1995.
11.16. Белецкий В. В., Левин Е. М. Динамика космических тросовых систем.
М.: Наука, 1990. 329 с.
К очерку двенадцатому
12.1. Аким Э.Л., Энеев Т. М. Определение параметров движения космиче¬
ского летательного аппарата по данным траекторных измерений //
Космич. исследования. 1963. Т. 1. № 1.
12.2. Аким Э.Л. Определение поля тяготения Луны по движению искус¬
ственного спутника Луны «Луна-10» // Космич. исследования. 1966.
Т.4. №6.
Литература
417
12.3. Белецкий В. В., 3оное Ю. В. Вращение и ориентация третьего совет¬
ского спутника // Искусственные спутники Земли. 1961. Вып. 7.
12.4. Белецкий В. В., Голубков В. В., Степанова Е.Л., Хацкевич И. /■. Опреде¬
ление ориентации искусственных спутников по данным измерений.
Препринт / Ин-т прикл. матем. АН СССР. Часть I: Метод. М., 1967;
Часть И: Результаты. Анализ движения. М., 1968.
12.5. Белецкий В. В., Голубков В. В., Лавровский Э. К., Трушин С. Я.,
/севи*/ Я. Г. Определение ориентации и вращения искусственных
спутников по данным измерений // Космич. исследования. 1967.
Т. 5. № 5.
12.6. Белецкий В. В., Голубков В. В., Хацкевич И. Г. Анализ вращения и ори¬
ентации спутника «Протон-2» // Ргос. XVII1 International Astronau-
tical Congr., Belgrad, 1967. Pergamon Press, 1968.
12.7. Голубков В. В., Хацкевич Я. Г. Определение ориентации искусствен¬
ных спутников Земли по заданной системе измерений // Космич.
исследования. 1969. Т. 7. №4.
12.8. Белецкий В. В., Голубков В. Я, Степанова Е. А., Хацкевич Я. У". Резуль¬
таты определения ориентации спутника «Протон-2» и описание его
движения относительно центра масс // Космич. исследования. 1969.
Т. 7. №4.
12.9. Белецкий В. В. Оценка характера взаимодействия аэродинамического
потока со спутником по анализу движения спутника «Протон-2»
относительно центра масс // Космич. исследования. 1970. Т. 8. № 2.
12.10. Энеев Т. А/., Платонов А. ККазакова Р. К. Определение параметров
орбиты искусственного спутника поданным наземных измерений //
Искусственные спутники Земли. 1960. Вып. 4.
12.11. Белецкий В. В. Движение искусственного спутника относительно
центра масс. М.: Наука, 1965.
27 Заказ 1667
Комментарии к рисункам
И. В. Новожилова
Стр. 18. Быстрое развитие цивилизации в системе одиночной звез¬
ды. В роли Ньютона — коллега художника В. Андреев.
Стр. 20. Медленное развитие цивилизации в системе двойной звез¬
ды. В роли троглодита — друг автора и художника Г. Р. Сазыкин.
Стр. 65. Задача о двух массах на чисто мнимом расстоянии друг от
друга. Авторы задачи (слева направо): Е. П. Аксенов, Е. А. Гребени-
ков, В. Г Демин.
Стр. 69. Добавочные члены ньютоновского потенциала подбирает
В. В. Белецкий.
Стр. 90. В. В. Белецкий изыскивает интегралы уравнений движения.
Стр. 120. М. JI. Лидов не дает Луне упасть на Землю.
Стр. 134. Герои книги А. А. Милна «Вини-Пух и все, все, все» удру¬
чены душераздирающим зрелищем инвариантного тора.
Стр. 148. «Луна, тебе — мой поцелуй». В. И. Левантовский, первый
издатель данной книги, в роли Мефисто.
Стр. 160. Т. М. Энеев — сеятель галактик.
Стр. 173. Марс (Г. Р. Сазыкин) и его спутники (В. С. Семячкин и
В. В. Белецкий).
Стр. 181. Ринограденция на орбите.
Стр. 197. Забрел в науку изысканный жираф из поэзии Н. Гумилева.
Стр. 249. По траектории «малой тяги» летит автор книги.
Стр. 272. Полет (автора) под солнечным парусом. Солнышко —
Н. А. Парусников, на парусе — портрет Г. Р. Сазыкина.
Стр. 294. Барон Мюнхгаузен (В. В. Белецкий) знает, как и почему
можно вытянуть себя из космического болота.
Комментарии к рисункам И. В. Новожилова
419
Стр. 296. Пародия на придуманный автором (подвешен с якорем)
«гравилет». На платформе В. В. Лунев и Н. А. Парусников — одно¬
курсники художника и автора.
Стр. 298. Еще один вариант гравилетного эффекта. Портрет В. А. Его¬
рова.
Стр. 313. Малые тяги. Слишком долго летел. Ср. с рисунком
на стр. 249.
Стр. 366. Иллюстрация к теме «Болеадорас в космосе». В морде
быка — явный намек на автора книги. Охотники: Д. Е. Охоцимский
и Е. Т. Новикова.
Стр. 377. Орбитальная связка тел (двойной автопортрет художни¬
ка — И. В. Новожилова).
Стр. 391. Автор в роли космического Дон Кихота.
Стр. 405. Заключительный портрет автора.
Именной указатель
Аким Э. Л. 394
Аксенов Е. П. 64, 70, 71, 418
Алексеев В. М. 71
Арнольд В. И. 8, 14, 51, 117, 125,
130-133, 135, 138, 146, 154,
174, 383, 385, 386
Балк М. Б. 59, 60
Белецкий В. В. 8, 9, 14, 15, 182,
194, 218, 219, 241, 243, 245,
248, 299, 300, 321, 352, 418
Беляев П. 360
БиркгофДж. (BirkhofTG.) 135
Блехман И. И. 140
Боголюбов Н. Н. 35
Брауэр Д. (Brower D.) 66
Брэкуэлл Дж. (Breakwell J. V.) 185,
189
Брюно А. Д. 62, 140, 166
Винти Дж. (Vintiit J. Р.) 66, 71
Волосов В. М. 35
Воробьев И. И. 305
Воронцов-Вельяминов Б. А. 161
Гиверц М. Е. 290, 299
Голдстейн (Goldstein R. L.) 213
Голубев В. В. 13
Голубков В. В. 311, 339, 394
Гольдрейх П. (Goldreich Р.) 213,
227
Гребеников Е. А. 64, 70, 71, 418
Гродзовский Г.Л. 271, 311, 348
Гумилев Н. 418
Дайс (Dyce R. В.) 212
Девянин Е. А. 378
Демин В. Г. 13, 51, 64, 66, 70, 71,
86, 125, 163, 418
Депри (Deprit А.) 154
Депри-Бартоломе (Deprit-Barto-
lome А.) 154
Дубошин Г.Н. 23, 33, 51, 66, 114
Евтушенко Ю. Г. 265
Егоров В. А. 147, 155, 157-159,248,
311,321,364,419
Ершов В. Г. 311
Ефимов Г. Б. 264
Зауэр (Sauer С. G.) 346
Зельдович Я. Б. 8, 14, 385
Зигель K.J1. (Siegel К. L.) 135
Зиолковский К. 14
Зонов Ю. В. 394
Иванов Ю.Н. 271, 311, 348, 386
Ишлинский А. Ю. 124, 183
Казакова Р. К. 394
Карпентер (Carpenter R. L.) 213
Кассини Дж.Д. 214-216, 222
Кеплер И. (Kepler I.) 19, 23, 215
Кислик М. Д. 66, 71
Кларк A. (Clarke А. С.) 270, 275—
279
Клеменс Дж. (Clemence G.) 66
Козлов Н.Н. 161, 242, 384, 385
Колмогоров А. Н. 130-132, 135,
146
Коломбо Дж. (Colombo G.) 212,
218, 220, 233
Коникова Н. С. 13
Кордылевский К. 155
Именной указатель
421
Космодемьянский А. А. 13
Котельников В. А. 213
Крылов Н. М. 35
Куницын A. J1. 14
Кэйн Т. P. (Kane Т. R.) 189
Лавровский Э. К. 394
Лагранж (Lagrange J. L.) 27, 87,
153, 177, 217
Лаплас (Laplace Р. S.) 157, 217
Левантовский В. И. 147, 159, 418
Леонов А. 360-362
Леонтович А. М. 154
ЛидовМ.Л. 106, 109, 122-124, 157,
218, 418
Лунев В. В. 419
Лурье А. И. 33
Ляпунов А. М. 172, 174, 176, 177,
184
Маркеев А.П. 154, 211
Маршак С. Я. 88
Мельбурн (Melbourn W. G.) 346
Меус 108
Мещерский И. В. 87
Милн А. А. 418
Митницкий А. Б. 302
Митропольский Ю.А. 35
Мозер Ю. (Moser J.) 135, 146
Моисеев Н.Д. 27, 122
Моисеев Н. Н. 45
Молчанов А. М. 136, 138, 142, 146
Нам Тум По 193
Нейштадт А. И. 218
Нехорошев Н. Н. 135
Новикова Е.Т. 352, 378, 419
Новожилов И. В. 9, 13-15,418,419
Ньютон И. (Newton I.) 13, 19, 215,
418
Охоцимский Д. Е. 13, 59, 157, 184,
245, 258, 419
Парусников Н.А. 13, 418, 419
Петтенгил Дж. (Pettengffll G. Н.)
212
Пиил С. (Peale S.J.) 213, 218, 227
Платонов А. К. 349, 394
Прингл Р (Pringle R.) 185, 189
Птолемей 19, 405
Пуанкаре A. (Poincare Н.) 35, 135
Румянцев В. В. 180
Сазыкин Г. Р 13, 418
Сарычев В. А. 61, 184
Седов Л. И. 60, 159
Селерье 87, 88
Семячкин B. C. 418
Сен-Жермен 87, 88
Скиапарелли (Sciaparelli) 211, 212
Скопцов А. П. 271
Солоненко В. П. 300
Степанова Е.А. 13
Сюняев РА. 161, 384, 385
Таратынова Г П. 59
Тесленко Н. М. 157
Токарев В. В. 271, 311, 348
Торжевский А. П. 211, 221, 222
Трушин С. И. 201, 222, 394
Хабибулин Ш.Т. 217
Хацкевич И. Г. 394
Хентов А. А. 236, 240, 241, 243
Черников Ю.А. 106, 108, 109
Черноусько Ф. Л. 198, 201, 207,
220, 221
Четаев Н.Г. 13, 142, 144, 172
Шапиро (Schapiro 1.1.) 212, 233
Шефер (Schaefer J. F.) 290
Шмидт О. Ю. 213
Штюмпке (Stumpke Н.) 183
Эйлер Л. (Euler L.) 63, 64
Эльясберг П. Е. 59
Энеев Т. М. 13, 59, 161-163, 166,
242, 320, 384, 385, 394, 418
Предметный указатель
Активная система стабилизации
183
Алгоритм статистической
обработки информации 392
Амплитуда (функция) 81
амплитудно-фазовая траектория
43
Аномалия истинная 22
— эксцентрическая 23
Апогей 22
Аргумент перигея 25
— широты 25
Арнольда теорема 133, 135, 154
Асимптотические методы
нелинейной механики 35-37,
45, 46, 57
Бесселя функции 43
Большая полуось эллипса 22
Быстрые вращения 191
— переменные 37
Вековые возмущения 30, 33
Вектор кинетического момента 193
— Лапласа 24, 117
— управления 314
Взаимодействующие галактики 161
Возмущение 179
Возмущенное движение 133, 195
Восходящий узел орбиты 24
Вращение Венеры 213, 227, 242
— Луны 170, 171
— спутника 167, 389
быстрое 191
— типа лунного 209, 211
Меркурия 210, 211, 226
Вырождение предельное 132
— собственное 132
Галактики взаимодействующие 161
Гамильтона уравнения 74, 383
— функция 58, 73, 113
Гамильтона—Якоби уравнение 74
Гипотеза Молчанова 136
Главные центральные моменты
инерции 170
оси инерции 170
Гравилет 301
Гравитационная стабилизация 183
Гравитационный потенциал 167
Давление световое 88, 105, 270
Дальность угловая 335
Датчики ориентации 390
Двигатели малой тяги см. Полет с
малой тягой
Движение в окрестности спутника
331
— возмущенное 26, 133
— вращательное см. Вращение...
— кеплеровское 21
— космонавата относительно
спутника 357
— лагранжево планет 118
— невозмущенное 26, 172, 179, 192
— относительное 332, 351
— среднее 23
— условно-периодическое 131
— центра масс связки 353
Делоне элементы 33, 36, 113
Дельта амплитуды 82
Предметный указатель
423
Долгота восходящего узла 25
Допустимые управления 314
Задача двух неподвижных центров
64
обобщенная 71
— о сближении двух космических
объектов 331
— ограничения движения относи¬
тельно центра масс 356
— оптимального управления 312,
314
— тех тел ограниченная 64, 118,
147
круговая 147
Задача п тел 110
Закон площадей 22
— сохранения энергии 23
— тяготения ньютоновский 16
Законы Кассини 171, 214, 217
Звезды кратные 19
Знакоопределенная функция 174,
175
Знакопостоянная функция 174
Зона резонансная 209
— срыва 369
Зонд космический возвратный 363
Изохронные производные кепле-
ровского движения 331
Импульсы обощенные 73
Интеграл Лапласа (обощенный) 89
— Лежандра первого рода нормаль¬
ный эллиптический 81
— площадей 22, 28, 89
— полный эллиптический перво¬
го рода 81
— энергии 23, 89
— Якоби 150
Истинная аномалия 22
Канонические уравнения движе¬
ния 37, 50, 74, 114
Кассини законы 171, 214, 215, 217
— — обобщенные 214, 222-225,
231, 241
— щель 215
Кеплера уравнение 23
Кеплерова орбита 22
Колебания спутника 37
нелинейные 184
Коррекция межпланетных траек¬
торий 348
Косинус эллиптический 82
Лагранжа треугольные точки либ¬
рации 153
— уравнения первого рода 352, 353
Лагранжево движение планет 118
Лапласа вектор 24, 117
— теорема 51, 115, 116, 118
Лежандра интеграл первого рода
нормальный эллиптический
81
— полиномы 56, 67
Линия узлов 24, 117
Лиувилля теорема 383
Локально-оптимальное управление
солнечным парусом 275, 282
Ляпунова теорема 175
— функция 175
Медленные переменные 37
Метод наименьших квадратов 393
— осреднения 49
— точечных отображений 372
— транспортирующей траектории
320
Методы асимптотические нелиней¬
ной механики 35-37, 45, 46,
57
Модуль эллиптического интеграла
81
Молчанова гипотеза 136
Момент прохождения через пери¬
гей орбиты 23
Моменты инерции главные цен¬
тральные 170
424
Предметный указатель
Наклонение 25
Невозмущенное движение 26, 172,
192
Нелинейные колебания 184
Неограниченная функция 175
Неправильная система 176
Нисходящий узел орбиты 25
Нормальный эллиптический ин¬
теграл Лежандра первого ро¬
да 81
Область маловозмущенного дви¬
жения 125
Обобщенные импульсы 73
Ограничения 314, 316, 318
Ограниченная исчезающая функ¬
ция 175
Орбита кеплерова 21
Орбиты узел 24
— элементы 25
Ортимизация 314
Оси инерции главные централь¬
ные 170
Оскулирующая орбита экватори¬
ального спутника 27
Оскулирующий элемент 26, 27
— эллипс 33
Осреднение 50, 51
— канонических уравнений 37
Ось динамической симметрии
спутника 192
— спутника продольная 192
Относительное движение 351, 380
Отображение точечное 372
Парадокс разгона с малой тягой
251
— спутника аэродинамический 59,
60, 252
Параметр фокальный 22
Параметрический резонанс 42
Парус солнечный 270
наилучшей конструкции 271
Пассивная система стабилизации
183
Переменная быстрая 37
— медленная 37, 54
Перигей 22, 222
Плоскость фазовая 368
Поверхность Хилла 147
Полет к Луне 147
— ракеты оптимальный 316
— с малой тягой 87, 246
к Венере 338, 346
к Марсу 338, 339, 342,
344, 345, 348
к Юпитеру 346
между орбитами планет
311
с возвращением 344
— с малой тягой к Венере 338
Полиномы Лежандра 56, 67
Портрет фазовый 208, 370
Порядок резонанса 140
Постоянная тяготения
универсальная 16
Потенциал гравитационный 167
Поток фазовый 383
Правильная система 176
Предельное вырождение 132
Прецессия орбиты спутника 59
— спутника регулярная 192
Принцип максимума Понтрягина
314, 315
Продольная ось спутника 192
Производные изохронные кепле-
ровского движения 331
Пропеллирующий эффект 397
Пространство фазовое 383
«Протон» 389, 390, 394
Пуанкаре теорема 382-384
Равновесие относительное в гра¬
витационном поле 171, 172,
177
Радиолокация Венеры 141
Разгон с малой тягой 247
— с малой тягой монотонный 257
Резонанс 41, 53
— параметрический 42
Предметный указатель
425
Резонансная зона 209
Резонансность 132
— вращений Луны, Венеры, Мер¬
курия 141, 143
— систем спутников Юпитера,
Сатурна, Урана 139
— Солнечной системы 137
Решение асимптотическое 40
Ринограденция 180
Ряд Фурье 47, 54, 114, 237
Сближение космических
объектов 331
Световое давление 88, 105, 270
Связка двух тел на орбите 352, 365
— четырех тел на орбите 378
Сепаратриса 370
Сжатие Земли 28, 58
— Урана 124
Силовая функция 56, 112
Силы приливные 125
Синус эллиптический 82
Система координат транспортиру¬
ющая 321
— неправильная 176
— правильная 176
— стабилизации активная 183
пассивная 183
Скорость прецессии 193
— собственного вращения 193
Собственное вырождение 132
Солнечная система, устойчивость
110, 111, 116, 130, 138
Солнечный парус 270, 282
наилучшей конструкции 271
Спираль разгона 247
монотонная (универсальная)
257
Спутник в поле земного сфероида
56, 64
— гантелеобразный 288
— Луны 128
— полярный 84
— экваториальный 27
Спутники Урана 124
Среднее движение 23
Стабилизация спутников активная
183
пассивная 183
гравитационная 183
Сфера действия 128
Земли 128
Луны 128
Сферы гравитационные 130
Тень Земли 274
Теорема Арнольда 133, 135, 154
— Лапласа 115, 116, 118
— Лиувилля 383
— Ляпунова 175
— Пуанкаре 382, 383
Теория устойчивости Ляпунова 175
Тор п-мерный 131
— двумерный 131
Точечное отображение 372
Точки либрации 152, 153
треугольные 153
Траектория разгона спиральная
247
— сближения 155
— транспортирующая 321, 336
Тяга малая см. Полет с малой
тягой
Угловая дальность 335
Угол нутации 193
Узел орбиты 24
восходящий 24
нисходящий 25
Управление локально-оптимальное
солнечным парусом 275
— оптимальное 312
— ступенчатое малой тягой 339
Управления допустимые 314
Уравнение Гамильтона—Якоби 74
— Кеплера 23
Уравнения в оскулирующих эле¬
ментах 33, 34
— в элементах Делоне см. Элемен¬
ты Делоне
426
Предметный указатель
— возмущенного движения 172
канонические 37, 50, 113
— вращения спутника 60
— Гамильтона 74
— Лагранжа первого рода 352
— эволюционные 36, 51
вращения спутника 195, 196
Уран, его спутники 124
Ускорение малое, постоянное по
величине и направлению 87
— ньютоновской силы тяготения
21
Условно-периодическое движение
131
Устойчивость относительного рав¬
новесия в гравитационном
поле 177, 243
— Солнечной системы 110, 116,
130, 138
Фазовая плоскость 368
Фазовое пространство 383
Фазовый портрет 208, 370
— поток 383
Фокальный параметр 22, 29
Функции эллиптические Якоби 82
Функция Бесселя 43
— Гамильтона 58, 73, 113
— знакоопределенная 174, 175
— знакопостоянная 174
— Ляпунова 175
— неограниченная 175
— ограниченная 175
исчезающая 175
— тени 275
Фурье ряд 47, 54, 114, 237
Характеристическое число функ¬
ции 176
Хилла поверхность 150
Число характеристичное
функции 176
Эволюционные уравнения 36, 51,
222
Эйлера задача двух неподвижных
центров 64
Эйлера—Пуансо движение 192
Экваториальная орбита 32
Экспедиции межпланетные с ма¬
лой тягой 310
Экспериментальное определение
ориентации спутников 390
Эксцентриситет 22
Эксцентрическая аномалия 23
«Электрон» 394
Элементы Делоне 36
— орбиты 25
— оскулирующие 26, 27
Эллипс оскулирующий 27
Эллиптические функции Якоби 80
Эллиптический косинус 82
— синус 82
Эффект пропеллирующий 397
«Эхо» 88, 105, 108
Якоби интеграл 150
— эллиптические функции 77, 82,
83
е-поверхность 127, 128
е-сфера 128
nJ'SSMfl nj'SSHII IMSSUR nJSSHR
URSS
URSS:ru * " ryrss?fu^ ^ yjisslfIIWSS.ru
Представляем Вам наши лучшие книги:
Серия «НАУКУ — ВСЕМ! Шедевры научно-популярной литературы»
Перельман Я. И. Занимательная астрономия.
Липунов В. М. В мире двойных звезд.
Кононович Э. В. Звезда Солнце.
Колмогоров А. Н. Математика — наука и профессия.
Стинрод //., Чинн У. Первые понятия топологии.
Мизес Р. Вероятность и статистика.
Лебег А. Об измерении величин.
Харкевич А. А. Автоколебания.
Каганов М. И. Электроны, фононы, магноны.
Каганов М. И., Цукерник В. М. Природа магнетизма.
Тарасов Л. ВТарасова А. Н. Беседы о преломлении света.
Сазанов А. А. Четырехмерная модель мира по Минковскому.
Ашкинази Л. А. Электронные лампы: Из прошлого в будущее.
Гарднер М. Теория относительности для миллионов.
Кац Е.А. Фуллерены, углеродные нанотрубки и нанокластеры.
Оптика. Колебания и волны
Саржевский А. М. Оптика. Полный курс.
Майкельсон А. А. Исследование по оптике.
Шепелев А. В. Оптика. Готовимся к экзаменам, зачетам, коллоквиумам.
Федоров Ф. И. Оптика анизотропных сред.
Русинов М. М. и др. Вычислительная оптика: Справочник.
Шутов А. М. Методы оптической астрополяриметрии.
Фок В. А. Проблемы дифракции и распространения электромагнитных волн.
Харкевич А. А. Спектры и анализ.
Кабисов К С., Камалов Т. Ф., Лурье В. А. Колебания и волновые процессы.
Кравченко И. Т. Теория волновых процессов.
Добролюбов А. И. Бегущие волны деформации.
Добролюбов А. И. Скольжение, качение, волна.
Добролюбов А. И. Волновой перенос вещества.
Кнудсен В. О. Архитектурная акустика.
Старченко И. Б. Динамический хаос в гидроакустике.
Полников В. Г. Нелинейная теория случайного поля волн на воде.
Стрэтт (Рэлей) Дж. В. Волновая теория света.
Гончаренко А. М., Карпенко В. А. Основы теории оптических волноводов.
Гончаренко А. М. Гауссовы пучки света.
Вилля Г. Теория вихрей.
Абурджаниа Г. Д. Самоорганизация нелинейных вихревых структур и вихревой
турбулентности в диспергирующих средах.
Шаткое А. Г., Бубнов В. А., Янковский С. Ю. Волновые явления теплопроводности.
Бардзокас Д. И. и др. Распространение волн в электромагнитоупругих средах.
Гетлинг А. В. Конвекция Рэлея—Бенара. Структуры и динамика.
Иванов Б. Н. Мир физической гидродинамики.
URSS.ru URSS.ru URSS.ru URSS.ru
UWSS.ru UWSS.ru UWSS.ru UWSS.ru URSS.ru lUWSS.ru
URSS.ru URSS.ru URSS.ru URSS.ru
I
ее
ев
Ш
св
ев
ев
ев
ев
ев
ев
ев
,ь
а
ев
iee
Представляем Вам наши лучшие книги:
Учебники и задачники по физике
Капитонов И. М. Введение в физику ядра и частиц.
Иванов Б. Н. Законы физики. URSS
Воронов В. К., Подоплелов А. В. Современная физика.
Воронов В. КПодоплелов А. В. Современная физика: Конденсированное состояние.
Сапунов В. Т. Классический курс сопротивления материалов в решениях задач.
Кириллов В. М. и др. Решение задач по физике.
Колоколов И. В. и др. Задачи по математическим методам физики.
Жукарее А. С. и др. Задачи повышенной сложности в курсе общей физики.
Кронин Дж., Гринберг Д., Телегди В. Теоретическая физика. Сб. задач с решениями.
Варикаш В. М., Болсун А. И., Аксенов В. В. Сборник задач по статистической физике.
Кубо Р. Статистическая механика. Современный курс с задачами и решениями.
Галицкий В. М., Карнаков Б. М., Коган В. И. Задачи по квантовой механике. Ч. 1,2.
Бардзокас Д. И., Зобнин А. И., Сеник И. А., Фильштинский М.Л. Задачи по теории
термопьезоэлектричества с подробными решениями.
Самарский А. А. и др. Задачи и упражнения по численным методам.
Сурдин В. Г. Астрономические задачи с решениями.
Николаев О. С. Физика и астрономия: Курс практических работ для средней школы.
Физика элементарных частиц
Окунь Л. Б. Физика элементарных частиц.
Окунь Л. Б. Лептоны и кварки.
Борн М. Лекции по атомной механике.
Бояркин О. М. Введение в физику элементарных частиц.
Бояркин О. М. Физика массивных нейтрино.
Ляховский В. Д., Болохов А. А. Группы симметрии и элементарные частицы.
Бранский В. П. Теория элементарных частиц как объект методологического
исследования.
Бранский В. П. Значение релятивистского метода Эйнштейна в формировании
общей теории элементарных частиц.
Теория поля
Рубаков В. А. Классические калибровочные поля. Бозонные теории.
Рубаков В. А. Классические калибровочные поля. Теории с фермионами.
Некоммутативные теории.
Сарданашвили Г. А. Современные методы теории поля. Т. 1-4.
Иваненко Д. Д., Сарданашвили Г. А. Гравитация.
Коноплева Н. П., Попов В. Н. Калибровочные поля.
Богуш А. А. Введение в калибровочную полевую теорию электрослабых взаимодействий.
Богуш А. А., Мороз Л. Г. Ведение в теорию классических полей.
Прохоров Л. В., Шабанов С. В. Гамильтонова механика калибровочных систем.
Менский М. Б. Группа путей: измерения, поля, частицы.
Менский М. Б. Метод индуцированных представлений: пространство-время
и концепция частиц.
Визгин В. П. Единые теории поля в квантово-релятивистской революции.
И j
ев:
Ч
ее
ее
ев
09;
ее
и
св
ев!
ев
ев!
■
Т
URSS.ru URSS.ru URSS.ru URSS.ru
IIRSS.ru ll URSSiru IIRSS.ru URSS.ru URSS.ru URSS.ru
URSS.ru URSS.ru URSS.ru URSS.ru
Представляем Вам наши лучшие книги:
Термодинамика и статистическая физика
Квасников И. А. Молекулярная физика.
Базаров И. П. Заблуждения и ошибки в термодинамике. URSS
Крылов Н. С. Работы по обоснованию статистической физики.
Бриллюэн Л. Квантовая статистика.
Хинчин А. Я. Математические основания квантовой статистики.
Варикаш В. Л/., Болсун А. ИАксенов В. В. Сборник задач по статистической физике.
Баранов А. А., Колпащиков В. Л. Релятивистская термомеханика сплошных сред.
ШапкинА. ИСидоров Ю. И. Термодинамические модели в космохимии и планетологии.
Агеев Е. П. Неравновесная термодинамика в вопросах и ответах.
Дуров В. А., Агеев Е. П. Термодинамическая теория растворов.
Мюнстер А. Химическая термодинамика.
Зайцев Р. О. Введение в современную статистическую физику. Курс лекций.
Зайцев Р. О. Введение в современную кинетическую теорию. Курс лекций.
Поклонский Н. А., Вырко С. А., Поденок С. Л. Статистическая физика полупроводников.
Планк М. Теория теплового излучения.
Карно С., Клаузиус Р., Томсон-Кельвин В. и др. Второе начало термодинамики.
Теория относительности
Фок В. А. Теория пространства, времени и тяготения.
Фок В. А. Теория Эйнштейна и физическая относительность.
Угаров В. А. Специальная теория относительности.
Сацункевич И. С. Экспериментальные корни специальной теории относительности.
Вильф Ф. Ж. Логическая структура частной теории относительности.
Эддингтон А. Пространство, время и тяготение.
Эддингтон А. Относительность и кванты.
Эддингтон А. Теория относительности.
Вейль Г. Пространство. Время. Материя. Лекции по общей теории относительности.
Вяльцев А. Н. Дискретное пространство-время.
Фридман А. А. Мир как пространство и время.
История физики
Дорфман Я. Г. Всемирная история физики: С древнейших времен до конца XVIII века.
Дорфман Я. Г. Всемирная история физики: С начала XIX до середины XX вв.
Горобец Б. С. Круг Ландау: Жизнь гения.
Горобец Б. С. Круг Ландау: Физика войны и мира.
Горобец Б. С. Круг Ландау и Лифшица.
Горобец Б. С. Секретные физики из Атомного проекта СССР: Семья Лейпунских.
Абрамов А. И. История ядерной физики.
Богуш А. А. Очерки по истории физики микромира.
Хайтун С. Д. История парадокса Гиббса.
Бетяев С. К. Записки гидродинамика.
Тимошенко С. П. История науки о сопротивлении материалов.
Кадомцев С. Б. Геометрия Лобачевского и физика.
. URSS~ru - :URSS.ru У URSS.ru URSS.ru
URSS.ru URSS.ru I " URSS.ru URSSxu URSS.ru URSS.ru
URSS.ru
URSS.ru
URSS.ru
URSS.ru
JRSS
Представляем Вам наши лучшие «лиги:
Механика
Кирхгоф Г. Механика. Лекции по математической физике.
Якоби К. Лекции по динамике.
Уиттекер Е. Т. Аналитическая динамика.
Жуковский Н. Е. Аналитическая механика.
Жуковский Н. Е. Механика системы. Динамика твердого тела.
Жуковский Н. Е. Кинематика, статика, динамика точки: университетский курс.
Чаплыгин С. А. Исследования по динамике неголономных систем.
Кориолис Г. Математическая теория явлений бильярдной игры.
Малкин И. Г\ Методы Ляпунова и Пуанкаре в теории нелинейных колебаний.
Малкин И. Г. Некоторые задачи теории нелинейных колебаний.
Малкин И. Г. Теория устойчивости движения.
Пановко Я. Г., Губанова И. И. Устойчивость и колебания упругих систем.
Блехман И. И., Мышкис А. Д., Пановко Я. Г. Прикладная математика.
Пфейффер П. Колебания упругих тел.
Геккелер И. В. Статика упругого тела.
Новожилов В. В. Основы нелинейной теории упругости.
Победря Б. Георгиевский Д. В. Лекции по теории упругости.
Георгиевский Д. В. Устойчивость процессов деформирования вязкопластических тел.
Петкевич В. В. Основы механики сплошных сред.
Шмыглевский Ю. Д. Аналитические исследования динамики газа и жидкости.
Розенблат Г. М. Механика в задачах и решениях.
Розенблат Г. МПаншина А. В., Козлова 3. П. Теоретическая механика в решениях
задач из сборника И. В. Мещерского. Кн. 1-3.
Серия «Физико-математическое наследие: физика (механика)»
Вебстер А. Г. Механика материальных точек, твердых, упругих и жидких тел. В 2 т.
Кирпичев В. Л. Беседы о механике.
Квантовая механика
Фок В. А. Начала квантовой механики.
Фок В. А. Работы по квантовой теории поля.
Фок В. А. Квантовая физика и строение материи.
Бройль Л. де. Введение в волновую механику.
Кемпфер Ф. Основные положения квантовой механики.
Мотт Н., Снеддон И. Волновая механика и ее применения.
Тарасов Л. В. Основы квантовой механики.
Тарасов Л. В. Введение в квантовую оптику.
Грин X. Матричная квантовая механика.
Флюгге 3. Задачи по квантовой механике. В 2 кн.
Горбацевич А. К. Квантовая механика в общей теории относительности.
Килин С. Я. Квантовая оптика: поля и их детектирование.
Вильф Ф. Ж. Логическая структура квантовой механики.
Дирак П. А. М. Лекции по квантовой теории поля.
Стояновский А. В. Введение в математические принципы квантовой теории поля.
URSS.ru
URSS.ru
URSS.ru
URSS.ru
3
ът'л
619
09
тщ
L.
И
09
и
С/Э
JRSS.ru
URSSru
•■V- ^р^р
URSSiru
URSS.ru
09
09
«Ь.
09
оз
»Е
** ■
09
и
URSS
Представляем Вам наши лучшие книги:
Серия «Синергетика: от прошлого к будущему»
Пенроуз Р. НОВЫЙ УМ КОРОЛЯ. О компьютерах, мышлении и законах
физики. Пер. с англ.
Хакен Г. Информация и самоорганизация. Пер. с англ.
Малинецкий Г. Г. Математические основы синергетики.
Малинецкий Г. Г., Потапов А. Б. Нелинейная динамика и хаос: основные понятия.
Малинецкий Г. Г., Потапов А. Б., Подлазов А. В. Нелинейная динамика.
Малинецкий Г. Г. (ред.) Будущее России в зеркале синергетики.
Малинецкий Г. Г. (ред.) Синергетика: Исследования и технологии.
Арнольд В. И. Теория катастроф. •
Климонтович Ю. JI. Турбулентное движение и структура хаоса.
Безручко Б. П. и др. Путь в синергетику. Экскурс в десяти лекциях.
Данилов Ю.А. Лекции по нелинейной динамике. Элементарное введение.
Трубецков Д. И. Введение в синергетику. В 2 кн.: Колебания и волны; Хаос и структуры.
Быков В. И. Моделирование критических явлений в химической кинетике.
Чумаченко Е. Н. и др. Сверхпластичность: материалы, теория, технологии.
Редько В. Г. Эволюция, нейронные сети, интеллект: Модели и концепции
эволюционной кибернетики.
Чернавский Д. С. Синергетика и информация (динамическая теория информации).
Баранцев Р. Г. Синергетика в современном естествознании.
Баранцев Р. Г. и др. Асимптотическая математика и синергетика.
Анищенко В. С. Знакомство с нелинейной динамикой.
Тюкин И. Ю., Терехов В. А. Адаптация в нелинейных динамических системах.
Васильков Г. В. Эволюционная теория жизненного цикла механических систем.
Пригожий И. Неравновесная статистическая механика.
Пригожий И. От существующего к возникающему: Время и сложность в физических
науках.
Пригожий Я, Стенгерс И. Время. Хаос. Квант. К решению парадокса времени.
Пригожий Я, Стенгерс И. Порядок из хаоса. Новый диалог человека с природой.
Пригожий Я., Николис Г. Познание сложного. Введение.
Пригожий Я., Гленсдорф П. Термодинамическая теория структуры, устойчивости
и флуктуаций. *
Суздалев И. П. Нанотехнология: физико-химия нанокластеров, наноструктур
и наноматериалов.
Тел./факс:
(499) 135-42-46,
(499) 135-42-16,
E-mail:
URSS@URSS.ru
http://URSS.ru
Наши книги можно приобрести в магазинах:
«Библио-Глобус» (и. Лубянка, ул. Мясницкая, 6. Тел. (495) 625-2457)
«Московский дом книги» (м. Арбатская, ул. Новый Арбат, 8. Тел. (495) 203-8242)
«Молодая гвардия» (м. Полянка, ул. Б. Полянка, 28. Тел. (495) 238-5001, 780-3370)
«Дом научно-технической книги» (Ленинский пр-т, 40. Тел. (495) 137-6019)
«Дом книги на Ладожской» (м. Бауманская, ул. Ладожская, 8, стр.1. Тел. 267-0302)
«Гнозис» (м. Университет, 1 гум. корпус МГУ, комн. 141. Тел. (495) 939-4713)
«У Кентавра» (РГГУ) (м. Новослободская, ул. Чаянова, 15. Тел. (499) 973-4301)
«СПб. дом книги» (Невский пр., 28. Тел. (812) 448-2355)
URSSsPU,
URSS.ru
URSS.ru
;IIRSS:nu
URSS.ru URSS.ru I ; URSS.ru URSS.ru Г URSS.ru URSS.ru
URSS.ru
fn
URSS.ru
Щpi'll:
URSS.ru
URSS.il
Уважаемые читатели! Уважаемые авторы!
Наше издательство специализируется на выпуске научной и учебной
литературы, в том числе монографий, журналов, трудов ученых Россий¬
ской академии наук, научно-исследовательских институтов и учебных
заведений. Мы предлагаем авторам свои услуги на выгодных экономи¬
ческих условиях. При этом мы берем на себя всю работу по подготовке
издания — от набора, редактирования и верстки до тиражирования
и распространения.
URSS
Среди вышедших и готовящихся к изданию книг мы предлагаем Вам следующие:
Капитонов И. М. Введение в физику ядра и частиц.
Ишханов Б. С., Капитонов И. М., Тутынь И. Л. Нуклеосинтез во Вселенной.
Абрамов А. И. История ядерной физики.
Гейзенберг В. Философские проблемы атомной физики.
Гейзенберг В. Часть и целое (беседы вокруг атомной физики).
Окунь JI. Б. Физика элементарных частиц.
Окунь JI. Б. Лептоны и кварки.
Борн М. Лекции по атомной механике.
Бояркин О. М. Введение в физику элементарных частиц.
Бояркин О. М. Физика массивных нейтрино.
Ляховский В. Д., Болохов А. А. Группы симметрии и элементарные частицы.
Бранский В. П. Теория элементарных частиц как объект методологического
исследования.
Бранский В. 77. Значение релятивистского метода Эйнштейна в формировании
общей теории элементарных частиц.
Богуш А. А. Очерки по истории физики микромира.
Иванов Б. Н. Законы физики.
Воронов В. К., Подоплелов А. В. Современная физика.
Воронов В. К, Подоплелов А. В. Современная физика: Конденсированное состояние.
Гамов Г. Мистер Томпкинс исследует атом.
Хван М. П. Неистовая Вселенная: от Большого взрыва до ускоренного расширения,
от кварков до суперструн.
Горобец Б. С. Круг Ландау: Жизнь гения.
Горобец Б. С. Круг Ландау: Физика войны и мира.
Горобец Б. С. Круг Ландау и Лифшица.
Горобец Б. С. Секретные физики из Атомного проекта СССР: Семья Лейпунских.
Серия «Классический университетский учебник»
Ишханов Б. С., Капитонов И. А7., Юдин Н. П. Частицы и атомные ядра.
Квасников И. А. Термодинамика и статистическая физика. В 4 т.
Кононович Э. В., Мороз В. И. Общий курс астрономии.
Петровский И. Г. Лекции по теории обыкновенных дифференциальных уравнений.
Гнеденко Б. В. Курс теории вероятностей.
Колмогоров А. Н., Драгалин А. Г. Математическая логика.
По всем вопросам Вы можете обратиться к нам:
тел./факс (499) 135-42-16, 135-42-46
или электронной почтой URSS@URSS.ru
Полный каталог изданий представлен
в интернет-магазине: http://URSS.ru
Научная и учебная
литература
URSSsHl
URSS.ru
URSS.ru
URSS.ru
Об авторе Владимир Васильевич
БЕЛЕЦКИЙ
Один из ведущих специалистов в области небесной ме¬
ханики, динамики твердого тела, механики космического
полета. Доктор физико-математических наук, член-кор¬
респондент Российской академии наук, действительный
член Международной академии астронавтики и Россий¬
ской академии астронавтики им. К. Э. Циолковского, глав¬
ный научный сотрудник Института прикладной математики
им. М. В. Келдыша РАН, профессор механико-математиче¬
ского факультета МГУ им. М. В. Ломоносова, лауреат пре¬
мий им.Ф. А. Цандера (Россия) и им. А. фон Гумбольдта (Германия). Малой планете
№ 14790 присвоено имя Beletskij—2001.
Автор свыше 200 научных публикаций, в том числе более 20 монографий. Среди
них: «Движение искусственного спутника Земли относительно центра масс»
(1965), «Движение спутника относительно центра масс в гравитационном поле»
(1975), «Двуногая ходьба: модельные задачи динамики и управления» (1984),
«Динамика космических тросовых систем» (1990), «Регулярные и хаотические
движения твердыхтел» (2007).
В. В. Белецким была создана теория вращательных движений искусственных и
естественных небесных тел, учитывающая приливные эффекты, резонансные
вращения, динамику тросовых систем. Он доказал классическую теорему об
устойчивости пассивной гравитационной стабилизации; в теории космических
полетов есть «уравнение Белецкого», описывающее плоские колебания спутника
на эллиптической орбите; им исследовано соотношение хаотических и регулярных
траекторий в прикладных проблемах нелинейной гамильтоновой динамики.
Наше издательство предлагает следующие книги:
4652 ID 50797 НАУЧНАЯ И УЧЕБНАЯ ЛИТЕРАТУРА
785382
009827
Тел./факс: 7 (499) 135-42-16
Тел./факс: 7 (499) 135-42-46
E-mail:
URSS@URSS.ru
Каталог изданий
в Интернете:
http://URSS.ru
Любые отзывы о настоящем издании, а также обнаруженные опечатки присылайте
по адресу URSS@URSS.ru. Ваши замечания и предложения будут учтены
и отражены на web-странице этой книги в нашем интернет-магазине http://URSS.ru