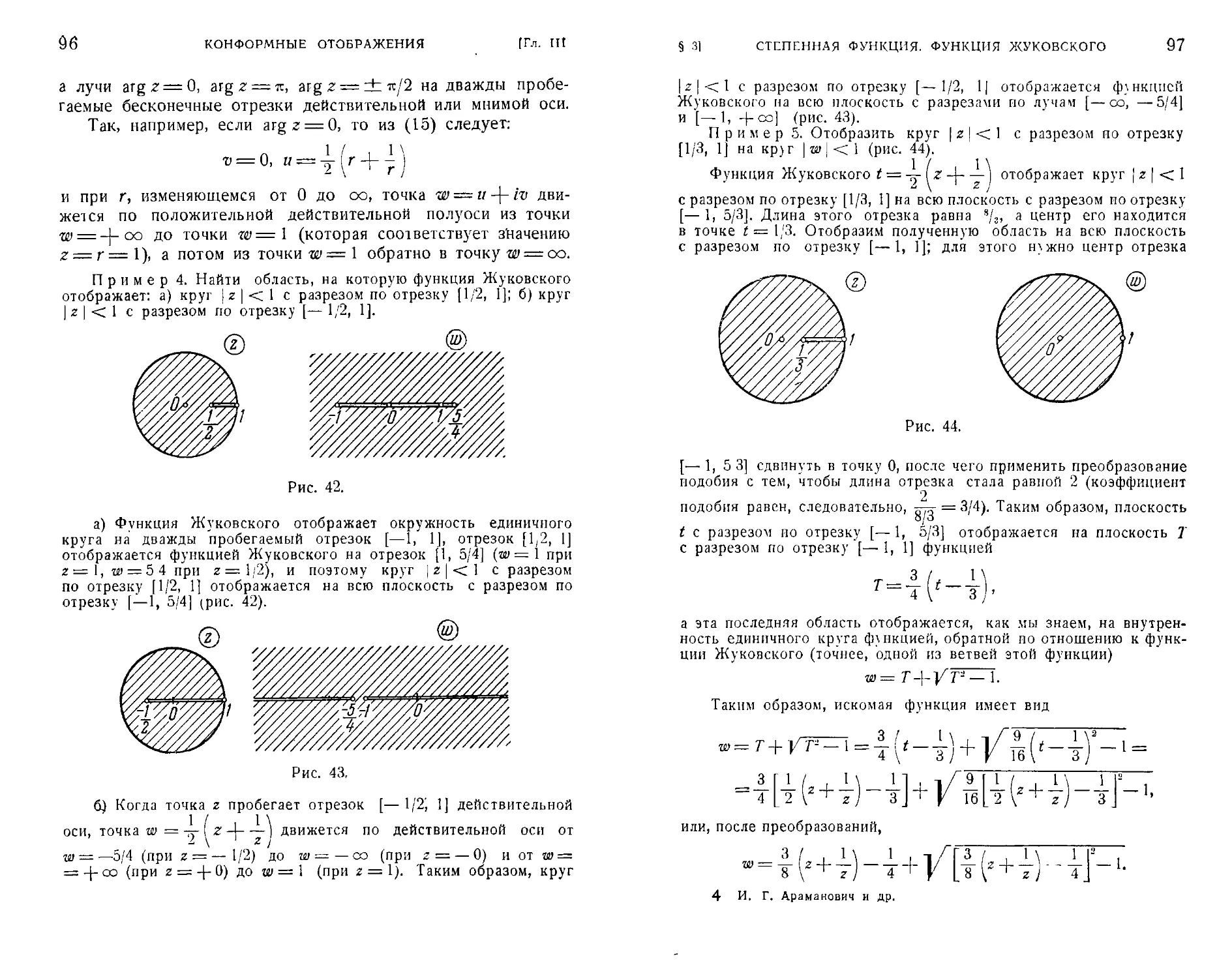
Текст
главы S
р
ВЫСШЕЙ ЛЪАТЕЛ^АТИКИ
для инженеров и студентов втузов
И.Г.АРАМАНОВИЧ,Г.АЛУНЦ,Л-3-ЗЛЬСГОЛЬЦ
ФУНКЦИИ
КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
ОПЕРАЦИОННОЕ
ИСЧИСЛЕНИЕ
ТЕОРИЯ
УСТОЙЧИВОСТИ
ИЗБРАННЫЕ ГЛАВЫ ВЫСШЕЙ МАТЕМАТИКИ
ДЛЯ ИНЖЕНЕРОВ И СТУДЕНТОВ ВТУЗОВ
И. Г. АРАМАНОВИЧ, Г. Л. ЛУНЦ,
Л. Э. ЭЛЬСГОЛЫД
ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ТЕОРИЯ УСТОЙЧИВОСТИ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего а среднего специального образования СССР
в качестве учебного пособия
для высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1968
517.2 @75)
A 79
УДК 517.53+517.432. 1+517.91 @75.8)
Функции комплексного переменного. Операционное
исчисление. Теория устойчивости. Изд-во «Наука»,
Главная редакция физико-математической литературы,
1968 г., стр. 416.
Книга посвящена трем разделам математики, знание которых не-
необходимо многим специалистам, работающим в области автоматики.
Изложение материала построено так, что вторая и третья части
могут изучаться независимо друг от друга.
В тексте подробно решено большое количество задач и при-
примеров. В конце каждой главы помещены задачи для' самостоятель-
самостоятельного решения.
Библиография — 13 назв., илл. 159, табл. 4.
Исаак Генрихович Арамановяч, Григорий Львович Лунц, Лев Эр/естови i Эльсгольц
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ. ТЕОРИЯ УСТОЙЧИВОСТИ
(Серив <Избранные главы высшей математики для инженеров и студентов вгузов>)
М., 1968 г., 416 стр. с илл.
Редактор М. М. Горячая.
Теин, редактор С. Я- Шкляр. Корректор М. Л. Липелис.
Сдано в набор 23/1V 1968 г. Подписано к печати 31'Vll 1968 г. Бумага 84 X'03 '/аз
Физ. печ. л. 13. Условн. печ. л. 21,84. Уч.-изд. л. 19.56. Тираж 45 000 экз. Т-09360.
Цена 78 к. Заказ № 1406.
Издательство <Наука».
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени Ленинградская типография Кз 1 «Печатный
Двор> имени А. М. Горького Главполиграфпрома Комитета по печати при Совете
Министров СССР, г. Ленинград, Гатчинская ул., 26.
2-2-3
16-68
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию 5
Из предисловия к первому изданию 6
ЧАСТЬ I
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Глава I. Комплексные числа и функции комплексного
переменного 7
§ 1. Комплексные числа и действия над ними G). § 2. По-
Последовательности комплексных чисел и функции комплекс-
комплексного переменного A6). § 3. Основные трансцендентные
функции B6). Задачи к главе 1 C6).
J Г л а в а И. Дифференцирование и интегрирование функ-
функций комплексного переменного 38
§ 1. Производная C8). § 2. Геометрический с^ы л аргу-
аргумента и модуля производной D5). § 3. Интеграл от ф)нк-
ции- комплексного переменного D9). '§ 4. Теорема Коши
E4). § 5. Интегральная формула Коши F2). Задачи к
главе II F8).
Глава III. Конформные отображения 70
§ 1. Линейная и дробно-линейная функции G0). § 2. Не-
Некоторые общие теоремы (83). § 3. Степенная функция.
Функция Жуковского (85). § 4. Основные трансцен-
трансцендентные функции (98). § 5. Конформное отображение полу-
полуплоскости на прямоугольник A07). Задачи к главе III A12).
Глава IV. Ряды и особые точки 114
§ 1. Функциональные ряды A14). § 2. Степенные ряды
A19). § 3. Ряд Тейлора A21). § 4. Ряд Лорана A28 ).
, § 5. Изолированные особые точки A36). § 6. Некоторые
Приемы разложения функций в ряд Лорана A43). Задачи
, к^ главе IV A44).
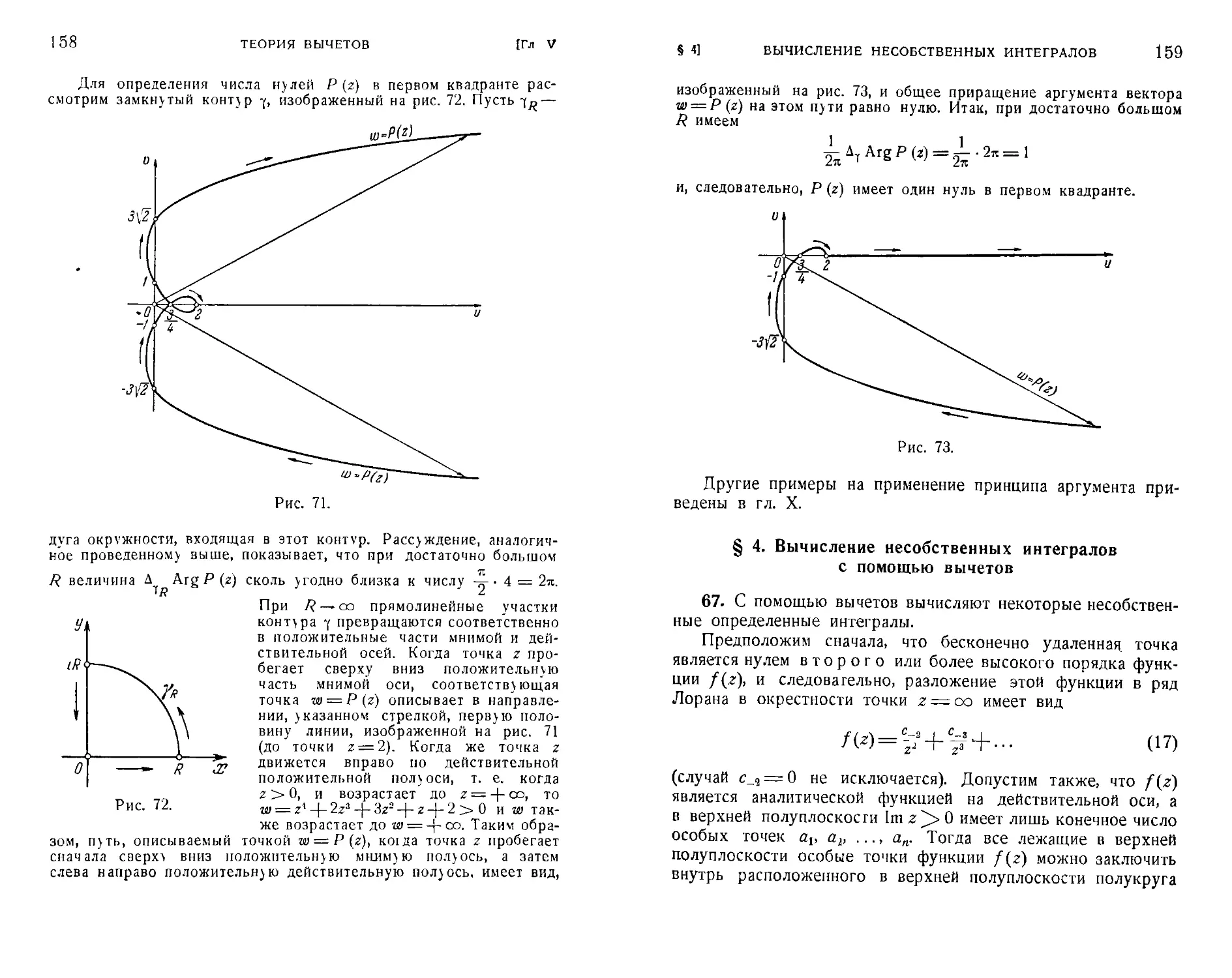
It'ki в а V. Теория вычетов
§ 1. Основная теорема о вычетах A46). § 2. Вычет относи-
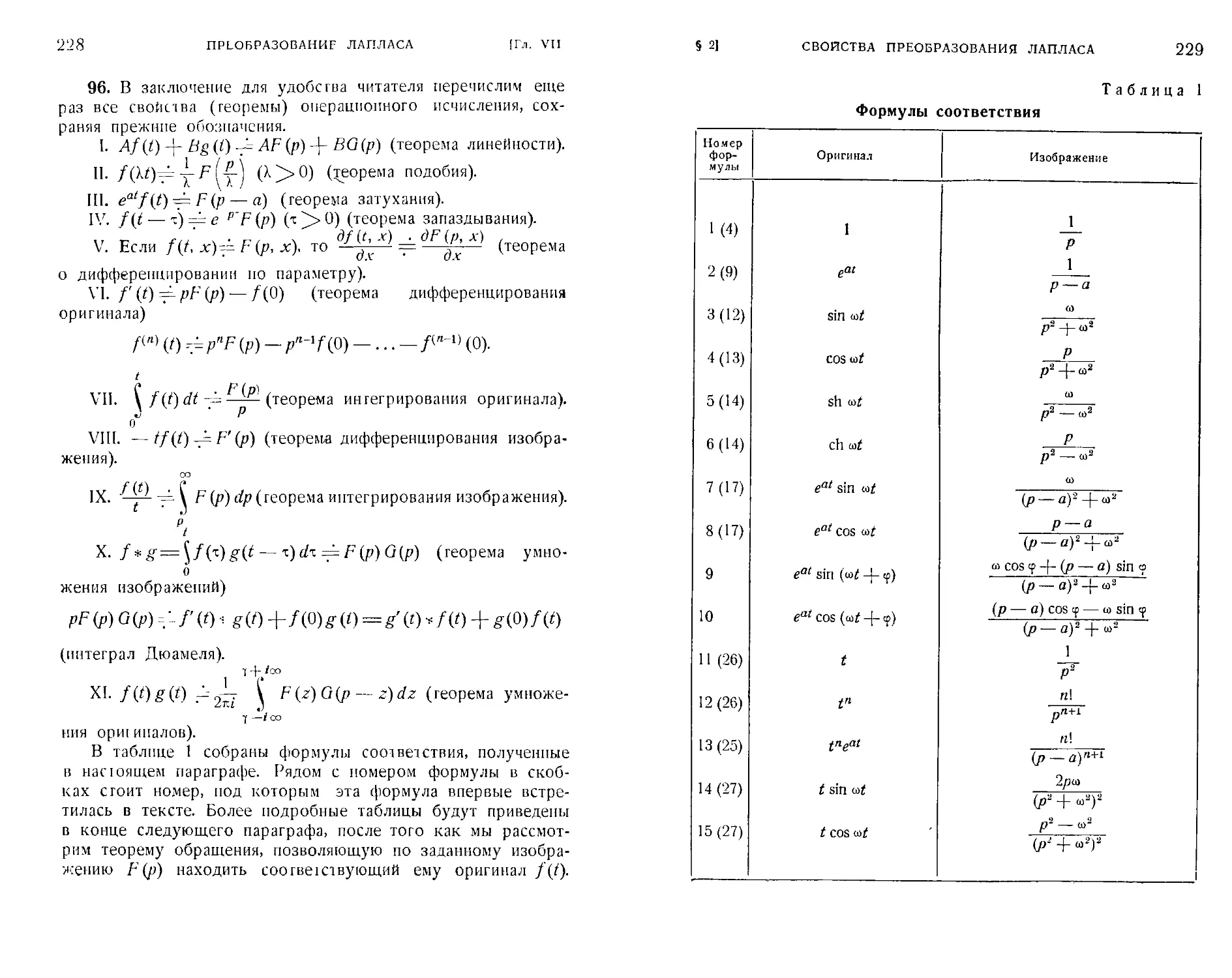
относительно полюса A49). §. 3. Логарифмические вычеты A52).
§ 4. Вычисление несобственных интегралов с помощью
'Вычетов A59). Задачи к главе V A63).
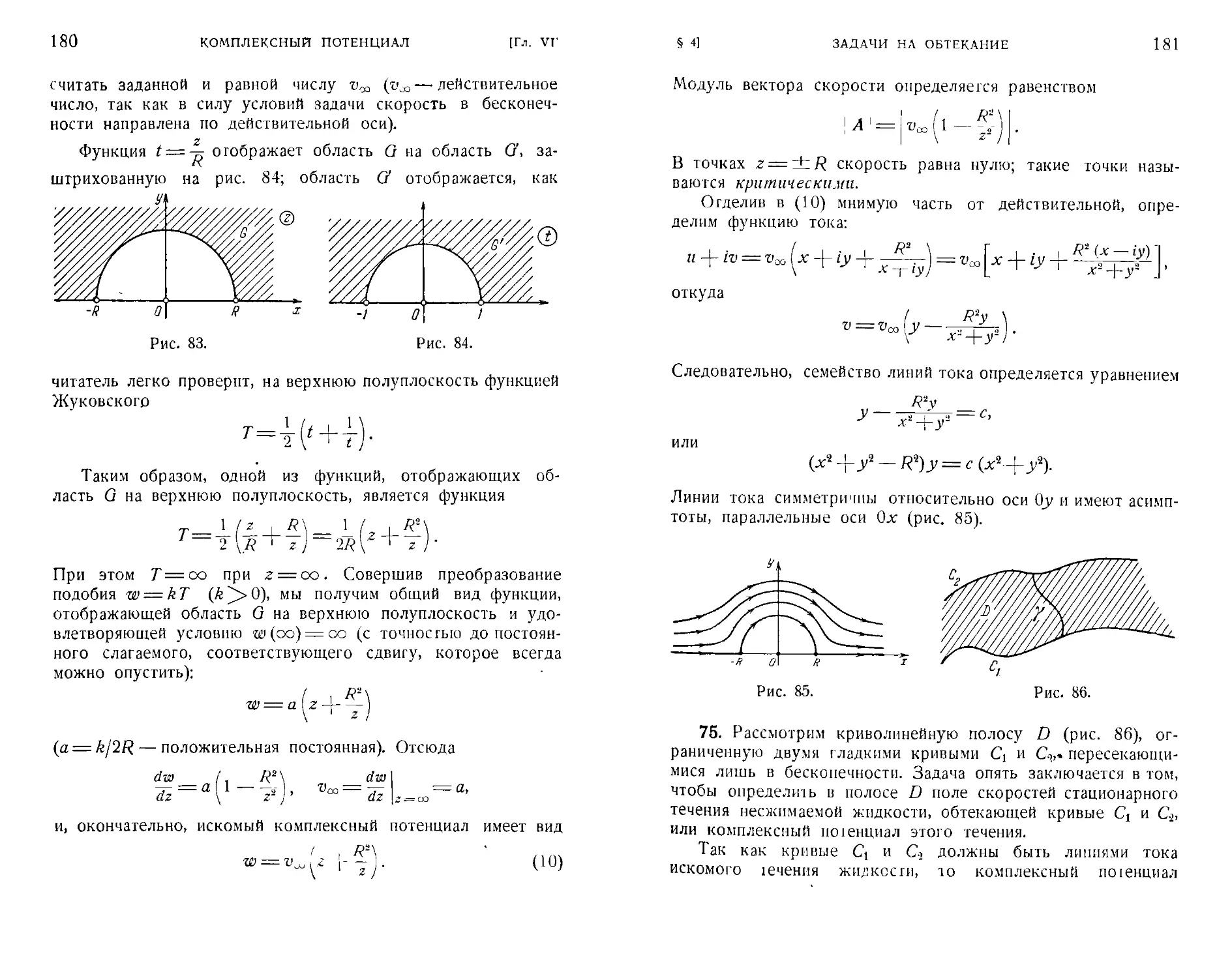
VI. Комплексный потенциал
Плоскопараллельные векторные поля A65). § 2. Коми-
146
165
ОГЛАВЛЕНИЕ
лексный потенциал A66). § 3. Комплексный потенциал
в гидродинамике A72). § 4. Задачи на обтекание
A78). § 5. Комплексный потенциал в электростатике и
термодинамике A85). Задачи к главе VI A89).
ч а с т ь 2
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Глава VII. Преобразование Лапласа 190
§ I. Определение преобразования Лапласа A90). § 2. Свой-
Свойства преобразования Лапласа A99). § 3. Теорема обраще-
обращения B30). §4. Преобразование Фурье B46). Задачи к гла-
главе VII B62).
Глава VIII. Применения преобразования Лапласа 263
§ 1. Решение дифференциальных уравнений B63). § 2. При-
Приложения операционного исчисления к задачам элек-
электротехники B77). § 3. Решение дифференциальных
уравнений с частными производными B85). Задачи к гла-
главе VIII B97).
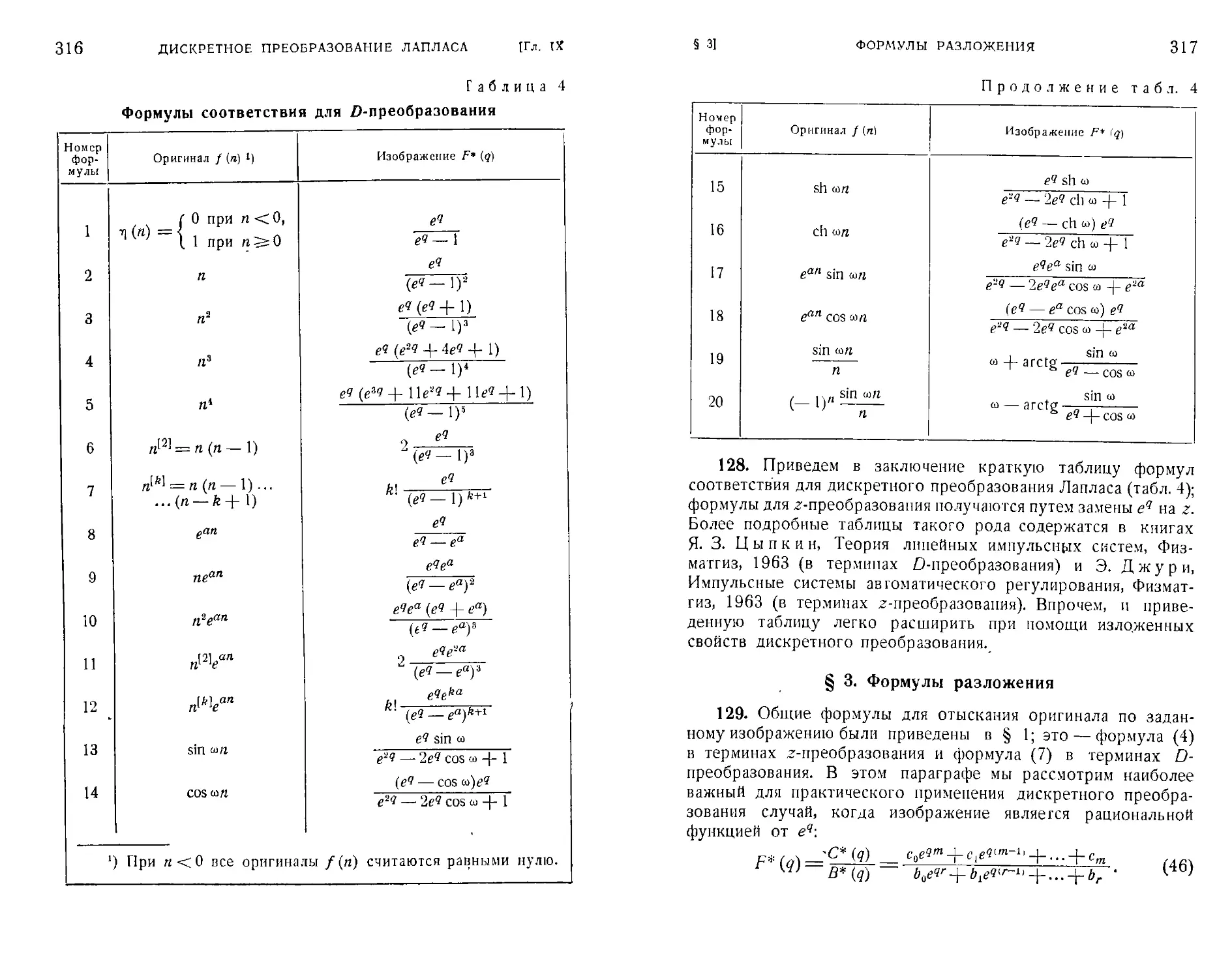
Глава IX. Дискретное преобразование Лапласа 298
§ 1. Определение дискретного преобразования B98).
§ 2. Свойства дискретного преобразования C04). § 3. Фор-
Формулы разложения C17). § 4. Связь между преобразова-
преобразованием Лапласа, /^-преобразованием и преобразованием Лап-
Лапласа—Стилтьеса C21). § 5. Решение разностных уравне-
уравнений C29). Задачи к главе IX C33).
часть 3
ТЕОРИЯ УСТОЙЧИВОСТИ
334
Введение
Глава X. Устойчивость решений линейных дифферен-
дифференциальных уравнений 337
§ 1. Линейные системы с постоянными коэффициентами
C37). § 2. Основные понятия теории устойчивости C46).
§ 3. УСЛОВИЯ УСТОЙЧИВОСТИ' ДЛЯ линрйныу <¦'"¦"" ' --
. .... j~ ,„^,1, д« линейных систем с по-
постоянными коэффициентами C52). § 4. Признаки отрица-
отрицательности действительных частей всех корней многочлена
C62). § 5. Устойчивость решений разностных уравнений
C77). Задачи к главе X C82).
Глава XI. Второй метод Ляпунова
§ 1. Основные теоремы второго метода Ляпунова C84).
§ 2. Устойчивость но первому приближению C97).
§ 3. Устойчивость при постоянно действующих возмуще-
возмущениях D00). Задачи к главе XI D04).
Ответы к задачам 406
Литература 416
384
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
При подготовке второго издания книга была подвергнута
довольно значительной переработке.
Вторая часть (операционное исчисление) пополнена новой
главой, посвященной дискретному преобразованию Лапласа,
широко применяющемуся в задачах автоматического регули-
регулирования.
Существенно переработана третья часть (теория устой-
устойчивости); в частности, упрощены доказательства теорем, свя-
связанных со вторым методом Ляпунова, за счет того, что
рассматривается в основном лишь случай автономных систем.
В третью часть включен также параграф об исследовании
устойчивости решений линейных разностных уравнений.
Внесены некоторые изменения и в первую часть (функции
комплексного переменного) — добавлен пункт о теореме един-
единственности аналитической функции.
В октябре 1967 г. трагически погиб в автомобильной ка-
катастрофе Лев Эрнестович Эльсгольц, талантливый ученый и
автор многих книг, пользующихся широкой известностью.
План переработки настоящей книги был обсужден всеми
авторами еще при жизни Л. Э. Эльсгольца.
И. Г. Араманович,
Г. Л Лунц
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Книга, предлагаемая вниманию читателя, рассчитана на
студентов тех специальностей, в программу которых входят
соответствующие разделы математики; мы полагаем также,
что она будет полезна широкому кругу инженеров. Для ее
чтения достаточно знания лишь общего курса математики
в объеме программы технических вузов. Книга состоит из
трех частей: 1. Функции комплексного переменного.1 2. Опе-
Операционное исчисление. 3. Теория устойчивости.
Знание всех трех разделов математики, которым посвящена
книга, необходимо многим специалистам, в частности, инже-
инженерам, работающим в области автоматизации производственных
процессов, и студентам факультетов автоматики. Однако,
имея в виду интересы и других категорий читателей, авторы
построили изложение так, чго вторая и третья части книги
могут изучаться независимо друг от друга.
Содержание книги несколько выхолит за рамки программы,
по которой в большинстве технических вузов изучаются
соответствующие разделы математики. Поэтому для удобства
пользования книгой весь ее текст разбит на пункты, причем
нумерация пунктов — сплошная для всей книги. В соответ-
соответствии с программой вуза всегда можно указать номера пунктов,
изучение которых обязательно.
ФУНКЦИИ
ЧАСТЬ 1
КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
ГЛАВА I
КОМПЛЕКСНЫЕ ЧИСЛА И ФУНКЦИИ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
§ 1. Комплексные числа и действия над ними
1. Число
= x-\-iy,
где х и у — любые действительные числа, а / — так назы-
называемая мнимая единица, называется комплексным числом.
Действительные числа х и у называются соответственно дей-
действительной и мнимой частями комплексного числа z и
обозначаются
x = Rez, y = \mz.
Два комплексных числа считаются равными, если равны
порознь их действительные и мнимые части, другими словами,
равенство
равносильно двум равенствам:
JC, = Хо, )>t =Уо.
Так как две точки, определенные своими координатами
в декартовой прямоугольной системе координат, совпадают
тогда и только тогда, когда они имеют равные абсциссы и
равные ординаты, то можно установить взаимно однозначное
соответствие между всевозможными точками плоскости, с одной
стороны, и всевозможными комплексными числами, — с другой.
Иначе говоря, будем изображать комплексное число z = x-\-iy
8
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. I
с помощью точки, абсцисса которой равна х, а ордината у;
тогда всякое комплексное число изобразится с помощью
определенной точки плоскости («комплексной плоскости»)
и, обратно, всякой точке (х, у) плоскости буцет соответство-
соответствовать определенное комплексное число z = x-\-iy (рис. 1).
В дальнейшем мы часто не будем делать различия между
комплексным числом и точкой, его изображающей.
Действительной и мнимой частям комплексного числа
можно также поставить в соответствие координаты вектора,
т. е. проекции на координатные оси вектора, начало которого
совмещено, например, с началом
координат, а конец — с данной точ-
точкой, и, следовательно, изображать
комплексные числа с помощью век-
векторов (см. рис. 1).
Комплексное число с мнимой
частью, равной нулю, т. е. л:4-Ю,
будем отождествлять с его действи-
действительной частью, х-\-Ю = х,к счичать
действительное число частным слу-
случаем комплексного. Действительные числа изображаются точ-
точками, лежащими на оси Ох; эту ось будем называть дей-
действительной осью. Аналогично будем писать 0-\-ty = iy.
Комплексные числа, действительные части которых равны нулю
(чисто мнимые числа), изображаются с помощью точек,
лежащих на оси Оу; эту ось будем называть мнимой осью.
Положение точки, изображающей комплексное число z,
можно определять также с помощью полярных координат г
и ср (см. рис. 1) или, что то же самое, с помощью длины
вектора, соответствующего комплексному числу, и величины
угла, образованного этим вектором с положительным направ-
направлением действительной оси. Числа г и ср будем называть
соответственно модулем и аргументом комплексного числа z
и пользоваться обозначениями
Рис.
' = \г\, <р =
Для действительного числа введенное здесь определение
модуля совпадает с определением абсолютной величины этого
числа. Модулем чисто мнимого числа является абсолютная
величина его мнимой части.
§ 1] КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ 9
Из определения модуля и аргумента следует, что если
г = х-\-1у, то
x = r cos <p = | z [ cos Argz, y = r sin <p = | z\ sin Argz A)
= tp-CB = -', COS CD =
sin <p = -
Величина Arg z многозначна и определена лишь с точ-
точностью до целого кратного числа 2т. В качестве главного
значения величины Arg z обычно выбирают значение, опре-
определенное неравенствами —т<^ Argz==c;T.
Главное значение аргумента z обозначают arg z. Если z —
действительное положительное число, то arg z = 0; если z —
действительное отрицательное число, то argz = it; если z—¦
чисто мнимое число с положительной мнимой частью, то
arg z = т/2, если z — чисто мнимое с отрицательной мнимой
частью, то arg 2 = — тг/2. При 2 = 0 величина Arg z не имеет
смысла.
Пользуясь формулами A), можно всякое комплексное
число, отличное от нуля, представить в так называемой
тригонометрической форме:
z = x-\~iy = r cos cp 4- ir sin cp = г (cos cp 4- / sin cp). B)
Например,
14-Z = VA2 fcos-^ + i sin ^), 1 = 1 (cosO-fi sinO),
i= 1 ( cos ~ -\-i sin yJ, —2 = 2(cos т 4-i sjht),
С помощью формулы Эйлера el<f = cos cp 4-i sin ср(см. [1],
гл. IV, § 6 или здесь, стр. 28) можно перейти от тригоно-
тригонометрической формы B) к показательной: z = reltf. Например,
—!=«
'«
10
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. Г
Два комплексных числа, имеющих одну и ту же действи-
действительную часть, а мнимые части равные по абсолютной вели-
величине, но противоположные по знаку, называются взаимно
сопряженными. Число, сопряженное числу z, обозначается 2.
Если г = х -\- iy, то z = х — iy. Из этого определения сле-
следует, что если w = z, го z = w и, следовательно, z = z.
Модули взаимно сопряженных чисел одинаковы, а аргу-
аргументы отличаются только знаком:
2 \— Z
Arg2= — Arg г ').
Всякое действительное число совпадает с числом, ему сопря-
сопряженным.
Сопряженные числа изображаются точками, симметрич-
симметричными относительно действительной оси.
2. Сложение и умножение комплексных чисел произво-
производится по правилам сложения и умножения алгебраических
многочленов: последнее из этих правил дополняется требо-
требованием замены Р числом — 1 (и, следовательно, /3 числом — I,
г4 числом 1, Р числом / и т. д.). При записи результата
действий, произведенных над комплексными числами, следует
отделить действительную часть от мнимой, т. е. собрать
отдельно члены, не содержащие множителя /, и члены, со-
содержащие этот множитель:
C)
-f ty2) = (xiXv — уi y2) + i (xi y2 -f- ** Vi)-
Из (З), в частности, следует, что произведение двух взаимно
сопряженных комплексных чисел является действительным
числом, равным квадрату модуля этих чисел:
иначе
z-z= z\\
J) Так как функция Argz неоднозначна, то равенство Arg 2 =
— — Argz надо понимать в том смысле, что множество значений,
определяемых левой частью этого равенства, совпадает с множе-
множеством значений, определяемых правой частью.
S П
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
И
Сумма двух взаимно сопряженных комплексных чисел также
является действительным числом:
т. е.
(х -f iy) -\-(x — iy) = 2лг,
z -f z = 2 Re z.
У
X
Вычитание определяется как действие, обратное сложению,
откуда следует, что
(лг, -f iyt) — fa + iyi) = (xi — х2) -\- i (yx — yt).
Итак, при сложении и вычитании комплексных чисел от-
отдельно складываются или вычитаются их действительные и
мнимые части. Если изобра-
изобразить комплексное число
с помощью вектора, то, как
мы уже знаем, действитель-
действительная и мнимая части этого
числа будут являться коор-
координатами вектора, а так как
при сложении и вычитании
векторов их координаты О
соответственно складывают-
складываются или вычитаются, то ело- Рис- 2-
жение или вычитание ком-
комплексных чисел сводится к сложению или вычитанию векто-
векторов, изображающих эти числа (рис. 2). Модуль комплексного
числа равен длине соответствующего вектора, поэтому модуль
суммы двух комплексных чисел меньше или равен сумме
модулей этих чисел:
Применяя это неравенство несколько раз, получим
\zl + zi-\-... + zn\^\zl\ + \zi\+... + \za\.
Знак равенства имеет место только тогда, когда векторы,
изображающие числа zt, zit ..., zn, лежат на одной прямой
и направлены в одну и ту же сторону, т. е. когда
arg Zi = arg гг =... = arg zn.
Модуль разности двух комплексных чисел равен расстоянию
между точками, изображающими эти числа (рис. 2). Если
12
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. t
i, то
I *« - *, | = W. - *i)e + (У, -Ух)*- .
Пусть Zi — данное комплексное число (данная точка), р —
данное действительное положительное число. Совокупность
точек г, удовлетворяющих уравнению
Z — Zx | = р,
образует окружность с центром в точке zx радиуса р. Не-
Неравенство \z — Zj j <^ p определяет множество точек, лежащих
внутри этой окружности {внутренность круга), а неравенство
| г — Zj|^>p — множество точек, лежащих вне окружности
(внешность круга).
Деление определяется как действие, обратное умножению.
Пользуясь свойствами сопряженных чисел, удобнее всего де-
деление комплексных чисел производить следующим образом:
сначала умножить делимое и делитель на число, сопряженное
делителю, после чего делитель станет действительным поло-
положительным числом, а затем произвести деление действитель-
действительной и мнимой частей отдельно:
Xi + ijli _ (Xi +1>,) (xs — iy2) __ (xtx2 +y,y2) -f- i (xsyt — х,уг) _
xa + iy-2 (xt + iy2) (xs — iy2)
.
3. Если воспользоваться тригонометрической формой
записи комплексных чисел:
z\ = fj (cos ?i +1 sin Ti)> zi = ri (cos Ь +' sm Ъ)>
то получим
ztZi = r-fi [(cos cpi cos cpa — sin cpt sin <p4) -f-1 (sin <ft cos tp9 -|-
+ cos cp, sin <ps)] = rjra [cos (cp, -|- tp4) -|- / sin (fj + <ps)]. D)
Следовательно, при умножении комплексных чисел их модули
перемножаются, а аргументы складываются:
Arg fazd = Arg zx -f Arg
') Обе части этого равенства многозначны. Множество значений
левой части этого равенства совпадает с множеством значений его
правой части; можно также записать, что Arg (г,г2) = Arg zt -\-
+ Argzs-f2*7c, где й —о, ± 1, ±2,...
§ И
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
13
Вектор, изображающий произведение zizi, может быть полу-
получен из вектора, изображающею число zlt поворотом на угол
еря, образуемый вектором г2 с положительным направлением
действительной оси, и умножением его длины на длину век-
вектора Zi (рис. 3). Например, число
i имеет модуль, равный единице,
а аргумент я/2, поэтому умноже-
умножение на i сводится к повороту
вектора на угол тс/2 в положи-
положительном направлении без изменения
его длины.
Число, модуль которого равен
единице, имеет вид cos'f -\-isiny,
или, в показательной форме, е'?.
Следовательно, вектор zelf может
быть получен поворотом вектора z около начала координат
на угол tp.
Деление комплексных чисел, заданных в тригонометри-
тригонометрической форме
Рис. 3.
= г у (cos
sin
— r2 (cos <
sin
приводит к формуле
j- = ^ [cos (cpi — 9..) + / sin (?i
*2 '2
т. е.
f1 = Ai g 2"! — Arg г2.
4. Из правила умножения D) следует правило возведения
в целую положительную степень: если z^r (cos у-\-i simp),
то z" = rn (cos ну-\-i sin ny), т. е.
| zn J = ; z \n, Arg (zn) — n Arg z -j- 2kx,
где A — любое целое число (& = 0, ±1, ±2,...).
Пользуясь правилом деления, нетрудно проверить, что эти
формулы остаются справедливыми и при целом отрицатель-
отрицательном п.
Извлечь корень целой положительной степени п из числа
z — значит найти такое число w = yrz , я-я степень которого
14
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. I
равна Z- В соответствии с правилом возведения в степень
имеем (при z ф 0):
\w\n=\z\, nkxgw = kxgz-\-2kr. (А = 0, it 1, ±2,...).
Если обозначить z = r (cos <p -(-isincp), w = p (cos9 —|— / sin б),
то получим
pn = r, nQ — <?-\-2kz (k = 0, ± 1, ±2,...).
Так как г и р — положительные числа, то первое из этих
равенств однозначно определяет р, а именно:
где скобки в правой части обозначают, что берется арифме-
арифметическое (действительное и положительное) значение корня.
Из второго равенства находим
и формула, с помощью которой можно извлекать корень из
любого комплексного числа, принимает такой вид:
= y r (coscp-(-/sin'.p) =
= (>/>)( cos °
• / sin •
я - ¦-- я <¦ E)
Хотя k — любое целое число, однако из этой формулы сле-
п,
дует, что имеется лишь я различных значений величины у z ,
которые можно получить, полагая k = 0, 1, 2,..., п—1.
Действительно, два значения k, отличающиеся друг от дру-
друга на я, а значит, и на любое кратное числа и, дают при
и _
подстановке в формулу E) одно и то же значение для У'z,
так как если k' — ? = и, то
2 (К — k) тс
п
и, следовательно,
cos *-^—.—- = cos '
sin -'
-=2ir.
= sin
п я ' """ я "" я
Как видно из формулы E), все л различных значений ве-
п/— п/
личины у z имеют один и тот же модуль, равный (у
§ И
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
15
А гак как
9 + 2/гк
л,
(аргументы двух значений у z , соответствующих значени-
значениям к и Де —|— 1, отличаются один от другого на 2тс/л), то точ-
п,
ки, соответствующие значениям у г, являются вершинами
правильного л-угольника,
вписанного в окружность
радиуса (j/1 z \) с центром
в начале координат.
Поэтому способ построе-
построения точек, соответствующих
значениям у г, таков (рис.4):
из начала координат, как из
центра, описываем окруж-
окружность, радиус которой ра-
равен (у \z\y, если arg2 = 'f-
то из начала координат про-
проведем луч под углом се/л
к положительному напра-
направлению действительной оси;
на пересечении этого луча
с окружностью мы найдем точку, соответствующую одному
из значений yz (для этой точки в формуле E) ? = 0);
вписав в окружность пранильный я-угольник так, чтобы одной
из его вершин была найденная точка, мы построим точки,
соответствующие остальным значениям корня.
Пример. Вычислить все значения Y — 8-
Имеем — 8 = 8 (cos тс + I sin nj, откуда
Рис. 4.
При /г = О, 1, 2 получим
-8 = { - 2,
—; у'З.
16 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [Гл. I
Если обозначить, как это принято для действительных чисел,
то действие возведения комплексного числа в степень ока-
окажется определенным для любого действительного рациональ-
рационального показателя степени. Заметим, однако, что такие обозна-
обозначения можно применять лишь в случае, когда несокра-
несократимая дробь, так как, например, Yz<i имеет четыре значения,
-. /—
тогда как у z — лишь два.
§ 2. Последовательности комплексных чисел
и функции комплексного переменного
5. Внутренность круга радиуса р с центром в данной точке
z0, т. е. совокупность точек, удовлетворяющих неравенству
|-i — ?0|<Ср> называется ^-окрестностью точки z0. Вообще,
под окрестностью точки понимают не обязательно круговую
область, а любую область, внутри которой лежит точка гй.
В дальнейшем мы будем пользоваться, однако, только кру-
круговыми окрестностями.
Число z0 называют пределом последовательности ком-
комплексных чисел zv zit..., zn,... и пишут Um zn = z0, если
я->со
для любого положительного числа е можно подобрать такое
число N(N зависит от г), что при n^N выполняется не-
неравенство \zn — ,го|<^?. Иначе говоря, равенство Ншгл=г0
л~»оа
означает, что как бы мала ни была г-окрестность точки z0,
вне этой окрестности может остаться лишь конечное число
точек последовательности, так как все точки zn последова-
последовательности, начиная с номера n = N, попадут внутрь этой
е-окрестности.
Если zn = xn-\-iyn и zu = xu-\-iyu, то, учитывая равенство
I *„ - *о \ = V(*п-*<,)* +(Уп-Уо?>
нетрудно заключить (непосредственно из определения), что
существование предела \imzn=z0 равносильно существова-
существованию двух пределов: п^са
lim хп =
и-юо
ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
17
Пусть последовательность zt, z.2,..., zn,... такова, что мо-
модули всех ее членов, начиная с некоторого, становятся больше
любого, сколь угодно большого, положительного числа (т. е.
как бы велико ни было положительное число М, к нему можно
подобрать такое Л/, что jz,,j^>Af при n~s^N). Тогда после-
последовательность, очевидно, предела нз имеет; однако в этом
случае удобно писать, что
lim zn = сю
и говорить, что предел последовательности бесконечен, а для
его изображения дополнить плоскость точкой, которую будем
называть бесконечно удаленной. Окрестностью бесконечно
удаленной точки будем называть внешность круга достаточно
большого радиуса. Если радиус этого круга равен R, а центр
находится в точке z = 0, то множество точек, образующих
окрестность бесконечно удаленной точки, определяется нера-
неравенством \z\~^>R. Чем больше радиус круга, тем «меньше»
окрестность бесконечно удаленной точки, являющаяся внеш-
.ностью этого круга.
Сопоставляя определение равенства Нтгя = оо с опреде-
п~*са
лением окрестности бесконечно удаленной точки, мы видим,
что если предел последовательности бесконечен, то как бы
«мала» ни была окрестность бесконечно удаленной точки, т. е.
как бы велик ни был радиус R круга, внешностью которого
эта окрестность является, все точки последовательности zv
2e, ..., zn, ..., за исключением конечного их числа (все точки
zn, начиная с n = N), попадут внутрь этой окрестности.
В таких терминах определение предела, по существу, одно
и то же как для случая, когда предел конечен, так и для слу-
случая, когда он бесконечен. В этом смысле бесконечно удален-
удаленная точка вполне равноправна с остальными точками пло-
плоскости.
Однако во многих случаях нас будет интересовать вопрос
о том, существует ли именно конечный предел последо-
последовательности. Последовательность, имеющую конечный предел,
называют сходящейся.
В дальнейшем комплексную плоскость, дополненную бес-
бесконечно удаленной точкой, будем называть расширенной пло-
плоскостью.
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
(Гл. I
функ-
функЗаметим, что в соответствии с введенным нами определе-
определением на комплексной плоскости имеется лишь одна беско-
бесконечно удаленная точка, тогда как, например, во многих раз-
разделах геометрии удобно считать, что имеется бесконечное
множество таких течек: каждому направлению соответствует
своя бесконечно удаленная точка.
6. Определение функции комплексного переменного ана-
аналогично определению функции действительного переменного.
Говорят, что на некотором множестве точек, изображаю-
изображающих значения комплексной переменной z, задана (определена)
функция w=f(z), если каждой точке z этого множества по-
ст?влено в соответствие одно (в случае однозначной функции)
или большее число (в слу-
случае многозначной
ции) значений w.
В дальнейшем, как
правило, будут рассматри-
рассматриваться функции, заданные
либо на всей плоскости,
либо на всей плоскости,
за исключением отдель-
отдельных ее точек, либо на части плоскости, ограниченной одной
(односвязная область, рис. 5, а) или несколькими (многосвяз-
(многосвязная область, рис. 5, б) гладкими или кусочно-гладкими')
кривыми. Из области могут быть удалены отдельные точки.
Так, например, функция w = zi однозначна и определена
во всей плоскости, так как с помощью формулы, по кото-
которой производится возведение комплексного числа в степень
(стр. 13), всякому комплексному числу z соответствует, и
притом только одно, значение z'2. Функция w = \rgz многв-
значна и определена на всей плоскости, за исключением точ-
точки z = 0 (см. стр. 9).
Так как задание комплексного числа z равносильно зада-
заданию двух действительных чисел х и у, являющихся соответ-
соответственно его действительной и мнимой частями (z = x-\-ly),
а числу w точно так же однозначно соответствует пара дей-
- 5.
') Дуга называется гладкой, если в каждой ее точке можно
провести касательную, причем направление касательной изменяет-
изменяется непрерывно при движении точки по кривой; дуга непрерывной
кривой, состоящая из конечного числа гладких дуг, называется ку-
кусочно-гладкой.
5 21
Последовательности комплексных чисел
19
ствительных чисел и и v (w = u-[-iv), то зависимость
w = f(z) между комплексной функцией w и комплексной
переменной z равносильна двум зависимостям:
и = и (х, у), v = v {x, у), F)
определяющим действительные величины и и v как функции
действительных переменных х и у.
Например, если w = гг. то, полагая z = x-\-iy,w = u-\-iv,
получим и -\- iv = (х -\- iyf = (х*—у^)-\-21ху, и, следова-
следовательно, равенство w = z*- равносильно равенствам
и = xi —
v = 2ху.
Если значения переменной z изображать с помощью точек
некоторой плоскости (плоскости z), а, значения функции w
с помощью точек другой плоскости (плоскости w), то функ-
функция w = f(z) устанавливает соответствие между точками пло-
плоскости г, в которых эта функция определена, и точками плог
скости те». Другими словами, функция w = f(z) осуществляет
отображение точек плоскости z па соответствующие точки
плоскости w.
Обозначим через g множество точек плоскости z, на ко-
котором определена функция w^f(z), а через G—множество,
состоящее из тех точек плоскости w, на которые с помощью
функции w = f(z) отображаются точки множества g. Точки
множества G называют образами соответствующих точек мно-
множества g при отображении w=f(z), а точки множества
g— прообразами соответствующих точек множества G. Выбрав
какую-либо определенную точку множества G, найдем те точки
множества g, которые отобразились в выбранную точку, т. е. все
прообразы выбранной точки. Таким образом, каждой точке мно-
множества G будет соответствовать одна или несколько точек
множества g. В соответствии с определением функции это
будет означать, что на множестве G определена некоторая
функция z = <f (w), которую называют обратной по отноше-
отношению к функции w=f{z).
Если функция w = f{z) однозначна, то каждой точке пло-
плоскости z, в которой функция определена, соогвегствуег одна
точка плоскости w. Пусть при этом некоторое множество то-
точек g плоскости z отображается взаимно однозначно на неко-
некоторое множество Gплоскости те1, т.е. функция w=f(z) такова,
что не только каждой точке множества g соответствует
20
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. Г
одна и только одна точка множества О, но и обратно,
каждой точке множества G соответствует в точности одна
точка множества g Тогда функция 2 = ср (w), определенная на
множестве G и отображающая его на множество g обратная
по отношению к функции w =f(z), также является однознач-
однозначной. В этом случае говорят, что функция w = f(z) одно-
однолистна на множестве g.
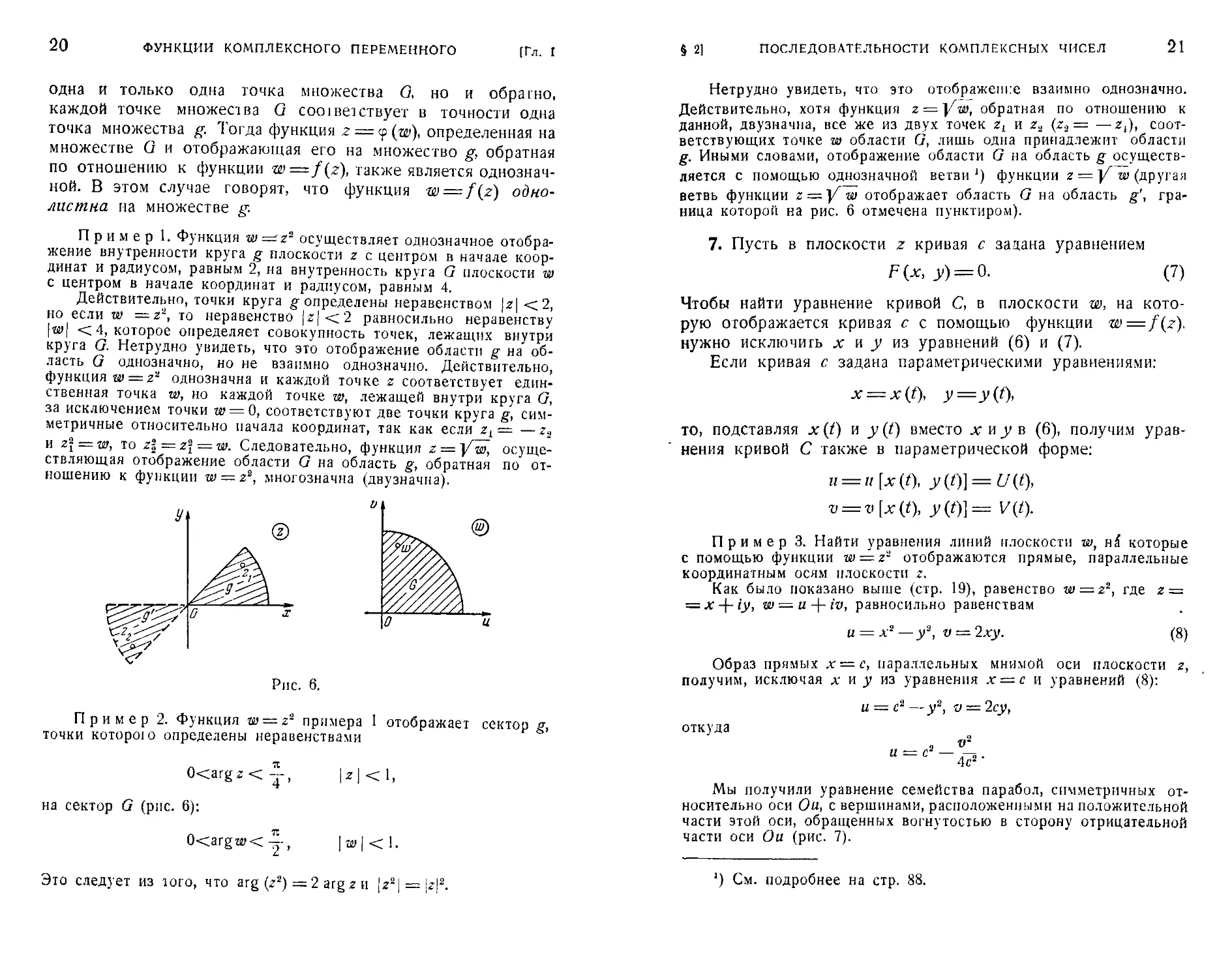
Пример 1. Функция w =?z2 осуществляет однозначное отобра-
отображение внутренности круга g плоскости z с центром в начале коор-
координат и радиусом, равным 2, на внутренность крута G плоскости w
с центром в начале координат и радиусом, равным 4.
Действительно, точки круга g определены неравенством \z\ < 2,
но если w =2а, то неравенство |г|<2 равносильно неравенству
\w\ < 4, которое определяет совокупность точек, лежащих внутри
крута G. Нетрудно увидеть, что это отображение области g на об-
область G однозначно, но не взаимно однозначно. Действительно,
функция w — z* однозначна и каждой точке z соответствует един-
единственная точка w, но каждой точке w, лежащей внутри круга G,
за исключением точки да = 0, соответствуют две точки круга g, сим-
симметричные относительно начала координат, так как если zL = —г2
и z\=w, то z\=z\=w. Следовательно, функция г = Y~w, осуще-
осуществляющая отображение области G на область g, обратная по от-
отношению к функции w — z2, многозначна (двузначна).
Рис. 6.
Пример 2. Функция а> = г2 примера 1 отображает сектор g,
точки которою определены неравенствами
0<argz •
на сектор G (рис. 6):
0<argH>< —,
< !
Это следует из юго, что arg (г2) =2 aigz и |г2| = 1г|2.
2]
ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
21
Нетрудно увидеть, что это отображение взаимно однозначно.
Действительно, хотя функция z = Yw, обратная по отношению к
данной, двузначна, все же из двух точек zL и z2 (z2 = — zt), соот-
соответствующих точке w области G, лишь одна принадлежит области
g. Иными словами, отображение области G на область g осуществ-
осуществляется с помощью однозначной ветви1) функции г = У w (другая
ветвь функции z — Yw отображает область G на область g', гра-
граница которой на рис. 6 отмечена пунктиром).
7. Пусть в плоскости z кривая с задана уравнением
F(x, y) = 0. G)
Чтобы найти уравнение кривой С, в плоскости w, на кото-
которую отображается кривая с с помощью функции w=f(z).
нужно исключить х и у из уравнений F) и G).
Если кривая с задана параметрическими уравнениями:
x = x{t), y=y{t),
то, подставляя x(t) и y(t) вместо хи_ув F), получим урав-
уравнения кривой С также в параметрической форме:
u = u[x{t), y{t)] = U(t),
v = v[x (t), y(t)]=V(t).
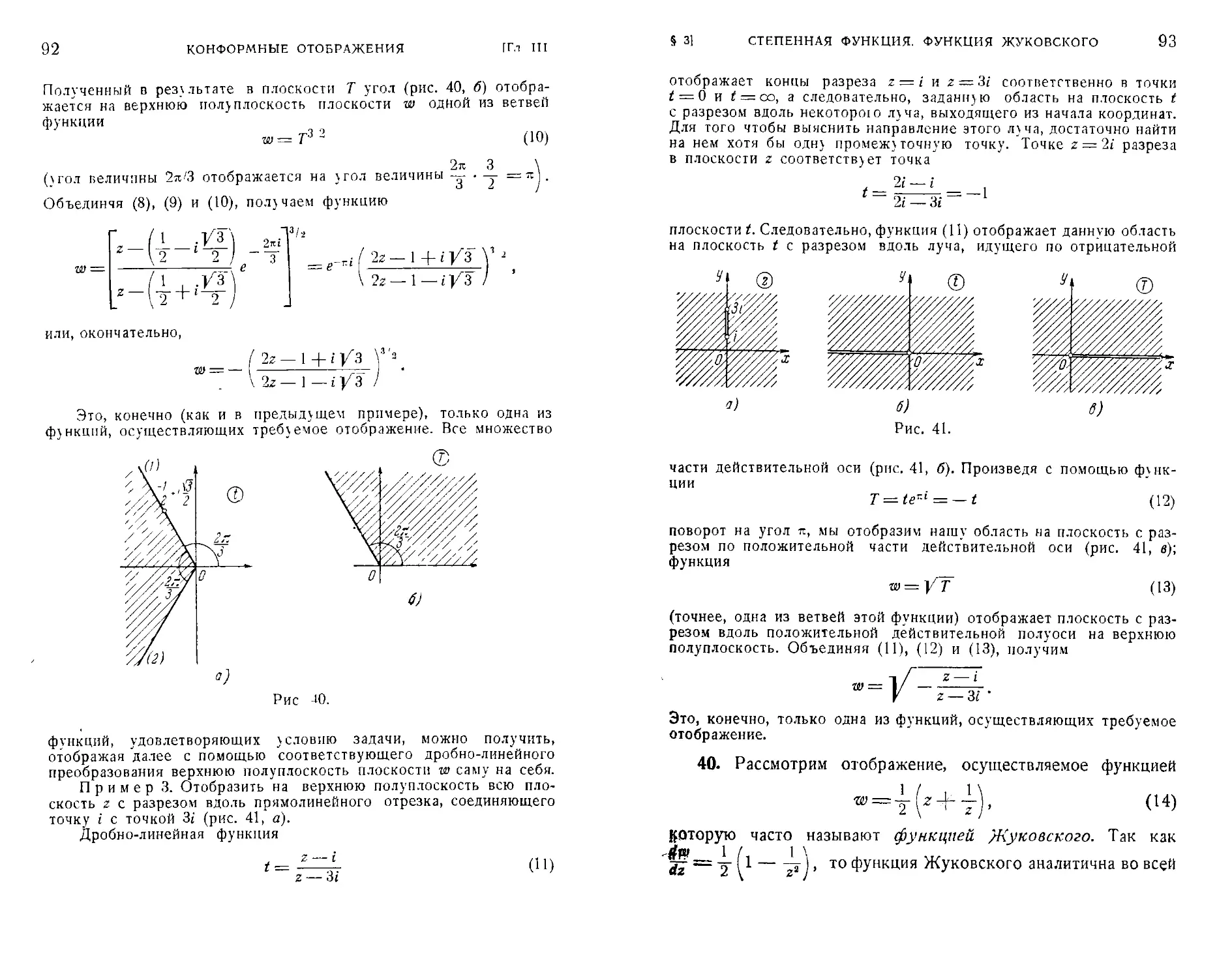
Пример З. Найти уравнения линий плоскости w, н& которые
с помощью функции w = z" отображаются прямые, параллельные
координатным осям плоскости г.
Как было показано выше (стр. 19), равенство w = z2, где z =
= x-\-iy, да = и -4-й», равносильно равенствам
и = х2 —у2
2xy.
(8)
Образ прямых х = с, параллельных мнимой оси плоскости г,
получим, исключая х и у из уравнения х = с и уравнений (8):
. = c«-^, v = :
откуда
Мы получили уравнение семейства парабол, симметричных от-
относительно оси Ои, с вершинами, расположенными на положительной
части этой оси, обращенных вогнутостью в сторону отрицательной
части оси Ои (рис. 7).
J) См. подробнее на стр.
22
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. 1
Мнимая ось х = 0 плоскости г отобразится на линию
и — —у2, v = 0.
(9)
Второе из этих равенств показывает, что линия (9) расположе-
расположена на оси Ои, а из первого следует, что и может принимать любые
неположительные значения, следо-
следовательно, мнимая ось х = 0 пло-
плоскости 2 отображается на отрица-
отрицательную часть действительной оси
плоскоеiи w:
, и sg 0^ v = 0.
Аналогичные рассуждения по-
показывают, что семейство прямых
у = с, параллельных действитель-
действительной оси плоскости 2, отобразится
в семейство парабол
_ «2
Рис. 7.
плоскости и), причем действительная ось у = 0 плоскости z отобра-
отобразится в положительную часть действительной оси плоскости w:
(рис. 7).
:0, 11=0
Следует заметить, что параметрические уравнения х =
= x(t), y=y(t) линии в плоскости г могут быть заменены
одним уравнением z — z(t), где z(t) = x(t)-\-ly{t).
Например, уравнение
z = cos t -\- i sin t
является уравнением окружности радиуса 1 с центром в на-
начале координат, так как оно равносильно уравнениям
х= cos t, у— sin t.
Уравнение кривой в плоскости w, на которую с помощью
функции w=f(z) отображается кривая z = z(t), имеет вид
w=f[z{t)\.
Пример 4. Найти образ прямой z = (\-\-i)t при отображе-
отображении И) = 2*.
Уравнение 2 = A -\-i) t равносильно системе уравнений
x = t, y = t
и определяет в плоскости z биссектрису первого координатно-
координатного утла у = х. С помощью функции w — z% эта биссектриса
§ 21
ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
23
отображается на линию w = (l -}-i)''t" или
то = (- 2 + 2«) t\
откуда
и = — 2t\ v = 2t\
Исключая параметр t, получим
v =— и
— уравнение биссектрисы второго координатного угла плоскости w.
8. Число w0 называют пределом функции f{z) при z,
стремящемся к za, и пишут
Wo= linn f(z),
если для любой сколь угодно малой е-окрестности точки wa
можно найти такую 8-окрестность точки z0, что для всех
точек z этой 8-окрестности (кроме, быть может, самой точки
za) соответствующие значения функции f(z) будут изобра-
изображаться точками е-окрестности точки w0.
В случае, если zQ и wQ — конечные числа, это определе-
определение равносильно следующему. Равенство
wQ= lim f(z)
означает, что как бы мало ни было положительное число е,
к нему можно подобрать такое положительное число 8, что
для всех значений z(z^?z0), удовлетворяющих условию
A0)
выполнено неравенство
(И)
Если z0 или Wo или оба вместе бесконечны, то в соот-
соответствии с определением окрестности бесконечно удаленной
точки неравенства A0) или A1), или оба вместе должны
быть заменены другими. Так, например, равенство
lim f(z) =
г-» оо
(wa конечно) означает, что, как бы мало ни было положи-
положительное число ?, к нему можно подобрать столь большое
24
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. I
положительное число А, что для всех значений г, для которых
\^А функция f(z) будет удовлетворять неравенству
Введенное нами определение предела функции ничем не
отличается от определения предела функции действительного
переменного, следовательно, все доказываемые в курсе матема-
математического анализа теоремы о пределах и бесконечно малых1)
остаются в силе для функций комплексного переменного.
9. Если функция w=f(z) определена в точке 2, ив не-
некоторой ее окрестности и предел lim f(z) не только суще-
z^za
ствует, но равен значению функции f{z) в точке г0, т. е.
lim /(*)=/(*„),
то функция f{z) называется непрерывной в точке z0. В соот-
соответствии с определением предела это значит, что функция
w=f(z) непрерывна в точке гф если как бы мало ни было
положительное число е, к нему можно подобрать такое число
8^0 что из неравенства
следует, что
z — г0' < 8
A2)
A3)
Если обозначить z — zu = Az, w — wo — Aw (Дг— прираще-
приращение независимой переменной, Ди' — приращение функции), то
неравенств-а A2) и A3) заменяются соответственно неравен-
неравенствами
Аг <3, A2')
Да'!<е, A3')
и определение непрерывности в точке гй функции w=f{z\
определенной в некоторой окрестности этой точки, сводится
к тому, что в точке гй выполняется равенство
lim Дш = 0.
') Функция f (г) называется бесконечно малой в окрестности
точки zg, если lim/(z)=0.
§ 21
ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
25
'Гак как сформулированное выше определение непрерыв-
непрерывности совпадает с определением непрерывности для функций
действительного переменного, то доказываемые в курсе мате-
математического анализа теоремы о непрерывности суммы, раз-
разности, произведения, частного') непрерывных функций, а также
непрерывной функции от непрерывной функции остаются
в силе для функций комплексного переменного.
Как уже указывалось выше (стр. 19), равенство w=f(z),
где w = u-\-iv, z = x-\-iy, равносильно системе равенств
и = и (х, у), v = v(x, у).
Если г0 —
то
yu)]-\-i[v{x, y) —
\Пг) -f(zo)\=
= /[»(х, у) — и (дг0, >'о)]'2 + [^ (х, y) — v (хЛ, у0)}*. A4)
Из определения непрерывности функции f(z) в точке z сле-
следует, что если точка (х, у) находится в достаточно малой
окрестности точки (хй, _у0), то выполняется неравенство A3),
и следовательно, в соответствии с.A4), выиолняклся нера-
неравенства
|н(л:, у)—п(х0, j'0)!<e,
\ v (х, у) — v (х0, )'о) < г,
которые означают, что функции и{х,у) и v (x,y) непрерывны
в точке (хй, у0). Таким образом, из непрерывности функции
комплексного переменного следует непрерывность ее дейст-
действительной и мнимой частей как функций двух действитель-
действительных переменных х и у. Справедливо и обратное утверждение:
из неравенств A5) и равенства A4) непосредственно следует,
что непрерывность функций и (х- у) и v(x, у) влечет за со-
собой непрерывность функции f(z).
Заметим, что если вспомнить способ (см. стр. 21), с по-
помощью которого, зная уравнение некоторой линии в плоско-
плоскости г, можно найти уравнение ее образа на плоскости w при
1) Если делитель не обращается в нуль.
26
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
(Гл. I
отображении w=f(z), то легко убедиться в справедливости
утверждения: непрерывная кривая отображается с помо-
помощью непрерывной функции на непрерывную кривую (или,
если /(г) постоянна вдоль заданной кривой, — в одну
точку).
§ 3. Основные трансцендентные функции
10. Ряд с комплексными членами
*1 +2*+ ... + *„-}-..., A6)
так же как и ряд с действительными членами, называется
сходящимся, если существует конечный предел его частич-
частичной суммы
$„ = *,+ Zi-\-...-\-zn
при я->оо. Этот предел называется суммой ряда:
S= lim Sn.
л~»оо
Ряд A6) сходится тогда и только тогда, когда сходится
как ряд
*i+Jffj + --- + -*ii + ---» A7)
членами которого являются действительные части членов
ряда A6), так и ряд
J'i+J's + ---+J'B + ..., A8)
составленный из мнимых частей членов ряда A6).
Это утверждение немедленно следует из того, что сходи-
сходимость последовательности комплексных чисел равносильна
сходимости двух последовательностей, одна из которых со-
составлена из действительных, а другая из мнимых частей чле-
членов данной последовательности. Отсюда, в частности, полу-
получаем, что в случае сходимости ряда A6)
lim zn = 0,
л~»оо
в силу того, что lim xn= lim yn = Q ввиду сходимости ря-
л —ю> л —ю>
дов A7) и A8).
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
27
Если сходится ряд
:*„!+.
составленный из модулей членов ряда A6), то ряд A6) также
сходится и называется абсолютно сходяшдмся.
Действительно, из очевидных неравенств
л л =?= %п > \Уп \ === zn
вытекает сходимость рядов A7) и A8), а следовательно, и
ряда A6).
Определения суммы, разности, произведения двух рядов и
теоремы о сходимости суммы, разности, произведения рядов
не отличаются от соответствующих определений и теорем для
рядов с действительными членами ([1], гл. XI, § 1).
П. Введем определения основных трансцендентных функ-
функций для комплексных значений независимого переменного.
Если показатель степени является комплексным числом, то
определение степени аг, вводимое в алгебре, теряет смысл.
.Точно так же известные из тригонометрии определения три-
тригонометрических функций sin z, cos z, tgz, ctg.2 неприменимы
при комплексных значениях z. Принимая во внимание извест-
известные для действительных значений х разложения функций е*,
sin х, cos x в степенной ряд, положим по определению
7~ 7п
Л- |
91 "Г • • • "Г „|
A9)
sin z =,
B1)
Ряды, стоящие в правых частях этих равенств, сходятся, и
притом абсолютно, при любом комплексном значении z. Дей-
Действительно, рассмотрим, например, ряд A9). Если z = r, где
г — любое действительное положительное число, то ряд A9),
как известно из курса анализа, сходится, по эю и значит,
что ряд A9) сходится абсолютно при z \ = г, а так как г
произвольно, то ряд A9) сходится абсолютно в любой точке
плоскости z. Аналогичные рассуждения применимы к рядам
B0) и B1).
Следовательно, равенсша A9) — B1) определяют но всей
плоскости комплексного переменного z функции ег, sin z,
28
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. Г
cos z, совпадающие при действительных значениях z с соот-
соответствующими функциями действительного переменного.
Функции ег, sin z, cos z связаны между собой формулой
Эйлера:
е'г = cos z -\-i sin z. B2)
Действительно, подставив в равенство A9) iz вместо z, по-
получим
Умножив, далее, обе части равенства B0) на I и почленно
сложив полученное равенство с равенством B1), убедимся
в справедливости формулы Эйлера.
Если в формуле Эйлера заменить z на — z, будем иметь
е~1г = cos z — I sin z. B3)
Из B2) и B3) получим
cos z = ~V ,
sin z —
B4)
B5)
Как уже указывалось на стр. 9, формула Эйлера позволяет
перейти от григоночегрической формы комплексного числа
к показательной:
z = г (cos <р -f-1 sin у) = re1".
Если Х\ и Хц — действительные числа, то, как известно,
Принимая во внимание, что
?.
получим
/ * 1 t Л1 1 [ л I
2!
(•V,
}-•••+
3]
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
29
Заметим, чго сходимость (и притом абсолютная) рядов, уча-
участвующих в равенстве B6), не нарушается при замене дей-
действительных чисел Х\ и х^ любыми комплексными числами zt
и г2 и что перемножение рядов с комплексными членами
производится по правилам перемножения рядов с действи-
действительными членами. Отсюда можно утверждать, что равенство
ezl + z1—-ezlezi B7)
справедливо при любых комплексных zt и z%. В частности,
если z = x-\-ty, где х и у — действительные числа, то
ег — ex+iy = е*е'У.
Но в силу B2) еь'= cosy-\-l sin у, следовательно,
е2 = ех (cos у -\- i sin у). B8)
Отсюда, в частности, следует, что |ег| = е* и. одно из зна-
значений Arg ег равно у.
Равенство B8) позволяе1 вычислять значения показатель-
показательной функции при любых комплексных значениях показателя.
Например,
ГС .
ei-3i = e* (COS з _ i sin 3); етЛ = — 1; e*' = L
Из равенства B8) следует, что функция ег периодична
и имеет период 2izi:
Действительно, если z = х -f- iy, то
= <?•*¦ (cos у -f- г sin j/) = ег.
В частности, e2*rI = e°=l, e<-ik+il™ = е" = — 1 (Л —целое
число).
Если /я — целое число, то из B8) получим
iff1 = \ex (cos _y -f i sin y)]m = emx (cos у -\-1 sin ^)m =
= ет v (cos my -f г sin ягу) = em ^+i ''> = emz.
Так как формула B8) позволяет вычислять значения показа-
показательной функции, то формулы B4) и B5) могут служить для
вычисления cos z и sin z при любом комплексном z.
30
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл. I
Поскольку показательная функция имеет период 2тл, пра-
правые части равенств B4) и B5) не изменятся при замене z
на z -\- 2тс:
U izi
следовательно,
cos [z -\- 2тс) = cos z, sin (z -)- 2тс) = sin г,
т. е. определенные с помощью B4) и B5) функции cos z и
sin z периодичны и имеют, как и в случае действительного
аргумента, период 2тс.
Нетрудно убедиться в том, что для функций sin г и cos г
при любых комплексных значениях z сохраняется основное
связывающее их тождество sin'2z-j- cos'2 2= 1. Действительно,
,'eiz — e~IZ
sin*z
U I e-iz \-2
¦ + ¦
Сохраняются также и другие основные тригонометрические
тождества. Например, на основании B4) и B5)
Sin Z\ COS Z.2 -j- COS 2j Sin 22 —
2i
2 1 2
= sin (Zi -(- z.2).
Функции tg z и ctg z определяются с помощью равенств
sin?
° COS Z j ieiz.
—
sin г
B9)
C0)
Гиперболические функции sh z, ch г, th z, cth г опреде-
определяют ся равенствами
thz =
sh z
cth 2 =
2
chz
bh z'
§ 3l
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
31
Принимая во внимание B4), B5), B9) и C0), заметим, что
гиперболические функции легко могут быть выражены через
тригонометрические:
sh z = — / sin iz, chz= cos iz, '
th z = — / tg iz, cth z = i ctg z.
Из этих тождеств следует, в частности, периодичность гипер-
гиперболических функций, причем периоды sh z и ch z равны 2тс/,
a th г и cth z равны тс/.
Пример 1. Найти cos i.
Принимая во внимание, 4tocosz = -
e-iz
COS 1 = -
- = ch Ь
2
= 1,543
получим
(таким образом, cos i — действительное число, большее единицы,
тогда как при х действительном всегда | cos* | ==; 1).
Пример 2. Найти sin A + 2i).
Имеем: sin A + 2«) = sin I cos 2i -j- cos 1 sin 2r, но cos 1i = ch 2,
sin 2i = i sh 2 и потому
. sin A + 2i) = ch 2 sin 1 + i sh 2 cos 1
(аргумент под знаком син\са и косин)са измеряется, конечно, в
радианах).
12. Логарифмическая функция определяется как функ-
функция, обратная показательной. Если ew^z, где zj±Q, то w
называется логарифмом числа z и обозначается
w = Ln z.
Если щ;=гг-1-й>, то из формулы B8) следует, что je°'| = eu
и ArgeB' = z»-f 2?tc (A = 0, ±1, ±2, ...). Так как в рас-
рассматриваемом случае ew — z, то e"=\z\, или н = 1п|г
(j г | — число действительное и положительное, и здесь имеется
в виду обычное определение логарифма), и a =
Итак,
Ln z = In !
I -f- / Arg г = In . z \ -j- / arg г -)- 2Лта C1)
(A = 0, +1, ±2, ...).
Ввиду многозначности величины Arg z логарифм является
многозначной функцией (действительная часть логарифма,
равная In J z |, определяется однозначно, а мнимая содержит
неопределенное слагаемое, кратное 2тс).
32
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
[Гл I
Главным значением логарифма числа z будем называп.
то значение, которое соо1вегсгпует главному значению apiy-
мента числа z. Следовательно, в формуле C1) главное зна-
значение логарифма получим при k = 0.
Если z = x— действительное положшельное число, то
z\ = x и arg z — 0, поэтому, согласно C1), главное значе-
значение логарифма действительного положительного числа является
числом действительным и совпадает со значением, обознача-
обозначаемым символом In л;, которое и приводится в таблицах лога-
логарифмов. Естественно поэтому символом In z обозначать глав-
главное значение логарифма любого комплексного числа z. Тогда
в соответствии с формулой C1) получим
In z = In | z | -\-1 arg z.
Пример 3. Найти ln ( — 1) и Ln ( — 1).
Модуль числа —1 равен 1, а главное значение аргумента равно
я, следовательно,
Ln(— \)=тЛ + 2Ы — Bк+ 1)~< (k = Q, ±1, ±2,...).
Пример 4. Вычислить In г и Ln Л
Модуль числа < равен 1, а главное значение аргумента равно
=- следовательно,
In i = 1
тЛ
= 0, ±1,ч 2,...).
Пример 5. Найти In C + 4г) и Ln C -4- 4/).
Модуль числа 3 -f— 4i равен |/32 -f- A- = 5, а главное значение
аргумента равно arctg q-, следовательно,
lnC + 40=ln5 + iarctgi,
Ln C 4- 40 = In 5 -f i arctg , + 2Ы (k = 0, ± 1, ± 2,...).
Так как
Arg B,2.,) = Arg 2, -f- Arg 2a, Arg ^ = Arg 2j — Arg Zi,
(k = 0, ± 1, ±2,...),
= - Arg
3]
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
33
in — целое число, положительное или отрицательное), то из
формулы C1) следует, что логарифмическая функция, обоб-
обобщенная нами на случай комплексных значений независимой
переменной, обладает следующими свойствами:
Ln
Z*) = Ln z1 -4- Ln z» Ln - = Ln' z, — Ln zit
z
Ln (zn) = n Ln z-\- 2Ы (k = 0, ±1, ±2, ...),
Ln \/~z = — Ln 2.
n
Формула B8) служит для возведения в комплексную степень
числа е. Переходя к определению действия возведения в степень
любого комплексного числа, заметим сначала, что в силу определения
логарифмической функции eLna = a для любого комплексного а.
Для действительных а и г при а > 0, очевидно, справедливо
тождество a* = ezina- Определим теперь выражение аг для любых
комплексных а к г формулой
a* = e*Ln". C2)
В силу многозначности логарифма выражение аг, определенное
равенством C2), многозначно. Его главным значением будем на-
называть то, которое получим, подставив в правую часть C2) In a
вместо Ln а. Только при целых действительных (положительных,
отрицательных или равных нулю) значениях г формула C2) опре-
определяет единственное значение величины az, так как в этом случае
неопределенное слагаемое вида 2k^i, входящее в Ln а, будучи умно-
умножено на целое число г, дает в показателе правой части равенства
C2) слагаемое вида 2К%\, где К — также целое действительное
число, и значения правой части C2), соответствующие различным
значениям К, совпадают.
Пример 6. Найти il.
' —е (fe = 0, ± 1, ± 2, ...)•
л *
Главное значение величины i' равно е 2.
Пример 7. Найти 2l+i.
2' + ' == е0+'I-п2 = g(I + i)(ln2+2*7tj) __
= ? = е (cos In 2 -j- i sin In 2)
(ft = 0, ± 1, ±2, ...).
13. Обратные тригонометрические функции опреде-
определяются как функции, обратные по отношению к тригономе-
тригонометрическим (см. определение обратной функции на стр. 19).
2 И. Г. Араманоаич и др.
34
ФУНКЦИИ КОМПЛЕКСНОЮ ПЕРЕМЕННОГО
[Гл. t
Если z=sinffi», 10 w называется арксинусом числа z
и обозначается
w== Arcsin z.
Аналогично, если z = cos w, то w называется арккосинусом z
и обозначается
w = .Arccos г;
если z = tgw, то и; называется арктангенсом z и обозна-
чается
ги = Arctg 2
и т. д.
Если z== sin то, то на основании B5) z = (elw — e~lw)j2l,
откуда
или
etw — liz — e~iw =
—2*ze'*—1=0.
Решив это уравнение, получим
eiw = i
т. е.
w
—г2)
= Arcsin z = — I Ln (iz -j- }Л — г2).
C3)
В силу многозначности логарифма и двузначности корня
в правой части C3), Arcsin г является функцией много-
многозначной. Если z — число действительное и | z | =sc 1, то вели-
величина у\ — г* также является действительной и
iz
— zQ<
=\.
Но в силу формулы C1) все значения логарифма числа, мо-
модуль которого равен 1, являются числами чисто мнимыми,
а так как перед знаком логарифма в правой части C3) стоит
множитель — I, то все значения Arcsin z будут в рассматри-
') Мы не пишем перед радикалом знака ;?, так как символом
обозначаем все значения корня.
§ 3]
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
35
ваемом случае, как и следовало ожидать, числами действи-
действительными; во всех прочих случаях значения Arcsin z дей-
действительными быть не могут.
На основании B9), если z = tgz, имеем
elw — e
,-iit
(el
откуда elw(\ —iz)=4 ш'О
) '
). или
Следовательно,
Tvw = Ln
1 -\-tz
, , i, 1 -f iz
w = Arctg z = — -j Ln y±-r^
C4)
Если z является любым действительным числом, то числа
1 -j- iz и 1 — iz будут сопряженными, поэтому их модули
одинаковы, следовательно, модуль выражения, стоящего под
знаком логарифма в правой части C4), равен 1 и в силу C1)
все значения этого логарифма чисто мнимые. В этом случае
ввиду наличия в правой части C4) множителя s- величина
Arctg z, как и следовало ожидать, действительна, в остальных
случаях эта величина действительной быть не может.
Аналогично можно получить
Arccos z = — I Ln (г -f- V~z3 — l),
Arcctg z = -j Ln j-рт-.
Пример 8. Найти Arcsin 2.
С помощью C3) и C1) пол>чим
Arcsin 2 = — i Ln B1 ± i /3) = — I Ln [B ± /3) i] =
= - i [in B + V3) + 11 + 2Ш J =
= 4-'lnt2- >Л3) -f- 2Ait (A = 0, + 1, ±2, ...),
36 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО [Гл. I
Пример 9. Найти Arctg 2/.
Arctg 2< = - Lu
- \ d/
==Т + |'^ + *'с (* = 0, +1, ±2,...).
Функции, обратные sh z, ch z, th z, cth z, называются об-
обратными гиперболическими функциями и обозначаются соот-
соответственно Arsh z, Arch г, Arth z, Aretha. Обратные гипер-
гиперболические функции многозначны. Действительно, если
w = Arsh z, то z — shw, или z = (ew— e~w)j'2, откуда
elw — 2zew — 1 = 0.
Решая это уравнение, получим ew = z + у z1 + I, откуда
w = Ln [z + j/F'+T) или
Arsh 2 == Ln (z + 1Л2+1).
Многозначность функции Arsh z является следствием мно-
многозначности логарифма и квадратного корня, стоящих в пра-
правой части последнего равенства.
Совершенно так же можно доказать, что
Arch2 = Ln(z + l/> — I), Arcth z = - Ln -^tL.
... 1 . 1+2
Arthz —у Ln t _ .
ЗАДАЧИ К ГЛАВЕ 1
1. Записать в тригонометрической форме числа:
d) 3i; б) — i; в) 2; г) —2; д) 1 + i; е) — 1— i;
ж) УЗ — i; з) 1—1 /3; и) 2 + 5i; к) — 2 + 5/; л) 2 — 5i;
м) —2 — 5/.
2. Где расположены точки г, для которых:
а) |г | >5; б)
3; в)
2; г) | г — 3 — 4i | = 5;
д) Re г > 3; е) 1га г г? 2; ж) j г — 2 | + [ г + 2 | = 5; з) | г — 2 | —
+ 2 | > 3; и) | г- — 1 | = а- (а > 0); к) Re z- — а1; л) | г — i \ =
5= 1; н) а < ary, г < ,3; о) arg (г — 0 = -j;
П) "й" < arS
ЗАДАЧИ К ГЛ 1
37
3. Доказать, что если г, тг, + 2, = 0, [г,
то точки г,, 22, г, являются вершинами правильного треугольника,
вписанного в кр\г радиуса 1 с центром в начале координат.
4. Найти:
а) f; б) jff, в)п^Г' г)(/з-о*;д)
5. Найти:
а) у^г; б) -^=^8; в)
у ^ 11; г) /п^1; д) ]/3+4i; е) ^ — 2 + 2/.
6. На какие линии плоскости oi отображаются с помощью
функции w = —(г — x-\-iy,
— u-\-iv) следующие линии пло-
пло= 1; в) ^» = лт; г) з» = 0; д)д:=1;
скости г:
а) х2+/ = 4;
е) (*-1J+У = 1?
7. Какие линии заданы уравнениями:
а) г = A+0*; б) z— acos t-\-ib sin t (a > 0,
в) г = < + -|; г) г = ^ + 1.?
8. Найти:
a) Ln(l + 0; 6) Ln(—0; в) Ln(—3 + 40-
9. Найти:
a) e 2; б) г 2; в) e'+l; r) «1+l; д) A+0'; e) 31.
10. Доказать тождества:
2 tg г
a) sin 2г = 2 sin г cos г; 6) tg 2z = i _ t » ! B) sin zi + s'n za =
= 2 sin ,-, cos -
" •
И. Найти:
a) sim'; б) cos A+0; в) tg B — ?); г) сгн; Д) sh (— 2 + 0;
е) sin (дг + (у); ж) cos (.дг + ty).
12. Доказать тождества:
а) sin х = — г sh ix; г) sin ('дг = i sh a:;
б) cos x = ch 1'л;; д) cos «л; = ch л-;
в) tg л: = — i th ix; e) tg ix = i th д:.
13. Найти:
a) Arcsin 3; 6) Arcsin/; в) Arcsin(^2 — 0; r) Arctg -=-;
д) Arctg A + 20; e) Arthi; ж) Arch (— 1).
ГЛАВА I!
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
§ 1. Производная
14. Определения производной и дифференциала функции
комплексного переменного дословно совпадают с соответ-
соответствующими определениями для функций действительного пе-
переменного. Поэтому почти все основные теоремы и формулы
дифференциального исчисления без изменения распростра-
распространяются и на функции комплексного переменного.
Однако дифференцируемые функции комплексного пере-
переменного обладают по сравнению с дифференцируемыми функ-
функциями действительного переменного многими дополнитель-
дополнительными свойствами, причина появления которых заключается
в том, что условие для существования производной функции
комплексного переменного, как будет видно из дальнейшего,
является несравненно более ограничительным, чем условие для
существования производной функции действительного пере-
переменного.
Дадим независимому переменному z = x-\-ty приращение
Дг = Дх-|-?Д_у и вычислим вызванное этим приращением
приращение Aw однозначной функции w=f{z):
Если существует предел отношения -г- при стремлении Az
к нулю по любому закону, то этот предел называется про-
производной функции f(z) в точке z и обозначается f' (z), w',
dw df
.— или -?-:
dz dz д
ПРОИЗВОДНАЯ
Требование существования предела отношения ~ и его
независимости от закона стремления Az к нулю накладывает
на функцию f(z) значительно более сильные ограничения,
чем аналогичное требование для функции у = <р(х) действи-
действительного переменного х. Так, если функция у = <р(х) имеет
производную, то это значит, что существует предел отноше-
отношения —- при приближении точки х -\- Ах к точке х по двум
направлениям: слева (при Дх<^0) и справа (при Ajc^>0),
и что эти пределы совпадают. Требование же существования
производной для функции /(г) комплексного переменного
Дда
означает существование предела отношения т- при прибли-
приближении точки z -\- Az к точке z по любому пути, в частности,
по любому из бесконечного множества различных лучей,
и совпадение всех этих пределов.
Пусть f{z) = u{x, y)-\-iv(x, у) и Az = Ax-{-iAy; тогда
Aw=f(z-\-Az) — f{z) = [u(x + Ax, у-\-Ау) — и{х, y)] +
-\- i [v (х -\-Ах, у-\- Ду) — v (х, у)} = Аи -J- iAv,
где
Ди = и (х -\- Ах, у -\- Ау) — и (х, у)
и
Av = v (х -}- Ах, у-\-Ау) — v(x, у).
В этих обозначениях
f'(z)= lim T-= Hm -A~~
A)
15. Пусть функция /(г) имеет производную в точке z;
тогда предел A) существует и не зависит от закона стрем-
стремления Az = &x-\-lAy к нулю; в частности, при Az = Ax,
т. е. при приближении точки z -\- Az к точке z по прямой,
параллельной оси Ох (рис. 8), получим:
Дг-О112 ДЖ-.0
\x
ди
dv
40
ДИФФЕРЕНЦИРОВАНА И ИНТЕГРИРОВАНИЕ
[Гл II
Выбрав Az = iAy, т. е. устремляя точку z -\- Дг к точке z
по прямой, параллельной оси Оу (рис. 9), получим:
ft, ч ,. Aw ,. Аи -\- iAv
I (z)= hm xr = llm —7T7.— =
= lim
/ — О
Ли , Av\ da . du
4У Ау/ дУ дУ
Aw
C)
Так как предел отношения -г- при Дг -*- 0 не должен зависеть
от закона стремления Az к нулю, то из B) и C) следует, что
ди , , dv dv . ди
или
дх
ди_
дх
dv
dv_
дх
D)
Эти условия, называемые условиями Коши — Римана или
условиями Даламбера — Эйлера, должны быть выполнены
У.
Рис. 8.
Рис. 9.
в каждой точке, в которой функция f(z) = u-\-iv дифферен-
дифференцируема (имеет производную).
При некоторых добавочных ограничениях, например, если
потребовать существование полных дифференциалов функций
и (х, у) и v (х, у), можно доказать, что условия Коши — Ри-
Римана не только необходимы, но и достаточны для диффе-
дифференцируемое™ функции /(г).
Действительно, если функции и (х, у) и v (x, у) имеют
полный дифференциал (см., например, [1], п. 110), то
ди k . ди
Ax +
dv
dv
_
§ И
ПРОИЗВОДНАЯ
41
где р = V (Axf -)- (ДуJ и Пт ?j = lim ?.2 = 0. Каково бы
Р-.0 р-»0
ни было Дг = Ах -\- iky, имеем
Да) Ди -4-iAv
Az =
" Ах -f- iA
ди .
дх '
ди .
,— Д v
.[dv
1\
dv . \
^1
Ax-\-iAy
Заменив на основании условий Коши — Римана в числителе
„ ди dv dv ди
правой части ^— на — ^-, а ,— на -j- , получим
Aw
Так как
d?(Ax + iAy) + id?(Ax + iAy)-
Р
du ,
дх
Az\ =
¦ dv | (e.
Ддг -\- гД_у
Дд; 4- «4.
Дл:-|-<Ду
+ «^ "
Р i Е 1 г-- i
E)
Но величина J sj -)- i?-i | стремится к нулю при р — 0, т. е.
при Az-^Q.
Следовательно, по какому бы закону приращение Az
ни стремилось к нулю, из E) получим
,. Aw л/ ч ди , . dv
'lm И~ == * (z) == л И Д~>
&Z—+0 ОЛГ GЛГ
и достаточность условий Коши — Римана для существования
/' (z) доказана. Мы снова пришли к формуле B), которая
показывает, что дифференцирование функции по комплексному
переменному (если оно возможно) равносильно вычислению
частной производной по х.
Если функция дифференцируема не только в данной
точке, но и в некоторой окрестности этой точки, то
она называется аналитической в данной точке.
Функция, аналитическая во всех точках некоторой
области, называется аналитической или голоморфной
в этой области.
Точки плоскости z, в которых однозначная функция f(z)
является аналшической, называют правильными точками этой
42
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
функции, а точки, в которых функция f{z) не является ана-
аналитической (в частности, точки, в которых f(z) не опреде-
определена), — особыми точками.
Пример 1. Выяснить, является ли ф)нкция и» = 22 анали-
аналитической?
Если и; = 22, то и -\-iv=(x -\-iy)'=xa—у'' -\- lixy и ц=л:2—у2,
v = 2ху, откуда находим
du n dv du _ dv
дх ду ' ду дх'
Условия D) выполнены во всех точках плоскости, следовательно,
функция z2 является аналитической во всей плоскости.
Пример 2. Выяснить, является ли функция ег аналитической?
Если w = ez, то и -f- iv = е*+'У = ех (cosy -f- i sin у) и а ¦=¦ ех cosy,
v = ex&my. Отсюда
да
dv ди
dv
с- = е cos у = ,- , -5— = — е* sin у = — з— .
ja: ay' ay ^ <?лг
Следовательно, условия Коши—Римана выполнены в каждой
точке. Функция ez является аналитической во всей плоскости.
Пример 3. Выяснить, является ли аналитической функ-
функция w= г.
Если w = г, то и -\- iv = .t — iy и « = ^r, о = — у, откуда
Следовательно, первое из условий D) не выполнено. Функция да = 5
не дифференцируема ни в одной точке плоскости.
Пример 4. Выяснить, является ли функция да = 2 Re г ана-
аналитической.
Если w = 2 Re 2, то и + го = (х -\- iy) х = х* + <Л'.У и « = д;3,
» = х_у, откуда
dv
дх
ду
дх
Условия D) выполнены только при х = 0 и _у = 0. Следовательно,
функция 2 Re 2 дифференцируема только в одной точке г = 0 и ни
в какой точке не является аналитической.
Так как основные теоремы о пределах сохраняются для
функций комплексного переменного, а определение произ-
производной функции комплексного переменного также не отли-
отличается от соответствующего определения для функции дей-
действительного переменного, то нетрудно проверить, что извест-
известные правила дифференцирования суммы, разности, произве-
произведения, частного, степени, функции от функции, обратной
ПРОИЗВОДНАЯ
43
функции остаются справедливыми и в случае функций комп-
комплексного переменного.
Легко проверить, что сохраняются и правила дифферен-
дифференцирования элементарных трансцендентных функций. Напри-
Например, если w = ez—ex+l" = ex{cosy -\-l sin у), то, пользуясь
формулой B), получим
-^ = ех (cos у -г I sin у) = е2.
С помощью формул B4) и B5) гл. I нетрудно проверить
справедливость известных формул дифференцирования три-
тригонометрических функций. Правило дифференцирования обрат-
обратной функции приведет нас к известным формулам дифферен-
дифференцирования логарифма и обратных тригонометрических функ-
функций. Предоставляем читателю самостоятельно проверить все
сделанные утверждения.
16. Действительная и мнимая части функции f(z) =
=:it-\-lv, аналитической в некоторой области D, являются
в этой области решениями уравнения
называемого уравнением Лапласа:
д2и . д-и __ - а2и , d2v
дх- ' ay2 ' a.vs "^ ау2
Действительно, функции и и х> связаны в области D усло-
условиями Коши — Римана:
ди dv ди dv
dx dy ' dy dx'
Дифференцируя первое из этих тождеств по х, а второе
по у и складывая, получим
ду2
') Существование и непрерывность частных производных вто-
второго порядка функций и (х, у) и v (x, у) следует из того, что ана-
аналитическую функцию можно дифференцировать любое число раз
(см. п. 27).
44
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ [Гл It
Дифференцируя первое из тех же тождеств по _у, а второе
по х и вычитая, будем иметь:
дх* I" dys "~
Решения уравнения Лапласа
называются гармоническими функциями. Следовательно, дей-
действительная и мнимая части аналитической функции являются
гармоническими функциями.
Однако, если и(х, у) и v(x, у) являются произвольно
выбранными гармоническими функциями, функция и(лг, _у)-|-
-\-iv(x, у), вообще говоря, не будет аналитической функ-
функцией, так как условия D), как правило, не будут выполнены.
Аналитическую функцию f(z) = u(x, y)-\-lv(x, у) мы
получим, если, произвольно задав одну из двух гармониче-
гармонических функций и{х, у) или v{x, у), подберем другую так,
чтобы удовлетворялись условия Коши — Римана ^- = ^—f
^¦ = —Д, т. е. определим другую из этих функций по ее
двум частным производным или, что то же самое, по ее пол-
полному дифференциалу. Как известно (см., например, [1], п. 115),
по полному дифференциалу функция определяется с точностью
до постоянного слагаемого. Следовательно, аналитическая
функция с точностью до постоянного слагаемого определяется
своей действительной или мнимой частью.
Две гармонические функции и (х, у) и v (х, у), удовлетво-
удовлетворяющие условиям Коши — Римана, следовательно, являющиеся
действительной и мнимой частями некоторой аналитической
функции f(z) = u(x,y)-\-lv(x,y), называются сопряженными.
Пример 5. Найти аналитическую функцию, если известна ее
мнимая часть и = 2л:8— 2уг-\-х.
Так как з^- =
дх
мана D) находим производные:
ди
-?- — — 4у, то из условий Коши —Ри-
ду
F)
ду
§ 21 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Из F) пол)чим
и — — \Aydx~ — Аху + <р СУ)|
45
(8)
где функция о (у) пока произвольна. Для определения функции <р (у)
дифференцируем (8) по у и подставляем в G):
4 + 'C) 4l
откуда а'(у) = —1, tf (у) = — у-\-С- Следовательно,
и = — Аху — у -)- С
Окончательно получаем
w = и + iv = — Аху — у + С + i Bх2 — 2у- + х)
= 21 (х2 -у> + 21ху) -\-Ц
где 2 = х -\- iy.
и
§ 2. Геометрический смысл аргумента и модуля
производной
17. Пусть в плоскости z задана точка z0 и проходящая
через эту точку кривая -у с уравнением z = z(t), где z{t) —
= х (t) -j- iy (t), причем точке z0 соответствует значение
У
ш'Ю
Рис. 10.
параметра tQ, т. е. z0 = z {tu). Предположим, далее, что при t = tu
существует не равная нулю производная функции z (f), т. е.
Отсюда следует, что величины х'(t0), У (t0) не могут быть
равны нулю одновременно и, следовательно, в точке г0 су-
существует касательная к кривой -у (рис 10), причем вектор
46
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
с координатами [х' (t0), у'(to)\ направлен по касательной
к этой кривой') (этот вектор изображает комплексное число
х' (tu) -\- iy' (to) = z' (t^j). Предположим, что функция f(z)
аналитична в некоторой окрестности точки z0 и /'(zo)^O.
Уравнение кривой •/'> являющейся образом кривой у ПРИ
отображении w — f(z), имеет вид w = f[z(t)]. Обозначим
f[z(t)) = w(t). Пусть
— образ точки zu при отображении w = f(z). Так как, в со-
соответствии с правилом дифференцирования сложной функции,
то в сцлу сделанных предположений w'{t^)^Q и, следова-
следовательно, в точке wu существует касательная к кривой -(. Из
равенства (9) имеем
Arg w' (О = arg /' (z0) -f Arg z' (t0)
(неопределенное слагаемое вида 2Aic(A = 0, zh 1, ±2, ...),
входящее в правую часть, можно отнести ко второму сла-
слагаемому, а в первом слагаемом взять, например, главное
значение аргумента). Величина /' (г0), а следовательно и вели-
величина arg/'(z0), зависит только от вида функции f(z) и точки
z0, поэтому если функция f(z) фиксирована, то
Arg w' (t0) = а 4- Arg z' (t0),
где величина a = argf'(z0) не зависит от выбора кривой т>
проходящей через точку z0.
Комплексные числа z'(t0) и w' (^0) изображаются векто-
векторами, направленными по касательным к кривым f и ¦(, про-
проведенным соответственно через точки г0 и да0; поэтому если
производная аналитической функции f(z) отлична от нуля
в точке 20, ю аргумент этой производной имеет следующий
геометрический смысл: он равен углу, на который
нужно повернуть касательную в точке z0 к любой кривой,
проходящей через эту точку, чтобы получить направле-
направление касательной в соответствующей точке w0 к образу дан-
данной кривой при отображении w = f(z) (если а = arg /' С?
')Cm. [11, n. 73.
21
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
47
то поворот происходит против часовой стрелки, если а<^0,
то по часовой стрелке).
Если через точку г0 провести какие-либо две кривые -^
и f.,, имеющие касательные в этой точке, то направления ка-
касательных к образам fi и 7-2 этих кривых мы получим путем
поворота касательных к самим кривым fi и ^ на один и
тот же угол а, поэтому угол 9 между кривыми fl и -^
тот же (как по величине, так и по направлению отсчега),
что и угол между кривыми fi и Тз (рис. 11).
Рис. И.
Отображение, сохраняющее углы между линиями, назы-
называют конформным; если при этом сохраняется и направле-
направление отсчета углов, то такое отображение называют конформ-
конформным отображением 1-го рода. Мы, таким образом, доказали,
что отображение, осуществляемое аналитической функцией,
является конформным отображением 1-го рода во всех
точках, в которых производная этой функции отлична
от нуля.
18. Для выяснения геометрического смысла модуля про-
производной заметим, что ] Дг | есть расстояние от точки z0 до
точки z0 -|- \z, а | kw | — расстояние между точками w0 и
w0 -j- Да». Следовательно, величина '. .да указывает, в каком
отношении в результате отображения изменяется расстояние
между этими точками.
Так как
lim
, Дг
= lira
Дда
48
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
то величину | /' (z0) \ естественно назвать коэффициентом рас-
растяжения в точке z0 при отображении w=f(z). Если ]/'(zo)|^>l,
то в достаточно малой окрестности точки г0 расстояния между
точками при отображении увеличиваются и происходит рас-
растяжение: если !/'(^0)|<^l, то отображение в окрестности
точки za приводит к сжатию.
Так как производная f (zQ) не зависит от того, по какому
закону точка zu -{- hz стремится к точке z0, то коэффи-
коэффициент растяжения в данной точке постоянен, т. е.
одинаков во всех направлениях; таково второе свойство
отображения, осуществляемого с помощью аналитической
функции.
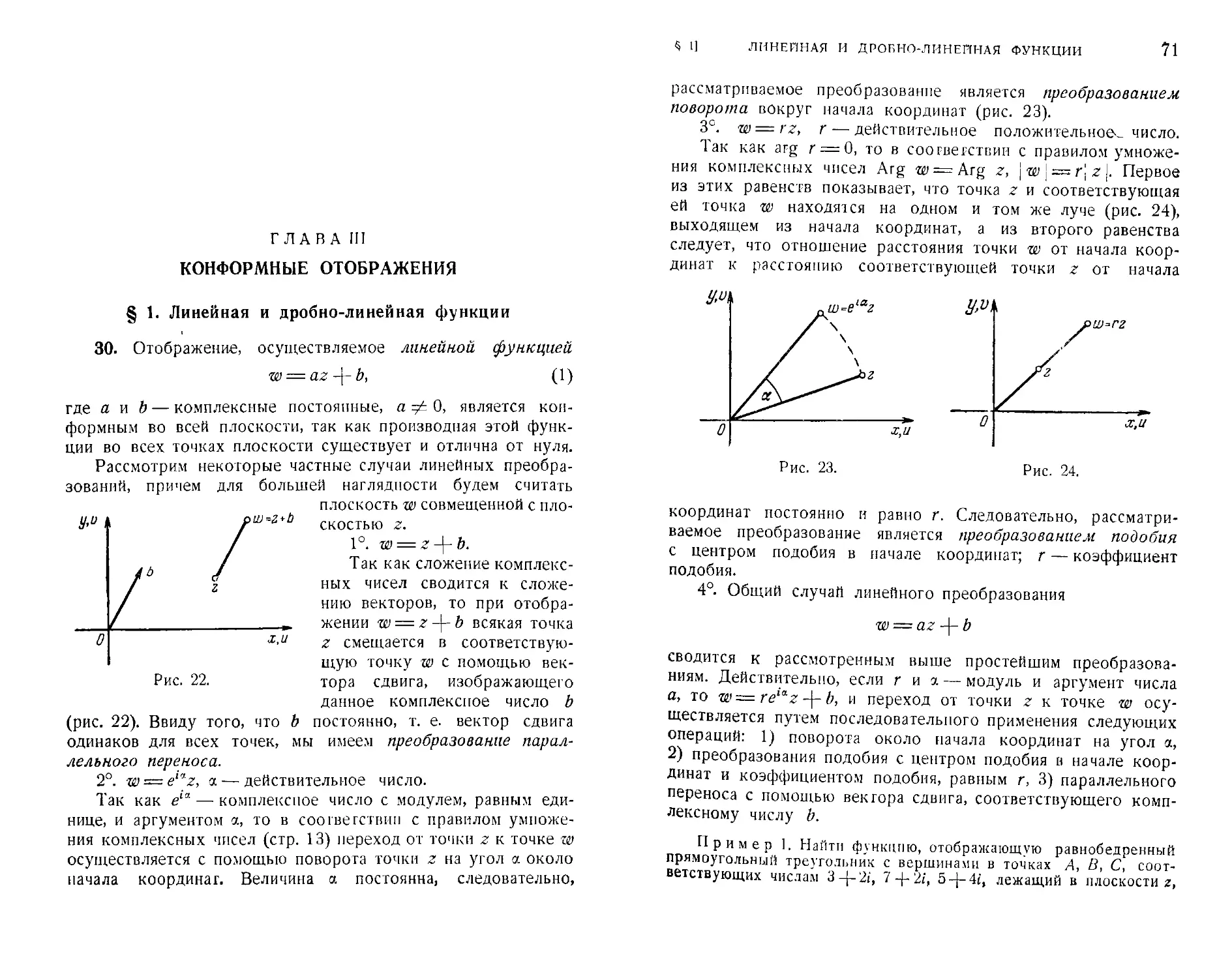
Пример 1. Рассмотрим отображение, осуществляемое функ-
функцией w = Зг.
Так как -=— = 3 -? 0, то отображение конформно во всей пло-
плоскости и коэффициент растяжения в любой тОчке равен 3.
Так как arg -j— = 0, то направления при отображении не изме-
изменяются.
Если учесть, наконец, что w = 0 при г = 0 и, следовательно,
начало координат остается при рассматриваемом отображении
неподвижным, то можно утверждать, что отображение с помощью
функции и = 3г сводится к преобразованию подобия с центром
подобия в нулевой точке и коэффициентом подобия, равным 3.
Пример 2. Отображение w = z" конформно во всех точках
плоскости 2, за исключением точки 2 = 0.
Действительно, -т-:=22, и лишь при 2=0 производная -— =0.
&Z U.Z
Так как
то лучи
(ft = O, ±1, ±2,
Arg 2 = а и Arg 2 = 3,
выходящие из точки г = 0 и образующие между собой угол, рав-
равный C — а, отображаются соответственно в лучи Argai = 2а и Arg w =
= 2C, образующие между собой угол 2 (fl—а).
Следовательно, в точке 2 = 0 конформность отображения нару-
нарушается: углы в этой точке не сохраняются, а удваиваются.
Конформное отображение, при котором углы сохраняются
только по абсолютной величине, по изменяют направление
отсчета на противоположное, называют конформным ото-
отображением 2-го рода. Таково, например, отображение, осу-
§31 ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 49
0
Рис. 12.
ществляемое функцией да = г. Действительно, если значения z
и w изображать точками одной и той же плоскости, то ввиду
того, что точки z и z симмет-
симметричны относительно действитель-
действительной оси (рис. 12), это отобра-
отображение сводится к преобразованию
симметрии относительно действи-
действительной оси. При этом не проис-
происходит никакого искажения мас-
масштаба (коэффициент растяжения
в каждой точке равен 1), а все
углы сохраняются по абсолют-
абсолютной величине, но изменяют на-
направление отсчета на противо-
противоположное.
В дальнейшем, говоря о конформном отображении, мы всегда
будем иметь в виду лишь конформное отображение 1-го рода.
§ 3. Интеграл от функции комплексного переменного
19. Предположим, что в плоскости z дана замкнутая или
незамкнутая дуга С, которую мы будем в дальнейшем считать
гладкой или кусочно-гладкой'). Граничные точки кривой С
обозначим 20 и Z; если кривая замкнута, то zo = Z. Одну из
этих точек, например zu, будем
считать начальной, а другую — ко-
конечной; тем самым мы установим
положительное направление на
кривой С, которое на чертеже
будем отмечать стрелкой (рис. 13).
Предположим, кроме того, что
функция f(z) непрерывна во всех
точках дуги С.
Разобьем дугу С произвольным
способом на п «элементарных»
дуг и занумеруем точки деления zh в направлении от на-
начальной точки к конечной, причем zn = Z (рис. 13). Введем
обозначения
0
Рис. 13.
') См. сноску на стр. 18.
50
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
Число Д-гй изображается вектором, идущим из точки zk_x
в точку 2ft, a \&zk\ — длина этого вектора, т. е. длина хорды,
стягивающей соответствующую элементарную дугу. Внутри
или на одном из концов каждой элементарной дуги выберем
по одной точке и обозначим эти точки Ci. Cq> • • ¦> Ся (точка Си
находится на элементарной
дуге с концами в точках zh^\
и zk). Составим сумму
Рис. 14. Предел этой суммы, вычис-
вычисленный при условии, что п -> оо,
а длина наибольшей из элементарных дуг стремится к нулю
(т. е. стремится к нулю максимальная из величин | Д^й |),
называется интегралом от функции f(z) no дуге Си обозна-
обозначается
\f(z)dz= lim
(Ю)
Из этого определения интеграла непосредственно получим
следующие его свойства'2):
^ [Л(*)±U(*)] dz=\A(z)dz±\f,(z)dz;
с ее
2)
где k — действительная или комплексная постоянная;
3) если дуга С геометрически совпадает с дугой С, но
имеет противоположное направление, то
так как при замене дуги С дугой С все множители
в правой части A0) изменят знаки на противоположные;
') Существование этого предела при ограничениях, наложенных
выше на функцию /(г) и дугу С, будет доказано на стр. 52.
2) Свойства 1)—5) могут быть также легко получены из фор-
формулы (И) или из формулы A4) (см. далее).
§ 3] ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 51
4) если дуга С состоит из дуг С\, С2, ..., Сп (рис. 14),
\f(z)dz = \ f(z)dz -\- \ f(z)dz+ ...+ \f(z)dz;
С C СС
то
5) ^dz = Z — 20, так как при /(г)=1 сумма в правой
с
части A0) принимает вид
6) если \f(z)
равна /, то
Действительно,
¦ • • "Г (^п — zn-i) — zn — г0 = Z — ZqJ
во всех точках дуги С и длина дуги С
/(С*)!
M
Ж/,
так как сумма
равна длине ломаной, вписанной
А1
в дугу С, и поэтому не больше, чем длина / дуги С.
20. Вычисление интеграла A0) сводится к вычислению
криволинейных интегралов от действительных функций дей-
действительных переменных. Пусть
z = x-\-ty, /"(г) = м + ^.
где и к v — функции переменных х и у:
а = и(х, у), v = v(x, у).
Тогда
^ /(г) dz = J и (х, y)dx — v (x, у) dy +
с с
u(x, y)dy. A1)
Формула A1) показывает, что для того, чтобы свести вы-
вычисление интеграла от функции комплексного переменного
к вычислению обычных криволинейных интегралов, следует
52
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. It
представить подынтегральную функцию в виде f(z) = и -\- iv
и умножить ее на dz = dx -\- idy. При этом подынтеграль-
подынтегральное выражение преобразуется к виду
f(z) dz = (u-\- iv) (dx ~\- i dy) = udx — v dy -j- t (v dx -f- и dy).
Докажем формулу A1).
Обозначим zk = + i
тогда
(*=1. 2.
где ДхЛ = %,-
то
Azk =
= [" B*. 1ft) Дл> — 0
следовательно,
^ / (г) Л = li m
il A-
=Уш— У к, а так как
(ib, in,) + 10 EА, i\k),
i [0 (=ft,
[в (Е*, ^) Axk - v (ik,
+
i lim
и в соответствии с определением криволинейного интеграла (см.,
например, [1], гл. IX, § 1) мы приходим к формуле (I ^..Существо-
^..Существование криволинейных интегралов в правой части формулы A1),
а следовательно и существование интеграла
\f(z)dz,
'С
следует из кусочной гладкости кривой С и из непрерывности вдоль
дуги С функций и (х, у) и 0 (л-, у), являющихся действительной и
мнимой частями непрерывной вдоль кривой С функции /(г).
Если дуга С задана параметрическими уравнениями
x = x(f), y=y(f),
A2)
а начальная и конечная точки дуги соответствуют при этом
значениям параметра ^ = ^0 и t=T:
то, как известно из правила вычисления криволинейного ин-
интеграла, подставив под знак интеграла вместо х и у функ-
§ 3] ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 53
ции, стоящие в правых частях уравнений A2), а вместо dx
и dy—: дифференциалы этих функций, можно свести вычис-
вычисление криволинейных интегралов в правой части A1) к вы-
вычислению определенных интегралов с нижним пределом tu и
верхним пределом Т. С другой стороны,уравненияA2) равно-
равносильны (см. стр. 22) одному уравнению в комплексной форме
z = z(t), A3)
где z (t) = х (t) -\- iy(t). Поэтому для вычисления интеграла
A1) достаточно подставить вместо z в подынтегральную
функцию z(t) из A3), а вместо dz — дифференциал этой
функции.
Следовательно, интеграл по комплексному переменному
можно вычислять, пользуясь формулой
т
\f(z)dz=\f[z(t)\z'(t)dt A4)
С /о
Пример. Вычислить интеграл
\ Re г dz,
С
где дуга С есть: 1) прямолинейный отрезок, соединяющий точку О
с точкой 1 + г; 2) ломаная, состоящая из прямолинейного отрезка,
соединяющего точку 0 с точкой 1, и прямолинейного отрезка, сое-
соединяющего точку 1 с точкой 1 + i.
Решение.
1) Уравнение отрезка, соединяющего точки 0 и 1+t в па-
параметрической форме, имеет вид x-=t, y = t, а в комплексной
форме г = (l + i) Л где действительное переменное / изменяется
от 0 до 1. Находим, далее, dz = A + i) dt и
l i
\ Re z dz = \ Re [A + i) t] A + 0 Л = A + 0 \tdt =
i: о сI -
1 1 -\-i
o = ~2~-
2) Уравнение отрезка, соединяющего точки 0 и 1, в комплекс-
комплексной форме имеет видг = ^, где t изменяется от 0 до 1; уравнение
в комплексной форме отрезка, соединяющего точки 1 и 1 + /, имеет
вид г = 1 -\-it, где t изменяется от 0 до 1. Итак,
11 11
и
б
54
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
(Ь If
§ 4. Теорема Кош и
21. Теорема Кош и. Если функция f(z)—аналитиче-
f(z)—аналитическая в односвязной области О, ограниченной замкнутым
контуром С, а также в точках этого контура, то
Предположим, что производная f'(z) данной функции не-
непрерывна на контуре Сив ограниченной им односвязной
области.
Напомним, что для того чтобы криволинейный интеграл
вида
\P(x,y)dx+Q(x,y)dy
с
не зависел от контура интегрирования (т. е. чтобы этот ин-
интеграл, взятый по любому замкнутому контуру, был равен
нулю), необходимо и достаточно, чтобы
ду дх'
В этом случае, как известно, подынтегральное выражение
является полным дифференциалом (см. [1], п. 141). При этом
предполагается, что функции Р и Q вместе со своими част-
частными производными непрерывны в некоторой односвязной
области, а контур С целиком лежит в этой области.
Согласно формуле A1)
jj f(z) dz = $ и dx — v dy -f- i jj v dx -\- и dy.
с с с
A5)
Так как функция f(z) аналитическая, то для нее выполняются
,, г, ди dv dv ди
условия Коши — Римана j-= — ^ , ^- = ^-( которые как
раз и являются условиями равенства нулю интегралов
§ и dx — v dy и ^ v dx -\- и dy, взятых по замкнутому кон-
с с
туру С. Непрерывность частных производных функций и
и v соблюдается, так как с самого начала предполагалось,
что производная /'(г) непрерывна.
Таким образом, каждый из двух интегралов в правой
части A5) равен нулю, и теорема Коши тем самым доказана.
S 4]
ТЕОРЕМА КОШИ
55
Можно доказать теорему Коши и без предположения
о непрерывности производной f'(z) на контуре Сив области,
ограниченной этим контуром, однако при этом доказательство
значительно усложнится.
22. Рассмотрим теперь многосвязную область О, ограни-
ограниченную внешним контуром Со и внутренними контурами Clt
Ct, ..., Сп (рис. 15), и предположим, что функция f(z) является
аналитической как в этой
многосвязной области,
так и на контурах Со, Q,
d, ..., С„. Пусть
\f(z)dz
(k = 0, I, 2, ..., п)
обозначает интеграл по
контуру Cft, обходимому
против часовой стрелки.
Соединим контуры Со, Cv Сь ..., С„ дугами Ti. Та Тя+1>
как показано на рис. 15; при этом область О окажется раз-
разбитой на две односвязные области. Контуры, ограничивающие
эти односвязные области, обозначим соответственно Г' и Г".
Так как функция f{z) является аналитической как на кон-
контурах Г' и Г", так и в областях, ограниченных каждым из
этих контуров, то по теореме Коши
\f(z
(z)dZ = O, \;
I" Г"
а следовательно, и
A6)
Г"
Если на каждом из контуров Г', Г" считать положитель-
положительным то. направление, при котором область, ограниченная этим
контуром, остается слева, то
$ $ f(z)dz =
Г'
$
Г"
= $ f{z)dz - \ f(z)dz - \ f(z)dz- ... - \f{z)dz A7)
56
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
(при сложении интегралов в левой части A7) интегралы по
дугам -fi> 7a> • • • > Тя уничтожаются ввиду того, что интегриро-
интегрирование по каждой из этих дуг будет производиться при вычи-
вычислении суммы в левой части A7) два раза в противополож-
противоположных направлениях).
Из A6) и A7) следует
\f(z)dz=\ f(z)dz
Со Cj С2
]f(z)dz. A8)
С
В частности, если функция f(z) является аналитической
на контурах Со и d (рис. 16) и в двусвязной области, огра-
ограниченной этими контурами, то из
A8) при я=1 получим
\f{z)dz=\f(z)dz. A9)
Со Ci
Равенство A8) будем называть
теоремой, Кошп для составного
Рис. 16. контура.
23. Если интеграл от функ-
функции f(z) по всякому замкнутому
контуру, расположенному в некоторой области G, равен нулю,
то интеграл по всякой дуге, находящейся внутри области Q,
зависит только от положения начальной и конечной точек
этой дуги и, следовательно, одинаков для всех дуг, имеющих
общую начальную и общую конечную точки. Другими сло-
словами, в этом случае интеграл не зависит
от пути интегрирования.
Действительно, если дуги С\ и С2 имеют
общую начальную точку г0 и общую ко-
конечную точку Z (рис. 17), то величина
\ f(z)dz~ $ f(z)dz B0)
с, с3
Рис. 17.
представляет собой интеграл от функции f{z) по замкнутому
контуру С, состоящему из дуги С] и дуги С8, геометрически
совпадающей с дугой С^, но противоположной ей по напра-
направлению. Если этот интеграл равен нулю, то равна нулю и
S 41 ТЕОРЕМА КОШИ
разность B0), откуда
57
Таким образом, из теоремы Коши следует, что если функция
аналитична в некоторой односвязной области О, то, какова
бы ни была дуга С внутри этой области, величина \ f(z) dz
с
зависит только от начальной точки zn и конечной точки Z
дуги С и, следовательно, для этого интеграла можно пользо-
пользоваться обозначением
z
\f{z)dz.
го
Докажем, что если функция f(z) аналитична в одно-
связной области Q, содержащей точки zQ и Z, причем
величина z0 постоянна, a Z изменяется, то в этой об-
области функция
= ]f(z)dz
B1)
является аналитической и
Положив, как и раньше, f(z) = u-\riv, где и = и(х, у),
v = v(x, у), и обозначив zo = xo-\-iyQ, Z = X-\-iY, получим
с помощью формулы A1)
2
F(Z) = \f{z)dz = U{X, Y) + IV(X, П
го
где
(X, Y)
U(X, Y)= \ udx — vdy, B2)
(*о..Уо)
(X, Y)
V(X, Y)= \ vdx-\-udy. B3)
Uo. .Уо)
') Очевидно, справедливо и обратное утверждение: если в не-
некоторой области интеграл от функции f (z) не зависит от пути
интегрирования, то интеграл по всякому замкнутому контуру, рас-
расположенному в этой области, равен нулю.
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
(Гл. 11
Основываясь на свойствах криволинейных интегралов от пол-
полных дифференциалов (см. [1], п. 142), можно утверждать,
что полные дифференциалы функций U(X, Y) и V(X, Y)
равны подынтегральным выражениям в правых частях равенств
B2) и B3). Поэтому
откуда
дЛ-а(Х Y) d^-
дХ— *• ' >' дУ —
dU_dV dU
дХ~дУ дУ''
-v(X, Y),
и(Х, Y),
dV
Но это означает, что для функции F(Z) выполнены условия
Коши—Римана, следовательно, эта функция является аналити-
аналитической в области Q. В соответствии с формулой B) имеем
что и требовалось доказать.
Если две функции имеют в некоторой области одинаковые
производные, то в этой области разность между функциями
постоянна.
Действительно, если ср (z) = Fj (z) — Fa (z) и F\ (z) = Fa (z),
то <p'(z) = 0. Но если y(z) = u(x, y)-\-iv(x, у), то
,, ч dv , , 'dv
и из равенства tp'(z) = O получим
ди _ n dv — r>
¦t— = U, 3— = U.
дх дх
Отсюда в силу условий Коши—Римана
ay oy
Следовательно, функции и(х, у), v{x, у), а значит, и функ-
функция <р (z), постоянны.
Пусть теперь Ф (Z) — какая-нибудь функция, для которой
§ 41
ТЕОРЕМА КОШИ
59
где f(Z) — аналитическая функция. Так как производная от
z
интеграла ^f(z)dz тоже равна /(Z), то по доказанному
z
где С—постоянная. Положив в этом равенстве Z = za, по-
получим 0 = ФB0)-)-С откуда С=—Ф(г0) и
z ' z
Эта формула совпадает с известной из интегрального исчи-
исчисления формулой Ньютона—Лейбница.
24. Вычислим интеграл
B4)
! — а)п
по замкнутому контуру С, если п является целым положитель-
положительным числом (если целое число п ^ 0, то по теореме
Коши \т^7а)Н— \ (z~ a)mdz = 0, так как т = — я^Ои
с с
подынтегральная ф}'нкция аналитическая во всей плоскости).
Если точка z = a находится вне области, ограниченной
контуром С, то подынтегральная функция — аналитическая
внутри и на контуре С и по теореме Коши
dz
; = 0.
Предположим теперь, что контур С один раз обходит
точку а, и будем считать, что направление обхода выбрано
так, что точка а остается слева. Тогда в силу теоремы Коши
(см. A9)) величина интеграла B4) не зависит от вида кон-
контура С, хотя, быть может, и отлична от нуля. Поэтому
в качестве контура С можно взять, например, окружность
радиуса R с центром в точке а. Уравнение такой окруж-
окружности в комплексной форме имеет вид
z — a —
60 ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
Отсюда dz = Rle'9 d<? и на основании A4)
[Гл. И
B5)
При
со о
\ (н = 2, 3, ...) получим
dz
С
(г —a)"
n~l «A—
.el(l-n)
1
1 — n) <p
— A_„)Д»-1
так как e2ltd — «)< = е° = 1.
Если же л = 1,, то из B5) следует, что
= 0,
2я
= t \ dtp = 2iu.
i — a i T
B6)
Итак, даже если точка а находится внутри контура С,
то интеграл B4) отличен от нуля только при н=1.
Из B6) следует, что если контур С
обходит k раз точку а в положитель-
положительном направлении (на рис. 18 k = 2), то
B7)
Рис. 18.
если же контур С обходит k раз точ-
точку а в отрицательном направлении, то
dz nL_: ^щ
25. Равенства B6) — B8) находятся в тесной связи с определе-
определением логарифмической функции. Действительно, для неопределен-
неопределенного интеграла имеем:
— In (z — я) -\-С.
г — а
Подынтегральная функция аналитична всюду, кроме точки г = а,
и поэтому в любой односвязной области, не содержащей точки
г = а, интеграл по f — дуге, принадлежащей этой области,
41
ТЕОРЕМА КОШИ
61
не зависит от пути интегрирования, а зависит только от начальной
точки 2j и конечной точки z.2 дуги т-
Допустим, для простоты, что д = 0, и рассмотрим интеграл
Пусть г, = 1 и г, = г являются соответственно начальной и конеч-
конечной точками дуги -у и пусть дуга -у не пересекает отрицательной
части действительной оси и не проходит через точку 2=0. Тогда
можно дугу -у включить в односвязную область, не содержащую
точки z = 0 и точек отрицательной части действительной оси;
7
Рис. 19.
в такой области функция In г б\дет непрерывной и аналитической
(отрицательная часть действительной оси является для функции
In г = In ]г| + ' argz линией разрыва, так как в сил\ определения
главного значения аргумента величина argz терпит разрыв при
действительных отрицательных значениях 2). При этих условиях
независимо от формы дуги f будем иметь
— = \ — = In z — In 1 = In z.
Если теперь соединить точку 1 с точкой z дугой f так, чтобы
дуги т и ]' образовывали замкнутый контур /, один раз окр)жаю-
щий точку z = 0, то в силу равенства B6) получим
Г dz „ .
если направление на контуре / выбрано против часовой стрелки.
Но так как (рис. 19)
S?
62
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл II
(знак зависит от того, какое из расположений, указанных на рис. 19,
имеет место, а именно: верхний знак относится к рис. 19, а, ниж-
нижний— к рис. 19, 6), то
Если дуга f' такова, что замкнутый контур, образованный ею и
дугой ¦[, k раз обходит точку г = 0, то на основании формулы B7)
или B8) получим
1'
Поэтому, если Г — любая не проходящая через точку z = 0 дуга
с начальной точкой 1 и конечной точкой г, то
причем выбор значения многозначной ф\нкции Lnz в правой части
этого равенства зависит от выбора дуги Г.
§ 5. Интегральная формула Коши
26. Предположим, что функция /(С) является аналитиче-
аналитической в односвязной области Q плоскости С, а также на кон-
контуре Г, ограничивающем эту область. Пусть, далее, z — лю-
любая точка внутри области О
(рис. 20). Описав из точки z,
как из центра, окружность f ра-
радиуса р так, чтобы она цели-
целиком лежала внутри области О,
в силу A9) получим
~. B9)
Рнс- 20- Теорема Коши для составного
конгура применима, так как
единственной особой точкой в области О для подынгеграль-
ной функции I является точка Л = 2 и, следовательно,
в двусвязной области между контурами Г и f эта функция
является аналитической. Заметим, чю в равенаве B9) ра-
ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
63
диус р окружности f может быть выбран произвольно, лишь
бы эта окружность лежала внутри области Q.
Так как функция /(С) является аналитической, а следо-
следовательно, и непрерывной в области О, то, как бы ни было
мало ?^>0, для любой точки С на окружности ? справедливо
неравенство
1/@ -/
если только радиус р окружности -у достаточно мал (напо-
(напоминаем, что точка z — центр этой окружности и, следова-
следова[С \
тельно,
С /(С)
С — z [ = р). Поэтому
dH
7 ' 7
C0)
Здесь мы воспользовались свойством 6) интеграла (стр. 51)
и тем, что ! С — z | = р на дуге f.
Так как е можно взять сколь угодно малым, то нера-
неравенство C0) означает, что
С/(ГОЛ
ГОЛ С/?)«?_
C1)
Но, как уже было отмечено, величина V
ПРИ
V ^yzi—
^
шении р не изменяется, поэтому знак предела в левой части
C1) можно опустить. Если учесть также, что в силу B6)
то из C1) будем иметь
Сопоставляя последнее равенство с равенством B9), полу-
получим" так называемую интегральную формулу Коши:
C2)
С —г *
64
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. I!
Величина, стоящая в правой части интегральной формулы
Коши^называется интегралом Коши. Для вычисления интег-
интеграла Лоши нужно знать значения функции /(г) только на
контуре Г, следовательно, интегральная формула Коши по-
позволяет находить значения аналитической функции в любой
точке, лежащей внутри области G, если известны значения
этой функции на контуре Г, ограничивающем область G.
Если точка z лежит вне области О, то интеграл Коши
равен нулю в силу теоремы Коши, так как в этом случае
подынтегральная функция в C2) является аналитической
в области Q.
27. Применяя интегральную формулу Коши, докажем, что
производная аналитической функции также является
аналитической функцией.
Пусть f(z) является аналитической функцией на замкну-
замкнутом контуре Сив ограниченной этим контуром области;
тогда, в соответствии с интегральной формулой Коши,
J^'—ы^ с-* •
где z — любая точка внутри рассматриваемой области.
Какова бы ни была внутренняя точка z данной области,
величину j ft 1 можно выбрать столь малой, что точка z-\-h
будет также лежать внутри этой области. Будем, например,
считать, что | ft | меньше кратчайшего расстояния точки z до
контура С. На основании интегральной формулы Коши
/(С)Л_
С
С—г —Л
А
-/(*)_ 1 С Г /@ _ Ш.
~~ 2nih
с
или, после несложных преобразований,
/(z + A)-/(z)_ I Г /(C)rfC
h — 2ти } (С— z — Л) (С — 2)'
с
При ft-^-О левая часть этого равенства стремится к /'(z),
f (С)
f (С)
f (С)
а подынтегральная функция в правой части — к / \2. Пре-
(<. — г)
ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
65
дельный переход под знаком интеграла в правой части C3)
приводит, таким образом, к формуле
f(z\— '
C4)
Справедливость этой формулы будет доказана, если будет до-
доказано, что
hm
Л
f / (С)
Для этого достаточно установить, что разность
C5)
стремится к нулю при Л —0.
Обозначим через Ь кратчайшее расстояние от точки z до кон-
контура С (рис. 21); тогда для любой точки С этого контура | С — г\
Так как сторона треугольника
не меньше разности двух других
его сторон, то для расстояния от
точки С контура до точки z-\-h
справедливо неравенство
(| Л | взят столь малым, что
| Л | < Ь). Пусть М — наиболь-
наибольшее значение модуля функ-
функции /(г) на контуре С, тогда для любой точки С этого контура
М
(8-| А I)
и на основании свойстеэ 6) интеграла (стр. 51)
Ml
I1 /(C)rfC
J (С-2-ЛМС-
i —1Л1
3 И. Г. Арамановнч и др.
66
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. I!
где I — длина дуги С. Но тогда на основании C5)
/(О «С
.М/
I - | h
при Л—»0, и формула C4) доказана.
Теперь, составив с помощью формулы C4) отношение
[f'(z-\-h)—f'(z)]jh и перейдя к пределу при h-+Q, можно
путем аналогичных выкладок доказать, что
7 W— 2ш ) (С-гK"
Так же доказывается, что при любом целом л
(С —2)»+I •
Равенство C6) получено при условии, что функция f(z)
является аналитической как па контуре С, так и в области,
ограниченной этим контуром. Но если функция f{z) является
аналитической в точке z, то всегда можно провести из этой
точки, как из центра, окружность С столь малого радиуса,
что функция f(z) остается аналитической на этой окруж-
окружности и в круге, ею ограниченном, и следовательно, на осно-
основании формулы C6) можно заключить, что в точке г и в лю-
любой другой точке достаточно малой окрестности точки z
существует производная любого порядка п этой функции.
Итак, из аналитичности функции в некоторой точке,
т. е. из существования первой производной данной функ-
функции в какой-либо окрестности этой точки, следует су-
существование в окрестности той же точка производных
данной функции любого порядка, а следовательно, и ана-
аналитичность этих производных.
28. Интегральная формула Коши и формула C6) могут
служить для вычисления интегралов по замкнутым контурам.
') Для удобства запоминания заметим, что формально фор-
формулы C4), C6) можно получить из интегральной формулы Коши,
дифференцируя обе ее части по г (в правой части дифференциро-
дифференцирование производится по параметру г под знаком интеграла).
§ 5]
ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
67
Пример
Вычислить интеграл
С e'dz
] z (г - 20 ¦
гае С — окружность радиуса 2 с центром в точке Зг.
Функция f (г) =— внутри круга, ограниченного окружностью
С, аналитична, поэтому, применяя интегральную формулу Коши,
получим (роль С играет г, а роль г — число 2i)
С С
Пример 2. Вычислить интеграл
cos z dz
где С — замкнутый контур, обходящий точку I один раз. Применяя
формулу C6) к функции/(г) = cos г, получим:
С cos z dz _ 2я j rf2 (cos г)
,) B-0' '
dz'1
= — ш cos i = — tc( ch 1.
\Z=l
Подробнее о вычислении интегралов по замкнутым кон-
контурам см. в гл. V.
29. Мы условились называть интеграл вида
C7)
интегралом Коши в предположении, что С— замкнутый контур,
а функция f(z) — аналитическая па контуре Сив области G,
ограниченной этим контуром. При этом оказалось что функ-
функция, определяемая интегралом C7), совпадает с f(z) внутри
области О и равна тождественно нулю вне контура С. Если
считать, что С—произвольная кусочно-гладкая дуга (или
даже совокупность нескольких таких дуг), а функция /(С)
задана только на контуре С и непрерывна на нем, то вели-
величину C7) принято называть интегралом типа Коши. Интеграл
Коши является, очевидно, частным случаем интеграла типа Коши.
Функция, определяемая интегралом типа Коши,
С
68
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
[Гл. II
определена всюду, кроме точек дуги С, так как в любой
точке z, не принадлежащей С интеграл типа Коши суще-
существует (подынтегральная функция ? ' остается непрерыв-
непрерывной на контуре С).
Дословно повторяя выкладки и рассуждения, с помощью
которых была обоснована формула C4), можно найти произ-
производную интеграла типа Коши в любой точке z, не принадле-
принадлежащей дуге С:
и тем самым доказать, что интеграл типа Коши является
функцией аналитической в любой точке, не лежащей на
дуге С. Для производной любого порядка п интеграла типа
Коши справедлива формула, аналогичная формуле C6):
ЗАДАЧИ К ГЛАВЕ II
1. Проверить условия Коши — Римана для следующих ф_\нкций:
a) w = sin 2; б) w = cos 2; в) w = Ln 2; г) w = Arcsin 2;
д) да = 2™ (,i — целое число).
2. Найти аналитическую функцию переменной z (z = x-\-iy),
действительная часть которой равна:
х — оху , и^ х —у —|— za, в^
д) 2?* sin _у.
3. Найти аналитическую функцию переменной г, мнимая часть
которой равна
а> —(->_[-ГK + у" б) 2л^+3х; в) arctg-j> *>0;
г) ех (у cosy + х sin _y) -\-x -\-y.
4. Найти угол поворота и коэффициент растяжения при отоб-
отображении с помощью ф)икцнй w = z2 и м) = 23 в каждой из сле-
следующих точек:
1 ^
а) 2=1; б) 2 = 1; в) г = -^; г) 2=
'; Д) г = УЗ-Л
5. Выяснить, какая часть плоскости г сжимается и какая растя-
растягивается, если отображение осуществляется функцией:
a) w = г2; б) w = —; в) w = z"-\-2z; г) w = e-; д) ai = ln B — 1).
ЗАДАЧИ К ГЛ. II
69
6. Вычислить ^ Im 2 dz, если путь интегрирования С:
С
а) является прямолинейным отрезком, соединяющим точку О
с точкой 2 + i;
б) состоит из прямолинейного отрезка, соединяющего точку О
с точкой /, и прямолинейного отрезка, соединяющего точку i
с точкой 2 + (.
7. Вычислить I | 2 | Й2, если путь интегрирования С является:
а) прямолинейным отрезком, соединяющим точку —1 с точ-
точкой 1;
б) полуокружностью радиуса 1 с центром в начале координат,
лежащей в верхней полуплоскости, причем точка —1 является на-
начальной, а точка 1 — конечной.
В задачах 8—13 следует пользоваться теоремой Коши, интег-
интегральной формулой Коши и формулами, получаемыми из интеграль-
интегральной формулы Коши дифференцированием. Направление вдоль кон-
контура С в этих задачах — против часовой стрелки.
С 2 d
8. Вычислить
р
С г2 dz
.) z — 2г
С
если:
а) С — окружность радиуса 3 с центром в начале координат;
б) С — окружность радиуса 1 с центром в начале координат.
. „ С sin 2 dz _
9. Вычислить \ . I ¦ , если С — окружность с центром
в точке — i.
10. Вычислить
dz
F+~9'
а) С — окружность радиуса 2 с центром в точке 11;
б) С — окружность радиуса 1 с центром в точке —11.
11. ВЫЧИСЛИТЬ \ г 4-Q1-' если:
а) С—окружность радиуса 2 с центром в точке 2«;
б) С — окружность радиуса 2 с центром в точке —2i.
12. Вычислить
замкнутого контура С.
13. Вычислить
С ez dz
\ /~ | 'ти > если точка г = — 2 находится внутри
dz
если:
а) С — окружность радиуса R < 2 с центром в точке 2 = 1;
б) С — окружность радиуса R < 2 с центром в точке 2 = —1;
в) С — окружность радиуса R> 1 с центром в точке 2=0.
ГЛАВА III
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
§ 1. Линейная и дробно-линейная функции
30. Отображение, осуществляемое линейной функцией
w = az-\-b, A)
где а и & — комплексные постоянные, о^О, является кон-
конформным во всей плоскости, так как производная этой функ-
функции во всех точках плоскости существует и отлична от нуля.
Рассмотрим некоторые частные случаи линейных преобра-
преобразований, причем для большей наглядности будем считать
плоскость w совмещенной с пло-
плоскостью г.
1°. w = z^rb.
Так как сложение комплекс-
комплексных чисел сводится к сложе-
сложению векторов, то при отобра-
отображении w = z -\-Ь всякая точка
z смещается в соответствую-
о
х,и
щую точку w с помощью век-
Рис. 22. тора сдвига, изображающего
данное комплексное число b
(рис. 22). Ввиду того, что b постоянно, т. е. вектор сдвига
одинаков для всех точек, мы инеем преобразование парал-
параллельного переноса.
2°. и) = е"\г, а — действительное число.
Так как е1Л — комплексное число с модулем, равным еди-
единице, и аргументом а, то в соответствии с правилом умноже-
умножения комплексных чисел (стр. 13) переход от точки z к точке w
осуществляется с помощью поворота точки z на угол а около
начала координат. Величина а постоянна, следовательно,
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕИНАЯ ФУНКЦИИ
71
рассматриваемое преобразование является преобразованием
поворота вокруг начала координат (рис. 23).
3°. w = rz, г — действительное положительное-- число.
Так как arg r = 0, то в соответствии с правилом умноже-
умножения комплексных чисел Arg w = Arg z, \w\ = r\z\. Первое
из этих равенств показывает, что точка z и соответствующая
ей точка w находятся на одном и том же луче (рис. 24),
выходящем из начала координат, а из второго равенства
следует, что отношение расстояния точки w от начала коор-
координат к расстоянию соответствующей точки z от начала
У.»
=гг
Рис. 23.
Рис. 24.
координат постоянно и равно г. Следовательно, рассматри-
рассматриваемое преобразование является преобразованием подобия
с центром подобия в начале координат; г — коэффициент
подобия.
4°. Общий случай линейного преобразования
w = az -\-b
сводится к рассмотренным выше простейшим преобразова-
преобразованиям. Действительно, если г и а — модуль и аргумент числа
а, то w = re'az -\- b, и переход от точки z к точке w осу-
осуществляется путем последовательного применения следующих
операции: 1) поворота около Е1ачала координат на угол а,
2) преобразования подобия с центром подобия в начале коор-
координат и коэффициентом подобия, равным г, 3) параллельного
переноса с помощью вектора сдвига, соответствующего комп-
комплексному числу Ъ.
Пример 1. Найти функцию, отображающую равнобедренный
прямоугольный треугольник с вершинами в точках А, В, С, соот-
соответствующих числам 3-(-2(, 7 + 2», 5+-4J, лежащий в плоскости г,
72
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гт III
на равнобедренный прямо}гольный тре)гольник с вершинами в точ-
точках О, В', С плоскости w, соответств)ющих числам 0, — 2/, 1 — i
(рис. 25).
Так как треугольники ABC и ОВ'С подобны, то отображение
может быть осуществлено с помощью линейной ф\нкции.
У
5-41
О
в'
Si
Рис. 25.
Отображение можно разложить на следующие операции:
1) параллельный сдвиг, смещающий точку А в начало коорди-
координат; этот сдвиг производится вектором Ад, соответствующим числ>
— C-1-20, и, следовательно, осуществляется функцией t = z —
-C-1-20;
2) поворот около начала координат на угол —тт, соответст-
соответствующий преобразованию
;. _
или Г = — it;
3) преобразование подобия с центром подобия в начале коор-
координат и коэффициентом подобия, равным 1,2; это преобразование
осуществляется функцией w = -у Т- Таким образом, окончательно
¦ C
], или » = -| + |'-
31. Точки А и В называются симметричными относи-
относительно окружности (рис. 26), если
1) они лежат на одном луче, выходящем из центра
окружности;
2) произведение их расстояний or центра окружности
равно квадрату радиуса окружности:
ОА-ОВ= R\
или
О А •
B)
И
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИИ
73
Рис. 26.
Отсюда, в частности, следует, что если точка А прибли-
приближается к окружности, то точка В также приближается к
окружности и всякая точка, лежащая на окружности, симмет-
симметрична самой себе относи-
относительно этой окружности. Из
B) следует также, что точ-
точкой, симметричной центру
окружности, является беско-
бесконечно удаленная точка.
Если центр О окружно-
окружности совпадает с началом
координат и одна из двух
симметричных относительно
окружности точек изобра-
изображает комплексное число z,
то другая соответствует числу R^/z. Действительно, модули
чисел z и R^jz удовлетворяют условию B), так как
R* _
и, кроме того, числа z и R^jz изображаются точками, лежа-
лежащими на одном луче, выхо-
выходящем из начала коорди-
координат, так как Arg -=—=
= — Arg z = Arg г.
В частности, точки z и
1/z симметричны относитель-
х но окружности единичного
радиуса с центром в начале
координат {единичной ок-
окружности), а так как точ-
точки 1/5 и 1/г симметричны
относительно действитель-
действительной оси, то преобразование
w=l/z состоит из двух симметричных отражений: относи-
относительно единичной окружности и относительно действительной
оси (рис. 27).
Функция w =1/2 осуществляет взаимно однозначное ото-
отображение расширенной плоскости z на расширенную плос-
плоскость w; при этом точке 2 = 0 соответствует точка щ> = оо,
Рис. 27.
74
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. [Ц
а точке и> = 0 соответствует точка 2 = со. Условимся счи-
считать, что угол между линиями в бесконечно удаленной точке
одной из плоскостей (z или w) равен углу между образами
этих линий в начале координат другой плоскости. Так как
во всех остальных точках производная w'=—Ijz1 не равна
нулю, то при указанном условии отображение будет конформ-
конформным во всей расширенной плоскости.
32. Дробно-линейная функции
W
__аг-\-Ь
C)
где а, Ь, с, d — комплексные постоянные и ad — be ф 0]),
осуществляет взаимно однозначное отображение всей расши-
расширенной плоскости г на всю расширенную плоскость w. Дей-
Действительно, разрешив C) относительно z, получим
г =
dw — b
— ew -j- a '
и следовательно, не только всякому z соответствует единст-
единственное значение w, но и каждому w соответствует единст-
единственное значение г. Точке z = — djc соответствует точка
w = co, а точке w = a/c— точка г = со.
Произвольное дробно-линейное преобразование C) может
быть получено с помощью последовательного применения
линейных преобразований и преобразования w=\jz. Дейст-
Действительно, преобразование C) легко приводится к виду
аг-\-Ь а (сг -\- d) -f- (be — ad) a . be — ad 1
W cz~\-d с (cz -f- d) T ' с cz~\-d'
Следовательно, к преобразованию C) можно прийти путем
последовательных преобразований:
be — ad
Т.
Отсюда следует, что если какое-нибудь свойство справедливо
при линейном преобразовании и при преобразовании w=\jz,
то оно справедливо и при дробно-линейном преобразовании
C). Например, можно утверждать, что отображение, осуще-
1) Если ad — be = 0, то а : с — Ь : d и w = k, где k — постоянная.
§ И
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИИ
75
ствляемое дробно-линейной функцией, конформно во всей
плоскости, так как этим свойством обладают отображения,
осуществляемые линейной функцией и функцией w=\jz.
33. Дробно-линейное преобразование обладает круговым
свойством, состоящим в том, что с помощью этого преобра-
преобразования окружность всегда отображается также на окруж-
окружность, если прямую считать частным случаем окружности —
окружностью бесконечного радиуса.
Для доказательства этого свойства достаточно проверить,
что круговое свойство выполнено при преобразовании w —
= \/z, так как для всех простейших преобразований, из ко-
которых состоит линейное преобразование (стр. 70—71), кру-
круговое свойство очевидно.
Считая z = x-\-iy, w = uJriv, перепишем равенство
w=\jz в виде u-\-iv = -—-j—r-, или
откуда
x-'riy '
u- -\- v-' J
и — iv
и- + v*'
D)
Уравнение произвольной окружности в плоскости z имеет
вид
A (jc2 + У)
C)
(при А = 0 имеем прямую — окружность бесконечного радиу-
радиуса). Подставив в (о) х и у из D), получим уравнение отобра:
женной линии
Cv
I n — о
или
v-\ a' + v*
А + Ви — Cv -j- D (и2 + v*) = 0,
являющееся также уравнением окружности (при D = 0 полу-
получим уравнение прямой), и круговое свойство доказано.
Всякая окружность делит всю плоскость на две области:
внутренность круга и внешность круга, если радиус окруж-
окружности конечен, и две полуплоскости, если радиус окружности
бесконечен. При отображении с помощью дробно-линейной
функции каждая из двух областей, ограниченных окружностью
76
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. Ш
в плоскости z, отображается на одну из двух областей, огра-
ограниченных соответствующей окружностью в плоскости w.
Так, например, из сказанного выше относительно ото-
отображения, осуществляемого функцией w=\jz, следует,
что с помощью этой функции единичная окружность |,г|=1
отображается сама на себя (т. е. на такую же окружное >ь
плоскости w), причем внутренность единичного круга пло-
плоскости z отображается на внешность единичного круга пло-
плоскости w, а внешность единичного круга плоскости z — на
внутренность единичного круга плоскости w. Вообще, для
того чтобы определить, на какую область плоскости w отобра-
отображается каждая из двух областей, ограниченных окружностью
в плоскости z, следует проследить за тем, в каком направ-
направлении движется точка w, когда соответствующая ей точка z
непрерывно перемещается по окружности. При этом та из
областей, ограниченных окружностью в плоскости г, которая
находится, например, слева от движущейся по окружности
точки, перейдет в область плоскости w, расположенную также
слева, если смотреть в сторону движения точки w. Это сле-
следует из того, что при конформном отображении углы сохра-
сохраняются не только по величине, но и по .направлению.
Если а, Ь, с, d — действительные числа, то дробно-линей-
дробно-линейная функция
az
"" _ cz-\-d
принимает при действительных значениях z действительные
значения, и следовательно, действительная ось плоскости z
отображается на действительную ось плоскости w. При этом,
так как действительная ось делит плоскость на две полу-
полуплоскости («верхнюю» и «нижнюю»), то верхняя полупло-
полуплоскость плоскости z отображается или сама на себя (т. е. на
верхнюю полуплоскость плоскости w), или на нижнюю полу-
полуплоскость, в зависимости от того, в каком направлении при
заданных а, Ь, с, d движется по действительной оси точка w,
если соответствующая точка z перемещается по действитель-
действительной оси, например, слева направо.
34. Область, ограниченная дугами двух окружностей,
в силу кругового свойства дробно-линейной функции, отобра-
отображается этой функцией или на облапь такого же вида, или
на область, ограниченную дугой окружности и прямолинейным
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИИ
77
офезком (внутренность или внешность кругового сегмента),
или на угол между двумя лучами. Для выяснения того, какой
из указанных случаев осуществляется в некотором конкрет-
конкретном примере, следует иметь в виду, чго если на данной окруж-
окружности (или прямой) расположена точка, отображающаяся в
бесконечно удаленную точку плоскости w, то эта окружность
(или прямая) отображается в прямую, в противном случае
она отобразится в окружность конечного радиуса. Поэтому
если, например, общая точка двух окружностей отображается
в бесконечно удаленную точку, область, ограниченная дугами
этих окружностей, должна отобразиться в угол.
Пример 2. Найти область плоскости w, на которую отобра-
отображается с помощью функции
z — l
заштрихованная на рис. 28, а область плоскости г, ограниченная
дугами окружностей радиуса 1/2 с центрами в точках — 1 и 1.
"К
Ok
6)
Рис. 28.
Окружности пересекаются в точках / и — i под прямым углом,
так как радиусы, идущие в точку пересечения окружностей, взаимно
перпендикулярны. Так как и; = со при г = — i, то одна из общих
точек окр)жностен отображается в бесконечно удаленную точку
плоскости w. Следовательно, заштрихованная область отображается
на угол.
Другая общая точка отображается в начало координат (ю = 0
при 2 = () и, таким образом, вершина утла, на который отобража-
отображается данная область, находится в начале координат. Величина угла
равна я/2, так как отображение конформно, а для тою чтобы опре-
определить положение угла, достаточно найти хотя бы одну точк) на
78
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
какой-нибудь из его сторон. Точка г = /2—1, как это видно из
рисунка, находится на дуге ¦(. При z = /2 — 1 имеем
'l- ' - О'
= 2A—/2L-2 A-/2') f _ (l-yr2
4 — 2/2
2-/2"
Эта точка, как нетрудно видеть, расположена в третьей четверти
на биссектрисе координатного угла (ее координаты одинаковы и
отрицательны). Следовательно, дуга ¦/ отображается в луч Г, иду-
идущий из начала координат по биссектрисе координатного угла в
третьей четверти (рис. 28, б). Так как углы сохраняются не только
по величине, но и по направлению, то для того чтобы получить
вторую сторону угла Г', следует луч Г повернуть около начала
координат на угол 90° по часовой стрелке, потому что в плоскости
2 при движении по дуге 7 от точки i (отображающейся в начало
координат плоскости w) заштрихованная на рис. 28, а область оста-
остается справа.
35. Дробно-линейная функция обладает свойством
симметрии: две точки, симметричные относительно
окружности С, отображаются с помощью дробно-линейной
функции в точки, симметричные относительно той окруж-
окружности, на которую отобра-
отображается окружность С.
Рис. 29.
Рис. 30.
Переходя к доказательству этого свойства, заметим сна-
сначала, что если окружность Г проходит через точки А к В,
симметричные относительно окружности С, то окружность Г
ортогональна к окружности С.
Действительно, пусть М (рис. 29) — точка пересечения Г
и С. Тогда в силу определения симметрии
§ И
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИИ
79
Но, в силу известной теоремы о касательной и секущей, от-
отсюда следует, что радиус ОМ касается окружности Г, и, сле-
следовательно, окружность Г ортогональна к С.
Докажем теперь, что если окружности 1\ и Г2, пересекаю-
пересекающиеся в точках А и В (рис. 30), ортогональны к окружности
С, то точки А п В симметричны относительно окружности С.
Действительно, проведем через одну из точек пересечения
Т1 с Г2, например, через точку А, луч ОА из центра окруж-
окружности С, и пусть В* — вторая точка пересечения этого луча
с окружностью Г\. Тогда, в силу ортогональности окружно-
окружностей Г\ и С, обозначив через М точку пересечения С и 1\,
с помощью теоремы о секущей и касательной получим
ОА ¦ ОВ* = ОУИ'2 = R*, следовательно, точка В* симметрична
с точкой А относительно окружности С. Те же рассуждения
применимы и к окружности Г.2, которая тоже проходит через
точку А и тоже ортогональна к С. Следовательно, та же
точка В*, симметричная точке А относительно С, лежит и на
окружности Г.2, а значит,
точка В* совпадает с точ-
точкой В.
Доказанное свойство
сохраняется, если окруж-
окружность С заменяется пря-
прямой. Читатель без труда
докажет, что все окруж-
окружности, проходящие через
точки А и В, симметрич-
симметричные относительно прямой,
ортогональны к этой пря-
прямой (рис. 31); и обратно:
если две окружности, проходящие через точки Л и В, ортого-
ортогональны к прямой С, то эти точки симметричны относительно С.
Свойство симметрии дробно-линейной функции следует из
доказанных предложений. Действительно, если точки А и В
плоскости 2, симметричные относительно окружности С
(рис. 32), с помощью некоторой дробно-линейной функции
отображены соответственно в точки А' и В' плоскости w, a
окружность С — в окружность С, то всевозможные окруж-
окружности, проходящие через точки А и В, отобразятся, в силу
кругового свойства дробно-линейной функции, на окруж-
окружности, проходящие через точки А' и В'. Но окружности.
Рис. 31.
80
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл III
проходящие через точки А и В, как было доказано выше,
ортогональны к окружности С, следовательно, ввиду кон-
конформности дробно-линейного отображения, окружности, про-
проходящие через точки А' и В', ортогональны к окружности С;
отсюда следует, что точки А' и В' симметричны относи-
относительно окружности С", и доказательство свойства симметрии
завершено. Применим свойство симметрии для решения двух
важных задач.
1. Найти дробно-линейную функцию, отображающую верх-
верхнюю полуплоскость на внутренность единичного круга (рис. 33).
°СС
Рис. 33.
При этом отображении некоторая точка ч верхней полу-
полуплоскости z должна отобразиться в центр единичного круга
(т. е. в начало координат плоскости w). В силу свойства
симметрии точка а, симметричная точке а относительно дей-
действительной оси, должна отобразиться в точку оо, симмет-
симметричную точке 0 относительно единичной окружности пло-
§ И
ЛИНЕЙНАЯ И ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИИ
81
скости w, так как действительная ось плоскости z, по усло-
условию, должна быть отображена на единичную окружность пло-
плоскости w. Дробно-линейная функция, удовлетворяющая пере-
перечисленным условиям (т. е. такая, что о> —0 при z = & и
да = оо при z — 5), имеет вид
где k — комплексная постоянная.
Величина k не вполне произвольна, гак как при действи-
действительном значении г точка w должна находиться на единич-
единичной окружное!и и, следовательно, *w = 1. С другой сто-
— 3.
роны, при действительном z должно бьпь ' z — а.
поэтому \k\ = \, т. е. k = e'f, где <р — любое действитель-
действительное число. Следовательно, отображающая функция имеет вид
Как и следовало ожидать, существует бесконечное
множество дробно-линейных функций, осуществляющих
требуемое отображение. Каждая из этих функций определя-
определяется значениями трех действительных параметров (параметра 9
и двух действительных параметров, определяющих комплекс-
комплексное число а).
2. Найти дробно-линейную функцию, отображающую внут-
внутренность единичного круга на себя (рис. 34)
Рис. 34.
Пусть а — точка внутри единичного круга плоскости z,
отображающаяся в центр круга (в начало координат) пло-
плоскости w. Тогда точка 1/а, симметричная точке о. относи-
относительно единичной окружности, должна отобразиться в точку,
симметричную центру круга, т. е. в бесконечно удаленную
82
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
точку плоскости w. Таким образом, w = 0 при z = i и
яу = оо при 2= 1/а. Дробно-линейная функция, удовлетворяю-
удовлетворяющая этим условиям, имеет вид
, z — a
W = k p=,
2 —
2 — a ,, 2 — i
I = Я =
az — 1 1 — a
где k' = — ka.
Постоянная k' не произвольна, так как точки единичной
окружности плоскости z отображаю 1ся в точки единичной
окружности плоскости w, и, в частности, при z—\ имеем
,, 1 — а
|а>!=1. Но при z=\ имеем w = k ,_-, а так как
= 1, то \kn = l, т. е. /г' = е"? (ср — действительное
1 —-
число). Таким образом, общий вид функции, отображающей
единичный круг на себя, таков:
1 = р"?.
В этом равенстве также участвуют три действительных
параметра. Произвольность параметра ср связана с тем, что
при повороте на любой угол вокруг центра круг отобража-
отображается сам на себя (умножение на е'? соответствует повороту
на угол tp вокруг начала координа(). Произвольность комп-
комплексного числа а( а <^ 1), которое определяется, как и вся-
всякое комплексное число, двумя действительными числами, оз-
означает, что можно, оюбражая единичный круг сам на себя,
потребовать еще, чтобы любая заданная точка, лежащая вну-
внутри круга, отобразилась в центр круга.
Пример 3. Найти центр и радиус окружности, на которую
функция
w —
(Im z-2 Ф 0,
отображает действительную ось.
При заданном отображении точка г = г2 переходит в точку
да = оо. Так как действительная ось отображается на окружность,
то точка 5о, симметричная точке г2 относительно действительной
оси, отобразится в точку, симметричную бесконечно удаленной точ-
точке относительно окружности, т. е. в центр окружности. Таким об-
образом, центр окружности находится в точке
Z л Z | Z 9 Z ] Z | Z о
— 21тг,
21т
НЕКОТОРЫЕ ОБЩИЕ ТЕОРЕМЫ
83
Чтобы найти радиус окружности, достаточно найти какую-нибудь
одну точку окружности и определить ее расстояние от центра.
Имеем
lim
—г.
Следовательно, точка г = оо на действительной оси переходит в
точку м=1 на окружности, и радиус окружности равен расстоя-
расстоянию этой точки от центра, т. е.
1 г„ —г,|
г., — г.,
2 1ГП2.
Можно было бы вместо образа точки г = со взять, например, об-
образ и» = —точки 2 = 0. Тогда /?= а»0 — — . Читателю рекомен-
рекомендуется проверить, что этим равенством определяется уже найден-
найденное значение R.
§ 2. Некоторые общие теоремы
36. Приведем без доказательства некоторые теоремы те-
теории конформных отображений.
а) Теорема Рпмана о возможности конформного и вза-
взаимно однозначного отображения одной односвязной области
на другую.
Теорема Р и м а н а утверждает, что существует ана-
аналитическая функция w=f(z), отображающая взаимно
однозначно и конформно одну односвязную плоскую об-
область О, на другую О.г, если только ни одна из областей
Qv G.2 не принадлежит к числу двух исключительных.
Одним из таких исключений является вся расширенная
плоскость, другим—вся плоскость с одной выключенной
точкой (например, вся плоскость с выключенной бесконечно
удаленной ючкой, т. е. вся конечная плоскость).
Можно, далее, доказать, что аналитических функций, осу-
осуществляющих отображение односвязной области G{ на одно-
связную область G2 (если, конечно, ни одна из них не при-
принадлежит к числу исключительных), бесконечное мно-
множество, и для того чтобы обеспечить единственность
отображающей функции w=f(z), достаточно в какой-нибудь
точке г0 области О, задать значения
84
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
Геометрически эго означает, что единственность отображе-
отображения будет обеспечена, если для некоторой точки za области
Ot будет указан ее образ w0 и задан угол, на который при
этом отображении поворачивается бесконечно малая окрест-
окрестность точки za.
б) Принцип взаимно однозначного соответствия границ.
- Пусть область G ограничена гладким или кусочно-
гладким контуром Г и пусть, далее, функция w=f(z),
аналитическая в О и на Г, отображает контур Г вза-
взаимно однозначно на некоторый контур V, ограничиваю-
ограничивающий область G', причем, когда точка z обходит контур
Г так, что область О остается слева, соответству-
соответствующая точка w обходит контур Г так, что область (У
также остается слева. В этом случае, утверждает прин-
принцип взаимно однозначного соответствия, об-
область О отобразится с помощью функции f(z) взаимно
однозначно и конформно на область (У.
'Следовательно, в тех случаях, когда этот принцип при-
применим, для отыскания области, на которую функция w =
= /B) отображает заданную область О, достаточно обойти
границу области О и найти контур, на который эта граница
отображается функцией f(z). В дальнейшем принцип взаимно
однозначного соответствия будет неоднократно использован.
в) Принцип симметрии.
Пусть область О, содержащая в составе своей границы
некоторый прямолинейный отрезок f (конечной или беско-
бесконечной длины), отображается функцией w — f(z) на область
Рис. 35.
(У так, что отрезок ? отображается на прямолинейный отре-
отрезок "f'> входящий в границу области О (рис. 35). Обозначим
соответственно через L и V прямые, на которых лежат от-
отрезки f и т'. Имеет место следующая теорема (принцип
симлегри и): если функция f\z) аналитична в области
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
85
О, а также во всех внутренних точках граничного от-
отрезка 7, то эта функция аналитична также в области
О*, симметричной с О относительно прямой L, и обла-
обладает тем свойством, что любые две точки z^ и г.ъ
из которых одна лежит в О, симметричные относитель-
относительно L, оторбажаются в точки и>, и w.i, симметричные
относительно прямой L' ').
Из принципа симметрии, в частности, следует, что функция
w=f(z) отображает область, состоящую из области О, об-
области G* и отрезка f> Ha область, состоящую из области (У,
симметричной с ней относшельно V области О*' и отрезка
¦\' (рис. 35).
Прямолинейные отрезки f и Т' с помощью соответству-
соответствующих дробно-линейных преобразований можно отобразить на
дуги окружностей, и так как для дробно-линейных преобра-
преобразований имеет место свойство симметрии, то принцип сим-
симметрии справедлив и в том случае, когда f и f' — /.ути ок-
окружностей.
§ 3. Степенная функция. Функция Жуковского
37. Отображение, осуществляемое степенной функцией
w = zn, F)
где целое положительное число «2=2, является конформным
во всей плоскости, кроме точки z = 0, так как производная
этой функции существует и отлична от нуля всюду, кроме
точки z'=0. В точке г —0, как будет показано ниже, кон-
конформность отображения нарушается.
Введя в плоскостях z и w полярные координаты z^re'9
и ¦sy = pe'e, получим из F), что ре'ь = rnel1li, и следовательно,
р = г", 6 = л<р.
Из этих равенств следует, что окружности г = const с
центром в точке z = 0 плоскости z отображаются на окруж-
окружности р = const с центром в точке w = 0 плоскости w
(рис. 36), причем единичная окружность отображается сама
:) Если функция /(г) не определена в области, симметричной
с Q относительно прямой, на которой лежит отрезок fi то ее можно
доопределить так, чтобы теорема осталась справедливой.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. Ill
на себя, а лучи <р = const, выходящие из начала координат
плоскости z, на лучи 0 = const, выходящие из начала коор-
координат плоскости w. При этом луч ср = О, идущий по поло-
положительному направлению действительной оси, отображается
V,
Рис. 36.
сам на себя, т. е. на луч 0 = 0; луч v = a. плоскости z ото-
отображается на луч 6 = да плоскости w, и угол 0<?<а пло-
плоскости г(а<2тс/л) с вершиной в начале координат отобра-
отображается на угол 0<^8<^иа плоскости w. Следовательно, кон-
конформность отображения действительно нарушается в точке
г_0: углы в этой точке увеличиваются при отображении
рис. 37.
в п раз. В частности, угол 0<>О/л величины тс/л пло-
плоскости z отображается с помощью функции w = z" на верх-
верхнюю полуплоскость 0<6<> плоскости w. Угол 0<ср<
<^2т/п величины 2тс/я отображается на угол 0<9<2тс, т.е.
па всю плоскость без действительной положительной полу-
полуоси (рис. 37). На эту полуось отображаются обе стороны
рассматриваемого угла плоскости z.
§ з]
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
87
Для того чтобы отображение было взаимно однозначным
не только внутри угла 0<^ср<^2тс/я, но и на его сторонах,
следует в плоскости w произвести «разрез» по положитель-
положительной части действительной оси и условиться считать, что луч
о = 0 отображается на верхний, а луч ср = 2тс/л на нижний
край этого разреза (если луч <р = а, вращаясь против часо-
часовой стрелки, приближается к лучу ср = 2тс/я, то соответству-
соответствующий луч в плоскости w приближается к действительной
части положительной полуоси снизу).
Если w = zn, то каждой точке z соответствует единст-
единственная точка w, но одной и той же точке w (w ф О,
w Ф со) соответствует (стр. 15) п точек плоскости z, рас-
расположенных в вершинах правильного я-угольника с центром
в нулевой точке: отображение плоскости z на плоскость w
не является, следовательно, взаимно однозначным. Всякие два
значения z, соответствующие одному и тому же w (т. е. всякие
два значения величины \/~w), имеют один п тот же модуль и
аргументы, отличающиеся на число, кратное 2тс/я. Если одно из
2kjU
этих чисел z, то другое ze п , где k — целое.
Область плоскости z, не содержащая никаких различных
точек, соответствующих одному и тому же w, т. е. не со-
содержащая никаких двух различных вершин правильного
«-угольника с центром в начале координат, отображается с
помощью функции w = zn на соответствующую область пло-
плоскости w взаимно однозначно, т. е. в ней функция zn одно-
однолистна. Этим свойством во всяком случае обладает любая об-
область, целиком заключенная внутри угла величины 2тс/л с
центром в начале координат. В частности, как указано выше,
угол 0 <^ ср <^ 2тс/я отображается взаимно однозначно на всю
плоскость w с разрезом по положительной части действи-
действительной оси, причем лучу <р = 0 соответствует верхний, а
Г)
лучу ср = — нижний край разреза. Угол 2тс/я <^ <р <^ 4тс/я с
помощью функции w = zn также отображается взаимно одно-
однозначно на плоскость w с тем же разрезом, причем лучу
(р = 2и/я соответствует верхний, а лучу сс = 4л/я нижний
край разреза. Такое же отображение получим для каждого
из углов, на которые разбивают плоскость z лучи <f = 2kizjn,
где k — целое число, причем при отображении угла
2(&— 1) Я/'/2 <^ ср <^ 2Атс/л (А= 1, 2, , . .) на плоскость
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл III
с описанным выше разрезом лучу ср = 2(А—1)я/я ссь
ответствует верхний, а лучу y^ik-Jn нижний край разреза.
Для того, чтобы область плоскости z взаимно однознач-
однозначно отображалась на соо1ветствующую область плоскости w
с помощью функции w = zn, необходимо и достаточно, как
было отмечено выше, чтобы эта область не содержала двух
различных вершин какого-нибудь правильного «-угольника с
центром в точке 2 = 0 (т. е. двух различных точек вида
Ikri
ze n , где k — целое действительное число). Область, внутри
которой находится начало координат или бесконечно удален-
удаленная точка, таким свойством заведомо не обладает, так как в
первом случае область содержит достаточно малые правиль-
правильные л-угольники с центром в начале координат, а во втором
случае содержит достаточно большие «-угольники указанного
вида, и, следовательно, отображение такой области с по-
помощью функции w^zn на соответствующую область пло-
плоскости w не является взаимно однозначным.
38. В любой односвязной области, не содержащей точек
w^O и w = oo, можно определиib, как будет показано, од-
однозначные ветви функции z^y^w. Это означает, что в та-
такой области можно определить несколько однозначных ана-
аналитических функций, по отношению к каждой из которых
функция te> = z" является обратной. Эти функции и называют
однозначными ветвями функции -\/~w.
Вообще, пусть функция w=f(z), аналитическая в неко-
некоторой области G, отображает эту область на область G* и
такова, что обратная функция z = y(w) многозначна в обла-
области О*; если существуют однозначные, аналитические в об-
области G* функции z = <fi(w), <p2(m')> •¦•' Для которых данная
функция w=f(z) является обратной, то функции fi(w),
<?.i(w), ... называются однозначными ветвями функции ср(иу),
определенными в области G*.
Пусть w — zn и z = re'9, w = peib; тогда
я/¦¦- 0 , 2Ы ,.
Г = у р, 9 = ¦ (')
Выберем в точке wa ф 0 какое-нибудь определенное значе-
значение 9 = 9О (например, будем считать, что % — главное значе-
значение аргумеша w0) и фиксируем также число k. Пусть неко-
§ 31
СТЕПЕННАЯ ФУНКЦИЯ ФУНКЦИЯ ЖУКОВСКОГО
юрая односвязпая область, которой принадлежит точка wQ,
не содержит точек щ> = 0, w=oo. При непрерывном пере-
перемещении точки w в этой облааи можно считать, что аргу-
ыет 9 величины w изменяется также непрерывно. При этом,
так как точка w не может совершить полный оборот вокруг
начала координат, то не только р, но и 8 определяется в
каждой точке облааи однозначно. Тем самым равенства G)
определяют непрерывную и однозначную функцию, которая и
является ветвью функции z = yrw. Различным фиксирован-
фиксированным в формуле G) значениям k(k = 0, 1, 2, ..., п—1) при
одном и том же выборе числа 60 соответствуют различные
п
ветви функции у w в данной ооласти.
Если точка w совершает один или несколько полных обо-
оборотов вокруг начала координат, ю непрерывное изменение ве-
величины 6 при этом движении точки w приводит к тому, что
точка w возвращается в исходное положение со значением
аргумента G, отличающимся от исходного на величину, крат-
кратную 2тс, а это соответствует изменению значения k во втором
равенстве G), т. е. переходу на другую ветвь функции у w.
Точка, обладающая тем свойавом, что обход вокруг нее
в достаточно малой окрестности влечет за собой переход ох
одной ветви многозначной функции к другой, называется
точкой разветвления (или точкой ветвления) рассматри-
рассматриваемой многозначной функции. Точками разветвления функции
Ухи являются точки гу = 0 и яу = оо. Следует также отме-
отметить, что в каждой из этих точек ветвления функция -\fw
имеет только одно значение ("j/~0 = 0 и у^со = оо), т. е.
различные ветви функции в этих точках совпадают.
39. Как уже отмечалось выше, угол величины а(а<^2л//г)
с вершиной в точке 2 = 0 (соответствующей точке развет-
разветвления а> = 0) 01 ображается функцией w = zn взаимно одно-
однозначно на угол с вершиной в точке w = 0 величины т. (в ча-
частности, угол с вершиной в точке z = 0 величины л/л ото-
отображается взаимно однозначно па полуплоскость). Это, отно-
относится и к тому случаю, когда число л дробное, так как угол
с вершиной в начале координат не содержит никакой окре-
окрестности нулевой точки (а также и бесконечно удаленной
точки), и следовательно, внутри такого угла может быть
90
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл III
определена однозначная ветвь отображающей функции. Но,
с другой стороны, с помощью дробно-линейной функции можно
отобразить на угол область, ограниченную дугами двух ок-
окружностей (или дугой окружности и прямолинейным отрез-
отрезкомI), поэтому, комбинируя дробно-линейную и степенную
функции, можно такую область отобразить на полуплоскость.
Пример 1. Отобразить на верхнюю полуплоскость верхний
единичный полукруг (т. е. область |г|<1, lm i>0).
Граница полукруга состоит из отрезка действительной оси и
дуги окружности, пересекающихся под прямым углом в точках
2 = ±1. Дробно-линейная функция
t= отображает одну из этих
точек в точку t = со, а другую в
точку t = 0 и, следовательно, задан-
заданную область — во внутренность }гла
между двумя взанмноперпендику-
лярными лучами с вершиной в точке
t = 0. Одна из сторон этого угла
пойдет по отрицательной части
действительной оси (если г дей-
действительное и —1-<2<;1) то
—со < t < 0), другая по положитель-
положительной части мнимой оси (так как
точка z = I, например, перейдет в
точку t = ;——т = /). Таким обра-
образом, функция t = . отображает
заданный пол\круг на угол, изобра-
изображенный на рис. 38. Остается по-
повернуть этот угол на 90° по часовой
стрелке, что соответствует отображе-
р „„ нию Т= —it (угол при этом совме-
стится с первым квадрантом), после
чего функция w=T- отобразит его
на верхнюю полуплоскость. Итак, требуемое отображение осущест-
осуществляется функцией
w = — i
J
') Для этого достаточно взять такую дробно-линейную функцию,
с помощью которой одна общая точка дуг окружностей отобража-
отображается в бесконечно удаленную точку. Если др\г)ю общую точку ото-
отобрази! ь в начало координат, то вершина угла будет находиться в
начале координат.
§ 3]
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
91
Пример 2. Отобразить на верхнюю полуплоскость область,
1 0 1 ( 39
рр р
общую двум кругам радиуса
Точки пересечения дут,
соо1ветствуют числам
р у
с центрами в точках 0 и 1 (рис. 39).
ограничивающих заданную область,
¦у
Z~2
1 ,
—f-
2 —
2
Дробно-линейная функция
у а
у
¦у [ ,'
(8)
отображает одну из этих точек ( г4 = — -(-
¦I -о-
точку t = оо, а другую
Рис. 39.
1 V3 ^
z2 =.— ( !-— 1 — в точку t = 0, и еле-
/
довательно, данную область — в угол
с вершиной в точке ? = 0. Величина этого угла равна 2тс/3. Для того
чтобы выяснить, как расположен в плоскости t этот угол, доста-
достаточно найти хотя бы одну точку на одной из его сторон. Выясним,
например, в какую точку отобразится точка г = 1, лежащая на одной
из дуг (/j), ограничивающих данную область. При z = l получим
t —
2
Следовательно, дуга lL плоскости г отображается на луч A) пло-
плоскости t, выходящий из начала координат и проходящий через
1 Уз
точку t = —о" ~т~' ^~ (рис. 40. а). Если идти по дуге 1У из точки
22, то отображаемая область окажется слева, следовательно, луч B)
плоскости t, являющийся отображением дуги /3, может быть получен
поворотом луча A) на угол 2я/3 против часовой стрелки.
Так как полученный в плоскости t угол предстоит отобразить
на верхнюю полуплоскость, то, прежде чем воспользоваться для
этой цели степенной функцией, следует произвести в плоскости t
поворот на угол 2л/3 по часовой стрелке с тем, чтобы луч A)
совместить с положительной частью действительной оси, которая
степенной функцией отображается сама на себя. Такой поворот
осуществляется функцией (см. стр. 70)
T = te~'M'3. (9)
92
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл III
Полученный в результате в плоскости Т угол (рис. 40, б) отобра-
отображается на верхнюю полуплоскость плоскости w одной из ветвей
функции
w=T32 (Ю)
2тс 3
(\гол величины 2я'3 отображается на \гол величины — . — =я
Объединяя (8), (9) и A0), пол>чаем функцию
2 \-F, I
2
2г — 1 + ' /3
2г — 1— i/3~
или, окончательно,
\ 2г — 1 — i /3
Это, конечно (как и в предыдущем примере), только одна из
ф}нкцпй, осуществляющих треб\емое отображение. Все множество
Ж
©
0
Рис JO.
функций, удовлетворяющих условию задачи, можно получить,
отображая далее с помощью соответствующего дробно-линейного
преобразования верхнюю полуплоскость плоскости w саму на себя.
Пример 3. Отобразить на верхнюю полуплоскость всю пло-
плоскость г с разрезом вдоль прямолинейного отрезка, соединяющего
точку i с точкой 3i (рис. 41, а).
Дробно-линейная функция
t —
¦Si
(П)
31
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
93
отображает концы разреза z = i и z = 3i соответственно в точки
i = 0 и t — co, а следовательно, заданную область на плоскость t
с разрезом вдоль некоторою луча, выходящего из начала координат.
Для того чтобы выяснить направление этого л\ча, достаточно найти
на нем хотя бы одн} промежуточную точку. Точке 2 = 2/ разреза
в плоскости г соответствует точка
Ъ. — Si ~"
плоскости t. Следовательно, функция A1) отображает данную область
на плоскость t с разрезом вдоль луча, идущего по отрицательной
4
WWa
'^Z^Z^y
yZyZyyyy,
w
Ш
©
yyyy.
i
Шх
Ш
6)
Рис. 41.
б)
части действительной оси (рис. 41, б). Произведя с помощью функ-
функции
T = teT-'l = — t A2)
поворот на угол я, мы отобразим нашу область на плоскость с раз-
разрезом по положительной части действительной оси (рис. 41, в);
функция
w = VT A3)
(точнее, одна из ветвей этой функции) отображает плоскость с раз-
разрезом вдоль положительной действительной полуоси на верхнюю
полуплоскость. Объединяя A1), A2) и A3), получим
w = I/ —
2 —3( -
Это, конечно, только одна из функций, осуществляющих требуемое
отображение.
40- Рассмотрим отображение, осуществляемое функцией
Которую часто называют функцией Жуковского. Так как
зт = -ij 1 2 > т0 функция Жуковского аналитична во всей
94
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
плоскости, кроме точки 2 = 0, и ее производная отлична от
нуля всюду, кроме точек z = ±l, которые соответствуют
точкам w^±\ плоскости w. Положив z = relf, найдем
= -j г (cos <р -\-i sin 9) + 7" (cos '¦? — i sin <p) =
откуда
1 / 1\ .
г» =T (r-T sin 9.
A5)
Всякая окружность радиуса r — R плоскости г отображается
функцией Жуковского на линию
^) cos
A6)
Нетрудно видеть, что при R jt 1 уравнения A6) представляют
собой параметрические уравнения эллипса
= 1
A7)
с полуосями
и фокусами в точках и = гЬ"|/а2— fe = dt I, г> = 0. Так как
¦гв»' (г) = 0 только при г = ± 1, то отображение, осущест-
осуществляемое функцией Жуковского, конформно при /?^ 1 во внеш-
внешl—во внутренности круга
ности круга \z\~^>R, а при
\z\KR1)-
') В точке 2 = 0, которая является особой точкой рассматрива-
рассматриваемой функции, отображение также конформно, так как мы усло-
условились (см. стр. 74) \глы в бесконечно удаленной точке измерять
так, что отображение w= \jz эти углы сохраняет.
S
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
95
Пусть для определенности /?^> 1; тогда по уравнениям
A6) нетрудно проследить, что если точка z движется по
окружности \z\ = R против часовой стрелки (т. е. Ь возрастает),
то точка w = u-\-iv движется по эллипсу A7) также против
часовой стрелки. Следовательно, в соответствии с принципом
взаимно однозначного соответствия, функция Жуковского
отображает конформно и взаимно однозначно внешность круга
z\^> R^> \ на внешность эллипса A7). Если /?^>1,
то \JR<^1, а так как замена R на ус сохраняет эллипс A7),
то одновременно на внешность эллипса A7) отображается
взаимно однозначно внутренность круга радиуса R\ = ljR<^ 1.
Действительно, при обходе его окружности против часовой
стрелки эллипс обходится по часовой стрелке (советуем
читателю это проверить).
Из уравнений A6) видно, что когда R=l, то v = 0,
и^ cos'f, и, следовательно, когда точка z обходит границу
единичного круга (| z \ = 1 и ср изменяется от 0 до 2ic), то
точка w = ir -)- iv дважды пробегает отрезок действительной оси
между точками 1 и — 1 и, в силу принципа взаимно одно-
однозначного соответствия, можно утверждать, что функция
Жуковского отображает как внутренность, так и внешность
единичного к,руга на всю расширенную плоскость с разрезом
по отрезку [— 1, 1].
Решив равенство A4) относительно z:
z2 — 2wz 4-1=0,
z = w -)- У wl — 1,
A8)
мы приходим к выводу, что одна ветвь функции z = z(w),
обратной по отношению к функции Жуковского, отображает
всю (расширенную) плоскость w с разрезом по отрезку
[—1, 1] на внутренность единичного круга, а другая — на
внешность единичного круга, причем выбор ветви функции
z{w) зависит от выбора ветви У W*—1 в равенстве A8).
Из равенств A5) легко заключить, что лучи arg,j = '.p
(ср ф 0, ± ir/2, ic) отображаются функцией Жуковского на
соответствующие ветви гиперболы:
и- v-
cos" <f sin"' <f
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. lit
а лучи argz = O, argz —тс, arg z = ± л/2 на дважды пробе-
пробегаемые бесконечные отрезки действительной или мнимой оси.
Так, например, если apgz = 0, то из A5) следует:
и при г, изменяющемся от 0 до оо, точка w = u-\-iv дви-
движется по положительной действительной полуоси из точки
w = -\-ca до точки w=\ (которая соответствует значению
z = r=l), а потом из точки 10=1 обратно в точку и> = оо.
Пример 4. Найти область, на которую функция Жуковского
отображает: а) круг \г | < 1 с разрезом по отрезку [1/2, 1]; б) круг
| г | < 1 с разрезом по отрезку [— 1/2, 1].
Рис. 42.
а) Функция Жуковского отображает окружность единичного
круга на дважды пробегаемый отрезок [—1, 1], отрезок [1,2, 1]
отображается функцией Жуковского на отрезок [1, 5/4] (w = 1 при
2=1, w = 5 4 при г=1/2), и поэтому круг |г|<1 с разрезом
по отрезку [1/2, 1] отображается на всю плоскость с разрезом по
отрезку [—1, 5/4] (рис. 42).
Рис. 43,
б) Когда точка г пробегает отрезок [—1/2; 1] действительной
оси, точка w = -j- ( г -] ) движется по действительной оси от
да = —5/4 (при z = — 1/2) до w = — со (при z = — 0) и от да =
= -т-°о (ПРИ г —+ 0) до w = 1 (при г = 1). Таким образом, круг
§ 31
СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ ЖУКОВСКОГО
97
| г | <; 1 с разрезом по отрезку [—1/2, 1| отображается функцией
Жуковского на всю плоскость с разрезами по лучам [—со", —5/4]
и [— 1, +оз] (рис. 43).
Пример 5. Отобразить круг | z | < 1 с разрезом ио отрезку
[1/3, 1] на кр)г | w | <; 1 (рис. 44).
Функция Жуковского t = -=- (z -I ] отображает круг | г | < 1
с разрезом по отрезку [1/3, 1] на всю плоскость с разрезом ио отрезку
[— 1, 5/3]. Длина этого отрезка равна 8/3, а центр его находится
в точке t = 1/3. Отобразим полученную область на всю плоскость
с разрезом по отрезку [—1, 1]; для этого н>жно центр отрезка
Рис. 44.
[— 1, 5 3] сдвинуть в точку 0, после чего применить преобразование
подобия с тем, чтобы длина отрезка стала равной 2 (коэффициент
подобия равен, следовательно, ^ = 3/4). Таким образом, плоскость
t с разрезом по отрезку [— 1, 5/3] отображается на плоскость Т
с разрезом по отрезку [— 1, 1] функцией
а эта последняя область отображается, как мы знаем, на внутрен-
внутренность единичного круга функцией, обратной по отношению к функ-
функции Жуковского (точнее, одной из ветвей этой функции)
Таким образом, искомая функция имеет вид
или, после преобразований,
4 И. Г. Араманович и др.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл III
§ 4. Основные трансцендентные функции
41. Отображение, осуществляемое функцией
конформно во всей плоскости, так как производная этой
функции существует и отлична от нуля во всякой конечной
точке плоскости z. Введя в плоскости z декартовы, а в пло-
плоскости w полярные координаты, т. е. положив z = x-\-iy,
¦да = ре'6, получим
ре'9 = ex+iyl = exelv.
Следовательно,
р = е\ 6= у. A9)
Из равенств A9) следует, что прямые, параллельные мнимой
оси Оу (рис. 45) плоскости 2(jc = const), переходят при
и,
0
%
ч
V-Уг
У У/
X
Рис. 45.
отображении т = ег в окружности с центром в нулевой
точке плоскости w (p = const), а прямые, параллельные дей-
действительной оси Ох (у = const) — в лучи, выходящие из на-
начала координат @ = const). Прямоугольник со сторонами
У=У\> У=У* х — х» x = xit
параллельными осям координат плоскости z, отображается
на область плоскости w, ограниченную лучами
§ 4) ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ 99
и дугами концентрических окружностей
Действительная ось плоскости z(y = 0) отображается
на действительную положительную полуось (8 = 0) пло-
плоскости w, прямая у = а — на луч 6 = а. Следовательно,
полоса ширины а(а<^2тс), прилегающая к действительной
оси, 0<^у<^а, отображается конформно и взаимно одно-
однозначно па угол 0<^6<^а величины а (в радианах) с верши-
вершиной в начале координат, одной из сторон которого является
действительная положительная полуось. В чааности, полоса
0<^_у<^1г ширины тс отображается функцией w = e* взаимно
однозначно на верхнюю полуплоскоаь, а полоса 0<^_у<^2тс
ширины 2т; — на всю плоскость с разрезом по положитель-
положительной действительной полуоси: 0<^6<^2тс.
Отображение всей плоскости z на плоскость w не
является взаимно однозначным- всякой точке w (кроме точек
w = 0 и т=оэ) соответс1вует бесконечное множество точек г:
z = Ln w = In | w | -j-1 Arg w = \n\w\-\-la.igw-{- 2 Arc/
(k = 0, ± 1, ±2,...).
Для того, чтобы область плоскости z отображалась функ-
функцией w = ez на соответствующую область плоскости w
взаимно однозначно, необходимо и достаточно, чтобы она
не содержала никаких двух
точек, абсциссы которых оди-
одинаковы, а ординаты огличают-
ся дру1 от друга на вели-
величину, крашую 2т., гак как
e2i = e2j лишь при z2 = zl-{-
4-2/Ы (k = 0, ± 1, ±2,...).
Такому условию, в частности,
удовлетворяет всякая область, ^^^^^'%%^
заключенная в полосе 2kr.<^
Если плоское1Ь z разбить
(рис. 46) на полосы
Рис. 46.
^{ \ 1)тс {k = Q, -±l I, ± 2,...), то каждая из этих полос
отобразится функцией w = ez взаимно однозначно на всю
плоскость w с разрезом вдоль положшельной части дейа-
вительной оси. Если в плоскости z прямая у = а поднимается
100
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
от положения y = 2kii до положения _у = 2(?-|-1):г, то
соответствующий луч б = а в плоскости w совершает
полный оборот против часовой стрелки от положения 6 = 2Атг
до положения 6 = 2(А —)— 1)тг. Поэтому, чтобы отображение
было взаимно однозначным и непрерывным не только внутри
полосы, но и на ее граничных прямых, достаточно усло-
условиться, что нижней границе у = 2кк соответствует верхний край
разреза в плоскости w, а верхней границе y = 2(k -j- l)u—
нижний край разреза.
42. В любой односвязной области, не содержащей точек
w = 0 ида = оо, можно определить однозначные ветви функции
z = Lnw. Для этого достаточно, положив яу = ре'в, фиксиро-
фиксировать в формуле
z = Ln w = In p + г9 -f- 2kri B0)
целое число k, выбрать в некоторой точке wa этой области
какое-либо определенное значение 0 = бо (например, положить
90 равным главному значению аргумента w0) и считать,
что 6 изменяется непрерывно при движении точки w по
непрерывной кривой. Различным значениям k(k = O, ± 1,
± 2,...) соответствуют различные однозначные ветви функции
Ln w. Это следует из рассуждений, аналогичных тем, которые
приводились на стр. 88 — 89 при изучении функции j/~w.
Если точка w совершает в своей плоскости один или несколько
полных оборотов вокруг начала координат, то она возвра-
возвращается в начальное положение со значением 6, отличающимся
от исходного на величину, кратную 2тг, а это равносильно
изменению значения k в равенстве B0), т. е. переходу на
другую ветвь функции Lntw. Следовательно, точка w = 0
является точкой разветвления функции Ln w; нетрудно убе-
убедиться, что точкой разветвления является также точка да = со.
В каждой из этих точек функция Ln w имеет только одно
значение (Ln 0 = оо, Ln со = со).
Характер точек разветвления функций z^\/~w и z =
= Lnw различен. После и-кратного обхода вокруг точки
10=0 мы вернемся к первоначальной ветви функции у/~щ
точки разветвления, обладающие таким свойством, назы-
называются алгебраическими точками разветвления порядка
п—1. Иначе обстоит дело с функцией Lnw. Любое конеч-
конечное число обходов (в одном и том же направлении) вокруг
§ 4]
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
101
точки а> = 0 не приведет вновь к первоначальной ветви
функции Ln w. Такие точки разветвления называются логФ
рифмическими.
43. Так как с помощью дробно-линейной функции об-
область, ограниченная двумя касающимися друг друга окруж-
окружностями (или окружностью и касающейся ее прямой), может
быть отображена на полосу между двумя параллельными пря-
прямыми (для этого достаточно, чтобы точка касания отобрази-
отобразилась в бесконечно удаленную точку), а полоса ширины л с
помощью показательной функции отображается на верхнюю
полуплоскость, то, комбинируя дробно-линейную и показа-
показательную функции, можно область указанного вида отобразить
на верхнюю полуплоскость.
Пример 1. Найти функцию, отображающую область, ограни-
ограниченную единичной окружностью С и прямом /, касающейся этой
окружности в точке z = / (рис. 47),
на верхнюю полуплоскость. ».
Функция *
I
А
Z+i
B1)
отображает общую для окружно-
окружности и прямой точку 2 = / (точку
касания) в бесконечно удаленную
точку плоскости t, следовательно,
в силу кругового свойства дроб-
дробно-линейной функции, как окруж-
окружность С, так и прямая / отобра-
отображаются этой функцией на прямые, Рис. >47.
параллельные друг другу (окруж-
(окружность С и прямая / имеют един-
единственную общую точку (, переходящую в со). Так как точка 2 =
= —i находится на окружности С и при 2= —/, t = 0, то пря-
прямая С плоскости t, соответствующая окружности С, проходит че-
через начало координат. Для того чтобы определить в плоскости t
положение прямой С, достаточно найти еще хотя бы одну точку,
лежащую на этой прямой. Возьмем, например, точку 2=1 на ок-
окружности С; ей соответствует на прямой С точка
Итак, прямая С проходит через точки f = 0 и t=i и, следова-
следовательно, совпадает с мнимой осью плоскости t (рис. 48, а). Чтобы
определить положение прямой /' плоскости t, на которую функция
102
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
B1) отображает прямую /, достаточно знать на прямой /' только
одну точку. Точке z=.\-\-i прямой / соответствует точка
прямой /'. Прямая /' проходит через точку I —]— 2г параллельно
мнимой оси и, следовательно, отстоит от этой оси на расстояние,
©
©
6)
Рис. 48.
равное 1. Итак, функция B1) отображает заданную область на по-
полосу ширины 1, прилегающую к мнимой оси.
Функция
х = nt B2)
отобразит эту полосу на полосу ширины % (рис. 48, б), прилегающую
к мнимой оси, а с помощью функции
Т = е x — h
B3)
эта полоса в плоскости т поворачивается на \гол к/2 против часо-
часовой стрелки и переходит в полосу, изображенную на рис. 48, в.
Эта последняя полоса ф)нкцией
w = ет B4)
отображается на верхнюю полуплоскость.
Объединяя B1) — B4), находим одну из функций, осуществ-
осуществляющих требуемое отображение:
w — e
2—i
П р и м е р 2. Отобразить на верхнюю полуплоскость полосу
0<д;<1 с разрезом по лучу х — 1/2, /гб?.у<со (рис. 49).
§ 4]
ОСНОВНЫЕ ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
103
Функция ег отображает на верхнюю полуплоскость полосу 0<
_ поэтому функция е1г отображает на верхнюю полуплоскость
полосу 0<х<я (замена г на iz соответствует поворот) на угол тс/2,
при котором вертикальная полоса 0
переходит в iоризонтальную
0<у<т.), а функция
полос)
отображает на верхнюю полуплоскость по-
полосу 0<л:<1/2. При этом точке
1
соответствует точка
2iti (\r+ih
Рис 49
и лучу х =1/2, —со <с_у < h, отмечен-
отмеченному на рис 49 пунктиром, соответствует
в плоскости t луч (— со, —e~'i7ih) на действительной оси,
отмеченный тонкой линией на рис. 50. Применяя принцип сим-
симметрии, мы приходим к выводу, что функция t = e2*iz отображает
область, состоящую из полосы 0<л-<1/2, симметричной с ней
относительно прямой л: =1/2 полосы 1/2<jc<1 и луча л; =1/2,
©
Рис. 51,
— со<_у</г, т. е. как раз заданную область (полосу 0 < х < 1 с
разрезом по лучу х—М2, й=^_у<со), на область, состоящую из
верхней полуплоскости плоскости t, симметричной с ней относи-
относительно действительной оси области (т. е. нижней полуплоскости),
и луча —со < t < — e~-'zh действительной оси, т. е. на всю плос-
плоскость t с разрезом по л\ч\ [ — e~2lzfl, + со) на действительной
оси (рис. 51). Функция r=/ + e"Sltft (сдвиг) отображает эту после>
нюю область на всю плоскость с разрезом по действительной поло-
положительной полуоси, а функция
10= V 1 =
,-irh
— на верхнюю полуплоскость. Итак, требуемое отображение осу-
осуществляется функцией
104
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл II t
44. Тригонометрические функции могут быть выражены
через показательную (см. стр. 28). Рассмотрим, например,
отображение, определяемое функцией
w = sin z = sin (x -)- iy) = sin x cos iy -f- cos x sin iy =
= smxchy -\- i cos x shy.
Возьмем в плоскости z полосу y~^> 0, —тс/2 <^ х <^ тс/2
(рис. 52, а). Если точка z находится на прямой х = т,то
w = — chy, B5)
и если точка г движется по прямой х = — тс/2 от_у= -|-оо
до_у = 0, то точка w перемещается по действительной оси
б)
Рис. 52.
от да= — сю до w^—1. На действительной оси у = 0,
поэтому
w = sin х, B6)
и если точка z передвигается по действительной оси от х=
= — тс/2 до х = тг/2, то соответствующая ей точка w пробе-
пробегает отрезок действительной оси от w= — 1 до да=1.
На прямой л; = тс/2
w = chy, B7)
и если точка z движется по прямой х = тс/2 от у = 0 до у =
= -|-оо, то соответствующая ей точка w перемещается по
действительной оси от w=l до w= -f-oo.
Итак, если точка z обходит границу полуполосы _У^>0,
— тс/2 <^jc<^tc/2 так, что эта полуполоса остается слева, то
точка w пробегает слева направо всю действительную ось,
и поэтому из принципа взаимно однозначного соответствия
§ 4]
ОСНОВНЫЕ ТРАНСЦЕНДГНТНЫЕ ФУНКЦИИ
105
следует, что функция w=sinz оюбражает рассматриваемую
полуполрсу на верхнюю полуплоскость (рис. 52, б).
Используя B5) — B7), нетрудно проверить, что если точ-
точка z обходит границу полуполосы _у<^0, —тс/2 <^ х <^ тс/2
(на рис. 53, а эта полуполоса заштрихована дважды) так, что
У
V/
(р.
§
©
Ш
Ш
\
А
Рис. 53.
эта полуполоса остается слева, то точка w пробегает всю дей-
действительную ось справа налево и функция w= sin z отобра-
отображает эту полуполосу на нижнюю полуплоскость, причем сто-
стороне полуполосы у<^0, х = — тс/2 соответствует отрезок
—1 действительной оси плоскости w, стороне
и сторо-
стороу = 0, —тс/2 <^х<^пГ2 — отрезок —
не у <^ 0, х = тс, 2 — от-
отрезок 1<^Щ)<^ОО.
Проведенное исследо-
исследование отображений рас-
рассмотренных полуполос
приводит к выводу, что вся
полоса — тс/2 <^ х <^ тс/2
(рис. 53, а) отображается
функцией f = sin г на
всю плоскость w с раз-
разрезами по действительной
оси от — сю до — 1 йог
1 до -\- сю (рис. 53, б),
причем верхним краям
этих разрезов соответствуют в плоскости z линии х = —у,
у~^>0 и х = ^г, у^>0, а нижним краям — линии х= — тс/2,
]|<^0 и х = тс/2, J»<^0.
Так как sin (z-{-2-k)= sin z и sin (z-|-tc)=— sin z, то
все полуполосы А (рис. 54) оюбражаклся функцией w= sinz
Рис. 54.
106
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
ГГл III
на верхнюю полуплоскость, а все полуполосы В — на ниж-
нижнюю полуплоскость плоскости w.
Пример 3. Найти функцию, конформно отображающую на
верхнюю полуплоскость полосу —я'2<л-<я/2 с разрезом вдоль
отрезка 0 *?:.*:< я/2 (рис. 55, а).
а,)
б)
Рис. 55.
Функция t = sin z отображает, как было показано выше, по-
лупрлосу — я/2 < х <; я/2, у > 0 на верхнюю полуплоскость. При
э*ом отрезок @, я/2) оси х переходит в отрезок @, 1) действитель-
действительной оси плоскости t, а отрезок ( — л/2, 0) оси х — в отрезок ( — 1, 0)
действительной оси. Отрезку 0<^<со прямой х= —я/2 соот-
соответствует отрезок (—оо, — I) действительной оси и отрезку 0<
<у<со прямой х = я/2 — отрезок A, со) действительной оси
плоскости t.
Применим принцип симметрии, выбрав в качестве отрезка -\ (см.
стр. 84 — 35) отрезок — л/2 < х < 0 действительной оси (ему соот-
соответствует, как указано выше, отрезок ( — 1, 0) действительной оси
плоскости t). На основании принципа симметрии можно утверждать,
что функция t = sin z отображает область, состоящую из «нижней»
полуполосы —я/2 <: х < я'2, у < 0, «верхней» пол> полосы —я/2<
<*<я/2, у > 0 и отрезка ( — я/2, 0) действительной оси, т. е.
данную в условии задачи область, на всю плоскость t с разрезами
по действительной оси вдоль отрезков (—оо, —1] м [0, со)
(рис. 55, б) (можно также сказать, что здесь имеется только один
разрез, идущий из точки г = 0 в точку г= —1 через бесконечно
удаленную точку).
Функция
t
отображает плоскость t с указанными разрезами на всю плоскость
с разрезом вдоль положительной действительной полуоси (в этом
читатель может убедиться самостоятельно). Наконец, функция w=-
= УГ, т. е-
¦V-
'sin 2
отображает заданную в условии задачи область на верхнюю полу-
полуплоскость.
§ 5]
ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
107
§ 5. Конформное отображение полуплоскости
на прямоугольник
45. Рассмотрим функцию
г
С = *(*) =
dt
B8)
где 0<^?<^1. Интеграл, стоящий в правой части этого ра-
равенства, называется эллиптическим интегралом первого рода
(см. [2], гл. IX). Особыми точками подынтегральной функции
/(?)=—:— х B9)
У(\— 22)A— *!aZa)
ЯВЛЯЮТСЯ ТОЧКИ 2 = ±1 И Z = ±ljk. ЭТИ ТОЧКИ ЯВЛЯЮТСЯ
точками разветвления, так как
/A — z2)(l — AV) = VT^~z V
— kz V
а точка да = 0 является точкой разветвления функции Уw
(см. стр. 89). Следовательно, выбор однозначной ветви функ-
функции f{z) возможен лишь в такой области, в которой нельзя
произвести обход вокруг точек ±1 и ± \jk. Для того чтобы
обеспечить выполнение указанных условий, будем считать,
что точка z в правой части B8) расположена в верхней по-
полуплоскости или на действительной оси (но не в точках ± 1
и ± Ijk) и что путь интегрирования тоже лежит в верхней
полуплоскости. Если в дальнейшем будет необходимо интег-
интегрировать по действительной оси, то будем обходить точки
dz I, ± l/k, например, по верхним полуокружностям с цент-
центрами в этих точках. При этих условиях функция C = <pB)>
определенная равенством B8). будет аналитической и одно-
однозначной во всей верхней полуплоскости, а также на действи-
действительной оси, за исключением точек ± 1, ± Ilk.
Для того чтобы функция C,:=tpB) была вполне опреде-
определена, нужно договориться о том, какую из двух ветвей
функции f(z) мы выбираем. Условимся брать ту ветвь функ-
функции f(z), для которой /@)= 1 (для другой ветви /@)= — 1).
Найдем линию в плоскости (,, на которую с помощью
B8) отображается действительная ось плоскости z. Точке
z = 0 соответствует, очевидно, точка 1 = 0. Если точка z
движется из положения г = 0 но действительной оси вправо,
108
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. III
то интеграл в правой части B8) является обычным опреде-
определенным интегралом функции действительного переменного,
причем пока z<^l, подынтегральная функция положительна,
а потому С тоже является положительной величиной, возрас-
возрастающей при возрастании z. При z=\ интеграл B8) стано-
становится несобственным. Этот интеграл сходится; обозначим:
i
dt
2
C0)
Величина u)i зависит от k и может быть найдена по таблицам
эллиптических интегралов. Продолжим теперь движение
точки z по действительной оси в положительном направ-
направлении. Точнее, пусть точка z, двигаясь от точки z = Q
в положительном направлении (вправо) и несколько не
дойдя до точки z=l, обходит ее по верхней полу-
полуокружности радиуса р (впоследствии нужно считать, что
р -*¦ 0), после чего точка z продолжает двигаться по
действительной оси в положительную сторону. При 1 <^z<^\/k
подкоренное выражение в знаменателе становится отрица-
отрицательным, а корень мнимым. Выясним, будет ли при этом мни-
мнимая часть знаменателя положительной или отрицательной. За-
Запишем
C1)
Для последних трех множителей точка z = 1 не является
точкой разветвления, и поэтому при переходе через эту точ-
точку аргумент каждого из этих множителей не изменяется.
Рис. 56.
Действительно, рассмотрим, например, }/~l-]-z. Число
1 -\-z = z — (— 1) изображается вектором, идущим из точки
— 1 в точку z. При 0<^z<^ 1 этот вектор (рис. 56) направ-
направлен по действительной оси в положительную сторону. Следо-
Следо§ 5]
ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
109
вательно, arg A -|— 2-) = 0. Когда точка z движется по полу-
полуокружности с центром в точке 2=1, вектор, изображающий
число 1 -\- z, сначала отклоняется от действительной оси, но
после того как точка z, описав полуокружность, вернулась
на действительную ось, направление вектора опять становится
прежним. Таким образом, обход вокруг точки z=\ не влия-
влияет на аргумент числа \ -\- г, а следовательно и числа
У 1 -|- z. Аналогично обстоит дело с множителями ]/l — kz
и Yl+kz.
Рассмотрим теперь первый множитель ]/"l — z. Число
1 — z изображается вектором, идущим из точки z в точку 1
(рис. 57). При 0<^2<^ 1 этот век-
вектор направлен по действительной
оси в положительную сторону и
arg A —z)=0. Но когда точка z
обходит по полуокружности точку
z=l, вектор поворачивается на
180° по часовой стрелке, следова-
/
Рис. 57.
р
тельно, его аргумент уменьшается на тг, и поэтому при
аргумент числа 1 — z нужно считать равным — и, а аргумент
числа У 1 — z равным соответственно „-. Так как аргументы
всех остальных множителей в C1) не изменились и остались
равными нулю, то аргумент всего произведения также станет
при \ <^z<^\/k равным —~. Произведение C1) стоит в
знаменателе подынтегральной функции B9), поэтому аргумент
этой функции при 1 <^z<^ \jk следует считать равным -j-ic/2,
т. е. величину f(z) нужно считать чисто мнимой с положи-
положительной мнимой частью. Это значит, что при I <^z<^ljk
удобнее писать:
/(*) = ¦
1
причем радикал в знаменателе положителен. Без предшеству-
предшествующих рассуждений нельзя было установить, справедливо ли при
\ <^z<^\jk равенство C2) или равенство
/(*) = -*:
1
to
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. lit
Итак, при
имеем
i
^ _ Г dt
-• C3)
Если точка z движется по действительной оси от 2=1
к z— l/k, то из C3) следует, что действительная часть С оста-
остается постоянной и равной Ш[/2, а мнимая часть положительна
и увеличивается, так как подынтегральная функция в послед-
последнем интеграле правой части C3) положительна. Это значит,
что точка ^ движется параллельно мнимой оси от точки
С = Tf до точки С = y -(- Мд, где ш.2 — несобственный интеграл
dt
вычисляемый с помощью таблиц эллиптических интегралов.
Рассуждениями, аналогичными приведенным выше, можно
убедиться, что после того как точка z обойдет по полу-
полуокружности точку l/k, аргумент f(z) увеличится еще на ~
и станет равным тс, т. е. величина f(z) станет действительной и
отрицательной. Это означает, что при z ^> I/k следует писать
/<*) = -,
-l)(/s2za — 1)'
причем радикал в правой части положителен. Следовательно,
при z^>l/k будем име1ь
г
dt
Если
-оо, то
dt
§ 5]
ОТОБРАЖЕНИЕ ПОЛУПЛОСКОСТИ
111
Пользуясь подстановкой t = -r-, dt = — ~ и учитывая,
что т=1 при t=\jk и т —>¦ 0 при t—у сю, получим
-1 4--1
в соответствии с обозначением C0). Следовательно, если
z -*¦ оо, то С —> 'ш^.
Итак, если точка z движется по действительной оси
от z = l/k до z=-}-oo, то точка ? движется параллельно
действительной оси от С = -у -|- Шз до С = /<о*
Продолжая аналогичные рассуждения, обнаружим, что
когда точка z движется по действительной оси от z = — оо
до z = —l/k, точка С продолжает перемещаться параллельно
действительной оси от ^ = Лп2до^ = — ~ -\- 1щ. Далее, отре-
отрезок действительной оси плоскости z между z = г-и
z = —1 оюбразится на отрезок, параллельный мнимой оси
плоскости (, между точками ? = — ^-)-ко2 и С = ^- и,
наконец, О1резок действи1ель-
ной оси между точками z = — 1
и 2 = 0 отобразится на отре-
отрезок действительной оси между
¦?-
?•
О),
2
Рис. 58
точками ? = — -^- и ?=0.
Таким образом, если точ-
точка z пробегает слева направо
всю действительную ось (верх-
(верхняя полуплоскость остается при
этом слева), то соогве1С1вующая точка С обходит про-
против часовой стрелки границу прямоугольника, изображенного
на рис. 58. Отсюда следует, что функция С = <р(^), опреде-
определенная с помощью B8), отображает конформно и взаимно
112
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
[Гл. Ill
однозначно верхнюю полуплоскость плоскости z на прямо-
прямоугольник со сторонами длины си, и со2 плоскости С- Обратная
функция z = /:(C) оюбражает прямоугольник плоскости С на
верхнюю полуплоскость плоскости г.
Если требуется отобразить верхнюю полуплоскость на
некоторый заданный прямоугольник, то сначала, пользуясь
таблицами эллиптических интегралов, следует подобрать
такое значение параметра k, при котором отношение to,: со.2
будет равно отношению сторон заданного прямоугольника.
При таком выборе парамефа k функция у(г), определенная
равенством B8), будет отображать верхнюю полуплоскость
на прямоугольник, подобный заданному. Для того чтобы
этот прямоугольник отобразить на заданный, достаточно
воспользоваться преобразованием подобия, а также, если это
понадобится, параллельным переносом и поворотом плоскости.
Все эти преобразования осуществляются линейной функцией.
Следовательно, функция w = сх", -|- с2, т. е.
Л
4-
при соответствующем выборе параметров k, ct и с,г отобра-
отображает верхнюю полуплоскость на любой заданный прямо-
прямоугольник.
В более подробных курсах рассматривается общая фор-
формула Шварца — Кристоффеля, позволяющая строить отобра-
отображение полуплоскости на любой заданный многоугольник.
ЗАДАЧИ К ГЛАВЕ Ш
1. Отобразить верхнюю полуплоскость плоскости г на круг
|ш|<1 так, чтобы точке z = j и направлению, идущему из этой
точки параллельно действительной оси в положительную сторону,
соответствовали точка в = 0 и выходящее из точки w = 0 положи-
положительное направление мнимой оси.
2. Найти функцию w=f(z), отображающую конформно и вза-
взаимно однозначно единичный круг на себя и такую, что:
а)/A)=0, aTg/'(i)=0; б) / (|) = 0, arg/Щ =-J ;
ЗАДАЧИ К ГЛ. III
113
3. Найти функцию, отображающую конформно на верхнюю
полуплоскость каждую из указанных областей:
а) сегмент 1ш z> I, \z\ > 2; б) область \г\ > 2, \г — У 2 | < У2\
в) каждую из областей /, //, ///, IV, ограниченных окружностями
|z| = l и |z-f-i| = l (рис. 59); г) сектор \г\ < 2, 0 < argz < -^-;
д) область |z|>2, 0<Argz<Y11; е) всю плоскость с разрезом
по прямолинейному отрезку, соединяющему точки 1 + / и 2 -f- 2i;
Рис. 60.
ж) всю плоскость с разрезами, указанными на рис. 60, вдоль бис-
биссектрис координатного угла; з) верхнюю полуплоскость с разрезом
по отрезку мнимой оси между точками г = 0 и z = ш (я > 0);
и) внешность единичного круга с разрезом по положительной ча-
части мнимой оси от г = i до г = со; к) внутренность единичного
круга с разрезом по радиусу от г = 0 до г=1; л) область |г|<2,
\г — 1|<1; м) область \г\ > 2, |г — 3| > 1; и) полосу а < Rez < й;
о) полуполосу Rez>0, 0<lmz<a; п) круг |zj<l с разрезом
по отрезку [1/2, 1]; р) круг |г]<1 с разрезами по отрезкам
[—1, О] и [а, 1] @<д<1).
4. На как\ю область плоскости w отображает функция да = cos г
полосу — я/2" < Re г < я/2?
5. На какую область плоскости да отображает функция
да = tg г полосу — л/4 < Re г <л/4?
6. Отобразить на верхнюю полуплоскость полуполосу 0<л:<п
j;>0 с разрезом по лучу х = п/2, Л^_у<оо (h > 0).
ГЛАВА IV
РЯДЫ И ОСОБЫЕ ТОЧКИ
§ 1. Функциональные ряды
46. Функциональный ряд, членами которого являются функ-
функции комплексной переменной z
- (i)
может в одних точках сходиться, в других расходиться.
Сумма такого ряда
где
является функцией переменной г, определенной в точках,
в которых ряд A) сходится. Множество точек, в которых
ряд A) сходится, будем называть областью сходимости
этого ряда. Остатком ряда A) называется разность
В каждой точке сходимосш ряда A)
Другими словами, если ряд в данной точке z сходится, то
для каждого е^>0 можно подобрать столь большое число N,
что при п^>N модуль ociaiKa ряда удовлетворяет нера-
неравенству
\Rni-) <-• B)
Наименьшее число N, определяющее номер п, начиная с
кошрого справедливо неравенство B), вообще говоря, зави-
5 И
Функциональные ряды
115
сит не только от е, но и от г, и не является, следовательно
одинаковым для всех точек области сходимости ряда; чтобы
подчеркнуть эту зависимость, вместо Л' пииту т N (г, z).
Предположим, что на некотором множестве точек Q
(в некоторой области, на некоторой дуге и т. д.) ряд A) не
только сходится, но и мажорируется некоторым сходящимся
числовым рядом Эт означает, что существует такой схо-
сходящийся ряд
Яо + fli + a<i + ¦ ¦ • + ап + ¦ ¦ • C)
с положительными членами, что во всех точках рассматри-
рассматриваемого множества
Будем в этом случае говорить, что на данном множестве точек
ряд A) сходится правильно. Очевидно, что в этом случае
|/?„(z)\ = |/я +,(z
т. е. модуль остатка данного функционального ряда не пре-
превосходит остатка гл числового ряда C). Но так как ряд C)
сходится, то, как бы ни было мало е^>0, найдется такое N
(зависящее только от е, так как ряд C) числовой и его
члены от z не зависят), что гп<^в при n^>N. Тем более
поэтому при п^>N имеем \Rn(z)\<^e. Таким образом, для
рядов, правильно сходящихся на некотором множестве точек,
неравенство B) имеет место при любом сколь угодно малом
е^>0, если n~^>N(t), где N (г) достаточно велико и зависит
только от е.
Ряды, для которых можно выбрать 7V не зависящим от г,
называются равномерно сходящимися на соответствующем
множестве точек. Правильно сходящиеся ряды принадлежат,
таким образом, к классу равномерно сходящихся рядов
(однако не всякий равномерно сходящийся ряд сходится пра-
правильно).
Нетрудно видеть, что если все члены ряда A), сходяще-
сходящегося правильно на некотором множестве О, умножить на одну
и ту же ограниченную по модулю функцию у (г), то полу-
полученный ряд
(z)/0 (г)
/, (г)
f-...
D)
116
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл IV
будет также правильно сходиться на О. Действительно, так
как функция <р (z) ограничена, то существует такая постоян-
постоянная М, что |<p(z)j<^/M во всех точках множества G, и так
как ряд A) мажорируется на G сходящимся рядом C), то
ряд D) будет мажорироваться сходящимся рядом
47. Докажем некоторые свойства рядов, сходящихся рав-
равномерно. Все эти свойства справедливы, тем самым, и для
правильно сходящихся рядов.
1. Если члены ряда
*) + ... E)
являются непрерывными функциями в некоторой области
О или на некоторой дуге L и ряд E) сходится в этой
области или на этой дуге равномерно, то сумма ряда
f(z) непрерывна в области О или на дуге L.
Пусть z и z-\-h — любые точки, принадлежащие рас-
рассматриваемому множеству (области G или дуге L), Sn(z) и
Rn(z) — частичная сумма и остаток ряда E). Имеем
f(z + A) -f(z) = Sn B + A) - Sn (z) + Rn (z + h) - Rn (z).
Ввиду равномерной сходимости ряда E), как бы ни было
мало ?^>0, можно найти такое я, что
откуда
следовательно,
Л) —
4- А) —
2г.
F)
Функция Sn(z), будучи суммой конечного числа непрерывных
функций, также непрерывна на данном множестве, и поэтому,
какова бы ни была точка z данного множества, величину \h\
можно взять столь малой (точка z-\-h также принадлежит
рассматриваемому множеству), чтобы
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
117
но тогда из F) получим
А) _/(*))< За,
а так как число е сколь угодно мало, то это и означает,
что функция f(z) непрерывна в любой точке z данного
множества.
2. Если члены ряда E) непрерывны на некоторой дуге L
и ряд сходится на этой дуге равномерно, то его можно
почленно интегрировать вдоль дуги L, т. е.
ILL L
В силу доказанного выше свойства функция f(z) непре-
непрерывна на дуге L и интеграл \f{z)dz существует. Пусть
L
an(z) — частичная сумма ряда в правой части G). Имеем
\f{z)dz-on(z) =
где Rn(z) — остаток ряда E). Так как ряд E) сходится на
дуге L равномерно, то можно выбрать N столь большим,
чтобы при n^>N неравенство \Rn(z)\<^z имело место во
всех точках дуги L. Тогда из последнего равенства получим
J f(z) dz - ся (z)\ = | \ Rn (z) dz | < e/,
L L
где /—длина дуги L. Так как г^>0 при этом сколь угодно
мало, то эго означает, что
lim J Rn [z)dz = 0,
п ->• ooi
т. е.
lim sn (z) =
я -» оо ?
что и требовалось доказать.
118
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
3. Если члены ряда E) — аналитические в некоторой
области G функции и ряд E) сходится в области О
равномерно, то его сумма f(z) также является функ-
функцией, аналитической в области О.
Выберем любую внутреннюю точку z области О и по-
построим круг столь малого радиуса с центром в этой точке, -
чтобы он целиком лежал внутри
области О (рис. 61). Пусть
С—окружность этого круга,
а С — любая точка на С. Имеем
_/.(?) | /.@
С —г ~? — г ~Г?-2
+ 7
-Ь... E)
Если z постоянно, а С нахо-
находится на окружности С, то вели-
Рис- 61- чина jC — z\ постоянна (равна
радиусу р окружности С).
Ряд E), по условию, сходится равномерно в области О и, тем
более, на окружности С. Поэтому ряд, стоящий в правой
части (8), также сходится равномерно на С (по отношению
к Г; напоминаем, что z постоянно), и, по доказанному, ею
можно вдоль С почленно интегрировать:
2тс(
С —z
_ 1 С/.(С)«К | 1 f/t(C)«ft
~2я J С — z ' 2м ) С — г
2w \ C —2 '"¦'•
Пользуясь интегральной формулой Коши, отсюда получаем
J
2*7 \ Z — z — JU^J
т. е. приходим к равенству
(9)
Функция /(г), будучи суммой равномерно сходящегося
аналитических и, следовательно, непрерывных функций, непре-
СТЕПЕННЫЕ РЯДЫ
119
рынпа в области О. Следовательно, интеграл, стоящий в пра-
правой части (9), является интегралом типа Коши и, по доказан-
доказанному выше (см. п. 29, гл. II), представляет функцию, анали-
аналитическую внутри окружности С, в частности, и в точке z.
Так как z — любая точка области G, то свойство доказано.
§ 2. Степенные ряды
48. Ряд вида
A0)
где с, — постоянные, называется степенным. Основной тео-
теоремой теории степенных рядов является теорема Абеля:
если степенной ряд A0) сходится в точке гй, то он
сходится и притом абсолютно во всех точках, лежащих
внутри окружности С с центром в точке z = 0 и про-
проходящей через точку гй (т. е.
во всех точках z, для ко- У
торых \ z ] <^ | гй I). При этом
во всяком круге z sg р (рис. 62)
радиуса р, меньшего, чем гй\,
ряд A0) сходится правильно.
Доказательство. Из
сходимости ряда A0) при z = гь
следует, что
lim cnz%^
Рис. 62.
и, следовательно, модули чле-
членов ряда A0) ограничены, т. е.
существует такая постоянная М, что \cnz%\<^M при любом п.
Пусть z — любая точка, лежащая внутри окружности С; тогда
M<|zol и ' " '
образовать:
= 9<Ч. Общий член ряда A0) можно пре-
Отсюда видно, что
120
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
следовательно, модули членов ряда A0) в точке z меньше
соответствующих членов геометрической прогрессии
М + Mq + Mq2 -f • • • + Щ" + ¦ ¦ •
со знаменателем q, меньшим единицы. Следовательно, ряд
A0) сходится в точке z абсолютно, и первая часть теоремы
доказана.
Возьмем теперь произвольный круг | z | =^ р (рис. 62),
лежащий внутри окружности С (р <^ ' г01). По доказанному,
ряд A0) сходится абсолютно во всякой точке, расположен-
расположенной внутри окружиос!и С, и в частности, во всякой точке,
лежащей на окружности выбранного нами круга радиуса р.
Итак, если z1 — какая-нибудь точка на окружности этого
круга (т. е. \z1'\-=p), то числовой ряд
сходится. Но для любой другой точки г, лежащей внутри
или на окружности круга | z \ ^ р справедливо неравенство
или на окружности круга
z I sg Zi\, следовательно
у ур
z \ ^ р, справедливо неравенство
с„г"
с„г
¦ п\
;р. где
при любом п. Этим доказано, что в круге | z
3 za', ряд сходится правильно.
49. Рассмотрим теперь любой луч, выходящий из нуле-
нулевой точки. Возможны три случая.
1) Ряд A0) сходится во всех точках этого луча. Тогда
в силу теоремы Абеля ряд A0) сходится внутри круга сколь
угодно большого радиуса, т. е. сходится во всей плоскости.
2) Ряд расходится во всех точках луча, кроме точки
2 = 0 (в точке z = 0 сходится всякий степенной ряд вида A0),
так как при 2 = 0 все члены ряда, кроме первого, обра-
обращаются в нуль). В этом случае ряд расходится во всех точ-
точках плоскости, кроме точки 2 = 0.
Действительно, из теоремы Абеля следует, что если
ряд A0) в некоторой точке z расходится, то он расходится
и всюду вне круга с центром в начале координат, окруж-
окружность которого проходит через точку г, так как из сходи-
сходимости ряда в некоторой точке вне такого круга следовала
бы сходимость его и в точке z. Следовательно, в рассматривае-
рассматриваемом случае ряд расходится вне круга сколь угодно малого ра-
радиуса с центром в нулевой точке, т. е. всюду, кроме точки z = 0.
§ з]
РЯД ТЕЙЛОРА
121
3) На луче имеются как точки сходимости, отличные
от г = 0, так и точки расходимости ряда A0). Как было
указано выше, из теоремы Абеля следует, что всякая точка
сходимости находится ближе к нулевой точке, чем всякая
точка расходимости. Следовательно, на
луче найдется точка г* (рис. 63), отде-
отделяющая точки луча, в которых ряд A0)
сходится, от точек, в которых ряд рас-
расходится. Сама точка z* принадлежит
или к числу точек сходимости или к чи-
числу точек расходимости ряда A0). Ряд
A0) будет сходиться внутри круга G
с центром в нулевой точке, окружность
которого проходит через точку г*, Рис. 63.
и расходиться вне этого круга.
Круг G называют кругом сходимости степенного ряда A0),
а его радиус—радиусом сходимости этого ряда. На окруж-
окружности круга сходимости могут лежать как точки сходимости,
так и точки расходимости ряда A0). В рассмотренных выше
случаях 1) и 2) можно считать, что радиус сходимости равен
соответственно бесконечности и нулю.
Так как во всяком круге, находящемся целиком внутри
круга сходимости, как было доказано выше, степенной ряд
сходится правильно, то из доказанного в предыдущем пара-
параграфе следует, что сумма степенного ряда внутри круга схо-
сходимости является аналитической функцией.
Радиус сходимости степенного ряда можно определять,
пользуясь известными признаками сходимости рядов (см. [1],
п. 189). Ряд
со -\- ci (z — а) ~Ь ci (z — af ~{~ •¦• ~\~ сп (z — а)п -{-..., A1)
где а — любое комплексное число, также называют степенным.
Этот ряд подстановкой z — a = t сводится к ряду A0), причем
точке ? = 0 соответствует точка z = a. Следовательно, обла-
областью сходимости ряда A1) является круг с центром в точке
г = а.
§ 3. Ряд Тейлора
50. Рассмотрим однозначную функцию f(z), аналитическую
внутри круга G, ограниченного окружностью С с цен гром в точке
z = а (рис. 64). Разложим эту функцию в степенной ряд вида A1).
122
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл IV
Пусть z—любая внутренняя точка круга О. Проведем
внутри круга О окружность С с центром в точке а так, что-
чтобы точка z оказалась внутри этой окружности. Тогда, если
С — точка на окружности С',
то в соответствии с интеграль-
интегральной формулой Коши имеем
Преобразуем один из множите-
множителей подынтегральной функции
1
1
С— 2~~t — а— (г — а)'
Рис. 64.
(С - а) 1 -
Модуль разности |С —а равен радиусу окружности С,
а так как модуль разности z — а\ равен расстоянию точки z
от центра окружности С, то, как бы ни перемещалась точ-
точка С по окружности С, величина
сохраняет постоян-
постоянное значение, меньшее единицы. Следовательно, функция
1
1-
является суммой геометрической прогрессии
1 —•
A4)
— а
сходящейся во всякой точке z внутри окружности С. Эта
прогрессия сходится правильно на окружности С относи-
относительно С. потому что при фиксированном z величина
С —а
= q постоянна на этой окружности и, следовательно, модули
членов ряда A4) совпадают с соответствующими членами
сходящегося числозого ряда
РЯД ТЕЙЛОРА
123
Этот последний ряд является, тем самым, мажорирующим
для ряда A4). Следовательно, подынтегральную функцию
в правой части A2) можно, пользуясь A3) и A4), предста-
представить в виде суммы ряда, сходящегося правильно на окруж-
окружности С (величина |/(С)| ограничена ма окружности С):
ffl _/(?) ¦ (z-а)/(С) | , (г-а)"/(С) ¦
С —z С — а I" (? —а)а "Г •••"Г (? _ a)«+i T«--
и произвести почленное интегрирование, что приводит к раз-
разложению функции f{z) в степенной ряд:
С-а
B - аJ
С
Р /(C)rfC .
\ (С — аK "" # *'
\ (С
С
с
A5)
(z — а)", ... вынесены за
(множители (г — a), (z — а)'2, ..
знаки соответствующих интегралов).
Итак, во всякой точке z, находящейся внутри круга G,
функция f(z) представлена с помощью A5) в виде суммы
степенного ряда
коэффициенты которого вычисляются по формулам
(
С — любая окружность с центром в точке z^=a, лежащая
внутри круга О, или любой другой простой замкнутый кон-
контур, однократно обходящий точку а в положительном направ-
направлении и лежащий внутри круга О, так как в силу теоремы
Коши величина интеграла A6) не зависит от выбора контура
С. Полученный ряд называется рядом Тейлора.
Пользуясь интегральной формулой Коши и вытекающей
из нее формулой C6) гл. II, можно для коэффициентов ряда
Тейлора получить иное представление:
*»'(а)
1 t* f (ХЛ dX, tt \ ' С /(SW- j
= ,,—. \ -pi-i— = J (а), сп = -~—. \ -jf yffj = •
С С'
(я=1, 2, ...)
124
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
и записать разложение в ряд Тейлора в форме, известной
из курса математического анализа для функций действитель-
действительной переменной:
Отсюда, в частности, легко получить известные разложения
элементарных функций
1пA+*) = *-? + ?-...,
и другие. Равенства
служившие нам для определения функций ег, sin z, cos z,
можно теперь рассматривать как разложения этих функций
в ряд Тейлора.
Всякая однозначная элементарная функция является ана-
аналитической во всех точках, в которых она определена.
Но может случиться, что ряд Тейлора для какой-либо эле-
элементарной функции сходится и в такой точке, в которой
эта элементарная функция не определена. Условимся в этом
случае приписывать рассматриваемой элементарной функции
в соответствующей точке значение, равное сумме ее ряда
Тейлора в этой точке.
Так, например, равенство
sin г
. г3 , г4
~ ~!+~5!~ •••
справедливо при любом z 9^ 0. Однако ряд, стоящий в его пра-
правой части, сходится и при 2 = 0, причем его сумма при 2 = 0
равна 1. Условимся поэтому считать, что ^"^=1 при 2 = 0.
РЯД ТЕЙЛОРА
125
Легко видеть, что при таком условии радиус сходимости
ряда Тейлора для всякой однозначной элементарной функции
f(z) равен расстоянию р от точки z = а, являющейся центром
круга сходимости, до ближайшей особой точки этой функции.
Действительно, в круге \z — а | <^ р функция f(z) анали-
тична и поэтому, по доказанному, в этом круге ее ряд Тей-
Тейлора сходится. С другой стороны, если бы радиус сходи-
сходимости ряда Тейлора был больше, чем р, то внутрь круга
сходимости попала бы особая точка функции f{z), которая
в силу принятого условия была бы особой точкой и для
суммы ряда Тейлора, что невозможно, так как сумма степен-
степенного ряда аналитична в круге его сходимости.
51. Если R—радиус круга сходимости ряда Тейлора функции
/(г) и эта функция ограничена в кр\ге сходимости, т. е. сущест-
сущестМ \f(\M ||^?
/() фу р р
вует такая постоянная М, что \f(z)\s^M при |г|-<^?, то, поль-
пользуясь интегральной формулой для коэффициентов ряда Тейлора и
выбрав в качестве пути интегрирования окружность |С — а| = р
с центром в точке г = а, получим (см. свойство 6) на стр. 51
1
м
м
Так как радиус р окружности С можно брать сколь угодно близ-
близким к радиусу круга сходимости R, то
\сп\^дП (п = 0, 1, 2, ...).
Эти неравенства называют неравенствами Коши для коэффициен-
коэффициентов ряда Тейлора.
Если функция/(г) является аналитической во всей плоскости,
то радиус кр}га сходимости ряда Тейлора бесконечен, и, следова-
следовательно, из неравенств Коши находим, что все коэффициенты сп,
кроме с0, равны нулю, и значит, /(г) = с0. Тем самым доказано,
что функция, аналитическая и в то же время ограниченная во
всей плоскости, постоянна (теорема Л и у в и л л я).
52. Ряд Тейлора можно почленно дифференцировать. Дей-
Действительно, если f(z) — аналитическая функция, то аналити-
аналитической является и ее производная f'(z); разложив по форму-
формуле A7) в ряд Тейлора функцию f'(z), получим
' К*} J V I л V" "¦) \ •¦¦П Тп П| V" "¦) \-"
Но к этому же равенству приводит почленное дифференци-
дифференцирование равенства A7). Полученный после дифференцирования
i26
РЯДЫ И ОСОБЫГ- ТОЧКИ
[Гл. IV
ряд имеет тот же круг сходимости, что и исходный ряд,
так как, с одной стороны, при дифференцировании степен-
степенного ряда модули его коэффициентов увеличиваются (коэф-
(коэффициент сп умножается на п) и поэтому радиус сходимости
не можег увеличиться, а с другой стороны, радиус сходи-
сходимости не может и уменьшиться, так как сумма ряда A7), а
следовательно, и ее производная являются функциями анали-
аналитическими во всякой внутренней точке круга сходимости
ряда Тейлора для функции f{z).
53. В качестве точки а в формуле A7) можно взять лю-
любую точку, в которой функция /(г) аналитична. Разложение
A7) называют разложением функции f(z) в окрестности
точки а. Если /(о) = 0, то точка а называется нулем функ-
функции /(г). В этом случае разложение функции в ряд Тейлора
в окрестности точки а имеет вид
так как cn = f(a) = 0. Если в разложении функции f(z) в
ряд Тейлора в окрестности точки а
cQ = c1 = ... = cn_i = О,
но сп rjz. О и, следовательно, разложение имеет вид
f(z) = ся(г — af + cn+i (z - af" + ..., A8)
то точка а называется нулем функции f{z) порядка, или
кратности, п. Если и=1, то нуль называется простым.
Продифференцировав A8), приходим к выводу, что если a—
нуль порядка п функции f(z), то эта же точка является
нулем порядка п — 1 для функции /' (г).
Из формул для коэффициентов ряда Тейлора следует, что
если точка а является нулем порядка п функции f{z), то
/(в) =/' (a) =... =^» (а) = О, но /W (а) ф 0.
Разложение A8) можно переписать в виде
f(z) = {г- af [сп + Cn+I {z - а) + ...]= (z ~ af ? (z),
где функция ср (z) определяется как сумма степенного ряда
=Р {г) — сп -|- сп+1 {z — а) -\-... ,
имеющего, очевидно, тот же круг сходимости, что и данный
ряд A8). Для функции <p(z) точка а уже не является нулем,
§ з]
РЯД ТРЙЛОРА
12'
так как ср (а) = сп ф 0. Справедливо и обратное утверждение.
всякая функция вида
где п — целое положительное число, у(а)фО, а ср (z) ана-
литична в точке а, имеет в этой точке нуль порядка п.
Действительно, разложив ср (z) в ряд Тейлора в окрест-
окрестности точки а, получим
ср {z) = ?0 -|- с1 (z — а) -\- ...,
где с0 = ср (а) ф 0. Отсюда
f(z) = {z- af ср (z) = Uz - af + с, (*
+ ...
Мы пришли к разложению вида A8), следовательно, точка
а является нулем порядка п функции f(z).
Пример. Точки z = + 2 являются для функции
f (z) = (г* — 4)* е*
нулями 3-го порядка, так как/(г) = (г — 2K (г + 2K ег, и если поло-
положить a (z) = (z-|-2K ег, то /(г) = (г— 2K а (г), причем <?B)ф0,
если же положить а (г) = (г — 2K ег, то /(г) = (г4-2)'ф(г) и
B)^0
54. Имеет место следующая теорема о единствен-
единственности аналитической функции:
Если значения аналитических в области Q функций
fi(z) и A(z) совпадают в некоторой бесконечной последо-
последовательности точек
zk,
(*)
сходящейся к точке а (Iim2ft = a), которая является
k -~ 00
внутренней точкой области G, то функции fx(z) и /4(г)
тождественны во всей области G: f\{z).z^fi{z).
Ограничимся доказательством теоремы в случае, когда
область О—круг, а точка а — ценгр этого круга. Пусть
/(г)=/, (г)— Л (г). Тогда /(zft) = 0 при любом k. Следо-
Следовательно, в силу непрерывности функции f(z) имеем /(а) =
= Umf(zk) = Q. Предположим теперь вопреки доказываемому,
128
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
что функция f(z) не равна тождественно нулю в круге О,
т. е. что не все коэффициенты разложения f(z) в ряд Тей-
Тейлора в окрестности точки а равны нулю. При этом предпо-
предположении точка а является нулем функции f(z) некоторого
порядка п и поэтому f(z) имеет вид A9). Множитель {z— а)'1
нигде, кроме самой точки а, нулю не равен, а функция со (г),
входящая в A9), отлична от нуля в точке а, а значит (в силу
непрерывности) и в некоторой ее окрестности. Поэтому в
некоторой окрестности точки а функция f(z) нигде, кроме
самой точки а, не равна нулю. Мы пришли к противоречию,
так как в любой окрестности точки а имеются точки из
последовательности (*), а в них /(,г) = 0. Итак, f(z) = 0,
а следовательно, f, (z) =- /, (z). Теорема доказана.
§ 4. Ряд Лорана
55. Предположим, что f(z) является однозначной анали-
аналитической функцией внутри кольца между концентрическими
окружностями С и С" с цен-
центром в точке z = a (рис. 65),
и пусть z — произвольная внут-
внутренняя точка эюго кольца.
Проведем окружности Г' и
Г" с центром в точке а так,
чтобы каждая из них находи-
находилась внутри данного кольца и
чтобы точка z оказалась между
Г и Г".
Опишем из точки г, как
из центра, окружность ¦(, на-
РИС_ 65. холящуюся в кольце между
Г' и Г". Пользуясь теоремой
Коши для составного контура, будем иметь
2iu 3 С —z ~2ra 3 С —z
_L 4 ШЛ
2tw J С —г *
Но, в силу интегральной формулы Коши,
2m ) Ч-г —
§41
и, следовательно,
РЯД ЛОРАНА
- _L f ПУЛ _ _L С /(О*'
— 2./Д С -г 2*0 С-а
129
B0)
Если С — точка на контуре Г", то |С — а | ^> | 2 — a| и
1 _ 1 1 _
* Г1 I z а | (г аJ | | (г °)" |_ 1
— С — а [ ' I" С — а 1" (С — аJ "" ''' ' (С — а)п г • • • J ¦
Ряд в правой части этого равенства сходится на окружности
Г" правильно (см. рассуждения в п. 50); умножив его по-
почленно на /(С) <К. и проинтегрировав вдоль Г", получим для
первого из интегралов в правой части B0) разложение
J_ f /(О Л L { /(Е)Д | г~а { Ш
2м 3 С — г ~ 2тс( J С — а ' 2л» J (С — а
Г" Г" Г"
3
Г"
(z-
-af ? /(C)rfC , , (г-а)" Р /(С)Д , _
2я» J (С — аK "" • • • "Г 2ni 3 (С — а)п+1 ~Г • • • —
Г" Г"
где
Г"
Если же точка С находится на контуре Г', то \z — а \
С —а
— а |, и следовательно,
_ ^ 1; поэтому для того
чтобы получить ряд, правильно сходящийся на V, преоб-
1
разуем
С-2
иначе:
I — z С — д — (z — а)
B-е) 1-
1 Г, , ? — а , (С — а)
= 1 -\ 1- т г
z — a I z — a \z — й)
5 И. Г. Араманович и др.
(z
-Д) ¦ 1
— а)" г •••]•
130
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
После такого преобразования для второго из интегралов в
правой части B0) получим:
5
Г'
~ z — а > (г _ ау ~Г ¦ ¦ •
где
= h \
Г'
= 1. 2,
B2)
В силу теоремы Коши для составного контура вместо
путей интегрирования Г" и Г' в B1) и B2) можно взять лю-
любую окружность Г с центром в точке а, лежащую в данном
кольце между С" и С".
Заметим также, что при замене я на — п подынтеграль-
подынтегральное выражение в правой части B1) переходит в подынтег-
подынтегральное выражение правой части B2), поэтому из B0) мы
получаем следующее разложение функции /(г), сходящееся
во всякой точке z внутри кольца между С' и С":
4-
^—4- -I — 1-
где коэффициенты сп, как при « = 0, 1, 2, ..., так и при
я — —1, —2, ... определяются формулой
г —A
л 2nl
B3)
а Г — любая расположенная в данном кольце окружность
с центром в точке 2 = а. Полученное разложение называют
рядом Лорана.
РЯД ЛОРАНА
131
Пример 1. Рассмотрим различные разложения в ряд Лорана
функции
/B) = -
выбрав д =0.
Функция/(г) имеет две особые точки: 2=1 и 2 = 2.
вательно, имеется три круговых «кольца» с центром в точке
в каждом из которых функция
аналитична, а именно (рис. 66):
1) круг \г\ < 1,
2) кольцо 1 < | z | < 2,
3) внешность круга | г | > 2.
В рассматриваемом примере
нетрудно получить разложение
в ряд Лорана в каждом из пере-
перечисленных «колец», не прибегая
к формулам для вычисления коэф-
коэффициентов.
1) Разложение в круге | z \ < 1.
Функцию /(г) можно предста-
представить в виде суммы двух элемен-
элементарных дробей:
Следо-
Следо2 = 0,
1
1
B—1) B —2) 2 — 2 2— Г
Так как
1
1
-, а функция ¦
Рис. 66
является суммой
геометрической прогрессии
модуль знаменателя которой |2/2|<1, то
1 1 _ г 22
2 —2~ 2 2а 23
Аналогично,
1 1 , ,
2—1 1 —2"
B4)
B5)
причем ряд в правой части сходится, так как | г | < 1. Складывая
B4) и.B5), получаем
132
РЯДЫ И ОСОБЫЕ ТОЧКИ
1Г.1 IV
т. е.
сп=^--^г (я=0, 1, 2, ...),
е-л = 0 (я=1, 2, ..)
Полученное разложение является рядом Тейлора.
2) Разложение в кольце 1 < | г | < 2
Ряд B4) остается сходящимся, так как | г \ < 2, но ряд B5)
расходится, потому что |г|> 1; поэтому разложение B5) заменяем
следующим:
1 _ 1 1 1 /, , 1 , 1
2— 1 ~ 2 ' . 1 ~~
I
B6)
В рассматриваемом кольце ряд B6) сходится, так как |г|>1 и,
следовательно, | 1 | г | < 1.
Складывая B4) и B6), получим
1 1 г г', г»
B-1) (г -2)
2"+''
1
т. е.
1
1
"г5"
е_* = -1 (я = 1,2,...).
3) Разложение в области |г|>2.
Равенство B6) сохраняется, так как если | г | > 2, то тем более
|г|>1; но ряд в правой части B4) 'расходится, и равенство B4)
заменяем следующим:
1
1
1
г —2'
?
-¦H'+f+?+¦••
Ряд в правой части B7) сходится, так как | г | > 2 и, следовательно,
; 1. Складывая B6) и B7), получаем:
(г-Л){г-2)
л. е.
с„^0 (я = 0, 1, 2, ...),
^„^г»-1-! (п = 1, 2, ...).
§ 41
РЯД ЛОРАНА
133
Пример 2. Выбрав л=1, найдем разложения в ряд Лорана
в различных областях функции, рассмотренной в примере 1:
/(*)=¦
B-1) B-2) •
В данном сл>чае построим два круговых «кольца» с центром
в точке 2 = 1 (рис. 67):
1) круг, из которого удален центр 0 <с | 2—1|-<1;
2) внешность круга \г— 1 | > 1.
В каждом из этих «колец» функция /(г) аналитична, а на гра-
границах имеет особые точки.
Разложим в каждой из этих
областей функцию /(г) по степе-
степеням разности (г — 1).
1) Разложение в области
0<|2— 1 |<1.
Как и в примере 1, получим
1
1
(z — 1)(г — 2) -"г^2
Далее,
1 _ 1 _
i^2 1 — (г— 1)
Г
Рис. 67.
+ •.. + B-1)" + ...],
причем ряд в правой части сходится, так как \г—1 | <1. Следо-
Следовательно,
1
1
B—1) B —2)
2—1
т. е.
— (г — 1)а —... —(г— 1)« —....
(/2 = 0, 1, 2, ...),
2) Разложение в области \г — 1 | > 1.
В этой области
1
1
1
; — 2~~ (г—1) —1 г —
-гЫ' + .4т+;
1.1.
1 —
2—1
2-1)
- +
B-1)
п ~г ¦¦• ,
134
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
причем ряд в правой части равенства сходится, так как \г — 1 |> 1
и, следовательно, ¦ т-г < 1. Итак,
1
(г—1)B —2) г — 2 г —1
к е.
¦ + •¦¦ +
с„ = 0 (л = 0, 1, 2, 3, ...),
1
B_1)«-Г"- .
56. Докажем единственность разложения функции в ряд Лорана,
т. е. разложения вида
f(n)=co + cl (г — а)+... + ся(г — a)» + ...
:-а т (г-аJ
(г —а)"
B8)
Иными словами, докажем, что если функция f (г) является в не-
некотором кольце с центром в точке г = а аналитической, то не
существует двух различных рядов указанного вида, сходящихся
в этом кольце и имеющих
своей суммой функцию /(г).
В самом деле, если в не-
некотором круговом кольце
г, < | г — а|<;га с центром в
точке г = а (рис. 68) ряд вида
B8) сходится, т. е. если в этом
кольце сходятся ряды
с0 + с, (г — а) + ... +
+ сп(г-а)" + ... B9)
г — а ' (г—аJ
C0)
Рис. 68.
то во всяком кольце p,sg|z —
— а | г^р2, лежащем внутри дан-
данного кольца (г, < Pi < р2 < г),
ряды B9) и C0) сходятся правильно. Для ряда B9) это следует из
теоремы Абеля, а для ряда C0) из следующих соображений: после
замены l/(z — а) = ? ряд C0) превращается в степенной ряд
а так как ряд C0) сходится во всем заданном кольце и, в частности,
на любой окружности \г—a j = p, где г1<р<:р1, то ряд C1) схо-
схоРЯД ЛОРАНА
135
дится на окружности |<|= 1/р и, в силу теоремы Абеля, сходится
правильно в кр)ге |<|=g|l/pj (так как 1 ,р_, < 1 р). Возвращаясь
к переменной г, мы приходим к выводу, что ряд C0) сходится пра-
правильно в области \г — a \^pt и тем более в кольце р, =g | г — а | ^ р2.
Из доказанного следует, в частности, что ряды B9) и C0) схо-
сходятся правильно на всякой окружности Г, лежащей в данном кольце,
с центром в точке а (рис. 68). Ряды B9) и C0), а следовательно,
и ряд B8), можно поэтому, в соответствии с доказанным, почленно
интегрировать вдоль Г.
В § 4 гл. II было доказано, что интегралы вида
где замкнутый контур Г однократно обходит в положительном на-
направлении точку г = а, равны нулю при всяком целом п, кроме
п = —1, а в этом последнем случае интеграл равен 2тц. Следова-
Следовательно, при почленном интегрировании ряда B8) исчезнут все члены,
кроме первого члена второй строки, и мы получим
откуда
С-|=;
Чтобы определить с_„, нужно до интегрирования умножить все
члены ряда B8) на (z — а)п~1. Тогда после интегрирования все ин-
интегралы, кроме одного, опять обратятся в нуль, и мы получим
(z) (z - а)"-> dz =
откуда
Аналогично, для того чтобы определить сп при п = 0, 1, 2, ...,
нужно, прежде чем печленно проинтегрировать ряд B8), разделить
его члены на (z — a)n+1. Тогда после интегрирования получим
z —
п
136
РЯДЫ И ОСОБЫЕ ТОЧКИ
Г.| IV
Мы пришли к формулам B1) и B2) для коэффициентов ряда Ло-
Лорана и тем самым доказали, что никакое другое разложение функ-
функции f (г) в ряд указанного вида невозможно. Так как ряд Тейлора
является частным случаем ряда Лорана, то доказана и единствен-
единственность разложения в ряд Тейлора.
§ 5. Изолированные особые точки
67. Особая точка z = a функции f(z) называется изо-
изолированной, если в некоторой окрестности этой точки функ-
функция f(z) не имеет других особых точек, т. е. если в неко-
некоторой окрестности точки z = а функция f(z) аналогична
всюду, кроме самой точки z = a. Разложение функции в ряд
Лорана, сходящийся к этой функции во всех точках круга с
центром в данной изолированной особой точке а, кроме этой
точки а (меньший радиус «кольца», в котором происходиi
разложение, равен нулю), будем называть разложением функ-
функции в ряд Лорана в окрестности данной изолированной
особой точки. Так, в примере 2 (стр. 133) первое из разло-
разложений является разложением в окрестности особой точки z = 1.
Будем называть ряд
co-\-c1(z — а) -|- • • • 4" сп (z — а)" -{-...
правильной частью, а ряд
С-' -I С-=1 L _| ?г2 L
г — а ~ (г — af ~ ' "' ~ (г — а)" ' ""'
главной частью ряда Лорана и выясним, как связано по-
поведение функции f(z) в окрестности точки z = a с разло-
разложением функции в ряд Лорана в окрестности этой точки.
Предположим сначала, что в некоторой окрестности точки
z = a функция f{z) ограничена, т. е. существует такая постоян-
постоянная М, что \f(z)\<^M во всех точках этой окрестности.
Если "обозначить через р радиус окружности Г, по которой
происходит интегрирование в формулах B3), получим
К„|= 2^т ^/(С)(С — а)п1с
г
т. е. | с_! | =ss Щг | с_21 «s: Мр1 и т. д. Так как в качестве Г
можно взять окружность сколь угодно малого радиуса р
с центром в точке z = а, то отсюда следует, что c_i = О,
51
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
137
с 2 = 0, ..., с_„^0,..., т. е. что главная часть ряда в раз-
разложении отсутствует и разложение имеет вид
f(z) — с0 + с, (г — а) + • • • + сп B — af -f... C2)
Это разложение имеет место во всех точках некоторой окре-
окрестности точки z = a, кроме самой точки z = а. Но правая
часть последнего равенства, будучи суммой степенного ряда,
аналитична и при z = a. Поэтому если под f(a) понимать сумму
ряда при z = а, т. е. положить /(а) = са, то z = а станет пра-
правильной точкой функции f(z) и разложение C2) бу-
будет разложением f{z) в ряд Тейлора в окрестности точки
z = а. Итак, если функция/(г) ограничена в некоторой окрест-
окрестности изолированной особой точки г = а, то мы можем всегда
считать эту точку правильной точкой функции, положив
^^ 124).
= cu (с
(см. пример с разложением ^-^ на стр. )
Пусть теперь функция f(z) неограничена в окрестности
изолированной особой точки г = а. В этом случае либо
lim f(z)^oo, либо при z—-а функция f(z) вообще не имеет
предела (ни конечного, ни бесконечного). В первом случае
будем точку z = a называть полюсом функции f(z), во вто-
втором — существенно особой точкой.
Если точка г = а является полюсом функции /(г), то
в достаточно малой окрестности этой точки \f(z)\^>M, как
бы ни было велико М, и поэтому уж во всяком случае f(z) ^ О
в некоторой окрестности точки z = а. Следовательно, функ-
функция F(z) = —г-г, будучи отношением двух аналитических функ-
функций (причем f(z) -ф 0), является также функцией аналитиче-
аналитической в некоторой окрестности точки г = а всюду, кроме са-
самой точки z = a. Но, по условию, lim /(z) = oo, следова-
следовательно, 2"а
lim F (z) — lim ^-ry = 0,
поэтому функция F(z) ограничена в некоторой окрестности
точки z = а и по доказанному эту точку можно считать пра-
правильной для F(z), положив F(a) = Q. Итак, если точка z = a
является полюсом функции f(z), то она является нулем функ-
функции ут-у. Будем точку z = a называть полюсом порядка п
138
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл. IV
функции f(z), если эта точка является нулем порядка п для
функции ут-г- В случае п = 1 будем полюс называть простым.
Как было доказано, точка z = a тогда и только тогда
является нулем функции -^-г- порядка п, когда
1
C3)
где <р (а) ^ 0 (функция <р (г) аналитична при z = а). Но из
C3) следует, что
или, если положить ф(г) =
?(Z) '
C4)
причем функция ф(г) также аналитична при г = а и if (а) ^ 0.
Итак, точка z = a тогда и только тогда является по-
полюсом порядка п функции f(z), когда f(z) можно предста-
представить в виде C4).
Так, например, точка z = — 2 является полюсом 3-го по-
рядка для функции
,
точки z = ±2i являются полю-
сами 1-го порядка для функции
cos г
так как г2 -j- 4 =
22 + 4'
= (z — 2i) (z -\- 2i), точка 2 = 0 —полюс 2-го порядка для
. sin z / sin z (sin г)/г sin г _ .
функции —Г 1так как —Г = ъ—-s—и-^—^U при z = (
Если числитель правой части C4) разложить в окрестности
точки z = a в ряд Тейлора, то получим
где со = ф(а
будем иметь
(г-а)»
Э. Отсюд?, произведя почленное деление,
f[z) = cn-\- cn+1 (z — а) + ся+2(г — а)9
§ 5]
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
139
Таким образом, если точка z = а является полюсом порядка п
функции f(z), то главная часть разложения этой функции
в ряд Лорана в окрестности точки z = a представляет собой
не бесконечный ряд, а конечную сумму, причем порядок
полюса равен наивысшему показателю степени выражения
(z — а) в знаменателях членов главной части разложения.
Обратно, предположим, что главная часть разложения
функции f(z) в ряд Лорана в окрестности точки z = a
содержит лишь конечное число отличных от нуля членов:
1 г — а ' (г— аK ' ' (г —а)" ^-»
Произведя приведение к общему знаменателю, получим
-а)™+...] = -(Шр, C5)
гае $(а) = с_пф0, и функция <рB), будучи суммой сходя-
сходящегося в некоторой окрестности точки z = a степенного
ряда, аналитична в этой точке. Сравнив C4) и C5), мы убеж-
убеждаемся в том, что точка z = а — полюс функции f(z) по-
порядка п.
Итак, главная часть разложения функции в ряд Ло-
Лорана тогда и только тогда содержит лишь конечное
число членов, когда точка, в окрестности которой про-
произведено разложение, является полюсом. Отсюда следует,
что главная часть разложения функции в ряд Лорана в ок-
окрестности существенно особой точки содержит бесконечное
множество отличных от нуля членов. Поведение функции
в окрестности существенно особой точки подчиняется следую-
следующей теореме, доказательство которой мы не приводим:
Теорема Сохоцкого — Вейерштрасса. Если
точка а является существенно особой точкой функции
f(z), то для любого заданного комплексного числа А най-
найдется последовательность точек, сходящаяся к точке а,
вдоль которой значения f(z) стремятся к А; для Л = оо
теорема также верна.
140
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл IV
Пример. Найти особые точки функции
их характер.
Принимая во внимание, что
и определить
получим
.'/г
— ' + , +
2!;
п\.
C6)
причем ряд в правой части сходится всюду, кроме точки z = 0.
Равенство C6) можно рассматривать как разложение функ-
функции е''г в ряд Лорана в окрестности точки 2 = 0, и так как его
главная часть содержит бесконечное множество членов, то точка z = 0
является существенно особой точкой функции е 'г.
Рассмотрим поведение функции el/z в окрестности точки z = 0.
При г — 0 вдоль положительной части действительной оси полу-
получим 1/г—»-f-oo и е'г — + оо; если z—>¦ 0 вдоль отрицательной части
действительной оси, то 1/г —> — оо и е]1г—* 0. Пусть теперь Л = re"? —
любое комплексное число, отличное от нуля и от бесконечности.
Из равенства
1/ = Ln Л
= Л или
находим
1
Ln Л In г + «<р + 2kni'
Полагая k — 0, ±\, ±2, ..., получим последовательность точек,
сходящуюся к точке z = 0, так как
llm ,
к-*±со 1П Г
2Й7СГ
. =0,
Г
причем функция eVz не только стремится к А вдоль этой после-
последовательности, но даже в точности равна Л в каждой точке рас-
рассматриваемой последовательности.
Других особых точек функция е''гне имеет.
68. Классификацию изолированных особых точек можно
распространить и на случай, когда изолированной особой
точкой является бесконечно удаленная точка. Назовем беско-
бесконечно удаленную точку изолированной особой точкой функ-
функции f(z), если в некоторой окрестности бесконечно удален-
удаленной точки, т. е. вне круга с центром в начале координат
достаточно большого радиуса, нет других особых точек функ-
функции f(z).
ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
141
Разложение функции в ряд Лорана, сходящееся всюду
вне круга достаточно большого радиуса с центром в точке
2 = 0 (кроме, быть можег, самой бесконечно удаленной точки),
будем называть разложением в окрестности бесконечно
удаленной точки. Последнее из разложений в примере 1
(стр. 132) является разложением функции -^г- ^- в ряд
B — I) (Z — I)
Лорана в окрестности бесконечно удаленной точки. Ряд C6)
является разложением функции е2 не только в окрестности
точки z = 0, но также и в окрестности бесконечно удален-
удаленной точки. При разложении функции в ряд Лорана в окрест-
окрестности бесконечно удаленной точки следует, в соответствии
с определением, считать в B8) а = 0. Запишем члены разло-
разложения в следующем порядке:
C7)
Назовем ряд
4- У ^п-
1 ^ L 2"
правильной частью, а ряд
—главной частью разложения C7). Такая терминология
вполне естественна, если учесть что при замене z=\jz ок-
окрестность бесконечно удаленной точки отображается на окрест-
окрестность точки 2 = 0 и разложение C7) превращается в разло-
разложение функции /"A/2) в ряд Лорана в окрестности точки
2 = 0:
2 Т" %i Т~ • • • Т ~п Т • • ¦ >
142
РЯДЫ И ОСОБЫЕ ТОЧКИ
(Гл. IV
в котором ряд с0 -f- Y] с_„2п является правильной частью,
а ряд 2_,С^к — главной частью.
л=1
Повторив рассуждения, аналогичные приведенным выше,
мы придем к выводу, что если в некоторой окрестности
точки 2 = со функция f(z) ограничена, то С] = с2 = -•• =
= ся = ...== О, разложение C7) принимает вид
и точку z = со можно считать правильной точкой функции
/(.г), положив /(со) = с0.
Если 2 = со— правильная точка функции f(z) и /(со) =
=0, то будем точку z = со называть нулем порядка т
функции /(г), если точка 2 = 0 является нулем порядка т
функции /A/2).
Если lim/B) = oo, будем точку 2 = со называть полю-
функции. Очевидно, что если точки 2 = со — полюс
функции /(г), то точка 2 = 0 — полюс функции /A/г). На-
Назовем точку 2 = со полюсом порядка т функции /B), если
точка 2 = 0 является полюсом порядка т функции /A/2).
В этом случае разложение функции f(z) в окрестности точки
z = со будет иметь вид
где стфЪ.
Если функция f(z) в окрестности точки 2 = со неограни-
чена и в то же время предел lim f{z), ни конечный, ни бес-
г-»со
конечный, не существует, то точку z = со назовем сущест-
существенно особой для /B). В этом случае главная часть разло-
разложения C7) содержит бесконечное множество отличных от
нуля членов, а поведение функции /(г) в окрестности точки
z=. со определяется теоремой Сохоцкого.
НЕКОТОРЫЕ ПРИЕМЫ РАЗЛОЖЕНИЯ В РЯД ЛОРАНА
143
§ 6. Некоторые приемы разложения функций
в ряд Лорана
59. Общие формулы B3) для коэффициентов ряда Лорана
обычно мало удобны для вычислений. В некоторых случаях
могут быть применены более простые приемы.
Для того чтобы разложить в ряд Лорана рациональную
функцию, достаточно воспользоваться представлением пра-
правильной рациональной дроби в виде суммы простейших дро-
дробей, как это было сделано в § 4 этой главы (примеры 1 и 2).
Простейшая дробь вида 1/B — а) разлагается в ряд, являю-
являющийся геометрической прогрессией, а дробь вида 1/B — a)k
(k^> I целое) — в ряд, полученный с помощью (k — ^-крат-
^-кратного дифференцирования геометрической прогрессии.
Заметим, что всякая правильная рациональная дробь может
быть разложена в сумму дробей вида A/(z — а)п, где А, а —
комплексные числа.
При разложении в ряд Лорана иррациональных и транс-
трансцендентных функций иногда можно использовать разложения
в ряд Тейлора функций ег, sin z, cosz, In A -\-z), биномиаль-
биномиальный ряд и другие известные разложения. Так, например, в
окрестности точки 2 = 2
cos
2 — 2 2! B — 2J t-'-^*- Ч Bя)! (г — 2J"'
Иногда следует предварительно преобразовать разлагае-
разлагаемую в ряд функцию.
Пример 1. Разложить в ряд Лорана в окрестности точки
г = 1 функцию sin •
1
Имеем:
• г
sin
г
in г = sin ( 1 -| г = sm I cos г -4- cos I sin г,
г— 1 \ г— 1/ 2 — 1 ' 2—1'
откуда
___
1)"
' (
Bл)! (г
(-1)"
1)! B
144
РЯДЫ И ОСОБЫЕ ТОЧКИ
[Гл IV
Если бесконечно удаленная точка является правильной
для функции f(z), то разложение в ряд в окрестности бес-
бесконечно удаленной точки сводится подстановкой z=l/'(, к
разложению функции /A/С) в ряд Тейлора в окрестности
точки С=0.
Пример 2. Разложить функцию
в окрестности точки z = оо.
в ряд Лорана
Положив z = y-, получим /(у] = e'1/i:)+2 =e1 + 2C t причем
точка С = 0 является для этой функции правильной точкой. Обо-
Обозначив / 1-р) = <р (?), будем иметь
(С) _
и т. д. Следовательно, ср @) = е, у' @)
Отсюда
2
¦ I+2C
i
—+- 4 1
: — 2е, ср" @) = 12<? и т. д.
т. е.
Ряд сходится вне круга радиуса R=2 (т. е. при | г | > 2), так как
единственной особой точкой функции является точка г = —2.
ЗАДАЧИ К ГЛАВЕ IV
1. Доказать, что ряд г -4- ™ -\-о? -f-...-\—а + --- сходится во
всем круге сходимости правильно.
2. Разложить в ряд Тейлора в окрестности точки г=1 любую
ветвь функции j/z. Каков радиус сходимости полученного ряда?
3. Разложить в окрестности нулевой точки в ряд Тейлора те
ветви функций Arctgz и Arcsinz, для которых ArctgO = ArcsmO =
= 0. Каков радиус сходимости полученных разложений?
4. Написать первые четыре члена разложения в ряд Тейлора
в окрестности нулевой точки функций:
а) в'Л!-*), б)
1
; вIпA+ег).
Каковы радиусы сходимости этих рядов?
ЗАДАЧИ К ГЛ IV
145
5. Найти нули функций и определить их порядки:
a) B2 + 9)(z2 + 4M; б) (I — ег) (г2 — 4K; в) г sin г, r) SLi:
6. Разложить в ряд Лорана функцию —. ^-. -г-:
а) в кольце | а \ < | г \ < Ь; б) в окрестности бесконечно уда-
удаленной точки; в) в окрестности точки а.
7. Разложить в ряд Лорана:
а) функцию 22е1/г в окрестности точки z = 0;
б) функцию cos
в окрестности точки 2 = 2.
8. Найти несколько первых членов разложения функции
sin | в ряд Лорана в окрестности бесконечно удаленной точки.
Какова область сходимости этого разложения?
9. Найти все конечные особые точки функций и определить
их характер (для полюсов указать порядок):
а) л,_-п^„ , п; б) л..', л»'. в) ~Г,\ г) tg2*
Д)
к)
sin z
е) cos;
1
1
ж) tg:
1
tg(z— 1) 1 — cosz.
z* ' ; ег — 2 •
10. Исследовать поведение функций в окрестности бесконечно
удаленной точки:
а) т-ГТг; б) ^ ~*+J ; lOg-i^; г) е"г; д) sin z;
5 —г*
е)е1/г + г2_4; ж) е1/г; з) е1/A-г); и) е~* + za + z — 2.
11. Является ли точка г = 0 изолированной особой точкой для
функции:
а) tg —",
' 6 Z '
sin —?
Z
12. Является ли бесконечно удаленная точка изолированной
особой точкой для функции:
а) е2; б) ctg z?
ГЛАВА V
ТЕОРИЯ ВЫЧЕТОВ
§ 1. Основная теорема о вычетах
60. Если точка z = a является правильной точкой или
изолированной особой точкой однозначной функции f(z), то
можно выбрать простой контур С, однократно обходящий
точку а в положительном направлении (например, окружность
достаточно малого радиуса), так, чтобы на контуре С и всюду
внутри этого контура, за исключением, быть может, самой
точки а, функция f(z) была аналитической. Величину
будем в этом случае называть вычетом функции f(z) от-
относительно точки а и писать:
Res
Из теоремы Коши для составного контура следует, что вычет
данной функции относительно заданной точки не зависит от
формы и размеров контура С, если этот контур удовлетво-
удовлетворяет указанным выше требованиям.
Если точка а является изолированной особой точкой
функции f(z), то коэффициент с_х первого члена главной
части разложения этой функции в ряд Лорана в окрестности
точки а (см. формулу B2) гл. IV) равен
§ 1]
ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ
147
и, следовательно, вычет функции f(z) относительно точки а
совпадает с коэффициентом с^ разложения этой функции в
ряд Лорана в окрестности точки а:
Res [/B); a] = c_l.
Если а является правильной точкой функции f{z), то все
коэффициенты главной части разложения в окрестности этой
точки равны нулю и, следовательно, вычет функции относи-
относительно правильной точки равен нулю (это следует' также из
теоремы Коши). Если а — полюс или существенно особая
точка функции f(z), то вычет относительно нее может быть
отличным от нуля, но может оказаться и равным нулю (если
0 = 0).
61. Пусть Со — простой замкнутый контур, на котором
функция f(z) аналигична. Допустим, что внутри контура Со
функция f(z) аналитична
всюду, за исключением п
изолированных особых то-
точек av аь ..., а„. Окружим
эти точки лежащими внутри
Со окружностями С\, С2, ...,
Сп (рис. 69) столь малых ра-
радиусов, чтобы внутри каж-
каждой из этих окружностей
находилось лишь по одной
особой точке функции f(z) Рис- 69.
и чтобы никакие две из этих
окружностей не имели общих точек. Тогда в силу теоремы
Коши для составного контура получим
— с„
С1
где при интегрировании все контуры обходят против часовой
стрелки.
Следовательно, величина ~--\f(z)dz равна сумме вы-
вычетов функции f(z) относительно всех особых точек
148
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
этой функции, находящихся внутри контура Со (основ-
(основная теорема о вычетах):
); **]¦
Вычетом функции относительно бесконечно удаленной
точки естественно считать величину
1
где С—окружность с центром в начале координат столь
большого радиуса, что вне этой окружности нет особых то-
точек функции f(z), отличных от бесконечно удаленной особой
точки. Направление интегрирования на окружности С сле-
следует выбрать так, чтобы при обходе контура бесконечно
удаленная точка оставалась слева, т. е. направление обхода
надо установить по часовой стрелке. Отсюда следует, что
если с_! является коэффициентом при — в разложении функ-
функции f(z) в ряд Лорана в окрестности бесконечно удаленной
точки, то
Res [f(z)\ со] = — с_,.
Если бесконечно удаленная точка функции f(z) правильная,
то вычет относительно нее не обязательно равен нулю. Так,
например, для функции
1
точка z = со является правильной, если считать /(со) = 2,
но c_i = 3, и, следовательно,
Res[/(z); oo] = —3.
Из сопоставления определения вычета относительно бес-
бесконечно удаленной точки с основной теоремой о вычетах
следует, что если функция имеет конечное число особых
точек, то вычет относительно бесконечно удаленной точки
равен взятой с обратным знаком сумме вычетов относительно
всех особых точек, расположенных в конечной части пло-
плоское т. Следовательно, сумма вычетов относительно всех осо-
особых ю'шк, включая и бесконечно удаленную точку, равна нулю.
ВЫЧЕТ ОТНОСИТЕЛЬНО ПОЛЮСА
149
§ 2. Вычет относительно полюса
62. Если точка а является простым полюсом функции f(z),
то в окрестности этой точки функция f(z) представима в виде
где функция <р (z), будучи суммой правильной части разло-
разложения функции f(z) в ряд Лорана в окрестности ючки а,
является аналитической и тем более непрерывной функцией
в точке а. Из A) имеем
и, переходя к пределу при z^-a, получим
<U = lim [(*-я)/(*)],
z-*a
так как вследствие непрерывности функции <?(z) в точке а
существует конечный предел lim q>(z) — <?(a) и
B)
относительно
г. Сле-
lim [{z — a)(f (z)] = 0.
г—>а
Итак, если а — простой полюс функции f(z), то
Res [/(г); o] = lira [(г-а)/(г)].
22
Пример 1. Вычислить вычет функции —
2 — 1*
точки г = 2.
Точка 2 = 2 является простым полюсом функции
довательно, в соответствии с B) имеем
Пример 2. Вычислить вычет функции
1
относительно
точки z = 0.
Точка г = 0 является простым полюсом функции ¦ ,
так как для ф)нкции япг эта точка является простым нулем. Сле-
Следовательно,
[—, 0 I = lim /г ——^i = 1.
[sill 2 J г->0\ sill 2/
150
ТЕОРИЯ ВЫЧЕТОВ
[Гл. V
Иногда для вычисления вычета относительно простого полюса
более удобна другая формула. Предположим, что точка z = a
является простым полюсом функции f(z) и что функция f(z)
представлена в виде
Л (г)'
где fi (z) и /2 (г) — функции, аналитические в точке а, при-
причем для функции fi(z) точка а является нулем первого по-
порядка, a /i (а) ф 0. В соответствии с B) имеем
Res
/s
lim
- a
Но так как /2(а) = 0, то в соответствии с определением
производной
Итак,
Res [f(z); *]=%$.
C)
Пример 3. Вычислить Res [ctg г; 0].
Имеем ctg г = -—. Точка 2 = 0 является нулем первого по-
SID 2
рядка для функции sin г и в соответствии с формулой C)
Res [ctg г; 0] = -^-j. = 1.
Пример 4. Вычислить
(z+1)rfz
22 + 4 '
где С — окружность | г | = 3, обходимая в положительном направ-
направлении.
Внутри контура С функция / (г) = \ ~\ имеет особые точки
г=±2«, являющиеся полюсами первого порядка, так как г2+ 4 =
= (г — 2г)(г + 2«). Пользуясь формулой C), получим
1— 21
Res [/(г); -2*]=
= — 2i
Res [/(г); 2i]=^±_
+ 2/
ВЫЧЕТ ОТНОСИТЕЛЬНО ПОЛЮСА
151
и, следовательно, с помощью основной теоремы о вычетах имеем
(z-\-\)dz _ 2п. /1 +2i _ \—2i\ = ы
Пример 5. Вычислить
С zdz
] 1—2 sin2 г'
с
где С — окружность радиуса 2 с центром в начале координат.
Так как
(V2 \ (V2 \
1 — 2 sin2 2 = 2 Мтт sin z V + sin г ,
то внутри контура С подынтегральная функция имеет два простых
полюса _в точках 2i = -j- и га = —j- (x>2)' B соответствии с
основной теоремой о вычетах
. ? Zdz г,.(г>Г г Ч I п [ Z пЪ
\ -, п ¦ ., = 2лг Res -, „ , , ; -т + Res , . ; г И- .
J 1—2smJz \ [1—2sinJz' 4J [1 — 2sin22' 4JJ
С
С помощью формулы C), учитывая, что A—2 sin2 г)' — — 2 sin 2г,
находим
Res
„ .«
2мпэг; 4 У
-2 sin [-у
Следовательно,
63. Если точка г = а является полюсом порядка/я функ-
функции f(z), то в окрестности этой точки
где функция <р (г) является суммой правильной части разло-
разложения в ряд Лорана и,- следовательно, аналитична в точке
152
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
z = а. Умножив обе части D) на (z — a)m, получим справед-
справедливое в некоторой окрестности точки а (кроме самой точки а)
равенство
(z - а)т f(z) = {г — а)т ср (г) -f c_x (z - а)т ' -f
Продифференцировав обе части этого тождества т — 1 раз,
получим
[(г -
= ^г [(г-а)" <р («
-!)!<:_,. E)
Для функции (z — а)т ср (z) точка z = а является нулем по-
порядка не ниже, чем т, следовательно, в точке а обращаются
в нуль производные этой функции во всяком случае до по-
порядка т—1 включительно. Поэтому при z = a первое сла-
слагаемое в правой части равенства E) равно нулю, и переходя
в E) к пределу при г-»-а, получим
а =•
Пример 6. Определить вычет функции
1
относи-
(+)
тельно точки г = I.
Точка 2 = i является полюсом третьего порядка данной функ-
функции, так как
1 1
В соответствии с F) получим
т i™i
§ 3. Логарифмические вычеты
1/
16 •
64. Если точка а является полюсом порядка т функции
f(z), то, как было показано выше (стр. 138), функция /(г)
представима в виде
j.. . ^ (г)
31
ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ
153
где функция <||B) аналитична и отлична от нуля в точке а.
Отсюда
т = [
Функция
•. — а
является аналитической в точке а, следовательно,
главная часть разложения функции : в ряд Лорана в ок-
т
рестности точки а состоит из одного члена -—, поэтому
G)
Если точка а является нулем порядка т функции f(z),
го эта же точка является полюсом порядка т функции
=7(SJ- Так как
Ln/(z) = —LnF(z),
то
(8)
Для функции F (z) точка а является полюсом порядка т,
следовательно, в соответствии с G)
отсюда на основании равенства (8) получим
ш> ahm-
Итак, вычет логарифмической производной функции f (z)
относительно точки, являющейся нулем функции f(z),
равен порядку нуля, а относительно точки, являющейся
полюсом функции f(z), — порядку этого полюса с обрат-
обратным знаком.
65. Предположим, что функция f(z) аналитична и отлична
от нуля во всех точках некоторого контура С, а внутри этого
контура имеет конечное число особых точек av a$, ..., ak,
причем все они являются полюсами. Обозначим через
154
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
oij, а,, ..., а„ нули функции /(г), расположенные внутри кон-
контура С. При этих условиях особыми точками функции *2',
расположенными внутри контура С, будут только точки аь а2,...
..., ak; Я], а2, ..., а„ и, в соответствии с основной теоремой
о вычетах,
Величину, стоящую в левой части этого равенства, называют
логарифмическим вычетом функции f(z) относительно кон-
контура С.
С другой стороны, как показано выше (см. (9)), величина
Res ,. ; <*J равна порядку нуля функции f(z) в точке <х?,
в частности, если нуль простой, то Res \ '; а?=1.
Если каждый нуль считать столько раз, каков его поря-
порядок, то сумма
?=1
будет равна числу нулей функции f(z), расположенных
внутри контура С. Аналогично, если ввести обозначение
и условиться каждый полюс функции f(z) считать столько
раз, каков его порядок, то из формулы G) следует, что
Р равно числу полюсов функции f(z) внутри контура С.
Записав равенство A0) с помощью введенных обозначений
в виде
A1)
приходим к следующей теореме о логарифмическом
вычете: при указанных выше условиях логарифмический
вычет функции относительно замкнутого контура равен
ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ
155
разности между количеством нулей и количеством по-
полюсов функции, расположенных внутри данного контура.
В частности, если внутри контура С функция f(z) не
имеет особых точек, то Р = 0 и логарифмический вычет
равен числу нулей функции /(г), расположенных внутри
контура С.
66. Если точка z пробегает дугу С с начальной точкой z0
и конечной точкой zb то соответствующая ей точка w =
= f(z) пробегает некоторую дугу Г плоскости w с началь-
начальной точкой wo=f(zo) и конечной точкой аI=/(г1).
Если аналитическая функция f(z) не обращается в нуль
вдоль дуги С, то в соответствии с правилом вычисления
интеграла от аналитической функции (§ 3 гл. II) получим
dz = Lx\f{zx) — Ln f(z0) = Lna»,-Lnw0, A2)
причем берется любая однозначная вдоль Г ветвь логарифма.
Если С — замкнутый контур (zt = z0), то Г также является
замкнутым контуром (wl^=w0), пробегаемым точкой w один
или несколько раз. Однако равенство нулю правой части A2)
только в том случае следует из того, что wt = w№,
когда вдоль Г можно определить однозначную ветвь функ-
функции Ln w, а это возможно лишь тогда, когда внутри области,
ограниченной контуром Г, не содержится точка w = 0.
Если же контур Г обходит точку w = Q, то, как было по-
показано в п. 42, к мнимой части логарифма прибавляется
приращение, полученное аргументом w Bл при каждом об-
обходе против часовой стрелки й — 2тс при обходе по часовой
стрелке). Поэтому, если контур Г т раз обходит точку
= 0, из A2) получаем
или
A3)
Если обозначить через Ас Argf(z) приращение, получаемое
аргументом величины w=f{z) при обходе точкой z контура С,
156 ТЕОРИЯ ВЫЧЕТОВ
то равенству A3) можно придать вид
[1л V
Сравнивая A3) с A1), приходим к иной формулировке
теоремы о логарифмическом вычете: разность между чис-
числом нулей и числом полюсов функции f{z) внутри кон-
контура С равна числу оборотов, которые делает в пло-
плоскости w вектор, идущий из точки ш = Ов точку w=f(z),
когда точка z описывает контур С (число оборотов счи-
считается при этом положительным, если вектор вращается
против часовой стрелки, и отрицательным в противопо-
противоположном случае).
В такой форме теорема о логарифмическом вычете но-
носит название принципа аргумента.
Пример. Найти количество нулей многочлена
равна
контура С
а) в правой полуплоскости; б) в первом квадранте.
Так как Р (г) не имеет полюсов, то величина л- Дс Arg P (z)
числу нулей Р (г) внутри контура С. Возьмем в качестве
границу полукруга с центром в точке г = 0, с диамет-
диаметром на мнимой оси и столь большого радиу-
радиуса R, чтобы все нули Р (г), лежащие в правой
полуплоскости, оказались внутри этого полу-
полукруга (рис. 70); применим к этому контуру
принцип аргумента и перейдем к пределу при
R—>co. Так как
-iff
то когда точка г описывает в положительном
направлении полуокружность С%, входящую
в выбранный нами контур,
Рис. 70.
а приращение аргумента второго множителя в правой части A4)
сколь угодно близко к нулю при достаточно большом R, так как
этот множитель близок к постоянной (единице).
Итак, Дс Arg P (z) — 4л при R —> со. Пусть теперь точка z двн-
жется по мнимой оси от z — U? до г = —iR. Положив z = it,
получим
Pitt) = и + iv = t* — З*2 -{- 2 +1 (— 2Г -1-1),
ЛОГАРИФМИЧЕСКИЕ ВЫЧЕТЫ
157
откуда
Для того чтобы представить себе вид линии, которую описывает
при этом точка w = P(z), найдем точки пересечения этой линии
с мнимой и действительной осями плоскости аи, для чего решим
уравнения
t* — 3t* + 2 = 0 A5)
и
— 2ta-{-t = 0. A6)
Первое из этих уравнений имеет корни t = ± j/2 , t = + 1, а вто-
второе t = 0, t = ±~— (так как при этом уравнения A5) и A6) не
имеют общих корней, то на мнимой оси плоскости г нет нулей
функции Р (z) и применение принципа аргумента к рассматриваемому
контуру законно). Расположим найденные корни в порядке убыва-
убывания (т. е. в порядке обхода контура):
]/2, 1, -L. °- —4=, —'. -/2
/2 V2
и найдем соответствующие значения и и г». Имеем:
о = — 3 1/2
_3_
«==0,
при
при
при
при
при
при
при
t=\;
t = —
Если, наконец, учесть, что при t = R—>аз имеем и-»-|-оо,
v
о--» — оо, '0, а при t = — R — — со имеем и—-{-со, V—--{-оэ,
>0, то можно утверждать, что линия, описываемая точкой w =
= P(z), когда точка z пробегает сверху вниз мнимую ось, имеет
вид, изображенный на рис. 71, и общее приращение аргумента век-
вектора да = Р(г) равно при этом нулю. Таким образом, при доста-
достаточно большом R имеем окончательно
2± Дс Arg P(z) = 2I. 4* = 2,
следовательно, Р (г) имеет два нуля в правой полуплоскости.
158
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
Для определения числа нулей Р (г) в первом квадранте рас-
рассмотрим замкнутый контур -у, изображенный на рис. 72. Пусть -[^ —
Рис. 71.
дута окружности, входящая в этот контур. Рассуждение, аналогич-
аналогичное проведенному выше, показывает, что при достаточно большом
R величина Д Arg P(z) сколь угодно близка к числу -=- • 4 = 2я.
При R — со прямолинейные участки
контура 7 превращаются соответственно
в положительные части мнимой и дей-
действительной осей. Когда точка z про-
пробегает сверху вниз положительную
часть мнимой оси, соответствующая
точка ta = P(z) описывает в направле-
направлении, указанном стрелкой, первую поло-
половину линии, изображенной на рис. 71
(до точки z = 2). Когда же точка г
¦^ движется вправо по действительной
положительной полуоси, т. е. когда
z > 0, и возрастает до z = -\-co, то
w = z4 -f- 2z3 -f- 3«s -f- z -f- 2 > 0 и w так-
также возрастает до ie = -f-oo. Таким обра-
образом, путь, описываемый точкой w = P(z), ко1да точка z пробегает
сначала сверх\ вниз положительную мнимую полуось, а затем
слева направо положительную действительную полуось, имеет вид,
О
Рис. 72.
§ 4]
ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
159
изображенный на рис. 73, и общее приращение аргумента вектора
a> = P(z) на этом пути равно нулю. Итак, при достаточно большом
R имеем
и, следовательно, Р (г) имеет один нуль в первом квадранте.
у»
Рис. 73.
Другие примеры на применение принципа аргумента при-
приведены в гл. X.
§ 4. Вычисление несобственных интегралов
с помощью вычетов
67. С помощью вычетов вычисляют некоторые несобствен-
несобственные определенные интегралы.
Предположим сначала, что бесконечно удаленная, точка
является нулем второго или более высокого порядка функ-
функции f(z), и следовательно, разложение этой функции в ряд
Лорана в окрестности точки z = со имеет вид
/(г) = ^ + ^ + ... A7)
(случай с_2 = 0 не исключается). Допустим также, что f(z)
является аналитической функцией на действительной оси, а
в верхней полуплоскости Im z ^> 0 имеет лишь конечное число
особых точек av ap ..., ап. Тогда все лежащие в верхней
полуплоскости особые точки функции f(z) можно заключить
внутрь расположенного в верхней полуплоскости полукруга
160
ТЕОРИЯ ВЫЧЕТОВ
(Гл. V
достаточно большого радиуса R с центром в начале коорди-
координат. В соответствии с основной теоремой о вычетах интеграл
\f(z)dz,
L
взятый по границе L этого полукруга, будет равен числу 2nl,
умноженному на сумму вычетов функции f{z) относительно
всех ее особых точек, распо-
расположенных в верхней полупло-
полуплоскости, причем при дальнейшем
увеличении R этот интеграл
изменяться не будет, так как
никакие новые особые точки
при этом внутрь полукруга не
попадут.
Пусть С# — полуокруж-
полуокружность, входящая в состав гра-
границы L указанного полукруга (рис. 74); тогда
R
\f{z)dz= \f{z)dz+ \f{x)dx.
L CR -R
На основании A7) имеем
-R
где <p (z) = с_ъ -|~ c~3 -j-... Для функции ср (z) бесконечно уда-
удаленная точка является правильной, причем lim cp(z) = c_s,
z -*-са
следовательно, функция <р (z) рграничена в окрестности бес-
бесконечно удаленной точки и, в частности, на полуокружности
CR, если ее радиус R достаточно велик, т. е. во всех точках
полуокружности Сд
где М — некоторое положительное число. Следовательно,
<f (z) dz
М
Мп
lim \f(z)dz=O.
§ 4] ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ 161
А так как
R со
lim \f(x)dx= \f(x)dx,
Й-ОО-О? -CO
то тем самым доказано, что если функция f(z) удовлетво-
со
ряет указанным выше условиям, то интеграл \ f(x)dx pa-
—со
вен произведению числа 2к1 на сумму вычетов функции
f(z) относительно всех ее особых точек, расположенных
в верхней полуплоскости.
со
Пример 1. Вычислить интеграл \ а а .
—со
имеет в бесконечности нуль четвертого
Функция
1
порядка; особыми точками функции являются полюсы второго по-
порядка в точках 2= + /, из них только первый находится в верхней
полуплоскости.
Имеем
Следовательно,
68. Интеграл
dx
Л 4Г21
\ f{x)dx
может быть вычислен с помощью теории вычетов и в неко-
некоторых других случаях. В частности, интегралы такого вида,
встречающиеся в операционном исчислении, часто удаегся
вычислить с помощью следующей леммы Жордана,
которую мы приводим без доказательства: пусть Cr — лежа-
лежащая в верхней полуплоскости дуга окружности радиуса R
б И. Г. Араманович ц др.
162
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
с центром в некоторой фиксированной точке z0 (рис. 75),
а функция f(z) имеет вид
причем f^>Q. Если функция F (z) аналитична на действи-
действительной оси, а в верхней полуплоскости имеет лишь
конечное число особых то-
ч\
чек и
) = 0, то
Рис. 75.
при достаточно большом R (см. рис. 75)
lim
Очевидно, что если а,,
а3, ..., ая — особые точки
функции f{z), лежащие в
верхней полуплоскости, то
); ak]
R
k=\
Очевидно также, что при R -> оо имеем xt -> — 00, дг2 ->¦ -}v оо>
и по лемме Жордана получим, переходя к пределу при
R-*-oo,
Res
); ak].
k= 1
_ _ „ f х cos x dx
Пример 2. Вычислить интеграл \ —а ~ i in •
—со
Функция
как нетрудно проверить, удовлетворяет условиям леммы Жордана.
Здесь t = 1 и F (г) = -g—Щ—i—=--. Особыми точками функции/(г)
z — 2.Z —р 10
являются полюсы первого порядка г = 1 —|— 3/ и г = 1 — Ы (эти точ-
точки являются нулями первого порядка для ф\нкции г2—2z —|— 10).
В верхней полуплоскости имеется1 единственная особая точка г =
= 1-|-3(. Вычислим относительно этой точки вычет функции /(г):
A-|~Зг)е-3-г*
W г-i+ai ~~ Й '
ЗАДАЧИ К ГЛ. V
163
Следовательно,
'XI
(' хе'х dx
) Т2-2д:-|-10 =
.
= -^ е~3 A +3«) (cos 1 +« sin 1) =
= -5- е (cos I — 3 sin 1) +«-5- е~3 C cos 1 —f— sin 1).
Сравнивая в обеих частях этого равенства действительные и мни-
мнимые части и учитывая, что
xeix dx
х cos x dx
—со
получим
х sin
2 — 2лг+10'
f х cos x dx
3 a-2 — 2.vr+10 =
-со
= ^з-е (cos 1 — 3 sin 1),
f A" SiD A" rf
J л-2- 2л- 4-
dx к
ЗАДАЧИ К ГЛАВЕ V
1. Найти вычеты следующих функций относительно каждого
из полюсов:
г- +1 е^г 1 г2"
а) ~т=2\ б) 7=Г' в) 7?ТТ)т; г) (^^ (">Ои целое);
)
д)
*' е)
z; к)
2. Найти вычеты относительно точки г = 0 функций:
а) ^1/г; б) cos—; в) sin —.
3. Вычислить \ , , . , если С — окружность х2 -f-у- = '2х,
С
проходимая однократно в положительном направлении.
4. Вычислить
г/г
164
ТЕОРИЯ ВЫЧЕТОВ
[Гл V
если С — окружность х- -{-у- = 2х-\-2у, проходимая однократно
в положительном направлении.
5. Вычислить
\(г-аПг-Ь)"
с
и целое),
если С — однократно проходимая в положительном направлении ок-
окружность |г| = 1, в следующих случаях:
а) |д|<|6|<1; б) ] а |< 1 < | * |; в) 1 < | а | < | * |.
6. Вычислить с помощью вычетов интегралы:
со со
С хй А-1 С dx
б)
целое); д)
dx
о
х sin
7. Определить, сколько нулей в каждом квадранте имеют мно-
многочлены:
а) 2г» — Зг'Ч-Зг2— 2+1; б) г4 + г3 -f 4z2 + 2z + 3.
ГЛАВА VI
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
§ 1. Плоскопараллельные векторные поля
69. Векторное поле
А = Ах(х, у, z, t)i-{-Ay(x, у, z, t)j-\-A2(x, у, z, f)k,
где i, j, k — единичные векторы, направленные по осям ко-
координат, a t—время, называется плоскопараллельным, если
все векторы поля параллельны не-
некоторой плоскости Р, причем в точ-
точках каждой прямой, перпендику-
перпендикулярной к этой плоскости, в любой
фиксированный момент времени t
векторы поля равны между со-
собой (рис. 76).
В дальнейшем мы будем счи-
считать плоскость Р параллельной
плоскости хОу. Тогда
Аг(х, у, z, 0 = 0
и
А = Ах(х,у, t)i + Ay{x, у, 0/
Очевидно, что изучение плоско-
плоскопараллельного векторного поля
сводится к изучению плоского
векторного поля в плоскости Р
или в любой другой параллель- Рис. 76.
ной ей плоскости.
Векторное поле называется стационарным, если оно
не изменяется с течением времени.
166
комплексный потенциал
[Гл VI
В этой главе мы будем paccinaipHuaib лишь плоские (или
плоскопараллельные) стационарные векторные поля
A = AAx,y)l+Ay(x,y)j. A)
Точку (х, у) в плоское 1 и хОу можно характеризовать
комплексным числом z = x-\-iy, а век юр
А = Ах(х, y)i-\-Ay(x, y)j
— комплексным числом Ах(х, y)-\-iAv(x, у). Поэтому наряду
с записью A) вектор можно представлять в виде
А = Ах(х, у)^1Ау(х,у). B)
Следовательно, векторное поле A) можно задать, указав две
функции действительных переменных Ах(х, у) и Ау{х, у)
или одну функцию комплексного переменного
<р (г) = Ах (х, у) -{- 1Ау (х, у).
§ 2. Комплексный потенциал
70. Напомним некоторые понятия векторного анализа (см.
[1], гл. IX, § 3) в применении к плоским стационарным
векторным полям A), или в комплексной форме B). Коор-
Координаты Ах(х, у) и Av(x, у) вектора А в области их опре-
определения будем считать непрерывно дифференцируемыми функ-
функциями, за исключением, бьпь может, конечного числа точек.
Циркуляцией век юра поля А вдоль замкнутого контура
С называется криволинейный интеграл
Tc = ]As(x, y)ds,
с
где Л, — проекция вектора А(х, у) на положительное на-
направление касательной к дуге С в точке (х, у) (положитель-
(положительное направление на касательной соогветствуег положитель-
положительному направлению обхода дуги С), ds — элемент дуги кри-
кривой С. Если ввести вектор ds = i dx -\-jdy (или в комплексной
форме ds — dx-\-idy), то по формуле для скалярного про-
произведения
As ds = A ds = Ах (х, у) dx -f- Ay (x, у) dy
и
Гс = \ A ds = \АХ {х, у) dx 4- Ay [х, у) dy. C)
С С
§ 21
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
167
Если в некоторой односвязной области циркуляция
по любому замкнутому контуру равна нулю, то подын-
подынтегральное выражение Ах(х, у) dx -\- Ау (х, у) dy в этой
области является полным дифференциалом некоторой
функции и(х, у), называемой потенциальной функцией.
По отношению к функции и(х, у) вектор А называется гра-
градиентом и обозначается
А — grad и (х, у).
Справедливо и обратное утверждение: если в C) подын-
подынтегральное выражение Ах(х, y)dx -\- Ay(x, y)dy является
полным дифференциалом некоторой функции и (х, у) в од-
односвязной области О,
т. е.
du (х, у) = Ах (х, у) dx + Ау (х, у) dy,
то циркуляция по любому замкнутому контуру С в этой
области равна нулю.
В рассматриваемом случае, т. е. при А = grad и (х, у),
векторное поле называется безвихревым или потенциальным.
Для того чтобы в C) подынтегральное выражение явля-
являлось полным дифференциалом и, следовательно, поле А =
= Ах(х, у) i -\- Ay (х, y)j было бы потенциальным, как извест-
известно, необходимо и достаточно, чтобы
дАх(х,у) dAv(x,y)
ду = ' дх ¦ <4)
Если условие D) выполняется во всех точках рассмат-
рассматриваемого поля, за исключением конечного числа точек zk,
в которых условие D) нарушается или теряет смысл из-за
обращения в бесконечность хотя бы одной из производных
дАх dAv
¦-%—, -jr-, то циркуляция по замкнутому контуру С, обхо-
обходящему какую-нибудь из этих точек или группу таких точек,
может быть отличной от нуля. Если циркуляция по контуру С,
ограничивающему область U, внутри которой находится лишь
одна из этих точек zk, отлична от нуля, то точка zk назы-
называется вихревой точкой. Если при эюм контур С одно-
однократно обходит точку zk в положительном направлении,
то число Yc называется интенсивностью вихря в точке zk.
168
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
Потоком вектора поля А через замкнутую или незамк-
незамкнутую кривую С называется криволинейный интеграл
где ds— элемент дуги кривой С, а Ап — проекция вектора
А (х, у) на положительное направление нормали к кривой С
в точке (х, у).
Вектор dn, направленный по нормали к кривой С в точке
(х, у) и по длине равный вектору ds — idx-\-jdy, направ-
направленному по касательной к той же кривой, можно записать
в виде
dn = ±(idy — Jdx).
Выбрав какой-нибудь из двух знаков перед скобкой в правой
части равенства, мы установим положительное направление
на нормали. Условимся в дальнейшем брать знак -}-, тогда
dn = idy— jdx. При этом условии для замкнутого контура С,
с направлением обхода против часовой стрелки, вектор dn
направлен по внешней нормали к контуру С.
Так как
Ап ds = A dn = Ах (х, у) dy — Ау {х, у) dx,
то
y)dy. E)
Если в некоторой области поток вектора через любой
замкнутый контур С равен нулю, то подынтегральное выраже-
выражение — Ау (х, у) dx -f- Ах (х, у) dy в E) является полным диффе-
дифференциалом некоторой функции v(x, у), называемой функцией
тока (это название связано с гидродинамическим смыслом
функции v, см. стр. 173),
dv = — Ау (х, у) dx -f Ах (х, у) dy,
ди . , ч dv . , ,
дх = — Ау (х, у), ?у = Ах (х, у).
В этом случае поле называется соленоидальным.
Необходимым и достаточным условием соленоидальности
поля является
дАу (х, у) _ дАх (х, у) ,йч
~~ ду 5л-
§ 21
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
169
Если условие соленоидальности F) выполняется во всех точ-
точках рассматриваемого поля, за исключением конечного числа
точек zk, в которых условие F) нарушается или теряет смысл
из-за обращения в бесконечность хотя бы одной из про-
производных
дАх (х, у) дАу (х, у)
или
дх
ду
то поток вектора поля через замкнутый контур, внутри
которого содержатся точки zk, может быть отличным
от нуля.
Если поток Nq вектора поля А через замкнутый контур С,
ограничивающий область, в которой содержится лишь одна
из этих точек zk, отличен от нуля, то точка zk называется
источником, если Лс^>0, и стоком, если Л/с<С^- При этом
предполагается, что контур С обходят в положительном напра-
направлении, т. е. при обходе контура С точка zk остается слева.
Если контур С однократно обходит точку zk в положитель-
положительном направлении, то число Nc называется обильностью
источника (если Nc^>Q) или стока (если Л^с<С0). Если
в области D, ограниченной контуром С, не проходящим
через точки zk, содержится несколько точек zk, то по-
поток Nc вектора поля через контур С, однократно прохо-
проходимый в положительном направлении, равен алгебраи-
алгебраической сумме обильностей всех источников и стоков,
находящихся в области D.
Аналогичная теорема, являющаяся следствием свойств кри-
криволинейных интегралов от полных дифференциалов, конечно,
справедлива и для циркуляции по контуру С в потенциаль-
потенциальном поле с конечным числом вихревых точек.
71. Предположим, что поле А {х, у) потенциально и солено-
идально, следовательно, существуют потенциальная функция
и(х, у) и функция тока v(x, у), определяемые с точностью до
постоянных слагаемых своими полными дифференциалами:
du = Ax(x, y)dx-\-Ay(x, y)dy,
dv — —Ay{x, y)dx-\- Ax{x, y)dy.
Рассмотрим функцию комплексного переменного
= u{x, y)-\-Lv(x, у),
170
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
называемую комплексным потенциалом. Функции и(х, у)
и v(x, у) удовлетворяют условиям Коши—Римана
гак
как
ди
дх
dv
~ду'
ди
ду —
dv
дх
ди
ди
Следовательно, комплексный потенциал f(z) = ti -\-iv является
аналитической функцией.
Весь превосходно разработанный аппарат теории аналити-
аналитических функций может быть использован для изучения потен-
циально-соленопдальных векторных полей, если их описы-
описывать с помощью комплексного потенциала.
Если известен комплексный потенциал f(z) = u(x, y)-\-
-\- iv (х, у), то соответствующее ему векторное поле А =
= Ах(х, у) -)-1Ау (х, у) легко определяется, так как
. , ч ди I dv\ . , ч ди I dv\
Ах (х, у) = -<-- = -г , Av (х, у) = т- — — -з- .
хУ ¦" дх \ ду]' Уу J' ду\ дх]
Принимая во внимание, что
~ iAy
получим
A=Ax(x,y)-\-lAv(x,y) =
G)
Следовательно, ] А (х, у) \ = \ f (г)', а аргумент вектора А (х, у)
отличается от аргумента вектора f'(z) знаком (так как
агё/'(г:):= — агё/'(г))- Линии уровня функций и a v
а(х, у) —с, v(x, y) = c
образуют ортогональную сеть, так как их образами в пло-
плоскости w при конформном отображении (сохраняющем углы)
w=f{z) являются взаимно-ортогональные семейства прямых,
параллельных осям координат и = с и v = c. Линии уровня
функции и(х, у) ортогональны вектору поля, так как вектор
поля А является градиентом функции и(х, у). Следовательно,
§ 2]
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
171
векюр поля А (х, у) направлен по касательным к линиям
уровня v(x, у) = с. т. е. линии уровня функции v(x, у) яв-
являются векюрными линиями рассматриваемого векторного поля.
Заметим, что
\ f (г) dz = 5 [Ах (х, у) - 1Ау (х, у)] {dx + idy) =
с с
= \ Ах (х, у) dx -f Ay (х, у) dy -\-
-i-l^—Av (х, у) dx -j- Ах (х, у) dy = Yc-\- iNo
с
где С—замкнутый контур (см. C) и E)).
Во многих прикладных задачах приходится изучать по-
потенциально-соленой, тальные векторные поля с изолированными
особыми точками zk, т. е. точками, в которых не выполнено
условие потенциальности
дАх дАу
ду дх
или условие соленоидалыюсти
dAv дАх
ду дх '
Среди точек z^ могут быть вихревые точки, источники и
стоки. Могут быть вихревые точки, которые одновременно
являются источниками или стоками; такие точки называются
вихреисточниками пли вихрестоками. Могут быть также
и иные особые точки, например, особые ючки, получающиеся
от слияния источника со стоком равной бесконечной обиль-
обильности (см. стр. 176—178).
Заметим, что если условия потенциальности D) и соле-
ноидалыюсги F) выполнены в многосвязной области О, то
потенциальная функция и(х, у) и функция тока v(x, у)
могут бьпь многозначными. Действшельно,
(х. \)
и(х, у)= \ Ах{х, y)dx-\-Ay(x, y)dy,
(8)
v (х, у) = \ - Ау (х, у) dx + Ах (х, у) dy, (9)
172
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
Рис. 77.
но в случае многосвязной облает О криволинейные nine-
гралы от полных дифференциалов могут до некоторой
степени зависеть от пути интегрирования, соединяющего
заданные точки А (х0, _у0) и В (х, у), а именно: интегралы
вида (8), определяющие функцию zz (х, у), не обязательно
одинаковы вдоль двух путей Q
и Со, идущих из точки А (ха, у0)
в точку В(х, у), если в области
между С) и Сг имеются особые
точки функции f(z); так же об-
обстоит дело и с интегралами вида (9),
определяющими функцию v(x, у).
На рис. 77 изображена дву-
связная область: круг, из которого
удалена точка М. Если точка М
является вихревой, то криволи-
криволинейные интегралы (8), взятые по
путям Q и С.,, очевидно, будут
отличаться на не равную нулю
циркуляцию вектора А по замкнутому контуру С, однократно
обходящему точку М. Точно так же, если точка М является
источником (или стоком), то криволинейные интегралы (9),
взятые по путям С\ и С2, будут отличаться на величину потока
вектора А через упомянутый выше замкнутый контур С, т. е.
на обильность источника (пли стока), находящегося в точке М.
§ 3. Комплексный потенциал в гидродинамике
72. Рассмотрим поле скоростей
А = Ах(х, y)i-\-Ay(x, y)j
стационарного плоскопараллельного движения несжимаемой
жидкости в области, не имеющей источников или стоков
жидкости.
В рассматриваемом случае поток Nc = ^ Ands вектора ско-
с
рости А через некоторую кривую С по абсолютной величине
равен в соответствующих единицах количеству жидкости,
протекающей в единицу времени через кривую С'). Если
') Точнее, количеству жидкости, протекающей через цилиндри-
цилиндрическую поверхность единичной высоты с образующими, параллель-
параллельными оси Ог, проекцией которой на плоскость хОу является кривая С.
§ 3]
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ГИДРОДИНАМИКЕ
173
в области D, ограниченной замкнутым контуром С, нет источ-
источников и стоков, то в силу несжимаемости жидкости ее коли-
количество внутри контура С не может изменяться и, следовательно,
количество втекающей в область D жидкости равно коли-
количеству вытекающей жидкости, т. е. поток вектора скорости
через замкнутый контур С равен нулю — поле соленоидально.
Если, кроме того, рассматриваемое поле скоростей дви-
движения несжимаемой жидкости потенциально, то для его изу-
изучения целесообразно ввести комплексный потенциал
f(z) = u(x, y)^-iv{x, у).
При этом векторными линиями v = c будут линии тока
жидкости, так как касательный к ним вектор А является век-
вектором скорости течения. Отсюда и происходит название
функции v—«функция тока». Названия «источник», «сток»,
«обильность» источника или стока также заимствованы из
рассматриваемой в этом параграфе гидродинамической интер-
интерпретации векторного поля.
Пример 1. Найти поле скоростей движения несжимаемой
жидкости, комплексный потенциал которого равен az, где действи-
действительное число а > 0.
Функция w=^az является аналитической во всей плоскости
и, следовательно, ее можно рассматривать как комплексный потен-
потенциал движения несжимаемой жидкости, в котором отсутствуют вих-
вихревые точки, источники, стоки и другие особые точки. Так как
dw
а а—число действительное и положительное, то вектор скорости
параллелен действительной оси, направлен в положительную сто-
сторону и по длине равен а во всех точках плоскости.
Пример 2. Найти иоле скоростей движения несжимаемой
жидкости, линии тока, линии уровня потенциальной функции
(эквипотенциальные линии), зная комплексный потенциал w = Ln z.
Для течения жидкости, определяемого комплексным потен-
потенциалом
w — Ln 2,
особой точкой является начало координат, так как 2 = 0 является
особой точкой функции
dw_ \_ ')
dz z
') Предполагается, что при дифференцировании выбирается
непрерывная в окрестности точки г (г ^0 ) ветвь функции Ln г.
174
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
Длина вектора скорости А в точке г в соответствии с G) равна
\А | =
Следовательно, модуль пектора скорости обратно пропорционален
расстоянию точки от начала координат.
Угол а, образованный направлением вектора скорости и поло-
положительным направлением оси Ох, согласно G) равен
а = - Arg — = Arg z,
и следовательно, направление вектора скорости в точке г совпадает
с направлением луча, идущего из начала координат в эту точку.
Очевидно, линиями тока яв-
являются лучи, выходящие из на-
начала координат (рис. 78), а ли-
линиями уровня потенциальной
функции ^ окружности с цент-
пом в начале координат.
К тому же выводу можно
было прийти, выделив из комп-
комплексного потенциала потен-
потенциальную функцию и функцию
тока
и -f- iv = Ln z = In (z | -f- i Arg z,
откуда (z = pe
и = In |
z | = In p,
v = Arg г = а.
Отсюда видно, что линии
рис 78. уровня потенциальной функ-
функции: р = с,, а линии тока:
<? = fs (с,, са — постоянные).
Начало координат является источником. Так как других особых
точек нет, то для подсчета обильности источника следует вычис-
вычислил, поток через любой простой замкнутый контур, содержащий
начало координат. Выбрав в качестве такого контура окружность С
радиуса г с центром в начале координат, получим
N
С С 1 ] С 1
= \ Ап ds — \ — ds =¦ — \ ds = — • 2кг = '.
с] с Г • Г
»
с
на окружности С всюду Ап — \А
Пример 3. Найти поле скоростей движения несжимаемой
жидкости, линии тока и эквипотенциальные линии, зная комплекс-
комплексный потенциал w — :'
§ 3)
комплексный потенциал в гидродинамике
175
Для комплексного потенциала
w = I Ln 2
единственной особой точкой является начало координат. Пусть
А—вектор скорости, а а. — угол, образованный этим вектором
с положительным направлением действительной оси. Тогда
dw
~dz'~
а = — Arg — = — -ту + Arg Z.
Модуль вектора скорости обратно пропорционален расстоянию
точки от начала координат, а направление вектора скорости (рис. 79)
перпендикулярно к лучу,
соединяющему точку г с на-
началом координат, т. е. сов-
совпадает с направлением ка-
касательной к окружности с
центром в начале коорди-
координат, проходящей через дан-
данную точку. Отсюда следует,
что линиями тока являются
окружности с центром в на-
начале координат, а линиями
уровня потенциальной функ-
функции — лучи, выходящие из
начала координат. К этому же
выводу можно было прийти,
выделив из комплексного
потенциала потенциальную
функцию и функцию тока.
Начало координат является вихревой точкой. Для того чтобы
вычислить циркуляцию вектора А по контуру С, обходящему вих-
вихревую точку (интенсивность вихря), проще всего взять в качестве
контура С окружность с центром в начале координат произвольного
радиуса г. Вектор скорости касателен к этой окружности и
Рис. 79.
(отрицательный знак указывает на то, что движение происходит
по часовой стрелке). Следовательно,
Г= [ Asds = — [ lrfs = —2u.
Пример 4. Найти линии тока движения несжимаемой жид-
жидкости, если комплексный потенциал равен w = (а -\- Ы) Ln z.
Из примеров 2 и 3 следует, что в движении, определяемом
комплексным потенциалом w ==¦ (а -\- Ы) Ln г, где а и b — действи-
176
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
тельные постоянные, начало координат является вихреисточником
(если а > О, Ь=60) или вихрестоком (если а < О, 6^0), причем
поток через контур, окружающий начало координат, равен 2ка,
а цирк)ляция равна —1~Ь- Линиями тока являются логарифмиче-
логарифмические спирали (рис. 80).
У\, Действительно, посколь-
поскольку 2 = ре'>,
w = (а + Ы) Ln г =
= (a + 6i)(lnp + !<?) =
= (a In р — йс) +
+ «" F In р + а?)-
Функция тока имеет вид
v — Ь In p -(- а», и линии
тока определяются урав-
уравнением Й1п р -f- ao = с,
i де с — постоянная, или
с а
1П р = -j- - -j- О,
откуда
Рис. 80.
Пример 5. Найти линии тока, эквипотенциальные линии и
особые точки движения несжимаемой жидкости, если комплексный
1
потенциал равен а> = —.
2
Движение, определенное комплексным потенциалом
_ 1 _ 1 _ х у
2 X-\-iy X--\-y X -\-у
имеет единственную особую точку 2 = 0.
Так как - = г, то в прежних обозначениях получим
Д — ч~ —
Уравнение семейства линий тока — ,-v-—5
или, полагая — = '1С,
= с, где с — постоянная,
т. е. линиями тока (рис. 81) являются окружности
§ з]
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ГИДРОДИНАМИКЕ
177
с центрами па оси Оу, касающихся оси Ох. Аналогичные вычисле-
вычисления показывают, что линиями уровня потенциальной функции (на
рис. 81 они обозначены пунктиром) являются окружности
(х-С)*+)>* = &
с центрами на оси Ох, касающиеся оси Оу.
Рис. 81.
Легко убедиться в том, что жидкость движется по линиям тока
в указанном на рис. 81 направлении. Для этого достаточно подсчи-
подсчитать величину угла а между вектором скорости и положительным
направлением оси O.v, например, для точек, лежащих на мнимой оси,
т. е. для точек г, \ которых arg г = ± тс/2.
Заметим, что комплексный потенциал
_ Ln (г -f- /г) — Ln г
при действительном положительном /г определяет течение жидкости
с источником в точке — h (см. пример 1) обильности 2я/Л и стоком
78
KOVimEKCHblli ПОТЕНЦИАЛ
[Гл VI
в начале координат обии.ности — 1т. h. Так как
lim
Ln (г -f- h) — Ln г __
то начало координат в течении жидкости, определяемом комшекс-
ным потенциалом w =—, можно рассматривать как точку, в кото-
pott совмещены сток и источник одинаковой «бесконечно большой»
обильности. Так\ю точку называют диполем1).
Нетрудно непосредственным вычислением проверить, что как
поток через любой замкнутый конт\р, окружающий диполь и не
содержащий друптх особых точек, так и циркуляция по такому
контуру равны н>лю.
§ 4. Задачи на обтекание
73. В задачах на обтекание требуется определить комп-
комплексный потенциал плоского поля скоростей безвихревого
течения несжимаемой жидкости, обтекающего заданные ли-
линии, т. е., если перейти к пространственной задаче, опреде-
определить комплексный потенциал плоскопараллельного поля ско-
скоростей безвихревого течения несжимаемой жидкости, обтекаю-
обтекающего заданные покоящиеся в жидкости цилиндрические твердые
тела, образующие которых перпендикулярны к плоскости
векторного поля (можно считать также, что эти цилиндриче-
цилиндрические тела движутся в покоящейся жидкости в направлении,
перпендикулярном к образующим цилиндрических поверх-
поверхностей).
Очевидно, течение жидкости не определяется одной только
формой обтекаемых тел, поэтому для единственности реше-
решения задачи на обтекание необходимо, кроме формы обтека-
обтекаемых тел, задать еще некоторые добавочные условия.
74. Рассмотрим гладкую кривую С, в обе стороны уда-
удаляющуюся в бесконечность (это означает, что при движении
точки z по кривой С в любую сторону г стремится к бес-
бесконечности). Эта кривая разбивает плоскость на две области
Д и D2 (рис. 82), называемые криволинейными полупло-
полуплоскостями.
') Впрочем, диполь можно рассматривать также как точку,
в которой совмещены две вихревые точки с одинаковыми беско-
бесконечно большими, но противоположными по знаку циркулчциями,
так как величину h можно считать мнимой (см. пример 3).
§ 4]
ЗАДАЧИ НА ОБТЕКАНИЕ
179
Задача заключается и тм, чтобы в одной из этих обла-
областей (например, /J,) определть комплексный пшенциал поля
скоростей бенвнхревого 1ечеипя несжимаемой жидкости, обте-
обтекающего кривую С, в котором orcyiCTByior источники и стоки.
Так как в точках кривой С
вектор скорости должен быть
направлен по касательной к
этой кривой, то кривая С должна
быть линией тока искомого
поля скоростей
v {х, у) = г/0,
Рис. 82.
где v0 постоянно. Функция тока v (x, у) определяется по своим
частным производным
dv
дх
dv
— А.ЛХу у), -г- = Ах(х, у)
ук ¦у>' ду хх ¦*'
лишь с точностью ло постоянного слагаемого. Следовательно,
можно считать vo = O.
Итак, искомый комплексный потенциал
w = n (x, у) -j- iv {x, у) = f(z)
должен отображать кривую С в прямую г/ = 0, а следова-
следовательно, область D\ должна отобразиться в полуплоскость
v~^>Q (или г'<0).
Существует (см. стр 81) бесконечное множество анали-
аналитических функций, осуществляющих указанное отображение.
Чтобы задачл стала вполне определенной, необходимы доба-
добавочные условия.
В задачах гидродинамики такими условиями обычно яв-
являются задание модуля вектора скорости в бесконечности,
т. е. задание \f'(z)\ при z = co и требование /(оо) = оо.
Рассмотрим в качестве примера безвихревое течение жид-
жидкости (без источников и стоков), обтекающей линию, состав-
составленную из луча —оо<^х-=с — R, верхней полуокружности
радиуса R с центром в точке г = 0 и луча /? «с; х<^ со
в области G (рис. 83), расположенной выше этой линии.
В соответствии со сказанным выше, комплексный потенциал
w=f(z) 1акого течения должен отображав ipannuy обла-
области О на действительную ось, а область О—на верхнюю (или
нижнюю) нолуплоскос1ь. Скорость в бесконечности будем
180
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. V!'
считать заданной и равной числу v^ (v^—действительное
число, так как в силу условий задачи скорость в бесконеч-
бесконечности направлена по действительной оси).
Функция ^ = -р отображает область О на область О', за-
заштрихованную на рис. 84; область G отображается, как
-R
0\ Т
Рис. 83.
Рис. 84.
читатель легко проверит, на верхнюю полуплоскость функцией
Жуковского
Таким образом, одной из функций, отображающих об-
область G на верхнюю полуплоскость, является функция
При этом Г=оо при г = оо. Совершив преобразование
подобия w = kT (&^>0), мы получим общий вид функции,
отображающей область G на верхнюю полуплоскость и удо-
удовлетворяющей условию та(оо) = со (с точностью до постоян-
постоянного слагаемого, соответствующего сдвигу, которое всегда
можно опустить):
г = &/2/?— положительная постоянная). Отсюда
/?2\ dw
и, окончательно, искомый комплексный потенциал имеет вид
A0)
§ 4] ЗАДАЧИ НА ОБТЕКАНИЕ
Модуль вектора скорости определяется равенством
181
В точках z = ±R скорость равна нулю; такие точки назы-
называются критическими.
Отделив в A0) мнимую часть от действительной, опре-
определим функцию тока:
откуда
Следовательно, семейство линий тока определяется уравнением
У
Х~+У
., = с,
-
или
Линии тока симметричны относительно оси 0_у и имеют асимп-
асимптоты, параллельные оси Ох (рис. 85).
Рис. 86.
75. Рассмотрим криволинейную полосу D (рис. 86), ог-
ограниченную двумя гладкими кривыми Q и С>,« пересекающи-
пересекающимися лишь в бесконечности. Задача опять заключается в том,
чтобы определить в полосе D поле скоростей стационарного
течения несжимаемой жидкости, обтекающей кривые Cj и Q,
или комплексный по1енциал этого течения.
Так как кривые С] и С.г должны быть линиями тока
искомого 1ечення жидкости, то комплексный по1енциал
182
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
(Гл VI
отображает линии С, и С, соо1ветсгвенно на прямые v = va и
т) = Т!|. Следона1ельно, определение искомого комплексного
по1енциала с[:одщся к нахождению анали-тической функции,
отображающей заданную криволинейную полосу D на пря-
прямолинейную полосу, ограниченную прямыми т> = т>0 и v = v{,
без ограничения общности можно считать г10 = 0.
Конечно, для однозначного определения комплексного по-
потенциала необходимы добаночные условия. Такими условиями
в гидромеханике обычно являются задание расхода жидкости,
т. е. потока Л/.( вектора скорости через кривую -у, соединяю-
соединяющую кривые С, и С2 (рис. 86), и тре&ование ограниченности
скорости при z —*¦ оо .
Заметим, чго задание расхода жидкости N^ определяет
величину разности г']—va. Действительно,
Щ = \ — Ау(х. y)dx-\-A*(x, y)dy = \dv = vi—vu.
Пример. Найти комплексный потенциал течения жидкости
в канале, берега которого (рис. 87) имеют форму парабол х =
= у~ j и ¦*" = ^ 1, если рас-
расход жидкости равен Q.
Функция w = \rz отображает
криволинейную полосу между
параболами х=-у2 -^ и л =
И
= J-j— 1 в полосу
мыми v = 1/2 и
1
между пря-
v = 1. Здесь
Рис. 87.
»| — °о= ' — -^ — ~2 ¦ Следова-
Следовательно, ф)нкция w = Уг является
комплексным потенциалом тече-
течения жидкости в заданном канале,
1
ко1да расход жидкости равен -у.
Функция w = 2Q У2, соответ-
соответствующая расходу Q, дает ре-
решение поставленной задачи.
76. Перейдем к задаче об обтекании замкнутого контура.
Найдем сначала комплексный потенциал плоскопараллельного
течения жидкости, обтекающего круговой цилиндр радиуса R,
предполагал, что в плоскости, перпендикулярной к оси ци-
§ 4]
ЗАДАЧИ НА ОБТЕКАНИЕ
183
линдра, течение симметрично относительно некоторой прямой,
проходящей через центр сечения цилиндра, а скорость в беско-
бесконечности направлена параллельно оси симметрии и равна г'оэ-
Выберем систему координат так, чтобы начало координат
находилось в центре сечения цилиндра, а направление скоросш
в бесконечности совпадало
с положительным направле-
направлением оси Од; (рис. 88). Из
условий задачи следует, что
линия, составленная из от-
отрезка — оо <^ х =g; — R дей- —^
ствительной оси, верхней —•-
полуокружности радиуса R
с центром в точке г = 0 и
отрезка R sg x <^ оо, должна
быть одной из линий тока,
и следовательно, дело сво- Рис. 88.
дится к задаче, уже решен-
решенной на стр. 179—181. Таким образом, комплексный потен-
потенциал в рассматриваемой задаче равен
Найдем более общее решение задачи. Выше было показано
(пример 3 на стр. 174), что функция w=:iLnz является
комплексным потенциалом течения с вихревой точкой в начале
координат и циркуляцией, равной — 2тс. Линиями тока в этом
случае являются окружности с центром в начале координат.
Для комплексного потенциала
w = ^- Ln г
A1)
величина циркуляции вокруг вихревой точки в начале коор-
координат равна Г, а скорость в бесконечности равна нулю. Так
как цилиндр радиуса R с центром в начале координат обте-
обтекается каждым из течений, определяемых комплексными по-
потенциалами A0) и A1), то течение с комплексным потенциалом
w = i
A2)
184
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл VI
будет также обтекать этот цилиндр. Скорость такого тече-
течения в бесконечности параллельна действительной оси и рав-
равна vm, циркуляция вокруг начала координат равна Г.
Если С — заданный замкнутый контур (рис. 89), а функ-
функция ? = cp(z) отображает внешность контура С взаимноодно-
взаимнооднозначно и конформно на внешность круга радиуса R с цент-
центром в начале координат, то в соответствии с A2) функция
A3)
является комплексным потенциалом течения, обтекающего С.
С помощью функции ? = cp(z) линии тока течения, обтекаю-
обтекающего в плоскости z контур С,
отображаются на линии тока
течения, обтекающего в плос-
плоскости t круг радиуса R; точка
t = co является при этом об-
общей для всех линий тока. По-
Потребовав, чтобы <?(оо) = оо,
мы получим в плоскости z
течение, обладающее тем же
свойством. Если потребовать еще, чтобы <р'(оо)=1 '), то ско-
скорость течения, определяемого комплексным потенциалом A3)
в бесконечно удаленной точке, окажется равной v&.
Рис. 89.
dw
~dz
dw
— Vrn- 1 —Vo
') Аналитическая ф>нкция, отображающая одн> односвязнмо
область на др\г\ю, определяется однозначно (см. стр. 83), если
задать в какой-либо точке отображаемой области значение отобра-
отображающей санкции и ар[)мент ее производнон. Поэтом) для опре-
определения единственной ф>нкции t = o(z), отображающей внешность
конт\ра С на внешность данного кр)га 11 | > R, достаточно, кроме
равенства ф(оэ)=оэ, задать только арг)мент числа о (оо), напри-
например считать этот аргумент равным нулю, т е. считать <р'(оо) дейст-
действительным положительным числом. Следовательно, вообще говоря,
невозможно найти функцию <р (t), осуществляющею треб)емое
отображение и )довлетворяющ\ ю }словиям
<f(co)=co, <р'(оо) =
(а)
если считать ради\с Kp\ia R в шоскости t заданным, но можно
найти такой ради>с R, при котором условия (а) б>д>т выполнены.
При атом число R в равенстве A3) определяется из условий (а).
§ 5]
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ЭЛЕКТРОСТАТИКЕ
185
§ 5. Комплексный потенциал в электростатике
и термодинамике
77. Плоское электростатическое поле, т. е. поле вектора
напряженности
является полем градиента
Е= — grad v (х, у),
где v — потенциал электростатического поля, и следовательно,
это поле потенциально. Во всех точках, в которых нет заря-
зарядов (заряды играют здесь роль источников и стоков в гидро-
гидродинамике), электростатическое поле соленоидально, и для его
изучения целесообразно воспользоваться понятием комплекс-
комплексного по1енциала. Однако, в отличие от гидродинамики, в зада-
задачах электростатики применяют несколько иные обозначения
и иную терминоло! ию. Комплексным потенциалом поля Е
называется функция
/ (z) = и (х, у) -)- iv (х, у),
где
dv = — [Ех {х, у) dx -f Ey {x, у) dy],
а
du — — Ey (x, у) dx -\- Ex {x, y) dy.
Функция и(х, у) называется силовой функцией, а функция
v(x, у), как уже упомянуто выше, — потенциалом электро-
электростатического поля. Имеем
откуда
= \f(z)\,
Линии уровня потенциальной функции v (x, у) называются
эквипотенциальными линиями, а линии уровня силовой функ-
функции и (х, у) — силовыми линиями.
Циркуляция векюра напряженности Е по замкнутому
контуру С
186
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл. VI
равна работе поля при перемещении единичного заряда по
замкнутому контуру и всегда равна нулю.
Поток вектора напряженности через замкнутый контур
в силу известной теоремы Гаусса, равен алгебраической сум-
сумме расположенных внутри контура С зарядов, умноженной
на 2тс (рассматривается плоский случай).
Пример 1. Выяснить характер электростатического поля, со-
соответствующего комплексному потенциалу f (z) = i Ln г.
Здесь (см. для сравнения пример 3 на стр. 174) ц = — Argz,
v = In | z \. Эквипотенциальными линиями являются окружности
| г | = с, силовыми линиями являются лучи Argz = C.
Найдем модуль и аргумент вектора напряженности:
1
Arg? = - [j
Это означает, что вектор напряженности направлен вдоль луча
Argz = С (вдоль силовой линии) к началу координат.
Единственной особой точкой является точка г = 0; в ней рас-
расположен заряд. Для того чтобы найти величину этого заряда,
следует вычислить поток вектора Е через замкнутый контур С,
однократно обходящий точку г = 0. Выбрав в качестве такого
контура окружность | г \ = г, получим
г '
откуда
= — \ — ds = —
и, в силу теоремы Гаусса, ветччина заряда равна —=—= — 1.
Отсюда следует, что комплексный потенциал, соответствующий
заряду -)-1 в точке г = 0, имеет вид
/B)=-П.пг
или
51
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ В ЭЛЕКТРОСТАТИКЕ
187
Пример 2. Выяснить характер электростатического поля,
соответствующего комплексному потенциал f(z) = i/z. Здесь (см
для сравнения стр. 176)
Эквипотенциальными линиями являются окружности с центрами
У
Рис. 90.
на оси Олг, касающиеся оси Оу (рис. 90), силовыми линиями — окруж-
окружности с центрами на оси Оу, касающиеся оси О.\г. Так как /' (г) =
= — i/z2, то вектор напряженности определяется равенствами
В особой точке г = 0 расположен диполь. Нетрудно (см. стр. 176)
убедиться в том, что рассмотренное электростатическое поле явля-
является предельным при Л —0 для поля, определяемого двумя зарядами:
одним — величины 1/Л, находящимся в точке 2 = 0, и другим —
величины — 1/А в точке —/г.
78. В поле скоростей течения жидкости вдоль обтекаемой
линии постоянна функция тока, в электростатическом поле,
188
КОМПЛЕКСНЫЙ ПОТЕНЦИАЛ
[Гл VI
аналогично, вдоль проводника постоянна потенциальная функ-
функция, поэтому нмесго гидродинамических задач на обтекание
в электростике возникают задачи об определении поля Е
или его комплексного потенциала в односвязных пли много-
многосвязных областях, ограниченных проводниками. Приведем
несколько 1ипов таких задач.
а) Определение электростатическою поля (или его ком-
комплексного потенциала) в области, ограниченной проходящим
через бесконечно удаленную точку проводником С, если
известны величина и направление вектора Е в бесконечности
(см. рис. 82).
б) Определение элек! роста: ического поля (или его ком-
комплексного по1епциала) в криволинейной потосе, ограниченной
двумя не пересекающимися на конечном расстоянии проводни-
проводниками С, и С2 в предположении, что разность потенциалов
между проводниками задана (см. рис. 86).
в) Определение электроаэтического поля во внешности
замкну!ого проводника С, если известны величина и направ-
направление вектора Е в бесконечности.
г) Определение поля между двумя замкнутыми непересе-
непересекающимися проводниками, если известна разность потенциалов
между ними.
Эти задачи решаются совершенно аналогично соответ-
соответствующим задачам на обтекание.
Комплексный гиленциал в задачах электростатики нахо-
находится так же, как и в задачах гидромеханики, как функция,
оюбражающая заданную область на стандартную область,
соответствующую пшу рассматриваемой задачи (полуплоскоаь,
полоса между параллельными прямыми, внешность круга,
кольцо).
79. В задачах термодинамики часто приходится рассмат-
рассматривать векторное поле
А = — k grad и (х, у, г)
или в плоском случае
А = — k grad it (x, у),
где и — температура соответственно в точке (х, у, z) или (х, у),
k — коэффициент внутренней теплопроводности, который мы
будем считать постоянным. Вектор А называется вектором
ЗАДАЧИ К ГЛ VI
189
потока тепла При постоянном k векторное поле
А = — k grad и = grad (— kit),
будучи полем градиента, потенциально. Это поле также и со-
леноидально во всех точках, в которых нет источников
и стоков тепла, ибо стационарный поток тепла через любой
замкнутый контур С, ограничивающий некоторую область D,
в которой нет источников и стоков тепла, должен быть равен
нулю (в противном случае количество тепла в области D
изменялось бы, и следовательно, изменились бы с течением
времени температура и и ее градиент, т. е. поле А не было бы
стационарным). Для изучения поля теплового потока также
целесообразно использовать понятие комплексного потенциала.
Задачи термодинамики, соответствующие основным задачам
на обтекание, формулируюкя и решаются так же, как и ана-
аналогичные задачи электростатики, только, говоря о провод-
проводниках, мы должны теперь иметь в виду не проводники элек-
электричества, а хорошие проводники тепла, а вместо разности
потенциалов теперь надо задавать разность температур.
ЗАДАЧИ К ГЛАВЕ VI
В задачах 1—4 требуется определить модуль и направление век-
вектора поля А, найти уравнения линий тока и линий уровня потен-
потенциальной функции по заданному комплексному потенциалу w.
1. w = z2.
2.Ш = 2+1.
3. w = A +0 Lnz.
4. w—yz— а (а — действительное число).
В задачах 5 и 6 требуется определить семейства линий тока
и линий уровня потенциальной ф\нкции, а также характер особых
точек по заданному комплексному потенциалу w.
z - г
5. w = Ln
6. w = i Ln
г—1
ЧАСТЬ 2
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
ГЛАВА VII
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
§ 1. Определение преобразования Лапласа
80. В этой главе мы рассмотрим определение и основные
свойства преобразования Лапласа, па базе которого
в последующем будет строиться операционное исчисление.
Для этого нам понадобятся уже известные сведения из теории
функций комплексною переменного. Именно применение этой
теории и обеспечит сравнительную простоту изучения свойств
преобразования Лапласа и использование этих свойств в таком
важном разделе математики, как решение дифференциальных
уравнений, и таком важном разделе электротехники, как
изучение переходных процессов в электрических цепях.
Начнем с определения. Преобразованием Лапласа функции
действительного переменного f(f) называется функция ком-
комплексного переменного F(p), определяемая формулой
Несобственный интеграл в правой части равенства, зави-
зависящий от комплексного параметра р, называется интегралом
Лапласа. Свойства интегралов, зависящих от комплексного
параметра, используемые в дальнейшем, аналогичны соответ-
соответствующим свойствам интегралов, зависящих от действитель-
действительного параметра (см. [1], гл. VIiI, § 3).
Прежде всего уаановим, какие функции f(t) мы будем
рассматривать и какие условия надо на них наложить, чтобы
несобственный интеграл A) сходился и действительно опреде-
определял некоторую функцию F(р). Будем предпола1ать следующее:
5 И
ОПРЕДЕЛЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАГП\СА
191
1) Функция f{t) — кусочно-непрерывная при t^O; эш
значит, что она или непрерывна, или имее1 точки разрыва
только первого рода (в каждом конечном интервале число
таких точек разрыва обязательно конечно).
2) Функция f{t) равна нулю при отрицательных значе-
значениях t
f{t) =
при
Так как в ишеграле Лапласа значения функции f{t) при
t<^0 вообще не участвуют, то не имеет значения, чему они
равны. Ка'к будет видно из дальнейшего (в п. 97), удобнее
считать, что они равны нулю. При изучении многих физи-
физических процессов роль переменной t играет время и сказан-
сказанное означает, что процесс начинается с некоторого момента
времени (удобнее всего считать, что в момент 2" = 0).
3) При возрастании t модуль функции f(t) может возрас-
возрастать, но не быстрее некоторой показательной функции, т. е.
\f(t)\^Me'lt, C)
где М и о. — постоянные.
Последнее условие обеспечивает, как мы вскоре убедимся,
сходимость интеграла Лапласа. Условию 3) удовлетворяют,
конечно, все ограниченные функции (в частности, sin t и cos f);
в этом случае а можно положить равным нулю: \f(t)\s^M.
Ему удовлетворяют и все степенные функции tk (?^>0),
так как любая такая функция растет медленнее, чем показа-
показательная функция е'\ применяя правило Лопиталя, легко про-
проверить, что lim -j—0. (При k<^0 соответствующие сте-
степенные функции имеют бесконечный разрыв при ^ = 0 и не
удовлетворяют первому условию.) Если чи1атель вспомнит, с
какими функциями ему приходилось сталкиваться при изуче-
изучении различных физических процессов, то он легко установит,
что почти для всех таких функций условие C) выполняется.
(В качестве примера функции, для коюрой условие C) не
выполняется, можно указать е1 .)
Любая функция f(t), удовлетворяющая сформулированным
выше трем условиям, называется оригиналом; функцию F(р),
определяемую формулой A), будем называть изображением
(для ясности иногда говорят «изображением по Лапласу»).
192
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
Соо]ветствие между оригиналом f{t) и изображением t
записывается в виде
или F(p)=f(t).
Употребляются также символы
f(t)oF(p),
= L{f(t)}.
Формула для обратного перехода от изображения F (р) к
оригиналу f(t) имеет более
сложный вид; мы ее приведем
и будем исследовать позже
(в третьем параграфе).
Приведем простой пример.
~t Пусть tj(?) — единичная функ-
функция
О, если t <^ О,
Рис. 91.
График ее приведен на рис. 91; ясно, что она является ори-
оригиналом. Для нее
О р'
at lst =e"J'. Последнее выражение стремится к нулю
со, если а^>0. Таким образом, интеграл Лапласа
причем последнее заключение можно сделать только в том случае:
когда e~pt-+0 при ^ —>• go. Если /? = а -)- is, то
при t
для единичной функции сходится при a = Re/?^>0, и ее
изображением является функция \,р.
Так как мы условились, чю всякий оригинал равен нулю
при t<^0, то для upocioibi будем писа1ь, что единичная
функция т](?)=1, и тогда соответс!вие запишется так:
1=1.
• Р
E)
Вообще в этой части книги, если речь идет о какой-то
функции f(t), например, о sin t, cos t, et и т. д., то всегда
ОПРЕДЕЛЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
193
подразумеваются следующие функции:
°' если t<0' Ш =
sin t, если a
°' если
cost, если
\ е', если
Графики этих функций приведены на рис. 92 (соответст-
(соответственно а, б, в). Видно, что функции /2(?) и f3(t) имеют
\1
Рис. 92.
в точке ^ = 0 разрывы первого рода. Функция fx(f) в точке 0
непрерывна (если fx @) = 0), но ее график имеет угловую точку.
С помощью единичной функции ч\(?) можно было бы
записать
/i @ = -П @ sin U U @ = т| @ cos t, h @ = fi @ e1,
однако для сокращения записи множитель ~q(t) мы будем
опускать и просто писать
/, @ = sin U А @ = cos t, f3 (t) = el.
Совершенно не обязательно считать, что оригинал f(t)
принимает только действительные значения. Функция f(t)
может быть и комплексной функцией действительного
переменного, т. е. иметь вид f{t)=fl(t)-\-ifi{t), где fx(f) и
fi(t) — соответственно действительная и мнимая части f(t).
При этом каждая из функций /,(?) и ft(t) должна удо-
удовлетворять первому условию, наложенному на оригинал. Ус-
Условия 2) и 3) формулируются совершенно одинаково для функ-
функций, принимающих как действительные значения, так и комп-
комплексные.
81. Перейдем теперь к доказательству того, что каж-
каждому оригиналу f(t) соответствует изображение F(p) и уста-
установим общие свойства изображения. Имеет место следующая
7 И. Г. Араманович и др.
194
ПРЕОБРАЗОВАНИР ЛАПЛАСА
[Гл VIГ
Теорема. Пусть функция fit) является оригиналом.
Тогда интеграл Лапласа
Fip)=\fif)e-P4t
о
сходится абсолютно для всех значений комплексной пере-
переменной р, удовлетворяющих условию Re/?^>a (/я. е. в полу-
полуплоскости Rep^xx), где а. — по-
'/////////////, стоянная, участвующая в усло-
условии 3), и определяет изобра-
изображение F(p), которое является
функцией, аналитической в полу-
полуплоскости Re/?^>a (рис. 93; па
этом рисунке а^>0, но, разумеет-
разумеется, а может быть и числом отри-
отрицательным, и нулем).
рис. 93. Чтобы доказать абсолютную
сходимость интеграла, восполь-
воспольПолуплоскость
'///. Rep* a
зуемся условием 3), согласно которому |/@|-
р = а-\- is, то | e^pl | = г'"' и поэтому
| fit) e~pt i »?S Me^e at = /We<*
Отсюда
; Me
*'-
a-Q)t
О о —
а — а
если
F)
G)
так как, по условию теоремы, а — о<^0 и потому е'а °>'—*-0
при ?—>оо. Неравенство G) и показывает, что интеграл
Лапласа сходится абсолютно.
Доказательство того, что изображение F(p)— функция
аналитическая, основывается на свойствах правильно (или рав-
равномерно) сходящихся интегралов (см. [1], п. 137); приведем
его мелким шрифтом.
Если Re рЭ=ао>а, то на основании формулы F) справедливо
неравенство \f(t)e~~pt | sg Me"l~'lo)t; функция в правой его части
не зависит от р и интеграл от нее в пределах от 0 до со сходится,
так как а — ао<;О. Этим доказана правильная сходимость интеграла
Лапласа при Rep^a,,. Производная подынтегральной функции
по параметру р равна — tf(t)e~pt. Ее модуль не превосходит функ-
функции Mte^ ~a°'', интеграл от которой также сходится (он легко
§
ОПРЕДЕЛЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
195
вычисляется и равен М'(а — а0J). Следовательно, и интеграл от
производной по параметру р сходится правильно, а отсюда и сле-
следует, что интеграл Лапласа можно дифференцировать по р, т. е.
что функция F (р) является аналитической. (В теоремах о правильно
сходящихся интегралах, на которые мы ссылаемся, требуется, чтобы
подынтегральная функция была непрерывна и по переменной
интегрирования t и по параметру р; можно доказать, что теоремы
справедливы и тогда, когда эта функция по t кусочно-непрерывна.)
В качестве примера найдем изображение функции eal, где
а = $-\- iy — любое комплексное число. Разумеется, согласно
нашему условию при t<^0 функция равна пулю. Условия 1)
и 3), очевидно, выполняются, причем в силу равенства-
„at
лучим
— е®' можно положить М=\ и <х=р. Интегрируя, по-
¦ip — a)
р — а'
если только е(ра)'->0 при ?->оо. Последнее же имеет
место при Re(p — a) —Re/* — Р^>0, т. е. при Rep^>p.
Таким образом,
(8)
• р — a
Если а = 0, то мы снова получаем формулу E):
1
• Р'
Крайне существенно то обстоятельство, что хотя теорема
утверждает сходимость интеграла Лапласа только при Re/?^>p,
в полученной формуле соответствия eat ф правая часть
является аналитической функцией при всех значениях/?, кроме
точки р^а, где она имеет полюс. Как мы увидим в даль-
дальнейшем, в большинстве случаев дело будет обстоять так же,
как и в приведенном примере. Функция F(p) оказывается
определенной и аналитической не только в полуплоскости
Rep^>a (где интеграл Лапласа сходится абсолютно), но и
в значительно большей части комплексной плоскости р, чаще
всего во всей плоскости, за исключением изолированных
особых точек. Пользуясь же приведенной теоремой, мы можем
лишь утверждать, что в полуплоскости Re/> ^> а функция
7*
196
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
не будет иметь особых точек: все они оказываются лежащими
или левее прямой Re/? = a, или на самой этой прямой.
Чтобы читателю стал более ясен смысл этого замечания,
приведем аналогичный пример, встречавшийся при рассмот-
рассмотрении рядов. Как известно, в единичном круге имеем
причем ряд слева (геометрическая прогрессия) сходится толь-
только при |z|<M; в то же время функция, стоящая справа,—
аналитическая при всех значениях г, кроме точки 2=1. Од-
Однако эта функция является суммой геометрической прогрес-
прогрессии только при \z\<^\. Так же обстоит дело и в приведен-
приведенном выше примере. Функция F(p) = з аналитическая
всюду, кроме точки р = а, однако то, что она выражается
со
интегралом § eate~ptdt, можно утверждать только при Re/T>Rea.
о
В дальнейшем нас, как правило, будет интересовать
только само изображение F(p), а вовсе не та область, в ко-
которой оно выражается интегралом Лапласа. Мы должны быть
всегда уверены только в одном: в какой-то полуплоскости
(безразлично какой) интеграл Лапласа сходится абсолютно.
Забегая вперед, укажем, что каждому изображению F(p)
отвечает единственный оригинал f{f), если только не обра-
обращать внимания на значения функции f(t) в точках разрыва.
Это означает также, что на изображение не влияют те значе-
значения оригинала, которые мы ему приписываем в точках разрыва.
82. Отметим еще поведение любого изображения F(p)
в бесконечно удаленной точке. Из неравенства G) следует, что
\F(P)\ =
М
где a — постоянная из условия 3) и a = Re р. Поэтому, если р
стремится к бесконечности так, что при этом и о —>- сю (на-
(например, вдоль положительной части действительной оси), то
F(p) стремится к нулю.
Если, в частности, F(p) — функция, аналитическая в беско-
бесконечно удаленной точке (см. п. 58), то дополнительное условие
ОПРЕДЕЛЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
197
a —> со не играет роли, и F (р) стремится к нулю при р стре-
стремящемся к бесконечности по любому закону:
lim F(p) =
(9)
Иначе говоря, если изображение F (р) аналитично в беско-
бесконечно удаленной точке, то оно обязательно имеет там
нуль.
83. Перед тем как перейти к изучению основных свойств
преобразования Лапласа, поясним основную идею его приме-
применения. Преобразование Лапласа устанавливает соответствие
между оригиналами f(t) и их изображениями F (р):
Оказывается, что определенным действиям, производимым
над оригиналами, будут соответствовать некоторые действия,
производимые над их изображениями, причем, как правило,
действия над изображениями будут проще, чем над оригина-
оригиналами (это будет показано в следующем параграфе). В этом
проявляется полная аналогия с основной идеей применения
логарифмов в элементарной математике. Роль оригиналов
там играют числа, а роль изображений — их логарифмы.
Действию умножения чисел соответствует сложение их лога-
логарифмов, действию возвышения числа в степень соответствует
умножение логарифма этого числа на показатель степени
и т. д. Таким образом, более сложные действия над числами
заменяются более простыми действиями над их логарифмами,
и схема применения логарифмов выглядит примерно так.
Чтобы, скажем, перемножить числа, мы сначала по таблице
находим их логарифмы и складываем их. Найдя логарифм про-
произведения, мы снова, пользуясь таблицами, возвращаемся к
числу и получаем искомый результат. Все это, разумеется,
хорошо известно читателю, и мы повторили это только для
того, чтобы более ясной стала рассматриваемая нами ана-
аналогия.
Именно, если имеется некоторое сложное соотношение
между оригиналами, то при помощи преобразования Лапласа
мы будем получать значительно более простое соотношение
между изображениями. Например, вместо дифференциального
198
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
уравнения относительно оригинала будет получаться алгебра-
алгебраическое уравнение относительно изображения. Решив это по-
последнее и перейдя затем от изображения назад к оригиналу,
мы и получим решение исходного дифференциального урав-
уравнения.
Приведенную аналогию с логарифмами можно продол-
продолжить. Ведь главное при действиях с логарифмами — это хо-
хорошо знать свойства логарифмов и правила логарифмиро-
логарифмирования. Само же соответствие между числами и логарифмами
устанавливается при помощи таблиц логарифмов, и можно
превосходно владеть методами вычислений, совершенно не
зная, как фактически составлялись логарифмические таблицы.
Точно так же обстоит дело и здесь. После того как мы в
следующем параграфе установим основные правила действия
над преобразованиями Лапласа и составим таблицу соответ-
соответствия между оригиналами и изображениями (своего рода
«аналог» таблицы логарифмов), нам уже не придется больше
вычислять интеграл Лапласа для различных оригиналов f(t),
и переход от оригинала к изображению и обратно — от изо-
изображения к оригиналу будет осуществляться при помощи
этой таблицы.
Таким образом, читатель е самого начала должен привык-
привыкнуть к тому, что интеграл Лапласа A) нужен главным обра-
образом для установления основных свойств и правил преобра-
преобразования Лапласа, или, как мы чаще будем говорить, свойств
и правил операционного исчисления.
Вообще под операционным исчислением понимают ме-
методы решения задач, основанные на следующих этапах:
1) от искомых функций переходят к некоторым другим
функциям — их изображениям;
2) над изображениями производят операции, соответствую-
соответствующие заданным операциям над самими функциями (отсюда
название — операционное исчисление);
3) произведя действия над изображениями и получив не-
некоторый результат, возвращаются к самим функциям.
В нашем курсе в качестве преобразования, позволяющего
перейти от функций к их изображениям, будет применяться
главным образом преобразование Лапласа. Несколько позже
(в § 4) мы вкратце коснемся еще одного преобразования —
преобразования Фурье, также играющего важную
роль при решении многих прикладных задач.
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
199
§ 2. Свойства преобразования Лапласа
84. В этом параграфе мы рассмотрим основные свойства
преобразования Лапласа и составим краткую таблицу,' уста-
устанавливающую соответствие между некоторыми оригиналами и их
изображениями. Для сокращения записи условимся, что ориги-
оригиналы будут обозначаться через/(f), g(t) и т, д., а их изображения
(аналитические функции комплексного переменного) соответ-
соответственно через F(p), G(p), ..., т.е.
• f(t)-r-F(p), g(t)~--O(p).
Напомним также, что мы уже
имеем формулу соответствия (8):
и, в частности,
1-
1
Рис. 94.
I. Теорема линейности. Для любых действитель-
действительных или комплексных постоянных А и В
Af(t)-\-Bg(t)=^AF(p)-{-BG(p), A0)
т. е. линейной комбинации оригиналов соответствует та-
такая же линейная комбинация изображений.
Доказательство немедленно следует из хорошо известного
свойства интеграла:
ОО ОО ОО
\ [Л/@ -f Bg(t)\ e'P'dt = A\f{f) e-P'dt -f В \ g{t) e^'dt.
0 0 0
Заметим только, что если интегралы справа абсолютно сходятся
в разных полуплоскостях: Re/?^>aj и Rep^>a.2, то интеграл
слева сходится в их общей части (покрытой двойной штри-
штриховкой на рис. 94). Но, как уже отмечено выше, нас не инте-
интересует, в какой полуплоскости сходится интеграл, лишь бы он
вообще где-нибудь сходился. Разумеется, теорема линейности
остается справедливой для любого конечного числа слагаемых.
В качестве применения этой теоремы найдем изображения
тригонометрических и гиперболических функций. По форму-
формулам Эйлера
sin ш^ = -
Ti
COS Uit = ¦
200
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
Полагая в формуле (8) а = ±ш и применяя теорему линей-
линейности, получим
1
sin сог^
COS СО/=-1-
2i \р — ш р-\- i«
1
р
sin
2 \ р — t'<i> ' p-\-i<a j р~ -f- <л" '
Опять пользуясь теоремой линейности, легко получим
coso-l-p sino
A1)
A2)
= sin w/coscp -|" cos«it sin ? == ¦
. p cos о — со sin 9
COS (wt -f- cp) =
ij i -
Совершенно аналогично, исходя из определения гиперболи-
гиперболических функций
shcor =
2
спо)Г = -
2
найдем, что
sh wt ==
ch (о/ -4:
Р" —
A4)
Заметим, что каждое из изображений A1) — A4) есть функ-
функция, аналитическая во всей плоскости р, с особыми точками
± ш (для sin ш/ и cos wt) или ± ш (для sh wi1 и ch tot).
В бесконечно удаленной точке все найденные изображе-
изображения аналитичны и, как легко проверить, обращаются в нуль;
это в точности соответствует общему положению о поведе-
поведении изображений F(p) в бесконечно удаленной точке (см. фор-
формулу (9)).
II. Теорема подобия. Для любого постоянного
A5)
ш. е. умножение аргумента оригинала на положительное
число X приводит к делению аргумента изображения и
самого изображения F (р) на то же число к.
В самом деле, по определению преобразования Лапласа
f№ =
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
201
Совершая в интеграле подстановку \t = tlt
лучим
= ^-dtv no-
так как безразлично, какой буквой обозначена переменная
интегрирования (t или /j).
Допустим, что нам была бы известна формула A1) только
для частного случая ш=1, т. е.
Тогда, воспользовавшись теоремой подобия, мы получили бы
sin ш/ == —
что в точности совпадает с формулой A1).
III. Теорема затухания1). Для любого действи-
действительного или комплексного числа а
ea'f(t)^F(p — a), A6)
т. е. умножение оригинала на функцию eat влечет за
собой «смещение» независимой переменной р. Поэтому тео-
теорему называют также теоремой смещения.
И здесь доказательство немедленно следует из определе-
определения преобразования Лапласа:
= \
= \f{t) e
= F{p — a).
Теорема затухания помогает расширить таблицу соответ-
соответствия между оригиналами и изображениями, позволяя по из-
известному соотношению f(t)==-F{p) находить изображение
') Названия теорем ясно подчеркивают связь рассматриваемых
вопросов с физическими представлениями. Смысл термина «зату-
«затухание» заключается в том, что если а < 0, то множитель eal в равен-
равенстве A6) убывает.
202 ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл VII
функции eatf(t). Например, из формул A1) и A2) получим
р — а
A7)
В обоих случаях мы заменили в выражении для изображения
переменную р на р — а.
Совершенно аналогично из формул A4) следует
(р — aJ—
A8)
Часто оказываются полезными формулы соответствия для
произведения оригинала f(t) на sin ш^ или cosco^. Применяя
теоремы затухания и линейности, читатель легко самостоя-
самостоятельно получит формулы:
/(Qcosurf = i- [F (p — ш) + F (р + ш)},
f(t) sin arf = 1- [F(p - w) - F (p + №)],
A9)
где f(t)==F(p). Ясно, что формулы A7) являются частными
случаями последних формул.
85. Перейдем к дальнейшим свойствам преобразования
Лапласа.
IV. Теорема запаздывания. Для любого посто-
постоянного ¦z ^> 0
f(t-^) = e^F(p). B0)
На этой теореме будет основано изображение многих
функций (в частности, функций, описывающих импульсные
процессы), и поэтому мы рассмотрим ее подробнее. Прежде
всего выясним смысл термина «запаздывание». Пусть график
функции f(t) изображен на рис. 95, а. Тогда график функ-
функции f(t — т), изображенный на рис. 95, б, будет сдвинут
относительно графика f(t) на т, причем на участке @, т) гра-
график совпадает с осью 0^, так как на этом участке t — т<^0
и поэтому функция / (t — т) равна нулю. Таким образом,
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
203
процесс, описываемый функцией fit — -:), начинается как бы
с опозданием на время т относительно процесса, описывае-
описываемого функцией f{t); отсюда и термин «запаздывание». Если,
например, t\(t)=\ (единичная функция), то график функции
f(t-t)
6)
Рис. 95.
r\(t — т) будет иметь вид, изображенный на рис. 96. На
рис. 97 сплошной линией изображен график функции f(t) = et
и пунктирной — график функции f(t — т), которая равна
е1''1 при t^>i и 0 при t<^z. Эту функцию коротко можно
записать так: ^~\{t — t).
Исходя из физического толко-
толкования, теорему запаздывания | / /
Рис. 96.
Рис. 97.
можно сформулировать так: запаздывание оригинала на время
т соответствует умножению изображения на е~рх.
Для доказательства теоремы запишем
так как на участке @, х) подынтегральная функция равна нулю.
Совершая подстановку t — ¦z==tl и замечая, что при этом
нижний предел интегрирования станет равным нулю, получим
\ f(t - -) с *dt = j f{tx)
204
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
Интеграл справа есть как раз F(р), и, таким образом, мы
доказали, что
Согласно этой теореме изображение оригинала f\(t — т),
график которого изображен на рис. 96 (единичная функция,
запаздывающая на время т), будет равно — <ГР", а оригинала
Р е р-
е , сдвинутого на х (пунктирная линия на рис. 97), есть . .
Применим теперь теорему запаздывания к построе-
построению изображения единичного импульса a (t), действующего
за промежуток времени х:
t
0, если
1, если
0, если
Рис. 98.
График его приведен на рис. 98.
Ясно, что этот единичный им-
импульс можно рассматривать как
разность двух оригиналов: единичной функции и единичной
функции, сдвинутой на х (рис. 91 и 96). Так как изображение
последней функции есть — е~р~, то, применяя теорему линей-
линейности, получим
. р р р К
B1)
Пусть теперь единичный импульс начинается не в момент
t = 0, а в некоторый момент t—T и по-прежнему действует
Т+х
г
1
T+t
гт
гт+х
г
t
Рис. 99.
Рис. 100.
в течение времени х (рис. 99). Снова применяя теорему запаз-
запаздывания, получим, что его изображение равно —A — е р")е~Рт.
Пусть, наконец, имеется периодическая система импульсов,
изображенная на рис. 100. Ясно, что эту систему можно
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
205
рассматривать как сумму импульсов, которые начинаются
в моменты времени п Т (я = 0, 1, 2, ...) и длятся время
^ (Т<С'О- Применяя теоремы запаздывания и линейности,
получим
Геометрическая прогрессия сходится, потому что \е~РГ\<^
<у-гГ<Ч, если только Rep^>a^>0. В том частном случае,
когда 7" = 2х, формула упрощается:
Если в указанном частном случае первый импульс начать не
с нуля, а с момента t = x, то
изображение опять умножится
на е~Р~ и будет равно
1
-7
2х
Зх
4х t
Рис. 101.
Рекомендуем читателю са-
самостоятельно проверить, что
для оригинала, изображенного на рис. 101, т. е. задаваемого
формулой
| 1, если Ъ,
\ — 1, если Bл-}-1)
имеет место соответствие
1 — е'Р
-р-л >
.A+е
после простых преобразований можно выразить че-
через гиперболический тангенс
Совершенно не обязательно, чтобы все импульсы были оди-
одинаковыми. Применяя предыдущие формулы, легко установить,
206
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
что система двух импульсов, показанная на рис. 102, имеет
изображение
—
р
р v
Можно также построить изображение и периодической си-
системы таких импульсов.
Аналогично строятся и
изображения синусоидальных
Л
Г ТЫ,
Рис. 102.
импульсов. Чтобы получить импульс в виде одной полу-
полуволны синусоиды sin i (рис. 103), нужно сложить два ориги-
оригинала, один из которых есть sin t, а другой — та же сину-
синусоида, запаздывающая на тс (сплошной и пунктирный графики
T-rt 2T t
Рис. 104.
Рис. 105.
на рис. 104). Применяя формулу A1) и теорему запаздыва-
запаздывания, получим изображение такой полуволны:
Такой же импульс, начинающийся с запаздыванием на Т, имеет
изображение
а периодическая система таких импульсов (рис. 105;
изображение
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ПАПЛАСА
207
В частности, если 7 = тс, т. е. рассматривался оригинал, рав-
равный | sin t\, то изображение равно
z\h-~-
о-ър
Значительно реже, чем теорема запаздывания, применяется
теорема опережения: если т^>0, то
B2)
Графики функций f{€) и f{t-\-T) изображены на рис. 106,
причем ординаты пунктирной части графика /(/ -f- т) должны
быть заменены нулем, так что график fit -\-t) остается как бы
срезанным. Это и приводит
к тому, что в формуле B2)
из F(р) вычитается интеграл ,*•'
в конечных пределах. ('
Для доказательства тео- !
ремы запишем ^
со
f(t + т) = \ f{t + т)
Рис. 106.
и совершим в интеграле подстановку t-\-x = ti. Тогда
f{t 4- т) = е<" ^ /(<,) в-"'1Л, = ерт [^ /@ е^Л - \ fit)
z 0 0
(мы переменную интегрирования вновь обозначили буквой t).
Так как первый интеграл в скобках есть как раз Fip), то
теорема доказана.
86. Для получения большого числа новых изображений
оказывается удобным рассматривать оригиналы и изображения,
зависящие от параметра. Пусть функция fit, x) при каждом
фиксированном значении х является оригиналом и ей соот-
соответствует изображение
ОО
F(p,x)=\fit,x)e-P'dt. B3)
Будем предполагать, что выполнены все условия, при
соблюдении которых интеграл B3), рассматриваемый как
208
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
функция параметра х, можно дифференцировать по этому
параметру под знаком интеграла; тогда
dF(p,x) ?df(t,x) c_p<dL
1 С
дх J дх
о
Указанное правило дифференцирования интеграла по параметру
позволяет сформулировать следующую теорему.
V. Теорема о дифференцировании по пара-
параметру. Если при любом значении х оригиналу fit, x) соот-
соответствует изображение F(p, x), то
dfjt,x) _^ dFjp.x)
дх • дх
B4)
Покажем, как следует применять эту теорему. Согласно
формуле (8)
„at.
¦ р — а
Здесь параметром является а; дифференцируя левую и пра-
правую части по этому параметру, получим новую формулу:
Продолжение дифференцирования приводит к соответствиям
2 f3ffit _l_ 3!
гт, . С С 7
и, вообще,
tneai = -
Полагая а = 0, получим
. 2
п\
п\
-Г" р2 , 1 — рЗ . • • • > 1 "Г" рП+1 •
B5)
B6)
Изображения дробных степеней tk будут получены позднее.
Совершенно аналогично, дифференцируя по параметру ш обе
части соответствий:
:_ Р
найдем
t cos ш —- -/-„—
t sin Ы ===-
B7)
2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
209
Рекомендуем читателю самостоятельно найти изображения для
функций t ch u>t и t sh wt.
87. До сих пор рассматривались те свойства преобразо-
преобразования Лапласа, которые применяются главным образом для
расширения таблицы оригиналов и изображений. Все выве-
выведенные формулы мы сведем в краткую таблицу, приведен-
приведенную на стр. 229—230; там же будут даны указания о более
подробных таблицах такого рода.
Теперь мы перейдем к наиболее важным свойствам преоб-
преобразования Лапласа, связанным с действиями дифференци-
дифференцирования и интегрирования.
Предварительно сделаем несколько замечаний. В предыду-
предыдущем параграфе были сформулированы три условия, при соб-
соблюдении которых функция fit) является оригиналом. Дальше
в качестве оригиналов будут рассматриваться производные
функции: f it), f" it) и т. д. Поэтому, не делая в дальнейшем
никаких оговорок, будем раз и навсегда считать, что если
какая-либо производная функция fit) принимается за ориги-
оригинал, то для нее выполняются все требуемые свойства. Кро-
Кроме того, если, например, в качестве оригинала выступает
первая производная, то будем считать, что сама функция
fit) при всех ^^>0 непрерывна. Если за оригинал прини-
принимается fit), то этому условию должна удовлетворять
первая производная f if) и т. д. В то же время, когда речь
пойдет о первообразной для функции fit), в частности об
t
интеграле с переменным верхним пределом \fit)dt, никаких
о
дополнительных оговорок делать не нужно. Можно показать,
что если функция fit) является оригиналом, то и интеграл
t
\fit)dt также является оригиналом,
о
Как мы уже видели (см. рис. 91, 92), часто случается,
что точка / = 0 является точкой разрыва оригинала. Так как
нам в дальнейшем придется говорить о значении /@), то
условимся всегда понимать под этим предел функции f(t)
при ^ — 0 справа, т. е.
B8)
(см. [1], гл. II, и. 33).
210
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
Аналогично, если точка ^ = 0 является точкой разрыва
для первой производной f (t), то условимся, что
/'@) = lim/'@- B9)
t>0
Так же поступим в случае производных высших порядков.
Во многих руководствах для предела B8) вводят специаль-
специальные обозначения /(-(- 0) или /@ -{-). Мы этого для сокращения
записи делать не будем, но всякий раз, как в тексте встретятся
выражения /@) или /'@). их надо определять по формулам
B8) и B9).
После сделанных оюворок перейдем к формулировке
и доказательству георем.
VI. Теорема дифференцирования оригинала.
Если f(t)==F(p), то
/'@ = ^ 00-/@). C0)
т. е. дифференцирование оригинала сводится к умножению
на р его изображения и вычитанию /@).
В частности, если /@) = 0, то
f'(t)=PF(p). C1)
Для доказательства запишем преобразование Лапласа для
производной f'(t):
/'@ = \П()
о
Интегрируя по частям и полагая
dv=f'(t)dt, ti=/@> получим
= е~р', du= —pe'ptdt,
О 0 0
Согласно условию роста оригинала, \f{t)\^Metti\ поэтому,
если Re/?^>a, то
' Me '"-к*"'' -+ 0
при ?->оо. Поэтому от первого слагаемого остается—/@),
и окончательно
что и требовалось доказать.
5 21
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
211
Применяя теорему повторно, получим
/" @ ^ р [pF (р) - ПО)} - /' @)=p*f (р) - Р№ - /' @),
/"' @ = р [p*F (р) - pf(O) - /' @)] - /" @) =
=p*F (j>) - ^/@) -pf @) -/" @),
и, вообще,
fW it) фрпрм-.рп-*/^ -p"-*f @) -.. .-/<»-» @). C2)
Самый простой случай — тот, когда все начальные значения
функции и ее производных равны нулю:
/@) =/@) = ...=/«--«) @) = 0;
тогда
f^{t)=pnF(p), C3)
т. е. при нулевых начальных значениях п-кратное диф-
дифференцирование оригинала сводится к умножению на рп
его изображения.
88. Подчеркнем, что условия, при которых теорема диффе-
дифференцирования справедлива, существенны. Возьмем функцию i\ (t — т),
график которой изображен на рис. 96. Производная Y (t — т) этой
функции равна нулю во всех точках, кроме точки t = i, где сама
функция разрывна и ее производная не существует. Так как
т|(*-т)= ~е~Р\
то по теореме дифференцирования мы получили бы
(при t = 0 функция т] {t — т) равна нулю). В тоже время, если ори-
оригинал (в данном случае — производная функции -i\{t — х)) во всех
точках, кроме одной, равен нулю, то и интеграл Лапласа от него
тоже равен нулю. Таким образом, соответствие (*) не верно! Сле-
Следовательно, наличие хотя бы одной точки, где оригинал разрывен,
может привести к тому, что теорема становится неприменимой.
В настоящее время широкое развитие получила теория обоб-
обобщенных функций, в которой вопросы, связанные с только что
рассмотренным примером, трактуются с другой точки зрения.
В этой теории часто встречается так называемая Ъ-функция, или
импульсная функция Дирака, определяемая следующим образом:
1)
2)
0, если t ф. т,
оэ, если t = 1;
212
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
где [а, Ь]—любой интервал, заключающий внутри себя точку т, а
f U) — оригинал, непрерывный в точке т. В теории обобщенных
функций 8 (t — т) рассматривается как производная сдвинутой еди-
единичной функции ц(г — •:). (Функции называются «обобщенными»,
потому что их свойства противоречат определению функции, при-
принятому в анализе.) Тогда
со
т{ (t — 1) = 3 (t — т) == $ 3 (t —- z) e~P<- dt = e~P;
о
что совпадает с результатом, полученным формальным применением
теоремы дифференцирования.
Теория обобщенных функций как раз и строится с таким рас-
расчетом, чтобы расширить область применимости основных теорем
обычного анализа. Эта теория принесла очень большую пользу
при решении ряда задач математики и физики ').
89. Из теоремы дифференцирования вытекают два важ-
важных следствия.
1. Если f'(t) является оригиналом, a F(p)— функция,
аналитическая в бесконечности, то
UmpF(p)=f{0).
p-rCO
C4)
Это следует из того, что (см. формулу (9)) любое изображе-
изображение, аналитическое в бесконечности, стремится при р->-оо к
нулю. Поэтому изображение производной f'(t) — функция
pF(p)—/@) — стремится к нулю при р-+со, откуда и вы-
вытекает равенство C4).
Аналогично, если и f"(t) — оригинал, то
lira \p*F(p)-pf@)]=f'(O).
Проверим формулу C4) на простых примерах.
Так,
Sin <ОГ— -3
И limp—J—| ; = 0= SHI 0.
= -г-т—; и limp-5-^—-=1 = '
Р- + <¦>" P^J р- + «-
') Краткие сведения об обобщенных функциях содержатся в
книге А. Д. Мышкиса, Лекции по высшей математике, «На}ка», 1967.
Читатель, заинтересовавшийся этими вопросами более серьезно,
должен обратиться к специальной литераторе.
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
213
2. Если f (t) является оригиналом и существует пре-
предел функции f(t) при t ->- со, то
р-«0 /-«оо
Действительно, согласно C0)
= \imf(t)=f(oo).
C5)
со
/' (О Ф J /' @ е-" dt = pF (p) - /@).
Перейдем к пределу при р —>0 (законность перехода к пределу
под знаком интеграла можно обосновать):
Нпф/7 (р) - /@)] = 5 /' @ dt = /(со) - /@),
р-*0 0
так как, по предположению, /(со) существует. Поэтому
откуда и следует C5). Заметим, что если ;? = 0 — пра-
правильная точка для F(p), то очевидно, что
UmpF(p) = 0.
Р-.0
Поэтому наибольший интерес формула C5) представляет тогда,
когда р = 0 — особая точка для изображения F(р).
Приведенным следствием нужно пользоваться с большой
осторожностью. Если с самого начала не проверить, чго су-
существует lim/(^)=/(co), то можно прийти к неверным ре-
/->00
зулыатам. Так,
sin (t>t = ¦
-, и lim
Л
в то же время lim sin cu^ не существует, и следовательно,
/-¦00
формула C5) здесь неприменима.
Для единичной функции -q(t) предел при t—>-схз равен 1,
формула C5) применима, и действительно,
lim р — = 1.
р-0 Р
214
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
Если f(t) = eai, то F(p)= _ . При а ф 0 точка р =
р — а
правильная и
Если а<^0, то \\meat = 0, и формула C5) справедлива;
если же а ^> 0, то оригинал при t —>¦ оо стремится к беско-
бесконечности и формула C5) теряет силу.
Рекомендуем читателю самостоятельно проверить, что если
а — комплексное число, то формула C5) справедлива для
функции eat при Rea<^0 и а = 0, и неприменима при Re а ^>
или при Rea = 0, Im а Ф 0.
90. VII. Теорема интегрирования оригинала.
t
Если /У)фР(р) и g{t)^=\f{f)dt, то
о
т. е. интегрирование оригинала в пределах от 0 до t при-
приводит к делению изображения на р.
Прежде всего заметим, что g'(t)=f(t) и g(Q) = 0 (ин-
(интеграл с одинаковыми нижним и верхним пределами). Поэ-
Поэтому, обозначая изображение g(t) через G(p), т. е. g{f)ф G(p),
и применяя теорему дифференцирования, получим
ё @ =/@ --pQip) ~ * @)=рО(р).
Но так как f (f) ф F (р), то F(p)—pG(p), откуда
Приведенные теоремы дифференцирования и интегриро-
интегрирования оригинала оправдывают замечание, сделанное в конце
предыдущего параграфа о том, что более сложным действиям
над оригиналами (в данном случае — дифференцированию и
интегрированию) соответствуют более простые действия над
изображениями (умножение и деление на р и в первом слу-
случае вычитание постоянного числа /@)).
Проверим теоремы VI и VII на простых примерах. Так,
е'ф-
1
¦ 1
отсюда
р-\
1
р-\ •
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
215
Исходя из соответствия cos t Ф
Ф /
, получим
(cosO' = -sln<=p-?^-r-l= —
PJ+l'
что опять-таки справедливо. Можно также записать, что
i
sin t= ^ cos tdt, и, применив теорему интегрирования, снова
получить sin t Ф —г—г. Вот более сложный пример: согла-
согласно формуле A7)
at ± . ш
eat sin oj^== — -7-,—=-.
Поэтому, дифференцируя левую часть и умножая правую
часть на р, получим соответствие
eat (a sin wt 4- <*> cos utf) = — ^Ц—^—
v ' (p — a) +ш
которое можно также проверить, воспользовавшись форму-
формулами A7) и A8) и теоремрй линейности.
91. Перейдем к теоремам дифференцирования и интегри-
интегрирования изображений.
VIII. Теорема дифференцирования изображе-
изображения. Если f(t)^F (p), то
C7)
т. е. дифференцирование изображения сводится к умноже-
умножению оригинала на — t. Формула C7) следует из правила диф-
оэ
ференцирования аналитической функции F (р) = ^ /(t) e~pt dt,
о
о котором мы уже говорили раньше: чтобы найти производ-
производную F'(р), т. е. производную по р от интеграла Лапласа,
нужно вычислить интеграл от производной по р подынтег-
подынтегрального выражения
F'(p}= y(t)( — t)e-P'dt.
о
Но это и означает, что
~tf(t)=-F(p).
216
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
Применяя теорему несколько раз, последовательно найдем
оригиналы для высших производных изображения F (р):
и, вообще,
C8)
Пользуясь формулой C8), легко найти изображения для сте-
степенных функций tk при целых значениях k, которые мы
раньше получали дифференцированием по параметру (тео-
(теорема V).
Исходя из формулы 1=— и применяя C8), последова-
, . I , . 1 ,, . 2
тельно найдем —г— 5, т. е. г = —;—t* ==— —j, т. е.
ра-' ¦ р^ р"
1 п\
t'1 -ф- -^ и, вообще, tn = —j^rL (формула B6)).
IX. Теорема интегрирования изображения.
со
Если интеграл ) F (г) dz сходится, то
р
со
F(z)dz, C9)
т. е. интегрирование изображения в пределах от р до оо
соответствует делению оригинала на t.
Эту теорему мы доказывать не будем и приведем лишь
несколько примеров.
Так как sin г=^ 2 , а \ 3, . = arctg,z
— arctgp = arcctg/?, то
sin t
= arcctg p.
Применяя еще теорему VII, найдем, что
t
? sin t ,, _^ arcctg p
2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
217
Интеграл, стоящий слева, не выражае1Ся при помощи эле-
элементарных функций, и определяет неэлементарную функцию
Si (t).
Из формул E) и (8) следует
. 1
р р —
Имеем
со
J \ г 2 — aj z — a
= 1п 1 — In —^-— ^ In .
р р — а р
Поэтому
1 — eat р — а
—i— -.— in .
t P
Отметим, что теорему IX нельзя применять к формуле
„at
=- , так как интеграл \ расходится; при
со
\
этом
р
и функция eat/t не будет оригиналом, так как она имеет
бесконечный разрыв при ^ = 0.
92. Теорема интегрирования изображения иногда позволяет со-
совершать интересные преобразования несобственных интегралов, об-
облегчающие их вычисление. Пусть
00
<? (О ф Ф (р) = \а (t) е-Р* dt.
Если заранее предположить, что [ <р (t) dt сходится, то
Ф @) = U (t) dt.
о
D0)
Отметим, что Ф @) может существовать и тогда, когда интег-
интеграл справа расходится. Так, если <f(t) = el, то Ф (р) = г и
со
Ф @) = —1, в то время как ^ e'dt, очевидно, расходится. Если же
и
218
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
1
[Гл VII
<р (t) = е~', то Ф (р) =||", интеграл \ е ' dt сходится и
о
Ф@) = 1 ').
равен
Применим формулу D0), положив у (t)—?-~- и считая, что
интеграл
V ~j-^
сходится,
где Ф (р) — изображение для оригинала —j^-'-
По формуле C9) это изображение равно § F (z) dz, где F (р) —
р
изображение f(t). Полагая /> = 0, найдем
ОО
Ф@)=Л
Подставляя в равенство (*) вместо Ф @) его значение, полу-
получаем искомое соотношение
CO CO
lMdt=[F(z) dz,
D1)
где f(t)=zF(p), и интеграл справа можно вычислить по положи-
оо
тельной полуоси. Так, если считать известным, что интеграл у —— dt
1) Это различие объясняется тем, что для оригинала е ' полу-
полуплоскость абсолютной сходимости интеграла Лапласа (Re/>>—1)
содержит точку р = 0, а для оригинала е' не содержит (полупло-
(полуплоскость Rej3>l). Для соответствия sin t = 2. . полуплоскость аб-
абсолютной сходимости Rep>0; точка р = О лежит на ее границе,
со
и формула D0) также неприменима: интеграл^ sin t dt расходится.
§ 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
219
сходится, то, исходя из соответствия sin t ==
sin t
dt =
dz
= arctgz
-, находим
T"
Точно так же, если предварительно доказать, что при л>0
оо
С e-at "e-bt
и й>0 интеграл
дем, что
f e-at _ g-ы
dt сходится, то по формуле D1) най-
най-!-= —:r4-il«fc = ln-
г -f й
z + b
= —In -j- = In —.
b a
93. Для того чтобы найти оригинал, соответствующий
произведению изображений, познакомимся сначала с одним
сравнительно простым действием над оригиналами — сверт-
сверткой. Начнем с определения.
Сверткой двух функций f(t) и g(t) называется интеграл
Этот интеграл является функцией переменной t, которая вхо-
входит в подынтегральное выражение и является также перемен-
переменным верхним пределом интеграла. Свертка функций обычно
обозначается символом f*g:
D2)
Покажем, что выражение для свертки не зависит от порядка,
в каком берутся функции f(t) и g(t) (как говорят, действие
t
свертки коммутативно). В интеграле § g(t)f(t — t)flft сде-
о
лаем подстановку t — z = zv тогда
/ о t
J gWfV - х) dx = $ g(t -
220 ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Следовательно,
g*f=f*g
[Гл VII
D3)
Приведем примеры отыскания свертки двух функций.
Пусть f(t) = ee и g(t) = t. Тогда
о
т. е.
Читатель может проверить, что то же самое получится при
t
вычислении t * е1 = \ те'"" dx. Приведем еще два примера:
b\i\t*t — \(t — х) sin х dx = — sin t-\~t,
о
t
cos t * t = [ (t — i) cost dx = — cos t -f-1.
Докажем, что если f(t) и g(t) — оригиналы, то и их
свертка также является оригиналом. Первые два свойства про-
проверить легко, а для доказательства третьего воспользуемся
тем, что существуют такие числа а! и а4, для которых
\f{t) | sS УИ,ем и ] g(t) | sg M^. Если обозначить через а наи-
наибольшее из двух чисел а! и а2, то подынтегральная функ-
функция в свергке при любом х (О^т^с^) не превосходит
где /C=AfiAfij. По теореме об оценке интеграла
так как t<^e' при всех t. Поэтому свертка удовлетво-
удовлетворяет и третьему условию. Теперь перейдем к формулировке
соответствующего правила операционного исчисления.
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
221
X. Теорема умножения изображений. Если
f(t)='=F(p) и g(t)==G(p), то свертке функций. f*g соот-
соответствует произведение изображений
f*g^F(p)Q(p). D4)
Доказательство этой теоремы несколько сложнее многих пре-
предыдущих. Прежде всего запишем ин-
интеграл Лапласа для свертки
ел t
о о
и будем рассматривать его как двои- _
ной интеграл, распространенный по
бесконечной области D, изображен-
изображенной на рис. 107. Пределы измене-
изменения г* от 0 до со, а х — от 0 до t.
Изменим порядок интегрирования, т. е. произведем внеш-
внешнее интегрирование по х в пределах от 0 до со, а внутрен-
внутреннее интегрирование по t в пределах от х до со:
Рис. 107.
Во внутреннем интеграле справа произведем подстановку
t — x = tv dt = dtv и вынесем множители f(x) и е~?~\ как
не зависящие от переменной интегрирования tv за знак внутрен-
внутреннего интеграла. Тогда получится двойной интеграл
который представляет произведение двух интегралов, так как
внутренний интеграл не зависит oi x. Первый из них есть
F(р), а второй О(р), а это и означает, что
Теорема доказана. Поскольку эта теорема будет приме-
применяться главным образом в приложениях, то мы ограничимся
пока только ее проверкой на уже известных изображениях.
На стр. 220 была вычислена свертка функций е1*г — ег — t—1.
222
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
1
По теореме умножения должно быть е1 * t = „ .,, и дей-
ствительно, ^ _ < - 1 = -L- _ ^ _ ± = f (Д_ {y Свертке
sin t * t должно соответствовать изображение -гцгт ~з- Про-
Проверка дает
J , 1 _. '
' + 1^"р2~Ра(^ + 1)-
Sin t * t = — Sin t-X-t =
Позже нам понадобится специальный случай теоремы
умножения. Именно, будем искать оригинал, соответствующий
произведению pF(p)G{p). Запишем это произведение в виде
Тогда первое слагаемое в правой части есть произведение
изображений, соответствующих оригиналам /'@ (теорема
дифференцирования оригинала) и g(t). Применяя теоремы
умножения и линейности, получим
pF(p)G(p)=f'(t)*g(t)^-f(O)g(t).
Если записать свертку в развернутом виде, то
D5)
(последнее равенство написано на основании свойства комму-
коммутативности свертки). Формула D5) называется интегралом
Дюамеля. В этой формуле можно поменять местами изо-
изображения F(p) и G(p), а следовательно, и оригиналы f(t)
и g(t); тогда получатся две новые формулы, записать которые
предоставляем читателю.
94. Подобно тому как произведению изображений соот-
соответствует свертка оригиналов, так и умножению оригиналов
соответствует определенное действие над изображениями —
свертка в комплексной области. Пусть
2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
223
и Re/»^>a — полуплоскость, в которой абсолютно сходятся
оба интеграла Лапласа, определяющие данные изображения.
Сверткой двух изображений называется интеграл
~ J F(z)Q(p-z)dz,
D6)
7 — ico
где путь интегрирования — вертикальная прямая
(рис. 108), ар—комплексная переменная, такая, что
Свертка D6) коммутативна, т. е. функции
F и О можно поменять местами. Теперь
сформулируем теорему.
XI. Теорема умножения ори-
оригиналов. Если f(t)=F(p) и g(t) = G(p),
то
7+
D7)
\y-ico
Рис. 108.
т. е. произведению оригиналов соответ-
ствует свертка изображений.
Доказательство эгой теоремы мы не приводим (оно
опирается на формулу обращения, которая будет рассматри-
рассматриваться только в следующем параграфе).
Важно отметить следующее: функции F(z) и G(z) анали-
тичны при Rez^>a. Функция G(p — z), где р фиксировано
и таково, что Rep^>f4~a> аналитичпа при Re2<^f> потому
что тогда Re(p — z)^>Rep — T^>a- Отсюда следует, что
если Rep достаточно велико, то линия интегрирования разде-
разделяет особые точки функций F(z) и Q(p — z): первые лежат
левее ее, а вторые — правее.
Положив g(t)=f(ty, получим из D7)
D8)
Интеграл в правой части формулы D7) обычно стараются
вычислить с помощью теоремы о вычетах. Приведем один
простой пример. Известно, что sin^— ,, , и е' — г.
224
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
ГГл VII
Вычислим по формуле D7) изображение произведения е' sin ^
и убедимся, что придем к известному результату (первая из
формул A7) при B=1 и ш=1). Имеем
1
2"+
— 2 — 1
dz.
7 -/со
Сразу замечаем, что <х=1, следовательно, f^> 1 и
Подынтегральная функция имеет при 2 = со нуль третьего
порядка; из доказанного на
стр. 160 следует, что интеграл
по любой дуге окружности
|z]=/? стремится к нулю при
/^-^оо. В области Di (рис. 109)
подынтегральная функция имеет
два полюса первого порядка:
2j = i И Zj = — /. ПОЛЮС Z3 =
= р—1 лежит правее прямой
Re z =¦ f, г. е. в области Dit
так как Re z3==Rep — 1 > 1 -f
рис. log. Применяя теорему о выче-
вычетах к контуру, ограничивающему
область ?>„ и переходя к пределу при /?-*оо, получим
J_ Г dz 1 , 1
2М j iz-'-f l)ip— 2— 1) 2( (р — (— 1) "Г — 2i(p-|-t— 1)
7 —/со
т. е. как раз нужную формулу.
Еще проще было применить теорему о вычетах к контуру,
ограничивающему область D2 (прямая и дуга С), так как
в Di лежит только один простой полюс z3=p— 1. Учшывая,
что контур обходим здесь в отрицательном направлении,
снова найдем
1
1 — /со
\)(р — г—
2] СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 225
95. Ранее было получено соответствие (формула B6))
где п — целое и положительное число. Значительно более слож-
сложным оказывается получить изображение оригиналов tk, где k — лю-
любое положительное число (если k < 0, то функция tk имеет бес-
бесконечный разрыв при t=0).
Сначала кратко познакомимся с одной очень важном функ-
функцией— гамма-функцией Эйлера. Она определяется несобственным
интегралом
D9)
который, как мы сейчас покажем, сходится при х > 0.
Пусть сначала jc5=1. Воспользуемся тем, что степенная функ-
функция t* с любым показателем степени х—1 при t —¦ do растет
медленнее, чем показательная функция e'J, где а — произвольное
положительное число, т. е.
tx~i
lim —-f = 0
(это легко проверить при помощи правила Лопиталя). Значит, отно-
шение —д- во всяком случае ограничено; поэтому г!-* sg Meat. Если
выбрать а < 1, то
где 3=1—а > 0. Подынтегральная функция положительна и
со со
0
tdt^M\ e~?dt = М
о
со М
о ~ТШ
Это и означает, что интеграл D9) сходится.
Если 0<х<с1, то функция tx~r обращается в бесконечность
при t = 0. Поэтому предварительно разобьем шпеграл D9) на сумму
несобственных ипте1ралов
со 1 со
\ tx^e-ldt = \ t'^e-'dt + \ f-'e-'dt.
о б t
Сходимость второго интеграла доказывается так же, как в случае
л:5=1, так как в интервале [1, со) приведенные выше неравенства
8 И. Г. Араманович и др.
226 ПРЕОБРАЗОВАНИЕ ЛАПЛАСА |Гл Vtt
остаются справедливыми. В первом же интеграле е~1 < 1 и поэтому
t 1
С , г*
V t*'1 е'1 dt<\ t*
*х 11 1
-> dt =— = —
(если лг^О, то этот интеграл расходится).
Итак, доказано, что интеграл D9) сходится при любом -t>0.
Предположим, что х> 1, и применим к интегралу D9) формулу
интегрирования по частям, полагая tx~l = и и e~'dt = dv:
tx-i e-t dt = — tx-i
со
--S
x-*e-' dt.
Так как внеинтегральный член в правой части равенства обращается
в нуль при (=сои при t = 0, то мы получаем рекуррентную
формулу
Г <*) = (*— 1) Г (дг— 1),
E0)
которая представляет важнейшее свойство гамма-функции. Поль-
Пользуясь этой формулой, легко вычислим значения гамма-функции
Г (х), когда л: равно целому положительному числу л. Заметим
предварительно, что
E1)
Далее, по рекуррентной формуле
Г (я) = (л — 1) Г (я — 1) = <я — 1) (л — 2) Г (я — 2) = ... =
= (я —1)(л —2)...2- 1 .ГA) = (я—1)!
Таким образом, для любого целого положительного числа я
Г (я) = (я— 1I E2)
Вычислим еще часто встречающееся значение Г (-у). Совершая
в интеграле, определяющем гамма-функцию, подстановку t = и2,
найдем
(*)
S 2]
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
227
(Мы воспользовались значением интеграла Пуассона ^ е~"а du =
o
= ^2~'< см- [ 1 ]. гл. VIII, п. 131.) Учитывая формулу E0), последо-
последовательно получим
8 ¦-
При других значениях х интеграл D9) может быть вычислен
только приближенными методами, и для значений гамма-функции
составлены специальные таблицы.
Теперь можно приступить к отысканию изображения функции tk.
По определению,
со
^ = j tk e'pt dt.
и
Вычислим последний интеграл, считая для простоты, что р — дейст-
действительное положительное число. Можно доказать, что пол)чаю-
пол)чающаяся формула справедлива и при р комплексном, если Re/>>0.
Сделаем подстановку pt = tu pdt = dtv Тогда
J
Следовательно,
E3)
При целых значениях к получается уже знакомая формула B6).
Заметим еще, что при —1 <Л<0 функция tk имеет бесконечный
разрыв в точке i = 0 и не является оригиналом. Однако правая
часть формулы E3) имеет смысл и при этих значениях к. Поэтому
функцию tk при —1 <й<0 мы будем считать как бы «особым»
оригиналом, а ее «изображение» находить по формуле E3).
В частности, учитывая формулу (*), получим
> #^) = /1и™^=4=. E4)
yt Ур у р *г-> ^ К '
Можно доказать, что к этим «особым» оригиналам и изображе-
изображениям применимы все теоремы операционного исчисления. Например,
по теореме затухания
eat ^ 1
' ур—а'
228
nPLOBPA3OBAHHF ЛАПЛАСА
[Гл. VII
96. В заключение для удобства читателя перечислим еще
раз все свойства (георемы) операционного исчисления, сох-
сохраняя прежние обозначения.
I. Af(t)JrBg(t)^AF{p)JrBG(p) (теорема линейности).
П. f (kt)= — F (j-) (x>°) (теорема подобия).
III. ea'f(t)= F(p — a) (теорема затухания).
iy_ f(t т) == е р F ip) (т^>0) (теорема запаздывания).
V. Если f(t, x)-^Fip, х), то д-^~ Ф —j^- (теорема
о дифференцировании по параметру).
VI. f (t) =L pF (р) — /@) (теорема дифференцирования
оригинала)
(») @ ^pnF{p)-
— ¦ ¦ ¦ —f^l) @).
VII. i f(f)dt -J=LS?l (теорема интегрирования оригинала).
•j P
о
VIII. —tf(t)-^F'(p) (теорема дифференцирования изобра-
изображения).
IX. lS*l^ki F{p)dp(теоремаинтегрирования изображения).
X. f*g=
о
жения изображений)
(георема умно-
(интеграл Дюамеля).
I. fit)git) .--J^ [ F(z)G(p — г)dz (георема умноже-
Z,TZt J
I
XI.
ния ори! ипалов).
В таблице 1 собраны формулы соответствия, полученные
в насюящем параграфе. Рядом с номером формулы в скоб-
скобках сгоит номер, под которым эта формула впервые встре-
встретилась в тексте. Более подробные таблицы будут приведены
в конце следующего параграфа, после того как мы рассмот-
рассмотрим теорему обращения, позволяющую по заданному изобра-
изображению F (р) находить соогвеювующий ему оригинал }{t).
СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА 229
Таблица 1
Формулы соответствия
Номер
фор-
формулы
1D)
2(9)
3A2)
4A3)
5A4)
6A4)
7A7)
8A7)
9
10
11 B6)
12B6)
13 B5)
14B7)
15B7)
Оригинал
1
eat
Sin at
COScoi
sh coj
ch a>t
eat sin let
eat cos v>t
eat sin {tot -\- if)
eat cos {tot + cp)
t
tn
tneat
t sin u>t
t COS tot
Изображение
P
1
р — а
Р
р2 — to2
р
р2 —со2
to
01 -в
(р — °JН
6) COS cp -f" (P —
(p — aJ-|
(p — a) cos cp -
¦ a) sin cp
- ш sin cp
P2
n\
230
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл. VII
Продолжение табл. 1
Номер
фор-
формулы
16
17
18
Оригинал
tshut
tchwt
tk(k> — \)
Изображение
2рш
(/>2-*-У
Р2 + ^
(Р2-«У
Г(* + 1)
§ 3. Теорема обращения
97. До сих пор, изучая соответствие f(t) ф F (р), мы
пользовались только интегралом Лапласа
выражающим изображение F(p) через оригинал f(t). Напом-
Напомним, что если |/@| ^Ме"', то интеграл Лапласа абсолютно
сходится при Re/>]>a. Теперь мы приведем формулу, выра-
выражающую теорему обращения и позволяющую по заданному
изображению F(p) отыскивать оригинал f(t).
Теорема обращения. Если функция f(f) является
оригиналом, a F(j>) — ее изображением, то в любой точке
t, где оригинал f(f) непрерывен, имеет место формула
1 TV~
= 25" \ F{p)e*dp,
t
E5)
\
7 — tea
где интегрирование производится по любой бесконечной
прямой Rejr> = f, лежащей в полуплоскости абсолютной
сходимости интеграла Лапласа от f(t) (см. рис. 108).
В связи с теоремой обращения заметим, что если нам
легко проверить, является ли' заданная функция f(t) ориги-
оригиналом, т. е. выполняются ли соответствующие три условия, то
относительно произвольно заданной аналитической функ-
функции F(p) нам заранее неизвестно, является ли она изображением.
§31
ГЕОРЕМА ОБРАЩЕНИЯ
231
Займемся прежде всего выяснением вопроса о том, при
каких условиях функция f(t), определенная формулой E5),
является оригиналом, а затем уже наметим доказательство
того, что F(p) является ее изображением. (Полное доказа-
доказательство теоремы требует значительно больших сведений
из анализа и выходит за рамки настоящей книги.)
Вычисление, интеграла E5) для произвольных аналитических
функций F(p) представляет большие трудности; мы ограни-
ограничимся некоторыми частными случаями, играющими, однако,
очень важную роль в приложениях. Именно, будем предпола-
предполагать, что F(p) — функция, аналитическая во всей комплек-
комплексной плоскостир, за исключением конечного числа особых
точек'), и удовлетворяющая условию
lim F(p) =
р -» оо
E6)
При этом предполагается, что в бесконечно удаленной точке
функция F (р) — аналитическая.
Напомним, что согласно формуле (9) условие E6) есть
необходимое условие того, что функция, аналитическая
в бесконечно удаленной точке, является изображением. Выбе-
Выберем прямую интегрирования Re^ = -f в интеграле E5) так,
чтобы все особые точки функции F(j>) лежали левее этой
прямой. Таким образом, правее этой прямой и на самой пря-
прямой, т. е. при Rep^si~[, функция F (р) особых точек не имеет.
В этих предположениях интеграл E5) легко вычисляется на
основании леммы Жордана (см. стр. 161). Так как эта
лемма понадобится нам в несколько измененном виде, то
сформулируем ее заново, по-прежнему не приводя доказа-
доказательства 8).
Лемма Жордана. Пусть функция F(р) стремится
к нулю при р—уоо. Тогда интеграл
\ F(p)e'"dp,
') Приводимый ниже результат верен и в более общем случае,
однако для наших целей вполне достаточно формулировки в тексте.
а) Если читатель сравнит приведенную формулировку с форму-
формулировкой, данной в п. 68, то он обнаружит их полное совпадение,
произведя замену р = iz.
232
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
где t^>0, взятый по дуге CR окружности \p\ = R, такой,
что на ней. Rep<f (рис ПО), стремится к нулю при
R-+CO-.
lim \ F(p)e»'dp = 0. E7)
R^C
Если t<^0, то стремится к нулю интеграл, взятый по
дополнительной к CR дуге Сд, в точках которой Re/?>f:
E8)
lim \ F(p)eptdp=:0.
RK
Возьмем теперь контур, состоящий из отрезка АВ прямой
и дуги CR, радиус которой выберем настолько
большим, чтобы все особые точ-
точки F(p) (а их по условию конеч-
конечное число) попали внутрь рассмат-
рассматриваемого контура (см. рис. 110).
По основной теореме о вычетах
$Р0?)ер'ф + $ F(p)e"'dp =
АВ CR
где ак — особые точки функции
F (р). Если t ^> 0, то при R -> со по
лемме Жордана § F (p) ept dp ->- 0,
Рис. ПО. cR
а интеграл по отрезку АВ перехо-
переходит в интеграл по всей бесконечной вертикальной прямой
? = f. Разделив обе части равенства на 2и/, получим
±
где ак — все особые точки функции F (/?). Если же t <^ 0,
то берем контур, состоящий из отрезка АВ и дуги C'R. Внутри
этого контура особых точек нет и по теореме Коши
\F(p)eptdp^r\ Г:(р)е>" dp = 0.
АВ С'
ТЕОРЕМА ОБРАЩЕНИЯ
233
По лемме Жордана второй интеграл при /?->оо стремится
к нулю; поэтому
т 4-«оо
\ F(p)eptdp = O при *<0,
7 — i оэ
т. е. f(t) = O приг!<^0. Таким образом, функция f{t) удовле-
удовлетворяет второму из условий, наложенных на оригинал.
Первое и третье условия просто проверяются в том
частном случае, когда все особые точки функции F(p) — по-
полюсы. (При сделанных предположениях F {р) — рациональная
функция. Доказательство этого факта мы приводить не
будем.)
Вспоминая формулы для вычисления вычетов (см. § 2 гл. V),
можно убедиться, чго функция f{f) при ^^>0 представляет
в этом случае линейную комбинацию показательных функций
a,t
еаь и произведений tm e * (подробнее об этом будет сказано
в п. 99), а любая из таких функций, разумеется, удовлетворяет
всем условиям, наложенным на оригинал.
В случае, когда F(p) имеет существенно особые точки,
доказательство более сложно, и мы его не приводим.
Приведем несколько примеров.
Пример 1. Пусть F(p) — — . Найти f (t).
Можно проверить, что все условия, налагаемые на функцию
F (р), выполняются, и функция /
7 +ioo
1 Т еР< .
7 — l оо
является оригиналом. Подынтегральная ф\нкция имеет один простой
полюс в точке /э = 0 с вычетом, равным 1. Поэтому при t>d
имеем/@=1, а при ?<0 функция /(t) = 0. Мы получили еди-
единичную функцию т] (t), что и следовало ожидать.
Пример 2. Пусть Р(р)=-
Найти fit).
V+1
Применяя сразу форм>лу E9), получим при
b
ept
e-it
234
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VIГ
98. Приведем теперь схему доказательства теоремы обращения.
Начнем с установленного выше соотношения
1 TY°v
i
\
7 — ioo
Если заменить t на t — х, где х>0, то получим функцию t\{t— х):
1
F0)
^ —
График функции n(t — x) изображен на рис. 96. Положим в фор-
формуле F0) последовательно x = xft и x = xft+] и вычтем из первого
равенства второе. Разность
ФУНКЦИЙ Г) (t — Xft) — Г] (t — Xk+1)
•(t)
t
t
Рис. 111.
представляет импульс, изображенный на рис. 111. Поэтому
vj_,-^ f 0, если t<xk,
еР<-(—'k> —epit~Tk+i)
dp = \ 1, если xft<^<xft+I, F1)
3 [ 0, если t > хк+1.
Числитель подынтегральной функции преобразуем к следующему
виду:
где ДтА = хА+1 — ih. Далее, раскладывая е рАгь в ряд, получим
I-,-'** 1-1+^*-%-+-
____ = _ ^A4,
если считать ДтЛ малой величиной и отбросить все члены, содер-
содержащие Дт^ в степенях выше второй; поэтому левая часть формулы
F1) примет вид
1
^ — ico
ТЕОРЕМА ОБРАЩЕНИЯ
235
Пусть теперь f(t) — произвольный оригинал. Заменим его ступен-
ступенчатой функцией /* (t) (рис. 112), которую представим себе как
сумму бесконечного числа импульсов в интервалах (xft, xft+1). Вы-
Высота каждого импульса равна /(х^,) и его можно записать как
1 — ico
Сумму таких импульсов, т. е. ступенчатую функцию /* (t), пред-
представим в виде
F2)
Заменим бесконечную сумму интегралов в формуле F2) интегралом
от суммы (этот шаг мы не обосновываем). Вынося еще ept за знак
суммы, получим
Y + i
Если Дхд, стремится к нулю, то величина хк будет пробегать все
значения от 0 до оо. Следовательно, можно считать, что сумма,
стоящая под знаком интеграла, будет стремиться к интегралу
$/(т) «-*»*,
который как раз и является изображением F (р) (и этот шаг остав-
оставлен нами без доказательства!) При этом ступенчатая функция f*(t)
с уменьшением основания каждой ступеньки будет стремиться
к функции f(t), и мы окончательно получим
7 —(со
т. е. формулу E5).
Рекомендуем читателю сравнить приведенное рассуждение
с тем, при помощи которого получается представление функции
интегралом Фурье (см. [1], гл. XII, п. 207), и убедиться в их полной
аналогии.
99. Применим формулу E9) к наиболее важному част-
частному случаю, когда F (р) — рациональная функция:
F3)
236
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
где А(р)и В(р) — многочлены, причем степень многочлена А (р)
меньше степени многочлена В(р). При этом условии
lim F(p)= lira -g-^-=0,
p->oo p~*-co {Pi
т. е. равенство E6) соблюдается. Функция F(p) имеет только
конечное число особых точек. Эти точки являются нулями
знаменателя В(р) и, следовательно, полюсами самой функ-
функций F{p). (Предполагается, что А(р) и В(р) не имеют общих
корней, т. е. что числитель и знаменатель дроби F3) не имеют
общих множителей, и дробь несократима.)
Л (р)
Согласно предыдущему функция Р[р) = щ-т является
изображением: соответствующий оригинал находится по фор-
формуле E9), в которой все особые точки ак — полюсы. При-
Применяя формулу для вычета в полюсе любого порядка, получим
где а/; —нули знаменателя В(р), а пк— их кратность. Диф-
Дифференцирование совершается по комплексной переменной р
при постоянном t. Формула F4) называется формулой раз-
разложения (или теоремой разложения).
При практическом использовании формулы F4) предел
вычисляют следующим образом: знаменатель В{р) содержит
множитель (р — ак)п>< и поэтому может быть представлен в виде
(р —
где Z?! (ак) ф 0. Тогда
1- Г/ \пь А (р) '
hm \(р — ак) к
- F5)
В том частном случае, когда все полюсы простые, фор-
формула F4) упрощается. Вычеты находятся по формуле C)
(стр. 150) и
А (р) _l_ f(A _ V A(ak)
/(<Jщ
ThOPLMA OHPAIUFHI-Ifl
237
Если р = 0 является корнем знаменателя, то В{р) можно
записать в виде pBi(p), где Вг @) ф 0 (все корни В{р) про-
простые!). Тогда
При этом В' @) = Bi @), а В' (ак) = акВ\ (ак), так как 5t (ак) =
= 0, поскольку все ненулевые корни многочленов В(р) и Вх(р)
совпадают. Выделяя из суммы F6) слагаемое, отвечающее
нулевому корню, получим
РВ1 (р)
-*"*'.
F7)
где сумма берется по всем ненулевым корням многочлена В(р),
т. е. по всем корням В^{р).
Отметим, что формула разложения иногда оказывается
применимой и в гораздо более общем случае, когда изобра-
изображение F{p) имеет бесконечное число полюсов. Однако, как
точная формулировка соответствующей теоремы, так и прак-
практическое ее применение выходят за рамки книги и мы отсы-
отсылаем чи!ателя к более специальной литературе [6], [7].
Пример 3. Пусть F(р) =
Здесь
Л (/э) = 1, В (р) = р (р-\-а) (р
Ь)
. Найти f{t).
¦Ь) и
Производная В[ (р) = (р-\- а) -4- (р + Ь). Корни знаменателя
р., = — а, рЛ = — Ь. По формуле F7) пол>чнм
p-at p-bt
1
ab ' a (a — b) ' b {b — а) '
Можно было бы пол)чить оригинал fit), разюжпв : •
Р (Р + а) (р + Ь)
на простейшие дроби и найдя оригинал для каждой такой дроби
С друтй стороны, обратно, формула F6) дает удобный способ
разложения дроби „ ' на простейшие, при условии, что все корни
знаменателя простые. Так, в приведенном примере, применив
к найденному оригиналу теорему линейности и формулу (8),
получим
ab p + a(a — b)
b{b — a)
т. е
1
!
L
!
ab р т а{а — Ь)
! !_
b (b — а) р + Ъ '
238
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
(Гл. VII
, Следует заметить, что если нам известно разло-
разложение дроби _ на простейшие (см. [1], гл. V, п. 82), то
оригинал находится сразу с помощью уже известных формул
соответствия. Простейшим дробям
соответствуют ори-
k~xeai
гиналы Aeat, а дробям , ^ — оригиналы tk~xe
(это следует из формулы 13 табл. 1).
Простейшую дробь а ... „ представим в виде суммы
Р т ЛР ~г е
¦+¦
N-
МА
где А = Б Г<^ (если Д^>0, то знаменатель раскла-
раскладывается на линейные множители), и применяем формулы 7
и 8 табл. 1, в которых нужно положить
Пример 4. Пусть
Представим F (р) в виде суммы простейших дробей
A Mp + N
р-2 +
и найдем неопределенные коэффициенты (предоставляем это сделать
читателю): А = 1, М = 2, УУ=3.
Записав F (р) в виде
F(p)=-
1
¦+¦
р-2
переходим по указанным выше формулам к оригиналу
/ (t) = е21 + 2<r2' cos 2t — у е-2' sin 2t.
(Можно было бы также воспользоваться формулами 11 и 12 табл. 2.)
ТЕОРЕМА ОБРАЩЕНИЯ
239
П р и м е р 5. Пусть F (Р) =
Здесь
А(р)=
. Найти / (t).
Р
(Р
Функция F (р) имеет два полюса: полюс /7 = 0 кратности 3
и р— 1 кратности 2. Применяя формулу F5), находим вычеты в этих
полюсах:
(При вычислении производной удобно воспользоваться формулой
Лейбница для производной произведения (uv)" = u"v-\-2u'v' -f-
-\-о"а (см. [1], гл. Ill, п. 54), положив ц= па й о = еК)
Далее,
Таким образом,
# (Й-8) *' + /• +5*+ 8.
Пример 6. Пусть
где а, Ь и с —действительные числа. Знаменатель В (р) имеет про-
простые комплексно-сопряженные корни ± ai и ± Ы. Производная
б' (р) = 2р(р* + б2) + 2/> (/>s + a2).
Вычисляя вычеты, получим
Res [F(р) еР', ai] = °!.Т': 8. е'а' = о ,.., зг-(а — cf) е'а',
1 2ш (о —а) 2а (о —в)
Res [f (p)^, -ai] =__1^±?__в-** =_
1
2а (й2 — а-1)
Заметим, что вычеты в комплексно-сопряженных полюсах ± at
также оказались комплексно-сопряженными. Их сумма равна удвоен-
удвоенной действительной части любого из них
240
ПРГОБРАЗОБАНИС ЛАПЛАСА
\П
Анаюгнчно, с)мма второп пары вычетов равна
— гт (cos bt -\--r- sm bt \,
и окончательно
f (t) = t~2 г cos at — cos bt -\- i
sin of sin bt
В связи с решением последнего примера сделаем к фор-
формуле F6) несколько замечаний. Чаще всею прихоцигся иметь
дело с функциями F{p)= f~-, у которых все коэффици-
коэффициенты многочленов А(р) и В(р) — дей с г в и те ль н ы е числа
(именно так было в примере 6). Toi да, как известно, комплекс-
комплексные корни многочлена В(р) (если они есть) попарно сопря-
сопряжены: наряду с комплексным корнем ак имеется и корень ак.
Поскольку все коэффициенты действительны, то комплексные
величины А{ак}\\ А(ак), В'(ак) и В'(ак), еаъ* и е' будут также
сопряжены друг с другом (предлагаем читателю это прове-
проверить). Следовательно, слагаемые в сумме F6), отвечающие
комплексно-сопряженным корням ак и ак, сопряжены, и их
сумма равна удвоенной действительной части любого из сла-
слагаемых:
h) abt _ о Dq А Ы at
А (ак)
В' Ы
a, t |
е к -j-
В' (ак)
В1 (ак)
Разбивая сумму F6) на две, получим (напоминаем, что все
корни В(р) считаются простыми):
А (а,)
в ы
гак' + 2 Re
А(ак)
В' (о*)
F8)
где первая сумма распространена па все дей ст в и те л ь н ы е
корни В(р), а вторая — па псе комплексные корни с по-
положительной (для определенности) мнимой частью.
Слагаемые второй суммы формулы F8) можно представить
в ином виде. Если ак = ук-\- ifik, то еа><* = еь1 (cos §ht -j-
-\- i sm ftkt). Полагая для кра гкости „ = Мк -\~ Шк, запишем
2 Re
los ?»* -
Mn
§ 31
ТЕОРГМА ОБРАЩЕНИЯ
241
Если ак = 0, т. е. корень ак — чисго мнимый, то ему соот-
соответствует ]ршопометрическая функция
2[Mkcos[ikt — Nksm[ikt].
Допустим, что все действительные корни знаменателя В(р)
отрицательны, а все действительные части комплексных
корней неположительны (или отрицательны, или равны
нулю). Как раз с таким случаем обычно приходится иметь
дело в теории колебаний. Тогда действительным корням
(РА = 0) соогве1С1вуют затухающие апериодические колебания,
комплексным корням с отрицательной действительной частью —
затухающие гармонические колебания и чисто мнимым кор-
корням {о.к = 0) — незатухающие гармонические колебания. Если
ecib нулевой корень, то ему соответствует постоянное откло-
отклонение. Таким образом, при t—-оэ все слагаемые формулы F8),
кроме тех, которые соответствуют нулевому и чисто мнимым
корням, стремятся к нулю. При больших значениях t сла-
слагаемые, стремящиеся к нулю, роли не играют. Если их от-
отбросить, то оставшиеся члены характеризуют установив-
установившийся колебательный процесс. Картина резко меняется, если
среди корней В(р) еаь корни с положительной дей-
действительной частью (или просто положительные). Слагаемые,
отвечающие таким корням, содержат множшель еа*'(аА^>0),
С1ремящийся к бесконечности1). Колебательная сис1ема в этом
случае, как говорят, теряет устойчивость. Подробно эти во-
вопросы будут рассматриваться в разделе, поснященном теории
устойчивости.
100. В заключение этого параграфа приведем таблицу,
в которой собраны оригиналы для наиболее часто встречаю-
встречающихся дробно-рациональных изображений. Таблица 2 noci роена
по следующему принципу: сначала идут рациональные функ-
функции р , . , у которых знаменатель В(р) — многочлен первой
') Если среди корней имеются кратные чисто мнимые корни
или кратный н) левой корень, то им также соответствх ют неогра-
неограниченные слагаемые: например, если F (р) = -й> то f(t)=t, или,
есш F (Р) = 1п ' . л , то /@=*е".
Р
— Ч
242
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
степени, затем второй степени и т. д. Во всех случаях в чи-
числителях стоят многочлены А(р), степени которых меньше
степени знаменателя. Как правило, многочлен В(р) уже счи-
считается разложенным на линейные или квадратичные мно-
множители. Более сложные примеры соответствия между ориги-
оригиналами и изображениями, в частности изображения некоторых
специальных функций, часто встречающихся в задачах мате-
математической физики, будут рассмотрены в § 3 гл. VIII.
Отметим, что существуют гораздо более подробные таб-
таблицы соответствия для преобразования Лапласа. Можно ука-
указать таблицы в книгах: Г. Дбч, Руководство к практическому
применению преобразования Лапласа, «Наука», 1965; В. А. Д и т-
кин и А. П. Прудников, Справочник по операционному
исшслению, «Высшая школа», 1965; В. А. Диткин и
А. П. Прудников, Справочная математическая библио-
библиотека (СМБ), Интегральные преобразования и операционное
исчисление, Физматгиз, 1961. При пользовании двумя послед-
последними книгами следует иметь в виду, что там операционное
соответствие основано на несколько ином преобразовании —
преобразовании Лапласа —Карсона, определяемом формулой
и отличающемся от преобразования Лапласа множителем р.
Если изображение для оригинала f(t) взято из таблиц преоб-
преобразования Карсона (обозначим его через Fk(p))> to чтобы
получить требуемое преобразование Лапласа F(p), надо его
разделить на р:
В более старых курсах электротехники часто пользова-
пользовались преобразованием Карсона, свойства которого совер-
совершенно аналогичны свойствам изученного нами преобразования
Лапласа.
В настоящее время предпочитают иметь дело с преобра-
преобразованием Лапласа, главным образом благодаря его тесной
связи с преобразованием Фурье, которое мы рассмот-
рассмотрим в § 4.
ТЕОРЕМА ОБРАЩЕНИЯ
243
Таблица 2
Оригиналы для дробно-рациональных изображений
Номер
фор-
формулы
Изображение
Оригинал
2
3
4
5
6
7
8
9
10
11
1
p — a
1
\+ap
1
p(p — a)
1
(p-af
1
(p — a) (p — b)
b + cp
p(p—a)
P
(p-af
P
(p-a) (p-b)
b + cp
/>2 —a2
1
_?1
T
„at
1
а
1
а
е
- е
(eat-
teat
at_t
а
-i)
,ы
aeat
с cos at-\ sin at
с chat -\ sh at
_ at
—— e г sin |/"Д t
Д
at
te
244
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл. VM
Продолжение табл. 2
Номер
фор-
формулы
Изображена
Орнгина п
12
13
14
15
16
17
18
19
a*
.-.-?-•
p-
(p
a)
-a)
1
(p — b)'1
1
(р — а) (р — Ь) (р — с)
(Р -
Р
(р — а) (p — bf
Р
(Р —а)(р — Ь) (р — с)
{р-ау
at
"T
— —^-= sin
, at
rb - —
]/ T<? 2 sin(|/A*-
e 2 (ch К— Д< —
а
— Д t
а—
еа<_ [1 -\-(а—Ь) t\ ebt
(а ~ ЪУ
(Ь —а) (с — а) ' (а — Ь) (с — Ь)
Pct
(a-c)(b-c)
~- t*eat
be1"
(b -а) (с —а) ' (a — b)(c —
(a-c)(b-c)
§ 3]
TEOPCMA ОБРАЩЕНИЯ 245
Продолжение табл. 2
Номер
фор-
му.и,i
Изображение
Оригинал
20
21
22
23
24
26
27
28
29
30
31
32
33
34
Pip2
(p -t-fe)
(/¦*"
1
— a2)
1
fp- -f- aa)
1
P4
(P*
iP2
iP2 + a-
— a*
P
— a'
1
1
1
0 (/>"' + b*-)
1
(p- — a-) (p- — b-)
1
ip^a-
iP2
p
—jr A — cos at)
„ , ,., ( e~bt — cos at A sin at)
a-Arb-\ ^ a j
--, A, :,— cos at A- 2b sm at
a- ' a2
, at . at
ch ——- sin
Л/2 Vl
, at at
— sh cos —-
У 2
1
т,—- (sh at — sin at)
1 . at at
— sin sh
-^—j (ch at — cos at)
7,-;j (sin at — at cos at)
75- , (ai ch a< — sh д<
1 ( sin 6i sin at
a- — b'1 \ b a
sh at sh bt
a- — b" \ a b
,'sh at sin W
а*-АгЬа-\ а
t
(P2 - a2J
t;— sin at
2a
- sh at
246
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл. VII
Продолжение табл. 2
Номер
фор-
формулы
Изображение
Оригинал
35
36
37
38
39
40
41
42
p(p*
Pip'
p(p>+<
p(P*-a
[P*
(P*
(P>
1
1
— a2K
1
1
1
1
— a2K
P
P
-f A — cos <z? =- Sln
772l2 +'
— b \ a
cos at
cos bt
1 1 (chat ch bt\
a2b2 'a2 — b2 \ a2 b2 '
g^j [C — aH2) sin at — 3at cos at]
gij [C + д2и2) sh at — 3at ch at]
t
8a1
(sin a? — at cos a?)
(р2 — а2K
8a3'
ch at — sh at).
§ 4. Преобразование Фурье
101. В этом параграфе мы укажем на другой пример
интегрального преобразования функции f{t), также играющего
важную роль в приложениях. Начнем с известного читателю
вопроса о разложении функции в ряд Фурье. Если функ-
функция f[t) определена в интервале (— it, к) и имеет кусочно-
непрерывную производную, то ее можно представить в виде
суммы ряда Фурье, который мы запишем в комплексной
форме (см. [1], гл. XII, п. 204):
=4 2
где
n=i $ f{t)eMdt.
F9)
S 4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
247
В случае произвольного интервала (— /. /) разложение запи-
записывается так:
где
" ldt.
G0)
G1)
5
. nnt
Каждая из функций е
и, как легко проверит
Поэтому сумма -к-
1 (я=1, 2, ...) периодична
11
читатель, имеет период Т——.
. Tflt
спе ' является периодической функ-
л= — оо
цией с периодом 7=2/ и чтобы разложение G0) было
справедливо на всей оси 0^, нужно считать, что функция f(t)
периодически продолжена на всю числовую ось.
Напомним еще, что в точках разрыва функции f(t) сумма
ряда Фурье равна полусумме предельных значений f(t) при
приближении аргумента к точке разрыва слева и справа.
Если значения функции f(t) на концах основного интер-
интервала (=—/, 0 не равны между собой: /(—/)^/@> то при
периодическом продолжении функции точки ± I становятся
точками разрыва и поэтому сумма ряда Фурье в этих точках
равна
2
Разложение в ряд Фурье с точки зрения физики можно
трактовать как представление периодического процесса
в виде суммы гармонических колебаний. Выражение для
гармоники с частотой ^— (я-й гармоники) мы получаем, взяв
сумму членов разложения, отвечающих значениям ±я и учи-
учитывая, что из формулы, определяющей с„, следует, что с_п = с^.
248
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
где (Jjrt =
т. е. сп=\сп
'
V Так как cn=an — ibm
где ап и Ьп — обычные коэффициенты Фурье, то tgi}in=-—.
Последовательность комплексных чисел сп называется
спектральной последовательностью функции f{t); последо-
последовательность действительных чисел сп —ее амплитудным
спектром и последовательность ф„ — фазовым спектром.
Мы особенно хошм подчеркнуть, что если известна функ-
функция f{t), то формулой G1) полностью определена ее спек-
спектральная последовательность, и наоборот, если задана спект-
спектральная последовательность сп, то функция f(t) может быть
восстановлена по формуле G0).
Таким образом, каждой функции f(t) (разумеется, удов-
удовлетворяющей условиям разложимости в ряд Фурье) ставится
в соответствие определенная последовательность комплексных
чисел — ее спектральная последовательность, и наоборот.
Если применить терминологию, принятую в операционном
исчислении, то функция f(t) играет роль оригинала, а ее
спектральная последовательность — роль изображения.
102. Приведем в качестве примера применения такого
соответствия следующую задачу. Пусть дано линейное диф-
дифференциальное уравнение (х означает производную ~)
diX =f(t),
G2)
где а\ и а3 — постоянные, a f(t) — периодическая функция;
для сокращения записи примем, что период 7=2тс. Требу-
Требуется найти частное решение уравнения G2) тоже периоди-
периодическое, того же периода. Функцию f(t) запишем в виде ряда
Фурье, считая, что известна ее спектральная последователь-
последовательность. Тогда
= -2- У
с е
G3)
Известно (см. [1], гл. X, п. 171), что если правая часть линей-
линейного дифференциального уравнения равна сумме нескольких
функций, то частное решение такого уравнения можно искать
в виде суммы частных решений уравнений с той же левой
частью, но с правыми частями, соответственно равными отдель-
§ 4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
249
ным слагаемым правой части данного уравнения. Учитывая
это, найдем сначала частное решение уравнения
Jt + aljb + aix = cneint, G4)
имеющее вид Aneint. Дважды дифференцируем функцию Aneint,
подставляем в уравнение G4) и сокращаем на eint:
отсюда
— пЧп -f- a{inAn + а.гАп = сп;
А — Сп
"'-~ na\-a]ian-
G5)
Читателя не должно смущать, что частное решение Апеи"
представляет комплексную функцию переменной t. Сгруп-
Сгруппировав слагаемые, отвечающие индексам zh n, мы получим
решение в действительной форме.
Легко видеть, что комплексные числа Ап представляют
спектральную последовательность искомого частного решения,
т. е. что это решение записывается в виде
¦=т 1
G6)
При этом мы должны еще доказать, что полученный ряд G6)
сходится. Это очень легко сделать в предположении, что ряд
абсолютно сходится. Из формулы G5) следует, что
А„\=-
откуда ясно, что при больших значениях \п\ имеет место
неравенство Ап | <^ | сп \. По признаку сравнения заключаем,
со
что ряд ^ Ап сходится абсолютно, а следовательно, абсо-
п = — со
лютно сходится и ряд G6), так как \е' \=\. Более слож-
сложными рассуждениями можно установить, что сходимость ряда
G6) имеет место и в более общих случаях. Отметим еще
250
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VU
что формула G5) может потерять смысл для какого-либо
n = k только в случае
aj = O и ai = ki;
тогда уравнение G4) примет вид
спе
Int
и частное решение, соответствующее слагаемым с индексами
±k, уже не имеет вида Akelkt (случай резонанса). Соот-
Соответствующие изменения решения в этом случае предоставляем
сделать читателю самостоятельно.
103. Рассмотренный пример играет очень важную роль при
изучении процессов в колебательных контурах под воздейст-
воздействием периодической несинусоидальной электродвижущей силы.
Как известно, дифференциальное уравнение для тока / (t)
в колебательном контуре имеет вид
G7)
где fl — сопротивление, L — индуктивность, С — емкость кон-
контура и v{t) — электродвижущая сила.
Дифференцируя обе части уравнения G7) по t, получим
линейное дифференциальное уравнение второго порядка
с постоянными коэффициентами:
G8)
Будем считать, что v(() имеет период Т =
т. е. что Е„ — спектральная последовательность напряжения.
Тогда легко получить выражения для спектральной последо-
последовательности установившегося тока — частного решения,
имеющего вид
- У
2 L
Ant
$ 4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
251
Название установившийся ток объясняется тем,
что общее решение соответствующего однородного уравнения
имеет вид
где \ и Ха — корни характеристического уравнения
Как легко видеть, корни \ и Х2 либо отрицательны (если
па 1 \
тгг'^Тс)' ЛИ^° являются комплексными числами с отрица-
/ Р" 1 \
тельной действительной частью если 7т»<Гттг . В обоих
\ 4Z.2 ^LC/
случаях модули \е^*\ и |еХа'| стремятся к нулю при t-+oo
и в цепи остается только вынужденный ток, который и
характеризует установившийся процесс (это полностью соот-
соответствует замечанию на стр. 241).
Если v (t) задано разложением G9), то уравнение G7)
примет вид (мы предполагаем, что ряд G9) можно почленно
дифференцировать):
d4(t),Rdi(t)\
1пЕ
Ге
ш
п = — оэ
Сначала отыскиваем решение вида Ine'nt для уравнения,
в правой части которого стоит одно слагаемое суммы: —~eint.
По формуле G5), в которой надо положить cn = ^rt, а^ =
R 1 L
= -j- и аа = 2т=". получим
/»=¦
1пЕ„
(80)
Пользуясь разложением G0), читатель легко проверит, что
если период Т=21 (а не 2тс), то в последней формуле на-
до п заменить на <ол = ~г. Если с учетом этого записать
формулу (80) в виде
1»= 7-^ ГГ. (81)
252
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
то она приобретает вид закона Ома для постоянного
тока. Разумеется, надо помнить, что Еп и /„ — это не напря-
напряжение и' ток, а комплексные числа, представляющие спек-
спектральные последовательности напряжения и тока. Выражение,
стоящее в знаменателе (81), называется комплексным сопро-
сопротивлением контура и обычно обозначается Zn:
(82)
В отличие от цепи постоянного тока, комплексное сопро-
сопротивление зависит от частоты шя соответствующей гармоники.
Таким образом, зная спектральную последовательность Еп на-
напряжения, мы при помощи формулы (81) находим спектраль-
спектральную последовательность установившегося тока, а следова-
следовательно, и сам ток:
=4 1
1пе
104. Перейдем теперь к случаю, когда/@ — неперио-
непериодическая функция, заданная на всей оси Qt, и будем счи-
считать, что она удовлетворяет следующим условиям:
1. В любом конечном интервале функция f(t) может быть
разложена в ряд Фурье.
2. Существует несобственный интеграл от абсолютной вели-
со
чины функции f(t), т. е. интеграл ^ \f{f)\dt сходится.
— со
Тогда функцию f{f) можно представить в виде инте-
интеграла Фурье, который мы запишем в комплексной форме
(см. [1], гл. XII, п. 209):
= й \
где
(83)
(84)
Так же как и для рядов Фурье, в точках разрыва функ-
функции fit) (они обязательно первого рода) интеграл Фурье
5 I] ПРЕОБРАЗОВАНИЕ ФУРЬЕ 253
равен полусумме предельных значений слева и справа:
2
г-
где t№ — точка разрыва, f(t0 — 0) — предельное значение слева
и f(t0 -}- 0) — предельное значение справа.
Если каждой периодической функции, как указано выше,
ставилась в соответствие ее спектральная последовательность,
то теперь непериодической функции f(t) мы поставим в соот-
соответствие комплексную функцию F(co), которую будем называть
спектральной функцией или преобразованием Фурье функ-
функции f{t).
Формула (84) позволяет по функции f(t) найти ее спек-
спектральную функцию F (ш), а формула (83), наоборот, по спек-
спектральной функции F(co) восстановить исходную функцию / (t).
Функция [ F (со) | называется амплитудным спектром (или
амплитудной характеристикой), а
ф (ш) = — arg F (со)
— фазовым спектром. При этом
аналогии с рядами Фурье, где
Cn = an — it>n='icnie~
(см.
Такая запись принята по
комплексный коэффициент
стр. 248).
Из формулы (84) следует, что F(—(о) = /7(а>) (функция
f(t) принимает только действительные значения). Поэтому
F( — ш) | = j Z7 (u>) [, т. е. амплитудный спектр есть четная
функция. Так как arg F(—ш)= •—arg F (со), то фазовый
спектр есть нечетная функция.
Говорят, что периодическая функция имеет дискретный
спектр (ей соответствует спектральная последователь-
последовательность), а непериодическая функция имеет непрерывный
спектр (ей соответствует спектральная функция).
С точки зрения физики это означает, что рассматривае-
рассматриваемый процесс уже нельзя построить из гармонических коле-
колебаний только с определенными изолированными частотами
ш„= —, теперь для его построения необходимы гармониче-
гармонические колебания всех частот.
254 ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл VII
Вернемся снова к дифференциальному уравнению G2):
и будем теперь считать, что f(t) — непериодическая функ-
функция, для которой известна ее спектральная функция F(<u).
Частное решение уравнения
ш
аух -\- ая_х = F (to) e
при любом фиксированном ш имеющее вид А(ш)е'ш', найдем
так же, как это сделано на стр. 249. При этом формула G5)
заменится следующей:
Если рассматривать правую часть уравнения G2), функ-
функцию f(t), как «сумму» всех ее составляющих F(<o)ela}t (по-
(поделенную на 2л), то и частное решение будет аналогичной
«суммой» составляющих А(ш)е1Ы. При этом, разумеется,
слово «сумма», поставленное в кавычки, означает предельный
переход от суммм по дискретным значениям со„ к интегралу
по непрерывно изменяющемуся параметру ш (именно такой
предельный переход совершается при переходе от ряда
Фурье к интегралу Фурье). Таким образом, мы нашли спект-
спектральную функцию искомою частного решения Л (со), а по
формуле (83) можем восстановить и само это решение:
l
(86)
Так же как и раньше, докажем абсолютную сходимость
интеграла (86) при условии, что абсолютно сходится интег-
интеграл от функции F(<u) и а^О. (Последнее означает, что ни
при каком значении ш знаменатель в формуле (85) не обра-
обращается в нуль, что соответствует отсутствию резонанса.)
Действительно, при этих условиях А (ш) определено при
всех значениях ш и
I А И I = 77т==Й=т=^=Г < I F H I
при достаточно больших значениях |ш[.
4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
255
Обращаясь к физической иллюстрации полученного реше-
решения, устанавливаем полную аналогию с тем, что было сказано
в п. 103. Разница только в том, что теперь установившийся
ток будет слагаться не из дискретных гармоник, а из гармо-
гармоник с непрерывно меняющейся частотой. Если раньше мы за-
заменяли напряжение v(t) суммой гармоник, то теперь за-
запишем, что
где E(w) — спектральная функция напряжения. Считая воз-
возможным дифференцирование под знаком интеграла, получим
±
Для отыскания спектральной функции тока ищем реше-
решение уравнения
R di(t) , 1 ,(.Л_Е(*)Ы
i L dt ~T~LC ()~ L '
dt2
имеющее вид 1(ш)еш'. Внося соответствующие изменения
в формулу (85), получим аналог формулы (80):
=Ш< (87)
где Z(<o) — комплексное сопротивление.
Спектральная функция тока найдена. По формуле (83) ток
равен
(88)
При этой аналогии надо только иметь в виду, что если
при периодическом процессе | lrl | давал амплитуду тока от-
отдельной гармоники, то при непериодическом процессе 11(ш)|
представляет закон распределения амплитуд в зави-
зависимости от частоты ш. Так как теперь нельзя выделить от-
отдельную гармонику, то нельзя говорить и об ее амплитуде
256
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
можно говорить лишь о гоке, представляющем совокупность
гармоник, частоты которых заполняют некоторый интервал.
105. Установим теперь связь между преобразованиями Лап-
Лапласа и Фурье. Для этого рассмотрим сначала одностороннее
преобразование Фурье. При этом преобразовании функция
f(t) считается равной нулю при t<^0. Тогда формула (84)
приобретает вид
Правая часть в точности совпадает с интегралом Лапласа,
если в последнем положить /? = /ои, т. е. считать комплекс-
комплексную переменную р чисто мнимой. Следует, однако, иметь
в виду, что преобразование Лапласа применяется для функций,
удовлетворяющих условию (см. стр. 191)
в то время как для существования одностороннего преобра-
преобразования Фурье требуется сходимость интеграла
\\m\dt
(89)
(первые два условия, которым удовлетворяют оригиналы,
совпадают с соответствующими условиями при преобразова-
преобразовании Фурье).
Ясно, что последнее условие (сходимость интеграла) на-
накладывает на функцию f(t) гораздо более жесткие ограни-
ограничения, чем условие быстроты ее роста. Даже для laiuix про-
простых и часто встречающихся функций, как единичная функ-
функция T](f), sin г1, cos t, не говоря уже о степенных функциях
t, t2, ..., интеграл (89) являекя расходящимся:
со со
5 \dt = со, \tdt==co;
о и
со са
геометрически ясно, что интегралы ^ | sin t \ dt и ^ J cos t' dt
также расходятся. В то же самое время все эти функции
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
257
имеют изображение по Лапласу '). Дело в том, что модуль
подынтегральной функции при преобразовании Лапласа
" -" (в = Re/0
отличается от модуля \f(t)\ быстро убывающим при ^
множителем е~"', который и обеспечивает абсолютную сходи-
сходимость интеграла Лапласа. Если в условии 3) оригинала счи-
считать, что постоянная а. <^0, то
М
а '
так как при а <^ 0 функция eat -> 0 при t -»¦ со . В этом
случае функция f(t) имеет как преобразование Лапласа,
так и преобразование Фурье (одностороннее). Условие а<4)
означает, что мнимая ось принадлежит области сходимости
интеграла Лапласа. Но тогда в формуле обращения E5)
7 — (
можно положить f = 0, р = /U)j dp == /^^ и
со
/@ = 5^ \ F(iu)eimtdw. (90)
— оо
Мы получили формулу обращения для преобразования
Фурье. Несущественное различие полученной формулы
и формулы (83) (вместо F(<o) стоит F(iui)) объясняется тем,
что для точного соответствия обозначений преобразование
Фурье следовало бы писать в виде F(lui), считая в интеграле
Лапласа р чисто мнимой величиной. Часто так и поступают.
Таким образом, можно сказать, что если оригинал f(t)
при преобразовании Лапласа дополнительно удовлетворяет
условию сходимости интеграла (89), то для него существует
и преобразование Фурье, и все свойства последнего немедленно
получаются из свойств преобразования Лапласа при замене
') Рассмотрение дифференциальных уравнений и связанных
с ними задач электротехники в случаях, когда правая часть урав-
уравнения G2) не допускает преобразования Фурье, но имеет преобра-
преобразование Лапласа, будет произведено в следующей главе.
9 И. Г. Араманович и др,
258
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
комплексной переменной р на чисто мнимую величину ш.
В частности, так будет всегда, когда а<^0 или когда ори-
оригинал f(t) отличен от нуля только на некотором конечном
интервале, скажем @, 7), а при всех t^>T он равен нулю
оо Т
(при этом \\f{t)\dt = \\f{t)\dt).
о о
106. Воспользуемся установленной связью между преоб-
преобразованиями Фурье и Лапласа, чтобы вывести важное для
приложений соотношение, являющееся аналогом формулы
Парсеваля для рядов Фурье. Напомним сначала эту фор-
формулу.
Пусть функция f(t) в интервале (— /, /) представлена
рядом Фурье:
со .Tint
=4 2 J~.
Умножим обе части равенства на f(t) и проинтегрируем
в пределах от — /до I:
= \ J f(t) 2 сае ' dt.
(91)
—I и=—со
Считая возможным почленное интегрирование ряда в пра-
правой части равенства и применяя формулу G1) для коэффи-
коэффициентов ряда Фурье, получим
I со
Деля на//2 и учитывая, что спс_п = спсп =' сп |а, мы приходим
к формуле Парсеваля '):
i
4$/w=2
(92)
') Так как | с_п | = | сп |, то правую часть можно записать и так:
оо
сл 12- Правая часть формулы (92) более симметрична
л=1
и поэтому предпочтительнее.
§ 4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
259
Пусть теперь f(t) — непериодическая функция, заданная
на интервале @, оо) и имеющая преобразование Фурье. По
предыдущему, если преобразование Лапласа функции f{t)
есть F(p), то ее преобразование Фурье запишется как f(/co).
Применим теорему умножения оригиналов в том частном
случае, когда оригиналы совпадают (формула D8), стр. 223):
7+ico
/'(O = 24i $ F(z)F(p-z)dz.
7—jco
Так как мнимая ось принадлежит теперь полуплоскости
сходимости интеграла Лапласа (это есть условие существо-
существования преобразования Фурье), то можно положить f = 0.
Заменяя еще z = ш, dz = ida>, получим
где F(iu>) — преобразование Фурье функции f(f). Предполо-
со
жим еще, что ]fq(f)dt сходится, и применим формулу D0),
о
полагая <o(t)=P(t) (тогда Ф(р) — изображение P{t));
получим
(t) dt = i- i F (Ш) F (— /CO) rf(O.
Замечая, наконец, что F{—m) = F{m), окончательно по-
получим
(93)
{формула Парсеваля для преобразования Фурье).
В заключение отметим, что важность преобразования
Фурье заключается в его тесной связи с физическими пред-
представлениями; в то же время применение преобразования
Лапласа оказывается более удобным благодаря возможности
использования теории аналитических функций комплексного
переменного.
9»
260
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл VII
107. Приведем некоторые примеры преобразований Фурье.
Пример 1. Пусть а>0 и
f(t)
(
e~al при ? >0,
0 при t <0.
Как было отмечено, функция / (t) имеет преобразование Фурье.
Сначала находим преобразование Лапласа:
„-at — .
¦ p-\-a
Заменяя теперь р на Ы, получим преобразование Фурье
1
Отсюда амплитудный спектр: | F (<и) | = ——
1
и фазовый спектр
у а- -j- ш2
ф (ш) = — arg-F (и) = arctg — .
Пример 2. Пусть f (t) —
единичный импульс, длящийся
время х:
Г 0, если t < 0,
f(t) = ) \, если 0 < t < т,
I 0, если «> т.
Согласно формуле B1) преоб-
преобразованием Лапласа этой функ-
функции служит — A — е~Рт). Так как при всех t > х функция f (t) равна
нулю, то ее преобразование Фурье существует и может быть
получено из преобразования Лапласа заменой р на гш:
2п
4л
6к
1 1Ч
?
Амплитудный спектр функции выражается формулой
хш
sin -^-
\F(*)\=2
при ш = 0 он имеет значение |F@)|=x. График его изображен
на рис. 113. При построении фазового спектра ф (а) приходится
§ 4]
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
261
быть осторожным в выборе значения argF (и>). По определению,
ф (ш) = — arg F (<а). Поэтому если 0 < ~ < я, то sin у > 0 и
, / ч Хсо хсй х<й тщ
9 (<°) = -ту ¦ ^сли же я < у < 2я, то sin -^- < 0 и ф Ы = я ¦).
Дальше функцию ф («и) следует
продолжить периодически, и ^б
мы получим разрывную функ-
функцию, график которой изображен
на рис. 114.
Пример 3. Пусть / (*) =
= sin t на интервале @, я) и
/(/)—0 при всех остальных ?
(синусоидальный импульс; см.
рис. 103). Для такой функции
преобразованием Лапласа служит функция
ванием Фурье
2л
г
г -
Рис. 114.
6Я Ь1
г
-, а преобразо-
Отсюда
При ш = 1 функция | F (ш) | не определена, и мы ищем предел:
2 cos -=-
= lim
— 2 у sin -y
— 2сс
2 •
Далее, при 0 < ш < 3 фазовый спектр ф(ш) = у) так как дробь
2 cos у
-j j- положительна. При 3-<а><;5 эта дробь отрицательна и
при 5 <а < 7 имеем
= -ц К
= -я 2п и т- Д-
') Мы не берем ф (ш) — "' -f- я, так как тогда ф (о>) > 2л.
262
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. VII
ЗАДАЧИ К ГЛАВЕ VII
1. Найти изображения оригиналов:
a) sin2i; б) cos2<o?; в) sin3 t\ г) cos41.
Указание. Пользуясь формулой Эйлера, выразить степени
синуса и косинуса через тригонометрические функции кратных дуг.
2. Найти изображения оригиналов:
a) sin It sin At; 6) sin t cos 3t; в) cos It cos At.
Указание. Преобразовать произведения тригонометрических
функций в суммы.
3. Пользуясь теоремой затухания (смещения), найти изобра-
изображения оригиналов:
a) e~t sin It sin At: 6) e~2t ch 3^; в) ch It cos t; r) sh at sin at.
4. Пользуясь теоремами дифференцирования и интегрирования
изображения, найти изображения оригиналов:
. sin At , sin21 «I,,
a) —— ; 6) t2 cos t; в) —-—; г) t- ch e<.
5. Найти изображения оригиналов:
!1, если 0 <zt < а,
— 1, если a<t<2a,
О, если t > 2а;
<, если 0 < t < 1,
2 — <, если 1 < t <. 2,
О, если г > 2;
О, если 0 < t < а,
? — а, если а < г < й,
й — а, если f > b.
в) /(<) =
6. Проверить формулы 14, 17, 20, 22, 25, 35, 42 табл. 2.
7. Пользуясь табл. 2 или формулами разложения, найти ориги-
оригиналы для следующих изображений:
б) 7^'
(/г — а2J
в)
4J
г)
- а2) (Я2 -
ГЛАВА VIII
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
§ 1. Решение дифференциальных уравнений
108. Одним из важнейших применений операционного
исчисления, связанных с преобразованием Лапласа, является
решение линейных дифференциальных уравнений с постоян-
постоянными коэффициентами. Возьмем неоднородное линейное диф-
дифференциальное уравнение второго порядка
A)
и найдем его частное решение при начальных условиях
х№ Jf@) = jt0. B)
Операционный метод решения такой задачи состоит в том,
что мы считаем как искомую функцию x(t), так и правую
часть f(t) оригиналами и переходим от уравнения A), связы-
связывающего оригиналы, к уравнению, связывающему их изо-
изображения X (р) и F (р). Для этого воспользуемся теоремой
о дифференцировании оригинала:
х (t) фргХ О) — рхъ — хй.
Применяя также теорему линейности, перейдем в уравнении A)
от оригиналов к изображениям:
р'Х (р) - рха - ха + а, [РХ (р) - ха] + а,Х (р) = F (р). C)
В результате мы получили уже не дифференциальное, а алгеб-
алгебраическое уравнение относительно неизвестного изображе-
изображения Х(р). (Рекомендуем читателю еще раз обратиться к
тексту на стр. 197.) Решая его, находим
Х- (Р) (Я2 + а\Р + «0
264
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIII
откуда
D)
Итак, изображение искомого решения найдено. Осталось
по таблицам, или, пользуясь теоремой обращения, по извест-
известному изображению X (р) найти соответствующий ему ориги-
оригинал x(t); он и будет являться искомым решением.
Операторное решение X (р) по формуле D) имеет особенно
простой вид при нулевых начальных условиях:
хй =0, хй = 0. E)
В этом случае
Изложенный метод применим к решению линейных диф-
дифференциальных уравнений с постоянными коэффициентами
любого порядка.
Пусть дано уравнение и-го порядка:
G)
с начальными условиями
х @) = х„, х @) = xv..., x^-V @) = j;i»-i). (8)
Применяя преобразование Лапласа и пользуясь общей фор-
формулой C2) теоремы дифференцирования, получим
(/>» X (р) -рп~ххй - рп-Ч0 -... - *<»-") + а, (Я^1 А" (р) -
= X(p) и
= F (р). Отсюда
где
Ир)
где L (р)—рп + а\Рп~У + • • • + ап-\Р + а«> а ф (/0 ~ многочлен
степени не выше, чем (я— 1), с коэффициентами, зависящими
от начальных значений х0, ха,..., х[п~$. Если, в частности,
все начальные значения равны нулю:
ТО Ф(р) —
=Ш
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
965
Переходя в формулах (9) или A0) от изображений к ориги-
оригиналам, получаем искомые решения.
При практическом решении вовсе нет нужды пользоваться
готовыми формулами (9) или A0). Нужно только помнить
метод их получения. Заметим еще, что если в формулах D)
или (9) считать начальные значения ха, ха, ... не заданными,
а произвольными постоянными, то мы получим не частное
решение, а общее. '
К сказанному сделаем только одно замечание. Так как
мы правую часть уравнения G), а также решение x(t) считаем
оригиналами, то при t<^0 их нужно считать равными нулю.
Таким образом, мы получаем, вообще говоря, решение x(t)
только при t :>= 0. Начальные значения х @), х @),... представ-
представляют при этом предельные значения соответственно x(t),
х(t),... при t —>• 0 справа. Как мы уже отмечали, при изуче-
изучении физических процессов нас, как правило, интересует толь-
только течение процесса начиная с некоторого момента времени,
который мы и принимаем за г^=0.
Впрочем, при решении конкретных примеров очень часто
получающееся решение оказывается справедливым при всех
значениях t (конечно, если и правая часть уравнения опре-
определена при всех ?), хотя это и требует проверки. Перейдем
к примерам.
В предлагаемых примерах мы рекомендуем в качестве
упражнения проводить самостоятельно все необходимые
выкладки.
Пример 1. Найти решение уравнения
удовлетворяющее нулевым начальным условиям
х @) = 0, х @) 5= 0.
Полагая x(t) = X(p) и находя изображение правой части
e3t = 5, составляем операторное уравнение
2
откуда
Х(р) =
¦р-3'
2
(Р - 3) (У - Зр + 2) (р—\)(р — 2)(р — 3) ¦
Функция X(р) имеет полюсы первого порядка в точках Pi = l,
ра = 2, Рз = 3 (корни знаменателя). Применяя формулу разложения
266
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIII
F6) гл. VII для случая простых полюсов, находим решение диф-
дифференциального уравнения:
х (t) = е< — 2е2' + e3i.
Функция х (t) удовлетворяет уравнению при всех значениях t.
При практическом решении дифференциальных уравнений опе-
операционным методом рекомендуется, конечно, пользоваться готовыми
таблицами соответствия между оригиналами и изображениями.
Чем эти таблицы подробнее, тем меньше придется делать допол-
дополнительных вычислений и преобразований. В частности, решение
примера 1 можно проверить по формуле 15 табл. 2.
Пример 2. Найти решение уравнения
X + 4х + 4х = t3 e~2t
при начальных условиях
= 1, х(Щ=2.
. 3!
Найдем прежде всего изображение правой части. Так как ts = —j
(форм}ла 12 табл. 1), то по теореме зат>хания
., _„, . 3!
1 (/> + 2L'
Учитывая, что
x(t)=pX(j>)-\ и x(t)=P2X(p)-p-2,
составим операторное )равнение:
р*Х(р)-р-2+4рХ(р)-4 + 4Х(р) = :
3!
отсюда
*{Р) = \
3!
Оригинал для первого слагаемого находим но формуле, указан-
указанной выше. Так как —j 7= tb< T0
(р + 2)» ^- 5!
(теорема затухания!).
Второе слагаемое запишем в виде
Тогда
2 -^ tie ,
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
267
и окончательно
х @ =
i*
Советуем читателю убедиться, что если решать данное уравнение
обычными методами, то это потреб)ет гораздо более длинных
выкладок.
Пример 3. Найти решение уравнения
при нулевых начальных условиях
х @) = х @) = х @) = х @) = 0.
Операторное ) равнение имеет вид
откуда
Х{Р) = ;
Для нахождения оригинала пользуемся общей формулой раз-
разложения. Так как коэффициенты в выражении для X (р) действи-
действительны, то вычеты в полюсах ± (' — сопряженные комплексные
числа. Вычисляем поэтому вычет только в точке р = i (см. стр. 240):
Взяв удвоенную действительную часть пол}ченного выражения,
находим л: (t):
^ ^ ?2
X (t) = 5~ t COS t 4-'—5 Sin t.
о о
Результат можно проверить по формуле 39 табл. 2.
Покажем на одном примере, кап след)ет поступать, если на-
начальные значения заданы не в точке а! = 0.
Пример 4. Найги решение уравнения
X-\-x = et
при начальных условиях лгA) = 1, л'A)=0.
Положим i!=T-f-l и л- (t) = x (т-|- 1) = лг, (х). Уравнение
и начальные условия терепишутся теперь в виде
_ . ,. / . dx, _ af2
268
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
(Гл VIIГ
(значению t = 1 соответствует т = 0). Переходя к операторному
уравнению, получим
от к \ да
X(P)=-
' p—\'
e p
Возвращаясь к оригиналам, найдем (соответствующие выкладки
читатель проделает самостоятельно или воспользуется формулой 22
табл. 2):
sx~4" sinx4-4-et-
Чтобы получить решение заданного уравнения, осталось заме-
заменить т на ( — 1:
l) + i--
109. До сих пор мы рассматривали дифференциальные
уравнения, у которых правая часть была непрерывной функ-
функцией и задавалась единым аналитическим выражением. Иногда
встречаются и такие случаи, когда правая часть уравнения
на различных интервалах задается разными аналитическими
выражениями (например, является функцией ступенчатого
вида) и имеет точки разрыва. Если правая часть является
оригиналом, то операционный метод решения применим. Оста-
Остановимся на некоторых особенностях решений таких уравнений
на примере уравнения второго порядка:
A)
Полагая x{t)r=X{p), мы дважды применяем теорему о диф-
дифференцировании оригинала. Согласно замечаниям, сделанным пе-
перед этой теоремой (см. стр. 209 — 210), как само решение x{t),
так и его первая производная x(t) должны Оьнь функциями
непрерывными. Поэтому из уравнения следует, что вторая
производная Х"@ будет иметь разрывы в тех же точках, что
и правая часть f(t). Разумеется, если fit) непрерывна, то
непрерывна и х (t). Поэтому функция x(t) будет удовлет-
удовлетворять уравнению A) во всех точках, где правая часть
fit) непрерывна. В точках же разрыва fit) проверку произ-
П
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
269
водить не имеет смысла, так как разрывна x(t). Перейдем
к примерам и начнем с уравнения первого порядка.
Пример 5. Найти при <>0 решение уравнения
1, если 0<? <2,
0, если t > 2,
при нулевом начальном )словии а'@)=0. График правой части
уравнения есть «ст)пенька», изоб-
изображенная на рис. 98.
Учитывая начальное условие
и формулу B1) гл. VII, состав-
составляем операторное \равнение
PX(p)+X(p) =
откуда
Xip) = '~
Для отыскания х (t) заметим, что
1
• == 1—e~l. Дтя изображения
довательно,
нал найдем по теореме запаздывания:
е-'Р
и еле-
орнги-
^(l_e-(/-sl)Yi(,_2)=/0'
I 1 — е~а~-\ есл
Окончательно,
если 0 < t < 2,
если * > 2.
x(t) =
(t) = \—ert—(\— <r"-2>) rt (t - 2),
1 — e'', если О < t < 2,
{1 — e~', ec1:
e-i<-si_e-( = g-((e2_i)) ec;
если (>2.
Как легко проверить, .г (?) — непрерывная функция, но ее произ-
производная в точке t = 2 имеет разрыв:
llm х (t) = V. 1>т -v @ = - -^
График функции х (t) при ? = 2 имеет углов)ю точку (рис. 115).
Если бы этот пример мы решай без помощи операционного
исчисления, то должны были бы сначала паитл решение уравнения
х-\-х=] при условии л'@) = 0. Это будет функция л-=1—е~К
Затем найти общее решение уравнения x-\-x^=Q — функцию х =
= Се~' и подобрать С так, чтобы A—e~*)t-a = (Се~%^.
При этом условии решение х (t) будет непрерывным при переходе
через точку ? = 2. Так как С — е2—1, то мы снова получаем
270
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл VIII
решение х (t) = e~l (е-—1) в интервале B, со). При большом числе
точек разрыва, а также в случаях уравнений высших порядков этот
способ приводит к весьма громоздким выкладкам, которых мы и
избегаем, пользуясь операционным методом.
Пример 6. Рассмотрим еще пример решения уравнения вто-
второго порядка. Найти при i>0 решение уравнения
(О, если 0 <.t < 1,
х -j- х = ) 1, если 1 < t < 3,
[о, если t > 3
при нулевых начальных условиях х @) = х @) = 0.
Правая часть дифференциального уравнения — та же «сту-
«ступенька», что и в примере 5, но запаздывающая на т=1. Поэтому
операторное уравнение примет
вид
или
Как и в предыдущем приме-
примере, сначала находим оригинал
для — 2 . . ¦ По формуле 20 табл. 2 имеем
—, о i ,ч = 1 — cos t¦
(это можно сразу получить и без таблицы, заметив, что
= ~—;-)• Тогда по теореме запаздывания
Р Р-+1 1
-=[1— cos (t— 1I i(t — :
е-зр
р{р*+\)
ф[\ — cos(t — 3)] г] (t —?3).
Окончательное решение х (t) таково:
@, если 0<<< 1,
1 — cos (t—\), если 1_< i < 3,
— cos (i — 1) + cos (г1 — 3), если t > 3.
Предоставляем читателю проверить, что в точках разрыва пра-
правой части t = 1 и ? = 3 решение х (t) и его производная х (t) не-
непрерывны, а х (t) в этих же точках имеет разрывы. Схематический
график функции х (t) приведен на рис. 116. При построении этого
графика учтено, что при f = 3 графики функций 1—cos (г!—1) и
§ И
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
271
cos{t — 3) — cos (t—1) = 2 sin 1 sin {t — 2) имеют общую каса-
касательную.
Пример 7. Приведем в заключение еще один пример, в ко-
котором правая часть представляет единичный синусоидальный импульс
(см. рис. 103). Найти при t>0 решение уравнения
sin t, если 0 < t < тс,
0, если t >тс,
при нулевых начальных условиях jt @) == jc @) = 0.
Операторное решение имеет вид
Х(р) =
Пусть сначала ш2^?1. Тогда по форм>ле 30 табл. 2 имеем
1 _^_ sin at — « sin t
и по теореме запаздывания
е~жР _;_ sin <o (t — я) — со sin (t — тс)
—*)¦
Таким образом, уравнение имеет решение
sin at — со sin t
x(t) =
@A— M2
_ COTC . / 71.
2 COS -^- Sin @ 11 ¦ j
если 0< i < тс,
@A—
если
Интересно отметить, что если со равно нечетному числу,
то при t > л имеем л- (<) = 0.
Пусть со8 = 1 (случай резонанса). Тогда по формуле 28 табл. 2
1 _^_ sin t t cos t
-, если 0 <t <тс,
Снова применяя теорему запаздывания, найдем
sin t — t cos t
x(t) = \
¦к cost
—2— . если * > я-
(То же самое можно получить, перейдя в решении для »^1 к пре-
пределу при со —. 1.)
Рекомендуем читателю самостоятельно убедиться в справедли-
справедливости полученных решений и построить их графики.
272
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIIГ
ПО. Покажем теперь, как при решении дифференциаль-
дифференциальных уравнений применяется теорема умножения и, в частности,
интеграл Дюамеля.
Введем сначала сокращенную запись линейного диффе-
дифференциального уравнения я-го порядка. Именно, будем симво-
символом L [х] обозначать левую часть уравнения G)
L [х] называется линейным дифференциальным оператором
п-го порядка. Числа (или функции, если речь идет об урав-
уравнениях с переменными коэффициентами) av аь...,ап называ-
называются коэффициентами оператора.
Из самого определения следует, что
L [ClXl + С2х,1 =
QZ. [x2],
A2)
т. е. что оператор от линейной комбинации функций ра-
равен линейной комбинации операторов от этих функций.
Отсюда, кстати, и происходит название — линейный оператор.
Неоднородное уравнение сокращенно запишется в виде
L[x]=№
A3)
Смысл применения теоремы умножения будет заключаться в
том, что если нам известно решение уравнения A3) при ка-
какой-то одной правой части, то мы получим возможность с
помощью свертки отыскивать решение при любой другой
правой части. Особенно удобно начинать со случая, когда
A4)
L[x] = l.
Начальные условия будем считать пулевыми:
= 0. A5)
Соответствующее решение обозначим через Х\ (t), а его
изображение — через Х\ (р). Операторное уравнение примет
вид
Xi(p)p" 1~ M"i С") А1 + ¦ • • 4^ аЛ (/>) =-,
или
A6)
§ И
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
273
где L (р) = р'1 -\- ахрп '• -\- ... -\- ап — характеристический
многочлен. Сокращенная форма записи уравнения с помощью
оператора L особенно удобна тем, что позволяет совер-
совершенно одинаково записывать как левую часть дифференциаль-
дифференциального уравнения, так и его характеристический много-
многочлен. При этом коэффициенты оператора и многочлена со-
совпадают.
Так как мы считаем, что решение Xi (t), а следовательно,
и его изображение Х\(р) уже известны, то из формулы A6)
можно найти
1
A7)
Возьмем теперь уравнение с любой правой частью L[x]=f{f)
при тех же нулевых начальных условиях. Его операторное
уравнение X (р) L (р) = F (р), где F(p)^f(t). Находя отсюда
А"^) и заменяя L(p) по формуле A7), получим
X(p)=pX1(p)F(p). -
Согласно формуле D5) гл. VII искомое решение x(t) равно
A8)
так как х1@) = 0 в силу начальных условий, или
х @ = х, (t) /@) + S /' СО xt (t - т) Л.
A9)
(Воспользовавшись коммутативностью действия свертки, мож-
можно написать еще две аналогичные формулы.) Отметим, что
для получения x(t) нам не нужно знать изображение F (р)
правой части уравнения.
Таким образом, зная решение для единичной правой
части, мы при помощи интегрирования находим решение для
любой правой части. Напомним только, что в обоих слу-
случаях начальные условия — нулевые. Полученные формулы
играют очень важную роль, которая будет разъяснена на
примере электротехнических задач в § 2.
274
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIII
Пример 8. Найти решение уравнения х-\~х = е ^ при
нулевых начальных условиях.
Изображения функции, стоящей в правой части, мы не знаем
и сначала решаем уравнение Х-{-х=\ при тех же нулевых на-
начальных условиях. Операторное уравнение
1
имеет решение Х1(р) =
- , 2 , ..; соответствующий ему оригинал
равен xL(t) = l — cost (см. формулу 20 табл. 2). Поэтому по фор-
формуле A8)
t
n sin х dx.
= \)
Выразить полученный интеграл при помощи элементарных функ-
функций нельзя.
Пример 9. Записать при помощи интеграла Дюамеля реше-
решение уравнения х — x=f(t) при нулевых начальных условиях.
Начнем, как и раньше, с уравнения х— х=1. Его оператор-
операторное уравнение имеет решение Xv (р) = 2 —- и
Р (Р — 1)
(формула 21 табл. 2). Поэтому
t
111. Операционный метод решения одного линейного диф-
дифференциального уравнения почти без всяких изменений пере-
переносится на решение систем линейных дифференциальных
уравнений с постоянными коэффициентами, как однородных,
так и неоднородных. Поэтому мы ограничимся рассмотрением
примеров.
Пример 10. Найти решение системы дифференциальных
уравнений
(
\
при начальных условиях х @) = 1, у @) = 1.
Если считать, что х (t) = Х(р) и у (t) =z Y (р), то по теореме
дифференцирования оригинала хфрХ—1 и y=ppY—1 (для крат-
краткости записи мы не пишем аргументы функций). Система опера-
операторных уравнений примет вид
рх— 1+х— >'=—Ц-, рУ— \+зх — 2/ = . 2
р-
p-V
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
275
или, после преобразования,
(p+\)X-Y =
р-\
В результате мы получили систему алгебраических линейных
уравнений относительно неизвестных изображений Х(р) и Y(p).
Решая эту систему, находим
и, возвращаясь к оригиналам,
x(t)=e*, y(t) = e(.
Операционный метод в равной мере применим и для решения
систем уравнений с производными высших порядков.
Пример 11. Найти решение однородной системы
\
[г+х+у-г=0
при начальных условиях
х @) = 1, х @) =у @) =--у @) = z @) = i @) =0.
Система операторных уравнений запишется в виде
f (p*-\)X+Y+Z=p,
\
Эту систему решим при помощи определителей. Определитель
системы равен
Д=
1
Вычислим его, опираясь на свойства определителей (сначала
к первому столбцу прибавим оба остальных столбца, а затем из
второй и третьей строк вычтем первую; в результате этих преоб-
преобразований определитель не изменится):
! + 1 1 1
'¦ — 1 1
о2 —2
276
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ГГл VIII
Вычислим определители Д ,
Р 1 1
'¦— 1 1
1 р2-
1
'— 1 р
1 0 1
1 0 р2 —
г — 1 1 I
'¦— 1 О
— IJ—1]=
= -/>(/>»-2),
= -/>(?"-2).
—2),
1 1 О
Теперь находим изображения искомых решений:
Для перехода к оригиналам воспользуемся формулой 32 табл. 2,
согласно которой (а = "|/2, 6=1):
1 (shVTt .
Применяя теорем) дифференцирования оригинала, находим
y(t)=2(t)= — -T (ch /2" t — cos 0-
о
Снова применяя эту же теорему, получим (каждый раз значение
оригинала при t = 0 равно нулю)
x(t)=^chY2t + -j cos t.
Мы напомнили читателю правило решения системы линей-
линейных уравнений при помощи определителей со следующей
целью. Часто в практических задачах, после того как система
уравнений составлена, нам оказываются нужными не все не-
неизвестные функции, а только некоторые из них. В этих слу-
случаях, воспользовавшись формулами Крамера, мы можем сразу
выписать выражения для нужных изображений, не отыскивая
остальных. Следует еще иметь в виду, что при большом
числе неизвестных функций для решения систем алгебраи-
алгебраических уравнений (а также для вычисления определителей)
применякнся специальные вычислительные приемы линейной
алгебры.
Можно рассматривать и такие неоднородные системы
дифференциальных уравнений, правые части которых имеют
§ 2]
ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОТЕХНИКИ
277
точки разрыва; при этом следует поступать так же, как при
решении примера 5.
Пример 12. Найти решение системы
( 1, еслиО<;<1,
I 0, если t > 1,
[, если 0 <t <2,
), если t > 2,
при нулевых начальных условиях л: @) =у @) =0.
Система операторных уравнений имеет вид
\—е-Р
Ее решение
Х(р) =
Y(p) =-
1
Р(р+\)
е~Р
Возвращаясь к оригиналам и применяя теорему запаздывания,
получим
1 —ег1, если 0<U< I,
x{t) = \ 1 — еч — sh (г1— 1), если1<<<2,
— е~' — sh (i — 1) -f- ch (t — 2), если t > 2y
1 — e~', если 0 < f < 1,
J» (<)=¦{ — e~'+ch(<— I), если 1 < t < 2,
¦e-' + ch (iJ— 1) —sh (< — 2), если * > 2.
Рекомендуем читателю построить графики найденных решений
и проверить, что решения непрерывны в точках t = \ и ? = 2, но
имеют разрывные производные.
§ 2. Приложения операционного исчисления
к задачам электротехники
112. В § 4 гл. VII уже рассматривались некоторые за-
задачи электротехники в связи с отысканием установившегося
тока в колебательном контуре при периодическом и непери-
непериодическом внешнем напряжении. Методы операционного
278
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [Гл. VIII1
исчисления позволяют с большим успехом рассчитывать любые
процессы в сложных электрических цепях при произвольном
внешнем напряжении. Эти методы ввел в электротехнику
английский инженер-электрик О. Хевисайд. Они оказались
настолько удобными для применения, что в настоящее время
в большинстве курсов электротехники и теории автоматиче-
автоматического регулирования занимают одно из центральных
мест при расчете электриче-
электрических цепей. Мы собираемся
познакомить читателя только
с принципиальной стороной
дела, совершенно не касаясь
специальных вопросов, кото-
R
\\
рые изучаются в курсах элек-
С тротехники.
Рис. 117. Начнем с простейшего слу-
случая — колебательного контура
(рис. 117), уравнение которого мы уже записывали на стр. 250:
B0)
Будем считать, что в начальный момент ток равен нулю:
г@) = 0. Последний член левой части уравнения преда ав-
ляет напряжение на обкладках конденсатора; его выражение
показывает, что при ^ = 0 это напряжение равно нулю, т. е.
что в начальный момент заряды на обкладках конденсатора
отсутствуют. Эти начальные условия соо1ветствуют задачам
включения. Более общий случай начальных условий мы
рассмотрим несколько позже.
Введем операторный ток I(p)~'-i{t) и операторное
напряжение V{p)=v(t). По теореме дифференцирования
оригинала
di .
так как г'@) = 0, а по теореме интегрирования
§ 2]
ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОТЕХНИКИ
279
Уравнение колебательного контура перепишем в операторном
виде
-±-
откуда
1 — Z(p) '
B1)
где Z (p) = R 4- Lp 4- -~ операторное сопротивление кон-
конь/7
тура. Комплексное сопротивление контура (формула (82) гл. VII)
получается из операторного сопротивления, если в последнем
положить р = Ы. Формула B1) называется операторной,
формой закона Ома.
По найденному операторному току 1(р), пользуясь теоре-
теоремой обращения, можно восстановить и сам ток:
B2)
7 — г
Разумеется, в конкретных задачах следует пользоваться таб-
таблицами или какой-либо из формул разложения.
Поясним сказанное примером. Пусть в колебательный
контур включается постоянный ток: v(t)^E. Тогда V(p) =
= — и формула B1) принимает вид
Е Е '
—
По формуле 11 табл. 2 получим:
~ 21
R
t\
1L
--A t.
280
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл VIII
В первом случае получаются затухающие гармонические ко-
колебания, во втором и третьем случаях затухающие апериоди-
апериодические процессы. В третьем случае для большей наглядности
ток i(t) лучше представить в ином виде. Корни трехчлена
р* + тр + тс равны *'•2 = - 2L ± У~т--?с> след°-
вательно, они действительны и отрицательны. Записывая опера-
Е 1
торный ток в виде 1(р)= >- -. ,-т^ ^г и применяя фор-
L (Р —ко (Р — к2>
мулу 5 табл. 2, получим
I (t) =
%= {е е),
Отсюда ясно видно, что i(t)
0 при
где Хх
t-yco.
Так же просто решае!ся задача о включении в кошур
синусоидального напряжения A sin <вм в этом случае 1/(р) =
= —гГг ). Можно рассматривать случаи, когда напряжение
v(t) — разрывная функция, и т. д. Все это полностью повто-
повторяет задачи решения дифференциальных уравнений, рассмот-
рассмотренные в § 1.
Особо остановимся на роли интеграла Дюамеля.
Пусть в контур включается постоянное единичное напряже-
напряжение
=l. Тогда Vt(p) = — и по формуле B1)
Следовательно, по формуле D5) гл. VII
Если теперь в контур включить любое напряжение v(t), то
B3)
B4)
B5)
или
§ 2]
ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОТЕХНИКИ
281
Таким образом, зная реакцию контура на единичное
напряжение, мы с помощью написанных формул можем вы-
вычислить реакцию контура на любое внешнее напряжение.
В полученные формулы не входят ни изображение напряже-
напряжения v\p), ни, что самое главное, операторное сопротивление
контура Z(p). Последнее означает, что мы можем рассчиты-
рассчитывать контур, фактически не зная его параметров, если только
нам удалось экспериментально получить ток iy (t) — реакцию
контура на единичное напряжение.
Перейдем к случаю ненулевых начальных условий. Во-
первых, будем считать, что в начальный момент в контуре
есть ток /@) = /0, и, во-вторых, что на обкладках конденса-
конденсатора есть начальный заряд #о- Последнее обстоятельство при-
приводит к некоторому изменению дифференциального уравне-
уравнения контура, именно, к падению напряжения на конденсаторе
добавится постоянное слагаемое -^К и уравнение примет вид
4r\ldt4-%- = i
B6)
Переходя к операторному уравнению и учитывая, что те-
теперь -Jr=pl{p) — /0, получим
откуда
Lplip) - Li, + Rl{p) + '^ + §¦ = V (р),
Ж
Z(p)
i; -и -9о
Zip)
B7)
где V(p)==v(f), a Z(j>) — операторное сопротивление кон-
контура.
Таким образом, к току, определяемому операторной
формулой j*
, добавится еще ток, операторное выражение
которого равно ^°РтТ5" • Этот ток соответствует заданным
начальным условиям и называется током короткого замы-
замыкания. Он получается, если в уравнении контура положить
v (t) = 0, т. е. накоротко замкнуть контур.
282
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIU
113. Преимущества операторного метода расчета сказы-
сказываются все больше и больше тогда, когда мы начинаем рас-
рассматривать не один контур, а сложную электрическую цепь.
Как известно, расчет цепей постоянного тока производится
на основании законов Кирхгофа.
1. Алгебраическая сумма всех токов, притекающих к
любой точке цепи, равна нулю.
2. Для каждого замкнутого контура цепи алгебраи-
алгебраическая сумма падений напряжений в отдельных ветвях
контура равна нулю.
В курсах электротехники доказывается, что если в цепи
протекает ток, изменяющийся во времени, то для оператор-
операторного тока и операторного напряжения оба закона Кирхгофа
остаются справедливыми. Первый закон формулируется совер-
совершенно одинаково, как для самих токов, так и для их изоб-
изображений, т. е. для операторных токов. Чтобы иметь возмож-
возможность пользоваться вторым законом Кирхгофа, мы должны
научиться вычислять операторное падение напряжения на
отдельных участках цепи.
R
L
Рис. 118.
¦to-
Рассмотрим простейшие участки цепи, изображенные на
рис. 118. Как известно, напряжение на концах участка с со-
сопротивлением R равно Vf( = Ri; на участке с индуктивностью
L равно vL = L-jp и на участке с емкостью С равно vc —
tt
t
= -=г \ idt (в последнем случае считается, что при ^ = 0 заряд
о
на обкладках конденсатора дп = 0).
Переходя к операторным токам и напряжениям и считая
для простоты, что начальный ток г0 равен нулю, получим
Все эти соотношения объединяются в единой форме опе-
операторного закона Ома
B8)
§ 21
ПРИЛОЖЕНИЯ К ЗАДАЧАМ ЭЛЕКТРОТЕХНИКИ
283
где Z(p) — операторное сопротивление участка цепи. На участ-
участках с сопротивлением R, индуктивностью L и емкостью С
соответственно имеем
= R, ZL(p) = Lp, Z(p)
Далее, при последовательном соединении участков це-
цепи (рис. 119) операторные
сопротивления, так же как
и обычные, складываются.
г,
Рис. 119.
Действительно, Vx^=Z\l, \
записи опускаем). Так как
Рис. 120.
2 = Zo/ (аргумент для краткости
то
т. е. операторное сопротивление всей цепи Z равно
Аналогично, при параллельном соединении (рис. 120)
и так как I (t) = ir (t) -\- ц (t), то
/ +
откуда для операторного сопротивления цепи Z имеем
Т
Z = -
7 7 \ 7-
или
284
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл VIIГ
Таким образом, операторное сопротивление цепи в случае
нулевых начальных условий может вычисляться по обыч-
обычным правилам соединения элементов цепи. С этой точки
зрения уравнение для колебательного контура получается
особенно просто. Мы имеем последовательное соединение
сопротивления, индуктивности и емкости и по только что
установленным правилам находим операторное сопротивление
контура
Z = R + Lp + ±.
Согласно второму закону Кирхгофа 11= V, и мы приходим
к знакомому уравнению B1).
Приведем более сложные примеры.
Пример 1. Найти операторное сопротивление участка цепи,
изображенного на рис. 121.
Рис. 121.
Рис. 122.
Для верхнего участка цепи Zi = R1-\-Lp, а для нижнего —
J2 = R3 -\- -q—. Следовательно,
Ср
JL = !___. .J
2 Rt-l-T* г
или
Пример 2. Найти ток в контуре, изображенном на рис. 122,
если при t = 0 включается постоянное напряжение Е.
Для параллельных ветвей, содержащих Си/?, операторное
сопротивление равно -=гр;—:—г-. Поэтому для всего контура
(Нр ~\- I
R
RCp-j-i
5 3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Операторный ток равен
285
Z(P)
Пользуясь табл. 2, легко перейти от операторного тока к его
оригиналу, т. е. к обыкновенному ток>.
Мы не останавливаемся на более специальных примерах,
а также на случае ненулевых начальных условий. Читатель
найдет их в курсах электротехники.
§ 3. Решение дифференциальных уравнений
с частными производными
114. В этом параграфе мы вкратце рассмотрим решение
некоторых дифференциальных уравнений с частными про-
производными — уравнений математической физики. Мы не
будем касаться вывода соответствующих уравнений, отсылая
читателя, например, к книге [4], а просто на нескольких
примерах покажем, как такие уравнения можно решать при
помощи операционного исчисления.
Начнем с задачи о распространении тепла в полубеско-
полубесконечном стержне. Требуется найти при х^>0 и ^^>0 реше-
решение уравнения теплопроводности
да .,й»и B9)
dt
дх2
удовлетворяющее краевому условию
к @, 0 = «о
и начальному условию
и(х, 0)=0 при
C0)
C1)
Решение этого уравнения при заданных условиях описы-
описывает процесс распространения тепла в полубесконечном од-
однородном стержне, боковая поверхность которого теплоизо-
теплоизолирована, если начальная температура стержня равна нулю,
а на его конце все время поддерживается постоянная темпе-
температура н0. Начальная температура и(х, 0) в точке х = 0
разрывна: при х = 0 она равна гг0, а при jc^>0 она равна нулю.
Будем считать, что искомое решение и(х, t) при любом
фиксированном л:(л:^>0) является оригиналом по перемен-
переменной t:
и(х, t)=U{x, p).
286
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [Гл. VIII
Тогда согласно теореме о дифференцировании оригинала
*!L=PU-n(x, Q)=pU.
C2)
Рассматривая х как параметр и применяя теорему о диф-
дифференцировании по параметру (разумеется, предполагая, что
все требуемые для этого условия соблюдены), получим
ди _^ dU
~дх~ ~ 7
дх* '
C3)
Подставив изображения для производных в уравнение B9),
перейдем к операторному уравнению:
pU=ai-rzT. C4)
Желая подчеркнуть, что в полученном уравнении р рас-
рассматривается как постоянная, мы вместо частной произ-
водной -5-3- пишем обыкновенную производную —^. В ре-
результате применения преобразования Лапласа мы перешли от
уравнения с частными производными к обыкновенному диф-
дифференциальному уравнению, в данном случае к линейному
уравнению второго порядка с постоянными коэффициентами.
Применяя также преобразование Лапласа к краевому ус-
условию
и@, 1) = щф-±,
C5)
получим соответствующее краевое условие для уравнения C4):
U\x^— p ¦
Общее решение уравнения C4) имеет вид
U[x, p)=Qe
C,e
C6)
C7)
Произвольные постоянные Cj и Q определим при помощи
условия C6) и вытекающего из физического смысла задачи
требования ограниченности решения и(х, t) при _к->оо. Из
последнего следует, что и изображение U(x, p) ограничено
при х -*¦ оо (доказательство мы опускаем). Это означает, что
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
287
Таблица 3
Изображения — иррациональные и трансцендентные функции,
встречающиеся при решении задач математической физики
Номер
фор-
формулы
Изображение
Оригинал
10
Vp
— е
Р
,-aYp
p + Vp
l —-
У nt
4^-в~»
2 f в-Я?гу=1_ф/ « V)
/я J \2Vt)
n't
У Tit
Л (О2)
Jo (it)
Л (О2)
Ml
t
л B Yrt
») Ф(^)=——- \ е у~ dy — интеграл-вероятностей.
2) Jo (t) и У) (t) — функции Бесселя первого рода порядка 0
и 1. Краткие сведения об этих функциях см. в [4], § 10.
288
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА (Гл VIII
Продолжение табл. 3
Номер
фор-
формулы
И
12
13
14
Изображение
а
Vp
а
pVp
а.
1 е~?
Vp
pVp
Оригинал
1 cos B У at)
У Tit
—J— Sin B Val)
]/ita
-i—chBV^F)
у nt
—}— shBy^F)
У ita
C, = 0. Подставляя условие C6) в общее решение C7), на-
находим, что С.2 = —. Следовательно, частное решение
Yp
C8)
Воспользуемся формулой 3 из табл. 3 (немного позже
будет показано, как эта формула получается), заменим в ней
а на — и перейдем к оригиналу, т. е. к искомому решению
=„' \
И . C9)
2а Yt
где Ф (?) = \е~'2 dy — интеграл вероятностей.
у* 5
Полученная формула в точности совпадает с формулой
A5.3") книги [4], только нужно в ней считать начальную
температуру стержня равной нулю (h^_0 = 0).
§ 31
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
289
Заметим, что решение C9) не определено при ^^0.
Поэтому начальное условие и(х, 0) = 0 следует понимать
так, что
lim и (х, t) = н0 [ 1 — Ф (со)] — 0.
Но именно такой смысл мы и условились придавать значе-
значению оригинала при t = 0 (см. формулу B8) гл. VII).
Получив решение при краевом условии н@, f) = z70,
легко при помощи 1еоремы умножения изображений перейти
к решению при общем краевом условии
и@, 0 = ?
D0)
по-прежнему считая, что в начальный момент ^ = 0 темпе-
температура точек стержня при х^>0 равна нулю: н(л*, 0) = 0.
Положим, что <p(t)=LF(p). Тогда краевое условие для
преобразованного уравнения C4) будет иметь вид
(J\x = o = F(p). D1)
Отыскивая произвольную постоянную Q в общем решении
C7) (напомним, что С, = 0), получаем, что Ca = F(p), т. е.
xYp
U{x, p) = F(p)e a . D2)
Согласно формуле 2 табл. 3, в ко юрой а заменено на
—, имеем
а . хе
е =
\аЧ
1а У lit"
(и эта формула будет получена позднее). Применяя теорему
умножения изображений, приходим к решению
В<*'') = ??^С
D3)
(Рекомендуем читателю сравнить полученное решение с фор-
формулой A7.17) указанной выше книги; для полной их тож-
тождественности надо в последней положиib /=0 и /J = a2.)
10 И. Г. Араманович и др.
290
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. УПГ
Функция и(х, t), определенная формулой D3), обращается
в нуль при х^>0 и ^ = 0, так что начальное условие соблю-
соблюдается. При х = 0 и t^>0 формула D3) функцию и(х, t)
формально не определяет, так как несобственный интеграл
f а (т) ,
\ ~~ Tud'z расходится (при x = t подынтегральная функция
обращается в бесконечность). Чтобы проверить условие D0),
преобразуем предварительно интеграл в правой части D3),
х х dz . v-a
положив -— =2, — — dz, x = t—
Тогда
4а (t — т)
ll{x>t)=Vl \ *(<-
2а VI
Теперь видно, что при л;=0 и
и@, t) = v{t)^
115. Наметим путь решения задачи в том случае, когда стер-
стержень конечный и задана начальная температура. Эта задача
приводится к решению уравнения теплопроводности
ди_
д2и
с краевыми условиями
"@, 0=?i@- u(l, t)=ys(t)
и начальным условием
и(х,0)=/(х) @<х<1).
Считая по-прежнему и (х, t) оригиналом, a U (х, р) — его изоб-
изображением, по формуле C2) получим
Преобразованное уравнение принимает вид
PU-f{x) = a*
dx*
или
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
291
т. е. становится неоднородным. Это уравнение нужно решить при
краевых условиях
где
Найдя изображение U(х, р) и перейдя к оригиналу и (х, t),
получим искомое решение.
Отметим, что в большинстве случаев изображение U(х, р) ока-
оказывается сложной трансцендентной функцией, и переход к ориги-
оригиналу совершить бывает нелегко.
Для читателя, знакомого с решением приведенной задачи мето-
методом Ф)рье, заметим, что операционный метод и метод Фурье
часто хорошо дополняют друг друга. Так, при помощи метода
Фурье удобно решать задачи с нулевыми краевыми условиями:
<pj (t) =<ра (t) = 0, и произвольным начальным условием. Операцион-
Операционный метод, наоборот, проще применять в случае нулевого началь-
начального условия и произвольных краевых условий.
116. Рассмотрим еще задачу о распространении электри-
электрических колебаний вдоль длинных линий. Как известно (см.,
например, [4], § 7), напряжение и(х, t) и ток i(x, t) в линии
связаны системой дифференциальных уравнений с част-
частными производными
ди , „. , . di „
^ 1" ' D4)
¦т—\- Gu -\- С -т- = 0,
дх ' ' dt
где R — активное сопротивление, L — индуктивность, О — про-
проводимость изоляции и С—емкость, рассчитанные на единицу
длины линии. Будем считать, чго в начальный момент напря-
напряжение и ток вдоль линии равны нулю:
и(х, 0) = 0,
, 0) = 0.
D5)
Не задаваясь пока краевыми условиями, составим опера-
операторные уравнения, положив
и (х, t)=U (х, р), I (х, t)=I (х, р)
и учитывая, что по 1еореме дифференцирования оригинала
ди . ,, di . ,
10*
292
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
[Гл. VIII
а по теореме о дифференцировании по параметру
ди ^ dU dl _^_ dl
дх ~r~ dx' дх ~ dx
(для изображений (J и / вместо частных производных по х
мы пишем обыкновенные). После простых преобразований
операторная система примет вид
D6)
^dx
Это система обыкновенных дифференциальных уравне-
уравнений относительно изображений U и /(р считается величиной
постоянной). Для решения системы проще всего исключить
одну из неизвестных функций, например /. Дифференцируя
первое из уравнений по х и заменяя -т- его выражением,
и, JC
получим дифференциальное уравнение вюрого порядка
d-II
1 "N'" -G)?/—0. D7)
Его общее решение
U(x, р) =
D8)
где X = \/{Lp -f- R) (Ср -\- О). Функцию / найдем из первого
уравнения системы D6):
,, ] dU
Чтобы найти произвольные постоянные А и В (в их вы-
выражения будет входить величина р), нужно задать краевые
условия, которые Moryi быть весьма разнообразны. Пусть,
например, напряжения в начале и в конце линии (при л: = 0
и при х = 1) являются заданными функциями времени
и@, 0 = <Pi@> «С 0 = <Pj(9- E0)
Применяя преобразование Лапласа, получим краевые усло-
условия для уравнения D7):
U\x^ = F1(p), U\x.l = Fi(p), E1)
где Fx (p) = ? i @ и Fi (p) = <?i (t).
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
293
Подставляя краевые условия E1) в общее решение D8),
можно найти А и В, а затем и сами изображения U и /.
Однако эти изображения оказываются в большинстве слу-
случаев слишком сложными, и чтобы перейти от них к ориги-
оригиналам, требуются специальные приемы (см., например, [3], [6]).
Сделаем упрощающее предположение, что линия очень
длинная, и положим /=со. Тогда второе из краевых усло-
условий E1) отпадает и заменяется требованием ограниченности
изображений U(x, p) и I (х, р) при лг^-со. Если X выбрано
так, что ReX^>0, то eXv стремится к бесконечности при
х —*• со, и последнее требование приводит к равенству А = 0.
Перепишем первое из условий E1) в виде U\x = o — F(p) и
подставим его (в 48); получим B^F(p). Таким образом,
(J(x, p) = F (р) е
E2)
Даже при сделанном предположении переход к оригина-
оригиналам оказывается все же очень сложным, и мы ограничимся
рассмотрением частных случаев.
1. Линия без потерь: R = 0, G—0. В этом случае
U (х, p) = F (р)е -Р* *п, I (х, р) = Yt U^x' Pi
Оригиналы находятся немедленно по теореме запаздывания:
и(х, t) = y(t — х ]/LC), если t~^>x\/LC,
и (х, t) = 0, если t < х \/1С
(<p(f) = H(O, f) — напряжение в начале линии). Ток равен
-.АС"
напряжению, умноженному на I/ у-.
Процесс распространения напряжения и тока носит волно-
волновой характер. Напряжение ср (t), приложенное к началу линии,
перемещается вдоль линии со скоростью v— _ (в точке
х напряжение возникает в момент t = x\^LC; значит, ско-
скорость распространения v = — =-—_,.
294
ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
ГГл. VIIT
2. Линия без искажений: RC=LG. После простых
преобразований получим
(Lp + R) (Cp +G) =
Поэтому
U(x, р) = е
XF (p)
/RG)\
, I(х, р) = ^Т
Перейдем к оригиналам:
и(х, t) = e-
и (х, 0 = 0,
если f>xV~LC,
если t < х /1С.
Гс
Как и в случае линии без потерь, имеем l(x, t)= I/ у- u(x, t).
Таким образом, в линии без искажений процесс распростра-
распространения напряжения и тока также носит волновой характер,
с тем только огличием, что по мере продвижения волн по
линии они затухают благодаря множителю е~^^а%. Скорость
распространения волн, а гакже о i ношение напряжения к току
остаются постоянными.
Если в линиях без noiepb и без искажений картина рас-
распространения напряжения и тока сравнительно проста, то
в остальных случаях она значительно сложнее. Приведем
лишь еще один пример.
3. Линия без утечки и индуктивности: G=0,
/. = 0. (Этот случай приближенно осуществляется в подземном
или подводном кабеле, где благодаря хорошей изоляции
утечка практически отсутствует, а индуктивность играет не-
незначительную роль по сравнению с емкостью.) Из общей
формулы E2) получим
Предположим для простоты, что напряжение в начале линии
постоянно: ср(О —ц@>
= ua. Тогда F(/>)==—
U(x, р)=1Ь
Р
^e
\p
§ 3] УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Оригиналы найдем по формулам 3 и 1 табл. 3:
295
117. В заключение этого параграфа покажем, как, можно полу-
получить некоторые формулы соответствия, приведенные в табл. 3.
Начнем с формулы
yvt
E3)
Предоставляем читателю проверить, что при t-~ 0 оригинал стре-
стремится к нулю.
Интеграл Лапласа от оригинала равен
4-
yt
dt.
Сделаем подстановку: pt — z2, dt = ; тогда
00
F(j>)=—= \
dz,
E4)
со p*
где р =-^г~ ¦ Введем обозначение /ф)=\е *2 Ли
вычис-
вычислим этот интеграл при помощи специального приема — дифферен-
дифференцирования по параметру. Найдем /' (fJ), взяв интеграл от произ-
производной подынтегрального выражения по fi:
Замена переменной — = и, —^—^- = du приводит нас снова к ин-
интегралу / (Р):
со , Р2
/' О) = — 2 5 e~"'~^rfM=—2/(Р).
В результате мы пришли к дифференциальном) )равнению
/' (р) = —2/ (fi); его общее решение:
296 ПРИМЕНЕНИЯ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА [Гл VIII
Чтобы найти С, положим р = 0. Тогда
(интеграл Пуассона). Окончательно
Подставляя выражение для /(Р) в E4) и заменяя |3 =
лучим
«У/»
по-
пот. е. как раз требуемое изображение.
Дифференцируя обе части соответствия E3) по параметру а
\-Tt rv=ne {~Vp)'
придем к форм>ле 2 табл. 3:
Применим теорему об интегрировании оригинала
} 2 Уnt3 e t ' Р
E5)
и преобразуем интеграл слева при помощи подстановки -т- = у2,
а- г- a dt ady
t =-г-5, К^^тп -7=== 2 , получаем
4у r ty Yt У
At
t
2 К^^
E6)
2 У/
ЗАДАЧИ К ГЛ VIII
297
Введем функцию Ф(х)=—— V e~yi dy—интеграл вероятно-
Уя J
о
от
стей. Так как Ф (со) = —=\ е~у" dy=\, то интеграл E6) равен
оо
-у2 I а \
' аУ^1~Ф[2~у1)'
IV t
и формула соответствия E5) перепишется в виде
2Vir Р
(формула 3 табл. 3).
Остальные формулы табл. 3 в тексте книги не встречались, и
мы их выводить не будем.
ЗАДАЧИ К ГЛАВЕ VIII
1. Решить дифференциальные уравнения при заданных началь-
начальных условиях:
а) X — 2х + х = ? V, х@) = х @) = 0;
б) ? -f Зх + Зх + х = бе"', х@)=х @) = X @) = 0;
в) X — 3x + 2x=\2e3t, x @) = 2, i@)=6;
г) ^ + 4.v = 3sin г;+1Oc°s3^, л: @) = — 2, Л@)=3;
д) Jf — х = 4 sin t + 5 cos 2г-, х @) = — 1, л; @) = — 2.
2. Решить системы дифференциальных уравнений при заданных
начальных условиях:
a) x + 2x-{-2y=\0e;!i,
i=x+y
-@) =— 1, з»@) = 1, г@)=0;
г) х — Зх — 4у + 3 = 0, t х @) = Л @) = 0,
5 = 0 [:у@)=^@)=0.
ГЛАВА IX
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
§ 1. Определение дискретного преобразования
118. Изучая преобразования Лапласа и Фурье, мы в ка-
качестве оригиналов /(/)рассматривали функции непрерывного
аргумента. Большой интерес представляет аналог операцион-
операционного исчисления для случая, когда оригиналами служат функ-
функции целочисленного аргумента или последовательности.
Это новое исчисление, опирающееся на дискретное преобра-
преобразование Лапласа, в настоящее время является математической
основой теории линейных импульсных систем, т. е. таких
систем, работа которых связана с передачей и преобразова-
преобразованием последовательностей импульсов').
Начнем со следующего определения. Пусть дана после-
последовательность действительных или комплексных чисел
аф alt аь .... ап, ...,
которую будем кратко обозначать символом {ап}.
z-преобразованием последовательности \ап\ называется
функция комплексного переменного F(z), определенная рядом
Прежде всего докажем, что если последовательность {ап)
удовлетворяет условию
| ап К Ме°п, B)
') Наиболее полное изложение всех вопросов, связанных
с импульсными системами, содержится в книге Я. 3. Цыпкина
«Теория линейных импульсных систем», Физматгиз, 1963.
И
ОПРЕДЕЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
299
где УИ^>0 и а. — постоянные, то ряд сходится при
где /? = еа. Действительно, ряд мажорируется геометрической
прогрессией
\М
которая сходится, если |z|^>ea. Из доказанного следует, что
функция F(z) — аналитическая при | z | ^> R, а разложение A) —
ее ряд Лорана в окрестности бесконечно удаленной точки
(см.п.58). Ясно, что.г = оо— правильная точка и F(oo)^au.
Приведем один простой, но важный для дальнейшего
пример. Пусть
где b — любое число, не равное нулю. Так как | ап \ = \ b" | =
= | b |" = enln *', то, сравнивая с B), видим, что ряд A) схо-
сходится при | z | ^> | b | (а^1п]й|). /-преобразованием последо-
последовательности {Ьп\ служит функция
-ьш
C)
Отметим, что хотя ряд, определяющий г-преобразование,
сходится только при | z j ^> | Ъ I, сама функция F (г) оказалась
определенной и аналитической во всей плоскости, кроме
точки z^b. С подобным же явлением мы встречались и при
изучении преобразования Лапласа (см. cip. 195).
Если г-преобразование некоторой последовательности {ап\
являекя заданной функцией F(z), аналитической в бесконеч-
бесконечности, то чтобы найти саму последовательность \ап} (т. е.
найти обратное z-преобразование), нужно разложить функцию
F(z) в ряд Лорана в окрестности бесконечно удаленной
точки; этот ряд будет содержать только правильную чааь
(см. п. 58).
1
Например, если F(z) = -
B-1,B-2)'
шением примера 1 па стр. 131 —132, получим
то, пользуясь ре-
Воспользовавшись общими формулами для отыскания
коэффициентов ряда Лорана, легко записать выражения для
300
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
членов последовательности {ап} через функцию F(z). Для
этого нужно в формуле B2) на стр. 130 положить а = 0
(это соответствует разложению как в окрестности начала
координат, так и в окрестности бесконечно удаленной точки)
и заметить, что теперь коэффициенты правильной части ряда
обозначены не через с_„, а через ап:
D)
Здесь С—любая замкнутая кривая, окружающая все особые
точки функции F(z), в частности, окружность' с центром в
начале координат и достаточно большого радиуса.
Если, как это часто бывает, функция F(z) является ана-
аналитической во всей плоскости, за исключением конечного
числа особых точек (лежащих внутри контура С), то может
оказаться, что более удобно вычислять коэффициенты ап,
отыскивая вычеты подынтегральной функции в особых точках.
119. Во многих случаях бывает удобно ввести новую
независимую переменную q, положив
г = е«. E)
Если обозначить F (z) = F (еч) = F* (q), то
F* (q) = а0
... + апе^ -4-... = fj апег"*. F)
Функция F* (q) называется дискретным преобразованием
Лапласа последовательности {ап).
Напомним (см. п. 41), что соответствие между точками
плоскостей z и q, определенное равенством z = e9, не
взаимно однозначно; все точки д-\-2/гш, где ? = 0, ± 1,
±2, ..., соответствуют одной и той же точке z. Это значит,
что функция F* (q) — периодическая с чисто мнимым перио-
периодом 2тг(:
Если взять в плоскости q любую полосу, параллельную
действительной оси и шириной 2тт, то соответствие между ее
точками и точками плоскости z станет взаимно однозначным.
Положим q = a-\-lx и выберем в качестве основной полосу
§ И
ОПРЕДЕЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
301
— тс ^ т sg: тс. Точки, лежащие на границах этой полосы, пере-
переходят в точки отрицательной части действительной оси:
ea±,ic== — еа. ПОЭТОМу ПОлоса отображается на всю пло-
плоскость z с разрезом по отрицательной части действительной
оси; также будут отображаться и все полосы, ей параллель-
параллельные (в п. 41 полосы, изображенные на рис. 46, выбирались
так, что разрез в плоскости z шел по положительной части
действительной оси).
Ясно, что в силу периодичности функцию F* (q) можно
рассматривать только в основной полосе; в остальных поло-
полосах ее значения будут повто-
повторяться.
Так как | z | = | ea + h\ =ea,
то из сходимости г-преобразо-
вания при | z | ^> в1 следует схо-
сходимость дискретного преобра-
зования Лапласа при а^>а.
Функция F* (q) апалитична в
полуплоскости а^>а, и в част-
частности, в полуполосе о^>а,
— tt^'is^t:, заштрихованной
на рис. 123. Может случиться, что существует функция, ана-
аналитическая во всей полосе —тге^теСтс, за исключением ко-
конечного числа особых точек, и совпадающая с F* (q) в указан-
указанной полуполосе. Будем тогда говорить, что функция F* (q)
продолжена на всю полосу — тг ^ т =g: it. Ее особые точки
могут лежать только левее прямой а = а и на самой этой прямой.
Посмотрим, как преобразуем формула D) при замене
z = eq. Если С — окружность | z \ = R' ^> е\ то в основной
полосе плоскости q ей соответствует прямолинейный отрезок
Y\ — /т, 7-(-/тс], где f = 1п/?'^>а. Учитывая, чго dz = eqdq,
получим
G)
-Kl
Рис. 123.
T— 1
120. Пусть теперь нам задана функция <p(t), определен-
определенная при t^sO, и члены последовательности {ап} являются
значениями этой функции для равноотстоящих друг ог друга
значений аргумента
302 ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА |Гл IX
Построенная для этой последовательности функция
оо
-пТд (8)
называется дискретным преобразованием Лапласа функции
<р@> соответствующим периоду повторения Т. Отметим,
что если функция <р (f) является оригиналом для обычного
преобразования Лапласа, то для последовательности {<?(пТ)\
условие B), очевидно, выполняется: <р(яГ) | sg Afel'rl", где /И
и а — постоянные, определяющие рост оригинала <р (t) (см.
стр. 191).
Не обязательно считать, что последовательность значений
аргумента пТ начинается с нуля; иногда приходится рассмат-
рассматривать «смещенные» последовательности: ап = <р (яТ -\- Д Т),
где ДГ—постоянное смещение, не зависящее от п, и такое,
что 0<Д7<7.
Всегда можно изменить масштаб по оси t так, чтобы
период повторения стал равным I; для этого нужно умень-
уменьшить масштаб в Т раз, т. е. положить y(Jt) = f(t). Тогда
f
Смещенная последовательность, соответствующая периоду
повторения I, будет иметь вид \f(n-\-z.)\, где е = Д7/7" —
относительное смещение @<^е<^1).
Последовательность {/(я)} будем, как правило, обозна-
обозначать проще: /(я); ее называют также решетчатой функ-
функцией. Итак, всякая функция f(t), являющаяся оригиналом для
обычного преобразования Лапласа, «порождает» решетчатую
функцию /(и), для которой определено дискретное преоб-
преобразование Лапласа F*(<?)• Соо1ветствие между f(n) (ориги-
(оригиналом) и F* (q) (изображением) будем записывать в виде
f(n)^-F*(q) или f(<?)^-/('0-
Дискретное преобразование Лапласа называют также
D-преобразованием и пишут F* (q) = D {/(«)}•
Решетчатая функция /(я) определена только при я = 0,
1, 2, ... В дальнейшем будем считав, чш /(я)—0 при
ОПРЕДЕЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
303
и = —1, —2, ... Тогда формула D) будет справедлива и
для целых отрицательных значений я. В самом деле, функ-
функция F(z) аналитическая в бесконечно удаленной точке, и
поэтому \F(z)\^M (М — постоянная) при z\^R, где R —
радиус окружности С, по которой производится интегриро-
интегрирование. Пользуясь простейшей оценкой модуля интеграла (см.
стр. 51), получим
ап! < ^ MRn~l • 21Z% = MRn -*¦ °
при R->oo, если л<^0. Это и значит, что /(я) = а„ = 0
при я<^0.
В дальнейшем мы всегда будем пользоваться следующими
обозначениями: я — номер члена последовательности {ап},
определяющей данную решетчатую функцию; в правой части
равенства F) ему соответствует слагаемое апе~щ. Аргумент
решетчатой функции принимает только целые значения, при-
причем для отрицательных значений аргумента решетчатая функ-
функция равна нулю. Так, например, если k — целое положитель-
положительное число, то fin — k) — решетчатая функция, равная нулю
при n<^k, и ее дискретное преобразование определяется
рядом
со оа
Ц /(«-*)*-»= 2 f(n-k)e.
Если же взять функцию /(я -)- k), то ее D-преобразова-
оо
ние будет иметь вид ^ f(n ~Ь *) e"q-
л=0
Заметим еще следующее. Значения порождающей функ-
функции f(t) при t = n-\-e. (п = 0, 1, 2, ...) или, что то же
самое, значения функции f(t-\-z) при ? = 0, 1, 2, ... @<^
<^е<^1) определяют смещенную последовательность, кото-
которую будем также называть смещенной решетчатой функ-
функцией и обозначать /е(я); соответствующее дискретное преоб-
преобразование Лапласа обозначим /%¦ (q). Для того, чтобы были
определены смещенные решетчатые функции /е(л), соответ-
соответствующие всевозможным значениям г @<^г<Ч), функция
f(t) должна быть определена при всех значениях ^^0,
тогда как сама решетчатая функция /(я) определяется только
значениями функции fit) при t=0, 1, 2, ... Поэтому любое
304
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
изменение порождающей функции f(t), при котором не изме-
изменятся ее значения при ? = 0, 1, 2, ..., не отразится на
решетчатой функции f(n).
Рассмотрим некоторые простые примеры.
Пример 1. Пусть f(t) = I] (t) — единичная функция: г) (^р= 1
при t^O и •<](?)= 0 при t <0. Воспользуемся найденным г-преоб-
разованием последовательности {Ьп\ (см. C)); положив 6 = 1 и
z — ei, получим требуемое соответствие
iW-A. (Ю)
Пример 2. Пусть / (t) = eat. Теперь нужно положить b = еа и
/>Q,fl • / 1 1 \
Для смещенной решетчатой функции/е («) =йа(Л+?1 получим
A2)
В левых частях соответствий A1) и A2) должны, строго го-
говоря, стоять функции, совпадающие соответственно с еап или
gatn+s) ПрН п==о, 1, 2, ... и равные нулю при п = — 1, —2, ...
Это замечание относится и к другим формулам соответствия и в
дальнейшем специально повторяться не будет.
Пример 3. Пусть /@) = а0и /(л) = 0 при «=1,2, ...В
соответствии с (9) изображение F* (q) = а0. Это значит, что посто-
постоянному изображению соответствует оригинал, значение которого
при п = 0 совпадает с изображением и который равен нулю при
всех других значениях п.
§ 2. Свойства дискретного преобразования
121. В этом параграфе будут рассмотрены основные свойства
дискретного преобразования Лапласа (D-преобразования). Ввиду
того, что эти свойства аналогичны соответствующим свойствам
обычного преобразования Лапласа, мы будем по возможности
кратки в их формулировках и особенно в доказательствах.
В дальнейшем, как правило, решетчатые функции-оригиналы
обозначаются символами /(я), g(n), ..., а их изображения —
соответственно F* (q), G* (q), ... Для обычного же преобра-
преобразования Лапласа оригиналы будут обозначаться fit), git), ...,
а их изображения — F(p), G(p), ...
I. Теорема линейности. Для любых действитель-
действительных или комплексных постоянных А и В
АЦп) -|- Bg(ri) -.- AF* (q) 4- BG" (q). A3)
§ 2]
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
305
Доказательство немедленно вытекает из самого определе-
определения преобразования. Пользуясь этой теоремой и формулой A1),
легко получить соответствие
sin шя ~^-
ei sin о)
е-ч — 2е<7 cos о + 1
A4)
При о> = 1С изображение тождественно равно нулю; так и
должно быть, потому что при этом и сама решетчатая функция
sin т.п равна нулю.
Предоставляем читателю найти изображения cos ши, sh од
и ch u)« (они приведены в табл. 4).
II. Теорема затухания (смещение независи-
независимого переменного в области изображения). Если
а — любое действительное или комплексное число, то
еап f (n) -r=- F* (q — a). A5)
И здесь доказательство сразу следует из определения (9):
оо
eanf(n) -^ 2 Л») еме-«п = F*(q — a).
Как и для обычного преобразования Лапласа, с помощью
этой теоремы легко получить изображения для произведе-
произведений тригонометрических и гиперболических функций на по-
показательную.
III. Теоремы запаздывания и опережения
(смещение независимой переменной в области
оригинала). Ее ч постоянная k — целое положительное
число, то
/(« _ k) - e-«kF* (q), A6)
fin + k) -~ e"k [F* iq) - 2 fir) e~*r]. A7)
Напомним, что под /(и — k) понимается решетчатая функ-
функция с аргументом п — k; она равна нулю при я — k<^0.
Так, например, если /(и) = еап, то /(и — 3) — решетчатая функ-
функция, равная нулю при п = 0, 1, 2 и равная еа ("~3' при п = 3, 4,...
Чтобы доказать формулу A6), запишем соответствие
306 ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Полагая под знаком суммы п — ? = г, получим
[Гл IX
(от обозначения индекса суммирования сумма не зависит).
Для доказательства формулы A7) произведем замену
п -\- k = г; тогда
f(n + k) - 2 f (n + k) e~«n =
k-\
/• = 0
Применяя формулы A6) и A0), получим изображение за-
запаздывающей единичной функции
1
' — 1
1
(еЧ— 1)
A8)
в частности, т](я — 1) -г=- q _ .
122. Пусть порождающая функция f(t, x) зависит не
только от основного переменного t, но и от параметра х;
тогда и соответствующая решетчатая функция /(«, х) также
зависит от этою параметра и
/(я, х)^- F*(q, х)=
Будем считать, что выполнены условия, при соблюдении
которых правую часть равенства можно почленно дифферен-
дифференцировать по х. Тогда
и мы получаем следующую теорему:
IV. Теорема о дифференцировании по пара-
параметру. Если f(n, х) -• Г* (q, x), то
dj(n, у) . dF'{q,x)
дх дх
B0)
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
307
Пусть роль параметра х играет относительное смеще-
смещение е, т. е. f(t, е) = /(t -\- е.) и, следовательно, /(я, s) =
^/е(п). Частная производная функции f(t-\-s) по параметру е
совпадает с производной этой" функции по всему аргументу,
т. е. с f'(t-\-z). Но функция f'(t-\-&) порождает смещенную
решетчатую функцию f\ (/г), и поэтому
123. Переходя к теоремам дифференцирования и интег-
интегрирования, изменим по сравнению с § 2 гл. VII порядок их
рассмотрения и начнем с соответствующих георем для изо-
изображения.
V. Теорема о дифференцировании изображе-
н и я. Дифференцирование изображения соответствует
умножению оригинала (решетчатой функции) на — п
-nf(n)~F*'(q). B2)
Теорема следует из возможности почленного дифференци-
дифференцирования ряда (9), определяющего изображение F* (<7); обосно-
обосновать эту возможность предоставляем читателю самостоятельно.
Повторное дифференцирование приводит к общей фор-
формуле
(—1)* я*/(л) — F* <*>(?). B3)
Применяя эту формулу к соответствию
довашльно получим
еч „ <
еЧ
—г, после-
— 1
Значительно более простой вид имеют изображения для
последовательностей, определяемых биномиальными коэффи-
коэффициентами
л (и— 1) . еЧ п(п — 1) (га — 2) . еЧ
2' " (еЧ—\у
Общая формула такова:
п(п—\) (п —
3!
от!
B4)
308
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл IX
Условимся произведение т множителей х(х—1)...(лг —
— т-\-\), из коюрых каждый следующий на единицу меньше
предыдущего, называть факториальной функцией и обозна-
обозначать символом х^тУ Тогда доказываемая нами формула B4)
кратко запишется так:
т\
B4')
Формулу B4) легко получить, сформулировав теорему о
дифференцировании изображения в терминах 2-преобразова-
ния. Согласно определению
со
F(z)= 2 anz'\
Последовательно дифференцируя, получим
F"{z)= ? п (п + \) anz~ ^\ ...
п=0
п=0
Отсюда видно, что
{пап} ^ - zF (z), \n{n-\-\)an}^-z'-F"{z), ...
). B5)
Произведя дифференцирование и заменив z на eq, получим
правые части соответствий в терминах D-преобразования (мы
пользуемся для D-преобразования и z-преобразования одним
и тем же символом соответствия).
Применим формулу B5) к единичной решетчатой функ-
функции \an}—ri{n); для нее а„=1 и F(z) = -^-r = I -f- г.
Последовательные производные равны
= (— \)mm\(z —
Поэтому
{n{n-\- 1). ..(n-\-m —
Воспользуемся еще теоремой запаздывания (см. формулу
A6)), положив k = m—1; при этом в последней формуле
нужно всюду заменить л на п — т-\-\. Расположив миожи-
§ 21
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
309
тели в обратном порядке и разделив на т\, приходим к фор-
формуле B4).
VI. Теорема об интегрировании изображе-
изображения. Если /@) = 0 и если принять, что
=0,то
B6)
Действительно, в силу условия теоремы
/1=1
Интегрируя и замечая, что \ e~qndq = , приходим к до-
ч
казываемой теореме (законность почленного интегрирования
ряда легко обосновывается).
1
Например, если /(п) = -г\(п—1), то F*(q) =
еЧ—\
dq -
-In
Заметим, что решетчатая функция ^? 1 соответствует по-
последовательности I—>.
124. Введем определение конечных разностей функции1).
Пусть f(t) — заданная функция и M — h — фиксированное
приращение независимого переменного t (шаг). Первой раз-
разностью или разностью первого порядка называется выра-
выражение
bf(t)=f(t + h)-f(t). B7)
Аналогично, разность второго порядка определяется как
ду @ = д д/(о=
J) Понятие конечной разности лежит в основе теории интерпо-
интерполяции и играет важную роль в численных методах анализа (см.,
например, книгу Б. П. Д е м и д о в и ч а и И. А. Марона, Основы
вычислительной математики, «Наука», 1967).
310
Дискретное преобразование лапласа
[Гл. IX
B8)
Так как Д/0-{-я)=/0 + Щ — f(t -fft), то
Д*/0) =/0 + 2/0 - 2/0 -f К) + /0).
, Вообще, разность k-то порядка равна
Д*/0) = ДД*/^) = Д*" 70 + н) — A*"V0). B9)
Все последовательные разности можно выразить через
значения функции /0) в точках t-\-rh (r = 0, 1,2,...). Так,
Д3/0) =/0 + ЗА) - 3/0 + 2/0 + 3/0 -f A) — fit).
Общая формула такова:
„г
где 0,=;
+ Clf{t + (А - 2) h) -... + (- \)k f(t), C0)
])(k r+\) k[r] л
!—-=—j биномиальные коэф-
коэфj
фициенты.
Обратно, значения функции /0) в точках t-\-h, t -j- 2ft,...
..., t-\-kh можно выразить через /0), Д/0) Д*/0)
Имеем /0 + А)/(О + Д/0)
и, вообще,
/0 + АЙ) = /0) + аД/0) + С1Д9/0) + ... + А*/0). C1)
Когда речь идет о конечных разностях решетчатой функ-
функции f(n), то шаг h считают равным 1 (периоду повторения)
и Д/(я) = /(л-(- 1)—f(n). Например, если f(n) = an, то
Д/(л) = а; все последующие разности этой функции, очевидно,
равны нулю.
Если f{n) = n\ то b.f(n) =
Да/(я) = 2, Д;1/(«) = Д4/(«) = ¦ ¦ ¦ = 0.
Легко проверть, чго последовательные разности функ-
функции /(л) = и* являются многочленами понижающихся степе-
степеней и \kf(n) = k\ Все последующие разности равны нулю.
Очень просю выражаются разности факториальных
функций:
они похожи на производные степенной функции.
свойства дискретного преобразования
311
Для показательной функции еап первая разность &еап =
— еа^< — еап — (еа~1)еап. Вторая разность AV" = (efl-
— IK ean и, вообще,
Д*еагг = (еа— \)kean.
125. Покажем, что при изучении дискретного преобразо-
преобразования Лапласа конечные разности играют роль, аналогичную
той, которую играют производные для обычного преобразо-
преобразования Лапласа.
VII. Теорема о разности решетчатой функ-
функции. Если f(n) -н- F* (д), то
Д/(я) -г- (е" - 1) F* {q) - еЩО). C2)
Доказательство следует из теоремы опережения (см. фор-
формулу A7)), согласно которой f(n-\-l)-^-e4[F*(g)—/@)].
Применяя к разности Д/(я)=/(я-|-1)—/(я) теорему ли-
линейности, поучаем требуемую формулу.
Повторно применяя формулу C2), получим сначала изоб-
изображение разности второго порядка:
А9/(я) ^- (е? —\fF* (q) — (eq — 1) е?/@) — е?Д/@), C3)
а затем и любого А-го порядка:
AV(«) ^- (е? - IL F* (?) - е9 [(ei — I)*-' /@) +
-Не'
Д/@) +... + (е" - 1) Д*"* /@) + Д* 1 /@)]. C4)
Можно было бы заменить все разности Дг/@) их выра-
выражениями через значения функции в соответствующих точках
по формуле C0), однако тогда формула соответствия при-
приняла бы более громоздкий вид. Заметим только, что если
/@) = 0, Д/@) = Д*/@) = ... = Д*-1/@) = 0(тогдаи/A) =
= /B) = . .. = /(?—1) = 0), то формула C4) упрощается,
^kf(n)-.--(eq—\)kF*(q). C5)
При обычном преобразовании Лапласа это соответствует
случаю, когда начальные значения оригинала /0) и его про-
производных равны нулю.
Если в анализе обратным действием по отношению к
дифференцированию является интегрирование, то при рассмот-
рассмотрении конечных разностей обратным действием образованию
первой разности является суммирование.
312
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл. IX
Суммой решетчатой функции /(я) называется решет-
решетчатая функция g(n), определенная следующим образом:
п-\
(я=1, 2,...). C6)
В частности, g(l)=/@), g-B) = /@) +/A),...
Ясно, что исходная функция /(я) служит для функции
g{n) первой разностью:
Д^-(я) = ^(я-|-1) — g{n)=f{n). C6')
VIII. Теорема о сумме решетчатой функции.
я-1
я-1
Пусть
Так как g-@) = 0, то по формуле C5) \g{ri)—f{ri)-r-{eq—
— l)Q*(<l) = F*(q), т. е.
и формула C7) доказана.
126. Между значениями решетчатой функции-оригинала и
ее изображения в нуле и на бесконечности имеют место со-
соотношения, подобные установленным в п. 89 для обычного
преобразования Лапласа. Напомним, что функция F(z), явля-
являющаяся ^-преобразованием последовательности /(я), анали-
тична в бесконечности (см. п. 118) и
Поэтому
C8)
Заметим, что если z-*co, то q-+oo, так что Re q -*¦ -|- со.
Это предполагается в формуле C8) и в других формулах,
на ней основанных. Из определения функции F (z) (см. равен-
§ 2] СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ 313
С1во A)) получаем также lim z [F (z) — а0]^а1=/A).Поэтому
Аналогично,
lim {e^ [F* (q) — /@)] - /A) е") =/B) и т. д.
Рассмотрим соответствие
со
если предположить, что ряд^ tp (я) сходится, то в этом со-
соответствии можно положить q = 0, и тогда
C9)
л=0
Так, в частности будет, если величина а, входящая в усло-
условие B) роста оригинала, отрицательна (см. также п. 92).
Пусть теперь функция ср (л) является первой разностью
решетчатой функции f(n), для которой существует предел
Тогда ряд C9) сходится, так как ^(n) =
п=0 , п=0 п=0
Поэтому Ф*@)=/(со)— /@).
Если /(я) -г=- F* (?), то по формуле C2)
Д/(л) = <р (я) -^ (е? - 1) F* (?) - /@) = Ф* (q).
Переходя к пределу при q->0 и пользуясь значением Ф*@),
получим
lim (е? — 1) F* (<?) = /(со). D0)
Отсюда, в частности, следует, что если ?^0 — правиль-
правильная точка для изображения F* (<?), то /(оо)^0. Предостав-
Предоставляем читателю самостоятельно подобрать примеры, иллюст-
иллюстрирующие выведенные предельные cooiношения.
314
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
127. Введем определение свертки решетчатых функций
D1)
/¦=0
Легко проверить, что свертка коммутативна, т. е. f*g=g*f.
Ясно, что свертка является решетчатой функцией.
IX. Теорема умножения изображений. Произве-
Произведению изображений соответствует свертка оригиналов
t(n)*g{n)---F*{q)Q*{q).
Для доказательства умножим обе части равенства
D2)
на F* (q) и внесем этот множитель под знак суммы:
По теореме запаздывания e~qrF* (q) -~ f (n — г), и по теоре-
теореме линейности
r=0
/-=0 /-=0
л значения /(/г — г) равны нулю. Теорема
так как при
доказана.
Сверткой изображений называется функция
1 Т
=2^ J F*{s)G*{<l-s)ds.
D3)
Предполагается, что функции F* и G* аналитичны в полу-
полуплоскости Re«7^>a и 7^>а- Тогда свертка аналитична в
полуплоскости Re q ^> a -j- 7. В этой полуплоскости Re(q—
— s)^>a, когда точка s находится на отрезке интегрирова-
интегрирования [f — /~, т -\- /л], и поэтому обе функции, стоящие под
знаком интеграла в правой части D2), — аналитические. Предо-
Предоставляем читателю проверить, что свертка изображений 1ак-
же обладает свойством коммутагивносш.
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ
315
X. Теорема умножения оригиналов. Произведе-
Произведению оригиналов соответствует свертка изображений:
f{n)g{n)~F*(q)*Q*{q). D4)
Доказательство этой теоремы удобнее провести в терми-
терминах ^-преобразования. Обозначим f(n) = an, g(n) = bn; тогда
п=0
= 2 bnz'n. Пусть оба ряда сходят-
ся при \z\~^>R.. Рассмотрим интеграл (называемый сверткой
г-преобразований)
i$f«G(!)f. D5,
С
где С — окружность |С | =R'^>R и \z[^>RR' (последнее
условие обеспечивает аналитичность G(-p) как функции С
на окружности С и внутри нее). Интеграл D5) сразу вычис-
вычисляется по теореме о вычетах, если заменить функции F и О
их разложениями и найти коэффициент при С-'
С и=0
п=0
— ао»о -У ~2 Г • • • "Г -^г + • ¦ •
Отсюда следует, что интеграл D5) яг;ляется ^-преобразованием
последовательности {anbn\, т.е. решетчатой функции f(n) g(n).
Переходя к D-преобразованию, положим ? = es, d\.=
— esds,z = ei. При этом F((,) = F* (s), Q(z/Q = G(e'1's) =
= Q* (q — s) и окружность С преобразуется в отрезок [7 — ^i,
"Y —j— -icij, где 7 = ?^'^>eff = a. Таким образом, интегралы D3)
и D5) равны между собой; это и значит, что свертка
F* (q) * G'* (q) есть D-преобразование произведения f(n)g(n).
Пользуясь результатами двух последних пунктов, чита-
читатель сможет самостоятельно доказать формулу Парсеваля
(см. п. 106) для дискретного преобразования Лапласа: если
со
для решетчатой функции f(n) сходится ряд ^ [f(n)f, то
7!=0
316 ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА [Гл. IX
Таблица 4
Формулы соответствия для ^-преобразования
[омср
фор-
улы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Оригинал / (п) ')
{0 при п <0,
1 при п^О
n()
пеап
sin «я
Изображение F* (<?)
gg—1
(gg — 1)а
—IM
— IK
{el — еау2
едеа (ед _[_ е
(gg — еаУ
е? sin <o
— 2еЧ cos м +
(gg COS tt>)gg
? — 2е« cos <й +
') При и<0 псе оригиналы /(и) считаются равными нулю.
§ 3]
ФОРМУЛЫ РАЗЛОЖЕНИЯ 317
Продолжение табл. 4
Номер
фор-
формулы
Оригинал / (п)
Изображение F* iq)
15
16
17
18
19
20
sh an
chwra
еап sin шп
еап cos ш/г
sin <яп
п
(_ 1)и sin мя
e2? — 2e? ch ш -f 1
(el — ch <o) ei
e"i — 2e4 ch ш +
sin <o
eL>? — 2e?ga cos <o
(el — ea cos а)
e2? — 2e? cos <o -[-
+ arctg -
»— arctg-
sin to
— cos со
sin <o
+ cos и
128. Приведем в заключение краткую таблицу формул
соответствия для дискретного преобразования Лапласа (табл. 4);
формулы для ^-преобразования получаются путем замены еч на г.
Более подробные таблицы такого рода содержатся в книгах
Я. 3. Цыпк и н, Теория линейных импульсных систем, Физ-
матгиз, 1963 (в терминах D-преобразования) и Э. Джури,
Импульсные системы автоматического регулирования, Физмат-
гиз, 1963 (в терминах ^-преобразования). Впрочем, и приве-
приведенную таблицу легко расширить при помощи изложенных
свойств дискретного преобразования.
§ 3. Формулы разложения
129. Общие формулы для отыскания оригинала по задан-
заданному изображению были приведены в § 1; это — формула D)
в терминах ^-преобразования и формула G) в терминах D-
преобразования. В этом параграфе мы рассмотрим наиболее
важный для практического применения дискретного преобра-
преобразования случай, когда изображение является рациональной
функцией от еч:
Г* W,) = g* ^ = J^riJrflf-iiO- _1_Л • ' °)
318
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА (Гл. IX
В терминах ^-преобразования этому соответствует отношение
двух многочленов
8 (г)— Ь
причем степень числителя не может превышать степени зна-
знаменателя (/я==сг), так как z = oo — правильная точка для
функции F (z) (см. п. 118).
Если т = г, то можно разделить числитель на знамена-
знаменатель и выделить целую часть; ясно, что она будет равна
ciyjba = F (оо) = F* (сю). В соответствии с формулой C8) на
стр. 312 это будет значение оригинала f{n) при п = 0. Остав-
Оставшаяся дробная часть F (z) представляет уже правильную дробь,
равную нулю на бесконечности; ей соответствует оригинал,
равный нулю при и = 0.
В дальнейшем всегда предполагается, что целая часть (ес-
(если она есть) уже выделена и дробь D7) — правильная, т. е.
/w</.
Как и в п. 99, требуемые формулы получаются путем
разложения рациональной функции F(z) = C(z)jB(z) на прос-
простейшие дроби. Пусть сначала все корни zk знаменателя В (г)
простые; они являются простыми полюсами функции F (z) и
поэтому ее разложение на простые дроби имеет вид
Коэффициенты dk — вычеты F (z) в простых полюсах, следо-
следовательно, dk = C (zk) j В' (zk).
Перейдем к-переменной <у(,г = е<?) и обозначим ,гА =
= е[а 2к — eq^\ тогда
С* (Я) _ V *k ия,
B*(q) ~~ Li e4 — e<>k- ^°>
Выражения для коэффициентов разложения можно записать
в виде
В* (q)
обозначая точкой дифференцирование по еч.
D9)
ФОРМУЛЫ РАЗЛОЖЕНИЯ
319
Применим теперь к уже встречавшемуся соответствию
еЧ
еап ~ q_ a теорему запаздывания, положив в формуле A6)
k=l:
1 ( 0, если л = 0,
^-^--^(я), где ф(я) = | .„,„_,, _._.. ^, E0)
Применив теорему линейности, получим из D8) и E0) фор-
формулу разложения
к=\
правую часть которой следует при п = 0 заменить нулем; в
последующих аналогичных формулах это будет всегда под-
подразумеваться.
Проследим, как ведут себя отдельные оригиналы-слагае-
оригиналы-слагаемые в сумме E1) при я->оо. Если ! zk \ = \ ечь |^> 1, то
гА|^>0 и je* | —»¦ оо при п->оо; значит, соот-
j р ; , соот
ветствующее слагаемое оригинала по модулю неограниченно
возрастает.
Если \zk\<^\, то Re^<^0, и соответствующее слагае-
слагаемое оригинала стремится к нулю: [ е?*™ | -> 0. В частности,
корнюгд,=^0 (при Re^ = — оо) соответствует в оригинале
слагаемое, равное dk при п=\ и 0 при /г^>1.
Наконец, если \zk\ = \, т. е. 2А = е"Ч то соответствую-
соответствующее слагаемое оригинала dke f*("~ ' — функция с постоянным
модулем | dk | и колеблющимся аргументом.
Если знаменатель B(z) имеет корень ,гй=1,тоон играет
ту же роль, что и корень /) = 0 в формулах разложения
обычного преобразования Лапласа. В этом случае ^A = 0, и
соответствующее слагаемое есть постоянная решетчатая фун-
функция dk-r\(n — 1).
Если один из корней знаменателя В (z) равен 1, то, вве-
введя обозначение B*(q) = (e4—\)B\(q), легко получить ана-
аналог формулы F7) п. 99:
А*{д)
Л* (qk)
E2)
320
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИИ ЛАПЛАСА
[Гл IX
Если коэффициешы многочленов C(z) и В (г) — дейС1ви-
тельпые числа, то комплексно-сопряженным корням знамена-
знаменателя В (z) соответствуют комплексно-сопряженные слагаемые
в суммах, входящих в правые части E1) или E2). Эги сла-
слагаемые можно объединить, получая линейные комбинации ре-
решетчатых функций е cos ря и еап sin ря с действительными
коэффициентами (это будет аналог формулы F8) п. 99).
Если все корни знаменателя В (z) простые и по модулю
не превосходят единицы, то слагаемые оригинала, соответст-
соответствующие корням с модулями, равными 1, характеризуют уста-
установившийся колебательный процесс, так как все остальные
слагаемые стремятся к нулю при «->со (см. стр. 241).
130. Перейдем к изучению общего случая, когда знамена-
знаменатель В (z) имеет кратные корни. Пусть, например, корень а
имеет кратность s. Запишем разложение функции F(z) в виде
4 ' а (г) z — cl- ¦ ^ —^ v- -/
E3)
где ®(z) — сумма всех остальных слагаемых, отвечающих
другим корням. Найдем прежде всего оригинал, соответствую-
соответствующий изображению (z — а)" или (еч — еау, где еа = <х. Бу-
Будем опираться на формулу B4'), полагая в ней яг = м—1:
Применим сначала теорему затухания (формула A5)):
е (ч— 1)! ~ (еЧ~а — \у (el —еа)-"
а затем теорему запаздывания (при k = \);
(v-1)!
(el — i
E4)
(числовой множитель е"^' перенесен в левую часть соот-
соответствия). Так как (я — I)!4 — 1 !=(,; — 1)(я — 2).. .(я — (v — 1)),
то оригинал в левой части равен нулю при я== 1, 2, ..., v— 1
(кроме того, он равен нулю и при л = 0). При ч=1 мы
снова возвращаемся к формуле E0), если условился, что
jct°l ===== 1 и 01=^1.
СВЯЗЬ МЕЖДУ ПРЕОБРАЗОВАНИЯМИ
321
Формула E4) позволяет найти оригиналы для каждого
слагаемого в разложении E3) на простейшие дроби и запи-
записать общий вид соответствия:
С*(д) ¦ V
B*(q) ¦
E5)
a v = l
где символ а под знаком внешней суммы означает суммиро-
суммирование по всем значениям а, соответствующим корням B(z).
Можно написать общие выражения для коэффициентов d4.
Переписав разложение E3) в виде
F^K*-*)* ==<*, + • ¦• + <*,(г-яГ' + ..•
...+ ^B-*)*-'+?(*)(*-а)*,
замечаем, что d, есть (s—v)-ft коэффициент разложения ле-
левой части в ряд Тейлора по степеням (г — а). Поэтому
_
«V —
B(z)
E6)
При v = l получаем d\ — вычет в кратном полюсе.
§ 4. Связь между преобразованием Лапласа,
^-преобразованием и преобразованием
Лапласа — Стилтьеса
131. Покажем, как можно прийти к дискретному пре-
преобразованию Лапласа, совершая некоторый предельный пере-
переход в обычном преобразовании Лапласа. Этот переход
в значительной мере выясняет физический смысл дискретного
преобразования решетчатых функций и его связь с работой
импульсных систем.
Возьмем некоторый оригинал f(t) и соответствующую
ему ступенчатую функцию /* (t), равную /(я) в каждом интер-
интервале [я, л —|— 1) (т. е. при л^t<^n-\- 1). Эту ступенчатую
функцию можно записать в виде суммы
f*(t) =
-л)-1('-(я+1)I-
E7)
л «О
Построение графиков функций f*(t) и tj(? — я) — т](? —
— (я-)-1)) показано на стр. 234 (нужно только на рис. 111
и 112 считать, что in = n).
11 И. Г. Арамановнч и др.
322
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
(Гл. IX
Каждый отдельный прямоугольный импульс — слагаемое
в формуле E5) — деформируем, не изменяя площади соот-
соответствующего прямоугольника, а именно: строим- прямоуголь-
прямоугольник, основанием которого служит отрезок между точками л
и я-f-x (длины х), а высота равна —/(л). Иначе говоря, мы
уменьшаем время действия импульса, сохраняя его величину.
Сумму таких деформированных импульсов обозначим через f*(t):
= 2
t1\(t— Я)— Y](< — I
E8)
Ясно, что в каждом из интервалов [л, л -j- х) функция /* (t)
равна —f{n), а вне этих интервалов она равна нулю.
Вспоминая формулу для изображения единичного импульса
(см. п. 85), будем иметь
е
рх
E9)
(это обычное, а не дискретное преобразование Лапласа!).
Перейдем формально к пределу при х—> 0; это означает,
что мы переходим к последовательности дискретных мгно-
мгновенных импульсов, равных по величине f(n). Так как
• 1 при х —0,
то в правой части формулы E9) получим ^/(п)е~рп, т. е.
п = 0
дискретное преобразование Лапласа решетчатой функции /(л)
(переменная, от которой зависит F*, обозначена теперь че-
через р, а не через д, как раньше).
Таким образом, дискретное преобразование Лапласа решет-
решетчатой функции /(л) в некотором смысле близко к обычному
преобразованию Лапласа функции /* (t) при малых т.
Осуществим только что указанный предельный переход
несколько иначе. Вместо функции/*@ возьмем функцию /Д0>
равную
-'0-1
F0)
л=0
§ 4]
СВЯЗЬ МЕЖДУ ПРЕОБРАЗОВАНИЯМИ
323
Отличие ее от функции /* (t) состоит в том, что на каждом
интервале [п, л —|— т) она равна не постоянной величине—/(и),
а —/@; в"е этих интервалов она тоже равна нулю1). До-
Довольно ясно, что если функция f(t) непрерывна, то при х—-0
получается та же дискретная последовательность импульсов,
что и раньше; поэтому можно считать, что изображения функ-
функций /ДО и f*(t) при т—-0 будут сближаться.
Функция /т (t) представляет собой произведение двух
оригиналов; через F (р) обозначим изображение первого множи-
множителя: /@ -= F (р). Второй множитель есть сумма единичных
импульсов, поделенная па длительность импульса х; изобра-
1р
жение такой суммы равно
(см. стр. 205; в дока-
дока——-.
занном там соответствии следует положить Т= 1).
По теореме умножения оригиналов для преобразования
Лапласа (см. п. 94)
F1)
1 —ICO
При х —0, как уже было отмечено, правая часть будет при-
приближаться к F* (р) — дискретному преобразованию Лапласа
решетчатой функции /(л):
да dz F2)
7 —ico
(последнее равенство написано в силу коммутативности
свертки).
') Предел правой части равенства F0) можно записать очень
компактно, если воспользоваться определением 8-функции, данным
в п. 88. Каждое слагаемое под знаком суммы при т-~0 представ-
представляет производную сдвинутой единичной функции, т. е. Ь (t — n).
GO
Поэтому lim /j (t) = У /@ 5 {t — п).
^о л=о
11»
324
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
(Гл IX
Как указано в п. 94, линия интегрирования разделяет осо-
особые точки обоих множителей в подынтегральном выражении.
Функция -г —г имеет бесконечное число особых точек (полю-
(полюсов первого порядка), лежащих на мнимой оси; это корни
уравнения 1—е'г = 0, т. е. точки 2ft = 2?i«, где ? = 0, ± 1,
±2, ... Если переменную z заменить на р—z, где р
фиксировано, то корнями
будут точки р -\- 2Ы1 (рис.
124). Пусть, далее, изобра-
изображение F(z) аналитично при
Rez^>a; так как f^>a, то
все особые точки F (z) ле-
лежат левее линии интегриро-
интегрирования.
Как обычно, вычисление
интегралов вида F2) поста-
постараемся свести к вычислению
интегралов по замкнутым
контурам (рис. 124). При
такой замене надо уметь вы-
вычислять интегралы по дугам
окружностей"; часто бывает,
что эти интегралы стремят-
стремятся к нулю при R — со (как это было, например, в лемме Жор-
дана). В нашем случае, если F(z) имеет на бесконечности нуль
второго или более высокого порядка, т. е. разложение F{z)
в ряд Лорана имеет вид
F3)
то интеграл по дуге CR радиуса R, расположенной левее
прямой Re z = 7> стремится к нулю при R—• со. Доказатель-
Доказательство этого совершенно аналогично приведенному в п. 67,
нужно только учесть, что в полуплоскости Rez<^i второй
множитель подынтегрального выражения ограничен.
С дугой С/? дело обстоит сложнее, так как она может
проходить через особые точки подынтегральной функции или
приближаться к этим точкам. Однако если выбрать только
такие значения R, для которых рассюяние особых точек
от дуги С'х превосходит некоторое положительное число,
Рис. 124.
§4]
СВЯЗЬ МЕЖДУ ПРЕОБРАЗОВАНИЯМИ
325
то можно доказать, что и на Cj? второй множитель подын-
подынтегрального выражения ограничен и интеграл также стремится
к нулю при R—¦ оо. (Именно об этом случае шла речь в за-
замечании на стр. 237; там же указаны книги, в которых сде-
сделанные утверждения доказываются.)
Рассмотрим контур, состоящий из прямой Re z = т и дуги
окружности С'%, выбранной как указано выше. Этот контур
обходится по часовой стрелке; вычеты подынтегральной функ-
функции в особых точках равны — F (p -f- ik-ni) (производная зна-
знаменателя по z при z^p -\- 2kizi равна — 1). Применяя основ-
основную теорему о вычетах и переходя к пределу при R — со,
получаем формулу
F*(P)= 2 ^ 0»+
F4)
выражающую дискретное преобразование Лапласа решетчатой
функции /(я) через обычное преобразование Лапласа функ-
функции f(t).
Из разложения F3) следует, что /@)= lim zF(z) = 0.
2 -~ ОЭ
Если бы было /@) ^ 0, то в правой части формулы F4)
появилось бы дополнительное слагаемое у/@) — не равный
теперь нулю предел интегралов по дугам С'ц при R — оо.
Интегрирование по контур), состоящем) из прямой и полуок-
полуокружности С„ и охватывающему особые точки изображения F(г),
не приводит к новым результатам: просто получается в несколько
ином виде формула обращения для дискретного преобразования
Лапласа, в частности, если F(г) — рациональная функция, то фор-
формула разложения.
132. Пусть на интервале [а, Ь\ заданы функции f(t) и <р (t),
причем функция /(t) на этом интервале непрерывна. Точки ^(« =
= 0, 1, 2 ft), выбранные так, что a = to<tl < t2 < ... < t^ = b,
определяют разбиение интервала [a, b\ на частичные интер-
интервалы [?;_j, t-,\. Диаметром разбиения назовем наибольшую из длин
этих частичных интервалов: max (ti — ^¦_1)=8. Выбрав произвольно
в каждом частичном интервале [^j_i, <;] точку *,• (?;_[ =?=tj ^tf), со-
составим интегральную сумму
/ Ы)
- Ч (<«-!)] =
F5)
326
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. ГХ
Предел этой суммы, вычисленный при условии, что 8 — 0, на-
называется интегралом Стилтьеса от функции f(t) и обозначается
lim 2/fa) д? С*) =5/@*? @-
F6)
Функцию <р (t) называют функцией распределения. Ясно, что инте-
интеграл Стилтьеса с функцией распределения <р (t) = t есть обычный
ь
определенный интеграл \f(t)dt. Заметим, что замена «о (t) на
а
<f(t)-\-C не влияет на значение интегральной суммы F5), а зна-
значит, и на значение интеграла.
До сих пор мы ничего не говорили о свойствах функции рас-
распределения «о (t), а именно с ними связан вопрос о существовании
интеграла Стилтьеса. Предположим, что существует такая постоян-
постоянная М, что при любом разбиении интервала [а, Ь] на частичные
к
соблюдается неравенство ^ | Ло (ti) \ <_М. Функции tp (t), обладаю-
щие таким свойством, называются функциями с ограниченной ва-
вариацией на интервале [а, Ь]. Например, любая монотонная огра-
ограниченная функция <\> (t) (безразлично, непрерывная или нет) будет
функцией с ограниченной вариацией; для такой функции М —
= |ф(й)-ф(в)|.
Можно доказать, что если <р (t)—функция с ограниченной ва-
вариацией на интервале [а, Ь], то для любой непрерывной функции f(t)
с)ществует предел интегральной суммы F5) при 8—»0, т. е. инте-
интеграл Стилтьеса. Этот предел не зависит ни от способа разбиения
интервала на частичные, ни от выбора промежуточных точек т;.
Если функция распределения <р (t) дифференцируема в интер-
интервале [а, Ь\ и ее производная о' (t) ограничена, то интеграл Стилтьеса
сводится к обычному интегралу
F7)
Однако для существования интеграла Стилтьеса совсем не обя-
обязательна дифференцируемость и даже непрерывность функции у (t)
как уже отмечено, функция с ограниченной вариацией может быть
и разрывной. Именно поэтому с помощью интеграла Стилтьеса
можно описывать процессы не только непрерывные, но и дискрет-
дискретные. С этим связаны многочисленные применения интеграла Стил-
Стилтьеса, в частности, в теории вероятностей.
Предположим, что 9 (t) является функцией с ограниченной ва-
вариацией на интервале [а, х] при любом х > а, т. е. что для любого х
существует такая величина М (.v), что
F8)
СВЯЗЬ МЕЖДУ ПРЕОБРАЗОВАНИЯМИ
327
при любых разбиениях интервала [а, х]. Тогда интеграл {f(t)d<?(t)
а
существует при всех х > а. Несобственный интеграл Стилтьеса
определяется, как обычно, с помощью предельного перехода
= lim
F9)
133. Интеграл
Ф (р) = \ е-Р> d'f (t),
G0)
где р— комплексный параметр, называется интегралом или пре-
преобразованием Лапласа — Стилтьеса (о (?) — оригинал, Ф (р) — изо-
изображение). *¦
Если функция <f (t) имеет ограниченную вариацию на любом
интервале [0, х] и функция М (х), входящая в неравенство F8),
такова, что М (х) < Се"х, где С и а — постоянные, то интеграл
Лапласа — Стилтьеса сходится в полуплоскости Яер>~а и функ-
функция Ф (р) в этой полуплоскости является аналитической. Доказа-
Доказательство этого утверждения мы не приводим, равно как и доказа-
доказательство того, что преобразование Лапласа — Стилтьеса обладает
многими уже известными нам свойствами обычного и дискретного
преобразований Лапласа.
Покажем теперь, что как обычное, так и дискретное преобра-
преобразования Лапласа являются частными случаями преобразовании
Лапласа — Стилтьеса. Пусть сначала функция <в (?) дифференцируема
и ее производная ср' @ может служить оригиналом для обычного
преобразования Лапласа. Тогда из равенства
f' (t)dt
G1)
следует, что в этом случае преобразование Лапласа — Стилтьеса
для функции <р (t) превращается в обычное преобразование Лапласа
для функции <?' (t).
Пусть теперь задана последовательность {ап}, удовлетворяю-
удовлетворяющая условию \ап\<. Кеа-п. Построим ступенчатую (кусочно-посто-
(кусочно-постоянную) функцию git), определив ее следующим образом: g(t) = O
при fsgO, g(t) = a0 при 0<*s?l, g(t) = ao + "i при 1 <t*S'2,...,
g(t)^=ao-\-al-\- ...-\- an при п <t^n-\-\. Функция g (t) постоянна
на каждом из интервалов (п, я+1].
Проверим, чю построенная функция g(t) удовлетворяет усло-
условию, обеспечивающему сходимость соответствующего ей интеграла
Лапласа — Стилтьеса. Действительно, если т — наибольшее целое
число, меньшее, чем х, то при любом разбиении интервала [0, х],
очевидно, справедливо неравенство
Считая,
32Я
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
что а>0 (при
я=о
т
I ап |
К
проверка совсем проста), получим
т
G2)
где С =
г. Поэтому \ е ptdg(t) сходится при Re/»>a.
1 jj
Составим для интеграла ^e~ptdg(t) интегральную сумму
о
г=1
G3)
Возьмем произвольное разбиение интервала [0, х] с диаметром 8,
меньшим единицы, и пусть ?,• — точки, определяющие это разбие-
разбиение. Так как t-L — <,-_, ^ 8 <с 1, то две соседние точки t[_t и ti либо
попадают в один и тот же интервал (п, и —|— 1J, где п — некоторое
целое число, и тогда соответствующее слагаемое интегральной
суммы равно нулю, либо ?,-_, и tt принадлежат соседним интерва-
интервалам п — 1 <ti_! ^ п и я< <г sg л + 1. и тогда g (<,-) —g (<f-i) = а„.
При этом соответствующее слагаемое интегральной суммы G3)
можно считать равным апе~рп, положив т,- = п. При таком выборе т;
интегральная сумма G3) для любого разбиения с 5 <; 1 становится
т
равной ^ апе~рп< где т — наибольшее целое число, меньшее,
л = 0
X
чем х. Поэтому [e~P'dg(t) также равен этой сумме и переходя
о
к пределу при х->оо, получим
G4)
Таким образом, преобразование Лапласа — Стилтьеса для по-
построенной функции g (t) совпадает с дискретным преобразованием
Лапласа для последовательности {а„}. Решетчатая функция, опре-
определенная последовательностью {а„}, порождается при этом функ-
функцией g(t+l) — g(t).
134. Пусть функция распределения <р (t) является оригиналом
для обычного преобразования Лапласа и <р@)=0. Примем без до-
доказательства, что для интеграла Стилтьеса справедлива формула
интегрирования по частям; тогда
e~Pl dy (t) = p
(t) dt
G5)
5]
РЕШЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЙ
329
(в правой части должно стоять еще слагаемое е~Р'о (t) | ^°, но ано
исчезает, так как <р @) = 0, а е~Р1 у (t) —»0 при t —. оо, если Rep
достаточно велико).
Если производная <р' (t) тоже является оригиналом, то, заменяя
интеграл в левой части по формуле G1), мы просто получим част-
частный случай теоремы о дифференцировании оригинала. Поэтому для
нас сейчас наиболее интересен случай, когда формула G1) непри-
неприменима, т. е. производная <р' (t) либо не существует либо не может
служить оригиналом.
Применим формулу G5) к кусочно-постоянной функции g(t)t
построенной выше для последовательности {«„} (легко проверить,
что g (t) является оригиналом для обычного преобразования Лапласа).
Тогда левая часть равенства G5) совпадает с ^-преобразованием
последовательности {ап} (см. формулу G4)) и тем самым Z)-npeo6-
разование сведется к преобразованию Лапласа — Карсона от функ-
функции g(t) (см. стр. 242).
Убедиться в справедливости сказанного можно и не пользуясь
теорией интеграла Стилтьеса. Для этого нужно обычным путем
найти преобразование Лапласа от функции g{t)', умножив его нар,
получим как раз D-преобразование последовательности {an\. Очень
рекомендуем читателю выполнить это самостоятельно.
В приложениях встречается и.такой случай, когда функция f(t)
представляет сумму двух слагаемых: непрерывной и дифференци-
дифференцируемой функции <р @ и кусочно-постоянной функции g(t), построен-
построенной для некоторой последовательности {an}. Тогда
СО СО 00
X е-Р* df (t) = \ е~Р< dy (t) + \ е-Р' dg (t) =
0 0 0
= J e-t* <p' (Г) Л + f] aHe-P*. G6)
0 , n = 0
Это значит, что преобразование Лапласа—Стилтьеса функции f(t)
свелось к сумме двух преобразований: обычного преобразования
Лапласа функции <р' С) и дискретного преобразования последова-
последовательности {an\').
§ б. Решение разностных уравнений
135. Уравнение вида
Ф [я, /(я), /(и + 1), .... /(л + k)] = О
Ф[п, /(я), Д/(п), ..., А*/(я)] = 0,
или
G7)
G8)
') Читателю, желающему подробно ознакомиться с теорией
преобразования Лапласа—Стилтьеса, рекомендуем обратиться к
монографии D. V, W i d d e r, The Laplace Transform, Princeton, 1946.
330
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
где /(л) — искомая решетчатая функция, называется разност-
разностным уравнением (или уравнением в конечных разностях
(см. п. 124)). Шаг разности будем всегда считать равным еди-
единице. Разности Д/(я), ..., Д*/(я) можно по формулам C0)
выразить • через значения /(я), /(я -{- 1),..., f(n -|- k) и свести
уравнение вида G8) к уравнению вида G7). Обратно, урав-
уравнение вида G7) сводится к уравнению вида G8) при помощи
формулы C1).
Мы ограничимся рассмотрением лишь линейных разност-
разностных уравнений ?-го порядка с постоянными коэффициентами
fin + k) + aj(n 4- k - 1) +... + akf{n) = ? (n). G9)
Здесь <р(я) — заданная решетчатая функция (если ср(я) = О,
то уравнение называется однородным), а коэффициент ak
отличен от нуля (если ak = 0, то положив п-\-\ =т, полу-
получим уравнение более низкого порядка).
Пусть заданы значения /@), /A), ..., f(k—1) (началь-
(начальные значения). Применяя к обеим частям уравнения G9)
дискретное преобразование Лапласа и пользуясь теоремой
опережения (формула A7)), получим уравнение, из которого
найдем изображение F* (q) искомой функции /(«). Далее,
пользуясь таблицей или формулами разложения (а в случае
необходимости — общей формулой обращения G)), получим
искомую решетчатую функцию /(/г). Если начальные значе-
значения /@), /A), ..., f(k— 1) не заданы, то, считая их про-
произвольными постоянными, получим общее решение уравне-
уравнения G9).
Если исходное линейное разностное уравнение записано
в виде
Д*/(я)
{n) + ... + bkf(n) = ср (я),
(80)
то метод его решения остается тем же, но для перехода от
оригинала к изображению в левой части уравнения вместо
теоремы опережения следует воспользоваться теоремой о раз-
разности решетчатой функции (формула C4)). При этом должны
быть заданы начальные значения /@), Д/@), ..., Д*~'/@);
если эти значения не заданы, то, считая их, как раньше, про-
произвольными постоянными, получим общее решение.
Указанный метод можно применять и при решении систем
разностных уравнений.
5]
РЕШЕНИЕ РАЗНОСТНЫХ УРАВНЕНИЯ
331
Дальнейшие вопросы, связанные с линейными разностными
уравнениями с постоянными коэффициентами, будут рассмот-
рассмотрены в ходе решения примеров.
Пример 1. Найти решение уравнения
/(n + 2)-5/(n+l)+6/H=0
при начальных условиях /@) =/0, /A) =/,.
Перейдем к изображениям, применяя формулу A7),
еЧ [р* (q) _/о _/1<г?] _ Ъея [F* (?) -/„1 + 6F* (q) = 0.
Отсюда
(81)
или после выделения целой части
C(z)
{г = ея, С (г) =/1г — 6/0, fi (z) = z2 — 5г
В (г) имеет корни г1 = 2, г, = 3; поэтому
J
В (г) г — 2 ~г г — 3 '
где dt = gig. = - 2 (/, - 3/0), rf8 =^| = 3 (Д - 2/0).
Итак, в соответствии с формулой D8)
' \4)—jo е?_2 ' еЧ — 3 '
и на основании формулы E1) заключаем, что решение f(n) раз-
разностного уравнения (81) при п >; 1 имеет вид
/ (я) = _ 2 (А - 3/0) 2»-' + 3 (А - 2/0) 3»-».
При « = 0 значение /(л) известно — оно равно /0 (напомним, что
оригинал для постоянного слагаемого /0 равен нулю при всех
я$=1)-
Если/0 и /, произвольны, то полеченное решение — общее.
Его можно записать также в виде /(я) = С{1п -\- С23Л.
Если бы выкладки, аналогичные приведенным в примере 1,
мы проделали в общем виде для однородного разностного
уравнения, соответствующего уравнению G9), то, как нетрудно
видеть, пришли бы к равенству
332
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
[Гл. IX
где
ям
В (г)
¦ правильная рациональная дробь и
Я (*) = ** +<!,**-* + ... +а*
(an ..., ак — коэффициенты уравнения G9)). Уравнение
B(z) = 0 называется характеристическим уравнением для
соответствующего разностного уравнения.
Решение /(«) однородного разностного уравнения вида
G9) представляет собой, в соответствии с результатами § 3,
линейную комбинацию показательных функций и произведе-
произведений степенных функций на показательные. При этом все по-
показательные функции, входящие в решение, имеют вид
enazb==z'k, где zk — корни характеристического уравнения.
Пример 2. Найти решение уравнения
Д*/(я)-24/(я)+/(л) = 2
при начальных условиях/@) = О, Д/@) = 1.
Здесь уравнение дано в форме (80). Применяя ?)-преобразова-
ние к обеим частям заданного уравнения и пользуясь формулой
C4), получим
(в правой части уравнения следовало бы, строго говоря, писать не
2, а 2т) (п), так как всегда предполагается, что оригинал равен ну-
нулю при п < 0). После простых выкладок найдем
F* (q) = -
' (е?— 1) (е? —2J~ (г— 1) (г — 2K '
Разлагая правую часть на простые дроби
где z = <
z2-\-z
1
6
(z —2J
±п-2\:
Заметим, что коэффициент при F* (q) в D-преобразова-
нии левой части уравнения (80) всегда равен
(г — 1)(г — 2J 2—1 г — :
и переходя к оригиналам, получим
f(n) =2 — 2»-
Соответственно, уравнение
является характеристическим для уравнения (80).
ЗАДАЧИ К ГЛ. IX
ЗАДАЧИ К ГЛАВЕ IX
1. Проверить формулы 9, 10, 11, 17—20 таблицы 4.
2. Найти решение разностного уравнения ,
при начальных условиях
333
3. Найти решение разностного уравнения
при начальных условиях
= 1, Д/@) = -
ЧАСТЬ 3
ТЕОРИЯ УСТОЙЧИВОСТИ
ВВЕДЕНИЕ
В практических задачах, сводящихся к интегрированию
дифференциальных уравнений, начальные значения обычно
являются результатом измерения и, следовательно, содержат
некоторую погрешность.
Поэтому естественно возникает вопрос о влиянии малых
изменений начальных значений на искомое решение данного
дифференциального уравнения.
Если окажется, что сколь угодно малые изменения началь-
начальных значений способны сильно изменить решение, то реше-
решение, определяемое неючными начальными значениями, обычно
не будет иметь прикладного значения, так как оно даже
приближенно не будет описывать изучаемое явление.
Следовательно, возникает крайне важный для приложе-
приложений вопрос о нахождении условий, при которых малое изме-
изменение начальных значений вызывает малое изменение опре-
определяемого этими условиями решения.
Рассмотрим например, дифференциальное уравнение пер-
первого порядка
X(t)=f(t, X). A)
Пусть x = o(t) — решение этого уравнения, определяе-
определяемое начальным условием cp(Y0) = cp0, a x = x(t) — решение,
соответствующее измененному начальному условию л;(г'0) = .г0.
Предполагается, что решения ср(г") и x(t) определены для
всех t ^з tu.
Решение ср (t) называется устойчивым в смысле Ляпу-
Ляпунова, если для любого г^О существует 8(е)^>0 такое, что
из неравенства
ВВЕДЕНИЕ
335
следует неравенство
|*(Э-?(<I<в
при t^tQ, это значит, что решения, близкие по начальным
значениям, остаются близкими и при всех t^t^.
Если решение cp(tf) устойчиво и существует 8± ^> 0 такое,
что из неравенства \x(t0) — cp(^o)|<C^i следует
lim [*(*)-?(*)] = О,
1-Ю)
то решение называется асимптотически устойчивым; ре-
решения, близкие по начальным значениям к асимптотически
устойчивому решению, не только остаются близкими к нему
при t^t0, но и неограниченно сближаются с ним при воз-
возрастании t.
Решение, не обладающее свойством устойчивости, назы-
называется неустойчивым.
Аналогично определяются понятия устойчивости, асимпто-
асимптотической устойчивости и неустойчивости для решения си-
системы дифференциальных уравнений первого порядка(см. § 2
гл. X).
Другая задача, рассматриваемая теорией устойчивости, свя-
связана с изучением влияния на решения уравнения A) малого
изменения функции f(t, x) — правой части уравнения. Этот
вопрос также весьма важен для приложений, так как для
описания какого-нибудь явления всегда приходится упрощать,
идеализировать это явление, учитывая лишь наиболее сущест-
существенные из влияющих на него факторов и отбрасывая осталь-
остальные, менее существенные. При этом всегда возникает вопрос,
удачно ли выбраны упрощающие предположения. Возможно,
что неучтенные факторы сильно влияют на изучаемое явле-
явление, значительно изменяя его количественные и даже качест-
качественные характеристики.
В конечном счете этот вопрос решается практикой — соот-
соответствием или несоответствием полученных теоретических
выводов с опытными данными, но все же во многих случаях
можно указать условия, при которых некоторые упрощения
заведомо недопустимы.
Например, если при сколь угодно малом изменении пра-
правой части уравнения A) решения могут сильно изменить-
измениться, то упрощающие предположения, сводящиеся к такому
336
ВВЕДЕНИЕ
изменению правой части в A), в большинстве случаев будут
недопустимы.
Исследование на устойчивость некоторого решения x=<f (t)
уравнения A) может быть заменой переменных у = х— y(t)
сведено к исследованию на устойчивость нулевого, или, как
часто говорят, тривиального решения _у = 0.
Поэтому в дальнейшем во всех случаях на устойчивость
исследуется тривиальное решение уравнений.
Заметим, что уравнение п-то порядка
x^=f(t, х, х, ..., х^) B)
с помощью введения новых вспомогательных функций x = xv
х = х,_, ..., х^~^ = хп^ может быть преобразовано в си-
систему п уравнений первого порядка:
= хг,
Xn_\=f(t, X, Х\, ..., Хп).
Точно так же можно свести систему дифференциальных
уравнений любого порядка к системе дифференциальных
уравнений первого порядка.
Поэтому в дальнейшем почти всюду на устойчивость ис-
исследуются системы уравнений первого порядка.
Для уравнения B) устойчивость некоторого решения <р(t)
будет означать близость при t^t0 решений x(t) иср(^)иих
производных до порядка п—1 включительно, если началь-
начальные значения этих решений и их производных до порядка
п—1 достаточно близки в начальной точке.
В дальнейшем предполагается, что читатель знаком с тео-
теорией дифференциальных уравнений (например, в объеме гл. X
книги [1]), и мы поэтому лишь напомним некоторые основ-
основные сведения.
ГЛАВА X
УСТОЙЧИВОСТЬ РЕШЕНИЙ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Линейные системы с постоянными коэффициентами
136. Общее решение линейного однородного дифферен-
дифференциального уравнения л-го порядка с непрерывными коэффи-
коэффициентами
имеет вид
X (t) = ClXl (t) +
=о
CnXn (t),
A)
B)
где с,— произвольные постоянные, a jtrt (f), jca (t),..., xn (t) —
линейно независимые частные решения.
Напомним, что система функций хх (t), хг (t), ..., хп (t)
называется линейно независимой на отрезке a^t^b, если
тождество
C)
на отрезке a^ts^b возможно лишь при равенстве нулю
всех постоянных а,.
Если же существуют а, не все равные нулю, при кото-
которых имеет место тождество C), то функции xt (t), x$ (t),...
...,xn(t) называются линейно зависимыми на отрезке а^.
^tss^b. Другими словами, линейная зависимость означает,
-что на отрезке as^t s^b хотя бы одну из функций xt (t),
хг(t),..., xn(t) можно представить в виде линейной ком-
комбинации остальных.
338
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Признаком линейной независимости решений xt, х& ... ,хп
уравнения A) может служить неравенство нулю определителя
Вронского:
W(xh...,xn) =
хх
...хп
...хп
(л—l)
Если же W(xv Xt,..., xn) = 0, то решения хь хь..., хп урав-
уравнения A) линейно зависимы. (Для краткости аргумент функ-
функций xt (t) часто не пишется.) Общее решение линейного не-
неоднородного уравнения и-го порядка с непрерывными коэф-
коэффициентами и непрерывной правой частью
^)+Л@^~1)+- +Pn(t)x = f(t) D)
равно сумме общего решения B) соответствующего одно-
однородного уравнения A) и какого-нибудь частного решения
x{t) неоднородного уравнения D):
х (t) = clXl @ +... + спхп @ 4- * (')¦
Пример 1. Уравнение х — х = 0 имеет очевидные линейно
независимые частные решения х — е* и х = е~*. Следовательно,
его общим решением является х = с^ -\-cse~l.
Пример 2. Уравнение х — х = 1—< имеет очевидное част-
частное решение x = t—1, следовательно, его общее решение имеет
вид
x-=-c1ei-\- с»еч -f-1 — 1.
Нахождение частных решений линейных однородных и не-
неоднородных уравнений является весьма сложной задачей, при-
причем часто приходится искать решения в виде сумм беско-
бесконечных рядов того или иного вида, однако для некоторых
классов уравнений, например для уравнений с постоян-
постоянными коэффициентами, эта задача решается сравнительно
легко.
137. Частные решения линейного однородного уравнения
с постоянными коэффициентами
аях = О
E)
ЛИНЕЙНЫЕ СИСТЕМЫ
339
можно искать в виде х = еш. Подставляя x = ekt в уравне-
уравнение E) и сокращая на ekt, получим для определения k так
называемое характеристическое уравнение
()
Если все корни kv k.2,..., kn этого уравнения различны, то
частные решения е , е ,..., е , как нетрудно проверить,
линейно независимы и, следова1ельно, оЗшим решением яв-
является
х=схе -\- ... -[-спе ".
Если среди корней характеристического уравнения F)
есть кратные, то можно доказать, что корню k кратности г
соответствуют г решений вида еы, tekt, ..., tr~lekt. Общее ре-
решение уравнения E) имеет при этом вид
i=i
G)
где т — число различных корней характеристического уран-
нения (G), a P{ (t) — многочлен с произвольными коэффици-
коэффициентами степени на единицу ниже кратности корня kl (в част-
частности, если kt — простой корень, то его кратность rt = \
и Pl{t) = ci).
Пример 3. Найти общее решение \-равнения х — 3x4-
+ 2а- = 0.
Корнями характеристического уравнения k2 — 3ft -\- 1 = 0 явля-
являются ft1 = 1, k.2 = 2, следовательно, общее решение имеет вид
Пример 4. Найти общее решение \ равнения х -\- Зх -f- Зх ~\-
+ .г = 0.
Характеристическое уравнение
ft1 + 3*° + 3ft+l=0, или (й+1M = 0,
имеет трехкратный корень klinti = —1. Следовательно, общим ре-
решением является
Если характеристическое уравнение F) имеет комплекс-
комплексные корни, то решение можно записывать в прежнем виде G),
но часто удобнее записать его с помощью формул Эйлера
в действительной форме.
340
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл X
Известно, что если уравнение A) с действительными
коэффициентами имеет комплексное решение u(t) -f- iv{t), то
отдельно действительная часть и (t) и отдельно мнимая часть
v(t) также являются решениями того же однородного урав-
уравнения A).
Поэтому комплексные решения уравнения E) вида
e^W = ept (cos qt ±i sin qt), соответствующие паре комп-
комплексных сопряженных корней k = p±qi характеристическо-
характеристического уравнения, могут быть заменены действительными реше-
решениями ept cos qt и еы sin qt.
Такая же замена возможна и в случае кратных корней:
решения вида tsei-p±ql)t = tsep'(cos qt ± i sin qt) заменяются
решениями tsept cos qt и tsept sin qt.
Пример 5. Общее решение уравнения
может быть записано в виде
или в виде
х = e~si
cos t + C2 sin t).
Пример 6. Общее решение уравнения
может быть записано в виде
х = cte~aU
cse
ait,
или х = С\ cos at -\- C2 sin at.
Для нахождения решений линейных уравнений с постоян-
постоянными коэффициентами, удовлетворяющих заданным началь-
начальным условиям, очень удобен операционный метод решения
§ 1, гл. VIII; читатель, изучающий часть III независимо от
части II, примеры 7 — 9 может пропустить).
Пример 7. Найти решение уравнения X — 2х -f- x = t2e*, удо-
удовлетворяющее условиям х @) = 0, х @)"= 0.
Применяя преобразование Лапласа, получим
2
(Р-1K'
откуда
X(p) = -
следовательно,
< 1] ЛИНЕЙНЫЕ СИСТЕМЫ
Пример 8. Проинтегрировать уравнение
X + x = smt, л:@) = 0, х @) = — i-.
Применяя преобразование Лапласа, получим
341
2 (p2+lJ' "¦'-'— 2 •
Пример 9. Проинтегрировать уравнение
х — Зх -4- 2х — 2e3t, х @) = 0, к @) = 0.
Применяем преобразование Лапласа:
*(/>) =
0» —1)(р —2H —3)
138. Систему линейных однородных дифференциальных
уравнений:
'¦*i @ = а» @ Jfi @ + а» @ Ь @ + • • • + flm @ ^ @-
¦*я @ = fl,, @ хх (i) + а22 @ *,(*) + ... + а2п @ х„ (t),
@ = eni @ хг (t) + ал2
(8)
¦ann(t)xn(t)
можно проинтегрировать путем сведения ее к линейному
уравнению более высокого порядка с одной неизвестной
функцией или путем подбора частных решений.
Решением системы называется совокупность функций
X1 = X1(t), Xi = Xi(t), ..., Xn = Xn{t),
удовлетворяющая этой системе, т. е. обращающая при под-
подстановке каждое уравнение системы в тождество. Если
имеется п частных решений системы (8) с непрерывными
коэффициентами ац (t):
— х21 (t), ..., xn =
= xni(t);
342 УСТОЙЧИВОСТЬ РЕШЕНИЙ [Гл. X
и определитель Вронского этой совокупности решений
\xn(t) xlq(t)... xln(t)
W =
,(/) xn(t)... **n(f)\
I xni (t) xni (t)... xnn if)
отличен от нуля, то общее решение системы (8) имеет вид
Х\ = СХХП if) -\- С.гХк @ + • • ¦ + СпХ\п Ц),
Хг = fiJfai @ + czx& @ + • • • + спХы @.
Хп = ClXni @ + CiXni it) -\- . . . -f" СпХпп if),
где С], сь ..., сп — произвольные постоянные.
Систему уравнений (8) удобно записывать в матричной форме
Х=АХ, (9)
где X и А — матрицы:
... а
/•*¦ \
\ап1 ап2 ... а„п/
\ =
(X можно рассматривать и как вектор с координатами .*•,, х2,..., хп).
Общее решение уравнения (9) (или системы (8)) имеет вид
где Xit Х2, ¦¦-, Хп — линейно независимые частные решения урав-
уравнения (9); каждое из них является матрицей-столбцом
,'Х,;
= l, 2, .... л).
/Матрицы (или векторы) Xt называются линейно зависимыми на
отрезке a^t-^b, если существуют такие постоянные аи а„, ... ,а„,
что
о (Ю)
при a^ti^b, причем не все а; равны нулю.
Если же тождество A0) справедливо лишь при а1 = а2 = ...=
— ап = 0, то1 матрицы (векторы) Xt называются линейно независи-
независимыми.
ЛИНЕЙНЫЕ СИСТЕМЫ
343
Заметим, что одно матричное (векторное) равенство A0) экви-
эквивалентно п скалярным равенствам:
1*11 + ^2Х12 + ¦ ¦ ¦ + "пХ1п = 0,
Л1 + аиХ«2 + ¦ ¦ ¦ + апх*п = 0,
l^nl + ЯЛ2 + - ¦ ¦ + апХПП =0.
(И)
В случае линейной зависимости матриц Хи Х2, ..., Хп система
п линейных однородных уравнений A1) с п неизвестными аи а„, ...,
ап имеет нетривиальное решение (т. е. решение, в котором не все
неизвестные а,- равны нулю), что, как известно, возможно лишь
в случае обращения определителя системы A1) в нуль.
Итак, необходимым условием линейной зависимости вектор-фун-
вектор-функций Хи ..., Хп является обращение в нуль определителя, состав-
составленного из координат этих векторов:
xt, ..., хп) =
Этот определитель для решения Хи ..., Хп системы уравнений
(9) (или (8)) и называется определителем Вронского для этой системы.
Можно доказать, что для системы (8) с непрерывными коэф-
коэффициентами в случае линейной независимости решений определи-
определитель Вронского W не обращается в нуль ни в одной точке.
Общее решение линейной неоднородной системы диффе-
дифференциальных уравнений
A2)
A (t) = an (t) Xl(t) + ... + ain (t) xn (t) + ft, (t),
x, (t) = agl (t) Xl (t) -\-... -f aln (t) xn (t) -t- ft, (t),
(все atl (t) и bi (t) непрерывны) рапно сумме общего решения
соответствующей однородной системы (8) и произвольного
частного решения неоднородной системы A2).
Подбор частных решений линейных однородных или не-
неоднородных систем уравнений весьма сложен, но для cucievi
уравнений с постоянными коэффициентами задача значи-
значительно упрощается.
344
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Частные решения линейной однородной системы с дей-
действительными постоянными коэффициентами
••• + аыхт
¦ ¦ • -~Г ainxn>
можно искать в виде
Xi = о.хеы,
хп =
A3)
A4)
где а,- и k — постоянные.
Подставляя A4) в A3), сокращая на еы и перенося все
члены в каждом уравнении в одну часть равенства, получим:
(ап —
A5)
— k)o.n — 0.
Линейная однородная относительно 0ц, аь ...,"¦„ система
уравнений A5) всегда имеет нулевое решение: al = o.<i==. ..=
= ал = 0, которому в силу A4) соответствует нулевое (три-
(тривиальное) решение системы дифференциальных уравнений A3)
Для того чтобы система A5) имела ненулевое решение,
т. е. такое решение, в котором не все а( равны нулю, не-
необходимо и достаточно, чтобы определитель системы A5)
был равен нулю:
" \ а11 — k ali • ¦ • ali
ап\
I Ri
=0.
A6)
Если это уравнение п-й степени относительно k, называемое
характеристическим, имеет различные корни kv kb ..., k№
то, подставляя в систему A5) по очереди какой-нибудь из
§ П
ЛИНЕЙНЫЕ СИСТЕМЫ
345
этих корней kt, находим соответствующие значения а1=аи,
а.2 = а3;, ..., ая^а„г и тем самым находим решение исходной
системы
Заметим, что в рассматриваемом случае система A5) опре-
определяет а; лишь с точностью до постоянного множителя. Не-
Нетрудно доказать линейную независимость этих решений. Сле-
Следовательно, общее решение системы A3) имеет вид
п п п
i—\ 1=1 i=l
где все с,- — произвольные постоянные.
Пример 10. Найти общее решение системы уравнений
(х = 2х— у,
Ищем решение в виде
x = a{eki, y = a.2ekt.
Для определения а, и а2 получаем систему уравнений
fB-*) aj-e, =0,
l3ai+ (— 2 — k)a2 = 0.
Определяем ft из уравнения
2 —ft —I
— 2 — k
= 0,
откуда k' — 1=0, ft,.2 = ± 1.
Следовательно, при k = 1 для определения ах и а8 получим
С а, — а2 = 0,
\3ai — 3as = 0.
Второе уравнение является следствием первого, поэтому Oj
остается произвольным, например, можно считать а, = 1, тогда
а3 = <*!=!. Следовательно, решением, например, будет:
х = е1, у = е'.
Аналогично при k = — 1 получим
3а, — а2 = 0,
346
устойчивость решений
[Гл. X
а., = 3а„ a otj остается произвольным; можно считать, например,
aj = 1, тогда a.j = 'Л. Следовательно, решением системы, например,
является х = е~', у = Зе~с. Поэтому общее решение имеет вид
Если характеристическое уравнение имеет некоторый ко-
корень k кратности г, то соответствующее ему решение систе-
системы A3) можно искать в виде
Xl=Pi{t)ekt, xi = Pi(t)ek', ..., xn = Pn{f)ekt, A8)
где все Pi(t) — многочлены степени г—1 с неопределенными
коэффициентами, которые вычисляют путем подстановки A8)
в A3); при этом ровно г коэффициентов останутся произ-
произвольными постоянными, а остальные выразятся через них.
Может случиться, что коэффициенты при старших членах не-
некоторых (или даже всех) многочленов Р,@ окажутся рав-
равными нулю. Тогда степени этих многочленов окажутся ниже,
чем г—1, и могут даже равняться нулю.
Если среди корней характеристического уравнения есть
комплексные, то можно преобразовать решения вида A4)
(или A8)) по формулам Эйлера и, взяв действительную и
мнимую части в отдельности, получить решения той же си-
системы A3) в действительном виде.
Частные решения неоднородной системы с постоянными
коэффициентами в простейших случаях легко подбираются,
а в более сложных случаях находятся операционными мето-
методами (см. § 2 гл. VIII) или методом вариации произвольных
постоянных.
§ 2. Основные понятия теории устойчивости
139. Рассмотрим систему дифференциальных уравнений
xl ==/l С> Х\, Х-2, . . ., X;,),
C-2 /<j (t, X\, X-i, ¦ . ., Хп),
A9)
Хп /„ (t, X\, X.j, . . ., Хп).
Пусть Xj = ?i@- х-1 = ?з @. ¦ • •. Хп = ?л @ — решение этой
системы, определяемое начальными условиями
21
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ
347
a j?i = хх (t), x<i = Хц(t),..., ха = хп (f) — решение, соот-
соответствующее измененным начальным условиям
Х1 (@) = Xl0> X-i (t0) = Xi(), ¦ . ., Хп (t0) = Хпй,
причем все функции <p;(f) и xt(t) определены при любых
Решение х-ь = <р,- (t) (i = 1, 2,..., п) назовем устойчивым
в смысле Ляпунова, если для любого в^>0 существует
такое §(г)^>0, что из совокупности неравенств
ИСо)-?,-Со)К8(?) (/=1,2 я)
следуют неравенства
|*i@ —fPiWIO (/=1,2,..., л)
при t^tu. Это значит, что в случае-устойчивости решения,
достаточно близкие по начальным значениям, остаются близ-
близкими при неограниченном возрастании аргумента t.
Решение <р; (?)(/= 1, 2,..., п) называется асимптоти-
асимптотически устойчивым, если оно устойчиво, и решения х,- (t),
достаточно близкие к решению ср; (t) по начальным значе-
значениям:'
неограниченно сближаются при возрастании t:
t~co
Решения, не обладающие свойством устойчивости, назы-
называются неустойчивыми.
Например, решение х = 0 уравнения
х = ах B0)
при постоянном а устойчиво, если а ^ 0, асимптотически
устойчиво, если а<^0, и неустойчиво, если а^>0.
Действительно, решение уравнения B0), удовлетворяю-
удовлетворяющее условию х (t0) = xQ, имеет вид
При asgO и t^st0 справедливо неравенство ео((^»'^1,
следовательно, | х | = | х01 еа^~1^ < г при t ^г ^, если | х0 \ < г.
348
УСТОЙЧИВОСТЬ РЕШЕНИЯ
[Гл X
- О при t—> со, и при любом
Если а<^0, то еа{-* *
получаем lim jk(O = O.
t — оо
Если же <2^>0, то при любом сколь угодно малом |j;0
(лишь бы хй ф 0) решение х = хаеа['~'°) при больших t не
может удовлетворять условию
f @ I
у
х @ I
при
<С г> так как
> оо.
На рисунках 125, 126 и
127 изображены семейства ин-
тегральных кривых уравнения
B0), соответствующие случаям
а = 0, а<0 и а>0.
В рассмотренном примере
при а<^0 решения уравне-
уравнения B0) стремятся при t-^сок решению х = 0 со скоростью
показательной функции eat. В этом случае иногда говорят, что
решение л; = 0 асимптотически устойчиво по показатель-
показательному закону.
Рис. 125.
Рис. 126.
Рис 127.
Решение ср, (if) A=1, 2,..., п) системы A9) называется
асимптотически устойчивым в целом, если
lim [*, @ — <
= 0,
где х, (?) — решение, определяемое любыми начальными
значениями х, (t0), а не только значениями, близкими к на-
начальным значениям <р, (^0). Для уравнения B0) при а<^0 ре-
S 2]
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ
349
шение х = 0 является асимптотически устойчивым в целом,
так как х (t) —*¦ 0 при t —> оо при любых ta и хй.
140. Рассмотрим систему уравнений
tili__.y и хх х )
Каждому решению этой системы
*, = <р,@ A=1, 2,...,и)
(/=1,2 л). B1)
B2)
соответств)ет интегральная кривая в (re-j- 1)-мерном про-
пространстве переменных t, xx, ..., хп. Часто удобно, независимо
от физического смысла переменных, рассматривать хь хъ ..., хп
как координаты точки в л-мерном пространстве, a t считать
временем. Тогда решение B2) можно рассматривать как закон
движения в этом пространстве.
Эти же уравнения B2) могут служить параметрическими
уравнениями (t—параметр) линии в пространстве перемен-
переменных хь ..., хф называемой траекторией.
Если система B1) ,имее1 решение хг = хлA= 1, -2,...,«),
где все х1й — постоянные, ю траекюрия сводится к одной
точке М (хы, ..., хп0), называемой в этом случае точкой по-
покоя системы B1). В частности, тривиальное (нулевое) решение
х, = 0 некоторой системы является ючкой покоя этой системы,
расположенной в начале координат.
Заметим, чго при исследовании на устойчивость тривиаль-
тривиального решения ср, (t) = 0 (i= I, 2, ...,«) определение устойчи-
устойчивости, данное на ар. 347, принимает вид: для каждого е^>0
найдется 8(е)^>0 1акое, чго из неравенств | xt (tu) \ <^Ь(е)
следует |x,@i<Ce "Ри t^^a (i= 1, 2,..., л).
Вместо этого определения устойчивости тривиального ре-
решения х, = 0 часго берут следующее ему эквивалентное:
точка покоя х, = 0 (г= 1, 2, ..., п) называется устойчивой,
если для каждого е^>0 существует 8(е)^>0 такое, что из
неравенства
следует
при
то есть если начальная точка находится внутри шара1)
радиуса 8 с ценфом в начале координат, то при t^tu траек-
траектория не выйдет за пределы шара радиуса s с тем же центром.
') Имеется в вид) шар в я-мерном пространстве При л = 3
это обычный шар, ир» п = 2 — кр>г, при а = 1 — интервал (— 8, 8).
350
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Определение асимптотической устойчивости для тривиаль-
тривиального решения jc; = 0 (i= 1, 2,...,«) сводится к требованию
устойчивости и, кроме того, к выполнению условий limjc;(^) —
/-.00
п I
= 0 (/= 1, 2,..., п) при 2x\(to)<^Ц(е). Это означает, что
j=i
траектории, начальные точки которых лежат внутри шара
достаточно малого радиуса ?>,, не только остаются внутри
шара радиуса ? при t^t0, но, кроме того, асимптотически
приближаются к центру шара (к началу координат) при
t -> со.
141. Исследуемое па устойчивость решение <р,- (i) (t=\,
2, ...,«) системы уравнений B1) можно преобразовать в три-
тривиальное решение _у; = 0 другой системы заменой уг = х-ь—
— <Р; (t). Смысл замены состоит в том, что за новые неизве-
неизвестные функции принимаются отклонения xt — <р» @ коорди-
координат, точки траектории, определяемой произвольным решением
системы B1), о г соответствующих координат точки на траек-
траектории, определяемой исследуемым решением ср,-(/). Отклонения
х,— <fi(t) также называют возмущениями.
При указанной замене система B1) преобразуется к виду
Ц =fi (t, J'l + «i, У, + ?„..., ya + cpj - -^
(/=l,2,...,n).
B3)
При этом ясно, что исследование устойчивости решения со,- (t)
системы B1) сводится к исследованию соответствующего ему
тривиального решения .У; = 0 системы B3).
Поэтому в дальнейшем всюду будет исследоваться на
устойчивость тривиальное решение.
Заметим, что если система уравнений B1) линейна,
7=1
bi (t)
(/= 1,2, ...,«), B4)
то, преобразуя любое его частное решение ft(t) (i= I, 2, ...
...,«) в тривиальное с помощью замены J\ = X; — <fi@>
получим соответствующую линейную однородную систему
уравнений.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ УСТОЙЧИВОСТИ
351
Действительно, при этом, как следует из B3), система B4)
преобразуется к виду
Но так как <р, (/), ср2 (г!),..., юп (t) — решение системы B4), то
i=\
и, окончательно,
(/=1,2,....л).
B5)
Следовательно, все частные решения системы B4)
в смысле устойчивости ведут себя одинаково, а именно,
так же как тривиальное решение соответствующей од-
однородной системы B5). (Разумеется, это относится и к тому
частному случаю, когда все &,•(?) = 0, т. е. система B4) одно-
однородна.) Например, все решения линейного уравнения
x~ax=f(t)
при постоянном а<@и непрерывной функции f(t) асимпто-
асимптотически устойчивы, так как при а<^0 асимптотически устой-
устойчиво тривиальное решение уравнения х — ах = 0 (см
стр. 347)
Пример 1. Исследовать на устойчивость решения уравне-
уравнения х-(-е'л" = 0.
Разделяя переменные и интегрируя, получим
In | х | = — е(-\-\пС, x = Ce"et.
Таким образом, тривиальное решение, а следовательно, и все ре-
решения асимптотически устойчивы в целом.
Пример 2. Исследовать на устойчивость решения системы
= X.
352
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл.- X
Интегрируя, полечим
х = «! cos t -j- c2 sin t, у = cl sin t — c2 cos t.
Все решения устойчивы, но асимптотической устойчивости нет: для
малых с, и с2 модули х и у остаются малыми при любых t^t0,
но х и у не стремятся к нулю при t — со.
Пример 3. Уравнение Jc-\-4x-{-5x = Q имеет общее решение
д: = е~п (с, cos * -f- c2 sin f).
Все решения устойчивы в целом; при любых с, и сг функции х и
х стремятся к нулю при ? — оо.
Пример 4. Исследовать на устойчивость решения уравнения
IV
X —
— А=0.
Это уравнение имеет очевидное решение е', а следовательно, и се-
семейство решений м', которые при любом с^О неограниченно воз-
возрастают по абсолютной величине, если t~«-оз. Значит, решение А" =
= 0 неустойчиво; поэтому неустойчивы и все другие решения.
§ 3. Условия устойчивости для линейных систем
с постоянными коэффициентами
142. Условием асимптотической устойчивости решений
динейного уравнения первого порядка с постоянным коэф-
коэффициентом
х = ах,
как было указано на стр. 347 — 348, является а<^0 или,
что то же самое, отрицательность корня характеристиче-
характеристического уравнения k—а = 0.
Рассмотрим теперь подробнее случай системы двух ли-
линейных уравнений с постоянными коэффициентами:
А = апх
U:
B6)
Согласно сказанному на стр. 344, ищем решение в виде
х = *1еы. у = о.фы- B7)
Подставляя B7) в B6) и сокращая на еы, получим для оп-
определения ci-i и а.2 систему линейных однородных уравнений
— k) a, -f- a12a2 = 0,
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
353
Для того чтобы система,B8) имела нетривиальные реше-
решения, ее определитель должен быть равен нулю:
ап — k
— k
B9)
Из полученного характеристического уравнения определяются
значения k.
Итак, решая уравнение B9), определяем два корня: k = k1
и k = k!i. Если kx^--kb то, подставляя эти корни по очереди
в систему B8), определяем cooiBercTByioiii.He этим корням две
пары значений о^ и а3, которые мы обозначим (яп, а..п) и
(aia> а2а)- Заметим, что так как определитель системы B8)
равен нулю при k=^kx или k = kb то одно из уравнений
является следствием дру! ого и поэтому at и а.2 определяются
лишь с точностью до постоянного множителя. Причина этого
вполне понятна: поскольку решения однородных линейных
уравнений можно умножать на произвольный постоянный мно-
множитель, то, следовательно, в решении вида B7) а.х и аа тоже
определены лишь с точностью до постоянного множителя.
В рассматриваемом случае {kt ф А2) общее решение си-
системы B6) имеет вид
= сх яи e*i' -f- c
c.2a..2iek''
C0)
(см. стр. 345), где ct и с.2 — произвольные постоянные.
Если корни характеристического уравнения комплексные
klti=p± qi, то общее решение C0) обычно удобнее записать
в действительной форме в виде
х = ept (cj cos qt -j- c2 sin qf),
у = ept (ci cos qt -(- c2 sin qt),
C1)
где Ci и c2 — некоюрые линейные комбинации произвольных
постоянных Ci и с%.
Рассмотрим следующие случаи:
) i^K *j<0, *а<0.
Точка покоя jc = O, y = 0, как видно из C0), асимпто-
асимптотически устойчива в целом, так как при любых значениях сх и
с$ все решения при t—>-oo стремя 1ся к нулю.
12 И. Г. Араманович и др.
354
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
При возрастании t точки на всех траекториях прибли-
приближаются к точке покоя х = 0, у = 0.
Две траектории, соответствующие значениям произволь-
произвольных постоянных ^ = 0, с2 Ф 0 и с2 = 0, ct ф 0, являются
прямыми линиями. В первом случае (ct = 0) исключение па-
параметра t приводит к уравнению апх — адУ = 0, а во вто-
втором (с2 = 0) — к уравнению аих — ац V = 0.
Если k\ <^ kit то отношение ^ стремится к нулю при
t -* со. Составляя отношение — и деля числитель и зна-
менатель полученной дроби по-
почленно на ек'', замечаем, что если
ф 0, то
стремится к —
Рис. 128.
при t—»¦ со, т. е. при стремлении
точки (лг, .у) к началу координат.
Это значит, что все траектории
(кроме прямой, соответствующей
с.г = 0) имеют в начале коорди-
координат общую касательную, а именно,
прямую а..пх — а1?_у = 0. Эта пря-
прямая тоже является траекторией;
для нее сх = 0. Заметим еще, что
если а,2 = 0, то этой прямой будет
ось ординат, а при а22 = 0 — ось
абсцисс. Соответствующее этому последнему случаю схема-
схематическое расположение траекторий в окрестности точки по-
покоя (начала координат) показано на рис. 128, причем стрел-
стрелкой указано направление движения точек по траекториям при
возрастании t. Точка покоя рассматриваемого типа называется
устойчивым узлом.
2) Ai ф kb ki > 0, А2 > 0.
Траектории не изменяются по сравнению с предыдущим
случаем (так как заменой параметра t = — tx этот случай
сводится к предыдущему), но только направление движения
по траекториям становится противоположным — с возраста-
возрастанием t все точки на траекториях удаляются от начала коор-
координат (рис. 129).
Точка покоя неустойчива. Она называется неустойчивым
узлом.
§ 3]
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
355
3) )
Из C0) видно, что точка, движущаяся по любой траек-
траектории, для которой сх Ф 0, с3 ^ 0 при t -> со (и при
t —i со), удаляется от начала
координат (рис. 130).
Если с, = 0, то, как и в слу-
случае 1), траекторией является пря-
прямая а.пх — а.пу = 0, по которой
точки при возрастании t прибли-
приближаются к началу координат, а если
с2 = 0, то прямая апх — аи_у = 0,
по которой при возрастании t
точки удаляются от начала коор-
координат.
Точка покоя такого типа на-
называется седлом. Она, очевидно, рис j2g.
неустойчива.
4) Корни характеристического уравнения чисто мнимы:
Общее решение (см. C1)) имеет вид
- Съ sin qt, \
- с2 sin qt, j
C2)
где с1! и с2—некоторые линейные комбинации произвольных
постоянных сх и с3.
Рис. 130.
Все решения являются периодическими функциями t, и
следовательно, траекториями являются замкнутые кривые.
Можно показать, что это эллипсы (в частных случаях —¦ ок-
окружности) с центром в начале координат (рис. 131).
12*
356
устойчивость решений
[Гл. X
Очевидно, что точки траекторий, близких по начальным
значениям к началу координат, остаются близкими к началу
координат при любых ^^>/0> но асимптотического приближе-
приближения к началу координат при t-*-co нет. Следовательно, рас-
рассматриваемая точка покоя, называемая центром, устойчива,
но не асимптотически.
Рис- 131.
Рис. 132.
5) Корни характеристического уравнения комплексные:
ki4=p±qi, причем р<^0, Цф§- Тогда из C1) находим,
что второй множитель изменяется периодически, а первый
с возрастанием i затухает по показательному закону. При из-
изменении t на величину периода второго множителя в C1)
траектория после обхода начала
координат не замыкается, как в
случае центра, а приближается
к началу координат. Следователь-
Следовательно, при t ->¦ со точки траекто-
траекторий по спирали приближаются к
началу координат (рис. 132). Точка
покоя такого типа называется
устойчивым фокусом. Она, оче-
очевидно, асимптотически устойчива
в целом.
6) Если k^=p±qi, /;>0,
q Ф 0, то расположение траекто-
траекторий не изменяется по сравнению со случаем 5), но дви-
движение по ним с возрастанием t происходит в противопо-
противоположном направлении (рис. 133). Точка покоя такого типа
называется неустойчивым фокусом. Она, очевидно, не-
неустойчива.
Рис. 133.
§ 3] СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 357
7) А, =
Как указывалось на стр. 346, общее решение в этом слу-
случае имеет вид
= К+ Р«0 «*''•/
C3)
На рис. 134 изображено расположение траекторий в слу-
случае C3) при fa и 8.2, не равных нулю одновременно; можно
Рис. 134.
Рис. 135.
заметить, что все без исключения траектории имеют в начале
координат общую касательную—-прямую fax — ^iV = 0.
Может случиться (см. стр. 346), что fa = fa = 0, и тогда
х = а.1е^', у = а.^ек'{, C4)
где o-i Hi) — произвольные постоянные; траекториями в этом
случае являются прямые а..гх — а,_у = 0 (рис. 135). В обоих
случаях точка покоя называется устойчивым узлом (в слу-
случае C4) устойчивый узел называется дикритическим).
Как видно из C3) и C4), обе точки покоя асимптотиче-
асимптотически устойчивы в целом (как известно, показательная функ-
функция eV при kx <^ 0 убывает значительно быстрее, чем воз-
возрастает степенная, и limfe*i' = 0 при любом i
8) ?, = 3>
Расположение траекторий такое же, как и в предыдущем
случае, но направление движения по траекториям противопо-
противоположно (рис. 136 и 137). Точка покоя, очевидно, неустойчива.
358
устойчивость решений
[Гл. X
Она называется неустойчивым узлом (в случае, изображен-
изображенном на рис. 137, неустойчивым дикритическим узлом).
9) /ц = 0, ?а<0.
Общее решение C0) имеет вид
V
V
х = с&и -\- с^пе , у = dOj! -f
При са = 0 решениями являются точки покоя х =
Рис. 136.
Рис. 137.
_y = c1aJ1, расположенные на прямой апх — aj]V = O. К этим
точкам покоя приближаются при t—>co точки, расположен-
расположенные на других траекториях
(с2 ф 0), которые, как легко
проверить, являются прямыми
линиями (рис. 138); их урав-
уравнения
Точка покоя х = 0, у = 0 ус-
устойчива, но не асимптотически;
Рис. 138. Траектории имеют такой же
вид, как и в предыдущем
случае, но движение по ним при возрастании t происходит
в противоположном направлении (рис. 139). Точка покоя не-
неустойчива.
31
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
359
Рис. 139.
11) А1 = /;8 = 0.
Общее решение имеет вид (см. C3)):
х = а.х + fat, у =
Траекториями являются прямые линии, причем при t—>co
точки по траекториям неограниченно удаляются от начала
координат; точка покоя
л: = 0, у = 0 неустойчива.
Однако возможно (см.
стр. 346), что C1 = C2 = О,
а аЛ и а2 остаются произ-
произвольными. В этом исклю-
исключительном случае общим
решением будет х = а1;
у = а^. Все точки плоскости
являются устойчивыми точ-
точками покоя, но асимпто-
асимптотической устойчивости нет.
143. Мы рассмотрели все возможные случаи для системы
двух уравнений. Приведем теперь общее правило для иссле-
исследования системы п линейных уравнений первого порядка
с постоянными коэффициентами
х{ = апХ1-\-ацХь-\- ... -\-ainxn (Z = l, 2, ..., п). C5)
1) Если все корни характеристического уравнения
имеют отрицательную действительную часть, то все
решения асимптотически устойчивы в целом.
Действительно, в этом случае, как указано на ар. 346,
все слагаемые общего решения содержат затухающие по
ReV
показательному закону при г->со множители е
Для системы двух уравнений это случай устойчивого
узла (&i<^0, &2<^0), устойчивого фокуса (kiti = p±ql,
р<^0) и устойчивого узла, соответствующего кратному отри-
отрицательному корню (k1 = ki<^0).
2) Если хотя бы один корень k характеристичес-
характеристического уравнения имеет положительную действительную
часть, то все решения системы C5) неустойчивы.
Действительно решения системы уравнений, соответствую-
соответствующие корню k, имеют вид xt = с а.^тек1, если k действительно
или
xt = с a/V" cos qt и xt = c fa^e1-' sin qt,
360
УСТОЙЧИВОСТЬ РЕШЕНИИ
[Гл. X
если k=p-{-iq, где р^>0- (Если корень k простой,
то т = 0.)
Эти решения при сколь угодно малых, отличных от нуля
значениях | с | (что эквивалентно выбору сколь угодно малых
начальных значений) с возрастанием t неограниченно возра-
возрастают по модулю или колеблются с неограниченно возраста-
возрастающей амплитудой. Для системы двух уравнений вида B6) этот
случай реализуется при 2) ?j^>0, A.2^>0 (неустойчивый узел),
3) kt > 0, ki < 0 (седло), 6) к1Л =p±qi, /* > 0, q ^ 0 (неустой-
(неустойчивый фокус), 8) kt = k.2^> 0 (неусюйчивый узел, соответствую-
соответствующий кратному положительному корню) и 10) kx = Q, ?2^>0.
3) Если характеристическое уравнение имеет простые
корни с нулевой действительной частью (т. е. чисто
мнимые или равные нулю корни), а остальные корни, если
они есть, имеют отрицательную действительную часть,
то все решения устойчивы, но асимптотической устой-
устойчивости нет.
Действительно, корням с отрицательной вещественной ча-
частью в общем решении системы C5) соответствуют затуха-
затухающие по показательному закону слагаемые, а чисто мнимым
простым корням rt ql и корню, равному нулю, соответствуют
слагаемые вида с a,- cos qt, c^-^rnqt и саь которые при ма-
малых значениях \с\ малы при любых t^ta, но не стремятся
к нулю при t —*¦ оо.
Для системы двух уравнений B6) этот случай реализуется
при 4) ?м = ±qi, q ф§ (центр) и 9) kx = 0, k^ <^ 0.
Остается нерассмотренным еще случай:
4) Характеристическое уравнение имеет кратные корни
с нулевой, действительной частью, а остальные корни,
если они есть, имеют отрицательную действительную
часть или являются простыми корнями с нулевой дейст-
действительной частью.
В этом случае все решения обычно неустойчивы, хотя
в виде исключения могут появиться случаи устойчивости, но
не асимптотической.
Действительно, слагаемые в общем решении системы C5),
соответствующие корням ±qi кратности ?^>1 с нулевой
действительной частью, имеют вид
C6)
§ 3]
СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
361
или
«о + Ч* +
aT-i
C7)
если характеристическое уравнение имеет нулевой корень
кратности 7-
Эти слагаемые при t —> оо или неограниченно возрастают
по модулю или колеблются с неограниченно возрастающей
амплитудой при сколь угодно малых начальных значениях.
Следовательно, все решения системы C5) неустойчивы.
Однако может встретиться исключительный случай (см.
стр. 346), когда ai = a.2=: ... =атЛ = 0, р, = р.2= ... =
= PT_.j = O; тогда слагаемые в C6) и C7) имеют такой же
вид, как и в случае простых корней с нулевой действитель-
действительной частью и, следовательно, как и в случае 3), все реше-
решения устойчивы, но асимптотической устойчивости нет.
Все пункты рассмотренного правила для исследования
систем линейных уравнений относятся, разумеется, и к одному
линейному дифференциальному уравнению высшего порядка
с постоянными коэффициентами, однако для одного уравнения
отмеченный в конце п. 4) исключительный случай невозможен.
Рассмотрим несколько примеров, в каждом из которых
надо исследовать решения на устойчивость.
Пример 1.
х = ау,
= — Ьх, а>0,
Корни характеристического уравнения
чисто мнимы:
— k a
— Ь —k
fei,j = ± i Vab,
следовательно, все решения устойчивы, но асимптотической устой-
устойчивости нет. Точка покоя х = 0, у = 0 является центром.
Пример 2.
Характеристическое уравнение
2-й —1
3 —2 —ft
х == 2х — у,
= 0,
имеет корень с положительной действительной частью й, = 1, сле-
следовательно, все решения неустойчивы. Так как корни имеют раз-
разные знаки, то точка покоя х = 0, у = 0 является седлом.
362 УСТОЙЧИВОСТЬ РЕШЕНИИ
Пример 3.
[Гл. X
(А)
Х-\-2х-\-2х = 0.
Это уравнение можно заменить системой
х=у, у = — 2у — 2х. (В)
Характеристическое j равнение системы (В) (уравнения (А)) таково:
Действительная часть всех корней отрицательна, следовательно,
все решения системы E) (и уравнения (А)) асимптотически устой-
устойчивы. Точка покоя системы (В) х = 0, у = 0 является устойчивым
фокусом.
П р и м е р 4. х = 0, у = х.
Оба корня характеристического уравнения ft2 = 0 равны нулю.
Общее решение системы имеет вид
Очевидно, что точка покоя х = 0, у = 0 неустойчива (lim у =оо
/->со
при любом с, ^0).
П р и м е р 5. х = 0, у = 0.
Как и в предыдущем примере, характеристическое уравнение
имеет вид ?2 = 0, следовательно, fet = k^ = 0. Однако теперь об-
общее решение
X = Ci, у = Са
таково, что точка покоя j;eO, у = 0 устойчива (но не асимптоти-
асимптотически). Здесь мы имеем дело именно с тем исключительным слу-
случаем, о котором шла речь в п. 4) правила.
§ 4. Признаки отрицательности действительных частей
всех корней многочлена
144. В предыдущем параграфе вопрос об устойчивости
решений линейных уравнений с постоянными коэффициентами
был сведен к исследованию знаков действительных частей
корней характеристического уравнения.
Если характеристическое уравнение имеет высокую сте-
степень, то его решение представляет значительные трудности,
поэтому большое значение имеют методы, позволяющие, не
решая уравнения, выяснить, будут ли все его корни иметь
отрицательную действительную часть или нет.
Докажем сначала следующую теорему: для того чтобы
действительные части всех корней многочлена с дейст-
действительными коэффициентами были отрицательны, необхо-
необходимо, чтобы все коэффициенты этого многочлена имели
одинаковые знаки.
§ 4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 363
Пусть
P(z) = a,zn-
ап,
где а0, аь ¦ ¦ ¦¦> ап~ъ ап — действительные числа. Предположим
для определенности, что а0 ^> 0 (если а0 <^ 0, то можно было
бы рассмотреть многочлен—Р (z)). Очевидно, что
[z - (а - РО] I* - (« + Ш = ^~ 2« + (а» + р2)
и при а<^0 коэффициенты квадратного трехчлена, стоящего
в правой части этого тождества, положительны. Положи-
Положительны также коэффициенты линейного двучлена z — а, если
0. Поэтому, если разложить многочлен Р (z) на множители
—*,)•••(* — *») C8)
(Zi, z% ..., zn — корни многочлена Р (z)) и объединить по-
попарно множители, соответствующие парам сопряженных ком-
комплексных корней, то правая часть C8) будет представлена
в виде произведения линейных и квадратичных множителей,
все коэффициенты и свободные члены которых положительны,
если все корни многочлена P(z) имеют отрицательные дей-
действительные части. Но произведение многочленов с положи-
положительными коэффициентами также является многочленом с по-
положительными коэффициентами, и теорема доказана.
Легко видеть, что положительность коэффициентов мно-
многочлена является необходимым, но отнюдь не достаточным
условием отрицательности действительных частей его корней.
В самом деле, у многочлена z3 -\~ z1 -\- 4z -f- 30 все коэффи-
коэффициенты положительны, но среди его корней ?! = ¦—3,2^3 =
= 1 ± 3/ два имеют положительную действительную часть.
145. Однако для квадратного трехчлена
г» + ai« + a« С39)
(или аог2 -}- axz -\- ait где а0 ^> 0) условия а{ ^> 0, а2 ^> 0 не
только необходимы, но и достаточны для того, чтобы все
его корни имели отрицательные действительные части. Дей-
Действительно, пусть Cj^>0, а^^>0. Если г^ и гг — корни мно-
многочлена C9), то z1-|-2ia = — fli и zx z9 —а2- Так как а2 ^> 0,
то, если корни действительны, они имеют одинаковые знаки,
а так как их сумма — ах отрицательна, то оба корня отри-
отрицательны. Если же корни комплексные, то z12 = a±p/, сле-
следовательно — a1 = Zi-\- Zz = 2a ик^О, так как ^
364
УСТОЙЧИВОСТЬ РЕШЕНИИ
[Гл. X
Если № -J- axk -\- аг = 0 — характеристическое уравнение
для некоторой системы двух линейных однородных диффе-
дифференциальных уравнений, то, с учетом доказанного в преды-
предыдущем параграфе, можно теперь утверждать следующее:
1) Если u( ^> 0, а.2^>0, то нулевое решение системы
асимптотически устойчиво.
2) Если а!^>0, а.2 = 0, то нулевое решение устойчиво,
но не асимптотически (один из корней характеристического
уравнения равен нулю, а другой отрицателен).
3) Если а, = 0, й.2^>0, то нулевое решение устойчиво,
но также не асимптотически (корни характеристического
уравнения — чист мнимые).
4) Во всех остальных случаях, если хотя бы одно из чи-
чисел at и а2 отлично от нуля, нулевое решение неустойчиво,
так как при этом по крайней мере один иа корней характе-
характеристического уравнения имеет положительную действитель-
действительную часть (когда а, = а^ = 0, решение также неустойчиво,
если только не имеет места исключительный случай, отмечен-
отмеченный ранее; см. пример 5 на стр. 362).
Пример 1. Выяснить, при каких значениях параметра а ус-
устойчиво нулевое решение системы
Характеристическое уравнение имеет вид
4 — а2 — ft 1
-C+a) -ft
= 0,
или, после упрощений,
В соответствии с доказанным, нулевое решение асимптотически
устойчиво, если
«, = а'2 — 4 > 0 и а2 = a -f- 3 > 0.
Но а2 — 4 > 0, если а ;> 2 или а<—2. Следовательно, нулевое
решение асимптотически } стоичиво при а > 2 и при — 3 < а < — 2.
При а = ± 2 и а =— 3 имеет место устойчивость, но не
асимптотическая, так как при этом о, = 0, а3 > 0 или at > 0,
а2 = 0. При всех остальных значениях а решение неустойчиво.
Пример 2. При каких а и р (в какой области плоскости па-
параметров а, р) устойчиво нулевое решение системы
X = p.v — ау,
2 + ft
I X = p.
U=l2
4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 365
Характеристическое уравнение имеет вид
2*
1 —ft — а
2 — a — k
= 0,
или, после упрощений,
k2 + (а — р — 2) ft
2 0 + а2) = 0.
Устойчивость или неустойчивость нулевого решения системы за-
зависит от знаков коэффициентов
aj = <x — p— 2, e2 = 2C-fa2).
Так как at и а2 являются непрерывными функциями от а и р, то
знаки at и а2 могут изменяться лишь там, где о, или о2 обра-
обращаются в нуль, т. е. на ли-
а —Р—2 = 0, р + «2=0.
Эти линии (прямая Р —
= а — 2 и парабола р= — а2),
пересекающиеся в точках
А( — 2, — 4) и 5A,-1),
разбивают плоскость (а, р)
на пять областей (рис. 140).
в каждой из которых знаки
а, и а2 неизменны. Взяв
поэтому в каждой из этих
областей произвольно по
одной точке, мы сможем
определить знаки коэффи-
коэффициентов а1 и а2 в каждой
из этих пяти областей.
Так, в области / для
точки о. = 0, р =— 3 полу-
получим ах = 1 >0, а2 =— 6<0.
В области // выберем точку
а = — 3, р = — 6, тогда
в] = 1 > 0, а2 = 6 > 0. В области /// для точки а = 3, р = 0 найдем
at = 1 > 0, а2 = 18 > 0. В области IV для точки а = 0, р = — 1 по-
л\чим «! = —1 < 0, а» =— 2 < 0. В области V для точки а = 0,
р=1 блдем иметь а1 = — 3 < 0, а, = 2 > 0.
Итак, «! > 0, о2 > 0 в областях // и /// и только в этих облас-
областях, т. е. при p-f-a2>0, а — р — 2;>0, нулевое решение данной
системы асимптотически устойчиво. Неасимптотическая устойчи-
устойчивость имеет место там, где в! = 0, а, > 0 или aL > 0, а2 = 0, т. е.
на границах между областями / и //, // и V, I и ///, /// и
К—всюду, кроме точек А и В; в этих точках аа=0 и а2 = 0,
поэтому корень ft=0 является кратным (ft! = fe2 = 0), и нулевое
решение неустойчиво.
В областях /, IV и V и на границах между ними решение не-
неустойчиво.
Рис. 140.
Збб
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Г г, X
146. Перейдем теперь к рассмотрению некоторых усло-
условий отрицательности действительных частей корней много-
многочленов любых степеней. Следующую теорему мы приводим
без доказательства.
Теорема Гурвица. Необходимым и достаточным
условием отрицательности действительных частей всех
корней многочлена с действительными коэффициентами
Р (г) = аага + в!*1-1 +... + в„_1 z + ап, а0 > О,
является положительность всех главных диагональных
миноров матрицы Гурвица:
аа 0 0 ... (\
а3 а2 а, а0... О
а4 аЛ а3... О
ай ав а4... О
0 0 0 0...а„/
По главной диагонали матрицы Гурвица стоят коэффици-
коэффициенты рассматриваемого многочлена в порядке и\ нумерации,
начиная с at до аа. Столбцы состоят поочередно из коэффи-
коэффициентов только с нечетными или только с четными индек-
индексами, включая и коэффициеш а0, причем все недостающие
коэффициент, г. е. коэффициенты с индексами, меньшими
нуля или большими п, заменяются нулями.
Элемент blk матрицы Гурвица, принадлежащий /-й строке
и к-щ столбцу, можно определить равенством ?1Д, = а2, k,
если 0 ==? 2/ — k sg п, и b,k = 0 в остальных случаях.
Обозначим главные диагональные миноры матрицы Гурвица:
0-1
Д1=а1, Д2 =
О
at
а0 О ...О
па п\ . . . О
0 0 0 ... а„
% 4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 367
Заметим, что так как Д„ = Ая_1а„, то последнее из условий
Гурвица Д]>0, Д25>0 ди^° может быть заменено
требованием а„^>0. Из условий Гурвица следует, что если
а0^>0, то и все остальные коэффициенты а? положительны,
но одной положительности всех коэффициентов, конечно, не-
недостаточно для выполнения всех неравенств Гурвица Д?^>0;
например, минор ?).-i = alai — айа3 может быть отрицательным
при положительных а0, аъ а2, а3.
Применим теорему Гурвица к многочленам 2, 3, 4-й сте-
степени с буквенными коэффициентами.
а) PB) = 2s + a,z-La].
Условия Гурвица сводятся к
а,>0, а2>0.
б) РB) = г3 + в1га + а,2+а,.
Условия Гурвица имеют вид
в) Р (г) = г* -г- а^ + 0,2» + a3z + a4.
Условия Гурвица имеют вид
at>0, aia2 — a, > 0, (ajuj — a,) a3 — a]
Заметим, что если заранее известно, что все коэффици-
коэффициенты многочлена Рп(г) положительны, то можно дока-
доказать следующее: для того чтобы все корна многочлена
имели отрицательную действительную часть, необходимо
и достаточно выполнение неравенств
0, Д„_3>0,...,
где п — степень многочлена,
С помощью этого признака соответствующие условия, на-
например для многочлена 4-й степени, примут вид
, a2>0, aa>0, a4>0,
— a3) a4 — a\a,t ^> 0.
Рассмотрим несколько примеров исследования на устой-
устойчивость решений дифференциальных уравнений с заданными
числовыми коэффициентами.
Пример 1. jcv+-v'V — 2а + 5^ + -*+'°^/@
Все решения не\стойчивы, так как один из коэффициентов ха
раюерисгического уравнения отрицателен.
368
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Пример 2. x + 2Jt-\-3x+\0x=f(t).
Все решения неустойчивы, так как один из главных диагональ-
/2 1 0\
ных миноров матрицы Гурвица 10 3 2 для характеристи-
\ 0 0 10/
ческого уравнения k3-\-2ki-\-3k->r 10 = 0 меньше нуля:
2
10
ПримерЗ. xni+x+ + + f()
Все решения асимптотически устойчивы, так как все коэффи-
коэффициенты положительны и
А, =
1
1
0
1
10
2
0
1
1
= 7 > 0, Д, = 1 > 0.
147. Критерий Михайлова. С помощью принципа
аргумента (см. стр. 156) найдем число корней многочлена
с положительной действительной частью.
Предположим, что P(z) не имеет нулей на мнимой оси..
Тогда принцип аргумента можно применить к полукругу
радиуса R с центром в начале координат, расположенному
в правой полуплоскости (рис. 141), границу которого обо-
обозначим CR.
При достаточно большом R все корни многочлена P(z)
с положительной действительной частью будут лежать внутри
этого полукруга и их число будет равно -s- Дс Arg P (г),
где ДС/? Arg P(z) — приращение аргумента P(z) при одно-
однократном обходе точкой z контура CR в положительном на-
направлении. При обходе полуокружности, входящей в состав
контура CR, аргумент множителя zn получает приращение
пк,с а аргумент множителя A + — + ...) получает при-
приращение сколь угодно близкое к нулю, так как этот мно-
множитель при \z\ = R сколь угодно близок к единице, если R
достаточно велико.
Переходя к пределу при R-+ оо и учитывая, что при этом
отрезок мнимой оси, входящий в состав конгура CR, пере-
S 4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 369
-Ri
Рис. 141.
ходит во всю мнимую ось, проходимую в отрицательном на-
направлении, приходим к выводу, что число N нулей много-
многочлена P(z) с положительной действительной частью равно
—5—, где kit — приращение аргумента многочлена Р (z) при
прохождении точкой z мнимой оси
в отрицательном направлении. В ча-
частности, многочлен Р (z) не имеет
нулей с положительной действитель-
действительной частью тогда и только тогда,
когда k= — п.
Если коэффициенты многочлена
P(z) действительны, то P(iy) и
Р( — 1у) — сопряженные числа, по-
поэтому образ мнимой оси при отобра-
отображении Р (z) симметричен относи-
тельно_ действительной оси и можно
ограничиться вычислением прираще-
приращения аргумента Р (z) лишь при дви-
движении по положительной части мни-
мнимой оси и удвоить это приращение. Ясно, что при изменении
направления движения приращение аргумента меняет знак.
Итак, для многочленов с действительными коэффициентами
справедлив следующий критерий (правило) Михай-
Михайлова. Если многочлен Р (г) не имеет нулей на мнимой
оси, то для отсутствия у него нулей с положительной
действительной частью необходимо и достаточно, чтобы
при прохождении точкой z положительной части мни-
мнимой оси снизу вверх приращение аргумента P(z) было
равно п -^-.
К критерию Михайлова можно прийти и с помощью
несколько иных рассуждений, опирающихся на геометриче-
геометрические представления. Разложим многочлен Р (г) на линейные
множители
Р B) = (*-*,) (Z-Zi)...(Z-Zn),
и напомним, что, по предположению, среди корней zit zb. ..,zn
не г лежащих на мнимой оси.
Пусть точка z = iy движется по мнимой оси снизу вверх.
Из рис. 142 ясно, что если Re^4<^0, то при изменении у
370
УСТОЙЧИВОСТЬ РЕШЕНИИ
[Гл. X
О
Рис. 142.
Ч/
от — оо до -f- оо вектор z— zk = ty— zk повернется на угол
к против часовой стрелки, и поэтому величина arg (z — zk)
получит приращение -)1- Поэтому если все корни P(z)
имеют отрицательные действительные части, то аргумент мно-
многочлена P(z) получит приращение яте, так как приращение
аргумента произведения равно сумме приращений аргументов
сомножителей. Если же хотя бы один
из корней Zj имеет положительную
действительную часть, то прираще-
приращение аргумента множителя (z — Zj),
когда точка z пробегает снизу вверх
всю мнимую ось, будет равно —тс
(соответствующий вектор поворачи-
поворачивается по часовой стрелке), и при-
приращение аргумента P(z) будет мень-
меньше чем пк.
Итак, для того чтобы все Re zk
были меньше нуля, необходимо и до-
достаточно, чтобы приращение аргу-
аргумента Р (z), когда точка z пробегает снизу вверх всю
мнимую ось, было равно п к. Так как коэффициенты
многочлена P(z) действительны, то приращение его аргу-
аргумента при движении точки z только по положительной
части мнимой оси будет в два раза меньше (я и/2), и мы
приходим к критерию Михайлова в приведенной выше фор-
формулировке.
Проследим за годографом вектора w = P(ly). Если все
Re.^^0, то коэффициенты многочлена P(z) положительны
(см. стр. 362), значит, Р@) = а„^>0, т.е. точка годографа,
соответствующая у = 0, находится на положительной части
действительной оси. При увеличении у от 0 до -j- оо вектор
w^P(iy) будет все время поворачиваться против часовой
стрелки, так как аргумент каждого множителя (z — zk) мо-
монотонно возрастает, и сделает п четверть-оборотов против
часовой стрелки. Если же среди корней есть корни с поло-
положительной действительной частью, то число оборотов годо-
годографа вектора w будет меньше.
Таким образом, если действительные части всех корней
многочлена отрицательны (и только в этом случае):
1) при увеличении у от 0 до -|- оо вектор w = P(iy) бу-
дет все время поворачиваться против часовой стрелки и, сле-
§4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 371
довательно, его годограф будет поочередно пересекать мни-
мнимую и действительную оси плоскости w;
2) общее число таких пересечений (включая пересечение
при у = 0) будет равно степени многочлена.
Отметим, что годограф вектора w не может проходить
через начало координат (щ> = 0), так как тогда при каком-то
значении у было бы Р(/_у) = 0, а по условию многочлен
Р (z) не имеет корней, лежащих на мнимой оси.
Выделим в многочлене
Р (iy) = (iy)" + а, (/у)»-' + • • • + а„_, W + ап
действительную часть и = и(у) и мнимую часть ¦и = 'о(_уI)
(ясно, что многочлен и (у) содержит только четные степе-
степени у, а многочлен v(y) — только нечетные и ¦э(О)^О).
Те значения у, при которых годограф вектора w — P(iy)
пересекает оси координат, являются действительными корнями
уравнений и(у) = 0 и v(y) = 0; так как P (iy) не может
равняться нулю, то общих корней эти уравнения не имеют.
Если вектор w = P(iy) поворачивается все время против
часовой стрелки, -jo он по очереди пересекает оси абсцисс
и ординат, а это означает, что между двумя любыми сосед-
соседними корнями одного из уравнений гг = О, v = 0 находится
в точности один корень другого. В таком случае будем гово-
говорить, что корни уравнений перемежаются.
Точке ¦ш = а„ на действительной оси соответствует ко-
корень у = 0 уравнения v (у) = 0. Далее уравнения и = 0, v = 0
имеют в общей сложности (п—1) положительных корней
(по числу точек пересечения с осями координат), а значит
и (п—1) отрицательных, так как и(—у) = и(у) и v(—_у) =
= — v(y). Таким образом, общее число всех действи-
действительных корней обоих уравнений, и(у) = 0 и v(y)=^0, дол-
должно быть равно 2я—1, где п—степень многочлена. Так
как одно из этих уравнений имеет степень п, а другое — сте-
степень п— 1, то это и значит, что все их корни действительны.
Проведенное исследование позволяет сформулировать кри-
критерий Михайлова в следующем, обычно более удобном для
проверки, виде.
!) и = а (у), v = v (у) — параметрические уравнения годографа
вектора w = P (iy).
372
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Если многочлен P(z) не имеет корней на мнимой оси,
то для того чтобы все его корни имели отрицательные
действительные части {лежали в левой полуплоскости),
необходимо и достаточ-
достаточно, чтобы 1
1) при возрастании у
вектор Р (iy) поворачивался
против часовой стрелки;
2) все корни уравнений
и = 0 и v = 0 были действи-
действительны и перемежались.
Если заранее известно,
что все коэффициенты много-
многочлена Р (z) положительны,
то, как можно доказать,
проверке подлежит только
\п-3
п.4
Рис. 143.
второе условие.
В предположении, что
все Re2,<^0, на рис. 143
изображены типичные годографы вектора w = P(iy),
0^у<^оо, для многочленов различных степеней: и=1,
2, 3, 4, 5.
Пример 4. Имеет ли многочлен
корни с положительными действительными частями?
Полагая z = iy, пол}чим
Р ^У) = —У* + 6У - 8/ + I + ' (/ - 5у3 + 4у),
и=
1, v—yb —
у—»оо
При достаточно большом у имеем и < 0, v > 0, причем
- = 0, нулями функции v=y(y* — 5у2 -(- 4) являются
Вычислим соответствующие значения и:
м@) = 1, «(±1)= -2, ц(±2) = 1.
Если еще учесть четность функции и и нечетность функции V,
то уже можно дать набросок образа мнимой оси при отображении
Р (г), довольно грубый, но достаточный для вычисления приращения
§41 ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 373
аргумента Р (iy) при у, изменяющемся от -\- оо до —со (рис. 144).
Из него видно, что приращение аргумента равно — 6л. Следова-
Следовательно, число N нулей многочлена Р (г) шестой степени, лежащих
в правой полуплоскости, равно
Пример 5. При помощи
критерия Михайлова выяснить,
устойчиво ли решение х = 0
уравнения
XIV -f x-\- 10.?+ 4* + 9х = 0.
Характеристический многочлен
имеет вид
Р (z) = z4 + z3 + 10z2 + 4z +
откуда
P(iy)=yi— 10у2 + 9 —
— i (у* — Ay).
Все корни уравнений
у _ Ау = О,
/,, _п „ h4i Рис. 144.
\У\ — и> 3*2,3 — — z/
действительны и перемежаются.
Все условия, указанные на стр. 372, выполнены, следовательно,
решение ,v = 0 рассматриваемого уравнения асимптотически устой-
устойчиво.
148. Метод D-p а з б и е н и й. Нули многочлена
являются непрерывными функциями его коэффициентов. Это
означает, что малое изменение коэффициентов многочлена
влечет за собой малое же изменение расположения его нулей
в комплексной плоскости').
Предположим, что коэффициенты многочлена Р (г) непре-
непрерывно зависят от каких-'io двух параметров аир. Любая
') Заметим, что это утверждение становится неверным, если
многочлен Р (z) взять в виде aozn -f- aizn~1 -4- ¦•¦ + оп — 0> но оно
остается справедливым, если в этом случае считать, что а0 не мо-
может обратиться в нуль.
374
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
пара значений этих параметров определяет некоторую точку
в плоскости (а, E) (плоскость параметров). Если при каких-то
значениях параметров аир многочлен Р (г) имеет чисто мни-
мнимый корень z = iy, то Р (iy) = 0. Таким образом, уравнение
Р (iy) = 0 определяет в плоскости параметров множество то-
точек — одну или несколько линий, соответствующих чисто
мнимым корням многочлена (и нулевому корню, который по-
получается при _у = 0). Линии Р(гу) = 0 разбивают плоскость
параметров на области gv gb ..., gk; это разбиение называют
D-разбпением. Всем точкам какой-то одной из этих облас-
областей gs соответствует одинаковое число нулей многочлена Р (г),
лежащих в правой полуплоскости. Действительно, как уже
отмечено, при непрерывном движении точки (а, р) в плоско-
плоскости параметров корни многочлена изменяются тоже непре-
непрерывно. Таким образом, переход корня из правой полуплоско-
полуплоскости в левую (или, наоборот, из левой в правую) может прои-
произойти лишь после пересечения корнем мнимой оси, что
соответствует переходу точки (а, |5) из одной области gs в
другую.
В более общем случае коэффициенты многочлена Р (z)
могут зависеть от любого числа параметров аь а2, ..., а.т.
Значения этих параметров определяют точку в /я-мерном
пространстве коэффициентов, а уравнению Р(/у)=0 соответ-
соответствуют некоторые «поверхности» в этом пространстве (гипер-
(гиперповерхности), разбивающие пространство коэффициентов на
области, причем опять-таки всем точкам какой-то одной из
этих областей соответствует одинаковое число нулей много-
многочлена P{z), лежащих в правой полуплоскости.
Особый интерес для теории устойчивости представляют
те области gs, точкам которых соответствуют многочлены,
не имеющие ни одного корня с положительной действитель-
действительной частью. Такие области gs будут областями асимпто-
асимптотической устойчивости для линейных однородных дифферен-
дифференциальных уравнений, для которых Р (г) является характери-
характеристическим многочленом.
Подсчитав в произвольно аыбранной точке некоторой
области g число корней с положительной действительной
частью любым методом, например при помощи критерия
Михайлова, мы тем самым определяем число таких кор-
корней для произвольных значений коэффициентов из этой
области.
§4] ОТРИЦАТЕЛЬНОСТЬ ДЕЙСТВ. ЧАСТЕЙ КОРНЕЙ МНОГОЧЛЕНА 375
Пример 6. Для многочлена
Р B) = z3 + «2 + az + 3
D1)
определить области плоскости a, f), в которых число нулей этого
многочлена, лежащих в правой полуплоскости, постоянно, и найги
для каждой области это чи-
число yv.
Полагая z = iy, получим
Р (iy) = — iy> — ays + lay + ?.
Уравнение Р (iy) = 0 равно-
равносильно системе двух уравнений
h
о
ml
ш
If
1 *
0B,1)
а
Рис. 145.
или
Следовательно, если Р (iy) = О,
то
у = О, Р = «У D2)
или
а —У = 0, 3 = ay. D3)
Из D2) получим 3 = 0 (ось
абсцисс в плоскости а, 3), а из
D3) 3 = з2, причем а=у>0
(правая половина параболы Р = а2). Линии Р (iy) = 0 разбивают всю
плоскость параметров на три области g,, g2, g^ указанные на рис. 145.
Возьмем какую-нибудь точку области glt например, в = 2, р = 1.
Тогда
да = РB)=г' + 222 + 2г+1.
Если точка г пробегает сверху вниз мнимую ось, то z = iy, ay
изменяется от -4-оэ до —оо,
D4)
откуда, отделяя мнимую и действительную части:
Если у -* + со, то а -> — оо, v -> — оэ, причем —- -> + со.
i V с
Если у — — оо, то и—« — со, v—--{-сои —— — со. Ьсли
учесть, наконец, что v = 0 при v = У2 , у — 0, у = — У2, при этом
соответственно и = — 3, и = 1, и = — 3, то уже можно приближенно
построить кривую (рис. 146).
При этом, как видно из чертежа, аргумент вектора w получает
приращение—Зге (вектор w делает полтора оборота по часовой
стрелке). Итак, k = — 3, п = 3 (многочлен Р (г) третьей степени),
376
УСТОЙЧИВОСТЬ РЕШЕНИИ
ГГл X
k-\- п
следовательно, N =: —~— =0, т. е. для значений параметров а, р,
соответствующих области gu многочлен Р (г) не имеет нулей с по-
положительной действительной частью.
В области gs возьмем точку а = 0, C = 1. При этом
Р(г)=г34-Ь w=u + iv = P (iy)=_iy + l,
откуда и = 1, v = —уг.
Очевидно, что когда у изменяется от -\-со Ь.о —со, точка
w = a -\-iv движется по прямой ц = 1 от о = — со до я =-|-°°
(рис. 147) и вектор и» поворачивается на угол я против часовой
стрелки, т. е. к=\, а так как п = 3, то N=^-2 = 2, следова-
следовательно, для значений параметров, соответствующих точкам области
Рис. 146.
Рис. 147.
g2, многочлен Р (z) имеет два корня с положительной действитель-
действительной частью. Еще проще было решить уравнение га+1=0.
Возьмем, наконец, в области g3 точку а = 0, р = —1. При этом
Р(г)=2«-1,
w = и -f- iv = Р (fy) = — iys — 1,
откуда и = — 1, о = — _у\
При _у, изменяющемся от -4-со до —со, точка a» = u-)-i» про-
пробегает прямую и=—1 снизу вверх и приращение аргумента век-
Ь _L"и
тора да при этом равно —тс, т. е. k = — 1 и Л^ = —I— = 1. Сле-
Следовательно, для значений параметров а, р, соответствующих точкам
области g-3, многочлен Р (г) имеет один корень с положительной
действительной частью (конечно, проще было найти корни ) равне-
равнения г3—1=0, но мы хотели еще раз показать читателю, как при-
применяются рассуждения, на которых основан критерий Михайлова).
51 УСТОЙЧИВОСТЬ РЕШЕНИЙ РАЗНОСТНЫХ УРАВНЕНИЙ 377
§ 5. Устойчивость решений разностных уравнений
149. Решение однородного линейного разностного урав-
уравнения порядка k с постоянными коэффициентами
|/(я4-а —1L~ ••• ~\~akf(n) — о D5)
где /(л) — искомая функция целочисленного аргумента, удобно
искать в виде /(л) = Хл. Подстановка этой функции в урав-
уравнение D5) приводит к равенству
Х"(^ + а1Х*-'+ ... +ак) = 0.
Значение X = 0 соответствует тривиальному (нулевому) ре-
решению /(л) = 0, а корни характеристического уравнения
X*4-^Х*-1 4- ... 4-аА = 0 D6)
определяют нетривиальные частные решения уравнения D5).
Если все корни Х4, Х2, ... lk характеристического уравне-
уравнения различны, то мы находим k частных решений Х^, X",...,
Х? уравнения D5), и можно доказать, что общее решение этого
уравнения имеет вид
где С\, Сц ck — произвольные постоянные. Эти постоян-
постоянные могут быть определены, если заданы начальные условия
/@)=/0, /A) =/„..., /(A-l)=/ftJ.
Если X — корень характеристического уравнения кратности
г, то ему, как доказывается, соответствует г частных реше-
решений вида X", п X",..., я'-'Х". Общее решение уравнения D5)
представляет собой линейную комбинацию решений, соответ-
соответствующих всем корням характеристического уравнения.
Если имеется простой комплексный корень X = fi,-j-b =
Jj elv характеристического уравнения, то соответствующее
ему решение можно преобразовать к виду Х"= jA)"(cos л<р -\-
-j-Zsin/ztp), где ср = arg X.
В случае, когда коэффициенты уравнения D5) — действи-
действительные числа, паре сопряженных корней р ± h соответст-
соответствуют действительные решения |Х|" cos (и arg X), |X|" sin (n argX).
Если X — кратный комплексный корень, ю соответствующие
ему решения б>ду1 содержать также и степенные множители.
= JXj
378
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
Общее решение неоднородного линейного разностного
уравнения
= g(n) D7)
представляет собой сумму общего решения соответствующего
однородного уравнения и какого-либо частного решения не-
неоднородного.
В § 4 гл. IX изложен способ решения линейных разностных
уравнений с постоянными коэффициентами, основанный на дискрет-
дискретном преобразовании Лапласа. Из него также следуют высказанные
утверждения о структуре и методе построения общих решений та-
таких уравнений.
Пример 1. Найти общее решение уравнения
/(л + 2)+3/(л + 1)-4/(я)=0, D8)
а также частное решение, удовлетворяющее условиям /@) = 0,
/A)=7
)
Характеристическое уравнение ).2-j-3X — 4 = 0 имеет корни
Х! = —4, А2 = 3. Общее решение уравнения D8) имеет вид
Из начальных условий получаем
откуда fj =—1, с2=1; следовательно, искомое частное решение
таково: / (л) = ( — l)n+1 4й+ 3".
Пример 2. Найти общее решение уравнения
/(и + 2)-4/(л+1)+16/(л) = 26л + 9. D9)
Характеристическое уравнение X2 — 4X-f-16 = 0 имеет корни
А,J = 2A ±iVS). Так как 2 11 ± i /3"| = 4, atg (l + i|/3") = л / 3, то
общее решение соответствующего однородного уравнения имеет
вид 4я с, cos —5—\- с2 sm —%- .
\ " о )
Частное решение неоднородного уравнения будем искать в виде
fa(n) = an-\-b. Так как /0 (п-\- I) = an + ч + Ь, /„ (и + 2) — an -f-
4- 1а -\- Ь, то после подстановки в уравнение D9) получим \3ап—¦
— 2а + 13* = 26л + 9. Отсюда а = 2, 6=1, т. е. /0 (л) = 2и + 1-
Общее решение уравнения D9) таково:
cos^ +casin y
Пример 3. Найти общее решение уравнения
/(л + 2)-4/(л + 1) + 4/(и)=0.
Характеристическое уравнение X3 — 4Х —|— 4 = 0 имеет двукрат-
двукратный корень }ч = Х2 = 2, и общее решение данного уравнения имеет
впд/(н) (с + сяJ«
§ 5] УСТОЙЧИВОСТЬ РЕШЕНИЙ РАЗНОСТНЫХ УРАВНЕНИЙ 379
150. Пусть /* (я) — решение разностного уравнения, по-
порядка k, определяемое начальными условиями /*@)=/q, ...
..., f* {k—l)=/fc_1, а /(и) — решение того же уравнения
при измененных начальных условиях /@) =/„,..., f(k — 1) =
= fk_l. Решение /* (и) называется устойчивым, если для
любого е^>0 существует такое 8(s)^>0, что из совокуп-
совокупности неравенств |/0—/*|<СЛ •••> I A-i — /l-i I <C8 следует
неравенство | f(n)—/*(и)|<^? при любом я^0. Если, кроме
того, Нт[/(я) — /*(«)] = 0, то решение /* (я) называется
rt-юо
асимптотически устойчивым.
Исследование на устойчивость решения /* (я) неоднород-
неоднородного линейного разностного уравнения D7) сводится с по-
помощью замены y(ri)=f(ri)—/* (я) к исследованию устойчи-
устойчивости тривиального (нулевого) решения однородного уравнения
<p(* + AL-fli?(« + *-l) + .-.+a*?(/i) = 0. E0)
Коэффициенты этого уравнения те же, что и уравнения D7).
Поэтому, как и в случае линейных дифференциальных урав-
уравнений, можно ограничиться исследованием устойчивости только
тривиальных решений однородных уравнений. Знание струк-
структуры общего решения таких уравнений (в случае, когда коэф-
коэффициенты постоянны) позволяет установить следующее общее
правило (оно аналогично правилу, приведенному в п. 143).
1) Если все корни характеристического уравнения по
модулю меньше единицы, то решение асимптотически
устойчиво.
Действительно, если |Х| <^ 1, то \\тп'"Кп = 0 при любом г.
га->со
Поэтому все слагаемые в общем решении стремятся к нулю
при и —• оо.
2) Если хотя бы один корень X характеристического
уравнения по модулю больше единицы, то решение не-
неустойчиво.
В самом деле, слагаемое в общем решении, соответству-
соответствующее этому корню, стремится к бесконечности при п—>-со.
3) Если характеристическое уравнение имеет, простые
корни с модулями, равными единице, а остальные корни,
если они есть, по модулю меньше единицы, то решение
устойчиво, но не асимптотически.
Действительно, если к — простой корень и |Х.| = 1, то
соответствующее ему в общем решении слагаемое ск" имеет
380
УСТОЙЧИВОСТЬ РЕШЕНИЙ
[Гл. X
постоянный модуль | с |, который будет мал, если малы но
абсолютной величине начальные значения. В то же время это
слагаемое не стремится к нулю при я-»-оо. Что же касается
слагаемых, соответствующих корням характеристического
уравнения, по модулю меньшим единицы, то они, как уже
было показано, стремятся к нулю при п-уоо.
4) Если характеристическое уравнение имеет хотя
бы один кратный корень с модулем, равным единице, то
решение неустойчиво.
В этом случае среди решений, соответствующих такому
корню, имеются решения вида пг\п, где |Х|=1 и г^>0, стре-
стремящиеся к бесконечности при п —»¦ оо .
Как уже отмечено выше, любое частное решение урав-
уравнения D7) в смысле устойчивости ведет себя так же, как и
тривиальное решение уравнения E0).
161. Приведенное общее правило исследования на устой-
устойчивость решений линейных разностных уравнений с постоян-
постоянными коэффициентами показывает, что все дело сводится к
выяснению того, каковы модули корней характеристического
уравнения. Покажем, что этот последний вопрос может
быть решен на основании уже известных нам признаков
отрицательности действительных частей корней многочлена.
Рассмотрим уравнение с действительными коэффициентами
\-a1z^+... + aa = Qi а„>0. E1)
Если отобразить комплексную плоскость z на комплексную
. да+1
плоскость w с помощью функции z =——г, то, как легко
проверить, внутренность единичного круга плоскости z отобра-
отобразится на левую полуплоскость плоскости w. Поэтому кор-
корням уравнения E1), лежащим внутри единичного круга (т.е.
по модулю меньшим единицы), будут соответствовать корни
преобразованного уравнения
лежащие в левой полуплоскости. Корни последнего уравне-
уравнения являются корнями многочлена
E2)
§ 5] УСТОЙЧИВОСТЬ РЕШЕНИЙ РАЗНОСТНЫХ УРАВНЕНИЙ 381
Коэффициенты bk выражаются через коэффициенты ак по
довольно громоздким формулам
-l)* Ckr],
где С =
— биномиальные коэффициенты, причем
"а! (8 —а)!
считается, что С*=1 и С^ = 0, если а<р или если
В частности,
После того как многочлен E2) будет построен, останется
применить к нему либо теорему Гурвица либо критерий Ми-
Михайлова.
Для случая л = 2, т.е. для характеристического уравнения
а0 г2 -(- ах z -\- а2 = 0, а0 ]> 0,
коэффициенты bk равны
Ьо = а0 -\- ах -f fla, b^ — 2 (а0 — а.3), bt
и условия Гурвица приводят к неравенствам
Предоставляем читателю проверить, что для п = 3 усло-
условия устойчивости запишутся в виде
а0 + fli + «a + «a > 0.
3 (а0 — аа) + а, — а2 > 0,
3 (а0 4" а») — ai — а« > 0,
«о — fli + аг — «з > 0,
382
УСТОЙЧИВОСТЬ РЕШЕНИИ
ЗАДАЧИ К ГЛАВЕ X
[Гл. X
1. Исследовать на устойчивость точку покоя х = 0, _у =
системы
х = — 2х — Зу,
х+у.
2. Исследовать на устойчивость точку покоя х = 0, у =0, z = 0
системы
= х — у — г,
= х+у-3г,
= 0, _у = 0, z =
3. При каких значениях а точка покоя х
системы
х = ах—у,
= аг — х
устойчива?
4. Какого типа точку покоя имеет система уравнений
5. Устойчиво ли решение A'sO уравнений
; = 0; 6)
+ — Зх + 4х = 0?
6. Какого тина точку покоя х = 0, _у = 0 имеет система урав-
уравнений
7. Найти периодическое решение уравнения
2i + 2* = sin С
и исследовать его на устойчивость.
8. Устойчивы ли решения уравнения
х -j- 1
ЗАДАЧИ К ГЛ. X
383
9. Устойчиво ли решение х = 0 уравнения:
a)'i + 3x + 3x + -« = 0; б) *IV + 2.?-|-;t = 0.
10. Найти области плоскости параметров а, [3, в которых устой-
устойчиво решение х = 0, у = 0 системы уравнений:
б) {!=.
11. Определить области плоскости а, Э, в которых число кор-
корней соответствующего многочлена Р (г), имеющих положительную
действительную часть, постоянно; найти для каждой области это
число N:
а) Р(г)=га + аг* + ^+1; б) рB)=2« + (в + р)а» + (в-рJ + а.
12. Найти область плоскости параметров а, [3, в которой устой-
устойчиво нулевое решение разностного уравнения
ГЛАВА XI
ВТОРОЙ МЕТОД ЛЯПУНОВА
§ 1. Основные теоремы второго метода Ляпунова
152. Выдающийся русский математик Александр Михай-
Михайлович Ляпунов в конце XIX века разработал весьма общий
метод исследования на устойчивость решений систем диффе-
дифференциальных уравнений
^—fi(t, хь хъ ... , хп) B = 1 , 2,..., л), A)
получивший в дальнейшем название второго метода Ляпу-
Ляпунова. Будем считать (см. п. 141), что система A) имеет три-
тривиальное решение х, = 0; это значит, что /,• (t, 0, 0,..., 0) = 0
при любом t.
Прежде чем давать точные формулировки, кратко изло-
изложим идею метода.
Предположим, что на устойчивость исследуется точка по-
покоя Xi = 0 A=1, 2,..., п) системы A). Если бы с возраста-
возрастанием t точки всех траекторий приближались к началу коор-
координат или хотя бы не удалялись от него, то, очевидно, рас-
рассматриваемая точка покоя была бы уетойчивой.
Проверка выполнения эюго условия не требует знания
решений системы A). Действительно, если р — расстояние от
точки траектории xi = xl(t)(i=\ , 2,..., л) до начала коор-
координат, р = 1/ 2 х' О' т0
*L _ \
dt ~Li
A
dt
B)
ОСНОВНЫЕ ТЕОРЕМЫ ВТОРОГО МЕТОДА ЛЯПУНОВА
385
Пр?вая чяс1Ь в B) являекя известной функцией t, хи х2, ¦ ¦ ¦ , хп,
и, еле товательно, можно исследовать ее знак. Если окажется,
da
чю - ^с 0, то ючки па всех траекториях не удаляю1ся or
начала координат при возрастании t и точка покоя jc; = O
(/=1, 2,..., п) устойчива.
Вмесю -J- обычно вычисляют для упрощения дифференци-
рования производную
da
со знаком -7Т-
dt
d (a2)
r
знак коюрой совпадает
Пример I. Дана система
х = — у — tx3,
Обозначим v = р2 = xs-\-y2; тогда производная v б\дет иметь вид
v = 2.\.x-{-2yy~=2x(— у — tx')-\-2y (x — ty") =—2t(xi-\-yi).
При всех х и у и при t^O справедливо неравенство v ^ 0. Следо-
Следовательно, точка покоя х = 0, у=0 )стойчива.
Однако точка покоя может быть устойчивой и даже асимг-
тотически устойчивой и при немонотонном приближении к ней
точек траекторий с возрастанием t; чтобы убедиться в этом,
достаточно взглянуть на изображение центра или устойчивого
фокуса на стр. 356. Поэтому вместо функции р или р2 А №. Ля-
Ляпунов ввел в рассмотрение функции v (t, хь х%,..., хп), не-
некоторые свойства которых схожи со свойствами расстояния
от точки траектории до начала координат — точки покоя.
Эти функции, применяющиеся для исследования вопроса
об устойчивости, получили название функций Ляпунова. В даль-
дальнейшем всегда предполагается, что функции Ляпунова непре-
непрерывны и непрерывно дифференцируемы в некоторой /«-ок-
/«-окрестности начала координат, т. е. в точках (хь хь ..., хп),
для которых 2-*гг<С'г2 и ПРИ всех ^===^o- Полная производ-
производная по t функции v(t, хъ x.h ..., хп), вычисленная в силу
системы (I) (вдоль интегральных кривых), равна
dv
dt ''
dv
dxi
Ht
dv
п
i
13 И. Г. Арамамович и др.
386
ВТОРОП МЕТОД ЛЯПУНОВА
[Гл XI
Эia производная показывает характер изменения функции v,
когда точка (хь хг, ..., хп) движется по траектории в сторону
возрастания t: если г>^>0, то функция v возрастает, а если
г><^ О, то убывает.
Особенно важным для приложений является случай, когда
в правые части системы дифференциальных уравнений A) не
входит независимая переменная t. Такие системы называются
автономными или стационарными. Они имеют вид
* •••> хп) (i=\, 1, ..., п).
D)
Для таких систем траектория движения полностью опре-
определяется начальной точкой и не зависит ог начального мо-
момента времени (см. [1], п. 177).
При исследовании на устойчивость автономных систем
можно ограничиться рассмотрением только таких функций
Ляпунова, которые явно от t не зависят, т. е. имеют вид
v(xb хь .... хп).
Производная по t от такой функции, вычисленная в силу
системы D) (вдоль интегральных кривых), равна
dv
di
dv \ dv f
dt — Zd d7tJi
b ¦ ¦ ¦' Xn>
E)
и также явно не зависит от t. Это обстоятельство во многом
упрощает исследование на устойчивость автономных систем.
Иногда и в случае неавтономных систем их исследование
на устойчивость удается провести при помощи функций Ляпу-
Ляпунова, не зависящих явно от t (как в примере 1), однако те-
теперь полная производная -г- будет явно зависеть от t. Это
видно из формулы C).
153. Введем важные для дальнейшего определения.
Функция v(x\, x<l, ..., хп) называется определенно поло-
положительной в /г-окрестности начала координат, если она по-
положительна во всех точках этой окрестности, за исключе-
исключением начала координат, где она равна нулю:
п
v(xlt ха, . , .*¦„)> О, если ^л';>0,
0, О,..., 0) = 0.
И
ОСНОВНЫЕ ТЕОРЕМЫ ВТОРОГО МЕТОДА ЛЯПУНОВА
387
= v(x,y)
Сказанное означает, что функция v имеет строгий мини-
минимум в начале координат. Если в этом определении нера-
неравенство v~^>0 заменить неравенством v<^0, то функция v
будет называться определенно отрицательной (ясно, что
в этом случае функция — v будет определенно положи-
положительной).
Например, расстояние р до начала координат есть функ-
функция определенно положительная. Определенно положитель-
положительными функциями двух пе-
переменных являются функции
v = ах* -\- by* и v = axi-\-
-f- Ay4 при а ^> 0 и b ^> 0.
Подчеркнем разницу
между определенно положи-
положительной функцией и функ-
функцией неотрицатель-
неотрицательной. Неотрицательная функ-
функция хотя и сохраняет по-
постоянный знак, но может
обращаться в нуль не только
в одной точке. Например,
функция v = (x—yf будет
неотрицательной, но не бу-
будет определенно поло-
положительной ни в какой /г-ок-
/г-окрестности начала координат,
так как v = 0 при у = х.
Если функция v принимает как положительные, так и
отрицательные значения, то говорят, что она знакоперемен-
знакопеременная.
Если я = 2, то поверхность z = v(x, у), где v — опре-
определенно положительная функция, в окрестности начала ко-
координат обычно имеет вид, изображенный на рис. 148. На
этом рисунке линии уровня функции v(x, у) представляют
замкнутые кривые, охватывающие начало координат.
Следует отметить, что поверхность z = v(x, у) и семей-
семейство линий уровня функции v(x, у) могут иметь гораздо
более сложную структуру.
Определенные выше понятия вводят и для функций, за-
зависящих от t. Функция v (t, Xi,..., xn) называется опреде-
определенно положительной в /г-окрестности начала координат и
13'
Рис. 148.
388
ВТОРОЙ МЕТОД ЛЯПУНОВА
[Гл. XI
при t^>ta, если существует такая не зависящая от t опре-
определенно положительная функция w {хь ..., хп), что v (t, X\...
..., xn)^w(Xi,..., xn) при всех указанных значениях аргу-
аргументов и v(t, О,..., 0) = 0.
154. Теорема Ляпунова об устойчивости.
Если система дифференциальных уравнений A) такова,
что существует функция Ляпунова v(t, xi,..., xn), оп-
определенно положительная при t^tu в некоторой h-ок-
рестности начала координат, производная которой, вы-
вычисленная в силу системы A), неположительна (v^O),
то точка покоя х; = 0 A=\,2,..., п) устойчива.
Мы докажем эту теорему в том частном случае, когда
функцию Ляпунова можно выбрать не зависящей от t, т. е.
в виде v(Xi,..., хп).
Возьмем произвольное положительное число е (меньшее,
чем п) и обозначим через С? границу е-окрестности начала
координат (при я=3 это поверхность шара радиуса г,
при п — 1 — окружность), а через т — наименьшее значение,
которое функция v принимает в точках границы СЕ; так как
функция v определенно положительна, то т ^> 0. Выберем
теперь 8 ^> 0 столь малым, чтобы в 8-окрестности начала
координат функция v была меньше т; это возможно, так как
функция v непрерывна и в начале координат равна нулю.
Пусть х10,..., хп о — произвольная точка выбранной 8-ок-
8-окрестности и xt = Xi (t) (/=1,2,..., и) — решение, опреде-
определенное начальными условиями х,- (t0) = х10. В начальной точ-
точке траектории') v (xi (t0),..., хГ1(гц))<^т. При увеличении
t, т. е. при движении точки по траектории, функция v не
может возрастать, так как ее производная v^.0 и поэтому
при всех t;>;?0 будет v(jq(t),..., хп(t))<^т. Отсюда следует,
что траектория при t ^ta не может выйти за пределы е-ок-
рестности, так как в противном случае она пересекла бы
границу Cs, а в точке пересечения функция v^m (m — наи-
наименьшее значение v на СЕ).
Таким образом, если начальная точка траектории нахо-
находится в 8-окрестности начала координат, то траектория не мо-
может выйти за пределы взятой s-окрестности. Так как г про-
произвольно, то это и значит, что точка покоя устойчива.
') Если система автономна, то траектория зависит только от
начальной точки и не зависит от начального момента времени.
ОСНОВНЫЕ ТЕОРЕМЫ ВТОРОГО МЕТОЛА ЛЯПУНОВА
389
Приведенное доказательство можно очень наглядно ил-
иллюстрировать при помощи рис. 149. На этом рисунке Се-ок-
ружность радиуса е с цент-
центром в начале координат,
Р — точка, в которой функ-
функция v(x, у) принимает наи-
наименьшее значение на Cs,
Г — линия уровня v (х, у) =
= т, проходящая через точ-
точку Р1), С5 — окружность,
ограничивающая 8-окрест-
ность начала координат,
в которой v<^m; ясно,
что С8 лежит внутри Г.
Если (х0, у0) — любая
точка, лежащая внутри
Q, то v(x0, _V0)<w, и
траектория, начинающаяся Рис. 149.
в этой точке, не может
пересечь окружность СЕ и даже, более того, линию Г.
Пример 2. Исследовать на устойчивость решение х = 0,
у = 0 системы
!х-=Ъу — 2х3,
(у = — Зх — 5у3.
Ищем функцию Ляпунова в виде v = ах2-\-$у2, где а > 0 и
постоянные; тогда
0
at
= 2ах
% = 2ах Eу - 2л'3) + 2f!y (_3лг - 5/') =
at
= — 2 [C3 - 5а) ху + 2*х< + 53у' 1.
Если выбрать аир так, чтобы 33 — 5а = 0 (например, считать
а = 3, 3 = 5), то все условия теоремы Ляпунова об устойчивости
будут выполнены, следовательно, решение х = 0, ;у = 0 устойчиво.
"Пример 3. Исследовать на устойчивость точку покоя х = 0,
у s 0 системы
\у = 1х — Ых2у.
!) Так как Р — точка условного экстремума функции v (х, у)
на окружности Се, то линия уровня Г и окружность С-с, как пра-
правило, 'касаются друг друга (см. [1], п. 124).
390
ВТОРОЙ МЕТОД ЛЯПУНОВА
[Гл. ХГ
Подбирая, как ив предыдущем примере, функцию Ляпунова в виде
v = ax2 -f- py, а>0, Р>0, получим
о = 7*2 + Зу2, — = 1 Ах (—Зу + bxf) -{- 6у Gл- — 14лг«у) es 0.
Условия теоремы Ляпунова выполнены, следовательно, точка покоя
х = 0, у = 0 устойчива.
Пример 4. Исследовать на устойчивость точку покоя х = 0,
>> = 0 системы:
x = a(t)x-j-kb(t)y,
a (t) s^O, c(t)s^0, постоянная k > 0.
Выбрав функцию Ляпунова v = л:2 -(- йу2, находим
^ = 2* [a (t) х + Aft @ Л-] + 2Ау [-6 @ х + с @ .у] =
= 2 [а @ л:2 + *й 00/
Условия теоремы Ляпунова выполнены, точка покоя л: = 0, jisO
устойчива.
Приведем несколько более сложных примеров. Они ин-
интересны также тем, что в исследуемые уравнения входят
произвольные функции и поэтому полученные результаты
можно будет применять ко многим конкретным задачам.
Пример 5. Исследовать на устойчивость решение х = 0 ура-
уравнения
x = —f(x), /@) = 0,
где функция f(x) непрерывна и в некоторой окрестности точки
л- = 0 имеет тот же знак, что и х, т. е. л/(л:)>0.
х
Возьмем функцию Ляпунова в виде v (х) = [ f (x) dx; она опреде-
о
ленно положительная в указанной окрестности. При х > 0 очевидно,
о
что г>>0; если же х < 0, то запишем, что v (х) = — f / (x) dx,
X
и так как в интервале (х, 0) функция f (х) < 0, то интеграл отри-
отрицателен, a v положительна. Далее,
Значит, точка покоя устойчива, так как все условия теоремы Ля-
Ляпунова выполнены.
Совершенно аналогично можно доказать устойчивость точки по-
покоя х, = 0 системы уравнений xi = —f{{xi),fi(fi) = 0 (« = 1, 2,..., и)
§ 1] ОСНОВНЫЕ ТЕОРЕМЫ ВТОРОГО МЕТОДА ЛЯПУНОВА 391
где все функции /; таковы, что л-/,- (х) >0 в некоторой окрестности
начала координат. Функция Ляпунова v выбирается теперь в виде
суммы
Л .V;
2 \fi (x) dx.
'=1
Например, для системы х = Зх2 — 2х,у= — siny функцией Ляпу-
Ляпунова можег служить v (х, у) = .V2 — х3 -\- I - - cos у.
Пример 6. Докажем устойчивость нулевого решения уравне-
уравнения
X + ax-{-f(x)=0, /@) = 0,
где a ^sO, а функция / (х) удовлетворяет тем же условиям, что и
в примере 5. _
Заменим уравнение системой
х=у, y = —ay
и возьмем функцию Ляпунова в виде
Ясно, что она определенно 'положительная; ее производная
Ь = / (х) у+у( -ау -/ (л-)) = -fljJ ^ 0.
Поэтому нулевое решение заданного уравнения устойчиво.
Можно рассмотреть более общее уравнение
X + g(x)*+f(x)=0,
где g{x)^Q, а функция /(х) удовлетворяет указанным выше ус-
условиям. И здесь, переходя к системе уравнений первого порядка
X
у2 С
и принимая за функцию Ляпунова v = =^- -f- \f(x) dx, легко дока-
о
зать устойчивость нулевого решения.
Пример 7. Докажем устойчивость нулевого решения уравне-
уравнения
Х + ч (*)-{-f(x)=0, f@) =0, /@) = 0,
рде функции (р и/в некоторой окрестности начала координат непре-
непрерывны и удовлетворяют условиям Ьр (?) > 0, ?/ E) > 0. Полагая
х =_у, получаем систему
х=у, у= —/W—
392
ВТОРОЙ MFTOfl ЛЯПУНОВА
[Гл ХГ
дл"я которой функцию Ляп) нова можно взять такой же, как и в
X
примере 6, т. е. v (л-, у) = -^ + \/(х) dx. Тогда
'о
v=fix)y+y(—f(x) — 4(y))= -
м, и в этом примере ну
э 8. Пусть дана систем;
(± _ du(xlt xa, .... хп)
= 0.
Таким образом, и в этом примере нулевое решение устойчиво.
Пример 8. Пусть дана система уравнений
dt
« = 1, 2, ..., я),
где функция и (xlt x3, ..., х„) имеет строгий максимум в начале
координат. Так как в точке максимума все частные производные
функции и равны нулю, то качало координат является точкой ио-
коя рассматриваемой системы. Докажем, что эта точка покоя
устойчива. Для этого возьмем функцию
v = u@, О, ..., 0) — u(xv x2, ..., хп),
которая, очевидно, равна нулю в начале координат и имеет в нем
строгий минимум. Производная
dv VI ди dx-t
~di ~~ ~ 2т l)x~i dt ~
ди
дХ;
Следовательно, начало координат является устойчивой точкой
покоя рассматриваемой системы.
Приведенные примеры показывают, что подбор функции
Ляпунова является весьма и весьма сложной задачей. Мож-
Можно доказать, что если точка покоя системы A) устойчива,
то функция Ляпунова, удовлетворяющая условиям теоремы
об устойчивости, всегда существует; неизвестно, однако, в
каком виде ее следует искать.
155. В дальнейшем для простоты изложения мы будем
рассматривать главным образом автономные системы уравне-
уравнений, т. е. системы вида D) и, соответственно, функции Ля-
Ляпунова выбирать не зависящими явно от t.
Теорема Ляпунова об асимптотической
устойчивости. Если система дифференциальных урав-
уравнений D) такова, что существует функция Ляпунова
v (хь х.2, ..., хп), определенно положительная в некоторой
h-окрестности начала координат, производная которой
v, вычисленная в силу системы D), определенно отрицатель-
отрицательна, то точка покоя xt = 0 асимптотически устойчива.
§ П
ОСНОВНЫЕ TFOPEMbI ВТОРОГО МЬТОДА ЛЯПУНОВА
393
Так как условия теоремы Ляпунова об устойчивости вы-
выполнены, то точка покоя устойчива; это значит, что для лю-
любого е^>0 (е<^/г) найдется 3(е)^>0 такое, что траектория
с начальной точкой (соответствующей 1 = 1Л) в 8-окрестно-
сти начала координат не выходит при t^tn за пределы
е-окрестности. Вдоль такой траектории при увеличении /
функция v убывает (г><^0), оставаясь ограниченной снизу:
0 2=0. Следовательно, при t->co она имеет предел
Umv(x1(t), д:,@, .... xa{t)) = i^0.
t-co
Если а = 0, т. е. lim v (x,(t), x2(Y), ..., xa(t)) = 0, то
/-.со
lim x, (t) = 0, так как функция v непрерывна и обращается
в нуль только при х; = 0; это и значит, что точка покоя
асимптотически устойчива.
Поэтому осталось доказать лишь, что случай а^>0 не-
невозможен. Допустим, вопреки доказываемому, что а^>0;
тогда при всех t^tb траектория находится в той области,
где о^а^>0, и, следовательно, вне некоторой р-окрестно-
сти начала координат. Рассмотрим кольцевую область, ле-
лежащую вне этой р-окрестности и внутри ранее выбранной
s-окрестности начала координат. В этой области и на ее
^0 |^0 П р>0
границах всюду
0. Пусть
— наименьшее
рц у ^, |^> у р>
значение | v \ в рассматриваемой кольцевой области; тогда
dv
F)
Интегрируя полученное неравенство в пределах от t0 до
t, получим
V (Xi (t), ..., хп (t)) - V (jci Цо), ..., xn (ta)) «S — P (t - to),
или
»(*,(*), •••, *,W)<- Ut — to)-\-v(xl(to), .... xa(t0)). G)
При достаточно большом t правая часть в G) отрицательна,
а следовательно, и v(xt(t), ..., xn(t))<^0, что противоре-
противоречит условию теоремы.
Итак, возможен лишь случай а = 0. Теорема доказана.
В примере 2 (стр. 389) все условия теоремы об асимпто-
асимптотической устойчивости выполнены; следовательно, исследуемая
Д94
?ТОРОЙ МЕТОД ЛЯПУНОВА
[Гл XI
точка покоя не только устойчива, но и асимпюгиче-
ски устойчива В примере 3 (ар. 389) производная v не
является отрицательно определенной она юждествешю рав-
равна нулю. Так как теорема даег лишь достаточные условия
асимптотической устойчивости, то из того, что ^ = 0, ко-
конечно, нельзя еще делать вывод, что точка покоя уаойчива
не асимптотически. Впрочем, небольшое дополнительное рас-
рассуждение уже позволяет сделать такое заключение. Действи-
Действительно, в этом примере v = Ix1 -)- 3_у2, а вдоль интегральных
кривых # = 0 и, следовательно, v = c. Таким образом, коор-
координаты точек любой траектории удовлетворяют уравнению
7х2 -|- ЗУ = с, где с — постоянная; семейство интегральных
кривых образуют эллипсы. Точка покоя х = 0, _у = 0 явля-
является центром; она устойчива, но асимптотической устойчивосш
нет: траектории не приближаются к началу координат
при / —*¦ сю.
Рассмотрим еще один пример.
Пример 9. Дана система
— ex — dfm+\
где постоянные а, Ь, с, d положительны, а т, п — целые неотрица-
неотрицательные числа
Легко проверить, что функция v = cxt-\-ay" удовлетворяет
всем условиям теоремы Ляпунова об асимптотической устойчиво-
устойчивости (ее производная ? = —2 [bcxin+- -\- adylm+i] определенно отри-
отрицательна). Следовательно, точка покоя л; = 0, jy = O асимптотиче-
асимптотически устойчива.
Теорема Ляпунова об асимптотической устойчивости мо-
может быть дополнена следующим утверждением, которое мы
приводим без доказательства.
Если функция v (xit Хч, ..., хп) определена во всем про-
пространстве, всюду удовлетворяет условиям теоремы об асимп-
асимптотической устойчивости и, кроме того, v стремится к беско-
п
нечности при
°> т0 решение х, = 0 (г = 1,2,..., п)
асимптотически устойчиво в целом.
Так, в примере 9 функция v = cxq-\-ау* удовлетворяет
всем указанным условиям, следовательно, ючка покоя асимп-
ютически устойчива в це ом
§ П
OCHOBHblF ТЕОРЕМЫ ВТОРОГО МЕТОДА ЛЯПУНОВА
395
У/
156. ТеоремаЧетаеваонеустойчивости. Пусть
для систе мы дифференциальных уравнений D) в некоторой
h-окрестности начала координат существует функция
Ляпунова v (хх, .. ,хп) и об-
область О, удовлетворяющие сле-
следующим условиям:
1) в области Q функция v
и ее производная v, вычисленная
в силу системы D), положи-
положительны: v^>Q, ii^>0;
2) в любой ^-окрестности
начала координат (р ^ h) имеет-
имеется область О, принадлежащая
области О, причем v = 0 на той
части границы Ор, которая ле-
лежит внутри ^-окрестности на-
начала координат; само начало координат находится либо
внутри области 0р, либо на ее границе.
Тогда точка покоя х, = 0 неустойчива
На рис. 150 для функции ъ = х^—у1 изображены об-
области, в которых х>^>0 и v<^0. Читателю рекомендуется
построить такие области для функ-
функций v = xi—у4 и v = (x—.у) X
Рис 150
Доказательство. Зафикси-
Зафиксируем некоторое положительное чи-
число p<^h. Внутри области Ор вы-
выберем точку А (х10 лгл0), лежащую
сколь угодно близко к началу ко-
координат (это возможно, так как на-
начало координат лежит либо внут-
внутри, либо на границе Ор). Пусть
v(xi0, ...,хп0) = а.; ясно, что а>0.
Возьмем решение системы D),
определяемое начальными условиями
х, (t0) — х1й, и рассмотрим соответ-
соответствующую траекторию, выходящую
из точки А (рис. 161). Пока эта
Рис 151.
траектория находится в области (Зр, вдоль нее й^>0, и, сле-
до1<а1ельно, функция v возрастает. Поэтому траектория не мо-
жег выйти за пределы области О, пересекая ее фаницу гам,
396
второй метод пяпунова
[Гл ХГ
где v=0, т. е. Buyipn р-окрестноаи начала координак Ос-
Остаются две возможности:
' 1) траектория все время остается внутри G;
2) траектория покидает область Gp, выходя одновременно
из фиксированной р-окрестности начала координат.
Покажем, что первая из этих возможностей на самом
деле неосуществима. Действительно, если траектория остается
в области Gp, то вдоль нее v^a, так как г» возрастает. По-
Поэтому траектория остается в той части области Go, где v^a.
Эта часть Gp лежит строго внутри области G, и производная
v имеет в ней положительный минимум (так как и^>0в О):
v^$:[i. Интегрируя это неравенство в пределах от t9 до t,
получим
@, ...,*„(О)-
„(to)
или
(8)
При t —> оо правая часть (8) стремится к бесконечности.
Значит, и v(x1(t), ..., x,l(t))-^-co, что невозможно, так как
функция v ограничена в области Gp (v непрерывна во всей
/г-окрестности начала координат).
Итак, необходимо имеет место вторая возможность, т. е.
как бы близко к началу координат ни была расположена на-
начальная точка А, траектория, начинающаяся в этой точке, по-
покидает фиксированную р-окрестность начала координат. Это
и означает, что точка покоя неустойчива.
Заметим, что если в некоторой окрестности начала ко-
координат функция v и ее производная v, вычисленная вдоль
интегральных кривых, обе определенно положительны, то все
условия теоремы Четаева выполнены. В этом частном случае
теорема была ранее доказана А. М. Ляпуновым.
Пример 10. Исследовать на устойчивость точку покоя х = 0,
у = 0 системы
х= —ау-\-х3, у = Ьх-{-у3, <2>0, й>0.
Функция v = Ьхй -(- ау2 определенно положительна; ее произ-
производная вдоль интегральных кривых v — 2 (bxi -f- яу4) также оп-
определенно положительна. Следовательно, выполнены все условия
теорем!.! Четаева и даже ее частного случая — теоремы Ляпунова;
точка покоя рассматриваемой системы неустойчива.
устойчивость по пирвому приближению
397
Пример 11. Исследовать на устойчивость точку покоя х = 0,
у = 0 системы
Х=уа-\-Х*, j) = A3 -f-y'\
Выберем v = л—_у4; тогда о>0 в области |.v|>|jv].
В этой же области Ь = 4 (л'8—jis)>0 Все >словия теоремы
Четаева выполнены, следовательно, точка покоя не\стойчпва
В заключение заме!им, что если мы исследуем на устой-
устойчивость вторым методом Ляпунова нулевое решение системы
дифференциальных уравнений, ю следует попытаться подоб-
подобрать функцию Ляпунова, удовле1воряющую условиям одной
из приведенных теорем, так как заранее неизвестно, устой-
устойчиво или нет исследуемое решение.
§ 2. Устойчивость по первому приближению
157.- Предположим, что на устойчивость исследуется три-
тривиальное решение системы
§ = /,(*!. **¦••, *«) (Л@> 0,..., 0)=0)
A=1, 2,..., и). (9)
Предположим также, что все /; дифференцируемы в неко-
некоторой окрестности начала координат. Выделяя в правой части
уравнений (9) линейную часть (что возможно в силу диффе-
ренцируемости функций /,), получим
dt
/=i v"";/o
где (-Д) —значение соответствующей частной производной
в начале координат. Функции Rt (хь хг,..., хп) при стремлении
точки (х,, х2,..., хп) к началу координат имеют порядок ча-
лости выше, чем р =
\ (это следует из определения
полною дифференциала; см. [1] п. 110).
Обозначив IJ-') =a-ij> перепишем A0) в виде
га
d.s,_'
dt
7=1
г,..., хп).
398
ВТОРОЙ МЕТОД ЛЯПУНОВА
(Гл. XI
Так как в окрестности точки покоя, т. е. при малых , xt \,
главными членами в правой части A1) являются линейные
члены, то естественно ожидать, что во многих случаях при
исследовании на устойчивость тривиального решения можно
в A1) пренебречь членами Rit заменив тем самым систему A1)
более простой линейной системой
dxi vi
-of = 2, auxJ
7=1
('¦=!. 2,..., я),
A2)
называемой системой первого приближения для системы (9).
Если исследование на устойчивость решения лг, = 0 сис-
системы (И) заменяе1ся исследованием на устойчивость решения
линейной системы A2), то говорят, что система A1) иссле-
исследуется на устойчивость по первому приближению.
Условия возможности такого исследования по первому
приближению были изучены А. М. Ляпуновым, доказавшим
следующие утверждения:
Систему A1) можно исследовать на устойчивость
по первому приближению, если:
1) все корни характеристического уравнения для урав-
уравнения первого приближения имеют отрицательные дейст-
действительные части; в этом случае точка покоя лг, = О (i= 1,
2,..., п) уравнения A1) асимптотически устойчива;
2) хотя бы один корень характеристического уравне-
уравнения имеет положительную действительную часть; в этом
случае точка покоя х, = 0 системы A0) неустойчива.
Указанные в теореме А. М. Ляпунова случаи 1) и 2) не
охватывают лишь так называемого критического случая:
3) существуют корни характеристического уравнения
с нулевой действительной частью, а остальные корни,
если они есть, имеют отрицательную действительную
часть.
В критическом случае исследование на устойчивость по
первому приближению, вообще говоря, невозможно: на устой-
устойчивость начинают влиять нелинейные члены Rt.
Например, точка покоя х = 0, у = 0 системы
х== —ау — х3, р = Ьх—У, A3)
где а^>0, b ^> 0, асимптотически устойчива, чак как функция
Ляпунова v = bx'~\-ayi удовлетворяет условиям теоремы
УСТОЙЧИВОСТЬ ПО ПЕРВОМУ ПРИБЛИЖЕНИЮ
399
об асимптотической устойчивости (v= —2 {bxk -\- <z_y4) опре-
определенно отрицательна).
В то же время точка покоя jc = O, _y = 0 системы
х=— ау^-х3, p = bx-{-y\ A4)
имеющей ту же самую линейную часть, неустойчива (см. при-
пример 10 на стр. 396).
Для рассматриваемых систем A3) и A4) характеристиче-
характеристическое уравнение для системы первого приближения
х = — ay, p = bx A5)
имеет чисто мнимые корни. Следовательно, для уравнений A3)
и A4) мы имеем дело с критическим случаем—действитель-
случаем—действительные части корней характеристического уравнения равны нулю.
Для системы первого приближения A5) начало координат
является центром (см. стр. 356). Добавление к линейной части
нелинейных членов в A3) и A4) приводит в окрестности
начала координат к малому изменению определяемого систе-
системой A5) поля направлений касательных к траекториям.
Однако даже малое изменение поля направлений приводит
к тому, что траектории, ранее замкнутые, после обхода
начала координат уже не замыкаются, а превращаются
в спирали в случае A3), приближающиеся к началу коорди-
координат и образующие в точке х = 0, у = 0 устойчивый фокус,
а в случае A4) — удаляющиеся от начала координат и обра-
образующие в начале координат неустойчивый фокус.
Итак, в критическом случае нелинейные члены могут
влиять на устойчивость точки покоя.
Приведем несколько примеров исследования на устойчи-
устойчивость по первому приближению точки покоя в начале коор-
координат.
Пример 1. jp + 2* + 2 sin x = Q.
Это уравнение можно заменить системой
х = у, у= — 2у — 2 sin х,
но в этом нет необходимости. Выделяем линейную часть непосред-
непосредственно в данном уравнении, разложив sin x по степеням х:
A6)
Уравнением первого приближения является
х -|- Ik -4- 2а = 0.
400
ВТОРОЙ МЕТОД ЛЯПУНОВА
[Гл XI
Корни характеристического уравнения /г,|2 = —1 ± < имеют огри-
цательн)ю действительна часть, следовательно, решение х ее О
уравнения A6), а значит и данного, асимптотически устойчиво.
Пример 2.
• = 1. A7)
Т + ""
Разлагая ех по степеням х
и выделяя линейн\ю часть, получим
В силу признака Гурвица (см. стр. 366) все корни характеристического
уравнения имеют отрицательные действительные части, следователь-
следовательно, решение х = 0 уравнений A8) и A7) асимптотически устойчиво.
Пример 3.
(х = х-\-еУ — cosy,
(у = Зх —у — sin у — хя.
A9)
Для характеристического уравнения системы первого прибли-
приближения
X = х -\-у, у = 3х — 2у B0)
один из корней положительный (fe1|2 = 1у-^-—), следователь-
следовательно, точка покоя лгееО, j> es 0 систем B0) и A9) неустойчива.
§ 3. Устойчивость при постоянно действующих
возмущениях
158. Составляя систему дифференциальных уравнений,
описывающую какой-нибудь процесс, мы всегда вынуждены
учитывать лишь основные влияющие на этот процесс факторы,
отбрасывая остальные, менее существенные. Такая идеализация
часто вызывается желанием упростить задачу, а кроме того,
мы почти никогда не знаем всех воздействующих на данный
процесс факторов, но имеем основания считать влияние не-
некоторых из них незначительным. Однако даже незначительно
влияющие на рассматриваемый процесс факторы при длитель-
длительном действии могут оказать на него заметное влияние.
Выяснению влияния таких малых посюянно дейс1вующих
возмущений и посвящен этот параграф.
§ з] устойчив, при постоянно дг.иств. возмущениях 401
Рассмотрим наряду с системой
Xi=fi(t, хь ..., хя) B1)
систему
Xi=fi(t, хь хь ..., xn)-\-Qi(t, хь хъ ..., хп), B2)
где функции Q{, называемые постоянно действующими
возмущениями, неизвестны, но известно, что они малы по
модулю и таковы, что возмущенная система B2), так же
как и сиаема B1), имеет единственное решение, определяемое
условиями
xi(ta) = xu> (/=1, 2, ..., л).
Как уже упоминалось выше (см. стр. 350), исследуемое
решение введением новых неизвестных функций может быть
преобразовано в нулевое, поэтому мы предположим, что на
устойчивость при постоянно действующих возмущениях ис-
исследуется нулевое решение уравнения B1).
Определение. Пусть для любого достаточно малого
е^>0 существуют такие 8^>0 и т)^>0, что каковы бы ни
были функции Qi(t, хь..., хп), лишь бы
Qi(t, xt,..., JCn) !<¦»),
я
когда t :>; ?0 и ^х*<^ е2, решение xt (i) возмущенной си-
стемы B2), определяемое начальными условиями л"; (^0) = xi(j,
п
где У]xf0<^8а, удовлетворяет при всех t^t^ неравенству
Тогда нулевое решение системы B1) называется устойчивым
при постоянно действующих возмущениях.
Иными словами, решение устойчиво при постоянно дей-
действующих возмущениях, если малые, но постоянно действу-
действующие возмущения вызывают лишь малые изменения решения
при сколь угодно больших значениях t.
159. Мы приведем теорему И. Г. Малкина, содержащую
достаточные условия устойчивости при постоянно действую-
действующих возмущениях. Для просюты сформулируем и докажем
402
ВТОРОЙ МЕТОД ЛЯПУНОВА
[Гл XI
эту теорему лишь в том частном случае, когда невозмущен-
невозмущенная система B1) автономна, т. е. имеет вид
х, ==/, (*, ..., хп). B3)
При этом возмущенной системой будет
¦*, =/i (JCi, • • •, ха) + Q, V, хь..., хп). B4)
Теорема М а л к и н а. Пусть для системы B3) суще-
существует функция Ляпунова v(xlt ..., хп), определенно поло-
положительная в некоторой h-окрестности накала координат,
производная которой v, вычисленная в силу системы B3),
определенно отрицательна. Тогда нулевое решение систе-
системы B1) устойчиво при постоянно действующих возму-
возмущениях.
Заметил!, что условия приведенной теоремы совпадают
с условиями теоремы Ляпунова об асимптотической устойчи-
устойчивости для автономных систем.
Доказательство. Возьмем любое е^>0 (s<^ft) и
обозначим через т наименьшее значение функции v(xh ..., хп)
на границе s-окрестности на-
начала координат — сфере Се
(см. рис. 152 для п =2).
Выберем, далее, какое-либо
положительное число 1<^т
и подберем 3^>0 так, чтобы
в S-окрестности начала ко-
координат и на ее границе Q'
имело место неравенство
v (xv ..., хп) <^ /. Это воз-
возможно, так как v @, ..., 0) =
= 0 и функция v непрерыв-
непрерывна. Очевидно, что 3<^а.
Рис. 152. В кольцевой области
между сферами Q и Сг и на
ее границах (на рис. 152 эта область заштрихована) производ-
производная функции v, вычисленная в силу системы B3), удовлетво-
удовлетворяет, будучи определенно отрицательной,неравенству
где k — некоторая положи1ельная посюянпая.
§ 3] УСТОЙЧИВ ПРИ ПОСТОЯННО ДЕЙСТВ ВОЗМУЩЕНИЯХ
403
Ввиду тою, что величины
дх,
в s-окрестности начала
координат ограничены, можно выбрать столь малое
что для всех функций Q, (t, xb ..., хп), для которых в е-ок-
реаности начала координат и при t^t0 имеют место нера-
неравенства | Qi l <^ 1\, справедливо также (при тех же t, хь..., хп)
неравенство
V
di;Qi
B6)
Из B5) и B6) следует, что в рассматриваемом кольце
(включая его границы) производная функции v, вычисленная
уже в силу возмущенной системы B4), удовлетворяет нера-
неравенству
1=1
1=1
Для завершения доказательства выберем точку А с коор-
координатами х, (t(,) = jci0 в 8-окрестности начала координат
и рассмотрим траекторию возмущенной системы B4), кото-
которая определяется этой начальной точкой; она не может выйти
за пределы сферы С,. Действительно, во всей 8-окрестности
(в чааности, й в точке Л) v s^.l<^m. Чтобы выйти за
пределы сферы Се, траектория должна сначала войти в кольцо
между Q и С?. Но в этом кольце вдоль траектории й<^0,
и поэтому функция v убывает; значит, траектория не может
пересечь сферу Са, так как во всех точках этой сферы
v 5= гп ~^> I.
Ввиду того, что s было выбрано произвольно, теорема
доказана.
Пример 1. Исследовать на устойчивость при постоянно дей-
действующих возмущениях тривиальное решение системы
х— ах — by3, у = су — fiU\
где а, Ь, с, d — положительные постоянные. Точка покоя х = 0,
jy = O устойчива при постоянно действующих возмущениях, так
как функция v = сх2 -|- ау2 удовлетворяет всем условиям теоремы
Малкпиа.
404
ВТОРОЙ МЕТОД ТЯПУНОВА
ГГл ХГ
о
t,
Рис. 153.
160. Мы предпола! али, чю возмущения действуют посто-
постоянно, т. е. Qt{t, jCi, ..., хп) могут быть отличными от нуля
при любом t^ta.
Естественно возникает вопрос, как влияют малые кратко-
кратковременные возмущения, т. е. как влияют в B2) малые по мо-
модулю функции Q; (t, хь ..., хп), отличные от нуля лишь на
небольшом интервале изменения
t, /,<f<tz. В силу малости
модулей Qi можно утверждать,
что их влияние сведется к тому,
что точка М в момент ^ будет
находиться где-то вблизи рассмат-
рассматриваемой траектории системы B1)
(рис. 153).
Для значений t^t^ Q, = 0
и, следовательно, надо рассмат-
рассматривать опять решение системы B1), но с несколько сме-
смешенными начальными значениями, т. е. возникает уже рас-
смофепная задача о нахождении условий устойчивости по
Ляпунову — устойчивости по отношению к возмущениям на-
начальных значений.
При этом возмущения начальных значений происходят не
в точке tlt а в точке tit однако легко видеть, что если ре-
решения уравнения определены при всех t^ti и непрерывно
зависят от начальных значений, то при исследовании на устой-
устойчивость безразлично, в какой точке происходят возмущения.
Действительно, решения, определяемые возмущенными началь-
начальными значениями в точке tv могут быть продолжены до точ-
точки ^2 (или, наоборот, от точки tt до ?]) и в силу непрерыв-
непрерывной зависимости решения от начальных значений малые воз-
возмущения начальных значений в точке tt будут вызывать ма-
малые возмущения, определяющие то же самое решение, в
точке t% (рис. 153).
ЗАДАЧИ К ГЛАВЕ XI
1. Исследовать на устойчивость н} левое решение л: = 0, у = 0
системы
х = — х sin21 -\- е'у,
у= — е'х —у cos41;
(х = — х sin2
а) {. ,
[у = — е'х —
.. f.* = 3v-jc',
ЗАДАЧИ К ГЛ XI
405
2. При каких значениях параметра а система
(х=у-{-ах — хъ,
имеет устойчивую точку покоя л; = 0, _у = 0?
3. Исследовать на устойчивость точку покоя
стемы уравнений
(х = х — 2 sin у —у3,
= 0, у =
си-
си4. Исследовать на устойчивость точку покоя дг = О, у = 0 си-
системы уравнений
С х = л: -f- еУ — cosy,
\у = 3х — у — sin у.
5. Устойчиво ли по отношению к постоянно действующим воз-
возмущениям решение х = 0, у = 0 системы уравнений
' = 5х —у7'?
6. Исследовать на устойчивость решение х sO уравнений:
а) х'" -\- 5х" -(- За-' + sin x = 0;
б) х'" + 4л:* + ох' + Зех = 3;
в) х'" -\- sin х
—С03 •* =
ОТВЕТЫ К ЗАДАЧАМ
ЧАСТЬ I
Глава I
1. а) 3 I cos -^ -\ I sin ~) ; б) cos l~ | j + I sin f — | j; в) 2 (cos 0 -f
-)-1 sin 0); г) 2 (cos n -[-«' sin я); д) /2 (cos -^ + i sin -" i;
з) 2Jcosf—^j + isinf—|j 1; и) /29 (cos arctg | + i sin arctg ^J;
к) /29 [cos (к - arctg |j + i sin ^ — arctg |)"|; л) /29 X
X cos f— arctg -gj + г sin (— arctg -^ j ; м) /29 cos (arctg -^ — лj -f
+ isin farctg -^ — л! .
2. а) Вне круга радиуса 5 с центром в начале координат;
б) внутри круга радиуса 3 с центром в точке i; в) вне круга ради-
радиуса 2 с центром в точке —21 и на окружности этого круга; г) па
окружности круга радиуса 5 с центром в точке 3 —f— 4i; д) ,справа
от прямой Л'= 3; е) ниже прямой у = 2 и на самой этой прямой;
ж) на эллипсе с фокусами в точках —2 и 2 и большой полуосью ^;
з) внутри левой ветви гиперболы с фокусами в точках —2 и 2 и
действительной полуосью -^; и) на лемнискате (х2—у"—1J +
-j- 4х2у- = а*; к) на гиперболе х2—у2 = а2; л) на перпендикуляре
к отрезку, соединяющему точки i и —2, восставленному из сере-
середины этого отрезка; м) на прямой х = -= и слева от нее; н) внутри
угла между лучами <р = а и <р = % выходящими из начала коорди-
нат; о) на луче, выходящем из точки i под углом —. к положи-
положительном} направлению действительной оси; и) внутри угла между
ОТВЕТЫ К ЗАДАЧАМ
407
лучами, выходящими из точки -2/ и образ) ющил'и с положитель-
положительным направлением действительной оси углы, равные соответст-
соответственно -г; И -= .
4. а) -I; б) -г; в) i +1 /; г) -16(/3 +'); д) -8;
5. a) 4 (V'3 ¦
- (/3" + 0, - V^2 i, 1Ц- (/3" - /); в) 1,
;
г) }/~2 (cos'f + ' sin ср), где « = -|-, -g-; д) 2 + t, — 2 —«;
е)/2
71 Ця 19Я
), где <? = ^, -у^ , TJ-
6. а)' ы2 + и2 = ^-; б) «2 + г»2= 1; в) « = —и; г) w = 0;
Д)(И—2-) + 0> = T"' e) " = Т"
а:2 у2 1
7. а) Прямая _у = а;; б) эллипс —г + тл = 1; в) гипербола _у = -;-;
г) ветвь гиперболы у = —, лежащая в первой четверти (л-> 0,
8. а) у In 2 + ^- i + 2Ы; б) — -^ i + 2fe7i/; в) In 5 —
— i arctg 4-4- Bй + 1) "' (k = 0, ±1, ±2, ...).
О
Указание. Главное значение аргумента числа —3 —J— 4i рав-
4
но л — arctg -5-.
9. а) — <; б) — el; в) е3 (cos 1 +1 sin 1); г) le
\ Yk ~ l) " / In 2 ... In 2\ . „ь, , .
д) еч cos^j- -j-ism-^ ; e) e2ft:c (cos In
+ /sinln3) (ft = 0, ± 1, ±2, ...).
в) гш 1 -1 'bh--'ij ¦''")cos 1; ll) '¦sin'ch 2 cos'sh 2;
408
OTBFTbl К ЗАДАЧАМ
е~У .
sin
еУ — е У
cos .v: или ch у sin х + i sh у cos x;
еу"-\-е-У . еУ — е-У .
ж) -к cos х — i ц sin х или спу cos х — i shy sin х.
13. а) Bй + т я — ПпC±2у2); бJАя —iln(j/2 —I),
Bft + l)rc —iln(/2~+l); в) гйя + аг^у'г — i [1и A +1^2 ) +
+ -2-ln(l+l/2~)l, Bft+l)^-arctgVA2"~i[ln (^Г—1) +
+ -у1и A +l/2 )]; г) fex + -y In 2; д) ftic + -^-arctg 2 + — In 5;
e) Ц + ftn^i; ж) Bfc+l)w (ft = 0, ± 1, ±2, ...)
Глава II
2. a) z*-\-Ci; 6)
д) — 2i^4-C«.
L
<; r) i. J-2гг 4-C/;
3. a)
4-C; б) га4-3(г4-С; в) 1пг4-С; r) ze* +
j
4-A 4-0 г + С.
4. а) Углы поворота 0 и 0, коэффициенты растяжения 2 и 3;
б) углы поворота 0 и 0, коэффициенты растяжения 1 и г; в) углы
1 3
поворота л и 0, коэффициенты растяжения ^ и у^; г) углы пово-
поворота т и R" , коэффициенты растяжения 2 |/2 и 6; д) углы пово-
поворота — -р и д-, коэффициенты растяжения 4 и 12.
5. а) Сжимается внутренность круга \z\<.-^-y растягивается
внешность круга |z|>2-; б) сжимается внешность круга | г | > 1,
растягивается внутренность круга [г|<;1; в) сжимается внутрен-
внутренность круга | г4-1 | < ?т', растягивается внешность круга | г4-1 I >
>5"; г) сжимается левая полуплоскость х < 0, растягивается пра-
правая полуплоскость а > 0; д) сжимается внешность круга | г — 1 | > 1,
растягивается внутренность круга \z— 1 | < 1.
6. а) 'Щ б) 2 4 .j.
7. а) 1; б) 2.
ОТВЕТЫ К ЗАДАЧАМ '
409
8. л) — 8тсг; 6) 0. 9. nie I = 2n sh 1.
.0. a) |; в)-|-. „.,)?; 6) _?. 12.
6) - —: в) 0.
&. 13. а) ^;
Глава III
1. » = ^-=p. 2. а) я»-^^; б) «> = i^
З1). а) и» = —
лгг .\ ;t
б) гг) =
в) w = i
2г _ /3 + i
для области /, да = —
Iт^
\2г - /3 +
для области //, w— I "Z ~*~ \._ ' | для области ///, го =
^-/3+ij
для области IV; г) да = ( -;
4. На верхнюю полуплоскость.
5. На внутренность единичного круга.
6. да ^^
cos 22+1 ¦
') В ответах к задачам 3 и 6 указана лишь одна функция,
удовлетворяющая условиям соответствующей задачи.
410
ОТВЕТЫ К ЗАДАЧАМ
Глава IV
2.
X
(^- —2) B7|
)
мости ранен 1.
... |, где ft = 0, 1, 2,..., т — 1. Радиус сходи-
•3 . , 1-3.5 . .
2! 2
" 23 • 7 ¦ 3!
3 -г 5 7 [ ¦¦;- i 2.3 ' 22-5-2Г
-... Радиус сходимости равен 1 в обоих случаях.
/ 3 13 \
4. а) е 1 -\- 2 + -ту 22 -f- -p- z3 -\-...), г = 1; б) sin I -f- cos
+ (cos 1 xy sin 1 j z- -\- \-^ cos 1 — sin
...;г=1;вIп2 + -|
5. a) z = ± 3/ — нули 1-го порядка, z = ± 2i — нули 5-го порядка;
6) 2 = 2йм (ft = 0, ± 1, ± 2,...) — нули 1-го порядка; z = ± 2 — нули
3-го порядка; в) 2 = 0— нуль. 2-го порядка, г = ft?c (ft = 0, ± 1,
± 2,...) — нули 1-го порядка; г) 2 = 0 —нуль 2-го порядка, z = кк
(ft = 0, ±1,±2,...) — нули 3-го порядка.
+ + +
1 д_» а
' г2 "Г(а — 6J3 ""(a
(а — 6) г" "т"""'
(а —
(а —
—а)'
б) cos
(-1)*
Bk) 1 B - 2)
(—1)"+J X
Х
8.-1-1-
2 2'
5 1
~-y—y-f —..., область сходимости |z]>l.
9. а) Полюсы 1-го порядка г = 0 и г = —1; полюс 3-го поряд-
ка 2=1; б) полюсы 3-го порядка ±.-Цр A —(); в) полюсы 1-го по-
порядка г — /гл (ft = 0, ± 1, ±2,...); г) полюсы 2-го порядка г =
2k 4- 1
=^=—^—тс (ft = 0, ±1, ±2,...); д) существенно особая точка
2 = 2i; е) существенно особая точка г = — /; ж) полюсы 1-ю по-
ОТВСТЫ К ЗАДАЧАМ
411
рядка 2=1
Bft
(¦'г=0, ± 1, ±2,...), г:-1—предельная
2ft + 1
точка для полюсов (неизолированная особая точка); з) 2=—А— я
(ft = 0, ± I, ±2,...) — полюсы 1-го порядка (г = 1—правильная
точка); и) особых точек в конечной части плоскости нет; к) 2 = 0 —
полюс 3-го порядка; л) 2= In2 -|- 2 k m (ft = 0, ± 1, ±2,...) —
полюсы 1-го порядка.
10. а) 2 = со — правильная точка,/(со) = 1; б) 2 —оо — полюс
3-го порядка; в) z = со — правильная точка (нуль 3-го порядка);
г) г = оо — существенно особая точка; д) г = со — существенно осо-
особая точка; е) 2 = со--полюс 2-го порядка; ж) z = co — правильная
точка, /(со) = 1; 3) г = оо — правильная точка, /(оо) = 1; и) 2 =
= со — существенно особая точка.
11. а) Нет; б) да. 12. а) Да; б) нет.
Глава V
1. а) 5; б) — 1; в) — 7^- (относительно точки г) и-т^ (относитель-
но точки— i);r) (— 1)" '
3)...Bй— 1Jп , «
J К ^ ; д) — j-
J_
; д) — j- (от-
(относительно точки i) и д- (относительно точки — ;'^е) 1 (относительно
1 4
точки 0) и =- (относительно каждой из точек ± 1); ж) -=- sin 2i;
з) — 1 (относительно каждой из точек Bft-)-1)-^-, й = 0, ± 1,±2,...);
и) 0 (относительно каждой из точек ftit, k =0, ± 1, ± 2, ... ); к) — 1
(относительно какдо;'! из точек кп (к = 0, + 1,± 2, ...)).
2. а) 1; б) 0; в) 1. 3.
77л-
izi
2 '5'
0; б) (—О" X
.. 2лBя — 2)! i _ . Bn — 2)! я
X [(n_1)!J»(e_u)M-i J в) 0. 6. а) я /2; б) 2'»-а[(л - I)!]2 '>
квадранте по одному нулю; б) во втором и третьем квадрантах по
два нуля.
Глава VI
Модуль вектора в точке г:
|з3 —
1. 2 I 2 I. 2.
3 2__ 4
I 2 | ' '
Угол между вектором в точке z и положительным направлением
действительной оси;
412
ОТВЕТЫ К ЗАДАЧАМ
1. —Argz. 2. 2 Argz— Arg (z-— 1). 3. Argz — -л-.
4. -^ Arg (z — а). Уравнения линий тока:
1. xy = С. 2. _y A 7-т—-j j = С, в полярных координатах
(р -) sinu = С. 3. р = Се-Р.
4. р = , если полярная система координат выбрана так,
sin2 ~
что z = a — полюс, а направление полярной оси совпадает с поло-
положительным направлением действительной оси.
Уравнения линий уровня потенциальной функции:
1. л—у- = с. 2. Л" i I -j——i—jj = c, в полярных координатах
р-) I cos (f = с. 3. р = cef. 4. р = , если полярная система
координат выбрана так же, как при определении линий тока (см. выше).
5. Семейство линий тока — пучок окружностей, проходящих
через точки г = U, г = 1. Линии уровня потенциальной функции —
окружности (л- — сJ -\-у- = с (с—1). Точка z = 0—источник обиль-
обильности 2л, точка z= 1 —сток обильности—2л.
6. Семейство линий тока — окружности (х — с)--{-у- = с (с— 1),
семейство линий \ровня потенциальной функции — пучок окруж-
окружностей, проходящих через точки г = 0, z=l; z = 0 — вихревая
точка интенсивности — 2к, z = 1 — вихревая точка интенсивности 2л.
2. а)—7
I P
3. а)
Глава VII
р2 -\- 2о>-
1а —I— :чвi» ' (n-i-w — я''
:1 \_(jj — ay-l-ш-
o2j2 — 412/?2
ОТВЕТЫ К ЗАДАЧАМ
413
2 (о — Лр) [
5. а)
г)
7. а) 1 + It + ту | е1; б) cos 2/ — t sin2i; в) ^ (sh at + a< ch a^);
a2 ch a^ — й2 ch bt
Глава VIII
/; г) x =
1. а) д- = -J2"; 6) x = f-e'1; в) л: = 4е' — !
sin< + sin2^ — 2 cos 3t; д) д: = — 2 sin/ — cos 2Л
2. a) x = e2', ji = 3e2/; 6) x = к от е4' + e' — j= cos /
5 22 2 4 1
-y= sin/; в) x — — e ',
>='еЧ z = 0;J'r) x=n—\7cht+ltsht, y = —12+12 chi —
Глава IX
2. /(я) = 2« fl + (- 1)" 2 —cos Щ — 2п — 1.
3. /(я) = A-я) 4*.
Глава X
1. Точка покоя асимптотически устойчива. 2. Точка покоя не-
неустойчива. 3. При а < — ^- точка покоя асимптотически устойчива,
при а = —5" устойчива, при а > — =- неустойчива. 4. Центр.
5. а) Точка покоя неустойчива, б) точка покоя асимптотически ус-
устойчива, в) точка покоя неустойчива. 6. Седло. 7. Периодическое
решение jtr = p-sin? — ^- cos/ асимптотически устойчиво. 8. Все
О О
решения асимптотически устойчивы. 9. а) Неустойчиво, б) неустой-
неустойчиво.
10. а) Решение устойчиво асимптотически в заштрихованной
на рнс. 154 области между прямой р = « н «верхней» ветвью ги-
гиперболы р (а — 1) =—1, на всей границе этой области решение
414
ОТВЕТЫ К ЗАДАЧАМ
устойчиво, но не асимптотически; б) решение устойчиво в заштри-
заштрихованной на рис. 155 области, лежащей под прямой В = —— л
О I/
?¦«¦
Рис. 154.
Рис. 155.
между ветвями гиперболы а2— 8s =1; решение устойчиво (но не
асимптотически) во всех точках границы этой области, кроме точек
Рис. 157.
11. а) В области а > 0, 8 >— (область / на рис. 156) N = 0,
а
в остальной части плоскости (область II) N = 2; б) в области
а> "~^г^2"^Т (область I на Рис- 157) N = 0, в области
ОТВЕТЫ К ЗАДАЧАМ
415
0<а <
А/
у + 1/р2+ ^-(область //) А/ = 2, в области, где а <
+^«< 0, р>0 (область///),
i- или 1_
=1; в области у— 1/ В2 + i- < а <0,В < 0 (область IV) N = 3.
12. а) Решение асимптотически устойчиво в области |а| — 1<
Э< 1 (треугольник, заштрихованный на рис. 158). Во всех точках
А
-? -;\
1
ш
%
-
Рис. 158.
Рис. 159.
границы, кроме точек А и В, решение устойчиво, но не асимпто-
асимптотически, б) Решение асимптотически устойчиво в заштрихованноп
на рис. 159 области а2 — 2а — 1 < В< 1—2а. Во всех точках гра-
границы, кроме точки (|/2,1 — 2 "|/2 ), решение устойчиво, но не асимп-
асимптотически.
Глаза XI
1. а) Решение устойчиво; б) Решение асимптотически \стойчиво.
Указание. Можно подобрать функцию Ляпунова вида ах3 -\-$у2-
2. При а^О точка покоя асимптотически устойчива, при а >. 0
неустойчива. 3. Точка покоя неустойчива. 4. Точка покоя неустой-
неустойчива. 5. Точка покоя устойчива по отношению к постоянно дейст-
действующим воз\1)щенням. 6. а) Решение асимптотически устойчиво;
б) решение асимптотически устойчиво; в) решение неустойчиво.
ЛИТЕРАТУРА
1. А. Ф. Б е р м а н т и И. Г. Араманович, Краткий курс
математического анализа, «Наука», 1967.
2. В. И. Смирно в, Курс высшей математики, т. III, Физ-
матгиз, 1958.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
3. А. А н г о, Математика для электро- и радиоинженеров,
«Наука», 1964.
4. И. Г. Араманович и В. И. Левин, Уравнения матема-
математической физики, «Наука», 1964.
5. Е. А. Барбашин, Введение в теорию устойчивости,
«Наука», 1967.
6. Г. Д е ч, Руководство к практическому применению преобра-
преобразования Лапласа, «Наука», 1965.
7. М. А. Лаврентьев и Б. В. Шабат, Методы теории
функций комплексного переменного, «На>ка», 1965.
8. И. Г. М а л к и н, Теория устойчивости движения, «Наука», 1966.
9. А. И. М а р к у ш е в и ч, Краткий курс теории аналитических
функций, «Наука», 1966.
10. П. И. Романовский, Ряды Фурье. Теория поля. Анали-
Аналитические и специальные функции. Преобразование Лапласа,
«Наука», 1964.
ЗАДАЧНИКИ
11. Л. И. В о л к о в ы с к и й, Г. Л. Лунц и И.Г.Арама-
н о в и ч, Сборник задач по теории функций комплексного
переменного, Физматгиз, 1960.
12. Н. И. Кожевников, Т. И. Краснощекова и
Н. Е. Ш и ш к и н, Ряды и интеграл Фурье. Теория поля. Анали-
Аналитические и специальные функции. Преобразование Лапласа,
«Наука», 1964.
13. М. Л. Краснов и Г. И. Макаренко, Операционное
исчисление. Устойчивость движения, «Наука», 1964.