Автор: Вельшенбах М.
Теги: языки программирования программирование криптография
ISBN: 5-89392-083-Х
Год: 2004
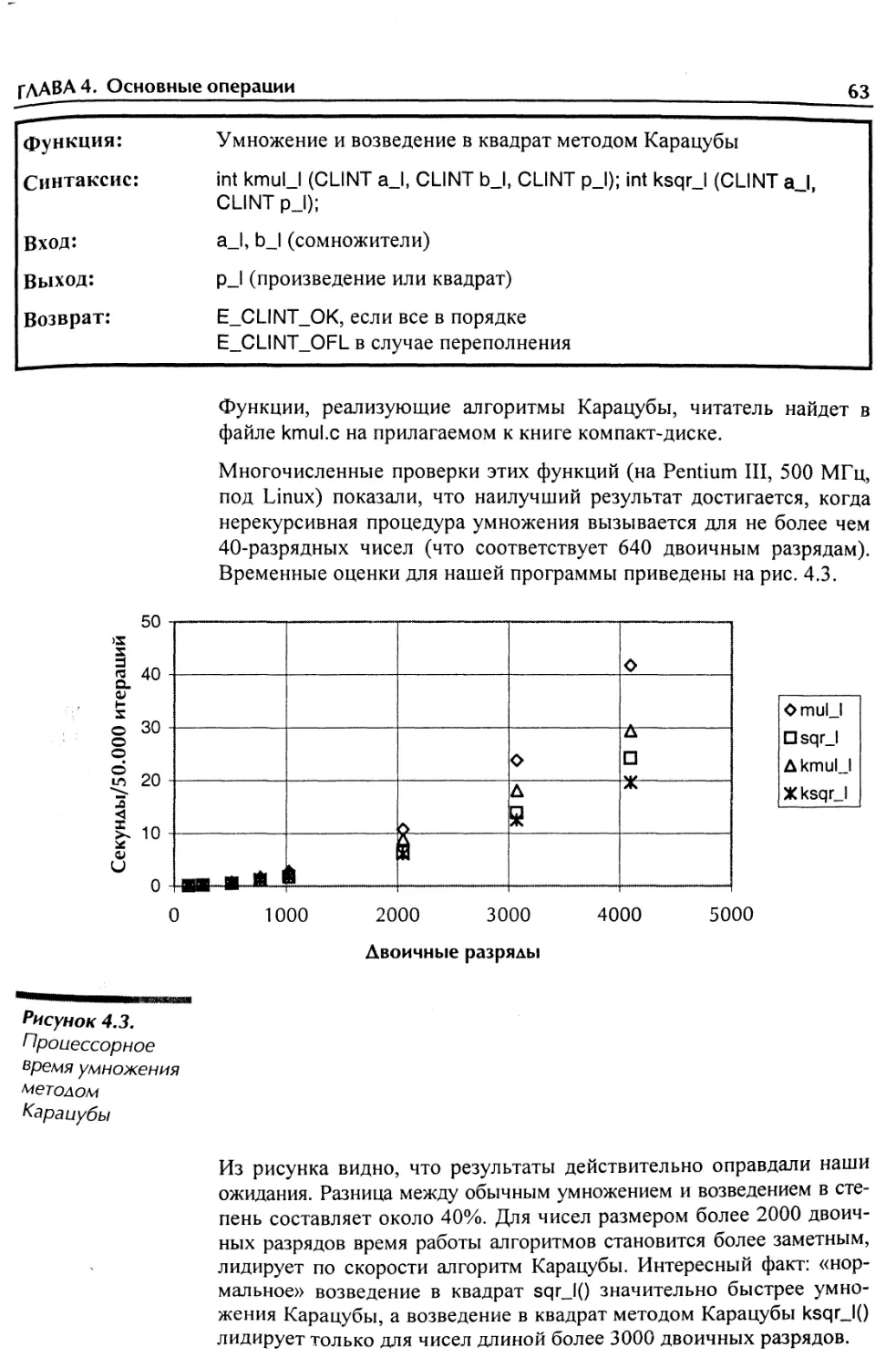
Текст
УДК 004.43
М. Вельшенбах
Криптография на Си и C++ в действии. Учебное пособие.—
М.: Издательство Триумф, 2004 — 464 с.: ил.
ISBN 5-89392-083-Х
ISBN 3-54042061-4 (нем.)
Несмотря на то, что настоящее издание содержит математическую
теорию новейших криптографических алгоритмов, книга в большей степени
рассчитана на программистов-практиков. Здесь Вы найдете описание
особенностей эффективной реализации криптографических алгоритмов на
языках Си и C++, а также большое количество хорошо документированных
исходных кодов, которые записаны на компакт-диск, прилагаемый к книге.
Купите книгу, и Вы легко сможете снабдить свои собственные
программные разработки сильной криптографической защитой.
Originally published in German.
Kryptographie in C und C++ by Michael Welschenbach.
Copyright © Springer-Verlag Berlin Heidelberg 1998, 2001.
Springer-Verlag is a company in the BertelsmannSpringer publishing group. All rights reserved.
ISBN 5-89392-083-X
ISBN 3-54042061-4 (нем.)
© Обложка, серия, оформление
ООО «Издательство ТРИУМФ», 2004
Fiir Helga, Daniel und Lukas
Посвящается Хельге, Даниэлу и Лукасу
Предисловие к русскому изданию
Криптография как наука имеет богатые традиции в России. Многие
широко известные результаты, особенно в области математических
основ современной криптографии, получены русскими учеными.
Один из самых известных (по крайней мере на Западе) мастеров
классической криптографии - Уильям (Вольф) Фридман (William
Friedman) (1891-1969) - родился в России. Он занимался криптоа-
нализом - искусством взлома шифров. Именно он является автором
термина «криптоанализ».
Искусство тайнописи веками совершенствовалось по всему миру.
В России секреты тайнописи талантливых самоучек (в том числе
родоначальников тайнописи - средневековых монахов и священно-
служителей) были поставлены на защиту интересов государства в
XVII веке. Возникла мощная дипломатическая служба, которая
распространила свое влияние на всю Европу и имела обширную
секретную переписку.
Криптография в России продолжала развиваться и после Октябрь-
ской революции 1917 года, в тяжелые годы Второй мировой войны,
во время «холодной» войны - но почти незаметно для западной
общественности. Падение Берлинской стены и объединение Герма-
нии лишь чуть приподняли завесу секретности над русскими мето-
дами шифрования, о русских методах взлома шифров по-прежнему
известно очень мало.
Сегодня, благодаря охватившей весь мир сети Интернет, любой
желающий может получить необходимую информацию практиче-
ски по любому вопросу. Однако доступность информации имеет и
оборотную сторону: как никогда легко отыскать информацию, как
никогда трудно ее защитить. В эпоху высокоскоростных вычисле-
ний и широкого общения роль криптографии неуклонно растет.
Достоянием широкой общественности она стала после сенсационной
публикации Уитфилда Диффи и Мартина Хеллмана, «открывших»
в 1976 году криптографию с открытым ключом.
Надеюсь, что эта книга позволит читателю познакомиться с совре-
менными криптографическими алгоритмами и понять, что и зачем
он делает. Я благодарен издательству «Триумф» за интерес, прояв-
ленный к этой книге. Особая признательность ее научному редак-
тору Павлу Семьянову за кропотливую работу.
Спасибо и тебе, читатель, держащий в руках эту книгу.
Кельн, Германия, март 2003
Michael Welschenbach
Предисловие ко второму изданию
Когда я ломаю голову над числами, я словно
зарываюсь в землю и ничего не вижу вокруг.
Стоит мне лишь отвлечься, взглянуть на море,
или на дерево, или на женщину - будь она
даже старухой, - и мои расчеты летят ко всем
чертям! Числа исчезают, обращаются в бегство,
а я пытаюсь догнать их.
Никос Казанзакис, Грек Зорба
Во второй редакции книга была пересмотрена и значительно рас-
ширена. Добавлено несколько криптографических алгоритмов, в
том числе протоколы Рабина и Эль-Гамаля; хэш-функция RIPEMD-
160 и форматы в реализации процедуры RSA приведены в соответ-
ствие с PKCS #1. Обсуждаются возможные источники ошибок,
способные привести к ослаблению процедуры. Введены дополне-
ния и пояснения по тексту, исправлены ошибки. Несколько усилена
дидактическая стратегия, в результате чего некоторые программы
на CD-ROM слегка отличаются от представленных в книге. Не все
технические подробности одинаково важны, поскольку быстро-
действие программы не всегда уживается с понятным исходным
текстом.
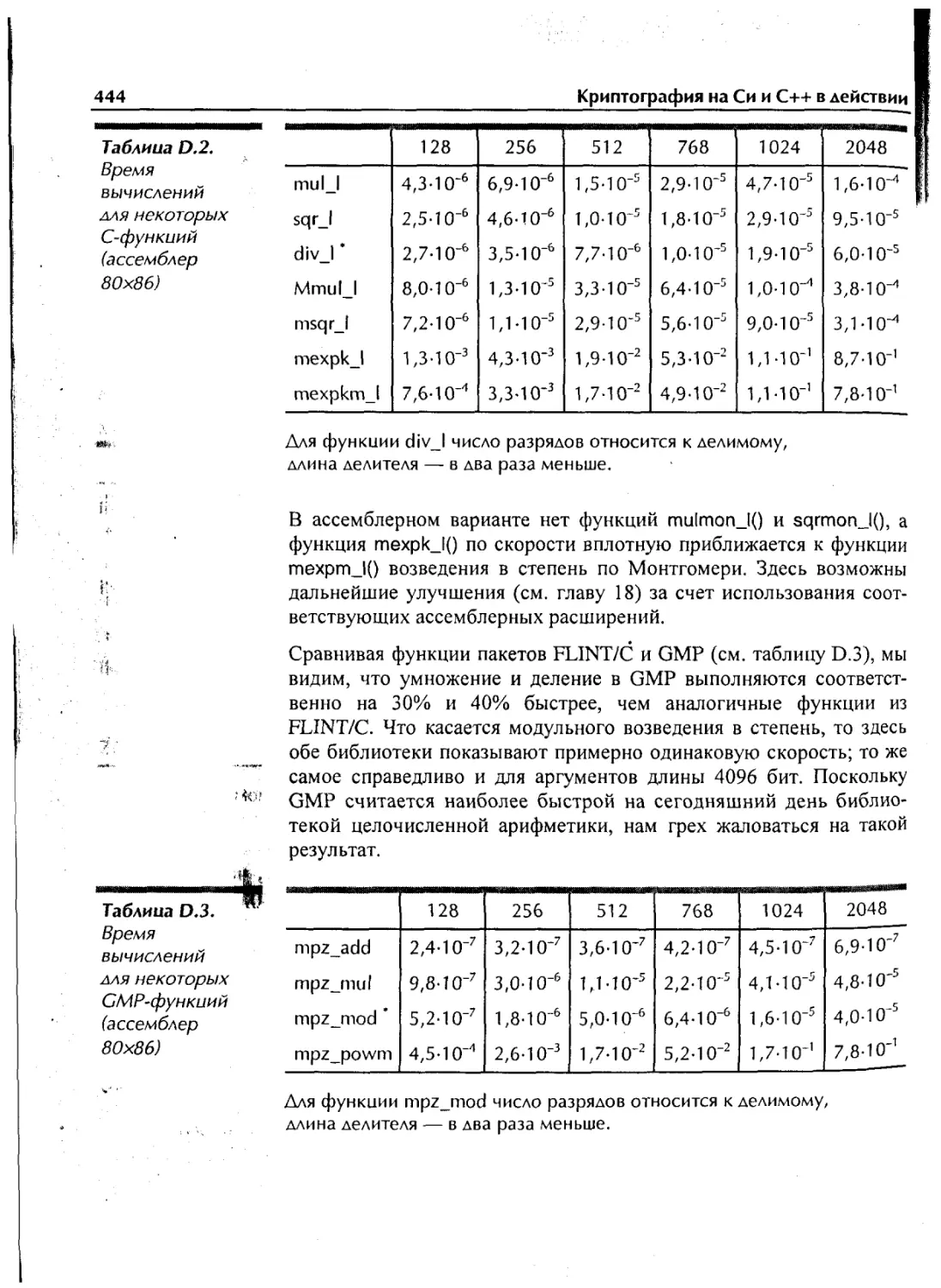
Кстати о быстродействии. В приложении D приведено сравнитель-
ное время вычислений для некоторых функций библиотеки много-
разрядной арифметики GMP (GNU Multi Precision Library). На их
фоне процедура возведения в степень пакета FLINT/C выглядит не
так уж плохо. Вдобавок в приложении F даны ссылки на некоторые
арифметические и теоретико-числовые пакеты.
Библиотека программ дополнена несколькими функциями, а мес-
тами существенно переработана, устранены многие ошибки и не-
точности. Разработаны новые тестовые функции, усилены имев-
шиеся ранее. Добавлен безопасный режим, теперь критические пе-
ременные в отдельных функциях уничтожаются путем затирания.
Все функции на С и C++ сгруппированы по приложениям и снаб-
жены примечаниями.
Поскольку разные современные компиляторы представляют разные
этапы разработки стандарта C++, модули на C++ пакета FLINT/C
построены так, что можно использовать как традиционные в C++
заголовки файлов вида xxxxx.h, так и новые ANSI-заголовки. Из тех
же соображений выполняется проверка при использовании оператора
new(): не возвращается ли пустой указатель. При такой обработке
ошибок, с одной стороны, не нужны исключения по стандарту ANSI,
а с другой стороны, она поддерживается современными компиля-
торами, тогда как метод, согласованный со стандартом (при кото-
ром new() сообщает об ошибке через throw()), годится не всегда.
8
Криптография на Си и C++ в действии
Хотя эта книга и посвящена в основном криптографии с открытым
ключом, недавнее утверждение алгоритма Rijndael Американским
национальным институтом стандартов и технологий (NIST) в каче-
стве нового стандарта шифрования (Advanced Encryption Standard -
AES) вдохновило меня на написание последней главы (глава 19),
содержащей подробное описание алгоритма. Я очень обязан Gary
Cornell из Apress, который обратил мое внимание на Rijndael и бла-
годаря которому книга была дополнена столь ценным материалом.
Хочу поблагодарить также Vincent Rijmen, Antoon Bosselaers, Paulo
Barreto и Brian Gladman, позволивших включить в компакт-диск,
прилагаемый к этой книге, программную реализацию алгоритма
Rijndael.
Спасибо всем читателям первого издания, особенно тем, кто сообщал
об ошибках, делал ценные замечания, предлагал пути улучшения
книги. Все такие контакты были для меня чрезвычайно полезны.
По-прежнему всю ответственность как за оставшиеся, так и за воз-
никшие ошибки в тексте книги или в программах несет исключи-
тельно автор.
Мои сердечные признания Hermann Engesser, Dorothea Glaunsinger
и Ulrike Stricker из издательства Springer-Verlag за безграничное
доверие и сотрудничество.
Я глубоко благодарен моему американскому переводчику Дэвиду
Крамеру (David Kramer), компетентно и самоотверженно потру-
дившемуся и давшему множество ценных советов, которые были
использованы и в немецком издании этой книги.
Предупреждение
Прежде чем где-либо использовать программы, содержащиеся в
этой книге, внимательно прочитайте руководство пользователя и
техническое описание соответствующего программного обеспече-
ния и компьютера. Ни автор, ни издательство не несут ответствен-
ности за ущерб, вызванный некорректным выполнением инструк-
ций и программ, содержащихся в этой книге, или ошибками в тек-
сте или в программах, которые, несмотря на тщательную проверку,
все же могут остаться. Программы, содержащиеся на CD-ROM,
защищены авторскими правами и не могут быть воспроизведены
без разрешения издательства.
Предисловие к первому изданию
'.н д) 1ШР: . )
<" я \/Н'.
~t< ж. wUr’-r, п
> |{1
.п.-. . . <
'.С’ЬН R04
him/МП Хл
< ’ • '< У'> 4'Иh'j
‘ -
" h ,• i i d 'I s ’ Г 'i
t 'aux
пр F4 ад
• .‘dW
. » : '>'.)'?/ ь ч
< /
•I, ЧЧ Ц, V •. *
ч '< .,uu - 1
л +*!М
-f)5>q ИЬ '.ЧЧ {
• X.1 ХЦНММ
‘ « /Л. и
lb Ow*!
Математика - царица наук, теория чисел -
царица математики. Иногда она снисходит до
того, чтобы помочь астрономии и другим есте-
ственным наукам, но при любых обстоятельст-
вах она - первая.
Карл Фридрих Гаусс
Зачем нужна книга по криптографии, посвященная в основном
арифметике целых чисел и ее реализации в виде компьютерных
программ? Насколько это важно по сравнению с теми большими
задачами, которые решает программист? Если ограничиться лишь
теми числами, которые могут быть описаны стандартными число-
выми типами какого-либо языка программирования, арифметика
будет делом довольно легким: обычные арифметические операции
задаются в программах обычными символами +,
Но как только нам нужны результаты, длина которых намного
больше 16 или 32 битов, все становится гораздо интересней. Для
таких чисел даже простые арифметические операции уже не годятся,
и приходится потрудиться над разрешением таких проблем, кото-
рые раньше и проблемами-то не казались. С этим сталкивается лю-
бой, будь то профессионал или любитель, кто занимается теорией
чисел: пытаясь применить школьные алгоритмы арифметики, мы
вдруг оказываемся втянутыми в невероятно запутанный процесс.
Читатель, который собирается разрабатывать программы в этой об-
ласти и не желает изобретать колесо, найдет в этой книге целый ряд
функций, оперирующих с большими числами, на языках С и C++.
Речь идет отнюдь не об «игрушечных» примерах, поясняющих «как
это работает в принципе», но о готовом пакете функций и методов,
удовлетворяющих профессиональным требованиям в части кор-
ректности, быстродействия и серьезной теоретической базы.
Цель этой книги - связать теорию и практику, перекинуть мост че-
рез пропасть, разделяющую теоретическую литературу и практиче-
ские задачи программирования. Последовательно, шаг за шагом мы
будем познавать фундаментальные принципы арифметики больших
натуральных чисел, арифметики конечных колец и полей, сложные
функции элементарной теории чисел, что позволит пролить свет на
многочисленные и разнообразные возможности применения этих
принципов в современной криптографии. Сведения из математики
приводятся здесь в объеме, необходимом для понимания пред-
ставленных программ; более глубокие знания можно почерпнуть
из обширного списка литературы. Все разработанные нами функ-
ции постепенно объединяются и многократно тестируются, так
что в итоге мы получаем полезный объемлющий программный
интерфейс.
10
Криптография на Си и C++ в действии
Мы начинаем с представления больших чисел и с изучения основ-
ных вычислительных операций, создавая для сложения, вычитания,
умножения и деления больших чисел мощные базовые функции.
Исходя из этого, мы поясняем модульную арифметику в классах
вычетов и реализуем соответствующие операции в виде библиотеч-
ных функций. Отдельная глава посвящена трудоемкому процессу
возведения в степень, те разрабатываются и программируются
различные специальные алгоритмы модульной арифметики.
После тщательной подготовки, включающей в себя также ввод и
вывод больших чисел и их преобразование в различных системах
счисления, мы рассматриваем элементарные теоретико-числовые
алгоритмы, используя для этого базовые арифметические операции,
а затем разрабатываем программы, начиная с вычисления наиболь-
шего общего делителя больших чисел. Следом идут такие задачи,
как вычисление символов Лежандра и Якоби, обращение и возве-
дение в квадрат в конечных кольцах. Мы знакомимся также с ки-
тайской теоремой об остатках и ее приложениями.
Попутно мы несколько подробнее останавливаемся на принципах
распознавания больших простых чисел и программируем мощный
тест простоты.
Следующая глава посвящена генерации больших случайных чисел,
разработке и проверке статистических свойств криптографически
стойкого генератора случайных битов.
Завершается первая часть тестированием арифметических и других
функций. Для этого, исходя из математических правил арифметики,
мы разрабатываем специальные методы проверки, а также обсуж-
даем реализацию эффективных внешних средств.
Во второй части мы шаг за шагом строим класс LINT (Large INTe-
gers - большие целые числа) на языке C++. Для этого функциям на
С из первой части мы придаем синтаксис и семантику объектно-
ориентированного языка C++. Значительное внимание уделено
форматированному вводу и выводу LINT-объектов с гибкими пото-
ковыми функциями и манипуляторами, а также обработке ошибок.
Элегантность, с которой алгоритмы формулируются на C++,
особенно поражает, когда начинают стираться границы между
стандартными типами и большими числами как LINT-объектами.
Отсюда - синтаксическое сходство, ясность и прозрачность реали-
зованных алгоритмов.
И наконец, мы иллюстрируем практичность разработанных мето-
дов на примере знаменитой криптосистемы RSA: для шифрования с
открытым ключом и цифровой подписи. Попутно мы приводим
теоретическое обоснование процедуры RSA как наиболее известного
представителя асимметричных криптосистем. Отдельно разрабаты-
вается расширяемое ядро, позволяющее применять этот ультрасо-
Предисловие к первому изданию
11
временный криптографический процесс, исходя из принципов объ-
ектно-ориентированного языка программирования C++.
В завершение мы кратко остановимся на дальнейших путях расши-
рения нашей библиотеки программ. Это, например, четыре функ-
ции умножения и деления на языке Ассемблера 80x86, которые
позволяют повысить производительность наших программ. В при-
ложении D приведена таблица типичного времени вычислений с
использованием Ассемблера и без него.
Я искренне призываю всех читателей этой книги присоединиться
ко мне на этом пути или хотя бы, в зависимости от наклонностей,
изучить отдельные параграфы или главы и испытать представлен-
ные там функции. Автор надеется, что читатели не обидятся за
слово «мы», под которым он подразумевал и их, и себя. Тем самым
он призывает читателей стать активными участниками увлекатель-
ного путешествия по бескрайним просторам математики и програм-
мирования, постичь эту науку и извлечь из этой книги максималь-
ную пользу. Что же касается программ - любой читатель сможет
удовлетворить свои амбиции, совершенствуя те или иные функции
для новых приложений.
Я благодарен издательству Springer-Verlag и, в частности, Hermann
Engesser, Dorotea Glaunsinger и Ulrike Striker за интерес, проявлен-
ный к этой книге, и за активное сотрудничество. Рукопись читали
Jorn Garbers, Josef von Helden, Brigitte Nebelung, Johannes Ueberberg
и Helga Welschenbach. Всем им - моя сердечная признательность за
высказанные критические замечания и предложения и, кроме того,
за внимание и терпение. Если, несмотря на все наши усилия, ошибки
в тексте и программах все еще остались, в них повинен только автор.
Большое спасибо моим друзьям и коллегам Robert Hammelrath,
Franz-Peter Heider, Detlef Kraus и Brigitte Nebelung, сумевшим
постичь связь между математикой и программированием, за долгие
годы сотрудничества, которые так много для меня значили.
Часть I
Арифметика и теория чисел на С
Легко понять, насколько важна арифметика и
вообще искусство математики: нет ничего, что
не было бы связано с числами, не имело бы
размеров; никакое искусство не может сущест-
вовать без измерений и пропорций.
Адам Райс, Вычисления, 1574
Типографские правила обработки литер сродни
арифметическим правилам обработки чисел.
Д.Р. Хофштадтер,
Гедель, Эшер, Бах: эта бесконечная гирлянда
Человеческий мозг никогда больше не отяготят
никакие вычисления! Талантливые люди снова
смогут думать, а не изводить бумагу на числа.
Стэн Надольный,
Открытие медлительности
ГЛАВА 1.
Введение
Целые числа сотворил Бог. Все остальное - дело
рук человеческих.
г . ( , Леопольд Кронекер
• С1' >г,к о ’
Если вы посмотрите на нуль, то не увидите ни-
/ ’ чего; но взгляните сквозь него - и вы увидите
\ • МИР-
Роберт Каплан,
Естественная история Нуля
к’ ! ".
В наши дни занятие криптографией волей-неволей влечет за собой
углубленное изучение теории чисел, а именно, изучение нату-
,, . * ральных чисел, которые представляют одну из занимательнейших
> , областей математики. Однако мы не станем уподобляться глубоко-
.. и, , водным ныряльщикам, чтобы добыть со дна математического океа-
,, и,-. на затонувшие сокровища, - для криптографических приложений
ч л ,rj это не требуется. Наша цель намного скромнее. С другой стороны,
внедрение теории чисел в криптографию беспредельно глубоко, и
; этому способствовали многие выдающиеся математики.
- Теория чисел уходит корнями в античность. Уже в VI веке до н. э.
’ ‘ пифагорейцы (греческий математик и философ Пифагор и его
; школа) серьёзно занимались целыми числами и достигли значи-
' • ' тельных математических результатов, например, таких как знаме-
нитая теорема Пифагора, известная сейчас каждому школьнику.
‘ С религиозным рвением они утверждали, что все числа соотносятся
; с натуральными числами, и оказались перед серьёзной дилеммой,
когда открыли существование иррациональных чисел, таких как
? . V2 , которые нельзя представить в виде частного двух целых. Это
м .. < , . • открытие до такой степени не укладывалось в представление пифа-
а ,г горейцев о мире, что они избрали достойную сожаления тактику
' * ' ’ г. . поведения, часто повторяющуюся в истории человечества, - поста-
< t : ... рались утаить знание об иррациональных числах.
От греческих математиков Евклида (III век до н.э.) и Эратосфена
. г Д' (276-195 гг. до н.э.) до нас дошли два древнейших алгоритма тео-
г" ’ ‘ рии чисел. Они тесно связаны с самыми современными алгоритма-
ми шифрования, которые мы используем повседневно для надеж-
ной связи через Интернет. Алгоритм Евклида и «решето» Эратос-
фена полностью отвечают целям нашей работы, и мы рассмотрим
их теорию и применение в пп. 10.1 и 10.5 данной книги.
16
Криптография на Си и C++ в действии
» t :.i;..fh
* 5 • 0 ГМ'
К числу главных основоположников современной теории чисел от-
носятся Пьер Ферма (1601-1665), Леонард Эйлер (1707-1783), Ад-
риен Мари Лежандр (1752-1833), Карл Фридрих Гаусс (1777-1855)
и Эрнст Эдуард Куммер (1810-1893). Их работы образуют фунда-
мент для современного развития этой области математики и, в
частности, таких интересных прикладных областей, как криптогра-
фия, с её несимметричными процедурами шифрования и формиро-
вания цифровой подписи (см. главу 16). Можно было бы упомянуть
еще многих, внесших важный вклад в эту область, кто и по сей день
участвует в зачастую драматических перипетиях эволюции теории
чисел. Тем, кому интересны захватывающие описания из истории
теории чисел, я настоятельно рекомендую книгу Саймона Сайна
«Последняя теорема Ферма» (Simon Singh, Ferma’s Last Theorem).
С самого детства мы воспринимаем счет как нечто само собой ра-
зумеющееся и легко принимаем на веру такие факты, как «два плюс
два равняется четырем». Поэтому нам покажутся неожиданными
абстрактные мысленные построения, к которым придется обратиться
для теоретического обоснования таких утверждений. Например,
теория множеств позволяет вывести существование и арифметику
натуральных чисел из почти ничего. Это «почти ничто» является
пустым множеством 0 := {}, то есть множеством, которое не со-
держит никаких элементов. Если допустить, что пустое множество
соответствует числу 0, тогда можно построить следующие допол-
нительные множества. Последующий элемент за 0 - 0+ соответст-
вует множеству 0+ := {0} = {0}, которое содержит единственный
элемент, а именно, пустое множество. Присвоим последующему
элементу 0 наименование 1. Для этого множества мы тоже можем
определить последующий элемент, а именно 1+:={0, {0}}. По-
следующему элементу 1, содержащему 0 и 1, присвоим наименова-
ние 2. Построенные таким образом множества, которым мы так
опрометчиво присвоили наименования 0, 1 и 2, мы отождествляем -
что неудивительно - с хорошо известными числами 0, 1 и 2.
Такой принцип построения, когда каждому числу х ставится в соот-
ветствие последующий элемент {%} посредством присое-
динения х к предыдущему множеству, можно продолжить далее.
Каждое полученное таким образом число, за исключением нуля,
само является множеством, чьи элементы представляют его пред-
шественников. Только нуль не имеет предшественников. Чтобы
гарантировать продолжение этого процесса до бесконечности, в
теории множеств сформулировано особое правило, называемое
аксиомой бесконечности', существует множество, которое содер-
жит 0, а также последующий элемент для каждого своего элемента.
ГЛАВА 1. Введение
17
Принимая без доказательства существование по крайней мере одного
так называемого последующего множества, которое, начиная с О,
содержит все последующие элементы, теория множеств выводит
существование минимального последующего множества IN, которое
само является подмножеством каждого последующего множества.
Это минимальное и однозначно определенное последующее мно-
жество IN называется множеством натуральных чисел, в которое мы
специально включаем 0 в качестве элемента.1
Натуральные числа можно охарактеризовать с помощью аксиом
Джузеппе Пеано (1858-1932), которые совпадают с нашим интуи-
тивным представлением о целых числах:
(I) Последующие элементы двух неравных натуральных чисел неравны:
Из п т следует, что м+ т+ для всех п, те IN.
(II) Каждое натуральное число, за исключением нуля, имеет предшест-
венника: IN+ = IN \{ 0}.
(III) Принцип полной индукции'. Если S с IN, 0 6 S, и из п G S всегда сле-
дует, что п G S , то S = IN.
Принцип полной индукции позволяет вывести интересующие нас
арифметические операции над целыми числами. Фундаментальные
операции сложения и умножения можно вывести рекурсивно сле-
дующим образом. Начнем со сложения:
Для каждого натурального числа и е IN существует функция sn:
IN —> IN, такая, что
(a) sn(0) = n
(б) 5,/хЭ = (^п(х))+ для всех натуральных чисел х е IN.
Значение функции sn(x) называется суммой п + х чисел них.
Однако существование таких функций sn для всех натуральных
чисел п е IN требуется доказать, так как бесконечно большое ко-
личество натуральных чисел не оправдывает априори такого допу-
щения. Для доказательства следует вернуться к принципу полной
индукции в соответствии с вышеупомянутой третьей аксиомой
Пеано (см. [Halm], главы 11-13). Операция умножения выводится
аналогичным образом:
1 При этом не имеет значения тот факт, что в соответствии со стандартом DIN 5473 нуль не отно-
сится к натуральным числам. В информатике, как правило, принято начинать счет с 0, а не с 1. Это
указывает на важную роль нуля как нейтрального элемента при сложении (аддитивное тождество).
18
Криптография на Си и C++ в действии
Для каждого натурального числа п е П\| существует функция рп: IN —» IN, такая, что
(а) Рп^ = 0
' (б) - л*, ‘ - . ' рп(х+) - рп(х) + п для всех натуральных чисел х е IN. Значение функции рп(х) называется произведением п • х чисел п и х. Как и следовало ожидать, умножение определено в терминах сло- жения. Для арифметических операций, определенных таким обра- зом, можно доказать, применяя повторно полную индукцию от х в соответствии с Аксиомой III, такие известные арифметические за- коны, как ассоциативность, коммутативность и дистрибутивность (см. [Halm], глава 13). Хотя обычно мы используем эти законы без
всяких церемоний, оговоримся, что будем очень часто обращаться к их помощи при тестировании FLINT-функций (см. главы 12 и 17). Подобным же образом получаем определение возведения в сте- пень. Мы приведем его здесь ввиду важности этой операции в дальнейшем. Для каждого натурального числа п G IN существует функция еп: IN —> IN, такая, что
(а) ^(0)=1
(б) г 4- ен(х+) = еп(х) • п для всех натуральных чисел х g IN. Значение функции еп(х) называется степенью х пх числа п. Используя полную индукцию, можно доказать правила возведения в степень пх- пу = пх+у,пх- mx=(ir т)х, (пх)у = пху, к которым мы вернемся в главе 6. В дополнение к вычислительным операциям, на множестве IN нату-
• г; --г -•. ральных чисел определено отношение порядка «<», позволяющее сравнивать два элемента н, те IN. Несмотря на важность этого факта в теории множеств, здесь мы отметим лишь, что отношение порядка обладает точно теми же свойствами, которые мы знаем и используем в нашей повседневной жизни. Начав с установления пустого множества в качестве единственного фундаментального блока для построения натуральных чисел, при- ступим теперь к изучению материалов, с которыми нам предстоит работать в дальнейшем. Теория чисел большей частью рассматри- вает натуральные и целые числа как данные и с ходу приступает
ГЛАВА 1. Введение
19
к изучению их свойств. Тем не менее, нам интересно хотя бы раз
взглянуть на процесс «математического клеточного деления» -
процесс, выдающий в результате не только натуральные числа, но
также арифметические операции и правила, с которыми мы будем
очень тесно взаимодействовать.
1.1.0 программном обеспечении
; Программное обеспечение, описанное в этой книге, в целом пред-
ставляет собой пакет, так называемую библиотеку функций, к ко-
торым часто обращаются. Название этой библиотеки - FLINT/C -
' * является аббревиатурой для «Functions for Large Integers in Number
Theory and Cryptography» (функции для больших целых в теории
чисел и криптографии).
FLINT/C содержит, среди всего прочего, следующие модули, кото-
рые можно найти в виде кода (текста программы) на сопроводи-
** ' м тельном CD-ROM.
/ J j
Таблииа 1.1. flint.h Заголовочный файл для использования
Арифметика и функиий из flint.c
теория чисел на С в директории flint/src flint.c Функции арифметики и теории чисел на языке С
kmul.h,c Функции для умножения и возведения
ripemd.h/C в квадрат по методу Каранубы Реализация хэш-функции RIPEMD-160
Таблииа 1.2. Арифметика и теория чисел на С++ в директории flint/src flintpp.h flintpp.cpp 'u, Заголовочный файл для использования функций из flintpp.cpp Функции арифметики и теории чисел на языке C++. Этот модуль использует функции из flint.c
Таблииа 1.3. Арифметический модуль на Ассемблере 80x86 (см. главу 18) в директории flint/src/asm mult.asm umul.asm sqr.asm div.asm Умножение, заменяет С-функнию mult() из flint.c Умножение, заменяет С-функиию umul() Возведение в квадрат, заменяет С-функиию sqr() Деление, заменяет С-функнию div_l()
20
Криптография на Си и C++ в действии
Таблииа 1.4. Арифметические библиотеки на Ассемблере 80x86 (см. главу 18) в директории flint/lib flinta.lib fl intavc.lib flinta.a libflint.a Библиотека ассемблерных функций в формате OMF Библиотека ассемблерных функций в формате COFF Архив ассемблерных функций для emx/gcc под OS/2 ' ' ' Архив ассемблерных функций для использования под LINUX
Таблииа 1.5. testxxx.clpp] Тестовые программы на С и C++
Тесты (см. п. 12.2
и главу 17)
в директории
flint/test
Таблииа 1.6.
Реализация RSA
(см. главу 16) в
директории
flint/rsa
rsakey.h Заголовочный файл для классов RSA
rsakey.cpp Реализация классов RSA RSAkey и RSApub
rsademo.cpp Пример применения классов RSA и их функций
Список отдельных составляющих программного пакета FLINT/C
можно найти в файле readme.doc на CD-ROM. Программы пакета
были протестированы с помощью указанных средств разработки на
следующих платформах:
✓ GNU gcc под Linux, SunOS 4.1 и Sun Solaris
✓ GNU/EMX gcc под OS/2 Warp, DOS и Windows (9x, NT)
✓ lcc-win32 под Windows (9x, NT, 2000)
✓ Cygnus cygwin B20 под Windows (9x, NT, 2000)
✓ IBM VisualAge под OS/2 Warp и Windows (9x, NT, 2000)
✓ Microsoft С под DOS, OS/2 Warp и Windows (9x, NT)
Microsoft Visual C/C++ под Windows (9x, NT, 2000)
✓ Watcom C/C++ под DOS, OS/2 Warp и Windows (3.1, 9x, NT).
Ассемблерные программы можно транслировать с помощью Micro-
soft MASM2 или Watcom WASM. Они содержатся в скомпилиро-
ванном виде на CD-ROM в виде библиотек в форматах OMF (фор-
мат объектного модуля) и COFF (общий формат объектного файла),
2 Вызов: ml /Сх /с /Gd <имя файла>
ГЛАВА#. Введение
21
соответственно, а также в виде LINUX-архива. Эти программы
можно использовать вместо соответствующих С-функций, когда
им при трансляции С-программ определен макрос FLINT_ASM и под-
ключены ассемблерные объектные модули из библиотек (архивов).
Типичный вызов компилятора, в данном случае для GNU gcc, вы-
н ! " глядит примерно так (пути к исходным директориям скрыты):
дсс -02 -DFLINT-ASM -о rsademo rsademo.cpp rsakey.cpp
’ ' л ,‘ flintpp.cpp flint.c ripemd.c-Iflint “lstdc++
Заголовочные файлы C++, соответствующие стандарту ANSI, ис-
пользуются, когда при компиляции определен макрос FLINTPP_ANSI;
в противном случае используются традиционные заголовочные
файлы xxxxx.h.
В зависимости от компьютерной платформы возможны отклонения,
касающиеся опций компилятора. Но для достижения максимальной
производительности всегда следует включать опции оптимизации
по скорости. Из-за требований к стеку для многих операционных
4. сред и приложений он должен быть правильно настроен3. Что каса-
i ется необходимого размера стека для конкретных приложений,
следует отметить замечание о функциях возведения в степень в
главе 6 и обзор на странице 140. Стековые требования можно
сделать менее жесткими, используя функцию возведения в степень с
J динамическим распределением стека, а также посредством реализа-
' ции динамических регистров (см. главу 9).
Функции и константы языка С описываются с использованием
n-,q нш - макросов
'Г4’ ‘Ь
sqru: ___FLINT_API Спецификатор для С-функций
1 J и ' ___FLINT_API_A Спецификатор для ассемблерных функций
v ___FLINT_API_DATA Спецификатор для констант
как например,
: - А
' ”'J extern int _FLINT_API add_l (CLINT, CLINT, CLINT);
- < гн extern USHORT_____FLINT_API_DATA smallprimes[];
OJ или, соответственно, при использовании ассемблерных функций
extern int _FLINT_API_A divj (CLINT, CLINT, CLINT, CLINT);
3 В современных компьютерах с виртуальной памятью, за исключением системы DOS, этот мо-
мент обычно не вызывает затруднений, особенно в случае операционных систем UNIX или
LINUX
22
Криптография на Си и C++ в действии
Эти макросы, в общем случае, определены как пустые комментарии
/* */. С их помощью, используя соответствующие описания, можно
создавать специфические для данного компилятора и компоновщи-
ка инструкции. Если используются ассемблерные модули, а компи-
лятор GNU gcc не используется, то макрос___FLINT_API_A опреде-
ляется как_________________________________cdecl, и некоторые компиляторы воспринимают, что
будет вызываться ассемблерная функции с соответствующими
С-именем и способом передачи параметров.
Для модулей, которые импортируют функции и константы библио-
теки FLINT/C из динамически подключаемой библиотеки (dynamic
link library - DLL) под Microsoft Visual C/C++, при трансляции
требуется определять макросы
-D_FLINT_API=_cdecl
и
-D__FLINT_API_DATA=___declspec(dllimport).
В заголовочном файле flint.h это уже учтено, и в этом случае для
компиляции достаточно определить макрос FLINTJJSEDLL. Для дру-
гих сред разработки следует представить аналогичные описания.
Небольшой объём работы, связанной с инициализацией DLL, ис-
пользующих FLINT/C, берет на себя функция FLINTInitJQ, которая
задает начальные значения для генератора случайных чисел4 и
генерирует набор динамических регистров (см. главу 9). Дополни-
тельная функция FLINTExitJO освобождает динамические регистры.
Вполне разумно, что инициализация производится не в каждом от-
дельном процессе, использующем DLL, а выполняется один раз при
старте DLL. Как правило, следует использовать функцию с опреде-
ленной разработчиком сигнатурой и способом передачи парамет-
ров, которая выполняется автоматически, когда исполняющая сис-
тема {run-time) загружает DLL. Эта функция может взять на себя
инициализацию FLINT/C и использовать две упомянутые выше
функции. Все это следует учитывать при разработке DLL.
Пришлось потрудиться, чтобы сделать программное обеспечение
применимым для приложений, критичных к безопасности. Для этого
в режиме безопасности локальные переменные функций, в частно-
сти CLINT- и LINT-объекты, удаляются после использования по-
F средством обнуления (записи на их место нулей). Для С-функций
это достигается с помощью макроса PURGEVARS_L() и соответст-
вующей функции purgevars_l(). Для С++-функций подобным же
образом устроен деструктор ~LINT(). Ассемблерные функции зати-
4 Эти начальные значения получаются из 32-разрядных чисел, задаваемых системными часами.
Для приложений, где безопасность критична, в качестве начальных значений советуем использо-
вать подходящие случайные значения из достаточно большого интервала.
ГЛАВА 1. Введение
23
рают свою рабочую память. За удаление переменных, которые были переданы функциям в качестве аргументов, отвечают вызывающие функции. Если из-за определенных дополнительных затрат времени все же нужно пропустить удаление переменных, следует определить мак- рос FLINTJJNSECURE. Во время выполнения функция char* verstrJO выдает информацию о режимах, установленных во время компиляции. При этом дополнительно к метке версии Х.х в строке символов выводятся литеры «а» для ассемблерной поддержки и «s» для режима безопасности, если эти режимы были включены.
1.2. Законные условия использования программного обеспечения Данное программное обеспечение предназначено исключительно для личного использования. В этих целях программное обеспече- ние можно использовать, изменять и передавать при следующих условиях: 1. Запрещается изменять или удалять замечание об авторских правах. 2. Все изменения должны быть снабжены комментариями. Любое другое использование, в частности, использование программного обеспечения в коммерческих целях, требует наличия письменного разрешения от издателя или автора. Программное обеспечение было разработано и протестировано всеми доступными средствами. Так как никогда нельзя полностью исключить наличие ошибок, то ни автор, ни издатель не несут от- ветственности за прямой или косвенный ущерб, который может быть вызван применением или неприменением программного обес- печения, вне зависимости от того, с какими целями оно использо- валось.
1.3. Как связаться с автором Автор будет рад получить сведения об ошибках и любую другую полезную критику или замечания. Пожалуйста, пишите по адресу kryptographie@welschenbach.de5.
5 Обо всех ошибках в русском издании, пожалуйста, сообщайте редактору по адресу:
Davel@semianov.com с пометкой «Криптография на С и C++» - Прим. ред.
ГЛАВА 2.
Числовые форматы:
представление больших чисел в языке С
ХкИ;'. .-г'"
(ГЦ; ,’ПЛ'ЬЬ
;п - vw
48
Итак, я придумал собственную систему записи
больших чисел и, пользуясь случаем, разъясню
ее в этой главе.
Айзек Азимов,
Дополнительное измерение
Процесс, который привел эту форму на более
высокую ступень организации, можно было
изобразить и по-другому.
Дж. Вебер,
Форма, движение, цвет
Приступая к созданию библиотеки функций для работы с большими
числами, в первую очередь следует определить, как представлять
и/ * эти числа в оперативной памяти компьютера. Эта задача требует
г тщательно продуманного решения, поскольку впоследствии пере-
смотреть его будет трудно. Конечно, всегда можно внести изме-
нения во внутреннюю структуру библиотеки программ, но пользо-
вательский интерфейс должен оставаться настолько стабильным,
насколько это возможно в смысле «совместимости снизу вверх».
Необходимо определить порядок размера чисел, которые придется
обрабатывать, и тип данных, который будет использоваться для ко-
дирования этих численных величин.
В основе всех программ библиотеки FLINT/C лежит обработка
многоразрядных натуральных чисел, длина которых (несколько
\ ' сотен разрядов) намного превосходит допустимый размер стан-
“ дартных типов данных. Таким образом, нам требуется логическое
/ упорядочение ячеек компьютерной памяти, с помощью которого
можно выражать большие числа и производить над ними различные
операции. В связи с этим можно было бы вообразить себе некие
структуры, создающие пространство именно такого размера, кото-
рый потребуется для представления этих чисел. Такие экономящие
оперативную память служебные средства поддерживались бы про-
граммой управления динамической памятью для больших чисел,
которая по мере необходимости выделяет или освобождает память
при выполнении арифметических операций. Конечно, такие сред-
ства можно реализовать (см. например, [Skal]), однако управление
памятью увеличивает время вычислений, поэтому в пакете
26
Криптография на Си и C++ в действии
FLINT/C для представления целых чисел предпочтение отдается
более простому их определению со статической длиной.
Большие натуральные числа можно представлять в виде векторов,
«М элементы которых являются каким-либо стандартным типом
данных. В целях эффективности предпочтительнее использовать
беззнаковый тип данных, который позволяет без потерь хранить
результаты арифметических операций в этом типе, как например
unsigned long (описанный в flint.h как ULONG), который является
наибольшим арифметическим стандартным типом данных в С
(см. [Harb], п. 5.1.1). Обычно ULONG-переменные можно целиком
представить регистровым словом процессора.
Наша цель заключается в том, чтобы свести при компиляции опе-
рации над большими числами по возможности непосредственно к
регистровой арифметике процессора, ибо операции с регистрами
компьютер выполняет, можно сказать, «в уме». Поэтому в пакете
FLINT/C большие целые числа представляются типом unsigned
short int (в дальнейшем USHORT). Мы полагаем, что тип USHORT
занимает 16 бит и что тип ULONG полностью воспринимает резуль-
таты арифметических операций с типами USHORT, то есть соотно-
шения размеров между этими типами можно выразить неформально
как USHORT х USHORT < ULONG.
Выполняются ли эти положения для отдельного компилятора, можно
узнать из заголовочного файла ISO limits.h (см. [Harb], пп. 2.7.1. и 5.1).
Например, в файле limits.h для компилятора GNU C/C++ (см. [Stlm])
появляются следующие строки:
#define UCHAR.MAX OxffU
#define USHRT_MAX OxffffU
#define UINT_MAX OxffffffffU
#define ULONG.MAX OxffffffffUL
Отметим, что фактически есть только три размера, которые раз-
личаются числом двоичных разрядов. Тип USHRT (в нашем пред-
ставлении соответственно USHORT) представляется 16-битовым
регистром; тип ULONG - 32-битовыми регистрами. Значение
ULONGJVIAX определяет величину наибольших беззнаковых целых
чисел, представимых скалярными типами (см. [Harb], стр. ИО)1.
Наибольшая величина произведения двух чисел типа USHRT равна
Oxffff * Oxffff = OxfffeOOOl и, следовательно, представима типом
ULONG, где младшие 16 бит, в нашем примере 0x0001, можно
выделить операцией приведения типов к типу USHRT. Реализация
1 Без учета используемых на практике нестандартных типов, таких как unsigned long long в GNU
C/C++ и в некоторых других компиляторах С.
ГЛАВА 2. Числовые форматы
27
г/’ШШ
) .кОЛ »
ЙОГА'. Ж :
"Ч ТУГ' :
основных арифметических функций пакета FLINT/C основывается
на обсуждавшемся выше соотношении размеров между типами
USHORT и ULONG.
Аналогичным образом, используя типы данных длиной 32 бита и
64 бита вместо USHORT и ULONG, можно сократить время вычис-
лений для операций умножения, деления и возведения в степень
почти на 25 процентов. Такие возможности можно реализовать с
помощью функций, написанных на Ассемблере, с прямым досту-
пом к 64-битовым результатам машинных команд умножения и
деления, или с помощью процессора с 64-битовыми регистрами,
который также позволяет приложениям на языке С без потерь
хранить полученные результаты в типе ULONG. Пакет FLINT/C
содержит несколько примеров того, как можно ускорить получение
результатов, используя арифметические ассемблерные функции
(см. главу 18).
Следующий вопрос - как упорядочить USHORT-разряды внутри
вектора. Можно рассмотреть две возможности: слева направо, с
убыванием значения разрядов от меньшего адреса ячейки памяти к
большему, или наоборот, с возрастанием значения разрядов от
меньшего адреса к большему. Второй вариант, противоположный
нашей обычной системе обозначений, удобен тем, что размер чисел
с постоянным адресом можно изменять просто добавляя разряды и
не перемещая ничего в памяти. Таким образом, выбор ясен: разря-
ды нашего числового представления возрастают с возрастанием
адресов ячейки памяти или индексов вектора.
В дальнейшем число разрядов будет рассматриваться как часть
этого представления и храниться в первом элементе вектора. Таким
образом, представление чисел большой длины в памяти выглядит
так:
п = (1пхп2... 0 < I < CLINTMAXDIGIT, 0 < < В (z = 1, /),
где В обозначает основание числового представления; для пакета
FLINT/C В := 216 = 65536. Это значение В будет постоянно участво-
вать в дальнейшем изложении. Константа CLINTMAXDIGIT опреде-
ляет максимальное число разрядов в CLINT-объекте.
Нуль представляется длиной I = 0. Значение п числа, представляе-
мого FLINT/C-переменной nJ, вычисляется как
п_1[0]
если nJ[0] > О,
Z = 1
О, в противном случае.
Если п > 0, то младший разряд числа п по основанию В задается
nj[1], а старший разряд - nJ[nJ[0]]. Число разрядов nJ[0] в
дальнейшем будет считываться макросом DIGITS_L (nJ) и поме-
щаться в / макросом SETDIGITS_L (nJ, I). Соответственно макросы
28
Криптография на Си и C++ в действии
LSDPTR_L(n_l) и MSDPTR_L(nJ) обеспечивают доступ к младшему
и старшему разрядам п_1, причём каждый из них возвращает указа-
тель на запрашиваемый разряд. Использование макросов, описан-
ных в библиотеке flint.h, обеспечивает независимость от реального
представления числа.
Поскольку для натуральных чисел знак не нужен, у нас теперь есть
все элементы, необходимые для представления этих чисел. Соот-
ветствующий тип данных мы определяем следующим образом:
typedef unsigned short clint;
typedef clint CLINT[CLINTMAXDIGIT + 1];
В соответствии с этим, большое число описывается так:
CLINT nJ;
Описание параметров функции типа CLINT следует из записи CLINT
2
nJ в заголовке функции. Определение указателя myptrj на CLINT-
объект осуществляется посредством CLINTPTR myptrj или clint
*myptrj.
В зависимости от установки константы CLINTMAXDIGIT в flint.h
функции пакета FLINT/C могут обрабатывать числа длиной до 4096
бит, что соответствует 1223 десятичным разрядам или 256 разрядам
по основанию 216. Изменяя CLINTMAXDIGIT, можно устанавливать
требуемую максимальную длину. От этого параметра зависит опре-
деление других констант. Например, число USHORT-разрядов в
CLINT-объекте задается следующим образом:
#define CLINTMAXSHORT CLINTMAXDIGIT + 1
а максимальное число обрабатываемых двоичных разрядов опреде-
ляется посредством
#define CLINTMAXBIT CLINTMAXDIGIT « 4
Так как константы CLINTMAXDIGIT и CLINTMAXBIT часто исполь-
зуются, то для удобства будем обозначать их сокращенно МАХд и
МАХ2 (за исключением текста программ, где они будут приводиться
в своём обычном виде).
Из этого определения вытекает, что CLINT-объекты допускают це-
лочисленные значения из промежутка [0, ВМАХд -1], соответст-
2 В связи с этим сравните главы 4 и 9 чрезвычайно интересной книги [Lind], где приводится подроб-
ное объяснение, в каких случаях в языке С векторы и указатели эквивалентны, а в каких - нет, и,
что самое главное, к каким ошибкам может привести неправильное понимание этих случаев.
ГЛАВА 2. Числовые форматы
29
венно [О, 2МАХ2-1]. Обозначим величину 5МАХд-1 = 2МАХ2 ~ 1
через 7Vmax. Это наибольшее натуральное число, представимое
С LI NT-объектом.
Некоторым функциям приходится работать с числами, у которых
разрядов больше, чем допускается CLINT-объектом. Для этих слу-
чаев определяются следующие варианты CLINT-типа:
typedef unsigned short CLINTD[1+(CLINTMAXDIGIT«1)];
и
typedef unsigned short CLINTQ[1+(CLINTMAXDIGIT«2)];
которые могут содержать в два (соответственно в четыре) раза
больше разрядов.
В качестве вспомогательного средства при программировании
модуль flint.с определяет константы nul_l, onej и twoj, которые
представляют числа 0, 1 и 2 в CLINT-формате. В библиотеке flint.h
есть соответствующие макросы SETZERO_L(), SETONE_L() и
SETTWO_L(), которые устанавливают соответствующие значения
CLINT-объектов.
ГЛАВА 3.
Семантика интерфейса
В словах понятия сокрыты.
Гете, Фауст, часть 1
В дальнейшем мы установим основные свойства, касающиеся по-
ведения интерфейса и использования функций пакета FLINT/C.
Сначала мы рассмотрим текстуальное представление CLINT-
объектов и FLINT/C-функций, но прежде хотелось бы прояснить
некоторые основные принципы реализации, имеющие значение для
использовании этих функций.
Имена функций пакета FLINT/C оканчиваются на «J»; например,
addj обозначает функцию сложения. Обозначения CLINT-объектов
тоже оканчиваются на «_1». Далее для простоты, если позволяют
условия, мы будем приравнивать CLINT-объект nJ тому значению,
которое он представляет.
Представление FLINT/C-функций начинается с заголовка, который
содержит синтаксическое и семантическое описание интерфейса
функции. Такие заголовки функций обычно выглядят следующим
образом:
Функция: Краткое описание функции
Синтаксис: int fJ (CLINT aj, CLINT bj, CLINT cj);
Вход: a J, bj (операнды)
Выход: cj (результат)
Возврат: 0, если все в порядке предупреждение или сообщение об ошибке в противном случае
Здесь нужно различать между собой значения выхода и возврата.
В то время как выход относится к значениям, которые функция
хранит в переданных аргументах, под возвратом подразумеваются
значения, которые функция возвращает посредством команды
return. За исключением нескольких случаев (например, функции
ldj(), п. 10.3, и twofactj(), п. 10.4.1), значение возврата содержит
сведения о состоянии или сообщения об ошибке.
Другие параметры, не связанные с выходом, функция не изменяет.
Обращения вида f J(aJ, bj, aj), где aj и bj - аргументы и в конце
32
Криптография на Си и C++ в действии
-Oh > * •; hlW’JtA
..Д': /
•ol/J .’•« .
ггнь 'hO
Ж
'JO
'» “-Г1 .* s
1*1 4 - >
ЫГ, ; : ' U '/
I f / A,
вычислений прежнее значение a_l затирается результатом, вполне
допустимы, так как результат записывается в возвращаемую пере-
менную только после завершения операции. Применяя термин про-
граммирования на ассемблере, можно сказать, что в этом случае
переменная а_1 используется как сумматор. Этот прием поддержи-
вается всеми FLlNT/C-функциями.
В СLI NT-объекте nJ имеются ведущие нули, если для некоторого
значения I выполняется следующее условие
(DIGITSJ. (nJ) == I) && (I > 0) && (nj[l] == 0);
Ведущие нули являются избыточными, так как они увеличивают
длину представления числа, не влияя при этом на его значение.
Однако в системе обозначений числа ведущие нули допустимы,
поэтому их не следует просто игнорировать. Конечно, при реали-
зации ведущие нули являются обременительной деталью, но они
способствуют вводу данных с внешних источников и таким обра-
зом поддерживают стабильность всех функций. В пакете FLINT/C
все функции понимают CLINT-числа с ведущими нулями, но не
генерируют их.
Следующее положение относится к поведению арифметических
функций в случае переполнения, которое происходит, если резуль-
тат арифметической операции слишком велик для заданного типа.
Хотя в некоторых публикациях по С говорится, что поведение
программы при переполнении зависит от реализации, стандарт
языка С тем не менее точно регулирует случай переполнения
при арифметических операциях с беззнаковыми целыми типами
данных. Там утверждается, что следует применять арифметику
по модулю 2”, когда тип данных представляет целые длиной п
бит (см. [Harb], п. 5.1.2). Соответственно, в случае переполнения
основные арифметические функции, описываемые ниже, выдают
результат, приведенный по модулю (Nmax + 1), то есть остаток от
целочисленного деления на 2Vmax + 1 (см. п. 4.3 и главу 5). В случае
потери значимости (отрицательного переполнения), которая проис-
ходит при получении отрицательного результата, на выход выда-
ется положительный вычет по модулю (Nmax + !)• Таким образом,
FLINT/C-функции согласуются с арифметикой в соответствии со
стандартом языка С.
Если обнаруживается переполнение или потеря значимости, ариф-
метическая функция возвращает соответствующий код ошибки.
Этот код и другие коды ошибок, приведенные в таблице 3.1, описаны
в заголовочном файле flint.h.
ГЛАВА 3. Семантика интерфейса
33
Таблииа 3.7. Код ошибки Интерпретация
Колы ошибок
FLINT/C E_CLINT_BOR Недопустимое основание в str2clint_l()
(см. главу 8)
E_CLINT_DBZ Деление на нуль
E_CLINT_MAL Ошибка при распределении ресурсов памяти
E_CLINT_MOD Четные модули в умножении по Монтгомери
E_CLINT_NIOR Регистр недоступен (см. главу 9)
E_CLINT_NPT Пустой указатель в качестве аргумента
E_CLINT_OFL Переполнение
E_CLINT_UFL Потеря значимости
ГЛАВА 4.
Основные операции
Таким образом, вычисления можно считать ос-
новой всех искусств.
Адам Райс, Вычисления, 1574
А вы, бедные создания, совершенно бесполезны.
Посмотрите на меня - я нужна всем.
Эзоп, Ель и ежевика
Для выполнения «математических» трюков в
этой главе необходимо одно маленькое условие -
вы должны знать таблицу умножения до 10...
туда и обратно.
Артур Бенджамин, Майкл Б. Шермер,
Матемагия
Любой вычислительный пакет программ составляется из функций,
выполняющих основные арифметические операции: сложение, вы-
читание, умножение и деление. Производительность всего пакета
держится на двух последних операциях, поэтому нужно очень
аккуратно подходить к выбору и реализации соответствующих
алгоритмов. К счастью, во втором томе классического «Искусства
программирования для ЭВМ» Дональда Кнута можно найти боль-
шую часть из того, что требуется для этой части пакета FLINT/C.
Прежде чем заниматься основными функциями, введем операцию
cpyj(), копирующую один CLINT-объект в другой, и стр_1(), срав-
нивающую размер двух CLINT-значений. Более строгое описание
см. в п. 7.4 и в главе 8.
Отметим, что в этой главе мы строим основные арифметические
функции как единое целое, тогда как в главе 5 будет разумнее
«посмотреть что у них внутри» и ввести ряд дополнительных
операций: отбрасывание старших нулей, обработку переполнения и
потери значащих разрядов, - сохраняя неизменными синтаксис и
семантику этих функций. Но для понимания этой главы такие под-
робности не нужны - что ж, забудем пока о них.
36
Криптография на Си и C++ в действии
4.1. Сложение и вычитание
Понятие «дальнейшие вычисления» означает:
«к целому числу П! прибавить целое число п2»,
; . а результат этих дальнейших вычислений -
целое число s - называется «результатом сло-
жения» или «суммой ni и п2» и записывается
П1 + п2.
Леопольд Кронекер, Об идее чисел
Поскольку операции сложения и вычитания отличаются лишь зна-
ком, соответствующие алгоритмы практически одинаковы и могут
быть рассмотрены одновременно. Пусть операнды а и b заданы в
системе счисления с основанием В:
т-1
а~(ат_}ат_2...а0)в=^а:В‘ ’ 0<а,<В,
i=0
0 </>,< В,
/=0
и пусть для определенности а>Ь. Для операции сложения это
условие ни на что не влияет, поскольку слагаемые всегда можно
поменять местами. Для операции вычитания оно означает, что раз-
ность является неотрицательным числом и, следовательно, может
быть представлена CLINT-объектом без приведения по модулю
Mnax + 1-
Вот основные шаги сложения.
Алгоритм вычисления суммы а + Ъ
1. Положить i <— 0 и с <— 0.
2. Вычислить t <— сц + bi + с, <— t mod В и с <— [_t/BJ.
3. Положить i <— i + 1. При I < п - 1 вернуться на шаг 2. .
4. Вычислить t <— at + с, si <— t mod В и с <г- [t/BJ.
5. Положить i <— i + 1. При i < т - 1 вернуться на шаг 4.
6. Положить sm <— с.
7. Результат: 5 = (smsm_x.. .s^B.
На шаге 2 разряды слагаемых суммируются с переносом, при этом
младшая часть результата записывается в разряд суммы, а старшая
переносится в следующий разряд. Как только мы дойдем до старше-
го разряда одного из слагаемых, на шаге 4 все оставшиеся разряды
г
ГЛАВА 4. Основные операции 37
- э? второго слагаемого складываются со всеми оставшимися перено- сами. До тех пор пока не обработан последний разряд слагаемого, младшая часть записывается в разряд суммы, а старшая переносится в следующий разряд. И, наконец, самый последний перенос (если он есть) записывается в самый старший разряд суммы. В случае вычитания, умножения и деления шаги 2 и 4 имеют тот же вид. Соответствующий код типичен для арифметических функций: 1 s = (USHORT)(carry = (ULONG)a + (ULONG)b + (ULONG)(USHORT)(carry » BITPERDGT));
им*-1’ Промежуточное значение г, участвующее в алгоритме, представле- но переменной carry типа ULONG, в которую записывается сумма разрядов ah и переноса с предыдущей операции. Полученный новый разряд si записывается в младшую часть переменной carry и приведением типов преобразуется в значение типа USHORT. Возникающий перенос записывается в старшую часть переменной carry до следующего шага. При реализации этого алгоритма с помощью функции add_l() может возникнуть переполнение; в этом случае нужно привести сумму по модулю Nmax+ 1.
Функция: Сложение
Синтаксис: int addj (CLINT aj, CLINT bj, CLINT sj);
Вход: aj, bj (слагаемые)
Выход: sj (сумма)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения int addj (CLINT aj, CLINT bj, CLINT sj) { clint ss_l[CLINTMAXSHORT + 1]; clint *msdptra_l, *msdptrb_l; clint *aptr_l, *bptr_l, *sptrj = LSDPTR_L (ss_l); ULONG carry = OL; int OFL = 0;
Автор этого компактного выражения - мой коллега Robert Hammelrath.
38
Криптография на Си и C++ в действии
В цикле сложения используются указатели. Проверяется, у какого
из слагаемых число разрядов больше. Инициируются указатели
aptrj и msdaptrj, соответствующие самому младшему и самому
старшему разряду большего слагаемого (или а_1, если слагаемые
имеют равную длину). Аналогично, указатели bptrj и msdbptrj
соответствуют самому младшему и самому старшему разряду
меньшего слагаемого, или bj. Инициализация выполняется с
помошью макросов LSDPTR_L() для младших разрядов и
MSDPTR_L() для старших разрядов CLINT-объекта. Макрос
DIGITS_L (а_1) определяет число разрядов CLINT-объекта а_1, а
макрос SETDIGITS_L (а_1, п) устанавливает число разрядов сла-
гаемого а_1 равным п.
if (DIGITS J_ (а_1) < DIGITS J. (bj))
{
aptrj = LSDPTFLL (bj);
bptrj = LSDPTFLL (aj);
msdptraj = MSDPTFLL (bj);
msdptrbj = MSDPTFLL (aj);
SETDIGITS J_ (ssj, DIGITS J. (bj));
else
{
aptrj = LSDPTFLL (aj);
bptrj = LSDPTRJ- (bj);
msdptraj = MSDPTFLL (aj);
msdptrbj = MSDPTFLL (bj);
SETDIGITS_L (ssj, DIGITS_L (aj));
На первом цикле процедуры addj разряды переменных aj и bj
суммируются и записываются в результирующую переменную
ssj. Появление ведущих нулей не вызывает никаких проблем -
они участвуют в вычислениях и отбрасываются при копировании
результата в sj. Движение осуществляется от младших разрядов
слагаемого b J к старшим разрядам. Это в точности соответствует
школьному сложению в «столбик». Как и было обешано, исполь-
зуем перенос.
while (bptrj <= msdptrbj)
{
ГЛАВА 4. Основные операции 39
*sptrj++ = (USHORT)(carry = (ULONG)*aptrJ++
+ (ULONG)*bptrJ++ + (ULONG)(USHORT)(carry » BITPERDGT));
}
Преобразуем USHORT-значения *aptr и *bptr путем приведения
типов в ULONG и сложим. К полученной сумме прибавим пере-
нос из предыдущей итерации. Результатом является значение ти-
па ULONG, содержащее перенос в старшем слове. Это значение
ч присваивается переменной carry и хранится в ней до следующей
( ) итерации. Из суммы берем младшее слово - это и есть результи-
। руюший разряд типа USHORT. Перенос, хранящийся в старшем
® слове carry, после сдвига на BITPERDGT и преобразования типов
участвует в следующей итерации.
На втором цикле оставшиеся разряды переменной а_1 складыва-
ются с переносом (если он есть); результат записывается в s_l.
while (aptrj <= msdptraj)
{
*sptrj++ = (USHORT)(carry = (ULONG)*aptrJ++
+ (ULONG)(USHORT)(carry » BITPERDGT));
}
Если на втором цикле возникает перенос, то результат будет на
один разряд длиннее, чем слагаемое а_1. Если результат превышает
I максимальное значение Nmax, допускаемое типом CLINT, то его
z нужно привести по модулю (Nmax + 1) (см. главу 5), как это дела-
ется для стандартных беззнаковых типов. В этом случае возвра-
щается уведомление об ошибке E_CLINT_OFL.
if (carry & BASE)
{
*sptr_l = 1;
SETDIGITS J_ (ssj, DIGITS_L (ssj) + 1);
if (DIGITS_L (ssj) > (USHORT)CLINTMAXDIGIT)
/* Переполнение ? 7
ANDMAX_L (ssj);
OFL = E_CLINT_OFL;
/* Привести по модулю (Nmax +1)7
40
Криптография на Си и C++ в действии
} cpy_l (s_l, ss_l);
return OFL; }
I' I и Временная сложность t всех представленных здесь процедур сло- жения и вычитания равна t = 0(h), то есть пропорциональна числу разрядов большего операнда. Что ж, сложение мы рассмотрели, теперь перейдем к вычислению
‘1 разности двух чисел а и Ь, заданных в системе счисления с основа- нием В:
е а = (^/n-i^/n-2- • -ао)в ^b- (bn..ibn_2- • -Ьо)в Алгоритм вычисления разности а -Ь 1. Положить i <— 0 и с <— 1. 2. При с = 1 вычислить t <— В + иначе t <— В - 1 + at? - bj. 3. Положить Si <— t mod В и с <— \_t/BJ. 4. Положить i <— i + 1. При i < н - 1 вернуться на шаг 2.
г 5. При с = 1 вычислить t <— В + а,; иначе t <- В - 1 + 6. Вычислить Si <— t mod В и с <— [_t!BJ.
' О'- г . • 7. Положить i <— i + 1. При i < т - 1 вернуться на шаг 5. 8. Результат: 5 = (sm_xsm_2-• sq)b.
W* *С *,М' '4J Ч Вычитание реализуется так же, как и сложение, за исключением следующего: ✓ С помощью переменной carry типа ULONG мы «занимаем» из предыдущего старшего разряда уменьшаемого в том случае, если текущий разряд уменьшаемого меньше соответствующего разряда вычитаемого. V Здесь нужно следить уже не за переполнением, а за возможной потерей значащих разрядов; в этом случае результат вычитания вообще-то будет отрицательным; однако, поскольку тип CLINT ( беззнаковый, нужно выполнить приведение по модулю (Nmax+ 1) (см. главу 5). Эта ситуация выявляется, когда функция возвращает код ошибки E_CLINT_UFL. ✓ И последнее: все ведущие нулевые разряды отбрасываются. Таким образом, получается такая функция вычисления разности чисел а_1 и Ь_1 типа CLINT.
ГЛАВА 4. Основные операции 41
функция: Вычитание
Синтаксис: int subj (CLINT aaj, CLINT bbj, CLINT dj);
Вход: aaj (уменьшаемое), bbj (вычитаемое)
Выход: dj (разность)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_UFL в случае потери значащих разрядов
int
subj (CLINT aaj, CLINT bbj, CLINT dj)
{
CLINT bj;
clint a_l[CLINTMAXSHORT + 1];
/* Добавляем в a_l еще один разряд */
clint *msdptra_l, *msdptrb_J;
clint *aptrj = LSDPTFLL (aJ);
clint *bptrj = LSDPTFLL (bj);
clint *dptrj = LSDPTFLL (dj);
ULONG carry = OL;
intUFL = O;
cpyj (aj, aaj);
: cpyj (bj, bbj);
msdptraj = MSDPTFLL (aj);
msdptrbj = MSDPTFLL (bj);
Если aj < bj, то будем вычитать bj не из aj, а из максимально
возможного значения Nmax. К полученной разности прибавим
(уменьшаемое + 1), то есть все вычисления выполняем по модулю
(Nmax +1 )• Значение Nmax генерируем с помошью функции
setmaxJO.
if (LT_L (aj, bj))
{
setmax J (aj);
msdptraj = aj + CLINTMAXDIGIT;
42 Криптография на Си и C++ в действии
SETDIGITS-L (d_l, CLINTMAXDIGIT); UFL = E_CLINT_UFL; • } else { SETDIGITSJ. (dj, DIGITS_L (aj));
C: . В } while (bptrj <= msdptrbj) { *dptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++ - (ULONG)*bptrJ++ - ((carry & BASE) » BITPERDGT)); } while (aptrj <= msdptraj) *dptr_l++ = (USHORT)(carry = (ULONG)*aptr_l++ - ((carry & BASE) » BITPERDGT)); ) RMLDZRS_L (dj); Складываем разность Nmax - bj, записанную в d_l, с величиной (уменьшаемое + 1). Результат: dj.
'?м- * > '* л i if (UFL)
ь 'ф I { addj (d_l, aa_l, d_l); inc_l (dj);
' 4‘‘ .AW'»/ (« }
return UFL;
}
ГДАВА 4. Основные операции
43
Помимо рассмотренных функций add_l() и sub_l() введем еще две
специальные функции, второй аргумент которых имеет тип
USHORT, а не CLINT. Такие функции будем называть смешанными
и обозначать префиксом «и», например uaddj() и usubj(). Преобра-
зование значения типа USHORT в CLINT-объект осуществляется с
помощью функции u2clint_l(), с которой мы познакомимся в главе 8.
функция: Синтаксис: Вход: Выход: Возврат: Смешанное сложение переменных типа CLINT и USHORT int uaddj (CLINT aj, USHORT b, CLINT sj); aj, b (слагаемые) sj (сумма) E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения
int
uaddj (CLINT aj, USHORT b, CLINT sj)
{
int err;
CLINT tmpj;
u2clintj (tmpj, b);
err = addj (aj, tmpj, sj);
return err; }
Функция: Вычитание числа типа USHORT из числа типа CLINT
Синтаксис: int usubj (CLINT aj, USHORT b, CLINT dj);
Вход: a J (уменьшаемое), b (вычитаемое)
Выход: dj (разность)
результат: E_CLINT_OK, если все в порядке
E_CLINT_UFL в случае потери значащих разрядов
int
usubj (CLINT aj, USHORT b, CLINT dj)
{
int err;
CLINT tmpj;
44
Криптография на Си и C++ в действии
" u2clintj (tmpj, b); err = subj (aj, tmpj, dj); return err; } Еще два важных частных случая сложения и вычитания: увеличе- ние и уменьшение CLINT-объекта на 1 (инкремент и декремент). Реализуем их в виде функций incj() и decj() в виде процедуры- сумматора: новое значение операнда будем записывать на место старого - очень практичный способ, используемый во многих алго- ритмах. Неудивительно, что реализация функций incj() и decj() осуществ- ляется по аналогии с функциями addj() и subj(). Они точно так же контролируют переполнение и потерю значащих разрядов, возвра-
щая соответствующие коды ошибки E_CLINT_OFL и E_CLINT_UFL.
Функция: Увеличение CLINT-объекта на 1
Синтаксис: int incj (CLINT aj);
Вход: aj (слагаемое)
Выход: aj (сумма)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения int incj (CLINT a J)
{ clint ‘msdptraj, ‘aptrj = LSDPTR_L (aj); ULONG carry = BASE; int OFL = 0; msdptraj = MSDPTFLL (aj);
• * ,, while ((aptrj <= msdptraj) && (carry & BASE)) { ‘aptrj = (USHORT)(carry = 1UL + (ULONG)‘aptrJ); aptrj++; }
if ((aptrj > msdptraj) && (carry & BASE))
. Основные операции
45
{ *aptrJ = 1; SETDIGITS J_ (aj, DIGITS J_ (aj) + 1); if (DIGITS J_ (aj) > (USHORT)CLINTMAXDIGIT) /* Переполнение ? 7 { SETZERO_L (aJ); /* Привести по модулю (Nmax +1)7 OFL = E_CLINT_OFL; } } return OFL; )
Функция: Уменьшение CLINT-объекта на 1
Синтаксис: int decj (CLINT aj);
Вход: aj (уменьшаемое)
Выход: aj (разность)
Возврат: EJDLINT_OK, если все в порядке E_CLINT_UFL в случае потери значащих разрядов
int
d tv:.
decj (CLINT aj)
clint *msdptraj, *aptr_l = LSDPTR_L (aj);
ULONG carry = DBASEMINONE;
if (EQZ_L (aj))
/* Потеря значащих разрядов ? 7
/* Привести по модулю maxj 7
setmax J (aj);
return E_CLINT_UFL;
msdptraj = MSDPTRJ. (aj);
while ((aptrj <= msdptraj) &&
Криптография на Си и C++ в действии
(carry & (BASEMINONEL « BITPERDGT)))
{
*aptrj = (USHORT)(carry = (ULONG)*aptrJ - 1L);
aptr_l++;
}
RMLDZRS_L (aJ);
return E_CLINT_OK;
2. Умножение
Если все слагаемые nb n2, n3, ..., nr равны од-
ному и тому же целому числу п, то сложение
называется «умножением числа г на целое чис-
ло п» и обозначается гц + п2 + п3 + ... + пг = гп.
Леопольд Кронекер, Об идее чисел
Функция умножения играет основную роль в пакете FLINT/C, яв-
ляется одной из наиболее трудоемких и вместе с функцией деления
определяет время работы многих алгоритмов. В отличие от сложе-
ния и вычитания, с которыми мы уже знакомы, сложность класси-
.. . „ ческих алгоритмов умножения и деления - квадратичная от числа
разрядов аргументов, недаром Дональд Кнут назвал одну из глав
«Искусства программирования для ЭВМ» «Как быстро мы можем
умножать?».
На сегодняшний день в литературе опубликовано множество мето-
дов умножения больших и очень больших чисел, среди которых
есть и весьма трудные. Одним из самых трудных является алго-
ритм, предложенный А. Шёнхаге и В. Штрассеном, в основе кото-
рого лежит быстрое преобразование Фурье над конечными полями.
Время работы этого алгоритма оценивается величиной
О(п log п log log и), где и - число разрядов аргументов (см. [Knut],
п. 4.3.3). Недостаток этого и подобных алгоритмов заключается в
том, что выигрыш по скорости по сравнению с классическими
методами сложности О(п2) достигается лишь когда длина сомножи-
телей составляет порядка 8000-10000 двоичных разрядов. До ис-
пользования таких чисел к криптографии пока еще очень далеко.
Сначала реализуем в пакете FLINT/C основной «школьный» метод
умножения, основанный на «Алгоритме М» Кнута (см. [Knut],
п. 4.3.1), и попробуем «выжать» из него максимальную скорость.
Затем плотно займемся возведением в квадрат - многообещающей
рЛАВА 4. Основные операции 47
операцией в смысле снижения вычислительных затрат - и для обоих случаев попробуем применить алгоритм Карацубы, асимптотически более быстрый, чем <Э(п2).2 Алгоритм Карацубы весьма любопытен и привлекателен своей кажущейся простотой, так что желающие могут заняться его реализацией как-нибудь (дождливым) воскрес- ным днем. А пока мы посмотрим, дает ли что-либо этот алгоритм для библиотеки FLINT/C. 4.2.1. Школьный метод Рассмотрим умножение чисел а и Ь, заданных в системе счисления с основанием В: т-1 а:=(а„_1ат.2...а0)в = У^а,В', 0<а; <В, i=0 b-.= (bn_xbn_2...b0)B=!yjbiBi, Q<bt<B. i=0 Как нас учили в школе, произведение ab можно вычислить по схеме рис. 4.1 (для т = п = 3).
Рисунок 4.1. Вычисления при умножении (Д2Д1^о)д ‘ (Ь2Ь\Ьо)В с20 Р20 Р10 Р00 + С21 Р21 Рн Poi + с22 Р22 Р12 Р02 <Р5 Р4 Рз Р2 Р1 Ро)в Сначала вычисляем частичные произведения (д2Я1Яо)я ’ для j = 0’ 1, 2: значения - это младшие разряды значения (яД + перенос), где apj - внутреннее произведение, а с2; - старшие разряды значе- ния p2j. Затем суммируем частичные произведения и получаем про- изведение р = (p5P4P3P2PlPo)fi- В общем случае произведение p = ab равно п-1 т-1 р = J=0 /=0 Произведение двух операндов длины т и п имеет длину не менее т + п - 1 и не более т + п разрядов. Число элементарных умноже- ний (в которых операнды меньше основания В) равно нт.
2 Когда про алгоритм говорят, что он асимптотически более быстрый, это означает, что чем боль-
ше входные значения алгоритма, тем больше заметно увеличение скорости. Однако не следует
преждевременно впадать в эйфорию - для наших целей это улучшение может вообще не играть
никакой роли.
48
Криптография на Си и C++ в действии
Функцию умножения можно реализовать по указанной схеме, то есть сначала вычислим и запомним все частичные произведения, а затем просуммируем их, домножая на соответствующую степень основания В. Этот школьный метод вполне годится для вычисления с карандашом и бумагой, но для компьютерной реализации он слишком громоздкий. Более эффективная альтернатива - сразу при- бавлять внутренние произведения atbj и переносы с с предыдущих шагов к результирующему разряду pi+j. Итоговое значение для каж- дой пары (/, J) записываем в переменную t:
t <— pi+j + ciibj + с, где t представимо в виде t = kB + /, 0 <к, 1 < В.
V Тогда pi+j + aibj + с<В-1 + (В- 1)(В - 1) + В - 1 = =(В - 1)В + В- 1 = В2 — 1 <в2.
ж.* он . Текущие значения разрядов результата определяются из представ- ления переменной t присваиванием pi+j <— 1. Выполняем новый перенос: с «— к. Таким образом, теперь наш алгоритм умножения включает только внешний цикл, вычисляющий частичные произведения а^Ь^Ь^... Ьо)в> и внутренний цикл, вычисляющий внутренние произведения a^bj, где j = 0, ..., п - 1, и значения t и р/±/. Вот этот алгоритм. Алгоритм умножения 1. Для i = 0, ..., п - 1 положить pt <— 0. 2. Положить 1 <— 0. 3. Положить j <— 0 и с <— 0. 4. Положить t <— pi+j + aibj + с, pi+7 <-1 mod В и с <- \_t/BJ. 5. Положить j <r-j + 1. При j < n - 1 вернуться на шаг 4. 6. Положить pi+n «— с. 7. Положить i <— i + 1. При i < т - 1 вернуться на шаг 3.
8. Результат: р = (рт+п_\рт+п_2.• -Ро)/?- Этот основной цикл является ядром следующей реализации алгорит- ма умножения. В соответствии с полученными оценками, на шаге 4 для переменной t требуется точное представление чисел, меньших В1. Так же как и в случае сложения, представим внутренние произ- ведения t типом ULONG. Заметим, что переменная t используется
ГЛАВА 4. Основные операции 49
неявно, а разряды произведения pi+j и переносы с выделяются внут-
ри одного и того же выражения так же, как это делалось в функции
сложения (см. стр. 37). Начальные значения будем задавать более
эффективной процедурой, чем на шаге 1 алгоритма.
функция: Умножение
Синтаксис: int mulj (CLINT f1 J, CLINT f2J, CLINT ppj);
Вход: f1 J, f2J (сомножители)
Выход: ppj (произведение)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения
int
mulj (CLINT И J, CLINT f2J, CLINT ppj)
{
register clint *pptr_l, *bptr_l;
CLINT aaj, bbj;
CLINTD pj;
clint *aj, *b_l, *aptrj, *csptr_l, *msdptra_l, *msdptrbj;
USHORT av;
ULONG carry;
int OFL = 0;
Сначала опишем переменные: результат будем записывать в pj,
то есть эта переменная должна быть двойной длины. Сначала
рассмотрим случай, когда один из сомножителей (а значит и про-
изведение) равен нулю. Иначе заносим сомножители в аа_1 и bbj
и убираем ведущие нули.
+ 1 if (EQZ_L (f1 J) || EQZ_L (f2_l))
{
SETZERO_L (ppj);
return E_CLINT_OK;
}
cpyj (aaj, f1 J);
cpyj (bbj, f2J);
50
Криптография на Си и C++ в действии
В соответствии с описанием задаем указателям а_1 и Ь_1 адреса
аа_1 и bb_l. Если число разрядов в аа_1 меньше, чем в bb_l, вы-
полняем логическую перестановку: указатель а_1 всегда соответ-
ствует операнду с большим числом разрядов.
if (DIGITS J_ (aaj) < DIG ITS J_ (bbj))
{
a J = bbj;
bj = aaj;
}
else
{
a J = aaj;
bj = bbj;
}
msdptraj = a J + *aj;
msdptrbj = bj + *bj;
Для экономии времени не выполняем инициализацию, указанную
выше, а вычисляем циклически частичное произведение
Ь0)в • а0 и заносим результат в pn, pn_lz ..., рп.
л’ carry = 0;
av = *LSDPTRJ_ (aJ);
for (bptrj = LSDPTRJ. (bj), pptrj = LSDPTRJ. (pj);
bptrj <= msdptrbj; bptrj++, pptrj++)
*pptr_l = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l +
(ULONG)(USHORT)(carry » BITPERDGT));
}
*pptr_l = (USHORT)(carry » BITPERDGT);
Дальше идет вложенный иикл умножения, начиная с разряда
а_1[2] переменной а_1.
ГЛАВА 4. Основные операции 51
for (csptrj = LSDPTR_L (рJ) + 1, aptrj = LSDPTR J. (aj) + 1;
aptrj <= msdptraj; csptrj++, aptrj++)
' {
carry = 0;
un
ut: av = *aptrj;
'V'
for (bptrj = LSDPTRJ- (bj), pptrj = csptrj;
bptrj <= msdptrbj;
> bptrj++, pptrj++)
{
t 4 *PPtrJ = (USHORT)(carry = (ULONG)av * (ULONG)*bptrJ +
(ULONG)*pptrJ + (ULONG)(USHORT)(carry » BITPERDGT));
*pptrj = (USHORT)(carry » BITPERDGT);
}
Максимально возможная длина результата равна сумме длин а_1 и
bj. Случай, когда длина результата оказывается на единицу мень-
ше, выявляется макросом RMLDZRSJ-.
SETDIGITS J_ (pj, DIGITS J. (aj) + DIGITS J. (bj));
RMLDZRSJ. (pj);
Если результат превышает допустимые размеры для объектов типа
CLINT, то он приводится по модулю (Nmax + 1), а флагу ошибки
OFL присваивается значение E_CLINT_OFL. Приведенный по мо-
дулю результат записывается в ppj.
if (DIGITSJ_ (pj) > (USHORT)CLINTMAXDIGIT)
/* Переполнение ? 7
{
ANDMAX_L (pj); /* Привести по модулю (Nmax +1)7
OFL = E_CLINT_OFL;
г
52 Криптография на Си и C++ в действии
cpyj (pp_l, рJ);
return OFL;
}
Время t = O(mri) выполнения умножения пропорционально произ-
ведению длин т и п операндов. Для умножения, как и для сложе-
ния, можно реализовать смешанную функцию, первый аргумент
которой имеет тип CLINT, а второй - тип USHORT. Укороченная
версия CLINT-умножения требует О(п) процессорных умножений.
Однако этим результатом мы обязаны не какому-то усовершенст-
вованию алгоритма, а просто малой длине USHORT-аргумента. Мы
еще вернемся к этой функции, когда будем возводить в степень
число типа USHORT (см. главу 6, функцию wmexpJO).
Для реализации функции umul_() воспользуемся слегка модифици-
рованной функцией mulj().
Функция: Умножение CLINT-объекта на число типа USHORT
Синтаксис: int umulj (CLINT aaj, USHORT b, CLINT ppj);
Вход: aaj, b (сомножители)
Выход: ppj (произведение)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения
int
umulj (CLINT aaj, USHORT b, CLINT ppj)
{
register clint *aptrj, *pptrj;
CLINT aj;
CLINTD pj;
clint *msdptraj;
ULONG carry;
int OFL = 0;
cpyj (aj, aaj);
if (EQZ_L (aJ) || 0 == b)
{
ГЛАВА 4* Основные операции
SETZERO J_ (ppj);
53
return E_CLINT_OK;
}
Предварительная подготовка завершена, теперь в цикле выпол-
няем умножение CLINT-аргумента на USHORT-аргумент, перенос
записываем в старший USHORT-разряд CLINT-аргумента.
msdptraj = MSDPTR_L (aj);
carry = 0;
for (aptrj = LSDPTR_L (aJ), pptrj = LSDPTRJ (pj);
aptrj <= msdptraj;
aptrj++, pptrj++)
{
><.; *pptr_l = (USHORT)(carry = (ULONG)b * (ULONG)*aptr_l +
(ULONG)(USHORT)(carry » BITPERDGT));
}
Km
' ' *pptr_l = (USHORT)(carry » BITPERDGT);
SETDIGITS J_ (p_l, DIGITSJ. (a_l) + 1);
RMLDZRS_L (p_l);
'►!№
if (DIGITSJ- (pj) > (USHORT)CLINTMAXDIGIT)
ns Oiiv /* Переполнение ? 7
{
ANDMAXJ. (pj); /* Привести по модулю (Nmax + 1)7
OFL = E_CLINT_OFL;
}
cpyJ (ppJ, pJ);
return OFL;
)
54 Криптография на Си и C++ в действии
4.2.2. А возведение в квадрат - быстрее |
Возведение большого числа в квадрат требует значительно меньше!
го числа умножений, чем умножение двух больших чисел, благодаря
симметрии операндов. Это наблюдение становится еще более важ-
? ' * * ным, когда дело доходит до возведения в степень, и нам требуется
? ъ ' не одно, а сотни возведений в квадрат - тогда можно получить значи-
j а '' тельное увеличение скорости. Снова обратимся к хорошо известной
схеме умножения, на этот раз с двумя одинаковыми сомножителя-
ми (я2<21Яо)д (см. рис. 4.2).
(«2«1^о)д ‘
Рисунок 4.2.
Вычисления
при возведении
в квадрат
+ Я2а0 (цац
a2ai «1«1 аоа{
+ ^1^2 «0^2
(Р5 Р4 Рз Р2 Pi Ро)в
Заметим, что внутренние произведения ащ вычисляются, во-
первых, однократно для i = j (выделены полужирным шрифтом на
рис. 4.2), и, во-вторых, дважды для i Ф j (на рисунке они обведены
прямоугольниками). Таким образом, вместо девяти умножений
можно выполнять всего три, удвоив слагаемые ащВ1^ при i < j.
Тогда сумму внутренних произведений при возведении в квадрат
можно переписать как
л-1 л-2 л-1 л-1
р = = 2£ YaiajBi+J
i,j=Q i=0 j=i+l j=Q
Таким образом, число элементарных умножений по сравнению со
«школьным» методом сокращается с п2 до и(и + 1 )/2.
Вычисление последнего выражения для р естественно алгоритми-
чески реализовать в виде двух вложенных циклов.
V Ц 4 ’лё Алгоритм 1 возведения в квадрат
1. Для i = 0, ..., п - 1 положить<— 0.
2. Положить i <- 0. !
3. Положить t <— p2l + аД P2i <— t mod В и с <- \j/BJ.
4. Положить j «— i + 1. При j = n -1 перейти на шаг 7.
5. Положить t <— Pi+j + 2a щ + с, pi+J- <— t mod В и с <—
6. Положить j <— j' + 1. При j < n - 1 вернуться на шаг 5.
7. Положить pi+n <— с.
ГЛАВА 4. Основные операции 55
8. Положить i <— i + 1. При i < п - 1 вернуться на шаг 3.
9. Резул ьтат: р = (p2n-iP2n-2 -Ро)в-
Выбирая типы данных для представления переменных, следует
учесть, что t может принимать значение
(В - 1) + 2(5 - I)2 + (В - 1) = 2В2 - 2В.
(на шаге 5 алгоритма). Это означает, что для представления t в сис-
теме счисления с основанием В понадобится больше чем два разряда,
поскольку В2 - 1 < 2В2 -2В < 2В2 - 1, то есть типа ULONG для пред-
ставления t будет недостаточно (из неравенства выше следует, что
требуется еще один двоичный разряд). При реализации на Ассемб-
лере это не вызывает никаких проблем, поскольку всегда можно
воспользоваться процессорным разрядом переноса. Но в языке С
все не так просто. Для разрешения проблемы будем на шаге 5 алго-
ритма 1 выполнять умножение на 2 в отдельном цикле. Тогда для
шага 3 потребуется свой цикл. Небольшие усилия, затраченные на
разбирательство с циклами, окупятся появлением дополнительного
двоичного разряда. Вот измененный алгоритм.
Алгоритм 2 возведения в квадрат
1. Инициализация: для i = 0, ..., п - 1 положить р, <— 0.
2. Вычисление произведения разрядов с неравными индексами:
положить i <г- 0.
3. Положить j <— / + 1 и с <— 0.
4. Положить t <— pi+J + a^j + с, pi+j <— t mod В и с <— \j/BJ.
5. Положить j <r-j + 1. При j < n - 1 вернуться на шаг 4.
6. Положить pi+n <— с.
7. Положить i <г- i + 1. При i < п - 2 вернуться на шаг 3.
8. Удвоение внутренних произведений: положить i <— 1 и с <— 0.
9. Положить t <— 2pi + с, pi <— t mod В и с <— [_t!BJ.
10. Положить i <— i + 1. При i < 2n - 2 вернуться на шаг 9.
11. Положить ргп-\ <— с.
12. Суммирование внутренних квадратов: положить i <- 0 и с <— 0.
13. Положить t <— p2t + а,2 + с, ри <— t mod В и с <— L^/Bj.
14. Положить t <— p2i+\ + с, Р2/+1 <— t mod В и с <— l_t/BJ.
15. Положить i <— i + 1. При i < п - 1 вернуться на шаг 13.
16. Положить р2п_х <- р2и-1 + с. Результат: р = (р2п-\Р2п-2-• -РоЪ-
56
Криптография на Си и C++ в действии
При реализации на С вместо шага 1, по аналогии с умножением,
вычисляем и запоминаем первое частичное произведение 6z0(tf„-i
«л_2.. .а\)в.
Функция: Синтаксис: Вход: Выход: Возврат: Возведение в квадрат nt sqr_l (CLINT fJ, CLINT ppj); LI (операнд) ppj (квадрат) E-CLINTJDK, если все в порядке E_CLINT_OFL в случае переполнения
int sqrj (CLINT fJ, CLINT ppj) i
А/- — register clint *pptrj, *bptrj; CLINT aj; CLINTD pj; clint *aptrj, *csptrj, *msdptraj, *msdptrbj, *msdptrcj; USHORT av; ULONG carry; int OFL = 0;
п". s cpyj (aj, fJ); if (EQZ_L (aj))
Q —а э w I ..." • j ТШП i'J - (} , t SETZERO_L (ppj); return E_CLINT_OK; } msdptrbj = MSDPTR_L (aj); msdptraj = msdptrbj - 1;
( Инициализация результирующего вектора по указателю pptrj вы- полняется путем вычисления частичного произведения a0(an_ian_2--- aJB, по аналогии с умножением. Разряду р0 здесь не присваива- ется никакое значение; он должен быть нулевым.
LSDPTRJ. (р_1) = 0;
ГЛАВА 4. Основные операции
57
carry = 0;
av = *LSDPTRJ_ (aj);
for (bptrj = LSDPTFLL (a_l) + 1, pptrj = LSDPTFLL (pj) + 1;
bptrj <= msdptrbj;
bptrj++, pptrj++)
{
*pptrj = (USHORT)(carry = (ULONG)av * (ULONG)*bptrJ +
(ULONG)(USHORT)(carry » BITPERDGT));
}
*pptrj = (USHORT)(carry » BITPERDGT);
Цикл суммирования внутренних произведений а,а;.
for (aptrj = LSDPTRJ_ (aj) + 1, csptrj = LSDPTR_L (pj) + 3;
aptrj <= msdptraj; aptrj++, csptrj += 2)
{
carry = 0;
av = *aptrj;
for (bptrj = aptrj + 1, pptrj = csptrj; bptrj <= msdptrbj;
bptrj++, pptrJ++)
{
‘pptrj = (USHORT)(carry = (ULONG)av * (ULONG)*bptr_l +
(ULONG)‘pptrJ + (ULONG)(USHORT)(carry » BITPERDGT));
}
‘pptrj = (USHORT)(carry » BITPERDGT);
}
msdptrcj = pptrj;
Умножение промежуточного результата из pptrj на 2 выполняем
с помошью сдвига (см. также п. 7.1).
carry = 0;
for (pptrj = LSDPTRJ. (pj); pptr_l <= msdptrcj; pptrj++)
{
58 Криптография на Си и C++ в действии
*pptrj = (USHORT)(carry = (((ULONG)*pptr_l) « 1) +
(ULONG)(USHORT)(carry » BITPERDGT));
}
*pptr_l = (USHORT)(carry » BITPERDGT);
/ Теперь вычисляем «главную диагональ».
carry = 0;
for (bptrj = LSDPTR_L (aj), pptrj = LSDPTR_L (pj);
bptrj <= msdptrbj;
bptrj++, pptrj++)
{
*pptrj = (USHORT)(carry = (ULONG)*bptrJ * (ULONG)*bptrJ +
(ULONG)*pptrJ + (ULONG)(USHORT)(carry » BITPERDGT));
pptrj++;
*pptrj = (USHORT)(carry = (ULONGfpptrJ + (carry » BITPERDGT));
}
Все остальное - так же, как в умножении.
SETDIGITS J_ (р J, DIGITS J. (aj) « 1);
RMLDZRS.L (pj);
if (DIGITSJ_ (pj) > (USHORT)CLINTMAXDIGIT) /* Переполнение? 7
{
ANDMAX-L. (pj); /* Привести по модулю (Nmax +1)7
OFL = E_CLINT_OFL;
}
cpyj (ppj, pj);
return OFL;
ГЛАВА 4. Основные операции
59
Время работы процедуры возведения в квадрат равно О(м2), то есть квадратичное от длины операнда. Однако, поскольку здесь требуется п(п + 1)/2 элементарных умножений, эта функция почти в два раза быстрее, чем умножение. 4.2.3. Поможет ли метод Карацубы?
/к ,vi Дух умножения и деления разрушил все вокруг и устремился к отдельной части целого. Стэн Надольный, Бог дерзости Как мы и обещали, рассмотрим метод умножения, носящий имя русского математика А. Карацубы, опубликовавшего несколько вариантов этого метода (см. [Knut], п. 4.3.3). Пусть числа а и Ь - натуральные длины п = 2к разрядов в системе счисления с основа- нием В. Представим а и b в системе счисления с основанием Вк: а = b = Если умножать а на b традиционным спосо- бом, то для вычисления произведения ab = В kci\b\ + В (aob\ + ci\Ьо) + требуется четыре умножения по основанию Вк и, следовательно, п2 = 4к2 элементарных умножений по основанию В. Однако если положить Со := aobo, := €ZiZ?i, <?2 := (aQ + tfi)(Z>o + bf) -cQ- сь
/ с то ab = Вк(Вкс\ + с%) + Со- Оказывается, теперь для вычисления произведения ab нужно всего три умножения чисел по основанию Вк или, что то же самое, 3£2 умножений по основанию В плюс несколько операций сложения и сдвига (умножение на Вк можно реализовать сдвигом на к разрядов в системе счисления с основанием В; см. п. 7.1). Предположим, что число п разрядов сомножителей а и b является степенью числа 2. Тогда, рекурсивно применяя указанную процедуру для вычисления частичных произведений, можно свести алгоритм к выполнению только элементарных умножений по основанию В. Откуда получаем 31оё2Л -/г10^3 =/г1>585 элементарных умножений вместо п2 (в класси- ческом методе); дополнительное время потребуется еще для опера- ций сложения и сдвига. Применительно к возведению в квадрат этот процесс несколько уп- рощается. Если
Со := «о .
60
Криптография на Си и C++ в действии
Cl := a2 ,
г'Д . I-.'. . ci(«о + fli)2 - cq- Ci, TO Cl2 = B^^B^Ci + C2) + Cq.
’ /pUH J--? f • На нас работает еще и то, что при возведении в квадрат оба сомно- жителя всегда имеют одну и ту же длину, что далеко не всегда выполняется в случае умножения. Следует, однако, помнить, что рекурсия тоже требует определенных затрат времени, так что наде- яться на какие-либо преимущества перед классическим методом, не обремененным рекурсией, можно лишь при работе с большими числами.
. (НИ Чтобы иметь полную информацию о реальной производительности алгоритма Карацубы, рассмотрим функции kmul() и ksqr(). Деление сомножителей на две части выполняется на месте, то есть копиро- вать их не нужно. А вот что нужно, так это, во-первых, снабдить сомножители указателями на младшие разряды и, во-вторых, де- лать это для каждого сомножителя отдельно (так как длины сомно- жителей могут различаться).
H's :r O" ; f В качестве эксперимента мы реализовали смешанную функцию, объединившую в себе рекурсивную процедуру для умножения чисел, длина которых превышает некоторое число, определяемое макросом, и обычное умножение и возведение в степень для ма- леньких чисел. Для нерекурсивного умножения в функциях kmul() и ksqr() будем использовать вспомогательные функции miilt() и sqr(), в которых умножение и возведение в квадрат реализовано в виде базовых (kernel) функций, не поддерживающих тождествен- ные адреса аргументов (режим сумматора) и приведение по модулю в случае переполнения.
Функция: Метод Карацубы умножения двух чисел а_1 и bj длиной 2к разря- дов в системе счисления с основанием В
Синтаксис: void kmul(clint *aptrj, clint *bptr_l, int len_a, int len_b, CLINT pj);
Вход: aptrj (указатель на младший разряд сомножителя а_1) bptrj (указатель на младший разряд сомножителя bj) 1еп_а (число разрядов сомножителя а_1) len_b (число разрядов сомножителя bj)
Выход: pj (произведение)
void
kmul (clint *aptr_l, clint *bptr_l, int len_a, int len_b, CLINT pj)
ГЛАВА 4. Основные операции 61
CLINT cO1J, C10J;
clint cOJ[CLINTMAXSHORT + 2];
clint d J[CLINTMAXSHORT + 2];
clint c2J [CLINTMAXSHORT + 2];
CLINTDtmpJ;
г йфг clint *a1ptr_J, *b1ptrj;
w int I2;
> if ((len_a == len_b) && (len_a >= MUL_THRESHOLD) &&
(0 == (len_a & 1)) )
{
Если оба сомножителя имеют одно и то же четное число разря-
дов, превышающее значение MUL_THRESHOLD, то используем
рекурсию, разбивая сомножители на две половины, младшим
разрядам каждой из которых соответствуют указатели aptrj,
а1 ptr_l, bptrj, Ы ptrJ. Эти половины мы не копируем и тем са-
мым экономим время. Значения с0 и С] вычисляются рекурсив-
ным вызовом функции kmul() и присваиваются переменным cOj
и d J типа CLINT.
I2 = len_a/2;
alptrj = aptrj + 12;
blptrj = bptrj + 12;
kmul (aptrj, bptrj, 12,12, cOJ);
kmul (alptrj, blptrj, 12,12, c1 J);
При вычислении значения c2 = (a0 + а7)(Ьо + bj - c0 - Cj выполня-
ем два сложения, один вызов функции kmul() и два вычитания.
Аргументами вспомогательной функции addkar() являются указа-
тели на младшие разряды и число разрядов двух слагаемых рав-
ной длины, значением функции - сумма этих слагаемых, имею-
щая тип CLINT. __
addkar (alptrj, aptrj, 12, cO1 J);
addkar (blptrj, bptrj, 12, c10J);
62
Криптография на Си и C++ в действии
kmul (LSDPTR_L (с01 J), LSDPTR_L (c10J),'
DIGITSJ. (c01 J), DIGITSJ. (c10J), c2J);
sub (c2J, c1 J, tmpj);
sub (tmpj, cOJ, c2J);
Выполнение функции заканчивается вычислением значения
Bk(Bkd + с2) + с0. Для этого используем функцию shiftaddO,
которая при сложении сдвигает влево первое из двух слагаемых
типа CLINT на заданное число позиций в системе счисления с
основанием В.
shiftadd (d J, c2J, I2, tmpj);
shiftadd (tmpj, cOJ, I2, pj);
}
Если хотя бы одно из входных условий не выполнено, прерываем
рекурсию и вызываем нерекурсивную функцию умножения
mult(). Для вызова функции mult() необходимо перевести части
aptrj и bptrj в формат CLINT.
д
else
{
memcpy (LSDPTRJ. (c1 J), aptrj, len_a * sizeof (clint));
memcpy (LSDPTRJ. (c2J), bptrj, len_b * sizeof (clint));
SETDIGITS J. (c1J, len_a);
SETDIGITSJ_ (c2J, lenjD);
mult (c1 J, c2J, pj);
RMLDZRS.L (pj);
}
}
Возведение в квадрат методом Карацубы выполняется аналогично,
поэтому не будем его описывать подробно. Для вызова функций
kmul() и ksqr() используем функции kmuIJO и ksqrj(), имеющие
стандартный интерфейс.
ГЛАВА 4. Основные операции
63
функция: Умножение и возведение в квадрат методом Карацубы
Синтаксис: int kmulj (CLINT aj, CLINT b_l, CLINT pj); int ksqrj (CLINT aj CLINT pj);
Вход: aj, bj (сомножители)
Выход: pj (произведение или квадрат)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения
Функции, реализующие алгоритмы Карацубы, читатель найдет в
файле kmul.c на прилагаемом к книге компакт-диске.
Многочисленные проверки этих функций (на Pentium III, 500 МГц,
под Linux) показали, что наилучший результат достигается, когда
нерекурсивная процедура умножения вызывается для не более чем
40-разрядных чисел (что соответствует 640 двоичным разрядам).
Временные оценки для нашей программы приведены на рис. 4.3.
Рисунок 4.3.
Процессорное
время умножения
метолом
К аранубы
Из рисунка видно, что результаты действительно оправдали наши
ожидания. Разница между обычным умножением и возведением в сте-
пень составляет около 40%. Для чисел размером более 2000 двоич-
ных разрядов время работы алгоритмов становится более заметным,
лидирует по скорости алгоритм Карацубы. Интересный факт: «нор-
мальное» возведение в квадрат sqr_l() значительно быстрее умно-
жения Карацубы, а возведение в квадрат методом Карацубы ksqrJO
лидирует только для чисел длиной более 3000 двоичных разрядов.
64
Криптография на Си и C++ в действии
Функции, реализующие алгоритмы Карацубы для маленьких чисел,
значительно ускорены по сравнению с первым изданием этой книги,
но в них все еще есть что улучшать. Заметные скачки во времени
работы функции kmulj() показывают, что рекурсия прерывается
раньше, чем это определено пороговым значением, если длина
сомножителей - нечетное число. В худшем случае это происходит в
самом начале процедуры умножения, и даже для очень больших
чисел нам не остается ничего лучшего, как применять обычное
умножение. Как нам кажется, стоит обобщить функции, реализую-
щие алгоритм Карацубы так, чтобы они могли обрабатывать аргу-
менты разной (в том числе нечетной) длины.
Дж. Зиглер (J. Ziegler) [Zieg] из Института Марка Планка
(г. Саарбрюкен, Германия) разработал для 64-разрядного процессора
(Sun Ultra-1) переносимую программу, которая реализует алгоритмы
умножения и возведения в степень методом Карацубы и «обгоняет»
обычные методы на числах длины 640 двоичных разрядов. Возве-
дение в квадрат работает на 10% быстрее для 1024-битных чисел и
на 23% - для 2048-битных.
Еще раз отметим, что алгоритмы Карацубы в том виде, в каком
они есть, не дают значительного преимущества для криптографиче-
ских приложений, так что мы предпочитаем вернуться к традицион-
ным функциям mulj() и sqrj() умножения и возведения в степень.
Если для ваших приложений функции, реализующие алгоритмы
Карацубы, подходят, просто воспользуйтесь ими, а не функциями
muIJO и sqr_l().
4.3. Деление с остатком
- У тебя осталось что-нибудь в кармане? ;
I
- Нет, - отвечала Алиса грустно. - Только на- |
переток. j
Льюис Кэррол,
Приключения Алисы в Стране Чудес,
(Перевод с английского Н. Демуровой)
Заложим в наше здание основных арифметических операций над
большими числами последний камень - деление - наиболее труд-
ную из всех операций. Поскольку мы работаем с натуральными
числами, то и результат мы можем выражать только натуральными
числами. Принцип деления, которым мы собираемся заняться,
называется делением с остатком и основан на следующем
соотношении. Для данных чисел a, b G 72L, Ь>0, существует
единственная пара целых чисел q и г таких, что а = qb + г, где
О < г < Ь. Будем называть q частным, а г остатком от деления а на Ь.
Чаще всего нас интересует только остаток, так что о частном мож-
но не беспокоиться. В главе 5 мы узнаем, как важно уметь вычис-
ГЛАВА 4. Основные операции 65
* t с: лять остаток - эта операция используется о многих алгоритмах, всегда одновременно со сложением, вычитанием, умножением и возведением в степень. Так что нам нужно постараться разработать как можно более быстрый алгоритм. Самый простой способ деления с остатком для натуральных чисел а и b - вычитать делитель b из делимого а, пока остаток г не будет меньше делителя. Подсчитав число вычитаний, мы получим част- ное. Частное q и остаток г равны: q = \_albJ и г = а - [_alb^b.3
f ? ’ Согласитесь, делить с остатком с помощью вычитания очень скучно. Даже в школьном методе деления «в столбик» используется значи- тельно более эффективный алгоритм: разряды частного определя- ются последовательно, делитель умножается на каждый из них, а полученные частичные произведения вычитаются из делимого. Пример работы этого алгоритма приведен на рис. 4.4.
Рисунок 4.4. Схема деления с остатком 354938:427=831, остаток 101 - 3416\|/ = 01333 - 1281 ф = 00528 - 427 = 101
«So.. :S : Уже при вычислении первого разряда частного - 8 - нам нужно попытаться угадать его или определить методом проб и ошибок. Ошибка выявляется либо если произведение (разряда частного на делитель) слишком велико (в нашем примере - больше, чем 3549),
либо если разность разрядов делимого и частичного произведения больше, чем делитель. В первом случае выбрано слишком большое
число (разряд частного), во втором - слишком маленькое; как бы то ни было, придется его исправлять.
При разработке программы эвристический образ действия следует заменить чем-нибудь более определенным. Попробуем же, вслед за Д. Кнутом (см. [Knut], п. 4.3.1), «отшлифовать» наши грубые вы- числения. Обратимся к нашему примеру. Пусть натуральные числа а = (am+n-\am+n_2- • -ао)в и Ь = (Ьп_1Ьп_2---Ьо)в представлены в системе счисления с основанием В и Ьп_\ > 0 (стар- ший разряд). Будем искать частное q и остаток г такие, что a - qb + г, где 0 < г < Ь. Действуя согласно методу деления «в столбик», на каждом шаге получаем значение qj.= \_Rlb\<B, где число R = (ат+п_\ат+п-2-•-вк)в образовано старшими разрядами делимого, а значение к выбрано из
Заметим, что для а < 0, когда q = -Г\a\/b\ и r = b- (|а| + qb), если а ]( b ,и г = 0, если а | Ь, деление
с остатком сводится к случаю a, b g IN.
66
Криптография на Си и C++ в действии
условия 1 < [_R/bJ (в примере выше на первом шаге получаем т + н-1 = 3 + 3-1=5, & = 2, 7? = 3549). Далее полагаем R := R - qjb\ разряд qj частного определен правильно, если выполнено условие 0 < R < Ь. Теперь заменяем R на сумму RB + (следующий разряд де- лимого) и вычисляем следующий разряд частного как После того как пройдены все разряды делимого, процесс останавливается. Остаток от деления равен последнему найденному значению R. Чтобы запрограммировать эту процедуру, нам необходимо уметь для заданных больших чисел R = (гпгп^...го)в и b = (Ьп.\Ьп-ъ^Ь^в таких, что [.RibJ < В, находить частное Q := [_RlbJ (разряд гп может быть и нулевым). Воспользуемся аппроксимацией q для Q, вычис- ляемой по старшим разрядам числа В и В, из книги Кнута. Пусть
(4.1) q := min- Г"--+ Г'1~1 , В -1 . IL J J Если bn_\ > [.RibJ, то q удовлетворяет двойному неравенству (см. [Knut], п. 4.3.1, Теоремы А и В): q -2<Q< q. В предположении, что старший разряд делителя достаточно велик по сравнению с В, аппроксимация q превышает истинное значение Q не больше чем на 2 и никогда не бывает слишком мала. Этого всегда можно добиться, «растянув» операнды а и Ь. Выберем число d > 0 так, чтобы dbn_\ > [_В12] и положим d:=ad = (am+ndm+n_x...do)B, b\=bd = (Ьп_{Ьп_2 ,,.bQ)в . Значение d выбираем так, чтобы число разрядов в b не превышало числа раз- рядов в Ь. При этом мы учли, что а может содержать на один раз- ряд больше, чем а (если это не так, полагаем ат+п = 0). Как бы то ни было, значение d лучше выбрать равным степени двойки, по- скольку в этом случае «растягивание» операндов осуществляется простым сдвигом. Так как оба операнда умножаются на одно и то же число, частное не изменится: ^А_|= LV^J- Прежде чем применять аппроксимацию q из формулы (4.1) к «рас- тянутым» операторам а (соответственно г) и b , уточним ее, чтобы получить q = Q или q = Q +1 : если для выбранного значения q вы- полняется неравенство bn_2q >(rnB + rn_x - qbn_x)B + гп_2 , то умень- шаем q на 1 и снова проверяем выполнение неравенства. Так мы отсеиваем все случаи, когда q превышает истинное значение на 2;
ГЛАВА 4. Основные операции 67
в очень редких случаях q будет превышать истинное значение на 1 (см. [Knut], п. 4.3.1, Упражнения 19, 20). Последняя ситуация выяв- ляется, когда мы вычитаем частичное произведение делителя на разряд частного из того, что осталось от делимого. В этом случае в последний раз уменьшаем q на 1 и корректируем остаток. Приве- дем теперь алгоритм деления с остатком.
Алгоритм деления с остатком числа а = (ат+п^ат+п^»»ао)в > 0 на число b = ^о)в > 0 1. Определить множитель d как описано выше. 2. ПОЛОЖИТЬ Г .— (.^m+n^m+n-i^m+n-2' • «Го)/? • ^о)в* 3. Положить i<— т + n,j <— т.
4. Положить q<r- minJ rjB+rj_l Vl , В -1 k где q, Г;Ч, - разряды
ПЧ ЯГ г* 5. соответствующих векторов, умноженных на d (см. выше). Если bn_2q > (J]В + Г/-!-qbn_x)B + rz_2 , то положить q^-q-1 и по- вторить проверку. Если г - bq < 0, то положить q <— q -1.
• - A.R •, 6. Положить г := (г/^.. -Г1-п)в - bq И qj <-q .
К/’’ . ' v - л- .W 7. 8. Положить i <— i - 1 и j <— j - 1. При i > п вернуться на шаг 4. Результат: q = (,qmqm-\.. .qo)B и г = (r„-ir„_2...r0)B.
Если делитель состоит всего из одного разряда то процедуру можно сократить, задав в самом начале г <— 0 и поделив двухразряд- ное число (га,)в с остатком на Ь$. Тогда в г записывается остаток: г <- (га,)в - a cq пробегает все разряды делимого. По окончании процедуры остаток будет равен г, а частное - q = (qmqm-\.. .<?о)в- Теперь, когда у нас есть все необходимое для реализации деления, напишем на языке С функцию, соответствующую рассмотренному выше алгоритму.
Функция: Синтаксис: Вход: Выход: Возврат: Деление с остатком int divj (CLINT d1 J, CLINT d2J, CLINT quotj, CLINT remJ); d1 J (делимое), d2J (делитель) quotj (частное), remJ (остаток) E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
Криптография на Си и C++ в действи!
int
divj (CLINT d1 J, CLINT d2J, CLINT quotj, CLINT remJ)
{
register clint *rptrj, *bptrj;
CLINT bj;
/* Допускаем остаток двойной длины плюс 1 разряд */
clint rj[2 + (CLINTMAXDIGIT « 1)];
clint *qptrj, *msdptrbj, *lsdptrrj, *msdptrrj;
USHORT bv, rv, qhat, ri, ri_1, ri_2, bn, bn_1;
ULONG right, left, rhat, borrow, carry, sbitsminusd;
unsigned int d = 0;
int i;
Присваиваем значения делимого a = (ат+п_1ат+п_2...а0)в и делителя
b = (Ьп_|Ьп_2...Ь0)в переменным rj и bj типа CLINT. Отбрасываем
все ведушие нули. Если при этом делитель равен нулю, то завер-
шаем функцию с кодом ошибки E_CLINT_DBZ.
Длина делимого может достигать удвоенного числа разрядов,
заданного в МАХВ. Позже это позволит нам использовать деление
в функциях модульной арифметики. Для хранения частного
двойной длины следует выделить память, которая всегда должна
быть доступна.
cpyj (r_I, d1 J);
cpyj (bj, d2J);
if (EQZ_L (bj))
return E_CLINT_DBZ;
Проверяем тривиальные ситуации: делимое = 0, делимое меньше
делителя или делимое равно делителю. В любом из этих случаев
завершаем процедуру.
if (EQZ_L (rj))
{
SETZERO J_ (quotj);
SETZERO J_ (remJ);
return E-CLINTJDK;
ГЛАВА 4. Основные операции
69
i = cmpj (r_l, bj);
if (i ==-1)
{
cpyj (remJ, rJ);
SETZERO J. (quotj);
return E_CLINT_OK;
}
else if (i == 0)
SETONE_L (quotj);
SETZERO-L (remJ);
return E_CLINT_OK;
На следующем шаге проверяем, не состоит ли делитель всего из
одного разряда. В этом случае строим ветвь более быстрого де-
ления, которую мы опишем позже.
if (DIGITSJ. (bj) == 1)
goto shortdiv;
Теперь начинаем собственно деление. Сначала задаем множитель
d как степень двойки. Пока bn_| > BASEDIV2 := L.B/2J, сдвигаем
\ старший бит Ьп_| делителя влево на один бит, при этом увеличи-
\ J ваем d каждый раз на 1 (начинаем с d = 0). Затем устанавливаем
У указатель msdptrbj на старший разряд делителя. Впоследствии
мы будем часто пользоваться значением BITPERDGT-d, так что
запишем его в переменную sbitsminusd.
msdptrbj = MSDPTRJ. (bj);
bn = *msdptrbj;
while (bn < BASEDIV2)
{
d++;
bn «= 1;
70
Криптография на Си и C++ в действии
}
sbitsminusd = (int)(BITPERDGT - d);
Если d > 0, то вычисляем два старших разряда bn_xbn_2 числа db
и записываем их в bn и Ьп_1. Здесь следует различать случаи,
когда делитель b имеет ровно два разряда и больше чем два раз-
ряда. В первом случае справа в Ьп_2 дописываем двоичные нули,
во втором случае младшими битами числа Ьп_2 становятся биты
числа Ьп.3.
к
if (d > 0)
{
bn += *(msdptrbj - 1) » sbitsminusd;
if (DIGITS_L (bj) > 2)
{
bn_1 = (USHORT)(*(msdptrbJ - 1) « d) + (*(msdptrbj - 2) »
sbitsminusd);
}
else
{
bn_1 = (USHORT)(*(msdptrbJ - 1) « d);
}
}
else
{
bn_1 = (USHORT)(‘(msdptrbJ - 1));
}
В CLINT-векторе г J, куда будем записывать остаток от деления,
устанавливаем указатели msdptrrj и IsdptrrJ на старший и млад-
ший разряды числа (am+nam+n_1...am+1)B соответственно. Разряд
am+n переменной г_1 полагаем равным 0. Устанавливаем указатель
qptrj на старший разряд частного.
msdptrbj = MSDPTR_L (bj);
msdptrrj = MSDPTRJ. (rj) + 1;
IsdptrrJ = MSDPTRJ. (rj) - DIGITS_L (bj) + 1;
ГЛАВА 4. Основные операции
71
*msdptrrj = 0;
qptrj = quotj + DIGITS J_ (rj) - DIGITS_L (bj) + 1 ;
Переходим к основному циклу. Указатель IsdptrrJ пробегает раз-
ряды ат, ат_2, а0 делимого в rj, а (неявный) индекс i - значе-
ния i = т + п, п.
while (IsdptrrJ >= LSDPTFLL (гJ))
{
Готовимся к вычислению q . Умножаем три старших разряда час-
ти (aiai_1...ai_n)B делимого на d и присваиваем полученные значе-
ния переменным ri, rij и ri_2. Отдельно рассматриваем случай,
когда указанная часть делимого состоит ровно из трех разрядов.
При первом проходе цикла имеем как минимум три разряда: в
предположении, что сам делитель b состоит как минимум из двух
разрядов, существуют старшие разряды am+n_| и am+n_2 делимого, а
разряд am+n мы положили равным нулю при инициализации век-
тора rj.
ri = (USHORT)((*msdptrrJ « d) + (*(msdptrrj - 1) » sbitsminusd));
nJ = (USHORT)((*(msdptrrJ - 1) « d) + (*(msdptrrj - 2) »
sbitsminusd));
if (msdptrrj - 3 > rj) /* Четыре разряда делимого */
{
ri_2 = (USHORT)((*(msdptrrJ - 2) « d) + (*(msdptrrj - 3) »
sbitsminusd));
}
else /* Только три разряда делимого */
{
ri_2 = (USHORT)(*(msdptrrJ - 2) « d);
}
Теперь дело дошло до вычисления аппроксимации qf которой
соответствует переменная qhat. Будем различать случаи ri Ф bn
(частый) и ri = bn (редкий).
72
Криптография на Си и C++ в действии
..-WMRiW-
if (ri != bn)
/* Почти всегда */
qhat = (USHORT)((rhat = ((ULONG)ri « BITPERDGT) +
(ULONG)ri_1) / bn);
right = ((rhat = (rhat - (ULONG)bn * qhat)) « BITPERDGT) + ri_2;
Неравенство bn_1 * qhat > right означает, что qhat превышает
истинное значение минимум на 1 и максимум на 2.
if ((left = (ULONG)bnJ * qhat) > right)
qhat-;
Уменьшив qhat на 1, повторяем проверку только тогда, когда
rhat = rhat + bn < BASE (в противном случае и так выполняется
неравенство bn_1 * qhat < BASE2 < rhat * BASE).
if ((rhat + bn) < BASE)
if ((left - bn_1) > (right + ((ULONG)bn « BITPERDGT)))
{
qhat-;
}
else
Во втором, более редком случае ri = bn сначала полагаем значе-
ние q равным BASE - 1 = 216 - 1 = BASEMINONE. Тогда для rhat
получаем: rhat = ri ♦ BASE + ri_1 - qhat ♦ bn = ri_1 + bn. Если
rhat < BASE, то проверяем, не слишком ли велико значение qhat.
В противном случае и так выполняется неравенство
bn_1 * qhat < BASE2 < rhat * BASE. Проверку повторяем при том
же условии, что и выше.
{
qhat = BASEMINONE;
операции 73
right = ((ULONG)(rhat = (ULONG)bn + (ULONG)ri_1) «
BITPERDGT) + ri_2;
if (rhat < BASE)
{
if ((left = (ULONG)bn_1 * qhat) > right)
{
qhat-;
if ((rhat + bn) < BASE)
{
if ((left - bn_1) > (right + ((ULONG)bn «
BITPERDGT)))
{
qhat-;
}
Вычитаем произведение qhat • b из части u := (aiai_1... a^Je дели-
мого, которая заменяется полученной разностью. Продолжаем
умножение и вычитание, сдвигаясь каждый раз на один разряд.
Здесь нужно помнить вот о чем. Произведение qhat • Ь, может
быть и двухразрядным. Оба разряда до поры до времени хранятся
в переменной carry типа ULONG. Старший разряд переменной
carry рассматривается как перенос при вычитании следующего
по старшинству разряда.
В том случае, когда разность u - qhat • b отрицательна (то есть
значение qhat больше истинного на 1), следует вычислить значе-
ние uz := Bn+1 +и - qhat • b и рассматривать результат по модулю
Bn+1 как В-дополнение й значения и. После вычитания старший
разряд u'i+1 числа и' записываем в старшее слово переменной
borrow типа ULONG.
Неравенство u'i+i 0 в точности означает, что значение qhat
слишком велико. В этом случае исправляем результат, вычисляя
сумму u <—u'+ b по модулю Bn+1. Случай корректировки рас-
смотрим несколько позже.
borrow = BASE;
carry = 0;
74
Криптография на Си и С-ь+ в действии
for (bptrj = LSDPTFLL (bj), rptrj = IsdptrrJ;
bptrj <= msdptrbj;
bptrj++, rptrj++)
{
if (borrow >= BASE)
{
*rptrj = (USHORT)(borrow = ((ULONG)*rptrJ + BASE -
(ULONG)(USHORT)(carry = (ULONGfbptrJ *
qhat + (ULONG)(USHORT)(carry » BITPERDGT))));
}
else
‘rptrj = (USHORT)(borrow = ((ULONG)‘rptrJ + BASEMINONEL-
(ULONG)(USHORT)(carry = (ULONG)'bptr_l * qhal + |
(ULONG)(USHORT)(carry » BITPERDGT))));
} 1
}
if (borrow >= BASE) j
{ I
*rptrj = (USHORT)(borrow = ((ULONG)*rptrJ + BASE -
(ULONG)(USHORT)(carry » BITPERDGT)));
}
else
*rptrj = (USHORT)(borrow = ((ULONG)*rptrJ + BASEMINONEL - |
(ULONG)(USHORT)(carry » BITPERDGT)));
Запоминаем разряд частного на случай если понадобится кор-
ректировка.
rqptrJ = qhat;
ГЛАВА 4. Основные операции
75
Как и было обешано, проверяем, не превышает ли разряд частно-
го истинное значение на 1. Этот случай встречается чрезвычайно
редко (ниже мы введем для него специальную проверку) и прояв-
ляется в том, что старшее слово переменной borrow типа ULONG
равно нулю, то есть borrow < BASE. Тогда нужно положить
и <— u' + b по модулю Bn+1 (см. выше).
if (borrow < BASE)
carry = 0;
for (bptrj = LSDPTRJ. (bj), rptrj = IsdptrrJ;
bptrj <= msdptrbj;
bptrj++, rptrj++)
{
*rptrj = (USHORT)(carry = ((ULONG)*rptrJ +
(ULONG) (*bptrj) +
(ULONG)(USHORT)(carry » BITPERDGT)));
}
*rptrj += (USHORT)(carry » BITPERDGT);
(*qptrj)-;
}
Устанавливаем указатели на остаток и частное и возвращаемся к
началу основного никла.
msdptrrj--;
IsdptrrJ-;
qptrj-;
Определяем длины частного и остатка. Число разрядов частного
может не больше чем на 1 превышать разность между числом
разрядов делимого и делителя. Длина остатка не может превы-
шать длины делителя. В обоих случаях определяем истинную длину,
отбрасывая все ведущие нули.
76
Криптография на Си и C++ в действии
SETDIGITSJ. (quotj, DIG ITS J_ (rj) - DIGITS J_ (bj) + 1);
RMLDZRSJ. (quotj);
SETDIGITSJ. (rj, DIGITSJ_ (bJ));
cpyj (remJ, rj);
return E_CLINT_OK;
В случае «короткого деления» делитель состоит всего из одного
разряда Ьо, на который делится двухразрядное число (raj)B, где а;
пробегает все разряды делимого. Устанавливаем начальное зна-
чение остатка: г <— 0, а затем полагаем равным разности
г <— (ra;)B - qb0. Значение г представлено переменной rv типа
USHORT, значение (raj)B - переменной rhat типа ULONG.
shortdiv:
rv = 0;
bv = *LSDPTR_L (bj);
for (rptrj = MSDPTRJ. (rj), qptrj = quotj + DIGITS J. (rj);
rptrj >= LSDPTR_L (rj);
rptrj-, qptrj-)
{
*qptrj = (USHORT)((rhat = ((((ULONG)rv) « BITPERDGT) +
(ULONG)*rptrJ)) I bv);
rv = (USHORT)(rhat - (ULONG)bv * (ULONG)*qptrJ);
}
SETDIGITSJ. (quotj, DIGITS J. (rJ));
RMLDZRSJ. (quotj);
u2clintj (remJ, rv);
return E_CLINT_OK;
Время t = O(mn) работы функции деления то же, что и для умно*
жения, где тип- числа разрядов соответственно делимого и дели-
теля в системе счисления с основанием В.
ГЛАВА 4. Основные операции 77
Теперь мы хотим представить на суд читателя несколько разновид- ностей алгоритмов деления с остатком, основанных на только что рассмотренной универсальной функции. Прежде всего, введем смешанную версию деления, когда делимое имеет тип CLINT, а делитель - тип USHORT. Для этого обратимся к подпрограмме для делителей малой длины функции div_l(). В ней практически ничего менять не надо, поэтому приведем только интерфейс.
функция: Деление переменной типа CLINT на переменную типа USHORT
Синтаксис: int udivj (CLINT dvj, USHORT uds, CLINT qj,CLINT rj);
Вход: dv_l (делимое), uds (делитель)
Выход: qj (частное), rj (остаток)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
Как уже отмечалось, в ряде случаев вычислять частное не нужно, а интересен только остаток. Это не дает большой экономии времени, но, по крайней мере, таскать указатель к ячейке, где хранится част- ное, не имеет смысла. Тогда логично было бы написать самостоя- тельную функцию для вычисления остатков, или «вычетов». Мате- матическую подоплеку использования этой функции нам предстоит подробно изучить в главе 5.
Функция: Вычисление остатка (вычета по модулю п)
Синтаксис: int modj (CLINT dj, CLINT nJ, CLINT rj);
Вход: dj (делимое), nJ (делитель или модуль)
Выход: rJ (остаток)
Результат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
Остаток вычисляется значительно проще, если модуль равен сте-
пени двойки, а именно 2к, так что и для этого случая сгодится своя
собственная функция. Остаток делимого от деления на 2 полу-
чается отбрасыванием всех двоичных разрядов после к-го, при
этом отсчет начинается с 0. Такое отбрасывание соответствует
побитной логической операции AND (см. п. 7.2) делимого и числа
2*-1= (111111... 1)2, состоящего из к двоичных единиц. Самым
важным объектом при выполнении этой операция является тот раз-
ряд делимого, представленного в системе счисления с основанием
В, который содержит к-й бит. Все более старшие разряды делимого
нас не интересуют. Делитель в соответствующей функции modj()
представлен только показателем к.
78
Криптография на Си и C++ в действии
функция: Вычисление остатка от деления на степень двойки (вычисление вычета по модулю 2*)
Синтаксис: int mod2J (CLINT dj, ULONG k, CLINT rj);
Вход: dj (делимое), k (показатель степени делителя или модуля)
Возврат: г_1 (остаток)
.. 4 int mod2J (CLINT dj, ULONG k, CLINT rj) {
int i; ”
Lot" •**;'*м { | Поскольку 2k > 0, проверять случай деления на 0 не нужно. Сна- чала копируем значение dj в rj. Если к превышает максималь-
ную двоичную длину, допускаемую типом CLINT, то завершаем
процедуру.
cpyj (rj, dJ);
.si / i hO : , > ' * ’ if if (k > CLINTMAXBIT)
return E_CLINT_OK;
I § ,f 1 Определяем тот разряд переменной rj, в котором нужно что-то
менять, и присваиваем его номер переменной i. Если значение i
превышает число разрядов в г J, то завершаем процедуру.
i . ; • i = 1 + (k » LDBITPERDGT); if (i > DIGITSJ_ (rj))
return E_CLINT_OK;
Теперь применяем логическую операцию AND к разряду пере-
I I менной г J (отсчитываем с 1), определенному на предыдущем шаге, и значению 2kmod BITPERDGT _ 1 (= 2kmod16_ 1 в нашей реализации).
Новое значение i числа разрядов переменной rj запоминаем в
rJ[0]. Удаляем нулевые старшие разряды и получаем результат.
гJ[i] &= (1U « (к & (BITPERDGT — 1))) — 1U;
SETDIGITSJ. (rj, i);
RMLDZRSJ. (rj);
ГЛАВА 4. Основные операции__________ ______________ 79
—— return E-CLINTJDK;
}
В смешанном варианте функции вычисления вычетов делитель имеет тип USHORT, остаток тоже представляется типом USHORT. Здесь мы опять приводим только интерфейс; сами функции чита- тель сможет найти в исходных текстах пакета FLINT/C.
функция: Вычисление остатка, деление переменной типа CLINT на перемен- ную типа USHORT
Синтаксис: USHORT umodj (CLINT dvj, USHORT uds);
Вход: dvj (делимое), uds (делитель)
Возврат: > неотрицательный остаток, если все в порядке OxFFFF в случае деления на 0
При тестировании программ, реализующих деление, - да и любых
других программ вообще, - следует учесть некоторые моменты
(см. главу 12). В частности, шаг 5 нужно проверять подробно, по-
скольку для случайно выбранных контрольных значений он выпол-
няется лишь с вероятностью 2/В (= 2“15 в нашем случае) (см. [Knut],
п. 4.3.1, Упражнение 21).
Следующие контрольные значения делимого а и делителя b (с уже
вычисленными частным q и остатком г) подобраны так, что та часть
программы, которая реализует шаг 5, выполняется дважды. Еще
несколько таких контрольных значений читатель найдет в тестовой
программе testdiv.c.
Контрольные значения даны в шестнадцатиричном виде, разряды
идут справа налево в порядке возрастания, длина не указана.
Контрольные значения для шага 5 алгоритма деления
а = еЗ 7d За Ьс 90 4b ab а7 а2 ас 4b 6d 8f 78 2b 2b f8 49 19 d2 91 73
47 69 Od 9e 93 de dd 2b 91 ce e9 98 3c 56 4c f1 31 22 06 c9 1e 74
d8 Ob a4 79 06 4c 8f 42 bd 70 aa aa 68 9f 80 d4 35 af c9 97 ce 85
3b 46 57 03 c8 ed ca
b = 08 0b 09 87 b7 2c 16 67 c3 0c 91 56 a6 67 4c 2e 73 e6 1a 1f d5 27
d4 e7 8b 3f 15 05 60 3c 56 66 58 45 9b 83 cc fd 58 7b a9 b5 fc bd
cO ad 09 15 2e 0a c2 65
q = 1c 48 a1 c7 98 54 1a eO b9 eb 2c 63 27 Ы ff ff f4 fe 5c 0e27 23
r = ca 23 12 fb b3 f4 c2 3a dd 76 55 e9 4c 34 10 Ы 5c 60 64 bd 48 a4
e5 fc c3 3d df 55 3e 7c b8 29 bf 66 fb fd 61 b4 66 7f 5e d6 b3 87 ec
47 c5 27 2c f6 fb
рЛАВА 5.
Модульная арифметика:
вычисление в классах вычетов
- А вы можете исчезать и появляться не так
внезапно? А то у меня голова идет кругом.
- Хорошо, - сказал Кот и исчез - на этот раз
п: очень медленно. Первым исчез кончик его
хвоста, а последней - улыбка; она долго
парила в воздухе, когда все остальное уже
пропало.
- Д-да! - подумала Алиса. - Видала я котов без
улыбок, но улыбка без кота!
Льюис Кэррол,
. Приключения Алисы в Стране Чудес
Начнем эту главу с основных правил деления с остатком. Попы-
таемся объяснить важность деления с остатком, его возможные
v приложения и способы вычисления. Ну а для начала - немного
4. алгебры, чтобы читатель смог понять те функции, которые мы вве-
t. дем позже.
Мы уже знаем, что при делении с остатком целого числа ае Z на
натуральное число 0 < т g DN существует единственное представ-
ление
а = qm + г, 0 < г < т.
Число г называется остатком от деления а на т, или вычетом по
модулю т. При этом число т делит разность а - г, обозначается как
т | (а - г).
К. Гаусс ввел для этого соотношения другое обозначение: 1
а = г mod т (читается «а сравнимо с г по модулю т»).
Сравнимость по модулю натурального числа т является отноше-
нием эквивалентности на множестве целых чисел. Это означает,
что множество R:={(a,b)\ a = b mod т} пар целых чисел таких,
что т | (д - /?), обладает следующими свойствами:
(a) Rрефлексивно', для любого целого числа а пара (д, д) лежит в R;
то есть а = a mod т.
Карл Фридрих Гаусс (1777-1855) - один из величайших математиков всех времен. Сделал мно-
жество важных открытий в математике и естественных науках. В возрасте 24 лет опубликовал зна-
менитую работу Disquisitiones Arithmeticae, послужившую основой для современной теории чисел.
82
Криптография на Си и C++ в действии
(б) R симметрично', если (a, b) G R, то (Z?, a) 6 R',
то есть из а = b mod т следует, что b = a mod т.
(в) R транзитивно', если (a, Z?) g R, (/>, с) е R, то (я, с) G 7?;
то есть из а = b mod т и b = с mod т, следует, что а = с mod т.
Доказательство этих свойств следует непосредственно из опреде-
6’ ^ ления операции деления с остатком. Отношение эквивалентности R
делит множество целых чисел на непересекающиеся подмножества,
называемые классами эквивалентности', для данного остатка г и
натурального числа т > 0 множество
г := {а | а = г mod ш},
или, в других обозначениях, r + ш^, называется классом вычетов
числа г по модулю т. Элементами этого класса являются все целые
числа, дающие при делении на т один и тот же остаток г.
' Например, пусть ш = 7, г =5; тогда множество целых чисел, даю-
щих при делении на 7 остаток 5, - это класс вычетов
5 = 5 + 7 -2 = {...,-9,-2,5, 12, 19, 26, 33, ...}.
Два класса вычетов по модулю фиксированного числа т либо
совпадают, либо не пересекаются.2 Следовательно, класс вычетов
однозначно определяется любым из своих элементов. Элементы
класса вычетов называются представителями', любой элемент
может служить представителем класса. Равенство классов вычетов
эквивалентно сравнимости представителей этих классов по данному
модулю. Поскольку при делении с остатком остаток всегда меньше
делителя, для любого целого т существует конечное число классов
вычетов по модулю т.
Теперь мы, наконец, вплотную приблизились к сути наших рассу-
ждений. Классы вычетов - это такие объекты, в которых можно
выполнять арифметические действия, оперируя лишь с представи-
* телями. Вычисления в классах вычетов играют огромную роль в
алгебре и теории чисел, а значит, незаменимы в теории кодирова-
ния и современной криптографии. Далее мы попытаемся пояснить
v fCi алгебраические аспекты модульной арифметики.
’ ' Пусть а, Ъ и т - целые числа, т > 0. Для классов вычетов а и b по
' модулю т определим операции «+» и «•», которые назовем сложени-
ем и умножением (классов вычетов), поскольку определяются они по
аналогии с соответствующими операциями над целыми числами:
а + b := а + b (сумма классов равна классу суммы);
а • Ъ := а • b (произведение классов равно классу произведения).
2 Множества называются непересекающнлшся, если у них нет общих элементов или, иначе, если
их пересечение есть пустое множество.
ГЛАВА 5. Модульная арифметика: вычисление в классах вычетов
83
Обе операции определены корректно, поскольку в обоих случаях
результат является классом вычетов по модулю т. Множество
7Lm := { г | г - вычет по модулю т} классов вычетов по модулю т,
на котором определены эти две операции, называется конечным
коммутативным кольцом +, •) с единицей, что, в частности,
подразумевает выполнение следующих аксиом:
(а) Замкнутость по сложению:
Сумма двух элементов множества является элементом множе-
ства
(б) Ассоциативность сложения:
Для любых а, Ь, с из справедливо а + (6 + с) = (а + й) + с .
(в) Существование нулевого элемента:
Для любого а из справедливо а + 0 = а .
(г) Существование противоположного элемента:
Для любого а из существует единственный элемент b из та-
кой, что а + b = 0 .
(д) Коммутативность сложения:
Для любых а, b из Жт справедливо а + b = b + а .
(е) Замкнутость по умножению:
Произведение двух элементов множества является элементов
множества
(ж) Ассоциативность умножения:
Для любых а, Ь, с из справедливо a-(b-c) = (а-Ь)-с.
(з) Существование единичного элемента:
Для любого а из справедливо а • 1 = а .
(и) Коммутативность умножения:
Для любых а, b из справедливо а • b = b • а .
(к) В кольце +, •) выполняется закон дистрибутивности'.
а-(Ь +с) = а‘Ь + а-с.
На основании свойств 1-5 можно заключить, что множество (Жт, +)
является абелевой группой, где термин «абелева» означает комму-
тативность сложения. Свойство 4 позволяет определить на множе-
стве операцию вычитания как сложение с противоположным
элементом: если элемент с является противоположным к Ь, то
b + с = 0, а значит, для любого а е ~ZLm
а - b := а + с.
84
Криптография на Си и C++ в действии
•’ Ж-'* На множестве (Z„2, •) справедливы групповые законы 6-9 для опе- рации умножения, единицей является элемент 1. Однако не для каждого элемента множества Жт обязательно существует обратный, то есть (Z„2, •), вообще говоря, является не группой, а лишь комму- тативной полугруппой с единицей.3 Но если исключить из все элементы, не взаимно простые с т (в том числе и 0), то полученная структура будет абелевой группой по умножению (см. п. 10.2). Обозначим ее через (Z/zl*, •)• Значимость алгебраических структур, аналогичных группе (Zw*, •), можно пояснить на примере некоторых хорошо известных комму- тативных колец. Множество Z целых чисел, множество Q рацио- нальных чисел и множество [R вещественных чисел - все это ком- мутативные кольца с единицей, которые, в отличие от (Z„2 , •), бес- конечны (на самом деле, множество вещественных чисел является полем, то есть обладает некоторыми дополнительными свойствами). Все арифметические правила, приведенные выше для конечного кольца, хорошо нам известны - ведь мы пользуемся ими каждый
-ВТ у ЛОТ . : день. В главе 12 они будут нам верными помощниками, когда при- дет время тестировать арифметические функции. А пока соберем о них важную информацию. При вычислении в классах вычетов мы оперируем исключительно с представителями этих классов. Из каждого класса вычетов по мо- дулю т выбираем ровно по одному представителю и получаем таким образом полную систему вычетов, в рамках которой и будем прово- дить все вычисления. Система наименьших неотрицательных выче- тов по модулю т представляет собой множество Rm := {0, 1, ..., ш-1}. Множество чисел г, удовлетворяющих неравенству ~т<г<±т, будем называть системой абсолютно наименьших вычетов по модулю т. В качестве примера рассмотрим кольцо Z26 = { 0,1,..., 25 }. Систе- мой наименьших неотрицательных вычетов по модулю 26 будет множество 7?2б={0, 1» 25}, системой абсолютно наименьших вычетов - множество {-12, -И, ..., 0, 1, ..., 13}. Поясним связь между арифметикой в классах вычетов и модульной арифметикой в системах вычетов: равенство 18 + 24 = 18 + 24 = 16 эквивалентно сравнению 18 + 24 = 42 = 16 mod 26;
3 Множество (Н, операция *. *) является полугруппой, если на множестве Н определена ассоциативная
ГЛАВА 5. Модульная арифметика: вычисление в классах вычетов 85
равенство
9-15 = 9 + 11 = 20
эквивалентно сравнению
9- 15 = 9 + 11 = 20 mod 26.
Сопоставляя английскому алфавиту кольцо классов вычетов Z26
или множеству ASCII-символов кольцо Z256, можно производить
вычисления с символами. Юлию Цезарю приписывают простей-
шую систему шифрования, в которой каждая буква открытого тек-
ста складывается по модулю 26 с некоторым фиксированным эле-
ментом кольца Z26 (у Цезаря это был элемент 3). Таким образом,
каждая буква алфавита сдвигалась на три позиции вправо, при этом
X переходил в A, Y в В и Z в С. 4
Для вычислений в классах вычетов можно составить таблицы сло-
жения и умножения. Покажем, как это делать на примере кольца
Z5 (таблицы 5.1 и 5.2 соответственно).
Таблииа 5.1. + 0 1 2 3 4
Таблииа сложения 0 0 1 2 3 4
по модулю 5 1 1 2 3 4 0
2 2 3 4 0 1
3 3 4 0 1 2
4 4 0 1 2 3
Таблииа 5.2. 1 2 3 4
Таблииа
1 1 1 3 4
умножения
по модулю 5 2 2 4 1 3
3 3 1 4 2
4 4 3 2 1
То, что множество классов вычетов является конечным, дает нам
значительные преимущества по сравнению с такими бесконечными
структурами, как кольцо целых чисел, поскольку при выполнении
арифметических операций в компьютерной программе у нас нико-
гда не возникнет переполнения, если только будут выбраны подхо-
дящие представители классов вычетов. Операция обработки ре-
зультата, например функцией mod_l(), называется приведением
Aulus Gellius, XII, 9 и Suetonius, Caes. LVI.
Криптография на Си и C++ в действии
(по модулю /и). Теперь мы можем вычислять сколько душе угодно,
ограничив лишь представление чисел и функций пакета FLINT/C
полной системой вычетов по модулю т, где т < 7Vmax. Будем всегда
оперировать с положительными представителями и работать в рам-
ках системы неотрицательных вычетов. Свойства классов вычетов
позволяют нам работать в пакете FLINT/C с большими числами ти-
па CLINT. Трудности могут возникать лишь в отдельных ситуациях,
которые мы специально обсудим.
Довольно теории об арифметике в классах вычетов. Займемся те-
перь функциями, реализующими модульную арифметику. Сначала
вспомним функции modj() и mod2J() из п. 4.3, вычислявшие оста-
ток от деления на т и 2к соответственно, а затем перейдем к функ-
циям модульного сложения, вычитания, умножения и возведения в
квадрат. Модульному возведению в степень, как особенно сложной
теме, будет посвящена отдельная глава.
Для удобства в обозначении класса вычетов будем опускать черту и
вместо а писать а.
Принцип работы функций модульной арифметики заключается в
следующем: к операндам применяется соответствующая обычная
(«немодульная») функция, а затем результат делим с остатком на
модуль. Следует, однако, отметить, что размер промежуточных
результатов может достигать 2МАХВ разрядов, а в случае вычита-
ния могут появляться отрицательные числа, что недопустимо в типе
CLINT. Ранее мы назвали такие ситуации переполнением и потерей
значащих разрядов соответственно. В основных арифметических
функциях предусмотрен механизм обработки этих ситуаций: про-
межуточные результаты рассматриваются как вычеты по модулю
(Mnax + 1) (см. главы 3 и 4). Этот же метод можно применять и сей-
час, в случаях, когда конечный результат модульной операции имеет
тип CLINT. Чтобы получить верный результат в случаях перепол-
нения и потери значащих разрядов, позаимствуем из уже
рассмотренных нами в главе 4 функций базовые функции
void add (CLINT, CLINT, CLINT); 1
void sub (CLINT, CLINT, CLINT); I
void mult (CLINT, CLINT, CLINT); ;
void umul (CLINT, USHORT, CLINT); ;
void sqr (CLINT, CLINT); |
Эти функции, выделенные из функций addj(), sub_l(), muIJO #
sqr_J(), с которыми мы работали раньше, служат для выполнения
собственно арифметических операций. Остальные операции: уда-
ление старших нулевых разрядов, заполнение сумматора и обра-
ботка возможного переполнения или потери значащих разрядов -
все, что осталось на долю ранее введенных функций. Их синтаксис
ГЛАВА 5. Модульная арифметика: вычисление в классах вычетов 87
и семантика не изменяются, то есть мы по-прежнему можем ими пользоваться. Рассмотрим это преобразование на примере функции умножения mulj() (сравните с реализацией этой же функции на стр. 49).
функция: Умножение
Синтаксис: int mulj (CLINT f1 J, CLINT f2J, CLINT ppj);
Вход: f1 J, f2J (сомножители)
Выход: ppj (произведение)
Возврат: E-CLINTJDK, если все в порядке E_CLINT_OFL в случае переполнения
int
mulj (CLINT f 1 J, CLINT f2J, CLINT ppj)
{
CLINT aaj, bbj;
CLINTD pj;
int OFL = 0;
Удаление ведущих нулей и заполнение сумматора.
cpyj (aaj, f1 J);
cpyj (bbj, f2J);
Вызов базовой функции умножения.
mult (aaj, bbj, pj);
Обработка переполнения, если таковое имеется.
if (DIGITSJ. (pj) > (USHORT)CLINTMAXDIGIT) /* Переполнение ? 7
88 Криптография на Си и C++ в действии
г ANDMAX_L (р_1); /* Привести по модулю (Nmax +1)7 OFL = E_CLINT_OFL;
'9Ж. I'b 1 } cpyj (ppj, pj);
jV r^W<**** *«*’*»*’ *» 9 ’*^f i » return OFL; } Аналогично изменяем и остальные функции: addj(), sub_l() и sqr_l(). Сами по себе базовые арифметические функции не содержат новых компонентов и поэтому здесь не приводятся; подробнее см. реали- зацию на flint .с. Базовые функции не вызывают переполнения, поэтому приведение
i»< «»«'«» «»>» '< ’ ' по модулю (Атах + 1) в них не выполняется. Они являются внутрен- ними компонентами функций пакета FLINT/C и поэтому имеют описатель static. Работая с базовыми функциями, следует помнить, что они не могут оперировать с числами с ведущими нулями и что их нельзя использовать в режиме сумматора (см. главу 3). Функция sub() предполагает, что разность положительна. В про- тивном случае результат не определен, поскольку такая ситуация функцией sub() не предусмотрена. И наконец, при вызове базовых функций следует выделить пространство под промежуточные ре-
’ t‘ зультаты большой длины. В частности, для представления резуль- *тата функции sub() требуется по крайней мере столько же памяти, сколько для представления уменьшаемого. Что ж, теперь у нас есть все, чтобы разработать основные функции
W4 -1 t модульной арифметики: madd_l(), msubj(), mmul_l() и msqr_l().
Функция: Модульное сложение
Синтаксис: int maddj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ);
Вход: aaj, bbj (слагаемые), mJ (модуль)
Выход: cj (остаток)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0 int maddj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ) { CLINT aj, bj; ( clint tmpJ(CLINTMAXSHORT + 1];
рддВА 5. Модульная арифметика: вычисление в классах вычетов
if (EQZ_L (mJ))
{
return E_CLINT_DBZ;
}
cpyj (aj, aaj);
r cpyj (bj, bbj);
sr- if (GE_L (aj, mJ) || GE_L (bj, mJ))
{
add (aj, bj, tmpj);
mod J (tmpj, mJ, cj);
}
else
] Если обе переменных aj и bj меньше модуля mJ, то делить с
остатком не нужно.
{
add (aj, bj, tmpj);
if (GE_L (tmpj, mJ))
subj (tmpj, mJ, tmpj);
/* Исключаем потерю значащих разрядов */
В предыдущем вызове функции subJO мы немного подстрахова-
лись, введя переменную tmpj. Эта переменная, где лежит сумма
переменных aj и bj, может лишь на один разряд превышать
константу МАХВ. Внутри функции subJO никаких нарушений
быть не должно, поскольку память для хранения дополнительного
разряда мы выделили. Таким образом, результат мы записываем
8 tmp J, з не сразу в cj, как можно было бы ожидать. Зато после
выполнения функции subJO переменная tmpj у нас имеет не
больше МАХВ разрядов.
90
Криптография на Си и C++ в действии
cpyj (cj, tmpj);
}
return E_CLINT_OK;
} I
Функция модульного вычитания msubJO оперирует только с неот-
рицательными промежуточными результатами функций addj(),
subj() и modj(), то есть мы не выходим за рамки системы наи-
меньших неотрицательных вычетов.
Функция: Модульное вычитание
Синтаксис: int msubj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ);
Вход: aaj (уменьшаемое), bbj (вычитаемое), mJ (модуль)
Выход: cj (остаток)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
int
msubj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ)
{
CLINT aj, bj, tmpj;
if (EQZ_L (mJ))
{
return E_CLINT_DBZ;
}
cpyj (aj, aaj);
cpyj (bj, bbj);
Будем различать случаи aj > bj и aj < bj. В первом случае
поступаем как обычно; во втором случае вычисляем разность
(bJ - aj), приводим ее по модулю mJ и вычитаем полученное
положительное число из mJ.
if (GE_L (aj, bJ)) /* aj - bj > 0 7
91
j-ддВА 5. Модульная арифметика: вычисление в классах вычетов
sub (aj, bj, tmpj);
mod J (tmpj, mJ, cj);
}
else /* a J - b J < 0 7
{
sub (bj, aj, tmpj);
modj (tmpj, mJ, tmpj);
if (GTZ_L (tmpj))
{
sub (mJ, tmpj, cj);
}
else
{
SETZERO J. (cj);
}
}
return E_CLINT_OK;
}
Теперь перейдем к функциям mmul_l() и msqr_l() модульного умно-
жения и возведения в квадрат.
Функция: Модульное умножение
Синтаксис: int mmulj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ);
Вход: aaj, bbj (сомножители), mJ (модуль)
Выход: cj (остаток)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
int
mmulj (CLINT aaj, CLINT bbj, CLINT cj, CLINT mJ)
{
CLINT aj, bj;
CLINTD tmpj;
if (EQZ_L (mJ))
{
92 Криптография на Си и C++ в действии
return E_CLINT_DBZ; } cpyj (aj, aaj); cpyj (bj, bbj); mult (aj, bj, tmpj); mod J (tmpj, mJ, cj); return E_CLINT_OK; } Функция модульного возведения в квадрат строится аналогично, поэтому для нее приведем только интерфейс.
Функция: Модульное возведение в квадрат
Синтаксис: int msqrJ(CLINT aaj, CLINT cj, CLINT mJ);
Вход: aaj (множитель), mJ (модуль)
Выход: cj (остаток)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0
Для каждой из этих функций (разумеется, за исключением возведе- ния в квадрат) можно определить соответствующую смешанную
функцию, у которой второй аргумент имеет тип USHORT. Пока- жем, как это делается, на примере функции umaddj(). Функции umsubJO и ummuIJO строятся по образу и подобию, так что их приводить не будем.
Функция: Модульное сложение переменных типа CLINT и USHORT
Синтаксис: int umaddj (CLINT aj, USHORT b, CLINT cj, CLINT mJ);
Вход: aj, b (слагаемые), mJ (модуль)
Выход: cj (остаток)
Возврат: E_CLINT_OK, если все в порядке E-CLINTJDBZ в случае деления на 0 int umaddj (CLINT aj, USHORT b, CLINT cj, CLINT mJ) { int err; CLINT tmpj;
ГЛАВА 5. Модульная арифметика: вычисление в классах вычетов 93
Д’ u2clintJ (tmpj, b); err = maddj (aj, tmpj, cj, mJ); return err; } В следующей главе мы пополним нашу коллекцию смешанных функций с аргументом типа USHORT еще двумя функциями. А за- канчивая эту главу, мы бы хотели, используя модульное вычитание, построить еще одну полезную вспомогательную функцию, которая определяла бы, являются ли две переменные типа CLINT представи- телями одного и того же класса вычетов по модулю т. В основу функции mequj() положено определение отношения сравнимости: а = b mod т <=> т | (а - Ь). Чтобы выяснить, сравнимы ли два CLINT-объекта по модулю mJ, нам нужно всего лишь применить функцию msubj(aj, bj, rj, mJ)
и проверить, равен ли нулю полученный остаток rj.
Функция: Проверка сравнимости по модулю т
Синтаксис: int mequj (CLINT aj, CLINT bj, CLINT mJ);
Вход: aj, bj (операнды), mJ (модуль)
Возврат: 1, если (aJ == bj) по модулю mJ
0 в противном случае int mequj (CLINT aj, CLINT bj, CLINT mJ) { CLINT rj; if (EQZ_L (mJ)) { return E_CLINT_DBZ; } msubj (aj, bj, rj, mJ); return ((0 == DIGITS_L (rj))?1:0); ~x }
рЛАВА 6.
Все дороги ведут к...
модульному возведению в степень
- Скажите, пожалуйста, куда мне отсюда идти?
- А куда ты хочешь попасть? - ответил Кот.
- Мне все равно... - сказала Алиса.
- Тогда все равно, куда и идти, - заметил Кот.
- ...только бы попасть куда-нибудь, - пояснила
Алиса.
- Куда-нибудь ты обязательно попадешь, - ска-
зал Кот. - Нужно только достаточно долго
идти.
Льюис Кэррол,
'! Приключения Алисы в Стране Чудес,
(Перевод с английского Н. Демуровой)
В дополнение к правилам вычисления суммы, разности и произве-
дения в классах вычетов определим операцию возведения в сте-
пень, где показатель указывает, сколько раз основание умножается
само на себя. Как правило, возведение в степень реализуется рекур-
сивным вызовом операции умножения: для а из кольца справед-
ливо а := 1 и а := а • а .
Легко видеть, что для операции возведения в степень в выпол-
няются обычные правила (см. главу 1):
ае • af= ae+f, а" be = (а b)e, (А'/ = а!.
6.1. Первые шаги
Самый простой способ модульного возведения в степень - рекур-
сивно применять указанное выше правило, умножая основание а
само на себя е раз. Для этого требуется е - 1 модульных умноже-
ний, а это для наших целей уж слишком много.
Более эффективный способ иллюстрируется следующими примера-
ми, в которых рассматривается двоичное представление показателя:
&
л15
23+22+2+1
= а
[а2
а] а.
а16 = а2
а2
96
Криптография на Си и C++ в действии
Здесь для возведения основания в 15-ю степень требуется всего
шесть умножений, тогда как в первом способе нам потребовалось
бы 14 умножений. Половина из них - это возведение в квадрат, для
которого, как мы знаем, нужно примерно вдвое меньше машинного
времени по сравнению с обычным умножением. Для возведения й
16-ю степень требуется всего 4 возведения в квадрат. j
Как мы увидим, алгоритмы вычисления экспоненты ае по модулу
т, использующие двоичное представление показателя, как правило^
намного более предпочтительны, чем первый подход. Но прежде
следует отметить, что промежуточные результаты многократного
целочисленного умножения быстро занимают столько памяти, что
их не в состоянии хранить ни один компьютер в мире, поскольку
из р = аь следует log р = b log а, таким образом, число разрядов
экспоненты аь есть произведение показателя на число разрядов
чг основания. Однако эту проблему можно решить, если проводить
вычисления в кольце классов вычетов Zzn посредством модульного
умножения. Фактически в большинстве прикладных задач требуется
возведение в степень именно по модулю т, так что эту ситуацию и
будем рассматривать.
Пусть е = (en_ien_2- • -ео)2, где e„_i > 0, - двоичное представление по-
казателя е. Тогда следующий бинарный алгоритм требует Llog2eJ = п
модульных возведений в квадрат и 8(e) - 1 модульных умножений,
где
5(e);=Sei
i=0
есть число единиц в двоичном представлении показателя е. Если
считать, что каждый разряд принимает значение 0 или 1 равноверо-
ятно, то можно сказать, что среднее значение 8(e) = п/2 и алгоритм
требует всего |Qog2 умножений.
Бинарный алгоритм вычисления ае по модулю т J
1. Вычислить р<г-ае,,~' и/«—л-2.
2. Положить р <— р mod т.
3. Если е, = 1, то положить р р • a mod т.
4. Положить I <г- i - 1; при i > 0 вернуться на шаг 2. ?
5. Результат: р. !
Следующая функция, реализующая этот алгоритм, дает хорошие
результаты уже для малых показателей степени, представимых ти-
пом USHORT.
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень 97
_—-
функция: Смешанное модульное возведение в степень с показателем типа USHORT
Синтаксис: int umexpj (CLINT basj, USHORT e, CLINT pj, CLINT mJ);
Вход: basj (основание)
e (показатель) mJ (модуль)
Выход: pj (вычет по модулю mJ)
Возврат: E-CLINTJDK, если все в порядке E_CLINT_DBZ в случае деления на 0
int
umexpj (CLINT basj, USHORT e, CLINT pj, CLINT mJ)
{
CLINT tmpj, tmpbasj;
USHORT к = BASEDIV2;
int err = E_CLINT_OK;
if (EQZ_L (mJ))
{
return E-CLINT-DBZ; /* Деление на нуль */
}
if (EQONE_L (mJ))
{
SETZERO.L (pj); /* Модуль = 1 ==> Остаток = 0 */
return EJDLINTOK;
}
if (e == 0) /* Показатель = 0 ==> Остаток = Г/
SETONE_L (pj);
return E_CLINT_OK;
}
if (EQZ_L (basj))
{
SETZEROJ_ (pj);
Криптография на Си и C++ в действии]
return E_CLINT_OK; I
} I
modj (basj, mJ, tmpj); 1
cpyj (tmpbasj, tmpj); 1
После различных проверок определяем позицию старшего еди-
ничного разряда показателя е. Переменная к используется в ка-
честве маски отдельных двоичных разрядов показателя е. Затем к
сдвигается еше на одну позицию вправо, что соответствует опе-
рации i <— п - 2 на шаге 1 алгоритма.
while ((е & к) == 0)
{
к »= 1;
}
к »= 1;
Для остальных разрядов показателя е выполняем шаги 2 и 3.
Маска к служит в качестве счетчика циклов и каждый раз сдвига-
ется на один разряд вправо. Затем выполняется умножение на
основание экспоненты по модулю mJ.
while (k != 0)
{
msqrj (tmpj, tmpj, mJ);
if (e & k)
{
mmulj (tmpj, tmpbasj, tmpj, mJ);
}
k »= 1;
}
cpyj (pj, tmpj);
return err;
Преимущества бинарного алгоритма возведения в степень особенно
видны, если основание степени мало. Для основания, имеющего
j-дАВА 6. Все дороги ведут к... модульному возведению в степень
99
тип USHORT, все умножения р <— р • a mod т на шаге 3 бинарного алгоритма имеют тип CLINT * USHORT по модулю CLINT. Это дает существенное увеличение скорости по сравнению с другими алго- ритмами, которые в этом случае потребовали бы умножения двух переменных типа CLINT. Конечно, возведения в квадрат (шаг 2) ис- пользуют объекты типа CLINT, но здесь мы можем использовать более быструю функцию. Таким образом, попробуем реализовать функцию возведения в сте- пень wmexpJO, парную к функции umexpJO и применяемую для основания типа USHORT. Выделение по маске разрядов показателя степени - хорошее подготовительное упражнение с точки зрения последующих «больших» функций возведения в степень. По суще- ству, мы последовательно сравниваем все разряды показателя с переменной Ь, первоначально имеющей 1 в старшем разряде, затем сдвигаем b вправо и повторяем процедуру до тех пор, пока b не станет равным 0. Для оснований и показателей длиной до 1000 бит функция wmexpJO работает примерно на 10% быстрее, чем универсальные функции, которыми мы займемся позже.
Функция: Модульное возведение в степень основания типа USHORT
Синтаксис: int wmexpj (USHORT bas, CLINT ej, CLINT restj, CLINT mJ);
Вход: bas (основание), ej (показатель) mJ (модуль)
Выход: restj (вычет baseJ по модулю mJ)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0 int wmexpj (USHORT bas, CLINT ej, CLINT restj, CLINT mJ) { CLINT pj, zj; USHORT k, b, w; if (EQZ_L (mJ)) { X return E_CLINT_DBZ; Г Деление на нуль */ }
100
Криптография на Си и C++ в действии
if (EQONE.L (mJ))
{
SETZERO J- (restj);
return E_CLINT_OK;
}
if (EQZ_L (e J))
{
SETONEJ. (restj);
return E_CLINT_OK;
}
if (0 == bas)
{
SETZERO.L (restj);
return E_CLINT_OK;
/* Модуль = 1 ==> Остаток = 0 */
SETONEJ. (pj);
cpyj (zj, ej);
Разряды показателя zj обрабатываются, начиная co старшего
ненулевого разряда в старшем слове показателя; при этом мы
всегда выполняем сначала возведение в квадрат, а затем, если
нужно, умножение. Проверка разрядов показателя осуществляется
в выражении if ((w & b) > 0) путем их маскирования поразрядной
операцией AND.
Ь = 1 « ((IdJ (zj) - 1) & (BITPERDGT - 1UL));
w = zJ[DIGITS_L (zJ)];
for (; b > 0; b »= 1)
{
msqrj (pj, pj, mJ);
if ((w & b) > 0)
101
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
ummulj (pj, bas, pj, m_l);
л lx: }
}
) Затем обрабатываются оставшиеся разряды показателя.
for (k = DIGITSJ- (zj) - 1; к > 0; к-)
{
w = zj[k];
for (b = BASEDIV2; b > 0; b »= 1)
{
msqrj (pj, pj, mJ);
if ((w & b) > 0)
{
ummulj (pj, bas, pj, mJ);
}
}
}
cpyj (restj, pj);
return EJDLINTJDK;
}
6.2. М-арное возведение в степень
Обобщив бинарный алгоритм со стр. 96, можно еще уменьшить
число модульных умножений при возведении в степень. Суть под-
хода состоит в том, чтобы записать показатель в системе счисления
с основанием, большим 2, и заменить умножение на а на шаге 3
умножением на степени числа а.
Итак, пусть показатель е представлен в системе счисления с осно-
ванием М\ е - (еп^еп_2---ео)м, где число М мы определим позже. Для
вычисления степеней ае mod т используется следующий алгоритм.
102 Криптография на Си и C++ в действии
М-арный алгоритм вычисления ае по модулю т
1. Вычислить и запомнить таблицу значений a2 mod т, a3 mod т, ..
a4'1 mod т.
' 2. Положить р <— ае,,~1 и / <— п - 2.
3. Положить р <г-рм mod т.
4. Если е[ Ф 0, то положить р <— pa ' modm .
5. Положить i «— i - 1; при i > 0 вернуться на шаг 3.
6. Результат: р.
Понятно, что число умножений зависит от числа разрядов показа-
(6.1) (6.2) теля е и, следоватег Поэтому определил бы как можно боль ре выше для 216. Т численные на шаге памяти на хранение Исходя из первого М= 2к. Согласно в рассматриваем как Потребуем, чтобы ь |_logM еJlog2 м = |_1< возведений в квадр; LlogM еJpr<>, * °) = [ЬНО, от 4 ЧИСЛО ше возв огда чи 1, буд таблиц услови порому функци ia шаге 3g2<d it, а на log2e Л выбора основания системы счисления М. М так, чтобы на шаге 3 использовалось рдений в квадрат, как это было в приме- :сло умножений на степени числа а, вы- ет минимальным, что оправдает затраты ы. я, выбираем М равным степени двойки: условию, число модульных умножений ю от М: 3 выполнялось j шаге 4 в среднем ; РГ(6; Ф 0) j. 1-
модульных умножений, где ; рГц^о)=1-Е <! м есть вероятность того, что разряд с{ показателя е ненулевой. Учи-
тывая, что для построения таблицы предвычислений нужно М - 2
(6.3) умножений, получаем, чт ц,(£):= 2к - 2 + [log2 еJ+ о 1 М-арный алгоритм требует в среднем Og2gf, И к Д 2к )
(6.4) — 2^ — 2 + [_log2 ^J+ модульных возведи f 2к -Р 1 к2к J ний в квадр ат и умножений.
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
103
j
В таблице 6.1 приведены значения числа модульных умножений для
вычисления ae mod m, когда показатель е и модуль m имеют длину
512 бит и М = 2к. Там же даны затраты памяти на хранение таблицы
предвычислений степеней a mod ш, обусловленные вычислением
произведения (2к - 2) * CLINTMAXSHORT * sizeof(USHORT).
Таблииа 6.1.
Требования
при возведен и и
в степень
к Число умножений Память (в байтах)
1 766 0
2 704 1028
3 666 3084
4 644 7196
5 640 15420
6 656 31868
in
• ; -
Как видно из таблицы, среднее число умножений достигает ми-
нимального значения 640 при к = 5, тогда как объем требуемой
памяти увеличивается при каждом следующем к примерно вдвое.
А как же будут меняться временные затраты для больших показа-
телей степени?
На этот вопрос отвечает таблица 6.2, в которой приведено число
модульных умножений, выполняемых при возведении в степень,
при различных длинах показателя и различных М = 2к. В таблицу,
помимо степеней двойки, включено значение 768, поскольку ключ
такой длины часто используется в криптосистеме RSA (см. главу 16).
Наименьшие значения для числа умножений выделены жирным
шрифтом.
При рассмотрении диапазонов чисел, для обработки которых был
разработан пакет FL1NT/C, оказывается, что при к = 5 мы получаем
универсальное основание М = 2к системы счисления. Но в этом
случае нам потребуется довольно много памяти (15 кбайт) для хра-
нения таблицы предвычислений и2, я3, ..., и31. Согласно работе
[Cohe], п. 1.2, М-арный алгоритм можно улучшить, выполняя на
этапе предвычислений не М - 2, а только М/2 умножений, то есть в
два раза сократить затраты памяти. И теперь наша задача - вычис-
лить ае mod m, где е = (^_1^-2«--<?о)л/ - представление показателя в
системе счисления с основанием М = 2к.
104
Криптография
на Си и C++ в действии
Таблииа 6.2. Число двоичных разрядов показателя
Число умножений к 32 64 128 512 768 1024 2048 4096
1 45 93 190 766 1150 1534 3070 6142
для типичных
длин показателя 2 44 88 176 704 1056 1408 2816 5632
и различных оснований 2к 3 46 87 170 666 996 1327 2650 5295
4 52 91 170 644 960 1276 2540 5068
5 67 105 181 640 945 1251 2473 4918
6 98 135 209 656 954 1252 2444 4828
7 161 197 271 709 1001 1294 2463 4801
8 288 324 396 828 1116 1404 2555 4858
Л/-арный алгоритм возведения в степень с сокращенной
таблицей предвычислений
Вычислить и запомнить таблицу
7 2к -1
a mod т, ..., a mod т.
значений
a3 mod in, a5 mod т
2. Если еп^ = 0, то положить р <— 1.
Если еп^ Ф 0, то представить еп_\ в виде еп.\ = 2гм, где и
ное. Вычислить р <— ali mod т.
нечет
В обоих случаях положить i <— п - 2.
3. Если
О, то положить Р rnodm
вычислив
f-ИГ.)1
mod т (k-кратное возведение в квадрат по мо
Дулю т).
Если е> * 0, то представить в виде et = 2'п, где и
положить р <— р mod/н, затем р <— pa mod т
- нечетное
и, наконец
р р2 rnodm .
4. Положить i <— i - 1; при i > 0 вернуться на шаг 3.
5. Результат: р.
Весь секрет этого алгоритма состоит в разделении операций возве
дения в квадрат на шаге 3 таким образом, что возведение а в сте
пень регулируется четным делителем 2' числа в/. Вместе с возведе
ниями в квадрат остается и возведение числа а в нечетную степень
Баланс между операциями умножения и возведения в степень сме
щается в сторону более
предпочтительного возведения
в степень
и
причем вычислять и хранить нужно лишь степени числа а с нечет
ным показателем.
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
105
Теперь нам нужно однозначно представить разряд показателя в
виде ei = 21и, где и - нечетное. Чтобы всегда иметь под рукой числа
tn и, можно составить таблицу (см., например, таблицу 6.3 для к = 5).
Таблииа 6.3. ej t и е; t u ej t u
Значения 0 0 11 0 11 22 1 11
параметров
в разложении 1 0 1 12 2 3 23 0 23
разрядов 2 1 1 13 0 13 24 3 3
показателя
в произведение 0 3 14 1 7 25 0 25
степени двойки 4 2 1 15 0 15 26 1 13
и нечетного 0 5 16 4 1 27 0 27
числа
1 3 17 0 17 28 2 7
7 0 7 18 1 9 29 0 29
. ; 8 3 1 19 0 19 30 1 15
:я> 9 0 9 20 2 5 30 0 31
г; 10 1 5 21 0 21
Для вычисления этих значений воспользуемся вспомогательной
функцией twofactJO, которая будет введена в п. 10.4.1. И прежде
чем запрограммировать Л/-арный алгоритм, нам осталось решить
всего одну проблему: как, исходя из двоичного представления по-
казателя или представления в системе счисления с основанием
В = 216, быстро перейти к представлению с основанием М = 2к для
произвольного к > 0? В этом нам поможет небольшой «трюк» с ин-
дексами, позволяющий получить требуемые разряды et представле-
ния в системе счисления с основанием М из представления е в сис-
теме счисления с основанием В. Итак, пусть (ег_1Ег-2---£о)2 - пред-
ставление показателя е в системе счисления с основанием 2 (оно
потребуется нам для определения числа г двоичных разрядов).
Пусть (eH_i^M_2...e0)fi - представление показателя е как числа типа
CLINT в системе счисления с основанием В = 216 и (е'п-1е'п^“е'о)м -
представление показателя е в системе счисления с основанием М = 2 ,
к < 16 (М не должно превышать основания В). Представление пока-
зателя е в памяти как CLINT-объекта е_1 задается последовательно-
стью значений ej[i] типа USHORT для 1=0, ..., и + 1: [и + 1], [е0],
[ej, ... , [ем_1], [0]. Заметим, что здесь мы добавили ведущий нуль.
Пусть f := |_-~J и пусть sf := [_^-J и := ki mod 16 для i = 0,
Справедливы следующие утверждения:
1. Число разрядов в представлении (e'n_ie'n_2• • •е'о)м равно/+ 1, то есть
/г - 1 =/.
Л еК w _ ,
2. Разряд ' содержит младший бит разряда е j.
106
Криптография на Си и C++ в действии
3. Значение di указывает позицию младшего бита разряда е\ в е
(отсчет позиций начинается с нуля). Если i </и dt > 16 - к, то не все
биты разряда е\ входят в ех ; оставшиеся (старшие) биты разряда е t
входят в es,.+1. Таким образом, интересующий нас разряд соответ-
ствует к младшим двоичным разрядам числа
Таким образом, для вычисления разряда е h i Е {0, ...,/} получаем
। следующее выражение:
И.............
(^5) e'i = ((e_l[s, + 1] | (e_l[s, + 2] « BITPERDGT)) »</,) & (2* - 1);.
Если для простоты положить ej[sy + 2] <— 0, то это выражение
v будет справедливо и для i =f
1 5 Таким образом, мы нашли эффективный способ доступа к разрядам
i ; показателя в его CLINT-представлении (это стало возможным бла-
годаря тому, что в нем они представлены в системе счисления с ос-
нованием 2\ к < 16), сэкономив явные преобразования показателя.
Теперь число умножений и возведений в квадрат равно .
(6.6) , , । / 2*-1^ S
ц2(&) := 2*~ +|_log2ej 1 + —- , !
и по сравнению с Ц1(&) (см. стр. 102) затраты на предвычисления
сократились вдвое. Теперь таблица, задающая наиболее подходя-
щие значения к (таблица 6.4), несколько изменилась.
Таблииа 6.4. Число двоичных разрядов показателя
Число умножений к 32 64 128 512 768 1024 2048 4096
1 47 95 191 767 1151 1535 3071 6143
лля типичных
ллин показателя 2 44 88 176 704 1056 1408 2816 5632
и различных оснований 2к 3 44 85 168 664 994 1325 2648 5293
4 46 85 164 638 954 1270 2534 5062
5 53 91 167 626 931 1237 2459 4904
6 68 105 279 626 924 1222 2414 4798
7 99 135 209 647 939 1232 2401 4739
8 162 198 270 702 990 1278 2429 4732^
Начиная с показателя длины 768, наиболее подходящие значения к
стали на 1 больше, чем в предыдущей версии алгоритма возведения
в степень (см. таблицу 6.2), тогда как число необходимых модульных
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
умножений заметно сократилось. Вероятно, эта процедура в целом
более предпочтительна, чем предыдущий вариант. Теперь цичто не
мешает нам реализовать алгоритм.
- Продемонстрируем реализацию рассмотренных принццпов на
примере адаптивной процедуры, использующей соответс‘гВуЮ1дее
оптимальное значение к. Для этого вновь сошлемся на Ко^а [Cohe]
и вслед за ним найдем наименьшее целое к, удовлетворяющее
неравенству
(6.7) Д
log2 е <
к(к + 1)22к
2м-к-2
которое выводится из приведенной выше формулы ц2(£) Для числа
необходимых умножений и условия |i2(^+l) - \^i(k) > 0. Константа
Llog2<?J, определяющая число модульных возведений в кв^драт во
всех рассмотренных выше алгоритмах, сократилась; остались ТОлько
«настоящие» модульные умножения, то есть те, где сомножители
различны.
При реализации процедуры возведения в степень с перченным
значением к требуется большой объем оперативной пад1ЯТИ для
хранения таблицы предвычислений (степеней числа я); Для £ = 8
необходимо около 64 кбайт для 127 переменных типа CLjnt (это
получается в результате умножения (27 - 1) * sizeof(USHoRT) *
CLINTMAXSHORT), при этом два автоматически возникаю1цих поля
CLINT не учитываются. Для приложений, использующих процесс0рЫ
или модели памяти с сегментированной 16-разрядной архитекту-
рой, это уже максимально допустимый предел (по этому поводу
см., например, [Dune], глава 12, или [Petz], глава 7). В
В зависимости от используемой платформы осуществлять доступ к
памяти можно по-разному. Память, необходимая для функции
mexp5J(), берется из стека (как и для всех переменных тищ CLINT),
тогда как под каждый вызов функции mexpkJO выделяет^ дина-
мическая память. Дабы избежать сопутствующего этому увели-
чения затрат, можно зарезервировать максимально необ^0ДИМуЮ
память при однократной инициализации и освободить ее тоЛЬКо по
окончании всей программы. В любом случае можно подчинить рас-
пределение памяти конкретным требованиям и обращал на них
внимание в комментариях к соответствующему коду.
Еще одно замечание по реализации: всегда рекомендуется прове-
рять, достаточно ли для данного приложения основания _ 25.
Экономия времени при увеличении к оказывается не так у^ велика
по сравнению с общим временем вычислений и с тем, чтоб^ оправ-
дать большие расходы памяти и, соответственно, затраты ее рас_
пределение. Типичные оценки времени, затрачиваемого разяичными
алгоритмами возведения в степень, приведены в Прило^ении d
108
Криптография на Си и C++ в действии
Исходя из этих оценок, можно решать, каким из указанных алго-
ритмов пользоваться.
Для М = 25 алгоритм реализован в виде функции mexp5J() в пакете
FLINT/C. Макрос EXP__L() позволяет установить используемую
функцию возведения в степень: mexp5_l() или mexpk_l() с перемен-
ным значением к.
Функция: Модульное возведение в степень
Синтаксис: int mexpkj (CLINT basj, CLINT expj, CLINT pj, CLINT mJ);
Вход: basj (основание) expj (показатель) mJ (модуль)
Выход: p_l (вычет по модулю mJ)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0 E_CLINT_MAL, если функция malloc() выдала ошибку
Начинаем с построения таблицы, в которой записаны значения
е; = 2fu, где и - нечетное, 0 < е, < 28. Таблииа представляется в
виде двух векторов. Первый вектор twotab[] содержит показатели
t числа 2\ элементами второго - oddtabf] - являются нечетные
множители и разряда 0 < е^ < 25. Целиком таблица, разумеется,
хранится в исходном коде FLINT/C.
static int twotab[] =
{0,0,1,0,2,0,1,0,3,0,1,0,2,0,1,0,4,0,1,0,2,0,1,0,3,0,1,0,2,0,1,0,5, ...};
static USHORT oddtab[] =
{0,1,1,3,1,5,3,7,1,9,5,11,3,13,7,15,1,17,9,19,5,21,11,23,3,25,13, ...};
int
mexpkj (CLINT basj, CLINT expj, CLINT pj, CLINT mJ)
{
В описаниях зарезервирована память под показатели степени
плюс ведущий нуль. Кроме того, необходимо будет еше выделить
указатель clint **aptrj, который будет содержать указатели на
вычисляемые степени переменной basj. В асс_1 будут храниться
промежуточные результаты.
109
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
CLINT aj, a2J;
clint eJ[CLINTMAXSHORT + 1];
CLINTD accj;
clint **aptrj, *ptrj;
int noofdigits, s, t, i;
unsigned int k, Ige, bit, digit, fk, word, pow2k, k_mask;
Затем выполняется обычная проверка деления на 0 и приведения
по модулю 1.
if (EQZ_L (mJ))
{
return E_CLINT_DBZ;
if (EQONE.L (mJ))
{
SETZERO J_ (pj);
return EJDLINT-OK;
}
/* Модуль = 1 ==> Остаток = 0 */
Копируем основание и показатель в рабочие переменные aj и
ej и убираем все ведущие нули.
cpyj (aj, basj);
cpyj (ej, expj);
Теперь обрабатываем тривиальные случаи а0 = 1 и 0е = 0 (е > 0).
if (EQZ_L (ej))
{
SETONE_L (pj);
110
Криптография на Си и C++ в действии
return E_CLINT_OK;
}
if (EQZ_L (aJ))
{
SETZERO J_ (pj);
return E_CLINT_OK;
}
Далее определяем оптимальное значение к; значения 2к и 2к-1
хранятся в pow2k и в k_mask соответственно. Для этого исполь-
зуем функцию которая возврашает число двоичных разря-
дов аргумента.
Ige = Id J (e_l);
k = 8;
while (k> 1 && ((k- 1) * (k « ((k-1)« 1))/((1 « k) - k- 1))
>= Ige - 1)
{
-k;
}
pow2k = 1U « k;
k_mask = pow2k - 1U;
Выделяем память под указатели на степени величины aj. Осно-
вание aj приводится по модулю mJ.
if ((aptrj = (clint **) malloc (sizeof(clint *) * pow2k)) == NULL)
{
return E_CLINT_MAL;
modj (aj, mJ, aj);
aptrj[1] = a J;
. Все дороги ведут к... модульному возведению в степень
111
При к > 1 выделяем память под таблицу предвычислений. При к = 1
этого делать не нужно, поскольку тогда никаких предвычислений
не требуется. В приведенных ниже присваиваниях указателю
aptrj[i] следует помнить, что при сложении смешения с указате-
лем компилятор сам правильно масштабирует результат, так как
он оперирует с объектами типа «указатель на р».
Как уже отмечалось, оперативную память можно выделять и при
однократной инициализации. В этом случае указатели на CLINT-
объекты должны содержаться в глобальных переменных вне
функции или в переменных класса static в функции mexpkJO.
if (k> 1)
{
if ((ptrJ = (clint *) malloc (sizeof(CLINT) *
((pow2k »1)-1))) == NULL)
{
return E_CLINT_MAL;
}
aptrj[2] = a2J;
for (aptrj[3] = ptrj, i = 5; i < (int)pow2k; i+=2)
{
aptrJ[i] = aptrJ[i - 2] + CLINTMAXSHORT;
}
Теперь выполняем предвычисления степеней переменной а, хра-
нимой в aj. Вычисляются значения а3, а5, а7, ..., а1 1 (а2 играет
лишь вспомогательную роль).
msqrj (aj, aptrj[2], mJ);
for (i = 3; i < (int)pow2k; i += 2)
{
mmulj (aptrj[2], aptrj[i - 2], aptrJ[i], mJ);
112
Криптография на Си и C++ в действии
На этом кончаются отличия случая к > 1. К показателю добавля-
ется нуль в старшем разряде.
й
(MSDPTFLL (е_1) + 1) = 0;
Определяем значение f (представленное переменной noofdigits).
noofdigits = (Ige - 1 )/k;
fk = noofdigits * k;
Для разряда ej определяем слово Sj (переменная word) и бит dj
(переменная bit).
word = fk » LDBITPERDGT; /* fk div 16 7
bit = fk & (BITPERDGT-1U); /* fk mod 16 7
Вычисляем разряд е^ по приведенной выше формуле; еп_! пред-
ставлен переменной digit.
switch (к)
т*
case 1:
case 2:
case 4:
case 8:
digit = ((ULONG)(eJ[word + 1]) » bit) & k_mask;
break;
default:
digit = ((ULONG)(eJ[word + 1] | ((ULONG)eJfword + 2]
« BITPERDGT)) » bit) & k_mask;
f-ддВА 6. Все дороги ведут к... модульному возведению в степень
113
В первый раз проходим шаг 3 алгоритма в случае digit = e^, 0.
if (digit != 0) /* k-digit >07
{
cpyj (accj, aptrj[oddtab[digit]]);
Вычисляем p2 •, значение t устанавливаем по таблице twotabfenJ -
число 2 в максимальной степени, деляшей е^; число р
представлено переменной accj.
t = twotabfdigit];
for (; t > 0; t-)
{
msqrj (accj, accj, mJ);
}
else /* k-й разряд == 0 7
{
SETONE_L (accj);
}
Цикл no noofdigits, начиная c f - 1.
for (-noofdigits, fk -= k; noofdigits >= 0; noofdigits-, fk -= k)
Для разряда ej определяем слово s, (переменная word) и бит dj
(переменная bit).
word = fk » LDBITPERDGT;
bit = fk & (BITPERDGT - 1U);
/* fk div 16 7
/*fk mod 16 7
114
Криптография на Си и C++ в действии
Вычисляем разряд е; по приведенной выше формуле; е, представ*
лен переменной digit.
switch (к)
case 1:
case 2:
case 4:
case 8:
digit = ((ULONG)(eJ[word + 1]) » bit) & k_mask;
break;
default:
digit = ((ULONG)(eJ[word + 1] | ((ULONG)eJ[word + 2]
« BITPERDGT)) » bit) & k.mask;
}
Проходим шаг 3 алгоритма для случая digit = е, 0;
значение t устанавливаем по таблице twotab[ej.
if (digit != 0) /* к-digit >07
{
t = twotab[digit];
2^”^ и
Вычисляем p а в accj. Для вычисления au определяем не-
четный делитель и разряда е; по таблице aptr j [oddtab[ej]].
for (s = к -1; s > 0; s-)
msqrj (accj, accj, mJ);
mmulj (accj, aptrj[oddtab[digit]], accj, mJ);
рддВА 6. Все дороги ведут к... модульному возведению в степень
115
Вычисляем р2 ; значение р по-прежнему представлено перемен-
ной accj.
for (; t > 0; t--)
{
msqrj (acc J, асе J, mJ);
}
}
else /* k-digit == 0 */
{
2^
Шаг 3 алгоритма для случая ej = 0: вычисляем р .
for (s = k; s > 0; s-)
{
msqrj (accJ, accJ, mJ);
}
}
}
Цикл заканчивается; результат accj является степенью по моду-
лю mJ.
cpyj (pj, accj);
И наконец, освобождается выделенная память.
free (aptrj);
if (ptrj != NULL)
free (ptrj);
return E_CLINT_OK;
116
Криптография на Си и C++ в действии
Поясним алгоритм М-арного возведения в степень на численном
примере. Для этого вычислим 1234667 mod 18577 с помощью функ-
ции mexpkj().
1. Предвычисления
Представим показатель е = 667 в системе счисления с основанием
2кс к = 2 (см. Л7-арный алгоритм возведения в степень на стр. 102),
получим е = (1010 011011)2?.
Значение a mod 18577 равно 17354. Больше никаких степеней чис-
ла а вычислять не требуется: 2к- 1 = 3.
2. Основной цикл
Разряд показателя е-,= 2*и 21-1 2'-1 2°-1 2’-1 2°-3
р <— р2 mod п - 14132 13261 17616 13599
22 р +- р mod п - - 4239 - 17343
р <— p-au mod п 1234 13662 10789 3054 4445
р <— р2 mod п 18019 7125 - 1262 1
3. Результат I
р = 1234667 mod 18577 = 4445.
Рассмотрим частный случай возведения в степень, когда показатель
является степенью двойки: 2к. Как мы видели ранее, это легко мож-
но сделать путем ^-кратного возведения в квадрат. Показателю к в
2к будет соответствовать переменная к.
Функция: Модульное возведение в степень в случае, когда показатель явля- ется степени двойки
Синтаксис: int mexp2J (CLINT aj, USHORT k, CLINT pj, CLINT mJ);
Вход: aj (основание) k (показатель к в 2k) mJ (модуль)
Выход: pj (вычет aj2k по модулю mJ)
Возврат: E_CLINTJ3K, если все в порядке E_CLINT_DBZ в случае деления на 0
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень 117
int
mexp2J (CLINT aj, USHORT k, CLINT pj, CLINT mJ)
J {
CLINT tmpj;
if (EQZ_L (mJ))
{
Y‘( return E_CLINT_DBZ;
}
При k > 0 возводим k раз a l в квадрат по модулю mJ.
if (k > 0)
{
cpyj (tmpj, aj);
while (k- > 0)
{
msqrj (tmpj, tmpj, mJ);
}
cpyj (pj, tmpj);
}
else
В противном случае, при k = 0, нужно выполнить лишь приведе-
ние по модулю mJ.
{
modj (aj, mJ, pj);
}
return E_CLINT_OK;
}
118
Криптография на Си и C++ в действии
6.3. Аддитивные цепочки и окна На сегодняшний день опубликовано множество алгоритмов возве- дения в степень: одни удобны лишь для частных случаев, другие универсальны. Но цель всегда одна и та же - по возможности со- кратить число умножений и делений, как это было при переходе от бинарного к Л/-арному алгоритму. Алгоритмы бинарного и Л/-арного возведения в степень, в свою оче- редь, являются частными случаями аддитивных цепочек (см. [Knut], п. 4.6.3). Мы уже знаем, что при возведении в степень можно пред- ставить показатель в виде суммы: е = k + 1 => ае = ам = ака1. Пред-
ПК** ' ставляя показатель в двоичной системе счисления: , ^к-2 . . е — ек_\ • 2 + ек_2 • 2 + ... 4- во, можно выполнить возведение в степень с помощью возведений в
л квадрат и умножений (см. стр. 96): ' (( \2 Л У аеты\п= ... У1 ... ae°modn. Элементами соответствующей аддитивной цепочки являются пока- затели при степенях числа а: ^к-Ь ек-\' Ъ вк-\' 2 + в^_2, (в^_г 2 + ек^' 2, (в^_г 2 + в^-2)* 2 + e^-з, , ((Q-r 2 + в£_2)’ 2 + в£_3)- 2, (•••(Q-Г 2 + в^)’ 2 + ••• + в])- 2 + в0. Если для некоторого значения j показатель в7 = 0, то соответствую- щие элементы последовательности опускаются. Например, для числа 123 результатом бинарного метода будет аддитивная цепочка из 12 элементов: 1, 2, 3, 6, 7, 14, 15, 30, 60, 61, 122, 123. В общем случае последовательность чисел 1 = aQ, ах, а2, ...,аг= е,ъ которой для каждого i = 1, ..., г существует пара чисел (/, к) таких, что j < к < i и at = aj + ак, называется аддитивной цепочкой длины г для числа е. М-арный метод обобщает представление показателя на случай про- извольного основания. Цель у обоих методов общая - получить наи- более короткие аддитивные цепочки и тем самым снизить вычисли-
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
119
тельные затраты на возведение в степень. Для числа 123 23-арный
метод дает аддитивную цепочку 1, 2, 3, 4, 7, 8 1 5, 30, 60, 120, 123-
24-арный метод - 1, 2, 3, 4, 7, 11, Д 28,’ 56, 112, 123. Эти две цепоч-
ки значительно короче, чем цепочка в бинарном методе; для боль-
ших чисел разница будет еще более значительной. Однако, раз уж
мы говорим^ о временных затратах, следует отметить, что база
данных а . а . а ..... а “, которую мы строим при инициализации
Л/-арных методов, включает в себя и те степени ci. которые не нуж-
ны для представления е по основанию М или для построения адди-
тивной цепочки.
Наихудшим случаем построения аддитивной цепочки является би-
нарное возведение в степень: здесь цепочка имеет максимально
1 t возможную длину log2e + Н(е) - 15 где через //(<?) обозначен хем-
мингов вес числа е. Снизу длина аддитивной цепочки ограничена
числом log2e + log2//(e) - 2,13, более коротких цепочек быть не
должно (см. [Scho] или [Knut], п. 4.6.3, упражнения 28, 29). В на-
; шем случае это означает, что длина самой короткой аддитивной
. цепочки для е - 123 не может быть меньше 8, а значит, приведен-
и ные выше результаты Л/-арных методов далеко не самые лучшие.
До сих пор не существует полиномиального алгоритма, решающего
задачу поиска кратчайшей аддитивной цепочки. Эта задача принад-
лежит классу сложности NP, то есть относится К задачам, которые
могут быть решены за полиномиальное время недетерминирован-
ными методами. Иначе говоря, решение этих задач за полиноми-
альное время можно лишь «угадать», в отличие от задач класса Р,
w ; которые будут решены детерминированно. Неудивительно, что Р
является подмножеством NP, поскольку все задачи, решаемые за
полиномиальное время детерминированными методами, могут
быть решены за то же время недетерминированными методами.
Определение кратчайшей аддитивной цепочки является NP-полной
задачей, то есть задачей, сложность которой не хменьше, чем слож-
ность любой другой задачи из класса NP (см. [HKW], стр. 302). NP-
полные задачи тем более интересны, что если хотя бы одна из них
будет решена детерминированными методами за полиномиальное
время, то и все остальные задачи из NP будут решены за полино-
миальное время. В этом случае можно будет сказать, что классы Р
и NP - это одно и то же множество задач. Задача о том, совпадают
ли множества Р и NP, является основной нерешенной задачей тео-
рии сложности. Однако в настоящее время превалирует мнение о
том, что Р NP.
Если число п в двоичной системе счисления имеет вид ц = (пк_хпк-2-• -п0)^ то #00 =
(см. [HeQu], Глава 8).
120
Криптография на Си и C++ в действии
Теперь ясно, что при практической реализации процедуры генерации
аддитивных цепочек мы должны опираться на некие эвристики, то
есть те приближенные математические методы, которые в данном
случае работают эффективнее других: как, например, в случае с
определением показателя к для 2^-арного возведения в степень.
Например, в 1990 г. Я. Якоби (Y. Yacobi) [Yaco] установил связь
между построением аддитивных цепочек и сжатием данных по
методу Лемпеля-Зива (Lempel-Ziv); в его работе приведен также
алгоритм возведения в степень, основанный на таком сжатии и
М-арном методе.
Для поиска кратчайшей аддитивной цепочки возможно дальнейшее
обобщение М-арного метода возведения в степень, чем мы сейчас и
займемся. В методах окна, в отличие от М-арного метода, показа-
тель представляется не разрядами в системе счисления по фиксиро-
ванному основанию М, а разрядами переменной двоичной длины.
Так, например, разрядом показателя может быть длинная последо-
вательность двоичных нулей, называемая нулевым окном. Вспом-
ним М-арный алгоритм со стр. 104: ясно, что для нулевого окна
длины I потребуется /-кратное возведение в степень, то есть третий
шаг алгоритма примет вид:
3.
2^
Положить р р
modw =
(/ раз)
mod т.
Ненулевые разряды обрабатываются либо как окна фиксированной
длины, либо как изменяемые окна максимальной длины. Как и в
М-арном случае, для любого ненулевого окна (называемого далее, не
совсем удачно, «1-окном») длины t помимо повторного возведения
в квадрат выполняется еще дополнительное умножение на некото-
рый элемент таблицы предвычислений:
3'. Положить р <— р2 mod т, а затем р «— paei modm.
Число элементов таблицы предвычислений зависит от допустимой
максимальной длины 1-окна. Отметим, что младший разряд 1-окна
всегда равен 1, то есть 1-окно всегда нечетно. Таким образом, нам
не надо здесь раскладывать разряд показателя, как на стр. 104, на
четный и нечетный множители. С другой стороны, при возведении
в степень мы двигаемся слева направо, а это значит, что, прежде
чем возводить в степень, нам потребуется полностью разложить
показатель на множители и, кроме того, помнить это разложение.
Тем не менее, если мы начнем раскладывать показатель со старшего
разряда и будем двигаться слева направо, то можно обрабатывать
каждое 0- или 1-окно сразу же по мере заполнения. Отсюда, оче-
видно, следует, что у нас получатся и четные 1-окна, но этот случай
алгоритмом допускается.
в. Все дороги ведут к... модульному возведению в степень 121
По существу, разложение показателя на 1-окна и в том, и в другом
направлении выполняется одним и тем же алгоритмом. Сформули-
руем его для разложения справа налево.
Разложение целого числа е на 0- и 1-окна
t фиксированной длины 1
1. Если младший двоичный разряд числа е равен 0, то начать 0-окно
и перейти на шаг 2; в противном случае начать 1-окно и перейти
на шаг 3.
2. Пока не появится 1, добавлять следующие по старшинству дво-
ичные разряды в 0-окно. Как только появится 1, закрыть 0-окно,
начать 1-окно и перейти на шаг 3.
3. Собрать следующие I - 1 двоичных разрядов в 1-окне. Если по-
следующий разряд равен 0, то начать 0-окно и перейти на шаг 2;
в противном случае начать 1-окно и перейти на шаг 3. Алгоритм
заканчивает работу после того, как пройдены все разряды числа е.
При разложении слева направо начинаем со старшего двоичного
разряда и действуем по аналогии. Если предположить, что в числе е
нет начальных нулей, то алгоритм не может закончиться на шаге 2,
а только на шаге 3. Приведем два примера.
✓ Пусть е = 1896837 = (111001111000110000101 )2 и I = 3. Раскладыва-
ем е, начиная с младшего двоичного разряда:
е = 111 001 111 00011 0000 101.
м При I = 4 получаем разложение
’ •ta е = 111 00 1111 00011 0000101.
Рассмотренный выше 2*-арный метод при к = 2 дает разложение
е = 01 И 00 11 11 00 01 10 00 01 01.
Таким образом, при I = 3 получаем в разложении числа е пять 1-окон,
а при I = 4 только четыре; в обоих случаях требуется одно и то же
число дополнительных умножений. Разложение по 22-арному методу
содержит восемь 1-окон, требует в два раза больше дополнитель-
ных умножений, чем в случае I = 4 и, значит, вряд ли заслуживает
внимания.
✓ При выполнении той же процедуры слева направо, начиная со
старших разрядов, при I = 4 и е = 123 получаем разложение
е = 1110 0 1111 000 ПОР 00 101,
также с четырьмя 1-окнами, среди которых, как уже отмечалось,
есть четные.
Теперь мы, наконец, можем сформулировать алгоритм разложения
показателя методом окон с учетом обоих направлений разложения.
122
Криптография на Си и C++ в действ|
Алгоритм вычисления вычета ае mod т с разложением
показателя е на нечетные 1-окна (максимальной) длины I
1. Разложить показатель е на 0- и 1-окна длины
соответственно.
2. Вычислить и запомнить я3 mod m, я5 mod /и, я7 mod ш, я2*
mod т.
3. Положить Р mod т и i <— к - 2.
4. Положить Р р'1 mod т.
5. Если со, * 0, то положить Р Ра^1 mod т.
6. Положить i <— i - 1; при i > 0 вернуться на шаг 4.
7. Результат: р.
Если среди 1-окон есть четные, то вместо шагов 3-7 выполняются
следующие: J
3'. Если avi = 0, то положить а
(ik-i
Если Щи Ф 0, то представить ccvi в виде = 2 я, где и - нечет-
ное; положить р <— аи mod т, а затем р <— р2' mod т . В обоих
случаях положить i <— к - 2.
4'. Если СО, = 0, то положить
Если со, Ф 0, то представить сог в виде со, = 2'я, где и - нечетное;
положить р <— р2' гаъ&т, затем р <— раи mod т и, наконец»
р <— р2 mod т .
5'. Положить i <— i - 1; при i > 0 вернуться на шаг 4Z.
6'. Результат: р.
6. Все дороги ведут к... модульному возведению в степень 123
6.4- Приведение по модулю и возведение в степень
методом Монтгомери
Теперь оставим аддитивные цепочки и обратимся к другому подхо-
ду, интересному, прежде всего, с точки зрения алгебры. Этот под-
ход позволяет заменить умножение по модулю нечетного числа п
умножением по модулю 2*, которое не требует деления в обычном
понимании и, следовательно, является более эффективным, чем
с приведение по модулю произвольного числа п. Этот замечательный
метод был опубликован в 1985 г. П. Монтгомери (Р. Montgomery)
[Mont] и с тех пор широко применяется. В основе метода лежит
следующее свойство.
Пусть пит- взаимно простые целые числа; г"1 мультипликативно
обратно к г по модулю и; и-1 мультипликативно обратно к п по мо-
дулю г. Пусть п := -/Г1 mod г и т := tn mod г. Для любого целого t
справедливо сравнение
(6.8) t + mn ч
1 ' ------= tr mod п .
г
Заметим, что при вычислении левой части сравнения мы оперируем
со сравнениями по модулю г (поскольку t + тп = 0 mod г, остаток
“° от деления на г равен нулю), но не по модулю п. Если выбрать в
* ' качестве г степень двойки 25, то 5 младших битов числа х и будут
задавать остаток от деления х на г, а деление х на г выполняется
простым сдвигом числа х на 5 бит вправо. Таким образом, вся пре-
'• лесть сравнения (6.8) состоит в том, что его левая часть вычисляет-
ся значительно быстрее, чем правая. Здесь нужны всего две опера-
ции, для выполнения которых можно воспользоваться функциями
mod2J() (см. п. 4.3) и shiftJO (см. п. 7.1).
Такая процедура вычисления вычета по модулю п называется
преобразованием Монтгомери. Поскольку здесь требуется, чтобы
числа п и г были взаимно простыми, число п должно быть нечетным.
Ниже мы покажем, что с помощью преобразования Монтгомери
можно выполнять модульное возведение в степень значительно
быстрее, чем предыдущими методами. А пока уточним некоторые
моменты.
Корректность сравнения (6.8) можно проверить довольно просто.
Подставим в левую его часть вместо т значение tn mod г (см. фор-
мулу (6.9)), затем заменим tn mod г на tn - r[_tn7 г]е7 (получим
(6.10)), наконец, выразим п в виде целого числа (г г - 1)/ п для
некоторого г G 77 и получим (6.11). Результатом приведения по
модулю п будет формула (6.12):
(6.9) t + тп = t + n(tn mod г)
г
г
124 Криптография на Си и C++ в действи
(6.10) t + ntn tn ж = п .ц* г |_ г J И.
(6.11) _t + t(rr' -1)
(6.12) = tr~x mod и. W Пусть n, t, re НОД(и, r) = 1 и n := -n~x mod г. Тогда из формулы (6.8) следует, что для
(6.13) ДО := t + (tn mod г) п справедливо
(6.14) ДО = t mod п, яН
(6.15) ДО = 0 mod г. W К этому результату мы еще вернемся. Чтобы применять преобразование Монтгомери, будем проводить вычисления по модулю п в полной системе вычетов (см. главу 5): R := R(r, п) := {ir mod п | 0 < i < п} с подходящим г := 2s > 0, таким, что 25-1 < п < 2Л. Определим произ- ведение Монтгомери «х» чисел а и b из R как а х b := abr~x mod п, где через г"1 обозначено число, мультипликативно обратное к г по модулю п. Имеем а х b = (ir)(jr)r~x = (ij)r mod п е R, то есть произведение х двух элементов множества R тоже принад- лежит множеству R. Произведение Монтгомери вычисляется с помощью преобразования Монтгомери. Поскольку числа п и г вза- имно просты, расширенным алгоритмом Евклида (см. п. 10.2) по- лучаем линейное представление их наибольшего общего делителя: 1 = НОД(и, г) = г'г-пп, где п := -/Г1 mod г. Тогда из линейного представления : 1 = г г mod п и 1 == -ни mod г,
ведут к... модульному возведению в степень 125
то есть число г = г-1 mod п мультипликативно обратно к г по моду-
лю п, а число п = -n~l mod г, взятое со знаком «-», мультиплика-
тивно обратно к п по модулю г (здесь мы немного забежали вперед;
см. п. 10.2). Произведение Монтгомери вычисляется по следующему
алгоритму.
Вычисление произведения Монтгомери а X Ъ в R(r, п)
1. Положить t <— ab.
2. Вычислить т <— tn'mod г.
3. Вычислить и <— (/ + тп) / г (деление выполняется нацело;
см. выше).
4. Если и > п, то результат: и - п; иначе результат: и. Параметры
алгоритма выбраны так, что а, b < п и т, п < г, тогда и < 2п
(см. формулу (6.21)).
Этот алгоритм требует вычисления трех произведений больших чисел:
одно на шаге 1 и два на этапе приведения (шаги 2, 3). Поясним алго-
ритм на маленьких числах. Пусть а = 386, b = 257, п = 533. выберем
г = 210. Тогда п = -n~l mod г = 707, т = 6,t + тп = 102400 и и = 100.
Теперь можем вычислять произведение ab mod п, где число п не-
четное, следующим образом. Сопоставим числам а и b элементы
множества R: а <— ar mod п, b' <— br mod /1, затем найдем произве-
дение Монтгомери р' <— а х b' = a'b'f1 mod п и, наконец, выполним
обратное преобразование: р <— р' х 1 = p'r~l = ab mod п. Можно
обойтись и без обратного преобразования, если сразу вычислить
р <— a xb, тем самым избавившись и от необходимости преобразо-
вывать Ь. В результате получаем следующий алгоритм.
Вычисление р =ab mod п (для нечетного и) с помощью
произведения Монтгомери
1. Подобрать г := 2s такое, что 25-1 < п < 2s. Найти линейное пред-
ставление 1 = r'r-п'п расширенным алгоритмом Евклида.
2. Положить а' <— ar mod п.
3. Вычислитьр «— a'xb, результат: р.
Опять поясним алгоритм на маленьких числах. Пусть а = 123,
b = 456, н = 789, г = 210. Тогда п =-n~{ modr = 963, «' = 501 и
р = а' х b = 69 = ab mod п.
Вычисление значений г и п на шагах 1, 2 и вычисление произведе-
ния двух больших чисел все же требуют значительно больших вре-
менных затрат, чем «обычное» модульное умножение, поэтому при
126
Криптография на Си и C++ в действии
однократном модульном умножении алгоритмом Монтгомери
пользоваться не стоит.
Когда же нам нужно вычислить много модульных произведений
по одному и тому же модулю, то есть когда указанные трудоем-
кие предвычисления выполняются всего один раз, результаты более
впечатляющие. Алгоритм Монтгомери особенно хорош для мо-
дульного возведения в степень, нужно лишь немного изменить
М-арный алгоритм. Опять представим показатель е и модуль п в
системе счисления с основанием В = 2к: е = (ет-\ет_2---ео)в и
п = Следующий алгоритм вычисляет степени ае mod п
в кольце где п нечетное, с помощью произведения Монтгомери,
Возведение в квадрат сводится к вычислению а х а.
Возведение в степень по модулю п (для нечетного п) с помощью
произведения Монтгомери
1. Положить г<—В/ = 2*/. Найти линейное представление \=г'г-пп
расширенным алгоритмом Евклида.
2. Положить а <— ar mod п. Вычислить и запомнить а\а5, ...,а2 -1
с помощью произведения Монтгомери х в /?(г, и).
3. Если ет-1 * 0, то найти разложение ет_] = 2'u, где и нечетное.
Положить р <— (ри J .
Если em_i = 0, то положить р <— г mod п .
В любом случае положить i <— т - 2.
4. Если =0, то положить =^...^p2jJ ...^ (к раз воз-
вести в квадрат: р2 ~Р*Р).
Если е,- * 0, то найти разложение е, = 2'и, где и нечетное. Поло-
жить р <— [р2 xauJ .
5. При i > 0 положить i <— i - 1 и вернуться на шаг 4.
6. Результат: произведение Монтгомери Р х 1.
Дальнейшее усовершенствование этого алгоритма возможно, скорее,
за счет модификации алгоритма умножения Монтгомери, чем алго-
ритма возведения в степень, что и сделали С.Р. Дуссе (S.R. Dusse)
и Б.С. Калиски (B.S. Kaliski) в работе [DuKa]. Вычисляя произве-
дение Монтгомери алгоритмом со стр. 125, можно избежать вы-
полнения присваивания т <— tn mod г на шаге 2. Кроме того, прй
выполнении преобразования Монтгомери можно оперировать с
6. Все дороги ведут к... модульному возведению в степень 127
и. nQ := п mod В, а не с п. Вычислим разряд mz <— tyi'o mod В, умно- жим его на и, затем на В1 и прибавим результат к t. Чтобы найти произведение чисел а, b <п по модулю п, представим, как и рань- ше, п - (п^пи.. .по)в и положим г := В1, rr - пп = 1 и н'о := п' mod В.
к’ Алгоритм Дуссе и Калиски вычисления произведения Монтгомери axb 1. Положить t <— ab, и о и'mod В, i <— 0. 2. Вычислить ш, <— tyi'o m°d В (гщ будет одноразрядным целым числом).
3. Положить t <— t + пцпВ'.
4. Положить i <- i + 1; при i < I - 1 вернуться на шаг 2 5. Положить t <— t / г.
• 6. Если t > п, то результат: t - п; иначе результат: t, В работе Дуссе и Калиски утверждается, что рассмотренное упро- щение основано на том, что t рассматривается как кратное числа г, однако доказательство не приводится. Прежде чем использовать эту процедуру, уточним, почему она действительно вычисляет про- изведение axb. Следующие рассуждения основаны на результатах Кристофа Бурникеля [Zieg]. На шагах 2 и 3 алгоритма вычисляется последовательность / по рекурсивной формуле:
(6.16) t^ = ab,
(6.17) Г0+1) !_ Bi i = Q ...J-l, Bl где Д7) = t + ((r mod B) (~n~x mod B) mod B) n - уже знакомая нам функция (см. формулу (6.13) при г<—В). Эле-
(6.18) менты последовательности обладают следующими свойствами: = 0 mod В',
(6.19) = ab mod и,
(6.20) /о = abr 1 mod n, r
128
Криптография на Си и C++ в действцц
(6.21) < 2n. r Свойства (6.18) и (6.19) следуют непосредственно из (6.14)—(6.17); из (6.18) получаем В1 |г(/) <=> г | г(/). Отсюда и из сравнения t(l) = ab mod п следует (6.20). Неравенство (6.21) выводим из соот- ношения
r(/) =z(0)+n£W;B' <W, 1=0 поскольку /0) = ab < п2 < пВ1.
Теперь скорость приведения по модулю определяется скоростью умножения чисел, по порядку величины близких к модулю. Такой вариант умножения по Монтгомери можно элегантно реализовать с помощью функции, аналогичной mulj (см. стр. 49).
Функция: Умножение по Монтгомери
Синтаксис: void mulmonj (CLINT aj, CLINT bj, CLINT nJ, USHORT nprime, USHORT logB_r, CLINT pj);
Вход: aj, bj (сомножители а и b) nJ (модуль n > a, b) nprime (11 mod B) logB_r (логарифм числа г по основанию В = 216; должно выполняться неравенство в|09В-г"1 < п < В|О9В-Г)
Выход: р_1 (произведение Монтгомери а х Ь = а • b • г"1 mod ri)
i
.* а •
void
mulmonj (CLINT aj, CLINT bj, CLINT nJ, USHORT nprime,
USHORT logB.r, CLINT pj)
{
CLINTD tj;
clint *tptrj, *nptrj, *tiptrj, *lasttnptr, *lastnptr;
ULONG carry;
USHORT mi;
int i;
mult (aj, bj, tj);
lasttnptr = tj + DIGITS_L (nJ);
lastnptr = MSDPTR_L (nJ);
ведут к... модульному возведению в степень
129
Используя функцию mult(), мы гарантируем отсутствие пере-
полнения (см. стр. 86) при вычислении произведения чисел а_1 и
b_l. Для возведения в квадрат по Монтгомери используем sqr().
Результат записывается в tj, где места для него достаточно.
Затем t_l дополняется нулевыми старшими разрядами до длины, в
два раза большей, чем длина nJ.
for (i = DIGITS J_ (tj) + 1; I <= (DIGITS J_ (nJ) « 1); i++)
{
tJ[i] = O;
}
SETDIGITSJ. (tj, MAX (DIGITSJ_ (tj), DIGITS.L (nJ) « 1));
При выполнении следующего двойного никла последовательно
вычисляются и складываются с t l частичные произведения т^пВ1,
где mi := tjnz0. Здесь тоже текст программы аналогичен функции
умножения.
for (tptrj = LSDPTRJ. (tj); tptrj <= lasttnptr; tptrJ++)
{
carry = 0;
mi = (USHORT)((ULONG)nprime * (ULONGftptrJ);
for (nptrj = LSDPTFLL (nJ), tiptrj = tptrj;
nptrj <= lastnptr; nptrj++, tiptrj++)
{
‘tiptrj = (USHORT)(carry = (ULONG)mi ‘ (ULONG)‘nptrJ +
(ULONG)‘tiptrJ + (ULONG)(USHORT)(carry » BITPERDGT));
}
В следующем внутреннем цикле при возникновении переполне-
ния перенос записывается в старший разряд переменной tj, по-
этому tj и содержит один дополнительный разряд. Этот шаг
очень важен, поскольку в начале основного никла переменной tj
присваивалось значение, в отличие от переменной pj, которая
была инициирована путем умножения на 0.
130
Криптография на Си и C++ в действии
for (;
((carry » BITPERDGT) > 0) && tiptrj <= MSDPTR.L (tj);
tiptrj++)
tiptrj = (USHORT)(carry = (ULONG)*tiptrJ +
(ULONG)(USHORT)(carry » BITPERDGT));
if (((carry » BITPERDGT) > 0))
*tiptrj = (USHORT)(carry » BITPERDGT);
INCDIGITS_L (tj);
Далее следует деление на В1, для чего мы сдвигаем tj на logB_r
бит вправо, т.е. отбрасываем младшие logB_r бит переменной tj.
Затем модуль nJ при необходимости вычитается из tj, и tj воз-
вращается в р_1 в качестве результата.
tptrj = tj + (logB_r);
SETDIGITSJ. (tptrj, DIGITSJ_ (tj) - (logB.r));
if (GE_L (tptrj, nJ))
sub J (tptrj, nJ, pj);
+
else
cpyj (pj, tptrj);
1 .
Функция sqrmonj() возведения в квадрат по Монтгомери несуш^"
ственно отличается от только что рассмотренной: в вызове функции
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень
131
нет переменной bj, а вместо функции умножения mult(a_l, bj, tj) используется функция sqr(aj, bj), точно так же пренебрегающая возможным переполнением. Однако здесь следует отметить, что при возведении в квадрат по Монтгомери вслед за вычислением р <— а х а выполняется обратное преобразование р <— р х 1 = р'г~{ = = a2 mod п (см. стр. 125).
Функция: Возведение в квадрат по Монтгомери
Синтаксис: void sqrmonj (CLINT aj, CLINT n_l, USHORT nprime, USHORT logB_r, CLINT pj);
Вход: a_J (множитель a) nJ (модуль n > a) nprime (n mod B) logB_r (логарифм от г по основанию В = 216; должно выполняться неравенство в*°9В-г”1 < п < В|О9В_Г)
Выход: р J (вычет а2 • г~{ по модулю и) В своей статье Дуссе и Калиски приводят также следующий вари- ант расширенного алгоритма Евклида (его мы еще будем рассмат- ривать в п. 10.2) для вычисления п0 = п mod В, который снижает сложность предвычислений. Этот алгоритм использует арифметику больших чисел для вычисления вычета -/Г1 mod 2Л, где 5 > 0. Алгоритм вычисления обратного значения -и"1 mod 2s, где s > 0, п нечетное 1. Положить х <— 2, у <— 1, i «— 2. 2. Если х < пу mod х, то положить у <— у + х. 3. Положить х<— 2х и i <— i + 1; при i < s вернуться на шаг 2. 4. Результат: х - у. Методом математической индукции можно доказать, что на шаге 2 рассмотренного алгоритма всегда выполняется сравнение уп = 1 mod х и, значит, у = /г-1 mod х. Как только на шаге 3 пере- менная х примет значение 2Л, мы получаем нужный результат: 2Л - у = -nl mod 2s, если только выбрать 5 из условия 2s = В. Этот алго- ритм реализован в виде небольшой функции invmomJO на FLINT/C. Аргументом функции является модуль п, результатом - значение -n~l mod В. Все эти соображения подтверждаются при построении функций mexp5mj() и mexpkmJO, для которых мы приводим здесь только интерфейс и численный пример.
132
Криптография на Си и C++ в действии
Функция: Модульное возведение в степень в случае нечетного модуля (25-арный или 2*-арный метод с умножением по Монтгомери)
Синтаксис: int mexp5m_l(CLINT basj, CLINT expj, CLINT pj, CLINT mJ); int mexpkmJ(CLINT basj, CLINT expj, CLINT pj, CLINT mJ);
Вход: basj (основание) expj (показатель) mJ (модуль)
Выход: pj (вычет по модулю mJ)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_DBZ в случае деления на 0 E_CLINT_MAL, если функция malloc() выдала ошибку EJ3LINT_MOD в случае четного модуля
В этих функциях для вычисления произведения Монтгомери ис-
пользуются процедуры invmonJO, mulmonj() и sqrmon_l(). В основе
—- их реализации - функции mexp5_l() и mexpkJO, модифицированные
в соответствии с описанным выше алгоритмом возведения в степень.
। Поясним алгоритм возведения в степень по Монтгомери функцией
, mexpkmJO на том же численном примере, который мы рассматри-
вали при М-арном возведении в степень (см. стр. 116). Приведем
основные этапы вычисления 1234667 mod 18577.
1. Предвычисления
Представим показатель е = 667 в системе счисления с основанием
2к с к = 2 (см. алгоритм возведения в степень по Монтгомери на
стр. 126), получим
е= (1О1ОО11О11)22.
Значение г, используемое в преобразовании Монтгомери, равно
г = 216 = В = 65536.
Значение п'о (см. стр. 127) теперь равно п0 = 34703. ;
Преобразуем основание а в элемент системы вычетов R(r, л)
чэг ч (см. стр. 124):
а = ar mod п = ПМ • 65536 mod 18577 = 5743.
Значение элемента а3 множества В(г, и) равно а3 = 9227. Показа-
тель мал, поэтому дальнейшие степени числа а вычислять не нужно.
рддВАб. Все дороги ведут к... модульному возведению в степень 133
2. Основной цикл
Разряд показателя е, = 2'и 2'-1 2’-1 2°-1 2’-1 2°-3
р<-р2 - 16994 3682 14511 11066
la. г la. - - 6646 - 12834
р рхаи 5743 15740 8707 16923 1583
т 9025 11105 - 1628 -
3. Результат
Значение р после обратного преобразования:
р = р х 1 = pr~l mod и = 1583г"1 mod и = 4445.
Читателя, интересующегося подробностями программной реализа-
ции функций mexp5m_l() и техркт_1()и численного примера для
функции mexpkmJO, мы отсылаем к исходному тексту программы
на FLINT/C.
В начале главы мы ввели функцию wmexp_l(), удобную в случае
малых оснований и требующую только умножений вида
р pa mod т переменных типа CLINT * USHORT mod CLINT. Эту
функцию также можно ускорить, заменив модульное возведение в
квадрат аналогичной процедурой по Монтгомери, как мы это делали
в mexpkmJO. Здесь мы будем использовать быструю функцию об-
ращения invmonJO, а умножение оставим без изменений. Это можно
сделать, поскольку при возведении в квадрат по Монтгомери и
обычном умножении по модулю п
(а2г-1) b = (а2/?) г-1 mod п
мы остаемся в рамках системы вычетов /?(г, л) = {ir mod п | 0 < i < п}.
В результате получаем две функции: wmexpmJO и umexpmJO,
аргументами которых являются показатели типа USHORT, для
нечетных модулей. Эти функции являются значительно более бы-
стрыми по сравнению с «обычными» функциями wmexpJO и
umexpJO. Для них мы снова приводим лишь интерфейс и числен-
ный пример, а читателя отсылаем за подробностями к исходному
тексту программы на FLINT/C.
134
Криптография на Си и C++ в действии
функция: Модульное возведение в степень с использованием преобразования Монтгомери для основания (или показателя соответственно) типа USHORT и нечетного модуля
Синтаксис: int wmexpmj (USHORT bas, CLINT ej, CLINT pj, CLINT mJ); int umexpmj (CLINT basj, USHORT e, CLINT pj, CLINT mJ);
Вход: bas, basj (основание) e, ej (показатель) mJ (модуль)
Выход: pj (вычет baseJ по модулю mJ, соответственно вычет basje по модулю mJ)
Возврат: E_CLINTJ3K, если все в порядке E_CLINT_DBZ в случае деления на 0 E_CLINT_MOD в случае четного модуля
Функция wmexpmJ заготовлена специально для алгоритма проверки
на простоту из п. 10.5, где мы, наконец-то, пожнем плоды тепереш-
них усилий. Проиллюстрируем эту функцию на уже знакомом нам
примере: вычислим 1234667 mod 18577.
1. Предвычисления
и . Двоичное представление показателя: = (1010011011 )2.
Значение г, используемое в преобразовании Монтгомери:
: г=2,6 = В = 65536.
Значение п'о (см. стр. 127) вычисляется, как и раньше: п'о = 34703.
Определяем начальное значение р <— pr mod 18577.
2. Основной цикл
Двоичный разряд показателя 1 0 1 0 0 1 1 0 1 1
р рхр в 7?(г, /z) 9805 9025 16994 11105 3682 6646 14511 1628 11066 9350
р ь-~ра mod /z 5743 - 15740 - - 8707 16923 1349 1583
3. Результат
Значение р после обратного преобразования:
р = р х 1 = pr~l mod/z = 1583г-1 mod/z = 4445.
Подробное исследование временной сложности преобразования
Монтгомери с учетом различного рода оптимизаций можно найти в
работе [Boss]. Мы обещали читателю 10-20%-ный выигрыш в ско-
рости от использования преобразования Монтгомери по сравнению
с традиционным возведением в степень. Приложение D, в котором
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень 135
приведены типичные оценки времени для функций на FLINT/C,
полностью подтверждает наши обещания. Мы ограничились случа-
ем возведения в степень по нечетному модулю. Тем не менее, для
многих прикладных задач, например, при зашифровании и рас-
шифровании, а также при вычислении цифровой подписи по алго-
ритму RSA (см. главу 16) можно воспользоваться функциями
mexp5mj() и mexpkmj().
Подведем итоги. В нашем распоряжении несколько функций мо-
дульного возведения в степень. Сведем их в таблицу 6.5 с учетом
особенностей и возможных областей применения.
Таблииа 6.5. Функция Область применения
функции возведения в степень в пакете FLINT/C mexp5J() Обшее 25-арное возведение в степень; не использует динамическое распределение памяти; значительные требования к стеку.
р mexpkJO Обшее 2к-арное возведение в степень, где значение к оптимально для чисел типа CLINT; использует динамическое распределение памяти; незначительные требования к стеку.
') • mexp5mJ0 25-арное возведение в степень по Монтгомери для нечетного модуля; не использует динамическое распределение памяти; значительные требования к стеку.
mexpkmJO 2^-арное возведение в степень по Монтгомери для нечетного модуля, где значение к оптимально для чисел типа CLINT длиной до 4096 двоичных разрядов; использует динамическое распределение памяти; незначительные требования к стеку.
umexpJO Смешанное бинарное возведение в степень для основания типа CLINT, показателя типа USHORT; незначительные требования к стеку.
umexpmJO Смешанное бинарное возведение в степень с исполь- зованием преобразования Монтгомери для основания типа CLINT, показателя типа USHORT и только для нечетного модуля; незначительные требования к стеку.
wmexpJO Смешанное бинарное возведение в степень для основания типа USHORT, показателя типа CLINT; незначительные требования к стеку.
wmexpmJO Смешанное бинарное возведение в степень с использованием возведения в квадрат по Монтгомери для основания типа USHORT, показателя типа CLINT и нечетного модуля; незначительные требования к стеку.
mexp2J() Смешанное возведение в степень с показателем вида 2е; незначительные требования к стеку.
136
Криптография на Си и C++ в действии
6.5. Криптографические приложения
модульного возведения в степень
На протяжении этой главы мы славно поработали над модульным
возведением в степень. Пора бы остановиться и спросить себя: а
для чего оно нужно в криптографии? Первое, что приходит в голову,
это, несомненно, вычисления в криптосистеме RSA, где показате-
: лями степени при зашифровании и расшифровании являются, соот-
ветственно, открытый и секретный ключи. Но пусть читатель набе-
рется немного терпения, поскольку для изучения криптосистемы
RSA у нас в следующей главе припасено кое-что еще, так что от-
ложим разговор до главы 16.
Для самых нетерпеливых приводим два очень важных алгоритма, в
* которых нужно возводить в степень. Это протокол обмена ключами,
предложенный в 1976 году Мартином Е. Хеллманом (Martin Е.
Hellman) и Уитфилдом Диффи (Whitfield Diffie) [Diff], и его обоб-
щение - протокол шифрования с открытым ключом Тахира Эль-
u i > ’ . Гамаля (Taher ElGamal).
Протокол Диффи - Хеллмана стал прорывом в области крипто-
графии. Это первая в истории криптосистема с открытым ключом,
или, иначе, асимметричная криптосистема (см. главу 16). Спустя
vV’r ? два года Ривест (Rivest), Шамир (Shamir) и Адлеман (Adleman)
опубликовали процедуру RSA (см. работу [Rive]). Сегодня различ-
ные разновидности протокола Диффи-Хеллмана используются для
ь о распределения ключей в Интернете и в защищенных протоколах
безопасности IPSec, IPv6 и SSL, предназначенных для безопасной
передачи пакетов на уровне протоколов и для передачи данных на
прикладном уровне (например, при электронных платежах). Трудно
переоценить практическую значимость этого принципа распреде-
ления ключей.2
Два участника протокола Диффи-Хеллмана, назовем их, к примеру,
А и В, могут очень просто установить секретный сеансовый ключ,
который впоследствии может быть использован для зашифрования
передаваемых сообщений. Сначала А и В выбирают большое про-
стое число р и примитивный корень а по модулю р (мы еще вер-
немся к этому позже). Протокол Диффи-Хеллмана выглядит так.
Протокол IP Security (IPSec), разработанный Рабочей группой инженеров Internet (Internet Engi-
neering Task Force; IETF), представляет собой всесторонне защищенный протокол и является ча-
стью будущего Internert-протокола IPv6. При разработке учитывалась возможность использова-
ния этого протокола и в текущем IPv4. Протокол безопасных соединений Secure Socket Layer
(SSL) разработан компанией Netscape на основе протокола TCP, обеспечивает оконечный безо-
пасный обмен в приложениях HTTP, FTP и SMTP (обо всем этом см. [Stal], Главы 13 и 14).
j-ддВА 6. Все дороги ведут к... модульному возведению в степень 137
Протокол обмена ключами Диффи-Хеллмана
1. А выбирает произвольное число хь<р- 1 и отправляет В свой
открытый ключ уд := а А.
2. В выбирает произвольное число хв < р - 1 и отправляет А свой
открытый ключ ув := а в.
3. А вычисляет секретный ключ за := у*А mod р.
4. В вычисляет секретный ключ зв := ух* mod р.
Поскольку выполняется равенство
з. - У** = « ГвЛа = yfB = з„ mod р ,
после шага 4 у А и у В оказывается один и тот же сеансовый ключ.
Значения аир, как и значения за и зв, передаваемые на шагах 1 и 2,
могут быть несекретными. Безопасность этого протокола зависит
от сложности задачи дискретного логарифмирования в конечных
полях, а взлом криптосистемы эквивалентен задаче вычисления
значений ха и хв, зная значения уд и ув в 3 Утверждение о том,
что вычислить аху, зная ах и ау, в конечной циклической группе
(задача Диффи-Хеллмана) так же трудно, как вычислить дискрет-
ные логарифмы, и, следовательно, об эквивалентности этих задач,
общепринято, но не доказано.
Таким образом, чтобы гарантировать безопасность протокола,
нужно выбирать число р достаточно большим (не менее 1024 бит,
еще лучше 2048 и больше; см. таблицу 16.1). Кроме того, число
р - 1 должно иметь большой простой делитель, близкий к числу
(р- 1)/2, чтобы нельзя было применить специальные методы реше-
ния задачи дискретного логарифмирования (процедура выбора таких
простых чисел будет рассмотрена в главе 16, где мы поговорим о
генерации сильных простых чисел для криптосистемы RSA).
Достоинством протокола Диффи-Хеллмана является то, что сек-
ретные ключи можно вырабатывать по мере надобности и не нужно
хранить в течение длительного времени. Кроме того, для использо-
вания протокола не требуется никаких дополнительных элементов
для согласования параметров а и р. У этого протокола есть и недос-
татки, самый серьезный из которых - отсутствие доказательства
подлинности предаваемых параметров уд и ув. Это делает протокол
уязвимым по отношению к «человек посередине», когда наруши-
тель X перехватывает истинные открытые ключи уд и ув и заменяет
их своим поддельным ключом ух. В этом случае А и В вычисляют
«секретные» ключи з' .- у*А mod р и з' .- у* mod р , а X, в свою
3 О задаче дискретного логарифмирования см. работы [Schn], п. 11.6 и [Odly].
138
Криптография на Си и C++ в действии
очередь, вычисляет ключ s'k ухк = ах*х* = ах*х* = у** = s'k mod р и,
аналогично, ключ 5' . Теперь вместо одного протокола между А и
В получается два протокола: между X и А и между X и В. Таким об-
разом, нарушитель X может перехватить сообщение, переданное
участником А, дешифровать его и отправить участнику В поддель-
ное сообщение (то же в обратном направлении). Катастрофа заклю-
чается в том, что с точки зрения криптографии А и В даже не будут
подозревать о том, что произошло.
Для использования в Интернете были предложены различные вари-
анты и обобщения протокола Диффи-Хеллмана, в которых не-
сколько сглажены недостатки и одновременно сохранены достоин-
ства этого протокола. Какова бы ни была версия этого протокола,
всегда следует обеспечить возможность проверки подлинности
ключевой информации. Это можно сделать, например, так. Участ-
ники протокола подписывают цифровой подписью свои открытые
ключи и вместе с ключом посылают сертификат, выданный серти-
фицирующим органом (см. стр. 374, п. 16.3) с использованием про-
токола SSL. В протоколах IPSec и Ipv6 реализована сложная проце-
дура под названием ISAKMP/Oakley,4 в которой устранены все не-
достатки протокола Диффи-Хеллмана (подробности см. в работе
[Stal], стр. 422-423).
Определить примитивный корень по модулю р (иначе - первооб-
разную), то есть такое число а, множество степеней которого
a! mod р, i = 0, 1, ..., р - 2, совпадает с мультипликативной группой
= {1, ...,р- 1} (см. п. 10.2), можно следующим алгоритмом (см.
[Knut], п. 3.2.1.2, теорема С). Предполагается, что известно разло-
жение на простые множители числа р - 1 - порядка мультиплика-
тивной группы р -1 = рр ... р[к .
Вычисление примитивного корня по модулю р
1. Выбрать случайное целое число а из интервала [0, р - 1] и по-
ложить i <- 1.
2. Вычислить t <г- a{p^Pi mod р .
3. Если t = 1, то вернуться на шаг 1. Иначе положить i <— i + 1. При
i < k вернуться на шаг 2. При i > k результат: а.
Реализуем алгоритм в виде следующей функции.
|-ддВА 6. Все дороги ведут к... модульному возведению в степень
139
I——
функция: Генерация примитивного корня по модулю р (р > 2 и простое)
Синтаксис: int primrootj (CLINT aj, unsigned noofprimes, clint **primesj);
Вход: noofprimes (число различных простых делителей числа р - 1 - по- рядка мультипликативной группы) primesJ (вектор указателей на CLINT-объекты, сначала идет р - 1, а затем простые делителирь ..рк числа р-1 = р^ ...ркк , к = noofprimes)
Выход: а_1 (первообразный корень по модулю pj)
Возврат: E_CLINT_OK, если все в порядке -1, если число р - 1 нечетное и, следовательно, число р составное
int
primrootj (CLINT aj, unsigned int noofprimes, clint *primesj[])
ж. {
CLINT pj, tj, junkj;
ULONG i;
..0)1
'.«ж- if (ISODDJ- (primesJ[0]))
return -1;
primes J[0] содержит число p - 1, из которого мы получаем мо-
л / дуль в р_1:
cpyj (pj, primesJ[0]);
inc J (pj);
SETONE.L (aj);
do
{
inc J (aj);
140
Криптография на Си и C++ в действии
Искомый примитивный корень а - это натуральное число, боль-
шее либо равное 2, поэтому рассматриваем только такие числа.
Если а является полным квадратом, то оно не может быть перво-
образным корнем, поскольку тогда а(р1)/2 = 1 mod р и порядок
элемента а меньше, чем 0(р) = р -1. В этом случае увеличиваем
значение переменной aj. Проверка того, является ли aj полным
квадратом, выполняется с помошью функции issqrJO (см. п. 10.3).
if (issqrj (aj, t_l))
{
inc_l (aj);
}
Значение t <— a^p x^Pi mod p вычисляем в два этапа. Проверяем
все простые делители р; по очереди; используем возведение в
степень по Монтгомери. Найденный первообразный корень за-
писывается в а_1.
do
{
divj (primes_J[0], primesJ[i++], tj, junkj);
mexpkmj (aj, tj, tj, pj);
while ((i <= noofprimes) && !EQONE_L (t_l));
}
while (EQONEJ- (tJ));
return E_CLINT_OK;
}
Еще одним примером приложения, использующего возведение в
степень, является протокол шифрования Эль-Гамаля. Этот прото-
кол является обобщением протокола Диффи-Хеллмана, его стой-
кость также определяется сложностью задачи дискретного лога-
рифмирования, то есть взлом протокола эквивалентен решению за-
дачи Диффи-Хеллмана (см. стр. 137). С помощью протокола Эль-
Гамаля осуществляется управление ключами во всемирно известной
ГЛАВА 6. Все дороги ведут к... модульному возведению в степень 141
системе Pretty good privacy (PGP), разработанной Филом Циммер-
маном (Phil Zimmermann) и используемой для зашифрования и
подписи сообщений электронной почты и электронных документов
(см. [Stal], п. 12.1).
Л. Участник А выбирает открытый и соответствующий секретный
ключ следующим образом.
Генерация ключей для протокола Эль-Гамаля
1. Участник А выбирает большое простое число р такое, что число
р- 1 имеет большой простой делитель, близкий к (р - 1)/2
(см. стр. 363), и примитивный корень а из мультипликативной
группы Zp*, как указано выше (см. стр. 138).
2. Участник А выбирает случайное число х такое, что 1 < х < р - 1,
и вычисляет b := ах mod р с помощью алгоритма Монтгомери.
3. Открытым ключом участника А является тройка (р, а, соот-
ветствующим секретным ключом - тройка (р, а, х)А-
•‘НХ-
Теперь участник В с помощью тройки (р, а, Ь)а может зашифровать
сообщение Me {1, р- 1} и отправить его участнику А. Прото-
кол выглядит так.
я Протокол Эль-Гамаля шифрования с открытым ключом
1. Участник В выбирает случайное число у такое, что 1 < у < р - 1.
2. Участник В вычисляет а := ау mod р и
Р := Mix mod р = М(ахУ mod р.
3. Участник В отправляет участнику А шифрограмму С := (а, Р).
4. Участник А вычисляет из шифрограммы С открытый текст:
М = p/ocv mod р.
Рассмотренная процедура корректна, поскольку
— = д/-----= М mod р .
аЛ (ау)х (ах)у
Значение р/осЛ вычисляется как произведение РосГ1"* по модулю р.
Размер числа р должен быть не менее 1024 бит, в зависимости от
приложения (см. таблицу 16.1). Кроме того, при зашифровании
двух разных сообщений и М2 следует использовать разные слу-
чайные числа yi у2, поскольку в противном случае равенство
_ M,by = Мх
Р2 М2ЬУ “ М2
142
Криптография на Си и C++ в действии
позволяет из сообщения вычислить сообщение М2. При практи- ческой реализации этого протокола нужно учитывать, что шифро- грамма С в два раза длиннее, чем открытый текст М, то есть объем передаваемых данных здесь больше, чем в других протоколах.
•'•ХЭэ Протокол Эль-Гамаля в том виде, как он приведен здесь, обладает весьма любопытным недостатком, благодаря которому нарушитель может получить сведения об открытом тексте, располагая лишь незначительным объемом информации. Циклическая группа
on- V '< содержит подгруппу U := {дх| число х четное} порядка (р - 1)/2 (см. [Fisc], глава 1). Если, b = ах или ос = ау - элемент подгруппы U, то и аху - элемент подгруппы U. Если еще и шифртекст 0 является элементом подгруппы U, то М = тоже принадлежит подгруппе U. Аналогичное рассуждение справедливо и в том случае, если ни аху\ ни Р не лежат в подгруппе U. В двух оставшихся случаях, - ко- гда в лишь один из элементов аху и Р не лежит в U, - открытый
ОЭ ’ текст М также не лежит в U. Распознать эту ситуацию позволяет следующий критерий: 1. аху g U <=> (ах g U или ау е U). Эту ситуацию, как и то, лежит ли Р
в U,можно проверить так: 2. Для любого и е включение ие U выполняется тогда и только тогда, когда = 1.
ЖН Насколько же серьезно то, что нарушитель получит такую инфор-
- Ц >v 'г г мацию о сообщении Л7? С точки зрения криптографии это совер- шенно неприемлемо, поскольку в этом случае множество сообще- ний, по которому ведется перебор, легко сокращается вдвое. На практике допустимость такой ситуации определяется приложением. Отсюда становится понятно, почему не стоит скупиться при выборе
} длины ключа.
C'VQM VI Можно предпринять еще некоторые шаги по устранению указанного недостатка, если не бояться внести новые и неизвестные. На шаге 2 умножение Mb? mod р можно заменить зашифрованием V(H(axy), М) с помощью подходящего симметричного алгоритма V (это может быть тройной DES, IDEA или новый стандарт шифрования AES; см. главу 19) и хэш-функции Н (см. стр. 373), сжимающей значение аху до размера ключа в алгоритме V. 1 ' Разумеется, это далеко не все приложения, в которых может исполь- зоваться модульное возведение в степень. В теории чисел (а значит, и в криптографии) это стандартная операция, и с ней мы еще не раз встретимся в дальнейшем, особенно в главах 10 и 16. Множество прикладных примеров можно найти в работе [Schr] и, конечно, в энциклопедических трудах [Schn] и [MOV].
Г Л А В A 7.
Поразрядные и логические функции
- ... совсем наоборот, - подхватил Труляля. -
Если бы это было так, это бы ещё ничего, а
если бы ничего, оно бы так и было, но так
как это не так, так оно и не этак. Такова ло-
гика вещей.
Льюис Кэрролл,
Алиса в Зазеркалье,
(Перевод с английского Н. Демуровой)
В этой главе мы представим функции, реализующие поразрядные
операции над CLINT-объектами, а также познакомимся поближе с
функциями, которыми мы уже отчасти пользовались - для опреде-
ления равенства и размера CLINT-объектов.
К поразрядным функциям относятся и операции сдвига, которые
сдвигают CLINT-аргумент в двоичном представлении, изменяя по-
зиции отдельных битов, и некоторые другие функции от двух
CLINT-аргументов, дающие возможность непосредственно работать
с двоичным представлением CLINT-объектов. То, как эти функции
можно применить в арифметических целях, наиболее наглядно по-
казывают операции сдвига, описываемые ниже. Мы также видели в
п. 4.3, как можно использовать поразрядную операцию AND для
приведения по модулю, равному степени двойки.
7.1. Операции сдвига
Всем движет необходимость.
Франсуа Рабле
Самый простой способ умножить число а, представленное по осно-
ванию В в виде а = (ап-1ап.2...а0)в, на Ве ~ это сдвинуть а влево на е
разрядов. Для двоичного представления это происходит точно так
же, как и для хорошо нам известной десятичной системы:
аВ — (ап+е-\ап+е.-2- •
где
^п+е-1 » ^п+е-2 &п-2’ • • •» 0, • • •, CIq 0.
Для В - 2 это соответствует умножению числа в двоичном пред-
ставлении на 2 для В = 10 - умножению на степень десяти в деся-
тичной системе.
144
Криптография на Си и C++ в действии
] 1 ’Ч 3 аналогичной процедуре для целочисленного деления на степень 3 разряды числа сдвигаются вправо: а . е \^п-1 • • •^п-е^п-е-\^п-е-2’ • *^0/Zb В
ще
L/-1 — ... — С1п~е — 0, С1п_е_\ — С1п-\, С1п_е_2 — йл_2, .. а0 — ае.
J Цля В = 2 это соответствует целочисленному делению числа в дво- е 4чном представлении на 2 , для других оснований получается ана- югичный результат.
] Гак как разряды CLINT-объектов в памяти представлены в двоич- ном виде, эти объекты можно легко умножать на степени двойки юсредством сдвига налево всех разрядов поочередно, при этом ос- гавшиеся справа пустые разряды заполняются нулями. Аналогичным образом CLINT-объекты можно делить на степени двойки, сдвигая каждый двоичный разряд вправо в сторону млад- лих разрядов. Оставшиеся в конце свободные разряды или запол- няются нулями, или игнорируются как ведущие нули. При этом на <аждом шаге (сдвиге на один разряд) самый младший разряд те- ряется. Преимущества этого процесса очевидны. Процедуры умножения и деления CLINT-объектов на 2 легко выполнимы и требуют не более 4"logBa"| операций сдвига, чтобы переместить каждую величину
j Л ' j ] гипа USHORT на один двоичный разряд. Умножение и деление на 5 использует только |~logBa"] операций для записи USHORT- зеличин.
( . W' J м * j НГО” ( ] ( 1 ( Цалее мы рассмотрим три функции. Функция shl_1() выполняет бы- строе умножение CLINT-числа на 2, а функция shrJQ выполняет де- 1ение CLINT-числа на 2 и возвращает целое частное. И, наконец, функция shiftJO умножает или делит число а типа е 3LINT на 2 . Вид выполняемой операции определяется знаком пока- зателя степени е, который передается функции в качестве аргумента. Если показатель положительный, выполняется умножение, если отрицательный - деление. Если е имеет представление е = В- k + /, ' < В, то функция shiftJO выполняет умножение или деление за 7 + 1) [~logBfl~] операций над USHORT-величинами.
] ( ( I I Зсе три функции выполняют вычисления над объектами типа 3LINT по модулю (Утах + 1)- Они реализованы как функции- сумматоры, то есть изменяют значение своих операндов, записывая з операнд результат вычислений. Функции проверяют наличие лереполнения и потери значимости. Однако при сдвигах потери d
рдДВА 7. Поразрядные и логические функции 145
значимости не возникает, так как если величина сдвига оказыва- ется больше количества разрядов, то в результате получается нуль. В этом случае значение состояния E_CLINT_UFL для потери значи- мости просто показывает, что было меньше сдвигов, чем требова- лось. Другими словами, степень двойки, выступающая в качестве делителя, оказалась больше, чем делимое, и поэтому частное рав- няется нулю. Три указанные функции реализованы следующим образом.
функция: Сдвиг влево (умножение на 2)
Синтаксис: int shlj (CLINT aj);
Вход: a J (множитель)
Выход: aj (произведение)
Возврат: E_CLINT_OK, если все в порядке
E_CLINT_OFL в случае переполнения int shlj (CLINT aj) г
1 t clint *ap_l, *msdptraj; ULONG carry = OL; int error = E_CLINT_OK; RMLDZRSJ. (aj); if (IdJ (aj) >= (USHORT)CLINTMAXBIT)
{ SETDIGITS.L (aj, CLINTMAXDIGIT); error = E_CLINT_OFL; } msdptraj = MSDPTRJ. (aj); for (apj = LSDPTR_L (aj); apj <= msdptraj; apj++) { *apj = (USHORT)(carry = ((ULONG)*apJ « 1) | (carry » BITPERDGT));
146
Криптография на Си и C++ в действии
if (carry » BITPERDGT)
{
if (DIGITS.L (aj) < CLINTMAXDIGIT)
{
*ap J = 1; SETDIGITSJ- (aj, DIG ITS J. (aj) + 1);
error = E_CLINT_OK;
}
else
I {
i error = E_CLINT_OFL;
}
L— } RMLDZRSJ. (aj);
return error; fl
}
Функция: Сдвиг вправо (целочисленное деление на 2)
Синтаксис: int shrj (CLINT a J);
Вход: aj (делимое)
Выход: a J (частное)
Возврат: E_CLINT_OK - если все в порядке E_CLINT_UFL - в случае потери значимости
int
shr_l (CLINT aj)
{
clint ‘apj;
USHORT help, carry = 0;
if (EQZ_L (aj))
return E_CLINT_UFL;
for (ap_l = MSDPTR_L (a_J); apj > aj; ap_l-)
j-ддВА 7. Поразрядные и логические функции 147
' HU { help = (USHORT)((USHORT)(*apJ » 1) | (USHORT)(carry « (BITPERDGT-1)));
-к carry = (USHORT)(*apJ & 1U); *apj = help; J
RMLDZRS.L (а_1);
return E_CLINT_OK;
Функция: Сдвиг влево/вправо (умножение/деление на степень двойки)
Синтаксис: int shift J (CLINT nJ, long int noofbits);
Вход: nJ (операнд), noofbits (показатель степени двойки)
Выход: nJ (произведение или частное, в зависимости от знака noofbits)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_UFL в случае потери значимости E_CLINT_OFL в случае переполнения
int
shift J (CLINT nJ, long int noofbits)
{
USHORT shorts = (USHORT)((ULONG)(noofbits < 0 ? -noofbits :
noofbits) / BITPERDGT);
USHORT bits = (USHORT)((ULONG)(noofbits < 0 ? -noofbits :
noofbits) % BITPERDGT);
long int resl;
USHORT i;
int error = E_CLINT_OK;
clint *nptrj;
clint *msdptrnj;
RMLDZRSJ. (nJ);
resl = (int) IdJ (nJ) + noofbits;
148 Криптография на Си и C++ в действии
П ; Если nJ == 0, нужно лишь правильно установить код ошибки и работа закончена. Аналогично для случая noofbits == 0:
if (*nj == 0) { return ((resl < 0) ? E_CLINT_UFL : E_CLINT_OK); 1 if (noofbits == 0) Я { . . 1 return E_CLINT_OK;
( 1 и Далее проверяется наличие переполнения или потери значимости. Затем, в зависимости от знака noofbits, выбирается сдвиг влево или вправо:
if ((resl < 0) || (resl > (long) CLINTMAXBIT)) 1 I error = ((resl < 0) ? EJDLINTJJFL : E_CLINT_OFL); /* Потеря значимости или переполнение?*/ Ц 1 if (noofbits < 0) {
Если noofbits < 0, тогда nJ делится на 2noofb,ts. Число сдвигаемых
разрядов в nJ ограничено DIGITSJ. (nJ). Сначала сдвигаются
целые разряды, а затем оставшиеся биты с помошью shrj():
shorts = MIN (DIGITSJ_ (nJ), shorts);
msdptrnj = MSDPTRJ- (nJ) - shorts;
for (nptrj = LSDPTFLL (nJ); nptrj <= msdptrnj; nptrj++)
рддВА 7. Поразрядные и логические функции
149
‘nptrj = ‘(nptrj + shorts);
SETDIGITSJ. (nJ, DIGITS J. (nJ) - (USHORT)shorts);
for (I = 0; I < bits; I++)
{
shrj (nJ);
}
}
else
' ' . "'I
\ /
i T
Если noofbits > 0, to n_l умножается на 2noofb,ts. Если число shorts
сдвигаемых разрядов больше, чем МАХВ, тогда результат равен
нулю. В противном случае сначала определяется и сохраняется
число разрядов нового значения и затем сдвигаются целые раз-
ряды, а освободившиеся разряды заполняются нулями. Чтобы
избежать переполнения, начальная позиция ограничивается
n_l + МАХВ и хранится в nptrj. Как и раньше, последние биты
сдвигаются по отдельности с помошью shl J():
if (shorts < CLINTMAXDIGIT)
{
SETDIGITS_L (nJ, MIN (DIGITS_L (nJ) + shorts,
CLINTMAXDIGIT));
nptrj = nJ + DIGITSJ_ (nJ);
msdptrnj = nJ + shorts;
while (nptrj > msdptrnj)
{
*nptrj = *(nptrj - shorts);
-nptrj;
}
while (nptrj > nJ)
{
150
Криптография на Си и C++ в действие
*nptr_l- = 0;
}
RMLDZRSJ. (nJ);
for (i = 0; i < bits; i++)
{
shlj (nJ);
}
}
else
{
SETZERCJL (nJ);
}
return error;
7.2. Все или ничего: битовые соотношения
Пакет FLINT/C содержит функции, позволяющие использовать
бинарные С-операторы &, |, Л и для типа CLINT. Однако прежде
чем рассмотреть программы, реализующие эти функции, хотелось
бы понять, что нам дает их реализация.
С математической точки зрения мы рассматриваем соотношения
обобщенных булевых функций /: {0,1}^ —» {0,1}, которые отобра-
жают набор из к чисел (хь ..., хк) 6 {0, 1 }* в 1 или в 0. Действие
булевых функций обычно представляется таблицей значений
(см. таблицу 7.1).
Таблииа 7.1.
Значения
булевых
функиий
X] х2 хк Лхъ хк)
0 0 0 0
1 0 0 1
0 1 0 0
1 1 1 1
рддВА 7; Поразрядные и логические функции
151
В случае битовых соотношений между CLINT-типами сначала бу-
дем рассматривать в качестве переменных вектора битов (хь ...»хл),
и формировать значения булевых функций последовательно. Таким
образом, мы имеем функции
/:{0, 1}"х{0, 1}л—>{0, 1}",
< / 1 1 к
которые отображают n-битовые переменные х1 :=(хр х2,..., хл) и
2 2 2
х2 := (%!> *„) в п-битовую переменную (хь хп) следующим
образом:
- 12
где/(хь х2) :=/л, xz). Полученный таким образом вектор (хь ..хп)
понимается в дальнейшем как число типа CLINT.
Решающее значение при выполнении функции f имеет описание час-
тичных функций f, которые определены в терминах булевой функ-
ции/. Булевы функции, реализуемые CLINT-функциями and_l(), ог_1()
и хог_1(), задаются следующим образом (см. таблицы 7.2 - 7.4).
Таблииа 7.2. Значения Ху Х2 fUi, х2)
0 0 0
CLINT-функиии
and_l() 0 1 0
1 0 0
1 1 1
Таблииа 7.3. Значения Ху х2 Лху, х2)
0 0 0
CLINT-функиии
orj()
0 1 1
1 0 1
1 1 1
Таблииа 7.4. Значения Ху х2 /Ixi, х2)
0 0 0
CLINT-функиии
xorj() 0 1 1
1 0 1
1 1 1
152 Криптография на Си и C++ в действии
: ' ?' 1 U4 ' Реализация этих булевых функций тремя С-функциями andjQ or_l() и хог_1() происходит не поразрядно, а посредством обработку разрядов CLINT-переменных стандартными С-операторами &, | и а Каждая из этих функций допускает три аргумента типа CLINT, при. чем первые два являются операндами, а последний - результирую- щей переменной.
Функция: Реализация поразрядного AND
Синтаксис: void and J (CLINT aj, CLINT bj, CLINT cj);
Вход: a J, b_l (обрабатываемые аргументы)
Выход: cJ (результат операции AND) void andj (CLINT a_l, CLINT bj, CLINT c_l) 1 1 CLINT dj; I clint *rj, *s_l, *tj; R clint *lastptr_l;
- ’ о ь Вначале указатели r_l и s_l устанавливаются на соответствующие разряды аргументов. Если аргументы имеют разное количество разрядов, то s_l указывает на аргумент меньшей длины. Указатель msdptraj - на последний разряд этого аргумента. if (DIGITS.L (а_1) < DIGITS.L (bj)) { rj = LSDPTR.L (bj); sj = LSDPTR.L (aj);
lastptrj = MSDPTR.L (a J); } else { 1 rj = LSDPTFLL (a_l); ; | s_l = LSDPTFLL (bj); i ; lastptrj = MSDPTFLL (bj); b
В A 7. Поразрядные и логические функции
153
Теперь указателю tj ссылается на значение первого разряда ре-
зультата, а максимальная длина результата хранится в dJ[O]:
tj = LSDPTRJ- (dj);
SETDIGITS_L (dj, DIGITS.L (sj - 1));
Сама операция выполняется в следующем цикле над разрядами
к 1 аргумента меньшей длины. При этом результат не может иметь
большее количество разрядов.
while (sj <= lastptrj)
{
*tj++ = *rj++ & *sj++;
}
После того как результат переписывается в с_1 (ведушие нули при
этом отбрасываются), функция заканчивает работу.
cpyj (сJ, dj);
}
Функция: Реализация поразрядного OR
Синтаксис: void orj (CLINT aj, CLINT bj, CLINT cj);
Вход: aj, bj (обрабатываемые аргументы)
Выход: cj (результат операции OR)
void
orj (CLINT aj, CLINT bj, CLINT cj)
{
CLINT dj;
clint *rj, *sj, *tj;
clint *msdptrrj;
clint *msdptrsj;
154
Криптография на Си и C++ в действие
Указатели rj и s_l задаются так же, как и выше.
if (DIGITS.L (aj) < DIGITSJ- (bJ))
rj = LSDPTR.L (bj);
sj = LSDPTFLL (aj);
msdptrrj = MSDPTRJ. (bj);
msdptrsj = MSDPTR.L (aJ);
}
else
{
rj = LSDPTR.L (aj);
sj = LSDPTR.L (bj);
msdptrrj = MSDPTRJ. (aj);
msdptrsj = MSDPTRJ. (bj);
tj = LSDPTR.L (dj);
SETDIGITS.L (dj, DIGITS.L (rj - 1 ));
Сама операция происходит в цикле над разрядами аргумента
меньшей длины:
while (sj <= msdptrsj)
{
*t_l++ = *r_l++ | *s_l++;
}
Далее берутся остающиеся разряды аргумента большей длины.
После того как результат переписывается в с_1 (с отбрасыванием
начальных нулей), функция завершает работу:
while (rj <= msdptrrj)
7. Поразрядные и логические функнии 155
1 { *tj++ = *г_1++;
} cpyj (cj, dj); }
функция: Реализация поразрядного исключающего OR (XOR)
Синтаксис: void xorj (CLINT aj, CLINT bj, CLINT cj);
Вход: aj, bj (обрабатываемые аргументы)
Выход: cJ (результат операции XOR)
void xorj (CLINT aj, CLINT bj, CLINT cj) { CLINT dj; clint *rj, *sj, *tj; clint *msdptrrj; clint *msdptrs_l;
if (DIGITS_L (aj) < DIGITS_L (bj)) { rj = LSDPTFLL (bj); sj = LSDPTFLL (aj); msdptrrj = MSDPTFLL (bj); msdptrsj = MSDPTFLL (aj); } else
{ rj = LSDPTR J. (a_l); sj = LSDPTFLL (bj); msdptrrj = MSDPTFLL (aj); msdptrsj = MSDPTFLL (bj); } tj = LSDPTFLL (dj); SETDIGITSJ_ (dj, DIGITS_L (rj - 1));
156
w
Криптография на Си и C++ в действци
Теперь выполняется непосредственно операция. Данный никл
обрабатывает разряды аргумента меньшей длины.
while (s_l <= msdptrsj)
{
*tj++ = *r_l++ л *sj++;
}
Оставшиеся разряды другого аргумента переписываются, как ука-
зано выше:
while (r_l <= msdptrrj)
{
*t_l++ = *rj++;
}
cpyj (c_l, dj);
}
Функцию andJO можно использовать для приведения числа а по мо-
дулю степени двойки 2^, задавая CLINT-переменной а_1 значение а,
CLINT-переменной bj значение 2^ - 1 и вычисляя andj (aj, b_l, cj).
Однако эту операцию можно выполнить быстрее с помощью соз-
данной для этой цели функции mod2J(), в которой учитывается тот
факт, что двоичное представление числа 2^ - 1 состоит исключи-
тельно из единиц (см. п. 4.3).
7.3. Прямой доступ к отдельным двоичным разрядам
В некоторых случаях оказывается полезной возможность обра-
щаться непосредственно к отдельным двоичным разрядам для того,
чтобы прочитать или изменить их. В качестве примера можно упо-
мянуть присваивание CLINT-объекту значения степени 2, которое
легко осуществляется заданием значения одного бита.
Далее мы подробно рассмотрим три функции, setbitJ(), testbit_J() 11
clearbit_l(), которые соответственно задают, проверяют и удаляют
значение отдельного бита. Функции setbit_J() и clearbit_l() возвра-
щают состояние указанного бита до выполнения операции. Пози-
ции битов отсчитываются от 0, и заданную позицию можно пред-
рддВА 7. Поразрядные и логические функции 157
ставить как логарифм степени двойки: если nJ равно 0, то setbitj
(nJ, 0) возвращает значение 0 и после выполнения операции nJ
о
имеет значение 2=1. После обращения к функции setbitJ(nJ, 512)
512
nJ принимает значение 2 .
функция: Проверка и задание значения бита в CLINT-объекте
Синтаксис: int setbitj (CLINT aj, unsigned int pos);
Вход: a J (C LI NT-аргумент), pos (позиция бита, считая от 0)
Выход: aJ (результат)
Возврат: 1 - если значение бита в позиции pos уже было задано 0 - если значение бита в позиции pos не было задано E_CLINT_OFL - в случае переполнения
int
setbitj (CLINT aj, unsigned int pos)
{
int res = 0;
unsigned int i;
USHORT shorts = (USHORT)(pos » LDBITPERDGT);
USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1));
USHORT m = 1U« bitpos;
if (pos > CLINTMAXBIT)
{
return E_CLINT_OFL;
}
if (shorts >= DIGITSJ. (aJ))
{
( | При необходимости a J заполняется нулями пословно, и новая
А длина сохраняется в a J[OJ:
for (i = DIGITSJ. (aj) + 1;i <= shorts + 1; i++)
{
aJ[i] = 0;
158 _____________________________________Криптография на Си и C++ в действии
} SETDIGITS_L (a_l, shorts + 1); }
Разряд числа а_1, содержащий позицию указанного бита, прове- ряется посредством наложения заранее заданной маски т, и
t( / w после этого бит принимает единичное значение сложением OR соответствующего разряда с т. По окончании работы функция возврашает предыдущее значение бита. if (aj[shorts + 1] & m) (
i res = 1; aj[shorts + 1] |= m; return res; }
Функция: Проверка двоичного разряда CLINT-объекта
Синтаксис: int testbitj (CLINT aj, unsigned int pos);
Вход: aj (CLINT-аргумент), pos (позиция бита, считая от 0)
Выход: 1 - если значение бита в позиции pos задано О-в противном случае int testbitj (CLINT aj, unsigned int pos)
-w { int res = 0;
USHORT shorts = (USHORT)(pos » LDBITPERDGT);
USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1)); if (shorts < DIGITSJ_ (aj)) I { 1 if (aj[shorts + 1] & (USHORT)(1 U « bitpos)) 1 res = 1; 1 } 1
рЛАВА 7- Поразрядные и логические функции 159
return res;
функция: Проверка и обнуление бита CLINT-объекта
Синтаксис: int clearbitj (CLINT aj, unsigned int pos);
Вход: aj (CLINT-аргумент), pos (позиция бита, считая от 0)
Выход: aJ (результат)
Возврат: 1— если значение бита в позиции pos было задано до удаления О-в противном случае
int
clearbitj (CLINT aj, unsigned int pos)
{
int res = 0;
USHORT shorts = (USHORT)(pos » LDBITPERDGT);
USHORT bitpos = (USHORT)(pos & (BITPERDGT - 1));
USHORT m = 1U « bitpos;
if (shorts < DIGITS.L (aJ))
{
Если a_l имеет достаточное количество разрядов, то разряд числа
а_1, содержащий позицию указанного бита, проверяется посред-
ством наложения заранее заданной маски m и бит принимает ну-
левое значение с помощью операции AND соответствующего
разряда с т. По окончании работы функция возвращает преды-
дущее значение бита.
Ш** 4
if (a_l[shorts + 1] & m)
{
res = 1;
}
ajfshorts + 1] &= (USHORT)(~m);
RMLDZRSJ. (aJ);
}
return res;
160
Криптография на Си и C++ в действии
7.4. Операции сравнения
В каждой программе приходится проверять условия равенст*
ва/неравенства или соотношения величин арифметических пере*
менных. Это требование справедливо и при работе с CLINT*
объектами. Здесь мы тоже исходим из того, что программист не
обязан знать внутреннюю структуру СLINT-типа, и то, как соотно-
сятся друг с другом два CLINT-объекта, определяют специально
разработанные для этих целей функции.
Основная функция, осуществляющая сравнение, - это функция
cmp_l(). Она определяет, какое из соотношений выполняется для
двух CLINT-величин a.I и b.l - a.I < b_l, a_l == b.l или a_l > b_l.
С этой целью сначала сравнивается количество разрядов CLINT-
объектов, из которых предварительно исключаются ведущие нули.
Если количество разрядов операндов одинаково, тогда работа на-
чинается со сравнения старших разрядов. Как только обнаружива-
ется несовпадение, сравнение заканчивается.
Функция:
Синтаксис:
Вход:
Возврат:
Сравнение двух CLINT-объектов
int cmpj (CLINT aj, CLINT b.l);
a J, bj (аргументы)
-1 - если значение aj < значения bj
О - если значение a.I = значению b.l
1 - если значение а_1 > значения bJ
int
cmpj (CLINT a.I, CLINT b.l)
{
clint *msdptra_l, *msdptrb_l;
int la = DIGITS.L (a.I);
int lb = DIGITS.L (b.l);
Первый тест проверяет, не равны ли нулю длины (а, следовательно,
и значения) обоих аргументов. Затем исключаются ведущие нули
и делается попытка принять решение, исходя из числа разрядов:
if (la == 0 && lb == 0)
{
return 0;
7. Поразрядные и логические функции
161
while (а_1[1а] == 0 && 1а > 0)
{
--1а;
}
while (b J[lb] == 0 && lb > 0)
{
-lb;
}
if (la == 0 && lb == 0)
{
return 0;
}
if (la > lb)
{
return 1;
}
if (la < lb)
{
return -1;
}
Если операнды имеют одинаковое количество разрядов, то необ-
ходимо сравнить их значения. Сравнение начинается со старших
разрядов и происходит поразрядно вплоть до младших разрядов,
пока не обнаруживаются два неравных разряда:
msdptraj = a_l + la;
msdptrbj = b_l + lb;
while ((*msdptraj == *msdptrbj) && (msdptraj > aj))
{
msdptraj-;
msdptrbj-;
162
Криптография на Си и C++ в действии
Теперь сравниваем эти два разряда и делаем вывод. Функция при
этом возврашает соответствующее значение:
if (msdptraj == a_l)
return 0;
if (*msdptraj > *msdptrbj)
return 1;
else
return -1;
Если нас интересует равенство двух CLINT-величин, то применение
функции cmpj() влечет за собой выполнение излишних операций.
Для этого случая имеется более простой ее вариант, где отсутствует
сравнение размеров.
Функция: Сравнение двух CLINT-объектов
Синтаксис: int equj (CLINT aj, CLINT bj);
Вход: a J, bj (аргументы)
Возврат: 0 - если значение aj значению bj 1— если значение aj = значению bj
int
equj (CLINT aj, CLINT bj)
{
clint *msdptraj, *msdptrbj;
int la = DIGITSJ. (aj);
int lb = DIGITSJ- (bj);
if (la == 0 && lb == 0)
j-дДВА 7. Поразрядные и логические функции 1 53
{
return 1;
}
while (aJ[la] == 0 && la > 0)
J г „ {
--la;
?т"'Ч j
' ‘"6 while (b_l[lb] == 0 && lb > 0)
{
-lb;
}
if (la == 0 && lb == 0)
{
return 1;
if (la != lb)
{ .
return 0;
}
Л К}
msdptraj = aj + la;
msdptrbj = bj + lb;
while ((*msdptraj == *msdptrbj) && (msdptraj > aj))
{
msdptraj-;
msdptrbj-;
}
return (msdptraj > a J ? 0 : 1);
164
Криптография на Си и C++ в действий
-----------------------------------------------------------
Применение пользователем этих двух функций в непосредственном
виде легко приведет к многочисленным ошибкам. В частности,
смысл результатов функции cmpj() необходимо твердо запомнить,
или же придется их периодически освежать в памяти. В качестве
средства против ошибок было разработано множество макросов,
с помощью которых можно представить условия сравнения в более
удобном виде. (см. Приложение С, «Макросы с параметрами»).
Например, есть следующие макросы, в которых объекты а_1 и bj
приравниваются к их величинам:
GE_L (a_l, b J)
EQZ_L (a J)
возвращает 1, если а_1 >= Ь, и 0 - в противном
случае;
возвращает 1, если а_1 == 0, и 0, если а_1 > 0.
f Л AB A 8.
Операции ввода, вывода,
присваивания и преобразования
Теперь числа из двоичной системы в десятич-
ную преобразовывались автоматически... 881,
883, 887, 907... знакомые простые числа.
Карл Саган, Контакт
В начале этой главы рассмотрим самую простую и одновременно
самую важную функцию - присваивание. Для того чтобы присвоить
CLINT-объекту а_1 значение другого CLINT-объекта Ь_1, нам нужна
функция, которая копирует разряды Ь_1 в область памяти, отведен-
ную под а_1, то есть выполняет действие, которое мы будем назы-
вать поэлементным присваиванием. Нельзя обойтись простым ко-
пированием адреса объекта bj в переменную а_1, так как в этом
случае оба объекта будут ссылаться на одну и ту же ячейку памяти,
а именно на ячейку bj, и любое изменение в aj будет отражаться
на объекте bj и наоборот. К тому же доступ к области памяти, на
которую ссылается а_1, может оказаться потерянным.
Мы вернемся к проблеме поэлементного присваивания во второй
части этой книги, когда коснемся вопроса реализации оператора
присваивания «=» в языке C++ (см. п. 13.3).
Присваивание значения одного CLINT-объекта другому выполняется
функцией сру_1():
Функция: Копирование CLINT-объекта как операция присваивания
Синтаксис: void cpyj (CLINT destj, CLINT srcj);
Вход: srcj (присваиваемое значение)
Выход: destj (объект назначения)
void
cpyj (CLINT destj, CLINT srcj)
{
clint * *lastsrcj = MSDPTFLL (srcj);
*destj = *srcj;
На следующем шаге находятся ведушие нули, которые потом от-
брасываются. Одновременно устанавливается количество разря-
дов в выходном объекте.
Криптография на Си и C++ в действии
166
while ((*lastsrcj » 0) && (*destj > 0))
-lastsrcj;
-*dest_l;
Теперь значимые разряды исходного объекта копируются в объ-
ект назначения. После этого функция заканчивает работу:
while (srcj < lastsrcj)
{
*++destJ = *++srcJ;
} - ' ;
) / <
Обмен значениями двух CLINT-объектов осуществляется с помо-
щью макроса SWAP_L (FLINT/C-варианта макроса SWAP), который
весьма интересным способом выполняет эту задачу посредством
операций XOR, не вводя временные переменные для промежуточ-
ного хранения:
#define SWAP(a, b) ((а)Л=(Ь), (Ь)Л=(а), (а)Л=(Ь))
#define SWAP J_(aJ, bJ) \
(xorj((aj), (bj), (aj)),\
xorj((bj), (aj), (bj)),\
xorj((aj), (bj), (aj)))
Недостатком этих макросов является то, что если их входные аргу-
менты являются некоторыми выражениями, то могут возникать
побочные эффекты их повторного вычисления и отсюда труднооб-
наружимые ошибки. Для SWAP_L это не так критично, так как эта
функция может работать только с указателями на CLINT-объекты, и
любое выражение при вызове этой функции все равно должно быть
преобразовано в такой указатель. В необходимых случаях вместо
макроса можно использовать функцию fswapJQ.
Функция: Перестановка значений двух CLINT-объектов
Синтаксис: void fswapj (CLINT aj, CLINT bj);
Вход: aj, bj (переставляемые значения)
Выход: a J, bj
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования 167
Хотя функции библиотеки FLINT/C для ввода и вывода чисел в дос-
тупном для понимания виде не принадлежат к числу поражающих
воображение, все же во многих приложениях без них не обойтись.
1 Из практических соображений вид этих функций выбирался таким
5 образом, чтобы ввод и вывод осуществлялся в виде строк символов
i (векторов типа char). Для этого были разработаны две по существу
। дополняющие друг друга функции str2clint_J() и xclint2str_1(): первая
преобразует строку цифр в CLINT-объект, а вторая, наоборот, пре-
образует CLINT-объект в строку. При этом задается основание для
представления строк, причем допускаются представления по осно-
ванию в интервале от 2 до 16.
Функция str2clintj() осуществляет преобразование представления
в объект типа CLINT из представления по заданному основанию.
Такое преобразование выполняется посредством последовательных
умножений и сложений по основанию В (см. [Knut], п. 4.4). Функ-
ция отмечает все случаи переполнений, использования недопусти-
мого основания и передачи пустых указателей и возвращает соот-
ветствующие коды ошибок. Любые префиксы, характеризующие
представление числа - «ОХ», «Ох», «ОВ» или «ОЬ» игнорируются:
Функция: Преобразование строки в CLINT-объект
Синтаксис: int str2clintJ (CLINT nJ, char *str, USHORT base);
Вход: str (указатель на последовательность типа char) base (основание числового представления строки, 2 < base < 16)
Выход: nJ (выходной CLINT-объект)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_BOR, если base < 2 или base > 16, или в str есть разряды, большие, чем base E_CLINT_OFL в случае переполнения E_CLINT_NPT, если в str передан пустой указатель
int
str2clintj (CLINT nJ, char *str, USHORT base)
{
clint baseJ[10]; y { . . J
USHORT n; /
int error = E_CLINT_OK; • |
" J
if (str == NULL)
{
168
Криптография на Си и C++ в действии
о return E_CLINT_NPT; ) if (2 > base || base > 16) { return E_CLINT_BOR; Г Ошибка: недопустимое основание */ } u2clint_l (base_l, base); SETZERO_L (nJ); if (*str == ’0‘) r
. «о ' t if ((tolowerj(‘(str+1)) == ’x') || (tolowerj(*(str+1)) == *b’)) !* Игнорировать любой префикс */ { ++str;
++str; }
: Rqo.q 4 i . } while (isxdigit ((int)*str) || isspace ((int)*str)) r
t if (iisspace ((int)*str)) { n = (USHORT)tolowerJ (*str); Многие реализации функции tolowerO из С-библиотек, несовмес-
Q wr тимых с ANSI, возврашают неопределенные результаты, если символ не является заглавным. FLINT/C-функция tolowerJO об- ращается к tolowerO только в случае заглавных A-Z, в противном случае возвращает символ неизмененным.
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования 169
switch (n) { case 'a':
. i •Г J case *b‘: case 'c': case 'd‘:
case ‘e’: case T: n -= (USHORT)Ca’ - 10); break; default:
n -= (USHORT)*0'; }
"*• - if (n >= base) { error = E_CLINT_BOR; break; }
V if ((error = mulj (nJ, basej, nJ)) != E_CLINT_OK) { break; } if ((error = uaddj (nJ, n, nJ)) != E_CLINT_OK) { break; .Г } } ++str; } return error;
170 Криптография на Си и C++ в действии
Функция xclint2strj(), обратная к функции str2clintj(), возвращает указатель на внутренний буфер класса памяти static (см. [Harb], п. 4.3), который сохраняет полученное численное представление и его значение до следующего вызова функции xclint2str() или до окончания работы программы. Функция xclint2strj() выполняет требуемое преобразование CLINT- представления в представление по заданному основанию путем
последовательных делений с остатком на основание В.
Функция: Преобразование CLINT-объекта в строку символов
Синтаксис: char * xclint2strj (CLINT nJ, USHORT base, int showbase);
Вход: nJ (преобразуемый CLINT-объект) base (основание численного представления искомой строки) showbase (значение Ф 0: численное представление имеет префикс «Ох» для base = 16 или «0Ь» для base = 2. Значение = 0: префикса нет).
Возврат: указатель на полученную строку символов, если все в порядке NULL - если 2 < base или base > 16 static char ntable[16] = {Ю717273,,,47576,,7,,,8,,'9,,,а,,,Ь,,,с*,,с1',‘е,,Т}; char * \ xclint2strj (CLINT nJ, USHORT base, int showbase) { CLINTD uj, rj; 1 clint baseJ[10]; | int i = 0; static char N[CLINTMAXBIT + 3]; if (2U > base || base > 16U) { return (char *)NULL; /* Ошибка: недопустимое основание 7
u2clintj (basej, base);
cpyj (uj, nJ);
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования 171
do
{
(void) div_l (uj, basej, uj, r_l);
if (GTZ_L (r_l))
N[i++] = (char) ntable[‘LSDPTR_L (r_l) & OxffJ;
}
else
"" {
N[i++] = 'O';
}
}
while (GTZ_L (uj));
if (showbase)
{
switch (base)
{
case2:
N[i-+-h] ='b';
N[i++] = ,°’;
break;
v.,. case 8.
N[i++] = '0';
t break;
case 16:
N[i++] = *x*;
N[i++] = '0';
break;
}
N[i] = '\0';
172 Криптография на Си и C++ в действии return strrevj (N); II } Для совместимости с функцией clint2strj() в первом издании книги clint2str_l (nJ, base) описывается как макрос, вызывающий функ- цию xclint2str(nj, base, 0). Кроме того, были разработаны макросы HEXSTR_L(), DECSTR_L(), OCTSTR_L() и BINSTR_L(), которые, используя в качестве аргумента переданный CLINT-объект, создают строку символов без префикса с численным представлением, заданным именем макроса. Таким об- разом, основание представления исключается из числа аргументов (см. приложение С). В качестве стандартной формы для вывода CLINT-значений мы располагаем готовым макросом DISP_L(), аргументами которого являются указатель на строку символов и CLINT-объект. Строка символов содержит, в зависимости от своего назначения, информа- цию о выводимом далее CLINT-значении, например, такую: «Произ- ведение aj и bj имеет значение...». CLINT-значение выводится в шестнадцатиричном формате, то есть по основанию 16. Дополни- тельно DISP_L() выводит с новой строки количество значимых дво- ичных разрядов (без учета начальных нулей) указанного CLINT- объекта (см. приложение С). В случае преобразования друг в друга байтовых векторов и СLINT- объектов можно применить пару функций byte2clintj() и clint2byte_l() (см. [IEEE], 5.5.1). Предполагается, что байтовые вектора осуще- ствляют численное представление по основанию 256 с возрастаю- щими справа налево значениями. Подробную реализацию этих функций читатель найдет в файле flint.c. Здесь мы приводим только их заголовки.
Функция: Преобразование байтового вектора в CLINT-объект
Синтаксис: int byte2clintJ (CLINT nJ, UCHAR *bytestr, int len);
Вход: bytestr (указатель на последовательность типа UCHAR) len (длина байтового вектора)
Выход: nJ (выходной CLINT-объект)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения E_CLINT__NPT, если в bytestr был передан пустой указатель
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования
173
функция: Преобразование CLINT-объекта в байтовый вектор
Синтаксис: UCHAR * clint2bytej (CLINT nJ, int *len);
Вход: nJ (преобразуемый CLINT-объект)
Выход: len (длина генерируемого байтового вектора)
Возврат: указатель на полученный байтовый вектор NULL, если в len передан пустой указатель
И наконец, для перевода значений типа unsigned в численный фор-
мат CLINT можно использовать две функции: u2clint_l() и ul2clintj().
Функция u2clintj() преобразует аргументы типа USHORT (а функция
ul2clintj() - аргументы типа ULONG) в численный формат CLINT.
Например, функция u2clintj() в дальнейшем будет описываться
следующим образом:
Функция: Преобразование значения типа ULONG в CLINT-объект
Синтаксис: void ul2clintJ (CLINT numj, ULONG ul);
Вход: ul (преобразуемое значение)
Выход: numj (выходной CLINT-объект)
void
ul2clintj (CLINT numj, ULONG ul)
{
*LSDPTR_L (numJ) = (USHORT)(ul & Oxffff);
*(LSDPTR_L (numJ) + 1) = (USHORT)((ul » 16) & Oxffff);
SETDIGITS J. (numj, 2);
RMLDZRSJ. (numj);
}
Завершая эту главу, рассмотрим функцию, которая выполняет про-
верку правильности числового формата CLINT-объекта. Контроль-
ные функции этого типа вызываются всякий раз, когда в систему
вводятся «чужеродные» величины для дальнейшей обработки в под-
системе. Такой подсистемой может оказаться, например, какой-
либо криптографический модуль, который перед каждой обработ-
кой входных данных должен проверить их допустимость. Динамиче-
ская проверка входных значений функции весьма полезна в практике
программирования, так как она позволяет избегать неопределённых
ситуаций и имеет решающее значение для стабильной работы при-
ложений. При тестировании и отладке эта проверка обычно проис-
ходит с помощью утверждений (assertions), проверяющих условия
174
Криптография на Си и C++ в действии
во время выполнения. Утверждения вставляются в программу как макросы, и при фактическом выполнении программы, обычно во время компиляции, их можно отключить посредством #define NDEBUG. В дополнение к макросу assert стандартной библиотеки языка С (см. [Plal], глава 1) имеется ещё несколько подобных реа- лизаций, которые выполняют различные действия в случае жестких условий тестирования, например, такие как распечатка обнаружен- ных исключительных ситуаций в файл регистрации, с завершением (или без завершения) работы программы при появлении ошибки. Подробную информацию по этому вопросу читатель может найти в [Magu], главы 2 и 3, а также в [Murp], глава 4.
• мик»м*мм>:>. »s ыамг i Защита функций из библиотеки программ (такой как пакет FLINT/C) от передачи значений, не входящих в область определения соответ- ствующих параметров, может происходить внутри или самих вызы- ваемых функций, или функций, их вызывающих. В последнем слу- чае вся ответственность возлагается на программиста, пользующе- гося этой библиотекой. Исходя из соображений эффективности, при разработке FLINT/C-функций мы не проверяли каждый пере- даваемый CLINT-аргумент на правильность адреса и на возмож- ность переполнения. Представив многократные проверки формата числа для тысяч операций модульного умножения или возведения в степень, автор решил переложить эту задачу на сами программы, использующие функции из FL1NT/C. Исключением является пере- дача делителей с нулевым значением. Здесь проверка имеет прин- ципиальное значение, и обнаружение нуля подтверждается сооб- щением о соответствующей ошибке во всех функциях, реализую- щих арифметику классов вычетов. Текст всех этих функций прове- рялся особенно тщательно, чтобы удостовериться, что библиотека FLINT/C генерирует только допустимые форматы (см. главу 12).
Для проверки правильности формата CLINT-аргументов была раз- работана функция vcheckj(). Она предназначена для защиты FLINT/C-функций от передачи недопустимых параметров в качестве CLINT-величин.
Функция: Проверка правильности числового формата CLINT-объекта
Синтаксис: int vcheckj (CLINT nJ);
Вход: nJ (проверяемый объект)
Возврат: E_VCHECK_OK - если формат правильный сообщение об ошибке в соответствии с таблицей 8.1
int
vcheckj (CLINT nJ)
unsigned int error = E_VCHECK_OK;
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования
175
Проверяем наличие нулевого указателя: самая ужасная из ошибок.
if (nJ == NULL)
{
error = E_VCHECK_MEM;
}
else
{
Проверяем наличие переполнения: не слишком ли много у числа
разрядов?
if (((unsigned int) DIGITSJ- (nJ)) > CLINTMAXDIGIT)
{
error = E_VCHECK_OFL;
}
else
{
---------------------------------------------------------1
Проверяем наличие ведущих нулей: с ними можно жить. |
if ((DIGITSJ. (nJ) > 0) && (nJ[DIGITS_L (nJ)] == 0))
{
error = E_VCHECK_LDZ;
}
}
return error;
176
Криптография на Си и C++ в действии
Возвращаемые функцией значения описаны как макросы в файле
flint.c. Их объяснение приводится в таблице 8.1.
Таблииа 8.1. Сообшения функиии vc heckJO о результатах проверки Возврашаемое значение Сообщение Интерпретация
E_VCHECK_OK Format is OK Число имеет допустимое представление, и его значение лежит в пределах CLINT-типа.
E_VCHECK_LDZ leading zeros Предупреждение: число обладает ведущими нулями, однако его величина лежит в допустимых пределах.
-м. . E_VCHECK_MEM memory error Ошибка: передан нулевой указатель
ъ --h ' E_VCHECK_OFL genuine overflow Ошибка: переданное число слишком большое; его нельзя представить как CLINT-объект.
Численные значения кодов ошибок меньше нуля, поэтому доста-
точно простого сравнения с нулем, чтобы отличить ошибки от пре-
дупреждений (или от допустимого случая).
.4ТНЖ
ste /ллшкж» <, -аг
рЛАВА 9.
Динамические регистры
- От глупости этой машины я впадаю в депрес-
сию, - сказал Марвин и поковылял прочь.
Дуглас Адамс,
Ресторан на краю Вселенной.
Кроме автоматических или, в исключительных случаях, глобаль-
ных CLINT-объектов, используемых до сих пор, иногда оказывается
полезным умение создавать и уничтожать CLINT-переменные авто-
матически. С этой целью разработаем несколько функций, которые
позволят нам генерировать, использовать, удалять и перемещать
совокупность CLINT-объектов - так называемый банк регистров -
как динамически распределенную структуру данных. Мы восполь-
зуемся схемой, представленной в [Skal], и приспособим её для ра-
боты с CLINT-объектами.
Будем разделять эти функции на закрытые функции управления и
открытые функции. Последние будут доступны другим внешним
функциям для работы с регистрами. Однако сами CLINT-функции
не используют эти регистры, так что полный контроль над исполь-
зованием регистров могут обеспечить функции пользователя.
При выполнении программы должно быть установлено число дос-
тупных регистров. Для этого нам требуется статическая переменная
NoofRegs, принимающая значение числа регистров, которое опре-
деляется встроенной константой NOOFREGS.
static USHORT NoofRegs = NOOFREGS;
Теперь определим центральную структуру данных для управления
банком регистров:
struct clint_registers
{
int noofregs;
int created;
clint **reg_l; /* указатель на вектор CLINT-адресов */
Структура clint_registers содержит: переменную noofregs, которая
описывает число регистров, помещенных в наш банк; переменную
created, которая указывает, выделена ли эта совокупность регист-
ров; указатель reg_l на вектор, содержащий начальные адреса от-
дельных регистров.
static struct clint_registers registers = {0, 0, 0};
178
Криптография на Си и C++ в действии
Теперь рассмотрим закрытые функции управления: allocate_regj()
чтобы создать банк регистров, и destroy_reg J() - чтобы уничтожить
его. Сначала создается область хранения адресов выделяемых реги-
стров и устанавливается указатель на переменную registers.regj.
После этого выделяется память для каждого отдельного регистра
посредством вызова malloc() из стандартной библиотеки языка С.
Тот факт, что CLINT-регистры являются единицами памяти, выде-
** ' ленными с помощью malloc(), играет важную роль при тестирова-
нии FLINT/C-функций. В п. 12.2 мы увидим, что благодаря этому
можно проверять память на наличие любых возможных ошибок,
я 7
static int
allocate_regj (void) Я
{ w
USHORT i, j;
Сначала выделяем память для вектора с адресами регистров.
if ((registers.regj = (clint **) malloc (sizeof(clint *) *
< NoofRegs)) == NULL)
return E_CLINT_MAL;
}
Теперь выделяем отдельные регистры. Если в процессе работы
вызов mallocO завершится ошибкой, все регистры, выделенные
до этого, очишаются и возврашается код ошибки E_CLINT_MAL:
for (i = 0; i < NoofRegs; i++)
{
if ((registers.reg J[i] = (clint *) malloc (CLINTMAXBYTE)) == NULL)
{
for (j = 0; j < i; j++)
{
free (registers.reg_J[j]);
}
return E__CLINT_MAL; /* ошибка: malloc */
}
fдАВА 9. Динамические регистры 179
}
return E_CLINT_OK;
)
Функция destroy_reg_l() по существу является противоположной
функции create_regj(). Сначала обнуляется содержимое регистров.
Затем память, выделенная под каждый регистр, возвращается с по-
мощью free(). Наконец, освобождается область памяти, на которую
указывал registers.regj.
static void
u destroy_regj (void)
• 1? > (
Г USHORT i;
4
- г- for (i = 0; i < registers.noofregs; i++)
;/ {
memset (registers.reg_l[i], 0, CLINTMAXBYTE);
wr free (registers.regJ[i]);
TC'{ }
4 и free (registers.regj);
’.30’1
Теперь рассмотрим общие функции для управления регистрами.
С помощью функции create_reg_J() образуем совокупность отдель-
ных регистров, число которых определяется константой NoofRegs.
Это осуществляется с помощью обращения к закрытой функции
allocate_reg_l().
Функция: ' Выделение совокупности регистров CLINT-типа
Синтаксис: " int create_regJ (void);
Возврат: E_CLINT_OK - если все в порядке
E CLINT MAL - в случае ошибки, связанной с malloc()
int
create_regj (void)
{
int error = E_CLINT_OK;
180
Криптография на Си и C++ в дей<
if (registers.created == 0) *. { error = allocate_reg_l (); registers.noofregs = NoofRegs; } if (lerror) { ++registers.created; ) return error; } Структура registers включает в себя переменную registers.created, которая используется для подсчета числа требуемых регистров. В результате вызова функции free_regj(), описанной ниже, получа- ем совокупность регистров, которые освобождаются только в том случае, если значение registers.created равно 1. В противном случае registers.created просто уменьшается на 1. Используя этот меха- низм, называемый семафором, мы предотвращаем ситуацию, когда совокупность регистров, выделенных одной функцией, может быть без всякого указания освобождена другой функцией. С другой сто- роны, каждая функция, которая запрашивает совокупность регист- ров, вызывая create_reg_l(), должна освобождать их посредством опять же free_reg_l(). Более того, нельзя допускать, чтобы после вы- зова функции регистры содержали конкретные значения. Переменную NoofRegs, определяющую число регистров, создаваемых функцией create_regj(), можно изменять посредством функции set_noofregs_J(). Однако это изменение остаётся действительным
только до тех пор, пока не будет освобождена текущая выделенная совокупность регистров и создана новая с помощью create_reg_J().
Функция: Задание числа регистров
Синтаксис: void set_noofregsj (unsigned int nregs);
Вход: nregs (число регистров в банке регистров) void set_noofregsj (unsigned int nregs)
ГДАВЙЙ- Динамические регистры____________________________________________181
NoofRegs = (USHORT)nregs; ) Теперь, когда мы умеем выделять совокупность регистров, можно задаться вопросом, как получить доступ к отдельным регистрам. Для этого необходимо выбрать динамически выделенное функцией create_regj() поле адреса regj в описанной выше структуре
clint_registers. Эта задача выполняется посредством функции get_regj(), представленной ниже, которая возвращает указатель на отдельный регистр из совокупности, при условии, что выделенный регистр обозначается определенным порядковым числом.
функция: Вывод указателя на регистр
Синтаксис: clint * get_reg_l (unsigned int reg);
Вход: reg (номер регистра)
Возврат: указатель на требуемый регистр reg, если он выделен NULL, если регистр не выделен clint * get_reg_l (unsigned int reg) /
•j'-h (j 1 if (’.registers.created || (reg >= registers.noofregs)) f
t return (clint *)NULL; } return registers.regj[reg];
} Так как размер совокупности регистров и её расположение в па-
мяти может измениться, то не рекомендуется сохранять уже счи- танные адреса регистров для использования их в дальнейшем. Намного предпочтительнее каждый раз заново получать адреса регистров. В файле flint.c можно найти несколько встроенных макросов вида #define rOJ get_reg_l(O); С помощью этих макросов можно вызывать регистры по их факти- ческим текущим адресам, не прибегая к дополнениям в тексте про- граммы. Используя функцию purge_reg_l(), можно очистить от- дельный регистр совокупности путём затирания его содержимого.
182 Криптография на Си и C++ в действии
” .
функция: Очистка CLINT-регистра из банка регистров с помощью заполнения его нулями
Синтаксис: int purge_reg_l (unsigned int reg); j j
Вход: reg (номер регистра)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_NOR, если регистр не выделен
int
purge_reg_l (unsigned int reg)
{
if (Iregisters.created || (reg >= registers.noofregs))
{
return E_CLINT_NOR;
}
memset (registers.regj[reg], 0, CLINTMAXBYTE);
return E_CLINT_OK;
}
Подобным же образом с помощью функции purgeall_reg_l() можно
очистить всю совокупность регистров.
Функция: Очистка всех CLINT-регистров с помощью записи в них нулей
Синтаксис: int purgeall_regj (void);
Возврат: E_CLINT_OK, если все в порядке
E CLINT NOR, если регистры не выделены
int
purgeall_reg_l (void)
{
USHORT i;
if (registers.created)
{
for (i = 0; i < registers.noofregs; i++)
{
memset (registers.regj[i], 0, CLINTMAXBYTE);
ГЛАВА 9. Динамические регистры 183
f?*- return E_CLINT_OK; } return E_CLINT_NOR; } В программировании считается хорошим стилем и проявлением профессиональной этики освобождать выделенную память, когда она больше не нужна. Имеющуюся в наличии совокупность регист- ров можно освободить с помощью функции free_reg_l(). Однако,
как мы уже объясняли выше, перед освобождением выделенной памяти семафор registers.created в структуре registers должен быть установлен в 1:
’94 < , t Г! Г ’ ' ’JKi .h* void free_regj (void) { if (registers.created == 1) { destroy_regj ();
' П.00 07
.nv он ж
' r!TR‘ if (registers.created) { -registers.created;
П } Теперь рассмотрим три функции, которые создают, очищают и ос- вобождают отдельные CLINT-регистры, по аналогии с управлением всей совокупностью регистров.
Функция: Выделение регистра CLINT-типа
Синтаксис: clint * createj (void);
Возврат: указатель на выделенный регистр, если все в порядке NULL в случае ошибки, связанной с malloc()
clint *
createj (void)
{
184 Криптография на Си и С+4* в действии
return (clint *) malloc (CLINTMAXBYTE); } При этом важно не «потерять» возвращаемый функцией createJQ указатель, так как иначе будет невозможно получить доступ к соз- данному регистру. Последовательность clint * do_not_overwritej; clint * lost I; 1 do_not_overwritej = createJO;
/* ... */ do_not_overwritej = lost J; выделяет регистр и хранит его адрес в переменной с соответст- вующим именем do_not_overwritej {не затирать). Если эта пере- менная содержит только ссылку на регистр, то после выполнения команды do_not_overwritej = lost J; регистр оказывается висячим (или потерянным, на него больше ничто не ссылается). Это типичная ошибка, которую можно допус- тить, блуждая «в дебрях» управления динамической памятью. Регистр, как и любую другую CLINT-переменную, можно очистить
с помощью представленной ниже функции purgeJO, посредством которой зарезервированная для указанного регистра память запол- няется нулями и таким образом очищается.
Функция: Очистка CLINT-объекта с помощью заполнения нулями
Синтаксис: void purgej (CLINT nJ);
Вход: nJ (CLINT-объект)
void
purgej (CLINT nJ)
{
if (NULL != nJ)
{
memset (nJ, 0, CLINTMAXBYTE);
|-дДВА 9. Динамические регистры
185
Следующая функция после очистки регистра к тому же освобождает выделенную для него память. После этого к регистру больше нельзя получить доступ.
функция: Очистка и освобождение CLINT-регистра
Синтаксис: void free_l (CLINT reg J);
Вход: regj (указатель на CLINT-регистр) void freej (CLINT reg_l) { if (NULL != regj) { memset (regj, 0, CLINTMAXBYTE); free (n_l); }
fjjABA 10.
Основные теоретико-числовые функции
Я ужасно хочу это услышать, поскольку я всегда
считал теорию чисел Королевой Математики -
самым чистым направлением математики -
единственным направлением, НЕ имеющим
прикладного значения!
Д.Р. Хофштадтер, Гедель, Эшер, Бах
Вооруженные целым арсеналом арифметических функций, разра-
ч ботанных в предыдущих главах, обратимся теперь к реализации не-
: ,J которых фундаментальных алгоритмов из теории чисел. Коллекция
* теоретико-числовых функций, которые нам предстоит обсудить, с
одной стороны, позволяет уяснить прикладные аспекты арифметики
больших чисел, а с другой стороны, является этапом на пути к более
; сложным теоретико-числовым вычислениям и криптографическим
*, приложениям. Рассматриваемые функции допускают сколь угодно
широкое обобщение, так что из них можно «собрать» вычислитель-
ный модуль почти для любого приложения.
Алгоритмы, на основе которых написаны программы, приведенные
в этой главе, взяты в основном из работ [Cohe], [HKW], [Knut],
пг [Kran] и [Rose]. Как и раньше, нас особенно интересует эффек-
та,. тивность и как можно более широкий спектр действия этих
алгоритмов.
* Что касается математической теории, то здесь мы приведем лишь
тот минимум, который необходим для уяснения представленных
функций и обоснования возможности их применения, - в конце
концов, можно и отдохнуть. Те же, кто ожидал более радикального
введения в теорию чисел, смогут найти его в книгах [Bund] и
[Rose]. Алгоритмические аспекты теории чисел ясно и кратко из-
ложены в работе [Cohe]. Информативный обзор теоретико-
числовых приложений дан в [Schr], а криптографические аспекты
теории чисел - в [КоЫ].
4 В этой главе, помимо всего прочего, мы рассмотрим способы вы-
числения наибольшего общего делителя и наименьшего общего
кратного больших чисел, мультипликативные свойства кольца
! классов вычетов, научимся распознавать квадратичные вычеты и
‘ извлекать квадратные корни в кольцах классов вычетов, научимся
ё применять китайскую теорему об остатках для решения систем ли-
I нейных сравнений и тестировать числа на простоту. Теоретические
' сведения будут подкреплены практическими примерами. Кроме
того, мы разработаем несколько функций, реализующих описанные
алгоритмы, и укажем приложения, в которых эти функции могут
быть полезны.
188 Криптография на Си и C++ в действии
----.
10.1. Наибольший обший делитель
То, что школьников учат использовать для вы-
числения наибольшего общего делителя двух
целых чисел метод разложения на простые
множители, а не более естественный способ -
алгоритм Евклида, - позор для нашей системы
образования.
. >. У. Хейс, П. Кватроччи,
Информация и теория кодирования, 19831
Наибольшим общим делителем (НОД) целых чисел а и b называ-
ется положительный делитель чисел а и Ь, делящийся на любой
другой общий делитель этих чисел. Таким образом, наибольший
общий делитель определен однозначно. В математических обозна-
чениях число d является наибольшим общим делителем двух не-
нулевых целых чисел а и b, d = НОД(«, Z?), если d > 0, d\a, d\b и
если для некоторого целого d' выполняются условия d' | а и d' | Ь,
< * то d' | d.
Это определение удобно дополнить, введя в рассмотрение случай
НОД(0, 0) := 0.
г.. Таким образом, мы определили наибольший общий делитель для
всех пар целых чисел, в частности, для всех чисел, представимых
CLINT-объектами. Выполняются следующие свойства:
г - .d (а) НОД(а, Ь) = НОД(Ь, а),
(10.1) (б) НОД(а, 0) = |а| (абсолютное значение числа а),
(в) НОД(а, Ь, с) = НОД(л, НОД(й с)),
(г) НОД(а, Ь) = НОД(-а, Ь),
из которых лишь первые три применимы к CLINT-объектам.
Сначала непременно следует рассмотреть классический алгоритм
л ‘ ' вычисления наибольшего общего делителя, которым мы обязаны
греческому математику Евклиду (III в. до н. э.) и который Д. Кнут
уважительно называет «дедушкой» всех алгоритмов (см. [Knut],
стр. 316 и далее). В основе алгоритма Евклида лежит повторное де-
ление с остатком: вычисляется вычет a mod b, затем b mod (a mod Й
и так далее, пока остаток не будет равен нулю.
1 Что удивительно, в России то же самое. - Прим, перев.
189
ГЛАВА 10» Основные теоретико-числовые функции
Алгоритм Евклида вычисления НОД(а, Ь) для а, b > О
А; 1. Если b = 0, то результат: а и алгоритм заканчивает работу.
НН . *1 Г. fX t 2. Положить г <— a mod b, а <— b, b <— г и вернуться на шаг 1. Для натуральных чисел а2 процесс вычисления наибольшего общего делителя по алгоритму Евклида выглядит так: = «2^1 + а3, 0 < я3 < а2, а2 = а3$2 + а4> 0 < Лд < Я3,
«з = a4q3 + а5, 0 < а5 < а4,
. Y£r-- * Г.С —у , •= О"’ Cltn-2 ^m-\Qm-2 < ^/п-Ь ^т-\ ~ Результат:
ЭР) ' ' Т НОД(яь а2) = ат.
п.*'- В качестве примера вычислим НОД(723, 288):
'W С ТЛ 723 = 288- 2+ 147, 288 = 147- 1 + 141, 147 = 141 • 1+6, 141=6- 23 + 3, 6 = 3- 2. Результат:
НОД(723, 288) = 3.
Эта процедура хороша как для вычисления вручную, так и для про- граммной реализации. Соответствующая программа короткая и бы- страя; кроме того, при ее написании трудно ошибиться. Следующие свойства целых чисел и наибольшего общего делителя открывают - по крайней мере теоретически - новые возможности для улучшения программной реализации алгоритма: (а) если числа а и b четные, то НОД(а, Ь) = НОД(а/2, Ь/2) • 2,
(Ю.2) (б) если а четное и b нечетное, то НОД(я, Ь) = НОД(а/2, Ь),
190
Криптография на Си и C++ в действии
(в) НОД(а, Ь) = НОД(л - Ь, Ь),
(г) если числа а и b нечетные, то а - b четное и |а - Ь\ < шах(а, Ъ).
Преимущество следующего алгоритма, опирающегося на эти свой*
ства, состоит в том, что в нем используются лишь операции срав-
нения длин, вычитания и сдвига CLINT-объектов, не требующие
особых временных затрат. Для их реализации у нас есть хорошие
функции; кроме того, здесь не нужно делить. Бинарный алгоритм
Евклида вычисления наибольшего общего делителя можно найти
также в книгах [Knut] (п. 4.5.2, Алгоритм В) и [Cohe] (п. 1.3, Алго-
ритм 1.3.5) почти в такой же форме.
Бинарный алгоритм Евклида вычисления НОД(а, Ь) для а, Ъ > О
1. Если а < Ь, то поменять местами а и Ь. Если b = 0, то результат:
а и алгоритм заканчивает работу. В противном случае положить
к<г-0 и, пока числа а и b оба четные, полагать к<г-к+1,
а <— л/2, b «— Z?/2. (Свойство (а) исчерпано; хотя бы одно из чи-
сел а и b стало нечетным.)
2. Пока а четное, повторять а <— а/2, пока а не станет нечетным.
Или, если b четное, повторять b <— /?/2, пока b не станет нечет-
ным. (Свойство (б) исчерпано; числа а и b теперь оба нечетные.)
3. Положить t <г- (а - Z?)/2. Если t = 0, то результат: 2ка и завершить
алгоритм. (Здесь мы использовали свойства (б), (в) и (г).)
4. Пока t четное, повторять t <—1/2, пока t не станет нечетным.
Если t > 0, то положить а <— f; иначе положить b <----t. Вер-
нуться на шаг 3.
Этот алгоритм легко превращается в программу. Воспользуемся
предложением Коха [Cohe] и выполним на шаге 1 дополнительное
деление с остатком, положив г <— a mod b, а <— b и b <— г. Тем
самым мы уравняли длины операндов а и Ь, поскольку различие в
размерах могло бы неблагоприятно сказаться на времени работы
программы.
Функция: Наибольший общий делитель
Синтаксис: void gcdj (CLINT aaj, CLINT bbj, CLINT ccj);
Вход: aaj, bbj (операнды)
Выход: ccj (наибольший общий делитель)
void
gcdj (CLINT aaj, CLINT bbj, CLINT ccj)
{
10. Основные теоретико-числовые функции
191
CLINT aj, b_l, г J, tj;
unsigned int k = 0;
int sign_of_t;
Шаг 1. Если аргументы не равны, то меньший аргумент записы-
вается в b_l. Если значение b_l равно 0, то наибольшим обшим
делителем будет а_1.
if (LT_L (aaj, bbj))
{
cpyj (aj, bbj);
cpyj (bj, aaj);
}
else
{
cpyj (aj, aaj);
cpyj (bj, bbj);
if (EQZ_L (bj))
{
cpyj (ccj, aj);
return;
Выполняем деление с остатком, «укорачивая» больший операнд
aj. Затем исключаем из aj и bj степени двойки.
(void) divj (aj, bj, tj, rj);
cpyj (aj, bj);
cpyj (bj, rj);
if (EQZ_L (bj))
{
cpyj (ccj, aj);
192 Криптография на Си и C++ в действии
return; } while (ISEVENJ. (aJ) && ISEVENJ- (bj)) I
' SV.. • t ++k;
„j..- • ’I--. shrj (aj); shrj (bj); }
Шаг 2.
while (ISEVENJ. (aj))
{
shrj (aJ);
}
while (ISEVENJ. (b_l))
(
shrj (bj);
}
Шаг 3. Здесь мы сравниваем aj и Ь_1 и учитываем, что разность
этих чисел может быть отрицательной. Абсолютную величину
разности записываем в tj, а знак разности - в целочисленную
переменную sign_ofJ. Как только tj == 0, алгоритм завершается.
do
{
if (GE_L (aj, bj))
{
subj (aj, bj, tj);
sign_ofJ = 1;
}
else
193
рдАВА 10. Основные теоретико-числовые функции
{
subj (bj, a J, tj);
sign_ofj = -1;
if (EQZ_L (tJ))
{
cpyj (ccj, aj); /* ccj <- a 7
shiftj (ccj, (long int) k);/* ccj <- ccj*2**k 7
return;
}
( ] Шаг 4. В зависимости от знака переменной tj записываем ее либо
\ в aj, либо в b_l.
while (ISEVENJ- (tj))
{
shrj (tj);
}
if (-1 == sign_of J)
{
cpyj (bj, tj);
}
else
{
cpyj (aj, tj);
}
}
while (1);
}
Все используемые здесь операции линейно зависят от числа разря-
дов операндов, однако тестирование показывает, что обычный ал-
горитм Евклида из двух строк (см. стр. 189), реализованный в виде
функции FLINT/C, значительно медленнее, чем только что рас-
смотренный вариант. Это странное явление мы можем объяснить
194
Криптография на Си и C++ в действии
' - лишь тем, что, во-первых, наша программа деления не слишком эффективна, а во-вторых, последняя версия алгоритма имеет не- сколько более сложную структуру. Вычисление наибольшего общего делителя для большего числа ар- гументов можно осуществлять путем многократного применения функции gcdj(), так как, согласно свойству (10.1, (в)), общий слу- чай рекурсивно сводится к случаю двух аргументов:
(10.3) НОД(пь .... пг) = НОД(пь НОД(п2,иг)).
Используя наибольший общий делитель, определим наименьшее общее кратное (НОК) двух CLINT-объектов aj и b_l. Наименьшим общим кратным ненулевых целых чисел иь ..., пг называется наи- меньший элемент множества {т е BN+ | и, делит ш, где i = 1, ..., г}. Это множество непусто, поскольку содержит по крайней мере про- изведение П;=1И1 • Наименьшее общее кратное двух чисел a, b е 7L
равно частному от деления абсолютной величины произведения на наибольший общий делитель:
(10.4) НОК(я, Ь) • НОД(я, b) = \ab\.
Воспользуемся этим соотношением для вычисления наименьшего общего кратного чисел aj и bj.
Функция: Наименьшее общее кратное (НОК)
Синтаксис: int IcmJ (CLINT aj, CLINT bj, CLINT cj);
Вход: a J, bj (операнды)
Выход: cj (наименьшее общее кратное)
Возврат: E_CLINT_OK, если все в порядке E_CLINT_OFL в случае переполнения
int
lcm_l (CLINT aj, CLINT bj, CLINT c_l)
{
CLINT gjjunkj;
if (EQZ_L (aj) || EQZ_L (b_l))
{
SETZERO_L (cj);
return E_CLINT_OK;
}
|-дДВА 10. Основные теоретико-числовые функции 195
gcdj (aj, bj, g_l); divj (aj, gj, gj, junkj); return (mulj (gj, bj, cj)); }
* 1 , ; СУ"' Случай вычисления наименьшего общего кратного для большего числа аргументов также можно рекурсивно свести к случаю двух аргументов:
(10.5) НОК(пь .... пг) = НОК(пь НОК(и2,пг)).
с'. П но формула (10.4) не может быть расширена на большее, чем 2, число аргументов, как видно из простейшего примера:
Г. НОК(2, 2, 2) • НОД(2, 2, 2) = 4 Ф 23. Тем не менее, соотношение ме- жду наибольшим общим делителем и наименьшим общим кратным можно обобщить на случай большего числа аргументов:
(10.6) НОК(а, Ь, с) НОД(аЬ, ас, be) = |aZ><?| И
(10.7) НОД(а, Ь, с) • НОКЖ ас, be) = \abc\ Интересная связь между наибольшим общим делителем и наи- меньшим общим кратным проявляется в следующих формулах, отражающих двойственность этих функций в том смысле, что, если поменять наибольший общий делитель и наименьшее общее крат- ное местами, формулы по-прежнему будут верны, как в случаях (10.6) и (10.7). Справедлив дистрибутивный закон:
(10.8) НОД(а, НОЖ с)) = НОК(НОД(я, Ь), НОД(я, с)),
(10.9) НОЖ НОД(6, с)) = НОД(НОЖ Ь), НОЖ с))> и, в довершение всего (см. [Schr], п. 2.4),
(10.10) НОЖ НОД(6, с)) = НОД(НОЖ Ь), НОЖ с)), Эти формулы не только завораживают своей симметрией, но и пре- красно подходят для тестирования функций, касающихся наи- большего общего делителя и наименьшего общего кратного, когда неявно тестируются и арифметические функции (о тестировании см. главу 12). Не вините тестировщиков в том, что они нахо-
дят ваши ошибки.
Стив Мэгью
196
Криптография на Си и C++ в действии
...................1 ... .. 1 11 ..................
10.2. Обращение в кольце классов вычетов
В отличие от множества целых чисел, в кольце классов вычетов
при определенных условиях можно находить мультипликативно
обратные элементы. Точнее, в кольце для элемента а е (во-
обще говоря, не для каждого) существует элемент xg такой,
что а • х = 1. Равенство для классов вычетов эквивалентно сравне-
нию а • х = 1 mod п или, иначе, равенству а • х mod п = 1. Например,
в кольце Zu элементы 3 и 5 мультипликативно обратны друг другу,
поскольку 15 mod 14 = 1.
Существование мультипликативно обратных элементов в кольце
не очевидно. В главе 5 (стр. 84) мы определили, что (Z„, •) является
лишь конечной коммутативной полугруппой с единицей 1. Доста-
точное условие того, чтобы для элемента ае 71п существовал
мультипликативно обратный, можно вывести из алгоритма Евклида.
Преобразуем предпоследнее равенство алгоритма (см. стр. 189)
^т-2 ~ 0 < Clm < ат_\, II
к виду
^т ~ & т-2 ^m-\Qm-2'
(1)
Продолжая в том же духе, получаем последовательно
О-т-Х ~ & т-3 ~~ ^т-2^т-3^ (2)
Я т-2 = &т-4 ~ (3)
а3 = ах -a2qi. (in -2)
Подставим в формулу (1) выражение для ат_\ из правой части фор-
мулы (2):
@т ~ & т-2 ~ Ят-1(^т-3 ~ Ят-3^т-2)
ИЛИ
&т = (1 + Ят-ЗЯт-2)^т-2 ~ Ят-2^т-3-
Продолжив выкладки, получим в формуле (ш-2) представление
числа ат в виде линейной комбинации начальных значений а\ и а*
коэффициентами при которых будут неполные частные qt из алго-
ритма Евклида.
Таким образом, получаем представление наибольшего общего де-
лителя g = НОД(я, Ь) = и- а + у- Ьв виде линейной комбинации чи-
сел а и b с целыми коэффициентами миг, причем и по модулю alg
и v по модулю b/g определены однозначно. Если же для элемента
a G 7Ln выполняется условие НОД(а, п) = 1 = и • а + v • п, то отсюда
рдДВА 10. Основные теоретико-числовые функции 197
сразу же следует 1 = и • a mod п или, что то же самое, а • и = 1.
В этом случае вычет и mod п определен однозначно и, следова-
тельно, и является обратным к а в кольце Попутно мы нашли
условие существования и вывели процедуру вычисления мультип-
ликативно обратного к элементу кольца 2Л. Рассмотрим пример.
Из проведенных ранее вычислений наибольшего общего делителя
НОД(723, 288) после переупорядочения получаем:
3 = 141-6- 23,
6=147-141- 1,
141 =288- 147- 1,
147 = 723-288- 2.
Отсюда получаем линейное представление наибольшего общего
делителя:
3= 141-23- (147- 141) = 24- 141-23- 147 =
= 24- (288 - 147) - 23 • 147 = -47- 147 + 24- 288 =
=-47- (723-2- 288) + 24 • 288 = -47- 723+ 118- 288.
Быстрая процедура поиска линейного представления наибольшего
общего делителя подразумевает вычисление и запоминание непол-
< ( ных частных (что мы только что и сделали) и восстановление с их
п помощью коэффициентов линейного представления. Эта процедура
., r v требует много памяти, а значит, непрактична. И вот перед нами ти-
ч г, личная задача, возникающая при разработке и реализации алгорит-
м мов: найти компромисс между требуемым временем вычисления и
объемом памяти. Для начала нам нужно так изменить алгоритм Евк-
лида, чтобы вычислять наибольший общий делитель и коэффици-
енты линейного представления одновременно. Как мы видели, для
a G 72-п существует обратный элемент хе если НОД(я, п) = 1.
Верно и обратное утверждение: если для элемента ае Д сущест-
1 т вует мультипликативно обратный, то НОД(л, и) = 1 (строгое дока-
1 г зательство этого утверждения см. в работе [Nive], доказательство
н теоремы 2.13). Отсюда становится понятно, почему так важен во-
прос об отсутствии общих делителей (о взаимной простоте) чисел:
подмножество 2Л* := { а е 2Л | НОД(я, п) = 1} кольца 2Л, состоящее
из элементов a g взаимно простых с и, с определенной на нем
операцией умножения является абелевой группой. В главе 5 мы
обозначили эту группу через (Д,*, •)• На группу (£л\ •) переносятся
все свойства абелевой полугруппы (^л, •) с единицей:
✓ ассоциативность,
✓ коммутативность,
✓ существование единицы: для любого a G выполняется а • 1 = а.
198 Криптография на Си и C++ в действиц
Условие существования мультипликативно обратного также вы-
полняется для всех элементов, поскольку именно такие элементы
мы и выбирали. Так что теперь нам осталось проверить лишь замк-
нутость по умножению, то есть что для любых элементов a, b
кольца 7Ln произведение а • Ъ тоже будет элементом кольца
Замкнутость доказывается легко: если элементы аиЬ взаимно про-
сты с и, то произведение ab не может иметь нетривиального общего
делителя с числом п, то есть произведение а • b должно принад-
лежать множеству 7L* • Группа (Z„*, •) называется группой классов
вычетов, взаимно простых с л2.Число элементов группы или,
что то же самое, число целых чисел из множества {1,2, ..., п - 1},
взаимно простых с н, определяется функцией Эйлера ф(л). Для чис-
ла и, представленного в виде произведения п = ррру ...р? различ-
ных простых чисел рь ..., ph где числа положительны, функция
Эйлера вычисляется как
Ф(п) = ПрГ1(р,-1)
/=1
(см., например, [Nive], пп. 2.1 и 2.4). Отсюда, в частности, следует,
s ж что если число р простое, то в группе ровно р - 1 элементов.3
Если НОД(д, /0=1, то согласно теореме Эйлера, которая, в свою оче-
редь, является обобщением малой теоремы Ферма, дф(л) = 1 mod и,
*’ так что, найдя значение дф(л)-1 mod п, тоже можно определить муль-
типликативно обратное кд.4 Например, если п = р • q, где числа р и
q простые, р* q и а е Zn*, то = 1 mod п и, следовательно,
вычет mod п является мультипликативно обратным к а по
модулю п. Однако для вычисления этим способом нужно даже в
лучшем случае знать значение <ф(/г), кроме того, сложность модуль-
ного возведения в степень равна <?(log3n).
Мы воспользуемся более практичным алгоритмом, который, во-
первых, имеет сложность <9(log2/i), а во-вторых, не требует знания
функции Эйлера. Для этого объединим приведенную выше проце-
дуру с алгоритмом Евклида. Рассмотрим две переменных и и v, для
которых следующий инвариант
д, = Ui • а + V/ • b, 11
2 Чаще эта группа называется мультипликативной группой кольца. - Прим, перев.
3 В этом случае Z/7 является полем, поскольку обе группы (Z/7, +) и (2Р*, •) = (Zp \ {0}, •) являются
абелевыми (см. [Nive], п. 2.11). Конечные поля используются, например, в теории кодирования, а
уж их роль в современной криптографии трудно переоценить.
4 Малая теорема Ферма утверждает, что если число р простое, то для любого целого а справедливо
ар = a mod р. Если а не делится на р, то ар~х = 1 mod р (см. [Bund], глава 2, §3.3). Малая теорема
Ферма и ее обобщение — теорема Эйлера — стоят в ряду наиболее важных теорем в теории чисел.
ГЛАВА 10. Основные теоретико-числовые функции 199
будет справедлив на каждом шаге процедуры, описанной на
стр. 189, где
ам = «/-i mod
По завершении алгоритма этот инвариант и даст нам коэффициенты
линейного представления наибольшего общего делителя чисел а и Ь.
Эта процедура называется расширенным алгоритмом Евклида.
Следующий алгоритм заимствован из книги [Cohe], п. 1.3, Алго-
ритм 1.3.6. Переменная v присутствует в нем неявно и вычисляется
лишь в конце алгоритма как v := (d - и • a)/b.
Расширенный алгоритм Евклида вычисления НОД(а, Ь)
и чисел и и v таких, что НОД(а, Ь) = и • а + v • b, для а, Ь > 0
1. Положить и <— 1, d <— а. Если b = 0, то положить у <— 0 и завер-
шить алгоритм; иначе положить vj <— 0 и v3 <— b.
2. Вычислить q и Z3 такие, что d = q • v3 + t3 и t3 < v3, поделив d с ос-
татком на v3. Положить t\ <— и - q • vb и <— vb d <— v3, Vi <— tx и
v3 <—t3.
3. Если v3 = 0, то положить v <— (d - и • d)lb и завершить алгоритм;
иначе вернуться на шаг 2.
Построим функцию xgcdJO с использованием вспомогательных
функций sadd() и ssub(), вычисляющих знаковое сложение и вычи-
тание (в исключительных случаях). Каждая из этих функций пред-
варительно определяет знак своего аргумента, а затем вызывает ба-
зовые функции add() и sub() (см. главу 5), выполняющие, соответ-
ственно, сложение и вычитание без учета переполнения или потери
значащих разрядов. Кроме того, на основе функции деления divj(),
определенной для натуральных чисел, создадим вспомогательную
функцию smod() для вычисления вычета a mod b, где a, b 6 Z и
b > 0. Эти вспомогательные функции еще пригодятся нам при по-
строении функции chinremJO, реализующей китайскую теорему об
остатках (см. п. 10.4.3). При возможном обобщении библиотеки
FLINT/C на целые числа этими функциями можно воспользоваться
для работы со знаковыми типами.
Порядок использования функции xgcdJO следующий: если оба ар-
гумента удовлетворяют условию а, Ь> Атах/2, то в значениях и и v,
возвращаемых функцией xgcdJO, может возникнуть переполнение.
Для разрешения подобных ситуаций следует запасти место для
этих значений, которые в этом случае будут объявлены вызы-
вающей программой как переменные типа CLINTD или CLINTQ
(см. главу 2).
200
Криптография на Си и C++ в действии
Функция: Синтаксис: Вход: Выход: Расширенный алгоритм Евклида вычисления линейного представ- ления НОД(а, Ь) = и • а + v • b для натуральных чисел а, b void xgcdj (CLINT aj, CLINT bj, CLINT gj, CLINT uj, int *sign_u, CLINT vj, int *sign_v); a J, bj (операнды) g_l (наибольший общий делитель чисел aj и bj) uj, vj (коэффициенты при a_J и bj в линейном представлении числа gj) *sign_u (знак коэффициента u J) *sign_v (знак коэффициента vj)
void
xgcdj (CLINT aj, CLINT bj, CLINT dj, CLINT uj, int *sign_u,
- ‘ Ы f' . . CLINT vj, int *sign_v) { CLINT v1 J, v3J, t1 J, t3J, qj;
CLINTD tmpj, tmpuj, tmpvj; int sign_v1, sign J1;
Г") Шаг 1. Задание начальных значений.
cpyj (d_l, а_1);
cpyj (v3J, bj);
if (EQZ_L (v3J))
{
SETONEJ- (uj);
SETZERO J- (vj);
*sign_u = 1;
*sign_v = 1;
return;
}
SETONEJ- (tmpuj);
*sign_u = 1;
10. Основные теоретико-числовые функции
SETZERO J. (v1_l);
sign_v1 = 1;
201
Шаг 2. Основной цикл; вычисление наибольшего обшего делителя
и коэффициента и.
while (GTZ_L (v3J))
{
divj (dj, v3J, qj, t3J);
mulj (v1 J, qj, qj);
signjl = ssub (tmpuj, *sign_u, qj, sign_v1, t1 J);
cpyj (tmpuj, v1 J);
*sign_u = sign_v1 ;
cpyj (dj, v3J);
cpyj (v1 J, t1 J);
sign_v1 = signjl;
cpyj (v3J, t3J);
}
Шаг 3. Вычисление коэффициента v и завершение процедуры.
mult (aj, tmpuj, tmpj);
*sign_v = ssub (dj, 1, tmpj, *sign_u, tmpj);
divj (tmpj, bj, tmpvj, tmpj);
cpyj (uj, tmpuj);
cpyj (vj, tmpvj);
return;
202
Криптография на Си и C++ в действии
Поскольку обработка отрицательных чисел в пакете FLINT/C тре-
бует дополнительных затрат, здесь нам полезно заметить, что для
вычисления мультипликативно обратного к классу вычетов а е %*
из линейного представления 1 = и • а + v • b нам нужен только
коэффициент и. Найдя для и соответствующий положительный
представитель, мы избавимся от необходимости оперировать с от-
рицательными числами. Следующий алгоритм представляет собой
вариант предыдущего, учитывает наше замечание и полностью ис-
ключает вычисление коэффициента v.
Расширенный алгоритм Евклида вычисления НОД(а, Ь)
и мультипликативно обратного к a mod п для а > 0, п > О
1. Положить и «— 1, g <— a, <— 0 и и v3 <— п.
2. Вычислить q и Г3 такие, что g = q • v3 + t3 и < v3, поделив d с ос-
татком на v3. Положить t\ <— и - q • Vi mod и, и <— vb g <— v3,
Vi <— ti и v3 <— Z3.
3. Если v3 = 0, то результат: g = НОД(я, b), элемент и мультиплика-
тивно обратный к a mod п и алгоритм завершен. Иначе вернуться
на шаг 2.
Шаг Ц <— и - q • vj mod п гарантирует, что числа vi и и будут неот-
рицательными. По окончании алгоритма получаем: и е {1, ..., п - 1}.
Реализуем этот алгоритм в виде следующей функции.
Функция: вычисление мультипликативно обратного в кольце ~ZLn
Синтаксис: void invj invJ(CLINT aj, CLINT nJ, CLINT gj,CLINT ij);
Вход: a J, nJ (операнды)
Выход: gj (наибольший общий делитель чисел aj и nJ)
ij (обратный элемент к aj mod nJ, если он существует)
void
invj (CLINT aj, CLINT nJ, CLINT gj, CLINT ij)
{
CLINT v1 J, v3J, t1 J, t3J, qj;
Проверка операндов на равенство нулю. Если хотя бы один из
операндов равен 0, то обратного элемента не существует, чего
нельзя сказать о наибольшем обшем делителе (см. стр. 188).
В этом случае результирующая переменная ij не определена и
полагается равной нулю.
рдДВА 10. Основные теоретико-числовые функции 203
if (EQZ_L (aJ))
if (EQZ_L (nJ))
-ле-ч {
SETZERO J. (gj);
SETZERO J. (ij);
return;
}
else
{
cpyj (gJ, nJ);
SETZERO J. (ij);
i. return;
}
}
else
{
if (EQZ_L (nJ))
cpyj (gj, aj);
pr SETZERO J. (i J);
return;
}
Шаг 1. Задание начальных значений.
cpyj (gj, aj);
cpyj (v3J, nJ);
SETZEROJ_ (v1 J);
SETONEJ- (t1J);
do
{
204
Криптография на Си и C++ в действии
Шаг 2. После деления осуществляем проверку в GTZ_L(t3j), что
позволяет избежать лишнего вызова функций mmuljО и msubJO
при последнем прохождении цикла. До окончания цикла пере-
менной i J ничего не присваиваем.
divj (gJ, v3J, qj, t3J);
if (GTZ_L (t3J))
{
mmulj (v1 J, qj, qj, nJ);
msubj (t1 J, qj, qj, nJ);
cpyj (t1 J, v1 J);
cpyj (v1 J, qj);
cpyj (gj, v3J);
cpyj (v3J, t3J);
}
}
while (GTZ_L (t3J));
Шаг 3. Выполняем последнее присваивание. В качестве наиболь-
шего общего делителя берем значение переменной v3j, и если
оно равно 1, то в качестве обратного к aj берем значение пере-
менной v1 I.
cpyj (gj, v3J);
if (EQONEJ. (gj))
cpyj (ij, v1 J);
''***' else
SETZEROJ- (ij);
ГЛАВА 10. Основные теоретико-числовые функции 205
10.3. Корни и логарифмы
В этом параграфе мы научимся вычислять целую часть квадратного корня и логарифмы по основанию 2 для объектов типа CLINT. Сна- чала рассмотрим вторую из этих функций, а затем с ее помощью будем вычислять первую: для натурального числа а будем искать число е такое, что Т < а < 2e+I. Число е = |_Iog2 a J есть целая часть
- логарифма числа а по основанию 2 и равно уменьшенному на 1 числу значащих битов числа а. Для этого используется функция ldj(), входящая в состав многих других функций пакета FLINT/C, которая игнорирует ведущие нули и считает только значащие дво- ичные разряды CLINT-объекта.
функция: Число значащих двоичных разрядов CLINT-объекта
Синтаксис: unsigned int IdJ (CLINT aj);
Вход: aj (операнд)
Выход: Число значащих двоичных разрядов числа aj
unsigned int
Ek IdJ (CLINT nJ) /
i unsigned int 1; USHORT test;
f "I .VI .4 ? М Шаг 1. Определяем число значащих разрядов в системе счисления | по основанию В.
* пш-
I = (unsigned int) DIGITS_L (nJ);
while (n J[l] == 0 && I > 0)
{
-i;
}
if (I == 0)
{
return 0;
}
206
Криптография на Си и C++ в действии
Шаг 2. Определяем число значащих битов в старшем разряде.
Константа BASEDIV2 - это число, имеющее единичный старший
бит и остальные нули (то есть 2BITPERDGT1).
test = nj[l];
I «= LDBITPERDGT;
while ((test & BASEDIV2) == 0)
test «= 1;
-I;
}
return I;
}
Теперь перейдем к вычислению целой части квадратного корня из
натурального числа. Воспользуемся классическим методом Ньюто-
на (называемым еще методом Ньютона-Рафсона), который обычно
применяется для определения нулей функции путем последова-
тельных приближений. Пусть функция Дх) дважды непрерывно
дифференцируема на интервале [а, Ь] так, что первая производная
f'(x) на этом интервале положительна и
max 1«Л] < 1
f'M2
Тогда, если хп е [а, Ь] - приближение к числу г, где/(г) = 0, то
значение xn+i := хп -ftxn)lf'(x^ будет к г ближе, чем хп. Последова-
тельность приближений хп сходится к г (см. [Endl], п. 7.3).
Если положить /(%) := х2 - с, где с > 0, то для х > 0 функция Дх)
будет удовлетворять условиям сходимости метода Ньютона, а по-
следовательность
х -х .. 1 .л+1‘ " /U) 2 с х„ + — Хг.
будет сходиться к Vc. Таким образом, получаем эффективную
процедуру для приближения квадратных корней рациональными
числами.
Нас интересует только целая часть г числа 4с , где г2 < с < (г + I)2,
а число с натуральное, поэтому при вычислении элемента последо-
вательности приближений ограничимся только целой его частью.
10. Основные теоретико-числовые функции
207
.we»'-- В качестве начального приближения выберем > 4с и будем про- должать до тех пор, пока для некоторого п не получим т,1+1 > хп, то- гда хп и будет искомым значением. Естественно выбрать начальное
приближение как можно ближе к 4с . Для значения с типа CLINT и
^3 , е := |_log2cJ получаем, что значение [2(с+2)/2 J всегда больше, чем
4с , то есть начальное приближение можно легко вычислить с по-
мощью функции Id_1(). А вот и алгоритм. Алгоритм вычисления целой части г квадратного корня из
’ * ’ натурального числа с > 0 1. Положить х <— [_2(f+2)/2 J, где е := llog2cJ. 2. Положить у е-|_(х + с/х)/2_|. 3. Если у < х, то положить х <— у и вернуться на шаг 2. Иначе ре- зультат: х и алгоритм завершен.
Доказательство корректности алгоритма не представляет труда. Зна-
чение х изменяется монотонно и всегда является натуральным чис- лом. Следовательно, алгоритм в конце концов остановится. По завер-
О •-ТЛ1Г шении гс ПpeдпoJ х2 > с иг Однако, у-х = что пре предпог Следую алгоритма пожим, чтс 1и, иначе, с (х + с/х) 2 ггиворечит южение не щая ф; будет ) х > г :-х2 < - х = уело] верно /нкция выполи + 1. Из; :0. с-х2 2х зию зав и х = г. [ КО| яться условие у = |_(х + с/х)/2_]> х . условия х > г + 1 > д/с следует, что <0, ершения алгоритма. Значит, наше эректно вычисляет значение
r h: „ у <-[_(х + с/х)/2_], используя целочисленное деление с остатком.
Функция: Целая часть квадратного корня из CLINT-объекта
Синтаксис: void irootj (CLINT nJ, CLINT floorj);
Вход: Выход: nJ (операнд > 0) floorj (целое число - квадратный корень из nJ)
void
irootj (CLINT nJ, CLINT floorj)
208
Криптография на Си и C++ в действии
CLINT xj.yj, rj;
unsigned I;
Используя функцию Id JO и оператор сдвига, полагаем I равным
L( Llog2(n_l)J + 2)/2J. Используя функцию setbitJO, полагаем у |
равным 2*.
I = (IdJ (nJ) + 1) » 1;
SETZERO_L (yj);
setbitj (yj, I);
do
{
cpyj (xj, yj);
Шаги 2 и 3. Аппроксимация методом Ньютона и проверка усло-
вия завершения алгоритма.
divj (nJ, xj, yj, rj);
addj (yj, xj, yj);
shrj (yj);
}
while (LT_L (yj, xj));
cpyj (floorJ, xj);
Чтобы выяснить, является ли число п квадратом какого-либо числа,
достаточно возвести в квадрат с помощью функции sqrj() значение
функции irootJO и сравнить полученный результат с п. Если числа
не совпадают, то, очевидно, п не является квадратом. Признаем, все
же, что это не самый лучший метод. Существуют критерии, позво-
ляющие во многих случаях распознать, является ли число квадра-
том, без вычисления квадратного корня. Один из таких алгоритмов
приведен в работе [Cohe]. Строятся четыре таблицы: q\l, q63, qiA
и q65, в каждой из которых квадратичные вычеты по модулю П,
63, 64 и 65 помечены единицей «1», а квадратичные невычеты -
нулем «О».
<- 0 для к = 0, ..., 10,
<?63[£] 0 для к = 0, ..., 62,
ql 1[Л2 mod 11] <- 1 для£ = 0.......5,
q63[k2 mod 63] <— 1 для к = 0, ..., 31,
209
рдАВА 10. Основные теоретико-числовые функции
<?64[А:] <— 0 для к = 0, 63, д64[£2 mod 64] <— 1 для к = 0, 31,
д65[к] <— 0 для к = 0, ..., 64, g65[&2 mod 65] <— 1 для к = 0, ..., 32.
Нетрудно заметить, что, рассматривая кольцо классов вычетов как
систему абсолютно наименьших вычетов (см. стр. 84), получаем
' таким образом все квадраты.
Алгоритм, определяющий, является ли целое число п > О
полным квадратом. Если да, то результат алгоритма -
квадратный корень из числа п (|Cohe], Алгоритм 1.7.3)
1. Положить t <— п mod 64. Если q64[f] = 0, то число п не является
полным квадратом и алгоритм заканчивает работу. Иначе поло-
жить r<—n mod (11 • 63 • 65).
2. Если q63[r mod 63] = 0, то число п не является полным квадра-
том и алгоритм заканчивает работу.
3. Если q65[r mod 65] = 0, то число п не является полным квадра-
том и алгоритм заканчивает работу.
4. Если qll[rmod И] = 0, то число п не является полным квадра-
том и алгоритм заканчивает работу.
5. Вычислить q <г- |_VnJ с помощью функции iroot_l(). Если q2 Ф п,
то число п не является полным квадратом и алгоритм заканчи-
вает работу. Иначе п является полным квадратом и результат:
q - квадратный корень из п.
На первый взгляд этот алгоритм может показаться странным: что за
константы 11, 63, 64, 65? Внесем ясность: если целое число п явля-
ется полным квадратом целого числа, то оно будет полным квадра-
том и по модулю произвольного целого числа к. Воспользуемся об-
ратным утверждением: если п не является квадратом по модулю к,
то оно не является квадратом и в целых числах. Таким образом, на
шагах 1-4 мы проверяем, является ли п квадратом по модулям 64,
63, 65 и И. Всего существует 12 квадратов по модулю 64, 16 квад-
ратов по модулю 63, 21 квадрат по модулю 65 и 6 квадратов по
модулю 11, то есть вероятность пропустить за четыре шага число,
не являющееся полным квадратом, равна
^^Yl-—Yi-—Y1-—1 = — 16 21 6 6
641 631 65^ 11J~64 63 65 11 715'
Только в таких относительно редких случаях выполняется проверка
на шаге 5. Если проверка проходит успешно, то п является полным
квадратом и квадратный корень из п определен. Очередность моду-
лей на шагах 1-4 определяется соответствующими вероятностями.
Появление следующей функции мы предвидели в п. 6.5, когда ис-
ключали числа, являющиеся полными квадратами, из множества
потенциальных первообразных корней по модулю р.
210 Криптография на Си и C++ в действии
функция: Является ли число nJ типа CLINT полным квадратом
Синтаксис: unsigned int issqrj (CLINT nJ, CLINT rj);
Вход: nJ (операнд)
Выход: rj (квадратный корень из nJ или 0, если nJ не является полным квад- ратом)
Возврат: 1, если nJ - полный квадрат,
0, в противном случае
static const UCHAR q 11 [11 ]=
{1, 1,0, 1, 1, 1,0, 0, 0, 1,0};
static const UCHAR q63[63]=
{1, 1,0, 0, 1,0, 0, 1,0, 1,0, 0, 0, 0, 0, 0, 1,0, 1,0, 0, 0, 1, 0, 0, 1,0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1,0, 0, 0, 0, 0, 1,0, 0,
’ЗС1Г-»' п* 1,0, 0, 1,0, 0, 0, 0, 0, 0, 0, 0, 1,0, 0, 0, 0}; static const UCHAR q64[64]=
•‘МТУ* {1, 1,0, 0, 1,0, 0, 0, 0, 1,0, 0, 0, 0, 0, 0, 1, 1,0, 0, 0, 0, 0, 0, 0, 1,0, 0, 0, 0, 0, 0, 0, 1,0, 0, 1,0, 0, 0, 0, 1,0, 0, 0, 0, 0, 0, 0, 1,0, 0, 0, 0, 0, 0, 0, 1,0, 0, 0, 0, 0, 0};
static const UCHAR q65[65]=
{1, 1,0, 0, 1,0, 0, 0, 0, 1, 1,0, 0, 0, 1,0, 1,0, 0, 0, 0, 0, 0,
0, 0, 1, 1,0, 0, 1, 1,0, 0, 0, 0, 1, 1,0, 0, 1, 1,0, 0, 0, 0, 0,
0, 0, 0, 1,0, 1,0, 0, 0, 1, 1,0, 0, 0, 0, 1,0, 0, 1};
unsigned int
issqrj (CLINT nJ, CLINT rj)
CLINT qj;
USHORT r;
if (EQZ_L (nJ))
{
SETZERO J- (rj);
return 1;
п
рдДВА 10. Основные теоретико-числовые функции 211
г' ' : U. 1. ; ; if (1 == q64[*LSDPTR_L (nJ) & 63]) /* q64[nj mod 64] */ { r = umodj (nJ, 45045); /* nJ mod (11 • 63- 65) 7 if ((1 == q63[r % 63]) && (1 == q65[r % 65]) && (1 == q11 [r % 11])) /* Условия проверяются слева направо, см. [Harb], п. 7.7 7
{ irootj (nJ, r_l); sqrj (rj, qj); if (equj (nJ, qj)) { return 1; } }
SETZERO_L (г_1);
; return 0;
}
10.4. Квадратные корни в кольце классов вычетов
Итак, мы научились вычислять квадратные корни (по крайней мере,
их целые части) из целых чисел. Теперь вновь обратимся к кольцам
классов вычетов, в которых займемся тем же самым, а именно,
вычислением квадратных корней. При некоторых ограничениях в
кольце классов вычетов существуют квадратные корни, вообще
говоря, определенные неоднозначно (то есть может существовать
несколько квадратных корней из одного элемента). Говоря на языке
алгебры, задача состоит в том, чтобы выяснить, существуют ли
для элемента а 6 Жт корни b е такие, что Р = а. Или, в тео-
ретико-числовых обозначениях (см. главу 5), есть ли решения у
сравнения второй степени
х2 = a mod т,
и если да, то какие.
Если НОД(я, ni) = 1 и существует решение b такое, что b2 = a mod ли,
то число а называется квадратичным вычетом по модулю т. Если
212
Криптография на Си и C++ в действии
сравнение неразрешимо, то а называется квадратичным невыче.
том по модулю т. Если b - решение сравнения, то b + т тоже
решение, то есть можно ограничиться рассмотрением вычетов
отличающихся на т.
Поясним ситуацию на примере. Число 2 является квадратичным
вычетом по модулю 7, поскольку З2 = 9 = 2 (mod 7); число 3 является
квадратичным невычетом по модулю 5.
Если число т простое, то найти квадратные корни по модулю т до-
вольно просто, позже мы приведем все необходимые для этого
функции. Трудность вычисления квадратных корней по модулю со-
ставного числа п определяется тем, известно ли разложение числа
т на простые множители. Если разложение неизвестно, то вычис-
ление квадратных корней для большого числа т является матема-
тически сложной задачей из класса NP (см. стр. 119), лежащей в
основе безопасности ряда современных криптосистем.5 Мы еще
вернемся к этому вопросу в п. 10.4.4.
Определение того, является ли число квадратичным вычетом, и вы-
числение квадратных корней - это две разные задачи, для решения
каждой из которых существуют свои методы. В следующих пара-
графах мы приведем реализацию этих методов с подробными ком-
ментариями. Сначала рассмотрим процедуры, позволяющие опре-
делить, является ли число квадратичным вычетом по модулю дан-
ного числа. Затем научимся вычислять квадратные корни по моду-
лю простых чисел и, наконец, по составным модулям.
10.4.1. Символ Якоби
Сразу начнем с определения. Пусть число р Ф 2 простое и число а
целое. Символ Лежандра (у) (читается «а по р») равен 1, если а -
квадратичный вычет по модулю р, и -1, если а - квадратичный не-
вычет по модулю р. Если а делится на р, то (у):= 0. Это определе-
ние пока вряд ли нам поможет, поскольку для того, чтобы знать
значение символа Лежандра, нужно знать, является ли а квадратич-
ным вычетом по модулю р. Однако символ Лежандра обладает за-
мечательными свойствами, которые и позволят нам оперировать с
ним и, что особенно важно, вычислять его значение. Чтобы не
5 Аналогию между математической и криптографической сложностью следует проводить очень
осторожно: согласно работе [Rein], вопрос о справедливости неравенства Р Ф NP весьма мало ка-
сается практической криптографии. Полиномиальный алгоритм разложения на множители с вре-
менной сложностью (9(и20) бессилен даже перед относительно небольшими значениями числа п,
( И0,1
тогда как экспоненциальный алгоритм сложности (9 k I справится даже с большими значе-
ниями модуля. Безопасность криптографических алгоритмов на практике не зависит от того,
совпадают или нет множества Р и NP, несмотря на то, что часто встречается именно такая фор-
мулировка.
ГЛАВА М. Основные теоретико-числовые функции 213
сбиться с пути, не будем вдаваться в теоретические дебри. Заинте-
ресованный читатель может обратиться, например, к работе [Bund],
п. 3.2. Но все же нам придется привести здесь некоторые свойства,
дающие основное представление о правилах вычислений с симво-
лом Лежандра.
(а) Число решений сравнения х2 = a (mod р) равно 1 + (7).
(б) Число квадратичных вычетов и невычетов по модулю р одинаково
и равно (р - 1)/2.
(в) Если а = b (mod р), то (7).
(г) Символ Лежандра обладает свойством мультипликативности:
(Д) §(t)=o.
/=1
(е) а(р"1)/2 = (-^-)(modp) (критерий Эйлера).
(ж) Если число q нечетное простое и q^p, то (~)= (-1)(/’~1)(<7"1)/4^)
(квадратичный закон взаимности Гаусса).
(з) (f)=(-l)<p’l)/2, (|)=(-1)(',2-1)/8, У=1.
Доказательство этих свойств можно найти в стандартной литерату-
ре по теории чисел, например, в [Bund] или [Rose].
, 1 nr '
Сразу же приходят в голову два способа вычисления символа
Лежандра. Во-первых, воспользоваться критерием Эйлера (свойст-
во (е)) и вычислить ар~^12 (mod р). Для этого потребуется выпол-
нять модульное возведение в степень (со сложностью <9(log3p)).
, u Во-вторых (и это более разумное решение), с помощью квадратич-
ного закона взаимности реализовать следующую рекурсивную про-
цедуру, основанную на свойствах (в), (г), (ж) и (з).
Рекурсивный алгоритм вычисления символа Лежандра
для целого а и нечетного простого р
1. Если а = 1, то (7) = 1 (свойство (з)).
2. Если а четное, то (^)= (-1)(р'-1)/8(^) (свойства (г), (з)).
3. Если аФ 1 и а = qx...qk - произведение нечетных простых
<7ь---,дьто
214
Криптография на Си и C++ в действии
Для каждого i вычисляем
j _ 1У Р-1)(<7/ -1)/4 (р inod Qi
с помощью шагов 1-3 (свойства (в), (г) и (ж)).
Прежде чем заняться программной реализацией этого алгоритма,
рассмотрим обобщение символа Лежандра. Это позволит нам обой-
тись без разложения на простые множители, которое необходимо
при использовании квадратичного закона взаимности в виде свой-
ства (ж) и для больших чисел занимающее чересчур много времени
(о задаче разложения см. стр. 225). А для этого обратимся к нере-
курсивной процедуре и введем еще одно определение. Для целых
чисел а и b =р{...рк9 где числа простые, но не обязательно раз-
личные, символ Якоби (называемый также символом Якоби - Кро-
некера, или символом Кронекера - Якоби, или символом Кронекера)
(f) определяется как произведение символов Лежандра :
fe):=nk).
/=1
где
О, если а четное,
М-=
\2/’ ,2 п/о
(-iya -V , если я нечетное.
Для полноты картины определим (f):=l для а е Z; (f):=l, если
а = ±1, и (§•):= 0 в противном случае.
Если число b нечетное простое (то есть k= 1), то значения симво-
лов Лежандра и Якоби совпадают. В этом случае символ Якоби
(Лежандра) показывает, является ли а квадратичным вычетом по
модулю Ь, то есть существует ли число с такое, что с2 = a mod b.
Если такое с существует, то (f) = 1, иначе (f)=-l (или (f) = 0, ес-
ли а = 0 mod b). Для составного числа b (при к > 1) число а является
квадратичным вычетом по модулю b тогда и только тогда, когда
НОД(я, b) = 1 па является квадратичным вычетом по модулю всех
простых чисел, делящих Ь, то есть когда для всех / = 1,...» к.
Ясно, что это не эквивалентно равенству (f)=l. Например, срав-
нение х2 = 2 mod 3 неразрешимо, то есть (|)= -1. Но по определе-
нию (|)= 1 > хотя сравнение х2 = 2 mod 9 также неразрешимо.
Обратно, если (g-)= -1, то а в любом случае является квадратичным
рддВА 10. Основные теоретико-числовые функции
215
невычетом по модулю Ь. Равенство (f) = 0 равносильно тому, что
НОД(л,/>)*1.
Пользуясь свойствами символа Лежандра, выведем свойства сим-
вола Якоби:
(a) и, если/, •<?*(), то (^)=(fXf)-
(б) Если а = с mod b, то (%) = (f) •
(в) Для нечетных b > 0 справедливы равенства
Й=(-1)М1. (i)=i
(см. свойство (з) символа Лежандра).
(г) Для нечетных а и Ь, где b > 0, выполняется квадратичный закон вза-
имности (см. свойство (ж) символа Лежандра): (f) = (-l)(a“1)(Z,-1)/4
Из этих свойств (доказательство см. в литературе, указанной выше)
получаем следующий алгоритм Кронекера (см. [Cohe], п. 1.4) вы-
числения символа Якоби (или, в зависимости от условий, символа
Лежандра) для двух целых чисел. Этот алгоритм нерекурсивный.
Кроме того, чтобы не зависеть от знаков этих чисел, положим
(тр):= 1 при а > 0 и (тр):= -1 при а < 0.
Алгоритм вычисления символа Якоби (f) для целых чисел а и Ъ
1. При b = 0 завершить алгоритм с результатом 1, если |а| = 1, и с
результатом 0 в противном случае.
2. Если оба числа а и b четные, то завершить алгоритм с результа-
том 0. Иначе положить v <— 0 и, пока b четное, выполнять:
v <— v + 1 и b <— Ы2. Если теперь v четное, то положить к <— 1;
иначе положить к <— (-1)(а -1)^8. При b < 0 положить b <—Ь.
При а < 0 положить к <------к (см. свойство (в) символа Якоби).
3. При <7 = 0 завершить алгоритм с результатом 0, если b > 1, с
результатом к в противном случае. При а Ф 0 положить v <— 0
и, пока а четное, выполнять: v <— v + 1 и а <— а/2. Если теперь v
нечетное, то положить к <— (-1)(/? -1)/8 • к (см. свойство (в) сим-
вола Якоби).
4. Положить к <— (-1)(а-1)(/?~1)/4 • к , r<- |а|, а <— b mod г, b <— г и
вернуться на шаг 3 (см. свойства (б) и (г) символа Якоби).
Время работы этого алгоритма равно 6>(log2TV), где число N>a,b-
верхняя граница чисел а и Ь. Это значительно лучше, чем вычисле-
216
Криптография на Си и C++ в действии
ние по критерию Эйлера. А вот еще два штриха, улучшающие этот
алгоритм (см. [Cohe] п. 1.4):
✓ Для вычисления значений (~1)(а и -1)/8 на шагах 2 и 3
лучше заготовить таблицу предвычислений.
✓ Значение (-1)(а~1)(/,-1)/4 . £ На шаге 4 можно вычислить на языке С
как if (a&b&2) к = -к, где & - это поразрядная операция AND.
В обоих случаях не нужно явно возводить в степень, что, конечно,
благоприятно сказывается на времени работы алгоритма.
Остановимся на первом «штрихе» более подробно. Если на 2 мы
полагаем к равным (-1)(“ -1)/8, то а нечетное. То же справедливо в
отношении b на шаге 3. Для нечетного а
2 | (а - 1) и 4 | (я + 1)
или
4 | (а - 1) и 2 | (а + 1),
то есть 8 делит произведение (а - 1)(а + 1) = а2 - 1 и число (а2 - 1 )/8 -
целое. Кроме того, выполняется равенство (-1)(а“-1)/8 =
(для проверки достаточно подставить в показатель степени выра-
жение а = к • 8 + г). Следовательно, показатель определяется лишь
четырьмя значениями числа a mod 8 = ±1 и ±3, дающими соответ-
ственно результаты 1, -1, -1 и 1. Записываем их в виде вектора
{О, 1, 0, -1, 0, -1, 0, 1}, откуда, зная a mod 8, можем найти значение
(-!)((“ mtxisr-n/s заметим? что а mod 8 можно представить в виде
выражения а & 7, где & по-прежнему означает бинарную операцию
AND, то есть возведение в степень сводится к нескольким быстрым
процессорным операциям.
Для пояснения второго «штриха» заметим, что (а & b & 2) * 0 то-
гда и только тогда, когда числа (а - 1 )/2 и (b - 1 )/2, а значит и
(а - 1)(Z? - 1 )/4, нечетные.
И, наконец, введем вспомогательную функцию twofactJO для вы-
числения значений v и b на шаге 2 для четного Ь, а также v и а на
шаге 3 для четного а. Функция twofactJO находит представление
числа типа CLINT в виде произведения степени двойки и нечетного
числа.
ГЛАВА 10. Основные теоретико-числовые функции 217
функция: Представление CLINT-объекта в виде а = 2ки, где число и нечетное
Синтаксис: int twofactj (CLINT aj, CLINT bj);
Вход: aj (операнд)
Выход: bj (нечетная часть числа aj)
Возврат: к (логарифм по основанию 2 в разложении числа а_1)
. int twofactj (CLINT a_l, CLINT bj) { int k = 0; if (EQZ_L (aj)) SETZERO_L (bj); return 0; } cpyj (bj, aj); while (ISEVENJ- (bj)) { shrj (bj); ++k; }
fc*’ 1 return k; }
1 -аиаимймЧ' 4 • < Теперь мы вооружены всем необходимым для реализации функции jacobiJO, вычисляющей символ Якоби.
Функция: Вычисление символа Якоби от двух CLINT-объектов
Синтаксис: int jacobij (CLINT aaj, CLINT bbj);
Вход: aaj, bbj (операнды)
Возврат: ±1 (значение символа Якоби aaj по bbj)6
Нетрудно заметить, что она возвращает еще и 0. - Прим. ред.
218
Криптография на Си и C++ в действии
*—.
static int tab2[] ={0,1,0, -1, 0, -1,0,1};
int
jacobij (CLINT aaj, CLINT bbj)
CLINT aj, bj, tmpj;
long int k, v;
Шаг 1. Случай bbj == 0.
if (EQZ_L (bbj))
{
if (equj (aaj, onej))
{
return 1;
else
{
return 0;
}
}
t J Шаг 2. Удаляем четную часть переменной bbj.
if (ISEVEN_L (aaj) && ISEVENJ. (bbj))
{
return 0;
}
cpyj (aj, aaj);
cpyj (bj, bbj);
v = twofactj (bj, bj);
if ((v & 1) == 0) /* v четное? */
{
р\ДВА 10. Основные теоретико-числовые функции
к= 1;
}
else
{
к = tab2[*LSDPTR_L (aj) & 7]; /* *LSDPTR_L (aJ) & 7 == aj % 8 7
Шаг 3. Если a_l == 0, то завершаем алгоритм. Иначе удаляем чет-
ную часть переменной aj.
while (GTZ_L (aj))
v = twofactj (aj, aj);
if ((v& 1) 1=0)
к = tab2[*LSDPTR_L (bj) & 7];
Ul
.• '-’О
Шаг 4. Применяем квадратичный закон взаимности.
R
if (*LSDPTR_L (aj) & *LSDPTR_L (bj) & 2)
k = -k;
cpyj (tmpj, aj);
mod J (bj, tmpj, aj);
cpyj (bj, tmpj);
Km ! * }
GO’ e jf (GT_L one_|)J
{
k = 0;
}
return (int) k;
220
Криптография на Си и C++ в действие
10.4.2. Квадратные корни по модулю рк Теперь мы знаем, что целое число может быть квадратичным выче. том или невычетом по модулю другого целого числа. Более того, у нас есть эффективная программа, определяющая, какой из этих случаев имеет место. Но даже зная, что целое число а является
квадратичным вычетом по модулю целого /г, мы пока не умеем из- влекать квадратный корень из а, особенно если число п большое. Будем скромны и попытаемся сначала сделать это для простых п. Таким образом, наша задача - решить сравнение второй степени
(10.11) х2 = a mod р, где число р нечетное простое и а - квадратичный вычет по модулю р (это гарантирует нам, что сравнение разрешимо). Рассмотрим два случая: р = 3 mod 4 и р = 1 mod 4. В первом, более простом случае решением сравнения будет х := a(p+l)/4 mod р, поскольку
(10.12) х2 = а(р+>>12 = а ар^'>/2 = a mod р, где а(р~^2 = (-^)=lmodp мы вычислили по свойству (е) символа Лежандра (критерий Эйлера). Следующие рассуждения, заимствованные из [Heid], приводят нас
к общей процедуре решения сравнений второй степени, в том числе и в случае р = 1 mod 4. Представим р - 1 в виде р - 1 = 2kq, где к > 1 и число q нечетное. Найдем произвольный квадратичный невычет п mod р, выбирая случайное л, 1 < п < р, и вычисляя символ Лежандра Значение -1 мы получим с вероятностью у, то есть нужное п будет найдено довольно быстро. Положим х0 = я(</+1)/2 mod р,
(10.13) у о = п1 mod р, Zq = a1 mod р, г0 •= к. Согласно малой теореме Ферма a(p~i)/2 = x2(p~l)/2 = xp~i = 1 mod р, если х - решение сравнения (10.11). Кроме того, если п - квадратичный невычет по модулю р, то н^~1)/2 = -1 mod р (см. свойство (е) символа Лежандра, стр. 213). Тогда
10. Основные теоретико-числовые функции 221
azQ - хо mod /Л
' 'ГЛ Уо ° = -1 mod р, 2Г°-1 z0 = 1 mod р. Если zq = 1 mod р, то х0 будет решением сравнения (10.11). Иначе определим рекуррентные последовательности х,, yh zi, гь где
(10.15) azi = xj mod р, 2^/ ”1 у, = -1 mod p, 2r'-1 Zj = 1 mod p и г, > Сделав не более чем к шагов, получим Zi = 1 mod р, то- гда Xi будет решением сравнения (10.11). Для этого найдем т0 - 2т° 1 д наименьшее натуральное число, для которого zQ =1 mod р, то есть ш0 < го - 1. Положим
(10.16) х/+1 = xiyi mod р, yi+i = У, mod Р> z,+i = mod р, где г,+1 := /п, := min|/i > 11 z2” = 1 mod р}. Тогда
(10.17) 2 2 2r'~w' 2r,-w' xi+i = xi yi = “Wi = ^/+1 mod
z x2"''-1 2r,+1-i 2"’r-i ( 2ri-"4 ) 2/'“1 1 J Л+i =Л-+1 =1л- 1 =y> =-lmodp, Qtnj -1 7r/+l-l ( jn-пч \ 9W/-I zz+i =zi+i =^z,>,- j =-Zi ^Imodp, поскольку (z2 ' ) = zf ’ = 1 mod p , и значит, в силу минимально- сти mh возможен лишь случай zj ' = -1 mod р . Таким образом, доказана корректность алгоритма Д. Шенкса (D. Shanks), определяющего решение сравнения второй степени (см. [Cohe], Алгоритм 1.5.1).
222 Криптография на Си и C++ в действии
Алгоритм извлечения квадратного корня из целого числа а по модулю нечетного простого р 1. Записать р - 1 в виде 2kq, где число q нечетное. Найти случайное п такое, что (^-)= -1. 2. Положить х <— a(^I)/2 mod р, у <— nl mod р, z<r- а • х2 modр,
b' J (’ •.; ‘ > X 4 х <— а • х mod р и г <— к. 3. Если 2=1 mod р, то завершить алгоритм с результатом х. Иначе найти наименьшее т, для которого 22 =1 mod р . При т = г завершить алгоритм с результатом «а - квадратичный невычет по модулю р». 4. Положить t <— у2' т 1 mod р , у <— t2 mod р, г <— т mod р, х <г- х • t mod р, z <— z • у mod р и вернуться на шаг 3. Ясно, что если х - решение сравнения второй степени, то -х mod р тоже будет решением этого же сравнения, так как (-л)2 = х2 mod р. В следующей программной реализации, не задумываясь о практич- ности, для всех подряд натуральных чисел, начиная с 2, будем вы- числять символ Лежандра, надеясь найти квадратичный невычет по модулю р за полиномиальное время. Наши надежды оправдаются, если считать, что верна до сих пор не доказанная расширенная ги- потеза Римана (см., например, [Bund], п. 7.3, Теорема 12 или [КоЫ], п. 5.1 или [Кгап], п. 2.10). Насколько мы сомневаемся в справедли- вости расширенной гипотезы Римана, настолько является вероятно- стным алгоритм Шенкса. При построении функции prootJO не будем принимать во внимание эти соображения и просто будем считать, что время работы алго- ритма полиномиально. Дальнейшие подробности см. в работе [Cohe], стр. 33 и далее.
Функция: Извлечение квадратного корня из а по модулю р
Синтаксис: int prootj (CLINT aj, CLINT pj, CLINT xj);
Вход: aj, pJ (операнды, число pJ > 2 - простое)
Выход: x_l (квадратный корень из aj по модулю pj)
Возврат: 5 0, если aj - квадратичный вычет по модулю pj, -1 в противном случае
int
prootj (CLINT aj, CLINT p_l, CLINT xj)
{
CLINT b_l, q_l, t_l, y_l, z_l;
10. Основные теоретико-числовые функции
223
int г, т;
if (EQZ_L (pj) || ISEVENJ. (pj))
return -1 ;
Если aj == 0, то результат: 0.
if (EQZ_L (aj))
SETZERO J_ (xj);
return 0;
Шаг 1. Находим квадратичный невычет.
cpyj (qj, pj);
dec J (qj);
r = twofactj (qj, qj);
cpyj (zj, two J);
while (jacobij (zj, pj) == 1)
*W>
incj (zj);
mexpj (zj, qj, zj, pj);
Шаг 2. Инициализация рекуррентной последовательности.
cpyj (yJ, zj);
dec J (qJ)>*
224 Криптография на Си и C++ в действии
shrj (qj);
mexpj (aj, qj, xj, pj);
msqrj (xj, bj, pj);
mmulj (bj, aj, bj, pj);
mmulj (xj, a J, xj, pj);
c Шаг 3. Завершение процедуры; в противном случае находим наи- меньшее т, для которого z2 = 1 mod р .
modj (bj, pj, qj); while (lequj (qj, onej)) { m = 0; do {
++m;
msqrj (qj, qj, pj);
.f ' 1 \ * A *«; / while (lequj (qj, onej));
if (m == r)
{
return -1;
}
Шаг 4. Рекуррентная формула для х, у, z и г.
mexp2J (yj, (ULONG)(r - m -1), tj, pj);
msqrj (tj, yj, pj);
mmulj (xj, tj, xj, pj);
mmulj (bj, yj, bj, pj);
cpyj (qj, bj);
r = m;
11
f-дДВА 10. Основные теоретико-числовые функции 225
} return 0; }
С учетом результатов, полученных для модуля р, мы теперь можем извлекать квадратные корни по модулю рк. Для этого рассмотрим сначала сравнение
(10.18) х2 = a mod р2. Если %! - решение сравнения х2 = а mod р, то, полагая х :=xi+ р • х2, получаем < 2 Л 2 2 22 л 12 х - а = х{ - а + 2рхрс2 + р х2 = р — h 2хрс2 mod р , 1 р J то есть для решения сравнения (10.18) нам нужно найти решение х2
п • • ог . линейного сравнения _ х,2 - а ~ , х • 2xj + —! = 0 mod р . Р Продолжая рекурсивно, за конечное число шагов получаем решение сравнения х = a mod рк для любого к е IN.
р • .,, ОС. 10.4.3. Квадратные корни по модулю п Мы сделали важный шаг - научились извлекать квадратные корни по модулю простого числа - на пути к конечной цели - решению сравнения х = a mod п для составного числа п. Справедливости ради отметим, что эта задача не из легких. В принципе, она разрешима, но требует значительных вычислений, объем которых увеличивается экспоненциально с ростом п. Решить это сравнение трудно на- столько (в теоретико-сложностном смысле), насколько трудно раз- ложить число п на простые множители. Обе задачи лежат в классе NP (см. стр. 119). Следовательно, извлечение корней по модулю составных чисел связано с задачей, которая на сегодняшний день не разрешима за полиномиальное время. И вряд ли мы сможем ре- шить сравнение быстро для больших п. Тем не менее, если есть два сравнения второй степени: у2 = a mod г и z2 = a mod s, где числа г и 5 взаимно просты, то можно объединить ре- шения этих сравнений и получить решение сравнения х = a mod rs. В этом нам поможет китайская теорема об остатках’. Пусть натуральные числа mj, ..., тг попарно взаимно просты (то есть НОД(ть пц) = 7 при пц ^nij) и числа a]f ..., аг - произвольные целые. Тогда существует решение системы сравнений х =ai mod пц, причем это решение единственно по модулю произведения трп^-.т^
226 Криптография на Си и C++ в действия — Хотелось бы уделить немного времени доказательству этой теоре. мы, поскольку именно в доказательстве сокрыто обещанное реше- ние. Положим т := niiin2...mr и in j := mlnij. Тогда число nij целое и НОД(/н < nij) = 1. Из п. 10.2 мы знаем, что существуют целые числа Uj и Vj такие, что 1 = m'jUj + nijVj, то есть m'jUj = 1 mod nij для j = 1, ...
qVii г, и умеем их вычислять. Построим сумму x0:=X/zW/’ W J=1
тогда, в силу сравнения m'jUj = 0 mod ди, для i Ф j, получаем оконча- тельное решение:
(10.19) г хо := ^m'jujaj = = at mod mi . j=i Предположим, что существуют два решения: х0 = a, mod и Xi = a,} mod имеем х0 = -И m°d nih или, эквивалентно, разность %о - делится одновременно на все mh то есть на наименьшее об- щее кратное чисел п^. А так как числа попарно взаимно просты,
их наименьшее общее кратное есть не что иное как произведение всех этих чисел, и х0 = хл mod т. С помощью китайской теоремы об остатках будем искать решение сравнения х = a mod rs, при этом НОД(г, д) = 1, числа гид- нечет- ные простые и ни г, ни д не делят а. Пусть уже известны решения
’: 1 C шл сравнений у2 = a mod г и z = a mod д. Найдем общее решение срав- нений х = у mod г, х = z mod 5
. < - '< ij как xq := zur + yvs mod rs, где 1 = иг + vs - линейное представление наибольшего общего
, > 0! делителя чисел гид. Тогда х} = a mod г и х^ = a mod д, а так как НОД(г, s) = 1, то будет верно и сравнение х}=а mod rs и мы нашли решение сравнения второй степени. Как мы уже говорили, каждое из сравнений по модулю гид имеет два решения, именно ±У и ±z, тогда, подставляя эти значения в выражение для х0, получаем четыре решения сравнения по модулю rs:
(10.20) xq := zur + yvs mod гд,
(10.21) Х\ := -zur - yvs mod rs = -Xq mod гд,
гдДВА 10. Основные теоретико-числовые функции 227
***** (10.22) х2 := -zur + yvs mod rs,
”(10.23) x3 := zur - yvs mod rs = -x2 mod rs.
s И i Таким образом, мы можем свести решение сравнений второй сте- пени вида
х2 = a mod и, где число п нечетное, к случаю х2 = a mod р с простым р. Для этого найдем разложение п = pkl ...рк< и вычислим корни по модулям ph из которых с помощью рекурсивной процедуры п. 10.4.2 находим решения сравнений х2 = a mod р-1 . И последний аккорд: по китай- ской теореме об остатках объединяем эти решения в решение срав- нения х2 = a mod п. Функция, которую мы сейчас рассмотрим, находит решение сравнения х2 = a mod п именно таким способом. Единственное ограничение: мы предполагаем, что п= р • <у, где числа р и q - нечетные простые. Сначала ищем решения и х2
сравнений
х2 = a mod р,
х2 = а mod q,
а затем восстанавливаем из хл и х2 решения сравнения
•-АГЛЛу х = a mod pq рассмотренным выше методом. В качестве квадратного корня из а
по модулю pq берем наименьшее из полученных значений.
Функция: Извлечение квадратного корня из а по модулю р • q, где числа р и q - нечетные простые
Синтаксис: int rootj (CLINT aj, CLINT pj, CLINT qj, CLINT xj);
Вход: aj, p_l, qj (операнды, простые числа pj, qj > 2)
Выход: xj (квадратный корень из aj по модулю pj * qj)
Возврат: 0, если a J - квадратичный вычет по модулю pj * qj, -1 в противном случае
int
rootj (CLINT aj, CLINT pj, CLINT qj, CLINT xj)
{
CLINT xOJ, x1 J, x2J, x3J, xp_l, xq_l, n_l;
CLINTD uj, vj;
228
Криптография на Си и C++ в действии
clint *xptrj;
int sign_u, sign_v;
I Вычисляем корни по модулям pl и qj с помощью функции
prootJO. При а_1 == 0 результат: 0.
if (0 != prootj (а_1, р_1, хр_1) || 0 != prootj (aj, qj, xq_l))
{
return -1;
}
if (EQZ_L (aj))
{
SETZERO J- (xj);
return 0;
}
Для корректного применения китайской теоремы об остатках,
следует учесть знаки чисел uj и vl. Для задания этих знаков вве-
дем вспомогательные переменные sign_u и signv, значения ко-
торых будем вычислять с помощью функции xgcdJO. Результа-
том этого шага является корень х0.
? mulj (pj, qj, nJ);
I xgcdj (pj, qj, xOJ, uj, &sign_u, vj, &sign_v);
5 mulj (uj, pj, uj);
i
j mulj (uj, xqj, uj);
$
mulj (vj, qj, vj);
mulj (vj, xpj, vj);
' sign_u = sadd (uj, sign_u, vj, sign_v, xOJ);
smod (xOJ, sign_u, nJ, x0_l);
Теперь находим корни x1z x2 и x3.
subj (nJ, xOJ, x1 J);
msubj (uj, vj, x2J, nJ);
229
|-дДВА 10. Основные теоретико-числовые функции
subj (nJ, x2J, x3J);
Наименьшее значение берем в качестве результата.
xptrj = MIN_L (xOJ, х1 J);
xptrj = MIN-L. (xptrj, x2J);
xptrj = MIN_L (xptrj, x3J);
cpyj (xj, xptrj);
return 0;
’ЗОЯ
Теперь мы легко можем реализовать китайскую теорему об остат-
ках, обобщив только что рассмотренную функцию на случай боль-
шего числа переменных. Это и сделано в следующем алгоритме,
принадлежащем Гарнеру (Garner) (см. [MOV], стр. 612). Преиму-
щество этого алгоритма перед приведенным выше состоит в том,
что остатки вычисляются только по модулям а не по модулю
т = niim2...mr, что значительно сокращает время вычислений.
и
Алгоритм 1 решения системы линейных сравнений
х = mod mi9 1 < i < г, где НОД(/лг, mj) = 1 при i * j
1. Положить и <— «1, x <— и и i <— 2.
2. Положить Ci <— 1, j <- 1.
3. Вычислить и <— m/1 mod nii (расширенным алгоритмом Евклида;
см. стр. 202) и Ci <— uCi mod пц.
4. Положить j <—j + 1. При j < i - 1 вернуться на шаг 3.
/-1
5. Положить и <— (а, - х)С, mod п^ и х <— х + •
J=i
6. Положить i <— i + 1. При i < г вернуться на шаг 2. Иначе
результат: х
Вообще говоря, не очевидно, что этот алгоритм делает именно
то, что нужно. Докажем его корректность по индукции. Пусть г = 2,
тогда на шаге 5
х = «j + ((а2 - аС)и mod ni2)ni[.
Сразу видно, что х = сц mod пц. Чуть менее тривиально
х = «1 + (а2 - а^т^тС1 mod т2) = а2 mod т2.
230 Криптография на Си и C++ в действии
— Для выполнения индукционного перехода от г к г + 1 предположи^ что алгоритм выдает нужный результат хг для некоторого г >£ и добавим еще одно сравнение x = «r+i mod тг+\. Тогда на шаге 5 получаем
/7 г > А г х = хг+ (аг+1-х)П'»;' modmr+1 П"Ь К И - J J *• | По индукционному предположению, х = xr = a, mod m, для 1 = 1, ,,L r Кроме того, * 11 11 Х = хг+ (аг+1 - х)П"Ь • П"Ь • = аг+1 mod '«г+1 > к 7=1 •/=1 > что и требовалось доказать. Для практической реализации китайской теоремы об остатках вос- пользуемся одной очень хорошей функцией, в которой не нужно заранее задавать число сравнений - его можно ввести во время ра- боты программы. Модифицируем процедуру, приведенную выше. При этом мы, увы, теряем возможность вычислять только по моду- лям пщ но зато можем оперировать с переменным числом парамет- ров щ и nii системы сравнений при фиксированных затратах памяти. Вот этот алгоритм (см. [Cohe], п. 1.3.3). Алгоритм 2 решения системы линейных сравнений х = сц mod 1 < i < г, где НОД(т/, ал7) = 1 при i j 1. Положить i <— 1, т <— т\ и х <— а\. 2. Если i = г, то закончить алгоритм с результатом х. Иначе по- ложить i <— i + 1 и найти расширенным алгоритмом Евклида (см. стр. 199) ииу такие, что 1 = uni + упщ 3. Положить х <г— шпщ + утре, т <— пищ, х <— х mod пг и вернуться на шаг 2. Этот алгоритм становится понятен уже для случая трех сравнений: х = щ mod nii, i= 1,2, 3. Для i = 2 получаем на шаге 2 1 = U\l1l\ + У\Ш^, на шаге 3: jq = mod Ш1/И2. При следующем прохождении цикла для i = 3 обрабатываем пара- метры а3 и т3. Получаем на шаге 2 1 = U2Ul + У^Щ = U2nilni2 + V2^3
ГЛАВА 10. Основные теоретико-числовые функции 231
RN , s •/‘Г и на шаге 3 х2 - и2та2 + V2"^i rood тт\ - = + v2m2Uitnia2 + г2аизVim2ai mod /нрлг^з- Слагаемые u2wii/n2^3 и уходят, если взять вычет х2 mod т{. Кроме того, г2^з = vpn2 = 1 mod т\ по построению, сле- довательно, х2 = mod mi есть решение первого сравнения. Анало- гичными рассуждениями можно показать, что х2 является решени- ем двух других сравнений. Реализуем индуктивный способ построения решения в виде функ- ции chinrem_l(), позволяющей применять китайскую теорему об ос- татках с переменным числом сравнений. Строим вектор четной длины указателей на CLINT-объекты ah /щ, а2, т2, а2, ... - коэф- фициентов системы сравнений х = mod Поскольку ее решение имеет длину порядка ^.logm, , при большом числе сравнений или размере параметров может возникнуть переполнение. Такие ошиб- ки придется распознавать и сообщать о них при возвращении зна- чения функции.
Функция: Применение китайской теоремы об остатках для решения системы линейных сравнений
Синтаксис: int chinremj (int noofeq, clint **koeff_l, CLINT x_l);
Вход: noofeq (число сравнений) koeffj (вектор указателей на С LI NT-коэффициенты пц сравнений х = сц mod т^ где i = 1, ..., noofeq)
Выход: х_1 (решение системы сравнений)
Возврат: ' >'< л" E_CLINT_OK, если все порядке E_CLINT_OFL в случае переполнения 1, если значение noofeq равно 0 2, если числа не попарно взаимно просты int chinremj (unsigned int noofeq, clint** koeffj, CLINT xj) { clint *aij, *mij; CLINT gj, uj, vj, mJ; unsigned int i; int sign_u, sign_v, sign_x, err, error = E_CLINT_OK; if (0 == noofeq)
232
Криптография на Си и C++ в действии
{
return 1;
}
Инициализация. Обрабатываем коэффициенты первого сравнения.
cpyj (xj, *(koeffj++));
cpyj (mJ, *(koeffj++));
Если есть еше сравнения, то есть noofeq > 1, то обрабатываем
параметры остальных сравнений. Если хотя бы одно из значений
mij не взаимно просто с предыдущими модулями, входящими в
произведение mJ, то функция завершается с кодом ошибки 2.
for (i = 1; i < noofeq; i++)
{
aij = *(koeffj++);
mij = *(koeffj++); 4
xgcdj (mJ, mij, gj, uj, &sign_u, vj, &sign_v);
if (!EQONE_L(gJ))
{ ‘ ;
return 2; i
Будем сохранять ошибку переполнения. По завершении функции
код ошибки будет храниться в переменной error.
err = mulj (uj, mJ, uj);
if (E_CLINT_OK == error)
{
error = err;
233
ГЛАВА 10. Основные теоретико-числовые функции
err = mulj (uj, aij, uj);
if (E_CLINT_OK == error)
.1' {
uj/’' J- error = err;
4 \\ / q err = mulj (vj, mij, vj);
if (E_CLINT_OK == error)
- {
, error = err;
}
err = mulj (vj, xj, vj);
if (E_CLINT_OK == error)
error = err;
/
W'
Побеспокоимся о знаках sign_u и sign_v (или sign_x) переменных
uj и vj (или xj) и снова воспользуемся вспомогательными
функциями sadd() и smod().
м sign_x = sadd (uJ, sign_u, vj, sign_v, xj);
) д л err = mulj (mJ, mij, mJ);
•рК.'УЦ?
Пл, if (E_CLINT_OK == error)
{
error = err;
3i! Л ( ..
smod (xj, sign_x, m_l, x_l);
}
,v‘ ;ХиЛн>. '.i 1 ' rij' . 'X
return error;
234
Криптография на Си и C++ в действии
10.4.4. Квадратичные вычеты
в криптографии
А вот и обещанные (на стр. 212) примеры применения квадратич-
ных вычетов и квадратных корней в криптографии. Сначала рас-
смотрим протокол шифрования Рабина, а затем схему аутентифи-
кации Фиата-Шамира.7
Безопасность протокола шифрования, опубликованного в 1979 г.
Майклом Рабином (Michael Rabin) (см. [Rabi]), основана на слож-
ности задачи извлечения квадратных корней в кольце Очень
важно, что доказано, что эта задача эквивалентна задаче разложе-
ния на множители (см. также [Кгап], п. 5.6). Этот протокол весьма
прост в реализации, поскольку требует лишь возведения в квадрат
по модулю п.
Генерация ключей для протокола Рабина
1. Участник А генерирует два больших простых числа р ~ q и вы-
числяет пь = р • q.
2. Открытым ключом для А является число нд, секретным ключом -
пара (р, q).
Участник В может послать участнику А сообщение М Е £п, зашиф-
рованное на открытом ключе пд.
Протокол Рабина шифрования с открытым ключом
1. Участник В, используя функцию msqr_l() со стр. 92, вычисляет
С := М2 mod ид и посылает участнику А шифртекст С.
2. Чтобы расшифровать полученное сообщение, А вычисляет
четыре квадратных корня Mi из С по модулю ид (/ = 1, ..., 4) с
помощью функции rootj() (см. стр. 227), при этом функция
должна выдавать не наименьшее значение квадратного корня,
а все четыре значения.8 Один из этих корней и есть исходный
открытый текст М.
Теперь перед А встает вопрос: какой же из четырех корней Л/, соот-
ветствует открытому тексту ml Если А и В предварительно догово-
рятся о некоторой избыточности сообщения М, скажем, в сообще-
нии М последние г бит должны быть одинаковыми, то у А не будет
7 Основные понятия, необходимые для понимания криптографии с открытым ключом, читатель
по-прежнему найдет в главе 16.
8 Не умаляя общности, можно считать, что НОД(Л/, лд) = 1 и, значит, существует четыре различ-
ных корня из С. В противном случае отправитель В может разложить число пд на множители,
вычислив НОД(Л/, яд), что, разумеется, совершенно недопустимо.
ГЛАВА 10. Основные теоретико-числовые функции
235
л-т д е/
ОЩфМ!;
ИН'го Д
WtamqTOhr
проблем с выбором правильного текста (вероятность того, что оди-
наковыми будут г бит в одном из трех остальных текстов, пренеб-
режимо мала).
Кроме того, избыточность позволяет предотвратить следующую
атаку на протокол Рабина. Если нарушитель X выберет случайное
число Яе Z*a и сможет получить от А (не важно под каким пред-
логом) один из корней сравнения X := R2 mod ид, то с вероятно-
стью у будет выполняться сравнение Rj £ ±7? mod пк .
Из соотношений пА = р • q | (R2 - R2) = (7?z - 7?)(7?( + R) * 0 получа-
ем 1 * НОД(7? - Rb ид) е {/?, q}> то есть X может вскрыть ключ, раз-
ложив на множители число пА (см. [Bres], п. 5.2). Если же открытый
текст обладает избыточностью, то А всегда может понять, какой из
корней соответствует истинному открытому тексту. Максимум, что
может сделать А - это открыть нарушителю значение R (при усло-
вии, что R имеет нужный формат), совершенно для X бесполезное.
При практическом использовании этого протокола недопустим
умышленный или случайный доступ к значениям квадратных кор-
ней из шифртекста.
Еще один пример применения квадратичных вычетов в криптогра-
фии - протокол аутентификации Амоса Фиата (Amos Fiat) и Ади
Шамира (Adi Shamir), опубликованный в 1986 г. и специально
предназначенный для использования в смарт-картах. Пусть I - по-
следовательность символов, которые содержат информацию, иден-
тифицирующую пользователя А, т - произведение двух больших
простых чисел р и <?, fiZ, п) -> Ж!П - случайная функция, отобра-
жающая произвольные конечные последовательности символов Z и
натуральных чисел п в кольцо классов вычетов некоторым не-
предсказуемым образом. Простые делители р и q числа т известны
только удостоверяющему центру. Рассмотрим алгоритм генерации
удостоверяющим центром компонентов ключа по информации I и
пока еще не определенному числу к G IN.
Алгоритм генерации ключей для протокола Фиата-Шамира
1. Вычислить значения =/(/, /) е Zm для некоторого i > к 6 IN.
2. Выбрать к различных квадратичных вычетов из vz и
вычислить наименьшие значения 5,-,...,^ квадратных корней
из v,V,;1 в2и.
3. Сохранить значения I и sik с защитой от несанкциониро-
ванного доступа (например, на смарт-карте).
236
Криптография на Си и C++ в действии
Для выработки ключей можно воспользоваться функциями
jacobiJO и rootj(), а в качестве функции f взять одну из хэщ~
функций из главы 16 (например, RIPEMD-160). Как сказал однажды
на конференции Ади Шамир: «Сойдет любая безумная функция».
Используя информацию, хранящуюся у удостоверяющего центра
на смарт-карте, участник А может быть аутентифицирован участ-
ником В.
Протокол аутентификации а-ля Фиата-Шамира
1. Участник А отправляет участнику В значения I и ij, где j = 1, .
к.
2. Участник В генерирует значения = f(I,ij) g для j = 1,
к. Далее для т= 1, ..., t выполняются шаги 3-6 (значение t пока
не определено).
3. Участник А выбирает случайное число rTG 7Lm и отправляет
участнику В значение хх = гх .
4. Участник В отправляет участнику А двоичный вектор (^Т1 ’ • •»еч).
5. Участник А отправляет участнику В числа ух := rx =isz g Zw.
6. Участник В проверяет, что хх := ух J*J _^vi .
Если А действительно знает числа sik, то на шаге 6 выполня-
ется последовательность равенств в кольце
Ут ГЕ = Гг21Ъ'2 ’ ПУ = = Гг
(>Т(=1 ст.=1 fT.=l
и, таким образом, участник А может доказать свою подлинность
участнику В. Нарушитель, стремящийся узнать информацию об А,
может с вероятностью 2~kt угадать вектор (е,..е ), отправляе-
мый участником В на шаге 4, а для этого предусмотрительно по-
слать на шаге 3 участнику В значение хх = гт2Р[ _jVf-. Например,
при k = t= 1 вероятность успеха для нарушителя будет равна
То есть значения к и t нужно выбирать так, чтобы вероятность
успеха для нарушителя была практически нулевой и чтобы (в зави-
симости от приложения) получить подходящие значения для:
- длины секретного ключа;
- объема данных, передаваемых между А и В; J
- временной сложности, определяемой числом умножений. Я
ГЛАВА 10. Основные теоретико-числовые функции 237
Подходящие значения параметров приведены в работе [Fiat] для
различных к и t при kt = 72.
;'1' Итак, безопасность рассмотренного протокола определяется защи-
щенностью значений , выбором параметров к и t и сложностью
задачи разложения: тот, кто сумеет разложить модуль т на мно-
жители, сможет вычислить и компоненты секретного ключа.
Значит, модуль т нужно выбрать так, чтобы его трудно было разло-
жить на множители. И здесь мы снова отсылаем читателя к главе 16,
с где будет обсуждаться проблема генерации модулей для криптоси-
стемы RS А.
1 Отметим, что в протоколе Фиата - Шамира участник А может про-
ходить аутентификацию сколь угодно часто, не выдавая при этом
никакой информации о секретном ключе. Подобные алгоритмы
называются доказательством с нулевым разглашением (см., напри-
гг - мер, [Schn], п. 32.11).
10.5. Проверка на простоту
Не буду больше томить Вас неизвестностью -
самое большое число Мерсенна, Ml 1213, по-
моему, самое большое из известных на сегодня
простых чисел, содержит 3375 разрядов, то
есть равно примерно Т-281 4-.9
Айзек Азимов,
Дополнительное измерение, 1964
Число 26972593 - 1 - простое!!!
http://www.utm.edu/research/primes/largest.html
(Май 2000)'°
Изучение простых чисел и их свойств - одно из старейших направ-
лений в теории чисел и имеет огромное значение для криптографии.
Вроде бы безобидное определение: простое число - это натуральное
число, большее 1 и делящееся только на само себя и 1, - а сколько
оно породило проблем и вопросов. Вот некоторые из них: «Сколько
существует простых чисел?», «Как простые числа распределены
в множестве натуральных чисел?», «Как можно проверить число на
Через Т Азимов обозначает триллион - число 1012, то есть Т-281 ± равно 1012’ 281,25 = 103375 ~ 211211’ .
] В ноябре 2001 г. было найдено 39-е простое число Мерсенна - 213466917 - 1 http://www.mersenne.org -
Прим, перев.
238
Криптография на Си и C++ в действии
простоту?», «Как можно определить, что натуральное число не яв-
ляется простым (то есть составное)?», «Как разложить составное
число на простые множители?». Математики веками пытались их
решить, и многие вопросы до сих пор остаются без ответа.
2300 лет назад Евклид доказал, что простых чисел бесконечно мно-
го (см., например, [Bund], стр. 5, особенно доказательства: забавное
и серьезное, на стр. 39 и 40). Сформулируем еще одно важное
утверждение, которое до сих пор подразумевалось по умолчанию:
согласно основной теореме арифметики, каждое натуральное число,
большее 1, можно разложить в произведение конечного числа про-
стых чисел, причем это разложение единственно с точностью до
порядка сомножителей. Простые числа - это своего рода «кирпи-
чики» в здании натуральных чисел.
Не выходя за границы множества натуральных чисел и не отвлека-
ясь на слишком большие числа, мы можем эмпирически ответить
на ряд вопросов и получить конкретные результаты. Конечно, эти
результаты в значительной степени зависят от имеющихся вычис-
лительных мощностей и эффективности используемых алгоритмов.
Посмотрим на опубликованный в Интернете список самых больших
простых чисел - размеры чисел поистине впечатляющие (см. таб-
лицу 10.1)!
Таблииа 10.1. Самые большие Простое число Число разрядов Автор Год
известные простые числа (данные на май 26972593 _ j 2098960 Hajratwala, Woltman, Kurowski, GIMPS 1999
2001 г.) 23021377 _ 1 909526 Clarkson, Woltman, Kurowski, GIMPS 1998
^2976221 _ 1 895932 Spence, Woltman, GIMPS 1997
21398269 _ 1 420921 Armengaud, Woltman, GIMPS 1996
^1257787 _ 1 378632 Slowinski, Gage 1996
4859465536 + 1 307140 Scott, Gallot 2000
2859433 _ 258716 Slowinski, Gage 1994
2756839 _ 1 227832 Slowinski, Gage 1992
66 7071.2667071 -1 200815 Toplic, Gallot 2000
104187032768 + 1 197192 Yves Gallot 2000
Самые большие известные простые числа имеют вид 2Р - 1. Эти про-
стые числа называются числами Мерсенна, по имени Марина Мер-
сенна (Marin Mersenne) (1588-1648), открывшего их в процессе поис-
ГЛАВА 10. Основные теоретико-числовые функции
239
л ка совершенных чисел. (Совершенным называется натуральное число,
равное сумме всех своих делителей. Например, число 496 является
совершенным, так как 496 = 1+ 2 + 4 + 8+16 + 31 + 62 + 124 + 248).
Для любого делителя t числа р число 2' - 1 является делителем числа
2Р - 1, так как при р = ab
2Р - 1=(2а- 1)(2“(Ь~}) + 2"(Ь~2) + ... + 1).
Следовательно, число 2Р - 1 может быть простым только если чис-
; ло р простое. Сам Мерсенн в 1644 г. утверждал (правда, без доказа-
тельства), что для р < 257 простыми являются числа вида 2Р - 1, где
р Е {2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257}. Предположение Мерсенна
подтвердилось, за исключением р = 67 и р = 257, при которых число
2Р - 1 составное. Были получены результаты и для других показате-
лейр (см. [Knut], п. 4.5.4, и [Bund], п. 3.2.12).
Отсюда можно, казалось бы, заключить, что чисел Мерсенна бес-
конечно много, однако это утверждение до сих пор не доказано
(см. [Rose], п. 1.2). Интересный обзор нерешенных задач, связан-
ных с простыми числами, читатель найдет в работе [Rose], глава 12.
Особым вниманием простые числа стали пользоваться с появлением
криптографии с открытым ключом. Как никогда раньше выросла
популярность алгоритмической теории чисел и смежных направле-
ний математики. Наибольший интерес вызывают проблемы про-
верки чисел на простоту и разложения на простые множители.
Криптографическая стойкость многих криптоалгоритмов с открытым
ключом (прежде всего, системы RSA) зависит от того, насколько
трудна задача разложения (в теоретико-сложностном смысле),
которая, по крайней мере на сегодняшний день, не разрешима за
полиномиальное время. 11
г То же, в несколько более слабой форме, можно сказать и о распо-
знавании простых чисел: как формально доказать, что данное число
простое? Правда, существуют тесты, определяющие (с малой веро-
ятностью ошибки) простоту числа. Более того, если тест о данном
числе говорит, что оно составное, то это действительно так. Сомне-
ния в правильности результата теста компенсируются полиноми-
альным временем работы, а вероятность «неверного положительного
ответа», как мы увидим, можно сделать сколь угодно малой, стоит
лишь повторить тест нужное число раз.
Старинный, но все еще действенный метод получения всех простых
чисел, меньших заданного натурального числа N, придуман грече-
। ским философом и астрономом Эратосфеном (276-195 до н. э.;
см. также [Saga]) и назван в его честь решетом Эратосфена.
Обсуждение теоретико-сложностных аспектов криптографии можно найти в [HKW], глава 6, или
[Schn], пп. 19.3 и 20.8, см. также многочисленные ссылки в этих работах. Рекомендуем прочи-
тать также сноску на стр. 212.
240
_____________________________Криптография на Си и C++ в действу
Сначала выписываем все натуральные числа от 1 до N и исклю
чаем из этого списка все числа, большие 2 и кратные ему. Затем
обозначаем за р первое число из оставшихся, большее текущего
простого (т.е. больше двух в первый раз) и исключаем из списка
числа вида р(р + 2Z), / = 0, 1, ... и т. д. Продолжаем процесс до тех
пор, пока не найдем простое число, большее J~N . После заверше
ния процедуры в списке остаются простые числа, меньшие либо
равные N- их мы «поймали в решето».
Вкратце поясним, почему же решето Эратосфена работает так, как
надо. Во-первых, простейшая индукция показывает, что число, сле-
дующее за простым и оставшееся в списке, само является простым
поскольку иначе у него должен быть маленький простой делитель
и, следовательно, это число мы должны были отбросить раньше.
Поскольку мы исключаем только составные числа, мы не теряем ни
одного простого числа.
Во-вторых, достаточно исключить только числа, кратные тем про-
стым р, которые меньше либо равны , так как если Т - наи-
меньший собственный делитель числа N, то Т < <J~N . Если бы в
списке осталось составное число п < V/V , то наименьший простой
делитель р числа п должен был бы удовлетворять неравенству
р < и мы должны были отбросить п как кратное р, а это
противоречит нашему предположению. Теперь посмотрим, как мож-
но реализовать решето, а для этого нам нужен программируемый
алгоритм. Но сначала несколько замечаний. Поскольку, кроме 2,
других четных простых чисел нет, будем проверять на простоту
только нечетные числа. Вместо того чтобы выписывать нечетные
числа, составим последовательность/, где 1 < i <L(W- 1)/2_1, соот-
ветствующую простоте чисел 2/ + 1. Далее, пусть переменная р со-
держит текущее значение 2/ + 1 элемента (воображаемого) списка
нечетных чисел, а переменная л удовлетворяет соотношению
2s + 1 = р2 = (2/ + I)2, то есть 5 = 2i2 + 21. Теперь можно и сформу-
лировать алгоритм (см. [Knut], п. 4.5.4, упражнение 8).
Алгоритм поиска всех простых чисел, меньших либо равных
натуральному числу N (решето Эратосфена)
1. Положить L <- |_(7V - l)/2j и В <-1 V?7/2 |. Для 1 < i < L положить
/ <— 1. Положить i <— 1, р <— 3 и s 4.
2. Если / = 0, то перейти на шаг 4. Иначе результат: р и положить
к <— j.
3. При k<L положить fk<^~ 0, к к + р и повторить этот шаг.
4. Если i < В, то положить i «— i + 1, л <— 5 + 2р, р <— р + 2 и вер
нуться на шаг 2. Иначе закончить алгоритм.
Файл взят с сайта
www.kodges.ru,
на котором есть еще
много интересной
литературы
ГЛАВА 10. Основные теоретико-числовые функции
241
На основе этого алгоритма напишем программу, возвращающую
в качестве результата указатель на список значений типа ULONG,
содержащий все простые числа, меньшие заданной границы, в
порядке возрастания. Первый элемент списка - это число всех
найденных простых чисел.
функция: Генератор простых чисел (решето Эратосфена)
Синтаксис: ULONG * genprimes (ULONG N);
Вход: N (верхняя граница поиска)
Возврат: Указатель на вектор значений типа ULONG, содержащий простые числа, меньшие либо равные N. (На нулевой позиции - число най- денных простых чисел). NULL при ошибке процедуры malloc().
ULONG *
genprimes (ULONG N)
{
ULONG i, k, p, s, B, L, count;
char *f;
ULONG *primes;
Шаг 1. Задание начальных значений переменных. Лля вычис-
ления целой части квадратного корня из числа типа ULONG
используется вспомогательная функция ul_iroot(), см. соответст-
вующую процедуру в п. 10.3. Составные числа помечаем с помо-
щью вектора f.
В = (1 + uljroot (N)) » 1;
L = N » 1;
if (((N & 1) == 0) && (N > 0))
{
-L;
}
if ((f = (char *) malloc ((size_t) L+1)) == NULL)
{
return (ULONG *) NULL;
242
Криптография на Си и C++ в действии
for (i = 1; i <= L; i++)
P = 3;
s = 4;
На шагах 2, 3, 4 собственно и реализуем решето. Переменная i
соответствует численному значению числа 2i + 1.
for (i = 1; i <= В; i++)
{
if (f[i]>
, {
for (k = s; к <= L; к += p)
{
f [k] = 0;
s += p + p + 2;
P+= 2;
Теперь определяем число найденных простых чисел и выделяем
для переменных типа ULONG поле соответствующего размера.
for (count = i = 1; i <= L; i++)
{
count += f[i];
}
if ((primes = (ULONG*)malloc ((size_t)(count+1) *
sizeof (ULONG))) == NULL)
f ДАВА 10. Основные теоретико-числовые функции
243
return (ULONG*)NULL;
Оцениваем поле f[J; все числа вида 2i + 1, помеченные как про-
стые, храним в поле primes. Если N 2, то учитываем и число 2.
for (count = i = 1; i <= L; i++)
if (f[i])
primes[++count] = (i « 1) + 1;
if (N <2)
{
primes[0] = 0;
}
else
{
primes[0] = count;
primes[1] = 2;
free (f);
return primes;
Чтобы определить, является ли число п составным, достаточно
применить к нему метод пробного деления: проверить, делится ли п
на все простые числа, меньшие либо равные л/и (их можно найти с
помощью решета Эратосфена). Если п не делится ни на одно из
этих чисел, то оно простое. Однако этот метод непрактичен: число
простых чисел быстро растет с ростом п. А именно, справедлива
теорема о простых числах, сформулированная А. М. Лежандром,
согласно которой число п(х) простых чисел р, где 2 <р<х, асим-
птотически стремится к х/1пх при х—> (см., например, [Rose],
г
244 Криптография на Си и C++ в действии
• - —
глава 12) 12 *. Дадим некоторые оценки для числа простых чисел
меньших заданного х. В таблице 10.2 приведены и истинные
значения числа л(х) простых чисел, меньших либо равных х, и
.аппроксимация х/ln х. В последней клетке таблицы стоит знак
вопроса - может быть, читатель сам ее заполнит?
X ю2 104 * 10® ю’6 1018 10’°°
х/In X 22 1 086 5 428 681 271 434 051 189 532 24 127 471 216 847 323 4 • 1097
п(х) 25 1 229 5 761 455 279 238 341 033 925 24 739 954 287 740 860 ?
Таблииа 10.2.
Число простых
чисел для
различных
значений х
Сложность метода пробного деления растет почти по экспоненте с
ростом х. Следовательно, для проверки простоты больших чисел
этот метод совершенно не применим. Позже мы увидим, что метод
пробного деления играет важную вспомогательную роль в других
тестах.
В принципе, нам нужен такой тест, который проверял бы число на
простоту, не выдавая никакой информации о его делителях. В этом
нам поможет хотя бы малая теорема Ферма, согласно которой для
простого числа р и всех чисел а, взаимно простых с р, справедливо
сравнение ар~х = 1 mod р (см. стр. 198). На этом факте основан тест
Ферма: если найдется число а, для которого выполняется либо
НОД(а, п) Ф 1, либо НОД(я, n) = 1 и 1 an~x mod /?, то число п со-
ставное. Для возведения в степень an~x = 1 mod п требуется <9(log3n)
операций процессора. Опыт показывает, что уже после нескольких
попыток составное число будет распознано. Однако тест Ферма не
является универсальным и «пропускает» некоторые числа. Посмот-
рим, какие именно.
Следует признать, что утверждение, обратное к малой теореме Фер-
ма, вообще говоря, неверно: число п, для которого НОД(д, н) =
и an~x = 1 mod п, где 1 < а < п - 1, не обязательно будет простым.
Существуют составные числа /г, которые проходят тест Ферма для
любых а, взаимно простых с п. Это числа Кармайкла, названные по
12 Теорема о простых числах была доказана независимо в 1896 г. Жаком Адамаром и Шарлем-ЖаноМ
де ла Валле Пуссеном (см. [Bund], п. 7.3). (В 1849-1852 гг. аналогичные утверждения были
сформулированы П. Л. Чебышевым; в частности, Чебышев впервые доказал, что число л(*)
удовлетворяет двойному неравенству 0,921-^ < л(х) < 1,06-^ . - Прим, перев.) Я
ГЛАВА 10. Основные теоретико-числовые функции
245
имени открывшего их Роберта Дениэла Кармайкла (Robert Daniel Carmichael, 1879-1967). Вот первые три из этих загадочных чисел: 561 = 3- 11- 17,1105 = 5- 13- 17,1729 = 7- 13- 19.
. К Любое число Кармайкла представляет собой произведение не менее трех различных простых чисел (см. [КоЫ], глава 5). Лишь в начале 1990-х гг. было доказано, что чисел Кармайкла бесконечно много
1,:' ЙГЛК?г..~ Ы ' (см. [Bund], п. 2.3). Относительная частота, с которой встречаются числа, меньшие п и взаимно простые с п, задается формулой
(10.24) ;; j<?" | . Г ' ’ s . ' А П &! /' St .. m'v t Ф(я) н-1 ’ где ф(л) - функция Эйлера (см. стр. 198), то есть доля чисел, не вза- имно простых с п, близка к 0 при больших п. Следовательно, в большинстве случаев, чтобы распознать число Кармайкла, прихо- дится много раз проходить тест Ферма. Заставляя а пробегать весь диапазон 2 < а < п - 1, мы в конце концов найдем наименьший про- стой делитель числа л, равный а. Помимо чисел Кармайкла существуют и другие нечетные состав- ные числа л, для которых найдутся натуральные а такие, что НОД(я, п) = 1 и ап~х = 1 mod п. Эти числа называются псевдопро- стыми по основанию а. Справедливости ради отметим, что лишь немногие числа являются псевдопростыми по основаниям 2 и 3, а в интервале от 1 до 25 • 109 существует всего 1770 целых чисел, псев- допростых по основаниям 2, 3, 5 и 7 одновременно (см. [Rose], п. 3.4). Но факт остается фактом - не существует общей оценки для числа решений сравнения Ферма для составных чисел. Таким обра- зом, к недостаткам теста Ферма можно отнести, во-первых, сомне- ние в том, действительно ли число, прошедшее тест, является про- стым, а во-вторых, невозможность оценить число проходов теста
для распознавания составного числа. Этих недостатков лишен следующий тест, основанный на критерии Эйлера (см. п. 10.4.1): если р нечетное простое, то для всех чисел а, не кратных р, выполняется сравнение
(10.25) ^(р-п/2 s mocj ? , где (у)=±1 mod р означает символ Лежандра (Якоби). По аналогии с малой теоремой Ферма, критерий проверки на простоту получаем из следующего утверждения: если для натурального числа п суще- ствует целое а такое, что НОД(я, и) = 1 и а(п~^2 = (f) mod п, то число /г, вероятно, простое. Временная сложность соответствующего теста совпадает со сложностью теста Ферма и равна <7(log3H).
246 Криптография на Си и C++ в действии
— Опять же, как и для теста Ферма, существуют составные числа ц удовлетворяющие критерию Эйлера для некоторого а. Эти числа называются эйлеровыми псевдопростыми по основанию а. Например число п = 91 = 7 • 13 эйлерово псевдопростое по основаниям 9 и 1о' так как 945 = (jf)= 1 mod 91 и 1045 = (>)=-! mod 91.13 Эйлерово псевдопростое по основанию а всегда является псевдопро- стым по тому же основанию (см. стр. 245), так как, возводя почленно в квадрат сравнение а{п~х^2 = (^)mod п , получаем ап~[ = 1 mod п. К счастью, для критерия Эйлера не существует чисел, аналогичных числам Кармайкла, а следующие наблюдения, отмеченные Р. Соло- вэем (R. Solovay) и В. Штрассеном (V. Strassen), позволяют значи- тельно сузить круг составных чисел, удовлетворяющих критерию Эйлера.
(а) Для составного числа п число целых чисел а, взаимно простых с для которых б7(л-1)/2 =(f)modn, не превышает уф(и) (см. [КоЫ], п. 2.2, упражнение 21). Отсюда следует, что:
(б) Вероятность для составного п и случайно выбранных к чисел ..., ак, взаимно простых с и, получить а^'1^2 = (y)mod п , где 1 < г < п, не превышает 2~к.
Теперь мы можем реализовать критерий Эйлера в виде вероятност- ного теста, где термин «вероятностный» означает, что результат «число п не простое» является безусловным, а говорить о том, что п является простым мы можем лишь с определенной вероятностью ошибки. Вероятностный алгоритм проверки натурального числа п на простоту (тест Соловэя-Штрассена)
' - • о, 1. Выбрать случайное число 2 < а < п - 1 такое, что НОД(я, ri) = 1- 2. Если a(n~l)^2 =(f)modn, то результат: «Число п вероятно про-
PX‘Rt; '-Я f ' стое»; иначе результат: «Число п составное». Возведение в степень и вычисление символа Якоби выполняется за время <?(log3n). Многократно повторяя этот тест, можно уменьшить вероятность ошибки в смысле свойства (б). Например, при к = $ вероятность ошибки пренебрежимо мала - меньше, чем 2”60 ~ Ю Как отмечает Д. Кнут, это меньше, чем случайная аппаратная ошибка, вызванная, например, альфа-частицей, попавшей в пронес' сор или память компьютера и изменившей значение бита.
13 В кольце Z9i элемент 3 имеет порядок 9, а элемент 6 — порядок 10, поэтому 93 = 106 = 1 mod 91-
Поэтому 945 — 93 15 = 1 mod 91 и 1045 = 106 7+3 = Ю3 =-1 mod 91.
ГЛАВА 10. Основные теоретико-числовые функции
247
Казалось бы, мы должны быть довольны этим тестом: мы можем
контролировать вероятность ошибки и у нас есть эффективные ал-
горитмы для выполнения всех необходимых вычислений. Однако
существует ряд результатов, позволяющих получить более мощный
тест. Чтобы лучше понять суть наиболее широко используемых на
сегодняшний день тестов, проведем некоторые рассуждения.
Предположим, что число п простое. Тогда по малой теореме Ферма
для всех целых чисел а, не кратных л, имеем: я""1 = 1 mod п. Квад-
ратный корень из an~l mod п может принимать лишь значения 1 и -1,
поскольку это единственные решения сравнения х2 = 1 mod п
(см. п. 10.4.1). Вычислим последовательно один за другим квадрат-
ные корни
а(п~^2 mod п, а(п~^4 mod и, ..., а(п~^2 mod и,
пока не получим нечетное число (п - 1)/2г. И если на некотором
шаге мы получим вычет, не равный 1, то он должен быть равен -1
(иначе п не может быть простым, что противоречит нашему пред-
положению). Если же квадратный корень, предшествующий 1,
будет равен -1, то мы можем по-прежнему верить, что число п яв-
; ляется простым. Составные числа п, обладающие таким свойством,
называются сильными псевдопростыми по основанию а. Сильное
псевдопростое число по основанию а всегда является эйлеровым
псевдопростым по тому же основанию (см. [КоЫ], глава 5).
‘ . Сведем полученные результаты в следующий вероятностный тест. Из
соображений эффективности сначала вычислим b = а{п~х^2 mod п с
г нечетным показателем (п - 1)/2', и если b * 1, будем возводить b в
квадрат, пока либо не получим ±1, либо не достигнем д(л-1)/2 mod п.
Во втором случае либо b должно быть равно -1, либо число п со-
ш ставное. Укороченный вариант алгоритма, без выполнения послед-
него возведения в квадрат, взят из книги [Cohe], п. 8.2.
Вероятностный алгоритм проверки нечетного числа n > 1
на простоту (тест Миллера-Рабина)
1. Определить q nt, где п - 1 = 2 g, число q нечетное.
2. Выбрать случайное число а из интервала 1 < а < п. Положить
е <— 0, b <г- a1 mod п, При b = 1 завершить алгоритм с результа-
том «Число п вероятно простое».
3. Пока b £ 1 mod п и е < t - 1, вычислять b b2 mod п и
е <r- е + 1. Если теперь b п - 1, то результат: «Число п состав-
ное»; иначе результат: «Число п вероятно простое».
Время возведения в степень равно <9(log3/z), поэтому сложность
теста Миллера-Рабина (или, короче, MP-теста) та же, что и слож-
ность теста Соловэя-Штрассена.
248
Криптография на Си и C++ в действии
” ——
Существование сильных псевдопростых чисел подразумевает, чТо
лишь результат «Число п составное» теста Миллера-Рабина является
безусловным. Число 91, представленное выше как эйлерово леев-
допростое по основанию 9, является также - вновь по основанию 9 -
сильным псевдопростым. Вот еще сильные псевдопростые числа:
2152302898747 = 6763 • 10627 • 29947,
3474749660383 = 1303 • 16927 • 157543.
Кроме них до 1013 не существует больше чисел, псевдопростых по
основаниям 2, 3, 5, 7 и 11 одновременно (см. [Rose], п. 3.4).
К счастью, оснований, по которым псевдопростое число является
таковым, не больше, чем само это число. М. Рабин доказал, что
число оснований а, 2 < а < п, по которым данное составное число п
является псевдопростым, гораздо меньше, чем л/4 (см. [Knut],
п. 4.5.4, упражнение 22, и [КоЫ], глава 5). Отсюда получаем, что
при /с-кратном повторении теста для случайно выбранных основа-
ний аь ..., ак сильное псевдопростое число будет распознано как
простое с вероятностью, меньшей чем 4”\ Следовательно, при том
же числе операций тест Миллера-Рабина всегда более предпочти-
телен, чем тест Соловэя-Штрассена, для которого вероятность
ошибки при к повторах равна 2~к.
На практике тест Миллера-Рабина ведет себя гораздо лучше, по-
скольку реальная вероятность ошибки в большинстве случаев
значительно ниже, чем это гарантирует теорема Рабина (см. [Schn],
п. 11.5).
Прежде чем перейти к реализации теста Миллера-Рабина, укажем
два способа улучшения алгоритма.
Во-первых, разумнее сначала применить к тестируемому числу ме-
тод пробного деления, то есть проверить, не делится ли это число
на маленькие простые числа. Если делитель будет найден, то нечего
и применять тест Миллера-Рабина. Но тогда сразу встает вопрос:
сколько нужно таких маленьких простых чисел, прежде чем мы
сможем применить MP-тест? Воспользуемся рекомендациями
А. К. Ленстры: наибольший эффект достигается, если проверить
делимость на 303 простых числа, меньших 2000 (см. [Schn], п. Н-Я
Откуда взялись такие цифры, становится ясно, если заметить, что
относительная частота появления нечетных чисел, которые не
кратны простым числам, меньшим п, примерно равна 1,Г2/1пи-
Проверяя делимость на простые числа, меньшие 2000, мы отбрИ
сываем 85% составных чисел без всякого теста Миллера-Рабина,
а его используем лишь для проверки оставшейся доли чисел.
Проверка делимости на маленькое простое число требует лиШЧ
О(1п п) элементарных операций. Для этого в методе пробного делв1
ния будем использовать специальную процедуру, особенно эфФеК1
тивную при делении на маленькие числа. |
ГЛАВА 10. Основные теоретико-числовые функции
249
Реализуем метод пробного деления в виде функции sieve_l(), кото- рая, в свою очередь, использует простые числа, меньшие 65536, для хранения которых выделим поле smallprimes[NOOFSMALLPRIMES]. Простые числа будем хранить в виде разностей, то есть под каждое простое число требуется лишь один байт памяти. Ограниченный доступ к этим числам не создает особых проблем, поскольку мы рассматриваем эти числа в естественном порядке. Особо следует выделить случай, когда само тестируемое число является малень- ким простым и содержится в таблице. Во-вторых, в тесте Миллера-Рабина будем использовать не слу- чайные основания, а маленькие простые числа 2, 3, 5, 7, 11, ... < В. Это значительно ускоряет работу функции возведения в степень (см. главу 6) и, как показывает опыт, ничуть не ухудшает результа- ты теста. И вот, наконец, метод пробного деления. Процедура деления на маленькие числа реализована в виде функции divj().
Функция: Метод пробного деления
Синтаксис: USHORTsieveJ(CLINT aj, unsigned no_of_smallprimes);
Вход: а_1 (тестируемое число) no_of_smallprimes (число простых чисел, на которые мы делим, без учета числа 2)
Возврат: Простой делитель, если таковой найден 1, если тестируемое число само является простым 0, если делитель не найден
USHORT sievej (CLINT aj, unsigned int no_of_smallprimes) { clint *aptrj; USHORT bv, rv, qv; ULONG rdach; unsigned int i = 1;
I Для полноты картины сначала проверяем, не является ли а_1 кратным 2. Если а_1 равно 2, то возвращаем 1; если же а_! четное,
I в большее 2, то возвращаем 2 в качестве делителя. if (ISEVEN_L (aj)) { if (equj (aj, two J))
250
Криптография на Си и C++ в действии
• У,
{
return 1;
}
else
{
return 2;
}
}
bv = 2;
do
{
Определяем простые делители, последовательно суммируя числа
из smallprimes[], сумму записываем в bv. Первое простое число,
проверяемое в качестве делителя, - это 3. Для деления на число
типа USHORT используем код из соответствующей быстрой про-
граммы (см. п. 4.3).
rv = O;
bv += smallprimes[i];
for (aptrj = MSDPTFLL (aJ); aptrj >= LSDPTFLL (aj); aptrj-)
{
qv = (USHORT)((rdach = ((((ULONG)rv) « BITPERDGT) +
(ULONG)*aptrJ)) / bv);
rv = (USHORT)(rdach - (ULONG)bv * (ULONG)qv);
}
}
while (rv != 0 && ++i <= no_of_smallprimes);
Если найден несобственный делитель (rv == 0 и bv aj; иначе aj
само простое!), то он и будет результатом. Если а_1 само является
простым, то результат: 1; в противном случае результат: 0.
if (0 == rv)
if (DIGITSJ- (aJ) == 1 && *LSDPTRJ_ (aj) == bv)
251
ГЛАВА 10. Основные теоретико-числовые функции
bv = 1;
}
/* else: Результат в bv является простым делителем числа aj 7
}
else /* Делитель числа aj не найден 7
{
bv = 0;
}
return bv;
}
С помощью функции sieveJO можно находить простые делители,
меньшие 65536, объектов типа CLINT. Для этого в flint.h имеется
макрос SFACTOR_L(n_l), вызывающий функцию sievej(nj,
NOOFSMALLPRIMES), которая, в свою очередь, проверяет, делится
ли nJ на простые числа из базы smallprimes[]. Макрос SFAC-
TORJ-(nJ) возвращает то же значение, что и функция sievej.
Многократно вызывая макрос SFACTOR_L(nJ) и тем самым после-
довательно определяя простые делители, мы можем найти полное
разложение чисел, меньших 232, то есть представимых стандартны-
ми целочисленными типами.
И вот уже primeJO - вполне созревшая функция, объединяющая в
себе метод пробного деления и тест Миллера-Рабина. Для прида-
ния ей большей гибкости будем рассматривать число простых де-
лителей в предварительном пробном делении и число проходов
теста Миллера-Рабина как параметры. В прикладных задачах для
простоты можно использовать макрос ISPRIME_L(CLINT nJ), кото-
рый, в свою очередь, вызывает функцию primeJO с наперед задан-
ными параметрами. Возведение в степень будем осуществлять с
помощью функции wmexpmj(), сочетающей в себе всю прелесть
приведения по Монтгомери и малых оснований степени (см. главу 6).
Функция: Вероятностный тест Миллера-Рабина с использованием метода
пробного деления
Синтаксис: int primej (CLINT nJ, unsigned no_of_smallprimes, unsigned
iterations);
^Х°Д«* nJ (тестируемое число)
no_of_smallprimes (число простых чисел в методе пробного деления)
iterations (число итераций теста)
возврат: 1, если тестируемое число «вероятно» простое
0, если тестируемое число составное или равно 1
252
Криптография на Си и C++ в действии
int
primej (CLINT nJ, unsigned int no_of_smallprimes,
unsigned int iterations)
{
CLINT dj, xj, qj; <
USHORT i, j, k, p; t
int isprime = 1; J
if (EQONE.L (nJ))
{
return 0;
}
Теперь выполняем пробное деление. Если делитель найден, то
функция завершается с результатом 0. Если функция sieveJ0 вы-
дала 1 (это означает, что число nJ простое), то функция завер-
шается с результатом 1. В противном случае выполняем тест
Миллера-Рабина.
k = sievej (nJ, no_of_smallprimes);
if (1 == к)
return 1;
}
if (1 < к)
{
return 0;
}
else
Шаг 1. Используя функцию twofactJO, находим разложение
n - 1 = 2kq, где число q нечетное. Значение п - 1 записываем в dj-
253
ГЛАВА 10. Основные теоретико-числовые функции
cpyj (dj, nJ);
dec J (dj);
k = (USHORT)twofactJ (dj, qj);
|L isprime = 1;
do
{
Шаг 2. Из прирашений, хранящихся в поле smallprimes[], форми-
руем основания р. Для возведения в степень используем функ-
цию Монтгомери wmexpmj, поскольку основание всегда будет
иметь тип USHORT и, кроме того, после предварительной про-
верки методом пробного деления числа nJ, всегда будет нечет-
ным. Если в результате степень (xj) равна 1, то переходим к сле-
дующей итерации.
р += smallprimes[i++];
wmexpmj (р, qj, xj, nJ);
if (!EQONE_L (xj))
hO'. {
I Шаг 3. Пока xj отлично от ±1 и пока число итераций не превы-
шает к - 1, выполняем возведение в квадрат.
hL
while (!EQONE_L (xj) && !equj (xj, dj) && ++j < k)
{
' ‘ msqrj (xj, xj, nJ);
}
if (!equj (xj, dj))
{
isprime = 0; ~
254
Криптография на Си и C++ в действии
Пикл по числу итераций теста.
ЭДИ-
while ((--iterations > 0) && isprime);
return isprime;
}
}
Открытым остается вопрос о том, сколько итераций теста Миллера-
Рабина следует провести, чтобы получить достоверный результат.
Рекомендации самые разные: [Gord] и [Schn] считают, что доста-
точно пяти итераций (для криптографических приложений), алго-
ритм в [Cohe] включает 20 итераций. Д. Кнут [Knut] говорит о том,
что при 25 итерациях вероятность ошибочно определить число как
простое будет меньше, чем 10~6 для миллиарда «кандидатов», хотя,
вообще-то, он не настаивает на числе 25, а вместо этого задает фи-
лософский вопрос: «А так ли уж нужно строгое доказательство
простоты?». 14
В том случае, если нам нужен утвердительный ответ, можно вос-
пользоваться тестом APRCL (L. Adleman, С. Pomerance, R. Rumely,
Н. Cohen, А. К. Lenstra), опубликованным в 1981 г. X. Ризель
(Н. Riesel) назвал этот тест прорывом, доказавшим, что быстрые
универсальные достоверные алгоритмы проверки на простоту дей-
ствительно существуют (см. [Ries], стр. 131). Этот тест распознает
простоту числа п за время <9((1п п)с1п,п1п") для некоторой подходя-
щей константы С. Поскольку на практике показатель In In In п ведет
себя как константа, этот тест можно считать полиномиальным.
Теперь можно проверять на простоту целые числа длиной в не-
сколько сотен десятичных знаков за такое время, которое раньше
могли показать только вероятностные тесты. 15 Алгоритм, исполь-
зующий аналог малой теоремы Ферма для более сложных алгеб-
раических структур, довольно сложен теоретически и труден в реа-
14 В статье «Генерация вероятно простых случайных чисел» (Р. Beauchemin, G. Brassard, С. Сгёреаа»
С. Goutier и С. Pomerance, Journal of Cryptology, Vol. 1, No. I, 1988) говорится о том, что утвер
ждение Д. Кнута верно лишь потому, что вероятность ошибки для большинства составных ни
сел гораздо меньше 14. В противном случае оценка, данная Кнутом, будет значительно больше,
чем 1(Г6.
15 Коэн (Cohen) в этой связи замечает, что, хотя практический вариант алгоритма APRCL также ве
роятностный, существует и менее практичная, детерминированная его версия (см. [Cohe], глава 9)-
ГЛАВА 10. Основные теоретико-числовые функции
255
лизации. Более подробную информацию см. в [Cohe], глава 9, в
[Ries] или в указанной выше оригинальной статье.
Читатель может спросить, получим ли мы достоверно простое число,
применяя тест Миллера-Рабина для большого числа оснований.
Согласно результату Г. Миллера (G. Miller), нечетное натуральное
число п является простым тогда и только тогда, когда тест Мил-
лера-Рабина определяет его как простое для всех оснований а
таких, что 1 < а < С • 1п2л (в [КоЫ], п. 5.2, указано, что С- 2), в пред-
положении, что верна расширенная гипотеза Римана (см. стр. 222).
При таких условиях тест Миллера-Рабина является детерминиро-
ванным и полиномиальным и за 2,5 • 105 итераций дает достовер-
ный результат для чисел длины 512 бит. Если на каждую итерацию
отводится 10”1 секунд (время возведения в степень на быстрых ПК;
см. Приложение D), тогда достоверный тест займет около семи
часов. Однако, принимая во внимание, что этот тест основан на не-
доказанной гипотезе, а также учитывая довольно длительные вы-
числения, можно ожидать, что такой теоретический результат не
устроит ни «чистых» математиков, ни программистов-прагматиков,
любящих быстрые программы.
Генри Коэн, отвечая на процитированный выше вопрос Д. Кнута,
был категоричен ([Cohe], п. 8.2): «Все же проверка на простоту тре-
бует строгих математических доказательств».
ГЛАВА И.
Большие случайные числа
Математика полна псевдослучайности, которой
вполне хватит всем изобретателям-мечтателям
на все времена.
Д.Р. Хофштадтер, Гедель, Эшер, Бах
Последовательности «случайных» чисел широко используются в
статистических процедурах, в вычислительной математике, в физике,
а также в теоретико-числовых приложениях, когда нужно либо за-
менить ими статистические наблюдения, либо автоматизировать
процесс ввода каких-то переменных величин. Случайные числа
могут пригодиться:
✓ если мы хотим выбрать несколько случайных элементов из боль-
шого множества;
✓ в криптографии для генерации ключей и работы защищенных про-
токолов;
✓ в качестве начальных значений при генерации простых чисел;
✓ для тестирования компьютерных программ (к этой теме мы еще
вернемся);
для развлечения
и много для чего еще. При компьютерном моделировании естест-
венных процессов случайными числами можно представлять из-
меряемые величины (методы Монте-Карло). Случайные числа
полезны и в том случае, если нам нужны произвольные, случайным
образом выбранные, числа. Прежде чем приступить в этой главе к
разработке каких-либо функций генерации больших случайных чи-
сел, которые нам понадобятся, в частности, для криптографических
приложений, проведем некоторую методологическую подготовку.
Существует множество способов получения случайных чисел, однако
мы сразу условимся разделять истинно случайные числа, возникаю-
щие в результате случайных экспериментов, и псевдослучайные числа,
выработанные алгоритмически. Истинно случайные числа можно
получить, подбрасывая монету или кость, вращая («честное») колесо
рулетки, наблюдая процесс радиоактивного распада на специальном
измерительном оборудовании. Напротив, псевдослучайные числа вы-
рабатываются алгоритмами, с помощью генераторов псевдослучайных
чисел, которые, в свою очередь, являются детерминированными и,
вследствие этого, предсказуемыми и воспроизводимыми. Таким
образом, псевдослучайные числа не являются случайными в строгом
смысле слова. Этим обстоятельством, однако, можно пренебречь,
если у нас есть алгоритмы, производящие «высококачественные»
случайные числа. Поясним, что мы понимаем под этим словом.
-1697
258
Криптография на Си и C++ в действии
(11.1)
Прежде всего, обратим внимание читателя на то, что бессмысленно
говорить о «случайности» какого-то одного числа. Математические
критерии случайности всегда применяются к последовательности
чисел. Д. Кнут говорит о последовательности независимых случайных
чисел с определенным законом распределения, в которой каждый
элемент вырабатывается случайно и независимо от всех других членов
последовательности и принимает значение из некоторого диапазона
с определенной вероятностью (см. [Knut], п. 3.1). Слова «случайно»
и «независимо» используются здесь, чтобы подчеркнуть, что харак-
тер и способ взаимодействия событий, определяющих выбор кон-
кретного числа, слишком сложен, чтобы распознать его статисти-
ческими или какими-либо другими тестами.
Теоретически достичь этого идеала детерминированными процеду-
рами невозможно. Цель же многочисленных алгоритмических
средств генерации чисел - как можно ближе приблизиться к этому
идеалу. Параллельно разрабатываются теоретические и эмпириче-
ские тесты для распознавания характера и структуры последова-
тельностей псевдослучайных чисел и, следовательно, для оценки
качества алгоритмов генерации этих последовательностей. Не бу-
дем слишком этим увлекаться: теория здесь слишком глубока и
сложна. Хороший обзор на эту тему желающие смогут найти в книге
[Knut], а исчерпывающие теоретические оценки генераторов слу-
чайных чисел - в работе [Nied], Ряд прагматических идей по тести-
рованию последовательностей случайных чисел есть в [FIPS].
Из множества существующих способов генерации псевдослучайных
чисел (для краткости будем иногда опускать слово «псевдо» и гово-
рить просто «случайные числа», «случайные последовательности»
и «генераторы случайных чисел») уделим сначала немного времени
проверенному и часто используемому методу генерации линейных
конгруэнтных последовательностей. По заданному начальному
значению Хо элементы последовательности определяются из линей-
ного рекуррентного соотношения:
Х;+1 = (Хр + b) mod m.
Эта процедура была предложена Д. Лемером (D. Lehmer) в 1951
году и с тех пор завоевала большую популярность. Несмотря на
кажущуюся простоту, линейные конгруэнтные последовательности
обладают хорошими свойствами случайности. Их качество, как.
нетрудно догадаться, зависит от выбора параметров а, b и т. В книге
[Knut] показано, что линейная конгруэнтная последовательность с
тщательно подобранными параметрами проходит испытания стати-
стическими тестами «на ура», однако случайный выбор параметров
почти всегда приводит к плачевным результатам. Мораль сей басни
такова: при выборе параметров будьте осторожны!
Выбор в качестве т степени двойки обладает очевидным преимУ'
ществом: вычислять вычет по модулю т можно с помощью мате-
ГЛАВА 11. Большие случайные числа
259
магической операции AND. Но, как всегда, есть и недостаток -
младшие двоичные разряды генерируемых чисел характеризуются
гораздо меньшей случайностью, чем старшие, а значит, надо быть
очень аккуратным при работе с такими числами. Да и вообще,
числа, полученные из линейной конгруэнтной последовательности
приведением по модулю простого делителя числа т, проявляют
весьма посредственные свойства случайности, поэтому следует
рассмотреть возможность выбора в качестве т простого числа, так
как в этом случае любые двоичные разряды ничуть не хуже, чем
любые другие.
Выбор чисел а и т влияет на периодичность последовательности:
поскольку элементы последовательности могут принимать конеч-
ное число, а именно т, различных значений, последовательность
начнет повторяться самое позднее на (пг + 1)-м элементе. То есть,
эта последовательность периодическая. (Говорят также, что после-
довательность входит в цикл). Точка входа в цикл - не обязательно
начальное значение Хо, это может быть и некоторое более позднее
значение Хц. Числа Хо, Х2, ...» Х^. образуют «хвост» последова-
тельности. Поведение такой последовательности схематично изо-
бражено на рис. 11.1.
Рисунок 11.1. у
Повеление .
~ ~ «Хвост» Пикл
псевдослучайной «лыдл»
последова- f \
тельности I I I
V
Поскольку повторение чисел с коротким периодом совершенно
г. . ( не подходит ни под какие критерии, мы должны приложить все
а. п усилия, чтобы максимально увеличить длину цикла или даже
построить генератор, вырабатывающий только последовательности
с максимальной длиной цикла. Сформулируем критерий, позволяю-
г’ щий создавать именно такие линейные конгруэнтные последова-
тельности с параметрами a, b и т. Итак, должны выполняться сле-
дующие условия:
(а) НОД(/>,ш)=1.
(б) Если р | т, то р | (а - 1) для любого простого числа р.
(в) Если 4 | т, то 4 | (а-1).
Доказательство и дополнительные подробности см. в [Knut], п. 3.2.1.2.
Стандарт ISO-С рекомендует использовать для функции rand() сле-
дующую линейную конгруэнтную последовательность, параметры
которой удовлетворяют указанному критерию:
Xi+i = (Xi -1103515245 + 12345) mod m,
9*
г
260
Криптография на Си и C++ в действии
где т = 2к, где к выбирается так, чтобы 2к ~ 1 было наибольшим
числом, которое можно задать типом unsigned int. Значением функ-,
ции rand() является не Х/+ь a X/+i/216 mod (RAND_MAX +1), то есть
все значения функции rand() заключены между 0 и RAND_MAX.
Макрос RAND_MAX определен в файле stdio.h и должен быть по
крайней мере не меньше, чем 32267 (см. [Plal], стр. 337). Здесь,I
очевидно, учтены рекомендации Д. Кнута обходиться без младших
двоичных разрядов, когда модуль равен степени двойки. Легко
проверить, что условия (а)-(в) выполнены, а значит, указанная по-
следовательность имеет максимально возможный период длины 2к.
Удовлетворяет ли указанным условиям конкретная реализация на
языке С, исходный текст которой, как правило, неизвестен,1 можно
при благоприятных условиях с помощью следующего алгоритма
Р. П. Брента. Этот алгоритм вычисляет длину X периода последова-
тельности, вычисленной по рекурсивной формуле X/+i = F(XZ) с по-
мощью порождающей функции F : D —» D из начального значения
Хо G D. Для этого требуется не более 2 • тах{ц, X} раз вычислить
функцию F (см. [HKW], п. 4.2).
Алгоритм Брента определения длины X периода
последовательности вида XI+1 = F(XZ) с начальным элементом Хо
1. Положить у <— Хо, г <- 1 и к <- 0.
2. Положить х <г- у, j <— к и г <— г + г.
3. Положить к <— к + 1 и у <- F(y). Повторять этот шаг, пока не по-
лучится х = у или к>г.
4. Еслих Ф у, то вернуться на шаг 2. Иначе результат: X = k-j.
Процесс завершится успехом, если на шаге 3 рассматривать реаль-
ные значения F(y), и неудачей, как для ISO-рекомендации, если
вместо значений будут лишь их старшие разряды.
Этот тест можно дополнить критерием хи-квадрат (пишут также
«критерий %2»), который устанавливает, насколько эмпирически
полученное распределение вероятностей соответствует теорети-
чески ожидаемому распределению. При использовании критерия
хи-квадрат вычисляют статистику
Библиотеки GNU-C от Free Software Foundations и ЕМХ-С Эберхарда Маттеса (Eberhard Mattes)
являются приятным исключением. В функции rand() библиотеки ЕМХ используются параметры
а = 69069, b = 5 и т = 232. Число а = 69069, предложенное Дж. Марсальей (G. Marsaglia), показы-
вает в сочетании с модулем т = 232 хорошие статистические результаты и максимальную длину
периода (см. [Knut], стр. 102-104).
ГЛАВА 11. Большие случайные числа
261
(11.2) 2 ^(H(Xl)-nP(Xi))2
(11.3) IU : Я? • > где для t различных событий Xt через H(XZ) обозначена наблю- даемая частота события Хь через Р(Х;) - вероятность появления события X,-, а п - это объем выборки. Для распределения, соответст- вующего указанному, математическое ожидание статистики %2, рассматриваемой как случайная величина, равно Е(%2) = г-1. Пороговые значения, при которых мы отвергаем гипотезу о равен- стве распределений с заданной вероятностью ошибки, можно опре- делить по таблицам хи-квадрат распределения с t - 1 степенями свободы (см. [Bosl], п. 4.1). Проверка критерия хи-квадрат применяется для проверки соответ- ствия результатов многих эмпирических тестов теоретически вы- численным распределениям. Особенно легко применять критерий хи-квадрат к последовательностям равномерно распределенных (это и есть гипотеза теста!) случайных чисел Xt из диапазона значе- ний {0, w- 1}. Мы считаем, что каждое из чисел множества W может быть взято с одной и той же вероятностью р = 1Лг, и таким образом предполагаем, что среди п случайных чисел Xt каж- дое число из W встречается примерно nlw раз (мы считаем п > w). Однако это не обязательно так, поскольку вероятность Рк того, что среди п случайных чисел X,- заданное значение w е W появится в точности к раз, вычисляется как рк = скрк(1 -Ргк = Рк(1 -ру-к 2 ; к\(п-к)\
(11.4) Это биномиальное распределение действительно принимает наи- большее значение при к ~ n/w, но вероятности Ро = (1 ~р)п и ?п = рп не равны нулю. Следовательно, в предположении, что последо- вательность Xi ведет себя как случайная, мы можем ожидать, что частоты hw отдельных значений we W будут распределены по биномиальному закону. Так ли это на самом деле, проверяется по критерию хи-квадрат: Г ;Г /=о п i=Q Проверка повторяется для нескольких случайных выборок (отрезков последовательности Xz). Грубая аппроксимация ^-распределения по- зволяет нам сделать вывод, что в большинстве случаев результат
Ск — биномиальный коэффициент. — Прим. ред.
262
Криптография на Си и C++ в действии
должен лежать в интервале [w-2y/w, vv + 2Vw]. В противном слу-
чае данную последовательность можно считать недостаточно слу-
чайной. Отсюда следует, что вероятность ошибки, то есть вероят-
ность признать действительно «хорошую» последовательность
«плохой» на основании результатов теста хи-квадрат, равна при-
мерно 2%. Подчеркнем, что этот тест корректен только для доста-
точно большого числа выборок: это число должно быть по крайней
мере равно п = 5w (см. [Bos2], п. 6.1), а в идеале - как можно больше.
Линейный конгруэнтный генератор из стандарта ISO-С, который
мы рассматривали выше, проходит этот простой тест, как и другие
генераторы псевдослучайных чисел, которые нам еще предстоит
реализовать в пакете FLINT/C.
После такого краткого экскурса в статистику вспомним о том, что
случайные последовательности должны удовлетворять, помимо
статистических, и другим критериям, в зависимости от области
применения. Случайные последовательности, используемые для
криптографических приложений, должны быть такими, чтобы без
знания некоторой дополнительной (секретной) информации их
невозможно было предсказать или восстановить по нескольким
заданным элементам. То есть нарушитель не должен иметь воз-
можности воспроизвести криптографический ключ или последова-
тельность ключей, вырабатываемых с помощью псевдослучайной
последовательности. Хорошо зарекомендовал себя в этом смысле
генератор BBS Л. Блюм (L. Blum), М. Блюма (М. Blum) и М. Шуба
(М. Shub), основанный на результатах теории сложности. Сначала
опишем, а затем реализуем этот генератор, при этом не будем
углубляться в теорию (читатель может с ней ознакомиться в [Blum]
или [HKW], глава 4 и п. 6.5).
Нам понадобятся два простых числа р и q такие, что р = q = 3 mod 4,
их произведение - число п, а также число X взаимно простое с п.
Вычислив Xq := X2 mod п, получаем начальный элемент Хо п0‘
следовательности чисел, получаемых рекуррентным возведением
в квадрат:
X/+i = X,2 mod п .
В качестве случайного числа берем младший бит элемента X/.
Полученная таким образом случайная последовательность битов
является безопасной с точки зрения криптографии: предсказать
следующий бит из уже вычисленных можно только зная делители/?
и q числа л. Если же эти два числа хранятся в секрете, то для пред-
сказания последующих битов с вероятностью, большей у, или ДДЯ
восстановления неизвестных отрезков последовательности нужно
разложить на множители число и. В основе безопасности генератора
BBS лежат те же принципы, что и в криптосистеме RSA. За доверие
к генератору BBS приходится заплатить трудностью вычисления
ГЛАВА 11. Большие случайные числа
263
случайных битов: для каждого бита нужно возводить в квадрат по
модулю большого целого числа, чем и обусловлено длительное
время генерации больших случайных последовательностей. Если
нужны короткие последовательности случайных чисел, например
при генерации отдельных криптографических ключей, это обстоя-
тельство не столь важно. Здесь играет роль лишь вопрос безопасно-
сти, хотя при ее оценке следует учитывать и процесс получения на-
чальных значений. Генератор BBS детерминированный, поэтому
«чистая случайность» может быть достигнута только при тщатель-
ном выборе начального значения. Для этого можно использовать
дату или время, статистические характеристики системы (напри-
мер, число «тиков» системных часов при выполнении заданного
процесса), числовые характеристики внешний событий, таких как
время между нажатием клавиши клавиатуры или мыши, и многие
другие методы, которые лучше всего сочетать друг с другом (сове-
ты по выработке начальных значений читатель найдет в работах
[East] и [Matt]).3
Теперь вернемся к теме, которой и посвящена эта глава, и на
имеющейся базе построим два генератора случайных чисел формата
CLINT. В качестве отправной точки на пути к генерации простых
чисел научимся, например, создавать большие числа заданной дво-
ичной длины. Для этого старший бит полагаем равным 1, а осталь-
ные биты генерируем случайным образом.
Сперва построим линейный конгруэнтный генератор и из элемен-
тов полученной последовательности будем выбирать разряды слу-
чайного числа типа CLINT. Параметры а = 6364136223846793005 и
т = 264 для нашего генератора возьмем из таблицы результатов
спектрального теста (см. [Knut], стр. 102-104). Тогда последова-
тельность Xf+i = (X,• • а + 1) mod т будет иметь максимальную длину
периода X = т и обладать хорошими статистическими свойствами,
что можно заключить на основании результатов, представленных в
таблице. Реализуем генератор в виде функции rand64J. При каждом
вызове функции rand64J очередной элемент последовательности
генерируется и записывается в глобальный CLINT-объект SEED64,
объявленный как static. Параметр а хранится в глобальной пере-
менной А64. Функция возвращает указатель на SEED64.
Функция: Линейный конгруэнтный генератор с периодом 264
Синтаксис: clint * rand64J (void);
Возврат: Указатель на SEED64 с полученным случайным числом
В критических приложениях для генерации начальных значений или всей случайной последова-
тельности всегда следует использовать истинно случайные числа, полученные с помощью под-
ходящих аппаратных компонентов.
264
Криптография на Си и C++ в действии
clint * rand64J (void) { mulj (SEED64, A64, SEED64); incj (SEED64);
( J Для приведения по модулю 264 просто устанавливаем нужную дли-
ну поля в SEED64, что не требует почти никаких временных затрат. SETDIGITS-L (SEED64, MIN (DIGITS.L (SEED64), 4)); return ((clint *)SEED64); } Теперь нам нужна функция, задающая начальные значения для rand64J(). Назовем ее seed64J(). На вход этой функции поступает переменная типа CLINT, из не более чем четырех старших разрядов которой берется начальное значение переменной SEED64. Преды- дущее значение переменной SEED64 копируется в статическую пе- ременную BUFF64 типа CLINT, а возвращает эта функция указатель на BUFF64.
Функция: Задание начальных значений для функции rand64J()
Синтаксис: clint * seed64J (CLINT seedj);
Вход: seedj (начальное значение)
Возврат: Указатель на переменную BUFF64, содержащую предыдущее зна- чение переменной SEED64 clint * seed64J (CLINT seedj) { int i; cpyj (BUFF64, SEED64); for (i = 0; i <= MIN (DIGITS_L (seedj), 4); i++) { SEED64[i] = seedj[i];
ГЛАВА 11. Большие случайные числа
return BUFF64;
}
Еще один вариант функции seed64J() с аргументом типа ULONG
Функция: Задание начальных значений для функции rand64J()
Синтаксис: clint * ulseed64J (ULONG seed);
Вход: seed (начальное значение)
Возврат: Указатель на переменную BUFF64, содержащую предыдущее зна_ чение переменной SEED64
clint *
ulseed64J (ULONG seed)
{
cpyj (BUFF64, SEED64);
ul2clintj (SEED64, seed);
return BUFF64;
}
«)И Следующая функция возвращает случайные числа типа ULONG. В процессе генерации каждого числа происходит обращение к функции rand64J(), при этом для построения числа нужного типа используются старшие разряды переменной SEED64.
Функция: Синтаксис: Возврат: генерация случайного числа типа unsigned long unsigned long ulrand64J (void); Случайное число типа unsigned long
ULONG ulrand64J (void) { ULONG val; USHORT 1; rand64J(); 1 = DIGITS-L (SEED64); switch (1) {
266
Криптография на Си и C++ в действии
case 4:
case 3:
case 2:
val = (ULONG)SEED64[I-1];
val += ((ULONG)SEED64[I] « BITPERDGT);
break;
case 1:
val = (ULONG)SEED64[I];
break;
default:
val = 0;
}
return val;
}
В пакете FLINT/C есть дополнительные функции ucrand64J(void) и
usrand64J(void) для генерации случайных чисел типа UCHAR и
USHORT соответственно. Здесь мы их обсуждать не будем, а рас-
смотрим лучше функцию ranf_l(), вырабатывающую случайные
числа типа CLINT с заданным числом двоичных разрядов.
Функция: Генерация случайного числа типа CLINT
Синтаксис: void randj (CLINT rj, int I);
Вход: I (число двоичных разрядов - длина генерируемого числа)
Выход: r l (случайное число из интервала 21"1 < r l < 21 - 1)
void
randj (CLINT rj, int I)
{
USHORT i, j, Is, Ir;
Сначала ограничиваем число двоичных разрядов I максимально
допустимым значением для типа CLINT. Затем определяем тре-
буемое число разрядов типа USHORT (Is) и позицию (Ir) старшего
двоичного разряда в старшем USHORT-разряде.
ГЛАВА 11. Большие случайные числа
267
I = MIN (I, CLINTMAXBIT);
Is = (USHORT)I » LDBITPERDGT;
lr = (USHORT)I & (BITPERDGT - 1UL);
aV’l ХГ
Теперь последовательно генерируем разряды числа rj, каждый
раз вызывая функцию usrand64_l(). Таким образом, младшие
двоичные разряды числа SEED64 при построении CLINT-разрядов
не используются.
for (i = 1; I <= Is; i++)
rj[i] = usrand64J ();
Далее идет «ювелирная обработка» значения r_l - задание стар-
шего бита. Если lr > 0, то бит на (1г-1)-й позиции (Is + 1 )-го
USHORT-разряда полагаем равными 1, а все более старшие -
равными 0. Если же lr = 0, то ставим 1 в самый старший бит
USHORT-разряда с номером Is.
if (lr > 0)
rj[++ls] = usrand64J ();
j = 1U « (lr- 1); /* j <- 2A(lr- 1) */
r_l[ls] = (r_l[ls]|j)&((j«1)-1);
else
r_l[ls] |= BASEDIV2;
SETDIGITSJ_ (rj, Is);
И завершим эту главу реализацией генератора BBS. Для этого с
помощью функции primeJO найдем простые числа р и q такие, что
р = q == 3 mod 4 примерно с одним и тем же числом двоичных раз-
рядов (это нужно для того, чтобы разложить модуль на множители
было максимально трудно, на чем, собственно, и основана крипто-
графическая стойкость генератора BBS, см. стр. 363). Из этих чисел
268
Криптография на Си и C++ в действии
t J > г.л - w. составляем модуль п = pq. Модуль такого вида длиной 2048 бит читатель найдет в пакете FLINT/C, хотя числа р и q там не указаны (их знает только автор). В static-переменные XBBS и MODBBS будем записывать соответст- венно элементы последовательности Xz и модуль п. Из них функция randbit() вычисляет случайный бит следующим образом.
" 41 < Функция: Синтаксис:* * Возврат: Псевдослучайный генератор Блюм-Блюма-Шуба int randbitj (void); Элемент множества {0, 1}
; ЛТЛЭ ’ ( О*' J 1 Й . > . i WW. « ‘ ‘ » Й? , static CLINT XBBS, MODBBS; static const char *MODBBSSTR = "81 aa5c..."; /* Модуль как строка символов */ int randbitj (void) { msqrj (XBBS, XBBS, MODBBS);
с В качестве результата берем младший бит числа XBBS.
return (*LSDPTR_L (XBBS) & 1); } Для инициализации генератора BBS воспользуемся функцией seedBBSJ().
Функция: Синтаксис: Вход: Задание начальных значений для функций randbitJO и randBBSJO int seedBBSJ (CLINT seedj); seedj (начальное значение)
int
seedBBSJ (CLINT seed J)
CLINT gcdj;
ГЛАВА 11. Большие случайные числа
269
str2clint_l (MODBBS, (char JMODBBSSTR, 16); gcdj (seedj, MODBBS, gcdj); if (IEQONEJ. (gcdj)) { return-1; i
) msqrj (seedj, XBBS, MODBBS);
return 0;
}
Функция ulrandBBS_l(), которую тоже можно использовать для
генерации случайных чисел типа ULONG, аналогична функции
ulrand64J().
Функция: Генерация случайного числа типа unsigned long
Синтаксис: unsigned long ulrandBBSJ (void);
Возврат: Случайное число типа unsigned long
ULONG
ulrandBBSJ (void)
{
ULONG i, r = 0;
for (i = 0; i < (sizeof(ULONG) « 3); i++)
{
r = (r« 1) + randbitJO;
}
return r;
}
Нам не хватает еще функции randBBS_l(CLINT г J, int I), генери-
рующей случайные числа r_l длины ровно I двоичных разрядов,
то есть r_l из интервала 21"1 < r_l < 21 - 1. Мы не приводим здесь ее
описание, поскольку она во многом совпадает с функцией rand_l().
Но разумеется, эту функцию читатель найдет в пакете FLINT/C.
ГЛАВА 12.
Стратегия тестирования LINT
Не обвиняйте компилятор.
Дэвид А. Спулер,
C++ и С: Отладка, тестирование
и достоверность кода
В предыдущих главах не раз упоминалось о тестировании отдель-
ных функций. Без проведения осмысленных тестов, удостоверяю-
щих качество нашего пакета, вся проделанная нами работа оказа-
лась бы бесполезной, ибо чем ещё можно обосновать нашу уверен-
ность в надежности разработанных функций? Поэтому сейчас мы
собираемся посвятить всё внимание этой важной теме, и с этой
целью поставим перед собой два вопроса, которыми должен зада-
' ваться каждый разработчик программного обеспечения:
✓ Как удостовериться, что функции нашего программного обеспече-
ния ведут себя в соответствии с их спецификацией, которая в на-
шем случае означает в первую очередь то, что они математически
корректны?
✓ Как достичь стабильности и надёжности функционирования нашего
программного обеспечения?
4 Несмотря на то, что эти два вопроса тесно связаны, фактически они
•Р относятся к двум различным областям. Функция может быть мате-
матически некорректна, например, если был неправильно реализо-
ван базовый алгоритм, и всё же она может надёжно и стабильно
воспроизводить эту ошибку и постоянно выдавать один и тот же
неправильный результат для заданного входного значения. С дру-
гой стороны, функции, возвращающие правильные на вид резуль-
таты, могут быть подвержены ошибкам другого рода, например
... таким, как переполнение длины вектора или использование непра-
вильно инициализированных переменных, что приводит к неопре-
р делённости поведения. Причём эта неопределённость остаётся
невыявленной после удачного (или лучше сказать неудачного?)
завершения отладки.
4J>. Итак, мы должны иметь в виду оба эти аспекта и утвердить методы
4 < разработки и тестирования, которые позволят нам доверять как кор-
ректности, так и надёжности наших программ. Существуют много-
численные публикации, в которых обсуждается значение и послед-
’ ствия таких требований для всего процесса разработки программ-
ного обеспечения и где углублённо изучается проблема качества
программ. Такое почтительное внимание к этой теме нашло выраже-
ние в международной тенденции внедрять в производство про-
граммного обеспечения стандарт ISO 9000. Теперь больше не гово-
рят просто о “тестировании’" или “обеспечении качества”, вместо
этого слышны разговоры об “управлении качеством” или о “полном
272
Криптография на Си и C++ в действии
управлении качеством”. Отчасти это просто результат эффективного
маркетинга, но, тем не менее, эти формулировки должным образом
освещают проблему, состоящую в том, чтобы рассматривать про-
цесс создания программного обеспечения во всей его многосторон-
ней полноте и посредством этого улучшать его. Часто употребляе-
мое выражение “проектирование программного обеспечения”, или
“программирование” не может скрыть тот факт, что этот процесс,
л гид. если уЧесть его отношение к предсказуемости и точности, едва ли
может соперничать с классическим инженерным искусством.
।
Это сравнение должным образом характеризуется следующим
анекдотом. Три инженера - механик, электрик и программист -
решили вместе прокатиться на автомобиле. Они уселись в машину,
но та отказалась заводиться. Механик сразу же заявил: «Проблема с
мотором. Засорена форсунка инжектора». «Чепуха, - возразил элек-
4; трик. - Виновата электроника. Определенно отказала система зажи-
гания». После чего программист предложил: «А давайте все выле-
зем из машины и опять залезем. Может, тогда она заведется».
Оставим трех отважных инженеров с их дальнейшими разговорами
_ j и приключениями и рассмотрим некоторые опции, которые были
реализованы при создании и тестировании пакета FLINT/C. Прежде
всего, упомянем те литературные источники, которыми мы пользо-
кьд’ вались. Они не утомляют читателя абстрактными рассуждениями и
руководящими указаниями, а оказывают конкретную помощь в ре-
шении конкретных проблем, не упуская из виду общей картины1.
Каждая из этих книг содержит многочисленные ссылки на другую
важную литературу по этой теме:
✓ [Dene] - стандартная работа, рассматривающая процесс разработки
программного обеспечения во всей полноте. Книга содержит много
методологических указаний, основанных на практическом опыте
автора, а также много наглядных и полезных примеров. Снова и
снова затрагивается тема тестирования в связи с разнообразными
этапами программирования и системного интегрирования, при этом
основные концептуальные и методологические правила рассматри-
ваются совокупно с практической точки зрения, и всё это объеди-
нено тщательно спроектированной системой примеров.
✓ [Harb] - содержит полное описание языка программирования С и
стандартной библиотеки С, а также даёт много ценных указаний и
замечаний по поводу стандарта ISO. Это необходимое справочное
пособие, к которому можно обращаться на каждом шагу.
✓ [Hatt] - очень подробно, в деталях, описывает создание в языке С
систем программного обеспечения с критической надёжностью.
Указанные здесь источники представляют личную, субъективную выборку автора. Существует
много других книг и публикаций, которые также можно было бы включить в этот список, однако
за недостатком места и времени они были опущены.
ГЛАВА 12, Стратегия тестирования LINT
273
Типовые примеры и источники ошибок демонстрируются с помо-
щью конкретных примеров и статистики - а ведь язык С опреде-
лённо предоставляет много возможностей для ошибок. Также при-
водятся исчерпывающие методологические советы, следуя которым,
можно укрепить доверие к продуктам программного обеспечения.
✓ [Lind] - превосходная, занимательно написанная книга, показы-
вающая глубокое понимание автором языка программирования С.
Кроме того, автор знает, как передать своё понимание читателю.
Многие рассматриваемые темы можно было бы снабдить подзаго-
ловком «А вы знаете, что...», и очень немногие читатели смогли бы
честно, положа руку на сердце, ответить утвердительно.
✓ [Magu] - рассматривает проектирование подсистем и поэтому
представляет для нас особенный интерес. Здесь идёт речь об интер-
претации интерфейсов и принципах работы с функциями, имею-
щими входные параметры. Разъясняются также отличия между
рискованным и защитным программированием. Ещё одна сильная
сторона этой книги - эффективное использование утверждений
(см. стр. 173) в качестве средств тестирования и во избежание
неопределённых программных состояний.
✓ [Murp] - содержит описание множества средств тестирования,
которые можно, не прилагая больших усилий, применить на прак-
тике при тестировании программ и немедленно получить успеш-
ные результаты. Помимо всего прочего к этой книге прилагается
дискета с библиотеками для реализации утверждений, тестирова-
ния обработки объектов динамической памяти, и отчёта о выпол-
нении тестов. Эти библиотеки также использовались для тестиро-
вания FLINT/C-функций.
✓ [Spul] - предлагает для обозрения методы и средства тестирования
программ на языках С и C++ и даёт многочисленные указания по
их эффективному применению. Книга содержит широкий обзор ти-
пичных для С и C++ ошибок программирования и рассматривает
способы их обнаружения и устранения.
12.1. Статический анализ
Методологические подходы к тестированию можно разделить на
две категории: статическое тестирование и динамическое тести-
рование. К первой категории относится проверка кода (текста про-
граммы). При этом исходный текст внимательно просматривается и
i проверяется построчно на наличие таких проблем, как отклонения
, от спецификации (в нашем случае это выбранные алгоритмы),
ошибки в рассуждениях, неточности в расположении строк или в
t стиле, сомнительные конструкции и ненужные кодовые последова-
тельности.
274
Криптография на Си и C++ в действии
Для проверки кодов используются аналитические средства, такие
как хорошо известная в Unix программа lint, которые в значительной
степени автоматизируют эту трудоёмкую задачу. Первоначально
одним из главных применений lint было компенсировать существо-
вавшие ранее в языке С недочёты при проверке согласования пара-
метров, которые передавались функциям в транслируемые по от-
дельности модули. Тем временем появились более удобные, чем
классический lint, продукты, которые могли обнаруживать огром-
ное количество потенциальных проблем в коде программы. Причём
синтаксические ошибки, не позволяющие компилятору трансли-
ровать код, представляли лишь малую часть этих проблем. Ниже
приводятся несколько примеров проблемных областей, которые
можно обнаружить путём статического анализа:
✓ синтаксические ошибки,
✓ пропущенные или несогласованные прототипы функций,
✓ несогласования при передаче параметров функциям,
✓ ссылки на несовместимые типы или соединение таких типов,
✓ использование неинициализированных переменных,
✓ непереносимые конструкции,
✓ необычное или неправдоподобное использование отдельных языко-
вых конструкций,
✓ недостижимый код.
Настоятельным условием строгой проверки типов автоматизиро-
ванными средствами является использование прототипов функций.
С помощью прототипов ISO-совместимый компилятор языка С
может проверять во всех модулях типы передаваемых функциям
аргументов и определять несогласования. Многие компиляторы
тоже можно настроить на анализ исходного кода, если включены
соответствующие уровни предупреждений. Например, компилятор
языка C/C++ gcc из проекта GNU Free Software Foundation обладает
весьма мощными анализирующими функциями, которые можно
активировать с помощью опций -Wall -ansi и -pedantic2 3.
При установке FLINT/C-функций, кроме тестов, выполняемых
множеством разных компиляторов, для статического тестирования
прежде всего применялись продукт PC-lint из Gimpel Software
(версия 7.5; см. [Gimp]) и LCLint из MIT (версия 2.4; см [Evan]) •
2 Этот компилятор содержится в различных дистрибутивах Linux, а также его можно приобрести
на http://www.leo.org.
3 LCLint можно скачать из Интернета. Домашняя страничка LCLint находится по адресу
http://www.sds.lcs.mit.edu/pub/lclint/. По анонимному ftp можно скачать LCLint для Linux И
Windows 9x/NT по адресу ftp://sds.lcs.mit.edu/pub/lclint/. I
ГЛАВА 12. Стратегия тестирования LINT
275
PC-lint оказался весьма полезным инструментом для тестирования
программ как на языке С, так и на C++. Ему известны примерно две
тысячи отдельных проблем, и он использует механизмы, которые
извлекают из кода значения, загруженные в динамические локальные
переменные во время выполнения, и включают их в сообщения об
ошибках. Таким путём уже во время статического анализа можно
открыть многие ошибки, такие как превышение границ векторов,
которые обычно обнаруживаются - если обнаруживаются вообще -
только в процессе выполнения (и можно надеяться, что во время
тестирования, а не после него).
Помимо этого, доступный для широкого пользования LCLint был
переделан для работы под операционной системой Linux. LCLint
различает четыре режима (weak, standard; check, strict), каждый из
которых связан с определёнными предварительными установками.
Эти режимы выполняют тесты различной степени точности. Кроме
типовых для lint функций, LCLint делает возможным проверку
программ на наличие отдельных спецификаций, которые вставля-
ются в исходный текст в виде особым образом форматированных
комментариев. Таким способом можно сформулировать граничные
условия для реализации функций и их вызовов и проверить их
соответствие спецификациям. Имеются также дополнительные
возможности для семантического управления.
Для программ без дополнительных спецификаций в качестве
стандарта рекомендуется установка режима с опцией -weak. Тем
не менее, в руководстве упоминается о специальной награде для
того, кому впервые удастся написать «настоящую программу»,
не выдающую ошибок при использовании LCLint в режиме -strict.
При использовании этих двух инструментов для тестирования
FLINT/C-функций оказалось целесообразным предварительно
проверять, какие именно опции используются, и создавать файлы
параметров пользователя, чтобы сконфигурировать инструменты
для индивидуального применения.
После тщательной проверки FLINT/C-кода, по окончании теста ни
один из этих двух продуктов не выдал никаких предупреждений,
которые можно было бы счесть серьёзными. Это позволяет нам
надеяться на успешное выполнение поставленных выше условий,
гарантирующих качество FLINT/C-функций.
12.2. Динамические тесты
Цель динамических тестов в том, чтобы доказать, что отдельный
«кирпичик» какой-либо части программного обеспечения выполняет
свою спецификацию. Чтобы придать этим тестам выразительность и
силу для оправдания затраченных на них времени и денег, нам при-
дётся предъявить к ним те же требования, что и к научному экспери-
менту. А именно: они должны быть полностью документированы,
276
Криптография на Си и C++ в действии
а их результаты должны быть воспроизводимы и доступны для про-
верки сторонними наблюдателями. Полезно делать различие между
тестированием отдельных модулей и тестами интегрированных
систем, хотя границы здесь весьма подвижны (см. [Dene], п. 16.1).
Для достижения этой цели тесты, или контрольные примеры, сле-
дует конструировать таким образом, чтобы можно было проверять
функции предельно исчерпывающим образом или, иными словами,
достигать максимально возможного охвата тестируемых функций.
Критерии, или метрики, для охвата тестов могут быть различными.
Например, в случае СО-охвата оценивается доля инструкций функ-
ции или модуля, которые на самом деле выполняются или, если
конкретно, какие инструкции не выполняются. Есть критерии
большего размера, чем СО, которые учитывают долю использую-
щихся ветвей программы {С 1-охват) или даже долю пройденных
путей функции. Последний значительно сложнее первых двух.
В каждом случае целью является достижение как можно большего
охвата с помощью тестов, которые полностью контролируют пове-
дение программы. Здесь есть два аспекта, слабо связанных друг с
другом. Тестировщик, просматривающий все ветви функции, всё
же может не обнаружить некоторые ошибки. С другой стороны,
можно сконструировать контрольные примеры, в которых тести-
руются все свойства функции, даже если некоторые её ветви не
рассматриваются. Таким образом, качество теста можно оценивать
по крайней мере двумя измерениями.
Тестовые значения, основанные только на знании спецификации,
выполняют так называемые тесты на уровне черного ящика. Если
для достижения высокой степени охвата тестов этого недостаточно,
тогда необходимо при конструировании контрольных примеров
учитывать подробности реализации, и в этом случае мы получим
так называемые тесты на уровне белого ящика. Примером случая,
когда мы создавали тесты для особой ветви функции только на ос-
нове спецификации, является алгоритм деления на стр. 67: чтобы
протестировать шаг 5, используются специальные тестовые данные,
указанные на стр. 79, в результате чего выполняется соответст-
вующий код. С другой стороны, необходимость специальных тес-
товых данных при делении с меньшими делителями становится
очевидной, только если учитывать, что этот процесс выполняется
особой частью функции divj(). Здесь подразумевается именно поД'
робность реализации, которую нельзя вывести из алгоритма.
На практике обычно всё сводится к смешанному применению ме-
тодов чёрного и белого ящиков, которое в работе [Dene] называется
соответственно тестирование серого ящика. Однако, никогда нельзя
ожидать достижения стопроцентного охвата, как показываю?
следующие рассуждения: допустим, что мы генерируем просты6
числа с проверкой по тесту Миллера-Рабина с большим число*1
итераций (скажем, 50) и соответствующей вероятностью ошибки
кАВА 12. Стратегия тестирования LINT
277
((1/4)“50 ~ 10~30, см. п. 10.5) и затем проверяем эти простые числа
ещё одним, детерминированным, тестом на простоту. Поскольку
управление передаётся той или иной ветви программы, в зависимо-
сти от исхода этой второй проверки, у нас практически нет реаль-
ного шанса достичь той ветви, переход к которой следует только
после отрицательного результата проверки. Однако вероятность
того, что эта вызывающая подозрение ветвь будет выполняться при
действительном использовании программы, также нереальна,
поэтому, наверное, легче обойтись без этой части теста, чем вно-
сить в код семантические изменения ради искусственного создания
возможности тестирования. Таким образом, на практике всегда
можно встретить ситуации, где требуется отказаться от стопро-
центного тестового охвата, чем бы он ни измерялся.
Тестирование арифметических функций пакета FLINT/C, который
? г реализован главным образом с математической точки зрения -
весьма сложная задача. Как установить, выдают ли правильные ре-
зультаты операции сложения, умножения, деления или возведения
в степень больших чисел? Карманные калькуляторы, как правило,
вычисляют только порядок величины, эквивалентной вычисляемой
' стандартными арифметическими функциями С-компилятора, по-
этому значимость этих вычислений ограниченна.
Конечно, имеется вариант, при котором можно применить в качест-
ве теста другой арифметический программный пакет. Разработаем
необходимый интерфейс, преобразуем числовые форматы - и пусть
! функции «соревнуются» друг с другом. Однако против этого под-
хода есть два «но»: во-первых, это не развлечение, а во-вторых,
r ' почему нужно доверять чьим-то разработкам, о которых известно
значительно меньше, чем о собственном продукте? Поэтому по-
ищем другие возможности тестирования, и с этой целью применим
математические структуры и законы, достаточно мощные, чтобы
п; распознать вычислительные ошибки в программе. С обнаружен-
ными ошибками затем можно будет разобраться с помощью допол-
нительного вывода тестовых результатов и современного символь-
uiv ного отладчика.
* . , Поэтому мы избирательно применим метод черного ящика и будем
надеяться, что к концу этой главы мы составим практичный план
проведения динамических тестов, который будет придерживаться
того курса проведения тестирования, который применялся к
4 ' FLINT/C-функциям. В ходе этого процесса у нас была цель достичь
наибольшего С1-охвата, хотя никакие измерения в этом отношении
не производились.
Перечень свойств FLINT/C-функций, которые нужно протестиро-
вать, не особенно велик, но затрагивает существенные вопросы.
В частности, мы должны убедиться в следующем.
✓ Все результаты вычислений корректны над всей областью опреде-
ления всех функций.
278
Криптография на Си и C++ в действии
✓ Все входные значения, для которых внутри функции имеются спе-
циальные последовательности команд, обрабатываются правильно.
✓ Осуществляется правильное управление переполнением и потерей
значимости. То есть все арифметические операции выполняются по
модулю Nmax + 1.
✓ Ведущие нули допускаются, не влияя на результат.
✓ Вызовы функции в режиме сумматора с идентичными объектами
памяти в качестве переменных, например, такие как addj(nj, nJ,
nJ), возвращают правильные результаты.
✓ Все деления на нуль распознаются, и выдаётся соответствующее
сообщение об ошибке.
Имеется много отдельных тестовых функций, необходимых для ра-
боты с этим списком, функций, которые вызывают тестируемые
FLINT/C-операции и проверяют их результаты. Эти функции соб-
раны в тестовых модулях, и их самих проверяют каждую по от-
дельности, прежде чем применить к FLINT/C-функциям. Для
проверки тестовых функций используются те же самые критерии и
те же самые средства статического анализа, что и для FLINT/C-
функций. Более того, выполнение тестовых функции следует
просмотреть пошагово по крайней мере на имеющейся в наличии
контрольной базе с помощью символьного отладчика для того,
чтобы проверить, тестируют ли они то, что нужно. Чтобы опреде-
лить, действительно ли тестовые функции должным образом реаги-
руют на ошибки, полезно встроить в арифметические функции
ошибки, приводящие к неправильным результатам (а после этапа
тестирования удалить их, не оставив и следа!).
Поскольку мы не можем протестировать каждое значение из области
определения CLINT-объектов, нам требуются, кроме фиксированных
заданных заранее тестовых значений, случайным образом сгенери-
рованные входные значения, которые равномерно распределены по
всей области определения [0, Л/тах]. С этой целью используем нашу
функцию randj(rj, bitlen), при этом выбираем число двоичных раз-
рядов bitlen, с помощью приведения функции usrand64J() по модулю
(МАХ2 + 1) случайным образом из интервала [О, МАХ2]. Первыми
должны проходить тестирование функции для генерации псевдослу-
чайных чисел, которые были рассмотрены в главе 11, где среди
прочего мы применяли описанный там критерий %2 для проверки
статистических свойств функций usrand64J() и usrandBBSJO- Кр°*
ме этого, мы должны убедиться, что функции randJO и randBBSjO
правильно генерируют числовой формат CLINT и возвращают числа
точно той длины, которая предопределена. Эта проверка необходима
и для других функций, выдающих CLINT-значения. Для распозна-
вания ошибочных форматов CLINT-аргументов у нас есть функция
vcheckj(), которую поэтому следует поместить в начало последова-
тельности тестов.
ГЛАВА 12. Стратегия тестирования LINT
279
ОН
-к -qu
1 „ \
* >[»-? *'А-
Ещё одно условие для большинства тестов - это возможность оп-
ределения равенства или неравенства и сравнения размеров целых
чисел, представленных CLINT-объектами. Мы должны также про-
тестировать функции IdJ(), equj(), mequj() и cmpj(). Это можно
осуществить, используя как определённые заранее, так и случайные
числа, при этом следует проверять все случаи - равенство, так же
как и неравенство - с соответствующими соотношениями размеров.
Ввод заранее заданных значений производится, в зависимости от
цели, либо посредством функции str2clint_l(), либо в виде типа
unsigned посредством функции преобразования u2clintj() или
ul2clintj(). Функция str2clintj(), обратная к функции xclint2strj(),
используется для генерации выходного результата теста. Поэтому
эти функции должны стоять следующими в нашем списке тести-
руемых функций. При тестировании строковых функций мы вос-
пользуемся их взаимодополняемостью и проверим, получается ли в
результате выполнения одной функции после другой исходная
строка символов или, при выполнении в другом порядке, выходное
значение в CLINT-формате. Далее мы неоднократно будем возвра-
щаться к этому правилу.
Теперь остается проверить только динамические регистры и их
управляющие механизмы, описанные в главе 9, которые вообще хо-
телось бы включить в тестовые функции. Использование регистров
как динамически распределённой памяти помогает нам тестировать
FLINT/C-функции, при этом мы дополнительно реализуем отладоч-
ную библиотеку для функций malloc() для распределения памяти.
Типовая функция таких пакетов, как общедоступных, так и коммер-
ческих (см. [Spul], глава 11), проверяет поддержание границ дина-
мически распределённой памяти. Имея доступ к CLINT-регистрам,
мы можем следить за нашими FLINT/C-функциями: о каждом
вторжении границы в чужую область памяти будет сообщаться.
Типовой механизм, предоставляющий такую возможность, перена-
правляет обращенные к malloc() вызовы специальной тестовой
функции, которая получает запросы на выделение памяти, по оче-
реди вызывает malloc() и таким образом выделяет значительно
больше памяти, чем требуется на самом деле. Этот блок памяти
регистрируется во внутренней структуре данных, а справа и слева
от первоначально запрашиваемой области памяти создаётся «барьер»
из нескольких бит, которые заполняется избыточным шаблоном,
таким как чередующиеся двоичные нули и единицы. Затем возвра-
щается указатель на свободную память внутри этого барьера.
Теперь обращение к функции free() также направляется сначала к
отладчику этой функции. Прежде чем освобождается выделенный
блок, выполняется проверка того, остался ли «барьер» неповреж-
дённым или шаблон уничтожен путём затирания, и в этом случае
генерируется соответствующее сообщение и область памяти вычёр-
кивается из регистрационного списка. Только потом в действитель-
ности вызывается функция free(). В заключение можно, используя
280
Криптография на Си и C++ в действии
внутренний регистрационный список, проверить, какие области
памяти не были освобождены. Настройка кода на передачу вызо-
вов, обращенных к malloc() и free(), их отладочным вариантам осу.
ществляется с помощью макросов, которые, как правило, описаны в
файлах #include.
Для тестирования FLINT/C-функций применяется пакет ResTrack
описанный в [Мигр]. Его использование даёт возможность обнару.
жить, при определённых обстоятельствах, трудно уловимые случаи
превышения векторных границ CLINT-объектов, которые иначе
могли бы остаться необнаруженными во время тестирования.
Теперь, когда мы закончили основные приготовления, рассмотрим
функции, выполняющие основные вычисления (см. главу 4).
add_l(), subj(), mulj(), sqrj(), div_l(), modj(), inc_l(), decj(), shlj(),
shr_l(), shiftJO,
включая базовые функции
add(), sub(), mult(), umul(), sqrQ,
смешанные арифметические функции с аргументами типа USHORT
uaddj(), usubj(), umulj(), udivj(), umodJO, mod2J(),
и, наконец, функции модульной арифметики (см. главы 5 и 6)
maddj(), msubj(), mmulj(), msqrj(),
и функцию возведения в степень
*mexp*J().
Правила вычислений, которыми мы будем пользоваться при тести-
ровании этих функций, вытекают из групповых законов для целых
чисел, которые уже приводились в главе 5 для кольца классов
вычетов 2Л. Здесь мы снова приводим подходящие правила ДяЯ
натуральных чисел и можем придумать тест в любом случае, если
между выражениями стоит знак равенства (см. таблицу 12.1).
Таблииа 12.1.
Групповой закон
лля целых чисел,
используемый
при
тестировании
Сложение Умножение
Т ождествен ность а + 0 = а а • 1 =а
Коммутативный закон а + b = b + а а . b = b • а
Ассоциативный закон (а + Ь) + с = а + (Ь + с) (а • Ь) . с = а • (Ь • d
ГЛАВА 12. Стратегия тестирования LINT
281
Сложение и умножение можно проверять относительно друг друга, используя определение
ПК"’ - • Э к := я, /=1 по крайней мере, для малых значений к. Следующие соотношения, которые поддаются тестированию, - это дистрибутивный закон и
иг- . J Г Л ‘j i первая формула бинома Ньютона. Закон дистрибутивности: а • (Ь + с) = а • b + а • с Формула бинома Ньютона: (а + b)2 = а2 + 2аЬ + Ь2 Законы сокращенного сложения и умножения предоставляют сле- дующие возможности для проверки сложения и вычитания, так же как умножения и деления: а +b = c=>c-a = b\\c~b = a И а • b = с => с/а = b и с!Ь = а. Деление с остатком можно проверить умножением и сложением, используя функцию деления, чтобы вычислить для делимого а и делителя Ь, сначала частное q и остаток г. Затем в игру вводятся умножение и сложение, чтобы проверить, выполняется ли равенство а = Ь- q + г. Для проверки модульного возведения в степень с помощью умно- жения для малых к мы прибегаем к помощи определения: /=1 Отсюда можно перейти к правилам возведения в степень (см. главу 1) ars = (аУ ar+s = а • а\
которые являются основой для проверки возведения в степень
умножением и сложением. Кроме этих и других тестов, основанных на правилах арифметиче- ских вычислений, мы используем специальные тестовые подпро- граммы, которые проверяют оставшиеся функции из вышеприве- дённого списка, и, в частности, поведение этих функций на грани- цах областей определения CLINT-объектов или в других ситуациях, критических для отдельных функций. Некоторые из этих тестов находятся в тестовом комплекте пакета FLINT/C, входящем в
282
Криптография на Си и C++ в действии
сопроводительный CD-ROM. Этот тестовый пакет содержит модули,
перечисленные в таблице 12.2.
Таблииа 12.2. Имя модуля Содержание теста
Тестовые testrand.с Линейные сравнения, генератор псевдослучайных
функции пакета
FLINT/C чисел
testbbs.c Генератор псевдослучайных чисел Блюм-Блюма-Шуба
testreg.с Управление регистрами
testbas.c Базовые функции cpy_l(), ld_l(), equ_l(), mequ_l(), cmpJO, u2clint_l(), ul2clint_J(), str2clint_l(), xclint2str_l()
testadd.с Сложение, включая inc_J()
testsub.с Вычитание, включая dec_l()
testmul.c Умножение
testkar.c Умножение методом Карацубы
testsqr.c Возведение в квадрат
testdiv.c Деление с остатком
testmadd.c Модульное сложение
testmsub.c Модульное вычитание
testmmul.c Модульное умножение
testmsqr.c Модульное возведение в квадрат
testmexp.c Модульное возведение в степень
testset.c Функции доступа к битам
testshft.c Операции сдвига
testboo I.c Булевы операции
testiroo.c Извлечение целого квадратного корня эд
testggt.c Вычисление наибольшего общего делителя и наименьшего обшего кратного
Мы вернемся к нашим теоретико-числовым функциям в конце вто-
рой части этой книги, где они приведены в качестве упражнении
для заинтересованного читателя (см. главу 17).
Часть II
Класс LINT: арифметика на C++
Анатомические находки, составляющие пред-
мет исследования науки, широко распростра-
нены в качестве украшений при создании объ-
ектов в различных географических зонах и
антропо-этнических группах. Добытый чело-
веком фрагмент, обычно кость, становится
функциональной деталью конструкции объек-
тов. Кость, как минимум, частично утрачивает
свою анатомическую индивидуальность, в том
смысле, что ее обрабатывают, обращаясь с ней
так, что она становится неотъемлемой частью
объекта, тем самым приобретая символическое
значение, выходящее далеко за пределы телес-
ной сущности.
Надпись на этикетке экспоната
национального музея Антропологии
и Этнологии, Флоренция, Италия.
ГЛАВА 13.
Пусть C++ облегчит Вашу жизнь
Детали разменяли нашу жизнь на мелочи...
Упрощайте, упрощайте.
А. Д. Торо, Вальден.
Язык программирования C++, разрабатывавшийся с 1979 года
Бьярном Страуструпом1 в Bell Laboratories, является расширением
языка С, и его роль становится преобладающей по отношению к
другим языкам в области создания программных продуктов. Язык
C++ поддерживает принципы объектно-ориентированного про-
граммирования, основой которого являются программы, а точнее
х сказать, процессы, включающие в себя множества объектов, кото-
рые взаимодействуют исключительно через их интерфейсы. То есть
они обмениваются информацией или принимают определенные
внешние команды и обрабатывают их как задачу. В этом интерфейсе
методы, с помощью которых выполняется задача, являются подза-
дачей, “определенной на” автономии единственного объекта.
Структуры данных и функции, которые представляют внутреннее
состояние объекта и эффект переходов между состояниями, явля-
11 ются частным делом объекта и не должны быть обнаружены со
стороны. Данный принцип, известный как намеренное скрытие
5 информации от пользователя, помогает разработчикам программ-
ного обеспечения сосредоточиться над задачами, в которых объект
' выполняется внутри структуры программы, что позволяет не вда-
ij ' ваться в детали реализации. (Говоря другими словами, мы заостряем
внимание на том, “что”, а не “как”).
‘„ю. •
п / Структурные единицы, которые имеют дело с «частными делами»
m объекта и содержат полную информацию об организации структур
данных и функций, называются классами. Наряду с этим создаются
я внешние интерфейсы объекта, которые и определяют набор пове-
vr дений, который объект может выполнять. Так как все объекты
1хг; класса имеют одинаковый самый структурный дизайн, они тоже
Интернет-страница Бьярна Страуструпа (hhtp://www.research.att.comfbs/), возможно, поможет
°тветить на вопрос «Как Вы произносите “Бьярн Страуструп”?»: “Это может быть затрудни-
тельным для людей, которые не являются скандинавами. Лучший совет, который я до сих пор
слышал, это ‘начать выговаривать имя и фамилию несколько раз на норвежском языке, затем
Набить горло картошкой и повторить это снова’:-). Оба моих имени произносятся по слогам:
Pjar-ne Strou-strup. Как В, так и J в моем имени не являются ударными, a NE - достаточно
Слабые, поэтому Be-ar-neh или Ву-ar-ne наталкивает на правильный путь. Первое U в моей фами-
лии на самом деле должно было быть V, первый конечный слог произносится глубоким гортан-
HbiM голосом: Strov-strup. Второе U слегка похоже на 00 в OOP, однако оно остается коротким;
в°зможно Strov-stroop подаст какую-нибудь идею. ” (Как видно, устоявшаяся русская транс-
крипция также имеет мало общего с оригиналом, имя должно звучать как что-то похожее на
^ьярне Стравструп» — Прим, перев.)
286
Криптография на Си и C++ в действии
обладают одним и тем же интерфейсом. Но как только объекты бы-
ли созданы (компьютерные разработчики говорят, что класс тира-
жирует (instantiate) объекты), они существуют независимо. Их
внутреннее состояние меняется независимо друг от друга, кроме
того, они запускают различные задачи в соответствии с их ролями в
программе.
Объектно-ориентированное программирование распространяет ис-
пользование классов в качестве стандартных блоков больших
структур, которые также могут являться классами или группами
классов, в готовые программы, так же, как и дома или автомобили
делаются из сборных модулей. В идеальном варианте, программы
могут быть собраны вместе из библиотек заранее созданных
классов без необходимости создания значимой части нового кода
(во всяком случае, не в такой степени, как для традиционной разра-
ботки программ). В результате этого проще разрабатывать про-
грамму применительно к текущей ситуации, прямо моделировать
текущие процессы, таким образом проходя последовательные
уточнения, пока результатом не будет набор объектов отдельных
классов и их взаимосвязей, причем все еще можно распознать
модель реальности, которая лежит в их основе.
Такой порядок выполнения действий достаточно хорошо известен
нам из многих жизненных аспектов, то есть мы не работаем напря-
мую с необработанными материалами, если мы хотим что-либо
создать скорее мы станем применять готовые модули, о конструк-
ции которых или внутренней разработке в деталях мы ничего не
знаем. Просто в этих знаниях нет необходимости. Опираясь на
имеющийся опыт, мы получаем возможность создания все более и
более сложных структур. В процессе создания программ предыду-
щий опыт разработок раньше не находил применения, разработчики
программных продуктов постоянно возвращались к тому, что соз-
давали ранее. Программы создавались с помощью элементарных
операций языка программирования (такой конструктивный процесс
обычно называют кодированием). Применение библиотек этапа
исполнения, таких как стандартная библиотека С, не улучшает
существенно эту ситуацию, так как функции, содержащиеся в
подобных библиотеках, являются слишком примитивными, чтобы
обеспечить связь с более сложными приложениями.
Любой программист знает, что структуры данных и функции, кото-
рые являются подходящим решением для некоторых проблем,
лишь изредка можно применить в похожих, но тем не менее разных
задачах без модификации. И как результат - практическое отсут
ствие выгоды от оттестированных и доверенных компонентов,
любое их изменение содержит риск появления новых ошибок - к
в проектировании, так и в программировании. (Это напомина
предупреждение в инструкции по эксплуатации любого товару
“Любое изменение, вносимое лицом, не являющимся авторизовав
ним специалистом, отменяет гарантию”).
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
287
С целью повторного использования программ в форме готовых
компонент, среди огромного количества других концепций был
разработан принцип наследования. Это дает возможность модифи-
цировать классы, для того чтобы удовлетворять новым требованиям,
фактически не изменяя их. Вместо этого необходимые изменения
будут внесены на уровне расширений.
Объекты, которые появились таким образом, помимо новых
свойств, приобретают все свойства старых объектов. Можно сказать,
что они наследуют эти свойства. Принцип скрытия информации
остается незыблемым. Вероятность ошибки значительно уменьши-
лась, а производительность возросла. Все это выглядит так, словно
сбываются мечты.
Как объектно-ориентированный язык программирования, C++
обладает всеми необходимыми механизмами для поддержки этих
принципов абстракции2. Тем не менее, эти механизмы представ-
ляют собой лишь возможность, а не гарантию того, что они будут
использоваться так, как принято в объектно-ориентированном
программировании. С другой стороны, переход от традиционной к
объектно-ориентированной разработке программного обеспечения
' требует значительной интеллектуальной перестройки. Особенно
явно это отражается в двух отношениях: с одной стороны, разра-
ботчик, который к настоящему времени достиг больших успехов,
вынужденно посвяшает значительно больше внимания фазам моде-
лирования и проектирования, нежели тому, что обычно требовалось
в традиционных методах разработки программ. С другой стороны,
при разработке и тестировании новых классов особое внимание
нужно обращать на то, чтобы компоновочные блоки были безоши-
3 бочны, так как они будут использоваться в множестве программ,
которые будут разрабатываться в дальнейшем. Также скрытие
ип информации может означать скрытие ошибок, Исказится цель идеи
f объектно-ориентированного программирования, если пользователю
Ир.'*класса придется знакомиться с внутренней его организацией для
|»г того, чтобы найти ошибку. Результатом этого являются ошибки,
Ьн содержащиеся в реализации класса, которые наследуются вместе с
|Вв 1. классом, и все подклассы становятся зараженными “наследствен-
ным заболеванием”. С другой стороны, анализ ошибок в объектах
* г ' класса может быть ограничен реализацией самого класса, что может
значительно уменьшить границы поиска ошибки.
В конечном счете нам следует отметить, что, хотя существует ус-
тойчивая тенденция в применении языка C++ в качестве языка про-
граммирования, принципы объектно-ориентированного програм-
мирования, воплощенные в чрезвычайно сложных элементах языка
C++ - не единственный объектно-ориентированный язык программирования. Например, есть
такие языки как Simula (предшественник всех объектно-ориентированных языков), Smalltalk,
Eiffel, Oberon, и Java.
288
Криптография на Си и C++ в действии
C++, часто многогранны и лежат за пределами понимания. Поэтому
пройдет много времени, прежде чем этот метод станет стандартным
для разработки программного обеспечения.
Таким образом, название данной главы отражает не столько объ-
ектно-ориентированное программирование и применение языка
C++ в целом, сколько механизмы, которые в ней предложены, и
их значение в нашем проекте. Они дают возможность описать
арифметически операции с большими числами настолько же есте-
ственно, как это было бы со стандартными операциями языка
программирования. Поэтому в последующих разделах мы рассмот-
рим не введение в язык C++, а рассуждения о разработке классов,
представляющих длинные натуральные числа и экспортируемые
функции для работы с ними в виде абстрактных методов3. Некото-
рые подробности о структурах данных будут скрыты как от пользо-
вателя, так и от клиента класса, так же как и реализации различных
арифметических и теоретико-числовых функций. Тем не менее,
прежде чем воспользоваться классами, они должны быть уже
созданы, поэтому нам следует иметь представление об их содер-
жимом. Однако ни для кого не должно быть неожиданностью то,
что мы не начнем с самого начала, а воспользуемся работой, кото-
рую мы уже завершили в первой части книги, и определим наш
арифметический класс как абстрактный уровень, или же оболочку,
над С-библиотекой.
Мы дадим нашему классу имя LINT (Long INTeger - длинное целое).
Он будет содержать структуры данных и функции как компоненты
с атрибутом открытый (public), который устанавливает возмож-
ность внешнего доступа. Доступ к структурам класса объявляется
как частный (private) и, с другой стороны, может быть выполнен
только функциями, которые являются членами класса или друже-
ственными функциями. Функции - члены класса LINT могут полу-
чить доступ к функциям и элементам данных объектов класса LINT
по имени. Требуются они для управления внешним интерфейсом
класса, обслуживания запросов к нему, а также являются основными
и вспомогательными для управления и обработки внутренних
структур данных. Функции-члены класса LINT всегда могут вы-
звать LINT-объект через неявный левый аргумент (его нет в списке
параметров). Функции - друзья класса не принадлежат самому
классу, но, однако, они имеют доступ к внутренней структуре класса.
В отличие от функций-членов, функции-друзья не содержат неяв-
ный аргумент.
Читатель может ознакомиться с несколькими традиционными работами по введению в язык С
и его обсуждению, а именно: [ElSt], [Strl], [Str2], [Deit], [Lipp] здесь перечислено несколько И3
наиболее важных названий. За основу попыток стандартизации ISO был взят [ElSt], который ст<
стандартом. ।
ГЛАВА 13. Пусть C++ облегчит вашу жизнь 289
>7’ ’•' Объекты генерируются как экземпляры класса при помощи конст- рукторов, которые осуществляют распределение памяти, инициа- лизацию данных и другие задачи управления перед тем как объект будет готов к выполнению работы. Нам потребуется несколько по- добных конструкторов для того, чтобы сгенерировать LINT-объекты из различного контекста. Наряду с конструкторами существуют и 5 : деструкторы, занимающиеся удалением объектов, которые больше не нужны, и ресурсов, которые были им выделены.
Вот элементы языка C++, которые мы обычно используем в разра- ботке наших классов: ✓ перегрузка операций и функций; ✓ усовершенствованные возможности, по сравнению с С, для ввода и вывода. В следующих частях рассматривается применение этих двух прин- ципов при разработке нашего класса LINT. Для того чтобы у чита- теля появилось представление о том, что из себя представляет класс LINT, мы покажем небольшую часть его объявления: class LINT г
i public: LINT (void); // Конструктор -LINT (); //Деструктор
' HI- К s - J » OX", ’ * • const LINT& operator (const LINT&); const LINT& operator+= (const LINT&); const LINT& operators (const LINT&); const LINT& operator*^ (const LINT&); const LINT& operators (const LINT&); const LINT& operator%= (const LINT&);
const LINT gcd (const LINT&);
const LINT Icm (const LINT&);
const int jacobi (const LINT&);
friend const LINT operator + (const LINT&, const LINT&);
friend const LINT operator - (const LINT&, const LINT&);
10'1697
290
Криптография на Си и C++ в действии
friend const LINT operator * (const LINT&, const LINT&);
friend const LINT operator / (const LINT&, const LINT&);
friend const LINT operator % (const LINT&, const LINT&);
friend const LINT mexp (const LINT&, const LINT&, const LINT&);
friend const LINT mexp (const USHORT, const LINT&, const LINT&);
friend const LINT mexp (const LINT&, const USHORT, const LINT&);
friend const LINT gcd (const LINT&, const LINT&);
friend const LINT Icm (const LINT&, const LINT&);
friend const int jacobi (const LINT&, const LINT&);
private:
clint *nj;
int maxlen;
int init;
int status;
};
Можно выделить в классе LINT типовое подразделение на два блока:
первый, открытый блок с конструктором, деструктором, арифмети-
ческими операторами и функциями-членами и друзьями данного
класса. Небольшой блок закрытых элементов данных присоединен
к открытому интерфейсу и идентифицирован меткой private. Такое
деление используется для большей ясности и хорошим тоном счи-
тается расположить открытый интерфейс перед закрытым блоком, а
метки public и private использовать только один раз внутри каждого
объявления класса.
Приведенный здесь список операторов, который фигурирует в раз-
деле объявления класса, очевидно, еще не совсем завершен. В нем
не хватает некоторых арифметических функций, которые не могут
быть представлены в качестве операторов, так же как и большинство
теоретико-числовых функций, которые нам уже известны как функ-
ции языка С. Более того, объявленные конструкторы представлены
так же мало, как и функции ввода и вывода объектов LINT.
В следующем списке параметров операторов и функций появляется
ссылочный оператор &, в результате применения которого объекты
класса LINT передаются не по значению, а по указателю на объект.
Аналогично происходит и при возврате. Такое использование &
недопустимо в С. Однако при более доскональном рассмотрении
ii
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
291
’ nWra<:
можно заметить, что только лишь определенные функции-члены
возвращают указатель на объект LINT, в то время как многие другие
возвращают в качестве результата само значение. Основным пра-
вилом, которое определяет, какой из двух методов используется,
является то, что функции, изменяющие один или более аргументов,
которые им передаются, могут вернуть результат в качестве ссыл-
ки, тогда как другие функции, не изменяющие входные параметры,
возвращают результат как значение. По мере изучения мы увидим,
в каких LINT-функциях используется какой способ.
Классы в языке C++ являются расширением сложного типа данных
«структура» в Си, и доступ к элементу х класса производится
синтаксически точно так же, как и к элементу структуры, то есть,
например, А.х, где А - указывает на объект, а х - на элемент класса.
Также следует отметить, что в списке параметров функции-члена
аргумент имеет неполное имя в отличие от точно так же названной
функции-друга, что показано в следующем примере:
friend LINT gcd (const LINT&, const LINT&);
в сравнении с :
LINT LINT::gcd (const LINT&);
Поскольку функция gcd() в качестве функции - члена класса LINT
принадлежит объекту А типа LINT, вызов gcd() должен происхо-
дить в форме A.gcd(b) без появления А в списке параметров. Однако
дружественная функция gcd() не принадлежит ни одному объекту и
таким образом не содержит неявных аргументов.
Мы наполним указанную выше упрощенную структуру нашего
класса LINT в следующих главах и выявим множество ее особенно-
стей, для того чтобы со временем у нас была окончательная реали-
зация класса LINT. Те, кому интересно узнать в общем о C++,
могут обратиться к следующим ссылкам: [Deit],[EISt],[Lipp], а
также [Meyl] и [Меу2].
13.1. Частное дело: представление чисел в классе LINT
Если мои идеи не похожи на их мнение,
Оставлю лучше их при своей точке зрения.
А. Е. Хаусман, Последние поэмы IX
Представление длинных чисел, которые были выбраны для нашего
класса, является расширением их представления на С, описанного в
I части. Оттуда мы возьмем расположение цифр натурального
числа как вектор значений типа clint, в котором наиболее старшие
10*
292
Криптография на Си и C++ в действии
разряды располагаются по старшему индексу (см. главу 2). Память,
которая требуется для этого, автоматически выделяется в момент
генерации объекта. Этот процесс осуществляется конструкторами,
которые вызываются как явно - в программе, так и неявно - при
компиляции с помощью new(). Поэтому в объявлении класса нам
потребуется переменная типа clint *nj, с которой в рамках одного
конструктора и ассоциируется указатель на размещаемую там
память. В качестве второго элемента нашего числового представле-
ния мы определяем переменную maxlen, которая хранит количество
памяти, выделенной конструктором отдельному объекту. Перемен-
ная maxlen определяет максимальное число clint-разрядов, которые
может иметь объект. Более того, мы хотим установить, был ли
LINT-объект инициализирован, то есть было ли ему присвоено’
какое-нибудь числовое значение перед тем как он был использован
. Bq
ж
справа от знака равенства в числовом выражении. Поэтому мы вво-
дим переменную init целого типа, которая изначально имеет значе-
ние 0 и устанавливается в 1, когда впервые объекту присваивается!
числовое значение. Мы реализуем наши функции и операторы
класса LINT так, чтобы сообщение об ошибке выдавалось в случае,
если не определены значения объекта LINT, а, как следствие, и
значение выражения.
Переменная status, строго говоря, не является элементом нашего
представления в числовом виде. Ее применяют для индикации
ситуации переполнения или потери значимости (см. стр. 32), если
оно происходит в результате выполнения операций над объектами
LINT. Типы и механизмы сообщений об ошибках и обработка оши-
бок подробно описаны в главе 15.
Таким образом, класс LINT определяет совокупность следующих
элементов для представления целых чисел и хранения состояний
объектов:
clint* nJ;
int init;
int maxlen;
int status;
Так как мы имеем дело с закрытыми элементами, доступ к этим
элементам класса возможен только лишь посредством функций-
членов или функций-друзей, а так же таких же операторов. В част-
ности, не существует возможности прямого доступа к отдельным
разрядам числа, которое было представлено объектом класса LINT.
ГЛАВА 13. Пусть C++ облегчит вашу жизнь______________________________ 293
13.2. Конструкторы.
Конструкторы - это функции для генерации объектов определенного
класса. Для класса LINT это может происходить как с инициал иза-
цией, так и без нее, причем в последнем случае объект будет создан
и требуемая для хранения числа память выделена, однако никакого
значения объекту не будет присвоено. Конструктору для этого не
нужно никаких аргументов и таким образом он играет роль конст-
руктора по умолчанию для класса LINT (см. [Strl], Раздел 10.4.2).
Следующий конструктор по умолчанию LINT(void) в файле
flintpp.cpp создает объект LINT без присвоения ему значения:
LINT::LINT (void)
{
nJ = new CLINT;
if (NULL == nJ)
{
panic (EJJNT.NHP, "конструктор 1", 0,_LINE_);
}
maxlen = CLINTMAXDIGIT;
init = O;
status = EJJNTJDK;
}
Если заново порожденный объект инициализируется числовым
значением, то подходящий конструктор должен способствовать
генерации объекта LINT, а затем присваивать ему заранее опреде-
ленный аргумент в качестве значения. В зависимости от типа аргу-
мента должны быть введены несколько перегружаемых конструк-
торов. Класс LINT содержит функции-конструкторы, которые
показаны в таблице 13.1.
Теперь мы хотим обсудить следующий пример конструктора LINT
вида LINT (const char* const), который генерирует объекты LINT и
ассоциирует с ними значение, взятое из строки ASCII-символов.
В строке может быть префикс, который содержит информацию об
основании числового представления. Если строка символов начи-
нается с Ох или ОХ, то ожидаются наборы символов в шестнадцати-
ричном виде из диапазонов {0,1,...,9}, {a,b,...,f} и {A, B,...,F}. Если
префиксом является 0Ь или 0В, то следует ожидать появления би-
нарных разрядов из множества {0,1}. Если префикса не существует
вовсе, то разряды интерпретируются как цифры в десятичном виде.
Конструктор использует функцию str2clintj() для того, чтобы пре-
294
Криптография на Си и C++ в действии
образовывать строку символов в объект типа CLINT, из которого на
втором шаге будет создан объект LINT:
LI NT:: LI NT (const char* const str)
{
nJ = new CLINT;
if (NULL == nJ) // ошибка в new?
{
panic (EJJNTJMHP, "конструктор 4", 0, _LINE_);
}
if (strncmp (str, "Ox", 2) == 0 || strncmp (str, “OX", 2) == 0)
int error = str2clintj (nJ, (char*)str+2,16);
}
else
{
if (strncmp (str, "Ob", 2) == 0 || strncmp (str, "OB", 2) == 0)
{
error = str2clintj (nJ, (char*)str+2, 2);
}
else
{
error = str2clintj (nJ, (char*)str, 10);
}
}
switch (error) // оценка кода ошибки
{
case 0:
maxlen = CLINTMAXDIGIT;
init = 1;
status = E_LINT_OK;
break;
case E_CLINT_BOR:
295
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
panic (E_LINT_BOR, ” конструктор 4”, 1,_LINE_);
break;
case E_CLINT_OFL:
panic (E_LINT_OFL," конструктор 4", 1,_LINE__);
break;
case E_CLINT_NPT:
panic (E_LINT_NPT," конструктор 4", 1,_LINE__);
break;
default:
panic (E_LINTJERR, ” конструктор 4”, error,_LINE );
}
}
Таблица 13.1. Конструкторы Конструктор Семантика: создание объекта LINT
LINT (void); LINT (const char* const, const unsigned char); LINT (const UCHAR* const, const int) LINT (const char* const); LINT (const LINT&); Без задания начального значения (конструктор по умолчанию) Из строки символов с основанием числового представления, заданной во втором аргументе Из вектора байтов с длиной, заданной во втором аргументе Из строки символов, возможно с префиксом ОХ для шестнадиатиричных чисел или ОБ для бинарных Для других объектов LINT (конструктор копирования)
LINT
тчг LINT (const int); Из значения типа char, short или int
НГ LINT (const long int); Из значения типа long int
k; I LINT (const UCHAR); Из значения типа UCHAR
LINT (const USHORT); Из значения типа USHORT
LINT (const unsigned int); Из значения типа unsigned int
LINT (const ULONG); LINT (const CLINT); Из значения типа ULONG Из объекта CLINT
Конструкторы позволяют проводить инициализацию объектов
LINT другими такими объектами, так же как и стандартными ти-
пами, константами и символьными строками, что и показано на
следующем примере:
Криптография на Си и C++ в действии
LINT а;
LINT one (1);
int i = 2147483647;
LINTb (i);
LINT c (one);
LINT d ("0x123456789abcdef0");
Функции-конструкторы вызываются явно для генерации объектов
типа LINT из заданных аргументов. Конструктор LINT, который,
например, преобразует значения типа unsigned long в объекты
LINT, реализован в следующей функции:
LINT::LINT (const ULONG ul)
{
nJ = new CLINT;
if (NULL == nJ)
{
panic (EJJNTJMHP, ’’Конструктор 11”, 0, _LINE_);
}
ul2clintj (nJ, ul);
maxlen = CLINTMAXDIGIT;
init = 1;
status = E_LINT_OK;
}
А теперь нам необходимо получить функцию-деструктор, которая
соответствует конструкторам класса LINT и которая дает возмож-
ность освободить объекты, в частности, связанную с ними память.
Вообще говоря, компилятор охотно создает деструктор по умолча-
нию, которым можно пользоваться, однако он освобождает только
память, которую занимают элементы объекта LINT. Дополнитель-
ная память, которая выделяется конструктами, не освобождается, в
результате чего идет утечка памяти. Следующий далее короткий
деструктор выполняет важную задачу освобождения памяти, зани-
маемой объектами LINT.
~LINT()
{
delete [] nJ;
ГЛАВА 13. Пусть C++ облегчит вашу жизнь 297
13.3. Перегрузка операторов.
Перегрузка операторов представляет собой достаточно мощный
механизм, позволяющий определить функции с одинаковыми име-
нами, но с различным списком параметров, то есть которые могут
выполнить отличающиеся операции. Компилятор использует спе-
циальный список параметров для того, чтобы определить, какая
функция имеется в виду. Чтобы сделать это, C++ использует стро-
гий контроль типов, который позволяет избежать двусмысленности
или противоречивости.
Перегрузка фукнций-операторов позволяет применять “обычный”
способ записи выражения суммы с = а + b с объектами а, b и с клас-
( са LINT вместо того, чтобы вызвать функцию, например, addjfaj,
bj, сJ). Это позволяет осуществить органичную стыковку класса с
? языком программирования, а также значительно повышает чита-
бельность программ. Для данного примера необходимо перегрузить
оператор “+” и присваивание “=”.
Существует всего несколько операторов в C++, которые нельзя пере-
гружать. Даже оператор “[ ]” который применяется для получения
доступа к векторам, может быть перегруженным, например, функци-
ей, одновременно проверяющей, не превышают ли запрошенный ин-
декс вектора его границ. Однако не нужно забывать, что перегрузка
операторов открывает путь к возможным неприятностям. В частно-
сти, не могут быть изменены операторы над стандартными типами
данных; так же не может быть изменен заранее определенный при-
оритет операторов (см. [Strl], Раздел 6.2) или “созданы” новые опе-
раторы. Но для отдельных классов вполне возможным является оп-
--------- ределение функции-оператора, не имеющего ничего общего с тем
и-----оператором, с которым он обычно ассоциировался. Для того, чтобы в
программах было проще разобраться, необходимо следовать следую-
щему совету - строже придерживаться смысла стандартных операто-
ров в C++ при перегрузке, чтобы избежать бесполезной путаницы.
Следует отметить, что в структуре класса LINT, отмеченной выше,
некоторые операторы выполнялись как функции-друзья, а другие
как функции-члены. Причиной этому послужило то, что мы хотели
- бы использовать, например, “+” или “*” в двух качествах: когда они
могут не только обрабатывать два эквивалентных объекта LINT, но
и, как альтернатива, принять один объект LINT и один из встроен-
ных целочисленных типов языка C++, более того, принять аргументы
в любом порядке, поскольку сложение является коммутативным.
Для этой цели нам потребуются ранее описанные конструкторы,
которые создают объекты LINT из целых типов. Комбинированные
выражения, такие как:
LINT а, Ь, с;
int number;
298
Криптография на Си и C++ в действии
И Инициализация а, b и number и какие-то вычисления
/I...
с = number * (а + b / 2)
также становятся возможными. В обязанности компилятора входит
автоматический вызов подходящих функций конструктора. Он
также следит за тем, чтобы преобразование целого числа number и
константы 2 в объекты LINT происходило в момент выполнения
программы, перед тем как будут вызваны операторы + и *. Таким
образом мы получим максимально возможную гибкость в приме-
нении операторов с .тем лишь ограничением, что выражения, со-
держащие объекты типа LINT, сами являются типом LINT и, соот-
ветственно, могут быть присвоены только объектам типа LINT.
Перед тем как мы углубимся в детали каждого отдельного операто-
ра, нужно получить общее представление об операторах, опреде-
ленных классом LINT, которые читатель может найти в Таблицах
13.2-13.5.
Таблииа 13.2, 4- Сложение
Арифметические операторы ++ Инкремент (префиксный и постфиксный)
класса LINT - Вычитание
- Декремент (префиксный и постфиксный)
* Умножение
/ Деление (частное)
fp. % Остаток
Таблииа 13.3. & Побитовое И
Побитовые операторы I Побитовое ИЛИ
класса LINT Л Побитовое исключающее ИЛИ (XOR)
« Сдвиг влево
j » Сдвиг вправо
i
Таблииа 13.4. == Равенство
Логические операторы != Неравенство
класса LINT </<= Меньше, меньше или равно
* >,>= Больше, больше или равно
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
299
Таблииа 13,5.
Операторы
присваивания
класса LINT
о <
ж
= Простое присваивание
+= Присваивание после сложения
-= Присваивание после вычитания
*_ Присваивание после умножения
/= Присваивание после деления
%= Присваивание после взятия остатка
&= Присваивание после побитового И
l= Присваивание после побитового ИЛИ
A— Присваивание после побитового исключаюшего ИЛИ
«= Присваивание после левого сдвига
»= Присваивание после правого сдвига
•/>пг '!
к
'ШЖШЙМ
Сейчас мы хотим обсудить реализацию функций операторов
которые могут служить примерами реализации
операторов LINT.
Сначала с помощью оператора можно увидеть, как выполняется
умножение объектов LINT с помощью функции С mulj(). Оператор
реализован как функция-друг, в которую оба сомножителя переда-
ются по ссылке. Так как функции-операторы не меняют своих
аргументов, ссылки объявляются как const (константы):
const LINT operator* (const LINT& Im, const LINT& In)
{
LINT prd;
int error;
Сначала нужно убедиться, инициализированы ли аргументы 1m и
In, переданные по ссылке. Если это не выполняется для обоих ар-
гументов, то включается обработка ошибок и вызывается функ-
ция-член panicO, которая объявлена как статическая (см. Главу 15)
if (llm.init) LINT::panic (E_LINT_VAL, 1, _LINE_);
if (lln.init) LINT::panic (E_LINT_VAL, "*", 2, _LINE_);
Вызывается С-функния mul_l(), в которую передаются в качестве
аргументов: векторы Im.nJ, In.nJ - как множители, a prd.nj -
как результат, куда будет помешено произведение.
error = mulj (Im.nJ, In.nJ, prd.nj);
Криптография на Си и C++ в действии
При опенке кода ошибки, который хранится в переменной error,
возможны 3 случая. Если error == 0, то все в порядке и объект
prd может быть отмечен как инициализированный. Это делается
присваиванием переменной prd.init 1 .Переменная статуса prf.status
уже была установлена конструктором в значение E_LINT_OK.
Если произошло переполнение в функции mul_l(), то переменная
error содержит значение E_CLINT_OFL. Поскольку в этом случае
вектор prd.n_l содержит правильное по формату число CLINT,
то prd.init установлен на 1, в то время как переменная статуса
prd.status содержит значение E_LINT_OFL. Если error не содержит
ни одного из этих двух значений после вызова mul_l(), то что-то
в этих функциях прошло не так, причем мы не имеем возмож-
ным определить более точно, какую именно ошибку мы сделали.
В этом случае вызывается функция panic() для дальнейшей обра-
ботки ошибки.
switch (error)
{
case 0:
prd.init = 1;
break;
case E_CLINT_OFL:
prd.status = E_LINT_OFL;
prd.init = 1;
break;
default:
LINT::panic (E_LINT_ERR, error, _LINE_);
}
Если ошибка не может быть исправлена функцией panicO, то и
возврат в эту точку не произойдет. Механизм распознавания
ошибок здесь приведёт к завершению, которое, в принципе,
лучше, чем продолжение работы программы в неопределенном
состоянии. И как заключающий шаг - поэлементный возврат
произведения prd.
return prd;
}
Поскольку объект prd существует лишь внутри контекста функции,
компилятор обеспечивает автоматическое создание временного
объекта, который представляет значение переменной prd вне функ-
ции. Данный временный объект создается с помощью конструктора
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
301
• лЯЬ !
он.
-Л'Ш
копирования LINT (const LINT&) (см. стр. 295) и существует до тех
пор, пока выражение, в рамках которого использовался оператор,
не будет обработано, то есть по достижении закрывающей точки с
запятой. Так как значения функции объявлены как const, компиля-
тор не воспримет такие бессмысленные конструкции как (а * Ь) = с.
Основной целью здесь является работа с LINT-объектами теми же
способами, как и со встроенными целых типов.
Мы можем расширить возможности функции-оператора, используя
следующие приемы: если сомножители одинаковы, то умножение
заменяется возведением в квадрат, и преимущество в скорости,
связанное с этой заменой, может быть применено автоматически
(см. п. 4.2.2). Однако придется затратить некоторые усилия на по-
элементное сравнение аргументов для того, чтобы определить их
равенство, что обходится нам дорого, и следует довольствоваться
компромиссом: возведение в квадрат следует выполнять только в
случае, если оба сомножителя ссылаются на один и тот же объект.
Таким образом, мы проверим, являются ли In и Im указателями
на один и тот же объект, и в этом случае вместо умножения выпол-
ним возведение в квадрат. Ниже приведен соответствующий текст
программы:
if (&lm == &ln)
a»:
error = sqrj (Im.nJ, prd.nj);
else
error = mulj (Im.nJ, In.nJ, prd.nj);
Этот взгляд назад на функции, реализованные в языке С в части I,
представляет собой модель для всех оставшихся функций класса
LINT, который сформирован как оболочка вокруг ядра функций С
и защищает его от пользователей класса.
Прежде чем мы обратимся к более сложному оператору присваива-
ния лучше, по-видимому, более подробно рассмотреть про-
стой оператор присваивания “=”. В части I мы уже определили, что
присваивание объектов требует особого внимания (см. главу 8).
Следовательно, как и в реализации на С, нужно четко обращать
внимание на то, чтобы при присваивании одного объекта класса
LINT другому присваивалось содержимое, а не адрес. Точно так же
нам нужно для нашего класса LINT определить специальный вари-
ант оператора присваивания который выполняет не только
простое копирование элементов класса: по тем же причинам, кото-
рые были описаны в главе 8, нам следует обратить внимание на то,
Криптография на Си и C++ в действии
что копируется не адрес числового вектора nJ, а разряды, на кото-
рые он ссылается.
Как только стало понятным основное требование к порядку дейст-
вий, дальнейшая реализация не будет очень сложной. Оператор “=”
реализован как функция-член и возвращает как результат ссылку
на неявный левый элемент. Вне всяких сомнений, мы будем ис-
пользовать внутри функцию С cpyj() для того, чтобы перенести
разряды из одного объекта в другой. Для того чтобы выполнилось
присваивание а = Ь, компилятор вызывает функцию-оператор “=”
в контексте а, которая берет на себя роль неявного аргумента, не
указанного в списке параметров функции-оператора. В рамках
функции-члена ссылка на элементы неявного аргумента может
быть выполнена просто по имени, без учета контекста. Более того,
ссылку на неявный объект можно сделать с помощью специального
указателя this, как показано в приведенном ниже примере реализа-
ции оператора
const LINT& LINT::operator= (const LINT& In)
{
if (lln.init) panic (E_LINT_VAL, 2, _LINE_);
if (maxlen < DIGITSJ_ (In.nJ))
panic (E_LINT_OFL, и=н, 1, _LINE—);
Сначала проверим, являются ли ссылки на правый и левый аргу-
менты одинаковыми, так как в этом случае нет необходимости
копировать. В противном случае, разряды числового представле-
ния In копируются в неявный левый аргумент *this, так же как
переменные init и status, а возвращается ссылка на неявный эле-
мент в виде *this.
if (&ln != this)
{
cpyj (nJ, In.nJ);
init = 1; j
status = In.status; J
}
return *this; И
} "
Возникает вопрос: нужно ли вообще оператору присваивания воз-
вращать какое-нибудь значение, так как после вызова LINT:.‘Operator =
(const LINT&) нужное присваивание вроде бы сделано. Однако ответ
ГЛАВА 13. Пусть C++ облегчит вашу жизнь
303
на данный вопрос достаточно очевиден, если вспомнить, что раз-
решено выражение в форме
f(a = b);
Согласно семантике языка C++, подобное выражение является
результатом вызова функции f с результатом присваивания а = b в
качестве аргумента. Таким образом, крайне необходимо, чтобы
оператор присваивания возвращал значение как результат, и для
большей эффективности это делается с помощью ссылки. Частным
случаем такого выражения является
а = b = с ;
где оператор присваивания вызывается два раза подряд. Когда он
вызывается второй раз, результат первого присваивания b = с при-
сваивается а.
В отличие от оператора оператор “*=” меняет самый левый
из двух сомножителей, записывая на его место значение произве-
дения. Смысл выражения а *= b как сокращенная запись выраже-
ния а = а * Ь, вне всякого сомнения, должен остаться верным для
объектов класса LINT. Следовательно, оператор как и опера-
тор может быть создан как функция-член, которая по причи-
нам, обсужденным выше, возвращает ссылку на результат:
const LINT& LINT::operator*= (const LINT& In)
{
int error;
if (Unit) panic (E_LINT_VAL, 0, _LINE_);
if (lln.init) panic (E_LINT_VAL, "*=и, 1, _LINE_);
if (&ln == this)
error = sqrj (nJ, nJ);
else
error = mulj (nJ, In.nJ, nJ);
switch (error)
{
case 0:
status = EJJNTJDK;
Криптография на Си и C++ в действии
break;
case E_CLINT_OFL:
status = EJJNTJDFL;
break;
default:
panic (EJJNT.ERR, "*=n, error, _LINE_);
}
return *this;
}
В качестве нашего последнего примера оператора LINT мы опишем
функцию “= =”, которая проверяет на равенство два объекта LINT:
в результате возвращается значение 1, если они равны, и 0 - в про-
тивном случае. Оператор = = также иллюстрирует реализацию дру-
гих логических операторов.
const int operator== (const LINT& Im, const LINT& In)
{ j|
if (!Im.init) LINT::panic (E_LINT_VAL, "==", 1, _LINE_);
if (lln.init) LINT::panic (E_LINT_VAL, "==”, 2, _LINE_);
if (&ln == &lm) I
return 1; И
else И
return equj (Im.nJ, In.nJ); И
ГЛАВА 14.
Открытый интерфейс LINT:
члены и друзья класса
Пожалуйста, примите мою отставку. Я не хочу
принадлежать какому-нибудь клубу, который
I . / г. примет меня в качестве члена клуба.
Гручо Маркс
f Каждый раз, когда я пишу портрет, я теряю
друга.
Джон Сингер Сарджент
В добавление к функциям-конструкторам и операторам, о которых
говорилось ранее, существуют и дополнительные функции LINT,
которые делают функции языка С, рассмотренные в части I, дос-
и тупными объектам LINT. На повестке грядущего обсуждения ле-
t жит следующее: мы сделаем приблизительное разделение функций
.. на “арифметические” и ’’теоретико-числовые” категории. Реализа-
цию функций мы обсудим вместе с примерами; в остальных случаях
мы ограничимся таблицей, которая требуется для их применения по
назначению. Также в следующих разделах мы дадим трактование в
более широкой форме функциям форматированного вывода объектов
’**'* LINT, для которых мы воспользуемся свойствами классов stream,
содержащихся в стандартной библиотеке C++. Во многих руково-
ди' дствах по языку C++ достаточно быстро расправляются со всевоз-
можными приложениями, особенно по форматированному выводу
объектов классов, которые определяются пользователем, и, пользу-
ясь случаем, мы собираемся раскрыть конструкцию функций, необ-
ходимых для вывода наших объектов класса LINT.
14.1. Арифметика
Следующие функции-члены выполняют основные арифметические
операции, так же как и модульные вычисления в кольце классов
вычетов колец в режиме сумматора: объект, к которому принадле-
жит вызываемая функция, содержит результат выполнения функции
как неявный аргумент после ее завершения. Функции-сумматоры
являются эффективными, так как они работают преимущественно
без внутренних вспомогательных объектов, таким образом экономя
лишние присваивания и вызовы конструкторов.
306
Криптография на Си и C++ в действии
В тех случаях, в которых присваивание результатов вычисления яв-
ляется неизбежным или же в которых автоматическая перезапись
неявно выраженного аргумента функции-члена результатом явля-
ется нежелательной, мы расширим их с помощью аналогичных
функций-друзей с похожими названиями вместе с дополнительными
функциями-друзьями. Мы не будем обсуждать это в дальнейшем в
данной главе, однако упомянем об этом в приложении В. Интер-
претация возможных ошибочных ситуаций в функциях LINT, кото-
рые могут возникнуть от применения функций CLINT, будет рас-
смотрена в полной мере в главе 15.
Прежде чем мы составим список открытых функций-членов, нам
предстоит рассмотреть пример их реализации в виде функции воз-
ведения в степень, для которой, увы, C++ не предоставляет никакого
оператора.
LINT& LINT::mexp (const LINT& е, const LINT& m);
и
LINT& LINT::mexp (const USHORT e, const LINT& m);
Функции mexp() построены так, что вызываемые ими С-функции
являются оптимизированными в зависимости от типа операндов
(а именно, mexpkJO, mexpkmJQ, umexpJO или umexpmJO), а в со-
ответствующих арифметических дружественных функциях мы бу-
дем обычно иметь дело с функциями возведения в степень
wmexpJO и wmexpmJO с основанием типа USHORT.
Функция: Модульное возведение в степень с автоматическим применением возведения в степень Монтгомери, если модуль оказался нечетным.
Синтаксис: const LINT& LINT::mexp (const LINT& е, const LINT& m);
Вход: неявный аргумент (основание) е (экспонента) m (модуль)
Возврат: указатель на остаток 1
Пример: a.mexp (е, т);
const LINT& LINT::mexp (const LINT& e, const LINT& m)
{
int error;
if (!init) panic (E_LINT_VAL, "mexp", 0,_LINE_);
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 3Q7
if (le.init) panic (E_LINT_VAL, "mexp", 1, _LINE_); if (Im.init) panic (EJJNT_VAL, "mexp", 2, _LINE_); err = mexpj (nJ, e.nJ, nJ, m.nj); /* mexpJ() использует mexpkJO или mexpkmJO */ switch (error) { case 0: status = E_LINT_OK; break; case E_CLINT_DBZ: panic (EJJNTJDBZ, "mexp", 2, _LINE_); break; default: panic (EJJNT.ERR, "mexp*’, error, _LINE_); } return *this; }
Функция: Модульное возведение в степень
Синтаксис: const LINT& LINT::mexp (const USHORT e, const LINT& m);
Пример: a.mexp (e, m); const LINT& LINT::mexp (const USHORT e, const LINT& m) г
1 int err; if (linit) panic (E.LINT.VAL, "mexp", 0, _LINE—); if (Im.init) panic (E.LINT.VAL, "mexp", 1, LINE ); err = umexpj (nJ, e, nJ, m.nj);
308
Криптография на Си и C++ в действии
switch (err) { И Здесь код, аналогичный вышеприведенному в техр (const LINT& е, const LINT& т) 1 return *this; } А теперь мы рассмотрим набор дополнительных арифметических и теоретико-числовых функций-членов.
Функция: сложение
Синтаксис: const LINT& LINT::add (const LINT& s);
Вход: неявный аргумент (слагаемое) s (слагаемое)
Возврат: указатель на сумму
Пример: a.add (s); выполняет операцию а += s;
Функция: вычитание
Синтаксис: const LINT& LINT::sub (const LINT& s);
Вход: неявный аргумент (уменьшаемое) s (вычитаемое)
Возврат: указатель на разность
Пример: a.sub (s); выполняет операцию а -= s;
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
309
Функция: умножение
Синтаксис: const LINT& const LINT& LINT::mul (const LINT& s);
Вход: неявный аргумент (множитель) s (множитель)
Возврат: указатель на произведение
Пример: a.mul (s); выполняет операцию а
Функция: возведение в квадрат
Синтаксис: const LINT& LINT::sqr (void);
Вход: неявный аргумент (множитель)
Возврат: указатель на неявный аргумент, который содержит квадрат
Пример: a.sqr (s); выполняет операцию а *= а;
Функция: деление с остатком
Синтаксис: const LINT& LI NT: :divr (const LINT& d, LINT& r);
Вход: неявный аргумент (делимое) d (делитель)
Выход: г (остаток от деления по модулю d)
Возврат: указатель на неявный аргумент, который содержит частное
Пример: a.divr (d, г); выполняет операцию а /= d; г = а % d;
310
Криптография на Си и C++ в действии
Функция: нахождение остатка
Синтаксис: const LINT& LINT::mod (const LINT& d);
Вход: неявный аргумент (делимое) d (делитель)
Возврат: указатель на неявный аргумент, который содержит остаток от деления по модулю d
Пример: a.mod (d); выполняет операцию а %= d;
Функция: нахождение остатка по модулю степени двойки
Синтаксис: const LINT& LINT::mod2 (const USHORT e);
Вход: неявный аргумент (делимое) е (показатель степени делителя)
Возврат: указатель на неявный аргумент, который содержит остаток от деления по модулю 2е
Пример: a.mod 2(e); выполняет операцию а %= d, где d=2e
Примечание: mod2 не может быть создана с помощью перегрузки ранее представ- ленной функции mod(), потому что mod() так же принимает аргумент USHORT, который автоматически приводится в объект LINT посред- ством подходящего конструктора. Поэтому из аргументов не ясно, какая функция имеется в виду, mod2() дается свое собственное имя.
Функция: проверка на равенство по модулю m
Синтаксис: const int ? LINT::mequ (const LINT& b, const LINT& m);
Вход: неявный аргумент a второй аргумент b модуль m
Возврат: 1, если a = b mod m, в противном случае 0
Пример: if (a.mequ (b, m)) //...
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
311
функция: модульное сложение
Синтаксис: const LINT& LINT::madd (const LINT& s, const LINT& m);
Вход: неявный аргумент (слагаемое) s (слагаемое) m (модуль)
Возврат: указатель на неявный аргумент, который содержит сумму по модулю m
Пример: a.madd (s, m);
Функция: модульное вычитание
Синтаксис: const LINT& LINTr.msub (const LINT& s, const LINT& m);
Вход: неявный аргумент (уменьшаемое) s (вычитаемое) m (модуль)
Возврат: указатель на неявный аргумент, который содержит разность по модулю m
Пример: a.msub (s, m);
Функция: модульное умножение
Синтаксис: const LINT& LINTr.mmul (const LINT& s, const LINT& m);
Вход: неявный аргумент (множитель) s (множитель) m (модуль)
Возврат: указатель на неявный аргумент, который содержит произведение по модулю m
Пример: a.mmul (s, m);
312
Криптография на Си и C++ в действии
Функция: модульное возведение в квадрат
Синтаксис: const LINT& LINT::msqr (const LINT& m);
Вход: неявный аргумент (множитель) г m (модуль) ?
Возврат: указатель на неявный аргумент, который содержит квадрат по модулю m
Пример: a.msqr (m);
Функция: модульное возведение в степень с показателем вида 2е
Синтаксис: const LINT& LINT::mexp2 (const USHORT e, const LINT& m);
Вход: неявный аргумент (основание) e (степень 2) m (модуль)
Возврат: указатель на неявный аргумент, который содержит степень по модулю m
Пример: a.mexp2 (е, m);
Функция: модульное возведение в степень (2к-арный метод, с преобразованием Монтгомери)
Синтаксис: const LINT& LINT::mexpkm (const LINT& е, const LINT& m);
Вход: неявный аргумент (основание) е (показатель) m (нечетный модуль)
Возврат: указатель на неявный аргумент, который содержит степень по модулю m
Пример: a.mexpkm (е, m);
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 313
Функция: модульное возведение в степень (25-арный метод, с преобразованием Монтгомери)
Синтаксис: const LINT& LINT::mexp5m (const LINT& е, const LINT& m);
Вход: и неявный аргумент (основание) е (показатель) • m (нечетный модуль)
Возврат: указатель на неявный аргумент, который содержит степень по модулю m
Пример: a.mexp5m (е, m);
Функция: левый/правый сдвиг
Синтаксис: const LINT& LINT::shift (const int noofbits);
Вход: неявный аргумент (множимое/делимое) (+/-) noofbits (число позиций, на сколько должны быть сдвинуты биты)
Возврат: указатель на неявный аргумент, который содержит результат операции сдвига
Пример: a.shift (512); выполняет операцию а «= 512;
Функция: проверка делимости на 2 объекта LINT
Синтаксис: const int LINT::iseven (void);
Вход: кандидат а как неявный аргумент
Возврат: ‘ 1, если а - нечетное, в противном случае 0
Пример: if(a.iseven ()) //...
314 Криптография на Си и C++ в действии
Функция: установка двоичного разряда объекта LINT в 1
Синтаксис: const LINT& LINT::setbit (const unsigned int pos);
Вход: неявный аргумент a pos - позиция того бита, который будет установлен (начиная с 0)
Возврат: указатель на а, с установленным битом в позиции pos
Пример: a.setbit (512);
Функция: проверка двоичного разряда объекта LINT
Синтаксис: const int LINT::testbit (const unsigned int pos);
Вход: неявный аргумент a pos - позиция того бита, который будет проверен (начиная с 0)
Возврат: 1, если бит находящийся в позиции pos установлен, в противном случае 0
Пример: if(a.testbit (512)) //...
Функция: установка двоичного разряда объекта LINT в 0
Синтаксис: const LINT& LINT::clearbit (const unsigned int pos);
Вход: неявный аргумент a pos - позиция того бита, который будет установлен (начиная с 0)
Возврат: указатель на а с нулевым битом в позиции pos
Пример: a.clearbit (512);
f
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
315
функция: обмен значениями двух объектов LINT
Синтаксис: const LINT& LINT::fswap (LINT& b);
Вход: неявный аргумент а второй аргумент b (значение, которое будет меняться на а)
Возврат: указатель на неявный аргумент со значением b
Пример: a.fswap (b); а и b обмениваются значениями
14.2. Теория чисел
; В отличие от арифметических функций, следующие теоретико- числовые функции-члены не перезаписывают первый неявный аргумент с результатом. Причиной этому является то, что при использовании более сложных функций, как показала практика, обычно не нужно перезаписывать аргумент, как это происходит в случае с простыми арифметическими функциями. Результаты следующих функций соответственно возвращаются как значения, а не как указатели.
Функция: вычисление наибольшего целого, меньшего или равного логарифму по основанию 2 от объекта LINT
Синтаксис: ’ const unsigned int LINT::ld (void);
Вход: неявный аргумент a
Возврат: целая часть log2 a
Пример: i = a.ld();
316
Криптография на Си и C++ в действии
Функция: вычисление наибольшего общего делителя двух объектов LINT
Синтаксис: const LINT LINT::gcd (const LINT& b);
Вход: неявно выраженный аргумент a второй аргумент b
Возврат: НОД(а, b)
Пример: с = a.gcd (b);
Функция: вычисление обратного значения по модулю п
Синтаксис: const LINT LINT::inv (const LINT& n);
Вход: неявный аргумент a модуль n
Возврат: обратная величина по модулю п (если результат равен нулю, то gcd(a, п) >1 и инверсии не происходит)
Пример: с = a.inv (b);
Функция: наибольший общий делитель чисел а и b и его представление g = ua+vb в виде линейной комбинации а и b
Синтаксис: const LINT LINT::xgcd (const LINT& b, LINT& u, int& sign_u, LINT& v, int& sign_v);
Вход: неявный аргумент a, второй аргумент b
Выход: множитель u в представлении НОД(а, b) sign_u - знак и множитель v в представлении НОД(а, Ь) sign_v - знак v
Возврат: НОД(а, Ь)
Пример: g = a.xgcd (b, u, sign_u, v, sign_v);
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 317
Функция: наименьшее общее кратное двух объектов LINT.
Синтаксис: const LINT LINT::lcm (const LINT& b);
Вход: неявный аргумент a, второй аргумент b
Возврат: HOK (a, b)
Пример: c = a.lcm (b);
Функция: решение системы линейных сравнений х = a mod m, х = b mod п
Синтаксис: const LINT LINTr.chinrem (const LINT& m, const LINT& b, const LINT& n);
Вход: неявный аргумент а, модуль m, аргумент b, модуль n
Возврат: решение x системы сравнений, если все в порядке (Get_Waming_Status() == EL1NTERR означает, что произошло переполнение или сравнения не имеют общего решения)
Пример: х = a.chinrem (m, b, n);
Функция-друг chinrem (const int noofeq, LINT** coeff) получает coeff - вектор указателей на объекты LINT, которые передаются как коэф- ’< фициенты aj, mlt а2, т2> а3, т3> ... системы линейных сравнений x^at mod mif i=l, ..., noofeq (см. Приложение В)
Функция: вычисление символа Якоби двух объектов LINT
Синтаксис: const int LINT::jacobi (const LINT& b);
Вход: неявный аргумент а, аргумент b
Возврат: Символ Якоби от двух входных значений
Пример: i = a.jacobi (b);
318
Криптография на Си и C++ в действии
Функция: вычисление целой части от квадратного корня
Синтаксис: const LINT LI NT::root (void);
Вход: неявный аргумент a
Возврат: целая часть от квадратного корня
Пример: с = a.root ();
Функция: вычисление квадратного корня по модулю простого числа р
Синтаксис: const LINT LI NT::root (const LINT& p);
Вход: неявный аргумент а, простой модуль p > 2
Возврат: квадратный корень из а, если а - квадратичный вычет по модулю р, в противном случае 0 (Get_Warning_Status() == E_LINT_ERR показывает, что а не является квадратичным вычетом по модулю р)
Пример: с = a.root (р);
Функция: вычисление квадратного корня объекта LINT по модулю а простого произведения р • q
Синтаксис: const LINT LINT::root (const LINT& p, const LINT& q);
Вход: неявный аргумент a простой модуль p > 2, простой модуль q > 2
Возврат: квадратный корень из а, если а - квадратичный вычет по модулю PQ> в противном случае 0 (Get_Warning_Status() == E_LINT_ERR показывает, что а не является квадратичным вычетом по модулю p*Q)
Пример: с = a.root (р, q);
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 319
Функция: проверка, является ли объект LINT квадратом
Синтаксис: const int LINTr.issqr (void);
Вход: кандидат а как неявный аргумент
Возврат: квадратный корень из а, если а является квадратом, в противном случае 0, если а == 0 или а не является квадратом
Пример: if(0 == (г = a.issqr ())) И...
Функция: вероятностная проверка объекта LINT на простоту
Синтаксис: const int LINT::isprime (void);
Вход: кандидат а как неявный аргумент
Возврат: 1, если а “вероятно” простое, в противном случае 0
Пример: if(a.isprime ()) //...
Функция: Разложение CLINT-объекта в виде а = 2еb
Синтаксис: const int LINT::twofact (LINT& b);
Вход: неявный аргумент а
Выход; b (нечетная часть а)
Возврат: показатель степени четной части а
Пример: е = a.twofact (b);
320
Криптография на Си и C++ в действии
14.3. Потоковый ввод/вывод объектов LINT
Классы, содержащиеся в стандартных библиотеках языка C++,
такие как istream и ostream, являются абстракциями устройств
ввода/вывода, полученных из базового класса ios. Класс iostreami
в свою очередь, получен из istream и ostream, и он позволяет писати
и читать из них объекты1. Ввод и вывод происходит с помощьк|
операторов поместить (insert) и извлечь (extract) “«” и ”»’]
(см. [Teal], глава 8). Они возникают при перегрузке оператором
сдвига, например, в выражении I
ostream& ostream::operator« (int i); I
istream& istream::operator>> (int& i); I
в котором они разрешают вывод и ввод, соответственно, целым
значений через следующие выражения: I
cout«i;
cin »i; I
В качестве специальных объектов классов ostream и istream, al
именно cout и cin, выступают те же самые абстрактные файлы, как!
объекты stdout и stdin стандартной библиотеки С.
Применение потоковых операторов “«” и ”»” для ввода и вывода
отменяет необходимость вникать в подробности используемой ап-
паратуры. В этом нет ничего особенного, к примеру, функция С
printf() ведет себя таким же образом: команда printf() должна всегда,
в независимости от платформы, возвращать одинаковый результат.
Однако лежащие за пределами изменяющегося синтаксиса, кото-
рый ориентирован на образное отображение вставки объектов в по-
ток, преимущества реализации потоков языка C++ лежат в строгой
проверке типов, которая в случае с printf() возможна лишь отчасти,
и своей собственной расширяемости. В частности, мы восполь-
зуемся последним свойством, перегрузив операторы “«” и
для того, чтобы они поддерживали ввод и вывод объектов LINT.|
Завершим класс LINT следующими потоковыми операторами:
friend ostream& operator« (ostream& s, const LINT& In);
friend fstream& operator« (fstream& s, const LINT& In);
Мы применяем это имя потоковых классов как синоним к тем, которые сейчас используются в
стандартной библиотеке C++, в которой имена класса, известные ранее, получили префикс basics
Настройка этого идет в самой стандартной библиотеке, в которой к ранее использовавшимся име-
нам классов можно обращаться через соответствующие объявления типов (typedef) (см. [KSchL
Глава 12)
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
321
friend ofstream& operator« (ofstream& s, const LINT& In);
friend fstream& operator» (fstream& s, LINT& In);
friend ifstream& operator» (ifstream& s, LINT& In);
Простая реализация перегрузки оператора “«” для вывода объек-
тов LINT могла бы выглядеть приблизительно следующим образом:
#include <iostream.h>
ostream& operator« (ostream& s, const LINT& In)
{
if (lln.init)
LINT::panic (E_LINT_VAL, "ostream operator«", 0,_____LINE___);
s « xclint2str (In.nJ, 16, 0) « endl;
s « Id (In) « " bit" « endl;
return s;
Таким образом, оператор “«” определяет выводы разрядов объек-
та LINT как шестнадцатиричных значений, добавляя при этом дво-
ичную длину числа на отдельной строке. В следующем разделе мы
рассмотрим возможности выражения появления вывода объектов
LINT с помощью функций форматирования, а также мы рассмот-
рим применение манипуляторов для того, чтобы вывод был на-
страиваемым.
14.3.1. Форматированный вывод
объектов LINT.
В данном разделе мы воспользуемся базовым классом ios стандарт-
ной библиотеки C++ и его функциями-членами для того, чтобы оп-
ределить наши собственные функции форматирования, подходящие
для LINT, с целью управления форматом вывода объектов LINT.
Л
Далее мы создадим манипуляторы, которые организуют настройку
формата вывода объектов LINT настолько просто, как это сделано
для стандартных типов, определенных в C++.
Ключевым моментом в создании форматированного вывода объек-
тов LINT является возможность установки спецификаций формата,
которые будут обрабатываться оператором Мы рассмотрим
механизм, обеспечиваемый классом ios (для более подробного рас-
смотрения см. [Teal], Глава 6, и [Р1а2], Глава 6), у которого функция-
11 _ 1AQ7
322
Криптография на Си и C++ в действии
член xalloc() в объектах классов, производных от ios, выделяет пе-
ременную состояния типа long и возвращает ее индекс того же типа.
Этот индекс хранится в переменной flagsindex. С помощью нее
функцию-член ios::iword() можно использовать для того, чтобы по-
лучить доступ по чтению и записи к выделенной переменной управ-
ления выводом (иначе, переменной состояния) (см. [Р1а2], стр. 125).
Для полной уверенности, что это происходит до вывода объекта
LINT, мы определяем в файле flintpp.h класс Lintlnit следующим
образом:
class Lintlnit I
<
public: I
Lintlnit (void);
};
Lintlnit::Lintlnit (void)
{
// получить индекс к переменной состояния в классе ios
LINT::flagsindex = ios::xalloc();
И установить состояние по умолчанию в cout и сегг
cout.iword (LINT::flagsindex) =
cerr.iword (LINT::flagsindex) =
LINT::lintshowlength|LINT::linthex|LINT::lintshowbase;
}
Класс Lintlnit в качестве своего единственного элемента содержит
конструктор Lintlnit::Lintlnit(). К тому же в классе LINT мы опреде-
ляем член элемента данных setup типа Lintlnit, который инициали-
зирован с помощью конструктора Lintlnit::Lintlnit(). Вызов xalloc()
происходит во время инициализации, а таким образом выделяемая
переменная состояния определяет стандартный формат вывода
объектов LINT. Далее мы покажем часть объявления класса LINT,
которая содержит объявление Lintlnit() как друга класса LINT, а
также объявление переменных flagsindex, setup и различных пере-
менных состояния в виде перечислимого типа (епит):
class LINT
{
J
public:
If...
enum {
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
323
lintdec = 0x10,
lintoct = 0x20,
linthex = 0x40,
lintshowbase = 0x80,
lintuppercase =0x100,
lintbin = 0x200,
lintshowlength = 0x400
};
n...
friend Lintlnit::Lintlnit (void);
//...
private:
H...
static long flagsindex;
static Lintlnit setup;
H...
};
Задание переменной setup как static означает, что эта переменная
существует только один раз для всех объектов LINT, и, таким обра-
зом, связанный конструктор Lintlnit() вызывается только один раз.
Здесь мы хотим ненадолго остановиться и рассмотреть всю проде-
ланную нами работу. Установку формата вывода можно с тем же
успехом организовать с помощью переменной состояния, с которой
как с членом класса LINT намного проще было бы иметь дело. Ос-
новным преимуществом метода, который мы выбрали, является то,
что вывод формата можно установить для каждого потока вывода
отдельно и независимо друг от друга, (см. [Р1а2], страница 125), че-
го нельзя сделать, используя внутреннюю для класса LINT пере-
менную состояния. Это организуется с помощью возможностей
класса ios, механизмы которого нам пригодятся для подобных целей.
Теперь, после того как были рассмотрены необходимые замечания,
мы сможем определить функции состояния как члены класса LINT.
Они отражены в Таблице 14.1.
Мы рассмотрим пример реализации функций состояния для функ-
ции LINT::setf(), которая возвращает текущее значение состояния
переменной типа long с ссылкой на поток вывода:
324
Криптография на Си и C++ в действии
Таблииа 14.1 Функция состояния Пояснения
Функиии- состояния класса LINT и результат их действия static long LINT::flags (void); static long LINT::flags (ostream&); Считывает переменную состояния, относящуюся к cout Считывает переменную состояния, относящуюся к заданному потоку вывода
static long LINT::setf (long); Устанавливает отдельные биты переменной состояния cout и возвращает предыдущее значение
static long LINT::setf (ostream&, long); Устанавливает отдельные биты переменной состояния заданного потока и возвращает предыдущее значение
static long LINT::unsetf (long); Восстанавливает отдельные биты переменной состояния cout и возвращает^ предыдущее значение |И
static long LINT::unsetf (ostream&, long); Восстанавливает отдельные биты переменной состояния заданного потока и возвращает предыдущее значение
static long LI NT:: restore! (long); Устанавливает переменную состояния cout и возвращает предыдущее значение
static long LINT::restoref (ostream&, long); Устанавливает переменную состояния заданного потока и возвращает предыдущее значение
long LINT::setf (ostream& s, long flag)
i..
long t = s.iword (flagsindex);
// Флаги для основания числового представления
взаимоисключающие:
if (flag & LINT: Jintdec)
{
s.iword (flagsindex) = (t & ~LINT::linthex & ~LINT::lintoct
& -LINT"lintbin) | LINT::lintdec;
flag *= LINT::lintdec;
}
if (flag & LINT::linthex)
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 325
s.iword (flagsindex) = (t & ~LINT::lintdec & ~LINT::lintoct & ~LINT::lintbin) | LINT::linthex; flag л= LINT::linthex; } if (flag & LINT::lintoct)
t s.iword (flagsindex) = (t & ~LINT::lintdec & ~LINT::linthex
& ~LINT::lintbin) | LINT::lintoct; flag л= LINT::lintoct; } if (flag & LINT::lintbin) { s.iword (flagsindex) = (t & ~LINT::lintdec & ~LINT::lintoct
& ~LINT::linthex) | LINT::lintbin; flag A= LINT::lintbin; } // Все остальные флаги являются взаимно совместимыми s.iword (flagsindex) |= flag;
..-и • • return t; } С помощью этой и оставшихся функций в Таблице 14.1 мы можем далее определить разные форматы вывода. Первоначально стан- дартный формат вывода представляет собой значение объекта LINT как шестнадцатиричное число в виде строки символов, которая
; ' 0 занимает столько строк на экране, сколько требуется для вывода всех цифр объекта LINT. В добавочной строке число цифр объекта LINT размещено слева от края. Были созданы следующие дополни- тельные режимы вывода объекта LINT:
‘Эсгдо 1. Основание представления цифр. Стандартным представлением цифр объектов LINT является шест- надцатиричное, а представлением длины - десятичное. Такие умолчания для объектов LINT могут быть установлены для стан- дартного потока вывода cout с определенным основанием системы счисления base с помощью вызова
326
Криптография на Си и C++ в действии
LINT::setf (LINT::base);
а на заданный поток
LlNT::setf (ostream, LINT::base);
где base может принимать одно из значений:
linthex, lintdec, lintoct, lintbin
которые
обозначают соответствующий
формат вывода.
Например
вызов LINT::setf(lintdec) устанавливает вывод формата цифр в деся-
тичной форме. Основание системы счисления для представления
длины может быть задано функцией
ios::setf (ios::iosbase);
с iosbase = hex, dec, oct.
2. Отображение префикса для числового представления
Для объекта LINT установкой по умолчанию является отображение с
префиксом, показывающим как он представлен. Следующие вызовы
LINT::unsetf (LINT::lintshowbase);
LINT::unsetf (ostream, LINT::lintshowbase);
меняют эту установку.
3. Отображение шестнадцатиричных цифр в верхнем регистре
По умолчанию установлено отображение шестнадцатиричных цифр
и префикса Ох для шестнадцатиричного представления в нижнем
регистре a b с d е f. Однако вызов
LINT::setf (LINT::lintuppercase);
LINT::setf (ostream, LINT::lintuppercase);
меняет их для того, чтобы они превратились в префикс ОХ и боль-
шие буквы А В С D Е F.
4. Отображение длины объекта LINT
По умолчанию установлено отображение двоичной длины объекте!
LINT. Это можно изменить, вызвав
LINT::unsetf (LINT::lintshowlength);
LINT::unsetf (ostream, LINT::lintshowlength);
для того чтобы длина не отображалась.
Г ЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
5. Восстановление переменной состояния
327
Переменную состояния для форматирования объекта LINT можно
восстановить в предыдущее значение oldflags с помощью вызова
двух функций
LINT::unsetf (ostream, LINT::flags(ostream));
LINT::setf (ostream, oldflags);
Вызовы этих двух функций собраны в перегруженной функции
restoref():
LINT::restoref (flag);
LINT::restoref (ostream, flag);
Флаги можно объединить, как показано в вызове
LINT::setf (LINT::bin | LINT::showbase);
Однако это разрешено только лишь для флагов, которые не являют-
ся взаимоисключающими.
Функции вывода, которые в конечном итоге и генерируют задан-
ный формат объекта LINT, являются расширением оператора
ostream& operator <<(ostream& s, LINT In), о котором в общих чертах
говорилось ранее. Он оценивает переменную состояния потока вы-
вода и генерирует соответствующий вывод. Для данного оператора
применяется вспомогательная функция Iint2str(), содержащаяся в
файле flintpp.cpp, которая в свою очередь вызывает функцию
xclint2strj() для того, чтобы представить числовое значение объекта
LINT как строку символов:
ostream& operator« (ostream& s, const LINT& In)
{
USHORT base = 16;
long flags = LINT::flags (s);
char* formattedjint;
if (lln.init) LINT::panic (E_LINT_VAL, "ostream operator«", 0, __LINE_);
if (flags & LINT::linthex)
{
base = 16;
Криптография на Си и C++ в действии
else
{
if (flags & LINT::lintdec)
{
base = 10;
}
else
{
if (flags & LINT::lintoct)
{
base = 8;
}
else
{
if (flags & LINT::lintbin)
{
base = 2;
}
}
}
}
if (flags & LINT::lintshowbase)
{
formattedjint = Iint2str (In, base, 1);
}
else
{
formattedjint = Iint2str (In, base, 0);
}
if (flags & LINT::lintuppercase)
{
struprj (formattedjint);
}
s «formattedjint«flush;
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса 329
if (flags & LINT::lintshowlength) { long -flags = s.flags (); //Получение текущего состояния s.setf (ios::dec); //установка флага для десятичного отображения s « endl « Id (In) « " bit" « endl; //восстановление предыдущего состояния s.setf (_flags); }
‘ к; U1 return s; } 14.3.2. Манипуляторы Опираясь на предыдущие механизмы, в данном разделе мы хотим достичь более подходящих вариантов для управления форматом вывода для объектов LINT. Для этого мы используем .манипуля-
торы, которые размещены прямо в потоке вывода, и, их эффект аналогичен тому, что мы получали при вызове ранее рассмотренных
функций состояния. Манипуляторы являются адресами функций, для которых существует специальный вид оператора поместить (“«”), который в свою очередь в качестве аргумента принимает указатель на функцию. Для примера мы рассмотрим следующую функцию: ostream& LintHex (ostream& s) г
t LINT::setf (s, LINT::linthex); return s;
1Ы } Данная функция вызывает функцию состояния setf(s, LINT::linthex) в контексте заданного потока вывода ostream& s и, таким образом, задает формат вывода объектов LINT в форме шестнадцатиричных чисел. Имя функции LintHex без круглых скобок рассматривается как указатель на функцию (см. [Lipp], страница 202), и он может быть направлен в поток вывода как манипулятор с помощью опера- тора “«” ostream& ostream::operator« (ostream& (*pf)(ostream&))
10
Криптография на Си и C++ в действи
return (*pf)(*this);
}
определенного в классе ostream:
LINT a ("0x123456789abcdef0");
cout « LintHex « a:
ostream s;
s « LintDec « a;
Функции-манипуляторы LINT работают по приведенному шаблону
как стандартные манипуляторы
dec, hex, oct, flush, и endl. Оператор “«”
в библиотеке языка C++,
например
пулятор функции LintHex()
или LintDecQ
просто
вызывает мани
подходящий
момент
Манипуляторы
обеспечивают установку флагов состояния,
принад
лежащих потокам вывода cout и, соответственно, s. Перегруженный
оператор “«” вывода объектов LINT переносит
объекта а типа LINT в запрошенную форму.
представление
Все установки
формата вывода объектов
LINT
могут быть
вы пол
йены с помощью манипуляторов, представленных в Таблице 14.2.
Таблииа 14.2. Манипулятор Результат вывода значений LINT
Манипуляторы LINT и результат LintBin как числа в бинарном виде
их выполнения LintDec как числа в десятичном виде
LintHex как числа в шестнадиатиричном виде
LintOct как числа в восьмеричном виде
LintLwr с символами нижнего регистра a, b, с, d, е, ( для шестнадцатиричного представления
LintUpr с символами верхнего регистра А, В, С, D, Е, F для шестнадцатиричного представления
LintShowbase с префиксом для числового представления (Ох или ОХ в шестнадцатиричном и 0Ь - бинарном)
LintNobase без префикса для числового представления
LintShowlength с отображение числа разрядов
LintNolength без отображения числа разрядов
В добавление к манипуляторам в таблице 14.2.,
которым
ется аргумент, доступны следующие манипуляторы:
LINT_omanip<int>
SetLintFlags (int flags)
в
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
331
и
LINT_omanip<int> ResetLintFlags (int flags)
Они применяются в качестве альтернативы функциям состояния
setf() и unsetf():
cout « SetLintFlags (LINT::flag) « // включить
cout « ResetLintFlags (LINT::flag) « // выключить
Реализацию этих манипуляторов читатель может найти в исходных
текстах (flintpp.h и flintpp.cpp), а пояснения по поводу класса-
шаблона class omanip<T> в [Pla2], Глава 10. Флаги LINT еще раз
показаны в Таблице 14.3.
Табл и на 14.3. Флаги LINT для форма тирования Флаг Значение
lintdec 0x010
вывода lintoct 0x020
linthex 0x040
lintshowbase 0x080
lintuppercase 0x100
lintbin 0x200
• 1 ю ;; . Э * lintshowlength 0x400
-С по Следующим примером мы внесем ясность в применение самих
’ •’! а*} . функций форматирования и манипуляторов:
' -f' • / н? Ж' #include "flintpp.h"
#include <iostream.h>
#include <iomanip.h>
main()
{
LINT n ("0x0123456789abcdef"); И число LINT с основанием 16
long deflags = LINT::flags(); И запомним флаги
cout « "Представление по умолчанию:" « n « endl;
332
Криптография на Си и C++ в действии
LINT::setf (LINT::linthex | LINT::lintuppercase);
cout « "Шестнадцатиричное представление символов
в верхнем регистре:" « n « endl;
cout « LintLwr « " Шестнадцатиричное представление символов
в нижнем регистре:" « n « endl;
cout « LintDec « "десятичное представление:" « n « endl;
cout « LintBin « "двоичное представление:" « n « endl;
cout « LintNobase « LintHex;
cout «"представление без префикса:" « n « endl;
cerr« "Представление в потоке сегг по умолчанию: ” « n « endl;
LINT::restoref (deflags);
cout« "представление по умолчанию:" « n « endl;
return;
}
14.3.3. Файловый ввод/вывод
для объектов LINT
Для реальных приложений не обойтись без функций вывода объ-
ектов LINT в файлы и ввода их из них. Классы ввода/вывода стан-
дартной библиотеки C++ содержат функции-члены, которые позво-
ляют помещать объекты в поток ввода и вывода для файловых опе-
раций, поэтому нам повезло в том, что мы можем использовать тот
же синтаксис, что мы применяли ранее. Операторы, необходимые
для файлового вывода, похожи на те, что были в последнем разделе,
однако мы можем обойтись без форматирования.
Мы определим два оператора
friend ofstream& operator« (ofstream& s, const LINT& In);
friend fstream& operator« (fstream& s, const LINT& In);
для потоков вывода класса ofstream и для потоков класса fstream,
который поддерживает оба направления, то есть как ввод, так и
вывод. Так как класс ofstream унаследован от класса ostream, мы
можем использовать его функцию-член ostream::write() для записи
неформатированных данных в файл. Поскольку сохранятся только
лишь те разряды объекта LINT, которые на самом деле использу-
ются, мы будем экономно расходовать место на носителе для запис)
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
333
данных. Разряды типа USHORT объекта LINT в действительности
будут записаны как последовательность значений типа UCHAR. Для
полной уверенности, что это происходит всегда в правильном
порядке, независимо от схемы представления чисел на конкретной
платформе, определим вспомогательную функцию, которая запи-
сывает значения USHORT в виде последовательности двух симво-
лов типа UCHAR. Функция устраняет эффект платформозависимого
расположения разрядов по основанию 256 в памяти, таким образом
позволяя данным, которые были записаны на одном типе компью-
теров, быть считанными на других, где, возможно, иначе распола-
гаются байты в слове или иначе интерпретируются данные при их
чтении с устройств чтения/записи. В качестве примера для данного
случая можно привести архитектуры с прямым (little-endian) и
обратным (big-endian) порядком байт, в первой из которых после-
довательное приращение адресов памяти выполняется в порядке их
возрастания, а во втором - в порядке убывания2 * *’
template <class Т>
int write_Jnd_ushort (Т& s, clint src)
{
UCHAR buff[sizeof(clint)];
unsigned i, j;
for (i = 0, j = 0; i < sizeof(clint); i++, j = i « 3)
{
bufffi] = (UCHAR)((src & (Oxff«j)) »j);
}
s.write (buff, sizeof(clint));
if (!s)
{
return -1;
}
else
{
return 0;
2 Два байта В, и B/+i с адресами i и /+1 интерпретируются в представлении little-endian как значение
USHORT w = 28В/и + В/, а в представлении big-endian как w=28B<+B/+1. Аналогичная ситуация рас-
сматривается для толкования значений ULONG.
334
Криптография на Си и C++ в действии
}
}
Функция writeJnd_ushort() в случае ошибки возвращает значение -1,
а когда выполнение операции является успешным, возвращается 0.
Она реализована как template (шаблон) для того, чтобы его можно
было использовать двумя объектами, как ofstream, так и fstream.
Функция readjnd_ushort() создана по аналогу предыдущей функ-
ции и обратна ей:
template <class Т>
int read_ind_ushort (Т& s, clint *dest)
{
UCHAR buff[sizeof(clint)];
unsigned i;
s.read (buff, sizeof(clint));
if (!s)
{
return-1;
}
else
*dest = 0;
for (i = 0; i < sizeof(clint); i++)
*dest |= ((clint)buff(i]) « (i « 3);
return 0;
}
}
Теперь операторы вывода используют этот промежуточный формат
для записи объекта LINT в файл. Чтобы прояснить ситуацию, мы
предоставим реализацию оператора для класса ofstream.
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
ofstream& operator« (ofstream& s, const LINT& In)
335
if (lln.init)
{
LINT::panic (E_LINT_VAL, "ofstream operator«", 0,_LINE___);
}
for (int i = 0; i <= DIGITS.L (In.nJ); i++)
if (writejnd-ushort (s, In.nJ[i]))
{
LINT::panic (E_LINT_EOF, "ofstream operator«",
0, _LINE_);
}
return s;
}
Прежде чем объект LINT будет записан в файл, файл должен быть
открыт на запись, для которого может быть использован конст-
руктор
ofstream:-.ofstream (const char *, openmode)
или функция-член
ofstream::open (const char *, openmode)
В каждом случае должен быть установлен флаг ios::binary, как пока-
зано в следующем примере:
LINT г ("0x0123456789abcdef");
И...
ofstream fout ("test.io", ios::out | ios::binary);
fout « r« r*r;
II...
fout.closeQ;
336
Криптография на Си и C++ в действии
Импорт объекта LINT из файла осуществляется в обратном порядке,
с операторами, аналогичными выводу объекта LINT в файл.
friend ifstream& operator» (ifstream& s, LINT& In);
friend fstream& operator» (fstream& s, LINT& In);
Оба оператора сперва считывают отдельное значение, которое опреде-
ляет число разрядов в сохраненном объекте LINT. Далее считывается
соответствующее число разрядов. Значения USHORT считываются
согласно описанию выше с помощью функции read_ind_ushort():
ifstream& operator» (ifstream& s, LINT& In)
{
if (readjnd_ushort (s, In.nJ))
{
LINT::panic (E_LINT_EOF, "ifstream operator»",
0, _LINE—); .
В
if (DIGITSJ- (In.nJ) < CLINTMAXSHORT) И
В
for (int i = 1; i <= DIGITSJ. (In.nJ); i++)
В
if (readjnd_ushort (s, &ln.nj[i]))
В
LINT::panic (EJJNTJEOF, "ifstream operator»", M
0, _LINE_); I
} , I
} I
}
// Никакой паранойи! Проверка импортируемого значения
if (vcheckj (In.nJ) == 0)
{
ln.init = 1;
}
else
337
ГЛАВА 14. Открытый интерфейс LINT: члены и друзья класса
In.init = 0;
return s;
}
Для того чтобы открыть файл, из которого будет считан объект
LINT, снова необходимо установить флаг iosz.binary:
LINT г, s;
//...
ifstream fin;
fin.open ("test.io", ios::in | ios::binary);
fin » r» s;
//...
fin.closeQ;
В процессе импорта объектов LINT оператор “»” проверяет, пред-
ставляют ли считанные значения числовое представление правиль-
ного объекта LINT. Если это не так, то величина init устанавливается
в 0, и, таким образом, целевой объект отмечен как “неинициализи-
рованный”. Следующую операцию над таким объектом LINT вы-
полнит обработчик ошибок, который мы рассмотрим более детально
в следующей главе.
ГЛАВА 15.
Обработка ошибок
О отвратительная ошибка, дитя меланхолии!
Шекспир, Юлий Цезарь
15.1. (Без) Паники ...
Функции C++, представленные в предыдущих главах, реализовы-
вают механизмы анализа того, произошла ли в процессе выпол-
нения вызванной С-функции ошибка или иная ситуация, которая
требует подробного ответа, или, по крайне мере, предупреждения.
Функции проверяют, были ли инициализированы переданные им
переменные и оценивают возвращаемое значение вызванных
функций С:
LINT f (LINT arg1, LINT arg2)
{
LINT result;
int err;
if (!arg1 .init) LINT::panic (E_LINT_VAL, "f”, 1, _LINE_);
if (!arg2.init) LINT::panic (EJ_INT_VAL, "f", 2, _LINE—);
И Вызвать С-функцию для выполнения операции,
код ошибки вернется в err
err = fJ (arg1 .nJ, arg2.nj, result.nJ);
..O'
switch (err)
{
case 0:
result.init = 1;
break;
case E_CLINT_OFL:
result.status = EJJNT_OFL;
340
Криптография
на Си
result, init = 1;
break;
case E_CLINT_UFL:
result.status = EJJNTJJFL;
* result.init = 1;
break;
default:
LINT::panic (EJJNT-ERR, T, err, _LINE_);
}
return result;
}
в
Если переменная status содержит значение E-LINT-OK, то это явля
ется наилучшем случаем. В более затруднительных ситуациях,
которых происходит переполнение или потеря значимости в функ
ции С, переменная status принимает соответствующие значения
E-LINT_OFL или E_LINTJJFL. Так как наши функции С реагируют
на потерю данных приведением по модулю Amax + 1 (см. стр. 32),
этом случае функции завершаются нормально. Значение перемен
ной status можно будет запросить функцией-членом
в
LINT-ERRORS LINT::Get_Warning_Status (void);
Кроме этого, мы видели, что функции LINT всегда вызывают
функцию с хорошо подобранным именем panic(), когда ситуация
накаляется так, что уже невозможно ее обработать внутри функции
Задача этой функции-члена сперва вывести сообщения об ошибках
чтобы пользователь программы осознал, что что-то проходит не
верно, и, во-вторых, убедиться в управляемом завершении про
граммы. Сообщения об ошибках LINT выводятся через поток сегг
они содержат информацию о природе произошедшей ошибки,
функции, обнаружившей ошибку, и об аргументах, ее иницииро
вавших. Чтобы вывести всю эту информацию, ее необходимо полу
чить от вызываемой функции, как показано в следующем примере:
о
LINT::panic (E_LINT_DBZ,"%", 2, _LINE_);
В данном выражении объявляется появление деления на ноль
операторе “%” в строке, заданной ANSI макросом_LINE__, кото
рое вызвано вторым аргументом этого оператора. Аргументы нуме
руются так: 0 - всегда обозначает неявный аргумент функции
члена, а все другие аргументы пронумерованы слева направо
ГЛАВА 15. Обработка ошибок
341
начиная с 1. Функция обработки ошибок LINT panic() выводит
сообщения об ошибках следующих типов:
Пример 1: Применение неинициализированного объекта LINT в
качестве аргумента.
уме i Critical run-time error detected by class LINT:
Argument 0 in Operator *= uninitialized, line 1997
ABNORMAL TERMINATION
Пример 2: Деление объекта LINT на значение О
Critical run-time error detected by class LINT:
Division by zero, operator/function/, line 2000
ABNORMAL TERMINATION
Функция и операторы класса LINT распознают ситуацию, рассмот-
ренную в Таблице 15.1.
Таблииа 15.1. Коды ошибки Код Значение Пояснение
функиии LINT E_LINT_OK 0x0000 Все в порядке
E_LINT_EOF 0x0010 Ошибка файлового ввода/вывода в поточном операторе « или »
E_LINT_DBZ 0x0020 Деление на ноль
E_LINT_NHP 0x0040 Ошибка выделения памяти: new вернул указатель NULL
E_LINT_OFL 0x0080 Переполнение в функции или операторе
E_LINT_UFL 0x0100 Потеря значимости в функции или операторе
E_LINT_VAL 0x0200 Аргумент функции не инициализирован или имеет недопустимое значение
EJJNT.BOR 0x0400 Неверное основание, переданное конструктору в качестве аргумента
E_LINT_MOD 0x0800 Четный модуль в mexpkm()
E_LINT_NPT 0x1000 Указатель NULL, переданный в качестве аргумента.
342 Криптография на Си и C++ в действии.
15.2. Обработка ошибок, определяемая пользователем 1
Как правило, бывает необходимо приспособить обработку ошибок
к определенным требованиям. Класс LINT предоставляет такие
возможности, позволяя пользователю заменить LINT-функцию
ошибки panic() на его собственные функции. В добавление к этому,
вызывается следующая функция, которая берет в качестве аргумента
указатель на функцию:
void
LINT::Set_LINT_Error_Handler (void (*Error_Handler)
(LINT_ERRORS, const char* const, const int, const int))
{
LlNT_User_Error_Handler = Error_Handler;
}
Переменная LINT_User_Error_Handler определена и инициализиро-
вана в файле flintpp.cpp как
static void (*LINT_User_Error_Handler)
(LINT_ERRORS, const char*, const int, const int) = NULL;
Если данный указатель имеет значение, отличное от NULL, то
установленная функция будет вызвана вместо panic() и ей будет
доступна та же информацию, что и panic(). Что касается реализации
пользовательской программы обработки ошибок, то тут фантазии
нет предела. Однако необходимо понимать, что ошибки, передан-
ные классом LINT, обычно отражают ошибки программы, которые
невозможно исправить в процессе выполнения. Совершенно не
имеет смысла возвращать управление в тот программный сегмент,
в котором имеют место подобные ошибки, поэтому, вообще говоря,
в подобных случаях единственным подходящим выходом из ситуа-
ции является завершение программы.
Возврат к программе обработки ошибок LINT panic() осуществля-
ется с помощью вызова
LINT::Set-LINT_Error_Handler(NULL);
Следующий пример демонстрирует интеграцию пользовательской
функции в обработку ошибок:
#include "flintpp.h"
void my_error_handler (LINT_ERRORS err, const char* str,
const int arg, const int line)
ГЛАВА 15. Обработка ошибок 343
{
//... Код
}
V-
main()
{
И активация пользовательского обработчика ошибок:
LINT::Set_LINT_Error_Handler (my_error_handler);
И... Код
И восстановление обработчика ошибок LINT:
LINT::Set_LINT_Error_Handler (NULL);
И ...Код
}
15.3. Исключения LINT
Механизм исключений языка C++ является инструментом, который
прост в применении, а следовательно, и более эффективен в обра-
4 ботке ошибок, нежели методы, предлагаемые С. Обработчик
ошибок LINT::panic(), который описан ранее, ограничен выводом
в сообщений об ошибках и контролируемым завершением программы.
Вообще говоря, нам важна информация не о функции деления, где
произошло деление на ноль, а о функции, которая вызвала деление
и тем самым спровоцировала ошибку. А такая информация в
LINT::panic() не передается. В частности, с LINT::panic() невозможно
он будет вернуться к этой функции для того, чтобы устранить ошибку
или отреагировать иным, характерным для данной функции обра-
?f! зом. С другой стороны, такие возможности предлагает механизм
х., исключений языка C++, и мы хотели бы здесь создать условия,
которые позволят сделать данный механизм пригодным для
класса LINT.
Исключения в C++ принципиально основываются на конструкциях
трех типов: блок try (попытка), блок catch (захват), и команда throw
(выброс), с помощью которой функция подает сигнал об ошибке.
У блока catch имеется функция локальной обработки ошибок
блока try: блоком catch, который следует за блоком try, будут выяв-
лены ошибки, находящиеся в try и объявлены с помощью throw.
344
Криптография на Си и C++ в действии
Дальнейшие команды блока try будут проигнорированы. Тип ошибки
будет отражен в значении команды throw в качестве параметра
сопроводительного выражения.
Связь между блоками try и catch может быть отражена следующим
образом:
try
{
• • • • // Если ошибка вызвана через оператор throw,
• • • • // то ее можно поймать
• • • • И следующим блоком catch
}
catch (argument)
{
• • • • // здесь находятся процедуры обработки ошибок.
}
Если ошибка произошла не прямо в блоке try, а в функции, которая
вызывалась из него, то данная функция завершает свое выполнение
и управление возвращается вызываемой функцией по цепочке
вызовов в обратном порядке, пока не будет достигнут блок try.
Начиная с этого момента, управление передается соответствующему
блоку catch. Если блок try не найден, то вызывается генерация про-
граммы обработки ошибок, добавленной компилятором, которая в
дальнейшем завершает программу, зачастую с каким-нибудь стан-
дартным выводом.
Вполне ясно, какие ошибки могут быть в классе LINT, поэтому со-
вершенно не составит труда вызвать throw с теми кодами ошибки,
которые были предоставлены методу panic() функциями и
операторами LINT. Однако следующее решение являются более
удобным: сперва мы определяем абстрактный базовый класс
class LINT_Error
{
public:
char* function;
int argno, lineno;
ГЛАВА 15. Обработка ошибок 345
virtual void debug__print (void) const = 0; // чистая виртуальная virtual ~LINT_Error() {}; V
df О j > точно так же, как классы следующего типа, основанного на нем: // деление на ноль м class LINT_DivByZero : public LINT_Error { public: LINT_DivByZero (const char* const tunc, const int line); void debug_print (void) const; }; LINT_DivByZero::LINT_DivByZero (const char* const func, const int line) { function = func; lineno = line; argno = 0; }
void LINT_DivByZero::debug_print (void) const { cerr« "LINT-Исключение:" « endl;
‘•ч-П’36 cerr« "деление на ноль в функции ” «function « endl; cerr« "в модуле:" « FILE « ", в строке:"
'' ЧЧУч/'- ; «lineno « endl; }
гг. Для любого типа ошибок существует класс, который, как показано в этом примере, может быть использован с throw LINT_DivByZero(function, line); для уведомления о конкретной ошибке. В целом, следующие под- классы базового класса LINT_Error определены как:
346
Криптография на Си и C++ в действии
class LINT_Base : public LINT_Error
{-);
class LINT_DivByZero : public LINTJError
class LINT_Emod : public LINT_Error
class LINT_File : public LINTJError
{-};
class LINT_Heap : public LINTJError
{-};
class LINTJnit: public LINT_Error
{-};
class LINT_Nullptr: public LINTJError
class LINTJ3FL : public LINT_Error
{ };
И неправильное основание
// деление на ноль
// четный модуль для
mexpkm
И ошибка при файловом
вводе/выводе
// ошибка выделения
памяти при new
И аргумент функции
И непредусмотрен
И или не инициализирован
И пустой указатель,
И переданный в качестве
И аргумента
// переполнение в функции
class LINTJJFL : public LINTJError // потеря значимости
в функции
{...};
С одной стороны, так мы можем отловить ошибки LINT, не различ:
специально, какая ошибка произошла, вставив блок catch
ГЛАВА 15, Обработка ошибок
catch (LINT_Error const &err)
{
//...
347
//Примечание: LINT_Error-
// абстрактный класс
err.debug_print();
//...
}
после блока try, с другой стороны, мы сможем сконцентрироваться
на поиске определенной ошибки, если зададим соответствующий
аргумент - класс ошибки - в операторе catch.
Необходимо отметить, что как абстрактный класс LINT_Error не
тиражируется как объекты, поэтому его аргумент err может быть
передан только с помощью ссылки, а не значения. Несмотря на то,
что все функции LINT содержат обработчик ошибок panic(), приме-
нение исключений вовсе не означает то, что мы должны изменять
все функции. Мы, скорее, объединим соответствующие операции
throw в процедуру panic(), где они вызываются в соответствии с той
ошибкой, о которой сообщается функции. Потом управление пере-
дается блоку catch, который принадлежит блоку try вызываемой
функции. Следующий фрагмент кода функции panic() проясняет
образ действия:
void
LINT::panic (LINT_ERRORS error, const char const * tunc, const int arg,
const int line)
{
if (LINT_User_Error_Handler)
{
LINT_User_Error_Handler (error, func, arg, line);
}
else
{
cerr« "Критическая ошибка во время исполнения,
обнаруженная классом LINT:\n";
switch (error)
{
case E_LINT_DBZ:
348 Криптография на Си и C++ в действии
сегг « "деление на ноль, оператор/функция "
«func « ", в строке " « line « endl;
#ifdef LINT.EX
throw LINT_DivByZero (func, line);
#endif
break;
//...
}
}
}
Поведение результатов в случае ошибки может полностью контро-
лироваться пользовательскими подпрограммами для обработки
' ошибок без необходимости вмешательства в реализацию LINT.
Кроме того, обработку исключений можно полностью отключить,
что является необходимым, когда этот механизм не поддерживается
. используемым компилятором C++. В случае описанной функции
panic() исключения должны быть явно включены с помощью опреде-
ления макроса LINT_EX, например, опцией компилятора -DLINT_EX.
Некоторые компиляторы требуют указания дополнительных опций
для того, чтобы активизировать обработку исключений.
Для более близкого рассмотрения рассмотрим небольшой пример,
демонстрирующий исключения LINT:
#include "flintpp.h"
main(void)
{
LINTa = 1,b = 0;
try
{
b = a / b; И ошибка: деление на ноль
}
catch (LINT_DivByZero error) И обработка ошибки
{ И деления на ноль
ГЛАВА 15. Обработка ошибок
error.debug_print ();
349
cerr« "деление на ноль в модуле" «_______FILE__
« ", в строке" «___LINE___;
}
}
Оттранслированная с помощью вызова GNU gcc
gcc -fhandle-exceptions -DLINT_EX divex.cpp flintpp.cpp flint.c -lstdc++
программа, в добавление к сообщениям об ошибках функции
panic(), выдаст следующий вывод:
LINT-Exception:
деление на ноль, оператор/функция /
в модуле: flintpp.cpp, в строке: 402
деление на ноль в модуле divex.cpp, в строке 17
Существенным отличием между этой и стандартной обработкой
ошибок без исключений является то, что мы выясняем с помощью
процедуры catch, где действительно произошла ошибка, а именно в
строке 17 модуля divex.cpp, хотя она проявилась в другом месте - в
модуле flintpp.cpp. Для отладки больших программ это является со-
вершенно необходимым источником информации.
ГЛАВА 16.
Практический пример:
криптосистема RSA
Напрашивался очевидный вопрос: Можно ли
это сделать с помощью обычного шифрования?
Можем ли мы создать защищенное зашифро-
ванное сообщение, которое смог бы прочитать
1 ‘ авторизованный получатель без какого-либо
1 предварительного обмена секретными ключами
и т.д.?» ... Я опубликовал теорему существо-
вания в 1970 году.
Дж. X. Эллис.
История несекретного шифрования, 1987
Наш рассказ близится к концу, и теперь нам хотелось бы проверить
то, что мы делали глава за главой, на живом современном примере,
- который бы показал нам связь разработанных нами многочислен-
ных функций с криптографией. После краткого экскурса в область
асимметричных криптосистем мы обратимся к классическому при-
меру такой системы - алгоритму RSA, который был изобретен и
опубликован в 1978 году Рональдом Ривестом, Ади Шамиром и
Леонардом Адельманом (см. [Rive], [Elli]) и который теперь ис-
пользуется во всем мире. 1 Алгоритм RSA запатентован в Соеди-
ненных Штатах Америки, однако срок патента истек 20 сентября
2000 года. Против свободного использования алгоритма RSA вы-
ступала компания RSA Security, обладавшая правами на фирменное
1 ! название «RSA», что вызвало неистовую дискуссию при работе над
стандартом Р1363 [IEEE]. Появлялись, порой, абсурдные предложе-
f " ния: переименовать процедуру RSA в «бипростую криптографию»
(biprime) или, менее радикально, FRA (former RSA algorithm -
бывший алгоритм RSA), RAL (по первым буквам имен авторов ал-
горитма - Ron, Adi, Leonard) и QRZ (RSA - 1 - каждая буква назва-
ния заменяется на предыдущую по модулю 26). По истечении срока
патента компания RSA Security вынесла следующий вердикт:
* Ясно, что словосочетания «алгоритм RSA», «алгоритм с открытым
о?! ключом RSA», «криптосистема RSA» и «криптосистема с откры-
• гг тым ключом RSA» прочно обосновались в стандартах и открытой
•I учебной литературе. Компания RSA Security не собирается запре-
щать использование этих терминов частными лицами или органи-
зациями, реализующими алгоритм RSA («RSA-Security - Behind the
Patent», сентябрь 2000).2
1 По данным http://www.rsasecurity.com, к 1999 году было продано более трехсот миллионов про-
дуктов, использующих алгоритм RSA.
2 http://www.rsasecurity.com/developers/total-solution/faq.htm (9/2000)
352 Криптография на Си и C++ в действии
16.1. Асимметричные криптосистемы
Идея, положенная в основу асимметричных криптосистем, была
опубликована Уитфилдом Диффи (Whitfield Diffie) и Мартином
Хеллманом (Martin Hellman) в революционной статье «Новые на-
правления в криптографии» (см. [Diff]). Асимметричные криптоси-
стемы, в отличие от симметричных алгоритмов, используют для
зашифрования и расшифрования сообщений не один секретный
ключ, а пару ключей для каждого участника протокола - открытый
ключ Е для зашифрования и не совпадающий с ним секретный
ключ D для расшифрования. Для этих ключей, последовательно
примененных к сообщению М, должно выполняться соотношение
(16.1) D(E(M)) = M.
Это соотношение можно рассматривать как замок, который можно
запереть одним ключом, а открыть другим.
Для безопасности такой системы секретный ключ D должен быть
таким, чтобы его нельзя было вычислить по открытому ключу Е
или чтобы указанное вычисление было неосуществимо из-за огра-
ничений времени и памяти.
В отличие от симметричных систем в асимметричных работать с
ключами несколько проще. Чтобы получатель А, владелец секрет-
ного ключа, смог расшифровать сообщение, зашифрованное отпра-
вителем В, по каналам связи нужно передать только открытый ключ
участника А.Этот принцип и определяет открытость сеанса связи:
для безопасного взаимодействия двух участников достаточно дого-
вориться об асимметричной процедуре шифрования и обменяться
открытыми ключами. Не нужно обмениваться никакой секретной
информацией. Однако прежде чем наша эйфория выйдет из-под
контроля, заметим все же, что в общем случае даже в асимметрич-
ных криптосистемах не удается избежать некоторого управления
ключами. Как участники предположительно безопасного сеанса
связи, мы должны быть уверены, что открытые ключи других уча-
стников подлинны, то есть, чтобы нарушитель, влекомый низмен-
ной идеей перехвата секретной информации, не смог незаметно
внедриться в сеанс связи и выдать свой ключ за открытый, будто
бы принадлежащий проверенному партнеру. Подлинность откры-
тых ключей гарантируется на удивление сложными процедурами, и
уже существуют законы на бумаге, регулирующие деятельность в
этой области. Ниже мы рассмотрим этот вопрос более подробно.
Принцип асимметричных криптосистем распространяется гораздо
дальше - он позволяет создавать цифровые подписи, в которых
ключевая функция переворачивается задом наперед. Для формиро-
вания цифровой подписи мы «зашифровываем» сообщение на сек-
ретном ключе и передаем то, что получилось, вместе с сообщением
ГЛАВА 16. Практический пример: криптосистема RSA
353
по каналу связи. Теперь любой, кто знает соответствующий откры-
тый ключ, может «расшифровать» «зашифрованное» сообщение и
сравнить результат с исходным текстом. Напротив, сформировать
цифровую подпись может только обладатель секретного ключа.
Отметим, что по отношению к цифровым подписям использование
терминов «зашифрование» и «расшифрование» не совсем кор-
ректно, поэтому будем говорить о «формировании» и «проверке»
цифровой подписи.
К асимметричным системам, формирующим цифровые подписи,
предъявляется следующее жесткое требование: зависимость значе-
ния D(M) от сообщения М должна быть проверяемой. Такая про-
верка возможна, если математические операции зашифрования и
расшифрования коммутативны, то есть результатом поочередного
их выполнения (неважно в каком порядке) должно быть одно и то
же, а именно исходное, сообщение М:
(16,2) D(E(M)) = E(D(M)) = М.
Применяя открытый ключ Е к значению £>(М), можно проверить,
является ли D(M) правильной цифровой подписью для сообщения М
Развитие цифровых подписей чрезвычайно важно сегодня в двух
аспектах:
3 ✓ Законы о цифровой (или электронной) подписи в Европе и США
создают предпосылки к дальнейшему использованию цифровых
подписей в легальных транзакциях.
✓ Растущая роль Интернета в электронной коммерции стимулирует
применение цифровых подписей для идентификации и аутенти-
н фикации участников коммерческой транзакции, аутентификации
цифровой информации и обеспечения безопасности финансовых
h транзакций.
Интересно отметить, что использование терминов «электронная
подпись» и «цифровая подпись» отражает два разных подхода к
законам о подписи. Для электронной подписи все идентифицирую-
f , щие средства: электронные символы, буквы и рисунки используются
для аутентификации документа. Цифровая подпись, напротив, явля-
г ется результатом электронной процедуры аутентификации, осно-
ванной на процессах информационных технологий, то есть призва-
г на проверять целостность и подлинность передаваемого текста. Эти
термины часто путают, смешивая, таким образом, два совершенно
разных технических процесса (см., например, [Mied]).3
Хотя законы об электронной подписи, как правило, оставляют от-
крытым вопрос об алгоритме цифровой подписи, большинство про-
В России к этому подошли просто - в стандартах фигурирует электронная цифровая (!) подпись. —
Прим, перев.
12_1 AQ7
354
Криптография на Си и C++ в действии
токолов идентификации, аутентификации и авторизации, как про-
ектируемых, так и уже применяемых для электронных транзакций
через Интернет, используют алгоритм RSA, который, вероятно, и
дальше никому не уступит в этой области. Таким образом, цифро-
вая подпись RSA как нельзя лучше подходит для реализации функ-
ций FLINT/C.
Автор отдает себе отчет в том, что эта глава служит лишь кратким
введением в чрезвычайно важный раздел криптографии. Однако
такая краткость оправдана наличием большого числа исчерпываю-
щих публикаций на эту тему. Читателю можно порекомендовать
[Beut], [Fumy], [Salo] и [Stin] в качестве вводных источников, более
разносторонние работы [MOV] и [Schn], а также математические
монографии [КоЫ], [Кгап] и [HKW].
16.2. Алгоритм RSA
Ложно почти все, что не более чем правдоподобно.
Рене Декарт
Теперь кратко опишем математические свойства алгоритма RSA и
посмотрим, как на его основе можно реализовать шифрование с от-
крытым ключом и цифровую подпись. Придерживаясь математиче-
ских свойств алгоритма RSA, разработаем классы C++ для каждой
из функций зашифрования сообщения, расшифрования сообщения,
формирования подписи и проверки подписи. А для начала поясним
пути реализации этих функций в нашем классе LINT.
Самым важным элементом алгоритма RSA является пара ключей,
имеющих конкретный математический смысл. Пара ключей RSA
формируется с помощью трех основных элементов: модуля п, ком-
понента е открытого ключа (для зашифрования) и компонента d
секретного ключа (для расшифрования). Открытым и секретным
ключом являются пары (е, п) и {d, п) соответственно.
Сначала сгенерируем модуль п как произведение п = pq ДВУХ
простых чисел р и q. Если ф(/г) = (р- 1)(р- 1) - функция Эйлера
(см. стр. 198), то для данного модуля п компоненту е открытого
ключа можно выбрать из условий е < ф(/г) и НОД(е, ф(и)) = 1 • Дек-
ретная компонента d вычисляется как d = е~х mod ф(и) - число,
мультипликативно обратное к е по модулю п (см. п. 10.2).
Проиллюстрируем этот принцип на небольшом примере. Выберем
Р = 7 и 4=11. Тогда „ = 77 и ф(„) = 22 • 3 • 5 = 60. Из условия
НОД(е, ф(„)) = 1 заключаем, что наименьшее число, которое можно
выбрать в качестве е, это 7, откуда получаем значение d = 43, по-
скольку 7 • 43 = 301 = 1 mod 60. С этими значениями можем применить
алгоритм RSA к игрушечному примеру: зашифровав «сообщение» 5,
ГЛАВА 16. Практический пример: криптосистема RSA
355
получаем 57 mod 77 = 47; расшифрованием 4743 mod 77 = 5 восста- навливаем исходное сообщение. Вооружившись такими ключами (вскоре мы обсудим, какой должна быть реальная длина различных компонент ключа) и подходящим программным обеспечением, мы теперь можем безопасно обмени- ваться информацией друг с другом. Чтобы проиллюстрировать процедуру RSA, рассмотрим процесс передачи сообщения, зашиф- рованного алгоритмом RSA, отправителем А получателю В: 1. Участник В генерирует свой ключ RSA с компонентами лв, t/в и ев, а затем сообщает открытый ключ (ев, пв) участнику А. 2. Пусть теперь участник А хочет отправить зашифрованное сообще- ние М (0<М<пв) участнику В. Получив от В открытый ключ, А вычисляет С = Л/В mod пв
it и посылает зашифрованное сообщение С участнику В.
р/ 3. Участник В, получив от А зашифрованное сообщение С, расшиф- ровывает это сообщение, вычисляя М = mod пв с помощью своего секретного ключа <е/в, пв). Теперь у В есть текст исходного сообщения М. Нетрудно видеть, почему это все работает. Так как d • е = mod ф(и), существует целое число к такое, что d • е = 1 + к • ф(и). Тогда
(16.3) с1 = = М1+к"Кп'> = М • (М^п})к = М mod п, при этом мы использовали теорему Эйлера, приведенную на стр. 198, согласно которой = 1 mod и, если НОД(Л/, п) = 1.
jpk , I' 1Э H.'i Ч • Ясно, что безопасность криптосистемы RSA зависит от того, на- сколько легко разложить число п на множители. Как только п раз- ложено в произведение чисел р и q, секретный ключ d сразу может быть вычислен по секретному ключу е. Обратно, легко найти раз- ложение числа и, если известны обе компоненты d и е. Действи- тельно, если положить к := de - 1, то число к будет кратным значе- нию ф(и) и, значит, к = г • 2', где число г нечетное и t > 1. Для любо-
‘ ч го g G справедливо gk = gtle~x s gg"x s 1 mod и, то есть gkl2 - квад- ратный корень из 1 по модулю п. Таких корней всего четыре: ±1 и ±х, где х — 1 mod р и х = -1 mod q. Таким образом, р | (х - 1) и q | (х + 1) (см. п. 10.4.3). Вычисляя р = НОД(х- 1, и), получаем делитель числа п (см. стр. 235). Сложность других атак на криптосистему RSA либо совпадает со сложностью разложения, либо использует слабости конкретных протоколов, но не самого алгоритма RSA. Современное состояние
356
Криптография на Си и C++ в действии
дел показывает, что атаки на алгоритм RSA возможны при сле-
дующих условиях:
1. Общий модуль I
Использование общего модуля для нескольких пользователей дает
очевидную уязвимость: учитывая то, что мы только что сказали,
каждый участник может с помощью своих компонент ключа е и d
разложить общий модуль п = pq. Зная множители р и q, а также
компоненты открытых ключей других пользователей, он может
вычислить и их секретные ключи.
2. Малый открытый показатель
Поскольку время вычислений в алгоритме RSA для данного модуля
целиком зависит от размера показателей е и J, очень хочется вы-
брать эти показатели как можно меньше. Например, при показателе,
равном 3 (наименьший возможный показатель), требуется всего
одно возведение в квадрат и одно умножение по модулю п - так
почему бы не сэкономить время вычислений?
Допустим, нарушитель смог перехватить три зашифрованных со-
общения Ci, С2 и С3, каждое из которых является шифрограммой
одного и того же открытого теста М, зашифрованного на трех раз-
ных ключах (3, и,) тремя разными отправителями:
Ci = М3 mod пь С2 = М3 mod n2, С3 = М3 mod н3.
Вполне вероятно, что НОД(н/, иД = 1 при i * j. Тогда нарушитель
может воспользоваться китайской теоремой об остатках (см. стр. 225)
и найти значение С, для которого
С = М3 mod Л1И2л3.
Поскольку верно и то, что М3 < npitfi?» отсюда получаем, что значе-
ние С в точности равно М3 и нарушитель может вычислить М про-
сто как корень Vc . Такого рода широковещательные атаки (broad'
cast attacks) всегда можно реализовать, если число шифрограмм С,
больше, чем открытый показатель. Кроме того, открытые тексты
даже не обязательно должны совпадать, а могут быть линейно
зависимы, то есть связаны соотношениями вида = а + b • Mj
(см. [Bone]). Таким образом, чтобы предотвратить такую атаку, не
нужно выбирать открытые показатели слишком маленькими (в лю-
бом случае, они должны быть не меньше, чем 216+ 1 =65537) и,
кроме того, прежде чем зашифровывать широковещательные со-
общения, в них следует внести случайную избыточность. Для этого
можно, например, «растянуть» сообщение до некоторого подходя-
щего числового значения, не превышающего модуль. Такой про-
цесс называется дополнением (см. стр. 370 и [Schn], п. 9.1).
ГЛАВА 16. Практический пример: криптосистема RSA
3. Малый секретный показатель
357
Еще хуже, если мал секретный показатель. Еще в 1990 году
М. Винер (М. Wiener) [Wien] показал, как, зная открытый ключ
(е, и), где 1 < е < ф(л), можно вычислить компоненту d секретного
ключа, если число d слишком мало. Результат Винера был недавно
усилен Д. Бонехом (D. Boneh) и Г. Дурфи (G. Durfee) [Bone], кото-
рые показали, что d можно вычислить из (е, н), если d < и0,292.
Существует гипотеза, что это же верно и для d < п0,5. Таким обра-
зом, для типичных размеров модуля RSA получаем следующие
ограничения на секретный показатель d:
п d
2768 2384
21024 2512
22048 21024
24096 22048
4. Уязвимости программной реализации
Помимо уязвимостей, обусловленных выбором параметров, суще-
ствует еще множество проблем, вызванных некорректной реализа-
цией, что также может сказаться на безопасности криптосистемы
RSA, да и любой другой криптографической процедуры. Нужно с
крайней осторожностью использовать чисто программную реали-
зацию, не защищенную от внешних атак какими-нибудь аппарат-
ными средствами. Чтение содержимого памяти, наблюдение за по-
ведением шины или состояниями процессора может привести к
раскрытию информации о секретном ключе. Минимум что нужно
делать - это сразу же после использования очищать оперативную
память от всех данных, так или иначе связанных с секретными
компонентами RSA (и любой другой криптосистемы). Это можно
сделать путем активной перезаписи (например, с помощью функ-
ции purgeJ(), которая появлялась на стр. 184).
В функциях пакета FLINT/C уже предприняты все необходимые
меры. В безопасном режиме локальные переменные и выделенная
память перед завершением функции перезаписываются нулями и,
таким образом, очищаются. Здесь надо быть очень осторожным,
поскольку у компиляторов бывают настолько большие возможно-
сти оптимизации, что простую команду, которая, по его мнению, не
влияет на завершение функции, он может и проигнорировать. И вот
еще: следует помнить, что вызовы функции memset() в стандартной
библиотеке языка С игнорируются, если компилятор «не понимает»,
зачем ее нужно вызывать.
Криптография на Си и О+ в действии
Проиллюстрируем все это на примере. В функции f_1() используют-
ся две динамические переменные: keyj типа CLINT и secret типа
USHORT. Перед завершением функции, содержание которой нас
больше не интересует, следует перезаписать память, присвоив О
переменной secret и, соответственно, вызвав функцию memset() для
переменной keyj. Вот соответствующая программа на С:
int
f_l (CLINT nJ)
I
CLINT keyj; И
USHORT secret; И
/* Переписываем переменные 7 И
secret = 0; И
memset (keyj, 0, sizeof (keyj)); H
return 0; M
}
И что же с этим делает компилятор (Microsoft Visual C/C++ 6.0,
компиляция с ключами cl -с -FAs -02)?
PUBLIC J
COMDATJ Ml
„TEXT SEGMENT H
_key_l$ = -516 H
_secret$ = -520 И
J PROC NEAR ;COMDAT H
;5 : CLINT keyj; H
;6 : USHORT secret; I
; 18 : /* Переписываем переменные 7
; 19 : secret = 0;
359
ГЛАВА 16. Практический пример: криптосистема RSA
; 20 : memset (keyj, 0, sizeof (keyj));
; 21 :
; 22 : return 0;
xor eax, eax
; 23 :}
add esp, 532
ret 0
J ENDP
;00000214H
_TEXT ENDS
Согласно созданной компилятором программе на Ассемблере,
команды удаления переменных keyj и secret не имеют никаких
последствий. С точки зрения оптимизации это, конечно, хороший
результат. Даже встроенная (inline) версия функции memset() при
оптимизации просто удаляется. Однако для приложений, обеспечи-
вающих безопасность, такая стратегия слишком умна.
Значит, динамическое удаление переменных, определяющих безо-
пасность, путем перезаписи нужно реализовать так, чтобы оно дей-
ствительно выполнялось. Отметим, что утверждения (см. стр. 173)
могут «подавить» проверку производительности, поскольку при их
наличии компилятор вынужден исполнять код программы. Как
только утверждения отключены, оптимизация возобновляется.
Следующая функция, реализованная в пакете FLINT/C, использует
переменное число аргументов и обрабатывает их, в зависимости от
размера, как стандартные целые типы, полагая их равными 0. Для
других структур данных вызывается функция memset() и выполня-
ется перезапись:
static void purgevarsj (int noofvars,...)
{
vajist ap;
sizej size;
va_start (ap, noofvars);
for (; noofvars > 0; -noofvars)
{
switch (size = va_arg (ap, size_t))
Криптография на Си и C++ в действии
{
case 1: *va_arg (ар, char *) = 0;
break;
case 2: *va_arg (ap, short *) = 0;
break;
case 4: *va_arg (ap, long *) = 0;
break;
default: assert (size >= CLINTMAXBYTE);
memset (va_arg(ap, char *), 0, size);
}
}
va_end (ap);
Функция рассматривает в качестве аргументов пары чисел (длина
переменной в байтах, указатель на переменную); в noofvars указы-
вается также число таких пар.
Обобщением этой функции является макрос PURGEVARS_L():
#ifdef FLINT-SECURE
#define PURGEVARS_L(X) purgevarsj X
#else
#define PURGEVARS_L(X) (void)O
#endif /* FLINT-SECURE 7
позволяющий при необходимости включать и отключать безопас-
ный режим. Удаление переменных в функции f() выполняется так:
/* Переписываем переменные 7
PURGEVARS_L ((2, sizeof (secret), &secret, sizeof (key_l), keyj));
Компилятор не может проигнорировать вызов этой функции исходя
из обычных принципов оптимизации, такое могло бы случится
только при проведении чрезвычайно мощной глобальной оптими-
зации. В любом случае, действенность таких средств защиты можно
проверить, просматривая код программы:
PUBLIC _f
EXTRN _purgevars_l:NEAR
; COMDAT _f
ГЛАВА 16. Практический пример: криптосистема RSA 361
_ТЕХТ SEGMENT _keyj$ = -516 _secret$ = -520 J PROC NEAR ; COMDAT ;9 :{ sub esp, 520 ; 00000208H
Л'.| 01 ; 10 : CLINT keyj; ; 11 : USHORT secret;
X г КЧ ; 18 : /* Переписываем переменные */ ; 19 : PURGEVARS_L ((2, sizeof (secret), &secret, sizeof (keyj), keyj));
/ ; lea eax, DWORD PTR _keyJ$[esp+532]
ЭУ -с? push eax lea ecx, DWORD PTR _secret$[esp+536] push 514 ;00000202H push ecx
я . п л push 2 push 2 call _purgevarsj
-К- ; 20 : ; 21 : return 0;
О'
хог еах, еах
;22 :}
Криптография на Си и C++ в действии
;00000228Н
add esp, 552
ret О
J ENDP
_TEXT ENDS
Для приложений, связанных с безопасностью, посоветуем еще ис-
пользовать такой исчерпывающий механизм обработки ошибок,
при котором даже в случае неверно заданного аргумента или в дру-
гих исключительных ситуациях не разглашается никакая критиче-
ская информация. Точно так же необходимо принять меры для про-
верки подлинности кодов программ, реализующих криптографиче-
ские приложения, чтобы предотвратить закладку троянских коней
(или хотя бы обнаружить их), прежде чем программа будет запу-
щена. Троянским конем (вспомним историю Троянской войны)
называется программа, измененная так, что внешне она функцио-
нирует корректно, но дополнительно имеет нежелательный эффект,
например, передает нарушителю через Интернет информацию о
секретном ключе.
Для решения указанных проблем на практике в криптографических
приложениях зачастую используются «блоки безопасности» («secu-
rity boxes», «S-блоки»). Реализующая их аппаратура защищена от
атак «внедрения» и снабжена детекторами или сенсорами.
Когда все эти ловушки нам удалось избежать, остается последняя
опасность: а вдруг модуль будет разложен на множители? Эту
угрозу также можно устранить, выбрав простые числа достаточно
большими. Разумеется, пока не доказано, что не существует других
методов взлома криптосистемы RSA, более легких, чем разложение.
Кроме того, нет доказательства и того, что задача разложения
больших чисел действительно сложная (как считается в настоящее
время). Однако эти вопросы пока никак не сказались на использо-
вании алгоритма: криптосистема RSA на сегодняшний день остается
самой популярной асимметричной криптосистемой во всем мире, а
ее применение в Интернете постоянно расширяется, особенно для
аутентификации.
Современные методы решения задачи о разложении предъявляют к
простым числам, образующим модуль RSA, следующие требова-
ния: числа р и q должны быть достаточно большими, примерно
одинаковыми по размеру, но, тем не менее, различаться в опреде-
ленном числе двоичных разрядов, поскольку при p~q~ Jn можно
быстро найти разложение числа и, пробуя в качестве делителей п
натуральные числа, близкие к .
В литературе часто рекомендуется в качестве р и q использовать
так называемые сильные простые числа, позволяющие противо-
стоять некоторым простым методам разложения. Простое число р
называется сильным, если
Г ЛАВА 16. Практический пример: криптосистема RSA
(а) число р - 1 имеет большой простой делитель г;
363
(б) число р + 1 имеет большой простой делитель 5;
(в) число г - 1 имеет большой простой делитель t.
Высказываются разные мнения о влиянии сильных простых чисел
на безопасность криптосистемы RSA. С недавних пор большинство
сходится на том, что, хотя использовать простые числа не вредно,
большой пользы от них тоже нет (см. [MOV], п. 8.2.3, а также
[RegT], Приложение 1.4). Некоторые считают, что эти числа ис-
» пользовать вообще не стоит ([Schn], п. 11.5). Поэтому в реализо-
ванной нами программе мы обойдемся без сильных простых чисел.
Для тех же, кому это интересно, приведем набросок процедуры
генерации таких простых чисел:
1. Чтобы получить сильное простое число р длиной 1Р двоичных
разрядов, сначала ищем такие простые числа s и t, что
log25 = log2r ~ j 1Р-logzip- Затем ищем такое простое число г, что
г - 1 делится на t, последовательно проверяя на простоту числа ви-
да г = к • 2t + 1, где к- 1, 2, ..., пока не получим простое число.
Это обязательно произойдет не более чем через |_2 In 2d шагов
(см. [НКW], стр. 418).
2. Теперь с помощью китайской теоремы об остатках (см. стр. 225)
находим решение системы сравнений х = 1 mod г, х = -1 mod 5:
Xq := 1 - 2r~ls mod rs, где число г"1 - мультипликативно обратное к г
по модулю S'.
3. Устанавливаем нечетное начальное значение: генерируем случай-
ное число z, число разрядов которого близко к длине искомого чис-
ла р, но меньше нужного значения (это иногда обозначается симво-
лом g), и полагаем л0 «— xQ + z +rs - (z mod rs). Если число xQ четное,
то полагаем х0 <— xQ + rs. По значению х0 начинаем определять р.
Проверяем числа вида р = х0 + к • 2rs, где £ = 0, 1, ..., пока мы не
получим нужного числа цифр 1Р и число р не будет простым. Если
ключ RSA должен содержать заданную открытую компоненту е, то
стоит еще проверить, что НОД(р - 1, ё) = 1. Такое число р удовле-
творяет всем необходимым условиям. Для проверки чисел на про-
стоту пользуемся тестом Миллера-Рабина, реализованным в виде
функции primej().
В любом случае, независимо от того, используются ли для ключей
сильные простые числа, нужно запастись подходящей функцией,
генерирующей простые числа заданной длины или из заданного
интервала. Соответствующая процедура, дополнительно гаранти-
рующая, что сгенерированное простое число р удовлетворяет усло-
вию НОД(р-1,/)= 1 для заданного числа/, приведена в [IEEE],
стр. 73. Мы приведем слегка измененный алгоритм.
364
Криптография на Си и C++ в действии
Алгоритм генерации простого числар такого, чторпйп <р<р^х 1. Сгенерировать случайное число р такое, что pmin <р < ртах. 2. Если р четное, то положить р k-p + 1. 3. Если р > ртах, то положить р «- pmin + р mod (pmax + 1) и вернуть- ся на шаг 2. 4. Вычислить d := НОД(р - 1,/) (см. п. 10.1). При d = 1 проверить р на простоту (см. п. 10.5). Если число р простое, то завершить алгоритм с результатом: р. Иначе положить р <— р + 2 и вер- нуться на шаг 3. Реализацию этого алгоритма в виде функции на языке C++ чита- тель найдет в пакете FLINT/C (файл flintpp.cpp).
Функция: Генерация простого числа р из интервала [pmin, PmaxL дополни- тельно удовлетворяющего условию НОД(р - 1,/) = 1, где число f- целое положительное нечетное
i (,, Синтаксис: const LINT findprime (const LINT& pmin,
const LINT& pmax, const LINT& f);
Вход: pmin: наименьшее допустимое значение ртах: наибольшее допустимое значение f: целое положительное нечетное число, которое должно быть взаимно простым с р - 1
Возврат: простое число р типа LINT, проверенное вероятностным алгорит- мом (см. п. 10.5), где НОД(р - 1,/) = 1 const LINT findprime (const LINT& pmin, const LINT& pmax, const LINT& f) { if (Ipmin.init) LINT::panic (E_LINT_VAL, "findprime", 1, LINE ); if (Ipmax.init) LINT::panic (E_LINT_VAL, "findprime", 2, LINE ); if (pmin > pmax) LINT::panic (E_LINT_VAL, "findprime", 1, LINE—); if (If.init) LINT::panic (EJJNT_VAL, "findprime", 3, _LINE_); // 0 < f должно быть нечетным if (f.iseven()) LINT::panic (E_LINT_VAL, "findprime", 3, _LINE_);
365
ГЛАВА 16. Практический пример: криптосистема RSA
LINT р = randBBS (pmin, ртах);
LINT t = ртах -pmin;
if (p.iseven())
{
++p;
}
I
if (p > ртах)
{
p = pmin + p % (t + 1);
}
while ((gcd (p — 1, f) != 1) || !p.isprime())
{
++p;
++p;
while (p > ртах)
{
p = pmin + p % (t + 1);
if (p.iseven())
{
; ++P!
}
}
)
return p;
}
Кроме того, функцию findprime() можно перегрузить так, чтобы
вместо границ pmin и ртах задавать двоичную длину числа р.
366
Криптография на Си и C++ в действии
функция: Генерация простого числа р из интервала [2м,21 - 1], дополни- тельно удовлетворяющего условию НОД(р - 1,/) = 1, где число /- целое положительное нечетное
Синтаксис: const LINT findprime (const USHORT 1, const LINT& f);
Вход: 1: требуемая двоичная длина f: целое положительное нечетное число, которое должно быть вза- имно простым с р - 1
Возврат: простое число р типа LINT, где НОД(р - 1,/) = 1
Что касается выбора длины ключа, наиболее информативными здесь
будут сведения о попытках разложения чисел на множители. В ап-
реле 1996 года после нескольких месяцев совместной работы ряда
университетов и исследовательских лабораторий США и Европы
под руководством А. К. Ленстры (А. К. Lenstra) 4 для RSA-модуля
RSA-130 = 18070820886874048059516561644059055662781025167
69401349170127021450056662540244048387341127590
812303371781887966563182013214880557
длины 130 десятичных разрядов было найдено разложение вида
RSA-130 = 39685999459597454290161126162883786067576449112
810064832555157243
х 45534498646735972188403686897274408864356301263
205069600999044599.
Затем в феврале 1999 года модуль
RSA-140 = 21290246318258757547497882016271517497806703963
27721627823338321538194998405649591136657385302
1918316783107387995317230889569230873441936471
был разложен на два 70-разрядных множителя:
RSA-140 = 33987174230284385545301236276138758356339864959
69597423490929302771479
х 62642001874012850961516549482644422193020371786
23509019111660653946049.
4 Lenstra Arjen К.: Factorization of RSA-130 using the Number Field Sieve,
http://dbs.cwi.nl.herman.NFSrecords/RSA-130; см. также [Cowi],
ГЛАВА 16. Практический пример: криптосистема RSA
367
Эти результаты были достигнуты группами исследователей из
Нидерландов, Австралии, Франции, Великобритании и США под
руководством Германа Дж. Дж. те Риля (Herman J. J. te Riele) из
Национального научно-исследовательского института математики
и информатики CWI (Centrum voor Wiskunde en Informatica) в Ни-
дерландах. 5 Числа RSA-130 и RSA-140 взяты из списка 42 модулей
RSA, опубликованного в 1991 г. компанией RSA Data Security, Inc.
в помощь исследователям в области криптографии.6 Вычисления
по разложению RSA-130 и RSA-140 были распределены между
большим числом рабочих станций, затем результаты были сопос-
тавлены. Разложение числа RSA-130 заняло около 1000 MIPS-лет,
RSA-140 - 2000 MIPS-лет.7
Вскоре после этого, в конце августа 1999 года, мир был поражен
известием о разложении числа RSA-155. Работы опять проводились
интернациональной командой под руководством Германа те Риля и
заняли около 8000 MIPS-лет. С разложением числа
RSA-155 = 10941738641570527421809707322040357612003732945
44920599091384213147634998428893478471799725789
12673324976257528997818337970765372440271467435
31593354333897
на два 78-разрядных множителя
RSA-155 = 10263959282974110577205419657399167590071656780
8038066803341933521790711307779
х 10660348838016845482092722036001287867920795857
5989291522270608237193062808643
был пересечен магический рубеж в 512 бит - ключи такой двоич-
ной длины долгие годы считались надежными.
Вопрос о том, ключи какой длины использовать для алгоритма
RSA, пересматривается после каждого очередного сообщения об
успехах в области разложения чисел. А. К. Ленстра (А. К. Lenstra) и
Эрик Р. Верхуль (Eric R. Verheul) [LeVe] разработали модель опре-
деления длины ключа для различных типов криптосистем. Эта
модель основана на ряде проверенных устоявшихся предположений
и учитывает современные достижения в области разложения чисел.
5 Сообщение получено по электронной почте от Herman.te.Riele@cwi.nl по сети Number Theory
Network 4 февраля 1999 г. См. также http://www.rsasecurity.com/rsalabs/html/status.html
6 http://www.rsasecurity.com/rsalabs/html/factoring.html.
7 MIPS = mega instruction per second (миллион инструкций в секунду) - единица измерения быстро-
действия компьютера. Считается, что со скоростью 1 MIPS работает компьютер, выполняющий
700 000 сложений и 300 000 умножений в секунду.
368
Криптография на Си и C++ в действии
Результаты, представленные в виде таблицы (см. таблицу 16.1),
позволяют определить минимальную длину ключа, рекомендуемую
в недалеком будущем, для асимметричных криптосистем RSA,
Эль-Гамаля и Диффи-Хеллмана.
Таблииа 16.1. Год Адина ключа (в битах)
Рекомендуемая длина ключа 2001 990
по Ленстре и Верхулю 2005 1149
2010 1369
2015 1613
2020 1881
2025 2174
Таким образом, чтобы сегодня обеспечить критическому приложе-
нию приемлемый «запас прочности», длина ключа RSA должна быть
не менее 1024 бит. При этом следует помнить, что успехи в решении
задачи разложения постепенно будут отодвигать эту границу, то есть
за развитием науки надо следить. В зависимости от назначения, для
особо чувствительных приложений могут потребоваться числа дли-
ны 2048 бит и более (см. [Schn], Глава 7, и [RegT], Приложение 1.4).8
Имея в распоряжении пакет FLINT/C, мы легко можем генериро-
вать ключи такой длины. Нас не очень волнует, что сложность раз-
ложения падает с ростом скорости новых компьютеров - ведь на
этих же компьютерах мы можем генерировать все более длинные
ключи. Таким образом, можно считать, что безопасность криптоси-
стемы RSA зависит в основном от развития методов разложения.
Сколько же существует таких ключей? Хватит ли их, чтобы раздать
каждому из живущих на Земле мужчин, женщин и детей (а может
даже кошек и собак) хотя бы по одному ключу RSA? На эти вопросы
дает ответ теорема о простых числах: число простых чисел, мень-
ших заданного х, примерно равно х/1пх (см. стр. 244). Модуль дли-
ны 1024 генерируется как произведение двух простых чисел, длины
512 бит каждое. Таких чисел примерно 2512/512, то есть около 10 ;
каждые два из них образуют модуль. Если обозначить N= 10151, то
существует А(А- 1)/2 таких пар, около Ю300 различных модулей,
причем каждое из этих чисел можно выбрать в качестве компонента
секретного ключа. Чтобы было легче осознать всю мощь этого числа,
скажем лишь, что вся обозримая Вселенная содержит «всего»
1О80 элементарных частиц (см. [Saga], Глава 9). Или еще пример.
Если каждому жителю Земли выдавать каждый день по десять новых
8 Удобно выбирать длину ключей RSA в битах кратной 8, чтобы число байтов было целым.
ГЛАВА 16. Практический пример: криптосистема RSA____________________369
модулей, то модулей хватит на 10287 лет, при этом ни разу не будет
повторений. Ну а сегодня нашей планете «всего» несколько милли-
ардов лет.
И, наконец, очевидно, что произвольный текст можно представить
в виде положительного целого числа. Сопоставляя каждой букве
алфавита единственное число, текст можно представить в виде це-
лого числа сколькими угодно способами. Традиционным является
представление символов в ASCII (American Standard Code for
Information Interchange)-кoдax. Рассматривая код каждого символа
как разряд в системе счисления с основанием 256, можно сопоста-
вить ASCII-закодированному тексту целое число. Вероятность при
этом получить число М такое, что НОД(Л/, п) > 1, то есть что М
будет делиться на один из делителей р или q ключа и, пренебрежимо
S j мала. Если текст М слишком велик, чтобы служить в качестве
ix модуля п или ключа, то есть больше, чем п - 1, то его можно раз-
бить на блоки, численные значения Л/ь Л/2, Л/3, ... которых будут
уже меньше, чем п. Каждый из этих блоков зашифровывается по
отдельности.
Если текст сообщения достаточно длинный, то указанный процесс
становится весьма утомительным, поэтому RSA редко используется
для шифрования длинных текстов. Для этого лучше подойдет сим-
метричный криптоалгоритм (например тройной DES, IDEA или
Rijndael; см. главу 19 и [Schn], главы 12, 13, 14), выполняющий
шифрование гораздо быстрее с неменьшей стойкостью. Больше
всего алгоритм RSA подходит для зашифрования ключа симмет-
ричного криптоалгоритма, передаваемого по каналам связи.
16.3. Цифровая подпись RSA
«С позволения Вашего Величества, - сказал
Валет, - я этого письма не писал, и они этого
4 не докажут. Там нет подписи».
Льюис Кэррол,
'Ю- < Приключения Алисы в Стране Чудес
Ж;?.
Объясним теперь, как используется RSA для формирования циф-
ровой подписи. Пусть участник А отправляет участнику В сооб-
щение М, подписанное цифровой подписью, а В проверяет пра-
вильность этой подписи.
1. Участник А генерирует компоненты па, t/д и ед ключа RSA и пере-
дает участнику В свой открытый ключ (ед, пд).
2. Участник А хочет отправить участнику В сообщение Л/, подписанное
цифровой подписью. Для этого А вырабатывает значение R = ц(М),
70
Криптография на Си и C++ в действии
где R < пь, с помощью функции избыточности ц (см. ниже). Затем
А вычисляет подпись
„ ~^А 1
S-R mod па
и отправляет участнику В пару (Л/, 5).
3. У участника В уже есть открытый ключ (ед, на) участника А. Полу-
чив от него сообщение М и подпись 5, В вычисляет
R = р(М),
R' = 5*а mod ид
с помощью открытого ключа (е&, ид).
4. Наконец, В проверяет равенство R' = R. Если оно выполняется, то В
считает подпись участника А правильной. В противном случае под-
пись считается неверной.
Цифровая подпись, для проверки которой необходимо передавать и
само сообщение М, называется цифровой подписью с приложением.
Цифровые подписи с приложением используются в основном для
сообщений переменной длины, численное значение которых пре-
вышает модуль, то есть М > и. В принципе, можно, конечно, как мы
это делали выше, разбить сообщение на блоки Л/ь Л/2, М3, ... под-
ходящей длины Mi < и, а затем зашифровать и подписать каждый
блок в отдельности. Оставим в стороне вопрос о том, что сообще-
, ние можно «перемешать», просто изменив порядок блоков и под-
писей. Здесь есть более веские причины, побуждающие нас вместо
блоков использовать функцию ц, которую мы назвали функцией
избыточности.
Во-первых, функция избыточности ц: М —» отображает произ-
вольное сообщение М из пространства сообщений М в кольцо клас-
сов вычетов в соответствии с чем сообщения обычно сжимаются
с помощью хэш-функции (см. стр. 373) до значений z 2160. Затем
такому значению сопоставляется заранее заданная последователь-
ность символов. Для вычисления значения jll(AJ) требуется выпол-
нить один шаг процедуры RSA, а значение хэш-функции вычисля-
ется быстро в соответствии с своим назначением, поэтому второй
вариант гораздо предпочтительнее с точки зрения скорости.
Во-вторых, алгоритм RSA обладает следующим «нехорошим» для
цифровых подписей свойством: любые два сообщения и М2 свя-
заны мультипликативным соотношением
(16.4)
(M]M2)d mod п = (MdMd) mod п ,
позволяющим подделать подпись, если, конечно, не предприняты
никакие меры защиты.
AABA16. Практический пример: криптосистема RSA 371
Благодаря этому свойству - гомоморфизму - функции RSA можно, не используя избыточность R, получать сообщения со «скрытой» подписью. Пусть нарушитель выбрал секретное сообщение М и с помощью некоторого безобидного сообщения Мх сформировал еще одно сообщение М2 := ММ\ mod ид. Некий пользователь или удо- стоверяющий центр А подписывает ему сообщения и Л/2: =Л//Л mod nA , S2 = М2К mod нА . С помощью этих подписей нарушитель может вычислить подпись mod иА для сообще- ния М, которое А, конечно же, подписывать не собирался, да он и не будет об этом знать, формируя подписи S] и S2- В этом случае говорят, что у сообщения М скрытая подпись. Разумеется, с большой вероятностью сообщение М2 не будет со- держать никакого осмысленного текста, и, кроме того, А настоя- тельно рекомендуется не подписывать никакие Мл и М2, не ознако- мившись с их содержанием, тем более по просьбе незнакомых лиц. И все же не стоит уповать на человеческое благоразумие и говорить потом о недостатках криптографического протокола, тем более что эти недостатки можно устранить, например, введя в сообщение избыточность. Для функции избыточности ц должно выполняться условие
'16.5) для всех Mi, М2 G М, тогда сама функция подписи не будет обладать нежелательным свойством гомоморфизма. Помимо подписей с приложением существуют другие методы, в которых подписанное сообщение извлекается из самой подписи, - это так называемые цифровые подписи с восстановлением сообщения (см. [MOV], глава 11, [ISO2] и [ISO3]). Цифровые подписи с вос- становлением сообщения, основанные на алгоритме RSA, особенно хороши для коротких сообщений, двоичная длина которых меньше половины двоичной длины модуля. В любом случае нужно тщательно исследовать безопасность функ- ции избыточности. В 1999 году Корон (Согоп), Наккаче (Naccache) и Штерн (Stern) опубликовали способ атаки на такие функции, который заключается в следующем. Нарушитель набирает доста- точное количество подписей RSA, соответствующих сообщениям, целочисленное представление которых делится исключительно на маленькие простые числа. При такой структуре сообщений нару- шитель при благоприятных условиях может, не зная ключа под- писи, формировать новые подписи и выдавать их за подлинные (см. [Coro]). На это открытие незамедлительно отреагировала ISO: в октябре 1999 года рабочей группой SC 27 стандарт [ISO2] был изъят из обращения со следующим уведомлением:
Криптография на Си и C++ в действии
«Учитывая многочисленные атаки на схемы цифровой подписи RSA ...» ISO/IEC JTC 1/SC 27 приняли единогласное решение: стандарт IS 9796:1991 больше не обеспечивает независимым от приложений цифровым подписям достаточной защиты и должен быть отменен» 9, Отмена стандарта касается цифровых подписей, в которых функция RSA применена непосредственно к короткому сообщению. К подпи- сям с приложением, использующим хэш-функцию, это не относится. Широкое распространение получила схема включения избыточности формата PKCS #1 от RSA laboratories, для которой атака Корона, Наккаче и Штерна имеет в лучшем случае теоретическое значение и не представляет реальной угрозы (см. [RDS1], [Coro], стр. 11-13 и [RDS2]). Формат PKCS #1 определяет вид так называемого блока зашифрования ЕВ, подаваемого на вход оператора зашифрования или формирования цифровой подписи: ЕВ = BTUPSdl ••• IIPS/IIOOIIDJI ... ||Dn. В начале стоит байт ВТ, указывающий тип блока (01 для операций с секретным ключом, т.е. формирования подписи; 02 для операций с открытым ключом, т.е. зашифрования). Затем следуют не менее восьми байтов-заполнителей PSi, ..., PS/, l> 8, имеющих значения FF (в шестнадцатиричном виде) в случае формирования подписи и случайные ненулевые значения в случае зашифрования. За ними идет байт-разделитель 00 и, наконец, байты данных Db ..., D„ - так сказать, полезная нагрузка. Число / байтов-заполнителей PSZ зави- сит от размера модуля т и числа п байтов данных. Если значение к таково, что
:6) 28<i-l) </и < 28\ ТО И
'•7) 1 = к-2-п. Минимально значение 8 < 1 байтов-заполнителей выбрано для зашифрования из соображений безопасности. Даже для маленького сообщения нарушитель не сможет зашифровать все возможные значения и сравнить результат с данной шифрограммой, надеясь определить открытый текст без знания секретного ключа. Здесь важно, чтобы значения PS, были случайными и определялись зано- во для каждой операции зашифрования. Для единообразия то же минимальное число байтов-заполнителей сохранено и для подписи, откуда следует неравенство для числа п байтов данных:
JTC 1/SC27: Recommendation on the withdrawal of IS 9796:1991, 6 October 1991.
ГЛАВА 16. Практический пример: криптосистема RSA 373
(16.8) п<к-\0.
В случае подписи байты данных D, обычно включают в себя иден-
тификатор хэш-функции Я и ее значение (хэш-образ) Н(М), пред-
ставляющее подписываемое сообщение М. Итоговая структура
данных называется Digestinfo. В этом случае число байтов данных
, определяется постоянной длиной хэш-образа и не зависит от длины
у текста, что особенно выгодно, если М намного длиннее, чем Н(М).
Мы не будем вдаваться в подробности построения структуры
Digestinfo, а просто будем считать, что байты данных соответству-
м ют значению Н(М) (см. по этому поводу [RDS1]).
С точки зрения криптографии хэш-функция должна обладать рядом
основных требований, чтобы не снижать безопасность соответст-
t s вующей функции избыточности и тем самым поставить под сомне-
ние всю процедуру подписи. Исследуя применение хэш-функций
и функций избыточности в цифровой подписи, можно заметить
следующее.
До сих пор мы предполагали, что цифровая подпись с приложением
13 связана с избыточностью R = ц(М), основным компонентом кото-
3 рой является хэш-образ подписываемого сообщения. Два текста
М и М', для которых Н(М) = Н(М') и, следовательно, ц(М) = ц(Л/'),
будут иметь одну и ту же подпись S = Rd = [i(M)d = [i(M')d mod n.
Отсюда получатель подписи S к сообщению М может заключить,
что эта подпись на самом деле относится к сообщению М', что,
1 скорее всего, не входило в планы отправителя. Аналогично, отпра-
витель может думать, что он подписывает текст М', на самом деле
; подписывая М. А дело здесь в том, что всегда существуют тексты
М Ф М', для которых Н(М) = Н(М'), поскольку бесконечное мно-
э* жество текстов отображается в конечное множество хэш-образов.
Это та цена, которую мы платим за фиксированную длину хэш-
образов. 10
•Г Поскольку мы предполагаем, что для данной хэш-функции или
функции избыточности всегда существуют тексты, обладающие
иг одинаковыми подписями (для одного и того же ключа подписи),
встает вопрос о том, чтобы эти тексты трудно было найти или
ПОСТРОИТЬ.
Итак, хэш-функция должна быть легко вычислимой, в отличие от
{ обратного к ней преобразования. То есть, для данного значения Н
хэш-функции должно быть трудно найти прообраз, отображающийся
в Н. Функции, обладающие таким свойством, называются одно-
направленными (или вычислимыми в одну сторону). Хэш-функция
10 На языке математики мы бы сказали, что хэш-функция Н: М —> отображающая тексты произ-
вольной длины в элементы множества Z„, не инъективна.
74 Криптография на Си и C++ в действии
должна быть свободной от коллизий, то есть для данного хэш-
значения должно быть трудно найти два разных прообраза. На
сегодняшний день такими свойствами обладают такие мощные
функции как RIPEMD-160 (см. [DoBP]) и Secure Hash Algorithm
SHA-1 (см. [ISO1]).
Позволим себе не углубляться дальше в эту столь важную для
! криптографии тему. Заинтересованному читателю советуем обра-
титься к [Ргеп] или [MOV], глава 9, см. также ссылки в этих работах.
Алгоритмы преобразования текстов или хэш-образов в натураль-
t ные числа можно найти в [IEEE], глава 12 «Методы шифрования»
(хотя у нас уже есть соответствующие функции clint2bytej() и
byte2clintj(); см. стр. 172). Реализацию алгоритма RIPEMD-160
читатель найдет в файле ripemd.c на компакт-диске.
При ближайшем рассмотрении описанного выше протокола подпи-
* си мы немедленно задаемся вопросом: откуда В может знать, что
L ему прислали аутентичный (подлинный) открытый ключ участ-
ника А? Не будучи в этом уверен, В не может доверять и соответ-
ствующей подписи, даже если она удовлетворяет проверочному
соотношению. Эта проблема особенно актуальна, если А и В не
, знакомы друг с другом или если они не обменивались открытыми
ключами лично, что обычно и бывает при взаимодействии через
Интернет.
Для того чтобы В все же смог доверять цифровой подписи, А дол-
► жен предоставить ему сертификат от сертифицирующего органа,
s подтверждающий подлинность открытого ключа. Неформальная
«расписка», которой можно верить, а можно и не верить, здесь,
конечно же, не подходит. Сертификат - это набор данных, формат
которых соответствует определенному стандарту. 11 Эти данные,
( помимо всего прочего, несут информацию и об участнике А, и о его
открытом ключе, да и сами подписаны цифровой подписью серти-
фицирующего органа.
। Информация, содержащаяся в сертификате, позволяет проверить
1 подлинность ключей участников. Уже есть программные приложе-
ния, поддерживающие такую проверку. О будущем разнообразии
। таких приложений, в связи с развитием так называемой инфра-
структуры открытых ключей (public key infrastructure, PKI), пока
можно только догадываться. Сегодня они применяются для цифро-
вой подписи сообщений электронной почты, при проверке ком-
мерческих транзакций, в электронной и мобильной коммерции
• (т-соттегсе), в электронном документообороте и управлении
(см. рис. 16.1).
Часто используется стандарт ISO 9594-8 или, что то же самое, рекомендация X.509v3 от ITU-
(ранее CCITT).
Г ЛАВА 16. Практический пример: криптосистема RSA
375
L
Рисунок 16,1,
Структура
сертификата
Секретный ключ сертифицирующего органа
Если участник В знает открытый ключ сертифицирующего органа,
то он может проверить сертификат, предъявленный участником А,
а значит, и цифровую подпись участника А, и тем самым убедиться
в подлинности информации.
Этот процесс показан на рис. 16.2, где клиент получает извещение,
подписанное цифровой подписью банка, и сертификат банка, пре-
доставленный удостоверяющим центром.
Рисунок 16,2,
Сертификация
цифровой
подписи
Version
Serial Number
Signature
Issuer Name
Validity
Открытый
ключ
банка
ат-
Subject Name
Issuer Identifier
110111011110110001100
0001111000001101110...
W3-Bank
Состояние счета
Имя: Браузер,
Бернард
Счет: 1234567890
Баланс: $4286,37
Дата: 14.06.2000
Подпись:
11101011011010011100
011101010011100111...
Сертификат банка
Извещение банка,
подписанное цифровой
в проверяет сертификат, предоставленный банком, и с
помощью открытого ключа банка проверяет цифровую
подпись банка
376
Криптография на Си и C++ в действии
Такая форма извещения хороша тем, что извещение может быть
передано клиенту по любому электронному каналу связи (напри-
мер, по электронной почте), при этом его следует предварительно
зашифровать, чтобы сохранить конфиденциальность информации.
И все же проблема доверия никуда чудесным образом не исчезла, а
просто немного видоизменилась: теперь участник В должен проверять
подлинность не ключа участника А (то есть банка в примере выше), а
сертификата, представленного участником А. Подлинность сертифи-
катов нужно устанавливать заново при каждом появлении как нового
владельца сертификата, так и выдавшего ему сертификат сертифици-
рующего органа. Это можно сделать лишь при следующих условиях:
✓ открытый ключ сертифицирующего органа известен;
✓ сертифицирующий орган безупречно идентифицирует получателей
сертификатов и защищает их секретные сертификационные ключи.
Для достижения первой цели открытый ключ сертифицирующего
органа можно сертифицировать у другого, вышестоящего сертифи-
цирующего органа и т. д., то есть нужна иерархия сертифицирую-
щих органов и сертификатов. При такой структуре предполагается,
что открытый ключ самого высокого, корневого сертифицирующего
органа известен и может считаться подлинным. То есть доверие к
такому ключу должно подкрепляться другими средствами, в боль-
шей степени техническими и организационными мерами.
Второе условие, разумеется, выполняется для всех сертифицирующих
органов в указанной иерархии. Для придания подписи законной силы
сертифицирующий орган должен предпринять технические и орга-
низационные меры, предписанные законом или иными документами.
В конце 1999 года Европейским Союзом была принята директива,
устанавливающая схему использования цифровых подписей в
Европе (см. [EU99]). Предполагается также выработка положения,
которое объединило бы в себе различные национальные подходы к
цифровой подписи и послужило бы толчком к созданию Европей-
ского стандарта подписи, имеющего статус национального закона.
Пересмотренный закон о подписи в Германии намечен на 2001 год
(см. [SigG]). В США закон об электронных подписях (Electronic
Signatures Act) действует с октября 2000 года. Все эти законода-
тельные акты позволяют надеяться, что в ближайшем будущем на
основе многочисленных цифровых подписей разных стран будет
выработан единый механизм, который позволит надежно заверять
транзакции по всей Европе, а спустя некоторое время (почему бы|
и нет?) между Европой и Америкой. I
А сейчас оставим эту интересную тему, обсуждение которой чита-1
тель найдет на страницах [Bies], [Glad], [Adam], [Mied] и [Fegh], Й1
обратимся, наконец, к разработке на C++ классов функций, реали-1
зующих процессы зашифрования и расшифрования сообщений, а|
также формирования и проверки цифровой подписи. I
ГЛАВА 16. Практический пример: криптосистема RSA
377
16.4. RSA-классы на C++
В этом параграфе мы напишем на C++ класс RSAkey, включающий
в себя следующие функции:
✓ RSAkey:: RSAkey() - генерация ключа криптосистемы RSA;
✓ RSAkey: :export() - экспорт открытых ключей;
✓ RSAkey::decrypt() - расшифрование;
г ✓ RSAkey::sign() - формирование цифровой подписи с использовани-
1( ем хэш-функции RIPEMD-160;
а также класс RSApub для хранения и применения открытых клю-
< 1 чей, содержащий функции
✓ RSApub::RSApub() - импорт открытого ключа из объекта класса
RSAkey;
✓ RSApub::crypt() - зашифрование текста;
✓ RSApub::authenticate() - проверка цифровой подписи.
Идея заключается в том, чтобы оперировать с криптографическими
ключами не просто как с числами, обладающими определенными
г., криптографическими свойствами. Эти ключи мы будем рассмат-
ривать как объекты, подсказывающие пути их применения, делая
1 v их доступными внешнему миру и в то же время защищая персо-
"}нальные данные от прямого доступа. К объектам класса RSAkey
°' относятся открытая и секретная компоненты ключа RSA (закрытые
данные), а также общедоступные функции расшифрования и фор-
мирования подписи. Функции-конструкторы позволяют генериро-
вать ключи:
✓ фиксированной длины со встроенной инициализацией генератора
случайных чисел BBS;
✓ регулируемой длины со встроенной инициализацией генератора
случайных чисел BBS;
регулируемой длины с передачей через вызываемую программу на-
чального значения типа LINT для генератора случайных чисел BBS.
К объектам класса RSApub относится открытый ключ, импорти-
руемый из объекта класса RSAkey, а также общедоступные функ-
ции зашифрования и проверки подписи. То есть при создании объ-
екта класса RSApub уже должен существовать и быть инициализи-
рованным объект класса RSAkey. В отличие от объектов класса
RSAkey, объекты класса RSApub не считаются конфиденциальными,
при работе с ними допускается больше свободы. Объекты же класса
RSAkey, особенно в серьезных приложениях, могут храниться или
передаваться только в зашифрованном виде или будучи защищен- v
ними специальными аппаратными средствами.
378 Криптография на Си и C++ в действии
Прежде чем строить эти классы, введем некоторые ограничения,
которые позволят нам оставаться в разумных пределах времени и
памяти. Для простоты будем считать входное значение процедуры
зашифрования RSA всегда меньше модуля, то есть не нужно будет
разбивать входной текст на блоки. Кроме того, оставим в стороне
более трудоемкие функции функционирования и безопасности,
которые приходится решать при реализации полноценных классов
криптосистемы RSA (см. в этой связи стр. 357).
Не будем, однако, забывать о необходимости быстро реализовать
процедуры расшифрования и формирования подписи. Китайская
? теорема об остатках (см. стр. 225) позволяет выполнять операции с
секретным ключом d почти в четыре раза быстрее, чем при обыч-
ном способе возведения в степень. Пусть (d,n) - секретный ключ
RSA, где п = pq. Положим dp := d mod (р - 1), dq d mod (g - 1) и
расширенным алгоритмом Евклида найдем представление
; ' 1 = гр + sq, где значение г мультипликативно обратно к р по моду-
лю q (см. п. 10.2). Теперь с помощью чисел р, q, dp, d(p г можно
вычислить с = ml mod п:
1. Вычислить ах <— mdp mod р и а2 <— mdq mod <7 .
4 2. Положить с <— а\ + р((«2 - лi)r m°d qY
После шага 1 получаем ах = mdp = md mod р и а2 = in4 = md mod q
Чтобы это увидеть, достаточно вспомнить малую теорему Ферм*
(см. стр. 198), согласно которой п?~[ = 1 mod р и mq~l = 1 mod q со
ответственно. Из равенства d=l(p~ 1) + dp с целым I следует, что
(1&9) md ~m{p^dp = mdp = mdp mod p,
аналогичное выражение получаем и для m<l mod q. Применяя алго
ритм Гарнера (см. стр. 229) с гщ := р, т2 :=q иг := 2, сразу получаем
что значение с на шаге 2 и есть искомое решение. Быстрое расшиф
рование осуществляется с помощью вспомогательной функци!
RSAkey::fastdecrypt(). Все операции возведения в степень по моду
лямр, q ип выполняются с использованием алгоритмаМонтгомер!
функцией LINT::mexpkm() (см. стр. 312).
// Взято из файла rsakey.h
#include "flintpp.h"
#include "ripemd.h"
#define BLOCKTYPE_SIGN 01
#define BLOCKTYPE ENCR 02
ГЛАВА 16. Практический пример: криптосистема RSA 379
i И Структура ключа RSA со всеми ключевыми компонентами typeclef struct { LINT kpub, kpriv, mod, p, q, ep, eq, r; USHORT bitlen_mod; // длина модуля в битах USHORT bytelen_mod; // длина модуля в байтах } KEYSTRUCT; И Структура, содержащая компоненты открытого ключа typedef struct { LINT kpub, mod; USHORT bitlen_mod; //длина модуля в битах USHORT bytelen_mod; // длина модуля в байтах } pkeystruct; class RSAkey { public: inline RSAkey (void) {}; RSAkey (const int); RSAkey (const int, const LINT&); pkeystruct export_public (void) const; UCHAR* decrypt (const LINT&, int*); LINT sign (const UCHAR* const, const int);
private: keystruct key; // Вспомогательные функции int makekey (const int); int testkey (void); LINT fastdecrypt (const LINT&); }; class RSApub {
380
Криптография на Си и C++ в действии
public:
inline RSApub (void) {};
RSApub (const RSAkey&); I
LINT crypt (const UCHAR* const, const int); I
int authenticate (const UCHAR* const, const int, const LINT&); I
private: I
pkeystruct pkey; I
}; I
// Взято из модуля rsakey.cpp
#include "rsakey.h"
llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllini
// Функции-члены класса RSAkey
// Конструктор для генерации ключей RSA заданной двоичной длины
RSAkey::RSAkey (const int bitlen)
{
int done;
seedBBS ((unsigned longtime (NULL));
do
{
done = RSAkey::makekey (bitlen);
} I
while (Idone); I
} I
// Конструктор для генерации ключей RSA заданной двоичной длины!
// с инициализацией генератора случайных чисел randBBS() I
И заданным аргументом типа LINT I
RSAkey::RSAkey (const int bitlen, const LINT& rand) I
{ I
int done; I
ГЛАВА 16. Практический пример: криптосистема RSA ЗВ1
seedBBS (rand); do { done = RSAkey::makekey (bitlen); } while (’done); } И Функция, экспортирующая компоненты открытого ключа ; pkeystruct RSAkey::export_public (void) const { pkeystruct pktmp; pktmp.kpub = key.kpub; pktmp.mod = key.mod; pktmp. bitlen_mod = key.bitlen_mod; pktmp.bytelen_mod = key.bytelen_mod; return pktmp; } // Расшифрование no RSA UCHAR* RSAkey::decrypt (const LINT& Ciph, int* LenMess)
f :• ' sru . t И Расшифрование и преобразование открытого текста в вектор байтов UCHAR* Mess = Iint2byte (fastdecrypt (Ciph), LenMess); И Берем расшифрованные данные из блока зашифрования PKCS #1 return parse_pkcs1 (Mess, LenMess); } И Выработка цифровой подписи по RSA LINT RSAkey::sign (const UCHAR* const Mess, const int LenMess) { int LenEncryptionBlock = key.bytelen.mod - 1; UCHAR* EncryptionBlock = new UCHAR[LenEncryptionBlock]; if (NULL == format_pkcs1 (EncryptionBlock, LenEncryptionBLock, BLOCKTYPE_SIGN,
382
Криптография на Си и C++ в действии
ripemd160 ((UCHAR*)Mess, (ULONG)LenMess),
RMDVER » 3))
{
delete [] EncryptionBlock;
return LINT (0); // Ошибочный формат: слишком длинное
сообщение
}
И заменяем блок зашифрования на значение типа LINT
(конструктор 3)
LINT m = LINT (EncryptionBlock, LenEncryptionBlock);
delete [] EncryptionBlock;
return fastdecrypt (m);
}
llllllllllllinilllllllllllllllllllllllllllllllllllllllllllfllllllllllll
// Закрытые вспомогательные функции класса RSAkey
//... помимо всего прочего: генерация ключа RSA в соответствии
с IEEE Р1363, Annex А
int RSAkey::makekey (const int length)
{
// Генерируем простое p такое, что 2Л(т - г - 1) <= р < 2л(т - г), где
// т = [.(length + 1 )/2J, а г - случайное число из интервала 2 <= г < 13
USHORT т = (length + 1) » 1 - 2 - usrandBBSJ () % 11 ;
key.p = findprime (m, 1);
И Определяем границы qmin и qmax интервала для простого числа q £
И Полагаем qmin = |_(2A(length - 1 ))/р + 1J |
LINT qmin = LINT(0).setbit (length - 1 )/key.p + 1; |
// Полагаем qmax = |_(2Alength)/p)J |
LINT qmax = LINT(O).setbit (length)/key.p; I
И Генерируем простое число q > р нужной длины: ^^1
qmin <= q <= qmax
key.q = findprime (qmin, qmax, 1);
ГЛАВА 16. Практический пример: криптосистема RSA
383
// Вычисляем модуль p*q длины 2A(length - 1) <= p*q < 2Alength
key.mod = key.p * key.q;
И Вычисляем функцию Эйлера
LINT phi_n = key.mod - key.p - key.q + 1;
// Генерируем открытый ключ длины 64 бита
key.kpub = randBBS (64) | 1;
while (gcd (key.kpub, phi_n) != 1)
{
++key.kpub;
++key.kpub;
//Генерируем секретный ключ
key.kpriv = key.kpub.inv (phi_n);
II Генерируем секретные компоненты для быстрого расшифрования
key.ep = key.kpriv % (key.p - 1);
key.eq = key.kpriv % (key.q - 1);
key.r = inv (key.p, key.q);
return testkey();
// Функция для тестирования
int RSAkey: :testkey (void)
{
LINT mess = randBBS (Id (key.mod) » 1);
return (mess == fastdecrypt (mexpkm (mess, key.kpub, key.mod)));
}
И Быстрое расшифрование no RSA
LINT RSAkey::fastdecrypt (const LINT& mess)
{
LINT m, w;
m = mexpkm (mess, key.ep, key.p);
w = mexpkm (mess, key.eq, key.q);
w = w.msub (m, key.q);
384
Криптография на Си и C++ в действии
w = w.mmul (key.r, key.q) * кеу.р;
return (w + m);
}
llllllllllll/l/lllllllinillllllllll/lllllllllllllllllllllllinnillllll
И Функции-члены класса RSApub
//Конструктор RSApub()
RSApub::RSApub (const RSAkey& k) I
{
// Импортируем открытый ключ из k I
pkey = k.export(); I
}
И Зашифрование no RSA I
хлодфыщ LINT RSApub::crypt (const UCHAR* const Mess, const int LenMess) I
{ I
int LenEncryptionBlock = key.bytelen_mod - 1; I
UCHAR* EncryptionBlock = new UCHAR[LenEncryptionBlock]; I
// Форматируем блок зашифрования в соответствии с PKCS #1 I
if (NULL == format_pkcs1 (EncryptionBlock, I
LenEncryptionBlock, I
BLOCKTYPE_ENCR, I
Mess, I
(ULONG)LenMess)) I
{ I
delete [] EncryptionBlock; I
return LINT (0); // Ошибочный формат: слишком длинное I
сообщение I
I
И Преобразуем блок зашифрования в значение типа LINT В
(конструктор 3) В
LINT m = LINT (EncryptionBlock, LenEncryptionBlock); В
delete [] EncryptionBlock; В
ГЛАВА 16. Практический пример: криптосистема RSA 385
return (mexpkm (m, pkey.kpub, pkey.mod));
}
И Проверка цифровой подписи no RSA
int RSApub::authenticate (const UCHAR* const Mess,
const int LenMess, const LINT& Signature)
n {
int I, verification = 0;
UCHAR* m = Iint2byte (mexpkm (Signature, pkey.kpub, pkey.mod), &l);
UCHAR* h = ripemd160 ((UCHAR*)Mess, (ULONG)LenMess);
И Берем данные из расшифрованного блока зашифрования PKCS #1
m = parse_pkcs1 (m, &l);
И Сравниваем длину и значение расшифрованного текста
со значением хэш-функции
if (I == (RMDVER » 3))
{
р verification = !memcmp ((char*)h, (char*)m, RMDVER » 3);
}
return verification;
}
Классы RSAkey и RSApub содержат еще несколько операторов, ко-
торые мы здесь не обсуждаем:
! ’ RSAkey& operator^ (const RSAkey&);
friend int operator== (const RSAkey&, const RSAkey&);
friend int operators (const RSAkey&, const RSAkey&);
friend fstream& operator« (fstream&, const RSAkey&);
friend fstream& operator» (fstream&, RSAkey&);
и
RSApub& operator (const RSApub&);
13- 1697
386
Криптография на Си и C++ в действии^
friend int operator— (const RSApub&, const RSApub&);
friend int operator!^ (const RSApub&, const RSApub&);
friend fstream& operator« (fstream&, const RSApub&);
friend fstream& operator» (fstream&, RSApub&);
Это операторы поэлементного присваивания, проверки равенств d
неравенств, считывания ключей из внешнего носителя памяти и за4
писи ключей на него. Здесь следует помнить, что секретный ключ,
как и открытый, хранится в открытом виде. При практической реа4
лизации секретные ключи нужно хранить в зашифрованном виде.
Есть еще функции
RSAkey::purge (void),
RSApub::purge (void),
позволяющие перезаписывать ключи и устанавливать соответст-1
вующие LINT-компоненты в 0. Форматирование блоков сообщения
для зашифрования или формирования подписи в соответствии cd
спецификацией PKCS #1 осуществляется функцией
UCHAR* format_pkcs1 (const UCHAR* ЕВ, const int LenEB,
const UCHAR BlockType, const UCHAR* Data, const int LenData).
Для анализа блоков расшифрованного сообщения с проверкой
формата и извлечением полезных данных служит функция
UCHAR* parse_pkcs1 (const UCHAR* ЕВ, int* LenData).
Классы RSAkey и RSApub можно расширять как угодно. Например,
составить конструктор, который принимал бы открытый ключ в
качестве параметра и вырабатывал соответствующий модуль и сек-^
ретный ключ. При практической реализации могут понадобиться
дополнительные хэш-функции. Нужна и функция разбиения сооб4
щений на блоки. Этот список можно продолжать до бесконечности,
что выходит за рамки данной книги.
Тестовый пример для классов RSAkey и RSApub читатель найдет и
модуле rsademo.cpp в библиотеки FLINT/C. Программа транслируй
ется с помощью
дсс -02 -DFLINT_ASM -о rsademo rsademo.cpp rsakey.cpp
flintpp.cpp flint.c ripemd.c -Iflint -lstdc++
при использовании, например, GNU С/С++-компилятора дсс под
Linux и ассемблерных функций в библиотеке libflint.a.
ГЛАВА 17.
Сделайте это сами: Протестируйте LINT
90% времени уходит на написание 10% кода.
Роберт Седжевик, Алгоритмы
Мы уже обсуждали тему тестирования в главе 12, в которой мы
подвергли серьезной статической и динамической проверке основ-
ные арифметические функции из первой части книги. Сейчас нам
нужна подобная обработка для проверки правильности класса LINT
языка C++. Кроме этого, нам до сих пор необходимо обеспечить
тестирование теоретико-числовых функций С.
Подход статических тестов можно перенести прямо в класс LINT, в
котором такой инструмент как PC-lint (см. [Gimp]), используемый
для статического анализа функций С, может сослужить нам хоро-
шую службу, поэтому мы можем применять его для проверки на
синтаксическую грамотность и (в определенных рамках) на семан-
тическую достоверность элементов класса LINT.
Также нам предстоит рассмотреть функциональные особенности
реализации нашего класса: нам необходимо показать то, что мето-
ды, содержащиеся в классе LINT, возвращают верные результаты.
Тот способ, который мы использовали ранее, когда для выяснения
корректности применяли эквивалентные или взаимно обратные
операции, вне всяких сомнений, может использоваться и функ-
циями C++. В следующем примере данный способ реализован
функцией testdist(), которая объединяет сложение и умножение с
помощью закона дистрибутивности. Даже здесь можно заметить,
насколько меньше в ней синтаксически сложных операций по срав-
нению с функцией проверки в С. Ядро этой функции состоит из
двух строчек кода!
#include <stdio.h>
#include <stdlib.h>
#include "flintpp.h"
void report_error (LINT&, LINT&, LINT&, int);
void testdist (int);
#define MAXTESTLEN CLINTMAXBIT
#define CLINTRNDLN (ulrand64J()% (MAXTESTLEN + 1))
main()
13*
388
Криптография на Си и C++ в действии
testdist (1000000);
}
void testdist (int nooftests)
{
LINT a;
LINTb;
LINT c;
int i;
for (i = 1; i < nooftests; i++)
{
a = randl (CLINTRNDLN);
b = randl (CLINTRNDLN);
c = randl (CLINTRNDLN);
// проверка + и * применением дистрибутивного закона
if ((а + b)*c != (а*с + Ь*с))
report_error (а, Ь, с,_LINE_);
void report_error (LINT& a, LINT& b, LINT& с, int line)
{
LINT d = (a + b) * с;
LINT e = a*c + b*c;
cerr« "Ошибка в дистрибутивном законе в строке" « line « endl;
cerr« "а = " « а « endl;
cerr« "b = " « b « endl;
cerr« "(a + b) * c = " « d « endl;
cerr« "a * c + b * c = " « e « endl;
abort();
ГЛАВА 17. Сделайте это сами: Протестируйте LINT
389
А теперь мы предоставим читателю в качестве упражнения прове-
рить все операторы LINT таким же или подобным образом. Для
того чтобы двигаться в нужном направлении, можно взглянуть
на тестовую программу функций языка С. Однако существует
несколько новых аспектов, которые предстоит рассмотреть: такие
как префиксные и постфиксные операторы ++ и - - соответственно,
в равной степени, как оператор = =. Ниже приведены несколько
дополнительных примечаний:
✓ Тестирование программы обработки ошибок panic() со всеми опре-
деленными ошибками, без и с исключениями;
✓ Тестирование функций ввода/вывода, потоковых операторов и ма-
нипуляторов;
✓ Тестирование арифметических и теоретико-числовых функций.
Теоретико-числовые функции можно проверить согласно принци-
пам, схожим с арифметическими функциями. Для этих целей также
хорошо подойдет использование обратных функций, эквивалент-
ных функций или же различные реализации одной и той же функ-
ции, но независимые друг от друга насколько это возможно. Мы
приведем примеры каждого из этих вариантов:
✓ Если символ Якоби показывает, что элемент конечного кольца яв-
ляется квадратом, то этот факт можно проверить, взяв квадратный
корень. И, наоборот, вычисленный квадратный корень может быть
проверен простым возведением в квадрат по модулю.
✓ Функцию inv() для вычисления инверсии i относительно умноже-
ния целого числа а по модулю п можно проверить с условием, что
ai = 1 mod п.
Для вычисления наибольшего общего делителя двух целых чисел
можно использовать две функции FLINT/C gcd_l() и xgcd_l(), по-
следняя из которых возвращает представление наибольшего обще-
го делителя как линейную комбинацию аргументов. Результаты
можно будет сравнить один с другим, а полученная линейная ком-
бинация также должна быть согласована с наибольшим общим
делителем.
✓ Также существует избыточность в отношении между НОД и наи-
меньшим общим кратным: для целых а и b есть важное равенство
\ab\
НОК(л, Ь) =----,
НОД(а,Ь)
которое тоже может быть легко проверено. Дополнительные полез-
ные формулы, которые относятся к НОД и НОК, представлены в
разделе 10.1.
390
Криптография на Си и C++ в действии
✓ Наконец, для проверки теста на простоту, можно вызвать процеду-
ру RSA: если р или q не простые, то ф(л) 7^ (р - l)(g - 1). Функции
RSA будут работать корректно только если тест Ферма выдаст, что
р и q вероятно простые. Поэтому некоторые взаимно обратные
операции RSA и сравнение расшифрованного текста с первона-
чальным определенно выявят, что тест на простоту был реализо-
ван некорректно.
Таким образом, существует достаточно много различных подходов
к эффективному тестированию функций LINT. Читателю имеет
смысл разработать по крайней мере один подобный тест для функ-
ции LINT. Это будет очень полезно как для тестирования, так и в
качестве примера работы с пользовательским классом LINT, чтобы
понять, как он устроен и как его можно применять.
ГЛАВА 18.
Направления дальнейших исследований
Теперь, когда в нашем распоряжении уже есть пакет программ,
реализующий строго сформулированные и протестированные
функции, перед нами встает вопрос: в каком направлении двигаться
дальше? Здесь могут быть два пути: расширение функциональности
и повышение производительности. Что касается функциональности,
читатель может попробовать применить основные функции пакета
FLINT/C в тех областях, которые нами были лишь слегка затронуты
или не рассматривались вообще, например, для разложения числа
на множители или для арифметики эллиптических кривых. Послед-
ние, благодаря своим свойствам, находят все большее применение
в криптографии. Заинтересованный читатель найдет подробное
обсуждение этих тем в работах [Bres], [КоЫ] и [Мепе], а также в
неоднократно нами упоминавшихся и содержащих многочисленные
ссылки на литературу [Cohe], [Schn] и [MOV].
; Второе направление работ - искать пути повышения производи-
тельности. Прежде всего, увеличить размер основания системы
счисления с 16 до 32 бит (В = 232), а также использовать ассемблер-
ные функции и (на тех платформах, где это возможно) включить их
в текст на языке C/C++.
Разработка и тестирование, связанные со вторым направлением,
могут выполняться независимо от платформы, например, с ис-
u * пользованием GNU-компилятора gcc с типом unsigned long long:
J тип CLINT будет тогда определяться как typedef ULONG
CLINT[CLINTMAXLONG];. Кроме того, нужно будет скорректировать
некоторые константы, связанные с системой счисления внутреннего
представления целых чисел.
В функциях пакета FLINT/C все явные приведения типов и прочие
и ссылки на тип USHORT следует заменить на ULONG, a ULONG, в
свою очередь, на unsigned long long (или, после соответствующего
typedef, на, скажем, ULLONG). Отдельные функции, зависящие от
длины разряда в представлении данных, придется адаптировать.
... После тщательного тестирования и отладки, включая статическую
проверку синтаксиса (см. главу 12), пакет FLINT/C будет годиться
и для 64-разрядных процессоров.
Применение ассемблерных функций позволяет также работать с
32-битной длиной разряда и 64-битным результатом, это можно
сделать, если процессор является 32-разрядным, но тем нее менее
допускает 64-битный результат арифметических операций.
Используя ассемблерные функции, мы отказываемся от ранее при-
нятой стратегии независимости от конкретной платформы, а значит,
хорошо бы реализовать эти функции как узко специализированные.
Следовательно, нужно выбрать из пакета FLINT/C те функции, для
392
Криптография на Си и C++ в действии.
которых выигрыш от использования Ассемблера будет макси-
мальным. Определить их нетрудно. Это функции, имеющие квад-
ратичную сложность: умножение, возведение в квадрат и деление.
Поскольку базовые операции занимают большую часть времени
выполнения теоретико-числовых функций, улучшение должно
быть линейным, без непосредственного изменения алгоритмов.
В пакете FLINT/C мы воспользовались этим «запасом прочности»,
реализовав на 80x86 Ассемблере функции
mult(), umul(), sqr(), div_l().
Функции mult(), umul() и sqr() являются ядром для построения
функций mult_J(), umuIJO и sqr_l() соответственно (см. стр. 86). Эти
функции допускают аргумент длиной до 4096 двоичных разрядов,
то есть 256 (= МАХд) разрядов числа типа CLINT, и результат двой-
ной длины. Функции на Ассемблере, как и соответствующие функ-
ции на С, реализованы в соответствии с алгоритмами главы 4, при
этом регистр процессора позволяет обрабатывать арифметическими
машинными командами 32-разрядные аргументы и 64-разрядный
результат (см. главу 2).
Ассемблерные модули mult.asm, umul.asm, sqr.asm и div.asm вклю-
чены в пакет FLINT/C в виде исходных текстов. Их можно ассемб-
лировать с помощью Microsoft MASM (вызов программы: ml /Сх/с
/Gd <filename>) или Watcom WASM1, после чего заменить ими со-
ответствующие функции на С, транслируя модуль flint.c с помощью
-DFLINT_ASM2. Время вычислений, приведенное в приложении D,
позволяет непосредственно сравнить реализацию некоторых важ-
ных функций с использованием Ассемблера и без него.
Возведение в степень по Монтгомери (см. главу 6) дает дополни-
тельную экономию времени. Кроме того, можно реализовать на 32-
разрядном Ассемблере две вспомогательные функции mulmonJO и
sqrmon_l() (см. стр. 128). Отправной точкой для такой реализации
могут послужить модули mul.asm и sqr.asm. Для заинтересованного
читателя здесь широчайшее поле деятельности.
И это все, что мы знаем.
Джон Хайзмен, Колизей!
В зависимости от того, какой компилятор используется, идентификаторы mult, umul, sqr и divj
ассемблерных процедур следует снабдить символом подчеркивания (_mult, _umul, _sqr и _divj),
поскольку WASM его не генерирует.
2 Модули mult.asm, sqr.asm, umul.asm и div.asm работают на 80х86-совместимых платформах. Для
других платформ необходима соответствующая программная реализация.
ГЛАВА 19.
Rijndael: наследник стандарта
шифрования данных
Не знаю, есть ли у нас хоть малейший шанс.
Он умеет умножать, а мы можем лишь склады-
вать. Он - само воплощение прогресса, а я едва
волочу ноги.
Стэн Надольный, Бог дерзости
В 1997 году Американский Национальный институт стандартов и
технологий (National Institute of Standards and Technology, NIST)
объявил конкурс на разработку нового национального стандарта
(федерального стандарта обработки информации, FIPS) симмет-
ричного шифрования - улучшенного стандарта шифрования AES
(Advanced Encryption Standard). Хотя эта книга посвящена в основ-
ном асимметричной криптографии, этот стандарт настолько важен,
что мы уделим ему немного внимания (хотя бы из любопытства).
Для нового стандарта нужен был алгоритм шифрования, который
удовлетворял бы всем современным требованиям по безопасности
и с учетом всех аспектов построения и реализации мог бы свободно
распространяться по всему миру. И наконец, новый стандарт дол-
жен был прийти на смену действующему стандарту шифрования
данных DES (Data Encryption Standard), который, правда, в виде
тройного DES (triple DES) по-прежнему будет использоваться в
правительственных учреждениях. В дальнейшем предполагается
использовать AES в качестве основного криптографического
средства защиты уязвимых данных в административных учреж-
дениях США.
Конкурс на AES привлек всеобщее внимание как в самих Соеди-
ненных Штатах, так и за их пределами не только из-за того, что
любое событие в американской криптографии находит отклик по
всему миру, но потому, что участие зарубежных конкурсантов в
/ разработке новой процедуры блочного шифрования всячески по-
ощрялось.
Из пятнадцати кандидатов, вступивших в борьбу в 1998 году, в
1999 году международной группой экспертов десять было отверг-
нуто. А вот кто остался: алгоритм MARS фирмы IBM; RC6 от RSA
Laboratories; Rijndael Иоана Дамана (Joan Daemen) и Винсента Рай-
мана (Vincent Rijmen); Serpent Росса Андерсона (Ross Anderson),
Эли Бихама (Eli Biham) и Ларса Кнудсена (Lars Knudsen); Twofish
. Брюса Шнайера (Bruce Schneier) и др. Наконец, в октябре 2000 года
был объявлен победитель. Алгоритм Rijndael Иоана Дамана и
Винсента Раймана из Бельгии был назван будущим улучшенным
394
Криптография на Си и C++ в действии
стандартом шифрования (см. [NIST]). 1 Rijndael является наследни-
ком блочного шифра «Square» («Квадрат»), опубликованного ранее
этими же авторами (см. [Squa]), но оказавшегося не таким стойким.
При разработке алгоритма Rijndael особое внимание обращалось на
устранение слабостей Square. Институт NIST приводит следующие
доводы в пользу алгоритма Rijndael.
1. Безопасность
Все претенденты удовлетворяли требованиям по стойкости относи-
тельно известных атак. На фоне других алгоритмов Serpent и
Rijndael смогли с меньшими потерями противостоять таким атакам,
при которых информация извлекается из результатов измерения
времени работы аппаратуры (так называемые временные (timing)
атаки) и токовых импульсов (простые или дифференциальные
токовые атаки (power attacks)) 2. Снижение производительности,
вызванное наличием средств защиты от таких атак, меньше всего у
Rijndael, Serpent и Twofish, причем алгоритм Rijndael в этом плане
значительно лучше двух других.
2. Скорость
Rijndael зашифровывает и расшифровывает быстрее всех. Этот ал-
горитм отличается хорошей производительностью на любой плат-
форме: 32-разрядном процессоре, 8-разрядном микроконтроллере,
смарт-карте, а также при аппаратной реализации (см. ниже).
Rijndael быстрее всех вычисляет ключи раундов.
3. Затраты памяти
Rijndael требует небольших затрат памяти ОЗУ и ПЗУ и поэтому
лучше всего подходит для приложений с ограниченными ресурса-
ми. В частности, ключи раундов можно вычислять «на лету». Эти
свойства особенно важны для реализации на микроконтроллерах,
используемых, например, в смарт-картах. Структура алгоритма
такова, что в случаях, когда требуется только зашифрование или
только расшифрование, требования к памяти ПЗУ минимальны и
возрастают лишь при двунаправленном процессе. Тем не менее, по
сравнению с другими четырьмя претендентами, по затратам ресурсов
Rijndael вне конкуренции.
Слово-гибрид «Rijndael» составлено из начальных слогов фамилий авторов. Мне говорили, чт
правильное его произношение - это что-то среднее между «rain doll» и «Rhine dahl» (Райндол
Возможно, NIST все же включит в стандарт международную фонетическую транскрипцию этог
слова.
2 Токовые атаки основаны на зависимости потребляемой электроэнергии, затрачиваемой на выпол
некие отдельных команд или последовательностей команд, от отдельных битов или групп бито
секретного криптографического ключа (см., например, [KoJJ], [CJRR], [GoPa]).
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных 39*
4. Аппаратная реализация
Алгоритмы Rijndael и Serpent показали наилучшую производитель-
ность в части аппаратной реализации; Rijndael был немного лучше
в режимах обратной связи по выходу и по шифртексту.
NIST предложил следующие критерии отбора в пользу Rijndael
(см. [NIST], п. 7):
Никто не знает, в какой среде и на какой вычислительной платфор-
ме будет функционировать AES. Все качества алгоритма Rijndael:
безопасность, производительность, гибкость и простота реализации -
говорят о том, что этот алгоритм стоит использовать и сегодня, и в
будущем.
Прозрачный процесс выбора алгоритма и политический интерес к
Rijndael как алгоритму «европейского происхождения» позволяют
предположить, что не за горами всевозможные пересуды о скрытых
свойствах, потайных лазейках и умышленных встроенных уязвимо-
стях, которые преследовали (впрочем, без особого успеха) и алго-
’ PhtmDES.
Прежде чем заняться изучением работы алгоритма Rijndael, прове-
дем небольшой экскурс в арифметику полиномов над конечными
полями. Материал следующего параграфа в основном соответствует
работе [DaRi], п. 2.
19.1 . Полиномиальная арифметика
J Начнем с изучения арифметических операций в поле F2„ - конеч-
ном поле из 2п элементов. Любой элемент поля F л можно предста-
вить в виде полинома Дх) = ап^хп~1 + ап_2хп~2 + ...+ ахх + а0 с коэф-
фициентами а, из поля F2 (изоморфного полю Z2). Можно задать
каждый элемент и просто набором из п коэффициентов полинома.
Q ; У каждого из этих представлений есть свои преимущества. Пред-
ставление в виде полинома удобнее для обработки вручную, тогда
как представление набором коэффициентов хорошо «ложится» на
двоичное представление чисел в компьютере. В качестве примера
рассмотрим два представления поля F 3: в виде последовательности
из восьми полиномов и в виде восьми троек с соответствующими
численными значениями (см. таблицу 19.1).
396
Криптография на Си и C++ в действии
Таблииа 19.1. Полиномы в F 3 Тройки в DF23 Численное значение
Элементы ПОЛЯ
F23 0 ООО '00'
1 0 0 1 '0Г
X 0 1 0 '02'
X + 1 0 1 1 '03'
х2 1 0 0 '04'
х2 + 1 1 0 1 '05'
х2 + X 1 1 0 '06'
х2 + X + 1 1 1 1 '07'
Сложению полиномов соответствует сложение коэффициентов в F2:
если fix) := х2 + х и g(x) := х2 + х + 1, то fix) + g(x) = 2х2 + 2х + 1 = 1,
так как в поле F2 выполняется равенство 1 + 1=0. Сложение троек
в поле Р2з выполняется отдельно для каждого столбца. Например,
сумма (1 1 0) и (1 1 1) равна (0 0 1):
1 1 0
© 1 1 1
О 0 1
Сложение разрядов выполняется в кольце Z2, его не следует путать
с двоичным сложением, при котором могут возникать переносы.
Оно напоминает нам функцию XOR из п. 7.2, которая выполняет ту
же операцию в кольце для больших п.
Чтобы перемножить два полинома в поле IFp, каждое слагаемое
первого полинома нужно умножить на каждое слагаемое второго
полинома, затем сложить частичные произведения и найти остаток i
от деления полученной суммы на неприводимый полином степени 3 |
(в нашем примере модуль т(х) := х3 + х + 1):3
fix) • g(x) = (х2 + х) • (х2 + х + 1) mod (х3 + х + 1) = J
= х + 2х3 + 2х2 + х mod (х3 + х + 1) =
= х4 + х mod (х3 + х + 1) = I
= х2+1. I
3 Полином называется неприводимым, если он делится (без остатка) только на самого себя и на 1 •
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
397
Это соответствует произведению троек (1 1 0) • (1 1 1) = (1 0 1) или,
в шестнадцатиричном виде, ‘06’ • ‘07’ = ‘05’.
Элементы множества F23 образуют абелеву группу относительно
операции сложения, а элементы множества F23 \ {0} - относительно
операции умножения (см. главу 5). Выполняется и закон дистрибу-
тивности.
Структуру и арифметику поля F23 можно перенести и на поле F28 -
именно оно нам понадобится при изучении алгоритма Rijndael.
Сложение и умножение выполняются точно так же, как в примере
выше, с тем лишь отличием, что в поле F28 уже 256 элементов, а в
качестве модуля нужно взять неприводимый полином степени 8.
В Rijndael это полином т(х) := х* + х4 + х3 + х + 1, соответствующий
набор коэффициентов (10001 101 1), а шестнадцатиричное
число - ‘011В’.
Умножение полинома
fix) = a-jx1 + а^х6 + а$х5 + а^х4 + а^х3 + а2х2 + а\Х + aQ
на х (что соответствует умножению • ‘02’) выполняется особенно
просто:
fix) • х = я7.х8 + а^х1 + а$х6 + ЯфХ5 + а^х4 + а2х3 + а\Х2 + а$х mod mix),
где приведение по модулю mix) требуется лишь в случае а2 Ф 0, и
для этого нужно просто вычесть т(х), то есть вычислить сумму
коэффициентов по модулю 2 операцией XOR.
При программировании коэффициенты полиномов следует рас-
сматривать как двоичные разряды целого числа. Умножение на х
осуществляется как сдвиг влево на один бит, после чего (в случае
а2 * 0) результат суммируется по модулю 2 с восемью младшими
битами ‘1В’ числа ‘011В’, соответствующего модулю mix) (при
этом коэффициент а2 просто «забывается»). Операцию а • ‘02’ для
полинома f где а - это его численное значение, Даман и Райман
обозначили через b = xtime(a). Умножение на степени х выполняется
путем последовательного выполнения операции xtime.
Например, умножение полиномаДх) нах+ 1 (или на ‘03’) выполня-
ется как сдвиг двоичных разрядов числа а, соответствующего по-
линому f на одну позицию влево и сложение по модулю 2 (XOR)
результата с а. Приведение по модулю т(х) выполняется так же,
как и для функции xtime. Процедуре соответствуют две строчки на
языке С:
f л= f « 1; /* умножение f на (х + 1) 7
if (f & 0x100) f Л= 0x11 В; /* Приведение по модулю т(х) 7
398
Криптография на Си и C++ в действии
Умножение двух полиномов /и^вГ^Х {0} можно ускорить, ис-
пользуя дискретные логарифмы. Пусть полином g(x) является обра-
зующей4 группы F2g\{0}. Тогда существуют числа тип такие,!
что /= gm и h = g\ то есть/- h = gm+n mod т(х).
В переводе на язык программирования это означает, что можно
составить две таблицы, в одну из которых мы записываем 255
степеней образующей #(х) :=х+1, ав другую - логарифмы по
основанию <g(.x) (см. таблицы 19.2 и 19.3). Теперь, чтобы вычислить
произведение/ - /г, нужно обратиться к этим таблицам три раза:
из таблицы логарифмов берем значения тип, для которых gm =/и
gn -h. По таблице степеней находим значение g^nJrm} mod 255) (заметим,
что #огад =1).
1 3 5 15 17 51 85 255 26 46 114 150 161 248 19 53
95 225 56 72 216 115 149 164 247 2 6 10 30 34 102 170
229 52 92 228 55 89 235 38 106 190 217 112 144 171 230 49
83 245 4 12 20 60 68 204 79 209 104 184 211 110 178 205
76 212 103 169 224 59 77 215 98 166 241 8 24 40 120 136
131 158 185 208 107 189 220 127 129 152 179 206 73 219 118 154
181 196 87 249 16 48 80 240 11 29 39 105 187 214 97 163
254 25 43 125 135 146 173 236 47 113 147 174 233 32 96 160
251 22 58 78 210 109 183 194 93 231 50 86 250 21 63 65
195 94 226 61 71 201 64 192 91 237 44 116 156 191 218 117
159 186 213 100 172 239 42 126 130 157 188 223 122 142 137 128 I
155 182 193 88 232 35 101 175 234 37 111 177 200 67 197 84 1
252 31 33 99 165 244 7 9 27 45 119 153 176 203 70 202 1
69 207 74 222 121 139 134 145 168 227 62 66 198 81 243 14 I
18 54 90 238 41 123 141 140 143 138 133 148 167 242 13 23 I
57 75 221 124 132 151 162 253 28 36 108 180 199 82 246 1 1
Таблииа 19.2,
Степени
полинома
g(x) = х + 1
g является образующей группы F 8 \ {0}, если порядок элемента g равен 255. То есть степени
элемента g пробегают всю группу F 8 \ {0}.
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
0 25 1 50 2 26 198 75 199 27 104 51 238 223 3
100 4 224 14 52 141 129 239 76 113 8 200 248 105 28 193
125 194 29 181 249 185 39 106 77 228 166 114 154 201 9 120
101 47 138 5 33 15 225 36 18 240 130 69 53 147 218 142
150 143 219 189 54 208 206 148 19 92 210 241 64 70 131 56
102 221 253 48 191 6 139 98 179 37 226 152 34 136 145 16
126 110 72 195 163 182 30 66 58 107 40 84 250 133 61 186
43 121 10 21 155 159 94 202 78 212 172 229 243 115 167 87
175 88 168 80 244 234 214 116 79 174 233 213 231 230 173 232
44 215 117 122 235 22 11 245 89 203 95 176 156 169 81 160
127 12 246 111 23 196 73 236 216 67 31 45 164 118 123 183
204 187 62 90 251 96 177 134 59 82 161 108 170 85 41 157
151 178 135 144 97 190 220 252 188 149 207 205 55 63 91 209
83 57 132 60 65 162 109 71 20 42 158 93 86 242 211 171
68 17 146 217 35 32 46 137 180 124 184 38 119 153 227 165
103 74 237 222 197 49 254 24 13 99 140 128 192 247 112 7
Таблииа 19,3,
Логарифмы
по основанию
g(x) = х + 1
(например,
l°gg(x>2 = 25,
loggM255 = 7)
С помощью этого же механизма можно выполнять и деление поли-
номов в F28 \ {0}. А именно:
J _ _ gm(gnyx = gm n = g(w~',)mod255
h
Теперь поднимемся еще на одну ступеньку сложности и рассмот-
рим арифметику полиномов вида f(x) =fyc3 +fix2' +f\X +/0 с коэф-
фициентами fi из поля F 8, to есть сами коэффициенты - это тоже
полиномы. Каждый такой коэффициент можно представить в виде
четырехбайтового поля. Теперь еще интересней: сложение полино-
мов f(x) и g(x) по-прежнему выполняется путем побитового сложе-
ния коэффициентов по модулю 2, а вот произведение h(x) -f(x)g(x)
вычисляется в виде
h(x) = h^x6 + h$x5 + ЛдХ4 + hpc3 + h2x2 + h pc + ho,
400
Криптография на Си и C++ в действии
где коэффициенты hk := / 7; । gj, знак суммы означает сло-
жение © в поле F28.
Приводим полином h(x) по модулю полинома степени 4 и опять
> получаем полином степени 3 над полем F28.
В качестве такого полинома в Rijndael взят полином М(х) :=х4 + 1.
1 Поскольку V mod М(х) = х1 mod 4, вычет /i(x) mod М(х) можно вычис-
лить как
d(x) :=/W ® g(x) *•= b(x) mod М(х) = dyx3 + d2x2 + d\X + dQ,
где I
do = © a3 • bi © a2 • b2 © • b3,
di = ai • b0® aQ • bi ® a2 • b2® a2^ b^,
d2 = a2* bQ® сц • bi ® cio • b2® • b2i
d2 = • bo ® a2 • bi ® • b2 ® ao • b3.
Отсюда видно, что коэффициенты d^ являются результатом умн<
жения на матрицу в поле F28:
d2
d3
aQ a3 a2 ax
a\ a0 a3 a2
Cl2 6Zq
a3 a2 ax a0
bo
bi
b2
Ь3
Именно эта операция с фиксированным, обратимым по модули
М(х) полиномом а(х)'.= а^х3 + а2х2 + сцх + ао над полем IF 8, ПК
а0(х) = х, ai(x) = 1, а2(х) = 1 и а2(х) = х + 1, выполняется в так назы
ваемом преобразовании MixColumn - одном из основных компонен-
тов преобразования раунда в Rijndael.
19.2. Алгоритм Rijndael
Rijndael - это симметричный блочный алгоритм шифрования с пе-
ременной длиной блока и ключа. Длины блока и ключа могут при-
нимать значения 128, 192 и 256, причем в любой комбинации]
Варьируемое значение длины ключа составляет одно из достоинств!
стандарта AES, а вот «официальная» длина блока - только 128 бит.!
40
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
Каждый блок открытого текста зашифровывается несколько раз i
так называемых раундах (round) с помощью повторяющейся после
довательности различных функций. Число раундов зависит от ддинь
блока и ключа (см. таблицу 19.4).
Таблииа 19,4. Число раундов в алгоритме Длина ключа (в битах) Длина блока (в битах)
128 192 256
Rijndael 128 10 12 14
как функиия от длины блока 192 12 12 14
и ключа 256 14 14 14
Rijndael не относится к алгоритмам на сетях Файстеля, которые ха-
рактеризуются тем, что блок текста разбивается на левую и правую
половины, затем преобразование раунда применяется к одной
половине, результат складывается по модулю 2 с другой половиной,
после чего эти половины меняются местами. Самым известным
блочным алгоритмом из этой серии является DES. Rijndael, напро-
тив, состоит из отдельных уровней, каждый из которых по-своему
воздействует на блок в целом. Для зашифрования блока последова-
тельно выполняются следующие преобразования:
1. Первый раундовый ключ складывается с блоком по модулю 2 (XOR).
2. Выполняются Lr- 1 обычных раундов.
3. Выполняется завершающий раунд, в котором, в отличие от обычного,
отсутствует преобразование MixColumn.
Каждый обычный раунд на этапе 2 состоит из четырех отдельных
шагов, которые мы сейчас и изучим:
1. Подстановка. Каждый байт блока заменяется значением, которое
определяется 5-блоком.
2. Перестановка. Байты в блоке переставляются с помощью преобра-
зования ShiftRow.
3. Перемешивание. Выполняется преобразование MixColumn.
4. Сложение с раундовым ключом. Текущий раундовый ключ скла-
дывается с блоком по модулю 2.
14-1697
402
Криптография на Си и C++ в действии
Уровневые преобразования внутри одного раунда схематично изо-
бражены на рис. 19.1.
Подстановка
(S-блок)
ShiftRow
MixColumn
Сложение
с раундовым
ключом
Рисунок 19.1.
Уровни
преобразования
внутри одного
раунда алгоритма
Rijndael
Каждый уровень оказывает на каждый из блоков открытого текста
определенное воздействие.
1. Влияние ключа
Сложение текста с ключом до первого раунда и на последнем шаге
внутри каждого раунда влияет на каждый бит результата раунда.
В процессе зашифрования результат каждого шага в каждом бите
зависит от ключа.
2. Нелинейный уровень
Операция подстановки в S-блоке является нелинейной. Строение
S-блоков обеспечивает почти идеальную защиту от дифференци-
ального и линейного криптоанализа (см. [BiSh] и [NIST]).
3. Линейный уровень
Преобразования ShiftRow и MixColumn обеспечивают максимальное
перемешивание битов в блоке.
Далее в описании внутренних функций алгоритма Rijndael, через
Lb будем обозначать длину блока в четырехбайтовых словах, через
Lk - длину ключа пользователя в четырехбайтовых словах (то есть
Lb, Lk е {4, 6, 8}) и через Lr - число раундов (см. таблицу 19.4).
Открытый и зашифрованный тексты представлены в виде полей
байтов и являются соответственно входом и выходом алгоритма.
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
403
Блок открытого текста, обрабатываемый как поле т0, ..., ли4£ ь
представлен в виде двумерной структуры В (см. таблицу 19.5),
в которой байты открытого текста отсортированы в следующем
порядке:
/?2о ^0,0, т\ ^1,0» т2 ^2,0» т3 ^3,0» 1Щ ^0,Ь т5 ^1,1» •• •,
т.е. тп -> bij9
где i = п mod 4 и j = |_и/4J.
Таблииа 19.5. Представление k>Q,0 ^0,1 ^0,2 Ьо,з Ьо,4 Ьоль-1
блоков £>1,0 bl,2 £>1,3 £>1,4 ьщ-'
открытого текста ^2,0 ^2,1 ^2,2 ^2,3 Ь2,4 b2,Lb-y
Ьз,о Ьз,2 Ьз,з Ь3/4 bi.Lb-\
Доступ к структуре 8 в функциях алгоритма Rijndael осуществля-
ется по-разному, в зависимости от операции. S-блок оперирует с
битами, ShiftRow - со строками (Z?I>0, ...» b/^-i) структуры В,
а функции AddRoundKey и MixColumn - с четырехбайтовыми сло-
вами, обращаясь к столбцам b2j, b^J).
19.3. Вычисление ключа раунда
И для зашифрования, и для расшифрования требуется сгенериро-
вать Lr раундовых ключей, совокупность которых называется раз-
верткой ключа (key schedule). Развертка строится путем присоеди-
нения к секретному ключу пользователя рекурсивно получаемых
четырехбайтовых слов ki = (k^b k\^ k2>[, k^).
Первые Lk слов kQ, ..., развертки ключа - это сам секретный
ключ пользователя. Для Lke {4, 6} очередное четырехбайтовое
слово ki определяется как сумма по модулю 2 предыдущего слова
ki-i со словом ki_Lk. При i = 0 mod Lk перед операцией XOR нужно
применить функцию FLf(k9 /), которая включает в себя циклический
сдвиг к байтов влево (операция г(к)), подстановку S(r(k)) с исполь-
зованием S-блока алгоритма Rijndael (к этой операции мы еще вер-
немся) и сложение по модулю 2 с константой с (Lz/LjJ). Итоговое
уравнение функции F таково: FL (k, i) := S(r(k)) © c(L//lJ).
Константы c(j) задаются равенством c(j) := (rc(/), 0, 0, 0), где зна-
чения гс(/) определяются рекурсивно как элементы поля F^:
гс(1) := 1, гс(/) :=гс(/- 1) •х = х'"1. Или в виде численных значений:
гс(1) := ‘0Г, rc(/) := гс(/- 1) • ‘02’. Программно значение гс(/)
404
Криптография на Си и C++ в действии
реализуется (j - 1)-кратным рекурсивным вызовом упоминавшейся
выше функции xtime, с начальным значением аргумента, равным 1,
или более быстро - с использованием таблицы предвычислений
(см. таблицы 19.6 и 19.7).
Таблииа 19.6. 'ОТ '02' •04' '08' '10' '20' '40' '80' '1В' '36'
Константы rc(j) (в шестнадцати- '60 'D8' 'АВ' '4D' '9А' '2F' '5Е' 'ВС' '63' 'С6'
ричном виде) '97' '35' '6А' 'D4' 'ВЗ' '7D' 'FA' 'EF' 'С5 '91'
Таблииа 19.7. 00000001 00000010 00000100 00001000 00010000
Константы rc(j) (в двоичном 00100000 01000000 10000000 00011011 00110110
виде) 01101100 11011000 10101011 01001101 10011010
00101111 01011110 10111100 01100011 11000110
10010111 00110101 01101010 11010100 10110011
01111101 11111010 11101111 11000101 10010001
Для ключей длины 256 бит (то есть при Lk = 8) введена дополни-
тельная операция подстановки: при i = 4 mod Lk перед операцией
XOR значение к^ заменяется на S(^_i).
Таким образом, развертка ключей состоит из Lb • (Lr+ 1) четырехбай-
товых слов, включая и секретный ключ пользователя. На каждом
раунде i = 0, ..., Lr- 1 очередные Lb четырехбайтовых слова с ./
по kLb.(i+i) выбираются из развертки и используются в качестве ключа
раунда. Раундовые ключи рассматриваются, по аналогии с блоками
открытого текста, как двумерная структура (см. таблицу 19.8).
Таблииа 19.8. Представление ко,о ко а ко,2 ко,з кол
раундовых ключей к\ ,о к\а к\,2 к\,з куд
^2,0 ^2,1 ^2,2 ^2,3 к2л k2,Lb-y
^3,0 кза кз,2 кз,з кзд k3.Lb-y
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
405
Для ключей длины 128 бит процесс генерации ключа изображен на
рис. 19.2.
Секретный ключ
пользователя
Рисунок 19.2.
Диаграмма
раундовых
ключей
для Lk = 4
Пока не известны слабые ключи, использование которых неблаго-
приятно сказалось бы на стойкости алгоритма Rijndael.
19.4. S-блок
Блок подстановки, или S-блок алгоритма Rijndael показывает, ка-
ким значением следует заменять каждый байт блока текста на каж-
дом раунде. S-блок представляет собой список из 256 байтов. Сна-
чала каждый ненулевой байт рассматривается как элемент поля IF2s
и заменяется мультипликативно обратным (нулевые байты остаются
неизменными). Затем выполняется следующее аффинное преобра-
зование над полем F2 путем умножения на матрицу и сложения с
вектором (1 10 0 0 1 10):
’Уо~ ’1 0 0 0 1 1 1 Г Ч" т
11000111 Х| 1
У2 11100011 0
Уз 11110001 хз 0
+
У1 11111000 0
у5 01111100 xs 1
Уб 00111110 *6 1
_Ут_ 00011111 .хт - о
106
Криптография на Си и C++ в действии
Здесь через х0 и Уо обозначены младшие, а через х7 и у7 - старшие
биты в байте; вектор (1 10001 1 0) длины 8 соответствует шест-
надцатиричному числу ‘63’.
S-блок построен так, чтобы свести к минимуму чувствительность
алгоритма к дифференциальному и линейному методам криптоана-
лиза, а также к алгебраическим атакам. Последовательно применяя
приведенную выше процедуру к числам от 0 до 255, получаем таб-
лицу 19.9 (значения идут по строкам слева направо).
99 124 119 123 242 107 111 197 48 1 103 43 254 215 171 118
202 130 201 125 250 89 71 240 173 212 162 175 156 164 114 192
183 253 147 38 54 63 247 204 52 165 229 241 113 216 49 21
4 199 35 195 24 150 5 154 7 18 128 226 235 39 178 117
9 131 44 26 27 110 90 160 82 59 214 179 41 227 47 132
83 209 0 237 32 252 177 91 106 203 190 57 74 76 88 207
208 239 170 251 67 77 51 133 69 249 2 127 80 60 159 168
81 163 64 143 146 157 56 245 188 182 218 33 16 255 243 210
205 12 19 236 95 151 68 23 196 167 126 61 100 93 25 115
96 129 79 220 34 42 144 136 70 238 184 20 222 94 11 219
224 50 58 10 73 6 36 92 194 211 172 98 145 149 228 121
231 200 55 109 141 213 78 169 108 86 244 234 101 122 174 8
186 120 37 46 28 166 180 198 232 221 116 31 75 189 139 138
112 62 181 102 72 3 246 14 97 53 87 185 134 193 29 158
225 248 152 17 105 217 142 148 155 30 135 233 206 85 40 223
140 161 137 13 191 230 66 104 65 153 45 15 176 84 187 22
Таблииа 19.9.
Значения S-блока
При расшифровании порядок действий меняется на противопо-
ложный. Сначала выполняется обратное аффинное преобразование,
затем мультипликативное обращение в поле F28. Обратный S-блок
приведен в таблице 19.10.
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
407
Таблииа 19,10.
Значения
обратного S-блока
82 9 106 213 48 54 165 56 191 64 163 158 129 243 215 251
124 227 57 130 155 47 255 135 52 142 67 68 196 222 233 203
84 123 148 50 166 194 35 61 238 76 149 11 66 250 195 78
8 46 161 102 40 217 36 178 118 91 162 73 109 139 209 37
114 248 246 100 134 104 152 22 212 164 92 204 93 101 182 146
108 112 72 80 253 237 185 218 94 21 70 87 167 141 157 132
144 216 171 0 140 188 211 10 247 228 88 5 184 179 69 6
208 44 30 143 202 63 15 2 193 175 189 3 1 19 138 107
58 145 17 65 79 103 220 234 151 242 207 206 240 180 230 115
150 172 116 34 231 173 53 133 226 249 55 232 28 117 223 110
71 241 26 113 29 41 197 137 111 183 98 14 170 24 190 27
252 86 62 75 198 210 121 32 154 219 192 254 120 205 90 244
31 221 168 51 136 7 199 49 177 18 16 89 39 128 236 95
96 81 127 169 25 181 74 13 45 229 122 159 147 201 156 239
160 224 59 77 174 42 245 176 200 235 187 60 131 83 153 97
23 43 4 126 186 119 214 38 225 105 20 99 85 33 12 125
19.5. Преобразование ShiftRow
Следующий шаг раунда - перестановка байтов в блоке. Порядок
байтов меняется в строке ^,2, • ••> структуры В в со-
ответствии с таблицами 19.11-19.13.
Таблииа 19.11. Опера и и я ShiftRow лля До операции ShiftRow После операции ShiftRow
0 4 8 12
0 4 8 12
блоков длины 128 бит (Lb = 4) 1 5 9 13 5 9 13 1
2 6 10 14 10 14 2 6
3 7 11 15 15 3 7 11
408
Криптография на Си и C++ в действии
Таблииа 19.12. До операции ShiftRow После операции ShiftRow
Операиия ShiftRow для 0 4 8 12 16 20 0 4 8 12 16 20
блоков длины 1 5 9 13 17 21 5 9 13 17 21 1
192 бита (Lb = 6) 2 6 10 14 18 22 10 14 18 22 2 6
3 7 11 15 19 23 15 19 23 3 7 11
Таблииа 19,13.
Операиия
ShiftRow для
блоков длины
256 бит (Lb = 8)
До операиии ShiftRow После операиии ShiftRow
0 4 8 12 16 20 24 28 0 4 8 12 16 20 24 28
1 5 9 13 17 21 25 29 5 9 13 17 21 25 29 1
2 6 10 14 18 22 26 30 14 18 22 26 30 2 6 10
3 7 11 15 19 23 27 31 19 23 27 31 3 7 11 15
Все нулевые строки остаются без изменений. В строках /= 1, 2, 3
байты циклически сдвигаются влево на cL/u позиций: с позиции с
номером j на позицию с номером j - mod Lb, где значение
определяется по таблице 19.14.
Таблииа 19.14.
Размер сдвига
строк в операиии
ShiftRow
Lb
4 1 2 3
6 1 2 3
8 1 3 4
При обратном преобразовании позиция с номером j в строках
i = 1, 2, 3 сдвигается на позицию с номером j + cLjmod Lb.
19.6. Преобразование MixColumn
После того как выполнена последняя построчная перестановка, на
следующем шаге каждый столбец (Z?zj) блока текста, где i = 0, 3,
7 = 0, ..., Lb, представляется в виде полинома над полем F28 и умно-
жается на фиксированный полином а(х) := а3х3 + а2х2 + арс + До с
коэффициентами я0(*) =•*» aiM = 1» а2(х) = 1, а3(х) = х+ 1. Затем
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
409
вычисляется остаток от деления полученного произведения на мо-
дуль М(х) :=х4 + 1. Таким образом, каждый байт столбца взаимо-
действует со всеми остальными байтами столбца. При построковом
преобразовании ShiftRow на каждом раунде байты взаимодействуют
друг с другом в других комбинациях. То есть эти две операции
дают сильное перемешивание.
Мы уже видели (см. стр. 400), как этот шаг можно свести к умно- жению на матрицу:
__ _
bo,j '02' '03' '0Г '0Г“ bo,j
bU '0Г '02' '03' '0Г bU
b2J •or 'ОГ '02' '03' b2J
hi. _'03' ’0Г ’0Г '02' hi.
А Умножение на ‘02’ (соответственно на х) мы уже реализовали в
виде функции xtime. Умножение на ‘03’ (соответственно на х+ 1)
• тоже сделано по аналогии (см. стр. 397).
* Для обращения преобразования MixColumn умножаем каждый стол-
бец (/?1х7) блока текста на полином г(х) := г3х3 + г2х2 + гхх + г0 с коэф-
фициентами г0(х) = х3 + х2 + х, Г1(х)=х3+1, г2(х)=х3 + х2 + 1,
г3(х)=х3 + х+1 и приводим результат по модулю Л/(х):=х4+1.
ж Соответствующая матрица имеет вид:
'0Е' 'OB’ '0D' ’09’
'09' ’0Е’ 'OB’ '0D'
'0D' '09' ’0Е’ '0В'
'OB' 0D' '09' '0Е'
19.7. Сложение с ключом раунда
На последнем шаге цикла раундовый ключ складывается по моду-
лю 2 с блоком текста:
Ьц, b2J, b3j) <— (bOj, bij, b2j, b3j) Ф (koj, kij, k2J, k3J),
гдеу = 0, ...,Lb- 1.
Jill | *
19.8. Полная процедура зашифрования блока
Зашифрование по алгоритму Rijndael реализуется в виде следую-
щего псевдокода (см. [DaRi], пп. 4.2-4.3). Аргументы обрабатыва-
ются как указатели на поля байтов или четырехбайтовых слов.
Интерпретация полей, переменных и функций дана в таблицах
19.15-19.17.
410
Криптография на Си и C++ в действии
Таблииа 19.15, . Интерпретаиия переменных Переменные Интерпретация
Nk Nb Nr Длина Lk секретного ключа пользователя в четырех- байтовых словах Длина Lb блока в четырехбайтовых словах Число раундов Lr в соответствии с таблицами выше
Таблииа 19.16, Интерпретаиия полей Таблииа 19.17. Интерпретаиия I функиий г Переменные Размер в байтах Интерпретация
CipherKey ExpandedKey Rcon State RoundKey 4*Nk 4*Nb *(Nr+1) T4*Nb *(Nr+1 )/Nk"| 4*Nb 4*Nb Секретный ключ пользователя Поле четырехбайтовых слов под развертку ключа Поле четырехбайтовых слов под константы c(j) := (rc(j), 0, 0, 0) Поле ввода открытого текста и вывода зашифрованного текста Раундовый ключ, фрагмент ExpandedKey
Функция Интерпретация
KeyExpansion Rot Byte ByteSub Round FinalRound ShiftRow MixColumn AddRoundKey Генерация раундового ключа Сдвиг четырехбайтового слова влево на 1 байт: (abed) -> (beda) Подстановка в S-блоке всех байтов поля М Обычный раунд Н Последний раунд без преобразования MixColumn Преобразование ShiftRow Преобразование MixColumn Сложение с ключом раунда
Генерация ключа при Lk < 8:
KeyExpansion (byte CipherKey, word ExpandedKey)
{
for (i = 0; i < Nk; i++)
ExpandedKey[i] = (CipherKey[4*i], CipherKey[4*i + 1],
CipherKey[4*i + 2], CipherKey[4*i + 3]);
411
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
for (i = Nk; i < Nb * (Nr + 1); i++)
{
temp = ExpandedKey[i - 1];
if (i % Nk == 0)
temp = ByteSub (RotByte (temp))л Rcon[i/Nk];
ExpandedKey[i] = ExpandedKey[i - Nk] л temp;
}
}
Генерация ключа при Lk = 8:
KeyExpansion (byte CipherKey, word ExpandedKey)
{
for (i = 0; i < Nk; i++)
ExpandedKey[i] = (CipherKey[4*i], CipherKey[4*i + 1],
CipherKey[4*i + 2], CipherKey[4*i + 3]);
for (i = Nk; i < Nb * (Nr + 1); i++)
{
temp = ExpandedKey[i - 1];
if (i % Nk == 0)
temp = ByteSub (RotByte (temp))л Rcon[i/Nk];
else if (i % Nk == 4)
temp = ByteSub (temp);
ExpandedKeyfi] = ExpandedKey[i - Nk]л temp;
}
}
Раундовые функции:
Round (word State, word RoundKey)
{
ByteSub (State);
ShiftRow (State);
MixColumn (State);
AddRoundKey (State, RoundKey)
412
Криптография на Си и C++ в действии
FinalRound (word State, word RoundKey)
{
ByteSub (State);
ShiftRow (State);
AddRoundKey (State, RoundKey)
}
Полная процедура зашифрования блока текста:
Rijndael (byte State, byte CipherKey)
{
KeyExpansion (CipherKey, ExpandedKey);
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++)
Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}
Раундовый ключ можно заготовить и вне функции Rijndael, а
вместо ключа пользователя CipherKey использовать развертку
ключей ExpandedKey. Преимущества такого варианта очевидны,
когда для зашифрования текста длиной более одного блока нужно
несколько раз вызывать функцию Rijndael с одним и тем же ключом
пользователя.
Rijndael (byte State, byte ExpandedKey)
{
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++)
Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}
Для 32-разрядных процессоров раундовое преобразование лучше
вычислять заранее и хранить результаты в виде таблиц. Заменяя опе-
рации перестановки и умножения на матрицу обращением к таблице,
мы значительно сокращаем время работы как при зашифровании,
так и (как будет видно позже) при расшифровании. С помощью
таблиц вида
I
ГЛАВА 19. Rijndael: наследник стандарта шифрования данных
413
T0[w]:=
ВД :=
’S(w) • ’02’
S(w)
5(w)
_S(w) • 'O3'_
SM
S(w) • ’03*
5(w) • ’02’
5(w)
5(w) • ’03’
5(w) • '02*
S(w)
S(w)
ВД:=
5(w)
5(w)
S(w) • ’03’
S(w) • ’02’
каждая из которых содержит по 256 четырехбайтовых слов (здесь
w = 0, ..., 255; 5(w) - S-блок подстановки), преобразование блока
b = bij, b2j, b3j),j = O, ...,Lb- 1, можно быстро выполнить как
(^oj, bXj, b2j, b3j) <r- Tot^oj] ® Tj[^1Д1 j)] ® T2[Z?2//(2j-)] ® Т3[£?з ^(3j)] ф
где d(i, j) :=j + cL/ri mod Lb (cm. ShiftRow, таблица 19.14) и
kj= j» k3j) ~ J-й столбец раундового ключа.
Вывод этого результата см. в [DaRi], п. 5.2.1. На последнем раунде
преобразование MixColumn не выполняется, поэтому результат по-
лучается как
bj •= (bOj, b2j, b3J) <— (S(Z?oj), 5(^ix/(ij))> ^(^2,fZ(2j)), ^(Ьздзт))) © kj.
Конечно, можно воспользоваться таблицей из 256 четырехбайто-
вых слов, тогда
bj <г- T0[Z?0j] © r(To[Z?j,j(i J © r(T0[^2,r/(2j)] © КТоС^з.^з^]))) © kj,
где r(a, b,c,d) = (d, a, b, с) - циклический сдвиг вправо на один
байт. Для приложений с ограниченной памятью этот вариант чрез-
вычайно удобен, немного увеличится лишь время вычислений,
необходимое для выполнения трех сдвигов.
19.9. Расшифрование
г При расшифровании алгоритмом Rijndael процесс зашифрования
выполняется в обратном порядке с обратными преобразованиями.
Мы уже рассматривали преобразования, обратные к ByteSub,
ShiftRow и MixColumn; ниже они представлены в псевдокодах функ-
циями InvByteSub, InvShiftRow и InvMixColumn. Обратный S-блок,
размер сдвига для обращения преобразования ShiftRow и обратная
матрица для обращения преобразования MixColumn приведены на
стр. 407-408. Вот эти обратные функции:
InvFinalRound (word State, word RoundKey)
Криптография на Си и C++ в действии
AddRoundKey (State, RoundKey);
ГЛ
InvShiftRow (State);
InvByteSub (State);
}
InvRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvMixColumn (State);
InvShiftRow (State);
InvByteSub (State);
}
Полная процедура расшифрования выглядит следующим образом:
InvRijndael (byte State, byte CipherKey)
{ I
KeyExpansion (CipherKey, ExpandedKey); H
InvFinalRound (State, ExpandedKey + Nb*Nr); H
for (i = Nr - 1; i > 0; i-) I
InvRound (State, ExpandedKey + Nb*i); И
AddRoundKey (State, ExpandedKey);
}
Алгебраическая структура алгоритма Rijndael позволяет упорядо-
чить преобразования зашифрования так, что и для них можно
будет использовать таблицы. Заметим, что подстановка S и преоб-
разование ShiftRow коммутируют, поэтому внутри одного раунда их
можно поменять местами. Благодаря свойству гомоморфизма
Дх + у) =flx) + fiy) линейных преобразований, операции InvMixColumn
и сложение с раундовым ключом можно тоже поменять местами.
В пределах одного раунда это выглядит так:
InvFinalRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvByteSub (State);
InvShiftRow (State);
}
ABA 19. Rijndael: наследник стандарта шифрования данных
InvRound (word State, word RoundKey)
415
{
InvMixColumn (State);
AddRoundKey (State, InvMixColumn (RoundKey));
InvByteSub (State);
InvShiftRow (State);
}
Если порядок функций не менять, то их можно переопределить:
AddRoundKey (State, RoundKey);
InvRound (word State, word RoundKey)
{
InvByteSub (State);
InvShiftRow (State);
InvMixColumn (State);
AddRoundKey (State, InvMixColumn (RoundKey));
}
InvFinalRound (word State, word RoundKey)
{
InvByteSub (State);
InvShiftRow (State);
AddRoundKey (State, RoundKey);
}
Отсюда получаем структуру, аналогичную зашифрованию. Из сооб-
ражений эффективности в процедуре lnvRound() отложим примене-
ние функции InvMixColumn к раундовому ключу до вычисления
развертки, в которой первый и последний раундовые ключи из
InvMixColumn оставим без изменений. «Обратные» раундовые ключи
генерируются процедурой
InvKeyExpansion (byte CipherKey, word InvEpandedKey)
{
KeyExpansion (CipherKey, InvExpandedKey);
for (i = 1; i < Nr; i++)
И 6
Криптография на Си и C++ в действии
ГЛ
InvMixColumn (InvExpandedKey + Nb*i);
}
Теперь полная процедура расшифрования выглядит так:
InvRijndael (byte State, byte CipherKey)
{
InvKeyExpansion (CipherKey, InvExpandedKey);
AddRoundKey (State, InvExpandedKey + Nb*Nr);
for (i = Nr - 1; i > 0; i--)
InvRound (State, InvExpandedKey + Nb*i);
InvFinalRound (State, InvExpandedKey);
}
По аналогии с зашифрованием можно и для расшифрования соста-
вить таблицы предвычислений. С помощью
T0-'[w]:= ’S-'(M') • '0E'" S-'(w)*’0D* /'(и'Л’ОВ’ , Tf'Evv]- S_1(iv) •'OB' 5~'(w)»'0E' S''(w)*’O9* /-1(w) • '0D'
3~‘(w) •'0D'~ У’Мош’
T2-*M:= 5'‘(w)«’0E' . Тз-'М^ S"l(w)»'0D' S”l(w) •'OB'
S~l(w) • '09'_ -^‘(^•'ОЕ'
(где w — 0, 255; У1^) - обратный S-блок подстановки) получа-
ем результат обратного раундового преобразования блока
b = (bQxh bu, b2j, b3J)J = 0, 1:
bj To-'[Z>oj] © ТГ1 [/>,.,r>(1J Ф TfVwl Ф T3‘WoJ © к-',
где :=j - cL^ mod Lb (см. стр. 408) и k[x - j-и столбец «об-
ратного» раундового ключа.
Здесь на последнем раунде тоже не выполняется преобразование
MixColumn, и результатом последнего раунда будет
bj <- (S~l(boj), S-'ib^r^j), S-'tb^aj)), S-'ib^r^ © k-'
где; = 0, ...,Lb- 1.
ABA 19. Rijndael: наследник стандарта шифрования данных
417
Для экономии памяти для расшифрования также можно составить
таблицу всего из 256 четырехбайтовых слов, в которой
bj <- То’1 [М Ф Ф Г(ТО-‘[&2,,Г1(2Л] Ф
®r(T0’WW)))©V,
где r(a, b,c,d) = (d, а, b, с) - циклический сдвиг вправо на один байт.
Дальнейшие подробности описания, вопросов безопасности, ре-
зультатов криптоанализа, вычислительных аспектов, а также теку-
щую информацию об AES и Rijndael читатель найдет в источниках,
указанных по тексту этой главы, а также на Интернет-сайте NIST и
страничке Винсента Раймана, которые также содержат множество
полезных ссылок:
http://csrc.nist.gov/encryption/aes/aes_home.htm
http://www.esat.kuleuven.ac.be/~rijmen/rijndael
На прилагаемом к книге компакт-диске содержатся три реализации
алгоритма Rijndael, рекомендуемые читателю для лучшего понима-
ния процедуры и для дальнейших исследований. Программами
предусмотрены функции шифрования в режимах обратной связи
по шифртексту (Cipher Feedback Mode, CFB) и обратной связи по
выходу (Output Feedback Mode, OFB). Автор хочет еще раз побла-
годарить всех, кто предоставил исходные тексты программ, вклю-
ченные в эту книгу. Исходные файлы расположены в следующих
каталогах:
Каталог Реализация
rijndael\c_ref Эталонная реализация на С с набором тестов (авторы - Vincent Rijmen и Paulo Barreto)
rijndael\c_opt Оптимизированная реализация на С (авторы - Vincent Rijmen, Antoon Bosselaers и Paulo Barreto)
rijndael\cpp_opt Оптимизированная реализация на C++ (автор - Brian Gladman)
Часть III
С':
У-
Г
i!V Приложения
e^7<7-
ИГ
v 7 \
’7
&’•. < J- < и
V
7 . , 7' j.- , < •
i
Гарри с удивлением наблюдал, как Думбльдор
; ! : вставляет в замки третий, четвертый, пятый и
шестой ключи, и всякий раз в сундуке обнару-
*... ’ живается разное содержимое.
< ‘ Джоан К. Роулинг,
. . Гарри Поттер и Огненная чаша
Ьс .V.
7>.
7UN Y. й. 7
chod
vmtr i с
ПРИЛОЖЕНИЕ A.
Каталог функций на С
А.1 Ввод/вывод, присваивание,
преобразования, сравнения
void cpyj (CLINT dest l, CLINT srcj); Присваивание значения srcj переменной destl
void fswapj (CLINT aj, CLINT b_l); Перестановка aj и b_l
int equj (CLINT aj, CLINT b_l); Проверка равенства значений aj и bj
int cmpj (CLINT a_l, CLINT bj); Сравнение размеров переменных aj и b_l
void u2clintj (CLINT numj, USHORT ul); Преобразование типа USHORT в тип CLINT
void ul2clintj (CLINT numj, ULONG ul); Преобразование типа ULONG в тип CLINT
UCHAR* clint2bytej (CLINT nJ, int *len); Преобразование типа CLINT в вектор байтов (согласно IEEE, Р1363, 5.5.1)
int byte2clintj (CLINT nJ, char *bytes, int len); Преобразование вектора байтов в тип CLINT (согласно IEEE, Р1363, 5.5.1)
char* xclint2strj (CLINT nJ, USHORT base, int showbase); Преобразование типа CLINT в строку символов в системе счисления с основанием base, с префиксом или без него
int str2clintj (CLINT nJ, char *N, USHORT b); Преобразование строки символов в системе счисления с основанием b в тип CLINT
clint * setmaxJ(CLINT nJ); Присвоение целому числу nJ типа CLINT максимального значения Nmax
unsigned int vcheckj (CLINT nJ); Проверка правильности формата CLINT
char* verstrj (); p... Версия библиотеки FLINT/C в виде строки символов; идентификатор 'а' указывает, поддерживается ли Ассемблер, идентификатор 's' - безопасный режим библиотеки FLINT/C
422
Криптография на Си и C++ в действии
А.2 Основные арифметические операции
int addj (CLINT aj, CLINT b_l, CLINT s_l) Сложение: слагаемые a J и bj, сумма sj
int uaddj (CLINT aj, USHORT b, CLINT sj) Смешанное сложение: слагаемые a l и b, сумма sj
int incj (CLINT aj) Увеличение a_l на единицу
int subj (CLINT a J, CLINT bj, CLINT sj) Вычитание: уменьшаемое aj, вычитаемое bj, разность sj
int usubj (CLINT aj, USHORT b, CLINT sj) Смешанное вычитание: уменьшаемое aj, вычитаемое Ь, разность sj
int dec J (CLINT a J) Уменьшение а_1 на единицу
int mulj (CLINT aj, CLINT bj, CLINT pj) int umulj (CLINT aj, USHORT b, CLINT pj) int sqrj (CLINT aj, CLINT pj) int divj (CLINT aj, CLINT bj, CLINT qj, CLINT rj) int udivj (CLINT aj, USHORT b, CLINT qj, CLINT rj) Умножение: сомножители а_1 и bj, произведение pj Смешанное умножение: сомножители а_1 и Ь, произведение р_1 Возведение а_1 в квадрат, результат pj Деление с остатком: делимое а_1, делитель Ь_1, частное qj, остаток г_1 Смешанное деление с остатком: делимое а_1, делитель Ь, частное qj, остаток г 1
А.З Модульная арифметика
int modj (CLINT dj, CLINT nJ, CLINT rj); USHORT umodj (CLINT dj, USHORT n); int mod2J (CLINT dj, ULONG k, CLINT rj); int mequj (CLINT aj, CLINT bj, CLINT mJ); int maddj (CLINT aj, CLINT bj, CLINT cj, CLINT mJ); Вычет dJ по модулю nJ, результат rj Вычет d_l по модулю n - Вычет d J по модулю 2k Проверка сравнимости aj и b_l no модулю mJ Модульное сложение: сложение aj и b_l по модулю mJ, результат с_1
Приложение А
423
int
umaddj (CLINT aj, USHORT b,
CLINT cj, CLINT mJ);
int
msubj (CLINT aj, CLINT bj, CLINT cj, CLINT mJ);
int
umsubj (CLINT aj, USHORT b,
CLINT cj, CLINT mJ);
int
mmulj (CLINT aj, CLINT bj, CLINT cj, CLINT mJ);
void
mulmonj (CLINT aj, CLINT bj, CLINT nJ,
USHORT nprime,
USHORT logB_r, CLINT pj);
void
sqrmonj (CLINT aj, CLINT nJ, USHORT nprime,
USHORT logB_r, CLINT pj);
int
ummulj (CLINT aj, USHORT b,
CLINT pj, CLINT mJ);
int
msqrj (CLINT aj, CLINT cj, CLINT mJ);
int
mexp5j (CLINT basj, CLINT expj,
CLINT pj, CLINT mJ);
int
mexpkj (CLINT basj, CLINT expj,
CLINT pj, CLINT mJ);
int
mexp5mj (CLINT basj, CLINT expj,
CLINT pj, CLINT mJ);
int
mexpkmj (CLINT basj, CLINT expj,
CLINT pj, CLINT mJ);
int
umexpj (CLINT basj, USHORT e,
CLINT pj, CLINT mJ);
int
umexpmj (CLINT basj, USHORT e,
CLINT pj, CLINT mJ);
int
wmexpj (USHORT bas, CLINT ej,
CLINT pj, CLINT mJ);
Смешанное модульное сложение:
сложение aJ и b по модулю mJ,
результат с J
Модульное вычитание: разность aj
и bj по модулю mJ, результат с_1
Смешанное модульное вычитание:
разность aj и b по модулю mJ,
результат с J
Модульное умножение: умножение aj
на Ь_1 по модулю mJ, результат с_1
Модульное умножение aj на bj
по модулю nJ, произведение р_1
(метод Монтгомери,
glogB_r-1 < n J < fllogB.r)
Модульное возведение а_1 в квадрат
по модулю nJ, результат р_1 (метод
Монтгомери, 5logB-r"1 < nJ < 5logB-r)
Смешанное модульное умножение а_1
на b по модулю mJ, произведение pj
Модульное возведение aj в квадрат
по модулю mJ, результат с_1
Модульное возведение в степень,
25-арный метод
Модульное возведение в степень,
2*-арный метод, выделение
динамической памяти через malloc()
Возведение в степень по Монтгомери,
25- арный метод, нечетный модуль
Возведение в степень по Монтгомери,
2к-арный метод с параметром к,
нечетный модуль, оптимальное значение
для к определяется автоматически
Модульное возведение в степень,
показатель типа USHORT
Возведение в степень по Монтгомери,
нечетный модуль, показатель типа
USHORT
Модульное возведение в степень,
основание типа USHORT
424
int
wmexpmj (USHORT bas, CLINT e_J,
CLINT p_l, CLINT mJ);
int
mexp2j (CLINT basj, USHORT e,
CLINT pj, CLINT mJ);
int
mexpj (CLINT basj, CLINT ej,
CLINT pj, CLINT mJ);
Криптография на Си и C++ в действии
Возведение в степень по Монтгомери,
нечетный модуль, основание типа
USHORT
Модульное возведение в степень,
показатель е - степень числа 2
Модульное возведение в степень; если
модуль нечетный, автоматически
вызывается функция mexpkmj(), в
противном случае - функция mexpkjQ
А.4 Битовые операиии
int
setbitj (CLINT aj, unsigned int pos)
int
testbitj (CLINT aj, unsigned int pos)
int
clearbitj (CLINT aj, unsigned int pos)
void
and J (CLINT aj, CLINT bj, CLINT cj)
void
orj (CLINT aj, CLINT bj, CLINT cj)
void
xorj (CLINT aj, CLINT bj, CLINT cj)
int
shrj (CLINT aj)
int
shlj (CLINT aj)
int
shiftj (CLINT aj, long int noofbits)
Проверка и установка бита в позиции
pos в числе а_1
Проверка бита на позиции pos
в числе aj
Проверка и очистка бита на позиции
pos в числе а_1
Побитовая операция AND aj и bj,
результат с_1
Побитовая операиия OR aj и bj,
результат с J
Побитовое сложение по модулю 2
(XOR) а_1 и Ь_1, результат с_1
Сдвиг aj на один бит влево
Сдвиг aj на один бит вправо
Сдвиг aj на noofbits битов
влево/в право
А.5 Теоретико-числовые функции
unsigned
issqrj (CLINT aj, CLINT bj)
unsigned
irootj (CLINT aj, CLINT bj)
Проверка того, является ли aj полным
квадратом. Если да, то результат bj "
квадратный корень d
Нелая часть квадратного корня из aJB
результат Ь_1 В
Приложение А
425
void
gcdj (CLINT aj, CLINT bj, CLINT gj)
void
xgcdj (CLINT aj, CLINT bj, CLINT gj, CLINT u_l,
int *sign_u, CLINT v_l, int *sign_v)
void
invj (CLINT aj, CLINT n_J, CLINT gj, CLINT ij)
void
IcmJ (CLINT aj, CLINT bj, CLINT vj)
int
chinremj (unsigned noofeq, clint** koeffj, CLINT x_J)
int
jacobij (CLINT aj, CLINT bj)
int
prootj (CLINT aj, CLINT p_l, CLINT x_l)
int
root J (CLINT aj, CLINT p_I, CLINT q_l, CLINT xj)
Int
primrootj (CLINT xj, unsigned noofprimes,
clint** primesj)
USHORT
sievej (CLINT aj, unsigned noofsmallprimes)
int
primej (CLINT nJ, unsigned noofsmallprimes,
unsigned iterations)
Наибольший обший делитель чисел aj
и bj, результат gj
Наибольший обший делитель чисел
aj и Ь_1 и его представление
в виде линейной комбинации
с коэффициентами uj и vj, знаки
коэффициентов sign_u и sign_v
Наибольший обший делитель чисел
а_1 и nJ, а также обратное значение
к a J mod nJ
наименьшее обшее кратное чисел а_1
и bj, результат vj
Решение системы линейных
сравнений, результат х_1
Символ Лежандра (Якоби) aj по Ь_1
Квадратный корень из aj mod pj,
результат х J
Квадратный корень из aj mod pj*qj,
результат х J
Определение первообразного корня
по модулю п, результат х_1
Метод пробного деления; деление
числа а_1 на маленькие простые числа
Сочетание проверки на простоту
Миллера - Рабина с методом
пробного деления для числа nJ
А.6 Генерация псевдослучайных чисел
clint* Генератор случайных 64-разрядных
rand64j(void) чисел
void Линейный конгруэнтный генератор
rand J (CLINT rj, int 1) случайных чисел типа CLINT длины 1
UCHAR Генератор случайных чисел типа
ucrand64j (void) UCHAR
USHORT Генератор случайных чисел типа
usrand64J (void) USHORT
ULONG Генератор случайных чисел типа
ulrand64j (void) ULONG
426 Криптография на Си и C++ в действии
clint* seed64_l (CLINT seedj) clint* ulseed64j (ULONG seed) Инициализация функции rand64J() значением типа CLINT Инициализация функции rand64J() значением типа ULONG
int randbitj (void) void randBBSJ (CLINT rj, int 1) 1 - UCHAR ucrandBBSJ (void) Генератор BBS Генерация с помошью BBS случайного числа типа CLINT длины 1 бит Генерация с помощью BBS случайного числа типа UCHAR
USHORT usrandBBSJ (void) ULONG ulrandBBSJ (void) void seedBBSJ (CLINT seedj) void ulseedBBSJ (ULONG seed) Генерация с помощью BBS случайного числа типа USHORT Генерация с помощью BBS случайного числа типа ULONG Инициализация функции randbitjQ значением типа CLINT Инициализация функции randbitjf) значением типа ULONG
А.7 Управление регистрами
void set_noofregsj (unsigned int nregs) int create_reg_l (void) clint* get_regj (unsigned int reg) Установление числа регистров Создание банка регистров типа CLINT Создание ссылки на регистр reg банка регистров
int purge_regj (unsigned int int purgeall_regj (void) void free_regj (void) Очистка регистра банка регистров путем затирания Очистка всех регистров банка регистров путем затирания Очистка всех регистров банка регистров путем затирания с последующим освобождением памяти
clint* createj (void) Генерация регистра типа CLINT
void purgej (CLINT nJ) void free J (CLINT nJ); Очистка объекта типа CLINT путем затирания Очистка регистра путем затирания последующим освобождением памя'^И
ПРИЛОЖЕНИЕ В.
Каталог функций С++
.... ......................И.... """в
В.1 Ввол/вывод, преобразования, сравнения:
функции-члены класса
LINT (void); Конструктор 1: создается неинициали- зированный объект класса LINT
LINT (const char* const str, const int base); Конструктор 2: объект класса LINT создается из представления строкой разрядов в системе счисления с основанием base
LINT (const UCHAR* const byte, const int len); Конструктор 3: объект класса LINT создается из вектора байтов с разрядами в системе счисления с основанием 28согласно IEEE Р1363, младшие разряды слева
LINT (const char* const str); Конструктор 4: объект класса LINT создается из строки ASCII-символов, синтаксис как в языке С
LINT (const LINT&); Конструктор 5: объект класса LINT создается из объекта класса LINT (конструктор копирования)
LINT (const signed int); Конструктор 6: объект класса LINT создается из целого числа типа int
LINT (const signed long); Конструктор 7: объект класса LINT создается из целого числа типа long
i LINT (const unsigned char); Конструктор 8: объект класса LINT создается из целого числа типа unsigned char
LINT (const USHORT); Конструктор 9: объект класса LINT создается из целого числа типа unsigned short
LINT (const unsigned int); Конструктор 10: объект класса LINT создается из целого числа типа unsigned int
LINT (const unsigned long); Конструктор 11: объект класса LINT создается из целого числа типа unsigned long
lint (const clint); Конструктор 12: объект класса LINT создается из целого числа типа CLINT
428
Криптография на Си и C++ в действии
const LINT& operator = (const LINT& b); inline void disp (char* str); inline char* hexstr (void) const; inline char* decstr (void) const; inline char* octstr (void) const; inline char* binstr (void) const; char* Iint2str (const USHORT base, const int showbase = 0) const; Присваивание a <— b Отображение целого числа класса LINT (сначала выводится str) Представление целого числа класса LINT в шестнадцатиричном виде Представление целого числа класса LINT в десятичном виде Представление целого числа класса LINT в восьмеричном виде Представление целого числа класса LINT в двоичном виде Представление целого числа класса LINT в виде строки символов в системе счисления с основанием base с префиксом Ох (или 0b) при showbase > 0
UCHAR* Iint2byte (int* len) const; Преобразование целого числа класса LINT в вектор байтов, результат len - длина вектора, согласно IEEE Р1363, младшие разряды слева
LINT& fswap (LINT& b); void purge (void); static long flags (ostream& s); static long flags (void); static long setf (ostream& s, long int flags); Замена неявного аргумента а аргументом b Очистка неявного аргумента а путем затирания Чтение статической переменной состояния LINT потока ostream s I Чтение статической переменной 1 состояния LINT потока ostream cout 1 Установка битов переменной 1 состояния LINT для потока ostream s, 1 заданных в flags 1
static long setf (long int flags); Установка битов переменной состоя-| ния LINT для потока к ostream cout, заданных в flags
static long unsetf (ostream& s, long int flags); static long unsetf (long int flags); Очистка битов переменной состояния LINT потока ostream s, заданных в flags Очитка битов переменной состояния । LINT потока ostream cout, заданных I в flags 1
static long restoref (ostream& s, long int flags); static long restoref (long int flags); Сброс переменной состояния LINT I потока ostream s к значению flags 1 Сброс переменной состояния класса LINT, относящейся к ostream cout 1 к значению flags 1
Приложение В
429
В.2 Ввод/вывод, преобразования, сравнения:
функции-друзья класса
const int
operator == (const LINT& a, const LINT& b);
const int
operator != (const LINT& a, const LINT& b);
const int
operator < (const LINT& a, const LINT& b);
const int
operator > (const LINT& a, const LINT& b);
const int
operator <= (const LINT& a, const LINT& b);
const int
operator >= (const LINT& a, const LINT& b);
void
fswap (LINT& a, LINT& b);
void
purge (LINT& a);
char*
Iint2str (const LINT& a, const USHORT base,
const int showbase);
UCHAR*
Iint2byte (const LINT& a, int* len);
ostream&
LintHex (ostream& s);
ostream&
LintDec (ostream& s);
ostream&
LintOct (ostream& s);
ostream&
LintBin (ostream& s);
ostream&
LintUpr (ostream& s);
Проверка равенства a == b
Проверка того, что a != b
Проверка неравенства a < b
Проверка неравенства a > b
Проверка неравенства a <= b
Проверка неравенства a >= b
Перестановка а и b
Очистка путем затирания
Представление а в виде строки
символов в системе счисления
с основанием base с префиксом
Ох (или 0b) при showbase > 0
Преобразование а в вектор байтов,
результат len - длина вектора, соглас-
но IEEE Р1363 младшие разряды слева
Манипулятор для потока ostream
для вывода числа класса LINT
в шестнадцатиричном виде
Манипулятор для потока ostream
для вывода числа класса LINT
в десятичном виде
Манипулятор для потока ostream
для вывода числа класса LINT
в восьмеричном виде
Манипулятор для потока ostream
для вывода числа класса LINT
в двоичном виде
Манипулятор для потока ostream
для вывода числа класса LINT
в шестнадцатиричном виде
с использованием прописных букв
430
Криптография на Си и C++ в действии
ostream&
LintLwr (ostream& s);
ostream&
LintShowbase (ostream& s);
ostream&
LintNobase (ostream& s);
ostream&
LintShowlength (ostream& s);
ostream&
LintNolength (ostream& s);
LINT_omanip<int>
SetLintFlags (int flag);
LINT_omanip<int>
ResetLintFlags (int flag);
ostream&
operator « (ostream& s, const LINT& In);
ofstream&
operator « (ofstream& s, const LINT& In);
fstream&
operator « (fstream& s, const LINT& In);
ifstream&
operator » (ifstream& s, LINT& In);
fstream&
operator » (fstream& s, LINT& In);
Манипулятор для потока ostream
для вывода числа класса LINT
в шестнадцатиричном виде
с использованием строчных букв
Манипулятор для отображения
префикса Ох (соответственно 0b)
в шестнадцатиричном (соответственно
двоичном) представлении
целого числа класса LINT
Манипулятор для пропуска префикса
Ох или 0b в шестнадцатиричном
или двоичном представлении
целого числа класса LINT
Манипулятор для отображения
двоичной длины выдаваемого
целого числа класса LINT
Манипулятор для пропуска
двоичной длины выдаваемого
целого числа класса LINT
Манипулятор для установки битов
переменной состояния LINT
Манипулятор для очистки битов
переменной состояния LINT
Перегруженный оператор "поместить",
выдающий целые числа класса LINT
в выходной поток типа ostream
Перегруженный оператор "поместить",
записывающий целые числа класса
LINT в выходной поток типа ostream
Перегруженный оператор "поместить",
записывающий целые числа
класса LINT в поток типа fstream
Перегруженный оператор "извлечь",
читающий целые числа класса LINT
из входного потока типа ifstream
Перегруженный оператор "извлечь",
читающий целые числа класса LINT
из потока типа fstream
В.З Основные операции: функции-члены класса
const LINT&
operator ++ (void);
Префиксное увеличение
на единицу ++а;
Приложение В 431
const LINT operator ++ (int); Постфиксное увеличение на единицу а++;
const LINT& operator - (void); Префиксное уменьшение на единицу -а;
const LINT operator - (int); Постфиксное уменьшение на единицу а-;
const LINT& operator += (const LINT& b); Сложение и присваивание: а += Ь;
const LINT& operator -= (const LINT& b); Вычитание и присваивание: а -= Ь;
const LINT& operator *= (const LINT& b); const LINT& operator /= (const LINT& b); Умножение и присваивание а *= Ь; Деление и присваивание: а /= Ь;
const LINT& operator %= (const LINT& b); Вычисление остатка от деления и присваивание: а %= Ь;
const LINT& add (const LINT& b); Сложение: с = a.add (b);
const LINT& sub (const LINT& b); Вычитание: с = a.sub (b);
const LINT& mul (const LINT& b); Умножение: с = a.mul (b);
const LINT& sqr (void); Возведение в квадрат: с = a.sqr (b);
const LINT& divr (const LINT& d, LINT& r); Деление с остатком: quotient = dividend.divr (divisor, rest);
В.4 Основные операции: функции-друзья класса
const LINT operator + (const LINT& a, const LINT& b); Сложение: c = a + b;
const LINT operator - (const LINT& a, const LINT& b); Вычитание: c = a - b;
const LINT operator * (const LINT& a, const LINT& b); Умножение: c = a * b;
const LINT operator / (const LINT& a, const LINT& b); Деление: c = a / b;
const LINT operator % (const LINT& a, const LINT& b); Вычисление остатка отделения: с = a % b;
432
Криптография на Си и C++ в действии
const LINT
add (const LINT& a, const LINT& b);
const LINT
sub (const LINT& a, const LINT& b);
const LINT
mul (const LINT& a, const LINT& b);
const LINT
sqr (const LINT& a);
const LINT
divr (const LINT& a, const LINT& b, LINT& r);
Сложение: c = add (a, b);
Вычитание: c = sub (a, b);
Умножение: c = mul (a, b);
Возведение в квадрат: b = sqr (a);
Деление с остатком:
quotient = divr (dividend, divisor, rest);
B.5 Модульная арифметика: функции-члены класса
const LINT&
mod (const LINT& m);
const LINT&
mod2 (const USHORT u);
const int
mequ (const LINT& b, const LINT& m) const;
const LINT&
madd (const LINT& b, const LINT& m);
const LINT&
msub (const LINT& b, const LINT& m);
const LINT&
mmul (const LINT& b, const LINT& m);
const LINT&
msqr (const LINT& m);
const LINT&
mexp (const LINT& e, const LINT& m);
const LINT&
mexp (const USHORT u, const LINT& m);
const LINT&
mexp5m (const LINT& e, const LINT& m);
const LINT&
mexpkm (const LINT& e, const LINT& m);
const LINT&
mexp2 (const USHORT u, const LINT& m);
Вычисление остатка от деления
b = a.mod (m);
Вычисление остатка отделения на 2й
b = a.mod (и);
Сравнение вычетов а и b по модулю m
if (a.mequ (b, m)) ...
Модульное сложение
с = a.madd (b, т);
Модульное вычитание
с = a.msubfb, m);
Модульное умножение
с = a.mmul (b, т);
Модульное возведение в квадрат
с = a.msqr (m);
Модульное возведение в степень й
по Монтгомери для нечетного Я
модуля т, с = а.техр (е, т); $1
Модульное возведение в степень
по Монтгомери для нечетного
модуля m и показателя типа USHORT,
с = а.техр (и, т);
Модульное возведение в степень
по Монтгомери для нечетного
модуля т, с = а.техр5т (е, т);
Модульное возведение в степень
по Монтгомери для нечетного
модуля т, с = a.mexpkm (е, т);
Модульное возведение в степень для
показателя вида 2U, с = а.техр2 (и, т);
Приложение В
433
В.6 Модульная арифметика: функции-друзья класса
const LINT mod (const LINT& a, const LINT& m); Вычисление остатка от деления b = mod (а, т);
const LINT mod2 (const LINT& a, const USHORT u); Вычисление остатка отделения на 2й b = mod (а, и);
const int mequ (const LINT& a, const LINT& b, const LINT& m); Сравнение вычетов а и b по модулю m if (mequ (a, b, m)) ...
const LINT madd (const LINT& a, const LINT& b, const LINT& m); Модульное сложение с = madd (a, b, т);
const LINT msub (const LINT& a, const LINT& b, const LINT& m); Модульное вычитание с = msub(a, b, т);
const LINT mmul (const LINT& a, const LINT& b, const LINT& m); Модульное умножение с = mmul (а, Ь, т);
const LINT msqr (const LINT& a, const LINT& m); Модульное возведение в квадрат с = msqr (а, т);
const LINT mexp (const LINT& a, const LINT& e, const LINT& m); Модульное возведение в степень по Монтгомери для нечетного модуля т, с = mexp (а, е, т);
const LINT mexp (const USHORT u, const LINT& e, const LINT& m); Модульное возведение в степень по Монтгомери для нечетного модуля m и основания типа USHORT, с = mexp (u, е, т);
const LINT mexp (const LINT& a, const USHORT u, const LINT& m); Модульное возведение в степень по Монтгомери для нечетного модуля m и показателя типа USHORT, с = mexp (a, u, т);
const LINT mexp5m (const LINT& a, const LINT& e, const LINT& m); Модульное возведение в степень по Монтгомери, только для нечетного модуля т, с = техр5т (а, е, т);
const LINT mexpkm (const LINT& a, const LINT& b, const LINT& m); Модульное возведение в степень по Монтгомери, только для нечетного модуля т, с = mexpkm (а, е, т);
const LINT mexp2 (const LINT& a, const USHORT u, const LINT& m); Модульное возведение в степень для показателя вида 2U, с = техр2 (а, и, т);
B.7 Битовые операции: функции- члены класса
const LINT& XOR и присваивание
operator л= (const LINT& b); а л= Ь;
15-1697
434
Криптография на Си и C++ в действии
const LINT& operator 1 = (const LINT& b); OR и присваивание a 1= b;
const L1NT& operator &= (const LINT& b); AND и присваивание a &= b;
const L1NT& operator «- (const int i); Сдвиг влево и присваивание а «= i;
const LINT& operator »= (const int i); Сдвиг вправо и присваивание а «= i;
const LINT& shift (const int i); (rn 31V ' Сдвиг (влево или вправо) на i битов a.shift (i);
const LINT& setbit (const unsigned int i); (И! ИЗ Установка бита на i-ю позицию a.setbit (i);
const LINIT& clearbit (const unsigned int i); Очистка бита на i-й позиции a.clearbit (i);
const int testbit (const unsigned int i) const; •ВД'-ХТТ Проверка значения бита на i-й позиции a.testbit (i);
В.8 Битовые операции: функции-друзья класса
const LINT XOR
operator л (const LINT& a, const LINT& b); с = а л b;
const LINT OR
operator I (const LINT& a, const LINT& b); с = a 1 b; I
const LINT AND
operator & (const LINT& a, const LINT& b); c = a & b;
const LINT Сдвиг влево ।
operator « (const LINT& a, const int i); b = a « i;
const LINT Сдвиг вправо
operator » (const L1NT& a, const int i); b = a » i;
const LINT Сдвиг (влево или вправо) на i битов
shift (const LINT& a, const int i); / b - shift (a, i);
В.9 Теоретико-числовые функции-члены класса
const unsigned int
Id (void) const;
const int
iseven (void) const;
const int
isodd (void) const:
Вычисление Ilog 2 a J
Проверка того, делится ли а на 2:
true, если а четное
Проверка того, делится ли а на 2:
true, если а нечетное
435
Приложение В
const LINT цЩ.
issqr (void) const; ' ,f|?i
const int
isprime (void) const;
const LINT pnux
gcd (const LINT& b);
* I IM-r ’J’/
const LINT " f
xgcd (const LINT& b, LINT& u, int& sign_u,
LINT& v, int& sign_v) const;
const LINT
inv (const LINT& b) const;
const LINT
Icm (const LINT& b) const-
const int
jacobi (const LINT& b) const;
const LINT
root (void) const-
const LINT
root (const LINT& p) const;
const LINT
root (const LINT& p, const LINT& q) const; . n>
к ..
const int
twofact (LINT& odd) const;
const LINT
chinrem (const LINT& m,
const LINT& b, const LINT& n) const;
Проверка того, является ли а полным
квадратом
Проверка числа а на простоту
Вычисление наибольшего общего
делителя чисел а и b
Расширенный алгоритм Евклида,
вычисление наибольшего общего
делителя чисел а и b, и и v -
абсолютные значения коэффициентов
линейной комбинации
g = sign_u*u*a + sign_v*v*b
Вычисление мультипликативно
обратного к а по модулю b
Вычисление наименьшего обшего
кратного чисел а и b
Вычисление символа Якоби
Вычисление целой части квадратного
корня из а
Вычисление квадратного корня из а
по модулю нечетного простого числа р
Вычисление квадратного корня из а
по модулю p*q, числа р и q - простые
нечетные
Определение четной части числа а,
в odd - нечетная часть а
Вычисление решения х системы линей-
ных сравнений х = a mod m и х s b
mod п (если такое решение существует)
В.10 Теоретико-числовые функции-друзья класса
const unsigned Id (const LINT& a); Вычисление Llog 2(a)J
const int iseven (const LINT& a); Проверка того, делится ли а на 2: true, если а четное
const int isodd (const LINT& a); m?-" Проверка того, делится ли а на 2: true, если а нечетное
const LINT issqr (const LINT& a); '' - Проверка того, является ли а полным квадратом
436 Криптография на Си и C++ в действии
const int isprime (const LINT& a); const LINT gcd (const LINT& a, const LINT& b); const LINT xgcd (const LINT& a, const LINT& b, LINT& u, int& sign_u, LINT& v, int& sign_v); Проверка числа а на простоту Вычисление наибольшего обшего делителя чисел а и b Расширенный алгоритм Евклида, вычисление наибольшего обшего делителя чисел а и b, и и v - абсолютные значения коэффициентов линейной комбинации g = sign_u*u*a + sign_v*v*b
const LINT inv (const LINT& a, const L1NT& b); Вычисление мультипликативно обратного к а по модулю b
const LINT Icm (const LINT& a, const LINT& b); Вычисление наименьшего обшего кратного чисел а и b
const int jacobi (const LINT& a, const LINT& b); Вычисление символа Якоби
const LINT root (const LINT& a); Вычисление целой части квадратного корня из а
const LINT root (const LINT& a, const LINT& p); const LINT root (const LINT& a, const LINT& p, const LINT& q); Вычисление квадратного корня из а по модулю нечетного простого числа р Вычисление квадратного корня из а по модулю p*q, числа р и q - простые нечетные
const LINT chinrem (const unsigned noofeq, LINT** coeff); Вычисление решения системы линейных сравнений. В coeff содержится вектор указателей на объекты класса LINT как коэффициенты а-|, ГЛ], Й2, ГП2, Эз, ГПз, ... системы сравнений, состоящей из noofeq сравнений вида х s a, mod m(.
const LINT primroot (const unsigned noofprimes, LINT** primes); чЬ Вычисление первообразного корня по модулю р. В noofprimes содержится число различных простых делителей порядка группы - числа р - 1, в primes - вектор указателей на объекты класса LINT: сначала р - 1, затем простые 1 е1 делители рь ..., рА числа р - 1 = Pi р^, где к = noofprimes.
const int twofact (const LINT& even, LINT& odd); const LINT findprime (const USHORT 1); Вычисление четной части числа а, в odd содержится нечетная часть числа а. Генерация простого числа р длины I бит, то есть 21 - 1 < р < 21.
Приложение В
437
const LINT
findprime (const USHORT I, const LINT& f);
const LINT
findprime (const LINT& pmin, const LINT& pmax,
const LINT& f);
const LINT
nextprime (const LINT& a, const LINT& f);
const LINT
extendprime (const USHORT I, const LINT& a,
const LINT& q, const LINT& f);
const LINT
extendprime (const LINT& pmin, const LINT& pmax,
const LINT& a, const LINT& q, const LINT& f);
const LINT
strongprime (const USHORT I);
const LINT
strongprime (const USHORT I, const LINT& f);
const LINT
strongprime (const USHORT I, const USHORT It,
const USHORT Ir, const USHORT Is,
< const LINT& f);
const LINT
strongprime (const LINT& pmin, const LINT& pmax,
const LINT& f);
const LINT
strongprime (const LINT& pmin, const LINT& pmax,
const USHORT It, const USHORT Ir,
const USHORT Is, const LINT& f);
Генерация простого числа p
длины I бит, то есть 21 - 1 < р < 2*,
такого, что НОА(р - 1, f) = 1,
где число f - нечетное
Генерация простого числа р такого,
что pmin < р < ртах и НОД(р - 1, f) = 1,
где число f - нечетное
Генерация наименьшего простого
числа р, превышающего число а
и такого, что НОД(р - 1, f) = 1,
где число (- нечетное
Генерация простого числа р длины
I бит, то есть 21 - 1 < р < 21, такого,
что р “ a mod q и НОД(р - 1, f) = 1,
где число f - нечетное
Генерация простого числа р такого,
что pmin < р < pmax, р s a mod q и
НОД(р - 1, f) = 1, где число f - нечетное
Генерация сильного простого числа р
длины I бит, то есть 21 - 1 < р < 21.
Генерация сильного простого числа р
длины I бит, то есть 21 - 1 < р < 21,
такого, что НОД(р - 1, f) = 1,
где число f- нечетное
Генерация сильного простого числа р
длины I бит, то есть 21 - 1 < р < 21,
такого, что НОД(р - 1, f) = 1, где число
f- нечетное; при этом длины Ir, It, Is
простых делителей г числа р - 1, t числа
г - 1, s числа р + 1, соответственно,
удовлетворяют условиям: It g j, Is ~ Ir g S
двоичной длины числа p
Генерация сильного простого числа р
такого, что pmin < р < ртах
и НОД{р - 1, f) = 1,
где число f - нечетное; при этом
длины Ir, It, Is простых делителей г
числа р - 1, t числа г - 1, s числа р + 1,
соответственно, удовлетворяют
условиям: It g j, Is ~ Ir g S
двоичной длины числа pmin
Генерация сильного простого числа р
такого, что pmin < р < ртах и
НОД(р - 1, f) = 1, где число f - нечетное;
при этом Ir, It, Is - длины простых
делителей г числа р - 1, t числа г - 1,
s числа о + 1, соответственно.
438
Криптография на Си и C++ в действии
и
В.11 Генерация псевдослучайных чисел
void seedl (const LINT& seed); I Инициализация 64-разрядного линейного конгруэнтного генератора случайных чисел с помошью начального значения seed
LINT randl (const int I); i Генерация случайного числа класса LINT длины I бит
LINT randl (const LINT& rmin, const LINT& rmax); Генерация случайного числа г 1 класса LINT, где rmin < г < rmax 1
int seedBBS (const LINT& seed); ; Инициализация генератора BBS 1 случайных чисел с помошью 1 начального значения seed 1
LINT randBBS (const int I); ' i . хьгпп LINT randBBS (const LINT& rmin, const LINT& rmax); Генерация случайного числа 1 класса LINT длины 1 бит ' 1 Генерация случайного числа г 1 класса LINT, где rmin < г < rmax 1
В.12 Прочие функции
LINT_ERRORS
Get_Warning_Status (void);
static void :
SetLINTErrorHandler
(void (*)(LINT_ERRORS err,
const char* const/ const int, const int));
Запрос состояния ошибки объекта
класса LINT
Вызов пользовательской программы
обработки ошибок для LINT-операний.
Зарегистрированная программа
используется вместо стандартного
LINT-обработчика ошибок panic().
Отмена регистрации
пользовательской программы
и одновременное возобновление
использования программы panic()
осуществляется вызовом функции
Set_LINT_Error_Handler (NULL).
ПРИЛОЖЕНИЕ С. *
Макросы
С.1 Коды ошибок и значения состояний
E_CLINT_DBZ -1 Деление на нуль
E_CLINT_OFL -2 Переполнение
E_CLINTJJFL -3 Потеря значащих разрядов
E_CLINT_MAL -4 Ошибка распределения памяти
ECLINTNOR -5 Регистр недоступен
E_CLINT_BOR -6 Неверное основание в str2clint_l()
E_CLl NT_MOD -7 Четный модуль в процедуре приведения по Монтгомери
E_CLINT_NPT -8 В качестве аргумента передан нулевой указатель
E_VCHECK_OFL 1 Предупреждение функции vcheck_l(): число слишком большое
E_VCHECK_LDZ 2 Предупреждение функции vcheck_l(): нули в старших разрядах
E_VCHECK_MEM -1 Ошибка функции vcheck_l(): нулевой указатель
С.2 Дополнительные константы
BASE 0x10000 Основание В - 216 системы счисления в типе CLINT
BASEMINONE OxffffU S-1
DBASEMINONE OxffffffffUL S2-1
BASEDIV2 0x8000U Ls/2j
NOOFREGS 16U Стандартное число регистров в банке регистров
BITPERDGT 16UL Число двоичных разрядов
в CLINT-разряде
440
Криптография на Си и C++ в действии
LDBITPERDGT 4U Логарифм по основанию 2 от BITPERDGT
CLINTMAXDIGIT ,-Ж • 256U — Максимальное число разрядов в CLINT-объекте в системе счисления с основанием В
CLINTMAXSHORT (CLINTMAXDIGIT + 1) Число разрядов типа USHORT, выделенных под CLINT-объект
CL1NTMAXBYTE ' (CLINTMAXSHORT « 1) Число байтов, выделенных под CLINT-объект
CLINTMAXBIT (CLINTMAXDIGIT « 4) Максимальное число двоичных разрядов в CLINT-объекте
г0_1,..., г15_1 FLINTVERMAJ FLINT_VERMIN get_reg_l(O),..., get_reg_l(15) Указатель на CLINT-регистры 0, 15 Старшая цифра версии библиотеки FLINT/C Младшая цифра версии библиотеки FLINT/C
FLINT_VERSION ((FLINT.VERMAJ« 8) + FLINT.VERMIN) Номер версии библиотеки FLINT/C
FLINT-SECURE 0x73, 0 Идентификатор 's' или '' безопасного режима библиотеки FLINT/C
С.З Макросы с параметрами
clint2str_l (nJ, base) .CLINT2STR_L (n_l, base) xclint2str_l((n_l),(base),0) Представление CL I NT-объекта в виде строки символов без префикса
DISP_L (S, A) printf("%s%s\n%u bit\n\n", (S), HEXSTR_L(A), IdJ(A)) Стандартный вывод CLINT-объекта
HEXSTR_L (n_l) T a. xclint2strj((nj), 16, 0) . c IU Преобразование CLINT-объекта в шестнадцатиричное представление
DECSTR.L (n) : ж. ? яг xclint2str l((n), 10, 0) Преобразование CLINT-объекта в десятичное представление
OCTSTR-L(nJ) xclint2strj((nj), 8, 0) Преобразование CLINT-объекта в восьмеричное представление
Приложение С
441
BINSTR_L (nJ) xclint2strj((nj), 2, 0) Преобразование CLINT-объекта в двоичное представление
SET_L (nJ, ul) ul2clintj((nj), (ul)) Присваивание nJ ULONG ul
SETZEROJ. (nJ) (*(nj) = 0) Установить nJ в 0
SETONEJ. (nJ) u2clintj((nj), 1 U) Установить nJ в 1
SETTWO L (nJ) u2clintj((nj), 2U) Установить nJ в 2
ASSIGN J. (a J, bj) cpyj((aj), (b_D) Присваивание а_1 <— bj
ANDMAXJ. (aJ) SETDIGITS J_((aJ), (MIN(DIGITS_L(aJ), \ (USHORT)CLINTMAXDIGIT)); RMLDZRS_L((a_l)) Приведение по модулю (Nmax + 1)
DIGITS J. (nJ) (*(nj)) Прочитать число разрядов nJ в системе счисления с основанием В
SETDIGITSJ. (nJ, I) INCDIGITS J. (nJ) (♦(nJ) = (USHORT)»)) (++*(nj)) Установить число разрядов nJ в I Увеличить число разрядов на 1
DECDIGITS_L (nJ) (-♦(nJ)) Уменьшить число разрядов на 1
LSDPTRJ. (nJ) ((nJ) + 1) Указатель на младший разряд CLINT-объекта
MSDPTR_L (nJ) ((nJ) + DIGITS_L(nl)) Указатель на старший разряд CLINT-объекта
RMLDZRS_L (nJ) while((DIGITS_L(n_l) > 0) && (*MSDPTR_L(nJ) == 0)) {DECDIGITS J.(nJ);) Удаление ведущих нулей CLINT-объекта
SWAP (a, b) ((а)л=(Ь),(Ь)л=(а),(а)л=(Ь)) Перестановка
SWAP_L (aj, bj) (xorj((aj),(bj),(aj)), xorj((bj),(aj),(bj)), xorj((aj),(b_l),(aj))) Перестановка двух значений типа CLINT
LT J. (aj, bj) (cmpj((aj), (b_D) == -1) Проверка условия a_l < bj
LE_L (aj, b_l) (cmpj((aj), (bJ)) < 1) Проверка условия aj < bj
GT J. (a_l, bj) (cmpj((aj), (b_D) == 1) Проверка условия a l > bj
GE_L (a_l, bj) (cmpj((aj), (bj)) > -1) Проверка условия a_l > bj
GTZJ(aJ) (cmpj((aj), nulj) == 1) Проверка условия а_1 > 0
EQZ_L (aj) (equj((aj), nulj) == 1) Проверка условия a l == 0
EQONE_L (aj) (equj((aj), one J) == 1) Проверка условия a l — 1
442 Криптография на Си и C++ в действии
MIN_L (aj, Ь_1) (LT_L((a_l), (b_D) ? (a_l) :(b J)) Минимум из двух значений типа CLINT
MAX_L (aj, Ь_1) (GT_L((a_l), (bj)) ? (aJ) :(b_D) Максимум из двух значений типа CLINT
ISEVENJ. (nJ) (DIGITS JXn J) ==0 II (DIGITSJ_(nJ) > 0 && (*(LSDPTR_L(nJ)) & 1 U) = 0)) Проверка того, является ли nJ четным
ISODDJ. (nJ) (DIGITSJ_(nJ) > 0 && (*(LSDPTRJ_(nJ)) & 1U) == 1) Проверка того, является ли nJ нечетным
MEXP_L (a_l, ej, pj, nJ) mexpkj((aj), (ej), (pj), (nJ)) Возведение в степень
MEXFJL (aj, ej, p_l, nJ) mexp5J((aJ), (ej), (pj), (nJ)) mexpkmj((aj), (ej), (pj), (nJ)) mexp5mj((aj), (ej), (pj), (nJ)) Альтернативные варианты возведения в степень
INITRAND64_LT() seed64j((unsigned long) time(NULL)) Инициализация генератора rand64j() случайных чисел с помошью системных часов
INITRANDBBS_LT() seedBBSJ((unsigned long) time(NULL)) Инициализация генератора randbitj() случайных битов с помошью системных часов
ISPRIMEL (nJ) primej((nj), 302, 5) Проверка на простоту с фиксированными параметрами
ZEROCLINT J. (nJ) memset((A), 0, sizeof(A)) Затирание CLINT-переменной
ПРИЛОЖЕНИЕ D.
Время вычислений
В таблицах D.1 и D.2 приведено время вычислений для некоторых
функций пакета FLINT/C. Вычисления проводились на процессоре
Pentium III, 500 МГц, 64 Мбайт ОЗУ. Время измерялось для п опе-
раций, и результат делился на и. Число п, в зависимости от типа
функции, варьировалось от 100 до 5 000 000. В таблице D.3 приве-
дено для сравнения время вычислений для некоторых функций
библиотеки многоразрядной арифметики GNU GMP (GNU Multi
Precision Arithmetic Library, версия 2.0.2), см. стр. 448.
Таблииа D.1. 128 256 512 768 1024 2048
Время — вычислений aaaj 3,8-107 5,5-1 O’7 8,8-10"7 1,2-10“6 1,5-10G 2,2-10’6
лля некоторых mu| । 1,9-1 0 f' 5,1-1 O’6 1,6-10‘5 3,3-10“5 5,6-10 s 2,1-1 O’4
С-функний
(без ассемблера) s4rJ 1,5-10“6 3,7-10“6 < ,1-10 s 2,1-1 O'5 3,5-1O'5 L3-10-4
divj * 2,6-1 0"6 5,8-10"6 7,6-10"5 2,7-1 0-5 5,1-1 O'5 7,8-1 O’4
mmulj 7,5-1 O’6 2,1-1 0’5 6,6-1 0“s 1,4-10^ 2,3-Ю-4 8,9-1 0"4
msqrj 7,3-10‘6 1,9-10^ 6,1-1 o-5 1,2-10“4 2,1-Ю-4 8,1 -10"4
mexpkj 1,2-1 0“3 6,4-10~3 3,8-10-2 1,2-1 0й 2,1-10-’ 1,9
mexpkmj 5,4-10^ 2,9- 1(T3 1,7-1 O’2 5,2-10“2 1,2-Ю"’ 8,6-10’1
Для функции divj число разрядов относится к делимому,
длина делителя — в два раза меньше.
Сразу видно, что возведение в квадрат быстрее, чем умножение.
Видно даже преимущество функции mexpkmJO, использующей
возведение в квадрат по Монтгомери, - она работает почти в два
раза быстрее, чем функция mexpkJQ. Таким образом, один шаг ал-
горитма RSA с ключом длины 2048 бит при использовании китай-
ской теоремы об остатках (см. стр. 225) занимает четверть секунды.
В таблице D.2 приведены результаты, полученные при использо-
вании ассемблерных подпрограмм. В этом случае скорость мо-
дульных функций увеличивается примерно на 70%. Разрыв между
умножением и возведением в квадрат остается на уровне 50%.
444
Криптография на Си и C++ в действии
Таблица D.2. 128 256 512 768 1024 2048
Время вычислений mulj 4,3-1 O'6 6,9-1 O’6 1,5-10“s 2,9-1 O’5 4,7-1 O'5 1,6-Ю-4
лля некоторых Sqr | С-функиий 2,5-10"6 4,6-10"6 1,0-10*5 1,8-1 O’5 2,9-10-' 9,5'10’5
(ассемблер divj 2,7-10-6 3,5-1 O’6 7,7-10"6 1,0-1 o" 1,9-105 6,0-10's
80x86) Mmulj 8,0-1 O’6 1,3-10*5 3,3-10“5 6,4-10’5 1,0-1 0"4 3,8-Ю-4
msqrj 7,2-1 O’6 1,1-1 O’5 2,9-1 O'5 5,6-1 0"5 9,0-1O’’ 3,1-Ю-4
mexpkj 1,3-1 O’3 4,3-1 O’3 1,9-1 O’2 5,3-1 O’2 1,1-10’’ 8,7-10-'
mexpkmj 7,6-1 O’4 3,3-1 O’3 1,7-1 O’2 4,9-1 O’2 1,1-10’’ 7,8-10-’
Для функции divj число разрядов относится к делимому,
длина делителя — в два раза меньше.
В ассемблерном варианте нет функций mulmonJO и sqrmonj(), а
функция mexpkJO по скорости вплотную приближается к функции
mexpmJO возведения в степень по Монтгомери. Здесь возможны
дальнейшие улучшения (см. главу 18) за счет использования соот-
ветствующих ассемблерных расширений.
Сравнивая функции пакетов FLINT/C и GMP (см. таблицу D.3), мы
видим, что умножение и деление в GMP выполняются соответст-
венно на 30% и 40% быстрее, чем аналогичные функции из
FLINT/C. Что касается модульного возведения в степень, то здесь
обе библиотеки показывают примерно одинаковую скорость; то же
самое справедливо и для аргументов длины 4096 бит. Поскольку
GMP считается наиболее быстрой на сегодняшний день библио-
текой целочисленной арифметики, нам грех жаловаться на такой
результат.
— - , Таблица D.3. 128 256 512 768 1024 2048
Время вычислений mpz_add 2,4-10-7 3,2-10’7 3,6-Ю-7 4,2-10-7 4,5-10’7 6,9-10"7
лля некоторых mpzjiud 9,8-Ю’7 3,0-10-6 1,1-Ю-5 2,2-Ю’5 4,1-Ю’5 4,8-10’5
GMP-функиий
(ассемблер mpz_mod * 5,2-Ю’7 1,8-10”6 5,0-10’6 6,4-10-6 1,6-Ю-5 4,0-10’5
80x86) mpzpowm 4,5-Ю-4 2,6-Ю’3 1,7-10’2 5,2-10-2 1,7-10-' 7,8-10"У
Для функции mpz_mod число разрядов относится к делимому,
длина делителя — в два раза меньше.
ПРИЛОЖЕНИЕ Е.
Условные обозначения
IN множество неотрицательных целых чисел 0, 1, 2, 3, ...
IN+ множество положительных целых чисел 1,2, 3, ...
Z множество целых чисел -2, —1,0, 1,2, 3, ...
л, кольцо классов вычетов по модулю п надмножеством целых чисел (глава 5)
конечное поле из рп элементов
a класс вычетов а + nZ в кольце Z„
a ~ b а приблизительно равно b
a g 6 а приблизительно равно b и при этом меньше b
а <— b переменной а присвоить значение b
lai абсолютное значение а
a 1 b а делит b без остатка
а l Ь а не делит b
а = b mod n а сравнимо с b по модулю п, то есть n I {а - Ь)
at b mod n а несравнимо с b по модулю п, то есть n j (а - Ь)
НОД(а, b) наибольший общий делитель чисел а и b (п. 10.1)
HOK(a, b) наименьшее обшее кратное чисел а и b (п. 10.1)
ф(п) функция Эйлера (п. 10.2)
O(-) «О-болыиое». Для двух вещественных функций f и g, тле g(x) > 0, пишут f- O(g) и говорят «Гпорядка О-большое от#», если существует константа С такая, что f{x) < Cg(x) для всех достаточно больших х.
( a A символ Якоби (п. 10.4.1)
(7 J
bd наибольшее целое число, меньшее либо равное х
Ы наименьшее целое число, большее либо равное х
p множество вычислительных задач, которые могут быть решены за полиномиальное время
446
Криптография на Си и C++ в действии
NP
в ~
МАХе
МАХ2 -У'
^плах
множество вычислительных задач, которые могут быть решены
недетерминированным алгоритмом за полиномиальное время
логарифм по основанию b от х
В = 216, основание системы счисления для представления объектов
типа CLINT
максимальное число разрядов, допустимое для CLINT-объекта
в системе счисления с основанием В
максимальное число разрядов, допустимое для CLINT-объекта
в системе счисления с основанием 2
наибольшее натуральное число, представимое объектом типа CLINT
- < ...
.У'
мнадмрп'нд ibM
ПРИЛОЖЕНИЕ?.
Арифметические
и теоретико-числовые пакеты
Если читатель все еще сомневается в привлекательности и полезно-
сти алгоритмической теории чисел, ему стоит лишь посмотреть,
сколько веб-сайтов посвящено этой теме, - и сомнительными ока-
жутся уже сами сомнения. Просто наберите в Вашей любимой по-
‘V исковой системе строку «теория чисел» (или «number theory») -
появятся тысячи ссылок, лишь малая толика из которых упомянута
в этой книге. Многие из этих веб-сайтов содержат ссылки на пакеты
программ, кое-где их даже можно свободно скачать. Это разнооб-
разные функции, связанные с арифметикой больших целых чисел,
алгеброй, теорией групп и теорией чисел, созданные усилиями
многочисленных профессионалов и любителей.
Огромный список ссылок на такие пакеты можно найти на сайте
Number Theory Web Page, поддерживаемом Кейт Мэтьюс (Keith
Matthews) (University of Queensland, Брисбен, Австралия). Этот сайт
читатель найдет на
http://www.math.uq.edu.au/~krm/web.html,
с американский сайт-зеркало
' http://www.math.uga.edu/~ntheory/web.html
I
и британский сайт-зеркало
http://www.dpmms.cam.ac.uk/Number-Theory-Web/web.htmi.
Там же можно найти ссылки на университеты и исследовательские
институты, а также на публикации по различным вопросам теории
чисел. Этот сайт - просто драгоценный клад.
Перечислим теперь некоторые доступные программные пакеты:
✓ ARIBAS - интерпретатор, исполняющий арифметические и теоре-
тико-числовые функции с большими числами. В ARIBAS на языке
л Паскаль реализованы алгоритмы из [Fors]. ARIBAS может быть ис-
пользован как дополнение к этой книге, его можно получить через
анонимный ftp в каталоге pub/forster/aribas, ftp.mathematik.uni-
muenchen.de или на http://www.mathematik.uni-muenchen.de/~forster.
✓ CALC от Кейт Мэтьюс - программа, позволяющая проводить вы-
числения со сколь угодно длинными целыми числами. Команды
v вводятся в командной строке, CALC выполняет их и отображает
результат. CALC «знает» более 60 теоретико-числовых функций.
Пакет реализован на языке С версии ANSI С и использует для ана-
448
Криптография на Си и C++ в действии
лиза командной строки анализатор YACC или BISON. Calc можно
взять с ftp://www.maths.uq.edu.au/pub/krm/calc/.
Ь ✓ GNU МР, или GMP, из проекта GNU - это переносимая библиотека
. С, в которой реализована арифметика сколь угодно больших целых,
а также рациональных и вещественных чисел. Благодаря использо-
ванию ассемблера, библиотека GMP демонстрирует прекрасную
\ производительность для целого ряда процессоров. GMP доступна
через ftp на www.gnu.org,prep.ai.mit.edu, www.leo.org, а также на
сайтах-зеркалах проекта GNU.
- ✓ LiDIA - библиотека программ, разработанная в Техническом уни-
Ф , верситете Дармштадта (Technical University Darmstadt) для теорети-
ко-числовых вычислений. LiDIA - это целая коллекция оптимизи-
рованных функций, позволяющая выполнять вычисления в Z, Q, R,
Л1 С, Г2я, Оу, а также смешанные вычисления. Здесь реализованы также
современные алгоритмы разложения на множители, алгоритм ми-
нимизации базиса решетки, алгоритмы линейной алгебры, методы
п , вычислений в числовых полях, а также полиномиальная арифметика.
Д: LiDIA может взаимодействовать с другими вычислительными па-
кетами, в том числе с пакетом GMP. Собственный интерпретируе-
1 . мый язык LC пакета LiDIA поддерживает C++ и тем самым облег-
чает переход к транслируемым программам. Поддерживаются все
платформы, допускающие использование длинных имен файлов и
имеющие подходящий компилятор C++, в том числе Linux 2.0.x,
Windows NT 4.0, OS/2 Warp 4.0, HPUX-10.20, Sun Solaris 2.5.1/2.6.
v Есть и перенесенная версия для Apple Macintosh. Библиотеку LiDIA
можно найти на http://www.informatik.tu-darmstadt.de/TI/LiDIA.
✓ Numbers от Ivo Diintsch - это библиотека объектных файлов, со-
; Jmh ’ держащая основные теоретико-числовые функции для чисел дли-
ной до 150 десятичных знаков. Функции, написанные на Паскале,
и интерпретатор, также входящий в состав библиотеки, предна-
значены для студентов и позволяют получать нетривиальные
вычислительные примеры. Страница Numbers находится по адресу
http://archives.math.utk.edu/soflware/msdos/
number.theory/num202d/.html.
✓ PARI - теоретико-числовой пакет, разработанный Генри Коэном
(Henri Cohen) и др. В этом пакете реализованы алгоритмы, пред-
ставленные в [Cohe]. PARI можно использовать и в качестве интер-
претатора, и в качестве библиотеки функций для включения в про-
+*< граммы. Благодаря использованию ассемблера, пакет демонстрирует
1 + высокую производительность для различных платформ (UNIX,
Macintosh, PC и др.). PARI можно найти на www.parigp-home.de.
*
Литература
[Adam] Adams, Carlisle, Steve Lloyd: Understanding Public Key Infrastructure Concepts,
Standards & Deployment, Macmillan Technical Publishing, Indianapolis, 1999.
[BaSh] Bach, Eric, Jeffrey Shallit: Algorithmic Number Theory, Vol. 1, Efficient Algorithms,
MIT Press, Cambridge (MA), London, 1996.
[BCGP] Beauchemin, Pierre, Gilles Brassard, Claude Crepeau, Claude Goutier, Carl Pom-
erance: The Generation of Random Numbers that are Probably Prime, Journal of
Cryptology, Vol. 1, No. 1, pp. 53-64, 1988.
[Beut] Beutelspacher, Albrecht: Kryptologie, 2. Auflage, Vieweg, 1991.
[Bies] Bieser, Wendelin, Heinrich Kersten: Elektronisch unterschreiben - die digitale Signatur
in der Praxis, 2. Auflage, Hiithig, 1999.
[BiSh] Biham, Eli, Adi Shamir: Differential cryptanalysis of DES-like cryptosystems, Journal
of Cryptology, Vol. 4, No. 1, 1991, S. 3-72.
[Blum] Blum, L., M. Blum, M. Shub: A Simple Unpredictable Pseudo-Random Number Gene-
rator, SIAM Journal on Computing, Vol. 15, No. 2, 1986, S. 364-383.
[BMBF] Bundesministerium fur Bildung, Wissenschaft, Forschung und Technologie (Hrsg.):
luKDG - Informations- und Kommunikationsdienste-Gesetz -Umsetzung und
Evaluierung-, Bonn, 1997.
[BMWT] Bundesministerium fur Wirtschaft und Technologie; Entwurf eines Gesetzes uber
Rahmenbedingungen fur elektronische Signaturen - Diskussionsentwurf zur Anhorung
und Unterrichtung der beteiligten Fachkreise und Verbande, April 2000.
[Bone] Boneh, Dan: Twenty Years of Attacks on the RSA-Cryptosystem, Proc. ECC 1998.
[Bosl] Bosch, Karl: Elementare Einfiihrung in die Wahrscheinlichkeitsrechnung, Vieweg,
1984.
[Bos2] Bosch, Karl: Elementare Einfiihrung in die angewandte Statistik, Vieweg, 1984.
[Boss] Bosselaers, Antoon, Rene Govaerts, Joos Vandewalle: Comparison of three modular
reduction functions, in: Advances in Cryptology, CRYPTO 93, Lecture Notes in
Computer Science 773, S. 175-186, Springer-Verlag, New York, 1994.
[Bres] Bressoud, David M.: Factorization and Primality Testing, Springer-Verlag, New York,
1989.
[BSI1] Bundesamt fur Sicherheit in der Informationstechnik: Geeignete Kryptoalgorithmen.
In Erfiillung der Anforderungen nach §17 (1) SigG vom 16. Mai 2001 in Verbindung
mit §17(2) SigV vom 22. Oktober 1997. In: Bundesanzeiger 158 (2001). S. 18.562.
[BSI2] Bundesamt fiir Sicherheit in der Informationstechnik: Anwendungshinweise und In-
terpretation zum Schema (AIS). Funktionalitatsklassen und Evaluationsmethodo-
logiefur physikalische Zufallszahlengeneratoren. AIS 31. Version 1. Bonn, 2001.
[Burt] Burthe, R. J. Jr.: Further Investigations with the Strong Probable Prime Test, Mathe-
matics of Computation, Volume 65, pp. 373—381, 1996.
450. Криптография на Си и C++ в действии
[Bund] Bundschuh, Peter: Einfiihrung in die Zahlentheorie, 3. Auflage, Springer-Verlag,
Berlin, Heidelberg, 1996.
[BuZi] Burnikel, Christoph, Joachim Ziegler: Fast recursive Division, Forschungsbericht
MPI-I-98-1-022, Max-Planck-Institut fur Informatik, Saarbrucken, 1998.
[Char] Chari, Suresh, Charanjit Jutla, Josyula R. Rao, Pankaj Rohatgi: A Cautionary Note
Regarding Evaluation of AES Candidates on Smart Cards, http://csrc.nist.gov/encryp-
tion/aes/roundl/conf2/papers/chari.pdf, 1999.
[Cohe] Cohen, Henri: A Course in Computational Algebraic Number Theory, Springer-
Verlag, Berlin, Heidelberg, 1993.
[Coro] Coron, Jean-Sebastien, David Naccache, Julien P. Stern: On the Security of RSA
Padding, in M. Wiener (Ed.), Advances in Cryptology, CRYPTO '99, Lecture Notes
in Computer Science No. 1666, S. 1-17, Springer-Verlag, New York, 1999.
[Cowi] Cowie, James, Bruce Dodson, R.-Marije Elkenbracht-Huizing, Arjen K. Lenstra,
* Peter L. Montgomery, Joerg Zayer: A world wide number field sieve factoring re-
cord: on to 512 bits, in K. Kim and T. Matsumoto (Ed.) Advances in Cryptology,
ASIACRYPT '96, Lecture Notes in Computer Science No. 1163, pp. 382-394,
Springer-Verlag, Berlin 1996.
[DaLP] Damgard, Ivan, Peter Landrock, Carl Pomerance: Average Case Error Estimates for the
Strong Probable Prime Test, Mathematics of Computation, Volume 61, pp. 177-194,
1993.
[DaRi] Daemen, Joan, Vincent Rijmen: AES-Proposal: Rijndael, Doc. Vers. 2.0,
http://www.nist.gov/encryption/aes, Sept. 1999.
[DR02] Daemen, Joan, Vincent Rijmen: The Design of RijndaeL: AES - The Advanced En-
cryption Standard, Springer-Verlag, Heidelberg, 2002.
[Deit] Deitel, H. M., P. J. Deitel: C++ How To Program, Prentice Hall, 1994.
[Dene] Denert, Ernst: Software-Engineering, Springer-Verlag, Heidelberg, 1991.
[deWe] de Weger, Benne: Cryptanalysis of RSA with small prime difference, Cryptology
ePrint Archive, Report 2000/016, 2000.
[Diff] Diffie, Whitfield, Martin E. Hellman: New Directions in Cryptography, IEEE Trans.
Information Theory, S. 644-654, Vol. IT-22, 1976.
[DoBP] Dobbertin, Hans, Antoon Bosselaers, Bart Preneel: RIPEMD-160, a strengthened
version of RIPEMD, in D. Gollman (Hrsg.): Fast Software Encryption, Third Interna-
tional Workshop, Lecture Notes in Computer Science 1039, S. 71-82, Springer-
Verlag, Berlin, Heidelberg, 1996.
[DuKa] Dusse, Stephen R., Burton. S. Kaliski: A Cryptographic Library for the Motorola
DSP56000, in: Advances in Cryptology, EUROCRYPT ’90, Lecture Notes in Com-
puter Science No. 473, S. 230-244, Springer-Verlag, New York, 1990.
[Dune] Duncan, Ray: Advanced OS/2-Programming: The Microsoft Guide to the OS/2-kerneI
for assembly language and C programmers, Microsoft Press, Redmond, Washington,
1981.
Литература_______ .___________________________________________________451
[East] Eastlake, D., S. Crocker, J. Schiller: Randomness Recommendations for Security, RFC1750,1994.
[Elli] Ellis, James H.: The Possibility of Secure Non-Secret Digital Encryption, 1970, http://www.cesg.gov.uk/about/nsecret/home.htm
[ElSt] Ellis, Margaret A., Bjarne Stroustrup: The Annotated C++ Reference Manual, Addi- son-Wesley, Reading, MA, 1990.
[Endl] Endl, Kurth, Wolfgang Luh: Analysis I, Akademische Verlagsgesellschaft Wiesbaden, 1977.
[Enge] Engel-Flechsig, Stefan, Alexander RoBnagel (Hrsg.): Multimedia-Recht, С. H. Beck, Munchen, 1998.
[EESSI] European Electronic Signature Standardization Initiative: Algorithms and Parameters for Secure Electronic Signatures, V.1.44 DRAFT, 2001.
[EU99] Richtlinie 1999/93/EG des Europaischen Parlaments und des Rates vom 13. Dezem- ber 1999 tiber gemeinschafthche Rahmenbedingungen fur elektronische Signaturen.
[Evan] Evans, David: LCLint Users Guide, Version 2.4, MIT Laboratory for Computer Sci- ence, April 1998.
[Fegh] Feghhi, Jalal, Jalil Feghhi, Peter Williams: Digital Certificates: Applied Internet Se- curity, Addison-Wesley, Reading, MA, 1999.
[Fiat] Fiat, Amos, Adi Shamir: How to prove yourself: Practical Solutions to Identification and Signature Problems, in: Advances in Cryptology, CRYPTO '86, Lecture Notes in Computer Science 263, S. 186-194, Springer-Verlag, New York, 1987.
[FIPS] Federal Information Processing Standard Publication 140 - 1: Security requirements for cryptographic modules, US Department of Commerce/ National Institute of Stan- dards and Technology (NIST), 1992.
[FI81] National Institute of Standards and Technology: DES Modes of Operation, Federal Information Processing Standard 81, NIST, 1980.
[F197] National Institute of Standards and Technology: ADVANCED ENCRYPTION STANDARD (AES), Federal Information Processing Standards Publication 197, November 26, 2001
[Fisc] [Fors] [Fumy] [Gimp] [Glad] Fischer, Gerd, Reinhard Sacher: Einfiihrung in die Algebra, Teubner, 1974. Forster, Otto: Algorithmische Zahlenthorie, Vieweg, Braunschweig, 1996. Fumy, Walter, Hans Peter RieB: Kryptographie, 2. Auflage, Oldenbourg, 1994. Gimpel Software: PC-lint, A Diagnostic Facility for C and C++. Glade, Albert, Helmut Reimer, Bruno Struif (Hrsg.): Digitale Signatur & Sicherheits- sensitive Anwendungen, DuD-Fachbeitrage, Vieweg, 1995.
[Gldm] Gladman, Brian: A Specification for Rijndael, the AES Algorithm, http://fp.glad- man.plus.com, 2001.
452 Криптография на Си и C++ в действии
[GoPa] Goubin, Louis, Jacques Patarin: DES and Differential Power Analysis, in Procee- dings of CHES '99, Lecture Notes in Computer Science, Vol. 1717, Springer-Verlag, 1999.
[Gord] Gordon, J. A.: Strong Primes are Easy to Find, Advances in Cryptology, Proceedings of Eurocrypt '84, S. 216-223, Springer-Verlag, Berlin, Heidelberg, 1985.
[Halm] Halmos, Paul, R.: Naive Mengenlehre, 3. Auflage, Vandenhoeck & Ruprecht, Got- tingen, 1972.
[Harb] Harbison, Samuel P, Guy L. Steele jr.: C, a reference manual, 4th Edition, Prentice Hall, Englewood Cliffs, 1995.
[Hatt] Hatton, Les: Safer C: Developing Software for High-integrity and Safety-critical Systems, McGraw-Hill, London, 1995.
[Henr] Henricson, Mats, Erik Nyquist: Industrial Strength C++, Prentice Hall, New Jersey, 1997.
[Heid] Heider, Franz-Peter: Quadratische Kongruenzen, unveroffentlichtes Manuskript, Koln, 1997.
[HeQu] Heise, Werner, Pasquale Quattrocchi: Informations- und Codierungstheorie, Springer- Verlag, Berlin, Heidelberg, 1983.
[HKW] Heider, Franz-Peter, Detlef Kraus, Michael Welschenbach: Mathematische Metho- den der Kryptoanalyse, DuD-Fachbeitrage, Vieweg, Braunschweig, 1985.
[Herk] Herkommer, Mark: Number Theory, A Programmers Guide, McGraw-Hill, 1999.
[HoLe] Howard, Michael, David LeBlanc: Writing Secure Code, Microsoft Press, 2002.
[IEEE] IEEE Pl363 / D13: Standard Specifications For Public Key Cryptography, Draft Version 13, November 1999.
[1SO1] ISO/IEC 10118-3: Information Technology - Security Techniques - Hash-functions- Part 3: Dedicated hash-functions, CD, 1996.
[ISO2] ISO/IEC 9796: Information Technology - Security Techniques - Digital signature scheme giving message recovery, 1991.
[ISO3] ISO/IEC 9796-2: Information Technology - Security Techniques - Digital signature scheme giving message recovery, Part 2: Mechanisms using a hash-function, 1997.
[Koeu] Koeune, F., G. Hachez, J.-J. Quisquater: Implementation of Four AES Candidates on Two Smart Cards, UCL Crypto Group, 2000.
[Knut] Knuth, Donald Ervin: The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd Edition, Addison-Wesley, Reading, MA, 1998.
[Kobl] Koblitz, Neal: A course in number theory and cryptography, Springer-Verlag, New York, 2nd Edition 1994.
[Kob2] Koblitz, Neal: Algebraic Aspects of cryptography, Springer-Verlag, Berlin, Heidel- berg, 1998.
[KoJJ] Kocher, Paul, Joshua Jaffe, Benjamin Jun: Introduction to Differential Power Analy- sis and Related Attacks, 1998, http://www.cryptography.com/dpa/technical/
Литература .453
[Kran] Kranakis, Evangelos: Primality and Cryptography, Wiley-Teubner Series in Com-
puter Science, 1986.
[KSch] Kuhlins, Stefan, Martin Schader: Die C++-Standardbibliothek, Springer-Verlag, Ber-
lin, 1999.
[LeVe] Lenstra, Arjen K., Eric R. Verheul: Selecting Cryptographic Key Sizes, www.crypto-
savvy.com, 1999.
[Lind] van der Linden, Peter: Expert C Programming, SunSoft/Prentice Hall, Mountain
View, CA, 1994.
[Lipp] Lippman, Stanley, B.: C++ Primer, 2nd Edition, Addison-Wesley, Reading, MA,
1993.
[Magu] Maguire, Stephen A.: Writing Solid Code, Microsoft Press, Redmond, Washington,
1993.
[Matt] Matthews, Tim: Suggestions for Random Number Generation in Software, RSA Data
Security Engineering Report, December 1995.
[Mene] Menezes, Alfred J.: Elliptic Curve Public Key Cryptosystems, Kluwer Academic
Publishers, 1993.
[Mess] Messerges, Thomas S.: Securing the AES Finalists Against Power Analysis Attacks,
Fast Software Encryption Workshop 2000, Lecture Notes in Computer Science,
Springer-Verlag.
[Meyl] Meyers, Scott D.: Effective C++, 2nd Edition, Addison-Wesley, Reading, Mass.,
1998.
[Mey2] Meyers, Scott D.: More Effective C++, 2nd Edition, Addison-Wesley, Reading,
Mass., 1998.
[Mied] Miedbrodt, Anja: Signaturregulierung im Rechtsvergleich. Ein Vergleich der Regu-
lierungskonzepte in Deutschland, Europa und den Vereinigten Staaten von Amerika,
Der Elektronische Rechtsverkehr 1, Nomos Verlagsgesellschaft, Baden-Baden, 2000.
[MOV] Menezes, Alfred J., Paul van Oorschot, Scott A. Vanstone, Handbook of Applied
Cryptography, CRC Press, 1997.
[Mont] Montgomery, Peter L.: Modular Multiplication without Trial Division, Mathematics
of Computation, S. 519-521,44 (170), 1985.
[Murp] Murphy, Mark L.: C/C++ Software Quality Tools, Prentice Hall, New Jersey, 1996.
[Nied] Niederreiter, Harald: Random Number Generation and Quasi-Monte Carlo Methods,
SIAM, Philadelphia, 1992.
[NIST] Nechvatal, James, Elaine Barker, Lawrence Bassham, William Burr, Morris
Dworkin, James Foti, Edward Roback: Report on the Development of the Advanced
Encryption Standard, National Institute of Standards and Technology, 2000.
[Nive] Niven, Ivan, Herbert S. Zuckerman: Einfiihrung in die Zahlentheorie Bd. I und II,
Bibliographisches Institut, Mannheim, 1972.
454 Криптография на Си и C++ в действии
[Odly] Odlyzko, Andrew: Discrete logarithms: The past and the future, AT&T Labs Re- search, 1999.
[Petz] Petzold, Charles: Programming Windows: The Microsoft Guide to Writing Applica- tions for Windows 3.1, Microsoft Press, Redmond, Washington, 1992.
[Plal] Plauger, P. J.: The Standard C Library, Prentice-Hall, Englewood Cliffs, New Jersey, 1992.
[Pla2] Plauger, P. J.: The Draft Standard C++ Library, Prentice-Hall, Englewood Cliffs, New Jersey, 1995.
[Pren] Preneel, Bart: Analysis and Design of Cryptographic Hash Functions, Dissertation an der Katholieke Universiteit Leuven, 1993.
[Rabi] Rabin, Michael, O.: Digital Signatures and Public-Key Functions as Intractable as Factorization, MIT Laboratory for Computer Science, Technical Report, MIT/LCS/TR-212, 1979.
[RDS1] RSA Data Security, Inc.: Public Key Cryptography Standards, PKCS#1: RSA En- cryption, RSA Laboratories Technical Note, Version 2.0, 1998.
[RDS2] RSA Security, Inc.: Recent Results on Signature Forgery, RSA Laborato- ries Bulletin, 1999, http://www.rsasecurity.com/rsalabs/html/sigforge.html .
[RegT] Regulierungsbehorde fiir Telekommunikation und Post (RegTP): Bekanntmachung zur digitalen Signatur nach Signaturgesetz und Signaturverordnung, Bundesanzeiger Nr. 31, 14.02.1998.
[Rein] Reinhold, Arnold: P-7NP Doesn’t Affect Cryptography, http://world.std.com/~rein- hold/p=np.txt, Mai 1996.
[Ries] Riesel, Hans: Prime Numbers and Computer Methods for Factorization, Birkhauser, Boston, 1994.
[Rive] Rivest, Ronald, Adi Shamir, Leonard Adleman: A Method for Obtaining Digital Sig- natures, Communications of the ACM 21, S. 120-126, 1978.
[Rose] Rose, H: E.: A course in number theory, 2nd Edition, Oxford University Press, Ox- ford, 1994.
[Saga] [Salo] Sagan, Carl: Cosmos, Random House, New York, 1980. Salomaa, Arto: Public-Key Cryptography, 2nd Edition, Springer-Verlag, Berlin, Hei- delberg, 1996.
[Schn] Schneier, Bruce: Applied Cryptography, 2nd Edition, John Wiley & sons, New York, 1996.
[Scha] Schonhage, Arnold: A Lower Bound on the Length of Addition Chains, Theoretical Computer Science, S. 229-242, Vol. 1, 1975.
[Schr] Schroder, Manfred R.: Number Theory in Science and Communications, 3rd ed., Springer-Verlag, Berlin, Heidelberg, 1997.
[SigG] Gesetz Uber Rahmenbedingungen fUr elektronische Signaturen und zur Anderung weiterer Vorschriften, unter http://www.iid.de/iukdg, 2001.
Литература
455
[SigV] Verordnung zur elektronischen Signatur (Signaturverordnung - SigV) vom 16. No- vember 2001.
[Skal] Skaller, John Maxwell: Multiple Precision Arithmetic in C, in: Schumacher, Dale (Editor): Software Solutions in C, Academic Press, S. 343-454, 1994.
[Spul] Spuler, David A.: C++ and C Debugging, Testing and Reliability, Prentice Hall, New Jersey, 1994.
[Squa] Daemen, Joan, Lars Knudsen, Vincent Rijmen: The Block Cipher Square, Fast Soft- ware Encryption, Lecture Notes in Computer Science 1267, Springer-Verlag, 1997, S,149-165.
[Stal] Stallings, William.; Cryptography and Network Security, 2nd Edition, Prentice Hall, New Jersey, 1999.
[Stin] Stinson, Douglas R.: Cryptography - Theory and Practice, Prentice Hall, New Jersey, 1995.
[Stlm] [Strl] Stallman, Richard M.: Using and Porting GNU CC, Free Software Foundation. Stroustrup, Bjarne: The C++ Programming Language, 3rd Edition, Addison-Wesley, Reading, MA, 1997.
[Str2] Stroustrup, Bjarne: The Design and Evolution of C++, Addison-Wesley, Reading, MA, 1994.
[Teal] [Wien] Teale, Steve: C++ lOStreams Handbook, Addison-Wesley, Reading, MA, 1993. Wiener, Michael: Cryptanalysis of short RSA secret exponents, in: IEEE Transac- tions on Information Theory, 36(3): S. 553-558, 1990.
[Yaco] Yacobi, Y.: Exponentiating faster with Addition Chains, in: Advances in Cryptology, EUROCRYPT '90, Lecture Notes in Computer Science 473, S. 222-229, Springer- Verlag, New York, 1990.
[Zieg] Ziegler, Joachim: Personliche Kommunikation 1998, 1999.
: ' '..ам
Содержание
а -......
.1............ Предисловие к русскому изданию............6
* Предисловие ко второму изданию............7
Предисловие к первому изданию..............9
ЧАСТЬ I. АРИФМЕТИКА И ТЕОРИЯ ЧИСЕА НА С
ГЛАВА 1. Введение...................................15
1.1.0 программном обеспечении..............19
1.2. Законные условия использования
программного обеспечения...............23
1.3. Как связаться с автором...............23
ГААВА 2. Числовые форматы:
представление больших чисел в языке С......25
ГЛАВА 3. Семантика интерфейса.......................31
ГААВА 4. Основные операции..........................35
4.1. Сложение и вычитание..................36
4.2. Умножение..........,..................46
4.2.1. Школьный метод...................47
4.2.2. А возведение в квадрат - быстрее.54
4.2.3. Поможет ли метод Карацубы?.......59
4.3. Деление с остатком....................64
ГЛАВА 5. Модульная арифметика:
вычисление в классах вычетов...............81
ГЛАВА 6. Все дороги ведут к...
моду..............льному возведению в степень...........95
6.1. Первые шаги...........................95
458 Криптография на Си и С+ + в действии Д
6.2. М-арное возведение в степень 6.3. Аддитивные цепочки и окна 1011 им
6.4. Приведение по модулю и возведение в степень методом Монтгомери 123В
6.5. Криптографические приложения модульного возведения в степень 136 j
Поразрядные и логические функции 143 '
Г 7.1. Операции сдвига 143 •’
7.2. Все или ничего: битовые соотношения 15о|
7.3. Прямой доступ к отдельным двоичным разрядам... 1561
7.4. Операции сравнения 160' А
ГЛАВА 8. Операции ввода, вывода, присваивания и преобразования 165 !
ГЛАВА 9. Динамические регистры.............................177
ГААВА 10. Основные теоретико-числовые функции.................187
10.1. Наибольший общий делитель.................188
чЛ 1 10.2. Обращение в кольце классов вычетов..........196
10.3. Корни и логарифмы.........................205
10.4. Квадратные корни в кольце классов вычетов.211
10.4.1. Символ Якоби.........................212
10.4.2. Квадратные корни по модулю рк........220
10.4.3. Квадратные корни по модулю п.........225
10.4.4. Квадратичные вычеты в криптографии...234
; 10.5. Проверка на простоту....................237
ГЛАВА 11. Большие случайные числа.................257
ГЛАВА 12. Стратегия тестирования LINT.............271
12.1. Статический анализ.............................273
12.2. Динамические тесты.............................275
Содержание 459
ЧАСТЬ II. КЛАСС LINT: АРИФМЕТИКА НА C++
ГЛАВА 13. Пусть C++ облегчит Вашу жизнь......................285
. 13.1. Частное дело: представление чисел в классе LINT.291
13.2. Конструкторы.................................293
13.3. Перегрузка операторов...................... 297
ГЛАВА 14. Открытый интерфейс LINT:
члены и друзья класса..............................305
14.1. Арифметика...................................305
14.2. Теория чисел.................................315
14.3. Потоковый ввод/вывод объектов LINT...........320
14.3.1. Форматированный вывод объектов LINT.....321
14.3.2. Манипуляторы............................329
14.3.3. Файловый ввод/вывод для объектов LINT...332
ГЛАВА 15. Обработка ошибок...................................339
15.1. (Без) Паники.................................339
15.2. Обработка ошибок, определяемая пользователем.342
15.3. Исключения LINT..............................343
ГЛАВА 16. Практический пример: криптосистема RSA...351
16.1. Асимметричные криптосистемы..................352
16.2. Алгоритм RSA........................... 354
16.3. Цифровая подпись RSA.........................369
16.4. RSA-классы на C++............................377
ГЛАВА 17. Сделайте это сами: протестируйте LINT..............387
ГЛАВА 18. Направления дальнейших исследований...................391
ГЛАВА 19. Rijndael: наследник стандарта
шифрования данных..................................393
19.1 . Полиномиальная арифметика...................395
19.2 . Алгоритм Rijndael...........................400
460 Криптография на Си и C++ в действии
193. Вычисление ключа раунда 403
19.4. S-блок 405
1. S 19.5. Преобразование ShiftRow 407
Ri ТИЦ - 19.6. Преобразование MixColumn 408
.. 19.7. Сложение с ключом раунда 409
го; ‘ 19.8. Полная процедура зашифрования блока 409
ГЛАВА 7. 19.9. Расшифрование ... .413
ЧАСТЬ III. ПРИЛОЖЕНИЯ
Приложение А. Каталог функций на С....................•...............421
АЛ Ввод/вывод, присваивание, преобразования, сравнения.421
А.2 Основные арифметические операции...............422
АЗ Модульная арифметика............................422
А.4 Битовые операции...............................424
А.5 Теоретико-числовые функции.....................424
t J А.6 Генерация псевдослучайных чисел....................425
rj А.7 Управление регистрами........................ 426
Приложение В. Каталог функций C++......................................427
ВЛ Ввод/вывод, преобразования, сравнения: I
функции-члены класса...........................4271
В.2 Ввод/вывод, преобразования, сравнения: I
функции-друзья класса..........................4291
... ВЗ Основные операции: функции-члены класса.........4301
В.4 Основные операции: функции-друзья класса......4311
В.5 Модульная арифметика: функции-члены класса....4321
В.6 Модульная арифметика: функции-друзья класса...433|
В.7 Битовые операции: функции-члены класса.........433
12* Битовые операции: функции-друзья класса..............434
В.9 Теоретико-числовые функции-члены класса.........434
ВЛ 0 Теоретико-числовые функции-друзья класса........435
ВЛ 1 Генерация псевдослучайных чисел.................438
ВЛ2 Прочие функции...................................438
Содержание
461
Приложение С. Макросы....................................................439
С.1 Коды ошибок и значения состояний.................439
С.2 Дополнительные константы.................................................... 439
С.З Макросы с параметрами............................440
Приложение D. Время вычислений...........................................443
Приложение Е. Условные обозначения.......................................445
Приложение F. Арифметические
и теоретико-числовые пакеты..............................................447
Литература...........................................449
Об авторе.......................................... 456
< f W