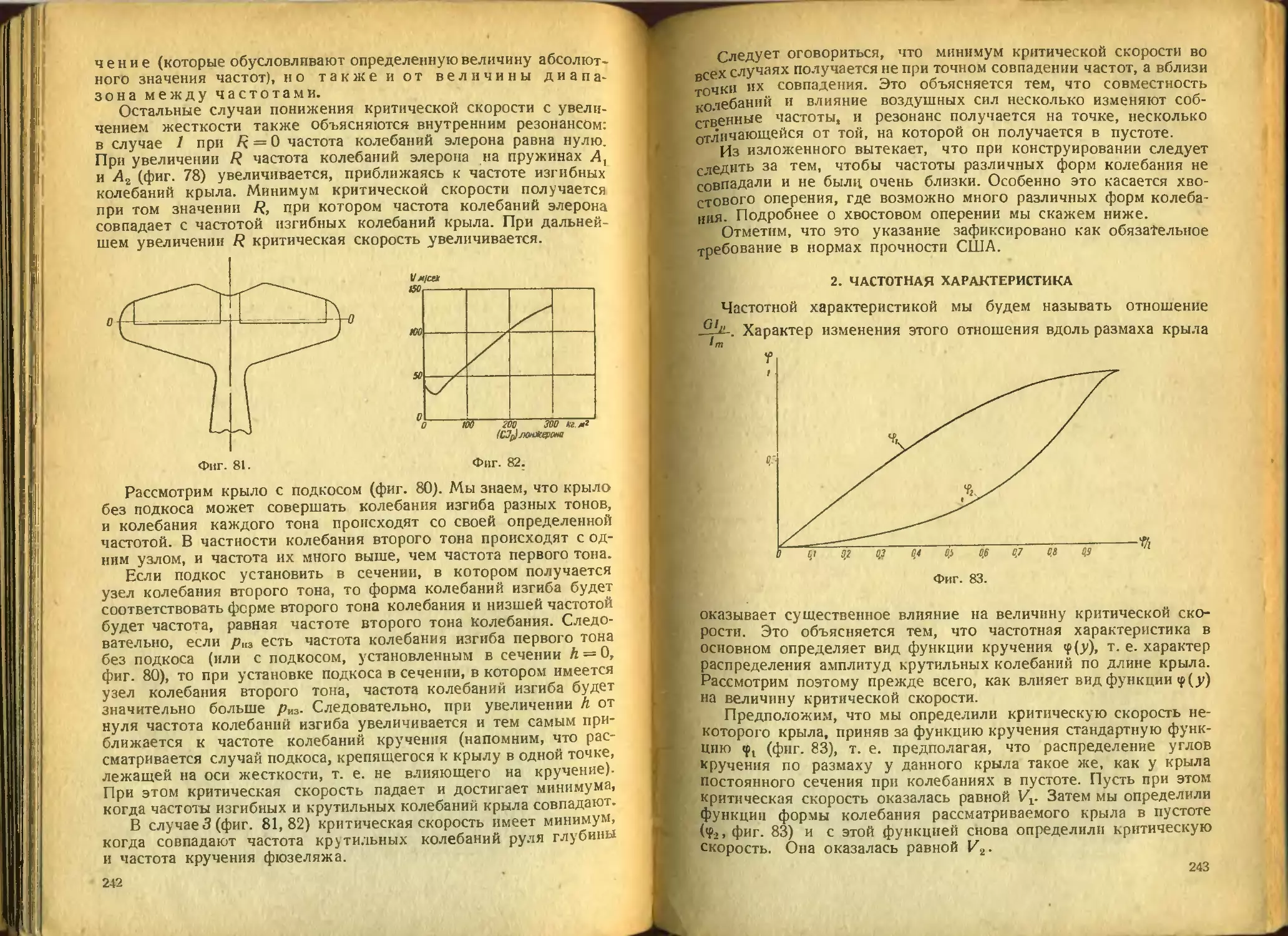
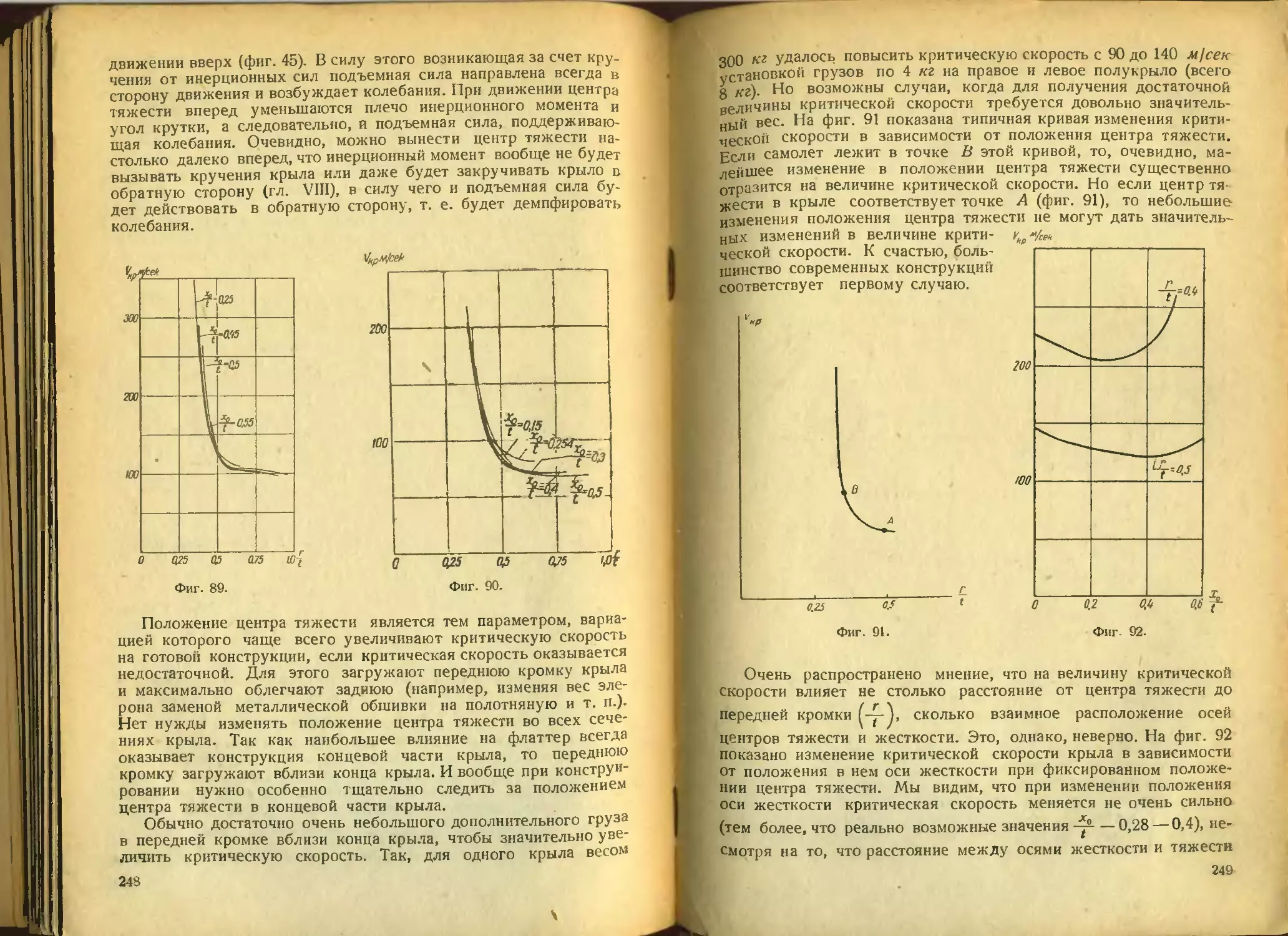
Текст
Е.п. Гроссман
К У Р с
ВИБРАЦИЙ ЧАСТЕЙ
САМОЛЕТА
ОБОРОНШЭ • IQ 40
Е. П. ГРОССМАН 5.V 6DI
КУРС
ВИБРАЦИЙ ЧАСТЕЙ
САМОЛ ЕТА
Утверждено ГУ УЗ НКАП
в] качестве учебного пособия
для авиационных втузов
Читальный зал Ль 1
Цена 10 р. в пер.
Киевсн-> Инегуг?
БИБЛИОТЕК*
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ОБОРОННОЙ ПРОМЫШЛЕННОСТИ
МОСКВА 1940
Книга Е. П. Гроссмана, утвержденная ГУУЗ НКАП в
качестве учебного пособия для втузов, содержит 14 глав.
Первые 6 глав посвящены вопросам расчета собственных
колебаний крыла, экспериментальным методам определения
собственных частот крыла и хвостового оперения, а также
расчету аэродинамических воздействий на крыло, вибриру-
ющее в потоке воздуха.
Последующие 7 глав автор отводит вопр.сам расчета
критической скорости флаттера крыла системы крыло—эле
рон и хвостового оперения. Он подробно аиадизирует при-
чины флаттера и влияние конструктивных параметров на
критическую скорость изгибно-крутнльиого флаттера крыла.
В последней 14-й главе рассказано о летных испытаниях
самолетов, т. е. о методах определения критической скоро-
сти самолетов в полете.
ОГЛАВЛЕНИЕ
Стр.
Предисловие..................................................... . 5
Условные обозначения •........................................... 7
Глава I. Системы с конечным числом степенен свободы................ 9
Уравнения Лагранжа............................................. —
Глава II. Крутильные колебания крыла.............................. 22
1. Основные уравнения......................................... —
2. Колебания крыла постоянного сечения в пустоте. Метод Фурье. . 24
3. Приближенные методы для крыла произвольного сечения......... 28
а. Метод Релея.............................................. 30
б. Метод Ритца...........................•.................. 31
в. Метод Галеркина.......................................... 35
4. Определение функции формы колебания и частоты методом после-
довательных приближений........................................... 42
а. Определение формы и частоты основного тона колебания ... 43
б. Определение функции формы и частоты для обертонов колебаний 50
5. Основные характеристики колебания.......................... 54
6. Колебания крыла с сосредоточенными грузами -............... 67
Глава III. Колебания изгиба крыла в пустоте....................... 79
1 . Основные уравнения........................................ —
2 Колебания изгиба крыла постоянного сечения в пустоте........83
3 . Колебания изгиба крыла произвольной формы в пустоте....... 87
4 Изгибные колебания крыла в пустоте при наличии сосредоточен-
ных масс ......................................................... 95
Глава IV. Совместные колебания крыла в пустоте....................104
1. Характер движения и основные уравнения...................... —
2. Приближенный способ определения частот совместных колебаний
крыла в пустоте...................................................109
3. Приближенный способ определения частот совместных колебаний
в случае наличия иа крыле сосредоточенных масс....................123
4. Применение метода последовательных приближений к расчету
совместных колебаний..............................................124
Глава V. Экспериментальные методы определения собственных частот
крыла и хвостового оперения.......................................126
Глава VI. Аэродинамические воздействия иа вибрирующее крыло . . . 133
1 Общие положения............................................. —
2. О вычислении аэродинамических сил, действующих на крыло при
неустановившемся движении.....................................«... 134
3. Аэродинамические воздействия на крыло.....................139
4. Аэродинамические характеристики крыла с элероном в плоском
потоке............................................................143
5. Аэродинамические характеристики крыла конечного размаха с эле-
роном ............................................................147
6. Крыло без элерона........................................ 154
Глава VII. Критическая скорость и способы ее определения..........156
2. Метод определения критической скорости изгибно-крутильиого
флаттера крыла и дивергенции........................................163
3. Стандартный способ расчета................................174
3
4. Применение метода последовательных приближений для расчета
колебаний крыла в потоке воздуха . ................................175
5. Выбор функции формы Колебаний при расчете флаттера. Опреде-
ление критической скорости крыла с сосредоточенными массами .... 183
6. Чисто изгибные н чисто крутильные колебания крыла в потоке
воздуха............................................................184
7. Приближенный метод определения критической скорости крыла
с элероном............................................................
Глд_ра VIII. Причины возникновения флаттера................... . 204
I Анализ причин возникновения флаттера.......................... —
2. Анализ энергообмена между вибрирующим крылом и потоком ..211
А. Колебания крыла в пустоте................................. —
Б. Колебания крыла в неподвижной среде.......................213
В. Колебания крыла в потоке воздуха.........•................ —
а) Изгнбно-крутильиые колебания крыла, подвергнутого начальной
б) Изгибно-крутильиые колебания крыла, подвергнутого начальной
деформаций кручения..........................................215
в) Третий цикл энергообмена.................................. —
г) Общий случаи. Уничтожение притока энергии . . ...........210
Г. Меры предотвращения флаттера..............................220
Глава IX. Теория подобия и исследование флаттера в аэродинамической
трубе............................................................ 222
Глава X. Влияние конструктивных параметров на критическую скорость
изгибно-крутильного флаттера крыла.................................236
1. Влияние жесткости крыла на критическую скорость............... —
2. Частотная характеристика................................• . 243
3. Положение оси центров тяжести по размкху крыла . . . • .... 247
4. Невибрирующая конструкция...................................250
5. Влияние масс и массовых моментов инерции крыла..............253
6. Влияние формы крыла в плане.................................254
7. Изменение критической скорости с высотой полета . . • .... 255
Глава XI. Влияние элерона иа флаттер крыла.........................257
Г л а в а XII. Вибрации воздушных винтов ..........................266
Глава XIII. Вибрации хвостового оперения...........................272
1. Баффтинг хвостового оперения................................273
2. Флаттер хвостового оперения.................................275
Глава XIV. О летных испытаниях.....................................301
Приложение. О численном интегрировании ............................305
ПРЕДИСЛОВИЕ
Вопросы вибраций частей самолета за последнее время при-
обретают все большее значение. При проектировании современ-
ных скоростных самолетов на эти вопросы приходится обра-
щать существенное внимание. Опыт последних лет показал, что
если антивибрационные мероприятия не предусмотрены при про-
ектировании самолета, то это может привести к печальным
последствиям. С другой стороны, теория вибраций частей само-
лета развилась только за самое последнее время, и литература
по этому вопросу разбросана в отдельных специальных статьях,
что весьма затрудняет применение результатов теории в кон-
структорской и расчетной практике. В авиационных вузах, по
нашему мнению, преподаванию вопросов вибрации уделяется не-
достаточное внимани^, и молодые инженеры, приходя на завод,
встречаются с целым рядом затруднений в этой области.
Настоящая книга представляет собой попытку систематически
изложить основы теории вибраций частей самолета, достаточные
для решения встречающихся в практике конструктора и расчет-
чика вопросов. Кроме того, книга содержит ряд вопросов общей
теории вибраций (методы Галеркина, Ритца и т. д.), а потому
может служить подготовительным материалом для изучения
специальной литературы по вибрациям.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
El кг м2 — жесткость крыла на изгиб.
Glp кг м2 — жесткость крыла иа кручение.
Z м—длина полукрыла.
t м —хорда крыла.
х0 м — расстояние от центра жесткости в рассматриваемом сечении до
передней кромки крыла.
а м — расстояние от оси жесткости до центра тяжести в рассматри-
ваемом сечении.
гм — расстояние от центра тяжести до передней кромки крыла в рас-
сматриваемом сечении.
По определению
г = Хо + о.
xf —расстояние ст фокуса до передней кромки.
т кг • сек21м2 — погоииая масса крыла.
1т кг сек2 — погонный массовый момент инерции относительно оси жесткости.
1т кг • сек2 — погонный массовый полярный момент инерции относительно
центра тяжести.
х м — радиус инерции относительно центра тяжести.
По определению:
Лл. = т2?>
Лп=Лп. + '«'’2-
Cv — коэфициеит подъемной силы.
Ст — коэфициеит аэродинамического момента относительно носка профиля.
СтЕ—коэфициеит аэродинамического момента относительно оси жесткость.
По определению:
^тЕ = + ^у
7
Все аэродинамические характеристики отнесены к pSV’. Подъемная сила —
C.,?SV2, момент относительно носка — CmpSV2.
" V м/сек—скорость полета.
укр м/сек — критическая скорость.
р кг-сек2/м*—плотность воздуха.
а—угол атаки.
6 — угол кручения.
Zm — прогиб оси жесткости крыла.
р — угол отклонения элерона относительно крыла.
с сек. —• время.
Оу — ось, направленная по размаху крыла вдоль оси жесткости.
Ог — ось, перпендикулярная к плоскости хорд крыла (направлена
вверх от летчика).
Ох — ось, перпендикулярная к двум предыдущим (направлена назад).
Начало координат берется в 'плоскости крепления крыла к фюзеляжу.
Положительное направление всех углов и моментов выбрано в сторону вра-
щения от оси Oz к оси Ох (положительный момент—кабрирующий; фиг. II).
Т сек.—период колебаний.
р 1/сек. — частота.
q 1/сек. — логарифмический декремент затухания.
п 1/сек.— число колебаний в секунду.
По определению р = 2пл.
о9 м — расстояние от центра тяжести элерона до его оси вращения.
тэ кг • сек2/м2 — погонная масса элерона’.
/тшкг-сск2—погонный момент инерции массы элерона относительно его
оси вращения.
Точками над соответствующими величинами обозначается диференцирова-
ине по времени.
ГЛАВА I
СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
УРАВНЕНИЯ ЛАГРАНЖА
Рассмотрим движение какой-либо системы в пространстве
Декартовы координаты какой-либо z-й точки системы обозначим
xit Vi> zt- Число точек системы может быть либо конечным (на-
пример математический маятник),
либо бесконечно большим (н£- 0---------------х
пример упругая балка). Рассмот-
рим системы, в которых пере- у' \
мещения частиц, составляющих .z V
систему, не вполне независимы, / \
а подчинены некоторым огра- ( \
ничениям, которые могут быть •м(х,у,г)
выражены уравнениями между
координатами частиц. Случаи,
когда уравнения ограничения (так
называемые уравнения связей) гфиг (
заключают не только координа-
ты, но также и скорости частиц и время, мы рассматривать не
будем.
В качестве примера таких систем может быть приведен,
например, сферический маятник (фиг. 1). Расстояние частицы
Л1 от начала координат О должно во время движения оставаться
постоянным и равным длине Z маятника. Поэтому координаты
х, у, z точки М не являются независимыми — они должны удов-
летворять уравнению
x2 + y2 + z2 = Z2,
и одна из координат всегда может быть выражена через две
других.
В качестве второго примера рассмотрим колебания пластины
АВ (фиг. 2) на оси Е, которая сама совершает колебания в на-
правлении оси z на пружинах П. Пластина прикреплена к оси
Е спиральной пружиной С1. Массы пружин по сравнению с массой
пластины АВ настолько малы, что ими можно пренебречь. В этом
случае число точек системы бесконечно велико. Но вследствие
1 Эта схема грубо изображает изгибно-крутильные колебания крыла.
&
того, что все точки должны лежать на прямой АВ (фиг. 2),
между их координатами существует соотношение
z = — tg О,- х + Z, (1)
где Z = ОЕ—перемещение оси Е. Так как этому соотношению
должны удовлетворять координаты л,- и любой точки пластины,
то имеется бесконечно большое число уравнений связей. Движе-
ние в рассматриваемом случае будет полностью определено,
«ели будут известны Всего две величины: Z и 6.
Отметим, что кроме уравнения (1) координаты любой точки
пластины должны также удовлетворять условию неизменности
расстояния данной точки от
оси Е:
fc? + (Z-zi)2 = 3i,
где с,- — неизменное рассто-
яние от i-й точки систе-
мы до оси Е.
Если декартовы коор-
динаты точек системы не
являются независимыми, то
часто бывает удобно опре-
делить положение системы
при помощи каких-либо
других величин, независя-
щих друг от друга. Число
таких независимых пара-
метров, полностью опреде-
ляющих положение систе-
• мы, называется числом
степеней свободы системы. Вовсе не обязательно, -чтобы эти
параметры имели измерение длины, как координаты. Например,
в случае, изображенном на фиг. 2, за независимые величины,
определяющие положение системы, удобнтр принять перемеще-
ние Z оси Е и угол закручивания 0.
Такие независимые величины, выбранные для выражения
положения системы, называются обобщенными координатами.
Декартовы координаты любой точки системы можно выразить
как функции обобщенных координат.
Xi = Xi(qlf q2, ... qn)~
?2. ••• ЯпУ
(2)
^i = zi(ql, Я* ЯпУ,
i — 1, 2, ..., k, где А? —число точек системы* 1; п — число обоб-
--- *4.
1 Ограничиваем рассмотрение тем случаем, когда эти уравнения явно ие
содержат скоростей обобщенных координат qr и времени т.
10
щенных координат. Например, если для случая, изображенного
на фиг. 2, за обобщенные координаты выбрать Z и 6, эти уравнения
будут:
х, = g,-cos9; |
rr . Л I W
z,- = Z — af sin 0. J
При решении многих задач динамики системы, подчиненной
связям, удобно исходить из принципа возможных перемещений.
Принцип возможных перемещений состоит в том, что работа
всех сил на каждом виртуальном перемещении системы (малые
возможные перемещения системы) должна быть равна нулю.
Пусть ох„ оу, oz,— составляющие возможного перемещения i-й
точки системы, mi — масса этой точки и Xit Yit Z,— составляю-
щие равнодействующей внешних си?1, действующих в рассматри-
ваемой точке. Составляющие силы инерции, действующей на
частицу т„ будут —т^, —т^у,, —т^, и работа всех сил в
точке m-t на перемещении ох;, оу, oz,- напишется в следующем
виде:
(X; — тус) 'jX, + ( К, — да,у) оу + (Z,--ZHjZ,) OZf.
Суммируя эту работу по всем точкам системы, получим пол-
ное выражение работы /? сил, приложенных к системе, на пути
возможных перемещений, которое и приравниваем нулю:
*
R = £ [(Л) — тус) ох,- + (У, — т1 у) оу + (Z, — да Д', ) oz,] = 0. (4)
i=l
Неудобство этого выражения состоит в том, что в случае
наличия связей составляющие перемещения ох,-, оу, oz,- не явля-
ются независимыми. В самом деле, пусть какое-либо уравнение
связи есть
f(*i, J'i. х2, уг, z2 ;...)= 0. (5)
Возможные перемещения — это такие, которые допускаются
связями. Поэтому координаты . точки после перемещения также
должны удовлетворять уравнениям связей:
f U1 + Ут. + Zx + oz,; х2 + ох2, у., + оу,, z2 + oz2;...) = 0.
Разлагаем левую часть в ряд Тейлора и отбрасываем члены
выше первого порядка малости. Тогда, принимая во внимание
уравнение (5), будем иметь:
< Ч + < гЛ + £ гг, + < и, + »А + % гЛ +... = о.
Таких уравнений будет столько, сколько уравнений связей,
и они выражают совместность данного возможного перемещения
со связями системы. Следовательно, в случае наличия связей
составляющие перемещений не будут независимыми. Между тем
часто несравненно удобнее пользоваться независимыми вели-
чинами, т. е. обобщенными координатами. Пользуясь для точек
11
системы выражениями (2) обобщенных декартовых координат,
преобразуем выражение (4) для работы сил на пути возможных
перемещений.
Варьируя уравнения (2), находим
«*)
и аналогично оу,- и Sz,..
Подставляем эти значения в выражение (4). Тогда
+ (гг - + Л. + -g- г<7„) +
+ (2/ - гЯ1 + iq2 +...+^ ] =
•(7)
Сумму, стоящую в фигурных скобках, обозначим через Sr.
Кроме того, введем обозначение
k
°-=Z(xH&+r.<+z<)- <«>
i=l
Тогда
k
Sr=Q^mi^+y^+^
1=1
k
= Qr^^yml^+y,^l +i,^-) +
d~ { A l\ 1 dqr vqr 1 OqrJ
i=l
r=l
Суммы, стоящие справа, могут быть преобразованы при по-
мощи соотношений (2). Диференцируя эти соотношения по
времени, получаем:
• дХ: • , дХ: • , , дх; ’
х‘ = ^^ + ^;^+ +~дГпдп’ ( 0)
и аналогично для j, и г,-
Таким образом мы убеждаемся, что в рассматриваемом слу-
чае [когда в выражение (2) время явно не входит] скорости из-
12
менения декартовых координат суть линейные однородные функ-
ции от обобщенных скоростей qr, причем коэфициенты в этих
функциях (д—, ...) суть, вообще говоря, функции обобщенных
\0<h oq2
координат qx, qo,...
Диференцируя обе части выражения (10) частным образом
по qr, находим:
dxt_djq и dyi dyt dij dzt
dqr dqr dqr dqr dqr dqr
Диференцируя же обе части выражения '(10) частным обра-
зом по qr, получаем:
dxt _ d2xt • , ФХ, • , д
dqr dqxdqr dq2dqr ' dqndqr ^n' '
С другой стороны,^ есть функция qv q,...qn, и, диферен-
цируя ее по времени, как неявною функцию, будем иметь:
d (дхл __ d2x-t • (Pxj • . d2Xj •
dz ydq'r) ~ dqrdqx dqrdq2 dqrdqn
Сравнивая это выражение с выражением (12), заключаем, что
дх -, _ d f дх Л
dqr dz \dqr)
(13)
и также
dyi d (dy\ dZ{ d_(dz;
dqr dz\dqrJ' dqr dz\dqr
Пользуясь выражениями (11) и (13), запишем выражение (9)
в следующем виде:
к
dAdqr) + dqr’
(14)
(15)
где
k
т = nil (х 2i + i>i + zl)
i=l
есть кинетическая энергия системы. При помощи соотношений (2)
она может быть выражена через обобщенные координаты, но мы
на этом останавливаться не будем.
Значение Sr из выражения (14) подставляем в выражение
(7) и находим окончательное выражение работы сил на пути
во. ожных перемещений:
= (16)
Ldr \ dqrJ dqr J
Пспринцнпу возможных перемещений! /?=0. Так как iqr неза-
ви 1мы и произвольны, то это может быть только, если выпол-
ни тся равенства1 * * *:
=о. (17)
dt dqr) dqr
г = 1, 2. . . п
ЭТ)— уравнения движения в форме Лагранжа. Как видно из
выода, эта форма уравнений движения самым тесным- образом
сизана с принципом возможных перемещений.
Найдем еще физическое значение обобщенных сил, для чего
р; смотрим работу приложенных к системе сил. Пользуясь вы-
ражением (6), легко убеждаемся, что эта работа Ж будет:
k
9i + УрУ, + = Qis(7i + Qis?2 4--+Q„3«7„. (18)
i=l
Рассмотрим перемещение, соответствующее приращению толь-
кс одной какой-либо координаты Zq^ В этом случае работа при-
ложенных сил будет:
9i\ = Qsqr.
Следовательно, обобщенная сила Qr есть тот коэфициент, на
который нужно помножить приращение обобщенной координаты,
чтобы получить соответствующую этому приращению работу
Приложенных сил.
Рассмотрим еще частный случай, когда приложенные к си-
стеме силы имеют потенциал. Пусть существует такая функция
У1, Zlt...,xk, yk, zft), что
(19>
В силу соотношений (2) мы можем рассматривать U, как
функцию обобщенных координату, q2,...,qn,. Подставляя значе-
ния сил из (19) в выражение (8), находим:
k
q ди dxt . dU ду, . dU dz,__dU
~~ /. dXj dqr "I" dyi dqr ' dZi dqr ~ dqr’
1 Уравнение (17) можно получить, например, если в выражении (16>
положить а все остальные вариации обобщенных координат равными
нулю. Делая это предположение поочередно для г = 1, 2, . . ., л, получи»
все уравнения системы (17).
14
т. е. эта функция будет служить также потенциалом и для
обобщенных сил. Уравнения Лагранжа в этом случае записыва-
ются в следующем виде:
+ = <20)
dt \ OqrJ dqr ддг
Г = 1. 2, . . п
К уравнениям такого вида приводит, например, задача о ко-
лебаниях крыла в пустоте, так как в этом случае приложенными
силами будут силы упругости, которые, как известно, имеют
потенциал. Уравнениями вида (17) приходится пользоваться при
изучении колебания крыла в потоке воздуха, так как в этом
случае к силам упругости добавляются еще аэродинамические
силы, уже не обладающие потенциалом.
Работу приложенных сил в случае наличия потенциала легко
найти по формуле (18):
\}dU . ...
^ = ~Xdqr(i(]r=~rjU-
г=1
Величина U, как известно, называется потенциальной энергией
системы.
Наконец, если одна часть сил обладает потенциалом, а дру-
гая часть не обладает им, то уравнение Лагранжа можно написать
в виде:
а дТ \ dU — Q /91)
^\д'Чг) дЧг { ’
где Qr определяется формулой (8); в этом случае под Xh Z,
следует понимать проекции сил, не имеющих потенциала; U —
потенциал остальных сил.
Если приложенные силы обладают потенциалом, то это озна-
чает, что полная энергия системы (кинетическая плюс потен-
циальная) во все время движения остается неизменной:
Т + U = const. (22)
Система в этом случае называется консервативной.
Для доказательства уравнения (22) умножим уравнения (20) соответственно
иа dqr и сложим. Будем иметь:
15>
я предыдущее равенство принимает вид:
V дТ я’ V дТ я
г=1 Г=1 Г=1
п
★Еъ*'-0- <23)
г=1
Подставляя значения скоростей (10) в выражение кинетической энергии (15),
убедимся, что Г есть однородная квадратичная форма относительно обобщенных
скоростей:
r“SXevU. (23а)
5=1 г=1
яоэфициенты as r которой будут, вообще говоря", зависеть от обобщенных ко-
ординат. Поэтому
п п
Г=1 Г=1
С другой стороны, потенциальная энергия U не зависит от обобщенных скоро-
стей и есть только функция координат. В самом деле, при изменениях всех
координат qr на величину dqr декартовы координаты в силу выражений (2)
изменятся ца величины dXi, dyif dzt. При этом приращение функции
Щх» уи zv..., xk, yk, zk) будет:
k
^rT ди A ди ди A 1 4 : f >4
dU =1 dXi+dyi + ~^dZi’
i=l
Определяя dx-t, dyi, dzt из выражений (2), получим:
. дх; . , дх: , дх: .
dXi “ dQl dqi + dq2 d42+---+^dqr,
и аналогично dyt, dzt.
Подставляя эти значения в уравнение (а), находим:
л г *
V л V ( ди dxi . ди дУ1 . ди dzi')
2Л^+^т;7+-ъъ;) “
Г=1 i=l J
r^i
Пользуясь выражениями (24) и (25), представляем выражение (23) в сле-
дующем виде:
Г = 1
или, интегрируя:
\1Л дТ\
/, ~д^)~ т+и° const W
16
Но так как Т — однородная функция второй степени относительно обоб-
щенных скоростей [формула (23а)], то по теореме Эйлера об однородных
функциях имеем:
Яг
дТ
dqr'~
2Т,
и выражение (26) получает вид,
Т 4- U — const,
что и требовалось доказать.
В случае колебаний крыла в потоке воздуха система не будет
консервативной [условие (22) не выполняется], так как либо
поток поддерживает колебания, и количество энергии в вибри-
рующей системе увеличивается, либо поток гасит (демпфирует)
колебания, и количество энергии в вибрирующей системе умень-
шается, так как часть энергии уходит на преодоление демпфи-
рующих воздействий аэродинамических сил.
В качестве примера применения уравнений Лагранжа рас-
смотрим систему, изображенную на фиг. 2, и изучим ее колеба-
ния в пустоте.
Пользуясь выражениями (3), легко вычислить кинетическую
энергию системы:
Т = mi (xi + г-) = 4~S mtZ*—5} Z 6 cos 9 +
(
где суммы распространены по всем точкам пластины АВ (фиг. 2).
Обозначим через М — массу пластины, Im—массовый момент
инерции ее относительно оси Е, □ — расстояние от центра
тяжести пластины до оси Е, и дополнительно предположим, что
колебания малы, т. е Z и 0 малы; тогда
7=4- MZ*— MiZ 0 -b 7m Q 2. (27)
Потенциальная энергия системы есть энергия деформации
пружин П и С (фиг. 2). Пусть k — жесткость пружины П и h —
жесткость пружины С. Тогда при деформациях 2и6— сила, раз-
виваемая пружинами П, будет kZ а момент пружины С будет ЛО.
Работа, совершаемая при деформациях пружин, есть потенциаль-
ная энергия системы:
U = 4- AZ2 + 4- ЛО2. (28)
Пользуясь выражениями (27) и (28), составляем уравнения
„Лагранжа (20) по обобщенным координатам Z и 9:
рвений Институт raqjl£ — Жаб 4-kZ = 0;
БИБЛИОТЕКА-+ Ае = 0-
)Л₽°ссман—15—2 s- л л
Эти уравнения движения могут быть легко проинтегрированы,
и движение системы полностью определено. Для примера выполним
это интегрирование. Так как уравнения (29) линейные с постоян-
ными коэфициентами *, то будем искать их решение в виде:
Z = Ae\ б = (30)
где А, В и X подлежат определению.
Подставляем эти выражения в уравнения (29). Тогда полу-
чаем для определения А и В:
(Ж2 + k) А + (- МЛ?) В = 0; |
(_ Д4зХ2) А + (ZmX2 + й) В = 0. j 1
Это — система линейных однородных уравнений, и чтобы она
имела отличные от нуля решения, определитель ее Д должен
равняться нулю, что приводит нас к уравнению для определе-
ния X, которое называется обычно характеристическим уравне-
нием,. или уравнением частоты (смысл последнего названия будет
разъяснен несколько ниже):
Д (МХ2 ф- k) (Jm\2 + h) — = 0. * (32)
Можно доказать, что это уравнение дает для X2 два отрица-
тельных корня. В самом деле, полагая Х2 =—со и Х2 = 0, убе-
ждаемся, что для обоих значений Д положительно. В то же время
k h
прн Х2 = — или Xs =------j- величина Д отрицательна. Следова-
тельно, если мы начертим кривую Д в функции X2, то эта кривая
между точками Х2 = — со и Х2 = 0 пересечет ось абсцисс дважды
(больше двух точек пересечения быть не может, так как урав-
нение биквадратное); при этом точки пересечения будут лежать
I л Л I
вне интервала ——р .
Пусть корни характеристического уравнения X2 и X2; обе эти
величины, как мы доказали, отрицательны. Обозначим:
= -Pl-
Тогда рг и р.2 — величины положительные.
Из любого уравнения системы (31) находим отношение -g-:
А МаХ3 1т№ + Л , опч
~В ~ ~М\3 +Т = AhV-’ 1 '
или для корня X2 = — р3
Мар?
А = ~ -Ь М2В’ > = ^=±^1.
R —Мр^
где I ;
1 Можно и в общем виде показать, что для случая малых колебаний урав
иення Лагранжа всегда будут линейными с постоянными коэфипиеитами. Ин-
тересующиеся найдут изложение этого вопроса в курсе «Теоретической меха-
ники* под редакцией Розе.
18
для корня Х2 = — р2
Мер* _
А =---------В, X = Х2 = 4- ip,,
k — Mpl 2 - г.,
причем В, конечно, в обеих формулах может быть различным.
Составляем теперь частные интегралы, например для корня Хх
по формулам (30):
Xj = + iPy
)i = — ‘Pi
R Мср'
1 k — Mp*
eip'z
Z2=-Ba
Mop*
k — Mp*
e~iPt'
b^B.e'^
b, = B2e-,p"
Аналогично можно составить частные решения для корня X.,.
Так как уравнения (29) — линейные, им будет удовлетворять
также сумма частных интегралов:
Z = - lBt е"”+ В2 e~ip‘ ] -
-^lT[B3ei^+
k — Mp2
6 = В,е,р‘'+ В2е~,р'л-\- взeitv+ Bt e~ip'\ (34)
Таким образом интегралы уравнений (29) найдены в комплекс-
ной форме. Так как физический смысл могут иметь только дей-
ствительные решения, то Вх и В,, а также В3 и Bt должны быть
сопряженными величинами:
В, — G -(- iDr
B, = Cx — iDA
В3 = С, *Т ID,
В4 = С,- iD,
(35)
В том, что Вк и В2, а также В3 и Bt должны быть сопряжен-
ными, можно убедиться и непосредственно, определяя эти по-
стоянные из начальных условий. Например, при т = 0
2 = Zo, Ь = 0О;
. Z = Z0, 0 = 6о,
где Zo, 60, Zo, % — известные значения деформации и скоростей
в начальный момент времени. Эти четыре условия служат для опре-
деления четырех произвольных постоянных интеграции. В спра-
ведливости выражений (35) можно убедиться непосредственным
вычислением.
Подставляя значения (35) в общий интеграл (34) и выражая
показательные функции через тригонометрические по известным
формулам:
е1* = cos х + i sin л;
е~‘х = cos х— i sin x,
19
находим: >
Z = ~ [CtCOSp^ —DiSin/?^] -
Afop»
— k_^ Iе2cos p2 т — D2 sinр2т];
6 = Cx cos pj t — £\ sin рхт + C2 cos p2T — O2 sin p2t,
где вместо 2CV 2Охи т. д. пишем просто Clt Dx..., так как эти
постоянные произвольны. Как уже указывалось, они могут быть
определены из начальных условий. Введем новые постоянные,
которые определим через Сх, Dx, С2, D2 следующим образом:
Сх cos otx б?2 — Т2 cos ot2
Dx = Lx sin ax D„ = L., sin a2.
Тогда
Afap? Afap?
Z = LX C0S + ai) + Li V m„* COS {piT + “2); /яйч
k — Mpi k—Mp2 (36)
в = Lx cos (p^ + ai) + T2 cos (p2T + a2).
Таким образом движение состоит из наложения двух гармо-
нических колебаний1,—первого с периодом Тх——, второго с пе-
Pi
риодом Г2= Все характеристики движения могут быть до
конца вычислены по приведенным формулам.
Каждое цз составляющих гармонических колебаний соответ-
ствует определенному корню уравнения частоты. Такое колеба-
ние, соответствующее определенному корню уравнения частоты,
называется стоячим колебанием, и мы в дальнейшем уви-
дим, что всякое гармоническое колебание может
быть представлено как сумма стоячих колебаний.
Число стоячих колебаний всегда равно числу степеней свободы
системы.
В дальнейшем мы еще вернемся к рассматриваемой задаче,
причем нужны будут некоторые свойства обоих стоячих коле-
баний, которые мы здесь и отметим.
Мы выше указывали, что решения характеристического урав-
Г k Ain
нения лежат вне диапазона ——у- . Положим для опреде-
k h m
ленности, что <-т-. Тогда
/И 1т
n k - h л
р1<лГ<Тт<Р1
1 Гармоническим называется колебание, происходящее по закону синуса
или косинуса.
20
и в силу уравнения (33) для Х® = —pf будет < 0, а для =
д
= — Pl будет -g-> 0. Следовательно, обращаясь к выражению (30)
или (36), заключаем, что в первом стоячем колебании положи-
тельному Z соответствует отрицательное 6, а во втором — поло-
жительному Z соответствует положительное 6. Кроме того, из вы-
ражения (36) видно, что в обоих стоячих колебаниях Z и 6
одновременно достигают максимума [когда cos (рт-f-a) = 1] и одно-
Фиг. 3. Фиг. 4.
временно обращаются в нуль [когда cos(/n -}- а) = 0]. В силу ска-
занного крайние положения при первом стоячем колебании
происходят так, как показано на фиг. 3, а при втором — как
показано на фиг. 4. В дальнейшем мы воспользуемся этими ре-
зультатами.
Прием, примененный при решении данной задачи, почти без
изменений будет в дальнейшем использован и в более сложных
случаях.
ГЛАВА II
КРУТИЛЬНЫЕ КОЛЕБАНИЯ КРЫЛА
1 ОСНОВНЫЕ УРАВНЕНИЯ
При изучении собственных колебаний крыла в пустоте будем
предполагать, что фюзеляж является абсолютно жесткой задел-
кой и крыло схематизируется как консольная балка с одтам
заделанным и другим свободным концом. Кроме того, предпо-
лагается, что самые колебания кручения выражаются в повороте
сечений крыла вокруг оси жесткости, и деформации сечений
не происходит.
В настоящей главе мы ограничимся рассмотрением такого
случая, когда центр тяжести в каждом сечении крыла совпадает
с центром жесткости. Как
будет показано далее,
если этого ограничения
не ввести, то колебания
будут обязательно сов-
местными, т. е. будут
иметь место не только
закручивание сечений
около оси жесткости, но
Фиг- 5- также и изгиб крыла.
Совместные колебания
будут изучены ниже, в настоящей же главе мы ограничимся рас-
смотрением чисто крутильных колебаний.
Пусть 0 — угол закручивания какого-либо сечения крыла. Он
изменяется вдоль размаха крыла и, кроме того, при колебаниях
меняется в каждом сечении крыла со временем. Поэтому 6
есть функция двух переменных у и т (ось оу на фиг. 5 направ-
лена вдоль оси жесткости крыла).
Составим уравнение движения колеблющегося крыла, для
чего рассмотрим элемент крыла между двумя соседними сече-
ниями тп и (фиг. 5) и составим условие равновесия действую-
щих на этот элемент моментов.
При колебаниях в пустоте на каждый элемент крыла дей-
ствуют инерционные и упругие силы, и для составления условия
равновесия моментов мы приравняем нулю сумму моментов
инерционных и упругих сил относительно оси жесткости.
22
Упругие скручивающие моменты, действующие на рассматри-
ваемый элемент крыла тптхпх, будут:
в сечении тп:
~GIpW'
в соседнем сечении тхпх.
где О/р — жесткость крыла на кручение в рассматриваемом се-
чении1. Если предположить, что центр тяжести в каждом сечении
крыла совпадает с осью жесткости, то легко написать также
выражение момента инерционных сил, действующих на элемент
гпптхпх.
т дх2
где 1т—погонный полярный момент инерции массы крыла отно-
сительно оси жесткости и, следовательно, lmdy— момент инерции
массы рассматриваемого элемента.
Приравняв нулю сумму всех моментов, получим уравнение
крутильных колебаний крыла:
<»
Для полного определения задачи к этому уравнению необхо-
димо добавить граничные и начальные условия.
Граничные условия. Так как крыло рассматривается
как консольная балка, жестко заделанная в корне, то в корневом
сечении крыла (.у—0) угол закручивания равен нулю. На свободном
же конце (_у=/) должен быть равен нулю крутящий момент.
Таким образом граничные условия будут:
6 = 0 при у = 0,
дб А
01 р= 0 при _у= /.
Начальные условия заключаются в том,чтобы задать рас-
пределения углов кручения и скоростей по размаху крыла в на-
чальный момент движения. Следовательно, для того чтобы до
конца определить все характеристики движения, нужно задать
ч и как функции у при т = 0; например:
при т—0
e = 0o(j); (3)
1 Не следует понимать, что Сесть модуль сдвига и 1р—полярный момент
инерции сечения крыла; это верно только для сплошного круглого сечения
Для крыла же Glp есть просто условное обозначение жесткости на кручение,
которая определяется специальными методами.
23
где 60 и 6г должны быть известными функциями у. Но обычно
эти функции неизвестны, так как зависят от характера и вели-
чины начального импульса, вызвавшего колебания; поэтому при
расчете не определяют полностью колебательное движение крыла,
а ограничиваются только определением некоторых характеристик,
не зависящих от начальных условий, что для практических це-
лей, как будет показано ниже, вполне достаточно.
Вообще говоря, GIp и 1т являются функциями у (изменяются
по размаху крыла). Уравнение (1) может быть точно проинте-
грировано только при некоторых частных видах зависимости GIp
и 1т от у. В общем же случае его интеграция возможна лишь
приближенными методами, главнейшие из которых будут ука-
заны ниже.
2. КОЛЕБАНИЯ КРЫЛА ПОСТОЯННОГО СЕЧЕНИЯ В ПУСТОТЕ
Метод Фурье. Простейшим случаем крыла является крыло
постоянного сечения, у которого GIp и 1т одинаковы во всех
сечениях. Для этого случая уравнение (1) принимает вид:
(4)
1т ду» 1 '
Для интегрирования этого уравнения можно применить метод
Фурье, заключающийся в следующем. Ищем частное решение
уравнения в виде произведения двух функций, из которых одна
зависит только от координаты у, другая только от времени т:
е = <р(у)-9’(т). (5)
После подстановки этого значения в уравнение (4) перемен-
ные разделяются, и мы получаем:
GIPdy^_d^ (6)
<т. Т 4
Так как левая часть уравнения зависит только от у, а правая
только от т, то каждая из них должна быть равна постоянной
величине1. Эту постоянную обозначим через р2. Приравнивая
порознь левую и правую части уравнения (6) этой постоянной,
получим два независимых уравнения для определения <р (у) и <?("):
а?+Л=0;
g»+-^ = o, (8)
где
________ — urZ- (9)
1 В самом деле, фиксируем т и будем изменять у. Тогда правая часть
уравнения (6) остается постоянной, так как от у оиа ие зависит; следовательно,
при изменении у должна оставаться неизменной и левая часть уравнения (6).
Частные интегралы уравнения (7) можно взять в различном
виде, например: qx= sin/к, <7„=cospT или ёг', q2 = е~,р\
где i=1 и е — основание натуральных логарифмов. Тогда
q (т) — А sin/м 4- В cos р~ (10)
или
д(т) = С e‘pz-±D е~‘р\ (И)
где А, В, С, D—произвольные постоянные.
Всегда можно сделать переход от выражения (11) к выраже-
нию (10) или обратно, пользуясь известными формулами Эйлера:
ёрх= cos рх 4- i sin рх\
-ipx . П2>
е F = cos рх — i sin рх.
Точно так же, интегрируя уравнение (8), находим:
<р (у) = М sin >у ф- N cos у. (13)
Произвольные постоянные Л4 и N Ъпределяем из граничных
условий. Подставляя в уравнение (2) значение 6 из выражения
(5), приходим к следующим условиям для функции <р(у):
<? (у) = 0 при у == 0,
^=0при^ = /. (14)
Подставляя сюда значение ъ(у) из выражения (13), придем к
следующей системе уравнений, определяющих М и JV:
N =
/И cos vl — N sin 4 = 0. (а)
В силу первого из этих условий второе распадается на два:
М = 0; cos 4 = 0. (b)
В первом случае из выражения (13) будем иметь ?(у) = 0, а
следовательно, согласно выражению (5) и 6 (у, т)е0. Это—три-
виальное решение, которое имеет место для любого однородного
диференциального уравнения и не представляет интереса, так
как соответствует в данном случае отсутствию вибраций.
Во втором случае находим:
4 = п^-, (15)
где ч может быть любым целым нечетным числом. Подставляя
сюда значение v из уравнения (9), находим:
25
Принимая во внимание выражения (14) и (15), находим окон-
чательное значение функции <р (у). Этих функций будет беско-
нечное множество, соответственно различным значениям п. Будем
обозначать через <р„(у) значение функции <р(у), соответствующее
определенному значению п. Соответствующее этому п значение р
будем обозначать через р„. Тогда
T„(j)=7M„sIn«^; (17)
п = 1, 8, 5, ...
и соответствующее значение ^(т) по выражению (10):
?n(T) =^nsinp„t-bBncosp„T. (18)
По формуле (5) находим соответствующее значение 6 (у, т):]
О'.т) = sin it (Ап sin-J- Вп cos р„т); (19)
п = 1, 3, 5, .
Постоянная Мп включена в Ап и Вп, так как эти величины про-
извольны.
Общий интеграл уравнения (4) составляется как сумма част-
ных:
6 (У, = ^sin n g- (А„ sinp„T cosp„t); (20)
И п
П « I, ?. ь, . . - »
Постоянные А„ и В„ могут быть определены из начальных
условий (3). Например, если при т = 0: в = б0 (у) и = то
W) = #«sin п^-.
И
ei(j) = ^Anpn sinn-^t
п
(21)
откуда Ап и Вп определяются методом, обычным для определения
коэфициентов ряда Фурье, а именно: чтобы получить Ат и Вт,
умножаем уравнения (21) на sinm-^ и интегрируем в пределах
от нуля до I. Все члены, кроме содержащих Ат и Вт, обра-
тятся в нуль, и мы найдем:
i 1
An= I (у) • sin т ~tdy, Bm = -^-f % (у) sin т ^dy.
6 о
Из выражения (20) мы видим, что движение может быть
представлено как сумма бесконечно-большого ч исла частных
26
движений. Каждое такое движение есть гармоническое колебание
2к
с периодом —.
Рп
В самом деле, рассмотрим значение 6Я [формула (19)] в мо-
менты времени т = и т = + —. Легко видеть, что значения
Рп
также скоростей и ускорений в эти моменты
одинаковы и, следовательно, интервал времени Т—^р- есть пе-
риод колебания. Число колебаний в секунду п — ~f= Вели-
чина рП называется круговой частотой колебания. Для
краткости в дальнейшем будем рп называть просто частотой. Рас-
2/
смотрим сечения крыла, находящиеся на расстоянии от
корня крыла, где k — любое целое число. (Легко видеть, что
число таких точек внутри интервала 0<_у < I, т. е. на крыле,
будет равно л 2~). В рассматриваемых точках при любом т зна-
чение 6„ обращается в нуль
[что непосредственно видно,
если подставить у = ук в вы-
ражение (19)], т. е. рассматри-
ваемое частное движение в
этих сечениях крыла отсут-
ствует. Такие точки называются
узлами колебания. Узлы
сохраняют свое положение во
все время движения. Сече-
ния крыла, находящиеся спра-
ва и слева от узла, двигаются в разные стороны.
Каждое частное движение, соответствующее какому-либо
значению п, называется стоячим колебанием, и формула (20)
дает разложение колебательного движения крыла по стоячим
колебаниям. Как мы увидим ниже, любое гармоническое коле-
бание можно представить как сумму конечного или бесконеч-
но-большого числа стоячих колебаний.
Стоячее колебание, соответствующее наименьшему значению
п, называется основным тоном колебания, а все осталь-
ные стоячие колебания называются обертонами1. В рассмат-
риваемом случае основной тон колебания происходит без узлов.
Как ясно из выражения (16), частота первого обертона пре-
восходит частоту основного тона в 3 раза, частота второго обер-
тона— в 5 раз и т. д.
На фиг. 6, 7 и 8 показаны формы колебания, т. е. распреде-
ление углов кручения по размаху крыла, для основного тона
1 Обертоны называют также соответственно вторым, третьим и т. д. тоном
колебания.
27
(фиг. 6), а также первого (фиг. 7) и второго (фиг. 8) обертонов,
построенное по формуле (17). Каждое стоячее колебание про-
исходит так, что в каждой данной точке крыла с течением времени
меняется величина угла закручивания, но закон изменения углов
кручения по размаху крыла сохраняется.
3. ПРИБЛИЖЕННЫЕ МЕТОДЫ ДЛЯ КРЫЛА ПРОИЗВОЛЬНОГО СЕЧЕНИЯ
Таким образом задача колебаний консольной балки постоян-
ного сечения до конца решается методом Фурье. Но если жест-
кость балки и момент инерции изменяются вдоль ее длины по
произвольному закону, задача значительно осложняется, так как
уравнение, определяющее функцию формы <₽ (у), обычно не уда-
ется проинтегрировать.
В самом деле, если выражение (5) частного интеграла под-
ставить в уравнение (1) колебаний балки переменного сечения,
то после разделения переменных будем иметь:
-L(Gi
dy \ р dy) d-t3
Так как слева стоит функция только у, а справа функция
только т, то, следовательно, каждое из отношений является
постоянной величиной. Обозначая эту постоянную через —р",
получим для определения <р(у) и q(y) уравнения:
g + Л-0; (22)
ф-(о/р$)+Л» = 0- <23>
Уравнение (23) может быть проинтегрировано в замкнутом виде
лишь в небольшом числе частных видов зависимости GIp и 1т
от у. Обычно же жесткость и момент инерции крыла заданы
таблично и аналитический закон их изменения по размаху крыла
неизвестен. В этом случае для определения частоты и формы
колебаний применяются различные приближенные способы.
28
Прежде всего сделаем некоторые предварительные замечания
общего характера. Уравнение (23) — второго порядка и потому
имеет два частных интеграла, которые обозначим <рх(у) и <р„(у).
Тогда уравнение (23) удовлетворится функцией:
<? (у) = Ж<рг (у) + N <?.2 (у). (24)
функция <р (у) должна удовлетворять граничным условиям (14).
Эти условия приводят к следующей системе уравнений для оп-
ределения постоянных интегрирования Ж и N:
Ж<Р1(0) + ^2(0) = 0; |
ж(^) + =о. | (25)
kdy 7j=o \dy Jy^o J
Эта система однородных линейных уравнений может иметь от-
личное от нуля решение тогда, и только тогда, когда ее опре-
делитель равен нулю, что приводит к следующему условию:
(»,-.= °- <26>
Так как и <р., — интегралы уравнения (23), коэфициенты
которого зависят от р, то и сами функции и <р2 будут зави-
сеть от р. Поэтому уравнение (26) можно рассматривать как
условие для определения р. Это уравнение называется уравне-
нием частоты (или характеристическим уравнением), так как р
есть не что иное, как частота колебания. В этом легко убе-
диться, проинтегрировав уравнение (22), совпадающее с уравне-
нием (7), которое мы выше рассмотрели, а затем определив пе-
риод колебания так же, как выше было сделано для крыла
постоянного сечения. [Для крыла постоянного сечения системой
(25) являются уравнения (а), а характеристическим является
уравнение (Ь)].
Из приведенного рассуждения видно, что уравнение (23) может
иметь интеграл, удовлетворяющий граничным условиям не всегда,
а только при некоторых частных значениях параметра р, входя-
щего в Это уравнение [именно только при значениях р, являю-
щихся корнями уравнения (26)]. Значения параметра, при которых
уравнение (23) имеет интеграл, удовлетворяющий граничным
условиям, называются собственными значениями пара-
метра, а функции <₽ (Д’), являющиеся интегралами уравнения (23)
и удовлетворяющие граничным условиям, называются собст-
венными функциями рассматриваемого диференциального
уравнения.
Уравнение (26) может иметь ряд корней: рх, р„,...,рп (число
корней может быть и бесконечным). Соответственно каждому
м
значению частоты находим отношение постоянных из любого
Уравнения системы (25) и затем, подставляя найденное значение
Р в выражения срг и <f2, находим по формуле (24) соответствующую
29
данному собственному значению р=р„ собственную функцию <р —
=<рп(у). Интегрируя уравнение (22) прир=р„, найдем также соответ-
ствующее данному р значение функции <7=9„(т)Таким образом
каждому р = рп будет соответствовать свое значение угла за-
кручивания крыла 6Л = »„(у)-?п (т), и общее решение опять будет
найдено как сумма:
«=хв-
причем сумма эта будет содержать столько членов, сколько кор-
ней имеет уравнение частоты. Каждое составное движение бп
есть стоячее колебание и, следовательно, для крыла произволь-
ного сечения мы также можем разложить движение по стоячим
колебаниям.
Как мы видим, этот путь полностью повторяет путь решения,
примененный нами для крыла постоянного сечения. Однако для
того, чтобы воспользоваться изложенным приемом решения,
необходимо проинтегрировать уравнение (23), что не всегда пред-
ставляется возможным. В последнем случае для определения
частоты и функции <f (у), дающей форму колебания, пользуются
различными приближенными методами.
а. Метод Релея. Метод Релея заключается в том, что делают
определенное предположение относительно формы колебания
балки. Частоту тогда находят из рассмотрения энергии колеблю-
щейся системы.
В самом деле, предположим, что функция формы колебания
известна. Тогда, согласно выражению (5), движение будет пол-
ностью определено, если будет известна функция <?(т). Эту вели-
чину принимаем за обобщенную координату и составляем урав-
нение Лагранжа по этой координате [уравнение (20), гл. I].
Потенциальная энергия упругих сил системы определяется
известной формулой сопротивления материалов для энергии за-
крученной балки:
и и
Кинетическая энергия
<28)
о о
Составляем уравнение Лагранжа [уравнение (20), гл. I]; получаем
, j'^dy + q [01 р ffldy = 0. (29)
о о
1 Постоянные интеграции при этом могут быть найдены из начальных
условий.
30
Это уравнение линейное относительно </, с постоянными коэ-
фициентами. Решение его возможно в виде q — cos pt или q =
= sin р т или q — е'р~, причем каждая из этих функций имеет пе-
риод [То же выражение для q получается и при решении
уравнения (2?)]. Подставляя значение q в уравнение (29), найдем
соотношение, из которого и определяется р:
№
р‘=—,---------- (30)
f Inrfdy
О
Если бы было известно точное значение функции формы
ф (у), то это выражение определяло бы точное значение частоты
р. Задавая функцию ср (у) из каких-либо соображений прибли-
женно, мы получаем по формуле (30) и приближенное значение
частоты. Обычно, если задать функцию ср (у) так, чтобы она удо-
влетворяла граничным условиям задачи (14), то значение часто-
ты по формуле (30) довольно близко совпадает с точным зна-
чением, даже если выбранная функция формы и не очень близка
к действительной. Ниже мы приведем примеры, иллюстрирую-
щие это.
Метод Релея неудобен тем, что дает возможность определить
только частоту колебаний, а не форму их. Кроме того, точность
определения частоты зависит от более или менее удачного вы-
бора функции <p(j'), а для такого выбора никаких способов не
дается. От этих недостатков свободен метод Ритца, который
является дальнейшим развитием метода Релея.
б. Метод Ритца. Метод Ритца с успехом применяется для
приближенного решения ряда задач математической физики, ко-
торые сводятся к задаче отыскания такой функции <с (у), кото-
рая обращает в минимум интеграл
ь
1= f Р(У, (31)
а
где ср'= и /-' — известная функция от у, э, Ниже мы по-
кажем, что к такой же задаче можно свести и задачу об опре-
делении интеграла диференциального уравнения (23), т. е. задачу
об определении функции формы колебаний балки.
В вариационном исчислении доказывается1, что функция, об-
ращающая в минимум функционал /, определяется как инте-
грал диференциального уравнения Эйлера:
--- 4
1 М. А. Лаврентьев и Л. А. Л юс терна к, Курс вариационного
исчисления. ГОНТИ, 1938 г.
в-К. Смирнов, В. Н. Крылов, Л. В. К а нт о ров и ч, Вариационное
исчисление. Кубуч, 1933 г.
31
= <32)
« таким образом задача о нахождении функции, обращающей в
минимум функционал, сводится к задаче интегрирования дифе-
ренциального уравнения. Развернув первый член левой части
уравнения, легко убедиться, что оно будет второго порядка и,
следовательно, его интеграл будет зависеть от двух произволь-
ных постоянных. Для их определения должны быть заданы два
условия (граничные условия).
Однако уравнение Эйлера не всегда может быть точно реше-
но. В этих случаях для приближенного определения <р часто
удобно применить способ Ритца, заключающийся в следующем.
Выбираем последовательность функций ^(j), <р2(у)..., каждая
из которых удовлетворяет граничным условиям, и ищем <p(j’) в
виде линейной комбинации первых п функций ©,(у):
(У) = + «2?2 + • • • + ап?п. (33)
Коэфициенты at подбираются таким образом, чтобы функция,
определяемая рядом (33), обращала в минимум интеграл (31).
Подставляя значение ср (у) из выражения (33) в ряд (31), найдем
/ как функцию конечного числа неизвестных alt а2,...,ап.
{av а2,...,ап).
Составляем условия минимума этой функции:
д[
= ........„. <34>
Таким образом получаем систему п уравнений, из которых
и определяются п неизвестных коэфициентов аъ а2,...,ап. Сле-
довательно, идея метода Ритца состоит в сведении задачи об
отыскании минимума функционала к задаче отыскания минимума
функции конечного числа переменных.
Можно доказать, что при неограниченном увеличении числа
членов ряда (33) определяемая этим рядом функция стремится к
функции, дающей точное решение поставленной задачи1 2, т. е.
стремится к точному решению уравнения (32).
Применим изложенный метод к нахождению функции формы
колеблющейся балки. Эта функция определяется уравнением (23)
и граничными условиями (14). Прежде всего заметим, что урав-
нение (23) является уравнением Эйлера для функционала:
'=Л0/Л^У-ргМр5>
1 В. И. Смирнов, В. И. Крылов, Л. В. Канторович, Вариацион-
ное исчисление, Кубуч, 1933
2 В самом деле, составляя
— получим в точности
уравнение (32), приняв F(y, ?, <р') =
уравнение (23).
32
Следовательно, функция формы колебания обращает этот
интеграл в минимум.
Ищем <f(y) в виде ряда (33). За функции <pt, <р2,при
этом можно принять, например, систему функций получен-
ных при решении задачи о колебаниях балки постоянного се-
чения [формула (17)], т. е.
Ъ (У) = sin У- (36)
Но возможны и другие способы выбора (у). Подставляем зна-
чение ?(у) из выражения (33) в формулу (35) и затем составляем
уравнения (34). Получим:
<37>
о
k = 1, 2.п.
или, выполняя в действительности подстановку выражения (33j:
где
£ (Д,й — p2Bffc)az = 0;
«= 1
k = J, 2, . .., п.
о
I
B.k =
О ч
(38)
(39)
Система (38) однородных линейных уравнений служит для
определения коэфициентов at. Система линейных однородных
уравнений может дать решения, отличные от нуля, только в том
случае, если определитель системы равен нулю. Это условие
приводит к уравнению частоты, из которого можно определить
р. Уравнение частоты будет порядка п относительно р2 и, сле-
довательно, имеет п корней. Можно доказать, что все эти корни
будут действительными и положительными и, следовательно,
получить п значений частоты. Каждому значению соответствует
своя форма колебаний, определяемая формулой (33), которая
/о°ожет быть найдена после того, как вычислены а, из системы
(38) для определенного значения частоты р.
Если в методе Ритца ограничиться первым приближением,
т. е. ряд (33) оборвать на первом члене, то от системы (38)
останется лишь одно уравнение:
ГР°Ссман—15—3
I
dy — p2f Im<t\dy
и
«1 = 0,
[/ч(^У
33
откуда
где, следовательно, (у) — заданная функция формы колебания.
Эта формула совпадает с выражением (30), которое было
получено при определении частоты методом Релея. Можно,
следовательно, сказать, что по методу Релея получается то же
значение частоты, как и в первом приближении по методу Ритца.
Весь метод Ритца для задач колебаний можно получить как
непосредственное обобщение метода Релея.
Задавая в методе Релея каким-либо образом функцию
мы тем самым накладываем ограничения на возможные формы
колебания балки, т. е. накладываем на колеблющуюся систему
дополнительные связи. Такие дополнительные связи как бы уве
личивают жесткость системы и потому частота, получаемая по
способу Релея, всегда несколько выше ее точной величины.
Точное значение функции с? (_у) обращает выражение (30) в ми-
нимум. Поэтому, выбирая (у) в виде ряда (33) и подставляя его
в формулу (30), мы найдем значение частоты ближе всего к
истинному значению, если выберем коэфициенты ак так, чтобы
выражение (30) обращалось в минимум. Это условие приводит
к следующей системе уравнений для определения коэфициен-
тов ак.
‘а°—1--------= 0:
./ 1т^У
"о
k = 1, 2.Л,
ИЛИ
faw ~ °-
о и о о
Замечаем, что согласно выражению (30)
о о
Тогда получим из предыдущего уравнения:
£-J[Gr? dy=°’
о
34
т. е. как раз систему (37) уравнений Ритца. Таким образом
способ Ритца является непосредственным обобщением способа
Релея.
Из этого рассуждения видно, что, определяя частоты коле-
баний методом Ритца, мы в каждом последующем приближе-
нии будем получать меньшее значение частоты, чем в предыду-
щем, т. е. будем приближаться к точному решению сверху.
Метод Ритца обычно сходится весьма быстро, так что одного,
двух приближений бывает вполне достаточно для получения
практически достаточной точности при определении частоты ос-
новного тона.
Следует подчеркнуть, что сходимость метода Ритца доказана
во всех случаях, когда уравнение, определяющее функцию формы
колебаний, представляет собой уравнение Эйлера для некото-
рого функционала.
в. Метод Галеркина. Метод Ритца, как выше было указано,
применим в тех случаях, когда искомая функция такова, что
обращает в минимум некоторый функционал. При этом состав-
ляется выражение данного функционала, и путем приближенного
задания искомой функции в виде
? (J) = ai4>i + ae<f2 + • - • + ап^п (40)
задача отыскания минимума функционала сводится к задаче на-
хождения минимума функций от п переменных (av а2, ..., aj.
Видоизменением метода Ритца является метод Галеркина,
который, во-первых, позволяет избежать составления выражения
функционала и, во-вторых, по своей форме может быть приме-
нен и в тех случаях, когда не. существует функционала, обраща-
емого искомой функцией в минимум.
Применим метод Галеркина на примере колебаний кручения
произвольного крыла. Будем предполагать, что кроме упругих
и инерционных сил на элемент крыла (фиг. 5) действует еще
момент М, пропорциональный угловой скорости колебания:
Mdy = K~dy, (41)
где коэфициент К, вообще говоря, различен для различных се-
чений крыла (т. е. является функцией у).
Такой момент возникает, например, если при колебаниях
имеются силы трения, пропорциональные скорости колебания.
В этом случае уравнение движения будет отличаться от урав-
нения (1) только тем, что в правой части добавится еще момент
М, и мы будем иметь:
'.£=£(<^W-
Делаем подстановку:
6 = <Р(У) •
(43)
35
Тогда для определения функции формы ср (у) получим уравнение:
W.f-UCf-^(Of,^)-a (44)
Метод Галеркина для приближенного определения функции
формы <р и величины X заключается в следующем. Функция ср (у)
определяется, как и в методе Ритца, в виде ряда (40), где <р, (у)—
заданные функции, удовлетворяющие граничным условиям. Урав-
нения для определения коэфициентбв этого ряда получаются
следующим путем. Подставляем выражение (40) в уравнение (44).
Затем полученное уравнение умножаем поочередно на <рх dy,
<?2dy,..., <fndy и интегрируем по длине крыла. Получим систему п
уравнений:
1=1 10
i i
ImWj dy-l f K'Wtjdy
о о
= 0,
(45)
7= 1,2......И,
из которых и находим коэфициенты а,-. Так как система (45)
есть система линейных однородных уравнений относительно ко-
эфициентов ait то она имеет отличные от нуля решения только
в том случае, когда определитель системы равен нулю. При-
равнивая этот определитель нулю, получаем характеристическое
уравнение, из которого определяется X.
Покажем, что уравнения (45) суть не что иное, как условия
равенства нулю работы на пути возможных перемещений колеб-
лющегося крыла, и метод Галеркина по существу сводится к
принципу возможных перемещений при наличии некоторых
ограничений свободы движения.
В самом деле, если движение представить как сумму стоячих
колебаний, то 6 будет иметь следующий вид:
6 = + <7г'-?2 +• - • + qn4n + • • •. (46)
где «р,— функции только у, a qt—’функции только времени.
Если предположить функции <ргСу) известными, то движение
будет полностью определено, если будут определены ?f(t). Эти
величины выберем за обобщенные координаты (см. гл. I). Ряд
(46), вообще говоря, содержит бесконечно большое число чле-
нов, так как упругая система является системой с бесконечным
числом степеней свободы (каждая точка системы может двигать-
ся независимо от другой при соблюдении) только условия от-
сутствия разрывов). Будем искать приближенное значение 9,
ограничиваясь в ряду (46) первыми п членами:
6 = <7i?i + + • • + <7„<Р„. (47)
Этим самым мы наложили ограничения на свободу движения
системы и свели задачу колебания упругого тела к задаче ко-
лебания системы с конечным числом п степеней свободы. По-
зе
кажем теперь, что, определяя приближенное значение 6, со-
гласно выражению (47), исходя из принципа возможных переме-
щений, мы получим тот же результат, как и исходя из метода
Галеркина.
В главе I было указано, что уравнения Лагранжа представ-
ляют собой условия равенства нулю работы на пути возможных
перемещений. Составим уравнение Лагранжа для нашего случая.
Кинетическую энергию и потенциальную энергию упругих
сил вычисляем, как и выше, по формулам (27) и (28):
Подставляя сюда значение 6 из выражения (47), находим:
п I
т"=2 У Я Л if
i,j = l О
v=i (48)
i, j— 1
Кроме упругих сил, на
крыло еще действует мо-
мент М [см. уравнение (41)].
Вследствие этого имеются
также обобщенные силы,
которые вычисляем по фор-
муле (8) гл. I. Пусть (фиг. 9)
MN — профиль крыла в ка-
ком-либо сечении до воз-
никновения движения и
M'N'— тот же профиль во
время движения. Пусть
xEz — неподвижная система
координат, начало которой Е
выбираем в точке, вокруг которой происходит закручивание крыла.
Тогда декартовы координаты произвольной точки А' крыла бу-
дут:
xft = oftcos(Tft-|-e);
^=-°*sin(7ft+0).
Обобщенные силы по формуле (8) гл. I будут:
= 2 (Х“Э? + Z>^) = £ И. SI» h. + ’) +
+ Z4cos(i, + 0)|^,
37
где суммирование распространено по всем точкам крыла. Выра-
жение, стоящее в квадратных скобках, есть не что иное, как
проекция силы на нормаль (п) к отрезку ak (фиг. 9), соединяю-
щему рассматриваемую точку с началом координат. Если при-
нять еще во внимание, что, согласно выражению (47), = <р7,
то выражение обобщенной силы можно переписать в виде:
где Mk — есть момент сил, действующих в произвольной точке
A'k крыла относительно оси вращения Е. Но У, если сум-
мирование производить только по точкам одного сечения крыла,
равна <ру7И dy, vny М — момент сил, действующих в сечении.
Суммируя далее по всем сечениям крыла и подставляя значение
М по формуле (41), находим:
Q/ = f
О
или согласно выражению (47):
п I
Q7=S?z
‘ ~1 о
(49)
Пользуясь выражениями (48) и (49), составляем уравнение
Лагранжа [см. уравнение (21) гл. I];
rf (дТ\ дТ ди = п .
dz k fy) d(]j +
/ = i, a.n.
или, подставляя значения T, U и Qy:
г z z z n
4if fK^, dy + qifGlp dy
о о 0
= 0
Это — система линейных диференциальных уравнений отно-
сительно обобщенных координат. Интегрируем ее подстановкой
gf. = а.е>т; (50)
i = 1, 2, ...» п.
Тогда для определения коэфициентов at получаем систему
уравнений:
п г 1 1 1 т
S °' I ’’ f'-wdy -’• Aw +А'- ЙН-а (51 >
i = 1 L о О О J
/ = 1, 1, . . . , п
38
Приравнивая нулю определитель этой системы, получаем
характеристическое уравнение, из которого находим X.
Предположим, мы нашли какой-либо корень К характеристи-
ческого уравнения. Затем из системы (51) определяем для най-
денного X значения а,-. Тем самым определяются и значения <?,
по выражению (50). Подставляя эти значения в уравнение (47),
находим: i
6 = ?(у).ех\
г
? (У) = ^191 + + • • • + а„ф„.
Решение будет полностью совпадать с решением по методу
Галеркина, если будет доказано, что системы уравнений (45) и
(51), из которых определяется at и X, тождественны. Непосред-
ственно видно, что это будет иметь место, если
-Л (Ч Э) =foip^} (%) dy. (52)
о о
Чтобы это доказать, проинтегрируем левую часть по частям:
- Л (4$) | Ч £ ъ +./Ч (§') ($') dy.
о 0 0
Но проинтегрированный член исчезает в силу граничных
условий (14), которым должны по условию удовлетворять функции
и <ру, что и доказывает справедливость выражения (52). Легко
проверить, что проинтегрированный член исчезает не только
в случае консольной балки, но и во всех других случаях закреп-
ления концов, т. е. решения методом Галеркина, и по принципу
возможных перемещений тождественны и в других случаях
закрепления концов балки.
Рассмотрим теперь частный случай, когда ZC = 0, т. е. когда
на крыло не действуют никакие силы, кроме сил упругости и
инерции. Этот случай мы выше решали методом Ритца.
Легко видеть, что в этом случае система уравнений (45) совпа-
дает с системой (38), которая была получена методом Ритца, т. е.
в этом случае методы Ритца и Галеркина дадут тождественные
результату. И вообще, если функция формы колебания дает
минимум некоторому функционалу, то методы Ритца и Галер-
кина приводят к одним и тем же результатам. Так как доказа-
тельство сходимости метода Ритца имеется, то тем самым
в этих случаях доказывается и сходимость метода Галеркина.
Но метод Галеркина можно применять также и в случае, если
функция формы не дает минимума никакому функционалу (как,
например, в рассмотренном случае, когда имеются силы, про-
за
порциональные скорости колебания). Доказательство сходимости
метода Галеркина для этих случаев не опубликовано1.
Пример. Требуется определить частоту собственных коле-
баний для крыла полуразмахом / = 975 см\ значения жесткости
кручения и момента инерции это^о крыла вдоль размаха указаны
на фиг. 10.
Решаем задачу, ограничиваясь вторым приближением. В каче-
стве функций и <р2, которыми необходимо задаться при решении,
возьмем функцию первого и второго тонов для крыла постоян-
ного сечения [формула (42)], и, следовательно, функция формы
по формуле (40) будет иметь вид:
<Р (У) = 0=1 sin + a., sin 3 Ц. (53)
Чтобы получить систему уравнений для определения ах и а2
подставим это выражение в уравнение (23), определяющее
функцию формы.
Получим:
0127 Гу ( GIp ™T) + a£ify( GIp cos 3 Ю + Sin +
+ p2Ima„sin 3^ = 0.
Это уравнение умножаем поочередно на каждую из двух
выбранных функций: первый раз на sinвторой — на sin3^,
1 В работах акад. Крылова имеются указания на существование такого
доказательства, но само доказательство не приведено.
40
и результаты интегрируем в пределах от пуля до I. Проделав
указанные вычисления, придем к следующей системе уравнений:
(_ 84,8 • Ю5 + 2,8 • 103р2) Oi-f- (— 115,9 • 105 + 2,45 • 103р2) а., = 0;
115,9 -105 + 2,45 • 103р2) at+ (-479 • 105 + 5,47 - 103р2) а2 = 0. (54)
Все интегралы были определены численно, значения GIP и 1т
брались из графика фиг. 10. При вычислении интегралов, в которые
входит GIp, их предварительно интегрируют по частям, чтобы осво-
бодиться от производных от жесткости, входящих под знак интег-
рала, как это было выше указано [формула (52)]. Например:
J .f£y (GrP C0S 2") Sin S’ dy = - fG/P C0S’- % dy-
о о
Система уравнений (54) соответствует системе (38). Приравни-
вая нулю определитель системы (54), получаем уравнение частоты;
(— 84,8 -105 4- 2,8 - 103р2) (— 479 • 105 + 5,47 • 103р2) —
— (- 115,9 • 105 + 2,45 • 103р2)2 =~ 0.
Решаем это уравнение и находим два корня:
р2 = 2775 и р* = 10 485,
или по извлечении корня:
рг = 52,6 и р,— 102,2.
Соответственно числа колебаний в секунду для первого и
второго тонов колебания будут:
= £ = 8,4—- и п.,=р£ = 16,3 —.
1 2п ’ сек. - 2я ’ сек.
Если бы желательно было получить также частоты более
высоких обертонов, необходимо было бы задаться в ряду (53)
соответственно большим числом функций.
Функцию формы колебания для первого и второго тонов
находим по формуле (53), для чего предварительно из любого
уравнения системы (54) определяем отношение —:
для первого тона
— = —6,82;
«2
Для второго тона
— = —0,6728.
а2
Функцию формы ряда (53) представим в виде:
(у) = a, g sin g' + sin 3 gQ. (55)
4i
Так как а, остается произвольным, выберем этот коэфициент
таким образом, чтобы значение <р(у) на конце крыла было равно
единице [<р(0 = !]• Функция <р (у), вычисленная для первого и
второго тонов по формуле (55), приведена на фиг. 11.
Укажем, что точное решение данной задачи возможно методом
последовательных приближений (см. п. 4 этой главы); оно дает
для основного тона значение р2, — 2730 и, соответственно, число
колебаний в секунду п = 8,33, что хорошо согласуется с найден
ным выше значением п — 8,4.
Фиг. II.
Заметим также, что если ограничиться первым приближением
|т. е. вместо ряда (53) принять = d^sin^], что соответствует при-
менению формулы Релея, то будем иметь:
и соответственно
п = 8,75 колебаний в секунду.
Следовательно, даже первое приближение по методу Галеркина
дает уже неплохое совпадение с точным решением.
4. ОПРЕДЕЛЕНИЕ ФУНКЦИИ ФОРМЫ КОЛЕБАНИЯ И ЧАСТОТЫ
МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Распределение углов кручения крыла по размаху опреде-
ляется функцией формы (у), которая должна быть найдена
интегрированием уравнения (23) при граничных условиях (14).
У меть находить функцию формы необходимо, во-первых, для
определения частоты колебания, которая, если функция у
известна, легко находится по формуле (30) Релея, и, во-вторых,
12
для расчета флаттера. Как мы ниже увидим, при расчете флат-
тера, как и в методе Релея, необходимо задаться формой колеба-
ния, и затем можно определить частоту и скорость полета, при
которой флаттер возникает. Задавать же формы колебания при
флаттере естественно на основе допущения, что эта форма сов-
падает с формой собственных колебаний крыла; вот почем)
определять собственную функцию необходимо также и для
расчета флаттера.
Наиболее часто употребляется для определения собственных
функций метод последовательных приближений.
а. Определение формы и частоты основного тона колебания.
Для определения функции ?(_у) необходимо проинтегрировать
диференциальное уравнение:
(56)
при граничных условиях
<f (у) — 0 при у — 0;
А / (57)
Гу = ° при J = /.
Прежде всего заметим, что функция <р(у) диференциальным
уравнением (56) и граничными условиями (57) определяется
только с точностью до постоянного множителя.
В самом деле, если функция <? (у) удовлетворяет диферен-
циальному уравнению (56) и граничным условиям (57), то функция
А-<р(у), где А — произвольное постоянное число, будет также
удовлетворять указанному уравнению и граничным условиям.
Если <?(у) — известна, то значение частоты можно найти по
формуле Релея:
./'"-(ST"*'
р‘ = °—;--------. (58)
f
О
Умножение функции <р(у) на произвольный множитель А не
отразится на величине частоты, так как числитель и знаменатель
в формуле Релея приобретут одинаковый множитель, который
сократится.
Следовательно, мы вправе сокращать (или умножать) функ-
цию ср (у) на любой постоянный множитель. Этим в дальнейшем
мы воспользуемся.
Перенесем в уравнении (56) последний член в правую часть
и проинтегрируем уравнение в пределах от произвольного у до I.
Разделив результат на GIp, получим:
g = (59>
43
Нижний предел выбран таким образом, чтобы было удовле-
творено второе из граничных условий (57). Интегрируем выра-
жение (59) в пределах от нуля до у. Нижний предел выбран
равным нулю для того, чтобы удовлетворить первому из усло-
вий (57). Будем иметь:
? (j) = J ту = р2 fAp f1^ аУ- (60)
о о р I
Пользуясь формулами (59) и (60), можно определить функцию
<р Су) следующим образом. В качестве исходного приближения
задаемся какой-либо функцией <? = <f0(y) и вычисляем соответ-
ствующее значение частоты р = р0 по формуле (58). Для полу-
чения следующего (первого) приближения подставляем значения
о == <р0 (_у) и р = р0 в правую часть формулы (59). Выполнив указан-
ные действия1, найдем в первом приближении. Интегрируя
найденное значение [формула (60)],. найдем первое приближе-
ние для функции (у), которое обозначим через <рг (у).
Совершенно так же определяются следующие приближения.
Для получения второго приближения подставляем <f = <?i (у)
в формулу Релея (58) и находим соответствующее значение
частоты р = рг. Затем найденные значения <р ='<?! и р — рг подбав-
ляем в правую часть формулы (59) и находим новое значение .
Интегрируя его, находим второе приближение для функции <? (у).
Этот процесс продолжаем до тех пор, пока функции (у),
полученные при двух последовательных приближениях, не совпа-
дут. Обычно для этого бывает достаточно двух-трех приближений.
Весь процесс последовательных приближений можно значи-
тельно упростить, если воспользоваться сделанным выше заме-
чанием, что функцию <р (у) мы вправе сокращать на' любой
постоянный множитель. Будем сокращать функции, получаемые
в каждом из последовательных приближений, на множитель р2.
(Это — величина постоянная, т. е. не зависит от у). Тогда вместо
формул (59) и (60) мы будем иметь для получения л-го прибли-
жения из (п — 1)-го следующие формулы:
= (61)
’.“/«‘'J'- (62)
О
Таким образом отпадает необходимость в каждом приближении
определять частоту. Только после того, как процесс окончательно
сошелся, р, если это необходимо, определяется по формуле (58).
1 Интегрирование, очевидно, ведется числовым методом. Простейший
способ числового интегрирования будет указан ниже.
44
Таблиц.! I
Вычисление третьего приближения Производная
XVI XVU XVIII XIX XX
/XV XVI/II JXVII А XVIII В XVII
?» dtp, dy
62.2 0,628-10-8 0 0 0,82-10—3
59,58 0,605-10-8 1,233-10-8 0.0785 0.79-10—3
'—7— 53 3 0,588-10~8 2,426-ю-8 0.1541 0.768-10—3
45,8 0.664-10“8 3,68-10-8 0,234 0.865-10- 3
37,7 0.91-Ю~8 5.25-10~8 0.334 1,19-10~3
28 95 0.943-10-8 7 105 10“8 0.452 1.23 IO-3
19,68 0.915-10~8 8,96-10“8 0.571 1 195-10—3
11.21 0.947-10-8 10 83-10“8 0.690 1,24-10-3
5,32 1 04-10-8 12,8-10-8 0 816 1,36-1 о-3
1,974 0.914-10~8 14.77-10—8 0,938 1,19-(О-3
0 0 1568 Ю“8 1.0 0
А=-------!-----=0.0636 108 д —-о |307 • 10С
15,68 10-8 1 ,
Для удобства сравнения между собой функций, получающихся
в различных приближениях, будем всегда умножать их на такой
множитель, чтобы получать на конце крыла (при у = 1) одно и
I то же значение <р (0 = 1-
В качестве исходного приближения для функции <р (у) можно
задаться, например, функцией первого тона колебаний крыла
I постоянного сечения [см. формулу (17)]:
<p0(j) = sin^f.
(62а)
Интегралы в формулах (61) и (62) проще всего вычислять методом,
указанным в приложении.
Пример. Вычислить методом последовательных приближений
функцию формы колебания и частоту для крыла полуразмахом
1=975 см, жесткость кручения и момент инерции которого
показаны на фиг. 10. Выше это же крыло было рассчитано
методом Галеркина. (Вычисление формы колебания приведено
в табл. 1.)
Порядок вычислений следующий. Все крыло делится на 10
равных частей. В сечениях, разделяющих эти части и отстоящих,
следоватеЛЬно, друг от друга на 10% размаха, вычисляются
значения жесткости на кручение (GIp) и погонного массового
момента инерции (/„) относительно оси жесткости. Эти значе-
ния заносятся в графы II и III табл. 1. В графу IV заносятся
значения функции <р0, вычисленные для принятых значении —
по формуле (62а).
Приступаем к вычислению первого приближения по формулам
(61) и (62). Под номерами граф в табл. 1 обозначено действие,
в результате которого получены цифры данной графы. Так,
например, в графе VII стоит обозначение VI/1I. Это значит, что
числа, стоящие в графе VII, получены в результате деления
соответствующих (стоящих в одной и той же строке) чисел
графы VI на числа графы II.
В графе V вычисляется подинтегральное выражение (/„,%)
интеграла, входящего в формулу (61). Числа графы VI получены
в результате интегрирования функции 1ту0. Это интегрирование
проведено способом, указанным в приложении г. Так как, со-
гласно формуле (61), в результате этого интегрирования полу-
чается величина GIp^~, а значение-^ при у = 1 есть нуль, то
интегрирование ведется от конца крыла к началу (см. приложе-
ние).
Кроме того, так как мы можем сокращать функцию на любой
постоянный множитель (как это ^ыло указано выше), мы резуль-
таты суммирования не умножаем на множитель I, что соответ-
1 Для понимания последующего знакомство с приложением I необходимо.
45
ствует сокращению функции <р, на множитель -—^1. Таким обра-
зом все интегрирование выполняется следующим образом. В строке
-7- = 1 (последней строке) графы VI ставим нуль в силу гранич-
ного условия (57). Складываем числа, стоящие в строках -у- = 1
и -у- = 0,9 графы V и результат (2,026) вписываем в строку
— 0,9 графы VI. К полученному числу прибавляем числа,
стоящие в строках = 0,9 и = 0,8 графы V (т. е. числа
1,21 и 2,52) и результат (5,76) вписываем в строку — 0,8 графы
VI. К этому числу прибавляем числа,.стоящие в строках -^- = 0,8
и — = 0,7 графы V (т,- е. числа 2,52 и 4,72), и результат (13,00)
вписываем в строку -у- = 0,7 графы VI. Этот процесс продолжаем,
пока вся графа VI не окажется заполненной. у
Полученные числа дают значения выражения J* I yQdy =
= GIp-~ в выбранных сечениях по размаху крыла (сокращен-
ные на множитель I, что в данном случае значения не
имеет)1. Для получения значений очевидно, нужно полу-
ченные числа разделить на G/p. Результат этого деления приве-
ден в графе VII. Следовательно, числа этой графы есть значения
(с точностью до множителя Z), вычисленные по фор-
муле (61).
Для вычисления обращаемся к формуле (62). Чтобы полу-
чить <рп необходимо проинтегрировать Результаты этого ин-
тегрирования приведены в графе VIII. Интегрирование выполнено
тем же методом, каким были получены значения GIp , с той
разницей, что сейчас интегрирование ведется от начала крыла
к концу, так как граничное условие (57) определяет значение <?
в начале крыла (<р = 0 при у — 0). Повторим описание процесса
интегрирования, так как он очень часто встречается при различ-
ных расчетах, связанных с вибрациями. •
В строку -у- = 0 графы VIII ставим заданное значение = 0.
Складываем числа, стоящие в строках ~ =0 и ^-—0,1 графы
VII (числа 0,981 • 10—8 и 0,938-10-®), и результат (1,919-10—®)
1 См. приложение.
46
вписываем в строку — = 0,1 графы VIII. К этому результату
прибавляем числа, стоящие в строках -у-= 0,1 и—=0,2графы
VII. Полученное значение вписываем в строку ~ — 0,2 графы
VIII и т. д., продолжая этот процесс (см. приложение) до тех
пор, пока вся графа VIII не будет заполнена.
Числа, стоящие в графе VIII, дают значение первого прибли-
жения <ft для функции <р. Однако удобнее брать за функцию,
которая, как и исходная, имеет при у=1 на конце крыла значение,
равное единице. Для этого полученные в графе VIII значения
умножаем на постоянный множитель А, который подбираем
так, чтобы при получить <рх=1. Для этого достаточно за А
принять число, получающееся в результате деления единицы на
последнее число, стоящее в графе VIII (20,1 • 10~8). Будем иметь:
А ------!—г = 0,0496 • 10s-
20,1 • IO-*8
Умножаем все числа графы VIII на этот множитель, и резуль-
тат, представляющий собой окончательное значение функции
первого приближения вписываем в графу IX.
Процесс вычисления второго и третьего приближений мы
описывать не будем, так как он совпадает с только что описан-
ным вычислением первого приближения. Разница заключается
только в том, что если для вычисления <рг мы в качестве исход-
ной брали функцию %, то для вычисления <f3 мы в качестве
исходной берем функцию первого приближения и»! и для вычи-
сления <р3 в качестве исходной берем функцию <f3. Процесс по-
следовательных приближений продолжаем до тех пор, пока две
последовательно полученные функции не совпадут.
В пояснениях нуждается только последняя (XX) графа табл. 1.
После того как функция <р определена (в данном случае для этого
оказались необходимы три приближения), нужно еще определить
производную этой функции, так как она нужна для вычисления
частоты р по формуле (58). Эту производную найти чрезвычайно
просто: функция, значения которой приведены в графе XVIII
(для краткости условимся называть ее функцией графы XVIII),
получена путем интегрирования функции графы XVII, без учета
множителя ~1. Следовательно, функция графы XVII есть произ-
водная функции графы XVIII, содержащая лишний множитель
Функция графы XIX (<р3) получена умножением функции
графы XVIII на постоянного множителя А. Следовательно, произ-
водной функции <р3 будет производная функции графы XVIII,
умноженная на А. Поэтому, чтобы получить производную функ-
ции ф3, необходимо функцию графы XVII умножить на А и раз-
делить для исключения лишнего множителя на 2Q I, т. е. умно-
47
жить на множитель В, где
В = -jA- = в’0*336 - 108. = 0,1307 • 10®.
20‘975
05
io
ч
Фиг 12
0 0,1 0,2 0,3 0,4 0,5 0,0 0,7
Выполнив это
действие, получаем
значения искомой
производной, приве-
денные в графе XX.
На фиг. 12 пока-
заны результаты рас-
чета. На этой фи-
гуре приведена ис-
ходная функция %
qa 0,9 lOy/l И функции <?,, <f3,
полученные в раз-
личных приближе-
ниях. Мы видим,
что в данном случае окончательная функция = <р3 довольно
сильно отличается от исходной.
Имея значения Т и легко определить частоту колебаний
кручения рассматриваемого крыла по формуле (58). Вычисление
определенных интегралов J" (“йу ) и входящих в
o' ' '
эту формулу, производим методом трапеции, как это указано
в табл. 2, а именно: вычисляем значения подинтегральных функ-
ций GIp У и/т <р2 (графы IV и VII табл. 2) в одиннадцати выбран-
ных сечениях (соответствующих делению крыла на десять равных
частей) и затем суммируем их, причем в суммы и 5]2) вклю-
чаем половинки значений при-у- = 0 и -у- = 1, а остальные зна-
чения— полностью. Чтобы получить значения интегралов, доста-
точно найденные суммы Vi и умножить на длину интервала
между соседними сечениями, т. е. на -^1 (см. табл. 2). Объяс-
нение этого способа вычисления интегралов дано в приложе-
нии. Затем вычисляем частоту р по формуле (58):
_ 1/ 0,357 1О’ _ 9 „
Г 13,08 102 — °2’
Период колебаний кручения
Т= —
Р
= 0,12 сек.
18
Таблица 2
Вычисление интегралов
l I
f G/₽(^y) ау н f Im^dy
о ' ’о
/ tfo \
(Значения о и взяты из табл. 1; I = 975J
I II III IV V VI VII
у/1 % d-s dy rm <? I Ф2 1 щ.
0 99.2 108 0.82-Юг"3 66.5- IO2 0,32-Ю2 0 0
0,1 98,5-108 0,79-10“3 61,5-102 0.32-102 0,0785 0,1974
0,2 90,5-108 0,768-Ю-3 53.3-102 0.227-IO2 0.1541 0,54
0,3 69- Ю8 0,865- Ю~3 51,6-Ю2 0,157-IO2 0,234 0,86
0.4 41,4-Ю8 1,19-10- 3 58.7-102 0,1234-Ю2 0,334 1,378
0.5 30,7'Ю8 1,23-l0“3 46,5 -Ю2 0,097-Ю2 0.452 1,983,
0,6 21,5-108 1,195-10~3 30,8-Ю2 0.0817-102 0,511 2,66
0,7 11.82-Ю8 1.238- 10г-3 18,1-Ю2 0,053-102 0.69 2,52
0,8 5.12-108 1,358-10-3 9.42-102 00265-Ю2 0.816 1,765
0,9 2,165-108 1,191-10-3 3,07-Ю2 00I23-102 0.938 1,073
1,0 0,591 -Ю8 0 0 0,00816-Ю2 1,0 0.816
Si =366,1-IO2 ^8 = 13 39
I
[GlP (^)2rfy=SI-1^Z=366,l -102 • 97,5 = 0.357- Ю7 ;
О
I
f Zm®2tfy=S2-j’()Z=l3,39-97,5=13.08-102 .
О
Число колебаний в секунду
п = — = 8>33-
Выше (на стр. 38) мы определили функцию формы и частоту
для этого же крыла методом Галеркина, ограничившись вторым
приближением. Частота была п = 8,4 колебания в секунду. Срав-
нение функций формы приведено на фиг. 13. Как для частоты,
Гроссман—15—4 49
так и для функции формы по методу Галеркина получаются
значения, весьма близкие к найденным методом последовательных
приближений.
Как видно из этого примера, второе приближение по методу
Галеркина дает результаты вполне достаточной точности.
б. Определение функции формы и частоты для обертонов
колебаний. Пусть <$Х’), <[(”>— функции формы соответст-
венно для первого, второго и т. д. тонов колебаний1. Прежде
Фиг. 13. удовлетворяют урав-
нению \'56), причем
каждой функции соответствует свое значение частоты р (которое
может быть определено, например, по формуле Релея). ОбозьД-
чаем через значение р, соответствующее собственной функ-
ции фб), и напишем тождества, получающиеся в результате
подстановки <&<*> и <рО> и соответствующих частот в уравнение (56):
Умножим первое тождество на <р(д, второе на <р(,) и, вычтя
одно из другого, проинтегрируем результат по интервалу 0, /-
Будем иметь:
о
+ (P(i,s ~Р/)2) f dy = 0. (64)
О
1 Здесь и в дальнейшем индексом сверху обозначен порядок тона колеба-
ния, индексом снизу — номер приближения.
50
Так как
то первый интеграл легко вычисляется:
О
В силу граничных условий (57), которым должна удовлетворять
каждая из функций и величина, стоящая справа, обра-
щается в нуль, и так как qtpU>, то из выражения (64) выте-
кает условие ортогональности (63). Процесс последовательных при-
ближений для определения формы обертонов колебаний строится
таким образом, чтобы условие ортогональности выполнялось
в каждом приближении. Если же не требовать выполнения этого
условия, то процесс последовательных приближений сойдется к
функции формы, соответствующей наименьшему значению ча-
стоты, т. е. к функции формы основного тона.
Второй тон колебания1. В качестве исходного прибли-
жения принимаем
^(у) = Л0[«>0(» + С^^)О)1,
где % (у*) — произвольная функция, за которую можно, например,
принять ту же функцию <f0 (у) = sin —, которой мы задавались
в качестве исходной при определении функции первого тона
колебания; еще проще принять <?oCv)—1; ^(j) —функция пер-
вого тона колебания, способ определения которой был указан
выше. Постоянную подбираем так, чтобы выполнялось усло-
вие (63) для функции второго и первого тонов:
f'm<?o2)(y<p)(1>(y)dy = O.
О
Подставляя сюда значение получим соотношение, из кото-
рого и определим Со15:
f {y)dy
. (65)
J fmk(1)(y)l2ay
1 Излагаемый метод разработан М. Келдыш и А. Камаем.
51
Удовлетверялось условие (63) и
(63) нахе дставляя выРажение (69)
' 7’ 'ходим:
i
(y)^(y)dy + ^j
и о
Постоянную же До определим таким образом, чтобы функция
<fo равня->^ась единице на конце крыла:
т(о2)Ю = До [% (О + <Я =1 <66>
[так же, ^ак фуккция первого тона <р(1>СУ) определялась нами
таким обр^азОМ, чтобы <р(1)(/) — 1].
Соотно бдения (65) и (66) определяют обе постоянных Со и Д.
Перейт от и— 1-го приближения к следующему (и-му) можно
было бы, Пользуясь формулами (59) и (60), но при этом в каж-
дом прибх?1ижении пришлось бы определять частоту. Так как
функция с)диференциальным уравнением (56) и граничными
условиям^ С57) определяется только с точностью до постоянного
множителе т0 вместо уравнений (59) и (60), как и при вычисле-
нии функ^ первого тона, будем пользоваться уравнениями
(61) и (62*у эт0 даСт возможность избежать вычисления частоты
в каждом приближении.
Подстл вляя в правую часть выражения (61) значение п 1-го
приближе вия и произведя указанные действия по фор-
муле (61)^ а затем (62)> получим новое значение функции, кото-
рое обоза м ч з ф<2)(у). Следовательно, фГ (у) вычисляется
по форму лам;
(67>
ГМ™
(68)
Функция Ю£) еще не будет n-ным приближением для функции
Ф(2‘ (У). как не удовлетворяет условию ортогональности, но Ч
мы опред<елим ^)(у) через следующим образом:
,«(>) = А. [ >“ W + W1' (69>
где попрЮжнему^11^)—функция первого тона колебания, а
постояннее и А„ нужно определить таким образом, чтобы
'’>(у) было равно единице при
в условие ортогональности
рш[»(1)(У)]3^=О- (70)
Кромер того, запишем условие у (п2>(/) == 1;
аЛФп’ю + ^Ч^1- (71)
Из Системы уравнений (70) и (71) определяются постоянные
Д„ и Сп после чего функция ч^2) (у) может быть полностью вы-
числена п0 ф0рМуле (69).
52
Таким образом схема вычислений следующая:
1. Задаемся исходным значением функции <f>o3)(j) по формуле
(64), причем вычисляем Ао и Со0 из систем (65) и (66).
2. Подставляя значение у™ (У) в правую часть уравнения (67),
Л|Я га
вычисляем а затем по формуле (68) находим фг (у). Распо-
лагать вычисления при этом удобно так же, как при нахождении
функции первого тона.
3. Из системы уравнений (70) и (71) находим значения и
Ci1*, после чего по формуле (69) вычисляем первое приближение
^’’(у) для функции </2)(у).
4. Процесс вычисления повторяем, приняв за исходную функ-
цию <pi2 (у), которую мы нашли [т. е. подставляем эту функцию
в правую часть уравнения (67) и т. д.(.
5. Процесс последовательных приближений повторяем до тех
пор, пока функции, определенные двумя последовательными
приближениями, не совпадут.
Мы не останавливаемся здесь на доказательстве сходимости
описанного метода последовательных приближений. Интересую-
щиеся могут найти это доказательство в книге А. И. Камай,
Труды ЦАГИ.
Высшие тона колебания. Описанный выше метод после-
довательных приближений обобщается на случай нахождения функ-
ции формы для любого лп-го тона колебания. При этом исход-
ная функция <fom) задается в виде:
<е(от)(у) = А0[<р0 (у) + C^w(y) + С^Чу) + ...+
+ C<om-1)<f(m-1)(y)], (72)
где <р(1) (у), ф<2 (у),... </m—4 (у) — функции соответственно первого,
второго и т. д. тонов колебания. Постоянные определяются
таким образом, чтобы было выполнено условие ортогональности
(63) между функцией <f>om)(y) и каждой из т — 1 первых собст-
венных функций:
i
О
/ г
f О') • Ч>(2)(У) dy = 0;
О
I
О
аЗ
Если подставить в эти условия значения (у) из уравнения
(72), то получится система линейных уравнений для определения
т — 1 постоянных Со0, Cj,50,.. . С<Г“°. Для определения постоян-
ной До к этой системе добавляется еще условие <р(™’(/) = 1, кото-
рое в развернутом виде запишется на основании уравнения (72)
следующим образом:
Л [<Fo (О + + С<2> 4- ... 4- СР"0] = 1.
От п — 1-го приближения к n-му переходим следующим образом.
Определяем функцию <рр°по формулам (67) и (68), только сверху
вместо индекса 2 пишем пг, так как в настоящем случае мы
ищем лг-й, а не второй тон колебания. Затем определяем функ-
цию по формуле:
e’(j) = 4„№р(у) 4- С^(у) 4- с^^)(у) 4-... 4- ср-» "(у)],
и постоянные СР определяем из условия (63), а Д„—из условия
?(пт)(0=1.
Условие ортогональности (63) при этом должно выполняться
между функцией (у) и каждой из первых т — 1 собственных
функций: ?(1)(у), <р(2)(_у).(у). Это дает т — 1 уравнение;
кроме того, еще одно уравнение получается из условия ^р)(^)=1.
Таким образом имеем т уравнений, определяющих т неизвест-
ных: д„, cP,c(n2),..., d-nm~v.
Частота любого тона колебания может быть определена по
формуле (58), причем за <? (у) следует принимать функцию формы
соответствующего тона колебания.
5. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАНИЯ
Вернемся к рассмотрению задачи о колебаниях крыла с пе-
ременными по размаху характеристиками при наличии сил, про-
порциональных угловой скорости колебательного движения. В п. 3
этой главы было получено диференциальное уравнение движения
для данного случая:
—;г(0/ЛЧ+*?- + /т?^=0- (73)
оу \ Р dyj от тот2 4 '
» »
Будем искать частное решение данного уравнения в виде:
О = ¥(у)е>\ (74)
Подставляя это выражение в уравнение (73), найдем уравне-
ние, определяющее функцию формы <₽ (у):
“ ® (Чф) + + Vs) ? - 0. (75)
В дальнейшем мы покажем, что X будет, вообще говоря, комп-
лексной величиной, и уравнение (75) будет содержать комплекс-
54
tibie коэфициенты. Поэтому интеграл его может также оказаться
комплексным. В дальнейшем мы исследуем, в каких случаях ?
будет комплексной и в каких — действительной величиной, а
также, что физически означает комплексность функции <? (у).
В общем случае интеграл уравнения (75) можно записать в
таком виде:
f(j') = ?i(j) + «?2(y)> (76)
где i—V— 1, a <pj (у) и <р2(у)— две действительные функции. В
частном случае какая-либо одна из них может быть и нулем.
Если <р2(_у) = 0, то <р(у) оказывается действительной величиной,
как это имеет место, например, при колебаниях крыла в пустоте
без сил трения.
Наряду с функцией <f(y) будем 'рассматривать сопряженную
с ней функцию
<р(У) —7®2(Г)-
Заметим, что функция <р(_у) должна удовлетворять граничным
условиям задачи (57), а следовательно, ^г(у) и <р2(у) порознь
должны удовлетворять тем же граничным условиям. Вследствие
этого и функция <р(у) также будет удовлетворять граничным ус-
ловиям (57).
Так как выражение (76) есть интеграл уравнения (75), то
после подстановки выражения (76) в уравнение (75) получим
тождество. Это тождество умножим на <f (_у) dy и проинтегри-
руем по интервалу О, I.
Получим:
i i i
-fdy dy + }fKvt dy + ) 2/dy = °- (77)
0 0 0
Первый интеграл левой части этого выражения преобразуем
интегрированием по частям:
(0/- = -[<*, гЯ + А а^=
о о
= [GL~a~dy. (77а)
J Р dy dy '
о
Вследствие того что функции <р(у) и «р(v) удовлетворяют гранич-
ным условиям (57), проинтегрированная часть обращается в нуль.
Для краткости введем следующие обозначения:
О
55
о
с = fjmVfdy-
b
Тогда соотношение (77) можем переписать в виде:
а + 1Ь + tfc = 0. (78)
Так как произведение любой комплексной величины на сопря-
женную с ней есть величина действительная, то а, Ь, с — вели-
чины действительные и выражение (78) представляет собой
квадратное уравнение относительно X с действительными коэфи-
циентами. Решив это уравнение, найдем два корня
__ ь ± Vb* — 4ac
71'2==-----2с-------•
Величина Ь~— 4ас может быть, вообще говоря, как положи-
тельной, так и отрицательной. Рассмотрим сперва случай»
& — 4ас <0. г
Тогда для X получаются два комплексных значения:
= <’ + “’] (79)
Х2 = <? — ip, J
где ________
Я = Р = ^4ас-Ь*.
Заметим следующее: если значению X = q + ip соответствует
функция <р(у), то значению \ — q— ip соответствует сопряженная
функция <р(у).
В самом деле, подставляя в уравнение (75) значение X = q + ip,
мы получим уравнение:
- ", (°Х гр) + !«(« + 'Р) +<« + W1Ч = °-
определяющее функцию со (у) = <pt(y) -р 7<х»3(_у). Подставляя это вы-
ражение функции в уравнение и разбив затем получающееся вы-
ражение на действительную и мнимую части и приравнивая нулю
каждую в отдельности, получим систему двух уравнений для
определения функций ^(у) и <f2(y):
- iy (G/$) + + 4 (<?8-/>*)]ъ-(f<p + Шр)ъ=0; (Ь)
- ± (GIpd£) + [Кд + Im (д*-р*)] ъ + (Кр + 1т2др)Т1 = о.
56
Подставим теперь в уравнение (75) сопряженное значение X =
q — ip. Тогда для определения ?(у) получим уравнение:
- dy (GZ4j) + [^-^) + 4>(?-^)2]<f = o. (С)
Покажем, что если уравнению (а) удовлетворяет функция
tp = ?, + где ¥i и ?2 определяются системой (Ь), то уравнению
(с) будет удовлетворять сопряженная функция ? = ?х — l'f2 ПРИ
тех же самых значениях <fx и ?2. Для доказательства достаточно
в уравнение (с) подставить ф = <р==(?1 — % и приравнять нулю
действительную и мнимую части получающегося выражения по
отдельности. В результате мы придем опять к той же системе
(Ь) и, следовательно, если ?! и <р2 этой системе удовлетворяют,
то уравнению (а) будет удовлетворять функция ?х + *?2> а уравне-
нию (с) — функция ?! — г?2.
Таким образом получаем два решения:
1) X = q 4- Ip — соответствующее значение функции ? = ?i+i?2;
2) X = q — ip — соответствующее значение функции ? = ?j— i?2.
Подставляя эти значения в выражение (74), находим два част-
ных решения:
Oj = (фх + /ф2) е(<Жр) « ; е2 = (?! — 1?2) .
Таким образом частные решения уравнения крутильных коле-
баний в рассматриваемом случае получены нами в комплексной
форме. Но угол кручения является, конечно, величиной действи-
тельной, и мы получим его выражение, составив решение урав-
нения (73) как сумму частных решений:
О = + ба = (?х + /?.,) 4- (<рх — /'£,) g(«—(80}
Так как и 02 — величины сопряженные, то их сумма будет
величиной действительной. Отметим это важное обстоятельство,
с которым нам и дальше придется неоднократно сталкиваться:
хотя частное решение записывается в комплексной форме, но
существует сопряженное решение, и потому окончательный ре-
зультат, выражающийся как сумма частных решений, будет дей-
ствительным. В дальнейшем мы часто будем изучать колебатель-
ное движение на основе изучения частного решения, записанного
в комплексной форме. При этом всегда следует помнить, что
существует также сопряженное решение.
Упростим выражение (80), пользуясь известными формулами
Эйлера:
eix + е ~‘х . е1х — ё~’х
COS X =---’ sin х ~-------2ZJ--•
Выражение (80) легко преобразовать к виду: |
0 = [?! (у) cos pt — ?2 (у) sin pt}. (81 >
57
(82)
(83)
выра-
(84)
Введем новые функции Ф(у) и Ф(у), которые определим через
функции ^(у) и <f.,(y):
2<^(у) = Ф (у) cos Ф(у); 1
2<ря Су) = Ф (У) sin Ф (у). 1
Из этих соотношений Ф(у) и Ф(У) определяются легко:
Ф2(у) = 4[с12(у)4-^2(у)];
tg 'Г (У) =
s 7 Ф1О')
Подставляя выражения (82) в интеграл (81), получим
жение для угла закручивания в еще более удобном виде:
0 = Ф (у) е“~ • cos [рт + ф О)].
При анализе движения можно пользоваться любой из форм за-
писи: (80), (81) или (84).
Произведем подробный анализ полученного решения.
Косинус является периодической функцией, имеющей период.
2~. Чтобы аргумент косинуса в выражении (84) изм^шлсц на *
2к, необходимо, чтобы время т изменилось на величину
j, _ 2п
* :
Этот промежуток времени, через который косинус в выраже-
нии (84) принимает прежние значения, называется периодом
колебания. Найдем число колебаний в секунду п: за Т секунд
происходит одно колебание, следовательно, за одну секунду бу-
Л,ет происходить = колебаний, а потому
Величинар называется круговой частотой колебания,
или, просто, частотой колебания. Подчеркиваем, что для
того, чтобы получить число колебаний в секунду, надо частоту
разделить на 2~.
Максимальная величина угла закручивания называется амп-
литудой крутильных колебаний. Так как максимальное
значение cos [рт 4- Ф (у)] {есть единица, то, согласно выражению
(84), максимальное значение 0 (амплитуда 0) есть:
Ат 0 = Ф (у) • ег-. (85)
Следовательно, амплитуда зависит как от у, так и от т, т. е.
амплитуда, во-первых, различна в различных сечениях крыла,
а во-вторых, в одном и том же сечении она меняется во времени.
Функция Ф(у) дает закон распределения амплитуд по размаху
крыла. Величина q характеризует закон изменения амплитуды
колебаний во времени.
58
Рассмотрим следующие случаи: 1) q — положительное число,
2) q — отрицательное число и 3) q = 0.
1) q > О. В этом случае при увеличении т, согласно выраже-
нию (85), амплитуда 6 будет неограниченно возрастать. Если мы
рассматриваем колебания какого-либо определенного сечения
крыла (у — фиксировано), то, согласно выражению (84;, угол за-
кручивания будет представлять собой произведение двух функций:
периодической [cos (pi + W)]
этому изменение 0 во вре-
мени будет итти так, как
показано на фиг. 14, и мы
будем иметь непрерывно
возрастающие колебания,
при которых амплитуда на-
растает по закону
2) q < 0. Так как
ё1', то при отрицательном
q величинам- будет неогра-
ниченно уменьшаться при
увеличении времени т. Сле-
довательно, амплитуда ко-
лебаний с ростом времени
уменьшается и стремится к
нулю при т—>оо. Колебания
в данном случае будут зату-
хающими, как показано на
фиг. 15.
3) q = 0. В этом случае
= ] и, следовательно,
амплитуда колебания [см.
формулу (85)] от времени
зависеть не будет. Колебания происходят с постоянной ампли-
тудой, как это показано на фиг. 16, т. е. имеют место чисто
гармонические колебания с постоянной аплитудой.
Таким образом величина q характеризует нарастание или
затухание колебаний. Она называется логарифмическим
декрементом затухания.
Напомним, что мы искали решение уравнения’движения в
виде равенства (74). При этом было получено уравнение, опре-
деляющее X, и мы нашли
l=q + ip.
Таким образом, при решении уравнения движения в виде равен-
ства (74) действительная часть X есть логарифмический декремент
затухания, а коэфициент при мнимой части есть частота коле-
бания. Если действительная часть X положительна, то движение
будет происходить с нарастающей амплитудой, если отрицательна,
т° движение будет затухающим. Наконец, если X будет величи-
59
Величина 'Г(_у) называется фазой колебания. Если в выра-
жении (74) <р(_у) будет действительной функцией, т. е. <р2(у) = О,
то, согласно выражению (83), Ч'(у) = 0. В этом случае все сече-
ния крыла одновременно проходят через положение равновесия
и одновременно достигают максимального отклонения от этого
положения. Движение совершается без сдвига фаз между коле-
баниями различных сечений. В частности такой случай имеет
место, если в уравнении (73) К = 0, т. е. при свободных колеба-
ниях в пустоте, которые были подробно изучены в предыдущих
параграфах.
Следовательно, комплексная часть функции <р(у) характери-
зует сдвиг фаз между колебаниями различных сечений.
Рассмотрим несколько примеров на определение характеристик
колебания.
Пример 1. Колебания некоторого определенного сечения
крыла подчиняются закону:
О = cos 60т -)- -i- sin 60т) е~".
Определить характер колебаний. Вычислить период и число
колебаний в секунду. Определить, во сколько раз изменяется
амплитуда за одну секунду и через сколько времени после на-
чала колебания амплитуда угла закручивания станет, меньше 1°.
Так как формула дает закон колебания только в некотором
определенном сечении крыла, то переменная у в формуле отсут-
ствует. Поэтому определить распределение углов кручения по
размаху не представляется возможным, и такая задача не ста-
вится.
По формуле сразу можно определить величины q = — 1 и
р = 60. Так как q<0, то колебания будут затухающими. Число
колебаний в секунду
п = = 9,55.
Период колебания
Т — — = 0,105 сек.
п ’
Найдем выражение для амплитуды колебания. Запись дана в
форме уравнения (81), причем 2^=-^-, 2<ра =—g-. *
Вводим, согласно выражению (82), новые величины Ф и Т', оп-
ределив их следующим образом:
1 -г. 11-
„ = ф COS ч }
4- = Ф sin ’F,
О
62
откуда
’=)z( 5)!+ЫУ -с-373.
tg 'Г = ; 'F = 26°34' = — 0,464 (в радианах).
Тогда выражение для угла кручения можем записать в форме
уравнения (84):
б = 0,373 е~' • cos (60т — 0,464).
Следовательно, амплитуда угла кручения
Ат0 = 0,373 еЛ (а)
Определим, во сколько раз уменьшается амплитуда за одну
секунду. В момент времени амплитуда Ат10= 0.373 ё~\ а одну
секунду спустя амплитуда будет Ат20 = 0,373 е—(Х1+1). Отноше-
ние амплитуд вычислить легко:
АгМ = 0,373 = е~1 - 0,368.
Ami 9 0,373 е
Это отношение не зависит от выбранного момента времени т-
и, следовательно, за каждую секунду амплитуда уменьшается в
0368 ~ 2,7 раза.
Определим, через сколько времени амплитуда угла закручи-
вания достигнет величины 1°. Так как равенство (а) дает значе-
ние амплитуды в отвлеченных единицах (радианах), то надо пе-
ревести в радианы также и 1°; 1° = 0,01744 радиана. Согласно
равенству (а), амплитуда достигнет величины 0,01744, если
0,373 е—' = 0,01744
ИЛИ *
е^1 = 0,0467.
Логарифмируя это выражение, находим:
т = - In 0,0467 = 3,06 сек.
Следовательно, примерно через 3 сек. после начала движения
амплитуда уменьшится до 1°. В начальный момент времени ам-
плитуда равна 0,373 = 21 °24'.
Пример 2. Определить характер движения, заданного зако-
ном:
0 = 0,1 е-3’cos 60-г + 0,15 е-0,1’sin 200 т. (Ь)
В данном случае движение состоит из суммы двух гармони-
ческих колебаний с периодами
Л = = 0,105 сек. и Г2= = 0,0314 сек.
63
и с числами колебаний в секунду
«! = =!-=9,55, /г2 =-J—= 31,8.
Н *2
Следовательно, второе составляющее колебание происходит
со значительно большей частотой, чем первое. Оба колебания—
затухающие, так как q < 0. Но декремент затухания первого ко-
лебания (<7 = — 3) очень велик. Так, если в начальный момент
амплитуда первого колебания 0,1, то через 1 сек. амплитуда бу-
Лет уже 0,1 е—8 = 0,00498, т. е. уменьшится примерно в 20 раз.
Амплитуда второго колебания за тот же промежуток времени
уменьшится всего на 10% против первоначальной величины 0,15.
Поэтому уже через короткий промежуток времени длинно-перио-
дическое колебание станет практически незаметным и останутся
только коротко-периодические колебания, даваемые вторым чле-
ном формулы (Ь).
В приведенных примерах были определены характеристики
колебательного движения по аналитическому выражению закона
движения. Поставим теперь обратную задачу: пусть требуется
найти характеристики колебательного движения по эксперимен-
тальной записи колебательного движения.
Пр'имер. Запись колебательного движения некоторого се-
чения стержня показана на фиг. 18. Требуется определить харак-
теристики колебательного движения.
Период колебания определяется как время, за которое про-
исходит одна волна колебания. Непосредственно по масштабу
64
оси т читаем время, например между точками А и В или Си D-
Т = 4 сек. •
Следовательно,
р = —= 1,57.
Декремент затухания определяется по измерениям амплитуд
в двух каких-либо местах записи. Например, пусть в момент тх
амплитуда была Ап^О, а в момент т2 — амплитуда имеет значе-
ние Ат30. Тогда, согласно выражению (85):
Ат. 6 = ег-‘ =
Amt 6 еч~' ’
откуда, логарифмируя, находим:
Для данных фиг. 18: Апыб = 0,061; Атг0 = О,О91; х. = 7,5 сек.;
— 3,5 сек., вышеприведенная формула дает:
1 1 °’061 л 1
9 — 7,5 —3,5 1П 0,091 ~
Например в точке т = 3,5 сек. имеем Ат 0 = 0,091, и следовательно,
по формуле (85):
Фе" •зл =0,091,
откуда, так как q — — 0,1,
ф =0,129.
Это и есть значение функции Ф в том сечении крыла, запись
которого приведена на фиг. 18.
Рассмотрим наименьшее значение т, при котором 0 = 0. Со-
гласно выражению (84), это имеет место в том случае, если
cos {р~ 4- ’F) = О, и следовательно, р~ + 'Г = .
По фиг. 18 6 = 0 при т = 0,5 сек.
Имея в виду, что р — 1,57, находим:
0,5-1,57+ ’F=~,
откуда определяем значение функции ’Г(у) в рассматриваемом
сечении крыла:
’Г = 0,785.
Собирая полученные результаты, можем по формуле (84) за.
яисать'закон движения, график которого показан на фиг. 18, в виде.
О = 0,129 0,1 cos (1,57x4-0,785).
Выше мы подробно исследовали движение в случае Ь-—4ас<0,
т- е. когда уравнение (78) имеет два комплексных сопряженных
Г₽оссман—15—5 65
корня. Но может быть также и другой случай, когда Ь-—4ас>0,
и оба корня уравнения (78) действительны:
'К1=91> )"2 ~ 9з‘
В этом случае уравнение (75) не будет содержать комплекс-
ных коэфициентов, и его интеграл может быть взят также в виде
действительной функции [в таком случае интегрировать уравне-
ния (75) можно, например, методом последовательных приближе-
ний, изложенным в п. 4 настоящей главы]. Пусть значению
соответствует функция <Р1СУ), а значению Z2 — q„— функция <р2(у).
Общий интеграл, согласно уравнению (74), возьмем в виде:
9 = Т1(у) е9*\ (86)
Рассмотрим следующие случаи: 1) q2 и q2— положительны, 2) ql
и q2~ отрицательны и 3) одно из значений, например qlt— от-
рицательно, другое — д.2— положительно.
1) >0, q2 > 0. В этом случае оба Слагаемых в выражении
(86) — монотонно возрастающие функции времени. Угол кручения
будет монотонно возрастать до тех пор, пока не произойдет по-
ломки крыла.
2) q2 <0, q2 < 0. Оба слагаемые в выражении (86) — монотонно
убывающие функции времени. Угол крученая 0 будет монотонно
убывать, пока крыло не вернется в положение равновесия (при
т—> со, 0 -> 0).
3) 91 <0, q2> 0. Первое слагаемое в выражении (86) будет с
течением времени уменьшаться, а второе — увеличиваться. При
достаточно большом значении ~ влияние первого члена в выра-
жении (86) станет весьма малым, и величина угла кручения бу-
дет определяться вторым членом, который будет монотонно уве-
личиваться. Угол кручения, следовательно, будет возрастать,
пока не произойдет поломки крыла. Таким образом, если оба
корня уравнения (78) действительны [в выражении (74) величина
/. — действительное число], то движение не будет колебательным,
а будет апериодическим, либо возрастающим, либо убывающим.
При этом, если среди значений X есть хоть одно положительное,
угол крученйя будет увеличиваться вплоть до поломки крыла. В
последнем случае движение носит название дивергенции.
Следовательно, как в случае колебательного, так и в случае
апериодического движения крыло вернется к положению равно-
весия только в том случае, если действительные части всех зна-
чений X отрицательны. В этом случае говорят, что конструкция
крыла устойчива. Конструкция крыла будет неустойчивой, если
среди значений X есть хотя бы одно с положительной действи-
тельной частью.
В дальнейшем будет показано, что все эти выводы приме-
нимы не только к случаю кручения крыла, но и к другим
видам движения (например изгибные колебания или совместные
колебания).
С6
6. КОЛЕБАНИЯ КРЫЛА С СОСРЕДОТОЧЕННЫМИ ГРУЗАМИ
Выше были рассмотрены крутильные колебания крыла в пред-
положении, что крыло можно схематизировать как ненагружен-
ную консольную балку. Однако практически весьма часто прихо-
дится сталкиваться с крыльями, на которых имеется значитель-
ная сосредоточенная масса. Например, весьма часто на крыле
имеется мотор, на крыльях гидросамолетов имеются поплавки, в
крыле часто помещают бензиновые баки и т. д. При колебаниях
крыла силы инерции, развиваемые
сосредоточенной массой, весьма
существенно влияют на характер
колебаний, и сосредоточенную
массу необходимо учесть при
расчете вибраций.
Ограничимся рассмотрением
случая, когда на крыле имеется
только одна сосредоточенная мас-
са. Методы расчета такого крыла
без всякого изменения переносят-
ся также и на случай несколь-
ких сосредоточенных масс. В ка-
честве упражнения можно рекомендовать читателю вывести
расчетные формулы для случая, скажем, двух сосредоточенных
масс, находящихся на полукрыле.
Напомним, каким образом было получено основное уравне-
ние (1) крутильных колебаний крыла (п. 1 настоящей главы). Мы
вырезали элементарный отсек крыла шириной dy и приравнивали
нулю сумму действующих на этот отсек моментов (упругих и
инерционных). Очевидно, есть ли или нет на крыле сосредоточенной
массы, условие равенства нулю моментов во всех сечениях крыла,
за исключением того, в котором имеется сосредоточенная масса,
будет одинаковым. Поэтому основное уравнение движения для
крыла с сосредоточенной массой будет тем же, что и для крыла
' без сосредоточенной массы [уравнение (1)]. Точно так же сохра-
няются и граничные условия (2). Дополнительно только следует
написать так называемые условия сопряжения в том сечении,
гле имеется сосредоточенная масса.
Пусть сосредоточенная масса находится в сечении крыла, на-
ходящемся на расстоянии у — А от корня (фиг. 19). Момент инер-
ции сосредоточенной массы относительно оси жесткости крыла
обозначим через /. Первое условие сопряжения заключается в
том, что при переходе через сечение у —h угол кручения 6
Должен изменяться непрерывным образом. Поэтому
0* + = 6 л —>
гДе через 6л + обозначено значение величины 6 при подходе к
сечению y — h справа (со стороны конца крыла; фиг. 19) и че-
рез 6Л —значение 0 при подходе к сечению у = А слева. При
67
движении от конца крыла к корню при переходе через сечение
у = h крутящий момент будет меняться скачком. В самом деле,
крутящий момент в любом сечении создается действием инерци-
онных сил всей лежащей справа от сечения части крыла. При
переходе через сечение у = h к моменту от сил инерции лежа-
щей справа части прибавляется момент сил инерции сосредото-
ченной массы. Поэтому разность между крутящим моментом
слева от сечения у —h и справа от него равна моменту сил
инерции сосредоточенной массы. Это дает второе условие сопря-
жения:
<8?>
Это условие можно получить и иначе, если рассматривать сосредоточенную
массу как предельный случай некоторой распределенной массы. П^сть сосре-
доточенная масса распределена равномерно» иа интервале от у = h—£ до
у— h +где е—некоторая мадая величина (фиг. 19). Погонный момент инер-
ции распределенной таким образом массы, очевидно, будетТогда мы име-
ем крыло без сосредоточенной массы, момент инерции которого имеет интен-
сивность 1т на участках от нуля до Л — ей от h 4-е до I и интенсивность
hn на участке от h — е до Л + е, где 1т — погонный момент инерции са-
мого крыла без сосредоточенной массы. Диференциальное уравнение колеба-
тельного движения (1) на последнем участке принимает вид:
= 0.
GI'^
рду
= 0.
ду~\ р ду
Проинтегрируем это выражение в пределах от h — г до h-|-e и затем пе-
рейдем к пределу при е-»0. После интегрирования получим:
Л+в Л-f-e
............. ( (-«А'
Л-в ' ' ' Л—е
Первый интеграл вычисляется непосредственно, второй вычисляем, пользуясь
теоремой о среднем* 1. Получаем:
(о,
\ рду)у=п-*. \ pdy)y=*h+t.
7
2г
следует понимать значение этой величины в некоторой
где под
точке, лежащей в интервале h—е, ft-J-e.
Переходя теперь к пределу при г—>0 п перенеся последний член в пра-
вую часть, найдем:
Р ду
= — /
y=h’
что совпадает с условием (87).
Таким образом окончательно имеем следующие основные
уравнения задачи:
а
1 Согласно теореме о среднем J'/(x)dx = /($) (Ь— а), где /(6)—значе-
а
ние функции /(х) в некоторой точке х = $ интервала а, Ь.
68
1) уравнение движения:
д (гг де\ . . е2е п
ду \Р^Рду ) + тЪ& ~
2) граничные условия:
6=0 при у = 0;
57 = 0 при y = Z;
3) условия сопряжения при y — h\
(88)
6Л+ = 6ft
Для решения этой системы уравнений применяется тот же
метод последовательных приближений, который выше был при-
менен к случаю колебаний крыла без сосредоточенной массы.
Частное решение уравнения (стоячее колебание) будем искать
в следующем виде:
0 = <р(у)еЧ (89)
Выше мы неоднократно уже применяли подстановку 6=ср(у)ет
и указывали, что колебательное движение может быть представ-
лено как сумма движений, записанных в этом виде. При этом
было доказано, что К может быть, вообще говоря, комплексной
величиной. Но если действительная часть X отлична от нуля,то
движение будет происходить либо с нарастающей, либо с умень-
шающейся амплитудой (в зависимости от знака действительной
части X). При исследовании настоящей задачи естественно сразу
предположить, что движение будет происходить с постоянной
амплитудой, так как движущаяся система является консерватив-
ной (см. гл. I), поскольку приложенные к ней силы (упругие)
обладают потенциалом. Следовательно, энергия системы сохра-
няется во все время движения и потому амплитуда не будет ни
возрастать (для этого необходимо сообщить движущейся системе
энергию извне), ни убывать (для этого энергия движущейся си-
стемы должна рассеиваться). Раз так, то X должно быть величи-
ной чисто мнимой (>. = ip, где р — частота колебаний, как было
показано в предыдущем параграфе), и потому мы сразу ищем 6
в форме выражения (89).
Подставляя выражение (89) в основные уравнения (88), найдем:
1) уравнение, определяющее функцию формы:
(90а>
2) граничные условия:
=0 при _у = 0;
^2- = 0 при v — I; (90b)
69
3) условия сопряжения:
(о/,»,,+-(о'р$).-=-"г^'4>- (И*)
Если функция <?(_у) известна, то легко определить частоту коле-
бания. Прежде всего выведем формулу для определения частоты.
Умножим уравнение (90а) на 4(y)dy и проинтегрируем ре-
зультат по длине крыла:
о о
Интеграл, стоящий в левой части, будем интегрировать по ча-
стям. Так как функция GIp~, производная которой стоит под
знаком интеграла, имеет разрыв в точке у = h [в*силу второго
условия сопряжения (90с)], то предварительно интервал интегри-
рования нужно разбить на две части: от нуля до h и от h до /,
и произвести интегрирование каждой части отдельно. Имеем:
i /Г I
J г, (°', ч dy +f ?y (°'.£) • =
О 0 h
h h ll
-14 foi„ (»’ Jy+ j atr^ , - f 01,,( £ ) dy.
О О ' ft ft
Оба интеграла, стоящие в правой части, опять соединяем в
один. Далее замечаем, что величина Glp (-^7) • <F в силу гранич-
ных условий (90b) обращается в нуль при у = 0 и у —I; получаем:
f д (ОЛЛ2-) f dy ~(GIpи' f) — f 0Гр(чт)“ dy.
J dy \ PdyJr y \ Pdy )y^h—\ Pdy‘Jv=iiy- J P\dyJ
о 0
В силу условий сопряжения (90с) можем записать:
/ £ (р',£)чЧу= fVW-j or, )>.
О о
Подставляем это значение в выражение (а) и определяем из
полученного уравнения частоту. Найдем
О
I
f Im ^dy + I^-W
(91)
70
Эта формула служит для определения частоты колебания,
если функция формы <р(я известна. Функции у(у) может быть
определена методом последовательных приближений подобно
тому, как определялась функция формы для крыла без сосредо-
точенной массы.
Интегрируя уравнение (90а) в пределах от произвольного
у > ft до /, находим.
Ч dy =Р2//"*аУ- (92а)
I
При y>h интегрирование выполняется, как обычно. При приб-
лижении у к h справа (со стороны конца крыла) имеем:
h
(G/p^y\ + = P2fI^dy. №
i
На основании условия (90с) имеем:
л
( 01 р \ _ = Р2 J Ап Ф dy+ Р2 Ztf (А), (92с)
I
а при у < h
°'Г (92d)
Л
Формулы (92а), (92b), (92с) и (92d) определяют величину Glp ~
на всем диапазоне 0, I. Функция <? непрерывна на всем диапазоне
[в том числе и в сечении у = Л, на основании первого условия (90с)];
следовательно:
V
(93)
О
Заметим, что граничные условия (90b) удовлетворены в силу
выбора пределов интегрирования.
Метод последовательных приближений состоит в том, что в
правую часть уравнений (92а), (92b), (92с) и (92d) подставляется
какая-либо функция <?0(у), затем выполняются все действия и на-
ходится значение-^. Далее по формуле (93) определяется новое
значение функции <р(у). Это значение опять подставляется в пра-
вую часть формулы (92) и т. д.; этот процесс продолжается до
тех пор, пока для функции <р(_у) два раза подряд не получится
одно и то же значение. Однако, если непосредственно пользовать-
ся формулами (92), в каждом приближении пришлось бы вычи-
слять значение частоты р [что можно сделать по формуле (91)].
Можно и упростить вычисления, заметив, что функция <р(у)
основными уравнениями задачи (90а), (90b), (90с) определяется
с точностью до произвольного множителя. Поэтому можно в каж-
71
дом приближении сократить функцию <р(у) на р2 (так же, как
было сделано в случае колебаний крыла без сосредоточенной
массы). Это соответствует тому, что в формулах (92) принимается
р2 = 1. Функции v(y) в каждом приближении умножаем на пос-
тоянное число А, которое выбираем таким образом, чтобы <р(у)
на конце крыла (для у — /) было равно единице. Функцию, полу-
чающуюся в результате вычисления по формулам (92) и (93), до
умножения на А будем обозначать через ф.
Следовательно, окончательно для получения n-го приближе-
ния из п — 1-го имеем следующие формулы:
для у > h
= (94а)
для у = h
h
. <94Ь>
I
=(GI^\ + /%, Ah)\ (94с)
\ Р dy Jh— \ р dy /л + т" —14 ' ’
для у < h
V
<94d>
h
и функция будет:
(94е)
О
'?„(.У)=МП (у), Д = (941)
Практически при выполнении вычислений по формулам (94)
опускают постоянные множители, появляющиеся при этом, что
возможно, так как (у) определена лишь с точностью до посто-
янного множителя.
Схема расположения вычислений показана в табл. 3.
Крыло разбито на 10 равных частей. В одном из сечений (в
табл. 3 в сечении у = 0,2) находится мотор. Если мотор не попа-
дает ни в одно из выбранных сечений, то крыло надо разбить
на большее число частей, чтобы мотор находился в одном из
сечений. Способ вычислений одинаково применим при делении
крыла на любое число равных частей.
В графе II помещены значения /т<₽, где <р— исходная функ-
ция, которой мы задались. В качестве исходной можно взять
обычную стандартную функцию крыла постоянного сечения по
формуле (62а).
72
Таблица 3
J П III IV V VI VII
у т Ли? V Glp p Ф ч>
0 (Ап®)о Vo (Glp)0 GB Фе ?0
0,1 UmVh V, (Glp\ Vi Ф1 Ф1
0,2 (^m’s)2 v; G', 4-2 Фз
v;
0,3 (Лп?)з v2 <GIp)a Ga Фз ®3
0,4 V4 (Glp), ut Ф« ъ
0,5 (An4)s VB (Gfph Gs Фз Ч>3
0,6 (An'f)e Ve (G/P)e Ge Фв Те
0,7 Um?)? V7 (Glp), u, Ф? <?7
0,8 V8 (Glp)a GB Фв Те
0,9 V„ (GIp), G, Ф» 4»
(Wlo Vlo (GIp)J0 Glo Ф1О Y1O
В графе III вычисляется значение GIp по формулам (94а),
(94b), (94с), (94d). Как обычно, интегрирование ведется по способу
трапеций (см. приложение). На основании уравнения (94а) мы
можем записать значения GIp ~ в сечениях крыла при у > Л,
приближенно, следующим образом:
(^^’~dy~\0 = 0 силУ граничного условия (90Ь)];
(°'я= (°4 4»,.,+Т КШ.+Й •
(ч w),=(°'Д").+1 (('-«>•+и
(Ч », += (Ч &), + 4 К'-А + «лМ W •
Чтобы получить значение
мулой (94):
G/p » воспользуемся
фор-
(GLd%n) = (gL^\ + I's(h),
\ Р dy Jh — \ Р dy Jh + ‘
73
где о (Л) — значение исходной функции у (у) в сечении y = h
(для табл. 3 в сечении ~ = 0,2).
Далее интегрирование ведем на основании уравнения (946)
опять по способу трапеций:
(Ч ^). = (°'- “ф )»- +1 [(/"А + то
(°', ^). - (0/- +4 [«'-"Л+то •
Вычисления значительно упрощаются, если при выполнении
интегрирования опускать общий множитель у^. Обозначим
через Vm значение , разделенное на 1 ‘у Эти значе-
ния и вычисляются в графе III табл. 3. Величина Ут в сечении
у = Л, где расположен мотор, имеет два значения* vm — значе-
ние Vm при подходе к сечению y = h справа (у = Л+) и Vm —
значение Vm при подходе к сечению у = h слева (у = Л_).
Разделив предыдущие формулы для вычисления на
1 1
получим следующие значения:
« IU
И1о=0;
И8-И9 + (/„,?)а + (/стТ)8;
^ = ^з + (/,пт)3 + (/т?)2;
^=K + (/m<Fh+(<M;
К — Ц + (An?)l + (Лл)о-
теля -тг
В графе IV табл. 3 выписываем значения Glp в выбранных
сечениях крыла.
Деля построчно числа, стоящие в графе III, на числа, стоя-
щие в графе V, находим значения (с точностью до множи-
____1 й У
____у которые обозначены через Um:
U — ____I7™— .
есть с точностью до постоянного мно-
. Интегрируя функцию U согласно
У' т I . _
| Напоминаем, что Vm
жителя значение
\ р dy ... .
равенству (94е), получаем функцию Опуская опять множи-
74
тель \ можем записать, произведя интегрирование по пра-
вилу трапеций (см. приложение 1):
ф0 = О [в силу граничного условия (90Ь)];
Фх = Фо + ^0 + СД;
Фг = Ф1 +
Фз — Фг + ^4 "Ь
Фл = Фз + U3 + Ui-
Значение функции <р в следующем приближении получаем
согласно уравнению (94f), причем, очевидно, для того, чтобы
иметь ош='1, следует выбрать
Найдя значение (у) в следующем приближении, подставляем
это значение снова в графу II и опять делаем все вычисления
сначала. Так продолжаем до тех пор, пока два следующих друг
за другом приближения практически не совпадут.
Для вычисления частоты по формуле (91), а также при рас-
чете на флаттер, необходимо иметь значение производной функ-
ции <p(j). Эта производная вычисляется обычно для последнего
приближения по формуле:
' ?у=и-А-г~Г’ W
2 ’ 10
где U— функция, значения которой вычислены в графе V. Вы-
вод этой формулы очевиден: ф есть интеграл от U, но разделен-
ный на множитель ? (при интегрировании этот множитель
отбрасывается). Следовательно, производная функция & есть t U
2 ’ 16
Так как = Дф, то производная <р есть производная ф Ат. е. t \
\ 2’ Тб/
Умноженная на А, откуда и получается формула (а). Как мы ви-
da , d'-s
АИМ’ dy имеет разрыв в сечении у = Л, ив этом сечении имеет
Два значения.
Итак, метод последовательных приближений для крыла с со-
средоточенной массой по существу не отличается от изложенного
в § 4 настоящей главы метода для крыла без сосредоточенных
Часе. Точно так же и для вычисления обертонов колебания
применяется метод, во всем аналогичный методу для крыла без
сосредоточенных масс.
75
Мы кратко опишем способ вычисления второго тона колеба-
ния, так как для крыла с сосредоточенной массой при расчете
флаттера всегда приходится проводить это вычисление.
Описанный выше метод последовательных приближений всегда
приводит к функции первого тона, независимо от того, какой
исходной функцией* задаться. Для получения функции второго
тона необходимо принять во внимание условие ортогональности
между функциями первого и второго тонов:
i
f dy 4- /<£, М (А). (А) = о,
О
где ч-(1>(у) — функция первого тона, способ вычисления которой
указан выше, и (у)—функция второгогтона колебания. Это
условие можно получить следующим образом.
Подставляя в основное уравнение (90а) один раз <р = а>(1) и,
соответственно, р = pv а другой раз и р = р2(рг— частота
первого и р,— частота второго тона колебания), получим:
Умножаем первое уравнение на <fw, а второе — на затем
вычитаем одно из другого и результат интегрируем в пределах
от нуля до I. Будем иметь:
о
(Ь)
о
Интеграл, стоящий в левой части, легко вычислить, если
заметить, что под знаком интеграла стоит полная производная
некоторой функции. Обозначая этот интеграл дпя краткости
письма одной буквой S, находим:
[~(с'
J dy\ p dy * p dy * ) y
Так как имеет разрыв в сечении у — h, то разбиваем
интервал интегрирования на две части: 0 — h и h — I и интегри-
руем по каждой части в отдельности. Получаем:
76
h
5 = Кч^п(!|-0'»С>*"’) +
0
+ (чС »'”-4 w
h
Принимая во внимание условия (90b) и (90c), будем иметь:
s = (о'р^гХ _?''№-( G4^),_T’UW-
[ - (0/, +<*> + ( 0/» ^).+W =
= p-fyM (ft) «-<=) (ft) — (ft) o(i> (ft) =
= (р!-р?)^(1)(Л)^2>(Л).
Подставляя найденное значение интеграла S в выражение (Ь),
находим указанное выше условие ортогональности первой и вто-
рой собственных функций.
Процесс последовательных приближений ведется таким обра-
зом, чтобы условие ортогональности выполнялось в каждом при-
ближении. Так как в данном случае метод по существу совпа-
дает с изложенным в п. 4 настоящей главы методом для крыла
без сосредоточенных масс, мы его подробно не излагаем, а огра-
ничиваемся лишь указанием порядка вычислений.
Исходная функция ф =<?0(у) задается в виде:
То^) = л[(У)2-^)|,
(d)
где ф(1) (у) — функция первого тона колебания, которая должна
быть заранее вычислена. Вместо (р ) можно, вообще говоря,
взять произвольную функцию у. Коэфициеит В определяется из
условия ортогональности между функцией о0 (у) и функцией
первого тона колебания ?'1) (у). Это условие дает для В следую-
щее выражение:
//га[ф(1,]2йу + /[?(П(Л)1*
о
Постоянная А определяется таким образом, чтобы на конце
крыла ф0(у) равнялось единице. Это условие дает значение
А =
1
1 — В
п
так как ср(1) 2 определено выше таким образом, что з(1> (/)=!. Сле-
довательно, исходная функция (rf) определена полностью.
Для определения n-го приближения по п— 1-му прежде всего
определяется функция фп,— так же, как это делалось для пер-
вого тона, т. е. по формулам (94). Вычислять эту функцию, как
уже было сказано, удобно, пользуясь расположением вычисле-
ний, указанным в табл. 3. Разница в вычислении для второго
тона заключается только в том, что задается по формуле (d).
Функция n-го приближения для второго тона колебания ф(п2> опре-
деляется через '!>„ следующим образом:
^ = Ап^п-Вп^),
где <Ь„ — найденная согласно уравнению (94) функция, ^(1>—Функ-
ция для первого тона колебания. Постоянная Вп определяется
из условия ортогональности:
i
f lmbn^dy -ь /ф(А) ?(1) (Л)
О
I
,pmk(1)l2dy + H°(1)(A)l3
о
а Ап определяется таким образом, чтобы <?„(/) = 1:
А — 1 •
п Ф„(О-В„
Приближения для вычисляются до тех пор, пока не со-
впадут два следующих друг за другом приближения. Последнее
из полученных приближений принимается за функцию кручения
второго тона. Частота колебаний второго тона определяется также
по формуле (91), причем, если вычисляется по табл. 3, то про-
изводная функция второго тона определяется формулой:
1 \
£ / dy " Г
2 " 10 7
dy
Отметим, что для получения необходимой точности при вы-
числении функции первого тона достаточно разбить крыло на
10 отсеков, в то время как для вычисления функции второго
тона этого часто бывает недостаточно, и приходится число де-
лений увеличивать до 15 — 20.
ГЛАВА 111
КОЛЕБАНИЯ ИЗГИБА КРЫЛА В ПУСТОТЕ
1. ОСНОВНЫЕ УРАВНЕНИЯ
Как и выше, будем схематизировать крыло как консольную
балку, жестко заделанную в фюзеляже. Для получения уравне-
ния колебательного движения такой балки воспользуемся извест-
ным диференциальным уравнением упругой линии стержня, на-
груженного распределенной нагрузкой интенсивности $:
где Е1 — жесткость балки (крыла) на изгиб и Z(y, -г)— прогиб
балки. В случае крыла под Z(_y, т) будем понимать прогиб оси
жесткости крыла.
При колебаниях на крыло действуют силы инерции, и под s
следует понимать интенсивность их распределения по длине
крыла. Обозначим через т погонную массу крыла; тогда будем
d2Z
иметь $ = —тга-^-, и уравнение упругой линии примет следу-
ющий вид:
(1)
Для полного определения задачи к этому уравнению необходимо
добавить граничные и начальные условия. В дальнейшем мы
будем интересоваться только теми характеристиками колебатель-
ного движения, которые не зависят от начального импульса,
и потому начальные условия нам будут не нужны. Напишем
граничные условия. В корне крыла в любой момент времени
прогиб должен равняться нулю, так как крыло предполагается
жестко закрепленным в фюзеляже. Кроме того, касательная
к упругой линии крыла в корне должна все время совпадать
Р осью у, так как упругая линия крыла не может иметь излома,
ли .КОнце крыла изгибающий момент и перерезывающая сила
лжны быть равны нулю.
19
Таким образом граничные условия для уравнения (1) полу-
чаются следующими:
для у = 0 должно быть Z = 0; -д— = 0;
У (2)
/ * &Z п d(PId*Z\ п ''
для у = / должно быть El-gyi = 0; \Ьл J = 0,
где L — расстояние от корня до конца крыла.
Для решения уравнения (1) могут быть применены все те
методы, которые были применены в предыдущей главе к случаю
крутильных колебаний. Так как все эти методы были изложены
весьма подробно, мы в настоящей главе ограничимся сравнитель-
но кратким изложением наиболее часто встречающихся приемов
решения.
Будем искать частное решение уравнения fl) в виде произве-
дения двух функций, из которых одна зависит только от у,
а другая — только от времени ':
Z=f{y)q^. • (3)
Подставляем это значение в уравнение (1) и разделяем в нем
переменные:
dy*\ dy"-) _ dz-
tnf q
(a)
Так как слева стоит функция только у, а справа — функция
только т, и они равны друг другу при любом значении у и т,
то каждая часть полученного выражения должна быть равна
постоянной величине (см. стр. 22). Эту постоянную обозначим
через X2. В дальнейшем будет показано, что при колебаниях
в пустоте X—чисто мнимая величина. Пока же будем считать, что
X может принимать любое комплексное значение.
Приравнивая каждую часть уравнения (а) постоянной X2, по-
лучим два уравнения для определения функций /(у) и <?('):
g—х’у-О; (>)
$) + *"/= °- ©
Граничные условия для функции /(у) получаются из гранич-
ных условий (2). Предполагая, что жесткость изгиба на конце
крыла не обращается в нуль, будем иметь:
при у = 0 должно быть /=0, = 0; |
, . (Pf г, d3f п j
при у = I должно быть 0, = 0. I
Прежде всего покажем, что если на крыло не действуют
никакие другие силы, кроме сил упругости и инерции, то X будет
80
величиной чисто мнимой. Как и в случае крутильных колебаний,
это будет означать, что имеют место колебания с постоянной
амплитудой, тогда как если К — комплексная величина, то коле-
бания происходят с нарастающей или убывающей амплитудой,
в зависимости от знака действительной части X (см. п. 5, гл. II).
Предположим сначала, что X может быть комплексной вели-
чиной и интеграл уравнения (5) есть комплексная функция
(7)
Подставляя значение интеграла в уравнение (5), получаем
тождество^ которое умножим на f(y)dy и проинтегрируем по
размаху [/(у) —комплексная функция, сопряженная с функцией
/(у), а именно: 7(y)=A(j)-//,(>)].
Будем иметь:
I i
= (8)
О о
Первый интеграл преобразуем, интегрируя два раза ?по частям.
Тогда, принимая во внимание граничные условия (6), получим:
С»
и о
Подставляя это значение в уравнение (8) и определяя из по-
лучившегося равенства X2, находим:
d-f d*T .
JEI dy* dy* dy
X2 = -°----p—-------. (10)
f mffdy
О
Так как произведение любой комплексной величины на сопря-
женную с ней есть величина действительная и положительная,
то из этого выражения непосредственно видно, что X2 есть отри-
цательная величина, а следовательно X есть величина чисто
мнимая. Поэтому можем написать:
\ = ip. (П)
Но если X—чисто мнимая величина, то уравнение (5) не будет
содержать комплексных коэфициентов, так как его можно на осно-
вании равенства (11) переписать в следующем виде:
[. <12>
Интеграл этого уравнения может быть взят в действительной
форме (ниже будет указан метод последовательных приближений
г Россман—15— б 81
для его вычисления). Следовательно, функция /(у) является дей-
ствительной и /(у) = /(у).
Тогда формула (10) примет такой вид:
PS=-----7-------• (13)
J тр dy
о
Для выяснения физического значения величины р обратимся
к уравнению (4). Подставляя в это уравнение Х = ip, найдем:
д+р2?=о. (к)
Это уравнение совпадает с уравнением (7) гл. II. В этой главе
было показано, что интегралом уравнения (14) является периоди-
ческая функция q (т) = A sin рт -ф В cos pt с периодом
Т = 2я, (15)
и, следовательно, р есть частота колебания. Число колебаний
в секунду выражается формулой:
(16)
Следовательно, изучаемое движение является гармоническим
колебанием с круговой частотой р. Формула (13) дает возмож-
ность вычислить частоту колебания, если известна форма коле-
бания (закон распределения прогибов крыла по размаху), ха-
рактеризуемая функцией /(у).
В тех случаях, когда уравнение (12) удается проинтегрировать,
решение задачи можно вести следующим образом.
Проинтегрировав уравнение (12), найдем четыре его частных
интеграла /„ /2, /3, /4, которые будут функциями независимого
переменного у и будут зависеть от р, как от параметра. Состав-
ляем общий интеграл уравнения (12):
/(У) = Afv(y, р) + Bf2(y, т) + Cf3 (у, р) 4- Dft(y, р), (17)
где А, В, С, D — произвольные постоянные, подлежащие опре-
делению из граничных условий. Подставляя выражение (17)
в граничные условия (6), получим для определения А, В, С, D
систему четырех линейных однородных уравнений, коэфициенты
которых будут функциями параметра р. Система линейных одно-
родных уравнений, как известно, может иметь отличные от нуля
решения тогда, и только тогда, когда определитель ее равен
нулю. Приравнивая определитель системы нулю, получим урав-
нение, из которого вычисляем р. Уравнение это называется
характеристическим уравнением, или уравнением
82
частоты. Когда значение р определено, можно из линейной
системы определить постоянные А, В, С, D, а затем по уравне-
нию (17) — окончательное выражение функции f(y).
Из сказанного ясно, что метод решения вполне аналогичен
методу, которым решалась задача о крутильных колебаниях крыла
(см. стр. 27). В частности, так же, как и в той задаче, уравне-
ние, определяющее функцию формы колебаний [/(j)j [уравне-
ние (12)], имеет решение, удовлетворяющее граничным условиям
не всегда, а только при некоторых определенных значениях па-
раметра р, которые называются собственными значениями пара-
метра 1 для диференциального уравнения (12). Функции, соответ-
ствующие собственным значениям р, называются собственными
функциями данного диференциального уравнения.
Изложенный метод решения, однако, можно применять лишь
в тех случаях, когда уравнение (12) удается проинтегрировать
аналитически. К сожалению, это возможно лишь в весьма огра-
ниченном числе случаев, при соответствующих законах распре-
деления жесткостей и масс крыла по размаху. Если же, как
обычно, закон изменения EI и т по размаху задан таблично,
при решении задачи приходится пользоваться различными при-
ближенными методами. Здесь можно пользоваться всеми теми
методами (Галеркина, Ритца и т. д.), применение которых к ре-
шению задачи крутильных колебаний было показано в предыду-
щей главе. Так как применение этих методов к задаче изгибных
колебаний ничем по существу не отличается от способа их при-
менения к задаче крутильных колебаний, мы не будем специ-
ально останавливаться на этом вопросе. Поэтому в настоящей
главе из всех приближенных методов будет изложен только наибо-
лее часто применяющийся—метод последовательных приближений.
2. КОЛЕБАНИЯ ИЗГИБА КРЫЛА ПОСТОЯННОГО СЕЧЕНИЯ
В ПУСТОТЕ
Одним из частных случаев, когда уравнение (12) может быть
проинтегрировано аналитически, является крыло постоянного се-
чения (у которого EI и т одинаковы во всех сечениях, т. е.
пе зависят от у). Рассмотрим прежде всего этот частный случай.
Рассмотрим крыло, у которого жесткость изгиба и погонная
масса по размаху не меняются. Для этого случая уравнение (12)
принимает такой вид:
I $-*V=o, <18>
где
1 Как указано выше, собственные значения р определяются характеристи-
ческим уравнением.
83
W I
Легко проверить, что частными решениями этого уравнения
являются sinAy, cos ky, sh&y и ch&y, и потому общий интеграл
будет:
/(у) = A sin ky 4- В cos ky + С sh ky 4* D ch ky. (20)
Подставляя это значение /(у) в граничные условия (6), придем
к следующей системе линейных однородных уравнений для опре-
деления постоянных А, В, С, D:
5 4-0 = 0;
А 4- С =0;
(21)
— A sin kl— В cos kl 4- Csh kl 4* D ch kl = 0;
— A cos kl+ В sinkl 4- C ch kl 4- D sh kl — 0.
Приравняв нулю определитель этой системы, получим харак-
теристическое уравнение, определяющее параметр k [а тем самым,
согласно уравнению (19), и р]. После некоторых несложных преоб-
разований характеристическое уравнение примет следующий вид:
cos kl - ch W = — J. (22)
Первые шесть корней этого уравнения в последовательном
порядке даны в табл. 4.
Таблица 4
*1/ kJ . kJ kJ kJ kJ
1.875 4,694 7,855 10,996 14,137 17,279
Решение для s > 2 можно приближенно представить формулой
ksl = ^r..
Следовательно, уравнение частоты (22) имеет бесчисленное
множество корней. Для каждого из корней ks системы (21) может
быть определена своя система постоянных и своя функция /(у) =
— fs(y). Таким тбразом существует бесчисленное множество
частных решений в форме (20). Для каждого значения корня ks
может быть определено по формуле (19) значение частоты ps
и затем интегрированием уравнения (14)—значение функции ^(') —
= qs(y). Далее по формуле (3) находим частное решение, соот-
ветствующее корню k6: Zs=fs(y)-qs(y). Общее решение найдем,
как сумму частных:
= (23)
5=1
Отметим, что при интегрировании уравнения (14) войдут две
произвольные постоянные и потому выражение Z(y, содержит
84
постоянные, которые пока остались неопределенными. Они опре-
деляются начальными условиями так же, как и соответствующие
постоянные в задаче о крутильных колебаниях (см. стр. 24).
Формула (23) показывает, что движение, совершаемое кры-
лом, может быть представлено как сумма гармонических ко-
лебаний,— каждое с соответствующей частотой ps. Каждое такое
колебание называется стоячим колебанием, и формула (23)
дает разложение колебательного движения по стоячим колеба-
ниям. Как и в случае крутильных колебаний, стоячее колебание,
соответствующее наименьшему значению частоты (kJ = 1,875),
называется основным тоном колебания, а все другие
стоячие колебания называются обертонами, или высшими то-
нами колебания.
Вычислим до конца функцию формы и частоту основного
тона колебания. Наименьшее значение р, согласно уравнению (19),
будем иметь при наименьшем значении k. Поэтому основному
тону соответствует наименьший положительный корень характе-
ристического уравнения, т. е.:
kl = 1,875. (24)
Решая систему (21), находим соответствующую данному корню
систему значений постоянных Л, В, С, D. Так как система одно-
родная, то одна из постоянных остается неопределенной:
А _ cos kl + ch kl _ п 7ои
В ~ sin/г/+ sh/г/~ U,/64,
О = — В, С = —А.
Подставляя эти значения в формулу (20), будем иметь:
f(y) — В [(cos ky — ch ky) + 0,734 (sh ky — sin ky)].
Величина В осталась произвольной. Это естественно, так как
с самого начала очевидно, что уравнение (12) вместе с гранич-
ными условиями (6) определяет функцию f(y) только с точностью
до постоянного множителя Ч Принято брать В = — 1 (отрицатель-
ное значение В принимается для того, чтобы f(y) была поло-
жительна). Тогда, подставляя также значение k из уравнения (24),
окончательно получаем:
/(у) = [ch (1,875 ^-) - COS (1,875 f)] -
— 0,734[sh (1,875 —sin (1,875 -)].
(25)
1 В самом деле, если /(у) удовлетворяет диференциальному уравнению
и граничным условиям, то и функция AJ (у), где А — любая произвольная
постоянная, будет им удовлетворять. Неопределенность функции/(у) объяс-
няется тем, что в задаче надо найти в конце концов прогиб крыла Z{y, ')
[частное решение Z = J (у) • q (т)], и остающаяся произвольной постоянная
мо>кег быть включена в функцию q (т). Постоянные же, входящие в функцию
4 (т), до конца определяются начальными условиями.
85
Числовые значения этой функции, которыми приходится поль-
зоваться в ряде задач (как будет показано ниже), приведены
в табл. 5. На фиг. 20 показан график функции первого тона
т 6 5 (I тон).
а лица Также можно вычислить функции,
У 1 f(y} соответствующие обертонам колеба- ния. На фиг. 20 приведены функции, соответствующие первому, второму
и третьему тонам колебания. Так как
0 0,1 0,2 0 00335 каждая из функций определена с точ-
<)’1277 ноэгыо до произвольного постоянного
0,3 0,2641 множителя, то последний во всех слу- чаях мы.выбрали так, чтобы получить
0,4 0,4598
0,5 0,6 0,7 0,6789 0 9222 одно и то же значение функции /(у)
1J816 на конце крыла (при у = Г).
0,8 1,4519 Из фиг. 20 видно, что функции
0,9 1,7246 формы для второго и третьего тонов
1,0 2,0 колебания обращаются в нуль в неко- торых сечениях крыла. Следовательно, прогиб Z (у, -с) для стоячего колебания,
соответствующего рассматриваемому тону, будет в этих точках ну-
лем, независимо от значения времени -с. Это значит, что при колеба-
ниях по второму или третьему тонам имеются сечения крыла,
Фиг. 20.
в которых прогиб равен нулю во все время колебания. Такие
сечения называются узлами колебания. Можно доказать,
что узлы колебания имеются не только при колебаниях второго
или третьего тонов, но и при колебаниях любого более высокого
тона, причем число узлов тем больше, чем более высок порядок
тона колебания.
Частота колебаний определяется по формуле (19), где k есть
решение характеристического уравнения (22).
Для основного тона
1,875 Vi/EI
Р I J V т ’
(26)
86
Для первого обертона
f 4,694 \2 ]/£/
Р \ I ) V т
и т. д. Период колебания и число колебаний в секунду опреде-
ляются по формулам (15) и (16).
Пример. Вычислить число колебаний первого тона в се-
кунду для модели крыла постоянного сечения по следующим
данным:
Размах I = 0,55 м.
Жесткость изгиба £7=1,48 кгм-.
Погонная масса т = 0,0461 —.
По формуле (26) находим, что
/1,875V j/ТЖ ссс
Р \ 0,557 У 0,0461 — 65>6>
и число колебаний в секунду
п = - 10,5 — .
2л ’ сек.
Пример. Консольная балка постоянного сечения с длиной
консоли 5 м и весом 100 кг имеет период колебания 0,1 сек.
Определить жесткость изгиба балки.
Период колебания определяется формулой:
r=z=4^)‘F¥-
Отсюда находим выражение жесткости изгиба через период ко-
лебания:
£7 _ 4,з ( 1 V Л
11,875/ Г2"
Вычисляем погонную массу балки:
т-----------------------!90_ _oQ4^ceK2
9,81 • 5 м* ’
Жесткость изгиба балки равна:
= 4я2 (Т875г) ’ (0,1)2 = 4,06 ‘ 1(^° кгм2‘
3. КОЛЕБАНИЯ ИЗГИБА КРЫЛА ПРОИЗВОЛЬНОЙ ФОРМЫ
В ПУСТОТЕ
Рассмотрим теперь способ определения формы и собственной
частоты изгибных колебании произвольного крыла. В общем
случае (при произвольном законе изменения Е1 и т по размаху)
Уравнение (12) проинтегрировать в аналитической форме не
Удается. Для его интегрирования применяется тот же способ
последовательных приближений, который применялся при изуче-
нии колебаний кручения.
87
Сначала мы изложим метод последовательных приближений
без каких-либо упрощений, а затем укажем на возможные упро-
щения, чрезвычайно облегчающие расчет.
Перепишем уравнение (12) в следующем виде:
{.ИН"'' (27)
Если бы нам был известен точный интеграл этого уравнения,
мы сразу могли бы определить частоту по формуле (13). Однако,
поскольку нам этот интеграл неизвестен, мы сперва задаемся его
приближенным значением f = f0(y). Вообще говоря, за функцию
f0(y) можно принять любую функцию, но чем менее похожа эта
функция на истинное значение интеграла, тем больше прибли-
жений нам придется вычислять. Поэтому желательно задаться
f0(y) так, чтобы она возможно больше походила на точный инте-
грал уравнения (27), так как тогда количество необходимых
вычислений будет минимальным. Удобно в качестве f0(y) задаться
функцией, найденной нами в предыдущем параграфе для крыла
постоянного сечения [формула (25)], график которой приведен
на фиг. 20 (I тон), а значения — в табл. 5.
Задавшись функцией f=/0(j), вычисляем по формуле (13)
соответствующее значение р = р0. Затем подставляем вместо
f(y} и Р в правую часть уравнения (27) f0(y) и р0. Таким обра-
зом в правой части будет стоять известная нам функция у.
Интегрируя после этого полученное выражение два раза, найдем:
E/^ = p^F0(y), (28)
где
(У)=// т/о(у) dy dy. (29)
F0(j) является известной нам функцией у. Обе части выраже-
ния (28) делим на EI, после чего результат опять дважды инте-
грируем. Будем иметь:
/=Хо(Л (30)
где
/.о (у) = p20fdydy- (31)
легко может быть найдена любым методом приближенного инте-
грирования.
Значение функции /, найденное таким образом, мы обозначим
через /10'); это и есть значение искомого интеграла в первом
приближении. Для получения следующего приближения повто-
ряем весь процесс, приняв за исходную1 функцию f = fi(y)-
В результате мы найдем функцию f=f2{y) (второе приближе-
ние). Берем эту функцию за исходную, опять повторяем весь
1 Здесь, как н в дальнейшем, будем называть исходной функцию, кото-
рой мы задаемся для получения следующего приближения.
88
процесс и т. д. Вычисления следует вести до тех пор, пока два
последовательные приближения не дадут одного и того же зна-
чения для функции f(y). Обычно для этого бывает достаточно
двух-трех приближений.
Расчет значительно облегчается, если принять во внимание,
что определение функции f(y) достаточно вести с точностью до
постоянного множителя. В самом деле, если умножить функцию f(y)
на постоянное число А, то числитель и знаменатель в фор-
муле (13) получат одинаковый множитель А, ив результате
частота не изменится. Как будет показано ниже, для расчета
крыла на флаттер также достаточно знать функцию /(у) с точ-
ностью до постоянного множителя. Кроме того, функция, умно-
женная на произвольный постоянный множитель, также удовлетво-
ряет уравнению (27) и граничным условиям (6).
Вследствие вышеизложенного мы можем сокращать функ-
цию /о(у) на любое постоянное число, так как тогда по
уравнению (30) и f(y) разделится на то же число. Сократим у0(у)
на величину р& а в последующих приближениях будем сокра-
щать хх(у), /2(у),... соответственно на р2, р2.... Тем самым
отпадает необходимость при каждом приближении определять р-.
Это равносильно тому, чтобы полагать р2 = 1, т. е. вместо
уравнения (27) интегрируем уравнение:
dy2 \. dy2J J'
куда не входит неизвестная величина р2. Интегрирование ведем
при помощи вышеуказанного процесса последовательных прибли-
жений, и лишь после того, как функция /(у) окончательно
определена, находим частоту по формуле (13).
Для сравнения функций, полученных в различных приближе-
ниях, их нужно как-то нормировать, так как функция формы,
как мы уже указывали, диференциальным уравнением и гранич-
ными условиями определяется только с точностью до постоян-
ного множителя. Принято нормирование функций производить
умножением функций, полученных в различных приближениях,
на постоянных множителей таким образом, чтобы значения ft(y) на
конце крыла (для у = /) были одинаковы во всех приближениях.
Кроме того, при выполнении интегрирований по формулам
(29) и (31) следует заботиться о выполнении граничных условий
в каждом приближении. Каким образом это делается, указано в
приведенном ниже примере на вычисление указанным методом
функции формы (/(у)] и частоты колебаний.
Пример. Вычислить функцию /(у) и период колебаний
изгиба для крыла, расчетные данные которого приведены в табл. 6.
Метод интегрирования и расположение вычислений принци-
пиально ничем не отличаются от способа расчета колебаний
кручения (табл. 1). Вычисления’расположены в табл. 6. Таблица
разбита на ряд частей. В первой расположены исходные данные,
которые, как и в случае кручения, заданы в одиннадцати равно
89
отстоящих друг от друга по размаху крыла точках, что соответ-
ствует делению интервала интегрирования (О, Z) на 10 равных
частей. В следующих частях таблицы расположены вычисления
функции /(у) в различных приближениях и в последней — вычи-
сление второй производной которая необходима для вычи-
сления частоты по формуле (13). w
Под номерами граф в таблице указано то действие, в резуль-
тате которого данная графа получена. Так, например, обозначе-
ние III • IV означает, что числа, стоящие в графе, над которой
стоит этот знак (графа V), получены в результате построчного
перемножения чисел, стоящих в графах Ill и IV.
В дополнительных пояснениях нуждается только символ
/V, /VI и т. д. Этот символ означает, что числа графы, над
которой стоит знак, например, / VI (графа VII), получены в рез> ль-
тате интегрирования функции, значения которой стоят в графе VI,
но без учета множителя Способ получения этих интегралов
не отличается от способа интегрирования, примененного в случае
кручения, и мы на нем отдельно останавливаться не будем.
Нули, стоящие в конце граф VI, VII и в начале граф IX, X,
поставлены в силу граничных условий, которым должна удовле-
творять функция /(у). Эти же условия учитываются и при
вычислении следующих приближений.
Множитель А подбирается таким образом, чтобы в каждом
приближении функция /(у) на конце крыла равнялась 2, так как
исходная функция /0(у) [формула (25)] на конце крыла (при у=1
равна 2. Окончательные значения функций /(у), получении
в различных приближениях, приведены на фиг. 21.
Производная также вычисляется аналогично тому, как вы-
числялась производная при расчете на крутильные колебания-
91
90
Продолжение табл. 6
Вычисление второго приближения
I XII XIII XIV XV XVI XVII XVIII
III. XI /ХИ /XIII XIV/11 fxv /XVI XVII А
'У 1 m/i /з
0 0 0,5679.10-2 7,383-10-2 0,090-10-11 0 0 0
0,1 0.00338.I0-2 0,5645-10-2 6,251 10-2 0 0815-10-11 0 1715-10-“ 0 1715-10-“ 0,0192
0,2 0,00996-10- 2 0,5510.10-2 5 135-Ю-2 0,079-10~11 0,3300-10-“ 0,675-10-“ 0 0755
0,3 0,0162-10“2 0,5250.10-2 4 059-10-2 0,0821-10““ 0,4933-10-“ 1,500-10-“ 01628
0,4 0,0237.10-2 0.4850.10-2 3,049-10-2 0,0874-10”11 0,6028-10-“ 2,656-10““ 0,2970
№ 0 0329-10~2 0 4285 ] О”2 2J36-10-2 01047-10““ 0 8549-JO-11 4174-10-“ 0 4670
о,6 0,0442.10-2 0,3514.10-2 1,356-10-2 0,1093-10-“ 1,0629-10-“ 6,098 10““ 0,6810
0,7 0,0491-10-2 0 2581-10-2 0 746-Ю-2 0,1130-10-“ 1,2510-10-“ 8,457-10-“ 0 9450
0,8 0,0444-10-2 0,1646-10-2 0 324-10“ 2 0,1060-10-“ 1,5100-10-“ 11,259-10-“ 1,2600
0,9 0,0407 IO-2 0,0795-10-2 0,0195-10“2 0,0688-10-“ 1,6850-10-“ 14,454-10-“ 1,6170
1 0,0388-10-2 0 0 0 1,7538-10-“ 17,893-10-“ 2,000
Л-17,893 2|0~“-0’"19'10"
Продолжение табл. 6
Вычисление третьего приближения Производная
I XIX XX XXI XXII XXIII XXIV XXV XXVI
III-XVIII /XIX /XX XXI/II /ххп /XXIII XXIV-A XXII В
У_ 1 m/s • /з аЧз d)’2
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 0 0,00324-10-2 0,00955-10-2 0,01559-10-2 0,02285-10-2 0,03200-10-2 0,04300-10-2 0,04815-10-2 0,04370-10-2 0,04040-10-2 0,03880-10-2 0,5550-10-2 0,5522-10-2 0,5394-10-2 0,5143-10-2 0,4758-10-2 0,4210-10-2 0,3460-10-2 0.2550 IO”2 о.юзз-ю-2 0,0792-10-2 0 7.248-10-2 6 140-Ю-2 5 049-Ю-2 3,995-Ю-2 3,005-10-2 2,108-10-2 1,341-10-2 0,740-10-2 0,322 -10“2 0,079-10-2 0 0,0884-10-“ 0,0800-10-“ 0,0777-10-“ 0,0810-10-“ 0,0860-10-“ 0,1032-10““ 0,1081-10-“ 0,1120-10-“ 0,1054-10-“ 0,0685-10““ 0 0 0,1684-10““ 0,3261-10““ 0,4848-Ю-11 0,6518-10-“ 0,8410-10““ 1,0520-10““ 1.2720-10““ 1,4898-10““ 1,6637-10““ 1,7320-10““ 0 0.1684-10““ 0,6629-10““ 1,4740-10““ 26106-10““ 4,1030-10““ 5.9960-10““ 8,3200-10““ 11,0820-10““ 14,2360-10““ 17,6320-10““ 0 0,01912 0,0752 0,1673 0,2960 0,4650 0.6800 0,9420 1,2580 ' 1,6180 2,0000 0,421 Io- О.382-10“5 0,371 -Ю-5 0,386-10“5 0,410-Ю-5 0 491 Iff-5 0.516-Ю“5. 0,535-10“5 0,504-10“5 0.327-10“5 0 В
А=—- 17 632 „-=0,1136-10“ 10““ __ 0,1136-10“ 0,238-104 =0,477-Ю7
После вычисления функции f(y) переходим к определению
частоты колебаний по формуле (13). Входящие в эту формулу
интегралы вычислены в табл. 7. в
По табл. 7 получено
о
I
J mJ2 dy = 0,252.
о
Таблица 7
Вычисление интегралов
( d2f Л
Значения / и т взяты из табл. 6 j I * * * У *
I II III IV V VI VII
у/1 / d2/ dy2 - Ш m / mf2
0 82-Ю9 0.421 • Ю“5 1,450 0,168-10-2 0 0
0,1 76.8.10е 0.382-IO-5 1,122 0,168-10“2 0.01912 0,0617-10“5
0,2 64,9-109 0,371-IO-5 0.890 0,126-Ю-2 0.0752 0,7150-10“5
0,3 49.4-109 0,386-IO-5 0.736 0,093-10“2 0.1637 2,600-10“5
0,4 34.9-109 0,410-10-5 0.586 0,077-10“2 0,2960 6,740-10“5
0,5 20.4-109 0.491 -IO-5 0,495 0,068-10“2 0 4650' 14,80-10“f
0,6 12.4-109 0.516-10-5 0.330 0,063-10“2 0,6800 29.20-10“5
0,7 6.61 -Ю9 0,535-10—5 0,189 0.051-10“2 0.9420 45,35-10“5
0,8 3,05-Ю9 0,504-IO-5 0,077 0,035-Юг-2 1.2580 54,90-10“5
0,9 1,16-109 0,327-10“5 0,012 0,025-10“2 1.6180 65,50-10“5
1,0 0,31-109 0 0 0,019-1O~2 2.000 77,50-10“5
Ej=5,159 E2=258,6-10“5
I
С „ 1
J Е1 Уйу2) dy = Xi-'1O1-5,159-97,5 - 504.
о
I
У mf- dy = Е,-= 258,6-10”5-97,5= 0,252.
и
f]o формуле (13) находим:
P-/S = «.7;
период колебаний изгиба
Т= 2"= 0,1405 сек;
Р
число колебаний в секунду
п = 4-= 7,1.
4. ИЗГИБНЫЕ КОЛЕБАНИЯ КРЫЛА В ПУСТОТЕ ПРИ НАЛИЧИИ
СОСРЕДОТОЧЕННЫХ МАСС
Если на крыле имеются сосредоточенные грузы (моторы,
поплавок и т. п.), то основное уравнение (1) и граничные усло-
вия (2) остаются справедливыми, так как уравнение (1) есть
условие равновесия сил в каждом сечении крыла; это условие
должно выполняться для всех сечений, за исключением того, в
котором приложен сосредоточенный груз. Граничные условия
целиком вытекают из условий заделки крыла и потому также
сохраняются. Но в отличие от случая крыла без сосредоточен-
ных грузов уравнение (1) следует интегрировать отдельно на
участках 0, h и h, I, где y — h— сечение, в котором находится
сосредоточенный груз. При интегрировании войдут четыре про-
извольных постоянных на первом участке и столько же на вто-
ром. Для определения всех восьми постоянных наряду с че-
тырьмя граничными условиями (2) должны быть использованы
условия сопряжения в сечении y — h. Условия эти следующие.
Во-первых, при у = h должны быть непрерывны прогиб крыла,
касательная к упругой линии (т. е. упругая линия крыла не мо-
жет иметь излома) и изгибающий момент. Перерезывающая сила
при переходе через сечение у = h изменяется скачком, причем
величина скачка равна перерезывающей силе (т. е. силе инерции)
от сосредоточенного груза. Следовательно, имеем следующие
условия сопряжения:
Zy=h-\- — Zy=h—;
(£U"(fU> (32)
д (F.d-Z\_____d__, F,d-Z\____Ml-Z\
dy \ cy*)y=h+ dy ' dy-/y=h— k
Здесь индекс у = h 4- есть значение соответствующей величины
при подходе к сечению у = А справа (со стороны конца крыла),
а У — h — значение той же величины при подходе к этому
сечению слева (со стороны корня крыла) (см. гл. II и фиг. 19).
Через М обозначена масса сосредоточенного груза.
95
Подставляя в уравнение движения/1), в граничные усло-
вия (2) и в условия сопряжения (32) выражение Z, согласно
формуле (3), где в силу уравнения (4) и равенства (11) сразу
можно принять q(z) = ep\ получим уравнение движения в виде
уравнения (12), граничные условия в виде выражений (6) и
условия сопряжения в виде:
fy=h+ ~~ Jу=h—'
(<),.,,+= (<Ь-; <33>
dy к dy- Jy=h+ dy к dy2 Jy=h— r J ' ’
Пусть ЛОО,/гO'), /з00, Л (у) —частные интегралы уравне-
ния (12). Очевидно, они будут зависеть от р, как от параметра.
Общий интеграл можем написать в следующем виде:
для 0 <_у < h
f(y) = Су) + (у) + с1/з (у) + ад (у);
для h <у < I
f(y)=(у) + ад (у) + ад (у) + адо).
Постоянные интегрирования будут различными на участках
О, h и h, I. Все восемь постоянных определяются из четы >ех
граничных условий (6) и четырех условий сопряжения (33).
Отметим, что для определения постоянных мы получим систем)
линейных однородных уравнений и, следовательно, отличные от
нуля решения будут существовать только в том случае, если
определитель этой системы будет равен нулю. Приравнивая
этот определитель нулю, получим условие, из которого найдем
частоту р.
Решение указанным методом возможно в тех случаях, когда
известны частные интегралы уравнения (12). Но это уравнение
удается в аналитической форме проинтегрировать лишь в весьма
небольшом числе частных случаев. Например, такое решение
возможно для крыла постоянного сечения. Если мы проведем ре-
шение до конца, то получим 1 частоту колебаний:
P = k*V^T> <34)
где k является корнем характеристического уравнения:
Л • Л2(k) - F3 (k) • F, (k) = 0; (35)
1 Вывод приводимых ниже формул может служить хорошим упражнением
для усвоения излагаемых методов.
96
здесь
Fi (k) = [ch kl + cos kl] +
+ ~ kl [ch kh — cos kh] [sh&(/ —A)4~sin&(/ — Л)];
F2 (&) = [ch kl + cos kl] 4-
+ 2^ kl [sh kh — sin kh] [ch k (I — A)-f-cos k(l — A)];
F3 (k) — [sh kl — sin kl] 4-
4- j —cosAA] [ch&(/ — A)4-cos&(/ — A)];
Ft (k) = [sh kl 4- sin kl] 4-
4- ~ kl [sh kh — sin kh\ [sh k (I — h) 4- sin k (I — A)];
у.— отношение массы сосредоточенного груза
крыла:
к массе всего
(36)
При [л —0 характеристическое уравнение переходит в уравне-
ние (22) для крыла постоянного сечения без сосредоточенных
грузов.
Форма колебания крыла постоянного сечения с сосредото-
ченным грузом будет:
Для 0 <у < h
f(y) = (eh ky — cos ky) 4- D (sh ky — sin ky).
Для h <_y <1
f CO = (eh ky — cos ky) 4- D (sh ky — sin ky) 4-
(37)
4- kl • -£- [(ch kh — sh kh) 4-
4- D (sh kh — sin kh)] [sh k (y — h) — sin k(y — A)].
Постоянная D имеет следующее значение:
= (Зв)
Наименьшие корни уравнения (35) в зависимости от h и р даны
на фиг. 22. При подстановке в формулу (34) наименьшего зна-
чения k получим частоту основного тона колебания крыла по-
стоянного сечения с одной сосредоточенной массой.
В тех случаях, когда уравнение (1) нельзя проинтегрировать
Ючно, для определения частоты и формы колебания приме-
няется тот же метод последовательных приближений, который
применялся выше для крыла без сосредоточенных масс.
Гроссман—15—7
97
Прежде всего найдем формулу для определения частоты ко-
лебания, если известна функция ффрмы f(y). Функция формы
является интегралом уравнения (12), поэтому после подстановки
в это уравнение получаем тождество, которое умножаем на
f(y)dy и интегрируем по размаху крыла. Будем иметь:
-М-г/ ^“у = 0.
и о
(39)
Преобразуем первый интеграл двукратным интегрированием
по частям. Так как является функцией, имеющей
разрыв в сечении у = h [в силу последнего из условий (33)], то
интервал интегрирования разбиваем на две части: 0, h и h, I, и
интегрирование проводим на каждом интервале отдельно:
I h I
-к>у -
о о л
h
Я W • +
о
п
98
Принимая во внимание граничные условия и условия сопря-
жения для функции f(y), можем переписать это выражение в
виде:
о
о
I
=-p*Mf*(h) + J Elfffldy.
о
Подставляем это значение в уравнение (39)
f mfdy+Mfih)
о
и определяем р:
(40)
Легко убедиться в том, что это выражение можно получить
также из принципа возможных перемещений. В самом деле, ле-
вая часть уравнения (1) есть не что иное, как сумма погонных
сил, действующих в некотором сечении крыла. Чтобы получить
сумму сил, действующих на элементарный отсек крыла между
сечениями у и у + dy, умножим левую часть (1) на dy. Затем,
умножив результат на Z, получим работу сил, действующих на
элементарном отсеке при прогибе крыла. Интегрируем резуль-
тат по длине крыла. Получим выражение работы всех сил, дей-
ствующих на все отсеки крыла, которое приравниваем нулю на
основании принципа возможных перемещений:
о
Если мы в это выражение подставим значение Z =f(y)e'P'c,
то придем к уравнению (39), из которого определялась частота.
Следовательно, прием умножения уравнения для функции формы
на саму функцию с последующей интеграцией по длине крыла,
которым мы уже пользовались выше и часто будем пользо-
ваться в дальнейшем, есть по существу составление условия
равенства нулю работы на пути возможных перемещений.
Математическим выражением принципа возможных переме-
щений, как было показано в гл. I, являются уравнения Ла-
гранжа. Естественно, что, исходя из них, также можно получить
выражение (40). В самом деле, потенциальная энергия колеблю-
щегося крыла по общей формуле сопротивления материалов для
99
потенциальной энергии изогнутой балки будет:
г/»®*'»- «»
о
Кинетическая энергия рассматриваемой колеблющейся си-
стемы слагается из кинетической энергии собственно крыла
i
„ 1 г , dZ \2 ,
и
и кинетической энергии колеблющегося сосредоточенного груза
Кинетическая энергия всей колеблющейся системы:
Г = Л + Т2 = 4/ + «)_»• (42)
о
Ищем Z в форме выражения (3j: Z=f (у)q(z). При известной
функции /(у) движение полностью будет определено, если бу-
дет известна функция q (у). Следовательно, q (") является пара-
метром, полностью определяющим движение, и эту функцию
можно принять за обобщенную координату. Подставляя Z=f(y)q(x)
в выражения кинетической и потенциальной энергии, найдем:
! <4з)
Г = 4-[/mf*dy+Mf*(h)\.
О '
Составляем теперь уравнение движения в форме Лагранжа:
d / дт_\ _ ат ди _ п
d- V dq J dq ' dq
Будем иметь:
q [ J'nf* dy 4- Mf (A)] + q f dy = 0. (44)
о 0
Это линейное диференциальное уравнение с постоянными
коэфициентами относительно неизвестной функции <7(~). Как
известно, такое уравнение интегрируется подстановкой
q& = eip\
Подставляя это выражение в уравнение (44), получаем:
i i
-p^nif-dy+Mf^+q J Ef^ydy=O.
О о
Решая это уравнение относительно р, опять получаем фор-
мулу (40). Таким образом по формуле (40) можно определить
частоту колебания крыла, если будет известна функция формы-
100
Для ее определения применяется обычный метод последователь-
ных приближений. От метода, изложенного в п. 3 настоящей
главы, он отличается только тем, что при выполнении интегри-
рования необходимо соблюдать условия сопряжения в сечении,
в котором находится сосредоточенная масса [аналогично тому,
как соблюдались условия сопряжения в случае крутильных
колебаний крыла с сосредоточенной массой (см. гл. II, п. 6)].
Так как мы много раз уже излагали аналогичные методы, огра-
ничимся здесь только указанием способа расчета, не давая по-
дробных объяснений.
Расположение вычислений показано в табл. 8.
Таблица 8
Схема вычисления функций формы изгибных колебаний крыла
с сосредоточенным грузом
1 1 11 ш IV V 1 V1 I Vll VIII IX Примечание
_У_ 1 V и El и El w Q f
0 (т/)о Vo и0 «.. & ). uz0=o Qo=O ...
0,1 Vi ... & )t Q1 ...
0,2 у; у; ... & 2 q, ... Сечение, в кото- ром находится сосредоточенный груз
0,3 W)s у. и, IPs Qs ...
0,4 ("А V, Ut ... (й) 4 Qt ...
0,5 ("А У5 Us ... о irs Qs ...
0,6 (m/)e у« Ut ... («: 1. Q, ...
0,7 ("А у. U, (-£) VZ7. Q, ...
0,8 W)8 Уз ия ... (-Й) 3 IVB Q« ...
0,9 ("А у» ... (£) 3 IV, <2, ...
1 У1О U1B ... (£) 10 MZ,o A ...
101
Эта таблица составлена в соответствии с формулами (28)—(31),
которые вытекают из основного уравнения (27). Способ вычисле-
ний отличается от способа, изложенного в п. 3 настоящей главы,
только тем, что кроме соблюдения граничных условий следует
при выполнении интегрирования заботиться о выполнении усло-
вий сопряжения.
При вычислении функции формы в формулах (28)—(31) можно
положить р2 = 1 и затем нормировать полученные значения таким
образок^ чтобы всегда на конце крыла /(у) принимало одно
и то же значение. Вычисление функции формы ведется сле-
дующим образом. Все крыло делится равно отстоящими друг
от друга сечениями на k частей (в табл. 8 k = 10) и отме-
чается деление, в котором находится сосредоточенный груз
(в табл. 8 груз находится в сечении = 0,2). В графе II
таблицы помещаются значения mf в выбранных сечениях, где f—
функция, которой задались в качестве исходной [удобно в каче-
стве исходной принимать функцию для крыла постоянного сече-
ния по формуле (25), числовые значения которой приведены
в табл. 5]. В графе III полагаем 1^0 = 0 [в силу граничного усло-
вия = 0 для у = zj и интегрируем обычным способом
до сечения с сосредоточенным грузом:
И1о = 0;
Vn — Ип+1 + (mfin+l + (m/)„.
В строке, соответствующей положению сосредоточенного груза,
в соответствии с последним условием сопряжения (33) выписы-
ваем две цифры:
Иа = И3 -Ь (/«/)з +
V[ = V2+Mf(h)™,
где М — масса сосредоточенного груза, y — h— сечение, в кото-
ром груз находится, и k — число делений интервала 0, Z. Множи-
2/е
тель -у- появился вследствие того, что функция, значения кото-
рой стоят в графе III табл. 8, есть интеграл f mfdy, деленный
на и этот делитель нужно ввести для соблюдения последнего
равенства (33) также и в член, зависящий от сосредоточенного
груза.
Дальше интегрирование идет опять обычным путем:
K1=IZa-|-(zra/)2 + O«/)i;
К> = К + (mf)i +
В графе IV в силу граничного условия полагаем
(710 = 0
102
и интегрируем вверх обычным способом до сечения с сосредо-
точенным грузом:
Un = Un 1 + V'n+i + V п.
В сечении с сосредоточенным грузом полагаем
U2=U3+ v3+v't
и дальше
U^U2+ И + Hf,
^о = ^1 + И1 + Ко.
Для получения графы VII интегрируем функцию графы VI обыч-
ным способом сверху вниз:
UZo = 0;
.,+(-&),•
Графа VIII получается интегрированием функции графы VII:
Qo = 0;
Q„=Qn_i+ Wn^+ Wn.
Для получения функции f нормируем функцию Q таким обра-
зом, чтобы получить на конце крыла /(Z) = 2. Для этого цифры,
полученные в графе VIII, делим на ^.10:
/=Qn-J-
Найденную таким образом функцию f подставляем в графу II
табл. 8 и вновь повторяем все вычисления. Вычисления ведутся
до тех пор, пока два следующие друг за другом приближения
практически не совпадут.
Вторая производная функции /, которую необходимо знать
при вычислении частоты, вычисляется по формуле:
rf3/ _ 2 (2k \2 / и \
4У2- Qio\ I J \El)’
причем Ql0 и берутся из таблицы вычисления последнего
приближения.
ГЛАВА IV
СОВМЕСТНЫЕ КОЛЕБАНИЯ КРЫЛА В ПУСТОТЕ
1. ХАРАКТЕР движения и основные уравнения
Выше были рассмотрены чисто крутильные и чисто изгибные
колебания крыла в пустоте. Однако в действительности такие
колебания могли бы существовать только в том случае, если бы
центр тяжести и ось жесткости в каждом сечении крыла сов-
падали. Если это условие не соблюдено, то колебания крыла
Фиг. 23.
будут обязательно сов-
местными, «т. е. крыло
будет испытывать од-
новременно и дефор-
мации изгиба, и де-
формации кручения.
Чисто изгибных и чи-
сто крутильных коле-
баний у крыла не бы-
вает, но совместные
колебания, как мы уви-
дим ниже, протекают
таким образом, что
обычно как по форме,
так и по частоте мало
отличаются от чисто изгибных и чисто крутильных. Поэтому
часто не производят расчета совместных колебаний крыла, а
характеристики (частоту и форму), полученные из расчета чисто
изгибных и чисто крутильных колебаний, принимают за харак-
теристики действительного колебательного движения крыла.
Рассмотрим колеблющееся в пустоте крыло, центр тяжести
которого С находится на расстоянии з от оси жесткости Е
(фиг. 23). Пусть xoz — неподвижная в пространстве система коор-
динат, выбранная таким образом, что ось oz проходит через
ось жесткости крыла Е и по направлению совпадает с направ-
лением изгибной деформации крыла. Движение совершается
таким образом, что центр жесткости во все время движения
остается на оси oz, так как жесткость крыла в лобовом направ-
лении бывает настолько велика, что деформацией крыла в на-
правлении оси ох можно пренебречь. Мы рассматриваем эле-
104
ментарный отсек крыла ширины dy, так что высоту крыла над
чертежом фиг. 23 следует представлять себе равной dy.
Покажем, что, даже если начальный импульс, вызвавший
движение, был чисто изгибающий, или чисто крутящий, коле-
бания крыла все равно будут совместными.
Пусть на крыло подействовал чисто изгибающий импульс,
например мы крыло изогнули и затем предоставили его самому
себе. Под действием сил упругости крыло начнет двигаться
d2Z
к своему положению равновесия с ускорением где Z—
прогиб крыла. При этом на каждую точку /И,- крыла, в которой
сосредоточена масса пц, будет действовать сила инерции, рав-
/)2^
ная — Равнодействующая всех сил инерции рассматри-
ваемого элементарного отсека крыла будет:
п V d2z . ...
pt= (О
где суммирование идет по всем точкам отсека.
Здесь т — погонная масса крыла в рассматриваемом сечении
и, следовательно, mdy—общая масса отсека.
Но силы инерции, вызванные изгибным движением, дадут
не только силу, направленную параллельно оси oz, но также
и момент относительно оси жесткости, который, очевидно,,
равен:
где л,-—абсцисса точки 7И,-. Знак „минус" перед суммой взят
потому, что моменты считаются положительными при вращении
от положительной оси z к положительной оси х, в то время
как сила —вращает в обратную сторону (фиг. 23). Из
статики известно выражение координаты центра тяжести си-
стемы точек с массами т^.
где а—'Координата центра тяжести. При помощи этого выра-
жения легко преобразуется выражение момента сил инерции,
взятого относительно оси жесткости:
d2z V d*z (О\
Но, поскольку момент относительно оси жесткости отличен
от нуля, неизбежно возникнет кручение крыла. Таким образом
имеем следующую схему возникновения крутильных колебаний
при первоначальном чисто изгибающем импульсе: так как из-
гибное колебательное движение происходит с определенным
Ускорением, в каждой точке крыла возникнут силы инерции;
10&
эти силы дадут около оси жесткости некоторый момент, кото-
рый и вызовет скручивание крыла — возникнут крутильные ко-
лебания. Легко видеть, что если центр тяжести крыла совпа-
дает с его осью жесткости (з = 0), то момент от сил инерции
также обращается в нуль и, следовательно, у крыла с совме-
щенными осями жесткости и центров тяжести возможны чисто
изгибные колебания. У крыла с несовмещенными осями чисто
г изгибные колебания невозмож-
ны,— они обязательно перейдут
в совместные.
Точно так же, если линия цент-
£ ров тяжести и ось жесткости крыла
не совпадают, невозможны и чисто
крутильные колебания крыла: они
также неизбежно перейдут в сов-
местные. В самом деле, предполо-
с-----------------1 жим, что мы закрутили крыло на не-
фНГ 24. который угол и предоставили его са-
мому себе. При этом возникнут кру-
- Э26
тильчые колебания, происходящие с угловым ускорением-^ , где
попрежнему 0 — угол закручивания крыла. Тогда каждая точка
/и,- крыла будет испытывать линейное ускорение —[где
si — расстояние от точки /И,- до оси жесткости Е (фиг. 24)] и,
следовательно, на эту точку будет действовать сила инерции
Момент этих сил относительно оси жесткости получим,
если умножим каждую силу на соответствующее плечо (з,) и
затем произведем суммирование по всем точкам отсека:
/ц2 = — V ,„.4 = — Imdy -g-, (3)
где 1т — погонный массовый момент инерции крыла относительно
оси жесткости в рассматриваемом сечении.
Но силы инерции, действующие на различные точки рас-
сматриваемого отсека крыла, имеют также равнодействующую,
слагающая которой по оси z отлична от нуля. Эта слагающая
и вызовет изгиб крыла в направлении оси z и, таким образом,
вызовет изгибные колебания крыла. Легко подсчитать величину
этой силы. Слагающая по оси z силы инерции mpi , дей-
б20
ствующей в точке, Л4,-есть/пгХ;-д^-. Суммируя эти силы по всем
точкам крыла, находим равнодействующую по оси z всех сил
инерции от крутильных колебаний:
п V <*2о , д2з
р3= (4)
100
Если з=0 (ось жесткости совпадает с центром тяжести),
то Р„ — 0 и, следовательно, в этом случае равнодействующая
по оси z сил инерции, возникших от кручения, равна нулю и
изгибные колебания крыла не возникнут.
Отметим, что все силы и моменты: Р2, Л4,, ТИ2, являются
периодическими, так как при колебательном движении ускоре-
ние является периодическим.
Таким образом ясно, что вследствие несовпадения центра
тяжести и жесткости сечений крыла изгибные и крутильные
колебания связаны между собой, и один вид колебаний неиз-
бежно вызывает другой.
Для получения уравнений движения, как и выше, будем
исходить из обычных уравнений упругой линии:
для изгиба
и для кручения
(5)
Здесь s — погонная нагрузка и у. — погонный крутящий момент1.
При вибрациях крыло нагружено силами инерции и под s
следует понимать сумму погонных сил инерции, а поду — сумму
их моментов относительно оси жесткости. Выше [формулы (1),
(2), (3) и (4)] мы нашли выражения сил инерции, действующих
на отсек крыла шириной dy, и их моментов. Чтобы получить
погонные значения сил и моментов, т. е. величины сил и момен-
тов, приходящихся на единицу длины крыла, делим соответству-
ющие выражения на ширину отсека dy. Таким образом находим,
что при совместных колебаниях на крыло действуют следующие
погонные инерционные силы и моменты (погонные значения
будем обозначать той же буквой, как и значения для элементар-
ного отсека, но с чертой сверху):
1 Вторая формула получается следующим образом. Из сопротивления
материалов известно, что крутящий момент в любом сечении крыла будет:
МКР — GIP ду
Но крутящий момент внешних сил Мкр в любом сечении крыла у созда-
ется действием сил, находящихся на всей части крыла от сечения у до
конца I. Если у — погонный крутящий момент, то Л4кр = J* ydy и, следова-
у
тельно,
Gr^==f'idy'-
у
Диференцируя это выражение по у, приходим ко второй формуле (5).
107
сила инерции, возникающая вследствие изгибных
колебаний крыла
сила инерции, возникающая вследствие колебаний
кручения крыла
(6)
момент сил инерции
момент сил инерции
от изгибных колебаний
от крутильных колебаний
УЙ2 = — Im
т дт2
Следовательно, при вибрациях в пустоте имеем:
s = P14-P2 = —4-ws-^;
-ЯГ , ЭПГ d-Z , д29
р. = Л1г +/И2 =/Из-~2
m й,2 •
(6а)
Подставляя эти значения в уравнения (5), получаем систему
уравнений движения при совместных колебаниях крыла в пу-
стоте :
д? + т
7у(О/р^-~т-
д-z <xi п
тт — № тт = °;
От2 о.
. d2Z / Э29 _ п
dt2 "* ‘т дх* U‘
(7)
Заметим, что уравнения (5) справедливы также и для крыла,
колеблющегося в потоке воздуха. В последнем случае только
следует учесть, что в s и р. входят, кроме инерционных [фор-
мулы (6)], такдсе и аэродинамические силы и момент. Ниже мы
|ПОлучим эти уравнения.
Система уравнений движения (7) в случае о = 0 (совпадение
Оси центров тяжести и оси жесткости) распадается на два не-
зависимых уравнения, которые были изучены в предыдущих
главах: уравнение чисто изгибных и уравнение чисто крутиль-
ных колебаний.
। Как и выше, граничные условия для Z и 6 будут: при у = О
в месте заделки крыла) сечение защемлено, следовательно, про-
1иб и угол кручения равны нулю (Z = 0, 0 = 0), и упругая ли-
'ия не может иметь излома (^==о)‘> ПРИ У = (на конце
рыла) изгибающий и крутящий моменты ^Е/-^ и (Лр-~^ и
Г д ( d2Z\\ ,
перерезывающая сила | д- \Е1| должны быть равны нулю.
Таким образом получаем следующую систему граничных условий:
при у = О
Z = 0, ~ = 0, 0 = 0;
при у = I
E/^=Q, -^-(еГ^) = О, GIp~ = 0.
ду2 ’ оу \ ду2 J ’ Р ду
Уравнения (7) вместе с граничными условиями (8) служат
для определения прогиба Z и угла кручения 6 при совместных
колебаниях крыла в пустоте. Проинтегрировав эту систему,
можно определить все характеристики колебательного движения,
в том числе и частоту. Однако для определения частоты коле-
баний чаще употребляется другой, приводимый ниже способ,
не требующий интегрирования системы уравнений движения.
2. ПРИБЛИЖЕННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТ СОВМЕСТНЫХ
КОЛЕБАНИЙ КРЫЛА В ПУСТОТЕ
Для приближенного определения частот совместных колеба-
можно применить метод Галеркина или Ритца или любой
ний
другой из приближенных
методов, изложенных в
гл. И.
Как было показано, ме-
тод Галеркина приводит
к тем же результатам, как
и принцип возможных пе-
ремещений, математическим
выражением которого яв-
ляются "уравнения Лагранжа
Фиг. 25.
(см. гл. I). Из этих уравнений
мы и будем исходить при определении частоты. .
Для составления уравнений Лагранжа необходимо опреде-
лить кинетическую и потенциальную энергию вибрирующего
крыла.
Вырежем элемент крыла 7W7V (фиг. 25), находящийся между
двумя близкими сечениями, расположенными на расстоянии dy
Друг от друга, и рассмотрим движение этого элемента. Пусть
{фиг. 26) MN — положение рассматриваемого элемента крыла
в состоянии равновесия. Выберем начало координат Е в центре
жесткости рассматриваемого сечения, ось z направим по на-
правлению изгибных колебаний крыла и ось х — перпендику-
лярно к ней. В некоторый момент времени во время колебаний
профиль MN займет положение M'N'. Как всегда, обозначаем
через Z прогиб оси жесткости крыла и через 6 — угол, на ко-
торые! закрутился рассматриваемый элемент (фиг. 26). Некоторая
точка профиля MN займет положение Д;, причем, так как
109
деформации сечений не происходит, расстояние а, от точки Az
до оси жесткости остается неизменным. Обозначим через
угол между отрезком А,С в положении равновесия и осью.х.
Предполагая кривизну профиля малой, можем считать малым.
Напомним, что деформации Z и 0 также считаются малыми1.
Обозначим через zf координаты точки А/ в рассматриваемый
момент времени. Тогда по обычной формуле теоретической ме-
ханики кинетическая энергия рассматриваемого элементарного
отсека крыла будет:
Эта сумма распространяется на все точки рассматриваемого от-
сека; здесь /дг — масса, сосредоточенная в каждой точке. Легко
составить выражения координат любой точки А,- (фиг. 26):
cos (ъ + 0); (10)
z, ~ Z — <3j sin (т,- + 0).
Диференцируя эти выражения по времени и подставляя ре-
зультат в формулу (9), находим: j
dT — 4- У mtZ2 + 4 V mpt 62 — V nipi cos (у, + 0) Z‘). (11)
Очевидно,
V т1 = т dy и V = Im dy.
Последний член выражения (11) также легко упрощается,
так как Е mpi cos (у,- + 0) = Е mixi [согласно уравнению (10)], а по
обычной формуле статики Е mixi = лц. т Е mit где лц.т — абсцисса
1 Малость углов означает, что можно принять сннус соответствующего
угла равным самому углу, а косинус равным единице. У всех практически,
встречающихся профилей значение у, этому условию удовлетворяет.
ПО
центра тяжести рассматриваемого элемента. Так как углы -у,
и 6 малы и начало координат находится в центре жесткости,
то можно принять, что Лц.т = ° равно расстоянию от центра
тяжести до осн жесткости крыла; тогда окончательно имеем:
v/И;Л. — a/n rfy. Подставляя в выражение (11) значения сумм,
получим:
dT = у Z2//z dy + 4 62/m dy — ZVms dy.
Чтобы получить полную кинетическую энергию всего крыла,
необходимо просуммировать кинетическую энергию отдельных
отсеков. Будем иметь:
i i i
T -^~fz2mdy + ^f $Чт dy — fzЬтзdy. (12)
О 0 0
При одновременном действии изгиба и кручения потенциаль-
ная энергия слагается из потенциальной энергии изгиба и по-
тенциальной энергии кручения. Поэтому выражение потенциаль-
ной энергии при совместных колебаниях будет:
о и
Первый член дает потенциальную энергию изогнутого, а второй —
закрученного стержня1.
Отметим, что найденные нами выражения потенциальной и
кинетической энергии, как ясно из самого способа их получе-
ния, не зависят от того, колеблется ли крыло в пустоте или
в потоке воздуха. Они остаются справедливыми и в последнем
случае, и мы ими будем пользоваться также в дальнейшем при
изучении колебаний крыла в потоке воздуха.
Будем искать значения прогиба Z(y, т) и угла кручения
6(j, т) в виде рядов:
Z(y, + ••• +?„(')• fM + •••;
e(j, -)=-чСО• ?i(j) + gCO• чМ + •+ rn(~) <tM + • • •
Эти ряды дают разложение колебательного движения по стоя-
чим колебаниям.
Для приближенного определения частоты и формы колебания
ограничиваемся в этих рядах первыми п членами и ищем зна-
чения Z и 6 в виде:
z (У, *) = (j) + Я 2 (")Л (У) + • • • + qn (~)fn (у); | . _
Г (*л)
°СУ, t) = ri(")?i(j) +G(")(f,2(y) + +г„(т)ср„(у). 1
1 Тимошенко, Курс сопротивления материалов.
Hi
Будем считать функции fk(y) и <₽ft(y) известными. При кон-
кретных расчетах их заранее задают из тех или иных рацио-
нальных соображений, о которых мы скажем ниже. Заметим
только, что для удовлетворения граничных условий (8) функции
Jk(y) н ?*(у) выбираются так, чтобы было:
при у — О
А=0; > = °; f« = 0’]
при у — I I (15)
d~tk _ n. __ n. dyk (
dy2 2 dy3 ’ dy I
K=l, 2,. . .n. I
Тогда, если будут известны функции времени qk(r) и rfc(t),
движение будет полностью определено. Эти функции примем за
обобщенные координаты вибрирующей системы и составим по
этим координатам уравнения Лагранжа [уравнения (20) гл. I].
Подставив значения(14) в выражения (12) и (13), найдем:
2 In 2
Q*fk1 т dy + f ( rk<fk ) Zm dy -
' ° k^l
In n
-f )(Zwk)"”dy;
0 'Si 1 'Si '
In 2 t n 2
b 'k=i 'o' '
Далее составляем уравнения Лагранжа:
d ( dT\ _ дТ . dU = 0.
d- k dqj J dqj + dqj ~ 2
d f dT\ _ df . dU = 0. >
d~ k di-j J drj drj
у = 1, 2,... л.
После подстановки в эти уравнения значений Т и U из
жений (16) будем иметь:
= 0;
1 1 1
— 'Як f ^fkfj dy + rk J l/n^j dy 4- rjc/p dy = 0;
о о о J
i = 1. 2. . . . n.
(16)
(17)
выра-
" Г ( 1 1
£ I /mfbfjdy- rk fm^kf.dy+ qk jEl^-^2 dy
.-1 «- и о О '
(18)
Так как функции fk и известны (ими при расчете задаются),
то все входящие в эти уравнения интегралы можно вычислить.
Уравнения (18) представляют собой систему линейных дифе-
112
ренциальных уравнений второго порядка с постоянными коэфп-
циентами относительно неизвестных функций qk(y) и гк(т). Как
известно, такая система уравнений интегрируется подстановкой
qk(^=AkelP--,
rk^)^Bke‘^ ;
fc=l, 2, ... Л.
(19)
Подставляя эти значения в уравнения (18), придем к системе
линейных однородных алгебраических уравнений относительно
подлежащих определению постоянных Ак и Вк:
г 1 '
л, -У /'»лл^+ /е/ ^dy +
L о о > J
Приравнивая нулю определитель этой системы, получим ха-
рактеристическое уравнение, из которого определяется р. Это
уравнение будет порядка 2п относительно р2. Каждое значение
р3 соответствует определенному тону совместных колебаний. Для
каждого значения р2, т„ е. для каждого тона колебания, из урав-
нений (20) могут быть определены свои значения постоянных Ак
и Bk, а затем по формулам (19) и (14) — значения прогиба Ди угла
кручения 6. Например, пусть р — ps —корень характеристического
уравнения. Тогда из уравнений (20) найдем соответствующие
этому корню значения постоянных
ДМ, ДО,..., ДМ;
ДО ВМ, ...,ДМ;
и согласно уравнениям (19)
гДт)=ВМ^-
А—1, 2..л.
Подставляя эти значения в уравнения (14), находим соответ-
ствующие значения Z и б:
z(y, у) = zs о-, т) = [дм/ду)+д<*>/3оо + • • + ;
6 (у, *) = 9, О', О = [во? 1 О') + <р> (у) + • • • + W к 0)1
Гроссман—15—8 113
Таким образом корню p — ps характеристического уравнения
соответствует стоячее колебание с частотой ps и формой:
fs(y)=A^f1(y) + A^f2(y} + •
?л (У) = В'ръ. (у) + (у)+ ... +BW (у),
т. е.
Zs{y,
Mb T) = M>)(’"V;
Заметим, что прогиб и угол кручения получены нами в комп-
лексной форме. Но так как из характеристического уравнения
определяется р2, то наряду с корнем р = р6 существует корень
р = — ps. Легко доказать, что если значению р = ps соответ-
ствуют значения Z = ZS и 0 = 6S., то значению р = — ps будут
соответствовать комплексные значения Z = Zs, 6 — 65, где Zs, 0s—
комплексные величины, сопряженные соответственно значениям
Zs и 6S. Поэтому, когда будем составлять общий интеграл как
сумму частных:
Z=£(Z,-|-Z,);
то комплексность исчезнет и окончательные значения Z и 0 бу-
дут действительными величинами.
Изложенный метод определения частоты и формы колебания
исходит из уравнений Лагранжа, т. е. в конечном итоге бази-
руется на принципе возможных перемещений. Ранее мы уже
указывали, что метод Галеркина приводит к тем же результатам,
что и принцип возможных перемещений, и все расчетные фор-
мулы можно получить методом Галеркина непосредственно из
системы уравнений движения (7), что позволяет избежать со-
ставления выражений кинетической и потенциальной энергии
системы. Для этого поступаем следующим образом. Подставим
в уравнения (7) значения Z и 0 из уравнений (14). Затем первое
из уравнений (7) умножим поочередно на • • • >/„, а второе —
на <р2, и результат проинтегрируем по длине крыла (по
переменному у в пределах от нуля до /). Получим следующую
систему уравнений:
114
Эта система отличается от системы (18) только последними
членами. Но если Д и <pfe удовлетворяют граничным условиям,
то интегрированием по частям легко доказывается, что
о о
- ( d (Glp <₽. dy = / GZdy.
J av 1 р dy j -У J р dy dy -у
о о
Тем самым доказывается, что система уравнений (21) тожде-
ственна системе уравнений (18) и, следовательно, методом Галер-
кина мы приходим к тем же результатам, которые дают и урав-
нения Лагранжа.
Способ составления уравнений (21) по Галеркипу позволяет
непосредственно видеть, что уравнения (21) представляют собой
не что иное, как условия равенства нулю работы на пути воз-
можных перемещений. В самом деле, заметим, что вместо умно-
жения на Д и <fk мы могли бы умножать уравнения (7) на
и гкук. От этого результат не изменился бы, так как
шрвое из уравнений (21) приобретает общего множителя qk,
а второе гк и этих общих множителей в дальнейшем можно
сократить. Но прогиб Z в силу уравнений (14) представляет
собой сумму элементарных прогибов qkfk, а угол круче-
ния 6 — сумму элементарных углов закручивания гкук. Напом-
ним, что первое из уравнений (7) есть условие равенства
нулю сил, действующих на элементарный отсек крыла, а вто-
рое — условие равенства нулю их моментов относительно оси
жесткости. Умножая первое уравнение на элементарный прогиб
qkfk, мы в левой части получаем работу сил при прогибе рас-
сматриваемого элементарного отсека на величину qkfk и, инте-
грируя результат по длине крыла, получаем работу всех сил
на крыле при перемещении qkfk. Точно так же умножение вто-
рого уравнения (7) на элементарный угол закручивания r^k и
последующее интегрирование результата по длине крыла дает
выражение работы момента сил при закручивании крыла на
угол rkyk.
Система (21), следовательно, выражает, что работа сил и
моментов при изгибе крыла по каждому из элементарных про-
гибов и закручивании на каждый из элементарных углов равна
нулю. Таким образом непосредственно ясно, что уравнения (21)
выражают принцип возможных перемещений.
При конкретных расчетах обычно за Д(у), Д(_У), • •
принимают соответственно функции формы первого, второго и
т- Д. тона чисто изгибных колебаний того же крыла в пустоте;
За 'Ft (.У), ФгСи), •••>'Fn(j) принимают соответственно функции
формы первого, второго и т. д. тона чисто крутильных колебаний
того же крыла в пустоте. Тогда перед расчетом совместных
115
колебаний требуется определить собственные функции чисто
изгибных и чисто крутильных колебаний, что делается методом
последовательных приближений, изложенным в гл. II и HI. Не-
сколько меньшая точность обычно получается, если за f(y) и
и у (у) принять функции чисто изгибных и чисто крутильных
колебаний крыла постоянного сечения [формулы (17), гл. II, и
(25), гл. III].
Практически для определения частоты ограничиваются первым
приближением, когда в выражениях (14) сохраняются только
первые члены:
Z(y, т) = ?(')/(»; 1 /22)
Цу, = r(')'f(J')- I
Напишем полностью расчетные формулы для этого случая. Под-
ставляя значения (22) в выражения (12) и (13), найдем:
где
г = 4 + у + c^qr'
U = ^auq2 + ~aarz,
I
Сц = J mfdy,
О
I
о
(24)
I
*22 = fCn^y;
0
0
I
и
Составляем уравнения Лагранжа по обобщенным координа-
там q и г [см. уравнения (17)]:
cnq + *«/+ anq = 0;
с.л<7 4- с21г + а„г = 0.
(25)
Интегрируем эту систему уравнений подстановкой
q = А е‘Р'-, г = В е’р\ (26)
Иб
Тогда для определения А и В получаем систему уравнений:
А (ап — Ап) + в Р2сг.) = 0; |
Л (— р2с21) + В (а21 — р2с22) = 0. I
(27)
Так как это система однородная, то она имеет решения,
отличные от нуля, только тогда, когда определитель системы
равен нулю. Приравнивая определитель системы нулю, получаем
характеристическое уравнение для определения частоты коле-
баний р-.
Д = («11 — All) («22 — Р2«2г) - А12«21 = 0 (28)
или
где
Л^—Cji2 4-^ = 0,
— «11^22 «12«21 *
= ^11^22 4" «22«11>
Ел —
(29)
(30)
Таким образом приближенно частоту совместных колебаний
определяют следующим образом. Прежде всего рассчитывают
чисто изгибные и чисто крутильные колебания рассматривае-
мого крыла и определяют их форму (см. гл. II и III). Найденные
таким образом функции формы первого тона f(y) (для изгибных)
и Ч'(у) (Для крутильных) колебаний считаются мало отличающи-
мися от функций формы совместных колебаний и принимаются
за основу при определении частоты1. Затем определяют коэфи-
циенты (24) и из уравнения (29) — частоту.
Уравнение (29) дает два значения для р2, т. е. два значения
частоты совместных колебаний. Прежде всего покажем, что
одно из этих значений всегда меньше частоты чисто изгибных
колебаний, а другое больше частоты чисто крутильных колеба-
ний. В обозначениях (24) значения частот чисто изгибных и
чисто крутильных колебаний, согласно формулам (58) гл. II и
(13) гл. III, запишутся в следующем виде:
раз =
Ркр =
(31)
гДе риз — круговая частота чисто изгибных и ркр — круговая
частота чисто крутильных колебаний. Для всех современных
крыльев частота чисто изгибных колебаний значительно меньше
’Заметим, что так как f(y) и tp(y) определены с точностью до постоянного
множителя, мы здесь, как и в гл. II и 111, выбираем его так, что для первого
тона/(у) > 0 и <р у) > 0.
117
частоты чисто крутильных колебаний. Мы хотим показать, что
если Pi — меньший и р2— больший корни уравнения (29), то
Pi <Риз <ркр < Рг • (32)
Для доказательства прежде всего важно заметить, что всегда
А1 = с11с22— с12с21> 0. Этот факт мы также используем ниже, при
составлении условий устойчивости для крыла, колеблющегося
в потоке воздуха. Кинетическая энергия всегда является вели-
чиной положительной [что ясно хотя бы из формулы (9)].
Поэтому, воспользовавшись выражением (23), можно написать:
Г = -’/2к11?4-2с12=-фс22]>0,
где через ; обозначена величина -Я-. На основании сказанного
величина, стоящая в квадратных скобках, должна быть поло-
жительна при любых значениях 5. Непосредственно видно, что
при 5 = 0 это условие соблюдается. При изменении 5 от нуля
величина Т изменит свой знак при значении $, равном корню
трехчлена г1Х;2 -ф 2с12; -ф с.,.,, т. е. если
, C12 i С12 С11С12
5 =--------------------. (33)
Си
Чтобы Т сохраняло знак при любых значениях 5, необходимо
и достаточно, чтобы оба корня трехчлена сцВ2 4- 2с135 -ф с22 были
комплексными. Тогда ни при каком действительном значении i
Т не может изменить знака, а так как 7 >0 при 5 = 0, то Т
останется положительным и при всех других значениях 5. Со-
гласно уравнению (33), корни трехчлена комплексны, если
сп czt <
или, так как
С12 = С21 1
то
= Сц^22 ^12^21 > 0. (34)
Следовательно, неравенство А1 > 0 выражает тот факт, что
кинетическая энергия колеблющегося крыла всегда положительна.
Переходим к доказательству положения (32). Для этого заме-
тим, как изменяется величина Д согласно уравнению (28) при
изменении р от нуля до -ф оо. Непосредственно видно, что Л > 0
при р = 0. Будем увеличивать р\ при этом, очевидно, Л будет
изменяться непрерывно как функция р. Когда р достигнет
величины р2 — Р23 =-—-, величина А будет:
А = —/74с12с21 < 0.
Так как Д есть непрерывная функция р и Л>0 при р =0, Д<0
при р = ркз, то, следовательно, Д должно по крайней мере один
118
раз обратиться в нуль при р, лежащем между нулем и риз - Та-
ким образом доказано, что один из корней (pj уравнения (28;
(или, что то же, уравнения (29)] лежит между р = 0 и р = риз :
б Р1 Риз •
Точно так же легко видеть, что А <0 при р2 = р2р = -— и
А>0 при р = + со [в силу неравенства (34)]. Следовательно, А
обращается также в нуль между р = ркр и р = 4--^и второй
корень (р2) уравнения <28) больше ркр : ркр < рг .
Таким образом положе-
ние (32) доказано. На фиг.
27 показано изменение А в
зависимости от р2 в соответ-
ствии с теми результатами,
которые мы только что по-
лучили.
Рассмотрим
движения при
р = р2- Для этого из
нений
шение
характер
Р = Pi и
урав-
отно-
(27; определим
А
В :
Я11 Р С11
А = _^-P2Gg (b) |
Zf р-с21 )
Если р определено как корень уравнения (28), то обе формулы
дают одно и то же значение для \ Согласно выражениям (22)
(26) приближенное значение прогиба и угла закручивания
исследуемом случае будет:
Z = Af (у) е',р~- ;
6 = Въ(у)е*-.
А _
В ~
(35)
и
в
(36)
Если p = Pi, то в силу выражений (31) и (32) ап—р2си>0,
и тогда по уравнению (35а) ^-<0[так как с12<0; см. обозна-
чения (24)]. Согласно выражениям (36), это означает, что положи-
тельному прогибу соответствует отрицательный угол кручения
и отрицательному прогибу—'положительный угол кручения. Если
Р = р2, то о22—р2с22<0 и, согласно уравнению (35в), > 0 .
Значит, в этом случае положительному прогибу соответствует
1 Разделив уравнение (23) на величину (ап — р2си) с21р2 и перенеся второй
член в правую часть, получаем:
^22”” Р Too _
СцРг alt— Р2Сц ’
что и доказывает тождественность обеих формул (35).
с,,р2
119
также положительный угол закручивания и отрицательному
прогибу — отрицательный угол закручивания. Следовательно,
колебания в обоих случаях происходят так, как показано на
фиг. 28, а и Ь. (Положение колеблющегося крыла построено
через »/8 периода).
Отметим, что отношение = ие зависит от времени.
Это значит, что нулевые и максимальные положения для Z
и И достигаются в одно и то же время, т. е. нет сдвига фаз
между изгибными и крутильными колебаниями.
Нужно подчеркнуть, что мы рассматриваем только частное
решение основных уравнений, т. е. стоячее колебание. Общее
решение, являющееся суммой стоячих колебаний с различными
частотами, может не обладать отмеченными выше свойствами,
которыми обладает каждое из стоячих колебаний в отдельности.
В действительности у крыла оси центров тяжести и центров
жесткости не совмещены, и потому все колебания, которые
наблюдаются в действительности, являются совместными. Однако
и к этим колебаниям условно применяются термины „изгибные
колебания" и „крутильные колебания", причем под изгибными
колебаниями понимаются совместные колебания, происходящие
с меньшей (pj, а под крутильными — с большей (р2) частотой.
Это объясняется тем, что произведение с12с21 всегда бывает
мало по сравнению с величиной а потому коэфициеит
уравнения (29) мало отличается от величины спс2г. Если бы
Ац — снс22> то уравнение ,(29) имело бы корни р2 — — и р; =
= —> т. е. в силу равенств (31) pj — р2з и р2 = р;р. Но так
120
как Аг, хотя и мало, но отличается от cuf22, то корни уравне-
ния (29) мало отличаются от рнз и рКр . Поэтому частоты сов-
местных колебаний мало отличаются: меньшая—от частоты
изгибных колебаний и большая — от частоты крутильных коле-
баний (ниже будут приведены числовые примеры). Соответст-
венно и формы колебаний мало разнятся: при частоте р^— от
формы чисто изгибных колебаний и при частоте р2— от формы
чисто крутильных колебаний. Это значит, что при частоте р = рх
амплитуда изгибных колебаний велика, а при частоте р = р?
мала по сравнению с амплитудой крутильных колебаний.
Особенно это ясно при экспериментальных исследованиях
вибрирующего крыла: при частоте р = рг на-глаз невозможно
заметить кручения, даже при весьма значительной амплитуде
изгибных колебаний. При частоте р = р2 почти незаметно изгиба
и в то же время крутильные колебания происходят весьма
интенсивно. Но все же следует всегда помнить, что термины
„изгибные" и „крутильные" колебания являются условными,—
в действительности колебания всегда совместные. В дальнейшем
колебания с частотой pY мы будем называть совместными изгиб-
ными колебаниями, а колебания с частотой р2— совместными
крутильными колебаниями. Следовательно, совместные изгибные
колебания—это совместные колебания первого тона с преоблада-
нием амплитуды изгибных колебаний, а совместные крутильные
колебания — это совместные колебания второго тона с преобла-
данием амплитуды крутильных колебаний.
Пример. Вычислить частоты совместных колебаний крыла,,
расчетные данные которого приведены в табл. 9.
В гл. II, п. 4 для данного крыла был произведен расчет кру-
тильных колебаний (табл. 1 и 2), а в гл. III, п. 3 — расчет чисто
изгибных колебаний (табл. 6 и 7). Значения функций соответ-
ствующих форм колебания приведены в табл. 9. В этой же таб-
лице произведено вычисление коэфициента с12 = с21. Коэфициенты
ои и с,! вычислены в табл. 7, а коэфициенты а22 и с22— в табл. 2-
В результате имеем:
ou = 504; си = 0,25.2;
а,2 = 0,357 • 107 ; с,2 = 13,08 • 102 ;
' ^'21 = 7,91.
Вычисляем коэфициенты по формулам (30):
Л. — сис22— CioCoi = 0,267 • 103 ;
Ci = спд22 + С22°п — 0,1558 • 107;
= аиа22 = 0,1798 • 1010.
Определяем по уравнению (29) частоту:
С1=:/С®-4А1Л1
Р- - 2А- .
«Я
9
Таблица 9
У 1 Конструктивные параметры крыла (вкг-см сек) Функции формы колебания (см. табл. 1 и 6) Вычисление с12
Е1 GIJ> т а / mif<f
0 82-Ю9 99.2-108 0,1687 -КГ2 0.32-102 80 0 0 0
0.1 76,8-109 98,5-Ю8 0.1687-10—2 0,32-102 80 0,01912 0.0785 0,02025-10~2
0.2 64.9-109 90,5-108 0,1265-10-2 0.227-Ю2 80 0,0752 0,1541 0.1175- IO-2
0,3 49.4-10° 69 -108 0.0928-10~2 0157-I02 80 0,1673 0,234 0,2915-10-2
0,4 34.9-109 41,4-Ю8 0.0770-10-2 0.1234-102 72,8 0.296 0,3 0 555-10-j
0.5 20.4-109 30.7-108 0 0684-Ю-2 0,097-102 64,9 0,465 0 452 0.931 Ю-2
Об 12,4-109 21,5-Ю8 0 0632-10-2 0.0817-Ю2 56,9 0,680 0.511 1,396-10“2
0,7 6 61-Ю9 11.82-Ю8 0,0510-10-2 0,053-102 48,9 0.942 0.69 1,621-10“2
0,8 3,05-109 5.12-108 0,0347-10—2 0,0265- Ю2 40,9 1,258 0.816 1,46-10-2
0,9 1,16-Ю9 2.165-108 0.0250-10“2 0,0123-102 32.8 1.618 0,938 1.244-10“2
1,0 0,31-109 0.591-108 0,0190-10—2 0,00816-102 24 8 2,000 1,0 0,964-10-2
1=975 1 2=0,08118
с12 = с21 = —J ffla/w </у=2-97,5=—7,91.
О
Подставляя числовые значения, находим:
А = 39,2;
А = 65,1.
Число совместных изгибных колебаний в секунду равно:
= -g- = 6,25.
Число совместных крутильных колебаний в секунду равно:
л, = g- = Ю,4.
Для сравнения приведем частоты чисто изгибных и чисто кру-
тильных колебаний (см. гл. II и III):
Риз = /^ = 44,7; ркр = = 52,3,
с-ц г ^22
откуда число чисто изгибных и чисто крутильных колебаний в
«секунду будет:
«из = 2”3 = 7,1; Пкр = = 8,33.
422
з ПРИБЛИЖЕННЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТ СОВМЕСТНЫХ
КОЛЕБАНИЙ В СЛУЧАЕ НАЛИЧИЯ НА КРЫЛЕ СОСРЕДОТОЧЕННЫХ
МАСС
Если на крыле имеются сосредоточенные грузы, то метод
определения частот совместных колебаний, изложенный в пре-
дыдущем параграфе, по существу остается без изменения; только
к кинетической энергии крыла необходимо добавить кинетичес-
кую энергию сосредоточенного груза. Определим эту энергию.
Рассмотрим точ-
ку Kj сосредоточен-
ного груза, в кото-
~'рой находится мас-
са иг,- (фиг. 29). Пусть
Д — расстояние от
точки Kj до оси же-
сткости крыла и Д—
угол, образованный
осью х и отрезком,
соединяющим центр
жесткости сечения
y= h, в котором на-
ходится сосредото-
ченный груз, с точ-
кой К^
В некоторый мо-
мент времени точка
К, займет положе-
ние К'г В этот мо-
мент координаты этой точки будут:
xi — cos (?< + ®>=л); Zj = — Д sin (3; -f- 6у=й),
где Zv=h и 6,,=л — значения прогиба и угла кручения в сечении
y=h. Кинетическая энергия сосредоточенного груза будет:
'Л. г = — У т, (х/ + 2*) = V т^у л-Ь mfii —
—У/пД. cos(3 -l-0)Zy^h‘0y-h= 1Ьу л—M'jZy^h by=h,
где М — масса сосредоточенного груза, /—его момент инерции
относительно оси жесткости крыла и о — абсцисса его центра
тяжести. Добавляя кинетическую энергию сосредоточенного
груза к кинетической энергии крыла [выражение (12)], находим
кинетическую энергию всей вибрирующей системы:
I i
Т = -2 fznZ2rfy+ 2 MZ2y~h+ 4f I^-dy-Y
O 0
I
( + 2 j tnzZbdy — Mtiy^hZy h. (37)
123
Можно повторить вывод всех расчетных формул предыдущей
главы, пользуясь этим выражением кинетической энергии. Так
как это не представляет труда, то мы для сокращения места
сделаем выводы только для того случая, когда расчет ограни-
чивается первым приближением, т. е. Z и 0 берутся в виде ра-
венств (22). Подставляя эти значения в выражение (37), найдем,
что Т можно опять записать в виде уравнения (23), но только
значения сц, с22 и с12 будут другие. Вместо формул (24) для этих
коэфициентов будем иметь:
cu = jmf-dy + Mf-(hy,
О
I
<22 = f te^y+W);
и
(38)
i
<1з = <2i =~ dy - W(/z) f (Л)-
О
Частота определяется опять из уравнения (29). Для данного
случая функции f(y) и о (у) определяются с учетом сосредото-
ченной массы (гл. П, п. 6, и гл. III, п. 4).
4. ПРИМЕНЕНИЕ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
К РАСЧЕТУ СОВМЕСТНЫХ КОЛЕБАНИЙ
Полученные выше формулы для определения частот совмест-
ных колебаний вполне точны, если функции /(у) и <?(у), при
помощи которых выражаются коэфициенты сп, с22, с12; пп, а22,
будут интегралами диференциальных уравнений движения. Для
определения их может быть применен метод последовательных
приближений. На основании выражений (22) и (26) частное ре-
шение можем искать в виде:
Z = Af(y)eipT;
в = B<?fy)eip\
Подставляя эти выражения в диференциальные уравнения
движения (7), получим систему уравнений для определения
функций формы /(у) и <р(у):
$ (£/?) ]’ I
j <39)
При отсутствии сосредоточенных масс эти уравнения вместе
с граничными условиями (15) полностью определяют функции /(у)
и <f(y). Если на крыле имеются сосредоточенные массы, то при
определении f и 7 должны быть еще приняты во внимание усло-
вия сопряжения.
124
Процесс определения f и ср протекает следующим образом:
задаемся какими-либо значениями / = /о(у) и-р = %(у) (например,
за /0 можно принять функцию чисто изгибных колебаний для
крыла постоянного сечения, а за <р0 — функцию крутильных ко-
лебаний крыла постоянного сечения). Для выбранных значений
функций определяем частоту р из уравнения (29) и отношение
j в из формул /35) [для крыла без сосредоточенных масс cik опре-
деляются по формулам (241, для крыла с сосредоточенными мас-
сами— по формулам 38)]. Функции / = /0(у), ? —To(J') и соот-
ветствующие им значения р и ~ подставляем в правые части
уравнений (39), которые после этого становятся известными
функциями у и могут быть вычислены. Интегрируя после этого
первое из уравнений (39) четыре, а второе — два раза по у,
находим новые значения f и <р. При выполнении этого интегри-
рования должны быть приняты во внимание граничные условия,
а для крыла с сосредоточенными массами—также условия со-
пряжения.
Для найденных таким образом функций /(_у) и <p(jy) вновь
определяем частоту р и отношение -у. Затем опять вычис-
ляем правые части уравнений (39) и после интегрирования новые
значения f и '-р. Таким образом процесс продолжаем до тех пор,
пока функции, определенные в двух следующих друг за другом
приближениях, практически не совпадут. Для удобства сравне-
ния между собой функций, получающихся в различных прибли-
жениях, нормируем их: функции f и <р умножаем на одинаково-
го постоянного множителя1, который подбираем так, чтобы на
конце крыла <p(Z)= 1.
В случае чисто изгибных и чисто крутильных колебаний
метод последовательных приближений всегда сходится. Но
в случае совместных колебаний вышеописанный метод сходится
не всегда, и возможны такие конструкции, для которых этот
метод расходится. Например, если на крыле имеются сосредо-
точенные массы, то иногда может оказаться, что колебания без
узлов вообще невозможны и уже первый тон совместных коле-
баний будет происходить с узлом. В этом случае изложенный
метод последовательных приближений неприменим, и приходится
применять более сложные методы2.
1 Легко видеть, что уравнения (39) вместе с граничными условиями и
условиями сопряжения определяют / и с только с точностью до произволь-
ного постоянного множителя (одн >го и того же для обеих функций).
2 Точно так же, как, например, приходится применять более сложные
методы для получения формы обертонов чисто крутильных (или чисто изгибных)
колебаний, которые происходят с узлами (см. гл. II, п. 6). Изложение этих
специальных методов интересующиеся найдут в книге А. И. К а май, Труды
НАГИ.
ГЛАВА V
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ СОБСТВЕН-
НЫХ ЧАСТОТ КРЫЛА И ХВОСТОВОГО ОПЕРЕНИЯ
Наиболее часто для экспериментального определения частот
собственных колебаний применяется резонансный метод. Метод
этот состоит в том, что крыло (оперение) подвергается действию
периодической возмущающей силы. Изменяя частоту возмущаю-
щей силы, добиваются того, что крыло (оперение) вступает
в резонанс. Резонанс, очевидно, наступает тогда, когда частота
возмущающей силы равна частоте собственных колебаний крыла
(оперения). Так как частота возмущающей силы известна, тотем
самым определяется и собственная частота крыла (оперения).
Возмущающая сила создается с помощью вибратора (фиг. 30).
Простейший вибратор 1 представляет собой эксцентричный
маховик 2, скрепленный с гибким валом 3, вращающимся от
мотора. При вращении маховика возникает центробежная сила.
Вследствие того, что центр тяжести маховика не находится на
оси вращения, проекция этой силы на любую ось будет изме-
няться периодически, причем период изменения ее будет равен
числу оборотов мотора. Если такой вибратор закрепить на крыле,
то при непрерывном увеличении числа оборотов мотора (от
минимальной величины) мы достигнем того, что при некотором
числе оборотов наступит резонанс — амплитуда колебаний резко
возрастет. Обычно первый резонанс происходит с частотой
совместных изгибных колебаний, под действием вертикальной
компоненты центробежной силы вибратора.
Так как число* оборотов мотора можно измерить, то тем
самым измеряется и частота возмущающей силы, равная в момент
резонанса собственной частоте колебаний крыла. При дальнейшем
126
Фиг. 31.
1—крепящие пластины; 2—стягивающие бол-
ты; 3— хомут; 4—соединительный вал; .7—на-
правляющая стойка; б—вибратор; 7—гибкий*
вал; 8—мотор; 9—вибратор.
увеличении числа оборотов мотора интенсивные изгибные коле-
бания прекращаются. Если число оборотов мотора увеличивать,
дальше, то наступает новый резонанс — когда число оборотов-
мотора совпадет с собственной частотой второго тона совместных
колебаний, т. е. с частотой совместных крутильных колебаний
(центробежная сила от вибратора создает периодический крутящий,
момент около оси жесткости кры-
ла). На более высоких числах
оборотов возникают резонансы
с обертонами изгибных и кру-
тильных колебаний, а иногда так-
же с частотой колебаний крыла
в плоскости хорд. Но на прак-
тике обычно ограничиваются
определением собственных ча-
стот основного тона изгибных и
крутильных колебаний.
Чтобы вызвать колебания крыла, вибратор должен сообщать
достаточную силу. Однако эта сила не должна быть излишне
велика, так как вибрации могут быть столь интенсивны, что
вызовут поломку крыла. Величина возмущающей силы достигается
подбором массы маховика
вибратора и его эксцентри-
ситета. Обычно на крыло в
одном и том же сечении его
устанавливают одновременно
два вибратора, находящиеся
на общем валу (фиг. 31). Для
крепления вибраторов к крылу
на него надевается деревянный
хомут. Мотор устанавливается
на отдельном постаменте, что-
бы лишняя масса не изменя-
ла собственной частоты коле-
баний крыла; вращение к ви-
браторам, как сказано выше,
передается при помощи гиб-
кого вала.
Для получения изгибных колебаний оба вибратора регулируются
так, чтобы центры их находились по одну сторону вала (фиг. 32, а).
Тогда возмущающие силы обоих вибраторов в каждый момент
времени направлены в одну сторону. Для получения крутильных
колебаний маховик одного из вибраторов поворачивают на 180°,
так что центры обоих вибраторов оказываются по разные
стороны вала (фиг. 32, Ь). Так как при этом возмущающие силы
вибраторов оказываются направленными в каждый момёнт вре-
мени в противоположные стороны, и вибраторы укреплены по
разные стороны оси жесткости (фиг. 31), то на крыло действует
возмущающая пара, которая и вызывает крутильные колебания^
127
Для обычных конструкций частота изгибных колебаний лежит
приблизительно в пределах 400—700 колебаний в минуту, частота
крутильных колебаний в пределах 1200—1600 колебаний в минуту.
Во время опыта следует внимательно следить за формой
колебаний, так как в пределах 400—2000 колебаний в минуту,
кроме основных резонансов изгибных и крутильных колебаний,
могут находиться резонансы с различными обертонами основных
форм колебания. При невнимательном проведении опыта их
легко спутать с основной формой колебаний.
Так как на крыле приходится укреплять вибраторы и поддержи-
вающий хомут (фиг. 31), то по существу измеряется собственная
частота не крыла, а системы крыло—хомут—вибраторы. Естественно,
что дополнительные массы, которые приходится устанавливать
на крыле (хомут и вибраторы), снижают частоту колебаний, и заме-
ренная резонансным методом частота оказывается меньше истинной.
Для учета влияния дополнительных масс применяется следующий
способ: испытание проводится несколько раз (обычно четыре раза)
< различными дополнительными грузами. Пусть, например, масса
хомута вместе с вибраторами будет /Ио. Проведя испытания, мы
нашли частоту р0. Затем поочередно на хомуте укрепляются
различные добавочные массы Мх, Мг, Мя и каждый раз измеряется
частота системы крыло—хомут—вибраторы—добавочные грузы.
Пусть массе /И0 + Л1г соответствует частота р,. Строим график
изменения частоты в функции дополнительной массы, находя-
щейся на крыле (фиг. 33. сплошная кривая). Затем кривую про-
должаем до пересечения с осью ординат (фиг 33, пунктир) и на
-оси р читаем значение частоты, соответствующее нулевому значе-
нию дополнительной массы. Это значение и принимается за зна-
чение собственной частоты крыла. Однако нет уверенности, что,
экстраполируя значение р от точки, соответствующей Л10, до точ-
128
ки, соответствующей нулевому значению дополнительной массы,
мЬ1 правильно проводим кривую. Весьма часто при этом допус-
каются очень значительные ошибки, доходящие в некоторых слу-
чаях до 50 и более процентов от искомой величины. Объяс-
няется это тем, что истинная кривая зависимости частоты от со-
средоточенной массы вблизи оси ординат часто имеет участок с
весьма крутым подъемом1 (фиг. 34, сплошная кривая). Между тем,
если бы частоты при различных значениях сосредоточенной
массы были измерены экспериментально (точки А, В, С, D, фиг. 34),
а затем была произведена экстраполяция (фиг. 34, пунктир), то
было бы получено значение частоты р± вместо р2, имеющейся в
действительности.
Существуют более точные2 методы экстраполяции, но они
связаны с довольно громоздкими вычислениями
и все же не гарантируют необходимой точ-
ности.
Изложенный резонансный метод дает доста-
точно точные результаты только в том случае,
если массы и моменты инерции дополнительных
грузов (хомут, вибраторы) невелики по сравне-
нию с массой и моментом инерции испытывае-
мого объекта (крыла или оперения). Следова-
тельно, этим методом можно пользоваться, на-
пример, при испытаниях крыльев больших
самолетов. При испытаниях же небольших
от.
/
Фиг. 35.
//
крыльев или оперений рекомендуется применять более совер-
шенный метод, который сравнительно недавно разработан в
ЦАГИ А. В. Смрчеком.
Прежде чем излагать метод А. В. Смрчека применительно
к крылу или оперению, изложим его идею на простом примере.
Пусть имеются две упругие системы I и II (грузы, подвешенные
на пружинах, фиг. 35), одна из которых имеет массу т1 и же-
сткость kv другая — массу т2 и жесткость k„. Пусть масса
выведена из положения равновесия и затем предоставлена самой
себе. Она начнет совершать колебания. Уравнение движения
массы мы получим, если приравняем нулю сумму действу-
ющих на нее сил со включением сил инерции. Будем иметь:
miZy + k1Zl = 0.
(40)
Здесь первый член — проекция на ось z силы инерции, второй—
упругой силы, действующих на массу т\ — отклонение массы
от положения равновесия. Интегрируя уравнение (40), как обычно,
подстановкой
Zr = А^,
1 См. фиг. 22.
2 И. В. Ананьев, К экспериментальному определению частот авиацион-
ных конструкций. .Технические заметки", ЦА1 И, вып. 175.
Гроссман—15—9 129
найдем частоту системы /:
A-FT <«>
Точно так же найдем частоту системы II:
<42>
Предположим, что обе системы настроены в резонанс, т. е.
имеют одинаковую частоту. Тогда
_ ^2
/Л/
Составляя производную пропорцию, получим:
Из этого равенства следует, что, если две системы обладают
одинаковой частотой, то новая система, масса которой равна
сумме масс этих систем, а жесткость — сумме жесткостей, имеет
ту же частоту, что и первоначальные системы.
На этом свойстве и базируется метод А. В. Смрчека. Пред-
положим, что мы хотели бы измерить частоту системы / (фиг. 35),
для чего на массу т1 нужно было бы поставить соответствующий
прибор массы т2. Для того чтобы вес прибора не влиял на ча-
стоту исследуемой системы, достаточно было бы на основании
сказанного выше подвесить прибор на дополнительной пружине
жесткости k,, подобранной так, чтобы частота массы т2, под-
вешенной на пружине k2, равнялась частоте основной системы /.
Жесткость пружины Л, подбирается последовательными при-
ближениями. Опишем, как ведется эксперимент.
Пусть требуется замерить неизвестную частоту системы I (на
фиг. 35 система I играет роль крыла) при помощи массы при-
бора и, (при испытаниях крыла роль массы т9 играют хомут
и вибраторы).
1. Подвешиваем прибор т2 на пружине жесткости k2 и изме-
ряем частоту полученной таким образом системы II. Эта частота
поддается непосредственному измерению, так как в систему вклю-
чен регистрирующий прибор т2.Пусть частота системы //есть р0.
2. Составляем новую систему, масса которой равна ту + т2,
и эту массу подвешиваем на пружине жесткости + k2. Если
бы частота системы / равнялась также р0, то новая система
имела бы эту же частоту. Так как этого, вообще говоря, нет,
то новая система будет иметь частоту р1г которая может быть
измерена, так как в систему включен регистрирующий прибор.
3. Опять подвешиваем прибор тй на отдельной пружине,
которую подбираем так, чтобы частота новой системы // рав-
нялась pv
130
4. Снова образуем систему с суммарной массой и суммарной
жесткостью; измеряем частоту,— она оказывается равной р2.
5. Подбираем жесткость пружины системы II так, чтобы ча-
стота ее равнялась р2, и т. д.
Опыт продолжается до тех пор, пока частоты системы 7/
и суммарной системы не совпадут. Тогда в силу пропорции (43)
искомая частота системы I будет равна частоте системы //.
Можно доказать, что описанный процесс всегда сходится и
сходится к частоте системы /, т. е. lim рп = р, где р — частота
системы /.
Опишем теперь, как практически осуществляется эксперимент
по определению частоты колебания крыла или оперения. Схема
установки изображена на фиг. 36. Крыло 1 вблизи свободного
конца охватывается хомутом 2. Хомут 2, кроме того, поддержи-
вается двумя плоскими пружинами 3. При желании верхнюю
и нижнюю половины хомута можно раздвинуть при помощи
болтов 9 и, установив деревянные подкладки 11, закрепить при
помощи подкладок 72 и болтов 10 на пружинах 3. В этом по-
ложении хомут не соприкасается с крылом и, так как он ук-
реплен на пружинах, представляет собой отдельную упругую
систему с определенной частотой. Каждая из пружин 3 охваты-
вается добавочной парой пружин 4, зажатых, в свою очередь,
между швеллерами 5. Швеллеры закреплены на стойках 6. Вы-
двигая на различную величину пружины 4, можно менять жест-
кость всей системы. На хомуте 2 крепятся два вибратора 7, ко-
торые приводятся в действие мотором 8.
Опыт производится так же, как было описано применительно
к грузу на пружине. В данном случае системой I является крыло,
системой II — хомут с вибраторами, укрепленный на пружинах
3 и 4. Вынимая подкладки 77 и 12 и стягивая обе половины
хомута болтами 9, мы соединяем обе системы, т. е. получаем
суммарную систему, масса которой равна общей массе систем 7 и //,
а жесткость — общей жесткости этих систем.
131
Опыт проводим следующим образом:
1. Укрепляем хомут на крыле и отъединяем от пружин 3;
обычным резонансным методом измеряем частоту системы хомут—
крыло; получаем частоту pt.
2. Раздвигаем хомут и устанавливаем на пружинах 3; выдвигая
различным образом пружины 4, добиваемся того, чтобы частота
колебаний хомута на пружинах оказалась равной
3. Вынимаем подкладки 11 и 12 и стягиваем хомут; измеряем
частоту системы крыло — хомут — пружины, которая получается
равной р2.
4. Раздвигаем хомут и укрепляем его на пружинах; регули-
ровкой пружин 4 добиваемся того, чтобы частота системы хомут—
пружины оказалась равной р.,.
5. Опять соединяем хомут с крылом и опять измеряем ча-
стоту всей системы крыло — хомут—пружины и т. д.
В конце концов окажется, что частоты систем хомут—пру-
жины и крыло—хомут—пружины будут равны. Согласно сказан-
ному выше, такую же частоту будет иметь и изолированное
крыло, т. е. частота крыла будет определена.
Практически можно ускорить сходимость процесса настрой-
кой системы хомут — пружины не на частоту предыдущего при-
ближения, а несколько иным образом1. На этом мы останавли-
ваться не будем, так как нашей целью является только изложе-
ние основной идеи метода.
о 1 С м р ч е к, Экспериментальное определение частот собственных колеба-
ний авиационных конструкций методом компенсирующей жесткости. Труды
НАГИ, вып. 411, 1939 г.
ГЛАВА VI
АЭРОДИНАМИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА ВИБРИРУЮЩЕЕ
КРЫЛО
1. ОБЩИЕ ПОЛОЖЕНИЯ
Теория неустановившегося движения крыла в плоско-парал-
лельном потоке идеальной жидкости была впервые разработана
Бирнбаумом1 в 1923 г. Решение Бирнбаума в 1929 г. было видо-
изменено Кюсснером2и применено им к задаче об определении
критической скорости крыла. В СССР первая работа, посвящен-
ная вопросу о неустановившихся движениях крыла, принадле-
жит С. А. Чаплыгину3. В 1933 г. М. В. Келдыш и М. А. Лав-
рентьев4 дали новое решение той же задачи и получили расчет-
ные формулы в несравненно более простом и удобном для
пользования виде, чем Кюсснер (Кюсснер получил решение в
виде рядов, весьма сложных для вычислений, в то время как
М. В. Келдыш и М. А. Лаврентьев дали окончательные формулы
в замкнутом виде). Позже указанных авторов то же решение
независимо было найдено Теодорсеном5.
Бирнбаум, Кюсснер, Келдыш, Лаврентьев и Теодорсен решают
задачу теоретически вполне строго®. Рассматривается крыло в
плоском потоке, двигающееся с переменными скоростями и и v
(в проекциях на оси координат) и, кроме того, вращающееся
с переменной угловой скоростью ш вокруг некоторого связан-
ного с крылом центра вращения. При таких условиях циркуля-
ция вокруг крыла будет меняться во времени и с крыла будет
сбегать вихревая пелена, влияние которой на крыло необходимо
учесть.
Однако до самого последнего времени не было теории, поз-
воляющей учесть влияние конечности размаха на аэродинами-
ческие силы, действующие на вибрирующее крыло.
1 W. Birnbaum, Das ebene problem des schlagenden Fliigels. ZAMM,
1923 г. стр., 290; ZAMM, 1924 г„ стр. 227.
3 G. Kiissner, Schwingungen von Flugzeugfliigefn. .Luftfahrtforschung", Bd.
4, H. 2, 1929 r.
3 С. А. Чаплыгин, О влиянии плоско-параллельного потока воздуха
на движущееся в нем цилиндрическое крыло. Труды ЦАГИ, вып. 19, 1926 г.
* М. В. Келдыши М. А. Лаврентьев, К теории колеблющегося
крыла. Технические заметки ЦАГИ, №45, 1935 г.
3 Т. Teodo г sen , General Theory of Aerodynamic and the Mechanism of
Flutter. NACA. Rep. № 496.
e С точностью до бесконечно-малых высших порядков.
133
Формулы для подъемной силы и момента, которые получа-
ются в результате решения данной проблемы, очень неудобны
для использования при вычислении критической скорости виб-
раций. Расчет получается настолько громоздким и сложным,
что практически пользоваться им в настоящее время весьма
затруднительно. Кроме того, конечность размаха сказывается
при вибрациях настолько значительно, что результаты расчета
по теории крыла в плоском потоке (т. е. без учета конечности
удлинения) плохо согласуются с опытом.
Поэтому появился ряд работ1, также посвященных вопросам
вычисления аэродинамических сил, действующих на вибрирую-
щее крыло, в которых принимается определенная гипотеза о
структуре потока около вибрирующего крыла. Эта гипотеза
(гипотеза стационарности) сводится к пренебрежению влиянием
части вихревой пелены, сходящей с крыла вследствие измене-
ния циркуляции во времени. При этом выражения аэродинами-
ческих сил получаются настолько простыми, что пользование
ими не представляет никаких затруднений.
Гипотеза стационарности. Аэродинамические характе-
ристики крыла в неустановившемся движении с переменной ско-
ростью V и угловой скоростью <о заменяются в каждый момент
времени характеристиками того же крыла, движущегося с по-
стоянными линейной и угловой скоростями V и ш; V и ш в каж-
дый момент времени равны скоростям действительного движения
в тот же момент времени, причем наклон I/ к профилю также
считается постоянным и равным действительному наклону в
рассматриваемый момент времени.
Следует сказать, что эта гипотеза очень часто применяется
в технических расчетах (например в расчетах, связанных с дина-
микой полета), хотя иногда и не высказывается в явной форме.
Гипотеза стационарности, следовательно, сводится к тому, что
в каждый момент времени истинный поток около крыла заме-
няется установившимся. Тогда (если рассматривать плоское дви-
жение) циркуляция в каждый момент времени будет неизменной
(но в различные моменты времени она будет различной, так как
скорости движения, соответствующие каждому моменту, раз-
личны), и потому с крыла не будет сходить вихревая пелена.
Это обстоятельство весьма сильно упрощает как решение за-
дачи, так и окончательные формулы.
2. О ВЫЧИСЛЕНИИ АЭРОДИНАМИЧЕСКИХ СИЛ, ДЕЙСТВУЮЩИХ
НА КРЫЛО ПРИ НЕУСТАНОВИВШЕМСЯ ДВИЖЕНИИ
При вычислении подъемной силы крыла в установившемся
потоке идеальной жидкости обычно пользуются теоремой Жу-
ковского. Однако известно, что для случая неустановившегося
1 Подробнее об этих работах см. Е. П. Гроссман, Флаттер. Труды
НАГИ, вып. 284, 1937 г.
134
движения теорема Жуковского становится несправедливой.
В настоящем параграфе мы покажем, что, если в каждый момент
времени поток около крыла считать установившимся (гипотеза
стационарности), то с точностью до малых высших порядков
подъемную силу и при наличии угловой скорости можно вычис-
лять по теореме Жуковского. Этой теоремой мы и будем поль-
зоваться в следующих параграфах для вычисления аэродинами-
ческих сил.
Для вычисления снл, действующих на крыло при неустановлвшемся дви-
жении, будем пользоваться прямоугольной системой координат хоу, неподвижно
скрепленной с ,'крылом и движущейся вместе с ним. Напишем интеграл
Лагранжа уравнений движения жидкости в этой системе координат.
Пусть х1о1у1—неподвижная в пространстве система координат (фиг. 37).
Для области потенциального движения жидкости при отсутствии внешних
массовых сил интеграл Лагранжа в неподвижной системе координат, как из-
JbecTHO, имеет вид:
---1~у>, (1)
где /(т)—некоторая функция, зависящая только от времени;
? 1*1. У1> ') — потенциал скоростей;
V — полная скорость жидкости в рассматриваемой точке;
р —• плотность жидкости;
р — давление.
Между координатами х1гуг неподвижной и координатами х, у подвижной
системы координат имеем зависимость:
Х1 = Х1(х,у,т);|
> (2)
У1-=УЛх,У,^- )
135
При помощи этих соотношении потенциал скоростей <р (х,, yt, -t) можно выра-
зить через координаты подвижной системы. Поэтому можем записать:
<?(-*.>> т) = <P(xi. Л.'). (3)
где X! и j»! связаны с х и у соотношениями (2).
и „ ду (х, у, т)
Найдем производную —~ Прн данном диференцировании коор-
динаты х, у считаются фиксированными и, следовательно, ищется изменение
потенциала скоростей <р во времени для точки, положение которой фиксиро-
вано в подвижной системе координат. Диференцируя уравнение (3) и учиты-
вая, что хх и у»! зависят от времени, согласно уравнению (2) имеем:
д<р(*. У, t) = (xlt Ji, т) (xt, т) дхг dytx^y,, -t) dji
дт д~ дх1 Эт dpi dz'
По определению потенциала скоростей, очевидно, что
d? (A, Vi. ~) ду (хг, yt, т)
dxi и
суть проекции скорости частицы жидкости на неподвижные оси координат:
(*i, У1. *) _ v
дхг
(*!, J>t, Т) =
„ дх1 ду.
Согласно уравнениям (2), производные и ^х, вычисляемые при фи-
ксированных х, у, суть проекции на неподвижные Ъсн координат скорости
переносного движения (скорости движения подвижной системы координат):
(6)
__
dz
где® — скорость движения рассматриваемой точки М вместе с системой
координат хоу.
В силу уравнений (5) и (6)
ду(хиУ1,1) dr, , d?(x„ т) dyi
dXt dt дуг dz х' '_'Л‘
есть скалярное произведение векторов V (-абсолютная скорость частицы жид-
кости) и® (скорость движения подвижной системы координат нли, что то же,
скорость движения крыла). Так как скалярное произведение не зависит от
выбора системы координат, то в проекциях на подвижные оси мы можем
записать его в следующем виде:
. dxt ду(хъ У1. т) dy, _
dxt dz + dyt dz~ Vr *x + vy "У
Пусть V®, V® — проекции на оси хну скорости движения начала
подвижной системы координат и ш — угловая скорость вращения этой систе-
мы. Тогда, очевидно,
< = V® + шу;
®> = V®-<oX.
136
Подставляя эти значения в соотношение (7) и результат в выражение (4),
будем иметь:
т)- = + (8)
д<? (-*«, >1» t)
Из этого равенства определяем производную ----------- и подставляем
ее в уравнение (1). Принимая во внимание, что V’ = Vj + Vy, будеД иметь:
у- р = / (’) - д?(У Т) + (VxV ° + Vy Vj) +
+ (^ху - <*Vyx) - -L (V« + vj). (9)
Вычисляем силы, действующие на крыло.
Пусть крыло, движущееся в потоке идеальной жидкости, обладает сле-
дующими скоростями: основной скоростью V, постоянной по величине и на-
правлению, направленной под небольшим углом к хорде, добавочными пере-
менными скоростями и, v, направленными по основной скорости и перпен-
дикулярно к ней, а также переменной угловой скоростью <о около центра,
лежащего на крыле. Добавочные скорости и угловую скорость будем пола-
гать малыми по сравнению со скоростью V основного движения.
Выберем определенным образом оси координат, неподвижно связанные с
крылом. Начало координат о выберем в центре вращения крыла, ось х напра-
вим по скорости основного движения крыла назад, а ось_у — перпендикулярно
к ней (фиг. 38).
Скорости частицы жидкости Vr н Vy в этой системе координат мы можем
записать так:
Vx=V + n;
Vy = v, (Ю)
где и и v малы по сравнению с V.
Вводим гипотезу стационарности: считаем, что в каждый момент времени
поток относительно крыла, т. е. в системе координат хоу, установился. Это
означает, что в каждый момент времени
у. т) (п)
дт
137
Подставляя уравнения (10) и (11) в интеграл Лагранжа (9) и отбрасывая
члены ^ime первого порядка малости, получим:
yr=/(’) + |W; +«V° +«V°)+wVy-~l-(V2 + 2«V). (12)
Будем обозначать индексом значения величин, относящихся к струе,
проходящей над крылом, и индексом »—• значения величин, относящихся к
струе, проходящей под крылом. Напишем уравнение (12) один раз для час-
тицы жидкости, проходящей непосредственно над элементом ds крыла (фиг. 38),
н другой раз для частицы, проходящей -под тем же элементом. Будем иметь:
-|-Р+=/(х) + (tfv°4-H+V° + vV°)+uVy- ~ (У=+2ц+У);
4-Р_= / (-) + (VV®+И_У®. + vV$)+«Vy- 4 (V2+2«_V).
(13)
Так как наклон профиля к скорости V и кривизна профиля считаются
малыми, то элемент ds можно считать совпадающим с элементом оси х, что
вносит ошибку второго порядка малости. Так как жидкость ие может проте-
кать сквозь профиль, то нормальная к ds компонента скорости частицы жид-
кости одинакова сверху н снизу профиля и равна нормальной компоненте
скорости движения элемента ds. С точностью до малых второго порядка эту
нормальную компоненту можно принять равной v, и потому в равенствах (13)
учтено, что V с точностью до величин второго порядка малости.
Вычитая одно из равенств (13) из другого, находим
(V-V®)(«+—«_)= (Р-—Р+). (14)
Профиль считается тонким, так что его можно схематизировать одной
линией. Эту линию можно рассматривать, как вихревую поверхность с цир-
куляцией вихрей на элементе дуги профиля ds (фиг. 38), равной r(x)ds [в
следующем параграфе будет показано, каким образом подобрать 7 (х) так,
чтобы вихревая поверхность вполне заменяла крыло]. Тогда, беря малый
контур s, сколь угодно близко окружающий элемент ds, будем иметь
7 (х) ds = J vs ds,
s
где vs — проекция скорости частицы жидкости на контур S. Так как над
элементом ds скорость жидкости с точностью до малых второго порядка есть
V 4- и+, а под элементом V+u_ и в обоих случаях она направлена по каса-
тельной к элементу (так как интегрирование идет в положительную сторону
над ив отрицательную под элементом), то будем иметь
7 (х) ds = j vs ds = (V-J- ы+) ds — (V + «_)ds,
s
откуда
7(x) = «+— n_. (15)
Подъемная сила P, действующая на элемент ds профиля, очевидно, будет:
(Р_~Р4) ds. (16)
На основании уравнений (15) и (16) можно записать уравнение (14) в сле-
дующем виде:
P=pV07dx, (16а)
138
где Vo = V—V® — скорость жидкости относительно крыла (в направлении
основного движения). Выражение (16а) есть не что иное, как теорема Жуковского.
Таким образом доказано, что если в каждый момент времени
движение относительно крыла считать установившимся (гипо-
теза стационарности), то для такого крыла силы можно вычислять
по теореме Жуковского (с точностью до малых высших порядков).
3. АЭРОДИНАМИЧЕСКИЕ ВОЗДЕЙСТВИЯ НА КРЫЛО
Рассмотрим тонкий профиль ММ (фиг. 39), произвольным
образом двигающийся в потоке жидкости и при этом деформирую-
щийся по произвольному закону (примером деформирующегося
профиля может служить, например, крыло, снабженное элероном).
Пусть xoz — неподвижная в пространстве прямоугольная система
координат, ось ох которой ориентирована по скорости основного
потока. Уравнение профиля в этой системе координат
z = z(x,t). (17)
Пусть х0 — расстояние от передней кромки профиля до на-
чала координат, отсчитываемое вдоль оси х; t — хорда профиля.
На крыло набегает поток, обладающий вдали от крыла основ-
ной скоростью V, направленной вдоль оси х. Около крыла ча-
стицы жидкости обладают, кроме того,добавочными скоростями:
ч — направленной по основной скорости потока и ч)— перпенди-
кулярно к ней, которые вызваны влиянием крыла. Как и выше,
будем считать эти скорости малыми по сравнению со скоростью
основного потока. Точно так же считаем малой амплитуду
отклонений профиля от оси х (z мало по сравнению с хордой).
Если бы профиль был неподвижным, то, так как поток обте-
кает профиль без срыва, вертикальная слагающая частицы
Жидкости около профиля была бы (фиг. 39) (V-|-u) Но так
как частица движется вместе с профилем с вертикальной ско-
ростью то общая вертикальная скорость частицы равна:
139
Ограничиваясь членами первого порядка малости, имеем:
+ (18)
дх 1 дх ' ’
Введем новую переменную ф, связанную с х зависимостью:
х + х0= у (1 — соэф). (19)
При изменении х от — х0 до t—х0 (вдоль профиля) ф будет
изменяться от нуля до я.
Заменим профиль непрерывной вихревой пеленой с напряже-
нием вихрей на элементе dx, равным y(x)cfx. Функцию у(х)
под.берем, исходя из того условия, чтобы поток, создаваемый
вИкревой пеленой, совпадал с действительным потоком около
ирОфиля. Как и в стационарной теории тонких профилей1,
gy^eM искать у(х) в виде тригонометрического ряда
се
7(x) = 2V'{H0ctg^- + ^4„sin/Hpj. (20)
1
Найдем вертикальную скорость от вихревой пелены и опре-
де1им неизвестные коэфициенты Д;, исходя из того условия,
чт,>бы эта скорость совпадала со скоростью v действительного
посока.
Так как профиль предполагается мало отличающимся от оси л,
тО при вычислении поля скоростей системы вихрей у (л), заме-
няющих профиль, делается допущение, что вихри расположены
п0 оси х. Тогда скорость, индуцированная вихрями в точке
профиля с координатой х, будет
Приравнивая эту скорость вертикальной скорости действи-
те(ьного потока {уравнение (18)], получаем условие, определяю-
щее распределение циркуляции у (л):
[ ' 1 = v — -I- —
J 2-п (xt — х) У дх ' dz"
Подставляем в левую часть у(х,) из выражения (20). Делая
за ем замену переменных х на ф по уравнению (19j, можем
вЫ1ислить интеграл, стоящий в левой части2. Будем иметь:
(21)
1 Глауэрт, Теория крыльев и винта.
2 Подробное вычисление этого интеграла имеется в книге Г л а у э р т а,
Те(рия крыльев и винта.
141
Из этого соотношения легко определить коэфициенты At ме-
тодом, которым обычно определяются коэфициенты при разло-
жении какой-либо функции в ряд Фурье. Умножаем поочередно
обе стороны уравнения (21) на dty, cos^db, cos20d<p,... и инте-
грируем в пределах от нуля до ~. В результате находим:
Таким образом коэфициенты Л,- определены и тем самым
определена циркуляция ч(х). Дальше уже не представляет за-
труднения, пользуясь теоремой Жуковского, определить силы,
действующие на крыло.
Подъемная сила, действующая на крыло, будет:
t—-Vo
Р =f pVi(x)dx.
Подставляя сюда значение ч(х) из выражения (20) и заменяя
затем х через Ф, после выполнения интегрирования получим:
откуда
C„^(Ao + 4^)- (23)
Аналогично вычисляется момент подъемной силы относи-
тельно начала координат (напомним, что начало координат от-
стоит на расстоянии х0 от передней кромки):
Z—л.
М = — у р V? (л) • X dx = — р V2tx0 Т (Ло ф- ~ А^ —
-_1рУ»^(Л0 + Л1-|Л8),
ИЛИ
Af=Cm£pt2V2,
где
СтЕ = —£ (А + Ла) + (4° - 4) Су. (24)
Таким же образом могут быть вычислены и силы, действую-
щие на какую-либо часть крыла. Например, если крыло обла-
дает элероном, передняя кромка которого находится на рассто-
янии х*, а шарнир — на расстоянии лш от передней кромки
U1
крыла, то шарнирный момент элерона может быть вычислен по
формуле: *
Мш = J pl/y (л) (л — хш + xu) rfx, (25)
так как л — лш+л-0 есть расстояние от произвольной точки
элерона с координатой х до шарнира (фиг. 40).
Определим ф* и фш так, чтобы
Л* = 4(1 -созф*);
(26)
Подставляем в формулу (25) значение к(х) и заменяем пере-
менное х на ф. Получаем:
71 I 00 -1
Л1Ш = — у J [Л0 ctg у + S АП Sin ft<P] (C0S --C0S '?) Sin I1
1
или
Ж = -l^V4~VAnBn, (27)
где
у (cos ф ш — cos ф) sin ф dty-,
(27a)
sin nd) (cos фш — cos ф) sin ф d'\.
Полученные формулы пригодны при любом законе движения
профиля. Для получения аэродинамических характеристик в каж-
дом конкретном случае, когда известен закон движения (17),
вычисляются сперва коэфициенты Ап по формулам (22), а затем
142
подъемная сила по формуле (23) и момент по формуле (24).
Проделаем эти вычисления для случая, интересующего нас
с точки зрения изучения флаттера.
4 АЭРОДИНАМИЧЕСКИЕ характеристики крыла с элероном
В ПЛОСКОМ ПОТОКЕ
Пусть (в плоско-параллельном потоке) MIJJN (фиг. 41) — про-
филь крыла в статическом положении (до возникновения ви-
браций). Выберем начало координат в точке Е профиля, от-
стоящей на х0 от передней кромки (в дальнейшем, при изучении
флаттера, будет удобно за эту точку принять центр жесткости
крыла), ось х направим по скорости основного потока и ось
z — перпендикулярно к ней. Через Ш обозначен шарнир эле-
рона, а через А — его передняя кромка. Расстояние от шарнира
до передней кромки крыла обозначено через лш, расстояние от
передней кромки элерона до той же точки—через л*.
Вычислим аэродинамические характеристики крыла, когда со-
вершаемое движение слагается из перемещения в направлении,
перпендикулярном основной скорости потока, вращения около
какой-либо точки, лежащей на профиле, и отклонения элерона.
Пусть M}LLlxNt—положение движущегося профиля в какой-либо
момент времени. Точка Е заняла положение Е1г причем расстоя-
ние EEt обозначим через Z и будем в дальнейшем называть
прогибом крыла, угол закручивания крыла около точки Et обо-
143
значим через 0, а угол отклонения элерона относительно крыла —
через ₽. Все эти величины считаются малыми, точно так же, как
и ординаты профиля в статическом положении, которые мы обо-
значим через zCT. Составим выражение (17).
Ординаты точек профиля в произвольный момент времени
можно с точностью до малых высших порядков выразить сле-
дующим образом:
на крыле (для —х0 < х <х* —х0)
z = zCT + Z — х 6;
на элероне (для х*— х0<х<£— х0)
z - zCT + Z — х 6 — (х — хш 4- х0)8.
Подставляем эти значения в формулы (22). Так как z имеет
различные значения в интервале — х0<х<х*— х0 и в интер-
вале х*—х0<х<£ —х0, то интервал интегрирования разби-
вается на два участка и интегрирование ведется отдельно по
каждому участку. Получаем:
г ф*
а« = 4/[lT-e-^+Az]cos„6^ +
и
, 2 fl^CT X . 1 - Х-Х ш + .г0 .1
+ т J га—е—v-e + -yz-₽----------v~ ИСО8 =
ф.
2 /•[ dz х . 1.1
= ----е—v ° + v zjcosn^-
о
— / [₽ + + *° ₽ ] cos гЦ d-'i,
и аналогично Ао.
Заменяем х через ф по формулам (19) и (26), после чего
интегрирование выполняется легко. В результате получаем:
Ап = АПст + С„9 4- Dn6 4- 4- Л + Kn^Z, (28)
где
к .
1 г dz
дОст = __ J-~d^;
О
2 г dz
Ал ст = — j cos лф dty,
О I
и величины Сп, Dn, Еп, Fn, Кп приведены в табл. 10.
144
(29)
Таблица 10
II с„ Вп Ег_ Fn Кп
0 1 1 х0 2 t [cos фш (к — Ф*) + sin ф* j — 1
1 0 1 "2 2 sin ip* К [2 cos фш sin<p* + . . sin 2ф* 1 +(« / ] 0
и >2 0 0 2 sin яр* nit 1 Г sin лф* 2я[2сО5Фш J sin (л—1)ф* sin (п + 1) ф* | 0
л — 1 л + 1 |
Легко видеть, что коэфициенты А„ст —значения коэфйци-
ентов Ап для профиля в статическом положении. Следовательно,
в силу уравнений (23), (24) и (27) можно написать:
О ст
•у ст у
vo
t
(у ст — СтЕ ст >
(30)
-^УЧГ£Аа„Вп = Мш. сТ,
и
где Суст, СтЕсс и /Иш. ст—соответственно коэфициент подъем-
ной силы, коэфициент момента относительно точки Е (фиг. 41)
и шарнирный момент элерона для профиля в статическом по-
ложении.
Принимая это во внимание, после подстановки в формулы
(23) и (24) значений коэфициентов Ао, Аи А2 согласно выраже-
нию (28) и данным табл. 10, получим окончательные выражения
для коэфициентов подъемной силы и момента крыла в рас-
сматриваемом случае:
С, = С,„ + ,ф + (|-ЗД в + <5₽ + //4₽—^];
с.г=с^„ —£4'в+/₽+'/4ё + (т‘_т)с‘”
(31)
где
С^пЕ ст = — (А ст + Аг с г)
согласно уравнению (24) представляет собой значение Ст£ для
неподвижного профиля в статическом положении при СуСт = 0.
Гроссман—15—10 *45
Величины G, Н, I, J зависят от характеристик элерона:
G— — ф*-|-sin ф*];
Н= ~ [(к — ф* + sin ф*) • cos фш + sin ф* + у (я—Ф*)~ 4 sin 2Ф*] ;
/==—-j-sin ф* [1 —cos ф*];
J — у [— (п — ф*) — 2 cos фш sin ф* + cos фш sin 2ф* +
+ у sin 2ф* — sin ф* — у sin Зф*]. (32)
При вычислении G, Н, /, J величины ф* и фш определяются
по формулам (26). Шарнирный момент элерона может быть
получен по формуле (27). Подставляя в эту формулу значения Ап
из формулы (28j, находим:
Л1Ш = 2ИШ. ст - [ sxe 4- s3 4 ё + 2з? + 4 ₽ + й5 4 Ц <33>
где
Si=4£c„B„; о
о о
оо оо
es=l^D„B,; а,= -^*Л
О о
со
2,= ^ед,;
О
Подставляя выражения Сп, Dn, Еп, Fn и Кп из табл. 10 и В„
из равенств (27а), после соответствующих вычислений получим:
2i=y[(n—ф*)(со8фш — у) — sin ф* (cos фш — 1) +4‘sin2'^];
О — О' I ХО О'.
И2— ~2 I t W2>
--2= У [ (к — Ф*) (3 COS фш — 1) + у Sin 2Ф* (Cos фш + 1) +
+ ~ sin ф* —у sin Зф* — 2 sin ф* cos фш J
2з= ^[(' — ф*)2 (cos фш — у) +(к — ф^) sin ф* 4-у 81П2ф*1;
<24= Ф*)со8фш 4-8й1ф*р;
й5= -2г.
146 * ’
Таким образом подъемная сила, момент крыла и шарнирный
момент полностью определены. Напомним, что все выводы сде-
ланы для случая крыла бесконечного удлинения. Покажем
теперь, как полученные формулы изменятся при переходе к крылу
конечного размаха.
5. АЭРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ КРЫЛА КОНЕЧНОГО
РАЗМАХА С ЭЛЕРОНОМ
Статическое значение Су в плоско-параллельном потоке всегда
может быть, как известно, представлено в виде:
Су СТ = ~ (®*СТ %), (35)
где аСт — угол атаки хорды профиля и а0 — угол атаки, при кото-
ром Су = 0. Это выражение может быть получено и непосред-
ственно из вышенаписанных формул.
Пусть (фиг. 42) MN—профиль крыла в статическом положении и xEz —
прямоугольная система координат, ось х которой ориентирована по скорости V
набегающего потока. Введем в рассмотрение также систему координат хгМг1г
начало которой совпадает с передней кромкой профиля п ось Л4 х направлена
по хорде его. Угол между хордой профиля и скоростью V набегающего
потока есть статический угол атаки аст, очевидно равный углу между осями х
и хг. Между координатами точек профиля в обеих системах координат имеем
зависимость:
и в силу равенств (29)
dz _ dzx______
dx ~~ dXi а<:т
(35а)
147
Подставляя значения До ст и Л1ст в первую из формул (30), будем иметь
СV ст = л <аст ао)>
где
К ч
а«=П ?д(,~со5ф)^
"о
зависит только от формы профиля. Таким образом формула (35) доказана.
Введя выражение (35) в формулу (31) для Су при неустано-
вившемся движении крыла, мы убеждаемся, что формула для Су
сохранит такую же структуру, как и формула (35), но только
вместо аст будем иметь величину а, где
а = аст + е + (|—+ <36>
Тогда
Су = ^(а-а0). (37)
Величину а можно рассматривать как мгновенное значение
угла атаки при движении крыла. Так как выражение (37) имеет
такую же структуру, как выражение (35) для статического
значения Cv, переход к конечному размаху можно совершить
так же, как это обычно делается в случае установившегося
движения.
При переходе к крылу конечного размаха к геометрическому
углу атаки1 добавляется еще угол скоса Да, возникающий вслед-
ствие влияния вихревых шнуров, сходящих с крыла. Добавляя
угол скоса в выражение (37), получаем значение С, для крыла
конечного размаха:
Су = *(а —а0—Да).
Это выражение представляем в следующем виде:
Величина 1 — ~1 есть, как известно, значение для
крыла конечного размаха, и мы имеем:
Си = ^ (38)
Вообще говоря, отношение - будет меняться по размаху.
В дальнейшем мы будем заменять это отношение неким средним
значением и считать не меняющимся вдоль размаха. За эту
dCv
величину принимается значение полученное из продувок
модели крыла в аэродинамической трубе.
1 Угол между направлением скорости набегающего потока в бесконечности
и хордой крыла.
148 ,
Таким образом, подставляя в выражение (38) значение а из
формулы (36), затем вычисляя приращение С относительно ста-
тического значения, имеем для крыла конечного размаха:
Г ’ + (т-т) v6+°₽:+ г 4 <39>
При вычислении момента крыла и шарнирного момента для
крыла конечного размаха мы воспользуемся тем обстоятель-
ством, что при угле атаки, при котором С — 0, около крыла нет
циркуляции, а следовательно, и нет сходящей с крыла вихревой
пелены. Следовательно, при угле атаки нулевой подъемной силы
аэродинамические характеристики крыла не зависят от удлине-
ния. Значение коэфициента момента относительно точки Е при
Су—0, согласно уравнению (31), будет:
с£е = Ч.е„--У* + /Р + 4₽-
Эта часть момента не зависит от удлинения. Для того же,
чтобы получить момент крыла конечного размаха при Су, от-
личном от нуля, нужно только в формулу (31) подставить со-
ответствующее значение С для крыла конечного размаха*.
Получаем:
СтЕ = С^ +(^-|) [Су ст + ACJ, (39а)
где ACV выражается формулой (39). Подставляя в это выраже-
ние значения СйтЕ и &Су и вычисляя приращение СтЕ по сравне-
нию со статическим значением, находим значение момента для
крыла конечного размаха:
®+'?+-'г₽+^(т-т)[в +
+ (t-t)v’ + °? + W (W)
Несколько сложнее осуществляется переход к конечному
размаху в выражении для шарнирного момента. Приращение
шарнирного момента по сравнению со статическим значением
для крыла в плоско-параллельном потоке, согласно уравнению
(33), равно:
д/иш =-P^[s1o-|-e21 ё + + l₽+2s^-zj. (41)
1 Для случая установившегося движения известно, что Ст есть линейная
Функция Су, причем ‘ ’ не зависит от удлинения, как и Ст- Здесь мы
имеем то же самое, так 'как в каждый момент времени поток считается уста-
новившимся (гипотеза стационарности), следовательно, не зависит от
Удлинения. У
149
В дальнейшем для краткости условимся вместо „приращение
силы (или момента) по сравнению со статическим значением"
говорить просто „сила" (или момент).
Выражение (41) представляет собой значение шарнирного мо-
мента на единицу длины элерона. Шарнирный момент на эле-
ментарном отсеке элерона шириной dy вдоль размаха (фиг. 43)
имеет, очевидно, следующее значение:
ЛЛ4Ш = - PZV2 [ 2хе 4- 23 4 б + 23? + S4 + S5±z]dy. (42)
Фиг. 43.
отсека крыла конечного размаха
Если элерон имеет
конечный размах, зна-
чения 2, будут отлич-
ны от вычисленных по
формулам (34), так как
эти формулы выведены
в предположении плос-
ко-параллельного по-
тока. Обозначим зна-
чения 2,- для крыла
конечного размаха че-
рез 2f. Тогда значение
шарнирного момента
для элементарного
будет:
=_p^v2[216 4-y2l 6 + 23p + 24l₽4-28iJ-Z]dy. (43
Для установления связи между коэфициентами 2- и 2; поль-
зуются экспериментальными данными.
1. При продувках в аэродинамической трубе определяется
коэфициент Сш, причем шарнирный момент относят к площади
элерона 5э и его моментной хорде
—Сшр5э^м^2. (44)
В этой формуле взят знак минус, так как при продувках
знак момента берется обратным принятому у нас.
Выше [формулы (42) и (43)] мы относили шарнирный момент
на каждом элементарном отсеке элерона к общей площади от-
сека всего крыла t dy (фиг. 43) и хорде крыла в данном сечении t.
В этом случае коэфициент момента будет отличаться от стан-
дартного Сш; его обозначают через Кш. Элементарный шарнир-
ный момент, отнесенный к площади элементарного отсека крыла
и к хорде крыла, запишется в следующем виде:
dMm =~КшрУЧЫу, . (45)
150
где /Сш — безразмерный коэфициент. Легко установить связь
между этим коэфициентом и известными из продувок значе-
ниями С
Суммируя элементарные моменты (45) по всем отсекам эле-
рона, получаем шарнирный момент, действующий на весь эле-
рон:
Уа
мш = —/СшрН2 f dy. (46)
У>
Сравнивая различные выражения (44) и (46) для одного и того
же шарнирного момента элерона, находим связь между Сш и Кш:
(47)
f t2 dy
yi
Таким образом, зная значения Сш из опыта, по этой формуле
можно вычислить и значения Кш.
Приращение элементарного шарнирного момента (45) вслед-
ствие колебательного движения можно записать в виде:
ДЛ)Ш = — д/<ш рИ^Му. (48)
Наша цель — найти зависимость между ЬКш, которое можно
выразить через экспериментально известные значения Сш, и вы-
ражением
^х0 +ё2^-ё +s3p + s4^₽+s5J-z.
Эту зависимость можно найти непосредственно, так как
истинный шарнирный момент (48) и теоретический (43) отнесены
к.одним и тем же характеристикам крыла.
2. Рассмотрим случай статического закручивания крыла,
когда
6 = p = p = Z = O; 0 ф 0.
Тогда выражение (43) сразу дает
Д/Иш = — р V42 2Х0 dy. (49)
Но закручивание крыла на угол 0 равносильно изменению угла
атаки хорды на тот же угол. Согласно уравнению (45), при уве-
личении угла атаки на величину Да = 0 получается приращение
шарнирного момента
Д/Иш = - Р У2*20 dy. (50)
0(2
__ Сравнивая выражения (49) и (50), находим, что коэфициент
определяется следующим равенством:
П, = (51)
151
3. Если мы рассматриваем
6 = 0 = р = Z = 0; ₽ ф О,
т. е. статическое отклонение элерона, то, рассуждая подобно
предыдущему, найдем, что
- “з— ар
4. Рассмотрим теперь случай чисто изгибных колебаний крыла,
когда
(52)
г
Фиг. 44.
0 = 6 = ₽ = ₽ = О: Z^O.
Если крыло (фиг. 44) движется вверх со скоростью Z, то
воздух относительно крыла движется вниз со скоростью — Z.
Складывая эту скорость
со скоростью набегающего
потока (фиг. 44), убеждаем-
ся, что аэродинамический
эффект изгибного движе-
ния сводится к изменению
угла атаки на величину
Даг = —FZ’
Приращение шарнирного
момента для крыла конечного размаха при таком изменении
угла атаки получим по формуле:
АЛ4Ш = — — ?V42dy=d-^- VZ& dy.
С другой стороны, в рассматриваемом случае 6 — р — 0 =
= ₽' =0 по формуле (43) находим:
Д7ИШ = — pVZ25£2 dy.
Сравнивая оба движения, получаем значение 25:
да
S
(53)
5. Переходим к отысканию коэфициента 23. Рассмотрим слу-
чай
0 = p=p=Z = O; 6^:0,
т. е. когда крыло вращается с определенной угловой скоростью
О, а отклонение элерона и изгиб отсутствуют. Значение шар-
нирного момента для элемента крыла бесконечного размаха в
этом случае находим по формуле (42);
Д/Иш =-PW3S26dy. (54)
152
В данном случае для перехода к крылу конечного раз-
маха воспользуемся высказанным выше положением о независи-
мости аэродинамических характеристик крыла при Су = 0 от
размаха, что объясняется отсутствием циркуляции около крыла
при Cj, = O.
Таким образом переход к конечному размаху осуществляется
следующим образом. Имеем вращающееся крыло бесконечного
размаха с элероном, обладающее шарнирным моментом [фор-
мула (54)] и определенным значением ЬСу, которое найдется по
формуле (31):
Поворачиваем крыло на угол ДО, который подберем таким
образом, чтобы 4(^ = 0. После поворота ЬСу, согласно уравне-
нию (31), будет равно:
и чтобы ACj, = 0, очевидно, необходимо, чтобы
М = -(4—т)4*- (55>
В новом положении значение шарнирного момента найдется по
формуле (42):
ДЛ4шо = - Р V4" [ 2Х • де 4- е
Согласно высказанному положению, этот момент одинаков
как для крыла конечного, так и для крыла бесконечного
размаха. Чтобы получить полное значение шарнирного момента
для крыла конечного размаха в рассматриваемый момент вре-
мени, нужно повернуть крыло обратно на угол—Д6. Этот по-
ворот для крыла конечного размаха, согласно формуле (43), из-
менит шарнирный момент на величину:
дЛ4ш = — ? У2/22х (- ДО) dy,
и полное значение шарнирного момента для элемента крыла
конечного размаха, следовательно, будет:
АЛ4Ш = дли 4- = — оV2*2 [(&х - йх) до 4- е2^ о].
То же значение по формуле (43) будет:
ДЛ4Ш = -РИ2/24£Л
, Сравнивая оба выражения, после подстановки ДО из выра-
жения (55) -находим:
й,= е,-(4-?)(в*-5"> =
= С=-(|-7)(а>-^)' <56)
153
6. Аналогично определяется значение 24. Рассматривается
случай
9 = 9= р = 2 = 0; р^О.
Значение ДС5, для рассматриваемого режима находим по фор-
муле (31). Затем поворачиваем элерон на угол Др таким обра-
зом, чтобы получить значение ДСу = 0. Согласно формуле (31),
находим, что Др будет определяться равенством:
ДСу = «[<7.ДЗ + А/7?]=О,
откуда
Ap=-^gp. <57)
По формуле (42) находим значение шарнирного момента для
крыла бесконечного размаха после поворота (согласно сделан-
ному предположению, оно сохранится без изменения и для
крыла конечного размаха):
ДЛ1шо = - р ИГ- [ез\р 4- 24 ' р] dy. (58)
Поворачиваем элерон обратно на тот же угол. Тогда для
крыла уже конечного размаха получим полное значение шарнир-
ного момента:
ДЛ4Ш = Д/Иш0 — 23р/2 V2 (— Др) dy.
Подставляя сюда значения ДЛ4ш0 из формулы (58) и Др из
равенства (57) и сравнивая полученное значение со значением
шарнирного момента в рассматриваемом случае, которое дается
формулой (43):
ДЛ/Ш =—
находим значение С4:
= S., - 4 (2з - 2з) = 2« - 4 (2з ~ <59>
Таким образом значения 2, полностью определены.
6. КРЫЛО БЕЗ ЭЛЕРОНА
Отметим здесь частный случай, когда на крыле отсутствует
элерон. Соответствующие формулы получаются из формул
(39) и (40) при р=р_ 0. Имеем:
154
Если ось вращения Е лежит на 25% хорды от передней
кромки — -j-J, то коэфициеит момента принимает значение
i^CmEO— ]g- у-6. (61)
Как известно, точка, лежащая на 25% хорды от передней
кромки, называется фокусом крыла и отличается тем свойством,
Что момент аэродинамических сил относительно этой точки не
меняется с изменением угла атаки и зависит исключительно от
формы профиля.
Существование фокуса легко доказывается следующим образом.
Согласно второй формуле (30), коэфициеит статического момента относи-
тельно точки, отстоящей иа 25% хорды от передней кромки может
быть записан в виде:
^тЕ ст ,= g— 6^1 ст + ^2 ст)’
причем, как выше указывалось, С®£ст не зависит от удлинения, так как это
есть момент, который получается при произвольном если Су = 0. Под-
ставляя в выражение С^Лст значения Д1СТ и Л2сг из формул (35а), убеж-
даемся, что С°£ст зависит исключительно от формы профиля.
Положение фокуса, найденное нами теоретически на 25% хорды для всех
профилей, в действительности для профилей различных форм несколько
изменяется, колеблясь в пределах 0,23 — 0,26 хорды. Для целей расчета иа
флаттер это незначительное изменение можно не учитывать.
Таким образом формула (61) дает изменение момента отно-
сительно фокуса профиля. Полное изменение момента при дви-
жении профиля [формула (60)] слагается из двух частей; из
изменения момента относительно фокуса профиля и изменения
за счет приращения подъемной силы.
Существенно отметить, что момент относительно фокуса
[формула (61)] всегда направлен в сторону, противоположную
направлению угловой скорости вращения профиля. Поэтому
при вибрациях этот момент является демпфирующим, т. е.
стремящимся гасить колебания.
ГЛАВА VII
КРИТИЧЕСКАЯ СКОРОСТЬ И СПОСОБЫ ЕЕ ОПРЕДЕЛЕНИЯ
1. ФЛАТТЕР КОНСТРУКЦИИ
В главах II — IV были изучены колебания крыла в пустоте.
Было показано, что если не учитывать явлений трения в кон-
струкции, то колебания
в пустоте будут гармо-
ническими с постоянной
амплитудой, т. е., раз
начавшись, будут про-
должаться вечно. Это
объясняется тем, что
энергия вибрирующей
системы остается посто-
янной — никуда не расхо-
дуется и не возрастает.
Если учесть потери энер-
' гии на трение в конструк-
ции и в материале (ги-
стерезис), то окажется,
что колебания будут за-
тухать (гл. II, п. 5). Меж-
ду колебаниями изгиба и
кручения существует
связь (за счет несовпа-
дения линии центров
тяжести и оси жесткости
крыла) такого рода, что
один вид движения не-
избежно порождает дру-
гой. Это означает, что
энергия изгиба трансфор-
мируется в энергию кру-
чения и обратно (гл. IV,
п. 1). Однако связь между колебаниями изгиба и кручения в
пустоте такова, что она не может изменить общего коли-
чества энергии в вибрирующей системе.
Картина меняется, если колебания крыла происходят в потоке
воздуха. При этом на крыле развиваются аэродинамические силы
156
(гл. VI), которые могут как поддерживать, так и противодей-
ствовать колебаниям.В первом случае колебания будут происхо-
дить с нарастающей амплитудой, во втором — колебания будут
затухающими. Колебания с нарастающей амплитудой, возни-
кающие в потоке воздуха под действием аэродинамических сил,
носят название колебаний типа флаттер. Они весьма опасны,
так как амплитуда колебаний нарастает весьма быстро, и кон-
струкция ломается. Ниже мы подробнее остановимся на характере
колебаний типа флаттер и их причинах, здесь же укажем только
на возможность их возникновения. Предположим, что крыло
вследствие какой-либо случайной причины (резкое движение
элеронами, воздушная яма и т. п.) изогнулось. Некоторое сече-
ние крыла при изгибе из положения равновесия ох (фиг. 45)
перейдет в положение I. После прекращения действия изги-
бающего импульса крыло под действием силы упругости начнет
двигаться к своему положению равновесия. Это движение будет
ускоренным и потому на точки крыла будут действовать силы
инерции, направленные в сторону, противоположную ускорению.
Напомним (см. гл. VI, п. 1), каким образом инерционные силы от
изгибного движения вызывают закручивание крыла. На точку А,
крыла, в которой сосредоточена масса /п,, очевидно, действует
&Z
сила инерции —Эта сила создает около оси жесткости
момент mixi где л£ — абсцисса точки At. Момент всех сил
инерции, действующих на элементарный отсек крыла между
сечениями у и у ф- dy, будет:
.. V д-Z &Z ,
= Д /«Л Й2 = dy. (1)
i
Этот момент вызовет крученье крыла. При этом существенно
отметить, в какую сторону будет закручиваться крыло. В поло-
жениях I—III (фиг. 45) крыло движется ускоренно к положе-
нию равновесия, т. е. отрицательно. Вейлу выражения (1)
момент Л4И будет отрицателен, следовательно, крыло перекру-
тится в сторону отрицательных углов атаки. После того как
крыло перейдет по инерции положение равновесия, знак уско-
рения переменится, следовательно, переменится и знак крутя-
щего момента — крыло будет раскручиваться (положения III—V).
Достигнув крайнего положения V, крыло под действием сил
упругости опять начнет двигаться ускоренно к положению
равновесия (положения V' VII)', ускорение будет положитель-
ным и, следовательно, крыло закрутится в сторону положитель-
ных углов атаки. В положениях VII—IX знак ускорения пере-
менится, и крыло будет раскручиваться.
Существенно подчеркнуть, что при движении вниз (фиг. 45)
Угол атаки крыла за счет кручения уменьшится, а при движе-
нии вверх — увеличится. Вследствие изменения угла атаки изме-
157
г
нится и подъемная сила, действующая на крыло. Дополнитель-
ная подъемная сила, которая получится за счет закручивания
крыла, будет направлена вниз при движении крыла вниз (положе-
ния I— V) и вверх при движении крыла вверх (положения V—IX,
фиг. 45). Таким образом эта подъемная сила усиливает дефор-
мацию изгиба, так как направлена всегда в ту же сторону,
в которую направлено изгибное движение крыла. Увеличение же
изгибных колебаний вызывает увеличение ускорения и тем
самым крутящего момента Л4И [формула (1)], что, в свою очередь,
вызовет увеличение кручения крыла, а следовательно, и подъем-
ной силы. Получается, что колебания изгиба вызывают такого
рода силы, которые стремятся дальше увеличить деформацию,
а это, в свою очередь, увеличивает силы, и так далее до тех пор,
пока не произойдет поломки крыла.
Схематически сказанное можно представить следующим
образом:
—> Вследствие случайного изгибаю- щего им- пульса воз- никают из- гибные ко- лебания Появляются силы инер- ции -> Силы инер- ции созда- ют момент около оси жесткости -> Крыло за- кручивает- ся под дей- ствием мо- мента инер- ционных сил -> Происхо- дит при- ращение подъемной силы, так как круче- ние изме- няет угол атаки —>
Происходит силы усиление изгибных колебаний под действием подъемной
Таким образом мы показали, что при колебаниях в потоке
воздуха появляются силы, стремящиеся эти колебания увели-
чить. Здесь мы рассмотрели далеко не все силы и моменты,
действующие на крыло во время колебаний в потоке воздуха.
Ниже мы дадим более полный и точный анализ причин возникно-
вения флаттера, здесь же мы хотели только показать, что флат-
тер возможен, и указать на качественную природу порождающих
его причин.
Возникает вопрос: если при любой случайной деформации
крыла всегда возникают силы, вызывающие- колебания с нара-
стающей амплитудой, то почему же вообще не разрушаются
крылья у каждого самолета? Объясняется это тем, что наряду
с возбуждающими силами при колебаниях в потоке воздуха
всегда имеются и демпфирующие силы. Например, демпфирую-
щей является аэродинамическая сила, зависящая от скорости
изгибных колебаний. Мы видели, что при движении крыла
вниз (положения /—V, фиг. 45) крыло перекручивается таким
образом, что угол атаки его уменьшается и вследствие этого
возникает дополнительная подъемная сила, действующая в сторону
движения. Но угол атаки будет изменяться не только за счет
перекручивания крыла, а также и вследствие того, что при дви-
158
женин крыла вниз относительная скорость воздуха будет на-
правлена вверх. Складывая эту скорость (очевидно, равную ско-
рости изгибных колебаний в данный момент времени и на-
правленную противоположно) со скоростью набегающего потока
(фиг. 45, внизу), мы убедимся, что угол атаки крыла изменится
на величину
(2)
. 1 dZ
да =-----—
V <3-’
причем угол атаки увеличивается (Ля > 0) при движении крыла
вниз (фиг. 45, внизу слева) и уменьшается (Да < 0) при движе-
нии крыла вверх (фиг. 45, внизу справа1). Вследствие этого из-
менения угла атаки также появится дополнительная подъемная
сила, которая будет направлена вверх при движении крыла вниз
(так как Аа>0) и вниз при движении крыла вверх (так как
Да < 0). Эта подъемная сила, в отличие от подъемной силы,
возникающей за счет кручения крыла, всегда направлена против
движения, т. е. она гасит (демпфирует) колебания.
Более детальный анализ показывает, что имеются и другие
возбуждающие и демпфирующие силы и моменты (например, за
счет угловой скорости крутильных колебаний). Все эти силы, как
и всякие аэродинамические силы, зависят от скорости набегаю-
щего на крыло потока воздуха. При малых скоростях обычно
возбуждающие воздействия бывают меньше, чем демпфирующие,
и потому возникающие колебания затухают2. Но с ростом ско-
рости возбуждающие воздействия растут быстрее, чем демпфи-
рующие, и, начиная с некоторой скорости, превосходят их. На-
чиная с этой скорости полета, возникающие колебания перестают
затухать. Скорость полета, с которой возникающие колебания
перестают затухать, носит название критической скорости
флаттера.
Опыт показывает, что при достижении критической скорости
амплитуда колебаний весьма быстро нарастает и происходит
разрушение конструкции. Поэтому в процессе проектирования
необходимо обеспечить конструкции такую критическую ско-
рость, которая лежала бы выше скорости, какой когда-либо
сможет достигнуть данный самолет. Для этого, очевидно, необ-
ходимо уметь определять критическую скорость конструкции,
а также знать, каким образом она зависит от различных кон-
структивных параметров. Решение этих двух вопросов и будет
нашей ближайшей задачей.
1 Так как ось Z направлена вверх (фиг. 45), то < 0 при движении вниз и
dZ Л
> 0 при движении вверх.
2 Ниже мы укажем примеры, когда возбуждающие силы превышают
Демпфирующие уже при сколь угодно малых скоростях. Однако эти случаи
Представляют только теоретический интерес.
159
Расчет на флаттер, т. е. определение критической скорости,
осложняется тем обстоятельством, что каждый самолет имеет
ряд критических скоростей. Мы показали, что изгибно-крутиль-
ные колебания крыла в потоке воздуха могут происходить с
нарастающей амплитудой. Но с нарастающей амплитудой могут
происходить не только изгибно-крутильные, но и другие виды
колебаний. Предположим, например, что крыло является абсо-
лютно жестким на кручение, но учтем, что на крыле имеется
элерон, могущий отклоняться относительно крыла (за счет упру-
гости проводки, люфтов и т. д.). В этом случае возможны сов-
местные колебания
крыла (изгибные) и
элерона, также с на-
растающей ампли-
тудой.
Пусть (фиг. 46)
крыло выведено из
положения равнове-
сия ох в положение /.
После прекращения
действия изгибаю-
щего импульса кры-
ло под действием
сил упругости нач-
нет двигаться уско-
ренно к своему по-
ложению равновесия
(положения I— III).
Так как центр тя-
жести элерона на-
ходится позади его
оси вращения, то под
действием сил инер-
ции элерон откло-
нится вверх относи-
тельно крыла. После
того как крыло по
инерции перейдет
положение равновесия (положения III—V), упругие силы начнут
действовать в обратную сторону, крыло будет двигаться замед-
ленно, и центр тяжести элерона будет по инерции догонять в
своем движении крыло. Из сказанного ясно, что при движении
крыла вниз элерон будет отклонен вверх. В следующем этапе
движения (положения V7' — IX), когда крыло будет двигаться
вверх, элерон по инерции будет отклоняться вниз.
За счет отклонения элерона возникнет дополнительная подъем-
ная сила, которая, очевидно, будет направлена вниз, если элерон
отклонен вверх,—и вверх если элерон отклонен вниз. Таким образом
в рассматриваемом случае подъемная сила, возникающая за счет
160
отклонения элерона от инерции, будет всегда направлена в ту
же сторону, куда движется крыло. Эта подъемная сила будет
стремиться увеличить колебания и вызвать флаттер1. Наряду
с возбуждающей в данном случае также имеется и демпфирующая
сила того же происхождения, как и в случае изгибно-крутиль-
ных колебаний. С увеличением скорости полета возбуждающая
сила растет быстрее демпфирующей и при достаточно большой
(критической) скорости возбуждающие воздействия превысят
демпфирующие,— возникнет флаттер, т. е. незатухающие коле-
бания с нарастающей амплитудой. Флаттер этой формы носит
название изгибно-элеронного.
Очевидно, критическая скорость изгибно-крутильного и кри-
тическая скорость изгибно-элеронного флаттера, вообще говоря,
различны. Это ясно хотя бы из того, что они зависят от различ-
ных параметров: критическая скорость изгибно-крутильного флат-
тера должна зависеть от жесткости крыла на кручение, в то
время как скорость изгибно-элеронного флаттера от жесткости
крыла на кручение не зависит, так как при изгибно-элеронном
флаттере крыло предполагается незакручивающимся. Критическая
скорость изгибно-элеронного флаттера должна зависеть от аэро-
динамической компенсации элерона, в то время как критическая
скорость изгибно-крутильного флаттера от аэродинамической
компенсации элерона не зависит, так как элерон предполагается
неотклоняющимся и т. д. Таким образом мы нашли две кри-
тических Скорости, которыми обладает крыло. Но, кроме этих двух,
могут быть и другие критические скорости: скорость крутильно-
элеронного флаттера (отсутствует изгиб крыла, но имеют место
закручивание крыла и отклонение элерона) и скорость изгибно-
крутильно-элеронного флаттера (крыло одновременно изгибается
и закручивается, а элерон отклоняется относительно крыла).
Таким образом крыло обладает четырьмя критическими скоро-
стями.
Хвостовое оперение обладает еще большим количеством кри-
тических скоростей, так как может испытывать больше различных
видов деформаций (изгиб и кручение стабилизатора, отклонения
Рулей, изгиб и кручение фюзеляжа и т. д.).
Резюмируя, можем сказать: различные части самолета могут
иметь множество различных форм совместных колебаний. Целый
Ряд форм совместных колебаний, вообще говоря, может перейти
во флаттер, т. е. в колебания, автоматически самоподдерживаю-
Щиеся за счет аэродинамических сил, и каждая из этих форм
обладает своей критической скоростью.
Конструктора, очевидно, интересует только наименьшая кри-
тическая скорость, так как уже она должна быть выше макси-
1 Подчеркиваем, что мы нигде не доказали, что движение будет происхо-
дить именно так, как мы выше изложили. Но для целей настоящей главы нам
Достаточно того, что такое движение возможно, а, следовательно, возможен
флаттер соответствующей формы. Более подробно и строго механизм воз-
икиовения флаттера будет рассмотрен ниже.
Троссман—15—и 161
мально достижимой для данного самолета скорости полета. Но,
к сожалению, не существует способа, который давал бы возмож-
ность заранее определить, какая из критических скоростей яв-
ляется наименьшей. Поэтому для каждой конструкции прихо-
дится на основе качественных соображений и статистических дан-
нух определять минимальное число расчетных случаев и произ-
водить расчет на каждый из них. Более подробно о выборе рас-
четных случаев мы скажем ниже.
Из изложенного вытекает способ построения расчетного ме-
тода. Мы установили, что критическая скорость — это такая
скорость полета, при которой возникающие колебания перестают
затухать. Следовательно, чтобы ее определить, необходимо прежде
всего предположить, что колебания существуют, и найти их ха-
рактеристики. Эти характеристики будут зависеть от скорости
полета, поскольку от нее зависят силы, действующие на вибрирую-
щую конструкцию. Затем необходимо рассмотреть, как меняется
характер колебаний в зависимости от скорости, и найти такую
скорость, при которой возникающие колебания перестают зату-
хать. Нарастание или затухание колебаний характеризуется лога-
рифмическим декрементом затухания (см. гл. II, п. 5), и крити-
ческая скорость — это такая скорость, при которой логарифмиче-
ский декремент затухания обращается в нуль (на меньшей
скорости он отрицателен — колебания затухают, на большей поло-
жителен,— колебания происходят с нарастающей амплитудой).
Но если декремент затухания равен нулю, то колебания будут
гармоническими — не нарастающими и не затухающими.
Таким образом мы получаем новое определение критической
скорости: критическая скорость—это такая скорость
полета, при которой возможны гармонические ко-
лебания с постоянной амплитудой.
При всякой другой скорости колебания будут либо затухаю-
щими, либо возрастающими.
Мы знаем, что каждое колебание можно разложить на сумму
стоячих колебаний. Каждое из стоячих колебаний обладает своим
декрементом затухания. При очень малых скоростях все декре-
менты затуханий, соответствующие различным стоячим коле-
баниям, отрицательны, поэтому конструкция может совершать
только затухающие колебания.
Пусть при увеличении скорости полета первым на некоторой
скорости V = обратился в нуль декремент затухания, соот-
ветствующий n-му тону колебания. Тогда при полете на ско-
рости все стоячие колебания за исключением и-го тона затух-
нут, и конструкция будет совершать гармонические колебания
формы n-го тона стоячих колебаний. Поэтому при определении
критической скорости можно найти ее для каждого стоячего
колебания в отдельности, а затем из всех найденных критиче-
ских скоростей определить наименьшую.
162
Подчеркнем здесь также, что критическая скорость не зави-
сит от начальных условий, т. е. от величины начального импульса.
Если скорость полета превышает критическую, то как бы ни был
мал начальный импульс, колебания будут происходить с на-
растающей амплитудой. Наоборот, если скорость полета меньше
критической, то каково бы ни было начальное возмущение, оно
будет затухать. Следовательно, определение критической скорости
есть задача устойчивости: на скорости, меньшей критической, кон-
струкция крыла устойчива (т. е., если дать крылу малое возму-
щение, то с течением времени последнее будет затухать и кон-
струкция вернется к положению равновесия), на скорости больше
критической — конструкция крыла неустойчива (т. е., если крыло
испытывает малое возмущение, то с течением времени это воз-
мущение нарастает вплоть до поломки крыла).
В теории флаттера ограничиваются определением критической
скорости и изучением зависимости этой скорости от конструк-
тивных параметров. Поэтому теория флаттера строится на основе
теории малых колебаний. Предполагается, что начальный импульс
вызывает малую деформацию, и определяется область устойчи-
вости конструкции.
Критическая скорость—это скорость, разграничивающая ско-
рости, при которых конструкция устойчива, от скоростей, при
которых конструкция неустойчива. Но, поскольку колебания
предполагаются малыми, теория флаттера не дает ответа на ряд
вопросов, например на вопрос о напряжениях, возникающих в кон-
струкции при флаттере, об изменении амплитуды колебаний во
времени и т. д. Теория не может дать ответа на эти вопросы,
так как при флаттере амплитуда колебаний нарастает весьма
быстро и достигает настолько значительной величины, что пред-
положение о малости колебаний теряет силу. Однако для практи-
ческих целей вполне достаточно из всех характеристик флаттера
знать только критическую скорость.
2. МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ СКОРОСТИ ИЗГИБНО-КРУТИЛЬ-
НОГО ФЛАТТЕРА КРЫЛА И ДИВЕРГЕНЦИИ
Для приближенного определения критической скорости флат-
тера можно воспользоваться принципом возможных перемещений.
При этом способ расчета аналогичен тому, который применялся
при вычислении частоты совместных колебаний в пустоте (гл. IV,
п. 2). Пусть крыло совершает изгибно-крутильные колебания
в потоке воздуха. Рассмотрим стоячее колебание. Значение про-
гиба и угла кручения, как всегда [см. формулы (221, гл. IV],
берем в виде:
2=/(у)^(т);| (3)
Считая форму колебаний f(y) и <р (г) известной, можем при-
нять q (') и г(') за обобщенные координаты. Составим уравнения
163
Лагранжа поэтам координатам. Так как при колебаниях в потоке
воздуха на крыло действуют внешние (аэродинамические) силы,
то уравнения Лагранжа берем в форме выражений (21), гл. I:
d ( ОТ \ дТ . ди _ п .
--1 —— j — — Wq,
dt \ dq J dq dq
d / дТ\ дТ , dU _ п ' '
d~ V dr ) dr dr r
Здесь T—кинетическая и U—потенциальная энергия вибрирую-
щего крыла, a Q(/, Qr—обобщенные силы, определяемые форму-
лами (8), гл. I:
где Рл;, Pzl — компоненты по осям координат внешней силы, дей-
ствующей в r-й точке колеблющейся системы, х„ z;—декартовы
координаты этой точки. Суммы распространяются по всем точкам
вибрирующей системы.
Выберем систему координат так же, как при изучении сов-
местных изгибно-крутильных колебаний крыла в пустоте (фиг. 26,
гл. IV) и сохраним те же обозначения. Выражение кинетической
и потенциальной энергии вибрирующего крыла было найдено
в гл. IV [см. формулы (12) и (13) этой главы]. Подставляя в эти
выражения значения Z и 6 из формул (3), находим:
т=4 спч2+4с^2+с^'г'
1G4
Для вычисления обобщенных сил воспользуемся выражением
декартовых координат произвольной точки Д' вибрирующего
крыла [гл. IV, формулы (10) и фиг. 26]. Подставляя
жения значения Z и 6 из
формул (3), находим:
х, = oj cos (у, + ?г);
2,- =fq — <J,sin (у,- + ©г).
Подставляем эти значения
в выражения (5). Будем
иметь:
в эти выра-
A
N
Фиг. 47.
где dPz— равнодействую-
щая всех внешних сил,
действующих на рассматри-
ваемый элементарный отсек
MN (фиг. 25, 26) вибрирую-
щего крыла:
Qr = — S 3< [p*isin <1+ °) + pzi cos (T, + 0)] ?.
Величина, стоящая в квадратных скобках, есть проекция силы
(с компонентами PXi, Р.. по осям), действующей в точке А'.
(фиг. 26 и 47) на нормаль (я) к отрезку о,, соединяющему точку А’.
с осью жесткости Е'. Для пояснения на фиг. 47 воспроизведена
фиг. 26 с добавлением компонентов внешней силы. Следовательно,
выражение
3, [Рх, sin (7г+ 6) + Pzt cos (к,- + 0)]
есть момент внешней силы, действующей в Д’г относительно оси
жесткости Е', но взятый с обратным знаком, так как положи-
тельное направление моментов нами выбрано в сторону увеличе-
ния угла атаки (от положительной оси z к положительной оси х).
Суммируя далее моменты сперва по всем точкам элементарного
отсека /WV (фиг. 25), а затем по всем элементарным отсекам
крыла, находим:
i
Or=f^-dME, (10)
о
где dME — результирующий момент относительно оси жесткости
всех внешних сил, действующих на элементарный отсек крыла ’.
1 Как всегда, в выражение dPz и dME нужно включать только силы и мо-
менты, возникшие вследствие вибраций, не учитывая статических значении.
Объясняется это тем, что до возникновения вибраций (в положении равновесия)
крыло находилось в равновесии и, следовательно, статические значения сил
и моментов сами собой уравновешиваются.
165
Внешними силами в рассматриваемой задаче являются силы аэро-
динамические, поэтому
dPz = SC^tV2dy, 1
dME = \CmE[i2V2dy, I
(И)
где ЬСу и ЬСтЕ— коэфициенты подъемной силы и ее момента
относительно оси жесткости, появившихся вследствие колебаний
крыла. Выражения их указаны в формулах (60) гл. VI. Подставляя
эти выражения в формулы (11), находим:
(12)
—Lz]}r4V2<Zj/.
Заменяя здесь 0 и Z их значениями из формул (3) и под-
ставляя результат в формулы (9) и (10), находим окончательные
выражения обобщенных сил:
Qtl ^-b^r—d^Vr-d^q-, I
Qr =— b22V2r - di2Vr—d2lVq, |
(13)
166
Пользуясь формулами (6) и (13), составляем уравнения Ла-
гранжа (4); получаем для определения q(~) и г(т) систему урав-
нений:
+ duVq + a^q + c12r + d12Vr + &l2V2r = 0; I
... ... } (15)
c2i<7 + d2lVq + a.,„r + c22r + d22Vr + b22V2r = 0. J
Это — линейная система диференциальных уравнении с посто-
янными коэфициентами. Как обычно, такая система интегрируется
подстановкой
q = Ае';
г = Be',
(16)
где А, В, I. — постоянные, подлежащие определению. Их нужно
определить так, чтобы выражения (16) удовлетворяли уравне-
ниям (15). Подставляя выражения (16) в уравнения (15), полу-
чаем систему линейных однородных алгебраических уравнений
для определения неизвестных А и В-.
А (си>-2 + + ап) + В (с^ + d13lA + 6121/2) = 0;)
А (c2J? + d2in.) + В (а2, 4- с2Л- + d22 4- b22I/2) = 0. j ( ’
Отличные от нуля значения А и В, удовлетворяющие этой си-
стеме уравнений, существуют тогда и только тогда, когда опре-
делитель системы равен нулю. Приравнивая нулю определитель
системы (17), получаем уравнение для определения 1:
где
Д0л‘ + 50)-3 + С0^ + ЦЛ + £о = 0, (18)
До — Д;
B0 = BLV-
С0=С14-С3И2;
£>„ = 2?^+ ZZV3;
£0 = E1+EaV2;
(1
^1 — Cll^22 ^*12^21»
== ^11^22 ^*11^22 * 12^21 ^*21^12 >
Cx = cna22 + a цС-221
~ d^O.22 4" G11^22> (20)
C, = cnb2i — bl2c214- dud22—d12d2l-,
Di^d^—b^d^
Найдя из уравнения (18) К, можем из системы (17) опреде-
лить А и В\ тем самым определяются q и г по формулам (16).
167
Подставляя значения (16) в формулы (3), находим:
Z = Af(y)e'\ I
I (21)
О = By (у) A J
В гл. II, п. 5 было показано, что если К — комплексное число
k - v + ip, (22)
то действительная часть к, т. е. величина >, есть логарифмический
декремент затухания, а коэфициент при мнимой части (р)— кру-
говая частота колебаний.
Уравнение (18), вообще говоря, имеет комплексные корни,
следовательно, колебания происходят с нарастающей (если v > 0)
или уменьшающейся (если v < 0) амплитудой. Найдем, при каком
условии уравнение (18) имеет чисто мнимый корень У=1р, т. е.
возможны гармонические колебания. Подставляя к — ip в урав-
нение (18), находим:
Л0р4 — 1В^рэ — С0р2 + iDop + Ео = 0. (23)
Это выражение разбиваем на действительную и мнимую части:
—СоР2 + ^о=О; I
p(Bop2-Da) = O. I
Рассмотрим сперва случай рфО. Тогда из второго уравне-
ния (24) находим:
Р2=%- (25)
Подставляя это значение в первое уравнение (24), приходим к сле-
дующему условию:
B0C0D0—в20е0 - D;a0 = 0. (26)
Если это условие выполнено и р определяется уравнением (25),
то система (24) удовлетворяется, а значит, удовлетворяется и
уравнение (23). Следовательно, в этом случае существует чисто
мнимое значение к, т. е. возможны гармонические колебания
с постоянной амплитудой.
Итак, колебания с постоянной амплитудой возможны, если
между коэфициентами характеристического уравнения (18) суще-
ствует зависимость (26). Но коэфициенты 50, Со, О0, Еи зависят
от скорости полета V. Следовательно, если определить скорость
так, чтобы условие (26) выполнялось, то при полете на этой ско-
рости будут возможны гармонические колебания с постоянной
амплитудой. По определению,— это будет критическая скорость.
Таким образом критическая скорость определяется из уравне-
ния (26). Запишем это уравнение в развернутом виде. Подставляя
значения (19) в уравнение (26), приходим к следующему урав"
нению:
V\L Vi + MV2 4- N) = 0, (27)
168
где
L = ВХСЛЕ — DlA»
M = B£DV + Bfifi., - B{E2 - 2D,D.,A^
N = BfiJ^- Bfo - dMx.
(28)
Уравнение (27) имеет корень V = 0. Этот корень соответ-
ствует гармоническим колебаниям в пустоте, в чем можно непо-
средственно убедиться из рассмотрения уравнений (24). Второе из
этих уравнений при V — 0 удовлетворяется тождественно (так
как Вй = Dn = 0), а первое дает:
Д1р4-С1р2 + £'1=0,
т. е. опять уравнение (29) гл. IV, из которого мы определяли
частоты совместных колебаний в пустоте. Естественно, что ко-
рень V = 0 должен был получиться, так как мы искали скорость,
при которой возможны гармонические колебания постоянной
амплитуды. В частности такие колебания возможны в пустоте,
т. е. при V = 0. Этот корень будет отсутствовать, если учесть
силы трения в конструкции и гистерезис материала.
Колебания в пустоте были подробно изучены выше, и мы в
дальнейшем корнем И = 0 интересоваться не будем. Тогда для
определения критической скорости флаттера остается уравнение:
ZVr*4-AIVr2 + A^ = 0. (29)
По этому уравнению мы можем вычислить критическую ско-
рость, если будут известны коэфициенты L, М, N. Все величины,
необходимые для их вычисления, известны, за исключением
функций формы колебания f(y) и ^(у), которые входят в выра-
жения коэфициентов (7) и (14). При расчетах эти функции за-
дают приближенно, на основе предположения, что форма коле-
баний крыла в потоке воздуха мало отличается от формы ко-
лебаний его в пустоте. Если это так, то можно вычислить форму
колебаний крыла в пустоте одним из методов, указанных в
гл. II—IV, и найденные таким образом функции принять за ос-
нову при расчете критической скорости.
Уравнение (26), определяющее критическую скорость, мы могли
Получить непосредственно на основе общих теорем об устойчи-
вости. Мы видели, что движение будет устойчиво тогда и только
тогда, когда уравнение (18) имеет все корни с отрицательной
вещественной частью. Известно, что уравнение (18) четвертой
степени будет иметь все корни с отрицательной вещественной
частью только в том случае, когда все его коэфициенты и ди-
скриминант Рута R = В0СаГ)й—В%Е0—D~A0 будут одного знака.
Так как Ап> 0 (см. стр. 117), то значит, мы имеем следующие усло-
вия устойчивости:
Boz>0', Со > 0; L>o>0; Е0>0; (26а)
R = В0С0Do - В* Ео - D* Ао = V\L И+Л1 V*+N) >0. J1
169
Легко видеть, что условия А0>0 и В0>0 выполняются при
всех скоростях. При очень малых скоростях, как известно, флат-
тера нет, а потому должны выполняться и остальные условия
устойчивости. С ростом скорости первыми могут обратиться в
нуль только Ео или /?, так как при Со=0 или Do = 0 величина
R уже отрицательна. Следовательно, критическая скорость оп-
ределяется либо из уравнения Ео = 0, которое будет рассмотрено
ниже, либо из условия /? = 0, что приводит к уравнению (29).
Таким образом имеем следующую схему определения крити-
ческой скорости изгибно-крутильного флаттера крыла:
1. Определяются функции [/(у) и 9(у)] формы колебаний
крыла в пустоте. Методы определения этих функций изложены
в гл. II, III и IV. Удобнее всего пользоваться методом последо-
вательных приближений.
2. Когда /(у) и фСу) определены, вычисляются коэфициенты
по формулам (7) и (14).
3. По формулам (20) вычисляются коэфициенты характери-
стического уравнения, и затем по формулам (28) определяются
L, М, N.
4. Определяется критическая скорость решением биквадрат-
ного уравнения (29).
Анализируя систему (24), мы рассмотрели случай р ф 0. Пред-
положим теперь, что р— 0. Как было показано в гл. II, п. 5,
движение в таком случае носит характер дивергенции — аперио-
дического отклонения от положения равновесия. При этом удов-
летворяется второе из уравнений (24). Чтобы было удовлетво-
рено также и первое уравнение (24), необходимо, чтобы
£о = О. (30)
Это условие служит для определения критической скорости
дивергенции. Подставляя в него £0 из обозначений (19), а затем
Ех и Е2 из обозначений (20), находим значение критической ско-
рости дивергенции:
Удив = / - . (31)
Ниже мы подробно остановимся на явлении дивергенции и не-
посредственно из рассмотрения физических причин, порождаю-
щих ее, опять получим выражение критической скорости дивер-
генции. В настоящей же главе ограничимся изучением флаттера.
Уравнение (26), определяющее критическую скорость, можно
было получить несколько проще.
Для определения <7(~) и г(т) мы получили систему (15),
решение которой мы искали в виде (16). Решение в этом виде
существует при любой скорости полета. Но можно было сразу
искать решение в виде:
q = Ае1р'-,
r — Belpz, (32)
170
т е. заранее
колебанияи
.-.яженпи (3~)
предположить, что крыло совершает тар ионические
ктоянной амплитуды. Однако решение в виде вы-
существует не всегда, а только в том случае, если
Скорость полета равна критической. Поэтому, если мы ищем ре-
шение системы (15) в виде (32), мы должны также получить ус-
ловие, при котором такое решение существует.
Подставляя значения (32) в систему (15), получим для опре-
деления А и В вместо системы (17) следующие уравнения:
А (— OiР2 + УР + «и) + В(—с12 p2+i5f12Vp+ b12Е2)=0; |
A (—Oi Р2 + idn Vp) + В (а22 — с22 р* + id22 Vp + b22 И2) = 0. J(
Приравнивая нулю определитель этой системы, получим опять
сравнение (23). Приравнивая действительную и мнимую части
полученного уравнения по отдельности нулю, приходим к си-
стеме (24). Как мы уже видели, удовлетворить обоим уравнениям
этой системы одновременно можно только значением р, опреде-
ленным по уравнению (25), и значением V, определенным по
уравнению (26;.
Пример расчета изгибно-крутильного флаттера. Требуется опре-
делить критическую скорость изгибно-крутильного флаттера
крыла, расчетные данные которого приведены в табл. 11.
Таблица II
Расчетные данные крыла
_____(в кг см сек) *
У 1 Е1 GIP m ' t О / (СМ. табл. 6) <р (см. табл. 1)
0 82-109 99.2-10s 0.168-10-2 0.32-102 500 80 0 0
0.1 76.8-109 98.5-10s 0,168-Ю-2 0,32-Ю2 500 80 0,01912 0,0785
0,2 64.9-109 90.5-108 0,126-Ю-2 0.227-102 500 80 0,0752 0,1541
0.3 49.4-10° 69-10s 0,093-Ю-2 0.157-Ю2 500 80 0.1637 0.234
0,4 34.9-109 41,4-10s 0,077-10-2 0.1234-Ю2 455 728 0,296 0,334
0.5 20.4-109 30,7-108 0,068-IO-2 0.097-102 405 64.9 0,465 0,452
0.6 12,4-109 21,5-108 0,063-Ю-2 0.0817-102 355 56.9 0,680 0.511
0.7 6,61 Ю9 11,82-10s 0,051-I0-2 0.053-102 305 48.9 0.942 0.690
0.8 3,05-109 5,12-108 0,035-КГ2 0.0265-Ю2 255 40.9 1,258 0.816
0.9 1.16-Ю9 2.165-108 0,025-10-2 0.0123-102 205 32,8 1,618 0.938
1 0.31 -109 0.591 • 108 0,019-Ю-2 0.00816-Ю2 155 24.8 2.000 1.0
х0 0,313 /; /=675;
-СЧ=1,99; р=0,125-10-9;
да
171
в
Вычисления коэфициентов по данным табл. 11 Таблица 12
VI IX >4 ы» v> m ю ю vs 41 VSl oooooooooo о ’И- Ю Г- —• tO —• CO m Ю -rf - m — ?i cc -t Tf н x ° Q о о о о о о И оо о 1 2,558-10’
ei VIII • IX X 0 0 0077-108 0 02975-108 0.0685-1 О’ 0 104-Ю8 0,136-108 0 146-Ю8 0 135-Ю8 0,111-Ю8 0.076-108 0,0372-Ю8 0,8326-1 О’
1 XI — ccoomm л О О СМ Ш — ОП > р GO ооо-рш О 00 о о о о о о о о о о ~
-»w 111Л со оо со со » со сс <» оо ® до ООООООООООО ю*п*пюсотг-ю-— ооо'Ч-®.0- сооо
1 ICP *г1р > - 1 VI! I ю vs ю vj щ ю vs «а vs io_ о о о о о о о о о о f-.mcioo'o-i-cninciooo u t- c.o-txcorjr re о О el К -г о 'P'C c gdedo'oo'oo о" I 3,322-10’
Cl V! ю *» vs m v> щ *» v? ю «о w ООООООООООО ЮЮЮЮЬ-тЮП - тг о о
I IV > см см ю о со см — ш — со о СОЮ с ю о С CN о Is* ’t о П О о — СО СО О Г- ОСО см — см то О 00 см оо о
т от т со о о 'С /-.от оо f о см о т ^оосмсо—ооооо — о^о оо см со т о о с о 6 с о о о ci 4
9 Ill — с 1^ со ю с о со о тid т т г- со" см —«о -ТГООСООО — — — — СМ СО С" 1 о см см о
I т о см Л --OOOCQ 00 00 о — оо о —«оотсм — ооооосм со тот о о о о о о о о — — см
1 *>» *—* ооооттттттт оооотототот тттт^^сососмсм*-
••Ml 1 0 0.1 02 0.3 0.4 05 0,6 0,7 0.8 09 1,0
•22
В гл. II был произведен расчет этого крыла на чисто кру-
тильные колебания (табл. 1 и 2). В табл. 2 были вычислены коэ-
фициенты аэо И ^*22* Было получено:
а2, = 0,357 • 107; г22 = 13,08 • 102.
Расчет этого крыла на чисто изгибные колебания произведен
в гл. III (табл. 6 и 7). В табл. 7 вычислены
ап = 504; си =0,252.
произведен расчет совместных колебаний этого
<
с12 = с21 —7,91.
вычислению остальных коэфициентов [обозна-
За функции f и if принимаем соответствующие
В табл. 9 был
крыла и найдено:
Приступаем к
чения (7) и (14)].
функции формы изгибных (табл. 6) и крутильных (табл. 1) коле-
баний. Вычисление всех коэфициентов произведено в табл. 11 и 12.
результате получено:
0,296- 10~3;
du = 0,444 • КГ*;
du = —0,0353;
d.n = 0,00509;
d.,, = 1,44;
d22 = —0,00391.
Далее вычисляем коэфициенты (20):
= гис22— с12с21 = 0,267 • 10я;
— ^11^*22 “Р ^llP-2 C^-^dyn —• 0,704,
= cua22 + аис22 = 1,558 -10е;
D, = d.,a„„ + a.,d^ = 0,231 • 104;
Ег = anai2 = 0,1798 • 1010;
С2 = С11622— &i2c2i + ^н^22— ^12^21 = —0,2506 • 10-®;
©2 — — bi2da — — 0,23 10“®;
Д2 = au&22 = —1,97.
формулам (28) имеем:
L = B^D., -DlAt = 0,3918 • 10-8;
M = + B^D» - Д2 Д2 — 2DJXA' = — 3,068;
W = B£J\ -BlEi-D'A^QZVZ-W.
По
173
Затем вычисляем критическую скорость по уравнению (29):
= „0,651.1С«,
откуда по извлечении квадратного-корня
V = 0,807 10* см /сек = 80,7 м/сек = 293 км/час.
3. СТАНДАРТНЫЙ СПОСОБ РАСЧЕТА
Для прикидочного расчета критической скорости изгибно-кру-
тильного флаттера крыла можно воспользоваться так называе-
мым стандартным методом расчета. Метод этот состоит в том,
что в качестве функций/(у) и ?(у) выбираются функции формы
колебаний крыла постоянного сечения в пустоте (гл. II, формула
(17) и гл. III, формула (25)]. Числовые значения этих функций и
их производных могут быть вычислены раз навсегда, и тем са-
мым расчет сильно сокращается, так как отпадает необходимость
определять функции формы колебания в пустоте. Функции формы
колебаний крыла постоянного сечения в пустоте носят название
стандартных функций. Их числовые значения и числовые значе-
ния их производных приведены Ь табл. 13.
Таблиц а 13
ф| /(У) ?(У) /ф /• /* Ч>* (<Р*)3 j (/*)2
0 0 0 0 0 0 2,0 1 1 4.0
0.1 0,0335 0,1564 0,00524 0.00112 0,02446 1,718 0,9875 0.975 2,93
0.2 0,1277 0,309 0.03946 0,01631 0.09548 1,448 0,951 0,905 2.095
0,3 0,2641 0,4539 0.1119 0,06975 0.206 1,190 0.891 0.794 1,417
0,4 0,4598 0,5877 0,2702 0.2114 0,3454 0,921 0,809 0,655 0848
0.5 0,6789 0,707 0,4801 0,4609 0.5 0,6875 0707 0.5 0.4725
0,6 0,9222 0.809 0,7461 0 8505 0.6546 0,4585 0.588 0,346 0,2095
0.7 1,1816 0.891 1,0528 1.3962 0,7939 0.273 0,443 0.196 0,0745
0,8 1,4519 0.951 1,3808 2.108 0,9044 0,1277 0,308 0.095 0,01629
0.9 1,7246 0,9876 1,7032 2.9742 0,9754 0,0333 0,1518 0,023 0,00111
1,0 20 1.0 2.0 *7 / 4,0 1 875 у 1,00 ' ’ dy 0 л , = 2/И 0 0 0
Г74
Стандартный метод расчета основан на том, что, как выясни-
лось в результате расчетов ряда крыльев, функции формы коле-
бания различных крыльев отличаются от стандартных не настолько,
чтобы это различие значительно сказалось на величине крити-
ческой скорости. Однако это справедливо не всегда, и встречаются
такие конструкции, для которых вид функций формы сильно от-
личается от стандартных и критическая скорость которых сильно
зависит -от вида функций. Поэтому применение стандартного ме-
тода расчета критической скорости возможно только в процессе
предварительных прикидок, чтобы быстрее выявить влияние кон-
структивных параметров крыла. Окончательный расчет всегда
должен быть произведен с функциями, определенными для дан-
ного крыла расчетом колебаний в пустоте. Это тем более необ-
ходимо, что стандартный метод расчета обычно дает завышенное
значение критической скорости и потому не обеспечивает без-
опасности.
Подробнее влияние вида функций на величину критической
скорости будет рассмотрено в гл. X.
г
4. ПРИМЕНЕНИЕ МЕТОДА ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
ДЛЯ РАСЧЕТА КОЛЕБАНИЙ КРЫЛА В ПОТОКЕ ВОЗДУХА
Для получения уравнений движения крыла, колеблющегося в
потоке воздуха, будем исходить из тех же уравнений упругой
линии, как и в случае совместных колебаний крыла в пустоте
[(гл. IV, формулы (5)]:
fKId*Z\ )
I (34)
ШО—I
где s — погонная нагрузка, а р- — погонный крутящий момент. В
случае колебаний в пустоте крыло было нагружено только си-
лами инерции. Величина s являлась суммой погонных сил инер-
ции, а р. — суммой их моментов относительно оси жесткости
[формулы (6а), гл. IV]. В случае колебаний в потоке воздуха
в величину s следует включить также погонную подъемную силу,
а в р.— погонный аэродинамический момент относительно оси
жесткости. Поэтому имеем:
s = — т—^ + та + ±Cy?tV~,
d2Z I I г /21/2
и = Ш —jp,---
Подставляем сюда значения ДСу и ЛСт£- [формулы (60), гл. VI],
а затем полученный результат — в формулы (34). Получаем >рав-
175
нения движения крыла, колеблющегося в потоке воздуха:
d20 dCv|fi .
~тсы - diTJ +
-v-d1|^2=0’
. . d20 f n t dO .
"*f 16" ~V d-1'
~ IT ^2l/2=:0-
V dz V dz If •
d2Z
dz2
;0\ JL^8
! ) V dz
d2Z
m?
I СГд?\ I
3-s ( El 5-5-) + m
dy" к dy1 ) '•
d <?0 \
dy ( P dy ) 1
dCv / x- 1 \r . (
(35)
Л»
Условимся в дальнейшем для краткости называть эти уравне-
ния уравнениями флаттера.
В п. 2 настоящей главы был получен приближенный метод
определения критической скорости, базирующийся на уравнениях
Лагранжа, т. е. на рассмотрении работы сил на пути возможных
перемещений. Можно составить выражение работы, не пользуясь
уравнениями Лагранжа, а непосредственно исходя из уравнений
движения (35) (метод Галеркина).
Первое из уравнений (35) есть условие равенства нулю сил,
действующих в каждом сечении крыла, а второе — моментов от-
носительно оси жесткости. Умножим левые части обоих’ уравне-
ний на dy, получим выражения сил и моментов, действующих
на элементарный отсек крыла длиной dy вдоль размаха. Чтобы
получить работу этих сил при деформации, умножим выражение
сил на прогиб Z, а выражение моментов — на угол кручения 6.
Затем просуммируем работу по всем элементарным отсекам крыла,
т. е. проинтегрируем результат в пределах от нуля до I. При-
равнивая работу всех действующих на крыло сил нулю, получаем:
и
+ ( 4—v)4-£~T-£]
Г( д / г, &\\ d2 *Z . r d20 ( zz I дО ,
J { dy р dy) mZ dz2 + mdz2 I IG V dz +
0 '
(36)
+S’(t—4)[е+(т-?)г"-р-ЯкНв^“0-
Если теперь подставить в эти выражения значения Z и 0 из
формул (3) и воспользоваться обозначениями^?) и (14), мы опять
придем к системе уравнений (15). Следовательно, применение мето-
да Галеркина к уравнениям флаттера приводит к тем же резуль-
татам, к каким мы пришли, базируясь на уравнениях Лагранжа1.
1 Заметим, что уравнения (35) мы могли умножить не на Z и в, а на f<y)
и 5f(y). Результаты были бы те же. так как Z = f(y)q(z) и 0 = <р(у) г(")-
Множители q(z) и r(t) в уравнениях (36) сокращаются.
176
Изложенным методом определения критической скорости
нельзя найти форму колебаний крыла в потоке воздуха. Кроме
того, этот метод дает приближенное значение критической ско-
рости, так как закон изменения по размаху крыла прогиба f(y)
и угла кручения <?(_у) принят приближенно. Чтобы получить бо-
iee точное значение критической скорости, можно применить
метод последовательных приближений.
Решение уравнений (35), как и всегда, будем искать в виде;
Z = Af(y)eip--
6 = By (_у) е!р\
(37)
Таким образом Z и 0 ищутся как гармонические функции
времени, т. е. заранее предполагается, что крыло совершает гар-
монические колебания с постоянной амплитудой. Как мы знаем,
это возможно только при скорости полета, равной критической,
и следовательно, решение в виде (37) существует только при
V = Икр.
При изучении чисто крутильных колебаний крыла (гл. II, п. 5)
мы убедились, что, если уравнение колебаний содержит член с
первой производной от угла кручения по времени, то движение
происходит со сдвигом фазы колебания между отдельными се-
чениями крыла. Математически это характеризуется тем, что
функция (?(_у) комплексна. Пользуясь тем же методом, которым
мы пользовались при рассмотрении чисто крутильных колебаний,
можно доказать, что выражения (37) могут удовлетворять уравне-
ниям (35) только при комплексных значениях функций f(y) и (_у).
Постоянные А и В также будут комплексными. Ниже мы уви-
дим, почему это так, и убедимся, что комплексность функций
f(y) и ср(_у) означает, что колебания как изгиба, так и кручения
происходят со сдвигом фаз между отдельными сечениями крыла,
т. е. максимальные амплитуды и нулевые положения в различ-
ных сечениях достигаются в разное время.
Итак, пусть
/(у)=А(у) + ^.(у)\]
А = А, -НА.,; )
В=В1+,К.) <39)
Подставляя эти значения в уравнения (37), получим Z и 0 в
виде комплексных функций от у и т. Легко доказать, как это
МЫ доказывали для случая чистого крученйя, что уравнения (37)
дут иметь и сопряженное решение:
Z = Af(y)e-p'-,
в = В <f (у)е~и ,
(40)
Гроссман—15—12
177
где
/Су)=/1(3') — ifi(y)-,
?0') = чЛу) — 1Ъ(У\,
А — At — М2;
В = Вг — iB.,.
(41)
Беря сумму обоих решений, найдем решение, выраженное
через действительные функции:
Z = 2 (ДjA— A,/,) cos р-. - 2 (A2ft + AJ2) sin pz- I
6 = 2(Д<р,— Z?,<p2) cos pt— 2 (£?.,(?!+ #!<(>,) sin/n. J
Введем новые функции f0(y), 40(y), '?i(_y)> tyjy), выражающиеся
через ЛОО, ЛОО, 'PiOO, fa(v) следующим образом:
ЛОО = 2 /И1Л - л=Л)2 + И2Л + AJJ ;
?о GO = 2 V (^ifi — B^ + (BMi + ;
t&’J'iO) =
^2 А “Ь ^ifz
^2/2
(43)
tg'?2(J') =
В2Ч1 + B\'~2
В,<р! — B2<p2
Тогда формулы (42) могут быть переписаны в следующей форме:
Z = f0(y)- cos [рх 4-ф1(з/)]; 1
6 = ТоОО • cos [pt + (.у)]. I
(44)
Из этих формул характер движения виден совершенно ясно.
Движение, конечно, гармоническое с периодом Т = у. Сущест-
вует сдвиг фаз между отдельными сечениями крыла как в коле-
баниях изгиба, так и в колебаниях кручения, т. е. максимальная
амплитуда в различных сечениях достигается в различные мо-
менты времени.
В самом деле, приравнивая нулю угловую скорость крутиль-
ных колебаний и скорость линейных колебаний найдем из
полученных таким образом уравнений значения т. Это и будут
те моменты времени, в которые достигается максимальная ампли
туда:
“аг = —Л О') • Р • sin [р- + бДу/)] = 0;
~ 'f'oG')-Р-sin [рт + '!>2 0')] = О.
178
Из этих уравнений находим, что максимальная амплитуда из-
гибных колебаний достигается в моменты:
Ттах из = — Ф1(у) 4 р ,
а максимальная амплитуда крутильных колебаний — в моменты:
* _ _ 1 I /.Л I П7С
"Стах кр---— у2 (У) -j ~
(п — любое целое число).
Из этих выражений видно, что максимальная амплитуда как
тех, так и других колебаний достигается в разных сечениях
крыла в разное время ("тах зависит от у), т. е. существует сдвиг
фаз между колебаниями различных сечений. Сдвига фаз не будет,
если (у) и ф2 (у) обратятся в постоянные (не будут зависеть
от у), что, очевидно, будет иметь место, если f2{y} — 0 и <р,(у) =0,
т. е. если уравнения (35) имеют интегралы в виде выражений (37),
содержащие вещественные функции /(у) и (у). Как мы уже ука-
зывали выше,’ можно доказать, что f и <р обязательно должны
быть комплексными и, следовательно, сдвиг фаз колебания между
отдельными сечениями при флаттере всегда имеет место.
Второе следствие, которое вытекает из выражений для ттах,
заключается в том, что в каждом сечении крыла максимальные
амплитуды изгиба и кручения достигаются в различное время
[так как функции <рг(у) и ф2(у) различны] и, следовательно, сдвиг
фаз существует не только между колебаниями различных сече-
ний, но также и между изгибными и крутильными колебаниями
одного и того же сечения.
Выяснив таким образом физический смысл получаемых реше-
ний, приступаем к изложению метода последовательных прибли-
жений для расчета флаттера.
Выражения (37) в силу значений (38) можно переписать в
следующем виде:
Z = A\fx{y)^ifMeip'-, ]
} (4у)
6 = B[<fi(y) + to2(y)]ev'. j
Прогиб Z и угол кручения 6 должны удовлетворять тем же
граничным условиям, которым они удовлетворяли и при колеба-
ниях в пустоте [гл. IV, формулы (8)]. В силу этого имеем сле-
дующие граничные условия для функций Л (у), Л (у), ?i(y), ?2(у)
При у = 0
А=о;
/.=<>; ->=0; л“°-
При у = I
- О’ = 0’ — = О’
и’ dy dy ", (4б)
У“=0; -^ = 0; ?v2 = 0.
су* djf3 dy
179
Подставляя выражения (45) в уравнения движения (35), получим:
4 »+г +ад+
+2'р'/«р(А+ад)+ ,
+ а{тзр2(о1 + /ф.)— —
-§^2(т-7;Ы’,> + ад1 =0;
a {»»m+ад+—г)(/.+ад}+
+®(—" (Ч€) ^-'„Ал+ад-
т Р- 4-) (т,+ад - fvpip (а - 4) [4 -
10 I —. I I
да \ t 4 / -*
Как уже было сказано, мы интегрируем уравнения методом
последовательных приближений. Этот метод состоит в том, что
мы задаемся какими-либо значениями функций /1( /2, <рг, <р,2 и
затем, исходя из заданных, ищем новые значения функций,
ближе соответствующие точному решению уравнения (35). Сле-
довательно, полагаем, что функции нам известны, — мы ими
задались.
Умножим первое из уравнений (47) на ft — if,, второе —на
<рх — iv, и результат проинтегрируем в пределах от нуля до /.
Придём к следующей системе уравнений, определяющих А и В:
А [ап - сир2 + idnp И] + В [- с12р2 + Ь^У2 + idlzpV +
+ i (— с12р2 + b'^V" + id[2pV)] = 0;
Al~ cnP2 + id2ipy + i (— c2iP2 + «АцрИ)] +
(48)
где
+ В [a22— c,,p2 + Ь2„У2 + id,2pV] = 0,
(49)
180
р.1* (/л + a<?2) dy ’
0
dC 1
b'i2=- ~d<h JA?i) dy;
0
»=— т p fr- (т-4) «+fi)4y,
0
I
~da=^J‘(f,+ftdy
0
I
da=-‘^-t J> (I - -;)(/,?,+ ЛЫ dy,
0
I
(t-4") -f^dy,
0
z
<*a=^P ft’-^-^ff^+f^dy,
0
I
(49)
1
c2i = Си = — / +f№)dy;
0
I
<1 = — ^'2 = J tnz^^—f^dy,
Ci~ =J fm(^+^)dy.
0
и В.
этим
Уравнения (48) служат для определения неизвестных А
Но значения А и В, отличные от нуля и удовлетворяющие ---
Уравнениям, существуют только тогда, когда равен нулю опре-
делитель этой системы.
Приравниваем нулю определитель системы (48) и, разбив
Получившееся равенство на действительную и мнимую части,
181
находим уравнения, которым должны удовлетворять р и I/, чтобы
существовали решения исходных уравнений в заданной форме:
Аг(Р, К)=0;|
Д2(р, Г) = 0. J
(50)
Решив систему (50), находим значения р и V, соответствую-
щие тем функциям, которыми мы задались. Когда р и V опре-
делены, подставляем их в уравнения (48) и находим отношение
&. Это отношение получается в виде комплексного числа:
А , . .,
В ~~ + l'J-‘
Обращаемся к уравнениям (47). Делим первое уравнение
на А, второе на В, и в каждом уравнении в отдельности при-
равниваем нулю действительную и мнимую части. В результате
получим четыре уравнения:
= R- d (gi = Ф, •
dy2 I dy2 J dy \ p dy ) n
ay2 = f2-, dl dy\ =ф«. (51)
А
где функции Flt F.,, Ф„ Ф2 зависят от Д, f.,. <р2, р, V, -&
и конструктивных параметров крыла.
Задавшись исходными функциями Д, Д, <р2, мы вычислили
соответствующие им значения р, И и у. Подставляя эти зна-
чения вместе с исходными функциями в правые части урав-
нений (51), мы можем вычислить значения F.,, Фь Ф2 в каж-
дом сечении крыла. Таким образом правые части уравнений (51)
теперь нам известны. Интегрируем каждое из уравнений (51)
тем же способом, каким интегрировались уравнения чисто изгиб-
ных и чисто крутильных колебаний (гл. И и III). При этом инте-
грировании должны быть приняты во внимание граничные усло-
вия (46). Так, например, интегрируя первое из уравнений (51) и
выбирая при этом пределы интегрирования так, чтобы удовле-
творить граничным условиям, получаем:
у v у у
Л = f ^dydy,dydy.
0 0 I I
В результате интегрирования уравнений (51) находим новые
значения функций Д, Д, <рг, <?2.
С найденными таким образом значениями Д, Д, <?lt <р.2 повто-
ряем сначала весь процесс вычислений. Находим соответствую-
щие вновь найденным функциям значения частоты р, критиче-
ской скорости V и отношения „ . Затем опять подставляем эти
О
значения в правые части уравнений (51) и в результате инте'
182
грирования этих уравнений находим новые значения функций
/и Л» fi> Чг- Процесс вычислений повторяем до тех пор, пока
функции, полученные в двух следующих друг за другом при-
ближениях, не совпадут. Значение критической скорости, полу-
ченное в последнем приближении, и дает точное решение задачи \
В дальнейшем (для крыла с элероном, хвостового оперения
и т. д.) мы не будем излагать методов точного решения задачи,
так как они весьма громоздки и редко применяются на практике.
Все эти методы строятся вполне аналогично изложенному методу
интегрирования уравнений изгибно-крутильного флаттера крыла.
5. ВЫБОР ФУНКЦИЙ ФОРМЫ КОЛЕБАНИЙ ПРИ РАСЧЕТЕ ФЛАТТЕРА.
ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СКОРОСТИ КРЫЛА С СОСРЕДОТОЧЕН-
НЫМИ МАССАМИ
В п. 2 настоящей главы был изложен приближенный метод
определения критической скорости изгибно-крутильного флат-
тера крыла. Чтобы вычислить этим методом критическую ско-
рость, необходимо задать функции f и <р формы колебаний
крыла. Как известно, крыло может совершать колебания раз-
личных тонов. Если мы зададимся функциями, соответствую-
щими n-му тону колебания, то получим критическую скорость,
соответствующую этому тону. Каждый тон колебания имеет
соответствующую ему критическую скорость, т. е. такую ско-
рость, при которой колебания этого тона перестают затухать.
Естественно, что практический интерес представляет наимень-
шая из всех критических скоростей. Но, к сожалению, до сих
пор не существует способа для определения тона колебания,
представляющего наибольшую опасность для исследуемого крыла,
т. е. обладающего наименьшей критической скоростью. На осно-
вании ряда расчетов различных крыльев без сосредоточенных
масс было установлено, что наименьшую скорость дает первый
(основной) тон колебания и поэтому ц расчетах за функции/(у)
и <р(у) принимают функции основного тона колебания. Однако
нельзя считать доказанным, что никогда не встретится конструк-
ция, для которой наименьшую скорость даст не основной, а ка-
кой-либо другой тон колебания.
Для крыла с сосредоточенными массами большей частью наи-
меньшую скорость дает второй тон колебания (первый обертон).
Поэтому расчет критической скорости для крыла со значитель-
ными сосредоточенными массами (моторы, поплавки) произво-
дится в двух вариантах. В одном расчете за исходные функции
принимаются функции формы колебания (/ и ъ) основного тона,
определенные для крыла с учетом сосредоточенных масс (гл. II,
1 Мы получаем тонное решение задачи в смысле точного удовлетворения
основных уравнений флаттера. Сами уравнения остаются, конечно, прибли-
женными.
В развернутом виде все расчетные формулы для изложенного метода по-
следовательных приближений интересующиеся найдут в книге Е. П. Гросс-
мана, Флаттер. Труды ЦАГИ, вып. 284, 1937 г.
183
п. 6 и гл. 111, п. 4). Второй расчет производится с той же функ-
цией изгиба первого тона, но с функцией кручения <о,соответ-
ствующей первому обертону колебаний кручения. Эти функции
приближенно соответствуют первому обертону совместных коле-
баний. Таким образом определяются две критических'скорости
и меньшая из них принимается за критическую скорость самолета.
В остальном расчет критической скорости крыла с сосредо-
точенными грузами совпадает с методом расчета крыла без со-
средоточенных грузов (п. 2 настоящей главы), за исключением,
однако, коэфициентов сц, с12, с22. Эти коэфициенты, определяю-
щие кинетическую энергию колеблющегося крыла [формулы (6)
и (7)], будут другими, так как при определении кинетической
энергии необходимо учесть кинетическую энергию сосредоточен-
ных масс. Вследствие этого вместо формул (7) для подсчета
коэфициентов си, с12, с23 следует применять формулы (38) гл. IV.
К вопросу о критической скорости различных тонов колеба-
ния мы вернемся в гл. X, где будет дано физическое объясне-
ние того факта, что для крыла с сосредоточенными массами
критическая скорость второго тона колебания часто оказывается
ниже критической скорости первого тона.
6. ЧИСТО ИЗГИБНЫЕ И ЧИСТО КРУТИЛЬНЫЕ КОЛЕБАНИЯ КРЫЛА
В ПОТОКЕ ВОЗДУХА
В предыдущих параграфах были рассмотрены совместные
изгибно-крутильные колебания крыла в потоке воздуха. Рас-
смотрим теперь чисто изгибные и чисто крутильные колебания
крыла в потоке воздуха и докажем, что такие колебания не
имеют критической скорости, т. е. являются затухающими при
любой скорости. Объясняется это весьма просто.
При колебаниях в пустоте, без учета сил трения, колебания
с одной степенью свободы будут чисто гармоническими. При
колебаниях в воздухе дополнительно возникают аэродинамиче-
ские силы, причем от чисто изгибных колебаний возникает
демпфирующая сила (т. е. сила, всегда направленная против
движения), а от чисто крутильных колебаний — демпфирующий
момент (т. е. момент, всегда направленный против направления
угловой скорости движения). Совместные же колебания могут
происходить с нарастающей амплитудой, потому что от изгиб-
ных колебаний возникает возбуждающий момент, поддерживаю-
щий крутильные колебания, а от крутильных колебаний — аэро-
динамическая сила, поддерживающая колебания изгиба. Вообще
можно доказать, что флаттер возможен только при наличии
нескольких (не менее двух) степеней свободы вследствие аэро-
динамических связей между различными компонентами движе-
ния. Поэтому невозможен, например, флаттер одного элерона на
неподвижном крыле, но возможны совместные нарастающие ко-
лебания крыла с элероном.
Рассмотрим прежде всего чисто крутильные колебания. Чтобы
получить уравнение таких колебаний, нужно приравнять нулю
184
сумму моментов относительно оси жесткости всех сил (инерцион-
ных, аэродинамических и упругих), действующих в каждом се-
чении крыла при чисто крутильных колебаниях. Условием ра-
венства нулю моментов при совместных колебаниях является
второе из уравнений (35). Отбрасывая в этом уравнении все
члены, зависящие от изгиба, получаем уравнение движения
в случае чисто крутильных колебаний:
---<L ( qi _i_ i if — (—- *64-
dy p dy) I 16 V ~
+^(т-т)[в + (т-т)т’1}^1'2-0-- <52>
Первый член этого уравнения есть погонный крутящий момент
упругих сил, второй —инерционных и третий — аэродинамических.
Рассмотрим колебания при произвольной скорости полета.
Решение будем искать в виде:
Ь^В^(у)ег\ (53)
л может быть величиной комплексной, так как колебания могут
происходить с изменяющейся амплитудой (дальше будет пока-
зано, что они обязательно являются затухающими), а <р (у), вообще
говоря, комплексная функция, так как колебания могут происхо-
дить со сдвигом фаз между различными сечениями крыла.
Подставляя выражение (53) в уравнение (52), получаем урав-
нение, определяющее неизвестную функцию w(y):
+§ (т - т) [’ + (т - т) v *»]}* р=°- (54)
Предположим, что <f (у) является точным решением этого
уравнения. Тогда выражение (54J есть тождество. Умножим его
на <f(y)dy, где <р(у)— комплексная функция, сопряженная с (у),
и проинтегрируем результат по длине крыла в пределах от нуля
до I. Получим соотношение, определяющее X:
сХ2 Ч- d\V Ч- (bV2 Ч- а) = 0, (55)
185
Так как функция <₽ должна удовлетворять граничным усло-
виям <р = 0 при у = 0 и = 0 при у = I, то этим же условиям
должна удовлетворять и функция \ Поэтому, интегрируя вы-
ражение а по частям и принимая во внимание граничные усло-
вия, находим1 2:
a=S°'^di‘,y- ,(56а>
и
Так как произведение любой комплексной величины на сопря-
женную есть величина действительная и положительная3, то
непосредственно видно, что все коэфициенты a, b, с, d являются
действительными числами; кроме того, а и с — положительны.
Нас в первую очередь интересует знак величины d, который, оче-
n dCv / х0 I \ ( 3 х0 \
видно, зависит от знака количества -jg- 1 —t-J (-----I .
Легко видеть, что это количество всегда положительно, незави-
симо от положения оси жесткости крыла (т. е. независимо от
величины
гс дСу / -Vq 1 \ / 3 Xq \ _дСу 1 / гс__ 1 \ у
”16 ~ д*ГО Tj ГУ да ieldq, 1
\ да /
+ (^-Я]>0. »
так как всегда Следовательно, коэфициенты (56) всегда
положительны:
ОО; с>0; d > 0. (57)
Что касается коэфициента Ь, то он отрицателен, если, как
обычно, ось жесткости располагается дальше 25% хорды от
(X 1 \
> -j-) , и положителен, если ось жесткости на-
ходится ближе 25% хорды от передней кромки.
Решая уравнение (55), находим:
X = -4 Г ± /(4 и)-4-(^2 + а) . (58)
» у J С-
Рассмотрим сперва случай, когда подкоренное количество
отрицательно. Тогда X будет комплексным числом с отрицатель-
1 Пусть <р = <рх + Z<p„; тогда <р = — гэ2. Если <р удовлетворяет граничным
условиям, то этим условиям будут удовлетворять функции и <р2 по отдель-
ности, а следовательно, и функция <р.
’См. формулу (77а), гл. II.
3 (<Р1 + 'Та) («1 — <4>а) = <Pi + ®2 •
186
ной вещественной частью. Следовательно (гл. II, п. 5), колебания
будут затухающими.
Если подкоренное количество положительно, то ). — величина
чисто действительная, и движение будет апериодическим. Таким
образом колебания с нарастающей амплитудой невозможны ни
при какой скорости полета.
Рассмотрим, как происходит при различных скоростях аперио-
дическое движение, которое, как мы установили, имеет место при
(4к)~т^’/2+а>>0- <59>
Если bV2 -f- а > 0, то при соблюдении условия (59) оба значе-
ния X, согласно уравнению (58), будут отрицательны. Следова-
тельно, движение — устойчивое, и после возмущения крыло апе-
риодическим движением вернется к положению равновесия (гл. II,
п. 5). Если &V'24-a<0, то одно из значений X будет положи-
тельным, и крыло апериодически будет удаляться от положения
равновесия, т. е. закрутится вплоть до поломки.
Следовательно, критическим случаем будет № 4- # = О, и из
этого уравнения получаем критическую скорость апериодической
неустойчивости (дивергенции):
(60)
При этой скорости оба значения X, согласно уравнению (58), будут
действительными числами. Следовательно, уравнение (54), опреде-
ляющее функцию (у), не будет содержать комплексных величин,
и его интеграл может быть взят в виде действительной функции.
Но если (у) — действительная функция, то (у) = (v), и тогда
а = а.,2 и b = Ь22 [формулы (7) и (14)]. Выражение (60) можно
переписать в следующем виде:
и мы опять пришли к формуле (31), найденной нами выше из
иных соображений. Мы видим, что эта формула дает скорость
апериодического скручивания крыла.
Тем же методом, каким только что были исследованы чисто
крутильные колебания, можно было бы исследовать и чисто
нзгибные колебания крыла в потоке воздуха. Однако в этом нет
необходимости, так как непосредственно из физических сообра-
жений можно заключить, что чисто изгибные колебания крыла
в потоке воздуха при всех скоростях полета будут затухающими.
Полагая 6 = 0 в первой из формул (60; гл. VI, найдем значе-
ние ДС„ при отсутствии кручения, т. е. при чисто изгибных ко-
лебаниях
<61)
187
Непосредственно видно, что знак ЬСу всегда противоположен
знаку Z, т. е. подъемная сила всегда направлена в сторону,
противоположную направлению скорости движения. Следова-
тельно, эта сила будет демпфировать колебания. Мы знаем, что
изгибные колебания крыла в пустоте будут гармоническими
с постоянной амплитудой. При колебаниях в потоке воздуха
к силам, действовавшим в пустоте, прибавляется всегда демпфи-
рующая, как мы выяснили, аэродинамическая сила. Следовательно,
в потоке воздуха колебания будут всегда затухающими.
Происхождение демпфирующей подъемной силы (61) моодо
объяснить весьма просто. Пусть крыло совершает изгибные коле-
бания в потоке воздуха. Рассмотрим какое-либо сечение крыла
(фиг. 48), которое в рассматриваемый момент времени движется
со скоростью Z. Аэ-
родинамически это
эквивалентно тому,
что воздух движется
относительно крыла
с той же скоростью
в обратном направле-
нии (т. е. со скоро-
стью —Z ). Склады-
вая относительные
скорости воздуха:
х скорость набегающе-
го потока И и ско-
ф1,г’ 48’ рость — Z, находим
результирующую скорость воздушного потока Рр (фиг. 48). Таким
образом угол атаки крыла изменится за”счет скорости изгибного
движения на величину Да. Ввиду малости угла Да можно счи-
тать tgAa^Aa и ИР~И.
Тогда
Да=-----JrZ.
Изменение угла атаки на величину Да изменит коэфициеит
подъемной силы на величину
^Да= —
У да da V
Это и есть приращение коэфициента подъемной силы за счет
изгибных колебаний [(ср. с выражением (61)]. Непосредственно
видно, что приращение подъемной силы будет всегда направлено
против движения крыла, так как при движении крыла вверх
угол атаки уменьшается (фиг. 48), а при движении вниз — уве-
личивается.
Таким образом можно считать доказанным, что чисто изгиб-
ные и чисто крутильные колебания крыла в потоке воздуха
всегда будут затухающими. Можно показать и для других слу-
188
чаев движения (колебания элерона, рулей и т. д.), что колебания
с одной степенью свободы в потоке воздуха всегда будут зату-
хающими. ,
7. ПРИБЛИЖЕННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ СКОРОСТИ
КРЫЛА С ЭЛЕРОНОМ
Крыло с элероном обладает тремя степенями свободы1: изгиб
крыла, кручение крыла и отклонение элерона. В соответствии
с этим возможны четыре вида флаттера: 1) изгибно-крутильный
флаттер, 2) изгибно-элеронный флаттер, 3) крутильно-элеронный
флаттер, 4) изгибно-крутильно-элеронный флаттер.
Фиг. 49.
В первом случае элерон движется вместе с крылом, и его
нужно рассматривать как часть конструкции крыла. Метод опре-
деления критической скорости изгибно-крутильного флаттера
изложен в п. 2 настоящей главы. Критическую скорость осталь-
ных форм флаттера определяют тоже, исходя из принципа воз-
можных перемещений, т. е. составляют уравнения Лагранжа, из
которых и определяют критическую скорость и частоту флаттера.
Для составления уравнений Лагранжа необходимо вычислить ки-
нетическую и потенциальную энергию системы, чем мы в первую
очередь и займемся.
Пусть MCN (фиг. 49)—профиль крыла с элероном CN, на-
ходящийся в положении равновесия, и M'C'N'— тот же профиль
в какой-либо момент времени во время колебаний. Центр жест-
кости Е профиля MN выбираем за начало координат, ось Ех
направляем по направлению скорости набегающего потока и ось
1 Термин „степень свободы" здесь употребляется в условном смысле. Строго
гэворя, крыло с элероном,как и всякая упругая система, обладает бесконечно
большим числом степеней свободы. Но мы условимся под термином „степень
свободы* понимать вид деформации, которую может совершать исследуемая
система.
189
Ez—перпендикулярно к ней. Направление изгибных колебаний
считаем совпадающим с направлением оси Ez. Обозначим через Z
прогиб оси жесткости крыла, через в — угол поворота всего крыла
и через U— угол отклонения элерона относительно статического
положения (фиг. 49). Произвольные точки Д, крыла и В, элерона
момент времени займут соответственно поло-
Координаты их в этот момент времени будут:
для точек, расположенных на крыле (на участке М'С'у
в рассматриваемый
жения At и Bi.
z, = Z — 3/sin(T/+9);
X; = 3; COS (f,. + 0);
для точек/ расположенных на элероне (на участке C'N'):
zt = Z — sin (^ ф-6) + р,- sin (8 + 6) — p; sin (8 +&);
x; = 3,. cos (у,- 4-6) — p; cos (8 4- 0) p; cos (B 4- U).
Обозначения входящий в эти формулы величин ясны из фиг. 49.
Через з(- обозначено расстояние от произвольной точки контура
M'N’ до оси жесткости Е’, через р,- — расстояние от произволь-
ной точки элерона до его шарнира Ш'.
Кинетическая энергия рассматриваемого отсека крыла опре-
деляется по общей формуле:
dT = ~ V]mi(х/ 4- zf), (63)
где суммирование распространяется на все точки рассматриваемого
отсека крыла и элерона (z/z, — масса, сосредоточенная в i-й точке).
Определяя л,- и г,- диференцированием по времени выражений (62)
и подставляя их в выражение (63), находим:
ат = X V m,+ -L es я„’ + АН/ ; + J. V mf’ _
К К 3 э
— Z 6 V mpl cos 4-6) 4- Z6 V т,-р; cos (о 4- б) —
к Т (64)
— Zii у m,p, cos (8 4- 0) — б2 у mippi cos (J — к) 4-
4- 6U у rnpip, cos (3 4- & — — 6) — 6 О У т$ cos (ft —6).
э э
Индекс „к”, стоящий под знаком суммы, означает, что дан-
ная сумма распространяется на все точки рассматриваемого се-
чения крыла вместе с элероном (контур М’С'ЕГ, фиг. 49), ин-
декс „э“,— что суммирование идет только по точкам элерона
(контур C'N', фиг. 49).
190
Очевидно, что
V m( = mdy,
к
т — погонная масса всего крыла вместе с элероном в рассма-
триваемом сечении;
^m£=Imdy,
К
[п—погонный массовый момент инерции относительно оси жест-
кости всего крыла вместе с элероном в рассматриваемом сечении^
У, = ^/пш ^У,
Фиг. 50.
Лтгш — погонный полярный массовый момент инерции элерона
в рассматриваемом сечении относительно оси вращения элерона.
Так как a, cos (7,- + 6) = л; — абсцисса точки крыла^ M’N*, то-
У /И,-3; COS (у,- -Т е) = S miXi = т^У Лц- т == Z7Z3 COS fr + ^У’
к к
где а — расстояние от центра тяжести сечения крыла вместе
с элероном до оси жесткости и 7 — угол между прямой, соеди-
няющей центр тяжести с осью жесткости, и осью х.
Аналогичным рассуждением находим:
У, /и, pz cos (8 -f- 6) = тэ зэ cos (о 4-0) dy,
э
та — погонная масса элерона, аэ— расстояние от центра тяжести»
рассматриваемого сечения элерона до оси вращения;
У tnfit cos (8 4- ft) = тэ зэ cos (8 4- 0) dy.
э
Рассмотрим теперь сумму
У cos (8 4-0 — ъ—О).
191
На фиг. 50 изображен профиль крыла M'C'N' с элероном^Ь'ДГ
в рассматриваемый момент времени. Пусть В, — произвольная
точка элерона. Расстояние от нее до оси жесткости крыла мы
обозначили через о;, а расстояние от нее до шарнира элерона LLT—
через рг. Обозначим расстояние между осью вращения элерона ИГ
и осью жесткости крыла Е’ через рш. Из фиг. 50 непосредствен-
но видно, что угол E’BiIir между отрезками а; и р; равен (о -J-S) —
— (7/4-6). Из /^Е'В'Ш' находим:
*
Рш = я? + Pi — 2о;р,- cos (о + & — -у,- — 6),
откуда
o;pz cos (о + & — 7. — б) = ~ (з- + р,? — рш).
В силу этого
У cos (о 4- У — ъ — 0) = У 4- р? — pL) =
Э 9
— ~2~ И"1 э Е 4~ 1тш Рш ] dy,
где ImsEdy^^nifh —момент инерции элерона относительно оси
э
жесткости крыла. Подчеркиваем, что 1тЭЕ—момент инерции для
элерона в отклоненном положении.
Тем же путем находим, что
\ COS (5-------- 7i) --[Ли эЕ 4“ Im ш рш^э ] dy,
2
где ГтзЕ — момент инерции элерона, относительно крыла, но
вычисленный для элерона, не отклоненного относительно крыла.
Так как угол отклонения элерона предполагается малым, то
в дальнейшем будем считать/шэе = Лиэ е; также всюду в даль-
нейшем косинусы малых углов заменены единицей.
Учитывая все сказанное, с точностью до величин второго по-
рядка малости по деформациям, можем переписать выражение (64)
в следующем виде:
dT = [4-тГ- 4- 4-(/и - 1тэЕ 4- /Лэ Рш) б2 4- -^1тш & 4"
4- (— /из 4- /Лэ ®э ) Z б — тэ зэ Z& 4-
4- 2 (,1т эЕ-------In ш /Лэ рш ) бд I dy.
192
Суммируя кинетическую энергию по всем отсекам крыла,
находим общую кинетическую энергию вибрирующей системы.
Г = + тэ?2ш)^ + 4г/тш^ +
О
+ (— то + тэ зэ ) Z8 — тэ аэ ZQ 4-
4 2~ (^ э е — 1т ш т3 рш ) в 1} I dy. (Go)
При выполнении интегрирования характеристики, относящиеся
к элерону (тэ , 1тэЕ, 1тш. Зэ и т. д.), следует на интервале, где
нет элерона, принимать равными нулю.
Потенциальную энергию системы легко написать сразу:
4 «»’• <вб)
о о
Первый член этого выражения дает потенциальную энергию
деформации изгиба, второй — деформации кручения. Наконец,
третий член представляет собой потенциальную энергию, возни-
кающую при отклонении элерона. Через R обозначен момент,
который, будучи приложен к элерону, отклоняет его на один
радиан. Об определении величины R подробнее будет сказано
ниже.
Как обычно, приближенный метод определения критической
скорости основан на том предположении, что форма колебания
системы известна. Если дополнительно предположить, что элерон
является абсолютно твердым и собственных деформаций элерона
не может быть, то стоячее колебание системы можно записать
в следующем виде:
6=<р(у)г(т); (67)
& = »(.).
$ не зависит от у, так как предполагается, что элерон откло-
няется от положения равновесия, вращаясь вокруг своей оси, как
твердое тело.
Подставляя выражения (67) в уравнения (65) и (66), найдем:
Т = у си?2 4- + у сзз{'2 + с12?г4-
и=4 «1# + у а^2 + Т
где
i
Сц = f mpdy,
* о
Гроссман—15—13
(68)
1&3
I У1
С*2 ~ J lm*%~ dy ' Um з E рш“) dy\
О У1
У;
c33 — J Im ш dy,
J1 l Уг
ci2 = C2i = — f mtfr? dy +fm° ъ/f dy,
О У.
с^з = C31 = tnB оэ f dy,
yi
1 л
C;3 — C30 — ~2 J Um э E Im ш— tTls рш“) ф dy J
У1
»»=M>
0
(69)
о
азз = 7?.
Пределы интегрирования показаны на фиг. 51.
Чтобы составить уравнения Лагранжа
по обобщенным координатам q, г, &,
необходимо еще вычислить обобщен-
ные
силы [формулы (8), гл. I]:
xi dr
(70)
> dXi
xi д»
Px и P- —компоненты по осям x
внешних сил, действующих в i-й
где
и z
точке системы.
Подставляя значения (67), в формулы
(62), найдем выражения декартовых ко-
ординат %,-, zz произвольной точки вибри-
рующей системы через обобщенные координаты q, г, U.
Подставляя затем результат в формулы (70), находим:
к
194
О, = - S =г sin (ъ-Н)+Рг/ COS (7i + 6)] <P +
К
+S Pi И5*- sin + ®) + ?z- cos (s +e)] ?;
э 1 1
Q» = - S Pi Ipx; sin (3 + ») + P2i COS (8 + »)].
Э
Пусть (фиг. 52) M'C'N' профиль крыла с элероном C'N’ в
какой-либо момент времени. В произвольной точке В/ прило-
жена внешняя сила, компоненты которой по осям координат мы
2
обозначили через Рх. и Рг . Проведем из точки В-' три нормали.
Нормаль п' к отрезку з,-, соединяющему В' с осью жесткости
Е’; нормаль л'— к отрезку р,-, соединяющему -В', с осью враще-
ния элерона Ш'. На фиг. 52 пунктиром ZZ/'Л/' показано положе-
ние, которое занимал бы элерон, если бы он не отклонялся
относительно крыла. Третья нормаль п'" проведена к отрезку
Ш'Л/". Тогда легко видеть, чтб
Ря. sin (-у,- + 6) + Рг. cos (7,- + 6) = Рп’ ;
Р,. sin (8 + 6) + Pz. cos (8 + 6) = Pn.„-
Px. sin (3 + И) + P2. cos (3 + ft) = Pn.,
где Pn. , p„., Pn„, — проекции внешней силы соответственно на
нормали л' л", л"'. Ввиду малости угла £ между CN' и C'N”
(фиг. 52) можно считать, что Рпт = Рп-- Принимая это во внима-
ние, можем выражения для обобщенных сил записать в следую-
щем виде:
Q.=S₽..-/;
195
Qr = — • Pn- <p + У, PiA»'?;
к Э
Q,>= —£p,P„--
Э
Суммируя силы сперва по всем точкам рассматриваемого се-
чения, а затем по всем сечениям крыла, найдем:
о
I
Qr = f4(dME~dMluy, } (71)
О
I
Q& == J d \ ш.
о
Здесь dPz — равнодействующая внешних сил, действующих
на элементарный отсек крыла с элероном по оси г, dME — момент
относительно оси жесткости крыла внешних сил, действующих
на крыло и элерон, dMm— момент внешних сил относительно
оси вращения элерона, действующих на элерон. Вне .интервала
у.,, в котором расположен элерон, dMm = 0. Внешними силами
являются силы аэродинамические; значения их были найдены в
гл. VI. Эти значения для элементарного отсека крыла между
сечениями у и у + dy будут:
dP^^tv^v, ( (72)
dME = bCmE^V2dy, I
где значения ДСу и ЬСтЕ определяются формулами (39) и (40) гл. VI:
АСх = й-[6+ +G? +H4-P-1Z];
+ /₽ + -/^+^(т-т)[б +
(73)
+(4- т) v6+G‘3+-44
Значение совпадает со значением ЛЛ4Ш, указанным в
формуле (43) гл. VI:
^Мш = -рГ-ИЧ216 +ё3уё4-оз ₽4-^4-p + 26Azjdy. (74)
Величины 9г, /, J, G, Н имеют значения, указанные в гл. VI.
В формулах (73) и (74) за координату, определяющую поло-
жение элерона, принят угол р отклонения элерона относительно
крыла (фиг. 49). Из фиг. 49 непосредственно видно, что
р =0 - 0. (75)
196
'Подставляя это значение В в формулы (73) и (74) и резуль-
тат в (72), находим:
+ G8 + Н±- b—^-Z^tV'-dy,
dME = {-Ih-(^ + j)l-k+^ + J-Lb +
+£(?->-«)’+
+ (4- 7° - + ы + н 4-& - Z |}р^Иа dy-
амш = - - s3)e+(22- ё4Ц ё +
(76)
+ Q3&+ 2, < & + 264z] pf-V-dy.
Подставляя сюда значения Z, 6, & из формул (67) и получен-
ный результат — в выражения (71), находим окончательные зна-
чения обобщенных сил:
Qq = ~daVq - b^r—d^Vr — b13V^—d13Vb-,
Qr = — d21Vq — &22 Var — z/22I< r — bwV2$ — d23 V<>;
Q8 =-d3lVq— b32V2r—d32Vr—b33V2ft — d^Vil,
где
b
1
dii = d^ pj(-t°—ri^dy — p j Q^fydy-,
u >.
^31 = P j ^s^2/dy\
y'
dCv ff 3 x. \
^12 = - aT p J(~T—Г ~
o' /
I
d22 = P f(~iQ + t\2 dy —
(77)
(78)
Уз
— p J (Q. — Q^t^-dy-
1OT
л _ )
d32 = ?j [Q2—Qt)t-\dy,
yi
0Л J
У1
У’ лГ Ь. . X
rf»=-P J Jt^dy-^j tf-T)»M-
У, У^
— pf QJ^dy;
yi
^33 = P f Q^dy;
У1
i
^"S'p f (l-G)tfydy;
us •'
0
= P f dy - p / -1)(1 - G) tW dy- } (78)
y, a y>
-p J'^-Q^tYdy;
У1
Уз —
&33 ~ P J~ (^i ^з) dy,
У1
613=-p^ f Gtfdy;
oa J
yt •
&23=-P / f (y-y) GC-fdy-
У, У1
-pf Q^2ftdy,
yi
^зз = P У Q3t~dy.
y' '
Имея выражения кинетической энергии, потенциальной энер
гии и обобщенных сил, можем составить уравнения Лагранжа:
d __ , dU _ q
d~\dq) dq dq Q’
и такие же уравнения по координатам г и &. Подставляя в эти
уравнения найденные выше значения кинетической и потенци-
198
альной энергии [формулы (68)] и обобщенных сил [формулы (77)],
находим диференциальные уравнения, определяющие обобщен-
ные координаты q, г, «> в функции времени:
спЧ 4- СтУQ 4- аиЯ 4" г12г 4" 4“ VZr 4"
4-^4-^1зИ>4-&13И2»= 0;
+ d2lVq + с2пГ + d,o V г b„ V2r 4- а^г 4-
". (79)
+ «за» + 4- b23V-'^ = 0;
<"31<7.Ф- d21Vq 4- с32 г 4- d32V г 4- 632И3г 4-
4- гзз'^ 4_^зз^4_ М^3 — О*
При произвольной скорости полета V эта система может быть
решена подстановкой
q = Ае г = Be' ; 0 = Се1'.
Мы найдем X в виде комплексного числа и движение будет
затухающим или с возрастающей амплитудой, в зависимости от
знака действительной части X. Критическая скорость, по опре-
делению, есть такая скорость полета, при которой колебания
будут происходить с постоянной амплитудой, следовательно X
будет чисто мнимым числом. Поэтому сразу будем искать ре- *
шение системы (79) в виде:
q = Aeijn; г = Beip'; l> = Ceipz (80)
и значение скорости V, при котором такое решение возможно.
После подстановки выражений (80) в уравнения (79) время
исключится, и мы получим систему линейных однородных урав-
нений для определения постоянных А, В, С. Чтобы эта система
имела отличные от нуля решения, необходимо и достаточно, чтобы
определитель ее равнялся нулю. Приравнивая нулю этот опре-
делитель, получим комплексное уравнение для определения
частоты р и критической скорости V:
au —CuP^+duipV, bl3V2—c12p2+dl3lpV, bl3V2—cl3p2+dt3ipV
—c2.iP2Jrd3tipV, a22 4-i>22V2—c22p24-d22rpV', b33V2—c„3p2+d23ipV
—c31P2+dsi'P v, b3„V2~Cs3p2+d32ipV, aas+bs^—Ca^+dsaipV
Разбивая этот определитель на действительную и мнимую
части и приравнивая нулю каждую в отдельности, получим два
уравнениях:
Щр, V) = 0;
Д2(р, Г) = 0,
(81)
Р 1 В развернутом виде эти уравнения интересующиеся найдут в книге
, П. Гроссмана, М. В Келдыша и Я. М. Пархомовс кого, Вибра-
ции крыла с элероном, Труды ЦАГИ, вып- 337, 1937 г.
199
из которых и определяются критическая скорость и частота
флаттера.
Таким образом вычисление критической скорости для рас-
сматриваемого случая ведется следующим образом:
1. Определяются функции / и <р формы колебаний крыла
в пустоте. Считается, что форма колебаний крыла в воздухе
мало отличается от формы его колебаний в пустоте, и эти функ-
ции принимаются за исходные при расчете флаттера.
2. Вычисляются по формулам (69) и (78) коэфициенты. При
этом значения О, Н, I, J определяются по формулам, приве-
денным в гл. VI.
3. Составляются и решаются уравнения (81).
Изложенный метод определения критической скорости
вибраций крыла с элероном с тремя степенями свободы в за-
водской практике вследствие громоздкости употребляется срав-
нительно редко. Чаще крыло с элероном проверяют на и з-
гиб но-элеронный флаттер, т. е. считают, что крыло не
подвержено деформации кручения. Обычно этот случай опреде-
ляет необходимую величину весовой балансировки элерона.
Если крыло все же вызывает сомнения в смысле вибрационных
свойств, дополнительно проводят также расчет крутильно-эле-
ронного флаттера.
Изложим вкратце метод определения критической скорости
изгибно-элеронного флаттера.
Полагая в формулах (68) г = 0 (кручение отсутствует), нахо-
дим выражения кинетической и потенциальной энергии при
изгибно-элеронных колебаниях:
Т = 2 *“ -2~
=4’°и?2+’ 2 а^2’
где попрежнему
i
cu = [ mf-dy,
О
У»
С33=/,
У.
<аз = с31 = -/ tn3'3fdy
I у‘
0ц = fEI
о
а33 = /?.
200
Обобщенные силы находим по формулам (71). Так как кру-
чение отсутствует, мы должны положить Qr — 0. В выражениях
для dPz и dMm следует отбросить члены, зависящие от круче-
ния. Поэтому значения dPz и dMm мы получим, полагая в пер-
вой и третьей формулах (76) 6 = *5 = 0:
dP, -4*2 |Р№^;
dM„, =_[ё,»+В4 у» + zJ't’V’dy.
Подставляя эти значения в формулы (71), находим обобщен-
ные силы при изгибно-элеронном флаттере:
Qg = -duVq-bl3V4-d13V^ |
„ - . ? (°4)
<4 = - 4?31 Vq - ь33 v2a - d33 га, I
где
i
dCv Г
du = tf- dy-
u
У2
d3i = pf Sst2fdy;
У1
va
dis=-pd-^'f HPfdy-
У1
dn^p f QtFdy;
У1
v2
dCv Г
bi3--p-^J Gtfdy-
У1
b33 = p f Q3t2dy. 1
y>
Составляем уравнения Лагранжа:
d ( дТ \ дТ . dU п
— ( - J — —п-----= U z
d-c \dq J dq dq 9
rf ( dT\ _ ar ,dU _
dz < ) db Ф —
(85)
201
Подставляя в эти уравнения значения Т и U из формул
(82) и Q?, Q& из формул (84), получим:
G19 + ЛиУ Я + аиЯ + с1з!> + <4з W = °;
c31q + Я + сзз^ + 4~ b33V2b 4~ а33»> = 0.
Интегрируем эту систему подстановкой
, q = Ae,p\ b = Ceip\
Тогда для определения А, С получаем систему линейных одно-
родных уравнений, определитель которой должен быть равен
нулю:
j — GiP3 + ipVd^ -Ь au, — с13р2 + ip Vd# 4- b13IZ2. = Q
I — c3iP2 + ip Vd3v — c33p2 + ipVd33 4- b33V2-\- a33.
Развернув этот определитель, получим:
А0Р4 — ip3B3 — С0р3 4- ipD0 -Ь Ео = 0, (86)
где
Ао -- At;
в0 = ву-
° 1 (87)
Q = C14-CSVS;
D0 = Dy+D2V3;
Ео = 4- By2.
В свою очередь Ар Ви... имеют следующие значения:
Аг = СцГ3з СкзГзь
Bi = сnd4~ ^uc33 C3idy3 d3lci3,
Bi — ^н^зз 4~ r11a33;
B^i — ацЛзз + d^a^', (ggj
B\ = °иазз;
C2 = dnd33 4“ сцЬзз dl3d3l b13c3i\
Dn — dub33 b^d33',
B3 = аиЛзз-
Приравнивая в выражении (86) нулю действительную и мни-
мую части по отдельности, получим два уравнения для опреде-
ления критической скорости V и частоты р. Исключая из этих
уравнений р, найдем условие для определения V:
B0C0D0-B'0E0-DlA0 = 0,
(89)
202
и р определится равенством:
• (ад
Если подставить в уравнение (89) значения величин А, В, С, D, Е
из выражений (87) и обозначить
L^B&D'-D^-
М = S1C2O14- B&D- — — 20^,4;
N = В^ - Bfa-Dfr,
то уравнение для определения критической скорости можно бу-
дет записать в виде:
LVi 4- /ИИ2 4- N = О,
откуда определяется V.
Этим и решается задача определения критической скорости,
так как коэфициенты L, М, N, равно как и А, В,могут быть
вычислены для каждого конкретного случая, если известна функ-
ция f (у), необходимая при вычислении исходных коэфициентов
по формулам (83) и (85). Как всегда, эта функция считается
совпадающей с функцией формы изгибных колебаний рассмат-
риваемого крыла в пустоте.
ГЛАВА VIII
ПРИЧИНЫ ВОЗНИКНОВЕНИЯ -ФЛАТТЕРА
1. АНАЛИЗ ПРИЧИН ВОЗНИКНОВЕНИЯ ФЛАТТЕРА
Неоднократно наблюдались случаи, когда в полете неожиданно
возникали весьма интенсивные вибрации крыла или хвостового
оперения, в большинстве случаев в течение нескольких секунд
приводившие к разрушению вибрировавшей части. Предположе-
ние о том, что причиной подобных вибраций является резонанс
с мотором, должно быть отвергнуто, во-первых, потому, что раз-
рушительные вибрации наблюдались и при остановленном моторе
(при пикировании), и, во-вторых, потому, что подобные вибрации
всегда наступали на определенной скорости полета, строго
определенной для каждого самолета, независимо от числа оборотов
мотора. Остается предположить, что причиной возникновения
подобных вибраций, которые получили название „флаттер",
являются аэродинамические силы.
На крыло или оперение летящего самолета всегда действуют
разные возмущающие силы. Природа этих сил может быть самой
различной: резкое движение элеронами (рулями), воздушная яма,
вихри, сбегающие с винта, мотор, — все эти причины порождают
силы, которые воздействуют на крыло и хвостовое оперение.
Силы эти вызывают небольшие деформации изгиба и кручения
или даже незначительные вибрации крыла.
Возникшие за счет начального импульса деформации происхо-
дят с определенными скоростями и влекут изменение аэродина-
мических сил, действующих на крыло. Появляются дополнительные
аэродинамические силы, которые могут быть разбиты на две
категории: одни, которые носят название демпфирующих, дей-
ствуют в сторону, противоположную возникшей деформации, и
стремятся вернуть крыло в положение равновесия; другие, так
называемые возбуждающие, действуют в том же направлении,
в каком идет деформация, и стремятся ее увеличить. На малых
скоростях демпфирующие силы значительно превосходят воз-
буждающие, но с ростом скорости возбуждающие силы растут
быстрее и, наконец, наступает такая скорость, когда они стано-
вятся равными демпфирующим. Эта скорость называется крити-
ческой скоростью. Если скорость полета превышает критическую,
то малейшая деформация, возникающая от любой случайной
204
причины, порождает возбуждающие силы, превосходящие демп-
фирующие, и возникает флаттер.
Конечно, это описание может служить лишь для грубого
уяснения причин возникновения флаттера. Более подробный
анализ причин флаттера будет приведен дальше.
Таким образом задача определения критической скорости
есть задача устойчивости: необходимо определить скорость, при
которой крыло теряет устойчивость, т. е. такую скорость, при
превышении которой возникающие деформации порождают силы,
автоматически увеличивающие деформации.
В настоящей главе мы исследуем причины, порождающие
флаттер, и наметим пути его устранения. При исследовании мы
постараемся по возможности избежать
сложного математического анализа и
ограничимся только качественной
стороной явления. Такой способ ис-
следования дает возможность доста-
точно хорошо уяснить внутренний
механизм (или, как часто говорят, фи-
зический смысл) изучаемого явления.
Количественный же анализ флаттера
проводится путем расчетов методом, изложенным в предыдущей
главе. Для простоты мы будем рассматривать плоскую задачу,
т. е. твердое крыло, подвешенное на упругих пружинах (фиг. 2,
гл. I). Колебания такого крыла в пустоте рассмотрены в гл. I.
Все качественные выводы, которые мы получим, без изменения
могут быть применены и к упругому крылу, так как каждое
сечение последнего колеблется так же, как твердое крыло.
Известно, что флаттер поддерживается за счет энергии
набегающего на крыло потока воздуха. Поток воздуха создает
два рода сил и моментов: демпфирующие и возбуждающие, и
-флаттер имеет место только тогда, когда энергия, получаемая
колеблющимся крылом из потока за счет возбуждающих воздей-
ствий, больше энергии, затрачиваемой им на преодоление демп-
фирующих воздействий.
В предыдущей главе было показано, кроме того, что флаттер
с одной степенью свободы невозможен и потому поток должен
давать такого рода воздействия, которые поддерживают и изгиб
и кручение. Рассмотрим в первую очередь воздействия потока
на изгибные колебания.
При изгибном движении крыла вниз угол атаки будет уве-
личиваться на величину Да = у- (фиг. 53), так как для получения
результирующей скорости воздушного потока необходимо сложить
скорость V набегающего потока со скоростью относительного
потока, получающегося около крыла, вследствие движения
последнего со скоростью Z. Так как угол атаки при движении
крыла вниз увеличивается, то будет увеличиваться и подъемная
сила. Следовательно, получится приращение подъемной силы,
205
демпфирующее колебания. Легко видеть, что при движении
крыла вверх приращение подъемной силы будет направлено
вниз, т. е. подъемная сила опять будет демпфировать колебания.
Таким образом та часть подъемной силы, которая получается
за счет скорости изгибных колебаний, всегда является демпфи-
рующей, независимо от формы колебаний, и всегда присутствует,
коль скоро существуют колебания изгиба.
Флаттер, очевидно, возможен только в том случае, если
существует возбуждающая сила, обладающая достаточной вели-
чиной для преодоления демпфирующих воздействий. Рассмотрим,
может ли существовать такая сила, если форма колебаний при
флаттере совпадает с какой-либо формой колебаний в пустоте.
В гл. IV было показано, что стоячее колебание в пустоте
может иметь только одну из форм, изображенных на фиг. 28.
[В гл. IV мы показ'али, что таковы же будут форма колебаний
каждого сечения упругого крыла (фиг. 28), совместные изгибные
колебания в пустоте (фиг. 28, а) и совместные крутильные
колебания в пустоте (фиг. 28,&)].
Мы видели, что часть подъемной силы, которая зависит от
скорости изгибных колебаний, всегда является демпфирующей.
Остается рассмотреть те части подъемной силы, которые зависят
от изменения утла атаки вследствие кручения крыла и от ско-
рости крутильных колебаний.
Если бы колебания в потоке воздуха имели форму, совпадаю-
щую с формой совместных изгибных колебаний в пустоте
(фиг. 28, а), то часть подъемной силы, зависящая от величины
угла кручения, была бы возбуждающей в первой (положения
1—1П, фиг. 28,а) и третьей (положения V — VII) четвертях
периода и демпфирующей во второй (положения III—V) и
четвертой (положения VII — IX) четвертях периода колебаний.
Вследствие симметрии колебаний относительно среднего положе-
ния ясно, что работа этой силы за каждую четверть периода
одинакова по абсолютной величине. Поэтому, хотя эта сила
в первой и третьей частях периода является возбуждающей,
т; е. сообщает энергию колеблющейся системе, но на ее преодо-
ление во второй и четвертой четвертях периода тратится точно
такое же количество энергии. В целом за период рассматриваемая
часть подъемной силы не сообщает колеблющемуся крылу ника-
кой энергии и, следовательно, за ее счет колебания поддержи-
ваться не могут.
Аналогично можно доказать, что также и при флаттере крыла
формы, соответствующей совместным колебаниям кручения
в пустоте (фиг. 28, Ь), та часть подъемной силы, которая зависит
от скорости колебаний изгиба, является демпфирующей, т. е. на
ее преодоление должна затрачиваться энергия колеблющейся
системы; часть же подъемной силы, зависящая от кручения,
в некоторые моменты будет демпфирующей, а в некоторые —
возбуждающей. Однако вследствие симметрии колебаний в те
моменты, когда эта часть силы является возбуждающей, она
206
будет сообщать системе ровно столько энергии, сколько система
должна затем затратить на преодоление этой силы, в то время
когда она является демпфирующей. Опять эта часть • силы не
дает энергии для поддержания колебаний.
Таким образом единственным возможным источником воз-
буждающих воздействий остается та часть подъемной силы,
которая зависит от скорости крутильных колебаний. Для того
чтобы возник флаттер, необходимо, чтобы эта сила сообщала
колеблющемуся крылу не меньше энергии, чем оно затрачивает
на преодоление демпфирующих воздействий. Если мы будем
предполагать, что критическая скорость отлична от нуля, то при
скорости полета, меньшей критической, затрата энергии на демп-
фирующие "воздействия будет больше, а при скорости, большей
критической,— меньше, чем работа возбуждающей силы. При
увеличении скорости от нуля флаттер возникнет тогда, когда
общая работа подъемной силы за период будет равна нулю, т. е.
начало флаттера возможно только при условии
т
RCy = f*Cy.pSV*gdz = Q, (1)
О
где Rcy — работа подъемной силы за период колебания Т и УСу —
полное приращение подъемной силы при вибрациях. Как мы
видели, это условие может выполняться только, если имеется
возбуждающая энергия, даваемая частью <\CV, зависящей от
угловой скорости колебаний кручения. Поэтому, кроме условия (1),
при выполнении которого возможны незатухающие колебания
изгиба, должно еще выполняться условие поддержания колебаний
кручения, так как в противном случае исчезнет источник воз-
буждающей энергии. Последнее условие, очевидно, будет:
т
RcmE = /^СтЕ pS V-tM g dt > о, (2)
О
где RcmE — работа аэродинамического момента относительно оси
жесткости за период Т и — моментная хорда крыла.
На основании формул (60) гл. VI выражение RcniE можно
представить в виде:
=f\- ’ / £ + -4)4CJ£Л-
О
Если колебания происходят без сдвига фаз (фиг. 28, а и 28, Ь),
то отношение -у не зависит от времени (гл. IV, стр. 119); значит,
® = FZ, где коэфициент F не зависит от времени и, следовательно,
а; == F^. Поэтому предыдущее выражение можно записать
207
в следующем виде:
о о
Второй член исчезает в силу уравнения (1), и необходимое
условие незатухания крутильных колебаний принимает вид:
— £ V 'SV4« f (S’ * > °’ <3>
О
чего, очевидно, быть не может1, а потому колебания кручения
будут неизбежно затухать; вместе с ними прекратится и источник
энергии для колебаний изгиба, и последние тоже затухнут.
Таким образом доказано, что гармонические колебания без
сдвига фаз (фиг. 28, а и 28, Ь) в потоке воздуха невозможны.
Итак, форма колебаний при флаттере должна отличаться
от формы колебаний в пустоте таким образом, чтобы как подъем-
ная сила, так и момент создавали возбуждающие воздействия,
превышающие воздействия демпфирующие. Мы уже видели, в чем
заключается принципиальное отличие формы колебаний при
флаттере от формы колебаний в пустоте: Ури флаттере обяза-
тельно наблюдается сдвиг фаз между изгибом и кручением, в то
время как при колебаниях в пустоте сдвиг фаз отсутствует.
Покажем теперь, что именно наличие сдвига фаз делает возмож-
ным флаттер, так как создает дополнительные источники энергии
за счет той части подъемной силы и момента, которые зависят
от изменения угла атаки вследствие деформации кручения.
Рассмотрим форму колебаний, близкую к крутильной, но
пусть максимумы изгиба и кручения (также и нулевые положе-
ния) достигаются не в одно время, а несколько сдвинуты, т. е.
имеется сдвиг фаз.
На фиг. 54 изображены кривые изменения прогиба Z и угла
кручения 6 по времени для гармонических колебаний при раз-
личном сдвиге фаз. Во всех случаях прогиб Z изображен одной
и той же кривой (косинусоидой). Углы кручения изображены
различными кривыми:
1) Изменение угла кручения 6 изображено косинусоидой А.
Максимумы и нулевые положения Z и 6 достигаются в один и
тот же момент времени, т. е. сдвиг фаз отсутствует, причем
знаки деформаций совпадают. Этот случай соответствует сов-
местным колебаниям кручения крыла в пустоте.
2) Изменение угла кручения по времени изображено кривой В
(косинусоида). Максимумы и нулевые положения Z и 6 сдвинуты,
т. е. имеется сдвиг фаз. Кручение достигает нулевого положения
раньше, чем изгиб, т. е. кручение опережает изгиб.
1 Выражение (3) есть не что иное, как работа момента, взятого относительно
фокуса крыла (см. гл. VI, п. 6). В гл. VJ 'мы уже отмечали что этот момент
является демпфирующим и, естественно, он не может поддерживать колебания.
208
3) Изменение угла кручения изображается косинусоидой С.
Опять имеется сдвиг фаз, причем изгиб опережает кручение.
На той же фиг. 54 изображены положения крыла через каж-
дую 1/в периода для указанных трех случаев движения. Для
построения этих положений значения прогиба Z и угла кру-
чения 6 снимались с вышеуказанных кривых. Рассмотрим, как
в каждом случае действует та часть подъемной силы, которая
получается вследствие деформации кручения. Для краткости
будем эту часть подъемной силы называть просто „подъемной
силой".
Фиг. 54
Непосредственно из фиг. 54 видно, что в случае А подъемная
сила является возбуждающей при положениях III—И и VII — IX
и демпфирующей при положениях I — Ill и V—VII. Вследствие
симметрии колебаний работа ее за период будет равна нулю.
В случае В подъемная сила является возбуждающей в поло-
жениях // — V и VI- IX и демпфирующей в положениях I и
V'. Непосредственно видно, что возбуждающее воздействие должно
превышать демпфирующее, так как подъемная сила почти все
время направлена по скорости изгибных колебаний и лишь
незначительное время (положения / и V) является демпфирую-
щей. Флаттер этой формы, очевидно, возможен.
В случае С действие подъемной силы будет обратно ее дей-
ствию в случае В. Большую часть периода (положения I — IV
и V — VIII) она будет демпфировать колебания и лишь незна
нительную часть времени (положения V и IX) возбуждать их.
Работа демпфирования явно превысит энергию возбужден..''
т- е. флаттер в этом случае невозможен.
гРоссман—15—14 209
Таким образом мы установили, что в случае сдвига фаз
появляется дополнительный источник энергии колебаний и, оче-
видно, именно это обстоятельство делает флаттер возможным.
Флаттер возможен именно вследствие наличия сдвига фаз и
именно в том случае, если сдвиг фаз таков, что кручение опе-
режает изгиб. Только этот случай мы и будем в дальнейшем
рассматривать. Мы выше рассмотрели только влияние сдвига
фаз на изгибные колебания. Не останавливаясь подробно, ука-
жем лишь, что за счет сдвига фаз появляется также и возбуж-
дающий момент, т. е. будут возбуждаться также и колебания
кручения.
Очевидно, при непрерывном изменении скорости полета сдвиг
фаз будет непрерывно увеличиваться от нуля. При этом превы-
шение энергии возбуждения над энергией демпфирования, кото-
рая возникает от частей подъемной силы и момента, появляю-
щихся от кручения (')), будет также непрерывно увеличиваться
от нуля. Когда сдвиг фаз достигнет такой величины, что энергия
возбуждения превысит всю энергию, которая затрачивается на
преодоление всех демпфирующих воздействий (от скорости из-
гибных колебани-й, от гистерезиса и т. д.), возникающие коле-
бания перестанут затухать, т. е. будет иметь место флаттер
крыла. Следовательно, существует какая-то критическая
величина сдвига фаз, определяемая скоростью полета (сдвиг
фаз зависит от скорости полета и имеет место на любой ско-
рости). Очевидно, это та величина, которой достигает сдвиг фаз
при критической скорости. Выводы не изменятся, если мы учтем
еще и части подъемной силы и момента, зависящие от угловой
скорости колебаний кручения. Эти части находятся в линейной
зависимости от скорости полета (как и демпфирующие воздей-
ствия от скорости изгибных колебаний), в то время как части,
зависящие от деформации кручения, пропорциональны квадрату
скорости полета. Поэтому при достижении достаточной величины
скорости полета возбуждающие воздействия могут превысить
демпфирующие, и'возникнет флаттер.
Интересно отметить следующие случаи: сдвиг фаз равен у,
, п к
больше y и меньше у, т. е. нулевое положение изгибных коле-
баний запаздывает по сравнению с крутильными на четверть
периода, больше четверти периода и меньше четверти периода.
Эти случаи изображены на фиг. 55, принцип построения которой
таков же, как и принцип построения фиг. 54. Изменение прогиба
по времени во всех случаях изображается косинусоидой Z, а
изменение угла кручения 6 —кривыми: кривая А — сдвиг фаз
равен у, кривая В — сдвиг фаз меньше-^- и кривая С — сдвиг
фаз больше -£•. Положения крыла через каждую х/8 периода,
соответствующие каждому из этих случаев, построены на той же
фигуре. Мы видим, что превышение возбуждающих воздействий
210
иад демпфирующими возможно в каждом из этих случаев и,
следовательно, возможен флаттер каждой из указанных форм.
Рассмотрим подробнее часть подъемной силы, зависящую от
\тловой скорости крутильных колебаний:
— 1см- УРавнение (6°). гл- VI].
Легко видеть (так как ось жесткости в современных кон-
1 х 1 \
струкциях всегда расположена так, что < -j- < что эта
часть подъемной силы направлена вниз при вращении профиля
в сторону уменьшения угла а гаки и вверх при вращении про-
филя в сторону увеличения угла атаки, т. е. она всегда направ-
лена в ту сторону, куда при вращении движется передняя кромка
профиля. Поэтому при форме колебаний, изображенной на фиг. 28, а
(совместные изгибные колебания), эта часть подъемной силы
будет демпфирующей, а при форме колебаний, изображенной на
фиг. 28, Ь (совместные колебания кручения), — возбуждающей. По-
видимому, этим объясняется, почему флаттер трансформируется
именно из совместных колебаний кручения, и кручение при флат-
тере играет основную роль.
2. АНАЛИЗ ЭНЕРГООБМЕНА МЕЖДУ ВИБРИРУЮЩИМ КРЫЛОМ
И ПОТОКОМ
А. Колебания крыла в пустоте
Рассмотрим прежде всего колеблющееся в пустоте крыло,
Центр тяжести которого в каждом сечении находится на рас-
211
стоянии а от его оси жесткости. Как было выяснено в гл. IV,
колебания такого крыла будут обязательно совместными изгибно-
крутильными, независимо от того, был ли первоначальный импульс
чисто изгибающим, чисто крутящим или комбинированным.
Мы видели (гл. IV), что если первоначально возникли изгиб-
ные колебания, то вследствие несовпадения центра тяжести
и оси жесткости возникнет крутящий периодический момент
d2Z ..
который вызовет крутильные колебания крыла. Если же
крыло совершает колебания кручения, то появится периодиче-
ская сила ms которая вызовет изгибные колебания.
Таким образом вследствие того, что центр тяжести сечения
крыла и его центр жесткости не совпадают, изгибные и кру-
Фиг. 56.
тильные колебания связаны между со-
бой, и один вид колебаний неизбежно
вызывает другой. Мы можем поэтому
говорить о наличии двух инерционных
связей: инерционной связи изгиба на
кручение (инерционный периодический
d-Z
крутящий момент/из ^-2, появляющийся
вследствие изгибных колебаний и вызы-
вающий колебания кручения) и инер-
ционной связи кручения на изгиб
(периодическая сила инерции ms
появляющаяся вследствие колебаний
кручения и вызывающая колебания из-
гиба). Эти инерционные связи вызы-
вают переход энергии из движений из-
гиба в движения кручения и обратно,
но они не могут увеличить общий запас
энергии в колеблющейся системе крыла.
Если бы затухания, вызванного гистерезисом конструкции,
не существовало, то колебания крыла в пустоте, раз начавшись,
продолжались вечно, так как запас энергии, сообщенный крылу
первоначальным импульсом, никуда исчезнуть не может.
В действительности же эта энергия будет расходоваться на
гистерезис, и колебания крыла в пустоте будут обязательно
затухающими.
Схематически энергообмен в колеблющейся системе крыла
можно представить диаграммой, показанной на фиг. 56. Запа<
энергии, сообщенный крылу первоначальным импульсом, непре'
рывно перераспределяется между движениями изгиба и кручения
ввиду наличия инерционных связей, изображенных стрелками-
АВ — инерционная связь изгиба на кручение и CD — инерционна _
связь кручения на изгиб. Стрелки О к О' показывают рассеина
ние энергии колеблющейся системы на внутренний гистерези
212
Б. Колебания крыла в неподвижной среде
Колебания крыла в неподвижной среде протекают так и е, как
и в пустоте, и также будут затухающими. Затухание в этом
случае произойдет еще быстрее, так как энергия, сообщенная
крылу первоначальным импульсом, будет затрачиваться не только
на внутренний гистерезис, но и на преодоление сопротивления
среды.
Как выше было выяснено, причина появления инерционных
связей лежит в несовпадении центра тяжести и центра жесткости
в каждом сечении крыла. Если оба эти центра совместить (соот-
ветствует з=0), то инерционные связи исчезнут (при а=0 как/пз ,
д2д чо
так и /из обращаются в нуль). В крыле с совмещенными осями
тяжести и жесткости кочебания изгиба и кручения разделяются.
Такое крыло может совершать как чисто изгибные (без кручения),
гак и чисто крутильные (без изгиба) колебания.
В. Колебания крыла в потоке воздуха
Из опыта известно, что при помещении крыла в поток воздуха
(например в аэродинамической трубе) иногда могут возникнуть
колебания, амплитуда которых непрерывно нарастает вплоть до
поломки крыла. Так как всякие колебания крыла как в спокой-
ном воздухе, так и в потоке связаны с расходованием энергии
(на внутренний гистерезис, на преодоление сопротивления среды
и т. д.), то, если амплитуда колебаний остается неизменной или
увеличивается, мы должны предположить, что существует источ-
ник энергии, сообщающий энергию колеблющемуся крылу. Таким
источником энергии может быть только поток воздуха. Выясним,
каким образом происходит энергообмен между потоком воздуха
и колеблющимся крылом.
а) Изгибно-крушильные колебания крыла, подвергнутого
начальной деформации изгиба. Мы выяснили, что если крыло
совершает только изгибные или только крутильные колебания,
го они обязательно затухнут.
Рассмотрим теперь крыло, у которого ось жесткости не сов-
мещена с осью центров тяжести, а находится впереди нее. Пусть
такое крыло, находясь в потоке воздуха, набегающего на крыло
со скоростью V, подверглось действию изгибающего импульса.
Мы уже установили, что вследствие инерционных связей даль-
нейшие колебания будут изгибно-крутильными. Но если крыло
находится в потоке воздуха, то, кроме инерционных, имеются
еШе и аэродинамические связи.
В самом деле, мы видели, что наличие скорости изгиб-
ных колебаний вызовет изменение угла атаки на величину
. 1 dZ
213
(4)
Фиг. 57.
Такое изменение в свою очередь изменит не только подъем-
ную силу, но и аэродинамический момент МЕ относительно оси
жесткости на величину
дМЕ дС_р dZ
ЛМр — Да = —-у - pSt V
с да оа * о
Этот момент будет периодическим, меняющим свой знак вместе
dZ tz
со знаком и может вызывать крутильные колебания. Крутиль-
ные колебания в данном случае черпают свою энергию из набе-
гающего потока, так как момент [формула (4)] создается не за
счет энергии, накопленной колеб-
лющейся системой вследствие на-
чального импульса, а за счет энер-
гии набегающего потока.
Итак, вследствие колебаний из-
гиба появляется внешний крутящий
аэродинамический момент, перио-
дически меняющий свой знак и
вызывающий крутильные колеба-
ния. Но как только образовались
крутильные колебания, появляется
сила инерции тз (инерционная
связь кручения на изгиб), вызываю-
щая дальнейшее увеличение изгиб-
ных колебаний. Таким образом
часть полученной от потока энергии через инерционную связь пере-
ходит из движения кручения в движение изгиба. Но увеличение
изгибных колебаний вызывает увеличение и, как следствие,
дальнейшее увеличение аэродинамического момента \МЕ. Тем
самым увеличиваются крутильные, а через инерционную связь
и изгибные колебания. Этот цикл энергообмена, непрерывно
продолжаясь, приводит к непрерывному притоку энергии из
потока в крыло, и если количество притекающей энергии ста-
новится больше, чем ее расход (на гистерезис, на преодоление
вышеуказанных демпфирующих аэродинамических сил и т. д-).
то возникают колебания с непрерывно нарастающей амплитудой
(флаттер).
Мы установили таким образом процесс, который приводит к
увеличению энергии в колеблющейся системе. Характер этого
процесса таков, что приток энергии в систему создает предпо-
сылки для дальнейшего притока энергии. Приток энергии воз-
никает благодаря наличию аэродинамической связи, которую мы
назовем аэрод инамичес кой связью изгиба на кру-
чение (приток энергии получается вследствие того, что дви-
жение изгиба порождает аэродинамический крутящий момент).
Найденный нами цикл энергообмена мы назовем первым
циклом. Схематически первый цикл изображен на фиг. 57. На
214
этой схеме.не показано рассеяние энергии, которое непременно
также имеет место.
б) И'згибно-крушильные колебания крыла, подвергнутого
начальной деформации кручения. Пусть под влиянием началь-
ного импульса возникли крутильные колебания. Вследствие ко-
лебаний кручения происходит изменение подъемной силы за
счет: 1) деформации кручения (что в аэродинамическом отноше-
нии эквивалентно изменению угла атаки) и 2) скорости крутиль-
ных колебаний (как показывает анализ, изменение скорости кру-
тильных колебаний эквивалентно изменению угла атаки хорды
крыла с одновременным изменением кривизны его средней линии)
Получающаяся за счет колеба-
ний кручения подъемная сила
будет, очевидно, менять свой
знак вместе с изменением знака О,
т. е. будет силой периодиче-
ской. Эта сила вызовет изгибные
колебания крыла.
Здесь мы имеем дело с но-
вой связью — аэродинамической
связью кручения на изгиб. Бла-
годаря колебаниям кручения на-
бегающий поток создает подъ-
емную силу, которая вызывает
колебания изгиба, т. е., иначе го-
воря, колебания возникают за счет Фчг- 58.
энергии набегающего потока.
Но как только возникнут колебания изгиба, образуется инер-
„ d-z .
ционный момент тз • — - (инерционная связь изгиба на круче-
ние), который дальше увеличивает колебания кручения, чем
опять создается предпосылка для дальнейшего перехода энергии
от потока к крылу.
Здесь мы имеем второй цикл энергообмена, в котором есть
звено (аэродинамическая связь кручения на изгиб), создающее
переход энергии из потока в колеблющуюся систему.
Схематически этот цикл представлен на фиг. 58.
в) Третий цикл энергообмена. Рассматривая колебания крыла
'без набегающего потока, мы показали, что, если в крыле сов-
мещены оси тяжести и жесткости, то инерционные связи между
колебаниями изгиба и кручения отсутствуют. Оба рассмотрен-
ные выше цикла энергообмена в этом случае оказываются на-
рушенными. Однако значит ли это, что в данном случае не
существует такого процесса перехода энергии от потока к крылу,
который, раз начавшись, создавал бы предпосылки для даль-
1 См. Е. П. Гроссман, С. С. Кричевский и А. А. Борин, К воп-
росу о потере устойчивости конструкцией крыла в полете. Труды ЦАГИ,
вып. 202, 1935 г.
215
нейшего перехода энергии? Оказывается, такой процесс все же
существует.
Пусть первоначально возникли колебания изгиба. За счет
скорости этих колебаний, как мы видели выше, образуется пери-
одический аэродинамический крутящий момент, меняющий свой
знак вместе с д~; этот момент вызовет колебания кручения.
Колебания кручения, как было показано, вызывают периодиче-
ское изменение подъемной силы, вызывающее, в свою очередь,
колебания изгиба. Таким образом и при отсутствии инерционных*
связей все же существует замкнутый цикл энергообмена через
две аэродинамические связи (третий цикл), причем здесь переход
энергии из потока в крыло происходит в двух звеньях, что
схематически показано на фиг. 59. Следовательно, совмещения
осей центров тяжести и жесткости
Фиг. 59. Фиг. СО.
г) Общий случай, уничтожение притока энергии. Обычно
крыло сконструировано таким образом, что при его колебаниях
имеются налицо все указанные выше связи. Энергообмен совер-
шается при этом сразу через все четыре связи (т. е. все три
цикла имеют место одновременно), что представлено схемой
фиг. 60.
На этой схеме мы нанесли такие стрелки, показывающие
расход энергии на внутренний гистерезис конструкции и на
преодоление аэродинамических демпфирующих сил.
Три цикла энергообмена, рассмотренных выше, схематически
представлены контурами:
первый цикл — контуром АА&СА;
второй цикл — контуром DJDBB^Dp,
третий цикл — контуром AAJ\DA.
216
Хотя в крыле имеются налицо все четыре связи, однако это
еще не значит, что флаттер обязательно должен возникнуть.
опыта известно, что вибрации с нарастающей амплитудой
могут возникнуть только при скорости набегающего потока,
превосходящей некоторую строго определенную для данного
крыла величину (критическую скорость). Чем объясняется на-
личие этой скорости?
Мы видели, что наряду с притоком энергии происходит и ее-
рассеивание. Количество притекающей и расходуемой энергии
зависит и от конструкции крыла (взаимного расположения осей
тяжести, жесткости и
фокусов, величины же-
сткостей изгиба и кру-
чения, величины масс,
моментов инерции и
т. д.) и от скорости
набегающего потока.
Для возникновения ви-
браций типа „флаттер"
недостаточно только
притока энергии бла-
годаря связям, — необ-
ходимо еще и чтобы
количество притекаю-
щей энергии было
больше количества рас-
ходуемой энергии. И
вот это-то обстоятельство имеет место только при некоторых
дополнительных условиях.
Сами связи также не обязательно вызывают приток энер-
гии, — они могут вызывать и дополнительный ее расход. Рас-
смотрим, например, аэродинамическую связь кручения на изгиб.
Действие этой связи, как было указано, вызывает возникно-
вение дополнительной подъемной силы вследствие изменения
угла атаки крыла от кручения1. Направление этой подъемной
силы может быть различным. Если крыло при движении вниз
перекручивается на отрицательные углы атаки, а при движении
вверх — на положительные (фиг. 45), то появляющаяся подъем-
ная сила будет при движении вниз направлена также вниз, а при
движении вверх вверх, т. е. подъемная сила будет все время
направлена по направлению движения изгиба и будет его уси-
ливать. Этот случай соответствует разобранному выше дей-
ствию аэродинамической связи вручения на изгиб. Но возможен
и другой случай. Крыло может быть сконструировано таким
образом, что при движении вниз оно перекручивается в сторону
положительных углов атаки, а при движении вверх в сторону
1 Для простоты мы опускаем здесь влияние на подъемную силу угловой
скорости колебаний.
217
отрицательных (фиг. 61). Тогда подъемная сила будет при дви-
жении вниз направлена вверх, а при движении вверх — вниз,
т. е. все время будет противодействовать движению изгиба’
Рассмотрим, при какой конструкции крыла будет иметь место
первый случай, при какой — второй.
Рассмотрим сперва крыло, у которого ось жесткости распо-
ложена впереди центра тяжести. Выше мы указывали, как это
крыло будет закручиваться при изгибных колебаниях вследствие
появляющегося момента инерционных сил (фиг. 45). В этом
случае подъемная сила будет направлена всегда по направлению
движения изгиба.
Иначе происходит движение, если ось жесткости крыла рас-
положена позади его центра тяжести. При движении такого
Энергия копеЬаний изгиба
Энергий колебании кручение
крыла под действием упругих сил по
направлению к положению равновесия
(ускоренно) центр тяжести будет
вследствие инерции отставать от оси
жесткости, и так как он находится
перед осью жесткости, то крыло
будет закручиваться, как показано
на фиг. 61. В этом случае подъемная
сила будет противодействовать дви-
жению изгиба.
Итак, подъемная сила, получаю-
ф11г 69 щаяся вследствие кручения крыла от
инерции, будет увеличивать колеба-
ния, если центр тяжести расположен позади оси жесткости, и
будет им противодействовать (демпфировать), если центр тя-
жести расположен впереди оси жесткости.
Второй цикл энергообмена в последнем случае не будет
давать притока энергии, а будет дополнительно рассеивать ее.
Схематически это изображено на фиг. 62.
Покажем, что первый цикл энергообмена путем соответствую-
щей конструкции крыла можно превратить в источник демпфиро-
вания колебаний. Для этого достаточно поместить ось жесткости
впереди фокуса крыла. В самом деле, пусть крыло закручи-
вается в сторону увеличения угла атаки. При увеличении угла
атаки приращение аэродинамического момента будет положи-
тельным, т. е. будет действовать в сторону дальнейшего увели-
чения угла атаки, если ось жесткости расположена за фокусом;
приращение момента будет отрицательным, если ось жесткости,
к которой мы относим момент, будет расположена впереди фо-
куса.
В первом случае момент будет стремиться закрутить крыло
дальше в сторону увеличения угла атаки (именно этот случай
действия аэродинамической связи изгиба на кручение мы и рас-
сматривали во всех предыдущих схемах); во втором случае
момент будет противодействовать движению. Очевидно, что при
218
кручении крыла в сторону отрицательных углов атаки картина
будет та же; если ось жесткости расположена за фокусом, аэро-
динамический момент будет помогать кручению; если же она
расположена впереди фокуса, возникает аэродинамический мо-
мент, демпфирующий движение кручения.
Схема первого цикла энергообмена в крыле с осью жест-
кости, расположенной перед фокусом, показана на фиг. 63.
1
Фиг. 63. Фиг. 64.
Схема действия аэродинамической связи изгиба на кручение
в этом случае такова: при движении крыла вниз угол атаки
увеличивается. При этом возникает аэродинамический момент,
стремящийся уменьшить угол атаки, благодаря чему и сам момент
по' абсолютной величине уменьшается. При движении крыла
вверх угол атаки уменьшается, но возникает аэродинамический
момент, стремящийся его увеличить. Таким образом момент,
возникающий в этом случае, создает предпосылки для своего
собственного уничтожения, в то время как при расположении
оси жесткости за фокусом действие аэродинамического момента
обратно: при увеличении угла атаки создается момент, стремя-
щийся этот угол увеличить, дальше и тем создающий предпо-
сылку для своего дальнейшего роста.
На фиг. 64 изображена схема энергообмена в крыле, у ко-
торого действие обеих аэродинамических связей обращено, для
чего, очевидно, необходимо и достаточно поместить центр тя-
жести крыла перед осью жесткости и ось жесткости—перед
осью фокусов. Поскольку крыло, сконструированное таким об-
разом, не поглощает энергию из набегающего потока воздуха,
оно не может быть подвержено вибрациям типа „флаттер
Мы не будем останавливаться на многих промежуточных
случаях, могущих представиться при различных конструкциях
крыла, так как метод анализа достаточно ясен, и читатель
легко может провести этот анализ самостоятельно.
219
Г. МЕРЫ ПРЕДОТВРАЩЕНИЯ ФЛАТТЕРА
Выше мы уже указали идеальную конструкцию крыла, при
которой флаттер становится невозможным: для этого достаточно
в каждом сечении крыла поместить центр тяжести перед центром
жесткости и центр жесткости перед фокусом. При этом действие
аэродинамических связей обращается, и поток создает дополни-
тельные демпфирующие силы.
Однако указанное расположение осей чрезвычайно трудно
осуществить конструктивно. В современных конструкциях крыльев
они расположены как раз обратно: центр тяжести находится по-
зади оси жесткости, а ось жесткости — позади фокуса. (Можно
сказать, что в среднем для крыльев обычной конструкции, на-
Фиг. 65.
пример типа ЦАГИ, фокус на-
ходится на 25%, центр жесткости
на 32 — 36% и центр тяжести
на 44—50% хорды от передней
кромки).
Для предотвращения флаттера
достаточно не обращать связи,
а нарушить замкнутость циклов
энергообмена; тогда невозможен
будет периодический процесс,
при котором переход энергии от
потока к крылу создает предпо-
сылки для дальнейшего перехода
этой энергии. Достаточно совме-
стить все три центра в каждом
сечении крыла (тяжести, жест-
кости и фокусов) в одной точке;
тогда будут отсутствовать обе
инерционные связи, благодаря чему разрушатся первый и вто-
рой циклы энергообмена.
Рассмотрим, что произойдет при этом с аэродинамической
связью изгиба на кручение. Эта связь создается благодаря тому,
что при изгибных колебаниях происходит изменение угла атаки,
влекущее за собой изменение аэродинамического момента отно-
сительно оси жесткости. Не фокус крыла есть такая точка,
момент относительно которой не зависит от угла атаки, и если
ось жесткости совпадает с осью фокусов крыла, то изменение
угла атаки не вызовет никакого изменения момента относи-
тельно оси жесткости. Следовательно, в данном случае аэро-
динамическая связь изгиба на кручение отсутствует, и замкну-
тость третьего цикла энергообмена также нарушается.
Диаграмма эиергообмена крыла с тремя совмещенными осями
.показана на фиг. 65. Движение кручения в данном случае только
рассеивает свою энергию и потому непременно затухнет,—тем
самым оборвется аэродинамическая связь кручения на изгиб,
220
прекратится приток энергии в движение изгиба, и оно также
затухнет.
Таким образом при совмещении трех осей крыла в одной
точке флаттер также становится невозможным.
Указанные выше пути устранения флаттера основаны на
возможности создать такую конструкцию крыла, при которой
полностью прекращается приток энергии по крайней мере в один
из видов движения. Возможен и другой путь устранения опас-
ности флаттера, основанный на количественном анализе энерго-
обмена. Для предотвращения флаттера нет необходимости пол-
ностью прекращать приток энергии в колеблющуюся систему, —
достаточно, чтобы количество притекающей энергии было меньше,
чем ее рассеивание. В этом случае колебания также будут за-
тухающими. Кроме того, нет необходимости конструировать
крыло так, чтобы оно ни при каких условиях не было подвер-
жено флаттеру. Достаточно, чтобы флаттер становился возможным
только при скоростях, значительно превосходящих максималь-
ную скорость самолета.
Количество притекающей и расходуемой при колебаниях
крыла энергии зависит от жесткостей изгиба и кручения крыла,
его масс, моментов инерции, формы крыла и т. д., а также от
скорости полета. Каковы должны быть эти факторы для преду-
преждения возникновения флаттера в диапазоне возможных
скоростей, мы увидим из дальнейшего количественного анализа
явления.
Укажем лишь, что учет расходуемой энергии позволяет
сделать тот вывод, что возможна конструкция крыла, у которого
ось жесткости совмещена с фокусом, а центр тяжести находится
позади нее, и которое тем не менее не подвержено флаттеру
ни при каких скоростях. В самом деле, у такого крыла приток
энергии в движение кручения получается только через инерци-
онную связь изгиба на кручение. Если центр тяжести находится
на небольшом расстоянии от оси жесткости, то этот приток
энергии невелик и может быть сделан меньше, чем ее расход,
благодаря чему флаттер станет невозможным.
ГЛАВА IX
ТЕОРИЯ ПОДОБИЯ И ИССЛЕДОВАНИЕ ФЛАТТЕРА
В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ
Одним из основных затруднений при изучении флаттера яв-
ляется трудность изучения этого явления на натуральных объек-
тах. Объясняется это тем, что при флаттере чрезвычайно быстро
(часто в течение долей секунды) наступает разрушение вибри-
рующей части и потому доводить самолет до скоростей, при кото-
рых возникает флаттер, слишком опасно. С другой стороны,
все существующие теории флаттера базируются на тех или
иных произвольных допущениях (например, гипотеза стационар-
ности) и потому являются приближенными, поэтому их экспери-
ментальная проверка совершенно необходима. Одним из путей
такой проверки является исследование вибраций упругой модели
в аэродинамической трубе.
Прежде чем изложить теорию моделирования явления флат-
тера, напомним некоторые понятия общей теории подобия. Если
имеются два тела и все линейные размеры одного из них в оди-
наковое число раз меньше соответственных линейных размеров
другого тела, то эти тела называются геометрически по-
добными. Меньшее тело при этом называется моделью боль-
шего. Постоянное для всех линейных размеров отношение какого-
либо линейного размера модели к соответственному линейному
размеру большего тела (натуры) называется масштабом мо-
дели (kL).
Рассмотрим теперь какое-либо явление, протекающее во вре-
мени. Предположим, что это явление заснято на киноленту и
кинолента пропущена через киноаппарат с иной скоростью, чем
при съемке. При этом на экране будет воспроизведено заснятое
явление, но будут изменены по сравнению с действительностью
не только геометрические размеры тел, на которых изучается
явление, но и время, протекающее между какими-либо событиями
в нем. В таком случае говорят, что на экране мы видим явле-
ние, кинематически подобное действительному. Таким образом
кинематическое подобие есть подобие по двум масштабам: по
длине (kL) и времени (/?-).
Наиболее общим случаем подобия двух явлений является
подобие динамическое, когда одно явление может быть
получено из другого изменением трех масштабов: длины (kr),
222
времени (&-) и сил (&0). Так как единица измерения любой ве-
личины составляется из единиц измерения длины, времени и
силы, то при динамическом подобии каждая величина (например
плотность воздуха, масса и т. д.) будет иметь свой масштаб,
определяющийся указанными выше тремя масштабами: (?£, k-,kQ .
Пусть F— какая-либо величина, характеризующая с какой-
нибудь стороны явление флаттера. Будем обозначать через
значение этой величины для модели, через FH — значение той же
величины для натуры и через kp- масштаб изменения этой ве-
личины:
Тогда имеем следующую систему масштабов:
масштаб масштаб масштаб масштаб масштаб масштаб масштаб длины ь “ . RL- L ’ скоростей k --М. v" VH ’ жесткости на изгиб h -Е± жесткости иа кручение к - G • Е~ Glpu ’ погонных масс k погонных моментов инерции . т м . *‘ = I ’ т н времени тм “н • (1>
масштаб плотности воздуха k = Р Рн 4
Основным свойством всех этих масштабов, если соблюдено
Динамическое подобие, является их постоянство на всем про-
223
»
странстве, в котором изучается явление, .и во все время проте
кания явления.
Предположим, что мы имеем модель, геометрически подоб-
ную крылу натурального самолета, с теми же граничными усло-
виями, т. е. с теми же условиями заделки крыла. Выведем те
условия, при которых явления флаттера для натуры и модели
будут динамически подобны, а также укажем, каким образом
критическую скорость, полученную при испытаниях модели в
аэродинамической трубе, можно пересчитать на натуру.
Прежде всего заметим, что при флаттере коэфициенты аэро-
динамической силы \CV и момента ЛСт£ должны зависеть от
характеристик колебания, в частности от частоты. Но так как
и ACV и ДС’тЕ величины безразмерные, то и частота должна
входить в их выражения в безразмерной комбинации с другими
параметрами, от которых могут зависеть \Су и ЬСтЕ- Такой
безразмерной комбинацией является число Струхаля , функ-
цией которого и являются аэродинамические силы1. Таким обра-
зом, кроме геометрического подобия модели и натуры, для ра-
венства коэфициентов аэродинамических сил необходимо еще
потребовать и равенства чисел Струхаля:
Рм^Ы _ Рн^Н
2VM ~ 2V~'
Если мы заменим частоты через соответствующие периоды
колебания, то будем иметь:
2я/м 2к/н
= 2'/нЛ,’
где Тн и Тн — периоды колебания соответственно для модели
и натуры.
1 То, что ДС,, и ДСт£ зависят от числа Струхаля, легко обнаружить н
непосредственно нз формул (60) гл. VI. Так как колебания при флаттере гар-
монические, то
0 = в0 • cos (рт + a), Z = ZBt cos рх,
где а—угол сдвига фаз, Го—амплитуда крутильных колебании (очевидно, без-
размерная, так как измеряется в угловых единицах) и ZB—безразмерная ампли-
туда изгибных колебаний в долях хорды. Подставляя эти выражения в фор-
мулы (60) гл. VI, найдем:
ХСу — Ф, cos (рт 4- а) ф2 sin (рх -р а) + Ф3 sin рх,
где Фь Фг и Ф3 — безразмерные функции, зависящие только от безразмерных
амплнтуд и числа Струхаля. Выражение для ЬСт1,- получается такого же вида-
Важно отметить, что нз соображений теории подобия аэродинамические силы
будут зависеть от числа Струхаля не только, если их вычислять на основе
гипотезы стационарности, ио и в том случае, если бы эта теория была вполне
точной. Поэтому теория подобия, излагаемая в настоящей главе, остается
справедливой, какой бы теорией аэродинамических сил мы не пользовались
224
Делим правую и левую части равенства на 2l/ Тогда,
пользуясь обозначениями масштабов (I), находим первое усло-
вие динамического подобия, которое необходимо соблюсти для
подобия аэродинамических сил у натуры и у модели:
(Если ввести в рассмотрение вязкость и сжимаемость воздуха,
н^жно также требовать равенства чисел Рейнольдса и Берстоу.)
Явление флаттера в натуре управляется системой диферен-
циальных уравнений движения, которые были получены в гл. VII:
д- Г &Z„
' л 2 Е/ц 2
<4
д-
Ф'н
— — [<7/,
Ф'н L
Рн
дУ»
Ч~ /Ин ~ n — /ИН5Н ——7; ДС, pH ^H V H — 0;
dx" -H
d22H d2BH 2 3_____
.» “b im о pH tn V H — 0.
dz" и dz" н
H H
(4)
Напишем также систему диференциальных уравнений движе-
ния для модели, для чего достаточно в уравнениях (4) заменить
j всех величин индекс „н“ на „м“. Заметим, что при соблю-
дении условия (3) коэфициенты аэродинамических сил для мо-
дели и натуры одинаковы &СтЕн — Затем
в системе уравнений движения модели заменим все величины
их выражениями через соответствующие величины для натуры
и переходные масштабы, согласно обозначениям (1) (например
— tu = kLtH, так как все линейные размеры уменьшены
У модели по сравнению с натурой в Ад раз и т. д.). Тогда си-
стема диференциальных уравнений движения для модели
иметь вид:
будет
kE
kl
д-
дУ»
kl дун
o-Z,
Е1п
GE
'н
^32н kmk^ о-0,
Ч----tn« -------------75“ Wh3h “7.
kt д-.-л kt дх,
k..kLkv ^CvjatHVl = 0;
kl
^~2ц
/Ин3н “ТУ
k,
k
д
*4тобы;явление флаттера у модели было подобно явлению флат-
геРа у натуры, необходимо, чтобы оно управлялось теми же
^иференцнальными уравнениями, т. е. система (5) должна сов-
гРоссчан—15_15 225
падать с системой (4). Это будет иметь место, если
k2
^Я — ^2 — K-.KLKV,
кЕ kmkL _ 3' _ А. ь2ь2
,п — ~п — .2 — KpR'LRV*
kl k; kx
(6)
(7)
Необходимость условий (6) и (7) при динамическом подобии
модели и натуры следует также из того, что первое из урав-
нений (5) — есть уравнение равновесия сил, а второе — уравнение
равновесия моментов. Так как необходимым условием динами-
ческого подобия является то, что все силы и все линейные раз-
меры (а следовательно и плечи моментов) изменяются в одина-
ковое число раз, то, следовательно, все члены уравнения сил
(и уравнения моментов) должны измениться в одинаковое число
раз. Это также приводит к условиям (6) и (7).
Делим соотношение (7) на ki. Тогда последние части ра-
венств (6) и (7) становятся равными, ’и, соединяя оба условия (6)
и (7) в одно, получаем:
^Е kmkL 2 A;
= ~~ь2" = k^kLkv = =
Кг К~ К в К kj
(8)
Эти равенства вместе с соотношением (3) дают полную систему
условий динамического подобия при флаттере.
Из уравнения (8) прежде всего следует, что
Ад = kE, (9)
т. е. что для соблюдения динамического подобия необходимо-
жесткости на изгиб и кручение по сравнению с натурой изме-
нять в одинаковое число раз. Считая условие (9) выполняю,
щимся, можем в дальнейшем отбросить последнее из равенств (8)
Пользуясь условием (3), можем исключить из системы (8)
масштаб времени А-: из условия (3) следует, что k- — ;
подставляя это значение в систему (8), а затем деля результат
^Е
на получим:
_ АтАд*у k^kLky kik2v .
kE - kE ~ kE •
Отсюда прежде всего следует, что:
или
А^Ад — АрАд А,,
Ащ kr.kL, ]
А, — k.,kb. ।
(И)
226
При выполнении этих условий последние три отношения системы
(10) будут равны между собой. Чтобы исчерпать систему (10),
остается только приравнять какое-либо из отношений единице.
Будем иметь:
kE
откуда
С2)
Но kv — -гг- и, следовательно,
*н
(13)
kL Г k?
По этой формуле критическая скорость, измеренная во время
опыта с динамически подобной моделью, может быть пересчи-
тана на натуру.
Если модель проектируется для испытаний в трубе обычного
типа, в которой плотность воздуха такова же, как и в атмо-
сфере, то k? — 1, и мы будем иметь следующие условия подобия.
km = kl; k;= kt\
Напоминаем, что, кроме этих условий, необходимо еще со-
блюдение подобия всех линейных размеров. В частности рас-
стояние от центра тяжести до оси жесткости и расстояние от
оси жесткости до передней кромки у модели должны быть
уменьшены по сравнению с натурой в такое же число раз, как
и все линейные размеры.
На основе продувок динамически подобной модели в аэро-
динамической трубе можно точно указать величину критиче-
ской скорости для натурального крыла, и с этой точки зрения
постройка динамически подобной модели дает радикальное ре-
шение вопроса о флаттере. Продувки динамически подобной
модели могут также указать способ увеличения критической
скорости, для чего необходимо только проверить, как меняется
критическая скорость с изменением параметров модели.
Однако возможность точного экспериментального изучения
флаттера не умаляет значения теории. Построить динамически
подобную модель можно только после окончания проектирова-
ния крыла, после того, как все параметры крыла точно известны.
Между тем предусмотреть вопросы безопаснрсти от флаттера
227
желательно еще до того, как крыло спроектировано, так как
если критическая скорость окажется слишком малой, менять
готовую конструкцию весьма сложно. Поэтому расчеты на
флаттер необходимо производить еще в период предваритель-
ного проектирования.
Практически осуществить динамически подобную модель
весьма сложно, так как требуется осуществить подобие по
весьма большому числу параметров.
Один из возможных способов конструирования динамически
подобной модели следующий1: модель осуществляется в виде
отдельных отсеков, надетых на лонжерон и крепящихся к нему
каждый в одной точке. Благодаря такой конструкции вся жест-
кость модели создается одним лонжероном и обшивка, жест-
кость которой обычно очень трудно учесть, исключается из
работы.
Жесткости лонжерона на изгиб и кручение определить не
представляет труда, так как лонжерон модели представляет
собой сплошной стержень, обычно прямоугольного сечения.
Выбором размеров поперечного сечения добиваются нужной
величины жесткостей на изгиб и кручение, причем для соблю-
дения условия подобия (9) необходимо, чтобы у модели жест-
кости на изгиб и на кручение были изменены по сравнению
с натурой в одинаковое число раз. Масштаб жесткостей kl:
подбирают таким образом, чтобы критическая скорость модели
была ниже максимальной скорости потока воздуха в аэродина-
мической трубе, в которой предполагается испытывать модель.
Таким образом соответствующим выбором лонжерона полно-
стью решается вопрос подобия по жесткостям. При описанной
конструкции также легко решается вопрос о положении оси
жесткости модели: она, очевидно, совпадает с осью лонжерона,
и поэтому нетрудно соблюсти требование подобного размеще-
ния оси жесткости в модели по сравнению с натурой,—для
этого только нужно ось лонжерона в модели поместить на том
же проценте хорды, на котором располагается ось жесткости в
натуре.
Соблюдение подобия по массам и моментам инерции [первые
два условия (14)], а также соответствующее расположение ли-
нии центров тяжести в модели осуществляется следующим об-
разом: отсеки, составляющие модель, строят предварительно
с соблюдением только геометрического подобия и по весу легче,
чем требуется по условию подобия по массам. Затем внутри
каждого отсека располагают два дополнительных груза. Веса
этих дополнительных грузов и их расстояние от оси лонжерона
подбирают таким образом, чтобы оказались выполненными
условия подобия по массам, моментам инерции и положению
центра тяжести.
1 Описываемый способ разработан Л. С. Поповым и Н. Альхимовнчсм,
которые осуществили первую динамически подобную модель.
228
Критическая скорость натуры определяется по найденной в
аэродинамической трубе критической скорости модели путем
пересчета по последней из формул (14).
Описанный способ моделирования имеет тот недостаток, что
прочность модели (которая создается только одним лонжероном)
получается весьма небольшой. Поэтому модель не может вы-
держивать сколько-нибудь значительных аэродинамических на-
грузок, и все испытание в аэродинамической трубе приходится
проводить на углах атаки, близких к углу, соответствующему
Cv = 0. Поэтому исследовать, например, влияние угла атаки на
критическую скорость на такой модели не представляется воз-
можным.
Теория подобия позволяет доказать важные положения, ко-
торые дают возможность установить влияние на критическую
скорость некоторых конструктивных параметров крыла:
1. Если жесткости крыла на изгиб и кручение изменяются в
п раз, причем все остальные параметры крыта сохраняются, то
критическая скорость изменяется в Vп раз. ф
Положение это следует из условий (14). В самом деле, при
изменении жесткостей и сохранении всех других параметров
крыла мы получаем новое крыло, динамически подобное первому,
причем, согласно последнему, из условий (14) критическая ско-
рость второго крыла будет:
l/2= Ц/щ
так как масштаб изменения жесткостей есть по условию и(1/1 —
критическая скорость исходного крыла). Это равенство и дока-
зывает высказанное положение.
2. Изменение всех геометрических размеров крыла (и его
* деталей) в произвольное число раз, если материал, из которого
изготовлено крыло, остается неизменным, не влечет за собой
никакого изменения критической скорости.
Предположим, что все линейные размеры изменились в kL раз.
Если при этом материал, из которого изготовлена каждая де-
таль крыла, сохраняется, то, очевидно, погонные массы изменят-
ся в k2L раз, радиусы инерции — в ki, а погонные моменты инер-
ции в k* раз, т. е. первые два условия (14) динамического по-
добия будут выполнены. Так как жесткости пропорциональны
четвертой степени линейного размера (при одинаковом мате-
риале, т. е. при одинаковых модулях упругости), то из последней
формулы (14) следует, что критическая скорость не изменится.
Выше мы изложили теорию моделирования явления флаттера.
Однако осуществление динамически подобных моделей требует
настолько большой затраты сил и труда, что в тех случаях,
когда это не является абсолютно необходимым, для испытания
в аэродинамической трубе применяются упругие модели, постро-
229
енные по тому же принципу, что и динамически подобные (из
отдельных отсеков), но без соблюдения всех критериев подобия.
Такие модели применяют в первую очередь для проверки ре-
зультатов приближенных методов расчета, а также для выявле-
ния влияния конструктивных параметров. Так как без соблюде-
ния критериев подобия модель имеет обычно небольшие числа
Струхаля (порядка <о = 0,3), в то время как в действительности
реальные конструкции имеют иногда значительно большие числа
Струхаля (от w=0,l до <0=1,5*), то проверка теории на неподоб-
ных моделях не может считаться достаточной. В последнее время
разработаны методы изучения флаттера в натуре, о чем будет
сказано в гл. XIV.
Фиг. 67
На фиг. 66 и 67 показаны две модели, испытывавшиеся в аэро-
динамической трубе. Каждая модель состоит из жестких (фанер-
ных) отсеков, надетых на общий дуралюминовый лонжерон и
крепящихся к нему каждый в одной точке. Так как массы, мо-
менты инерции и т. д. можно определить для каждого отсека в
отдельности, жесткости же создаются одним лонжероном, то все
параметры такой модели можно определить очень просто и с
1 Для крыла переменного сечения число Струхаля меняется по размаху,
так как меняется хорда. На конце крыла число Стрххаля бывает значительно
меньше, чем в корне, и доходит до 0,1.
230
большой точностью» что чрезвычайно важно для сравнения ре-
зультатов расчета с опытом. Кроме того, такая конструкция
обладает тем удобством, что вследствие очень большой гибко-
сти крыла модель может выдерживать, не ломаясь, весьма боль-
шие амплитуды колебаний.
На фиг. 68 показана установка модели в аэродинамической
трубе для испытания на вибрации. На фиг. 69 показаны кадры
киносъемки вибрирующей модели; скорость съемки —16 кадров
в секунду; на фиг. 70 показан вид вибрирующей модели спе-
реди. На фиг. 71 показана киносъемка вибрации другой модели.
Фиг. 68-
Эти кадры были засняты киноаппаратом „Рапид" со ско-
ростью примерно 120 кадров в секунду, следовательно, 18 кад-
ров, показанные на фиг. 71, засняты за 0,15 секунды.
На всех фигурах ясно видны как изгиб, так и кручение.
В некоторых случаях модель делают сплошной, а не из от-
дельных отсеков. На фиг. 72 показано несколько снимков вибри-
рующей сплошной модели. Сплошные модели почти всегда ло-
маются вскоре после возникновения флаттера. На последних
кадрах фиг. 72 видно начало поломки: на обшивке образовались
волны и у корня началось разрушение модели.
Из предыдущих фигур можно видеть, что амплитуда углов
кручения плавно нарастает от корня к концу крыла. Однако
^сли жесткость модели к концу сильно падает, то характер
Распределения амплитуд меняется: части крыла, примыкающие
к корню, в этом случае остаются почти неподвижными, в то
231
Фиг 69.
Фиг. 79.
232
время как концевые части ви-
брируют весьма интенсивно. Ви-
брации такого характера показа-
ны на фиг. 73. При исследовании
влияния конструктивных парамет-
ров крыла на величину крити-
ческой скорости мы специально
остановимся на случае, когда
возможен такой характер вибра-
ции. Конструкция крыла, в ко-
торой распределение амплитуд
крутильных колебаний носит
такой характер, как на фиг. 73,
должна быть с точки зрения
флаттера признана неудачной.
Подробнее этот вопрос будет
исследован ниже. На опытах в
аэродинамической трубе, а в
дальнейшем и путем летных ис-
следований (см. гл. XIV), была
выяснена точность, даваемая ме-
тодом расчета, основанным на
гипотезе стационарности. Можно
считать, что расчет дает зна-
чение критической скорости,
отклоняющееся от действитель-
ного не более, чем на 15 — 20%.
Такую точность нужно приз-
нать достаточной, тем более что
расчетные данные (жесткости,
моменты инерции, положение оси
жесткости и т. д.) практически
известны конструктору не с боль-
шей точностью.
Метод расчета, основанный
на нестационарной теории аэро-
динамических сил (т. е. когда
учитывается вихревая пелена,схо-
дящая с крыла за счет измене-
ния циркуляции во времени) в
применении к реальным конст-
рукциям в некоторых случаях
дает значительные отклонения
от опыта. Это может быть объяс-
нено тем, что в настоящее время
при расчете по нестационарной
теории не учитывается влияние
конечности удлинения на аэро-
фиг. 71.
динамические силы, а это влияние, повидимому, значительно.
23»
Фиг 72. Фиг. 73
Поэтому пользоваться нестационарной теорией практически не
представляется возможным до тех пор, пока не будет разрабо-
тана нестационарная теория аэродинамических сил для крыльев
конечного удлинения. Дальнейшее развитие теории флаттера
упирается в первую очередь именно в эту проблему.
Следует отметить, что во всех случаях, когда вычисленные
по стационарной теории критические скорости сравнивались с
опытом, оказывалось, что теория дает несколько заниженные
значения критической скорости, т. е. ошибка идет в сторону
безопасности.
ГЛАВА X
ВЛИЯНИЕ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ НА КРИТИЧЕ-
СКУЮ СКОРОСТЬ ИЗГИБНО-КРУТИЛЬНОГО ФЛАТТЕРА КРЫЛА
Изложенный выше метод определения критической скорости
позволяет определить скорость по заданным конструктивным
параметрам крыла. Однако для конструктора этого мало. Если
по расчету оказалось, что критическая скорость крыла слишком
низка, конструктор должен знать, какие параметры и в какую
сторону наиболее целесообразно изменять, чтобы увеличить
критическую скорость. Кроме того, нужно выяснить, за какими
параметрами в первую очередь должен следить конструктор в
процессе проектирования, чтобы обеспечить безопасность кон-
струкции от флаттера.
Оказывается, что основными параметрами, которые может
менять конструктор для увеличения критической скорости, явля-
ются: жесткость конструкции, частотная характеристика и поло-
жение оси центров тяжести по размаху. В первую очередь мы
остановимся на влиянии этих основных параметров, а затем
кратко укажем также и на влияние остальных конструктивных
параметров (массы, формы крыла и т. д.); однако последние
параметры обычно не удается менять по желанию, так как их
изменение требует капитальной переделки конструкции.
1. ВЛИЯНИЕ ЖЕСТКОСТИ КРЫЛА НА КРИТИЧЕСКУЮ СКОРОСТЬ
В гл. IX было установлено следующее положение: одновре-
менное изменение в п раз жесткости крыла на изгиб и кручение
влечет за собой изменение критической скорости в уЛг раз.
Укажем, что эта теорема справедлива не только в отношении
крыла, но и в отношении любой системы, подверженной флат-
теру (например крыло с элероном, хвостовое оперение): увели-
чение (уменьшение) всех жесткостей системы в п раз влечет за
собой увеличение (уменьшение) критической скорости в х^п
раз.
Однако для практического применения такого общего положе-
ния недостаточно: конструктору интересно знать, какие элементы
конструкции выгоднее ужестчать,— например лонжероны (что уве-
личивает главным образом жесткость изгиба) или обшивку (что
увеличивает главным образом жесткость кручения;. При исследо-
236
вании физических причин возникновения флаттера (гл. VIII)
было установлено, что основную роль при флаттере играет
вручение. Поэтому всегда параметры, характеризующие кручение,
влияют на критическую скорость сильнее, чем параметры, харак-
теризующие изгиб. Это правило сохраняется и в данном случае:
жесткость кручения влияет . на критическую скорость гораздо
сильнее, чем жесткость изгиба крыла.
На фиг. 74 показана типичная кривая изменения критической
скорости в зависимости от
циент — это то число
раз, в которое изменена
жесткость кручения. Взя-
то некоторое крыло, для
которого критическая
скорость равна 155 м/сек.
Затем жесткость круче-
ния этого крыла изме-
нена в *1 раз (одинаково
по всему размаху), а все
остальные параметры
крыла (в том числе и
жесткость изгиба) сохра-
нены. При этом критиче-
ская скорость в зависи-
мости от г; менялась так,
как показано на фиг. 74.
Исходный вариант крыла,
следовательно, соответст-
вует т]=1. С достаточной
жесткости крыла на кручение. Коэфи-
критической скорости в зависи-
точностью закон изменения
мости от изменения жесткости кручения для данного крыла
можно представить формулой:
т г ту 0,556
ИкР=И071 ,
где 1/0— критическая скорость исходного варианта крыла (в дан-
ном случае = 155 м/сек).
Вообще из большого числа расчетов было установлено, что
с достаточной для практики точностью можно принять, что кри-
тическая скорость изменяется пропорционально корню квадрат-
ному из жесткости кручения. Следовательно, если какое-либо
крыло имело критическую скорость , а жесткость кручения
крыла была изменена в tq раз (одинаково по всему размаху) и
получилась критическая скорость 1Л>, то можно считать, что
= (1)
Следует подчеркнуть, что сказанное будет справедливо только
в том случае, если частота крутильных колебаний крыла значи-
тельно выше частоты изгибных колебаний, как практически и
бывает. Ниже будет подробно выяснен смысл этой оговорки.
231
Формула (1) позволяет, с одной стороны, быстро прикинуть
значение критической скорости, которое получается при измене-
нии жесткости кручения крыла, а с другой стороны, определить
величину необходимого изменения жесткости, чтобы получить
заданную величину критической скорости.
Пример 1. При расчете некоторого крыла была получена
критическая скорость в 250 км/час. Эта скорость была признана
недостаточной и для ее увеличения было решено увеличить
толщину обшивки крыла. После увеличения толщины обшивки
жесткость кручения возросла по всему размаху крыла в 1,7 раза.
Требуется определить критическую скорость крыла после утол-
щения обшивки.
По формуле (1) сразу находим:
Уа= 250./1?7 = 326 км/час.
Пример 2. При расчете некоторого крыла была получена
критическая скорость в 300 км/час. Между тем по нормам проч-
ности данный самолет должен иметь критическую скорость не
менее 360 км/час. Во сколько раз нужно увеличить жесткость
крыла на кручение, чтобы получить требуемую скорость?
Из формулы (1) находим:
или, подставляя числа,
/360\2
71 = \зоо) = *’44 Раза‘
238
Формула (1) является приближенной. Более точно ее следо-
аЛо бы написать в таком виде:
= (2>
где для разных крыльев р может изменяться в пределах 0,5 —
0 65. Для более точных подсчетов можно рекомендовать прини-
мать »! =0,56. На фиг. 75 показана диаграмма зависимости кри-
тической скорости от Tj для двух крыльев и двух моделей.
Сплошные линии построены путем точного расчета, по методу,
изложенному в гл. VII. Точки, отмеченные кружочками, полу-
чены по формуле (2) при р = 0,56. Как видно из этой диаграммы,
приближенная формула дает вполне удовлетворительную точ-
ность.
Рассмотрим теперь влияние на критическую скорость,
жесткости крыла на изгиб. На] фиг. 76 и 77 показано,
что происходит с критической скоростью крыла (фиг. 76 по-
строена для крыла одного реального самолета, фиг. 77 — для пря-
моугольной модели), если жесткость изгиба меняется в £ раз. На
первый взгляд получается неожиданная картина: увеличение же-
сткости на изгиб ведет сначала к уменьшению критической ско-
рости; при каком-то значении жесткости изгиба критическая
скорость принимает минимальное значение и только при даль-
нейшем увеличении жесткости изгиба критическая скорость
увеличивается. Прежде чем дать объяснение факту уменьшения
критической скорости с увеличением жесткости изгиба, укажем,
что и в других случаях наблюдается аналогичная картина: уве-
личение какой-либо жесткости в колеблющейся системе умень-
шает критическую скорость. Укажем на три таких факта: 1) крыло
с элероном, 2) крыло с подкосом и 3) хвостовое оперение.
1) Будем рассматривать вибрации крыла с элероном с двумя
степенями свободы: изгиб крыла и отклонение элерона. Предпо-
ложим, что элерон упруго прикреплен к крылу, как это показано
на фиг. 78. Жесткость пружин и А2 обозначим через R, т. е.
пружины таковы, что при отклонении элерона на угол р создает-
ся упругий восстанавливающий момент R$. На фиг. 79 показано,
как изменяется критическая скорость изгибно-элеронного флат-
тера крыла с элероном при изменении жесткости пружин R.
Точка R = 0 соответствует свободно болтающимся элеронам (пру-
жины отсутствуют). При этом нафиг. 79 VKp=18 м)сек. При
увеличении жесткости пружин критическая скорость сначала
Уменьшается, достигая минимума при /?=г:15 кг-см., после чего
начинает увеличиваться. Опять мы сталкиваемся с фактом умень-
шения критической скорости при увеличении жесткости.
2) На фиг. 80 показано изменение критической скорости крыла
с подкосом в зависимости от расстояния подкоса от заделки крыла.
Точка h = 0 соответствует отсутствию подкоса. Мы видим, что
возможны такие положения подкоса, при которых критическая
скорость крыла, подкрепленного подкосом, значительно меньше
критической скорости неподкрепленного крыла. Существенно
239
чэо/и ' ^ээ/и^д
20 Я кг см
240
тметить, что диаграмма фиг. 80 построена для того случая,
когда подкос крепится к крылу в одной точке, лежащей на оси
жесткости крыла. Поэтому подкос влияет не на кручение крыла,
з только на изгиб.
3) Исследован случай вибрации хвостового оперения. Виб-
рации происходили с двумя степенями свободы: кручение фюзе-
ляжа и несимметричные отклонения рулей глубины. Рули глу-
бины имели общий лонжерон 00 (фиг. 81), и, следовательно, при
вибрациях происходило скручивание лонжерона рулей таким
образом, что в то время, когда
правая половина руля отклоня-
лась вниз, левая отклонялась
вверх и обратно. Критическая
скорость в зависимости от жест-
кости на кручение лонжерона
руля глубины [(О/p )ЛОн ] изобра-
жается кривой, показанной на
фиг. 82. В данном случае при
увеличении жесткости лонже-
рона руля критическая скорость
вначале также уменьшается, до-
стигает в некоторой точке ми-
нимума и при дальнейшем увели-
чении жесткости возрастает.
Таким образом в ряде слу-
чаев приходится сталкиваться с
фактом уменьшения критической
скорости при увеличении же-
сткости системы. Во всех этих
случаях имеет место одно и то
же явление.
В гл. VII, п. 6 было показано,
Фиг. 80.
что флаттер с одной степенью
свободы невозможен. Во всех вышеописанных случаях движение
совершалось с двумя степенями свободы. В случае изменения
изгибной жесткости крыла (фиг. 76 и 77) флаттер происходит
со степенями свободы: изгиб крыла и кручение крыла. Крыло
имеет две собственных частоты колебания: частоту изгибных
колебаний и частоту крутильных колебаний, причем частота
колебаний изгиба всегда меньше частоты колебаний кручения.
При увеличении жесткости изгиба (£7) частота изгибных коле-
баний увеличивается и при достаточно большом значении EI
становится равной частоте крутильных колебаний. Оказывается,
критическая скорость изгибно-крутильного флаттера крыла имеет
минимум именно при том значении жесткости, при котором сов-
Падают частоты изгиба и кручения. Явление это носит название
ВнУтреннег’о резонанса. Следовательно, величина кри-
тической скорости зависит не только от абсолют-
ной величины жесткостей крыла на изгиб и кру-
Г₽°ссман—15—16
241
чение (которые обусловливают определенную величину абсолют-
ного значения частот), но также и от величины диапа-
зона между частотами.
Остальные случаи понижения критической скорости с увели-
чением жесткости также объясняются внутренним резонансом:
в случае 1 при R = 0 частота колебаний элерона равна нулю.
При увеличении R частота колебаний элерона на пружинах А,
и А2 (фиг. 78) увеличивается, приближаясь к частоте изгибных
колебаний крыла. Минимум критической скорости получается
при том значении R, при котором частота колебаний элерона
совпадает с частотой изгибных колебаний крыла. При дальней-
шем увеличении R критическая скорость увеличивается.
Рассмотрим крыло с подкосом (фиг. 80). Мы знаем, что крыло
без подкоса может совершать колебания изгиба разных тонов,
и колебания каждого тона происходят со своей определенной
частотой. В частности колебания второго тона происходят с од-
ним узлом, и частота их много выше, чем частота первого тона.
Если подкос установить в сечении, в котором получается
узел колебания второго тона, то форма колебаний изгиба будет
соответствовать ферме второго тона колебания и низшей частотой
будет частота, равная частоте второго тона Колебания. Следо-
вательно, если р„3 есть частота колебания изгиба первого тона
без подкоса (или с подкосом, установленным в сечении h — 0,
фиг. 80), то при установке подкоса в сечении, в котором имеется
узел колебания второго тона, частота колебаний изгиба будет
значительно больше риз. Следовательно, при увеличении h от
нуля частота колебаний изгиба увеличивается и тем самым при-
ближается к частоте колебаний кручения (напомним, что рас-
сматривается случай подкоса, крепящегося к крылу в одной точке,
лежащей на оси жесткости, т. е. не влияющего на кручение).
При этом критическая скорость падает и достигает минимума,
когда частоты изгибных и крутильных колебаний крыла совпадают.
В случае 3 (фиг. 81,82) критическая скорость имеет минимум,
когда совпадают частота крутильных колебаний руля глубины
и частота кручения фюзеляжа.
242
Следует оговориться, что минимум критической скорости во
всех случаях получается не при точном совпадении частот, а вблизи
точки их совпадения. Это объясняется тем, что совместность
колебаний и влияние воздушных сил несколько изменяют соб-
ственные частоты, и резонанс получается на точке, несколько
отличающейся от той, на которой он получается в пустоте.
Из изложенного вытекает, что при конструировании следует
следить за тем, чтобы частоты различных форм колебания не
совпадали и не былц очень близки. Особенно это касается хво-
стового оперения, где возможно много различных форм колеба-
ния. Подробнее о хвостовом оперении мы скажем ниже.
Отметим, что это указание зафиксировано как обязательное
требование в нормах прочности США.
2. ЧАСТОТНАЯ ХАРАКТЕРИСТИКА
Частотной характеристикой мы будем называть отношение
Характер изменения этого отношения вдоль размаха крыла
‘т
оказывает существенное влияние на величину критической ско-
рости. Это объясняется тем, что частотная характеристика в
основном определяет вид функции кручения <₽(у), т. е. характер
распределения амплитуд крутильных колебаний по длине крыла.
Рассмотрим поэтому прежде всего, как влияет вид функции (у)
на величину критической скорости.
Предположим, что мы определили критическую скорость не-
которого крыла, приняв за функцию кручения стандартную функ-
цию <pt (фиг. 83), т. е. предполагая, что распределение углов
кручения по размаху у данного крыла такое же, как у крыла
постоянного сечения при колебаниях в пустоте. Пусть при этом
критическая скорость оказалась равной Vv Затем мы определили
функции формы колебания рассматриваемого крыла в пустоте
(<f2, фиг. 83) и с этой функцией снова определили критическую
скорость. Она оказалась равной И2.
243
Ряд произведенных расчетов показал, что если функции е
и <f3 имеют такой характер, как показано на фиг. 83, то V2 бу.
дет меньше, чем V\. Эго можно объяснить следующим.
Фиг. 84.
При колебаниях кручения по закону <f2 амплитуды на конце
крыла1 относительно велики по сравнению с амплитудами в
корневой части. Жесткость же кручения обычно сильно падает
к концу крыла (фиг. 84). Поэтому большие амплитуды получаются
в тех сечениях крыла, где относительно невелика жесткость. Крутя-
„Г ОТ
щий момент в сечении крыла, как известно, имеет выражение »
и следовательно, крутящий момент пропорционален величине
GIp-~ . Если взять распределение жесткостей, указанное на
фиг. 84, и вычислить крутящие моменты Л1кр = GIp ^ДЛЯ1Р = ®1
1 Напомним, что функция ср дает закон распределения амплитуд крутиль
ных колебаний по размаху крыла.
244
и <р == <р2, то получится картина, изображенная на фиг. 85. Хотя
в корне крутящие моменты для функции значительно выше,
чем для функции <р2, ио эти крутящие моменты воспринимаются
теми сечениями, в которых велика жесткость крыла. На конце
же крутящие моменты для функции <р2 значительно больше кру-
тящих моментов, соответствующих функции фР Поэтому кон-
цевая часть крыла во втором случае начинает вибрировать на
значительно меньшей скорости.
Кроме того, следует помнить, что возбуждающие аэродина-
мические силы пропорциональны углу атаки крыла, а следова-
тельно, и углу закручивания. Поэтому относительное увеличение
угла кручения на конце означает сильное относительное увели-
чение* возбуждающих аэродинамических сил и моментов на конце
крыла (в сечениях с малой жесткостью), что также ведет к
уменьшению критической скорости.
Функция с? зависит от закона распределения по размаху крыла
жесткости на кручение и момента инерции (см. гл. II). Следова-
тельно, от закона распределения этих величин по размаху будет
зависеть и критическая скорость. Одни средние величины жест-
кости крыла на кручение и момента инерции недостаточны для
характеристики крыла с точки зрения вибраций. Можно указать
примеры, когда крыло с меньшей средней жесткостью кручения
имеет большую критическую скорость за счет рационального
закона изменения жесткости кручения по размаху.
Судить о том или другом законе изменения жесткости кру-
чения по размаху крыла можно по коэфициенту
о
(3)
который характеризует потенциальную
крыла. Жесткость кручения влияет на
только через этот коэфициент, причем
энергию закрученного
критическую скорость
чем он больше, тем
больше критическая скорость. Приближенно можно считать, что
при изменении только одного коэфициента а22 критическая ско-
рость пропорциональна у а22. Очевидно, что для функции фг
(фиг. 83) коэфициент а22 значительно больше, чем для функ-
ции <р2, так как подинтегральная функция в коэфициенте (3) в
первом случае значительно больше, чем во втором. Это объ-
de>
ясняется тем, что в первом случае значение в корневых
частях крыла значительно больше, чем во втором, и, следова-
тельно, большие значения жесткости умножаются на квадрат
а во втором случае на квадрат малой
большой величины
величины ( )• Следовательно, во втором случае участки крыла
с большой жесткостью не использованы так, как это нужно,
что находится в соответствии со сказанным выше относительно
245
распределения крутящих моментов; во втором случае участки
с ббльшей жесткостью нагружаются малыми моментами, а
участки с малой жесткостью (концевая часть крыла) — относи-
тельно ббльшими моментами. Таким образом, если даже средняя
жесткость крыла велика, может оказаться, что за счет нерацио-
нального закона распределения жесткости по размаху эта боль-
шая жесткость не используется, а в основном работает при
вибрациях концевая часть крыла (фиг. 73).
Поэтому при конструировании следует избегать появления
участков с весьма крутым падением жесткости на кручение
(фиг. 86, /) и стремиться к воз-
у- можно более плавному изме-
нению жесткости от корневой
___— —" части к концу (фиг. 86, 2).
—"" Однако при крутильных
колебаниях важна не только
абсолютная величина жест-
кости, но и соотношение меж-
ду жесткостью кручения и
моментом инерции. Чем боль-
__________________________ ше момент инерции, тем
ф)1г gg___________________большие инерционные силы
развиваются при колебаниях и,
следовательно, тем более жестким должно быть крыло. Поэтому
отношение -GJP можно взять за характеристику, если можно так
‘т
выразиться, „вибростойкости" конструкции. В большинстве со-
временных конструкций отношение G.Ip по размаху крыла имеет
‘т
характер, указанный на фиг. 87, т. е. понижается к концу крыла.
Это говорит о том, что конец крыла относительно перетяжелен
по сравнению с корневой частью, т. е. жесткость кручения
к концу крыла убывает быстрее, чем момент инерции.
Естественно, что при этом на конце крыла амплитуда коле-
баний будет относительно велика, т. е. кривая <р(у) будет иметь
246
характер, изображенный на фиг. 83 (?2) и критическая скорость
будет снижена за счет малой „вибростойкости“ конца крыла.
Следует стремиться к тому, чтобы частотная характеристика
(С.Гр) к концу крыла не снижалась, а если возможно, то даже
увеличивалась (фиг. 88). Если при том на крыле нет участков
с резким падением жесткости, то вид функции <₽ будет прибли-
жаться к (фиг. 83). Поэтому при проектировании следует
особенно тшателыю следить за величинами Glp и /т на конце-
вой части крыла.
Особо нужно подчеркнуть, что переделать характер изменения
по размаху частотной характеристики на готовой конструкции
почти невозможно, а потому за этой величиной нужно следить
в стадии проектирования.
3. ПОЛОЖЕНИЕ ОСИ ЦЕНТРОВ ТЯЖЕСТИ ПО РАЗМАХУ КРЫЛА
В гл. VIII на основании качественных соображений было по-
казано, что критическая скорость существенным образом зависит
от положения в крыле трех осей: фокусов, центров жесткости и
тяжести. Из этих трех осей сильнее всего влияет на величину
критической скорости положение оси центров тяжести.
На фиг. 89 и 90 показано изменение критической скорости
двух крыльев в зависимости от положения оси центров тяжести
Для различных положений оси жесткости • В. обоих
крыльях расстояние от центра тяжести сечения до передней
кромки (г) в процентах от хорды t, а также расстояние от оси
жесткости до передней кромки (х0) в процентах хорды считает-
ся одинаковым по всему размаху. Из рассмотрения этих диа-
грамм можно сделать следующий вывод: если центр тяжести
крыла расположен не далее 50—60% хорды от передней кромки,
то положение центра тяжести весьма сильно влияет на величину
критической скорости. Передвижение оси центров тяжести сече-
ний крыла вперед всего на 1% хорды дает значительное увели-
чение критической скорости. Так, например (фиг. 89), переме-
щение оси центров тяжести с 42 до 41% хорды увеличивает
критическую скорость на 11 м)сек, т. е. почти на 40 км[час. Так
как почти у всех современных крыльев центр тяжести распо-
ложен ближе 50% хорды от передней кромки, то из приведен-
ных .диаграмм следует вывод: в современной конструкции крыла
следует бороться за каждый процент в положении центра тя-
жести, с тем чтобы помещать центр тяжести как можно ближе
к передней кромке.
Такое сильное влияние центра тяжести вполне понятно: инер-
ционные силы создают крутящий момент при вибрациях за счет
несовпадения оси центров тяжести с осью жесткости (гл. IV), и
так как центр тяжести находится позади оси жесткости, этот
момент закручивает крыло в таком направлении, что угол атаки
уменьшается при движении крыла вниз и увеличивается при
247
движении вверх (фиг. 45). В силу этого возникающая за счет кру-
чения от инерционных сил подъемная сила направлена всегда в
сторону движения и возбуждает колебания. При движении центра
тяжести вперед уменьшаются плечо инерционного момента и
угол крутки, а следовательно, й подъемная сила, поддерживаю-
щая колебания. Очевидно, можно вынести центр тяжести на-
столько далеко вперед, что инерционный момент вообще не будет
вызывать кручения крыла или даже будет закручивать крыло в
обратную сторону (гл. VIII), в силу чего и подъемная сила бу-
дет действовать в обратную сторону, т. е. будет демпфировать
колебания.
Положение центра тяжести является тем параметром, вариа-
цией которого чаще всего увеличивают критическую скорость
на готовой конструкции, если критическая скорость оказывается
недостаточной. Для этого загружают переднюю кромку крыла
и максимально облегчают заднюю (например, изменяя вес эле-
рона заменой металлической обшивки на полотняную и т. п.).
Нет нужды изменять положение центра тяжести во всех сече-
ниях крыла. Так как наибольшее влияние на флаттер всегда
оказывает конструкция концевой части крыла, то переднюю
кромку загружают вблизи конца крыла. И вообще при конструи-
ровании нужно особенно тщательно следить за положением
центра тяжести в концевой части крыла.
Обычно достаточно очень небольшого дополнительного груза
в передней кромке вблизи конца крыла, чтобы значительно уве-
личить критическую скорость. Так, для одного крыла весом
248
300 кг удалось повысить критическую скорость с 90 до 140 м/сек
установкой грузов по 4 кг на правое и левое полукрыло (всего
8 кг). Но возможны случаи, когда для получения достаточной
величины критической скорости требуется довольно значитель-
ный вес. На фиг. 91 показана типичная кривая изменения крити-
ческой скорости в зависимости от положения центра тяжести.
Если самолет лежит в точке В этой кривой, то, очевидно, ма-
лейшее изменение в положении центра тяжести существенно
отразится на величине критической скорости. Но если центр тя
жести в крыле соответствует точке А (фиг. 91), то небольшие
изменения положения центра тяжести не могут дать значитель-
ных изменений в величине крити-
ческой скорости. К счастью, боль-
шинство современных конструкций
соответствует первому случаю.
Очень распространено мнение, что на величину критической
скорости влияет не столько расстояние от центра тяжести до
передней кромки сколько взаимное расположение осей
центров тяжести и жесткости. Это, однако, неверно. На фиг. 92
показано изменение критической скорости крыла в зависимости
от положения в нем оси жесткости при фиксированном положе-
нии центра тяжести. Мы видим, что при изменении положения
оси жесткости критическая скорость меняется не очень сильно
(тем более, что реально возможные значения —0,28 — 0,4), не-
смотря на то, что расстояние между осями жесткости и тяжестк
249
— r — x0) меняется очень значительно. Даже совмещение осей
жесткости и тяжести (точки кривых фиг. 92, для которых r=_x0)
не дает заметного изменения критической скорости, если поло-
жение оси центров тяжести относительно передней кромки крыла
(г) фиксировано. Между тем при одном и том же положении
оси жесткости изменение г от г = 0,4 до г = 0,5 (фиг. 92) изме-
няет критическую скорость чуть ли не вдвое.
Незначительность влияния, которое оказывает на величину
критической скорости положение оси жесткости в крыле, объяс-
няется просто: почти всегда ось жесткости в крыле лежит между
линиями центров тяжести и фокусов профилей крыла (линия
центров жесткости обычно располагается на 33—36% хорды от
носка, линия центров тяжести сечений крыла—на 43—49% хорды,
а линия фокусов—на 25% хорды от носика крыла). Поэтому при
движении оси жесткости назад инерционные характеристики
крыла улучшаются (уменьшается расстояние между осями жест-
кости и центров тяжести), но аэродинамические характеристики
ухудшаются (увеличивается расстояние между осями фокусов и
жесткости). При движении оси жесткости вперед, наоборот,
улучшаются аэродинамические, но ухудшаются инерционные
характеристики г. В результате борьбы противоположно действую-
щих влияний критическая скорость существенно не меняется
(при практически возможных изменениях в положении оси жест-
кости). Поэтому при конструировании можно особенно не забо-
титься о положении в крыле оси жесткости.
4. НЕВИБРИРУЮЩАЯ КОНСТРУКЦИЯ
В гл. VIII на основе качественных соображений было пока-
зано, что всегда можно подобрать в крыле взаимное положение
осей тяжести, жесткости и фокусов таким образом, чтобы крыло
не вибрировало ни при каких скоростях. Мы переходим к вы-
воду количественных критериев, которым должно удовлетворять
расположение этих осей, чтобы крыло было абсолютно невиб-
рирующим.
Прежде всего рассмотрим частный случай,— крыло, у кото-
рого ось жесткости совмещена с осью фокусов крыла. Напом-
ним, что фокусом профиля называется такая точка, аэродинами-
ческий момент относительно которой не меняется при изменении
угла атаки крыла. В гл. VI мы выяснили, что фокус находится
на 25% хорды от носика профиля и потому в рассматриваемом
частном случае мы принимаем:
-?Ч-- <4)
1 Инерционные и аэродинамические характеристики, о которых идет речь,
представляют собой не что инее, как аэродинамические и инерционные связи,
рассмотренные в гл. VIII.
250
Для рассматриваемого случая, согласно формулам (14) гл. VII,
будем иметь:
— 0 5
d2i = °; , (5)
^2 = --Гб?
о
В силу этого по формулам (20) гл. VII находим, что для
крыла с осью жесткости на 25% хорды
Г. = 0; )
| £s = 0. f
Поэтому в формулах (28) гл. VII получается:
£ = 0;
Af = 51C2D1; (7)
N — В1Ек — D* А1г
и критическая скорость, вместо уравнения (29) гл. VII,
лится из уравнения:
ЛП/2фА^ = 0,
откуда
= __________________________________
М BtC2Dt ‘
опреде-
(8)
Формула (8) позволяет определить положение линии центров
тяжести крыла, при котором критическая скорость перестает су-
ществовать.
Так как условие устойчивости (26а) гл. VII при очень малых
скоростях выполняется, то, следовательно, должно быть N > 0
(как это всегда при конкретных расчетах и бывает). С др) гой
стороны, из того, что условие (26а) гл. VII должно при очень
малых скоростях выполняться, следует, что Вх > 0 и DL > 0.
Таким образом скорость, определяемая формулой (8), может
существовать только в том случае, если
С2<0, (9)
причем, если имеет место равенство С2 — 0, то КР = оо, а при
С2>0, ИКр — мнимая величина. Если для критической скорости
получается мнимое или комплексное значение, то это означает,
что гармонические колебания с постоянной амплитудой не могут
существовать ни при какой действительной скорости. А так как
при очень малых скоростях колебания обязательно затухающие
(т. е. декремент затухания отрицателен), то, значит, они будут
затухающими и при любых скоростях (декремент затухания как
непрерывная функция V не может стать положительным, не
251
перейдя через нуль, а нулем он не может быть ни при какой
скорости, так как иначе при этой скорости были бы колебания
постоянной амплитуды).
Если при выполнении условия (9) критическая скорость су-
ществует, то при
С2>0 (10)
крыло будет устойчиво при всех скоростях. Условие (10) и оп-
ределяет те положения центра тяжести, при которых флаттер
невозможен ни при каких скоростях.
Пользуясь уравнениями (20) гл. VII, а также условиями (5)
настоящей главы, можем записать условие (10) в развернутом
виде:
или, подставляя значения b12, c21,du, из уравнений (7) и (14) гл. VII
и d22 из уравнений (5) настоящей главы:
z i ос 1
— f tfydy- j in°fydy + -^ p J'tf-dy - j t3^dy>0. (11)
OO 0 0
Напомним, что мы рассматриваем случай, когда ось жесткости
совпадает с осью фокусов профилей крыла, т. е. х°- = -д-, по-
1 ОИй.' 4
этому
з = г—J-/. (12)
Подставляя выражение (12) в условие (11), находим условие,
которому должно удовлетворять положение линии центров тя-
жести сечений крыла, чтобы оно не могло быть подвержено флат-
теру ни при каких скоростях:
i i z
j rmju dy -Jtfy dy < 4 J mth dy J th dy +
0 0 OU
I I
+ ^?J f t3^dy- <13)
b о
Если расстояние от центра тяжести до передней кромки в до-
лях хорды по всем сечениям крыла одинаково = const), то
это условие можно переписать в следующем виде:
i i
J1 tf1 dy f t3a2 dy
r . 1 . Л ° О /1Д)
T<T + l6P-i----------Г— •
f mtfo dy -f tf-f dy
о о
252
Предположим теперь, что положение линии центров тяжести
сечений крыла удовлетворяет условию (13) или (14), но ось
жесткости не совпадает с линией фокусов, а сдвинута назад.
Передвижение оси жесткости назад уменьшит кручение крыла
от инерционных сил или даже (если ось жесткости окажется
позади линии центров тяжести) вызовет кручение крыла в такую
сторону, что аэродинамическая сила, появляющаяся за счет
кручения (аэродинамическая связь кручения на изгиб), будет
демпфировать колебания вместо того, чтобы их возбуждать
(см. гл. VIII). Возбуждение же колебаний за счет увеличения
плеча аэродинамического момента будет происходить более
интенсивно. Однако ряд расчетов, произведенных для раз-
личных крыльев, показал, что влияние инерционных характери-
стик сильнее, чем аэродинамических, и, если условия (13) или
I ха 1
(14) выполнены, т. е. если при = у критическая скорость от-
сутствует, то она будет отсутствовать и при у > -р Следова-
/ хо 1
тельно (так как у <^- реально
выполнение условия (13) или
(14) обеспечивает крыло
от флаттера при любых
скоростях и при всех
реально встречающих-
ся положениях оси же-
сткости.
5. ВЛИЯНИЕ МАСС И МАССОВЫХ
МОМЕНТОВ ИНЕРЦИИ КРЫЛА
не бывает), можно считать, что
Увеличение масс и особен-
но моментов инерции крыла
ведет к уменьшению крити-
ческой скорости (при фикси-
рованном положении линии
центров тяжести сечений кры-
ла). На фиг. 93 показано влия-
ние на критическую скорость
радиуса инерции крыла отно-
сительно центра тяжести (х).
Средние значения х для совре-
менных конструкций —26—
30% хорды. Мы видим (фиг.93),
что даже небольшие изменения в величине радиуса инерции (при
фиксированном положении линии центров тяжести) могут дать
Заметные изменения в величине критической скорости. Подчер-
киваем, что радиус инерции характеризует размещение масс по
А°Рде крыла при фиксированной величине самых масс и их центра
253
г
тяжести. С точки зрения вибраций можно было бы рекомендо-
вать максимально облегчать крыло, но такая рекомендация бес-
полезна, так как всегда крыло бывает уже облегчено настолько,
насколько это возможно. Во всяком случае, учитывая влияние
массовых характеристик в целом, следует еще раз подчеркнуть
необходимость размещения всех масс в крыле возможно ближе
к передней кромке и максимального облегчения элеронов.
6. ВЛИЯНИЕ ФОРМЫ КРЫЛА В ПЛАНЕ
Форма крыла в плане во многом уже предопределяет вели-
чину остальных конструктивных параметров крыла. Поэтому,
чтобы исследовать влияние ее на крити-
ческую скорость, необходимо задаться
определенной зависимостью между формой
крыла в плане и его жесткостью, массой,
расположением осей тяжести и жесткости
и т. д.
Рассмотрим серию крыльев, имеющих
в плане форму трапеции, одинаковую
площадь и размах. Тогда форму крыльев
можно охарактеризовать отношением кон-
цевой хорды крыла к корневой, которое
обозначим через Н. Этот параметр харак-
теризует сужение крыла.
Задавая различные значения с, мы бу-
дем получать различные крылья рассмат-
риваемой серии (фиг. 94). На основании
существующей статистики можно прибли-
женно считать, что конструктивные пара-
метры крыла связаны с его формой сле-
дующим образом:
жесткость изгиба и кручения пропор-
циональна четвертой степени хорды;
масса (погонная) пропорциональна квад-
рату хорды;
расстояния от оси жесткости до перед-
ней кромки, от центра тяжести до оси же-
сткости, а также радиус инерции пропор-
циональны хорде.
При этих условиях критическая скорость для различных
крыльев рассматриваемой серии в долях от критической скорости
прямоугольного крыла серии (; = 1) будет такой, как показано
на фиг. 94. Следовательно, с точки зрения вибраций из серии
крыльев одинакового размаха и площади наилучшим является
крыло, наиболее сильно суживающееся к концу.
Этот вывод и следовало ожидать: флаттер вызывается аэро-
динамическими силами, которые тем меньше, чем меньше хорда
крыла. Сужение крыла с сохранением площади и размаха ведет
254
к уменьшению хорды, следовательно, и аэродинамических сил,.
на концевой части, т. е. именно там, где жесткость крыла наи-
„рнывая. Это, естественно, влечет за собой увеличение крити
ческой скорости.
Следует еще отметить, что сильно коническое крыло может
быть сделано относительно более жестким, чем крыло менее
суживающееся.
7. ИЗМЕНЕНИЕ КРИТИЧЕСКОЙ СКОРОСТИ С ВЫСОТОЙ ПОЛЕТА
С высотой полета изменяется плотность воздуха р, а следо-
вательно, и критическая скорость. Выяснить влияние высоты
полета необходимо, так как необходимо проверить, обеспечит
ли расчет критической скорости, проведенный для определенной
высоты, безопасность полета и на других высотах.
Чтобы получить метод пересчета критической скорости с одной
высоты на другую, обратимся к формулам (20) гл. VII.
Введем обозначения:
^2 4l^22 ^12^21 i
С2 — ^12^21
(15)
Тогда [см. формулы (20), гл. VII]
са = с; + с;. (16)
Далее введем следующие обозначения:
L' = B&D., - DW1, L" = Дгс;г>2; )
; (17)
АГ = Bfi'. + B^D. - B}E., 2DrDAx\ М” = В.С'^. |
Тогда в силу формул (28) гл. VII:
L =L'+L"-,
М^М' + М";
N = N.
(18)
Легко непосредственно убедиться в том, что L' пропорционально
р’, L" пропорционально р5, М’—р3, Ми— р’, W— р2. Поэтому, если
вычислены значения L", М', М", N для какой-либо высоты /
полета И, которой соответствует значение плотности воздуха рл,
п затем по формулам (18) определены L, М, N и из уравнения
(29), гл. VII критическая скорость на этой высоте, то для по-
лучения критической скорости на высоте Hlt которой соответ-
ствует плотность^воздуха р7/, поступаем следующим образом.
255
-
Умножаем L' на f—\ L" — на f—, М’ — на (—Y М" — на
\Ря/ \Р«/ \Ря/ d
(Рл/
у3J ; 2V оставляем без изменения. Затем определяем L, М, 1\/
по формулам (18) и критическую скорость на новой высоте по
уравнению (29), гл. VII.
Если С' мало по сравнению с С', что обычно и бывает, то
можно считать, что
ЪтЛ = (
Ун / \ Р/Д/
где VHl — критическая
— критическая
.делах 0,35 — 0,5.
скорость на высоте /7г;
скорость на высоте Н и а лежит в пре-
ГЛАВА XI
ВЛИЯНИЕ ЭЛЕРОНА НА ФЛАТТЕР КРЫЛА
Большинство случаев возникновения флаттера крыла в полете
до сих пор наблюдалось у самолетов, снабженных несбалансиро-
ванными в весовом отношении элеронами. Роль таких элеронов
при флаттере чрезвычайно велика.
Фиг. 95.
Рассмотрим крыло, снабженное элероном, центр тяжести
которого лежит позади его оси вращения. Временно предположим,
что элерон точно аэродинамически компенсирован, т. е. при его
отклонениях 1 не возникает никакого аэродинамического шарнир-
ного момента.
Пусть крыло вследствие какого-либо внешнего импульса2
отклонилось от своего положения равновесия (фиг. 95, положе-
ние /; крыло с элероном представлено схематически прямыми
линиями). Под действием упругих сил крыло начнет ускоренно
двигаться по направлению к положению равновесия.
При этом центр тяжести элерона вследствие инерции будет
отставать от движения крыла, так как элерон обычно обладает
1 Напоминаем, что мы считаем все отклонения как элерона, так и крыла
от положения равновесия малыми, что в действительности и имеет место
в начальный момент возникновения флаттера.
2 Такой импульс в полете всегда возможен, например от мотора, порыва
ветра и т. п.
Гроссман—15—17 257
некоторой свободой движения относительно крыла (за счет
упругости управления, возможных люфтов, а также за счет того,
что ручка управления, сдерживаемая только летчиком, не может
считаться жестко закрепленной). Вследствие отставания центра
тяжести (по инерции) элерон отклонится так, как показано на
фиг. 95 (положение II). После того, как крыло по инерции перей-
дет положение равновесия, упругие силы начнут действовать
в обратную сторону, крыло начнет двигаться замедленно, и центр
тяжести элерона начнет догонять в своем движении крыло
(фиг. 95, положение IV). Из сказанного ясно, что при движении
вниз элерон будет отклоняться относительно крыла вверх. В сле-
дующих этапах движения (фиг. 95, положения V — IX), когда
крыло будет двигаться вверх, элерон вследствие инерции будет
отклоняться вниз.
• Otb вращения эяерона
х Центр тяжести элерона
Фиг. 96.
За счет отклонения элерона возникает дополнительная подъем-
ная сила, которая, очевидно, будет направлена вниз, если элерон
отклонен вверх, и вверх, если элерон отклонен вниз. Таким
образом в рассматриваемом случае (когда центр тяжести элерона
находится позади его оси вращения) подъемная сила, возникаю-
щая за счет отклонения элерона вследствие инерции, будет
всегда направлена в ту же сторону, куда движется крыло. Эта
подъемная сила будет стремиться дальше увеличивать колебания
и вызывать флаттер.
Здесь мы опять имеем замкнутый цикл энергообмена между
системой крыло — элерон и потоком: возникшие изгибные колеба-
ния крыла вызывают отклонения элерона, вследствие чего возни-
кает сила, увеличивающая изгибные колебания. Когда увеличи-
ваются изгибные колебания, увеличивается и отклонение элерона,
вследствие чего еще более увеличивается и сила, усиливающая
колебания. Таким образом мы имеем в данном случай* непрерыв-
ный процесс перехода энергии к крылу такого характера, при
котором переход этой энергии сам по себе создает предпосылки
258
для дальнейшего увеличения переходящей энергии. Флаттер
становится возможным.
Обратную картину мы имеем, если центр тяжести элерона рас-
положен перед его осью вращения. На фиг. 96 показано, как в этом
случае будет отклоняться элерон за счет инерционных сил при из-
гибных движениях крыла: при движении вниз элерон будет откло-
няться относительно крыла также вниз, а при движении вверх эле-
рон также будет отклоняться вверх. Подъемная сила, возникающая
вследствие отклонения элерона, будет в этом случае направлена
всегда в сторону, проти-
воположную движению
крыла, и будет демпфи-
ровать колебания.
Наконец, если центр
тяжести элерона совме-
щен с его осью враще-
ния, то элерон вовсе не
будет отклоняться при
движении крыла (при ус-
ловии точной аэродина-
мической компенсации) и
не окажет никакого влия-
ния на вибрации послед-
него.
Из сказанного ясно,
что конструкция элерона
должна быть такой, чтобы
центр тяжести его лежал
перед осью вращения
или, по крайней мере,
был совмещен с ней \
Очевидно, чем дальше
расположен центр тяже-
сти элерона от его оси вращения, тем на больший угол будет
отклоняться элерон и тем большей величины достигнет сила,
усиливающая колебания. Поэтому критическая скорость флат-
тера тем ниже, чем дальше расположен центр тяжести элерона
от оси его вращения и чем интенсивнее флаттер протекает.
Эти выводы целиком подтверждаются экспериментами, про-
веденными как за границей, так и у нас в ЦАГИ. Результаты
одного испытания показаны на фиг. 97. На этой фигуре нане-
сен график экспериментально полученной зависимости Икр от аэл,
где аэл — расстояние от центра тяжести элерона до его оси вра-
щения. В месте, где расположен центр тяжести, хорда испыты-
вавшейся модели крыла имела размер tKp = 274 мм и хорда
элерона t9n = 56 мм. Таким образом каждый миллиметр рас-
стояния от центра тяжести элерона до оси вращения составляет
В некоторых странах это требование обязательно.
239
приблизительно (довольно грубо) х/8% хорды крыла, или 2%
хорды элерона. Испытания крыла снимались на кинопленку при
помощи лупы времени. Расшифровка этих съемок показала,
что движение носило именно такой характер, какой мы выше
описали (изгиб крыла — отклонение элерона). Кручение крыла
было совершенно незаметно.
На фиг. 97 ясно видно, что величина зэ., чрезвычайно сильно
влияет на величину критической скорости. Так, если центр
тяжести элерона расположен на 5,3% хорды элерона от его оси
вращения, то VKp = 66 м/сек, а если центр тяжести элерона
передвинут на 1,8% назад, то 1/кр понизится до 44 м!сек,
т. е. на 16,7%. В зависимости от величины сэл критическая
скорость изменяется от 66 до 19,5 м/сек. Скорости больше
66 м/сек в аэродинамической трубе не могли быть достигнуты.
Все это показывает, что в современной конструкции следует
бороться за каждый процент приближения центра тяжести эле-
рона к его оси вращения.
Однако, как мы увидим в дальнейшем, в настоящее время
нельзя считать крыло гарантированным от флаттера, если его
элерон'не сбалансирован полностью. Интересно отметить, что
в наблюденных случаях вибрации крыла с элероном при двух
степенях свободы: изгиб крыла — отклонение элерона протекают
гораздо менее интенсивно, чем изгибно-крутильный флаттер
крыла. При увеличении скорости потока сверх критической
амплитуда колебаний вначале увеличивается, а затем сохраняет
свою величину, несмотря на возрастание скорости. Разрушения
не наступает. Кроме того, резко заметно, что амплитуда коле-
баний (интенсивность флаттера) тем меньше, чем ближе центр
тяжести элерона к оси его вращения.
Не менее четкие результаты получены при испытаниях
в аэродинамической трубе второй модели крыла с элероном.
На этой модели с закрепленными элеронами изгибно-крутильный
флаттер наступал при скорости 40 м/сек. Со свободными эле-
ронами, но при точной балансировке последних (центр тяжести
на оси вращения) флаттер наступал на той же скорости (^л/сек)
и носил совершенно тот же характер (изгиб—кручение крыла).
Влияния элерона в этом случае совершенно не было заметно.
В обоих случаях вибрации протекали весьма интенсивно.
При несбалансированном элероне картина резко изменилась:
флаттер наступил уже при скорости 18 м/сек, но носил совер-
шенно другой характер, — кручение крыта отсутствовало, имели
место только отклонение элерона и изгиб Крыла. Флаттер носил
несравненно менее интенсивный характер, чем в предыду’ гем
случае, с небольшой частотой и амплитудой. При увеличении
скорости сверх критической (сверх 18 м/сек) амплитуда колебаний
сначала возрастала, а затем даже начала уменьшаться. Частота
постепенно увеличивалась. Когда скорость достигла 39 м/сек
(почти такая же скорость, как та, при которой наступал изгибно-
крутильный флаттер при сбалансированных элеронах), моментально
260
возникли чрезвычайно интенсивные вибрации с тремя степенями
свободы (изгиб—кручение крыла и отклонения элерона) с очень
большой частотой и амплитудой, и в течение одной-двух секунд
модель была разрушена.
В табл. 14 показаны результаты опытов с другой моделью.
Таблица 14
Способ закрепления элерона Скорость м/сек Характер движения
Элерон свободен и не сбалансирован 3,05 Изгиб—кручение крыла и отклонение элерона
14 Кручей не крыла и отклонение элерона
Элерон свободен и сбалансирован 15,6 Изгиб—кручение крыла
Элерон связан с крылом и не сбалан-’ сирован 16 Изгиб—кручение крыла
Из приведенного экспериментального материала можно сде-
лать ряд выводов.
Колебания крыла с элероном всегда совершаются не менее
как с двумя степенями свободы.
Этот вывод следует и из теории: можно доказать, что коле-
бания с одной (безразлично какой) степенью свободы обязательно
будут затухающими, так как в этом случае невозможны такие
замкнутые циклы энергообмена, которые автоматически непре-
рывно увеличивают приток энергии из потока в колеблющуюся
систему.
Поэтому, колебания крыла с несбалансированным элероном
могут иметь следующие формы:
а) изгиб—кручение крыла и отклонение элерона;
б) изгиб крыла и отклонение элерона;
в) кручение крыла и отклонение элерона;
г) изгиб—кручение крыла.
Каждая форма колебаний имеет свою критическую скорость,
что ясно следует из тех опытов, результаты которых приведены
выше. Какая из критических скоростей является наименьшей,
и, следовательно, какой формы колебания возникнут во время
полета раньше всего,— сказать заранее нельзя.
Разные формы колебаний представляют и различную опас-
ность в смысле разрушения. Из ряда опытов мы вывели заклю-
чение, что наибольшую опасность разрушения представляют те
формы колебаний, где одновременно участвуют изгиб и круче-
261
ние крыла (формы колебаний „а“ и „г“). Формы колебаний „6“ и „в“
представляют меньшую опасность. Объясняется это, невидимому,
тем, что в последнем случае основной причиной колебаний слу-
жат силы, порождаемые отклонениями элерона. Так как площадь
и масса элерона невелики по сравнению с площадью и массой
крыла, то эти силы не могут внезапно вызвать большие дефор-
мации крыла. Необходимо некоторое время, пока элерон „рас-
качает" крыло. За это время летчик может успеть снизить скорость
полета и прекратить колебания. Но те же силы, которые недо-
статочны, чтобы быстро раскачать крыло, могут привести к бы-
строму нарастанию амплитуды колебаний самого элерона и к его
поломке. Этим объясняется то обстоятельство, что во многих
случаях элероны ломались от вибраций, в то время как само крыло
оставалось совершенно целым.
Если элерон сбалансировать в весовом отношении, то при
условии полной аэродинамической компенсации он не будет
менять своего положения относитель-
но крыла ни при изгибе, ни при
-------------7^—-—». кручении последнего. Эффект полу-
1 —--------------чается тот же, как и при полном
закреплении элерона относительно
крыла. В этом случае формы колеба-
Ф"г. 98. ний „а“, „б“ и „в“ становятся невоз-
можными, и остается только возмож-
ность изгибно-крутильных колебаний крыла.
Это положение также подтверждается экспериментом: и кри-
тическая скорость, и характер движения одинаковы как у крыла
с закрепленным, так и у крыла со свободным, но сбалансированным
элероном (при условии полной аэродинамической компенсации).
Итак, избавиться от критических скоростей, соответствующих
типам колебаний „а“, „б“ и „в“, можно либо жестким закрепле-
нием элерона относительно крыла, либо весовой балансировкой.
Увеличением жесткости управления возможно лишь повысить
критическую скорость1 форм „а“, „б“ и „в“, но не избавиться
от нее, так как в конце концов ручку управления удерживает
летчик, а руку последнего никак нельзя считать абсолютно жест-
кой. Кроме того, в тягах управления элероном почти всегда есть
не абсолютно жесткие звенья.
Весовая балансировка элерона неприятна по двум причинам:
во-первых, она увеличивает вес элерона и тем самым передви-
гает центр тяжести всего крыла назад, а во-вторых, в случае,
если балансирующий груз выносится на специальных кронштей-
нах наружу (схематически это показано на фиг. 98), увеличивает
лобовое сопротивление (хотя и весьма мало). Все же последнему
способу балансировки следует отдать предпочтение перед спо-
собом закладки груза в носок элерона, так как в этом случае
1 В некоторых случаях увеличение жесткости крепления элеронов может
даже повести к понижению критической скорости—см. стр. 239.
262
требуется значительно меньший дополнительный груз, и центр
тяжести всего крыла значительно менее оттягивается назад,
вследствие чего это менее неблагоприятно отражается на кри-
тической скорости самого крыла.
Строго говоря, нужно балансировать каждое сечение по от-
дельности. Но этого можно достигнуть, только помещая груз
в носок элерона, что, как выше указано, невыгодно. При поста-
новке балансиров в одной точке цель будет достигнута только
в том случае, если конструкция элеронов достаточно жестка
и гарантирует от деформаций (перекосов) самого элерона. На это
обстоятельство следует обратить существенное внимание, так как
жесткость, достаточная для обеспечения от возникновения боль-
ших деформаций при статических нагрузках, может оказаться
недостаточной при нагрузках динамических.
Что дает частичная балансировка элерона? При частичной
балансировке можно увеличить критическую скорость в случаях
„а“, „б“ и „в“, но не уничтожить возможности этих форм ко-
лебания.
На фиг. 99 показана типичная кривая изменения критической
скорости изгибно-элеронного флаттера в зависимости от поло-
жения его центра тяжести. Нижняя ветвь кривой соответствует
критической скорости начала флаттера, верхняя — прекращению
флаттера.
а
Мы видим, что только при < 1% критическая скорость
*9Л
изгибно-элеронного флаттера перестает существовать. Измене-
263
ние же 4^- в пределах от 5% и выше не дает значительного
увеличения критической скорости. Поэтому всегда следует стре-
миться к полной балансировке элерона. Если же этого нет, то
расчет изгибно-элеронного флаттера следует производить обяза-
тельно, так как для крыла с неуравновешенным элероном изгибно-
элеронный флаттер часто бывает более опасным, наступает на
меньшей скорости, чем изгибно-крутильный.
Выше мы подробно рассмотрели элерон, который аэродина-
мически точно компенсирован. Если этого нет, то при вибрациях
крыла возникает, кроме инерционного, еще аэродинамический
шарнирный момент, также вызывающий отклонение элерона, и,
как следствие, дополнительную подъемную силу и крутящий
момент. Чтобы этого избежать, следует стремиться к точной
аэродинамической компенсации элерона.
Так как точно достигнуть этого на всех скоростях вряд ли
возможно, то следует отдельно остановиться на различных спо-
собах аэродинамической компенсации.
Следует всячески избегать местной перекомпенсацич, когда
одна какая-либо часть элерона компенсирует всю остальную
часть. Особенно такой тип компенсации становится опасным,
если элерон разрезан и состоит из отдельных частей. Известен
случай, когда авария была вызвана тем, что элерон состоял из
двух частей, причем одна часть была перекомпенсирована, а дру-
гая недокомпенсирована. С этой точки зрения ненадежной яв-
ляется роговая компенсация, так как на роге получается пик
нагрузок, и это обстоятельство вызывает перекос элерона, тем
более, что качалку управления ставят обычно достаточно далеко
от рога х.
Известны также случаи, когда причиной вибрации являлась
плохая конструкция серворулей. Серворули добавляют новую
степень свободы, вследствие чего появляются ряд новых возмож-
ных форм колебаний (например, отклонение элерона — отклонение
серворуля) и соответствующие критические скорости, которые
часто бывают весьма невелики. Серворули тем более опасны,
что их устанавливают на органах управления, которые сами
по себе не жестко закреплены. Кроме того, часто кривая шар-
нирных моментов для органов, снабженных серворулями, имеет
в области малых отклонений перегиб, что говорит о переком-
пенсации в области малых углов.
Наилучшей формой аэродинамической компенсации является,
несомненно, осевая.
Из очевидных мероприятий следует также напомнить о том,
что желательно избегать тросового управления; предпочтитель-
нее ставить жесткие тяги.
По возможности следует также облегчать конструкцию орга-
нов управления (элеронов и рулей), что облегчает их баланси-
1 Особенно следует избегать роговой компенсации иа хвостовом оперения-
264
ровку и дает выигрыш в положении центра тяжести крыла (или
стабилизатора). Известен случай, когда одна иностранная фирма
построила три совершенно одинаковых серии истребителей, и
самолеты одной из этих серий гибли от вибраций хвостового
оперения, в то время как остальные две серии прекрасно летали.
Анализ этого явления показал, что у серии, подверженной виб-
рациям, была металлическая обшивка рулей, в то время как
у остальных — полотняная. И этого оказалось достаточно для
возникновения флаттера.
С принципиальной стороны действие рулей на хвостовом
оперении при вибрациях ничем не отличается от действия эле-
ронов на крыльях. Все выводы, сделанные относительно элерона,,
могут быть перенесены на рули.
ГЛАВА Xli
ВИБРАЦИИ ВОЗДУШНЫХ винтов
Винт постоянно подвергается действию периодических импуль-
сов и потому вопросы вибрации лопастей воздушных винтов
приобретают все больший практический интерес. В эксплоата-
ционной практике зарегистрировано немало случаев поломок
винта вследствие вибраций, и страховка от разрушительных
колебаний становится насущной задачей конструктора при про-
ектировании.
Разрушительные колебания винта могут наступить, например,
если собственная частота колебаний лопасти совпадает с часто-
той внешних возмущающих сил (лопасть попадает в резонанс).
Источником последних является мотор, а также аэродинамические
силы (например, лопасть получает импульс при прохождении
перед крылом). До настоящего времени нельзя считать оконча-
тельно установленным, какие именно частоты имеют возбуждаю-
щие импульсы. В работе Hansen und Messner1, например, указы-
вается, что число возбуждений от мотора, которое получает
лопасть за один оборот, будет:
ч; -4-; 2Q лля четырехтактного мотора;
Q; 2Q; -j-; 3Q; 4Q для двухтактного мотора,
где Q — число цилиндров мотора. Значения чисел возбуждений
расположены в порядке убывающей интенсивности их. Эти дан-
ные нуждаются еще в тщательной проверке; во всяком случае
можно думать, что приведенные числа не исчерпывают всех воз-
можных частот возмущений, но, к сожалению, достаточно полных
данных о числе и величине возбуждающих импульсов в настоя-
щее время еще нет.
Лопасть можно схематизировать как стержень, обладающий
определенной закруткой. При определении частот колебания
закрученностью лопасти обычно пренебрегают, и мы в дальней-
шем изложении также не будем учитывать ее.
Лопасть может колебаться в плоскости наименьшей жесткости,
в плоскости наибольшей жесткости, а также совершать крутиль-
1 Luftschraubeschwingungen, ZFM, № 11, 1933 г.
266
ные колебания. Частоты последних двух видов колебаний для
современных лопастей обычно настолько велики, что лежат зна-
чительно выше оборотности мотора. Поэтому достаточно рассчи-
тать винт только на изгибные колебания, определив для этого
частоту основного тона и первого обертона изгибных колебаний
лопасти в плоскости наименьшей жесткости.
Расчет изгибных колебаний ведут в такой последовательности:
сперва определяют частоту колебаний остановленного винта, а
затем вносят поправку, учитывающую влияние центробежных
сил, действующих на лопасть при вращении. Расчет изгибных
колебаний лопасти ведут на основе следующих упрощающих
предположений:
1) лопасть рассматривается как стержень переменного сечения,
•абсолютно жестко заделанный у втулки;
2) не учитывается совместность колебаний, т. е. влияние кру-
тильных колебаний на частоту изгиба; последнее допущение
оправдывается тем, что у винта собственные частоты изгибных
и крутильных колебаний лопасти весьма далеки друг от друга,
а потому взаимное влияние изгиба и кручения не может сущест-
венно отразиться на величине частот.
Расчет изгибных колебаний неподвижной ло-
пасти производится методом последовательных приближений,
изложенным в гл. III. Для определения жесткости изгиба EI ло-
пасть как бы раскручивают, т. е. под / в данном случае пони-
мают наименьший главный момент инерции сечения лопасти;
Е — модуль Юнга. Если попрежнему обозначить через Z — прогиб
лопасти, ось z направить по оси вращения винта, ось у—вдоль
лопасти и принять, как обычно,
Z=/(y)-e4 (1)
то уравнение изгибных колебаний лопасти:
<2>
совпадает с уравнением изгибных колебаний стержня [гл. III
уравнение (12)] и может быть решено методом, изложенным в
гл. III, п. 3. При такой постановке задачи не учитывается влия-
ние втулки, а также упругость вала, на который насажен винт.
Учет влияния центробежных сил на частоту
колебаний. В результате решения уравнения (2) методом по-
следовательных приближений находится функция формы f и
частота р0 колебания невращающейся лопасти. При вращении
лопасть находится в поле центробежных сил, а потому частота
вращающейся лопасти будет отличаться от частоты колебания
лопасти неподвижной.
Для приближенной оценки влияния центробежных сил при-
меним принцип возможных перемещений. Будем также предпо-
лагать, что направление изгиба совпадает с направлением оси
винта oz (фиг. 100).
267
Кинетическая энергия вибрирующей лопасти
R
о
(3)
где R— радиус лопасти и т — погонная масса ее.
Потенциальная энергия вибрирующей лопасти состоит из двух
частей:
(4)
u=uY + u2,
где UY — потенциальная энергия упругой деформации (равная
работе упругих сил при изгибе) и U2— потенциальная энергия
центробежной силы.
Как обычно,
R
о
Для определения рычислим работу центробежных сил при
изгибе лопасти. Пусть (фиг. 100j точка А при изгибе переме-
стилась и заняла по-
ложение Вычи-
слим радиальное пе-
ремещение Ьу точки
А. Так как лопасть
предполагается не-
растягивающейся.то
У длина ОСА равна
длине дуги изогну-
той лопасти ОС.Д,,
Фиг. 100. т. £
у
у -ф Ду = J ds, (6)
О
где ds — элемент дуги изогнутой лопасти (фиг. 100). По обычной
формуле _________
Ввиду малости величины (как и везде, мы рассматриваем
только малые колебания) можно разложить правую часть по
биному Ньютона и ограничиться членами наименьшего порядка
малости. Получим:
Подставляя это выражение в уравнение (6), будем иметь:
У У
О о
26Я
откуда
у
О
На элемент винта между сечениями у и yA~dy, имеющий
массу т dy, действует центробежная сила mw-y dy, направленная
параллельно оси у (ш—-угловая скорость вращения винта). При
перемещении сечения из положения А в положение работа,
производимая этой силой, будет:
mu-ydy-by = m^dy- J (^y)~dy.
и
Суммируя работу центробежных сил по всем элементам винта,
находим потенциальную энергию центробежных сил:
к у
^/"уД^у-
о о
Полагая, как обычно,
Z=f(y>q^ (7)
и учитывая формулы (3), (4), (5) и (7), находим выражения ки-
нетической и потенциальной энергии вибрирующей лопасти через
обобщенную координату q'.
. R
T=^-fmfdy,
О
г /? я У
[^Ш“у + ^уШ^у
1-и 0 0 J
Составляем уравнение Лагранжа по координате q:
R г R Ry
q f mf-dy +q fEI (Jr)2^+“>2 f myf (^у^У аУ
О О 0 0
Интегрируя это уравнение, как обычно, подстановкой
q = Ае,р,
находим выражение частоты колебания р:
(8)
f mj2dy J mfdy
о о
269
При расчете за функцию / в этой формуле принимают функцию
формы, определённую в результате расчета невращающейся ло-
пасти. 1
Легко видеть, что первый член формулы (8) представляет
собой не что иное, как квадрат частоты колебания невращаю-
щейся лопасти. В самом деле, умножая уравнение (2) на f(y) dy
и интегрируя результат в пределах от нуля до R, найдем:
fmf*dy
о
где р0 — частота колебаний неподвижной лопасти [см. также
формулу (13) гл. III]. Поэтому формулу (8) можно переписать
в следующем виде:
Р2 = Ро+«п2Л, (9)
где через k обозначен безразмерный коэфициент:
« у
------------ (10>
f mf* dy
О
Формулой (9) и следует пользоваться при определении ча-
стоты колебания вращающейся лопасти. Как видно из этой фор-
мулы, частота колебания вращающейся лопасти вследствие влия-
ния центробежных сил всегда больше, чем частота колебания
лопасти неподвижной.
Задача учета влияния центробежных сил сводится, следова-
тельно, к определению коэфициента k. Оказывается, что вели-
чина этого коэфициента мало зависит от параметров, определяю-
щих форму лопасти. Приводим ниже значения коэфициента k,
полученные различными авторами (табл. 15).
При конкретных расчетах коэфициент k рекомендуется под-
считывать для каждого винта по формуле (10). Для грубой оценки
влияния центробежных сил можно принять k — 1,4.
Флаттер винта. Вращающаяся лопасть представляет со-
бой несущую поверхность, на которую действуют аэродинами-
ческие силы. Как и в случае крыла, может встать вопрос о флат-
тере лопасти, т. е. о колебаниях с нарастающей амплитудой, воз-
никающих и поддерживающихся за счет энергии набегающего
на лопасть потока воздуха. Метод расчета критического числа
оборотов, т. е. числа оборотов, при котором возникает флаттер
лопасти, разработан П. М. Ризом1. Числовые расчеты, проведен-
ные Ризом, показали, что для лопастей нормальной толщины
1 П. М. Риз, Флаттер воздушных винтов. Труды ЦАГИ, вып. 391, 1938г.
270
Таблица i5
Автор Значения коэфициента k Примечание
Основной тон коле- бания 1-й обертон 2-й обертон
Berry 1,19 — — Стержень постоянного сечения
Webb and Swain 1,3 — -% Суживающийся клин
Southwell and Gough 1,52 — — —
Swain 1,17—1,19 — — Усеченный клин
Hohenemser 1,08 3,9 12,2 61 2 II •*4 Е II Е
Риз 1,44—1,47 ~3,6 — т=те (1 —^У;0,8<₽< 1,8
Page (результаты опы- тов) 1,04—1,54 — — Первая цифра для узких лопа- стей, вторая—для широких
Hansen u. Messner (результаты опы- тов) 1,45 4,4 — Эксперименты на моделях
флаттер в области доступных чисел оборотов не может иметь,
места. Объясняется это, невидимому, весьма высокой частотой
крутильных колебаний, которую имеют современные винты. По-
этому нормально расчет винта на флаттер не производится. Од-
нако заключение о невозможности флаттера винта не следует
рассматривать как абсолютное: с ростом окружных скоростей
(а также для тонких профилей), возможно, придется столкнуться
с проблемой флаттера винта.
Вопросы усталости для винта играют особенно важную
роль, так как винт все время работает под динамической на-
грузкой. Почти все поломки винтов происходят именно от уста-
лости. Сравнительно редки случаи разрушения новых винтов,,
в большинстве случаев разрушение винтов от вибраций происхо.-
дит после длительной эксплоатации винта, т. е. от усталости.
ГЛАВА XIII
ВИБРАЦИИ ХВОСТОВОГО ОПЕРЕНИЯ
Очень часто на практике приходится сталкиваться с вибра-
циями хвостового оперения. Следует различать три основных
типа вибраций хвостового оперения, которые отличаются как
по причинам их возникновения, так и по способам их устранения.
1. Резонансные колебания. Причина этих колебаний
кроется в совпадении собственной частоты- колебания какой-
либо части оперения с частотой импульсов от мотора. Особенно
часто резонансным колебаниям подвержены тяги управления
рулями, кронштейны балансиров и т. п.
2. Колебания типа „баффтинг". Эти колебания по-
рождаются вихрями, сбегающими с лежащих впереди частей
самолета (с крыла, обычно в месте его сопряжения с фюзеля-
жем, с моторных коков, при плохой их обтекаемости и т. п.).
Сорвавшийся вихрь налетает на оперение, последнее под дей-
ствием удара вихря деформируется и приходит в колебательное
состояние. Эти колебания имеют тенденцию к затуханию, но
следующий сорвавшийся вихрь, ударив по оперению, опять
заставляет последнее деформироваться и колебаться. Таким
образом баффтинг — это тряска оперения (часто даже не пери-
одического характера, если не наблюдается периодичности в
срыве вихрей) под действием ударов вихрей, срывающихся с
каких-либо находящихся впереди оперения частей самолета.
3. Колебания типа „флаттер". Оперение, так же как
и крыло, может быть подвержено колебаниям типа „флаттер",
т. е. колебаниям, порождающим такого рода аэродинамические
силы, которые эти колебания увеличивают дальше. Флаттер
оперения, как и крыла, происходит с очень быстрым нараста-
нием амплитуды и, как правило, ведет к разрушению оперения,
в отличие от баффтинга и резонансных колебаний, которые вызы-
вают разрушение лишь в очень редких случаях.
В дальнейшем мы будем рассматривать только баффтинг
и флаттер хвостового оперения, так как способы расчета и унич-
тожения резонансных колебаний очевидны: следует определить
собственную частоту колеба’ния вибрирующей части, а затем
изменить ее (путем изменения жесткости и массы) таким обра-
зом, чтобы устранить возможность резонанса. Определение соб-
272
J
ственной частоты производится либо расчетом (методами, из-
ложенными в гл. I—IV), либо, что более рационально, экспери-
ментальным путем, при помощи вибраторов (см. гл. V).
1. БАФФТИНГ ХВОСТОВОГО ОПЕРЕНИЯ
Баффтинг оперения летчиком воспринимается как тряска или
вздрагивание хвостового оперения, сопровождающаяся подерги-
ванием рычагов управления. Выше мы указывали, что эта тряска
возникает под действием вихрей, налетающих на оперение.
Очевидно, для возникновения баффтинга необходимы два усло-
вия: 1) нужно, чтобы существовали срывающиеся вихри и 2)
нужно, чтобы оперение попало в их зону. Отсюда и два основ-
ных способа уничтожения баффтинга: улучшение обтекаемости
тех частей, с которых срываются вихри, и установка приспо-
соблений (например закрылков), отклоняющих срывающиеся
вихри под стабилизатор.
В некоторых случаях баффтинг носит периодический харак-
тер и происходит с вполне определенной частотой. Это объясняется
тем, что в сорванной зоне имеется определенная пульсация ско-
рости, и при совпадении собственной частоты колебания опере-
ния (частота изгиба стабилизатора или частота колебаний фюзе-
ляжа и т. д.) с частотой пульсации скорости оперение попадает
в резонанс. Экспериментально установлено, что основная частота
пульсаций в сорванной зоне, если срыв происходит с крыла,
может быть выражена формулой:
Ип '= k •
t sin а* ’
где k = 0,12—0,15; t—хорда крыла; а* — геометрический угол
атаки
Следует избегать того, чтобы собственная частота оперения
совпадала с п„, или же располагать оперение относительно
крыла таким образом, чтобы оно не попадало в сорванную зону.
Кроме частоты лп , в сорванной зоне в разных случаях могут
существовать и другие частоты, но величина их до сих пор
точно не выяснена.
Поскольку баффтинг порождается срывающимися вихрями,
а срыв обычно усиливается с увеличением угла атаки, баффтинг
чаще всего наблюдается на больших углах атаки, а следова-
тельно на малых скоростях при планировании, спиралях с убран-
ным газом, а также при некоторых фигурах высшего пилотажа.
Предвидеть баффтинг в процессе проектирования в большин-
стве случаев не удается, и он обнаруживается при летных ис-
пытаниях готовой машины. Поэтому приходится готовую машину
подвергать переделкам, обеспечивающим уничтожение баффтинга.
Нельзя указать общих конкретных рецептов для этого, но все
мероприятия по уничтожению баффтинга в основном сводятся
к отысканию причин, порождающих срыв вихрей (путем снятия
спектра обтекания самолета), и уничтожению этих причин. Мы
Гроссман—15—18 273
остановимся на нескольких конкретных случаях баффтинга, из
описания которых можно установить, какие меры рациональнее
применять в том или ином случае.
1. Двухмоторный, низкоплан. Баффтинг наблюдался на плани-
ровании и спиралях с убранным газом при скоростях от 140 км/час
и меньше. Колебания происходили в основном за счет скручи-
вания конца фюзеляжа. Амплитуда колебаний возрастала при
уменьшении скорости, так что при планировании на скорости
120—115 км/час колебания становились настолько опасными,
что грозили разрушить оперение.
Снятием спектра было установлено, что вследствие плохой
обтекаемости (отсутствие зализов) на центроплане, в основном
между моторным коком и бортом фюзеляжа, наступал срыв
вихрей уже при угле атаки в 7—8°. При увеличении угла атаки
срыв увеличивался. Так как с правого и левого крыльев вихри
срывались не одновременно, то правая и левая половины стаби-
лизатора подвергались ударам вихрей в различные моменты
времени, вследствие чего происходило скручивание фюзеляжа.
Периодичности в колебаниях не наблюдалось — они носили ха-
рактер тряски. Период между двумя последовательными вздра-
гиваниями оперения менялся в пределах (приблизительно) от
0,25 до 1,1 сек. Собственная частота оперения ~0,2 сек., т. е.
резонанса здесь быть не могло.
Баффтинг был устранен установкой управляемых закрылков
вдоль центроплана. При обычном моторном полете эти закрылки
устанавливались в нейтральное положение (приблизительно па-
раллельно хорде крыла), чтобы уменьшить их сопротивление.
При полете на скоростях меньше 140 км/час закрылки отклоня-
лись вниз под углом в 30° к хорде. Закрылки, во-первых, затя-
гивали срыв (который после их установки начинался только на
углах 12—13°), а, во-вторых, заставляли срывающиеся с крыла
вихри отклоняться вниз и проходить под стабилизатором, не
задевая последний.
2. Также двухмоторный низкоплан. Течение баффтинга и
причина его — того же характера, как и в предыдущем случае,
но только баффтинг начинался на больших скоростях (примерно
на 180 км/час и ниже). В данном случае закрылки значительно
уменьшили интенсивность баффтинга, увели начало его на мень-
шие скорости, но окончательно уничтожить баффтинг при их
помощи не удалось. Устранить баффтинг окончательно удалось
установкой щитков и зализов. При закрытых щитках благодаря
зализам баффтинг не наблюдался на скоростях, больших 140 км/час.
При планировании на меньших скоростях приходилось откры-
вать щитки.
3. Многомоторный самолет. Наблюдался баффтинг оперения
при выходе парашютистов на крыло. Причиной срыва вихрей
здесь являлись тела людей.
4. Двухместный, биплан. Баффтинг происходил с малыми
амплитудами. Причиной срыва вихрей являлся плохо обтекае-
274
мый уступ фюзеляжа, имевшийся за вторым сидением. Баффтинг
удалось устранить увеличением жесткости фюзеляжа.
5. Гидросамолет с моторной установкой над крылом. Причи-
ной срыва вихрей являлись стойки моторной установки. Вихри
срывались в месте крепления стоек к крылу. Баффтинг был
устранен установкой обтекателей на места сопряжения стоек
с крылом.
6. В нескольких случаях причиной появления баффтинга яв-
лялись юбки капотов, плохая форма моторных коков и т. п.
В этих случаях улучшали обтекаемость соответствующей части.
2. ФЛАТТЕР ХВОСТОВОГО ОПЕРЕНИЯ
Уже при вибрациях крыла, снабженного элероном, имеются
три степени свободы и соответственно четыре возможных формы
колебаний. Все эти формы колебаний могут иметь место и
при вибрациях хвостового оперения. Роль крыла при этом играет
стабилизатор, или киль, роль элерона — руль. Поэтому все
сказанное выше относительно влияния конструктивных парамет-
ров на критическую скорость, относительно влияния элерона и
т. д. может быть качественно перенесено и на хвостовое опе-
рение. Количественные соотношения будут, конечно, иными, но
меры предотвращения флаттера для оперения следует искать
в том же направлении, как и для крыла.
Хвостовое оперение обладает рядом специфических особен-
ностей, чрезвычайно затрудняющих теоретический анализ явле-
ния. Прежде всего хвостовое оперение обладает большим ко-
личеством степеней свободы, чем крыло. Только фюзеляж
добавляет три новых степени свободы: кручение фюзеляжа,
изгиб фюзеляжа в горизонтальной плоскости и изгиб фюзеляжа
в вертикальной плоскости. Таким образом, если мы даже отбро-
сим влияние вертикального оперения, а будем рассматривать
только фюзеляж, снабженный горизонтальным оперением, все же
мы будем иметь чрезвычайно много возможных форм колебаний:
а) изгиб—кручение стабилизатора и отклонение рулей;
б) изгиб стабилизатора и отклонение рулей;
в) кручение стабилизатора и отклонение рулей;
г) изгиб— кручение стабилизатора;
д) изгиб фюзеляжа в вертикальной плоскости и отклонение
рулей;
е) изгиб фюзеляжа в вертикальной плоскости и кручение
стабилизатора;
ж) изгиб фюзеляжа в вертикальной плоскости, кручение ста-
билизатора и отклонение рулей;
з) изгиб фюзеляжа в вертикальной плоскости и изгиб кру-
чение стабилизатора;
и) изгиб фюзеляжа в вертикальной плоскости, изгиб—круче-
ние стабилизатора и отклонение рулей;
к) кручение фюзеляжа, кручение стабилизатора;
275
л) кручение фюзеляжа, отклонение рулей;
м) кручение фюзеляжа, изгиб—кручение стабилизатора;
н) кручение фюзеляжа, кручение стабилизатора, отклоне-
ние рулей;
о) изгиб—кручение фюзеляжа, кручение стабилизатора, от-
клонение рулей и т. д.
Нет смысла перечислять дальше. Каждая из форм колебании
обладает своей критической скоростью, и нет возможности пред-
сказать заранее, какая^из этих критических скоростей окажется
наименьшей.
Учет вертикального оперения добавляет еще ряд степеней
свободы и намного увеличивает список возможных форм коле-
Фпг. 101.
баний (всего возможных
критических скоростей для
оперения имеется несколь-
ко сотен).
Мы видим, насколько
громоздка и сложна задача
определения критической
скорости хвостового опере-
ния. Эта задача оконча-
тельно до настоящего вре-
мени не решена.
Громадное большинство
известных случаев вибраций
хвостового оперения имели
причиной наличие несба-
лансированных в весовом отношении рулей, а также рулей,
снабженных флеттнерами. Весовая балансировка рулей с> вер-
шение необходима. Если она осуществлена правильно, то сразу
делаются невозможными все формы колебаний, в которых
участвует отклонение рулей. Мы сознательно говорим: „если
она осуществлена правильно14, так как очень часто весовая
балансировка хотя и существует, но осуществлена она таким
образом, что не дает желаемого эффекта.
Цель весовой балансировки рулей—достигнуть того, чтобы
руль не отклонялся вследствие инерционных сил, возникающих
при каких-либо движениях стабилизатора, так как от отклоне-
ния рулей возникают аэродинамические силы, раскачивающие
оперение (точно так же, как от отклонения несбал нсиро-
ванного элерона возникают аэродинамические силы, раскачива-
ющие крыло).
Будем рассматривать руль (фиг. 101), как абсолютно твердое
тело Ч Тогда при вращении фюзеляжа около оси ОО' все точки
руля будут испытывать одно и то же угловое ускорение; обо-
значим его через &. При этом на произвольную точку С,- руля
1 Все решение относится как к вертикальным, так и к горизонтальным
рулям.
276
будет действовать сила инерции где у,— расстояние от
точки С, до оси вращения фюзеляжа и w?;—масса этой точки.
Сила инерции тур создаст около оси вращения руля АА' мо-
мент турх(, где xt — расстояние от рассматриваемой точки до
оси АА'. Общий момент, вращающий руль около его оси вра-
щения, когда фюзеляж вращается около своей оси, будет:
V] т,хур,
где суммирование распространяется по всем точкам руля. Легко
видеть, что
N ^П/Ху/ = Imxy,
где Imxy—центробежный момент инерции массы руля относи-
тельно осей ОО' и АА'.
Чтобы исключить неблагоприятное влияние руля при вибра-
циях, необходимо добиться уничтожения момента, вращающего
руль. Это можно сделать, поместив впереди оси вращения руля
массу М, находящуюся на расстоянии Е от оси АА' и на рас-
стоянии 1) от оси ОО', так, чтобы было выполнено условие:
М'Т] = Imxy • (О
Этим условием необходимо руководствоваться при конструи-
ровании балансиров. Очевидно, прн этом остается достаточно
большой простор для выбора; можно задаваться по произволу
любыми двумя из величин М, Е, »), и тогда третью необходимо
определять по формуле (1). Дальше мы укажем еще одно ус-
ловие, которое несколько сузит свободу выбора.
Если сбалансировать каждое сечение руля, параллельное оси
ОО', в отдельности так, чтобы в каждом сечении центр тяже-
сти руля (вместе с балансирующим грузом) расположился на
оси вращения АА', то условие (1) будет выполнено.
Если центры тяжести различных сечений руля находятся на
одинаковом расстоянии от его оси вращения, то для выполне-
ния условия (1) достаточно поместить груз в сечении, где рас-
положен центр тяжести всего руля, и подобрать этот груз та-
ким образом, чтобы общий центр тяжести (самого руля и балан-
сирующего груза) находился на оси вращения.
Довольно часто в конструкциях самолетов повторяется одна
и та же ошибка: с целью уменьшения лобового сопротивления
балансиры устанавливают в таком месте, чтобы их можно было
спрятать в фюзеляже. Очевидно, этого можно достигнуть, только
установив балансиры весьма близко к оси ОО'. При этом вели-
чина т] оказывается весьма малой и нужно увеличить весьма
сильно М и с. Но этого не делают, считая, что достаточно, если
произведение АД равно произведению 7ИРЕР (где Мр — масса
руля и Ер — расстояние от центра тяжести руля до его оси вра-
щения), т. е. если общий центр тяжести руля и балансирую-
щего груза находится на его оси вращения. О величине не
заботятся. Конечно, такие балансиры при кручении фюзеляжа
277
почти не действуют, так как возникающие при вращении фюзеляжа
инерционные силы дают около оси вращения руля момент, вовсе не
погашающийся моментом от балансирующего груза.
Мы еще вернемся к вопросу о наивыгоднейшем месте поста-
новки балансиров после того, как укажем второе условие
балансировки. Это второе условие получается при рассмотрении
изгибных колебаний фюзеляжа.
Если ось АА' (фиг. 101) перемещается параллельно самой
себе, перпендикулярно плоскости чертежа \ с линейным уско-
рением w, то на каждую точку С, руля будет действовать сила
инерции m/w. Эта сила инерции дает около оси вращения руля
момент и общий момент от всех точек руля будет:
где суммирование идет по всем точкам руля. Очевидно,
V} = 7И р Ер.
Чтобы погасить полученный момент, необходимо поставить впе-
реди оси вращения руля балансирующий груз массы 7И так,
чтобы
= (2)
где Е, как и прежде, расстояние от балансирующего груза до оси
руля вращения. Условие (2) означает, что общий центр тяжести
груза и руля должен находиться на оси вращения руля2.
Будем называть условие (2) условием статической баланси-
ровки, а условия (1) и (2) вместе — условиями динамической
балансировки.
Исключив из выражений (1) и (2) произведение 7И;, находим:
Так как при установке балансиров необходима динамическая
балансировка, то условие (3) должно определять место поста-
новки балансиров.
Следовательно, при конструировании балансиров одну из
величин — М или Е — выбираем произвольно. Тогда другая опре-
делится из условия (2), а место постановки балансиров — по
формуле (3).
Если ограничиваться только рассмотрением условия (2), что
обычно и делается, но чего недостаточно, то место установки
балансиров не определяется. Если рассматривать только усло-
1 Так как амплитуда колебаний фюзеляжа мала по сравнению с его дли-
ной, то такое представление о перемещении оси АА' практически соответ-
ствует действительности.
1 Если балансирующий груз расположен не в плоскости руля, то под Е
следует понимать проекцию расстояния груза от оси вращения руля иа плос-
кость хорд руля.
278
вие (1), то наилучшей кажется установка балансиров на конце
руля. Но условие (3) показывает, что оба решения неверны, и
балансиры следует ставить не ближе строго определенного рас-
стояния от оси фюзеляжа *. Если это не исполнено, рули не
могут считаться сбалансированными на 100%.
Нет смысла пренебрегать условием (3), так как оно не тре-
бует увеличения веса, поскольку вес балансиров целиком опре-
деляется условием (2).
Часто имеет смысл устанавливать не один, а несколько ба-
лансирующих грузов, например если на руле имеется роговая
компенсация и желательно часть балансирующего груза устано-
вить в роге 1 2. Легко написать соответствующие формулы и для
этого случая.
Пусть оперение балансируется при помощи п грузов,
массы которых М1г /И2, ...,/И„. Пусть расстояния от грузов до
оси вращения руля (вернее, проекции этих расстояний на плос-
кость хорд руля) будут Et, и расстояние от этих грузов
до оси вращения фюзеляжа тдт, т(2, Тогда для полной балан-
сировки необходимо соблюдение условий:
М& + М& +... + М„-п = УИрЕр;
М&ъ + ЛУЛг + • • • + = ^тху-
В данном случае, очевидно, свобода выбора масс и расположения
балансирующих грузов будет весьма большой.
Условия балансировки, которые мы выше указали, выведены
в предположении, что руль является абсолютно твердым телом.
Если руль сам может деформироваться, то и при соблюдении ука-
занных условий он может вызвать вибрации, а потому все рули
должны быть по возможности жесткими. Именно из опасения
собственных деформаций руля следует избегать постановки ба-
лансиров слишком далеко от фюзеляжа (особенно, если учесть,
что кабанчик, к которому идут тяги управления, обычно рас-
полагается возле фюзеляжа). Поэтому лучше при определении
места постановки балансиров пользоваться именно тем значением,
которое получается из формулы (3), хотя если бы руль был
абсолютно твердым, можно было бы допускать большие (но не
меньшие) значения *], чем предусматривает формула (3).
Постановка нескольких балансиров, при правильном их рас-
положении с точки зрения возможных деформаций руля лучше,
чем постановка одного.
Полученные условия балансировки не учитывают инерцион-
ных сил, появляющихся на руле при вращении стабилизатора
(киля), которое неизбежно имеет место при изгибе фюзеляжа,
1 Весовая перебалансировка не опасна, а просто излишня. Установка ба-
лансиров слишком далеко от оси фюзеляжа нежелательна, так как может по-
вести к перекосам руля, о чем речь будет ниже.
а Роговая компенсация руля, как и элерона, нежелательна, но все же ею
до настоящего времени иногда пользуются.
279
и потому нуждаются в уточнении. Ниже мы вернемся к этому
вопросу.
Если руль динамически сбалансирован, он может повора-
чиваться около своей оси только под действием аэродинамиче-
ких сил. Чтобы исключить это влияние, следует стремиться
к точной аэродинамической компенсации руля. Из всех типов
компенсации наилучшей с точки зрения безопасности от вибра-
ций является осевая. К аэродинамической компенсации руля
можно применить все те выводы, которые были сделаны при
рассмотрении способов компенсации элерона.
Следует упомянуть еше одно мероприятие, уменьшающее
возможность возникновения несимметричных вибраций горизон-
тального хвостового оперения1— это установление по возможности
жесткой связи правого и левого рулей глубины между собой.
Правильная весовая балансировка и аэродинамическая ком-
пенсация исключают возможность появления таких вибраций,
при которых руль отклонялся бы2.
Обратимся теперь к вопросу о возможности предотвращения
вибраций, возникающих из-за деформации стабилизатора.
Вибрации, как неоднократно указывалось, не могут проис-
ходить с одной степенью свободы. Поэтому,если рули сбалан-
сированы, изгибным колебаниям фюзеляжа обязательно должны
сопутствовать крутильные колебания стабилизатора (или киля),
тем более, что центр тяжести горизонтального оперения обычно
лежит достаточно далеко позади его оси жесткости, так как
к стабилизатору подвешен тяжелый руль. В настоящее время
для предотвращения крутильных колебаний стабилизатора (киля)
практически возможен один путь — всемерное повышение его
жесткости па кручение. Кроме того, следует стремиться поме-
щать центр тяжести стабилизатора (киля) с подвешенным рулем,
как и крыла, возможно ближе к передней кромке.
Переходим к вопросу о расчете оперения на флаттер.
Как уже отмечалось, оперение имеет очень много критических-
скоростей, и произвести расчеты для определения всех их нет
никакой возможности. Повидимому, для горизонтального опере-
ния можно ограничиться расчетом на три формы колебания:
1) изгибно-рулевой флаттер с двумя степенями свободы: из-
гиб фюзеляжа в вертикальной плоскости и отклонение руля
высоты (обе половинки руля высоты отклоняются в одну сторону);
2) крутильно-рулевой флаттер с двумя степенями свободы:
кручение фюзеляжа и несимметричные отклонения руля высоты
(обе половинки руля высоты отклоняются в разные стороны, т. е.
лонжерон руля высоты скручивается);
/ Несимметричными вибрациями называются такие вибрации, когда пра-
вый и левый рули отклоняются в разные стороны. При таких вибрациях
существенную роль играет кручение фюзеляжа.
2 Если, конечно, они не вызываются серворулями, щелью между рулем и
стабилизатором и тому подобными причинами. Все эти причины можно преду-
смотреть и устранить.
280
3) безрулевой флаттер с двумя степенями свободы: изгиб
фюзеляжа в вертикальной плоскости и изгиб—кручение стабили-
затора.
Аналогичные случаи следует рассмотреть также и для вер-
тикального оперения. Однако при различных схемах оперения
вопрос о сравнительной опасности того или иного вида колеба-
ния может быть подвергнут пересмотру, и окончательное уста-
новление расчетных случаев должно быть произведено в каждом
конкретном случае отдельно. Так, например, для некоторых
истребителей при очень коротком и жестком фюзеляже можно
считать фюзеляж абсолютно жесткой заделкой и ограничиться
расчетом стабилизатора с рулем как крыла с элероном.
Фиг. 102.
Методы, указанные в гл. VII для крыла, можно с успехом
применить и для определения критической скорости хвостового
оперения. Методы эти базировались на том, что задавалась форма
колебаний системы, а критическая скорость определялась затем
из условия равенства нулю работы на пути возможных переме-
щений при гармонических колебаниях постоянной амплитуды.
Для примера изложим метод расчета изгибно-рулевого флат-
тера (со степенями свободы: изгиб фюзеляжа и отклонение руля).
Построение расчетных методов для вибраций оперения с другими
степенями свободы вполне аналогично.
Рассмотрим фюзеляж с укрепленным на нем горизонтальным
оперением. Фюзеляж будем считать жестко заделанным в месте
сопряжения его с крылом.
На фиг. 102 показаны данный фюзеляж и оперение в положе-
нии равновесия.
Пусть теперь вследствие какого-либо случайного импульса
фюзеляж изогнулся (фиг. 103, положение /). Предоставленный
затем самому себе фюзеляж будет ускоренно двигаться к поло-
жению равновесия (фиг. 103, положение II). Если при этом центр
тяжести руля высоты находится позади его оси вращения, руль
будет по инерции отставать и отклонится вверх относительно
стабилизатора. После перехода через положение равновесия
(положение III) фюзеляж под действием сил упругости будет
двигаться замедленно, в то время как центр тяжести руля по
инерции будет стремиться сохранить приобретенную скорость
и будет нагонять в своем движении стабилизатор (положения
IV и V). Следовательно, .при движении фюзеляжа вниз руль
относительно стабилизатора оказывается отклоненным вверх.
Точно так же легко показать, что при движении стабилизатора
вверх руль будет отклоняться вниз. За счет отклонения руля
281
возникнет дополнительная подъемная сила, которая будет все
время направлена в ту же сторону, куда движется фюзеляж,
и будет стремиться усилить колебания последнего, т. е. вызвать
флаттер.
Конечно, приведенная схема может служить только для гру-
бого уяснения причин, вызывающих изгибно-рулевой флаттер, так
как она не учитывает некоторых важных факторов, например
вращения стабилизатора, получающегося за счет отклонения фю-
зеляжа (угол 6, фиг. 103), но и она уже показывает, насколько
важную роль при флаттере оперения играет положение центра
тяжести руля. Как будет ясно из последующего, расстояние от
центра тяжести руля до его оси вращения является одним из
основных параметров, характеризующих оперение с точки зрения
Переходим к изложению расчетного метода для определения
критической скорости оперения.
Выберем начало координат о в месте заделки фюзеляжа
(фиг. 104), ось ох направим вдоль фюзеляжа в недеформирован-
ном его состоянии, ось oz — перпендикулярно к ней, вниз.
Пусть оС (фиг. 104) — положение колеблющегося фюзеляжа в
какой-либо момент времени; С — точка прикрепления стабилиза-
тора к фюзеляжу; Ш — шарнир руля. Обозначим через 6 угол
поворота стабилизатора, получающийся за счет деформации фю-
зеляжа, р — угол отклонения руля относительно стабилизатора,
Z — прогиб фюзеляжа. Углы и моменты считаются положитель-
ными при повороте от положительной оси х к положительной
оси z.
Очевидно,
282
где /ф — длина фюзеляжа от места защемления о до места
крепления стабизатора С. Расстояние между точкой С и шар-
ниром руля Ш обозначим рш. Прогиб конца фюзеляжа усло-
вимся обозначать через Zo:
^0 ““
(5)
Будем считать, что руль соединен со стабилизатором упруго,
так что при отклонении руля на угол р создается упругий восста-
навливающий момент /?3.
Прежде всего рассмотрим колебания изучаемой системы в
пустоте.
Колебания в пустоте. Для получения уравнений движе-
ния приравниваем нулю сумму моментов (упругих и инер-
ционных), действующих на руль высоты относительно его оси
вращения, и сумму проекций на ось oz сил, действующих на
элементарный отсек фюзеляжа между сечениями х и х + dx.
Будем иметь:
д2 d2Z\ , d2Z n.
дхг dx*J + '”ф дт2 °’ .
(6)
^ + ^р3р20+/тр(₽+б)+Л1рзрршб=о,
где £7Ф — жесткость изгиба фюзеляжа;
/лФ — погонная масса фюзеляжа;
Мр—масса руля высоты;
<зр — расстояние от центра тяжести руля высоты до его
оси вращения;
Imp — массовый момент инерции руля высоты относительно
его оси вращения.
Уравнение движения фюзеляжа [первое из уравнений (о)[
совпадает с уравнением изгибных колебаний крыла [см. гл. III,
уравнение (1)1, что вполне естественно, так как и фюзеляж
283
и крыло схематизируются как стержень, закрепленный одним
концом.
Первое из уравнений (6) составляется так же, как уравнение
изгибных колебаний крыла, и в дополнительных разъяснениях
не нуждается. Что касается второго из уравнений (6), то
представляет восстанавливающий упругий момент при отклоне-
нии руля на угол ?. Остальные члены уравнения дают момент
инерционных сил на руле при колебаниях относительно его оси
вращения. Для получения этого момента рассмотрим какую-либо
точку At на руле (фиг. 105). Обозначим через а, р — расстояние от
точки до оси вращения руля Ш и через mi — массу, сосре-
доточенную в точке А,. Координаты z,. точки Ai (фиг. 105)
будут:
xi — h + рш COS 6 + з,-р COS(₽ 4-6); I
Zi — Zo 4- Рш sin 6 4- s, р Sin (Р 4- 6). J
Слагающие силы инерции точки А{ по осям ох и oz, очевидно,
равны: — — т^. Момент силы инерции относительно оси
вращения руля Ш (фиг. 105):
— (— Si р sin (₽4-0)+{—mlzi) р cos (₽ 4- 0).
Суммируя моменты сил инерции по всем точкам руля, полу-
чаем общий инерционный момент руля:
р =S Н(— mix>) 3i Р sin (₽ 4-е) 4- (— ^,z,) 5,- р cos (В 4- 0)], (8)
где суммирование распространяется по всем точкам руля.
284
Диференцируя выражения (7) дважды по времени, находим:
xt = — рш sin 6 • 6 —рш cosO • б2 — aip sin (3 4- 0)((3 4- ®) —
— =iPCOS (? + 6) (3 4- б)2;
z( = Zo + рш cos в - 0 — рш sin о - б2 + af р cos (3 4- 0) (Р 4-6) —
— р sin (.3 4- 0) (3 + 6)2.
Подставляя эти выражения в формулу (8) и пренебрегая
членами выше первого порядка малости по деформациям и ско-
ростям, получаем:
/И, р == ГП^1 pZp рРш ® p (P “F" 6) =
=— jWpGpZo — /ИрЗррш 6— /mp(.8 4-9). (9)
Приравнивая нулю сумму инерционного Л4,р и упругого — /?,3
моментов, приходим ко второму уравнению (6).
Чтобы полностью определить задачу, необходимо наряду
с уравнениями движения (6) написать граничные условия. При
колебаниях в пустоте условия эти будут следующими:
1) В месте заделки фюзеляжа прогиб равен нулю;
при х = О
Z = 0. (10а)
2) В месте заделки фюзеляжа касательная к упругой линии
фюзеляжа не может иметь излома; •
при х = 0
< = «• (10b)
3) Перерезывающая сила на конце фюзеляжа равна сумме
инерционных сил всех масс (горизонтальное и вертикальное опе-
рения, костыльная установка и т. д.), сосредоточенных на конце
фюзеляжа;
при х — /ф
—^-(£7Ф g) = - M0Z0-M0^-Mpap р. (Юс)
4) Изгибающий момент на конце фюзеляжа (в точке С,
фиг. 104) равен сумме инерционных моментов всех масс, сосре-
доточенных на конце фюзеляжа, относительно оси, парал-
лельной размаху стабилизатора и проходящей через точку С;
при х = /ф
£'ф g = - Af030Z0- 1т об - (Лир 4- Мр =р р")?. ( 10d)
Здесь Мо — сумма всех масс, [сосредоточенных на конце ста-
билизатора (горизонтальное и вертикальное опе-
рения с рулями, костыльная установка и т. д.);
285
о0—расстояние от центра тяжести масс, входящих
в Л10, до конца фюзеляжа; а0 считается положи-
тельным, если центр тяжести лежит позади конца
фюзеляжа;
Imo—момент инерции масс, входящих в 7И0, относи-
тельно оси, параллельной ' размаху стабилизатора
и проходящей через конец фюзеляжа С.
Инерционные силы и моменты, входящие в выражения усло-
вий (10с) и (10d), могут быть получены тем же методом, ка-
ким мы выше подсчитывали момент инерционных сил руля
[формула (9)]. С физической стороны, например, в условии
(10с) первый член правой части дает силу инерции масс 7И0
при прогибе конца фюзеляжа на Zo, второй — силу инерции,
возникающую за счет вращения масс Мо вместе с концом ста-
билизатора на угол 6 (при этом центр тяжести масс Л10 дви-
жется с линейным ускорением зо0) и последний член — силу
инерции масс, приходящихся на руль высоты Л1Р при вращении
последнего относительно стабилизатора на угол 8.
Уравнения (6) вместе с граничными условиями (10) дают
возможность полностью решить задачу о колебаниях в пустоте
рассматриваемой системы.
Будем искать решения системы (6) в виде:
Z = A^(x)eipz, в = Ве‘р\ (11)
Р не зависит от у, так как руль предполагается абсолютно твер-
дым и отклоняющимся как твердое тело. Так как система урав-
нений (6) и граничные условия (10) однородны, то они опреде-
А
ляют не обе постоянные А и В, а только их отношение . По-
О
этому одну из постоянных (Д или В) можно задать произвольно.
Выберем константу А таким образом, чтобы
(12)
Поэтому в дальнейшем вместо Д'?(л) будем всюду писать про-
сто ф(х), помня, что эта функция должна быть подчинена
условию:
№) = 1. (13)
1огда
Z = 6(x)eip\ $ = Beljn,
и в силу выражений (4) и (5) /,44
Функцию й(х) формы колебаний фюзеляжа и частоту коле-
бания системы р определим методом последовательных прибли-
жений.
286
Подставляя значения (14) в выражения (6) и (10), получаем
[принимая во внимание выражения (5) и (13)]:
<а)
RB - р2Мр а-РЧтр [В 4-й)^]-
-pW а„Ря(Й = 0. (Ь)
р р гш \, dx /х<=1$
При X = 0
4» = 0; (а)
4 = «- (Ь)
При х = /ф
• Л 2) = '’’["о + »-] • (с)
(15)
(16)
£/ф = р2 [ли + /то (5)^, + В (1т р + Мр ар рш )] . (d)
Исключаем из систем (15) и (16) величину В. Для этого
из уравнения (15b) находим:
°₽ + ( dz)*»/* ^mP+AfpopPm’
р _ -2 4 ' Ф_________
и подставляем это значение в граничные условия (16). В резуль-
тате для определения функции ф(х) будем иметь уравнение (15а)
граничные условия.
При х = 0
При х = /ф
ф = 0;
*=0.
ах
(а)
(Ь)
и
2)=р2 {<++
^р ар + ( d )х=;ф р + ^р ар Рш]
в-Рггтр
Л4р3р
(с)
(17)
EI* di -Р2 {M°3° + ( dx )х=гф +
(d)
MV°P + {jdx)x=^l 1/тр + Мр3Р₽ш1 I
---------- R -P4mp-------------- (/mp+Mp Op Рш) f •
287
Для определения «]> (л) поступаем следующим образом. Задаемся
каким-либо значением ф(х) = ф„(х) [за фп(л) можно взять, вообще
говоря, любую функцию, удовлетворяющую условию (13)].
Например можно взять для исходного приближения «1>п(х) =
= ~. Подставляем ф(х) = фп (х) в правую часть уравнения (15а)
£ф
и дважды интегрируем получающееся соотношение:
'ф
^-(£Z*S)=-^2 Г'Пф’№ + С1 = Р^(х) + Сх;
, Х (18)
(Ф
О = - Р2 J dx - - *) + Q = рЧ2>- Q(/ф-х)+с2,
где
'ф
фп’(х) = — [ m^n(x)dx-,
X
'ф
фп ’ (х) = — J (х) dx.
(19)
Постоянные Q и С2 подлежат определению из граничных ус-
ловий (17).
Делим последнее из соотношений (18) на £7Ф и результат
еще раз интегрируем. Получим:
XX х
dil г Ф(2) (’ 1л.— X Г 1
dx+cd kdx+c>-
о b о Ф
Из условия (17b) сразу находим С3 = 0, а потому это уравне-
ние можно переписать в следующем виде:
й = Р2 № (*) - с± я» {х) + с.^> (4 (20)
где
^’(Х)= [ ~Ef^~dx'’ ’l(l,W = f E'rdx. (21)
о о *
288
Интегрируем еще раз соотношение (20). Получим:
ф = p2J (x)dx — Е<х> (x)dx 4- С2Уrp\x)dx 4r С<;
ООО
Из условия (17а) находим С4 = 0, а потому
Ф = Р2Ф(„4,(х) - С^) (х) + с2т^)(х), (22)
где
Ф(„4>(х) = f Wdx; &>(x) = f^(x)dx-
о о
т|<2)(х)= jr^»(x)dx. (23)
о
Постоянные Clt С2 и частота р должны быть определены
из условий (17с), (17d) и (13). Эти условия дают:
с1=.-г|Л5«+Л1"°»(^-Ф +
М? °р +
/л = /ф l^mp +^р °р Рш)
(24)
С2 — р ]Л10з0
*='ф
Mv °р +
+ />2-^-
к = 1ф(Апр +мр ор рш1
Р — рг/------------(^₽ + -МрарРш,
ф (/ф ) = р2ф<4> (/ф ) - (/*)+ад аФ)=1.
J (25)
Подставляя значения Сг и С2 из формул (24) в выражение
(25), находим уравнение, из которого определяем частоту р. За-
тем по формулам (24) вычисляем постоянные Сх и С2. Зная р,
Съ С2, можно по формуле (22) вычислить ф. Это значение и
будет значением искомой функции в следующем приближении.
Далее, приняв найденную функцию за исходную, повторяем все
вычисление сначала (т. е. последовательно вычисляем ф^1), 4(п\
Фп3) и Фп)» а затем Р> £i> ^г)-
Функции £(1>(х), 3S)(x), ^(х), к](г>(х) одинаковы для всех
приближений, так как зависят только от конструктивных пара-
метров фюзеляжа, но не от искомой функции.
Таким образом вычисления повторяем до тех пор, пока функ-
ции ф(х), найденные в двух следующих друг за другом прибли-
жениях, практически не совпадут. Обычно для этого бывает до-
статочно двух-трех приближений.
Гроссман—15_19 2^9
Найденная таким образом функция формы колебаний фюзе-
ляжа ф(х) используется в дальнейшем для определения крити-
ческой скорости флаттера.
Определение критической скорости. При определении кри-
тической скорости, как уже указано, будем исходить из принципа
возможных перемещений. Для составления уравнений Лагранжа
нам, как обычно, нужно подсчитать кинетическую и потенциаль-
ную энергию хвостового оперения и обобщенные силы. Решение
будем искать в виде:
Z=<J)(z)- ^(т); |
₽ = ₽С0. I
(26)
За ф(х) примем функцию прогиба фюзеляжа при колебаниях
в пустоте, метод определения которой был изложен выше. Так
как ф(/ф)= 1, то в силу условий (4) и (5)
20 = q Сч;
6
[<ь • ?(')•
ф
(27)
Переходим к вычислению кинетической энергии вибрирую-
щей системы. Эта кинетическая энергия составляется из кине-
тической энергии руля высоты, стабилизатора, фюзеляжа и
дополнительных масс. Под дополнительными массами мы подразу-
меваем вертикальное оперение, костыльную установку и другие
массы, находящиеся на конце фюзеляжа.
Кинетическая энергия руля высоты. Выше были
определены координаты произвольной точки руля высоты [фор-
мулы (7)]. Пользуясь этими формулами, легко вычислить кине-
тическую энергию руля высоты. С точностью до малых второго
порядка по деформациям:
гр = 1V /пг (;,3 + z?) = 1V т$№ +1V + 6? +
+ V + У т^1р Zo(? 4~ 6)-}- V т,рш Zo6 4-
+ У т^ща.р 6 (₽ 4- б’),
где суммирование идет по всем точкам руля высоты. Выполнив
суммирование, находим:
Л> == Рш + ~2 (Р ^)2/тр 4" Zo ТИр 4~
+ + & )AfpOp 4-zo ё/Иррш 4-Л'1раррш 6 (3 4-6). (28)
290
Кинетическая энергия стабилизатора. Координа-
ты произвольной точки на стабилизаторе могут быть записаны
в виде (фиг. 105):
xi = +a,cos6; )
zf = Zo 4-af sin 6, J (29)
где через а. обозначено расстояние от рассматриваемой точки
стабилизатора до оси, параллельной размаху стабилизатора и
проходящей через точку С.
Кинетическая энергия стабилизатора равна:
Гст = i У.т‘ & + =
= _1_ V /иД2 4-1 £ 4- £ те.3Де,
или, производя суммирование по всем точкам стабилизатора:
7ст = “2 ^CT-Zo 4—у ^тст "Ь /WCTOCTZo6 , (30)
где /ист — момент инерции стабилизатора относительно оси, па-
раллельной его размаху и проходящей через точку С-
5ст — расстояние от его центра тяжести до точки С;
Л1ст — масса стабилизатора.
Кинетическая энергия фюзеляжа
Т* = 1 j m^ZPdx . (31)
О
Кинетическая энергия дополнительных масс.
Координаты произвольной точки /^дополнительной массы (фиг. 104)
xt = 1ф 4- a-t cos 6 4- bt sin 6 ;
z; = Zo 4- sin 6 — bt cos 6
(значения a,, см. на фиг. 104). Кинетическая энергия дополни-
тельных масс будет:
Тд. м =у Vm,- + # ) = у +
4- 4s m‘a^ +4s 4~ s =
— > /14д. mZo 4" у Im д. м Ь 4" /Ид. м3д. , (32)
где /Ид. и — дополнительная масса, Im д м — ее момент инерции отно-
сительно оси, проходящей через конец фюзеляжа С, параллельно
размаху стабилизатора, и зд м — расстояние от центра тяжести
дополнительных масс до точки С, отсчитываемое параллельно
хорде стабилизатора.
291
Суммируя кинетическую энергию по формулам (28), (30), (31)
и (32) и подставляя значения Z, Zo, 6, ₽ через обобщенные ко-
ординаты q, 3 из формул (26) и (27), найдем общую кинетическую
энергию вибрирующей системы:
Т = Тр + Тст + ?ф + ?д. м >
т=4 +4-с^ъ> (33)
где
гФ
G1 = /Ио + /то (^) л=/ф + 2/ИоСо (5)л=/ф +
Cis = С21 = /Ир 5р + (/тр 4- /Ир Эр рш) (44л=г ; (34)
Сг22 = Лир.
Значения всех величин те же, что и в формулах (10).
Потенциальная энергия вибрирующей системы U склады-
вается из работы упругих сил при изгибе фюзеляжа и при
отклонении руля:
'ф
О
// = 4йи?2 + т^2’ (35)
где
(ф
«И = f Е 1ф (-2 ) dX 5 «22 = R- (36>
и
Приступаем к определению обобщенных сил. Они подсчиты-
ваются по обычным формулам (8) гл. I:
где PXi, Рг. —компоненты внешней силы, действующей в точке
системы с координатами л;, zf по осям х и z. Суммирование
распространяется на все точки вибрирующей системы.
В рассматриваемом случае внешними силами являются силы
аэродинамические. Так как этн силы действуют только на руле
и стабилизаторе, то PXi и P2i равны нулю во всех точках си-
стемы, кроме точек руля и стабилизатора, и, следовательно,
в данном случае суммирование в формулах (37) нужно вести
только по точкам руля и стабилизатора.
292
Подставляя выражения (26) и (27) в формулы (7) и (29), на-
ходим выражение декартовых координат точек системы через
обобщенные координаты:
на руле высоты
х^/ф + Рш- cosf^)^- 9] + з,р . cos[₽ + (-g)^.
Zi = q +Рш. sin [(^-)г=,ф• g] + з/р • sin [₽ + (-^Цф- д];
на стабилизаторе
= '* + ’<-“S [(л)»,.'?]'-
z,= « + <,. sin |(^
Пользуясь этими выражениями, вычисляем обобщенные силы
[выражения (37)]. Суммирование ведем отдельно по точкам руля
и по точкам стабилизатора:
Q, = У РЧ + Zf- [- Р„ • sin в + р,: cos 0| • ( 2 +
р р
+ 2а,р Ь p-fsin +6) + рч cos (Р + 0)1 (-й-)х=1 +
р *
+ £ рг/+ S 3i f- P*i • Sin 0 + рг{ • COS 6] =
ст ст
Qp = °ip [— PXl sin (? + 6) + Pz. cos (₽ + 6)],
p
где — суммы, распространяющиеся на точки руля
р
мы, распространяющиеся на точки стабилизатора.
и
S —сум-
СТ
Выражение
на основанин формулы (27) всюду под знаком cos
и sin заменено через 6.
Преобразуем выражения Q9 и Q?; очевидно,
р ст
(39)
где Рг — равнодействующие всех внешних сил, действующих на
горизонтальное оперение (стабилизатор вместе с рулем) в на-
правлении оси z.
Выражение
— Р sin 6 4- Pz cos 6,
293
где Рх, Pz — компоненты внешней силы, действующей в произ-
вольной точке руля (фиг. 106), есть не что иное, как проек-
ция Рщ- внешней силы, действующей в точке Bh на нормаль п'
к линии ОО' (фиг. 106).
Поэтому
2 Рш[- /\sin 9 + Р2. cos 6) (-g) =
р ф
= (40)
где РЛр — равнодействующая внешних сил, действующих на
точки руля в направлении нормали к ОО' (нормали к стабили-
затору).
Фиг. 106.
__ Далее, — PX;sin (Р 4- cos (Р 4- 6) = Р1П- — проекция внеш-
ней силы, действующей в точке 5, руля (фиг. 106) на нормаль п”
к хорде руля. Поэтому
£ р sm (р 4- 6) 4- Рг. cos (р 4- 0)] (-^Ц, =
р ф
= (4.)
р
где Л1ш — шарнирный момент всех сил на руле.
Точно так же (фиг. 106)
^Д-P..sta» +₽,.cose] (2Цф-
= У°Л-(£) ,•
ЛшЛ \ах / .»=1ф \ах j *=/ф
(42)
294
где Pin-проекция внешней силы, действующей в точке At
стабилизатора на нормаль п'" к ОО', и МЕ ст — момент всех
внешних сил на стабилизаторе относительно оси, параллельной
его размаху и проходящей через точку С.
В силу формул (39), (40), (41) и (42) можно записать выра-
жение (38) в виде:
Qq — Р2 + (Рш^д р + /Иш4- М£ст) =
= Рг+м£(-^) (43)
\ ах /х=1ф
Q.3 = Л1ш, I
где М-е — момент внешних сил, действующих на все горизон-
тальное оперение относительно оси, параллельной размаху ста-
билизатора и проходящей через точку С.
Так как стабилизатор с рулем в аэродинамическом отно-
шении эквивалентен крылу с элероном, то для вычисления Pz,
Me и Л1ш можно воспользоваться формулами (39), (40) и (43)
гл. VI, в которых только следует изменить знаки в соответствии
с новым направлением оси1. Под л0 в данном случае следует
понимать расстояние от передней кромки стабилизатора до оси,
параллельной его размаху и проходящей через точку С, так
как к этой оси мы относим прогиб стабилизатора, и следова-
тельно, она играет такую же роль, как ось жесткости при под-
счете аэродинамических сил на крыле. Будем иметь:
Д = -2/^!{-^-[в+-г(4-т)6 + °₽ +
О
+ -^(1—т)[в+т-(т-т)®+°₽+н4?+гМ^;
Л4ш = - 2 + S2 2-6 + S8p + 2-р-25-~- 4,] dy.
h
Всюду поставлен коэфициент 2, так как интегрирование должно
быть распространено и на правую и на левую половины гори-
зонтального оперения.
Подставляя эти значения в формулы (43), находим, пользуясь
формулами (26) и (27):
Qq=-buV*q-bl2V*?-duVq-d^-
Qr = — &21V2? — - d2lVq — cf22V₽,
1 В гл. VI ось z была направлена вверх, теперь же положительное на-
правление оси z мы выбрали вниз.
295
где
(45)
296
Пользуясь выражениями (33), (35) и (45), составляем урав-
нения Лагранжа:
d (дт\ ОТ . dU = о
dr \ дЧ ) dq ' dq '*4’
и аналогично по координате 8. Будем иметь:
сйя + 4~ «п<7 4- + &12Г2р + duq V + rfj V = 0;
c2lq 4* 4"«22Р 4~ ^2iV2q 4~ Ь221/2? ~Ь d2XqV -|- d^sV — 0.
Интегрируя эту систему обычной подстановкой q — Ае1р\ 3 = Ве,р',
приходим к системе линейных однородных уравнений для опре-
деления постоянных А и В. Приравнивая нулю комплексный оп-
ределитель этой системы, получаем уравнение для определения
критической скорости V и частоты р-.
• | «И — «11Р3 + 61У2 + d^ip V, — с12р2 ч- fel2P2 + d12ipV _
--«21Р2 + ^21^2 + «22--C2>P2 4" b2.V2 + d.22ipV ~~
Разбивая это уравнение на действительную и мнимую части
и исключая р из получающейся системы, находим уравнение,
определяющее критическую скорость:
LVi + /ИГ2 4- N = 0,
(46)
где
L = C2D2B2-A2D}-E2B^
М = BYCJX + B£XD2 — 20^/1, — в\е2,
N = BfiJX- D^A.- B\Elt
(47>
и в свою очередь
Ay = «Н«22 «12«2П
^1 = «11^22 4“ «22^11 «21^12 «12^21 ?
Cj = СцЛ22 4" «22«11>
~ CU^22 4" «22^11 —«21^12 — «12^21 4* <41^22 ^12^21»
= ^7ц«22 4* ^22«11>
Z)2 = ^11^22 4" «^22^11 ^21^12 ^12^21»
= а11а22г
^2 = «11^22 4" ^11«22>
Ез — ЬпЬ22 ^21^12'
Таким образом схема определения критической скорости хво-
стового оперения (для двух степеней свободы: изгиб фюзеляжа
и отклонение руля высоты) следующая:
(48}
297
!) определяют методом последовательных приближений функ-
цию формы изгиба фюзеляжа и значение ее производной на
конце фюзеляжа; 2) находят коэфициенты по формулам (34) и
,45); 3) определяют по формулам (46), (47) и (48) критическую
скорость.
Мы изложили метод расчета критической скорости флаттера
хвостового оперения со степенями свободы: изгиб фюзеляжа и
-отклонение руля высоты. Расчетные методы для определения
критической скорости вибраций с иными степенями свободы
строят совершенно аналогично: задаются формой колебаний из
расчета колебаний в пустоте и затем определяют критическую
скорость из принципа возможных перемещений (т. е. состав-
ляют уравнения Лагранжа и находят скорость, при которой эти
уравнения имеют чисто периодическое решение). Мы не будем
останавливаться на изложении всех этих методов, так как это
было бы слишком громоздко и никаких новых приемов изучения
вибраций из рассмотрения этих методов вынести нельзя.
Остановимся теперь на вопросе о влиянии конструктивных
параметров оперения на его критическую скорость. Надо сказать,
что до конца этот вопрос до сих пор не изучен и потому осве-
тить его во всех деталях не представляется возможным.
Прежде всего остановимся на стабилизаторе. Его конструк-
тивные параметры влияют на критическую скорость оперения,
•по крайней мере качественно, так же, как параметры крыла.
Поэтому при конструировании стабилизатора, так же как и при
конструировании крыла, следует обращать внимание особенно
на его жесткость кручения, положение центра тяжести и частот-
ную характеристику (т. е. на рациональное распределение жест-
кости кручения и момента инерции стабилизатора по его раз-
маху). Частотная характеристика для стабилизатора играет осо-
бенно существенную роль.
При изучении влияния конструктивных параметров крыла на
-его критическую скорость мы обращали внимание на недопусти-
мость совпадения частот изгиба и кручения крыла (явление
внутреннего резонанса). Оперение совместно с фюзеляжем может
иметь весьма много различных форм колебания с соответствую-
щими частотами. Опасность совпадения частот различных форм
колебания для оперения гораздо актуальнее, чем для крыла. При
совпадении частот некоторых форм колебания у оперения по-
лучается внутренний резонанс и кинетическая скорость резко
падает (см. фиг. 82). Поэтому определение собственных частот
различных форм колебания оперения и фюзеляжа для каждой
опытной машины надо признать необходимым.
Если наблюдается совпадение частот каких-либо форм, то
весьма желательно изменить конструкцию таким образом, чтобы
избежать этого явления, и, во всяком случае, обязательно про-
извести расчет критической скорости вибраций с этими формами
колебания. В США требование несовпадения частот различных
форм колебания оперения обязательно.
298
Особо остановимся на вопросе о весовой балансировке и
аэродинамической компенсации рулей, так как именно рули
чаще всего вызывают флаттер оперения. Выше (стр. 276—279)
мы вывели формулы статической и динамической балансировки
рулей. Эти формулы выведены без учета влияния поворота ста-
билизатора вследствие изгиба фюзеляжа (угол 0, фиг. 103).
Кроме того, учет аэродинамической компенсации, от которой
зависят вращающие руль моменты аэродинамических сил, также
существенно сказывается на величине критической скорости. На
фиг. 107 показана критическая скорость модели хвостового опе-
рения в зависимости от степени весовой балансировки рулей при
различной аэродинамической компенсации (результаты эти получе-
ны расчетом с последующей экспериментальной проверкой).
299
Из фиг. 107 ясно, что увеличение аэродинамической ком-
пенсации полезно во всех случаях.
V м/сек
30
20-
to
О
0.03
002
QOi
Расстояние оси Орошения от перед кромки
Фиг. 108.
Увеличение весовой ба-
лансировки (увеличение
величины а, фиг. 107) bq
всех случаях повышает
критическую скорость, но
чтобы получить гарантию
от флаттера, необходимо
увеличить весовую балан-
сировку настолько, чтобы
уйти из области, где флат-
тер вообще возможен (на-
пример для положения
оси /— фиг. 107—необхо-
димо а > 0,074). Для рас-
сматриваемой модели во
всех случаях для этого
необходимо перебаланси-
ровать рули, т. е. необхо-
димо, чтобы Яр —расстоя-
ние от центра тяжести
руля до соответствующей
оси вращения — было от-
рицательным. Однако это
не является общим пра-
вилом, существуют опе-
рения, для которых пере-
балансировки не требу-
ется.
Из сказанного можно
сделать только тот вывод,
что одна полная весовая
балансировка не во всех
случаях дает гарантию от
флаттера и потому не
освобождает от необхо-
димости расчета.
На фиг. 108 показана критическая скорость того же опере-
ния (но с несбалансированными рулями) в зависимости от сте-
пени аэродинамической компенсации руля. Оказывается, 100%-ной
аэродинамической компенсации рулей достаточно для предотвра-
щения флаттера, даже без весовой балансировки.
Таким образом для вибраций оперения основными факторами,
влияющими на критическую скорость, являются весовая балан-
сировка и аэродинамическая компенсация рулей. Решение проб-
лемы флаттера в каждом конкретном случае следует искать в
рациональном подборе этих двух факторов
1 Мы не останавливаемся на вопросе о специальных демпфирующих при-
способлениях.
300
ГЛАВА XIV
О ЛЕТНЫХ ИСПЫТАНИЯХ
При испытании новых самолетов часто возникает необходи-
мость проверить безопасность машины в смысле вибраций. Ви-
брации в большинстве случаев возникают внезапно и ведут
к разрушению весьма быстро. Поэтому, если довести в полете
самолет до критической скорости, нельзя гарантировать, что он
не будет разрушен. Метод определения критической скорости
в полете должен позволять определить ее, не доводя самолет
до вибраций.
Фиг. 109.
Мы выше указывали, что задача определения критической
скорости есть задача устойчивости: математически явление опи-
сывается системой диференциальных уравнений, которая имеет
отличные от нуля решения только при строго определенных
значениях скорости и частоты. До достижения критической ско-
рости колебания с нарастающей амплитудой не могут иметь
места.
Аналогичное явление имеет место, например, при разрушении
сжатых стержней. Если сжимающая сила не превосходит кри-
тической величины, все спокойно. Но как только сжимающая
сила превосходит критическую величину, малейший толчок вы-
зывает разрушение стержня. Чтобы избежать этого разрушения
при испытаниях, можно было бы поступить следующим образом:
приложить сжимающую силу с некоторым первоначальным экс-
центриситетом и, таким образом, заведомо создать небольшой
301
первоначальный изгиб (фиг. 109). При возрастании нагрузки
прогиб будет возрастать сначала пропорционально нагрузке, за-
тем все быстрее и, наконец, мы получим весьма быстрое воз-
растание прогиба. При приближении к критической силе прогиб
будет стремиться к бесконеч-
z л ности. Изобразив зависимость
1 /1 прогиба от сжимающей силы,
/I / I получим кривую фиг. 110.
I I \ Так как заранее известно,
/ 'I / I что эта кривая уходит в беско-
J 11 У i \ нечность при приближении сжи-
----' , 4—у | р мающей силы к критической, то
р л>, мы можем не доводить стержень
до разрушения, а закончить
Фиг. 111. испытание в тот момент, когда
кривая начнет увеличиваться
достаточно быстро, чтобы можно было наметить положение вер-
тикальной асимптоты, существование которой заранее известно.
Положение этой асимптоты (фиг. НО) определяет значение кри-
тической силы. Таким образом критическая сила определена,
стержень же не доведен до разрушения.
Тот же принцип Шлиппе кладет в основу метода определения
критической скорости. Вместо прогиба он предлагает замерять
амплитуду колебаний, вызываемых искусственным путем.
На крыло или оперение устанавливается вибратор, который
состоит из эксцентрика, вращающегося от мотора. Изменяя
число оборотов мотора, мы тем самым изменяем частоту воз-
буждающей силы. Когда эта частота становится равной частоте
собственных колебаний, наступает резонанс и амплитуда коле-
302
баний резко возрастает. Максимальная амплитуда при резонансе
наступает при вполне определенной частоте. Эта частота, как.
и величина максимальной амплитуды, зависит от скорости полета.
Если скорость полета считать постоянной и менять частоту
возбуждающей силы (число оборотов вибратора), то получится
диаграмма зависимости амплитуды колебаний от частоты их, изо-
браженная на фиг. 111. На этой диаграмме для простоты принято,
что система колеблется с двумя степенями свободы.
При изменении скорости полета И места резонанса меняют
свое положение, а максимальные амплитуды — свою величину.
Если последовательно — ступенями — менять скорость и на каждой
ступени пробегать всю область частот, то получится семейств
кривых (фиг. 112). При увеличении скорости амплитуда первого»
резонанса, соответствующего частоте изгибных колебаний крыла,
все время уменьшается; амплитуда второго резонанса, соответ-
ствующего крутильным колебаниям, вначале уменьшается, а за-
тем увеличивается, и при V = 1/кр обращается в бесконечность.
Если мы построим максимальную амплитуду при резонансе
в зависимости от скорости (соответствующую второму резо-
нансу), то получим диаграмму, изображенную на фиг. 113 (эта
диаграмма аналогична диаграмме фиг. 110 для продольного из-
гиба стержня).
Следовательно, испытание - в полете производят следующим
образом: скорость полета увеличивают ступенями, причем на
каждой ступени вызывают путем резонанса колебания крыла
и замеряют их максимальную амплитуду. Строят график макси-
мальной амплитуды по скорости. Если на графике начинается
быстрое нарастание амплитуды, то испытание прекращают, так
как критическая скорость близка. Затем ищут положение асим-
птоты (фиг. 113, пунктир), которая определяет значение крити-
ческой скорости.
Метод этот был проверен и экспериментально и дал хорошие
результаты. На фиг. 114 показана кривая максимальных ампли-
303‘
туд, полученная Шлиппе для колебаний оперения одного само-
лета в натуре.
Метод Шлиппе все же не является безопасным. Вызывать
Фиг. 114.
резонансные колебания вблизи критической скорости, да еще
доводить их до максимальной амплитуды (замер которой не-
обходим для построения кривой), конечно, несколько рискованно.
Но, к сожалению, абсолютно безопасного метода испытаний
самолета на флаттер в натуре, не существует.
ПРИЛОЖЕНИЕ
О ЧИСЛЕННОМ ИНТЕГРИРОВАНИИ
Одной из главных работ при расчете крыльев на вибрацию
является вычисление целого ряда определенных и неопределен-
ных интегралов, причем подинтегральные функции обычно бывают
заданы или в виде таблиц или графически. В подобного рода
случаях приходится, как известно, пользоваться различными
приближенными методами численного интегрирования. Наиболее
простым и в то же время достаточно точным для наших расчетов
является способ, известный под названием „способа трапеций".
Он может быть применен для вычисления как определенных
интегралов, так и неопределенных.
Вычисление определенных интегралов
Пусть требуется вычислить определенный интеграл
i
о
Это значит — вычислить площадь, ограниченную кривой (у),
осью абсцисс и ординатами крайних точек (фиг. 115).
„Способ трапеций" состоит в том, что весь интервал интегри-
рования делят на несколько (мы выбираем 10) равных частей;
в точках деления (0; 0,1/; 0,2/; 0,3/;... ;0,9/; /) определяют значения
Гроссман—15—20 305
функции (%, Ф1, ф2,- --Лю) и вычисляют интеграл, как сумму
площадей десяти полос (фиг. 115), которые принимаются за
трапеции, т. е.
ft Ы dy = Ч1' -а + Ч* • w + • • + 4
о
или
I
/*Ф(У)^У = + •-4-'{»э+-у) jp • (1)
о
Итак, для того чтобы вычислить Таблица 1
определенный интеграл, следует просто сложить все ординаты кривой в выбран- ных одиннадцати точках, причем крайние ординаты разделить предварительно на 2 ц полученную сумму умножить на 0,1 интервала интегрирования. Ясно, что это вычисление можно про- делать, и не вычерчивая графика функции Ф(у): достаточно иметь численные зна- чения функции в точках у=0, у = 0,1/, у = 0,21,..., у = 1,ч. е. заданные таблично. Пример. Даны (табл. I) значения не- У// Ф О')
0,0 0.1 0,2 0.3 0.4 0.5 0,6 0.7 0.8 0.9 1 4 12 36 76 132 204 292 - 396 516 G52 804
которой функции в одиннадцати равно отстоящих друг от друга точках по размаху крыла. Размах крыла 1 = 40. Требуется вычислить £ = 2720 значение
интеграла f ф (у) ^У • 0
Подсчитываем значение суммы, стоящей в правой части
формулы (I), складывая все данные в таблице значения функций,
причем первые, т. е. соответствующие^- = 0, и последние = 1)
предварительно делим пополам. Полученную сумму £ — 2720
согласно формуле (1) нужно умножить на
Ю 10 ‘40 4’
Тогда получим:
i
(У) dy = ^--^ 1 = 2720-4=10880.
О
Вычисление неопределенных интегралов
Задача сводится к тому, чтобы по таблице значений функций
(у), заданных в нескольких равцо отстоящих друг от друга точках
(для нескольких значений у), найти значения интеграла этой
функции:
Т(У) = / ^(y)dy,
300
в тех же точках (для тех же значений у), т. е, получить таблицу
значений функции ’Г (у).
Как известно, всякая функция имеет бесчисленное количество
неопределенных интегралов, отличающихся друг от друга на
постоянные величины. Значение постоянной интегрирования
определяется для каждого отдельного случая (каждой конкретной
задачи). Для этого должно быть заранее известно значение
искомого интеграла в какой-нибудь одной точке (для какого-
нибудь одного значения независимой переменной).
В расчетах на вибрации крыла встречаются интегралы, кото-
рые обращаются в нуль либо в начале (_у = 0), либо в конце
(у = I) интервала, в котором бывает задана функция (в корневом
сечении или на конце крыла).
Рассмотрим сперва случай, когда требуется найти интеграл
ч;(_у)=f Ф (y)dУ
и заранее известно, что
Ф(0) = 0.
В этом случае неопределенный интеграл Ч'(у) представляет
собой площадь, ограниченную кривой ф(у), осью абсцисс, орди-
натой ф(0) и переменной ординатной >{/(у) (фиг. 116). В самом
деле,
f ''Ay)dy = ВД - ф‘(0) = ВД,
о
так как Ч'(0) =0 по условию. И, следовательно, значение неопре-
деленного интеграла в точке у равно значению определенного,
взятого в пределах от нуля до у:
'*’(у)=j'i>ty)dy-
о
Как и в случае вычисления определенного интеграла, можно
воспользоваться „способом трапеций". Обозначим, как и прежде,
значение функции ф(у) в точках у = 0; у — 0,1/; У = 0,21',..• ;у — /
соответственно через ф0, фр ф2,..., ф10 (заданы в таблице), а зна-
307
I
чсиия неопределенного интеграла — соответственно через Ч‘(),
’i2,..*Г10 (их требуется найти).
Тогда
'Го=О (задано);
о.п yi=J ’ИУ)<Ъ' = О 0.2/ 'V2=f Ф0')^ = 0 0,3/ Ф3 = у <b(y)dy = и Фо‘+ Ф1 J . 2 10 ’ Фо + Ф1 J. । Ф1 + Фо t «• 1 Ф1 + Фо 1 . 2 10 1 2 10 1 г 2 10 ’ Фо + Ф1 1 1 Ф1 + Фо 1 Фо + фа 1 2 10 1 2 10 1 2 10 "
_ ip- I Ф^ + Фз .
“ - ' 2 10
i
ф _ f — 'f'o + ’i'l 1 । Ф1 + Фо 1 i i Фо + Фю 1 _
2 10 + 2 10 + ••• 4 —10 “
о
_ »y I Фо + Фю I
J8T 2 10*
Удобнее эти формулы представить в несколько ином виде.
Обозначим
(2)
Тогда для вычисления ‘Г (_у) в различных точках интеграла будем
иметь следующие формулы:
'Го = 0 (начальное условие);
Ч'1 =Фо + (Ь1; Ф2=*'1 + Ф1+ф2; =’Г2 + ф2+ф3; (3)
*4 io='4 g 4- фй 4- ф10..
Найдя по этим формулам значения 'Р(у), находим по фор-
муле (2) значения 'F(j):
(4)
и задача решена.
Пример. Даны (табл. I) значения функций 4> (у) в одиннадцати
равно отстоящих друг от друга точках по размаху крыла. Размах
308
крыла / = 40. Найти неопределенный интеграл
f’'Ay)dy
по размаху крыла при условии 4(0) = 0.
По формулам (3) получим: (
То = 0; Ч’5 = 384 + 132 + 204 = 720;
= 4 + 12 = 16; = 720 + 204 + 292 = 1216;
^2 = 16 + 12 + 36 = 64; Г, = 1216 + 292 + 396 = 1904;
iT3 = 64 + 36 + 76 = 176; 4^=1904 + 396 4-516 = 2816;
<F4 = 176 + 76 + 132 = 384; = 2816 + 516 + 652 = 3984;
+I0 = 3984 + 652 + 804 = 5440.
По формуле (4) находим:
W =20*^ = -20 = 2*О0.
Вычисления удобно располагать в виде следующей таблицы
(табл. II) [стрелочками показан порядок суммирования, причем
первое число 4 (у) задано].
Таблица II
УН (у) Ч (v) J 4(У)^ = ФСУ) = 20 4
0 4 0 0
01 12 16 32
0.2 36 > 64 128
0,3 76 > 176 352
0,4 132 384 768
0,5 204 > 720 1440
0,6 0,7 292 1216 2432 3 808
396 1904
0.8 516 2816 5632
0,9 652 —> 3984 7 968
1,0 804 —> 5440 10880
309
В результате получаем искомый интеграл f ty(y)dy, т. е.
функцию *1 (у), заданную таблицей.
Рассмотрим теперь случай, когда требуется найти неопреде-
ленный интеграл
'•‘(J) = J 4(y)dy
при условии
Ф(/) = О
(интеграл обращается в нуль на конце интервала при у = /).
В этом случае неопределенный интеграл *1'(у) представляет
собой площадь, ограниченную кривой ty(y), осью абсцисс, орди-
натой 'р(/) и переменной ординатой Л(У).
Ясно, что, применяя „способ трапеций", площади полос сле-
дует вычислять, начиная не с начала [как в случае, когда было
задано условие Ч (0) =0], а с конца интервала, в котором задана
функция ф(у/). При этом значения интеграла получаются с обрат-
ным знаком, так как
f b(y)dy =У(1)-Ч(у)=-'Цу)
У
в силу того, что Ч (/) — 0 по условию. Следовательно, неопре-
деленный интеграл выражается через определенный следующим
образом:
^(y) = -f'^(y)dy.
у
В этом случае формулы (3), очевидно, должны быть заменены
следующими:
Ч?‘1О = 0 (задано);
Ч9 ~ Ч’ 10 4- фю + ?9 »
=Ч + ф9 + %;
ч\ =^ + 9., + ^;
4*0 = Ч’ 1 + <!>! +;%.
Соотношение (4) остается, конечно, тем же:
Пример. По данным табл. I при условии
‘F(Z) = 0
вычислить неопределенный интеграл
Ч‘(у) ^j'\(y)dy.
310
Все вычисления сведены в табл. Ill, где стрелочками указан
порядок суммирования.
Таблица III
1 —
<Ю0 4>(у) ‘Ку) = -20
— 10880
0 4| ' —5440
01 — 10848
12 ' —5424
0.2 > — 5376 — 10 752
Ло|
0.3 — 10528
— 52Ь4
0,4 > — 5056 — 10 112
132 ।
0,5 — 9 440
0,6 — 8448
2У2 । г —
0.7 — 7072
г —
0,8 516 । - > — 2624 — 5 248
0,0 652 > — 1456 — 2 912
1,0 ОЛ. I 0
Описанный метод численного интегрирования является
конечно, приближенным. Но так как в расчете на вибрации
точность определения исходных расчетных данных (жесткостей,
моментов инерции, погонного веса и т. д.) весьма невелика, то
бессмысленно гнаться за большой точностью вычислений Для
расчетов на вибрации точность, даваемая „способом трапеций",
вполне достаточна.