Robert I. Soare
Recursively Enumerable
Sets and Degrees
A Study of Computable Functions
and Computably Generated Sets
Springer-Verlag
Berlin Heidelberg New York
London Paris Tokyo

Роберт И. Соар
Вычислимо перечислимые
множества и степени
Изучение вычислимых функций
и вычислимо перечислимых множеств
Перевод с английского
под редакцией
М. М. Арсланова
Казань
«Казанское математическое общество»
2000

УДК 519.5
ББК 22.14
Соар Р. И.
Вычислимо перечислимые множества и степени: Пер. с англ. —
Казань: Казанское математическое общество, 2000. — 576 с., ил.
ISBN 5-900975-22-3
Книга профессора Чикагского университета Р. И. Соара, являющаяся
наиболее популярной книгой по теории вычислимости. В ней систематически
излагается современное состояние теории вычислимости, приводятся открытые
проблемы и описываются перспективные направления исследований.
Материал дополнен большим количеством упражнений.
Книга рассчитана на читателей, интересующихся современными
проблемами математической логики и теории вычислимости.
Издание осуществлено при финансовой поддержке Российского фонда
фундаментальных исследований согласно проекту № 98-01-14012
ISBN 5-900975-22-3 (рус.)
ISBN 3-540-15299-7 (англ.)
ISBN 0-387-15299-7 (англ.)
© М. М. Арсланов, 2000
© Springer-Verlag
Berlin Heidelberg, 1987
Заказ П-15. Формат бОхЭО1/^- Тир. 700 шт. Объем 35,75 п. л.
Тип. ЧАТШИТЛГ тел. 92-23-31, 92-23-92
Лицензия № 0252 от 23.03.99 г.

Моим родителям Маргарет и Ирвингу,
и моим «вторым родителям» Верил и Лауренсу
Только если его собственная
чаша когда-то с любовью была
наполнена, он сможет передать
любовь другому

Содержание
Предисловие редактора перевода 12
Предисловие автора к русскому изданию 14
Введение 17
Часть А. Фундаментальные понятия теории
вычислимости 23
Глава I. Вычислимые функции 25
§ 1. Неформальное описание 26
§ 2. Формальные определения вычислимых функций 27
2.1. Примитивно рекурсивные функции 27
2.2. Диагонализация и частично вычислимые функции 28
2.3. Вычислимые по Тьюрингу функции 30
§ 3. Основные результаты 34
§ 4. Вычислимо перечислимые множества и неразрешимые проблемы 39
§ 5. Вычислимые перестановки и теорема Майхилла об изоморфизме 46
Глава II. Основания вычислимо перечислимых множеств и
теорема рекурсии 51
§ 1. Эквивалентные определения вычислимо перечислимых множеств
и их основные свойства 51
§ 2. Равномерность и индексы вычислимых и конечных множеств . . 58
§ 3. Теорема рекурсии 62
§ 4. Полные, продуктивные и креативные множества 68
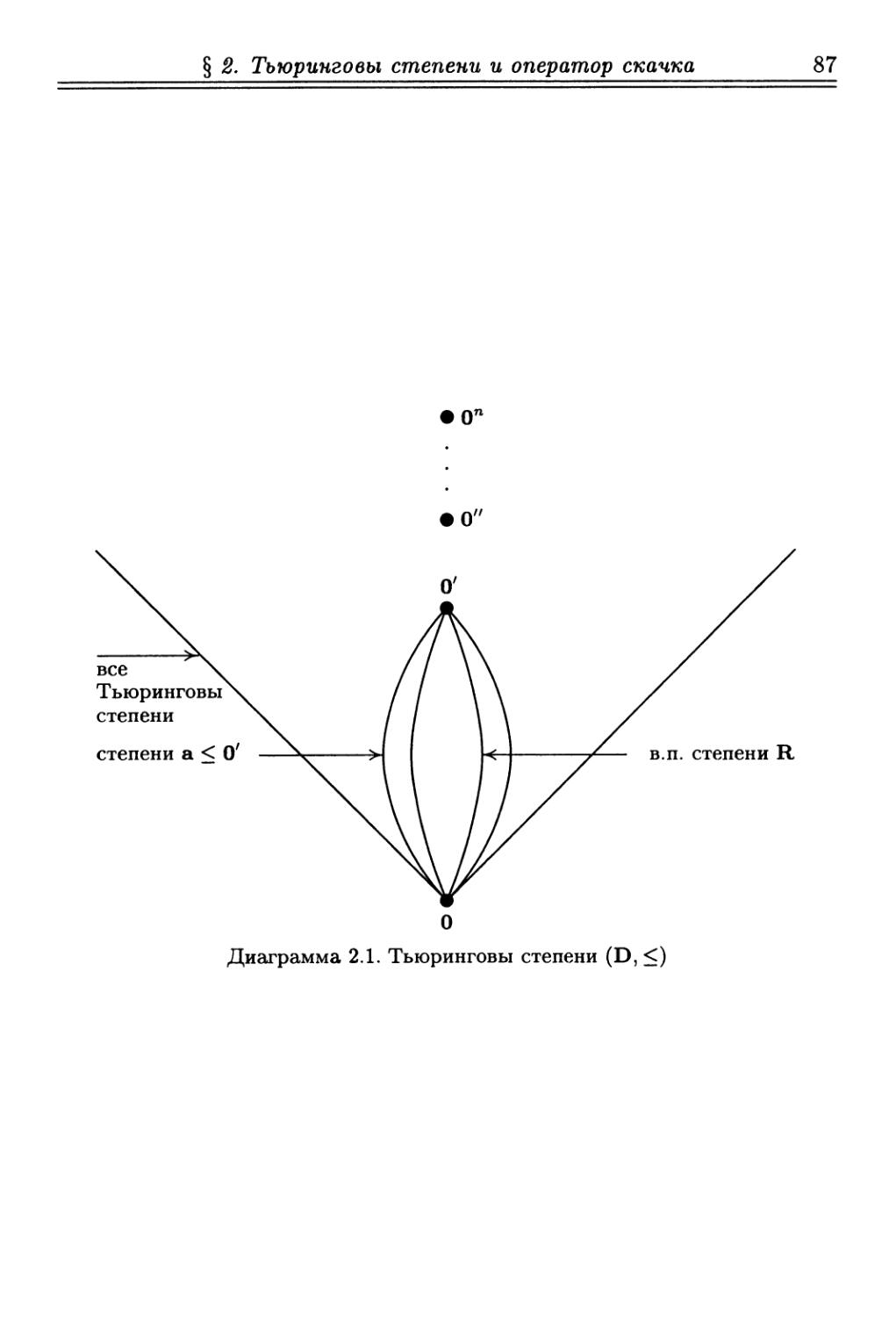
Глава III. Тьюринговая сводимость и оператор скачка 76
§ 1. Определения относительной вычислимости 76
§ 2. Тьюринговы степени и оператор скачка . . 84
§ 3. Леммы о модуле и о пределе 89

8
Содержание
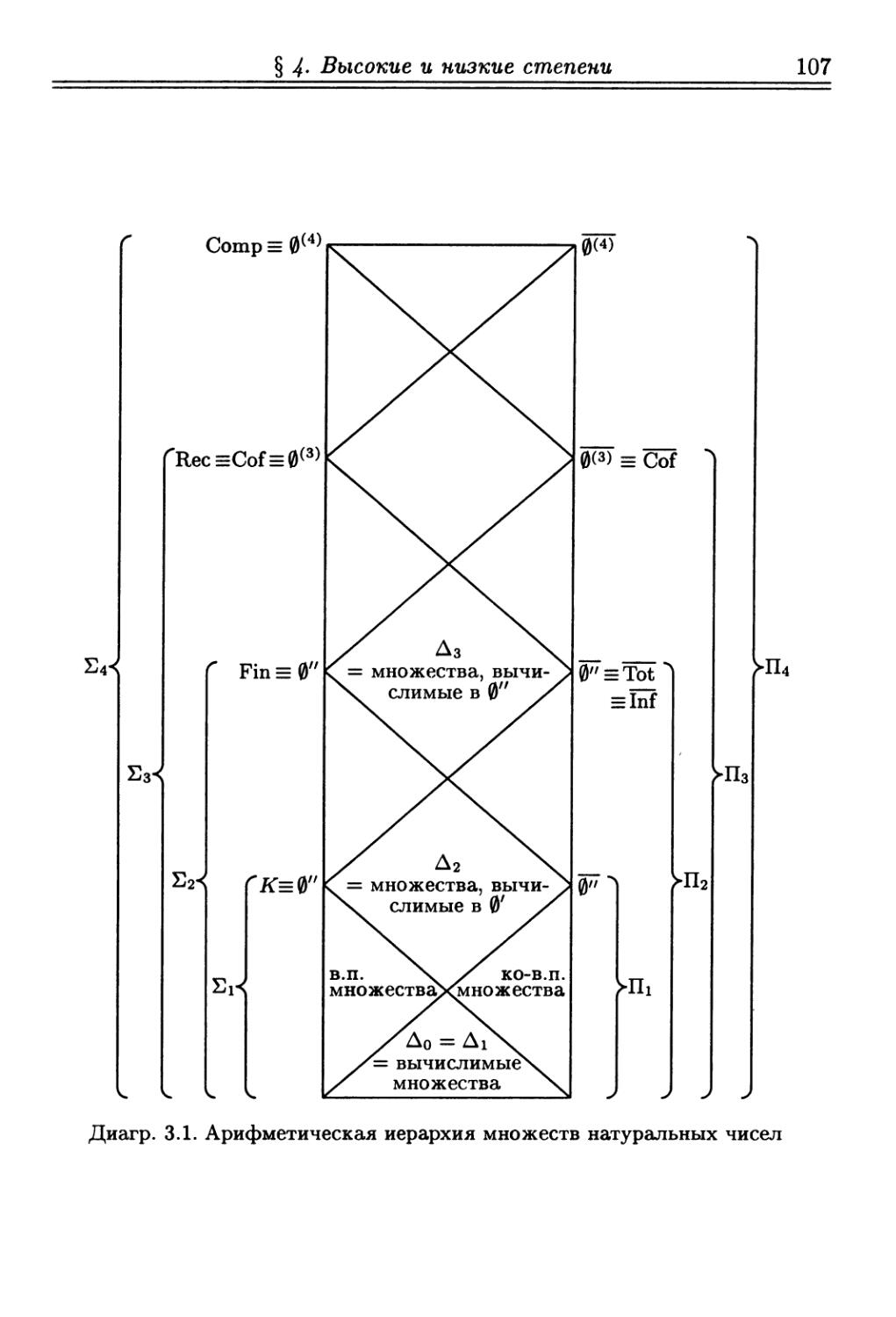
Глава IV. Арифметическая иерархия 94
§ 1. Уровни вычислимости в арифметической иерархии 94
§ 2. Теорема Поста и теорема об иерархии 98
§ 3. Еп-полные множества 101
§ 4. Релятивизованная арифметическая иерархия. Высокие и низкие
степени 106
Часть В. Проблема Поста, оракульные конструкции и
метод приоритета с конечными нарушениями 111
Глава V. Простые множества и проблема Поста 113
§ 1. Иммунные и простые множества. Конструкция Поста 114
§ 2. Гиперпростые множества и мажорирующие функции 117
§ 3. Метод разрешения 123
§ 4. Полнота эффективно простых множеств 126
§ 5. Критерий полноты для в. п. множеств 127
Глава VI. Оракульные конструкции не в. п. степеней 133
§ 1. Пара несравнимых степеней ниже О' 134
§ 2. Избегание конусов степеней 138
§ 3. Обращение скачка 139
§ 4. Верхние и нижние грани степеней 143
§ 5. * Минимальные степени 147
Глава VII. Метод приоритета с конечными нарушениями 156
§ 1. Низкие простые множества 157
§ 2. Исходная теорема Мучника-Фридберга 166
§ 3. Теоремы о разложении 170
Часть С. Бесконечные методы построения в. п. множеств
и степеней 179
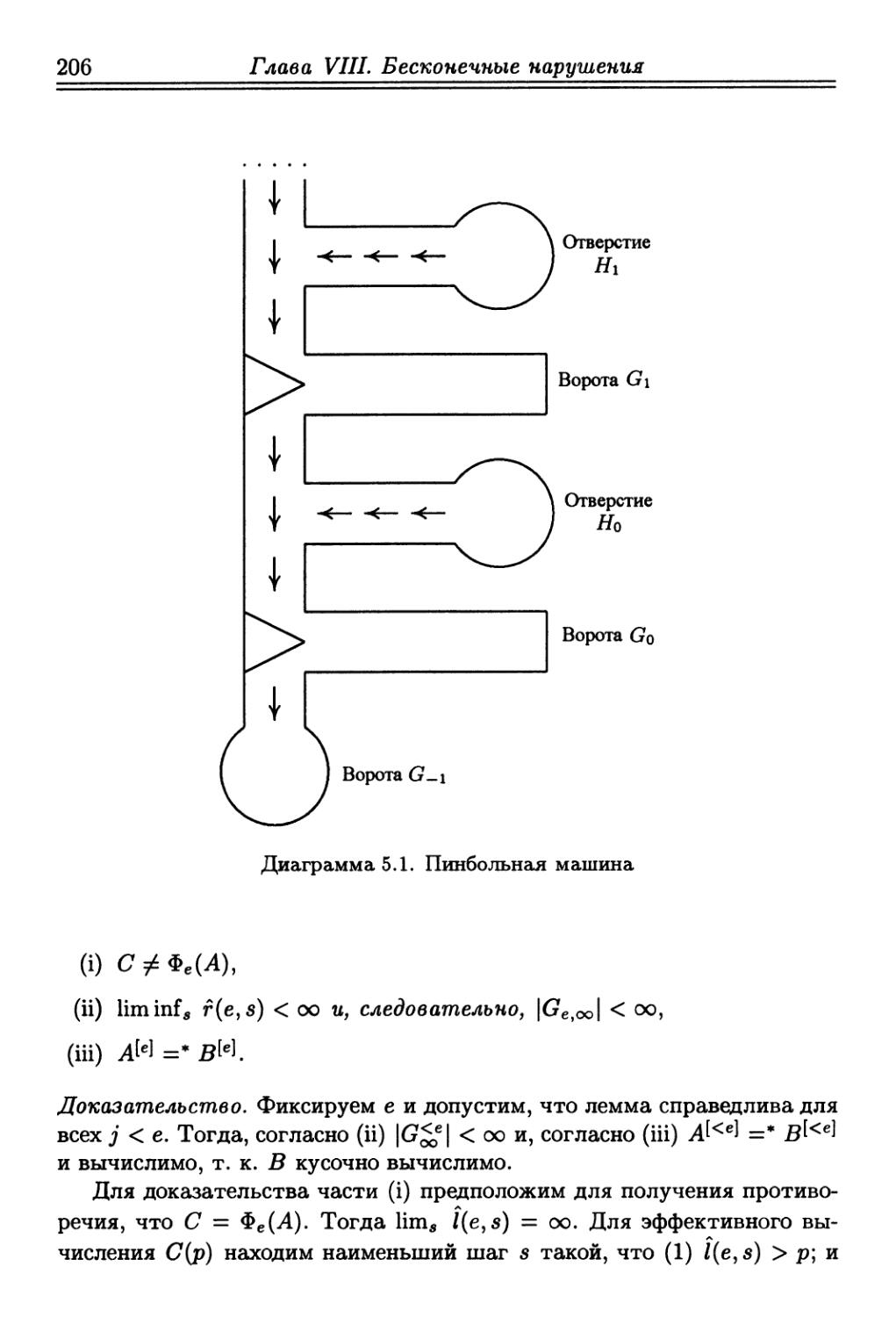
Глава VIII. Метод приоритета с бесконечными нарушениями 181
§ 1. Препятствия в методе приоритета с бесконечными нарушениями
и лемма о густоте 182
§ 2. Леммы о нарушениях, об окнах и о сильной густоте 187
§ 3. Теорема о скачке 192
§ 4. Теорема плотности и стратегия кодирования Сакса 198
§ 5. * Модель пинбольной машины для метода бесконечных нарушений204
Глава IX. Метод минимальных пар и вложение решеток в в. п.
степени 208
§ 1. Минимальные пары и вложение ромба 209
§ 2. * Вложение дистрибутивных решеток 216
§ 3. Теорема о невложимости ромба 222

Содержание
9
§ 4. * Неветвящиеся степени 231
§ 5. * Недополняемые вниз степени 238
Глава X. Решётка в. п. множеств относительно включения 243
§ 1. Идеалы, фильтры и факторрешетки 243
§ 2. Теоремы о разложении и булевы алгебры 247
§ 3. Максимальные множества 255
§ 4. Мажорные подмножества и г-максимальные множества 260
§ 5. Безатомные r-максимальные множества 266
§ 6. Безатомные гг-простые множества 271
§ 7. * Ез-булевы алгебры, представимые в виде решеток надмножеств 275
Глава XI. Связи между структурой в. п. множества и его
степенью 281
§ 1. Характеризация Мартина высоких степеней в терминах функций-
доминант 282
§ 2. Максимальные множества и высокие в. п. степени 293
§ 3. Низкие в. п. множества похожи на вычислимые множества .... 304
§ 4. Не 2-низкие в. п. степени содержат безатомные в. п. множества 312
§ 5. * 2-Низкие в. п. степени не содержат безатомных в. п. множеств 317
Глава XII. Классификация индексных множеств в. п. множеств 326
§ 1. Классификация индексного множества G(A) = { х : Wx =т А } . 327
§ 2. Классификация индексных множеств <7(^ А), <7(^ А) и G(\ А) 332
§ 3. Равномерное перечисление в. п. множеств и Ез индексные
множества 341
§ 4. Классификация индексных множеств п-высоких, п-низких и
промежуточных в. п. множеств 348
§ 5. Неподвижные точки по тьюринговой эквивалентности 361
§ 6. Обобщение теоремы рекурсии и критерия полноты на все уровни
арифметической иерархии 364
Часть D. Дальнейшие разделы и современные области
исследования в. п. степеней и решетки в. п. множеств 371
Глава XIII. Быстро простые множества. Совпадение классов в. п.
степеней, и алгебраическое разложение в. п. степеней 373
§ 1. Быстро простые множества и степени 374
§ 2. Совпадение классов быстро простых степеней, недополняемых
вниз степеней, и эффективно недополняемых вниз степеней .... 382
§ 3. Разложение в. п. степеней на непересекающееся объединение
определимого идеала и определимого фильтра 391
§ 4. Дополняемые наверх степени и совпадение быстро простых и
низко дополняемых наверх степеней 393

10
Содержание
Глава XIV. Метод деревьев и О'"-приоритетные рассуждения 398
§ 1. О'-приоритетные рассуждения 399
§ 2. Метод деревьев в приоритетных рассуждениях и классификация
0', 0" и 0'" -приоритетных методов 403
§ 3. Метод деревьев в О"-приоритетных рассуждениях 409
3.1. Деревья в обычном 0" -приоритетном рассуждении 409
3.2. 0"-приоритетное рассуждение, требующее метод деревьев. . . . 410
§ 4. Метод деревьев с О'7'-приоритетными рассуждениями: теорема
Лахлана о неограничении 418
4.1. Предварительные сведения 418
4.2. Основной модуль для удовлетворения подтребования
(конструирование компьютерного чипа) 419
4.3. Приоритетное дерево (вычислительная архитектура машины) 424
4.4. Интуитивные описания приоритетного дерева и доказательство 430
4.5. Построение (операционная система машины) 431
4.6. Верификация 436
Глава XV. Автоморфизмы решетки в. п. множеств 446
§ 1. Инвариантные свойства 446
§ 2. Некоторые основные свойства автоморфизмов S 450
§ 3. Неинвариантные свойства 455
§ 4. Формулировка теоремы о расширении и его мотивация 458
§ 5. Удовлетворение условий теоремы о расширении для
максимальных множеств 467
§ 6. Доказательство теоремы о расширении 4.5 473
6.1. Машины 473
6.2. Построение 477
6.3. Требования и мотивация правил 478
6.4. Правила 481
6.5. Проверка 484
Глава XVI. Дальнейшие результаты и открытые вопросы о в. п.
множествах и степенях 491
§ 1. Автоморфизмы и изоморфизмы решётки в. п. множеств 491
§ 2. Элементарная теория S 498
§ 3. Элементарная теория в. п. степеней 503
§ 4. Алгебраическая структура R 506
Литература 510
Список обозначений 549
Предметный указатель 562

Содержание
11
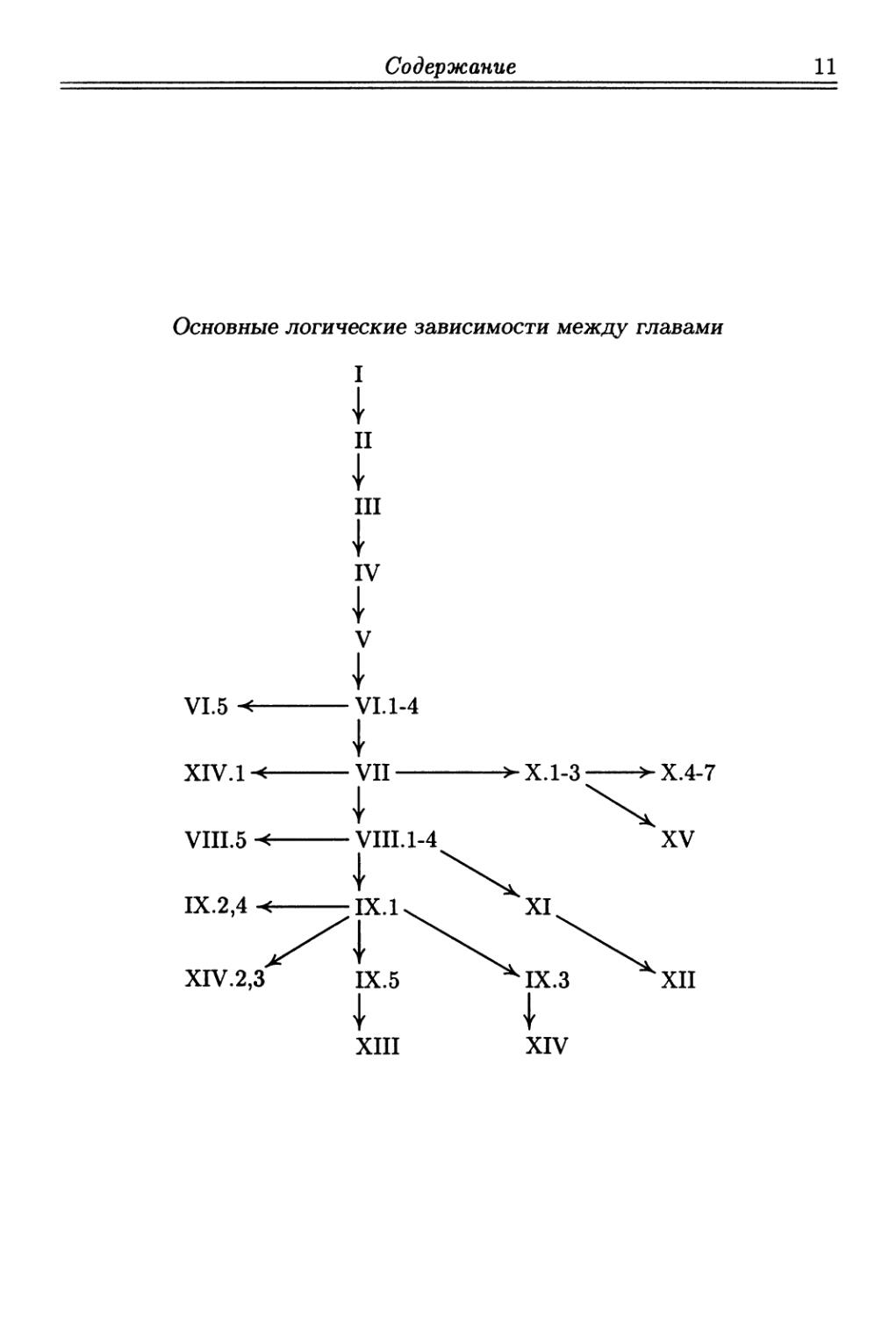
Основные логические зависимости между главами
I
I
II
III
I
IV
V
I
VI.5 -< VI. 1-4
I
XIV. 1 -< VII >
I
VIII.5 VIII. 1-4
Х.1-3 *
XIV
Х.4-7
XV
XII

Предисловие редактора перевода
Предлагаемая вниманию читателей книга написана известным
американским ученым, профессором Чикагского университета Робертом И.
Соаром. На сегодняшний день книга Соара является лучшей книгой в
мировой литературе для первоначального ознакомления с теорией
вычислимости и уже более десяти лет используется в университетах как
учебное пособие для студентов старших курсов и аспирантов. Она
может рассматриваться и как монография, содержащая все наиболее
значительные результаты теории, полученные ко времени издания книги на
языке оригинала в 1987 году, и способная вплотную подвести читателя
к передней линии современных исследований в этой области.
Профессор Соар известен российскому читателю своими
основополагающими работами в области теории вычислимости. В главе XV книги
излагаются его известные работы по построению автоморфизмов
решетки £ вычислимо перечислимых множеств, в частности, описывается его
знаменитый метод расширения. Большинство известных результатов об
автоморфизмах £ получаются с помощью этого метода. В последние
годы совместно с Харрингтоным, Лахланом, Чолаком Соар получил целый
ряд глубоких результатов, некоторые из них отвечают на поставленные
в главе XVI вопросы.
Профессор Соар является также одним из самых страстных
пропагандистов теории вычислимости. В последнем десятилетии по его
инициативе ведется большая работа по уточнению терминологии теории.
В частности, названия «рекурсивная функция» и «рекурсивно
перечислимое множество» меняются на «вычислимая функция» и «вычислимо
перечислимое множество», которые, по убеждению автора книги,
наиболее полно отражают суть теории как с исторической, так и с научной и
практической точек зрения (подробнее об этом см. предисловие автора к
русскому изданию). По пожеланию автора в русском издании книги мы
приводим новую терминологию.
Мы благодарны Р. Соару за постоянное внимание к работе над пере¬

Предисловие редактора перевода
13
водом и всестороннюю поддержку. Мы весьма признательны Стеффену
Лемппу, по инициативе которого был осуществлен перевод. Его
энергичное вмешательство в разных стадиях работы позволило довести эту
работу до завершения. М. Г. Перетятькин помог нам при
изготовлении диаграмм, кроме того, он, И. А. Лавров и А. С. Морозов сделали
многочисленные замечания по улучшению качества перевода. П. Чолак,
С. Лемпп, А. Ниис, К. Джокуш, Р. Доуни, Т. Сламан, Р. Шор и Б.
Купер помогли нам с определением современного статуса перечисленных
в книге открытых проблем. Всем им редактор перевода выражает свою
признательность.
Над переводом книги работали А. А. Голубев и Д. Ю. Харитонов
(введение, глава I), А. А. Ефремов (главы Х-ХН, XIV), И. Ш. Калимул-
лин (главы III, XIII, VI), Е. В. Липачева (главы II, IV, V), А. С. Морозов
(главы XV-XVI) и В. Д. Соловьев (главы VII-IX). Оригинал-макет
издания составили А. А. Голубев, И. Ш. Калимуллин и Д. Ю. Харитонов.
Финансовую поддержку при приобретении авторского права на
перевод книги оказала Ассоциация символической логики. Российский фонд
фундаментальных исследований оказал финансовую поддержку издания
перевода, Академия наук Татарстана поддержала работу над переводом.
В список литературы добавлены издания, на которые есть ссылки в
примечаниях редактора перевода (главным образом они касаются
современного состояния перечисленных в книге открытых проблем). Все они
отмечены звездочкой. Кроме того там, где это было возможно, мы
привели библиографическое описание источников, в оригинале помеченных
знаком [ta].
Переводчики и редактор перевода поправили большое количество
опечаток и неточностей, вкравшихся в оригинал. Исправления
совершенно очевидных опечаток в тексте не отмечены.
М. Арсланов

Предисловие автора к русскому изданию
Мне доставляет большое удовольствие увидеть мою книгу от 1987 года
по теории вычислимости на русском языке. Россия всегда была одним
из мировых центров исследований по теории вычислимости и ее
приложениям. Эти исследования берут начало от ранних работ Маркова и
Мальцева по теории алгоритмов и ее связям с алгеброй, ознаменовались
решением проблемы Поста Мучником. Эти исследования сегодня
продолжаются на очень высоком уровне во многих научных центрах России и
других стран бывшего Советского Союза, таких, как Новосибирск,
Казань, Алма-Ата и другие. Я надеюсь, что появление этой книги будет
способствовать их продолжению новыми поколениями российских
студентов.
За истекшие со времени выхода книги четырнадцать лет эта область
науки получила значительное развитие. Многие новые студенты
защитили диссертации по теории вычислимости и заняли преподавательские
и исследовательские позиции. С успехом проводятся конференции,
журналы завалены многочисленными хорошими работами, ждущими
публикации. Произошел ряд значительных продвижений вперед в различных
областях и самой теории вычислимости. Кроме того, недавно были
найдены приложения теории вычислимости в топологии и геометрии рима-
новых поверхностей по модулю диффеоморфизмов.
Оригинал книги только что разошелся в количестве 4000
экземпляров, и теперь стоит вопрос о втором ее издании. Во втором издании
книга будет значительно переработана, будет изменено и ее название.
Новое название книги отражает широко распространенную в последнем
десятилетии тенденцию к уточнению терминологии, как это описано у
Соара [1996]. В 1935 году Чёрч и Клини, отходя от своей ранней
вычислительной модели A-исчисления, ввели названия «рекурсивная
функция» и «рекурсивно перечислимое множество», что через несколько лет
привело к появлению нового предмета, по аналогии названного «Теория
рекурсивных функций» (Recursive Function Theory), а также к термину

Предисловие автора к русскому изданию
15
«рекурсивный» (recursive), который начали использовать в смысле
«разрешимый» (decidable) или «вычислимый» (computable). При появлении
модели вычисления Тьюринга особого стимула к изменению названия не
было, да и название «компьютер» (computer) в 1936 году означало нечто
другое, чем то, что мы под этим сейчас подразумеваем.
Тьюринг и Гёдель, изобретатели двух формализаций понятия
вычислимости посредством «машин Тьюринга» и «рекурсивных функций»,
слово «вычислимый» использовали только в этом контексте и
никогда не использовали слово «рекурсивный» в смысле «вычислимый» или
«разрешимый». Поэтому по причинам историческим, научным и
практическим в 1995 году нам показалось целесообразным вернуться к
исходной терминологии «вычислимый», как это понимали Гёдель и Тьюринг
в 1936 году, и, как это становится общепринятым сегодня, использовать
понятие «рекурсивный» только для определений по рекурсии. Изменение
названия предмета из «Теории рекурсии» в «Теорию вычислимости» и
соответствующее изменение названия новой книги, а также русского
издания этой книги, отражают эту тенденцию.
Трудно описать все достижения теории вычислимости с 1987 года, но
я укажу обзорные статьи для одной ее области. В главе XV книги
описан метод порождения автоморфизмов вычислимо перечислимых (в. п.)
множеств и доказано, что все максимальные множества автоморфны. С
1987 года был осуществлен большой прогресс в изучении автоморфизмов
и определимых свойств, и большая часть проделанной работы описана
в обзорных статьях Соара [1999] и [2000].
Теперь мы имеем World Wide Web (www) -страницы, которых в 1987
году еще не было. Статьи и уточненная информация будут направляться
на мои www-страницы, которые приводятся ниже, и я приглашаю
читателей их использовать для ознакомления с более свежей информацией.
Я хочу поблагодарить всех, кто способствовал осуществлению
русского издания моей книги. Прежде всего, это — Комитет по переводам
Ассоциации символической логики, взявший на себя инициативу
издания книги на русском языке, а также Ассоциация символической логики,
уплатившая издательству Шпрингер-Верлаг за передачу авторских прав
российскому издателю. Я очень благодарен многим россиянам, которые
под руководством Марата Арсланова организовали и осуществили
перевод книги. Я также благодарю Российский фонд фундаментальных
исследований за финансовую поддержку издания книги, Академию наук
Татарстана за финансовую поддержку перевода книги. Я особо
благодарен Марату Арсланову и Стеффену Лемппу за их энергию, энтузиазм
и решительность, которые помогли довести этот проект к успешному

К)
Предисловие автора к русскому изданию
завершению.
[ta] R. I. Soare, Computability Theory and Computable Enumerable
Sets, Springer-Verlag, Heidelberg, to appear.
[1996] R. I. Soare, Computability and recursion, Bulletin of Symbolic
Logic, 2 (1996), 284-321.
[1999] R. I. Soare, An overview of the computably enumerable sets, In:
Handbook of Computability Theory, ed. E. Griffor, North-Holland,
Amsterdam, 1999, 199-248.
[2000] R. I. Soare, Extensions, Automorphisms, and Definability, in:
P. Cholak, S. Lempp, M. Lerman, and R. Shore, (eds.)
Computability Theory and its Applications: Current Trends and
Open Problems, American Mathematical Society, (Proceedings of
Workshop in Boulder, Colorado, June, 1999).
Математический Факультет
Чикагский Университет
Чикаго, Йллиноис, 60637-1546
E-mail: soare@math.uchicago. edu,
или soare@cs.uchicago.edu
Анонимный ftp: cs.uchicago.edu: ftp/pub/users/soare
World Wide Web:
http://www. cs. uchicago. edu/~ soare
Роберт И. Coap
Чикаго, Йллиноис
13 Января, 2000

Введение
Эта книга прежде всего является введением в теорию вычислимых
функций и вычислимо перечислимых множеств. Некоторые параграфы в
частях А, В и С могут использоваться для семестрового или годового курса
лекций. Точный выбор материала зависит от интересов лектора и
продолжительности курса. Хотя большая часть книги и не предполагает
знакомства с логикой, читателю будет полезно её знание. Тот минимум
математических знаний, который нужен для чтения этой книги, обычно
студенты получают на курсе современной алгебры, читаемом студентам
на младших курсах. Более продвинутые разделы и упражнения частей С
и D содержат изложение некоторых наиболее серьезных новых
результатов и методов, относящихся к в. п. множествам. Они предназначены для
того, чтобы вплотную подвести читателя к современным исследованиям
в этой области.
Первые три части книги отражают три основных исторических
периода, которые определяются по времени получения основных результатов
и разработки техники доказательства. Конечно, это достаточно
условная классификация, так как не все результаты, отнесенные на тот или
другой период, именно тогда и были получены. Однако, вообще говоря
они могли быть получены в то время, так как методы, позволяющие это
сделать, тогда уже были известными.
Часть А соответствует периоду в 1931-1943 гг., и начинается со
времени использования примитивно рекурсивных функций в доказательстве
теоремы Гёделя о неполноте в 1931 году. Она содержит различные
определения вычислимых функций и в. п. множеств, их фундаментальные
свойства, теорему Клини о рекурсии и её приложения, относительную
вычислимость и степени неразрешимости, а также арифметическую
иерархию.
Часть В покрывает период в 1944-1960 гг., который начинается с
послания Поста от 1944 года Американскому Математическому Обществу
о в. п. множествах и проблем распознавания их элементов. Она содер¬

18
Введение
жит формулировку проблемы Поста и предпринятых Постом попыток
решения этой проблемы с помощью простых множеств. Далее, часть В
содержит «оракульные конструкции» Клини и Поста [1954] не в. п.
множеств, в которых сложное условие вида «Л не вычислимо
относительно J5» разбивается на бесконечную совокупность { Rn : п Е и } более
простых условий, называемых «требованиями», например, условий
вида А ф {п}в, каждое из которых удовлетворяется раз и навсегда на
некотором шаге конструкции. Проблема Поста была решена с помощью
метода приоритета с конечными нарушениями, разработанным Фрид-
бергом [1957] и, независимо, Мучником [1956а]. Этот метод комбинирует
тип требований Клини-Поста с эффективными построениями Поста,
позволяя, таким образом, построить в. п. множества (а не только
множества, вычислимые относительно некоторого оракула). Ключевое
нововведение метода состоит в том, что любому действию, совершенному на
некотором шаге для удовлетворения некоторого требования i?m, позднее
разрешается «портиться» под действием некоторого другого требования
i?n,n < m, более высокого приоритета, так что требование Rm
приходится удовлетворять снова на более позднем шаге.
Часть С покрывает период, который начинается с 1961 года и
продолжается до настоящего времени 1. В ней основное внимание уделяется
построениям, которые имеют дело с требованиями бесконечного действия.
Например, это могут быть «положительные требования», которые
заставляют бесконечно много элементов перечислиться в конструируемое
в. 	п. множество А, или это могут быть «отрицательные требования»,
которые сдерживают бесконечно много элементов от их перечисления в
А. Эта часть содержит хорошо известный метод приоритета с
бесконечными нарушениями и метод минимальной пары, направленные на
изучение свойств в. п. степеней R. Здесь же излагаются конструкция Фрид-
берга максимального множества и её дальнейшее развитие Лахланом и
другими для изучения решетки £ в. п. множеств по включению. После
рассмотрения каждой из совокупностей R и £ по отдельности, особое
внимание уделяется изложению определенных элегантных результатов,
относящихся к имеющимся связям между алгебраической структурой
множества А Е £ и его степенью в R (точнее, степенью информации,
носителем которой оно является).
Определения и обозначения. Разделы или теоремы, помеченные
знаком *, не предусмотрены для первого чтения, они содержат либо
более трудный, либо вспомогательный материал. Упражнения распадают¬
*Ко времени издания книги в США в 1987 году. — Прим. редактора.

Введение
19
ся на три группы. Те, которые не помечены никакими знаками,
решаются непосредственно (по крайней мере после чтения соответствующего
указания). Более трудные упражнения помечены знаком о, а очень
трудные — знаком оо.
Мы имеем дело с множествами и функциями, заданными на
множестве неотрицательных целых чисел ш = { 0,1,2,... }, иногда для
удобства в него добавляется число —1. Малые латинские буквы а, Ь, с, d, е, г, j,
k,...,y,z обозначают числа; для обозначения всюду определенных
функций из шп в ш при п ^ 1 используются буквы /,£, h (а иногда и другие
малые латинские буквы); как правило, заглавные и малые греческие
буквы Ф, Ф, 0, (р, ф, в обозначают частичные функции над ш (т. е.
функции, областью определения которых являются подмножества ш);
наконец, заглавные латинские буквы А, В, С,..., X, У, Z используются для
обозначения подмножеств ш. Композиция двух функций / и g
обозначается через fog или просто как fg; запись fn{x) означает результат
n-кратной подстановки функции f(x) в себя; запись ip(x)l означает, что
ip(x) определено, а запись (р(х) I = у означает, что, кроме того,
значением (р(х) является число у; (р(х) f означает, что tp(x) не определено;
<р = ф означает равенство частичных функций (р и ф (часто в других
книгах и статьях это записывается как (р ~ ф), а именно, для
любого х, (р(х) I тогда и только тогда, когда ф(х) и если tp(x) тогда
(р(х) = ф(х); через dom tp и ran tp соответственно обозначаются область
определения и область значений функции (р; характеристическая
функция множества А обозначается через ха, часто мы её отождествляем
с самим множеством А, записывая просто как А(х)\ для обозначения
ограничения функции / к значениям аргументов у < х пишем / [ х, а
запись А \ х означает ха [ я; мы говорим, что / мажорирует g, если
g(x) ^ f(x) для всех х, и / доминирует g, если g(x) ^ f(x) для всех, за
исключением конечного числа, х. Мы говорим, что функция / является
«1:1-функцией», если она является взаимно-однозначной (инъективной),
и что она является «1:1 и на», если / является биективной.
Кроме обычных теоретико-множественных обозначений, мы будем
использовать запись А С* В для обозначения того, что А С В за
исключением быть может конечного числа элементов (т. е. А — В конечно);
пишем Ас В, если А С J5, но А ф В; дополнение множества А
обозначается через А; запись А — В означает А П В; Мы пишем А =* J5, если
А С* В и В С А. Мощность множества А обозначается либо через \А\,
либо через card (А); наибольший элемент конечного множества А
обозначается через тах(А), если А не 0, в противном случае тах(А) = 0;
запись А Соо В означает, что А С В и \В — А\ = оо. В пункте П.2.9

20
Введение
мы также определяем Wx \ Wy и Wx \ Wy. (Первую запись не
надо путать с теоретико-множественной разностью Wx — Wy.)
Выражение (х, у) обозначает упорядоченную пару, состоящую из х и у в таком
порядке; х означает n-ку (xi,x2,... ,хп); образ (х,у) под стандартной
функцией пары |(х2 + 2ху + у2 -I- Зх -I- у) из ш х ш на ш обозначается
через (х,у); запись (х1,х2,хз) означает ((х1,х2),хз), и аналогично для
(xi,x2,... ,хп), как это определено в 1.3.6; через [n,m] обозначается
замкнутый интервал {xin^x^m}, а [п,оо) = {х : п ^ х}. Иногда
последовательность {fn}neи мы записываем как {/n}, a limn6a; /п(х)
как limn /п(х). Запись о/*7 используется для обозначения множества всех
функций из ш в о;; 2й* множество всех подмножеств о;; для
обозначения множества всех конечных последовательностей над ш используется
запись а 2<и} означает все конечные последовательности,
состоящие из 0 и 1. В главах III, VI и XIV для обозначения конечных строк
(т. е., строк из u)<ui или из 2<и) используются р, а, т, г/, а функция
длины lh(a) = рх[х £ dom а] = card(dom а). Через \а\ обозначается lh(a)\
0 (иногда А) означает пустую строку либо из 2<и;, либо из
конкатенация строк а и т (в этом порядке) обозначается через <r"Y; запись
а С т {а С AJ) означает, что а является начальным сегментом т
(соответственно A,f). Если а С т, но а ф г, то пишем а С т. В
главе X через а обозначается «е-штат» (который можно отождествлять
со строкой из 2<и). Новые предикаты образовываем, используя
обычные логические знаки &, V, =$►, 3, V, /хх, которые соответственно
означают «и», «или», «не», «влечет», «существует», «для каждого» и
«наименьший х». Кроме того, запись 3°°х означает «существует
бесконечно много х таких, что», двойственный квантор «для почти всех х»,
т. е. (Зхо) (Vx ^ хо), обозначается через (а. е. х). При определении
частичных функций используются обычные A-обозначения Чёрча. А
именно, пусть [.. .х ...] является выражением, в котором при любом
значении х выражение имеет самое большее одно значение. Тогда Ах[... х...]
означает соответствующую частичную функцию. A-обозначения также
будут использоваться для записи частичных функций от многих
переменных, в этом случае вместо Ах пишем Axix2 .. . х& для некоторого к.
Часто вместо х < w, у < w и z < w сокращенно пишем x,y,z < w.
В частично-упорядоченном множестве запись х | у означает, что х и у
несравнимы, то есть х ^ у и у ^ х.
Каждая глава разделена на параграфы, определения и теоремы
пронумерованы внутри каждого параграфа сквозной нумерацией. Так,
например, теорема Ш.2.2 отсылает на теорему 2.2 главы III, а запись § III.2

Введение
21
означает параграф 2 главы III. Некоторые строки текста имеют номера,
зависящие от соответствующего параграфа. Например, запись II (3.1)
означает строку с номером (3.1) в § 3 главы II. Если ссылка
производится на теорему или строку в той же главе, то номер главы
опускается. Таким образом, ссылка на теорему 2.2 главы III внутри главы III
производится как на теорему 2.2, а во всех других случаях — как на
теорему III.2.2. Часто мы это записываем в сокращенном виде — 2.2
и III.2.2, соответственно. Аналогично, на строку (3.1) главы III внутри
главы III ссылаемся как на строку (3.1), а в остальных случаях — как
на строку III (3.1).

Часть А
Фундаментальные
понятия теории
вычислимости

Глава I
Вычислимые функции
Часть А содержит основные определения и методы, разработанные в
начальный период развития теории вычислимых функций с 1931 по 1943
гг. Сюда же включены также результаты, которые хотя и были
получены намного позднее, но по духу и методам соответствуют именно
этому периоду. Знаменитая теорема Гёделя о неполноте [1931] привлекла
внимание к классу примитивно рекурсивных функций, которые Гёдель
в 1934 году расширил до класса общерекурсивных функций.
Эквивалентные определения были даны в середине 1930-х годов Клини,
Тьюрингом и другими. В соответствии с Тезисом Чёрча эти определения
теперь принимаются за описание класса алгоритмически вычислимых
функций. В главе I мы рассмотрим определения Клини и Тьюринга, а в
дальнейшем будем опираться на машины Тьюринга, отсылая читателя
для формального доказательства эквивалентности этих определений к
соответствующей литературе. Мы коротко изложим доказательства
теоремы о перечислении и s-m-n теоремы, которые для нас существенны,
а также рассмотрим проблему классификации неразрешимых проблем,
в частности, тех проблем, которые возникают в связи с вычислимо
перечислимыми (в. п.) множествами.
После краткого неформального описания частичных вычислимых
функций мы приведём два их формальных определения, а в § 3
сформулируем первоначальные основные результаты, такие как теорему о
нумерации и s-m-n теорему, существенные для большей части
дальнейшей работы. Мы даем только краткие наброски доказательств этих
результатов, отсылая читателя к соответствующей литературе для более
детального изучения. Далее рассматриваются вычислимо перечислимые
множества, устанавливается существование неразрешимых проблем, а
позднее последние классифицируются в терминах «степеней»,
используя s-m-n теорему.

26
Глава I. Вычислимые функции
Мы хотим подчеркнуть, что содержащиеся в книге результаты не
зависят от выбора конкретного формального определения вычислимых
функций, т. к. можно показать, что все хорошо известные определения
этих функций порождают в точности один и тот же класс функций.
После выбора конкретного формального определения эти результаты не
зависят (согласно упражнению 5.9) от конкретного эффективного
кодирования функций из этого определения.
§ 1. Неформальное описание
Неформально, алгоритм (для функции / на и) это конечное множество
инструкций, которые по заданному входу х через конечное число шагов
позволяют получить выход у = f(x). Алгоритм должен точно указать,
как получить в процессе вычисления каждый следующий шаг, зная все
предыдущие шаги и входное значение. В общем случае алгоритм может
вычислять частичные функции. Например, пусть ф(х) = ру\р{х,у) = 0],
где р(х, у) — какой-нибудь полином с целочисленными коэффициентами,
а рхР(х) означает «наименьший х такой, что Р(ж)». Тогда ф может
быть определена для некоторых, но не для всех значений х.
Алгоритмическая частичная функция, определенная для всех значений аргумента
(т. е. тотальная функция), называется общерекурсивной или
вычислимой функцией.
Для определенности приведем две точные математические
формулировки класса вычислимых функций: рекурсивные функции и функции,
вычислимые по Тьюрингу. Эти и некоторые другие формальные
определения порождают один и тот же класс функций, который, как теперь
общепринято считать, в точности описывает неформальный класс
алгоритмически вычислимых функций. Поэтому для нас не имеет значения,
какое из этих определений выбрано. Мы выберем формулировку
Тьюринга. Читатель, знакомый с какой-нибудь моделью вычисления, может
просто воспринимать (рп как частичную функцию, вычисляемую п-м
алгоритмом (программой) Рп при некотором эффективном
перечислении всех алгоритмов, и перейти к § 3 для ознакомления с простейшими
основными результатами.

§ 2. Формальные определения вычислимых функций
27
§ 2. Формальные определения вычислимых функций
2.1. 	Примитивно рекурсивные функции
Название «рекурсивно» отражает определение по рекурсии, когда
новая функция / определяется заданием каждого нового значения f(x + 1)
в терминах предыдущих значений /(0),/(1),...,/(ж), а также ранее
определенных функций. Например, соотношения /(0) = 1 и f(x + 1) =
(х -I- 1 )f(x) определяют х\ в терминах умножения. Примитивно
рекурсивные функции образуют очень большой класс алгоритмически
вычислимых функций, включая почти все функции, определенные на о; и часто
встречающиеся в математике.
2.1 	Определение. Класс примитивно рекурсивных функций —
наименьший класс С функций, замкнутый относительно следующих схем.
(I) 	Функция следования Хх[х -I-1] принадлежит С.
(И) Константные функции Хх\,... ,хп[т] принадлежат С, 0 ^ n,m.
(III) Тождественные функции (также называемые проекциями)
Xxi,..., хп[х{\ принадлежат С, 1 ^ n, 1 ^ i ^ п.
(IV) (Композиция). Если gi,g2, • • h G С, то
/(^1) • • • > Хп) = h(gi {xi, . . . , Xn)i • • • j gm{% 1 j • • • j Xn))
принадлежит С. Здесь gi,.. .,gm — функции от n переменных, a h —
функция от m переменных.
(V) (Примитивная рекурсия). Если g, h G С и п ^ 1, то / Е С, где
/(0? ®2» • • • » Я'п) = д{%2) • • • j %п))
f(x\ + 1, #2} • • • ) %п) = h(x\ , /(Х\ , Х2ч • • • , #п)> ^2) • • • j Sn).
Здесь функции (/и/ютп-1 ип + 1 переменных соответственно. (Если
п = 1, то 0-арная функция д является константной функцией и по схеме
(II) принадлежит С.)
Таким образом, функция примитивно рекурсивна, если для нее
существует вывод, а именно такая последовательность /i, /г? • • •, fk — />
что каждая /*, г ^ к, является либо одной из начальных функций (т. е.
функцией, полученной по одной из схем (I), (И) или (III)), либо /*
получается из { fj : j < г} применением схемы (IV) или (V). Например,
функция f(x\,X2) = Х\ -I- Х2 имеет такой вывод:
/i = Хх[х -I- 1] по (I)

28
Глава I. Вычислимые функции
h = Аж[х]
/з = \xix2x3[x2]
/4 = /1 о /3
/б(0, х2) = /2(2:2)
/5(2:1 + 1,х2) = /4(2:1, /5(2:1, х2), х2)
по (III)
по (III)
по (IV)
по (V)
Аналогично можно показать (Клини [1952а, глава IX, с. 217-232]),
что все обычные функции, определенные на а;, примитивно рекурсивны,
включая х • у, ху, ж! и
Предикат (отношение) примитивно рекурсивен, если примитивно
рекурсивна его характеристическая функция. Например, можно показать,
что отношение R = { х : х — простое число } примитивно рекурсивно.
Пусть рсьРь • • • — простые числа в порядке возрастания. Каждое число
х Е и имеет единственное представление в виде
где только конечное число Xi ф 0. Можно показать, что функция
является примитивно рекурсивной функцией от х. Таким образом, для
любой конечной последовательности положительных чисел { ao,ai,...,
ап } существует единственное «кодовое» число а = Pq0+1 ... p£n+1 такое,
что каждое а* = (а)* может быть получено примитивно рекурсивно из а.
Важность этого наблюдения станет понятнее в § 3.
2.2. 	Диагонализация и частично вычислимые функции
Класс примитивно рекурсивных функций не содержит все
алгоритмически вычислимые функции, хотя и включает в себя все обычные
функции из элементарной теории чисел. Любой вывод примитивно
рекурсивной функции является конечной последовательностью символов
некоторого фиксированного конечного алфавита, таким образом, все
выводы могут быть эффективно перечислены. Пусть /п означает функцию,
соответствующую n-му выводу в этом перечислении. Тогда функция
g(x) = fx(х) + 1 не может быть примитивно рекурсивной, т. к. д ф fx
х — у, если х ^ у,
0, если х < у.
(2.1)
(а:),- = экспоненте х* при pi в (2.1)
(2.2)

§ 2. Формальные определения вычислимых функций
29
для всех ж, но она очевидным образом алгоритмически вычислима:
чтобы вычислить д(п) мы «вызываем» n-ю примитивно рекурсивную
«программу», предъявляем ей входное значение п и прибавляем к выходному
значению число 1.
Это рассуждение (известное как диагонализация) можно применить
к любому эффективному множеству схем, порождающему всюду
определённые функции (т. к. в этом случае х-я функция на аргументе х
всегда выдает некоторое выходное значение). Таким образом, для
описания всех алгоритмически вычислимых функций мы вынуждены
использовать и частичные функции, т. е. функции, которые могут быть
определены не на всех значениях аргумента. Теперь диагонализация уже
не является препятствием. Например, пусть фп — частичная функция,
порожденная n-м алгоритмом при некотором эффективном
перечислении всех алгоритмов, и пусть ip(x) = фх(х) -h 1, если фх(х) определена,
и (р(х) не определена в противном случае. Теперь если (р соответствует
хо~у алгоритму списка, диагонализация не приводит к противоречию,
т. к. ^xoixo) может быть неопределенной.
Существуют и другие хорошие доводы в пользу рассмотрения
частичных функций. Мы хотим охватить все алгоритмические функции,
а некоторые алгоритмы работают только на собственных
подмножествах си. На самом деле существуют вычислимые частичные функции,
которые нельзя доопределить до вычислимой всюду определенной функции
(см. упражнение 4.21), следовательно, вычислимые частичные функции
не являются ограничениями всюду определенных вычислимых функций
на свои области определения. Наконец, мы хотим иметь теорему о
нумерации для вычислимых функций (теорема 3.4), а это возможно только
для вычислимых частичных функций.
2.2 	Определение (Клини). Класс частично вычислимых (ч. в.)
функций — наименьший класс функций, замкнутый относительно схем (I)-
(V) для класса примитивно рекурсивных функций, а также следующей
схемы (VI). Функция называется общерекурсивной (мы говорим
вычислимая функция), если она является всюду определенной частично
вычислимой.
(VI) 	(Неограниченный поиск). Если в(х\,... ,хп,у) является
частично вычислимой функцией от n + 1-переменной, и
ф(х1,...,хп) =
цу[в(х1,...,хп,у)1 = 0 & (Vz ^ у) [9{xi,...,x„,z)i)), (2.3)
то ф является частично вычислимой функцией от п переменных.

30
Глава I. Вычислимые функции
(В соотношении (2.3) существенно второе условие, т. к. иначе ч. в.
функции не замкнуты относительно /i-оператора, см. упражнение 4.24.)
Каждая ч. в. функция, получаемая по схеме (VI), очевидным образом
вычислима и в интуитивном смысле: для того, чтобы вычислить ф(х)
мы просто подряд пытаемся вычислить все 9(х, 0),9(х, 1),..., пока не
найдется (если вообще найдется) первый у такой, что в(х, у) =0. Тогда
на выход подается ф{х) = у. Таким образом, каждая ч. в. функция
интуитивно вычислима. В § 3 мы приведем аргументы и в пользу обратного
утверждения. Типичным примером применения \х оператора является
доказательство частичной вычислимости функции ф(х) = ру\р(х,у) =
0], где р(х,у) — полином с целочисленными коэффициентами,
следовательно, значение р(а, Ь) может быть вычислено примитивно рекурсивно
для всех а и Ь. Именно возможность неограниченного поиска в схеме (VI)
отличает вычислимые функции от примитивно рекурсивных, т. к.
можно показать, что функция, имеющая вид
{(ру < д(х)) [h(x,y) = 0], если такой у существует,
0 в противном случае,
является примитивно рекурсивной, если примитивно рекурсивны
функции д и h (см. упражнение 2.8).
Определение 2.2 применимо, в частности, к в, когда в является
всюду определённой вычислимой функцией. Мы, однако, не хотим
ограничить определение 2.2 условием всюду определенности функции 9, т. к.
по предложению 4.4 и теореме 4.10 мы не можем по номеру частично
вычислимой функции в эффективно определить, является функция в всюду
определенной или нет.
2.3 	Определение. Отношение R С п ^ 1, является вычис¬
лимым (примитивно рекурсивным, обладает свойством Р), если его
характеристическая функция XR вычислима, (соответственно
примитивно рекурсивна, обладает свойством Р), где xr(xь • • • >хп) = 1, если
(х\,... ,хп) Е R, и = 0 в противном случае. В этом определении
множество А С ш соответствует случаю n = 1, поэтому мы здесь имеем и
определение вычислимого множества.
2,3. 	Вычислимые по Тьюрингу функции
Вторая характеристика частичных вычислимых функций принадлежит
Тьюрингу. Машина Тьюринга М содержит бесконечную двустороннюю

§ 2. Формальные определения вычислимых функций
31
подвижная читающая головка
текущее состояние
бесконечная в две стороны лента
конечная
Тьюрингова
программа
В
1
1
1
1
в
в
в
Диаграмма 2.1. Машина Тьюринга
ленту, разделенную на клетки, читающую головку, которая обозревает
в каждый момент времени одну из клеток ленты, и конечное
множество внутренних состояний Q = {go,gi, • • • ,Яп }, и ^ 1. Каждая клетка
либо пустая (В), либо содержит символ 1. За один шаг работы машина
может совершить одновременно следующие действия: (1) перейти с
одного состояния в другое; (2) изменить обозреваемый символ s на другой
символ s' G S = {1,В}; (3) передвинуть читающую головку на одну
клетку вправо (R) или влево (L). Работа М определяется частичным
отображением S : Q х S —> Q х S х {R, L }; оно может на некоторых
аргументах быть неопределенным. Если (g, s, q' ,s',Х) G <5, то это означает,
что машина М, находясь в состоянии q и обозревая символ s,
переходит в состояние д', меняет s на s' и переводит читающую головку на
одну клетку вправо, если X = R (влево, если X = L). Это отображение
S, рассматриваемое как конечное множество таких пятерок, называется
тьюринговой программой. Входное число х представляется строкой из
хН- 1-й единицы, расположенных последовательно (все остальные клетки
пустые). Машину Тьюринга можно изобразить так:
В начале работы машины Тьюринга М читающая головка находится
около левой крайней клетки, содержащей 1, в начальном состоянии gi.
Если в процессе работы машина перейдет к заключительному
состоянию до, то мы говорим, что М останавливается и подает на выход
число у — общее количество содержащихся на ленте единиц. (Без
ограничения общности можно предположить, что М после достижения
заключительного состояния д0 не производит никаких действий; другими
словами, область определения S не содержит элементов вида (go, s).) Мы
говорим, что М вычисляет частичную функцию ф, если ф(х) = у тогда

32
Глава I. Вычислимые функции
и только тогда, когда М, начав работать со входным числом х, рано или
поздно остановится и подаст на выход число у. Например, следующая
машина вычисляет функцию /(х) = х + 3.
На любом шаге вычисления по тьюринговой программе дальнейшая
работа машины М полностью определяется: (1) текущим значением qi
внутреннего состояния машины; (2) символом so обозреваемой
читающей головкой клетки; (3) символами $i, s2, • • •, sn, расположенными на
ленте правее символа $о> ДО последней единицы включительно; (4)
символами s_m,..., s_2, s-i, расположенными на ленте левее символа so,
до первой единицы включительно. Последовательность
называется конфигурацией машины Тьюринга на этом шаге. Например,
машина (2.4) в процессе вычисления со входным числом х = 0
проходит через конфигурации gil, lq\B, llq2B, lllqoB и подает на выход
число у = 3. (Напомним, что входное число х кодируется х + 1-й
единицей, расположенными последовательно, в то время как выходное
число у определяется как общее количество находящихся на ленте единиц.
Заметим также, что в начале работы машины Тьюринга лента
содержит только конечное число непустых клеток, и это условие сохраняется
на каждом шаге вычисления, независимо от того, остановится машина
когда-нибудь или нет. Таким образом, числа п и т в (2.5) определены.)
Тьюринговым вычислением согласно тьюринговой программе Р со
входным числом х называется последовательность со, с\,..., сп
конфигураций машины Тьюринга, где со — конфигурация, соответствующая
начальному состоянию q\, когда читающая головка находится возле
левой крайней единицы, сп — конфигурация, соответствующая
заключительному состоянию qo, и для всех i < п переход с* —> c*+i задается
программой Р. Таким образом, в дальнейшем под вычислением мы
всегда будем понимать останавливающееся вычисление, т. е. вычисление,
которое завершается переходом в заключительное состояние. С каждой
машиной Тьюринга М мы также ассоциируем частичную функцию от
п переменных, записывая значения аргументов (xi,X2,... ,хп) в виде
начальной конфигурации qia\Ba2 .. Вап, где щ состоит из х» + 1
последовательных единиц.
Qi 1 Qi 1 R
qi В q2 1 R.
#2 В qo 1 R
(2.4)
S — m • • • 2 S_i qi Sq S\ S2 • . • Sn
(2.5)

§ 2. Формальные определения вычислимых функций
33
2.4-2.11 Упражнения
2.4. Пользуясь определением 2.1 напишите примитивно рекурсивные
выводы для следующих функций: f(x,y) = х • у, g(x,y) = ху, h(x) =
х\ (Например, неформальными примитивно рекурсивными равенствами
для / являются: х • 0 = 0, х • (у + 1) = х • у + х.)
2.5. Опираясь на примитивную рекурсивность функции х — у
покажите, что функция sg(x) также примитивно рекурсивна, где sg{x) = 1,
если х = 0, и sg(x) = 0 в противном случае.
2.6. (Определение разбором случаев) Покажите, что если <71 (ж),...,
9п(х) — примитивно рекурсивные функции, a R\{x),..., Rn(x) —
примитивно рекурсивные взаимно исключающие и исчерпывающие
отношения, тогда следующая функция / примитивно рекурсивна: f(x) = gi(x),
если Ri(x), f(x) = <72(я), если R2(x), • • •, и }{х) — дп(х), если Rn(x)
2.7. Докажите, что если / примитивно рекурсивна, то конечные сумма
Yjy<z f(x'V) и произведение /(х> 2/) также примитивно рекурсив¬
ны.
2.8. Докажите, что если R примитивно рекурсивное отношение, то
следующие отношения от z также примитивно рекурсивны: (V?/ < z)R(y),
(Зу < z)R{y) \ что следующая функция / примитивно рекурсивна: f(z) =
(ру < z)R(y), если у существует, и f(z) —zb противном случае.
2.9. Напишите машины Тьюринга, вычисляющие функции Ах[0], Ах[к],
2х, х + г/, х -у.
2.10. (а) Используйте (2.1) для присвоения кодового номера каждой
тьюринговой программе. Сперва присвойте номер каждой пятерке
программы, например, (<7ь $j, si, гт) получает номер
plo+ip\+jpl+kpl+lp\+m,
где го = R и 7*1 = L. Аналогично используйте (2.1) для присвоения
номеров всем возможным конечным последовательностям пятерок,
следовательно, всем тьюринговым программам. Пусть Ре является тьюринговой
программой с кодовым номером е.

34
Глава I. Вычислимые функции
(b) 	Хотя это отображение 1:1 и эффективно, оно не является
отображением на и. Предложите такое кодирование тьюринговых программ,
которое являлось бы также и отображением «на».
2.11. (а) Покажите, что мы можем, используя (2.1), каждой возмож¬
ной конфигурации с в (2.5) эффективно присвоить кодовый номер #(с).
(Например, пусть #(с) = 21+г31+^^°^5г7/, где г = Ylj>iPf^Sj\ I —
и #(s) = если 8 = В, и = 1 в противном случае.) Эти
кодовые номера называются также гёделевскими номерами.
(Ь) 	Определите кодовый номер тьюрингового вычисления со, с\,...,
сп, соответствующее Ре, равным у = 2е • Yli<nPf+i'^ - Покажите, что
предикат Т(е,х,у), который утверждает, что «у является кодовым
номером вычисления по тьюринговой программе Ре со входным
значением ж», вычислим в интуитивном смысле. (На самом деле он примитивно
рекурсивен; см. Клини [1952а].)
§ 3. Основные результаты
В этом параграфе мы установим основные результаты о приведенных
определениях, которые будут необходимы для нашей работы. Мы
опускаем подробные доказательства, которые можно найти в книгах
Клини [1952а] и Хермеса [1969]. Известно, что определения Клини и
Тьюринга из § 2 (так же, как и многочисленные другие определения)
описывают в точности один и тот же класс частичных функций. Тезис Чёрча
утверждает, что этот класс совпадает с классом интуитивно
вычислимых функций. Мы принимаем Тезис Чёрча и в дальнейшем термины
«частично вычислимая (ч. в.)», «вычислимая по Тьюрингу»,
«вычислимая» используем как синонимы.
Так как каждую программу машины Тьюринга можно записать в
виде конечного набора пятерок, мы можем пронумеровать все программы
машин Тьюринга так, что для любой программы можно эффективно
находить ее номер в этой нумерации и наоборот. Зафиксируем такую
эффективную нумерацию, например, как в упражнении 2.10. (Из
упражнения 5.9 следует, что не имеет значения, какая из них выбрана.)
3.1 	Определение. Пусть Ре — машина Тьюринга с гёделевым
номером е (иногда говорят индекс е) в этой нумерации, и пусть означает
частичную функцию от п переменных, вычисляемую на Ре, где (ре —
(1)
сокращенная запись для ipye .

§ 3. Основные результаты
35
3.2 	Лемма о множестве индексов. Каждая частично вычислимая
функция (рх имеет No номеров машин Тьюринга, кроме того, для
каждого х можно эффективно найти бесконечное множество Ах номеров
для этой частичной функции (т. е. ipy = ipx для всех у Е Ах).
Доказательство. К программе Рх, имеющей внутренние состояния
{<70, • • •, Яп }, добавляем новые команды qn+iB qn+iB R, gn+2B qn+2B R,
... для того, чтобы получить новые программы для вычисления той же
функции. О
3.3 	Теорема о нормальной форме. (Клини) Существуют такие
вычислимые (даже примитивно рекурсивные) предикат Т{е,х,у)
(называемые Т-предикатом Клини) и функция U(y), что
(ре(х) = U(цу Т(е,х,у)).
Доказательство (набросок). Предикат Т(е,х,у) утверждает, что
«число у является номером некоторого тьюрингового вычисления (в смысле
упражнения 2.11), соответствующего программе Ре со входным
значением ж». Для проверки истинности предиката Т(е,х,у) сначала по е
находим программу Р€ (см. упражнение 2.10), а затем по у находим тью-
ринговое вычисление со, с\,..., сп (см. упражнение 2.11), если у является
номером такого вычисления. Затем проверяем, верно ли, что со, с\,..., сп
является вычислением, проводимым по программе Ре со входом х в со-
Если да, то U(у) просто вычисляет количество единиц в
заключительной конфигурации сп. Примитивную рекурсивность Т и U можно
доказать, изучая нумерацию из упражнений 2.10 и 2.11 (см. Клини [1952а]).
(Это — не исходные определения Т и U, которые первоначально
были сформулированы на языке выводов в исчислении равенств (см.
Клини [1952а, с. 281]). Но эти определения проще и используются аналогии-
НО.) О
Из теоремы о нормальной форме следует, что каждая вычислимая по
Тьюрингу частичная функция частично вычислима. Для
доказательства обратного утверждения строится машина Тьюринга в соответствии
со схемами (I)-(VI) (см. Клини [1952а]). То, что эти два определения
описывают один и тот же класс функций, непосредственно следует из
Тезиса Чёрча. Такой же анализ, какой был проведен в доказательстве
теоремы 3.3, можно использовать и для неформального «подтверждения»
Тезиса Чёрча (см. Шёнфилд [1967, с. 120], где произвольные алгоритмы
и конфигурации шагов в их вычислениях заменяют программы машин

36
Глава I. Вычислимые функции
Тьюринга и их конфигурации. Заметим, что из теоремы 3.3 следует, что
каждая частично вычислимая функция может быть получена из двух
примитивно рекурсивных функций одним применением /х-оператора.
В дальнейшем мы будем описывать алгоритмы для вычислимых
функций в обычных математических терминах, предоставляя
читателю самому убедиться, что они могут быть преобразованы в одно из
вышеизложенных формальных определений. Такие доказательства будут
называться «доказательствами с помощью Тезиса Чёрча».
3.4 	Теорема о нумерации. Существует такая ч. в. функция от
двух переменных <^2^(е,я), что (р¥\е,х) = (ре{х). Это
утверждение справедливо и для ч. в. функций от п переменных (см.
упражнение 3.13).
Доказательство. По теореме 3.3 мы можем определить (р^(е,х) =
U(fiyT(e,x,y)). Другое неформальное доказательство следующее.
Программа Pz по данному входу (е,я) эффективно восстанавливает
программу Ре и применяет её к входу х до тех пор, пока (если вообще
когда-нибудь) некоторый выход не будет получен. Q
3.5 	Теорема параметризации (s-m-n теорема). Для любых т,
п ^ 1 существует такая 1:1-вычислимая функция s™ от m + 1
переменных, что для всех я, у\, г/2> • • •, Ут
Ч>
(п)
ят
Azi,..., zn\v(™+n\yu. ..,ym,zu..., zn)].
Доказательство (неформальное). Для простоты рассмотрим случай
т = п = 1. Программа Psj(X)2/) на входе z сначала находит
программу а затем применяет Рх к входу {y,z). Так как мы задали
эффективную процедуру вычисления Psi(x,y) по данным х и ?/, то по Тезису
Чёрча функция s — s\ является вычислимой. Если s не является 1:1-
функцией, то с помощью леммы 3.2 о множестве индексов она
следующим образом может быть заменена вычислимой 1:1-функцией s' такой,
что ips(x,y) = определяем s'(x,y) в порядке возрастания (я,г/),
где (я, у) является значением функции пары из обозначения 3.6 на
аргументе (я, у). D
Как утверждает s-m-n теорема, у можно рассматривать как
фиксированный параметр в программе Ps(Xty)> работающей с z, более
того, номер s(x,у) этой программы может быть найден эффективно по я

§ 3. Основные результаты
37
и у. Простым применением s-m-n теоремы является существование
такой вычислимой функции /(ж), что <Pf(x) = 2<^х. Действительно, пусть
ф{х,у) = 2<рх(у). Тогда, по Тезису Чёрча, ф{х,у) = <р¥\х,у) для
некоторого е. Положим /(х) = s}(e,x). Другие приложения этой теоремы мы
получим в § 4. (Грубо говоря, теоремы о нумерации и параметризации
являются взаимообратными в том смысле, что первая позволяет
«поднять индексы» в переменные, в то время как вторая дает возможность
«опустить переменные» в индексы.)
3.6 	Обозначения. Через (х,у) обозначим образ (х, у) относительно
стандартной функции пары |(х2 4- 2ху 4- у2 4- За; 4- у), которая является
вычислимой 1:1-функцией из ш хш на и. Через 7Ti и 7г2 обозначим
обратные функции 7Ti((ж,у)) = х, и 7г2((х,2/)) = у. Через (xi,x2,x3) обозначим
((xbx2),x3), ачерез (хьх2,... ,хп) — (• • • ((xi,x2),x3),... ,хп). (Все эти
функции, очевидно, вычислимы и даже примитивно рекурсивны.)
3.7 	Соглашение. Для отношения R С cjn, п > 1, мы говорим, что
оно имеет некоторое свойство Р (такое как, например, вычислимость,
в. п. Ei и т. д.) тогда и только тогда, когда множество { (xi,... ,хп) :
Д(хьх2,... ,хп) } имеет свойство Р. (Заметим, что это согласуется с
определением 2.3 о том, что отношение R вычислимо тогда и только
тогда, когда функция XR вычислима.)
3.8 	Определение. Мы пишем <^e>s(x) = у, если х,г/,е < s и у
является значением функции </?е(я)5 полученным за < 5 шагов работы по
программе Тьюринга Ре. Если такой у существует, то мы говорим, что
(/?е,«(ж) определена и пишем <^e,s(x) | , в противном случае (pe,s(x)
доопределена {(feyS{x) f ). Также мы пишем (ре(х)1 , если для некоторого
s j и пишем <ре(х)1 = у, если и <^е(х) = у. Аналогично
ДЛЯ <pe,s(x)l = У•
Эти упрощенные определения и мы используем только в
главе I и в § 1 главы II для того, чтобы читатель привык к конечным
аппроксимациям. Начиная с главы II мы будем пользоваться
соглашением II.2.6, согласно которому (pe,s и We>8 могут быть определены с
помощью упражнения 3.11 вместо определения 3.8, так что мы сможем
предположить, что условие (3.3) выполнено для We,s в силу
определения 4.1.

38
Глава I. Вычислимые функции
3.9 	Теорема, (i) Множество {(e,a;,s) :ipe,s(x)l} вычислимо.
(ii) 	Множество { (e,x,y,s) : <pe,s{x) = у} вычислимо.
Доказательство. Истинность утверждений (i) и (й) выводится из
Тезиса Чёрча следующим образом: мы производим вычисление до тех пор,
пока либо оно не завершится, либо не будут пройдены s шагов
вычисления. Ц
3.10-3.13 Упражнения
3.10. Докажите, что если R(xyy) вычислимо, то отношение (3у ^
z)R(x,y) также вычислимо по х и z.
3.11. Определим ipe,s(x) = у рекурсией по s следующим образом:
положим </?е,o(^)t Для всех х• Положим <£e)S+i(x) = у тогда и только тогда,
когда (feyS{x) = у или s = (е,ж,г/,£) для некоторого t > 0, и у является
выводом ipe{x), полученным за ^ t шагов работы программы
Тьюринга Ре.
Докажите, что это альтернативное определение ipe,s(x) = у
удовлетворяет теореме 3.9 и обладает следующими удобными свойствами:
(pe,s(x) = у => е,х,у < S, (3.1)
и
(Vs) (3 не более одного (е,ж,г/)) [ч>еАх) = У & ^e,s-i(^)t ], (3.2)
следовательно,
(Vs) (3 не более одного (е,х)) [х Е We,s+i — We,s], (3.3)
где WefS определяется по <peyS согласно определению 4.1. (Начиная с
соглашения И.2.6, будем предполагать, что в определениях ipe,s и WetS
используется упражнение 3.11, поэтому (3.3) имеет место для WeyS-)
3.12. Покажите, что следующее альтернативное определение <^e,s
также удовлетворяет теореме 3.9 и свойствам (3.1), (3.2) и (3.3):
{U((fj,z < s)T(e,x,z)), если (3z < s) T(e,x,z),
неопределена в противном случае.
3.13 (Теорема о нумерации). Модифицируйте доказательство
теоремы 3.4, чтобы показать, что для любых п ^ 1 существует такая ч. в.
функция <pZn (е, xi у..., хп) от (п + 1)-ой переменной, что <pZn (е, х\,...,
хп) = {х\,..., хп) для всех е и Х\,..., хп.

§ 4• Неразрешимые проблемы
39
§ 4. Вычислимо перечислимые множества и
неразрешимые проблемы
4.1 	Определение, (i) Множество А вычислимо перечислимо (в. п.),
если А является областью определения некоторой ч. в. функции.
(й) Обозначим е-ое в. п. множество так:
We = dom ipe = {х : (pe(x)i } = {х : (Зу)Т(е,х,у) }.
(iii) 	We>s = dom <peiS. (Напомним, что если х Е We,8, то х,е < s.)
Отметим, что <ре(х) = у тогда и только тогда, когда (3s) [pe,s(x) =
у], и х Е We тогда и только тогда, когда (3s) [х Е Wet8], Заметим
также, что каждое вычислимое множество является в. п. множеством,
т. к. если А вычислимо, то А = dom ф, где ф(х) = 1, если ха(х) = 1,
и ф(х) f в противном случае. Мы покажем (теорема И. 1.8), что
непустое множество в. п. тогда и только тогда, когда А является областью
значений вычислимой функции (т. е. тогда и только тогда, когда
существует алгоритм для порождения элементов А). Обилие в. п.
множеств в других областях математики и существование невычислимых
в. п. множеств, таких как определенное ниже множество К, позволило
получить целый ряд результатов о неразрешимости. Сюда, например,
относятся работы Дэвиса , Матиясевича, Путнама и Дж. Робинсон о
неразрешимости десятой проблемы Гильберта о диофантовых уравнениях
и теорема Буна-Новикова о неразрешимости проблемы равенства слов
для конечно-определенных групп (см. Девис [1973], Бун [1955-57], [1959]
и Новиков [1955]).
4.2 	Определение. Пусть К = {х : фх(х) определена} = {х : х G
Wx}.
4.3 	Предложение. Множество К является в. п. множеством.
Доказательство. Множество К является областью определения
следующей ч. в. функции:
х, если <рх(х) определена,
неопределена в противном случае.

40
Глава I. Вычислимые функции
Функция ф ч. в. по Тезису Чёрча, т. к. значение ф(х) можно
вычислить, применяя к входу х программу Рх и подавая на выход число ж,
если <рх(х) определена. Более формально, К = dom в, где в(х) = ср^(х,х),
(2)
&ipz — ч. в. функция, определенная в теореме 3.4 о нумерации.
4.4 	Предложение. К не вычислимо.
Доказательство. Если бы множество К имело вычислимую
характеристическую функцию хк, то следующая функция была бы вычислима:
{<Рх(х) 4- 1, если х е К,
0, если х f К.
Однако / не может быть вычислимой, поскольку / ф ipx для
любого х. Q
Таким образом, не существует алгоритма проверки условия х Е К.
Это — наш первый пример неразрешимой проблемы.
4.5 	Определение. Ко = { (ж, у) - х Е Wy }.
Заметим, что Ко также в. п. Действительно, Kq = dom 0, где
в((х,у)) = ip¥\y,x), а (р^ — как в теореме 3.4.
4.6 	Следствие. Ко не вычислимо.
Доказательство. Заметим, что х Е К тогда и только тогда, когда
(ж,т) Е Ко. Таким образом, если Ко имеет вычислимую
характеристическую функцию, то К также вычислимо, что противоречит
предложению 4.4. О
Проблема остановки должна решать для произвольных х и ?/,
определена ли (рх{у), т. е. останавливается ли когда-либо программа Рх с
входом у. Следствие 4.6 утверждает неразрешимость проблемы
остановки. Доказательство этого следствия описывает один косвенный метод
установления неразрешимости новых проблем путем сведения
множества К к этим проблемам.
4.7 	Определение, (i) А много-одно сводимо (т-сводимо) к В (пишется
А Б), если существует такая вычислимая функция /, что f(A) С В
и /(-А) С В, т. е. х Е А тогда и только тогда, когда f(x) Е В.
(ii) 	A is одно-одно сводимо (1-сводимо) кВ (A 5), если А В
посредством вычислимой 1:1-функции.

§ 4• Неразрешимые проблемы
41
Доказательство следствия 4.6 устанавливает, например, что К
Ко посредством функции f(x) = (х,х). Заметим, что если А В
посредством /, то А В также посредством /. Очевидно, что отношения
дующие отношения эквивалентности.
4.8 Определение, (i) А =т В, если А В и В А.
(ii) А =1 В, если А В и В А.
(iii) degm(j4) = {В : А=т в}.
(iv) deg1(i4) = {B:i4=1B}.
Классы эквивалентности по =ш и =i называются т- степенями и
1-степенями, соответственно.
4.9 Предложение. Если А В и В вычислимо, то А также
вычислимо.
Доказательство. Если А В посредством /, то ха{х) = Хв{1{^)),
поэтому ха вычислимая функция, если В вычислимо. О
Предложение 4.9 позволяет доказать неразрешимость большого
числа проблем. Например, таких, как проблема проверки для данного х,
является ли функция ipx константой, всюду определенной функцией,
dom<^x ф 0, (рх доопределяема до (всюду определенной) вычислимой
функции, и т. д. Если мы можем свести одну неразрешимую проблему
А к некоторой проблеме В, то В также неразрешима.
4.10 Теорема. К ^i Tot =dfn { х : рх всюду определенная функция }.
Доказательство. Определим функцию
Ясно, что ф ч. в., т. к. следующая программа вычисляет %l)(x,y)\
сначала вычисляем <рх(х); если рх(х) не определена, то на выход ничего
не подается; если же (рх(х) определена, то при любом аргументе у на
выход подается 1. По s-m-n теореме существует такая вычислимая 1:1-
функция /, что iff(x){y) — ф{х,у). Именно, выбираем такое число е, что
<ре(х,у) = ф(х,у), и определяем f(x) = Ax[sJ(e,a;)]. Теперь / является
1:1-функцией, так как 1:1-функцией является s\. Далее заметим, что
и рефлексивны и транзитивны, следовательно, порождают сле¬
неопределена в противном случае.
х е К => (Pf(x) = Аг/[1] => <Pf(x) всюду определена

42
Глава I. Вычислимые функции
=> f(x) е Tot,
х £ К => <Pf(x) = Ау [неопределена]
=> <Pf(x) не всюду определенная => f(x) £ Tot.
Заметим, что это доказательство устанавливает, что проблема
определения по данному х, является ли ipx постоянной функцией, или
даже проблема проверки условия dom^ ф 0, являются неразрешимыми
проблемами. Заметим также, что в этом доказательстве множество К
можно заменить на произвольное в. п. множество А. Предположим, что
А = dom в, где в ч. в. Тогда предыдущая программа начинается с
вычисления в(х) вместо <рх(х)- Однако мы не можем заменить К на
произвольное we-в. п. множество А, потому что в этом случае не существует
эффективного аналога для этого первого шага программы вычисления
фу а. ф должна быть частично вычислимой функцией.
Таких применений s-m-n теоремы, какие мы приводили выше, очень
много. Читатель в каждом случае должен проверять, являются ли
эффективными инструкции для вычисления ф(х,у). В дальнейшем мы
будем просто писать ipf(x)(y) вместо ф(х,у), без специального упоминания
s-m-n теоремы. Метод предыдущего доказательства применим к ряду
других множеств А вместо Tot, необходимо лишь, чтобы свойства, с
помощью которых задается Л, были свойствами функций, а не
свойствами определенных индексов функций, т. е. если А является «индексным
множеством».
4.11 Определение. Множество А С ш называется индексным
множеством, если для любых х и у
[х е А & ipx = <Ру] => у € А.
4.12 Теорема. Если А — нетривиальное индексное множество, т. е.
Аф 0,а>, тогда либо К А, либо К А.
4.13 	Следствие (теорема Райса). Пусть С — произвольный класс
частично вычислимых функций. Тогда множество {п : ipn Е С}
вычислимо тогда и только тогда, когда либо С = 0, либо С — класс всех
частично вычислимых функций. []
Доказательство (теоремы 4-12). Выберем ео такое, что ipeo(y)
неопределена для всех у. Докажем, что если ео Е А, то К ^ А. (Если

§ 4• Неразрешимые проблемы
43
ео Е А, то К А доказывается аналогично.) Так как А ф 0, то
существует ei Е А. Теперь <^ei 7^ <£ео, т. к. А является индексным множеством.
По s-m-n теореме определяем такую вычислимую 1:1-функцию /, что
X € К V (Pf(x) — <Рео ^ /(ж) £
Последняя импликация в каждой строке истинна, т. к. А является
индексным множеством. Ц
Для некоторого индексного множества А могут выполняться обе
сводимости К А и К А, например, для множества Л = Tot. (см.
упражнения ниже.)
4.14 	Определение. Кроме К и К0 мы будем рассматривать
следующие индексные множества, которые соответствуют естественным
неразрешимым проблемам, о которых говорилось выше.
Fin = { х : Wx конечно };
Inf = lj — Fin = { x : Wx бесконечно };
Tot = { x : фх всюду определенная } = { х : Wx = ш };
Con = { х : срх всюду определена и постоянна };
Cof = { х : Wx коконечно };
Rec = { х : Wx вычислимо };
Ext = {х : ipx доопределима до (всюду определенной)
Из всех приведенных выше индексных множеств наиболее
полезными для дальнейшей работы окажутся множества К, Fin, Inf, Tot, и Cof.
Каждое из них является нетривиальным индексным множеством,
поэтому невычислимо по теореме Райса. Из них только RT, Ко и К\ —
в. п. множества, и все они принадлежат одной 1-степени (см.
упражнение 4.18). Следовательно, по теореме 5.4 все три множества вычислимо
изоморфны и могут быть одинаково использованы для всех наших целей.
<РеЛу), если х Е К,
неопределена, если х £ К.
Теперь
х € К => ipf(x) = <pei => f(x) е Ау
Кх = {x:Wx^9};
вычислимой функции}.

44
Глава I. Вычислимые функции
4.15 	Определение. В. п. множество А 1-полно, если для любого в. п.
множества We имеем We А.
Очевидно, что Ко 1-пол но, так как х Е We тогда и только тогда,
когда (х,е) Е Kq. Поэтому по упражнению 4.18 К и К\ также являются
1-полными. В §1 главы II мы докажем, что остальные из названных
индексных множеств, а также их дополнения, не в. п. В главе IV мы
покажем, что
Inf =i Tot =i Con, и Cof =i Rec =i Ext.
Важной задачей теории вычислимости является задача точной
классификации, «насколько неразрешима» данная проблема, путем
вычисления её «степени» неразрешимости относительно других проблем.
Например, если А =г В, где г = 1,т или более общей тьюринговой (Т-)
сводимости из главы III, то А и В имеют одинаковую г-степень и
интуитивно «кодируют одинаковую информацию». Если А <г В, то В имеет
r-степень более высокую, чем А, и кодирует больше информации.
В главе IV мы дадим другую характеристику этих множеств в
терминах арифметической иерархии. Для каждого п Е со уровень п этой
иерархии состоит из множеств, принадлежащих одной Т-степени.
Например, вычислимые множества находятся на уровне 0; множества К,
Ко, и К\ на уровне 1; Inf, Con и Tot на уровне 2; Cof, Rec, и Ext на
уровне 3 и т. д. Множества более высоких уровней имеют строго большую
Т-степень, чем те, которые находятся на нижних уровнях.
4.16 	Определение. Сочленением множеств А и В (пишется А 0 В)
называется множество
{2х : х € A} \J {2х + I : х € В }.
4.17-4.27 Упражнения
4.17. 	Докажите, что m-степень А 0 В является наименьшей верхней
гранью (н. в. г.) m-степеней А и В, а именно,
(a) А А® В, В А 0 В, и
(b) если А С и В С, то А 0 В С.
(1-степени, даже 1-степени в. п. множеств, не всегда имеют н. в. г. или
наибольшую нижнюю грань (н. н. г.).)

§ 4• Неразрешимые проблемы
45
4.18. Докажите, что К =i Ко =i К\. (Заметим, что доказательство
теоремы 4.10 автоматически устанавливает, что К А, где А = К\,
Con, или Inf. Используйте тот же метод с Ко вместо К, чтобы показать,
что Ко К и, следовательно, что Ко К К\, поэтому К и К\
являются 1-полными.)
4.19. Докажите непосредственно (без использования теоремы Райса),
что К Fin. Указание. Пусть <Pf(x)is) неопределена, если х G KSJ и
Pf(x)is) = 0, если х £ Ks, где Ks = We s для некоторого е такого, что
K = We.
4.20. Для любого х покажите, что К {у : (рх = Ц>у } и К ^ {у :
Wx = Wy }. Указание. Рассмотрите отдельно случаи, когда Wx конечно
и когда Wx бесконечно, и используйте метод упражнения 4.19. (см.
также упражнение 11.4.10(b) для того, чтобы убедиться, что это сведение
не может быть сделано равномерным.)
4.21. Покажите, что Ext ф и. (Следовательно, не каждая частично
вычислимая функция может быть продолжена до всюду определенной
вычислимой функции.)
4.22. (а) Непересекающиеся множества А и В вычислимо
неотделимы,, если не существует такого вычислимого множества (7, что А С С
и С П В = 0. Докажите, что существуют непересекающиеся вычислимо
неотделимые в. п. множества. Существование таких множеств весьма
полезно, например, в упражнении 5.9, а также в теории моделей.
Указание. Пусть А = { х : (рх(х) = 0 }, В = { х : (рх(х) = 1}. Рассматривая
<рх(х) докажите, что никакая (рх не может быть характеристической
функцией вычислимого множества (7, отделяющего А от В.
(b) Дайте альтернативное доказательство того, что Ext ф ш.
(c) Для множеств А и В из части (а) докажите, что К =i А и К =i
В.
4.23. 	Множество А называется цилиндром, если (VI?) [В А =>
В А].
(a) Покажите, что любое индексное множество является
цилиндром.
(b) Покажите, что любое множество вида Ах ш является цилинд¬
ром.

46
Глава I. Вычислимые функции
(с) 	Покажите, что А является цилиндром тогда и только тогда,
когда A =i В х и, для некоторого множества В.
4.24. Покажите, что частично вычислимые функции не замкнуты
относительно /i-оператора, т. е. существует такая ч. в. функция t/;, что
Лх[р,у[ф(х,у) = 0]] не ч. в. Указание. Определите ф(х,у) = 0, если либо
у = 1, либо у = 0 и (рх(х)1 •
4.25. Если А вычислимо и В, В ф 0, то А В. (Следовательно, если
пренебречь тривиальными множествами 0 и существует наименьшая
т-степень.)
4.26. 	° Докажите, что Inf =i Tot =i Con. Указание. Используйте
s-m-n теорему как в теореме 4.10 или как в упражнении 4.18. Например,
для доказательства Inf Con определите
По s-m-n теореме выберете такую вычислимую функцию /, что
4>f(e){x) — ф(е,х) и покажите, что е Е Inf тогда и только тогда,
когда f(e) Е Con.
4.27. 	Докажите, что Fin Cof. Указание. Покажите, что Fin Cof
посредством функции /, определенной следующим образом:
§ 5. Вычислимые перестановки и теорема Майхилла
об изоморфизме
5.1 	Определение, (i) Вычислимой перестановкой называется
вычислимая 1:1-функция из о) на ш.
(й) Свойство множеств вычислимо инвариантно, если оно
инвариантно под действием всех вычислимых перестановок.
t, если We,s+1 - WetS ф 0,
0 в противном случае.
Примеры вычислимо инвариантных свойств:

§ 5. Теорема Майхилла об изоморфизме
47
(i) А вычислимо перечислимо (в. п.);
(ii) А состоит из п элементов (пишется \А\ = п);
(Ш) А вычислимо.
Следующие свойства не вычислимо инвариантны:
(i) 2 GA;
(ii) А состоит из чётных целых чисел;
(iii) А — индексное множество.
5.2 	Определение. Множество А вычислимо изоморфно множеству
В (пишется А = В), если существует такая вычислимая перестановка
р, что р(А) = В.
5.3 Определение. Классы эквивалентности по = называются
типами вычислимого изоморфизма.
Мы попытаемся классифицировать множества по вычислимому
изоморфизму также, как алгебраисты классифицируют структуры по
обычному изоморфизму. Одной из причин введения отношения в § 4 (когда
для результатов о неразрешимости вполне достаточно иметь отношение
^ш) является следующая теорема, эффективный аналог классической
теоремы Шрёдера-Бернштейна о кардинальных числах.
5.4 Теорема Майхилла об изоморфизме. А = В A =i В.
Доказательство. ( => ) Очевидно.
( <= ) Пусть A В посредством / и В ^ А посредством д.
Поэтапно определим вычислимую перестановку ft так, чтобы ft(А) = В.
Положим ft = |JS fts, где ho = 0 и hs — часть ft, определенная на этапе s.
Мы определим h8 так, что, в частности, сможем эффективно проверять
принадлежность любого числа множествам dom hs и ran ft5, которые
будут конечными.
Этап s -1-1 = 2ж + 1. (Определяем h(x).) Предположим, что hs
является 1:1-функцией, dom hs конечна, и у € А тогда и только тогда, когда
hs(y) Е В для всех у Е dom hs. Если hs(x) определена, то ничего не
делаем. В противном случае перечисляем множество { /(ж), f(hjlf(x)),...,
f{hjxf)n{x),... } до тех пор, пока не найдем первый элемент у, ещё не
принадлежащий ran hs. Положим hs+i(x) = у. Заметим, что такой у
должен существовать, т. к. / и hs являются 1:1-функциями и х £ dom hs.

48
Глава I. Вычислимые функции
Более того, х Е А тогда и только тогда, когда у € В, по предположениям
об / и hs.
Этап s + 1 = 2х + 2. Подобным образом определяем /г—1 (ж), заменив
/, hs, dom и ran на <7, ftj1, ran и dom, соответственно. []
Следующее определение понадобится в упражнении 5.7 и, позднее, в
главе XI (см. также определение V.2.2).
5.5 	Определение. Функция / доминирует функцию <7, если (Зто)
(Va; > жо) [/(я) ^ d(x)]i т- е- если f(x) ^ д(х) для почти всех (всех, за
исключением конечного числа) х Е ш.
Понятие допустимой нумерации частично вычислимых функций,
приведённое в упражнение 5.9, является очень важным. Несущественно,
какая конкретная допустимая нумерация изначально выбирается, т. к.
большинство естественных нумераций допустимы, и две допустимые йу-
мерации отличаются только вычислимой перестановкой.
5.6-5.11 Упражнения
5.6. Докажите, что множество вычислимых перестановок образует
группу относительно операции подстановки.
5.7. Докажите, что примитивно рекурсивные перестановки не
образуют группу относительно операции подстановки. Указание. Сначала
постройте, используя идеи из определения 2.2, эффективную и,
следовательно, вычислимую функцию <ре, которая доминирует любую
примитивно рекурсивную функцию. Определите функцию g следующим обра-
зом: ^(0) = цу T(e,0,y); g(x + l) = \iy Т(е, z+l, у), если цу Т(е,х + 1,у) >
д{х), и д(х + 1) = д(х) + 1 в противном случае. Здесь Т(е,х,у) и U(y)
примитивно рекурсивные предикат и функция из теоремы 3.3. Заметим,
что д также доминирует все примитивно рекурсивные функции, т. к.
U(у) ^ у для всех у. Постройте такую примитивно рекурсивную
перестановку /, что f(g(x)) — х, если х — чётное число. Заметим, что по
данному у мы можем определить, используя только примитивно
рекурсивные процедуры, существует ли такое число ж, что д(х) = у.
5.8. Пусть и) — IJпАп — IJпВп, где последовательности {An}n^UJ и
{ Вп Jneu, попарно не пересекаются. Пусть / и д — такие вычислимые
1:1-функции, что f{An) С Вп и д(Вп) С Ап для всех п. Покажите, что
построение из теоремы 5.4 определяет такую вычислимую перестановку
Л, что h(An) = Вп для всех п.

§ 5. Теорема Майхилла об изоморфизме
49
5.9 	(Роджерс). Пусть V — класс частично вычислимых функций от
одной переменной. Нумерацией ч. в. функций является отображение 7г
из ш на V. Нумерация {ipe }е€а; из § 3 называется стандартной
нумерацией. Пусть 7Г — другая нумерация и пусть фе обозначает 7г(е).
Тогда 7г называется допустимой нумерацией, если существуют такие
вычислимые функции / и д, что (i) <Р/(Х) = Фх и (й) ^у(х) = 4>х-
Покажите, что для любой допустимой нумерации п существует такая
вычислимая перестановка р на ш, что (рх = фр(х) для всех х. Указание.
(Джокуш) Согласно упражнению 5.8 с подходящими определениями Ап
и Вп достаточно преобразовать / и д на вычислимые Т. 1-функции Д и
#1, удовлетворяющие (i) и (ii). Чтобы определить Д по /, используйте
лемму 3.2 о множестве индексов. Чтобы определить д\(х) мы должны
уметь (равномерно по ж) эффективно порождать такое бесконечное
множество индексов SXJ чтобы для каждого у 6 Sx иметь фу = фд(х)- Далее
возьмите два вычислимо неотделимых в. п. множества А и В как в
упражнении 4.22 и определите
и, аналогично, определите <Pi(x,y) с 1 вместо 0. Пусть Сх = {к(х,у) :
у е А) и Dx = {1(х,у) : у е А}. Если (рх ф Az[0], то д(Сх) не
может быть конечным, иначе А и В вычислимо отделимы. Следовательно,
множество Sx = д(Сх) U g(Dx) бесконечно. Заметим, что мы не можем
эффективно сказать, какое из условий ipx ф Ая[0] или <рх ф Xz[l] имеет
место. Нам это и не нужно знать, чтобы убедиться, что множество Sx
бесконечно. (Для доказательства, использующего теорему рекурсии, см.
упражнение П.4.11.)
5.10. Продолжая терминологию упражнения 5.9 скажем, что ф
является эффективной нумерацией класса ч. в. функций V тогда и
только тогда, когда ф ч. в. и {фе : е € ш} = V, где фе = Ах[ф((е,х))].
Эффективная нумерация ф допустима, если множество {фе : е G и }
допустимо в терминах упражнения 5.9, т. е. тогда и только тогда,
когда существует вычислимая функция g, удовлетворяющая условию (ii)
упражнения 5.9, т. к. существование /, удовлетворяющей условию (i)
упражнения 5.9, следует непосредственно из определения ф и s-m-n
теоремы для { (ре : е G и }.
<Px(z),
если у € А,
если у G В,
Vk(x,y)(z) = < 0,
неопределена в противном случае,

50
Глава I. Вычислимые функции
(a) Покажите, что эффективная нумерация ф допустима тогда и
только тогда, когда для каждой другой эффективной нумерации в
существует такая вычислимая функция £, что для всех е ве = фце)-
(b) (Роджерс). Покажите, что эффективная нумерация ф допустима
тогда и только тогда, когда она удовлетворяет s-m-n теореме при т =
п — 1, а именно, существует такая вычислимая функция s, что ф8{е,х) —
^у[Фе({х,у))\ для всех е, х и у.
(c) (Мактей и Янг). Покажите, что эффективная нумерация ф
допустима тогда и только тогда, когда существует такая вычислимая
функция с(р, q), что фс(р,д) = фрофд. Указание. Выберите i и j так, чтобы
ф{ — Аг/[(0, г/)] и фj = \ху[(х + 1,1/)]. Определите для ф s-l-1-функцию
s(p, ж), рассматривая фр о фу •фj о ф{, где подстановка функции фj в
себя встречается х раз.
5.11. Постройте эффективную нумерацию ф, не являющуюся
допустимой, следующим образом: пусть
ф( о,д) (0) = неопределена,
^<Р+1,9>(°) =Р»
Ф(Р,д)(х) - ¥>д(х), если X > 0.
Покажите, что { фп }n€u> =Vn что ф не может быть допустимой.
Указание. Покажите, что если существует такая вычислимая функция д, что
Фд(х) = 4>х, то мы могли бы решить проблему остановки. (Для другого
примера определите такую вычислимую функцию /, что { (р/(р) : р Е и; }
состоит в точности из частичных функций с непустой областью
определения, и положите фр+\ = <Pf(p), Фо{у) = Ау [неопределена].)

Глава II
Основания вычислимо перечислимых
множеств и теорема рекурсии
Назначение этой главы состоит в том, чтобы помочь читателю получить
более глубокое восприятие в. п. множеств. Мы приведем несколько
эквивалентных описаний в. п. множеств и докажем их наиболее полезные
свойства. Мы также докажем теорему рекурсии, которая окажется очень
полезным инструментом, и используем её для доказательства теоремы
Майхилла о том, что все креативные множества изоморфны.
§ 1. Эквивалентные определения вычислимо
перечислимых множеств и их основные свойства
В § 4 главы I мы определили в. п. множество А как область определения
ч. в. функции. Теперь покажем, что это определение эквивалентно
следующему, интуитивно более понятному: множество в. п., если существует
алгоритм перечисления его элементов. (См. теорему 1.8 о перечислении.)
Третье полезное определение в. п. множества: множество А в. п., если
оно является Ei-множеством.
Напомним наше соглашение 1.3.7: отношение R С шп обладает
некоторым свойством Р (например, быть вычислимым, в. п., или
Ei-отношением) тогда и только тогда, когда множество А = { (xi,X2, • • • »£п) :
R(x 1, #2, • • •»хп) } обладает этим свойством Р.
1.1 	Определение, (i) Множество А называется проекцией отношения
R С и) х cj, если А = { х : (3y)R(x,y)} (т. е. геометрически А является
проекцией двухмерного отношения R на ось х).
(й) Множество А имеет Ei -форму (или «А является
Ei-множеством»), если А является проекцией некоторого вычислимого отношения

52
Глава II. Основания в. п. множеств
R С и х и. (Основанием для обозначения Ei является то, что
соответствующий предикат для А состоит из одного квантора 3 и
следующего за ним вычислимого предиката. Формы ЕП,ПП и Дп,п ^ 0, будут
определены в главе IV об арифметической иерархии. В литературе эти
формы обычно обозначаются Е^,П^ и Д^, чтобы отличить их от форм
аналитической иерархии и А1 где подсчет ведется по функцио¬
нальным кванторам. См. Роджерс [1967] или Хинман [1978].)
Следующая теорема эквивалентна теореме 1.3.3 о нормальной форме
для частично вычислимых функций.
1.2 Теорема о нормальной форме для в. п. множеств. Множество
А в. п. тогда и только тогда, когда А имеет Еi-форму.
Доказательство. {=>) Если А в. п., то А = We —djn dom </?е для
некоторого е. Следовательно,
х G We <==> (3s)[a; G WeiS\ <==> (3s)T(e, x, s).
По теореме 1.3.9(i) отношение { (e,x,s) : x G WeyS } вычислимо, а
предикат T(e,x,s) даже примитивно рекурсивен.
(<f=) Пусть A = { x : (3y)R(x, у) }, где R — вычислимое отношение.
Тогда А = dom ф, где ф(х) = (fiy)R(x,y). О
1.3 Теорема о сжатии кванторов. Если существует такое
вычислимое отношение R С шп+1, что
А = {х : (3yi)...(3yn)R(x,yi,...,yn)},
то А является Ei -множеством.
Доказательство. Определим вычислимое отношение S С и2
следующим образом:
S(x,z) <p=$dfn R(x,(z)i,(z)2,...,(z)n),
где г = р[: *1 •... — разложение числа г на простые сомножители,
как в пункте (2.1) главы I.
(3z)S(x,z) <=> (3z)R(x,(z)i,(z)2,...,(z)n)
•£=>• {3yi)(3y2)...(3yn)R(x,yi,y2,...,yn). Q
1.4 	Следствие. Проекция в. п. отношения также является в. п.
отношением.

§ 1. Свойства в. п. множеств
53
1.5 Определение. Графиком (частичной) функции ф называется
отношение
(х,у) е graph ф ф{х) = у.
Из теоремы 1.3 (или следствия 1.4) вытекает, что множество А в. п.,
если оно имеет вид
{х: (Зуг)... (3yn)R(x,yi,... ,уп) },
где R С wn+l вычислимо. Это свойство полезно при доказательстве вы-
числимой перечислимости различных множеств. Например, с помощью
теоремы 1.3.9 теперь можно показать, что следующие множества и
отношения являются вычислимо перечислимыми:
(1.1) К = { е : е € И'е } = { е : (Э*)(Эу)[фе,,(е) = у] },
(1.2) К0 = { (х, е) : х € We } = { (х, е) : (3s)(3y)[<^e,s(^) =*/]},
(1.3) Кг = { е : We ф 0 } = { е : (3s)(3z)[z € We,s] },
(1.4) rng (fie = { у : (3s)(3:r)[pe,s(:r) = у) },
(1.5) graph <pe = { (x,y) : (3s)[yje,s(a:) = y] }.
1.6 Теорема униформизации. Если отношение R С w2 в. п., то
существует такая ч. в. функция ф (называемая функцией выбора для
R), что
ф(х) определена <=> (3y)R(x,y),
и в этом случае (х,ф(х)) Е R. (Более того, индекс функции ф может
быть найден эффективно по в. п. индексу отношения R.)
Доказательство. Так как R в. п. и, следовательно, Ei-отношение, то
существует такое вычислимое отношение 5, что R(x,y) тогда и только
тогда, когда (3z)S(xyyyz). Определим ч. в. функцию
в{х) = (nu)S(x,(u)i,{u)2),
И ПОЛОЖИМ ф(х) = (0(x))i. О
В теореме униформизации существенно не то, что функция ф
существует (это очевидно), а то, что ф частично вычислима.
1.7 Теорема о графике. Частичная функция ф тогда и только тогда
частично-вычислима, когда её график в. п.

54
Глава II. Основания в. п. множеств
Доказательство, (=$►) График (ре в. п. по теореме 1.2 и
соотношению (1.5).
{<=) Если график гр в. п., то, как видно из определения 1.5, гр
является ч. в. функцией выбора своего графика, т. к. R = graph гр в качестве
своей функции выбора может иметь только функцию гр. Q
Следующая теорема является основной теоремой о в. п.
множествах и обосновывает интуитивное описание в. п. множества А как
множества, элементы которого могут быть эффективно перечислены: А =
{ao,ai,a2,... }. (З.аметим, что это перечисление может иметь
повторения и не обязано быть перечислением в порядке возрастания.)
1.8 Теорема о перечислении. Множество А в, п. тогда и только
тогда, когда А = 0 или А является областью значений всюду
определенной вычислимой функции /. Более того, как выясняется в
упражнении 1.25, функция f может быть найдена равномерно по номеру
множества А.
Доказательство. (4=) Если А = 0, то А в. п. Теперь предположим, что
А = rng /, где / — вычислимая функция. Тогда А в. п., согласно (1.4).
{=>) Пусть A = We ф$. Найдем такое наименьшее число (a, t), что
а € Weyt• Определим вычислимую функцию / следующим образом:
если х Е W€yS+i - WeyS,
в противном случае.
(Заметим, что каждое х Е Wei х ф а, перечисляется как значение
функции / только один раз.) Ясно, что А = rng /. Действительно, если
х Е We, то пусть s — такое наименьшее число, что х Е We,s+\. Тогда
f((s,x)) = я, поэтому х Е rng /. О
1.9 Теорема об объединении. В. п. множества равномерно
эффективно замкнуты относительно операций объединения и пересечения, а
именно, существуют такие вычислимые функции f и g, что Wf(x у) =
WxUWy uWg{Xty) = WxnWy.
Доказательство. С помощью s-m-n теоремы определим f(x,y)
следующим образом: перечисляем z в Wf(XyV), если (3s)[z Е WXyS U WVyS], и
аналогично для g с П вместо U. Q
1.10 Следствие (принцип редукции для в. п. множеств). Для
любых двух в. п. множеств А и В существуют такие в. п. множества

§ 1. Свойства в. п. множеств
55
Ai С А и Bi С Я, что Аг П Вх = 0 и Аг U Вг = A U В.
Доказательство. С помощью теоремы 1.9 определим в. п. отношение
R =djn А х {0} U В х {1}. Пусть ф является ч. в. функцией выбора
для отношения Я, которая существует по теореме 1.6 униформизации.
Тогда Ах = { х : ф(х) = 0 }, Вх = { х : ф(х) = 1}. (см. также
упражнение 2.10(d).) Q
1.11 Определение. Множество А находится в А\-форме (или <аА
является Дх-множеством»), если как А, так и А являются Ех-множествами.
Следующая теорема, связывающая в. п. множества с вычислимыми,
была доказана Постом.
1.12 Теорема о дополнении. Множество А вычислимо тогда и
только тогда, когда как А, так и А в. п. (т. е. если Ае Ах).
Доказательство. (=>)• Если А вычислимо, то и А вычислимо,
следовательно, А и А оба в. п. _
(Ф=). Пусть A = We, A = W{. Определим вычислимую функцию
f(x) = (fis)[x е WeyS или X е wiyS\.
Ясно, что х G А тогда и только тогда, когда х Е И^е,/(х)5 следовательно,
А вычислимо. О
1.13 Следствие. Множество К не в. п.
Доказательство. По теоремам 1.4.3 и 1.4.4 К в. п., но не вычислимо. Q
Легко показать, что если К А, то А не в. п., отсюда можно
заключить, что многие множества, такие как Tot, Fin и Cof, не являются
в. п. (см. упражнение 1.16.)
1.14 Определение, (i) Решёткой С = (L;^,V, А) называется такое
частично упорядоченное (ч. у.) множество, в котором любые два
элемента имеют наименьшую верхнюю грань (называемую также супремумом
или объединением) и наибольшую нижнюю грань (называемую также
инфимумом или пересечением). Если а и Ь — элементы решётки £, то
а V Ь обозначает наименьшую верхнюю грань (н. в. г.) элементов а и
Ь, и а А Ь обозначает их наибольшую нижнюю грань (н. н. г.). Если С
содержит наименьший и наибольший элементы, то они соответственно
называются нулевым 0 и единичным 1 элементами. В такой решётке а
называется дополнением Ь, если aV b = I и а ЛЬ = 0.

56
Глава II. Основания в. п. множеств
(ii) 	Решетка называется дистрибутивной, если все её элементы
удовлетворяют законам дистрибутивности: (а V Ь) А с = (а А с) V (Ь А с) и
(aAb)V с = (aV с) A(bV с).
(ш) Решетка называется решёткой с дополнениями, если каждый ее
элемент имеет дополнение.
(iv) 	Дистрибутивная решётка с дополнениями, содержащая по
крайней мере нулевой и единичный элементы, называется булевой алгеброй.
(у) Ч. у. множество, замкнутое относительно супремума и
необязательно замкнутое относительно инфимума, называется верхней полу-
решёткой.
(vi) М — (M;^,V, Л) называется подрешёткой в £, если М С L и
М замкнуто относительно операций V и Л в £.
(vii) Непустое подмножество / С L образует идеал X — (/; ^,Л, V) в
£, если I удовлетворяет условиям:
(1) [aeL&ca^bel] => a Е /, и
(2) [ael kbel]=>avbel.
(viii) Аналогично, подмножество D С L образует фильтр (также
называемый дуальным идеалом) V = (D; V,A) в £, если оно удовлетво¬
ряет двойственным условиям:
(3) [aeLka^beD]=>aeD, и
(4) [ае D & b е D]=> аЛЬ е D.
(Ясно, что идеалы и фильтры в С являются подрешётками в С.)
(ix) Пусть С — верхняя полу решётка. Тогда определения идеала и
фильтра для С те же самые, за исключением того, что мы требуем
выполнения условия (4) только в том случае, когда а А Ь существует в С.
Далее, скажем, что V — сильный фильтр в £, если V удовлетворяет
условию (3) и условию:
(5) [a G D & b G D] => (Зс G D)[c ^ а & с ^ Ь].
(Ясно, что любой сильный фильтр является фильтром.)
Например, множество всех подмножеств и образует булеву алгебру
N = (2u;;C,U,fl) с 0 в качестве наименьшего элемента и о; в качестве
наибольшего элемента. Конечные множества образуют идеал Т в И и
ко-конечные множества А (т. е. такие множества А, дополнение которых
А конечно) образуют фильтр С в И.
1.15 Определение, (i) Согласно теореме 1.9, в. п. множества образуют

§ 1. Свойства в. п. множеств
57
дистрибутивную решётку £ по включению с наибольшим элементом со
и наименьшим элементом 0.
(ii) 	По теореме 1.12, в. п. множество А € £ вычислимо тогда и только
тогда, когда А Е £. Следовательно, вычислимые множества образуют
булеву алгебру 71 С £, состоящую в точности из тех элементов £,
которые в нем имеют дополнения. (По следствию 1.13 7Z ф £.)
В III.2.1 мы определим тьюринговы степени (D,^) и в. п. степени
(R, относительно частичного порядка, индуцированного тьюринго-
вой сводимостью • Они будут образовывать только верхние полуре-
шётки. Идеалы и фильтры в R изучаются в главах IX и XIII, а идеалы
и фильтры в £ — в главах X и XI.
1.16-1.25 Упражнения
1.16. (а) Докажите, что если А В и В в. п., то А также является
в. п. множеством.
(b) Покажите, что множества Fin и Tot не в. п.
(c) Покажите, что множество Cof не в. п.
1.17. Докажите, что если множество А в. п. и — ч. в. функция, то
ф{А) и ф~1(А) оба в. п. Указание. Запишите ф(А) в Ех-форме.
1.18. Докажите, что если / — (всюду определенная) вычислимая
функция, то graph / является вычислимым множеством.
1.19. Функция / называется возрастающей , если f(x)<f(x + 1) для
всех х. Покажите, что бесконечное множество А вычислимо тогда и
только тогда, когда А является областью значений некоторой
возрастающей вычислимой функции.
1.20. Докажите, что любое бесконечное в. п. множество является
областью значений вычислимой 1:1-функции.
1.21. Докажите, что каждое бесконечное в. п. множество содержит
бесконечное вычислимое подмножество.
1.22. Множество А называется ко-в. п. (или, что эквивалентно, Щ-
множеством), если А является в. п. множеством. Используйте
упражнение 1.4.22, чтобы показать, что принцип редукции (следствие 1.10) не
имеет места для И\ -множеств.
1.23. Для класса С множеств имеет место принцип отделения, если для

58
Глава II. Основания в. п. множеств
любых А, В G С таких, что А П В = 0, существует такое множество
(7, что (7, С Е С, Л С (7 и В С (7. Согласно упражнению 1.4.22
принцип отделения не имеет места для класса в. п. множеств. Используйте
следствие 1.10, чтобы показать, что принцип отделения имеет место для
класса ко-в. п. множеств.
1.24. Докажите, что если A В, А и В в. п. и А бесконечно, то A В
посредством некоторой функции / такой, что f(A) = В.
1.25. Покажите, что доказательство теоремы 1.8 равномерно по е в том
смысле, что существует такая ч. в. функция t/^(e, г/), что если We Ф 0, то
Ху/ф(е^ у) всюду определена и We = { ^(е, у) : у Е со }. Эта равномерность
нужна, например, для упражнения 2.11.
§ 2. Равномерность и индексы вычислимых и
конечных множеств
В теореме 1.9 об объединении мы описали эффективную процедуру /,
которая по данным индексам х,у множеств, упоминаемых в условии,
выдает индекс f(x,y) множества, упоминаемого в заключении. Будем
говорить, что теорема имеет место равномерно, если такая
эффективная процедура существует. Процедуры могут быть также равномерными
для некоторого собственного подмножества S множества о;, например,
множества таких ж, что Wx ф 0 (см. упражнение 1.25), или таких ж,
что Wx вычислимо (см. теорему 2.2). Подробные доказательства
равномерности обычно используют s-m-n теорему. В случае, когда мы имеем
дело с в. п. множеством А, которое оказывается вычислимым или
конечным, удобнее ввести некоторые более сильные индексы, дающие больше
информации о множестве А.
2.1 	Определение, (i) Говорят, что число е является Ei-индексом (в. п.
индексом) множества А, если А = We = {х : (3у)Т(е,х,у)}.
(й) Число (е,г) является -индексом вычислимого множества А,
если А = We и А = W{.
(iii) 	Число е является До-индексом (характеристическим индексом)
множества А, если <ре является характеристической функцией
множества А.
Ясно, что по До-индексу вычислимого множества А можно
эффективно получить Дх-индекс А. Из доказательства теоремы 1.12 о допол¬

§ 2. Равномерность и индексы множеств
59
нении следует, что можно равномерно переходить от Дх-индекса
множества А к его До-индексу. Однако, как устанавливает следующая
теорема, в общем случае мы не можем равномерно перейти от Ех-индекса
вычислимого множества А к его Дх-индексу.
2.2 Теорема. Не существует ч. в. функции ф такой, что если Wx = А
и А вычислимо, то ф{х) определена и = А. (Другими словами,
не существует равномерного способа перехода от Ех-индексов к Д0-
индексам вычислимых множеств.)
Доказательство. Определим вычислимую функцию / следующим
образом:
цг _ Г и, если х Е К,
/(ж) “ I 0 в противном случае.
Имеем
х Е К => Wf{x) = ш =Ф> W^/(x) = 0,
и
х & К => Wf(x) = 0 => W$f(x) = ш.
Следовательно,
х е к <=► Wj,f(X) Ф 0 <*=> (3y){Bs)[y е и^/(ж))5],
поэтому К является Ех-множеством и, следовательно, в. п., что
противоречит следствию 1.13. Поэтому такой функции ф не существует. О
2.3 Следствие. Вычислимые множества замкнуты относительно
операций U, Г) и взятия дополнения. Замыкания относительно
операций U и П являются равномерными как относительно Е\-индексов,
так и относительно Дх -индексов. Замыкание относительно операции
взятия дополнения является равномерным только относительно Дх -
индексов. Q
Конечные множества, будучи вычислимыми, имеют как Ех-индексы,
так и До-индексы. Однако, даже последние не дают эффективного
способа определения максимального элемента множества А, или хотя бы
мощности множества А. Поэтому для каждого конечного множества
вводится третий индекс, который позволяет явно определить все элементы
множества А.
2.4 Определение, (i) Для конечного множества А = {х\,х2,... ,Xk },
где х\ < х2 < ... < Xk, число у = 2X1 + 2Х2 -I- ... -I- 2Хк называется

60
Глава II. Основания в. п. множеств
каноническим индексом множества А. Пусть Dy обозначает конечное
множество с каноническим индексом г/, и Do обозначает 0.
(ii) 	Последовательность { i2/(x) }x€u> Для некоторой вычислимой
функции / называется вычислимой последовательностью , или сильной
таблицей конечных множеств.
Если число у задано в двоичной записи, то элементами множества
Dy являются те её позиции, где стоит цифра 1. Например, двоичной
записью числа 5 является 101 и D$ = {0,2}. Ясно, что существуют
такие вычислимые функции / и д, что f(y) = таx{z : z G Dy } и
g{y) = \Dy\. Однако, не существует такой ч. в. функции t/;, что если ipx
является характеристической функцией множества Dy, то i/>(х)
определена и 'ф(х) \Dy\. (Если бы такая существовала, то яр о / была бы
характеристической функцией множества К, где функция / определена
так: <Pf(x)(s) = 1, если х Е Ks+\ — Ks, и <Pf(x)(s) = 0 в противном
случае.) Следовательно, не существует эффективного способа перехода от
До-индекса конечного множества к его каноническому индексу.
2.5 Определение, (i) Последовательность { Vn }П€и> в. п. множеств
называется равномерно в. п. (р. в. п.) или, что эквивалентно,
одновременно в. п. (о. в. п.), если существует такая вычислимая функция /, что
Vn = Wf(n) для всех п.
(ii) 	Последовательность { Vn }neu; вычислимых множеств называется
равномерно вычислимой, если существует такая вычислимая функция
^(х,п), что Ах[д(х,п)\ является характеристической функцией
множества Vn для всех п. (См. также определение III.2.4 для релятивизованных
версий этих понятий.)
2.6 Соглашение. С настоящего момента будем полагать, что функция
ipe,s и множество We)S определены с помощью упражнения 1.3.11, а не как
в определении 1.3.8, так что выполняется условие (3.3) главы I. Это
значит, что на каждом шаге s самое большее одно множество We получает
новый элемент. (В дальнейшем это условие будет часто
использоваться. Его выполнения можно добиться, определяя множество We>s как в
упражнении 2.10(d).)
2.7 Определение. Вычислимое перечисление (обычно называемое
просто перечислением) в. п. множества А состоит из такой сильной таблицы
{ As }s€u; (конечных множеств), что As С As+i и А = (J As.

§ 2. Равномерность и индексы множеств
61
Например, как мы увидим в упражнении 2.12, { We,s }s€u, является
перечислением в. п. множества We, хотя, вообще говоря, в. п. множество
А может иметь и такое перечисление { As }s€u;, которое ни для какого i
не совпадает с WifS-
2.8 	Определение, (i) Одновременным (вычислимым) перечислением
р. 	в. п. последовательности { Vn }neu>. в. п. множеств называется такая
сильная таблица { VniS }n,«€w, что для всех s и п G ш выполняются
условия:
(1) Vn,8 Я Vn,s+U
(2) |Vn>s+1 - Vni8\ ^ 1, и
(3) Vn = и vn,a.
s£u>
(ii) 	Стандартным перечислением (в. п. множеств) называется
одновременное перечисление {Уп}п€и;> где { Vn }П€а; — некоторая
допустимая нумерация в. п. множеств (см. упражнение 1.5.9).
Например, существует такой простой способ построения
одновременного перечисления произвольной р. в. п. последовательности {Уп}п^и:
выбираем вычислимую 1:1-функцию / с областью значений { (ж,п) : х G
Vn } и определяем
Vn,s = {х : (3t < s)[/(0 = (ж,п)] }.
Определение 2.9 будет иметь смысл и последующие построения
также будут действительны, если даже опустить условие (2) в
определении 2.8(i). Но это очень полезное условие, поэтому мы его принимаем в
соглашении 2.6 и в определении 2.8.
2.9 	Определение. Пусть {Xs }s€u; и { Ys }s€u; — вычислимые
перечисления в. п. множеств X и У.
(i) Определим X\Y = { z : (3s)[z G Xs — Ys\} — множество
элементов, которые перечисляются в X раньше, чем они перечисляются (если
вообще перечисляются) в Y.
(ii) Определим X \ Y = (Х\У)Г)У — множество элементов, которые
сначала перечисляются в X, а позднее — в У.
(Множество X\Y отличается от множества X — У, которое означает
X П У. Заметим, что определения множеств X\Y и!\У зависят не
только от самих множеств X и У, но и от их конкретных вычислимых
перечислений {Xs}sEu; и {У« }«€„,.)

62
Глава II. Основания в. п. множеств
Мы используем эти обозначения в упражнении 2.10, при
доказательстве теоремы Х.2.1, и в главе XV об автоморфизмах.
2.10-2.13 Упражнения
2.10. (а) Для данных вычислимых перечислений {Xs}s€u; и {Vs}s€u;
в. п. множеств X и Y докажите, что как X\Y, так и X \ Y являются
в. п. множествами.
(b) Докажите, что X\Y = (X — Y) U (X \ Y).
(c) Докажите, что если X - Y не в. п. , то X \ Y бесконечно.
(d) Приведите альтернативное доказательство теоремы 1.10, полагая
А1 = Wx\Wy и Вх = Wy\WXj где Wx=AnWy = B.
(e) Пусть / является вычислимой 1:1-функцией, отображающей и на
К0 = { (х, е) } : х € We }. Определим
We,3 = {x:(3t^s)[f(t) = (x,e)}}. (2.1)
Докажите, что { WeyS : е, s G ш } удовлетворяет условию I (3.3).
2.11. Докажите, что существует такая вычислимая функция /, что
{ wm }пеи> состоит в точности из всех вычислимых множеств.
(Следовательно, мы можем эффективно перечислять все Ех-индексы
вычислимых множеств, но не можем это сделать для их Дх-индексов.) Указание.
Получите И^(п) С Wn, перечисляя Wn и помещая в Wf(n) только те его
элементы, которые в нем появляются в порядке возрастания, и
примените упражнение 1.19. Заметим, что мы здесь пользуемся равномерностью,
о которой говорилось в упражнении 1.25. (См. также упражнение 3.17.)
2.12 Докажите, что существует такая вычислимая функция /(e,s), что
Df(e,s) = We,s и, следовательно, We = |J^/(e,s)-
s
2.13 Докажите, что существуют такие вычислимые функции f и д, что
Dx U Dy — Df(X y^ и Dx П Dy = Од^х у}.
§ 3. Теорема рекурсии
Следующая теорема Клини, известная как теорема рекурсии или
теорема о неподвижной точке, является одним из наиболее элегантных и
важных результатов теории. Идейно она является сильным
расширением схемы (V) для примитивно рекурсивных функций, поскольку
позволяет установить вычислимость некоторых неявно определенных функций.

§ 3. Теорема рекурсии
63
Её очень короткое доказательство использует только s-m-n теорему и
на первый взгляд кажется несколько мистическим.
3.1 	Теорема рекурсии (Клини). Для каждой вычислимой функции f
существует такое число п (называемое неподвижной точкой функции
f), что ч>„ = ¥>/(„).
Доказательство. Определим «диагональную» вычислимую функцию
d(u) следующим образом:
^Vu(u)
неопределена
если (ри{и) определена;
в противном случае.
(3.1)
Заметим, что согласно s-m-n теореме функция d является взаимно
однозначной и всюду определенной. Заметим также, что d не зависит от
/•
По заданной функции / выберем такой индекс и, что
(fv = f о d. (3.2)
Мы утверждаем, что число п = d(v) является неподвижной точкой для
/. Сначала заметим, что если / всюду определена, то fd = <pv также
всюду определена. Таким образом, (pv(v) определена и
Теперь имеем
4>п - <Pd(v) = VWv) = 4>fd(v) - 4>f{n)- (3.3)
Второе равенство следует из (3.1), а третье равенство — из (3.2). Ц
3.2 	Следствие. Для каждой вычислимой функции f существует
такое число п, что Wn = W/(n)*
Вышеприведенное доказательство удобно представить как неудав-
шееся диагональное рассуждение [Оуингс, 1973]. В обычном
диагональном доказательстве имеется квадратная таблица объектов {ах,и }X)lt€u;
и строится такая последовательность D1 = {а^}, где х € и>, что для
каждого х а'х ф аХ)Х, где D = {аХуХ}х^ — диагональная
последовательность и, следовательно, D* не совпадает ни с одним из рядов
Ru = {&х,и}хеи>> Теперь рассмотрим таблицу, в которой aXfU = ^u(x),
полагая aX)U и ^р(Ри(х) нигде неопределенными функциями, если <ри(х)
неопределена. Из s-m-n теоремы вытекает, что диагональная
последовательность D = { ах>х }хеи совпадает с одной из строк, а именно, с

64
Глава II. Основания в. п. множеств
е-й строкой Re = { ф<рЛ(х) }жеи>} где фе = d. Любая вычислимая
функция / индуцирует некоторое преобразование строк Ru = {ip<pu(x)
этой таблицы, при котором Ru отображается на строку }х€и>-
В частности, / отображает «диагональную» строку Re = {ipd(x) }xeu> на
Rv = {(ffd(x) }iew Так как Re — диагональная последовательность, то
v-й элемент этой последовательности, а именно, <fd(v) = Vipv{v), остается
неизменным под действием / и, следовательно, ipd(v) —
Типичным примером применения теоремы рекурсии является
доказательство существования такого числа п, что Wn = { п }. (Определяем
с помощью s-m-n теоремы Wf (ж) = { х } и по теореме рекурсии
находим такое число п, что Wn = Wf^n) = {п}.) Так же можно показать,
что существует такое п, что <рп = Ах[п]. Выше мы сформулировали
теорему рекурсии в её простейшей форме, хотя, в действительности, её
доказательство дает нам значительно больше полезной информации, и
мы сейчас это явно сформулируем.
3.3 Предложение. В теореме рекурсии число п может быть найдено
эффективно по индексу f с помощью вычислимой 1:1-функции д.
Доказательство. Пусть v(x) — такая вычислимая функция, что (pv(x) =
<рх о d и д(х) = d(v(x)). По s-m-n теореме как d, так и v являются 1:1-
функциями. О
3.4 Предложение. В теореме рекурсии для функции f существует
бесконечное в. п. множество неподвижных точек.
Доказательство. По лемме 1.3.2 о множестве индексов существует
бесконечное в. п. множество V таких индексов v, что <pv = / о d. Но d —
взаимно однозначная функция, поэтому в. п. множество { d(v) }vgv
бесконечно. Q
Для более тонких применений таких, как теорема Майхилла из § 4,
мы нуждаемся в следующей форме теоремы рекурсии с параметрами.
(Нумерацией конечных последовательностей рассмотрение можно
свести к одному параметру.) Доказательство использует равномерность
предыдущего доказательства и ему аналогично.
3.5 Теорема рекурсии с параметрами (Клини). Если f(x,y) —
вычислимая функция, то существует такая вычислимая функция п(у),
Что <рп(у) = ^/(n(y),y)-
Доказательство. Определим вычислимую функцию d следующим об-

§ 3. Теорема рекурсии
65
разом:
Ффх{х,У){2)ч
неопределена
если <рх(х,у) определена;
в противном случае.
Выберем такой индекс v, что ч>У{х,у) = 2/),2/)- Тогда п(у) =
d{v,y) — неподвижная точка, т. к. (Pd(v,y) = <P<pv(v,y) = Vf{d{v,y),y)-
Первое равенство следует из определения функции d, второе — из
определения V. П
Заметим, что равномерности, содержащиеся в утверждениях 3.3 и 3.4,
присутствуют и в теореме 3.5. На неформальном уровне применение
теоремы рекурсии позволяет определять ч. в. функцию ipn (или в. п.
множество Wn) заранее, как часть алгоритма, используя в определении ее
(его) собственный индекс n, ipn(z) : ...п Это достигается с помо¬
щью теоремы рекурсии следующим образом. Сначала с помощью s-m-n
теоремы определяем функцию /(ж), <Pf(x)(z) : ...ж..., а затем берем
её неподвижную точку, ipn(z) = <Pf(n)(z) : •••и Единственное огра¬
ничение на этот неформальный метод состоит в том, что мы в этой
программе не можем использовать никакие специальные свойства </?п
(такие, как «ipn всюду определена», или Wn ф 0). Например, если для
каждого х функция ц>/(х) окажется всюду определенной, то, очевидно,
и неподвижная точка <Р/(п) = 4>п будет всюду определенной функцией.
Однако инструкции для вычисления (р/(х) не должны содержать таких
слов, как «ждите до тех пор, пока (px(z) не определится, и тогда
возьмите значение v = <px(z),..Более того, эти инструкции должны быть
применимы к произвольной функции ipx.
Такое неформальное использование теоремы рекурсии в
литературе встречается часто и значительно упрощает доказательства, которые
иначе были бы технически весьма громоздкими. Мы проиллюстрируем
этот метод, приведя альтернативное доказательство теоремы 2.2. (По
замечанию, предшествующему теореме 2.2, эта теорема равносильна
теореме 3.6.)
3.6 	Теорема. Не существует ч. в. функции гр такой, что если Wx
вычислимо у то ф(х) определена и (р^(х) является характеристической
функцией множества Wx. (Не существует равномерного
эффективного способа перехода от Ei -индекса вычислимого множества к его
До -индексу.)
Доказательство. Используя теорему рекурсии, определим вычислимое

66
Глава II. Основания в. п. множеств
множество
если ф(п) I и <^,(„)(0) 1= О,
в противном случае.
Ясно, что <р-ф(п) не может быть характеристической функцией множества
Wn, потому что О G Wn тогда и только тогда, когда <р<ф(п){0) =0- D
Следующая теорема усиливает теорему 3.5, замещая всюду
определенную функцию f(x,y) частичной функцией ф{х,у), и имеет такое же
доказательство. Такая её форма нам понадобится позднее.
3.7 	Теорема. Если ф(х,у) — частично вычислимая функция, то
существует такая вычислимая функция п(у)1 что
Доказательство. Используйте то же самое доказательство, что и в
теореме 3.5. D
3.8-3.18 Упражнения
3.8. Множество А называется самодвойственным, если А А.
Например, если А = В 0 В, то А самодвойственно.
(a) Используя теорему рекурсии докажите, что никакое индексное
множество А не может быть самодвойственным.
(b) Приведите короткое доказательство теоремы 1.4.13 Райса.
3.9. Покажите, что для любой ч. в. функции ф(х,у) существует такое
число п, что ipn(y) = *Ф(п,у)-
3.10. Покажите, что следствие 3.2 эквивалентно следующему
утверждению: для каждого в. п. множества А справедливо (3n)[Wn = { х : (х, п) G
А}]. Указание. Определите в. п. множество Ап = {х : (х,п) G А} и
сравните последовательности { Ап }п€а; и { Wn }П€и;-
3.11. Используя неформальную технику теоремы 3.6 покажите, что не
существует такой ч. в. функции (ре, что если ipx — характеристическая
функция конечного множества F, то ipe(x) 1= max(F). Указание.
Определите <pn(t + 1) = 1, если t = (fis)[(pei8(n) JJ, и (рп{х) = 0 в противном
случае, и примените строку (3.1) главы I.
3.12. Покажите, что не существует такой вычислимой функции /(x,s),
что для всех х f(x)= lims f(x,s) существует и f(x) является характе¬
(Уу)[ф(п(у),у) 4.=* ¥>„(,) = фф(п(у),у)\'

§ 3. Теорема рекурсии
67
ристической функцией множества Tot (см. определение Ш.3.1).
Указание. Предположите противное и определите (pn(s), используя {/(n, t)}t^s
таким образом, что (pn(s) | тогда и только тогда, когда f{n,t) = 0 для
некоторого t ^ s.
3.13. Пусть / — вычислимая функция. Покажите, что существует такое
число п, что: (i) Wn вычислимо и (ii) {py)[Wy = Wn\ > /(п). Указание.
Перечисляйте конечное множество Wn следующим образом: сначала
вычислите /(п), а затем определите Wn = К } (f(n) + 1), где А } х
означает ограничение множества А на элементы у < х.
3.14. (а) Используя вычислимую перестановку р в упражнении 1.5.9
докажите, что теорема рекурсии верна для допустимой нумерации {гре }ееи,
тогда и только тогда, когда она верна для стандартной нумерации
{ Фе }е6и> •
(b) Пусть гре — частично вычислимая функция, график которой
получается применением теоремы 1.6 унйформизации к отношению Re =
{{х,у) : (ж,у) е We}, и пусть Wh{e) = {(х,у) : гре{х) = у). (Будем
говорить, что W€ является однозначным множеством, если Re —
однозначное отношение.) Докажите, что {гре }е€и является допустимой
нумерацией.
(c) Используя (а) и (Ь) докажите, что из следствия 3.2 вытекает
теорема 3.1. Указание. Для того, чтобы по данной функции / найти такое
число п, что грп = VV(n)> примените следствие 3.2 к функции ho f oh.
(Заметим, что мы не можем применить следствие 3.2 непосредственно к
функции / и затем использовать функцию h, т. к. из того, что We = Wi,
не обязательно следует Wh(e) = Wад-)
3.15 	(Теорема парной рекурсии — Смальян).
(a) Докажите, что для любых вычислимых функций f{x,y) и д(х,у)
существуют такие числа а и Ь, что ipa = 4>/{а,ъ) и ц>ь = <рд(а,ь)- Указание.
С помощью теоремы 3.5 найдите такую вычислимую функцию а{у), что
<Ра(у) = ^/(о(у),2/)* Затем определите а = а(Ъ), где Ъ — неподвижная точка
ВЫЧИСЛИМОЙ функции h(y), где (рцу) = Ч>д(а{у),У)-
(b) Используя в точности такой же метод докажите теорему парной
рекурсии с параметрами, а именно, что для любых вычислимых функций
f(x, у, z) и д(х, у, z) существуют такие вычислимые функции a(z) и b(z),
что
4>a{z) — <Pf(a(z),b(z),z) и *Pb(z) ~ lPg(a(z),b(z)tz)'

68
Глава II. Основания в. п. множеств
3.16. 	Используя теорему рекурсии докажите, что К не является
индексным множеством.
3.17 (Лахлан). Пусть { Z* }г,$€и; — стандартное перечисление некоторой
допустимой нумерации { }*€и; в. п. множеств (см. определение 2.8).
Докажите, что для любого обычного перечисления WiyS,
удовлетворяющего соглашению 2.6, существует такая вычислимая функция ft, что
W{ = Zh(i) для любого г, и элементы множества Wi появляются при
перечислении { Wi>8 }г,$еи> в том же самом порядке, как и при перечислении
{ Zh(i),s Указание. Поскольку {Zi}ieiV является допустимым пе¬
речислением в. п. множеств, то, согласно упражнению 1.5.9, существует
такая вычислимая функция д, что Wi = Zg^ для любого i. Используя
теорему рекурсии с параметрами определите вычислимую функцию /(г)
следующим образом. Пусть элементы множества Wi = { ai,a2,... }
перечислены именно в таком же порядке (при перечислении {Wii8}seuf)-
Положите а\ в Wf^y Затем перечисляйте an+i в Wf^ тогда и только
тогда, когда существует такой шаг s, что Zg^f^yi8 = { ai, a2,..., ап }, и
все элементы a*, i ^ п, появились в множестве Zg^f^y именно в этом
порядке (при перечислении { Zg^f^yiS}se w). Положите h(i) = g(f{i)).
3.18 (Лахлан). Пусть нумерация { Z* }i,seu> определена как в
упражнении 3.17. Определим вычислимые множества Vi следующим образом:
Vi = {n : (3s)[n € Z?+1 - Z\ & n > max(Z?)] }.
(См. также упражнения 1.19 и 2.11.)
(a) Используя упражнение 3.17 докажите, что последовательность
{ Vi единственна в следующем смысле. Если { Z* }г,$еи> — другая
одновременно в. п. (о. в. п.) таблица, удовлетворяющая условиям (1)-(3)
определения 2.8, и {V*}^ — соответствующая ей последовательность
вычислимых множеств, то на ш существует такой вычислимый
изоморфизм ft, ЧТО Vi = Vh(i)-
(b) Докажите, что для любой вычислимой функции / Vn = V)(n) для
некоторого п, другими словами, теорема рекурсии верна для
вычислимых множеств { Vn }П£
§ 4. Полные, продуктивные и креативные множества
В § 3 главы I мы определили сводимости и . В главе III мы
определим более общую тьюрингову сводимость •

§ 4• Полные, продуктивные и креативные множества
69
4.1 Определение. Пусть г = 1,т или Т. Множество Л называется
г-полным , если А в. п. и А для любого в. п. множества Ж
4.2 Теорема. Множества К, Zfo u являются 1-полными (и,
следовательно, по теореме 1.5.4 Майхилла Ко = К\ = К).
Доказательство. Каждое из этих множеств в. п. согласно (1.1), (1.2)
и (1.3). Более того, множество Ко = { (х, у) : х Е Wy} 1-полно, т. к.
х Е Wy тогда и только тогда, когда (х,у) Е Ко. Пусть Ж —
произвольное в. п. множество. Определим, как в теореме 1.4.10, вычислимую
1:1-функцию /:
Теперь, если х € W, то W/(x) = ^ и /(ж) Е if П Zfi. Если х Е то
Wf(x) = 0 и /(ж) ^ (jK Uifi). Таким образом, W К и W К\
посредством /. Ц
4.3 	Определение, (i) Множество Р называется продуктивным, если
существует такая ч. в. функция ф(х), называемая продуктивной
функцией для Р, что
(ii) 	В. п. множество С называется креативным, если С продуктивно.
Например, множество К является креативным, т. к. К —
продуктивное множество с тождественной продуктивной функцией 'ф(х) = х.
Поскольку, по теореме 4.2, К = К0 = К\, то множества Ко и К\ также
креативные. (Заметим, что если Wx С К, то х Wx и х £ К.)
Креативное множество С является «эффективно невычислимым» в том смысле,
что для любого множества Wx, кандидата на роль С, ф(х)
предоставляет эффективный контрпример, поскольку ф(х) ЕС — Wx. Пост [1944]
назвал эти множества креативными, т. к. их существование
подтверждает «положение о том, что любая символическая логика неполна и
может быть расширена до совокупности предложений», необходимой для
задания отношения {(х,у) : х Е Wy }. Далее Пост отмечает: «С
неизбежностью напрашивается вывод о том, что даже в такой конкретной и
естественной математической системе математическое мышление
является, и должно оставаться, в значительной степени творческим.»
{
ш, если х Е W,
0 в противном случае.
(Vx)[Wx С Р=> [ф{х) | & ф(х) Е Р - Wx]].

70
Глава II. Основания в. п. множеств
4.4 Теорема. Для любого продуктивного множества Р существует
всюду определенная вычислимая продуктивная 1:1-функция р.
Доказательство. Пусть множество Р продуктивно с продуктивной
функцией ф. Сначала определим всюду определённую продуктивную
функцию q для Р следующим образом. Пусть g — такая вычислимая
функция, что
W - / Wx’ если Ф(х) 4>
glx> \ 0 в противном случае.
Определим q(x) либо как ф(х), либо как ф(д(х)), в зависимости от
того, что из них вычислится первым. Если Wx С Р, то ф(х) определена
и Wg(x) = Wx, поэтому оба числа ф(д(х)) и ф(х) принадлежат Р — Wx.
Теперь преобразуем функцию q в продуктивную 1:1-функцию р.
Пусть Wh(x) = Wx U { q(x) }. Заметим, что справедливо
Wx CP=>Wh{x) CP. (4.1)
Пусть р(0) = g(0). Чтобы определить р(х + 1), перечисляем
множество { q(x Н- 1), qh(x + 1), qh2(x + 1),... } до тех пор, пока либо не
встретится некоторый элемент у, не принадлежащий {р(0),... ,р(ж) }, либо
не случится повторение. В первом случае определяем р(х + 1) = у. Во
втором случае в силу (4.1) имеем W^+i £ -Р? и мы можем определить
р(* +1) = (м)[у £ {р(о),...,р(ж) }]. D
4.5 Теорема, (i) Если Р продуктивно, то Р не в. п.
(ii) Если Р продуктивно, то Р содержит бесконечное в. п.
подмножество W.
(iii) Если Р продуктивно и Р <^т А, то А также продуктивно.
Доказательство, (i) Очевидно.
(ii) Пусть Wn = 0, и Wh(x) = WXU {р{х) }. Определим
W = {p(n),ph(n),ph2(n),...}.
(iii) Пусть Р А посредством функции /, и р — продуктивная
функция для множества Р. Пусть Wg[x) = f~1{Wx). Тогда fpg —
продуктивная функция для множества А. О
Теорема 4.5(iii) позволяет находить новые продуктивные множества
Р, используя продуктивность множества К. Для этого достаточно
установить, что К <^т Р. Ниже с помощью теоремы рекурсии мы докажем,

§ 4• Полные, продуктивные и креативные множества
71
что каждое продуктивное множество обладает этим свойством.
Отсюда непосредственно следует, что все креативные множества 1-полные и,
следовательно, вычислимо изоморфны множеству К.
4.6 	Теорема (Майхилл [1955]). (i) Если множество Р продуктивно,
то К Р.
(ii) 	Если множество С креативно, то С 1-полно и С = К.
Доказательство. (i) Пусть р — всюду определенная продуктивная 1:1-
функция для Р. Определим вычислимую функцию / следующим
образом:
Wf(xty)
Г{р(х)}, если у € К,
\ 0 в противном случае.
По теореме 3.5 рекурсии с параметрами существует такая вычислимая
1:1-функция п(р), что
^пы
— W/(n(y),y) —
f{p(n(y))}>
\0
если у £ К,
в противном случае.
Имеем
(4.2)
У е к => Wn{y) = {рп(у) } =* Wn(y) £Р=> рп(у) е Р, (4.3)
У ек=> Wn(y) = 0 => Wn{y) С Р => рп(у) е Р. (4.4)
В обеих строках первая импликация следует из (4.2). Из того, что р
является продуктивной функцией для Р, следует вторая импликация в (4.3)
и третья импликация в (4.4). Но из (4.3) и (4.4) следует, что К Р
посредством функции Ау\рп(у)\.
Часть (ii) сразу следует из (i) и теоремы 1.5.4 об изоморфизме. О
4.7 	Следствие. Следующие условия эквивалентны:
(i) Р продуктивно;
(ii) ЯЧ1 Р\
(Ш) К Р. Q
4.8 	Следствие. Следующие условия эквивалентны:
(i) С креативно;
(ii) С 1-полно;
(Ш) С m-полно. Q

72
Глава II. Основания в. п. множеств
Следующее определение нам понадобится ниже в упражнении 4.15 и
в главе IV.
4.9 Определение. Пусть (А1}А2) и (BlfB2) — две пары множеств
таких, что Ai П А2 = 0 = В\ П В2. Тогда (Bi,B2) (Ах,А2), если
существует такая вычислимая функция /, что f(B\) С А\, f(B2) С
А2 и f{Bi U В2) С А\ U А2. Мы пишем «^1», если / является взаимно
однозначной.
4.10-4.17 Упражнения
4.10. Пусть Ах = { у : (ру = (рх }.
(a) Докажите, что для каждого х множество Ах продуктивно.
Указание. Соедините следствие 4.7 и упражнение 1.4.20.
(b) (Фейер). Покажите, что сведение К Ах не равномерно по х,
а именно, не существует такой вычислимой функции f(x,у), что для
любого х число у Е К тогда и только-тогда, когда f(x,y) Е Ах.
Указание. Выберите у о Е К, рассмотрите функцию Xx[f(x,yo)] и используйте
теорему рекурсии для /.
4.11. Используя теорему рекурсии, приведите альтернативное
доказательство упражнения 1.5.9 (что любые две допустимые нумерации ч. в.
функций переводятся друг в друга подходящими вычислимыми
Перестановками). С этой целью докажите, что для каждой вычислимой
функции д, удовлетворяющей условиям упражнения 1.5.9, существует такая
вычислимая функция </i, что для всех х справедливо фд(х) = Фдх{х) и
gi(x -t-1) > gi(x). Указание. Для того, чтобы найти </i, сначала
определите такую вычислимую функцию Л, что
(i) (Vx)[¥»fc(e,*) = <ре] И
(ii) (Vx)(Vy)[x фу=> gh(e, х) ф gh(e, j/)].
Для фиксированного е определите функцию h(e,k) индукцией по к.
Пусть ft(e, 0) = е. Положите Вь = {gh(e, 0),... ,gh(e, к) }. Используя
теорему рекурсии, определите
<Pe(z),
неопределена
если g(n) i Вк,
в противном случае.
Если д(п) £ В*, то пусть h(e,к-I-1) = п. В противном случае (ре = (рп =
Az[f], и /г(е, к -I-1) можно определить с помощью упражнения 4.10(a).

§ 4• Полные, продуктивные и креативные множества
73
4.12. Докажите, что если К А посредством функции / и множество
А не в. п., то существует 2**° множеств В таких, что К В
посредством /. Следовательно, существует 2**° продуктивных множеств.
Указание. Если множество А не в. п., то 5 = А — f(K) бесконечно.
4.13. Пара (А, В) непересекающихся в. п. множеств называется
эффективно неотделимой, если существует такая частично вычислимая
функция ф, называемая продуктивной функцией для (А, В), что для
всех х и у справедливо
(a) Используя метод теоремы 4.4 докажите, что функцию ф можно
выбрать всюду определенной и взаимно однозначной.
(b) Докажите, что в. п. множества А = {х : <рх(х) = 0} и В = {х :
(рх(х) = 1} эффективно неотделимы. Указание. Определите функцию ф
следующим образом:
Напомним, что Wx\Wy обозначает множество элементов, перечисленных
в Wx раньше, чем в Wy (см. определение 2.9).
(с) 	Покажите, что если (А, В) — пара эффективно неотделимых в. п.
множеств, то оба множества А и В являются креативными.
4.14 (Хэй). Пусть Ах определено как в упражнении 4.10. (а) Докажи¬
те, что если (ра и щ различные ч. в. функции, то Аа и Аь
эффективно неотделимы. Указание. Используя теорему рекурсии определите
<^/(®,з/)(2;) = если /(яг,у) Е Wx\Wy (см. определение 2.9), и опреде¬
лите <Pf(x,y) подходящим образом в остальных случаях.
(Ь) Предположим, что щ собственно расширяет <ра. Докажите, что
существует такое в. п. множество W Э Аь, что W П Аа = 0, но не
существует такого в. п. множества V Э Аа, что V П Аь = 0.
4.15 (Смальян). Пусть (А\, А2) — пара эффективно неотделимых в. п.
множеств с продуктивной функцией р. Докажите, что если (Bi, В2) пара
непересекающихся в. п. множеств, то (В^Вг) ^1 (Ai, А2) (см.
определение 4.9). Указание. Используя теорему 3.15(b) парной рекурсии с одним
[А С WxhB С WyhWx nWy=9]
=> т*> у» I У» t Wx и wy\.
1, 	если z е Wx\Wy,
0, 	если z е Wy\Wx,
t в противном случае.

74
Глава II. Основания в. п. множеств
параметром, определите такие вычислимые 1:1-функции g(z),h(z), что
и
w.(*) = {
WHz) = {
М и{р«$(*),Л(*)»}.
Ах
{p{{g{z),h{z)))},
а2
если z £ В2,
в противном случае,
если z £ 2?i,
в противном случае.
Далее, рассмотрите функцию f(z) = p((g(z),h(z))) и покажите, что
(Яь-Ва) (i4i,i42) посредством функции /.
4.16° (Лахлан). (а) Докажите, что если К А х В и одно из множеств
А или В в. п., то /Г Л или К J5.
(Ь) Сделайте вывод, что не существует пары несравнимых в. п. т-
степеней, н. в. г. которых является m-степенью множества if. (Указание.
Имейте в виду, что А® В А х В.)
Указание для (а). Предположим, что К А х В и множество J5
в. п. Постройте такое в. п. множество D, что D А х В, и либо
if А, либо /Г D ^m J5. Используя теорему рекурсии можно
предположить, что в начале построения мы имеем индекс множества D
и, следовательно, такие вычислимые функции /, <7, что х £ D тогда и
только тогда, когда f(x) £ А & £ J5. Назовем элемент ж хорошим
на шаге 5, если ж ^ Ds и <7(2;) £ J5*. Следовательно, х £ D тогда и
только тогда, когда f(x) £ А. Пусть G = • • •} — вычислимое
перечисление элементов, хороших на некотором шаге (будем называть
их просто хорошими элементами). Если множество G бесконечно, то мы
должны добиться, чтобы г £ if тогда и только тогда, когда Xi £ D.
Таким образом, г £ if тогда и только тогда, когда f(xi) € А и,
следовательно, К А. На произвольном шаге s, если i £ ifs и элемент ж*
существует, то кладите Xi в D. Кроме того, если г £ ifs и г не является
хорошим на шаге s, кладите i в D. Если множество G бесконечно, то
г £ if тогда и только тогда, когда Xi £ D, а х\ £ D тогда и только тогда,
когда f{xi) £ А. Таким образом, if А. Если множество G конечно,
то почти для любого я, х £ D тогда и только тогда, когда д(х) £ В
и D =* if (т. е. симметрическая разность множеств D и if конечна),
таким образом, if В. (Это — первый пример доказательства,
где мы следуем двум стратегиям одновременно. Стратегия о\
пытается добиться if D А, как только появляется хороший элемент.
Стратегия а2 пытается добиться К =* D В. Действие стратегии
02, т. е. построение функции h, сводящей К к В, «нарушается», когда

§ 4• Полные, продуктивные и креативные множества
75
появляется новый хороший элемент, и сг2 начинает все сначала с новым
кандидатом на роль сводящей функции D В.)
4.17. 	(Джокуш-Морхер). Пусть А — произвольное в. п. множество,
отличное от и. Докажите, что множество А креативно тогда и только
тогда, когда
(Vb. п. В)[А С\В = Ъ=>А = АиВ].

Глава III
Тьюринговая сводимость и оператор
скачка
Ранее изучавшиеся сводимости в этой главе обобщаются посредством
более широкого понятия тьюринговой сводимости, которая
формализует понятие вычислимости множества В относительно другого
множества А. Это понятие будет одним из главных объектов нашего изучения.
Большинство основных результатов § 3 главы I могут быть обобщены
на их релятивизованные формы с примерно такими же
доказательствами. В § 2 мы рассмотрим верхнюю полурешетку тьюринговых степеней
и введем оператор скачка через релятивизацию определения 1.4.2
невычислимого в. п. множества К. В § 3 будут изучены взаимосвязи этих
двух объектов, мы докажем лемму о модуле и лемму о пределе, которые
окажутся чрезвычайно полезными при изучении в. п. степеней и
степеней ниже О'.
§ 1. Определения относительной вычислимости
Неформально, множество В вычислимо относительно множества Л,
сокращенно, В Ау если существует алгоритм распознавания
принадлежности чисел х множеству В, предполагая известными ответы на
любые вопросы вида «верно ли, что у Е А?». Например, если В А
посредством /, то х Е В тогда и только тогда, когда f(x) Е А. Хотя т-
сводимость — первая и наиболее естественная сводимость, она является
весьма ограниченной. Например, ясно, что для любого множества А его
допролнение А вычислимо относительно А, т.к. х € А х £ А, но не
существует невычислимого в. п. множества, удовлетворяющего условию
А А. Этот пример побудил Поста [1944] ввести определенные
промежуточные сводимости, такие как ^tt и ^ttl которые мы вместе с неко¬

§ 1. Определения относительной вычислимости
77
торыми другими изучим в упражнениях § 2 главы V, они впоследствии
окажутся полезными. Теперь обратимся к наиболее важной сводимости
^т> для которой приводим два эквивалентных формальных определения,
полученные релятивизацией двух формальных определений § 2 главы I.
1.1 Определение. Пусть А С и. Частичная функция называется
частично вычислимой относительно А, если она получена по правилам
(i)-(vi) § 2 главы I, где \А добавлена к функциям (i)-(iii) как новая
исходная функция.
Возможно, на интуитивном уровне легче воспринимается
определение, основанное на модифицированном понятии машины Тьюринга, и на
нем в дальнейшем наши формальные построения и будут основываться.
Машиной Тьюринга с оракулом является обычная машина Тьюринга с
встроенной, открытой «только для чтения» внешней лентой, называемой
оракульной лентой, на которой напечатана характеристическая
функция некоторого множества А (называемого оракулом) и символы
которой нельзя изменить. Лента самой машины Тьюринга будет называться
рабочей лентой, и она будет устроена так же, как и раньше.
Читающая головка будет двигаться вдоль обеих лент одновременно. Пусть по-
прежнему Q — конечное множество состояний, Ei — алфавит
оракульной ленты {J5,0,1}, — алфавит рабочей ленты {J5,1}, и { Д, L} —
операции, означающие движения головки направо и налево. Тьюринго-
вой программой теперь будет называться частичное отображение
6 : Q х Ei х Е2 —У Q х Е2 х { Я, L },
где S(q,a,b) = (р, с, X) означает, что если машина находится в
состоянии q, считывает символ а на оракульной ленте и символ Ъ на рабочей
ленте, то она переходит в состояние р, печатает символ «с» вместо «6»,
и читающая головка сдвигается вправо (влево) на обоих лентах в случае
X = R (X = L, соответственно). Остальные элементы описания
машины Тьюринга будут такими же, как в § 2 главы I, за исключением того,
что в начальный момент читающая головка находится на той клетке
оракульной ленты, которая кодирует хл(0) (см. диаграмму 1.1).
Пусть у А- 1 — количество непустых клеток оракульной ленты,
содержимое которых считывалось читающей головкой в процессе
вычисления. (А именно, у — это наибольшее число, принадлежность которого
множеству А проверялось в процессе вычисления.) Мы говорим, что в
вычислении были использованы элементы z ^ у. (См. определение 1.7.)

78
Глава III. Тъюринговая сводимость и оператор скачка
(Заметим, что машина Тьюринга может двигаться влево от начальной
точки, так что общее количество просматриваемых машиной клеток
рабочей ленты в ходе вычисления может быть намного больше, чем у.)
Эти программы машины Тьюринга с оракулом , т. е. конечные
множества шестерок, составленных из вышеперечисленных символов,
могут быть эффективно пронумерованы почти так же, как в
упражнении 1.2.11(b). Обозначим через Ре программу, имеющую номер е в такой
эффективной нумерации. Отметим, что Ре не зависит от оракула А.
1.2 Определение, (i) Частичная функция ф вычислима по Тьюрингу
относительно множества А (А-вычислима по Тьюрингу), пишется как
ф А, если существует такая программа Ре, что если на оракульной
ленте машины Тьюринга записана функция хл, то для всех х и у имеем
ф(х) = у тогда и только тогда, когда программа Ре при входном
значении х останавливается и выдает у как выходное значение. В этом случае
мы пишем ф = {е}л, или, что эквивалентно, ф = Ф£, или ф = Фе(А).
Мы говорим, что ф(х) расходится (записывается как ф(х) f), если Ре с
поданным входным значением х никогда не останавливается.
(ii) 	Мы также в качестве оракула допускаем (всюду определенные)
функции, определяя { е как { е }л, где А = graph(/).
1.3 Теорема. Частичная функция ф A-частично вычислима тогда
и только тогда, когда ф A-вычислима по Тьюрингу.
Мы опускаем доказательство этой теоремы, которое может быть
найдено в Клини [1952а]. Совпадение этих двух формальных определений,

§ 1. Определения относительной вычислимости
79
а также ряда других является свидетельством в пользу истинности ре-
лятивизованного Тезиса Чёрча, который утверждает, что функция ф
^4-частично вычислима тогда и только тогда, когда ф вычислима
относительно А в интуитивном смысле. Поэтому мы будем в
дальнейшем употреблять термины «A-частично вычислима», «А-вычислима по
Тьюрингу» и «А-вычислима» как синонимы.
Результаты главы I легко релятивизовать с теми же
доказательствами, заменяя вычислимые функции на A-частично вычислимые.
Например,
1.4 	Релятивизованная теорема о нумерации. Существует
такое число z G что для всех множеств А С ш и для всех х,у G ш
A-частично вычислимая функция Ф£(х,у) удовлетворяет соотноше-
нию Ф*(х,у) = Ф£(у).
1.5 Релятивизованная s-m-n теорема. Для всех m,n ^ 1
существует такая вычислимая 1:1-функция т+ l-й переменной s™, что для
всех множеств А С и и для всех х, у\, у2,..., ут € и
Ф<(х,, гп[Ф^(у1,..., ym,zu ... ,zn)\.
(Отметим, что s™ является вычислимой, а не только А-вычислимой
функцией.)
Доказательство. Пусть т = п = 1, обозначим s™ через s. Новая
программа Р8(х,у) ПРИ данном входном значении z применяет программу Рх
с входным значением (у, z). Это позволяет определить s(x,y) как
вычислимую функцию, т. к. программа Р8(х,у) не зависит от оракула А. Ясно,
что s можно сделать 1:1-функцией, используя идею доказательства
леммы 1.3.2 о множестве индексов. []
1.6 Релятивизованная теорема рекурсии (Клини). (i) Для всех
множеств А С и и для всех х,у Е если f(x,y) является
А-вычислимой функцией, то существует такая вычислимая функция п(у), что
^п(у) ^f(n(y),y)'
(ii) 	Более того, п(у) не зависит от оракула А, а именно, если
f(x,y) = { е }А(х,у),

80
Глава III. Тьюрипговая сводимость и оператор скачка
то вычислимая функция п(у) может быть найдена равномерно по е.
Доказательство. Применяем доказательство теоремы И.3.5. Заметим,
что функция п(у) будет вычислимой (а не только А-вычислимой),
поскольку вычислимой является s-m-n функция s(x,y) из теоремы 1.5.
Поэтому можем определить вычислимую функцию d(x,y) так же, как и
в теореме II.3.5, релятивизовав все частичные функции к оракулу А. Ц
Отметим, что строки сг, состоящие из 0 и 1, т. е. a Е 2<ц;, могут
рассматриваться как конечные начальные сегменты
характеристических функций. Мы отождествляем множество А с его
характеристической функцией и пишем а С А, если как частичная функция а С ха,
т. е. а(х) = ха(я) Для всех х Е domсг. Длиной строки а (записывается
как lh(a)) называется число |domcr|. Заметим, что lh(a) = цх[сг(х) t]«
Фиксируем некоторую эффективную нумерацию строк а Е 2<и) и
отождествляем а с его номером. Напомним, что А [ х означает ограничение
А на аргументах у < х и, аналогично, для а \ х. Заметим, что если
п = lh(a), то а = a f п.
1.7 	Определение, (i) Мы пишем {e}f(x) = у, если ж,г/,е < s, s > 0,
и {е}А(х) = у вычисляется за < s шагов, соответствующих программе
Ре, причем в вычислении используются только числа z < s. (Сравните
это с определением 1.3.8.)
(и) use-функцию u{A\e,x,s) определяем как 1 -I- наибольшее число,
использование е в вычислении, если { е }f(x) и и(А] е, ж, s) = 0 в
противном случае. Определим также use-функцию и{А\ е,*а;), которая
совпадает с и(.А; е, ж, s), если {е}^(ж) I для некоторого s, и неопределена, если
{e}A(*)t-
(iii) Будем писать { е (х) = г/, если { е }^(х) = у для некоторого А Э сг,
причем в вычислении используются только числа z < lh(a). Если такая
а совпадает с А [ и, то мы также пишем {е}^и(ж) = у.
(Определение (ii) построено так, что если {e}f(x) = у, то {е}°{х) = у, где
сг = А [ u(A;e,x,s).)
(iv) Запись {е}сг(х) = у означает, что (3s)[{е}£(я) = у].
Отметим, что это определение гарантирует, что
{ е 0*0 =y=i>x,y,e<s; и(А; е, х, s) ^ s, (1.1)
{ в }^0*0 = У => (Vi ^ s)[{ е }f(x) = у & и(А) е, х, t) = и(А; е, х, в)],
(1.2)
И

§ 1. Определения относительной вычислимости
81
так что определение и(А;е,х) в 1.7 (ii) не зависит от s.
Заметим, что если А вычислимо, то и{А\ е, х, s) является вычислимой
функцией, и её индекс может быть найден равномерно по Д0-индексу А.
В последующих главах мы определяем в. п. множество А = {Js As, где
{ As }sev — вычислимая последовательность конечных множеств
(определяемых, скажем, по каноническим индексам). В этом случае заметим,
что Xxs[u(As] е, х, s)] является вычислимой функцией.
1.8 Главная теорема о перечислении.
(i) Множество {(е,сг, х, s) : (е}£(х) 1} вычислимо;
(ii) Множество L = {(е,сг,х) : {е}<7(х) 1} в. п.
Доказательство, (i) Совершаем тьюрингово вычисление по программе
Ре с входным значением х и со строкой сг, записанной на оракульной
ленте, пока либо не получим выходное значение, либо не будет сделано
s шагов в вычислении.
(й) {е}°’(х) (3s)[{e}£(x) |], так что L является Ei-множеством
и, следовательно, L — в. п. множество. О
1.9 Теорема (use-принцип).
(О {е}А(х) = у^ (3«)(3<т С А)[{е}'(х) = у];
(ii) 	{ е }£(х) =y=^(\/t^ s)(Vr D о-)[{ е }[(z) = у);
(ш) { е }* (х) = у=$>(УАЭ о-)[{ е }А(х) = у].
Доказательство. Любое сходящееся вычисление сходится за конечное
число шагов, используя при этом только конечное число элементов.
Следовательно, (i) выполнено. Утверждения (ii) и (ш) следуют из
определения вычисления с оракулом. Q
Для большинства из последующих теорем use-принцип окажется весьма
важным, поскольку (i) утверждает, что если { е }А(х) = у, то { е }ст(х) =
у для некоторого сг С А, причем можно полагать а = А [ и, где
и = и(А\е,х) — use-функция из определения 1.7 (й). Более того, (Ш)
утверждает, что { е }в(х) = у для любого В Э а (а именно, use-принцип
утверждает, что Фе непрерывно, см. упражнение 1.18). Из (1.1) и use-
принципа следует, что
[{ е }^(х) = y& J4fu = Bfu]=*{e }f (х) = у, (1.3)
где и = u(A;e,x,s), т. к. (1.1) утверждает, что в вычислении
используются только числа z < и.

82
Глава III. Тъюринговая сводимость и оператор скачка
1.10 Обозначения, (i) Пусть WA — с!от{е}л. Аналогично
определяем WAS1 W° и W°8 по {e}f, {е}а и {е}£, соответственно.
(и) Пусть Ф£(х) = Фе{А\х) = \ е}А(х) и ФА3{х) = Фе1в(А;а:) = {е}^(х).
(Ш) Обозначим {е}®(х) через { е }(ж). (См. упражнение 1.14.)
1.11 Определение, (i) Множество В вычислимо относительно
(сводится по Тьюрингу к) А, пишем В А, если В = { е }А для
некоторого е. (Мы отождествляем множества с их характеристическими
функциями.) Пусть В <т А означает, что В А, но А В.
(ii) 	Множество В вычислимо перечислимо относительно А, если В =
WeA для некоторого е.
(ш) Множество В представимо в Е]4-форме (или В является
Е^4-множеством), если В = {х : (3y)RA(x,y)} для некоторого А-вычислимого
предиката RA(x,y). (По теореме II.1.3 о сжатии кванторов это
эквивалентно утверждению, что В = {х : (3y)RA(x,y) } для некоторого такого
предиката Ra.)
Все результаты § 1 главы II о в. п. множествах можно релятивизовать
к соответствующим утверждениям об A-в. п. множествах с фактически
такими же доказательствами, заменяя лишь слова «в. п.» и
«вычислимость» на «A-в. п.» и «А-вычислимость». Например,
1.12 Релятивизованная теорема о дополнении. В А тогда и
только тогда, когда В и В в. п. относительно А.
1.13 Теорема. Следующие утверждения эквивалентны:
(i) В в. п. относительно А;
(ii) В = 0 или В является областью значений некоторой А-вычислимой
всюду определенной функции;
(Ш) В является Ej4 -множеством.
Доказательство. Доказательства (i)<£> (ii) и (i) <=> (Ш) являются
релятивизациями соответствующих доказательств § 1 главы II. Например,
для доказательства (i)=> (Ш) предположим, что В = WA.
Следовательно, по use-принципу 1.9 имеем
х 6 В & (3s)(3cr)[cr С А & х Е W°J. (1.4)
Отношение х Е Wf s является вычислимым отношением четверок (е,сг,
ж, s) по теореме 1.8 (i); с другой стороны, отношение а С А является А-
вычислимым отношением на сг, т. к. а С А (V?/ < lh(a))[cr(y) = А(у)].

§ 1. Определения относительной вычислимости
83
Следовательно, (1.4) представляется в форме (3s) (Зсг)Д(е, cr,a;, s), где R
является А-вычислимым отношением. []
1.14-1.20 Упражнения
1.14. Используя метод упражнения 1.2.10, определите эффективную
нумерацию программ { Ре }е€а; и докажите, что относительно этой
нумерации фе =dfn { е }0 будет допустимой нумерацией всех частично
вычислимых функций (см. упражнение 1.5.9). Поэтому мы в дальнейшем
будем часто использовать функции { е }(ж), е £ ш, вместо ipe(x), е £ со.
1.15. (а) Докажите, что множество { (е, сг, х, г/, s) : {е}°(х) = у }
вычислимо.
(Ь) Докажите, что { (е, сг,х,у) : {е }<7(ж) = у } в. п. и что это множество
и множество L из теоремы 1.8 (ii) являются 1-полными и, следовательно,
вычислимо изоморфными К.
1.16. Для данных множеств В и А докажите, что В ^ А тогда и
только тогда, когда существуют такие вычислимые функции / и <7, что
х £ В (3a)[cr £ Wf(x) & сг С А],
х £ В (3cr)[a £ Wg(x) & сг С А].
Указание. Если В = {е}А, то используйте упражнение 1.15(b) при
у = 1 и у = 0 для получения / и g соответственно. Для доказательства
обратного утверждения примените теорему о дополнении 1.12.
1.17. Для данных в. п. множеств В и А докажите, что В А тогда
и только тогда, когда существует такая вычислимая функция ft, что
х £ В (Зг>)[г> Е Wh(x) & Dv С А].
Указание. Предположим, что В = { е }А. Пусть g получена из
упражнения 1.16 и
Wh(x) = {v : (За)[а £ Wg(x) & Dv = {у : а(у) = 0} & {у : а (у) = 1} С А]},
где Dv — как в определении II.2.4.
1.18. Рассмотрим пространство Бэра сои с обычной топологией, где
базисные открытые множества состоят из множеств Ua = {f : f £

84
Глава III. Тъюринговая сводимость и оператор скачка
cju & а С /} при а Е и)<ш. Используя use-принцип 1.9 покажите, что
частичное отображение Фе из в является непрерывным
отображением и, более того, эффективно непрерывным отображением в том
смысле, что Ф7l(U(y) = U{ UT : т Е V }, где V — в. п. множество
номеров строк т Е ш<и>.
1.19. В релятивизованной s-m-n теореме мы получили вычислимую (а
не только А-вычислимую) функцию s. С другой стороны, обычные
релятивизации теорем глав I и II позволяют находить только ^-вычислимые
функции. Постройте, например, множество А и A-вычислимое
отношение RA(x,y) такое, что теорема униформизации II.1.6 при R — RA не
выполнена ни для какой частично вычислимой селекторной функции.
1.20. Докажите, что если гр частично вычислима относительно Y Си,
то существует вычислимая функция / такая, что
(Vz € Aomxl>)[Wj{x) = W^(x)).
Более того, индекс функции / может быть найден равномерно
вычислимо по е, где гр = {е}у. Указание. Определим / так, что для всех
х Е uj
WY _ Г W${x), если ф(х) I,
^х'1 \ 0 в противном случае.
А именно, программа машины Тьюринга Р/(х) использует оракул Y,
пытаясь вычислить гр(х), и не выдает никаких выходных значений до
тех пор, пока не вычислится гр(х) = z. Затем Pf(x) начинает перечислять
элементы из Wj.
§ 2. Тьюринговы степени и оператор скачка
2.1 	Определение, (i) Определим А =т В, если А ^т В и В ^т А.
(Отметим, что ^т рефлексивно и транзитивно, так что =т является
отношением эквивалентности.)
(й) Тьюринговой степенью (или, иначе, степенью неразрешимости)
множества А назовем deg(A) = { В : В =т А].
(ш) deg(A) U deg(2?) = deg(A 0 В).
(iv) 	Степени обозначим строчными полужирными буквами а, Ь, с. Через
D обозначим класс всех степеней.
(у) Степени из D образуют частичный порядок относительно отношения

§ 2. Тъюринговы степени и оператор скачка
85
deg(A) ^ deg(R) <=>dfn А В. Пишем deg(A) < deg(R), если А <т В,
т. е. если А В и В А.
(vi) Степень а называется вычислимо перечислимой, если она содержит
в. п. множество. Обозначим через R класс всех в. п. степеней и введем
в R такой же порядок, что и в D.
(vii) Степень а называется вычислимо перечислимой относительно Ь,
если а содержит множество Л, вычислимо перечислимое относительно
некоторого множества В Е Ь.
Если два множества имеют одинаковую степень, то мы можем
считать, что они кодируют одну и ту же информацию и, следовательно,
их одинаково трудно вычислить. С другой стороны, а < b означает,
что множества степени b труднее вычислить, чем множества степени а.
Кроме того, deg(A 0 R), как легко видеть, является наименьшей
верхней гранью для deg(^) и deg(R) относительно указанного порядка (см.
упражнение 2.6). Таким образом, степени образуют верхнюю пол у
решетку (см. определение И. 1.14) (D, U). К сожалению, наибольшая нижняя
грань двух степеней не обязательно существует (следствие VI.4.4), более
того, она может не существовать даже у в. п. степеней (следствие IX.3.3
и упражнение IX.3.12). Следовательно, ни D, ни R не образуют
решетку.
В главе I мы путем диагонализации получили невычислимое в. п.
множество К. Релятивизация этой процедуры применительно к
множеству А дает такое множество КА, вычислимо перечислимое
относительно А, что А <т КЛ.
2.2 Определение, (i) Пусть КА = {х : ФА(х) |} = {х : х 6 WA }.
Множество КА называется скачком множества А и обозначается А1
(читается как «А штрих»).
(ii) 	п-Последовательным применением операции взятия скачка получаем
А(п\ п-й скачок А. Таким образом, А= А, = (А^)'.
Из релятивизованной s-m-n теоремы 1.5, доказательства
теоремы 1.5.4 и теоремы 1.5.4 Майхилла об изоморфизме вытекает, что КА =
КА = КА, где КА = { (х,у) : ФА{х) сходится} и КА = {х : WA ф 0}.
Эти альтернативные характеристики скачка весьма полезны.
В следующей теореме приведены наиболее важные свойства
оператора скачка.
2.3 Теорема о скачке, (i) А! в. п. относительно А.
(ii) 	А! А.

86
Глава III. Тьюринговая сводимость и оператор скачка
(iii) В в. п. относительно А тогда и только тогда, когда В А'.
(iv) Если А в. п. относительно В и В С, то А в. п. относительно
С.
(v) В А тогда и только тогда, когда В' А!.
(vi) Если В =т А, то В' =i А' (и, следовательно, В1 =т А!).
(vii) А в. п. относительно В тогда и только тогда, когда А в. п.
относительно В.
Доказательство. Части (i)-(iii) следуют из релятивизаций
доказательств соответствующих теорем главы I и главы И, однако
доказательство (iii) ( => ) использует КА = КА.
(iv) Если А ф 0, то А является областью значений некоторой
В-вычислимой функции и, следовательно, С-вычислимой функции, т. к. В ^т С.
(v) ( => ) Если В А, то В1 в. п. относительно А по (iv), т. к. В'
в. п. относительно В по (i). Из (Ш) следует, что В' А!.
(v) ( <= ) Если В1 А', то В и В в. п. относительно А в силу (iii)
(т. к. В, В В1). Следовательно, В А по теореме 1.12 о дополнении.
(vi) Следует непосредственно из (v).
(vii) Следует непосредственно из (iv). О
Пусть а' = deg (А'), если A G а. Отметим, что а' > а и а' в. п.
относительно а. По теореме 2.3 (vi) скачок корректно определен на степенях.
Пусть 0(n) = deg(0(n)). Таким образом, мы имеем бесконечную
иерархию степеней 0 < 0' < О" < • • • < < • • • Первые несколько степеней в
этой иерархии имеют особое значение и могут рассматриваться как
степени определенных неразрешимых проблем, рассмотренных в главе I.
О = deg(0) = { В : В вычислимо }.
О' = deg(0'), где 0' =dfn К9 = К = К0 = Кг.
О" = deg(0") = deg(Fin) = deg(Tot).
O'" = deg(0,,/) = deg(Cof) = deg(Rec) = deg(Ext).
По определению, 0 является наименьшей степенью, состоящей в
точности из вычислимых множеств. Степень 0' (читается «нуль штрих»)
является степенью проблемы остановки и также проблемы { х : Wx ф 0 },
т. к. К = К\. Вышеуказанные характеристики для 0" и 0Ш будут
доказаны в главе IV, однако, используя уже имеющиеся методы, можно
показать, что 0" = Fin (см. упражнение 2.9).
2.4 	Определение. Пусть А С ш и а = deg (А). Релятивизуя
определение II.2.5 к множеству А, назовем последовательность множеств

§ 2. Тъюринговы степени и оператор скачка
87
• Оп
• О"
Диаграмма 2.1. Тьюринговы степени (D, <)

88
Глава III. Тьюринговая сводимость и оператор скачка
{ Уп }пеи равномерно вычислимой относительно А (равномерно
степени ^ а), если существует такал А-вычислимая функция д(х,п), что
Ах[д(х, п)] является характеристической функцией для Vn при каждом
значении п.
2.5-2.9 Упражнения
2.5. Используя аксиому выбора докажите, что существует самое
большее 2«о
степеней. (Используя методы главы VI можно доказать, что
существует по крайней мере 2**° степеней, поэтому существует в
точности 2**° степеней. Для этого строится 1:1-отображение из
множества всех подмножеств и во множество степеней, см. упражнение VI.1.8.)
Указание. Для произвольного А существует только No множеств В
таких, что В А Но по аксиоме выбора Nq • к = к для всех к ^ No-
2.6. Покажите, что deg(A 0 В) является наименьшей верхней гранью
для deg(A) и deg(2?) в (D,^,U).
2.7. Пусть { Ау }У€и> — счётная последовательность множеств.
Определим бесконечное сочленение как
0{ Ау }уеш =dfn { (я, у) : х Е Ау & у Е и }.
Обозначим множество ®{Ау}уеи; через tByAy. Докажите, что
deg(®уАу) является равномерной наименьшей верхней гранью { deg(Ау) :
у Е и)} в том смысле, что если существует множество С и вычислимая
функция / такие, что Ау = { f(y) }с для всех г/, то ®УАУ С.
2.8. Докажите, что 0' = К. (Напомним, что { е }0 является допустимой
нумерацией в силу упражнения 1.14.)
2.9. 	° Докажите, что Fin =i К' (и, следовательно, Fin = К1).
Указание. Для сводимости Fin К' заметим, что х Е Fin тогда и только
тогда, когда (3y)[Wx П [у, оо) = 0], так что Fin является Ех-множеством
относительно К\. Чтобы показать К' Fin, полагаем Ks = WitS для
некоторого i такого, что Wi = К. Отметим, что
е € А! & { е }А(е) l<* (Эа)(Эв)[о- С А & { е }°{е) |].

§ 3. Леммы о модуле и о пределе
89
Определим вычислимую функцию
( lh(a), где а = {цт)[т С К8 к { е }£(е) ф],
h(e, s) = <
если такой т существует,
если не существует такого т.
Пусть Wf(e) = {х : (3s)[a; ^ Л(е,в)]}. Покажите, что е Е К' тогда и
только тогда, когда /(е) Е Fin.
§ 3. Леммы о модуле и о пределе
Хотя для нас важны все степени, мы особо интересуемся степенями,
расположенными ниже 0', а среди них, в особенности, в. п. степенями.
Покажем теперь, что deg(A) ^ 0' тогда и только тогда, когда
существует такая вычислимая функция f{x,s), что Хл{х) = lim5/(х, s), т. е.
deg (А) ^ 0' эквивалентно тому, что А может быть вычислимо
аппроксимируема. Далее, степень множества А является вычислимо
перечислимой тогда и только тогда, когда / может быть выбрана так, что / имеет
модуль сходимости тп А. Эти характеристики, особенно первая, нам
очень понадобятся.
3.1 	Определение, (i) Последовательность (всюду определенных)
функций { fs (х) }s€u; сходится (поточечно) к f(x) (записывается как f(x) =
lim5/5(ж)), если fs(x) = f(x) для почти всех s (т. е. за исключением
конечного числа) при любом значении х.
(й) Модулем (сходимости) для { f8 }5€а; называется такая функция т(а;),
что fs(x) = f(x) для всех s ^ т(х). (Следовательно, fm(x)(x) = fix)•)
Функция т(х) = (fis)(Vt ^ s)[ft(x) — f(x)] называется наименьшим
модулем.
(ш) Последовательность { fs(x)}seu вычислима, если существует
вычислимая функция f(x,s) такая, что fs(x) = f(x,s) для всех x,s.
Пусть { fs(х) }seu) — вычислимая последовательность. Заметим, что
наименьший модуль вычислим относительно любого модуля. Если / =
lim5 fs и т — произвольный модуль сходимости, то
/ то, (3.1)
т. к. fm(x)(x) = f(x). Однако, т / обычно не выполняется даже
для наименьшего модуля. Примечательно, что в силу следующей леммы,

90
Глава III. Тьюринговая сводимость и оператор скачка
если / имеет в. п. степень, то т ^т / выполнено для некоторого модуля
сходимости определенной вычислимой последовательности.
3.2 	Лемма о модуле. Если А в. п. и f ^т А, то существуют
вычислимая последовательность { fs }s€u; такая, что lims fs = /, и
вычислимый относительно А модуль сходимости для {fs}sew
Доказательство. Пусть А в. п. и / = {е}А. Выберем г таким, чтобы
А = Wi. Положим As = Wii8. Определим следующие функции:
/ Лр) _/{*}?■(*), если {е }*•(*) J,,
s \ 0 в противном случае,
ш(х) = (ns)(3z ^ s)[{e}^*^(x) I k As \ z = А \ z\.
Ясно, что { fs }seu, — вычислимая последовательность. Кроме того, т
является А-вычислимой, т. к. предикат {e}^z(x) I вычислим, а
предикат As \ z =■ А \ z является А-вычислимым, поскольку А в. п.
Наконец, т является модулем, т. к. по use-принципу 1.9 для всех s ^ т(х)
справедливо
{ в = { е }^*(х) = { е }А(х) = /(*). О
3.3 	Лемма о пределе. Для любой функции f f А* тогда и
только тогда, когда существует такая A-вычислимая
последовательность { fs }seч> ( т• е• найдется A-вычислимая функция /(х, s) = /s(x)),
что f = lime /5.
Доказательство. (=>►) Пусть f ^ А'. Известно, что А' в. п.
относительно А. Следовательно, А-вычислимая последовательность { fs }«еи;
существует по лемме о модуле, релятивизованной к А.
(Ф=) Пусть / = lim8 f8• Определим
Ах = { s : (3*)[s ^ t k ft(x) ф ft+i(x)] }.
Множества Ах конечны, множество В = 0ЖАХ = { (s, х) : s Е Ах }
принадлежит классу Е]4, поэтому В является А-в. п. и В А1.
Таким образом, по данному х мы можем В-вычислимо (и, следовательно,
А'-вычислимо) вычислить наименьший модуль т(х) = (/xs)[s ^ Ах].
Следовательно, /^т^Ф^^т^Ф^^т Q

§ 3. Леммы о модуле и о пределе
91
В частности, / 0; тогда и только тогда, когда / = lims f8 для
некоторой вычислимой последовательности { fs Этот факт является
самой полезной характеристикой степеней ниже 0'. Так как не все
степени ниже 0' содержат в. п. множества, то нижеприводимое следствие
выделяет в. п. степени среди степеней ^ О'.
3.4 	Следствие. Функция f имеет в. п. степень тогда и только
тогда, когда f является пределом вычислимой последовательности
функций { fs с модулем сходимости т /•
Доказательство. (=$►) Пусть / =т А и А в. п. Применяем лемму о
модуле для получения т ^т А =т /•
(<Ф=) Пусть / = lim5 fs с модулем т ^т /• Определим в. п. множество
В как в доказательстве леммы о пределе и напомним, что / В. С
другой стороны В /• Следовательно, / =т В и / имеет в. п.
степень. Q
3.5-3.13 Упражнения
3.5. Покажите, что т, определенная в лемме о модуле, необязательно
является наименьшим модулем. Дайте явное определение А-вычислимого
наименьшего модуля.
3.6. Множество D называется разностью в. п. множеств (d-e. п.
множество), если D = А — В, где А и В в. п. множества. Покажите,
что d-в. п. множества замкнуты относительно пересечений.
3.7. Определим Сп = { е : \We\ = п }.
(a) Покажите, что Сп является d-в. п. множеством при п ^ 0.
(b) Покажите, что Сп не в. п. при п ^ 0. Указание. Убедитесь в том,
что К Сп.
3.8. 	Множество А К называется п-в. п. множеством, если А =
\ims As для некоторой вычислимой последовательности { А3 }8еш такой,
что для всех х выполнено А0(х) = 0 и card{s : А8(х) ф As+i(x) } ^ п.
Например, только пустое множество может быть О-в. п., 1-в. п.
множества— это обычные в. п. множества, класс всех 2-в. п. множеств совпадает
с классом всех d-в. п. множеств.
(а) 	Докажите, что для каждого п существует (n -I- 1)-в. п. множество,
не являющееся п-в. п. множеством. Следовательно, d-в. п. множества не

92
Глава III. Тъюринговая сводимость и оператор скачка
замкнуты относительно объединения. Указание. Заметим, что
аппроксимация {As }seu> может быть выбрана так, что предикат п G As
примитивно рекурсивен, поэтому все такие аппроксимации равномерно
вычислимы.
(b) Покажите, что А является (2п 4- 2)-в. п. тогда и только тогда, когда
А получено (n -I- 1)-кратным объединением d-в. п. множеств.
(c) Покажите, что А является (2п 4- 1)-в. п. тогда и только тогда,
когда А получено объединением некоторого в. п. множества с п-кратным
объединением d-в. п. множеств.
3.9. 	Пусть В — наименьшая булева алгебра, содержащая £ (т. е.
булева алгебра, полученная замыканием класса в. п. множеств относительно
операций дополнения, объединения и пересечения).
(a) Докажите, что A G В тогда и только тогда, когда А является
объединением конечного числа d-в. п. множеств.
(b) Покажите, что существует множество А К такое, что А £ В.
3.10 (Джокуш и другие). Докажите индукцией по п, что если А
является п-в. п. множеством, то либо А, либо А содержит бесконечное в. п.
множество.
3.11. Предположим, что А и В — в. п. множества и А невычислимо.
Докажите, что А х А В 0 В. Указание. (Джокуш) Для получения
противоречия предположим, что для всех х и у
хеАкуеА<& /(х, у) G В 0 В.
Определим С = { у : (3х)[/(х, у) G В00] }. Покажите, что С в. п., С С А
и что существует a G А — С. Далее убедитесь, что для всех х
х G А 4=> /(х, a) G 0 0 В,
так что А является ко-в. п. множеством.
3.12. (а) Покажите, что К х К является d-в. п.
(b) Покажите, что если D является d-в. п., то D К х К
(следовательно, К х К является 1-полным на d-в. п. множествах).
(c) Покажите, что К 0 К является d-в. п.
(d) Используя упражнение 3.11, убедитесь, что сводимость К х К
К 0 К невозможна (значит, К 0 К не может быть ни 1-полным, ни т-
полным среди d-в. п. множеств), (см. упражнение VII.2.4, где показано,
что существует d-в. п. степень, не являющаяся в. п. степенью.)

§ 3. Леммы о модуле и о пределе
93
3.13. 	Дайте альтернативное доказательство того, что КхК К®К,
установив, что КхК =m A =dfn { х : Wx = { 0 } } и что А =£т А по
теореме рекурсии.

Глава IV
Арифметическая иерархия
В предыдущей главе оператор скачка позволил нам определить
иерархию степеней 0 < 0' < ... < < В этой главе мы определим
другую иерархию множеств А, связанную со сложностью кванторной
приставки в синтаксическом определении множества А. В § 2 будет
доказана теорема Поста, которая свяжет эти иерархии друг с другом. Все
это позволит нам классифицировать в обеих иерархиях неразрешимые
проблемы (невычислимые индексные множества), упомянутые в главе I.
Затем мы рассмотрим высокие и низкие в. п. степени, которые будут
играть важную роль в классификации степеней и в изучении
алгебраической структуры в. п. множеств.
§ 1. Уровни вычислимости в арифметической
иерархии
Определим Еп- и Пп-множества. (Классы множеств Еп и Пп иногда
обозначаются в литературе как Е® и П®, чтобы отличить их от классов
Е* и аналитической иерархии.)
1.1 	Определение, (i) Множество В принадлежит классу Ео(По) тогда
и только тогда, когда В вычислимо.
(ii) 	Множество В принадлежит классу Еп (обозначаем В Е Е„ и
говорим также, что В является Еп-множеством), где п ^ 1, если
существует такое вычислимое отношение R(x, у\, у2, • • • , 2/п)> что
хеВ <=> {3yi)(Vy2){3y3) ...{Qyn)R(x,yi,y2,..-,yn),
где Q является квантором 3, если число п нечётно, и квантором V,
если число п чётно. Аналогично, множество В принадлежит классу Пп

§ 1. Уровни вычислимости в арифметической иерархии
95
(обозначаем В Е Пп и говорим также, что В является Пп-множеством),
если
* е В <=}> (4yi)(3y2){Vy3)...(Qyn)R(x,yi,2/2,-.-.J/n),
где Q является квантором 3 или квантором V, в зависимости от того, п
чётно или нечётно, соответственно.
(ш) Множество В принадлежит классу Дп, если В Е En П Пп.
(iv) 	Множество В называется арифметическим1, если
в е U№„ и пп).
п
Заметим, что множество В является арифметическим тогда и только
тогда, когда В может быть получено из вычислимого отношения
применением конечного числа операций взятия проекции и дополнения. (См.
упражнение 1.9.)
1.2 	Определение. Зафиксируем множество А. Заменяя всюду в
определении 1.1 слово «вычислимый» на сочетание «А-вычислимый», получим
определение множества В, являющегося Еп -множеством
относительно А (обозначаем В Е Е^), Пп-множеством относительно А
(обозначаем В Е П^), Дп-множеством относительно А (обозначаем В Е Д^)
и арифметическим множеством относительно А.
Формулу назовем Еп-формулой (Пп-формулой), если она на
множестве своих свободных переменных определяет отношение, принадлежащее
классу Еп (Пп). Мы предполагаем, что читатель знаком с обычными
правилами элементарной логики, позволяющими преобразовывать
формулу в эквивалентную ей формулу, находящуюся в пренексной
нормальной форме. Это означает, что она состоит из кванторной приставки
(префикса) и формулы без кванторов (бескванторной части), причем
последняя в нашем случае должна быть вычислимым отношением. Используя
эти правила, мы докажем приведенные ниже утверждения, которые
будут часто использоваться при доказательстве того, что некоторое
множество является Еп- или Пп-множеством. Здесь единственным
нетривиальным утверждением является (vi), касающееся ограниченных
кванторов. Ограниченным квантором называется квантор вида (Qx ^ y)F,
являющийся сокращенной записью формулы (Уя)[х ^ у =$ F], если Q
является квантором V, или формулы (Зж)[х ^ у & F], если Q является
1 Автор не объясняет происхождение этого определения. О связи арифметической
иерархии с предложениями элементарной арифметики читатель может найти в книге
Роджерса [1972, §§ 4,5 главы 14]. — Прим, редактора.

96
Глава IV. Арифметическая иерархия
квантором 3. Утверждение (vi) означает, что ограниченные кванторы
могут передвигаться вправо и располагаться после обычных кванторов
и, таким образом, могут игнорироваться при подсчете сложности кван-
торной приставки формулы.
1.3 Теорема, (i) А € Еп <=> А € Пп;
(ii) А € £„(ПП) =Ф> (Vm > п)[Л € £т П Пт];
(Ш) А, В € £П(ПП) ==^ A U В, А П В G Sn(nn);
(iv) [il€En&n>0&.<4 = {a;: (Э y)R(x, у) }] =Ф> А € £п;
(v) [В А & А € Еп] В € Еп;
(vi) Если R G Е„(ПП), и множества А и В определены следующим
образом:
(х,у)еА <?=> (Vz < y)R(x,y,z),
{х,у)еВ «=> (3z <y)R(x,y,z),
то А, В € Е„(П„).
Доказательство, (i) Если А = {х : (Зг/i)(Vj/2) • • • R(x,у) }, то
А = {х : (Vyi)(3y2) • ..~'R{x,y)}.
(И) Например, если А = {х : (3yi)(Vy2)R(x,y1,y2) }, то
А = {х : (3yi)(4y2)(3y3)[R(x,yi,y2) & у3 = Уз] }•
(iii) Пусть А = { х : (3yi)(Vy2)... R(x, у)}, и
В = {х: (3zi)(Vz2).. .S(x,z) }.
Тогда
xeAlSB «=>■ (Зу\){Уу2) ...R{x,y) V(3zi)(Vz2)...S(x,z),
<=>• (3yi)(3zi)(Vy2)(Vz2)... [R(x,y) V S(x,z)],
<=> (3«i)(Vw2)... [R(x, (ui)0, («2)0, • • •)
V5(x,(«i)i,(«2)i,...)],
где обозначение (u)o такое же, как в строке 1(2.2). То же справедливо и
для АпВ.
(iv) Непосредственно следует из правила сжатия кванторов, как в
(Ш) или в теореме II. 1.3.
(v) Пусть А = {х : (3yi)(Vy2)... R(x,y)} и В ^го А посредством /.
Тогда
В = {х : (3yi)(Vy2)...R(f(x),y) }.

§ 1. Уровни вычислимости в арифметической иерархии
97
(vi) 	Доказательство ведем индукцией по п. Если п = 0, то А и 2?,
очевидно, вычислимы. Для п > 0 предположим, что R Е Еп и допустим,
что (vi) справедливо для всех т < п. Тогда, согласно (iv), В Е Еп.
Далее, существует такое S Е Пп_1, что
(х,у)еА <=}> (Vz < y)R(x,y,z),
<=> (Vz < y)(3u)S(x,y,z,u),
<=> (3<t)(Vz < y)S(x,y,z,a(z)),
где а пробегает множество ш<ш. Теперь, по предположению индукции
(Vz < y)S Е Пп_1, поэтому А Е Еп. Случай, когда R Е Пп, сводится к
случаю R Е Еп с помощью (i). О
1.4 Предложение. Fin Е Ег-
Доказательство.
х Е Fin <=> W* конечно
<=> (3s)(Vt)[t ^ s V = WXt8].
Отношение в квадратных скобках, зависящее от x,s,t, является,
очевидно, вычислимым. D
1.5 Предложение. Cof Е Е3.
Доказательство.
х Е Cof <=Ф> конечно,
(3y)(Vz)[z ^ у V z € W,],
<=► (3y)(Vz)(3e)[z ^ у V z € W*,,]. D
Так как окончательный префикс зависит только от типа и
относительного расположения кванторов и пропозициональных связок, мы
часто будем сокращать эти вычисления, заменяя ранее определенные
предикаты соответствующей строкой кванторов, указывающей классы, к
которым они принадлежат.
1.6 	Предложение. { (х,у) : Wx С Wy } Е П2.
Доказательство.
WxCWy
(Vz)[z G Wx => z € Wy],
(Vz)[z ^.Vze W„],
(V^)[V V 3],
W3[...],
V3[...]. D

98
Глава IV. Арифметическая иерархия
1.7 Следствие, (i) { {х,у) : Wx = Wy } G П2.
(ii) Tot = { У : Wy = ш } G П2.
Доказательство, (i) следует из утверждения 1.6 и теоремы 1.3(iii); (ii)
следует из утверждения 1.6, где Wx = ш. О
1.8 Следствие. Rec G Е3.
Доказательство.
х G Rec
Wx вычислимо,
(3y)[Wx =Wy),
(3y)[Wx nlfs = «&№,Ulfy^],
3[V & V3], по следствию 1.7,
3V3[...]. D
1.9-1.13 Упражнения
1.9. 	Докажите, что A G (J(En U Пп) тогда и только тогда, когда мно-
п
жество А может быть получено из вычислимого отношения применением
конечного числа операций взятия проекции и дополнения.
1.10. 	Докажите, что Ext G Е3, где множество Ext описано в определении
1.4.14.
1.11. Докажите, что {(ж,у) : Wx и Wy вычислимо отделимы } G Е3.
(Напомним, что множества Wx и Wy вычислимо отделимы, если Wx С
R и Wy С R для некоторого вычислимого множества R.)
1.12. Пишем А С* Д, если А — В конечно, т. е. если А С В за
исключением конечного числа элементов. Пишем А =* В, если А С* В и
В С* А. Докажите, что
{ (*,</> : С* } € Е3 & { (*,2/> : =* Wy } G Е3.
1.13. 	Покажите, что {х : Wx креативно} G Е3.
§ 2. Теорема Поста и теорема об иерархии
2.1 	Определение. Множество А называется Еп-полным (Пп-полным),
если A G ЕП(ПП) иВ^А для любого 2? G ЕП(ПП). (Из упражнений 2.6

§ 2. Теорема Поста и теорема об иерархии
99
и 2.7 следует, что в определении Еп-полноты и Пп-полноты множества
А безразлично, какую запись использовать, «В А» или «В А».)
Заметим, что множество А является Ei-полным тогда и только
тогда, когда А является 1-полным (см. определение II.4.1). Поэтому
множество К является Ei-полным и множество К является Щ-полным.
Следующая фундаментальная теорема связывает иерархию степеней,
определенную при помощи операции скачка в главе III, с арифметической
иерархией.
2.2 	Теорема Поста. Для любого п ^ О
(i) 	В Е En+i В в. п. относительно некоторого Ип-множества
В в. п. относительно некоторого Т,п-множества, по
теореме Ш.2.3(у й);
(й) Если п > 0, то множество 0(п) Еп -полно;
(iii) В Е En+i <=> В в. п. относительно 0(п);
(iv) В Е Дп+1 <=> В 0(п).
Доказательство, (i) (=$►) Пусть В Е En+i. Тогда х Е В (3у)
R(x,y) для некоторого множества R Е Пп. Следовательно, В
является Ei-множеством относительно R и поэтому в. п. относительно Д, по
теореме III. 1.13.
(i) (<£=) Предположим, что множество В является в. п. относительно
некоторого Пп-множества С. Тогда для некоторого е
х € В <=> х е Wg ,
<=> (Эв)(Э<г)[о- С С & х <Е W"s).
По теореме III. 1.8 отношение х Е W%8 вычислимо. Поэтому, согласно
теореме 1.3(iv), достаточно показать, что отношение а С С является
En_|_i -отношением. Имеем
асС «*=► (Уз/ < 1Ца))[а(у) = С{у%
<=> (Vy < lh(a))[[a(y) = 1 & у е С] V [ст(у) = 0 & у $ С}},
^ (Уу<ВД)[П„У£п],
т. к. С Е Пп. Следовательно, а С С является En+i-отношением, по
теоремам 1.3(ii), 1.3(iii) и 1.3(vi).
(ii) доказывается индукцией по п и очевидно для п — 1. Фиксируем
п ^ 1 и предположим, что множество 0(п) Еп-полно, следовательно,

100
Глава IV. Арифметическая иерархия
множество 0(п) Пп-полно. Далее,
В Е £n+i <=Ф> В в. п. относительно некоторого
£п-множества, по (i),
<==> В в. п. относительно №п\
по индуктивному предположению,
<=Ф> В 0(Л+1),по теореме III.2.3(vii),
Таким образом, множество 0(n+1) £п+1-полно.
(ш) По (i) и (ii), так как 0(Л) Пп-полно.
(iv)
ВеАп+1 <=> J3,J3E£n+i,
<=Ф> В, В в. п. относительно 0(n), по (in),
<=> В^Т№п)- D
2.3 	Следствие (теорема об иерархии). (Vn > 0)[Д» С Е„ и Д„ С
П„].
Доказательство. 0(п) Е Еп —Пп (по теоремам 2.2(ii), 2.2(iv) и III.2.3(ii))
и, аналогично, 0(n) Е Пп - Еп. О
2.4-2.7 Упражнения
2.4. Напомним, что число е называется Ei-индексом множества А, если
А = We. В этом случае число е назовем также и Их -индексом
множества А. Назовем число е En+i -индексом множества А и Пп+1 -индексом
множества А, если А = {х : (32/)2?(ж,2/) } и е является Пп-индексом
для В. Докажите, что А имеет П2-индекс е тогда и только тогда, когда
А = {х : (Vyi)(3y2)3T(e,<a?,yi),y2) }•
2.5. По теореме 2.2(iv) и лемме Ш.З.З следующие условия эквивалентны:
(а) 	А Е Д2; (Ь) А ^т К; (с) А = lim8fs для некоторой вычислимой
последовательности { fs }8еи- Докажите, что можно эффективно перейти
от индекса одной характеристики к индексу любой другой. (Д2 -индексом
множества А называется такое число (е,г), что е является Е2 -индексом
множества А и i является П2-индексом множества А\ индексом в (Ь)
является такое число е, что А = {е}^; индексом в (с) является такое
число е, что ipe(s,x) = fa(x).)
2.6. Докажите, что если В А и А = 0(п) для n ^ 1, то В А.
Указание. Используйте лемму 1.3.2 о множестве индексов. Для другого

§ 3. Еп -полные множества
101
доказательства покажите, что В Е Еп. Отсюда по теореме 2.2(ш) В в. п.
относительно 0(n-1) и можно применить теорему Ш.2.3(ш).
2.7. 	Докажите, что если В = 0(Л) для п ^ 1 и В А, то -В А.
(Следовательно, для доказательства Еп-полноты множества А не
обязательно показывать, что 0(Л) А, достаточно показать, что 0(л) А,
хотя наши доказательства обычно устанавливают первое, т. к.
функция s в s-m-n теореме 1.3.5 является взаимно однозначной.) Указание.
Используйте следствие II.4.7.
§ 3. Еп-полные множества
Мы показали, что для всех п множество 0(п) является Еп-полным
множеством. Однако, существуют другие Еп-полные множества с
естественными определениями, которые будут полезны нам в дальнейшем.
Например, мы уже выяснили, что К, Ко и К\ являются Ei-полными
множествами. Теперь покажем, что множество Fin является Ег-полным, а
множества Cof и Rec являются Ез-полными. Раньше мы определяли
принадлежность множества А к классу Еп с помощью метода из § 1, теперь
мы увидим, что наилучшим способом доказательства Еп-полноты
множества А является доказательство того, что В А для некоторого
множества J5, о котором уже известно, что оно Еп-полно. Согласно
определению И.4.9, {А, В) {C,D) посредством /, если f(A) С C,f(B) С D
и f(AU В) С CUD. Мы пишем <<^i>>, если / является взаимно
однозначной.
3.1 Определение. Для п ^ 1 положим (ЕП,ПП) (C,D), если
{A, A) (C,D) для некоторого Еп-полного множества А, и,
аналогично, для вместо . В этом случае мы также пишем En С
и Пп D. (Так же, как в определении 2.1, не имеет значения, какую
запись мы здесь используем, «^ш» или «^i».)
(На первый взгляд такое обозначение может показаться странным,
т. к. в нем Еп и Пп являются классами множеств, а не множествами, но
оно оправдано тем, что если (ЕП,ПП) (C,D), то (А, А) ^го (C,D) и
{В, В) ^го (C,D) для любых Е„-множества А и П„-множества В. Такое
обозначение окажется удобным в главе XII.)
3.2 Теорема. (Е2,Пг) (Fin,Tot). Таким образом, множество Fin
является Е2-полным, а множества Inf и Tot являются Щ-полными, и

102
Глава IV. Арифметическая иерархия
Inf = Tot.
Доказательство. По утверждению 1.4 и следствию 1.7 Fin Е Е2 (так что
Inf Е П2) и Tot Е П2. Пусть А € Е2, тогда А Е П2, и, следовательно,
существует такое вычислимое отношение Д, что
хеА <=> (iy){3z)R{x,y,z).
Используя s-m-n теорему 1.3.5, определим вычислимую 1:1-функцию /
следующим образом:
Vf{*
0,
t
если (Vy ^ u)(3z)R(x,y,z),
в противном случае.
Теперь _
х Е А => W/(*) = ш => f{x) Е Tot,
и
х € А => Wf(x) конечно => f(x) Е Fin. О
3.3 Определение. Comp = {х : Wx =т К }, т. е. Comp является
множеством индексов полных (по Тьюрингу) в. п. множеств.
3.4 Теорема. (Ез,Пз) (Cof, Comp) (Rec,Comp).
3.5 Следствие. Cof является Ез -полным множеством.
Доказательство. Следует из утверждения 1.5 и теоремы 3.4. Ц
3.6 Следствие (Роджерс). Rec является Ез -полным множеством.
Доказательство. Вытекает из следствия 1.8 и теоремы 3.4, поскольку
Cof С Rec и Rec П Comp = 0. О
В следствии XII. 1.7 мы покажем, что Comp является Е4-полным
множеством.
Доказательство теоремы 3.4• Зафиксируем вычислимое перечисление
{Ks}seu; множества Д, и пусть множество А Е Е3. Существует такое
отношение R Е П2, что х Е А тогда и только тогда, когда (3y)R(x, у).
Так как Д Е П2, то по теореме 3.2 существует такая вычислимая
функция 0, что R(x,y) истинно тогда и только тогда, когда Wg(x^y)
бесконечно. Следовательно,
х € А 4==> i^y)\Wg{x,y) бесконечно].
(3.1)

§ 3. £п-полные множества
103
Определим в. п. множество Wf(x) = (J5 ^f(x) по шагам, гДе ^f(x) со~
стоит из элементов, перечисленных в Wf(x) к концу шага s и таких, что
х € А тогда и только тогда, когда множество W/(x) является коконеч-
ным.
Шаг s = 0. Положим = 0.
Шаг s + 1. Положим И^(х) = { Ьх0 < • • • < Ьху <•••}. Для каждого
У ^ s такого, что Wg(Xiy)t8 ф И^(Х|У)|в+1 или у € K8+i -К8, перечисляем
bsx у в Если такого у не существует, то положим = W^xy
Теперь, если х 6 А, то для некоторого у множество беско¬
нечно, limsbxy = оо, поэтому |W/(X)| ^ у и, следовательно, Wf(x)
конечно. Если х А, то для любого у множество конечно, поэтому
ЬХуУ =dfn Итв Ь8х у < оо, W/(X) = { Ьх>3/ и W/(ж) бесконечно. Более
того, если х £ А, то К ^т Т* к- Для каждого у мы можем Wf^xy
вычислимо найти такой шаг s(y), что Ь8Х$ = Ьх>у. Заметим теперь, что
по построению у £ К тогда и только тогда, когда у £ Kg^). Q
Эту конструкцию можно наглядно представить следующим образом.
Зафиксируем число х и перечисляем в. п. множество Wf(x), на каждом
шаге рассматривая его дополнение и используя множество «подвижных
маркеров» {ГХ)3/ }у€а;. На шаге 0 соотносим маркер Гх>у с числом у.
Маркеры перемещаются с сохранением порядка всегда с меньших
элементов на большие, и любой элемент, с которым не соотнесен ни один
маркер, перечисляется в W/(x). Таким образом, к концу шага s маркер
ГХ|У соотносится с (у + 1)-м элементом множества W*f(xy (Отсюда
видно, число Ьах у в вышеприведенном доказательстве обозначает положение
маркера ГХ)3/ в конце шага s.) На шаге s + 1 в W/(X) перечисляем
текущую позицию маркера Гж>у для каждого у ^ s такого, что либо
мощность множества Wg(XiV) только что увеличилась, либо у только что
перечислился в К; затем перемещаем все маркеры с позиций, больших или
равных позиции смещённого маркера, на позиции, ещё не перечисленные
в Wf[x), сохраняя порядок расположения маркеров. Таким образом, мы
рассматриваем Wg(XiV) как некоторое «выбрасывающее» множество,
которое заставляет у-й маркер ГХ|У перемещаться на всех шагах s > у, на
которых мощность множества Wg(x%y) возрастает. Если х £ А, то для
некоторого у множество Wg(XiV) бесконечно, поэтому маркер Гх>у
перемещается («выбрасывается») бесконечно много раз. Поэтому W/(х)
конечно и |W/(х)| = уо для наименьшего такого уо. Если же х £ А, то каждое
множество Н^(Х)У) конечно, поэтому каждый маркер Гх>3/ перемещается

104
Глава IV. Арифметическая иерархия
только конечное число раз, и множество Wf (ж) бесконечно. Метод
подвижных маркеров является одним из наиболее важных инструментов в
наглядном представлении более сложных конструкций в. п. множеств и
в дальнейшем будет часто использоваться.
В теореме XII. 1.7 мы усиливаем теорему 3.4, доказав, что множество
Comp является даже Е4-полным. В главе XII классифицируется на
более высоких уровнях арифметической иерархии большое число других
индексных множеств в. п. множеств.
Следующее утверждение вероятно дает лучшую для Ез-множества
А аппроксимацию «угадывания» того, что х € А. Оно может
рассматриваться как усиление (3.1).
3.7 Следствие. Если А € Ез, то существует такая вычислимая
функция д, что
X € A <=i> (а. е. y)[Wg{XtV) = и\
(3.2)
х £ А <*=*• (Vj/)[VF9(XiJ/) конечно].
(3.3)
Доказательство. Пусть А Cof посредством функции /. Определим
функцию д следующим образом:
2 6 Wg(x,y) «=> (Vu)[y ^ Z => и € РУ/(х)].
Следовательно,
х е А => Wf(x) коконечно => (3y)(Vz ^ y)[z € W/(x)]
и
х € А => Wf(x) кобесконечно => (Vy)(3z ^ y)[z £ Wf(x)]
=> (V2/)[Wp(x,y) конечно]. Q
Чтобы «угадать» принадлежность элемента х Ег-множеству А, мы
имеем такую вычислимую функцию /, что х Е А тогда и только тогда,
когда множество Wf(x) конечно. Для Ез-множества А следствие 3.7
предоставляет двумерный аналог, когда множество Wg(Xty)
рассматривается как у-я строка матрицы. Если х Е А, то почти все строки совпадают
с cj, в противном случае все они конечны.

§ 3. Еп -полные множества
105
3.8-3.13 Упражнения
3.8. Докажите, что (Ез,Пз) (Cof,Ext) и, следовательно, множество
Ext является Ез -полным. Указание. Используйте обозначения и метод
теоремы 3.4, чтобы построить такую функцию <Р/(Х), что если х € А,
то f(x) G А С Cof, и если х £ Cof, то из того, что ipy всюду
определена, следует, что <Pf(x)(z) Ф 4>y{z) для некоторого z < bXfV. Здесь
ЬХ}У — конечная позиция подвижного маркера ГЖ)3/, как описано после
доказательства теоремы 3.4. Измените движение маркера ГЖ)У
следующим образом. Пусть Ь8х у обозначает элемент, на котором остановился
маркер Гх>у в конце шага s. Как и раньше, если мощность
множества Wg(XyV) возросла на шаге s + 1, то положите Ьху в Wf^, определяя
^/(х)(Ьх,у) и перемещая маркер ГЖ)У на свободный элемент. Кроме того,
если (py,s(bXfy) 1= v и
^ ^X,y)VPf{x),s{Z) -1Ф Фу,8&)\,
то определите <Pf(x)(bXty) = и переместите маркер ГХуУ на
свободный элемент. (Упражнение 3.8 понадобится в теореме XII.3.4.)
3.9. Докажите, что множество {(х,у): Wx и Wy вычислимо
неотделимы} является Ез-полным. Указание. Определите функцию <ff(x) из
упражнения 3.8 так, чтобы она принимала значения из множества {0,1}.
3.10. Докажите, что оба множества {(ж, у) : Wx С* Wy } и {(х,у) :
Wx =* Wy } являются Ез-полными.
3.11. Докажите, что множество {х : ipx всюду определена & -«[limj,
<Рх(у) = оо]} является Ез-полным. Указание. Для доказательства Ез-
полноты используйте следствие 3.7 и определите
iPf{x){s) = (w)[^p(x,y),s+l Ф Wg(x,y),s V У = 5].
3.12. Определим слабый скачок На соотношением На = { х : Wx П А ф
0 }. Докажите, что если множество А является Пп-полным, то На
является En+i -полным. (Это дает нам интересную последовательность
множеств, полных на каждом уровне.) Заключите отсюда, что множество
tfinf —dfn {х : (Зу)[у eWx & Wy бесконечно}
является Ез-полным.

106
Глава IV. Арифметическая иерархия
3.13. 	Покажите, что если А — в. п. множество, то Gm(A) £ Е3, где
@т{А) —dfn { X • Wx —т А }.
§ 4. Релятивизованная арифметическая иерархия.
Высокие и низкие степени
Классы EjJ (П£) определяются так же, как классы Еп (Пп) в
определении 1.1, за исключением того, что вычислимый предикат R заменяется
на A-вычислимый. Если а = deg(A), то используется также обозначение
EjJ вместо EjJ, поскольку класс EjJ не зависит от конкретного
представителя А £ а.
Все результаты этой главы могут быть релятивизованы
относительно произвольного множества А, сохраняя фактически те же самые
доказательства и заменяя Еп, Пп и 0(п) на и А^п\ соответственно.
Например,
4.1 Релятивизованная теорема Поста . Для любого п ^ 0
справедливо следующее:
(i) Если п > 0, то множество А^ является -полным;
(ii) В £ Е^+1 <=Ф> В в. п. относительно А^;
(Ш) В ^Т А<—> В £ Д„+1 =dfn En+i ^ nji+i*
Определим множества Fin"4,Tot"4 и Cof"4 так же, как Fin, Tot и Cof,
заменяя только We на W*.
Фактически в § 3 было установлено, что множество Fin"4 является
Е^-полным, Tot"4 является П^-полным, Cof"4 и Rec"4 — Е^-полными и
т. д. Следовательно, если а = deg(A), то а' = deg(A'), а" = deg(Fin"4) и
а'" = deg(CofA).
Было бы полезным уметь классифицировать степени в терминах их
скачков. По теореме Ш.2.3, если а ^ Ь, то а' ^ Ь'. Следовательно, если
О ^ а ^ 0', то 0' ^ а' ^ 0".
4.2 Определение, (i) Степень а ^ 0' называется низкой, если а' = 0'
(т. е. если скачок а' имеет наименьшую возможную степень), и высокой,
если а' = 0" (наибольшее возможное значение).
(ii) 	Множество А ^т 0; называется низким (высоким), если deg(A)
является низкой (высокой). (См. также упражнение 4.5 и определение 1.3
главы VII.)

§ 4• Высокие и низкие степени
107
Диагр. 3.1. Арифметическая иерархия множеств натуральных чисел

108
Глава IV. Арифметическая иерархия
На интуитивном уровне высокие множества — это множества с
большим объемом информации («близкие» к полным множествам), а
низкие — это множества с маленьким объемом информации (подобно
вычислимым множествам). Нетривиальные высокие и низкие в. п.
множества будут найдены в главах VII и VIII, и они сыграют большую роль
при классификации в. п. степеней, а также при установлении связи
алгебраической структуры в. п. множества с его степенью. Для этих
предстоящих приложений будут полезными следующие описания низких и
высоких множеств.
4.3 	Теорема. Для множества А 07, следующие условия
эквивалентны:
(i) А — низкое множество;
(ii) С Пг£_
(Ш) A' 0(2) = Tot.
Доказательство.
А низкое
А' 0',
А' е Л2, по теореме 2.2 Поста,
Ej4 С Д2, т. к. А1 Е^-полно,
Е]4 С т. к. Ej4 С Е?# = Е2,
A! 0(2), т. к. 0(2) П2-полно. О
4.4 	Теорема. Для множества А ^т 07, следующие условия
эквивалентны:
(i) 	А — высокое множество;
(ii) Е2СП^;
(Ш) 0(*> AM
(т. е.
Fin TotA).
Доказатель ство.
А высокое
0" А',
0" е АА, по теореме 4.1,
Е2 С Аа, т. к. 0" Е2-полное,
Е2 Q ПА, т. к. , очевидно, Е2 С ЕА,
А(2), т. к. AW П^-полное.
4.5-4.11 Упражнения

§ 4• Высокие и низкие степени
109
4.5. Заметим, что если а ^ 0', то 0(Л) ^ ^ 0^л+1\ Пусть п >
0. Назовем степень а ^ О' п-низкой (п-высокой), если а^п) =
(а(л) = 0(л+1)), и множество А ^т 07 п-низким (п-высоким), если
степень deg(j4) n-низкая (n-высокая). Пусть Ln (Нп) обозначает
совокупность п-низких (п-высоких) в. п. степеней. Для удобства скажем, что
множество А является 0-низким (0-высоким), если А =т 0 (А =т 0')»
т. е. Lo = { 0 } и Но = { 0'}. Вместо термина 1-низкое (1-высокое)
пишем просто низкое (высокое), в соответствии с определением 4.2. (Для
получения большей информации о n-низких и п-высоких в. п. степенях
см. определение VII.1.3, упражнение VII.1.6, следствие VIII.3.4 и
следствие VIII.3.5.) Для множества А ^т 07 докажите, что для любого п > 0
справедливо следующее:
(a) А n-низкое <=Ф> Ej* С Пп_|_1 <=Ф> А^ 0(Л+1);
(b) А n-высокое <=Ф> En+i С П£+1 0<п+1> А^1);
(c) А 2-низкое «=>• Fin"4 Cof;
(d) А 2-высокое <*=> Cof Cof"4.
(См. доказательство теоремы XI.5.1, где утверждение (с) будет
использовано.)
4.6. (а) Для любого множества А С ш определим слабый скачок На =
{ е : We П А ф 0 }. Покажите, что На Ка-
(Ь) 	Назовем множество А полунизким, если На 07- (Согласно
(а), если множество А низкое, то А полунизкое.) Докажите, что если
На 07> то А ^т 07* (Для получения большей информации о кобес-
конечных в. п. множествах А таких, что А является полунизким, см.
упражнения XI.3.5 и XI.3.6 и замечание ХШ.1.15.)
4.7. Пусть А — в. п. множество. Докажите, что следующие условия
эквивалентны:
(a) множество А полунизкое;
(b) существует такое вычислимое перечисление { As }seu) множества
Л, что для любого е справедливо:
(3°°s)[We,s - As Ф 0] =* We - А Ф 0;
(c) существует такая вычислимая функция /, что для любого е
справедливо:
(1) WenA = Wf(e)nA и
(2) We П А = 0 => ^/(е) конечно.

no
Глава IV. Арифметическая иерархия
Указание. Чтобы показать, что из (а) следует (Ь), определите,
используя лемму Ш.З.З о пределе, такую вычислимую функцию g(e,s),
что д(е) = \ims д(е, s) является характеристической функцией
множества Н-д. Выберите такое число г, что W% = А. Для каждого е ^ s, если
х G We,8+1 - We,s, определите
te = (fit ^ s)[z G Wi,t или tf(M) = 1]
и пусть As.|_i = Wit, где * = max{te : e ^ s}. (См. также
упражнение XI.3.6.)
4.8. Докажите, что в упражнении 4.7(c) (2) условие We П А = 0 может
быть заменено на We П А =* 0.
4.9. Используя метод из упражнения 4.7, докажите, что если множество
А в. и., то А является низким множеством тогда и только тогда, когда
существует такая вычислимая функция /, что для любого j
справедливо:
(1) (V±)[B* С А -> [х G Wj <=> х G Wm]] и
(2) { х : Dx С А & х G } = 0 =>► W/y) конечно.
Сформулируйте и докажите эквивалентное условие о перечислении,
аналогичное условию (Ь) из упражнения 4.7.
4.10. Докажите, что для каждого в. п. множества А существует такое
в. п. множество В =т А, что Н^ =т А!. (Следовательно, если А не
низкое, то В не полунизкое.) (Упражнение 4.10 используется в
упражнении ХИ.4.22.) Указание. Пусть В = { п : Dn П А ф 0 }.
4.11. Докажите, что для каждого в. п. множества А существует
такое в. п. множество В =т А, что В — полунизкое множество.
Указание. Пусть { As }5€u, — вычислимое перечисление множества А. Пусть
{ Df(n) }п€а; — такая каноническая последовательность непересекающих-
ся конечных множеств, что \Df^\ = п + 1 и ипВдп) = ш. Пусть
Г| = fix[x G We,s — В8], если такой х существует, и Г| = 0 в противном
случае. Если п G As+1 — ASl то положите
хп = цх[х € £>/(„) - |J{ Г* : е < п }]
и перечислите хп в В5+ь Покажите, что п G А тогда и только тогда,
когда Df(n) П5^0. Таким образом, А =т В.

Часть В
Проблема Поста,
оракульные конструкции
и метод приоритета с
конечными
нарушениями

Глава V
Простые множества и проблема Поста
Часть А содержала первоначальные результаты и методы, получившие
развитие за период с 1931 года по 1943 год. Часть В содержит такой же
материал, но относящийся приблизительно к периоду с 1944 по 1960 гг.
Оба раздела включают также результаты, полученные позднее, но
доказательства которых проводятся с помощью методов, разработанных за
обозначенный период. В своей основополагающей работе Пост [1944]
отказался от формализма, характерного для развития теории вычислимых
функций в 1930-е гг., и в ясном неформальном стиле изложил основные
свойства в. п. множеств и их применения к теореме Гёделя о неполноте.
Он также предпринял попытку классифицировать в. п. множества и их
степени. Им был поставлен вопрос (ставший известным как проблема
Поста) о существовании более чем двух в. п. степеней. Пытаясь решить
эту проблему, Пост определил различные классы простых множеств,
которые изучаются в этой главе. Эта глава также содержит очень
привлекательное обобщение теоремы рекурсии и критерий полноты для в. п.
множеств, который был получен намного позднее Мартином, Лахланом и
Арслановым. Попытки положительного решения проблемы Поста
введением обеспечивающего неполноту свойства в. п. множеств в духе
определения простого множества, оказались безуспешными. Между тем, К лини
и Пост [1954] исследовали верхнюю полурешетку тьюринговых степеней
в общем случае (т. е. включающую не только в. п. степени) и, используя
диагональные рассуждения с оракулами (т. е. невычислимые
построения), доказали существование несравнимых степеней ниже О7. Эти
методы описываются в главе VI вместе с критерием полноты Фридберга и
построением Спектора минимальной степени. Наконец, Фридберг [1957]
и, независимо, Мучник [1956] с помощью изобретенного ими метода
приоритета с конечными нарушениями решили проблему Поста. Этот метод
является наиболее тонкой и эффективной версией метода К лини и Поста,

114
Глава V. Простые множества и проблема Поста
когда построение должно быть эффективным, чтобы производить в. п.
степени. Эти результаты включены в главу VII вместе с теоремой
Сакса о разложении, метод доказательства которой позднее окажется весьма
полезным. По поводу решения проблемы Поста в стиле самого Поста см.
замечание после следствия 2.6. О недавнем решении проблемы Поста, не
использующем метод приоритета, см. замечание VII. 1.9.
§ 1. Иммунные и простые множества. Конструкция
Поста
Пока единственными в. п. степенями, о существовании которых мы
знаем, являются 0 и О7. Проблема Поста заключалась в построении
других в. п. степеней, т. е. в построении такого в. п. множества А, что
0 <т А <т 0'. Программа Поста построения такого множества А
заключалась в нахождении некоторого легко определяемого свойства для
А (совместимого с невычислимостью множества А), которое
гарантировало бы неполноту (К А)-
Напомним, что (по теореме II.4.5) для множества К (и,
следовательно, для любого креативного множества) существует бесконечное в. п.
множество (и, следовательно, бесконечно много бесконечных в. п.
множеств), содержащееся в его дополнении. Предложенная Постом идея
построения неполного множества А состояла в том, чтобы заставить его
дополнение А быть достаточно «жидким» относительно свойства
«содержать бесконечные в. п. множества» с тем, чтобы К не сводилось по
Тьюрингу к А.
1.1 Определение, (i) Множество называется иммунным , если оно
бесконечно и не содержит бесконечного в. п. подмножества.
(ii) 	Множество А называется простым, если А в. п. и А является
иммунным.
1.2 Предложение. Если множество А простое, то:
(0
А
не вычислимо;
(И)
А
не креативно;
(iii)
А
не т-полно (т. е. К А)
Доказательство, (i) А не может быть в. п. множеством, т. к. в
противном случае оно содержало бы бесконечное в. п. множество (а именно,
3).

§ 1. Простые множества и конструкция Поста
115
(ii) 	Дополнение любого креативного множества содержит бесконечное
в. п. подмножество (по теореме И.4.5).
(Ш) Если К А, то А креативно (по следствию И.4.8). Q
1.3 Теорема (Пост [1944]). Существует простое множество S.
Доказательство. Пусть А = {(е, х) : х G We & х > 2е }. Тогда А —
Ei-множество и, следовательно, в. п. Пусть гр — какая-нибудь ч. в.
функция выбора для множества А (в смысле теоремы II. 1.6 униформизации)
и пусть S = rng ip. (Говоря неформально, перечисляем множество We до
тех пор, пока не появится первый элемент ip(e) > 2е, и затем
перечисляем ip(e) в 5.) Из (1)-(3) вытекает, что множество 5 простое.
(1) Множество S в. п. (5 является областью значений ч. в. функции.)
(2) S бесконечно. Чтобы понять это, заметим, что 5 содержит самое
большее е элементов из множества { 0,1,2,..., 2е }, а именно, ip(0),
ip( 1),..., ip(e — 1). Следовательно, е + 1 ^ card(5 [ (2е -h 1)), поэтому 5
бесконечно.
(3) Если We бесконечно, то We П 5 ф 0, поскольку (е,ж) G А для
некоторого х > 2е. Следовательно, гр(е) определена и гр(е) G SC\We. О
Другой полезный метод построения простого множества приведен в
упражнении 1.6.
1.4 Определение. Простое множество А называется эффективно
простым, если существует такая вычислимая функция /, что
(Ve)[WeCl=>|^eK/(e)]. (1.1)
Заметим, что простое множество Поста является эффективно
простым с функцией /(е) = 2е +1, т. к. если We С 5, то We С {0,1,...,2е}.
1.5-1.10 Упражнения
1.5. Пусть S — класс простых множеств, и С — класс коконечных
множеств. Докажите, что S U С является фильтром в £. (В упражнении 2.8
мы докажем это и для класса гиперпростых множеств, а в
упражнении Х.2.17 — для класса гипергиперпростых множеств.)
1.6. Опишите построение простого множества А с помощью
«подвижных маркеров», удовлетворяя для е G ш следующим требованиям:
Ре : We бесконечно => We П А ф 0,
Ne: \A\2e.

116
Глава V. Простые множества и проблема Поста
Указание. Пусть А = (Js Aa, где As состоит из элементов,
перечисленных во множество А к концу шага s следующей вычислимой процедуры.
(Таким образом, последовательность {As}s€u; будет вычислимой,
поэтому А в. п. Действительно, х G А тогда и только тогда, когда (3s) [х G
А3].) Пусть Ао = 0. По данному As полагаем As = {ag < af < ...}.
(Под а* подразумеваем позицию в конце шага s подвижного маркера
Гп.) На шаге s -1-1 находим наименьший элемент е ^ s такой, что (1)
WetS П As =0, (2) a* G WetS для некоторого п ^ е. Перечисляем asn
в А. Если такого е не существует, то переходим к следующему шагу.
Заметим, что пункты (1) и (2) гарантируют, что Ит5а* < оо, таким
образом, требование Ne удовлетворяется.
1.7. Покажите, что множество А, построенное с помощью конструкции
из указания к упражнению 1.6, является эффективно простым с
функцией /(е) = 2е.
1.8. Докажите, что множество {е :We простое} является Пз-полным.
(См. также следствие ХП.4.8(й).) Указание. Скомбинируйте методы из
упражнения 1.6 и следствия IV.3.7 следующим образом. Пусть
множество А Ез-полно и функция д такая же, как в следствии IV.3.7. Постройте
такую вычислимую функцию /, что если х G А, то Wf(x) коконечно, и
если х £ А, то Wf(х) просто. Wf(x) стройте, используя маркеры { Г* }n€a,
как в упражнении 1.6, но, кроме того, как только новый элемент
перечисляется в Wg(ж>п), маркер Г® также передвигается.
1.9. Докажите, что если А 5 и А является одним из множеств
вычислимо неотделимой пары (как определено в упражнении 1.4.22) в. п.
множеств, то S не простое. Заметим, что К = { х : (рх(х) = 0 }, и,
следовательно, по упражнению П.4.13, К является одним из множеств
эффективно неотделимой (и поэтому вычислимо неотделимой) пары в. п.
множеств. (Следовательно, простое множество не может быть т-полным.)
Указание. Пусть (А, В) — вычислимо неотделимая пара в. п. множеств,
где A S посредством /. Рассмотрите f{B).
1.10. Докажите, что следующее множество S минимальных индексов
ч. в. функций не является в. п.:
S =dfn { х : “43t/ < х)\(рх = ipy] }.
Указание. Используйте теорему рекурсии.

§ 2. Гиперпростые множества
117
§ 2. Гиперпростые множества и мажорирующие
функции
Пост доказал, что простые множества не могут быть m-полными (см.
упражнение 1.9) и даже полными относительно промежуточной
сводимости btt (определение см. в упражнении 2.13). Однако, он понимал,
что простые множества могут быть полными по Тьюрингу.
Действительно, в § 4 мы покажем, что Т-полным является каждое эффективно
простое множество. Поэтому Пост продолжал определять классы кобес-
конечных в. п. множеств с ещё более жидкими дополнениями, названные
им гиперпростыми (г-простыми) и гипергиперпростыми (гг-простыми).
Хотя эти множества также оказались непригодными для решения
проблемы Поста, они, как было выяснено позднее, имеют очень интересные
характеристики, позволяющие получить значительную информацию о
структуре невычислимых в. п. множеств и о связях между в. п.
множеством и его степенью. (Напомним, что Dy обозначает конечное множество
с каноническим индексом у, по определению II.2.4.)
2.1 	Определение, (i) Последовательность { Fn }пеи> конечных множеств
называется сильной (слабой) таблицей, если существует такая
вычислимая функция /, что Fn = Df(n) (Fn = Wf(n)). (См. также
определение П.2.4.)
(ii) 	Таблица называется таблицей без пересечений, если её элементы
попарно не пересекаются.
(ш) Бесконечное множество В называется гипериммунным,
сокращенно г-иммунным (гипергипериммунньгм, сокращенно гг-иммунным ),
если не существует такой сильной (слабой) таблицы без пересечений
{ Гп }neu>i что Гп П В ф 0 для любого п.
(iv) В. п. множество А называется гиперпростым, сокращенно г-
простым (гипергиперпростым, сокращенно гг-простым), если А г-
иммунно (гг-иммунно).
Идея, стоящая за определениями г-простого и гг-простого множеств,
заключается в том, что вместо выделения в. п. множества { ап }пеи> Я Д
мы выделяем такую в. п. последовательность конечных непересекаю-
щихся множеств { Fn }П£и, что каждое Fn содержит некоторый элемент
х € А, хотя мы и не можем точно сказать, который х G Fn
обладает таким свойством. В сильной таблице мы можем явно вычислить как
max(Fn), так и все его элементы, но в слабой таблице мы можем
только перечислять элементы Fn. Легко доказывается (см. упражнение 2.18),

118
Глава V. Простые множества и проблема Поста
что из гг-простоты множества вытекает его г-простота, а из г-простоты
множества вытекает его простота. Позднее мы докажем, что эти
импликации необратимы.
2.2 Определение, (i) Всюду определенная функция / мажорирует
функцию д, если f(x) ^ д(х) для любого х, и / доминирует над g,
если f(x) ^ д(х) для почти всех х. (См. также определение 1.5.5.)
(ii) 	Если множество А = { а® < ai < аг < ...} бесконечно, то
функция ра, где рл(п) = ап, называется главной функцией множества А.
(ш) Функция / мажорирует (доминирует) бесконечное множество
А, если / мажорирует (доминирует) ра• Аналогично, множество А
мажорирует (доминирует) функцию /, если это делает р^.
2.3 Теорема (Кузнецов, Медведев, Успенский). Бесконечное
множество А тогда и только тогда г-иммунно, когда никакая вычислимая
функция f не мажорирует А.
Доказательство. (<Ф=) Пусть {Dg^ }хви> — такая сильная таблица
без пересечений, что Dg(x) П А ф 0 для любого х. Положим f(x) =
max((J{ Dg(y) Тогда f(x) ^ рд(х) для любого х.
(=>) Предположим, что / — такая вычислимая функция, что f(x) ^
рл(х) для любого х. Положим Dg(о) = [0,/(0)], где [n,m] = {n,n +
1,..., m } при п < т. Допустим, что мы уже определили р(0), р(1),...,
д(п). Пусть k = 1 + max(|J{ A,(i) }г^п)- Определяем Д,(п+1) = [&,/(&)]•
Теперь к ^ рА(к) ^ /(*), поэтому рд(А;) G A,(n+i) П A. Q
2.4 Следствие. Кобесконечное в. п. множество А является
гиперпростым тогда и только тогда, когда никакая вычислимая функция
не мажорирует А.
Заметим, что простое множество S Поста из теоремы 1.3 не
является гиперпростым, поскольку S мажорируется функцией f(x) = 2х.
Если А в. п. и pj доминирует над любой вычислимой функцией, то А
называется плотно простым и, как мы позднее увидим, имеет высокую
степень. (См. упражнение XI. 1.11.) Это контрастирует со следующей
теоремой, которая утверждает, что гиперпростые множества существуют
в каждой ненулевой в. п. степени.
2.5 Теорема (Деккер [1954]). Для любого невычислимого в. п.
множества А существует г-простое множество В =т А.
Доказательство. Пусть А = ran / для некоторой вычислимой 1:1-

§ 2. Гиперпростые множества
119
функции / и as = f(s), As = { /(0),..., f{s) }. Определим В = {s :
(3t > s)[a* < a*]} — дефицитное множество А для перечисления /.
Ясно, что В — Ei-множество и, поэтому, в. п. Кроме того, В
бесконечно. Заметим, что из определения множества В и того, что х ^ ар_(х),
вытекает:
X € А <*=*• х е {a0,ai,...ap_(:i:)}. (2.1)
Следовательно, А ^т В. Далее, В г-иммунно, т. к. если некоторая
вычислимая функция g мажорирует то по (2.1) х G А тогда и только
тогда, когда х G { ao,ai,...ag(x) }• Это означает, что множество А
вычислимо. Наконец, В А, т. к. для проверки условия s G В достаточно
А-вычислимо найти такое наименьшее число t, что At [ а8 = А [ а8.
Теперь заметим, что s G В тогда и только тогда, когда t > s, т. е.
s G В тогда и только тогда, когда s G Bf. Более того, В ^tt А (см.
упражнение 2.12). Ц
В определении дефицитного множества В существенным является
то, что любой недефицитный шаг s G В является «истинным» шагом
перечисления { А3 }8еш множества А в том смысле, что As f f(s) = А [
f(s). Такие шаги окажутся очень полезными в главе VIII при изучении
метода приоритета с бесконечными нарушениями.
2.6 	Следствие. Каждая невычислимая в. п. степень содержит
простое (на самом деле г-простое) множество.
Из следствия 2.6 вытекает, что свойство г-простоты множества не
гарантирует его неполноту. Несмотря на то, что г-простые множества
легко строятся (см. упражнение 2.9), не так очевидно, как построить
гг-простые множества. И действительно, первым и наиболее
естественным примером такого множества оказалось максимальное множество,
которое мы построим в главе X. Мы увидим, что максимальное
множество имеет наиболее жидкое дополнение, возможное для кобесконечных
в. п. множеств. Тем не менее, Ейтс [1965] построил полное максимальное
множество, тем самым опровергнув предположение Поста о том, что
неполные в. п. невычислимые множества могут быть найдены среди
кобесконечных в. п. множеств с очень жидкими дополнениямм. Позднее
Марченков [1976] нашел совокупность свойств в духе предположения Поста,
гарантирующую неполноту множества, но для доказательства
существования множеств с такими свойствами требуется метод приоритета с
конечными нарушениями, разработанный первоначально Фридбергом и
Мучником для решения проблемы Поста. Этот метод мы изложим в гла¬

120
Глава V. Простые множества и проблема Поста
ве VII. Решение Марченкова этой проблемы в духе предположения Поста
можно найти в работе Одифредди [1981].
2.7-2.18 Упражнения
2.7. Множество S называется интросводимым, если S ^т Т для любого
бесконечного Т С S. Докажите, что для дефицитного множества В из
теоремы 2.5 множество В интросводимо.
2.8. Покажите, что г-простые множества вместе с совокупностью коко-
нечных множеств образуют фильтр в £. (В упражнении 1.5 это было
доказано для простых множеств.)
2.9. Постройте г-простое множество прямой конструкцией, с
привлечением «подвижных маркеров». Указание. Модифицируйте конструкцию
из упражнения 1.6, заменив требование Ре на требование
Ре : { РЫх) }хеч; — сильная таблица без пересечений =>►
(3x)[DVe(x) С А].
Стратегия удовлетворения требования Ре заключается в нахождении на
шаге s -1-1 такого х, что
(Vy ^ х)[^е,Лу) 4].
(Уу>2 ^ Х)[^<Ре,.(у) 13 = 0]|
И
#*>«,.(*) ^ [ае+1.00)‘
Тогда в А перечисляются все элементы множества D(Pe a(xy
2.10. Докажите, что множество {х : Wx г-просто} Щ-полно. (См.
указание к упражнению 1.8.)
2.11. Покажите, что любое кобесконечное в. п. множество В имеет г-
простое надмножество А. Указание. Если В не является г-простым, то
по теореме 2.3 существует такая возрастающая вычислимая функция /,
что [/(п),/(пН-1))ПД Ф 0 для любого п. Пусть Fn = [f(n),f(n-1-1)).
Используем стратегию из упражнения 2.9 с тем изменением, что каждому
маркеру Ге сопоставляется некоторое множество Fn вместо числа п.
Когда х перечисляется в J5, то он перечисляется и в А. Кроме того, если
окажется, что множество Fn не сопоставлено никакому маркеру, то все

§ 2. Гиперпростые множества
121
его элементы перечисляются в А. В начале построения каждый маркер
Ге связывается с множеством Fe. Чтобы удовлетворить требованию Ре
из упражнения 2.9, ждем такого я, что ipe{x) I и Аре(ж) П Fn = 0 для
любого Fni связанного в настоящий момент с маркером Г», г ^ е. Для
каждого у G D<pe{x) находим такое число п, что у G Fn, перечисляем все
элементы множества Fn в А и передвигаем маркер, связанный с Fn (если
такой существует), на некоторое множество Fm, т ^ п, которое ещё не
является подмножеством множества А. Докажите, что каждый маркер
Ге передвигается конечное число раз и останавливается окончательно
на некотором множестве Fn таком, что Fn П А ф 0. Следовательно, А
бесконечно. (Заметим, что описанная процедура построения множества
А не является равномерной по В.)
2.12. Множество А таблично сводится (сокращенно, tt-сводится) к
множеству В (А ^tt В), если существуют такие вычислимые
функции / и 0, что х G А тогда и только тогда, когда В \ f{x) = Dy
для некоторого у G Dg(x)- (В табличном представлении каждая строка
соответствует одному из возможных вариантов значений
характеристической функции множества В f(x). Множество Dg(ж) содержит
кодовые номера у тех строк, где «да» является верным ответом для
данной строки на вопрос: «верно ли, что х G Д?».) Докажите, что В ^tt А,
где В — дефицитное множество для А из теоремы 2.5.
2.13. Множество А ограниченно-таблично сводится к множеству В
(пишем А ^ьи В), если существуют некоторое число п (называемое
нормой этой сводимости) и такие вычислимые функции / и </, что для
любого х выполнены условия: (1) |£>/(ж)| ^ п и (2) х G А тогда и
только тогда, когда В П ^/(ж) = Dy для некоторого у G Dg(x)-
(Например, для любого множества А, А ^ьи А.) Пусть В — булева
алгебра, порожденная в. п. множествами, как в упражнении Ш.3.9.
Докажите, что A G В тогда и только тогда, когда А ^ьы К. (Заметим, что
А В => А ^ьи В => A ^tt В, кроме того, сводимости и
рефлексивны и транзитивны, и поэтому они индуцируют отношения
эквивалентности =ьи и =tt •)
2.14. Докажите, что если множества А и В в. п. не равны ш и 0 и
А ^ьи В с нормой 1, то А В.
2.15°° (Кобзев). Докажите индукцией по норме п, что если А В
и А является одним из множеств вычислимо неотделимой пары в. п.

122
Глава V. Простые множества и проблема Поста
множеств, то В не простое. Для п = 1 используйте упражнения 2.14
и 1.9. (Схему доказательства см. у Одифредди [1981, теорема 8.2].)
2.16 (Фридберг и Роджерс [1959]). Множество А слабо таблично
сводимо к множеству В (пишем А ^wtt В), если А = {е}в для некоторого е,
и существует такая вычислимая функция /(х), что /(х) ^ и(В;е, х), где
и — use-функция вычисления { е }в(х) из определения III. 1.7. (Это
определение похоже на определение A ^tt В из упражнения 2.12 с тем
отличием, что здесь нет функции д.) Эту сводимость также называют
ограниченной тьюринговой сводимостью и иногда обозначают А ^ьт В.
Можно также определить g ^wtt h для функций g и h, используя в
вышеприведенном определении их графики , как это было сделано для
g ^т h в определении III.1.2(ii). Покажите, что ни для какого г-простого
множества Н не выполняется К ^wtt Н . Указание (Оуингс).
Предположим, что К = { е }я и функция / определена так же, как выше.
Достаточно показать, что для каждого интервала [0, у], пересекающегося с Н,
можно равномерно по у найти такое число z > у, что [у -I- 1, z] П Н ф 0.
Положим F — Н П [0, у]. Пусть множество Wn состоит из всех х таких,
что
(За)[{ е }*(х) = 0 & (Vi> < lh(a)[[a(v) = 0 => v G F]
& [<т(г>) = 1 => v € Я]]].
К множеству Wn применяем продуктивную функцию для К и затем
применяем функцию /, чтобы получить zF. Полагаем z = max{zF :
FQ[0,V])-
2.17 (Миллер и Мартин [1968]). Степень а называется гипериммунной,
если а содержит гипериммунное множество, в противном случае а
называется гипериммунно-свободной .
(a) Используя теорему 2.3, докажите, что если а гипериммунна и
а < Ь, то b также гипериммунна.
(b) Покажите, что степень а гипериммунна тогда и только тогда,
когда существует функция степени ^ а, которая не мажорируется
никакой вычислимой функцией.
(c) Покажите, что если (За)[а < b ^ а'], то b гипериммунна.
(Используйте (Ь) и лемму о пределе.)
(d) Покажите, что любая ненулевая степень, сравнимая с 0',
гипериммунна.
2.18. (а) Докажите, что любое г-простое множество просто.

§ 3. Метод разрешения
123
(b) 	Докажите, что любое гг-простое множество г-просто. (Обратное
неверно, т. к. по теореме XI. 1.7 гг-простые множества имеют высокие
степени, а по теореме 2.5 в каждой ненулевой в. п. степени есть г-простые
множества.)
§ 3. Метод разрешения
Фридберг [1975b] и Ейтс [1965] ввели следующий простой способ
построения в. п. множества А, вычислимого относительно данного
невычислимого в. п. множества В. Элемент х перечисляется в А на некотором
шаге s, только если множество В разрешает элементу х это сделать
в том смысле, что некоторый элемент у < х перечисляется в В на
шаге s. Комбинируя подобное «разрешение» с кодированием множества В
в А, часто удается построить в. п. множество А той же степени, что
и множество J5, но обладающее некоторыми специальными
свойствами. Например, сейчас мы построим простое, негиперпростое множество
заданной ненулевой в. п. степени. (В упражнении 5.6 мы увидим, что
в доказательстве подшаг 2 на самом деле не является обязательным и
достаточно только подшага 1.)
3.1 Предложение. Если {As }s€u; и — такие вычислимые
перечисления в. п. множеств А и В, что из х Е As+\ — As следует
(3у < х)[у Е В - В8], то А В.
Доказательство. Чтобы Д-вычислимо определить, верно ли, что х € А,
находим такой шаг s, что В8 [ х = В х. Теперь х Е А тогда и только
тогда, когда х Е А3. []
3.2 Теорема. Для любого невычислимого в. п. множества В
существует простое негиперпростое множество А =т В.
Доказательство. Фиксируем вычислимую 1:1-функцию / с областью
значений В. Положим
Bs = {f(0),...,f(s)}.
Пусть А8 обозначает множество элементов, перечисленных в А к концу
шага s. На шаге s = 0 ничего не делаем. Предположим, что As = { ag <
af < ...}.
Шаг s + 1.

124
Глава V. Простые множества и проблема Поста
Подшаг 1. (Который делает множество А простым, не нарушал
условия А ^т В.) Для всех е (разумеется, е ^ s) таких, что Wet8 П As = 0
и
(Зж)[ж > Зе к ж Е We,s & f{s 4-1) < ж], (3.1)
перечисляем в А наименьший такой элемент ж, который соответствует
числу е. Если такого е не существует, то ничего не делаем. В любом
случае переходим к подшагу 2.
Подшаг 2. (Который кодирует множество В в А.) Перечисляем
аЗ/(Н-1)+1 в А- __
Заметим, что \А П [0,3е]| ^ е, т. к. самое большее е элементов у ^
Зе могут быть перечислены в А в под шаге 1 (по одному для каждого
W{, i < е), и самое большее е элементов — в подшаге 2 (по одному для
каждого i € В, г < е: действительно, у ^ а*, поэтому, если в подшаге
2 у Е As.|_i - As , то у = азх+1, где х Е Bs+\ — Bs, следовательно Зе ^
г/ ^ Зж + 1 и, следовательно, е > х). Таким образом, А мажорируется
функцией f(x) = Зж, поэтому А бесконечно и А не г-просто.
Заметим, что из третьего коньюнкта в (3.1) и того, что у ^ а*,
следует, что если В8 I х = В х, то As ^ х = А [ х.
Следовательно, А ^т В по предложению 3.1. Убедимся в справедливости В ^т А.
Действительно, для любого х можно Л-вычислимо найти такое s, что
аЗж+1 = ^mt аЗх+1* Ясно, ЧТО х € В тогда и только тогда, когда х Е 2?s.
Покажем, что А просто. Предположим противное: пусть We
бесконечно и We П А = 0 для наименьшего такого е. Тогда, как следует из
подшага 1, множество
Ue = { х : (3$)[ж Е & /(s + 1) < ж] }
конечно, что противоречит невычислимости множества В. Ц
«Разрешение» в предложении 3.1 является «разрешением» самого
простого вида и обеспечивает, фактически, более сильную сводимость
А ^wtt В, определенную в упражнении 2.16. Более общее и полезное
«разрешение» используется там, где элементу ж «разрешается»
появиться в множестве А на шаге s + 1, только если некоторый элемент у <Г%,
появился в Б на шаге s+1. Здесь Г* — позиция маркера Гх к концу шага
s, который движется к некоторому пределу и который может сдвинуться,
только если некоторый меньший элемент перечисляется в В. Например,
в главе XI нам будет нужна главная функция «разрешающего»
множества В, поэтому мы определяем Г* = Ь*, где Bs = { < 6f <...}. В
следующем предложении под f(x,s) подразумевается Г*.

§ 3. Метод разрешения
125
Предложение 3.3. Пусть {>ls}seu; и {J5s}s€u, — вычислимые
перечисления в. п. множеств А и В. Пусть f{x,s) — такая вычислимая
функция, что для любых х и s
(i) f(x, s) ф f(x, s + 1) =* (By < f(x, s))[2/ G Bs+l - Bt],
(ii) f(x) =dfn lim, f(x, s) < со, и
(iii) x G Л,+1 - As => (3y < /(x, s))[y G Bs+i - Bs].
Тогда A ^т В.
Доказательство. Для каждого х В-вычислимо находим такое число t,
что В [ f(x,t) = Bt [ f(x,t). Теперь f{x,t) = limSf(x,s) и x G A
тогда и только тогда, когда х е At. (Заметим, что пункты (i) и (ii) в
отдельности обеспечивают f В.) Ц
Мы должны рассматривать это «разрешение» как попытку
построения тьюринговой сводимости Ф такой, что А = Ф(В). Время от времени
мы получаем величину Ф(Bs;x) = у и определяем use-функцию /ф(х,в)
для аргумента х. А именно, перечисляем в некоторое в. п. множество
Уф, которое определяет Ф, «аксиому» (а,х,у), где а — Bs [ ^{x^s). Это
означает, что Ф°(х) = у с use-функцией ^(x^s). На последующем шаге
t -1-1 мы сможем изменить наше представление о величине у или
переопределить use-функцию, только если Bt+\ [ V>(a;,s) Ф Bt\ t/>(a;,s), так
что а (ф Bt+1.
Полезно сравнить этот метод разрешения Ейтса с методом
разрешения Мартина из § 2 главы XI, где строится в. п. множество А,
удовлетворяющее некоторым положительным требованиям бесконечного
действия и расположенное ниже заданного высокого в. п. множества. См.
замечание XI.2.6.
3.4-3.6 Упражнения
3.4. 	Докажите, что «разрешение» в предложении 3.3 является
«разрешением» наиболее общего вида в том смысле, что для любых данных
невычислимых в. п. множеств А и В таких, что А ^т В, можно найти
вычислимые перечисления и вычислимую функцию /, удовлетворяющую
пунктам (i), (й) и (iii) из предложения 3.3. Указание. Пусть А = {е}в.
Зафиксируем вычислимые перечисления { At} teu и {Bt}te w множеств
А и В. Для данных А8, Bs, bs G В и {f(x,s) }x€u, найдем такое
наименьшее число t, что As С At, { bs } U Bs C Bt и At(y) = { e }fl(y) для
всех у ^ s. Положим As+i = At и Bs+1 = Bt. Для каждого у ^ s такого,

126
Глава V. Простые множества и проблема Поста
что Bt f f(y,s) ф Bs f f(y,s), определим f(y,s + 1) = u(Bt;e,y,t), где
функция и была задана в определении IIIЛ.7. Пусть 1 — некоторый
элемент из В — Bt. Для у > s определим /(у, s + 1) = 1 + bs+1.
3.5 	(Ейтс). В. п. множество А называется полукреативным, если
существует такая вычислимая функция /, что если Wx С А, то W^(x) С А
и Wf(x) %. Wx. Покажите, что для каждого невычислимого в. п.
множества В существует полукреативное множество А =т В. Указание.
Чтобы обеспечить А ^т В, на шаге s + 1 перечисляем 2х • Зу в А, как
только 2х Зу G WX}8 и Bs+1 ^ г/ ^ ^ у. Пусть Wf(x) = { 2х Зу : г/ G и }.
(См. также упражнения VII.2.7, XI.2.10 и замечание XI.2.19.)
3.6. 	Используя метод разрешения докажите, что в каждой невычислимой
в. п. степени существует гиперпростое множество.
§ 4. Полнота эффективно простых множеств
Пост построил и полное простое множество, однако он не предполагал,
что полным является даже простое множество, построенное им
первоначально, также как и все эффективно простые множества.
4.1 	Теорема (Мартин [1966а]). Если А эффективно просто, то А
полно.
Доказательство. Пусть {Ks}seш — вычислимое перечисление
множества К и в(х) — такая ч. в. функция, что в(х) = (p>s)[x G К8\, если
х € К, и в(х) расходится в противном случае. Пусть множество А
эффективно просто с функцией /, { Aa }eew — перечисление множества А и
As = {< а* < а2 <...}. Используя теорему рекурсии с параметрами,
определим вычислимую функцию h следующим образом:
Wh(x)
к
.•(*) „•(*>
>“i
.•(*)
гЩх)
если х € К,
в противном случае.
(4.1)
Положим r(x) = (l*s)[asfh^ = afh(х)]. Тогда г А, т. к. функции / и h
вычислимы. Теперь, если х G К и г(х) ^ в(х), то W^x) С А и |И//1(а.)| =
fh(x) -f- 1, что противоречит выбору функции /. Следовательно, для
любого х € К, г(х\ > 0(х). Таким образом, для любого х, х G К тогда
и только тогда, когда х G Кг(ху Поэтому К A. Q
4.2-4.4 Упражнения

§ 5. Критерий полноты для в. п. множеств
127
4.2. 	Множество А называется эффективно иммунным , если А
бесконечно и существует такая вычислимая функция /, что если Wx Q А,
то \WX\ < f{x). Докажите, что если множество А эффективно иммунно,
В в. п. и А В, то В =т 0'. Указание. Используйте лемму Ш.3.2 о
модуле и модифицируйте доказательство теоремы 4.1.
4.3 (Смальян-Мартин). (а) Докажите, что если множество А
эффективно просто, А С В Соо о; и В в. п., то В также эффективно просто.
(Напомним, что запись X Соо У означает, что X С Y и Y — X
бесконечно.)
(Ь) Покажите, что существует эффективно простое гиперпростое
множество. (Используйте упражнение 2.11. Заметим, что простое
множество Поста S из теоремы 1.3 эффективно просто, но не гиперпросто.)
4.4 (Шёнфилд [1957]). Множество А называется квази-креативным,
если А в. п. и
(3 вычислимая f)(4x)[Wx С А => [Df(x) С Л & ^/(ж) £ Wx]\.
Докажите, что если А квази-креативно, то А полно. (Используйте
теорему рекурсии в духе теоремы 4.1 или теоремы П.4.6.)
§ 5. Критерий полноты для в. п. множеств
Мартин [1966а] на самом деле доказал значительно более сильный
результат, чем теорема 4.1, сформулировав достаточное условие полноты
для в. п. множеств. Его условие применимо к ряду других множеств,
которые являются «эффективно» невычислимыми в. п. множествами,
включая креативные, квази-креативные и таблично полные множества.
Лахлан [1968а] модифицировал условие Мартина так, что оно стало
необходимым и достаточным. Затем Арсланов [1977] преобразовал условие
Лахлана к следующему виду, который может рассматриваться как
обобщение теоремы рекурсии. Оно утверждает, что не только вычислимые
функции, но также и все функции произвольных в. п. степеней,
меньших, чем 0', обладают неподвижными точками. (Ниже приводится
более простое доказательство теоремы 5.1, принадлежащее Соару, впервые
опубликованное Арслановым в [1981]. Первоначальное доказательство
Арсланова, использующее критерий полноты Лахлана (Лахлан [1968е]),
можно найти в работе Арсланова, Надырова и Соловьёва [1977].)
5.1 	Теорема (Критерий полноты Арсланова) (Арсланов [1981]).

128
Глава V. Простые множества и проблема Поста
В. п. множество А полно тогда и только тогда, когда существует
такая функция f А, что Wf(x) ф Wx для любого х.
Доказательство. (=$►) Напомним, что {х : Wx = 0} =т 0', по
теореме Н.4.2. Определим функцию / 0; следующим образом:
w _ Г 0, если Жх ф 0,
/(*) \ { 0 } в противном случае.
{<=) Предположим (Vx)[Wf(x) ^ W*], где / А. По лемме о модуле
существует такая вычислимая функция f(x,s), что f(x) = \im8f(x,s)
для любого х, и последовательность { Axf(x, s) }5€u, имеет модуль m ^т
А. Пусть { Ks }sgu> — вычислимое перечисление множества К. Пусть
в{х) = (fis)[x G К8], если х € К, и в(х) расходится в противном
случае. Используя теорему рекурсии с параметрами, определим
вычислимую функцию h следующим образом:
Wh(x) = / ^f{h{x),9{x)Y еСЛИ Х е
w \ 0 в противном случае.
Теперь, если х € К и 0(х) ^ m(h(x)), то f(h(x),6(x)) = f(h(x)) и
n^/(/i(®)) = И^(х), что противоречит выбору функции /. Следовательно,
для любого х
хеК <=> х € Km(h(xj),
так что К -4- Q
5.2 	Следствие (Арсланов [1981]). Для любой в. п. степени а а < О7
тогда и только тогда, когда для каждой функции / G а существует
такое число п, что Wn — Wf(n). Q
Заметим, что условие вычислимой перечислимости множества А в
теореме 5.1 является необходимым (см. упражнение 5.9). Далее, если
функция / не имеет такой неподвижной точки п, что Wn = Wf (п), то
мы, по крайней мере, можем надеяться на её * -неподвижную точку
(почти неподвижную точку), а именно, на такое число п, что Wn =* Wf(ny
Упражнение 5.5(a) является аналогом теоремы рекурсии, т. к. оно
устанавливает, что любая функция / 0' имеет *-неподвижную точ¬
ку, а упражнение 5.10 содержит критерий 0"-полноты, который
является аналогом теоремы 5.1, и в котором используются *-неподвижные
точки вместо неподвижных точек. Наконец, если функция / не имеет

§, 5. Критерий полноты для в. п. множеств
129
почти неподвижных точек, то мы можем надеяться, что / имеет
хотя бы неподвижную по Тьюрингу точку, а именно, такое число п, что
Wn =т Wf(n). В следствии ХИ.5.2 будет доказано, что это справедливо
для всех функций / 0^- В § б главы XII мы расширим теорему
рекурсии и критерий полноты до аналогичных предложений для всех
уровней арифметической иерархии. Усиление теоремы 5.1 см. в
следствии ХИ.6.5.
5.3-5.10 Упражнения
5.3. 	Для каждого из следующих свойств определите подходящим образом
функцию / и, используя теорему 1.5, докажите, что множество А полно.
(a) А креативно.
(b) А квази-креативно (определение см. в упражнении 4.4).
(c) А эффективно просто.
(d) В из упражнения 4.2.
5.4 (Моррис-Гилл). В. п. множество А называется субкреативным (М.
Блюм), если существует такая вычислимая функция g, что для любого
ху если Wx П А конечно (возможно, пусто), то Л С Wg^ С A U Wх. С
помощью теоремы 5.1 докажите, что каждое субкреативное множество
полно. Указание. Найдите такое наименьшее число s, что либо (Ву)[у Е
— А], либо WXf8 Ф 0. В первом случае положите Wf(x) = {у},
а во втором — ^/(®) = 0* Покажите, что / А и / удовлетворяет
теореме 5.1.
5.5 (Арсланов, Надыров и Соловьёв [1977]). Число п называется почти
неподвижной точкой для функции /, если W/(n) =* Wn.
(a) Покажите, что для любой функции t/>, частично вычислимой
относительно 0', существует такая вычислимая функция /, что
(VsedomVOtW^*) =*wf(x)).
(Обобщение см. в теореме ХП.6.2.) Указание. Выберите такую всюду
определенную вычислимую функцию f(x,s)y что 'ф(х) = lims f(xys) для
любого х Е dom<ф. Определите
(b) Покажите, что любая функция / 0; имеет почти неподвижную
точку. (См. также теорему ХП.6.3.)

130
Глава V. Простые множества и проблема Поста
(с) Используя (Ь) покажите, что ни для какого кобесконечного в. п.
множества А не существует такой функции / 07, что для любого
х такого, что А С Wx, справедливо: (1) Wx П Wf(х) =* А; (2) Wx U
Wf(x) =* а). (В связи с этим отметим, что в следствии Х.2.7 мы докажем,
что множество А гг-просто тогда и только тогда, когда С* (А) является
булевой алгеброй, а именно, существует функция /, удовлетворяющая
(1) и (2). А из этого упражнения следует, что / не может Т-сводиться
к 0'.)
5.6 (Джокуш-Соар [1972а]). Предположим, что в теореме 3.2 множество
А строится только с помощью шага 1 (где условие «х > Зе» заменяется
на условие «х > 2е») без использования шага 2, кодирующего В в А.
Используя метод теоремы 4.1 докажите, что условие В А
выполняется автоматически. (Это — пример известного «принципа максимальной
степени», который, грубо говоря, утверждает, что любое
конструируемое в. п. множество А всегда имеет наибольшую возможную степень,
если только такая возможность явно не исключается в процессе самого
построения.) (См. также упражнение XI.2.9 и замечание XI.2.19.)
Указание. Определим функции h и г так же, как в (4.1), используя только
f(x) = 2х вместо f(x) и В вместо К. Положим В = {х : х € В — Дг(ж) }.
Заметим, что В в. п. относительно А. Рассмотрим по отдельности
случаи, когда В конечно и В бесконечно. Если В конечно, то, очевидно,
В А. Если же В бесконечно, то соотношение В А докажем
следующим образом. Ясно, что В в. и. относительно А. Для произвольного
числа у вычислимо относительно А находим такое число х Е В, что
2h(x) > у. Пусть s — такой первый шаг, что множество И^(х)>в
содержит число z > 2h(x). Для дальнейшего сначала покажите, что такое
число z существует, а затем, что у Е В тогда и только тогда, когда
у Е В9. (Заметим, что если у перечисляется в В позднее, то z позднее
перечисляется в А, но Wh(x) = { a£(l),..., aef^x) } С А, т. к. х G В-Вг(х),
поэтому |И^/1(а.)| = 2h(x) +1 > f(x).) (См. также упражнение XI.2.9 и
замечание XI.2.19.)
5.7 (Лахлан [1968а]). (а) В. п. множество А называется слабо
креативным, если существует такая функция / А, что для любого х, если
Wx С А, то f(x) Wx U А. Докажите, что в. п. множество А слабо
креативно тогда и только тогда, когда А полно.
(Ь) (Мартин). В. п. множество S называется слабо эффективно
простым, если S бесконечно и существует такая функция f S, что для

§ 5. Критерий полноты для в. п. множеств
131
любого х, если Wx С 5, то /(х) > \WX\. Покажите, что любое слабо
эффективно простое множество является полным.
(с) 	Покажите, что любое полное простое множество является слабо
эффективно простым.
5.8 (Джокуш). Докажите, что для произвольного множества А
следующие условия эквивалентны:
(a) (3/ A)CVe)[We Ф Wf{e)],
(b) (39 А)1уе)[<ре ф ¥>9(е)],
(c) (ЭЛ A)(4e)[h(e) ф <ре(е)\-
Указание. Для доказательства того, что из (Ь) следует (с),
определите вычислимую функцию d так же, как в доказательстве теоремы
рекурсии II.3.1, и положите h(e) = gd{e). Для доказательства того, что из
(с) 	следует (а), зафиксируйте такую ч. в. функцию ф, что если We ф 0,
то ф(е) G We. Выберите такую вычислимую функцию q, что для любого
е справедливо ipq(e) = Ау[ф(е)\. Положите Wf(e) = { h(q(e)) } для любого
е. (Заметим, что импликация (а) => (с) является обобщением теоремы
рекурсии.)
5.9 (Арсланов [1979] и [1981]). Покажите, что существуют множество
А 07, А1 =т 0' и такая функция / А, что (Ve)[We Ф ^/(е)]-
Указание (Джокуш). Докажите, что класс С, состоящий из таких {0,1}-
значных функций ft, что (Ve)[ft(e) ф <^е(е)], является П^-классом (как
определено в VI.5.11). Примените теорему о низком базисе VI.5.13, чтобы
получить функцию ft низкой степени, ft G С, затем примените
упражнение 5.8.
5.10 Критерий 0,,-полноты (Арсланов [1981]). Пусть A G Ег и 0'
А. Докажите, что
А =т 0" <=» (3/ A)Q/e)[We ф* Wf{e)\.
(Следовательно, эта теорема связана с упражнением 5.5(a) так же, как
теорема 5.1 связана с теоремой рекурсии.) См. теорему XII.6.5 для
обобщения. Указание (Джокуш). Сначала, используя метод из
упражнения 5.5(a), покажите, что если ф — частично вычислимая относительно
0' функция, то существует такая вычислимая функция #(е), что
(Ve G dom ф)[УГ+(е) =* Wg{e)}.
Замените построение теоремы 5.1 на 0'-построение. Пусть В = Fin.
Тогда В вычислимо перечислимо относительно 0'. Пусть {As}s€uJ и

132
Глава V. Простые множества и проблема Поста
{ В8 }8еи; 0; — вычислимые перечисления множеств А и В. Определите
функцию в(х) следующим образом: в(х) = fis[x Е Bs\, если iGB, и в(х)
расходится в противном случае. Имея / = {е}Л, определите функцию
/ так же, как в теореме 5.1. Имеем / W• Тогда /(у,в(х)) является
функцией, частично вычислимой относительно 0', поэтому существует
такая вычислимая функция д{у,х), что справедливо
(V*)(Vy)[[/(y,0(*)) Whyfi(x)) =* Wt(v,x)]
& [/(у,0(*)) W9(yiX) = 0]].
Теперь примените теорему рекурсии с параметром х к функции д, чтобы
получить такую вычислимую функцию h(x), что для любого ж справед-
ливо Wh(x) = Wg{h{x)iX). Тогда
(V* е B)[WHx) = Wg(h(x),x) =* WHh(xle{x))]. (5.2)
Теперь доказательство завершается так же, как и в теореме 5.1.

Глава VI
Оракульные конструкции не в. п. степеней
Более общим вопросом, чем проблема Поста, является проблема
существования между 0 и 0' каких-либо (не обязательно в. п.) степеней. Кли-
ни и Пост [1954] на этот вопрос дали положительный ответ,
построив несравнимые по Тьюрингу множества А, В 0;- Использованный
ими метод состоит в замене сложного условия типа А фт В
бесконечной последовательностью {Re}eeu> более простых условий, называемых
требованиями, где требование Re имеет вид А ф {е}в.
Характеристические функции множеств А и В строятся последовательно, по шагам:
Ха = IJsfSj хв = В процессе удовлетворения некоторому фикси¬
рованному требованию на шаге s определяются частичные функции fs
и gs. Каждому требованию в соответствии с его расположением в этой
последовательности присваивается определенный приоритет, и однажды
удовлетворенное требование остается удовлетворенным и впоследствии
(а именно, оно впоследствии не будет нарушено). Такие рассуждения
часто называются «диагональными рассуждениями», доказательствами
с помощью методов «жди и смотри», «начальных сегментов», или
доказательствами «Клини-Поста», чтобы отличить их от доказательств,
использующих метод приоритета с конечными нарушениями, изучаемых в
главе VII. В этих доказательствах действия, совершенные на некотором
шаге s построения при удовлетворении требования Де, впоследствии
могут быть разрушены для удовлетворения требования Ri более
высокого приоритета, г < е, так что процесс удовлетворения требования Re
приходится начинать сначала.
В главах IV и V мы строили в. п. множество А как объединение
конечных множеств {A5}5Gu;. При этом построение As на шаге s было
вычислимым. В этой главе построение f8 на шаге s не будет
вычислимым, а потребует привлечения некоторого оракула (7, например, (7 = 0'.
Такое построение называется С-вычислимым оракульным (или просто

134
Глава VI. Оракулъные конструкции не в. п. степеней
С-вычислимым построением). Кроме того, мы обеспечим выполнение
условия fs С /в+1. Если при этом для любого s множество dom fs
конечно, то мы называем это построением с конечными расширениями (как
ниже в§ 1, § 2 и § 3), в противном случае — построением с бесконечными
расширениями (как в § 4).
В седьмой и последующих главах мы построим вычислимо
перечислимые множества с похожими свойствами. Для этого нам придется
отказаться от оракульных построений и использовать более сложные апрок-
симирующие их вычислимые построения. В этих построениях
требования могут нарушаться и, следовательно, будут требовать внимания,
многократно. Фундаментальная стратегия удовлетворения каждому из
этих требований является такой же, поэтому для лучшего понимания
мы их сначала изучим в виде более простых оракульных построений.
В пределах этой главы малые латинские буквы с индексами fs, gs,...
будут использоваться для обозначения строк и частичных функций, в
то время как буквы fug без индексов по-прежнему будут обозначать
только всюду определенные функции. Малые греческие буквы р, сг, т и v
обозначают строки из w<UJ или из 2<и}. Через сг~т обозначается строка,
являющаяся конкатенацией строк а и т (т пишется вслед за сг). Символ
0 используется для обозначения пустой строки; сг С т означает, что сг
является начальным сегментом т, сг с т означает, что сг С т и сг ф т;
обозначения сг С р,т (а ^ 6, с) являются сокращениями для «сг С р» и
«сг С т» («а ^ 6» и «а ^ с» соответственно).
§ 1. Пара несравнимых степеней ниже О'
1.1 Предложение. Пусть / — всюду определенная функция, и / =
Us 'Фв, где { ф3 }seu> является A-вычислимой последовательностью
частичных функций (т. е. ^(х) = 0(x,s) для некоторой частичной А-
вычислимой функции в). Тогда функция f является А-вычислимой.
Доказательство. Для вычисления f(x) с помощью оракула А находим
такое s, что i/>s(x) определена. Тогда f(x) = i/>s(x). О
1.2 Теорема (Клини-Пост). Существуют такие степени a, b ^ О',
что а несравнима с Ь (пишется а|Ь, что означает a^b ub ^ aj.
Поэтому 0 < a, b ua,b<0'.
Доказательство. Множества А, В ^т 0; построим по шагам методом
конечных расширений с привлечением 0'-оракульного построения так,

§ 1. Пара несравнимых степеней ниже О7
135
что ха = [Jsfs и Хв = где fs 9s — строки из 2<и конечной
длины ^ s, рассматриваемые как начальные сегменты функций ха и
Хв- Так как построение строк fs и д8 на шаге s будет вычислимым
относительно 07, то { fs }seu> и {<7*}5еи> будут 07-вычислимыми
последовательностями и, следовательно, А, В ^т 0; по предложению 1.1. Нам
достаточно для каждого е удовлетворить требованиям
Re:A?{e}B,
И
Se:B?{e}A,
чтобы обеспечить А фт В и В фт А. Тогда а = deg(A) и b = deg(2?)
будут несравнимыми. (Существует ещё неявное требование того, чтобы
(Js fs и (Jsgs были всюду определенными функциями, но оно
удовлетворяется за счет выполнения условий fs С fs+i И 9s С gs+i-)
Шаг s = 0. Пусть f0=g0 = 0.
Шаг s+ 1 = 2е + 1. (Удовлетворяем Re). Имеем fs,gs € 2<ц; длины ^
s. Пусть п = lh(fs) = (fix)[x ф dom/s]. С помощью 07-оракула проверяем
условие
(30(Зст)[с7Э^&{е}Ип)|]. (1.1)
Условие « a D д8э> является вычислимым отношением относительно
аргументов а и д81 а вторая часть условия (1.1) вычислима по Ш.1.8,
поэтому (1.1) является Ei-утверждением и может быть проверено эффективно
относительно 07.
Случай 1. Предположим, что (1.1) верно. Перечисляем вычислимое
множество
{<М> : {е}^(п) 4},
и выбираем наименьшую пару (cr7,£7), удовлетворяющую бескванторной
части (1.1). Полагаем gs+1 = а1 и fs+i(n) = 1 — {е(п).
Случай 2. Предположим, что (1.1) неверно. Определяем fs+i(lh(fs)) =
0 и gs+i(lh(gs)) = 0. (А именно, полагаем fs+i = fs 0 и д8+г = д8 0.)
В обоих случаях имеем lh(f8+i), lh(gs+i) ^ s-1-1, поэтому ха = U* Л
И Хв = Us9s определены для всех значений аргументов. В обоих
случаях, если / D fs+1 и 9 О 9s+1, то f(n) ф {е}9(п) по use-принципу
Ш.1.9.
Шаг s+l=2e+2. (Удовлетворяем 5е). Производим точно такие же
действия, что и выше, переставляя / и д. Q

136
1.3 	Теорема (Релятивизованный вариант). Для любой степени с
существуют такие степени а и Ь, что с ^ a,b; а, b ^ с1 и а|Ь.
Доказательство. Выберем С Е с. Релятивизуем предыдущее
доказательство, используя оракул С", для построения множеств А и В таких,
что АфС\тВ®С и А,В С'. Вместо (1.1) используем С' для проверки
(ЗгХЗпХЭтзНп D д8 & Т2 С С & {е }tTl®T2(«) 4], (1-2)
где т\ 0 гг определяется как кратчайшая строка р Е 2<и;, для которой
р(2х) = т\(х) и р(2х -h 1) = Т2{х). Очевидная модификация случаев 1
и 2 обеспечивает А ф { е}ВфС. На шаге 2е + 2 добиваемся выполнения
условия В ф {е }ЛфС. Затем полагаем а = deg(A 0 С) и b = deg(B 0
С). D
1.4 	Определение. Счётная последовательность множеств {А*}^
называется вычислимо независимой, если для каждого i выполнено
А{ фт ®{ Aj : j ф г }, где операция 0 определена в III.2.7.
1.5-1.8. Упражнения
1.5. 	Модифицируя доказательство теоремы 1.2, постройте вычислимо
независимую последовательность { Aj }j€u, множеств, вычислимых
относительно 0' (на самом деле j V)- Указание. Используйте 0'-
вычислимое построение с конечными расширениями, чтобы построить
на шаге s такие строки { /? }s€u;, что если Aj = \JS /?, то для каждого
ей i выполняется требование
Мф{е}
На шаге s = 0 для всех j положите = 0. На шаге s + 1 = (е,г) + 1
удовлетворяйте требованию R(e,i) следующим образом. По данным
строкам {//}jeu>, только конечное число из которых непусты, положите
п = lh{ff) и используйте оракул 0' для проверки существования
числа тп и конечной последовательности строк а\, ст2,..., сг*. таких, что
{е }0{'ЯЛ«>(П) 1= тп & (V? ^ k)\j ф г => // С *;]. (1.3)
Теперь, если условие (1.3) выполняется, действуйте как в случае 1
теоремы 1.2 (полагая //+1(n) = 1 — m и /?+1 = aj для j ф i). В противном
случае — как в случае 2. (Не забудьте сделать все /* всюду
определенными.)

§ 1. Пара несравнимых степеней ниже О'
137
1.6. Частично-упорядоченное множество V = (Р^р) называется
счётно универсальным, если каждое счётное частично-упорядоченное
множество изоморфно некоторому подпорядку V. Докажите
существование вычислимого счётно универсального частичного порядка на
и. Указание. Одно из решений можно получить, рассматривая
вычислимо представимую безатомную булеву алгебру, а другое — путем прямой
конструкции, в которой на шаге s -I-1 по данному конечному множеству
Р8 элементов из ^я множество Ps+1 строится путем добавления
нового элемента для каждого возможного порядкового типа над Р8. Булева
алгебра В = ({ bi }ieu>; V, Л/ ) называется вычислимо представимой,
если существует вычислимое отношение Р(г, j) и вычислимые функции
/, g и h такие, что P{i,j) истинно тогда и только тогда, когда hi ^ bj,
и такие, что bf^j) = bi V bj, bg^j) = bi A bj и bhp) = b\.
1.7. Докажите, что для любого счётного частично-упорядоченного
множества V = (Т,^р) существует сохраняющее порядок 1:1-отобра-
жение из Р в D(^ O') — степени ^ 0'. Указание. Как следует из
упражнения 1.6, можно предположить, что Р = со и ^р — вычислимое
отношение. Пусть { А\ }tGa, — последовательность, полученная в
упражнении 1.5. Определите / : ш —> D(^ O'), полагая /(i) = а* = deg(® Aj :
j ^p ъ). Покажите, что если i ^p j, то a* ^ (используя определение и
то, что отношение ^р вычислимо), и что если г ф.р j, то а* ф. a j (из-за
вычислимой независимости { А{ }геа;)-
1.8. Докажите, что существует 2Н° попарно несравнимых степеней.
Указание. Используя определения 5.11 и обозначения упражнения 5.12,
постройте такое дерево Т С 2<и}, что f\rg для любой пары /, <7 G [Г], / ф
д. Пусть Т = ‘Je Те, где Te+i Э Те, причем дерево Te+i состоит из 2е+1
несравнимых строк таких, что для всех сг, т G Те+1, если афт, то
(V/ Э <т)(Уд D т)[{ е }/ Ф д & { е }э ^ /]. (4.1)
Пусть То = {0}. По данному дереву Те определите множество Ье
листиков дерева Те следующим образом:
Ье = {а : а еТе k (Vt D а)[т £Те)}.
Затем определите
5 = {сг 0:aeLe}U{a 1 : a G Ье}.

138
Глава VI. Оракульные конструкции не в. п. степеней
Предположим, что S = {pi : i ^ 2e+1 }. Зафиксируем i,j ^ 2е+1,г ф j.
Пользуясь методом доказательства теоремы 1.2, замените pi и pj на
строки a D pi,r D Pj, удовлетворяя (1.4). Повторите эту процедуру для
всех i,j ^ 2е+1,г 7^ j.
§ 2. Избегание конусов степеней
Все построенные нами до сих пор степени (такие как или степени,
расположенные ниже 0') были сравнимыми с О'. В этом параграфе мы
покажем, как построить степень а, несравнимую с заданной степенью
b > 0. Для этого а должна находиться вне нижнего конуса степеней
{ d : d ^ b } и вне верхнего конуса { d : d ^ b }. Стратегия
удовлетворения последнего требования (мы ей следуем на чётных шагах) будет
использована в § 4 и § 5 этой главы, а после некоторого уточнения мы
её часто будем использовать и в различных построениях в. п. степеней,
например, в теореме VII.3.2 Сакса о разложении.
2.1 	Теорема. Для любой степени b > 0 существует степень а < Ь'
такая, что а|Ь.
Доказательство. Пусть В Е Ь. Характеристическую функцию /
множества А мы построим с помощью В'-вычислимого построения с
конечными расширениями, / = |Jsfs, удовлетворяя всем требованиям Re и
Se из теоремы 1.2.
Шаг s = 0. Полагаем /0 = 0.
Шаг s-f-1 — 2е + 1. (Удовлетворяем Re : А ф { е }в.) Пусть п = lh(fs).
С помощью оракула В' проверяем, определено ли значение { е }в{п) (т. е.
верно ли, что (n, е) Е Кв = Кв = В1). Если «да», то полагаем /s+i(n) =
1 — (е}в(п). В противном случае полагаем /s+i(n) = 0.
Шаг s -1- 1 = 2е + 2. (Удовлетворяем Se : В ф { е }А.) Пусть дано fs.
С помощью оракула 0' проверяем, верно ли следующее:
(3a)(3r)(3x)(3y)(3z)(3t)[f8 С а, г & { е }?(х) I ( .
= у Ф Z = {е}Цх) I].
Если «да», то одно из чисел y,z должно отличаться от В(х).
Полагаем /s+1 равной первой строке a D fs такой, что {е}а(х) ф В(х)
для некоторого х. (Все это 2?'-вычислимо, т. к. В 0 0' В'.) Если
же (2.1) неверно, то полагаем /s_j_i = fs 0. В этом случае мы
утверждаем, что если f D fs и функция { е = д является всюду определенной,

§ 3. Обращение скачка
139
то д вычислима. (Поэтому {е}* ф В, т. к. 0 <т В). Для
вычисления д(х), вычислимо перечисляем L из теоремы III. 1.8 до тех пор,
пока не перечислится первая a D fs такая, что {е}°’(а;) сходится. Тогда
д(х) = {е}*(х) = {е}а(х), т. к. в противном случае для некоторого т,
f8 С т С /, { е }т(ж) 1Ф { е }ст(ж), что удовлетворяет (2.1). О
2.2-2.3 Упражнения
2.2. Пусть {Ьп }печ> — произвольная счётная последовательность
невычислимых степеней. Докажите, что существуют такие попарно
несравнимые степени {ап}п€а;, что an|bm для всех n,m G w. Указание.
Соедините построения теорем 1.2 и 2.1 так, чтобы удовлетворить для
всех е,т и п требованиям вида R(e,n,m) : Ап ф {е}Вт, S(e>n,m) : Вш ф
{ е }Ап, а также Т(6>П)Ш) : Ап ф { е }Атп для пфтп.
2.3. Докажите, что если 0'-вычислимая последовательность
невычислимых множеств {Вп}пеш равномерно вычислима относительно 0', то
существует такое множество А, 0 <т А <т 07, что (Уп)[Вп фт А].
Указание. Стратегия на чётных шагах теоремы 2.1 использует только
оракул множества 0' 0 В.
§ 3. Обращение скачка
Заметим, что для любой степени а справедливо 0 ^ а, поэтому 0' ^ а7,
т. е. скачок любой степени расположен выше 0'. Таким образом,
оператор скачка, рассматриваемый как отображение совокупности степеней,
имеет область значений, содержащуюся в совокупности {Ь : b ^ О'}.
Приводимая ниже теорема утверждает, что это — отображение на все
множество {b : b ^ О7}. Степень а называется полной, если а ^ О7,
поэтому теорема дает также некоторый критерий полноты для степени
а.
3.1 	Теорема (Критерий полноты Фридберга). Для любой
степени b ^ О7 существует такая степень а, что а7 = a U О7 = Ь.
Доказательство. Пусть множество В Е Ь. Мы построим
характеристическую функцию / множества А через совокупность её начальных
сегментов {fs}seиспользуя В-вычислимое построение с конечными
расширениями.
Шаг s = 0. Полагаем /0 = 0.

140
Глава VI. Оракулъиые конструкции не в. п. степеней
Шаг s + 1 = 2е + 1. (Проверяем, будет ли е G А1.) Мы удовлетворим
требованию
Re ■ (Эст С Л)[{ е (е) I V(Vr Э <г)[{ е }т(е) t]]- (3-1)
(Если А удовлетворяет Де, то мы говорим, что А вынуждает скачок
для аргумента е.) По данному /5 используем оракул 0' для проверки
истинности соотношения
(Эа)(Э*)[/,Са&{е}?(еН]. (3.2)
(Заметим, что бескванторная часть формулы вычислима, поэтому (3.2)
является Ei-условием и, следовательно, вычислимо относительно О').
Если (3.2) выполняется, то полагаем /5+1 равной первой такой а
(например, той строке сг, которая быстрее остальных перечислится во
множестве L из теоремы III. 1.8, относительно стандартного перечисления
L). Если нет, то полагаем fs+i = fs.
Шаг s+l=2e+2. (Кодируем В(е) в А.) Пусть п = lh(fs). Полагаем
fs+i(n) = В(е). (Это завершает построение.)
Функция f = Usfs всюду определена, так как lh(f2e) ^ е. Пусть А =
{х : f(x) = 1} и а = deg(A). Все построение вычислимо относительно
J5, так как на нечётных шагах мы используем оракул 0', а на чётных —
оракул В, и 0' <^ТВ. Так как для любого А имеем А 0 0' А\ то для
доказательства А! =т В =т А 0 0' достаточно доказать следующие две
леммы.
Лемма 1. А В.
Лемма 2. В А 0 0'.
Доказательство леммы 1. Так как все построение В-вычислимо, то
и последовательность { fs }5€u, является В-вычислимой. Чтобы
определить принадлежность элемента е множеству А', В-вычислимо
проверяем, используя 0' В, выполняется ли (3.2) для fs, s = 2е. Если «да»,
то е G А', в противном случае е £ А'у так как ни для какого о Э fs
значение {е}<7(е) неопределено.
Доказательство леммы 2. Так как В(е) является последним элементом
строки /ге+2} то достаточно показать, что последовательность { fs }s€u;
является А 0 0'-вычислимой. Доказательство проводится индукцией по
s. По данному множеству { fs • s ^ 2е } с помощью оракула 0'
вычисляем /2е+1- Если п = lh(f2e+1), ТО /2е+2 = /2е+1 А{п) И /2е+2 МОЖНО
вычислить по /ге+i с помощью оракула A. D

§ 3. Обращение скачка
141
3.2 Теорема (Релятивизованный критерий полноты Фридбер-
га). Для любой степени с имеет место
Fx (с) : (Vb)[b ^ с' =* (За) [а ^ с & a' = c'Ua = b]].
Доказательство. Повторяется доказательство теоремы 3.1 с заменой О
и 0' соответственно на с и с'.
3.3 Следствие. Для любого n)l и любой степени с справедливо
Fn{с) : (Vb)[b ^ с<п> (За)[а ^ с & a<n> = c(n) U а = Ъ]].
Доказательство. Чтобы доказать (Vc)Fn(c) для любого n ^ 1,
используем индукцию по п и то, что Fn+i(c) следует из Fn(c) и ^(с^). Q
Несмотря на то, что теорема 3.1 демонстрирует одно из хороших
свойств оператора скачка, из нее также следует другое, неприятное
свойство скачка, а именно то, что этот оператор не является
1:1-отображением. Чтобы в этом убедиться, применим теорему 3.1 при b = 0" и
получим такую а, что а' = aUO' = 0". Очевидно, а | 0', но скачки этих
степеней совпадают. В упражнении 3.5 мы увидим, что также могут
одновременно иметь место условия а < b и а' = Ь'.
3.4-3.10 Упражнения
3.4. Докажите, что
(Vb ^ 0')(3ao)(3ai)[ao|ai & а^ = а0 U O' = b = ах U 0' = a'J.
Указание. Объедините построения из теорем 1.2 и 3.1, чтобы
одновременно работать с требованиями четырех видов (два вида из теоремы 1.2
и два — из теоремы 3.1).
3.5. Используя упражнение 3.4 докажите, что (3а)[0 < а < 0' & а' =
0'], т. е. существует невычислимая низкая степень (в теореме VII. 1.1 мы
увидим, что такая степень может быть вычислимо перечислимой ).
3.6 	(Джокуш-Познер). Множество А называется 1 -генерическим, если
оно удовлетворяет для любого е требованию Re из теоремы 3.1.
Докажите, что если множество А является 1-генерическим, то А 0 0' =т А1.

142
Глава VI. Оракульные конструкции не в. п. степеней
3.7 (Джокуш-Познер). Докажите, что А является 1-генерическим тог¬
да и только тогда, когда для любого в. п. множества строк We оно
удовлетворяет требованию
Se : {За С А)[а G We V (Vr D а)[т $ We]]. (3.3)
Указание. Для данного е определим вычислимую функцию /(е)
следующим образом:
{/(е)П*) = {
1,
неопределено
если (3s ^ \а\)(3т С а)[т G We,s\,
в противном случае.
Покажите, что если А удовлетворяет требованию Rf(e) из (3.1), то оно
удовлетворяет и Se.
3.8 	(Джокуш-Познер). Пусть А — 1-генерическое множество.
(a) Докажите, что А иммунно. Указание. Пусть V — в. п.
подмножество А. Определите We = {а : (За; G V)[a{x) = 0] } и, используя
требования Se из (3.3), покажите, что V конечно.
(b) Докажите, что А гипериммунно.
(c) Докажите, что не существует невычислимого в. п. множества
V А. Указание. Пусть V = {i}A. Определите
We = { а : (За;)[{ г }а{х) = 0 & х G V] }
и примените Se из (3.3), чтобы показать, что V вычислимо перечислимо.
(d) Докажите, что множества Ао и ii, где Ао{х) = А{2х) и А\{х) =
А(2х 4- 1)], несравнимы по Тьюрингу. Указание. Для доказательства
А0 Ф { е }Al рассмотрите в. п. множество строк
Ve = {а : (Зж)[{ е }ai (х) а0{х)] },
где сг0(а;) = сг(2а;) и а\(х) = а(2х 4- 1).
(e) Докажите, что существуют такие множества Bi ^т A,i G и;, что
для любого г выполнено В{ фт ®{Bj • j ф i }•
3.9.° Докажите, что если V невычислимое в. п. множество, то
существует 1-генерическое множество А ^т V. Указание. (Шор) Определим
функцию вычисления для множества V как функцию
с(п) = {fis)[V8 [ п = V [ п\

§ 4- Верхние и нижние грани степеней
143
Заметим, что с =т V. Чтобы удовлетворить требованиям Re из
теоремы 3.1, заменим 0'-вычислимое построение на шаге s -1-1 следующим
^-вычислимым построением. Выбираем наименьшее е ^ s такое, что
{е}{*(е) t и (3cr)k|^c(s)[/e С а и {e}*(e)(e) J.].
Если такое е существует, то пусть Д+i равна первой соответствующей
этому е строке а. Если требование Re не удовлетворено, то покажите,
что с является вычислимой функцией. Для этого на шаге s + 1 надо
эффективно вычислить: (1) такую строку as Э /5, что {е}°’в(е) (2)
c(s); (3) f8+1. (Заметим, что это доказательство напоминает
доказательство теоремы V.3.2, в котором методом разрешения строилось простое
множество S V- В обоих случаях, если V или с не дают
достаточно быстрого «разрешения», тем самым мешая проведению стандартного
построения, то устанавливаем, что V вычислимо.).
3.10 	(Джокуш-Шор [1983]). Докажите, что для любого г G о; и любого
множества В, для которого верно 0' В, существует такое А, что
А 0 WA =т А 0 0; =7" В.
(Заметим, что теорема 3.1 является частным случаем этого
утверждения, когда число г выбирается таким, чтобы W* — X1). Указание.
Повторите доказательство теоремы 3.1, заменив в (3.1) { е }р(е) | на е G W?
для р = а или р — т. (Это построение равномерно по В и по любому j
такому, что { j }в = 0'.)
§ 4. Верхние и нижние грани степеней
Из § 2 главы III следует, что любое конечное множество степеней имеет
наименьшую верхнюю грань (н. в. г.). В этом параграфе мы покажем,
что это неверно для наибольшей нижней грани (н. н. г.). Таким образом,
степени не образуют решетку, а образуют лишь верхнюю полу решетку.
4.1 Определение. Для произвольного множества А определим его и;-
скачок: А^ = {(i,n):xG А^ }, и пусть = deg(A^^) для A G а.
Бесконечная последовательность степеней { an }n€u; называется
возрастающей, если an < an+i для всех п. Например, последовательность
0,0^), 0<2>,.. . — возрастающая, а 0^^ является для нее естественной
верхней гранью, однако по следующей теореме эта последовательность
не имеет наименьшей верхней грани.

144
Глава VI. Оракулъные конструкции не в. п. степеней
4.2 Теорема (Клини-Пост-Спектор). Для любой возрастающей
последовательности степеней { ап }П€о; существуют такие верхние
грани Ь,с (называемые точной парой для этой последовательности), что
(Vd)[[d ^ b & d ^ с] =» (3n)[d ^ ап]]. (4.1)
4.3 Следствие. Никакая возрастающая последовательность не
имеет наименьшей верхней грани.
4.4 Следствие. Существуют степени b и с, не имеющие
наибольшей нижней грани.
Перед тем, как приступить к доказательству теоремы 4.2 приведем
несколько определений и введем новое обозначение.
4.5 Обозначения. Для произвольного множества А С и определим
его у -сечение:
д[у] _ | z) : (х, z) е А & z = у },
и положим
Л[<у] =и{Л[г] :z<y}.
(Используя функцию пары мы можем отождествлять А с подмножеством
ljxuj, и рассматривать А^ как у-ю строку множества А. Мы используем
обозначение с квадратными скобками А^ для того, чтобы избежать
путаницы с ?/-кратным скачком А^УК)
4.6 	Определение. Подмножество В С А называется густым
подмножеством А, если для каждого у выполняется следующее требование
(называемое также требованием густоты):
Ту : в№ =* ЛЧ
где X =* Y означает, что симметрическая разность X AY = (X - Y) U
(Y — X) конечна.
Здесь, также как и в последующих построениях в. п. множеств и
степеней из главы VIII, изучение густых подмножеств оказывается весьма
полезным (см., например, лемму о густоте VIII. 1.1).

§ 4• Верхние и нижние грани степеней
145
4.7 	Определение. Частичные функции называются
совместимыми (записывается как corapa£(0, i/>)), если они имеют общее
расширение, т. е. не существует такого числа х, что ф{х) и в(х) определены и
неравны.
Доказательство теоремы J^.2. Выберем Ау G в.у для каждого у и
определим А = { (х,у) : х G Ау }, так что (х, у) G & х G Ау. Мы
построим характеристические функции / и д множеств БиС, густых
подмножеств А (так, что Ау =т В^у] В, и аналогично для множества
С). По этой причине степени b = deg(J5) и с = deg((7) будут верхними
гранями для { an }nGu,. В дополнении к требованиям густоты
тв . В[У] _* Л1у]9
и
Тус : С[у] =* Ah1
мы должны удовлетворить для всех ей i требованиям
R(e i) : {е)В — {г}с = h — всюду определенная функция =>
(Э»)[Л Ау]
путем нахождения «е-расщеплений», аналогично доказательству
теоремы 2.1.
Пусть f8,9s)B8 и С8 — части f,g,B и С соответственно,
определенные к концу шага s следующего построения.
Шаг s = 0. Полагаем f0 = д0 = $.
Шаг s -1-1. Предположим, что f8 и д8 определены на всех элементах
из аЛ<51, и что
(Уз/ ^ s)[BM =• см =* лМ],
(dom/s — =* 0 =* (domgg — аДО).
Подшаг 1. (Удовлетворяем R(e,i) для s = (е,г).) Если
(3cr)(3r)(3x)(3£)[compat(cr, f8) & compat(r,^s) &
(e}"(aO № {*}*(*) 4-],
то пусть а и т — первые строки с такими свойствами. Расширяем f8
до / = f8 U а и gs до g = g8 U т. В противном случае полагаем / = fs и
g = gs. Заметим, что по (4.2) и (4.3) f8 =т =т gs• Следовательно,
compat(cr, /в) является -вычислимым отношением от а. (Заметим,
что для s > 0 этот подшаг требует использования оракула A,s_1 =т
(AK'ly.)
(4.2)
(4.3)
(4.4)

146
Глава VI. Оракулъные конструкции не в. п. степеней
Подшаг 2. (Удовлетворяем Тв и .)
Пусть /s+i(x) = f(x) для х Е dom/. Для всех х Е o;tsl - dom /
положим fs-i-i(ж) = А(х). Аналогично, полагаем gs+i(x) = g(x) для х Е
dom g, а для всех х Е — domg полагаем <7s+i(a;) = А(х).
По (4.3) fs (и, следовательно, /) определена лишь на конечном
множестве элементов из иД5! (то же самое верно и для #), так что 2?^ =*
=* и функции / и g определены на элементах из Этим
описание построения завершается.
Если (4.4) верно, то {е}в ф {г}с. Если (4.4) неверно и {е}в =
{i }с = h — всюду определенная функция, то для s = (е, г) покажем, что
h A<sl. Заметим, что ^т А, т. к. A<s 1 =т А°10.. .0AS-11 =т
Aq 0 ... 0 As-1 А- Для вычисления h(x) с помощью оракула A<s 1,
находим первую в некотором перечислении множества :{ а : { е }а(х) |}
строку а такую, что compat(cr, fs) и полагаем h(x) = {е}сг(х). Теперь
h(x) = {е}^(х)1 иначе для некоторого а1 С / верно compat(cr/, fs) и
{е}а (х) 1= у ф {е}°’(а;), так что (4.4) выполняется либо для сг, либо
для а1 при любом выборе строки г С С такой, что { г }т(ж) сходится. []
4.8-4.11 Упражнения
4.8. 	Покажите, что в доказательстве теоремы 4.2 множества В и С
автоматически оказываются вычислимыми относительно @{А'у: у Ecj}.
4.9. Покажите, что в доказательстве теоремы 4.2 можно положить
В — А и соответствующим образом изменить шаги 1 и 2 так, чтобы В
и С удовлетворяли тем же требованиям, что и прежде.
4.10. Пусть I — счётный идеал, содержащийся в верхней по л у решетке
тьюринговых степеней D. Докажите, что существуют такие степени Ь,
с, что для всех а Е D
а Е I <=> [а ^ b & а ^ с]
(Мы назовем b и с точной парой для I.)
4.11.° (Теорема Шёнфилда об обращении скачка.) Пусть S —
такое множество, что 0' 5 и 5 в. п. относительно 0'. Постройте
такое А ^т 0;, что А' =т S. (В теореме VIII.3.1 мы, используя
другое доказательство, усилим этот результат, сделав А в. п.) Указание.

§ 5. * Минимальные степени
147
Определяем 0'-последовательность { fs }s€u; частичных функций со
значениями из {0,1} такую, что fs С /s+1 и limsfs = ха• Для
выполнения 5 А' для каждого у обеспечиваем limхА((х,у)) = xs{y)- Для
выполнения условия А1 ^т S будем вынуждать скачок {е}А(е).
Фиксируем такое 0'-вычислимое перечисление { Ss множества 5, что
\Ss+i — Ss | = 1. Пусть /о = 0. Последующее является 0'-построением.
Шаг s +1. Предположим, что если у Е Ss, то /5((ж, г/)) = 1 для почти
всех ж, а в противном случае /Д(х, г/)) 1= 0 не более чем для конечного
числа х таких, что (х,у) < s, и /5((я,2/)) f для всех остальных х.
Подшаг 1. Теперь f8.ц имеет вычислимую область определения и
вычислима на dom fs. Следовательно, для каждого е ^ s, ещё не
«подчиненного» А', мы можем с помощью оракула 0' проверить справедливость
условия
(3t)(Зет)[compat(сг, fs) к { е YT{e) I (4.5)
& (Vy < e)(Vx)[(x,y) £ dom fs => °{(x,y)) = 0]].
Если «да», то выбираем наименьшее такое е и наименьшую
соответствующую строку сг. Полагаем gs+i = fsUa и говорим, что е подчинено
А1. В противном случае полагаем g8+1 = fs.
Подшаг 2. Перечисляем следующий элемент z Е Ss+i-Ss. Определим
/s+l((x,y»
, ffs+i(<®) !/>), если (x,y) € dom0s+b
< 1, если у = z к (x,y) £ dom<7s+i,
0, если у <£ Ss+1 ,(г,!|)Ои
. <ж, J/) £ dom0s+i.
Последнее условие в (4.5) обеспечивает то, что если у £ S, то
limx А((х, ?/)) = 0. Далее, для доказательства А1 ^т S зафиксируем
произвольное е. Предполагая, что для всех i < е значение ха'(i) уже
известно, найдем такой шаг s, что Ss [ е = S f е. Покажите, что если
число е не было подчинено А! на шаге s, то оно уже никогда не будет
подчинено А1.
§ 5. * Минимальные степени
Этот параграф содержит один из немногих фундаментальных методов
теории вычислимости над о;, который возникает не в связи с в. п.
множествами и степенями. Он включен в главу только для придания
завершенности ранее изложенным методам и может быть опущен без каких-
либо неудобств при чтении последующих глав. Различные вариации
этого метода породили много важных результатов, касающихся степеней

148
Глава VI. Оракульные конструкции не в. п. степеней
и их начальных сегментов. Они могут быть найдены в книге Лерма-
на [1983], изданной в той же серии, что и эта книга, и дополняющей ее
в тех областях теории вычислимости, которые не связаны с в. п.
множествами и их степенями. Кроме того, большое количество ссылок на
теоремы, использующие построение минимальной степени, можно найти
в библиографии, содержащейся в конце книги Эпштейна [1979].
5.1 Определение. Степень а называется минимальной, если а > 0 и
не существует такой степени Ь, что 0 < b < а.
Существование минимальных степеней доказал Спектор [1956], а
Сакс [1963а] доказал, что они существуют и среди степеней ниже О'.
Наше доказательство будет существенно совпадать с доказательством
Шёнфилда [1966], которое в свою очередь является упрощением
доказательства Сакса. Для начала приведем некоторые термины и леммы,
которые окажутся полезными при построении минимальных степеней.
Пусть а, /3,7 Е 2<{л} — строки. Будем говорить, что /3 и 7 расщеп-
ляюта, если аС/3,аС7, и/3и7 несравнимы в смысле
определения 4.7. Назовем f-деревом такую частично вычислимую функцию
Т : 2<ш 2<ш, что если хотя бы одно из значений Т(а 0),Т(а 1) опре¬
делено, то каждое из Т(а),Т(а 0), Т(а 1) также определены, и при
этом Т(а 0) и Т(а 1) расщепляют Т(а). (Например, тождественная
функция Id(cr) = а является f-деревом.)
Мы пользуемся термином «f-дерево» (читается: «функциональное
дерево»), чтобы отличать это понятие от стандартного понятия дерева,
как множества вершин Т С ш<и>, замкнутого относительно начальных
сегментов (см. определение 5.11). Связь между этими понятиями
следующая: если Т — всюду определенное вычислимое f-дерево, то Т\
(замыкание rng Т относительно начальных сегментов) будет вычислимым
деревом. Понятие f-дерева встречается только в этом параграфе, в то
время как деревья и вычислимые деревья будут использоваться часто.
(См. упражнения 5.12-5.14, главу X и главу XIV.)
Будем говорить, что строка а лежит на Т, если о Е rngT. Множество
А лежит на Т, если а С А для бесконечно многих а на Т. (Как
обычно, мы отождествляем множество А с его характеристической
функцией ха из 2и.) f-Дерево Т\ называется суб-/-деревом Т (обозначается
как Т\ СТ), если каждая лежащая на 7\ строка лежит на Т
(следовательно, каждое лежащее на 7\ множество лежит на Т). Строки р и т
е-расщепляют а на Т (и а е-расщепляется наТ), если р и т лежат на

§ 5. * Минимальные степени
149
Т, сг С р, сг С т, и { е }р и { е }т несовместимы, а именно:
(Зх)(Эу)(Зг)(Э*)[{е}£(х) i=iI к {e}Tt(x) ±= z к у ф z] (5.1)
(Ясно, что если (5.1) выполняется, тор и т должны расщеплять сг.)
5.2 Лемма. Если А лежит на Г, а С А, а не е-расщепляется на Т,
и {е}А всюду определена, то {е}А вычислима.
Доказательство. Предположим, что { е }А = g всюду определена. Для
того, чтобы эффективно вычислить д(х), найдем любую строку т на Т,
т Э сг, такую, что {е}Т(х) сходится, и положим д(х) = {е}т(ж). Такая
т существует, т. к. {е}^(а;) сходится, значит, {е}р(ж) сходится для
некоторой р на Т, (7 С р с А. Более того, {е}р(я) = {е}т(х), т. к.
сг не имеет е-расщеплений на Т. Таким образом, {е}т{х) = {е}л(х).
Наконец, д вычислима, так как Т ч. в. функция, поэтому rngT в. п. и
оно может перечисляться до тех пор, пока т не будет найдена. Q
/-Дерево Т называется е-расщепляющим, если из того, что Т(а 0)
и Т(а 1) определены, следует, что они е-расщепляют Т(а).
5.3 Лемма. Если f-дерево Т является е-расщепляющим, множество
А лежит на Т, и { е }А = д- всюду определенная функция, то А ^т g•
Доказательство. Зафиксируем g в качестве оракула и р-вычислимо
найдем такую последовательность строк { а8 }s€u; на Т, что А = as.
Шаг s = 0. Пусть сг0 = Т(0).
Шаг s +1. Предположим, что мы имеем а8 = Т(а) для некоторой а
длины s такую, что а8 С А. Вычислим р = Т(а 0) и г = Т(а 1) (оба эти
значения существуют, т. к. а8 расширяема). Теперь р и т е-расщепляют
а8, поэтому для них верно (5.1). В точности одно из значений у или z
в (5.1) совпадает с д{х), потому что { е }А(х) = д(х), и либо { е }л(ж) = у,
либо { е }л(я) = z. Перечисляем все четверки (х, у, z, t) до тех пор, пока
не найдется первая четверка, удовлетворяющая (5.1). Полагаем as+1 = р,
если р(х) = у, и crs_|_i = т, если р(х) = z. Теперь as+\ С А, т. к. только
одна из строк р и т может быть продолжена до А, и { е }А = д(х). О
5.4 Определение. Для данного /-дерева Т, строки сг на Т и числа
е G cj определим Ti = Т(Т, сг, е), е-расщепляющее суб-f -дерево дерева Т
над сг индукцией по //г(а) следующим образом. Полагаем Ti(0) = сг.
Если Т\(а) = v определено, перечисляем все шестерки (р, т, £, ж, у, z) такие,

150
Глава VI. Оракулъные конструкции не в. п. степеней
что v С р, т, р и т лежат на Т, до тех пор, пока не будет найдена
первая шестерка, удовлетворяющая условию (5.1). Определяем 7\(а 0) = р
и Т\{а 1) = т. Если же такой шестерки не существует, то Т(а г) не
определено.
5.5 	Лемма. Следующие свойства Т\ вытекают непосредственно из
определения:
(i) Ti является f-деревом;
(ii) Т\ С Т (а именно, любая строка, лежащая на 7\, лежит и на
Т);
(iii) а лежит на Т\;
(iv) Если т лежит на Т\, mo а С г;
(у) Т\ является е -расщепляющим;
(vi) 	Если т лежит на Т\ и е -расщепляется на Т, то т е
-расщепляется на Т\.
5.6 	Теорема (Спектор [1956]). Существует минимальная степень а.
(Более того, а ^ 0,;.)
Доказательство. По Леммам 5.2 и 5.3 достаточно построить А С и,
удовлетворяя для всех е требованиям:
(Минимальность) Re : А лежит на f-дереве Т, и либо
Т е-расщепляющее, либо
существует строка а С А
такая, что а не
расщепляется на Т;
(Невычислимость) Se : А ф { е }.
На шаге s -1-1 мы построим всюду определенное /-дерево Ts+1 и
строку as.|_! на нем так, чтобы А = сг8, причем
<tsC<ts+1, (5.2)
Ts D Ts+1, (5.3)
и
либо Ts-i-i s-расщепляющее, либо as.|_! не
s-расщепляется на Т8+\.
(5.4)
Заметим, что А лежит на Т8 для каждого s в силу (5.2) и (5.3).
Следовательно, по (5.4) А удовлетворяет Re для каждого е.
Шаг s = 0. Полагаем сг0 = 0, То = Id.

§ 5. * Минимальные степени
151
Шаг s + 1. Имеем а8 на Т8.
Подшаг 1. (Удовлетворяем S8.) Выбираем такую сг' на TSi что сг' Э а8
и сг' несравнима с { s }, если { s } всюду определена, в противном случае
сг' = сг. Это можно сделать, т. к. Т8 всюду определена, поэтому дерево Т8
имеет расщепление над crs. (Заметим, что этот подшаг требует оракула
0" для проверки, всюду ли определена { s }.)
Подшаг 2. (Удовлетворяем Rs.) Проверяем, верно ли
(Зт)[т на Т8 & сг' С т & т не имеет s-расщеплений на Т8]. (5.5)
Это утверждение является Е!| -утверждением и, следовательно, его
истинность может быть проверена эффективно относительно 0", т. к. Т8
всюду определена.
Если (5.5) верно, то полагаем crs+1 равной первой такой т, и
полагаем Т5+1 = Т8. Процедура нахождения т по сг' в. п. относительно 0'
и, следовательно, вычислима относительно 0". Если же (5.5) не верно,
то полагаем crs+1 = сг' и Te+1 = T(TS, сг', s). В этом случае все
строки т Э сг', лежащие на Т81 s-расщепляются на Т8, поэтому Т8.|_i всюду
определено и является s-расщепляющим по лемме 5.4 (vi).
Ясно, что А = (J5cr5 имеет минимальную степень и А ^т 0,;, т. к.
все построения вычислимы относительно 0". О
5.7 	Теорема (Сакс). Существует минимальная степень а < О'.
Доказательство. На каждом шаге s, используя оракул множества 0',
будем определять строку а8 и /-деревья Т/, е ^ s, так, чтобы Те+1 =
lims Т/+1 существовало и удовлетворяло требованию Re для множества
А = (Js <rs. В данном построении /-деревья Т/ могут быть частичными.
Пусть Tq = Id для всех s € ш. Отметим, что следующее построение
будет обеспечивать rng(T65+1) С rng(Tes).
Шаг s = 0. Полагаем сг0 = 0.
Шаг s + 1.
Подшаг 1. (Удовлетворяем Ss.) Пусть п8 —наибольшее натуральное
число ^ s такое, что а8 имеет расщепление р, т на Т*л. (Т. к. Т£ = Id, то
такое п8 существует. Более того, п8 может быть найдено с
использованием оракула 0', т. к. каждое Т/, е ^ s, является частично вычислимым
/-деревом.) Далее, используя оракул 0' определяем crs+1 = р, если { s }
и р несравнимы или {s}(a;) f Для некоторого х < lh(p), и crs+i = т в
противном случае.
Подшаг 2. (Удовлетворяем Rs.) Полагаем Т/+1 = Те5 для всех е ^
ns. Если п8 = s, то пусть Т/+1 = T(T/+1,cr5+i, s). Если же п8 < s,

152
Глава VI. Оракульные конструкции не в. п. степеней
то выбираем а такую, что Т*л(а) = as+i. Теперь пусть Т^г(7) =
для всех 7 и Т*+\ = Т(Т/+1,0-в+i,e) для п8 <e^s.
Этим построение завершается. Пусть A = \Jsas. Заметим, что А ^т
0', т. к. подшаг 1 требует 0'-оракул, а на подшаге 2 оракул не
используется вообще.
(Неформально построения на подшаге 2 можно описать следующим
образом. Построение начинается с определения Т* как О-расщепляющего
суб-/-дерева Т£. Если позднее на шаге s + 1 оракул 0' укажет, что над
а8 на Т* более нет О-расщеплений, то полагаем п8 = 0, отбрасываем
старое О-расщепляющее /-дерево Т* и определяем Т/-1"1 как ограничение
Tq"1"1 на вершины, продолжающие сг5+1, а именно, полагаем Т15+1(7) =
То+1(а~7) для всех 7. Теперь Г/"1"1 более не представляет трудностей в
нахождении расщеплений, т. к. их не представляет дерево Tq. Заметим,
что этим изменением в Т/+1 мы переключаем стратегию удовлетворения
До со способа, представленного в лемме 5.3, на способ, представленный
в лемме 5.2. Естественно, все старые /-деревья Т/ при е > 1 должны
быть заменены на новые /-деревья Т/+1, вложенные в новое /-дерево
Т*+1.)
Наконец, индукцией по е докажем, что для всех е
Те = lims Т/ существует
(5.6)
и
п8 ^ S
(5.7)
для почти всех s.
Ясно, что все это верно для е = 0. Фиксируем е^Ои
положением индукции, выберем такое наименьшее se,
, пользуясь пред-
что
(Vs ^ se)[Te°+1 = Ге*‘ ип^ е].
(5.8)
Теперь (5.8) верно и для е+1, если только на каком-то шаге t ^ se не
окажется, что щ = е. В этом случае выбираем такую а, что Т*(а) = сг*_ц.
Тогда (7) = Tl{oT7) для всех 7. Индукцией по s ^ £+1
доказывается, что для всех s ^ t+1 имеет место Т/+1 = и что все расщепления
сг5 на Т/ сохраняются и на Т/+1. Таким образом, (5.8) выполняется для
е+1 с заменой se на $ + 1. Следовательно, Te+i либо е-расщепляющее
дерево (если se+1 = se)> либо не содержит е-расщепляющих вершин (если
se+i > se)- D
(Внимательный анализ этого построения убеждает в том, что здесь
на самом деле приводится приоритетное построение с конечными
нарушениями, использующее оракул 0', но мы отложим такой анализ до

§ 5. * Минимальные степени
153
главы VII, так как приведенное доказательство вполне понятно и без
явного упоминания метода приоритета.)
5.8-5.15 Упражнения
5.8 	(Познер-Эпштейн). Покажите, что в доказательстве теоремы 5.6
при удовлетворении всем требованиям минимальности Re, е G си, мы
автоматически удовлетворим и всем требованиям 5е, е е си Указание.
Предположим, что А вычислимо. Определим вычислимый функционал
{i }х следующим образом:
Покажите, что требование Ri не удовлетворено.
5.9 	(Сакс). Покажите, что любая счётная возрастающая
последовательность степеней bo < bi < ... имеет минимальную верхнюю грань
а. 	(Другими словами, степень а является верхней гранью и не
существует другой верхней грани d < а). Указание. Выберем для каждого п
множество Вп G Ьп. Используйте теорему 5.6 для нахождения всюду
определенного вычислимого /-дерева Ti, удовлетворяющего Ro.
Определяем всюду определенное So-вычислимое /-дерево Т\ С Т\у все ещё
удовлетворяющее Ro, и такое, что В0 ^т А для любого А на 2\.
Определяем Т8(а) индукцией по |а| следующим образом. Пусть Ti(0) = Ti(0).
Предположим, что Ti(a) уже определено и равняется Т\{р) для
некоторого р. Если \а\ = п, то положим Т\{а^%) = Т\{р^Во{п)^г) для i = 0,1.
Выберем соответствующую о\ на Ti, |cri| ^ п. Обобщая, примените
описанную выше процедурок Тп, чтобы получить Вп-вычислимое
всюду определенное /-дерево Тп+1 С Тп такое, чтобы Тп+\ удовлетворяло
Rn и Вп А для каждого множества А на Тп+\. Затем выберите
<7n+i G Тп+1 так, чтобы ап С <тп+Положите А = (Jn ап-
5.10.° Докажите, что существует 2**° различных степеней. Указание.
Соедините методы упражнения 1.8 и теоремы 5.6, используя дерево /-
деревьев.
Следующие упражнения используют понятие дерева, которое слегка
отличается от приведенного выше, и требуют рассуждения с конечными
и бесконечными расширениями.
{*}"(*) =
сг(х), если а несовместна с А,
неопределено, если а С А.

154
Глава VI. Оракульньге конструкции не в. п. степеней
5.11 Определение, (i) Множество Т С ш<и; называется деревом, если
для всех а и т справедливо [a Е Т & т С а] =Ф_т Е Т.
(ii) Если Т — дерево, то пусть [Т] = { / : (Vx)f(x) Е Т } — множество
бесконечных путей вдоль Т, где f(x) = (мы
отождествляем вершину / f хЕГ с его кодовым числом f{x)).
(iii) Дерево называется вычислимым, если предикат «а Е Т» вычислим,
где сг отождествляется с его номером a(lh(a)), где а(х) =
1+<7(ж-1)
• • • Рх — 1
(iv) Если R вычислимый предикат от одной переменной, то класс всех
функций /Ей/*', удовлетворяющих условию (Vx)R(f(x)), называется
П ^-классом.
5.12. (а) Докажите, что для любого П^-класса С Си/*' существует
такое вычислимое дерево Т, что С = [Т]. (Обратное очевидно.)
(b) Пусть Т С 2<ш — бесконечное вычислимое дерево. Докажите, что
если [Т] = { / }, то функция / вычислима.
(c) Пусть Т С 2<и — бесконечное вычислимое дерево. Докажите, что
[Т] содержит элемент, имеющий в. п. степень. Указание. Используйте
следствие III.3.4.
5.13 Теорема о низком базисе (Джокуш-Соар [1972b]). Докажите,
что любой непустой П°-класс С С 2Ы имеет элемент / низкой степени.
Указание. К классу С примените упражнение 5.12, получая вычислимое
дерево Т С 2<и такое, что С = [Т]. Определите последовательность
бесконечных вычислимых деревьев { Те }ееа; и выберите / Е П{ Ре] }ееи-
Дерево Te+i будет обладать следующим свойством: { е }9(е) определена
либо для каждой g Е [Te+i], либо не определена ни для какой g Е [Те+1].
Пусть То = Т. Предположим, что Те уже определено. Положим
Ue = {(т : {e}°h(<(T){e) неопределено},
и заметим, что Ue образует вычислимое дерево. Пусть Те+1 = Те, если
Те П Ue конечно, и Те+1 = Те П Ue в противном случае. Выберите / Е
ГК [^е] }ееи> и покажите, что deg(/') = О7, т. к. все построение вычислимо
относительно О'.
5.14. 	Докажите, что существует эффективно иммунное множество низ-^
кой степени и, следовательно, существует функция / низкой степени без
неподвижных точек. (Таким образом, предположения о вычислимой
перечислимости в упражнении V.4.2 и теореме V.5.1 были необходимы).

§ 5. * Минимальные степени
155
Указание. Пусть S — простое множество Поста из теоремы V.1.3,
которое эффективно просто, но не гиперпросто. Пусть { Df ^ }хеи> —
сильная таблица попарно непересекающихся конечных множеств, каждое из
которых имеет непустое пересечение с 5. Определим
С = { А : А С S и (Va?)[D/(x) П А ф 0] }.
Покажите, что С является непустым П°-классом и примените
теорему о низком базисе.
5.15 (Джокуш-Соар). Докажите, что если Т — бесконечное вычисли¬
мое дерево, то [Т] содержит гипериммунно-свободную степень
(определение см. в упражнении V.2.17). Указание. Определите
последовательность вычислимых деревьев {Те}ееи; и выберите / Е р|{ [Те] }б€а;. По
данному Те определите Щ = { а : { е } Гл(о-) (х) неопределено}. Если Те П
Щ конечно для всех ж, то пусть Te+i = Те. В противном случае пусть
Те-|_i = Те П 17* , где х1 — такое наименьшее число, что
соответствующее дерево является бесконечным. Используйте упражнение V.2.17 (Ь)
для доказательства того, что deg(/) является гипериммунно-свободной.

Глава VII
Метод приоритета с конечными
нарушениями
В конечном итоге положительное решение проблемы Поста было
получено Мучником [1956а] и независимо Фридбергом [1957а]. В предложенном
ими методе для выполнения определенных требований {Дп}пеим
аналогичных требованиям главы VI, искомое в. п. множество А строится
по шагам. Однако, теперь построение должно быть вычислимым, чтобы
обеспечить вычислимую перечислимость А. Если п < т, то требованию
Rn отдается приоритет перед Дш, и мы говорим, что Rn имеет более
высокий приоритет, чем Rm. Действия, предпринятые для
удовлетворения Rm на некотором шаге s, на более позднем шаге t > s могут быть
стать недействительными из-за действий для удовлетворения Rnj
нарушающих требование Rm на шаге t. Доказательства в этой главе
отличаются тем, что каждое требование нарушается самое большее конечное
число раз. Позднее мы рассмотрим более сложные методы, допускающие
и бесконечные нарушения.
В последующих трех параграфах мы приведем три различных
результата, каждый из которых даёт решение проблемы Поста, и при
доказательстве каждого из них будет в различных вариациях
использоваться метод приоритета с конечными нарушениями. Все три метода
имеют фундаментальное значение и будут существенны для получения
результатов в последующих главах. Они располагаются в порядке
возрастания их технической сложности: если /(е) — количество нарушений
требования Де, то /(е) ^ е в § 1, /(е) ^ 2е — 1 в § 2, а в § 3 функция
f(e) не будет даже вычислимо ограниченной.

§ 1. Низкие простые множества
157
§ 1. Низкие простые множества
Вероятно, простейший путь решения проблемы Поста — построение
низкого простого множества А. Простота гарантирует, что А в. п. и
не вычислимо, а то, что А низкое {А1 =т 07) гарантирует его
неполноту, т. е. что А <т 0'. Кроме того, в этом построении требования могут
быть разделены на положительные требования Ре, которые пытаются
положить элементы в А, и отрицательные требования Ne, которые
пытаются не допустить попадания элементов в А. Как мы увидим в
главе XI, низкие множества и степени имеют ряд полезных
структурных свойств.
1.1 Теорема. Существует простое множество А, являющееся
низким (А1 =т 0').
1.2 Следствие (Мучник-Фридберг). Существует невычислимая
неполная в. п. степень а (0 < а < 0').
Доказательство теоремы 1.1. Достаточно построить кобесконечное
в. п. множество А, удовлетворяющее для всех е требованиям:
где (3°°s)Q(s) означает «существует бесконечно много таких s, что
<2(s)>>, As состоит из элементов, перечисленных в А к концу шага s, и
А = \JS As. Примем следующее приоритетное упорядочение требований:
iVo,-F()}Ni,Pi,... (Так как построение будет вычислимым, то
последовательность конечных множеств { As }s€u, будет вычислимой, а именно,
существует вычислимая функция / такая, что f(s) является
каноническим индексом As.)
Требования {iVe}e€u, гарантируют А1 ^т 0;- Действительно,
определим вычислимую функцию g равенством
Если требование Ne выполняется для всех е, то g(e) = lims д(е, s)
существует для всех е. Но д 0; по лемме Ш.З.З о пределе, и д является
характеристической функцией А', поэтому А! 0;-
(А простое) Ре : We бесконечно => We П А ф 0,
(А низкое) Ne : (3°°s)[{ е }f'(e) |] =*► { е}А(е) |,
О в противном случае.

158
Глава VII. Конечные нарушения
Вспомним из определения 1.7 главы III use-функцию u(As; е, ж, s),
равную 1+ максимальному элементу, использованному при вычислении
{е}^л(х), если {е}^л(ж) и 0 в противном случае. Для выполнения
требования ЛГе, по данному As определим для всех е следующую
функцию:
(запрещающая функция) r(e, s) = u(As; е, е, s).
Функция r(e, s) является вычислимой, т. к. {As }s€u; — вычислимая
последовательность. Для удовлетворения Ne мы пытаемся запретить с
приоритетом Ne любые элементы х ^ r(e, s) от попадания в 1. (Дело
в том, что если {e}£s(e) I, г = u(As,e,e,s) и iVe успешно
предотвращает все х ^ г от их попадания в дальнейшем в А, то А [ г = As [ г
и, значит, {е}А{е) J,). Таким образом, такие элементы могут попасть в
А только из-за требований Pi с большими приоритетами (а именно, при
i < е). Стратегия удовлетворения Pi такая же, что и при построении
простого множества Поста в теореме V.I.3.
Конструкция А.
Шаг s = 0. Пусть Ао — 0.
Шаг s + 1. Пусть As уже построено, таким образом значение r(e,s)
определено для всех е. Выберем наименьшее i ^ s такое, что
WitSnAs =0, (1.1)
и
(Зх)[ж Е & а; > 2г & (Ve ^ z)[r(e,s) < ж]]. (1.2)
Если такое г существует, выберем наименьшее х, удовлетворяющее
(1.2). Перечисляем ж в -A5+i, и скажем, что требование Pi получило
внимание. Таким образом, W^8 П As+1 ^ 0, поэтому Pi удовлетворено,
(1.1) 	ложно на шагах > s + 1 и, следовательно, Pi больше никогда не
будет обрабатываться. Если такого i не существует, то ничего не делаем,
так что As-|_i = As.
Полагаем А = \JS As. Это завершает построение.
Будем говорить, что х нарушает Ne на шаге s + 1, если х Е ^4s+i —
и х ^ r(e, s). Определим множество нарушений для Ne
Ie = {х : (3s)[ж Е As+1 - As & х ^ r(e,s)] } =
= { а: : х нарушает Ne на некотором шаге s 4-1 }.
(Положительные требования, конечно, никогда не нарушаются.)

§ 1. Низкие простые множества
159
Лемма 1. (Ve)[/e конечно]. (Именно, Ne нарушается только конеч¬
ное число раз.)
Доказательство. Каждое положительное требование Pi вынуждает нас
перечислить в А самое большее один элемент по (1.1). Но согласно
последней конъюнкции в (1.2) Ne может быть нарушено из-за Pi, только
если г < е. Следовательно, \1е\ ^ е.
Лемма 2. Для каждого е требование Ne удовлетворяется, и г(е) =
lims r(e, s) существует.
Доказательство. Зафиксируем е. По лемме 1 выберем такой шаг se,
что Ne не нарушается ни на каких шагах s > se. Следовательно, если
{е}^а(е) сходится для s > se, то индукцией по t ^ s, r(e,t) = r(e,s)
и {e}f*(e) = {е}^а(е) для всех t ^ s, так что А ^ г = As г при
г = r(e, s) и, значит, {е}А(е) определено по use-принципу III.1.9.
Лемма 3. Для каждого i требование Pi удовлетворяется.
Доказательство. Пусть г такое, что Wi бесконечно. По лемме 2
найдется такое s, что
(Vt ^ s)(Ve ^ i)[r{e,t) = г{е)\.
Выберем s' ^ s так, что все Pj, j < i, не получают внимания после шага
s'. Теперь пусть t > s' такое, что
(Зх)[х Е Wij > 2г& (Ve ^ i)[r(e) < х]].
Теперь либо Wi,t П At Ф 0, либо Pi получает внимание на шаге t + 1. В
любом случае Wift П At+i Ф 0, так что Pi удовлетворяется к концу шага
t -f* 1.
По второй конъюнкции (1.2) А бесконечно. Следовательно, А
является простым и низким множеством. Q
В этом и последующих построениях r(e,s) можно представлять как
некоторую «стену», установленную требованием Ne, и охватывающую
интервал от 0 до r(e,s). Стена r(e,s) при фиксированном е не
является монотонно возрастающей по s, т. к. после того, как она
воздвигнута, прорыв этой стены некоторым х, нарушающим Ne, может вызвать
{е}^1^) и тогда стена опускается до 0. Если Pi хочет положить
некоторый элемент х в А, то х должен быть расположен выше всех
стен r(e, s), е ^ г. Главной особенностью всех построений с конечными

160
Глава VII. Конечные нарушения
нарушениями является то, что каждая стена может разрушаться самое
большее конечное число раз и, таким образом, рано или поздно
стабилизируется. Но тогда каждое положительное требование удовлетворяется,
т. к. для этого достаточно выбрать элемент, находящийся выше всех
стен, имеющих более высокий приоритет.
В определении IV.4.2 мы назвали высокими (низкими) такие в. п.
степени, первый скачок которых имеет наибольшее (наименьшее)
возможное значение. В упражнении IV.4.5 мы продолжили эту иерархию,
заменив первый скачок n-м скачком, следующим образом.
1.3 	Определение. Для каждого п ^ 0 определим следующие
подклассы класса в. п. степеней R:
Hn = {d : d € R и d<n) = 0(n+1>}
И
Ln = {d:deRHdM=0(n)},
где d° = d; обозначим Ln = R—Ln. Заметим, что Но = { 0' }, Lo = { 0 },
и что Hi(Li) просто высокие (низкие) в. п. степени из определения
IV.4.2. Для п > 1 мы будем называть степени из Hn(Ln) п-высокими
(п-низкими). Мы пишем и для соответствующих классов, реля-
тивизованных относительно произвольного оракульного множества В.
Ясно, что Hn С Hn+i и Ln С Ln+i для всех п. Из теоремы 1.1
следует, что Lo Ф Li, а в упражнении 1.6(c) мы покажем, что Н0 Ф Hi, т. е.
что существует неполная высокая в. п. степень. В следствии VIII. 1.2 мы
докажем это с помощью исходного метода Сакса, используя метод
приоритета с бесконечными нарушениями. Приведенное здесь доказательство
является комбинацией двух построений с конечными нарушениями.
Обобщая эти методы мы можем показать, что все включения Ln С Ln+i
и Hn С Hn+i строгие. (См. упражнение 1.6(d) или следствие VIII.3.4.)
Более того, существует такая в. п. степень а, что
(Vn)[0(n) < а(п) < 0(п+1)],
т. е. а € R—(Jn(HnULn). (См. упражнение 1.6(e) или следствие VIII.3.5.)
Такая степень называется промежуточной (см. упражнение VIII.3.9).
1.4-1.7 Упражнения
1.4. В доказательстве теоремы 1.1 замените требования Ре
требованиями упражнения V.2.9 для получения прямого построения низкого
гиперпростого множества.

§ 1. Низкие простые множества
161
1.5. 	Комбинируя метод доказательства теоремы 1.1 с методом
разрешения § 3 главы V, покажите, что для любого не вычислимого в. п.
множества В существует низкое простое множество А В.
1.6 	(Джокуш-Шор [1983]). Для е G со и Y С и определим Je{Y) =
Y 0 Wj.
(а) 	Докажите, что для любого е существует невычислимое в. п.
множество А такое, что Je(A) =т 0'- (Этот результат относится к
теореме 1.1 так же, как упражнение VI.3.10 относится к критерию полноты
Фридберга VI.3.1.) Мы скажем, что А =т В посредством (fco,&i)5 если
А = {ко}в и В = {к\}А. Покажите, что это доказательство равномерно
по е и может быть релятивизовано относительно любого оракула У С о;,
т. е., что существуют вычислимые функции / и g такие, что для всех
е £ си и Y С ц
Je(Jf(e)(Y)) =т Y' посредством д(е). (1.4)
Указание. Для построения множества А и функции h ^т А 0
используйте метод теоремы 1.1. Множество А стройте, удовлетворяя для
всех х требованиям
Nx : (3°°s)[x € WAJ} =*xeWeA-,
P2x :x € К <*=>■ (3y ^ h(2x))[y € w[2a:1 и у € A};
И
P2x+1 : А ф Щ.
На шаге s + 1 по данному As определите вычислимые функции
Г u(As;e,x,s),
l о
если { е }А‘ (х)
в противном случае,
и h(x, s) =
(цу)[у G & h(x -1, s) < у k h(x, s - 1) ^ у & (Vj ^ rc)[r(j, s) < y]]
Для каждого x G Ks+1 - Ks перечислите h(2x,s) в As+i. Далее, для
каждого x < s, если Wx,s П As = 0 и h(2x + l,s) G Wx,s, то
перечислите h(2x + l,s) в As.|_i, в противном случае ничего не делайте. Это
определяет А.
Покажите, что lim5 h(x, s), limSr(xys) и K(x) могут быть найдены
вычислимо относительно А 0 .

162
Глава VII. Конечные нарушения
(b) Используйте равномерность доказательства пункта (а), чтобы
показать, что существует вычислимая функция h такая, что для всех Y и
е выполнено Je{Jh(<e){Y)) =т^'иУ <т Л(е)00-
(c) (Сакс). Покажите, что существует неполное высокое в. п. множес¬
тво А. Указание. (Джокуш-Шор) Заметим, что теорема 1.1 может быть
релятивизована относительно произвольного множества Y для
получения такого индекса ei, что Y <т и Y1 =т т. е. является
низким над Y. Примените часть (а) к е\ для получения А. (Отметим,
что если 0' является низким над А, то А высокое.)
(d)  . (Сакс [1963с]). Докажите, что для любого п в Hn+i — Нп и Ln+i —
Ln существуют в. п. степени. Указание. Заметим, что в части (с) мы
получаем такой индекс ег, что для любого множества У, W£ является
высоким над У, т. е. У <т <т У7 и (W£)' =т Y". Примените (а)
к в2 для получения 2-низкого в. п. множества Л, далее используйте то,
что У' является n-низким над С тогда и только тогда, когда С является
п-высоким над У.
(e) (Мартин, Лахлан, Сакс). Докажите, что существует в. п. сте¬
пень а, которая не принадлежит Нп или Ln ни для какого п.
Указание (Джокуш-Шор [1983]). Примените релятивизованную теорему
рекурсии III. 1.6 к вычислимой функции h части (Ь) для получения
такого числа ё, что = W? для всех У. (Так как У <т Je{V) и
Je{Je(y)) =т У1, то мы можем представить себе как «пол-скачка»,
хотя у нас и нет оснований утверждать, что она инвариантна
относительно степеней.) Покажите, что J?n(Y) =т Y^n\ так что J?n(Y) <т
j2n+i(y) <т j2n+2(у) И) значиТ) j2n{y) ^LVUH[
1.7° (Джокуш-Шор). По данным е, г Е ш найдите в. п. множество А
такое, что: (i) A®W^ имеет в. п. степень; и (ii) At&W^QW-* =т К.
Указание. В доказательстве упражнения 1.6(a) будем рассматривать h(x,s)
как позицию «подвижного маркера» Гх, который движется так, что его
позиция превосходит use-функцию для х Е и позицию маркера
Гж_1. Дополнительно к этим «е-маркерам» {Гх }хеш мы имеем список
{ Лх }хеч> г-маркеров, которые ведут себя аналогичным образом для
вычисления х Е за исключением того, что г-маркеры должны пе¬
редвигаться на множестве позиций е-маркеров. Если х перечисляется
в К, мы перечисляем текущую позицию Лх в А. Для доказательства
(ii) заметим, что по множеству А 0 0 мы можем вычислить
use-функции для х Е weA и х Е WД конечную позицию всех маркеров,
и, таким образом, выяснить, принадлежит ли х множеству К. Чтобы
проверить, что А0 имеет в. п. степень, заметим, что передвижение

§ 1. Низкие простые множества
163
Г-маркеров такое же, как в упражнении 1.6(a) и, следовательно, каждое
А удовлетворяет всем тем отрицательным требованиям Nx. По нашей
конструкции, существует функция т А 0 такая, что для всех
s ^ т(ж), х Е W£ тогда и только тогда, когда х Е . Следовательно,
А 0 имеет в. п. степень по лемме III.3.2 о модуле.
1.8 	Замечания. Упражнение 1.6 может быть использовано для
короткого доказательства, в стиле метода приоритета с конечными
нарушениями, теоремы VIII.3.1 Сакса о скачке, которая в обозначениях
упражнения 1.6 утверждает, что
(У*)(Эр)Ш0))' М<Ь')}
Доказательство (М. Симпсон [1985]). Пусть дано г, и / и д
удовлетворяют (1.4). Тогда, положив У = 0 в (1.4), мы имеем для всех е
Je{Jf(e)(9)) =Т 0; посредством д(е). (1.5)
Очевидно, что существует такая вычислимая функция ft, что
В =т 0' посредством к => Jh^(B) =т Jri(0/)- (1.6)
Из (1.5) и (1.6) при В = J6(Jyr(e)(0)) имеем
Jh9{e)(Je(Jf(e)(m =Т МП (1-7)
Мы хотим, используя (1.4), преобразовать левую часть (1.7) так,
чтобы получить скачок в. п. множества. С этой целью, сперва заменим в
(1.7) 	е на /(е):
Jhgf(e)(Jf(e)(Jff(e](Q))) =Т М0')- (1-8)
Далее, применяя теорему рекурсии к hgf получим ео такое, что для
всех У С си
whgf(eо) = WI0 и> следовательно, Jeo{Y) = Jhgf(eo](Y). (1.9)
Подставляя ео вместо е в (1.8), из (1.8) и (1.9) получим
=Т МП
(1.10)

164
Глава VII. Конечные нарушения
Следовательно, по (1.10) и (1.4) при Y = J//(eo)(0) получим
(Jff(eo)m' =т J0). (1.11)
Положим р = ff(eо). (Отметим также, что р может быть
найдено равномерно по г в виду того, что в (1.6) мы можем заменить h(k)
вычислимой функцией Л(г, к), и теорема рекурсии с параметрами
позволяет получить ео равномерно по г. Заметим также, что примечание 1.8
выполняется в релятивизованной версии с Y вместо 0.)
Чтобы лучше понять упражнение 1.6 и примечание 1.8, представим
себе Je(Y) как «подскок» У, т. к. он ведет себя как некоторое подобие
пол-скачка. Согласно упражнению 1.6 для любого выбора второго
подскока существует первый подскок такой, что два подскока эквивалентны
(по Тьюрингу) одному скачку. Теорема Сакса о скачке говорит, что
скачок, сопровождаемый каким-либо подскоком, эквивалентен некоторому
подскоку, сопровождаемому скачком. Согласно вышеизложенному, оба
они эквивалентны последовательности из трех подходящим образом
выбранных подскоков.
1.9 	Замечания. Недавно А. Кучера нашел следующее решение
проблемы Поста, не использующее метод приоритета и, следовательно, не
содержащее нарушений требований. Скажем, что / является функцией без
неподвижных точек, если РУдх) ф Wx для всех х (см. теорему V.5.I.)
1.10 	Теорема (Кучера [1986]). Если / ^т 0; и / — функция без
неподвижных точек, то существует простое множество А /•
1.11 	Следствие. Существует низкое простое множество А.
Доказательство. Согласно упражнению V.5.9 существует функция /
без неподвижных точек, принадлежащая низкой степени. Применяя
теорему 1.10, получим А /• (Заметим, что упражнения V.5.8, V.5.9 и
VI.5.13 не используют метод приоритета, а только конструкции с
оракулом. Следовательно, нет и нарушений требований.) []
Доказательство теоремы 1.10. Так как / 0', мы можем^выбрать
вычислимую функцию f{x,s) так, что f(x) = limSf(x,s). Достаточно
построить кобесконечное в. п. множество А f такое, что для А
выполняются все требования Ре теоремы 1.1. С этой целью мы используем

§ 1. Низкие простые множества
165
теорему рекурсии, чтобы определить вычислимую функцию Л(е),
которая играет ту же роль, что и ft(e) в теореме V.5.I.
Конструкция А.
Шаг s = 0. Положим Aq — 0.
Шаг s + 1. Найдем наименьшее е (если оно существует) такое, что
W€fS (1AS = 0, и
(3у)[у Е We,5 & у > 2е & у > h(e) & .
№)v*t&[f(h(e),t)=f(h(e),a)]]. ’ '
Перечислим в As+\ наименьшее у, удовлетворяющее (1.12). Используя
теорему рекурсии, определим h(e) так, чтобы Wh(e) = Wf(h(e) «)• (Если
Ре никогда не получит внимания, то W^e) =0.)
Лемма 1. Если We бесконечно, то We П А ф 0.
Доказательство. Выберем у Е И^е так, что у > 2е, у > h{e), и
у > m(h(e)), где т(я) — функция модуля для {/(я,s)}seu,
(определение Ш.3.1). В конце концов у (или другой элемент We) будет перечислен
в А.
Лемма 2. А /•
Доказательство. Определим «слабую» функцию модуля для
{ f(x, s) }8еш следующим образом
с(у) = (/*<? > J/)(Vx ^ y)[f(x,s) = f(x)\.
Ясно, что с /• Мы утверждаем, что для всех у у Е А тогда и
только тогда, когда у Е Ас(у), так что А /• Предположим противное,
что у Е А-Ас(у). Пусть у Е и у е А из-заРе. Тогда /(ft(e),£) =
f(h(e),s) для всех t, у ^ ^ s. Но у < с(у) < s (по определению с(у) и
предположению относительно у соответственно). Следовательно,
Wh(e) = Wf(h(e),s) = ^/(/i(e),c(3/)) = ^/(M«))> (1*13)
что противоречит тому, что / функция без неподвижной точки. (Первое
равенство в (1.13) следует из определения ft, а последнее — из
определения с(у) и того факта, что ft(e) ^ у.) Q

166
Глава VII. Конечные нарушения
1.12 	Замечания. Заметим, что если / имеет вычислимо
перечислимую степень, тогда т ^т / как это было в теореме V.5.1, и мы можем
доказать К ^т /• Далее, т. к. / имеет лишь Д§ степень, мы уже не
можем доказать, что m ^т /, но только то, что слабая функция модуля
удовлетворяет условию с ^ /. Поэтому, если We бесконечно, то мы в
конце концов получим некоторое у, удовлетворяющее условию (1.12),
которое войдет в А, но мы не можем априори указать конкретное
такое у. Это значит, что мы не можем добиться, как ранее, выполнения
условия К /•
Используя более тонкое рассуждение, Кучера дал доказательство
теоремы 2.1 о существовании двух несравнимых в. п. степеней, также без
использования метода приоритета.
§ 2. Исходная теорема Мучника-Фридберга
Мучник и Фридберг первоначально решили проблему Поста, построив
в. п. множества А и В несравнимых степеней, удовлетворяя при этом в
точности требованиям теоремы VI. 1.2. В отличие от требований из § 1,
эти требования, например, А ф { е }в, имеют как положительную, так и
отрицательную компоненты, т. к. они пытаются положить элементы в А
и одновременно предотвратить попадание некоторых элементов в В. Мы
опишем сперва стратегию для удовлетворения отдельного требования,
а затем как такие стратегии могут сочетаться.
2.1 	Теорема (Мучник [1956а]-Фридберг [1957а]). Существуют
такие в. п. множества А и В, что А \т В (т. е. А В и В А) и,
значит, 0 <т А, В и А, В <т 0'.
Доказательство. Достаточно вычислимо перечислять множества А и
В так, чтобы удовлетворить для всех е требованиям:
Я2е : ^7^{е}В.
Д2е+1 : Вф{е)А.
Стратегия удовлетворения единственного такого требования i?2e
состоит в том, чтобы прикрепить к /?2е потенциального «свидетеля» ж, все
ещё не перечисленного в А, и ждать такого шага s + 1, что
{e}f‘(*H=0. (2.1)
(Если такого шага не существует, то мы нвдего не делаем, и R2e
автоматически удовлетворяется свидетелем ж, т. к. А(х) — 0, и либо { е }в(я) t>

§ 2. Исходная теорема Мучника-Фридберга
167
либо { е }в(х) 0.) Если же шаг s + 1 существует, то мы скажем, что
/?2е требует внимания на шаге s + 1. Тогда /?2е получает внимание, и
мы (1) перечисляем х в As+1, (2) определяем ограничивающую функцию
(т. е. «стену») r(2e,s + 1) = u(Bs\e,x,s), и пытаемся (с приоритетом
i^2e) ограничить все числа у ^ г = r(2e,s + 1) от последующего
попадания в В. Если мы достигнем последней цели, то В [ г = Bs [ г и, по
use-принципу,
{ е }В(х) = { е }B(V(:r) = { е }B^r(z) = 0.
Однако А(х) = 1, так что требование /?2е удовлетворено. (Стратегия
для удовлетворения i?2e+i такая же, но А и В меняются ролями.)
Для одновременного выполнения всех требований мы должны время
от времени, но только конечное число раз, изменять свидетелей хе
требований Re. Пусть х\ — аппроксимация свидетеля хе к концу шага s, и
хе = lim5 xse. (Число xse можно представлять себе как позицию
движущегося маркера Ге, стабилизирующегося на хе, к концу шага s.) Для того,
чтобы свидетели различных требований были различными, мы
выбираем в качестве свидетелей требования Re числа из = { (х, у) : у = е },
так что xse ^ А, если только он не попадает в А для выполнения Re.
Если Re получает внимание на шаге s + 1, мы переопределим всех
свидетелей х\ для всех % > е, выбирая х\^1 > г = r(e,s + 1). Таким
образом, только требования Ri с большими приоритетами (г < е) позднее
могут нарушить Re, перечислив некоторые х ^ г в А или в В. После
того, как каждое Д», г < е, перестает получать внимание, Re получит
внимание самое большее однажды, и в этот момент оно будет
удовлетворено и останется удовлетворенным навсегда.
Конструкция А и В.
Шаг s = 0. Положим А0 = Во = 0, х°е = (0,е) и г(е,0) = -1 для всех
е.
Шаг s -1-1. Требование R^e требует внимания, если
{е}?‘(х2е) 4-= 0 & r{2e,s) = -1, (2.2)
и /?2е+1 требует внимания, если (2.2) выполняется с As и 2е + 1
вместо Bs и 2е. Выберем наименьшее г ^ s такое, что Ri требует
внимания. Мы скажем, что Ri получает внимание. Допустим, что г =
2е. Перечислим х^е в As+1, положим xf^1 = xs2e и установим стену
r(2e,s -f 1) = u(Bs;e,X2e,s). Это действие удовлетворяет требованию

168
Глава VII. Конечные нарушения
R2e. Для j < 2е положим r(j, s + 1) = r(j,s) и Xj+l = xSj, что оставляет
неизменными все предыдущие стены и действия, связанные с
требованиями с большими приоритетами. Для j > 2е положим r(j,s -1-1) = —1
и определим а^+1 как наименьшее у Е такое, что у & As+1 U Bs+1,
у > max{r(A;,s + 1) : A; ^ 2e} и у > xsj. (Таким образом, действия,
предпринятые ранее для удовлетворения требований Rj с более
низкими приоритетами (j > 2е), аннулируются, а стены r(j,s-1-1) полагаются
равными — 1. Это означает, что Rj в будущем снова может потребовать
внимания, тогда позиции маркеров Xj+l поменяются на новые
элементы, большие текущей стены для R2e, с тем, чтобы их возможное
последующее вхождение в В не помешало произведенным вычислениям для
Д2е.) Если г = 2е + 1, то делаем то же самое, поменяв А и В
местами. Если такого i не существует, то полагаем As+\ = As, Bs+i = Bs,
r(e, s -I-1) = r(e, s) и xp~l = xse для всех e.
Лемма. Для любого i требование Ri получает внимание самое
большее конечное число раз и, в конце концов, удовлетворяется.
Доказательство. Зафиксируем i и предположим, по индукции, что
лемма выполняется для всех j < г. Выберем наименьшее s такое, что
никакое Rj, j < i, не получает внимания на шаге t ^ s. Значит, для всех
t ^ s, х\ = х\ — Х{, и Х{ ^ As U В8. Допустим, что г = 2е. (Случай
нечётного г аналогичен.) Если требование R2e после шага s никогда не
получает внимания, то А(х2е) = 0 и неверно, что {е}в(х2е) |= 0. Если
R2e получает внимание на некотором шаге t -I-1 ^ s, то { е }t * (х2е) 1= 0,
х2е £ At+i - At и Bt \ г = В [ г для г = u(Bt;e,x2e,t), так что
{ е }в{х2е) |= 0 Ф 1 = А{х2е). В последнем случае R2e никогда не
требует и, следовательно, не получает внимания ни на каком шаге v > t -1-1.
Заметим, что Ri может нарушаться самое большее 2г — 1 раз.
2.2-2.7. Упражнения
2.2. (а) Покажите, что существует в. п. последовательность в. п. мно¬
жеств {Ai}^ такая, что для любого г, А\ ф{ А? : 3 Ф О- Ука-
зание. Модифицируйте конструкцию теоремы 2.1 для удовлетворения
требований R(e,i) упражнения VI. 1.5.
(Ь) Покажите, что любое счётное частично-упорядоченное множество
может быть вложено в в. п. степени (R, отображением, сохраняющим
порядок. (См. указание к упражнению VI. 1.7.)

§ 2. Исходная теорема Мучника-Фридберга
169
2.3 (Соар [1972]). Докажите, что в. п. множества А и J5, построенные в
теореме 2.1, автоматически являются низкими и К ^т АфВ. Указание.
Для доказательства К А 0 В убедитесь в том, что функция \е[хе\
вычислима относительно А 0 В (действительно, х8е ф ж|+1, только если
некоторое у < х8е на шаге 5 + 1 входит в А или в В) и что
существует такая вычислимая функция /, что для любого е, е Е К тогда и
только тогда, когда требование Л2/Ге) вынуждает я2/(е) перечислиться
в А. Здесь для всех у и X { /(е) }*(у) = 0, если е € К, и { /(е) }х(у)
неопределена в противном случае. Чтобы доказать, что А и В низкие,
сперва определите следующую вычислимую функцию h: для всех X и е
{ е }*(е) +=> (Vj/)[{ Л(е) }*(у) = 0], (2.3)
{ е }х(е) (Vj/)[{ Л(е) }*(y) fl, (2.4)
Далее, пусть (j(e, s) — следующая вычислимая функция:
g(e, S) = [ 60111/1 Iл(е) i= °>
5 \ 0 в противном случае.
Покажите, ?то ограничивающие функции в конструкции теоремы 2.1
гарантируют, что д(е) =dfn lime^(e, s) существует. Теперь по (2.3) и
(2.4) 	д является характеристической функцией А'.
2.4 (Купер-Эпштейн-Лахлан). Постройте такую пару в. п. множеств
А и В, что степень d-в. п. множества D = А — В не является в. п.
Указание. Для всех е, г, j удовлетворите требованиям
R{e<itj) : D ф {i}w‘ или We ф { j}D■
Для удовлетворения единственного требования R(eyi,j) возьмите х, не
принадлежащий А или В, и ждите такого шага 5, что
О = { i }^“(*) & We.. N = { j }^V f U
для некоторых и и vy Ds — Ал — Bs. Перечислите x в и запретите
D от изменений на любых других элементах ^ v. Требование R(e,ij)
удовлетворено по первому конъюнкту до тех пор, пока не найдутся такой
шаг t ^ 5 + 1 и такое число у < и, что у Е Weyt - Wey8. В этом случае
перечислите х в Bt, так что Dt [ v = Ds [ v и {j}^^(2/) = WeyS(y) ф
WeAv)-

170
Глава VII. Конечные нарушения
2.5 	(Трахтенброт). Множество А автосводимо, если существует такое
е, что А(х) = { е }А~^Х 1 для всех х . (Идея состоит в том, что { е }
распознает принадлежность х к множеству А, задавая вопросы к оракулу
«2/ G А ?» только при х ф у.)
(а) Постройте в. п. множество Ау которое не автосводимо. Указа¬
ние. Для каждого е выберем свидетеля х и попытаемся удовлетворить
А(х) ф (е}Л"ж(х), ожидая такого шага s, что { е 1= у для
некоторого s. Тогда (1) перечисляем х в А тогда и только тогда, когда
у = 0; (2) пытаемся запрещать элементы z ^ u(As-,e,x,s) от попадания
в А.
(б) Для любого невычислимого в. п. множества В постройте в. п.
множество А фт В такое, что А не автосводимо. (Ладнер [1973а]
показал, что этот результат нельзя усилить до А =т В. Он доказал, что
А автосводимо тогда и только тогда, когда А является митотическим
множеством, т. е. А является объединением непересекающихся в. п.
множеств Ао и А\ таких, что А =т Ао =т А\. В статье Ладнера [1973b]
доказано, что существует ненулевая в. п. степень, содержащая только
митотические в. п. множества.)
2.6. Вспомните определения ^tt и фми из упражнений V.2.12 и V.2.16.
Заметим, что если Ао и А\ непересекающиеся в. п. множества, тогда
Ai фwtt Ао U А\, % = 0,1. Используйте метод приоритета для построения
непересекающихся в. п. множеств Ао и А\ таких, что А{ фи А0 U А\,
i = 0,1. Указание. Подберите свидетеля х для удовлетворения
требования, что Ai фи Ао U Ai посредством е-го ^-сведения; ждите, пока оно
сойдется на Aq>s U AifS U { х }; для получения противоречия положите х
в Ао или А\.
2.7. Соедините метод разрешения теоремы V.3.2 с конструкцией Муч-
ника-Фридберга из теоремы 2.1, чтобы доказать, что для любого
невычислимого в. п. множества С найдутся несравнимые по Тьюрингу
в. п. множества А, В фт С. (В теореме 3.2 мы добьемся даже большего
АиБ = (7и ЛПБ = 0, так что deg(A) U deg(2?) = deg(C).)
§ 3. Теоремы о разложении
Вскоре после доказательства теоремы 2.1 Фридберг [1958а] установил
(см. теорему Х.2.1), что любое невычислимое в. п. множество В может
быть представлено как объединение непересекающихся невычислимых

§ 3. Теоремы о разложении
171
множеств А0 и А\. Сакс [1963b] затем обобщил эти две теоремы Фрид-
берга, установив, что Aq и А\ могут быть выбраны не только
невычислимыми, но даже несравнимыми отнсительно тьюринговой сводимости.
Если С — невычислимое в. п. множество, то метод Сакса построения
в. п. множества А со свойством С ф { е }А состоит скорее в сохранении
согласованности между Cs и {е}^% чем в достижении
несогласованности в стратегии Фридберга. Достаточно долгое сохранение
согласованности между ними будет гарантией того, что если С = { е}А, то
С вычислимо в противоречии с предположением. Этот мощный метод
будет существенно использоваться в следующей главе при бесконечном
числе нарушений требований. Для раздельного рассмотрения этих
ключевых идей, которые будут развиваться в главе VIII, мы сперва докажем
более слабый результат, который иллюстрирует метод, а затем
полностью докажем теорему Сакса о разложении.
3.1 	Теорема (Сакс). Для любого невычислимого в. п. множества С
существует такое простое множество А, что С А (и,
следовательно, 0 <т А <т 0'Л
Доказательство. Ясно, что достаточно построить кобесконечное
множество А, удовлетворяя для всех е требованиям:
Ne:C?{e}A;
и
Ре : We бесконечно => WeC\A^$.
Пусть { Cs }seu; — вычислимое перечисление С.
Конструкция множества А.
Шаг s = 0. Положим Ао = 0.
Шаг s -1-1. Так как А3 уже определено, мы можем определить для
всех е
(функцию длины) l(e, s) = max{ х : (Vj/ < х)[{ е (у) |= Cs(y)] },
(функцию запрета) г(е, s) = max{ u(As\e,x, s) : x ^ l(e,s)}. Мы ска-
жем, что Pi требует внимания на шаге s + 1, если г ^ s, Wi,s П As = 0
и
(Зх)[х Е Wi,s & х > 2г & (Ve ^ г)[г(е,$) < х]].
(3.1)

172
Глава VII. Конечные нарушения
Для каждого Pi, которое требует внимания на шаге 5+1, мы
перечисляем в А8+1 наименьшее такое х, и скажем, что Pi получает внимание
на шаге 5 + 1.
Замечание. Фиксируем е. Предположим, что никакое Pj, j < е, не
получает внимания на шаге 5 + 1.
(i) 	Пусть у < 1{е,з) и z € As+i — As. Тогда z > u(As;e,y,s), так что
(е}£Г(у) 1= {е)?-+1(у) ;= {е}?'Ы = С.Ы,
и u(A8+\\e,y,s + 1) = u(A8;e,y,s).
(й) Пусть у = l(e, s) и z G — As. Тогда z > и(А8; e, у, 5) согласно
части «х ^ /(е, 5)» в определении г(е, 5), так что если { е }А*(у) то
{ е }£Г (V) 1= { е Х= { е }?‘(у) ф С,(у),
и u{As+i\e,y,s + 1) = u(At-,e,y,s).
Справедливость замечания следует немедленно из определения.
Отрицательное требование Ne нарушается на шаге 5 + 1 элементом х,
если х ^ г(е, з) и х G А8+\ — А*. Эти элементы образуют в. п.
множество
(множество нарушений) /е = { х : (35)[х G & х ^ г(е, 5)] }
Заметим, что как и в § 1 каждое 1е конечно (в действительности даже
\1е\ ^ е), так как Ne нарушается каждым из Pi, i < е, самое большее
один раз, после чего Pi навсегда удовлетворяется, как и в теореме 1.1.
Лемма 1. (Ve)[C ф { е }А].
Доказательство. Предположим противное С = {е}А. Тогда lim5 l(e, s)=
00. Выберем s' так, что Ne после шага s’ никогда не нарушается.
Докажем, что С вычислимо, в противоречии с предположением. Для
вычисления С(р) для некоторого р G ш, найдем наименьшее s > s' такое, что
1(е, з) > р. По индукции для t^s имеем
(Vi ^ s)[l(e, t) > р & r(e, i) ^ max{ u(Ae; е, х, 5) : х ^ р }]] (3.2)
и, следовательно, {е}А*(р) = {е}А*(р) = {е}А{р) = С(р). Значит, С
вычислимо. Чтобы доказать (3.2) предположим, что это выполняется
для некотрого i. В силу предыдущего замечания из определения r(e, i)

§ 3. Теоремы о разложении
173
и условия s > s' следует, что At+i [ z = At [ z для всех чисел z,
использованных в вычислении { е }А* (х) = у для всех х ^ р. Поэтому
{ e}t+V(x) = 2/> так что либо l(e,t + 1) > р, либо C*+i(x) ^ С*(х) для
некоторого а: < /(е,£). Но, если С*(х) ^ С8(х) для некоторого t ^ s и
х ^ р, где х минимально, то несогласованность Ct(x) ф {е}£*(х) в
противоречии с предположением С = { е }Л будет иметь место на всех
следующих шагах, так как в определении r(e, t) мы использовали
неравенство /(е,£)» вместо «< /(е,£)». (Заметим, что хотя стратегия
Сакса и описывается, как сохраняющая согласованность,
принципиально важно, что мы сохраняем по меньшей мере одну несогласованность,
как только это удается сделать. Причина, по которой несогласованность
сохраняется, в следующем: т. к. С в. п., то С8{х) может измениться
только с 0 на 1, и никогда не наоборот.) (См. упражнение 3.8 для обобщения
на случай С 07 вместо вычислимой перечислимости С.)
Лемма 2. (Ve)[lims r(e, s) существует и конечен].
Доказательство. По лемме 1 выберем р = (рх)[С(х) ф {е}А(х)]. Далее
выберем s1 достаточно большим так, что для всех s ^ s'
(1) (V*<p)[{e}^(*) = {e}A(*)];
(2) (V* 0)[<7s(z) = ОД];
(3) Ne не нарушается на шаге s.
Случай 1. (Vs ^ s')[{e}As(p) t]* Тогда r(e,s) = r(e,s') для всех s ^
s'.
Случай 2. {e}f*(p) I для некоторого t ^ s'. Тогда {е}А*(р) =
{e}fl(p) для всех s ^ t, т. к. l(e,s) ^ р и, значит, по определению
r(e,s) и того факта, что Ne не нарушается после шага t, вычисление
{e)t (р) сохраняется навсегда. Таким образом, {е}А(р) = {е}Аа(р).
Но С(р) ф (е}л(р). Значит,
(Vs ^ ЩСв(р) ф (е}^*(р)] & l(e,s) = р & r(e,s) = r(e,t)].
Следовательно, r(e,t) = lim5r(e,s).
Лемма 3. (Ve)[We бесконечно => W€Ci А Ф$].
Доказательство. По лемме 2 пусть r(i) = lim5 r(i, s) для г ^ е, и R(e) =
max{ r(i) : i ^ e }. Если
(3x)[x €We & x > 2e & x > i?(e)],

174
Глава VII. Конечные нарушения
то We П А ф 0.
Заметим, что А бесконечно по условию «х > 2е» в (3.1).
Следовательно, А просто. О
3.2 Теорема (Теорема Сакса о разложении )(Сакс [1963b]). Пусть
В и С — такие в. п. множества, что С невычислимо. Тогда
существуют такие низкие в. п. множества Ао w Ai, что:
(1) А0 U Ах = В и А0 П Ai = 0, и
(2) С А{ для i = 0,1.
3.3 Предложение. Если в. п. множество В является объединением
непересекающихся в. п. множеств А0 и А\, то В =т А0 0 А\.
Доказательство. Сперва заметим, что А\ В для г = 0,1, и, значит,
Ао 0 А\ <^Т В: чтобы определить принадлежность х к множеству А{,
выясняем принадлежность х множеству В. Если х G В, то перечисляем
Ао и А\ до тех пор, пока х не появится в одном из них. Обратное сведение
В А) 0 А\ очевидно. О
3.4 Следствие. Если b произвольная ненулевая в. п. степень, то
найдутся несравнимые такие низкие в. п. степени ао и ai, что Ь =
ао U ах.
Доказательство. Пусть в. п. множество В G Ь. Применяем теорему 3.2
при С — В для получения А0 и А\. Тогда А0, А\ <т В. По утверждению
3.3, 	В =т Ао 0 А\. Степени множеств Ао и А\ не' могут быть
сравнимыми ввиду того, что если, скажем, Ао А\, то А\ =т В. Положим
а0 = deg(j40) и а, = deg(i4i). Q
3.5 Следствие. Низкие в. п. степени порождают все в. п.
степени при замыкании относительно операции взятия наименьшей верхней
грани.
3.6 Следствие. Не существует минимальных в. п. степеней.
3.7 Следствие. Для любой в. п. степени с, 0 < с < (У , существует
в. п. степень, не сравнимая с с.
Доказательство. Пусть В = К и С G с — в. п. множество. Применим
теорему 3.2. Одно из множеств Ао, А\ должно иметь степень, не
сравнимую с с, иначе Ао С и А\ ^т С, так что К С, в противоречии
с С <т Г Q

§ 3. Теоремы о разложении
175
Заметим, что в следствии 3.7 мы получаем не сравнимое с С
множество А не равномерно по С, а указываем лишь пару множеств Aq,
А\, одно из которых искомое. В теореме VIII.4.3 мы сможем найти А
равномерно по С.
Доказательство теоремы 3.2. (Мы можем предположить, что В
бесконечно, иначе результат тривиален. Это предположение, однако, не
влияет на равномерность получения Aq и А\ по В и С.) Пусть {Bs}seu,
и {С8 }s€u; — такие вычислимые перечисления В и (7, что Во = 0
и \Bs+i — Bs\ = 1 для всех s. Мы укажем вычислимые перечисления
* = 0,1, удовлетворяющее единственному положительному
требованию
Р : х е Bs+1 - Bs => [х € Ao,«+i V х G Ait3+1],
и отрицательным требованиям для г = 0,1, и всех е,
Ще^-Сф{е)А*.
(Ниже поясняется, что условие «Ai низкие множества» будет
автоматически следовать из требований N(e^.)
Шаг s = 0. Положим Ai)0 = 0, г = 0,1.
Шаг s -1-1. По данным AiyS определим вычислимые функции P(e,s)
и гг(е,«), также как в доказательстве теоремы 3.1, но с AiiS вместо As.
Пусть х £ Bs+1 — Bs. Выбираем (е7,г7), как наименьшее (е,г) такое, что
х ^ гг(е,s), и перечисляем х в Ai-i>iS+i. (Именно, выбираем требование
N(e'ti>) с наивысшим приоритетом, которое нарушается перечислением
ж в Aj/, и перечисляем х в «другую часть» Ai-i>.) Если такого (е7,г')
не существует, то перечисляем х в Ао.
Чтобы убедиться в успешности этой конструкции, определим
множество нарушений 1\ как в доказательстве теоремы 3.1, но с А{ вместо
А. Индукцией по (е, г) доказываем, что для г = 0,1 и всех е
(1) 1\ конечно
(2) Сф{е}А<
(3) гг(е) = lims гг(е, s) существует и конечно.
А именно, фиксируем (е,г) и предполагаем, что (1), (2) и (3)
выполняются для всех (k,j) < (е,г). Согласно (3) выберем t так, чтобы
ri(k,s) = г7 (А;) для всех (k,j) < (е,г) и всех s ^ t.

176
Глава VII. Конечные нарушения
Пусть г больше, чем все такие г*7(А;). Выберем v > t так, чтобы
В \ г = Bv \ г. Теперь Л^(е,г> никогда не нарушается после шага v, так
что (1) выполняется для (е,г). Теперь (2) и (3) выполняются для (е,г) в
точности так же, как в леммах 1 и 2 теоремы 3.1.
Чтобы убедиться, что каждое А{ является низким, определим
вычислимую функцию д следующим образом:
{ о(е) }Х(у) = [ С'^’ eC™ У = ° И ^ 6 ^Х^ Ь
х 1 \ неопределено в противном случае.
Заметим, что для г = 0,1,
е € А• <*=> {e}Ai(e) {д(е) }Ai(0) = С(0) <*=*• Ит,Г(^(е),s) > О,
тах что А\ Е Д® ввиду того, что Iх и д вычислимые функции и
существует lims 1г(д(е), s) и, следовательно, А!{ 07* D
Отметим, что множество нарушений 1\ хотя и конечно, но не имеет
очевидной ограничивающей функции, как в §§ 1 и 2. В действительности,
вообще не существует такой вычислимой функции /, что \Ц\ ^ /(г,е).
3.8-3.11 Упражнения
3.8. Докажите, что теоремы 3.1 и 3.2 выполняются при условии «(7
0' и С невычислимо» вместо «С в. п. и С невычислимо». Указание. С
помощью леммы III.3.3 о пределе выберите вычислимую каноническую
последовательность { С8 }seu> конечных множеств такую, что С = lim5 С8.
По данным А8 и /(e,s) в теореме 3.1 определите
(функцию наибольшей длины) га(е, s) = тах{ l(e,t) : t ^ s}.
Далее, используйте m(e,s) вместо /(e,s) в определении r(e,s), и
покажите, что вышеприведенное доказательство остается справедливом.
(Ключевой точкой является использование m(e,s) для доказательства
(3.2), т. к. использование l(e,s) в данном случае не достаточно.)
3.9. Докажите, что если {Cj }j£<jj — вычислимая последовательность
невычислимых Д£ -множеств, и В — в. п. множество, то существуют
такие непересекающиеся в. п. множества Aq и А\, что В = А0 U А\ и
Cj М для j Е о;, г Е { 0,1}. Сделайте вывод, что не существует такой
вычислимой нумерации { Ai }iGu, в. п. (Д^-) множеств, что { deg(A{) }ieuJ
состоит в точности из ненулевых в. п. (соответственно Д!]-) степеней.

§ 3. Теоремы о разложении
177
Указание. Замените отрицательные требования в теореме 3.2 на :
Cj ф { е }Ai и используйте тот же метод.
3.10. По данной (как в упражнении 3.9) последовательности { Cj }j€u,,
найдите бесконечную последовательность { Ai }ieu, пар несравнимых по
Тьюрингу в. п. множеств, удовлетворяющую всем требованиям
упражнения 3.9.
3.11. Докажите, что существуют такие низкие в. п. степени ао и ai,
что для любой в. п. степени с найдутся в. п. степени Ь0 ^ ао и bi ^ ai
такие, что с = bo U bi. Указание. Фиксируйте We £ с и примените
теорему 3.2 к Ко = { (х,е) : х £ We } для получения А0 и А\.

Часть С
Бесконечные методы
построения в. п.
множеств и степеней

Глава VIII
Метод приоритета с бесконечными
нарушениями
Метод приоритета с бесконечными нарушениями был предложен
Шёнфилдом [1961] и, независимо, Саксом [1963а, 1963с и 1964а]. Шён-
филд доказал несколько более слабую версию леммы о густоте из § 1 (а
именно, для случая С = 0') и использовал её для построения неполной
в. п. теории, в которой представимы все вычислимые функции. Сакс
использовал другой подход и соединил его со своим методом сохранения из
теоремы VII.3.1 для получения большого числа новых сильных
результатов о в. п. степенях, наиболее сильной из которых является теорема 4.1
о плотности, которая утверждает, что для любых в. п. степеней d < с
существует такая в. п. степень а, что d < а < с. Другая версия
метода с бесконечными нарушениями была предложена Ейтсом [1966b] для
изучения индексных множеств, которые мы обсудим в главе XII.
Обычно в построениях, использующих метод приоритета с
бесконечными нарушениями, отрицательные требования, такие как
требования Ne : С ф {е}А теоремы VII.3.1, могут нарушаться бесконечно
часто (т. е. множество нарушений 1е может быть бесконечным), в
результате чего для ассоциированной запрещающей функции r(e,s)
может быть limsupe г(е, з) = оо, даже если мы добиваемся, чтобы было
lim infs r(e, s) < оо. Таким образом, положительное требование вида Р*
может иметь серьезную трудность при попытке перечисления
некоторого элемента х Е A*+i — А8, если будет продолжать оберегать
запрещающие функции с большими приоритетами (т. е. продолжать
контролировать выполнение условия х > r(e, s) для всех е ^ г).
Существуют два способа преодоления этой трудности. Во-первых,
может существовать элемент х, ассоциированный с Р* (называемый
последователем Pi), возвращаемый каждым требованием с большим прио¬

182
Глава VIII. Бесконечные нарушения
ритетом Ne (рассматриваемым как некоторые «ворота») для ожидания,
пока соответствующая «стена» r(e, s) не станет ниже х, тем самым
позволяя х пройти в следующие ворота. Этот подход близок к исходному
методу и описывается в § 5 в виде модели «пинбольной машины»,
успешно используемой и во многих других построениях. Второй, в
некоторой степени более глубокий подход, состоит в возможности порождения
бесконечной последовательности «истинных шагов» перечисления А, во
время каждого из которых все запрещающие функции r(e,s), е ^ г,
сбрасывают свои значения одновременно, тем самым позволяя числу х,
последователю требования Р*, сразу пройти все ворота и немедленно
попасть в As-ц. Мы будем придерживаться второго подхода, который
был сперва предложен Лахланом [1973], а затем усовершенствован Соа-
ром [1976].
Мы начнем в § 1 с леммы о густоте, которая является самым простым
примером построения с бесконечными нарушениями. В § 2 доказывается
более сильная версия, а также выделяются и доказываются ключевые
компоненты метода, а именно, леммы о нарушениях и об окнах. Они
применяются в § 3 и § 4 для доказательства элегантных и полезных
теорем Сакса о скачке и о плотности.
§ 1. Препятствия в методе приоритета с
бесконечными нарушениями и лемма о густоте
В этой главе нам будет удобнее вместо {е}^а(х) использовать
обозначение Фe,s{As\x). Пусть С — невычислимое в. п. множество. В самом
простом применении метода приоритета с бесконечными нарушениями
мы хотим построить в. п. множество А с теми же отрицательными
требованиями, что и в теореме VII.3.1, а именно, Ne : С ф Фе(.А), а
положительные требования имеют вид
Ре : wm с* А,
(где X С* Y означает, что X — Y конечно, и где р — вычислимая
функция), так что фиксированное положительное требование Ре может
перечислять в А бесконечно много элементов. В простейших случаях
все в. п. множества { Wp(6) }ееи окажутся вычислимыми. Для
каждого требования Ne мы хотели бы иметь такую запрещающую функцию
r(e,s), которая, подобно функции r(e, s) из теоремы VII.3.1, позволяет
для удовлетворения требования Ре перечислить элемент х в As+i
только тогда, когда х Е Wp(e))5+х и х > r(z,s) для всех i ^ е. Теперь от¬

§ 1. Лемма о густоте
183
рицательное требование Ne может нарушаться требованиями Р{ при
i < е бесконечное число раз, но то, что множество Wp(i), i < е,
вычислимо, окажется достаточным для удовлетворения Ne, как это было
в лемме 1 теоремы VII.3.1. Главная трудность состоит в том, что
некоторое Ре остается неудовлетворенным из-за запрещающей функции
г(г,$),г ^ е, которая в этом методе может быть неограниченной по s
(т. е. limsup5 г(г,$) = оо). Ясно, что для удовлетворения требования Ре
достаточно определить функцию r(e, s) так, чтобы выполнялось условие
liminf R(e,s) < оо, (1.1)
S
где R(e,s) = тах{г(г,$) : г ^ е}. Действительно, тогда Ре бесконечное
число раз получает «окна» сквозь запреты отрицательных требований.
Первое препятствие к выполнению (1.1) заключается в том, что
если мы определим r(e,s) как r(e,s) в теореме VII.3.1, то может для
некоторого е оказаться lim5 r(e,s) = оо. (Предположим, например,
что Ф1^(Х;0) = (7(0), если п X для некоторого чётного п < s,
п > liminfs R(0,s), но Pq в конце концов перечисляет все такие числа в
А, так что $i(A;0) не определена. Тогда N\ удовлетворено из-за этой
неопределенности $i(A;0), но может случиться, что (7(0) = $i)5(As;0)
для почти всех s, поэтому lim5 и(А8\ 1,0, s) = оо, lims r( 1, s) = оо, и Pi
не удовлетворено.) Такая трудность возникает только при условии, что
существует бесконечно много таких шагов s, что As \ и ф As+\ [ м, где
и = и{А3\ 1,0, s). Мы увидим, что от этого первого препятствия можно
легко избавиться, просто заменив Фе,5 всюду на Фе,$, определяемую
ниже, и положив r(e, s) равной итоговой запрещающей функции. Мы тогда
сможем показать, что если С Ф Ф6(.А), то liminf5 r(e,s) < оо.
Второе препятствие к выполнению (1.1) заключается в том, что
lime R(e,s) может быть бесконечным даже несмотря на то, что
liminfs r(i,s) < оо для каждого i ^ е. (Например, N\ и N2 вместе
могут держать под запретом все элементы, т. к. их запрещающие функции
свои значения одновременно никогда не сбрасывают.) Удивительно, но,
как впервые заметил Лахлан [1973], использование Фе>5 для преодоления
первого препятствия автоматически устраняет и второе.
Допустим, что мы хотим организовать вычислимое перечисление
{ As в. п* множества А. По данному { At }t^s определим
{/jlx[x € As - Аа±1], если As - AsJ_x ф 0,
max(A5 U { s }) в противном случае;

184
Глава VIII. Бесконечные нарушения
х)
{Фе,8 (А8; х), если она определена и
и(А8;е,х,з) < а8,
не определена в противном случае;
и
й(А8\е,х,з)
{и(А8\е,х,з), если Фе,8(А8;х) определена,
О в противном случае;
Т = {s: А8 \ а8 = А \ а8}.
Если { А8 }8еш — произвольное вычислимое перечисление
бесконечного в. п. множества А, то назовем множество Т множеством истпиннных
(недефицитных) шагов в этой нумерации. Заметим, что Т бесконечно и
Т =т А равномерно относительно (перечисления) А. Если Фе(А;х) = у,
то, очевидно, как и раньше lim* Фе,8(А8;х) = у. Решающим моментом
относительно Фе,« является то, что на любом истинном шаге t любое
текущее вычисление Фе,*(Л*;х) = у является и истинным вычислением
Фе(А;х) = у. А именно, мы имеем
(\/teT)fie,t(At;x) = y =* (1.2)
(Vs ^ t) [Феу3(А,;х) = Фе{А\х) -у k vi(As;e,x,s) = u(At\e,x,t)%
т. к. если Фeit(At;x) определена, то u(At;e,x,t) ^ at, и At [ at = А [ at.
Простейшим применением этого метода является лемма о густоте.
Напомним для заданных А С ш и у £ ш определения VI.4.5 и VI.4.6 у-
секции: AM — { (х, z) : (х, z) G А & z = у }, А^<у 1 = |J{ AM : z < у }, и
подмножество А С В называется густым подмножеством, если А\уJ =*
В№ для всех у . Мы скажем, что В кусочно вычислимо, если В^
вычислимо для всех у. (Следующая лемма была доказана Шёнфилдом [1961]
для частного случая С = 0', но для произвольных невычислимых в. п.
множеств С требуется метод сохранения Сакса из § 3 главы VII в
сочетании с методом приоритета с бесконечными нарушениями, что и было
первоначально разработано Саксом [1963а и 1963с].)
1.1 	Лемма о густоте (Шёнфилд). Для любого невычислимого в. п.
множества С и любого кусочно вычислимого в. п. множества В
существует такое густое в. п. подмножество А множества В, что
С£т А.
Доказательство. Зафиксируем вычислимые перечисления {В8 }8еи) и
{ С9 }«ец, множеств В и С. Пусть Aq = 0. По данному { At опре¬

§ 1. Лемма о густоте
185
делим Фе,5(А*) как выше. Определим оставшиеся функции как в
теореме VII.3.1 с Фe,s вместо Фe,s, а именно,
(функция длины)
l{e,s) = max{ х : (Vy < х) [Cs(y) = Фе,3(А3;у)1] },
(запрещающая функция)г (е, s) = тах{й(.Л*;е,х,5) : х ^ l(e,s) },
(множество нарушений) Ie — /е>5,
где
ie,s = { X : (3v ^ s) [х ^ f(e, v) & х G - Av] }.
Для удовлетворения требований
Ре : ЯН =* и Ne\C Ф Фе(Л),
мы перечисляем а: в как только a: G и х > r(i,s) для всех
г ^ е. Пусть А = \JS As.
Заметим, что Ie С А^<е\ т. к. Ne нарушается требованием Pi только
при i < е. Следовательно, мы имеем 1е А\<е\ т. к. если х G л<ч
скажем х G А^е\ то х G 1е только если х G Ie,s-
Выберем е и допустим по индукции, что С Ф Ф{(А) и АМ =*
для всех г < е. Тогда j4J<61 =* J5f<el вычислимо и, следовательно, /е
вычислимо, т. к. /е А^<е\ Следующие леммы аналогичны леммам
теоремы VII.3.1, но с множеством истинных шагов Т вместо всех шагов.
Лемма 1. С ф Фе(А).
Доказательство. Предположим, для получения противоречия, что С =
Фе(А). Тогда \ims l(e,s) = оо. Покажем, что С 1е> Так как 1е
вычислимо, то это будет означать, что и множество С вычислимо, в
противоречие с предположением. Для вычисления С(р), р G с помощью
оракула /е, найдем некоторое s такое, что Z(e,s) > р и
(Vx ^ р) (Vz) [z ^ u(As; е, х, s) => [z £ 1е или z G As]].
Такое s существует, т. к. С = Фе(.А). С теми же замечаниями, как и в
лемме 1 теоремы VII.3.1, индукцией по t ^ s доказывается, что
(У* ^ s) [Z(e, t) > р & r(e, £) ^ max{ u(As; e, x, s) : x ^ p }] (1.3)
и,значит,
Фв|.(А.;р) = Фс(АнР) = ФеИ;р) = С(р).

186
Глава VIII. Бесконечные нарушения
Лемма 2. Пусть Т — множество истинных шагов в перечислении
{As}seu; множества А. Тогда \imter ?(e,t) < оо. (Следовательно,
если С ф Фi(A) для всех г ^ е, то limter R(e,t) < оо, где R(e,s) =
max{ r(z,s) : г ^ е}, тем самым удовлетворяя (1.1).)
Доказательство. По лемме 1 имеем С ф Фе(А)- Определим
р = рх[С(х) ф Ф6(.А;х)]. Выберем s' G Т таким большим, чтобы для
всех s ^ s'
(Vx < р) [Фе,*(.А5;х) = Фе{А;х)] & (Vx ^ р) [<75(х) = С(х)\.
Случай 1. (VZ ^ s') [t G Т =$> $ej(At;p) f]. Тогда для любого t ^ s'
такого, что t G Г, мы имеем l(e,t) = р и r(e,£) = max{ u(.A5/;e,x, s') :
х < р}.
Случай 2. (3Z ^ s') [t е Т & Фе,*(А*;р) I]. Тогда Фе{А\р) =
Фe,s(As\p) для всех s ^ t согласно (1.2). Но С(р) ф Фе(А]р).
Следовательно, мы имеем
(Vs ^ £) [Z(e, s) = р & r(e, s) = r(e, Z) = max{ u(A5; е, х, s) : х ^ р }].
(1.4)
Лемма 3. (Ve) [А^ =* ДМ].
Доказательство. Любое х G £tel такое, что х > Д(е) =dfn Нт*€т R(e,t)
перечисляется в А)е\ []
Следующее утверждение является двойственным к теореме VII. 1.1 о
существовании невычислимого низкого в. п. множества.
1.2 	Следствие (Сакс [1963с]). Для любого невычислимого в. п.
множества С существует в. п. множество А такое, что А' =т 0" (т. е.
А является высоким) и С А (и, следовательно, А неполно).
Доказательство. По теореме IV.2.2 Поста любое множество 5, которое
является в. п. относительно 0' (такое, как 0"), может быть представлено
в Ег-форме и, следовательно, по теореме IV.3.2 существует такая
вычислимая функция h(y), что для всех у, у G 5 влечет, что конечно, а
у £ S влечет, что = ш. Для каждого S с таким свойством опреде¬
лим в. п. множество Bs следующим образом: Bs = {(x,j/):xG ^h(y) }•
Если А густое подмножество Bs, то

§ 2. Леммы о нарушениях, об окнах и о сильной густоте 187
у G 5 => В^ конечно => конечно => Иш А((х,у)) — О,
° х
И
у i S =*■ вУ'1 = «М =ф AW =* Jy] => lim А{(х,у)) = 1.
X
Функция f(y) = l\mx A({x,y)) вычислима относительно А! по лемме о
пределе, так что S ^т А!. Выберем теперь 5 = 0" и применим
теорему 1.1 к Bs для получения A. Q
(Заметим, что метод приоритета с положительными требованиям^
конечного действия может быть соединен с требованиями § 1 главы VII,
необходимыми для построения низких множеств, с целью построения
в. п. низкого множества. Поэтому не удивительно, что для построения
неполного высокого множества мы нуждаемся либо в положительных
требованиях бесконечного действия теоремы 1.2, либо в построении с
конечными нарушениями, действующим над другим таким построением,
как в упражнении VII. 1.6 (с), либо как в упражнении VII. 1.8 в сочетании
с теоремой VII. 1.1, релятивизованной относительно 0'. Эти построения,
как показывает тщательный анализ, равнозначны методу приоритета с
положительными требованиями бесконечного действия.)
§ 2. Леммы о нарушениях, об окнах и о сильной
густоте
Для доказательства теорем о скачке и о плотности нам потребуется не
столько лемма о густоте, сколько более общие версии лемм 1 и 2 § 1,
которые мы сейчас сформулируем и докажем. По данному 0 <т С 0;
фиксируем вычислимую последовательность (с каноническими
индексами) конечных множеств такую, что С(х) = \ims С8(х).
Предположим, что А = где { As }s€u; — вычислимая последователь¬
ность конечных множеств, либо заданная априорно, либо определенная
нами в ходе некоторого вычислимого построения. По данному { Av
определим
(функция длины)
l(e,s) = max{ х : (Vy < х) [Ca(y) = Фе,«(Л;у)] };
(модифицированная функция длины)
m(e, s) = тах{ х : (3i> ^ s) [х ^ Z(e, v) &

188
Глава VIII. Бесконечные нарушения
(Vy ^ х) [Л* f и = Av f «]] }, где и = й(Ау; е, у, v);
(запрещающие функции)
r(e, s) = max{ й{А8\е, х, s) : х ^ m(e, s) };
R(e, s) = max{ f(г, s) : г ^ e };
(множество нарушений)
/е = где Je,s = {х : (3i> < s) [х ^ r(e,i>) & х G Av+i - Av]}.
Назначение m — поддерживать длину соглашения, установленного
на некотором шаге v так долго, что «Фе(А) сторона» не меняется даже
тогда, когда изменение «(7 стороны» на некотором шаге s > v может
привести к Z(e, s) < Z(e, v). Использование rh необходимо для
доказательства леммы 1.1с более слабой гипотезой С ^т 07 вместо «С в. п.», что
по (1.2) позволяет немедленно получить некоторые удобные свойства,
такие как
(VZ G Т) (Vs ^ t) [rh(e,t) ^ m(e,s) & R(e,t) ^ Я(е, s)]. (2.1)
(С этого момента мы будем понимать г, Я и 1е в смысле
вышеприведенных определений, а не в смысле определений § 1.) Метод приоритета
с бесконечными нарушениями зависит от следующих двух лемм, чьи
доказательства в главных чертах похожи на доказательства лемм 1 и 2 из
§1-
2.1 Лемма о нарушениях. Если С фт Дм mo С ф Фе(Л).
2.2 	Лемма об окнах. Пусть Т — множество истинных шагов в
перечислении {As}seiV в. п. множества А. Если С Ф Фе(А), то
lim*£T r(e,t) < оо. (Значит, если С ф Фi(A) для всех i ^ е, то
1пп*ет Я(е,£) < оо.)
Доказательство леммы о нарушениях 2.1. Повторяем
доказательство леммы 1 § 1 с новыми функциями r(e,s), Д(е, s), /6 и функцией т
вместо I в (1.3). 0

§ 2. Леммы о нарушениях, об окнах и о сильной густоте 189
Доказательство леммы об окнах 2.2. Повторяем доказательство
леммы 2 § 1 с новыми функциями r(e, s), R(e, s) и 1е. Теперь случай 2
леммы 2 из § 1 доказывается как в § 1, случай 1 из^§ 1 леммы 2 также
доказывается как выше, благодаря использованию Фе,$. Таким образом,
в случае 2 согласно (2.1) мы имеем дополнительно к (1.4) ещё и
(Vs ^ t) [m(e,t) = m(e,s) & R(e,t) = R(e,s)]. 0 (2*2)
Мы сейчас получим более сильную форму леммы о густоте.
Аналогичные версии явно или неявно были установлены Робинсоном, Шёнфил-
дом, Саксом и Ейтсом.
2.3 	Лемма о густоте — сильная форма. Для данных 0 <т С 0;
и в. п. множества В существует в. п. множество А С В такое, что
А В,
(i) 	(Ve) [С Bt<el] => [С А & А густое подмножество В] и, в
действительности,
(u) (Ve) [С Я[<е] => (Vj ^ е) [С ф Ф,-(А) & =* ВЩ.
Более того, номер множества А может быть вычислен равномерно по
номерам множеств В и С.
Доказательство. Достаточно доказать (ii), т. к. (ii) влечет (i).
Фиксируем вычислимые последовательности конечных множеств {Bs}seuJ и
{ Cs bew такие, что В = \JS Bs и С = lims Cs. Определим А точно как
в теореме 1.1, но с новыми определениями функций r(e,s), R(e,s),n Ie.
Заметим, что как и раньше, имеем
/е<тЛ[<е]. (2.3)
Для данного е предположим, что
[С &<% (2.4)
и допустим по индукции, что С ф Ф*(.А) и AW =* ВМ для всех к < е.
Тогда A.t<el =* Bt<el, поэтому по (2.3) /е В^<еУ Отсюда, из (2.4) и
леммы о нарушениях следует, что С ф Фе(А). Таким образом, по лемме
об окнах, Ит*ет R(e,t) < оо и, следовательно, АМ =* B^l по
построению. Это доказывает (й). То, что А В, вытекает из следующей
леммы, которая будет полезной и в дальнейшем. О

190
Глава VIII. Бесконечные нарушения
2.4 	Лемма. Пусть последовательность { С8 }$ео> определена как
выше, и пусть { As }s€u, — вычислимое перечисление в. п. множества А.
Напомним, что А^е^ = |J{ А$ : i < е}. Определим
Те = {t: А1<еЦ at = А[<е] fa*},
где at определяется как в § 1 с л[<е^ вместо At. Тогда
Те А^<е} равномерно по е (2.5)
и, если
/е С А^<е\ (2.6)
то
(Vt € Те) (V* ^ ш(е, 4)) (V») [Ф,,«(А*; х) = у => Фе(Л; х) = у\ (2.7)
и
(Vt G Те) (Vs ^ t) [m(e,t) ^ m(e, s) & R(e,t) ^ Я(е, s)]. (2.8)
Доказательство. Ясно, что (2.5) получается как условие Т А в § 1.
Теперь (2.7) выводится как (1.2), с помощью (2.6) и того, что m (а не I)
используется в определении r(e, s) и, следовательно, и в определении /е.
Наконец, (2.8) получается для Те, как (2.1) для Т. Q
2.5 	Лемма. Для множеств А, В и С, удовлетворяющих условиям
лемм 2.3 и 2.4, включая условие (2.6), автоматически имеем А^.т В.
Доказательство. Фиксируем е и допустим, что для всех i < е мы
имеем 2?-вычислимо найденное д(г) такое, что АМ = Фд^(В). Тогда В-
вычислимо определяем л<«] и Те. Далее, если х G скажем х G
то положим t' = ^ s & £ G Те]. Теперь R(e,tr) = min{R(e,v) : t' ^
и}, согласно (2.8). (А именно, R(e,t') теперь так мала, какой она
никогда позднее не будет.) Следовательно, по построению At*+1, х G А№
только если х G 4' '+1- D
Многие результаты о в. п. степенях легко вытекают из леммы о
сильной густоте, как, например, следующая теорема.

§ 2. Леммы о нарушениях, об окнах и о сильной густоте 191
2.6 Теорема (Сакс [1963с]). Пусть d0 < di < d2 < • • • — бесконечная
равномерная возрастающая последовательность в. п.
степеней. Тогда существует в. п. степень а такая, что d0 < di <
• • • < а < O'. (Следовательно, O' не является минимальной верхней
гранью этой последовательности.)
Доказательство. Фиксируем вычислимую функцию h такую, что для
всех х deg (W^x)) = d^. Определим в. п. множество В так: ВМ =
{ (х,у) : х Е Wh(y) }• Пусть С = 0'. Применим лемму 2.3 (i) для
получения такого густого в. п. подмножества А С. В, что С А. Ввиду
густоты Wh(x) =т ВМ =* А)х\ потому что di < deg(A) для всех г. О
В противоположность теореме 2.6 Купер [1972а] показал, что
существует в. п. степень а и возрастающая в. п. последовательность в. п.
степеней { di }ieu, такие, что а является минимальной верхней гранью
этой последовательности. Другой результат, который легко вытекает из
леммы 2.3 о сильной густоте, теорема XII.1.5 Ейтса об индексном
множестве. Из нее можно получить короткое и элегантное доказательство
теоремы 4.1 Сакса о плотности, как мы покажем в теореме III. 1.8.
2.7 Упражнение
2.7 	(Интерполяционная теорема) (Сакс). Докажите, что если С и
D такие в. п. множества, что D <т С, тогда существует такое в. п.
множество А, что D А <т С и А* =т С. Указание.
Фиксируем вычислимые перечисления {Cs }5еа; и { Ds }eGw множеств С и D, и
определим вычислимую функцию
h(x, s)
х, если ФХ'8(Са;х)1,
s в противном случае .
Это — каноническое представление для скачка С1 в. п. множества
С, т. к. ввиду вычислимости h мы имеем lim5 h(x, s) < оо <=> х G С.
Пусть = { (п, 0) : п £ D } и J5ty+1l = { (п, у -I-1) : (3s) [n ^ h(y, s)] }.
Примените лемму 2.3 для получения А из В и С и докажите, что
у € С <=4- lim А((х,у -f 1)) = 0.
X
Для получения А ^т С и А! С1 необходимо доказать, что В С.
(Для более сильной версии см. теорему 4.4 — интерполяционную теорему
скачка.)

192
Глава VIII. Бесконечные нарушения
§ 3. Теорема о скачке
Если А в. п. и S = А!, то ясно, что S в. п. относительно 0' и 0' S.
Теорема Сакса о скачке утверждает, что эти условия на 5 и достаточны
для того, чтобы 5 =т А! для некоторого в. п. множества А и, кроме того,
для данного 0 <т С 0; можно добиться, чтобы С А. Исторически
это было первое применение Саксом метода приоритета с бесконечными
нарушениями.
3.1 	Теорема Сакса о скачке [1963с]. Для данных множеств S и С
таких, что S в. п. относительно 0', 0' 5, и 0 <т С 0', сущест¬
вует невычислимое в. п. множество А такое, что А' =т S и С А.
Более того, номер множества А может быть найден равномерно по
номерам S и С.
Доказательство. Любое множество S, в. п. относительно 0', является
Ег-множеством, поэтому по теореме IV.3.2 существует такая
вычислимая функция Л, что
У € S => Wh(y) конечно, и у £ S => Wh(y) = ш.
Определим в. п. множество В = { (х,у) : х е у) }, так что для всех у
у е S => вМ конечно, и у i S =» ДМ =а>1. (3.1)
Заметим, что т. к. 0' S, то существует такая S-вычислимая функция
/, что <Pf(y) является характеристической функцией множества в№.
Мы построим густое подмножество А множества В такое, что С
А, удовлетворяя для всех е требованиям
К:Сф{е)А
И
Ре : л[е1 =* рМ.
Требования густоты гарантируют, что S А', т. к.
F(y) =dfn Ит А((х,у))
X
существует для всех у и является характеристической функцией S. Это
следует из (3.1) и из того, что по лемме о пределе F А'.

§ 3. Теорема о скачке
193
Чтобы удержать скачок внизу и быть уверенным, что 5, мы
вводим для каждого е G со отрицательное «псевдо-требование»
де:(Зто5)[Фе,*(Лв;еН] =» {е}Л(еН,
и соответствующую ему запрещающую функцию q{e,s) =dfn u(As;e,
e,s). Если 0' <т S, то мы не можем рассчитывать удовлетворить для
всех е требованиям Qe, иначе А1 =т 0', как в теореме VII. 1.1. Тем не
менее, мы пытаемся удовлетворить Qe в точности так же, как в
теореме VII.1.1, позволяя Pi нарушить Qe (а именно, перечислить некоторый
элемент х ^ q(e,s) в As+1) только если г < е. Мы затем докажем, что
нарушения Qe (хотя, возможно, и бесконечно частые) имеют достаточно
хорошее поведение, чтобы мы могли доказать А! S, используя
предположение 0' S. Для этого мы определим S-вычислимую функцию д
такую, что для любого е, ч>д{е) является характеристической функцией
AM.
Построение А. Фиксируем вычислимые последовательности { Bs }s€u; и
{C'sbeu; такие, что В = \JSBS и С == lims Cs. По данному { At }t^s
определим r(e,s) и u(As;e,x,s) как в § 2 и q(e,s) — как выше. Пусть
А0 = 0. Перечисляем х в А^х тогда и только тогда, когда х G и
х > тах{ г(г, s), д(г, s) } для всех г ^ е. Пусть А = (Js As.
Лемма 1. Для всех е АМ =* в№ и С ф Фе{А). (Значит, С фт А и
S А1.)
Доказательство. Пусть Т — множество истинных шагов в
перечислении {A5}s€u;. Фиксируем е и допустим, что Pi и N{ выполняются
для всех i < е. Множество А^<е^ =* J5t<el вычислимо (т. к. В
кусочно вычислимо), Ne выполняется согласно лемме 2.1 о нарушениях и
Нт^ет В(е, t) < оо по лемме 2.2 об окнах. Кроме того, q(h t) < оо
для всех г ^ е, согласно (1.2). Следовательно, по построению АIе! =*
ВМ.
Лемма 2. А! S.
Доказательство. Пусть Те — множество истинных шагов в
перечислении { А^е^ }5би; (как в аналогичной лемме 2.4). По построению
требования Ne или Qe могут быть нарушены некоторым элементом х только
если х G А^<е 1. Значит, (2.6) выполняется. Таким образом, как в (2.7) и
(2.8), мы теперь имеем
(Vf € Те) [Фе,*(Л*;еН =* Фе(А;е)|],
(3.2)

194
Глава VIII. Бесконечные нарушения
и
(Vf G Те) (Vs ^ t) [Q(e, t) ^ Q(e, s) & Д(е, t) ^ Д(е, в)], (3.3)
где Q(e, s) = max{ q(i, s) : i ^ e }.
Фиксируем e и допустим, что для всех i < е мы имеем S-вычислимо
найденный номер g(i) такой, что AW имеет (вычислимую)
характеристическую функцию <pg(i)- Используя это мы можем S-вычислимо найти
номер для (вычислимой) характеристической функции А^<е^ и, значит,
для Те согласно (2.5). Для вычисления д(е) мы прежде всего, как
выше, S-вычислимо находим номер f(e) для вычислимой
характеристической функции 2?te 1. Если х G В^е\ скажем х G В^\ то определяем
t' = (fit > s) [t G Те]. Тогда, согласно (3.3) х G А^ 4=> х G At>+Это
завершает определение д.
Для доказательства А! S заметим, что т. к. 0' S, и S
позволяет, используя д равномерно по е вычислить номер (вычислимой)
характеристической функции множества Те, то мы можем с помощью
оракула S определить, выполняется ли условие е G А’, т. к. по (3.2)
имеем
е G А! Фе(А;е)1 <=> (31) [teTe & Фе,*(.А*; е)1]. (3.4)
Фиксируем геделевский номер характеристической функции
множества Те и заметим, что (3.4) является Ei-формулой. Следовательно, её
истинность проверяется эффективно с оракулом 0' (а не только с
оракулом S). Это — решающий момент всего доказательства и его следует
хорошо понять, прежде чем идти дальше. (Если бы бескванторная часть
последнего условия в (3.4) была невычислимой, а только S-вычислимой,
то для установления истинности (3.4) потребовался бы оракул
множества S'.)
Для проверки, что А невычислимо, заметим, что мы можем
предположить 0' <т S (в противном случае теорема 3.1 немедленно следует из
теоремы VII.3.2 Сакса о разложении). Следовательно, А не вычислимо,
т. к. А! =т S. Мы можем также привести равномерное построение
невычислимого в. п. множества А, удовлетворяющего условиям теоремы 3.1,
добавляя к вышеприведенному построению положительные требования
конечного действия вида Re : А ф {е}. В этом случае для
удовлетворения Re надо, как в главе VII, использовать какого-нибудь свидетеля
х G не меняя стратегии удовлетворения вышеприведенных
требований Pi и Ni. О

§ 3. Теорема о скачке
195
Для последующих ссылок заметим, что с помощью условий 0' S
и (3.3) мы имеем, что
R(e) = liminf R(e,s) является S-вычислимой функцией. (3.5)
S
(Так как мы знаем, что ИmteTe R(e,t) < оо, то для каждого t Е Те
выясняем, будет ли выполняться условие
(Э*' > t) [t' еТе & R(e,t) < R(e,t%
пока не получим отрицательный ответ. Каждый такой вопрос
записывается в виде Ei-формулы, т. к. Те вычислимо.)
3.2 Примечание (Сакс). Пусть S и С определены как в теореме 3.1.
Если D — такое в. п. множество, что D1 S и С D, то мы можем
добавить к заключению теоремы 3.1 условие D А.
Доказательство. Заменим В на в. п. множество Д, где = { (х,0) :
х Е D } и (х,у -I- 1) Е В <=Ф> (я, у) Е В. Построение и доказательство
теперь такие же, что и выше, за исключением того, что А и В теперь
«кусочно вычислимы относительно D» вместо «кусочно вычислимы»,
т. к. j4i°l =* в№ =т D. Лемма о нарушениях остается применимой в
лемме 1, т. к. /е А^<е^ D и С D. Теперь Те D,
поэтому в (3.4) мы должны использовать вместо 0'-оракула D'-оракул. Так
как D1 5, доказательство леммы 2 является простой релятивизацией
относительно D. О
3.3 Примечание. Пурть S и С определены как в теореме 3.1. Мы
можем получить множество А непосредственно, применяя лемму 2.3 о
густоте к множествам В и С без введения второй запрещающей функции
q(e,s).
Доказательство. Определим по данному (7(0) вычислимую функцию h
равенством
Ф /Х.у\ _ / С'(О), если у = 0 и Фе(Х;е)1,
л(ед ’ У> | неопределена в противном случае.
Следовательно,
Фе(Л;е)4- •<=>• Фд(е)(А;0) = (7(0) <=> liminf l(h(e),s)> 0
-«=► (Э*) [t е Тл<«> & ФМе)ДЛ4;0) = (7(0)],
согласно (3.4). Ц

196
Глава VIII. Бесконечные нарушения
В определении IV.4.2 мы ввели высокие (низкие) в. п. степени как
степени, чьи первые скачки являются самыми высокими (низкими) из
возможных. В определении VII.1.3 (и упражнении IV.4.5) эта иерархия
была расширена заменой первого скачка на n-й скачок. В результате
для п ^ 0 возникают классы н„ и Ln. Следующий результат
устанавливает, что все эти классы различны и не исчерпывают множество
всех в. п. степеней R. (Альтернативные доказательства можно найти в
упражнениях VII.1.6(d) и VII.1.6(e).)
3.4 Следствие. Для всех п € ш Lп ф Ln+i и Нп ф Hn+i.
Доказательство. Релятивизуя следствие 1.2 и теорему VII. 1.1
относительно 0(п) и используя теорему 3.1 о скачке получаем, что для всех п
Нп ф Hn+i и Ln ф Ln+i. []
Мартин [1966d], Лахлан [1965d] и Сакс [1967] доказали, что
объединение этих классов не исчерпывает R. Мы приводим доказательство
Сакса.
3.5 Следствие (Мартин, Лахлан, Сакс). Существует такая в. п.
степень а, что для всех п [0^n^ < < 0(n+1)], т. е.} a G R-Un(HnU
Ln). (Такая степень а называется промежуточной степенью.)
Доказательство. (Сакс [1967]) Равномерность теоремы 3.1 о скачке
вместе со следствием 3.4, обе релятивизованные по произвольному
множеству Y Си, дают такую вычислимую функцию д(х), что для всех х G
и и Y С ш имеем:
Y<tW?{x)<tY' и (W?(x)y =T(WD®Y'. (3.6)
Теперь, применяя релятивизованную теорему III. 1.6 рекурсии,
находим такую неподвижную точку п, что = W% для всех Y С ш.
Положим а = deg(lV^). (Заметим, что q(x) является вычислимой 1:1-
функцией, а не просто У-вычислимой функцией согласно релятивизо-
ванной теореме Ш.1.6(й) рекурсии.) Q
В главе XII нам будет полезно следующее усиление (3.6). Мы
доказываем определенное утверждение (Уп) (УУ) Pn(Y) индукцией по п.
Наибольший интерес для нас будет представлять нерелятивизованная
версия Рп(0)> но для доказательства индуктивного шага нам понадобится
релятивизованная индуктивная гипотеза (VУ) РП(У). Этот тип
доказательства похож на релятивизованные индуктивные доказательства
следствия VI.3.3 и упражнения VII. 1.6. В доказательстве теоремы XII.4.4 мы
будем пользоваться следующим следствием.

§ 3. Теорема о скачке
197
3.6 	Следствие. Пусть q(x) определена, как в следствии 3.5. Тогда
для всех х Е ш, У Сц и п ^ О
Y <т W*{x) <т Г & (И£(ж))(п) =т W?n) ф У<">. (3.7)
(Напомним, что qn(x) означает п-ю итерацию функции q(x).)
Доказательство. Через Рп(У) обозначим формулу (3.7), начинающуюся
с «(Уж)». Докажем предложение (VY) Рп(У) индукцией по п. При п = 1
это просто (3.6). Заметим, что Pn+i(y) следует из Pn(Y') и Pi(Y). Q
3.7 	Предложение. Существует такая вычислимая функция f{i,x),
что для всех Y Сш и i,x Е ш
где, по определению, Wj^ х^ = 0, если <рУ (х) не определена.
Доказательство. Оракульная тьюрингова программа Pf(i,x) из § 1
главы III сначала с помощью оракульной ленты (содержащей
характеристическую функцию множества Y) вычисляет (рУ (х) = z, а затем
перечисляет . Пока (рУ (х) не определилась, полагаем = 0. Q
3.8-3.9 Упражнения
3.8. 	Докажите, усилив (3.7), существование такой вычислимой
функции q(n,i,x), что для всех Y С со, п ^ 1 и i,x Е со
у <Т w^niiix) <Т У & (W^„,ilI))(n) =т W*£hx) 0 (3.8)
Указание. Скомбинируйте следствие 3.6 с предложением 3.7.
3.9 	(Мартин, Лахлан). Покажите, что существуют такие в. п. степени а
и Ь, что для всех п a| b(n). Указание. Модифицируйте
доказательство теоремы 3.1 и формулу (3.6) так, чтобы получить такие вычислимые
функции р{х,у) и q{x,y), что для всех х,у € ш и Y Си
(W^y)y =т (жГ)еП
К..Л 1т К.„У
Далее используйте теорему парной рекурсии (теорема II.3.15).

198
Глава VIII. Бесконечные нарушения
§ 4. Теорема плотности и стратегия кодирования
Сакса
Для доказательства теоремы плотности Сакс [1964а] скомбинировал
приведенный выше метод бесконечных нарушений с найденной им новой
стратегией кодирования, позволяющей удовлетворять положительным
требованиям. Эта стратегия кодирования является основной идеей в
следующем доказательстве и имеет множество других применений. (Другое
доказательство, предложенное Ейтсом и использующее индексные
множества, приводится в теореме XII. 1.8.)
4.1 	Теорема плотности (Сакс [1964а]). Для любых данных в. п.
множеств D <т С существует такое в. п. множество А, что D <т
А <т О.
Доказательство. Зафиксируем вычислимые нумерации {Cs и
{ Ds }s€u; множеств Си Д положим D0 = 0. Определим = { (х,0) :
х G Ds }, так что D ^т А. Мы будем добиваться А С, как в
лемме 2.5, находя такую (7-вычислимую функцию g, что для всех е
AM = Фр(е)((7). Чтобы сделать оба неравенства строгими, достаточно
удовлетворить для всех е > 0 требованиям
АГе:С^Фе(А), И Ре '.Аф Фе(£>).
(Достаточно рассмотреть только случай е > 0, вместо е ^ 0, т. к.
любое тьюрингово сведение имеет бесконечное множество индексов.) Для
удовлетворения Ре попытаемся так закодировать С в Aiel, что если
А = Фе(Б), то С D, что противоречит первоначальному
предположению.
Положим Ао = 0. По данным для е > 0 определим r(e,s)
как в § 2, Д(е, s) = max{ г(г, s) : 0 < г ^ е }, и положим
lD(e,s) = max{ х : (Vj/ < х) [As(y) = Фe,s(Ds;y)\ }•
(Напомним, что по определению 1.3.6 под (х, s, е) мы понимаем ((х, s), е).)
Для всех t ^ s и е таких, что 0 < е ^ s, перечисляем (х, £, е) в As+1
тогда и только тогда, когда (x,t, е) > R(e,s), х G Cs+1 и х < lD(e,v) для
всех v, t ^ s. Положим A = \JSAS. (Это завершает построение А.)
(Наглядно эту стратегию кодирования можно представить себе
следующим образом. Для фиксированного е элементы {(х,у,е) : х,у G со }

§ 4• Теорема плотности и стратегия кодирования Сакса 199
расположены на плоскости. Если lD(e,t) > х на шаге £, то
(неподвижный) «маркер кодирования» присваивается числу (x,t,e). Если позднее
на некотором шаге s > t мы имеем lD(e, s) ^ х, то этот маркер
удаляется. Если х Е С8+и то все числа вида (ж, £, е), £ ^ s, все ещё обладающие
маркерами на шаге s и не запрещённые требованиями более высокого
приоритета, перечисляются в А8.ц.)
Чтобы убедиться в том, что А удовлетворяет всем требованиям, мы
проверим все требования индукцией по е и одновременно определим С-
вычислимую функцию д(е) так, чтобы А№ = Фд(е){С). Ясно, что ^(0)
существует, т. к. А^ =т D <т С. Зафиксируем е > 0 и предположим,
что следующие формулы верны для всех г, 0 < г < е:
С^Фг(А), (4.1)
АфФг(П), (4.2)
А^ вычислимо, (4.3)
и
Л'1 = %Ц)(С), где g(i) находится С-вычислимо. (4.4)
Лемма 1. С ф Фе{А).
Доказательство. Имеем А^<е^ D, т. к. множество AW вычислимо
для каждого г, 0 < г < е. Пусть 1е — множество нарушений Ne,
определенное в § 2. Тогда Ie С At<el по построению и, следовательно, как
в (2.3), имеем 1е A^<eh Отсюда 1е А^<е^ D <т С. Поэтому,
С ф Фе(А) по лемме 2.1 о нарушениях.
Лемма 2. А ф Фе(1)).
Доказательство. По лемме 1 и лемме 2.2 об окнах
R(e) =dfn liminf R(e,s) < оо.
s
Если А = Фe(D), то lim5/D(e,s) = оо. Определим функцию модуля
М(х) = (fis) [х < lD(e, s) & Ds и = D [ и],
где и = таx{u(D8;e,y1s) : у ^ х}. Теперь, т. к. D в. п. , М D по
лемме Ш.3.2 о модуле. Однако, также справедливо
М{х) = (fis) (yt ^ s) [х < lD(e,t)],

200
Глава VIII. Бесконечные нарушения
т. к. для всех s ^ М(х) и для всех у ^ я, Фe,s(Ds\y) = Фe(D\y),
так что если А(у) ф А3(у), то Фe(D) ф А, что противоречит
нашему предположению. Для каждого х D-вычислимо выбираем
наименьший ух > max{ M(x),R(e)}. Теперь х G С тогда и только тогда, когда
(я,2/х,е) G А. Следовательно, С A0D D, что противоречит
предположению.
Лемма 3. Множество АМ вычислимо.
Доказательство. По лемме 2 А ф Фe(D). Пусть ре = {fix) [А(х) ф
Фe(D]x)\. Тогда liminf8lD(e,s) = ре. При х ^ ре для данных х и t
находим такой шаг s ^ t, что lD(e,s) = ре. Теперь, (x,t,e) G А тогда
и только тогда, когда (x,t,e) G As+1. Для х <ре зафиксируем такой s',
что С8> [ ре = С ре, Ре ^ /D(e,£) и Д(е) ^ R(e,t) для всех t ^ s'. По
данному £ определим
vt = (рг>) [v ^ s' & v ^ £ & R(e,v) = R{e)].
Тогда для t ^ s', (xyt,e) G А тогда и только тогда, когда (х, £,e) G
Avt+i-
(Заметим, что для проверки условия (x,£,e) G А граница по s
существует по разным причинам: если х ^ ре, то она существует потому,
что lD(e,s) сбрасывает свое значение; если же х < ре (и t достаточно
велико), то она существует потому, что lD(e, s) со временем станет > х
и lim inf 5 R(e,s) = R(e). Это означает, что описанная разрешающая
процедура не равномерна по е.)
Лемма 4. Можно так С-вычислимо определить д(е), что А^ =
Фд(е)(С) равномерно по е.
Доказательство. Определим Те для множества { А^<е' }seu, как в
лемме 2.4. Исходя из {р(г) : i < е}, (7-вычислимо находим At<el и,
следовательно, Те. Зафиксируем (x,t,e). Если х £ (7, то (х,£,е) £ А. Если же
a: G С, то выберем такой s, что Crs^a:-|-l = C'^a:-fl, и определим
v' = (/iv) [u^&v^s&vG Т€].
Тогда (x,t,e) G А тогда и только тогда, когда (х,£,е) G A„/+i, потому
что R(e,v') ^ R(e,v) для всех v ^ v1. Q

§ 4- Теорема плотности и стратегия кодирования Сакса 20i
4.2 Замечание. Заметим, что в отличие от леммы 2 теоремы 3.1
здесь мы не утверждаем, что (4.3) и (4.4) можно скомбинировать для
построения такой С-вычислимой функции g, что для всех е > 0 <р9(е)
- характеристическая функция множества А^е\ в нашем случае просто
Д[е] = Ф^е)(С). Дело в том, что даже несмотря на то, что А\е 1
вычислимо для всех е > 0, доказательство вышеприведенной леммы 3 зависит
от параметров ре и Д(е), которые не могут быть найдены С-вычислимо
равномерно по е, и доказательство леммы 4 для каждого х очевидно
использует оракул множества С. Это тонкое различие существенно для
теоремы 4.4 и объясняет разницу между упражнениями 4.5 и 4.6.
Приведенная выше стратегия кодирования, позволяющая избежать
нижние конусы, имеет множество других приложений, такие, как
следующая равномерная версия следствия VII.3.7.
4.3 Теорема (Ейтс [1966b]). Пусть С — такое в. п. множество, что
0 <т С <т 0*- Существует такое в. п. множество А, что А |т С.
Более того, номер множества А может быть найден равномерно по
номеру множества С.
Доказательство. Для доказательства теоремы достаточно для всех е >
О удовлетворить требованиям:
Ие:СфФе(А) и Ре:АфФе(С).
Пусть К = {е:е Е We } =т 07. Вместо предположения D <т С
теоремы 4.1 мы используем предположение С <т К, поэтому С и К играют,
соответственно, роли D и С. Пусть Aq = 0. По данным перечислениям
{ С8 }seи>, { Ks }seu и {At }t^s как обычно определяем:
lc{e,s) = max{ х : (Vy < х) [As(y) = Фе,*(С'*;у)]}.
Для t ^ s перечисляем (ж,£,е) в As+1 только когда (я,£,е) > Д(е,$),
х Е Ks+1, и х < Iе(е, и) для всех v, t ^ s. Пусть А = |J5 As.
Зафиксируем е и предположим по индукции, что для всех г < е, С ф
фi(A), А ф Фг(С), и вычислимо. Приведенные выше доказательства
устанавливают (с С и К вместо D и С соответственно в леммах 2 и 3)
следующее: С ф Фе(А), А ф Фе(С) и А^е 1 вычислимо. Q
Возникает естественный вопрос: до какой степени предыдущая
теорема может быть скомбинирована с теоремой 3.1 о скачке так, чтобы
выполнилось A! =j S для некоторого S. Ейтс [1969] доказал, что это

202
Глава VIII. Бесконечные нарушения
может быть сделано для 5 =т 0", причем все ещё сохраняется
равномерность теоремы 4.3. Позднее Робинсон [1971b, следствие 3] расширил
этот результат до любого S, в. п. относительно 0' такого, что 0' ^т S, но
без условия равномерности Ейтса. Эти результаты приведены в
упражнениях 4.5 и 4.6.
Мы также можем использовать стратегию кодирования для
одновременного комбинирования результатов теоремы о скачке, теоремы
плотности и теоремы 2.7 об интерполяции. Для данных в. п. множеств D <т
С предположим, что D <т А <т С и S =т А'. Что мы можем сказать
про 5? Ясно, что необходимо, чтобы D* S и чтобы S было в. п.
относительно С. Следующая теорема показывает, что эти необходимые
условия являются также и достаточными. Это одна из наиболее важных
и широко используемых теорем теории вычислимости.
4.4 Интерполяционная теорема о скачке (Робинсон [1971b]). По
данным в. п. множествам D <т С и множеству S, в. п. относительно
С такому, что D1 S, найдется такое в. п. множество А, что
D <т А <т С и А1 =т S.
Доказательство. Так как S в. п. относительно С (и, следовательно,
S С"), мы можем применить метод интерполяционной теоремы 2.7,
чтобы найти такое в. п. множество В С, что В^ =т D и для всех х >
0, если х Е S, то вМ конечно, и если х £ S, то вМ = иМУ Стратегия
перечисления элементов в А^е 1 такая же, что и для требования густоты
Pi упражнения 2.7 (с определенным выше множеством В), если е = 2г,
и для требования Р{ из теоремы 4.1 о плотности, если е = 2* + 1.
Так как В ^т С, мы можем вычислить (как в лемме 4 теоремы 4.1)
(7-вычислимую функцию g такую, что АIе! = Ф9(е)(С) для всех е ^ 0.
Так как D' *?, то мы можем также вычислить, как в теореме 3.1,
лемме 2 и упражнении 4.5, некоторую S'-вычислимую функцию h(e)
такую, что iph(e) является характеристической функцией А^е 1. Остальное
как в предыдущих доказательствах. Ц
4.5-4.10 Упражнения
4.5 (Ейтс [1969]). Для данного в. п. множества С такого, что 0 <т С <т
0' и любого в. п. относительно 0' множества S такого, что С ^т S,
существует такое в. п. множество А, что А! =т S и А |т С. Более того,
номер А может быть найден равномерно по номерам С и S. Указание.
Стратегия перечисления элементов в А№ такая же, что и для Р* в
теореме 4.3, если е = 2г, и для Pi в теореме 3.1, если е = 2i + 1, при

§ 4• Теорема плотности и стратегия кодирования Сакса 203
использовании обычной запрещающей функции R(e,s). В предыдущих
доказательствах достаточно было только показать, что существует S'-
вычислимая функция g такая, что <р9(е) является характеристической
функцией AM для всех е ^ 0. Далее действуем, как в теореме 3.1,
лемме 2, если е нечётно, и как в теореме 4.3, лемме 3, если е чётно.
(Заметьте, что параметры R(e) и ре в лемме 3 как функции от е S-вычислимы.
Для этого используйте (3.5) и условие С1 S.)
4.6 	(Робинсон [1971b]). Докажите, что для любого в. п. множества С
и любого множества S таких, что 0 <т С <т 0', S' в. п. относительно 0'
и 0' S, существует такое в. п. множество А, что А |т С и А' =т S.
Указание. Используя теорему VII.3.2 Сакса о разложении найдите такие
непересекающиеся в. п. множества D0, D\, что: (1) К = D0 U D\, (2)
С фт для i = 0,1, и (3) D[ =т 0* для г = 0,1. Покажите, что одно из
этих множеств, скажем Do, несравнимо с С, и примените замечание,3.2
при Do вместо D.
4.7 (Робинсон [1971а, следствие 3]). Предположим, что D и С в. п.,
D <т С, { U }i€a, 0', { 9i }гбо; С, и /j $£т А С 5^т 9i для всех г.
Докажите существование в. п. множества А такого, что D <т А <т С
и /г А, А 9i для всех *• (Запись {<7г}геи> С означает, что
существует функция h С такая, что Ax[h(i,x)] = gi.) Указание.
Сначала рассмотрите по одной функции / и д.
4.8 (Робинсон [1971а]). Пусть D <т С. Конечная, последовательность
{ А\,..., Ап } независима относительно D иС, если Z)0(0{ Ai }i^n) <т
С и А{ D 0 (0{Aj : j ф г}). Используйте упражнение 4.7 и
метод, позволяющий избежать верхние конусы, чтобы показать, что если
D <т С в. п. множества, и { А{ }^п — конечная последовательность в. п.
множеств, независимая относительно D и С, то существует в. п.
множество An+i такое, что {Ai,...,An, Ап+\ } независима относительно D
и С. Заметим, что нам требуется нечто большее, чем упражнение 4.7,
чтобы показать, например, что Ai ф { е }ф{Aj bv*.
4.9 (Робинсон [1971а]). Для данных в. п. множеств D <т С
покажите, что существует бесконечная в. п. последовательность в. п. множеств
{ Ап }neu; такая, что D <т Ап <т С и Ап фТ ®{ Аш }ш^п для всех п.
Указание. Сначала неоднократно примените упражнение 4.8 для
получения в. п. последовательности {Вп }nea; в. п. множеств, равномерно

204
Глава VIII. Бесконечные нарушения
вычислимой относительно С, и такой, что {Bi независима
относительно D и С для каждого п. Пусть В = 0nJ5n. Используйте метод
из леммы 2.3 для построения в. п. множества А С JB, А Д,
удовлетворяя требованиям Ре : АМ =* В^, и N: ВМ ф 4>e(0j^i.A^)-
Пусть Ап = А^п 1. Рассмотрите одновременное перечисление всех в. п.
множеств { Ai}i£u>, {Bibe*;, и рассмотрите истинные шаги для этого
комбинированного перечисления.
4.10 	(Робинсон [1971а, следствие 7]). Докажите, что если d и сг- в. п.
степени и d < с, то любое счётное частично упорядоченное множество
может быть вложено в в. п. степени между степенями d и с с
сохранением верхней грани. Указание. Используйте упражнение 4.9 и метод
упражнений VI. 1.7 и VII.2.2. (Робинсон [1971а] доказал, что если dr-
низкая степень, то это вложение сохраняет наибольший и наименьший
элементы, если только они существуют (см. замечания XI.3.7).)
§ 5. * Модель пинбольной машины для метода
бесконечных нарушений
Модель пинбольной машины является альтернативным методом для
того, чтобы справиться со второй трудностью (описанной в § 1),
возникающей в построениях с бесконечными нарушениями. Это несколько более
громоздкий, но более гибкий метод, чем метод истинных шагов,
описанный выше. Он может быть использован для получения результатов о
минимальных парах в главе IX и действительно существенен для
понимания некоторых более сложных построений в. п. степеней. Более того,
этот метод необходим в доказательствах, использующих определенные
построения, с привлечением более одного в. п. множества, где метод
«истинных шагов» § 1 и § 4 недостаточен. См. упражнение XII.2.13.
Решающим моментом в модели пинбольной машины является то, что
мы позволяем свидетелям положительных требований проходить
отрицательные требования с большими приоритетами одно за другим,
вместо ожидания, когда запрещающие функции одновременно сбросят свои
значения, как это было в § 1. (Подобный подход был использован в
первоначальных доказательствах Сакса [1963а], Ейтса [1966] и других, но
явное описание модели пинбольной машины впервые была приведено
Лерманом [1973].) Для демонстрации этого метода мы приведем
альтернативное доказательство леммы 1.1 о густоте. Пусть В, С, {Bs}s€u;,

§ 5. * Модель пинболъной машины
205
{С8 }seu> и г(е,5) определены, как в § 1. Как и раньше, создаем
требования Ре : АМ =* ВМ и Ne:C^ Ф е(А).
Пинбольная машина имеет отверстия Не, соответствующие
положительным требованиям Ре, и ворота Ge, соответствующие
отрицательным требованиям iVe. Они располагаются поочередно в порядке
убывания их приоритетов Go, Но, G\, Hi,... , как показано на
диаграмме 5.1. Ворота G_ 1, соответствующие карману на дне машины,
добавляются ради удобства.
Неформально построение выглядит следующим образом. Если х
перечисляется в В^ на шаге 5 + 1, тогда х падает через отверстие Не на
поверхность машины (называемой столом), х движется в направлении
стрелок (вниз) и останавливается у первых ворот G», i ^ е, таких, что
х ^ r(i,s). Если на более позднем шаге t + 1 мы имеем r(i,t) < х, то
х освобождается воротами Gi и проходит к следующим воротам Gj,
j < i, таким, что х ^ r(j,t). Таким образом происходит движение числа
х, пока х не застрянет навсегда в некоторых воротах или не достигнет
последних ворот G_i, в которых оно перечисляется в А. Пусть Ge,$
обозначает числа, находящиеся в воротах к концу шага 5, и Ge,<х> — числа,
застрявшие в Ge навсегда. Пусть Gfe = Ui<e Gits и G<e = Ui<e Ф,оо.
Как и в § 1, используем r(e,s) (вместо r(e,s)) для обеспечения того,
что если С ф Фе(А), то liminfs r(e, s) < оо; следовательно, |Ge,oo| < оо и
Ре удовлетворено. Более того, требование Ne также выполняется, т. к.
все Pi, i < е, создают только вычислимое множество нарушений к
требованию Ne и, кроме того, |G^f| < оо. Теперь приведем формальное
доказательство.
Альтернативное доказательство леммы 1.1 о густоте. Фиксируем
вычислимые последовательности { В8 }зеи, и { С8 }в6о; такие, что В =
U* В8 и С = \J8 С8. Пусть А0 = 0. По данным { At }*<£« определим l(e, s)
и r(e,s), как и в § 1.
Шаг 5 + 1.
Подшаг 1. Для каждого е и х Е — В$ освобождаем х из
отверстия Не и помещаем в ворота Ge.
Подшаг 2. Для каждого х, находящегося в воротах Ge (включая и
только что помещённых), если r(e,s) < х, то Ge освобождает х.
Находим наибольшее i < е такое, что х ^ r(i,s) и помещаем х в G{. Мы
полагаем г(—1,5) = оо, так что такое i существует. Если х окажется в
G_i, то перечисляем его в As+1.
Лемма. Для всех е

206
Глава VIII. Бесконечные нарушения
Отверстие
Ворота G\
Отверстие
Но
Ворота Go
Диаграмма 5.1. Пинбольная машина
(i) С ф Фе(А),
(ii) liminf5 r(e,s) < оо и, следовательно, |Ge,oo| < °о>
(Ш) А& =* £Н.
Доказательство. Фиксируем е и допустим, что лемма справедлива для
всех j < е. Тогда, согласно (ii) \G<f\ < оо и, согласно (iii) А^<е^ =* 2?[<е1
и вычислимо, т. к. В кусочно вычислимо.
Для доказательства части (i) предположим для получения
противоречия, что С = Фе(.А). Тогда lim5 l(e,s) = оо. Для эффективного
вычисления С(р) находим наименьший шаг s такой, что (1) l(e,s) > р\ и

§ 5. * Модель пипбольной машины
207
(2) 	для всех z < и =dfn таx{v,(As;e,x,s) : х ^ р}, если z G А^<е^ U Gfe,
то z G As U Такой шаг s существует, т. к. С — Фе(А), и мы можем
найти его эффективно, т. к. А^<е^ вычислимо и G<f конечно, так что
его канонический индекс может быть выбран заранее. (Заметим, что,
таким образом, эта процедура не равномерна по е.) Индукцией по t ^ s
следует, что
(W ^ s) [l{e,t) > р & г(е,£) ^ и].
Тогда С(р) = Фе,в(Ав;р), т. к. любой элемент х, который
перечисляется в А после шага s, сперва должен быть освобожден воротами Ge на
некотором шаге t ^ s, на котором х > r(e, t) ^ и. Таким образом, С
вычислимо, в противоречие с предположением. Следовательно, С Ф Фе(А).
Для доказательства (и) пусть р = рх[Фе{А\х) ф С(х)]. Выберем s'
таким большим, что для всех s ^ s' справедливо
(V® < р) [Фе,*(Л5;х) = Фе(А;х)] & (Ух ^ р) [С8(х) = С(х)].
Случай 1. Фe(A;p)t • Тогда, из-за использования Фе вместо Фе,
существует бесконечно много шагов s таких, что Фe,s(As\p) не определено.
На каждом таком шаге s, Z(e, s) = р и г(е, s) = r(e, s').
Случай 2. Фе(А\р)1 . Тогда для почти всех s, Z(e,s) = р и r(e, s) =
r(e,s').
Часть (iii) следует немедленно из (ii), т. к. каждый х G
принадлежит либо Afel, либо Gi>00 для некоторого i ^ е. Q
Заметим, что в модели пинбольной машины требования с более
сильными «приоритетами» располагаются ниже требований с более
слабыми приоритетами. Так, если i < j, мы говорим, что требование Ri имеет
более сильный приоритет, чем Rj (а не «более высокий приоритет», как
это принято в литературе), чтобы избежать неточностей здесь и в
дальнейшем.

Глава IX
Метод минимальных пар и вложение
решеток в в. п. степени
Пусть L(^,U,0,1) — язык для описания верхних полурешеток, таких,
как класс в. п. степеней R, где ^ и U интерпретируются обычным
образом, а под константами 0 и 1 подразумеваются, соответственно,
наименьший и наибольший элементы. После того, как теорема VIII.4Л Сакса о
плотности стала известна, Шёнфилд [1965] сделал попытку
алгебраического описания R. Он сформулировал предположение, заключающееся в
том, что класс R, рассматриваемый как верхняя полурешетка, является
плотной структурой, аналогично тому, как линейно упорядоченное
множество рациональных чисел образует плотную структуру относительно
всех счётных линейно упорядоченных множеств. Предположение Шён-
филда утверждает, что если а Е R удовлетворяет диаграмме D(x),
и если D\{x,y) — любая непротиворечивая диаграмма в L(^,U, 0,0'),
расширяющая Dy то существует b Е R такая, что Di(a,b). В
дополнение к теореме Сакса о плотности, Шёнфилд сформулировал два
следствия этой гипотезы:
(0.1) Если a, b Е R несравнимы, то они не имеют наибольшей нижней
грани в R;
(0.2) Для данных в. п. степеней 0 < b < а существует в. п. степень
с < а такая, что а = bUc, т. е. что любая такая степень b может быть
нетривиально дополнена наверх к а. (см. определение ХШ.4.1.)
Позднее выяснилось, что оба эти следствия неверны (поэтому
неверна сама гипотеза Шёнфилда). Как Шёнфилд и предвидел, эти
исследования привели к постановке двух новых типов задач и разработке новых
методов доказательства. В этой главе мы изучим первый тип задач,
связанных с проблемой вложения решеток в R. В замечаниях ХШ.4.4 мы

§ 1. Минимальные пары и вложение ромба
209
будем обсуждать задачи второго типа, изучение которых впоследствии
привело к известным теоремам о дополняемости и о недополняемости
наверх, а затем — и к доказательству неразрешимости элементарной
теории R.
Метод приоритета с конечными нарушениями позволяет строить
вложения в в. п. степени R произвольных счётных частично упорядоченных
множеств (ч. у. множеств) Р (с сохранением порядка), см.
упражнение VII.2.2. Более того, с помощью метода приоритета с бесконечными
нарушениями можно доказать, что существует вложение ч. у. множества
Р в любой наперед заданный интервал [а, Ь], где a,beRna<b (см.
упражнение VIII.4.9). В случае, когда Р является решеткой, легко
видеть, что вложения из VII.2.2 и VIII.4.9 сохраняют наименьшие верхние,
но не обязательно наибольшие нижние, грани.
В следующих двух параграфах мы получим новый метод,
позволяющий получать вложения некоторых решеток в R с сохранением как
наименьшей верхней, так и наибольшей нижней граней. Пусть о —
четырехэлементная булева алгебра, называемая также ромбом. В § 1 мы
доказываем, что ромб может быть вложен в R с сохранением не только
точных граней, но также и наименьшего элемента. В § 2 мы заменяем
ромб произвольной счётной дистрибутивной решеткой. С другой
стороны, в § 3 мы докажем, что даже ромб, рассматриваемый как решетка,
не может быть вложен в R с сохранением наибольшего и наименьшего
элементов. Отсюда будет следовать, что в. п. степени не замкнуты
относительно операции взятия точной нижней грани и поэтому не образуют
решетку. В § 4 и § 5 мы рассматриваем неветвящиеся и недополняемые
вниз степени, свойства которых прямо противоположны свойствам
степеней, построенных в § 1 и § 2.
Техника вложения из § 1 (называемая методом минимальных пар в
соответствии с определением 1.1) рассматривает требования
бесконечного действия. Однако, она сильно отличается от метода из главы VIII.
Представленное здесь доказательство (в основном соответствующее
статье Лахлана [1973]) использует специальные шаги, аналогичные
недефицитным шагам (т. е. истинным шагам) главы VIII, на которых
отрицательные запреты снимаются одновременно. Это доказательство будет
напоминать метод приоритета с конечными нарушениями.
Альтернативное доказательство в стиле § 5 главы VIII будет дано в упражнении 1.7.
§ 1. Минимальные пары и вложение ромба

210
Глава IX. Метод минимальных пар
1.1 	Определение. Вычислимо перечислимые степени а и b образуют
минимальную пару, если а, b > 0 и
1.2 Теорема (Лахлан [1966Ь]-Ейтс [1966а]). Существует
минимальная пара в. п. степеней а и Ь.
1.3 Следствие. Ромб может быть вложен в R с сохранением
точных нижних и верхних граней и наименьшего элемента.
Доказательство. Пусть с = a U Ь, где аи b — степени из теоремы 1.2.
Тогда ромб вкладывается в { 0, a, b, с }. Q
Доказательство теоремы 1.2. Достаточно построить в. п. множества
А и В, удовлетворяющие для всех е,г, j требованиям
Следующее замечание позволяет упростить форму отрицательных
требований.
1.4 	Замечание (Познер). Чтобы удовлетворить все i,j G ш,
достаточно удовлетворить для всех е требование
N'e : {е}А = {е}в = f всюду определена => / вычислима.
Доказательство. Из требований { N'e }ееи) и { Ре }ееи) непосредственно
следует, что А ф В, например, no G А — В. Для всех г и j существует
индекс е такой, что
(V в. п. с) [с ^ а & с ^ b => с = 0].
Р2е ■ А ф {е},
Р2е+1 : в ф { е }
И
: {г }А = {j }в = / всюду определена =>► / вычислима.
Отсюда мы немедленно получаем требуемое. []

§ 1. Минимальные пары и вложение ромба
211
С этого момента мы заменим все отрицательные требования,
аналогичные эквивалентными им требованиями N'e, и обозначим по¬
следние через Ne.
По данным { At и { Bt определим, как обычно, функции
(функция длины) l(e,s) = max{ х: (Vj/ < х) [{е}f'(y) | = {е I ] },
(функции наибольшей длины) m(e, s) = тах{ l(e, t) : t ^ s }.
Шаг s называется О-расширяющим, если s = 0 или если Z(0, s) > m(0, s —
1). Определим запрещающую функцию г следующим образом.
(Заметим, что такое определение запрещающей функции вполне
корректно, т. к. в силу соглашения III (1.1), которое следовало после
определения III. 1.7, для каждого числа z, использованного при вычислении
{е}Аз, выполнено z < u(A8-,e,y,s) < s.)
Стратегия сг0 удовлетворения одиночного отрицательного
требования Nq состоит в том, чтобы позволять элементу х перечислиться в А
или В на шаге s + 1, только если х ^ г(0, s), и при этом самое большее
в одно из множеств А и В. Таким образом, если перечисление элемента
х будет разрушать одно из вычислений { О (р) = q или { 0 }f* (р) = q
для некоторого р < 1(0, s), например, { 0 }^л(р) = q, то другое
вычисление, {0}fJ(p) = q, мы пытаемся сохранить до тех пор, пока не будут
восстановлены оба равенства {0}^(р) = q и {0 }f‘(p) = g, где t > s.
Тогда, если [0}А = {0}в = f — всюду определенная функция, то
функция / будет вычислимой. (Чтобы вычислить f(p), достаточно
будет найти наименьшее s такое, что р < 1(0, s). Тогда f(p) = {0}^л(р).)
Кроме того, liminfs r(0,s) < оо, т. к. либо liminfs r(0,s) = 0, либо
существует наибольший О-расширяющий шаг t и, поэтому, r(0, s) = t для
всех s ^ t.
Эта фундаментальная стратегия, пытающаяся на каждом шаге
сохранить хотя бы одно из вычислений, применима и к остальным
отрицательным требованиям Ne, е > 0. Но для этого мы должны изменить её
так, чтобы запреты отрицательных требований снимались
одновременно, создавая, таким образом, «окна» через запреты, как и в главе VIII.
'0,
наибольший О-расширяющий
, шаг t < s
если шаг s
О-расширяющий,
в противном случае.

212
Глава IX. Метод минимальных пар
Например, стратегия удовлетворения N\ должна знать значение к =
liminfs г(0, s), чтобы её запреты снимались одновременно с запретами
стратегии для No. Поэтому, для удовлетворения требования Ni
необходимо иметь бесконечное число стратегий erf, для каждого
возможного значения к Е ш. (См. объяснения в главе XIV, § 3.1, где
используется метод деревьев для определения r(e,s).) Каждая стратегия erf
действует так же, как и стратегия сг0, но она уже не будет
активизироваться на всех шагах, а лишь на шагах, принадлежащих множеству
Sk = {s : г(0,s) = А;}, на которых определены соответствующие
функции I и т. Это позволяет erf чаще открывать свое окно, т. к. её функции
длины игнорируются на шагах из ш — Sk. Работа стратегии erf не будет
нарушаться, если её запреты не будут игнорироваться другими
стратегиями на промежуточных шагах s £ S'*, на которых erf бездействует.
Поэтому, если на шаге s будет к = г(0, s), то мы работаем со стратегией
erf, учитывая и сохраняя все запреты, установленные ранее
бездействующими стратегиями crj, i < А;, а запреты, установленные стратегиями
а{, j > к, снимаем. Тогда, если к = liminf5 r(0,s), то: (1) стратегия
erf приводит к удовлетворению требования N\; (2) стратегии crj, г < А;,
смогут установить лишь конечное число запретов; (3) запреты
стратегий erf, j > А;, снимаются на всех шагах s Е Sk. Таким образом, для
общего запрета r(l,s), установленного требованиями No и N\ вместе,
имеет место liminf5 r(l,s) < оо.
Построение А и В.
Шаг s = 0. Ничего не делаем.
Шаг s + 1. По данным А3 и В8 определим запрещающую функцию
r(e, s) для Ne индукцией по е следующим образом. Определим r(0, s)
так же, как и раньше. Назовем шаг s (е + 1 )-расширяющим , если s = 0
или
(W < s) [r(e, t) = r(e, s) => l(e + 1, t) < l(e -I- 1, s)].
Полагаем r(e + l,s) равным наибольшему из
(0 r(e,s),
(й) тех t < s, для которых r(e,t) < r(e, s),
(iii) 	тех (е + 1)-расширяющих шагов t < s, для которых r(e, t) = r(e, s)
в случае, если шаг s не (е + 1)-расширяющий.
(В соответствии с § 3 главы XIV мы могли бы рассматривать это
построение как построение на дереве. Часть (i) учитывает требования

§ 1. Минимальные пары и вложение ромба
213
N{, i ^ е; часть (ii) учитывает вершины к', расположенные левее к =
r(e,s), т. е. те стратегии, которые предполагают, что г(е) = кг < к] и
часть (Ш) учитывает запреты вершины к на не-(е 4- 1)-расширяющих
шагах, т. е. запреты стратегии, предполагающей, что г(е) = к.)
Будем говорить, что требование Рче требует внимания, если
i(3y) [у € As & {e}s(j/)4- = 0], (1.1)
И
(Зх) [{ е }5(х)| = 0 & r(2e, s) < х & х Е о^2е1]. (1.2)
Аналогично, Рге+i требует внимания, если выполнено то же самое,
но с В вместо А и 2е +1 вместо 2е. Выберем требование Ре наивысшего
приоритета, которое требует внимания, и наименьшее х,
удовлетворяющее (1.2) для этого е. Перечислим х в А, если е чётно (в В, если е
нечётно). (Заметим, что АГ\В = 0, т. к. любой свидетель х для Ре лежит
в а/М.)
Лемма 1. (Ve) [liminfs r(e,s) < оо].
Доказательство. Доказательство ведется индукцией по е. Пусть
сначала е = 0. Если существует бесконечно много 0-расширяющих шагов, то
по определению существует бесконечно много s таких, что r(0,s) = 0,
и, следовательно, liminf5 r(0, s) — 0. Если существует только конечное
число 0-расширяющих шагов, то пусть v — наибольший из них. Тогда
lim5 r(0, s) = v. Для очередного индукционного шага выберем е и
предположим k = liminfs r(e,s). Тогда существует только конечное число
шагов s таких, что r(e, s) < к. Пусть t — наибольший из них. Положим
5 = { s : r(e, s) = к }. Тогда либо существует бесконечно много (е -I- 1)-
расширяющих шагов из S, на которых liminf* r(e + l,s) = max{£,A;},
либо существует наибольший (е -f 1)-расширяющий шаг v G S, на
котором liminf5 r(e -f- l,s) = max{£,k,v}.
Лемма 2. Любое положительное требование Ре удовлетворяется,
причем действует только один раз.
Доказательство. Рассмотрим требование Рге (Лге+i рассматривается
аналогично). Если А = { е }, то по построению ни один элемент из
не может перечислиться в А, так что А П оД2е1 = 0. Следовательно,
существует такой х £ АП аЛ2е1, что {е}(х)| = 0их> liminfs r(2e,s).
Ясно, что некоторый такой х рано или поздно перечислится в А,
удовлетворяя тем самым требование Рге- Легко видеть, что по (1.1) Рге
действует самое большее один раз.

214
Глава IX. Метод минимальных пар
Лемма 3. (Ve) [Требование Ne удовлетворяется].
Доказательство. Фиксируем е, и пусть k = liminf5 г(е — 1, s), S = {s :
r(e — l,s) = А:}. (Если e = 0, то полагаем 5 = ш и к = 0.) Выберем
такой шаг s', что ни одно требование Р*, i < е, не действует после
шага s', и r(e — l,s) ^ к для всех s ^ s'. Предположим, что {е}А =
{ е }в = / всюду определенная функция. Для того, чтобы эффективно
вычислить /(р), р Е cj, найдем е-расширяющий шаг s" Е 5, s" > s1
такой, что l(e,s") > р. Ясно, что таких шагов существует бесконечно
много, поскольку {е}А = {е}в. Полагаем q = (р) = (р).
Докажем индукцией по i, что для всех t ^ s" либо
(!) {e}t‘(p) = Ч, либо
(2) {е}?'(р) = д,
и, следовательно, f(p) = q. Пусть si < S2 < • • • — е-расширяющие шаги
из 5, большие или равные s". Оба утверждения (1) и (2) выполнены при
t = si, т. к. si = s". Фиксируем п и предположим, по индукции, что (1)
и (2) выполняются для t = sn (и что либо (1), либо (2) выполняются
при всех t, si ^ t ^ sn). На шаге sn + 1 в А или Р перечисляется не
более одного элемента, так что самое большее одно вычисление из (1)
и (2) при t = sn разрушается, а другое, например (1), выполняется для
t = sn + 1. По выбору s" имеем
(Vi) [[sn < t < sn+1 & t £ 5] => r(e — 1,0 > A;]
и, следовательно,
(Vi) [[sn < i < Sn+i] —к r(e,i) ^ 5n],
согласно утверждениям (ii) и (iii) в определении r(e,i), а именно,
применяем (ii) при i ^ 5, и (iii) при t E S'. (Если e = 0, то достаточно
применить лишь (ii).) Следовательно, для всех £, sn ^ t ^ sn+i> имеем
At [ sn = ASn l sn & {e}^'(p) = {e}£"(p) = q,
так что (1) выполняется при t = sn+i. Но шаг sn+i является е-рас-
в
ширяющим, так что значение { е }«пл+^1 (р) должно быть определено и
совпадать с q. Таким образом, (2) также выполняется при t = s„+i. Q

§ 1. Минимальные пары и вложение ромба
215
В § 3 главы XIV можно найти другую версию этого доказательства,
основанную на методе деревьев, которая проясняет взаимосвязи между
различными стратегиями, работающих с одинаковыми требованиями.
При этом определение r(e, s) из предыдущего доказательства становится
более наглядным.
1.5-1.7 Упражнения
1.5. Постройте минимальную пару в. п. степеней а, b такую, что а и
b (и даже aUb) низкие. Указание. Добавьте в построение минимальной
пары отрицательное требование Ne из теоремы VII. 1.1, которое
обеспечит, что a U b — низкая степень.)
1.6. Построите в. п. последовательность в. п. степеней { a* }i€u, такую,
что каждая пара степеней a*, aj при i ф j является минимальной.
1.7 	(Лерман [1973]). Получите доказательство теоремы 1.2, используя
модель пинбольной машины из § 5 главы VIII. Чтобы удовлетворить
требования Ре и Ne из § 1, поставьте в соответствие Ре отверстие #е, а
Ne — ворота Ge• Определите г(0, s) аналогично, как и выше, a r(e, s) —
точно также, но с заменой 0 на е. Заметим, что r(e) = liminfs r(e,s) <
оо.
Шаг з = 0. Для каждого е поместим все элементы х Е шМ над
отверстием Не. Будем говорить, что они ещё не реализованы.
Шаг s + 1. Последователь х требует внимания, если  1 2(1) х расположен над некоторым отверстием Не, х пока не реализован,
х > у для всех уже реализованных последователей у, и {e}s(x) I
= 0; или
(2) х лежит в некоторых воротах Ge и r(e, s) < х.
Случай 1. Если хотя бы один последователь х требует внимания,
выберем наименьший такой х, и уничтожим (навсегда) все реализованные
последователи у > х. Если для х выполнено условие (1), то ж
становится реализованным. В противном случае, выберем наибольший г, г ^ е,
такой, что х ^ r(i,s), и переместим х в ворота G\. (Чтобы такой г
существовал, полагаем r(—l,s) = оо.) Если х попадает в GLi из
отверстия Hj при чётном j, то перечисляем х в А. Если х попадает в G-\ из
отверстия Hj при нечётном j, то перечисляем х в В. В обоих случаях
мы удовлетворяем Pj.

216
Глава IX. Метод минимальных пар
Случай 2. Если ни один последователь не требует внимания, то
выберем наименьший j такой, что Pj не удовлетворено и не имеет
нереализованных последователей, и определим как (нереализованный)
последователь Pj наименьшее у G , большее, чем любой из ранее определенных
последователей. Уничтожим последователи всех требований Pky к > j.
Это завершает построение А и В.
Как и в § 5 главы VIII покажем, что Ge,оо, множество последователей,
оставшихся в воротах Ge навсегда, конечно; что каждое Pj
удовлетворяется и порождает конечное число последователей; и что каждое Ne
удовлетворяется. В любой момент времени мы рассматриваем
реализованные, но не уничтоженные последователи, как активные (т. е.
находящиеся на поверхности машины). Заметим, что если в некоторый момент
времени последователь х требования Pi и последователь у требования
Pj активны, то, в соответствии с процедурой реализации и уничтожения
последователей, х < у тогда и только тогда, когда i < j. Следовательно,
мы можем доказать индукцией по г, что для любого i последователь Р{
получает внимание самое большее конечное число раз.
§ 2. * Вложение дистрибутивных решеток
Используя довольно простую модификацию метода из предыдущего
параграфа, мы докажем аналог теоремы 1.2 для произвольной счётной
дистрибутивной решетки. Так как любая счётная дистрибутивная
решётка может быть вложена в счётную безатомную булеву алгебру, то
достаточно доказать следующее утверждение.
2.1 	Теорема (Лахлан-Лерман-Томасон). Счтная безатомная
булева алгебра В может быть вложена в в. п. степени R с сохранением
точных верхних и нижних граней и наименьшего элемента.
Доказательство. Пусть { a* }i€u; — произвольная равномерно
вычислимая последовательность вычислимых множеств (т. е. { (ж, г) : х G щ } —
вычислимое отношение), которая образует безатомную булеву алгебру В
относительно операций U, П, и дополнения, содержит элемент и
имеет 0 в качестве единственного конечного элемента. Сначала для каждого
г G ш построим в. п. множество А{. Затем для каждого а € В положим
Аа = {(iyx) : х € А{ & i G а} для a G В. Тогда мы немедленно
получаем
deg(A,u/3) = deg(j4Q) U deg^),
(2.1)

§ 2. * Вложение дистрибутивных решеток
21?
а С /3 => deg(Аа) ^ deg(^),
deg(AQn^) ^ deg(AQ),deg(A/9).
(2.2)
(2.3)
Мы должны удовлетворить для всех г,), а,/3 требованиям:
P{i,j) : Ф Wj,
N(a,(3j) • { j }Аа = {j}A(3 = f — всюду определена ==> / ЛаП/з-
Эти требования гарантируют, что
Заметим, что из (2.1)—(2.5) следует, что отображение а -> deg{Аа)
является искомым вложением, а из (2.5) следует инъективность этого
отображения. (Чтобы убедиться в том, что отрицательные требования
обеспечивают справедливость (2.5), допустим, что: (1) deg(>lQ) ^ deg(Ap);
но (2) а 2 Р- Пусть i е а-(3. Тогда deg(>lj) ^ deg(>lQ) ^ deg(A/g) в силу
(1) и определения Аа, но deg(Ai) ^ deg(A-p) в силу выбора г и
определения Аа. Следовательно, по (2.4) deg(Ai) ^ deg(^n^) = deg(^0) = О,
что противоречит невычислимости А{.)
Стратегия удовлетворения отрицательных требований в об¬
щих чертах повторяет стратегию из теоремы 1.2. Обозначаем
требование через Ne, где а = /3 = ai2, и е = (ii,i2,j). Далее,
мы определяем запрещающую функцию r(e,s) и е-расширяющие шаги
индукцией по е в точности как в § 1, но с Аа, Ва, и j вместо А, В и
е, используемым в § 1. Но теперь появляются новые трудности при
доказательстве леммы 3 (утверждающей, что Ne удовлетворяется), и они
требуют более аккуратного перечисления элементов для удовлетворении
положительных требований. Для удовлетворения требования P(ij) мы
установим последователи х Е названные так из-за того, что
перечисление элемента х в А{ будет удовлетворять P(ij) (хотя х, возможно,
будет и удален из нашего рассмотрения до того, как это случится). Мы
говорим, что последователь х требования Pi имеет больший приоритет,
чем последователь у требования Pj, (обозначается как х < у), если либо
г < j, либо г = j и х был принят к рассмотрению до того, как это
было сделано для у. Наше построение будет устроено так, что на каждом
шаге s для всех неудаленных последователей х и у, рассматриваемых
на шаге s, х -< у будет иметь место тогда и только тогда, когда х < у.
deg(-Aan/j) = deg(j4a) Г) deg(А0),
(2.4)
deg(Aa) ^ deg(4a) => а С (3.
(2.5)

218
Глава IX. Метод минимальных пар
Построение А{, г Е ш:
Шаг s = 0. Ничего не делаем.
Шаг s + 1. Требование P(ij) удовлетворено, если А^8 П Wj,s Ф 0.
Требование P(ij) требует внимания, если P(ij) не удовлетворено, и
либо
х Е Wjt8 и х > r((i,j),s)
для некоторого неудаленного последователя х (2.6)
требования P(ij),
либо
ж Е
для каждого неудаленного последователя х (2.7)
требования ^(ij) •
Пусть P(ij) — требование с наивысшим приоритетом, которое
требует внимания. Мы говорим, что P(ij) получает внимание (действует)
на шаге s + 1. Если для P(ij) выполнено (2.6) для некоторого ж, то
перечисляем наименьший такой х в А{. Если (2.6) не имеет места, а (2.7)
истинно, то будем считать х = s +1 последователем P(ij)- В обоих
случаях удаляем всех последователей у с меньшими, чем х, приоритетами
(т. е., х -< у). (Если никакое P(ij) не требует внимания, то ничего не
делаем.)
Лемма 1. (Ve) [liminfs r(e,s) < оо].
Доказательство. В точности такое же, как и в лемме 1 из § 1.
Лемма 2. (Ve) [Требование Ре получает внимание самое большее
конечное число раз и удовлетворяется].
Доказательство. Фиксируем е и выбираем такое sq, что не существует
требования Ре'> е' < е, получающего внимание после шага so- Пусть
k = liminfs r(e,s) согласно лемме 1. Пусть е = Если P(ij) по¬
лучает внимание бесконечно часто, то некоторый х > к назначается
последователем P(ij) и никогда не удаляется. Поэтому, согласно (2.7)
х Е Wj. Следовательно, найдется шаг t + 1 > so такой, что r(e,t) < х
и х Е Wjyt. Тогда либо сам элемент ж, либо некоторый меньший
последователь требования Ре перечисляется в Л на шаге t+ 1. Поэтому в
данном случае Ре удовлетворено, и это требование никогда не будет
требовать внимания на последующих шагах. Следовательно, Ре получает
внимание самое большее конечное число раз.

§ 2. * Вложение дистрибутивных решеток
219
Для завершения доказательства остается заметить, что если
требование P(ij) не удовлетворено, то Ai = Wj и, следовательно, х Е Wj для
каждого неудаленного последователя х требования P(ij), так что P(ij),
согласно (2.7), получает внимание бесконечно часто.
Лемма 3. (Va) (V/3) (Vj) [Требование удовлетворяется].
Доказательство. Фиксируем Ne = N^^jy Пусть k, S и шаг s'
определяются так же, как и при доказательстве леммы 3 из § 1. Предположим,
что { j }Аа = {j }А(3 = / — всюду определенная функция. Назовем
вычисление { j }^,л(ж) А$-корректным, если А#у8 I и = As [ и, где
и = u(Ayy,j,x,s).
Для АаПр -вычислимого определения значения f(p) находим е-расши-
ряющий шаг s Е S, s > s1, такой, что l{e,s) > р, и оба вычисления
{j }^a,a(p) — Я и О }^’Чр) = Я являются л4аПд -корректными. Докажем
индукцией по £, что для всех £ ^ s мы имеем либо
{j}ta,(p) = Q, (2-8)
либо
{j}t*4p)=q (2-9)
посредством АаПр-корректного вычисления. Если х, перечислившись на
шаге £ 4- 1 в множество Aa Ui/j, разрушает одно из вычислений (2.8)
и (2.9), то £ Е 5, причем £ должно быть е-расширяющим (как и в
лемме 3 из § 1), так что оба эти вычисления имеют место к концу шага £.
По индуктивному предположению, по крайней мере одно из вычислений,
скажем (2.8), АаПр-корректно. Предположим, что х перечисляется в Аа
на шаге £ 4- 1, разрушая соответствующее вычисление. Тогда х
удаляет на шаге £4-1 всех последователей у таких, что х < у (т. к. это в
точности те последователи у, для которых х -< у). Далее, z > £ 4- 1 ^
up =dfn u(Aptt'ij)t,p) для любого последователя z, назначенного позднее.
Но х < иа =dfn u(Aaj', j, t,p), т. к. Аа-вычисление разрушается
элементом х. Кроме того, Aanpit [ иа = АаП@ [ иа, т. к. Аа-вычисление (2.8)
было АаПр-корректно. Следовательно, Aanptt ^ (£ 4- 1) = Аапр [ (£4-1),
и up ^ £4-1, так что А ^-вычисление (2.9) продолжает оставаться Aa^p-
корректным. Этот факт является решающим новым элементом
доказательства.

220
Глава IX. Метод минимальных пар
2.2-2.6 Упражнения
2.2. Докажите, что вложение в теореме 2.1 в действительности
является вложением В в m-степени. (Оно может быть сделано и вложением
в 1-степени заменой А$ на бесконечное вычислимое множество с
бесконечным дополнением.)
2.3. Назовем в. п. степень с ветвящейся, если существуют такие в. п.
степени а,b > с, что с = aflb, и неветвящейся в противном случае.
Например, теорема 1.2 утверждает, что 0 — ветвящаяся. Примените
теорему 2.1 чтобы показать, что существуют ветвящиеся степени с > 0.
(См. § 4, где приводятся примеры неветвящихся степеней.)
2.4. (а) (Лахлан). Приведите прямое построение ненулевой ветвящейся
степени с, ветвями которой являются степени а = deg (А 0 С) и b =
deg(2? 0(7). Для этого постройте множества А, В, (7, удовлетворяющие
требованиям: {е}с Ф А, {е}с ф В, {е} ф С и
{ е }ЛфС = { е }ВфС = / всюду определена => / С.
(Ь) 	(Фейер). Комбинируя это построение с методом разрешения из
§ 3 главы V покажите, что для любой в. п. степени d > 0 существует
ненулевая ветвящаяся степень с < d.
2.5 (П.Ф. Коэн [1975]). Замените в определении ветвящихся степеней Т-
сводимость гу^-сводимостью из упражнения V.2.16, получая тем самым
определение wtt-ветвящейся степени. Докажите, что любая в. п. wtt-
степень с < 0' является wtt-ветвящейся. Указание. По данному в. п.
множеству С 6 с постройте в. п. множества А и В, степени которых
образуют ветви. Для удовлетворения условия { е }с ф А используйте
стратегию кодирования Сакса из теоремы VIII.4.1.
2.6 (Лахлан [1972а]). (а) Докажите, что если А, В к С — такие в. п.
множества, что А В 0 С, то А является объединением непересека-
ющихся в. п. множеств Д, А\ таких, что Aq ^wtt В и А\ ^wtt С.
(Ь) Докажите, что недистрибутивные решетки М5 и iV5 из
диаграммы 2.1 не могут быть вложены в в. п. гу^-степени отображением,
сохраняющим точные грани. Известно, что любая недистрибутивная решетка
содержит в качестве подрешеток изоморфные копии М5 или iV5 (см.
Биркгоф [1967, сс. 13, 39]). Следовательно, никакая недистрибутивная

§ 2. * Вложение дистрибутивных решеток
221
Диаграмма 2.1. Специальные недистрибутивные конечные решётки
решетка не может быть вложена в в. п. ги^-степени. Указание.
Используйте (а).
(с) 	Покажите, что из доказательства теоремы 2.1 следует, что любая
счётная дистрибутивная решетка может быть вложена в wtt-степени.
Следовательно, (Ь) и (с) дают полную характеризацию решеток, которые
могут быть вложены в wtt-степени.
2.7 	Замечание. Томасон [1971] и независимо Лерман (неопубликова-
но) доказали, что все конечные дистрибутивные решетки могут быть
вложены в R. Лахлан и независимо Лерман расширили этот
результат на счётные дистрибутивные решетки. Случай недистрибутивных
решеток, однако, оказался более трудным. Лахлан [1972а] доказал, что
недистрибутивные решетки М5 и iV5 из диаграммы 2.1 могут быть так
вложены в R. Робинсон [1971а, с. 313] и Шёнфилд [1975, с. 976]
предположили, что в R может быть вложена любая конечная решетка. Лахлан
и Соар [1980] опровергли это предположение, доказав, что решетка S&
из диаграммы 2.1 не может быть вложена в R. Дальнейшие
результаты о невложимости решеток были получены Амбос-Шпиисом и Лер-
маном [1986]. Известны также и другие частичные результаты, однако
общей характеристики вложимых решеток не найдено.

222
Глава IX. Метод минимальных пар
§ 3. Теорема о невложимости ромба
Можно было бы попробовать расширить теорему 2.1 построением
решеточного вложения, которое сохраняло бы как наибольший, так и
наименьший элементы. Следующий неожиданный результат показывает,
что это невозможно сделать даже для ромба. Однако это можно
сделать, если заменить в. п. степени Д^-степенями (см. Купер [1972b] и
Познер и Робинсон [1981]).
3.1 	Теорема о невложимости ромба (Лахлан [1966b]). Если а и Ь
невычислимые в. п. степени такие, что aUb = O', то существует
такая невычислимая в. п. степень с, что с ^ а и с ^ Ь.
Доказательство. Пусть А и В — в. п. множества из степеней а и
Ьсоответственно такие, что А содержит только чётные, а В только
нечётные числа, так что A U В = А 0 В =т 0;- Пусть { as }s€u, и { bs }s€u,
- вычислимые перечисления А и В. Пусть As = { at : t ^ s } и Bs = { bt :
t ^ s}. Построим такие в. п. множества с бесконечными дополнениями
Е, Fo, Fi, F2,... , что хотя бы одно из них имеет требуемую степень с.
Мы пытаемся удовлетворить для каждого i и j требованиям
Pij : Е DWi ф 0 или F{ П Wj ф 0.
Мы будем строить также вспомогательное в. п. множество D. Так
как deg(^ U В) — 0', можно считать (используя теорему рекурсии),
что заранее известен такой индекс е, что D = {е}АиВ. (Заметим, что
здесь условие «D в. п.» не обязательно, достаточно, чтобы D было Д^-
множеством. Этот факт используется в упражнении 3.8.) Через u(k, s)
обозначим use-функцию u(As \J Bs;e,k, s). (Для каждого X = D, Е или
Fi запись Xs означает совокупность элементов, перечисленных в
множество X к концу шага s.)
Чтобы получить Е А и Е В, будем перечислять число х в
Е на шаге s, только если какие-нибудь числа ^ х уже перечислились
в оба множества А и В. Пусть, например, необходимо удовлетворить
требованию Ri : Wi П Е ф 0. Предположим, что на некотором шаге s
имеет место х G Wi,s, as ^ т, и и < х, где и = u(fc,s) для какого-
нибудь к fi Ds такого, что {e}AaUBa(k) = 0. Мы можем попытаться
удовлетворить это требование перечислением атакующего числа к в D.
Так как D = { е }АиВ, то некоторое число z < и должно перечислиться
или в Л, или в В. Если z перечисляется в В, то наша атака оказалась
успешной, и тогда мы перечисляем х в Е, удовлетворяя Ri навсегда.

§ 3. Теорема о невложимости ромба
223
Если существует бесконечно много безуспешных попыток
удовлетворить Ri, то будем строить множество F{ таким, чтобы F{ П Wj ф 0
для всех бесконечных Wj. Поэтому мы будем предпринимать описанные
выше атаки только в тех случаях, когда существует шаг t < s со
свойством у G Wj-,*, bt < у, и и < у. Если после такой атаки некоторое z
перечислится в Л, то мы можем перечислить у в множество F{.
Действуя подобным образом, мы сможем обеспечить F{ ^т А и F{ В.
Таким образом, мы не атакуем непосредственно само требование Щ ,
а лишь требование Pitj посредством атакующего числа к = (i,j). Одна
из попыток удовлетворить требованию Pij завершается успешно, после
чего новые попытки не предпринимаются.
Построение.
Шаг s — 0. Ничего не делаем.
Шаг s +1. Требование Pij требует внимания, если Pij ещё не
удовлетворено (т. е. Es П WifS = 0, Fi,s П WjiS = 0), и существует
упорядоченная пара {х,у), удовлетворяющая условиям:
{ е }f‘uB‘((i,j)) = 0,
(3.1)
х>2г, as, u((i,j),s),
(3.2)
х € Wits,
(3.3)
существует некоторое t < s такое, что:
(3.4)
(a) у > 2j, bt, u((i,j),t),
(b) у G WjtU
(c) (4иБ5)| u((i,j),t) = (AtUBt) [ u((i,j), t),
n{e}^((i,j))=0.
(Заметим, что из условия (3.4)(с) следует, что u((i,j),t) = u((i,j),s).)
Выберем наименьшее (г, j) такое, что Pij требует внимания, и
затем — наименьшую соответствующую пару (х,у). Перечислим (i,j)
в D. Перечисляем А и В до тех пор, пока первое число z < и —
u((i,j),t) = u((i,j),s) не появится в A U В. (Т. е. мы «ускоряем»
перечисление А и В.) (Если такое г не появится, мы больше ничего делать
не будем. Однако, если е — индекс, полученный по теореме рекурсии,

224
Глава IX. Метод минимальных пар
для которого выполнено D = {е}АиВ, то такой элемент z должен
появиться.) Если z появится в Л, то перечислим у в F{. Если z появится в
В, то перечислим х в Е. В этом случае мы говорим, что Pij получает
внимание.
Лемма 1. Множества Е и F{, г G ш, имеют бесконечные
дополнения, Е ^т A, F В и F{ ^т А.
Доказательство. Эти м-ножества имеют бесконечные дополнения
ввиду условий х > 2г, у > 2j из (3.2) и (3.4)(а). Требуемые тьюринговы
сводимости получаются применением обычного метода разрешения.
Например, Е ^т А, т. к.
(Vs) (Уж) [As I х = А I х => Es+1 [ х = Е [ х].
Такие же рассуждения дают Е В и F{ А.
Лемма 2. Если Е вычислимо и Е = то
(i) F{ невычислимо и
(И) Fi В.
Доказательство (i). Если Fr вычислимо, то выберем наименьшее j та-
кое, что Wj = F{. Выберем so такое, что ни одно требование Рт,п
при (m,n) < (i,j) не получает внимания ни на каком шаге s ^ sq.
Если D((i,j)) = 1, то Pij получает внимание. Следовательно,
можно предполагать, что 0 = D((i,j)) = {e}AuB((i,j)). Выберем теперь
v ^ So так, что для всех s ^ v, u((i,j),s) = u((i,j),v) > 0, и
(A U В) [ и = (Av U Bv) I и, где и = u((i,j),v). Из невычислимости
В и бесконечности Wj (в силу леммы 1) получаем, что существуют
такие у > и и t > v, что у G Wjit, причем множество В разрешает числу
у перечислиться в F{ на шаге t, т. е. такие, что условия (3.4)(а), (Ь), и
(с) 	выполняются для у и любого s > t. Но так как А невычислимо, то
существует бесконечно много элементов х G Wi, удовлетворяющих
условиям (3.1), (3.2) и условию (3.3) при некотором s > t. Следовательно,
требование Pij получает внимание и либо EC\Wi ф 0, либо FiDWj ф 0,
что противоречит предположению.

§ 3. Теорема о невложимости ромба
225
Доказательство (ii). Чтобы определить, верно ли, что у € Fi, найдем
наибольшее t такое, что bt ^ у. Рассмотрим все j со свойством у Е Wjj-
Для каждого такого j найдем наименьший Sj ^ t такой, что либо
(ASj U BSj) I u((i,j), t) ф (AtUBt) I' u((i,j),t) (3.5)
(в этом случае утверждение (3.4) (с) не позволяет требованиям P{j
перечислить число у в множество F{ на последующих шагах), либо
требование Pij получает внимание на шаге Sj. (3.6)
В любом из этих случаев у будет принадлежать множеству F{ тогда и
только тогда, когда у Е i^s+b где s = max{ Sj : у Е Wjj }• Заметим,
что если условие (3.5) не имеет места, то (3.6) должно выполняться,
поскольку в этом случае мы, как и в части (i) доказательства, будем
иметь бесконечно много х Е Wi, удовлетворяющих (3.1), (3.2) и (3.3), и
поэтому требование Pij получит внимание посредством упорядоченной
пары (ж, у) для некоторого х. (Заметим, что здесь используется
условие (3.4)(с), т. к. достаточно только ждать такого первого шага s, что
некоторый х Е Wi,s будет образовывать пару с у, посредством которой
мы пытаемся атаковать Pij. Мы поступаем так до тех пор, пока
имеет место (3.4)(с).) Изложенное выше рассуждение, показывающее, что
Fi В, например, посредством F{ — Фв для некоторого Ф,
называется задержанным разрешением, т. к. если bt ^ у, то несмотря на то,
что старое вычисление ^^-i{y)i = 0 становится недействительным, мы
задерживаем переопределение Ф^(у) до некоторого шага > s. []
3.2 	Теорема (Лахлан [1966b]). Пусть даны в. п. степени а, b и
степень Атакая, что d ^ а и d ^ Ь. Тогда существует такая в. п.
степень с, что d ^ с, с $ a u с ^ b.
Доказательство. Фиксируем в. п. множества А Е а, В Е b и индексы
ей i такие, что {е}А = {г }в = D для некоторого множества D Е d.
Пусть {А8}8^ш и {Ss}s€u; — вычислимые перечисления А и В
соответственно. Для каждого х определим конечное множество Сх «плохих
шагов» следующим образом. Если {е}^а(а;) = {г}?*^) = у, и для
некоторого шага t > s ни одно из равенств {e}fl(x) = ?/, {i}fl{x) = у
не выполнено, то на шаге t перечислим все числа v ^ s в Сх. Пусть
С = ®Х{(7Ж : х Е о;}. Ясно, что С является в. п., т. к.
перечисление каждого Сх происходит равномерно по х. Кроме того, D С,
т. к. для того, чтобы вычислить D(x), мы можем найти такой s Е Сх,

226
Глава IX. Метод минимальных пар
что {е}^а(х) I = {г}?л(ж) = у. Тогда D(x) = у. Сведение С А
также имеет место, т. к. для каждого х достаточно найти такой £,
что {е I = у и At [ и = А [ и, где и = u(At‘,e,x,t). Тогда
{ е v(x) = у для всех v ^ £, так что никакие новые s не могут входить
в Сх после шага t. Сведение С В доказывается аналогично. О
См. упражнение 3.5., где приведены аналогичные результаты для
более сильных сводимостей.
3.3 Следствие (Лахлан [1966Ь]-Ейтс [1966а]). Существуют
несравнимые в. п. степени а и Ь, не имеющие наибольшей нижней грани.
Таким образом, в. п. степени не образуют решетку. (См. также
упражнения 3.10 и 5.7.)
Доказательство. Пусть а и b - любые несравнимые низкие в. п.
степени, такие, что aUb = O'. (Они могут быть получены из теоремы
Сакса о разложении, или из исходной теоремы Мучника-Фридберга в силу
упражнения VII.2.3.) Пусть степень d является произвольной нижней
гранью степеней а и Ь. Тогда d' = O', т. к. а' = 0'. Поэтому при
релятивизации относительно d теоремы 3.1 мы получаем такую степень
с > d, что с < а, с < Ь. По теореме 3.2 можно предполагать, что с
является в. п. Следовательно, а и b не имеют точной нижней грани в
верхней полурешетке в. п. степеней, и даже в верхней полурешетке всех
степеней. []
Основываясь на теореме 3.1, Лахлан [1966b, с. 568] и Робинсон [1971а,
с. 	313] предположили, что, возможно, в. п. степени а и b такие, что
aUb = O', никогда не будут иметь точной нижней грани. Это
предположение было опровергнуто Шёнфилдом и Соаром [1978] и, одновременно,
Лахланом [1980]. На самом деле Лахлан получил следующий приятный
результат, обобщающий теорему VII.3.2 Сакса о разложении.
3.4 Теорема (Лахлана о разложении) (Лахлан [1980]). Пусть А —
невычислимое в. п. множество. Тогда существуют в. п. множества
Во, Si и С такие, что:
(i) С <т А,
(п) В0 U Bi = А и Во П J3i = 0,
(iii) Bi-i $£т Bi 0 С, для г = 0,1, и
(iv) deg(C) = deg(50 ®С)П deg(J5i 0 С).

§ 3. Теорема о иевложимости ромба
227
Следовательно, для любой в. п. степени а > 0 существуют
несравнимые в. п. степени bo — deg(£?o Ф С) и bi = deg(J5i 0 С), наименьшей
верхней гранью которых является а, а наибольшей нижней — степень
с = deg(C). Доказательство этой теоремы мы не приводим. Оно
интересно использованием нового метода (отличного от изложенных в § 1 и
§ 2) получения наибольшей верхней грани степеней. Идея здесь состоит
в том, чтобы добиться выполнения условия bo flbi = с, не только
запрещая, как в § 1 и § 2, перечислять элементы в Во и Bi, но и перечисляя
новые элементы в С.
В противоположном направлении Амбос-Шпиис (упражнение XI.3.4)
получил интересное обобщение теоремы 3.1 о иевложимости ромба для
произвольных низких в. п. степеней. Он заметил, что отсюда
непосредственно следует, что никакая низкая степень не может быть дополнена
наверх относительно 0' половиной минимальной пары, и что для любой
низкой в. п. степени а существует b Е R такая, что степени а П b не
существует.
3.5-3.12 Упражнения
3.5. (а) Докажите аналог теоремы 3.2, где Т-сводимость заменена на
w^-сводимость (определенную в упражнении V.2.16). А именно, что если
А и В в. п. D ^wtt А, и D ^wtt В, то существует в. п. множество Е ^wtt
А, В такое, что D ^wtt Е. Указание. Для получения D ^wtt Е замените
С на множество Е = 0Х{ Ех }, где Ех = card({ s : Cs(x) ф С8+\{х) }).
(b) Докажите, что при замене на или этот результат
получается тривиально. (Фейер и Шор [1988] показали, что для ^-сводимости
аналог теоремы 3.2 не имеет места.)
3.6. Дайте альтернативное доказательство теоремы 3.1, используя
функции-доминанты вместо теоремы рекурсии. Указание. Зафиксируем
е такое, что {е}АфВ всюду определена, и {e}A®B(j) ^ {n}(z,j), если
гг, г ^ j и {п }(г, j) I . Определим частично вычислимую функцию { п },
полагая {гг }(г, j) = 1 + { е (j), где s+1 — первый шаг (если такой
существует), на котором Pij требует внимания посредством некоторой
пары (ж, у). В этом случае присоединяем наименьшую такую пару (ж, у)
к требованию Pij. Если j ^ гг, то некоторый г < u(j,s) должен позднее
появиться либо в А, либо в В. Как только это произойдет, действуем с
(х,у) как раньше, перечисляя либо х в jE, либо у в F{. Тогда,
игнорируя конечное число требований Pij, j < п, начиная с некоторого шага
будет задействована каждая пара (ж, ?/), присоединенная к Pij. Поэтому
доказательство можно завершить так же, как и ранее.

228
Глава IX. Метод минимальных пар
3.7 	(Амбос-Шпиис). Покажите, что в доказательстве теоремы 3.1
можно обойтись без применения теоремы рекурсии следующим образом.
Постройте в. п. множества Ее и Ff для всех е,г Е ш, удовлетворяя
требованиям:
P(e,ij) • [D = {е}ЛфВ и Wi, Wj бесконечны]
=>[WiHEe^9 или WjnFf^Q].
Для этого перечислите (e,i,j) в D в качестве атакующего числа
требования P(e,itj)> если (3.1)-(3.4) удовлетворены, но не перечисляйте А и В
до тех пор, пока не перечислится некоторое z ^ и. Затем продолжайте
построение в стиле доказательства теоремы 3.1, заканчивая очередную
попытку удовлетворения Pij в том (и только в том) случае, когда такой
z отыщется. (Если D = {е}АфВ, то это обязательно должно
произойти.) Так как D в. п., то D = { е }АфВ для некоторого е. Докажите, что
P(e,ij) удовлетворяется для всех г и) и этого е.
3.8. Покажите, что в доказательстве теоремы 3.1 мы можем
ограничиться построением только двух в. п. множеств Е и F, одно из
которых имеет требуемую степень с. Указание. Замените Pij требованием
РГ : Е П Wi Ф 0 или F DWj ф 0, которое мы пытаемся
удовлетворить для всех г и j, i < j\ замените атакующее число (i,j) на число j, а
u((i,j), s) - на u(j, s). Разрешите D быть только Д^- (а не в. п.)
множеством, т. к. атакующее число j может включаться или исключаться из
D (в зависимости от того, какой случай имеет место: {e}£a®Ba (j) = О
или = 1) всякий раз, когда делается попытка удовлетворить Р( • для
i < j. Так как попытка удовлетворить РГ делается самое большее один
раз, каждое j включается или исключается из D конечное число раз
(один раз для каждого г < j), так что D является Д§-множеством и
D = { е }ЛфВ для некоторого е. (Эта версия доказательства подробно
описана в работе Соара [1980а, § 6].)
3.9. Докажите, что использование по меньшей мере двух множеств Е
и F в теореме 3.1 и упражнении 3.8 необходимо, т. к. не существует
равномерной процедуры получения с по а и Ь. А именно, докажите,
что не существует вычислимых функций / и g таких, что для данных
невычислимых в. п. множеств А = Wa, В = Wb, и е,
определяемого равенством К = {е}ЛфВ, имеет место следующее: Е невычислимо
и Е — {/(а,b,e)}A = {g(a,b,e)}B. Указание. Примените теорему
рекурсии к доказательству того, что для любого отдельного требования

§ 3. Теорема о невложимости ромба
229
минимальной пары вида
Nf,g :{/}i4 = {<7}B = ft всюду определена => h вычислима,
мы можем построить невычислимые в. п. множества А и S,
удовлетворяющие N/,0, такие, что К А®В. Как только х перечислится в К, мы
перечисляем некоторое у ^ За; или в А, или в S, тем самым обеспечивая
К А 0 Б, и позволяя одновременно множествам А и В иметь
бесконечные дополнения и быть простыми. Определим (/, д)-расширяющий
шаг аналогично тому, как мы определили О-расширяющий шаг в § 1.
Если х Е Ks+i — К8, и s не (/, 0)-расширяющий, можно предположить,
что одно из вычислений { / }Л, { д }в, полученных на наибольшем (/, д)-
расширяющем шаге t < s, оказалось неразрушенным к концу шага s.
Пусть, например, оказалось неразрушенным вычисление {/}^л. Тогда
x можно перечислить в другое множество (т. е. в В). Одновременно мы
должны удовлетворять положительным требованиям Ре из теоремы 1.2,
иначе могло бы быть либо А =т К и В =т 0, либо наоборот.
3.10 	(Джокуш). Пусть М = { а : а = 0 или а в. п. и является половиной
минимальной пары }. Пусть М+ — идеал R, порожденный М (т. е.
множество степеней замкнутое относительно конечных объединений и
следующего отношения: х Е М+ их)у => у Е М+). Докажите, что
0' ^ М+. Указание. Рассмотрите в. п. множества Ai, А2, A3, Si, S2, S3
такие, что К Ai 0 А2 0 A3, и такие, что deg(Aj) и deg(S;) образуют
минимальную пару для г = 1,2,3. Постройте в. п. множество D так же,
как и в теореме 3.1, и заметьте, что можно считать заранее известным
индекс е, для которого выполнено D = {е}Л1фЛ2фЛз. Постройте в. п.
множества S, F*, Gjj, удовлетворяя требованиям Pij,k : Wi П Е ф 0,
или Wj П F( ф 0, или Wk П Gij Ф 0. Атака требования Pijyk теперь
будет состоять в следующем: сначала находим шаг to, на котором
{e}A'o^((i,j,k})=0 = D((i,j,k}),
где А = А\ 0 А2 0 Аз- Затем находим ti ^ to и хз 6 Wk,ti такие, что
Х3 ^ u,2fc, Х3 разрешается множеством S3 на шаге ti,Wkjx = 0,
и Atx [ u = At0 [ u. После этого находим <2 ) М ^2 Е Wjj2
такие, что Х2 ^ u,2j, Х2 разрешается S2 на шаге ^, И^2 П F,^2 = 0, и
Af2 и = А*0 ii. Наконец, находим ^ ^ <2 и xi Е Wj.f3,a;i ^ u.2i,
xi разрешается Si на шаге t3,Wij3 П Ets = 0, и Af3 ^ и = А*0 д.
Положим (г, j, к) ъ D. Перечисляем Ai U А2 U А3, пока не перечислится
некоторое число z < и. Если z Е Ах (Аг, A3), перечисляем rri {л'2,хз) в

230
Глава IX. Метод минимальных пар
Е (Fi,Gii3 соответственно). Ясно, что Е А\, Е Дь F Я2,
и Gij ^т Я3. Если бы Е было невычислимым, то утверждение
упражнения было бы доказано. В противном случае полагаем Е — W{. Чтобы
получить F{ используйте невычислимость множества В\. Если
бы F{ было невычислимым, то тогда мы опять получили бы
утверждение упражнения. Поэтому предполагаем F{ = Wj. Используя
невычислимость В\ и В2 покажите, что Gij Дз- Таким образом, для
каждого к такого, что Wk бесконечно, Pij,k должно быть атаковано и
удовлетворено, поэтому Wk П Gij = 0. (См. упражнение XI.3.4(b),
результат которого связан с этой тематикой, а также теорему ХШ.3.1,
которая утверждает, что неожиданно выполнено М = М+.)
3.11 (Харрингтон). Докажите, что существует низкая в. п. степень,
которая не принадлежит классу М+, определенному в упражнении 3.10.
Указание. Примените теорему VII.3.2 Сакса о разложении, чтобы
представить множество К в виде объединения непересекающихся низких в. п.
множеств А и В и примените упражнение 3.10. (См. также
упражнение XIII. 1.14, теорему XIII.2.2 и теорему ХШ.3.1, которые совместно
дают тот же результат.)
3.12 (Джокуш [1981]). Используя метод теоремы 3.1, дайте простое пря¬
мое доказательство следствия 3.3 о том, что существуют несравнимые
в. п. степени а и Ь, не имеющие точной нижней грани среди в. п.
степеней. Указание. Пусть { 0 }е€и> и { (Фе, Фе) }е€и> — перечисления всех
тьюринговых сведений и всех пар тьюринговых сведений
соответственно. Пусть { Ze }e€u; — любое допустимое перечисление в. п. множеств
и { Ze,s — одновременное вычислимое перечисление { Ze }е£и- По¬
стройте в. п. множества А, В и { V€ }е£ип удовлетворяя требованиям
ЩеЛ) : Фе(А) = Ze = Фе(В) => [Ve ^т А & Ve В & V€ ф Qi(Ze)}.
Выберите свидетеля х = (е,г,&) для требования Ждите такого
шага s + 1, что для некоторых и и v выполнено
&i(Ze,s I щх) = 0&(Vy < и) [Фе,«(Лв f v;y)l = Фе,«(Я« f v;y) = Z6iS(y)\.
Положите х в As+i и запретите Bs [ v с приоритетом Дождитесь
шага t > s такого, что либо
(а) (3у <и)[у е геЛ - ze<t-1], либо

§ 4- * Неветвящиеся степени
231
(b) некоторое требование с более высоким приоритетом получает
внимание, либо
(c) (Vy < и) [Фe,t(At h Z\y)i}.
Если выполняется условие (а), то запретите Bs [ v (для получения
Ze ф Фе(В)); если выполняется (Ь), то начинайте работать заново,
выбирая нового свидетеля; если выполняется (с) и Фe,t(At) [ и ф Фe,s(Bs) [ и,
то запретите At [ z и Bs [ v\ если (с) выполняется и имеет место
Фe,t{At) [ и = Фe,s(Bs) ^ и, то перечислите х одновременно и в Ve и
в В, запрещая At [ z, и удовлетворяя тем самым требованию R(e,i)-
В последнем случае Ve В устанавливается обычным методом
разрешения. Покажите, с помощью метода «задержанного разрешения» из
леммы 2(ii) теоремы 3.1, что V€ А.
3.13 	Замечание. В связи с теоремой 3.4 Амбос-Шпиис [1980, § 6]
исследовал решетки, вложимые в в. п. степени отображениями, переводящими
их наибольшие элементы в 0'. Он доказал, что любая счётная
дистрибутивная решетка может быть вложена таким образом, так же как и
некоторые недистрибутивные решетки, такие, как N5 из диаграммы 2.1.
Доказательство теоремы 3.1 о невложимости ромба впервые было
опубликовано в работе Лахлана [1966Ь]. Приведенная здесь упрощенная
его форма найдена в результате дискуссий автора с Лахланом, Джоку-
шем и Стобом.
§ 4. * Неветвящиеся степени
4.1 	Определение. Пусть а— в. п. степень. Тогда а называется
ветвящейся, если существуют в. п. степени b и с, отличные от а и такие,
что а является наибольшей нижней гранью степеней b и с. В противном
случае а называется неветвящейся.
Например, в § 1 мы использовали метод минимальных пар для
доказательства того, что 0 ветвящаяся, а из теоремы 2.1, упражнения 2.3
или упражнения 2.4 следует, что существует бесконечно много
ветвящихся степеней. Перейдем к рассмотрению неветвящихся степеней.
Существование нетривиальных таких степеней было установлено
Лахланом [1966b, с. 554]. Обобщения метода этого доказательства сыграли
ключевую роль в опровержении гипотезы о вложении [Лахлан-Соар,

232
Глава IX. Метод минимальных пар
1980], а именно, при доказательстве того, что любая в. п. степень,
которая является наибольшим элементом решетки вида М5 из
диаграммы 2.1, должна быть неветвящейся. Фейер в [1980] и [1983], комбинируя
построение неветвящейся степени с теоремой плотности, доказал
теорему о плотности для неветвящихся степеней. А именно, что для любых
в. п. степеней с < d существует такая неветвящаяся (в. п.) степень а ,
что с < а < d. Отсюда следует, что неветвящиеся степени порождают
(относительно U) все ненулевые в. п. степени. Это было первое
нетривиальное подмножество в. п. степеней, для которого показано, что оно
плотно, и, следовательно, что оно порождает все в. п. степени.
Определим на множестве в. п. степеней порядковую топологию, предложенную
Лерманом, в которой предбаза открытых множеств состоит из
интервалов R(< а) = {Ь:Ь<а}и R(> a) = {b:b>a}. Тогда все
ветвящиеся степени вместе с 0' будут образовывать класс всех изолированных
точек этой топологии. Из вышеприведенной теореме о плотности Фей-
ера для неветвящихся степеней следует, что ранг Кантора-Бендиксона
класса в. п. степеней относительно этой топологии равен 1 (см.
упражнение 4.5). См. замечание 4.8 о теореме Сламана, утверждающей, что
ветвящиеся степени также плотны.
Сейчас мы изложим основной метод построения неветвящихся
степеней. Это — метод приоритета с конечными нарушениями,
напоминающий метод Мучника-Фридберга для удовлетворения требований вида
В ф { е }А, но он также использует метод разрешения, чтобы обеспечить
вычислимость В относительно некоторых множеств W{, Wj.
4.2 	Теорема (Лахлан [1966b, с. 554]). Для любой невычислимой в. п.
степени с существует неветвящаяся (в. п.) степень а ф с.
Доказательство. Займёмся построением в. п. множества А, после чего
положим а = deg(A). Для обеспечения С фт А мы должны
удовлетворить для каждого е отрицательному требованию
Ne \ С Ф {е }А,
в точности так же, как и в теореме VII.3.1, используя при этом такую же
запрещающую функцию r(e,s). Для любого в. п. множества We
определим We = We 0 А. Для того, чтобы А было неветвящимся, мы должны
добиться следующего: если
А <т Wi и А <т Wj,
(4.1)

§ 4- * Неветвящиеся степени
233
то deg (А) не является наибольшей нижней гранью для степеней deg(Wi)
и deg(Wj), а именно, существует такое в. п. множество Bij, что
Bi,j Wi и Bij Wj (4.2)
И
Bij фт -А- (4.3)
Для выполнения (4.3) мы должны удовлетворить для каждого е
требованию
Ще,и) :В^ф{е}А. (4.4)
Дадим сначала набросок стратегии удовлетворения единственного
такого требования Rn, п = (e,i,j), для фиксированных е, г, и j. Для
удобства обозначений будем опускать индексы i,j в Bi j и в маркере Гх,
который мы определим ниже.
Будем пытаться удовлетворить Rn в точности так же, как в обычной
конструкции Мучника-Фридберга. А именно:
(1) выбираем нового свидетеля х Е с(не запрещённого какими-либо
требованиями с более высокими приоритетами),
(2) ждем такого шага s, что { е }^а(ж)4, = О,
(3) определяем запрещающую функцию
q{n, s 4-1) = и8х =dfn u(As\e, х, s),
и запрещаем с приоритетом Rn перечислять числа у ^ q(n, s) в А,
(4) перечисляем х в Bs+1, тем самым обеспечивая В(х) ф {е}л(х).
Трудность здесь состоит в том, что для выполнения В ^ и В
Wj мы вынуждены одновременно с перечислением х в В перечислить в
А (и, следовательно, в ^ и Wj) некоторый след ух. Однако поступать
так будет бесполезно из-за установленного в (2) запрета, т. к. если ух ^
usx, то вычисление {e}fa(x) = 0 будет разрушено. Определим теперь
для каждого х «подвижной маркер» Гх, позиция которого к концу шага
s, Г*, будет обозначать число, выбранное нами в качестве текущего
значения следа ух. Движение маркера Тх будет удовлетворять условиям:
Г‘+1 Ф К
(3z ^ х) [z € Wi>s+1 - Wi,s],
(4.5)

234
Глава IX. Метод минимальных пар
и
х Е Bs+1 - Bs => Г*+1 Е As+1 — Ад. (4.6)
Из (4.5) следует, что Гх передвигается только конечное число раз, так
что Г£° =dfn Ит5 Г* < оо. Согласно (4.5) функция Аж[Г£°]
вычислима относительно Wi. Более того, из (4.6) следует, что В т. к.
х Е В тогда и только тогда, когда х Е Bs, где s = fit[At [ (Г£° + 1) =
А [ (Г- + 1)]. Сведение В ^т Wj получаем при помощи обычного
метода разрешения, а именно,
х Е Bs+1 - Bs => Wj,s-1_1 \ х ф WjtS I х.
Условие А <т Wi будет использоваться для того, чтобы перед
применением описанной выше процедуры Мучника-Фридберга для
удовлетворения Ль можно было передвинуть Гх (не нарушая условие (4.5)) на
некоторую новую позицию ух > usx. Сейчас мы объясним, как это будет
сделано.
На шаге s = 0 помещаем (для каждого у) маркер Гх на позицию
(ж,п), т. е. на х-й элемент из и^п\ и полагаем Ао = Во = 0.
Шаг s + 1.
Подшаг 1. Для Rn найдем такой наименьший х е wM - Bs,
х ^ s (если он существует), что
{е }?'(*); = О (4.7)
И
Wi,g+\ \ х ф Wi,s ^ х (т. е., Wi разрешает элемент х). (4.8)
Передвинем Гх на наименьшее у Е иЛп1 — As такое, что: у > usx =
u(As\е, ж, s); у ^ Г*; и у не запрещается большим приоритетом (т. е.
у > max{ r(m, s), q(m, s) } для всех т ^ п). Также передвигаем все
маркеры Г2, z > х, сохраняя их порядок, на новые свободные позиции из
(>1 ~ Ад.
Подшаг 2. Скажем, что х — подходящее число, если х ^ s;
х Е — Bs \ (4.7) выполняется для х\ и
u(As\e,x,s) < Г*+1. (4.9)
Выберем наименьшее подходящее х (если оно существует) такое, что
для всех т ^ п
Г*+1 > тах{ r(m, s),q(m, s) }

§ 4- * Неветвящиеся степени
235
и
Wj,s+1 [ х ф Wj,s [ X. (4.10)
Если такое число х существует, то будем говорить, что Rnjrnpedyem
внимания. Перечисляем Г*+1 в А (и, следовательно, в Wi и Wj);
определяем g(n, 5 +1) = u(As; е, ж, s) и перечисляем х в В. В этом случае мы
будем говорить, что требование Rn получило внимание на шаге s + 1.
Если Rn получает внимание, оно остается удовлетворенным и не
получает внимания в дальнейшем до тех пор, пока не будет нарушено
требованием более высокого приоритета. Чтобы показать, что Rn в_конце
концов получит внимание, предположим, что А <т Wi и А <т Wj, но
В = {е}А. Для каждого х пусть их = lims u(As;е,х,s) и sx = {fit) (Vs ^
t) [их = u(As;е, s, ж)]. Так как Aa;[sx] является Л-вычислимой функцией,
следующее множество является А-в. п.:
и = {х : х € иД"] & (3s ^ sx) [W<,.+1 f х ф Wi}S f х] }.
Если U конечно, тогда Wi А, т. к. для почти всех z, z Е Wi тогда и
только тогда, когда z Е WiiSx, где х = (/i?/ > z) [у Е оДп1]. Следовательно,
U бесконечно. Под шаг 1 выполняется для каждого х Е U на некотором
шаге tx ^ sx их является подходящим на любом шаге s ^ tx. Так как
{tx : а; Е J7 } является А-в. п., то таким же является и множество
V = {х : х € U к {3s^tx) [Wjt8+i [ х ф WjtS [ х) }.
Но V бесконечно, т. к. в противном случае Wj ^т А. Следовательно,
существует лишь конечное число таких жЕК, что число Г** запрещено
от попадания в А с приоритетом большим, чем Rn. Следовательно, Rn
в конечном итоге получит внимание посредством некоторого х Е V — В
и, следовательно, будет удовлетворено, оставаясь с этого момента
удовлетворенным навсегда (пока не будет нарушено требованием с большим
приоритетом Дш, m < п). (Отметим, что мы не запрещаем А [ их, если
при выполнении подшага 1 Гх передвигается из-за требования Rn.
Следовательно, требования с меньшими приоритетами могут перечислить
элементы z < их в А. Таким образом, х может неоднократно
становиться подходящим и переставать быть им до тех пор, пока окончательно не
выполнится подшаг 2.)
Это завершает описание стратегии для единственного требования.
Для того, чтобы удовлетворить все требования одновременно, снова
будем писать индекс е и индексы г, j при В\ -, и индексы е, г, jf при Г*,м'.
На шаге s + 1 выполняем подшаг 1 для каждого требования Rn, п ^ s.
На подшаге 2 выбираем наименьшее п такое, что Rn требует внимания
и подшаг 2 выполняется на Rn.

236
Глава IX. Метод минимальных пар
Лемма. (Vn) [n = (e,z,jf) & С ф {п}А & [А <т Wi &
А <т Wj => Bij ф { е }"*] & Rn получает внимание самое большее
конечное число раз].
Доказательство. Зафиксируем п и предположим, что для всех т < п
вышеприведенные утверждения выполняются. Тогда пределы r(m) =
lims r(m,s) и q(m) = lim* g(m,s) существуют для всех т < п. Более
того, Rn нарушается самое большее конечное число раз, так что в
конечном итоге удовлетворяется навсегда. Тогда Nn нарушается конечное
число раз и в конце концов удовлетворяется, в точности так же, как в
§ 3 главы VII. Q
4.3-4.7 Упражнения
4.3. Покажите, что доказательство теоремы 4.2 в действительности
показывает, что для любого невычислимого в. п. множества С существует
в. п. множество А, С фт А, такое, что для всех г и j Go;,
[Wi А & Wj з£т А) =►
(3 в. п. Bij A) [B{j А 0 W{ & Bi j Wj].
4.4 (Амбос-Шпиис [1980, § 8]). Постройте равномерно в. п.
возрастающую последовательность в. п. степеней ао < ai < • • •, которая не
имеет точной пары в. п. степеней в смысле теоремы VI.4.2. Указание.
Постройте в. п. множества Ап и Bi j для всех iyj, п G и, удовлетворяя
следующим требованиям, где Ап = 0{ Аш : т ^ п }:
5е,п : An+i ф { е }^п;
Ri,j,n • [Wi фт Ап & Wj Ап] =>
[Bij Ао 0 Wi & Bij Wj & Bij ^т Ап].
Требования 5е>п удовлетворяются обычным методом Мучника-Фрид-
берга путем перечисления элементов в Ап+\ и запрещением элементов
вне Ап. Требования Rij,n удовлетворяются так же, как и в построении
неветвящихся степеней из теоремы 4.2, перечислением элементов в Ао с
целью удовлетворения для всех е требованиям Rij,n,e • Bij ф { е }Ап.
4.5 (Фейер [1980]). Пусть на R задана порядковая топология,
определенная в начале § 4. Если a G R, то пусть R(^ а) обозначает { х : х G
R и х ^ а} и, аналогично, для R(^ а).

§ 4- * Неветвящиеся степени
237
(a) Докажите с помощью теоремы VII.3.2 Сакса о разложении, что
для любой в. п. степени а > О R(^ а) является открытым множеством.
(b) Докажите индукцией по п, что если а = inf (bi,b2,... ,bn), где
п ^ 2, Ъ{ > а и — в. п. для всех г ^ гг, то а — ветвящаяся степень.
(c) Докажите, что а является ветвящейся тогда и только тогда, когда
R(^ а) — открытое множество, что, в свою очередь, имеет место тогда
и только тогда, когда а - изолированная точка.
(d) Докажите, что множество ветвящихся степеней вместе с 0' в
точности совпадает с множеством изолированных точек.
(e) Пусть R1 — первая производная Кантора-Бендиксона
топологического пространства R, а именно, R1 = R— { изолированные точки R }.
С помощью теоремы Фейера о плотности (Фейер [1983]), утверждающей,
что для данных в. п. степеней d < с существует неветвящаяся степень
а такая, что d < а < с, и используя (а), покажите, что R1 не
имеет изолированных точек. Таким образом, процесс Кантора-Бендиксона
останавливается после первого шага.
4.6.° Используйте метод разрешения, чтобы доказать, что для любой
ненулевой в. п. степени d существует неветвящаяся степень а ^ d.
4.7 	(Амбос-Шпиис). Используя теорему Фейера [1983] о плотности для
неветвящихся степеней, докажите, что решетка N& из диаграммы 2.1
может быть вложена в R. Указание. Пусть а и b - минимальная пара
степеней. Выберите неветвящуюся с с условием 0 < с < а. Выберите d
такую, что d<a, c<dnd<cUb. Существование такой степени d
следует из того, что имеет место аП (cUb) ф с. Рассмотрите 0, b, с, d
и с U b.
4.8 	Замечание. Фейер не только установил плотность
неветвящихся степеней [1983], но также получил частичный результат о
плотности ветвящихся степеней, доказав в [1980] и [1982], что существует
ветвящаяся степень над произвольной низкой в. п. степенью. Позднее
Сламан [1991] доказал плотность ветвящихся степеней, используя 0'"-
приоритетную конструкцию, наподобие описанной в главе XIV.
Теорема 4.2 была первоначально доказана Лахланом в виде, приведенном в
упражнении 4.6, которое содержит более сильной результат, вошедший
также в монографию Шёнфилда [1971, с. 106].

238
Глава IX. Метод минимальных пар
§ 5. * Недополняемые вниз степени
5.1 Определение, (i) В. п. степень а называется дополняемой вниз,
если существует в. п. степень b > 0 такая, что а П b = 0. В противном
случае а называется недополняемой вниз (н. в.).
(И) Пусть Мг- класс дополняемых вниз степеней (т. е. О вместе с теми
в. п. степенями, которые являются половинами минимальных пар).
(ш) Пусть NC (= R—М) — класс недополняемых вниз в. п. степеней.
Легко видеть, что NC образует фильтр в R ( см. упражнение 5.4).
В теореме XIII.3.1 будет показано, что М образует идеал (а именно,
М = М+ в соответствии с обозначением из упражнения 3.10), так что
М и NC цают первый пример алгебраического разложения R на два
непересекающиеся класса, определимые в (R, ^), один из которых
является идеалом, а другой — фильтром, на самом деле сильным фильтром.
(См. определение II. 1.14 идеалов, фильтров и сильных фильтров в
верхних полу решетках.)
Чтобы убедиться, что класс NC не тривиален, дадим простое
построение с конечными нарушениями неполной степени из NC. Это
построение также окажется полезным, т. к. при изучении степеней из NC
и их алгебраических свойств в полурешетке R оно легко комбинируется
со многими другими известными построениями. Например,
предполагалось, что в отличие от м, где обнаружено много патологий, степени из
NC настолько хорошо устроены, что, возможно, даже удовлетворяют
гипотезе Шёнфилда. Это предположение опровергается в упражнении 5.6
построением ветвящейся степени из NC.
5.2 Теорема (Ейтс [1966а]). Для любой в. п. степени с > 0
существует недополняемая вниз в. п. степень а такая, что с ^ а.
Доказательство. Пусть С — любое невычислимое в. п. множество.
Построим в. п. множество А, удовлетворяя для всех е и г требованиям
Ne-.Ф е{А)фС-
P(e,i) : We невычислимо => [А^ ^т We & A^ 7&Wi\.
(Заметим, что требования P(e,i) гарантируют, что А невычислимо.) Для
Ne определим ограничивающую функцию r(e, s) так же, как в
теореме VII.3.1. С целью удовлетворить требование P(e,i)i перечисляем на
шаге s + 1 некоторое х вида х = (п,г,е) в АIе', если:
ЛИ П Wi,s = 0,
(5.1)

§ 5. * Недополняемые вниз степени
239
х е wiyS,
1 \ X ф We,s f Ху
W ^ (e,t)) [r(j,s) < x],
(5.2)
(5.3)
(5.4)
причем x — наименьшее число с такими свойствами. Из-за P(e,i) в
множество А кладется не более одного элемента, так что Ne может
нарушаться лишь конечное число раз и, следовательно, r(e) = lims r(e, s)
существует, как в теореме VII.3.1. Условие (5.3) обеспечивает сведение
Aie] we) а сведение А№ А очевидно. Если We невычислимо,
то требование P(e,i) в конце концов получит внимание (и будет после
этого удовлетворено), т. к. здесь применимо стандартное
доказательство, которое мы использовали при доказательстве методом разрешения
результатов главы V § 3. (А именно, если А№ = Wi, выберем
возрастающую в. п. последовательность элементов х\ < Х2 < • • • в W\ вида
(п,г,е) такую, что Х\ > r(j) для всех j ^ (е,г). Выберем шаг t такой,
что r(j) = r(jys) для всех s ^ t и всех j ^ (е,г). Выберем наименьшее
Sk такое, что Sk > t и Xk Е W^Sfc. Тогда We,Sk [ Xk = We [ Xk, поэтому
We вычислимо.) Q
5.3 	Определение, (i) В. п. степень а называется эффективно недо-
полняемой вниз (э. н. в.), если существуют в. п. множество A G а и
вычислимые функции f,gnh такие, что Wf(e) = {g(e) }А = { h(e) }We,
и если 0 <т Wej то 0 <т W/(e).
(ii) 	Пусть ENC - класс всех эффективно недополняемых вниз (в. п. )
степеней.
Заметим, что в теореме 5.2 на самом деле построена э. н. в.
степень, т. к. можно полагать Wf(e) = А^е 1. Э. н. в. степени обладают
более изящными свойствами, чем н. в. степени. Например, можно
показать, что они образуют сильный фильтр (см. упражнение 5.5), и что
строго ниже любой э. н. в. степени существует другая э. н. в. степень.
Из теоремы ХШ.2.2 будет следовать, что любая н. в. степень является
э. н. в. Этот факт очень удивителен, поскольку в теории вычислимости
эффективные варианты понятий редко совпадают с неэффективными.
Например, в. п. множество А невычислимо тогда и только тогда, когда
А не имеет дополнений в S, но А креативно тогда и только тогда, когда
А эффективно недополняемо. Более того, существует четыре других,
казалось бы, не взаимосвязанных друг с другом, классов в. п. степеней,
совпадающих, однако, с NC. Эти результаты главы XIII используют

240
Глава IX. Метод минимальных пар
только материалы главы IX (за исключением теоремы XI.3.4 о невло-
жимости ромба для низких степеней), и поэтому заинтересованный
читатель может обратиться непосредственно к главе XIII, минуя главы X,
XI и XII.
5.4-5.8 Упражнения
5.4 (Амбос-Шпиис [1980, § 1]). Докажите, что степени NC образуют
фильтр в R, а именно: (1) если а < b и а Е NC, то b Е NC; и (2) если
a, b Е NC ис = аПЬ существует, то с Е NC.
5.5 (Амбос-Шпиис [1980]). Докажите, что э. н. в. степени образуют
сильный фильтр, а именно, они замкнуты вверх, и если а,Ь э. н. в. то
существует такая с < а, Ь, что с является э. н. в. (Следовательно, по
теореме 5.2 для любой э. н. в. а существует э. н. в. b < а.) Указание.
Пусть fi и /2 — вычислимые функции из определения 5.3 для А Е а и
Be b, соответственно. Пусть С = 0{ Wf2^f^e)) : е Е ш }. Докажите, что
f = f2 о fi удовлетворяет определению 5.3 для С.
5.6 (Амбос-Шпиис [1980, теорема 1.1]). Докажите, что существует
ветвящаяся э. н. в. степень а. (Следовательно, для степеней NC не
выполняется гипотеза Шёнфилда.) Указание. Скомбинируйте методы
упражнения 2.4 и теоремы 5.2 для построения в. п. множеств А, В и С таких,
что А удовлетворяет требованиям P(e,i) из теоремы 5.2 и А, В и С
удовлетворяют требованиям:
11е:Вф{е}А & Сф{е}А
И
Ne : { е }ВфЛ = { е }СфЛ = / всюду определена => / ^т А.
Пусть приоритетное упорядочение требований таково: АГ0, До, АГ1?...
Для удовлетворения требования Re выбираем свидетелей, которые были
выбраны для В и С в методе Мучника-Фридберга из § 2 главы VII. Для
требования Ne определим ограничивающую функцию r(e, s) так же, как
в§1с2?0Аи(70А вместо А и В, и разрешим последователю у
требования Re перечислиться на шаге s +1, только если у > r(e, s). Для P(e,i)
выберем последователи х = (гх,0) с целью перечислить их на некотором
шаге в А так же, как в теореме 5.2. Эти действия не будут учитывать
запрещающую функцию r(e, s). Однако, как только последователь х
назначается или перечисляется, все последователи с меньшими
приоритетами (это в точности последователи у > х) уничтожаются. Далее, если

§ 5. * Недополняемые вниз степени
241
х назначен на шаге s, то х > s. Эти предосторожности гарантируют,
что Ne будет удовлетворено так же, как в теореме 2.1. Уничтожение
последователей сохраняет A-вычисления, необходимые для удовлетворения
требований Re. Последователь х требования P(e,i)y однажды
назначенный, позднее реализуется на шаге s -1-1, если существует некоторое
у > х вида (т, г, е -I-1), такое, что для у выполнены следующие условия:
(5.1) 	с Ate+1l вместо (5.2), (5.3). В этом случае мы перечисляем и
х, и у в As+1. (Причиной, по которой нам необходимы оба числа х и у,
является то, что наша техника ветвления для Ne подразумевает, что,
возможно, последователь х реализуется лишь по истечении
значительного отрезка времени после того, как х назначается. Однако, если We
вычислимо, то можно назначить бесконечно много последователей P(e,i)
в ожидании, что один из них удовлетворит (5.3). Но тогда P(e,i) будет
бесконечно часто уничтожаться последователями с меньшими
приоритетами.)
5.7° (Амбос-Шпиис [1984b, следствие 1]). Постройте в. п. степень а,
О < а < 0', являющуюся строго недополняемой вниз, а именно такую,
что не существует в. п. степеней b и d с условием а | b и аПЬ =
d. Указание. Пусть С — произвольное невычислимое в. п. множество.
Постройте в. п. множество А, удовлетворяя следующие требования для
всех е, где е = (eo,ei,e2):
Ме:Сф{е}А,
Ре'.Аф We,
Re : [Weo = {в! }A k A Weo & We2 A]
=> (3Ee) [Ee We2 & Ee^T A & Ee Weo].
Для удовлетворения Ne используйте стратегию Сакса сохранения
равенства и ограничивающие функции r(e,s) теоремы VII.3.1. Для
удовлетворения Re используйте метод построения неветвящихся степеней
теоремы 4.2. А именно, попытайтесь удовлетворить требование R(e,i) '•
Ее Ф {г }We°. Если мы перечисляем х в Ее на шаге s -1-1 для Я(е,;>, то
надо перечислить некоторый след /е(ж, s) в А для обеспечения Ее А.
Однако, мы это делаем, только если { г }Weo<a^u(x) = 0, и { е\ [ и =
Weo,s [ так что, запрещая As [ v, можно сохранить Weo-вычисление
на х. Этот запрет f((e,i),s), накладываемый требованием R(ej) на

242
Глава IX. Метод минимальных пар
As [ ix, будет конфликтовать с перечислением следа в А. Поэтому,
используя Weo <т А, определяем 7(2,0) = 0,
7/(х>s + 1)
s + 1, если As+1 [ х ф As ^ ж,
7(a;,s) в противном случае.
Определим
/e(z,s) = (гг,тах{гх(Ав;е,у,*) : у ^ j(x,s) к t^s}).
Покажите, что предел lims 7(0;, s) существует, является вычислимым
относительно А и что, если {ei}A всюду определена, то fe(x) =
lims /e(a:,s) существует и вычислим относительно А. Сведение Ее
We2 получим, используя обычный метод разрешения, а также то, что
We2 $£т А. Скажем, что Ще,г) требует внимания на шаге s + 1 тогда и
только тогда, когда существует х € (дКе+1’1» такой, что:
f((e,i),s) = 0; (5.5)
{* }Г,*°’*(а:) = 0 & х £ Ееу, (5.6)
7(x,s)^u, где и = u(We0ta;i,x,s)\ (5.7)
Weo,s I и = { ei I' it; (5.8)
fe{x,s) ^ max({ r(k, s), f(j, s) : к ^ (e,t) и j < (e,i) }); (5.9)
И
(3y<x)\yeWe2ts+l-We2ta]. (5.10)
Выберите требование с наибольшим приоритетом, которое требует
внимания на шаге s + 1, и действуйте с ним согласно описанной стратегии.
Покажите, что если условия R(e,i) выполняются, то существует шаг, на
котором Д(е,г) получает внимание и больше не нарушается.
5.8° (Амбос-Шпиис [1984b, теорема 2]). Для данной в. п. степени с > О
докажите, что существуют строго недополняемые вниз в. п. степени ао
и ai такие, что с ^ ао, ai и ао U ai =0'.

Глава X
Решётка в. п. множеств относительно
включения
В главах VII-IX изучалась структура верхней полурешетки в. п.
степеней R и особое внимание уделялось тьюринговым вычислениям. В этой
главе рассматривается решетка в. п. множеств £, и особое внимание
уделяется алгебраической структуре в. п. множества в решетке в. п.
множеств. В главе XI эти два направления исследований будут
объединены с целью изучения взаимосвязей между алгебраической структурой
в. п. множества и его тьюринговой степенью.
Двумя основными темами главы X являются методы теоремы о
разложении (§ 2) и построение максимального множества, использующее
понятие е-штата (§ 3). Как вариации и расширения этих методов
получаются остальные результаты главы, включая классификацию булевых
алгебр, которые можно представить в качестве решетки надмножеств
некоторого в. п. множества (§7).
§ 1. Идеалы, фильтры и факторрешетки
Напомним, что в определении И. 1.14 были введены понятия решетки
£ = (L; V, А, 0,1) с наибольшим и наименьшим элементами 1 и 0
соответственно, дистрибутивной решетки, булевой алгебры, идеала и
фильтра. Большинство решеток, которые мы рассматриваем, будут являться
подрешетками или факторрешетками N = (2W; С, U, П, 0,ы) — решетки
всех подмножеств множества натуральных чисел. Особый интерес
будут представлять решетка в. п. множеств £ С N и булева алгебра TZ
вычислимых множеств, которые были введены в определении II. 1.15.
Отметим, что идеал или фильтр сам образует решетку
относительно индуцируемых операций. Например, решетка конечных множеств Т

244
Глава X. Решётка в. п. множеств
образует идеал в 7£, 8 или в Л/", а совокупность коконечных множеств
С образует фильтр в каждой из них. Мы уже видели (упражнение V.1.5
и V.2.8), что простые множества совместно с С образуют фильтр в 8, и
аналогично для гиперпростых множеств. (Это же верно и для гиперги-
перпростых множеств (упражнение 2.17)). Если С — решетка и a G £,
то
1(a) = {b Е С : b ^ а }
и
V(a) — { 6 Е £ * Ь ^ а}
называются, соответственно, главным идеалом и главным фильтром в
£, порожденными элементом а. Идеал (фильтр) является главным тогда
и только тогда, когда он представим в виде 1(a) (V(a)) для некоторого
a Е С. Ни Т, ни С не являются главными.
Следующая теорема показывает, что идеалы и фильтры позволяют
нам получать факторрешетки.
1.1 Теорема. Пусть С — дистрибутивная решетка, ICC (VC
С) — идеал (фильтр). Мы говорим а =х Ъ (а =х> Ь), если для
некоторых c,d el (из V) aV с = by d (а А с = bAd). Тогда =х и =v
определяют конгруэнции, чьи множества классов эквивалентности образуют
дистрибутивные решетки. Эти решетки обозначаются через С/1 и
C/dl соответственно, где jd означает, что используется дуальный
идеал (фильтр).
Доказательство, см. упражнение 1.5. Q
Легко видеть, что если С — под решетка N такая, что С замкнута
относительно симметрической разности, и 1 — идеал в £, то A =j В
тогда и только тогда, когда ААВ Е Z, где ААВ — симметрическая
разность А и В.
1.2 Определение. Обозначим через £*, Л/"*, 8* и TV
факторрешетки С/Т, N(Т, 8jT и 7Z/T соответственно, где 1 — идеал конечных
множеств. Будем писать А =* В вместо А =? В, и пусть А* = { В :
А =* В } и А С* В тогда и только тогда, когда А* ^ В*, а именно, если
А — В конечно.
Часто бывает более удобным изучать вместо решетки 8 факторре-
шетку 8*. Автоморфизмом решетки С называется взаимно однозначное
отображение С на £, которое сохраняет упорядочение С (и,
следовательно, сохраняет операции точной нижней и точной верхней граней).

§ 1. Идеалы, фильтры и факторрешетки
245
1.3 	Определение. Свойство Р в. п. множеств (в. п. множеств по
модулю конечных множеств) называется инвариантным или
теоретикорешеточным (т. р. ) в £ (в £*) тогда и только тогда, когда оно
инвариантно относительно всех автоморфизмов £ (£*). Свойство Р
называется элементарно теоретико-решеточным (э. т. р. ), если
существует формула с одной свободной переменной (без параметров) языка
Z/(^,V,A,0,1), которая определяет класс множеств в £ (в £*),
обладающих свойством Р. Здесь 0 и 1 интерпретируются соответственно как
наименьший и наибольший элементы решетки.
Очевидно, что любое э. т. р. свойство является также т. р., т. к.
любой автоморфизм должен сохранять отношение включения. Легко
видеть, что обратное неверно, т. к. обычные мощностные рассуждения
показывают, что существует несчётное множество т. р. свойств £* (см.
упражнение 3.10(d)), но очевидно, что существует только счётное
множество э. т. р. свойств. Следующие формулы показывают, что свойства
вычислимости и конечности являются э. т. р. как в £, так ивГ:
1.4 	Определение. Вычислимо перечислимое множество М
называется максимальным, если М* является коатомом в £*, т. е., если М
бесконечно и не существует в. п. множества W такого, что \W П Ml =
\WDM\ = оо.
Легко показать (см. упражнение 1.7), что если Р — некоторое
свойство в. п. множеств, замкнутое относительно конечных разностей, то Р
является э. т. р. в £ тогда и только тогда, когда Р э. т. р. в £*. Так
как все свойства Р, которые мы рассматриваем, замкнуты
относительно конечных разностей, то, чтобы доказать, что Р является э. т. р. в £,
достаточно доказать, что Р э. т. р. в Г, и это доказательство обычно
бывает проще и элегантнее, чем для £. Например, простота является
э. т. р. в £* так же, как и свойство множества А быть максимальным,
что устанавливается следующими формулами:
Rec(x) = (Зу)[х V у = 1&ж А у = 0],
(1.1)
Fin(a:) = (Vy)[y ^ х => Rec(y)].
(1.2)
Sim(a:) = х < l&(Vy)[y > О х А у > 0],
(1.3)
И
Мах(ж) = х < 1 &(Vi/)[a; < у => у = 1].
(1.4)

246
Глава X. Решётка в. п. множеств
Хотя из первоначального определения гипергиперпростого
множества совсем не очевидно, что оно является э. т. р., неожиданная их
характеризация из следствия 2.7 показывает, что гипергиперпростота на
самом деле является э. т. р. в £* (и, следовательно, в £).
Самый простой способ убедиться, что некоторое свойство Р не
является э. т. р. состоит в том, чтобы показать, что оно не является т. р.,
а это требует использования метода порождения автоморфизмов £ из
главы XV. Например, там доказывается, что гиперпростота не
является т. р. (теорема XV.3.1), и что любые два максимальные множества
лежат в одной и той же орбите (теорема XV.4.6). Показывается также,
что любой автоморфизм £* индуцирован некоторым автоморфизмом £
(следствие XV.2.6). Следовательно, любое свойство Р в. п. множеств,
замкнутое относительно конечных разностей, является т. р. в £ тогда и
только тогда, когда Р т. р. в £*. Это способствует отождествлению £
и £* с алгебраической точки зрения.
1.5-1.9 Упражнения
1.5. Докажите теорему 1.1. (Это можно также найти в книге
Роджерса [1967а, с. 225].)*
1.6. Докажите, что если А — бесконечное в. п. множество и 1 —
порождаемый им главный идеал в £, то X = £.
1.7. (а) Используя (1.1) докажите, что идеал Т и отношение А —* В
являются определимыми над £.
(б) 	Докажите, что если свойство Р в. п. множеств замкнуто
относительно конечных разностей (т. е., является хорошо-определенным на
£*), то Р является э. т. р. в £ тогда и только тогда, когда Р э. т. р. в £*.
Указание. Для данной формулы Ф*, определяющей Р над £*, получите
Ф, определяющую Р над £, заменяя атомные формулы х = г/, для чего
используйте определимость А =* В в (а).
1.8. Найдите формулы, которые показывают, что свойства множества
А быть простым или максимальным являются э. т. р. в £. (Используйте
упражнение 1.7 и формулы (1.3) и (1.4).)
1.9. Докажите, что £* не является плотно упорядоченной тогда и
только тогда, когда £* содержит максимальный элемент. Указание. Если
С. 288 русского издания. — Прим, редактора.

§ 2. Теоремы о разложении и булевы алгебры
247
£* не является плотно упорядоченной, выберите множества В, А Е £,
В* < А* так, что не существует С такого, что В* < <7* < Л*, где
X* < Y* означает, что X С* Y, по Y <£* X. Выберите взаимно
однозначную вычислимую функцию / такую, что f(u) = А, и докажите, что
множество2 D = /_1(2?) является максимальным.
1.10 Замечания. Майхилл [1956] был первым, кто предложил
изучать решётки 5 и Г, он же поставил вопрос о существовании
максимальных элементов в £*. Фридберг [1958а] опубликовал три теоремы
о вычислимой перечислимости: теорему 2.1 Фридберга о разложении,
теорему 3.3 о существовании максимального множества и теорему о
возможности вычислимого перечисления в. п. множеств без повторений.
§ 2. Теоремы о разложении и булевы алгебры
Хотя теорема VII.3.2 Сакса о разложении и содержит в себе слабую
форму следующей теоремы Фридберга о разложении (из теоремы Сакса
следуют только пункты (i) и (й)), значительно более простое
доказательство Фридберга дает более сильное свойство (ш), необходимое для
разрешающей процедуры Лахлана [1968d] проверки истинности Vlf —
предложений в £*. (Конечно, из теоремы Фридберга теорема Сакса не
вытекает, т. к. первая касается только алгебраических свойств Ао и
А\ и не имеет дела со свойством, позволяющим избежать конуса
теоремы VII.3.2(ii).)
По данным вычислимым перечислениям { Xs }s€u; и {Ys}s€u, в. п.
множеств X и Y определяем в. п. множества X\Y и X \ Y так же,
как в определении И.2.9. Заметим, что Х\Y = (X - Y) U (X \ Y) (см.
упражнение 11.2.10(b)). Следовательно,
X — Y не в. п. => X \ Y бесконечно , (2.1)
потому что X\Y и X \ Y оба являются в. п. множествами (см.
упражнение 11.2.10(a)).
2.1 Теорема Фридберга о разложении. Для любого
невычислимого в. п. множества В существуют такие непересекающиеся в. п.
множества Ао и А\, что
2В оригинале это множество названо «pullback», см. также упражнения 4.8 и
XI.1.18. — Прим, редактора.

248
Глава X. Решётка в. п. множеств
(i) 	В = А0 U Ai и
(И) Ао и А\ невычислимы.
Кроме того, если W — произвольное в. п. множество, то
(iii) 	W — В не в. п. => W - Ai не в. п., для г — 0,1.
(Конечноу из (Ш) следует (й), если положить W = ш.) Далее, в. п.
индексы множеств Ао и А\ могут быть найдены равномерно по в. п.
индексу множества В.
Доказательство. Пусть / — взаимно однозначная вычислимая функция
с областью значений В и Bs = { /(0),..., f(s) }. Чтобы добиться
выполнения (ii) будем стараться удовлетворить для всех е, i требованиям
Ще,%) - We Ф А{. Описываемая ниже стратегия добивается выполнения
условия
We \ В бесконечно => We П А{ ф 0, для i = 0,1.
По (2.1) это автоматически выполняет (Ш), т. к. в (2.2) f(s + 1) Е We \
В.
Шаг s = 0. Перечисляем /(0) в Ао>
Шаг s -1-1. Выбираем такое наименьшее число (е,г), что
f(s + 1) Е We,s и W€fS П Ait8 = 0. (2.2)
(Напомним, что по определению We,8 справедливо е < s.) Перечисляем
f{s+ 1) в А{ (тем самым We>5n Ai,s+\ ф$ и R(e,i) удовлетворено
навсегда). Заметим, что f(s + l) Е We \ В, и это пригодится в упражнениях,
подобных 2.19. Если такого (е, г) не существует, то перечисляем f(s 4-1)
в А0.
Пусть Ai = г = 0,1. Очевидно, что Ао и А\ являются не-
пересекающимися в. п. множествами, которые удовлетворяют (i). Для
того, чтобы доказать (iii), предположим противное, и пусть W является
контрпримером для (iii). Следовательно, W—Ai вычислимо перечислимо
и справедливы импликации
W - В = (W - Ai) - В не в. п.
==> (W - Ai) \ В бесконечно по (2.1),
=> (W - Ai) П Ai ф Q по построению.
Получили противоречие. []

§ 2. Теоремы о разложении и булевы алгебры
249
2.2 Определение. Для множества S С и определим £(S) = { W П
S : W в. п. } — решетку (относительно включения) в. п. множеств,
ограниченных на S. Для W Е £ пусть Ws обозначает множество W П S
из £(S). Элемент As из £(S) называется дополняемым в £{S), если
существует такое в. п. множество В, что As U Bs = S и As П Bs = 0.
В противном случае As называется недополняемым в £(S). (Заметим,
что £(S) является булевой алгеброй, если каждый её элемент является
дополняемым.)
Наша цель состоит в том, чтобы дать алгебраическую
характеризацию понятий гипергипериммунности и гипергиперпростоты (см.
определение V.2.1), доказав следующую теорему:
2.3 Теорема (Морли-Соар). Бесконечное А^-множество S гиперги-
периммунно тогда и только тогда, когда £(S) является булевой
алгеброй.
Доказательство. Вытекает из леммы 2.4 и упражнения 2.10. О
2.4 Лемма (Лахлан). Если множество S (не обязательно из А^)
бесконечно и £(S) является булевой алгеброй, то S гипергипериммунно.
Доказательство. Если S не является гипергипериммунным и слабая
таблица { И^/(п) }пеш непересекающихся в. п. множеств для некоторой
вычислимой функции / представляет негипергипериммунность 5, то
пусть А = \J{Wn П Wf(n) }пеw Тогда А в. п. и As является
недополняемым в £(S). Действительно, если В = Wn, то пусть х Е ^/(п) П S.
Либо х Е А П В, либо х Е А Г) В, поэтому Bs не является дополнением
As в £(S). D
При доказательстве теоремы 2.3 в обратном направлении в
упражнении 2.9 показывается, что если S принадлежит Дз, то любой недопол-
няемый элемент As из £(S) может быть равномерно разложен на не-
пересекающееся объединение Bs и Cs недополняемых элементов. (Эта
равномерность, которую мы особо подчеркиваем в теореме 2.5 и
упражнении 2.9, существенна для получения повторных разложений в
следствии 2.7 и упражнении 2.14.) Теорема Фридберга устанавливает это для
S = ш, а следующая теорема делает это для любого множества S с в. п.
дополнением. Мы приводим первоначальное доказательство этой
теоремы (похожее на доказательство Фридберга), т. к. оно дает более сильное
свойство (Ш), полезное в разрешающих процедурах, а упражнение 2.9
его не дает.

250
Глава X. Решётка в. п. множеств
2.5 	Теорема Оуингса о разложении. Пусть С С В — такие в. п.
множества, что В — С не является ко-в. п. (т. е. Bs является
недополняемым в £{S) для S = С). Тогда существуют такие непересе-
кающиеся в. п. множества Ао и А\ (чьи индексы могут быть получены
равномерно по индексам В и С), что
(i) В = Ао U А\ и
(ii) А{ — С не является ко-в. п., для i — 0,1.
(Т. е. (Ai)s являются недополняемыми в £{S) для S = С.) Более того,
для любого в. п. множества W имеет место импликация
(iii) С U (W — В) не в. п. => С U (W - Ai) не в. п.} для % = 0,1.
(Очевидно, что при W — uj из (iii) вытекает (ii).,)
Доказательство. Пусть / — вычислимая 1:1-функция с областью
значений В и Bs — { /(0), /(1),..., f(s) }. Пусть { Cs }S£u, — некоторое
вычислимое перечисление С. Чтобы выполнить (i) и (ii), будем стараться
удовлетворить следующим требованиям:
Ps : f(s) G Аоч8 U Ai,s, s G cj;
R(e,i) : We Ф Ai - C, e e uj, i = 0,1.
Тогда наша стратегия автоматически обеспечивает выполнение (iii).
Для требования Ще^) используем вычислимую функцию g(e,i,s),
которую можно рассматривать как позицию подвижного маркера Г(ел) к
концу шага s.
Шаг s = 0. Перечисляем /(0) в А0, и определяем g(e, i, 0) = 0 для
всех е и г.
Шаг s 4- 1.
Подшаг 1. Если существует х ^ g(e,i,s) такой, что х G We%8 П
Ai,s П Сs, то пусть g(e,i, s + 1) = g(e, i, s). В противном случае g(e,i, s +
1) = s + l.
Подшаг 2. Пусть у = f(s + l). Выбираем такую наименьшую пару
(е,г), что
yeWe^s и y^g(e,i,s),
и перечисляем у в Ai. Если таких (e,i) нет, перечисляем у в Aq.
Пусть Ai = (JsAijS, где i = ОД. Очевидно, (i) выполнено. Чтобы
доказать (iii), предположим, что для некоторых е, г и W мы имеем

§ 2. Теоремы о разложении и булевы алгебры
251
CU(W — Aj) = We. Мы должны показать, что C\J(W — В) в. п. Выбираем
s' настолько большим, что для всех (е7, г'), меньших, чем (е,г), если
lims д(е', г', s) < оо, то g(el,i,,st) = lims д(е', г', s). Пусть г — максимум
этих пределов. (Заметим, что limSg(elil,s) < оо тогда и только тогда,
когда требование R(e> у) удовлетворено навсегда.) Выбираем шаг s" ^ s'
таким, что f(s) > z для всех s ^ s". Теперь limSg(e,i,s) = оо, потому
что We П (А{ — С) = 0. Определим в. п. множество
Ve = { х : (3s ^ s")[x Е W€tS - BsSzx ^ д(е, г, s)] }.
Имеем Ve П В = We П Б, т. к. lims д(е, г, s) = оо. Следовательно, VeDB =
We П В, поскольку Ai,C С В. Кроме того, Ve П (В - С) = 0.
Действительно, для получения противоречия предположим, что х Е Ve П (В — (7),
например, пусть а; Е — Bs, а; ^ g(e,i,s), и а; = /(s 4- 1) для
некоторого s ^ s". Тогда, согласно нашему построению, либо требование
R(e,i), либо требование R(e>у) при (е7, г7) < (е,г), lims д(е', г', s) = оо,
на шаге s + 1 выбирает элемент х. Но это означает, что х не может
быть постоянным представителем R(e>^) (иначе предел является
конечным), поэтому х должен войти в С после шага s + 1. Следовательно,
Ve П (В - С) = 0 и Ve П В = W П В. Поэтому С U Ve = С U (W - В)
является в. п. множеством. О
2.6 Определение. Для любого в. п. множества А определим главный
фильтр С(А) = {В:А С В & В Е £}.
Заметим, что если А — в. п. множество, то С(А) = £(А), посредством
соответствия WeUA*+ We П А. Используя определение 1.2 будем писать
С* (А) и £*(А) для обозначения результата факторизации решеток С(А)
и £ (А) по идеалу конечных множеств Т.
2.7 Следствие (Лахлан). Пусть С — кобесконечное в. п.
множество. Тогда С гипергиперпросто тогда и только тогда, когда £(С)
(или, эквивалентно, С(С)) образует булеву алгебру.
Доказательство. (<=) По лемме 2.4.
(=£►) Предположим, что В D С, В — в. п. множество и В является
недополняемым в С(С), т. е. В - С не ко-в. п. Неоднократно
применяем теорему 2.5, чтобы получить таблицу непересекающихся множеств
{ wf(n) }n€u;> которая обеспечит негипергипериммунность множества С.
А именно, применяем теорему 2.5 к множествам В и С, чтобы получить
Ао и Л\. Полагаем Wf(0) = Aq и применяем теорему 2.5 к множествам

252
Глава X. Решётка в. п. множеств
А\ и CilAi, чтобы получить Aq и А\. Полагаем Wf( 1) = А\ и применяем
теорему 2.5 к А\ и СГ\А\, и так далее. В силу равномерности теоремы 2.5
последовательность { Wf(n) }пеи> является вычислимо перечислимой,
состоящей из непересекающихся множеств, причем Wf(n) ПС ф 0 для всех
п. П
2.8 Следствие (Лахлан). Свойство «быть гипергиперпростым»
является элементарно теоретико-решеточным в £.
Доказательство. Если A Е £, то А является гипергиперпростым тогда
и только тогда, когда
(VX Э A){3Y Э А)[Х PiY = AkXUY = uj\. Q
В упражнении 2.9 дается другой способ доказательства следствия 2.7,
использующий вместо теоремы 2.5 теорему Сакса о разложении.
2.9-2.19 Упражнения
2.9 (Морли-Соар). Докажите следующее обобщение теоремы Сакса о
разложении.
Для любого множества 5 Е и любого в. п. множества В, если Bs
является недополняемым элементом в £ (5), то существуют непересека-
ющиеся в. п. множества А0 и А1, индексы которых могут быть найдены
равномерно по индексам В, такие, что:
(i) b = a°ua1,
(й) А*§ и А$ являются недополняемыми в £(5), и
(Ш) А0 и А1 несравнимы по Тьюрингу.
Указание. Покажите, что достаточно удовлетворить следующим
требованиям для е Е ш, i Е { 0,1 }:
Ri:Wf C\S фБОБ.
Например, если А0 П S = Wj П 5, то W^ = Wj П А1, что
противоречит R\. Чтобы удовлетворить этим требованиям, возьмите
вычислимую последовательность конечных множеств { Ss }$еим такую, что

§ 2. Теоремы о разложении и булевы алгебры
253
S = lims 5S. Пусть / — вычислимая 1:1-функция с областью значений В
и В8 = { /(0),..., f(s) }. Определим вычислимые функции для г = 0,1:
/(г, е, s) = max{ х : х ^ s&(Vt/ < a;)[y G =* [г/ G W^i] <=> у & B8]\ },
т(г, e, s) = max{ /(г, e, £) : t ^ s },
г(г,е,$) = max{z : (3s)[a: ^ т(г,е, s)&a; G WeJ&z ^ u(j4* ; e,ar, s)] }.
Перечисляем /(0) в А0. На шаге s+1 находим наименьшее число (e, г)
такое, что /(s + 1) ^ г(г, е, s), и перечисляем /(s + 1) в А1~г. Покажите,
что каждая ограничивающая функция гг(е, s) нарушается самое большее
конечное число раз, и каждое требование Щ удовлетворяется, т. к. в
противном случае Bs является дополняемым.
2.10. Используйте упражнение 2.9 и метод следствия 2.7, чтобы
завершить доказательство теоремы 2.3.
2.11. Докажите, что каждое максимальное множество гипергиперпрос-
то.
2.12. Используйте следствие 2.7, чтобы показать, что кобесконечное
в. п. множество С гипергиперпросто тогда и только тогда, когда для
каждого в. п. множества В Э С существует такое вычислимое
множество Д, что В ПС = RH С.
2.13. Если А и В — в. п. множества, то пусть А < В означает, что
АсВпВ — Ане ко-в. п. Докажите, что если А < В, то А < С < В
для некоторого в. п. множества С.
2.14. 	Докажите, что если С С В — в. п. множества и В - С гиперги-
периммунно, то В — С ко-в. п. Указание. Если это не так, то В является
недополняемым в £(С), и мы можем, согласно теореме 2.5, применить к
В - С процедуру разложения из доказательства следствия 2.7.
2.15 	(Робинсон [1967а]). Докажите, что кобесконечное в. п.
множество А гипергиперпросто тогда и только тогда, когда для каждой слабой
таблицы непересекающихся конечных множеств { И^п) }n€u;
существует такое число п, что для всех m ^ n, |W/(m) П А\ ^ т. Указание.

254
Глава X. Решётка в. п. множеств
Предположим, что существует слабая таблица {И^/(п) }n€u>>
нарушающая это условие. Постройте слабую таблицу непересекающихся
множеств { Wg^ }пеим которая ввиду определения V.2.1 обеспечит негипер-
гиперпростоту А. Постарайтесь поместить по меньшей мере один
элемент из Wf(n) Г\А (если такой элемент существует) в каждое множество
И^(т), т^п.
2.16 	(Ейтс [1962]). Бесконечное множество В называется сильно гипер-
гипериммунным (сгг-иммунным), если не существует равномерно в. п.
(р. в. п.) последовательности { Wf(n) }П€и> попарно непересекающихся
в. п. множеств таких, что Wf(n) Г\В ф 0 для каждого п. (Разница между
этим определением и определением гг-иммунного множества состоит в
том, что в определении V.2.1 все в. п. множества И^(п) должны быть
конечными.) Докажите, что если А — кобесконечное в. п. множество, то
А гг-иммунно тогда и только тогда, когда А сгг-иммунно.
2.17. Используйте следствие 2.7, чтобы доказать, что если А и В
являются гг-простыми, то А Г) В также гг-просто. (Следовательно, гг-
простые и ко-конечные множества образуют фильтр. В упражнениях 1.5
и 2.8 главы V показано, что это же верно для простых и г-простых
множеств.) Указание. Пусть А и В — гг-простые множества, а С —
в. п. множество. Докажите, что (А П В) U С в. п.
2.18. Докажите, что если А в. п., кобесконечно и не гг-просто, то £*
вложима в С*{А). Указание. Пусть условие гг-иммунности А не
выполнено для { Sn }пеw Рассмотрите
Wn = \J{Sm:meWn}.
2.19 	(Шор [1978а]). В. п. множество В называется нигде не простым,
если для каждого в. п. множества С такого, что С — В бесконечно,
существует бесконечное в. п. множество W С С —В. Докажите, что каждое
в. п. множество В может быть представлено в виде непересекающегося
объединения нигде не простых в. п. множеств А0 и А\. Указание.
Измените конструкцию теоремы 2.1 так, чтобы удовлетворить требованиям
R(e,i,n) : Поместить п элементов из We в Л;.
На шаге s поместите f(s) в Ai для того, чтобы выполнить
неудовлетворенное требование наивысшего приоритета. Чтобы показать, что Л о

§ 3. Максимальные множества
255
нигде не просто, фиксируйте е такое, что We — Aq бесконечно.
Рассмотрите случаи, когда We П А\ бесконечно, и когда We \ В конечно.
2.20 	Замечания. Теорему 2.1 доказал Фридберг [1958а]. Следующим
важным продвижением явилась неожиданная характеризация гг-прос-
тых множеств, найденная Лахланом [1968с] в следствии 2.7. Он это
доказал другим методом. После появления препринта, содержащего
доказательство Лахлана, Оуингс [1967, с. 174] доказал теорему 2.5 и показал,
как её использовать для получения следствия 2.7. Позднее Мор ли и Соар
[1975] доказали результат из упражнение 2.9 и теорему 2.3.
§ 3. Максимальные множества
Фридберг решил упомянутый в замечаниях 1.10 вопрос Майхилла,
построив максимальное множество, т. е. коатом в £*. Это было
существенным достижением по нескольким причинам. Пост ввел понятие гг-
простого множества, но не смог их построить. Так как максимальные
множества, очевидно, являются и гг-простыми, этот результат Фрид-
берга дает первое (и до сих пор самое простое) доказательство
существования гг-простого множества. Построение легко изменить для того,
чтобы сделать это максимальное множество полным по Тьюрингу. Так
как среди в. п. множеств максимальные множества имеют самые
«жидкие» дополнения, то это обрекает на провал программу Поста (глава V)
нахождения свойства «жидкости» дополнения А вычислимо
перечислимого множества А, гарантирующего неполноту А. (Позднее все же были
обнаружены другие свойства такого рода, гарантирующие неполноту;
см. замечания 3.13.) Наконец, из существования максимального
множества следует (см. упражнение 1.9), что решетка £* не является плотно
упорядоченной. (Самым близким к плотному упорядочению свойством,
которое можно осуществить, является свойство из упражнения 2.13.)
3.1 	Определение. Бесконечное множество С называется сжатым,
если не существует такого в. п. множества W, что W П С и W П С оба
бесконечны.
Таким образом, по определению 1.4 в. п. множество А максимально
тогда и только тогда, когда А сжато. Заметим, что сжатое множество
гг-иммунно и множество А максимально тогда и только тогда, когда
А* — коатом в £*. Легко привести неэффективное построение
сжатого множества (см. упражнение 3.4). Для того, чтобы построить макси¬

256
Глава X. Решётка в. п. множеств
мальное множество, мы эффективизируем эту стратегию. Для этого нам
понадобится следующее техническое средство, которое будет часто
использоваться.
3.2 	Определение, е-штатом элемента х на шаге s называется
множество
сг(е, ж,$) = {г:г^е&а;Е Wi,s }.
Мы отождествляем каждый е-штат со строкой из 2<и} длины е+1,
которая является начальным сегментом его характеристической функции.
Для фиксированного е существует 2е+1 е-штатов, которые упорядочены
лексикографически. Мы читаем е-штаты слева направо, так что,
например, е-штат 100 показывает, что х Е Wo, х $ х $ Когда при
таком упорядочении а больше, чем т , то будем говорить, что а является
более высоким (или более сильным) е-штатом, чем т, что записывается
как а > т. Например, 010 > 001. Положим для удобства <т( —1 ,x,s) = 0
для всех х и s, и пусть а(е,х) = lims сг(е, ж, s). Этот предел, очевидно,
существует.
3.3 	Теорема (Фридберг [1958а]). Существует максимальное
множество А.
Доказательство. Достаточно построить в. п. множество А, которое
удовлетворяет для всех е требованиям
Ne :\А\^е
и
Ре:А С* We или А С* We.
Чтобы построить А, используем последовательность маркеров { Гп }П€и;,
обозначая через asn позицию маркера Гп к концу шага s, и где
As = {ag <aj < •••}.
Стратегия для удовлетворения Ро состоит в том, чтобы выбрать на
шаге s + 1 такое наименьшее е (если оно существует), что ase ^ Wo,s, но
af Е Wo,s Для некоторого г > е, и передвинуть Ге на позицию а\. (А
именно, каждый маркер сдвигается так, чтобы максимизировать
(поднять) его 0-штат.) Очевидно, что эта стратегия эффективна и
удовлетворяет требованию Ро, потому что если Wo П А бесконечно, то каждый

§ 3. Максимальные множества
257
маркер окончательно останавливается на элементе из Wo, и,
следовательно, А С Wo. Функция е-штатов состоит в том, чтобы дать
возможность соединить стратегию удовлетворения Р{+1 со стратегиями для Р,
г' ^ г. А именно, каждый маркер Ге двигается так, чтобы
максимизировать его е-штат. Таким образом, каждый маркер двигается не более чем
конечное число раз, но все маркеры Г*, г ^ е, принимают во внимание
требование Ре. Множество А строится следующим образом.
Шаг 5 = 0. Полагаем А = 0 и а° = п для всех п.
Шаг 5 + 1. Выбираем наименьшее е такое, что для некоторого г е <
г ^ 5 и cr(e,af,5) > cr(e,af,5). Для этого е выбираем наименьший такой
г. 	Передвигаем маркер Ге на элемент af и сдвигаем маркеры Г^, j > е,
сохраняя их порядок, на элементы aj, к > г, тем самым перечислив
элементы af, af+1,... ,а*_г в А. (Если такого е нет, то ничего не делаем.)
Лемма 1. Для каждого е маркер Ге передвигается не более чем
конечное число раз. (Следовательно, множество А бесконечно.)
Доказательство. Фиксируем е и предположим, что лемма верна для
всех г < е. Выберем 5о таким, что для всех г < е, а*0 = a* =dfn lims af.
После шага во маркер Ге сдвигается только к элементу с более высоким
е-штатом. Но существует лишь 2е+1 различных е-штатов и,
следовательно, после шага во маркер Ге передвигается не более чем 2е+1 — 1
раз. Q
Лемма 2. (Ve)[A С* W€ или А С* We).
Доказательство. Фиксируем е и предположим, что лемма верна для
всех i < е. Выберем п ^ е таким, что для всех т ^ n, а(е — 1 ,am) =
а(е — 1 ,an). Теперь предположим противное: пусть We П А и Wе П А
оба бесконечны. Выберем р, q такими, что п < р < q, ар £ We и
aq G We, а шаг 5 таким, чтобы для всех т q было ат = а8т
и cr(e,am) = cr(e,am,5). Однако a(e,aq) > а(е,ар) и, следовательно,
а(р>ая) > Таким образом, некоторый маркер Гг, г ^ р, пе¬
редвигается на шаге 5 + 1, что противоречит выбору 5. Ц
3.4-3.12 Упражнения
3.4. (а) Постройте сжатое множество С следующим образом. Пусть
Z-1 = и. Для данного Zn, n ^ -1, пусть Zn+i = ZnfWn, если последнее
множество бесконечно, и Zn+i = ZnC\Wn в противном случае. Выберите
со G Zo, ci G Zi и со < ci ..., и положите С = { с* }*€и;. Покажите, что
множество С является сжатым.

258
Глава X. Решётка в п. множеств
(б) 	Покажите, что любое бесконечное множество имеет сжатое
подмножество.
3.5. Покажите, что со является объединением счётного числа непере-
секающихся сжатых множеств, но не является объединением конечного
числа таких множеств.
3.6. (а) Соедините построения теоремы 3.3 и упражнения V.1.6, чтобы
сделать множество А максимальным и эффективно простым
(следовательно, полным).
(б) 	Постройте полное максимальное множество А, перечисляя asn
в As-|_i, если п G Ks+\ — Ks, и используя построение из теоремы 3.3.
3.7. Будем говорить, что частичная функция ф доминирует
частичную функцию 0, если для почти каждого п
в(п) [ф(п) | & в(п) ^ ф(п)].
Докажите, что если ф доминирует каждую ч. в. функцию, то 0' ^т Ф-
Указание. Рассмотрите ч. в. функцию в(х) = fis[x G Ks\.
3.8 	(Ейтс [1965]). Измените доказательство теоремы 3.3 так, чтобы
построить такое максимальное множество А, что главная функция pj
доминирует каждую ч. в. функцию (следовательно, А полно). Указание.
Передвигайте маркер Гп, как только необходимо сделать, чтобы </?e(n) ^
ап для всех е ^ п таких, что (ре(п) и одновременно двигайте Гп, чтобы
максимизировать его п-штат.
3.9. Покажите, что для каждого бесконечного в. п. множества А
существует в. п. множество В С А, которое является максимальным в А
в том смысле, что А — В сжато. (Заметим, что из упражнения 2.14
вытекает, что А — В должно быть ко-в. п.) Указание. Рассмотрите /(М)
для взаимно однозначной вычислимой функции / с областью значений
А и максимального множества М.
3.10. Множество А называется квазимаксимальным, если оно является
пересечением конечного числа максимальных множеств.
(а) Докажите, что кобесконечное в. п. множество А
квазимаксимально тогда и только тогда, когда С* (А) конечно.
(б) Докажите, что каждое квазимаксимальное множество гг-просто.

§ 3. Максимальные множества
259
(в) Докажите, что для каждого п, если все А*, 1 ^ г ^ п, являются
такими максимальными множествами, что А* ф Aj для г ф j, и Вп =
р|{ А{ : г ^ п }, то С*(Вп) является булевой алгеброй, мощность которой
есть 2п.
(г) Используйте (в), чтобы показать, что существует 2К° свойств Р,
которые являются теоретико-решеточными в £*. Указание. Для каждой
/ Е 2^ пусть свойство Р/ включает Рп тогда и только тогда, когда
/(«) = !•
3.11. (Тенненбаум) Докажите, что существует вычислимое линейное
упорядочение <l целых чисел порядкового типа ш + ш* (где есть
порядковый тип отрицательных целых чисел), которое не содержит таких
бесконечных в. п. последовательностей, что они либо строго возрастают,
либо строго убывают в <l .
Указание. Постройте упорядочение, удовлетворяя для всех е Е и и
г < 2 требованиям
/?2e+i : We бесконечно ==> WeПAiф 0,
где Ао — начальный сегмент порядкового типа и и А\ = Aq. Пусть Ls
обозначает часть <l, определенную к концу шага s, и пусть —
позиции подвижных маркеров на Ls. Пусть I* = {х : ase ^l3 х bse }.
Предположим, что к концу шага s у нас есть такие L-интервалы Ц для
е ^ s, что ase <l 1 <l &e+i <l bse для e < s, и по крайней мере все
х Е [0,2s] уже L-упорядочены. Однако, в L-упорядочении может быть
больше элементов, чем {а|}е^, {bl}e^s. Если /?2е является
неудовлетворенным на шаге s + 1 и существует х Е /|е П Wet8, то удовлетворяем
Я2е, определив а*£1 = х и используя новые элементы, вошед¬
шие в L — упорядочение из интервала II*1, в качестве крайних точек
для интервалов /?+1, е < j ^ s -I-1 и добиваясь, чтобы I^\ С /?.
3.12. (а) Докажите, что не существует такого вычислимого
упорядочения L порядкового типа и + ш*, что его начальный сегмент А
порядкового типа ш является сжатым множеством. (Следовательно, по
симметрии финальный сегмент порядкового типа и* также не является
сжатым.) Указание. По мере перечисления элементов L будем их
окрашивать в красный и синий цвета так, чтобы в. п. множества R и В
красных (синих) элементов удовлетворяли требованиям Д2е : |ДП А\ ^ е
и Я2е+1 : |В П А\ ^ е.
(б) (Д.А. Мартин). Выполните часть (а) с «гг-иммунно» вместо
«сжато». (см. Джокуш [1968а, следствие 4.5].)

260
Глава X. Решётка в. п. множеств
3.13 	Замечания. Первый пример максимального множества
построил Фридберг [1958а] он же определил е-штаты. Упрощенное построение
теоремы 3.3 принадлежит Ейтсу [1965], который первым построил и
полное максимальное множество (упражнение 3.8). Отсюда следует, что не
существует такого свойства «жидкости» дополнения А в. п. множества
Ау которое бы гарантировало неполноту А. Однако, Марченков [1976а]
нашел другой тип свойства множеств в стиле Поста, который уже
гарантирует их неполноту. Таким свойством является свойство быть rj-
максимальным множеством, которое является также нижним
сечением некоторого вычислимого линейного упорядочения и. ^-максимальное
множество — это такое множество, которое является максимальным,
если в его определении натуральные числа заменить классами
эквивалентности по некоторому в. п. отношению эквивалентности. Для
доказательства см. Одифредди [1981].
§ 4. Мажорные подмножества и r-максимальные
множества
Если А С. В являются в. п. множествами и В ф* Л, то существует
несколько способов формализации того, что множество А расположено
«близко к» множеству В. Например, А является максимальным в В в
смысле упражнения 3.9, или А может быть дополнено до о; в точности
теми же в. п. множествами, которые с точностью до конечных множеств
дополняют В до и.
4.1 	Определение. Для в. п. множеств А С В множество А
называется мажорным подмножеством В (пишется А Ст В)у если В — А
бесконечно и для каждого в. п. множества W справедлива импликация
BC*W=>AC*W. (4.1)
(Заметим, что (4.1) эквивалентно условию В С W => А С* W.)
Если А и В такие в. п. множества, что A Coo By то А Ст В
тогда и только тогда, когда не существует такого вычислимого
множества Я, что R С В и R — А бесконечно (следствие II. 1.10 и
упражнение II. 1.23). Мажорные подмножества полезны при разработке
разрешающих процедур для определенных подклассов элементарной теории
в. п. множеств, они также дают простые примеры нетривиальных г-
максимальных множеств, определение которых подсказано определением
максимального множества.

§ 4• Мажорные подмножества
261
4.2 Определение, (i) Бесконечное множество С называется г-сжатым,
если не существует такого вычислимого множества R, что RDC и RDC
оба бесконечны.
(ii) 	В. п. множество А называется r-максимальным, если А г-сжато.
4.3 Предложение. Предположим, что А Соо В и В г-максимально.
Тогда А Сm Д тогда и только тогда, когда А г-максимально.
Доказательство. (=>) Предположим, что А Ст В. Чтобы убедиться,
что А является г-максимальным, зафиксируем произвольное
вычислимое множество R. Пусть R — We и R = W{. Тогда We U Wi = и> Э В,
поэтому либо Wef)B, либо WiDB бесконечно. Пусть, например,
выполнена первая возможность. Тогда В С* We ввиду г-максимальности В.
Отсюда А С* We, потому что А Ст В. Следовательно, Wi П А конечно
и поэтому R не расщепляет А.
(<=) Теперь пусть А — r-максимально, но А (£т В. Выберем
такое в. п. множество W Э В, что |W П (Д — .А)| = оо, и произвольное
бесконечное вычислимое множество R С W. Из существования такого R
следует, что А не r-максимально. О
4.4 Следствие. Если В г-максимально и А Ст В, то А
г-максимально, но не максимально.
Доказательство. Из утверждения 4.3 вытекает, что А г-максимально,
но А не максимально, т. к. А Соо Д Соо D
Очевидно, что любое максимальное множество Д r-максимально,
поэтому следствие 4.4 дает пример г-максимального множества, которое
не является максимальным, т. к. по теореме 4.6 любое невычислимое
в. п. множество Д имеет мажорное подмножество.
4.5 Предложение. Если А r-максимально и гг-просто, то А
максимально.
Доказательство. Если А r-максимально, то С*(А) не содержит
нетривиальных дополняемых элементов, но т. к. А гг-просто, то каждый
элемент из С* (А) является дополняемым. Следовательно, С* (А) изоморфна
двухэлементной булевой алгебре, и А максимально. О
В. п. множеств А Ст В таких, что А максимально в Д, не
существует, т. к. по упражнению 2.14 последнее означает, что В - А ко-в. п.
Таким образом, для данного невычислимого в. п. множества Д мы не

262
Глава X. Решётка в. п. множеств
можем надеяться построить А Ст В тем же способом, что и в § 3, но
неожиданно то же самое построение работает, если только
модифицировать таблицу, с помощью которой измеряются е-штаты.
4.6 	Теорема (Лахлан). Для каждого невычислимого в. п. множества
В существует такое в. п. множество А, что А Ст В.
Доказательство. Используем последовательность подвижных маркеров
{ Гп }neu>, такую же, как в теореме 3.3, за исключением того, что теперь
В — А = {do < d\ < •••}, где dsn — позиция Гп к концу шага s, и
dn = lims dsn. Будем удовлетворять требованиям
Ne : маркер Г6 двигается не более конечного числа раз ,
Ре : В С We => А С* We.
Определим в. п. таблицу конечных множеств { Ve^s }seu, (которые
могут может быть заданы своими каноническими номерами из
определения II.2.4) следующим образом:
х G Ve,s =dfn х G W€fS & (Vy ^ x)[y G W6fS U B8],
Пусть Ve = \JS Ve,s. Смысл этого определения состоит в том, что
в С We => к = we,
(4.2)
В ^ We =>- Ve конечно .
(4.3)
Теперь определяем е-штаты a(e,x,s) точно так же, как в
определении 3.2, но с Vet8 вместо Wei8. Выберем вычислимую 1:1-функцию /
с областью значений В и построим А Ст В следующим образом.
Шаг s = 0. Положим Aq = 0. d§ = /(0)» и Для всех е > 0 пусть
(Ре = — 1 (это значит, что маркеры Ге являются неприкрепленными).
Шаг s 4-1. Пусть у = f{s + 1). Выберем наименьшее е такое, что
dse < 7/, -1 < dse_x < у и либо cr(e,y,s) > cr(e,df,s), либо dse = -1.
Положим df+1 = у, d*+1 = — 1 для всех г > е и d?+1 = df для всех г < е,
тем самым перечисляя в As+i все df, г ^ е, если df > -1. (Если такого
е не существует, то перечисляем у в Ля+1.)
Лемма 1. Каждый маркер Ге двигается не более чем конечное число
раз, и в конце концов навсегда остается прикрепленным к некоторому
х > —1. (Следовательно, В — А бесконечно.)

§ 4• Мажорные подмножества
263
Доказательство. Фиксируем е и предположим, что Г* окончательно
установились для каждого г < е. Теперь Ге будет прикреплен к
некоторому ж, потому что В бесконечно, и с этого момента Ге передвинется
не более 2е+1 — 1 раз, каждый раз к элементу, вновь перечисленному
в В. о
Лемма 2. (Ve)[5 С We => А С* We].
Доказательство. Фиксируем е и предположим, что по индуктивному
предположению для всех г < е утверждение леммы выполняется. Пусть
а = {i : i < е Sz В CWi}.
По (4.2) и (4.3) для i < е имеем
ie(T=>Vi = Wi
и
г £ а => Vi конечно.
Отсюда, и по предположению индукции заключаем, что существует т
такое, что для всех п > т имеет место а{е — 1 ,dn) = а. Положим Va —
П{ Vi : г G а }. Тогда Va вычислимо перечислимо и В С Va, т. к. В С V
для каждого г G о. Предположим, что В С We. Тогда Ve = We, и в. п.
множество U =dfn Var\Ve содержит В. Но В не является ко-в. п., поэтому
U \ В бесконечно, а именно,
(3°°s)(3a;)[a; G Bs+1 — Bs & a(e - 1, ж, s) = a & x G ^е>5]. (4.4)
Но если V€C\(B — А) бесконечно, то мы получаем противоречие таким же
образом, как в лемме 2 теоремы 3.3, рассматривая dp G Ven(B — A), m <
р, и замечая, что Гр передвинется к некоторому элементу ж, который
удовлетворяет бескванторной части (4.4). Следовательно, (В — А) С*
ve. D
4.7-4.12 Упражнения
4.7. Докажите, что если А Сш В и В Cm С, то А Ст С.
4.8. Пусть А Сщ В и / — взаимно однозначная вычислимая
функция с областью значений В. Рассмотрим «pullback» множества А: А =
ГЧА).
(а) Докажите, что А ^т А.

264
Глава X. Решётка в. п. множеств
(б) Покажите, что А не имеет гг-простых (а значит, и максимальных)
надмножеств. Указание. Неоднократно примените теорему 2.5.
4.9 (Лерман). Для r-максимальных множеств А и В будем писать
А ~ В, если A U В Соо и-
(а) Докажите, что ~ является отношением эквивалентности на г-
максимальных множествах.
(б) Докажите, что для r-максимальных множеств А, В, если А ф* В,
то А ~ В тогда и только тогда, когда А Г) В Ст A\J В.
4.10 Определение, (i) Пусть даны в. п. множества А Соо В.
Множество А называется маленьким в В (что записывается в виде A Cs В),
если для каждой пары в. п. множеств X, Y из X П (В — А) С Y следует,
что Y U (X — В) в. п.
(ii) Множество А называется маленьким, если A Cs В С о; для
некоторого в. п. множества В. (Интуитивно это значит, что В — А настолько
велико, что если Y содержит X П (В — А), то Y содержит часть X,
достаточную для того, чтобы Y U (X — В) являлось в. п.)
4.11 (Стоб [1979]). Докажите следующие утверждения:
(a) Если А С В и А вычислимо, то A Cs В.
(b) Если А С В и В вычислимо, то A Cs В.
(c) Если А С С С В и A Cs С, то A Cs В.
(d) Если А С С С В и С Cs В, то A Cs В.
(e) Если A Cs В vi В невычислимо, то A U В не в. п.
4.12° (Лахлан [1968d]). Покажите, что если В в. п. и невычислимо, то
В имеет маленькое мажорное подмножество А (что будет записываться
в виде А Сsm В), а именно, A Cs В и А Ст В. Указание. Постройте
А Соо В, удовлетворяя требованиям Ре из доказательства теоремы 4.6,
а также требованиям
Ni : У D Xi П (В - A) => (X* - В) U Y{ в. n. ,
где { (Xj, Y{) — перечисление всех пар в. п. множеств. Приоритетное
упорядочение требований — iV0, Ро, Ni, Pi, Фиксируем вычислимые
перечисления { Xj>s }s€u; и { Yi^s множеств Xi и У*. Для
удовлетворения Ni определите индукцией по s g(i,s) и где д играет роль,
подобную роли д из теоремы 2.5 Оуингса о разложении. Для s = 0 пусть

§ 4■ Мажорные подмножества
265
g(i, о) = о, Zi,о
g(i,s + 1) :
= 0. Для s + 1 пусть
(/хж)[ж G (Ps-fi -^-s)
n(ZjjS — У^)],
к s -f 1
если такой х существует,
в противном случае.
Здесь ZiiS+1 = {х : х е XiyS+i к х ^ #(г,s + 1) } U ZiyS.
Элементы из (J3e+i — ^s)n(Zj5S+i — Yi,s) называются запрещёнными с
приоритетом N{ от перечисления в А8+\. (Заметим, что только
конечное число элементов являются навсегда запрещёнными с приоритетом
N{, потому что, если Z{ бесконечно, то lims g(i,s) = оо.) Измените шаг
s + 1 из теоремы 4.6, выбирая такое наименьшее е, что dse < у, и для
некоторого j ^ е
- l,y,s) = <r{j - l,€,s),
< °{j,dse,s)
и нет чисел d|, k ^ s, запрещённых какими-нибудь Ni, i ^ j.
Затем определите d|+1 = ?/ и перечисляйте в As+i (ради Pj) все
элементы d£, е ^ к. (Если такого е не существует, то перечисляйте у
в А8+\.) Тогда каждое требование Pj удовлетворяется, т. к. каждое Nt
навсегда запрещает не более конечного числа элементов. Чтобы
проверить iVj, зафиксируйте i и положите а — {e:e^ikBC We }. Тогда
В С Va, поэтому А С* Va. Выберите хо такое, что х G A U Va для всех
х ^ х0 и определите
Uiy8 = {х : х е Хиз - Bs к х ^ g(i, s)
& (Vy)[z0 V^)] }.
Предположим, что Yi D Xif) (В — А). Тогда limSg(i,s) = оо, и поэтому
Х{ — В С* Ui, и, следовательно, Х( — В =* Ui — В. Теперь докажите, что
Ui UY{ =* (Х{ - В) UY{, поэтому последнее множество в. п. и TV,
удовлетворено. (Чтобы закончить это рассуждение, следует заметить, что уже
имеется включение * D . Чтобы получить включение С*, используйте
запрет, устанавливаемый Ni против элементов х G f/j,s П (J35+i - Л5),
которые перечисляются в Л до того, как они появляются в У*, замечая,
что UUs С Этот запрет не будет нарушен никаким Pj, j < г, т. к.
каждый х G Uit8 находится уже в!^. К тому же lims g(i,s) = оо.
Следовательно, Ui П В С* у;, что и доказывает требуемое включение С* .)

266
Глава X. Решётка в. п. множеств
4.13 	Замечания. Лахлан доказал теорему 4.6 в работе [1968с], а
затем в [1968d] — более сильный результат (упражнение 4.12), который
был необходим в его разрешающей процедуры для V3 — предложений,
истинных в £*. В § 2 главы XVI обсуждение этой темы будет
продолжено.
§ 5. Безатомные r-максимальные множества
5.1 Определение. Кобесконечное в. п. множество А называется
безатомным, если А не имеет максимального надмножества.
В упражнении 4.8 было показано, что безатомные множества
существуют. В упражнении 5.5 приводится простое прямое доказательства
этого факта, г-максимальные множества, с которыми мы до сих пор
встречались, не являются безатомными, т. к. они являются мажорными
подмножествами максимальных множеств. В этом параграфе мы построим
безатомные г-максимальные множества, а в следующем — безатомные
гг-простые множества. Эти построения похожи на построение
максимального множества, но используют маркеры, упорядоченные в
определенные нелинейные конфигурации, а также е-штаты, работающие с
некоторыми новыми сильными таблицами взамен стандартных
перечислений { WeiS}.
Для последующих теорем желательно изменить наше интуитивное
представление о подвижных маркерах. Вместо изображения маркеров
{ Гп }пеи; движущимися по элементам, мы теперь их будем представлять
в виде неподвижных «окон», в которых появляются элементы, причем
они время от времени могут меняться (увеличиваться). Мы
продолжаем использовать dsn для обозначения элемента, связанного с Гп к концу
шага s. Основное действие, в котором маркер Гп рассматривался как
передвигающийся с позиции dsn на позицию dsn+k, теперь читается как
«окно Гп притягивает dsn+k на шаге s +1». В построениях, когда
маркеры упорядочены в определенные геометрические конфигурации (такие,
как квадратная таблица или вершины дерева) и движение элементов
частично определяется их текущей позицией, представление о
последовательности { dsn }пеи> становится более понятным, хотя её
математическая сущность остается неизменной.
5.2 Определение (Робинсон [1967а]). Последовательность (не
обязательно в. п.) { Нп }пеи> в- п- множеств образует башню, если [Jn Нп = uj,
и для всех п имеем Нп Соо Нп+\.

§ 5. Безатомные г-максимальные множества
267
5.3 	Лемма (Робинсон [1967а]). Если А — в. п. множество,
{ Нп }neu> — такая башня, что A Coo Я(ь и требование
Рп : Wn С* Япили А С* Wn
выполняется для каждого п, то А является безатомным и
г-максимальным.
Доказательство. Чтобы проверить, что А является безатомным,
предположим, что Wn кобесконечно и Wn Э А. Тогда Wn С* Нп Соо
Яп+1 Coo cj, и Яп+1 является свидетелем того, что Wn не
максимально. Чтобы проверить, что А является г-максимальным, предположим,
что R — вычислимое множество, например, R = W{ и R = Wj. Если
R разбивает А на бесконечные части, то при п = i,j второе
предложение требования Рп не выполняется. Поэтому Wi С* Я*, Wj С* Hj
и ш = Wi U Wj С* Я*, где k = max{z,jf}, что противоречит условию
Н-к Соо Нк+\* D
5.4 	Теорема (Лахлан [1968с], Робинсон [1967а]). Существует
безатомное г-максимальное множество А.
Доказательство. Мы имеем маркеры { Г^-) }ijzим упорядоченные в
виде квадратной таблицы, где dsn означает элемент, связанный с Гп к концу
шага s, dn =dfn Иms dsn, As = { dsn }n€u, и A = { dn }n€u;. Для каждого n
мы должны удовлетворить требованиям:
Nn : dn - lims dsn < oo,
Pn : Wn С* Hn или А С* 1УП
и
Дп : Яп — в. п. множество,
где для каждого г мы определяем столбцы,
cl - beи,
Ci — { d(ij) }j€u>
И
Нп = л udJfCj : i ^ n}).
Чтобы удовлетворить этим требованиям, определим сильную
таблицу { Сn,s }n,seu> и проведем с небольшими изменениями, объясняемыми

268
Глава X. Решётка в. п. множеств
ниже, построение Фридберга максимизации е-штатов относительно
множеств Un,s- Затем положим Un = {JsUn,s• Определим множества
Un,s = {х : {3t ^ s)[x = d^^kx Е Wn,tkn < i\ }
и
сг(е, Ху s) = {i : i ^ ekx Е } — е-штат элемента х на шаге s.
Шаг s = 0. Определяем (Рп—п.
Шаг s + 1. Находим такое наименьшее е, что для некоторого г, е <
i ^ s, выполняется cr(e,df,s) > cr(e,d|,s). Выбираем г > е, г ^ s с
насколько это возможно большим cr(e,df,s), и определяем d|+1 = df.
Будем говорить, что Ге притягивает df. (Если такого i не существует,
то ничего не делаем.) Перечисляем d£, где е ^ k ^ s, к ф г, в А. (По
техническим причинам теперь необходимо перечисление в А всех этих
элементов, а не только dj, е ^ /г < г. Эту процедуру будем называть
сбросом.) Для всех j < е положим d^+1 = d*, и для всех к > 0 dse^_ 1к =
Цель сброса состоит в следующем. Если z Е то z < s ^ d*, и
поэтому либо z < d8e у либо z = d|+1, либо, в противном случае, z Е ^4s+i.
Таким образом, как будет показано в лемме 3, отсюда следует, что если
Ге притягивает элемент у = d\ на шаге s + 1, то на шаге s у должен
был увеличить свой е-штат. (см. также объяснение для (6.5).)
Лемма 1. Для каждого п dn = lim5dsn существует и А = {dn }п€а;.
Доказательство. Доказательство того, что lims dsn существует,
проводится индукцией по п точно так же, как в лемме 1 из теоремы 3.3 или в
теореме 4.6.
Лемма 2. (Vn)[Wn С* Нп или А С* Wn\.
Доказательство. Доказательство проводится индукцией по п.
Отметим, что Uo бесконечно тогда и только тогда, когда А С Uq. (Если Uo
бесконечно, то из определения Щ и построения А следует, что А С {/0. В
другую сторону это получается сразу, так как по лемме 1 А бесконечно.)
Зафиксируем п > 0 и предположим, что для всех т < п выполняется
Um П А конечно или А С* Um. (5.1)
Пусть а = {т : т < п k А С* Um } — истинный (п — 1)-штат (почти
всех элементов) А, и пусть Uo- = f){Um : га Е сг}. Если Un П Ua =*

§ 5. Безатомные г-максимальные множества
269
0, то Un П А =* 0 и, по определению С/п, имеем Wn С* Нп. Но, если
Un П U(j бесконечно, то по построению А С* Un. Таким образом, (5.1)
выполняется и для т = п.
Лемма 3. (Ve)[#e — в. п. множество].
Доказательство. Фиксируем е. Пусть а = {i : i ^ е & А С* [/*}.
Выберем такое п, что для всех т ^ п выполняется сг(е, dm) = сг. Затем
выберем такой шаг s, что для всех т ^ п имеем dm = dsm. Определим
в. п. множество Не, перечисляя у = сРк в Ле на шаге £ + 1 > s, если
только п ^ к ^ t, и выполняются условия:
(3»)(3j)[* = (t,j)&i^e], (5.2)
(Vm)[n ^ т к => a(e1dtm1t) = а] (5.3)
(Vm ^ fc)[4, = 4J-1]. (5.4)
Мы утверждаем, что если у = сРк перечисляется в Не на шаге t + 1,
то либо у = с4, либо у € А. Если у ф dk, то выберем такой первый шаг
v > t + 1, что некоторый маркер Гш, где т < к, притягивает некоторый
элемент z. Теперь по условиям (5.3), (5.2), выбору s и определению Upy
для всех р ^ е элемент у G UPyt тогда и только тогда, когда у G UPyV.
По (5.2), выбору s и определению Up для всех р > е элемент у G UPit
тогда и только тогда, когда у G UPyV. Но по условию (5.4) Гш не
притягивает у на шаге £ + 1, поэтому он не притягивает у и на шаге v.
Следовательно, у Ф z, поэтому по свойству операции сброса будет у G Av,
т. 	к. у = (ft ^ dvvZ\- Следовательно, согласно сформулированному выше
утверждению Не U А =* Не и поэтому Не в. п. Ц
5.5-5.10 Упражнения
5.5 	(Мартин [1963]). Дайте простое прямое доказательство
существования безатомного в. п. множества А, удовлетворяя для каждого е
требованиям
Ре : [А С We & А £* Же] => (3°°n)[|Fn П We\ > 2],
где { Fn }П£и; — фиксированная сильная таблица непересекающихся
конечных множеств, в объединении дающих и таких, что для каждого
п выполняется |Fn| = n + 1. Указание. На шаге s + 1 для каждых е и
n, е < п ^ s, для которых выполняется |Fn — (Же>в U А8)\ = 1, пусть

270
Глава X. Решётка в. п. множеств
х(п,е) — единственный элемент из Fn - (WefS U As). Тогда
перечисляем х(пуе) в А. (см. также упражнение XI.2.8, где доказывается, что
множество А может иметь произвольную высокую в. п. степень.)
5.6. Покажите, что множество А из теоремы 5.4 не имеет гг-простого
надмножества.
5.7. (а) Используя доказательство леммы 3, убедитесь, что в
теореме 5.4 фактически показано, что для любого столбца С{ = { d^j\ }j€u,
множество AuCi в. п. (Действительно, пусть R — произвольное
вычислимое множество, для которого существует такое п, что если (г, j) Е Д,
то г ^ гг. Докажите, что A U { d* : k Е R } в. п.)
(б) Сделайте вывод, что определенная в (1.3) из § 1 формула (Зж)
Sim(a;) ложна в С*(А).
5.8. Измените построение из теоремы 5.4 так, чтобы получить такое
безатомное г-максимальное множество Л, что предложение (3a;)Sim(a;)
истинно в £*(.А). (Из упражнений 5.7 и 5.8 сделайте вывод о
существовании таких безатомных r-максимальных множеств А\ и Аг? что в С*(А\)
и в £*(Лг) не выполняются одни и те же предложения первого порядка.)
Указание. Добейтесь, чтобы Но являлось простым в £*(Л),
удовлетворяя для каждого п требованию
Qn : | Wn П А\ = оо => |Wn П (Я0 - А)| = оо.
Конфликт с требованиями вида Рп из теоремы 5.4 разрешается при
помощи следующего приоритетного упорядочения: Ро> Qoi Ни Qь
5.9. Докажите, что если В — r-максимальное множество и A CSm В
(как определено в упражнении 4.12), то предложение (3s)Sim(x)
истинно в С*(А). (Заметим, что по предложению 4.3 множество А г-
максимально.)
5.10 	(Лахлан [1968с, теорема 8]). Приведите альтернативное
построение безатомного г-максимального множества А в стиле упражнения 5.5.
Пусть {Fj — таблица таких непересекающихся конечных
множеств, что \Fj\ = 2J j. Пусть Fj^s = Fj — As. Для каждого г < j на
первом шаге, когда Wi,s содержит не менее половины элементов из FjtS,
перечисляем остальные элементы из FjiS в А8+Наконец, чтобы
максимизировать е-штаты, пусть маркеры из теоремы 3.3 вместо целых чисел

§ 6. Безатомные гг-простые множества
271
двигаются по множествам Fj,s, причем в данном случае е-штатом
множества F на шаге s является
сг(е,F,s) = {i : i ^ е к F С Wi,s }•
Докажите, что А г-максимально и не имеет гг-простого надмножества.
Указание. Чтобы проверить, что А г-максимально, предположите, что
вычислимое множество R расщепляет А. Пусть We = R и W{ = R,
где е < г. Покажите, что если для бесконечно многих j выполняется
е Е сг(е, F/), то это верно и для почти всех jf, и аналогично для г.
5.11 	Замечания. Безатомные r-максимальные множества были
построены Робинсоном [1967а] и, независимо, Лахланом [1968с], хотя
приведенное здесь построение отлично от обоих этих построений. Она была
придумана Джоном Норстадом и появилась в статье Лермана и Соа-
ра [1980b, теорема 2.15], в связи с расширением разрешающей процедуры
Лахлана для одного фрагмента элементарной теории решетки £ *.
§ 6. Безатомные гг-простые множества
В следствии 2.7 мы видели, что кобесконечное в. п. множество А
является гг-простым тогда и только тогда, когда С(А) образует булеву
алгебру. Естественно спросить: какие именно булевы алгебры реализуются
таким образом. Во-первых, легко показать (см. упражнение XV.2.12),
что тип изоморфизма С* (А) определяет его и для С(А), и поэтому
достаточно классифицировать первый из них. Сейчас мы построим такое
в. п. множество Д, для которого С* (А) является счётной безатомной
булевой алгеброй. В § 7 этот метод будет модифицирован, чтобы показать,
что произвольная булева алгебра с достаточно эффективным
представлением изоморфна С* {В) для некоторого в. п. множества В.
6.1 Теорема (Лахлан [1968с]). Существует безатомное гг-простое
множество А.
6.2 Следствие. Существует такое в. п. множество А, что С*(А)
является счтной безатомной булевой алгеброй.
Доказательство. Если для множества А из теоремы 6.1 булева алгебра
С*{А) содержит атом С*, то его дополнение в С*(А) является коатомом
D*, поэтому D является максимальным надмножеством множества А,
а это противоречит тому, что А безатомно. О

272
Глава X. Решётка в. п. множеств
Доказательство теоремы 6.1. Зафиксируем эффективное
1:1-кодирование / из 2<и} на uj такое, что если lh(a) < lh((3), то f(a) < /(/3). Пусть
щ — dfn /_1(0- Для каждого г Е и) мы имеем маркер Г*, расположенный
на вершине а* бинарного дерева 2<и}. Для каждой вершины а Е 2<ш
длины е определим е-регион вершины Ra = {/3:аС/3}и
соответствующие конусы элементов:
Са — { d\ : оц Е Rq }
и
Cq — { di . ot{ Е Rqc })
где, как обычно, df — натуральное число ж, связанное с маркером Г;
к концу шага s, и d\ = — 1, если такого х не существует; d* = limsd*
и А = { di }ieu>- Договоримся, что df > — 1 тогда и только тогда, когда
г ^ s.
Лемма 1. Чтобы построить требуемое множество Ау достаточно
удовлетворить следующим требованиям:
Ре : lh(a) =e=>[CQnWe=* <й или Са С* We],
и
Na : A U Са — в. п. множество.
Доказательство. Предположим, что А С We и We максимальное
множество. Тогда Wе бесконечно, и поэтому для некоторого а со
свойством lh{a) = е имеем Са 2* И^е и поэтому, благодаря требованию Ре,
Сс* П И^е =* 0. Выберем /3 D а. Тогда ввиду требования Np имеем
В = A U Ср U We — в. п. множество и We Coo В Coo что
противоречит максимальности множества We. Таким образом, А — безатомное.
Теперь предположим, что А С We. Чтобы заключить, что А — гг-
просто, по следствию 2.7 достаточно показать, что AuWe в. п.
Определим
V, = A U (lj{ Са : lh(a) = е k We П Са =* 0 }).
Тогда, благодаря требованиям iVa при lh(a) = е, получаем, что Ve в. п.,
а вследствие требования Ре должно быть Ve =* A U Wе. Это завершает
доказательство леммы 1.
При построении множества А ситуация, позволяющая нам
произвести позитивное действие, называется «Г* хочет притянуть dsj из-за
(ради) Ре на шаге s + 1 » и определяется в виде конъюнкции следующих
условий:
е ^ г;
(6.1)

§ 6. Безатомные гг-простые множества
273
г < 3\
(6.2)
И
си a.j лежат в одном и том же е-регионе.
(6.4)
(е-штаты cr(e,a;,s) определяются обычным образом, как в
определении 3.2.)
Говорят, что целое число, которое ещё не прикреплено ни к какому
маркеру и не перечислено в А, является свободным.
Шаг s = 0. Определяем d^ = 0.
Шаг 5 + 1.
Этап 1 (а) (Притягивание). Выбираем наименьшее г, затем
наименьшее е и затем наименьшее j такие, что выполняется условие: е, i,j ^
5 и Гг хочет притянуть dj из-за Ре. Определяем d?+1 = dsj. Мы говорим,
что Гг притягивает dSj.
(б) (Сбрасывание). Для каждого к такого, что i ^ Ц s и i / j,
перечисляем (сбрасываем) dsk в А. (Если таких е, г, j не существует, то
для всех к ^ s определяем d*k+1=d°k.)
Этап 2. Каждому маркеру Г^, где к ^ s + 1, не прикрепленному
на данный момент ни к какому элементу из Л, в порядке увеличения к
назначаем первый свободный элемент > 5 + 1. Перечисляем в все
свободные элементы, которые ^ 5 -1-1.
Построение на этом завершается.
Целью дополнительного сброса на этапе 1(6) ( при котором в А кроме
элементов dsk, г ^ к < j, перечисляемых при обычных условиях,
перечисляются и элементы dsk1 где j < к ^ s) является выполнение следующего
свойства, необходимого при доказательстве леммы 3.
Если dts+1 ф d? и г ^ к ^ 5, то у = dsk перечисляется
в А на шаге 5 + 1, если только у не является (6.5)
элементом, который притягивают.
Отсюда следует, что элемент у может быть притянут ради Ре только
в том случае, когда он только что изменил е-штат, т. к. если некоторый
Гг хочет притянуть его в этот момент, то либо у сразу притягивается
маркером Г*',, для некоторого г' ^ г, либо у сбрасывается в А, потому
что Г*' притягивает некоторый z ф у. Соответствующая модификация
этого факта будет играть ключевую роль в § 7, особенно в лемме 2.

274
Глава X. Решётка в. п. множеств
Ютметим, что когда свободный элемент у назначается маркеру на
некотором шаге s + 1, то е-штатом элемента у является 0, потому что
у > s + 1. Следовательно, до тех пор, пока элемент у не будет
назначен маркеру и затем не изменит свой е-штат, он не хочет, чтобы его
притягивали.)
Лемма 2. Для каждого п dn = lims dsn существует, и А = {dn }neu>-
Доказательство. Первая часть получается индукцией по гг, как в
доказательстве леммы 1 теоремы 3.3 или в доказательстве теоремы 4.6.
Вторая часть вытекает из того, что каждое число в конечном счете либо
назначается некоторому маркеру, либо перечисляется в А.
Лемма 3. Для каждого е требование Ре удовлетворяется.
Доказательство. Зафиксируем е и предположим, что для всех i < е
требование Pi выполняется. Зафиксируем а длины е. Так как почти
все элементы х Е Са имеют один и тот же (е — 1)-штат сг, мы можем
выбрать такое п > е, что для всех т ^ п, если dm Е СQ, то выполняется
сг(е — 1 ,dm) = а. Предположим, что W€ расщепляет Са на бесконечные
части. Выберем такие j > i > п, что cr(e,dj) = сг, a(e,dj) = a U {е},
а С OLi и а С otj. Затем выберем такой шаг s, что для всех k ^ j
dsk — dk и cr(e,dfc,s) = a(e,dk). Тогда на шаге 5-1-1 маркер Г; хочет
притянуть d* для Ре, поэтому для некоторого к ^ j имеем dp'1 ф dsk,
что противоречит выбору 5.
Лемма 4. Для каждого а АиСа в. п. множество.
Доказательство. Зафиксируем а и пусть е — lh(a). По лемме 3 для
каждой вершины /3 длины е существует такой е-штат сг^, что для почти
всех х G С@ выполняется сг(е,а;) = сг^. Выберем такое n, е ^ n, ап G i?Q,
что для всех т ^ п выполняются
ШЩР) = е & dm е С!3] (6.6)
и
(WP)[[lh(l3) = е k dm € Сц] => <r(e,dm) = <j$\. (6.7)
Выбираем такой шаг v, что для всех т ^ п выполняется
dm = dvm и cr(e, d,n) = a(e,dvm,v). (6.8)
Определяем в. п. множество Са, перечисляя у = d*k в Са на шаге
t 4- 1 > v, если только выполняются условия: к ^ n, а С cr(e, y, t) =

§ 6. Ез -булевы алгебры
275
сга, и нет маркера Г*, который хотел бы на шаге t +1 притянуть элемент
у. Мы утверждаем, что АиСа =* АиСа, и поэтому последнее множество
является в. п. Очевидно, что Са С* Са, т. к. каждый dm Е Са, т ^ п,
в конце концов перечисляется в CQ.
Чтобы удостовериться, что Са С (7QUA, покажем, что не существует
элемента у = d£, перечисленного в (7а на шаге £+1, который позднее мог
бы покинуть е-регион Ra, не будучи перечисленным в А. Для получения
противоречия предположим, что 5 + 1 — наименьший шаг > t + 1, где ?/
переходит в другой е-регион. Тогда по (6.4) Г* притягивает у = dj ради
Ре' на шаге 5 + 1 для некоторых г, jf, е7 таких, что i<j^kne'<e.
Кроме того, по (6.5) для всех т < j имеем dsm = бьт, в противном случае
у Е As. В частности, d? = dj и, скажем, они равны х.
По определению Са теперь имеем, что Г* не хотел притянуть у ни
для какого Р6", е" ^ е' на шаге t + 1, поэтому a(e’,x,t) ^ a(e',y,t).
Но затем он сделал это на шаге 5 + 1, и поэтому по (6.3) <j(e',x,s) <
cr(e,52/5s)- Следовательно, cr(e,y,s) > a(e,y,t) = crQ, и поэтому по (6.7)
Гп хочет притянуть у на шаге 5 + 1. Таким образом, для некоторого т ^
п Гш притягивает некоторый элемент на шаге 5 + 1, что противоречит
условию (6.8). D
6.3 	Замечания. Первоначальное построение Лахлана [1968с] в
доказательстве теоремы 6.1 использовало е-штаты, работающие вместо
{ We,s } с более сложной таблицей { Ve,s }, и позволило притянуть
элемент у ради Ре только на таком шаге, когда у увеличивает свой е-
штат. Изложенная здесь измененная версия, предложенная М. Стобом,
использует для выполнения (6.5) дополнительный сброс. Это
значительно упрощает доказательство в § 7.
§ 7. * £3-булевы алгебры, представимые в виде
решеток надмножеств
7.1 Определение. Счётная булева алгебра В = ({bi}i€u>, ^,и,П/)
называется Hz-булевой алгеброй, если существуют такие вычислимые
функции / и $ и Ез-отношение R, что bi U bj = b/(*,j) 9 С bj = bg
и bi ^ bj тогда и только тогда, когда R{i,j). (В перечислении {bi
любой элемент из В может появляться более одного раза.)
Если А гг-просто, то по теореме П.1.9 и упражнению IV.1.12 С* (А)
является Ез-булевой алгеброй. Теперь мы докажем, что когда А про¬

276
Глава X. Решётка в. п. множеств
бегает по всем гг-простым множествам, С* (А) пробегает по всем Е3-
булевым алгебрам.
7.2 	Теорема (Лахлан [1968с]). Пусть В — произвольная
Е3-булева алгебра. Тогда существует такое гг-простое множество Ау что
С* (А) изоморфно В.
Доказательство. Пусть В = (В, С, U, П/ ) — Е3-булева алгебра с
нулевым элементом 0. Говорят, что последовательность { Ьо»Ьь • • • }
элементов из В порождает В, если их замыкание относительно операций
объединения, пересечения и взятия дополнения совпадает с В. Отображение
F из 2<и} в {0,1} называется представлением В, если существует
такая порождающая последовательность { Ьо> &1» • • • }» что F(a) = 0 тогда
и только тогда, когда Ьа = 0, где
ba =dfn (Р|{ bi : a(i) = 1}) П (Qf 6- : a(i) = 0 }). (7.1)
Теперь каждый элемент из В представим в форме \J{ba : а Е 5} для
некоторого конечного множества S С 2<и}. В частности,
bi = |^J{ ba : lh(a) = i -1-1 и a(i) = 1}.
Легко видеть, что если В0 и В1 — две счётные булевы алгебры с
общим представлением F, то В0 и В1 изоморфны. (Пусть {b® }, { b\ } —
соответствующие порождающие последовательности, тогда просто
отображаем Щ на Ь\.)
Очевидно, что последовательность В = {bo,b\,...} порождает В.
Исходя из вычислимых функций для объединения и пересечения, можно
найти такие вычислимые функции / и д, что
Ь/'(а) = ГНЬг : а(*) = !}. И Ъ9(ос) = : °(*) = °}-
Следовательно, будем иметь
F(a) = 0 «=> bf{a) П Ь'§{а) =0<=> Ь;{а) ^ bi(a).
Так как третье отношение есть Ез-отношение, то таковым является и
первое, и поэтому, по следствию IV.3.7 об аппроксимации Ез-отношений
существует такая вычислимая последовательность в. п. множеств {Ха,у :
а Е 2<и & у Е cj}, что
F(a) = 0 => (Зуо)(Уу ^ Уо)[Ха,у = ш\ & •
& F(a) = 1 => (Vy)[Xa,v =* 0]-
(7.2)

§ 7. * Из-булевы алгебры
277
Теперь определим вычислимую последовательность в. п. множеств
{Za : а е 2<и> } следующим образом:
Za = {J{X0<y:f3Caky^ lh(a)}.
Заметим, что Zp С ZQ, если (3 С а, и если F{(3) = 0, то существует
такой ?/, что \Za\ = оо для всех a Э /3, Z/i(a) ^ у. Таким образом,
множества ZQ обладают следующими свойствами, которые будут нам
необходимы:
F(a) = 0 <==> [Zy = ш\ (7.3)
для почти всех 7 D а, и
=* 0 => (V/3 С а)[^ =* 0]. (7.4)
(При доказательстве (7.3) (<£=) используется тот факт, что если F(a) =
1 и е > lh(a), то существует некоторая /3 Э a, lh(P) = е такая, что
также выполняется F(/3) = 1.) Каждую вершину а* отождествим с её
кодовым числом г, как это сделано в теореме 6.1, и вместо Zai будем
писать Z{. Пусть { Z{iS }г,$еи> — одновременное вычислимое перечисление
множеств { Zi }.
Сохраним все обозначения, соглашения и требования Ре, Na из
теоремы 6.1. Кроме того, будем предполагать, что We,s определено так же,
как в упражнении 1.3.11, и поэтому, как в I (3.3), справедливо
утверждение
(Vs)(3 не более одного (е,х))[х Е We,s+i - We,s]- (7.5)
Приводимое здесь построение множества А очень похоже на построение
из теоремы 6.1, за исключением того, что с Г* связывается введенное
выше «пинающее множество» Z», и как только в Z{ на шаге s появляется
новый элемент, мы перечисляем (пинаем) d\ в А. Это обеспечивает, что
предел di = lims df существует тогда и только тогда, когда Z{ конечно,
поэтому F является представлением С*(А).
То обстоятельство, что di = lims d\ не всегда существует, делает
необходимым внести в первоначальное построение несколько
изменений. Во-первых, мы будем позволять Г* притягивать dj, если только
\Zi,s\ < j• Это гарантирует, что если di не определено (т. е. Z\
бесконечно), то ни для какого j > г Г* не притягивает d* бесконечно число
раз. (В противном случае бесконечное притягивание маркером могло
бы заставить dj стать неопределенным, хотя Zj при этом могло быть
конечным.) Во-вторых, если когда-либо по какой-нибудь причине
выполняется d°+1 ф di, то мы перечисляем (сбрасываем) в А все такие

278
Глава X. Решётка в. п. множеств
элементы dj ^ ds8 (возможно за исключением dj+1), что \Z{y8\ < j, т. е.
все элементы dj ^ dj, которые Г* может быть позднее захочет
притянуть. Это обеспечивает выполнение соответствующего аналога свойства
(6.5), который необходим в лемме 3.
Будем говорить, что Г* хочет притянуть dj ради Ре на шаге s + 1,
если выполняются условия (6.1)—(6-4), а также
\Zits\<j- (7.6)
Шаг s = 0. Определяем d{] = 0.
Шаг s + 1.
Этап 1. (Притягивание) (То же самое, что и этап 1(a) из
доказательства теоремы 6.1.) Выбираем наименьшее г, затем наименьшее е
и затем наименьшее j такие, что выполняется условие: е, г, jr ^ s и Г*
хочет притянуть dj из-за Ре. Определяем dj+1 = dj и перечисляем dj
в А. Будем говорить, что Г* притягивает dSj.
Этап 2. (Пинок) Для каждого k, k^snk^j такого, что
Zk,s+i ф Zk,s, перечисляем (пинаем) dsk в А.
Этап 3. (Выбрасывание) Для всех р ^ s в порядке увеличения р
делаем следующее. Если d* был перечислен в А на шаге s + 1 и \ZPiS\ <
q ^ s, то перечисляем dsq в А, если только q не совпадает с j из этапа 1.
Этап 4• То же самое, что и этап 2 из доказательства теоремы 6.1.
Построение на этом завершается.
Лемма 1. Для всех j предел dj = lims dj существует тогда и только
тогда, когда Zj конечно и А = {dj
Доказательство. Зафиксируем j и для рассуждения по индукции
предположим, что для всех г < j лемма выполняется. Если Zj бесконечно, то
для бесконечно многих s к dSj применяется этап 2, и поэтому lims dj не
существует. Если Zj конечно, то этап 2 применяется к dj только
конечное число раз, и, например, после шага и уже не применяется никогда.
Пользуясь индуктивным предположением, выберем такой шаг v > и,
что для всех г < j выполняется либо dj = dj, либо \ZiyV\ ^ j. Теперь
ввиду условия (7.6) ни один Гг не может притянуть dj ни на каком шаге
s > v, поэтому после шага v связанный с элемент меняется не более
2J'+1 раз, и, следовательно, lims dj существует.
Лемма 2. Если какой-нибудь Г; хочет притянуть у = dj из-за Ре на
шаге s + 1, гао сг(е, г/, s) ф сг(е, ?/, s — 1), и, следовательно, для некоторого
г' ^ i маркер Г;' притягивает у.

§ 7. * Ез -булевы алгебры
279
Доказательство. Доказательство проводится индукцией по s.
Предположим, что лемма верна для всех шагов t ^ s. Рассмотрим шаг s + 1
и предположим, что Г* хочет притянуть у = d* из-за Ре на шаге s + 1.
Следовательно, ^ \Z^8\ < j• Для получения противоречия пред¬
положим, что cr(e,2/,s) = сг(е, г/, s — 1). К тому же ст(е,г/,$) ф 0, и поэтому
2/ не был назначен маркеру в качестве свободного элемента в конце
шага s. Следовательно, для некоторого k ^ j имеет место у = dsk~l.
Более того, d\ = d^~l, т. к. в противном случае в ходе выполнения этапа 3
на шаге s у был бы перечислен в А. Следовательно, Г* хотел притянуть
у на шаге s. По индукционному предположению для некоторого г' ^ г
Г*/ притягивает у на шаге s, что противоречит равенству у = dj.
Следовательно, a(e,yys) ф a(e,y,s — 1). Но на каждом шаге свой е-штат
меняет не более одного элемента у, поэтому число j на этапе 1 является
единственным. Это означает, что у притянут на шаге s + 1.
Лемма 3. lh(a) = е => [Са П We =* 0 шш <7Q С* We], где <7а = { di :
a Cqj u di существует }.
Доказательство. Это доказательство похоже на доказательство
леммы 3 из теоремы 6.1 за исключением того, что мы рассматриваем только
такие ш, для которых dm существует. Выбираем е, г и j как в лемме 3
из теоремы 6.1, за исключением того, что теперь дополнительно
требуется, чтобы di и dj существовали и выполнялось j > \Z{\. (Так как di
существует, то по лемме 1 Z\ конечно, и поэтому для каждого
соответствующего г такой j существует.) Так как у = dj имеет более высокий,
чем d{, е-штат, то Г* хочет притянуть у на всех достаточно больших
шагах. Следовательно, по лемме 2 у в конце концов окажется утянутым
от Tj, что противоречит равенству у = dj.
Лемма 4. Для каждой вершины а множество AVJCa является в. п.
Доказательство. Зафиксируем а и пусть е = lh(a). Выберем ар и п
как в доказательстве леммы 4 из теоремы 6.1, за исключением того, что
теперь должен существовать предел dn, и условия (6.6) и (6.7)
применяются только к тем dm, которые существуют. (Такой п существует,
потому что если dm существует только для конечного числа ат Е Ra,
то Са является конечным и, очевидно, A U Са в. п.). Выбираем шаг v,
удовлетворяющий условию (6.8) для всех таких т ^ п, для которых dm
существует, \ZUyV\ = \Zn\ и, к примеру, равно р, и выполняется
утверждение
(Vm ^ p)[dm существует
dvm = dm].
(7.7)

280
Глава X. Решётка в. п. множеств
(Так как dn существует, то по лемме 1 Zn конечно, и поэтому v
существует.) Используя v как и раньше, определяем Са. Теперь доказательство
является таким же, как и в лемме 4 из теоремы 6.1, потому что, хотя
больше и не выполняется свойство (6.5), мы знаем, что если Г*
притягивает у = dj на шаге s + 1 > £ + 1, то \Z{iS\ < j и, следовательно, d\ = d\,
т. к. в противном случае в ходе выполнения этапа 3 у был бы сброшен.
Как и ранее, мы утверждаем, что не существует элемента у = d\,
перечисленного в Са на некотором t +1, который позднее мог бы
покинуть е-регион Ra, не будучи в конце концов перечисленным в А. Для
получения противоречия предположим, что s + 1 > £ + 1 — наименьший
шаг > t + 1, где у переходит в другой е-регион. Тогда Г* притягивает
у = dSj ради Ре> на шаге s+ 1 для некоторых г, j, е1 таких, что г < j ^ к
и е' < е. Но, так как df = d\ и Г* не хотел притянуть у на шаге £,
то у должен был увеличить свой е-штат между шагами s + 1 и t + 1.
К тому же \Zn\ < j, т. к. в противном случае из-за условия (7.7) у в
конечном счете перечислится в А. Следовательно, Гп хочет притянуть
у на шаге s + 1, и поэтому по лемме 2 некоторый Гш, т ^ п,
действительно притягивает у на шаге s + 1. Но если lims dsm не существует,
то у позднее войдет в Л; а если limsdsm существует, то это
противоречит предположению о том, что d^ = dm для всех т ^ п таких, что dm
существует.
Используя лемму 4, легко построить последовательность {В* }i^u
элементов из £*, которая порождает С* {А) и имеет в качестве
представления отображение F. А именно, по лемме 4 для каждой вершины
a G 2<и} множество Ва = A U Са является в. п. Тогда в равенстве (7.1)
в роли Ьа выступает Ва, и поэтому мы можем положить
Bi = [J{ Ва : lh(a) = i + 1 & а(г) = 1 }. О
7.3 	Замечания. Для в. п. множеств, для которых С* (А) не является
булевой алгеброй, алгебраических интерпретаций, подобных теореме 7.2,
не известно. Но так как по упражнению 2.18 £* вложима в
произвольную бесконечную С* (А) такого вида, то кажется вероятным, что любая
подобная характеризация должна оказаться сложной.

Глава XI
Связи между структурой в. п. множества и
его степенью
В главах I-IX мы изучали свойства в. п. степеней R, в частности, в
упражнениях IV.4.5, VII.1.6 и следствиях VIII.3.4 и VIII.3.5 изучались
классы Нп и Ln n-высоких и n-низких степеней. В главе X мы изучали
алгебраические свойства в. п. множеств, рассматривая их как
элементы дистрибутивной решетки по включению £. В этой главе мы
соединяем эти два направления, изучая взаимосвязь между алгебраической
структурой в. п. множества и его тьюринговой степенью (то есть, его
«объемом информации»). Мы рассматриваем высокие (низкие) степени
как степени, имеющие большой (соответственно незначительный) объем
информации.
Построенное в теореме Х.3.3 максимальное множество потребовало
сложной конструкции, и как с алгебраической, так и с вычислительно-
сложностной точек зрения может рассматриваться как сложное. В § 1
мы доказываем, что максимальные множества обязаны иметь высокую
степень (и, следовательно, большой объем информации), а в § 2 — что и
каждая высокая в. п. степень содержит максимальное множество.
Следовательно, deg{М : М — максимально} = Hi. Более того, все эти
результаты остаются в силе, если свойство «быть максимальным»
заменить на другие свойства, такие, как «быть гг-простым», «мажорным
подмножеством» и многие другие.
С другой стороны, в § 3 мы доказываем, что поведение низких в. п.
множеств и степеней как в £, так и в R очень похоже на поведение
вычислимых множеств. Например, свойство С{А) = £ справедливо для
каждого кобесконечного низкого в. п. множества А, а не только для
вычислимого множества А. Теорема Сакса о разложении справедлива при
разложении заданной степени на степени, которые располагаются над

282
Глава XI. Структура и степень в. п. множества
произвольной низкой в. п. степенью, а не только над 0. Пусть А означает
класс степеней кобесконечных в. п. множеств, являющихся
безатомными (не имеющими максимального надмножества). В § 4 мы продолжим
начатое в §§ 1 и 2 исследование, доказав теорему Шёнфилда о том, что
A D Ь2. В § 5 мы усиливаем результат Робинсона из § 3 о том, что
А П Li = 0, а именно докажем теорему Лахлана, утверждающую, что
А П Ь2 = 0, и, следовательно, А = Ь2.
§ 1. Характеризация Мартина высоких степеней в
терминах функций-доминант
Описанная в главе V программа Поста состояла в том, чтобы построить
кобесконечные в. п. множества А с все более и более «жидкими»
дополнениями А, с тем, чтобы в конечном итоге найти такое сильное условие
«жидкости» А, которое бы гарантировало неполноту А. Построив
полное максимальное множество, Ейтс [1965] доказал невозможность этой
программы, т. к. дополнение максимального множества является
наиболее жидким, насколько это возможно, ко-в. п. множеством. Напомним,
что Ейтс сделал это (упражнение Х.3.8), построив такое максимальное
множество М, у которого главная функция дополнения М
доминирует каждую частично вычислимую функцию, т. к. по упражнению Х.3.7
любая функция, доминирующая каждую частично вычислимую
функцию, должна быть полной.
Опираясь на этот факт, Тенненбаум [1961] высказал предположение,
противоположное программе Поста, а именно, что если М
максимально, то М должно быть настолько жидким, что pjj доминирует каждую
ч. в. функцию, и тем самым М является полным. Однако Сакс опроверг
предположение Тенненбаума, построив с помощью метода приоритета с
бесконечными нарушениями из главы VIII неполное максимальное
множество. Мартин [1966b] и, независимо, Тенненбаум [1962] спасли верное
ядро программы Тенненбаума, доказав, что если М максимально, то
pjf доминирует все тотальные вычислимые функции (см.
предложение 1.2). По аналогии с упражнением Х.3.7 Мартин [1966b] затем связал
это свойство доминант с высокими степенями и с его помощью доказал,
что высокие в. п. степени являются в точности степенями максимальных
множеств (см. теоремы 1.3 и 2.3).
1.1 	Определение. Функция / называется доминантой, если /
доминирует каждую (тотальную) вычислимую функцию.

§ 1. Характеризация Мартина высоких степеней
283
1.2 Предложение (Мартин [1966b] — Тенненбаум [1962]). Если
множество М максимально, то главная функция pjj для М является
доминантой. (А именно, каждое максимальное множество является
плотно простым, как это определено в упражнении 1.11.)
Доказательство. Для получения противоречия предположим, что pjj
не доминирует некоторую вычислимую функцию /. По следствию V.2.4
/ не доминирует pjj. Следовательно, существует бесконечно много
таких «точек пересечения» х, что f(x) < pj^(x), но Pj^(x 4-1) ^ f{x 4-1)
и, значит, card(MD/x) ^ 2, где Ix = (f(x),f(x 4-1)]. Пусть {М8}8еи —
вычислимое перечисление М. Положим t/j{x,s) = ру[у G 1Х - М8\, если
такой у существует, и пусть ф(х, s) не определена в противном случае.
Тогда, перечисляя z в As+i, если z G М8, или z G {^(a;,s) : х ^ s},
получаем вычислимое перечисление { As }seiV такого в. п. множества А,
что М Соо А Соо
1.3 Теорема (Мартин [1966b]). Множество А удовлетворяет
условию 0" А' тогда и только тогда, когда существует функция-
доминанта / А. (Заметим, что здесь не требуется, чтобы
степень А была в. п., или даже чтобы она была вычислимой относительно
г.;
Доказательство. Из теоремы IV.3.2 мы знаем, что Tot =т 0;/-
Следовательно, по лемме III.3.3 о пределе, релятивизованной относительно
А, имеем, что 0" ^т А' тогда и только тогда, когда существует
такая A-вычислимая функция g{x,s) с множеством значений {0,1}, что
НшSg(x,s) = XTot, где XTot — характеристическая функция индексного
множества Tot.
(=£►) Предположим, что 0" ^т А1. По данной функции g{x,s) из
предыдущего абзаца мы определяем функцию-доминанту / А
следующим образом.
Шаг s. (Определение /($).) Для всех е ^ s определяем
t(e) = {nt ^ s)[(Vz ^ s)[ye,t{x) I] или g(e,t) = 0]
И положим
f(s) = max{ t(e) : е ^ s }.
Заметим, что t(e) существует, потому что если ipe не всюду определена,
то g(e, t) = 0 для почти всех t. Если <ре всюду определена, то для почти
всех t будет g(e,t) = 1, и, следовательно, для почти всех s имеем f{s)>
<pe(s).

284
Глава XL Структура и степень в. п. множества
{<=) Предположим, что / А является функцией-доминантой.
Определим такую А-вычислимую функцию g(x,s), что lims g{x,s) =
XTot:
Тогда, если ipx всюду определена, то всюду определена и следующая
функция фх:
Таким образом, / доминирует фх, и тогда для почти всех s имеем
g(x,s) = 1. Если ipx не всюду определена, то для некоторого у ipx(y)
расходится. Поэтому фх{у) тоже расходится, и для всех s ^ у имеем
Напомним, что высокие и низкие множества, классы степеней Нп и
Ln определялись в IV.4.2 и VII. 1.3.
1.4 Следствие. Вычислимо перечислимая степень а является
высокой (a Е hi; тогда и только тогда, когда существует такая
функция-доминанта /, что deg(/) ^ а.
1.5 Следствие. Каждое максимальное множество имеет высокую
степень.
Доказательство. Для доказательства используем утверждение 1.2 и
следствие 1.4. О
Интересно заметить, что не только максимальные множества
должны быть высокими, но и многие другие классы множеств,
рассмотренные в главе X, такие, как гг-простые, г-максимальные множества,
мажорные подмножества, должны также быть высокими. Однако, в
отличие от максимальных множеств, не все они обязаны иметь дополнение-
доминанту, и поэтому вначале мы должны заменить утверждение 1.2
на более гибкое утверждение, связывающее структурные свойства
множеств со свойством быть высоким множеством.
1.6 Лемма. Пусть А — кобесконечное не высокое в. п. множество и
h(x) — произвольная строго возрастающая вычислимая функция.
Тогда А имеет ft-диагонально верное вычислимое перечисление { As }s€u, в
том смысле, что
1, если (Vz ^ s)[<Pxj(s){z) 4];
О в противном случае.
Фх(у) = (/xs)(Vz ^ y)[VxAz) -И-
5(a:,s)=0. О
(3 s)[o/,(s) —
где As = { ag < af < • • • } и A = { ao < ai <•••}.
(1.1)

§ 1. Характеризация Мартина высоких степеней
285
Доказательство. Пусть Wi — А для некоторого г. Пусть Bs — Wi,s,
Bs = {bo < bi <•••}. и ff(x) = - ah(x)]- Тогда 5<т1и, еле-
довательно, по следствию 1.4 д не доминирует некоторую вычислимую
функцию /. Определим As = Bf(sy Следовательно, для всех х имеем
О® = bt(a). Теперь, если f(s) ^ g(s), то ash{t) = = b9hfy = ah{s).
Таким образом, свойство (1.1) выполняется. Q
(см. доказательство теоремы 5.1 для применения леммы 1.6.)
1.7 Теорема (Мартин[1966Ь]). Если А гг-просто или г-
максимально, то А является высоким множеством. (Более того, если А конечно
сильно гиперпросто, как это определено в упражнении 1.8, то А
также является высоким.)
Доказательство. Предположим, что А не является высоким.
Применяем лемму 1.6 с функцией h(s) = s, чтобы получить вычислимое
перечисление { As }S£u; для А со свойством (1.1). Теперь построим такую
равномерно вычислимую (см. определение II.2.5(ii)) последовательность
{ Уп }пби> попарно непересекающихся конечных множеств, что для всех
п будет выполняться Vn П А ф 0. Из существования такой
последовательности { Vn }n€u> будет следовать, что множество А не может быть
гипергиперпростым. Так как эта последовательность является
равномерно вычислимой, то множество R = (Jn V2п будет вычислимым, а это
означает, что множество А не г-максимально.
Мы построим последовательность { Vn }n€u> по шагам, обозначая
через V„ множество элементов, перечисленных к концу шага s, и пусть
Fs = (J{V^:n^s}. На шаге s +1 элемент ass перечислится в точности
в одно из множеств Vn. Следовательно, \VS\ = s и, т. к. вычислимая
функция f(s) = ass является строго возрастающей, последовательность
{ Уп }new является равномерно вычислимой. Положим = 0 для всех
п.
Шаг s + 1. Определяем
п = (/im ^ s)[V£ П { а\ : * < s } = 0]
и перечисляем ass в V^f+1. (Заметим, что такой п существует, т. к. Vf =
00
Лемма. (Vn)[Vn П А ф 0 и Vn конечно].
Доказательство. Зафиксируем п и предположим, что лемма верна для
вгех т < п. Пусть г — такой шаг, что для всех т < п выполняется

286
Глава XI. Структура и степень в. п. множества
квази-максимальные
(5) I
максимальные
(4)/ \(1)
г-максимальные
(2)
гг-простые
<7>1
плотно простые
<8>1
г-простые
(10)
простые
(6)
>- сг-простые
(9)
(3)
■ конечно сильно г-простые
Диаграмма 1.1
= Vm. Пусть t = (ps > r)[ass = as]. Теперь либо существует
некоторый х < t такой, что а* = ах уже принадлежит V^, либо, в противном
случае, а\ = at перечисляется в V^+1. В любом случае V^+1 ПА ^ 0, и
для всех s ^ t + 1 имеем V£ = V^+1. []
На самом деле доказательство теоремы 1.7 устанавливает больше,
чем утверждает эта теорема. Янг [1966] и Д.А. Мартин [1966b]
определили новый класс в. п. множеств, называемых конечно сильно
гиперпростыми (ксг-простыми), который содержит как гг-простые, так и
r-максимальные множества, и к ним применимо доказательство
теоремы 1.7 (см. упражнение 1.8). Мартин также ввел понятие плотно
простого множества (см. упражнение 1.11). Утверждение 1.2 на самом деле
устанавливает, что максимальные множества являются плотно
простыми. Янг [1966] определил также сильно гиперпростые множества.
Следующая диаграмма суммирует взаимоотношения между этими классами
простых множеств, а также между классами множеств, рассмотренных
в главе X. Отметим, что «Р —> £?» означает, что свойство Р влечет
свойство Q, а отсутствие стрелки означает, что соответствующая
импликация неверна. Необходимые определения, импликации и отсутствие
обратных импликаций приведены в упражнениях ниже.

§ 1. Характеризация Мартина высоких степеней
287
1.8—1.24 Упражнения
1.8. 	Бесконечное множество В называется сильно гипериммунным
(сг-иммунным), если не существует такой равномерно вычислимой (см.
определение II.2.5) последовательности { Vn }пе^ попарно непересекаю-
щихся вычислимых множеств, что Vn П В ф 0 для всех п, и
множество V = Un Vn вычислимо. (Это понятие отличается от понятий гг-
иммунности и г-иммунности, приведенных в определении V.2.1 прежде
всего тем, что в первом случае мы требуем существования индекса
для Vn, во втором — канонического индекса для Уп, а здесь —
характеристического индекса для Vn в соответствии с определениями И.2.1
и И.2.4.) В. п. множество А называется сильно гиперпростым (сг-прос-
тым), если А сг-иммунно. Далее, В называется конечно сильно
гипериммунным (ксг-иммунным), а А — конечно сильно гиперпростым (ксг-
простым), если к предыдущим условиям мы добавим требование, что
каждое Vn является конечным множеством.
(a) Докажите, что бесконечное множество В является сг-иммунным
(ксг-иммунным) тогда и только тогда, когда не существует такой
равномерно в. п. (р. в. п.) последовательности { И^(п) }П€и; попарно непере-
секающихся в. п. (конечных) множеств, что Wf(n) Г) В ф 0 для всех п и
и пП/ы=ш-
(b) Докажите, что кобесконечное в. п. множество А является сг-прос-
тым (ксг-простым) тогда и только тогда, когда не существует такой
р. в. п. последовательности { Wf(n) }neu> попарно непересекающихся в. п.
(конечных) множеств, что для всех п выполняется Wf(n) П А ф 0 и
3cunw>(n).
(c) Д.А.Мартин [1966b, с. 306] назвал кобесконечное в. п. множест¬
во А суперпростым, если не существует такой равномерной
вычислимой последовательности { Vn }пеи> попарно непересекающихся конечных
множеств, что для всех п УпГ)Аф$. (А именно, снимается
вышеупомянутое условие о вычислимости множества V = (Jn Vn.) Докажите, что А
суперпросто тогда и только тогда, когда А ксг-просто. Указание (Лер-
ман-Шор). Пусть { Vn }П€и> — последовательность, которая
обеспечивает, что А не суперпросто. Положим д(п) = ® • Определим
Un = tj{ Vi : д(п) ^ i < д(п + 1) } - {0,1,...,п - 1}.
(Следовательно, Uo = Vo, U\ — V\ U V2 — {0}, и т. д. ) Докажите, что
последовательность { Un }П€и> обеспечивает не ксг-простоту множества
А.

288
Глава XL Структура и степень в. п. множества
1.9. 	Докажите импликации (2), (3), (6) и (9) из диаграммы 1.1.
Заметим, что импликации (1), (4), (5) и (10) вытекают из упражнения Х.3.10
и определений из глав V и X. (Для импликаций (7) и (8) см.
упражнение 1.11.)
1.10 	(Робинсон [1967а]). Пусть В — бесконечное множество.
Докажите, что главная функция рв является доминантой тогда и только тогда,
когда для каждой сильной таблицы { Fn }пеи> (конечных множеств)
выполняется условие
(3m)(Vn ^ m)[\Fn П В\ ^ п]. (1.2)
Указание. Если существует таблица, не удовлетворяющая условию (1.2),
то легко показать, что рв не является функцией-доминантой.
Обратно, предположим, что рв не доминирует некоторую строго
возрастающую вычислимую функцию /. Определяем новую строго
возрастающую вычислимую функцию д следующим образом: #(0) = /(0) и
д(п 4-1) = f(g{n) + п 4-1). Положите Fn = (д(2п),д(2п 4- 2)] и покажите,
что { Fn }печ> нарушает условие (1.2). Если рв(х) ^ /(ж) > #(1), то
найдите такой г/, что д{у) < f(x) ^ д(у 4- 1), и докажите, что д(у — 1) < х.
Докажите, что
card (В Г) (д(у - 1 ),д{у + 1)]) ^ у.
Далее, рассмотрите отдельно случаи г/ = 2пиг/ = 2п4-1, чтобы
удостовериться, что существует не менее п элементов из В, которые
принадлежат либо Fn-1, либо Fn.
1.11 	(Мартин). Кобесконечное в. п. множество А называется плотно
простым (Мартин [1966b]), если его главная функция p-j является
доминантой. (Например, предложение 1.2 устанавливает, что максимальные
множества являются плотно простыми.) Сейчас мы докажем
импликации (7) и (8) из диаграммы 1.1 и, таким образом, учитывая
упражнение 1.9, будут доказаны все импликации.
(a) Докажите, что плотно простые множества являются г-простыми.
(См. теорему V.2.3.)
(b) (Мартин [1963, с. 273]). Докажите, что гг-простые множества
являются плотно простыми. Указание. Если А не плотно просто, то пусть
{ Fn }n€u> — последовательность из упражнения 1.10, нарушающая усло-
зие (1.2) при В — А. Постройте слабую таблицу {УП}П£Ш,
гарантирующую, что А не является гг-иммунным. С этой целью всякий раз,
как только это возможно, добивайтесь, чтобы для каждого п множество

§ 1. Характеризация Мартина высоких степеней
289
Fn — As имело непустое пересечение с каждым из Vm, т < п.
(Заметим, что согласно упражнению Х.2.16 не имеет значения, является Vn
конечным или нет.)
Можно также дать прямое доказательство упражнения 1.11 (без
использования упражнения 1.10), построив такую строго возрастающую
функцию /, что для бесконечно многих п выполняется условие pj(n) <
f{n). Строим по шагам таблицу { Vi }ieiV и полагаем
— множество элементов, перечисленных в таблицу к концу шага s. На
шаге s + 1 выбираем такое наименьшее г ^ s, что
(Зп)[2г < п ^ s & V* П As [ f(n) = 0
& (3x)[f(2i) ^х< f(n) kxe AsnVs]\.
Наименьший такой x перечисляем в V7*+1. Докажите, что для каждого
i множество Vi конечно и V П А ф 0.
1.12 (а) (Мартин [1966b, теорема 3]). Покажите, что доказательство
теоремы 1.7 устанавливает, что каждое ксг-простое множество является
высоким.
(b) Покажите, что каждый класс в. п. множеств из диаграммы 1.1,
за исключением классов простых и г-простых множеств, содержится в
классе высоких множеств.
(c) Докажите, что импликации (8) и (9) из диаграммы 1.1 не могут
быть обращены. Указание. Используйте теорему V.2.5.
1.13 (Лахлан и Робинсон). Докажите, что существует г-максимальное
множество без плотно простого надмножества. Сделайте вывод, что в
диаграмме 1.1 больше не существует никаких стрелок, идущих к
«плотно простым» множествам, кроме показанных. Указание. Покажите, что
если в конструкции безатомного г-максимального множества из
упражнения Х.5.10 выполняется условие Fj П А ф 0, то верно |Fj П А\ ^ j, и
затем используйте упражнение 1.10.
1.14 (Робинсон [1967а]). Докажите, что мы можем модифицировать
доказательство теоремы Х.5.4 так, чтобы сделать множество А плотно
простым. Указание, см. упражнение Х.3.8. Это дает пример г-макси-
мального (и, следовательно, сг-простого) множества, которое является

290
Глава XI. Структура и степень в, п. множества
плотно простым, но не имеет гг-простого надмножества.
Следовательно, импликации (6) и (7) из диаграммы 1.1 не могут быть обращены, и
не существует стрелки, идущей от г-максимальных к гг-простым
множествам. (Последнее также вытекает из следствия Х.4.4 и
предложения Х.4.5.)
1.15 	(Мартин [1966b, с. 306]). Докажите, что существует не ксг-
простое плотно простое множество А. Указание. Используйте
подвижные маркеры { Гп }neu> так, чтобы Гп окончательно останавливался на
ап, где А = { ао < а\ < • • •}. Если г ^ п и (fi(n) то передвиньте Гп
дальше за (fi(n). Пусть Vn — множество позиций маркера Гп. Чтобы
сделать последовательность { Vn }neu> равномерно вычислимой,
передвигайте Г ? на шаге s + 1 только на элементы, большие max{ Vs }.
1.16. Янг [1966, с. 80] показал, что существует ксг-простое не сг-
простое множество, и поэтому импликация (3) из диаграммы 1.1 не
может быть обращена. Докажите, что не существует дополнительных
стрелок, которые можно было бы добавить в диаграмму 1.1. Указание.
Используйте упражнения 1.12, 1.13, 1.14, 1.15, 1.16 и результаты,
полученные в главах V и X.
1.17 	(Робинсон [1967а]). Докажите, что кобесконечное в. п. множество
А является сг-простым тогда и только тогда, когда для каждой слабой
таблицы { Wf(n) }пеим чье объединение содержит А, существует такое
т, что для всех п ^ т множество Wf(n) Г\А конечно. (Сравните это с
подобными характеристиками плотно простых и гг-простых множеств из
упражнений 1.10 и Х.2.15.) Указание. Используйте упражнение 1.8(6).
1.18.° Пусть А Ст В и А — «pullback» множества А, определенный
в упражнении Х.4.8.
(а) (Робинсон [1968, с. 344]). Докажите, что А является плотно
простым (и, следовательно, высоким), и не содержится ни в каком сг-простом
множестве. (Стоб и Херманн заметили, что на самом деле А не
содержится ни в каком ксг-простом множестве.)
(б] (Стоб [1979, теорема 1.2.5] и Херманн [1978, с. 191]). Докажите,
что А является мажорным подмножеством некоторого в. п. множества.
1.19 (Джокуш [1973а]). Докажите, что если А Ст В, то А высокое.
Указание. Положим с(п) = (fis)(3x > п)[х Е Bs — А]. Тогда с А
и, поэтому, если А не является высоким, то функция с не доминирует

§ 1. Характеризация Мартина высоких степеней
291
некоторую вычислимую функцию /. Пусть R = U^LoС®/(п) — [0, п]).
Докажите, что R нарушает условие А Ст В.
1.20 (Робинсон [1968]). Пусть { As }s€u; — (вычислимое)
перечисление в. п. множества А. Вычисляющая функция этого перечисления са(х)
определяется как
сА(х) = (/xs)[A, f X = А f ж].
Мы говорим, что А является доминантой по перечислению (е-доминан-
той), если оно имеет перечисление, у которого вычисляющая функция
является доминантой.
(a) Пусть са(х) > { ^8 }s€u> и А будут прежними и g(x) ^wtt са(х).
(см. определение ^wtt в упражнении V.2.16.) Докажите, что если са(х)
не является доминантой, то и д(х) ею не является.
(b) Докажите, что если в. п. множество является е-доминантой по
вычисляющей функции для одного перечисления, то оно является и е-
доминантой по вычисляющей функции для каждого перечисления.
(c) Докажите, что если А является е-доминантой, В — в. п.
множество и А ^wtt В, то В также является е-доминантой.
(d) Докажите, что каждое гу^-полное множество является
е-доминантой.
1.21 (Робинсон [1968]). Докажите, что каждая в. п. степень содержит
в. 	п. множество, не являющееся е-доминантой. (Другие сведения о е-
доминантах см. в упражнении 2.7.)
1.22 (Робинсон [1968]). Для произвольного перечисления { As в. п.
множества А определим дефицитное подмножество (множества А) как
В = { х : (3s)(Зу < х)[х G As & у Е А - As] }
и дефицитное множество
D = { s : As С As—i UB}.
(Заметим, что если для всех s \As+i - As\ = 1, то D совпадает с
дефицитным множеством Деккера из теоремы V.2.5.)
(а) 	Докажите, что бесконечное в. п. множество А является е-доминан-
той тогда и только тогда, когда каждое дефицитное подмножество В
множества А является мажорным подмножеством множества А.

292
Глава XI. Структура и степень в. п. множества
(b) Докажите, что если { As }s€u; перечисляет е-доминанту А, то
соответствующее дефицитное множество D является плотно простым и не
содержится ни в каком сг-простом множестве.
(c) Докажите, что если { As }s€u, перечисляет креативное множество,
то D является безатомным кобесконечным в. п. множеством.
1.23° (Робинсон [1968]). Докажите, что существуют максимальные
множества, как являющиеся, так и не являющиеся е-доминантами.
1.24 (Купер [1972с]). (а) Докажите, что если В ^т 0;, то В является
гг-иммунным тогда и только тогда, когда В является сгг-иммунным.
(Используйте доказательство из упражнения Х.2.16.)
(Ь) 	Покажите, что в теореме 1.7 Мартина предположение о
вычислимо перечислимости множества А не является необходимым. А именно,
докажите, что если В гг-иммунно и В 0;, то В является высоким.
Указание (Джокуш). Предположим, что В гг-иммуннно. Релятивизуем
критерий Арсланова (теорема V.5.1) и упражнение V.5.8(c)
относительно 0'. Для того, чтобы показать 0" В', достаточно найти такую
функцию h ^т В', что для всех х верно h(x) ф (х). Определим
вычислимую функцию
д/х s\ _ / <Px,t(x)> если она определено,
\ О в противном случае.
Для каждого х определяем слабую таблицу { Vn }neu>5 полагая Vn = { s :
д(х, s) = п }. Так как В сгг-иммунно, то для некоторого п имеем Vn С В.
Чтобы вычислить такое п, используем множество В', и затем замечаем,
что п ф <Рх{х).
1.25 Замечания. Упражнение 1.14 является усилением одной
теоремы Лахлана и Робинсона и было предложено Робинсоном [1967а], в то
время как упражнение 1.13 использует конструкцию Лахлана [1968с] и
характеристику Робинсона [1967а]. Робинсон [1968] назвал е-доминанты
упражнения 1.20 высокими множествами, а множества, не являющиеся
е-доминантами, низкими, но к настоящему времени термины «высокий»
и «низкий» принято использовать в смысле определения IV.4.2.
1.26 Открытый вопрос (Джокуш). Удовлетворяет ли каждое сжатое
множество С (или даже может быть каждое сгг-иммунное множество)

§ 2. Максимальные множества и высокие в. п. степени 293
условию 0" С" ? 1 Известно, что это не так для гг-иммунных
множеств В, если только мы не добавим, как в упражнении 1.24,
предположение, что В 0;-
§ 2. Максимальные множества и высокие в. п. степени
По следствию 1.5 каждое максимальное множество имеет высокую
степень. В этом параграфе мы хотим доказать, что верно и обратное
утверждение: каждая высокая в. п. степень d содержит максимальное
множество и, поэтому, содержится в каждом классе, показанном на
диаграмме 1.1. Пусть D G d — в. п. множество. Из упражнения V.3.6 мы
знаем, как использовать метод разрешения Ейтса для построения такого
в. п. множества А ^т D, чтобы А удовлетворяло определенным
положительным требованиям конечного действия, достаточным для
обеспечения простоты или гиперпростоты множества А. Чтобы обеспечить
максимальность множества А, мы должны, как в теореме Х.3.3,
удовлетворить определенным положительным требованиям Ре бесконечного
действия, где каждое Ре может требовать перечисления в А
бесконечного множества Se элементов перечислиться в А, например, если Ре
является требованием вида Se С* А. Мы можем удовлетворить этому
новому требованию Ре, добиваясь выполнения следующих условий: (1)
Se вычислимо, (2) D является высоким множеством. Метод,
позволяющий достичь этого, называется методом разрешения Мартина, и он
будет проиллюстрирован в следующих двух теоремах, являющихся
подготовительными для главного результата, теоремы 2.3.
2.1 	Теорема. Если А — высокое в. п. множество, то существуют
такое в. п. множество D =т А и такое вычислимое перечисление
{ Ds }$еи> множества D, что вычисляющая функция Ср{х) является
доминантой. Здесь D = {do < d\ <•••}, Ds = {dg < d\ < •••} и
c-p(x) = fJ>s[dx — dx\.
Доказательство. Так как А — высокое, то по теореме 1.3 существует
функция-доминанта / ^т А. Пусть / = { е }А, и { As }seu> —
вычислимое перечисление множества А. Положим g(x,s) = {е}^а(а;), если
последнее вычисление определено, и g(x, s) = 0 в противном случае. Пусть
функция сд(х) — наименьший модуль для д, а именно
сд(х) = (/is)(Vt ^ s)[g{x,t) = g(x,s)].
1 Джокуш и Штефан [1993],[1997] отрицательно ответили на этот вопрос, построив
2-низкое сжатое множество. — Прим, редактора.

294
Глава XL Структура и степень в. п. множества
По лемме III.3.2 о модуле имеем сд ^т А и, к тому же, сд является
доминантой, т. к. если сд не доминирует некоторую вычислимую функцию
ft, то / не доминирует вычислимую функцию g(x,h(x)) 4- 1. Определим
последовательность { Ds }seu, по шагам. Положим Do = 0.
Шаг s -1-1.
Этап 1. (Обеспечиваем сд(х) Ор(а;)). Если g(x,s 4- 1) Ф g(x,s) и
х ^ s, то перечисляем dx в Ds+\. (Заметим, что Ds+\ конечно.)
Этап 2. (Обеспечиваем А ^т D). Если х Е .As+i—.As, то перечисляем
d* в jDs+i.
Так как / всюду определена, то \ims g(x,s) существует. Поэтому,
lim5 dx существует и Ср(х) определена для всех х. Тогда из-за этапа 1
функция сгр должна быть доминантой. Далее, D А, т. к. если для
данного х мы выберем такой шаг s > сд(х), что As+i [ х + 1 = А [ х + 1,
то dsx — dx. Окончательно имеем А ^т D, потому что если dx = dx, то
х € А тогда и только тогда, когда х Е As. О
(Заметим, что в условиях теореме 2.1 для существования lims д(х, s) для
всех х достаточно, чтобы функция / была всюду определенной, в
противном случае имеем \D\ < оо. Это используется в доказательстве
теоремы XII.4.13.) Одним из самых простых применений метода разрешения
Мартина является доказательство следующий вариации леммы VIII. 1.1
о густоте.
2.2 	Теорема. Если d высокая в. п. степень и В кусочно-вычислимое
в. п. множество, то существует такое густое в. п. подмножество
А множества В, что deg(A) ^ d.
Доказательство. Выберем в. п. множество D Е d и перечисление
{■D*}*ew множества D с функцией-доминантой как в теореме 2.1.
Пусть { Bs }s€u; — вычислимое перечисление множества В. Если х Е
Bs+1 — As, то перечисляем х в As+\ тогда и только тогда, когда dx+1 ф
dx. Очевидно, что А С В и А D. Мы утверждаем, что каждое
положительное требование Ре : А^е 1 =* В^е 1 удовлетворяется. Если это не
так, то выберем такое е, что В№ — А^е 1 бесконечно. Так как
вычислимо, мы можем определить вычислимую функцию
h(x) - ( €
если х Е В^€\
в противном случае.
Тогда для всех х Е Вtel — А^ выполняется dx^ = dx и, следовательно,
Ср(х) ^ h(x). Таким образом, если В^ — А^ бесконечно, то Ср{х) не
является доминантой. Q

§ 2. Максимальные множества и высокие в. п. степени 295
Теперь для данного множества D с доминантой мы хотим
построить максимальное множество А D, используя при этом конструкцию
максимального множества и систему обозначений из теоремы Х.3.3 так,
чтобы для каждого е удовлетворить положительному требованию
Ре : А С* We или ~А С* We.
Мы имеем подвижной маркер Ге, который к концу шага s
останавливается на элементе ase. Для того, чтобы максимизировать свой е-штат, Ге
может передвинуться на шаге s + 1 к некоторому элементу а?, е < г,
тогда мы перечисляем ase в As+i. Чтобы гарантировать сводимость
А D, мы разрешаем передвигаться маркеру Ге и, следовательно,
позволяем числу ase перечислиться в As+i — As, только если, как и в
теореме 2.1, выполняется условие d|+1 ф dse. Чтобы удостовериться, что
этот метод разрешения позволяет требованию Ре быть
удовлетворенным, рассмотрим случай е = 0. Определим функцию h(х) равной
такому наименьшему s, что либо х Е As U Wo,s, либо х = ase и Ге хочет
передвинуться к некоторому а\ Е WqiS, е < г, для того, чтобы
максимизировать свой 0-штат. Если Wo П А бесконечно, то h будет всюду
определенной и вычислимой. Но Ср{х) доминирует h(x), и поэтому
множество D разрешает почти всем маркерам передвинуться к элементам
множества Wo и, следовательно, АС* Wo. Отметим, что с того времени,
как маркер захотел передвинуться для максимизации своего 0-штата, он
будет продолжать хотеть этого до тех пор, пока его желание не будет
исполнено.
2.3 	Теорема (Мартин [1966b]). Если d высокая в. п. степень, то
существует максимальное множество А степени d.
2.4 	Определение. Если С С £, то пусть deg (С) = { deg(W) : W Е
С}.
2.5 	Следствие. Пусть Л4 означает класс максимальных множеств.
Тогда deg(A4) = Hi. Следовательно, для каждого класса С в. п.
множеств из диаграммы 1.1 за исключением классов простых и
гиперпростых множеств имеет место deg (С) = Hi.
Доказательство. Используйте упражнение 1.12, теорему 2.3 и
импликации из диаграммы 1.1. Ц

296
Глава XI. Структура и степень в. п. множества
Доказательство теоремы 2.3. Выберем в. п. множество D Е d, { Ds
и Ср(х), как в теореме 2.1. Строим множество А по шагам, используя
метод и обозначения теоремы Х.3.3. Пусть As = {ag < af < • • • } и
А = { ао < cli < • • •}. Для s = 0 положим Aq = 0, и поэтому а°п — п
для всех п. Если выполняются условия х,у Е ASi х < у, х = а* и
cr(z,a;,s) < cr(z,?/,s), то мы говорим, что на шаге s + lx тяготеет к у
ради Р{.
Шаг s + 1.
Этап 1 (для удовлетворения Pi). Выбираем такое наименьшее
число г, что выполняется
(3j > i)[<r(i,a?,s) < cr(i,aj,s)] (2.1)
И
(Зу ^ <)К+1 * (2-2)
Пусть (Т1 — наиболее высокий г-штат такой, что cr(i,a|,s) = <J\ для
некоторого j, i < j ^ s. Выбираем наименьший j, г < j ^ s, такой, что
cr(z,a*,s) = ах. Для всех к ф j, где г ^ А; ^ s, перечисляем число а£ в
As+1. Маркер Г* передвигаем к aj, а для всех к > 0 маркер 1^+* — к
элементу ass+k. (Заметим, что к концу этого перечисления не остается
элементов х ^ a*+1, которые тяготеют к какому-нибудь у > х). Если
такого г не существует, то ничего не делаем.
Этап 2 (для обеспечения D А). Выбираем z = (/if/)[d*+1 ф dsy).
Если во время этапа 1 некоторый элемент х ^ а*+1 был перечислен в
As+1, то ничего не делаем. В противном случае и если cr(z,a*+1,s) ^
a(z,asz,s) , перечисляем а\ в А8+\. Если же cr(z,a*+1,s) < cr(z,asz,s), то
перечисляем в As+] число а*+1. Если такого z не существует, то ничего
не делаем.
Замечание. При выполнении этапа 2 мы перечисляем в А один из двух
элементов а\ и а*+1, имеющий более низкий z-штат и, следовательно,
мы гарантируем, что если какой-то х ^ а\ тяготел к некоторому у Е
{ asz, a*+1 } до выполнения этапа 2, то и после выполнения этапа 2 х все
ещё тяготеет к оставшемуся элементу у1 Е {a*,a*+1 } — As+i.
Лемма 1. Для каждого е маркер Ге передвигается только конечное
число раз. (Следовательно, А бесконечно.)
Доказательство. Выбираем такой шаг £, что выполняется d\ — de.
Следовательно, на шагах s ^ t маркеры 1\, ъ ^ е, не могут передвигаться

§ 2. Максимальные множества и высокие в. п. степени 297
под воздействием этапа 2, а могут передвигаться лишь под воздействием
этапа 1.
Теперь, чтобы доказать, что после шага t маркер Ге передвигается
не более конечного числа раз, используется доказательство леммы 1 из
теоремы Х.3.3.
Лемма 2. А =т D.
Доказательство. Во-первых, D Д так как, из-за этапа 2, если
ах+1 = аж+1, то dx = dx. Во-вторых, А т. к. если dsx — dx, то
х е А тогда и только тогда, когда х Е As.
Лемма 3. (Ve)[.A С* Wе или А С* We].
Доказательство. Зафиксируем е и предположим, что для всех i < е
лемма выполняется. Выберем такое п ^ е, что для всех т ^ п
выполняется а(е — 1 ,am) = сг(е — 1 ,ап) = сг0. Положим cri = сто U {е}.
Выберем такой шаг что для всех т ^ п выполняется = ат и
c^(c,am,so) — сг(е, ат).
Для получения противоречия предположим, что оба множества И^е П
Д и Же П Л бесконечны. Определим вычислимую функцию h(x),
которая не доминируется функцией с^(ж), следующим образом. Для х ^ ап
положим h(x) = 0. Для х > ап определим
h(пгЛ = (tie .QaUt С- А . \/ гт(р пг /Тг»V/
(Если выполняется третий дизъюнкт из (2.3), то а; = а| тяготеет к
у = aSj в соответствии с требованием Ре.) Мы хотим показать, что если
и функция Ср(х) не доминирует функцию h(x) +1. Но если а; Е 1УеПА, то
для х должно выполняться (2.4), т. к. WeC\A бесконечно. Следовательно,
т. к. Wе П А бесконечно, то функция Ср{х) не является доминантой, что
противоречит предположению.
Зафиксируем х и допустим, что для х выполняется условие (2.4).
Чтобы доказать (2.5), достаточно проверить
h(x) определяется через третий дизъюнкт из (2.3)
& х Е А & lims а(е, х, s) = сг0,
(2.4)
ТО
(2.5)
(Vs ^ Л(а;))(ЗА;)[а; < а£ & <7i ^ cr(e,aj(,s)],
(2.6)

298
Глава XI. Структура и степень в. п. множества
а именно, проверить, что для всех s ^ h(x) х тяготеет к некоторому
у > х для удовлетворения требования Ре. Тогда из (2.6) вытекает (2.5),
т. к. в противном случае dp1 ф dx для некоторого s ^ h(x), и поэтому, в
силу условий (2.1) и (2.2), для некоторого z ^ х верно, что z Е As+1 - As
и, таким образом, либо х входит в As+i, либо х является новой позицией
для^ларкера Гр, который является наименьшим среди передвигающихся
на шаге 5 + 1. Первое не может произойти из-за условия (2.4). Последнее
тоже не может случиться, потому что предполагается, что х является
новой позицией для наименьшего из передвигающихся на шаге s + 1
маркеров Гр. Так как 5 + 1 > /i(a;) ^ 5о, мы должны иметь р > п ^ е. В
силу (2.6) существует такое А;, что выполняется х < ask и <ti ^ сг(е, а£, 5).
Так как сг(е,а;) = его, то мы имеем cr(p,x,s) < сг(р, a^,s), и поэтому х не
может быть новой позицией для Гр, который иначе предпочел бы вместо
х перейти к элементу ask.
Остается индукцией по s ^ h(x) доказать (2.6). Для s = h(x)
условие (2.6) очевидным образом выполняется при k = j из (2.3), т. к. мы
предполагаем, что для х справедливо (2.4). Зафиксируем s ^ h(x) и
предположим, что ак удовлетворяет условию (2.6) на шаге 5, но не на
шаге 5 + 1.
Случай 1. ак Е As+\ — As из-за этапа 1. Тогда для некоторых р и
<7, где п < р < q ^ s, некоторый (наименьший) маркер Гр на шаге
5 + 1 передвигается к элементу asq. Теперь р ^ к и к ф q, т. к. ак Е
As+1. Но х < asp, потому что х ф As+1. Таким образом, х < ар ^ ак и
ар < aq. Тогда на шаге 5 p-штат (а следовательно, и е-штат) элемента
а* должен быть по меньшей мере таким же высоким, как у элемента
а£, т. к. в противном случае Гр, вместо того, чтобы двигаться к ак,
передвинулся бы к aq. Таким образом, условие (2.6) выполняется на шаге
5 + 1 с элементом у = asq— ар'1.
Случай 2. ask Е ^4s+i — из-за этапа 2. Из замечания в конце этапа
2 следует, что условие (2.6) для элемента х на шаге 5+1
продолжает выполняться либо при у = а£+1, либо при у = (Точнее, пусть
г = (fJ>y)[dpl Ф d*]. Предположим, что z = к. Тогда z-штат, а
следовательно, и е-штат элемента aj+1, является по меньшей мере таким
же высоким, как у ак, поэтому условие (2.6) выполняется на шаге 5 + 1
при у = а£+1. Теперь предположим, что z = к — 1. Тогда a*. Е ^4s+i
влечет, что а (к — 1,а|,5) < сг (к — 1 ,а^_1?5). Следовательно, а; < и
ог^а^^в) ^ сгх, поэтому условие (2.6) выполняется при г/ = а^.)
Это завершает доказательство (2.6), доказательство леммы 3 и
доказательство теоремы. О

§ 2. Максимальные множества и высокие в. п. степени 299
2.6 	Примечание. Эту конструкцию можно наглядно представить
следующим образом. Если h(х) = s определяется в (2.3) через третий
дизъюнкт, то назначаем элементу х е-символ *е, означающий, что х
хочет войти в А ради Ре? как только D разрешит х это сделать.
По условию (2.6) х продолжает этого хотеть на всех шагах s ^ h(x).
Чтобы удовлетворить положительному требованию конечного действия
Ре, используя метод разрешения Ейтса (например, требованию Ре :
We бесконечно => We П А ф 0, чтобы А было простым), достаточно
показать, что по меньшей мере один элемент х с е-символом *е в конце
концов перечислится в А. Чтобы удовлетворить положительному
требованию бесконечного действия методом разрешения Мартина, мы должны
показать, что почти каждый х с символом *е в конце концов получает
разрешение (или теряет *е из-за cr(e,a;,s) = а\). Здесь решающим
моментом является то, что положительное требование Ре должно быть
таким, чтобы мы смогли определить вычислимую функцию Л(т), как
в (2.3), для того, чтобы заставить D дать разрешение почти каждому
элементу, сохраняющему символ *е. Точнее, Ре должен быть готов
действовать с элементом, помеченным звездочкой, на всех шагах s ^ h(x).
2.7-2.18 Упражнения
2.7° (Робинсон [1968]). Докажите, что каждая высокая в. п. степень d
содержит в. п. множество D, являющееся е-доминантой в смысле
определения из упражнении 1.20. (Для степеней множеств, не являющихся
е-доминантами, см. упражнение 1.21.) (Таким образом, если бы мы
вместо теоремы 2.1 сначала доказали упражнение 2.7, то могли бы в
теоремах 2.2 и 2.3 выбрать D и {Ds }s€u; так, чтобы функция с(х) (вместо
функции c-q{x)) являлась доминантой, где с(х) = (/is)[Ds [ х = D [ х].
Тогда мы могли бы использовать разрешающее условие Ds+\ \ х ф Ds [
х из главы V вместо здесь используемого d£+1 Ф dsx.) Указание.
Выберите в. п. множество А Е d. Достаточно построить D А так, чтобы
D было е-доминантой, поскольку тогда по упражнению 1.20(c)
множество At&D также будет е-доминантой. Пусть { As / и 9{хч s) будут
такими же, как в теореме 2.1. Положим D — [Js Ds, где
Ds = Ds-1 U { х : g(x, s) ф g{x, s + 1) & (Vy < Зх)[{ (ж)0 }e(y) i) }.
Очевидно, что D А. Чтобы доказать, что cd является доминантой,
используйте тот факт, что функция с9 является доминантой.

300
Глава XI. Структура и степень в. п. множества
2.8. (а) (Мартин [1967b]). Докажите, что для любой высокой в. п.
степени d существует безатомное в. п. множество Л, степень
которого ^ d. Указание. Чтобы добиться выполнения А -D, используйте
упражнение Х.5.5 и метод доказательства теоремы 2.3. Когда элемент
х = ж(п,е) захочет войти в А для удовлетворения Ре, назначьте
элементу х е-символ *е, и потом, при выполнении условия d*+1 ф dsx
перечисляйте х в As+i. Покажите, что если We является максимальным
надмножеством множества Л, то почти каждый элемент х с символом *е
войдет в Л. Далее, как в лемме 3 теоремы 2.2, определите вычислимую
функцию
h(x) = {fjLs)[x е As U W6yS V [х G Fn & |Fn - (W€yS U As)\ = 1]].
(b) Измените доказательство пункта (а) так, чтобы добиться
выполнения условия Л =т D. Указание. Выберите Fn так, чтобы |Fn| = п + 2
и, если п G Ds+1 — Ds, перечисляйте некоторый элемент множества Fn
в Л.
(c) Постройте Л G d так, чтобы Л не имело плотно простого
надмножества. (см. упражнения 1.13 и Х.5.10.)
2.9 (Джокуш-Соар [1972а]). (Новый пример «принципа максимальной
степени», сформулированного в упражнении V.5.6. см. также
упражнения 2.10, 2.11 и примечание 2.19.) Докажите, что пункт (Ь) из
упражнения 2.8 был излишним, потому что множество Л D из 2.8(a)
автоматически удовлетворяет условию Л =т D.
Указание. Пусть { As }seu> и { Ds }S€u> перечисления множеств AnD.
Пусть Fn определено как в упражнении Х.5.5. Положим т(х) = {fis)[x G
Ds], если х G D, в противном случае т(х) расходится. Как в
теореме V.5.1, с помощью теоремы рекурсии с параметрами определяем
вычислимую функцию h(x):
{Fh(x) ~ {у}, где
(:У = f*z)[z € Fh{x) - Ат{х)], если х € D,
0 в противном случае.
Положим д(х) = max(F/l(a.)), и пусть
r(x) = (vs)[As f д(х) = A f ^(аг)].
Как обычно, имеем г ^т Л, потому что д вычислима. Пусть D = { х :
х G D - Dr(x) }. Если D конечно, то D Л. Если D бесконечно, то

§ 2. Максимальные множества и высокие в. п. степени 301
доказываем D ^ А так. Очевидно, что D в. п. относительно А.
Фиксируем произвольное число у. Чтобы проверить, выполняется ли у G D,
находим х G D такой, что у < h(x). Пусть s — такой наименьший шаг,
что \Wh(x)iS\ = \Fh{x)\ — 1. Так как х G D, то т(х) > г(ж), и поэтому
для некоторого z 6 А имеем = Fh(x) — { z}. Покажите, что у G D
тогда и только тогда, когда у € Ds.
2.10.° Пусть А В — полукреативное множество, вычислимое
относительно невычислимого в. п. множества 2?, построенное методом из
указания к упражнению V.3.5. Докажите, что, как и в упражнении 2.9,
автоматически имеем В Л.
2.11° (Джокуш-Соар [1972а]). (а) Докажите, что в доказательстве
теоремы 2.3 этап 2 излишен, то есть, если множество А D строится
только с использованием этапа 1, то, как и в упражнениях 2.9 и V.5.6,
автоматически получаем D А. Указание. Пусть т(х) = (fis)[x G Ds],
если х G D, и т(х) неопределена в противном случае. Определите
вычислимую функцию h следующим образом:
Whlx) =
/ {“”(5+21 : ° < * < л(*) + !}.
\ 0
если х € D,
в противном случае.
(Ь) Докажите, что максимальное множество А из теоремы Х.3.3
автоматически является полным (без модификации Ейтса, приведенного в
упражнении Х.3.8).
2.12° (Лахлан [1968с, с.27]). Докажите, что конструкция в. п.
множества А из теоремы Х.7.2 (или, проще, в теореме Х.6.1) может быть
осуществлена в любой высокой в. п. степени.
2.13° (Лерман [1971а]). Покажите, что для любой высокой в. п. степени
d существует безатомное г-максимальное множество A G d.
2.14° (Лерман [1971а]). Докажите, что если d высокая в. п. степень и В
невычислимое в. п. множество, то существует мажорное подмножество
А множества В такое, что A G d. Используя упражнение 1.19, сделайте
вывод, что deg(C) = Нь где С = { А : (ЗХ)[А Cm X] }. Указание.
Соедините конструкцию теоремы Х.4.6 с методом разрешения теоремы 2.3.
Пусть Ve определено как в теореме Х.4.6 и Ue = Ve \ В.
Устанавливаемые на элементах множества Bs - As маркеры { Ге }ееч> максимизируют

302
Глава XL Структура и степень в. п. множества
е-штаты, измеряемые при помощи таблицы { Un}neu;• Маркеры
передвигайте таким образом, чтобы для всех е Е и) имело место Г| ^ Г|+1.
2.15° (Купер [1974b]). Докажите, что если d высокая в. п. степень,
то существует минимальная пара а, b в. п. степеней, каждая из
которых d. Указание. Пусть D Е d будет как в теореме 2.1. Постройте
А и В, используя метод «пинбольной машины», кратко описанный в
упражнении IX. 1.7. В дополнении к этому разделите каждые ворота Ge
на верхний уровень G+ и нижний уровень G~. Пусть Х2, -.. — эле¬
менты, прибывающие в Ge. Когда хп прибывает в Ge, например, на
шаге 5П, то он входит в G+ и ждет такого шага tn ^ sn, на котором
г(е,£п) < хп, и тогда хп падает в G“, и мы определяем fe{sn) — £п-
Затем хп ждет такого шага v ^ tn, что dvs+l ф dvSn, и тогда хп
падает в Ge-\. Определим fe{z) = 0, если z ^ {5n}nGu;, и заметим, что
если {хп }nGu; бесконечно, то /е будет вычислимой. Если хп остается
навсегда в G“, то fe{sn) > Cp(sn). Следовательно, G~ не может иметь
бесконечно много постоянных резидентов. Кроме того, если
последователь х находился над отверстием Не и затем реализовался на шаге s,
то, прежде чем упасть через отверстие Не к воротам Ge, х должен
дождаться такого шага t ^ s, что выполняется условие (Р+1 ф dx. Так как,
прежде чем х сможет покинуть любое отверстие или ворота, ему
требуется разрешение от множества D, то для каждого элемента х множество
D может вычислить его окончательное положение внутри пинбольной
машины. Следовательно, А, В ^т D.
2.16 	(Мартин [1967b]). Пусть А — кобесконечное не высокое в. п.
множество. Докажите, что А имеет кобесконечное в. п. надмножество В
такое, что главная функция р^ доминирует каждую частично
вычислимую функцию. Поэтому, в частности, множество В является плотно
простым. Указание. Используйте лемму 1.6.
2.17. (а) (Мартин и Миллер [1968]). Пусть А ^т 0', и { As }sGu, —
равномерно вычислимая последовательность вычислимых множеств
такая, что А(х) = lim5 As(x). Докажите, что если А невычислимо, то не
существует вычислимой функции /, которая доминировала бы са, где
са(х) = (ps ^ х) [As I х = А I х]. Указание. Чтобы вычислить А (ж),
найдите наименьшее такое п, что для всех s Е [n,f(n)] выполняется
As(x) = Af{n)(x).
(Ь) Используйте пункт (а), чтобы показать, что каждая ненулевая
степень, расположенная ниже (У, является гипериммунной.

§ 2. Максимальные множества и высокие в. п. степени 303
(с)° (Соар). Докажите, что предыдущее2 неверно, если мы ошибочно
определим
сА{х) = (fJ,s)[As f X = A f' ж].
(Заметим, что А является только Дг, а не Si-множеством.)
2.18° (Познер и Робинсон [1981]). Если 0 < с ^ 0' и 0 < b ^ 0', то
существует степень а со следующими свойствами: aUb = 0' ис^а.
Указание. Используйте упражнение 2.17. Отметим, что эти степени не
обязательно являются в. п.
2.19 Замечания. Способ обеспечения сводимости D ^т А
описанный в этапе 2 теоремы 2.3, принадлежит Лахлану, и делает
доказательство значительно проще, чем первоначальное доказательство
Мартина [1966b], которое использовало подшаги на каждом шаге.
Принцип максимальной степени в общих чертах утверждает, что
произвольное в. п. множество А, построенное таким образом, чтобы
оно обладало определенным свойством Р, автоматически будет иметь
степень, наивысшую среди степеней, совместимых со свойством Р.
Например, множества, полученные удовлетворением простых
отрицательных требований, как правило, оказываются полными. Такими являются,
например, множество К, простое множество Поста S (теоремы V.1.3
и V.4.1), сочленение А 0 В множеств А и В из теоремы Мучника-
Фридберга (упражнение VII.2.3) и максимальное множество
(упражнение 2.11(b)). см. также теорему V.5.1 — критерий полноты Арсланова .
Джокуш и Соар [1972а, с. 615] заметили, что при построении в. п.
множества А ^т D методом разрешения часто оказывается и D А (как,
например, в упражнениях 2.9, 2.10, 2.11 и V.5.6). Было бы интересным
сформулировать и доказать точную версию этого принципа.
Значительное количество информации о не в. п. степенях,
расположенных ниже 0', включая упражнения 2.17 и 2.18 и метод разрешения
Мартина для степеней ниже высокой (не в. п.) степени, может быть
найдено в работе Познера [1980].
2.20 Открытый вопрос. Если d — произвольная высокая в. п.
степень, и В — любое невычислимое в. п. множество, то существует ли
такое в. п. множество А Е d, что С*(А) = С*(В)? Результаты
этого параграфа, особенно теорема 2.3, упражнения 2.12, 2.13 и 2.14, да¬
2т. е. утверждение пункта (а). — Прим, редактора.

304
Глава XL Структура и степень в. п. множества
ют основание предположить, что ответ положителен.3 Маасе, Шор и
Стоб [1981] показали, что с более сильным заключением «А автоморфно
Б» это утверждение ложно. Соар [1982а] показал, что если А низкое, то
£*(А)^£*.
§ 3. Низкие в. п. множества похожи на вычислимые
множества
В § 1 мы видели, что множества с определенными сложными или
необычными структурными свойствами (такими, как свойства быть
максимальным, гг-простым множествами или мажорным подмножеством)
должны быть высокими, а в § 2 — что произвольная высокая в. п.
степень содержит в. п. множество с таким свойством. В этом параграфе
показывается, что низкие в. п. множества и степени имеют склонность
обладать очень равномерной структурой, похожую на структуру
вычислимых множеств. (В теореме 1.7 и упражнении 2.16 для в. п. множеств,
которые не являются высокими, мы уже убеждались в этом.)
Из теоремы VII.3.2 Сакса о разложении вытекает, что любая в. п.
степень b > 0 разложима над 0. В теореме 3.2 мы доказываем теорему
Робинсона о разложении, которая утверждает, что, более того, b
разложима над произвольной низкой в. п. степенью с < Ь. (Теорема Лахлана
о неразложении [1975а], известная как «теорема монстра», утверждает,
что, в общем случае, когда с не является низкой, это неверно.) В
упражнении 3.4 устанавливается обобщение теоремы Лахлана о невложимости
ромба над низкими в. п. степенями. В упражнении 3.5 показывается, что
каждое кобесконечное низкое в. п. множество С имеет максимальное
надмножество. На самом деле справедлив значительно более сильный
результат: для каждого такого С выполняется С(С) = £ (см.
примечания 3.7). Это дает очень сильное структурное сходство между низкими
в. п. множествами и вычислимыми множествами.
3.1 	Лемма. Если С — низкое множество (не обязательно в. п.), то
х =dfn и : (Зп € Wj)[Dn СС]}^т 0'. (3.1)
Доказательство. Очевидно, что X является Sf -множеством, и поэтому
X С. Если С — низкое, то С 0;, поэтому X 0;- О
3Действительно, ГГ Чолак [1995] установил, что ответ на этот вопрос
положителен. - Прим, редактора.

§ 3. Низкие в. п. множества
305
(Заметим, что индекс для тьюринговой сводимости в (3.1) находится
не равномерно по в. п. индексу для С. Для этого нам также нужно знать
индекс «низкости» множества С, т. е. такой индекс е, что С" = { е }0 .
см. упражнение XII.4.24.)
3.2 	Теорема (Робинсона о разложении). (Робинсон [1971а,
следствие 9]). Пусть b и с — такие в. п. степени, что с < b и с низкая.
Тогда существуют такие несравнимые низкие в. п. степени ао и ai, что
b = ао U ai и а* > с, г < 2.
Доказательство. Пусть 5 G b и С Е с — такие в. п. множества, что
В С 2и (множество чётных чисел), а С С 2и 4-1 (множество нечётных
чисел). Мы будем вычислимо перечислять в. п. множества Ао и А\ так,
чтобы выполнялись условия:
Ао U А\ — В и Ао П А\ — 0 (3*2)
и
В ^т Ai ф С для г < 2. (3.3)
Положим а^ = deg(А{(ВС). Тогда, по предложению VII.3.3 условие (3.2)
гарантирует, что b = ао Uai, а (3.3) гарантирует а^ < Ь, и,
следовательно, с < ai < b для i < 2. Условие, чтобы ai были низкими, может
быть обеспечено надлежащей модификацией нижеизложенной
конструкции, или соответствующей модификацией замечания в конце
доказательства теоремы VII.3.2. Так как Ai U С =т Ai ф С, то, начиная с этого
момента, мы будем использовать первое множество.
Пусть { Bs }sGa; и { Cs }sGu; — такие вычислимые перечисления
множеств В и С, что Во = 0, и для всех s \B8+i — В8\ = 1. Пусть g(e,s) —
такая вычислимая функция, что lims д(е, s) является
характеристической функцией множества X из условия (3.1). Как и в теореме VII.3.2
Сакса о разложении, мы дадим перечисления { AifS }sgu;? i € { 0,1 },
удовлетворяя единственному положительному требованию
Р : х е Bs+1 - Bs => [х € A),s+1 или х G j4i>e+i], (3.4)
и для г < 2 и всех е — отрицательным требованиям
N(e,i) ■ В Ф {е }А‘иС.
Фиксируем е, г их. Интуитивно, мы используем «низкость»
множества С, чтобы помочь следующим образом « С-удостоверить» вычисление

306
Глава XL Структура и степень в. п. множества
{ е Пусть Dn = С8[ и. Перечисляем п в в. п. множество
V, которое мы будем строить в процессе нашей конструкции. По теореме
рекурсии можно предположить, что у нас заранее есть такой индекс j,
что V = Wj. Находим такое наименьшее t ^ s, что либо Dn П Ct ф 0
(в этом случае, очевидно, вычисление некорректно), либо g(j,t) = 1,
в этом случае мы С-удостоверяем наше вычисление (и предполагаем,
что оно С-корректно). Позднее может оказаться, что мы были неправы,
и С и ф С8 it, но, по условию (3.1) и определению функции g, это
может случиться не более конечного числа раз. Так как при проверке
условия Dn С С мы на самом деле используем функцию g как
«оракул» для текущего равенства Dn = С8 гл, важно, чтобы не было ранее
перечисленных элементов т е V8, если условие DmГ\С8 ф 0 не
выполняется. Таким образом, как только С-удостоверенное вычисление станет
^-недействительным (из-за At \ и ф А8 \ и), мы оставляем прежнее
в. п. множество V и начинаем с новой версией V и, следовательно, с
новым индексом j таким, что Wj = V.
Этот процесс С-удостоверения лучше всего формализуется путем
преобразования функционала {е}*{у) в вычислимый функционал
Ф(X;e,y,s), который похож на функционал Ф из § 1 главы VIII.
Когда зафиксированы е и г, ради удобства будем писать
Ф5(ж) для обозначения Ф(А*>5 U С; е,ж, s), (3.5)
и
usx для обозначения u(AiiS U С; е, х, s). (3.6)
Если Ф5_1(ж) а Ф*(ж) 1\ будем говорить, что (е,г,х)-вычисление
Ф8-х(х) становится А-недействительным, если
(Э*<иГг)[*еЛ-л._1], (3.7)
и становится С-недействительным в противном случае. _
Зафиксируем е, г, х и s, и следующим образом определим Ф8(х).
Предположим, что нам даны A^t и Ct, t ^ s. Предположим также, что
выполняются условия
{e}s^‘uC'(*U=J/, (3.8)
И
->(32 < <_1)[г е (AitS U Cs) - (i4j,s_! U Cs-i)], (3.9)
(т. е. Фe(AifS U C8',e,x,s) определен, причем Ф имеет тот же смысл, что
и в § 1 главы VIII).

§ 3. Низкие в. п. множества
307
Положим Dn = С8 [ и8х. Перечисляем п в V£'l'x. Пусть v —
наибольший шаг < 5, на котором (е, г, х)-вычисление стало А-недействитель-
ным, и v = 0, если такого шага не существует. По теореме рекурсии
выберем j такой, что Wj — : v < t} Находим такой наимень¬
ший шаг t ^ 5, что выполняется либо
Dn П Ct ф 0,
(ЗЛО)
либо
= 1-
(ЗЛ1)
Если выполняется (3.11), то определяем Ф5(ж) = у. В противном
случае — Ф5(ж) t* Как обычно, определим вычислимые функции:
(функция длины)
1{е, г, s) = rnax{ х : (Vy < x)[Bs(y) = Ф(ЛМ U(7»;e, у, s)] },
(функция запрета)
r(e,i,s) = max{u(Ait8UC8;e,x,s) : х ^ l(e,i,s) & Фв(.А*|виС*;е,
и
1 Я) &) ■i' } 7
(множество нарушений)
/(е,г) = { ж : (3s)[z Е Aiy8+1 - А*,* & ж ^ г(е,г,$)] }.
Шаг 5 — 0. Для г < 2 определяем = 0-
Шаг s + 1. Для данных t 5, определяем l(e,i,s) и г(е,г,$), как
описано выше. Пусть ж Е — В8. Выбираем пару (е',*') так, чтобы
она была наименьшей (е,г) со свойством х г(е,г,$). Перечисляем ж в
^1-г' •
Чтобы доказать, что наша конструкция достигает цели, мы должны
индукцией по (е, г) доказать, что:
7(е,г) конечно,
(312)
Вф{е}А^с
(313)
и
г(е,г) =dfn limf(e,2,s) существует и конечен.
(ЗЛ4)
Зафиксируем (е,г) и предположим, что для всех (?, к) < (е,г)
выполняются (3.12), (3.13) и (3.14). Используя (3.14), выберем такой шаг $о, что
для всех s ^ so и (j, к) < (е, г) имеет место r(j, к) = f (j, /г, s). Определяем
г = 1 + таx{r(j,k) : (j,k) < (е,г) }.

308
Глава XI. Структура и степень в. п. множества
Лемма 1. /(е,г) конечно.
Доказательство. Выберем такой s\ > «о, что В [ г = В81 [ г. Тогда
после шага s\ требование iV(e,i) больше не нарушается.
Лемма 2. В ф {e}AiUC.
Доказательство. Для получения противоречия предположим, что В =
{e}AiUC. Тогда lim8t(e,i,s) = оо. Мы покажем, что В ^т С, что
противоречит предположению теоремы. Чтобы вычислить В(р) для р £ ш
с помощью оракула С, находим такое s > $i, что £(e,i,s) > р, и
каждое вычисление Ф8(ж), х ^ р, является С-корректным, а именно,
и8х = С it£. Как в лемме 1 из теоремы VII.3.1, индукцией по t ^ s
показывается, что
(V£ ^ s)[£(e,i,t) > р & г(е,г,£) ^ max{i4 : ж ^ р}],
и, следовательно, для всех t ^ s выполняется Ф*(р) = {e}AiL)C(р) =
В(р).
Лемма 3. Предел г(е,г) =dfn limSr(e,i,s) существует и конечен.
Доказательство. Используя лемму 2, выберем
р = (цх)[В(х) ф { е }л‘иС(х)].
Выберем шаг $2 ^ s\ таким большим, чтобы для всех s ^ 52 были
выполнены следующие условия:
< P)[^s(z) 4-= { е }AiUC(a;)],
(3.15)
(Vz ^ р)[Ве(х) = В(х)}.
(3.16)
Случай 1. { е }AiUC(p) В(р). Выберем такой шаг 53 ^ $2, что для
всех s ^ S3 имеет место ФДр) q ф В(р). Следовательно, Z(e,i,s) =
^(е,г,5з) и f(e,i,s) =г(е,г,5з) для каждого 5 ^ 53.
Случай 2. { е }А*иС(р) t • Мы найдем шаг v такой, что для всех s ^ v
будет выполняться Ф*(р) t • Следовательно, для любого шага s ^ v
будем иметь г(е, г, 5) = г (е,г, v).
Заметим, что если для какого-нибудь s ^ S2 верно Ф5(р) то
г(е, г, 5) ^ и®, и поэтому индукцией по t ^ s устанавливается, что
вычисление Ф*(р) = Ф8{р) сохраняется, пока оно остается С-действительным.

§ 3. Низкие в. п. множества
309
Пусть s' — такой наименьший шаг t, что ни на каком шаге ^ t (е,г,р)-
вычисление не становится A-недействительным. По теореме рекурсии
выберем индекс j такой, что
Wj=\J{Vr^:s^s'}
Так как { е }AiUC{p) 1\ то любое вычисление Ф8{р), s > s', на некотором
шаге t > s становится С-недействительным, и в этот момент для
каждого т Е Vf'hp выполняется DmnCt Ф 0- Следовательно, lim8g{j,s) = 0
в соответствии с (3.1). Выберем такой шаг v > 52, что Фv{p) t и для
всех s ^ v будет иметь место g(j, s) = 0. Мы утверждаем, что для всех
s ^ v Ф8{р) t • Предположим, что для некоторого s > v верно Ф8~\(р) t
и Ф«(р) I. Тогда перечисляем индекс п Е У/’г,р, где Dn = С [ и®, и
выбираем наименьший £ ^ s, удовлетворяющий условиям (3.10) или (3.11).
Но по выбору шага v (3.11) не может больше иметь места, поэтому
выполняется (3.10), и получаем Фs(p) t • О
3.3-3.6 Упражнения
3.3. С помощью метода, приведенного в конце доказательства
теоремы VII.3.2, докажите, что степени а*, г < 2, из теоремы 3.2
автоматически являются низкими.
3.4 	(Теорема о невложимости ромба для низких степеней, Амбос-
Шпиис [1984а]). (Эта теорема обобщает теорему IX.3.1 Лахлана о
невложимости ромба.)
(а) 	Докажите, что для в. п. степеней ао, аь bo, bi, если 0х = ао U ах
и степень b = bo U bi является низкой, то не существуют в. п. степеней
с» ф: bi таких, что а* П Ci Ь*, г = 0,1. Указание. Выберите непересека-
ющиеся в. п. множества Ai Е a*, Bi Е b*, Ci Е с*, г = 0,1. Предположим,
что множество В = BoUB\ низкое и выполняется К А = AoUAi. Как
и в доказательстве теоремы IX.3.1, перечисляйте в. п. множества F, F0,
Fi, F2, ..., стараясь добиться сводимостей Е Со, Ао и Fn Ci, А\
и удовлетворить для всех i и j следующим требованиям:
Pij :Еф{1}в° или Fi^{j}BK
Как и ранее, выберите для представитель-пару {х,у) такую, что
{ j }?1,л^и(у) |= 0 и {г }?0,^и(ж) 0, но, прежде чем атаковать требо¬
вание Pij-, перечисляя элемент (i,j) в D, используйте, как в
доказательстве теоремы 3.2, низкость множества В и 0'-оракул, чтобы проверить,
выполняется ли равенство В8 f и = В [ и.

310
Глава XL Структура и степень в. п. множества
(b) Используйте метод упражнения IX.3.10, чтобы в (а) заменить
условие г 1 на условие г п для произвольного п ^ 1.
(c) Полагая в пункте (a) ai = bi низкой и bo = О, докажите, что если
ai £ Li и d = ао G М+, то ai U d < O'. (В частности, если в. п. степень
d нетривиально дополняется вниз до 0, то d не может быть дополнена
наверх до 0' никакой низкой в. п. степенью. Обратное утверждение будет
доказано в теореме XIII.4.2.)
(d) Докажите, что если а £ Li и а ф 0, то существует такая в. п.
степень Ь, что аПЬ не существует.
3.5 	(Робинсон [1966а, теорема 5.3]). Докажите, что если С — кобеско-
нечное низкое в. п. множество, то С имеет максимальное надмножество
А. Указание. Используем даже более слабое предположение: множество
С является полу-низким (см. упражнение IV.4.6), а именно, выполняется
условие:
{ 3 : Wj П С ^ 0 } (3.17)
Пусть g(j, s) — такая вычислимая функция, что lims g(j, s) является
характеристической функцией множества из (3.17). Как и при
доказательстве теоремы Х.3.3, строим множество А при помощи маркеров { Ге }eGu,
таких, что к концу шага s маркер Ге находится на элементе а|, и в
конце концов останавливается на ае, где А = { ао < а\ < • • • }. Однако, если
теперь на шаге 5 + 1 маркер Го хочет передвинуться на элемент х > а|,
сначала перечисляем х в \4),s+i (как в теореме 3.2), а затем используем
теорему рекурсии, чтобы выбрать такой индекс j, что Wj — |Jf Vo,f-
Выбираем такой наименьший шаг t ^ s, что выполняется либо (1) х £ Ct,
либо (2) g(j, t) = 1. Если выполняется (2), то передвигаем Г0 на этот
С-удостоверенный элемент х.
Заметим, что
(Зх)[х £ Vo,5+i ~ Vo,s] => Vo,5 О Cs, (3.18)
так что в действительности функция g отвечает (возможно, после
конечного числа ошибок) на вопрос «выполняется ли ж £ С» для текущего
кандидата ж, а не для какого-нибудь предыдущего элемента у £ Vb,s*
В полной конструкции для каждого маркера Ге и е-штата а мы имеем
множество V/. Когда на шаге 5 + 1 маркер Ге хочет передвинуться на
элемент х > а|, где а(е, х, s) = а, перечисляем х в V°s+l. На каждом
шаге 5 + 1 для каждого маркера Ге и каждого е-штата <т, в возрастающем
порядке для е и убывающем порядке для а выполняем вышеизложенную
процедуру до тех пор, пока некоторый Ге не получит С-удостоверен и я

§ 3. Низкие в. п. множества
311
для передвижения. Чтобы получить для Vf аналог утверждения (3.18),
выберите такой индекс j(e,cr), что
= |J{ УеЛ ■ t > te },
где te — наибольший шаг ^ s, на котором некоторый маркер Г*, i < е,
изменяет свое положение.
3.6. 	Пусть С — в. п. множество, (см. также упражнение IV.4.7.)
(а) Докажите, что С является полу-низким тогда и только тогда,
когда существует вычислимая функция / такая, что для всех j
справедливо:
Wj ПС = WfU) ПС;
и
Wj П С — 0 => Wf(j) конечно.
(Ь) Докажите, что С является низким тогда и только тогда, когда
существует вычислимая функция / такая, что для всех j верно:
Wj П { п : Dn С С } = Wf(j) П {п : Dn С С}
и
Wj П { п : Dn С С } = 0 => Wf^j) конечно.
3.7 	Замечания. Теорема 3.2 появилась в статье Робинсона [1971а,
следствие 9], а упражнение 3.5 в статьях Робинсона [1966а, теорема 5.3] и
[1966Ь], хотя здесь приводятся более простые доказательства.
Использованный здесь метод был выработан в статье Соара [1982а, § 2], где дается
полное доказательство упражнения 3.5. Этот метод также использовался
в статьях Соара и Стоба [1982], Амбос-Шпииса [1984а].
Результат упражнения 3.5 был значительно обобщен Соаром [1982а]
и это обсуждается в теореме XVI. 1.1. Характеризация из упражнения 3.6
появилась в статье Соара [1977], где показано, что в. п. множество С
является неускоряемым (некоторое свойство сложности вычислений в
стиле М. Блюма) тогда и только тогда, когда С полу-низко. Обзор
некоторых таких вычислительно-сложностных свойств в. п. множеств и
их связь с быстро простыми множествами из главы XIII можно найти
в статье Соара [19826]. Грубо говоря, в. п. множество С является
неускоряемым тогда и только тогда, когда С «почти всюду» имеет самую

312
Глава XL Структура и степень в. п. множества
быструю программу (по модулю некоторой вычислимой функции). Если
С не имеет единственную самую быструю программу, то в этом случае
М. Блюм спрашивает, имеет ли С вычислимую последовательность
программ, кофинальную по времени выполнения всем программам для С.
Беннисон и Соар [1978] показали, что в. п. множество С обладает этим
свойством тогда и только тогда, когда С является 1.5-полу-низким, а
именно, выполняется условие { е : WeC\C бесконечно } $Cm Inf, что
является существенно более слабым условием, чем полу-низкость С. Затем
они обобщили результат упражнения 3.5, показав, что такое
множество С всегда имеет максимальное надмножество. Маасе [1983]
соединил этот метод с техникой расширения автоморфизма из статьи Соа-
ра [1982а], чтобы доказать, что кобесконечное в. п. множество С
удовлетворяет свойству С* (С) =eff £* тогда и только тогда, когда С является
1.5-полу-низким, что обобщает упражнение 3.5 и два упомянутых
выше результата (см. теорему XVI. 1.2). Можно сказать, что общий смысл
этих результатов состоит в том, что в. п. множество С имеет
небольшой объем информации (например, С является полу-низким или 1.5-
полу-низким) тогда и только тогда, когда С легко вычислить (с точки
зрения сложности вычислений), и тогда и только тогда, когда С имеет
равномерную алгебраическую структуру в £* (и иногда в R), похожую
на структуру вычислимых множеств.
Робинсон [1971а] доказал, что если а и b — в. п. степени и а < Ь, то
любое счётное частично упорядоченное множество вложимо в структуру
в. п. степеней между а и b с сохранением точной верхней грани, как
только она существует (см. упражнение VIII.4.10). Он также доказал,
что если степень а низкая, то существует такое вложение, которое к
тому же сохраняет наибольший и наименьший элементы, как только
они существуют. По теореме XVI.4.6 требование, чтобы а была низкой,
является здесь существенным.
§ 4. Не 2-низкие в. п. степени содержат безатомные
в. п. множества
Пусть А4, И и V означают, соответственно, классы максимальных, гг-
простых и плотно простых множеств. Из результатов §§ 1, 2 следует
deg(A4) = deg(7{) = deg(X>) = Hi. Для любого класса в. п. множеств С
обозначим через С# класс кобесконечных в. п. множеств, которые не
имеют надмножеств из С. Мартин показал (см. упражнения 2.8(b) и 2.16),
что также deg(X>#) = Hi. Пусть А = deg(A4#) — совокупность сте¬

§ 4• Не 2-низкие в. п. степени
313
пеней безатомных множеств. Из упражнения 2.8(a) мы уже знаем, что
Hi С А, а из упражнения 3.5 — что А П Li = 0. Лахлан [1968а] усилил
последний результат, показав, что А П 1»2 = 0, т. е. любое кобесконеч-
ное 2-низкое в. п. множество имеет максимальное надмножество (см.
теорему 5.1). Шёнфилд [1976] завершил классификацию А, показав, что
L»2 С А, откуда следует, что А = L2. На самом деле его доказательство
показывает, что каждая не 2-низкая в. п. степень d содержит кобесконеч-
ное в. п. множество А без гг-простого надмножества. Отсюда следует,
что также и deg(7{^) = L2.
4.1 	Теорема (Шёнфилд [1976]). Для каждой не 2-низкой в. п. степени
d существует такое кобесконечное в. п. множество A Е d, что А
не имеет гг-простого надмножества. Следовательно, L2 С А. Более
того, для данного в. п. множества В 6 d в качестве А мы можем
взять дефицитное множество Деккера для В.
Доказательство. Выбираем произвольное в. п. множество В Е d и
любую взаимно однозначную вычислимую функцию / с областью
значений В. Пусть А — дефицитное множество Деккера для В относительно
функции /, т. е.
A = {s:{3t> s)[f(t) < f{s)]}.
Напомним, что по теореме V.2.5 множество А в. п. г-просто и А =т В.
Мы покажем, что если А имеет гг-простое надмножество Н, то В" ^т
0", т. е. В является 2-низким.
Обозначим через Р множество TotB = {е : Wf = ш}. По реляти-
визованной относительно В теореме IV.3.2, Р является П^-полным, и
поэтому существует такая вычислимая функция g, что выполняется
ееР=>ШВе)=ш=> (Va:)(3u)[x е И$“] (4.1)
в i Р => W&) =* 0 =» (а.е. яНЭиН* € W%e)\ и]. (4.2)
Так как Р G П2В и В в. п., то Р G Пз. Предполагая, что А имеет гг-
простое надмножество Н, мы построим такой в. п. класс в. п. множеств
{ Ve^k }e,*eu;, ЧТО ДЛЯ ВСвХ б
е € Р <==> Ve коконечно, (4.3)
где Ve = Так как по теореме IV.3.5 Cof Ез-полно, то Ре Е3.
Следовательно, F Е А3, и поэтому по теореме IV.2.2 Поста Р 0//-
Так как множество Р является П^-полным, то В" $^т 0,;.

314
Глава XI. Структура и степень в. п. множества
Пусть Я — гг-простое надмножество множества В. Пусть Hs, Bs,
V* и V*k означают множества элементов, перечисленных к концу шага
s соответственно в Я, В, 14 и 14 Для всех е и к положим Н° = 14° =
К°к=9.
Шаг s 4- 1. Находим наименьшее к ^ s, для которого существует
такое t ^ 5, что
* * К', (4-4)
(Эи < /(*))[* € И^] (4.5)
С Я*. (4.6)
Перечисляем наименьшее t с этим свойством в 14,ь (Если таких к и t
не существует, то ничего не делаем.) Это завершает конструкцию мно-
жеств { Ve,k }e,fc€o,-
Отметим, что из (4.6) следует, что для каждого ей к
верно \Vetk - < 1.
Лемма. (Ve)[e Е Р <==> 14 коконечно ].
Доказательство. (=>) Зафиксируем е и предположим, что е Е Р. Так
как множества {14,* }*еи; попарно не пересекаются, а Я гг-просто, то
существует такое к, что 14,& С Я. (Из упражнения Х.2.16 следует, что
нет необходимости требовать, чтобы каждое 14,к было конечным.) Так
как е Е Я, то по (4.1) имеем (3u)[k Е Выберем такое to, чтобы
для каждого t ^ to выполнялось f(t) > и. Покажем, что каждое t ^ to
кладется в 14- Действительно, выберем такой шаг s ^ t, что к Е
выполняется (4.6) и
(W < $)[м < f(z) => z € V/]-
Теперь, на шаге 5 + 1 число t перечисляется либо в 14,либо в одно из
множеств 14,к1 < к, если только t не принадлежит уже множеству
Vs
(ф=) Предположим, что е ^ Р. Тогда по (4.2) конечно и
(3fc0)(Vfc ^ к0)^(3и)[к е И$“]. (4.7)
Далее, по (4.6) для всех к |14,fc — Н\ ^ 1. Мы утверждаем, что для всех
к ^ ко 14 * — Я = 0, следовательно, 14 С* Я, поэтому 14 кобесконечно.

§ 4- Не 2-низкие в. п. степени
315
Предположим, что число t на некотором шаге s + 1 > t перечисляется
в Ve,k, к ^ ко- Тогда для t, s, к и некоторого и выполняется (4.5).
Однако, ввиду (4.7), В \ и ф В8 \ и, поэтому для некоторого z > t
имеем f(z) и < f(t). Следовательно, позднее t войдет в А. Но Л С Я,
поэтому t Е Н. Ц
4.2-4.3 Упражнения .
4.2 	(Лахлан). Пусть А — гг-просто, А С В — в. п. множество, а =
deg(A) и b = deg(i?). Докажите, что существует такая в. п. степень с,
что а = bUc. (см. также упражнение 4.3 и следствие XII.3.8.) Указание.
Используйте следствие Х.2.7.
4.3 (Лахлан [1968а]). Пусть А — кобесконечное не гг-простое в. п.
множество, и пусть а = deg(A). Пусть b ^ а — произвольная в. п. степень.
Докажите, что существует в. п.
надмножество В Э А степени Ь. (см. также упражнение 4.2 и
следствие XII.3.8.) Указание. Выберите р. в. п. таблицу в. п. множеств
{Vejecu, которая обеспечивает негипергиперпростоту А, такую, что
для всех е выполняется е < шт(Уе). Выберите произвольное в. п.
множество С Е Ь. Положите i/>(e,s) = (/дг)[ж Е Ve,s - As]. Пусть
В = A U {^(е,s) : е € С & s € и}.
4.4 Замечания. Узнав о результатах, приведенных в упражнениях 3.5
и 2.8, Лахлан [1968а] их усилил, показав, что А П 1»2 = 0 и Н2 С А.
Доказательство Шёнфилда теоремы 4.1, более сильного утверждения
L2 С А, значительно проще. Дальнейших связей между Н2 и решеточ-
но определимыми классами в. п. множеств пока не найдено, и было бы
очень интересно обнаружить что-нибудь новое. Коэн и Джокуш [1975]
показали, что простое множество Поста S из теоремы V.1.3 безатомно.
Д. Миллер [1981b] использовал метод теоремы 4.1 для доказательства
того, что каждое //-максимальное полу-вычислимое множество является
2-низким. Эти множества были введены Марченковым [1976] в его
решении проблемы Поста в стиле Поста, путем нахождения такого
структурного свойства для А, что в. п. множество А с таким А не полно,
(см. Одифредди [1981, теорема 2.11].) Робинсон [1968] использовал
дефицитные множества примерно так же, как в теореме 4.1. (см.
упражнение 1.22.)

316
Глава XL Структура и степень в. п. множества
4.5 	Открытый вопрос. Класс в. п. степеней С называется инвариант-
ным, если С = deg(C) для некоторого класса С С £, инвариантного
относительно Aut£, группы автоморфизмов решетки £. По следствиям 2.5
и 5.2, классы Hi и L2 инвариантны. Конечно, Lo = R+ — R — { 0 }
является инвариантным, т. к. R+ = deg(C), где С — класс невычислимых
множеств (или класс простых множеств). Очевидно, что класс Lo = { 0 }
является инвариантным, т. к. он в точности состоит из вычислимых
множеств. Харрингтон показал (см. главу XV), что креативные множества
образуют орбиту, и, следовательно, Но = {(У } инвариантен.
Существуют ли какие-нибудь другие инвариантные классы вида Hn, Ln, Нп
или Ln? В частности, последовательность Lo, Hi, L2 наводит на мысль,
что, возможно, для каждого п классы Н2п и L271+1 являются
инвариантными, но других оснований для такого утверждения нет.4 Лерман
и Соар [1980а] опровергли предположение, что каждый инвариантный
класс представляется в одной из вышеприведенных форм. Они ввели
класс d-простых множеств (свойство, возникающее при изучении
автоморфизмов решетки £) и показали, что класс их степеней С расщепляет
Li. Маасе, Шор и Стоб [1981] усилили этот результат, введя
инвариантный класс SPH (состоящий из не-гг-простых множеств с определенным
свойством расщепления) и затем установив, что SPH расщепляет Нп
и Ln для каждого п. Амбос-Шпиис, Джокуш, Шор и Соар [1984]
показали, что SPH = PS (PS — совокупность степеней быстро простых
множеств из главы XIII), так что этот класс определим как в £, так и
bR, он образует фильтр в R и его дополнение является идеалом. Какие
другие классы в. п. множеств являются инвариантными? В частности,
инвариантен ли Е1?5Если это так, то возможно, что для
доказательства удастся найти какое-нибудь свойство в стиле теоремы 4.1. Если
нет, можно было бы постараться использовать автоморфизмы решетки
£ (как в главе XV), чтобы показать
(VA)[deg(A) Е L2 - Li => (ЭФ е Aut£)[deg($(A)) G Lx]].
Пусть С — класс кобесконечных в. п. множеств без г-максимальных
надмножеств. Классифицируйте deg(C) в иерархии Нп и Ln.
4Харрингтон и Соар [1996] и, независимо, Чолак [1995] доказали, что каждое
невычислимое в. п. множество автоморфно множеству высокой степени. Отсюда следует,
что для всех п > 0 классы Ln и н„ не инвариантны. Кроме того, Харрингтон
и Соар [ta] доказали, что Li также неинвариантен. Наконец, Харрингтон и
Чолак [ta] установили инвариантность классов Нп и Ln для каждого и ^ 2. — Прим,
редактора.
5см. предыдущее примечание. — Прим, редактора.

§ 5. * 2-низкие в. п. степени
317
§ 5. * 2-Низкие в. п. степени не содержат безатомных
в. п. множеств
Р. 	В. Робинсон показал (упражнение 3.5), что каждое кобесконечное 1-
низкое в. п. множество имеет максимальное надмножество и,
следовательно, AflLi =0. Лахлан улучшил этот результат, заменив Li на Ь2.
Это позволяет нам завершить классификацию А, как класса, равного
L2. Пусть, как и в § 4, для произвольного класса в. п. множеств С через
С# обозначается класс кобесконечных в. п. множеств, которые не имеют
надмножеств из С.
5.1 Теорема (Лахлан [1968а]). Если А — кобесконечное 2-низкое в. п.
множество (А" =т 0,;Л то А имеет максимальное надмножество М.
Следовательноу А П Ь2 =0.
5.2 Следствие. A =dfn deg(A4#) = deg(7{#) = L2.
Доказательство. Примените теоремы 4.1 и 5.1. Q
Доказательство теоремы 5.1. Дадим эффективную конструкцию, в
которой на шаге s определяется конечное множество М8, состоящее из
элементов, перечисленных в М к концу шага s. С помощью теоремы
рекурсии можно предположить, что заранее имеется некоторый индекс
для вычислимой последовательности { М8 }sGu;.
Напомним определение Х.3.2. Для каждого е е-штат а есть строка
из 2<и), такая что lh(o) = е + 1. На 2<ш задан порядок < . Если г < а,
то мы говорим, что о больше (выше), чем т.
В теореме Х.3.3 мы аппроксимировали дополнение максимального
множества, используя подвижные маркеры. В § Х.5, § Х.6 и § Х.7 мы
рассматривали маркеры как фиксированные «окна», через которые
проходят элементы. Теперь мы расширяем окна до блоков {Bj}jeu;, где
каждый блок делится на 2J+1 рядов, каждый из которых соответствует
одному из j-штатов а, и эти ряды расставлены в убывающем порядке
согласно упорядочению j-штатов. (См. диаграмму 5.1.) Блоки Во, В\,
В2,... упорядочены слева направо. В конце шага s + 1 каждый ряд а
блока Bj может содержать самое большее конечное число элементов х
из М8, удовлетворяющих условию a(j,x,s) = а. Движение элементов в
пределах блоков возможно вверх и влево. Точнее, после того как х
вошел в блок Bj, он может двигаться вверх по рядам блока Bj, по мере
того, как х растет в j-штате, х может двигаться влево к некоторому

318
Глава XL Структура и степень в. п. множества
Блок Во
Блок В\
Блок Bj
текущие
резиденты
в Во
0-штаты
*1, Х2
<7 = 1
Хз
<7 = 0
текущие
резиденты
Bi
1-штаты
<7 = 11
Х4, Х5, Xq
<7 = 10
Х7
гН
О
II
Ь
Х8
II
о
о
текущие
резиденты
в Bj
j- штаты
*11,*12
11...11
*13
11...10
*14, *15
00...01
*16
о
о
о
о
Движение данного элемента х >
вверх и влево
Диаграмма. 5.1. Расположение блоков {Ве}ееч>

§ 5. * 2-низкие в. п. степени
319
блоку Bk, к < j, или х может быть перечислен в А или М. В последнем
случае х навсегда удаляется из блоков. Постоянные резиденты блоков в
точности образуют М.
Пусть Bj,s — множество резидентов блока Bj к концу шага s, а
BjtOQ — множество постоянных резидентов Bj. Мы покажем, что BjiOQ
непусто и конечно для всех j, и М = Uj^Bj>00. Положим а(е,х) =
lims сг(е, ж, s), этот предел всегда существует.
Предположение, что А является 2-низким, мы используем
следующим образом. Во-первых, т. к. А не является 1-высоким, то по
лемме 1.6 при h(s) = s множество А имеет такое вычислимое перечисление
{ As }seu;? что выполняется
(3°°5)[а* = о.], (5.1)
где As = { ag < а{ < • • •}, и А = { ао < а\ < • • •}. Каждый такой шаг s,
при котором ass = as, называется истинным шагом.
Для каждого е Е и> и е-штата а мы определяем A-в. п. множество U£
следующим образом. Если s является истинным шагом, и выполняется
к card{ ж : х Е Ms+i & ж а® & а(е, ж, s) — о }, (5.2)
то перечисляем к в UТак как А является 2-низким, то П^ С Ез
(по упражнению IV.4.5(a)). Следовательно, по следствию 3.7 главы IV
существует такая равномерно вычислимо перечислимая таблица
множеств { Zy,a }Уеи;,<7е2<“> что для всех а и у
\и?\ = оо => (a.e.y)[zy’° = ш]
(5.3)
\Up\ < оо =>• ('iy)[Zv'<T конечно].
(5.4)
Для каждого у и а определим в. п. множество
Vy’° = (J{ Zy’T : т С а к (Вк > 0)[<r = т V] }.
На самом деле, ,4-в. п. множества U„ определяются в течение кон-
струкции, т. к. они зависят от того, как определяется
последовательность { Ms }se.u>* Однако, с помощью теоремы рекурсии можно
предположить, что у нас есть индекс для последовательности { М8 }sGu;, а
следовательно, и для последовательности { Vy,<T : у Е и, сг Е 2<tJ }, данный
нам до конструкции. Фиксируем некоторое одновременное вычислимое

320
Глава XL Структура и степень в. п. множества
перечисление { Vy,<T }s€a; последовательности { Vy,a }, такое что на
каждом шаге не более чем одно множество Vy,<T получает новый элемент.
(Интуитивно это можно представить следующим образом. Элемент
х является истинным, если х Е А. Цель блока Bj состоит в том, чтобы
поместить истинный элемент х j-штата а на наивысший возможный
ряд а. Если U£ бесконечно, то в распоряжении Bj имеется бесконечно
много истинных элементов j-штата о. Как только на шаге s +1 в
а следовательно и в V^a, появляется новый элемент, этот «оракул»
сообщает Bj, что U£ бесконечно, и поэтому лучше «сбросить» в Ms+i
все элементы х из Bj, менее желательные, чем элементы j-штата а, а
именно, все элементы х из Bj, принадлежащие j-штату v < а. Мы
выполняем этот сброс, если только Bj содержит какой-нибудь элемент в
некоторой строке т ^ а, так что Bj не становится пустым. Дальнейшие
интуитивные замечания мы приведем после доказательства.)
В следующей конструкции множества М элемент х является
неиспользованным в определенное время в течение шага s +1, если х ^ а®,
и х ещё не был перечислен в М или в Bjt8+i для некоторого j s.
Конструкция множества М.
Шаг 5 = 0. Пусть Mq = 0 = Bj$ для всех j.
Шаг s +1. Перечисляем в М все элементы х Е As такие, что х ass.
Для каждого j, 0 ^ j 5, выполняем подшаг j и затем переходим на
завершающий подшаг j = 5 + 1.
Подшаг j.
Этап 1. (Сброс элементов строк v < р). Если существует
такой j-штат р, что ф Vj,p, то перечисляем в М все
неиспользованные х такие, что х Е BjfS и a(j,x,s) < р.
Этап 2. (Модернизация). Перечисляем в BjyS+\ все
неиспользованные х Е Bj^s.
Этап 3. (Добавление одного). Если существует неиспользо¬
ванный х такой, что
a(j,x,s) > a(j,y,s)
для всех у, перечисленных в Bjy8+1, то сначала выбираем наибольший j-
штат для такого х, затем наименьший х в этом j-штате и перечисляем
х в Вj^g^.\.
Подшаг 5 + 1. (Завершающий подшаг). Перечисляем в М все
неиспользованные х. Определяем i?e,s+1 = 0 для всех е > 5.
Это завершает конструкцию.

§ 5. * 2-низкие в. п. степени
321
Из описанной конструкции для всех s их немедленно вытекают
следующие четыре утверждения:
X G #,>+1 => х G { а80 < а{ < • • • < а*8 }, (5.5)
х G ^ х ^ Qig ^ (5.6)
[5 — истинный шаг и х € ^ х € А, (5*7)
ж G #/,* => [ж G М8+1 V (3fc ^ j)[z G £*,*+1]]. (5.8)
Для каждого j определим
{наибольший j-штат а такой,
что |Vr-7’CT| = оо, если такой а существует,
наименьший j-штат в противном случае.
Лемма 1 (о стабилизации блоков). Для каждого j существует шаг
sj такой, что
(i) 	(it ^ *j)(V®)[[® G B^t & aj ^ a(j,x,t) & x G A\
—^ (Vv ^ t)\x € Bj^v]],
(ii) 	(3x)[x G A k gj ^ a(j,x,Sj) k (it ^ Sj)[z G Bjtt]],
(iii) 	(V* ^ sy)(Vz)[z G => <7, ^ a(j,x,t)],
(iv) 	(it ^ Sj)(Vz)[a: G - #/,* => x G А].
Доказательство. Предположим, что лемма 1 выполняется для всех е <
j. Мы определим г\ (соответственно 7*2, гз, 7*4) такой, что часть (i)
(части (ii), (iii), (iv), соответственно) выполняется для всех t^r\
(соответственно t ^ 7*2, t ^ гз, t ^ Г4), и затем выберем Sj > max{ 7*1,7*2,7*3,7*4 }.
Выберем г\ ^ тах{ «о,..., Sj-1 } таким образом, чтобы = V^’*7 для
всех о > Oj. Тогда по (iv) и (5.5) будем иметь
(Vt ^ ri)[(U i?e,t) ПАС {оо,.. .,оГ1_1 }]. (5.9)
e<j
Во-первых, мы утверждаем, что (i) выполняется для всех t ^ г\.
Зафиксируем t ^ г\ и х, удовлетворяющие условиям из (i). Тогда х не
перечисляется в М в начале шага i +1, т. к. х G А. Далее, х не
перечисляется в 5е,*+1 ни на каком подшаге е < j, поскольку (iv) выполняется
для всех е < j. Кроме того,

322
Глава XI. Структура и степень в. п. множества
т. к. 7*1 ^ t. Следовательно, х не сбрасывается в М на этапе 1 подшага
j. Таким образом, х Е Bjj+i-
Во-вторых, найдем х Е А и Г2 такие, что (ii) выполняется для всех
t^r2.
Случай 1. V*'0’ конечно. Таким образом, oj является наименьшим j-
штатом. Пусть г2 — истинный шаг ^ г\. Тогда по (5.6) агг22 — аГ2 МГ2,
аГ2 не перечисляется в М в начале шага г2 + 1, т. к. аГ2 Е А. Для всех
е < j в силу соотношения (5.9) имеем аГ2 ^ Де>Г2+1, т. к. аГ2 ^ аГ1.
Следовательно, на подшаге j существует неиспользованный х. Таким
образом, т. к. т*2 является истинным шагом, существует такое х Е А, что
х Е Bj,r2+1. Наконец, Gj ^ a(j,x,r2), поскольку oj является наименьшим
j-штатом.
Случай 2. V^aj бесконечно. Тогда Z*'a бесконечно для некоторого
е-штата сг, где е ^ j и gj — a 0J“e. Следовательно, U£ бесконечно и
выполняется
lim sup card{ х : х Е Ms+i & ж ^ а* & сг(е, ж, s) = сг} = оо.
s — истинный шаг
Заметим, что если сг(е,ж,$) = <т, то Gj ^ (j(j, x,s). Выберем такой
истинный шаг 7*2 ^ 7*1, что
card{ х : х € МГ2+1 & ж ^ &; ^ <j(j, ж, 7*2) } > т*х.
Так как на подшаге j шага 7*2 +1 имеем |(Ue<j #e,r2+i) С А\ ^ r*i, то
существует такое неиспользованный ж, что Gj ^ (j(j, ж, 7*2). Следовательно,
существует такое х Е Bj>2+i, что ^ <r(j, ж,т*2). Так как 7*2 является
истинным шагом, то по (5.7) имеем х Е Л.
Вне зависимости от того, какой из этих случаев имеет место, из (i)
следует, что х Е Bjj для всех t > г2 ^ г\.
В-третьих, найдем такой шаг т*з > г2, что (Ш) выполняется для всех
t ^ 7*з. Можно предположить, что Gj > наименьшего j-штата (т. к.
в противном случае (Ш) очевидным образом истинно). Следовательно,
V*'*’ бесконечно. Выберем т*з > г2 такой, что V^+i Ф Vrf3. Тогда
(Vx Е Bj^+x^Gj ^ аО’,аг,г3)].
Так как гз > г2, то, применяя те же самые рассуждения, что и для г2,
получим
(3x)[(jj ^ a(j,x,r3) & (Vi ^ r3)[x €
Следовательно, все элементы из -штатов > <jj, которые входят в Bj на
шагах t > гз, могут быть только новыми.

§ 5. * 2-низкие в. п. степени
323
В-четвертых, определим Г4 таким, чтобы (iv) выполнялось для всех
t^r\. Пусть
т = max{ a(j,y, s) : (3s ^ r3)[y е BjtS+i П А] }.
По (ii) г ^ aj. Выберем х и шаг г 4 ^ гз такими, чтобы a(j, x,ri) = т и
ж Е Д/>Г4+1 П А. Тогда по (i) для всех t > г4 имеем х Е #/,*. Теперь
предположим, что у Е Bjf+i —Bjf для некоторого у, где £ > Г4 и a(j, у, £) > т.
Тогда у Е А вследствие нашего выбора т. Лемма 1 доказана при Sj = Г4.
Лемма 2. Для каждого j множество BjyQO конечно и непусто.
Доказательство. Вытекает из леммы 1, части (ii) и (iv).
Лемма 3. М = \Jj<QO Bjy00.
Доказательство. (С) Пусть х Е М. Выберем такой истинный шаг s,
что х ^ а* = а8. Тогда для некоторого j получим х Е Bj,8+1 (в
противном случае х Е Me+i). Выберем наименьшее к такое, что для некоторого
шага t > s имеем х Е Bk,t- Теперь по (5.8) либо х останется в блоке Bk
навсегда, либо х перечислится в М. Следовательно, х Е Bk,<х>-
(Э) 	Если х Е Bjt00 Для некоторого j, то существует такой шаг s, что
для всех t ^ s верно х Е Bjj- Следовательно, х £ Mt для всех t ^ s.
Поэтому х ^ М.
Лемма 4. М максимально.
Доказательство. По леммам 2 и 3 М бесконечно. Предположим, что
М не является максимальным. Выберем такое наименьшее е, что
множества М П We и МП We оба являются бесконечными. Пусть а —
такой (е — 1)-штат, что а(е — 1 ,я) = <т для почти всех х Е М. Положим
о\ = а 1 и do = (7 0. Очевидно, что бесконечно. Следовательно,
(3fc)(Vj ^ k)[Z*'ai бесконечно]. (5.10)
Для каждого j ^ к из (5.10) рассмотрим V^ai °J *. Так как Z^ai С
V-ba 1 °J *, то все эти множества являются бесконечными.
Следовательно, (jj ^ (7i О*7-6. Поэтому не существует постоянных резидентов блока
Bjj имеющих е-штат ао. По леммам 2 и 3 \М П Wе| < оо.
Это завершает доказательство теоремы 5.1. О

324
Глава XL Структура и степень в. п. множества
Чтобы лучше понять это доказательство на интуитивном уровне,
рассмотрим только одно в. п. множество Wo. Пусть о\ — высокий 0-
штат, ох = 1, а во — низкий 0-штат, 0о = 0. Допустим, что каждый
блок Bj содержит только два ряда, по одному для каждого из 0о и 01.
Элемент х является истинным, если х £ А. Наиболее консервативная
стратегия для блока Bj состоит в том, чтобы заполнить обе его строки
0*, i = 0,1, элементами Х( со штатами 0*, но тогда Wo может
расщеплять М. Наиболее агрессивная стратегия состоит в том, чтобы
отвергать (сбрасывать) х = b8(j,ao) каждый раз, как только определится
у = b8(j, 0i), но в этом случае каждый такой у позднее может войти в
А, и поэтому Bj не будет иметь постоянного резидента. Следовательно,
требуется более разборчивая стратегия для заполнения рядов и
выбрасывания текущих резидентов.
Каждый Bj действительно хотел бы знать, выполняется ли |U^ \ =
оо, т. к. в этом случае в распоряжении каждого Bj будет существовать
бесконечно много истинных элементов со штатом 01. Это П^-вопрос и,
т. к. А является 2-низким, он является Ез-вопросом. Пусть { Z^a }
удовлетворяет условиям (5.3) и (5.4) при а = 0o,0i- Представляем Z*7’671 как
некий «оракул» для Bj, который всякий раз, как только Z^ai получает
новый элемент, «сообщает» Bj, что U^x бесконечно, и который по (5.3)
и (5.4) «ошибается» самое большее конечное число раз.
Чтобы помочь нашему воображению, мы представляем каждый блок
Bj как некоторую особу (произвольного пола), а числа х Е и> — как
представителей противоположного пола (п.п.п.). Последние делятся на
блондинов (если х Е 01) и брюнетов (если х Е 0о)- Брюнеты могут
превратиться (самое большее один раз) в блондинов, но не наоборот.
Каждый Bj предпочитает блондинов брюнетам, но главная цель
состоит в том, чтобы выбрать в качестве постоянного спутника по меньшей
мере одного истинного п.п.п. х (т. е. х Е А). На подшаге j Bj отвергает
резидента-брюнета, если: (1) Bj в данный момент уже имеет резидента-
блондина; и (2) оракул Z^ai блока Bj для блондинов получает новый
элемент, тем самым сообщая Bj, что Bj будет иметь в своем
распоряжении бесконечно много истинных блондинов. Bj всегда пытается
заполнить ряд блондинов 01, вне зависимости от наличия или отсутствия
брюнетов в блоке Bj, но Bj не получит нового брюнета, если он в
текущий момент уже имеет блондина. Однако, при заполнении пустого ряда
блондинов Bj должен быть очень осторожным, т. к. множество
истинных блондинов, хотя и бесконечно, может быть очень «расплывчатым».
Bj стремится сначала проверить, содержит ли его собственный ряд
брюнетов 0о какого-нибудь блондина х (т. к. брюнет может превратиться

§ 5. * 2-низкие в. п. степени
325
в блондина, даже находясь в Bj). Если это так, то Bj передвигает х в
ряд блондинов о\. Если нет, то Bj ищет следующего подходящего (ещё
не использованного) блондина.
Конечно, если \U^ \ < оо, то Bj может преуспеть только в
нахождении постоянного резидента-брюнета у, а не резидента-блондина х. Это,
однако, не мешает Bj старательно перебирать бесконечную
последовательность { хп }n€u; в поисках временного резидента-блондина (вместо
у), каждый из которых позднее оказывается ложным. (Да, в жизни
иногда лучшее оказывается эфемерным.) Между тем, т. к. оракульное (для
блондинов) множество Z^,<Tl множества Bj конечно, то Bj приходится
быть очень осторожным, чтобы нечаянно не отказаться от истинного
брюнета у во время посещения какого-нибудь транзитного блондина хп.
5.3 	Замечания. Первоначальное доказательство теоремы 5.1
появилось в статье Лахлана [1968а]. Приведенное изложение, использующее
блоки и множества Vy'a, было введено автором в первом черновом
варианте этого параграфа. После чтения ранней версии чернового варианта
этой главы С. Ахмад предложила дальнейшие упрощения и
исправления, которые мы здесь использовали.

Глава XII
Классификация индексных множеств в. п.
множеств
В главе IV мы видели, как арифметическая иерархия дает нам точную
меру для классификации индексных множеств и доставляет
значительно больше информации, чем примитивные методы глав I и И,
использовавшие только s-m-n теорему. В этой главе мы получим существенно
больше результатов о классификации индексных множеств, комбинируя
методы арифметической иерархии из главы IV с методами приоритета,
развитыми в главах VII, VIII, X и XI. Эти результаты об индексных
множествах, интересные сами по себе, часто имеют неожиданные и важные
применения. Например, теорема 1.5 Ейтса об индексном множестве
позволяет дать очень короткое и элегантное доказательство теоремы
Сакса VIII.4.1 о плотности. Совсем недавно Херманн [1983b] использовал
индексные множества для доказательства неразрешимости
элементарной теории £.
Мы начинаем § 1 с доказательства теоремы Ейтса об индексном
множестве. Она дает нам возможность показать, что если А в. п., то
G(A) =dfn { х : Wx =т А } Е^-полно. В § 2 мы продолжаем эту тему,
получая классификацию Ейтса для индексных множеств G($C А), G(^ А) и
G(|A), но заменяя первоначальное доказательство Ейтса новыми и более
сильными результатами, которые содержат больше информации.
В § 3 мы устанавливаем связь равномерно в. п. (р. в. п.)
последовательностей в. п. множеств с Ез-индексными множествами и 2-низкими
в. п. степенями. Здесь представлены результаты Джокуша о степенях,
в которых вычислимые функции (множества) являются равномерными
(соответственно субравномерными). Недавно выяснилось, что понятия
равномерности и субравномерности являются полезными при изучении
степеней моделей арифметики.

§ 1. Индексное множество G(A) = { х : Wx =т А }
327
В § 4 мы представляем некоторые новые красивые результаты с
неожиданно короткими доказательствами Шварца, Соловея и Джокуша о
классификации индексных множеств классов n-высоких и n-низких
множеств, и класса т. н. «промежуточных множеств» из следствия VIII.3.5,
введенных Лахланом, Мартином и Саксом. Из этих общих теорем
удивительно легко выводится П4 -полнота множества Max =dfn { х : Wx
максимально} и П5-полнота множества {х : Wx безатомное}. Вопрос о П5-
полноте для {х : Wx безатомное} оставался открытым до появления
этого метода.
В § 5 мы продолжаем исследование теорем о неподвижной точке,
которое началось с теоремы К лини о рекурсии (II.3.1) и продолжилось
теоремами Арсланова о неподвижной точке (V.5.1 и V.5.5). Мы покажем,
что для произвольной функции / $^т 0(2) существует такая
неподвижная по Тьюрингу точка п, что Wn =т ^/(п)-
В § б мы обобщаем как теорему рекурсии, так и критерий полноты
Арсланова на все уровни арифметической иерархии и даже на уровень
0^). Материал из параграфов 4, 5 и 6 является относительно новым,
он получен в 1982-1985 гг., и в большинстве своем ещё в печати не
появлялся1.
§ 1. Классификация индексного множества
G(A) = {x: WX=TA}
1.1 Определение. Если А — в. п. множество, то пусть G(A) = {х :
Wx =т А }.
В этом параграфе мы доказываем, что G(A) £3*-полно, а также
важную теорему Ейтса об индексном множестве, которая дает короткое и
элегантное доказательство теоремы VIII.4.1 Сакса о плотности.
1.2 Лемма (Ейтс [1966b]). Если А в. п., то G(A) Е Е^.
Доказательство. Мы используем методы главы IV. Заметим, что
ж G G(A) *=> {3e){3i)[Wx = { е }А & А = {i }w-] (1.1)
(Зе)(Эг)[{ е }А всюду определена (1.2)
& (г}{е всюду определена
k(Vy)[{y£Wx^{e}A(y) = l}
k{yeA^{i}w*(y) = l}]}.
хКо времени издания книги на языке оригинала в 1987 г. — Прим, переводчика

328
Глава XII. Индексные множества в. п. множеств
Остается заменить последнюю строку на следующую:
У £ А <=> (3s)(3<r)[{ г }£(</) = 1 ( .
k (V* < Ща))[{ е }f(z) |= а(х)]].
Тогда правая сторона в линии (1.3) находится в Е^4 форме, поэтому (1.2)
может быть легко представлено в Е^ форме. []
Следующая лемма о представлении для произвольного Е^ множества
S является основным инструментом этого параграфа.
1.3 Теорема о представлении (Ейтс [1966b]). Пусть А — в. п.
множество. Для произвольного множества S Е е? существует такая
р. в. п. последовательность в. п. множеств {Vk}keun равномерно
вычислимая относительно Л, что для всех к выполняется
к Е S => (3e0)[(Ve ^ eo)[V^ =т А] к (Ve < e0)[V^ вычислимо ]] (1.4)
и
к £ S => (Ve)[V^ вычислимо ]. (1.5)
1.4 Лемма. Если А в. п. и R Е П^, то существует такая р. в. п.
последовательность в. п. множеств {Ui}^, равномерно вычислимая
относительно Л, что для всех i
i е R => Ui =т Л (1.6)
и
i £ R => Ui вычислимо. (1.7)
Кроме того, индекс последовательности { Щ }iGu; может быть найден
равномерно по -индексу для R.
Доказательство теоремы 1.3 (с помощью леммы 1.4)• Зафиксируем
S Е Eg1. По теореме IV.3.2, релятивизованной относительно Л, выберем
такое R Е П^, что для всех к
ке S => (3e0)[(Ve ^ е0)[(А;, е) Е R] к (Ve < e0)[(fc, е) £ Л]] (1.8)
и
к <£ S => {Щ[(к,е) £ Д]. (1.9)
По лемме 1.4 выбираем р. в. п. последовательность { U(k,e) }к,ееил
равномерно вычислимую относительно Л и удовлетворяющую условиям (1.6)
и (1.7) для R. Определим V*. = ®eGu; £/(*,с>. D

§ 1. Индексное множество G(A) — {х \ Wx =т ^4}
329
Доказательство леммы 1.4. Фиксируем R Е П^. По теоремам IV.3.2
и III.1.5 существует такая вычислимая функция /, что для всех г
ieR=>wf{i)=w=> (Vy)[y 6 Wfa] (1.10)
i R
Wявляется начальным сегментом и (1.11)
=► (3fto)[(Vy ^ У0)[У i Wf(l)]
& (Vy < Уо)[у € W$f)]].
Для всех i и у определим множество
Li,v = {u:(3s^u)[yiW^us}}.
Очевидно, { Li^y является равномерно в. п. и равномерно вычис¬
лимой относительно А. Отметим, что
у е Wflfi => LiyV конечно
У t
^i,у — <*>•
(1.12)
(1.13)
Определяем
Ui = { (х, у) : у 6 А V х 6 (J LitZ }.
Заметим, что Ui ^т А равномерно по г, поскольку { Li>y } равномерно
вычислима относительно А. Теперь по (1.10) и (1.12)
*’еД=> (Vy)[y е Wf(i)\,
=> {\ty){LlAJ конечно],
=► Ui=TA,
потому что у G А тогда и только тогда, когда (Зт)[(а;, у) G U,}. Далее,
по (1.11), (1.12) и (1.13)
i*R => (3yo)[(Vy £ yo)[y i Wf{i)} k (Vy < y0)[y € Wf(i)]},
=> (3yo)[(Vy ^ Уо)[Ь.,у = w] & (Vy < yo)[bi,y конечно]],
=£► Ui вычислимо,
т. к. для у ^ yo имеем u\y^ = u^y\ а для у < y0, если у € А, то t/j2^ = u№\
и если у А, то t/N конечно. Q
Следующие важные результаты теперь оказываются простыми
следствиями теоремы 1.3 о представлении.

330
Глава XII. Индексные множества в. п. множеств
1.5 Теорема об индексном множестве (Ейтс [1966b]). Для данных
в. п. множеств С и D, если D <т С и S Е то существует такая
вычислимая функция g, что для всех к
(i) 	D Wg(k) С, и
(й) к е S <=> Wg(k) =т С.
Доказательство. Фиксируем S Е Е^, и пусть { Vk }кеи —
последовательность для S', существующая по теореме 1.3. Для каждого к
определим в. п. множество Bk посредством = {(ж, 0) : х Е D} и
= { (х,е + 1) : х Е }. (Заметим, что Bk С для всех к,
т.к. Vk С и D ^т С.) Для каждого к применяем к Bk и С
сильную лемму VIII.2.3(ii) о густоте, чтобы найти такое в. п. подмножество
Ak Q Bk, Ak ^т Bk ^т С, что Ak удовлетворяет заключению
леммы VIII.2.3(ii). Тогда D ^т Ak для каждого к, т. к. по лемме VIII.3.2(ii)
при е = 0 имеем =* В^ =т D. Из равномерности VIII.3.2 следует
существование такой вычислимой функции д(к), что Wg(k) = Ak.
Теперь, если к £ S, то по (1.5) для всех е > 0 В^ вычислимо, откуда по
VIII.2.3(i) С ^т Ak. Если к Е S, то по (1.4) и определению Bk можно
выбрать такое е, что
В^ =т С & (V7’)[0 < j < е => В$ вычислимо].
Следовательно, в\^е^ =т D <т С. Поэтому по VIII.2.3(ii) А$ =* В^ =т
<7, так что С Ak. Таким образом, Ak =т С, поскольку Ak Bk
с. о
1.6 Следствие (Ейтс). Если С в. п., mo G(C) 0,$-полно.
Доказательство. В силу леммы 1.2 имеем G(C) Е Е^. Далее, если С
вычислимо, применяем следствие IV.3.6., в противном случае применяем
теорему 1.5 с D = 0. Q
Напомним, что в IV.3.3 мы определили Comp = { х : Wx =т 0;} =
G(0'). В теореме IV.3.4 мы показали, что (Ез,Пз) (Cof,Comp), и это
значит, что A Comp для произвольного Пз-множества А. Теперь мы
улучшаем этот результат, показывая, что Comp Е4-полно.
1.7 Следствие. Comp Е4 -полно.
Доказательство. Применяем следствие 1.6 с С = 0' и замечаем, что по
теореме IV.2.2 Поста Ejf = Е4.

§ 1. Индексное множество G(A) = {х : =т А}
331
В качестве следствия теоремы 1.5 мы получим элегантное
доказательство теоремы VIII.4,1 Сакса о плотности.
1.8 Теорема о плотности (Сакс). Если D и С в. п. и D <т С, то
существует такое в. п. множество А, что D <т А <т С.
Доказательство. Пусть S = {х : Wx =т D}- Тогда по следствию 1.6
S Е £3* и тем более S Е Е37. Применяем теорему 1.5, чтобы найти такую
вычислимую функцию д(х), что D $^т Wg(x) ^т С и Wx =т D тогда и
только тогда, когда Wg(x) =т С. По теореме рекурсии П.3.1 выбираем
такое число п, что Wn = И^(п). Следовательно, D <т Wg(x) <т С. О
1.9-1.14 Упражнения
1.9 (Ейтс [1969]). Не существует такой р. в. п. последовательности
в. п. множеств { Ап}пеи;, равномерной относительно степени (У, что
для каждой в. п. степени d существует в точности одно п, для
которого d = deg(An). (В частности, в. п. степени не могут быть
вычислимо перечислены без повторения, хотя Фридберг [1958] показал, что это
может быть сделано для в. п. множеств.) Указание. Для получения
противоречия предположим, что { Ап }neu; является такой р. в. п.
последовательностью. Пусть { Вп } — в. п. последовательность, получаемая
из { Ап } изъятием единственного множества Aj, имеющего степень (У.
Таким образом,
G(0;) = {х : (Vn)[Wx ВД.
Покажите, что тогда G(0') G П4, что противоречит следствию 1.7 о £4-
полноте G(0').
1.10 (Ейтс [1966b]). (а) Докажите, что если С в. п., С ф 0, С ф и,
то индексное множество Gm(G) — dfn {х : Wx =т С} Е3-полно.
Указание. По упражнению IV.3.13 имеем Gm(C) Е Е3. Теперь докажите
£з-полноту Gm(G). Если С вычислимо, то утверждение вытекает из
упражнения 1.4.25 и следствия IV.3.6. Для невычислимого С выберем
S Е £3, и пусть д удовлетворяет следствию IV.3.7 при А — S. Для
каждого х определим в. п. множество
Вх = {(z,e) : z € С П Wg{x,e) }.
Примените доказательство усиленной леммы VIII.2.3(ii) о густоте к
множествам С и Дс, чтобы получить Wf(x) = Ах С Вх, и покажите,

332
Глава XII. Индексные множества в. п. множеств
что х Е S тогда и только тогда, когда f(x) Е Gm(C). Сокращая Ах
до А, мы должны так изменить предыдущее доказательство, что если
(z,e) Е 1 — As, то для всех е' > е и z' ^ z справедливо (z',e') ^ Л,
если только (z',e') уже не входит в As. Это гарантирует, что если х Е 5
и, скажем, е — такое наименьшее число, что Wg(eyX) бесконечно, то не
только А^ =т С, а также ^>el — вычислимое множество. Поэтому
С.
(Ь) Докажите, что {х : Wx креативно } Ез-полно. (см.
упражнение 1.12 для обобщения.)
1.11. 	Докажите, что если А в. п., то Gtt(A) =dfn {% : Wx =tt А}
Ез-полно.
1.12°° (Херманн [1986]). Если А в. и., бесконечно и кобесконечно, то
GM) =dfn {х :WX =i А}
Ез-полно. (Это обобщает упражнение 1.10(b).)
1.13 (Янг). Покажите, что два произвольных максимальных
множества либо m-несравнимы, либо имеют одну и ту же т-степень.
1.14 (Д.А. Мартин и С.Е.М. Ейтс). Докажите, что максимальные
множества степени 0' могут лежать в бесконечно многих различных т-
степенях. Указание. Применяем упражнение 1.13. Для получения
противоречия предположим, что они содержатся в конечном числе т-степенях,
чьи классы в. п. множеств запишем так: Ci, Сг,. •.,С*. Определите такую
вычислимую функцию /, что для всех х
Wx Е [J Ci => Wf{x) вычислимо
i^k
И
wxi U Ci => Wf(x) максимально и имеет степень (У.
i^.k
Чтобы получить противоречие, примените к / теорему рекурсии.
§ 2. Классификация индексных множеств
GU A), G&A) и G(\A)
По аналогии с определением 1.1 вводим следующие определения.

§ 2. Индексные множества G(^ A), G(^ А) и G(| А)
333
2.1 	Определение. Пусть А — в. п. множество, и а = deg(A).
Определяем
G(^a)=G(^ A) = {x:Wx^TA},
G{> a) = G(^) = {i:A^T^}
и
G(| a) = G(| A) = {x : Wx |T A }.
Верхние оценки для этих трех индексных множеств — S4 и П4,
соответственно, легко устанавливаются в следствии 2.3 и в
упражнениях 2.7 и 2.6. Сейчас мы докажем, что они (за исключением
тривиальных случаев А =т 0 и А =т 0/, когда G(^ 0) = и = G(^ 0') и
G(| 0) = 0 = G(| 0')) являются лучшими из возможных оценок.
Мы могли бы легко классифицировать последние два индексных
множества, доказав сначала следствие 2.4, которое является простым
следствием теоремы 1.3 и леммы VIII.2.3 о густоте, как мы показываем в
общих чертах в упражнении 2.8. Однако все три индексных множества
могут быть классифицированы при помощи следующей сильной
теоремы, доказательство которой использует стандартные методы с
бесконечными нарушениями из главы VIII. Как объясняется в примечании 2.17,
формулировка теоремы принадлежит Каллибекову, а доказательство —
Стобу. В этом рассуждении в доказательстве строки (2.6) из леммы 3
имеется новая интересная идея.
2.2 	Теорема (Каллибеков-Стоб). Пусть С и D — такие в. п.
множества, что
0 <т G <т 0'
и С $^т D. Пусть S Е Е^. Тогда существует такая р. в. п.
последовательность в. п. множеств {Ak что для всех к
к Е S => Ak —т D,
к i S => Ак \т С.
Доказательство. Пусть { Vk }fceu> определена как в теореме 1.3 о
представлении и удовлетворяет (1.4) и (1.5) с D вместо А. Пусть { Vk,s }к,stun
{ Cs }sGu;, { Ds }seu и { Ks }sGa; — вычислимые перечисления { V* }кеим
C, D и К, соответственно. Мы построим Ак- Конструкция будет
равномерной по А;, так что { Ak }кеи> Р- в. п.

334
Глава XII. Индексные .множества в. п. множеств
Если k £ S, то для того, чтобы гарантировать Ak |т С, мы для всех
е удовлетворяем требованиям
Ne :С^Фе(Ак)
и
Ре : Ак Ф Фе(С7).
Эти требования и стратегии для их удовлетворения выглядят в
точности как в теореме VIII.4.1 о плотности. Именно, для удовлетворения
Ре, мы пытаемся кодировать К в А^е+1\ если Фe,s(Cs) согласовано с
AkyS на достаточно длинных начальных сегментах. Таким образом, если
Фе(С) = Ak, то Ak =т К, следовательно, К $^т С вопреки
предположению о С. Эта стратегия кодирования устроена так, чтобы для всех е
А^е+1^ было вычислимо, чтобы не мешать выполнению требования Ne,
которое удовлетворяем как в главе VIII.
Мы также пытаемся устроить, чтобы выполнялось А^ =т Vj^.
Следовательно, если к £ S, то D Ak по (1.4). Если к £ 5, то это
дополнительное действие не конфликтует с Ne, т. к. тогда по (1.5)
вычислимо для каждого е. Однако, если к Е S, то мы не сможем
добиться выполнения условия А^ =т для каждого е, но нам достаточно
выполнить его хотя бы на одном из кобесконечно многих е таких, что
J =т D. Хитрость в этом случае будет заключаться в том, чтобы с
помощью (2.6) доказать Ak D.
Пусть /(e,s), r(e,s) и 1е определены как в лемме VIII.1.1, но с Ak
вместо А. Определим R(e,s) = max{ r(i,s) : i ^ 5} и R(—l,s) = 0 для
всех s. Аналогично теореме VIII.4.1 определим вычислимую функцию
ic(e,s) = max{ х : (Vy < x)[i4j.,s(y) = Фе.ДС^у)] }.
Построение Ak.
Шаг s -hi.
Этап 1. Перечисляем (ж,2е) в Ak,s+i тогда и только тогда, когда
(х,е) е Vk,s и R(e - 1,5) < (х,2е).
Этап 2. Перечисляем (x,t, 2е + 1) в Ak,s+i тогда и только тогда,
когда х € Ks, t ^ 5, R(e - 1 ,s) < (x,t,2e + 1) и х < lc(e,v) для всех
у, t ^ v ^ s. (Это то же самое, что и стратегия кодирования Сакса из
теоремы VIII.4.1.)

§ 2. Индексные множества G(^ A), G(^ А) и G(\A)
335
Лемма 1. Если вычислимо (и, следовательно, вычислимо
для всех j ^ е), то для всех j е
42j! вычислимо, (2.1)
<МС) ф Ак, (2.2)
Aj.2вычислимо, (2.3)
Ф,-(А*)^а (2.4)
Доказательство. Предположим, что (2.1)-(2.4) выполняются для всех
г < .7. Покажем, что они выполняются и для j. По (2.4) и лемме VIII.2.2
об окнах имеем
г ——dfn liminf R(j — 1,5) < 00.
s
Таким образом, если (x,2j) > г, то (х,2j) Е А* тогда и только тогда,
когда (ж,.?’) Е У* и, следовательно, (2.1) доказано. Для доказательства
(2.2) предположим, для получения противоречия, что Фj(C) = Ak.
Тогда, как в лемме 2 из теоремы VIII.4.1, мы можем добиться К $^т С, что
противоречит предположению С <т К. (А именно, вычисляем модуль
М(х) = (/xs)(Vt ^ s)[lc(j,t) > х] с помощью оракула С. Тогда из-за
этапа 2 нашей конструкции, если х > г, то х Е К тогда и только тогда,
когда (х, М(х), 2j 4- 1) Е Ak. Следовательно, К ^т Ak ^т С.) Далее,
(2.3) вытекает из (2.2), как в лемме 3 из теоремы VIII.4.1, но с А, С, D
и е, замененными на Ak, К, С и j, соответственно. Окончательно, как
в лемме VIII. 1.1, множество нарушений Ij С А^<2j’+2l и, следовательно,
Ij ^т а\^2^2^ =т 0- Таким образом, С ф $j(Ak) по лемме VIII.2.1 о
нарушениях, что устанавливает справедливость (2.4).
Лемма 2. Если к £ S, то Ak \т С.
Доказательство. По условиям (1.5), (2.2) и (2.4) леммы 1, Фj(C) Ф Ak
и Фj{Ak) ф С для всех j.
Лемма 3. Если к Е S, то Ak =т D.
Доказательство. Если к Е S, то по (1.4) существует такое
(наименьшее) число ео, что =т D. вычислимо для г < ео, поэтому по
лемме 1 (2.1)-(2.4) выполняются для всех г < ео. По (2.4) и лемме VIII.2.2
об окнах liminfs R(eо — 1 , s) < 00, пожтому А^е°^ =т V^ =т D.

336
Глава XIL Индексные множества в. п. множеств
Осталось только показать, что Ak ^т D. Так как С Ak, то
существует такое наименьшее число е\ (обязательно е\ ^ ео), что
Фei{Ak) — С. Мы покажем Ak D, установив, что выполняется
л^2е1 + 1] ^ D
(2.5)
4>2ei+i) D.
(2.6)
Чтобы доказать (2.5) заметим, что если е < е\, то Фe(Ak) Ф С, так
что liminfsR(e,s) < оо. Таким образом, для е ^ е\ А^ =т У^
D, Ф€(С) ф Ak, и А^е^ вычислимо по доказательствам (2.1)—(2.3) из
леммы 1. (Отметим, что доказательство (2.3) требует только (2.2), без
(2.1).) Это доказывает (2.5).
Чтобы доказать (2.6) заметим, что 1ег так что мы
можем /^-вычислимо определить, когда вычисление вида Фei,s(Ak,s\x)
не будет больше нарушаться. Таким образом, т. к. Фei(Ak) = С, для
данного у мы можем /^-вычислимо найти такой шаг s, что у < r(ei,s),
где r(ei,s) защищает длину соглашения Z(ei,s), которая после шага s
никогда больше не уменьшится. Поэтому если у = (x,t,e), е > 2ei -I- 1,
то у Е Ak тогда и только тогда, когда у Е Ak,s, поскольку у < r{e\,v)
для всех v ^ s. Это доказывает (2.6). О
2.3 Следствие (Ейтс). Если С в. п. и С <т 0х, то G(^ С) Е^-полно.
Доказательство. То, что G(^ С) Е Е^, доказывается при помощи того
же метода, что и в лемме 1.2. Далее, G($J G) Е^-полно по теореме 2.2
при D — С. (Случай G =т 0х тривиален, так как G(^ С) = и.) О
2.4 Следствие (Ейтс). Если С в. п. и 0 <т С <т 0х, то (Е4,П4)
(G(0'), G(| С)) и, следовательно, G(|G) П4 -полно.
Доказательство. Применяем теорему 2.2 при D = 0'. (Заметим, что
Е® = Е4.) К тому же по упражнению 2.6 G(| С) Е П4. О
2.5 Следствие (Ейтс). Если С в. п. и Ф <т С, то G(^ С) Yj^-полно.
Доказательство. По упражнению 2.7 G(^ С) Е Е4. Если С <т 0х, то
положим D — 0х и применим теорему 2.2. Если С =т 0х, то G(^ С) —
G(0') и Е4-полно по следствию 1.7. Q

§ 2. Индексные множества G(^ A), G(^ А) и G(\ А) 337
2.6-2.16 Упражнения
2.6 (Ейтс). Докажите, что если А в. п., то G(\A) Е Щ. Указание.
Используйте тот же метод, что и при сокращении бескванторной части
формулы в лемме 1.2.
2.7 (Ейтс). Докажите, что если А в. п., то G(^ А) Е £4. Указание.
см. метод из леммы 1.2.
2.8. 	Дайте простое прямое доказательство следствия 2.4, используя
вместо теоремы 2.2 лемму VIII.2.3 о сильной густоте. Указание.
Фиксируем S Е £4 = и применяем теорему 1.3 к К, чтобы получить р. в. п.
последовательность { Vk }*eu;? удовлетворяющую (1.4) и (1.5) (с К
вместо А). Выберем в. п. множество Е |т С и такую р. в. п.
последовательность { Bk }keun что для всех к =т Е и В=т V^. Применяем
лемму VIII.2.3 к С и {Bk }keu>, чтобы получить такую р. в. п.
последовательность { Ak }fceuM что если к Е 5, то Ak =т К, но если к ^ 5, то
Ak |т G.
2.9 (Ейтс). Пусть 0 <т С ^ и Di D2 ^т £*з • • • — такая
р. в. п. последовательность (в. п. множеств), что С ^ Di для всех г.
Докажите, что если 5 Е £4, то существует такая р. в. п.
последовательность { Ak }fcGu;j что для всех к и i D{ $^т Ak и
к Е S => Ak =т 0\
к £ S => С ^т Ak>
Указание. Доказательство такое же, как в упражнении 2.8, за
исключением того, что для каждого к мы определяем такое в. п. множество Bk,
что 42е] =т vle] и Б'2е+1] =т De.
2.10 (Ейтс). Пусть 0 <т С <т 0' и £>2 ^т D$ * • • — такая
р. в. п. последовательность, что С ^т Di для всех г. Докажите, что
существует такое в. п. множество А |т G, что Di А для всех г.
Указание. Положим S = G(^ G) Е £4- Применяем упражнение 2.9 к 5,
чтобы получить { Ak }*eu;- Используйте теорему рекурсии, чтобы найти
такое п, что Wn = Ап, и положите А = Ап.

338
Глава XII. Индексные множества в. п. множеств
2.11. Докажите другую версию теоремы 2.2 с дополнительным
предположением «С <т 13» и дополнительным заключением «{ Ak }кеи
равномерно вычислима относительно D». Указание. В доказательстве
теоремы 2.2 замените все вхождения К на D. Дело в том, что теперь с
помощью D мы можем определить, какие элементы хотят войти в
и какие хотят войти в А^ (как обычно, используя функцию запрета).
Доказательство того, что D теперь может вычислить А^ равномерно
по е, подобно доказательству леммы 4 из теоремы VIII.4.1.
2.12. Докажите, что для произвольного в. п. множества D
(Е?,П?) (G(D),G«D)).
Указание. Выберите некоторое в. п. множество <7, 0 <т С <т и
примените упражнение 2.11.
2.13 (Сламан). Покажите, что в теореме 2.2 мы можем изъять
предположение «С ^т £*», и тем не менее получить то же самое заключение
теоремы, что и в 2.2. Указание. Пусть { V* }^Еа; — как в доказательстве
теоремы 2.2. По доказательствам теоремы 1.3 и леммы 1.4 видно, что
существует такая вычислимая функция /, что для всех к и е
VF =т D=>W°e k)=u,
(2.7)
vie] =т 0 =» И$е,к) =* 0.
(2.8)
Определим вычислимую функцию
q{e, s) = max{ х : (Vty ^ х)[у 6 *)5 & Da f иу = Ds_i \ иу] },
при иу = u(Z)s_i;/(e,k),y,s - 1). Пусть Q(e,s) = max{g(z,s) : г ^ e}.
Заметим, что
wf(e,k) =* 0 [Q(e) =dfn lim inf5 Q(e,s) < oo & Q D], (2.9)
а также
Wf^e^k) = ^ => lim infs Q(e, s) = oo (2.10)
и m где т(ж) = (fis)(Vt ^ s)[Q(e,s) ^ ж]. Дело в том, что пред¬
положение «С ^т 13» использовалась только в лемме 3 для получения
такого ei, что lim infs l?(ei,s) = оо. Теперь мы просто выбираем ео как

§ 2. Индексные множества G(^ A), G(^ А) и G(\ А)
339
в лемме 3 и замечаем, что по (2.2) и (2.10) liminf* Q(e, s) = оо и m -D.
Это достаточно для доказательства леммы 3.
Поэтому в построении целесообразно потребовать, что если у —
(ж,2е) на этапе 1 (или у = (ж,£,2е 4-1) на этапе 2), то у > Q(e — l,s) в
дополнение к у > R(e — 1, s). Проблема в том, что liminf* Q(e, s)
достигается на истинных шагах перечисления {Z}s}sGu;, a liminfsR(e,s) —
на истинных шагах перечисления { Ak,s Ьеим так что liminfsP(e,s) не
обязан существовать, если Р(е, s) = max{ Д(е, s), Q(e, s) }.
Для получения решения мы используем метод пинбольной машины
из § 5 главы VIII. Пусть элемент у, который хочет войти в Ak для
удовлетворения положительного требования из теоремы 2.2, выпадает
из отверстия Не, если у = (х,е) для некоторого х. (см. диаграмму 5.1 из
главы VIII.) Разобьем ворота Ge, е ^ 0, на два воротика G\ и G\. Далее,
позволяем у проходить на шаге s 4-1 через G\, если у > <3(е, s), и через
Gg, если у > R(e,s). Если у достигает ворота G_i, то перечисляем ?/ в
Ak- Теперь используйте метод доказательства из § 5 главы VIII, чтобы
показать, что эта конструкция предоставляет нам возможность доказать
леммы 1 и 2 из теоремы 2.2. Лемму 3 докажите, используя Q(eо, s) вместо
R{ei,s).
2.14. Предположим, что D и С — такие в. п. множества, что 0 <т
D <т С <т 0; и D' =т G'. Докажите, что
(Sf,nf) = (Ef, n3D) sa (G(D), G(|x С) П G(> D)).
Указание- Заметим, что условие D' =т С' обеспечивает = Е^.
Примените доказательство упражнения 2.13, но для каждого к кодируйте D
в А^ так, чтобы для всех к выполнялось D $^т Ak- (Отметим, что без
условия D1 =т С‘ мы все ещё можем получить то же самое заключение,
но уже без первого равенства.)
2.15. Зафиксируем такое произвольное в. п. множество А, что 0 <т
А <т 0х-
(a) Докажите, что G(< А) е [Т,^ & П31]. Указание. Используйте
следствие 2.3 и лемму 1.2.
(b) (Сламан). Докажите, что: (i) Е31 G(< А); и (и) П£ G(< А).
Указание. Для (i) используйте упражнение 2.14 при А = G, замечая,
что G(D) С G(< С). Отметим, что по данному G, 0 <т С <т 0х, в
силу теоремы VIII.4.3 мы можем выбрать D так, чтобы 0 <т D <т С и
D1 =т G'. Для (ii) используйте упражнение 2.12 при А — D.

340
Глава XII. Индексные множества в. п. множеств
(с) 	Докажите, что: (i) Е4 G{> А) и (ii) П£ G(> А). Указание.
Для (i) используйте следствие 2.4, а для (ii) используйте упражнение 2.14
при А — D.
2.16. 	Назовем в. п. степень а т-верхушечной, если среди в. п. т-
степеней в а существует максимальная.
(a) (Джокуш [1972а]). Докажите, что произвольная неполная т-вер-
хушечная в. п. степень а является 2-низкой. Указание. Используйте
классификацию индексных множеств { е : We А } и {е :We ^4 }•
(b) 	° (Доуни и Джокуш). Никакая m-верхушечная (или даже
^-верхушечная) в. п. степень не является низкой.
(c) 	°° (Доуни и Джокуш). Существует такая ненулевая т-верхушеч-
ная в. п. степень а, что 0 < а < 0'. (Фактически, для каждой низкой
в. п. степени b существует такая т-верхушечная в. п. степень а, что
b ^ а < 0х.)
2.17 	Замечания. Каллибеков [1971, теорема 1] анонсировал теорему 2.2
и для её доказательства предложил новый остроумный метод
приоритетного рассуждения, который был также использован Кинбером [1977].
К сожалению, предложенное Каллибековым доказательство содержало
ошибку, которая казалась неустранимой. Позднее Стоб пробовал
доказать теорему 2.2 с помощью стандартного метода приоритета с
бесконечными нарушениями в стиле главы VIII, но натолкнулся на
трудности при доказательстве условия Ak D. Эти трудности он в [1982Ь]
преодолел с помощью необычного подхода к доказательству
соотношения (2.6) в лемме 3. Затем Сламан в упражнении 2.13 показал, как может
быть убрано предположении «С $^т £>». Результаты следствий 2.3, 2.4,
2.5 	и упражнений 2.6, 2.7, 2.9 и 2.10 содержатся в статье Ейтса [1969],
но с другими доказательствами. Доказательства, набросанные в
упражнениях 2.8, 2.9 и 2.10, содержатся в статье Соара [1976, § 6].
Каллибеков [1971] использовал теорему 2.2 для доказательства, что
если d — такая в. п. степень, что d < 0' и d" = 0'" (т. е. d Е Н2), то d
содержит бесконечную антицепь в. п. m-степеней и не содержит в. п. т-
степени, максимальной среди её в. п. m-степеней. (Каллибеков это также
доказал для ^-степеней вместо m-степеней.) Более того, Дегтев [1972а]
доказал, что каждая ненулевая в. п. степень содержит бесконечную
антицепь в. п. tt-степеней. Кобзев [1973b] показал, что каждая ненулевая
в. п. степень содержит бесконечно много минимальных в. п. ш-степеней.

§ 3. Равномерное перечисление в. п. множеств
341
§ 3. Равномерное перечисление в. п. множеств и Е3
индексные множества
Пусть С — класс в. п. множеств и G(C) = { х : Wx € С }. В этом
параграфе мы получим некоторые результаты о таких классах С, что G(C) Е Е3.
Это свойство особенно интересно и полезно потому, что оно
эквивалентно условию «С р. в. п.» (при предположении ТС С).
3.1 	Теорема (Ейтс [1969]). Пусть С — класс в. п. множеств,
содержащий класс Т всех конечных множеств. Тогда следующие условия
эквивалентны:
(i) С равномерно в. п.,
(ii) С равномерно вычислим относительно О',
(iii) G(C) Е Е3.
Доказательство, (i) => (й). Непосредственно, т. к. Ко = 0' и К0 1-
полно.
(й) => (iii). Выберем такую функцию / 0', что Ап — множество
с характеристической функцией Ax[f(n,x)] и С — {Ап}пеи;.
Следовательно,
k Е G(C) ^ (3n){Vx)[x Е Wk f(n,x) = 1 ].
Выражение в квадратных скобках вычислимо относительно 0' и,
следовательно, по теореме IV.2.2 Поста является Д2-множеством, поэтому
G(C) Е Е3.
(iii) 	=> (i). Если G(C) Е Е3, то выберем g как в следствии IV.3.7
и определим В(х^ = Wx П Wg(<X}y). Если х Е G(C), то - Wx для
почти всех у, и В(ХуУ) конечно для всех оставшихся у. Если х £ G(C),
то £(ж,у) конечно для всех у. Таким образом, { Вп }nGu; является р. в. п.
и совпадает с С, т. к. С Э Т. Ц
Из теоремы 3.1 следует, что класс вычислимых множеств р. в. п.
хотя это уже было установлено в упражнении II.2.11. Не так очевидно,
что это верно и для класса в. п. множеств, степени которых ^ а, если
а является 2-низкой. Следующий результат устанавливает, что условие
быть 2-низкой степенью является для а и необходимым условием.

342
Глава XII. Индексные множества в. п. множеств
3.2 Следствие (Ейтс). Если а < 0' — в. п. степень, то следующие
условия эквивалентны:
(i) 	класс в. п. множеств степени а является р. в. п.
(й) класс в. п. множеств степени ^ а равномерно вычислим
относительно О',
(iii) 	а^2) = О^2) (т. е. а является 2-низкой степенью).
Доказательство, (i) (й) по теореме 3.1.
(й) <=> (iii). Заметим, что по теореме 3.1 (й) выполняется тогда и
только тогда, когда G(^ a) G Ез, а это по следствию 2.3 возможно
тогда и только тогда, когда £3 = Е^. Но £3 = £^ и £^ = £f по
теоремам IV.2.2 и IV.4.1. Следовательно, £3 = T,f тогда и только тогда,
когда а^2) = О^2). Q
В отличие от следствия 3.2, ниже в следствии 3.5 мы увидим, что не
существует такой в. п. степени а < 0', что класс в. п. множеств
степени ^ а является равномерно вычислимым относительно а. Теорема 3.4
хорошо соотносится с теоремой Мартина XI. 1.3 о функциях-доминантах
и высоких степенях. Отметим, что введенные в определении 3.3
понятия оказались полезными в других областях теории вычислимости и в
моделях арифметики, см. например, Найт, Лахлан и Соар [1984].
3.3 Определение (Джокуш). Если / — двухместная функция, то /е
обозначает функцию Ап[/(е, п)]. Если С — класс (одноместных) функций
и а — степень, то С называется а-равномерным (в.-субравномерным),
если существует такая двухместная функция / степени ^ а, что
С — { fe • е € w } (соответственно, С С { fe : е € и}).
3.4 	Теорема (Джокуш [1972а]). Если а — произвольная степень, то
утверждения (i)-(iv) эквивалентны:
(О а'^0";
(й) вычислимые функции являются а-равномерными;
(iii) 	вычислимые функции являются а-субравномерными;

§ 3. Равномерное перечисление в. п. множеств
343
(iv) вычислимые множества являются а-равномерными.
Если а в. п. то каждое из утверждений (i)—(iv) эквивалентно (v):
(v) вычислимые множества являются а-субравномерными.
Доказательство. Импликации (ii) => (iii), (ii) => (iv) и (iv) => (v)
очевидны.
(i) => (ii). По теореме XI. 1.3 можем выбрать функцию-доминанту д
степени ^ а. Пусть /((е,г),ж) = (pe,i+g(x)(x), если <pe,i+9(y){y) I для всех
у ^ х, и /((е,г),ж) = 0 в противном случае. Тогда либо /(е>*) = (р€ —
всюду определенная функция, либо /(е,г) всюду равна нулю, кроме
конечного множества значений аргументов. В любом случае f^yi) вычислима.
Если (ре всюду определена, то д(х) доминирует с(х) = (fj,s)[(peyS(x) |],
поэтому (ре — /(e,i) для некоторого г.
(iii) => (i). Пусть f(e,x) — такая функция степени а, что
каждая вычислимая функция совпадает с некоторой /е. Определим д(х) =
max{ fe(x) : е х }. Тогда д — доминанта, поэтому а' ^ 0'' по
теореме XI.1.3.
(iv) => (i). По теореме IV.3.2 и упражнению IV.3.8 имеем
(Tot, Tot) (Ext, Ext)
посредством некоторой вычислимой функции д. Предположим, что /
имеет степень ^ а и функции {/e}eGu; в точности являются всеми
вычислимыми характеристическими функциями. Тогда для всех е:
е е Tot (3i)[/* продолжает (рд(е)],
<=* (3i)(Vx)(Vj/)(Vs)[^g(e)iS(a;) = у => fi(x) - у].
Таким образом, Tot 6 Следовательно, Tot € Д2 и поэтому 0" ^ а'
в силу теоремы IV.4.1.
(v) => (i). (Изложенное ниже напоминает доказательство того, что
класс вычислимых функций не равномерно вычислим.) Предположим,
что а в. п. , но (i) ложно и /(е,ж) — произвольная функция степени
а. 	Мы должны построить такую вычислимую функцию /, что h ф fe
для всех ей/ принимает только значения { 0,1}. Так как deg(/) ^ а,
то по лемме III.3.2 о модуле существуют вычислимая функция f{e,x,s)
и функция-модуль т(е,х) для / такие, что /(е,ж) = limSf(e,x,s) и
т(е,ж) имеет степень ^ а. Пусть р(х) = тах{т(е,(е,я)) : е ^ х}.
Так как deg(p) а и (i) не выполняется, то существует
вычислимая функция q(x), которую р(х) не доминирует. Определим h((e,x)) =

344
Глава XII. Индексные множества в. п. множеств
1—/(е, (е, х), q{x)). Тогда h — вычислимая функция и h((e,x)) ф
/е((е,ж)), как только х ^ е и q(x) ^ р{х). (Как следует из
упражнения 3.9, предположение «а в. п.» для доказательства (v) => (i) является
необходимым.) О
3.5 Следствие (Джокуш). Если а < (У в. п. то класс в. п. множеств
степени ^ а не является а.-равномерным.
Доказательство. Предположим, что а является контрпримером. Тогда
вычислимые множества являются а-субравномерными, и поэтому по (v)
=> (i) теоремы 3.4 а' = О". Однако, т. к. класс в. п. множеств степени
а является а-равномерным, он также и (У-равномерен, и поэтому по
следствию 3.2 имеем а" = О". О
Следующая теорема продолжает тематику £3 -индексных множеств,
начатую в теореме 3.1, и дает интересное следствие 3.8, которое имеет
отношение к упражнениям XI.4.2 и XI.4.3 о степенях в. п. подмножеств
произвольного в. п. множества.
3.6 Теорема (Стоб [1982b]). Если S — такое £3 -множество, что
k Е S => Wk не является бесконечным, кобесконечным . .
вычислимым множеством, ' ’ '
то существует такое простое множество А, что
[к Е S & Wk невычислимо] => Wk фт А. (3.2)
3.7 Следствие (Кинбер [1977, теорема l']). Пусть Т —
П2-множество, и ф — такая ч. в. функция, что если к Е Т, то ф(к) | и W^^k)
невычислимо. Тогда существует такое невычислимое в. п. множество
А, что если к Е Т, то W^k) ^т А.
Доказательство. Применяем теорему 3.6 к £з-множеству S = { ф(к) :
кет}. Q
(По теореме V.4.1 простое множество Поста полно, независимо от
того, какое вычислимое перечисление { WeyS }e,seu> в. п. множеств
используется в построении. В противоположность этому Джокуш и Соар [1973]
показали, что гиперпростое множество Н, построенное Постом [1944],
может быть полным или неполным в зависимости от того, какое
перечисление { We,s }e,sGu; используется. Они также поставили вопрос о том,
может ли Н при выборе подходящего перечисления иметь
произвольно заданную ненулевую в. п. степень. Кинбер [1977] с помощью
следствия 3.7 отрицательно ответил на этот вопрос.)

§ 3. Равномерное перечисление в. п. множеств
345
3.8 	Следствие (Стоб [1982b]). Если В — простое множество, то
существует такое невычислимое в. п. множество А, что если В С
С Ф* и>, то С фт А. Таким образом, кобесконечное в. п. множество В
является простым тогда и только тогда, когда В не может иметь
надмножества в каждой в. п. степени.
Доказательство. Пусть S = {е : В С We }. Тогда S — Пг-множество,
удовлетворяющее условию следствия 3.7, т. к. В просто тогда и
только тогда, когда никакое его бесконечное, кобесконечное надмножество
не является вычислимым. Следовательно, по 3.7 существует такое в. п.
множество А, что если В С W€ и We невычислимо, то We фт А. О
Доказательство теоремы 3.6. Фиксируем S Е Ез, удовлетворяющее
(3.1). Так как Inf Е Пг, мы можем предположить, что S С Inf, при
необходимости заменяя S на S П Inf. По следствию IV.3.7 фиксируем
р. в. п. последовательность { V* }к^и такую, что для всех к
к € S => (Эе)(Vi ^ e){vj?] = и] (3.3)
И
к £ S => (Ve)[VJ^ конечно]. (3.4)
Искомое множество А достаточно построить кобесконечным и
удовлетворяющим для всех ей к требованиям:
Ре : W€ бесконечно ==> A HWe ф 0;
N(e,k) : [V^ бесконечно Л Wk невычислимо ] => Фе(Л) ф Wk.
Выполнение требований N(e^) гарантирует (3.2). Действительно, если
к Е S и Wk невычислимо, то по (3.3) для почти каждого е = и
и, следовательно, Фе(л4) ф Wk по N(€tky Поэтому Wk Фт А, т. к. для
каждого тьюрингового сведения существует бесконечно много индексов.
Мы удовлетворяем N(Ciky используя стратегию сохранения
равенства из теоремы VII.3.1, при этом мы должны стремиться избежать
слишком большого запрета в случае, когда Wk коконечно. Определим
следующие вычислимые функции:
l((e,k),s) = max{ х : (Vy < ж)[Фе,»(А*;ж) = WA%s(x)] },
/((е, k),s), если m((e, k),s — 1) <
m((e, к), s — 1) в противном случае.
m((e,k),s) =

346
Глава XII. Индексные множества в. п. множеств
r((e, A;),s) = таx{u(As]e,x,s) : х т((е, A;), s) }.
Заметим, что I — обычная функция «длины соглашения», но т
модифицирована так, чтобы увеличиваться при увеличении \V^\ и \W k\-
Отметим также, что если выполняется первая строка определения т, то
т((е, к), s - 1) < /((е, к), s).
Шаг s -f 1. Выбираем наименьшее число i такое, что Wiy8 П А8 = 0 и
(Зж)[ж £ & 2i < х к (Vj < i)[r0’,s) < ®]]-
Перечисляем наименьший такой х в А и говорим, что Pi получает
внимание на шаге s + 1.
Лемма. Для каждой пары (е, А;)
(i) iV(e удовлетворяется,
(ii) lims m((e, A;), s) < oo,
(iii) lims r((e, A;), s) < 00.
Доказательство. Фиксируем (e,k). Выберем s0 так, что никакое Р*,
г (е,А;), не получает внимание ни на каком шаге s ^ so. Заметим, что
для s ^ so ни один х г((е, А;), 5) не входит в А на шаге 5 4-1, поэтому
если Фe}8(As]x) = у и х ^ m((e,A;),s), то для всех £ ^ s Фе>*(А*;:г) = 2/
и u(At',e,x,t) = u(As-,e,x,s). Таким образом, (и) влечет (iii), т. к. если
т = lims m((e, А;),5), то
lims r((e, A;), s) = max{ и(А\ е, х) : х ^ m }.
Следовательно, достаточно доказать (i) и (ii). Если конечно, то
(i) и (ii) очевидны по определениям. Таким образом, мы можем
предполагать, что бесконечно, поэтому по (3.3) и (3.4) имеем к £ S.
Случай 1. Wk невычислимо.
Тогда \Wk\ = 00, поэтому если N(6yk) не удовлетворяется и Фе(л4) =
VFfc, то lims Z((e, A;), s) = 00, lims m((e, A;), 5) = 00, и мы можем показать,
что Wk вычислимо, вопреки предположению. (Чтобы эффективно
определить, верно ли, что х £ Wk, находим s ^ so такое, что х < m((e, A;), s)
и Фе,8(А8] е,х, s) 4= у. Тогда х £ Wk тогда и только тогда, когда у — 1.)
Следовательно, (i), а значит, и (й) выполняются.
Случай 2. Wk коконечно.

§ 3. Равномерное перечисление в. п. множеств
347
Заметим, что (i) выполняется непосредственно. Предположим, что
(и) неверно. Тогда
lims m((e, к), s) — оо.
Выберем t > so такое, что m((e,A;),£) > m((e, к), t — 1) > \W к\- Положим
m = m((e, &),£). Тогда m = l((e,k),t) и, следовательно,
(Vx < т)[Фе,((Л(;х) = Wfe,t(x)].
Так как t > so, каждое из этих вычислений Ф€it(At;x) неизменно. Но
т > \Wк\, поэтому должен существовать х < m, х £ Wk,t, но х Е
для некоторого v > t. Следовательно,
О — Фе,г; (Дг; J Я') "ф- ^^k,v = 1
и поэтому это неравенство будет препятствовать увеличению либо
/((е, &),$), либо m((e,k),s) на любом шаге s > v.
Это завершает доказательство леммы. Теперь каждое
положительное требование Pi удовлетворяется по построению и части (iii) леммы.
Теорема доказана. О
3.9—3.10 Упражнения
3.9 (Джокуш). Покажите, что предположение «а в. п.» в
доказательстве импликации (v) => (i) из теоремы 3.4 является необходимым. Для
этого доказажите, что существует такая степень а, что а' = 0' и класс
всех вычислимых множеств а-субравномерен.
Указание. Примените теорему о низком базисе VI.5.12 к П^-классу
С С 2<и;, где
f еС <=> rng/ с {о, 1}
& (Ve)(Vx)fo>e(x) 4-=» f((e,x)) = min{ 1 ,<ре(х) }],
чтобы получить некоторую функцию / Е С низкой степени.
3.10 (Джокуш [1972а]). Покажите, что если а и b — в. п. степени,
b а и b < 0х, то следующие три утверждения эквивалентны:
(i) в. п. множества степени ^ b а-субравномерны;
(и) Ь" = а' = 0";
(iii) 	существует в. п. последовательность в. п. множеств, степени
которых равномерно а, состоящая в точности из в. п. множеств
степени < Ь.

348
Глава XII. Индексные множества в. п. множеств
§ 4. Классификация индексных множеств п-высоких,
n-низких и промежуточных в. п. множеств
4.1 Определение, (i) Пусть 0(u;+1) = (0^))' — скачок множества 0^).
(ii) Множество А является -множеством (П^+i-множеством), ес-
ли л е Ef“) (П?(и>).
(iii) 2^4.1- (П^х-) множество А называется -полным (П^+i-
полным), если 0(u;+1) А (соответственно 0(tJ+1) ^ А). (По тем же
самым замечаниям, что в определении IV.2.1 и упражнениях IV.2.6 и
IV.2.7, не имеет значения, используем ли мы в определении -полных
и П^+i-полных множеств «^ш» или «^i».)
4.2 Определение, (i) Highn = {х : Wx n-высокое},
(ii) Lown = { x : Wx n-низкое },
(iii) Low<CJ = L<u; - Un Lown и High<u; = H<u; = jjn Highn,
(iv) Int = { x : Wx промежуточное } = и — (L<u; U H<a;).
Так как = A, то очевидно, что Lowo = Rec, a High0 = Comp =
{x : Wx =т 0; }, как также определено в IV.3.3. В теореме IV.3.4 мы
видели, что (Ез,Пз) (Rec, Comp) — (Lowq, High0), а в следствии 1,7,
что Comp = High0 £4-полно. Теперь мы обобщаем эти результаты,
показывая, что для всех п ^ 0 Highn £„4.4-полно и
(£п+з,Пп+3) (Lown,Highn).
Также мы доказываем, что каждое из L<a; и Н<и; является £^4.1-полным,
а Int является П^4.1-полным. Начнем с установления некоторых простых
оценок.
Из них вытекает, что Lowi £4-полно, а Highx £5-полно. Эти
результаты существенны, т. к. часто нам по данному в. п. множеству Wx
желательно узнать, не является ли оно 1-низким. Многие построения
упрощаются, если мы работаем с 1-низкими в. п. множествами или их
степенями, (см. теорему XI.3.2, упражнения XI.3.4 и XI.3.5 и
примечания XI.3.7 для 1-низких, и теорему XI.5.1 — для 2-низких множеств.)
Однако, обычно бывает недостаточно знать, является ли Wx 1-низким,
требуется знать также его индекс низкости (см. упражнение 4.24).
4.3 Теорема, (i) Lown G £п+з равномерно по п;
(ii) Highn G £п+4 равномерно по п;
(iii) L<u; G Ец;+1 и H<u; G £^4.1;
(iv) Int G П^+i.

§ 4• Индексные множества Highn, Lown и Int
349
Доказательство. Заметим, что (Ш) следует из (i) и (ii), a (iv) — из (ш),
поэтому достаточно доказать (i) и (ii).
(i)
х G Lown <=> Wxn* 0*"^
(3e)m[[yewin) k {е}0<",(у) = 1]
V[yiW^n) к {е}0(")Ы = О]]
4=> 3V[[En+i к En+i] V [П„+1 к Е„+1]]
<==>■ 3[Пп+2 к П„+2]
(ii)
х € High„
0(n+D Wt]
(Зе)[{ е }lv")n> всюду определена
& •••]
<э.)[<-” ь •••]
Э[ПП+3 & • • •], потому ЧТО WxU^
<СТ 0<n+1>
Sn-f 4* D
4.4 	Теорема (Шварц [1982]). Для всех п ^ 0 Highn является Еп+4 —
полным равномерно по п.
Доказательство. Мы хотим определить вычислимую функцию /(n,fc)
так, чтобы
0(n+4) Highn
посредством Xk[f(n,k)]. В следствии 1.7 мы показали, что Но = Comp
Е4-полно. Релятивизуя это доказательство относительно 0(п) и
используя релятивизованную s-m-n теорему, получаем такую вычислимую
функцию g(n,fc), что Сотр0( * является Еп+4-полным посредством
\k[g(n,k)], а именно, для всех пик
к е 0(n+4) wf{”]k) =т 0(п+1). (4.1)
Пусть q(x) — вычислимая функция из теоремы Сакса о скачке,
удовлетворяющая условию VIII (3.6). По следствию VIII.3.6 при Y = 0 для
всех х и п имеем
0 <т WV(I) <т 0' к W(q:\x) =т wfn) ® 0(п). (4.2)
Определим f(n,x) = qn(g(n,x)). По (4.1) и (4.2) для всех пик
выполняется
к е 0(n+4) wffn,k) =т 0<п+1)-

350
Глава XII. Индексные множества в. п. множеств
Заметим, что доказательство устанавливает, что для всех Y С и и n,k €
uj
к е гп+4 <=> (w/v;n,,))(n) =т О
Далее Шварц [1982] примерно так же, как теорему 4.4, доказал
следствие 4.7, использовав в качестве исходного шага (Ез, Пз) (Rec, Comp).
Позднее Джокуш использовал метод Шварца, чтобы получить более
общий результат (следствие 4.10) о множествах, замкнутых относительно
п-го скачка. Следующая теорема слегка обобщает следствие 4.7 Шварца,
потому что в случае к G у(п+3) мы заменяем нижнюю оценку Y^ из
(4.6) на нижнюю оценку {Wj)из (4.4).
4.5 	Теорема (Джокуш). Существует такая вычислимая 1:1-функция
/(n,j, к), что для всех множеств Y С ш и целых неотрицательных
чисел n, j, к
(4.3)
к е У<”+3> => (W/[n>j>fc))<n> =т (wr)<»> (4.4)
U
к i у("+3> =► (Wj(nJtk))^ =т У(п+1). (4.5)
Доказательство. Релятивизуем теорему IV.3.4 относительно Y^ и
получаем такую вычислимую функцию g(n,k), что для всех п
(еГ\п3у'<П>) «П (Recyln,,CompK(n)) = (Low0v'(n),Highy<">)
посредством \k[g(n,k)]. Следовательно, для всех пик
к 6 у(«+») =► w^k) =т v(n) (4.6)
к i Y(n+3) => (4.7)
Определяем вычислимую функцию h:
<,!) = (V ф >0(п> ® <2) гт
Пусть f(n,k,j) = qn(h(n.k.j)). Теперь (4.3), (4.4) и (4.5) следуют из
(4.6)  , (4.7) и Следствия VIII.3.6. D

§ 4• Индексные множества Highn, Lown и Int
351
4.6 	Следствие (Джокуш). Для любого в. п. множества А
существует такая вычислимая функция g(n,k), что для всех пик
А именно, (Еп+з,Пп+з) (Gn(A),Gn(0')), где по определению
Gn(X) = {е: Wjn) =т Х(п)}-
Доказательство. В теореме 4.5 положим Y = 0 и g(n, А;) = f(n,j, А;) для
некоторого ^ такого, что IV) = А О
4.7 Следствие (Шварц [1982]). Для всех п ^ 0 выполняется
(£„+з,П„+з) <1 (Low„,Highn)
равномерно по п и, следовательно, Lown Еп+з-полко.
Доказательство. В теореме 4.5 положим V = 0 и = 0. Q
4.8 Следствие, (i) (Джокуш). A =dfn {х : Wx безатомное} Пь-полно.
(ii) Sim =def {х : Wx простое} Пз -полно. (См. упражнение V.I.8.)
(iii) HSim =dfn {х : Wx гиперпростое} Пз -полно. (См.
упражнение V.2.10.)
Доказательство, (i) Пусть для каждого у Wg(у) — дефицитное
множество Деккера для множества Wy (как определено в теореме V.2.5, но
используя стандартное перечисление { WViS }sGa; из упражнения 1.3.11 и
пропуская повторения). Применяя следствие 4.7 при п = 2 получим
посредством некоторой вычислимой функции h. Таким образом, по
теореме XI.4.1 и следствию XI.5.2 (Е5,П5) (А, А) посредством g о h.
Отсюда П5 $Ji А. Более того, т. к.
а по упражнению 4.21 Мах Е Щ, то A Е П5 и, следовательно, А является
П5-полным множеством.
(ii) и (iii). Применяя следствие 4.7 при п = 0 получим (Ез,Пз) ^
(Rec, Comp) посредством некоторой h. Следовательно, (Ез,Пз) (Rec,
HSim)посредством goh. При помощи методов глав IV и V легко показать,
что Sim, HSim Е П3. []
(Е5,П5) (Low2,High2)
х G А х $ Cof & -i(3t/)[t/ G Мах & Wx С Wy],

352
Глава XII. Индексные множества в. п. множеств
4.9 Определение, (i) Множество С замкнуто относительно п-го
скачка, если х Е С и WxU^ =т WyU>i влечет у € С.
(ii) Множество С и-замкнуто, если С замкнуто относительно п-го
скачка для каждого п.
4.10 Следствие (Джокуш). Предположим, что С и С Ф и.
(i) Если С замкнуто относительно п-го скачка, то либо 0(п+3)
С, либо 0(п+3) С.
(ii) Если С и -замкнуто, то С.
Доказательство. Для доказательства (i) предположим, что СП Comp =
0, и зафиксируем j Е С. По следствию 4.6
(ЕП+3,ПП+3) (С,С).
Заметим, что (ii) следует из равномерности в (i). О
4.11 Следствие (Соловей). 0й* L<u;, 0Ы Я<ш и 0^ Int.
4.12 Теорема (Джокуш). Теорема IV.3.4 равномерна в том смысле,
что существуют такие вычислимые функции fug, что (0(3\0(3))
(Cof, Comp) посредством функции /, и для всех х
х £ 0(3) => { g(x) = хк,
х Е 0(3) => Wf(x) =т 05
и
compat (xk,{9(x)}W,{u)),
где хк — характеристическая функция множества К. Если х Е 0^3\
то функция { g(x) будет частичной, даже с конечной областью
определения.
Доказательство. В доказательстве теоремы IV.3.4 процедура ф(у) =
{ 9(х) }Wf^{у)сначала находит такой наименьший шаг s(y), что Ъ*х$ =
Ъх,у, и затем выдает выход 1 или 0 в зависимости от того, у Е К8^
или нет. Если х $ 0(3\ то s(y) существует для всех у, поэтому ф
всюду определена. Если х Е 0^3^, то ф(у) определена только на конечном
начальном сегменте и, но если ф(у) определена, то ф(у) = К (у) по
построению Wf(x). о

§ 4• Индексные множества Highn, Lown и Int
353
4.13 	Теорема (Шварц), (i) (Е4,Щ) (Lowi,Max), где
Max =dfn {% • Wx максимальное }.
(ii) Max П4 -полно.
(iii) Для каждого из пяти других классов С, состоящих из простых
множеств, в диаграмме 1.1 главы XI (исключая классы простых,
гиперпростых и квазимаксимальных множеств) {х : Wx Е С } Щ -полно.
Сюда входят классы г-максимальных, сильно гиперпростых, конечно
сильно гиперпростых, гипергиперпростых и плотно простых множеств.
Доказательство. Части (ii) и (ш) немедленно следуют из (i) и
упражнения 4.21, потому что по упражнению XI. 1.12(б) deg(C) С Hi для каждого
такого класса С, поэтому deg(C) flLi = 0 и Л4 С С, где Л4 — класс
максимальных множеств. Таким образом, для класса С квазимаксимальных
множеств мы также имеем П4 { х : Wx Е С }, но этот класс не входит
в П4, а, более того, является Е5-полным (см. Лемпп [1986]). Все другие
упомянутые классы представляются в Щ-форме (см. упражнение 4.21),
за исключением классов простых и гиперпростых множеств, которые
являются П3-полными (см. упражнения V.1.8 и V.2.10).
(i) (Джокуш). Пусть по следствию 4.7 при п = 1
(£4,П4) (Lowi,Highi)
посредством некоторой вычислимой функции /. (Идея теперь состоит
в том, чтобы применить теорему Мартина XI.2.3, позволяющую
перейти от произвольного 1-высокого в. п. множества D к максимальному
множеству М =т D, но сначала нам нужно установить некоторые
равномерности.) Релятивизуем теорему 4.12 относительно 0' и применяем
теорему III.1.5, чтобы получить такие вычислимые функции g и F, что
для всех к
к $ 0<4> => 0<2> = { д(к) }^), (4.8)
к е 0(4) => W|'(jk) =т 0' (4.9)
И
compat(0^2), {д(к) }Wf^). (4.10)
Определим вычислимую функцию f(k) = q(F(k)), где q удовлетворяет
следствию VIII.3.6. Следовательно, Wp^ =т ^/(ж) и тьюринговы
сведения равномерны по к, поэтому в (4.8)—(4.10) мы можем заменить Wp^

354
Глава XII. Индексные множества в. п. множеств
на Wj(ky Достаточно получить функцию hk такую, что для всех к
hk всюду определена,
(4.11)
hk ^т Wf^k) равномерно по к,
(4.12)
к £ 0(4) => hk является доминантой,
(4.13)
потому что тогда мы сможем применить конструкцию Мартина из
теорем XI.2.1 и XI.2.3 при заданных Wf(x) и hk, чтобы получить в. п.
множество Ak =т являющееся максимальным, если hk — доми¬
нанта. Зафиксируем к и определим hk{x) следующим образом. Из (4.8)-
(4.10), леммы III.3.3 о пределе, примененной к { д(к) и из того,
что 0(2) =т Tot, получаем, что существует такая всюду определенная
функция m(k,x,s), вычислимая относительно Wf(k), что выполняются
к £ 0(4) => (Vz)[Tot(z) = limsm(A;,z,s)], (4.14)
и
[к Е 0^ & Фк(х) = lims т(к,х, s)] => compat(^*(a;),Tot(a;)), (4.15)
даже хотя фк{х) может быть не всюду определенной, если к Е 0^4^.
Теперь получаем hk, как в части (=£►) доказательства теоремы XI. 1.3 при
А, g(x,s) и /, замененными соответственно на Wf(x), m(k,x,s) и hk.
Заметим, что (4.15) гарантирует, что в XI. 1.3 значение t(e) существует,
даже если к Е 0^. Следовательно, hk всюду определена для всех к, вне
зависимости от того, к Е 0^4^ или нет. []
(Заметим, что в доказательстве теоремы 4.13 для того, чтобы мы
могли применить построение из теоремы XI.2.3, нам нужно, чтобы
функция hk была всюду определенной. Если это не так, то пусть hk(xо) t •
Тогда для каждого х ^ х0 мы можем иметь т(&, я, s) ф т(к, я, s +1) для
бесконечно многих s. Но на каждом таком шаге «4-1 элементу х
разрешается войти в Wf(x), согласно конструкции из теоремы XI.2.3, поэтому
мы можем получить Wf(k) =т 0;, даже если к Е 0^4). Этим объясняется
наша осторожность при использовании (4.10) и теоремы 4.12.)
Соловей ответил на вопрос Шварца о классификации множества Int
следующей теоремой, которая усиливает следствие 4.11. Доказательство
похоже на доказательство Сакса следствия VIII.3.5 о том, что Int ф 0.

§ 4• Индексные множества Highn, Lown и Int
355
4.14 	Теорема (Соловей). Int Пы+i -полно, и каждое из множеств
Н{jj и L<u; E^-j-i -полно.
Доказательство. По теореме 4.3 имеем Int Е П^+i, a L<u;,H<a; Е E^+i.
Пусть S — произвольное Ew+i -полное множество, например, 5 = 0(u;+1).
В упражнениях 4.15 и 4.16 мы устанавливаем следующие два
необходимых нам факта:
(3 вычислимая функция h)(Vy)[y Е S <==> (4-16)
<=» (Эп)[Л(»,п) € 0<Л>]],
(3i0)(Vn)[{ г0 }®<п>(0) = п]. (4.17)
По данным х, у и Y определяем вычислимую функцию д(х,у),
перечисляя W^x следующим образом.
Этап 1. Вычисляем {г'о}г(0). Пусть п — его значение (если оно
вообще существует). (Таким образом, если Y = 0^, то п — j.) Если же
{*о }r(0) t> то пусть W^x = 0. В противном случае делаем следующее.
Этап 2. Проверяем, верно ли h(y,n) Е Y.
Случай 1. Если «да», то определяем Wg(XtV) = Y'.
Случай 2. Если «нет», то определяем Wg^XtV) = W^xy где q(x) —
как в следствии VIII.3.6.
Теперь по релятивизованной теореме рекурсии с параметрами III. 1.6
существует такая вычислимая функция р(у), что
Kv) = W9Mv),v)- (4-18)
Мы утверждаем, что для всех у
yes=► (3n)[(Wjv,)<«> =Т 0(п+1)] (4.19)
И
у £ S => — промежуточное множество. (4.20)
Для каждого j определим dj = deg(W^yj). Если у Е 5, то выберем
наименьшее п такое, что h(y,n) Е Тогда для всех j п имеем
(Wp(y)Yj) =т <;• Следовательно, по случаю 2 этапа 2 и свойствам
функции q из следствия VIII.3.6 имеем
(Vi < n)[0«> < d,- < 0<j+1> & d' = dj+1}.
(4.21)

356
Глава XII. Индексные множества в. п. множеств
Но при j = п по случаю 1 этапа 2 имеем dn = 0(n+1) и, таким
образом, по (4.21) dpn^ = 0(n+1). Следовательно, d0 G Нп. Если у £ S',
то (Vn)[/i(y,n) 0^], поэтому (4.21) выполняется для всех п и, таким
образом, является промежуточным. Заметим, что (4.19) и (4.20)
устанавливают, что (E^+i,n^+i) (H<a;,Int) и, следовательно, H<u;
является -полным, а Int — П^+x-полным.
Чтобы доказать E^+i-полноту L<a;, в случае 1 этапа 2 полагаем
Wg(x,y) = Дальнейшее доказательство такое же и устанавливает, что
(£ц;+1, П^+х) (L<aMInt). Q
4.15-4.26 Упражнения
4.15. Докажите соотношение (4.16), предварительно установив
следующие факты:
(i) Существует такая вычислимая функция f(u,v), что для всех и и
v
[Du С 0<") & Dv П г(ш) = 0] <=► f(u,v) е 0(ы).
(ii) Существует такая вычислимая функция r(i,j,x), что
(Уж)(Уг, j)i<j[x е 0(,) r(i,j,x) е
Указание. По определению 0(u,+1) имеем у 6 0(^+1) .*=>. {y}0<u,)(j/) 4 •
Следовательно, по (i) существует такая вычислимая функция д(у), что
у е 0<"+1> <=» (3(а, Ь))[(а, Ь) € Wg(y) & a 6 0(ь)]. (4.22)
Используйте (ii) и И^(у), чтобы определить такую вычислимую
функцию А;(у), что
wk{y) = { .. • } бесконечно;
Vj < для всех j, и (4.22) выполняется с &(?/) вместо д(у). Пусть
{бо}г(^) не определена для всех У и г, так что для произвольного п
е0 ^ 0(п). Определите h(y,n) = если п = Vj для некоторого j, и = во
в противном случае. (См. также аналогичное доказательство леммы 1
из теоремы 6.2.)
4.16. (а) Докажите соотношение (4.17). Указание. Пусть {ei}y =
Az[0]. Для п ^ 1 определим {en+i }у = Az[0], если еп Е У, и Xz[\] в
противном случае. Заметим, что еп Е 0^ш^ в точности для 1 ^ п ^ т,

§ 4• Индексные множества Highn, Lown и Int
357
и функция g(n) = еп вычислима по s-m-n теореме. Для вычисления
{}г(0) ищем такое наименьшее п > О, что еп £ Y, и на выход подаем
п - 1.
(Ь) Докажите
(3i0)(3ei)(Vn)(VF)[{ г0 }(y-{ei })(п>(0) = п]. (4.23)
Указание. Определите ei, как в части (а). Доказательство для Z = Y —
{ е\ } такое же, что и для Z = 0 в (а).
4.17 (Джокуш). (а) Докажите, что класс С с^-замкнутых множеств С
является П^’0( ^классом (как определено в определении VI.5.11 и реля-
тивизовано относительно 0(ы)).
(b) Применив теорему о низком базисе VI.5.13 и следствие 4.10(ii),
сделайте заключение, что С имеет нетривиальный элемент А, низкий
над (т. е. А' =т 0(ы+1)).
(c) Докажите, что в отличие от теоремы 4.14 заключение
следствия 4.10(ii) не может быть усилено так, чтобы получить <<0(u;+1) С».
4.18 (Джокуш). Непересекающаяся пара (Aq, А\) 0^-в. п. множеств
называется 0^) -эффективно неотделимой, если определение из
упражнения II.4.13 выполняется при «0^^-в. п.» и «0^)-вычислимо» вместо
«в. п.» и «вычислимо», соответственно. Пусть V — класс множеств D,
которые отделяют некоторую фиксированную непересекающуюся пару с
таким свойством. Докажите, что если С — нетривиальное и-замкнутое
множество, то (3D Е D)[D С]. Указание. Пусть А0 и А\ — не-
пересекающиеся множества, в. п. относительно 0^) и 0^) -эффективно
неотделимы. Для i = 0,1 выберем вычислимую функцию hi,
удовлетворяющую (4.16) с Ai вместо S. Пусть С ил-замкнуто и нетривиально.
Выберем ео Е С и е\ £ С. Модифицируем определение в случае 1 этапа 2
из теоремы 4.14 следующим образом. Пусть
WY _ f WJ(i>ny если [Ы(у,п) eY k h!-i(y,n) ^Y],
9(x*y) I И^ж) в противном случае,
где z(i,n) выбирается так, чтобы = We^. Далее продолжайте,
как в доказательстве теоремы 4.14.
4.19 (Джокуш). Для А С и определим с^-замыкание множества А:
СМЛ) = { е : (3» G Л)(3п)[^п) =т Wjn>] }.

358
Глава XII. Индексные множества в. п. множеств
Заметим, что Cl^A) является наименьшим с^-замкнутым множеством,
содержащим А.
(a) Докажите, что если А в. п. относительно 0^, то С1а;(А) также
является в. п. относительно
(b) Докажите, что если А в. п. относительно 0^) и С1 и;(А) ф 0, и, то
С1 ш{А) =т 0^+1\ Указание. Используйте (а) и упражнение 4.16, чтобы
доказать, что С1ц,(А) 0(и;+1)-полно.
4.20 	(Джокуш). (а) Докажите, что если С С 2Ш — произвольный
непустой П? -класс и D отделяет пару эффективно неотделимых множеств,
то (3С Е С)[С $^т D]. Указание. Зафиксируем вычислимое дерево Т, как
в определении VI.5.11, такое, что [Т] = С. Пусть Та = {т € Т : а С т}.
Покажите, что с помощью оракула D можно вычислить такую функцию
/(а), что если [Та] ф 0, то также ] Ф 0.
(Ь) Релятивизуйте (а) относительно 0^) и комбинируйте с
упражнением 4.18, чтобы доказать, что для С из упражнения 4.17 и V из
упражнения 4.16 замыкание наверх степени deg(C) равно замыканию наверх
степени deg(V).
4.21. (а) Докажите, что Мах Е Щ.
(Ь) Для каждого из оставшихся пяти классов простых множеств С,
приведенных в диаграмме 1.1 главы XI, за исключением простых,
гиперпростых и квазимаксимальных множеств, докажите, что { х : Wx Е
С } Е П4. Сюда входят классы r-максимальных, сильно гиперпростых,
конечно сильно гиперпростых, гипергиперпростых и плотно простых
множеств.
4.22 	(Шварц). Докажите, что (Е4,Щ) (Lowi,NSemilow), где
NSemilow = { х : Wx не является полу-низким }.
Указание. Используйте следствие 4.7 при п — 1 и упражнение IV.4.10.
(Этот результат также следует из теоремы 4.13, потому что если А
максимально, то А не полу-низко.)
4.23. Дайте прямое, без использования теоремы 4.13,
доказательство того, что Мах Щ-полно. Указание. (Д.А. Мартин). Пусть S — Щ-
полное множество. Тогда существует такая вычислимая функция /, что
k Е S тогда и только тогда, когда {Vi)(3j)Wf(k,iyj) бесконечно. Мы
можем предположить, что 0) конечно и непусто для всех А; и г, и что

§ 4- Индексные множества Highn, Lown и Int
359
Wf(kyij) Я Wf(k,i,j') для J1 ^ 3- Построим такое в. п. множество Ак, что
если k € S, то Ak максимально, в противном случае Ak не является
даже конечно сильно гиперпростым. Пусть теперь к фиксировано, поэтому
не пишем нижний индекс к для Ak.
Используем построение максимального множества из теоремы Х.3.3,
где As = { ag < ai < • • • }, но предполагаем, что, как и в теореме Х.7.2,
lims а8п может существовать не для каждого п. На шаге 5 = 0 положим
= 2п. Элемент х является свободным на шаге 5+1, если х £ AsVJ{asn :
п Е и)}.
Шаг 5 + 1 = 2£ + 1. Если Wf(k,i,j),a+1 перечисляем ^ в
As+1. Это напоминает «пинок» на этапе 2 в теореме Х.7.2. (По
соглашению П.2.6 существует не более одной такой пары (i,j)-) Полагаем
равным наименьшему свободному числу и ар"1 = а®, если р ф (i,j).
Шаг 5 + 1 = 2£ + 2. Находим наименьшее n = (i,j) такое, что
некоторое т > гг, т = (г',j') удовлетворяет условиям:
(a) ^ пт.,
(b) a{i,asn,s) < a{i,asm,s),
(c) o{i,abm,s — I) ф a{i,a8m,s), или был свободным на шаге 5.
Если такое п существует, то перечисляем а8п в As+i, выбираем
наименьшее т, соответствующее этому гг, полагаем ар1 = а8т и а^1 —
наименьшему свободному числу. Пусть ар"1 = а8р для всех р Ф п (если
такой п не существует, то для всех р). (Условие (с) похоже на
условие X (7.6) из теоремы Х.7.2, которое обеспечивает, что если lims а8п
не существует, то не существует и т > п такое, что элемент а8т под
маркером m бесконечное число раз переводится на позицию маркера п.)
Докажите последовательно следующие утверждения:
(1) = lims асуществует тогда и только тогда, когда
конечно;
(2) (Vi)[fl(i>0> существует] и, следовательно, \Ак\ = оо, вне
зависимости от того, к Е S или нет;
(3)
(Vi)(3a0)(a.e.n)[n = (*', j')&i ^ i' => <r(i,an) =dfn lims a(i, an, s) = a0]\
(4) A: E S => Ak максимально;
(5) k £ S => Ак не является конечно сильно гиперпростым.
Для (5) выбираем такое наименьшее г, что {Vj)Wf(k,ij) конечно.
Пусть ао удовлетворяет (3). Для каждого j определяем
Vj = {x : (3s)[а; = as{iJ) = a£]j к o(i,x,s) = Сто] }.

360
Глава XII. Индексные множества в. п. множеств
Покажите, что множества Vj конечны, имеют непустые пересечения с
Ак и являются равномерно вычислимыми и непересекающимися.
4.24. Пусть в. п. множество А является 1-низким. Число е
называется индексом низкости для А, если А! = { е }0 . Для каждого п ^ 1
определим
Р« = { (а?) е) : = { е }0<л> }.
Покажите, что Рп является Пп+2-полным. Отсюда в частности
следует, что Pi является Пз-полным. Таким образом, один квантор в £4-
определении для Lowi можно убрать. Указание. Для доказательства
Pn Е Пп+2 заметим, что
(я, е) Е Рп <=> { е }0(п) всюду определена
& (V2/)[[y е win) k {e}0(n,(y) = 1]
V[y$win) к { е }®<п>(у) = 0]]
[П®<п) k (Vi/)[[En+1 & En+1] V [П„+1 к Е„+1]]].
4.25. Пусть в. п. множество А является 1-высоким. Число е
называется индексом высокости для А, если 0" = { е }л . Пусть
Qn = { (ж, е) : 0<п+1> — {е }и'*п> }.
Покажите, что Qn является Пп+з-полным. Указание. Для
доказательства Qn Е Пп+з заметим, что
(я, е) Е Qn { е }vr*n) всюду определена & (V?/)[- • •]
<=>■ пГ' ’ & (Vy)[- * •]
<=> [Пп+з к Пп+з], потому что W0*n+1*.
4.26. Докажите, что (Е4,Щ) (Lowi,Qi) ^1 (Lowi,Max), где Qi
определено в упражнении 4.25.
4.27 	Замечания. Шварц [1982] и [ta] доказал теорему 4.4, а затем
фактически с тем же доказательством и следствие 4.7, но используя
(Ез,Пз) (Rec,Comp) в качестве исходного шага. Шварц поставил
вопрос о классификации Int. После ознакомления с результатами
Шварца Соловей (частное сообщение) доказал теорему 4.14. Джокуш

§ 5. Неподвижные точки по Т-эквивалентности
361
(частное сообщение) расширил метод Шварца, чтобы получить
результаты 4.5, 4.6, 4.8, 4.10, 4.17, 4.18, 4.19 и 4.20. В конце 60-ых годов
Лахлан, Мартин, Р. В. Робинсон и Ейтс независимо друг от друга
доказали следствие 4.13(h) о ГЦ-полноте Мах (возможно, используя
метод из упражнения 4.23), хотя ни одно из этих доказательств не было
опубликовано. Таллос [1971] опубликовал полное и более сложное
доказательство П4-полноты множества Мах, он же получил верхние
оценки из упражнения 4.21. Доказательство Туллоса позднее было
упрощено Д.А. Мартином и приведено к виду, представленному в упражнении
4.23. Шварц [1982] использовал усложненный вариант метода из 4.23,
чтобы получить теорему 4.13 и упражнение 4.22. Затем Джокуш нашел
приведенное здесь элегантное доказательство теоремы 4.13(i),
использующее следствие 4.7 и теорему XI.2.3. Пусть QMax = {х : Wx квази-
максимальное }. Используя упражнение 4.21(a), легко установить, что
QMax Е Е5. Вопрос, является ли QMax Е5-полным, оставался
открытым со времени работы Таллоса [1971] и положительный ответ на него
был получен Лемппом [1986] только в 1986 году. Лемпп, кроме того,
обобщил понятие максимальности и квазимаксимальности до а-атомности
и а-квазиатомности и установил, что соответствующие индексные
множества являются Ща+2-полными и Ега+з-полными для произвольного
вычислимого ординала а (см. Лемпп [1986]).
§ 5. Неподвижные точки по тьюринговой
эквивалентности
Теорема рекурсии II.3.2 утверждает, что каждая вычислимая функция /
имеет неподвижную точку п, удовлетворяющую равенству Wn = Wf(ny
В следствии V.5.2 этот результат был обобщен на произвольную
функцию / в. п. степени < 0'. Поднимаясь на один уровень выше, мы в
упражнении V.5.5 видели, что каждая функция / 0х имеет *-неподвижную
точку п, удовлетворяющую условию Wn =* Wf{n). Теперь мы покажем,
что каждая функция / 0^ имеет тьюрингову неподвижную точ¬
ку, а именно число п, удовлетворяющее условию Wn =т И^(п). Это
утверждение является прямым следствием теоремы 5.1. Теорема 5.1 и
следствие 5.2 обобщаются соответственно в теоремах 6.2 и 6.3.
5.1 	Теорема (Арсланов). Если функция ф частично вычислима
относительно 0<2>, то существует такая вычислимая функция д, что

362
Глава XII. Индексные множества в. п. множеств
Wg(e) =т W^(e) для всех е Е Аотф.
5.2 	Следствие (Арсланов). Если / — всюду определенная функция,
вычислимая относительно 0^2\ то существует такое число п, что
Wn=TWf{n).
Доказательство следствия 5.2. По теореме 5.1 и теореме
рекурсии И.3.2. Q
Доказательство теоремы 5.1. Так как ф частично вычислима
относительно 0(2\ то дважды применяя лемму III.3.3 о пределе получим такую
вычислимую функцию /, что для всех е Е dom ф
ф(е) = limy lims f{e,y,s),
и lim Sf(e,s,y) существует для всех ей у. Для каждого е равномерно
по е построим в. п. множество Ае, следовательно, будет существовать
такая вычислимая функция g, что И^(е) = Ае. Кроме того, для всех
е Е dom ф будет выполняться Ае =т W^ey Сводимости между Ае и
И^,(е) не будут, однако, равномерными по е.
Мы определяем Ае = ФУА%, где у-я «строка» А\ — [)3ВеуУу8, где
Be,y,s строится следующим образом.
Шаг 5 — 0. Для всех е,у положим Ве,у>о = 0.
Шаг s > 0. Пусть ВеуУ,8 содержит все элементы х, удовлетворяющие
условиям
0) *еИ7(«,1м),.;
(ii) (вертикальное условие) (Vj ^ я)[/(е,2/, s) = /(е,2/ + .7,s)]; и
(Ш) (горизонтальное условие) (yt)x<^t^s [/(е, у, 0 = f(e,y,t + 1)].
Построение на этом закончено. (Заметим, что множество Ве,Уч8
конечно, так как
Beyy,s Я ^/(е,у,в),в»
что вытекает из (i).)
Фиксируем е Е Аотф. Определим у о и so следующим образом:
Уо = (w)(V* ^ y)[lime/(e,z,s) = </>(е)]
и
50 = (jis)(V* ^ s)[f{e,y0,t) = ^(е)].

§ 5. Неподвижные точки по Т-эквивалентности
363
(Мы думаем о всех строках Ауе, у ^ у0, как о хороших, а об А%, у < уо —
как о плохих. Ниже мы увидим, что Ау =* И^(с) при у = у0 (а также
и для каждой хорошей строки Ау), и в то же время условие (й)
гарантирует Ауе =* 0 для каждой плохой строки. Условие (Ш) обеспечивает
СВОДИМОСТЬ Ае ^т И^0(е).)
Лемма 1. (V?/ < уо)[Д^ конечно].
Доказательство. Фиксируем у < уо. По определению уо существует
такое ух, ?/ < 2/i ^ уо, что lim* /(е, yi, s) ф lim5/(e,y,s). Выберем такой
шаг 5, что f(e,z,t) = lims/(e, z,s) для всех t ^ s и z ^ yi. Пусть
к = ух — у. Выберем произвольный t ^ s. Тогда ни одно число х ^ к
не входит в из-за (ii), и поэтому Q [О, Л:). Следовательно,
конечно, т. к. Ау CUt<s5e,y>tU[0,/:).
Лемма 2. АУо =* И^(е) fu, следовательно, W^(e) $^т Ае).
Доказательство. Во-первых АУо С* И^(е), т. к. для каждого s ^ so
/(е,уо, «) = ф(е), и поэтому по условию (i) Be>yo>s С И^(е). Для проверки
И^(в) С* заметим, что ни одно число ж ^ so не удерживается из-
за (ш) от попадания в произвольное Be>yoj- Далее, для любого х ^ $о,
^ Е W^(e), выберем такой шаг £, что х Е И^(е)>< и для всех J ^ х
/(е,уо,£) = /(е, у0+ j, t). Тогда х Е Ле,У(Ь*, поэтому ж Е АУо. (Такой шаг
t существует, т. к. все хорошие строки Ау имеют lim* /(е,у,£) = ф(е).)
Лемма 3. Ае ^т И^(в).
Доказательство. По лемме 1 Uy<yo =* поэтому достаточно
доказать, что для каждого у ^ уо Ау $^т И^(е) равномерно по у. Фиксируем
у ^ уо. Для того, чтобы проверить, выполняется ли х Е Ау, сначала
проверяем, выполняется ли х Е W^ey
Случай 1. х Е И^0(в). Выбираем такой наименьший шаг 5 > «о, что
х Е И^(с)|в, и для ж выполняется условие (й) (т. е. /(е, у, s) = /(е, у+ j, s)
для всех j ^ х). Если х £ -Be,y,s? то это должно означать, что условие (Ш)
удерживает х от вхождения в ВеуУу8, но тогда условие (Ш) обеспечивает
х £ Ве%уЛ для любого t > s. Следовательно, х Е Ау тогда и только
тогда, когда х Е U *.Де,у,*.
Случай 2. х £ W^e). В этом случае а: Е только тогда, когда
х Е B€iy}S для некоторого 5 такого, что /(e,y,s) ^ ф{е). Выбираем такой
произвольный s > х, что /(e,y,s) = ф(е). (Такой 5 существует, потому

364
Глава XII. Индексные множества в. п. множеств
что у ^ уо.) Если х Е Be,y,t для какого-нибудь t > s, то f(e,y,v) ф
ф(е) для некоторого наименьшего v, s < v t. Но тогда условие (in)
препятствует выполнению х Е i?e,y>p для любого v. Ц
5.3 	Замечания. Теорема 5.1 впервые появилась в работе
Арсланова [1981]. Приведенное здесь доказательство является модификацией
переработки Л. Уэлша [1981]. Теорема 5.1 может быть также доказана при
помощи метода деревьев из главы XIV. Это требует больше рутинной
техники, но, возможно, дает более ясное проникновение в
доказательство.
§ 6. Обобщение теоремы рекурсии и критерия
полноты на все уровни арифметической иерархии
Теорема И.3.2 рекурсии утверждает, что каждая вычислимая функция
имеет такую неподвижную точку е, что We = Wf(e). В
упражнении V.5.5 и следствии 5.2 мы видели, что на более высоких уровнях
п = 1,2 каждая функция / $^т 0^ (/ 0^) также имеет некото¬
рую «неподвижную точку» е: либо такую, что We =* Wf(e) (уровень
п = 1), либо такую, что We =т Wf^e)) (уровень п — 2). В этом
параграфе мы докажем, что для произвольного п Е ш каждая функция / $^т 0^п^
имеет такую неподвижную точку е, что We ~n Wf(е) при подходящем
определении некоторых отношений эквивалентности ~n, п Е ш, на в. п.
множествах. Для этого, как и в теореме 5.1 для случая п = 2, мы
сначала докажем, что для каждой / ^т 0^ существует такая вычислимая
функция д, что для всех х выполняется Wf^ ~n Wg(xy На самом деле,
для того, чтобы доказать теорему 6.4 и следствие 6.5., мы формулируем
и доказываем последнее утверждение для частичных функций ф 0^
(вместо всюду определенных / $^т 0^п^).
Аналогично, критерий полноты Арсланова V.5.1 утверждал, что в. п.
множество А полно тогда и только тогда, когда существует функция
/ $^т А такая, что Wf(x) ф Wx для всех х. В упражнении V.5.10 этот
критерий был обобщен на уровень п — 1. Здесь мы распространяем
критерий полноты на все уровни 0(п) арифметической иерархии, используя
отношения эквивалентности ~п для всех п Е и). Приводимые здесь
результаты могут быть доказаны не только для а = п Е но также для
а = и, где и) рассматривается как ординал (также, как и множество
натуральных чисел) и под «а о;» подразумевается «а Е и) или а = и;».

§ 6. Обобщение теоремы рекурсии и критерия полноты 365
6.1 Определение. Для каждого а и определим следующие
отношения эквивалентности на подмножествах множества и :
(0
A
~o В,
если
А = В,
(ii)
A
~i В,
если
А =* В,
(iii)
A
~2 В,
если
cq
н
III
(iv)
A
~п+2
В, если А=т
Вдля п € и>
(v)
A
~u; В,
, если
(Зп)[Л ~п
в].
6.2 Теорема о моделировании вычислимого индекса. Для
каждого а си, если функция ф частично вычислима относительно 0(а\
то существует такая (всюду определенная) вычислимая функция g,
что
(Vx 6 dom^)[W9(l) ~а W^(x)).
6.3 Обобщенная теорема о неподвижной точке. Для каждого
а ^ о;,
/ 0(“> => (3e)[We Wf{e)}.
Доказательство теоремы 6.3. Для а = 0 — это теорема II.3.2
рекурсии. Случай 0 < а ш непосредственно следует из теоремы 6.2 и
случая а = 0. О
(Случаи а = 1 и 2 — это, соответственно, упражнение V.5.5 (б) и
следствие 5.2, они были доказаны Арслановым, Надыровым и
Соловьёвым [1977], Арслановым [1981] и Арслановым [1981]. Случаи 3 ^ а < и
были доказаны Джокушем, Лерманом, Соаром и Соловеем [1989].)
Доказательство теоремы 6.2. Рассмотрим различные значения а,
О а uj.
Случай а — 0. Пусть
цг _ / если ф{х) 4,
\ 0 в противном случае.
Случай а = 1. Это — упражнение V.5.5(a). Если ф частична, то надо
использовать функцию g из случая а = 0.
Случай а = 2. Это — теорема 5.1. Если ф частична, то снова надо
использовать функцию g из случая а = 0.

366
Глава XII. Индексные множества в. п. множеств
Случай 3 ^ а < со. (Джокуш). Фиксируем п ^ 1, и пусть дана
функция ф $^т 0(п+2). Мы хотим найти такую вычислимую функцию g, что
(V* 6 dom^g =т <(!)]. (6.1)
Сначала, исходя из ф, фиксируем такую частичную функцию в
0(п+2), что dom0 = domz/; и
(Vz е dom^)[C; = W$x)]. (6.2)
По теореме 5.1, релятивизованной относительно 0(п) и примененной к в,
имеем такую всюду определенную функцию <71 0^п\ что для всех ж
из dom0 выполняется
KZ) -т <,")'• (6-3)
По упражнению III.1.20 мы можем в (6.3) заменить д\(х) на (всюду
определенную) вычислимую функцию #2(я)- Теперь определяем вычислимую
функцию д(х) = <7п(#2(я))> где д(ж) — вычислимая функция,
существующая по теореме Сакса о скачке и удовлетворяющая следствию VIII.3.6.
Тогда для всех х Е dom ф
W
(п)
9{х)
=т <ы = <м ST = И';(„
л0(п) _ и/(п)
(6.4)
по следствию VIII.3.6, упражнению III. 1.20, (6.3) и (6.2) соответственно.
Это устанавливает (6.1).
Случай а = и. Пусть ф — частично вычислима относительно 0^.
Следующая лемма дает удобное представление для ф, а её
доказательство похоже на доказательство соотношения (4.16) из упражнения 4.15.
Лемма 1. Существует такая вычислимая функция h(x,y,n), что
для всех х и у
Ф(х) = у (3п ^ у)[Цх,у,п) е 0(п)].
Доказательство. Пусть д\ — такая вычислимая функция, что для всех
х и у
ф(х) = у <*=> (3(7 € Wgl(x<y))[a С 0(и,)],
a h\ и /^2 — такие вычислимые функции, что для всех а
а С 0(w) ■$=>• /ц(а) <= 0(Мст)).

§ 6. Обобщение теоремы рекурсии и критерия полноты 367
Наконец, пусть h3 — такая вычислимая функция, что для всех i,j,k
таких, что k ^ j,
г е 0^ h$(i,j,k) Е 0^.
Зафиксируем ао такое, что для всех п ао £ Определяем h(x,y,n)
следующим образом. Пусть гг = (m,s), и пусть а — строка из 2<и; с
номером т. Если h2{(T) < гг и a Е И^^у)^, то определяем h(x,y,n) =
h3(hi(a),h2{a),n). В противном случае полагаем h(x,y,n) = ао.
Лемма 2. (Зг0)(Уп)[{ г0 }0(п>(О) = гг].
Доказательство, см. упражнению 4.16.
По теореме IV.2.2 Поста очевидно, что
(3 вычислимая функция г)(Уг)(Уп)[И^ „) = W^]. (6.5)
Пусть /г, г‘о и г определены как выше. Пусть q(x) — вычислимая
функция из теоремы Сакса о скачке, удовлетворяющая следствию VIII.3.6.
Определим вычислимую функцию / следующим образом. Для
данных х и z пусть f{x,z) — такой индекс, что для всех Y
0,
если {го}у(0) t>
если {го }к(0) 4-= п к
З/о = (/*3/ ^ n)[/i(x,j/,n) 6 У],
%(.)•
если {г0 }к(0) = п
k -i(3y ^ n)[h(x,y,n) € Y],
(6.6)
По релятивизованной теореме III. 1.6 рекурсии с параметрами
существует такая вычислимая функция д, что
У тверж дение.
(Vx)(Vy)[W^>s(l)) = W*x)}.
(V* е dom^)[W^(!t) W®(a)].
(6.7)
Доказательство. Зафиксируем х Е dom^ и пусть, скажем, ф{х) = у.
Выберем
п = (/м ^ y)[h(x,y,i) е 0(,)].
Достаточно показать, что
Км)'”’ Зт wi">-
(6.8)

368
Глава XII. Индексные множества в. п. множеств
Для i < п по (6.7) и (6.6) имеем
Следовательно, для i < п
w:
0(*>
с;"
0(!) <Г)-
Таким образом, индукцией по г п имеем для всех г п
(О
<’) =т К.)) ■
(6.9)
Для i — п имеем
тду(п) — тд/0^п ^ тд/0^п ^ тд/0^ тду(п)
%(*) =Т ^(z) - Wf(x,g(x)) - Wr(y,n) - Wy
по (6.9), (6.7), (6.6) и (6.5) соответственно. Это доказывает (6.8) и,
следовательно, случай а = со. О
Мы теперь хотим с помощью теоремы 6.2 подобным образом
получить обобщение критерия полноты Арсланова V.5.1 в терминах ~п .
Сначала нам удобнее доказать следующую общую теорему. Она
аналогична результату Арсланова [1985а, теорема 2].
6.4 	Теорема. Пусть =е — отношение эквивалентности на в. п.
множествах. Пусть С и А — такие множества, что С $^т А <т
С1 и А в. п. относительно С. Предположим, что для произвольной
Ф, частично вычислимой относительно С, существует такая (всюду
определенная) функция g А, что
(Vz е domф)[Ш9(г) =Е WMz)\. (6.10)
Тогда для любой функции / Л существует такое число е, что
We =Б Wf(e).

§ 6. Обобщение теоремы рекурсии и критерия полноты 369
6.5 	Следствие (обобщенный критерий полноты). Пусть а ^ ш.
Предположим, что 0(а) А и А в. п. относительно Тогда
А =Т 0(а+1) (3/ <т A)(V*)-.[W7(X) ~Q Wx}.
Доказательство следствия 6.5. ( => ) Очевидно, т. к. {х : Wx ~а
0}<т 0(а+1).
( 4= ) Пусть А <т 0^а+1^. В теореме 6.4 положим С = 0^а\ и пусть
=е будет отношением эквивалентности . Теорема 6.2 гарантирует
выполнение условий теоремы 6.4, и, следовательно, 6.4 дает такое число
е, что Wf{e) D
(Заметим, что в следствии 6.5 случай а = 0 — это теорема V.5.1
(Арсланов [1981]), а случай а = 1 — упражнение V.5.10 (Арсланов [1981]).
Случай а = 2 также принадлежит Арсланову [1981, теорема 10]. Случай
3 а и; принадлежит Джокушу.)
Доказательство теоремы 6.4. Для получения противоречия
предположим, что / $^т А и
(Ve)[W, Wf(e)].
Достаточно определить такую Цт А что
(Ve)[/i(e) Ф {е}с(е)],
потому что тогда по теореме V.5.1 и упражнению V.5.8, релятивизован-
ным относительно С, мы можем заключить, что С' =т А, что
противоречит условию.
Так как Ае[{ е }с(е)] частично вычислима относительно С, то по
предположению теоремы существует А-вычислимая функция g со
свойством W^g(e) —Е ^{е}с(е) Для всех е таких, что { е }с(е) сходится. Так
как / не имеет =е-неподвижных точек, то для всех е имеем Wf^e))
И^(е). Пусть h(e) = f(g{e)), поэтому, h А. Тогда для всех е Е
dom({ е }с(е))
Wh(e) = Wf(9(e)) Wg(e) -Е Ще}с(е)>
W/i(e) ^Е VF{e}C(e),
поэтому
Це)ф{е}с\е),
что и требовалось.

370
Глава XII. Индексные множества в. п. множеств
6.7 	Замечания. Результаты 4.5, 4.6, 4.10, 4.11, 4.14, 4.17, 4.18 и с
6.1 по 6.5 сначала были получены названными выше лицами, а позднее
скомбинированы с некоторым числом других результатов, которые все
вместе появились в совместной статье Джокуша, Лермана, Соловея и Со-
ара [1989]. Среди других результатов этой статьи — теорема плотности
для и-классов в. п. степеней (где классами эквивалентности для А
являются множества { W : W А }), а также обобщение критерия полноты
Арсланова V.5.1, где условие «А в. п.» заменяется на условие «А d-в. п.»
(По упражнению V.5.9 оно не может быть заменено на «А € Д§>>.) Далее,
более сложное рассуждение приводит к следующему результату: если В
п-в. п. относительно 0(Q\ а ^ и, 0(а) В и функция / В не имеет
а-неподвижных точек (а именно, (Vx)-'[WX W/(x)])> то 0^Q+1^ $^т В.

Часть D
Дальнейшие разделы и
современные области
исследования в. п.
степеней и решетки в. п.
множеств

Глава XIII
Быстро простые множества. Совпадение
классов в. п. степеней, и алгебраическое
разложение в. п. степеней
Равенство классов ENC и NC , а также анонсированные в § 5 главы IX
алгебраические свойства М и NC наилучшим образом
устанавливаются введением понятия быстро простого множества. До сих пор все
свойства в. п. множества, которые мы ранее изучали, являлись
статическими свойствами, например, свойство креативности, простоты,
гиперпростоты и т.д. При изучении алгебраической структуры
решетки £ в. п. множеств и, в частности, ее автоморфизмов, требуются, как
стало ясно, их динамические свойства, учитывающие не только то, что
определенные элементы принадлежат множеству А, но также и то, как
быстро они в нем перечисляются (по сравнению с элементами, которые
перечисляются в другие в. п. множества относительно стандартного
одновременного перечисления всех в. п. множеств из 1.3.11).
Впервые такое динамическое свойство было сформулировано в
теореме о расширении Соара [1974Ь, с. 91], и оно оказалось необходимым для
построения автоморфизмов решетки £ . Лерман и Соар [1980а]
приблизили это динамическое свойство к статическому понятию плотно простого
множества, чтобы ответить на один вопрос Д. А. Мартина о классах
в. 	п. степеней. Маасе [1982] ввел изящное и очень плодотворное
динамическое понятие быстро простого множества, которое влечет плотную
простоту, а также и сложные динамические свойства из посылок
теоремы о расширении. Он использовал это понятие для получения и
расширения результатов из работ Соара [1974b] и [1982а] об автоморфизмах £
Вскоре стало ясно, что быстро простые множества выявляют весьма
важные и неожиданные связи в структурах в. п. множеств и степеней.
В § 1 мы определим быстро простые множества и соотнесем их свой¬

374
Глава XIII. Быстро простые множества
ства с простыми множествами, а также с методом разрешения, который
мы изучали в главе V. В § 2 мы докажем, что класс PS степеней,
содержащих быстро простые множества, неожиданно совпадает с недопол-
няемыми вниз степенями NC , а также с эффективно недополняемыми
вниз степенями ENC из § 5 главы IX. В § 3 мы докажем равенство
R = NC U М , что дает пример алгебраического разложения R на не-
пересекающееся объединение (строгого) фильтра и идеала. Это говорит
о том, что алгебраическая структура в. п. степеней более равномерна,
чем предполагалось. В § 4 мы докажем, что PS = LC , где LC —
класс низко дополняемых наверх степеней. На самом деле PS совпадает
с двумя другими, казалось бы, не связанными с ним, классами, это будет
обсуждаться в замечаниях 2.7. (Определения строгого фильтра, фильтра
и идеала см. в II.1.4.)
§ 1. Быстро простые множества и степени
Напомним, что мы принимаем соглашение II.2.6 относительно
перечисления { W€y8 }e,s€u>, что на каждом шаге s не более чем в одном из
множеств We, появляется самое большее один элемент.
1.1 Определение. Пусть { Ve,8 }e,s€u> — такое вычислимое
перечисление последовательности в. п. множеств, что Ve = UsV€iS. (Например,
Ve,8 = W€y8.) Тогда запись х € Ve> at s означает х Е Ve,8 - V^s-i, если
s > 0, и х Е Veyo, если 5 = 0.
Пост назвал кобесконечное в. п. множество простым, если WenA ф 0
для каждого бесконечного в. п. множества We. Для быстрой простоты А
требуется, чтобы некоторый элемент ж, перечисленный в We на шаге 5,
перечислился в А «быстро», а именно, к концу шага p(s) в перечислении
А, где р — некоторая вычислимая функция.
1.2 Определение. Кобесконечное в. п. множество А называется
быстро простым, если существуют такие вычислимая функция р и
вычислимое перечисление { А8 }8еи, множества А, что для каждого е
W€ бесконечно => (3s)(Зх)[х Е W€i at * П Ap(a)]. (1.1)
(Мы можем считать р неубывающей, т. к. можем, если необходимо,
заменить p(s) на тах{р(£) : £ ^ 5 }.)
Определение быстро простого множества не зависит от его
конкретного перечисления в следующем смысле.

§ 1. Быстро простые множества и степени
375
1.3 Предложение. Если А быстро просто, a {A8}8euJ и { Ve,8 }sGu;
являются такими сильными таблицами конечных множеств, что А =
U8А8, We = U8Ve,s, As Я Лн-1, Ve,8 Я Ve>8+\ U фунКЦЧЯ Шах{ в \ Ve,8 ф
0 } вычислимо ограничена, то существует такая вычислимая функция
q, что для всех е
We бесконечно => (3s)(3z)[z € Ve, at s П Aq(8)]-
Доказательство. Пусть А — быстро простое посредством р множество
относительно перечисления {As}s€u;. По данному s для каждого х £
Ve> at s вычисляем такое наименьшее t, что х £ We,t, и полагаем q(s)
равным такому наименьшему числу и, что Аи Э Ap(ty Ц
Большинство известных простых множеств, такие, как простое
множество Поста S в V.1.3, автоматически являются быстро простыми,
причем чаще всего в качестве функции р можно взять тождественную
функцию. Из следующей характеристики быстро простых множеств, в
которой перечисления в. п. множеств не упоминаются, вытекает, что
быстро простые множества вычислимо инвариантны. Эта
характеристика подобна аналогичной вычислимо инвариантной характеристике не-
ускоряемых множеств (см. Соар [1977, теорема 2.4]). Последние связаны
с быстро простыми множествами по теореме Маасса [1982, теорема 17],
которая гласит, что любые два множества, обладающие обеими этими
свойствами, автоморфны.
1.4 Теорема (Маасе). Для в. п. множества А следующие условия
эквивалентны:
(i) А является быстро простым;
(ii) А кобесконечно и существует такая вычислимая функция /,
что для всех е
Wf{e)cwe, (1.2)
Wf(e)nA = WenA (1.3)
и
We бесконечно => We - Wf(e) Ф 0, (1.4)
(iii) 	To же самое, что и (ii), если (1.4) заменить на
We бесконечно => We — Wf(€) бесконечно.
(1.5)

376
Глава XIII. Быстро простые множества
Доказательство, (i) => (ii). Поданному перечислению {As}s€a;
множества А и вычислимой функции р, удовлетворяющей (1.1), определим
wm = {x:(3s)[xe We,s - Ар{8)}}.
Теперь Wf(e) в. п. равномерно по е, и И^(е), очевидно, удовлетворяет
(1.2) 	и (1.3). По (1.1), если We бесконечно, то We — Wf(e) ф 0.
(ii) => (Ш). Пусть h — такая вычислимая функция, что
w _ Г We, если х = О,
Wh(e,x) — | ИЛ, _ {0, 1, . . . ,х - 1 }, еСЛИ X > О '
Если We бесконечно, то И^(е>я;) также бесконечно для каждого х.
Пусть (ii) выполнено с некоторой /. Определим /' следующим образом:
у^.х
Ясно, что Wf(h(e,y)) Я ^h(eyy) Я We, так что Wft(е) С We. Более
того, Wf'(e) П А = We П А, т. к. если х Е We П А, то х Е Wh(e,y) П А для
каждого у х. Но множество We — бесконечно, если только мно¬
жество We бесконечно, т. к. в этом случае множество И^(в|У) — Wfyi(e,y))
непусто, т. е. We — Wf^e) содержит элемент, больший у для каждого
фиксированного у.
(ш) => (i). По данному перечислению { А8 }sGu; множества А и
вычислимой функции / из (ш) определим функцию р, удовлетворяющую
(1.1). Пусть
p(s) - (pit)(Vx)(Ve)[x Е We,s => x € At U П/(е)}<].
Функция p вычислима, т. к. для каждого s существует лишь конечное
число таких пар ж,е, что х Е 1Уе>8, причем в силу (1.3) для каждой такой
пары найдется шаг t ^ s, на котором выполнено х Е AtUWf(e)tt- То, что
р удовлетворяет (1.1), следует непосредственно из (1.5) и определения р.
Следующая лемма будет необходимой в некоторых последующих
теоремах.
1.5 	Лемма (о замедлении). Пусть {UetS}seuJ — такая сильная
таблица конечных множеств, что Ue,8 Я £7e,s+i и Ue = UsUe,s. Тогда
существует такая вычислимая функция р, что для всех е выполнено

§ 1. Быстро простые множества и степени
377
Wg(e) = Ue и Wg(e)y8 П[/е, at s = 0 fm. е. любой элемент, перечисленный
в Ue, появляется в Wg(€) строго позднее).
Доказательство. С помощью теоремы рекурсии определим вычислимую
функцию </: W9(e) = { а: : (3s)[x е Ue,s - W9(e)t,)] }. О
В дальнейшем мы будем часто строить в. п. множество Ue по шагам
{Ue,s}seu;- По теореме рекурсии мы можем считать, что существует
такая вычислимая функция g, что Wg(е) = Ue. Суть леммы 1.5 о
замедлении заключена в том, что если мы перечисляем х в Ue на шаге s, то
для наименьшего t, удовлетворяющего х £ Wg(e)yt, выполнено t > s. Это
будет важно в теореме 1.6.
Быстро простое множество отличается от обычного простого
множества тем, что оно должно «быстро» пересекать любое бесконечное
в. п. множество. Теперь мы хотим получить более широкое свойство,
которое выполнено для всех в. п. множеств А из быстро простой
степени. Вспомним из § 3 главы V , что любое в. п. множество А из ненулевой
степени должно давать разрешение любому бесконечному в. п.
множеству в том смысле, что
(3x)(3s)[x € W€y at a & Aa \ X Ф A \ x\.
Следующая теорема характеризует в. п. множества из быстро
простой степени как такие множества, которые дают такое «разрешение
быстро».
l. 	6 Теорема (о быстро простой степени). Пусть А — в. п.
множество и {As }sGu; — вычислимое перечисление А. Тогда для того,
чтобы А имело быстро простую степень, необходимо и достаточно,
чтобы существовала такая вычислимая функция р, что для всех s
p(s) ^ s и для всех е
W€ бесконечно => (Эж)(3$)[ж £ Wey at s & As \ х ф ^4p(s) x], (1.6)
m. e. А «быстро разрешает:» некоторый элемент х £ W€.
Доказательство. (=>) Пусть В = {е}Л, где множество В быстро
простое посредством функции q{s), удовлетворяющей условию (1.1), и
пусть { Bs }sGu; — вычислимое перечисление В. Определим функцию р,
удовлетворяющую (1.6), и одновременно сильную таблицу { Ue,s }е,веим
к которой мы применяем лемму 1.5 о замедлении. Полагаем р(0) = 0.
Шаг s > 0. (Определяем p(s).) Выберем единственные е и х (если
они существуют) такие, что х £ W€t at s• Если существует у £^e,s-i

378
Глава XIII. Быстро простые множества
такое, что {е}£Л(у) |= В8(у) и u(As\e,y,s) < х, то перечисляем
наименьший такой у в ие,8. Найдем наименьшее t, при котором у Е И^(е),*,
где Wg(e) получено из { Ue,s }e,seu> по лемме 1.5. Полагаем p(s) равным
наименьшему v ^ q(t) такому, что Bv(y) = { е }^v(?/). Если такие е и ж
не существуют, то определим p(s) = p(s — 1) 4-1. (Этим заканчивается
описание конструкции.)
Теперь, если We бесконечно, то U€ бесконечно (т. к. В бесконечно
и В — {е}А). Следовательно, в силу быстрой простоты В, существует
у Е Wg(e), at t П Вф). Но у Е С/е, at а дпя некоторого s < t, так что
{ е }^*Ы 1= -ВДу) = 0. Теперь у € Bg(f) - Bs влечет и ф Ap{s) и,
где и = u(A8;e,y,s), т. к. p(s) ^ q(t). Но у попадает в Ue только из-
за некоторого х Е Wey at так что (1.6) выполнено для We. Заметим,
что при доказательстве импликации слева направо нам понадобилась
только сводимость В $^т А. Мы воспользуемся этим наблюдением при
доказательстве следствия 1.9.
(<=) По функции p(s), удовлетворяющей (1.6), мы построим В =т А
обычными методами разрешения и кодирования так, чтобы множество В
было быстро простым посредством тождественной функции. Мы должны
удовлетворить для каждого е требованиям
Р€ : We бесконечно => (Эж)(3$)[ж Е Wey at s П Bs].
Определим В0 = 0.
Шаг s > 0. Пусть В8-\ = { Ь^~г < Ь[~г <•••}.
Подшаг 1 (обеспечиваем быструю простоту). Выберем единственные
х и е (если они существуют) такие, что х Е We, at s. Если х > bse~l и
требование Ре ещё не удовлетворено, то вычисляем Ap(s) и, если As [
х ф Ар(8) I х, перечисляем х в В.
Подшаг 2 (кодируем А в В). Для каждого х Е As — As-\ перечисляем
К~1 в в.
Этим завершается описание перечисления В. Имеем В $^т А, т. к.
если х Е Bs — Bs-1, то А8-\ \ х ф А \ х. Множество В быстро простое,
т. к. если We бесконечно, то правая часть требования Ре выполнена
по построению, (1.6), и части (ii) => (Ш) теоремы 1.7,
сформулированной ниже (причем доказательство этой импликации не использует
теорему 1.6). Отметим также, что А $^т В, т. к. если bx = limsb8x и
В8 Ьх = В \ Ьх, то х Е А тогда и только тогда, когда х Е As. Q
Следующая теорема не применяется так часто, как теорема 1.6, но
тем не менее она дает некоторые дополнительные характеристики в. п.

§ 1. Быстро простые множества и степени
379
множества, имеющего быстро простую степень, и используется при
доказательстве теоремы 4.2.
1.7 	Теорема. Пусть А — в. п. множество и {As }sGa; — вычислимое
перечисление А. Тогда следующие условия эквивалентны:
(i) А имеет быстро простую степень.
(ii) Существует вычислимая функция р, удовлетворяющая (Тб).
(Ш) Аналогично (ii), если «(Эя)» в (1.6) заменить на «(Э°°я)», где
3°°х означает «существует бесконечно много», а именно,
We бесконечно => (3°°я)(Э5)[я Е We, at s & As [ x ф Ap(s) x]. (1.7)
(iv) Для любой сильной таблицы конечных множеств { Ue,s }e,sGu;
такой, что We = Us ^e,s и Ue,8 С Ue,8+1, существует вычислимая
функция р, удовлетворяющая (1.6), где «VFe,s» заменено на «C/e>s».
(v) То же самое, что и (ii), если «We бесконечно » заменить на
«We — о;».
Доказательство. (i)<£=>(ii) доказывается с помощью теоремы 1.6, а
импликация (iii)=>(ii) очевидна.
(ii) 	=>(iii). По значению q(s), удовлетворяющему (ii), определим p(s),
удовлетворяющее (iii). Применяя теорему рекурсии, определим
W9(e,„) = { х : х > п k (3s)[x G We<„ - Wg{e<n)tS] }.
Для каждого s находим такие х и е (если они существуют), что х Е
We, at s. Для каждого п < х находим такое наименьшее t, что х Е
Wg(e%n),t- Определим p(s) как максимальное значение q(t) по всем
таким t, если е и х существуют, и p(s) произвольное в противном случае.
Фиксируем п. Теперь, если We бесконечно, то Wg^e>n) бесконечно, так
что
(Эя)(3£)[я Е Wg(e n}^ at t & At \ ф Ag(t) [ х].
Но тогда х Е We, at s, Для некоторых s < t и х > п. Однако, q(t) ^ p{s),
так что
х Е We% at s и As [ х ф Ap{s) [ х.
Так как п произвольное, существует бесконечно много таких х, так что
р удовлетворяет (iii).
(iv) 	=> (ii). Определим Ue%s = W€nS.
(iii) =>(iv)• Пусть q(s) удовлетворяет (iii). Определим p(s) для
удовлетворения (iv). Применяя лемму 1.5 к { t/e,s }е,веим получаем g{e). По

380
Глава XIII. Быстро простые множества
данному s для всех ж и е s, х € Ue находим такое £, что х Е
W9le). at *, и полагаем p(s) равным максимальному значению q(t) по
всем таким t, если х и е существуют, и p(s) произвольное в
противном случае.
(ii) => (v). Непосредственно.
(v) 	=> (ii)- Пусть q(s) удовлетворяет (v). Мы определим p(s),
удовлетворяющее (ii), сначала построив сильную таблицу { UefS }e>sGa;, а потом
применив лемму 1.5. Если х Е Wej at s и х £ C/e>s_ 1 (где C/e,_i = 0), то
все у ^ х, у £ Ue,s-1, перечисляем в C/e,s. Если же такого ж не
существует, то полагаем C/e,s = £/e,s-i- Применяем лемму 1.5 к { C/e,s }e,sGo;j чтобы
получить д. По данному s находим х и е такие, что х Е Wef at s, а затем
такое t, что ж Е И^(е)> at t (т. к. И^(е) С 1Уе), и определим p(s) = q(t),
если такие х и е существуют. В противном случае p(s) произвольное.
Теперь, если We бесконечно, то Wg(е) = о;, так что
(3j/)(3f)[a; е W9(e), at t & -4* N ^ Aq(t) \ У]-
Выберем s таким, что у Е Ue, at s- Тогда s < t по определению д.
Выберем единственный ж Е We> at s. Теперь y^xns<t^ q(t) = p(s), так
что As \ x ф Ap(<s) [ x. D
1.8 	Определение. Обозначим через PS класс всех быстро простых
степеней.
1.9 	Следствие. Если b Е PS и b ^ а Е R, то а Е PS.
Доказательство. Пусть Во и А — такие в. п. множества, что Во быстро
простое и Bq $Ст А. Тогда, по доказательству части (=>) теоремы 1.6
существует функция р для А, удовлетворяющая (1.6). Следовательно, по
части (4=) теоремы 1.6 существует быстро простое множество В =т А.
1.10-1.14 Упражнения
1.10. Докажите, что простое множество Поста S из теоремы V.1.3
быстро простое.
1.11. Выведите непосредственно из определения 1.2, что если А быстро
простое множество посредством неубывающей вычислимой функции р' и

§ 1. Быстро простые множества и степени
381
вычислимого перечисления { As }s€u; множества Л, то существует такая
вычислимая функция р, что p'(s) ^ p(s) для всех s и для каждого е
We бесконечно => (3°°x)(3s)[x Е at s П Лр(в)]. (1.8)
Указание. Определим h как в доказательстве части (й)=>(ш)
теоремы 1.4. Определим р следующим образом:
р'(£), где t — такой наименьший шаг, что t > s и
(3e)(3z)(3t/)[a; 6 We, at « & x e УГцел)> at t]>
если такой £ существует,
p'(s) в противном случае.
p(s) = <
1.12. (i) Докажите, что если А С В, В в. п., кобесконечно и А быстро
простое, то В также быстро простое.
(ii) Докажите, что быстро простые множества замкнуты
относительно пересечения и, следовательно, они образуют фильтр в £. Указание.
Пусть А и В — быстро простые множества посредством функций p(s)
и q(s) соответственно, удовлетворяющим (1.8). Следовательно, если We
бесконечно, то Ue также бесконечно, где
Ue,s = { х • (^£ ^ s)[x £ at t Cl Лр(^)] }•
Пусть Wg^e) — Ue по лемме 1.5. Если Ue бесконечно, то
(Зх)[х Е Wg(e)t at t Cl Bq(f}].
Определите функцию, обеспечивающую быструю простоту множества
АПВ.
1.13. Пусть А — в. п. множество из быстро простой степени. Пусть
В — дефицитное множество для А (относительно некоторого
перечисления Л), которое было определено в упражнении V.2.5. Используя
теорему 1.6 докажите, что В быстро простое.
1.14. Постройте низкое быстро простое множество. Указание.
Совместите требования быстрой простоты с требованиями низкой степени из
теоремы VII. 1.1.

382
Глава XIII. Быстро простые множества
1.15 	Замечания. Определение 1.2 быстрой простоты было дано Маас-
сом [1982], где он доказал теорему 1.4 и упражнение 1.11, ввел понятие
в. п. генерического множества и показал, что каждое в. п.
генерическое множество должно быть одновременно низким и быстро простым.
Применяя технику автоморфизмов из статьи Соара [1974Ь и 1982а],
Маасе доказал, что любые два множества, являющиеся быстро простыми
и низкими (на самом деле, достаточно, чтобы их дополнения были по-
лунизкими в смысле упражнения IV.4.6(b)), автоморфны. Маасе, Шор
и Стоб [1981] получили результаты 1.9 и 1.12. Амбос-Шпиис, Джокуш,
Шор и Соар [1984] получили результаты 1.3, 1.5, 1.6, 1.7 и 1.13.
Другие понятия генеричности вычислимо перечислимых множеств
изучались Джокушем [1985] и Инграссиа [1981 и н.о.]. Джокуш ввел
новое понятие е-генеричности и показал, что, как и для генерических
множеств Маасса, е-генерические множества обладают многими
свойствами, получаемыми при применении метода приоритета с конечными
нарушениями, такими, как принадлежность множества к низкой степени
и быстрая простота. Однако, Джокуш [1985] также показал, что если а и
b несравнимые в. п. степени, имеющие наибольшую нижнюю грань с, то
ни одна из степеней а, Ь, с не может содержать е-генерическое
множество. Следовательно, е-генерические степени являются неветвящимися и
строго недополняемыми вниз. Кроме того, Харрингтон и Сламан [1996]
использовали быстро простые множества при доказательстве того, что
элементарная теория в. п. степеней (R, <) имеет степень 0Ы. (см. главу
XVI.)
§ 2. Совпадение классов быстро простых степеней, не-
дополняемых вниз степеней, и эффективно недо-
полняемых вниз степеней
Мы теперь покажем, что быстро простые степени PS из определения 1.8
совпадают с недополняемыми вниз степенями NC из IX.5.1, а также с
эффективно недополняемыми вниз степенями ENC из IX.5.3.
Следующий простой результат показывает, что PS С ENC, и этим
устанавливается первая связь между быстро простыми и недополняемыми вниз
степенями.
2.1 Теорема. Если а быстро простая степень, то а эффективно
недополняема вниз.
Доказательство. Фиксируем быстро простое множество A Е а, вычис¬

§ 2. Совпадение классов PS, NC и ENC
383
лимое перечисление { As }sGa;, и вычислимую функцию p(s),
удовлетворяющую (1.6), такую, что p(s) ^ s для всех s. Для каждого
невычислимого в. п. множества В мы найдем (равномерно по индексу В) такое
невычислимое в. п. множество <7, что С ^т А и С ^т В, причем эти
сводимости равномерны по индексам А и В. Для того, чтобы С было
невычислимым, мы добиваемся бесконечности множества С и выполняем
стандартные требования простоты:
Ре : We бесконечно => С П We ^ 0.
Для того, чтобы построить такое удовлетворяющее требованиям Ре
множество С $^т А, мы перечислим некоторое в. п. множество f/e,
предполагая, по теореме рекурсии, что U€ = Wg(е) для некоторой фиксированной
вычислимой функции д, существование которой следует из леммы 1.5 о
замедлении. Чтобы обеспечить сводимость С В, мы
дополнительно требуем равенства С [ х = Cs х на каждом шаге s, на котором
справедливо В [ х = В8 [ х. Предположим, что для каждого s разность
Bs+1 — Bs содержит в точности один элемент. Обозначим этот элемент
через Ь8. Инструкции по построению С состоят в следующем. Пусть
Со = 0.
Шаг s 4-1. Находим наименьшее е такое, что
Wei8+l О С8 — 0
и
(Зх)[х е We,8+i & х > 2е & х > Ъ8].
Перечисляем в i7e,s-fi наименьшее такое ж, удовлетворяющее х £ С/е>5.
Найдем такой шаг t, что х Е at t• Перечисляем теперь х в Cs+1 в
том и только в том случае, если Ар^) \ х ф As \ х. (Отметим, что такой
шаг t существует, поскольку Ue == Wg(e). Более того, в силу леммы 1.5 о
замедлении, для каждого х Е t/e>s+i ~ U€,s выполнено х Е Wg(e^ at t для
некоторого t > s + 1, так что p(t) > s.)
Теперь С ^т А, т. к. А8 [ х = А [ х влечет С8 \ х = С \ х. Каждое
требование Ре выполнено, т. к. в противном случае We бесконечно и,
поскольку В невычислимо, Wg(e) является бесконечным в. п. множеством,
а это означает, что для Аир условие (1.6) не выполнено при замене
индекса е на, д(е). О
Следующая наиболее трудная в этой главе теорема утверждает
справедливость равенства ENC = NC = PS, а также что все классы из

384
Глава XIII. Быстро простые множества
этого равенства образуют строгие фильтры. Её доказательство
интересно тем, что использует «гэп-когэп» конструкцию, которую можно найти
в 0,,/-приоритетных конструкциях, обсуждаемых в главе XIV. (см. § 2
главы XIV , где приводится классификация 0(п) -приоритетных
рассуждений.) Подобная же конструкция, в которой применяются «гэп-когэп»
рассуждения, была применена Фейером и Соаром [1980] при
доказательстве плюс-наверх теоремы. См. замечания 2.7 и теорему 4.2, где
приведены другие классы, совпадающие с PS.
2.2 Теорема. ENC = NC = PS.
2.3 Следствие. Каждый из классов ENC, NC и PS образует
строгий фильтр в R.
Доказательство. По IX.5.5 ENC образует строгий фильтр в R.
Доказательство теоремы 2.2. 1 Ясно, что ENC С NC. По теореме 2.1
NC С ENC. Достаточно показать, что NC С PS.
Фиксируем в. п. множество В и его вычислимое перечисление
{ Bs }sGu;. Мы построим в. п. множество А, определяя вычислимое
перечисление { As }s€u; так, что либо А невычислимо и deg(A) fldeg(R) = О,
либо В имеет быстро простую степень.
Мы пытаемся выполнить первую альтернативу, применяя
стандартный метод минимальной пары, представленный в § 1 главы IX. А именно,
мы построим множество А, удовлетворяя для каждого е £ и
требованиям
Ре : We бесконечно => We П А ф 0,
Ne : Ф^ = = fe всюду определена =Ф> /е вычислима,
где Фе определено в главе VIII.
По данным {At}^s и {Bt}t^8 определим вычислимые функции
Z(e,s) = max{ х : (Чу < я)[ф£‘(у) 4-= $£;(у)] }
И
m(e, s) — max{ Z(e, t) : t ^ s }.
Назовем s е-расширяющим шагом, если l{e,s) > m(e,s). (Таким
образом, если и Ф^ всюду определена, то существует бесконечно
много е-расширяющих шагов.)
хПри переводе в доказательство этой теоремы внесены предложенные автором
изменения. — Прим, редактора.

§ 2. Совпадение классов PS, NC и ENC
385
Одновременно с построением А мы для каждого е определяем
такую частично вычислимую функцию ре? что либо требование Ne
выполнится, либо функция ре будет всюду определенной, причем ре будет
удовлетворять для каждого i Е ш требованию
Re,i : Wi бесконечно => (3z)(3s)[z G Wif at s & B8 я ф BPe(<s) \ x],
откуда по теореме 1.6 будет следовать быстрая простота степени
множества В.
Перед тем, как привести полную конструкцию, мы кратко опишем
основной модуль для удовлетворения одного требования.
Фиксируем е. Мы пытаемся удовлетворить требованию
Re : Ne или (Vi)i2ejj.
Если мы удовлетворим Re по второй альтернативе, то В имеет
быстро простую степень посредством функции ре, так что мы можем не
выполнять требования Де, е ^ е'. Для каждого г мы определим такую
частично вычислимую функцию что если В не имеет быстро
простой степени, Ф^ = всюду определена и г такое наименьшее
число, что для ре требование Re,i не удовлетворено, то фе^ = Ф^, т. е.
требование Ne выполнено. С этой целью мы определим вычислимую
«запрещающую» функцию г(е, г, s), которая создает запрет, налагаемый
требованием Re>i. Он не позволяет перечислять элементы r(e,i,s) в
множество А. Определим функцию r(e,s) = тах{г(е,г,$) : г ^ Z(e,s)},
которая создает запрет, налагаемый требованием Re против
положительных требований меньшего приоритета Pj, j ^ е.
На шаге s 4- 1 мы открываем Де>*-гэп, выбирая такой наименьший
индекс г (если он существует), что Re,i ещё не удовлетворено и для
которого найдутся такие х Е W{, at s и у £ dom(ipe,i,s)i что у < l(e,s) и
иу < х. Здесь
иу = й(В8\е, у, s) =dfn max{ u{Bs; e, */',s) \ y' ^y}.
Определим фе^^-\-\{у) = Ф^Ы для наименьшего такого у и r(e,j,s +
1) = 0 для всех j ^ г. (Отсюда следует, что ipe,i,s+i{z) определена для
всех z < у в силу минимальности у, потому что z < у влечет z < у <
Z(e,s) и uz ^ иу < х.)
Этот гэп закрывается позднее на шаге £ +1, где t > s — следующий
после s е-расширяющий шаг. На шаге t + 1 мы определяем pe(s) = t и
полагаем г(е,г,£ 4- 1) = £, запрещая перечислять в А элементы, не
превосходящие t (т. к. по нашим допущениям u(As\e,y,t) < t). Отметим,

386
Глава XIII. Быстро простые множества
что если В8 \ иу ф Bt \ Uy, ТО Bs \ X ф Bt \ X, и поэтому ре
удовлетворяет требованию Де,г посредством элемента х. Таким образом, если
Rei никогда не выполнится, то любое значение фе^{у) = w,
определенное конструкцией, будет совпадать со значением Фf{y) из-за того, что
во множестве В на интересующем нас отрезке не будут
перечисляться новые элементы, и поэтому Ф^v{y) = w на всех гэп-шагах v, т. е.
s + 1 ^ v ^ t.
Следовательно, если Ф^ = Ф^ всюду определена и В не быстро
просто, то мы можем найти такой наименьший г, что Re^ не выполняется.
В этом случае бесконечно много Де,г~гэпов открываются и (затем)
закрываются. Тогда ipej = фй, т. к. если феАу) — w определяется на
некотором шаге, то все элементы, использованные при вычислении ,
сохраняются на всех последующих шагах, принадлежащих некоторому
Де,г~гэпу, а все элементы, использованные при вычислении Ф^,
сохраняются на протяжении соответствующих когэпов (интервалах между гэ-
пами). Более того, liminf* r(e, s) < оо, т. к. на каждом шаге, на котором
открыт Re,i-гэп, справедливо
r(e, s) = max{ r(e, j, s) : j < i }
(т. к. все запреты, наложенные требованиями Rej, j ^ i,
отменяются, как только требование Re>i открывает некоторый гэп). Конечно,
если бы не существовало такого г, что будет открываться бесконечное
Де>г-гэпов, то мы могли бы иметь lirninf* г(е, г, s) > 0 для каждого г и,
следовательно, был бы возможным случай liminfs г(е, 5) = оо, но
тогда при условии, что ф* = ф? всюду определенная функция, множество
В имело бы быстро простую степень и, значит, нам не нужно было бы
удовлетворять требованиям Де/, е' ^ е.
Рассмотрим теперь случай, когда не существует такой всюду
определенной функции /е, что /е = ф£ = . Пусть р = (/лх)-*[ф£(х) 4=
<£f(:r)4]. Тогда (3°°s)[l(e, s) = р]. Отметим, что если для некоторого
г открывается бесконечно много Де,г-гэпов, то в силу предыдущих рас-
суждений снова будет иметь место liminfs r(e, s) < 00. В противном
случае для каждого i < р только конечное число Де^-гэпов будут открыты.
Пусть Т = {s : /(e,s) = р}. Тогда, по определению r(e,s) существует
конечный предел lim5GT г(е, 5).
Таким образом, в любом случае имеем liminfs г(е, 5) < оо.
Этим завершается описание основного модуля для одного требования
Де.
Только что описанная стратегия сге, удовлетворяющая одному из тре¬

§ 2. Совпадение классов PS, NC и ENC
387
бований Де, скажем До, строит такую A-запрещающую функцию r(0, s),
что lim inf s r(0, s) < оо. Как и в конструкции минимальной пары в § 1
главы IX или в конструкции Фейера и Соара [1980], мы модифицируем
стратегию ое для Де при е > 0 так, чтобы различные запрещающие
функции r(j, s), j е, сбрасывали свои запреты одновременно, а
именно так, чтобы lim inf s r(0, s) < 00, где r(e, s) = ma,x{r(j, s) : j ^ e}.
Для этого требование Re должно угадать значение k = lim infs r(e — 1,5)
(максимум из запретов, налагаемых на шаге s требованиями Де/, е1 < е)
и одновременно запускать бесконечно много стратегий , по одной для
каждого возможного значения к, в точности так, как это было в § 1
главы IX.
Вдобавок мы будем позволять стратегии а* открывать Д*-гэп (и
отменять соответствующий запрет) только на шагах s Е , где S* =
{s : r(e — 1,5) = А;}. Мы полагаем r( — l,s) = 0 для всех 5.
Следовательно, Sq = и и Sq = 0 для А; > 0. Однако стратегии 0^
разрешается закрывать этот гэп на любом шаге £, если он является е-
расширяющим. Таким образом, в результате мы имеем достаточно
маленький итоговый запрет, так что если deg(i?) не быстро простая, то
liminfs г(е, s) < 00. Кроме того, мы закрываем эти гэпы достаточно
часто. А именно, если = *?, то каждый Д*-гэп закрывается на
следующем е-расширяющем шаге, что обеспечивает всюду определенность
Кроме того, чтобы обеспечить lim inf s г (е, s) < 00 мы должны быть
уверены в том, что пересечение с определенным выше множеством Т
было бесконечным. Для этого будем переопределять перечисления
множеств А и В, разрешая перечисляться новым элементам только на тех
шагах 5, для которых выполнено r(e — l,s) = А;. А именно, для каждой
пары (е, А:) определим А^е’^ = Ав, если r(e — l,s) = А;, и А*6’^ = А^!^
в противном случае. Множества В^е'к^ определяются аналогично.
Ясно, что если г(е — l,s) = к имеет место для бесконечно многих s, то
Us А^е'к>* = А и Us В$е*к^ == В. Определим теперь новую функцию
длины, учитывающую наши изменения в перечислениях множеств А и В:
l(e,k,s) = ma.x{x : (Уу < х)[ФеЛ ’(у) 4= J ] }-
Для дальнейшего обозначим максимум из запретов, налагаемых
требованиями Rj, j ^ е, через r(e,s) (вместо f(e,s)).
Конструкция А, и
Шаг 5 — 0. Ничего не делаем.
Шаг s + 1. Для каждого е ^ s выполняем в порядке возрастания е
следующие под шаги.

388
Глава XIII. Быстро простые множества
Подшаг 1. Пусть к — г(е — 1, s + 1). Для каждого j > к уничтожаем
все гэпы и запреты, созданные ранее стратегиями RJe i, для любого г.
Подшаг 2 (закрытие гэпов). Если s не является е-расширяющим
шагом, то переходим к подшагу 3. В противном случае, если существует
R?ei гэп, который был открыт на некотором шаге v-flCs-fln ещё не
был закрыт или уничтожен, то этот гэп объявляем закрытым.
Определяем pl{t) = s для всех t у, не принадлежащих области определения
pi, и стратегии R?ei в качестве A-запрета присваиваем число s (т. к.
s > u(As;e,y,s) для всех у < l(e,s)).
Подшаг 3 (открытие гэпов). Пусть s' = тах{ £ < s : г(е — 1 ,t) =
к}, если такие t существуют, и s' = 0 в противном случае. Выбираем
наименьшее i s такое, что Rке i ещё не удовлетворено, нет открытого
R%^-гэпа и
(3у)[(3х)[х Е Wit. - Wit9.] ку£ dom«i>s)
к l(e, s) > у к u(Bs\e,y,s) < x],
где
u(Bs;e, у, s) = max{ u(Bs; e,z,s) : z ^y}.
Выбираем наименьший такой у, затем выбираем наименьший х,
соответствующий этому у, и открываем Д*-гэп, определяя i>e,i,s+i(y) —
Ф(у) и уничтожая для каждого j ^ i все A-запреты, сделанные
стратегиями Rej- Если же такого г не существует, то ничего не делаем.
(Заметим, что некоторый Д* -гэп может быть закрыт на подшаге 2 и снова
открыт на подшаге 3. В этом случае любой А-запрет, наложенный Д* i
на подшаге 2, уничтожается на под шаге 3.) Полагаем r(e, s + 1) равным
наибольшему значению из текущих A-запретов, налагаемых
стратегиями Д£, где либо е' < е, либо е' == е и к1 < к, либо е = е', к = к1 и
i < 1(е, к, s).
Подшаг 4 (делаем А простым). Если W€tS+1 П = 0 и
(Ву)[у е w€}8+1 к у > 2е к у > г(е, 5 + 1)],
то выбираем наименьшее такое у и перечисляем его в А.
Этим описание конструкции завершено.
Предположим, что В не имеет быстро простой степени. Тогда для
каждого е существует такое г, что Де^ не выполнено. Покажем, что
требование Ne выполнено и liminfSr(e,s) < оо для всех е. Тогда из-за

§ 2. Совпадение классов PS, NC и ENC
389
под шага 4 конструкции отсюда автоматически следует, что А простое
множество.
Случай 1. = Фf — всюду определенная функция. Фиксируем е и
предположим по индукции, что Ne> выполнено для всех е' < е и
liminfsr(e — l,s) < оо.
Пусть k — liminf5 г(е — 1,5). Пусть = { s : r(e — 1, s) = к }.
Предположим, что = { ев } всюду определенная функция. Выберем
наименьшее i такое, что Wi бесконечно, но Д* i не выполнено. Так как мы имеем
бесконечное число Д* -гэпов, то функции { и рке всюду определены и
вычислимы. Выберем so такое, что для всех s ^ sq: (1) если к1 < к или
г1 < г, то на шаге s ни один Rk ^-гэп не открывается и не закрывается;
(2) если е' е, то Ре> на шаге s в А новый элемент не перечисляет.
Теперь предположим, что = w впервые определена на некотором
шаге, s Ч-1 > 5о- Докажем индукцией по v > 5, что либо
(!) {е}?”(2/) = ги, либо
(2) { е }£',(у) = w,
и, следовательно, /е(у) = w. (Таким образом, /,.(у) = ф^{у) почти для
всех у, так что Ne выполнено.)
Для проведения доказательства по индукции заметим, что на шаге
s -f 1 мы открываем Д*-гэп из-за у и некоторого х Е WiyS — WitS>, где
s1 определяется как в подшаге 3 конструкции. Выберем такой шаг v,
s' < v ^ 5, что ж Е И7* наг;. Для всех £, s' < t, значения p*s(£) ещё
не определены. (Отметим, что р*(£) определяется только тогда, когда
некоторый гэп, открытый на шаге ^ t, закрывается. Однако Д* ^-гэпы
открываются только на шагах Е S'*, a s' является последним таким
шагом < 5.) По выбору so, ни один Д* -гэп не уничтожается после шага
So, поэтому гэп, открытый из-за у и ж, должен закрыться на шаге t+ 1,
где t — следующий после s е-расширяющий шаг. Теперь pk(v) — t и
v ^ 5 < t, поэтому Д5 ж = Bt I х, т. к. Reyi никогда не удовлетворится.
Но u(Bs;e,y,s) < х, поэтому (1) имеет место для всех v, s + 1 ^ v ^ t,
т. е. для всех шагов v в этом Д*-гэпе.
Теперь на шаге t + 1 этот Д* -гэп, открытый из-за г/, закрывается,
и я* i налагает A-запрет t ^ u(At\e, г/, £). Но по выбору so все такие А-
запреты после шага so не нарушаются. Следовательно, этот А-запрет
продолжает действовать до тех пор, пока на шаге si + 1 ^ £4-1 из-
за 2/i = у -f 1 не откроется следующий Д*-гэп. Таким образом, (2)
имеет место для всех v, £4-l$J^$Jsi,a именно, для всех шагов v в

390
Глава XIII. Быстро простые множества
Re -когэпе. Но по той же причине (1) имеет место для всех шагов v в
Кг -гэпе, открытому из-за t/i, т. к. й(Х; е, yi, v) ^ u(X\e,y,v).
Таким образом,
(1) имеет место для всех v в Д* -гэпах и
(2) имеет место для всех v в Д* -когэпах.
Пусть, наконец, г(е) равен максимуму из Л и запретов,
наложенных требованиями Д*^,, где к1 < к или V < i. Теперь r(e,s) — г(е)
на каждом шаге s, на котором открыт Д*-гэп. Следовательно, г(е) =
lim inf s r(e,s) < оо.
Случай 2. Функции и либо не совпадают, либо не всюду
определены. В этом случае требование Ne выполнено автоматически. Далее,
можем считать, что существует число р = (/лх)-'[Ф^(х) (х) 4] (в
противном случае соотношение r(e) = liminfs r(e,s) < оо доказывается
также, как и в случае 1). Пусть Т = { s : /(е, A:, s) = р }. Тогда
существует бесконечно много таких шагов s Е Т, что г(е — 1, s) = к.
Доказательство соотношения r(e) = lim inf s r(e,s) < оо теперь проводится так же,
как и в рассуждениях, предшествующих описанию конструкции. []
2.4-2.6 Упражнения
2.4. Докажите, что существует такая вычислимая функция /, что
если deg(We) является половиной минимальной пары, то deg(iye) и
deg(H^(e)) образуют минимальную пару. Указание. Используйте
доказательство теоремы 2.2.
2.5. Докажите, что если A and В являются такими в. п. множествами,
что К ^wtt А® В и К £wtt В, то deg(A) недополняема вниз.
2.6. Докажите, что если в. п. степень с не является половиной
минимальной пары, то с ограничивает некоторую минимальную пару.
Указание. Если с не является половиной минимальной пары, то выберите
произвольную минимальную пару (а, Ь) и найдите минимальную пару
(ai, bi) под степенью с.
2.7 Замечания. Теорему 2.1 доказали Маасе, Шор и Стоб [1981]. Амбос-
Шпиис, Джокуш, Шор и Соар [1984] доказали результаты 2.2, 2.3, 2.4 и
2.5. 	Они также показали, что три других класса в. п. степеней
совпадают с PS , а именно, LC из теоремы 4.2, степени G из орбиты в. п.
генерических множеств, относительно автоморфизмов Е, и SPH степеней

§ 3. Разложение полурешетки в. п. степеней
391
не гипергиперпростых множеств, обладающих определенным свойством
расщепления, рассмотренного Маассом, Шором и Стобом [1981].
Строго говоря, доказательство теоремы 2.2 использует О'^-приори-
тетные рассуждения (в классификации главы XIV), т. к. для того, чтобы
в конце конструкции определить, каким образом каждое из требований
Re в конечном счете удовлетворяется, требуется 0;/,-оракул. Однако
описанная конструкция не использует деревья, в отличие от доказательств
главы XIV, а использует только метод группирования стратегий из
конструкции минимальной пары, описанной в § 1 главы IX. Более того,
если мы заранее знаем, что множество В не является быстро простым,
то требуется лишь 0"-оракул, чтобы в точности определить, как каждое
требование удовлетворяется.
§ 3. Разложение в. п. степеней на непересекающееся
объединение определимого идеала и определимого
фильтра
Теперь мы докажем, что NC и М образуют в R определимые фильтр и
идеал соответственно, следовательно, R = М U NC, что дает приятное
алгебраическое разложение R. Ясно, что М и NC определимы в
элементарной теории (R, ^). По следствию 2.3 NC образует строгий фильтр
в R.
3.1 	Теорема. М является идеалом в R.
Доказательство. По определению IX.5.1 если а Е М и b ^ а, то b G
М. Так как по теореме 2.2 М = PS, то достаточно показать, что PS
замкнуто относительно операции взятия наименьшей верхней грани, а
именно, что если a, b Е R и aUb Е PS, то а Е PS или b Е PS. Выберем
такие в. п. множества A,R,C, что С = A U В имеет быстро простую
степень посредством {Cs}sGu; и q(s), удовлетворяющих (1.6), А С
(чётные числа), и В С 2uj + 1 (нечётные числа).
Пусть { As }sGa; и { Bs }sGu; — такие вычислимые перечисления А и
В, что Cs = As U Bs. Определим вычислимую функцию p(s) и
частично вычислимые функции pl(t) для всех i Е и так, что либо А имеет
быстро простую степень посредством р, удовлетворяющей (1.6), либо
в противном случае любой свидетель W*, для которого (1.6) не
выполнено с функцией р, гарантирует, что рг является всюду определенной,
и В быстро просто посредством р\ удовлетворяющей (1.6). Применяя

392
Глава XIII. Быстро простые множества
теорему 1.6 мы попытаемся удовлетворить для всех i и j требованиям
Pi,j ■ (Зж) (Эе) [ж е Wi, at 8 & As \ хф Ap{s) f ж]
V(3 у) (Ш) [ж 6 Wj, at f & Bt \ уф Bpi(t) f у].
По ходу построения мы определяем в. п. множества Uij и
предполагаем, что g(i,j) — соответствующая функция, удовлетворяющая лемме
1.5. 	Множество Uij используется для «вынуждения» чисел быстро
перечисляться в множество С (и, следовательно, также в А или В).
Построение для р и рг.
Шаг 5 = 0. Полагаем р(0) = 0.
Шаг s > 0. Находим единственные х и i (если они существуют)
такие, что х Е Wif at s• Для каждого j ^ s находим наименьшие t < s и
у < s такие, что
У £ Wjt at t & t$ dom(p*) & Zij < y, (3.1)
где Zij = (pz) [z £ UijfS]‘ Если такие t и у существуют, то перечисляем
Zij в Uij,s+1, и полагаем Vij равным наименьшему v такому, что Zij Е
Wg(ij)yV', в противном случае полагаем Vij = s 4-1. (По лемме 1.5 имеем
5 < Vij.) Определяем p(s) = таx{q(vij) : j s } и рг(£) = p(s) для всех
t ^ 5, t £ dom(p*). Если такие х и г не существуют, то определяем
p(s) = p(s - 1) + 1.
Построение завершено.
Мы утверждаем, что если А не является множеством быстро простой
степени, то таким является В. Выберем г таким, что Wi бесконечно, но
для всех х
X Е at s ^ Ж = ^4p(s) X. (3*2)
Так как Wi бесконечно, то рг всюду определена. Если Wj бесконечно, то
Uij бесконечно, поэтому Wg^j) бесконечно. Следовательно, существуют
такие x,s и у, что х Е Wif at s, У удовлетворяет (3.1) и Cs [ Zij ф
Cq(v) [ Zij, где v = Vij. Но p(s) ^ q(v) и As [ х = Ap(s) ж. Поэтому
Bt I У ф Bpi{t) [ у, т. к. <ynt<s<v< q(v) ^ p(s) = pl(t).
Следовательно, Б имеет быстро простую степень посредством р\ О
Теорема 3.1 показывает, что наименьшая верхняя грань двух
дополняемых вниз степеней также дополняема вниз. Кроме того, по
теореме VII.3.2 Сакса о разложении и замкнутости класса М вниз любая

§ 4• Дополняемые наверх степени
393
а Е М совпадает с bUc для строго меньших степеней b,c G М. Однако,
в общем случае мы не можем выбрать степени b и с образующими
минимальную пару, так как Лахлан [1979] построил в. п. степень а, которая
не ограничивает ни одну минимальную пару степеней (см. § 4 главы
XIV). Легко видеть, что каждая в. п. степень d > 0 ограничивает
минимальную пару или является её частью, так что построенная Лахланом
степень а принадлежит М. Л. Уэлш показал [1981], что не существует
такой в. п. степени а < 0', что а ^ b для всех b Е М. Таким образом,
М не содержится ни в одном нетривиальном главном идеале полурешет-
ки R. С другой стороны, с помощью метода избегания конусов можно
непосредственно показать, что NC не содержится ни в каком
нетривиальном главном фильтре полурешетки R. Отметим также, что М не
является максимальным идеалом, т. к. по теореме 4.2 идеал,
порожденный Ми {а}, является собственным идеалом для каждой низкой в. п.
степени а. (Низкие в. п. степени а ^ М существуют. Действительно,
т. к. существует пара низких в. п. степеней, наименьшая верхняя грань
которых равна 0', то низкие в. п. степени могут быть низко
дополняемыми наверх и, следовательно, недополняемыми вниз.) Однако М является
простым идеалом (т. е. aflbGM влечет а Е М или b Е М), т. к. его
дополнением является фильтр NC.
3.2 	Упражнение
3.2. Докажите, что если ai,a2,... ,an Е М, то существует такая в. п.
степень b > 0, что а* П b = 0 для всех i п, причем индекс
представителя b может быть эффективно найден по индексам представителей
ах, аг,..., ап. Указание. Используйте упражнение 2.4 и теорему 3.1.
§ 4. Дополняемые наверх степени и совпадение
быстро простых и низко дополняемых наверх степеней
Определение 4.1 (i) В. п. степень а дополняема наверх, если
существует такая в. п. степень b < (У, что aU b = О'.
(ii) Кроме того, а низко дополняема наверх, если b может быть
выбрана низкой.
(iii) Пусть LC обозначает класс всех низко дополняемых наверх
степеней.
Ясно, что понятие степени, дополняемой наверх, является
двойственным к понятию степени, дополняемой вниз из IX.5.1. Свойства степеней

394
Глава XIII. Быстро простые множества
дополняемости наверх играют важную роль в изучении в. п. степеней,
а также в доказательстве неразрешимости R, что будет обсуждаться в
замечании 4.4. Например, Харринтон доказал интересную «вниз или
наверх» теорему (см. Фейер и Соар [1981, следствие 2.4]), которая
утверждает, что каждая в. п. степень либо дополняется вниз, либо дополняется
наверх, и что некоторая степень дополняется как наверх, так и вниз.
Мы теперь продолжим эквивалентность из теоремы 2.2, доказав, что
NC = LC, т. е. каждая в. п. степень либо дополняема вниз, либо
низко дополняема наверх, но не одновременно и то и другое, и тем самым
устраним возможность выполнения обоих альтернатив, в отличие от
теоремы Харрингтона.
4.2 	Теорема. NC = LC.
Доказательство. По теореме XI.3.4 о невложимости ромба для низких
степеней, не существует такой половины минимальной пары, которая
была бы низко дополняема наверх, так что LC С NC. Таким образом
достаточно доказать, что NC С LC. Вспомним, что по теореме 2.2
справедливо NC = PS.
Выберем множество В быстро простой степени, содержащееся в
множестве нечётных чисел 2и + 1, и вычислимую функцию p(s),
удовлетворяющую (1.6). Мы хотим построить такое низкое в. п. множество А С 2ш
(чётные числа), что К АфВ. Отметим, что А®В =т АиВ. Выберем
j таким, что Wj = К, и пусть Ks = Wj,8. Мы имеем набор
«кодирующих маркеров» { Гп }n€a;, и пусть Г* обозначает позицию маркера Гп к
концу шага s. Мы будем добиваться того, что для всех п и s, Г* чётно
и
(1 )пек-к, =► (A.UB.)l(Vn + l)*(AUB)HK + l),
(2) Г* ^ Г®+1 и Г® < Г*+1,
(3) Г® < Г*+1 => (A, U Bs) ^ (Г* + 1) ф (A U В) f (Г* + 1), и
(4) (Vn) [/(n) =dfn Пт, Г* < оо].
Ясно, что эти условия гарантируют К $^т АиВ, т. к. / $^т A U В
по (3) и (4), и для каждого п, если s такое, что (A U В) [ (f(n) + 1) =
(А8 U В8) (/(п) 4- 1), то п Е К тогда и только тогда, когда п € К8
по (1).
Для того, чтобы сделать А низким, выполняем для всех е
стандартные требования
Ne : (3°°s) [{ е }^л(е) сходится] => { е }л(е) сходится.

§ 4• Дополняемые наверх степени
395
С этой целью мы будем пытаться избавиться от всех маркеров Гп,
п ^ е, в A-интервале А [ u(As;e,e,s), использованном при вычислении
{е}^л(е). Для этого используем быструю простоту В, чтобы
спровоцировать изменение В [ Г®. По ходу построения определяем в. п.
множества С/е, е Е си. Пусть д — соответствующая вычислимая функция,
полученная по лемме 1.5.
Построение множества А.
Шаг 5 = 0. Пусть Г° = 2п для всех п Е ш.
Шаг s + 1.
Подшаг 1. Находим наименьшее е такое, что {е}^а(е) сходится и
Г* ^ u(A8\e,e,s).
(Если такого е не существует, то переходим к подшагу 2.)
Перечисляем Г| в Ue. Находим такой наименьший шаг t, что Г| Е Wg(e)j. (По
лемме 1.5 имеем s <t.)
Случай 1 (очищение от маркеров). В8 Г| ф Врщ [ Г®. Передвигаем
все маркеры Г*, г ^ е, сохраняя их порядок, на новые чётные позиции
в А8, превосходящие одновременно и u(As;e,e, s), и их старые позиции.
Случай 2 (временное разрушение). В8 [ Г| = Bp^t) Г|.
Перечисляем Г| в А (тем самым временно разрушая вычисление {е}^а(е)) и
передвигаем все маркеры Г*, % ^ е, сохраняя их порядок, на новые
чётные позиции в А8, большие их старых позиций.
Подшаг 2. Если п Е К8+\ — К8, то перечисляем текущую позицию
маркера Гп в А, передвигаем все маркеры Гш, т ^ п, на новые позиции,
ещё не перечисленные в А.
Конструкция завершена.
Лемма 1. (Vn) [f(n) = lims Г* < оо].
Доказательство. Если это не так, то находим наименьшее п такое, что
Гп бесконечное число раз передвигается, и выбираем такой шаг «о, что
Ks [ (п + 1) = К8о [ (п + 1) и = Игл* для всех т < п и
s > so. Так как Гп после шага $о передвигается бесконечное число раз,
то Wg(n) бесконечно, причем после шага so случай 1 никогда не имеет
места (иначе вычисление очищается от маркеров навсегда). На каждом
шаге s + 1 > $о, когда конструкция применяется к маркеру Г®, х = Г®
перечисляется в C/n,s+\ и, следовательно, для некоторого t > s в Wg(n)it.
Но Bt [ х = Bp(t) [ х, поэтому р не удовлетворяет (1.6) на бесконечном
в. п. множестве Wg(ny

396
Глава XIII. Быстро простые множества
Лемма 2. (Ve) [Ne выполнено] и, следовательно, А является низким
множеством.
Доказательство. Выберем шаг s такой, что {е}А*(е) сходится и для
всех г ^ е Г£ = Игл* Г*. Теперь Г® > и = u(As;e,e,s), т. к. в противном
случае некоторый Г*, i е, на шаге s 4- 1 передвинулся бы (здесь не
имеет значения, который случай имеет место), что противоречит выбору
s. Следовательно, As [ и = А [ и, поэтому {е}А(е) сходится. О
4.3 	Следствие (вниз или наверх теорема Харрингтона). Каждая в. п.
степень либо дополняется вниз, либо дополняется наверх. {]
4.4 	Замечания. Степень а Е R обладает свойством
антидополняемости наверх ( а. д. н.)п если существует такая в. п. степень b < а, что ни
для какой в. п. степени с < а справедливо а = bUc. Следствие IX (0.2) из
гипотезы Шёнфилда утверждает, что не существует а Е R со свойством
а. д. н. Лахлан [1966с] опроверг IX (0.2). Ладнер и Сассо [1975] доказали,
что каждая а Е R+ =dfn R — { 0 } имеет некоторого предшественника
b Е L»2nR+ со свойством а. д. н. Ейтс, Купер [1974а] и Харрингтон [1976]
показали, что 0' обладает свойством а. д. н. Харрингтон показал, что
таким свойством обладают все степени а 6 Hi, доказательство можно
найти в работе Д. Миллера [1981а]. Это доказательство имеет сакостоя-
тельный интерес, т. к. там ограничивающие функции r(e,s) такие, что
lim infs r(e,s) = оо. Эта трудность преодолевается при помощи модели
пинбольной машины из § 6 главы VIII, но теперь запреты
отрицательных требований Ne распределяются над всеми воротами Gj, г ^ е (а не
только на воротах Ge, как было раньше), так что по-прежнему на
каждых воротах Ge навсегда останавливаются лишь конечное число
последователей. Из следующего абзаца следует, что не каждая в. п. степень
имеет а. д. н. свойство, хотя точное описание таких степеней остается
открытой проблемой.
Полной противоположностью к свойству а. д. н. является свойство
плюс-дополняемости наверх, которым обладают степени а Е R, для
которых выполнено
(V b ^ а) (V d ^ а) [0 < b => (3с < d) [bUc = d]],
где кванторы действуют над R. Это свойство утверждает, что каждая
ненулевая степень b ^ а может быть нетривиально дополнена наверх к

§ 4• Дополняемые наверх степени
397
любой d ^ а. При помощи 0'"-приоритетного метода Лахлана [1975а],
который будет обсуждаться в главе XIV, Харрингтон [1978] построил
в. п. степень а > 0, обладающую свойством плюс-дополняемости
наверх. Если мы положим d = 0', то доказательство будет использовать
только методы, подобные методу минимальной пары из теоремы 2.2 и § 1
главы IX, а не конструкцию на полных деревьях главы XIV. Это
показано в работе Фейера и Соара [1981, теорема 2.1]. Из этой версии теоремы
можно непосредственно вывести «вниз или наверх» и «вниз и наверх»
теоремы Харрингтона. Последняя теорема утверждает, что некоторая
в. п. степень одновременно дополняема и вниз, и наверх. Дальнейшие
свойства дополняемости наверх в. п. степеней были получены
Харрингтоном и Шелахом при помощи 0'"-приоритетного метода [1982а и 1982Ь]
для доказательства неразрешимости элементарной теории полурешетки
(R,0.

Глава XIV
Метод деревьев и (^''-приоритетные
рассуждения
В главе VII мы описали метод приоритета с конечными нарушениями, а
в главах VIII и IX — метод приоритета с бесконечными нарушениями.
Как объясняется в § 2, эти методы называются также О'-приоритетным
и 0"-приоритетным методами соответственно. В [1975а] Лахлан ввел
новый, ещё более сильный метод, который может рассматриваться как
метод приоритета с конечными нарушениями, построенный над методом
приоритета с бесконечными нарушениями. Лахлан использовал этот
метод для доказательства своей теоремы «о неразложении», которая
гласит, что теоремы Сакса о разложении (VII.3.2) и плотности (VIII.4.1)
не могут быть соединены. Тогда этот метод трудно поддавался
пониманию, т. к. предложенное доказательство было построено в виде серии
технических приемов, расположенных один над другим, где назначение
каждого следующего — исправление недостатков своего
предшественника. В течение 1970-х годов на этот метод неформально ссылались как на
«метод монстра» из-за его громадной сложности.
Позднее некоторые из ключевых идей метода были отобраны и
использовались в других доказательствах; например, т. н. «гэп-когэп»
метод использовался в плюс-наверх теореме Харрингтона [1978] (см. также
Фейер и Соар [1981]), а позднее — в теореме XIII.2.2. Постепенно метод
становился более понятным (Харрингтон [1982]), а затем
использовался Харрингтоном и Шелахом [1982а и 19826] для исследования проблем,
связанных с определимостью внутри структуры в. п. степеней (R, <)
с тем, чтобы доказать неразрешимость ее элементарной теории. Этот
новый мощный метод теперь известен как 0"'-приоритетный метод. В
ближайшие десятилетия он обещает быть таким же полезным, каким
был 0"-приоритетный метод в течение 1960-х и 1970-х годов. Недавно

§ 1. О1-приоритетные рассуждения
399
он имел несколько новых важных применений, например, в
доказательстве теоремы Сламана [1991] о плотности ветвящихся степеней.
Чтобы продемонстрировать этот метод, мы приведем доказательство
теоремы Лахлана о неограничении [1979], которое, по-видимому,
является самым простым его применением. Метод существенно зависит от
использования деревьев в приоритетных рассуждениях. Использование
деревьев в доказательствах весьма полезно и само по себе, независимо
от 0ХХХ-приоритетного метода. Сначала, в § 1 и § 3, мы иллюстрируем
использование деревьев в 0х- и 0"-приоритетных рассуждениях, совместно
с некоторым общим обсуждением деревьев и классификацией в § 2 0^п^-
приоритетных построений. (Мы читаем «0х-приоритетный» как «нуль
штрих приоритетный», аналогично для .) Теорема о неограничении
доказывается в § 4.
§ 1. О'-приоритетные рассуждения
Для доказательства теоремы Мучника-Фридберга из VII.2.1 был
стандартным образом использован метод приоритета с конечными
нарушениями. Теперь мы изложим это доказательство на языке деревьев. В
данном конкретном случае особой пользы от использования деревьев нет, но
на этом очень простом примере мы ознакомим читателя с построениями,
использующими деревья.
Введем некоторую общую терминологию и обозначения для деревьев,
используемые в этой главе. Пусть Л — счётное (часто конечное)
множество с заданным линейным порядком <д . Определим Т как дерево
А<ш — множество всех конечных последовательностей элементов из Л, и
обозначим через [Т] множество всех бесконечных ветвей на Т (другими
словами, путей через Т), где h является бесконечной ветвью на Т, если
h [ п Е Т для всех п. Строчные греческие буквы а, (3, 7, ... обозначают
элементы Л<а;, a / и g — элементы Лы, |а| означает длину а. Запись
а С (3 (а С (3) означает, что строка (3 расширяет (собственно
расширяет) строку а, А означает пустую строку. Пусть (а) означает строку,
состоящую только из элемента а, а а"(3 означает конкатенацию строк а
и (3. Запись (/if3 С а)Р(/3) определяет строку (3 С а наименьшей длины,
удовлетворяющую предикату Р.
1.1 Определение. Пусть а, /3 Е Т.
(i) а находится слева от (3 (a <l /3), если
(За, b Е Л)(37 Е Т)[у"(а) С а & (b) С (3 & а <д Ь\.

400
Глава XIV. Метод деревьев
(ii) а (3, если a <ь Р или а С /3.
(iii) а < /3, если а ^ [3 и а ф /?.
Заметим, что отношение а /? является разновидностью
модифицированного упорядочения Клини-Брауэра. Если а С Р, то а называется
предшественником Р, а /? — последователем а. (Таким образом, мы
рассматриваем дерево Т как растущее сверху вниз, и А является его
верхней вершиной.)
Предполагается, что читатель знаком с обозначениями
теоремы VII.2.1, которую мы формулируем снова.
1.2 	Теорема (Мучник-Фридберг). Существуют в. п. множества А
и В такие, что А ^т В и В А.
Напоминаем, что достаточно для всех е удовлетворить следующим
требованиям теоремы VII.2.1:
Д2е : А ф{е}в,
И
Д2е+1 :Вф{е}А.
В этом параграфе мы полагаем А = { 0,1 }, где <д — обычный порядок,
и Т = А<и}. Для каждой вершины a G Т мы имеем a-стратегию, которая
является версией основной стратегии из теоремы VII.2.1 и которая будет
пытаться удовлетворить требованию Ri, где i = \а\. А именно, а
имеет кандидата (потенциального свидетеля) х (а) и запрет г (а), значения
которых к концу шага s обозначаются через x(a,s) и r(a,s)
соответственно. Теперь а требует внимания на шаге s + 1, если |а| = 2е и
{ е }f * (х(а, s)) 1= 0 & r(a, s) = -1, (1.1)
или |а| =2еН-1 и (1.1) выполняется с As вместо В8. На некотором
шаге s -f 1 определенная требующая внимания вершина а, предположение
которой «кажется верным», получает внимание (т. е. а действует),
и на этом шаге мы перечисляем x(a,s) в А, если \а\ = 2е (в В,
если |а| = 2е + 1 соответственно), устанавливаем r(a,s -f 1) = s, чтобы
сохранить вычисление, и инициализируем (следовательно, может быть,
нарушаем) все вершины Р > а (т. к. эти вершины дерева Т
соотносятся с требованиями более слабого, чем у а, приоритета), определяя
r(P, s + 1) = -1 и переопределяя х(Р, s + 1).

§ 1. О1-приоритетные рассуждения
401
Разница между этим и предыдущим построениями состоит в том,
что раньше некоторое требование Re могло действовать целых 2е раз,
т. к. после каждого нарушения требование Re начинало все сначала.
Теперь каждая из 2е строк а длины е действует не более одного
раза, т. к. теперь а снабжена «предположением» о результатах попыток
удовлетворения Ri для всех г < е, и а действует только тогда,
когда это предположение «кажется верным». В конечном счете требование
Re будет удовлетворено единственной вершиной а длины е с верным
предположением, а именно, а = f [ е, где / G 2W — истинный путь,
определяемый следующим образом.
1.3 	Определение. Истинный путь / G 2Ы на дереве Т (для ниже
описанного построения) определяется индукцией по п. Пусть а = f \ п.
Полагаем
Хотя / и не вычислима, очевидно, что / $^т 0', и на самом деле,
f(n) = lims6s(n), где мы определяем вычислимую последовательность
{ S8 }sGu; строк дерева Т (таких, что \Ss\ = s) индукцией по п < s
следующим образом. Пусть дано а = Ss [ п. Если п < s, то определяем
Заметим, что для каждого п п Ss [ п (т. е. при увеличении
s Ss никогда не двигается вправо), поэтому lims Ss(n) существует и
равен f(n). (В более общих 0"- и О'"-построениях на деревьях мы сможем
обеспечить только условие f(n) = lim inf8Ss(n) в смысле § 2, а именно,
/ будет являться самой левой ветвью, посещаемой вычислимой
последовательностью { S8 }sGa; бесконечно часто.)
Таким образом, каждая вершина a G Т может быть отождествлена
с предположением о том, какие /3 С а со временем будут действовать.
Именно, а предполагает, что (3 = а \ к будет действовать тогда и
только тогда, когда а(к) = 0. Если a С S8, то на шаге s -f 1 предположение
вершины а кажется верным, и а имеет возможность действовать.
(Отметим, что на таком шаге вершина а предполагает, что все вершины
/3 С а, которые могли когда-нибудь действовать, уже сделали это.)
Доказательство теоремы 1.2.
0, если (3s)[Ra действует на шаге s]
1 в противном случае.
0, если (3t ^ s)[Ra действует на шаге £],
1 в противном случае.

402
Глава XIV. Метод деревьев
Построение множеств А и В.
Для каждой вершины a Е Т мы имеем параметры х(а) и г (а),
значения которых к концу шага 5, обозначаются через х(а, s) и г(а, 5). Когда
параметру назначается некоторое значение, он сохраняет это значение
до тех пор, пока ему не будет назначено новое значение. Пусть
означает аДЛ1, где п является номером а при некоторой эффективной
нумерации элементов дерева Т. Инициализировать вершину а на шаге
s значит определить r(a, s) = —1, а ж(а,$) приравнять наименьшему
числу у Е у & А8 U В8, у > 5, и у > всех предыдущих значений
параметра х(а).
Шаг 5 = 0. Положим Ао = Во = 0 и инициализируем все а Е Т.
Шаг 5+1. Пусть а является С-минимальной вершиной 7 С Ss,
требующей внимания. Полагаем г(а, 5 + 1) = 5, перечисляем ж(а, 5) в А, если
|а| — чётное число, и в В, если |а| нечётное, и инициализируем все 7,
а < 7. Мы говорим, что а действует. (Если такой а не существует, то
ничего не делаем.)
Лемма 1. Для каждого i требование R{ удовлетворяется вершиной
а = f \ i.
Доказательство. Фиксируем г, положим а = f [ г и предположим, что
лемма выполняется для всех j < i. Так как <3v+i [ г ^ Sv [ г для всех
v, мы можем выбрать такой наименьший шаг 5, что а С St для всех
t ^ 5. Тогда г (а, 5) = — 1 и а после шага 5 никогда не
инициализируется. Пусть х = limtx(a,t) = x(a,s). Предположим, что i = 2е. Если а
больше никогда не действует, то { е }в(я) t или { е }в(я) 0. Если же
а действует на некотором шаге t > 5, то {e}f*^(x) |= 0 и At(x) = 1,
причем я(/3, £) > t для всех /3 > а, и поэтому /3 не может позднее
нарушить а добавлением некоторого у ^ t в Л U В. Кроме того, если /3 < а,
то /3 никогда не действует после шага t по предположению о шаге 5. В
любом случае { е }в{х) ф А(х). []
Отметим, что в этом построении вдоль истинного пути нарушений
не бывает. (Мы говорим, что вершина /3 нарушается на шаге t, если /3
действует на некотором шаге 5 < £, и затем на шаге t /3
инициализируется.) Именно, если а С /3 С /, то а никогда не нарушает /3, потому что
/3 имеет верное предположение о том, будет ли а когда-нибудь
действовать, и /3 действует только после того, как её предположение кажется
верным. Заметим, что здесь мы имеем даже большее: ни одна вершина
а С / никогда не нарушается никакой /3 Е Т. Для 0;/-построений это не
так.

§ 2. Метод деревьев в приоритетных рассуждениях 403
1.4—1.5 Упражнения
1.4. Дайте доказательство на дереве для теоремы VII. 1.1.
1.5. Дайте доказательство на дереве для теоремы VII.3.1.
§ 2. Метод деревьев в приоритетных рассуждениях и
классификация 0', 0" и (^''-приоритетных методов
Имея в виду простое доказательство на дереве из § 1, мы сделаем
сейчас некоторые общие замечания об использовании деревьев в методах
приоритета, перед тем как начнем изучать несколько более сложные
примеры. Некоторые из этих замечаний были предложены
Харрингтоном [1982], некоторые высказывались в частных разговорах, хотя деревья
с этой целью рассматривались ещё Лахланом [1975а], который их также
применил в своей статье [1979]. Мы принимаем некоторые обозначения,
терминологию и соглашения этой статьи, которые находим удобными,
хотя наше доказательство теоремы о неограничении в § 4 будет
отличаться от доказательства Лахлана.
При доказательстве какой-нибудь теоремы в теории вычислимости
сначала записывается список требований Щ, г Е и, достаточных для её
установления. Затем формулируется стратегия, называемая основным
модулем, для удовлетворения одного такого требования в отдельности.
Основной модуль может совершать бесконечное число действий и может
иметь несколько возможных окончательных выходов (возможно, даже
бесконечно много).
Пусть Л — множество символов для обозначения возможных
выходов, и <д — соответствующее упорядочение множества Лу обычно
выбираемое так, что если а <д b и а «оказывается верным» бесконечно
часто, то b не является правильным окончательным выходом.
(Например, в § 1 Л = { 0,1}, где выход 1 означает результат того, что { е }в(я) t
или {е}в(ж) 0; а выход 0 означает, что {е}в(ж) 0, и мы пере¬
числяем х в А.)
Если существует несколько различных типов требований (например,
положительные и отрицательные), нам могут для каждого из них
понадобиться разные типы основного модуля, и множество выходов Л будет
меняться в соответствии с типом требования. (Для простоты сначала
рассматриваем случай, когда существует только один тип основного
модуля и одно множество выходов Л. Другие типы могут быть легко
скомбинированы с этим методом обычным образом, как в § 4.)

404
Глава XIV. Метод деревьев
Далее, мы определяем приоритетное дерево Т = к<и) и
используем обозначения и терминологию для дерева Т, определенного в § 1,
в том числе и определение 1.1. Для каждой вершины a G Т
определим a-стратегию для удовлетворения требования Д*, где г = \а\. а-
стратегия является просто естественной модификацией основного
модуля, учитывающей тот факт, что для каждого к < |а|, стратегия а
должна «предполагать», что выходом /3-стратегии, где /3 = а [ к,
является а (А;) = а Е Л. (Это дает вершине а значительное преимущество
перед стандартной линейной версией того же самого рассуждения, где
Ri не имеет информации о выходах стратегий более высокого
приоритета Rj, j < г.) Отложим на время детализацию полного построения и
объяснение, когда именно вершине а разрешается действовать
По завершении построения мы определяем истинный путь / G Лш
индукцией по п, как это было сделано в § 1. Именно, если а = / I п,
то пусть f(n) Е Л означает окончательный выход a-стратегии. Полное
вычислимое построение представляем в виде С = (J{CQ : a Е Т}, где
Са — та часть построения, которая выполняется a-стратегией. Наша
основная цель состоит в следующем: мы должны добиться, чтобы то, что
Харрингтон [1982] называет построением вдоль истинного пути, т. е.
С = [){Са ot С f увенчалось успехом, для чего в конце построения
будем проверять выполнение условия
(Уг)[а = / [ г => а удовлетворяет требование Ri]. (2.1)
Конечно, С в действительности не является «построением» ни в
каком эффективном смысле, т. к. функция / не вычислима, а просто
является частью полного вычислимого построения С. Тем не менее, С
является единственной существенной частью С, потому что по (2.1) лишь
вершины а С / будут иметь для нас значение. Однако, т. к. в
процессе построения мы не можем эффективно распознавать эти а С /, то
мы должны описать возможные действия Са для каждой a G Т таким
образом, что если а С /, то а будет по крайней мере получать те
минимальные условия, требуемые основным модулем, которые позволят ей
достигнуть своей цели.
Насколько хорошо мы можем распознавать / в процессе построения?
В нашем примере из § 1 каждый из выходов Л = {0,1} был
конечным, и мы определяли такую вычислимую последовательность { 68
что f(n) = lims£s(n). В конструкциях с бесконечными нарушениями (а
именно, в 0;/-приоритетных конструкциях) множество выходов обычно
включает как бесконечные, так и конечные выходы. Например, в
лемме VIII. 1.1 о густоте, где мы строим в. п. множество А по данному В

§ 2. Метод деревьев в приоритетных рассуждениях
405
в. п. множеству такому, что либо В№ = аДе1, либо конечно, мы
имеем положительные требования вида Ре : =* А^е\ Если \а\ = г и
Ri = Ре, то окончательными выходами для а являются Л = { 0,1 }, где
1 означает, что Ri перечисляет самое большее конечное число
элементов в А, в то время как 0 означает, что Ri перечисляет в А бесконечное
число элементов. В таких случаях, как в построении минимальной
пары (IX. 1.2) или в лемме VIII. 1.1 о густоте, Ri может быть
отрицательным требованием Ne с соответствующей вычислимой функцией запрета
r(e, s) такой, что существует lim infs r(e, s). Множеством выходов для Ne
будет Л = lj, где выход к означает, что liminf* r(e, s) = к, как описано
в §3.1.
Мы должны определить вычислимую аппроксимацию функции /,
{6. }s€u;, где S8 Е A<UJ и \68\ — s. Фиксируем s и определим 68(п)
индукцией по п, для п < s. Пусть а = 68 [ п. Для вышеописанного примера
с леммой о густоте, если ДЛ есть Ne, то 68(п) = r(e,s). Если Rn есть
Ре, то 68(п) = 0, если — А^ ф 0, где t — такой наибольший шаг
< 5, что а С St, и 68(п) = 1 в противном случае. Здесь важно то, что /
является самой левой ветвью, посещаемой { 6S }sGu; бесконечно часто, а
именно, f [ п = liminfs£s п, для всех п G и, в том смысле, что если
а = f [ п, то выполняется
(3<°°s)[6, <L а], (2.2)
(3°°s)[a С 6,}. (2.3)
Кроме того, мы должны выполнять следующее правило:
(V/3)[JS <l /3 => (3 инициализируется на шаге s], (2.4)
где (3 инициализируется на шаге 5, как в § 1, путем переустановле-
ния всех её параметров и разрушения всякого ожидающего (3-действия.
Говорят, что на шаге 5-1-1 вершины а С 68 кажутся верными, а 5
называется а-шагом для таких а. Кроме того, вершине а разрешается
действовать только в том случае, когда она кажется верной, а именно,
(Va)(V5)[a действует на шаге 5 + 1 ==> a С 68]. (2.5)
(Картина такова, что в конце шага 5 те /3, которые расположены справа
от 68, т. е. 68 <l /3, инициализируются, и всякие ожидающие /3-действие
или /3-запрет разрушается. В течение шага 5 + 1 вершины a С 68 имеют
возможность действовать, т. к. их «предположения» согласуются с 68.

406
Глава XIV. Метод деревьев
Вершины (3 <l Ss на шаге s + 1 считаются «спящими», хотя и
ожидающими некоторого шага t > s -hi такого, что /3 С St- Пока (3 является
спящей, всякое ожидающее (3-действие или /3-запрет сохраняются, но
никаких новых /3-действий не предпринимается. Если а — f [ п, то,
подобно той принцессе, которая просыпается только раз в каждые сто
лет, а просыпается на каждом a-шаге из бесконечного множества таких
шагов, возможно предпринимает некоторые действия и снова засыпает,
и так до следующего a-шага, за этот интервал времени действия а
сохраняются. В процессе вычислимого построения С ни одна из тех (3,
|/3| = г, которые работают с Дг, не знает, которая из них нам
понадобится (именно, которая (3 станет a =def / [ г) и добьется удовлетворения
Ri. Другими словами, каждая (3 просто «выполняет свой долг перед
логикой», делая все возможное для удовлетворения Д*. Вершины (3 <l ol
будут действовать конечное число раз и, возможно, не удовлетворят Д*,
в то время как вершины /3, a <l /3, бесконечное число раз будут
инициализироваться и поэтому также возможно потерпят неудачу в
удовлетворении требования Д*, и только для а можно уверенно сказать, что
она добьется успеха.)
Зафиксируем а = / [ п и рассмотрим это построение с точки зрения
а. Как в работе Харрингтона [1982], разложим Т — { а } на непересека-
ющиеся множества вершин, лежащих слева, справа, выше и ниже а,
L = {/3 : /3 <i, а},
R — {0 : a <l
А = {0:0Сс
В = {0 : а С 0},
и пусть Сх = { С/з : (3 G X } для X С Т. По (2.2) и (2.5) существует
только конечное число таких шагов, на которых какая-нибудь (3 <ь сх
действует, скажем, ни одна из них не действует после шага $о, поэтому
Cl оказывает конечное воздействие на а. Вершины /3 G Д
непосредственно перед каждым a-шагом инициализируются, поэтому Cr не может
причинять никаких препятствий a-стратегии, когда последняя захочет
действовать. Окончательно, выберем si ^ so таким, чтобы для всех
/3 С а, если 0 действует только конечное число раз, то /3 не действует
на шагах s ^ s\. Любое действие, произведенное вершиной а на любом
а-шаге > s\, остается в силе до следующего a-шага. В большинстве из
0/;-построений можно показать, что основной модуль можно успешно
использовать в полном построении, если только он может действовать на
некотором бесконечном вычислимом множестве шагов (а именно, на а-
шагах > 5i) вместо того, чтобы действовать на всех шагах s G ш, и поэ¬

§ 2. Метод деревьев в приоритетных рассуждениях
407
тому a-стратегия также достигает цели. (Такая модификация —
основной момент в построении минимальной пары степеней из теореме IX. 1.2
и является существенной чертой любого 0"— или 0,,/— приоритетного
рассуждения на деревьях.) В 0'"-построениях a-стратегия требует не
только этого, но также активного «сотрудничества» со стороны С а, как
мы описываем ниже в § 4.4. Грубо говоря, ведущим принципом является
то, что Харрингтон [1982] называет золотым правилом, а именно,
чтобы а вела себя по отношению к (3 Е R (/3 Е В соответственно) так, как
множество L (соответственно А) могло бы вести себя по отношению к
а, с тем чтобы обеспечить, что предположения вершины /3 достаточно
часто становятся верными. Таким образом, а добивается
сотрудничества со стороны множества С а и активно сотрудничает с определенными
/3 Э а, когда (3 кажутся верными.
Метод деревьев классифицирует приоритетные рассуждения на (У,
0" или 0'"-рассуждения следующим образом. Если для того, чтобы в
конце построения определить, каким образом удовлетворяется каждое
требование i?j, в качестве оракула требуется 0(п\ то мы полагаем, что
построение С принадлежит уровню Во всех (даже 0'")
рассуждениях на дереве аппроксимация { Ss(n) }sGu; будет вычислимой как функция
от s и п. Для построений с конечными, как в § 1, нарушениями мы
имеем f(n) = lims5s(n), поэтому / 0', в то время как в построени¬
ях с бесконечными, как в (2.2) и (2.3), нарушениями мы имеем только
/ [ п = lim infs ds [ п, поэтому / 0". Но если а = / [ п, то f(n) яв¬
ляется истинным выходом a-стратегии, и а удовлетворяет Rn по (2.1).
Следовательно, рассуждения с конечными нарушениями имеют уровень
0', а с бесконечными нарушениями — уровень О".
В большинстве рассуждений на деревьях истинный путь /
вычислим относительно 0", т. к. по вышесказанному f \ п = liminfs£s
а { Ss }sgu; — вычислимая последовательность. Естественно возникает
вопрос, по какому признаку построение С можно отнести к уровню 0,,;?
Ответ заключается в том, что условие (2.1) здесь больше не
выполняется. А именно, в типичном 0Ш-построении (например, в том, который
излагается в § 4) требования Д* имеют более сложный вид. Например,
в нашем примере они имеют следующую логическую форму:
Л» = Piti V Pi,2 V ... V Pvn V (3Xi)[Ni(Xi) & (Vj)Rij(Xi)], (2.7)
где X{ — некоторый объект, который строится в процессе построения.
Это, например, в. п. множество, как в (2.8), или сведение по Тьюрингу,
как в статьях Лахлана [1975а] и Сламана [1991].

408
Глава XIV. Метод деревьев
Например, в теореме Лахлана о неограничении из § 4 для
построения невычислимого в. п. множества С, степень которого не
ограничивает минимальную пару степеней, мы должны для всех i удовлетворить
следующим требованиям:
Ri : Фр ф AiV Фр ф А{ вычислимо V Bi вычислимо V . .
V (3Di)[Di Ai к Di Bi к (Vj)[Di ф Wj}}, {Z'*}
где { В{, Фг, Ф*) — некоторое стандартное перечисление всех
четверок {А, В, Ф,Ф) таких, что А, В — в. п. множества, Ф, Ф — ч. в.
функционалы и Di — в. п. множество. (Заметим, что здесь (2.8) имеет
вид (2.7), где т = 4, к ^ 4, является А;-м дизъюнктом из (2.8), Ni
утверждает, что <<D{ $^т Ai и Di $^т Р*», а подтребование Rij
утверждает, что «Di ф Wj».)
Так как все требование Ri слишком сложное, чтобы его атаковать
сразу целиком, мы начинаем с того, что строим Di и описываем основной
модуль для удовлетворения Rij при фиксированных i и j. Множество
А = {s,g2,gl,w,l)0} всех возможных выходов двух модулей из § 4
будет содержать особое подмножество Ai = { #2, gl, 1}. В § 4 (определение
4.3) мы задаем приоритетное дерево Т С Л<и;, определенные
вычислимые функции истинный путь / £ [Т], где [Т] обозначает
множество бесконечных путей через Т. Каждой вершине a £ Т чётной
длины назначается проверка гипотез Фр — Ai и Фр = Bi для i = г (а). С
каждой вершиной a £ Т нечётной длины связывается вариант
основного модуля, который старается удовлетворить под требованию Ri(a),j{a)-
Назначение Ai = { g2,gl, 1} состоит в том, что если а С / и /(|а|) £ Ai,
то один из первых четырех дизъюнктов в (2.8) выполняется при i = г (а),
т. е. а свидетельствует в том, что Ri выполнено. Зафиксируем г. Если
ни одна а С / не является свидетелем в этом смысле удовлетворения
Ri, то для каждого j должна существовать некоторая нечётная /3 С /
с i(P) — i и j(P) = j такая, что (3 является свидетелем того, что
подтребование Ri(f3)j((3) удовлетворено и в таком случае f{\{3\) £ Л — Ль В
этом случае Ri удовлетворено пятым дизъюнктом из (2.8).
Теперь с помощью оракула 0'" можно точно определить, каким
образом удовлетворяется каждое требование Ri. Действительно, как обычно
имеем / 0//- Для проверки До с помощью оракула 0/// узнаем, су¬
ществует ли такая а С /, что г (а) = 0 и /(|а|) £ Ai. Если «да», то
обозначим через ао наименьшую такую а. Теперь можно точно
определить, который из первых четырех дизъюнктов в (2.8) истинен. Если
«нет», то пусть ао является наибольшей а С / чётной длины такой, что

§ 3. О" -приоритетные рассуждения
409
г (а) = 0. Теперь построение связывает с ао в. п. множество Do,
удовлетворяющее пятому слагаемому (2.8). Аналогично, по а* проверяем,
каким образом удовлетворяется требование Ri+1, отыскивая ai+i среди
а таких, что a* С а С /.
Интересной чертой такого построения является то, что если Ri
удовлетворяется через (*i как в первом случае, то мы рассматриваем такое
удовлетворение Ri как «нарушение» требований R# для г' > г. Мы
вынуждаем соответствующие стратегии для этих требований начинать
действовать заново на вершинах 0 D оц. Этот подход называется
«конечными нарушениями вдоль истинного пути» и объясняется далее в
§4.3.
§ 3. Метод деревьев в 0"-приоритетных рассуждениях
3.1. 	Деревья в обычном 0"-приоритетном рассуждении.
В теореме IX. 1.2 мы построили минимальную пару в. п. степеней. Теперь
мы изложим это построение на дереве, что поможет понять его лучше.
Примем определения и терминологию, использованные в IX. 1.2.
Определим функцию запрета r(e,s) с помощью дерева Т = Л<ы, где
Л = и) с естественным отношением порядка. Определим также
вычислимую последовательность строк { St }teu;? аппроксимирующую, как в § 2,
истинный путь /. Для a Е Т шаг s называется а-шагом, если а С. 5s
или 5 = 0. Пусть Sa — множество всех а-шагов. a-стратегия
определяется так же, как и основной модуль, но с Sa вместо ш. Именно, пусть
/(a, s) = Z(e,5), где е = |а|, и
m(a, s) = тах{ /(a, t) : t ^ s & t € Sa }.
Шаг s называется а-расширяющим, если либо 5 = 0, либо s является
a-шагом таким, что l(a,s) > m(a,5 — 1). Функция запрета для
единственной a-стратегии есть
' 0, если 5 «-расши¬
ряющий шаг,
наибольший а-расши-
, ряющий шаг t < 5 в противном случае.
(3.1)
Для 5^0 определим Ss Е Т, \Ss\ = 5, следующим образом. По данной
a = Ss [ е, е < 5, определим
Ss(e) = г(е, 5) =dfn тах{ r(0, s) : 0 ^ a }.

410
Глава XIV. Метод деревьев
Заметим, что для (3 <l ol значение r(/3, s) определяется через вторую
строку (3.1), поэтому Ss I е достаточен для определения r(/3,s) для всех
(3 ^ а. Теперь истинный путь / G Ли определяется как /(е) = r(e) =dfn
liminfs r(e, s). Имеем f f e = liminfs Ss [ e в смысле условий (2.2) и (2.3).
Дальше доказательство завершается так же, как в теореме IX. 1.2.
Это определение, по существу, задает такую же функцию запрета
r(e,s), какая была в теореме IX.1.2, но оно хорошо иллюстрирует, как
a-стратегии взаимодействуют. То, что в доказательстве, приведенном
в главе IX, оказалось возможным обойтись без использования деревьев,
можно объяснить так: в этом доказательстве рассуждение напоминает
марковский процесс, в котором единственной единицей информации, в
которой нуждается a-стратегия, является равенство а(е —1) = r(e — 1, s),
где е = |а|, т. к. мы добились выполнения условия r(e — 1, s) ^ r(j, s) для
всех j е — 1. В данном же рассуждении a-стратегии достаточно знать
только max{ r((3, s) : (3 < а }. Это верно и для многих других построений
таких, как, например, в плюс-наверх (см. Фейер и Соар [1981]). Однако
ряд других построений, имеющих такой же тип функций запрета r(e, s),
как в построении минимальной пары, а также содержащих
положительные требования бесконечного действия, лучше выполнять на деревьях.
Мы сейчас это увидим в следующей теореме, которая, возможно, дает
наиболее типичный пример 0"-приоритетного рассуждения,
использующего деревья.
3.2. 	0"-приоритетное рассуждение, требующее метод
деревьев
Лахлан в [1966b] построил два максимальных множества, степени
которых образуют минимальную пару. Из утверждения XI.2.5,
принадлежащего Мартину, следует, что совокупность степеней максимальных
множеств в точности совпадает с совокупностью высоких в. п.
степеней. Поэтому результат Лахлана означает существование минимальной
пары высоких в. п. степеней.
Для нас этот результат интересен своим доказательством, которое
приводится ниже. В нем мы построим в. п. множества А и В, и при
построении мы должны сделать предположение не только о значении
liminfs r(e, s), как это было в § 3.1, но также и об информации, какие
строки и В^е 1 бесконечны. Мы построим А и В как густые
подмножества некоторого в. п. множества С, так что для всех е выполняется
Ale 1 =* В^е 1 =* С^. На самом деле нам достаточно будет сделать
предположение = oj или С^е 1 =* 0. В этом параграфе будет использоваться

§ 3. О" -приоритетные рассуждения
411
следующее приоритетное дерево:
Т = {а : а € ш<ш к (Ve)[a(2e + 1) 6 {0,1}] }. (3.2)
Истинный путь / вдоль Г будет таким, что
/(2е) = r(e) =dfn lim infs r(e,s)
(3.3)
и
/(2e + 1) = |
0, если Ctel бесконечно,
1, если С М конечно.
(3.4)
Описанный в этом параграфе метод может быть адаптирован
практически ко всем стандартным построениям с бесконечными
нарушениями, например, построениям из глав VIII и IX. Что более существенно,
этот, использующий рассуждения на дереве, метод удобнее использовать
в 0"-приоритетных рассуждениях, требующих как выполнения
положительных требований бесконечного действия (как в обычных
рассуждениях с бесконечными нарушениями), так и при рассмотрении таких
запрещающих функций r(e,s), которые использовались в требованиях
минимальной пары из теоремы IX. 1.2), чем в рассуждениях с бесконечными
рассуждениями, таких как теоремы Сакса VIII.4.1 о плотности и VIII.3.1
о скачке с условием избегания верхнего конуса. В последних двух
случаях функции запрета могут быть определены таким образом, что они
одновременно сбрасывают свои значения при помощи метода «истинных
шагов» главы VIII § 1. А при построении минимальной пары для этой
цели требуется метод группирования стратегий теоремы IX. 1.2, и, таким
образом, требуется метод деревьев, если эта стратегия комбинируется с
положительными требованиями бесконечного действия. Поэтому метод,
описанный в этом параграфе, является более сильным, чем метод
работы с бесконечными нарушениями, описанный в главе VIII. Например,
метод деревьев может быть использован для доказательства
упражнения XII.2.13, в то время как метод «истинных шагов» главы VIII, § 1-§ 4,
для этой цели не достаточен, и были вынуждены совершать бесконечные
нарушения при помощи пинбольной машины, описанной в главе VIII § 5.
Метод деревьев позволяет также получить более ясное доказательство
теоремы XII.5.1 (см. упражнение 3.8).
3.1 	Теорема (Лахлан [1966b]). Существует минимальная пара
высоких в. п. степеней.

412
Глава XIV. Метод деревьев
Доказательство. Мы построим невычислимые в. п. множества А и В,
степени которых образуют минимальную пару, удовлетворяя для
каждого е следующему отрицательному требованию (как в теореме IXЛ.2):
Ne : {е}А = {е}в = g всюду определена => g вычислима.
Далее, аналогично множеству В из следствия VIII. 1.2, фиксируем
в. п. множество С такое, что для всех е выполняется
е Е 0" => С[е] конечно, (3.5)
е£0 "=>cM=Jel (3.6)
Для того, чтобы Ат В имели высокую степень, мы их построим как
густые подмножества С, а именно, А, В С С и для каждого е
удовлетворяется следующее положительное требование («требования густоты»):
Pf : AM =* С[е],
И
рВ : р[е) =* с^.
Отметим, что по лемме III.3.3 о пределе требования { РА }eGu; и { Рв }eGu,
обеспечивают справедливость 0" $^т А! и 0" В1, т. к. из (3.5) и (3.6)
следует, что
Ишж Л((ж, е)) = \imx В((х, е)) = 1 - 0"(е).
Пусть Т определено как в (3.2). Для каждого s мы определим Ss Е Т,
\Ss\ = 2s так, чтобы для всех п выполнялось / \ п = liminfs Ss [ п, как
В §2.
3.2 	Определение. Л-вычисление {е}£а(х) = у называется а-кор-
ректным, если
(Vi<e)[a(2i + 1)=0
=> (Vz)[[a(2t) < z ^ и(Л5; е,ж, s) k z € шЩ =Ф z £ Л«']],
и аналогично для В-вычисления (с Bs вместо As).
(Здесь смысл в том, что по (3.3) а предполагает, что
а(2г) = г(2г) =dfn liminfSr(i,s).

§ 3. О" -приоритетные рассуждения
413
К тому же по (3.4), (3.5), (3.6) и Р/4, если а(2i + 1) = 0, то а угадывает,
что С7М = и^г\ и, следовательно, А® =* Действительно, а исходит
из того, что все числа z > r(i), z G в конечном итоге войдут в А^.
Поэтому а «не верит в» вычисление до тех пор, пока эти элементы не
перечислятся в А.)
Теперь мы адаптируем основной модуль для вершины а € Т, |а| =
2е, определяя вычислимые функции
l(a,s) = max{ х : (Vy < ж)[{ е }^'(у) 4= {e}f‘(y) 4-
и эти вычисления а-корректны] }
ш(а, s) = max{/(a, t) : t ^ s & t G Sa }.
Шаг s является а-расширяющим, если либо 5 = 0, либо s > 0 и s
является a-шагом таким, что /(a, s) > т(а, 5 — 1). (Если |а| — нечётное
число, скажем 2е + 1, то эти три определения не имеют смысла, т. к.
вершине а назначены и Рев.)
Построение множеств А и В.
Шаг 5 = 0. Положим А0 — В0 — 0, г(а,0) = 0 для всех а G Г, и
r(a,s) = 0 для всех s и для всех а таких, что \а\ нечётная.
Шаг 5 -f 1. Сначала определяем Ss G Т, |JS| = 25, выполняя
этапы е < 5, описанные ниже, в порядке возрастания е. Далее, выбираем
наименьшее целое число х = (у, е) < s такое, что х G С[е^ — А$ или
х G с[е^ — В^ и х > r(e, s) = Js(2e). Перечисляем ж в А, если ж 0 As и в
В в противном случае. Если такого ж не существует, ничего не делаем.
Заметим, что на каждом шаге самое большее один элемент
перечисляется либо в А, либо в В, но не в оба сразу.
Этап е, 0 ^ е < 5. По данной а = Ss [ 2е определяем Ss(2e) и
Ss(2e + 1) следующим образом. Если (3 ^ а \(3\ чётная, то пусть
0,
r(/3, s) = <
наибольший /^-расширяющий
, шаг t < 5
если (3 С а и
5 — /^-расширяющий
шаг,
в противном случае.
(3.8)
Определяем
Ss(2e) = г(е, 5) =dfn max{ r(/3,5) : /3 ^ а }.

414
Глава XIV. Метод деревьев
Пусть 7 — 6S [ (2е + 1). Определяем
Г 0, если |с!е*| > |CjeI|,
6в(2е + 1) = 4 где t — наибольший 7-шаг < s,
t 1 в противном случае.
(Интуитивно, вершине 7 назначаются РеА и Рев, и 7 «просыпается»
только на 7-шагах. Если с тех пор, когда 7 просыпалась в последний раз,
мощность множества С№ увеличилась, то в этот момент нам кажется,
что Ctel является бесконечным, и мы поэтому определяем 5s{2e + 1) = О
согласно (3.4), РеА и Рев, а в противном случае определяем 6s(2e+l) = 1.)
Если е < 5 — 1, то переходим к этапу е + 1. В противном случае
определяем r(/3, s) = r(/3,s — 1) для всех (3 таких, что r(/3, s) ещё не
была определена, и завершаем шаг s + 1.
Лемма 1 (об истинном пути). Существует / G Л1^, называемая
истинным путем, такая, что
(i) (Vn)[/ l п = liminf5 Ss [ n, как определено в (2.2) и (2.3)],
(ii) (Ve)[/(2e) = r(e) =df„ liminfs r(e,s) < oo],
(iii) (Ve)[[/(2e + 1) = 0 <=> |(7lel| = oo]
&[/(2e + l) = l^|Ctel|<oo]].
Доказательство. Докажем (i), (ii), (iii), используя индукцию.
Фиксируем e ^ 0, обозначим a — f 2e и предположим, что (i) верно для
п — 2е, а (й) и (iii) — для всех е' < е. Выберем наименьшее to такое,
что не существует s > to такого, что 6S <l а. Пусть t\ > to
таково, что а С <!tl. Положим k = max{r(/3,£1) : /3 < а}. Теперь, как в
лемме 1 из теоремы IX. 1.2, если существует бесконечное множество а-
расширяющих шагов s, то на каждом таком шаге s имеем r(a, s) = О
и /(2е) = г(е) = к. В противном случае существует такой наибольший
шаг v, что r(a,s) = г; для почти всех 5, и г(е) = тах{А;,г;}. В любом
случае имеем (i) для п = 2е +1 и (ii) для е. Теперь пусть 7 = / [ (2е +1).
Если конечно, то Ss(2e-\-1) = 1 для почти всех s. Если же \С^\ = оо,
то существует бесконечно много s таких, что Ss D 7 (0), т. к.
существует бесконечно много 7-шагов. В любом случае имеем (i) для п — 2е + 2
и (iii) для е.

§ 3. О"-приоритетные рассуждения
415
Лемма 2. (Ve)[A^l —* =* В^Ц. (Точнее, для всех е С С^е\ и
С { 0,1,..., r(e) } U А^, и аналогично для вместо А^еУ)
Доказательство. Пусть х £ произвольное число такое, что х >
г(е). Выберем шаг so такой, что х £ CSo, и для всех у < х у € Аи В
тогда и только тогда, когда у £ ASq UBSq. На последующем шаге 5 +1 >
$о таком, что r(e,s) = г(е), х перечисляется в As+1, если х # As, и
перечисляется в Bs+\, если х £ As — Bs. В первом случае выбираем
следующий шаг t -f 1 > s 4-1 такой, что r(e, £) = г(е). Таким образом, ж
перечисляется в Bt+
Лемма 3. (Ve)[{ е }А — {е}в = g всюду определена => g вычисли¬
ма;].
Доказательство. Предположим, что {е}А = {е}в = д — всюду
определенная функция. Пусть а = f \ 2е. Покажем, что a-стратегия
удовлетворяет Ne. По лемме 1(Ш), а имеет правильное предположение о
|CM| для всех г < е, именно, а(2i 4-1) = 0 тогда и только тогда, когда
\сЩ = оо. По лемме l(i) выбираем a-шаг £ такой, что не существует
шага s ^ t со свойством <l а. Заметим, что по лемме 1 (ii) мы имеем
(V* < e)(Vs ^ i)[r(i) ^ s)]> (3-9)
и, следовательно,
(V* < e)(V® ^ r(i))[* е лМ иBw л[« ив{<>]. (ЗЛО)
По лемме 1(Ш) мы также имеем
(Уг < е)[<7^ конечно => с]1' = С^], (3.11)
т. к. если С7М конечно, то а(2г Ч- 1) = 1, и если какой-нибудь ж входит
в (7^1 на шаге v > t, то на некотором шаге s ^ v > t мы должны иметь
=2 (а 2i) (0), поэтому <l а, что противоречит выбору t. Теперь
предположим, что t выбран таким большим, что справедливо
(V* < е)[С?М конечно => [л[;] = Л^ к = вМ]].
Чтобы эффективно вычислить д(р), находим такой наименьший а-
расширяющий шаг v > t, что l(a,v) > р. Пусть д(р) = {e}^v(p).
Заметим, что такой шаг v существует, т. к. если { е }А{р) = q со значением
use-функции и, то вычисление {е}^л(р) = q будет а-корректным почти

416
Глава XIV. Метод деревьев
всегда, именно, оно будет корректным для всех таких s > t, что z € С s
для всех z Е для которых i < е, а(2 г + 1) = 0 и г (г) < г ^ w. То же
самое верно и для В-вычислений. Теперь, как в лемме 3 теоремы IX. 1.2,
индукцией по s ^ v следует, что для всех s ^ v
{ е }fa(p) = Q — а-корректное вычисление, (312)
или
{ е }fa(p) — Ч — а-корректное вычисление. (3.13)
К сказанному в лемме 3 теоремы IX. 1.2 можно добавить следующее.
Как видно из (3.10), (3.11) и определения а-корректного вычисления, мы
не можем иметь z Е — А$ или z Е г — в[г\ если i < е, s > t и
z использовано в процессе а-корректного вычисления { е }£a(p) — q или
{e}fa(p) = q• Как обычно, запрещающая функция r(e,s) не позволяет
никакому z Е и^г\ где i ^ е, перечислиться в A U В и разрушить
вычисление (3.12) или (3.13), если только s не является а-расширяющим
шагом. В последнем случае оба соотношения (3.12) и (3.13) справедливы
для s. О
3.3 	Примечание. При доказательстве теоремы 3.1 и по существу во
всех 0"-приоритетных построениях на деревьях мы могли бы так
модифицировать дерево, чтобы не существовало никаких нарушений в
«построении, проводимом вдоль истинного пути» С — (J{CQ : а С / }. А
именно, если (3 С а С /, то а-стратегия никогда не нарушается
стратегией (3 в следующем смысле.
Пусть а = / I 2е. Определим слегка модифицированную
функцию запрета r(/3, s) как в (3.8), но во второй строке (3.8) t заменяем
на наибольший элемент и, использованный в А- или ^-вычислении
на шаге t для какого-нибудь аргумента х < /(а,£). (Заметим, что
f (a, s) ^ г (а, 5), и этот запрет достаточен, чтобы обеспечить, что а-
стратегия достигает цели.) Мы говорим, что а нарушается па шаге
5+1, если z Е (^4s+i — As) U (Bs+1 — Bs) для некоторого z ^ f(a,5).
Кроме того, если z E cjM и (3 = Ss [ (2i + 1), то мы говорим, что (3
нарушает а.
Теперь а может нарушаться самое большее конечное число раз
такими (3 <l а. При доказательстве теоремы 3.1 а к тому-же может
нарушаться конечное число раз вершинами (3 С а, если \(3\ = 2 г + 1 и
а(2г + 1) = 1, т. к. а знает, что множество СМ конечно, но не знает в
точности его элементы. Это может быть исправлено заменой дерева Т

§ 3. О" -приоритетные рассуждения
417
из (5.1) на Т = и<и} и определение (3.4) на
/<2i+i)={°'+i.
если \СЩ = оо,
если CW = .Dfc,
где { Dk }кеи — обычная каноническая нумерация конечных множеств.
Теперь если а = / [ 2е, то а имеет достаточную информацию о для
всех i < е, и соответственно определяет а-корректные вычисления, так
что теперь а никогда не нарушается никакими (3 С а.
3.4 Примечание. В вышеприведенном построении в качестве прио¬
ритетного дерева мы могли бы взять просто Т = 2<а\ Тогда /(2е + 1)
определяется как раньше, по (3.4). Если а = / 2е, то /(2е) = 0, ес¬
ли существует бесконечно много a-расширяющих шагов, и /(2е) = 1, в
противном случае.
Построение и доказательство проходят как описано выше, за
исключением того, что при определении а-корректного вычисления в (3.7) мы
заменяем «а(2г) < z» на <<r(i,s) < z», где r(e,s) определяется как
раньше, a Ss(2e) определяется следующим образом. Если а = Ss [ 2е, то
положим <5s(2e) = 0, если s является a-расширяющим, и Ss(2e) = 1
в противном случае. Теперь лемма 1 (ii) справедлива, если г(е) имеет
прежнее значение, а /(2е) — только что определенное значение. При
доказательствах лемм информация о возможных выходах старших
требований не теряется, т. к. Ss(2e) = 1 и r(e, s) = к эквивалентно условияю
Ss(2e) = к в прежней теминологии. В частности, как раньше,
выполняются лемма 3 и соотношения (3.9), (3.10) и (3.11).
Такой подход имеет некоторые преимущества, потому что в
дальнейшем, особенно в 0Ш-приоритетных построениях, удобнее использовать
конечно ветвящиеся приоритетные деревья Т. (Тогда, однако, а может
не иметь полную информацию обо всех (3 С а, как было в замечании 3.3,
и поэтому а может нарушаться и такими (3.)
3.5-3.8 Упражнения
3.5 (Лахлан). Используйте метод теоремы 3.1, чтобы прямой
конструкцией построить два максимальных множества, степени которых
образуют минимальную пару.
3.6. 	Дайте доказательство на дереве для теоремы Сакса о скачке
(VIII.3.1.).

418
Глава XIV. Метод деревьев
3.7. 	(Шор). Соедините метод деревьев из теоремы 3.1 с идеями
главы XIII § 2 с тем, чтобы доказать, что для каждой в. п. степени b
b £ PS V (3 в. п. а) [а' = 0" к а П b = 0].
3.8 	(Сламан). Дайте новое доказательство теоремы ХИ.5.1, используя
метод деревьев из теоремы 3.1.
§ 4. Метод деревьев с 0'"-приоритетными
рассуждениями: теорема Лахлана о неограничении
4-1. Предварительные сведения.
Точное описание степеней а £ R+, ограничивающих минимальные
пары, остается открытым вопросом. Купер (упражнение XI.2.15) показал,
что это верно для высоких степеней а £ Hi. Сейчас мы докажем
теорему Лахлана, которая утверждает, что не каждая а £ R+ обладает этим
свойством. (См. также замечания, приведенные после теоремы XIII.3.1.)
4.1 	Теорема о неограничении (Лахлан [1979]). Существует в. п.
степень с > 0, под которой нет в. п. степеней, образующих
минимальную пару.
Мы примем некоторые обозначения из работы Лахлана [1979],
удобные для этих и других О'"-рассуждений. Заглавные греческие буквы
Фл, Фл, ...обозначают A-частично вычислимые функции, ранее
обозначаемые как { е}А, е £ и. Если в процессе вычислимого построения
определяется в. п. множество А или частично вычислимый функционал
Ф, то через A[s], Фе[$] обозначается результат этого построения,
полученный к концу шага s. (Ранее мы их обозначали как As, {e}s и т. д.)
Если т — некоторый параметр, то через m[s] обозначается его значение
к концу шага s. Мы будем снабжать буквой «[$]» и целые выражения.
Например, Ф^(а:)[5] обозначает Ф[5]^М(:г). Преимущество таких записей
состоит в том, что в процессе построения А, Ф, т,... рассматриваются
как в стадии формирования. На конкретном шаге (который может
состоять из множества подшагов) мы можем использовать ту же запись А
для обозначения множества элементов, перечисленных к этому моменту
в А, т — для обозначения текущего значения параметра т, и т. д. Для
избежания путаницы мы снабжаем эти обозначения номером шага s и

§ 4- Теорема Лахлапа о неограничении
419
пишем А[5], m[s] и Ф[s], чтобы обозначить соответствующий результат
?с концу шага 5.
Доказательство теоремы 4-Т Мы должны построить в. п.
множество <7, удовлетворяющее для всех i следующим требованиям:
Ri : [фр = Ai & Фр = Bi & Ai невычислимо & Bi невычислимо]
=> (3 в. п. Bi)[Bi ^т Ai & Bi ^т -Bi & Di невычислимо],
(4.1)
где { (Ai, Фг, Фг) }i€a; — стандартная эффективная нумерация всех
четверок (А,В,Ф,Ф) такая, что А и В — в. п. множества, а Ф и Ф —
частично вычислимые функционалы. Предполагается, что имеются
равномерные эффективные перечисления для Ai, Bi, Ф; и Ф*. Без
ограничения общности можем предположить, что для всех х и s
X € i4j[s] - v4j[s - 1] =Ф Фр (x)[s] = 1, (4.2)
И
x 6 Bi{s} - Bi[s - 1] =► Фр(х)[в] = 1. (4.3)
Для этого достаточно задержать перечисление числа х в Ai и Bi до
тех пор, пока Фр(ж) и Фр(ж) не примут значение 1. (Это можно
осуществить, т. к. как четверка (Ai, Bi, Фi, Ф*) интересует нас только, если
Ai = Фр и Bi = Фр.) Определим
1Ф( [в] = тах{ х : (Vy < х)[А<(у)[в] = Фр (у) [в]] }, (4.4)
и, аналогично, /ф*[$] с Bi и Ф; вместо А* и Ф^ Польза от соглашений
(4.2) 	и (4.3) заключается в том, что если на некотором шаге х < /ф‘,
то мы можем сохранить А{ [ х, сохраняя С [ и, где и — наибольший
элемент, используемый в вычислениях Фfl(y), у < х, и аналогично для
Bj ж.
^.2. Основной модуль для удовлетворения подтребования
(конструирование компьютерного чипа)
Чтобы понять нашу стратегию, удобно переписать требование Ri в
следующем виде:
Ri : Фр = Ai & Фр = В{ =>
[Ai вычислимо V Bi вычислимо
V (Э в. п. Di)[Di А{ k Di В{ & (Vj)[Bf ф Wj]]].
(4.5)

420
Глава XIV. Метод деревьев
Определим следующее подтребование
Rij (4.6)
Наша стратегия заключается в том, чтобы попробовать
удовлетворить R{ построением в. п. множества Di с целью удовлетворения
последнего дизъюнкта требования R{. Описанный ниже основной модуль
пытается это сделать для единственного под требования Rij (совмещая
это с обеспечением равномерной сводимости Di $^т Ai,B{). Либо он
достигает этой цели, либо в противном случае гарантирует, что одно из
множеств А{ или В{ вычислимо, а это значит, что требование R{
удовлетворяется сразу, и уже не нужно рассматривать подтребования Rij>,
j1 ф j. (Описываемый нами основной модуль отличается от
приведенного в статье Лахлана [1979], но он близок к тому, что имел в виду
Харрингтон [1982], хотя последний и не описал всех деталей. Этот основной
модуль приводит к более простому дереву выходов, чем у Лахлана, хотя
начальный модуль описывается сложнее, имея вместо одного два типа
гэпов.)
Зафиксируем г и j и опустим индексы у Ai, В{, Ф* и Ф*. У нас
имеются параметры х, гх, г2 и г, которые должны рассматриваться как
функции от шага s. Параметр, получивший однажды некоторое
значение, сохраняет его до тех пор, пока ему не будет назначено новое
значение. Через х мы обозначаем текущего кандидата для удовлетворения
Ri j, гх и 7*2 — функции запрета, которые препятствуют элементам
перечисляться в С для того, чтобы сохранить значения А [ х и В [ х
соответственно, а г — тах{ гх, 7*2, }. Переназначить кандидата х на шаге
s 4-1 означает следующее: отменить старого кандидата ж[$] и определить
x[s+1] как наименьшее у Е такое, что у > s +1 и у также больше
всех предыдущих кандидатов всех модулей. Инициализировать
(основной модуль) означает переназначить х и положить п = Г2 = 0. Мы
проводим такую инициализацию на шаге s = 0 и на любом
последующем шаге, когда некоторый элемент z ^ г входит в С (под воздействием
некоторого требования Р&), или когда наш модуль «нарушается» из-за
действия модуля более высокого приоритета, в этом случае основной
модуль начинает все сначала с новым кандидатом х.
Начиная с этого момента мы предполагаем, что в (4.5) выполняются
равенства Фс — А и Фс = В. Основной модуль состоит из следующих
этапов. (См. диаграмму 4.1.)
Этап 1. Ждем шага s такого, что х Е Wj[s]. На шаге s + 1
открываем А-гэп, устанавливая r\[s Ч-1] = 0, и переходим к этапу 2.

§ 4• Теорема Лахлана о неограничении
421
Диаграмма 4.1. Схема основного модуля как конечный автомат
Этап 2. Ждем наименьшего t ^ s -f 1 такого, что /ф[£] > х. На шаге
t + 1 закрываем А-гэп, выполняя этап 2(a) или 2(6) в зависимости от
того, который из них имеет место.
Этап 2(a). (Удачное закрытие.) Предположим, что A[s] [ х ф A[t] [
х. Открываем В-гэп, определяя Г2^Ч-1] = 0. (Заметим, что г\ остается
равным 0, поэтому r[t 4-1] = 0.) Переходим к этапу 3.
Этап 2(6). (Неудачное закрытие.) Предположим, что A[s] [ х =
A[t] [ х. Определяем r\[t 4- 1] = t (чтобы сохранить A[t\ [ х),
переназначаем х и переходим к этапу 1.
Этап 3. Ждем наименьшего v ^ £4-1 такого, что l*[v] > х. На шаге
v -f 1 закрываем В-гэп, выполняя этап 3(a) или 3(6) в зависимости от
того, который из них имеет место.
Этап 3(a). (Удачное закрытие.) Предположим, что B[v] \ х ф B[t\ [
х. Перечисляем х в D и останавливаемся.
Этап 3(6). (Неудачное закрытие.) Предположим, что B[v\ [ х =
B[t] I х. Определяем Г2[у 4- 1] = v (чтобы сохранить B[v] [ х),
переназначаем х и переходим к этапу 1.
(Заметим, что при открытии А-гэпа (Б-гэпа), сбрасывание
запрета 7*1 (г2) позволяет другим положительным требованиям перечислять
элементы в С, заставляя посредством этого измениться Фс (Фс) и, тем

422
Глава XIV. Метод деревьев
самым, сбросить значение /ф (/ф, соответственно).)
Сначала заметим, что если предположение (4.5) верно, то обе
сводимости D $^т А и D ^т В равномерны, потому что мы требуем оба А-
и ^-разрешения (т. е. изменения А [ х и В [ х), прежде чем х
перечислить в D. Требование Rij выполняется, если либо мы безрезультатно
ждем такого шага s, что х Е Wj[s], и поэтому D U Wj ф и, либо если
некоторый В-гэп удачно закрывается, и в этом случае х входит в D и
D П Wj Ф 0. Так как по предположению Фс = А (Фс = Б), то каждый
А-гэп (В-гэп) в конце концов должен быть закрыт.
Предположим, что существует бесконечно много (например) Б-гэпов,
открывающихся на шагах {tn }nGш и закрывающихся (обязательно
неудачно) на шагах {^п}п€им где to < vo < t\ < v\ <•••. Интервалы
{ s : tn ^ s < vn } называются В-гэпами, т. к. на шагах из этих
интервалов т*2 — 0, и мы свободно можем перечислить любое число в (7, в то
время как интервалы { s : vn s < tn+\ } называются В-когэпами, и на
шагах из этого интервала мы имеем г2 = vn.
Предположим, что основной модуль нарушается только конечное
число раз, именно, что существует шаг $о такой, что
(Vs > s0)(4z)[z Е C[s + 1] — C[s] => z > ф]]. (4.7)
Тогда вычислимость множества В можно показать следующим
образом. Для вычисления В(р) находим шаг t > so такой, что х = x[t] > р
и В-гэп открывается на шаге t + 1. Так как этот В-гэи позднее на
шаге v + 1 > £+1 неудачно закрывается, то B[t] [ х = B[v] [ х. Если
следующий В-гэп открывается на шаге t14-1 > v 4-1, то С-запрет г2
гарантирует, что B[v] [ х = B[t'] [ х. Теперь рассуждение продолжается с
заменой х на х* — x\b' + 1] > я, и приводит к тому, что B[t] [ х = В [ х.
Следовательно, р Е В тогда и только тогда, когда р Е B[t]. Заметим,
что Нт*ф] = оо, т. к. каждый новый кандидат превышает все
предыдущие.
Если существует только конечное число Б-гэпов, но бесконечно
много А-гэпов, то А вычислимо при помощи такого же рассуждения с 7*1, А
и Ф вместо 7*2, В и Ф соответственно, и с достаточно большим s\ > so,
чтобы удовлетворить (4.7), и превышающим все шаги, на которых
закрываются В-гэпы (чтобы после шага s\ каждый А-гэп закрывался
неудачно).
Наконец, заметим, что liminfs ф] < оо. Если существует только
конечное число А- и Б-гэпов, то lims ф] существует. Если существует
бесконечно много В-гэпов, то liminfsr[s] = 0, т. к. ф] = 0, если В-гэп

§ 4• Теорема Лахлапа о неограничении
423
открывается на шаге s. Если существует конечное число Б-гэпов и
бесконечно много А-гэпов, то существует к = limer2[s], поэтому r[s] = к
для всех шагов 5 > на которых открывается А-гэп, поскольку на
таких шагах справедливо ri [5] = 0.
Имеет смысл рассмотреть основной модуль как разновидность
конечного автомата М, состояниями которого являются {s,g2,gl, ги},
упорядоченные слева направо, а переходами между состояниями являются
переходы, описанные на этапах 1, 2(a), 2(6), 3(a) и 3(6) основного
модуля. А именно, М начинает действовать в начальном состоянии w,
пытаясь перейти влево в заключительное состояние s. Пока М находится
в состоянии w (д 1, #2), он ждет выполнения условия перехода,
связанного с соответствующим этапом 1 (2, 3). Затем М переходит влево или
вправо в новое состояние, согласно тому из этапов, который имеет
место. Заметим, что желательное продвижение влево по направлению к
заключительному состоянию s может прерываться неудачным закрытием
А-гэпа (В-гэпа) и, следовательно, возвращением в начальное состояние
w. Это может заставить М образовать бесконечные циклы, бесконечно
часто возвращаясь направо из состояния д 1 или #2, или из них обоих.
Пусть F[s] обозначает состояние автомата М к кону шага s.
Возможными выходами основного модуля являются
S = {s,g2,gl,w},
с отношением естественного (слева направо) порядка <5 . Они
делятся на конечные (O') выходы SFin = {$,д;} и бесконечные (0") выходы
5’Inf = {gl,g2 }.
Определим выход следующим образом. Если lims F[s] = а, то a G SFin
и выходом является а. Если же lim* F[s] не существует, тогда: если
существует бесконечно много В-гэпов (бесконечно много выходов вправо
из д2), то выходом является д2\ в противном случае (в этом случае
существует бесконечно много выходов вправо из <jl) выходом является д 1.
Состояния автомата М показаны на диаграмме 4.1 в виде
прямоугольников. (Таким образом, выходом основного модуля является <5-
наименыпий (т. е. самый левый) a G S такой, что автомат М либо
находится внутри прямоугольника а, либо на бесконечно многих шагах
проходит через него.)
Приведенная на диаграмме 4.2 таблица описывает результат работы
основного модуля по отношению к Ri и Rij, для каждого выхода a G S.
Фиксируя г и повторяя основной модуль для всех j Е о;, легко видеть,
что существует невычислимое в. п. множество С, которое
удовлетворяет единственному требованию Ri, имеющему вид (4.5), и такое, что D{

424
Глава XIV. Метод деревьев
Результат
S
02
01
W
Действие на Rt tJ
успех
нет
нет
успех
Действие на Ri
нет
в,
вычислимое;
Ri
выполнено
л.
вычислимое;
R.
выполнено
нет
Диаграмма 4.2. Анализ результатов
может быть найдено равномерно по каждому из А{ и В{. Тогда отсюда
по теореме рекурсии следует, что не существует равномерной
эффективной процедуры для перехода от индекса невычислимого в. п. множества
С к индексам в. п. множеств А, В $^т С, степени которых образуют
минимальную пару, и, одновременно, к индексам функционалов Ф и Ф,
которые сводят множества А и В к множеству С.
4-3. Приоритетное дерево (вычислительная архитектура
машины)
Если мы рассмотрим основной модуль из § 4.2 как определенный
элементарный «компьютерный чип», созданный для выполнения маленькой
конкретной задачи, то можно сказать, что в этом параграфе
описывается, как эти чипы «вместе плотно соединяются» и создают
вычислительную архитектуру всей машины. Эта архитектура включает в себя
распределение чипов в определенное дерево (приоритетное дерево) и затем
назначение каждому чипу конкретной задачи (требования), согласно его
позиции на дереве. Очень много информации можно получить, просто
изучая это приоритетное дерево, до перехода к построению. В § 4.5 мы
описываем построение, которое соответствует «операционной системе»,
определяя, что требуется сделать на каждом шаге, а именно, как
процесс контроля переходит от вершины к вершине по мере того, как мы
спускаемся вдоль определенного пути на дереве в течение одного шага
построения.

§ 4• Теорема Лахлана о неограничении
425
Рассмотрим требование Ri, определенное в (4.1). Отметим, что
первые две предпосылки
Ф? = ^ и фр = Ви (4.8)
ЯВЛЯЮТСЯ П2С -условиями. Мы будем аппроксимировать эти условия,
оценивая, будет ли lim sup минимума из /ф,'[$] и бесконечным на не¬
котором бесконечном множестве шагов. Нам этих аппроксимаций будет
достаточно, а они просто являются Пг-условиями. Следовательно,
подобно П2-условиям из § 3, каждое из них подходящим образом может быть
добавлено в виде вершины (3 на дереве над теми вершинами а, которые
предназначены для работы с подтребованиями Rij для фиксированных
j. Таким образом, а может исходить из того, что эти предположения
(4.8) 	удовлетворяются, и, следовательно, вершине а нужно действовать,
только когда это предположение «кажется верным». Для оценки,
когда предположения (4.8) «кажутся верными», мы определим следующие
вычислимые функции.
4.2 	Определение, (i) Пусть /ф*' [s] и [s] будут как в (4.4). Определяем
li[s] = min{/*i[s])rI'i[s]},
И
mla[s] = max{ li[t] : t ^ s & t + 1 € Sa },
где Sa будет определено в 4.9.
(ii) Шаг v является а-расширяющим, если либо v = 0, либо v = s-f 1,
s 4- 1 G Sa, и li[s] > mla[s — 1], где i = г (а), и г (a) определяется как в
4.4.
4.3 	Определение, (i) Пусть Л = { s,g2,gl,w,0,1} с заданным
естественным отношением порядка <д слева направо. (Это — множество
возможных выходов для всех стратегий всех вершин.)
(ii) Определим приоритетное дерево
Т = {а € Л<ы : (Vn)[a(2n) G { 0,1 } & а(2п + 1) 6 { s, g2, gl, w }] }.
(iii) [T] = {fc:/i6Au,& (Vn)[/i f n 6 T]}. Мы называем эти h € [T]
(бесконечными) путями через Т.
(iv) Вершина a £ Т является чётной, если число \а\ чётно, и
нечётной в противном случае.
Определим функции г, j : Т -» и). Каждая чётная вершина a £ Т
назначается к (Ф*, Ф*)-гипотезе (4.8), где i = i(a). Выход 1 для а-й

426
Глава XIV. Метод деревьев
стратегии приблизительно означает, что существует самое большее
конечное число a-расширяющих шагов, поэтому (4.8) для г не
выполняется и, следовательно, а верит, что R{ удовлетворено. Выход 0 означает,
что существует бесконечно много a-расширяющих шагов, и что,
следовательно, дальнейшие действия по удовлетворению Ri должны взяты на
себя вершины /3 D а.
Каждая нечётная вершина a Е Т назначается некоторому
подтребованию Rij с i = i(a) и j = j(a), а a-стратегией будет вариант
основного модуля, имеющий в качестве выходов { s,g2,gl,w }. Выход g2 (д 1)
означает, что существует бесконечно много Да-гэпов (бесконечно много
Аа-гэпов, но конечное число Да-гэпов), и что, следовательно, Ва (Аа
соответственно) вычислимо. Выход s (w) означает, что под требование
Rij удовлетворено, потому что Ица) П Wj(a) ф 0 (A(a) U Wj{a) ф и
соответственно).
4.4 	Определение. Определим частичные функции функ¬
ции Lo, L\ :Т -> Р(и>) = { X : X С и }, называемые списками,
индукцией по п = |а| следующим образом. Функция i будет всюду определенной,
а j будет определена только на нечётных вершинах.
Для п = 0. Определим г(А) = 0 и Lo(A) — Li(A) — со.
Для п > 0. Пусть a = (3 (а) для a Е Л. Предположим, что г(/3),
Lo(/3) и Ь\(Р) определены, а также что j(/3) определено, если /3
нечётная. Сначала определим Lo(a) и Li(a), как описано ниже. Далее, если
а чётная, определим г (a) = Е Lo(a)], a j(a) пусть остается не¬
определенным. Если а нечётная, определим г(а) = i0 и j(a) = jo, где
.(*Wo) = (а*п)[п € £а(а)]-
Определим Lo(a) и Li(a) следующим образом. Пусть г = г(/3) и, если
/3 нечётная, то пусть j = Я/?)-
Случай 1. (3 чётная.
Случай 1А. а = 1. Определяем
Ьо(о^) = (Ьо(/3) - {г }) U {г' : г' > г }
и
Li (a) = (Li (/3) - { (г, jfe) : jfe E a; }) U { (г', jfe) : i' > i k k E ш }.
Случай IB. a = 0. Определяем
L0(a)=L0(/3)-{i}
и
Ыа) = Li (/3).

§ 4• Теорема Лахлана о неограничении
427
Случай 2. (3 нечётная.
Случай 2А. a G { д2,д1}. Определяем L0(a) и Ь\(а) как в случае 1А.
Случай 2В. a Е { }. Определяем L0(a) = L0(/3), и la (a) = Iq(/?) —
{{U)h
Интуитивно это определение можно понимать так. По мере того, как
мы спускаемся по дереву Т вдоль произвольного пути h Е [Т], L$
представляет «список» индексов г, соответствующих (Ф*, Ф^-гипотезам из
(4.8), и которые будут назначены чётным вершинам a Е Т в
порядке уменьшения приоритета. «Список» Ь\ представляет индексы (г, j),
соответствующие подтребованиям Rij, и которые будут назначены
нечётным вершинам. Если а = /3 (а) и a Е {<jl,g2,1}, то а верит, что
Ri удовлетворено, поэтому при построении L0{a) (Li(a)) из Lo(/3) (из
Li(/3)) мы можем удалить г (соответственно {(г,А;) : к Е и;}). Однако
мы считаем это «действие» по удовлетворению Ri как «нарушающее»
Ri> для всех г' > г, поэтому такие V ({ (г', к) : к Е и } соответственно)
должны быть помещены обратно в Lo(a) (Li(a)), так что для всех таких
требований Ri>, г' > г, все действия начинаются сначала на вершинах
7 D а.
(Существует очевидная аналогия между процессом спуска вдоль
произвольного пути h Е [Т] и продвижением по шагам в построении с
конечными нарушениями, например таком, как в теореме VII.2.1. В последнем
случае мы начинаем на шаге 0 со списком Ьо = и индексов требований
Ri, которые должны быть удовлетворены. На каждом шаге s -f 1 мы
выбираем наименьшее г Е Ь8 такое, что Ri требует внимания. Мы
позволяем Ri действовать и определяем
Ts+1 — {Le {® }) С {i • i > i} ?
так как все R*/, г' > г, нарушаются на шаге s -f 1 и им должно быть
позволено действовать на шагах v > s + 1.)
4.5 	Определение. Пусть a Е Т.
(i) Определяем
г (a) = (/i/3 С а)[{3 чётная & г(/3) = г(а)
& -’(37bc7ca[*(7) < i(a) & а(1т1) € {52,51,1}]]-
Если таких (3 не существует, то пусть т(а) неопределено.

428
Глава XIV. Метод деревьев
(ii) Если т(а) определено, то для i = г(а) определяем г -регион,
содержащий а:
E(a,i) = {(3 : (3 Е Т к т(а) С 0 & т(/3) = т(а) & г(/3) = г(а) }.
(ш) Мы называем т(а) верхушкой г-региона Д(а,г), потому что она
является (относительно С) там наименьшей (т. е., С-наименьшей)
вершиной. Она также является единственной чётной вершиной в Е{а,г).
(iv) 	Мы называем 7 i-границей, если 7 = 0 (а), г = г(/3) и а Е
{52,31,1}.
4.6 Лемма. Пусть Е является i-регионом с верхушкой т и г = г(т)>.
Тогда ^
(i) ->(Э/3 Е £)[т С 0 = а (а) & г(а) < г & а Е { g2,gl, 1 }],
(ii) -«(3/3 Е Д)[т С (3 & /3 чётная & г(/3) = г].
Доказательство. Утверждение (i) следует непосредственно из
определений т(а) и Д(а, г). Для (ii) предположим, что /3 является С-минимальной
вершиной в Е, для которой (ii) ложно, и получим противоречие. Тогда
i Е L0(/3), но i £ L0(r+), где т+ = т (а) для а = /3(|т|). Следовательно,
по определению 4.4 существует некоторая вершина 7, т С 7 С /3, такая,
что 2(7) < г, и /3(|7|) Е {#2,gl, 1}, что противоречит (i). О
Интуитивно это можно представить так. Для произвольного i Е и), по
мере того, как мы спускаемся вдоль произвольного пути h Е [Т], в конце
концов приходим к некоторой чётной вершине т С h, для которой
определяем г(т) = г и, тем самым, открываем новый г-регион Е с верхушкой г.
Однако, если мы встречаем такую вершину 7, что rCnfChnry = 0 (а)
является г'-границей для некоторого г' < г, тогда (3 верит, что Zfy уже
удовлетворено (и это будет действительно так, если h = истинному
пути/), поэтому 0 нарушает нашу попытку удовлетворения Д*, и мы
начинаем новый г-регион с некоторой верхушкой т', 7 С т1 С h. После
конечного числа нарушений этот процесс стабилизируется на некоторой
r(h,i), Определяемой ниже, которая является верхушкой завершающего
г-региона, открываемого в процессе спуска вдоль h. Следующая лемма
утверждает, что для каждого г по мере того, как мы спускаемся вдоль
произвольного пути h Е [Т], мы пересекаем конечное число г'-границ,
для V < г, и поэтому E(h,i) (см. определение 4.8) существует.
4.7 Лемма о конечных нарушениях вдоль произвольного пути.
Для каждого пути h Е [Т] и каждого i Е ш выполняются условия

§ 4■ Теорема Лахлана о неограничении
429
(i) (3<оса С Л)[*(а) = i & h(\a\) € { д2,gl, 1}],
(ii) (3<оса С h)[i(a) = i & а чётная ].
Доказательство. Фиксируем Лиги предположим, что лемма верна
для всех г' < г. Выберем 0 С h такую, что для всех а, /3 С а С Л,
если г(а) < г, то а нечётная и h(\a\) £ {g2,gl,l}. Чтобы доказать
(i), предположим, что существует некоторая 7, 0 С 7 С Л, 2(7) = г, и
а Е {#2,#1,1 }, где а = Л(|7|). Пусть 7+ = 7 (а). Тогда индукцией по
длине а получаем, что
(Уа)7+Сасл[* i L0(а) & (Vfc)[(i,A:) £ Li(a)]]
и, следовательно,
(Уа)7+Сасл[*(«) < * => ММ) i {52,gl, 1}].
Чтобы доказать (ii), выберем такую наименьшую чётную 7? 0 Q 7 С
Л, что 1(7) = г. Пусть 7+ = 7 (Л(|7|)). Тогда по выбору 0 и
определению 4.4 имеем
(VO')^+gac/J,[^ ^ Lo(^)]?
следовательно,
(Va)7+cac/i[a чётная => г(а) > г].
Лемма 4.7 позволяет нам следующим образом определить
завершающий г-регион для h Е [Т].
4.8 	Определение. Фиксируем произвольные i Е w и путь h Е [Т].
Пусть a — такая С-максимальная чётная вершина 0 С Л, что г(/3) = г.
(По лемме 4.7 и определению 4.4 такая а существует.)
(i) Определяем E(h,i) = E(a,i), завершающий i-регион пути h.
(ii) Определяем т(Л,г) = т(а) = а, верхушку завершающего г-региона
E(h,i).
Заметим, что выполняется
(V7)[[т(Л,») С 7 С Л & 1(7) = »] => 7 Е Л5(Л,»)]. (4.9)
(О завершающем г-регионе Е = E(h,i) можно думать как о
некотором нижнем конусе вершин с верхушкой т = т(Л,г). Конечно, £
содержит намного больше вершин помимо тех 7, для которых т С 7 С Л,

430
Глава XIV. Метод деревьев
2(7) = г, в которых мы действительно заинтересованы. Однако Е не
является настоящим конусом (т. е. состоящим из всех 7^7, г(7) = г),
потому что может существовать такая /?, т С (3 <jt h, что г(/3) < i и
7 D/3 (а) для a Е { </2, </1,1}. В этом случае 7 ^ J3, даже если 2(7) = г.)
Интуитивные описания приоритетного дерева и
доказательство
В следующем параграфе мы индукцией по п определим истинный путь
/ Е [Т] для нашего построения, где a = f[nnf(n)— а означают,
что а является истинным выходом стратегии для а. Если а — нечётная
вершина, то истинный выход а Е {s,g2,gl,w} для а определяется как
в основном модуле из § 4.2. Если а — чётная вершина, то а = 0 тогда
и только тогда, когда существует бесконечно много а-расширяющих
шагов, в противном случае а — 1.
Истинный путь / дает нам возможность проверить, что каждое
требование Дг, определенное в (4.1), удовлетворено. Зафиксируем г и
рассмотрим завершающий 2-регион Е = E(f,i) с верхушкой т — т(/,г).
Если /(|т|) = 1, то limsupsG5r mlT[s] < 00, поэтому либо Фр ф
либо Фр ф Bi, и Д* немедленно удовлетворяется. В противном случае
/(|т|) = 0 и limsupsG5r mlT[s] = 00, поэтому каждая нечётная а Е Е при
г (а) = г, открывшая некоторый гэп, в конце концов его закроет.
Мы представляем т как место, с которого берет начало наша
стратегия построения невычислимого множество Di и вычислимых
функционалов = Di и = Di для удовлетворения правой части
требования Ri в (4.1). Чтобы гарантировать невычислимость Di, нам нужно
убедиться в том, что для почти каждого j существует такая нечётная
вершина а, т С а С /, что г(а) = г и j(a) = j. Если существует
такая нечётная вершина а, т С а С /, что г = г(а) и /(|а|) Е {^2,^1 },
то А{ или В{ вычислимо и Дг немедленно удовлетворяется. Таким
образом, если левая часть (4.1) выполнена, а а такова, что т С а С / и
г = г(а), то /(|а|) Е {s,w}, что означает, что подтребование Ri(a),j(a)
удовлетворено.
Предположим, что левая часть требования Ri в (4.1) выполнена и
т = т(/, г). Мы должны построить невычислимое в. п. множество DT
Ai,Bi. Определим
DT = { х(а) : а Е Д(/, г) & г(а) = г и ж(а)
перечисляется в Z)r по условию (4.14), чтобы удовлетворить
Ri(a),j(a) }•

§ 4• Теорема Лахлана о неограничении
431
Тогда DT в. п., т. к. E(f,i) — вычислимое множество вершин.
Далее, DT невычислимо, потому что для почти каждого j Е и существует
некоторая а, т С а С /, такая, что г(а) = г, j(a) = j и /(|а|) Е { s,il> },
следовательно удовлетворено. Наконец, Дг ^т А{,В{, т. к. для
произвольной нечётной a Е E(f,i) такой, что г = г(а), каждый однажды
открытый а-гэп в конце концов закроется. Поэтому для
произвольного a-кандидата х = х(а) существует такой шаг v, на котором х
либо отменяется, либо перечисляется в DT. Тогда значения функционалов
0f * (x)[v] и & fi (z)[v] могут быть переопределены, чтобы сделать их
равными DT(x)[v]. (Подробности см. в лемме 4.17.)
Здесь ключевым моментом является следующее. Так как (4.8)
истинно, то мы знаем, что т (0) С /, и для всех a Е E(f, г) имеем т (0) С а.
Следовательно, каждая а Е Д(/, г), для которой г = г (а), в конце концов
закроет любой открытый гэп, поэтому х(а) сможет выполнить свою
функцию. Для произвольной чётной ас i — г (а) такое рассуждение
не проходит, поэтому для удовлетворения заключению требования Ri в
(4.1) 	мы должны использовать вышеупомянутое множество DT.
Таким образом, настоящее нарушение требования Д*, по мере
того как мы спускаемся вдоль / Е [Т], состоит в следующем. Когда мы
открываем новый г-регион в некоторой чётной т С /, /, определяя
г(т) = г, мы выделяем кандидата (ДГ,0Г,0Г) для тройки (Di,Qi,Qi),
чтобы удовлетворить заключению из (4.1). Если позднее мы перейдем
г'-границу (3 для т С /3 С / и г' < г, то надо открыть новый г-регион
на некоторой т', (3 С т' С /, а также строить на т' нового кандидата
(DT>, 0Г/, 0Г/) для завершающей тройки. Значения леммы 4.7 и
определения 4.8 состоят в том, что по мере того как мы спускаемся вдоль
произвольного пути h Е [Т], этот процесс стабилизируется с окончательным
значением (ДГ,0Г,0Г) для т = r(h,i), следовательно, с окончательным
значением (ДГ,0Г,0Г) для тройки (Д*,01,0Г). (В процессе построения
прямое упоминание о 0* и 0* может быть опущено, т. к. они
определяются в лемме 4.17 при помощи задержанных А- и Д-разрешений.)
4-5. Построение (операционная система машины)
Обозначим множества А^а) и Д*(а) через Аа и Да, а функционалы Ф^а)
и ^г(а) — через Фа и Фа соответственно. Для каждого а Е Т у нас есть
стратегия, которая пытается удовлетворить требованию
Pa'.C^Wk

432
Глава XIV. Метод деревьев
где к = \а\. Кроме того, для каждой нечётной a Е Т мы имеем стратегию
удовлетворения подтребования
Га • -^г(а) Ф W'j(a)t
(Таким образом, существуют две различные стратегии, связанные с
каждой нечётной вершиной а.) Для последней у нас есть вариант
основного модуля, называемый а-модулем, который пытается удовлетворить
подтребованию Ri(a)j{a)-
В процессе построения мы считаем Аа, Ва, Фа, Фа, С, Wj и т. д.
находящимися в процессе формирования. Если в некоторый момент
времени в процессе построения мы пишем Аа, то мы имеем ввиду конечное
множество элементов, к тому времени перечисленных в Аа, аналогично
для Фа. Когда это необходимо во избежание путаницы, мы добавляем [s]
и пишем Аа [«] или Фа [s] для обозначения соответствующего результата
к концу шага s. Однако при последующей верификации после
построения мы снова используем обозначения Аа, Фа и т. д. как обозначения
для уже построенных множеств и функционалов.
Для описания построения полезно для нечётных вершин a Е Т иметь
следующие параметры (как в основном модуле) со следующими
значениями:
х(а) = текущий кандидат для а-модуля,
г (а, 1) = запрет, наложенный на С, чтобы сохранить Аа [ я(а),
г (а, 2) = запрет, наложенный на С, чтобы сохранить Ва [ х(а),
г (а) = та х{г(а, 1),г(а,2) },
F(a) = текущее состояние a G { s,g2,gl,w } а-модуля.
Значения этих параметров в процессе построения могут меняться.
Параметр, однажды получивший некоторое значение, сохраняет его до
тех пор, пока оно не будет переопределено. Пусть обозначает uj^n\
где п — номер а при некоторой эффективной нумерации вершин
дерева Т. Предположим, что a — нечётная вершина. Переназначить
кандидата х(а) на шаге s означает следующее: отменить предыдущего
кандидата х(a) [s — 1] (если s > 0) и определить х(а) [5] как
наименьший у Е cjtal такой, что у > s и у больше всех предыдущих
кандидатов. Инициализировать вершину а означает следующее:
переназначить х(а) и установить F(a) = ю, если F(a) ф s; установить
r(a, 1) = r(a,2) = r(a) — 0; отменить любые Аа- и Ва-гэпы;
удалить любые связки, которые в качестве низа имеют а. (Связки будут
определены позднее.) Если а чётная, то фраза «инициализировать вер¬

§ 4• Теорема Лахлапа о неограничении
433
шину а» означает удаление любых связок, которые в качестве
верхушки имеют а. Кроме того, для чётных а и для всех s определяем
г(а, 1 )[s] = г(а, 2 )[s] = r(a)[s] = 0.
По окончании построения мы определим истинный путь построения
/ Е [Т]. Мы будем аппроксимировать /, определяя в течение каждого
шага построения s строку $[s] € Т таким образом, чтобы можно было
доказать
/ = lim inf J[s],
s
а именно, для всех п выполняется f [ п = lim infs J[s] [ п, как определено
в (2.2) и (2.3). В течение шага s + 1 определяем S[s +1], используя ряд
подшагов t 5, на которых определяем строки St так, чтобы St С
а S[s + 1] является последней такой St. Только строке будет позволено
действовать на под шаге t.
4.9 Определение. Фиксируем произвольную a Е Т.
(i) Будем говорить, что s + 1 является а-шагом, если a С Ч- 1].
По определению шаг 0 также является a-шагом. Обозначим через Va
множество а-шагов.
(ii) Будем говорить, что s -f 1 является подлинным а-шагом, если
St = а на некотором подшаге t шага s +1, где определяется в процессе
построения. Обозначим через Sa множество подлинных а-шагов.
(Ш) Пусть для чётной а выполнено i = г (а). Будем говорить, что
v является а-расширяющим шагом, если v = 0 или v = s 4 1; s 4 1
является подлинным a-шагом и l{[s] > mla[s — 1].
Если на шаге s (нечётная вершина) а открывает Аа-гэп, мы
строим связку (т, а) с низом а и верхушкой (чётной вершиной) т = т(а)
В этом случае мы имеем т (0) С а и F(a)[s] = g 1. (Заметим, что в
соответствии с (4.13) вершина а может закрыть свой гэп только на т-
расширяющем шаге, причем т связана с (Ф*, Фг)-гипотезой (4.8) так, что
если она истинна, то существует бесконечно много т-расширяющих
шагов.) Связка (т, а) удаляется, если либо а закрывает Аа-гэп неудачно
(и тогда снова будет F(a) = ю), либо а закрывает Ва-гэи (удачно или
неудачно), либо вершина а инициализируется. (Удаленная связка (т, а)
позднее может быть восстановлена.)
4.10 Определение. Если на шаге 5-1-1 существуют связка (т, а) и
такой подшаг £ шага 5 4- 1, что = т и = а, то будем говорить,
что связка (т, а) действует на шаге 5 + 1.

434
Глава XIV. Метод деревьев
Связка (т, а) может рассматриваться как некий электрический
провод или короткое замыкание, берущее начало в т и идущее из т прямо
вниз к а. На шаге 5 + 1, если St = т и s + 1 является т-расширяющим
шагом, то мы вынуждаем связку (т, а) действовать, перемещаясь
непосредственно к вершине а, т. к. в этот момент а закрывает свой Аа-
или Ва-гэи. Цель связки состоит в том, чтобы при проверке
построения перейти от вершины т, где только что ещё разраз подтвердилась
(Фг, Ф*)-гипотеза (4.8) (т. е. s + 1 — т-расширяющий шаг), вниз к
некоторой вершине a D т (0), для которой г (а) = г(т) = г. При этом
некоторый гэп вершины а открыт и а нуждается в этой гипотезе для
того, чтобы закрыть этот гэп.
Действие этой связки может вынудить нас пропустить другие
вершины 7, т С 7 С а, более низкого глобального приоритета, 1(7) > г (а),
которые в противном случае получили бы внимание раньше а, если бы
мы просто спускались вдоль дерева без использования связок. Для
таких 7 шаг 5 + 1 является 7-шагом, но не подлинным 7-шагом, т. к. не
существует такого подшага t, что St[s + 1] = 7 и на котором 7 могла
бы действовать. Таким образом, чтобы определить, достигает ли данная
a-стратегия успеха, мы должны исследовать подлинные а-шаги вместо
просто а-шагов.
Описание построения.
Шаг 5 — 0. Инициализируем все вершины а Е Т. Определяем J[0] =
Л.
Шаг 5 + 1. Построение будет происходить по подшагам t ^ 5 + 1. Мы
ссылаемся на подшаг t шага 5+1 как шаг (5+I, t). Значение параметра р
к концу подшага t будет обозначаться через pt[s + 1], или, сокращенно,
через pt. К концу под шага t мы определим строку St £ Т такую, что
St С St+1 С (5[s + 1], £ ^5 5, причем на подшаге t действует только St.
Подшаг t = 0. Определяем = А. Переходим к под шагу 1.
Подшаг t +1 ^ 5 + 1. Пусть дана St и для всех нечётных a G Т имеем
текущее состояние a-модуля Ft(a) G { s,g2,gl,w }. Определяем сначала
<5*+i следующим образом.
Случай 1. St нечётная. Полагаем = St (Ft(St)).
Случай 2. St чётная.
Случай 2А. Шаг 5 + 1 не является St- расширяющим. Полагаем
— St (1).

§ 4• Теорема Лахлана о неограничении
435
Случай 2В. Шаг 5+1 является ^-расширяющим, но в данный
момент не существует связки с верхушкой St- Полагаем 5t+i = St (0).
Случай 2С. Шаг 5 + 1 является ^-расширяющим и в данный
момент существует связка с верхушкой St и низом некоторой (3 D St (0). (В
лемме 4.11 мы покажем, что такая /3 является единственной.) Полагаем
й+i — Р-
Пусть а = J*+i. Мы говорим, что а требует внимания на шаге
(5 + 1, t + 1), если выполняется одно из следующих условий (их точный
смысл будет разъяснен ниже):
а готова удовлетворить Ра,
а готова открыть Д*-гэп, , ч
а готова закрыть Ла-гэп, ^ ‘ '
а готова закрыть Ва-гэп.
Если а не требует внимания и t < 5, то переходим к подшагу t +
2. 	Если же а требует внимания, то выбираем первый из подходящих
пунктов (4.11)-(4.14) и выполняем указанное ниже действие. Если t < s
и а открывает некоторый Ла-гэп, или а удачно закрывает некоторый
Аа-гэи и открывает Д^-гэп, то переходим к подшагу t + 2. В противном
случае переходим к шагу 5 + 2, определив J[5 + 1] = J*+i.
(4.11) Вершина а готова удовлетворить Ра, если
(а) С П Wk — 0, где к = |а|,
(б) (3у)[у G Wk П & у > г(а)], где г(а) = max{ г(/3) : (3 ^ а }.
Действие. Перечисляем наименьшее такое у в С. Инициализируем
все (3 ^ а.
(4.12) Вершина а готова открыть Ла-гэп, если
(а) а нечётная,
(б) т(а) определена,
(в) Ft(a) = w,
(г) х{а) е Wj{a),
(д) х(а) < mL(a)[s].
Действие. (Это действие называется этапом 1.) Открываем Аа-гэп,
положив F(a) — д 1 и r(a, 1) = 0. Инициализируем все 7 такие, что
a (w) ^ 7. Создаем связку (т, а) с низом а и верхушкой г — т(а).
(4.13) 	Вершина а готова закрыть Аа-гэп, если

436
Глава XIV. Метод деревьев
(а) а нечётная,
(б) Ft(a)=gl,
(в) s -f 1 является т-расширяющим шагом, где т = т(а).
Действие. (Это действие называется этапом 2.) Пусть v + 1 < s +
1 — шаг, на котором был открыт текущий Ла-гэп, и пусть х — ж(а)[$].
Закрываем Д*-гэп, как описано ниже.
Этап 2А. (Удачное закрытие.) Если AQ[s] \ х ф Aa[v\ х, то
открываем Д*-гэп, положив F(a) — g2 и г(а, 2) = 0. (Поэтому также
г (а) = 0.) Инициализируем все 7 такие, что a (g 1) ^ 7.
Этап 2Б. (Неудачное закрытие.) Если AQ[s] f х = Aa[v] [ х, то
определяем F(a) = ю и r(a,l) = s (чтобы сохранить Аа [ х), переназначаем
х(а) и инициализируем все 7 такие, что а (ю) 7. Удаляем связку
(т,а).
(4.14) 	Вершина а готова закрыть Д*-гэп, если
(а) а нечётная,
(б) Ft(a) = д2,
(в) s 4-1 является т-расширяющим шагом, где т = т(а).
Действие. (Это действие называется этапом 3.) Пусть v + 1 < s +
1 — шаг, на котором был открыт текущий Д*-гэп, и пусть х = ж(а)[$].
Удаляем связку (т, а) и закрываем Д*-гэп, как описано ниже.
Этап ЗА. (Удачное закрытие.) Если Ba[s] \ х ф Д*[о] х, то
перечисляем х в £>г(а) и определяем F{a) — s. Инициализируем все 7,
а (д2) ^ 7. Устанавливаем r(a, 1) = г(а, 2) = 0.
Этап ЗБ. (Неудачное закрытие.) Если Д*[$] f х — Ba[v\ [ х, то
определяем F(a) = w и г(а, 2) = s (чтобы сохранить Ва х), переназначаем
х(а) и инициализируем все 7, a (gl) ^ 7. Удаляем связку (т,а).
Это завершает построение.
4-6. Верификация.
4.11 	Лемма о связках, (i) Если (р, 7) является связкой, то 7 2 Р (0).
Более того, р является чётной, а 7 является нечётной вершинами,
р = г(7) uju) и i(p) = i(7).
(ii) Любая однажды созданная связка (р, у) может действовать
самое большее дважды до того, как она будет удалена. (Однако после
её удаления на более позднем шаге может быть создана новая связка
(р, 7) с теми же верхушкой и низом.)

§ 4• Теорема Лахлапа о неограничении
437
(iii) Пусть (/9i,7i) — связка, созданная на некотором шаге 5,
причем позднее (либо на более позднем подшаге шага s, либо на более
позднем шаге), но до того, как она удаляется, создается новая
связка (р2,72) такая, что р\ (0) С • Тогда 71 С 72. Кроме того, еслгг
2(72) < г (71) и не существует такой V-границы (3, что 71 С (3 С 72
и г' < 2(72), mo /92 С /9ь В противном случае 71 С р2•
(Следовательно, одновременно существующие различные связки могут быть
вложены друг в друга, но не могут пересекаться. Причем, если связка
(/9i,7i) вложена в связку (/92,72), гая 2(72) < 2(71), поэтому внешняя
связка (р2,72) имеет более высокий приоритет и создается позднее,
чем внутренняя связка (pi,7i)J
(iv) Если связка (р, 7) удаляется на некотором шаге, то к концу
этого шага не существует связки (/91,71) с Pi С р и р С 71.
Доказательство, (i) Свойства, которые следуют после слов «более
того», вытекают непосредственно из процесса создания связок, который
может быть проведен только согласно (4.12) и только когда 7
открывает некоторый Ау-гэп. Докажем, что 7 Dp (0). Предположим, что
7 5 Р (1)* Пусть 2 = 2(7). Тогда по определению имеем р = т(7),
2 = i(p) и р чётная. Пусть р+ = р (1). По определению 4.4 г ^ Lo(p+)
и (2,^) ^ Li(p+) для всех j. Но, т. к. i = 2(7) и 7 является нечётной,
мы должны иметь (i,j) Е -^1(7) для некоторого j. По определению 4.4
это может произойти только в том случае, если существует такая £,
р+ С ( с 7, что г(£) < г и £ (а) С 7 для некоторого а Е {p2,pl, 1 }. Но
тогда по определению 4.5 т(7) ф р. Получили противоречие.
(ii) Предположим, что связка (р,7) создается на шаге (5 + 1,£ + 1).
Тогда 5t+1 =7, и 7 открывает Л7-гэп на шаге (5 + l,t + 1).
Следовательно, к концу шага 5 + 1 ^(7) = pi, что остается справедливым либо
всегда, либо до тех пор, пока 7 не будет инициализирована (в этом
случае связка (р, 7) удаляется), либо до тех пор, пока связка в следующий
раз на некотором шаге 51 + 1>5+1не будет действовать. В последнем
случае для некоторого подшага t\ + 1 имеет место <^1+1 =7, причем 7
закрывает Ау-гэп. (Это так, потому что действие связки
подразумевает, что Si + 1 является р-расширяющим шагом и р — т(7), поэтому все
условия для (4.13) удовлетворены.) Если А>-гэп закрывается неудачно
на шаге (s 1 + l,ti + 1), то связка (р,7) удаляется. В противном случае
7 открывает Ву-гэп на шаге (s\ + l,*i + 1), F(7)[si + 1] = g2 и
связка (р, 7) остается до тех пор, пока не будет удалена или не пройдется
в следующий раз на некотором шаге 52 + 1 > 5i + l. На этом шаге 7

438
Глава XIV. Метод деревьев
закрывает Ву-гэп и связка (р, 7) удаляется, вне зависимости от того,
было ли закрытие удачным или неудачным.
(iii) Предположим, что связка (pi, 71) создается на шаге (s, ti) и
условие (iii) остается истинным вплоть до того момента, когда создается
вторая связка (рг,72)- Тогда Stl = 71 и Ъ открывает Л71-гэп на шаге
(s,£i). Предположим, что другая связка (/92,72) создается на некотором
подшаге ^2 > h шага s. Тогда 71 С 72, потому что Stl С St2 = 72-
Так как 71 на шаге (s,£i) открывает А71-гэп, имеем 71 (gl) С 72 и по
определению 4.5 71 (gl) является г(71)-границей. Таким образом, если
г(71) < г(72), то по определению 4.5 71 С р2• Если г(72) = 2(71), то
по определению 4.4 должна существовать некоторая г'-граница /3 такая,
что 7i С /3 С 72 при г' < г(71). Поэтому 71 С р2 по определению 4.5,
т. к. 7i и 72 лежат в различных г(71)-регионах. Если же г(72) < i(7i),
то по определению 4.5 либо р2 С pi, либо существует такая г'-граница
13, что 7i С /3 С 72, при V < г(72). Отметим, что в последнем случае
имеем 7i С р2-
Теперь предположим, что связка (/92,72) с р\ (0) С 72 создается
на некотором шаге (г>,£), v > s, и условие (iii) выполняется на всех
предшествующих (v,t) шагах. Тогда v является р\ -шагом. Если этот
pi-шаг является подлинным, то связка (/9i, 71) действует на шаге (v,t')
для некоторого t' < t, т. к. v является pi -расширяющим шагом потому,
что он является подлинным 72-шагом и р\ (0) С 72. Поскольку на шаге
(v,t) связка (/91,71) не была удалена, то j47i- или Б71-гэпы вершины
7i остаются открытыми и, поэтому, 71 (дк) С 72 для некоторого к Е
{1,2}. Следовательно, проводя те же рассуждения, что и в предыдущем
абзаце, получим 71 С 72, причем по-прежнему выполнено либо условие
7i С /92, либо условие р2 С /91.
Предположим, что v не является подлинным pi-шагом. Но по
условию v — pi-шаг. Следовательно, должна существовать такая связка
(рз,7з), что рз С pi, pi (0) С 73 и связка (рз,7з) действует на шаге
v. Так как (Ш) выполняется до шага (v,t), то мы знаем, что 71 С 73, а
именно, что связка (pi,7i) вложена в (рз,7з)- Следовательно,
существует некоторый подшаг t! < t такой, что 6?[у] = рз, 6t>+i[v] = 73 и 73 С 72.
Так как в течение этого времени некоторый гэп вершины 71 остается
открытым, то имеем 71 (дк) С 72 для некоторого к Е { 1,2 }. Поэтому
здесь опять применимы приведенные выше рассуждения. Таким
образом, 7i С 72, и либо 7i С р2, либо р2 С рь
(iv) Предположим, что связка (р, 7) удаляется на шаге (s 4- l,t + 1).
Если 7 инициализируется на шаге s 4-1 из-за действия некоторой а < 7,

§ 4- Теорема Лахлапа о неограничении
439
то а < р, поэтому на шаге 5 + 1 инициализируется каждая вершина 71 Э
р и удаляется любая связка с низом 71. В противном случае на шаге 5+1,
St = р, £*+1 = 7, связка (р, 7) действует, и 7 либо неудачно закрывает
А7-гэп, либо закрывает В1-гэп. Так как связка (р,7) действует, то на
шаге (5 + 1,£) не существует никакой другой такой связки (pi, 71), что
Pi С р и р С 7i. По (i) и (iii) не существует никакой другой связки
(pi,7i) на шаге (5 + 1,t) с pi = р и 7i 7^ 7. Однако, т. к. связка (р,7)
удаляется на (5 + l,t + 1) под действием либо (4.13), либо (4.14), то
согласно построению, как описано между строками (4.10) и (4.11), мы
немедленно переходим к шагу 5 + 2 без дальнейших подшагов t' > t + 1.
Следовательно, в течение шага 5 + 1 после подшага t + 1 никаких новых
связок не создается. Это устанавливает (iv) и лемму 4.11. О
Теперь уточним неформальное определение истинного пути / из § 4.4.
4.12 	Определение. Истинный путь / Е [Т] для построения
определяется индукцией по п следующим образом. Пусть а — f \ п.
Случай 1. а чётная. Определяем
г / ч Г 0, если (3°°5)[5 является а-расширяющим],
' \1 в противном случае.
Случай 2. а нечётная. Определяем
если lim5 F(a)[5] существует и равен а Е { 5, w },
если liminfs F(a)[s] = дк, к Е {1,2}.
(Отметим, что соотношение limsF(a)[5] = дк, к Е {1,2} невозможно.
Однако, в случае 2 мы имеем liminfs F(a)[5] = р2, если а открывает
бесконечно много Д^-гэпов, и = gl, если а открывает конечное число
Д*-гэпов и бесконечно много Ла-гэпов.)
4.13 	Лемма о самом левом пути. Фиксируем произвольное п и пусть
а = / [ п.
(i) (Э<“*)№] <L a],
(й) Множество подлинных а-шагов (см. определение 4.9 (ii)) Sa
бесконечно.
Доказательство. Очевидно, что (i) и (й) выполняются при п — 0. Пусть
п ^ 0. Предположим, что (i) и (ii) выполняются для п. Положим (3 —
f { n, а = f(n) и а = 0 (а). Докажем (i) и (ii) для а.

440
Глава XIV. Метод деревьев
Фиксируем такой шаг s\, что для всех s ^ si:
Ф] *L /?,
если (3 нечётная, то F((3)[s] о,
если (3 чётная и а = 1, то s не является
/^-расширяющим шагом,
(4.15)
(4.16)
(4.17)
“'(ЗтШт ^ (3 V 7 = а] & Ру действует на шаге s]. (4.18)
(i) Если это не так, то J[s] <l а для бесконечно многих s.
Выберем Ь <д а такое, что /3 (Ъ) С S[s] для бесконечно многих s. Пусть
/3+ = (3 (Ъ). Тогда по (4.15) и (4.16) не существует подлинного /3+-шага
6 ^ 5i. Следовательно, существует бесконечно много таких шагов 5, на
которых некоторая связка (р, у) действует и
р С (3 к (3+ С 7.
(4.19)
По индуктивному предположению множество 5^ подлинных /3-шагов
бесконечно. Рассмотрим произвольный шаг 52 + 1 > 5Ь 52 -f 1 Е 5^.
Выберем t таким, что St[52 +1] = /3. На шаге (52 + 1, £) может существовать
самое большее одна связка (р, 7), удовлетворяющая (4.19), и мы должны
иметь р = /3. Кроме того, эта связка должна действовать на некотором
шаге 53 +1 ^ 52 -f 1 до того, как будет создана какая-нибудь новая связка,
удовлетворяющая (4.19). Тогда по лемме 4.11 (ii) связка (р, у)
действует самое большее дважды, после чего она удаляется. По лемме 4.11 (iv),
если связка удаляется на некотором шаге 54 4-1 ^ 52 +1, то не
существует связок, удовлетворяющих (4.19). Но т. к. не существует подлинного
/З^-шага ^ 5i, индукцией по s > 54 + 1 следует, что на каждом шаге
5 > 54 + 1
не существует связки (р,7), удовлетворяющей (4.19), (4.20)
(3+ £ ад. (4.21)
(ii) Мы должны доказать, что SQ бесконечно. Фиксируем к Е ш.
Достаточно найти шаг 53 Е Sa такой, что к ^ 53.
Случай 1. Вершина (3 нечётная.
Случай 1А. limsF(/3)[5] = a Е {s,w}. Выберем 52 ^ max{fc,5i}
такой, что F(/3)[s] = а для всех s ^ S2- Тогда для всех s ^ 52, если

§ 4• Теорема Лахлапа о неограничении
441
s G 5^, то s G SQ, т. к. если = (3 на шаге 5, то <5*+i = а по этапу 1 из
определения 6t+1.
Случай 1В. а = (3 (дк) для A; G {1,2}. Пусть к = 2. (Случай к =
1 разбирается аналогично.) Тогда /3 открывает бесконечно много Вр-
гэпов. Но если (3 открывает Вр-тэп на шаге (s,t), то s € 5^, = /3,
Ft(/3) = д2 и = а, поэтому s G 5а.
Случай 2. Вершина /3 чётная.
Случай 2А. а = 1. Используя (i) выбираем такой шаг $2 ^ $i, что
<$[s] а на любом 5 ^ 52. Выберем наименьший шаг S3 G s3 ^
max{fc,S2}. Выберем t таким, что St[s3] “ Тогда 53 не является
/3-расширяющим и, следовательно, 5t+i = ос по описанию случая 2А в
определении St+\. Таким образом, 53 G Sa.
Случай 2В. а — 0. Так как /3 (0) — а С /, то существует бесконечно
много /3-расширяющих шагов s' > к, и по определению 4.9(iii) каждый
такой s' является подлинным /3-шагом, поэтому St = 0 для
некоторого подшага t шага s'. Следовательно, либо 5t+i = а будет иметь место,
либо будет существовать такая связка (р, 7), что р — /3 и а С 7. Если
выполнено последнее, то по лемме 4.11 (ii) эта связка действует самое
большее два раза. Так как существует бесконечно много ^-расширяющих
шагов, то связка (р, 7) будет действовать до тех пор, пока она на
некотором шаге S2 > s' не будет удалена. По лемме 4.11 (iv) к концу шага $2
не существует связки (р', 7') с р' С (3 и а С 7', и это условие сохраняется
до следующего /3-расширяющего шага 53 > $2. Выберем t таким, что
St[s3}m = (3. Тогда (5*+i[s3] = ol по описанию случая 2Б в определении
й+i- D
4.14 	Лемма о запретах. Если а = f [ п и а+ — а (f{n)), то
r(a) =dfn lim{r(a)[s] : s G Va+ } существует,
где V1 — множество 7-шагов (см. определение 4-9 (г)), и), и
f(a)[s] =dfn тах{ r(/3)[s] : (3 ^ a}.
Доказательство. Зафиксируем a = / [ п. Пусть а~ будет
предшественником вершины а (если такая существует). Предположим по индукции,
что г(а~) существует, где по определению
r(a~) = lim{ f(a~)[s] : s G Va }.
Если a чётная вершина, то г (a) [s] = 0, поэтому лемма выполняется.
Предположим, что a — нечётная вершина. По лемме 4.13(i) выбираем

442
Глава XIV. Метод деревьев
v таким, что для всех s ^ v, J[s] фъ и если s 6 F, то r(a~)[s] =
г{(\~). Тогда, как в основном модуле из § 4.2, r(a) =dfn liminfs r(a)[s]
существует и r(a)[s] = г (а) на почти всех s таких, что a+ С d[s] (т. к.
если /(п) = дк для к Е {1,2}, то для такого шага s r(a,k)[s] = 0).
Следовательно, существует шаг z ^ v и число г (а) такие, что r(a)[s] =
г(а) для всех s Е Va+, s ^ z. О
4.15 Лемма о невычислимости. Множество С невычислимо.
Доказательство. Если это не так, то пусть С = Wk при некотором
к > 0. (Мы выбираем к > 0, потому что a = А никогда не действует.)
Выберем такую вершину а, что а С f и \а\ = к. Заметим, что = 0,
т. к. элементы из иФ°^ входят в С только для удовлетворения Pk = P\Q\.
Отсюда следует, что wj^ = сьДа1. По лемме 4.13(ii) можем выбрать у Е
у ^ Wk[s], у > r(a)[s], где s -f 1 является подлинным а-шагом
таким, что никакая вершина (3 < а не действует для удовлетворения
требования Рр (в соответствии с (4.11)) ни на каком шаге ^ s-f 1. Так
как C[s]nWk[s] = 0, то на шаге s-f 1 вершина а действует в соответствии
с (4.11), удовлетворяя Ра. Поэтому C[s +1]DWk[s +1] Ф 0, мы получили
противоречие. О
4.16 Лемма об истинных выходах. Пусть а = f \ п.
(i) Если f (п) = 1, то ->[Ф£ = Аа & Фр = £а].
(ii) Если f(n) = 0, то существует бесконечно много а-расширя-
ющих шагов. (Следовательно, limsupsG5a ma°^[s] = оо.)
(iii) Если f(n) = g2, то Ва вычислимо.
(iv) Если f(n) = g 1, то Аа вычислимо.
(v) Если f(n) — w и т(а) определено, то Dr(а) U Wj(Q) ф и.
(vi) Рели /(п) = 5, то DT(а) П И^(а) ф 0, а именно, х(а) Е Dr(a) П
Wj(Q), где ж(а) — (единственный) элемент, перечисленный в Dr(а) при
помощи действия из (4-Ц)-
Доказательство, (i) По лемме 4.13(ii) существует бесконечно много
подлинных a-шагов. По определению 4.12 для / существует только
конечное число a-расширяющих шагов. Следовательно, по
определению 4.9(iii) существует только конечное число г-расширяющих шагов
для i = г (а). Поэтому Фр ф Ai или Ф р ф В{.
(ii) Следует непосредственно из определения 4.12 истинного пути /.
(iii) Пусть f(n) = g2. Положим a+ = a (g2). Выберем шаг so
таким, что a+ S[s] для всех 5 ^ «о, и для всех 7 С а+ требования Р7

§ 4• Теорема Лахлана о неограничении
443
удовлетворены до шага sq , если они вообще когда-либо
удовлетворяются. Таким образом, вершина а не будет инициализироваться на шагах
s ^ so- Тогда для $о соотношение (4.7) выполняется при r(a)[s]
вместо r[s]. Теперь то же доказательство, которое приводилось в основном
модуле, устанавливает, что Ва вычислимо.
(iv) Доказательство подобно предыдущему, но с д1 и Аа вместо д2
и Ва.
(v) Пусть /(n) = w. Тогда оба предела существуют и lims F(a)[s] =
w, lims:r(a)[s] = x(a). Выберем so так, чтобы эти значения оставались
неизменными для всех s ^ so. По построению х(а) £ DT(ay
Предположим, что т(а) определено и х(а) Е Wj(a). Тогда для почти каждого
шага s все условия (4.12) (для того, чтобы а открыл Аа-гэи)
удовлетворены. Но по лемме 4.13(ii) существует бесконечно много подлинных
a-шагов, поэтому а открывает Аа-тэи на некотором шаге s > so,
вопреки предположению.
(vi) Если f(n) = 5, то на некотором шаге s применялось (4.14) и а
успешно закрыла некоторый Д*-гэп и перечислила х = :r(a)[s] в Z)r(Q).
Но тогда справедливо х Е Wj(Qys, т. к. на некотором шаге s' < s а
открыла Аа-гэи с кандидатом
х — :r(a)[s ] Е Wj^a^si. Q
4.17 	Лемма об г-регионе. Пусть г такое, что Фр = А{, Фр =
Bi, Ai и Bi оба невычислимы. Существует такое невычислимое в. п.
множество D, что D А{ и D В{.
Доказательство. По лемме 4.7 и определению 4.8 выберем т = т(/,г).
Пусть т = / \ т. Тогда по 4.7, 4.8, лемме 4.16(i) и предположениям
леммы 4.17 имеем, что f(m) = 0 и не существует 7 Dr (0) такой, что
2(7) ^ h 7 С /, и либо 7 чётная, либо 7 и /(I7I) Е {<?2, #1 }.
Очевидно, что D вычислимо перечислимо, т. к. E(a,i) —
вычислимое множество вершин. Докажем, что D невычислимо. Для получения
противоречия предположим, что D в. п. Найдем некоторую а, т С а С /,
такую, что г (а) = г и Wj(a) = D. Это возможно, т. к. по лемме 4.16 и по
предположениям леммы 4.17 не существует такой /3 С /, что i((3) — г и
/(|/3|) Е { д2,д\, 1}. Следовательно, по определению 4.4 для почти
каждого j Е uj существует такая нечётная а, т С а С /, что г (а) = г и
Да) = j. Пусть а = / гг. Имеем /(гг) Е {s,iu}. По лемме 4.16, если
/(гг) = 5, то х(а) е D П Wj(ay и если /(гг) = ги, то х(а) ^ Z) U Wj(a).
Следовательно, D ф Wj(ay Для этого достаточно доказать, что для всех

444
Глава XIV. Метод деревьев
нечётных а £ E{r,i) открытый на некотором шаге, позднее
закрывается или отменяется. Тогда, чтобы Ai-вычислимо проверить, выполняется
ли х £ D, находим такой шаг s, что Ai[s] [ х = Ai х. Пусть v > s
такой шаг, что для любой а £ Е(т,г), для которой выполнено ж(а)[$] = ж,
на шаге v имеем следующее: либо Аа-гэи закрывается неудачно, либо
закрывается Ва-гэп, либо вершина а инициализируется. Тогда х £ D
тогда и только тогда, когда х £ D[v\. (Доказательство D ^ Вi такое
же.)
Чтобы доказать, что каждый такой a-гэп в конце концов
закрывается или отменяется, зафиксируем произвольную нечетную a £ E(r,i)
и предположим, что а открывает Аа-гэп на шаге s. Тогда на шаге s
создается связка (т, а). Но т (0) С а и по лемме 4.16(ii) существует
бесконечно много т-расширяющих шагов. Таким образом, связка (т, а)
будет действовать на некотором шаге, а Аа-гэи на некотором шаге v > s
закрывается (если только она ещё раньше не будет отменена). На шаге
v либо х = х(а) отменяется, либо в противном случае открывается Ва-
гэп, который по тем же рассуждениям на некотором шаге z > v должен
закрыться.
Эта лемма завершает доказательство теоремы 4.1. \\
4.18 Упражнение
4.18° ( Доуни). Постройте такое высокое в. п. множество (7, что если
А и В являются в. п. множествами такими, что А ^wtt С и В ^wtt С, то
deg(A) и deg(i?) не образуют минимальную пару. Указание. Соедините
метод из § 4 с методом из теоремы 3.1 так, чтобы приоритетное дерево
имело три типа вершин: типы вершин из § 4 плюс раздваивающиеся на
две ветви вершины для требований густоты, как в теореме 3.1. Заметим,
что эта теорема контрастирует с результатом Купера для А $^т С и
В С из упражнения XI.2.15.
4.19 Замечания. Более ранняя версия доказательства теоремы 4.1
появилась в работе Соара [1985]. В представленной здесь версии учтены
предложения Сламана по использованию связок и четных вершин для
проверки Ф{- и Фг-гипотез. Это дало возможность исключить
некоторые чисто технические детали более ранней версии, сделав построение
и доказательство интуитивно более понятными. С. Лемпп и В. Хариза-
нова также внесли много исправлений и предложений.
Теорема 4.1 контрастирует с другим результатом Лахлана [1979] о
том, что существует такая ненулевая в. п. степень с, что для каждой

§ 4• Теорема Лахлана о неограничении
445
в. п. степени d со свойством 0 < d с существует минимальная пара
в. п. степеней ниже d. Последнее утверждение доказывается простой
модификацией метода минимальной пары. Купер показал, что под любой
высокой степенью с существует минимальная пара степеней, поэтому
теорема 4.1 о неограничении не может быть обобщена так, чтобы
сделать неограничивающую в. п. степень с высокой.1 (Это контрастирует
с упражнением 4.18, где ^т заменяется на ^wtt •)
хЭто предложение уточнено при переводе. — Прим, редактора.

Глава XV
Автоморфизмы решетки в. п. множеств
В этой главе мы изучаем группу Aut £ (Aut £*) автоморфизмов решетки
£ (£*) в. п. множеств. В § 1 мы, продолжая в духе главы X, докажем, что
свойство креативности является элементарно теоретико-решеточным и,
следовательно, инвариантным относительно группы Aut £\ в § 3 мы
применим простой метод приоритета с конечными нарушениями для
построения автоморфизмов, чтобы доказать, что гиперпростота не
инвариантна относительно Aut £. В § 2 мы приведем некоторые основные
сведения об автоморфизмах и докажем, что любой Ф £ Aut£*
индуцируется некоторой перестановкой р на ш и, стало быть, Ф индуцируется
некоторым Ф £ Aut£. Главная цель оставшейся части главы —
показать, что для любых двух максимальных множеств А и В существует
такой автоморфизм Ф решетки £, что Ф(А) — В. Доказательство
этого требует использования нового и существенно более трудного метода
построения автоморфизмов, который описывается в теореме о
расширении 4.5. В § 4 мы мотивируем и формулируем эту теорему, а в § 6 её
доказываем. В § 5 мы проверим условия теоремы о расширении для
случая максимальных множеств. Теорема о расширении является главным
инструментом для построения автоморфизмов решетки £ в том смысле,
что все известные трудные результаты об автоморфизмах £ либо из нее
следуют, либо являются ее модификациями. В § 1 главы XVI мы
сформулируем дальнейшие результаты и открытые вопросы об автоморфизмах.
§ 1. Инвариантные свойства
В определении II.1.15 отмечалось, что в. п. множества образуют
дистрибутивную решетку по включению, изучавшуюся в главе X и
обозначенную через £. В Х.1.2 мы определили £* как факторрешетку £ по идеалу
конечных множеств. Напомним, что согласно определению Х.1.3 свойст¬

§ 1. Инвариантные свойства
447
во Р в. п. множеств называется инвариантным или, другими словами,
теоретико-решеточным в £ (£*), если Р инвариантно относительно
Aut £ ( Aut £*), и Р называется элементарно теоретико-решеточным
свойством (э. т. р.), если Р определимо в £ (£*) формулой первого
порядка. В § 1 главы X мы показали, что любое свойство Р в. п. множеств,
замкнутое относительно конечных разностей, является э. т. р. в £ тогда
и только тогда, когда Р является э. т. р. в £*. В следствии 2.8 получим
аналогичное свойство для инвариантности вместо э. т. р.
Для некоторых э. т. р. свойств мы можем непосредственно указать
определяющую их формулу первого порядка, как, например, в случаях
вычислимого, простого, конечного и максимального множеств (см. § 1
главы X). В других случаях существование такого определяющего
свойства не очевидно, и для его нахождения требуется нетривиальное
доказательство, как, например, в случае гг-простого множества (см.
следствие Х.2.8). В этом параграфе мы приведем нетривиальное и неожиданное
доказательство элементарно теоретико-решеточности креативных
множеств.
1.1 	Теорема (Харрингтон). В. п. множество А креативно тогда и
только тогда, когда
(ЗС D A)(VB С C)(3R)[R вычислимо (1.1)
& R П С невычислимо &Д П А = Rn В],
где все кванторы действуют на £.
1.2 	Следствие (Харрингтон). Свойство креативности является
элементарно теоретико-решеточным.
1.3 	Определение, (i) Пусть Aut £ ( Aut £*) обозначает группу
автоморфизмов £ (£*)• Символы Ф, Ф обозначают автоморфизмы £ или
£*.
(й) Назовем множества А и В из £ автоморфными, если существует
Ф eAut £ ( Aut £*) такой, что Ф(А) = В (Ф(А*) = В*). Обозначим это
А=е В {А* В*).
(ш) Орбитой множества А € £ называется класс {В : А =£ В}.
Обозначим его через orbit (А).
(iv) 	Орбитой A* G £* называется класс { В* : А* =£* В* }.

448
Глава XV. Автоморфизмы решетки в. п. множеств
I. 	4 Следствие (Харрингтон). Креативные множества образуют
орбиту.
Доказательство. Это вытекает из следствия 1.2 и из того, что для
любых двух креативных множеств А и В существует вычислимый
изоморфизм, а следовательно, и автоморфизм решетки £, переводящий А в
В (см. теоремы 1.5.4 и П.4.8). Ц
Доказательство теоремы 1.1. (=>) Поскольку все креативные
множества вычислимо изоморфны, мы можем выбрать в качестве А любое
фиксированное креативное множество.
Пусть
А = { (х,у) : х € К к (х,у) 6 Wy }.
(Ясно, что по следствию II.4.8 множество А креативно ввиду того, что
К А, т. к. , выбрав Wyo = ш, мы получим х € К <=> (х,уо) £ А).
Далее, определим С = { (х,у) : х Е К}. По данному в. п. множеству
ВСС выберем уо таким, что Wyo = В. Пусть R = { (х,уо) : х Е и)}
Множество R Г) С = { (х,уо) : х € К } невычислимо и
R П А — R П В = { (х,у0) : х € К & (х,у0) Е Wyo = В },
т. к. В С С.
(<£=) (Это доказательства слегка напоминает упражнение II.4.16.)
Зафиксируем А и С, удовлетворяющие (1.1). Тогда А С С. Выберем
в. п. индексы а, с и к множеств А, С и К соответственно и
определим As = Wa,s4 С8 = Wc,s и Ks = Wk,s, имея ввиду соглашение
II. 	2.6. Мы хотим построить вычислимую функцию /, посредством
которой К $Cm А. С этой целью мы сначала построим в. п. множество ВСС,
задав его перечислением { В8 }sGu; так, чтобы имело место В \ С = 0
и, следовательно, В = С \ В (см. определение П.2.9), т. к. В С С, то
должно существовать вычислимое множество R = We,
удовлетворяющее бескванторной части утверждения (1.1). Для каждого е определим
ч. в. функцию фе так, чтобы мы смогли в качестве искомой сводящей
функции / взять функцию фео (или, по меньшей мере, функцию ^ для
некоторого г ео), где ео — наименьшее е, при котором R = We
удовлетворяет бескванторной части утверждения (1.1).
Основная стратегия для отдельного е состоит в следующем.
Предположим, что е — такое наименьшее число, что R = We удовлетворяет
бескванторной части (1.1). Тогда We П С невычислимо, откуда W€ - С
не в. п. и поэтому \We \ С\ = оо (как в (2.1) главы X ). Далее
We П А = We П В.
(1.2)

§ 1. Инвариантные свойства
449
По заданному е определим фе = / следующим образом. Пусть ф —
взаимно-однозначная вычислимая функция, областью значения которой
является бесконечное множество We \ С, вычислимо перечислимое в
силу упражнения II.2.10. Для каждого х, как только х перечисляется в
К, мы перечисляем значение ф(х) в Б, вынуждая в соответствии с (1.2)
перечислиться ф(х) позднее в А. Поэтому, х Е К Ф{х) € А по (1.2).
В этом заключается основная стратегия для отдельного е. Поскольку
мы не в состоянии определить упомянутое выше наименьшее число е,
мы вынуждены исполнять г-стратегии для всех г одновременно. Чтобы
стратегии i < е не мешали бесконечно много раз выполнению стратегии
е, определяем новое значение ф{,8+\(х) только в том случае, если
(Vy < x)[ipitS{y) 4- & [у 6 Ks «=> psii,a(y) е Л]]- (1-3)
Таким образом, действия стратегий г < е могут нарушить
справедливость к € К фе(к) € А только на конечном множестве элементов к.
Поэтому стратегия для минимального е достигает своей цели, как это
было описано выше.
Построение В и {ipi}ieи-
Шаг 5 — 0. Полагаем Во = 0 = ф{>0.
Шаг s -j-1.
Подшаг 1. Находим единственное z (если оно существует) такое,
что z Е Cs+1 — С8. Находим наименьшее г (если оно существует) такое,
что z Е Wi,s и для г выполнено (1.3), где х = {рьи)[фгу8{и) t]- Полагаем
Фi,s+l(x) = 2. Если z или г не существует, то ничего не делаем.
Подшаг 2. Для всех г, если х Е Ks+1 и фгу8+1{х) перечисляем
Фг,в+1(*) В В.
Конец построения.
Если г — такое наименьшее число, что ф{ всюду определена, то
К $СШ А посредством ф{. (Напомним, что г ^ е для наименьшего
числа е, для которого R = We удовлетворяет бескванторной части (1.1).)
Следовательно, А креативно по следствию II.4.8.
Заметим, что приведенное выше доказательство показывает, что
если А и С удовлетворяют (1.1), то А С<х> С. В самом деле, в этом легко
убедиться, положив В = 0 и заметив, что соответствующее множество
R удовлетворяет RC\A = 0, и RnC невычислимо. Поэтому RC\C С С-А
и R П С бесконечно. Более того, С — А не в. п., ибо в противном случае
при В — С — А получим, что для соответствующего множества R верно

450
Глава XV. Автоморфизмы решетки в. п. множеств
R П С = 0 (поскольку Rn С = (R П A) U (R П В), R П А = R П В и
АП В — 0), что противоречит невычислимости Rn С. О
1.5 	Замечания. Харрингтон (неопубликовано) сообщил, что он
доказал, что орбита креативных множеств — это единственная орбита,
состоящая из единственной невычислимой m-степени. Более того,
(VA Е £)[А не вычислимо и не креативно
<=> (ЭФ € Aut £)[Ф(А) ±т А]].
Этот результат был получен с использованием сложной техники работы
с автоморфизмами. Харрингтон также сообщил, что он доказал
существование не креативного множества А € £ такого, что
orbit(A) С {We :We =т К},
т. е. существует орбита, содержащая только полные по Тьюрингу не
креативные множества.
§ 2. Некоторые основные свойства автоморфизмов 8
2.1 	Определение. Перестановка р на и индуцирует автоморфизм Ф
на £ (£*), если для всех n p(Wn) = $(Wn) (соответственно (p(Wn)Y —
Очевидно, что каждая вычислимая перестановка тривиальным
образом индуцирует автоморфизм решетки £ и что каждый автоморфизм
решетки £ индуцирует автоморфизм решетки £*. Возникает
естественный вопрос: а существуют ли другие автоморфизмы решеток £ и £*?
Если да, то сколько их, все ли они индуцируются перестановками на
и и как соотносятся между собой автоморфизмы £ и £*. В этом
параграфе мы ответим на эти вопросы и приведем некоторые определения и
обозначения, которые будут использованы далее.
Кент (упражнение 2.11) использовал сжатые множества для
доказательства существования 2К° автоморфизмов £, но при этом все
соответствующие индуцированные автоморфизмы решетки £*
оказываются тождественными. Лахлан использовал следующее более точное, но,
тем не менее, несложное доказательство для получения аналогичного
результата для £*. Однако в методе Лахлана автоморфизм Ф Е Aut £*
индуцируется перестановкой р, которая возникает как результат
«склеивания» вычислимых перестановок невычислимым образом так, что для

§ 2. Некоторые основные свойства автоморфизмов £
451
любых А и В, если р(А) = В, то А = В. Таким образом, этот метод
не дает новых элементов £* -орбиты элемента А*, которые нельзя
получить посредством обычных вычислимых перестановок. Поэтому для
доказательства неинвариантности гиперпростоты в § 3 или теоремы о
максимальных множествах в §§ 4-6 потребовалось изобретение новых
методов.
2.2 	Теорема (Лахлан). Существует 2К° автоморфизмов решетки
£*.
Доказательство. Для каждого п определим вычислимое множество Rn
так, чтобы Rn С Rn~i, Rn бесконечно и Rn-\ - Rn бесконечно. Примем
для удобства К-\ = ш. Пусть Rn С Rn-\ - Wn, если Rn-iC\Wn конечно,
и Rn С Rn-i П Wn в противном случае. В любом случае Rn вычислимо,
бесконечно и Rn-\ —Rn также бесконечно. Заметим, что для всех п либо
Rn С Wn, либо Rn С Wn-
Для всех п € си и j Е {0,1} выберем частично вычислимые функции
ф™, являющиеся перестановками на Rn-i — Rn, так, что z/# —
тождественная перестановка и z/j™ отображает 5П в некоторое Т ф* Sn для
некоторого бесконечного в. п. множества Sn С Дп_х — Rn- Для
произвольной функции / : и {0,1} определим перестановку pf на cj так,
чтобы ограничение р/ на Rn-i — Rn совпадало с Ф^п)' Ясно, что Pf
всюду определена и поэтому является перестановкой на о;, поскольку
для каждого m найдется п такое, что Wn = {га}, откуда m 6 йп (и,
следовательно, га Е dom pf). Так как z/# (Sn) ф* то при / ^ р
перестановки pf и рд индуцируют различные автоморфизмы на £*.
Теперь достаточно доказать, что p/(VFn) и pJ1(Wn) являются в. п.
множествами для любого п. Ясно, что (J{ Ф}({) : ® ^ п) — частично
вычислимая функция с областью определения Rn- Следовательно,
Pf(Rn n Wn) = (J П Wn) : i ^ п|
для любого п, что является в. п. множеством. Далее, pf(Rn П Wn) =
Rn П Wn, поскольку либо Rn С VFn, либо Дп и Wn не пересекаются.
Таким образом,
Pf(W„) =pf(RnnWn)Upf(RnnWn)
— вычислимо перечислимо. В силу аналогичных рассуждений pj1 {И7,,)
является в. п. множеством. []

452
Глава XV. Автоморфизмы решетки в. п. множеств
2.3 Следствие. Не каждый автоморфизм решетки £* индуцируется
вычислимой перестановкой на ш.
С другой стороны, мы покажем, что каждый автоморфизм £*
индуцируется некоторой перестановкой на ш. Сначала нам нужен удобный
способ для описания произвольного Ф Е Aut £* относительно нашей
фиксированной нумерации {Wn}neu;.
2.4 Определение. Автоморфизм Ф Е Aut£* представляется
перестановкой h на и, если Ф(И^) = для всех п.
2.5 Теорема. Каждый Ф Е Aut £* индуцируется некоторой
перестановкой р на и). Более того, если Ф представим с помощью h, то р
может быть выбрана вычислимой относительно (h 0 0,)/.
Доказательство. Зафиксируем Ф Е Aut £* и пусть Ф представляется с
помощью h. Для каждого х Е ш определим е-штаты
а(е, х) = {% : г ^ е & х Е Wi },
<j(e, x) = {i:i^ebE Wh^) }.
Заметим, что множества а(е,х) равномерно вычислимы относительно
0', а множества <т(е,ж) — относительно h 0 0'. Пусть р = |Jnpn, где
конечные частичные функции рп определены следующим образом. Пусть
для удобства р-\ = 0 и а{ — 1,ж) = <т(—1,х) = 0 для всех х. Для чётных
п полагаем
хп = {fix)[x £ domPn-i],
еп = max{ е : -1 ^ е ^ п & (3?/)[2/ 0 rangpn_i
& <т(е,яп) = 5*(е,у)] },
Уп = (l*y)[v i ranpn_i & а(еп,жп) = a(en,j/)].
Определим рп = pn_i U {(жп,уп)}. Заметим, что еп, а
следовательно, и ?/п могут быть найдены вычислимо относительно (h 0 0,)/. Для
нечётных п полагаем уп = (/if/)[у $ rangpn_i], и далее
продолжаем как выше, поменяв местами хп и уп, а также and. Ясно, что
р = jjnpn является перестановкой и р $^т (/i00')'. Поскольку Ф Е Aut £*,
мы имеем limn еп = оо. Теперь индукцией по п легко убедиться, что
p(Wn) =* ЖЛ(п) для всех п. Q
2.6 Следствие. Каждый Ф Е Aut£* индуцируется некоторым Ф Е
Aut 5.
Доказательство. Вышеуказанная перестановка р индуцирует Ф Е
Aut£, который и индуцирует Ф. Q

§ 2. Некоторые основные свойства автоморфизмов £
453
2.7 Следствие. Если А и В бесконечны и кобесконечны, то А =£ В
тогда и только тогда, когда А* =£* В*.
Доказательство. Ясно, что из А =£ В следует А* =£* В*. Наоборот,
если А* =£+ В* посредством Ф, то в доказательстве теоремы 2.5 положим
Wo = А и Wh(o) = В, так что полученная перестановка р удовлетворяет
р(А) = В.
В силу следствия 2.7 для того, чтобы убедиться в справедливости
А =£ В, надо строить либо автоморфизм Ф Е Aut£, либо автоморфизм
Ф Е Aut£*, удовлетворяющий Ф(А*) = В*. Обычно мы будем делать
последнее, что, как правило, проще.
2.8 Следствие. Любое свойство в. п. множеств, которое
корректно определено в £*, инвариантно относительно Aut £ тогда и только
тогда, когда оно инвариантно относительно Aut £*.
Заметим, что в доказательстве теоремы 2.5 установлен следующий
факт, который в дальнейшем окажется полезным.
2.9 Следствие. По заданной перестановке h на и) определим а(е,х)
и а(е,х) как в доказательстве теоремы 2.5. Тогда h представляет
некоторый Ф Е Aut £* тогда и только тогда, когда для каждого е и
каждого е-штата <7о выполнено
{ х : а(е, х) = cfq } бесконечно { х : а(е, х) = &о } бесконечно.
Пусть С — произвольная счётная подрешетка в N = (2й7; С, (J, р|),
замкнутая относительно конечных разностей и содержащая 0 и и.
Теорема и её следствия, приведенные выше, очевидно остаются
справедливыми при замене £, £* и 0' на £, £*(= С/Т) и 0{А : А Е £}
(= { (m,n) : т Е Ап }) соответственно, где совокупность { Ап }nGa;
совпадает с С. Метод доказательства теоремы 2.5 может, таким образом,
быть применен для получения альтернативного (но похожего)
доказательства результата Лахлана (упражнение 2.12) о том, что для таких
подрешеток С\ и £2 условия £i=£2h£i=£2 эквивалентны.
Для того, чтобы задать некоторый автоморфизм Ф Е Aut
£*, очевидно, можно также задать функции / и д, удовлетворяющие
(Vn)pra = И7(п) & Ф-1^*) = w;(n)], (2.1)
что обычно бывает проще сделать. В этом случае мы говорим, что Ф
представлен парой (/, д). (По заданным / и д строится
соответствующее представление Л, вычислимое относительно /0р, с использованием

454
Глава XV. Автоморфизмы решетки в. п. множеств
леммы 1.3.2 о множестве индексов. Наоборот, если h задано, то полагаем
/ = h и д = Л-1.)
Построение автоморфизма Ф состоит в определении перестановки р
на и, которая индуцирует Ф, и в одновременном определении функций /
и д (не обязательно вычислимых), удовлетворяющих (2.1).
Перестановка р гарантирует, что требуемый Ф сохраняет включение (и является,
таким образом, 1:1 гомоморфизмом из £ в Л/*), в то время как функции /
и д обеспечивают, что р и р~1 отображают £ в £. Перестановка р часто
подразумевается неявно и получается по условию на е-штаты следствия
2.9.
2.10 Определение. Автоморфизм Ф решетки £* называется
эффективным, если Ф представим некоторой вычислимой перестановкой (или,
что эквивалентно, парой вычислимых функций (/,д)).
Ясно, что произвольная вычислимая перестановка индуцирует
эффективный изоморфизм, но не наоборот. Например, метод Мартина из
§ 3 позволяет строить только эффективные автоморфизмы, но тем не
менее он достаточен для доказательства не инвариантности
гиперпростых множеств. Однако эффективных автоморфизмов недостаточно для
получения результата о максимальных множествах из теоремы 4.6.
Поэтому необходимо также изучать и невычислимые представления h.
Например, можно было бы предположить, что существуют неэффективные
автоморфизмы, соответствующие представлениям h 0*, но это не
так по упражнению 2.13. Поэтому, мы в § 4 будем вынуждены изучать
представления h $^т 0".
2.11-2.13 Упражнения
2.11 (Кент [1962]). Докажите напрямую, без использования теоремы
2.2, 	что существует 2**° автоморфизмов решетки £. Указание.
Зафиксируем произвольное сжатое множество С. Рассмотрим класс
С — {р\ р — перестановка на и & (Ух)[х £ С => f(x) = х] }.
Покажите, что каждое р G С индуцирует автоморфизм на £ и что С
содержит 2**° элементов. Что представляет из себя индуцированный
автоморфизм на £ * для каждого такого р G С?
2.12 (Лахлан [1968с, лемма 14]). Пусть С\ и Со — счётные подрешетки
N, замкнутые относительно =* . Докажите, что С\ = £2 <=> С\ =
где £* означает факторрешетку £/Т.

§ 3. Неинвариантные свойства
455
2.13 	(Джокуш). Докажите, что если Ф Е Autf* представим
некоторой перестановкой h $^т 0', то Ф представим и некоторой вычислимой
перестановкой hi. Указание. Используйте лемму о пределе.
§ 3. Неинвариантные свойства
В § 1 главы X мы видели, что свойства вычислимости, простоты и
максимальности являются элементарно теоретико-решеточными и,
следовательно, инвариантными. В следствии Х.2.8 и теореме 1.1, пользуясь
более тонкими рассуждениями, мы получили инвариантность
гипергиперпростоты и креативности. В этом параграфе мы покажем, что
гиперпростота не инвариантна. Сравнительно простое доказательство этого
утверждения использует только метод приоритета с конечными
нарушениями. Оно также позволит нам лучше понять более трудный метод
построения автоморфизмов решетки £* из следующих параграфов
настоящей главы.
3.1 	Теорема (Д. А. Мартин). Существует гиперпростое множество
Ни Ф Е Aut£ такие, что Ф (Н) не гиперпросто.
Доказательство. Определим эффективно некоторую
последовательность вычислимых перестановок {ps}seш и возрастающую
последовательность конечных множеств { Н8 }sGu; так, чтобы Н = \JSH8 было
гиперпростым, р = Игл8р8 была перестановкой на u;, S = р(Н) не было
гиперпростым и р индуцировала бы автоморфизм решетки £.
Обозначим р8(Н8) через Ss. Мы будем иметь Ss С Ss+i для всех s, так что
S будет в. п. Пусть { F* }nGu; будет е-м кандидатом на роль сильной
таблицы таким, что множество F% конечно, и либо F* определено для
всех п, либо неопределено для всех п, больших некоторого т.
Мы говорим, что индекс е удовлетворяется на шаге s, если либо
некоторые F* и F^ определены к шагу s и F* f| ^ 0» т Ф п, либо
F* определено и является подмножеством Н8. Полный е-штат числа х
на шаге s — это пара е-штатов (а, т), где
(j = {i:i^e&iE Wi,8 },
и
r = {i:i^e & р8(х) £ W^8 }•
Построение p и H.
Шаг 5 — 0. Пусть ро — тождественная перестановка, Я0 = 0.

456
Глава XV. Автоморфизмы решетки в. п. множеств
Шаг s -f 1. Ищем индекс е, который ещё не удовлетворился на шаге
5, и такой, что существует элемент F* из е-й сильной таблицы, а также
такие х Е F* — Н8, что для некоторого у £ Н8\
(i) х и у имеют одинаковые полные е-штаты на шаге s;
(ii) min(x,y,ps(x),p,(j/)) ^ e;
(iii) pa{y) > 2x;
(iv) у > x.
Если такого e не существует, то полагаем ps+1 = и Я5+1 = Hs. В
противном случае пусть е8 будет наименьшим таким е, п8 —
наименьшим числом, соответствующим е8, а f/s — наименьшими числами,
соответствующими е8 и п8. Полагаем
Пусть Я5+1 = Я5 (J{zs }• На этом построение закончено. Заметим, что
Лемма 1. S = l)sSs кобесконечно и не гиперпросто.
Доказательство. Если z 6 S, то z = р8+\(х8) ф ps{xs) для подходящего
s. Для каждого s найдется самое большее одно z, z = ps{ys)- Условие (iii)
обеспечивает, что для всех п в S содержится п элементов меньших
2п, поскольку если z = Ps{ys) попадает в 5 на шаге s + 1, то х8 попадает
в Я и 2xs < z. Поэтому S не гиперпросто по теореме V.2.3.
Лемма 2. Для всех z существует p(z) = limsps(z).
Доказательство. Зафиксируем z и выберем t так, чтобы Ht [ (z + 1) =
Я (z-f 1). Пусть s ^ t Hpi+i(z) ф р8{z). Тогда z — xs или z = у8. Если
z = х8, то z Е Я*+1 - Я*, противоречие. Если z — у8, то по условию
(iv) 	некоторое х8 < у8 содержится в Я5+х — Н8, чего не может быть при
s ^ t. Таким образом, p(z) = pt(z).
Лемма 3. Если Н — [Js Н8 кобесконечно, то Я гиперпросто. Более
того, lims es — оо.
Доказательство. Предположим для получения противоречия, что
сильная таблица { F* )nGu; свидетельствует о не гиперпростоте множества
Я, и пусть е — наименьший возможный номер для такой таблицы.
Если г < е, то в силу минимальности е, г-й кандидат на сильную таблицу
=Ss\J{p8(y8)}.

§ 3. Неинвариантные свойства
457
конечен, в противном случае г должно быть удовлетворено. Выберем so
так, чтобы е8 ^ е для всех s ^ So-
Полный е-штат назовем хорошо населенным, если в нем навсегда
остается бесконечно много элементов из Н. Все элементы из Н, за
исключением лишь конечного их числа, лежат в хорошо населенных
полных е-штатах. Следовательно, найдется п такое, что либо F* С Н, либо
F* — Я ^ 0, и для каждого х € F* — Н выполнено х ^ е и р(ж) ^ е,
причем все такие х находятся в хорошо населенных полных е-штатах.
Выберем наименьшее такое п. Затем выберем наименьшее такое х.
Тогда существует бесконечно много шагов s, на которых найдется некоторое
у > х, что у ^ е, р(у) = р8{у) > 2х, р(р) > е, у g Н8, и у находится в
том же самом полном е-штате, что и х. Значит х будет в конце концов
перечислен в Н. Получили противоречие.
Чтобы доказать lims е8 = оо зафиксируем е и по индукции выберем
so такое, что е ^ е8 для всех s ^ $о* Теперь, если е8—е для бесконечно
многих s ^ so, то существует бесконечно много таких п, что множество
F* ПН содержит некоторый элемент хеп, который в любой момент будет
готов к перестановке его с каким- нибудь уп из того же полного е-штата.
Но в том же полном е-штате лежат бесконечно много таких хеп, поэтому
один из них будет переставлен с некоторым у и хеп попадает в Н.
Лемма 4. Число p~l(z) = limspJ1(z) существует для всех z.
Следовательно, р является перестановкой на ш по лемме 2.
Доказательство. Если p^+i ф p~l(z), то z = р8(х8), либо z = ps{ys) и
es ^ z по условию (ii). Тем не менее, е8 ^ z лишь для конечного числа
s в силу леммы 3.
Лемма 5. Н гиперпросто.
Доказательство. Н = p~l(S), поэтому Н кобесконечно. Затем
применяем лемму 3.
Лемма 6. Перестановка р индуцирует автоморфизм решетки £ и,
более того, эффективный автоморфизм решетки £*.
Доказательство. Вычислимо относительно 0' определим функцию к(е)
как такой наименьший шаг t, что е8 ^ е для всех шагов s ^ t.
Определим функции / и g как

458
Глава XV. Автоморфизмы решетки в. п. множеств
WW) = LK^Wn,*) : О Цп) }.
Ясно, что p(Wn) = W/(n) и p~l{Wn) = Wg(n) для всех п, поскольку по
условию (i) после шага к(п) р переставляет элементы в одном и том же
полном е-штате. Обе функции / и д вычислимы относительно 0'. Чтобы
убедится, что р индуцирует эффективный автоморфизм Ф Е Aut£*, мы
можем либо применить упражнение 2.13, либо, заменяя везде к(п) на
О, получить вычислимые функции / и д такие, что p(Wn) =* И^(п) и
p~4Wn) =* waln). О
Заметим, что в приведенном выше доказательстве е-ое
положительное требование, утверждающее, что F? С Я для некоторого j, будучи
однажды удовлетворенным, впоследствии никогда не нарушается,
хотя перед тем, как будет полностью удовлетворено, оно может конечное
число раз требовать внимания (чтобы поместить все F? в Я).
Отрицательное требование с номером е, утверждающее, что только элементы
из того же самого е-штата могут быть переставлены, может быть
нарушено г-м положительным требованием лишь в случае г < е.
3.2. Упражнение
3.2. Покажите, что для каждой ненулевой в. п. степени а существуют
гиперпростое множество Я, не гиперпростое множество 5, и
автоморфизм Ф Е Aut£ такие, что Я, S Е а и Ф(Я) = S. Указание.
Зафиксируем в. п. множество А Е а. Если условия (i)-(iv) теоремы 3.1 выполнены,
определим ps+\ как выше и назовем xs и ps(ys) последователями
требования Яе, при этом х8 не перечисляем в Я (и ps(ys) в S) до тех пор,
пока А не разрешит это сделать. Ясно, что S ^т Я $^т А, поскольку
х8 < PsiVs)• Для обеспечения эквивалентности по Тьюрингу,
закодируйте А в S.
§ 4. Формулировка теоремы о расширении и его
мотивация
Главной целью последующего материала этой главы станет
доказательство того, что для произвольных максимальных множеств А и В
существует такой Ф Е Aut£, что Ф(А) = В. Главным инструментом
для достижения этой цели является теорема о расширении, которую мы
сформулируем и мотивируем в настоящем параграфе. В § 5 мы докажем,

§ 4• Формулировка теоремы о расширении
459
что по данным максимальным множествам А и В могут быть получены
необходимые нумерации, удовлетворяющие теореме о расширении. В § 6
мы докажем теорему о расширении.
Зафиксируем два максимальных множества А и В и рассмотрим
некоторые наивные (и безуспешные) попытки построения Ф Е Aut£
такого, что Ф(А) = В. Сначала, имея ввиду упражнение 2.11, мы могли
бы попытаться найти такую перестановку р, что (i) р тождественна на
АП В, (ii) р(А) =* В, и (Ш) р индуцирует автоморфизм на £*. Однако
в силу упражнения 4.11 любая перестановка, удовлетворяющая (i) и (ii)
для невычислимых А и В таких, что Ар\В =* 0, не может
удовлетворять (ш). Далее, мы могли бы попытаться расширить метод Мартина
из теоремы 3.1 для того, чтобы построить Ф. Однако этот метод всегда
дает эффективные автоморфизмы. Мы же сейчас докажем, что
существуют максимальные множества, которые не эффективно автоморфны.
4.1 	Теорема (Соар [1974с]). Существуют такие максимальные
множества А и В, что для любого эффективного Ф Е Aut£* выполнено
Ф(А*) Ф В*.
Доказательство. Вспомним конструкцию Ейтса из теоремы Х.3.3 для
построения максимального множества А, в которой маркеры {Ге}е€а;
передвигаются с целью достигнуть максимальных е-штатов по
отношению к стандартному перечислению^ Uny8 }n,seu> (как определено в II.2.8).
Заметим, что в этой конструкции А С Uo <=> Uo\ А бесконечно.
Сначала мы покажем, как удовлетворить единственному требованию
Де, утверждающему, что если Ф — эффективный автоморфизм £* с
представлением <^е, то Ф(А*) ф В*. Опишем стандартные
перечисления { Un,s }n,sEu> и { Vn,8 }n,seu> всех в. п. множеств, и по ним построим
максимальные множества А и В соответственно, пользуясь методом
теоремы Х.3.3. Пусть Un+2 = Vn+2 = Wn для всех п. Определим С/0, U\,
Vo и V\ для удовлетворения Re. Пусть множество U\ = Wсовпадает
с множеством чётных чисел и перечисляется таким образом, что U\ \ А
бесконечно. Полагаем Vo = если <ре{ч) определено, и Vo = 0 в
противном случае. Определим
г все нечётные числа, если Vo\B бесконечно,
Uo = <
конечное подмноже-
, ство нечётных чисел в противном случае.
Предположим, что Uo перечисляется так, что Uq\A бесконечно

460
Глава XV. Автоморфизмы решетки в. п. множеств
V0\B бесконечно. Пусть Wi0 = U0 и Vl — И^е(*0), если <^е(г0) определено,
и V\ = 0 в противном случае.
Ясно, что А и В — максимальные множества. Предположим теперь,
что А* =£+ В* посредством Ф с представлением фе. Тогда ipe(iо) и
<pe(ii) определены, Ф{Щ) = V{ и Ф(С/х) = Vq . Докажем, что
множество Vo \ В бесконечно. Действительно, в противном случае множество
U0\A было бы конечным (по определению Uo). Поэтому А С* U\ (по
построению А, т. к. U\ \ А бесконечно) и, следовательно, В С* Vo (т. к.
Ф([/*) = Vq и Ф(Л*) = В*). Тогда множество Vo — В и, следовательно,
множество Vo \ В были бы бесконечными. Мы получили противоречие.
Теперь из бесконечности множества Vo \ В следует бесконечность
множества Uo \ А в силу определения Uo-
Но теперь из бесконечности Uo \ А и Vo \ В следует, что А С Uo и
В С Vo в силу построения теоремы Х.3.3. Так как А С Uo и Ф(Щ) = V{,
то имеем В С* Vi. Таким образом,
I? С* Vo П Fi =* Ф(Uo П Ui) =* 0,
что противоречит максимальности Б.
Этот метод можно следующим образом модифицировать, чтобы
удовлетворить всем требованиям йе, е 6 и). Равномерно вычислимо
перечислимые последовательности { Un }nGu; и { Vn }nGu, группируются в
семейства конечных последовательностей, называемых «е-блоками». 0-
блоками являются последовательности множеств Uo, Ui, U2 = Wo и
Vq, Vi, V2 = Wo соответственно, где C/o, U\, Vo и V\
определяются так же, как и выше при е = 0. Предположим, что для некоторого
е ^ 0 мы определили обе последовательности через е-блоки, и пусть
{ Un }n^.j и { Vn }n^.j для некоторого j будут получившиеся
последовательности. Обозначим через a(j,x,s) (a(j,x,s)) j-штат числа х
относительно { Un>s }n^.j (соответственно { VUyS }n^.j)- Тогда (е -f 1)-блоками
ИЗ { Un }nG о; И { Vn}nG4 будут последовательности Xi, Yi, Х2, У2, ...,
Хт, Ym, W€+1 И Xi,Yi, Х2, У2, Хт, Ут, We+1 соответственно.
Пары (Xfc,yjk) и (Хк,Ук) строятся также, как соответственно (Uo,U\) и
(Vo, Vi) в вышеприведенном доказательстве. Они соответствуют
фиксированному j-штату а к = о к и расположены в убывающем порядке
относительно порядка а к при обычном упорядочении j-штатов. Для
фиксированного j-штата 0*, 0 ^ А; ^ 2J+1 определим в. п. множество 1
Определения множеств Ск, C^ven и добавлено при переводе. — Прим,
редактора.

§ 4■ Формулировка теоремы о расширении
461
Си — { х : х е f|{ Wi : г е ст* }) \ А }, и для нумерации { с£ }п6а)
множества Ск \ А определим C%dd - { с%п+1 }n6u> и Cekven = { c£n }n€u>.
Пусть Ск — для некоторого г' такого, что W%> = Ск, если
<ре(г') определено, и пусть Ск = $ в противном случае. Заметим, что
если а к — истинный j-штат для (кобесконечно многих элементов) А,
то А С* С*. Таким образом, если А* =£* Б* с представлением <ре, то
В С* Ск, и поэтому Ск\ В бесконечно. Пусть X* = C£dd, У* = C|ven,
Xfc = И^,е(<1) flC'fc иУ^С И^,в(<0) ПС'л ПРИ = хк и Wij = Vfc. Тогда
в силу аналогичных рассуждений, как и выше, получаем, что Хк \ А
бесконечно Хк\В бесконечно.
Пусть ак> — истинный j-штат А. Как выше получаем, что для всех
к < к' множества Ск и, следовательно, Хк и Yk будут конечными.
Поэтому они рано или поздно перестанут препятствовать множествам Х&
и обеспечить А* ^£+ В* посредством представления ср€. Ц
4.2 	Определение. Равномерно в. п. (р. в. п.) последовательность в. п.
множеств { Un }nGш назовем скелетом, если
(Ve)(3n)[We =* Un],
Зафиксируем произвольных два максимальных множества А и В и
вернемся к проблеме доказательства А =£ В. Мы предпочтем работать
со скелетами { Un }nGu; и { Vn }nGu;, определенными для А и В
соответственно, чем напрямую с { Wn }nGu;. (Тем самым мы устраняем
препятствия теоремы 4.1). Автоморфизм Ф будет эффективным относительно
этих скелетов в том смысле, что мы определим перестановку р на о; и
вычислимые функции / и д такие, что р(А) = В и
(Vn)[p([/„) =* Wf(n) & p-l{Vn) =* Wg(n)\. (4.1)
Если { Un }nGu; и { Vn }n€u; являются скелетами, то существуют
такие (невычислимые) функции F и G, что
(\/n)[Wn =* UF{n) & Wn =* VG(n)]. (4.2)
Таким образом, автоморфизм Ф будет представлен (в смысле (2.1))
парой (/о F,д о G) (относительно нумерации { Wn }nGu;).
Неэффективность этого представления следует из того, что F и G не вычислимые, а

462
Глава XV. Автоморфизмы решетки в. п. множеств
всего лишь всюду определенные Ез-функции (т. к. отношение =* в (4.2)
принадлежит Ез), поэтому они вычислимы относительно 0".
В теореме 5.1 мы определим скелеты { Un }пеи и { Уп }пеи>
соответственно для А и В, и зададим одновременное перечисление всех этих
множеств. Предположим, что мы это уже сделали. Как теперь
определить / и д! В дальнейшем мы обозначаем Wf(n) через Un и Wg(n) через
Vn. Таким образом, наше предполагаемое соответствие выглядит так:
Ф : А^ В
Un Un (4.3)
Vn*Vn
Нам будет удобнее располагать двумя копиями множества и).
Первая — для работы с множествами А, C/n, Vn «на левой стороне»,
вторая — для работы с множествами В, f/n, Vn «на правой стороне», в
соответствии с (4.3). Проблема построения Un, Vn и р может быть
разделена на две части: часть «А в В», (4.4), соответствующая р(А) = В, и
часть «А в Б», (4.5), соответствующая р{А) — В. В них мы добиваемся
выполнения для всех п условий
р(А П Un) =* (В П Un) & р(А П Vn) =* (В П Vn), (4.4)
и
Р(А П ип) =* {В П Un) & р(А п Кп) =* (В П Кг). (4.5)
Как видно из следствия 2.9, мы можем проводить дальнейшее
доказательство без использования р, рассматривая полные е-штаты.
4.3 	Определение, (i) Пусть { Хе }е€и; и { Ye }ееи; — равномерно
вычислимо перечислимые последовательности в. п. множеств. Полным е-
штатом v(e,x) числа х относительно { Хе }eGa; и { Ye }eGa;
называется тройка (е,а, т), в которой о является е-штатом х относительно
{ Хе }ееал а т является е-штатом х относительно { Ye }eGa;.
(ii) Определим аппроксимацию для v(e,x) в конце шага s по данным
ОДНОВремеННЫМ Перечислениям { Хе>8 }e,sGu; И { Уе>5 }e,sGu; для { Хе }eGu;
и { Уе }ееи> следующим образом:
v{e,x,s) = (е,а(е,ж,5),т(е,ж,5)),
где
a(e,x,s) = Xi)S }

§ 4• Формулировка теоремы о расширении
463
и
т(е,я,$) = {*:i^e&a;€ }.
По следствию 2.9 часть «А в Б» (4.4) эквивалентна условию
(Vi/)[(3°°a; £ A)[v(e,x) = 1/ относительно
{ Un }n€cj и { К» }nGu>]
(3°°я £ B)[i/(e, х) = i/ относительно
{ Un }n€u; и { Fn }n€u>]]*
(4.6)
Часть «А в Б» (4.5) эквивалентна условию
(У1/)[(3°°ж £ A)[v{e,x) = i/ относительно
{ Un }nGu> и { Vn }nGu>]
(3°°я £ B)[v(e,x) = j/ относительно
{ }nGu; и { }n£u;]]*
В доказательстве теоремы о расширении в § 6 мы дадим
одновременные перечисления всех множеств А, В, { C/n }neu;> { Vn }ne}nGu;
и { Кг }nGtt»• Обозначения X\Y и X \ Y из определения П.2.9 здесь
понимаются относительно этих одновременных перечислений, которые
согласуются с порядком одновременного перечисления в теореме 5.2
определенных элементов в эти множества.
Все это может быть представлено как некоторая игра между
двумя командами: командой I, пытающейся построить автоморфизм Ф, и
командой II, которая хочет испортить Ф. В команде I имеются два
игрока: игрок 1а, отвечающий за выполнение (4.6), и игрок lb, отвечающий
за выполнение (4.7). Игрок 1а должен обеспечить перечисление в Un
и Vn достаточно много элементов, чтобы удовлетворить (4.6).
Однако 1а должен это делать с большой осторожностью, т. к. элементы, им
перечисленные в Un (Vn), могут быть позднее игроком II перечислены
в В (соответственно в Л), тем самым создавая трудности игроку 1Ь в
удовлетворении (4.7). Например, если
\U0 \ В\ = оо и Uo П А =* 0, (4.8)
то игрок lb немедленно проигрывает, даже не успев что-либо сделать, и
не имеет возможности удовлетворить (4.7).

464
Глава XV. Автоморфизмы решетки в. п. множеств
Пусть U+ (V+) обозначает множество элементов, перечисленных в
Un (Vn) игроком la, a U~ (V~) — множество элементов,
перечисленных игроком lb. Заметим, что U+ = Un\B и U~ = В \ Un, так что
Un = U~ и U+ и аналогично для Vn и А. Игрок 1а должен следить за
выполнением некоторых минимальных условий, таких как
\и+ \В\ = оо =» \и0 \ А\ = 00, (4.9)
и двойственного условия
\V+ \ А\ = оо => \V0\B\ = oo, (4.10)
чтобы избежать немедленного проигрыша игрока lb, подобного
описанному в (4.8). Суть теоремы о расширении 4.5 состоит в том, что если
игрок 1а достаточно осторожен при перечислении U+ и V*, добиваясь
выполнения этих минимальных условий, то игрок lb, перечисляя новые
элементы в U~, V~, может расширить U+ и V+ до Un и Vn, тем самым
удовлетворив (4.7). Это значит, что команда I достигает цели в
построении Ф. Все это чем-то напоминает доказательство детерминированности
открытых игр, т. к. если игроку удается избегать проигрыша в каждой
конкретной ситуации игры, то в результате он выигрывает игру.
Конечно, условия (4.9) и (4.10) должны быть заменены на другие,
учитывающие полные е-штаты вместо одиночных в. п. множеств, как
это сделано в (4.11) и (4.12). Такая замена одиночных в. п. множеств в
(4.9) 	на полные е-штаты дает необходимое условие (4.11), которое мы
называем так: «А покрывает Б». Двойственное условие (4.12)
утверждает, что «В ко-покрывает А». (Такая терминология найдет объяснение
в § 6.)
4.4 	Определение. Пусть даны полные е-штаты v — (е,сг,т) и v' —
(е1а,1т/). Обозначим через v ^ v* условие а С а' и т D т'. (Это
отношение читается как «... покрывается ...».) (Вспомним, что отношение
а С а1 означает, что «а содержится в а' как конечные подмножества
сj», а не как «а* является расширением а» как начальные сегменты в
2<и.)
4.5 	Теорема о расширении (Соар [1974а]). Пусть А и В —
бесконечные в. п. множества и {Un}neu>, {Vn}nGa;, { U+ }nGu; и { V+ }nGu,
— p. в. n. последовательности в. n. множеств. Предположим, что
существует такое одновременное перечисление всех этих множеств,
что для всех п
А \ V+ = 0 = В \ {/+.

§ 4• Формулировка теоремы о расширении
465
Для каждого полного е-штата v — (е,а,т) определим в. п. множества
DA =dfn { X : (3s) [х G As+1 - Aa k
х Е Ui,s } & т = {г : г ^ e &
•Df =dfn { a- : (3s) [a; € 5S+1 - Bs k
x £ {/} & т = {г:г^е &
Кроме того, предположим, что
о — {г : г е
*ev£}},
ст = {г : г ^ е
&
&
и
(Vi/) бесконечно => (3i/' ^ i/)
[Z)^, бесконечно]],
(Vi/) [£И бесконечно => (3i/' ^ v)
[.D% бесконечно]].
(4.11)
(4.12)
Тогда можно расширить в. п. множества {/+ до Un и V* до Vn так,
что выполняется соотношение (4-7)-
Теорема о расширении доказывается в § 6.
4.6 	Теорема (Соар [1974]). Для любых двух максимальных множеств
А и В существует такой автоморфизм Ф решетки £, что Ф(А) = В.
Доказательство. Зафиксируем максимальные множества А и В. В
теореме 5.1 мы определим скелеты { Un }neu> и {^пЬгеим которые будут
зависеть соответственно от А и В. В теореме 5.2 мы определим р. в. п.
последовательности { U+ }nGu, и { V+ }nGu;, удовлетворяющие (4.6), и
дадим одновременное перечисление всех вышеприведенных в. п. множеств,
удовлетворяющих условиям (4.11) и (4.12) теоремы о расширении. По
заключению теоремы о расширении и следствию 2.9 теперь существует
взаимно-однозначное отображение р из А в В, удовлетворяющее (4.7),
поэтому А* =£* В*. По следствию 2.7 А =£ В. []
4.7 	Следствие (Мартин). Тьюринговая степень не является реше-
точно инвариантной.
Доказательство. По теореме XI.2.3 существуют такие максимальные
множества А и В, что А =т 0; и В <т 0*.
Следствие 4.7 первоначально было доказано Мартином при помощи
рассуждения, похожего на приведенное в доказательстве теоремы 3.1.

466
Глава XV. Автоморфизмы решетки в. п. множеств
4.8 Следствие (Соар [1974а]). Пусть для к > О Ai, Аг,...,
Ak и В\, В2,..., Bk — последовательности, каждая из которых
содержит к максимальных множеств с попарно непересекающимися
дополнениями. Тогда существует такой автоморфизм Ф решетки £, что
Ф(А*) = Bi для всех i ^ к.
Доказательство. Найдем такие вычислимые множества Д*, 1 i ^ fc,
что и) = Я*, Д* П Дj =0 для г ф j и Д* Э А* для всех г ^ к.
Аналогичным образом найдем вычислимые множества Д*, г к, для
множеств Дг вместо А*. Применяя теорему 4.6, находим частичную 1:1-
функцию pi с областью определения Д*, отображающую Ri на Д*, и
такую, что Pi(Ai) = Bi и pi индуцирует изоморфизм из { Wn П Ri }nGa;
в { Wn П Ri }nGu;• Тогда р = — перестановка на о;, которая ин¬
дуцирует требуемый Ф. О
Множество А называется квазимаксимальным ранга п, если А
является пересечением п максимальных множеств с попарно непересекаю-
щимися дополнениями.
4.9 Следствие. Пусть А и В — два произвольных квазимаксималь-
ных множества одного и того же ранга. Тогда существует Ф 6 Aut £
такой, что Ф(А) — В.
4.10 Следствие. Для каждого к ^ 1 группа Aut £* к-кратно тран-
зитивна на коатомах решетки £*.
Доказательство. Применяем следствие 4.9 и также то, что если AJ,
А2,...,А£ — различные коатомы из £*, то существуют такие
максимальные множества В\, В2,..., Bk с попарно непересекающимися
дополнениями, что Bi Е А* для всех г ^ к. О
4.11 Упражнение
4.11. 	Пусть А и В — невычислимые в. п. множества такие, что
А П В ф* 0. Докажите, что не существует такой перестановки р на
о;, что (i) р является тождественной на А Г) Д, (ii) р{А) =* Д и (Ш) р
индуцирует автоморфизм решетки £*. Указание. Пусть С — мажорное
подмножество множества А. Докажите, что р{С) =* A U (С Г) Д) и р{С)
не может быть в. п.

§ 5. Удовлетворение условий теоремы о расширении
467
§ 5. Удовлетворение условий теоремы о расширении
для максимальных множеств
С этого момента фиксируем максимальные множества А и В. В
теореме 5.1 этого параграфа мы сначала определим скелеты { Un }nGu; и
{ Кг }П£и> соответственно для А и В. В теореме 5.2 определяем
последовательности { U+ }nGa; и {Уп }nGu;, удовлетворяющие (4.6), и даем
одновременное перечисление всех вышеупомянутых множеств,
удовлетворяющее условиям теоремы 4.5 о расширении.
Определим для произвольного в. п. множества С
С{С) = { We : С С We или We С* С }.
Заметим, что если С кобесконечно, то С* (С) = £* (а именно, С (С)
является скелетом) тогда и только тогда, когда С максимально. Для
упрощения доказательства теоремы 5.2 нам нужно организовать такое
одновременное перечисление последовательности { Zn}neu;, содержащей все
множества из С (С), которое сохраняет порядок расположения множеств
в этой последовательности в следующем смысле: для всех пит, если
п < т, то почти каждый ж, который, будучи пока в С, перечисляется в
обоих множествах Zn и Zm, то в Zn перечисляется раньше, чем в Zm.
Это очень сильное свойство может быть выполнено из-за того, что нам
достаточно рассматривать только такие Zi, для которых выполняется
условие Zi D С.
5.1 	Теорема о нумерации, сохраняющей порядок. Для любого
ко бесконечного в. п. множества С существует такая
последовательность { Zn }n€a; с Zo = С, что { Z* }nGu; = С*(С), и существует такое
её одновременное перечисление, что
(Vn) [Zn\C бесконечно <=> Zn - С бесконечно ( .
*=> ZnDC\, (5Л)
и
(Vn) (Vm > п) (а.е. х) [х € (Zn\C) П (Zm\C) =» „ч
х 6 (Zn\Zm)}. М
Доказательство. Фиксируем С. Определим такую последовательность
{ Уп }n€u)! ЧТО { У* }„€и> = С*(С), полагая У0 = С,
У2п+1 = П С,

468
Глава XV. Автоморфизмы решетки в. п. множеств
и
*2п+2 = {x:xewn & (Чу^х) [yeCuWn]}.
(Назначение множеств У2П+2 аналогично назначению множеств Ve из
теоремы Х.4.6 о мажорных подмножествах.) Фиксируем такое
одновременное перечисление последовательности { Уп }nGчто У2П+1 — С \ F2n+i
и
(Vn) [Уп\С бесконечно <==> Уп - С бесконечно Ф=> Уп D С], (5.3)
где С8 = Уо,«-
Теперь { Zn }nGu; определяются следующим образом. (Соотношение
(5.3) 	будет очевидным образом выполняться с Zn вместо Уп.) Пусть
%o,s = Уо,в для всех s.
Определим функцию F(e) так, чтобы F(0) = 0, %F{e) — Ye Для
каждого е, и Zn конечно для всех п £ rang F. Выбор функции F(e) будет
зависеть как от Уе, так и от (е — 1)-штата множества С относительно
{ Уп }пеим что определено корректно по (5.3). Для каждого е>0иаС
{0,1,...,е — 1} у нас имеется подвижной маркер Г£, который в конце
концов останавливается на таком индексе F{e), что ^F(e) — Ye, если
(е — 1)-штатом множества С относительно { Уп }nGu; является а. Число
п на некотором шаге называется свободным, если оно до этого не имело
никакого маркера. Теперь для всех е > 0 определим Ze,s по шагам s
следующим образом.
Шаг 5 = 0. Для всех е > 0 полагаем Ze$ = 0.
Шаг s 4-1. Перечисляем одну новую пару (хо,уо), где хо £ УУо. Если
у0 = 0, то переходим к шагу s + 2. В противном случае выполняем
следующие этапы.
Этап 1. Если хо Е Cs+1, то оставляем все маркеры на месте.
В противном случае те маркеры Г|Г, для которых уо < е и уо £ а,
передвигаем к первым свободным числам, сохраняя при этом их порядок.
Этап 2. Для каждого о С {0,1,...,5} прикрепляем маркер
Г£+1 к первому свободному числу в порядке возрастания 5-штата о.
Этап 3. Для каждого е, 0<е^5 + 1,и каждого а С
{ 0,1,..., е — 1} пусть F(e, <7, s + 1) обозначает текущую позицию
маркера Г£. Пусть (ж,,е,,0'/) — первая тройка (х,е,а) со свойствами (Р1)
и (Р2) (см. ниже). Если такая (х'.е^а1) существует, то перечисляем х1
в ^F(e',а',s+i),s+i• В противном случае переходим к шагу 5 + 2.
X £ Уе,в+1 & X ^ ^F(e,<T,s-fl),s•
(Р1)

§ 5. Удовлетворение условий теоремы о расширении
469
(Р2) Либо х Е С8+1, либо сг = 0, либо элементами множества о
являются ai < а2 < ••• < ак и (V? ^ А;) [ж Е ZF(a.^jiS+i)>s], где
<7j — { 0>\ , (22 ? • • • 7 Qj — l } •
Лемма 1. Для всех е и а маркер передвигается бесконечное число
раз тогда и только тогда, когда С CYy для некоторого у < е, у £ а.
Доказательство. По этапу 1 построения и (5.3).
Лемма 2. Для всех п, если Zn\C бесконечно, то некоторый маркер
в конце концов останавливается на таком числе п, что
(V»)[»eaU{e} => С CYy}.
Доказательство. По этапу 3 построения и (5.3).
Пусть теперь е\ < ег < • • • — пересчет всех е таких, что С С Ye.
Для всех е положим ре = { ej : ej < е }. По лемме 1 Г£е в конце концов
остановится на некотором числе, которое мы обозначаем через F(e), и
Zf{<>) — Ye по этапу 3. Маркеры Г£е, е € со, однажды назначенные,
остаются упорядоченными по е (по этапам 1 и 2), и, следовательно, для
всех г и е неравенство i < е имеет место тогда и только тогда, когда
F(i) < F(e). По леммам 1 и 2 для всех г ^ { F(ej) : j Е со } Z\C конечно.
Последняя часть свойства (Р2) этапа 3 гарантирует, что для почти всех
X если X е (ZF(ei)\C) П (ZF(e.)\C), где i < j, то х 6 ZF(ei)\ZF{ej).
Заметим, что (5.3) обеспечивает (5.1). А именно, если п — F(e) и
х Е Zn\C, то х Е Ye\C. Следовательно, если Zn\C бесконечно, то Ye\C
бесконечно, поэтому Ye D С по (5.3) и Zn D С, т. к. Ye = Zn. Если
п £ ran F, то Zn\C конечно по лемме 2. []
5.2 	Теорема. Пусть для максимальных множеств А и В {Un }nGu;
и { Vn }печ; — скелеты с одновременными перечислениями, полученные
по теореме 5.1 для А и В соответственно. Тогда существуют р. в. п.
последовательности {U* }nG и ^ { V* }nGu;, ^ одновременное
перечисление всех множеств А = U0, В = V0, { Un }nGu;, { Vn }ne{ Un }neи
и удовлетворяющие условиям теоремы о расширении и усло¬
вию (4-6), которое (т. к. А и В максимальны, Un Е С(А) и Vn Е С(В))
утверждает, что
(Vn) Р С Un *=* В С* U+] & [BCVn А С* V+}}. (5.4)

470
Глава XV. Автоморфизмы решетки в. п. множеств
Доказательство. Мы изменим данное перечисление, чтобы получить
новое, описываемое ниже в построении. Обозначим через Х8 конечное
множество элементов, перечисленных в множество X к концу шага s
в новом перечислении. К концу шага s мы определим C/n,s, Vn,8, U£s
и V+8. По данным As = Uo,s и Bs = Vo,s определим ф8 как
частичную 1:1-функцию с областью определения А8, в возрастающем порядке
отображающую As на Bs. Пусть ф-\ — тождественная функция на и).
Положим ф — lims ф8.
Для управления перечислениями множеств U+ и V+, будем
использовать ф. Мы должны перечислять U£ и V* так, чтобы удовлетворить
(5.4). Будем добиваться этого так, чтобы для почти всех х G А х G Un
имело место тогда и только тогда, когда ф(х) Е £/+, и аналогично для
В, Vn, и V+. Основной проблемой здесь является то, что мы можем
перечислить так много элементов в J7+, что нарушим (4.11). Решение этой
проблемы состоит в том, что мы не перечисляем элемент у в 17+ до тех
пор, пока штат v, до которого он поднимается, успешно не покроется
некоторым элементом, перечисляющимся в А. Мы можем это выполнить
из-за достаточной простоты множеств {Un}neu;, а именно из-за того,
что соотношение |С/ПП А\ = оо справедливо тогда и только тогда, когда
ACUn (аналогично для Vn и В), а также из-за сохраняющего порядок
перечисления из теоремы 5.1.
Построение.
Шаг s = At. Пусть х — элемент, перечисленный (игроком II) в
некоторое множество Ue на шаге t в процессе фиксированного
одновременного перечисления множеств { Un }nGu;. Перечисляем х в [7e>s. Положим
А8 — U()y8.
Шаг s = At 4-1. Поступаем, как на шаге At, но с Vn и В вместо Un и
А соответственно.
Шаг s = At 4- 2. Пусть (х‘,е') — первая пара (х,е) со свойствами
(Р1)-(Р4). Если такая пара (ж',е') существует, то перечисляем ф8-i(x')
в 8. В противном случае на этом шаге ничего не делаем.
(Р1) X е Ue,s-l - As-1 И ф8-г(х) $ U+S-1-
(Р2) (V* < е) [х е Ui,s-i <=► е U^s-il
(Vi < е) [a; £ Pj^»—i '' Фз—\{х) € Pi,»—1]•
(РЗ)

§ 5. Удовлетворение условий теоремы о расширении
471
Определим
СТо = {г : i ^ е & ф8-г(х) G Ui,s-i },
т0 = {г : г ^ х к ф8-х{х) G },
tx = (единственное t < s — 1) [х G C/e,t+i - t/e,*]-
(P4) (3v) (Зу) (Заг) (3ri) [tx < v < s - 1 & yG Ai>v+i - AiiV
& ai D { e } U & Ti С to
&а1 = {г:г^е & ?/ G UiyV }
& 7i = {г : i ^ x & у G }].
(Свойство (P4) утверждает, что после того, как х появляется в С/е, в
А появится некоторый элемент у, чья пара штатов {а\, Т\) в этот момент
времени покроет пару (<7о U {е},то), предназначенную для ф8-\(х) в
том смысле, что о\ Э U { е } и т\ С т0. Суть здесь в том, что &о
определяется относительно чисел i е. Если бы оно, как в случае с то,
определялось относительно i х, то мы могли бы получить слишком
большие запреты на перечисление ф8-\(х) в 17+, т. к. в общем случае
х > е. По свойству сохраняющего порядок перечисления это более слабое
предположение достаточно для доказательства леммы 1. Но мы можем
позволить себе наложить на т\ более сильное предположение «г ж».
Дело в том, что либо ф8-\(х) в конце концов перечислится в Vi, и тогда
это не приведет ни к какому запрету, либо в противном случае навсегда
ips-i(x) Е Vi, но тогда V* конечно и условие х Е V* действует не более,
чем на конечное число элементов х Е А.)
Шаг s = At 4- 3. Аналогично, пытаемся перечислить некоторый эле-
мент ф~\(х') в VettS, где A, Un, U+, Vn, V+ и ф3 ~\{х) из шага 4£ + 2
заменяются на В, Vn, V+, C/n, £/+ и ^^(ж) соответственно. Также в
(РЗ) (которое теперь имеет отношение к Ui и 17+) заменяем «(Уг < е)»
на «(Уг ^ е)», чтобы отразить более высокий приоритет Ue 17+ перед
V+OV*.
Лемма 1. Условия теоремы о расширении выполнены посредством
вышеприведенной р. в. п. последовательности и соответствующего
одновременного перечисления.
Доказательство. Очевидно, В \ {7+ = 0 = А \ V+ для всех гг,
потому что в J7+ мы перечисляем только элементы ф(х) (ф~1(х) в V^).
«Ускоряя» при необходимости перечисление множества А, мы можем
предположить, что существует бесконечно много х таких, что они в А
появляются до того, как появляются в каких-либо С/п, п > 0, или V*,

472
Глава XV. Автоморфизмы решетки в. п. множеств
п ^ 0, и аналогично для В, Vn и J7+. Таким образом, нам необходимо
проверить (4.11) и (4.12) только для штатов а ф 0. Достаточно
проверить (4.11), т. к. проверка (4.12) проводится аналогично.
Зафиксируем е и полный е-штат == (е,<7о>7о) при <то ^ 0.
Предположим, что D^x конечно для всех v\ ^ v$. Мы должны показать, что для
каждого Т\ С то только конечному числу элементов ж, чьи е-штаты
относительно { Vn }nGu; есть Ti, позволяется войти в U+Q =dfn П{ : п G
0о }• Так как е-штаты со временем увеличиваются, то отсюда следует,
что D^q также должно быть конечным.
Пусть ео = тах(ао). По условию (Р2) построения и свойству (5.2)
упорядоченного перечисления из теоремы 5.1 для { Un }nGu; следует, что
U*Q \ конечно для всех п < ео- Следовательно, если существует
бесконечно много х Е U*, то почти все такие х войдут в U+ только после
х Е и+, для всех n G о'о — { ео }. Но по условию (Р4) построения и
предположению, что D$x конечно для всех v\ ^ щ, не более чем конечному
числу элементов ж, уже принадлежащим р|{ U+ : п Е (Jq — { бо } }, будет
позволено войти в {/+, пока е-штат элемента х относительно { Vn }nGu;
будет некоторым т\ С то.
Лемма 2. Свойство (5.4) выполняется.
Доказательство. Докажем (5.4) индукцией по е. Фиксируем е и
предполагаем, что (5.4) выполняется для всех п < е. Если Ue 2 Д то Ue\A
конечно по (5.1) и, следовательно, U+\B и U+ — В конечны.
Предположим, что Ue 2 А. Выберем уо такое, что для всех х Е А, х ^ у о
влечет
(Vi < е) [[ж Е Ui ф(х) Е &*] & [х Е V* <=> ф(х) Е Vi]].
Мы утверждаем, что для произвольного х0 Е А, х0 ^ уо
влечет ф(х0) 6 U+. Пусть т = тах{е,ж0}. Выберем $о такой, что для
всех s ^ 5о, ф8(х) = ф8о(х), a xq и ф(хо) к шагу s0 достигли своих
окончательных т-штатов относительно каждой из последовательностей
{ Un }nGu;, { Ui }neu;,J Vn }nGu; и { V'+ }nGu;. Чтобы удостовериться, что
ф(хо) принадлежит U+, определим
То = {i : г ^ х0 & ф(х0) € V }.
Теперь если i <С xq и г £ то, то Vi - В конечно и, следовательно, УД В
конечно по (5.1). Но для произвольного г, из условия конечности
множества Vi\B следует, что УД\А также конечно. Следовательно, существуют

§ 6. Доказательство теоремы о расширении 4-5
473
такие о\ D gq и т\ С то, что
CVO (3w > t) (Эу) [уе Av+i Av
& <71 = {г:г^е & у е UiiV }
& 71 = {г : г ^ х0 & у G V£, }.]
Но тогда по (Р4) ?/>(х) в конце концов перечислится в U+. Случай
(Уе) =* V* разбирается аналогично. Из лемм 1 и 2 следует
теорема 5.2. \\
§ 6. Доказательство теоремы о расширении 4.5
6.1. Машины
Зафиксируем два списка натуральных чисел, и) и и. Пусть переменные
х, у,... (х, у,...) пробегают множество и; (о>). В соответствии с (4.3) мы
рассматриваем A, Un и Vn как подмножества си, а В, {Уп и Vn — как
подмножества и>. Начиная отсюда, мы измеряем полный е-штат числа
х £ uj относительно { Un }nGa; и { Vn }nGa;, а числа х Е с!) — относительно
{ Un }n€u> И { Уп }n£uM поэтому
u(e, х, s) = (e, {i < e : x e Ui<a }, {i ^ e : a: 6 VjiS })
И
i/(e, i,s) = (e,{i^e:iG^}, {г ^ e : x £ }),
где C/i,s, Vi5S, {У^5 и Vii8 будут определены в построении § 6.2.
Следовательно, i/(e,x) = lims j/(e,x,s) и i/(e,x) = lims j/(e,x,s).
В дополнение к определению 4.4 отношения v ^ v' нам понадобятся
следующие определения о штатах v.
6.1 	Определение. Пусть = (е,а,т) и и1 = (е/,о',,т/).
(i) i/ а-точно покрывает v' (и и1) тогда и только тогда, когда
е = е', а = а' и т' Э т.
(ii) i/ г-точно покрывает и1 {у i/') тогда и только тогда, когда
е =’е', т = т' и а' С а.
(iii) i/ является начальным сегментом v' [у < v') тогда и только
тогда, когда е ^ е', а = а1 П { 0,1,..., е } и т = т' П { 0,1,..., е }.
(iv) Длиной v, пишется |i/|, является е.
Мы говорим, что х (х) имеет к концу шага s штат и, если v <
i/(x,x,s) (и < i/(x,x,s)), и х имеет окончательный штат и, если I/ ^
i/(x,x) (i/ ^ i/(x,x)).

474
Глава XV. Автоморфизмы решетки в. п. множеств
Отношения из определений 4.4 и 6.1 в доказательстве имеют
существенное значение по следующей причине. Для достижения (4.7) мы хотели
бы рассматривать такие элементы х Е и) и у Е и, которые могут быть
приведены к одному и тому же окончательному штату v, привести и ж,
иук этому штату и затем связать их. Это трудно сделать потому, что
мы можем перечислять только множества {Un}neu; и { Уп }пеим в то
время как «оппонент» перечисляет все остальные множества.
Предположим, что х находится в штате V\ — (e,(Ji,ri) и у находится в штате
щ = (е,0о,то). Тогда мы можем привести х и у к одному и тому же
штату тогда и только тогда, когда V\ ^ v$. В этом случае мы сначала
мы поднимаем х до штата v2 — (e,0i,To), перечисляя х в Vn для всех
п Е то — Т\. Далее, мы поднимаем у до штата v2 Ць перечисляя у в
Un для всех п Е о\ —oq. Теперь х можно успешно связать с у. (Заметим,
что при у Е М мы пишем v(y,y,s), а не v(y,y,s).)
Перечисление х в Vn и у в Un на самом деле сложнее, чем
описано выше, и это лучше сделать с помощью двух одинаковых пинбольных
машин М и М. Элементы х Е uj (х Е си) действуют на машине М
(М). Как только х перечисляется в А (В), элемент х (х) помещается
над отверстием Н (Н) машины М (М). Машина М показана на
диаграмме 6.1. Машина М такая же, за исключением того, что над всеми
обозначениями в машине М присутствует знак Л (например, трек X и
правило Rn становятся треком X и правилом Дп), причем в правилах
Rn для машины М множества Un и Vn из соответствующих правил для
машины М заменяются на Vn и Un соответственно.
Поверхностью машины М является та часть диаграммы, которая
покрыта стрелками и разделена на треки С, Ci, С2 и D. Элемент х
первоначально входит в М через отверстие Н, когда х перечисляется
в А, и мы говорим, что с этого времени х находится в машине М. Далее
х выполняет ряд последовательных движений в направлении стрелок,
направленных вниз до тех пор, пока х не войдет либо в карман Р, либо
в карман Q. Карман Р подразделяется на такие ящики Bv, что каждый
элемент х G Ви удовлетворяет v ■< v(x,x,s), и Bv содержит не более,
чем конечное число постоянных резидентов (т. е. элементов, оставшихся
там навсегда). Точное движение х и его возможное перечисление в
множества Vn для некоторых п G и) управляются правилами Pi, R2, Рз и
Р4, которые будут описаны позднее.
После достижения кармана х позднее может быть удален и снова
помещён над отверстием Н при условии, что х перечисляется в Un для
некоторого п х. В этом случае позднее х передвигается через отверстие
Н к треку С, и описанный выше процесс повторяется. Так как х может

§ 6. Доказательство теоремы о расширении 4-5
475
помещаться над отверстием Н только после изменения в a(x,x,s), то
очевидно, что х передвигается к отверстию Н не более конечного числа
раз и, таким образом, в конце концов навсегда остается либо в кармане
Р, либо в Q.
При очень грубом приближении упомянутые выше повышение штата
и установление связи между элементами х и у осуществляются
машинами М и М следующим образом. Процесс связывания
устанавливается процедурой, состоящей из двух частей — «назад» и «вперед», где
часть «назад» — это связывание Р <-> Q элементов х Е Р с элементами
у Е Q, а часть «вперед» — аналогичное связывание Q <-> Р. (Ниже мы
описываем только первую часть процесса, т. к. вторая часть полностью
двойственна первой части с обычными изменениями, а именно, меняются
местами А и Р, х и я, C/n, Vn, Vn, Un и Уп, {/n, f/n, V"n соответственно.)
Большинство входящих в М элементов у достигнут кармана Q, из
которого они будут искать соответствующего «напарника» х среди
элементов, проходящих через трек D машины М. Пока у находится в
кармане Q, согласно правилу Д4 его штат поднимается с щ = (е,сго,то) до
некоторого ^2 = (e,^i,To), v2 путем перечисления у в Un для
77- £ <Тх — (Jo • (Выбор конкретного v2, используемого для у, основан на
частоте появления ^2 среди штатов элементов ж, прошедших до этого
через трек D.) Далее, различные элементы х в треке С2 машины М
поднимаются с некоторого штата v\ — т\ С то, до штата
v2 согласно правилу Дз, путем перечисления х в Vn для п G то — т\,
и тогда ж помещается в трек D. (Это перечисление х в Vn по правилу
Дз также управляется штатами предыдущих элементов у в М.)
Наконец, правило Д2 может удалить х из трека D и поместить х в ящик
Bv^ кармана Р при условии, что v2 -< iy(x,x,s) и некоторый элемент у
в Q со штатом v2 «требует» х в качестве своего напарника. Позднее
изменение в принадлежности элементов z в Q или изменение их штата
могут заставить отменить это требование. В этом случае х удаляется
из кармана Р. Обычно после этого х входит в карман Q, из которого он
ищет своего напарника z в кармане Р, тем самым изменив свой статус
«напарника, которого ищут» на «напарника, который ищет».
Далее, у может недовольствоваться тем, что имеет только одного
напарника х из BU2, и опасаясь потери х (из-за перечисления х оппонентом
в Un для некоторого п \v2\) может потребовать, чтобы конечное
число напарников х со штатом v2 были помещены в ящик В„2. Однако мы
гарантируем, что существует не более чем конечное число постоянных
резидентов ящика BV2, так что окончательное соответствие будет
«конечное число к одному» и необязательно «одно к одному». Но этого для

476
Глава XV. Автоморфизмы решетки в. п. множеств
Карман Q
Диаграмма 6.1. Машина М

§ 6. Доказательство теоремы о расширении 4-5
477
удовлетворения (4.7) достаточно.
6.2. 	Построение
Теперь мы дадим формальное описание построения, хотя её точное
изложение будет также зависеть от правил Дх, Д2, Д3 и Д4 (Дх, Д2,
Дз и Д4), которые будут даны в § 6.4. Зафиксируем определенное
условиями теоремы 4.5 о расширении перечисление и назовем его данным
перечислением C/n, Vn, V^, п Е ш. Как обычно, в построении мы
определяем новое перечисление, и пусть Xs обозначает множество
элементов, перечисленных в X к концу шага s в этом новом перечислении.
Чтобы элемент х имел свое окончательное положение внутри М, мы для
удобства удерживаем от вхождения в Un (Vn, Un, Vn) в случае 3 этапа 1
ниже конечное число элементов х п, так что каждый х перечисляется
только в конечном числе множеств. Это не оказывает никакого влияния
на (4.7), которое имеет дело с бесконечным поведением.
Построение.
Шаг 5 = 0. Ничего не делаем.
Шаг s 4- 1. Действуем в зависимости от того, какой из следующих
случаев выполняется первым.
Случай 1. Некоторый элемент х находится в треке С, Ci, С2 или D
(С, Ci, С2 или D) к концу шага s. (Такой элемент х будет
единственным.) Применяем правило Дх, если он находится в треке С (С), правило
Дз (Дз), если он находится в треке С2 (С2), и правило Д2 (Д2), если он
находится в треке D (D). Если х находится в треке Сх, то удаляем х
*из С\ и помещаем его в трек D на шаге s 4-1.
Случай 2. Некоторый элемент находится над отверстием Н (Н).
Находим наименьший такой элемент (если одинаково малые элементы
расположены над обоими Я и Я, то выбираем элемент, расположенный над
Н) и, если он был над отверстием Н (Д), то кладем его в трек С (С).
Случай 3. В противном случае.
Этап 1. Пусть данное перечисление зачисляет один новый элемент
х (х) в одно в. п. множество Y = Un или V+ (=Vn или J7+). Если п ^ х
(£), то перечисляем х (х) в Un {Vn), если Y = Un (Ki), и в Un (Vn),
если Y = U+ (V+).
Этап 2. Если Y — Uq — A (Vo = Д), то помещаем x (x) над
отверстием H (H). Мы говорим, что элемент х (£) на всех шагах ^ s + 1
находится в машине М (М).

478
Глава XV. Автоморфизмы решетки в. п. множеств
Этап 3. Если в данный момент элемент х (х) находится в ящике
Ви (Ви) кармана Р (Р), Y — Un (Vn) и п ^ \v\, то удаляем х {х) из
кармана Р (Р) и помещаем х (х) над отверстием Н (Я). Если х (х)
в данный момент времени находится в кармане Q (Q), то х (х) оттуда
удаляем и помещаем х (х) над отверстием Н (Я). В конце шага s + 1
к каждому элементу, находящемуся в данный момент в кармане Q (Q),
применяем правило Я* (Я*)- (Заметим, что в конце концов каждый
элемент х останавливается. Это происходит из-за того, что х снова может
помещаться над отверстием Я только если после того, как он последний
раз побывал над отверстием Я, в его ж-штате произошли изменения.)
Это завершает построение.
Это построение порождает одновременное перечисление всех мно-
жеств А = Uo, В = У0, {Un}n> 0, {V„}n>0, {Un }„6u> и {К}„6а,.
Если X — некоторое множество (карман или ящик), то пусть Xs
означает множество тех элементов, которые были перечислены в X к концу
шага s. Если X — карман или ящик, то пусть Х^ означает множество
постоянных резидентов X.
6.3. 	Требования и мотивация правил
Перед тем как дать точное описание правил, мы приведем некоторую
мотивацию. Наша цель состоит в том, чтобы достичь (4.7). Для этого
нужно для всех v удовлетворить следующее требование:
Sv : Если бесконечно много элементов В (А) имеют окончательный
штат I/, то существует хотя бы один элемент ^ \v\ в А(В),
который имеет окончательный штат v.
Смысл в том, что если бесконечно много элементов из В имеют
окончательный штат i/, то для всех k > \v\ найдется штат v\~ У v длины к
такой, что бесконечно много элементов В имеют окончательный штат
i/fc. Таким образом, при выполнении требования Svk в А найдется
элемент ^ к с окончательным штатом v\~.
Чтобы удовлетворить мы пытаемся соотнести каждый элемент
у G Q с хотя бы одним элементом х G Р с тем же штатом. Мы
располагаем элементы у G Qs на дереве штатов так, чтобы для каждой вершины
v и каждого шага s хотя бы один элемент, обозначаемый через q(v, s),
остается в вершине и q(y, s) имеет штат v.

§ 6. Доказательство теоремы о расширении ^.5
479
6.2 	Определение. Определим индукцией по \v\ функцию
q{u,s) = {fxy)[y eQskv < v{y,y,s) & (Vj/ -< v)[y > g(s, »/')]]•
Если у не существует, то q(v,s) неопределено (q(v,s) t), в остальных
случаях q(v, s) | .
Заметим, что для каждого у Е Qs существует штат v такой, что
у — q{v, s) (т. к. существует у +1 штат v для у и самое большее у из них
могут удовлетворять q(v, s) — z для некоторого z < у). Во время работы
машины мы стараемся найти партнера х для q(v,s), и мы помещаем х
в ящик Ви кармана Р в соответствии с правилом R2. Чтобы обеспечить
это соответствие, нам надо обеспечить для v два условия:
ф{у, s) t=> (Vs G BVj8)(3t ^ s)[x удаляется ( .
из ящика Bv на шаге £] \ )
и
\BUtQO\<oo. (6.2)
(Свойство (6.1) будет обеспечиваться шагом 1 правила 2. Свойство (6.2)
обеспечивается подшагом 3 случая 3 и шагами 2 и 3 правила R2.) Ввиду
(6.1) 	и (6.2), для того чтобы выполнить все Su, необходимо для каждого
v выполнить следующее ключевое условие:
Ru : Если карман Q(Q) содержит бесконечно много постоянных
резидентов с окончательным штатом v, то тогда карман Р(Р) имеет
как минимум один постоянный резидент с окончательным штатом
V.
Легко указать две стратегии для удовлетворения Ru. Первая
стратегия состоит в попытке найти постоянный элемент из Ви. (Это
делается правилом Д2.) Поскольку оппонент контролирует перечисление
множеств { Un }пеим это может оказаться невозможным, поскольку
каждое х из А в штате v впоследствии может быть поднято оппонентом до
некоторого окончательного штата v* v. Вторая стратегия
состоит в том,чтобы увеличить штат почти каждого элемента у в штате v
из Q до некоторого v' v, для которого мы сможем исполнить
первую стратегию. (Это делается посредством правила Д4.) Определение
того, какую стратегию исполнять и, во втором случае, до какого
штата v* v поднимать элементы у в штате v из Q, является главной
проблемой всего построения. Интуитивно, решение этой проблемы
будет состоять в следующем. На основе штатов элементов, которые перед

480
Глава XV. Автоморфизмы решетки в. п. множеств
этим прошли через трек D (и, таким образом, являются кандидатами в
ящик Ви) мы создаем некоторый список М8 (более точно определенный
в определении 6.6) из штатов i/, для которых представляется
возможным на шаге s удовлетворить требование Rv> по первой стратегии. По
Ms мы формально определим Vs следующим образом.
6.3 Определение. Определим
V, = { v : (3j/ € Ms)[v' и] }.
Интуитивно, Vs состоит из тех и, для которых на шаге s оказывается
возможным применить вторую стратегию, а потом и первую.
6.4 Определение. Определим
d(y, s) = max({ -1 } U { е ^ 0 : v{e, у, s) G Vs
& [d(y,t) ^ e на всех шагах i < s,
на которых у уже было в машине М] }).
Грубо говоря, d(y,s) является наибольшей длиной \v\ для таких v ■<
i/(f/,y,s), что на шаге s нам кажется, что мы можем исполнить хотя
бы одну из двух стратегий для удовлетворения Rv. Последняя часть
определения 6.4 обеспечивает, что As[d(y,s)] не возрастает по s после
шага, на котором у попадает в машину М. Таким образом, d(y) =dfn
lims d(y, s) существует.
Если на некотором шаге s в машине М есть элемент у в некотором
штате v (fc VS1 то кажется, что ни одна из двух стратегий не
удовлетворит Rv. В этом случае мы говорим, что требование Rv требует
внимания на шаге 5, и предпринимаем следующее важное действие. Мы
прекращаем все действия, ожидающие появления некоторых событий
(такие как создание списков) для удовлетворения требований Ru> для
\и'\ > |^|, нарушая таким образом все Ru> на шаге s + 1. Формально это
выглядит как исключение из Ms+i (по условию (а) в определении 6.6)
всех v' таких, что \v'\ > \v\. Вследствии этого, d(y,s-f 1) \v\ для
всех у G Qs+i и мы рассматриваем у с требованиями Ru>> такими, что
KI ^ 1И-
Правило Дз отвечает за то, чтобы требование Rv требовало
внимания конечное число раз. Как только Rv требует внимания, мы добавим
к списку % все штаты V\ v. Впоследствии элементы х из трека С2
могут быть подняты в штат V\ и могут быть помещены в трек D по

§ 6. Доказательство теоремы о расширении 4-6
481
правилу Дз. Это увеличит вероятность того, что V\ € Ms и,
следовательно, v G Vs, так что требование Rv не потребует внимания снова.
Важной здесь является лемма 5 из § 6.5, которая показывает, что если
Ru требует внимания бесконечно много раз, то это по правилу Лз
вынудит v принадлежать Vs для всех 5, за исключением их конечного числа,
и потому Rv не может требовать внимания более конечного числа раз.
6-4- Правила
Теперь мы дадим точное описание правил. Сначала нам необходимо одно
определение.
6.5 	Определение, (i) Пусть X (= С, С^Сг, или D) — трек машины
М. Если х в треке X в конце шага s, определим Ss(X) как
последовательность всех штатов и ■< v(x,x,s), и будем говорить, что х
обуславливает v в Ss(X). Пусть Ss(X) будет пустым множеством, если такого
х нет.
(й) Пусть X (= Р или Q) — карман в М. Определим
Sa(X) = { v : (3x)[v ■< u(x,x,s)
& [х G Xs - Xs-i V v(x, x, s) Ф v{x, x, s — 1)]] }.
Будем говорить, что x обуславливает v в Ss{X). (Напомним, ^то по
случаю 1 построения, если х в треке X на шаге 5, то х и X определены
однозначно.)
(Ш) Пусть S(X) — конкатенация последовательностей
Ss{X) для всех s G и. Будем говорить, что х обуславливает v в S(X),
если х обуславливает v в Ss(X) для некоторого s.
(iv) 	Если X — трек или карман М, то определим S^(X) и S(X)
аналогично, используя v(x,x,s). До конца этой главы пусть X будет
переменной, обозначающей треки С, Сг, или D, или карманы Р или
Q. 	Аналогичные значения будет принимать и X для треков и карманов
М.
Правило R\ очень похоже на теорему Фридберга о разложении Х.2.1
и служит для обеспечения того, что если v появляется конечное число
раз в 5(C), то v появляется бесконечно в 5(Ci) и 5(Сг), как мы
доказываем в лемме 1 из § 6.5. Для правила R\ мы фиксируем бесконечную
последовательность, называемую списком, 1Z такой, что для всех v и
каждого i Е { 1,2 } упорядоченная пара (и, i) появляется в 1Z бесконечно

482
Глава XV. Автоморфизмы решетки в. п. множеств
часто. Каждое вхождение {v,i) в R первоначально немаркировапо, но
впоследствии оно может стать и маркированным.
Правило R\. Пусть х находится в треке С в конце шага s. Пусть
(j/, г) — первый немаркированный элемент списка 1Z такой, что v -<
v(x,x,s). Маркируем (и, г) и помещаем х в трек С* на шаге s + 1.
Во время применения правила R2 мы определяем для каждого ящика
Bv кармана Р некоторый список C(BV) из штатов и'. Пусть С8(Ви)
обозначает штаты и', добавленные к C(BV) к концу шага s. Добавленное
к списку вхождение v' сначала не маркировано, но впоследствии может
стать и маркированным. Как правило, один и тот же штат v' может
появляться много раз в С(Ви). (Интуитивно, немаркированные штаты
v' Е С8(Ви) — это те штаты, для которых мы намереваемся добавить
новый элемент х со штатом и' в ящик Bv, если х должен появляться в
треке D и если q(v,s) требует этого.)
Правило R2. Пусть х находится в треке D к концу шага s. Пусть
s' < s будет наибольшим из предыдущих шагов меньших s таких, что
некоторый элемент был в треке D на шаге s'. (Если такого шага нет,
полагаем s' = 0.)
Шаг 1. Для каждого v такого, что
Ф q(v,8)],
удалим из кармана Р каждое у Е BUi8. Для каждого такого у, если
v(y,y,t') ф v{y,y,s), где t' — шаг, на котором у в последний раз был
помещён в карман Р, то поместим у в Н. В противном случае, поместим
у в карман Q.
Шаг 2. Для каждого v такого, что Ви^8 = 0 добавим v' к списку
C8+i{Bv) для всех v' таких, что v <v', |i/| ^ s и v' уже не появляется
немаркированным в списке C8{BV).
Шаг 3. Проверим, существуют ли штаты i/hi/' такие, что v -< v' ■<
i/(x,x,5), v' E £S4-i(Pi/), и и' в настоящий момент является
немаркированным в £s+i(Pl/). Если это так, выберем v наименьшей длины и
затем первый соответствующий немаркированный и' из С8+\(Ви).
Поместим х в ящик Bv кармана Р на шаге s + 1 и пометим это вхождение
и' в списке C8+\{BV). Если таких v и v' не существует, то поместим х
в карман Q.
Этим заканчивается описание правила Дг-

§ 6. Доказательство теоремы о расширении 4-5
483
6.6 	Определение. Для каждого шага s определим множество М8
штатов индукцией по s. Пусть Мо — 0 и
Ms+i = { v : \и Е М8 & v не исключено из A4s+i]
V[i/ £ & I/ 6 5e+i(Z?)] }.
Будем говорить, что v исключено из М8+г, если v 6 М8 и выполнено
одно из двух следующих условий:
Условие (a). (3*/)(ЭХ)[И < |„| & е 5S(X) -Я5].
Условие (Ь). (3i/ ^ = 0 & (V£)|l/|^*^s(Vi// Ч v')
По мы определим Vs и d(y, s) как в определениях 6.3 и 6.4. Пусть
также
= { v : (а.е. s)[v Е Л4в] },
и
Vu; - { v : (а.е. s)[i/ Е Я5] }.
(Мы определим множества штатов MS,VS и функцию d(x, 5) для х € Qs
аналогично, с обычными изменениями.) Этим завершается
определение 6.6.
Для правила Яз определим список Я штатов v следующим
образом. Пусть Н8 состоит из всех v(e,y,t) таких, что е ^ у, t ^ s,
у находится в машине М на шаге t, и для некоторого X мы имеем
v{e,y,s) Е S8(X) — Vs, где X = Ci, С2, С, D, Р или <3- Мы обозначаем
через Н конкатенацию Н8, s Е си, и через конкатенацию Я*, t ^ 5.
Правило Я3. Пусть ж находится в треке С2 к концу шага 5. Пусть
v — (е,£7, т) будет первым немаркированным шагом в Я^5 таким, что
v(e,x,s) ^ J/. Перечислим ж во множества V* для всех г Е т — т(е,ж,$)
и замаркируем это вхождение ^ в (Если такого v не существует,
мы не делаем перечислений.) Поместим х в трек D на шаге s 4-1.
Правило Я4. Пусть у находится в кармане Q к концу шага 5+1,
е = d(y,s) и v(e,y,s) = (е, а, т) ^ Л45. Среди штатов v' = {е,а',т) Е Л45
таких, что a' Э а, выберем 1/, который появлялся наиболее часто в
последовательности Ss(D). Для этого v' перечисляем у в Ui для всех
г Е а' - а.

484
Глава XV. Автоморфизмы решетки в. п. множеств
Мы задали правила R\, R2, R3 и Д4, необходимые для соответствия
Р 4+ Q. Правила R\, R2, R3 и R4 для соответствия Q Р
получаются теперь обычными изменениями. (Заметим, что это перечисление не
удовлетворяет условию (2) из определения И.2.8, поскольку правило R3
(Д4) может перечислить элемент х (несколько элементов у) в
несколько множеств Vi (Ui), а вовсе не обязательно один элемент в одно в. п.
множество. Этого можно было бы избежать добавлением новых шагов,
и это не будет наносить вреда всему построению, описанному выше.)
6.5. Проверка
Теперь мы проведем точный анализ построения с помощью ряда лемм,
получив в итоге (4.7). Тривиальное доказательство индукцией по
перечислению показывает следующее. Каждое х € А (х Е В) помещается в
отверстие Я (Я) на некотором шаге, после чего х (х) оказывается в
машине М (М). Ни одно число не остается навсегда в Я (Я). На каждом
шаге существует самое большее один элемент в одном из треков С, С\,
С2, Я, С, Ci, 62 или D. Это число передвигается вниз на следующем
шаге. Более того, элемент х Е А может двигаться вверх в машине М
(т. е. из кармана Р или Q в Я) только в случае, когда х
перечисляется в некоторое новое множество Ui для i х. Ни один элемент х не
перемещается напрямую из одного ящика Ви из Р в другой ящик Ви>,
хотя х может быть отправлен в отверстие Я и помещён в другой ящик
Ви>, когда х войдет вРв следующий раз. Следовательно, каждое х Е А
будет перемещаться по машине М лишь конечное число раз и в конце
концов остается навсегда либо в кармане Q, либо в одном из ящиков
Ви кармана Р. Аналогичное верно и для элементов у € В в машине М.
Следующие ниже леммы имеют дело лишь с первой половиной
требования Ru для соответствия Р Q. Леммы для соответствия Q <-> Р
доказываются аналогично.
Лемма 1. Каждый штат, входящий бесконечно много раз в S(C),
входит бесконечно много раз и в S(C\), 5(Сг), S(D).
Доказательство. Предположим, что v входит в S(C) бесконечно много
раз. Тогда правило обеспечит, что v появится в S(Ci)
бесконечное число раз для г Е { 1,2 }, поскольку каждое из конечного семейства
вхождений (и, i) в список 1Z в конце в концов будет маркировано, когда
какой-либо элемент х со штатом и на треке С будет помещён в трек Ci.
Но каждый элемент на треке Ci входит в трек D на следующем шаге.
Поэтому v входит в S(D) бесконечное число раз.

§ 6. Доказательство теоремы о расширении 4-5
485
Лемма 2. Для каждого у, постоянного резидента Q, существует
единственный штат v такой, что у = limSq(v,s). Этот штат v
удовлетворяет v < lims v(y, у, s). Более того, для каждого v, если
\imsq(v, s) существует, то и lims s) существует для каждого
v1 < V.
Доказательство. Зафиксируем у и предположим, что первая часть
леммы истинна для всех z < у. Выберем шаг s0 так, чтобы
(Vs ^ s0)(Vz < y)(Vi/)[[z € Qs г € <9*0]
k [q{v, So) = 2 =>• q[y, s) = z] _
k v{y,y,8о) = I'(y,y,s) ky e Q*].
Тогда для некоторого v у = q(v,so), и для всех v' -< v выполнено
q{v',sо) < У- Таким образом, для всех s > so выполняется у = q(v,s)
и q{v' ,s) = q{v',sq) для всех v' ^ i/.
Для второй части выберем $о так, чтобы у = q(v,s) для всех 5 ^
5о- Если i/ -< I/ и limeg(i/,s) не существует, то по определению 6.2
существует s\ > so такой, что у = q(v',s\) противоречие.
Лемма 3. Пусть v — такой штат, что лишь конечное число
штатов v' >Т v входит в S(D). Тогда существует лишь конечное число
шагов s, на которых v исключается из Ais+i в соответствии с
условием (Ь).
Доказательство. Пусть лемма не выполняется для v. Тогда по
определению Л4в+1, существует бесконечно много шагов s, на которых v Е
Л48+1 — Л48, и v впоследствии исключается из M.t+\ для некоторого
t > s. Следовательно, v появляется бесконечно много раз в S(D). Из
этого, в свою очередь, по условию (Ь) следует, что существует
некоторый Vq < v наименьшей длины такой, что ни один элемент не является
постоянным резидентом ящика BUQ и q(v') = lims q(v‘ ,s) существует для
всех v1 ■< vo. Следовательно, по шагу 3 правила R2 существует
бесконечно много шагов, на которых BVQ = 0. Таким образом, v входит конечное
число раз в список С(Вио) в соответствии с шагом 2 правила i?2*
Следовательно, бесконечно много элементов х в штате v попадают в ящик
Ви0 в соответствии с шагом 3 правила R2 (т. к. v появляется в S(D)
бесконечное число раз и v встречается в списке C{BV>) лишь конечное
число раз для каждого v* -< v в силу минимальности i^o). Но все эти
элементы х впоследствии покидают ящик BUQ. Ввиду того, что lims q(vо, s)
существует, лишь конечное число элементов х покинет Вио из-за шага 1

486
Глава XV. Автоморфизмы решетки в. п. множеств
правила R2, таким образом, в соответствии с шагом 3 случая 3, почти
все х покидают BVQ только тогда, когда они перечисляются в Un для
некоторого п \is0\. Каждое такое х покинет BUQ, имея некоторый штат
i^i >т 1/о и будучи помещённым в отверстие Н, а затем попадет в трек С,
все ещё имея штат v\. Следовательно, существует штат v' >Т is, is* У isx
такой, что is1 появляется в S(C) бесконечное число раз и поэтому is1
появляется в 5(D) бесконечно много раз по лемме 1, что противоречит
предположению о v.
Лемма 4. Зафиксируем е. Предположим, что существует самое
большее конечное число шагов таких, что некоторый штат is
длины е исключается из Ms+i по условию (а). Тогда
(Vt/)|H=e[(3°°s)[^ е Vs] => V 6 Тш\.
Доказательство. Предположим, что существует лишь конечное число
шагов s таких, что некоторый штат длины ^ е исключается из Ms+1 по
условию (а). Зафиксируем v длины е такое, что v G Vs для бесконечно
многих s. Заметим, что по определению 6.3,
v G Vs => (3i/ v)[v' G Ms]- (6.3)
Если v1 G Мш, to is € Vui- В противном случае, если v1 удовлетворяет
(6.3) 	для бесконечно многих s, то is* добавляется бесконечное число раз в
Ms+i и потом исключается. В этом случае v' входит в S(D) бесконечно
часто. Выберем v* v такое, что и1 входит в S(D) бесконечное число
раз и ни одно vn >т is1 не входит в S(D) бесконечное число раз. Теперь по
лемме 3 v' исключается из Ms+1 лишь конечное число раз посредством
условия (Ь). Следовательно, v' G Ми,, откуда получаем v G TV
Лемма 5. Пусть X — трек или карман машины М и X — трек или
карман машины М. Тогдаогдаогда
(i) (Vj/)(VX)[j/ входит бесконечное число раз в S(X) => v G VJ\,
(ii) (Vi/)(VX)[i/ входит бесконечное число раз в <S(X) => v G Vu}-
Доказательство. Доказываем одновременно (i) и (ii) индукцией по \и\.
Предположим, что (i) и (й) выполнены для всех v таких, что \v\ < е.
Тогда каждый штат длины е исключается из Ms+\ или Ms+i
посредством условия (а) лишь для конечного числа шагов s. Достаточно
доказать (i) для всех v длины е, поскольку (ii) ему двойственно.

§ 6. Доказательство теоремы о расширении 4-6
487
Предположим противное, т. е. (i) не выполнено для некоторого штата
v\ длины е. Зафиксируем некоторое X такое, что v\ входит в S(X)
бесконечное число раз. Следовательно, по лемме 4 v\ £ S8(X) — Vs для
бесконечно многих s. Следовательно,
(Vi')[v G Мш => \v\ < е], (6.4)
по условию (а) исключения из A4s+i.
Зафиксируем бесконечно много различных элементов yj и шагов tj,
j £ и, таких, что yj для всех j £ uj обуславливает v\ £ Stj(X) — Vtr
Пусть Tj будет конечной последовательностью штатов v таких, что
(3s tj)[yj в машине М на шаге s и v(e,yj,s) = v].
Пусть Т будет конкатенацией последовательностей Tj, j G ш. Поскольку
v\ входит в Т бесконечно много раз, следующие два утверждения (ниже
доказываемые отдельно) дают v\ £7^, что является противоречием.
Утверждение 1. Если v входит бесконечно много раз в Т и
некоторое v* ^ v входит бесконечно много раз в S(C), то некоторое v" v
входит бесконечно много раз в S(D) и v £
Доказательство утверждения 1. Штат v появляется в списке И для
правила Rz бесконечное число раз, поскольку v входит в Т бесконечное
число раз. Предположим, что и1 ^ v и и1 входит в S(C) бесконечное
число раз. Пусть v = (е,о,т) и is1 = (е,о‘,т;), причем о С о' и т D т1.
Тогда v' входит в 5(Сг) бесконечное число раз в силу леммы 1. Пусть
vn — (е^1 ,т), так что vn v. Теперь по правилу Rz бесконечно много
элементов х в треке Съ из штата v‘ поднимаются в штат v" и потом
помещаются в трек D. Таким образом, для бесконечно многих s, v" £
М8, и, следовательно, v £ Vs- Отсюда по лемме 4 имеем v £
Утверждение 2. Если v входит в Т бесконечное число раз, то и
некоторое и1 ^ v входит в S(C) бесконечное число раз.
Доказательство утверждения 2. Предположим противное, т. е. пусть
утверждение 2 ложно. Зафиксируем V2 = (6,02,72) такое, что 02
минимально и 72 минимально для 02 среди всех возможных V2, для
которых утверждение ложно. По гипотезе (4.11) о покрытии теоремы о
расширении 4.5 невозможно, чтобы бесконечно много yj были уже в
штате V2 в момент входа в машину М. Следовательно, существует штат
Vz — (е, 03,73) ф V2, бесконечное множество J С ш и шаги Sj tj, j £ J

488
Глава XV. Автоморфизмы решетки в. п. множеств
такие, что для каждого j Е J, yj находится в машине М на шаге Sj — 1,
v{sj - 1 ,e,j/j) = t/3 и i/(sj,e,yj) = v2.
По минимальности о 2 и 72 утверждение 2 выполнено для v3. Таким
образом, мы не можем иметь oz = 02 и тз С Т2, поскольку в этом
случае vз ^ ^2, и тогда утверждение 2 будет верно для V2, поскольку оно
верно для i/3. Поэтому мы можем считать, что о3 С^. Следовательно,
существует бесконечное множество J1 С J такое, что для всех j Е J'
правило Дз применяется к на шаге Sj (случай 1 ниже) или же для
каждого j Е J' правило R4 применяется к yj на шаге sj (случай 2 ниже).
Случай 1. Для каждого j Е </' правило Rz применяется к yj на
шаге sj. По предположению индукции существует лишь конечное
число v в списке Н для правила Rz таких, что \v\ < е.
Следовательно, для почти всех j Е J' во время применения правила Rz на шаге
Sj мы маркируем некоторое v' = (е',0'/,т/) в Ц такое, что е' ^ е и
(е,а' I4 (е 4- 1),т' I4 (е 4- 1)) ^ ^2- По определению И мы знаем, что
элемент х в машине М, обусловивший появление v' в Д, ранее прошел
трек С в некотором штате v" ^ и1 (а именно, когда он впервые
прошел трек С после достижения е-штата а1). Следовательно, некоторое
v2 ^ v2 появляется в <S(C) бесконечно много раз.
Случай 2. Для всех j Е J' правило R4 применяется к yj на шаге
Sj. Следовательно, для почти всех j Е J' выполнено d(yj,Sj — 1) ^ е
по минимальности 02 и утверждению 1. Сначала предположим, что
d{yj,sj — 1) > е для бесконечно многих j Е J'. Тогда для каждого из
этих j найдется некоторое v(j) у V2 из MSj~ 1 такое, что \v(j)\ > е.
По (6.4) ни одно из этих v(j) не лежит в Ми. Следовательно, для
бесконечно многих s некоторое v(j) у V2 добавляется к Л4в+1, и поэтому
v(j) появляется в Ss(D). Таким образом, некоторое v* ^ V2 входит
бесконечно много раз в S(C). Далее, предположим, что d(yj,Sj — 1) = е
для почти всех j Е J1. Поскольку утверждение 2 выполнено для vz,
некоторое v1 ^ г vз в силу утверждения 1 входит бесконечное число раз
в S(D). Выберем v" как максимальное и' относительно такое, что
и' обладает этим свойством. Следовательно, v" появляется в 5(D)
бесконечно много раз и v" Е Мш по лемме 3 и предположению индукции.
Но применив R4 к yj на шаге Sj — 1, мы поднимаем yj в штат v i/3,
v Е A4Sj-i, который появляется максимально часто в S(D). Ввиду этого
V2 входит бесконечное число раз в S(D), поскольку так же себя ведет
и v". Итак, некоторый v2 ^<7 Щ входит бесконечное число раз в 5(C),
т. к. произвольное х в треке D перед этим находилось в треке С в том
же самом a-штате. Это доказывает утверждение 2 и лемму 5.

§ 6. Доказательство теоремы о расширении 4-5
489
Лемма 6. (i) Для каждого е Е си существует только конечное число
элементов у Е В таких, что d(y) =dfn 1 ims d(y, s) < e.
(ii) Если у остается навсегда в кармане Q и d(y) ^ 0, то
limSv{d(y),y,s) Е Ми.
Доказательство, (i). Произвольное у € В в конце концов
стабилизируется, цолучая окончательный штат v(y,y) и попадая навсегда в карман
Р или Q, где оно обуславливает добавления всех v -< v(y,y) к S(P) или
S(Q). Следовательно, по лемме 5(i) и определению 6.4 условие d(y) < е
для всех е € си выполняется лишь для конечного числа у Е В.
(й). Возьмем шаг so, после которого у остается в кармане Q, d(y,s)
и v(y,y,s) уже не изменяются и d(£) ^ 0. Тогда для всех s ^ $о
lim, u(d(y),y,s) = v{d{y), у, s + 1) € Ms
из-за применения правила R4 на шаге s + 1.
Лемма 7. Для каждого и, если карман Q содержит бесконечно
много постоянных резидентов, имеющих окончательный штат и, то этим
же свойством обладает и карман Р. Более того, ящик Bv кармана Р
имеет лишь конечное число постоянных резидентов и каждый из них
имеет окончательный штат v.
Доказательство. Предположим, что S — бесконечное множествоство
постоянных резидентов кармана Q, имеющих окончательный штат v.
Достаточно показать, что ящик Bv кармана Р содержит хотя бы одного
постоянного резидента. (Этого уже достаточно, поскольку для каждого
k ^ \v\ найдется vk У v, \vk\ = к такое, что Q содержит бесконечно много
постоянных резидентов, имеющих окончательный штат vОтсюда по
доказанному выше ящик BUk имеет постоянного резидента.)
По лемме 2, для каждого у Е S найдется штат Vy такой, что у =
lims q(vy, s) и Vy ■< lims v(y, у, s). Поскольку никакие два элемента у Е S
не могут иметь одни и те же штаты Vy, v ■< Vy для почти всех у Е S.
Следовательно, по лемме 2 мы можем выбрать $о так, чтобы
(Vi/ ч i/)(Vs ^ So)[q(U,s) - g(v',So)]-
Пусть Т = { v : v = lim8v(d(y),y,s) & у Е S }. По лемме 6(ii), Т
является бесконечным подмножеством МВозьмем произвольное v\ Е
Т, |^i | ^ so и v < v\. Определим
£0 = ^ t)[vi Е М?].

490
Глава XV. Автоморфизмы решетки в. п. множеств
Тогда Bv^s ф 0 для всех s ^ to, поскольку в противном случае V\
исключается из М8+1 по условию (Ь). Следовательно, список С(Ви) конечен
по шагу 2 правила /?2- Поэтому лишь конечное число элементов
попадает в ящик Ви по шагу 3 правила Дг, т. к. каждый входящий элемент
маркирует некоторое вхождение подходящего v1 в списке C(BV). Значит,
некоторый элемент навсегда останется в ящике Bv. По шагу 3
правила и шагу 3 случая 3, каждый элемент х, попадающий в ящик Ви,
имеет штат v и сохраняет его на время пребывания в Bv (хотя х может
быть перечислен в Un для некоторого п > \и\). Таким образом, ящик Ви
имеет лишь конечное число постоянных резидентов, и каждый из них
имеет окончательный штат v.
Лемма 8. Для каждого и, если карман Р имеет бесконечно много
резидентов, имеющих окончательный штат v, то таким является и
карман Q.
Доказательство. Если карман Р содержит бесконечно много
постоянных резидентов х с окончательным штатом v, то почти для всех таких
х существует v' У v такое, что х — постоянный резидент ящика Bv<, и
каждый ящик Bv< по лемме 7 содержит лишь конечное число постоянных
резидентов. Для каждого такого и1 шаг 1 правила R2 обеспечивает, что
уи> = lims <?(*/, s) существует, и yv> находится в окончательном штате v'
по лемме 2.
Леммы 7 и 8 устанавливают (4.7) для соответствия Р <-> Q.
Доказательство для соответствия Р ы Q совершенно аналогично. Этим
завершается доказательство теоремы о расширении 4.5. О
6.7 	Замечания. Определения, обозначения и основные идеи
доказательства, представленные в параграфах 4, 5 и 6, взяты из работы Со-
ара [1974]. Различные упрощения и улучшения взяты из работы Ма-
асса [1983]. В изложении имеются также и другие, более поздние,
модификации. Существенные поправки и предложения по текущей версии
главы XV сделали В. Харизанова, С. Лемпп и М. Стоб. Дальнейшие
результаты и открытые вопросы по автоморфизмам содержатся в
главе XVI, § 1.

Глава XVI
Дальнейшие результаты и открытые
вопросы о в. п. множествах и степенях
В этой главе мы попытаемся привести без доказательств краткий обзор
некоторых дальнейших результатов и открытых вопросов о в. п.
множествах и в. п. степенях, которые были бы изучены более подробно в
этой книге, если бы позволяли время и объем. Читатель сможет увидеть
здесь, как комбинируются и обобщаются разнообразные результаты и
методы из глав VII-XV. Мы не ставим перед собой цель дать
исчерпывающее изложение всех вопросов теории вычислимости и исключаем из
рассмотрения многие её важные и активно исследуемые в настоящее
время области, например, такие, как общая теория тьюринговых степеней,
теория вычислимых моделей, эффективная математика, вычислительная
сложность и другие.
§ 1. Автоморфизмы и изоморфизмы решётки в. п.
множеств
Метод построения автоморфизмов из главы XV был расширен для
получения богатой информации о структуре в. п. множеств и об их
алгебраических свойствах в решетке £. Большинство из этих результатов
показывает скорее удивительную и очень приятную однородность
структуры £, чем ее патологические свойства, также, как и некоторые другие
результаты о в. п. множествах и степенях. Вспомним определение Х.2.6
решетки С{А) надмножеств А Е £. Робинсон (упражнение XI.3.5)
использовал метод оракулов для аппроксимации низких в. п. множеств А
при доказательстве того факта, что если низкое в. п. множество А ко-
бесконечно, то А имеет максимальное надмножество. Было замечено,
что метод Робинсона использовал ослабленную гипотезу «А полуниз¬

492
Глава XVI. Открытые вопросы
кое» (см. упражнения IV.4.7 и XI.3.6(а)) вместо «А низкое». Позднее
Соар использовал аналогичные рассуждения вместе с методом
построения автоморфизмов из главы XV для доказательства следующей
характеризации решетки С(А) для таких множеств.
1.1 Теорема (Соар [1982а]). Если А в. п. , кобесконечно и А полуниз-
кое (как определено в упражнении IV.4-6), то С(А) = £, более того,
С* (А) эффективно изоморфно £* (пишем С* (A) =eff £*) в смысле
определения XV. 2.10.
Этот результат показывает большое сходство низких в. п. множеств
и вычислимых множеств, поскольку очевидно, что C*(R) =eff £*, если
R вычислимо и кобесконечно. По аналогии с определением по л у низкого
(= 1-полунизкого) в упражнении IV.4.6 мы теперь будем говорить, что
множество S 1.5-полунизкое, если
{ х : Wx П S конечно} 0".
Если S полунизкое, то S является 1.5-полунизким, но не наоборот. Ко-
бесконечные в. п. множества А с полу низкими и 1.5-полу низкими
дополнениями изучались Беннисоном и Соаром [1978]. Ими была
обнаружена связь свойств индексных множеств таких множеств со свойствами
вычислительной сложности А в терминах последовательностей
сложности Мейера-Фишера (см. обзор у Соара [1982Ь]). Они также
показали, что каждое кобесконечное в. п. множество А такое, что А
является 1.5-полунизким, имеет максимальное надмножество. Маасе соединил
метод использования гипотезы «А 1.5-полунизкое» с расширением
техники автоморфизмов, использованной в теореме 1.1 для получения
следующей очень приятной характеризации в. п. множеств А со свойством
С* {A) =“eff £*.
1.2 Теорема (Маасе [1983]). Если А в. п. и кобесконечно, то С* [A) =eff
£* эквивалентно тому, что А является 1.5-полунизким.
В одну сторону это утверждение получается непосредственно, в то
время как другая часть требует дальнейшего развития техники
автоморфизмов из главы XV. В обеих теоремах 1.1 и 1.2, изоморфизму С(А) = £
ранее предшествовал более слабый результат о том, что множество А
имеет максимальное надмножество, если А бесконечно и по л у низко (1.5-
полунизко). Поэтому теорема XI.5.1 наводит на мысль, что следующий
открытый вопрос может иметь положительное решение.

§ 1. Автоморфизмы и изоморфизмы решётки £
493
1.3 Открытый вопрос. Верно ли, что если в. п., кобесконечное
множество А 2-низко, то С(А) = £ А
По теореме 1.2 мы не можем надеяться, что ответ на вопрос 1.3 будет
получен в виде С* (A) =eff £*, поскольку существуют кобесконечные в. п.
множества А такие, что А является 2-низким, но не 1.5-полунизким. Тем
не менее, изоморфизм мог бы быть эффективным при выполнении
некоторых дополнительных условий. Положительный ответ на вопрос 1.3
мог бы быть первым шагом в изучении вопросов XI.4.5 и, в частности,
в доказательстве строки ХЦ4.8). Заметим, что мы не можем надеяться
получить 1.3 для 3-низких в. п. множеств вместо 2-низких, т. к.
теорема XI.4.1 утверждает, что не 2-низкие в. п. степени содержат
безатомные в. п. множества, т. е. n-низкие в. п. множества при п ^ 3 не всегда
могут иметь максимальные надмножества.
Вспомним определение Х.2.2 решетки £(S) = {W C\S : W € £}
для S С и, а также то, что £{А) = С(А) для A Е £. В § 4 главы X
мы изучали свойства мажорных подмножеств В (обозначаем В Ст А)
в. п. множества А. Расширением техники автоморфизмов из главы XV
Маасе и Стоб показали, что существует единственный тип изоморфизма
интервалов, определяемых мажорными подмножествами.
1.4 Теорема (Маасе, Стоб [1983]). Если Bi Ст М и В2 Ст А2, то
£(А1-В1)^£(А2-В2).
1.5 Следствие. Если А и В г-максимальные множества с
максимальными надмножествами, то £(А) = £{В).
Следствие 1.5 однако не классифицирует типы автоморфизма г-мак-
симальных множеств с указанным свойством, т. к. по данному
максимальному множеству М мы можем найти мажорные подмножества А и
В такие, что А СSm М, но при этом неверно, что В Cs М (см.
определение Х.4.10 и упражнение Х.4.12), откуда А и В не могут быть ав-
томорфными. Другое доказательство этого факта вместе с дальнейшей
информацией о мажорных подмножествах можно найти у Маасса [1985Ь].
1.6 Открытый вопрос. Классифицировать типы автоморфизма г-
максимальных множеств.1  2
1 По-видимому, ответ на этот вопрос все ещё неизвестен. — Прим, редактора.
2Это пока ещё не сделано. Чолак и Ниис [1999] доказали существование
бесконечно много различных типов изоморфизма решеток Ь(А) в. п. надмножеств г-
максимального множества А. — Прим, редактора.

494
Глава XVI. Открытые вопросы
Очень важным вопросом, дающим простор для дальнейших
исследований, является следующий
1.7 Открытый вопрос. Если А,В€£ и С(А) = С(В), то при каких
условиях А автоморфно В (A =aut В).3
По замечанию, сделанному после следствия 1.5 мы знаем, что С(А) =
С(В) не всегда влечет существование автоморфизма между А и В.
(Наоборот, мы можем выбрать А низким и простым, а В вычислимым и
кобесконечным. Тогда по теореме 1.1 С(А) = £{В), но не А =£ В.) По
следствию XV.4.9 С(А) = С(В) влечет A =aut В, если С* (А) конечно
(и, следовательно, конечная булева алгебра). Но это уже неверно, если
С* (А) является бесконечной булевой алгеброй, даже если С* (А) ведет
себя настолько хорошо, что является счётной безатомной булевой
алгеброй.
1.8 Теорема (Лерман, Шор и Соар [1978]). Существуют неавто-
морфные в. п. множества А и В такие, что С{А) = £{В) и С*(А)
является счётной безатомной булевой алгеброй.
Мы будем писать С Crm D, если С Ст Г> и при этом С г-макси-
мяльно в D. Лерман, Шор и Соар доказали, что в. п. множество А имеет
rm-подмножество С тогда и только тогда, когда А имеет «Дз-функцию
предпочтения» (что является некоторым свойством А), а также
доказали существование множеств А и В, удовлетворяющих теореме 1.8 и
таких, что А имеет rm-подмножество, а В — нет. В положительном
направлении Маасе показал, что 1.7 выполняется в случае булевых алгебр,
если мы добавим следующую более сильную гипотезу об изоморфизме
С(А) = С(В).
1.9 Теорема (Маасе [1984]). Если А, В G £, С* (А) — булева алгебра и
С* (А) = С*(В) посредством некоторого Е° -изоморфизма, то А =£ В.
Теорема 1.9 не может быть усилена заменой Е§ на Е° ввиду
теоремы 1.8 и того факта, что если А и В — безатомные гг-простые
множества, то стандартная челночная конструкция дает Е4 -изоморфизм между
С*{А) и £*{В).
3Ответ на этот вопрос в том виде, как он здесь сформулирован, все ещё не получен.
П. Чолак [1995] установил, что для любого невычислимого множества А такого, что
С*(А) бесконечно, существует такое множество В, что С*(А) ^ С*(В), но А и В не
автоморфны. — Прим, редактора.

§ 1. Автоморфизмы и изоморфизмы решётки £
495
Будем говорить, что дополнение А в. п. множества А 2-полунизкое,
если
{ е : We П А бесконечно } ^т 0;/*
Многие классы в. п. множеств (например, безатомные гипергипер-
простые множества) содержат, в частности, таких представителей А,
что А является 2-полунизким. Из теоремы 1.9 следует, что если С(А) =
С(В), С*{А) безатомная булева алгебра, А и В являются 2 полунизки-
ми, то А =£ В. Херманн [1989] дал дальнейшую классификацию орбит
гг-простых множеств А с одинаковыми С(А) и показал, что они могут
содержаться в бесконечно многих различных орбитах.
Маасе [1982] дал альтернативное решение проблемы Поста, построив
в. п. множество, которое является генерическим в обычном
теоретикомножественном смысле, но где понятие вынуждения вводится
относительно малых универсумов. Маасе показал, что все в. п. генерические
множества А быстро простые и низкие (и поэтому А полу низкое) и,
следовательно, их тьюринговы степени лежат строго между 0 и О'.
1.10 	Теорема (Маасе [1982]). Если А и В быстро простые, кобеско-
нечные множества, имеющие полунизкие дополнения, то А =£ В.
Доказательство теоремы 1.10 несложно, но использует теорему 1.1
вместе с доказательством того, что в теореме о расширении XV.4.5 все
предположения выполняются одновременно, если оба множества А и В
быстро простые. Пусть G — класс степеней множеств, автоморфных в
£ в. п. генерическим множествам. Амбос-Шпиис, Джокуш, Шор и Со-
ар [1984] показали, что
G == ENC = NC = PS = LC,
где последние три равенства были установлены в теоремах XIII.2.2 и
XIII.4.2. Другие результаты о быстро простых множествах содержатся
в Маасе [1985а] и Маасе, Шор и Стоб [1981]. Новое понятие генеричнос-
ти для в. п. множеств, названное е-генеричностью, было введено Джо-
кушем [1985] и обобщено в Нероудом и Реммелем в [1985а] и [1985b]. С
е-генерическими множествами легче работать, чем с в. п.
генерическими множествами, и поэтому о е-генерических в. п. множествах известно
больше, чем о в. п. генерических множествах.
Теорема 1.10 применяется при доказательстве неинвариантности
того или иного свойства в. п. множеств. В теореме XV.3.1 и следствии 4.7
главы XV мы видели, что г-простые множества и тьюринговы степени

496
Глава XVI. Открытые вопросы
не являются инвариантными классами в £. Стоб [1982а] обобщил
теорему расширения для доказательства того, что плотная простота не
инвариантна в £. Позднее Маасе и Стоб заметили, что этот результат
можно получить и из теоремы 1.10, построив плотно простое, быстро
простое множество А такое, что А полу низкое, поскольку легко строится
быстро простое низкое множество В, которое по упражнению XI. 1.11 не
может быть плотно простым. Таким образом, орбита в. п. генерических
множеств содержит удивительно богатое многообразие в. п. множеств.
Вопрос об определимости этой орбиты (а в случае отрицательного
ответа — вопрос о характеризации её каким-либо другим образом) является
открытым. Свойство быстрой простоты не инвариантно относительно
Aut(£), поскольку можно построить максимальные множества А и В
такие, что А является быстро простым, а множество В — нет. Маасе, Шор
и Стоб [1981] показали однако, что свойство быстрой простоты влечет
некоторое свойство разложения, которое инвариантно.
1.11 Открытый вопрос. Существует ли A Е £ такое, что
deg{W : W~eA}= R+?4
Заметим, что теорема 1.10 не может быть использована для ответа
на этот вопрос, поскольку PS расщепляет R по теореме XIII.2.2.
Один из самых интересных вопросов о в. п. множествах —
классификация их орбит. В главе XV мы видели, что креативные и максимальные
множества образуют орбиты. Доуни и Стоб [1992] назвали невычислимое
в. п. множество А гемимаксимальным , если существует максимальное
множество М и невычислимое в. п. множество В такие, что М = АиВ и
АП В = 0 (например, если А и В получены из М по теореме Фридберга
о разложении Х.2.1). Они доказали следующий неожиданный результат:
1.12 Теорема (Доуни и Стоб [1992]). Любые два гемимаксималъных
множества АиВ автоморфны.
Идея доказательства состоит в том, чтобы сначала модифицировать
теорему XV.5.2 для установления С{А) — С(В) и одновременно
использовать невычислимость А и В для получения условий теоремы о
расширении XV.4.5. Пусть НМ — класс степеней гемимаксимальных
множеств. Доуни и Стоб показали, что Hi С НМ, R+ £ НМ и что для
4 Отрицательный ответ на этот вопрос получен Доуни и Харрингтоном [1996]. Они
доказали, что существуют такие в. п. степени а, b и с, что а является низкой, b и
с являются 2-высокими, и не существует в. п. множества, степень которого
принадлежит интервалу [а, Ь] и которое было бы автоморфно некоторому в. п. множеству
степени < с. — Прим, редактора.

§ 1. Автоморфизмы и изоморфизмы решётки £
497
каждой степени а Е R+ существует b Е НМ такое, что b а. Скачки
степеней гемимаксимальных множеств не изучены. Гемимаксимальные
множества дают первый пример определимого в £ класса, образующего
орбиту и содержащего низкие ненулевые степени. Заметим, что
гемимаксимальные множества являются примером того, что класс степеней
множеств, содержащихся в некоторой орбите невычислимых множеств,
не обязательно замкнут вверх в R.
1.13 Открытый вопрос. Пусть С — класс простых множеств,
образующих орбиту. Образует ли орбиту { А : А — половина фридбергова
разложения некоторого множества из С }, где множества Ао и А\
образуют фридбергово разложение В, если выполнены условия (i), (ii) и (iii)
теоремы Х.2.1.5
Этот вопрос был поставлен Доуни и Стобом [1993], которые
предложили начать его изучение с исследования фридберговых разложений
низких быстро простых множеств. Большим открытым вопросом является
следующее: верно ли, что каждая орбита (невычислимого множества)
содержит 0', а именно
1.14 Открытый вопрос. Верно ли, что для любого
невычислимого в. п. множества А существует такой автоморфизм Ф Е Autf, что
Ф(А) =Т 0'?6
Этот вопрос представляется довольно трудным. (Некоторые
частичные результаты были получены Доуни и Стобом [1992, теоремы 9 и 12];
из них следует, что каждое 2-низкое простое множество, каждое простое
А с 1.5—полунизким дополнением и каждое плотно простое множество
с максимальным надмножеством автоморфно некоторому полному
множеству.) Двойственный вопрос состоит в том, всякая ли орбита
содержит некоторую степень а < (У. По теореме XV. 1.1 это не может быть
истинным именно в такой формулировке. Действительно, Харрингтон
утверждает, что существует орбита, состоящая только из полных по
Тьюрингу, но не креативных множеств. Тем не менее, Харрингтон
также утверждает, что этот вопрос в несколько измененной формулировке
имеет положительный ответ. А именно, он утверждает, что если А в. и.
5Доуни и Стоб [1993] получили отрицательный ответ на этот вопрос. — Прим,
редактора.
6Харрингтон и Соар [1998а], [1998b] доказали, что ответ на этот вопрос
отрицателен. — Прим, редактора.

498
Глава XVI. Открытые вопросы
не вычислимо и не полно, то в орбите А существует множество В
такое, что В А. Следующий ослабленный вариант вопроса 1.14 также
открыт: верно ли, что каждое невычислимое в. п. множество содержит
в своей орбите некоторое высокое множество.7  8Теорема Мартина XI.2.3 о степенях максимальных множеств
наводит на мысль, что вопрос 1.14 может быть усилен доказательством того,
что каждая орбита, содержащая невычислимое в. п. множество,
содержит также множества из каждой высокой в. п. степени. Маасе, Шор
и Стоб [1981] опровергли это, доказав, что степени не гг-простых
множеств с некоторым свойством разложения (определимым в £)
совпадают со степенями PS быстро простых множеств из теоремы XIII.2.2,
а последние, как известно, нетривиально расщепляют Hi. Однако этот
вопрос все ещё остается открытым для С{А) вместо орбиты (А), и
представляет большой интерес, т. к. его решение дало бы самое сильное из
возможных обобщений теоремы Мартина.
1.15 	Открытый вопрос. Пусть A е £ и d — высокая степень.
Существует ли в. п. множество Bed такое, что С{А) = С(В)?в
В теореме XI.2.3 Мартина это подтверждается для двухэлементной
булевой алгебры £*(А), а Лахлан [1986, стр. 27] доказал это для случая,
когда С* {А) является произвольной булевой алгеброй. Харрингтон
сообщил, что для любого кобесконечного А е £ существует В е £ такое,
что 0 < deg(i?) < O' и С(А) = £(В), что в некоторой степени говорит в
пользу 1.15 (см. также XI.2.20).
§ 2. Элементарная теория S
Пусть ТЪ (£) (ТЪ (£*)) — элементарная теория решетки £(£*) в языке
L(C,n,U,0,1), где 0 и 1 интерпретируются как наименьший и
наибольший элементы решетки. Лахлан показал в [1968с, теорема 1], что
проблема разрешимости для ТЪ (£) сводится к той же проблеме для ТЪ (£*)
и наоборот. (На самом деле он доказал первое сведение для любой
подрешетки С в ЛГ, замкнутой относительно симметрической разности с
конечными множествами, где С* = С/Т. Первое сведение основано на
7Ответ на этот вопрос положителен, см. следующее примечание. — Прим,
редактора.
8Положительный ответ на этот вопрос получен Чолаком [1995] и, независимо,
Соаром и Харрингтоном [1996]. В этих работах также установлено, что множество
В можно выбрать таким, что А, кроме того, автоморфно В. — Прим, редактора.

§ 2. Элементарная теория £
499
элиминации кванторов, а второе является простым следствием того
факта, что конечные множества, как мы видели в главе X (1.2), определимы
в £.)
Первое крупное продвижение в решении проблемы для ТЪ (£) было
сделано Лахланом [1968d]. Вспомним, что В обозначает булеву
алгебру, порожденную £. Лахлан добавил к языку унарный предикат Е(х),
интерпретируемый над (£*,/?*) как «х Е £*». УЗ-предложения этого
языка имеют вид (Ух\)... (Vzn)(Eto/i)... (Зут)Р(х,у), где предикат Р не
содержит кванторов.
2.1 	Теорема (Лахлан [1968d]). Существует разрешающая процедура
для УЗ-предложений, истинных в В*, в которых кванторы пробегают
£\
Лахлан начал с доказательства того, что все совместные экзистен-
циональные предложения истинны в £*. Решётка С называется
отделимой, если для любой пары х, у элементов С в С существует пара
дизъюнктивных элементов х\ и у\ таких , что х\ х, у\ у и x\Uyi = xUy.
Ясно, что £* отделима. Лахлан свел проблему УЗ-разрешимости для £*
к следующему. Пусть даны конечные отделимые решетки L, L\, L2, ...,
Lk такие, что каждая Li — утончение L. В каких случаях будет верным,
что для всех подрешеток С в £* таких, что С = L, существует
подрешетка £' в £* такая, что одна из следующих диаграмм коммутативна
для 1 г fc?
С
L
С—
Диаграмма 2.1
Для каждой конечной отделимой решетки L Лахлан дает
«каноническую реализацию» С С £*,£ = L. Эти канонические реализации
обеспечивают необходимые условия коммутативности диаграммы. Для
построения канонической реализации Лахлану нужны лишь следующие факты
о £:
(1) принцип редукции (следствие П.1.10),
(2) для любого бесконечного А Е £, £(А) = £ (очевидно),
(3) существование бесконечного кобесконечного вычислимого
множества,

500
Глава XVI. Открытые вопросы
(4) существование максимального множества (теорема Х.3.3),
(5) теорема Фридберга о разложении (теорема Х.2.1) с условием (in),
(6) теорема о малом мажорном подмножестве (упражнение Х.4.12).
Например, если отделимая решетка L состоит из 0, х\, хг, х$, 1
таких, что х\ С 1, Х2,х$ С xi и Х2 П хз = 0, то метод Лахлана позволяет
получить решетку С = L, состоящую из в. п. множеств Ао, Ai, А2 и
Аз, где Ао = и, Ai — максимальное множество, В Csm Ai, а А2 и
Аз образуют фридбергово разложение Б. Эти канонические реализации
опровергают большой класс УЗ-предложений. Например, не существует
W Е 8 такого, что W расщепляет А\, и не существует F € £ такого, что
Ai С V, но В V. Теорема Лахлана об утончении [1968d, теорема 4]
показывает, что эти необходимые условия являются также и
достаточными. Он определяет понятие характеристики для конечных отделимых
решеток, которые их вполне упорядочивают. Его теорема об утончении
либо позволяет получить £' С £* такую, что диаграмма 2.1 коммутативна,
либо показывает, что контрпример уже содержится среди канонических
реализаций некоторого конечного эффективно определяемого множества
решеток характеристики меньшей, чем у L. В этом состоит суть
разрешающей процедуры. Используя сходный метод, Стоб [1979] получил
разрешающую процедуру для УЗ-предложений, истинных в 8(В — А),
где А Ст В. По теореме 1.4 есть только один тип изоморфизма для
таких интервалов. Результат Стоба может быть выведен из теорем 1.4
и 2.1.
Лерман и Соар [1980b] расширили метод Лахлана для
V3-предложений расширенного языка, истинных в 8*. Расширенный язык
содержит новые предикаты, такие как Мах(х) и Hhs(x), интерпретируемые
‘как «х — максимально» и «х — гипергиперпросто». Идея состоит в
том, чтобы построить канонические реализации и доказать теорему об
утончении, как у Лахлана. Однако, теперь каждый шаг разрешающей
процедуры будет более сложным и потребует новой структурной
информации о £, поскольку УЗ-предложения расширенного языка включают
утверждения типа «существует безатомное гипергиперпростое
множество с r-максимальным подмножеством» или «существует г-максимальное
множество».
Следующее важное продвижение — это доказательство
неразрешимости ТЪ (£), полученное Херманном и, независимо, Харрингтоном.
(Доказательство Харрингтона появилось позднее и существует лишь в
форме неопубликованных заметок.)
2.2 	Теорема (Херманн [1984b], Харрингтон [1983]). Теория первого

§ 2. Элементарная теория £
501
порядка решетки £ неразрешима.
Оба доказательства основаны на неразрешимости теории булевых
алгебр с выделенной подалгеброй (см. М. Рабин [1976] и Баррис и Мак-
кинзи [1981]). Булевой парой назовем пару (Ль Лг), где Л\ есть булева
алгебра, а Лг — её подалгебра, определяемая некоторым унарным
отношением Щх). Булева пара называется вычислимой, если обычные
булевы операции и предикат R(x) вычислимы. Баррис и Маккензи [1981]
построили класс булевых пар (изоморфных вычислимым булевым
парам) такой, что любое расширение этого класса имеет неразрешимую
теорию. Таким образом, если С — класс булевых пар, включающий все
типы изоморфизма вычислимых булевых пар, то теория С
неразрешима. Херманн доказал теорему 2.2, указав такой класс С булевых пар,
содержащий типы изоморфизма всех вычислимых булевых пар, что С
элементарно определим с параметрами (э. о. п.) в £. Херманн добился
этого после серии предварительных результатов об определимости в £,
содержащийся в его работах [1981], [1983], [1984b] и [1984с]. Например,
сначала он показал, что (Е4, Ез) э. о. п. в £, где Е4 — решетка всех
Е4-множеств вместе с унарным предикатом, выделяющим в точности
Ез-множества. Доказательство использует идеи метода Лахлана из
теоремы Х.7.2 для вложения Ез-отношений в £. Харрингтон доказал
теорему 2.2. показав, что любая булева пара (Ль Л2) из Д9-булевых алгебр
э. 	о. п. в £. По данным А\ и Л2, Харрингтон с помощью 0'"-конструкции
строит гипергиперпростое множество А ив. п. множество В С А,
определяющие (Ль А2) следующим образом. Пусть идеал, определяемый А
и В будет
1 = { X е £ : (3 выч. С С А) {3D Ст А) [X С С U В U (А - D)} }.
Для X Е £ (А) выберем произвольное вычислимое множество Yx такое,
что Yx — А = X. Он показал, что если Yx другое такое множество,
то Yx Д Yx Е X. Следовательно, отображение f{X) = Yx дает
решеточный гомоморфизм из £(А) в £{А)/Х. Харрингтон построил А и В
такие, что (ЛьЛг) — (£(Л)/Х, f(£(A))). Остается нерешенным
следующий важный вопрос о том, является ли степень неразрешимости Th(£)
максимально возможной (т. е. равной 0^).
2.3 	Открытый вопрос. Какова степень ТЪ(£)? В частности, равна ли
она 0^)?9
9Ниис и Харрингтон [1998] на этот вопрос дали положительный ответ. — Прим,
редактора.

502
Глава XVI. Открытые вопросы
Было бы также интересно классифицировать кванторный уровень, с
которого ТЪ(£) становится неразрешимой.
2.4 	Открытый вопрос. Существует ли разрешающая процедура для
3 V 3-предложений, истинных в £?10
Точный кванторный уровень в теореме 2.2, с которого ТЪ(£)
становится неразрешимой, пока ещё не определен, хотя он явно выше, чем
три блока перемен кванторов. С другой стороны, использовать
теорему 2.1 и результаты Лермана и Соара для случая 3V3
представляется довольно сложным. Любое продвижение в этой проблеме, похоже,
приведет к значительному количеству новой структурной информации
о £. Существуют также интересные открытые вопросы, касающиеся
определимости в £. Поскольку каждое в. п. множество А, А ^ 0 и
А ф и, содержит бесконечно много множеств в своей орбите,
определить единственное нетривиальное в. п. множество невозможно. Тем не
менее, мы видели, что различные классы в. п. множеств являются
элементарно теоретико-решеточными, такие как максимальные, гиперги-
перпростые, креативные и другие. Мощностные соображения
показывают, что существуют теоретико-решеточные свойства, не являющиеся
элементарно теоретико-решеточными. Более специфические результаты
могут быть выведены из результатов Лемппа [1986] и [1987]. Он
классифицировал индексные множества гипергиперпростых множеств А, у
которых £*(А) имеет фиксированный ранг относительно производной
Кантора-Бендиксона. Он также показал, что степени этих индексных
множеств проходят по всем уровням 0(Q) для всех вычислимых
ординалов а, являющихся последователями. Все эти классы в. п. множеств, у
которых индексные множества имеют степень 0^а^, а ^ о;, являются те-
оретико решеточными, но не элементарными теоретико-решеточными.
Наконец, Лемпп показал, что множество { х : Wx квазимаксимально }
£5-полно, но неизвестно, является ли класс квазимаксимальных
множеств элементарно теоретико-решеточным в £. Соображения
компактности показывают, что этот класс не может быть определимым в чистой
теории решеток, но, возможно, он определим в £ . Аналогичный вопрос
открыт и для других классов в нижних уровнях иерархии Лемппа, таких
как в. п. множества А, у которых £*(А) атомная булева алгебра (т. е.
10Это — все ещё открытый вопрос. Ниис [1992] доказал неразрешимость Щ-теории
Е. — Прим, редактора.

§ 3. Элементарная теория в. п. степеней
503
изоморфна булевой алгебре конечных и коконечных множеств), или
других сравнительно простых типов изоморфизма.
Поскольку алгебраическая структура решетки £ очень сложна,
было предложено сначала исследовать её различные факторрешетки. Лах-
лан [1968, стр. 36] предложил изучить факторрешетку £ по фильтру,
порожденному простыми множествами. Лерман [1976] предложил
мажорность и гипергиперпростоту в качестве конгруэнций для факторизации
£ (см. упражнение Х.4.9). Некоторые факторрешетки были изучены
Дегтевым [1978с]. Здесь предстоит сделать очень много.
§ 3. Элементарная теория в. п. степеней
Пусть Th(R) обозначает элементарную теорию верхней полу решетки
в. п. степеней (R, $С,и) в языке L($C,U). Экзистенциональная теория
R разрешима, поскольку по упражнению VII.2.2 любое совместное эк-
зистенциональное утверждение истинно в R. Имелись не очень
успешные попытки разработать разрешающую процедуру для некоторых V 3 -
предложений, истинных в R с использованием результатов и методов из
глав VIII-XIV. Следующим важным продвижением было
доказательство неразрешимости Th(R).
3.1 Теорема (Харрингтон и Шелах [1982а] и [1982b]). Th(R)
неразрешима.
Этот результат был улучшен Харрингтоном и Сламаном, которые
показали, что степень Th(R) — максимально возможная, а именно 0^).
3.2 Теорема (Харрингтон и Сламан [1996]). Теория Th(R) имеет
степень 0^.
Упрощенное доказательство теоремы 3.1 приводится в совместной
работе Харрингтона и Сламана [1996]. Доказательство использует
неразрешимость теории частичных упорядочений и использует
0'"-приоритетные рассуждения для кодирования произвольного частичного Д!>-
порядка в R с использованием четырех параметров. А именно, по
данному частичному Д°- упорядочению (Р, $Ср) можно определить в. п.
степени а, Ь, с и d, кодирующие (Р, $^р), следующим образом. Пусть S -
класс степеней х Е R , удовлетворяющих условиям
(1) х ^ а,
(2) xUc^b, и

504
Глава XVI. Открытые вопросы
(3) 	х максимально относительно степеней у Е R, удовлетворяющих
(1) и (2).
Пусть х = х U d, S = {x:x6S}. Тогда (S, — (Р, ^р).
3.3 Открытый вопрос. Разрешима ли теория в. п. степеней х таких,
что а х Ь, для любой пары в. п. степеней а < Ь? Имеет ли она
степень О^)?11
3.4 Открытый вопрос. Каковы разрешимые фрагменты Th(R)? В
частности, разрешима ли V3-теория R?12
Тесно связаны с этими вопросами и проблемы определимости в. п.
степеней. Степень d Е R называется определимой, если существует
такая формула первого порядка F(x) в языке L(^), что d — единственный
элемент, удовлетворяющий F(x) в (R, $С). Сламан и Харрингтон
поставили следующие вопросы.
3.5 Открытый вопрос. Существует ли определимая в. п. степень а
такая, что 0 < а < 0'? Определима ли любая в. п. степень?13
Этот вопрос имеет отношение к следующему вопросу, давно
поставленному Саксом [1967].
3.6 Открытый вопрос. Существует ли инвариантное относительно
степеней решение проблемы Поста, а именно, существует ли геделев
номер е такой, что для любых множеств X и Y С ш выполнено
X <т Wx <т X' k [X =т У =» wex =т Wx]714
11 Отрицательный ответ на первую часть вопроса получили Амбос-Шпиис, Хирш-
велдт и Шор [ta]. На вторую часть вопроса для непустых начальных интервалов
положительный ответ получил Ниис (частное сообщение). — Прим, редактора.
12 Ответ на этот вопрос все ещё неизвестен. Лемпп, Ниис и Сламан [1998] доказали
—> —> —>
неразрешимость V 3 V теории R. С этой проблемой связана трудная проблема
исследования решеток, вложимых в R. Сламан и Соар [1995] описали в R разрешающую
процедуру для предложений типа «расширений вложений» на языке, содержащем
отношение порядка, 0 и 1. Эти предложения имеют следующую форму: для всех
реализующих отношение порядка Р, существуют такие 2/i,.. ,2/m, что
®1,... ,агп,г/1,... ,г/т реализуют Q, где Р С Q. — Прим, редактора.
13Купер в [1994] опубликовал положительное решение второй части проблемы. Как
сообщил редактору Р. Доуни, модификацией некоторых идей Стоба можно доказать
существование таких в. п. степеней а > b > О, что b определимо в [О,а]. Кроме
того, Чолак, Доуни и Волк [ta] построили определимую антицепь степеней. — Прим,
редактора.
14 Ответ на этот вопрос все ещё неизвестен. — Прим, редактора.

§ 3. Элементарная теория в. п. степеней
505
Лахлан [1975] показал, что если такое решение существует, оно не
может быть равномерным в том смысле, что гёделевы номера второй
тьюринговой эквивалентности не могут быть получены равномерно по
индексам первой. Мартин предположил, что в контексте теории
множеств вопрос Сакса имеет сильно отрицательное решение. Для
дальнейшей информации о предположении Мартина и о некоторых частных
результатах см. Сламан и Стил [1988].
3.7 Открытый вопрос. Какие классы в. п. степеней определимы в
(R, ^)? В частности, определимы ли Нп или Ln для п > 0? (Остальные
открытые вопросы об Нп и Ln см. в XI.4.5.)15
Интересным также является отношение между в. п. степенями и Д§-
степенями. Сламан и Вудин [1986] показали, что класс в. п. степеней
определим с параметрами из -степеней. Вопрос об элиминации
параметров является открытым. Сламан [н.о.] также показал, что в. п.
степени не образуют Ei-подструктуру в Д°-степенях в языке L($C). Сламан
показал, что следующая До-формула F(x, у, z) с параметрами a, b, с Е R
выполнима на -степенях, но не на (R, $С):
0 < х ^ а & х ^.у & Ь ^у & с £у.
3.8 Открытый вопрос. Существуют ли нетривиальные
автоморфизмы (R, ^)?16
Харрингтон поднял вопрос о взаимной интерпретируемости (си, 4-, •)
и (R, $С). Интерпретация I из си в R состоит из множества S С R,
отношения эквивалентности на S, дающего классы эквивалентности [d]/,
d G S, и определимых операций 0,0 на этих классах эквивалентности
таких, что
(w) +, 0 — ({ [d]/ : d € S }, ф, ©).
Назовем d кодом в I для п £ си, если этот изоморфизм переводит п в [d],
Харрингтон и Сламан доказали теорему 3.2, построив интерпретацию си
в R.
15Ниис, Шор и Сламан [1998] доказали, что Нп определимы в (R, для всех
и что Ln определимы для всех п ^ 2. — Прим, редактора.
16Купер на конференции в Боулдере (июнь, 1999, США, Боулдер) сделал
сообщение, в котором, в частности, привел доказательство существования нетривиальных
автоморфизмов (R, ^). Насколько нам известно, его доказательство пока не
опубликовано. — Прим, редактора.

506
Глава XVI. Открытые вопросы
3.9 	Открытый вопрос. Существует ли интерпретация I из и в R
такая, что отношение R(а, b), определенное как
R{а, Ь) <=> а — код I для п и Wn Е b?
Если это так, то (R, — жесткая структура, и в таком случае ответ
на вопрос 3.8 является отрицательным.17
Если ах,..., ап € R, то п-типом (ах,..., ап) называется
множество всех формул первого порядка F(xi,... ,хп) в языке L(^) с п
свободными переменными, истинными на (a1?...,an) b(R, $С). Th(R) ^o'-
категорична, если для каждого п существует лишь конечное число п-
типов. Лерман, Шор и Соар [1984] показали, что существует бесконечно
много 3-типов в (R, и, следовательно, Th(R) не No-категорична.
(Последнее следует также из доказательства теоремы 3.1.) Амбос-Шпиис и
Соар [1989] использовали метод главы XIV для доказательства того, что
существуют неограничивающие в. п. степени { сп }nGa;, которые попарно
образуют минимальные пары. Отсюда следует существование
бесконечно много 1-типов в (R, $С), что отвечает на вопрос Лермана, Шора и
Соара [1984].
§ 4. Алгебраическая структура R
Возможно, наиболее важным открытым вопросом о структуре R
является следующий
4.1 	Открытый вопрос. Охарактеризовать конечные решетки, вло-
жимые в (R, $С,и,П) с сохранением наименьших верхних и наибольших
нижних граней.18
Известные результаты, имеющие отношение к этому вопросу,
приведены в замечаниях IX.2.7. Более подробное обсуждение этой проблемы
17Из результата Купера следует (см. предыдущее примечание) отрицательный
ответ на этот вопрос. В работе Нииса, Шора и Сламана [1998] (см. примечание 15 на
стр. 505) содержится частичный положительный ответ на этот вопрос. — Прим,
редактора.
18Эта проблема интенсивно исследовалась. В работах Лемппа и Лермана [1997],
Лермана [1998] можно узнать о последних достижениях в её решении. В частности,
ими найдено одно VB-условие, описывающее конечные решетки без т. н. «критических
точек», допускающие такое вложение. — Прим, редактора.

§ 4• Алгебраическая структура R
507
содержится в статье Лермана [1985а] и в недавних результатах Амбос-
Шпииса и Лермана [1986]. Техника вложимости и невложимости уже
достаточно сильно развита, но до сих пор не существует ни одного
ясного критерия вложимости. Заметим, что даже для описания экзистен-
ционалъных предложений языка L(^,U,fl), истинных в R(^,U,fl), нам
необходимо знать решение проблемы 4.1. Было бы также интересно
выяснить, какие конечные решетки плотны в R(^,U, П).
Одним из первоначальных доводов в пользу гипотезы Шёнфилда (см.
§ 1 главы IX) была теорема VIII.4.1 Сакса о плотности. После этого, при
появлении каждого нового свойства Р, например, такого, как свойство
быть ветвящейся или неветвящейся степенью (см. определение IX.4.1),
исследователи пытались определить, является ли это свойство плотным,
а именно, верно ли что для любых в. п. степеней а < b существует такая
в. п. степень d со свойством Р, что а < d < Ь. Например, Фейер [1983]
доказал плотность неветвящихся степеней, а Сламан [1991] доказал
плотность ветвящихся степеней. Подобное существование в каждом
интервале различных типов степеней дает надежду на положительное решение
вопроса 3.3, поскольку может оказаться возможным закодировать
некоторую интерпретацию и в интервале (а, Ь).
Другое следствие гипотезы Шёнфилда — это свойство сильной
дополняемости наверх IX (0.2), опровергнутое Купером и Ейтсом. Пусть
даны в. п. степени 0 < b < а. Будем говорить, что b дополняется
наверх до а, если существует в. п. степень с < а такая, что bUc = а. Если
такой с не существует, то b называется свидетелем недополняемости
для а. Будем говорить, что а недополняема (н. д.), если у нее есть
свидетель недополняемости. (Гипотеза IX (0.2) утверждает, что никакая в. п.
степень не является н. д.) Ладнер и Сассо [1975] доказали, что каждая
степень а € R+ имеет предшественника b Е 1»2 П R+ со свойством н. д.
4.2 Теорема (Купер [1974а] и Ейтс). О' имеет свойство н. д.
Рукописное доказательство Купера теоремы 4.2 было
модифицировано Харрингтоном таким образом, что свидетель b можно считать
низким. Затем Харрингтон усилил этот результат, установив, что
свидетель b может быть и высоким. Эти доказательства опираются на тот
факт, что (У содержит креативное множество. Затем Харрингтон
соединил эту технику с методом разрешения для высоких степеней Купера
(теорема XI.2.15) и получил следующее обобщение.
4.3 Теорема (Харрингтон). Каждая высокая в. п. степень а имеет
свойство н. д. с высоким в. п. свидетелем Ь.

508
Глава XVI. Открытые вопросы
Заметки Харрингтона [1976] никогда не публиковались, но
доказательство теоремы 4.3 появилось у Миллера [1981а]. Доказательства
теорем 4.2 и 4.3 интересны тем, что они используют такую запрещающую
функцию r(e,s), что liminfs r(e,s) = оо в отличие от запрещающих
функций из глав VIII, IX, и XIV.
С этим контрастирует другой результат Харрингтона о том, что не
каждая степень а Е R имеет свойство н. д.
4.4 	Плюс-наверх теорема (Харрингтон). Верно следующее
утверждение, в котором все кванторы берутся по R.
(За > 0) (Vb)0<b<a (Vd)a^d (3c)c<d [b U с = d].
Заметки Харрингтона [1978] о доказательстве этой теоремы
распространялись, но никогда не публиковались. Шёнфилд также
распространял свои заметки о доказательстве этой теоремы, которые также не
публиковались. В доказательстве используются 0ХХХ-приоритетные
рассуждения, аналогичные рассуждениям из главы XIV. Доказательство
частного случая этой теоремы (при d = 0х), приведенное в работе Фейера
и Соара [1981], использует только 0"-приоритетные рассуждения,
похожие на доказательство теоремы XIII.2.2. Методы построения степеней
со свойством дополняемости наверх сыграли ключевую роль при
доказательстве теоремы 3.1.
Другая группа результатов, представляющая сегодня интерес,
касается относительной перечислимости и структуры в. п. степеней с
дополнительным оператором скачка. Будем говорить, что а выше и в. п.
относительно (в. в. п. относительно) Ь, если а в. п. относительно b и
а ^ Ь. Купер [1972d] выдвинул гипотезу, что если а в. в. п.
относительно 0х, то а в. в. п. относительно любой высокой степени d ^ 0х. Это
было опровергнуто Соаром и Стобом [1982], которые показали, что для
любой с Е R+ существует не в. п. степень а, являющаяся в. в. п.
относительно с. (Это отвечает на вопрос Купера, поскольку теперь мы можем
релятивизовать этот результат с d вместо 0 и 0х вместо с.) Это
доказательство не может быть равномерным, оно определяет двух кандидатов
для с, ai и аг, один из которых и есть искомая степень а. Шор соединил
этот метод с 0ХХХ-приоритетными рассуждениями для доказательства
теоремы о необратимости, которая контрастирует с теоремами Шёнфилд а
(упражнение VI.4.11) и Сакса (теорема VIII.3.1) об обратимости
оператора скачка.

§ 4’ Алгебраическая структура R
509
4.5 Теорема о необратимости (Шор [1988]). Существуют такие
степени ао и ai в.в. п. относительно (У, что ао U ai < 0" и, если
и < (У, то неверно, что обе ао и ai в.в. п. относительно и.
Отсюда следует, что не всякая степень а, которая является в. в. п.
относительно (У, является скачком степени, являющейся половинкой
минимальной пары степеней. Это следствие также доказано Купером [1988]
с использованием 0'"-приоритетных рассуждений. Доказательство
теоремы 4.5 использует новую 0'"-приоритетную конструкцию, где дерево
стратегий является ш 4-1-ветвящимся, так что для определения
истинного пути требуется О'"-оракул.
В том же направлении Лемпп и Сламан [1989] доказали, что не
существует ненулевой в. п. степени а, которая является глубокой в том
смысле, что для всех w Е R, w' = (all w)'. Доказательство этой
теоремы также использует 0'"-приоритетное рассуждение. Этот результат
вместе с упомянутым результатом Соара-Стоба опровергает
существование невычислимых в. п. степеней с определенными «сильно низкими»
свойствами.
Теорема XI.3.2 о разложении Робинсона показала, что теорема VII.3.2
Сакса о разложении и теорема VIII.4.1 Сакса о плотности могут быть
соединены в интервале (с,Ь) в. п. степеней в том случае, когда нижняя
степень с является низкой. Лахлан доказал необходимость последнего
предположения.
4.6 Теорема Л[ахлана о неразложении (Лахлан [1975а]).
Существуют в. п. степени b и с такие, что с < b и для всех в. п. степеней
ао и ai
[с ^ а0, ai ^ b & b ^ а0 U ai] =Ф> [b ^ а0 V b ^ ах].
Доказательство теоремы 4.6 интересно, в частности, тем, что это —
первый пример применения (У"-приоритетного рассуждения. Эта
теорема обнаруживает сложность структуры (R, <) и позволяет провести
необходимое для доказательства теорем 3.1 и 3.2 кодирование.

Литература1
Аберт (О. Aberth)
[1971] The failure in computable analysis of a classical existence theorem for ordinary
differential equations, Proc. Amer. Math. Soc., SO (1971), 151-156.
[1980a] Computable Analysis, McGraw-Hill, New York, 1980.
Абрахам и Шор (Abraham, and R. A. Shore)
[1986] Initial segments of the Turing degrees of size Ni, Israel J. Math., 53 (1986),
1-51.
Аддисон (J. W. Addison)
[1958] 	Separation principles in the hierarchies of classical and effective descriptive set
theory, Fund. Math., 56 (1958), 123-135.
Аддисон, Хенкин и Тарский (J. W. Addison, L. Henkin and A. Tarski)
[1965] Symposium on the Theory of Models (editors), North-Holland, Amsterdam,
1965.
Амбое-Шпиис (К. Ambos-Spies)
[1980] 	On the Structure of the Recursively Enumerable Degrees, Dissertation,
University of Munich, 1980.
[1983] 	Automorphism bases for the r. e. degrees (abstract), in: Extended Abstracts
of Short Talks of the 1982 Summer Institute on Recursion Theory Held of
Cornell University, I. Kalantari, ed. special publication of Recursive Function
Theory Newsletter, (1983), 3-4. preprint.
[1984a] An extension of the non-diamond theorem in classical and а-recursion theory,
J. Symbolic Logic 49 (1984), 586-607.
[1984b] On pairs of recursively enumerable degrees, Trans. Amer. Math. Soc. 283
(1984), 507-531.
[1984c] Contiguous r. e. degrees, In: Richter et al. [1984], 1-37.
[1984d] On the Structure of the Polynomial Time Degrees of Recursive Sets, Habilita-
tionsschrift, University of Dortmund 1984.
Звездочкой отмечены работы, добавленные при переводе.— Прим, редактора.

Литература
511
[1984e] On the structure of polynomial degrees, In: STACS ’84, Symposium on
Theoretical Aspects on Computer Science (M. Fontet and K. Mehlhorn,
editors), Lecture Notes in Computer Science No. 166, Springer-Verlag, Berlin,
Heidelberg, New York, Tokyo, 1984, 198-208.
[1985a] Anti-mitotic recursively enumerable sets, Z. Math. Logik Grundlag. Math. 31
(1985), 461-477.
[1985b] Cupping and noncapping in the r. e. weak truth table and Turing degrees,
Arch. Math. Logik Grundlag. 25 (1985), 109-126.
[1985c] Generators of the recursively enumerable degrees, In: Ebbinghaus, Muller, and
Sacks [1985], 1-28.
Амбое-Шпиис, Джокуш, Шор и Соар (К. Ambos-Spies, С. G. Jockusch,
Jr., R. A. Shore and R. I. Soare)
[1984] An algebraic decomposition of the recursively enumerable degrees and the
coincidence of several degree classes with the promptly simple degrees, Trans.
Amer. Math. Soc. 281 (1984), 109-128.
Амбос-Шпиис и Лерман (К. Ambos-Spies and M. Lerman)
[1986] 	Lattice embeddings into the recursively enumerable degrees, J. Symbolic Logic
51 (1986), 257-272.
Амбос-Шпиис и Соар (К. Ambos-Spies and R. I. Soare)
[1989] The recursively enumerable degrees have infinitely many one types, Ann. Pure
and Applied Logic 44 (1989), 1-23.
Амбос-Шпиис и Фейер (К. Ambos-Spies and P. A. Fejer)
[1988] Degree theoretic splitting properties of recursively enumerable sets, JSL 53
(1988), 1110-1137.
Амбос-Шпиис, Хиршвелдт и Шор (К. Ambos-Spies, Hirschfeldt and
R. A. Shore)
[ta*] Undecidability and 1-types in intervals of the computably enumerable sets, to
appear.
Амбос-Шпиис и Шор (К. Ambos-Spies and R. A. Shore)
[1993*] Undecidability and 1-types in the recursively enumerable degrees. 9-th
International Congress of Logic, Methodology and Philosophy of Science (Uppsala,
1991). Ann. Pure Appl. Logic 63 (1993), no. 1, 3-37.
Арсланов M. M.
[1968] Две теоремы о рекурсивно перечислимых множествах, Алгебра и Логика,
7(1968), 4-8.
[1969] Об эффективно гиперпростых множествах, Алгебра и Логика, 8 (1969),
143-153.
[1970] О полных гиперпростых множествах, Изв. вузов. Мат., 95 No. 4 (1970),
30-35.
[1979] 	Слабо рекурсивно перечислимые степени и предельная вычислимость, Ве-
роятн. методы и киберн., 15 (1979), 3-9.

512
Литература
[1981] О некоторых обобщениях теоремы о неподвижной точке, Изв. Вузов. Мат.,
228 No. 5 (1981), 9-16.
[1982] Об одной иерархии степеней неразрешимости, Вероятн. методы и киберн.,
18 (1982), 10-17.
[1985а] Семейства рекурсивно перечислимых множеств и их степени
неразрешимости, Изв. Вузов. Мат., 275 No. 4 (1985), 13-19.
[1985b] m-сводимость и неподвижные точки, Межвуз. сб. ’’Сложностные проблемы
мат. логики”, Калинин, 1985, 11-18.
[1985с] Структурные свойства степеней ниже 0;, ДАН СССР, 283 No. 2 (1985),
270-273.
[1985d] Эффективно гипериммунные множества и мажоранты, Мат. Заметки, 38
No.2 (1985), 302-309.
[1985е] Об одном классе гиперпростых неполных множеств, Мат. заметки, 38
(1985), 872-874, 958.
Арсланов М. М., Надыров Р. Ф., Соловьев В. Д.
[1977] 	Критерий полноты рекурсивно перечислимых множеств и некоторые
обобщения теоремы о неподвижной точке, Изв. вузов. Мат., 179 No. 4 (1977),
3-7.
Бар-Хиллел (Y. Bar-Hillel)
[1970] Mathematical Logic and Foundations of Set Theory (editor), Proc. Intern.
Colloquium, Jerusalem, November 11-14, 1968, North-Holland, Amsterdam,
London, 1970.
Барвайс (К. J. Barwise)
[1977] Handbook of Mathematical Logic (editor), North-Holland, Amsterdam, New
York, Oxford, 1977. (Русский перевод: Справочная книга по
математической логике, в четырех частях. Москва, Наука, 1982,1983).
Барвайс, Кейслер и Кунен (К. J. Barwise, Н. J. Keisler and К. Kunen)
[1980] The Kleene Symposium (editors), Proc. Symposium held June 18-24, 1979 at
Madison, Wisconsin, U.S.A., North-Holland, Amsterdam, New York, Oxford,
1980.
Баррис и Маккинзи (S. Burris and R. McKenzie)
[1981] Decidability and Boolean representations, Memoirs Amer. Math. Soc., 32 No.
246, 1981.
Белеградек О. В.
[1978] m-степени проблемы равенства слов, Сиб. мат. журнал, 19 (1978), 1232-
1236.
Беннисон (V. L. Bennison)
[1976] 	On the Computational Complexity of Recursively Enumerable Sets, Ph.D.
Dissertation, University of Chicago, 1976.
[1979] Information content characterizations of complexity theoretic properties, In:
Theoretical Computer Science: Fourth G.I. Conference, Aachen, March 26-28,
1979, edited by K. Weihrauch, Lecture Notes in Computer Science No. 67,
Springer-Verlag, Berlin, Heidelberg, New York, 1979, 58-66,

Литература
513
[1980] 	Recursively enumerable complexity sequences and measure independence, J.
Symbolic Logic, ^5 (1980), 417-438.
Беннисон и Coap (V. L. Bennison and R. I. Soare)
[1978] 	Some lowness properties and computational complexity sequences, Theoret.
Comput. Sci., 6 (1978), 233-254.
Бёргер (E. Borger)
[1985] Berechenbarkeit, Komplexitat, Logik, Vieweg und Sohn, Wiesbaden, 1985.
Бикфорд (M. Bickford)
[1983] 	The Jump Operator in Strong Reducibilities, Ph.D. Dissertation, University of
Wisconsin, 1983.
Бикфорд и Миллс (M. Bickford and C. F. Mills)
[ta] Lowness properties of r. e. sets, J. Symbolic Logic, to appear.
Биркгоф (G. Birkhoff)
[1933] On the combination of subalgebras, Proc. Cambridge Philos. Soc., 29 (1933),
441-464.
[1967] 	Lattice theory, 3rd ed., Amer. Math. Soc. Colloquium Publications XXV,
Amer. Math. Soc., Providence, R.I., 1967. (Русский перевод: Биркгоф Г.
Теория решеток)
Бишоп (Е. Bishop)
[1967] Foundations of Constructive Analysis, McGraw-Hill, New York, 1967.
Блюм и Маркус (M. Blum and I. Marques)
[1973] 	On complexity properties of recursively enumerable sets, J. Symbolic Logic, 38
(1973), 579-593.
Бойд, Хенсел и Патнам (R. Boyd, G. Hensel and H. Putnam)
[1969] A recursion-theoretic characterization of the ramified analytical hierarchy,
Trans. Amer. Math. Soc., Ц1 (1969), 37-62.
Булитко В.К.
[1980] Сводимости линейными по Жегалкину таблицами, Сиб. мат. журнал, 21
(1980), 23-31, 235.
Булос и Патнам (G. Boolos and Н. Putnam)
[1968] Degrees of unsolvability of constructible sets of integers, J. Symbolic Logic, 33
(1968), 497-513.
Бун (W. W. Boone)
[1954-57] Certain simple unsolvable problems of group theory, I, II, III, IV, V, VI,
Nederl. Akad. Wetenschappen. Proc. Ser. A 57 (1954), 231-237 and 492-497;
ibid. 58 (1955), 252-256 and 571-577; ibid. 60 (1957), 22-27 and 227-232.
[1959] 	The word problem, Ann. of Math. (2), 70 (1959), 207-265.
[1966] Word problems and recursively enumerable degrees of unsolvability. A sequel
on finitely presented groups, Ann. of Math. (2), 84 (1966), 49-84.

514
Литература
Бун и Хигмен (W. W. Boone and G. Higman)
[1974] 	An algebraic characterization of groups with soluble word problem, J. Austral.
Math. Soc., 43 (1974), 41-53.
Бухараев H.P.
[1979] 	О свойствах предельной перечислимости дополнений рекурсивно
перечислимых множеств, Вероятн. мет. и киберн., 15 (1979), 10-16.
[1981] 	О Т-степенях разностей рекурсивно перечислимых множеств, Изв. вузов.
Мат., 228 No.5 (1981), 40-49.
Валидов Ф. И.
[1984] Рекурсивно перечислимые множества и дискретные семейства
общерекурсивных функций, Изв. вузов. Мат., 4 (1984), 6-11.
Вейнер (S. S. Wainer)
[1985] Subrecursive ordinals, In: Ebbinghaus, Muller, and Sacks [1985], 405-418.
Венквай и Нероуд (Huang Wen Qi and A. Nerode)
[1985] The application of pure recursion theory to computable analysis, Acta Mathe-
matica Sinica, 28 (1985), 625-636.
Вьюгин В. В.
[1974] 	Сегменты рекурсивно перечислимых m-степеней, Алгебра и Логика, 13
(1974), 635-654, 719.
Ганф ( W. Hanf)
[1965] Model theoretic methods in the study of elementary logic, In: Addison, Henkin,
and Tarski [1965], 132-145.
Гаттридж (L. Gutteridge)
[1971a] Some Results on Enumeration Reducibility, Ph.D. Thesis, Simon Fraser
University, 1971.
[1971b] The partial degrees are dense, preprint (unpublished).
Гейтинг (A. Hey ting)
[1959] Constructivity in Mathematics (editor), Proc. Colloquium held in Amsterdam
1957, North-Holland, Amsterdam, 1959.
Гёдель (К. Godel)
[1930] Die Vollstandigkeit der Axiome des logischen Funktionenkalkuls, Monatsh.
Math. Phys., 57(1930), 349-360, translated In: Van Heijenoort [1967], 583-591.
[1931] Uber formal unentscheidbare Satze der Principia Mathematica und verwandter
Systeme I, Monatsh. Math. Phys., 38 (1931), 173-198; translated in Davis
[1965], 4-38.
[1934] On undecidable propositions of formal mathematical systems, Notes by S.C.
Kleene and Barkley Rosser on lectures at the Institute for Advanced Study,
Princeton, New Jersey; reprinted in Davis [1965], 39-71.
[1946] Remarks before the Princeton Bicentennial Conference on Problems in
Mathematics, In: Davis [1965], 84-88.

Литература
515
Гжегорчик (A. Grzegorczyk)
[1953] 	Some classes of recursive functions, Rozprawy matematyczne no. 4, Instytut
Matematyczny Polskiej Akad. Nauk, Warsaw, 1953.
Гилл и Моррис (J. Gill and P. Morris)
[1974] On subcreative sets and S-reducibility, J. Symbolic Logic, 39 (1974), 669-677.
Гончаров С. C.
[1983] 	Универсальные рекурсивно перечислимые булевы алгебры, Сиб. мат.
журнал, 24 No. 6 (1983), 36-43
Грассин (J. Grassin)
[1974] Index sets in Ershov’s hierarchy, J. Symbolic Logic, 39 (1974), 97-104.
Дёгтев A. H.
[1970] Несколько замечаний о ретрассируемых, регрессивных и
точечно-разложимых множествах, Алгебра и Логика, 9 (1970), 651-660.
[1971] О гиперпростых множествах с ретрассируемым дополнением, Алгеьра и
Логика, 10 (1971), 235-246.
[1972а] Об m-степенях простых множеств, Алгебра и Логика, 11 (1972), 130-139,
239.
[1972b] Наследственные множества и табличныая сводимость, Алгебра и Логика,
11 (1972), 257-279, 361.
[1973] О tt- и m-степенях, Алгебра и Логика, 12 (1973), 143-161, 243.
[1975] Сводимость частично рекурсивных функций, Сиб. мат. журнал, 16 No. 5
(1975), 970-988.
[1976а] О частично упорядоченных множествах 1-степеней, содержащихся в
рекурсивно перечислимых m-степенях, Алгебра и Логика, 15 (1976), 249-266,
365.
[1976b] О минимальных 1-степенях и табличной сводимости, Сиб. Мат. Журнал,
17 (1976), 1014-1022, 1196.
[1977] 	Сводимость частично рекурсивных функций И, Сиб. мат. журнал, 18 No.
4 (1977), 765-774.
[1978а] Об m-степенях надмножеств простых множеств, Мат. Заметки, 23 (1978),
889-893.
[1978b] Три теоремы о tt-степенях, Алгебра и Логика, 17 (1978), 270-281.
[1978с] Разрешимость V3-теории некоторой фактор решетки рекурсивно
перечислимых множеств, Алгебра и Логика, 17 (1978), 134-143, 241.
[1979а] О сводимостях табличного типа в теории алгоритмов, Успехи мат. наук,
34 (1979), 137-168, 248.
[1979b] Несколько результатов о верхних полурешетках и т-степенях, Алгебра и
Логика, 18 (1979), 665-679, 754.
[1980] О сводимостях нумераций, Мат. сборник, 112(154) No. 2 (1980), 207-219.
[1981] Соотношения между полными множествами, Изв. вузов. Мат., 228 No. 5
(1981), 50-55.
[1982] Small degrees in ordinary recursion theory, In: Proc. of the Sixth International
Congress of Logic, Methodology, and the Philosophy of Science, Hannover 1979,
North-Holland, Amsterdam, New York, Oxford, 1982, 237-240.

516
Литература
ван Дейлен, Ласкар и Смайлей (D. van Dalen, D. Lascar and J. Smiley)
[1982] 	Proc. Logic Colloquium ’80: Papers intended for the European Summer
Meeting of the Association of Symbolic Logic planned for Prague, August
24-30, but never held, (editors), North-Holland, Amsterdam, New York,
Oxford, 1982.
Деккер ( J. С. E. Dekker)
[1953] Two notes on recursively enumerable sets, Proc. Amer. Math. Soc., 4 (1953),
495-501.
[1954] A theorem on hypersimple sets, Proc. Amer. Math. Soc., 5 (1954), 791-796.
[1955] Productive sets, Trans. Amer. Math. Soc., 78 (1955), 129-149.
Деккер и Майхилл (J. С. E. Dekker and J. Myhill)
[1958a] Some theorems on classes of recursively enumerable sets, Trans. Amer. Math.
Soc., 89 (1958), 25-59.
[1958b] Retraceable sets, Canad. J. Math., 10 (1958), 357-373.
[1960] 	Recursive equivalence types, University of California Publications in
Mathematics, New Series 3 (1960), 67-214.
Денисов С. Д.
[1970] 	Об m-степенях рекурсивно перечислимых множеств, Алгебра и Логика, 9
(1970), 422-427.
[1974] Три теоремы об элементарных теориях и tt-сводимости, Алгебра и Логика,
13 (1974), 5-8, 120.
[1978] 	Строение верхней полурешетки рекурсивно перечислимых m-степеней I,
Алгебра и Логика, 17 (1978), 643-683, 746.
Джокуш (С. G. Jockusch, Jr.)
[1968а] Semirecursive sets and positive reducibility, Trans. Amer. Math. Soc., 131
(1968), 420-436.
[1968b] Uniformly introreducible sets, J. Symbolic Logic, 33 (1968), 521-536.
[1969a] The degrees of hyperhyperimmune sets, J. Symbolic Logic, 34 (1969), 489-493.
[1969b] Relationships between reducibilities, Trans. Amer. Math. Soc., Ц2 (1969),
229-237.
[1969c] The degrees of bi-immune sets, Z. Math. Logik Grundlag. Math., 15 (1969),
135-140.
[1972a] Degrees in which the recursive sets are uniformly recursive, Canad. J. Math.,
24 (1972), 1092-1099.
[1972b] Ramsey’s theorem and recursion theory, J. Symbolic Logic, 37 (1972), 268-280.
[1972c] Upward closure of bi-immune degrees, Z. Math. Logik Grundlag. Math., 18
(1972), 285-287.
[1973a] Review of Lerman [1971a], Math. Reviews, ^5 (1973), No. 3200.
[1973b] Upward closure and cohesive degrees, Israel J. Math., 15 (1973), 332-335.
[1973c] An application of E® determinacy to the degrees of unsolvability, J. Symbolic
Logic, 38 (1973), 293-294.
[1974] IlJ classes and Boolean combinations of recursively enumerable sets, J.
Symbolic Logic, 39 (1974), 95-96.
[1975] Recursiveness of initial segments of Kleene’s O, Fund. Math., 87 (1975),
161-167.

Литература
517
[1977] Simple proofs of some theorems on high degrees, Canad. J. Math., 29 (1977),
1072-1080.
[1980] Degrees of generic sets, In: Drake and Wainer [1980], 110-139.
[1981] Three easy constructions of recursively enumerable sets, In: Lerman, Schmerl,
and Soare [1981], 83-91.
[1985] Genericity for recursively enumerable sets, In: Ebbinghaus, Muller, and Sacks
[1985], 203-232.
Джокуш и Mopxep (C. G. Jockusch, Jr. and J. Mohrherr)
[1985] Embedding the diamond lattice in the r. e. tt-degrees, Proc. Amer. Math. Soc.,
94 (1985), 123-128.
Джокуш и Калантари (C. G. Jockusch, Jr. and I. Kalantari)
[1984] 	Recursively enumerable sets and van der Waerden’s theorem on arithmetic
progressions, Pacific J. Math., 115 (1984), 143-153.
Джокуш, Лерман, Coap и Соловей (C. G. Jockusch, Jr., M. Lerman,
R. I. Soare and R. M. Solovay)
[1989] Recursively enumerable sets modulo iterated jumps and extensions of
Arslanov’s completeness criterion, J. Symbolic Logic, 54 (1989), 1288-1323.
Джокуш и Маклохлин ( C. G. Jockusch, Jr. and T. G. McLaughlin)
[1969] 	Countable retracing functions and П^ predicates, Pacific J. Math., 30 (1969),
67-93.
Джокуш и Патерсон (C. G. Jockusch, Jr. and M. Paterson)
[1976] 	Completely autoreducible degrees, Z. Math. Logik Grundlag. Math., 22 (1976),
571-575.
Джокуш и Познер (C. G. Jockusch, Jr. and D. Posner)
[1978] Double jumps of minimal degrees, J. Symbolic Logic, 43, 715-724.
[1981] 	Automorphism bases for degrees of unsolvability, Israel J. Math., 40 (1981),
150-164.
Джокуш и Симпсон (C. G. Jockusch, Jr. and S. G. Simpson)
[1976] A degree theoretic definition of the ramified analytical hierarchy, Ann. Math.
Logic, 10 (1976), 1-32.
Джокуш и Coap (C. G. Jockusch, Jr. and R. I. Soare)
[1970] Minimal covers and arithmetical sets, Proc. Amer. Math. Soc., 25 (1970),
856-859.
[1971] A minimal pair of nj classes, J. Symbolic Logic, 36 (1971), 66-78.
[1972a] Degrees of members of nj classes, Pacific J. Math., 40 (1972), 605-616.
[1972b] П® classes and degrees of theories, Trans. Amer. Math. Soc., 173 (1972), 33-56.
[1973a] Post’s problem and his hypersimple set, J. Symbolic Logic, 38 (1973), 446-452.
[1973b] Encodability of Kleene’s Q, J. Symbolic Logic, 38 (1973), 437-440.
Джокуш и Соловей (C. G. Jockusch, Jr. and R. M. Solovay)
[1977] Fixed points of jump preserving automorphisms of degrees, Israel J. Math., 26
(1977), 91-94.

518
Литература
Джокуш и Шор (С. G. Jockusch, Jr. and R. A. Shore)
[1983] Pseudo jump operators I: The R. E. case, Trans. Amer. Math. Soc., 275 (1983),
599-609.
[1984] Pseudo jump operators. II: Transfinite iterations, hierarchies, and minimal
covers, J. Symbolic Logic, ^9 (1984), 1205-1236.
[1985] REA operators, R. E. degrees, and minimal covers, In: Nerode and Shore [1985],
3-11.
Джокуш и Штефан (C. G. Jockusch and F. Stephan)
[1993*] A cohesive set which is not high, Math. Logic Quarterly, 39 (1993), 515-530.
[1997*] Correction to ”A cohesive set which is not high”, Math. Logic Quarterly 43
(1997), 569.
Доуни (R. G. Downey )
[1985] 	The degrees of r. e. sets without the universal splitting property, Trans. Amer.
Math. Soc., 291 (1985), 337-351.
[1987a] Localization of a theorem of Ambos-Spies and the strong antisplitting property,
Arch. Math. Logik Grundlag., 26 (1987) 127-136.
[1987b] Subsets of hypersimple sets, Pacific J. Math., 127 (1987), 299-319.
[1987c] A® degrees and transfer theorems, Illinois J. Math., 31 (1987), 419-427.
[1989] Intervals and sublattices in the r. e. wtt-degrees, part 1: Density, Ann. Pure
Appl. Logic, 49 (1989), 1-27.
Доуни и Джокуш (R. G. Downey and C. G. Jockusch, Jr.)
[1987] T-degrees, jump classes, and strong reducibilities, Trans. Amer. Math. Soc.,
301 (1987) 103-136.
Доуни и Куртц (R. G. Downey and S. A. Kurtz)
[1986] 	Recursion theory and ordered groups, Ann. Pure Appl. Logic, 32 (1986),
137-151.
Доуни и Стоб (R. G. Downey and M. Stob)
[1986] 	Structural interactions of the recursively enumerable T- and W-degrees, Ann.
Pure Appl. Logic, 31 (1986), 205-236.
[1992] Automorphisms of the lattice of recursively enumerable sets: Orbits, Advances
in Math., 92 (1992) 237-265.
[1993] Friedberg splittings of recursively enumerable sets, Annals Pure and Applied
Logic, 59 (1993), 175-199.
[1997] Minimal pairs in lower cones, Israel J. Math., 100 (1997), 7-27.
Доуни и Уэлш (R. G. Downey and L. V. Welch )
[1986] Splitting properties of r. e. sets and degrees, J. Symbolic Logic, 51 (1986),
88-109.
Доуни и Харрингтон (R. G. Downey and L. Harrington)
[1996*] There is no fat orbit, Ann. Pure Appl. Logic.80 (1996), 277-289.
Дрейк и Вейнер (F. Drake and S. S. Wainer)

Литература
519
[1980] 	Recursion Theory: Its Generalizations and Applications (editors), Proc. Logic
Colloquium ’79, Leeds, August 1979, London Math. Society Lecture Notes
Series No. 45, Cambridge University Press, Cambridge, U.K., 1980.
Дэвис (M. Davis)
[1958] 	Computability and Unsolvability, McGraw-Hill, New York (1958); reprinted in
1982 by Dover Publications, with an appendix which includes Davis [1973].
[1965] 	The Undecidable. Basic Papers on Undecidable Propositions, Unsolvable
Problems, and Computable Functions (editor), Raven Press, Hewlitt, New
York, 1965.
[1973] Hilbert’s tenth problem is unsolvable, Amer. Math. Monthly, 80 (1973),
233-269.
[1977] Unsolvable problems, In: Barwise, Keisler, and Kunen, 1980, 567-594.
[1982] Why Godel didn’t have Church’s Thesis, Inform, and Control, 54 (1982), 3-24.
Дэвис и Вейакер (M. Davis and E. Weyuker)
[1983] Computability, Complexity, and Languages: Fundamentals of Theoretical
Computer Science, Academic Press, New York, 1983.
Дэвис, Матиясевич и Робинсон (М. Davis, Ju. V. Matijasevic and
J. Robinson)
[1976] 	Hilbert’s tenth problem, Diophantine equations: positive aspects of a negative
solution, In: Mathematical Developments Arising From Hilbert’s Problems,
Proc. Symp. Pure Math., 27, 1976, Amer. Math. Soc., Providence, R.I., 1976,
323-378.
Дэвис, Патнам и Робинсон (М. Davis, Н. Putnam and J. Robinson)
[1961] The decision problem for exponential diophantine equations, Ann. of Math.
(2), 74 (1961), 425-436.
Ейтс (С. E. M. Yates)
[1962] Recursively enumerable sets and retracing functions, Z. Math. Logik Grundlag.
Math. 8 (1962), 331-345.
[1965] Three theorems on the degree of recursively enumerable sets, Duke Math. J.
32 (1965), 461-468.
[1966a] A minimal pair of recursively enumerable degrees, J. Symbolic Logic 31 (1966),
159-168.
[1966b] On the degrees of index sets, Trans. Amer. Math. Soc. 121 (1966), 309-328.
[1967] Recursively enumerable degrees and the degrees less than O', in Crossley [1967],
264-271.
[1969] On the degrees of index sets II, Trans. Amer. Math. Soc. 135 (1969), 249-266.
[1970a] Initial segments of the degrees of unsolvability, Part I: A survey, In: Bar-Hillel
[1970], 63-83.
[1970b] Initial segments of the degrees of unsolvability, Part II: Minimal degrees, J.
Symbolic Logic 35 (1970), 243-266.
[1972] 	Initial segments and implications for the structure of degrees, In: Hodges [1972],
305-335.
[1974] Prioric games and minimal degrees below O', Fund. Math. 82 (1974), 217-237.

520
Литература
[1976] Banach-Mazur games, comeager sets, and degrees of unsolvability, Math. Proc.
Cambridge Philos. Soc. 79 (1976), 195-220.
Ершов Ю. Л.
[1964] Разрешимость элементарной теории дистрибутивных структур с
относительными дополнениями и теории фильтров, Алгебра и Логика, 3 (1964),
17-38.
[1968а] Об одной иерархии множеств I, Алгебра и Логика, 7 (1968), 47-73.
[1968b] Об одной иерархии множеств II, Алгебра и Логика, 7 (1968), 15-47.
[1969] Гипергиперпростые m-степени, Алгебра и Логика, 8 (1969), 523-552.
[1970а] Об одной иерархии множеств III, Алгебра и Логика, 9 (1970), 34-51.
[1970b] О неотделимых парах, Алгебра и Логика, 9 (1970), 661-666.
[1970с] Об индексных множествах, Сиб. мат. журнал, 11 (1970), 326-342.
[1971] 	Позитивные эквивавлентности, Алгебра и Логика, 10 (1971), 620-650.
[1973] 	Иерархия А® множеств, In: Proc. of the Fourth International Congress of
Logic, Methodology, and the Philosophy of Science (Bucharest), North-
Holland, Amsterdam, 1973, 69-76.
[1975] 	Верхняя полурешетка нумераций конечных множеств, Алгебра и Логика,
Ц (1975) 258-284, 368.
[1977] Теория Нумераций, Москва, Наука, 1977.
[1980] Проблемы разрешимости и констуктивные модели, Москва, Наука, 1980.
Ершов Ю. Л. и др.
[1965] Элементарные теории, Успехи мат. наук, 20 (1965), 37-108.
Ершов Ю. Л. и Лавров И. А.
[1973] Верхняя полурешетка L(7), Алгебра и Логика, 12 (1973), 167-189, 243-244.
Иванов Л. Л. (Ivanov L.L.)
[1986] 	Algebraic Recursion Theory, Ellis Horwood Publishers, Chichester, U.K., 1986.
Инграссиа (M. Ingrassia)
[1981] P-Genericity for Recursively Enumerable Sets, Ph.D. Dissertation, University
of Illinois at Urbana-Champaign, 1981.
[h.o.] P-generic r. e. degrees are dense, unpublished.
[h.o.] Restricted notions of P-genericity for r. e. sets, unpublished.
Ишмухаметов Ш. T.
[1982] О семействах рекурсивно перечислиых множеств, Вероятн. методы и ки-
берн., 18 (1982), 46-53.
[1983] Об индексных множествах разностей рекурсивно перечислимых множеств,
Изв. вузов. Мат., 250 No. 3 (1983), 78-79.
[1985] О разностях рекурсивно перечислимых множеств, Изв. вузов. Мат., 279
No. 8 (1985), 3-12.
Калантари (I. Kalantari)
[1982] 	Major subsets in effective topology, In: Metakides [1982], 77-94.
Калантари и Вейткемп (I. Kalantari and G. Weitkamp)

Литература
521
[1985] Effective topological spaces I: A definability theory, Ann. Pure Appl. Logic, 29
(1985), 1-27.
Калантари и Реммел (I. Kalantari and J. B. Remmel)
[1983] 	Degrees of recursively enumerable topological spaces, J. Symbolic Logic, 4&i
610-622.
Каллибеков C.
[1971a] Индексные множества степеней неразрешимости, Алгебра и Логика, 10
(1971), 316-326.
[1971b] Индексные множества m-степеней, Сиб. мат. журнал, 12 (1971), 1292-1300.
[1973а] О степенях рекурсивно перечислимых множеств, Сиб. мат. журнал, 14
(1973), 421-426, 463
[1973b] О табличных степенях рекурсивно перечислимых множеств, Мат. заметки,
Ц (1973), 697-702.
Кат ленд (N. J. Cutland)
[1980] 	Computability: An Introduction to Recursive Function Theory, Cambridge
University Press, Cambridge, 1980.
Кейз (J. Case)
[1970] 	Enumeration reducibility and partial degrees, Ann. Math. Logic, 2 (1970),
419-439.
Келли (J. L. Kelley)
[1955] General Topology, D. van Nostrand, Inc., Princeton, New Jersey, 1955.
Кент (G. F. Kent)
[1962] Constructive analogues of the group of permutations of the natural numbers,
Trans. Amer. Math. Soc., 104 (1962), 347-362.
Кинбер (E. Kinber)
[1977] О тьюринговых степенях гиперпростых множеств, Латв. Мат. Ежегодник,
21, 164-170 (1971).
Клив (J. Р. Cleave)
[1961] Creative functions, Z. Math. Logik Grundlag. Math., 7(1961), 205-212.
К лини (S. C. Kleene)
[1934] Proof by cases in formal logic, Ann. of Math. (2), 35 (1934), 529-544.
[1935] A theory of positive integers in formal logic, Amer. J. Math., 57(1935), 153-173
and 219-244.
[1936a] General recursive functions of natural numbers, Math. Ann., 112 (1936),
727-742; reprinted in Davis [1965], 236-253.
[1936b] А-definability and recursiveness, Duke Math. J., 2 (1936), 340-353.
[1938] On notation for ordinal numbers, J. Symbolic Logic, 3 (1938), 150-155.
[1943] Recursive predicates and quantifiers, Trans. Amer. Math. Soc., 53 (1943),
41-73; reprinted in Davis [1965], 254-287.
[1950] A symmetric form of Godel’s theorem, Indag. Math., 12, 244-246. (Koninklijke
Nederlandse Akademie van Wetenschappen, Proceedings, Series A 53.)

522
Литература
[1952а] Introduction to Metamathematics, Van Nostrand, New York,
1952; Eighth reprint, Wolters-Noordhoff Publishing Co., Groningen and North-
Holland, Amsterdam, New York, Oxford, 1980.
[1952b] Recursive functions and intuitionistic mathematics, Proc. Intern. Congress
of Mathematicians, Cambridge, Mass., 1950, 679-685, Amer. Math. Soc.,
Providence, R.I., 1952.
[1955a] Arithmetical predicates and function quantifiers, Trans. Amer. Math. Soc., 79
(1955), 312-340.
[1955b] On the forms of the predicates in the theory of constructive ordinals (second
paper), Amer. J. Math., 77, 405-428.
[1955c] Hierarchies of number-theoretic predicates, Bull. Amer. Math. Soc., 61 (1955),
193-213.
[1959a] Recursive functionals and quantifiers of finite types I, Trans. Amer. Math. Soc.,
91 (1959), 1-52.
[1959b] Countable functionals, In: Heyting [1959], 81-100.
[1959c] Quantification of number-theoretic functions, Compositio Math., Ц (1959),
23-40.
[1963] 	Recursive functionals and quantifiers of finite types II, Trans. Amer. Math.
Soc., 108 (1963), 106-142.
[1981] Origins of recursive function theory, Ann. Hist. Comput., 3 (1981), 52-67.
К лини и Пост (S. С. Kleene and E. L. Post)
[1954] The upper semi-lattice of degrees of recursive unsolvability, Ann. of Math. (2),
59 (1954), 379-407.
К лот (P. Clote)
[1985] Applications of the low-basis theorem in arithmetic, In: Ebbinghaus, Muller
and Sacks [1985], 65-88.
Кобзев Г. H.
[1973a] О btt-сводимости, Алгебра и Логика, 12 (1973), 190-204, 244.
[1973b] О btt-сводимости И, Алгебра и Логика, 12 (1973), 433-444, 492.
[1973с] Полные btt-степени, Алгебра и Логика, 13 (1973), 22-25, 120.
[1975] О r-отделимых множествах, Исслед. по мат. логике и теории алгоритмов,
Тбилиси, 1975, 19-30.
[1976] Соотношения между рекурсивно перечислимыми tt- и w-степенями, Сообщ.
АН ГССР, 84 (1976), 585-587.
[1977а] Максимальные m-степени, Сообщ. АН ГССР, 85 No. 2 (1977), 325-327.
[1977b] Рекурсивно перечислимые bw-степени, Мат. Заметки, 21 (1977), 839-846.
[1978а] О tt-степенях рекурсивно перечислимых тьюринговых степеней, Мат.
сборник, 106 (1978), 507-514.
[1978b] О полурешетке tt-степеней, Сообщ. АН ГССР, 90 No. 2 (1978), 281-283.
[1979] 	О tt-степенях рекурсивно перечислимых тьюринговых степеней, Алгебра
и Логика, 18 (1979), 415-425.
Коэн (Р. F. Cohen)
[1975] Weak Truth-Table Reducibility and the Pointwise Ordering of 1-1 Recursive
Functions, Doctoral Dissertation, Univ. of Illinois at Urbana, 1975.

Литература
523
Коэн и Джокуш (Р. F. Cohen and С. G. Jockusch, Jr.)
[1975] A lattice property of Post’s simple set, Illinois J. Math., 19 (1975), 450-453.
Коэн (P. J. Cohen)
[1963] The independence of the continuum hypothesis I, Proc. Natl. Acad. Sci. USA,
50 (1963) 1143-1148.
[1966] Set theory and the continuum hypothesis, W. A. Benjamin, New York, 1966.
Крейг (W. Craig)
[1953] 	On axiomatizability within a system, J. Symbolic Logic, 18 (1953), 30-32.
Крейзел (G. Kreisel)
[1950] Note on arithmetic models for consistent formulae of the predicate calculus,
Fund. Math., 57(1950), 265-285.
[1953] A variant to Hilbert’s theory on the foundations of arithmetic, British J. Philos.
Sci., 4 (1953), 107-129, 357.
Крейзел, Лакомб и Шёнфилд (G. Kreisel, D. Lacombe and
J. R. Shoenfield)
[1959] 	Partial recursive functionals and effective operations, In: Heyting [1959],
290-297.
Крейзел и Сакс (G. Kreisel and G. E. Sacks)
[1965] Metarecursive sets, J. Symbolic Logic, 30 (1965), 318-338.
Крослей (J.N. Crossley)
[1967] Sets, Models, and Recursion Theory (editor), Proc. Summer School in
Math. Logic and Logic Colloquium, Leicester, England 1965, North-Holland,
Amsterdam, 1967.
[1981] 	Aspects of Effective Algebra (editor), Proc. Conference on Aspects of
Effective Algebra at Monash University, August 1979, Upside Down A Book
Company, Yarra Glenn, Victoria, Australia, 1981. (This contains an extensive
bibliography of effective algebra by J. N. Crossley and S. Miranda.)
Крослей и Нероуд (J. N. Crossley and A. Nerode)
[1974] 	Combinatorial Functors, Ergebnisse der Mathematik und ihrer Grenzgebiete,
Band 81, Springer-Verlag, Berlin, Heidelberg, New York, 1974.
Кузнецов A. В.
[1950] О примитивно рекурсивных функций большого размаха, ДАН СССР, 71
(1950), 233-236.
Купер (S. В. Cooper)
[1972а] Minimal upper bounds for sequences of recursively enumerable degrees, J.
London Math. Soc., 5 (1972), 445-450.
[1972b] Degrees of unsolvability complementary between recursively enumerable
degrees, Part I, Ann. Math. Logic, 4 (1972), 31-73.
[1972c] Jump equivalence of the A® hyperhyperimmune sets, J. Symbolic Logic, 37
(1972), 598-600.

524
Литература
[1972d] Sets recursively enumerable in high degrees, Notices Amer. Math. Soc., 19
(1972), A-20.
[1973] 	Minimal degrees and the jump operator, J. Symbolic Logic, 38 (1973), 249-271.
[1974a] On a theorem of C.E.M. Yates (handwritten notes).
[1974b] Minimal pairs and high recursively enumerable degrees, J. Symbolic Logic, 39
(1974), 655-660.
[1974c] An annotated bibliography for the structure of the degrees below O' with special
reference to that of the recursively enumerable degrees, Recursive Function
Theory Newsletter 5 (1974), 1-15.
[1982] Partial degrees and the density problem, J. Symbolic Logic, ^7 (1982), 854-859.
[1984] Partial degrees and the density problem. Part 2: The enumeration degrees of
the £2 sets are dense, J. Symbolic Logic, 4& (1984), 503-513.
[1987] 	Enumeration reducibility using bounded information: counting minimal covers,
Z. Math. Logic Grundlag Math., 33 (1987), 537-560.
[1988a] A jump class of non-cappable degrees, J. Symbolic Logic, 54 (1988), 324-353.
[1988b] The strong anti-cupping property for recursively enumerable degrees, J.
Symbolic Logic, 54 (1988), 527-539.
[1994*] Rigidity and definability in the non-computable universe, in “Proceedings of the
9th International Congress of Logic, Methodology and Philosophy of Science”
(eds. D. Prawitz, B. Skyrms, D. Westerstahl), North-Holland, Amsterdam,
1994, 209-236
[1996] Strong minimal covers for recursively enumerable degrees, Math. Logic
Quarterly, 42 (1996), 191-196.
[1997*] Beyond Godel’s theorem—the failure to capture information content, in
’’Complexity, Logic and Recursion Theory” (ed. A. Sorbi), Lecture Notes in
Pure and Applied Mathematics, vol. 187, Marcel Dekker, New York, 1997,
93-122
Купер и Эпштейн (S. В. Cooper and R. Epstein)
[1987] Complementing below recursively enumerable degrees, Ann. Pure Appl. Logic,
34 (1987), 14-32.
Куртц (S. A. Kurtz)
[1983] Notions of weak genericity, J. Symbolic Logic 48 (1983), 764-770.
Кучера (A. Kucera)
[1985] Measure, nj-classes and complete extensions of PA, In: Ebbinghaus, Muller
and Sacks [1985], 245-259.
[1986a] An alternative priority-free solution to Post’s problem, In: Twelfth Symposium
held in Bratislava, Czechoslovakia, August 25-29, 1986, edited by J. Gruska,
B. Rovan, and J! Wiederman, Lecture notes in Computer Science No. 233,
Proceedings, Mathematical Foundations of Computer Science ’86, Springer-
Verlag, Heidelberg, Berlin, New York, Tokyo, 1986.
[1986b] On the role of O' in recursion theory, Proc. of Logic Colloquium’86 (Drake,
Truss eds) North-Holland, 133-141.
Лавров И. A.
[1968] 	Ответ на один вопрос П. Р. Янга, Алгебра и Логика, 7 (1968), 48-54.

Литература
525
[1974] Некоторые свойства ретрактов нумераций Поста, Алгебра и Логика, 3
(1974), 662-675.
Ладнер (R. Е. Ladner)
[1973а] Mitotic recursively enumerable sets, J. Symbolic Logic, 38 (1973), 199-211.
[1973b] A completely mitotic nonrecursive recursively enumerable degree, Trans. Amer.
Math. Soc., 184 (1973), 479-507.
Ладнер и Cacco (R. E. Ladner and L. P. Sasso)
[1975] The weak truth table degrees of recursively enumerable sets, Ann. Math. Logic,
8 (1975), 429-448.
Лакомб (D. Lacombe)
[1954] 	Sur le semi-r6seau constitue par les degree d’indecidabilit6 recursive, Comptes
rendus hebdomadaires des seances de l’Academie des Sciences (Paris) Ser. A-B
239 (1954), 1108-1109.
[1959] Quelques proc6d6s de d6finition en topologie recursive, In: A. Heyting [1959],
129-158.
[1960] La th6orie des fonctions recursives et ses applications (Ехроэё d’information
g6n6rale), Bull. Soc. Math. France 88 (I960), 393-468.
Лахлан (A. H. Lachlan)
[1965a] Some notions of reducibility and productiveness, Z. Math. Logik Grundlag.
Math., 11 (1965), 17-44.
[1965b] On a problem of G. E. Sacks, Proc. Amer. Math. Soc., 16 (1965), 972-979.
[1966a] A note on universal sets, J. Symbolic Logic, 31 (1966), 573-574.
[1966b] Lower bounds for pairs of recursively enumerable degrees, Proc. London Math.
Soc., 16 (1966), 537-569.
[1966c] The impossibility of finding relative complements for recursively enumerable
degrees, J. Symbolic Logic, 31 (1966), 434-454.
[1967] The priority method I, Z. Math. Logik Grundlag. Math. 13 (1967), 1-10.
[1968a] Degrees of recursively enumerable sets which have no maximal superset, J.
Symbolic Logic, 33 (1968), 431-443.
[1968b] Distributive initial segments of the degrees of unsolvability, Z. Math. Logik
Grundlag. Math., Ц (1968), 457-472.
[1968c] On the lattice of recursively enumerable sets, Trans. Amer. Math. Soc., 130
(1968), 1-37.
[1968d] The elementary theory of recursively enumerable sets, Duke Math. J., 35
(1968), 123-146.
[1968e] Complete recursively enumerable sets, Proc. Amer. Math. Soc., 19 (1968),
99-102.
[1969] 	Initial Segments of one-one degrees, Pacific J. Math., 29 (1969), 351-366.
[1970a] On some games which are relevant to the theory of recursively enumerable sets,
Ann. of Math. (2), 91 (1970), 291-310.
[1970b] Initial segments of many-one degrees, Canad. J. Math., 22 (1970), 75-85.
[1971] 	Solution to a problem of Spector, Canad. J. Math., 23 (1971), 247-256.
[1972a] Embedding nondistributive lattices in the recursively enumerable degrees, In:
Hodges [1972], 149-177.

526
Литература
[1972b] Рекурсивно перечислимые m-степени, Алгебра и логика, 11 (1972),
326-358.
[1972с] Две теоремы об m-степенях рекурсивно перечислимых множеств, Алгебра
и Логика, 11 (1972), 216-229.
[1973] 	The priority method for the construction of recursively enumerable sets, In:
Mathias and Rogers [1973], 299-310.
[1975a] A recursively enumerable degree which will not split over all lesser ones, Ann.
Math. Logic, 9 (1975), 307-365.
[1975b] Uniform enumeration operations, J. Symbolic Logic, 40 (1975), 401-409.
[1975c] wtt-complete sets are not necessarily tt-complete, Proc. Amer. Math. Soc., 48
(1975), 429-434.
[1979] Bounding minimal pairs, J. Symbolic Logic, 44 (1979), 626-642.
[1980] Decomposition of recursively enumerable degrees, Proc. Amer. Math. Soc., 79
(1980), 629-634.
Лахлан и Лебёф (A. H. Lachlan and R. Lebeuf)
[1976] 	Countable initial segments of the degrees of unsolvability, J. Symbolic Logic,
41 (1976), 289-300.
Лахлан и Coap ( A. H. Lachlan and R. I. Soare)
[1980] 	Not every finite lattice is embeddable in the recursively enumerable degrees,
Adv. in Math., 57(1980), 74-82.
Лемпп (S. Lempp)
[1986] Topics in recursively enumerable sets and degrees, Ph.D. Dissertation,
University of Chicago, 1986.
[1987] Hyperarithmetical index sets in recursion theory, Trans. Amer. Math. Soc., 303
(1987), 559-583.
[1988] A high strongly noncappable degree, J. Symbolic Logic, 53 (1988), 174-187.
Лемпп и Лерман (S. Lempp and M. Lerman)
[1997*] A finite lattice without critical triple that cannot be embedded into the
enumerable Turing degrees, Ann. Pure Appl. Logic, 87 (1997), No. 2, 167-185.
Лемпп, Ниис и Сламан (S. Lempp, A. Nies A. and Slaman, T.A.),
[1998*] The Пз-theory of the computably enumerable Turing degrees is undecidable,
Trans. Amer. Math. Soc., 350 (1998), No.7, 2719-2736.
Лемпп и Сламан (S. Lempp and T. A. Slaman)
[1989] 	A limit on relative genericity in the recursively enumerable sets, J. Symbolic
Logic, 54 (1989), 376-395.
Лерман (M. Lerman)
[1970a] Recursive functions modulo co-r-maximal sets, Trans. Amer. Math. Soc., 148
(1970), 429-444.
[1970b] Turing degrees and many-one degrees of maximal sets, J. Symbolic Logic, 35
(1970), 29-40.

Литература
527
[1971а] Some theorems on r-maximal sets and major subsets of recursively enumerable
sets, J. Symbolic Logic, 36 (1971), 193-215.
[1971b] Initial segments of the degrees of unsolvability, Ann, of Math. (2), 93 (1971),
365-389.
[1973] Admissible ordinals and priority arguments, In: Mathias and Rogers [1973],
311-344.
[1976] Congruence relations, filters, ideals and definability in lattices of alpha-
recursively enumerable sets, J. Symbolic Logic, (1976), 405-418.
[1977] Automorphism bases for the semilattice of recursively enumerable degrees,
Notices Amer. Math. Soc., 24 (1977), A-251, Abstract # 77T-E10.
[1978a] Lattices of а-recursively enumerable sets, In: Fenstad, Gandy and Sacks [1978],
223-238.
[1978b] On elementary theories of some lattices of а-recursively enumerable sets, Ann.
Math. Logic, Ц (1978), 227-272.
[1980] The degrees of unsolvability: Some recent results, In: Drake and Wainer [1980],
140-157.
[1981] On recursive linear orderings, In: Lerman, Schmerl, and Soare [1981], 132-142.
[1983a] Degrees of Unsolvability, Perspectives in Mathematical Logic, Omega Series,
Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1983.
[1983b] The structures of recursion theory, In: Chong and Wicks [1983], 77-95.
[1985a] The embedding problem for the recursively enumerable degrees, In: Nerode and
Shore [1985], 13-20.
[1985b] On the ordering of classes in high/low hierarchies, In: Ebbinghaus, Muller, and
Sacks [1985], 260-270.
[1985c] Upper bounds for the arithmetical degrees, Ann. Pure Appl. Logic, 29 (1985),
225-254.
[1986] Degrees which do not bound minimal degrees, Ann. Pure Appl. Logic, 30
(1986), 249-276.
[1998*] A necessary and sufficient condition for embedding ranked finite partial lattices
into the computably enumerable degrees, Ann. Pure Appl. Logic, 94 (1998),
No. 1-3, 143-180.
Лерман и Реммел (M. Lerman, J. Remmel)
[1982] 	The universal splitting property I, In: van Dalen, Lascar and Smiley [1982],
181-208.
[1984] 	The universal splitting property II, J. Symbolic Logic, 49 (1984), 137-150.
Лерман и Розенштейн (M. Lerman and J. Rosenstein)
[1982] 	Recursive linear orderings, In: Metakides [1982], 123-136.
Лерман и Coap (M. Lerman and R. I. Soare)
[1980a] d-Simple sets, small sets, and degree classes, Pacific J. Math., 87 (1980),
135-155.
[1980b] A decidable fragment of the elementary theory of the lattice of recursively
enumerable sets, Trans. Amer. Math. Soc., 257(1980), 1-37.
Лерман и Шмерл (M. Lerman and J. H. Schmerl)
[1979] Theories with recursive models, J. Symbolic Logic, 44 (1979), 59-76.

528
Литература
Лерман, Шмерл и Соар (М. Lerman, J. Н. Schmerl and R. I. Soare)
[1981] 	Logic Year 1979-80: University of Connecticut (editors), Lecture Notes in
Mathematics, No. 859, Springer-Verlag, Berlin, Heidelberg, Tokyo, New York,
1981.
Лерман , Шор и Соар (М. Lerman, R. A. Shore and R. I. Soare)
[1978] 	r-Maximal major subsets, Israel J. Math., 31 (1978), 1-18.
[1984] The elementary theory of the recursively enumerable degrees is not No-
categorical, Adv. in Math., 53 (1984), 301-320.
Лолли (G. Lolli)
[1981] 	Recursion Theory and Computational Complexity (editor), Proceedings of
Centro Internazionale Matematico Estivo (C.I.M.E.), June 14-23, 1979, in
Bressanone, Italy, Liguori Editore, Naples, Italy, 1981.
Маасе (W. Maass)
[1981] A countable basis for sets anc* recursion theory on Hi, Proc. Amer. Math.
Soc., 82 (1981), 267-270.
[1982] Recursively enumerable generic sets, J. Symbolic Logic, ^7 (1982), 809-823.
[1983] Characterization of recursively enumerable sets with supersets effectively
isomorphic to all recursively enumerable sets, Trans. Amer. Math. Soc., 279
(1983), 311-336.
[1984] On the orbits of hyperhypersimple sets, J. Symbolic Logic, 4& (1984), 51-62.
[1985a] Variations on promptly simple sets, J. Symbolic Logic, 50 (1985), 138-148.
[1985b] Major subsets and automorphisms of recursively enumerable sets, in Nerode
and Shore [1985], 21-32.
[1986] Are recursion theoretic arguments useful in complexity theory ?, Proc. of the
Seventh International Congress of Logic, Methodology, and the Philosophy of
Science, Salzburg 1983, North-Holland, Amsterdam, New York, Oxford, 1986,
141-158.
Маасе и Стоб (W. Maass and M. Stob)
[1983] 	The intervals of the lattice of recursively enumerable sets determined by major
subsets, Ann. Pure Appl. Logic, 24 (1983), 189-212.
Маасе и Хумер (W. Maass and S. Homer)
[1983] 	Oracle dependent properties of the lattice of NP sets, Theoret. Comput. Sci.,
24 (1983), 279-289.
Маасе, Шор и Стоб (W. Maass, R. A. Shore and M. Stob)
[1981] Splitting properties and jump classes, Israel J. Math., 39 (1981), 210-224.
Мадан и Робинсон (D. В. Madan and R. W. Robinson)
[1982] Monotone and 1-1 sets, J. Austral. Math. Soc. (Series A), 33 (1982), 62-75.
Майхилл (J. Myhill)
[1953] 	Three contributions to recursive function theory, Actes du Xleme congres
international de philosophic, Bruxelles 20-26, Aout 1953 XIV, North-Holland,
Amsterdam, 1953, 50-59.
[1955] 	Creative sets, Z. Math. Logik Grundlag. Math., 1 (1955), 97-108.

Литература
529
[1956] 	The lattice of recursively enumerable sets, J. Symbolic Logic, 21 (1956), 220
(abstract).
[1959a] Finitely representable functions, In: A. Heyting [1959], 195-207.
[1959b] Recursive digraphs, splinters and cylinders, Math. Ann., 138 (1959), 211-218.
[1961a] A note on degrees of partial functions, Proc. Amer. Math. Soc., 12 (1961),
519-521.
[1961b] Category methods in recursion theory, Pacific J. Math., 11 (1961), 1479-1486.
[1971] 	A recursive function, defined on a compact interval and having a continuous
derivative that is not recursive, Michigan Math. J.,18 (1971), 97-98.
Майхилл и Шепердсон (J. Myhill and J. C. Shepherdson)
[1955] Effective operations on partial recursive functions, Z. Math. Logik Grundlag.
Math., 1 (1955), 310-317.
Маклохлин (T. G. McLaughlin)
[1965] On a class of complete simple sets, Canad. Math. Bull., 8 (1965), 33-37.
[1966] Retraceable sets and recursive permutations, Proc. Amer. Math. Soc., 17
(1966), 427-429.
[1968] A theorem on intermediate reducibilities, Proc. Amer. Math. Soc., 19 (1968),
87-90.
Мактей и Янг (M. Machtey and P. Young)
[1978] An introduction to the general theory of algorithms, Elsevier North-Holland,
Amsterdam and New York, 1978.
Макэвой (К. McEvoy)
[1985] 	Jumps of quasi-minimal enumeration degrees, J. Symbolic Logic, 50 (1985),
839-848.
Макэвой и Купер (К. McEvoy and S. В. Cooper)
[1985] 	On minimal pairs of enumeration degrees, J. Symbolic Logic, 50 (1985),
983-1001.
Мальцев А. И.
[1965] Алгоритмы и рекурсивные функции, Москва, Наука, 1965, 372 с.
Мальцев Ан. А.
[1984] 	О структуре семейств иммунных, гипериммунных и гипергипериммунных
множеств, Мат. сборник, 124 No. 7 (1984), 307-319.
Марков А. А.
[1947] 	О представлении рекурсивных функций, ДАН СССР, 58 (1947), 1891-1892.
[1951] Теория алгоритмов, Труды мат. инст. АН СССР, 38 (1951), 176-189.
[1954] Теория алгоритмов, Труды мат. инст. АН СССР, 4% (1954).
[1960] 	Неразрешимость проблемы гомеоморфии, Успехи мат. наук, 13 (1960), вып.
4(82), 213-216.
Маркус (I. Marques)
[1973] Complexity Properties of Recursively Enumerable Sets, Ph.D. Dissertation,
Univ. of California, Berkeley, 1973.

530
Литература
[1975] 	On degrees of unsolvability and complexity properties, J. Symbolic Logic, 40
(1975), 529-540.
Мартин (D. A. Martin)
[1963] A theorem on hyperhypersimple sets, J. Symbolic Logic, 28 (1963), 273-278.
[1966a] Completeness, the recursion theorem, and effectively simple sets, Proc. Amer.
Math. Soc., 17 (1966), 838-842.
[1966b] Classes of recursively enumerable sets and degrees of unsolvability, Z. Math.
Logik Grundlag. Math., 12 (1966), 295-310.
[1966c] On a question of G. E. Sacks, J. Symbolic Logic, 31 (1966), 66-69.
[1966d] The priority method of Sacks, mimeographed notes.
[1967] 	Measure, category, and degrees of unsolvability (unpublished manuscript), 16
pp.
Мартин и Пур-Эль (D. A. Martin and M. B. Pour-El)
[1970] Axiomatizable theories with few axiomatizable extensions, J. Symbolic Logic,
35 (1970), 205-209.
Марченков С. C.
[1975] Существование рекурсивно перечислимых минимальных табличных
степеней, Алгебра и Логика, Ц (1975), 442-429.
[1976а] Об одном классе неполных множеств, Мат. Заметки, 20 (1976), 473-478.
[1976b] К сравнению верхних полурешеток рекурсивно перечислимых табличных
и m-степеней, Мат. Заметки, 20 (1976), 19-26.
[1976с] О табличных степенях максимальных множеств, Мат. Заметки, 20 (1976),
373-381.
[1977] 	О рекурсивно перечислимых минимальных btt-степененях, Мат. сборник,
103 (Ц5) (1977), 550-562 и 631.
Матиас и Роджерс (A. R. D. Mathias and Н. Rogers)
[1973] 	Cambridge Summer School in Mathematical Logic (editors), held in
Cambridge, England, August 1-21, 1971, Lecture Notes in Mathematics 337,
Springer-Verlag, Berlin, Heidelberg, New York, 1973.
Матиясевич Ю. В.
[1970] Диофантовость перечислимых множеств, ДАН СССР, 191 (1970), 279-282.
[1971] Диофантово представление перечислимых множеств, Изв. ДАН СССР,
Серия матем., 35 (1971), 3-30.
Медведев Ю. Т.
[1955а] О неизоморфных рекурсивно перечислимых множествах, ДАН СССР, 102
(1955), 211-214.
[1955b] Степени трудности массовых проблем, ДАН СССР 104 (1955), 501-504.
Метакидес (G. Metakides)
[1982] 	Patras Logic Symposion (editor), Proceedings of the Logic Symposium held at
Patras, Greece, August 18-22, 1980, North-Holland, Amsterdam, New York,
Oxford, 1982.
Метакидес и Нероуд (G. Metakides and A. Nerode)

Литература
531
[1975] Recursion theory and algebra, In: Lecture Notes in Mathematics No. 450,
Springer-Verlag, Berlin, Heidelberg, New York, 1975, 209-219.
[1977] Recursively enumerable vector spaces, Ann. Math. Logic, 11 (1977), 141-171.
[1979] Effective content of field theory, Ann. Math. Logic 17 (1979), 289-320.
[1980] Recursion theory on fields and abstract dependence, J. Algebra 65 (1980),
36-59.
[1982] The introduction of non-recursive methods in mathematics, In: Troelstra and
van Dalen [1982], 319-335.
Метакидес, Нероуд и Шор (G. Metakides, A. Nerode and R. A. Shore)
[1985] 	Recursive limits on the Hahn-Banach theorem, Contemp. Math. 39 (1985),
85-91.
Миллар (T. Millar)
[1978] Foundations of recursive model theory, Ann. of Math. Logic 13 (1978), 45-72.
[1985] Decidable Ehrenfeucht theories, In: Nerode and Shore [1985], 311-321.
Миллер (C. F. Miller, III)
[1971] On Group-Theoretic Decision Problems and Their Classification, Ann. of Math.
Stud. 68, Princeton University Press, Princeton, N.J., 1971.
Миллер (D. Miller)
[1981a] High recursively enumerable degrees and the anti-cupping property, In:
Lerman, Schmerl, and Soare [1981], 230-245.
[1981b] The Relationship Between the Structure and Degrees of Recursively
Enumerable Sets, Ph.D. Dissertation, University of Chicago, 1981.
Миллер и Реммел (D. Miller and J. B. Remmel)
[1984] 	Effectively nowhere simple sets, J. Symbolic Logic 49 (1984), 129-136.
Миллер и Мартин (W. Miller and D. A. Martin)
[1968] 	The degree of hyperimmune sets, Z. Math. Logik Grundlag. Math. Ц (1968),
159-166.
Минский M. Л. (M. L. Minsky)
[1961] 	Recursive unsolvability of Post’s problem of “tag” and other topics in the theory
of Turing machines, Ann. of Math. (2) 74 (1961), 437-455.
Морлей и Coap (M. D. Morley and R. I. Soare)
[1975] Boolean algebras, splitting theorems and sets, Fund. Math. 90 (1975),
45-52.
Моррис (P. В. Morris)
[1974] Complexity Theoretic Properties of Recursively Enumerable Sets, Ph.D.
Dissertation, University of California, Irvine, 1974.
Mopxep (J. Mohrherr)
[1982] Index Sets and Truth-Table Degrees, Ph.D. Dissertation, University of Illinois
at Chicago Circle, 1982.

532
Литература
[1983] Kleene index sets and functional га-degrees, J. Symbolic Logic, 48 (1983),
829-840.
[1986] 	A refinement of lown and highn for the r. e. degrees, Z. Math. Logik Grundlag.
Math., 32 (1986), 5-12.
Мостовский (A. Mostowski)
[1947] On definable sets of positive integers, Fund. Math. 34 (1947), 81-112.
[1948] On a set of integers not definable by means of one-quantifier predicates, Annales
de la Societe Polonaise de Mathematique 21 (1948), 114-119.
Мучник A. A.
[1956a] Неразрешимость проблемы сводимости теории алгоритмов, ДАН СССР,
108 (1956), 194-197.
[1956b] Об отделимости рекурсивно перечислимых множеств, ДАН СССР, 109,
29-32.
[1958] Изоморфизм систем рекурсивно перечислимых множеств с эффективными
свойствами, Труды Моек. мат. общ., 7 (1958), 407-412.
Найт, Лахлан и Соар (J. Knight, А. Н. Lachlan and R. I. Soare)
[1984] Two theorems on degrees of models of true arithmetic, J. Symbolic Logic 49
(1984), 425-436.
Нероуд (A. Nerode)
[1961] Extensions to Isols, Ann. of Math. (2) 73 (1961), 362-403.
Нероуд и Манастер (A. Nerode and A. B. Manaster)
[1970] 	A universal embedding property of the RET’s, J. Symbolic Logic 35 (1970),
51-59.
Нероуд и Реммел (A. Nerode and J. B. Remmel)
[1982] Recursion theory on matroids, In: Metakides [1982], 41-65.
[1985a] Generic objects in recursion theory, In: Ebbinghaus, Muller, and Sacks [1985],
271-314.
[1985b] A survey of lattices of r. e. substructures, In: Nerode and Shore [1985], 323-375.
[1986] 	Generic objects in recursion theory II: Operations on recursive approximation
spaces, Ann. Pure Appl. Logic 31 (1986), 257-288.
Нероуд и Шор (A. Nerode and R. A. Shore)
[1980a] Second order logic and first order theories of reducibility orderings, In: Barwise,
Keisler, and Kunen [1980], 181-200.
[1980b] Reducibility orderings: Theories, definability and automorphisms, Ann. Math.
Logic 18 (1980), 61-89.
[1985] Recursion Theory (editors), Proc. Symp. Pure Math., ^2, Proceedings of AMS-
ASL Summer Institute on Recursion Theory, held at Cornell University, Ithaca,
New York, June 28 - July 16, 1982, Ainer. Math. Soc., Providence, R. I., 1985.
Ниис (A. Nies)
[1989] Coding Methods in Computability Theory and Complexity Theory.
Habilitationsschrift, Universitat Heidelberg. 106 pages.

Литература
533
Ниис, Шор и Сламан (A. Nies, R. A. Shore and Т. A. Slaman)
[1998*] Interpretability and definability in the recursively enumerable degrees, Proc.
London Math. Soc. (3), Proceedings of the London Mathematical Society. Third
Series, 77(1998), 2, 241-291,
Новиков П. C.
[1955] Об алгоритмической неразрешимости проблемы тождества слов, Труды
мат. инст. АН СССР 44 (1955).
Норманн (D. Normann)
[1980] Recursion on Countable Functionals, Lecture Notes in Mathematics No. 811,
Springer-Verlag, Berlin, New York, Heidelberg, 1980.
Одифредди (P. Odifreddi)
[1981] Strong reducibilities, Bull. Amer. Math. Soc. 4 (1981), 37-86.
[1983a] Forcing and reducibilities I, J. Symbolic Logic 4% (1983), 288-310.
[1983b] Forcing and reducibilities II: forcing in fragments of analysis, J. Symbolic Logic
48 (1983), 724-743.
[1985] 	The structure of ra-degrees, In: Ebbinghaus, Muller and Sacks [1985], 315-332.
[1989] Classical Recursion Theory, North-Holland, Amsterdam, New York, Oxford,
1989.
[h.o.] Recursion-Theoretical Aspects of Complexity Theory, unpublished.
[h.o.] Church’s Thesis: the extent of recursiveness in the universe and man,
unpublished.
Оманадзе P. Ш.
[1976] 	О полных рекурсивно перечислимых множествах, Сообщ. АН Груз. ССР,
81 (1976), 529-532.
[1978] On reducibilities for the class of recursively enumerable sets, Сообщ. АН Груз.
ССР, 91 (1978), 549-552.
Оуингс (J. C. Owings, Jr.)
[1967] 	Recursion, metarecursion, and inclusion, J. Symbolic Logic 32 (1967), 173-178.
[1970] Review of Lachlan [1968c, 1968d] and Robinson [1967a, 1967b], J. Symbolic
Logic 35 (1970), 153-155.
[1973] Diagonalization and the recursion theorem, Notre Dame J. Formal Logic 14
No. 1 (1973), 95-99.
Парис (J. В. Paris)
[1976] Survey of results on measure and degrees (preprint).
[1977] Measure and minimal degrees, Ann. Math. Logic 11 (1977), 203-216.
Петер (R. Peter)
[1967] 	Recursive Functions (third revised edition), Academic Press, New York, 1967.
Познер (D. Posner)
[1977] 	High Degrees, Doctoral Dissertation, University of California, Berkeley, 1977.
[1980] A survey of non-r. e. degrees ^ O', In: Drake and Wainer [1980], 52-109.
[1981] The upper semilattice of degrees ^ O' is complemented, J. Symbolic Logic 46
(1981), 705-713.

534
Литература
Познер и Робинсон (D. Posner and R. W. Robinson)
[1981] Degrees joining to O', J. Symbolic Logic 46 (1981), 714-722.
Познер и Эпштейн (D. Posner and R. Epstein)
[1978] Diagonalization in degree constructions, J. Symbolic Logic 43 (1978), 280-283.
Пост (E. L. Post)
[1936] Finite combinatory processes-formulation I, J. Symbolic Logic 1 (1936),
103-105; reprinted in Davis [1965], 288-291.
[1943] Formal reductions of the general combinatorial decision problem, Amer. J.
Math. 65 (1943), 197-215.
[1944] Recursively enumerable sets of positive integers and their decision problems,
Bull. Amer, Math. Soc. 50 (1944), 284-316; reprinted in Davis [1965], 304-337.
[1946] Note on a conjecture of Skolem, J. Symbolic Logic 11 (1946), 73-74.
[1947] Recursive unsolvability of a problem of Thue, J. Symbolic Logic 12 (1947),
1-11; reprinted in Davis [1965], 292-303.
[1948] Degrees of recursive unsolvability: preliminary report (abstract), Bull. Amer.
Math. Soc. 54 (1948), 641-642.
Пур-Эль (M. В. Pour-El)
[1965] “Recursive isomorphism” and effectively extensible theories, Bull. Amer. Math.
Soc. 71 (1965), 551-555.
[1968a] Effectively extensible theories, J. Symbolic Logic 33 (1968), 56-68.
[1968b] Independent axiomatization and its relation to the hypersimple set, Z. Math.
Logik Grundlag. Math. Ц (1968), 449-456.
[1974] 	Abstract computability and its relation to the general all purpose analogue
computer, Trans. Amer. Math. Soc. 199 (1974), 1-28.
Пур-Эль и Крипке (M. В. Pour-El and S. Kripke)
[1967a] Deduction-preserving “recursive isomorphisms” between theories, Bull. Amer.
Math. Soc. 73 (1967), 145-148.
[1967b] Deduction-preserving “recursive isomorphisms” between theories, Fund. Math.
61 (1967), 141-163.
Пур-Эль и Ричардс (M. В. Pour-El and I. Richards)
[1979] A computable ordinary differential equation which possesses no computable
solution, Ann. Math. Logic 17 (1979), 61-90.
[1981] The wave equation with computable initial data such that its unique solution
is not computable, Adv. in Math. 39 (1981), 215-239.
[1983a] Computability and noncomputability in classical analysis, Trans. Amer. Math.
Soc. 275 (1983), 539-560.
[1983b] Noncomputability in analysis and physics: a complete determination of the
class of noncomputable linear operators, Adv. in Math. 48 (1983), 44-74.
Рабин (M. О. Rabin)
[1960] Computable algebra, general theory and theory of computable fields, Trans.
Amer. Math. Soc. 95 (1960), 341-360.
Райс (H. G. Rice)

Литература
535
[1953] Classes of recursively enumerable sets and their decision problems, Trans.
Amer. Math. Soc. 74 (1953), 358-366.
[1954] Recursive real numbers, Proc. Amer. Math. Soc. 5 (1954), 784-791.
[1956a] Recursive and recursively enumerable orders, Trans. Amer. Math. Soc. 83
(1956), 277-300.
[1956b] On completely recursively enumerable classes and their key arrays, J. Symbolic
Logic 21 (1956), 304-308.
Реммел (J. В. Remmel)
[1978] 	Recursively enumerable Boolean algebras, Ann. Math. Logic Ц (1978), 75-107.
[1980] 	Recursion theory on algebraic structures with independent sets, Ann. Math.
Logic 18 (1980), 153-191.
[1989] Recursive Boolean Algebras, Handbook of Boolean Algebras, 3 (1989), North-
Holland, Amsterdam.
Рихтер, Бергер, Обершелп, Шинцель и Томас (М. М. Richter, Е. Borger,
W. Oberschelp, В. Schinzel and W. Thomas)
[1984] Computation and Proof Theory (editors), Proceedings of the Logic Colloquium
held in Aachen, July 18-13, 1983, Part II. Lecture Notes in Mathematics No.
1104, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1984.
Робинсон (J. Robinson)
[1968] Recursive functions of one variable, Proc. Amer. Math. Soc. 19 (1968), 815-820.
[1949] Definability and decision problems in arithmetic, J. Symbolic Logic 14 (1949),
98-114.
Робинсон (R. W. Robinson)
[1966a] The Inclusion Lattice and Degrees of Unsolvability of the Recursively
Enumerable Sets, Ph.D. Dissertation, Cornell University, 1966.
[1966b] Recursively enumerable sets not contained in any maximal set, Notices Amer.
Math. Soc. 13 (1966), 325. Abstract #632-4.
[1967a] Simplicity of recursively enumerable sets, J. Symbolic Logic 32 (1967), 162-172.
[1967b] Two theorems on hyperhypersimple sets, Trans. Amer. Math. Soc. 128 (1967),
531-538.
[1968] A dichotomy of the recursively enumerable sets, Z. Math. Logik Grundlag.
Math. Ц (1968), 339-356.
[1969] Review of Sacks [1964a], J. Symbolic Logic 34 (1969), 294-295.
[1971a] Interpolation and embedding in the recursively enumerable degrees, Ann. of
Math. (2), 93 (1971), 285-314.
[1971b] Jump restricted interpolation in the recursively enumerable degrees, Ann. of
Math. (2), 93 (1971), 586-596.
Роджерс (H. Rogers, Jr.)
[1959] Computing degrees of unsolvability, Math. Ann. 138 (1959), 125-140.
[1967a] Theory of Recursive Functions and Effective Computability, McGraw-Hill, New
York, 1967.
[1967b] Some problems of definability in recursive function theory, In: Crossley [1967],
183-201.

536
Литература
Россер (J. В. Rosser)
[1936] Extensions of some theorems of Godel and Church, J. Symbolic Logic 1 (1936),
87-91; reprinted in Davis [1965], 230-235.
Роуз и Юллиан (G. F. Rose and J. S. Ullian)
[1963] Approximations of functions on the integers, Pacific J. Math. 13 (1963),
693-701.
Рубин (M. Rubin)
[1976] 	The theory of Boolean algebras with a distinguished subalgebra is undecidable,
Ann. Sci. Univ. Clermont-Ferrand II Math. 13 (1976), 129-134.
Сакс (G. E. Sacks)
[1961a] A minimal degree less than O', Bull. Amer. Math. Soc. 67 (1961), 416-419.
[1961b] On suborderings of degrees of recursive unsolvability, Z. Math. Logik Grundlag.
Math. 7(1961), 46-56.
[1963a] Degrees of unsolvability, Ann. of Math. Stud. 55, Princeton University Press,
Princeton, N.J., 1963 (see revised edition, 1966).
[1963b] On the degrees less than O', Ann. of Math. (2) 77 (1963), 211-231.
[1963c] Recursive enumerability and the jump operator, Trans. Amer. Math. Soc. 108
(1963), 223-239.
[1964a] The recursively enumerable degrees are dense, Ann. of Math. (2) 80 (1964),
300-312.
[1964b] A maximal set which is not complete, Michigan Math. J. 11 (1964), 193-205.
[1964c] A simple set which is not effectively simple, Proc. Amer. Math. Soc. 15 (1964),
51-55.
[1966a] Degrees of unsolvability, rev. ed., Ann. of Math. Studies 55, Princeton
University Press, Princeton, N. J., 1966.
[1966b] Post’s problem, admissible ordinals and regularity, Trans. Amer. Math. Soc.
124 (1966), 1-23.
[1967] On a theorem of Lachlan and Martin, Proc. Amer. Math. Soc. 18 (1967),
140-141.
[1969] 	Measure theoretic uniformity in recursion theory and set theory, Trans. Amer.
Math. Soc. Ц2 (1969), 381-420.
[1971] 	Forcing with perfect closed sets, In: Scott [1971], 331-355.
[1976] 	Countable admissible ordinals and hyperdegrees, Adv. in Math. 19 (1976),
213-262.
[1977a] The fc-section of a type n-object, Amer. J. Math. 99 (1977), 901-917.
[1977b] R. e. sets higher up, In: Logic, Foundations of Mathematics and Computability
Theory, ed. D. Reidel, Dordrecht, Holland, 1977, 173-194.
[1982] Post’s problem in E-recursion, In: Nerode and Shore [1985], 177-193.
[1985] Some open questions in recursion theory, In: Ebbinghaus, Muller, and Sacks
[1985], 333-342.
[1986] The limits of E-recursive enumerability, Ann. Pure Appl. Logic 31 (1986),
87-120.
[h.o.] On Kucera’s solution to Post’s problem, unpublished.
Сакс и Симпсон (G. E. Sacks and S. Simpson)

Литература
537
[1972] The а-finite injury method, Ann. Math. Logic 4 (1972), 343-367.
Cacco (L. P. Sasso, Jr.)
[1970] A cornucopia of minimal degrees, J. Symbolic Logic 35 (1970), 383-388.
[1971] Degrees of Unsolvability of Partial Functions, Ph.D. Thesis, University of
California, Berkeley, 1971.
[1973] A minimal partial degree ^ O', Proc. Amer. Math. Soc. 38 (1973), 388-392.
[1974a] Deficiency sets and bounded information reducibilities, Trans. Amer. Math.
Soc. 200 (1974), 267-290.
[1974b] A minimal degree not realizing least possible jump, J. Symbolic Logic 39 (1974),
571-574.
[1975] 	A survey of partial degrees, J. Symbolic Logic 40 (1975), 130-140.
Селиванов В. Л.
[1978a] Об индексных множеств вычислимых классов конечных множеств,
Алгоритмы и Автоматы, изд-во КГУ, Казань, 10 (1978), 95-99.
[1978b] Некоторые замечания о классах р.п. множеств, Сиб. мат. журнал, 19 (1978),
153-160, 238.
[1979] О структуре степеней неразрешимости индексных множеств, Алгебра и
Логика 18 (1979), 463-480, 508-509.
[1982а] Об индексных множествах в иерархии Клини-Мостовского, Сб.:
Математическая логика и теория алгоритмов, Сиб. отд. АН СССР, 2, 1982,
Новосибирск, Наука, 1979, 135-158.
[1982b] Об одном классе сводимостей в теории рекурсивных функций, Вероятн.
методы и киберн., 18 (1982), 83-100.
[1984а] Об иерархии предельных вычислений, Сиб. мат. журнал, 25 (1984),
146-156.
[1984b] Индексные множества в гиперарифметической иерархии Сиб. мат. журнал,
25 (1984), 164-181.
[1985] Об иерархии Ершова, Сиб. мат. журнал, 26 (1985), 134-149.
Симпсон (М. Simpson)
[1985] Arithmetical Degrees: Initial Segments, u;-REA Sets and the o;-Jump Operator,
Ph.D. Dissertation, Cornell University, 1985.
Симпсон (S. G. Simpson)
[1977] First-order theory of the degrees of recursive unsolvability, Ann. of Math. (2)
105 (1977), 121-139.
[1978] Sets which do not have subsets of every higher degree, J. Symbolic Logic 43
(1978), 135-138.
[1980] Degrees of unsolvability: A survey of results, In: Barwise, Keisler, and Kunen
[1980], 631-652.
[1985] Recursion theoretic aspects of the dual Ramsey theorem, In: Ebbinghaus,
Muller, and Sacks [1985], 357-371.
Скотт (D. Scott)
[1962] Algebras of sets binumerable in complete extensions of arithmetic, Proc. Symp.
Pure Math. 5, Providence, R.I., 1962, 117-121.

538
Литература
[1971] Axiomatic Set Theory I (editor), Proc. Symp. Pure Math. 13, Los Angeles,
1967, Amer. Math. Soc., Providence, R.I., 1971.
Сламан (T. A. Slaman)
[1985] Reflection and the priority method in E-recursion theory, In: Ebbinghaus,
Muller, and Sacks [1985], 372-404.
[1991] The density of inflma in the recursively enumerable degrees, Ann. Pure and
Applied Logic 52 (1991), 155-179.
[h.o.] A recursively enumerable degree that is not the top of a diamond in the Turing
degrees, unpublished.
[h.o.] The recursively enumerable degrees as a substructure of the degrees,
unpublished.
Сламан и Вудин (T. A. Slaman and W. H. Woodin)
[1986] Definability in the Turing degrees, Illinois J. Math. 30 (1986), 320-334.
Сламан и Coap (T. A. Slaman and R. I. Soare)
[1995*] Algebraic Aspects of the Computably Enumerable Degrees, Proc. Nat. Acad.
Sci. U.S.A. 92 (1995), 617-621
Сламан и Стил (T. A. Slaman and J. R. Steel)
[1988] Definable functions on degrees, in Cabal Seminar 81-85, A. S. Kechris,
D. A. Martin and J. R. Steel eds., LNMS 1333, Springer Verlag, Berlin, 37-55.
[1989] Complementation in the Turing degrees, J. Simbolic Logic 54 (1989), 160-176.
Coap (R. I. Soare)
[1969a] Recursion theory and Dedekind cuts, Trans. Amer. Math. Soc. 140 (1969),
271-294.
[1969b] A note on degrees of subsets, J. Symbolic Logic 34 (1969), 256.
[1969c] Cohesive sets and recursively enumerable Dedekind cuts, Pacific J. Math. 31
(1969), 215-231.
[1972] The Friedberg-Muchnik theorem re-examined, Canad. J. Math. 24 (1972),
1070-1078.
[1974a] Automorphisms of the lattice of recursively enumerable sets, Bull. Amer. Math.
Soc. 80 (1974), 53-58.
[1974b] Automorphisms of the lattice of recursively enumerable sets, Part I: Maximal
sets, Ann. of Math. (2) 100 (1974), 80-120.
[1976] The infinite injury priority method, J. Symbolic Logic (1976), 513-530.
[1977] Computational complexity, speedable and levelable sets, J. Symbolic Logic 4%
(1977), 545-563.
[1978a] Recursive enumerability, Proceedings of the International Congress of
Mathematicians, Helsinki, 275-280.
[1978b] Recursively enumerable sets.and degrees, Bull. Amer. Math. Soc. 84 (1978),
1149-1181.
[1980] Fundamental methods for constructing recursively enumerable degrees, In:
Drake and Wainer [1980], 1-51.
[1981] Constructions in the recursively enumerable degrees, in Lolli [1981], 172-225.
[1982a] Automorphisms of the lattice of recursively enumerable sets, Part II: Low sets,
Ann. Math. Logic 22 (1982), 69-107.

Литература
539
[1982b] Computational complexity of recursively enumerable sets, Inform, and Control
52 No. 1 (1982), 8-18.
[1985] Tree arguments in recursion theory and the (^''-priority method, In: Nerode
and Shore [1985], 53-106.
Coap и Стоб (R. I. Soare and M. Stob)
[1982] 	Relative recursive enumerability, In: Proceedings of the Herbrand Symposium
Logic Colloquium ’81, ed. J. Stern, North-Holland, Amsterdam, New York,
Oxford, 1982, 299-324.
Соловьев В. Д.
[1974] Q-сводимость и гипергиперпростые множества, Вероятн. методы и ки-
берн., 10-11 (1974), 121-128.
Спектор (С. Spector)
[1955] Recursive well-orderings, J. Symbolic Logic 20 (1955) 151-163.
[1956] On degrees of recursive unsolvability, Ann. of Math. (2) 64 (1956), 581-592.
[1961] Inductively defined sets of natural numbers, In: Infinitistic Methods,
Proceedings of the Symposium on Foundations of Mathematics, Warsaw 1959,
Pergamon Press, Oxford, 1961, 97-102.
Стил (J. Steel)
[1975] Descending sequences of degrees, J. Symbolic Logic 40 (1975), 59-61.
[1982] A Classification of Jump Operators, J. Symbolic Logic ^7 (1982), 347-358.
Стоб (M. Stob)
[1979] 	The Structure and Elementary Theory of the Recursively Enumerable Sets,
Ph.D. Dissertation, University of Chicago, 1979.
[1982a] Invariance of properties under automorphisms of the lattice of recursively
enumerable sets, Pacific J. Math. 100 (1982), 445-471.
[1982b] Index sets and degrees of unsolvability, J. Symbolic Logic ^7 (1982), 241-248.
[1983] wtt-degrees and T-degrees of recursively enumerable sets, J. Symbolic Logic 48
(1983), 921-930.
[1985] Major subsets and the lattice of recursively enumerable sets, In: Nerode and
Shore [1985], 107-116.
Столтенберг-Хансен и Такер (V. Stoltenberg-Hansen and J. V. Tucker)
[ta] Computable Algebra: An Introduction to the Theory of Computable Rings and
Fields, to appear.
Таллос (R. E. Tulloss)
[1971] Some Complexities of Simplicity: Concerning the Grades of Simplicity of
Recursively Enumerable Sets, Ph.D. Dissertation, Univ. of California, Berkeley,
1971.
Тарский, Мостовский и Робинсон (A. Tarski, A. Mostowski and
R. M. Robinson)
[1953] Undecidable theories, North-Holland, Amsterdam, 1953.
Тенненбаум (S. Tennenbaum)

540
Литература
[1961] Degrees of unsolvability and the rate of growth of functions, Notices Amer.
Math. Soc. 8 (1961), 608.
[1962] Degrees of unsolvability and the rate of growth of functions, Proc. Sympos.
Math. Theory of Automata, Microwave Res. Inst. Sympos. Ser. 12, Polytechnic
Press, Brooklyn, New York (1962), 71-73.
Томасон (S. К. Thomason)
[1971] 	Sublattices of the recursively enumerable degrees, Z. Math. Logik Grundlag.
Math. 17 (1971), 273-280.
Трулстра и ван Дейлен (A. S. Troelstra and D. van Dalen)
[1982] 	The L. E. J. Brouwer Centenary Symposium, Proceedings of the Conference
held in Noordwijkerhout, 8-13 June 1981, North-Holland, New York,
Amsterdam, Oxford, 1982.
Тьюринг (A. M. Turing)
[1936-37] On computable numbers, with an application to the Entscheidungsproblem,
Proc. London Math. Soc. 4% (1936), 230-265; A correction, ibid. 4$ (1937),
544-546; reprinted in Davis [1965], 115-154.
[1937] Computability and A-definability, J. Symbolic Logic 2 (1937), 153-163.
[1939] Systems of logic based on ordinals, Proc. London Math. Soc. ^5 (1939),
161-228; reprinted in Davis [1965], 154-222.
Успенский В. A.
[1955a] О вычислимых нумерациях, ДАН СССР, 103 (1955), 773-776.
[1955b] Системы перечислимых множеств и их нумерации, ДАН СССР, 105 (1955),
1155-1158.
[1957] 	Несколько замечаний о перечислимых множествах, Z. Math. Logik
Grundlag. Math., 3 (1957), 157-170.
[1960] Лекции о вычислимых функциях, Москва, Издат. физ.-мат. лит., 1960.
Уэлш (L. Welch)
[1981] A Hierarchy of Families of Recursively Enumerable Degrees and a Theorem on
Bounding Minimal Pairs, Ph.D. Dissertation, University of Illinois at Urbana-
Champaign, 1981.
[1984] 	A hierarchy of families of recursively enumerable degrees, J. Symbolic Logic,
49 (1984), 1160-1170.
Фейер (P. A. Fejer)
[1980] The Structure of Definable Subclasses of the Recursively Enumerable Degrees,
Ph.D. Dissertation, University of Chicago, 1980.
[1982] Branching degrees above low degrees, Trans. Amer. Math. Soc. 273 (1982),
157-180.
[1983] The density of the nonbranching degrees, Ann. Pure Appl. Logic 24 (1983),
113-130.
Фейер и Coap (P. A. Fejer and R. I. Soare)
[1981] The plus-cupping theorem for the recursively enumerable degrees, In: Lerman,
Schmerl, and Soare, 1980, 49-62.

Литература
541
Фейер и Шор (Р. A. Fejer and R. A. Shore)
[1985] 	Embeddings and extensions of embeddings in the r. e. tt- and wtt-degrees, In:
Ebbinghaus, Muller, and Sacks [1985], 121-140.
[1988] Infima of recursively enumerable truth table degrees, Notre Dame Journal of
Formal Logic 29 (1988), 420-437.
[1990] 	A direct construction of a minimal recursively enumerable truth-table degree,
in: Recursion Theory Week, Proceedings Oberwolfach, 1989, K. Ambos-Spies,
G. H. Muller and G. E. Sacks, eds. Springer-Verlag, 1432 (1990), 187-204.
Фейнер (L. Feiner)
[1967] Orderings and Boolean algebras not isomorphic to recursive ones, Doctoral
Dissertation, M.I.T., Cambridge, Mass., 1967.
Фенстад (J. E. Fenstad)
[1980] General Recursion Theory: An Axiomatic Approach, Perspectives in
Mathematical Logic, Omega Series, Springer-Verlag, Berlin, Heidelberg, New
York, 1980.
Фенстад, Ганди и Сакс (J. Е. Fenstad, R. О. Gandy and G. E. Sacks)
[1978] Generalized Recursion Theory II (editors), Proceedings of the Second
Symposium on Generalized Recursion Theory, Oslo, 1977, North-Holland,
Amsterdam, New York, Oxford, 1978.
Феррант и Ракофф (J. Ferrante and C. W. Rackoff)
[1979] Computational complexity of logical theories, Lecture Notes in Math. No. 718,
Springer-Verlag, Berlin, Heidelberg, New York, 1979.
Феферман (S. Feferman)
[1957] Degrees of unsolvability associated with classes of formalized theories, J.
Symbolic Logic 22 (1957), 161-175.
Фрблих и Шепердсон (A. Frohlich and J. C. Shepherdson)
[1955] Effective procedures in field theory, Philos. Trans., Royal Soc. of London, Series
A 248 (1955), 407-432.
Фридберг (R. M. Friedberg)
[1957a] Two recursively enumerable sets of incomparable degrees of unsolvability,
Proc. Natl. Acad. Sci. USA 43 (1957), 236-238.
[1957b] The fine structure of degrees of unsolvability of recursively enumerable
sets, In: Summaries of Cornell Univ. Summer Institute for Symbolic Logic,
Communications Research Division, Inst, for Def. Anal., 1957, 404-406.
[1957c] A criterion for completeness of degrees of unsolvability, J. Symbolic Logic 22
(1957), 159-160.
[1958a] Three theorems on recursive enumeration: I. Decomposition, II. Maximal Set,
III. Enumeration without duplication, J. Symbolic Logic 23 (1958), 309-316.
[1958b] Un contre-exemple relatif aux fonctionnelles r6cursives, Comptes rendus
hebdomadaires des зёапсез de l’Acad6mie des Sciences (Paris) 247 (1958),
852-854.

542
Литература
[1958с] Four quantifier completeness: a Banach-Mazur functional not uniformly partial
recursive, Bulletin de l’Academie Polonaise des Sciences, Serie des sciences
math6matiques, astronomiques et physiques, 6 (1958), 1-5.
Фридберг и Роджерс (R. M. Friedberg and H. Rogers, Jr. )
[1959] Reducibility and completeness for sets of integers, Z. Math. Logik Grundlag.
Math. 5 (1959), 117-125.
Фридман (H. Friedman)
[1975] 102 Problems in mathematical logic, J. Symbolic Logic 40 (1975), 113-129.
Фридман, Макелун и Симпсон (Н. Friedman, К. McAloon and
S. G. Simpson)
[1982] 	A finite combinatorial principle which is equivalent to the 1-consistency of
predicative analysis, In: Metakides [1982], 197-230.
Харрингтон (L. Harrington)
[1974] Recursively presentable prime models, J. Symbolic Logic 39 (1974), 305-309.
[1976] On Cooper’s proof of a theorem of Yates, Parts I and II (handwritten notes).
[1978] 	Plus cupping in the recursively enumerable degrees (handwritten notes).
[1980] 	Understanding Lachlan’s monster paper (handwritten notes).
[1982] A gentle approach to priority arguments (handwritten notes for a talk at
A.M.S. Summer Research Institute in Recursion Theory, Cornell University,
July 1982).
[1983] The undecidability of the lattice of recursively enumerable sets (handwritten
notes).
Харрингтон и Ниис (L. Harrington and A. Nies)
[1998*] Coding in the partial order of enumerable sets, Adv. Math., 133, No.l (1998),
133-162.
Харрингтон и Сламан (L. Harrington and T. A. Slaman)
[1996*] Interpreting arithmetic in the Turing degrees of the recursively enumerable sets
(handwritten notes).
Харрингтон и Coap (L. Harrington and R. I. Soare)
[1996*] The A®-automorphism method and noninvariant classes of degrees, J. Amer.
Soc. 9, No.3 (1996), 617-666.
[1998a*] Codable sets and orbits of computably enumerable sets. J. Symbolic Logic, 63
(1998), No. 1, 1-28.
[1998b*] Definable properties of the computably enumerable sets. Conference on
Computability Theory (Oberwolfach, 1996). Ann. Pure Appl. Logic, 94 (1998),
No. 1-3, 97-125.
[ta*] Martin’s Invariance Conjecture and Low Sets, in preparation.
Харрингтон и Шел ax (L. Harrington and S. Shelah)
[1982a] The undecidability of the recursively enumerable degrees (research
announcement), Bull. Amer. Math. Soc. 6 No.l (1982), 79-80.
[1982b] The undecidability of the recursively enumerable degrees (handwritten notes).

Литература
543
Харрингтон и Шор (L. Harrington and R. A. Shore)
[1981] 	Definable degrees and automorphisms of V, Bull. Amer. Math. Soc. (new series)
4 (1981), 97-100.
ван Хейдженорт (J. van Heijenoort)
[1967] From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931,
Harvard Univ. Press, Cambridge, Mass., 1967.
Херманн (E. Herrmann)
[1978] Der Verband der rekursiv aufzahlbaren Mengen (Entscheidungsproblem),
Seminarbericht Nr. 10, Humboldt-Universitat Sektion Mathematik, Berlin,
1978.
[1981] Die Verbandseigenschaften der rekursiv aufzahlbaren Mengen, Seminarbericht
Nr. 36, Humboldt-Universitat Sektion Mathematik, Berlin, 1981.
[1983a] Major subsets of hypersimple sets and ideal families. Dissertation B, Humboldt-
Universitat Sektion Mathematik, Berlin, 1983.
[1983b] Orbits of hyper hyper simple sets and the lattice of £3 sets, J. Symbolic Logic
48 (1983), 693-699.
[1983c] Definable Boolean pairs in the lattice of recursively enumerable sets,
Seminarber. Humboldt-Univ. Berlin. Sek. Math., 49 (1983), 42-67.
[1984a] Classes of simple sets, filter properties and their mutual position, In:
Proceedings of the Conference on Model theory, Wittenberg, GDR, 1984,
Seminarbericht Nr. 49, 60-72.
[1984b] The undecidability of the elementary theory of the lattice of recursively
enumerable sets (abstract), In: Frege Conference 1984, Proceedings of the
International Conference at Schwerin (GDR), Akademie-Verlag, Berlin, 66-72.
[1984c] Definable structures in the lattice of recursively enumerable sets, J. Symbolic
Logic 49 (1984), 1190-1197.
[1986] 	The index set { e : We =1 X }, J. Symbolic Logic, 51 (1986), 110-116.
[1989] Automorphisms of the lattice of recursively enumerable sets and
hyperhypersimple sets, in Logic, Methodology and Philosophy of Science, VIII
(Moscow 1987), North-Holland, 1989.
Хермес (H. Hermes)
[1969] 	Enumerability, Decidability, Computability: An Introduction to the Theory
of Recursive Functions, Springer-Verlag, Berlin, Heidelberg, New York,
1969. (This is an English translation of: Aufzahlbarkeit, Entscheidbarkeit,
Berechenbarkeit, Grundlehren der mathematischen Wissenschaften, Band 109,
Springer-Verlag, Berlin, Heidelberg, New York, 1965.)
Хигмен (G. Higman)
[1961] Subgroups of finitely presented groups, Proceedings of the Royal Society of
London, Series A 262 (1961), 455-475.
Хинман (P. G. Hinman)
[1978] Recursion-Theoretic Hierarchies, Perspectives in Mathematical Logic, Omega
Series, Springer-Verlag, Berlin, Heidelberg, New York, 1978.
Ходжес (W. Hodges)

544
Литература
[1972] 	Conference in Mathematical Logic, London, 1970 (editor), Lecture Notes in
Mathematics No. 255, Springer-Verlag, Berlin, Heidelberg, New York, 1972.
Хоот (C. A. Haught)
[1985] Turing and truth table degrees of 1-generic and recursively enumerable degrees,
Ph.D. dissertation, Cornell University, 1985.
[1986] The degrees below a 1-generic degree and less than O', J. Symbolic Logic 51
(1986), 770-777.
[1987] Lattice embeddings in the recursively enumerable truth table degrees, Trans.
Amer. Math. Soc. 301 (1987), 515-535.
Хумер и Сакс (S. Homer and G. E. Sacks)
[1983] 	Inverting the half-jump, Trans. Amer. Math. Soc. 278 (1983), 317-331.
Хуторецкий А. Б.
[1969] 	Две теоремы существования вычислимых нумераций, Алгебра и Логика 8
(1969), 483-492 (Russian).
Хэй (L. Нау)
[1973а] The halting problem relativized to complements, Proc. Amer. Math. Soc. J>1
(1973), 583-587.
[1973b] The class of recursively enumerable subsets of a recursively enumerable set,
Pacific J. Math. 46 (1973), 167-183.
[1975] Spectra and the halting problem, Z. Math. Logik Grundlag. Math. 21 (1975),
167-176.
Хэй, Манастер и Розенштейн (Hay, A. Manaster and J. G. Rosenstein)
[1975] Small recursive ordinals, many-one degrees, and the arithmetical difference
hierarchy, Ann. Math. Logic 8 (1975), 297-343.
[1977] 	Concerning partial recursive similarity transformations of linearly ordered sets,
Pacific J. Math. 71 (1977), 57-70.
Цензер, Клот, Смит, Coap и Вейнер (D. Cenzer, P. Clote, R. Smith,
R. I. Soare and S. S. Wainer)
[1986] Members of countable П® classes, Ann. Pure Appl. Logic 31 (1986), 145-163.
Чёрч (A. Church)
[1936a] An unsolvable problem of elementary number theory, Amer. J. Math. 58 (1936),
345-363; reprinted in Davis [1965], 88-107.
[1936b] A note on the Entscheidungsproblem, J. Symbolic Logic 1 (1936), 40-41 and
101-102; reprinted in Davis [1965], 108-115.
Чолак (P. Cholak)
[1995*] Automorphisms of the lattice of recursively enumerable sets, Mem. Math. Soc.,
113, No. 541 (1995), viii+151.
Чолак, Доуни и Волк (Р. Cholak, R. Downey, R. and R. Walk)
[ta*] Maximal contiguous degrees, to appear.
Чолак и Ниис (P. Cholak and A. Nies)

Литература
545
[1999*] Atomless r-maximal sets, Israel J. Math., 113 (1999), 305-322.
Чолак и Харрингтон (P. Cholak and L. A. Harrington)
[ta*] On the definability of the double jump in the computably enumerable sets,
submitted
[ta*] Definable encodings in the computably enumerable sets, To appear in the Bull.
Symbolic Logic.
[ta*] On the definability of the double jump in the computably enumerable sets, to
appear.
[ta*] Definable encodings in the computable enumerable sets, To appear in the Bull.
Simb. Logic.
Чонг (С. T. Chong)
[1984] 	Techniques of Admissible Recursion Theory, Lecture Notes in Mathematics,
Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1106 (1984).
Чонг и Викс (С. Т. Chong and М. J. Wicks)
[1983] Proceedings of the Southeast Asian Conference on Logic (editors), North-
Holland, Amsterdam, New York, Oxford, 1983.
Чонг и Джокуш (С. Т. Chong and С. G. Jockusch, Jr.)
[1984] Minimal degrees and 1-generic sets below O', In: Richter et al. [1984], 63-77.
Чонг и Доуни (С. Т. Chong and R. G. Downey)
[1989] Minimal degrees recursive in 1-generic degrees, Victoria University of
Wellington, New Zealand, Research report 89-38 (1989).
Шварц (S. Schwarz)
[1982] 	Index Sets of Recursively Enumerable Sets, Quotient Lattices, and Recursive
Linear Orderings, Ph.D. Dissertation, University of Chicago, 1982.
[1984a] The quotient semilattice of the recursively enumerable degrees modulo the
cappable degrees, Trans. Amer. Math. Soc. 283 (1984), 315-328.
[1984b] Recursive automorphisms of recursive linear orderings, Ann. Pure Appl. Logic
26 (1984), 69-73.
[1989] Index sets related to prompt simplicity, Ann. Pure Appl. Logic 42 (1989),
243-254.
[ta] Index sets related to the high-low hierarchy, Israel J. Math., to appear.
Шепердсон и Штургис (J. C. Shepherdson and H. E. Sturgis)
[1963] Computability of recursive functions, J. Assoc. Comput. Mach. 10 (1963),
217-255.
Шёнфилд (J. R. Shoenfield)
[1957] Quasicreative sets, Proc. Amer. Math. Soc. 8 (1957), 964-967.
[1958a] The class of recursive functions, Proc. Amer. Math. Soc. 9 (1958), 690-692.
[1958b] Degrees of formal systems, J. Symbolic Logic 23 (1958), 389-392.
[1959] 	On degrees of unsolvability, Ann. of Math. (2) 69 (1959), 644-653.
[1960a] Degrees of models, J. Symbolic Logic 25 (1960), 233-237.
[1960b] An uncountable set of incomparable degrees, Proc. Amer. Math. Soc. 11 (1960),
61-62.

546
Литература
[1961] Undecidable and creative theories, Fund. Math. 4$ (1961), 171-179.
[1965] Application of model theory to degrees of unsolvability, In: Addison, Henkin,
and Tarski [1965], 359-363.
[1966] A theorem on minimal degrees, J. Symbolic Logic 31 (1966), 539-544.
[1967] Mathematical Logic, Addison-Wesley, Reading, Mass. (1967), 344 pp.
[1971] Degrees of unsolvability, Mathematics Studies 2, North-Holland, Amsterdam,
1971.
[1975] The decision problem for recursively enumerable degrees, Bull. Amer. Math.
Soc. 81 (1975), 973-977.
[1976] Degrees of classes of r. e. sets, J. Symbolic Logic J^l (1976), 695-696.
[1984] 	Strategies in the r. e. degrees (handwritten notes).
Шёнфилд и Coap (J. R. Shoenfield and R. I. Soare)
[1978] 	The generalized diamond theorem, Recursive Function Theory Newsletter 19
(1978), #219 (abstract).
Смальян (R. M. Smullyan)
[1964] Effectively simple sets, Proc. Amer. Math. Soc. 15 (1964), 893-895.
Шор (R. A. Shore)
[1977a] Determining automorphisms of the recursively enumerable sets, Proc. Amer.
Math. Soc. 65 (1977), 318-325.
[1977b] а-recursion theory, In: Barwise, Keisler, and Kunen [1980], 653-680.
[1978a] Nowhere simple sets and the lattice of recursively enumerable sets, J. Symbolic
Logic 43 (1978), 322-330.
[1978b] On the V3-sentences of а-recursion theory, In: Fenstad, Gandy and Sacks [1978],
331-354.
[1979] 	The homogeneity conjecture, Proc. Natl. Acad. Sci. U.S.A. 76 (1979),
4218-4219.
[1980a] £*(K) and other lattices of the recursively enumerable sets, Proc. Amer. Math.
Soc. 80 (1980), 143-146.
[1980b] Some constructions in а-recursion theory, In: Drake and Wainer [1980],
158-170.
[1981a] The theory of the degrees below O', J. London Math. Soc. Ser. II 24 (1981),
1-14.
[1981b] The degrees of unsolvability: global results, In: Lerman, Schmerl, and Soare
[1981], 283-301.
[1982a] Finitely generated codings and the degrees r. e. in a degree d, Proc. Amer.
Math. Soc. 84 (1982), 256-263.
[1982b] On homogeneity and definability in the first order theory of the Turing degrees,
J. Symbolic Logic 47 (1982), 8-16.
[1982c] The theories of the truth-table and Turing degrees are not elementarily
equivalent, In: van Dalen, Lascar, and Smiley [1982], 231-237.
[1983] The degrees of unsolvability: the ordering of functions by relative computability,
Proc. International Congress of Mathematicians, Warsaw 1983, 337-345.
[1984] The arithmetical degrees are not elementarily equivalent to the Turing degrees,
Arch. Math. Logik Grundlag. 24 (1984), 137-139.

Литература
547
[1985] 	The structure of the degrees of unsolvability, In: Nerode and Shore [1985],
33-51.
[1988] 	A non-inversion theorem for the jump operator, Ann. Pure Appl. Logic 40
(1988). 277-303.
Эббингхауз, Мюллер и Сакс (H.-D. Ebbinghaus, G. H. Muller and
G. E. Sacks)
[1985] 	Recursion Theory Week (editors), Proceedings of a Conference held
in Oberwolfach, West Germany (April 15-21, 1984), Lecture Notes in
Mathematics No. 1141, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo,
1985.
Эйленберг и Элгот (S. Eilenberg and С. C. Elgot)
[1970] 	Recursiveness, Academic Press, New York, London, 1970.
Элтон (D. A. Alton)
[1970] Uniformities in Recursively Enumerable Sets, Doctoral Dissertation, Cornell
Univ., Ithaca, N.Y., 1970.
[1971] Recursively enumerable sets which are uniform for finite extensions, J. Symbolic
Logic, 36 (1971), 271-287.
[1974] Iterated quotients of the lattice of recursively enumerable sets, Proc. London
Math. Soc., 28 (1974), 1-12.
[1975] A characterization of r-maximal sets, Arch. Math. Logik Grundlag., 17 (1975),
35-36.
Эпштейн (R. L. Epstein)
[1975a] Minimal Degrees of Unsolvability and the Pull Approximation Construction,
Memoirs Amer. Math. Soc. 3 No. 162, Amer. Math. Soc., Providence, R.I.,
1975.
[1975b] Review of S. B. Cooper [1972b], J. Symbolic Logic 40 (1975), 86.
[1979] Degrees of Unsolvability: Structure and Theory, Lecture Notes in Mathematics
759, Springer-Verlag, Berlin, Heidelberg, New York, 1979.
[1981] Initial Segments of Degrees Below O', Memoirs Amer. Math. Soc. 30 No. 241,
Amer. Math. Soc., Providence, R.I., 1981.
Эпштейн, Хаас и Крамер ( R. L. Epstein, R. Haas and R. Kramer)
[1981] Hierarchies of sets and degrees below O', In: Lerman, Schmerl and Soare [1981],
32-48.
Эш (C. J. Ash)
[1986] 	Stability of recursive structures in arithmetical degrees, Ann. Pure Appl. Logic,
32 (1986), 113-135.
[1986] Recursive labelling systems and stability of recursive structures in
hyperarithmetical degrees, Trans. Amer. Math. Soc., 298 (1986), 497-514,
correction (ibid) 310 (1988), 851.
[1987] Categoricity in hyperarithmetical degrees, Ann. Pure. Appl. Logic, 34 (1987),
No. 1, 1-14.
Эш и Гончаров (C. J. Ash and S. S. Goncharov)
[1985] 	Strong A® categoricity, Алгебра и Логика, 24 (1985), No. 6, 718-727.

548
Литература
Эш и Доуни (С. J. Ash and R. Downey)
[1984] Decidable subspaces and recursively enumerable subspaces, J. Symbolic Logic,
49 (1984), 1137-1145.
Эш и Нероуд (C. J. Ash and A. Nerode)
[1981] Intrinsically recursive relations, In: Crossley [1981], 26-41.
Юллиан (J. S. Ullian)
[1960] Splinters of recursive functions, J. Symbolic Logic 25 (1960), 33-38.
[1961] A theorem on maximal sets, Notre Dame J. Formal Logic 2 (1961), 222-223.
Янг (P. R. Young)
[1963] On the Structure of Recursively Enumerable Sets, Ph.D. Dissertation,
Massachusetts Institute of Technology, Cambridge, Mass., 1963.
[1966] Linear orderings under one-one reducibility, J. Symbolic Logic 31 (1966), 70-85.
[1985] Godel theorems, exponential difficulty and undecidability of arithmetic
theories: an exposition, In: Nerode and Shore [1985], 503-522.
Ясухара (A. Yasuhara)
[1971] 	Recursive Function Theory and Logic, Academic Press, New York, 1971.

Список обозначений
Введение
и
{0,1,2,...} 19
a,b,c,d,e,i,j,k,.. .,y,z
целые числа 19
f,9,h
тотальные функции из wn в w 19
Ф, Ф, ©, р, ф, 0
частичные функции на о; 19
Л, В, С ..., X, У, Z
подмножества и 19
fog или / д
суперпозиция двух функций / и д 19
/"(*)
n-кратная суперпозиция функции f(x) 19
<^(х) 4.
р(х) определена 19
1^(х) 4-= у
р(х) определена и равна у 19
v?(x) t
р(х) неопределена 19
v? = i> (v? ~ V)
равенство частичных функций (риф 19
dom v?
область определения ip 19
rng v?
область значений р 19
ХЛ
характеристическая функция А 19
Л(х)
характеристическая функция А 19
/|х
ограничение / на аргументах у < х 19
Afx
Хл|я 19
1:1
/ — инъекция 19
1:1, на
/ — биекция 19
А С* В
Л С В за исключением конечного
числа элементов 19
АС В
А С В, но А ф В 19
\A\
кардинальное число (мощность) А 19
card(i4)
кардинальное число (мощность) А 19
max(A)
максимальный элемент множества А,
если А ф 0, и 0 в противном случае 19
A Coo В
АСВи\А-В\=оо 19
A =* В
А С В и \В - А\ = оо 19, 144, 244
A
дополнение А 20
A-В
АП В, теоретико-множественная
разность А и В 20, 61
(*.y)
упорядоченная пара, состоящая из ж и у 20
X
(з?1,3?2) **')*£>г) 20

550
Список обозначений
(х,у)
{х 1) *^2 » 2»з)
[п,т\
[п, оо)
{/п}
limn fn(x)
2Ш
2<и
т, i/,a,/?,7,<*
или |<т|
0 или Л
(7 Т
(7 С Т
<7 С л, /
(7 С т
(7
&
V
—I
==>
3
V
рх
3°°х
(а.е. х)
Аж[... ж ...]
Ажхжг .. (bkl- • •]
x,y,z < и
х | У
образ (х,у) относительно стандартной
функции пары 20, 36
((ж1,Х2)хз) 20, 36
замкнутый интервал {х : п ^ х} 20
{х : п ^ ж} 20
последовательность {/n}n€w 20
limn<Eu> fn(x) 20
множество функций из о; в о; 20
множество подмножеств ш 20
конечные последовательности
элементов из ш 20
конечные последовательности из 0 и 1 20
строки из oi<w или 2<w 20
рх[х £ dom<7] = card(dom<7) 20, 80
пустая строка в 2<w или и)<UJ 20
конкатенация строк а и т 20
(7 — начальный сегмент т
(за исключением главы XV) 20
о- начальный сегмент А и
/ соответственно 20
(7 С Т, НО (7 ф т 20
е-штат (глава X) 20, 256
и 20
или 20
не 20
влечёт 20
существует 20
для любого 20
наименьший х 20
существует бесконечное множество х
таких, что ... 20
почти для всех ж,
а именно (3xo)(Va: ^ жо) 20
лямбда-обозначение Черча для определения
частичной функции 20
лямбда-обозначение для частичной
функции к переменных 20
х < ш, у < ш и z < и 20
х и у несравнимы 20
Глава I
(цх) Р(х)
х-у
(*)i
наименьший х такой, что Р(х) 26
ограниченная разность, а именно
х—у — х — у, если х ^ г/, и
х—у — 0 в противном случае 28
показатель Х{ при pi
в разложении из (2.1) 28

Список обозначений
551
Ре
#(с)
‘Ре
Т(е, х, у)
7Г1, 7Г 2
{х 1, Ж2 • • • > Хп)
We,s
4>e,s
<Ре,з(х) = У
<Ре,з(х) I
4>e,s(x) t
We
К
Ко
^ m
^1
А —т В
А =1 В
degm(A)
degi (А)
Ki
Fin
Inf
Tot
Con
Cof
Rec
Ext
A® В
Программа Тьюринга с кодовым
(гёделевым) номером е 34
кодовый номер конфигурации с 34
частичная функция п переменных,
вычисляемая на Ре 34
<Р(е1} 34
Т-предикат Клини 35
функции, обратные функции пары:
7Г1 (<ж,у>) = х и 7г2«ж,2/)) =2/ 37
(•.. ((ж!, ж2), з?з),..., Хп) 37
(см. соглашение И. 2. 6) 37, 39, 60
(см. соглашение II. 2. 6) 37, 60
(см. соглашение И. 2. 6) 37, 60
4>е,з(х) определена 37
(ре,з(х) неопределена 37
е-ое в. п. множество 39
{x:xeWx} 39,53
{(ж,у) : х € Wy} 40, 53
много-одно сводимость 40, 101
одно-одно сводимость 40, 101
А ^ m В И В ^ m А 41
Л^ВиВ^Л 41
{В :А=т В} 41
{В :А=! В} 41
{x:Wx^ 0} 43, 53
{ж : War конечно } 43
и — Fin = {х : Wx бесконечно } 43
{х : ipx всюду определена} =
{ж : Wx = а;} 43
{ж : v?ar всюду определена и постоянна } 43
{ж : War коконечно } 43
{ж : War вычислимо } 43
{ж : (рх доопределима до всюду
определенной вычислимой функции } 43
сочленение множеств А и В 44
вычислимый изоморфизм 47
Глава II
Si
класс Si (:
в. п. множеств) i
S п
класс Еп
52, 94
П1
класс П1 (ко-в. п. множеств)
Пп
класс Пп
52, 94
Ai
класс Ai
52, 94
Ап
класс Ап
52, 94
класс
52, 94
п°
класс П®
52, 94
к
класс А®
52, 94

552
Список обозначений
Si
класс Ei 52, 94
ni
класс Ili 52, 94
graphy>„
{(^, У) ' [<Pn(x) = 2/]} 53
С
решетка 55, 243
a V b
наименьшая верхняя грань а и Ь 55
a A b
наибольшая нижняя грань а и Ъ 55
X
идеал 56
V
фильтр (дуальный идеал) 56
M
булева алгебра подмножеств и 56, 2
e
дистрибутивная решетка
в. п. множеств 57, 243
T
идеал конечных множеств 56, 243
n
булева алгебра вычислимых
множеств 57, 243
Ei-индекс
(см. определение И.2.1) 58
A i-индекс
(см. определение И.2.1) 58
До-индекс
(см. определение И.2.1) 58
Dv
конечное множество с каноническим
индексом у 60
Do
0, пустое множество у 60
VeyS
(см. соглашение И.2.6) 60
We,,
(см. соглашение И.2.6) 60
X\Y
{z : (3s[z eXs- Ys})} 61
X\Y
(X\Y)C\Y 61
(Bi.Ba) (Ai,i42)
(см. определение И.4.9) 72, 101
(Bi,B2) (AuA2)
(см. определение И.4.9) 72, 101
Ax В
декартово произведение А и В 74
Глава III
Pe
е-я программа машины Тьюринга
с оракулом 78, 81
Тьюринговая сводимость 78, 82
фА
частичная функция, вычислимая на
машине Тьюринга с оракулом А
с программой Ре 78
Фе(А)
ФА 78
{e)A
78
{e}f
{e}graph(/) 78
{e}f(x) = y
(см. определение III. 1.7) 80
u(A\ e, ж, s)
use-функция 80
u(A\ е,ж)
(см. определение III.1.7) 80
{e}?(z)= У
(см. определение III. 1.7) 80
{eH*) = У
(3«)[{е}£(ж) = у] 80
WA
dom{e}A 82
{e}{x}
{е}0{ж} 82, 83
Z?
класс Е^ 82, 106
А =т В
А В и В Л 84

Список обозначений
553
deg {А)
тьюрингова степень А 84
deg(a)Udeg(£)
deg(j4 0 В) 84
а, b, с
степени 84
(0,0
класс тьюринговых степеней 57, 84.
(R,0
класс в. п. степеней 57, 85
кА
{х : ФА(х) 4} = {х : х € WA} 85
А'
скачок множества А 85
ам
n-кратный скачок множества А 85
а'
deg(i4') для А € а 86
о (п)
deg(0<n)) 86
0'
deg(0') 86
0
deg(0) 86
Ф{^у}у€и>> ФуАу
бесконечное сочленение 88
} = Uma }з
поточечная сходимость 89
В
наименьшая булева алгебра,
Глава IV
содержащая S 92
В £ Е„
В принадлежит классу En 94
В £ Пп
В принадлежит классу Пп 95
В £ Д„
В принадлежит классу Дп 95
(Vx ^ у) Р(х)
ограниченный квантор всеобщности
(Эх ^ у) Р(х)
ограниченный квантор существования
В €2*
В принадлежит классу £п
относительно А 95, 106
веп£
В принадлежит классу Пп
относительно А 95, 106
В 6 А*
В принадлежит классу Дп
относительно А 95, 106
Еп-полное множество
(см. определение VI.2.1) 98
Пп-полное множество
(см. определение VI.2.1) 98
(S„,n„) (С, D)
(см. определение VI.3.1) 101
(2»,П„) (C,D)
(см. определение VI.3.1) 101
Comp
{х : Wx =Т К} 102
Г (или Га:, ИЛИ riiy)
подвижной маркер 103, 105, 116, 167,
НА
слабый скачок 105, 109
Gm(A)
(см. определение IV.3.13) 106, 331
(см. с. 106)
Fin-4
множество Fin, релятивизованное
относительно А 106
Tot-4
множество Tot, релятивизованное
относительно А 106
CofA
множество Cof, релятивизованное
относительно А 106
H*,L£
классы Hn,Ln, релятивизованные
относительно оракула В 160

554
Список обозначений
n-высокое множество
классификация в иерархии
(степень)
высоких/низких множеств
(степеней) 109, 160
n-низкое множество
классификация в иерархии
(степень)
высоких/низких множеств
(степеней) 109, 160
L п
класс n-низких в. п. степеней 109, 160
Н п
класс n-высоких в. п. степеней 109, 160
Глава V
S
класс простых множеств 115
РА
главная функция А 118
табличная сводимость 121
ограниченная табличная сводимость 121
)tt
слабая табличная сводимость 122
ограниченная Тьюрингов ая сводимость 122
’"-неподвижная точка
такое число п, что Wn =* ^/(п) 128
Глава VI
• • •
строки и частичные функции,
только в главе VI 133
а|Ь
степени а и b несравнимы 134
D(^O')
класс степеней ^ 0 137
Ко
мощность множества и 137
АМ
а;-скачок А 143
а(")
deg(A(u>)) для А £ а 143
Л[#1
{(x,z) : (x,z) е А & z = 2/},
2/-сечение множества А 144
лк»)
: z < у} 144
compat(0, ф)
совместимость частичных функций
В и ip 145
Т
дерево Т С 2<ш или Т С
(в главе VI) 154
[Т]
множество бесконечных путей
вдоль дерева Т 154
П|-класс
(см. с. 154)
Глава VII
Ne
требование низкости
(только для теоремы VII. 1.1) 157
Ne
отрицательное требование С ф {е}А
(для теоремы VII.3.1 и главы VII) 171
r(e,s)
запрещающая функция
(для требования Ne) 158, 171
/е
множество нарушений
(для требования Ne) 158, 172

Список обозначений
555
H£,L£
классы Hn, Ln релятивизованные
к оракулу В 160
L„
R — L„ 160
МУ)
у е wY i6i
N(e,i)
отрицательное требование
(для теоремы VII.3.2) 175
г*(е, в)
запрещающая функция
(для требования N<e,t>) 175
п
множество нарушений
(для требования N(e,t>) 175
Глава VIII
Ne
отрицательное требование С ф {(-4)} (для
леммы VIII. 1.1 и VIII.2.3) 182
Ф еААз\х)
{е*‘(х)} 82,182
Ф е,з(Л3;х)
модифицированный тьюринговый
оператор 183
u(A3;e,x,s)
модифицированная use-функция 184
Т
множество истинных шагов (т. е.,
недефицитных шагов) (в главе VIII)
184, 186
l(e,s)
модифицированная функция
длины 185, 187
r(e,s)
модифицированная запрещающая
функция 185, 188
Л(е, з)
max{r(i, s) : i ^ е} 188
Ie,s
модифицированное множество
нарушений к концу шага з 185, 188
/е
модифицированное множество
нарушений 185, 188
Я(е)
limter R(e,t) 186, 188
m(e, s)
модифицированная функция длины
187
Те
{« : Л1<е1 fat = Л[<е) faj} 190
q(x)
вычислимая функция из
теоремы о скачке и из (3.6) 196
Не
е-ое отверстие в пинбольной машине
(для главы VIII §5) 205, 215
Ge
е-ые ворота в пинбольной машине
(для главы VIII §5) 205, 215
Ge,oo
множество постоянных резидентов
в воротах Ge 205
Глава IX
D(x)
диаграмма 208
О
решетка «ромб» 209
l(e,s)
функция длины (для теоремы IX. 1.2)
211

556
Список обозначений
m(e, s)
максимальная функция длины
(для теоремы IX. 1.2) 211
r(e,s)
запрещающая функция
(для теоремы IX. 1.2) 212
x -< у
х имеет более строгий приоритет, чем
ремы IX.1.2) 217
у (для тео-
M
{а : а = 0 или а в. п. является половиной
минимальной пары } 229, 238
м+
идеал R порожденный М 229
R(< а)
{х : х £ R & х < а} 232
R(>a)
{ж : х £ R & х > а} 232
R«a)
{ж : х £ R & х ^ а} 236
R(^a)
{ж : х £ R & х ^ а} 236
R1
первая производная
Кантора-Бендиксона для R 237
NC
класс недополняемых вниз
в. п. степеней 238
ENC
класс эффективно недополняемых
вниз (в. п. ) степеней 239
Глава X
X
{Ь е С : Ь ^ а} 244
V
{Ь е С : Ь ^ а} 244
c*
факторрешетка С/Т 244, 453
факторрешетка N jT 244
£*
факторрешетка Е/Т 244
n*
факторрешетка 'Я/Т 244
A*
{В : А =* В} 244
Rec(x)
(Зу)[х Уу = 1&схЛу = 0] 245
Fin(a;)
(Vy)[y ^ я => Rec (у)] 245
Sim(a;)
х < 1 & (Vj/) [у > 0 => х А у > 0] 245
Max (a?)
х < 1 & (V2/)[z < у => 2/ = 1] 245
£(S)
решетка {W С\ S : We. п. } 249
Ws
W П S в E(S) 249
C(A)
главный фильтр {В : А С В & В Е £}
251
<r(e, x, s)
е-штат числа х на шаге s 256
a > т
упорядочение е-штатов 256, 318
<r(—1, ж, s)
0, для всех х и s 256
77-максимальное множество
(см. с. 260)
A Cm В
А — мажорное подмножество В 260
ACS В
А — маленькое подмножество В 264
A (Zsm В
АСз В и A Cm В 264
Ез булева алгебра
(см. с. 275)
Глава XI
Са(х)
функция вычисления
(/ха)[А»|'х = А\х] 291,303
deg (С)
{ deg(W) : W е С] 295

Список обозначений
557
М
ФДя)
—eff
П
V
C#
А
SPH
PS
Глава XII
G(A)
Мах
Gtt(A)
Gi(A)
GK А)
GQ> А)
G(\A)
GK a)
G{> a)
G(|a)
G(C)
0(^+1)
A £ Ецг+i
Eo, 4-i-полное множество
Пц;-и-полное множество
Highn
Lown
Low<u,(L<u,)
High<u,(Н<Ш)
Int
A
Sim
HSim
класс максимальных множеств 295, 312
Ф{Аг,3 U Cs; е, х, s)
(для теоремы XI.3.2) 306
эффективный изоморфизм
(автоморфизм) 312
класс гг-простых множеств 312
класс плотно простых множеств 312
класс кобесконечных в. п. множеств,
которые не имеют
надмножеств С 312, 317
класс степеней deg(M#), безатомных
множеств 312, 318
класс степеней не-гг-простых
множеств с некоторым свойством
разложения 316, 390
класс степеней быстро простых
множеств 316, 380
{х : Wx =т А} 326, 327
{ж : Wx максимально} 327, 353
{х : Wx =tt А} 332
{х : Wx =i А] 332
{х : Wx А} 333
{х : А ^т Wx} 333
{x:A\TWx} 333
(см. с. 333)
(см. с. 333)
(см. с. 333)
\x:Wx е С] 341
(0^))', скачок множества 0^^ 348
А е 348
(см. Определение 12. 4. 1) 348
(см. Определение 12. 4. 1) 348
{х : Wx п-высокое} 348
{х : Wx п-низкое} 348
UnLown 348
U„Highn 348
{х : Wx промежуточное } =
и — {Z/<a; U 348
{х : Wx безатомно} 351
{х : Wx просто} 351
{ж : Wx гиперпросто} 351
если х 6 С и Win) = Win), то у Е С 352
множество, замкнутое
относительно n-го скачка
а;-замкнутое множество
множество, замкнутое относительно n-го скачка
для всех п 352

558
Список обозначений
0(^) -эффективно
неотделимые множества
cj-замыкание
С1Ш(А)
Та
NSemilow
QMax
А ~о В
A ~i В
А В
А ~п+г В
А В
Глава XIII
PS
G
LC
R+
Глава XIV
метод 0;-приоритета
метод 0"-приоритета
метод 0,,/-приоритета
метод 0(п)-приоритета
Л
<л
Т
[Г]
а,
f,9
И
аСР
а С/3
А
(а)
оГр
иф С а)Р(Р)
<*<L Р
а^Р
(см. упражнение XII.4.18) 357
(см. упражнение XII.4.18) 357
{е : (3t 6 Л)(Эп)[ж/п) =т We(n)]} 357
{т G Т : а С т} для дерева Т 358
{х : Wх не полунизко} 358
{х : Wx квази-максимально} 361
А — В 365
А =* В 365
А=т В 365
А(п) =т В(п\ для nEw 365
(3п)[А -п В] 365
класс степеней быстро
простых множеств 316, 380
степени множеств из орбит в. п.
генерических множеств относительно
автоморфизмов решетки S 390
класс низко дополняемых наверх
в. п. степеней 393
R - {0} 396
(см. с. 398)
(см. с. 398)
(см. с. 398)
(см. с. 399)
счетное (или конечное) множество 399
линейный порядок на А 399
приоритетное дерево
Т С А" 399, 404, 411, 425
множество бесконечных путей
вдоль Т 399
элементы из А<ш 399
элементы из 399
длина а 399
строка /? продолжает строку а 399
а С /? и а ф (3 399
пустая строка 399
строка состоящая из элемента а 399
конкатенация строк а и /? 399
имеющая наименьшую длину строка /? С а, на
которой предикат Р истинен 399
а левее /3 399
a <i /? или а С Р 400

Список обозначений
559
а < 0
lim infs &s Гя.
а-шаг
a-расширяющий (шаг)
a-корректное (вычисление)
l(ays)
m(a, 8)
a-стратегия
фА фД
a ^ 0 и a ^ 0 400
(cm. c. 405)
(cm. c. 405, 409)
(cm. c. 409, 413, 425)
(cm. c. 412)
(cm. c. 413)
(cm. c. 413)
(cm. c. 415)
А-частично вычислимые функции,
ранее обозначаемые через {е}А 418
A[s], Ф[з]
m[s]
»*'W
Ri
В-гэп
А-гэп
Ва-гэп
Аа-гэп
В-когэп
ПА
s
l^s]
m'a[s]
i,j : T —¥ w
Lo(a)
Li(a)
r(a)
г-граница
E(a,i)
E(h, i)
r(h,i)
значение к концу шага s конструкции 418
значение параметра т к концу шага s 418
(см. с. 419)
(см. с. 419)
требование 419
подтребование Я, 420
(см. с. 421)
(см. с. 421)
(см. с. 426)
(см. с. 426)
(см. с. 422)
(см. с. 423)
множество выходов {s,p2,pl,a;} 423
(см. с. 425)
(см. с. 425)
функции i и j 426
list Lo 426
list Li 426
(см. c. 427)
(cm. c. 428)
(cm. c. 428)
завершающий г-регион для h 429
вершина завершающего
г-региона для h 429
Pa
Rat.
Act
Bat
Ф a
Фа
x(a)
r(a, 1)
r(a, 2)
r(a)
F(a)
Va
Sa
(t, a)
положительное требование 431
подтребование 432
(см. с. 432)
(см. с. 432)
(см. с. 432)
(см. с. 432)
текущий кандидат для а-модуля 432
(см. с. 432)
(см. с. 432)
(см. с. 432)
(см. с. 432)
множество а-шагов 433
множество подлинных а-шагов 433
связка с низом а и верхушкой т 433

56U
Список обозначений
fe[T]
истинный путь / 439
f(a)
lim {r(a)[s] : s £ Va+} 441
r(oc)[s]
max {r(/3)[s] : (3 ^ a} 441
Глава XV
Aut £ (Aut £*)
группа автоморфизмов £ (£*) 446
AS*e В (A* B*)
существует Ф £ Aut £ (Aut £*) такое, что Ф(А) =
В (Ф(А*) = В*) 447
orbit (A)
класс {В : А ^£ В} 447
огЫЦА*)
класс {В* : А* $££+ В*} 447
c^eff
эффективный изоморфизм
(автоморфизм) 454
is(e,x)
полный е-штат х относительно
{Ae,s}e,s€u/ И {Ye,s}e,s€и/ 462
(е,(т,т)
полный е-штат 462
is(e,x,s)
(е,о-(е,х, s),r(e,x,s)) 462
(j(e, x, s)
{г : г ^ е & х £ 462
r(e,x,s)
{г : г ^ е & х £ Vi,s} 463
V/
v - (е, о-, т), у' = (е, о-7, т'), а С а1
и т Э т1 464
D?
(см. с. 465)
D5
(см. с. 465)
C(C)
{1Уе : С С 1Уе или 1Уе С* С} 467
Ci
(см. с. 473)
v(e,x,s)
(е, {г е : ж £ {г е : х £ Vi,s}) 473
v(e,x,s)
(е, {г ^ е : я £ {г ^ е : х £ ^,а}) 473
v о--точно покрывает v'(v
v')
е = е', и = и', и т' D т 473
v т-точно покрывает v'(y
v>)
е = е', т — т1, и а* С а 473
V <v'
е ^ е', о- = о-7 П {0,1,..., е}, и
г = г' П {0,1,..., е} 473
и
е = длина у, где (у = (е, (7, т)) 473
M, M
пинбольные машины 474
C,Ci,Ci,D
треки в машине М 474
H
отверстие в машине М 474
P,Q
карманы машины М 474
Bv
ящик внутри кармана Р 474
Sv
требование 478
q(v, s)
(м)[у 6 Qs и < и(у, у, S) &
(Vi/' Ч i/)[у > g(s,«/')]] 478
Ru
требование 479
Vs
: (З^' £ Ms)[y' И) 480
d(y,s)
(см. с. 480)
d(y)
lim5 d(£,s) 480
S,(X)
(см. с. 481)

Список обозначений
561
5(Х)
конкатенация последовательностей <Ss(X) для всех
s £ и 481
S(X)
конкатенация последовательностей
Ss(X) для всех s £ и 481
list 1Z
(см. с. 482)
list C{Bu)
(см. с. 482)
Ms
(см. с. 483)
и исключается из Л45
(см. с. 483)
Ми,
{и : (о.е. s)[v Э Л45]} 483
Vu,
{и : (а.е. s)[v Э Ps]} 483
Ms
(см. с. 483)
Vs
(см. с. 483)
d(x, s)
(см. с. 483)
list H
(см. с. 483)
Us
(см. с. 483)
Глава XVI
semi-lowi.5
{х : Wx П S конечно} 0” 492
semi-low2
{е : We П А бесконечно} 495
HM
класс степеней гемимаксимальных
множеств 496
Th(£) (Th(£*)
элементарная теория 498
Th(R)
элементарная теория верхней полурешетки в. п.
степеней Rc ^ 503

Предметный указатель
1-сводимость (1-reduciblicity), 40
1-степень (1-degree), 41
а-модуль (a-module), 432
а-шаг (a-stage), 405, 409, 433
— подлинный (genuine a-stage), 433
ЬТ-сводимость (bT-reducibility), см. ограниченная сводимость по Тьюрингу
btt-сводимость (btt-reducibility), см. ограниченнотабличная сводимость
До-индекс для вычислимого множества (До-index for a recursive set), 58
Ai-индекс для вычислимого множества (Ai-index for a recursive set), 58
е-доминанта (e-dominant), 291
е-расщепление (e-splitting), 145, 148
е-регион (e-region), 272
е-штат (e-state), 256
— полный (full e-state), 455
f-дерево (f-tree), 148
г-граница (г-boundary), 428
г-регион (г-region), 428
/х оператор (/x operator), 20
m-сводимость (m-reducebility), 40
га-степень (m-degree), 41
о;-скачок (a;-jump), 143
Ei-индекс (Ei-index), 58
tt-сводимость (tt-reducibility), см. табличная сводимость
T-предикат Клини (Kleene T-predicate), 35
Т-степень (T-degree), см. Тьюринговая степень
use-принцип (Use Principle), 81

Предметный указатель
563
use-функция (use function), 80
wtt-сводимость (wtt-reducible), 122
wtt-степень (wtt-degree), 122
у-сечение (y-section), 144
автоморфизм (automorphism), 244
аксиома выбора (Axiom of Choice), 88
алгоритм (algorithm), 26
Амбос-Шпиис (Ambos-Spies), 221, 227, 231, 236, 237, 240-242, 309, 311, 316, 382, 390,
495, 504, 506, 507
Арсланов (Arslanov), 113, 127-129, 131, 292, 303, 327, 361, 362, 364, 365, 368-370
Ахмад (Ahmad), 325
Баррис (Burris), 501
башня (tower), 266
Беннисон (Bennison), 312, 492
Блюм (Blum), 129, 311, 312
булева алгебра (Boolean algebra), 56
— безатомная (atomless Boolean algebra), 266, 271
— вычислимо представимая (computably presented Boolean algebra), 137
Бун (Boone), 39
верхушка г-региона (top of the i-region), 428
вершина
— нечётная (odd node), 425
— чётная (even node), 425
ворота (gate), см. отверстие
временное разрушение (capricious destruction), 395
Вудин (Woodin), 505
вход машины Тьюринга (Turing machine input), 31
вывод (derivation), 27
вынуждение (forcing), см. вынуждение скачка
— скачка (forcing the jump), 140
выход (outcomes), 423
выход машины Тьюринга (Turing machine output), 31
вычисление
— А-недействительное (А-invalid computation), 306
— С-удостоверенное (C-certified computation), 305
— истинное (true computation), 184
— машины Тьюринга (Turing machine computation), 32
— текущее (apparent computation), 184
— тьюрингово (Turing computation), см. вычисление машины Тьюринга
вычислимость
— относительно A (computable in А), 82
— равномерная (uniform computability), 60
вычислимый изоморфизм (recursive isomorphism), 47
Гёделев номер (Godel number), 34

564
Предметный указатель
Гёдель (Godel), 17, 25, 113
Гилл (Gill), 129
гипотеза Шёнфилда (Shoenfield’s conjecture), 208
график (graph), 53
гэп (gap), 420
Дёгтев (Degtev), 340, 503
действие (act), 400
Деккер (Dekker), 118, 291, 313, 351
дерево (tree), 154
— вычислимое (computable tree), 154
— приоритетное (priority method tree), 403
Джокуш (Jockusch), 49, 75, 92, 130, 131, 141-143, 154, 155, 161, 162, 229-231, 259, 290,
292, 293, 300, 301, 303, 315, 316, 326, 327, 340, 342, 344, 347, 350-353, 357,
358, 360, 361, 365, 366, 369, 370, 382, 390, 455, 495
диагональное рассуждение (diagonal argument), 28
доминанта (dominant), 282
— по перечислению (enumeration dominant), 291
дополнение элемента в £(S) (complemention in £(S)), 249
дополнение элемента решётки (complement of an element in a lattice), 55
Доуни (Downey), 340, 444, 496, 497, 504
Дэвис (Davis), 39
единичный элемент решётки (unit element of a lattice), 55
Ейтс (Yates), 119, 123, 125, 126, 181, 189, 191, 198, 201, 202, 204, 210, 226, 238, 254,
258, 260, 282, 293, 299, 301, 326-328, 330-332, 336, 337, 340-342, 361, 396,
459, 507
заключительное состояние машины Тьюринга (Turing machine halting state), 31
закрытие гэпа (closing a gap), 388
идеал (ideal), 56
— главный (principal ideal), 244
— дуальный (dual ideal), см. фильтр
иерархия
— аналитическая (analitical hierarchy), 52
— арифметическая (arithmetical hierarchy), 94
— — релятивизованная (relativized arithmetical hierarchy), 106
Инграссиа (Ingrassia), 382
индекс (index), 34
— высокости (highness index), 360
— канонический (конечного множества) (canonical index for finite set), 60
— низкости (lowness index), 348
— характеристический (вычислимого множества) (characteristic index of a compu¬
table set), 58
инициализировать (initialize), 400
• штерпретация (interpretation), 505
.шфимум (infimum), 55
.исление равенств (equational calculus), 35

Предметный указатель
565
Каллибеков (Kallibekov), 333, 340
каноническая реализация (canonical realization), 499
квантор (quantifier), 20
— ограниченный (bounded quantifier), 95
Кент (Kent), 450, 454
Кинбер (Kinber), 340, 344
класс
— а-равномерный (а-uniform class), 342
— а-субравномерный (a-subuniform class), 342
клетка машины Тьюринга (Turing machine cells), 31
Клини (Kleene), 17, 18, 25, 28, 29, 34, 35, 62-64, 78, 79, 113, 133, 134, 144, 327, 400
Клини-Пост (Kleene-Post), 18
коатом (co-atom), 255
Кобзев (Kobzev), 121, 340
когэп (cogap), 422
кодовое число (code number), 28
коконечный (cofinite), 43
композиция (composition), 27
— функций (composition of functions), 19
конструкция
— гэп-когэп (gap-cogap construction), 384
— оракульная (oracle construction), 113
— с расширениями
— — бесконечными (infinite extension of construction), 134
— — конечными (finite extension of construction), 134
конус степеней
— верхний (upper cone of degrees), 138
— нижний (lower cone of degrees), 138
конус элементов (cone of elements), 272
конфигурация машины Тьюринга (Turing machine configuration), 32
Коэн П. Ф. (Cohen P. F.), 220, 315
критерий
— 0"-полноты (0"-completeness criterion), 131
— полноты (Completeness Criterion), см. Критерий полноты Арсланова, Критерий
полноты Фридберга, 0"-критерий полноты
— — Арсланова (Arslanov’s Completeness Criterion), 127, 303, 327, 364
— — обобщённый (Generalized Completeness Criterion), 369
— — Фридберга (Friedberg Completeness Criterion), 139
— — Фридберга релятвизованный (relativized Friedberg Completeness Criterion),
141
Кузнецов (Kuznecov), 118
Купер (Cooper), 169, 191, 222, 292, 302, 396, 418, 444, 445, 504-509
Кучера (Kucera), 164, 166
Ладнер (Ladner), 170, 396, 507
Лахлан (Lachlan), 18, 68, 74, 113, 127, 130, 162, 169, 182, 183, 196, 197, 209, 210, 216,
220-222, 225, 226, 231, 232, 237, 247, 249, 251, 252, 255, 262, 264, 266, 267,
270, 271, 275, 276, 282, 289, 292, 301, 303, 304, 309, 313, 315, 317, 325, 327,
342, 361, 393, 396-399, 403, 407, 408, 410, 411, 417, 418, 420, 444, 450, 451,
453, 454, 498-500, 503, 505, 509

566
Предметный указатель
лемма
— об t-регионе (t-Region Lemma), 443
— о густоте (Thickness Lemma), 184
— — в сильной форме (Thickness Lemma in Strong Form), 189
— — сильная (Strong Thickness Lemma), см. Лемме о густоте в сильной форме
— о замедлении (Slowdown Lemma), 376
— об истинном пути (True Path Lemma), 414
— об истинных выходах (Huth of Outcome Lemma), 442
— о множестве индексов (Padding Lemma), 35
— об окнах (Window Lemma), 188
— о пределе (Limit Lemma), 90
— о самом левом пути (Leftmost Path Lemma), 439
— о связках (Link Lemma), 436
— о стабилизации блоков (Stable Block Lemma), 321
Лемпп (Lempp), 444
Лемпп (Lempp), 353, 361, 490, 502, 504, 506, 509
лента
— машины Тьюринга (Turing machine tape), 31
— оракульная (oracle tape), 77
Лерман (Lerman), 148, 204, 215, 216, 221, 232, 264, 271, 287, 301, 316, 365, 370, 373,
494, 500, 502, 503, 506, 507
лямбда обозначения (lambda notation), 20
Маас (Maass), 304, 312, 316, 373, 375, 382, 390, 391, 490, 492-496, 498
Майхилл (Myhill), 47, 51, 64, 69, 71, 85, 247, 255
Маккинзи (McKenzie), 501
маркер
— кодирующий (coding marker), 199
— подвижный (movable marker), 103
Мартин Д. A. (Martin, D. A.), 113, 122, 125-127, 130, 162, 196, 197, 259, 269, 282, 283,
285-290, 292-295, 299, 300, 302, 303, 312, 327, 332, 342, 353, 354, 358, 361,
373, 410, 454, 455, 459, 465, 498, 505
Марченков (Marchenkov), 119, 120, 260, 315
машина Тьюринга (Hiring machine), 30
— с оракулом (oracle Hiring machine), 77
Медведев (Medvedev), 118
Мейер (Meyer), 492
метод
— O'-приоритета (O'-priority method), 398
— 0"-приоритета (0"-priority method), 398
— O'"-приоритета (0"'-priority method), 398
— группирования стратегий (nested strategies method), 212
— деревьев (tree method), 398
— Мучника-Фридберга (Friedberg-Muchnik method), 166
— приоритета (priority method, priority argument), 156
— — с бесконечными нарушениями (infinite injury priority method), 181
— разрешения (permitting method), 123
— — Мартина (Martin’s permitting method), см. метод разрешения для высоких
степеней
— — для высоких степеней (high permitting method), 293

Предметный указатель
567
— — Ейтса (Yates permitting method), 123
— — задержанного (delayed permitting method), 225
— — обычного (usual permitting), см. метод разрешения Ейтса
Миллер (Miller D.), 122, 302, 315, 396, 508
минимальная верхняя грань (minimal upper bound), 153
множества
— автоморфные (automorphic sets), 447
— вычислимо
— — отделимые (computably separable sets), 98
множество
— 1-генерическое (1-generic set), 141
— l-полное (1-complete set), 44
— 1.5-полунизкое (semi-low 1.5 set), 312
— 2-полунизкое (semi-low2 set), 495
— d-в. n. (d. c. e. set), см. разность в. п. множеств
— е-генерическое (e-generic set), 382
— 77-максимальное (77-maximal set), 260
— m-полное (m-complete set), 69
— п-в. n. (n-c. e. set), 91
— п-высокое (highn set), 109
— cj-замкнутое (u;-closed set), 352
— П1-полное (IIi-complete set), 98
— n„ -полное (Пп-complete set), 98
— г-максимальное (r-maximal set), 261
— г-сжатое (r-cohesive set), 261
— Ei-полное (Ei-complete set), 98
— En-полное (En-complete set), 98
— автосводимое (autoreducibile set), 170
— арифметическое относительно A (arithmetical in A set), 95
— быстро простое (promptly simple set), 374
— в. n. (c. e. set), см. вычислимо перечислимое множество
— — генерическое (с. е. generic set), 382
— — неполное (incomplete с. е. set), 113
— — неускоряемое (nonspeedable с. е. set), 311
— высокое (high set), 106
— вычислимо
— — изоморфные (computably isomorphic sets), 47
— — неотделимые (computably inseparable sets), 45
— — перечислимое (computably enumerable set), 39
— — перечислимое относительно A (computably enumerable in A), 82
— вычислимое (computable set), 30
— — кусочно (piecewise computable set), 184
— гг-иммунное (hh-immune set), см. гипергипериммунное множество
— гг-простое (hh-simple set), см. гипергиперпростое множество
— гемимаксимальное (hemimaximal set), 496
— г-иммунное (h-immune set), см. гипериммунное множество
— гипергипериммунное (hyperhyperimmune set), 117
— — сильно (strongly hyperhyperimmune set), 254
— гипергиперпростое (hyperhypersimple set), 117
— гипериммунное (hyperimmune set), 117

568
Предметный указатель
— — конечно сильно (finitely strongly hyperimmune set), 287
— — сильно (strongly hyperimmune set), 287
— гиперпростое (hypersimple set), 117
— — конечно сильно (finitely strongly hypersimple set), 286
— — сильно (strongly hypersimple set), 287
— г-простое (h-simple set), см. гиперпростое множество
— дефицитное (deficiency set), см. дефицитное множество Деккера
— — Деккера (Dekker deficiency set), 119
— замкнутое относительно n-го скачка (n-jump closed set), 352
— иммунное (immune set), 114
— — эффективно (effectively immune set), 127
— индексное (index set), 42
— интросводимое (introreducible set), 120
— квази-креативное (quasi-creative set), 127
— квазимаксимальное (quasimaximal set), 258
— — ранга n (quasimaximal set of rank n), 466
— креативное (creative set), 69
— — слабо (weakly creative set), 130
— ксг-иммунное (fsh-immune set), см. конечное сильно гипериммунное множество
— ксг-простое (fsh-simple set), см. конечное сильно гиперпростое множество
— максимальное (maximal set), 245
— митотическое (mitotic set), 170
— нарушений (injury set), 158
— нигде не простое (nowhere simple set), 254
— низкое (low set), 106
— плотно простое (dense simple set), 118
— полунизкое (semi-low set), 109
— продуктивное (productive set), 69
— простое (simple set), 114
— — Поста (Post’s simple set), 114
— — слабо эффективно (weakly effectively simple set), 130
— — эффективно (effectively simple set), 115
— самодвойственное (self-dual set), 66
— сгг-иммунное (shh-immune set), см. сильно гипергипериммунное множество
— сг-иммунное (sh-immune set), см. сильно гипериммунное множество
— сг-простое (sh-simple set)), см. сильно гиперпростое множество
— сжатое (cohesive set), 255
— субкреативное (subcreative set), 129
— суперпростое (supersimple set), 287
— частично упорядоченное (partially ordered set), 55
— — счётно универсальное (countably universal partially ordered set), 137
— эффективно
— — невычислимое (effectively noncomputable set), 69
— — неотделимое (effectively inseparable sets), 73
модуль
— основной (basic module), 403
— сходимости (modulus of convergence), 89
— — функции (modulus of convergence function), 89
Морли (Morley), 249, 252, 255
Моррис (Morris), 129

Предметный указатель
569
Морхер (Mohrherr), 75
Мучник (Muchnik), 18, 113, 119, 156, 157, 166, 170, 226, 232-234, 236, 240, 303, 399, 400
Надыров (Nadirov), 127, 129, 365
наибольшая нижняя грань (greatest lower bound), 44
наименьшая верхняя грань (least upper bound), 44
— равномерная (uniform least upper bound), 88
Найт (Knight), 342
нарушение (injure), 133
начальное состояние машины Тьюринга (Turing machine starting state), 31
неограниченный поиск (unbounded search), 29
Нероуд (Nerode), 495
Новиков (Novikov), 39
Норстад (Norstad), 271
нулевой элемент решётки (zero element of a lattice), 55
нумерация
— допустимая (accepting numbering, acceptible numbering), 49
— стандартная (standard numbering), 49
— эффективная (effective numbering), 49
область значений (range), 19
область определения (domain), 19
ограничение функции (restriction of a function), 19
Одифредди (Odifreddi), 120, 122, 260, 315
окна (windows), 183
определение разбором случаев (definition by cases), 33
орбита (orbit), 447
отверстие (hole), 205
открытие гэпа (open a gap), 385
отношение
— вычислимое (computable relation), 30
— примитивно рекурсивное (primitive recursive relation), 28
Оуингс (Owings), 63, 122, 250, 255, 264
пара
— Булева (Boolean pair), 501
— минимальная (minimal pair), 209
— точная (exact pair), 144
перестановка (permutation), см. вычислимая перестановка
— вычислимая (computable permutation), 46
перечисление (enumeration), 60
— h-диагонально верное (h-diagonally correct enumeration), 284
— в. п. множества (enumeration of an c. e. set), 60
— вычислимое (computable enumeration), 60
— — одновременно (simultaneous computable enumeration), 61
— стандартное
— — в. п. множеств (standard enumeration of the c. e. sets), 61
пинбольная машина (pinball machine), 204
пинбольные машины M и М (pinball machines М and М), 474
подмножество

570
Предметный указатель
— густое (thick subset), 144
— мажорное (major subset), 260
— — маленькое (small major subset), 264
подрешётка (sublattice), 56
Познер (Posner), 141, 142, 153, 210, 222, 303
полнота (по Тьюрингу) (completeness, Turing completeness), 69
пол-скачка (half-jump), 162
полукреативность (semicreative), 126
полурешётка
— верхняя (upper semi-lattice), 56
— — тьюринговых степеней ((D, ^)) (upper semi-lattice of Turing degrees), 56
последователь (follower), 181
— реализованный (realized follower), 241
последователь (successor), 400
последовательность
— возрастающая (степеней) (ascending sequence of degrees), 143
— вычислимая (computable sequence), 60
— вычислимо независимая (множеств) (computably independent sequence of sets),
136
— независимая (independence sequence), 203
— равномерно вычислимая (в. п. множеств) (uniformly computable sequence of c. e.
sets), 60
Пост (Post), 18, 55, 69, 76, 94, 99, 106, 113-115, 133
построение
— С-вычислимое оракульное (C-computable oracle construction), 133
— вдоль истинного пути (construction along the true path), 404
поточечная сходимость (convergence pointwise), 89
правило
— Ri (Rule R\), 482
— Я2 (Rule R2 ), 482
— R3 (Rule Я3), 483
— R4 (Rule Я4), 483
предикат
— вычислимый (computable predicate), см. вычислимое отношение
— примитивно рекурсивный (primitive recursive predicate), см. примитивно рекур¬
сивное отношение
представление булевой алгебры (associate of a Boolean algebra), 276
предшественник (predecessor), 400
примитивная рекурсия (primitive recursion), 27
принцип
— максимальной степени (maximum degree principle), 303
— отделения (separation principle), 57
— редукции в. п. множеств (Reduction Principle for С. Е. Sets), 54
приоритет
— более высокий (stronger priority, higher priority), 156
проблема
— неразрешимая (unsolvable problem), 39
— остановки (halting problem), 40
— Поста (Post’s Problem), 114
программа

Предметный указатель
571
— машины Тьюринга (Turing machine program), 31
— машины Тьюринга с оракулом (oracle Turing machine program), 78
— Поста (Post’s Program), 114
проекция (projection), 27
производная Кантора-Бендиксона (Cantor-Bendixson derivative), 237
пространство Бэра (Baire space), 83
псевдотребование (pseudo-requirement), 193
путь
— вдоль дерева T (path through a tree T), 154
— истинный (true path), 401
Рабин (Rubin), 501
равенство функций (equality of functions), 19
равномерная эффективность (uniform effectiveness), см. равномерная вычислимость
равномерно в. п. семейство в. п. множеств (uniformly с. е. sequence of с. е. sets), 60
равномерность (uniformity), 54
разность в. п. множеств (difference of с. е. sets), 91
разрешение
— быстрое (promptly permits), 377
ранг Кантора-Бендиксона (Cantor-Bendixson rank), 232
рекурсия (recursion), 27
Реммель (Remmel), 495
решётка (lattice), 55
— в. п. множеств 8 (lattice of с. е. sets 8), 57
— дистрибутивная (distributive lattice), 56
— отделимая (separated lattice), 499
— с дополнениями (complemented lattice), 56
Робинсон Дж. (Robinson, J.), 39
Робинсон Р. В. (Robinson, R. W.), 189, 202-204, 221, 222, 226, 253, 266, 267, 271, 282,
288-292, 299, 303-305, 310-312, 315, 317, 361, 491, 509
Роджерс (Rogers), 49, 50, 52, 95, 102, 122, 246
ромб (diamond lattice), 209
Сакс (Sacks), 114, 138, 148, 151, 153, 160, 162-164, 171, 173, 174, 181, 182, 184, 186, 189,
191, 192, 194-196, 198, 203, 204, 208, 220, 226, 230, 237, 241, 247, 252, 281,
282, 304, 305, 326, 327, 331, 334, 349, 354, 366, 367, 392, 398, 411, 417,. 504,
507-509
Сассо (Sasso), 396, 507
сводимость
— много-одно (many-one reduciblicity), см. m-сводимость
— ограниченно-табличная (btt-сводимость) (bounded truth-table reducibility), 121
— одно-одно (one-one reducibility), см. 1-сводимость
— табличная (truth-table reducibility), 121
— — слабая (weak truth-table reducibility), см. wtt-сводимость
— Тьюринговая (Turing reducibility)
— — ограниченная (ЬТ-сводимость) (bounded Turing reducibility), 122
свойство
— а. д. h. (a.c. property), см. свойство антидополняемости наверх
— антидополняемости наверх (anticupping property), 396
— вычислимо инвариантное (computably invariant property), 46

572
Предметный указатель
— инвариантное (invariant property), 245
— решеточно-инвариантное (lattice invariant property), 245
— элементарно теоретико-решеточное в £ (elementary lattice theoretic property in
£), 245
— э. т. p. (e. 1. t. property), см. элементарно теоретико-решеточное свойство
связка (link), 433
Симпсон М. (Simpson М.), 163
скачок (jump), 85
— п-й, 85
— слабый (weak jump), 105
скелет (skeleton), 461
Сламан (Slaman), 232, 237, 338-340, 382, 399, 407, 418, 444, 503-507, 509
Смальян (Smullyan), 67, 73, 127
Соар (Soare), 127, 130, 154, 155, 169, 182, 221, 226, 228, 231, 249, 252, 255, 271, 300,
301, 303, 304, 311, 312, 316, 340, 342, 344, 365, 370, 373, 375, 382, 384, 387,
390, 394, 397, 398, 410, 444, 459, 464-466, 490, 492, 494, 495, 500, 502, 504,
506, 508, 509
Соловей (Solovay), 327, 352, 354, 355, 360, 365, 370
Соловьёв (Solov’ev), 127, 129, 365
состояние машины Тьюринга (Turing machine states), 31
сочленение (join), 44
Спектор (Spector), 113, 144, 148, 150
списки (lists), 426
степень
— d-в. п. (d. с. е. degree), см. разность в. п. множеств
— m-верхушечная степень (m-topped degree), 340
— n-высокая (highn degree), 109
— wtt-ветвящаяся (wtt-branching degree), 220
— быстро простая (promptly simple degree), 373
— ветвящаяся (branching degree), 220
— в. n. (c. e. degree ((R, ^))), 85
— — промежуточная (intermediate c. e. degree), 160
— высокая (high degree), 106
— гипериммунно-свободная (hyperimmune-free degree), 122
— глубокая (deep degree), 509
— дополняемая вниз (cappable degree), 238
— дополняемая наверх (cuppable degree), 393
— — низко (low cuppable degree), 393
— минимальная (minimal degree), 148
— неветвящаяся (nonbranching degree), 220
— недополняемая вниз (noncappable degree), 238
— — строго (strongly noncappable degree), 241
— — эффективно (effectively noncappable degree), 239
— неразрешимости (degree of unsolvability), 84
— низкая (low degree), 106
— тьюринговая (Turing degree), 84
Стил (Steel, J.), 505
Стоб (Stob), 231, 264, 275, 290, 304, 311, 316, 333, 340, 344, 345, 382, 390, 391, 490, 493,
495-498, 500, 504, 508, 509
стратегия (strategy), 74

Предметный указатель
573
— кодирования (coding strategy), 198
— — Сакса (Sacks coding strategy), 198
— сохранения равенства Сакса (Sacks preservation strategy), 171
супремум (supremum), 55
таблица (array), 117
— без пересечений (disjoint array), 117
— сильная (strong array), 60, 117
— слабая (weak array), 117
Таллос (Tulloss), 361
Тезис Чёрча (Church’s Thesis), 34
Тенненбаум (Tennenbaum), 259, 282, 283
теорема
— s-m-n теорема (s-m-n Theorem), 36
— — релятивизованная (relativized s-m-n Theorem), 79
— Буна-Новикова (Boone-Novikov theorem), 39
— вниз или наверх (Cup or Cap Theorem), 394
— вниз и наверх (Cup and Cap Theorem), 397
— интерполяционная Сакса (Sacks Interpolation Theorem), 191
— Матиясевича-Дэвиса-Путнама-Робинсона (Matijasevic-Davis-Putnam-Robinson
Theorem), 39
— о графике (Graph Theorem), 53
— о дополнении (Complementation Theorem), 55
— об иерархии (Hierarchy Theorem), 100
— об изоморфизме (Isomorphism Theorem), см. теорема об изоморфизме Майхилла
— — Майхилла (Myhill Isomorphism Theorem), 47
— об индексном множестве (Index Set Theorem), 330
— — Ейтса (Yates Index Set Theorem), 330
— о моделировании вычислимого индекса (Computable Index Simulation Theorem),
365
— о невложимости ромба (Non-Diamond Theorem), 222
— — Лахлана (Lachlan Non-Diamond Theorem), 222
— — для низких степеней (Low Non-Diamond Theorem), 309
— о необратимости Шора (Shore’s Non-Inversion Theorem), 509
— о неограничении Лахлана (Lachlan’s nonbounding theorem), 418
— о неподвижной точке (Fixed Point Theorem), см. теорема рекурсии
— — Арсланова (Arslanov’s Fixed Point Theorem), см. критерий полноты Арсланова
— — обобщенная (Generalized Fixed Point Theorem), 365
— о неполноте Гёделя (Godel’s Incompleteness Theorem), 25
— о неразложении (Nonsplitting Theorem), см. теорема о неразложении Лахлана
— — Лахлана (Lachlan Nonsplitting Theorem), 509
— о низком базисе (Low Basis Theorem), 154
— о нормальной форме (Nofmal Form Theorem), 35
— о нумерации (Enumeration Theorem), 36
— — релятивизованная (Relativized Enumeration Theorem), 79
— — сохраняющей порядок (Order-Preserving Enumeration Theorem), 467
— об обращении скачка Шёнфилда (Shoenfield’s Jump Inversion Theorem), 146
— об объединении (Union Theorem), 54
— о перечислении (Listing Theorem), 54
— о плотности Фейера (Fejer Density Theorem), 232

574
Предметный указатель
— о представлении (Representation Theorem), 328
— о разложении
— — Лахлана (Lachlan Splitting Theorem), 226
— — Оуингса (Owings Splitting Theorem), 250
— — Робинсона (Robinson’s Splitting Theorem), 305
— — Сакса (Sacks Splitting Theorem), 174
— — Фридберга (Friedberg Splitting Theorem), 247
— о расширении (Extension Theorem), 464
— о сжатии кванторов (Quantifier Contraction Theorem), 52
— о скачке (Jump Theorem), см. теорема о скачке Сакса
— — интерполяционная (Jump Interpolation Theorem), 202
— — Сакса (Sacks Jump Theorem), 192
— параметризации (Parameter Theorem), cm. s-m-n теорема
— парной рекурсии Смальяна (Smullyan’s Double Recursion Theorem), 67
— плотности (Density Theorem), см. теорема плотности Сакса
— — Сакса (Sacks Density Theorem), 198
— Плюс-наверх (Plus-Cupping Theorem), 508
— Поста (Post’s Theorem), 99
— — релятивизованная (relativized Post’s Theorem), 106
— Райса (Rice’s theorem), 42
— рекурсии (Recursion Theorem), 63
— — релятивизованная (relativized Recursion Theorem), 79
— — с параметрами (Recursion Theorem with Parameters), 64
— униформизации (Uniformization Theorem), 53
— Шрёдера-Бернштейна (Schroder-Bernstein Theorem), 47
типы вычислимого изоморфизма (types of computable isomorphism), 47
Томасон (Thomason), 216, 221
точка
— неподвижная (fixed point), 62
— — по тьюринговой эквивалентности (Turing fixed point), 129
— почти неподвижная (almost fixed point), 128
Трахтенброт (Trakhtenbrot), 170
требование (requirement), 133
— густоты (thickness requirement), 144
— отрицательное (negative requirement), 18, 157
— положительное (positive requirement), 157
— — бесконечного действия (infinitary positive requirement), 187, 293
— — конечного действия (finitary positive requirement), 293
— с более низким приоритетом (weaker priority requirement), 156
трек (track), 474
Тьюринг (Turing), 25, 26, 30-32, 34, 35, 37, 77, 78, 82, 84, 114, 129, 142, 164, 170, 252,
255, 327, 407, 450, 458, 465
Успенский (Uspenskii), 118
утончение решетки (refinement of a lattice), 499
Уэлш (Welch), 364, 393
фактор-решетка (quotient lattice), 244
Фейер (Fejer), 72, 220, 227, 232, 236, 237, 384, 387, 394, 397, 398, 410, 507, 508
фильтр (решётки) (filter of a lattice), 56

Предметный указатель
575
— главный (principal filter), 244
— сильный (strong filter of a lattice), 56
Фишер (Fischer), 492
Фридберг (Friedberg), 18, 113, 119, 122, 123, 139, 141, 156, 157, 161, 166, 170, 171, 226,
232-234, 236, 240, 247, 249, 255, 256, 260, 268, 303, 331, 399, 400, 481, 496
функция
— без неподвижной точки (fixed point free function), 164
— биективная (bijective function), 19
— возрастающая (increasing function), 57
— всюду определенная (total function), 19
— выбора (selector function), 53
— вычисления (computation function), 142
— вычислимая (computable function), 26
— — всюду определенная (total computable function), 29
— — по Тьюрингу (Turing computable function), 30
— — по Тьюрингу относительно A (A-Turing computable function), 78
— — частично относительно A (А-partial computable function, partial computable
function in A), 77
— главная (principal function), 118
— длины (length function), 171
— доопределяемая (extendible function), 41
— запрещающая (restraint function), 158
— инъективная (injective function), 19
— константная (constant function), 27
— максимальной длины (maximum length function), 176
— пары (pairing function), 20
— примитивно рекурсивная (primitive recursive function), 27
— продуктивная (productive function), 69
— слабая (модуля) (weak modulus function), 165
— следования (successor function), 27
— совместимые частичные (compatible partial functions), 145
— тождественная (identity function), 27
— характеристическая (characteristic function), 19
— частичная (partial function), 19
— частично вычислимая (partial computable function), 29
Харизанова, В. (Harizanov, V.), 444, 490
Харрингтон (Harrington), 230, 316, 382, 394, 396-398, 403, 404, 406, 407, 420, 447, 448,
450, 496-498, 500, 501, 503-505, 507, 508
Херманн (Herrmann), 290, 326, 332, 495, 500, 501
Хермес (Hermes), 34
Хэй (Hay), 73
цилиндр (cylinder), 45
Чёрч (Church), 20, 25, 34, 35, 79
читающая головка машины Тьюринга (Turing machine reading head), 31
шаг
— а-расширяющий (a-expansionary stage), 409

576
Предметный указатель
— е-расширяющий (е-expansionary stage), 212
— истинный (true stage), 119
— недефицитный (nondeficiency stage), см. истинный шаг
Шварц (Schwarz), 327, 349-351, 353, 354, 358, 360, 361
Шелах (Shelah), 397, 398, 503
Шёнфилд (Shoenfield), 35, 127, 146, 148, 181, 184, 189, 208, 221, 226, 237, 238, 240, 282,
313, 315, 396, 507, 508
Шор (Shore), 142, 143, 161, 162, 227, 254, 287, 304, 316, 382, 390, 391, 418, 494-496, 498,
504-506, 508
Эпштейн (Epstein), 148, 153, 169
Янг (Young), 50, 286, 290, 332