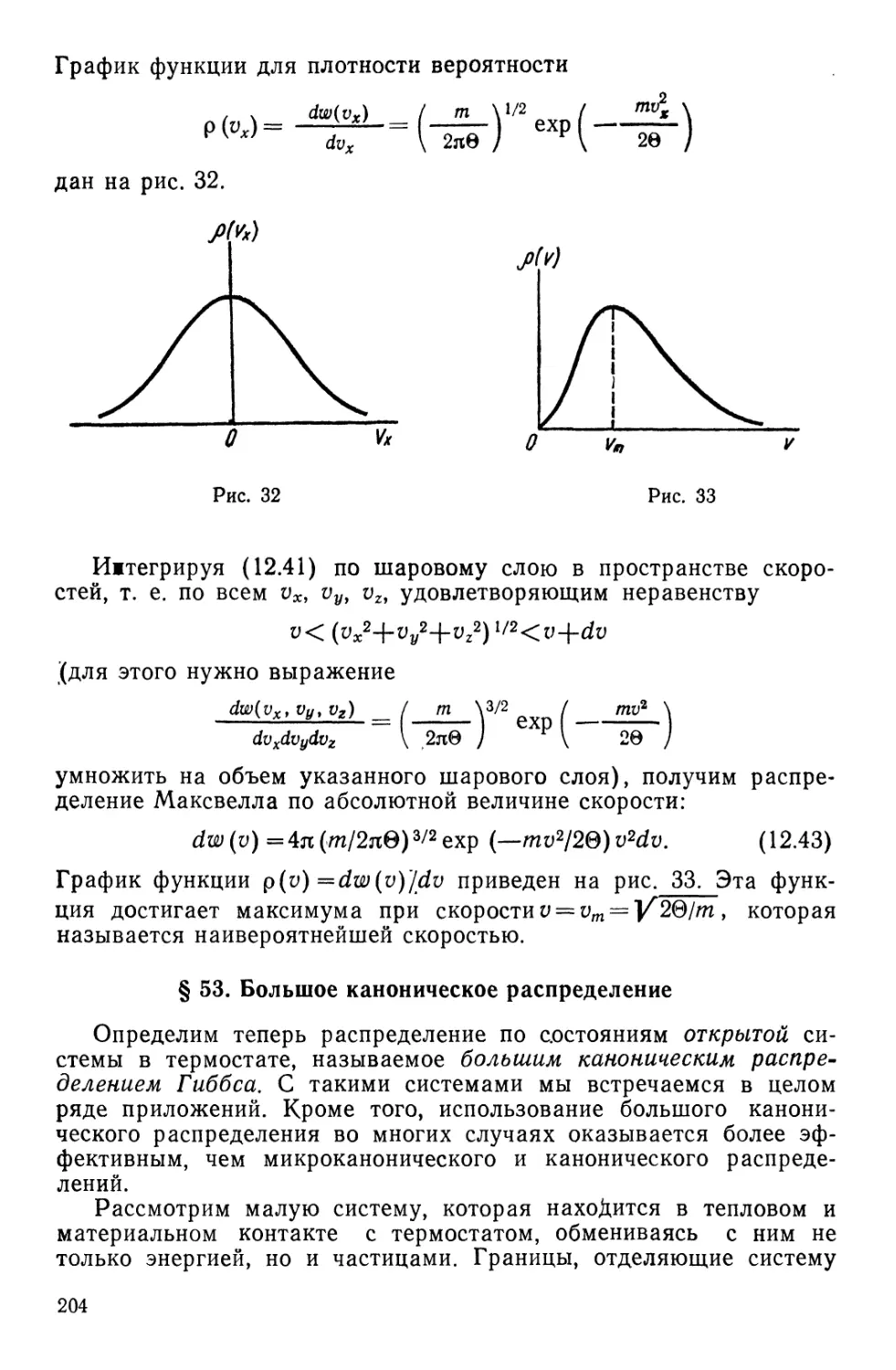
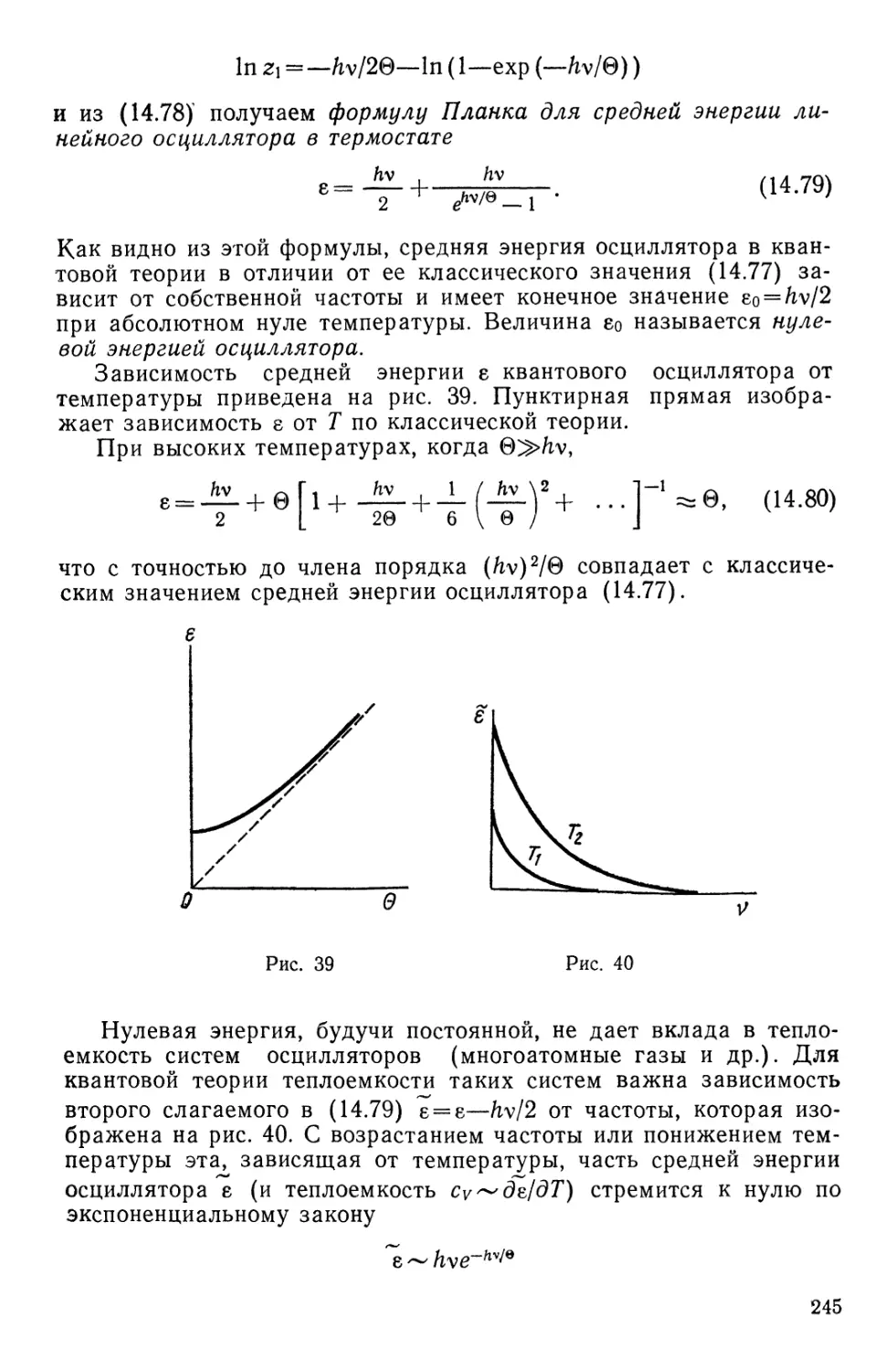
Текст
И. П. Базаров, Э. В. Геворкян,
77. Н. Николаев
ТЕРМОДИНАМИКА
И СТАТИСТИЧЕСКАЯ
ФИЗИКА
ТЕОРИЯ РАВНОВЕСНЫХ
СИСТЕМ
Допущено Министерством высшего и среднего
специального образования СССР в качестве
учебного пособия для студентов университетов,
обучающихся по специальности «Физика»
ИЗДАТЕЛЬСТВО МОСКОВСКОГО
УНИВЕРСИТЕТА 1986
УДК 536.7
Базаров И. П. и др. Термодинамика и статистическая физика.
Теория равновесных систем/ И. П. Базаров, Э В. Геворкян,
П. Н. Николаев. —М.: Изд-во МГУ, 1986.—312 с.
Систематически излагается термодинамика и статистическая тео-
теория многочастичных равновесных систем. В основу статистической фи-
физики равновесных идеальных и неидеальных систем положены метод
Гиббса и метод функций распределения Боголюбова. Излагается клас-
классическая и квантовая теория газа, твердого тела, равновесного излу-
излучения, статистическая теория плазмы и равновесных флуктуации. Об-
Обсуждаются методологические вопросы курса. В книре рассматрива-
рассматриваются также некоторые новые вопросы, еще не вошедшие в программу:
теория критических индексов, вариационный принцип Боголюбова, тер-
термодинамическая теория возмущений, интегральные уравнения для
функций распределения (уравнение самосогласованного поля, интег-
интегральное уравнение Боголюбова—Борна—Грина, уравнение Перкуса—
Йевика).
Ил. 49.
Рецензенты:
чл.-кор. АН СССР Н. Н. Боголюбов (мл.),
кафедра статистической физики ЛГУ им. А. А. Жданова
(зав. кафедрой профессор Ф. М. Куни)
Печатается по постановлению
Редакционно-издательского совета
Московского университета
1704020000-103 12786 @ Издатедьство
077@2)—86 Московского университета, 1986 г.
ОГЛАВЛЕНИЕ
Предисловие . . . в
Введение 7
Часть первая. ТЕРМОДИНАМИКА 9
Основы теории
Глава 1. Основные понятия и исходные положения термодинамики . 13
§ 1. Термодинамическая система и термодинамические параметры.
Термодинамическое равновесие с молекулярной точки зрения 13
§ 2. Исходные положения термодинамики и их обсуждение . 15
§ 3. Гомогенные и гетерогенные системы. Фазы и компоненты . 19
§ 4. Равновесные ц неравновесные процессы 21
§ 5. Внутренняя энергия системы, работа и теплота 22
§ 6. Термические и калорическое уравнения состояния .... 27
Глава 2. Основные законы и уравнения термодинамики. Первое начало
термодинамики 30
§ 7. Уравнение первого начала термодинамики 30
§ 8. Теплоемкости и теплоты изотермического изменения внешних
параметров 33
§ 9. Основные термодинамические процессы и их уравнения . . 36
§ 10. Связь модулей упругости с теплоемкостями 38
Глава 3. Второе начало термодинамики 40
§ 11. Общая характеристика и исходная формулировка второго на-
начала 40
§ 12. Обратимые и необратимые процессы 44
§ 13. Принцип адиабатной недостижимости и второе начало для
равновесных процессов. Энтропия и термодинамическая темпе-
температура 45
§ 14. Математическое обоснование существования энтропии и тер-
термодинамической температуры 48
§ 15. Основное уравнение термодинамики для равновесных процес-
процессов. Связь между термическим и калорическим уравнениями
состояния , 54
§ 16. Вычисление энтропии. Парадокс Гиббса 57
§ 17. Второе начало термодинамики для неравновесных процессов.
Основное уравнение и основное неравенство термодинамики . 62
§ 18. Цикл Карно и теоремы Карно. Прямое преобразование внут-
внутренней энергии в электрическую . 66
§ 19. Самопроизвольный переход теплоты , 70
§ 20. Пределы применимости второго начала термодинамики. На-
Направление времени ....... »...,, 71
Глава 4. Третье начало термодинамики * . 74
§ 21. Формулировка третьего начала термодинамики 75
§ 22. Некоторые следствия третьего начала термодинамики ... 76
Глава 5. Методы термодинамики * . , 80
§ 23. Метод циклов , 80
§ 24. Метод термодинамических потенциалов 82
§ 25. Термодинамические потенциалы сложных систем и систем с
переменным числом частиц 93
Глава 6. Условия равновесия и устойчивости термодинамических е^тем 98
§ 26. Общие условия термодинамического равновесия и устойчивости 98
§ 27. Условия равновесия двухфазной однокомпонентной системы . ЮЗ
§ 28. Условия устойчивости равновесия однородной системы . . Ю5
§ 29. Принцип Ле Шателье — Брауна 109
Глава 7. Термодинамика систем при отрицательных температурах . . ИЗ
§ 30. Существование состояний с отрицательной термодинамической
температурой ИЗ
§ 31. Система с отрицательной термодинамической температурой . 115
§ 32. Термодинамика систем с отрицательными температурами . . 118
§ 33. Условия устойчивости систем с отрицательными температурами 123
Применения термодинамики
Глава 8. Термодинамика некоторых физических систем 125
§ 34. Охлаждение газа при ' необратимом и обратимом адиабатных
расширениях , 125
§ 35. Термодинамика диэлектриков и магнетиков ...... 129
§ 36. Равновесие в гомогенной системе 133
§ 37. Равновесие в гетерогенной системе 139
§ 38. Термодинамика излучения 143
Глава 9<. Поверхностные явления 151
§ 39. Поверхностные натяжение и давление 151
§ 40. Равновесная форма монокристалла. Принцип Гиббса—Кюри и
теорема Вульфа 153
§ 41. Роль поверхностного натяжения при образовании новой фазы.
Зародыши 157
Глава 10. Фазовые переходы и критические явления 160
§ 42. Классификация фазовых переходов. Фазовые переходы первого
рода. Уравнение Клапейрона — Клаузиуса , 161
§ 43. Фазовые переходы второго рода. Уравнения Эренфеста . . 165
§ 44. Термодинамика сверхпроводящего перехода 166
§ 45. Критические и закритические явления 170
§ 46. Термодинамическая теория критических индексов . . . . 176
Часть вторая. СТАТИСТИЧЕСКАЯ ФИЗИКА РАВНОВЕС-
РАВНОВЕСНЫХ СИСТЕМ 181
Глава IK Исходные положения и основные уравнения статистической
физики 183
§ 47. Микроскопические и макроскопические состояния многочастич-
многочастичной системы. Основная задача статистической физики. Урав-
Уравнение Лиувилля . ,,......».,, 183
§ 48. Описание квантовых систем. Оператор плотности и уравнение
Неймана 187
Глава 12. Общие методы равновесной классической статистики . . . 194
§ 49„ Основное положение классической статистики. Микроканониче-
Микроканоническое распределение . . 194
§ 50. Каноническое распределение 197
§ 51. Теорема о равномерном распределении кинетической энергии
по степеням свободы и теорема о вириале 200
§ 52. Распределение Максвелла . . 203
§ 53. Большое каноническое распределение 204
§ 54. Термодинамическая эквивалентность канонических распреде-
распределений , 206
§ 55. Термодинамическая теория возмущений. Вариационный прин-
принцип Боголюбова . . 209
§ 56. Метод Боголюбова 211
Глава 13. Основы квантовой статистики 216
§ 57. . битовые микроканоническое и каноническое распределения 216
§ 58. Квантовое большое каноническое распределение . . . . 218
§ 59. ^Классический предел квантовой статистики 220
Глава 14. Статистическая теория идеальных систем ...... 226
§ 60. Классический одноатомный идеальный газ 226
§ 61. Квантовые одноатомные идеальные газы 229
§ 62. Распределения Бозе—Эйнштейна и Ферми—Дирака .... 230
§ 63. Термическое и калорическое уравнения состояния квантовых 233
газов 236
§ 64. Сильно вырожденный электронный газ 241
§ 65. Вырожденный бозе-газ. Бозе-эйнштейновская конденсация . . 243
§ 66. Осциллятор и ротатор в термостате 247
§ 67. Теория теплоемкости двухатомных газов 250
§ 68. Статистическая теория равновесного излучения - . 255
§ 69. Теория кристалла в гармоническом приближении .... 261
§ 70. Электрические и магнитные свойства идеальных систем . . 265
Глава 15. Теория классических неидеальных систем 266
§ 71. Реальный газ. Групповое разложение в теории газов . . . 272
§ 72. Уравнение Ван-дер-Ваальса 274
§ 73. Метод Боголюбова в теории газов 277
§ 74. Статистическая теория плазмы .
Глава 16. Интегральные уравнения для функций распределения в теории gg7
твердых тел и жидкостей 28«
§ 75. Уравнение самосогласованного поля
§ 76. Интегральное уравнение Боголюбова—Борна—Грина для ра-
радиальной функции распределения в суперпозиционном прибли-
жении *°°
§ 77. Уравнение Перкуса—Йевика ™г
Глава 17. Теория равновесных флуктуации ~~1
§ 78. Вычисление флуктуации методом Гиббса 292
§ 79. Вычисление флуктуации методом функций распределения . . ^95
§ 80. Квазитермодинамическая теория флуктуации 298
§ 81. Флуктуационные явления 304
Предметный указатель , , , » , , * . . , . . 308
ПРЕДИСЛОВИЕ
«Термодинамика и статистическая физика» является заверша-
завершающим курсом теоретической физики для студентов физических и
физико-математических факультетов университетов. В этом курсе
макроскопические тела, т. е. системы из большого числа частиц,
изучаются вначале термодинамическим методом, а затем метода-
методами статистической физики. Такая последовательность обусловле-
обусловлена постепенным переходом в процессе изучения от простого к бо-
более сложному методу познания. (В отличие от основного курса
спецкурсы по термодинамике и статистической физике можно
излагать в любом порядке.) Статистическая физика дает не толь-
только молекулярную интерпретацию термодинамических понятий и
законов термодинамики, но и позволяет получить более глубокие
знания о многочастичных системах.
В настоящем курсе вначале излагается термодинамика и ста-
статистическая физика равновесных систем, а затем теория нерав-
неравновесных систем. В данной книге рассматриваются равновесные
системы. Некоторые частные результаты, получение которых свя-
связано с конкретными расчетами, приводятся без вывода и отмеча-
отмечаются в книге звездочкой (*). Читателю предлагается либо само*
му провести их, либо обратиться к задачникам.
Поскольку университеты, как и высшая школа в целом, реша-
решают двуединую задачу — подготовку профессионально высококва-
высококвалифицированных специалистов и формирование у них диалектико-
материалистического мировоззрения^ в настоящем курсе обсуж-
обсуждаются теоретико-познавательные, методологические проблемы
физики, ибо без философского осмысления физических теорий их
знание не может быть по-настоящему глубоким.
Наш курс написан под научньГм и идейным влиянием акаде:
мика Н. Н. Боголюбова, которому мы выражаем глубокую благо-
благодарность за обсуждение многих вопросов термодинамики и ста-
статистической физики.
ВВЕДЕНИЕ
Последовательность различных курсов как общей, так и тео-
теоретической физики определяется прежде всего постепенным пере-
переходом к изучению все более сложных форм движения соответст-
соответствующих структурных видов материи (макротела, молекулы, ато-
атомы, элементарные частицы и поля). Механика изучает законо-
закономерности простейшей формы движения — 'относительного пере-
перемещения тел в пространстве во времени. Термодинамика и
статистическая физика рассматривают явления, обусловленные
совокупным действием огромного числа непрерывно движущихся
молекул или других частиц, из которых состоят окружающие нас
тела. Благодаря очень большому количеству частиц беспорядоч-
беспорядочное их движение приобретает новые качества: макроскопические
свойства систем из большого числа частиц в обычных условиях
совершенно не зависят от начального положения этих частиц, в
то время как механическое состояние системы существенно зави-
зависит от начальных условий. Это один из примеров диалектическо-
диалектического закона перехода количественных изменений в качественные:
возрастание количества механически движущихся частиц в систе-
системе порождает качественно новый вид движения — тепловое дви-
движение. Тепловое движение представляет собой изменения систе-
системы, обусловленные ее атомистическим строением и наличием ог-
огромного числа частиц; оно связано с молекулярным механическим
движением, но этим не исчерпывается его сущность. «Всякое дви-
движение, — писал Ф. Энгельс, — заключает в себе механическое
движение, перемещение больших или мельчайших частей материи;
познать эти механические движения является первой задачей нау-
науки, однако лишь первой ее задачей. Но это механическое движе-
движение не исчерпывает движения вообще. Движение — это не толь-
только перемена места; в надмеханических областях оно является
также и изменением качества. Открытие, что теплота представля-
представляет собою некоторое молекулярное движение, составило эпоху в
науке. Но если я не имею ничего другого сказать о теплоте кро-
кроме того, что она представляет собой известное перемещение мо-
молекул, то лучше мне замолчать» *. Определяющим для возникно-
возникновения теплового движения является не механическое движение от-
* Маркс К., Энгельс Ф. Соч., 2-е изд., т. 20, с. 567—568.
дельных частиц системы, а существование коллектива большого
числа частиц. Действительно, закономерности теплового движения
проявляются не только в атомно-молекулярных совокупностях, но
и в таких системах, как электромагнитное излучение, заключен-
заключенное в некотором объеме (см. § 38) **.
Термодинамика и статистическая физика изучают тепловую
форму движения материи. При этом вначале рассматриваются
закономерности теплового движения в системах, находящихся в
тепловом равновесии, когда в них отсутствуют макроскопические
перемещения одной части относительно другой. Как видно, пред-
предмет изучения термодинамики и статистической физики один и тбт
же. Существенное отличие их друг от друга состоит в методах
исследования, поэтому они излагаются последовательно.
Термодинамика изучает свойства равновесных физических си-
систем, исходя из трех основных законов, называемых началами
термодинамики, и не использует явно представлений о молекуляр-
молекулярном строении вещества, статистическая же физика при рассмотре-
рассмотрении этих свойств с самого начала опирается на молекулярные
представления о строении физических систем, широко применяя
методы математической теории вероятностей.
Феноменологический характер термодинамики (ее несвязан-
несвязанность с молекулярно-кинетической сущностью изучаемых ею за-
закономерностей) приводит, с одной стороны, к важным результа-
результатам в отношении свойств физических систем, а с другой стороны,
ограничивает глубину изучения этих свойств, так как не позво-
позволяет вскрыть природу исследуемых явлений. По этой причине
наряду с развитием термодинамики формировалась и молекуляр-
но-кинетическая теория свойств физических систем, и все иссле-
исследователи, имена которых связаны с термодинамикой, уделяли
большое внимание молекулярно-кинетическому обоснованию ее
результатов.
Термодинамика является первым шагом на пути к- изучению
закономерностей поведения системы непрерывно движущихся и
взаимодействующих частиц; для всестороннего и более глубокого
рассмотрения этих закономерностей необходимо применение ста-
статистических методов.
В настоящей книге излагается термодинамика и статистиче-
статистическая физика равновесных систем. Обобщение термодинамики и
статистической физики на неравновесные системы — неравновес-
неравновесные термодинамика и статистическая физика — составляет содер-
содержание второй части нашего курса.
** Тепловым движением обладают системы из большого числа частиц, от*
дельные же частицы имеют не тепловое, а механическое движение.
Часть первая
ТЕРМОДИНАМИКА
Термодинамика изучает закономерности теплового движения
в равновесных системах и при переходе систем в равновесие
(классическая, или равновесная, термодинамика), а также обоб-
обобщает эти закономерности на неравновесные системы (неравновес-
(неравновесная термодинамика, или термодинамика необратимых процессов).
Здесь рассматривается равновесная термодинамика (ее обыч-
обычно называют просто термодинамикой в отличие от неравновесной
термодинамики).
Хотя в конечном итоге все свойства физических систем опре-
определяются молекулярным движением в них, термодинамика позво-
позволяет установить многие из этих свойств, не прибегая к представ-
представлениям о молекулярном строении тел. Для решения многих прак-
практически важных задач достаточны методы термодинамики. Все
это обусловливает, с одной стороны, ограниченность термодина-
термодинамики, а с другой стороны, наделяет ее определенными преимуще-
преимуществами перед молекулярными теориями. Термодинамика позволя-
позволяет с помощью своих начал легко учитывать наблюдаемые на опы-
опыте закономерности и получать из них фундаментальные . след-
следствия.
Исторически термодинамика возникла из потребностей тепло-
теплотехники. Развитие производительных сил стимулировало ее созда-
создание. Широкое применение в начале XIX в. паровой машины поста-
поставило перед наукой задачу теоретического изучения работы тепло-
тепловых машин с целью повышения их коэффициента полезного дей-
действия. Это исследование было проведено в 1824 г. в первом сочи-
сочинении по термодинамике французским физиком и инженером
Сади Карно, доказавшим теоремы, определяющие наибольший
коэффициент полезного действия тепловых машин. Эти теоремы
позволили впоследствии сформулировать один из основных зако-
законов термодинамики — второе начало. В 40-х годах XIX в. ib ре-
результате исследований Майера и Джоуля был установлен механи-
механический эквивалент теплоты и на этой основе открыт закон сохра-
сохранения и превращения энергии, называемый в термодинамике ее
первым началом. Энгельс назвал его «великим основным зако-
законом движения» *.
* Маркс К., Энгельс Ф. Соч., 2-е изд., т. 20, с. 13.
Закон сохранения и превращения энергии имеет как количе-
количественную, так и качественную стороны. Количественная сторона
закона сохранения и превращения энергии состоит в утверждении,
что энергия системы является однозначной функцией ее состояния
и при любых процессах в изолированной системе сохраняется,
превращаясь лишь в строго определенном количественном соотно-
соотношении эквивалентности из одного вида в другой. Качественная
сторона этого закона состоит в никогда не утрачиваемой способ-
способности материального движения к новым превращениям.
Хотя закон сохранения и превращения энергии (как и само
понятие энергии — меры движения) применим только к физиче-
физическим формам движения (см. § 2) и неприменим к высшим фор-
формам движения материи (биологическое и общественное движе-
движение), тем не менее он имеет всеобщее значение. Это следует из
общности физических форм движения: всякая более высокая фор-
форма движения материи содержит в себе физические формы дви-
движения, хотя и не сводится к ним. И если при превращении одной
физической формы движения в другую одна из них исчезает (час-
(частично или полностью), а вторая количественно увеличивается
.{превращение механического движения в тепловое, электромаг-
электромагнитное и наоборот и т. д.), то при возникновении новой, более
высокой формы движения материи порождающие ее различные
физические формы движения не исчезают, а существуют как их
«высшее единство»*. Разрушение этого единства приводит к ис-
исчезновению более высокой формы движения и высвобождению
как самостоятельных, порождающих ее различных физических
форм движения, которые имеют своей мерой энергию.
Отсюда следует, что непосредственно закон сохранения и пре-
превращения энергии приложим только к физическим формам дви-
движения материи и устанавливает неуничтожимость и взаимопрев-
взаимопревращаемость только этих форм материального движения, но вмес-
вместе с тем он одновременно является естественнонаучным выраже-
выражением общефилософской идеи несотворимости и неуничтожимости
материи и движения: «Современное естествознание вынуждено
было заимствовать у философии положение о неуничтожимости
движения; без этого положения естествознание теперь не может
уже существовать»"*.
В виде оформленной научной системы, исходящей из работ
Карно и закона сохранения и превращения энергии, термодинами-
термодинамика появилась в 50-х годах XIX в. в трудах Клаузиуса и Томсона
(Кельвина), давших современные формулировки второго начала
и введших важнейшие понятия энтропии и абсолютной темпера-
температуры. Основным методом исследования в термодинамике XIX в.
был метод круговых процессов.
Большое значение для термодинамики имели появившиеся в
* Маркс К-, Энгельс Ф. Соч., 2-е изд., т. 2G, с. 566.
** Там же, с. 360.
10
конце XIX в. работы Гиббса, в которых был создан новый метод
термодинамических исследований (метод термодинамических по-
потенциалов), установлены общие условия термодинамического рав-
равновесия, развита теория фаз и капиллярности.
В XX в. термодинамика вышла за пределы первоначальных
требований теплотехники и стала изучать, как уже было сказа-
сказано, закономерности тепловой формы движения материи в основ-
основном в равновесных системах и при переходе их в равновесное со-
состояние.
Первое начало термодинамики выражает количественную сто-
сторону закона сохранения и превращения энергии в применении к
термодинамическим системам.
Второе начало термодинамики представляет собой закон об
энтропии. Проявлением действия этого закона является, напри-
например, самопроизвольный переход теплоты от тела с большей тем-
температурой к телу с меньшей температурой при соприкосновении,
невозможность процессов, единственным результатом которых
было бы превращение теплоты в работу, и др.
Так же, как и первое начало термодинамики, второе начало
имеет около десятка различных формулировок, большая часть ко-
которых эквивалентна одна другой и выражает полное содержание
самого закона. Разнообразие формулировок этих законов связано
с их проявлением в тех или иных конкретных случаях. Та из фор-
формулировок, которая выражает закономерность явления, наиболее
близкого к нашему опыту, практике, может быть принята за ис-
исходную при установлении и анализе каждого из законов.
В 1906 г. на основе многочисленных исследований свойств тел
при температурах, близких к 0 К, был установлен новый закон
природы — третье начало термодинамики. Согласно ему при тем-
температурах, стремящихся к 0 К, равновесные изотермические про-
процессы проходят без изменения энтропии. Третье начало термоди*
намики имеет большое значение при нахождении энтропийных и
химических констант, которые оказываются существенными при
любой температуре.
Основываясь на трех началах, термодинамика исследует свой-
свойства реальных систем, состоящих из большого числа частиц.
Неоценимый вклад в развитие термодинамики внесли наши
ученые. В конце XIX в. профессор Киевского университета
Н. Н. Шиллер дал новую формулировку второго начала термоди-
термодинамики, которая в 1909 г. была развита немецким математиком
Каратеодори. В 1928 г. Т. А. Афанасьева-Эренфест, критически
анализируя работы Шиллера и Каратеодори, впервые показала,
что второе начало термодинамики состоит из двух независимых
положений, являющихся обобщением данных опыта и относящих-
относящихся, с одной стороны, к состояниям равновесия, а с другой —
к неравновесным процессам.
Важна роль русских ученых и в изучении критических явле-
явлений. Само понятие критической температуры появилось впервые
у Д. И. Менделеева.
II
Менделеев установил, что при приближении к некоторой тем-
температуре поверхностное натяжение стремится к нулю и пропада-
пропадает различие между жидкостью и паром. Он назвал эту темпе-
температуру температурой абсолютного кипения. В дальнейшем изуче-
изучением критических явлений занимались А. Г. Столетов, М. П. Аве-
Авенариус и др. Русские ученые В. А. Михельсон и Б. Б. Голицын
внесли значительный вклад в термодинамику излучения. Голицын
первым ввел понятие температуры излучения, которое вошло в
науку и сохранилось до наших дней. Применением термодинами-
термодинамики к физической химии занимались Д. П. Коновалов, Н. С, Кур-
наков и др.
Большой вклад в термодинамические и статистические иссле-
исследования внесли работы Н. Н. Боголюбова по проблемам динами-
динамической теории в статистической физике, работы Л. Д. Ландау по
теории сверхтекучести, работы М. А. Леонтовича о термодинами-
термодинамических функциях неравновесных состояний, работы В. К- Семен-
ченко по теории растворов и критических явлений и др.
ОСНОВЫ ТЕОРИИ
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ
И ИСХОДНЫЕ ПОЛОЖЕНИЯ
ТЕРМОДИНАМИКИ
Прежде чем перейти к изложению основных законов и мето-
методов термодинамики и изучению свойств различных систем, рас-
раскроем содержание главных термодинамических понятий. Это поз-
позволит оценить значение и пределы применимости термодинамики.
§ 1. Термодинамическая система
и термодинамические параметры.
Термодинамическое равновесие
с молекулярной точки зрения
Всякий материальный объект, всякое тело, состоящие из боль-
большого числа частиц, называется макроскопической системой. Раз-
Размеры макроскопических систем всегда значительно больше раз-
размеров атомов и молекул.
Все макроскопические признаки, характеризующие такую си-
систему и ее отношение к окружающим телам, называются макро-
макроскопическими параметрами. К их числу относятся такие, напри-
например, величины, как плотность, объем, упругость, концентрация,
лоляризация, намагничивание и т. д. Макроскопические парамет-
параметры разделяются на внешние и внутренние.
Величины, определяемые положением не входящих в нашу си-
систему внешних тел, называются внешними параметрами at (i =
= 1, 2...): это, например, объем системы (определяемый располо-
расположением внешних тел), напряженность силового поля (зависящая
от положения источников поля — зарядов и токов, не входящих
в нашу систему) и т. д.
Следовательно, внешние параметры являются функциями ко-
координат внешних тел. Величины, определяемые совокупным Дви-
Движением и распределением в пространстве входящих в систему
частиц, называются внутренними параметрами bf (/=1, 2, ...);
это, например, плотность, давление, энергия, поляризованность,
намагниченность и др. (их значения зависят от движения и поло-
положения частиц системы и входящих в них зарядов).
Поскольку само пространственное расположение входящих в
систему частиц — атомов и молекул — зависит от расположения
внешних тел, то, следовательно, внутренние параметры определя-
13
ются положением и движением этих частиц и значением внешних
параметров *.
Совокупность независимых макроскопических параметров оп-
определяет состояние системы, т. е. форму ее бытия. Величины, не
зависящие от предыстории системы и полностью определяемые
ее состоянием в данный момент (т. е. совокупностью независимых
параметров), называются функциями состояния.
Состояние называется стационарным, если параметры системы
с течением времени не изменяются.
Если, кроме того, в системе не только все параметры постоян-
постоянны во времени, но и нет никаких стационарных потоков за счет
действия каких-либо внешних источников, то такое состояние си-
системы называется равновесным (состояние термодинамического
равновесия). Термодинамическими системами обычно называют
не всякие, а только те макроскопические системы, которые нахо-
находятся в термодинамическом равновесии. Аналогично термодина-
термодинамическими параметрами называются те Параметры, которые ха-
характеризуют систему в ее термодинамическом равновесии.
Внутренние параметры системы разделяют на интенсивные и
экстенсивные. Параметры, не зависящие от массы или числа час-
частиц в системе, называются интенсивными (давление, температу-
температура и др.); параметры, пропорциональные массе или числу частиц
в системе, называются аддитивными или экстенсивными (энергия>
энтропия и др.). Экстенсивные параметры-характеризуют систе-
систему как целое, в то время как интенсивные могут принимать опре-
определенные значения в каждой точке системы. Система, энергия
которой нелинейно зависит от числа частиц, не является термоди-
термодинамической, и ее изучение методами существующей термодинами-
термодинамики может быть, вообще говоря, лишь весьма приближенным
или даже совсем неправомерным.
Что представляют собой равновесные (термодинамические)
внутренние параметры с молекулярной точки зрения?
Для выяснения этого рассмот-
рассмотрим простейший пример. Пусть в
начальный момент времени газ на-
находится в неравновесном состоя-
_ нии, так что его плотность в раз-
, ных точках разная. С течением
-Г времени газ начинает приходить в
равновесное состояние (см. § 2) и
рис i его плотность р = пгоп (гп0 — масса
* Заметим, что в зависимости от условий, в которых находится система, од-
одна и та же величина может быть как внешним, так и внутренним параметром.
Так, при фиксированном положении стенок сосуда объем V является внешним
параметром, а давление Р — внутренним параметром, так как оно зависит от
координат и импульсов частиц системы; в условиях же, когда система нахо-
находится в сосуде с подвижным поршнем под постоянным давлением, давление Р
будет внешним параметром, а объем V — внутренним параметром, так как он
зависит от положения и движения частиц.
14
молекулы, п — концентрация молекул), изменяясь, приобретает
некоторое макроскопически постоянное, равновесное значение ро
{рис. 1). Оно может быть определено как среднее значение плот-
плотности р за большой промежуток времени Т:
Аналогично равновесное значение и любого другого внутреннего
параметра представляет собой среднее значение за большой про-
промежуток времени от соответствующей этому параметру функции
координат и скоростей.
Статистическая физика, исходя из определенной молекулярной
модели строения вещества, позволяет вычислять равновесные зна-
значения внутренних параметров. Однако, и не проводя этих вычис-
вычислений, можно выявить закономерности систем в равновесном со-
состоянии, имея в виду, что во многих случаях эти параметры могут
быть определены экспериментально. Этот первый этап в теории
равновесных состояний и представляет термодинамика.
Основанные на макроскопическом опыте представления об осо-
особенностях термодинамического равновесия конечных систем при-
принимаются в термодинамике в качестве постулатов, опираясь на
которые с помощью основных законов (начал) термодинамики
изучаются свойства равновесных систем и закономерности при их
приближении к равновесию.
§ 2. Исходные положения термодинамики
и их обсуждение
Физика изучает закономерности наиболее простых форм дви-
движения (механического, теплового, электромагнитного и др.) соот-
соответствующих структурных видов материи. Общая мера этих форм
движения при их превращении из одной в другую называется
энергией.
Система, не обменивающаяся с внешними телами ни энергией,
ни веществом (в том числе и излучением), называется изолиро-
изолированной.
В термодинамике постулируется, что у изолированной системы
существует состояние термодинамического равновесия, в которое
юна приходит с течением времени и из которого никогда самопро-
самопроизвольно выйти не может (первый, или основной, постулат тер-
термодинамики).
Являясь результатом обобщения опыта, это первое исходное
положение термодинамики, справедливое для изолированных си-
систем, может быть названо «общим началом термодинамики», так
как является основой всей термодинамики и определяет рамки ее
применимости.
15
В статистической физике, явно учитывающей движение частиц
в системе, смысл положения о ее термодинамическом равновесии
состоит в том, что у всякой (изучаемой термодинамикой) изоли-
изолированной системы существует такое определенное и единственное
макроскопическое состояние, которое чаще всего создается непре-
непрерывно движущимися частицами. Это есть наиболее вероятное со-
состояние, в которое и переходит изолированная система с течени-
течением времени. Отсюда видно, что постулат о самопроизвольном пе-
переходе изолированной системы в равновесие и неограниченно
долгое ее пребывание в нем не является абсолютным законом
природы, а выражает лишь наиболее вероятное поведение систе-
системы; никогда не прекращающееся движение частиц системы приво-
приводит к ее спонтанным отклонениям (флуктуациям) от равновесно-
равновесного состояния.
Вероятностное поведение макроскопических систем, состоящих
из громадного числа механически движущихся частиц, является
характерной особенностью теплового движения, качественно от-
отличающей его от классического механического движения с прису-
присущей ему однозначностью. Наличие огромного числа частиц в тер-
термодинамических системах обусловливает второстепенность меха-
механических закономерностей движения отдельных частиц и возник-
возникновение закономерностей их совокупного, массового движения.
Принимая основной (первый) постулат, термодинамика, таким
образом, ограничивает себя, исключая из рассмотрения систе-
системы, для которых равновесное состояние невозможно (процессы
в таких системах не завершаются наступлением равновесия), а
также все явления, связанные с большими самопроизвольными
отклонениями системы от равновесного состояния.
Основанием для принятия общего начала термодинамики яв-
является то, что, как показывают опыт и статистическая физика,
относительные спонтанные отклонения макроскопической системы
от равновесия при других равных условиях тем меньше, чем
больше частиц в системе. Так как термодинамические системы
состоят из громадного числа частиц N (N~1023), то флуктуация-
ми в большинстве случаев можно пренебречь, что и делается в
термодинамике.
В тех же случаях, когда флуктуации существенны, термодина-
термодинамический подход становится неправомерным и необходимо ста-
статистическое рассмотрение. При этом обнаруживается несогласо-
несогласованность выводов термодинамики и статистической физики, кото-
которая обусловливается ограниченностью и относительностью первого
исходного положения термодинамики. Уяснение этого обстоятель-
обстоятельства показывает, что термодинамическое и статистическое рас-
рассмотрения макроскопических систем не исключают, а дополняют
друг друга.
Второе исходное положение термодинамики (второй постулат)
связано с другими свойствами термодинамического равновесия
как особого вида теплового движения. Опыт показывает, чта
если две равновесные системы А и В привести в тепловой кон-
16
такт, то независимо от различия или равенства у них внешних:
параметров щ они или остаются по-прежнему в состоянии термо-
термодинамического равновесия, или равновесие в них нарушается,
и спустя некоторое время в процессе теплообмена (обмена энер-
энергией) обе системы приходят в другое равновесное состояние. Кро-
Кроме того, если имеются три равновесные системы А, В, С и если
системы А и В порознь находятся в равновесии с системой С, то
системы А и В находятся в термодинамическом равновесии и меж-
между собой (свойство транзитивности термодинамического равно-
равновесия).
Следовательно, состояние термодинамического равновесия си-
системы определяется не только ее внешними параметрами ait но и
еще одной величиной t, характеризующей ее внутреннее состоя-
состояние. Значения t при тепловом контакте различных равновесных
систем в результате обмена энергией становятся для них одинако-
одинаковыми как при продолжающемся тепловом контакте, так и после
его устранения *.
Свойство транзитивности состояний термодинамического рав-
равновесия позволяет сравнивать значения величины / у разных си-
систем, не приводя их в непосредственный тепловой контакт между
собой, а пользуясь одним каким-либо другим телом. Эта величи-
величина, выражающая состояние внутреннего движения равновесной
системы, имеющая одно и то же значение у всех частей сложной
равновесной системы независимо от числа частиц в них и опре-
определяемая внешними параметрами и энергией, относящимися к
каждой такой части, называется температурой. Будучи интенсив-
интенсивным параметром, температура в этом смысле является мерой ин-
интенсивности теплового движения.
Изложенное положение о существовании температуры как
особой функции состояния равновесной системы представляет
второе исходное положение термодинамики. Его иногда называв
ют «нулевым началом», так как оно, подобно первому и второму
началам, определяющим существование некоторых функций со-
состояния, устанавливает существование температуры у равновес-
равновесной системы.
Температура, как мы видим, является термодинамически рав-
равновесным параметром, так как существует только у термодинами-
термодинамически равновесных систем, притом у таких, части которых не
взаимодействуют друг с другом (т. е. энергия взаимодействия час-
частей много меньше их собственных внутренних энергий), так что
энергия системы равна сумме энергий ее частей. Следовательно,
согласно второму исходному положению термодинамики энергия
термодинамических систем является аддитивной функцией. Боль-
Большие гравитирующие системы не являются поэтому термодинами-
термодинамическими, так как для них принцип аддитивности энергии не вы-
выполняется вследствие дальнодействующего .характера гравитаци-
гравитационных сил.
* Энергия различных систем при этом, вообще говоря, различна.
17
Таким образом, в то время как первое исходное положение
термодинамики приводит к нижнему пределу ее применимости —
системе с малым числом частиц, второе ее исходное положение
ограничивает применение термодинамики к реальным системам
сверху, поскольку для систем галактических размеров это поло-
положение не имеет места.
Положение о существовании температуры может быть сформу-
сформулировано также следующим образом. В § 1 мы установили, что
равновесное состояние термодинамической системы характеризу-
характеризуется внешними и внутренними параметрами, причем внутренние
параметры зависят от положения и движения молекул системы
и значений внешних параметров. Положение же о существовании
температуры устанавливает, что состояние термодинамического
равновесия определяется совокупностью внешних параметров и
температурой.
Следовательно, внутренние параметры хотя и характеризуют
состояние системы, но не являются независимыми параметрами
равновесной системы.
Таким образом, все равновесные внутренние параметры систе-
системы являются функциями внешних параметров и температуры
(второй постулат термодинамики).
Так как энергия системы является ее внутренним параметром,
то при равновесии она будет функцией от внешних параметров и
температуры. Выражая с помощью этой функции температуру че-
через энергию и внешние параметры, второе исходное положение
термодинамики можно сформулировать также в следующем виде:
мри термодинамическом равновесии все внутренние параметры
системы являются функциями внешних параметров и энергии *.
Второе исходное положение термодинамики позволяет опреде-
определить изменение температуры тела по изменению какого-либо его
внутреннего параметра, на чем основано устройство различных
термометров.
Для установления того, какая температура больше, а какая —
меньше, вводится дополнительное условие: считается, что при со-
сообщении телу энергии при постоянных внешних параметрах его
температура повышается. Такое дополнительное условие для
уточнения понятия температуры означает, что для внутренней
энергии системы можно выбрать монотонно возрастающую функ-
функцию температуры; это действительно возможно вследствие выте-
вытекающей из опыта единственности распределения энергии по час-
частям системы и одновременного роста энергии частей при увели-
увеличении общей энергии системы (*).
При практическом определении температуры приходится поль-
пользоваться какой-либо определенной шкалой, связанной с тем или
* Равновесные системы, у которых внутренние параметры являются функ-
функциями внешних параметров и энергии, называются эргодическими. Термодина-
Термодинамика, следовательно, рассматривает эргодические системы.
IS
иным веществом. В качестве термометрического параметра обычно
используется объем этого вещества, а шкалу выбирают по Цель-
Цельсию: разность объемов тела при тепловом равновесии его с кипя-
кипящей водой при нормальном атмосферном давлении и тающим
льдом при том же давлении делят на 100; каждое деление соответ-
соответствует одному градусу, температура тающего льда принимается
за 0°С*.
Эмпирической температурой тела называют установленную*
опытным путем меру отклонения термодинамического состояния
тела от состояния теплового равновесия с тающим льдом, находя-
находящимся под нормальным атмосферным давлением.
Показания двух термометров с различными термометрически-
термометрическими веществами, вообще говоря, никогда не совпадают, кроме как
при 0°С и 100° С, поэтому такое определение температуры как,
объективной меры интенсивности теплового движения является
произвольным.
Эта произвольность отчасти устраняется, если в качестве тер-
термодинамического вещества использовать достаточно разреженные
(идеальные) газы. Их коэффициент теплового расширения а не
зависит ни от температуры, ни от природы газа. Шкала газовога
термометра градуируется так же, как и шкала Цельсия, но за
нуль температуры принимается —1/а градусов Цельсия (шкала
Кельвина).
Обозначим температуру, измеренную с помощью идеального
газа по шкале Кельвина, буквой Т: очевидно, T=l/a + ty где t —
температура по шкале Цельсия (см. § 14). Показания всех других
термометров приводятся к газовому термометру**.
Как будет впоследствии показано, второе начало термодина-
термодинамики полностью устраняет произвольность в определении темпе-
температуры, позволяя строго установить абсолютную шкалу темпера-
температуры (шкалу Кельвина), не зависящую ни от выбранного веще-
вещества, ни от того или иного термометрического параметра.
§ 3. Гомогенные и гетерогенные системы.
Фазы и компоненты
Все множество термодинамических систем разделяют на дваз
класса — гомогенные и гетерогенные.
Гомогенные — это такие системы, внутри которых свойства из-
изменяются непрерывно при переходе от одного места к другому.
Частным случаем гомогенных систем являются физически одно-
однородные системы, имеющие одинаковые физические свойства в лю-
* С 1954 г. термодинамическая температурная шкала (шкала Кельвина) оп-
определяется одной реперной точкой — тройной точкой воды (она воспроизводит-
воспроизводится с большей точностью, чем точка таяния льда), которой приписывается темпе-
температура 273,16 К. Температура плавления льда при нормальном атмосферном дав-
давлении по этой шкале равна 273,15 К.
** Газовый термометр вследствие относительной сложности устройства ис-
используется лишь в качестве эталона.
19»
бых, произвольно выбранных частях, равных по объему. Примера-
Примерами таких систем являются смеси различных газов и растворы,
как жидкие, так и твердые. В этих системах могут происходить ре-
реакции между составными частями смеси, диссоциация газа или
растворенного вещества, полимеризация (образование из простых
молекул более сложных, например из трех молекул С2Н4О одной
молекулы (С2Н4ОK или из двух молекул воды Н2О одной более
сложной молекулы воды (Н2ОJ) и т. д., и сольватация (ориента-
(ориентация молекул растворителя вокруг иона или другой частицы рас-
растворенного вещества). При равновесии в таких системах реакции
макроскопически прекращаются. Закономерности при равновесии
устанавливаются с помощью законов термодинамики.
Гетерогенными называются системы, которые состоят из не-
нескольких физически однородных, или гомогенных, тел, так что
внутри систем имеются разрывы непрерывности в изменении их
свойств. Эти системы представляют собой совокупности или раз-
различных агрегатных состояний одного и того же вещества (лед —
вода, вода — пар и т. д.), или различных кристаллических моди-
модификаций (серое и белое олово и др.), или различных продуктов
взаимного растворения (водный раствор соли — твердая соль —
пар), или продуктов химического взаимодействия различных ве-
веществ (жидкий сплав и твердое химическое соединение двух ме-
металлов).
Гомогенная часть гетерогенной системы, отделенная от других
частей поверхностью раздела, на которой скачком изменяются
какие-либо свойства (и соответствующие им параметры), назы-
называется фазой. Если система состоит из жидкости и пара, то жид-
жидкость представляет собой одну фазу, пар — другую. Нельзя пу-
путать и отождествлять агрегатные состояния с фазами. В то вре-
время как агрегатных состояний всего четыре — твердое, жидкое,
газообразное и плазменное, фаз — неограниченное число; даже
у одного и того же химически чистого вещества в твердом агре-
агрегатном состоянии может быть несколько фаз (ромбическая и мо-
моноклинная сера, серое и белое олово и др.). При небольших дав-
давлениях, когда газы мало отличаются от идеальных, в газообраз-
газообразном состоянии может быть только одна фаза, так как при таких
условиях все газы обладают способностью смешиваться друг с
другом в любых пропорциях, образуя однородную систему*.
В жидком состоянии в равновесии может находиться несколько
фаз, например вода и масло, керосин и вода и др.
Кроме фазы важное значение при исследованиях равновесия
термодинамических систем (как гетерогенных, так и гомогенных)
имеет понятие компонент. Это такая часть системы, содержание
которой не зависит от содержания других частей. Смесь газов
является однофазной, но многокомпонентной системой: компонен-
* При высоком давлении наблюдается ограничение во взаимной растворимо-
растворимости газов.
20
тов в смеси химически не реагирующих газов столько, сколько в
ней различных газов. Вода, лед также являются однофазными
системами, но однокомпонентными, так как водород и кислород
в них входят в определенном отношении: количество одного зави-
зависит от количества другого. И вообще, если в фазе имеется N
различных зеществ (химических элементов), между которыми су-
существует п химических реакций, то число компонентов (незави-
(независимых веществ) в такой фазе N—п.
Система с двумя компонентами называется бинарной или
двойной (смесь двух газов, жидкостей или твердых тел и др.)? с
тремя компонентами — тернарной или тройной и т. д.
§ 4. Равновесные и неравновесные процессы
До сих пор мы рассматривали свойства систем в термодина-
термодинамически равновесном состоянии, когда ни один параметр системы
со временем не изменяется и внутри системы нет никаких макро-
макроскопических движений.
Если некоторые параметры системы изменяются со временем,
то мы говорим, что в такой системе происходит процесс. Напри-
Например, при изменении объема происходит процесс расширения си-
системы; при изменении характеристик внешнего поля — процесс
намагничивания или поляризации системы и т. д. Если система
выведена из состояния равновесия и предоставлена самой себе,
то, согласно первому исходному положению термодинамики, через
некоторое время она снова придет в равновесное состояние. Этот
лроцесс перехода системы из неравновесного состояния в равно-
равновесное называется релаксацией, а промежуток времени, в тече-
течение которого система возвращается в состояние равновесия, на-
зывается временем релаксации *.
Процесс называется равновесным или квазистатическим, если
все параметры системы изменяются физически бесконечно мед-
медленно, так что система все время находится в равновесных со-
состояниях.
Физически бесконечно медленным или равновесным изменени-
изменением какого-либо параметра а называют такое его изменение со
временем, когда скорость da/dt значительно меньше средней ско-
скорости изменения этого параметра при релаксации; так, если при
релаксации параметр а изменился на Да, а время релаксации
равно т, то при равновесных процессах
da /y Да
dt х
* Для разных процессов время релаксации различно: от 10~16 с для уста-
установления равновесного давления в газе до нескольких лет при выравнивании
концентрации в твердых сплавах. В термодинамике берется наибольшее вре-
время релаксации, в течение которого устанавливается равновесие для всех пара-
параметров данной системы.
21
Если изменение какого-либо параметра а происходит^ за время
t, меньшее или равное времени релаксации т (^т), так что
da Да
то такой процесс называется неравновесным или нестатическим.
Сам процесс релаксации является, следовательно, неравновес-
неравновесным процессом.
Представление о равновесном процессе и все рассуждения,
связанные с ним, оказываются возможным лишь на основе обще-
общего начала термодинамики о самоненарушаемости равновесного
состояния. Действительно, направление равновесного процесса
вполне определено характером внешних воздействий только в
том случае, если исключены спонтанные изменения термодинами-
термодинамического состояния системы.
Изучение равновесных процессов важно потому, что, как ока-
оказывается (см. § 17, 18), при этих процессах ряд важных величин
(работа, коэффициент полезного действия машин и др.) имеет
предельные, максимально возможные значения. Поэтому выводы*
получаемые термодинамикой для равновесных процессов, играют
в ней роль своего рода предельных теорем.
§ 5. Внутренняя энергия системы,
работа и теплота
Всякая термодинамическая система состоит из огромного чис-
числа частиц. Энергия этих непрерывно движущихся и взаимодей-
взаимодействующих частиц называется энергией системы.
Полная энергия системы разделяется на внешнюю и веутрек-
нюю. Часть энергии, состоящая из энергии движения системы как
целого и потенциальной энергии системы в поле внешних сил,
называется внешней энергией. Остальная часть энергии системы
называется внутренней энергией.
В термодинамике не рассматриваются движение системы как
целого и изменение ее потенциальной энергии при таком движе-
движении, поэтому энергией системы является ее внутренняя энергия *.
В статистической физике внутренняя энергия системы состоит иа
энергии разных видов движения и взаимодействия входящих в
систему частиц: энергия поступательного и вращательного дви-
движений молекул и колебательного движения атомов, энергия мо-
молекулярного взаимодействия* внутриатомная энергия заполнен-
заполненных электронных уровней, внутриядерная энергия и др.
* Энергия положения системы в поле внешних сил входит в состав ее внеш-
внешней энергии при условии, что термодинамическое состояние системы при пере-
перемещении в поле сил не изменяется. Если же термодинамическое состояние при
ее перемещении в поле сил изменяется, то определенная часть потенциальной
энергии уже будет входить в состав внутренней энергии системы.
22
Внутренняя энергия Е является внутренним параметром и,
следовательно, при равновесии зависит от внешних параметров
а-ь и температуры Т: Е = Е (аи ..., ап\ Т).
Зависимость внутренней энергии от температуры почти у всех
встречающихся в окружающей нас природе систем такова, что с
неограниченным ростом температуры внутренняя энергия также
неограниченно растет. Это происходит потому, что каждая моле-
молекула или какой-либо другой элемент «обычной» термодинамиче-
термодинамической системы может иметь любое сколь угодно большое значение
энергии.
Несколько лет назад экспериментально было установлено су-
существование и таких систем, у которых внутренняя энергия с рос-
ростом температуры асимптотически приближается к конечному
граничному значению, так как каждый элемент системы лимити-
лимитирован в своей максимально возможной энергии. Такими «необыч-
«необычными» системами являются совокупности ядерных спинов неко-
некоторых кристаллов, т. е. совокупности закрепленных в узлах ре-
решетки и взаимодействующих друг с другом ядерных магнитных
моментов, когда их энергия взаимодействия с решеткой чрезвы-
чрезвычайно мала по сравнению с энергией спин-спиновых взаимодей-
взаимодействий.
При взаимодействии термодинамической системы с окружаю-»
щей средой происходит обмен энергией. При этом возможны два
различных способа передачи энергии от системы к внешним те-
телам: с изменением внешних параметров системы и без изменения
этих параметров.
Первый способ передачи энергии, связанный с изменением
внешних параметров, называется работой, второй способ — без
изменения внешних параметров, но с изменением нового термоди-
термодинамического параметра (энтропии) — теплотой, а сам процесс пе-
передачи энергии — теплообменом.
Энергия, переданная системой с изменением ее внешних пара-
параметров, также .называется работой W (а не количеством работы),
а энергия, переданная системе без изменения ее внешних пара-
параметров, — количеством теплоты Q. Как видно из определения
теплоты и работы, эти два рассматриваемых в термодинамике
различных способа передачи энергии не являются равноценными.
Действительно, в то время как затрачиваемая работа W может
непосредственно пойти на увеличение любого вида энергии (элек-
(электрической, магнитной, упругой, потенциальной энергии системы в
лоле и т. д.), количество теплоты Q непосредственно, т. е. без
лредварительного преобразования в работу, может пойти только
на увеличение внутренней энергии системы. Это приводит к тому,
что при преобразовании работы в теплоту можно ограничиться
только двумя телами, из которых одно тело (при изменении его
внешних параметров) передает при тепловом контакте энергию
другому (без изменения его внешних параметров); при превраще-
превращении же теплоты в работу необходимо иметь по меньшей мере три
тела: первое отдает энергию в форме теплоты (теплоисточник),
'23
второе получает энергию в форме теплоты и отдает энергию в
форме работы (рабочее тело), и третье получает энергию в форме
работы от рабочего тела.
Если система не обменивается с окружающими телами ни
энергией, ни веществом, то она, как уже было сказано, называет-
называется изолированной или замкнутой; если же система имеет такой
обмен, то она называется открытой. Система, не обменивающая-
обменивающаяся с другими телами веществом, но обменивающаяся энергией,
называется закрытой, а не обменивающаяся энергией только в
форме теплоты — адиабатно изолированной, или адиабатной, си-
системой.
Работа W и количество теплоты Q имеют размерность энергии,
а работа и теплота не являются видами энергии: они представля-
представляют собой два различных способа передачи энергии, рассматрива-
рассматриваемые в термодинамике, и, следовательно, характеризуют процесс
энергообмена между системами. Работа W и количество теплоты
Q характеризуют не только процесс, в котором участвует систе-
система; состоянию же системы не соответствует какое-либо значение
W или Q, и поэтому бессмысленно говорить о запасе теплоты или
работы в теле.
Принято считать работу W положительной, если она соверша-
совершается системой над внешними телами, а количество теплоты Q счи-
считается положительным, если энергия передается системе без из^
менения ее внешних параметров *.
При бесконечно малом равновесном изменении параметра а
работа, совершаемая системой, равна
где А — обобщенная сила, сопряженная внешнему параметру
а и являющаяся при равновесии функцией внешних параметров
at и температуры Т.
При неравновесном бесконечно малом изменении параметра а
работа 6№Нр, совершаемая системой, также равна
но в этом случае обобщенная сила Анр является функцией внеш-
внешних параметров аи внутренних параметров bi и их производных
по времени.
При изменении п внешних параметров работа системы
idai. A.1)
Как следует из определения работы и как видно из A.1), в.
выражение элементарной работы не входит дифференциал темпе-
* Входящие в уравнения термодинамики Q и W означают, как следует из;
предыдущего, не способ передачи, а энергию, полученную системой соответст-
соответствующим способом; часто их, однако, называют просто теплотой и работой и го-
говорят о превращении теплоты в работу и наоборот.
24
ратуры (т. е. коэффициент при dT равен нулю). Это приводит к
тому, что дифференциальное выражение A.1) не является полным
дифференциалом какой-либо функции параметров состояния си-
системы (*). По этой причине элементарную работу обозначают
6W9 а не dW.
Приведем примеры выражений для элементарной работы, со-
совершаемой системой в некоторых случаях.
При квазистатическом расширении системы, подверженной
действию всестороннего равномерного давления, элементарная
работа
где Р — давление газа или жидкости, dV — увеличение объема
системы; работа газа при расширении его в пустоту равна нулю,
так как при этом газ не преодолевает никакого сопротивления.
Работа сил поверхностного натяжения при изменении площа-
площади поверхности на <i2 равна
где a — поверхностное натяжение.
Поляризация диэлектрика в электрическом поле связана с оп-
определенной работой. В зависимости от характера задачи (что оп-
определяет выбор различных независимых переменных, характери-
характеризующих состояние диэлектрика в электрическом поле) для вычис-
вычисления этой работы приходится пользоваться различными выра-
выражениями (см. § 42).
Элементарная работа, совершаемая единицей объема диэлект-
диэлектрика, при изменении в нем напряженности & электрического по-
поля вследствие движения создающих его зарядов равна
6W ±-1<№ = 1- (gxd®x + $j&> + izd3)z)
4я 4я » у
(независимой переменной является в данной задаче индукция 2D),
так что ах=д)х, п2 = 2>У9 az=-?Dz, Ai = —<§У4я, A2 = —SI Л
— <Г*/4я.
—> —>¦
Для изотропного диэлектрика, когда ЭЬ\\8 эта работа
6Ц7 = -gd® (a=Z, A = Lg\
= -gd® (a=Z, A
4л \ 4л
\ /
Собственная работа поляризации (или работа поляризации в
собственном смысле) 6№с есть работа 8W без работы — й[*?2/8я]
возбуждения поля в вакууме:
Элементарная работа при изменении напряженности Ж в маг-
магнетике с индукцией $ равна
25
Для изотропного магнетика эта работа равна
Собетвенная работа намагничивания
где a=f — намагниченность, А = —Ж.
Элементарная работа однородной деформации единицы объ-
объема твердого тела равна
где oij — нормальные и сдвиговые компоненты напряжения, гц —
компоненты деформации (растяжения и сдвиги).
Работа, совершаемая системой при неравновесном переходе
системы из состояния 1 в 2, всегда меньше работы, производимой
ею при переходе из состояния 1 в 2 равновесным путем:
Это особенно хорошо видно на примере расширения или сжа-
сжатия газа. При неравновесном расширении газа внешнее давление.
Р' меньше исходного равновесного давления Р газа, поэтому
P'dV<PdV. При неравновесном сжатии, наоборот, внешнее дав-
давление Р" больше равновесного давления, и так как работа в этом
случае отрицательна, то и здесь P"dV<PdV.
В общем случае для любого неравновесного процесса эту тео-
теорему о максимальной работе при равновесных процессах можно
доказать лишь на основании второго начала термодинамики.
Несмотря на то, что между понятиями работы и .количества
теплоты существует глубокое качественное различие, они явля-
являются родственными: и то и другое выражают энергию, передан-
переданную системе или с изменением, или без изменения внешних пара-
параметров. Благодаря этому родству теплоту часто называют терми-
термической работой. Элементарное количество теплоты 6Q, получае-
получаемое системой при равновесных процессах, может быть записано,
подобно элементарной работе, в виде произведения обобщенной
силы Т (температуры) на изменение обобщенной координаты S
(энтропии):
26
Однако строгое обоснование этого выражения с доказатель-
доказательством однозначности энтропии может быть дано лишь вторым на-
началом термодинамики.
§ 6. Термические и калорическое
уравнения состояния
Второе исходное положение термодинамики о том, что равно-
равновесные внутренние параметры являются функциями внешних па-
параметров и температуры, привадит к существованию термических
и калорического уравнений состояния системы, т. е. уравнений,
связывающих температуру Т, внешние параметры щ и какой-либо
равновесный внутренний параметр Ьи\
bk=f(au ..., ап\ Т).
Если внутренним параметром Ьи является внутренняя энергия
Е (bk = E)t то уравнение
Е = Е(аи ..., an; T)
называется уравнением энергии или калорическим уравнением со-
состояния. Оно так называется потому, что с его помощью, как мы
увидим, можно находить теплоемкости и другие подобные вели-
величины, ранее обычно выражавшиеся в калориях.
Если внутренним параметром bk является сопряженная внеш-
внешнему параметру а,- обобщенная сила Л* {bk = Ai), то уравнения
Ai = Ai(au .... ап; Т) (i=l,2, ..., и)
называются термическими уравнениями состояния. Это название
обусловлено тем, что с помощью этих уравнений вычисляется тем-
температура.
Общее число термических и калорического уравнений состоя-
состояния системы равно числу ее степеней свободы, т. е. числу незави-
независимых параметров, характеризующих состояние системы.
Если калорическое и термические уравнения состояния извест-
известны, то с помощью начал термодинамики можно определить все
термодинамические свойства системы. Вывести сами уравнения
состояния на основе начал термодинамики нельзя; они или уста-
устанавливаются из опыта, или находятся методами статистической
физики. Это еще раз указывает, что термодинамика и статистиче-
статистическая физика дополняют друг друга и полностью отделить их не-
невозможно.
При изучении свойств равновесных систем термодинамика
прежде всего рассматривает свойства простых систем. Простой
называется система с постоянным числом частиц, состояние ко-
которой определяется только одним внешним параметром а и темпе-
температурой Т. Иначе говоря, простая система — это однофазная си-
система, определяемая двумя параметрами.
27
Термическое и калорическое уравнения состояния простой си-
системы имеют соответственно вид
А=А(а, Г), Е = Е(а, Т).
Если А = Р — давление и, следовательно, a=V — объем си-
системы, то уравнения состояния системы
P = P(V% Г), E=E(V, T). A.2)
Для такой простой системы, как идеальный газ, термическим
уравнением состояния является уравнение Клапейрона — Менде-
Менделеева *
PV=vRT, A.3)
где v = m/M — число молей газа массой m, M — молярная масса,
# = 8,314 Дж/К-моль.
Используя закон Джоуля о независимости внутренней энергии
газа от его объема при постоянной температуре
^-) =0, A.4)
получаем калорическое уравнение состояния идеального газа
где Cv — теплоемкость газа при постоянном объеме.
Для одноатомного идеального газа, как показывает опыт, теп-
теплоемкость Cv не зависит от температуры, поэтому
Е=СуТ+Е0.
Для реальных газов эмпирически установлено более 150 тер-
термических уравнений состояния. Наиболее простым из них и ка-
качественно правильно передающим поведение реальных газов да-
даже при переходе их в жидкость является уравнение Ван-дер-
Ваальса
(P + a/V2)(V—b)=RT.
Это уравнение отличается от уравнения Клапейрона — Менде-
Менделеева двумя поправками: на объем Ь самих молекул и на внут-
внутреннее давление а/ V2, определяемое взаимным притяжением мо-
молекул газа (а и Ь — константы, не зависящие от Т и Р, ,но разные
для разных газов; в газах с большим а при постоянных Т и V
давление меньше, а с большим Ь — больше).
Необходимость введения поправок на объем в уравнение A.3)
при применении его к реальному газу впервые обосновывал еще
* Объединяя законы Бойля—Мариотта и Гей-Люссака, Клапейрон в 1834 г.
получил уравнение состояния идеального газа PV=cTt где постоянная с для
данной массы газа зависит от его природы. На основе тех же законов и за-
закона Авогадро Д. И. Менделеев в 1874 г. установил уравнение состояния PV=
= (mlM)RT> где постоянная R одна и та же для всех газов.
28
М. В. Ломоносов, исходя из молекулярно-кинетических представ-
представлений о природе теплоты (теплового движения).
Более точными термическими уравнениями состояния реально-
реального газа являются (*) первое и второе уравнения Дитеречи
р (V—b) =RT exp[—a/RTVl
A.5).
{P + alV^){V— b)=RT\
уравнение Бертло
(P + a/V2T)(V—b)=RT
и др.
Как калорическое, так и термические уравнения состояния
для реальных газов могут быть теоретически выведены методами
статистической физики.
Термическое уравнение состояния для реальных газов может
быть записано в виде ряда со степеням плотности N/V для про-
произведения PV (вириальная форма уравнения состояния):
где В, С, D, ... являются функциями температуры и называются
вириалъными коэффициентами (соответственно вторым, третьим
и т. д.). Первый член вириального ряда соответствует идеально-
идеальному газу, в котором отсутствует взаимодействие между молекула-
молекулами, второй учитывает парное взаимодействие между молекула-
молекулами, третий — тройное взаимодействие молекул и т. д.
Уже из самого существования термического уравнения состоя-
состояния можно вывести важные следствия. Действительно, рассмат-
рассматривая такие изменения состояния простой системы, при которых
фиксирована одна из переменных, мы получаем три термических
коэффициента (расширения, сжатия, давления (упругости)):
a" i/0 Urjp'P- v0 (др)ту~ Ро [дт
где Vo и Ро — объем и давление системы при 0° С.
Существование уравнения состояния системы приводит к то-
тому, что эти коэффициенты не независимы друг от друга, а связа-
связаны между собой соотношением (*)
важным при определении у у твердых и жидких тел, так как этк
тела практически невозможно нагреть без изменения их объема.
Подобно трем термическим коэффициентам, употребляются
также три термодинамических коэффициента (расширения, сжа-
сжатия и давления):
а L(JL\ — 1 ( дР \
Vt— V \ дР )т Р \ дТ )v'
29
Глава 2
ОСНОВНЫЕ ЗАКОНЫ
И УРАВНЕНИЯ ТЕРМОДИНАМИКИ.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Термодинамика — дедуктивная наука. Ее основные успехи мо-
тут быть охарактеризованы тем, что она позволяет получить мно-
множество различных соотношений между величинами, определяющи-
определяющими состояние тел, опираясь на весьма общие эмпирические зако-
законы — начала термодинамики.
Обсудим содержание этих основных законов и соответствую-
соответствующих им основных уравнений термодинамики.
§ 7. Уравнение первого начала термодинамики
Первое начало термодинамики является математическим вы-
выражением количественной стороны закона сохранения и превра-
превращения энергии в применении к термодинамическим системам. Оно
было установлено в результате экспериментальных и теоретиче-
теоретических исследований в области физики и химии, завершающим эта-
лом которых явилось открытие эквивалентности теплоты и рабо-
работы, т. е. обнаружение того, что превращение теплоты в работу и
работы в теплоту осуществляется всегда в одном и том же строго
постоянном количественном соотношении.
Уже в XVIII в. была обнаружена невозможность механического вечного
двигателя (устройства, с помощью которого можно было бы периодически про-
производить механическую работу без внешнего воздействия на него).
В 1748 г. М. В. Ломоносов в письме к Эйлеру, высказывая мысль о зако-
законе сохранения вещества и распространения его на движение материи, писал;
«Тело, которое своим толчком возбуждает другое тело к движению, столько же
теряет от своего движения, сколько сообщает другому». В 1755 г. Француз-
Французская Академия наук «раз и навсегда» объявила, что не будет больше прини-
принимать каких-либо проектов вечного двигателя. В 1840 г. Г. Г. Гесс сформулиро-
сформулировал закон о независимости теплового эффекта химических реакций от промежу-
промежуточных реакций. В 1842—1850 гг. многие исследователи (Майер, Джоуль и др.)
пришли к открытию принципа эквивалентности теплоты и работы.
Установление принципа эквивалентности было последним этапом в форми-
формировании количественной стороны закона сохранения и превращения энергии,
вследствие чего дата установления этого принципа обычно отождествляется с
датой открытия первого начала термодинамики.
Из приведенной исторической справки видно, что потребовался ряд деся-
десятилетий, чтобы наука могла найти путь от простого убеждения о невозможности
-вечного двигателя до современной формы закона сохранения и превращения
энергии.
Первое начало термодинамики устанавливает: внутренняя
энергия системы является однозначной функцией ее состояния и
изменяется только под влиянием внешних воздействий.
В термодинамике рассматриваются два типа внешних воз-
воздействий: воздействия, связанные с изменением внешних парамет-
параметров системы (система совершает работу W), и воздействия, не
.30
связанные с изменением внешних параметров и обусловленные
изменением внутренних параметров или температуры (системе
сообщается некоторое количество теплоты Q).
Поэтому, согласно первому началу, изменение внутренней
энергии Е2—Е\ системы при ее переходе под влиянием этих воз-
воздействий из первого состояния во второе равно алгебраической
сумме Q и W, что для конечного процесса запишется в виде урав-
уравнения Е2—EX = Q—W, или
Q = E2-EX + W. B.1)
Для элементарного процесса уравнение первого^начала таково:
6Q = dE + 6W. B.2)
По первому началу изменение внутренней энергии dE при эле-
элементарном процессе перехода системы из одного состояния в бес-
бесконечно близкое есть полный дифференциал и, следовательно^
В
Рис. 2
Рис. 3
конечное ее изменение Е2—Е\ будет одним и тем же независима
от пути перехода системы из состояния 1 в 2 (на рис. 2 пути ус-
условно обозначены буквами а и ft), но Q и W могут быть при?
этом разными. Это означает, что W и Q в отличие от Е не явля-
являются функциями состояния системы, а характеризуют процесс,
испытываемый системой, т. е. являются функциями от линии, или
функционалами.. То, что выражение для элементарной работы 8W
не является полным дифференциалом, устанавливается в общем?
случае на основе второго исходного положения термодинамики
(*), а то, что дифференциальное выражение для 8Q не есть пол-
полный дифференциал, непосредственно следует из уравнения перво-
первого начала B.2).
Зависимость Q и W от пути видна на простейшем примере
расширения газа. Работа, совершенная системой при переходе ее
из состояния 1 в 2 (рис. 3) по пути а, изображается площадью,,
ограниченной контуром А1а2ВА:
T)dV,
31
а работа при переходе по пути Ъ — площадью, ограниченной кон-
контуром А1Ь2ВА:
2
Wb= JPA/, T)dV.
Kb)
Поскольку давление зависит не только от объема, но и от
температуры, то при различных изменениях температуры на пути
и или Ь при переходе из одного и того же начального состояния
(Ри V\) в одно и то же конечное (Р2, V2) работа получается раз-
разной. Отсюда видно, что при замкнутом процессе (цикле) 1а2Ы
система совершает работу, не равную нулю. На этом основана
работа всех тепловых двигателей.
Из первого начала термодинамики следует, что работа может
совершаться или за счет изменения внутренней энергии, или за
счет сообщения системе количества теплоты. В случае если про-
процесс круговой, начальное и конечное состояния совпадают,
Е2—?1 = 0 и W=Q, т. е. работа при круговом процессе может со-
совершаться только за счет получения системой теплоты от внеш-
внешних тел.
По этой причине первое начало часто формулируют в виде по-
положения о невозможности вечного двигателя первого рода, т. е.
такого периодически действующего устройства, которое бы совер-
совершало работу, не заимствуя энергии извне.
Положение о вечном двигателе первого рода допускает обра-
обращение: работу нельзя ни создать из ничего (без затраты энер-
энергии), ни превратить в ничто (без выделения энергии).
Уравнение первого начала в виде B.1) или B.2) справедливо
как для равновесных, так и для неравновесных процессов.
Учитывая выражение A.1) для 8W при равновесных процес-
процессах, уравнение B.2) первого начала для элементарного процесса
лринимает вид
или, поскольку состояние системы определяется внешними пара-
параметрами аь и температурой Г,
f) К B.4)
аи ... ,ап ^L\ да? Jak,T J
Из уравнения B.4) видно, что дифференциальное выражение
для 6Q представляет собой линейную форму в полных дифферен-
дифференциалах независимых переменных Г, аь ..., ап, т. е. форму Пфаф-
Пфаффа. Согласно первому началу B.2) — B.3) 8Q равно сумме полно-
полного дифференциала dE и неполного дифференциала 8W, и, следо-
следовательно, форма Пфаффа для 8Q не является полным дифферен-
дифференциалом какой-либо функции параметров состояния системы. Как
следует из B.1) — B.3), уравнение первого начала позволяет оп-
32
ределить внутреннюю энергию E(a\t ..., ап\ Т) в состоянии
(аи ..., ап; Т) только с точностью до аддитивной постоянной
Е(а\°, ..., ап°\ Т°), зависящей от выбора начального состояния
(п\0, ..., ап°\ Т°). Для термодинамики этого вполне достаточно,
так как в устанавливаемые ею соотношения входят лишь измене-
изменения энергии.
Рассмотрим теперь некоторые следствия и приложения перво-
первого начала.
§ 8. Теплоемкости и теплоты изотермического
изменения внешних параметров
Изучаемые в термодинамике свойства систем (и соответствен-
соответственно величины, характеризующие эти свойства) могут быть разде-
разделены на два класса — термические и калорические. Те свойства,
которые определяются только термическим уравнением состояния
системы, называются ее термическими свойствами, те же свойст-
свойства, которые определяются или только калорическим уравнением
состояния, или совместно калорическим и термическим уравне-
уравнениями состояния, называются калорическими свойствами. К кало-
калорическим свойствам (величинам) относятся прежде всего тепло-
теплоемкости и теплоты изотермического изменения внешних пара-
параметров.
Теплоемкость определяет количество теплоты, необходимое
для изменения температуры системы на 1 К, т. е.
Поскольку количество теплоты 6Q, необходимое для измене-
изменения температуры системы на dT, зависит от характера происходя-
происходящего при этом процесса, то и теплоемкость С системы также за-
зависит от условий, при которых определяется 8Q/dT. Это означает,
что теплоемкость является не функцией состояния системы, а
функцией процесса: одна и та же система в зависимости от про-
происходящего в ней при нагревании процесса обладает различны-
различными теплоемкостями. Численно величина С изменяется в пределах
от —оо до +оо. Наибольшее практическое значение имеют теп-
теплоемкости СР и Cv.
С определением теплоемкости тесно связано понятие о термо-
термостате, которое широко используется в термодинамике. Термо-
Термостат — тело с настолько большой теплоемкостью (С->оо), что
его температура при теплообмене с какой-либо системой не изме-
изменяется.
Когда говорят о системе, помещенной в термостат, то имеют
в виду систему, в которой при всех происходящих в ней процессах
{расширение, намагничивание и т. д.) температура поддержива-
поддерживается постоянной.
Первое начало термодинамики позволяет найти значения раз-
различных теплоемкостей и установить связь между ними, если из-
2 Зак. 245 33
вестны термическое и калорическое уравнения состояния систе-
системы. Действительно, пусть для простой системы, состояние кото-
которой определяется внешним параметром а и температурой Т, даны
уравнения состояния А=А(а, Т), Е=Е(а, Т). Тогда из уравнения
первого начала
или
получаем
dT \дТ )а [\ да )т J дТ'
откуда
(?) B-5>
B.6)
Если А=Р и a = V, то
Из этих выражений для теплоемкостей и их разности видно,
что для определения Су надо знать, лишь одно калорическое урав-
уравнение, для определения же Ср и СР—Cv надо знать и термические
и калорическое уравнения состояния вещества. Согласно опреде-
определению понятия «более высокая температура» в термодинамике
принимается Cv= (dE/dT)v>0 (и вообще Са= (дЕ/дТ)а>0).
Для идеального газа термическим уравнением состояния явля-
является уравнение Клапейрона — Менделеева A.3).
Калорическое уравнение состояния идеального газа можно
установить исходя из опытов Гей-Люссака и Джоуля — Томсона.
Согласно этим опытам при расширении- разреженного газа в пус-
пустоту без притока теплоты FQ = 0) его температура не изменяется.
Отсюда следует закон Джоуля: энергия идеального газа, находя-
находящегося при постоянной температуре, не зависит от занимаемого
им объема. Действительно, поскольку при таком расширении
6Q = 0, 8W = 0 и, следовательно, по первому началу, d? = 0, то при
dT = 0 (согласно опытам Гей-Люссака) из уравнения dE =
= (dE/dT)vdT+ (dEldV)TdV=0 получаем {dE/dV)T = 0. Поэтому
для идеального газа
dE= (dE/dT)vdT=CvdT, E = \CvdT.
Результаты опыта показывают, что у одноатомных газов теп-
теплоемкость Су не зависит от температуры, для других же идеаль-
34
ных газов существует слабая зависимость теплоемкости Су от
температуры, что нетрудно понять исходя из молекулярных пред-
представлений о многоатомных идеальных газах.
Считая Су для идеальных (одноатомных) газов постоянной,
получаем калорическое уравнение состояния
E = CVT+Eo. B.8)
На основании уравнения Клапейрона — Менделеева и закона
Джоуля для идеального газа находим
СР—Cv = vR,
откуда для молярных теплоемкостей (v=l)
для удельных теплоемкостей
Cp—Cv
для разности теплоемкостей на одну молекулу газа
здесь /? = 8,314 Дж/К-моль — молярная газовая постоянная; М —
молярная масса газа; Na — постоянная Авогадро; k —
= 1,38-10-23 Дж/К — постоянная Бюльцмана.
Помимо теплоемкостей другой важной калорической величи-
величиной является теплота изотермического изменения какого-либо
внешнего параметра системы — количество теплоты, необходимое
для увеличения этого параметра на единицу при постоянной тем-
температуре и других внешних параметрах:
1 ап;Т.
Например, при расширении она равна
lv= FQ/dV)ai а„;Г.
Из уравнения первого начала термодинамики
следует, что теплота «изменения внешнего параметра ((при 7=
= const)
) t (*=lf 2 n)f B.9)
а теплота изотермического расширения
~dVJat ап;г'
35
Очевидно, что для идеального газа теплота расширения чис-
численно равна давлению:
lv = P.
Используя полученные выражения для теплоемкости B.5) и
теплоты изменения внешнего параметра B.9), запишем диффе-
дифференциальное уравнение первого начала B.4) в виде
§ 9. Основные термодинамические процессы
и их уравнения
Во всякой термодинамической системе (простой или сложной)
возможны три процесса: изотермический (Т—const), адиабатный.
FQ = 0) и политропный (С = const). Число и характер других про-
процессов зависят от природы систем.
В простой системе с внешним параметром а и сопряженным
ему силовым параметром А кроме названных трех процессов мож-
можно наблюдать также процесс при а = const и процесс при А —
= const. В сложных системах возможно большее число различных
процессов. Если внешним параметром является объем -системы
(a=V и, следовательно, А = Р), то процесс при У=const называ-
называется изохорным, а при Р — const — изобарным. Эти пять процес-
процессов (изотермический, адиабатный, политропный, изохорный и
изобарный) считаются основными в термодинамике, причем адиа-
адиабатный процесс является, очевидно, частным случаем политроп-
ного.
Функциональная связь, возникающая в случае простой систе-
системы между двумя из величин Т, V, Р (т. е. между Т и 1/, Т и Р
Р и V) при том или ином процессе, называется уравнением этого
процесса. Уравнения изотермического, изохорного и изобарного
процессов непосредственно получаются (без использования перво-
первого начала) из уравнения состояния любой простой системы соот-
соответственно при T^const, l/=const и P = const.
Что касается уравнений адиабатного и политропного процессов,,
то их нельзя <найти, пользуясь лишь термическим уравнением со-
состояния. Уравнения этих процессов можно получить с помощью
первого начала термодинамики, используя также и калорическое
уравнение состояния (поскольку ни элемент количества теплоты
6Q, ни теплоемкость С, определяющие соответственно эти про-
процессы, не входят в термическое уравнение состояния).
Найдем уравнение политропы и его частный случай — уравне-
уравнение адиабаты для любой простой системы и для идеалыного газа.
При политропном процессе C = 8Q/dT = consi и 8Q = CdT (для
адиабатного процесса С = 0). По первому началу термодинамики,
для простой системы 8Q = dE+Ada, поэтому для политропы
36
Используя B.6), получаем
Если СфСа> то
Это дифференциальное уравнение политропы в переменных Т
и а. В переменных А и а дифференциальное уравнение политро-
политропы можно получить, если из уравнения состояния Т = Т(АУ а)
I dA + ( 1 da и подставить в формулу
ЗА ) а \ да ] а
B.10). Тогда
JL)da=o.
Са-С \ да )л
Отсюда дифференциальное уравнение адиабаты (С = 0) для
простой системы имеет вид
дЛ la \ да
где у = СА/Са.
Для интегрирования уравнений политропы и адиабаты необ-
необходимо знать как термическое уравнение состояния (при опреде-
определении (дТ/дА)а и ((ЭГ/5а)л), так и калорическое уравнение со-
состояния (при определении СА и Са).
Если система находится под действием силы всестороннего
давления (А = Р и a=V), то уравнениями политропы и адиабаты
соответственно будут
cv-c [ )
JL) dV=0. B.12)
В случае идеального газа СР и Су на основании закона Джоу-
Джоуля зависят только от температуры, причем для одноатомных га-
газов 7 = 5/3 и не зависит от Т, а для двухатомных газов у с увели-
увеличением Т уменьшается и при комнатной температуре равна 1,4.
Для одноатомного идеального газа, подставляя в дифферен-
дифференциальное уравнение политропы производные (дТ/дР)у и (dT/dV)Pt
определяемые из уравнения Клапейрона — Менделеева, после ин-
интегрирования получаем уравнение политропы
Р Vn -const,
где п= (СР—С)/(Cv—С) — показатель политропы.
37
Уравнение адиабаты этого газа
Р1Л = const B.13)
называется уравнением Пуассона. В переменных V и Т уравнение
адиабаты идеального газа имеет вид
Г1Л-1 = const,
а в случае одноатомного идеального газа
Г l/2/з = const.
Поскольку для одноатомного идеального газа теплоемкости Су
и Ср не зависят от температуры и являются постоянными, то для
него (и только для него) изохорный и изобарный процессы явля-
являются политропными.
Уравнения равновесных процессов можно изображать в виде
графиков (диаграмм) на плоскости с соответствующими коорди-
координатными осями. Одними из наибо-
наиболее употребительных в термодина-
мике являются рабочие диаграм-
диаграммы, которые изображаются на пло-
плоскости с координатными осями V
(ось абсцисс) и Р (ось ординат).
Элемент площади на этой плоско-
плоскости изображает рабоху.
Через каждую ючку на плоско-
плоскости V, Р можно провести изотерму
и адиабату. Наклон этих кривых к
оси абсцисс определяется соответ-
соответственно производными (dP/dV)T и
(дР/д!/)ад, которые вычисляются
Рис- 4 из термического уравнения состоя-
состояния и уравнения адиабаты данно-
данного вещества.
Для изотермы идеального газа (dP/dV)r =—P/V9 а для его
адиабаты (dP/dV)aa = —yP/V, поэтому
(dP/dV)n=y(dPfdV)T. B.14)
Поскольку y = CP/Cv>U то на плоскости V, Р адиабата иде-
идеального газа наклонена к оси абсцисс всегда круче изотермы
(рис. 4). В следующем параграфе будет показано, что соотноше-
соотношение B.14) справедливо не только для идеального газа, но и для
любого вещества.
§ 10. Связь модулей упругости
с теплоемкостями
Первое начало термодинамики позволяет установить связь
между модулями упругости и теплоемкостями системы.
38
Модуль упругости системы определяет изменение давления
(упругости), отнесенное к относительному (изменению объема, и
представляет собой величину, обратную коэффициенту сжимае-
сжимаемости:
дР
dV/V
дР
dV
Для того чтобы К было положительным (для устойчивых со-
состояний, как мы увидим, dP и dV имеют разные знаки), постав-
поставлен знак «минус». Модуль упругости определяется значением про-
производной dP/dV, зависящей от условий, при которых происходит
сжатие.
Наиболее употребительными модулями упругости являются
изотермический и адиабатный:
Отношение этих модулей таково:
(dP!dV)s
Из дифференциального уравнения адиабаты B.12) имеем
дР \ (дТ]дУ)Р
WJs~ У(дР/дТ)у'
а из уравнения состояния T=T(V, P)
dV jp \ дР )v
и для изотермического процесса (dT=0) получаем
/ дР\ _ (дТ1дУ)Р
[ dV )т~ (дТ1дР)у'
Поэтому
и, следовательно,
(dPjdV)T
B.15)
т. е. отношение адиабатного и изотермического модулей упругости
любого вещества равно отношению теплоемкостей CP/CV. Так как
Y>1 (см. § 15), то Ks>Kt и (dP/dV)s>-(dPldV)T. Измеряя экс-
экспериментально Ks и Кт можно найти у.
Из соотношения B.15) видно, что оно совпадает с B.14) для
идеального газа, причем на плоскости V, Р изотерма ни для ка-
39
кого вещества не может быть круче адиабаты и, следовательно,
иметь с ней несколько отдельных общих точек. Но она может,
помимо простого пересечения, касаться адиабаты с обязательным
пересечением, а также совпадать с ней на конечном участке.
Глава 3
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Первое начало термодинамики, как мы видели, устанавливает
существование у вся'кой системы однозначной функции состоя-
состояния — «внутренней энергии, которая не изменяется в отсутствие
внешних воздействий при любых процессах .внутри системы.
Второе начало термодинамики устанавливает существование
у всякой равновесной системы другой однозначной функции сос-
состояния — энтропии, которая, однако, в отличие от внутренней
энергии не изменяется у изолированной системы только при рав-
равновесных процессах и всегда возрастает при неравновесных про-
процессах; аналогично ведет себя энтропия и адиабатных систем.
Таким образом, если первое начало есть закон сохранения и
превращения энергии (его количественная сторона) в применении
к термодинамическим системам, то второе начало представляет
собой закон об энтропии.
§11. Общая характеристика и исходная
формулировка второго начала
Открытие второго начала связано с анализом работы тепло-
тепловых машин, чем и определяется его исходная формулировка.
Впервые работа тепловых машин была теоретически рассмотрена
в 1824 г. Сади Карно>, который в своем исследовании «Размыш-
«Размышления о движущей силе огня и о машинах, способных развивать
эти силы», доказал, что КПД тепловых машин, работающих по
предложенному им циклу (циклу Карно), не зависит от природы
вещества, совершающего этот цикл. Позднее Клаузиус и В. Том-
сон, по-новому обосновывая эту теорему Карно, почти одновре-
одновременно положили основание тому, что теперь входит в содержание
второго начала.
Так же, как и первое начало, второе начало термодинамики
является обобщением данных опыта. Многолетняя человеческая
практика привела к установлению определенных закономерно-
закономерностей превращения теплоты в работу и работы в теплоту (как
общих для «обычных» и «необычных» систем (см. § 5), так и
специфических для тех и других). В результате анализа этих
закономерностей и было сформулировано второе начало в виде
закона о существовании энтропии и ее неубывании при любых
процессах в изолированных (или только адиабатически изолиро-
изолированных) системах. Для того чтобы прийти к такому выражению
40
второго начала, примем за исходную такую его формулировку,
которая непосредственно' связана с особенностями превращения
теплоты в работу и работы в теплоту. При этом, вследствие ред-
редкости необычных систем (ими являются пока только лишь систе-
системы ядерных спинов), мы будем исходить из формулировки вто-
второго начала в применении к обычным, наиболее распространен-
распространенным системам *.
Из определения понятий теплоты и работы (см. § 5), следует,
что две рассматриваемые в термодинамике формы передачи энер-
энергии не являются равноценными: в то время как работа W может
непосредственно пойти на увеличение любого вида энергии, теп-
теплота Q непосредственно, без предварительного превращения в
работу, приводит лишь к увеличению внутренней энергии систе-
системы. Эта неравноценность теплоты и работы не имела бы значе-
значения, если бы можно было без каких-либо трудностей превратить
теплоту в работу. Однако, как показывает опыт, в то время как
при превращении работы в теплоту явление может ограничиться
изменением термодинамического состояния одного лишь тепло-
получающего тела (например, при нагревании посредством тре-
трения или при электронагреве), при преобразовании теплоты в ра-
работу наряду с охлаждением теплоотдающего тела происходит
изменение термодинамического состояния других тел, участвую-
участвующих в этом процессе: или рабочего тела при незамкнутом про-
процессе, или других тел в замкнутом круговом процессе, когда
этим телам рабочее тело непременно* отдает часть полученной им
от нагревателя теплоты. В качестве таких «других тел» в тепло-
тепловых машинах обычно служат холодильники.
Изменение состояния рабочего тела (если процесс незамкну-
незамкнутый) или отдача части теплоты рабочим телом другим телам в
изменение термодинамического состояния этих тел при круговом
процессе превращения теплоты в работу называется компенса*
цией. Результаты опытов показывают, что без компенсации ни
один джоуль теплоты в работу превратить нельзя. В то же самое
время работа в теплоту превращается полностью без всякой ком-
компенсации.
Такая неравноправность превращения теплоты в работу по
сравнению с превращением работы »в теплоту приводит к одно-
односторонности естественных процессов: самопроизвольные процессы
в замкнутой системе идут в направлении исчезновения потенци-
потенциально возможной работы. Например, в практике не обнаружено
случаев самопроизвольного перехода теплоты от холодного тела
к горячему. При тепловом (контакте двух тел различной темпе-
температуры теплота переходит от горячего тела к холодному до тех
пор, пока их температуры не станут равными.
* В § 32 будет установлена соответствующая закономерность для спино-
спиновых систем и установлен закон возрастания энтропии. Там же будет" приведена
и общая для обычных и необычных систем исходная формулировка второго
начала.
41
Назовем устройство, которое без компенсации полностью прев-
превращало бы периодически © работу теплоту какого-либо* тела,
вечным двигателем второго рода. Тогда исходная формулировка
второго начала, выражающая закономерности превращения теп-
теплоты в работу (И работы в теплоту (в случае обычных систем),
будет следующей: невозможен вечный двигатель второго^ рода,
причем это утверждение не допускает обращения.
Как известно, предложение о невозможности вечного двигателя первого ро-
рода допускает обращение. Эта особенность предложения о вечном двигателе пер-
первого рода не включается в формулировку первого начала, так как не играет ро-
роли для установления существования внутренней энергии системы как однознач-
однозначной функции ее состояния, что составляет содержание первого начала. Анало-
Аналогично для установления существования энтропии утверждение о невозможности
обращения предложения о вечном двигателе второго рода также не нужно.
Однако при установлении второго положения второго начала (положения о ро-
росте энтропии) приходится пользоваться утверждением о невозможности обра-
обращения предложения о вечном двигателе второго рода. Кроме того, это утверж-
утверждение, как теперь известно, не всегда справедливо. Все это приводит к необхо-
необходимости включения данного утверждения в исходную формулировку второго на-
начала (для обычных систем).
Это положение означает, что, в то время как теплоту нельзя
превратить в работу полностью без компенсации (невозможен
вечный двигатель второго рода), работу в теплоту можно прев-
превратить без всяких компенсаций, ибо не представляет «никаких
затруднений построить машину, вся деятельность которой своди-
сводилась бы к затрате работы и нагреванию резервуара (невозмож-
(невозможность обращения предложения о вечном двигателе второго рода)\
Иначе говоря, если теплота превращается в работу, и за
весь круговой процесс у какого-либо тела или у различных тел
было взято положительное количество теплоты Qi= § 6Q FQ>0),
а совершенная положительная работа равна W, то всегда Qi>W;
если же работа W(W>0) превращается в теплоту Qb то всегда
W = QX*.
Как видно из приведенных формул, второе начало термодина-
термодинамики представляет собой совокупность двух независимых поло-
положений:
Qi> W и W = Q{. . C.1)
Первое положение (Qi> W), как будет показано, (приводит
в случае равновесных систем к установлению существования тер-
термодинамической температуры и новой однозначной функции сос-
состояния — энтропии. Совместно первое и второе положения вто-
второго начала устанавливают односторонний характер изменения
энтропии при естественных процессах в замкнутых системах.
Таким образом (см. § 13, 17), второе начало термодинамики
выражает закон о существовании энтропии у всякой равновесной
* Стрелки указывают направление процесса.
42
системы и неубывании ее при любых процессах в изолированных
и адиабатно изолированных системах.
Первое положение второго начала указывает на (невозмож-
(невозможность с помощью замкнутого кругового процесса превратить теп-
теплоту в работу без компенсации. Понятие компенсации, как видно
из его определения, содержит отдачу части теплоты рабочим те-
телом другим телам и изменение термодинамического состояния
этих других тел при превращении теплоты в работу в замкнутом
круговом процессе. В случае обычных, наиболее распространен-
распространенных систем оба эти элемента компенсации совпадают, так как
отдача части теплоты рабочим телом другим телам при круговом
процессе в этом случае безвозвратна и автоматически влечет
изменение термодинамического состояния этих других тел. В слу-
случае спиновых систем эти элементы компенсации не совпадают,
вследствие чего с помощью спиновых систем теплоту какого-либо
тела можно целиком превратить в работу с помощью кругового
процесса без изменения термодинамического состояния других
тел. Однако такое превращение, как и в случае обычных систем,
обязательно сопровождается отдачей части теплоты рабочим
телом другим телам. Эта общая закономерность (общий элемент
компенсации) превращения теплоты в работу приводит к сущест-
существованию энтропии как у обычных, так и нео^бычных равновесных
систем.
Устройство, в результате действия которого периодически про-
производилась бы положительная работа только за счет охлажде-
охлаждения одного тела, без каких-либо других изменений в телах, назы-
называется вечным двигателем второго рода Томсона—Планка. Поль-
Пользуясь о^бычными системами, невозможно' осуществить вечный дви-
двигатель второго рода Томсона—Планка, но при наличии спиновых
систем такой двигатель вполне возможен. Однако устройство;
которое бы непрерывно превращало в работу теплоту какого-либо
тела без компенсации — вечный двигатель второго' рода, невоз*
можно ни в случае обычных, ни в случае спиновых систем *. При
этом если для обычных систем предложение о> вечном двигателе
второго рода не допускает обращения, то для спиновых систем
такое обращение возможно (см. § 32).
Для получения аналитического выражения второго начала
термодинамики рассмотрим второе начало термодинамики в от-
отдельности для равновесных и неравновесных процессов.
Исходя из второго начала термодинамики, рассмотрим преж-
прежде разделение всех процессов, испытываемых изолированной сис-
системой в целом, на обратимые и необратимые и установим отно-
отношение этих процессов к равновесным и неравновесным.
* Очевидно, что «вечный двигатель второго рода» и «вечный двигатель вто-
второго рода Томсона—Планка» в случае обычных систем совпадают.
43
§ 12. Обратимые и необратимые процессы
По второму (началу термодинамики в природе возможны про-
процессы, в которых превращение теплоты в работу связано с ком-
компенсацией, и невозможны процессы, в которых такое превращение
не сопровождается компенсацией. Это приводит к делению всех
процессов в замкнутой системе на обратимые и необратимые.
Процесс перехода системы из состояния 1 в 2 называется
обратимым, если возвращение этой системы в исходное состояние
из 2 в 1 можно осуществить без каких бы то ни было измене-
изменений в окружающих внешних телах. Процесс же перехода систе-
системы из состояния 1 в 2 называется необратимым, если, обратный
переход системы из 2 в 1 нельзя осуществить без изменений в
окружающих телах. Очевидно, что всякий квазистатический про-
процесс является обратимым. Действительно, при квазистатическом
процессе состояние системы в каждый момент полностью опреде-
определяется внешними параметрами и температурой, поэтому при рав-
равновесных изменениях этих параметров в обратном порядке систе-
система также в обратном порядке пройдет все состояния и придет в
начальное состояние, не вызвав никакого изменения в окружаю-
окружающих телах.
При процессах с трением, как мы отмечали, работа может
быть без компенсации превращена в теплоту; так как обратный
переход системы из конечного состояния в начальное связан с
переходом теплоты в работу, а это невозможно осуществить без
изменения в окружающих телах, то, следовательно, процессы с
трением необратимы. А так как всякий равновесный процесс об-
обратим, то необратимый процесс с трением неравновесен *.
Мерой необратимости процесса в замкнутой системе (см. § 17)
является изменение новой функции состояния — энтропии, суще-
существование которой у равновесной системы устанавливает первое
положение второго начала о невозможности вечного двигателя
второго рода. Однозначность этой функции состояния приводит
к тому, что всякий необратимый процесс является неравновесным
(см. § 17). Верно и обратное заключение: всякий неравновесный
процесс необратим, если в дополнение ко второму началу осу-
осуществляется достижимость любого состояния неравновесно, когда
оно достижимо из данного равновесно (вся современная практика
подтверждает выполнение этого условия; однако противополож-
противоположное условие (см. § 30) выполняется не всегда). Деление процес-
процессов на обратимые и необратимые относится лишь ж процессам,
испытываемым изолированной системой в целом; разделение же
процессов на равновесные и неравновесные с этим не связано.
* Это находится в соответствии с представлением о природе механическо-
механического трения. Трение между двумя соприкасающимися телами происходит вследст-
вследствие того, что поверхности этих тел не абсолютно гладки, а в большей или мень-
меньшей степени шероховаты; для того чтобы переместить одно тело относительно
другого, необходимо некоторое конечное усилие для преодоления сил, вызван-
вызванных шероховатостью этих поверхностей.
44
Приведем несколько примеров необратимых процессов.
1. Процесс теплопередачи при конечной разности температур
необратим, так как обратный переход связан с отнятием опреде-
определенного количества теплоты у холодного тела, превращением его
без компенсации (некомпенсированно) в работу и затратой ее на
увеличение энергии нагретого тела. Необратимость этого процес-
процесса видна также из того, что он нестатичен.
2. Расширение газа в пустоту необратимо, так как при таком
расширении не совершается работа, а сжать газ так, чтобы не
совершить работу, нельзя. Произведенная же при сжатии работа
идет на нагревание газа. Чтобы газ ие нагревался, нужно отнять
у него теплоту и превратить ее в работу, не невозможно без ком-
компенсации.
3. Процесс диффузии необратим. Действительно, если в сосуде
с двумя (различными газами, разделенными перегородкой, снять
лерегородку, то каждый газ будет диффундировать *в другой. Для
разделения газов каждый из них нужно сжимать. Чтобы они не
нагревались, необходимо отнять у них теплоту и превратить ее
в работу, что невозможно без изменения в окружающих те-
телах (*).
§ 13. Принцип адиабатной недостижимости
и второе начало для равновесных процессов.
Энтропия и термодинамическая температура
Применение второго начала термодинамики (его первой части
о невозможности вечного двигателя второго рода) »к равновесным
процессам позволяет установить, что около (Каждого- состояния
термически однородной * системы существуют такие состояния,
которые недостижимы из него адиабатным равновесным путем
(принцип адиабатной недостижимости Каратеодори).
Действительно, пусть из состояния 1 система равновесно пере-
переходит в состояние 2, получая из какого-либо тела положительное
количество теплоты FQ;>0) и совершая работу 8W, тогда
8Q = dE + 8W. C.2)
Предполагая, что из состояния 2 система адиабатно может
лерейти в состояние 1, совершив работу 8W\y находим
0=— dE + bWx. C.3)
Складывая уравнения C52) и C.3), получаем, что за весь
круговой процесс была совершена работа 6W+8W\ за счет неком-
некомпенсированного превращения теплоты
8Q = SW+8Wi>0. C.4)
* Термически однородная система — система, все части которой имеют оди-
одинаковую температуру (т. е. система, в которой отсутствуют теплонепроницаемые
{адиабатные) перегородки). Для термически неоднородной системы принцип
адиабатной недостижимости, вообще говоря, не выполняется (•&).
45
Так как, по второму началу термодинамики (ЗЛ), такой про-
процесс невозможен, то, следовательно, состояние 1 адиабатно не-
недостижимо из состояния 2.
Если ори равновесном переходе системы цв состояния 1 в сос-
состояние 2 8Q<0, то, предполагая возможном адиабатное возвра-
возвращение системы из 2 в 1, для всего кругового процесса, подобно
формуле C.4), получаем
Это неравенство указывает на отдачу системой за цикл количества теплоты
6Q за счет произведенной над ней работы. Такой круговой процесс не проти-
противоречит второму началу и, следовательно, возможен только при нестатическом
адиабатном возвращении системы из состояния 2 в 1. Действительно, если бы
процесс 2 — 1 был равновесным, то весь цикл был бы обратимым; проводя его
в обратном порядке, получаем формулу C.4), что противоречит второму нача-
началу (*).
Физический смысл принципа адиабатной недостижимости со-
состоит в утверждении, что у всякой равновесной системы сущест-
существует некоторая новая функция состояния а=а(Щу ..., ап; /), кото-
которая при равновесных адиабатных процессах не изменяется
(в (аи •••, ап\ 0=const при адиабатных .процессах). В этом мож-
можно убедиться исходя из следующих соображений.
Легко заметить, что положение о существовании температуры
t у всякой равновесной системы можно сформулировать в виде
принципа изотермической недостижимости: около каждого состоя-
состояния равновесной системы существуют такие состояния, которые
недостижимы изотермически (т. е. при условиях, когда система
все время находится в тепловом контакте с термостатом). Дей-
Действительно, из состояния системы с температурой t = t\ нельзя
изотермически перевести систему в состояние с температурой
i = t2. Аналогично этому невозможность адиабатно (т. е. в .усло-
.условиях, когДа система теплоизолирована) церевести равновесную
систему из состояния 1 в некоторое состояние 2 означает, что в
состоянии 1 система имеет значение некоторой функции состоя-
состояния a = ai, а в состоянии 2 — a=<S2?^O\, причем эта функция при
адиабатных равновесных процессах не изменяется (do = 0 при
6Q = 0).
Установление на основании принципа адиабатной недостижи-
недостижимости существования такой новой функции состояния a(du •.., cin;
t) приводит к тому, что пфаффова форма для элементарного ко-
количества теплоты 6Q, которая согласно первому началу не явля-
является полным дифференциалом, всегда имеет' интегрирующий
множитель, т. е. является голономной *.
Действительно, так как 6Q и da являются линейными диффе-
дифференциальными формами в полных дифференциалах одних и тех
же независимых переменных и одновременно обращаются в ц.уль,
то, следовательно', они пропорциональны:
* Пфаффовы формы, имеющие интегрирующий множитель, называются го-
лономными\ не имеющие интегрирующего множителя — неголономными.
46
Здесь К в оИццем случае зависит от всех параметров состояния
системы: Х = Х( о\, ..., ап\ t). Поэтому
т. е. пфаффова форма &Q голономна.
Можно показать (см. § 14), что среди интегрирующих дели-
делителей X дифференциальной формы 8Q имеется делитель, завися-
зависящий только от температуры. i = q(t), причем вид функции ср(/)
зависит от выбора эмпирический температуры t в данном состоя-
состоянии, а числовое значение — нет. Поэтому в каждом состоянии
системы функция ср(/) имеет некоторую абсолютную (не завися-
зависящую от выбора эмпирической температуры) величину. Принимая
значение функции ф(?) за меру температуры и обозначая ф(/)=7\
получаем
8Q/T dS. C.5)
\
Функция S, определяемая дифференциальным уравнением
C.5), называется энтропией, а не зависящая от выбора термо-
термометрического вещества температура Т — термодинамической тем-
температурой.
Из второго начала следует также, что энтропия S является
однозначной функцией состояния. Это означает, что ф 8QJT для
любого кругового равновесного
процесса равен нулю. Если бы это
не выполнялось, т. е. если бы энтро-
энтропия была неоднозначной функцией
состояния, то можно было бы осу-
осуществить вечный двигатель второго
рода.
В самом деле, неоднозначность
энтропии означает, что две разные
адиабаты Si и S2 могут пересекать-
пересекаться и, следовательно, возможен кру-
круговой процесс, изображенный от-
отрезками изотермы 1—2 и отрез-
отрезками пересекающихся адиабат 2—
3 и 3—1 (рис. 5). Если на участке
изотермического процесса 1—2 та-*
кого цикла у термостата берется теплота Q(Q>0), то по первому
началу за счет этой теплоты за цикл производится положительная
работа № = Q = j> 6Q и мы имеем, таким образом, вечный дви-
двигатель второго рода.
Невозможность вечного двигателя второго рода приводит к
невозможности пересечения адиабат, т. е. к однозначности энтро-
энтропии. Математически это 'выражается уравнением
Рис. 5
C.6)
при любом равновесном круговом процессе.
47
Если рабочее тело, совершающее круговой процесс, все время
находится в контакте с термостатом, то за такой цикл согласно
формулам C.5) и C.6)
т. е. работа при изотермическом круговом, процессе равна нулю *.
Положение о существовании у всякой термодинамической
системы новой однозначной функции состояния — энтропии S,
которая при адиабатных равновесных процессах не изменяется, и
составляет содержание второго начала термодинамики для рав-
равновесных процессов.
Математически второе начало термодинамики для равновес-
равновесных процессов записывается уравнением
-^- = dS, или 6Q=TdS. C.7)
Это выражение для элемента количества теплоты имеет такой
же вид, как и выражение A.3) для элементарной работы, причем
температура Т является интенсивным параметром теплопередачи
(термическая обобщенная сила), а энтропия 5 — экстенсивным
параметром теплопередачи (обобщенная координата).
Интегральным уравнением второго начала для равновесных
круговых процессов является равенство Клаузиуса
-^=0. C.8)
§ 14. Математическое обоснование
существования энтропии
и термодинамической температуры
Из 'принципа адиабатной недостижимости, как мы видели,
следует голоиомность дифференциальной формы 6Q, т. е. сущест-
существование у выражения для равновесного элемента теплоты 6Q
интегрирующего делителя X (или множителя 1Д). Покажем, что
среди этих интегрирующих делителей к есть такой, который за-
зависит только от температуры [(X=cp(^)] и определяет энтропию
8Q/(p(t) =dS системы, и что- числовое значение этой функции от
такого выбора не зависит, хотя вид функции ф(/) связан с выбо-
выбором эмпирической температуры t.
Существование энтропии. Пусть имеются две подсистемы, на-
находящиеся в тепловом равновесии. Состояние первой системы
определяется параметрами аи ..., ап\ ty состояние второй — па-
параметрами &i, ..., bm\ t, состояние всей системы — параметрами
аи ..., ап\ &ь ..., Ьт\ t.
* Для неравновесных процессов работа W за цикл при одном теплоисточ-
теплоисточнике может быть отрицательной (•&).
48
Пусть при* некотором равновесном процессе всей системе в це-
целом сообщается количество теплоты 6Q, которое распределяется
по подсистемам в количестве 8Qi и 6Q2, так что
C.9)
оэто-
C.10)
где
(ЗЛО7)
п\ Ьи ..., Ът\ t)
По доказанному все, эти элементы теплоты голономны, поэто-
поэтому они могут быть записаны в виде
соответствующие интегрирующие делители; в\ и а2 — функции,
состояния первой и второй систем соответственно.
Функции о\ и а2 можно взять в качестве независимых пере-
переменных «каждой из этих систем, например вместо параметра aL
первой системы и параметра Ь\ второй системы, та'к что
^i = A,i(ai; a2, ..., ап\ t), X2 = X2(a2; 62, ..., Ьт\ t),
l=l{ou a2; a2, ..., an; b2, ..., bm\ t),
C.11)
G = a(au a2; a2, • • •, ^; b2, ..., bm; 0;
« m
1 do ij , da * ^ do * , \^ да л . \*\ do AU
da= at H do, H da. + > dat + >; dbk.
i=2 k=2
С другой стороны, подставляя выражение C.10) в C.9), полу-
получаем
de=-^dG1 + ^-do2. C.12)
л л
Сравнивая формулы C.11) и C.12) находим^ что do/da\ = 'KilK
da/do2"=hlK а коэффициенты при dt, da2y ..., dan\ db2, ..., dbm
равны нулю. Отсюда, приравнивая смешанные производные, полу-
получаемые из формулы C.11), находим:
(f = 2, ..., п; й=2, ..., т).
Из формулы C.13) следует, что если в выражения C.10')
входит параметр /, то только в виде одной и той же функции
49
y так что
^2(а2, &2, .-., Ът)\
C.16)
а2, «2, • •> ап, Ь2, ..., ftm).
Поскольку A,i ее зависит от bk, а ^2 — от а*, то из формул
C.14), C.15) следует, что X не зависит от а,- и &*, М — от аи а
Л2 — от Ьк. Таким образом, из C.16) получаем
bi = <p(*)-M(Ti), ^=ф@-/2(а2), X-<p(O-f((Tb а2). C.17)
Входящие сюда функции /1@1), f2(a2) и /(аь а2) являются
произвольными, поскольку, как известно из математики, если
имеется хотя бы один интегрирующий делитель Х\ дифферен-
дифференциальной формы 6Qi, такой, что 6QAi = dab то произведение К\
на произвольную функцию W (cti) также будет интегрирующим
делителем.
Отсюда следует, что среди бесконечного- множества интегри-
интегрирующих делителей имеются и такие, для которых произвольные
функции fi (cti) =f2 (cri) = 1, т. е. делители, зависящие только от
температуры Я1 = Х2 = ф(^); при этом интегрирующий делитель X
также равен ф(^):
q>(f)=A,=Ai = A<2. C.18)
_ Действительно, рассмотрим три подсистемы (рис. 6), находя-
находящиеся в тепловом равновесии; согласно доказанному для каж-
каждой пары систем имеем: ?ц=Я2='ф(/),
А,2 = Яз = ф(О> ^==^з=::ф(О и, следовательно,
Х1 = Я2 = Я = ф(/) (^относится к системе 1,2).
Функция Si, определяемая уравнением
6QiAp(O =dSi, называется энтропией пер-
первой системы, а функция S2, определяемая
уравнением &Q2/q>(t)=dS2, называется эн-
энтропией второй системы.
Разделив выражение C.9.) на C.18),
Рис. 6 получаем
где S = Si + S2 — энтропия всей системы, равная сумме энтропии
отдельных подсистем. Энтропия, как видно из ее определения,
является аддитивной величиной, пропорциональной числу частиц
системы.
Таким образом, показано, что среди интегрирующих делителей
элемента теплоты 8Q имеется такой ф(?)> который зависит только
от температуры t и одинаков для произвольных систем, находя-
находящихся в тепловом равновесии.
Термодинамическая шкала температур. Употребляемая нами
до сих пор эмпирическая температура t определялась по измене-
изменено
нию кажого-йибо параметра (например, расширению) того или
иного термометрического вещества (ртути, спирта и т. д.). Как
мы уже отмечали, термометры с различными термометрическими
телами, кроме основных точек 0 и 100°С, показывают, вообще
говоря, во всех других случаях разиую температуру. Это особен-
особенно ясно указывает на произвольность и неудовлетворительность
такого определения температуры как объективной меры интен-
интенсивности теплового движения.
Второе начало термодинамики устраняет этот недостаток и
позволяет установить термодинамическую шкалу, температура па
которой не зависит от термометрического вещества и поэтому на-
называется абсолютной. В самом деле, поскольку интегрирующий
делитель ф(/) для элемента теплоты определяется только темпе-
температурой, он может служить мерой температуры. Температура
T = q>(t) и является термодинамической (абсолютной) температу-
температурой, поскольку, как мы покажем, числовое значение функции
ф(?) от выбора эмпирической температуры <не зависит, хотя вид.
этой функции зависит от выбора эмпирической температуры.
Найдем связь между термодинамической и эмпирической тем-
температурами. Пусть эмпирическая температура системы, измеряе-
измеряемая по величине какого-либо параметра некоторого термометри-
термометрического вещества, равна t, а ее термодинамическая температура
T = q)(t). Состояние термометрического вещества определяется
внешним параметром а и эмпирической температурой t или зна-
значением термодинамической температуры T = <p(t). Тогда для этого
вещества по первому еачалу bQ = dE + Ada, по второму началу*
&Q/T = dS и; следовательно,
откуда
Так как
то
или
Поскольку
откуда
После интегрирования получаем
51
In T - Г
t
e
(dE/da)t + A ' To
to
тогда
Г=Гов7, C.20)
где Г и Го — температуры по термодинамической шкале, соответ-
соответствующие эмпирическим температурам t и tQ.
Из выражения C.20) видно, что при равновесном переходе
системы из одного состояния в другое температура Т не может
изменить знака: она всегда или положительна, или отрицательна.
Доказать положительность или отрицательность термодинамиче-
термодинамической температуры нельзя. Ее знак определяется дополнительным
условием, связанным с определением того, какая температура
больше, а какая — меньше; считается, что в случае равновесного
сообщения телу теплоты при постоянных внешних параметрах его
температура увеличивается, т. е. Са= (дЕ/дТ)а>0 (см. § 2). Та-
Такое дополнительное условие приводит к положительной термоди-
термодинамической температуре (Г>0) (см. § 28).
Считая («в соответствии с принятым условием *, определяю-
определяющим, какая температура больше, а какая — меньше) темлера-
туру Т положительной, мы приходим к выводу, что обычные сис-
системы не могут иметь отрицательных термодинамических темпе-
температур.
Формулу C.20) для определения температуры Т можно преоб-
преобразовать. Для эмпирической температуры U термодинамическая
температура Т\ = Т ехр 1и откуда-
1-1), C.21)
1 J (dE/da)t + A
to
Разделим выражение C.20) на C.21):
Г/(Г1-Г0)=ехр//(ехр/1-1),
откуда
Г=(Г1-Г2)ехр//(ехр/1-1). C.22)
Выберем температурную шкалу такой, чтобы разности между
основными точками t\—^0 = 100°С и Тх—Г0=100К соответствова-
соответствовали друг другу. Тогда
7 = 100 ехр/ . C.23)
ехр /х — 1
* Это дополнительное условие приводит к формулировке второго начала
термодинамики для равновесных процессов в адиабатных системах в виде за-
закона возрастания энтропии (см. § 17).
52
Эта формула позволяет найти термодинамическую температу-
температуру Т по данной эмпирической температуре /, определяемой по
какому-либо свойству того или иного термометрического' ве-
вещества.
Покажем теперь, что термодинамическая температура Т в
данном состоянии не зависит от выбора термометрического тела.
Пусть состояние некоторой системы характеризуется помимо эм-
лирической температуры t еще другой эмпирической температу-
температурой т = т(?). Термодинамическая температура 0, определяемая с
помощью эмпирической температуры т (при той же разности
6i—9o=Ti—то= 100 между основными точками), равна
6 = 100
exp /1T — l
где
j } (dA/dx)adr _r (dA/dt)a-(dt/dx)dr _
x J(dE/da)x + A J (dE/da)f+A
To to
} (дА/дт)адт _C (dA/dt)a-(dt/dx)dT __
j
To
J
_
J(dE/da)x + A J (dE/da)t
и, следовательно, 8 = Г, т. е. температура по термодинамической
шкале не зависит от -выбора термометрического тела.
Поэтому для вычисления термодинамической температуры по
формуле C.23) в качестве термометрического тела можно взять
идеальный газ, находящийся под действием всестороннего* давле-
давления Л = Р, a=V. Для идеалыного газа при постоянном объеме
/> = Р0A+а0, где а = 0,003661 К = 1/273,15 К, t — температу-
температура по шкале Цельсия, (dE/dV)t = O. Интегралы / и 1\ в этом слу-
случае равны:
Z (dP/dt)vdt r' adt =ln j ln
J (dE/dV)t + P J 1 + at 1 + at0' x 1 + at0
h t
1 I ff j-
Подставляя / и 1г в формулу C.23), получаем Т = 100 —— ,
a (*i — ^о)
ж так как t\—to= 100°С, то
Абсолютный нуль температуры по шкале Цельсия равен
—273,15°С.
При сделанном нами выборе величины 100 для разности тем-
температур Тх—Го, соответствующих основным точкам, т. е. при вы-
выборе градуса Цельсия -в качестве единицы температуры, термо-
термодинамическая температура совпадает с газовой температурой,
53
измеренной по шкале Кельвина *. Если пользоваться градусом
Реомюра, т. е. если положить
/i—*0 = 80°R и Г!—Го = 80 Kr,
то
1/а= B73,15-80/100)Кн = 218,4 Kr и Г-(/ + 218,4)Kr.
Абсолютный нуль температуры по шкале Реомюра равен
—218,4° R.
§ 15. Основное уравнение термодинамики
для равновесных процессов.
Связь между термическим
и калорическим уравнениями состояния
По второму .началу термодинамики, для равновесных процес-
процессов 6Q = TdS. Объединяя это выражение с уравнением первого
начала термодинамики bQ = dE + J]Аьйа(, получаем основное
i
уравнение термодинамики для равновесных процессов
^idat. C.24)
i
Для простой системы, (Находящейся под всесторонним давле-
давлением Р, уравнение C.24) имеет вид
TdS = dE + PdV. C.25)
Уравнение C.24) является исходным при анализе всех равно-
равновесных процессов в термодинамических системах с постоянным
числом частиц.
Как мы видели, при вычислении многих величин необходимо
знать как термическое, так и калорическое уравнения состояния
системы. Экспериментально эти уравнения могут быть получены
независимо друг от друга. Уравнение C.24) позволяет установить
дифференциальную связь между ними, которая в некоторых слу-
случаях делает ненужным знание или калорического уравнения сос-
состояния, или только зависимости внутренней энергии от внешних
параметров. Действительно, из основного уравнения термодина-
термодинамики C.24) находим
ЛО i l ( дЕ \ AT _i_ l V ( ( дЕ \ _i_ A 1 A
dS = = — ( dl H > + Ai\ da;.
* Кельвин — 1/273,16 термодинамической температуры тройной точки воды.
Это определение было дано в резолюции Десятой Генеральной конференции па
мерам и весам A954). Вместе с тем по Международной практической темпе-
температурной шкале для тройной точки воды принята температура ?=0,01°С точно.
Поэтому формула перехода от практической к термодинамической темпе-
температурной шкале имеет вид Г=^°С + 273,15°С.
54
Тогда
дТ )а, Т \ дТ )at' \ да, )ап.Т Т [ \ да, )ап.т
(» = 1, 2, .... л),
откуда, подобно C.19), получаем дифференциальное уравнение,
связывающее термическое и калорическое уравнения состояния:
=(™-\ +At. C.26)
\д)т У '
дТ )at \да,)т
Для простой системы, подверженной действию силы всесто-
всестороннего давления А — Р, a=V, уравнение C.26) имеет вид
iL\ «(Ш +Р. C.27)
dTJv \дУ)т К '
Примем уравнение C.27) для определения 'внутренней энер-
энергии идеального газа, газа BaiH-дер-Ваальса и для вычисления
разности теплоемкостей различных систем.
Для идеального газа термическим уравнением состояния явля-
является уравнение Клапейрона—Менделеева
PV=RT.
Из этого уравнения (dP/dT)v = \R/V. Подставляя найденное выра-
выражение производной (dP/dT)v в формулу C.27), получаем закон
Джоуля (dEldV)r:=Q, который, как мы уже показывали, позво-
позволяет найти калорическое уравнение состояния газа, если дополни-
дополнительно известна температурная зависимость его теплоемкости:
Для одноатомного идеального газа с точностью до аддитивной
постоянной имеем
Е = СУТ. C.28)
Если воспользоваться значением молярной теплоемкости одноатомного иде-
идеального газа Cv = zkR> то из формул C.27) и C.28) можно получить алгебраи-
алгебраическую связь между его термическим и калорическим уравнениями состояния:
РУ=2/з?, C.29)
и
Р=2/зе, C.30)
тде e—E/V — плотность энергии одноатомного идеального газа.
Как устанавливается в статистической физике, связь C.29) между давле-
давлением Р и энергией Е существует не только в случае обычных (подчиняющихся
уравнению Клапейрона—Менделеева и называемых классическими) одноатомных
идеальных газов, но и в случае квантовых идеальных (нерелятивистских) как
€озе-, так и ферми-газов, когда кинетическая энергия частиц значительно меньше
их собственной энергии тс2 (с — скорость света). Для релятивистского идеаль-
идеального квантового газа, когда кинетическая энергия его частиц сравнима или зна-
55
чительно больше их собственной энергии, связь между уравнениями состояния
Р и Е имеет вид
PV=4*E, C.31)
так что Р=1/зЕ.
Для реального газа, термическим уравнением которого явля-
является уравнение Ван-дер-Ваальса Р= —, имеем
\ дТ )y V — b'
Подставляя эти выражения в уравнение C.27), получаем
(dE/dV)T = a/V2. Таким образом,
= BЦ dT+(—
\ дТ )у \ dV
dV,
V2
C.32)
—a/V.
Так как Су реальных газов слабо зависит от температуры, то
формулу C.32) можно записать в виде
E = CvT—a/V+E0.
Первое слагаемое в формуле C.32) представляет собой сред-
среднюю кинетическую энергию молекул газа, а второе — потен-
потенциальную энергию взаимодействия молекул, соответствующую
ван-дер-ваальсовым силам притяжения.
Первое начало для разности теплоемкостей СР—Cv дает
выражение B.7): СР—Cv= \( ) +Р \( | . Для вычисле-
[ V dV It J \ дТ I р
ния Ср—Су по1 формуле B.7) необходимо' знать как термическое
уравнение состояния Р = Р(Т, V), так и калорическое уравнение
состояния Е=Е(Т, V). Второе начало*, устанавливая связь между
этими уравнениями, позволяет найти разность СР—CV, зная
только одно термическое уравнение состояния. Действительно,
используя C.27)*, находим
Ср-Су = т(-?-\ № . C.33)
V \дТ )у\дТ jp V
Входящие сюда производные можно определить, зная лишь
термическое уравнение состояния Р = Р(Т, V) или измеряя непос-
непосредственно коэффициент объемного расширения а — ( )
Vo \ дт I p
, , о 1 / dV \
и коэффициент термического сжатия р = ) .
* В общем случае согласно формулам B.6) и C.26)
СА—Са^Т(дА/дТ)а(да/дТ)А. C.33')
56
Из тождества [ \ ( ) ( ) =—1 (*) и выражений для
\дТ )р\дР )v\dV )т К } У
аир находим
дР \ ( dV \ ( дР
дУ
/ дР \ __(_dV_
\дт)у~ [dT
Подставим эту производную в формулу C.33):
СР—Cv=VJa?l§. C.34)
Так как согласно условию устойчивости равновесного состоя-
состояния всегда (dV/dP)T<.0 и, следовательно, р>0, то из уравнения
C.34) находим, что Ср^Су. Равенство выполняется при ос = 0.
Например, у воды при 4°С и нормальном атмосферном давлении
ее плотность максимальна и а изменяет знак:
сс<0 при 0</<4°С,
а>0 при ?>4°С.
Такое поведение коэффициента объемного расширения у воды
приводит к такому ее аномальному свойству, что в интервале
температур 0<?<4°С при адиабатном сжатии она не нагревает-
нагревается, как другие жидкости и все газы, а охлаждается.
§ 16. Вычисление энтропии.
Парадокс Гиббса
Согласна основному уравнению термодинамики C.24) изме-
изменение энтропии при равновесном переходе системы из одного сос-
состояния в другое равно
C.35)
Для вычисления разности S2—Si по формуле C.35) необходи-
необходимо знать как термическое, так и калорическое уравнения сос-
состояния:
Ai = Ai{au ..., ап, Г), (i=l, 2, ..., п).
Е = Е(аи ..., а., Г).
Если, однако, воспользоваться дифференциальным уравнением
C.26), связывающим эти уравнения состояния, то
2 (dE/dT)aidT + V[(dE/dcn)T a +At]dat-
57
откуда видно, что для нахождения изменения энтропии S2—Si
(нужно знать только термическое уравнение состояния и зависи-
зависимость внутренней энергии лишь от температуры (знание ее зави-
зависимости от внешних параметров не требуется).
Для простой системы, находящейся под всесторонним внешним
давлением, из формулы C.36) находим
^. C.37)
Так как для моля идеального газа PV = RT и (dP/dT)v = R/V>
то для газа с CV=const находим
S2—SX = CVIn^- + RIn-?*- = CvIn-?- + ?In -Hz-,
П Vi Tt Vl'
где v\ v2 — объемы на одну частицу в начальном и конечном сос-
состояниях газа соответственно. Поэтому для энтропии моля газа
получим
S = CV In T+R In v + Sq, C.38)
где
So = Sl{Tu VJ—CvlnTx—Rlnvi. C.39)!
Энтропия v = N/NA молей идеального газа, занимающего при
температуре Т объем V, равна
S = v[CvIn T+R ln(V/N) +50], C.40)
где согласно равенству C.39) So не зависит от числа частиц N.
Выражение C.40) определяет зависимость S от N, Т, V.
Если имеется смесь различных идеальных газов, то с помощью
полунепроницаемых перегородок (т. е. перегородок, проницаемых
для одного газа и непроницаемых для другого) можно* обратимо
разделить эту смесь на составляющие ее .компоненты, каждый из
которых имеет объем смеси, без сообщения теплоты и затраты
работы и, следовательно, без изменения энтропии системы (*).
Это приводит к теореме Гиббса об энтропии газовой смеси: энт-
энтропия смеси идеальных газов равна сумме энтропии этих гйзов,
когда каждый из них в отдельности занимает при температуре
смеси тот же объем, что и вся смесь *.
Вычислим, пользуясь этой теоремой, увеличение энтропии при
смешении двух различных газов, разделенных вначале перего-
* Обратимо разделить смесь газов и, следовательно, доказать теорему Гибб-
Гиббса можно и без использования полупроницаемых перегородок (см. в кн.: Л о -
ренц Г. А. Лекции по термодинамике. М., 1941, § 70). Теорему Гиббса можно
также доказать, используя закон Дальтона (*).
58
редкой, занимающих объемы V\ и У2 и имеющих одинаковую
температуру Т (vi и V2 — число молей каждого газа).
Энтропия газов до смешения
Si = vx[CVt \nT + R\n(VJNJ + Sol] +
+ v2[CV2 \nT + RIn(V2/N2) + S02],
а после смешения, когда каждый газ занимает весь объем Уг + У2,
Su = v1 {CVt \nT + R\n[(Vx + VJ/tfJ + Sol} +
+ v2{CV2 \nT+R\n[(Уг + V2)/N2] + 502}. C.41)
Изменение энтропии системы после смешения
9 C.42)
откуда видно, что изменение энтропии при изотермическом смеше-
смешении идеальных газов определяется только конфигурационной (за-
(зависящей от объема) частью энтропии
Sk=vRln(V/N), C.43)
другие члены в формуле C.40) при этом роли ие играют. В част-
частном случае равных количеств газов (vi=V2=v = Ar/A/'A), находя-
находящихся до смешения в одинаковых объемах (V\ = V2=V)> для (кон-
(конфигурационной части энтропии системы получаем
Si=2vR\n(VIN)9 C.44)
Sn = 2v#lnBV7A0. C.45)
Изменение энтропии после смешения
AS = 2vR In 2 = 2kN In 2. C.46)
Из соотношений C.42), C.46) видно, что возрастание энтро-
энтропии при смешении двух идеальных газов зависит только от числа
молей газов, но не зависит от их природы. В предельном случае
смешения двух идентичных газов увеличения энтропии не должно
быть, так как при этом после удаления разделяющей перегород-
перегородки никакого термодинамического процесса в системе не происхо*-
дит. Таким образом, при расчете изменения энтропии смешение
двух идентичных газов нельзя рассматривать как предельный
случай смешения двух различных газов и, следовательно, при
переходе от смеси сколь угодно близких по своим свойствам и
разделимых из этой смеси газов к смеси одинаковых газов AS
испытывает скачок {парадокс Гиббса*).
* Парадокс является истинным утверждением, которое необычно, противо-
противоречит общепринятому и про которое хочется сказать, что этого не может быть.
Ошибочное утверждение, выглядящее правдоподобно, называется паралогиз-
паралогизмом. Паралогизм означает рассуждение, в котором ненамеренно сделана логи-
логическая ошибка.
59
Для вычисления изменения энтропии при смешении двух пор-
порций одного и того же газа надо пользоваться или непосредствен-
непосредственно выражением C.40) для энтропии химически однородного газа
(*), или видоизмененной теоремой Гиббса, согласно которой
энтропия газовой смеси двух одинаковых порций одного и того же
газа равна сумме энтропии обеих порций, когда каждая из них
в отдельности занимает весь объем, без 2UN In 2 '(*), или же учи-
учитывать в формуле C.45) для энтропии смеси разных газов ска-
скачок изменения их плотности в предельном случае смешения тож-
тождественных газов, т. е. при переходе к смешению тождественных
газов надо в формуле C.45) заменить плотность N/V на 2N/V
(*).
Решить парадокс Гиббса означает установить физическое ос-
основание скачка величины AS при переходе от смеси сколь угодна
близких газов к смеси одинаковых газов.
В литературе известна точка зрения, согласно которой пара-
парадокс Гиббса о разрывном поведении Д5 связывается с объектив-
объективной невозможностью непрерывного сближения параметров, харак-
характеризующих смешивающиеся газы.
Физическим основанием парадокса Гиббса является невозмож-
невозможность разделения на первоначальные порции смеси тождествен-
тождественных газов в отличие от допускаемого термодинамикой разделе-
разделения смеси сколь угодно мало отличающихся друг от друга газов,
В результате этой особенности смеси тождественных газов по
сравнению со смесью разных газов имеет место скачок плотности
смешиваемых газов при переходе от смешения сколь угодно
близких газов к смешению тождественных газов, который и при-
приводит к скачку изменения AS.
Вследствие этой особенности смеси тождественных газов в
общей формуле для энтропии смеси разных газов (см. C.41))
различие между газами нельзя стремить к нулю. Для вычисле-
вычисления с помощью формул C.41) и C.45) энтропии смеси в пре-
предельном случае смешения тождественных газов необходимо не
только параметр различия положить равным нулю, но и учесть
происходящий при этом скачок изменения плотности смешивае-
смешиваемых газов (*).
В тех же случаях, когда смесь тождественных газов не обла-
обладает отмеченной физической особенностью, т. е. когда газовую
смесь нельзя разделить не только при смешении одинаковых га-
газов, но и при смешении термодинамически разных газов, ника-
никакого скачка изменения плотности смешиваемых газов при пере-
переходе от смешения сколь угодно близких газов к смешению тож-
тождественных газов не происходит. Поэтому в формуле для" энтро-
энтропии смеси разных газов в этих случаях параметры их различия
можно стремить к нулю и этот второй вид смешения идеальных
газов не имеет отношения к парадоксу Гиббса (*)•
Обсудим в заключение вопрос о физическом смысле энтропии.
Однозначная функция состояния — энтропия, существование ко-
которой у равновесной системы устанавливает второе начало тер-
60
модинамики, не является (наглядной величиной: ее можно вычис-
вычислить, но нельзя непосредственно измерить подобно температуре
или объему — энтропиометро'В не существует.
Физический смысл энтропии можно выяснить жак при анализе
равновесных процессов, так и при изучении неравно-весных про-
процессов; при этом более глубокий термодинамический смысл энтро-
энтропии раскрывается при анализе неравновесных процессов. Смысл
этот состоит в том, что изменение энтропии является мерой необ-
необратимости процессов в замкнутой системе и характеризует нап-
направление естественных процессов в такой системе.
При анализе равновесных процессов понятие энтропии ,можег
быть в какой-то степени уяснено из следующих рассуждений, по-
поясняющих смысл уравнения
т *
определяющего дифференциал энтропии.
Первое начало устанавливает, что элемент теплоты 8Q не
является полным дифференциалом (см. § 7). Физический смысл
этого утверждения состоит в том, что
количество теплоты, необходимое при
переходе от одного состояния в дру-
другое, зависит от пути (т. е. условий пе-
перехода).
Рассмотрим переход системы из
состояния 1 в 2 по пути I или II
(рис. 7). Разобьем эти пути на эле-
элементы, на которых система получает
соответствующие количества теплоты
6Q при температуре Г. Полные коли-
количества теплоты, необходимые для перехода из состояния 1 в 2 по1
этим путям, соответственно равны
Рис. 7
(i) (И)
причем по первому началу, вообще говоря, Qj^Qn. Однако если
количество теплоты 6Q*, получаемое системой на некотором эле-
элементе какого-либо пути, разделить на температуру 7\, при (кото-
(которой сообщается эта теплота, и найти сумму (интеграл) этих
(приведенных) теплот по всему пути I и по всему пути II, то«
(согласно опыту или второму началу термодинамики для равно-
равновесных процессов) эти суммы (интегралы) приведенных теплот
для ©сех путей перехода одинаковы:
3 т ) т '
(I) (II)
C.47)
Это- указывает на существование некоторой однозначной функ-
функции состояния, изменение которой определяется интегралом
C.47) и называется энтропией:
St_Sl »(-*-. C.48)
Более глубокий смысл энтропии раскрывается в статистиче-
статистической физике, согласно «которой энтропия S системы в данном
состоянии характеризует вероятность этого состояния:
S = k\nw, C.49)
где k — постоянная Больцмана; w — термодинамическая вероят-
вероятность состояния, определяемая числом микросостояний, реали-
реализующих данное макросостояние. Соотношение C.49) выражает
принцип Больцмана. Односторонний характер изменения энтро-
энтропии -в замкнутой системе определяется переходом системы из ме-
менее вероятного состояния в более вероятное.
Как было установлено К. Шенноном, информация / о системе, получаемая
при наблюдении за системой, связана с происходящим при этом изменением
вероятности состояния системы таким же соотношением (с точностью до знака),
как и C.49). Это формальное сходство выражений для термодинамической энт-
энтропии S и уменьшения информации —/ («информационной энтропии» по Шен-
Шеннону) привело многих авторов к необоснованному отождествлению термодина-
термодинамической энтропии с «информационной энтропией», хотя последняя не является
термодинамическим параметром. Использование одного и того же термина (энт-
(энтропия) для различных величин лишь вводит в заблуждение.
§ 17. Второе начало термодинамики
для неравновесных процессов.
Основное уравнение и основное неравенство
термодинамики
Существование у равновесной системы новой однозначной
функции состояния — энтропии S — 'выражает второе начало
термодинамики для равновесных процессов. Сформулируем те-
теперь второе начало в применении
к неравновесным, необратимым
процессам.
Рассмотрим (рис. 8) два близ-
близких состояния равновесия 1 и 2 не-
некоторой системы. Пусть при нерав-
неравновесном переходе из одного состоя-
состояния в другое * системе сообщается
от какого-либо тела количество
рис. g теплоты 6QHP и она совершает ра-
* На рис. 8 неравновесный переход системы условно изображен совокуп-
совокупностью черточек, поскольку такие переходы нельзя изобразить на какой-либо
диаграмме.
<62
боту 6Wup, так что по первому началу
6QHp = d? + 6WV C.50)
Если же система переходит из состояния 1 в 2 равновесие и7
количество теплоты, получаемое ею от того же тела, равно* 6Q, а
совершенная работа 8W, то
C.51)
Первый переход является необратимым, поэтому возвращение
системы в начальное состояние без компенсации невозможно;
второй переход обратим и систему можно вернуть в исходное сос-
состояние без всяких изменений в окружающих телах. Вычитая из
уравнения C.50) уравнение C.51), получаем для кругового
процесса
SQhP—6Q = 6№HP—6W. C.52)
Эта разность не может быть равной нулю, так как в против-
противном случае это означало бы, что необратимый процесс перехода
системы из одного состояния в другое можно обратить равновес-
равновесно без изменения в окружающих телах (отдав теплоисточнику ко-
количество теплоты 6Q = 6QHp и произведя работу 6№=6WHp) • Раз-
Разность C.52) не может быть положительной, так как это означало
бы, что за круговой процесс системой была произведена работа
б^нр—6W>0 только^ за счет теплоты теплоисточника 6QHp—6Q>0
без всякой компенсации. Разность C.52) должна быть отрица-
отрицательной. Это соответствует тому, что при возвращении системы в
начальное состояние часть теплоты 6Q—6QHp>0 передается теп-
теплоисточнику за счет внешней работы 8W—б^нр, что по второму
началу (второй его части) возможно*: 6QHP—6Q = S№hp—8W>0.
Отсюда следует, что
6Q>6QHP, C.53)
&W>6W*p. C.64)
Так как 8Q = TdS, то из C.53) получаем TdS>6QHp; принимая
Г>О/С, имеем
dS>-^-, C.55)
5.-5х>]-р-. C.56)
Из выражений C.55) и C.56) заключаем:
* Если бы предложение о невозможности вечного двигателя второго рода
допускало обращение, т. е. если бы работу в теплоту также нельзя было превра-
превратить полностью без компенсации, то разность C.52) не могла бы быть и отри-
отрицательной. При выполнении первбго условия C.1) это означало бы, что при-
приведенный на рис. 8 замкнутый процесс невозможен. В настоящее время можно
привести пример такого случая (см. § 31).
63
1. Переход системы из одного состояния в другое, совершае-
совершаемый адиабатно равновесно FQ = 7\iS = 0), нельзя осуществить
адиабатно неравновесно FQHp = 0, dS>0) и наоборот.
Поэтому, хотя при адиабатных .процессах работа системы (как
при равновесном, так и при неравновесном процессах рав.на убы-
убыли внутренней энергии, однако даже при одном и том же умень-
уменьшении внутренней энергии при таких процессах работу 8W при
адиабатном равновесном процессе нельзя сравнивать с работой
6WHp при адиабатном неравновесном процессе, так как конечные
состояния при этих адиабатных процессах будут разные. Однако
если при адиабатном равновесном переходе системы из состояния
1 в 2 8W= —dE, то при неравновесном, «но уже не адиабатном
переходе из 1 в 2 ё1^нр< —dE (см. C.54)).
2. При адиабатном /неравновесном процессе FQHp = 0)
dS>0 и S2—Si>0, C.57)
т. е. при этом процессе система переходит в состояние с большей
энтропией: при адиабатных неравновесных процессах энтропия
системы возрастает.
То, что энтропия в неравновесных процессах в адиабатных системах возра-
возрастает, а не убывает, связано с условием, определяющим положительность термо-
термодинамической температуры. При другом дополнительном условии, приводящем к
Т<0К, мы имели бы из C.53) для неравновесных процессов в адиабатно изо-
изолированных (обычных) системах не закон возрастания, а закон убывания энт-
энтропии.
Таким образом, закон возрастания энтропии содержит в себе не только
объективную сторону (односторонность естественных процессов), но и субъек-
субъективный момент — знак термодинамической температуры, который придает объ-
объективной стороне лишь определенное выражение, не меняя ее существа. Отсюда,
между прочим, следует, что нельзя доказывать положительность термодинами-
термодинамической температуры исходя из закона возрастания энтропии, так как формули-
формулировка второго начала для необратимых процессов в адиабатно замкнутых
(обычных) системах в виде закона возрастания энтропии уже предполагает, что
термодинамическая температура положительна.
Это положение о возрастании энтропии в адиабатно замкну-
замкнутой системе при неравновесных процессах (закон возрастания
энтропии) выражает второе начало для неравновесных процессов.
Оно позволяет характеризовать энтропию как меру необратимо-
необратимости процессов в замкнутой системе. В этом состоит физический
смысл энтропии, если подходить « ней, учитывая особенности не-
равновесных процессов.
Поскольку все естественные, самопроизвольные процессы про-
проходят с конечной скоростью, т. е. неравновесны, то, следователь-
следовательно, при этих процессах в замкнутых системах энтропия всегда
возрастает. Таким образом, второе начало термодинамики для
неравновесных процессов указывает направление естественных
процессов: естественные процессы в изолированных. (или только
адиабатно изолированных) системах проходят в 'направлении
роста энтропии.
•64
Для неравновесного кругового процесса из формулы C.56) по-
получаем неравенство Клаузиуса
^<0. C.58)
Это неравенство, так же как и формула C.56), выражает вто-
второе начало для неравновесных процессов в адиабатно неизолиро-
неизолированных системах (в отличие от неравенств C.57), относящихся к
адиабатным системам).
Неравенства C.56) и C.57) не следует понимать в том смыс-
смысле, что при неравновесном переходе системы из состояния 1 в 2
изменение энтропии больше, чем при равновесном переходе из 1
в 2. Энтропия есть однозначная функция состояния, и » каждом
состоянии система .имеет одну определенную энтропию. Следова-
Следовательно, разность значений энтропии S2—«Si не зависит от того,
равновесным или неравновесным путем система перешла из сос-
состояния 1 в 2. Знак неравенства в формуле C.56) указывает на
та, что интеграл в правой части формулы, взятый по неравновес-
неравновесному пути, не определяет разности энтропии конечного' и началь-
начального состояний, а меньше ее. Аналогично неравенство C.57) вы-
выражает то, что адиабатная система может неравновесно* перехо-
переходить в такие состояния, в которых ее энтропия больше. В этом и
состоит смысл закона возрастания энтропии в адиабатных систе-
системах при неравновесных процессах в ней. Из всего этого следует,
что для определения изменения энтропии S2—S\ при неравновес-
неравновесном переходе системы из состояния 1 в 2 нужно перевести систе-
систему из 1 в 2 равновесно и по формуле C.35) вычислить S2—S\
(*). Неравенство dS>8Qnv/Ty а следовательно, и неравенство
Клаузиуса j> 6QHp/r<0 следуют из неравенства 6Q>6Qhp при
подстановке в него 8Q = TdS. Само же неравенство 6Q>6Qhp
получено из условия, что тело при равновесном и неравновесном
переходах в определенное 'конечное состояние получает теплоту от
одного и того же теплоотдатчика. Следовательно, Г в неравенстве
dS>6QHp/?1 и неравенстве Клаузиуса есть температура тепло-
теплоотдатчика, а не тела.
Неравенство C.54) уже использовалось в частном случае ра-
работы при равновесном и неравновесном расширении газа (см.
§ 5); здесь оно установлено на основании второго начала в об-
общем случае для любых .неравновесных процессов. Из формулы
C.54) видно, что если система равновесно перешла из состояния
1 в 2 без совершения работы F117=0), то осуществить переход
системы из 1 в 2 неравновесно без совершения работы F№Нр = 0)
невозможно. Поэтому при процессах перехода системы равновес-
равновесно и неравновесно из одного состояния в другое без совершения
работы затрачиваемые при этом соответствующие количества теп-
лот 8Q и 6Qnp нельзя сравнивать, так как конечные состояния
при таких переходах будут разные. Забвение этого следствия
второго начала может привести к ошибкам (*).
3 Зак. 24i 65
Второе начало для неравновесных процессов показывает отно-
относительность адиабатной равновесной недостижимости и устанав-
устанавливает абсолютную адиабатную недостижимость состояний с
энтропией S<50. Действительно, при адиабатных равновесных
процессах достижимы лишь состояния с неизменной энтропией
S=Sq=const и недостижимы все состояния как с S>50, так и с
S<cS0. С помощью неравновесных процессов можно достичь сос-
состояний с S>So, но нельзя достичь состояний с S<cS0. Таким об-
образом, состояния с 5<S0 абсолютно недостижимы адиабатно из
данного состояния с энтропией 50.
Основное уравнение и основное неравенство термодинамики,
выражающие первое и второе начала термодинамики, можно* те-
теперь записать © виде
TdS^dE + YtAidac, C.59)
i
где знак равенства относится к равновесным, ^ неравенства — к
неравновесным элементарным процессам.
Все дальнейшие приложения термодинамики базируются на ее
основных уравнениях и неравенстве C.59).
Прежде чем приступить >к решению конкретных физических
задач, основываясь на уравнении термодинамики C.59), рас-
рассмотрим некоторые следствия второго начала.
§ 18. Цикл Карно и теоремы Карно.
Прямое пребразование внутренней энергии
в электрическую
Как уже отмечалось, второе начало термодинамики было< ус-
установлено в результате анализа работы тепловых машин.
В первом сочинении по термодинамике, опубликованном
С. Карно в 1824 г., была поставлена и решена проблема возмож-
возможного повышения коэффициента полезного действия тепловых дви-
двигателей. Относительно КПД тепловых машин Карно установил
две теоремы, которые совместно эквивалентны второму началу
термодинамики. Докажем эти теоремы, исходя из второго
начала.
Коэффициентом полезного действия г) теплового двигателя на-
называется отношение работы W, производимой машиной за цикл,
к количеству теплоты Qb получаемому машиной за этот цикл:
По первому началу термодинамики,
где С?2 — абсолютное значение количества теплоты, отдаваемого
рабочим телом за цикл, поэтому
66
TdS
(§TdS)
Q1-Q2
Qi
dS>0
где интеграл (§ TdS)ds>o берется по участкам цикла, ;на которых
dS>0.
Для графического изображения процессов воспользуемся
энтропийной диаграммой на плоскости с осями координат S, Г.
На этой диаграмме величина W= ф 6Q = §TdS равна площади
цикла, a Q\=(j) TdS)ds>o определяет площадь, ограниченную пре-
предельными адиабатами 1А и ЗВ, осью абсцисс и элементами цикла
с dS>0 (часть кривой цикла 1, 2, 3 иа рис. 9).
;
т,
t
j
7
Рис. 9
Рис. 10
Вычислим КПД цикла Карно, состоящего из двух изотерми-
изотермических и двух адиабатных процессов. На диаграмме S, Т этот
цикл изображен на рис. 10. На изотерме 1—2 теплота Qi берет-
берется от теплоотдатчика, на изотерме 3—4 теплота отдается тепло-
приемнику. Эти теплоты и работа за цикл равны:
Q1 = r1(S2—Si), Q2=r2(S2-S1),
W=Ql-Q2=(Tl-T2)(S2-Sl),
и, следовательно, КПД цикла Карио
ri= (Qi-Q2)/Qi= {TX-T2)ITX. C.60);
Отсюда видно, что КПД цикла Карно не зависит от природы
рабочего вещества и предельных адиабат, а определяется только
температурами теплоотдатчика и тепло приемника (первая теоре-
теорема Карно). Из формулы C.60) следует также, что влияние изме-
изменения температур Т\ и Т2 на значение КПД- цикла Карно раз-
различно:
дц 7*2 дх\ 1 7\
дТх Т\ ' дТ2 Тх Т\ '
и так (Как Т\>Т2, то \дц1дТ\\<\дх\1дТ2\. Таким образом, изме-
67
нение температуры теплоотдатчика в меньшей степени влияет на
изменение КПД цикла Карно, чем изменение температуры тепло-
приемника.
Чем ниже температура Г2 теплоприемника при данной темпе-
температуре Тх теплоотдатчика, тем выше КПД цикла Карно. Однако
цикл Карно с температурой Т2 теплоприемника, равной О К, осу-
осуществить невозможно, так как это противоречило бы второму на-
началу термодинамики (теплота Qu взятая у нагревателя, в таком
цикле полностью превращалась бы в работу). Невозможность по
второму началу цикла Карно с температурой теплоприемника
Г2 = 0 К выражается не в том, что О К недостижим (этот вопрос
не решается вторым началом), а в том, что такой цикл или
нельзя замкнуть, или он вырождается в совокупность двух сов-
совпадающих адиабат и изотерм (*). Таким образом, второму нача-
началу не противоречит достижение О К, но цикл Карно с температу-
температурой теплоприемника Гг = 0 К невозможен.
По этой причине порочны все выводы и доказательства^ основывающиеся на
использовании и анализе цикла Карно с 72=0К. Например, неверным является
встречающееся в некоторых общих курсах физики утверждение о том, что для
осуществления полного превращения теплоты в работу с помощью периодиче-
периодически действующей тепловой машины надо было бы располагать холодильником,
температура которого равна О К, и что, поскольку такого холодильника нет, пе-
периодически действующая машина может превращать в работу только часть теп-
теплоты. В действительности же даже при наличии холодильника с температурой
О К вечный двигатель второго рода невозможен, так как при 72=0К цикл Кар-
Карно вырождается.
Как устанавливает третье начало термодинамики (см. гл. 4), О К недости-
недостижим, и поэтому цикл Карно с температурой холодильника 72=0К осуществить
тем более невозможно.
Заметим, что, допуская возможность цикла Карно с температурой холо-
холодильника 72=0К, можно прийти к неверному выводу о том, что уже по второ-
второму началу изотермический процесс при О К одновременно является и адиабатным.
В самом деле, предполагая, что цикл Карно с 72=0К осуществим, из форму-
формулы C.60) получаем
в то время как из второго начала этот вывод без дополнительных предположе-
предположений не следует.
Действительно, при элементарно^ изотермическом изменении какого-либо па-
параметра х по второму началу имеем
Отсюда видно, что если при 7->0К производная (dSJdx)T изменяется по за-
закону (dS/dx)T—c/T, где с=const, то изотермический процесс при температуре
7=0 К не будет адиабатным, если же (dSJdx)T-+o к-^const, то изотермический
процесс при температуре 7=0 К будет адиабатным. Сказать, как изменяется
S при различных процессах, когда 7~>0К, второе начало ничего не может, к
поэтому нельзя утверждать, что уже по второму началу все процессы при 0К
являются адиабатными. К такому выводу можно прийти или в результате не-
неверного предположения о возможности цикла Карно с 72=0К, или при до-
дополнительном предположении, что изменение энтропии (dSJdx)r при 0К конечно*
хотя и отлично от нуля. В гл. 4 показано, что по третьему началу
(dS/dx)T-+o к-Н), поэтому нулевая изотерма совпадает с нулевой изоэнтропой»
а следовательно, и с адиабатой.
68
Теорема Карно указывает путь повышения КПД тепловых
машин. Она сыграла руководящую роль в развитии основ тепло-
теплотехники. Хотя 1ни одна применяемая в технике тепловая машина
не работает по циклу Карно, значение этого цикла состоит в том,
что он имеет наибольший КПД по сравнению с циклами, работа-
работающими в тех же температурных пределах, и является мерой
КПД всех других циклов (*).
Если машина при заданных внешних условиях работает по
некоторому циклу и получает при необратимом цикле то же коли-
количество теплоты Qi, что и при обратимом, то, поскольку (см.
C.54)) работа WHp за необратимый цикл меньше работы W об-
обратимого цикла, КПД необратимой машины /nHeo6p=№Hp/Qi мень-
меньше КПД обратимой машины r\0QV=W/Q\ (вторая теорема Карно):
'Пнеобр<'Побр. C.61)
Проблема промышленной выработки электроэнергии является
одной из важнейших задач развития экономики. В настоящее
время основную часть электроэнергии (-80%) вырабатывают
паротурбинные электростанции и о^оло 20% — гидроэлектростан-
гидроэлектростанции. В турбинах внутренняя энергия топлива вначале преобразу-
преобразуется в механическую энергию вращения, а потом в генераторах
в электрическую энергию. Такое двухступенчатое преобразование
теплоты в электроэнергию, связанное с использованием быстро-
движущихся частей, не позволяет повысить температуру пара
выше 600—650°С, вследствие чего КПД паротурбинных электро-
электростанций не превосходит 40—42%. Поэтому уже давно* ведутся
исследования прямого (безмашинного) преобразования внутрен-
внутренней энергии в электроэнергию.
В настоящее время наибольшее научно-техническое развитие
получил магнитогидродинамический метод (МГД-метод) прямого
преобразования энергии. Идея этого метода основана на том, что
при пересечении проводником линий индукции в нем возникает
ЭДС. В МГД-генераторе таким проводником является электро-
электропроводящий газ (плазма). Высокотемпературный газ B500—
3000°С) в МГД-генераторе выполняет двойную роль: в сопле пе-
перед генератором внутренняя энергия газа преобразуется в кине-
кинетическую энергию потока, т. е. газ является термодинамическим
рабочим телом, а в генераторе кинетическая энергия потока пре-
преобразуется в электрическую энергию, т. е. газ выполняет роль
силовой обмотки электрической машины. Можно поэтому гово-
говорить, что МГД-генератор представляет собой совмещенную с теп-
тепловым двигателем электрическую машину, а термодинамический
цикл энергетической установки с МГД-генератором принципиаль-
принципиально ничем не отличается от известных циклов газо- и паротурбин-
паротурбинных установок. Использование высокой температуры рабочего
вещества (которую вполне выдерживают неподвижные части ге-
генератора) приводит к генерации электроэнергии МГД-методом с
КПД до 50-60%.
69
§ 19. Самопроизвольный переход теплоты
Второе начало термодинамики для нестатических процессов
указывает на определенное направление естественных процессов.
Это особенно хорошо видно из примера самопроизвольного пере-
перехода теплоты при тепловом контакте двух тел с различными
температурами Т\ и Т2.
Пусть при этом от первого тела ко второму за некоторое вре-
время dl перейдет количество теплоты 6Q>0 (для простоты записи
мы употребляем здесь 6Q вместо- 6QHp). По второму началу энт-
энтропия этой системы тел при таком (Процессе должна возрасти,
поэтому (*)
(±±) C.62)
откуда Т\>Т2, т. е. теплота самопроизвольно переходит от тела
с большей температурой к телу с меньшей температурой.
Определенная направленность, односторонность перехода теп-
теплоты при тепловом контакте двух тел с различной температурой
:является объективным законом природы. Однако конкретное
выражение этого закона зависит от определения понятия «боль-
«большая (меньшая) температура», или, что то же самое, от выбора
знака термодинамической температуры (для обычных систем).
Если принять отрицательную термодинамическую температу-
температуру (это соответствовало' бы тому, что при сообщении теплоты
обычному телу при постоянных внешних параметрах его темпера-
температура понижается), то второе начало для нестатических процессов
состояло бы в утверждении убыли энтропии системы при адиа-
адиабатных процессах. Тогда вместо неравенства C.62) мы имели бы
откуда Ti<r2, т. е. теплота самопроизвольно переходит от тела
с меньшей температурой к телу с большей температурой.
Приняв термодинамическую температуру положительной, по-
получаем выражение одностороннего характера самопроизвольного
перехода теплоты при тепловом контакте двух тел в виде C.62),
т. е. приходим к формулировке второго начала термодинамики
для иестатических процессов в виде утверждения о самопроиз-
самопроизвольном переходе теплоты от тела с большей температурой к
телу с меньшей температурой при их непосредственном тепловом
* Из изложенного видна ошибочность проводимого в некоторых курсах фи-
физики вывода о том, будто утверждение, что при непосредственном тепловом кон-
контакте двух тел теплота всегда переходит от тела более нагретого к телу менее
нагретому, не составляет содержание физического закона, а является просто
определением того, какое из двух тел условно называть более, а какое менее
нагретым.
70
В научной и учебной литературе часто приходится встречать
утверждения о том, что закон возрастания энтропии и закон о
существовании энтропии являются независимыми положениями,
и поэтому с последним вполне совместимо противоположное ут-
утверждение — «закон убывания энтропии» или какое-нибудь
другое. Необходимо, однако, заметить следующее. Как мы виде-
видели, если принять термодинамическую температуру (в случаях
обычных систем) положительной, то с законом существования энт-
энтропии совместим только закон возрастания энтропии и .несовмес-
.несовместим закон убывания энтропии. Если же считать термодинамиче-
термодинамическую температуру отрицательной, то все будет наоборот. Вывод
о том, что термодинамическая температура не может менять
знака (при квазистатических процессах), является следствием
существования энтропии у всякой равновесной системы, а выбор
знака зависит от определения понятия «большая (меньшая) тем-
температура».
Второе начало термодинамики действительно состоит из двух
независимых положений, которые выражаются или в виде
QX>W и W = Ql9
или — на языке энтропии — в существовании энтропии и одно-
одностороннем изменении ее при нестатических процессах в адиабат-
адиабатных изолированных системах.
§ 20. Пределы применимости
второго начала термодинамики.
Направление времени
Применимость начал термодинамики ограничивается прежде
всего рамками самой термодинамики — ее предметом и исход-
исходными положениями. Действительно, тепловое движение, законо-
закономерности которого изучает термодинамика, существует лишь в
системах из большого числа частиц. Поэтому законы термодина-
термодинамики неприменимы к микросистемам, размеры которых сравнимы
с размерами молекул. Это означает не то, что в таких системах
нарушается второе начало — вечный двигатель второго' рода осу-
осуществить нельзя с помощью любых систем *, а то, что говорить
* С первого взгляда может показаться, что наличие тепловых флуктуации
дает принципиальную возможность построения вечного двигателя второго рода.
Но это не так. Рассмотрим, например, флуктуацию плотности в газе. Может
показаться возможным «поймать» возникающие разности давлений с помощью
специальных клапанов и аппаратов, имеющих дело с отдельными молекулами
(такие устройства (существа) В. Томсон называл «демонами Максвелла»), и ис-
использовать их для совершения работы или разделения смеси газов. Однако это
не только практически, но и теоретически невозможно. Все наши аппараты, кла-
клапаны и т. д. сами состоят из молекул и сами обладают некоторыми колебаниями
около положения равновесия, притом совершенно независимыми от колебаний
плотности газа. Желаемый результат можно было бы получить в некоторый оп-
определенный момент времени, но в следующий же момент он компенсировался бы
снова колебаниями аппарата и газа.
71
о вечном двигателе второго рода как об устройстве, которое не-
компенсированно превращало бы теплоту в работу, в применении
к микросистемам лишено смысла, поскольку для них стирается
различие между теплотой и работой.
Таким образом, для второго начала, как и для всей термо-
термодинамики, существует нижняя граница его применимости: оно не-
неприменимо к микросистемам.
Верхняя граница применимости второго начала связана с огра-
ограничением применения термодинамики (из-за ее второго исходного
положения) к системам галактических размеров, поскольку у
таких систем внутренняя энергия не аддитивна (так как вслед-
вследствие дальнодействующего- характера гравитащшнных сил энергия
взаимодействия (микроскопических частей космических систем
сравнима с их внутренними энергиями), а понятия температуры и
энтропии в классической термодинамике определены для адди-
аддитивных систем. Поэтому без обобщения исходных положений тер-
термодинамики для неаддитивных систем второе начало нельзя при-
применять к большим участкам Вселенной и тем более ко Вселен-
Вселенной как целому.
Между тем некритическое перенесение закономерностей зем-
земного макроскопического опыта на Вселенную как целое приводило
к антинаучным выводам о «тепловой смерти» Вселенной.
В законченном виде концепция «тепловой смерти» Вселенной
была сформулирована около ста лет назад на основе работ Клау-
зиуса *, который, распространяя законы термодинамики на Все-
Вселенную как целое, писал: «Энергия мира остается постоянной,
энтропия мира стремится к максимуму». Это- означает, что Все-
Вселенная рано или поздно придет в состояние термодинамического
равновесия; тогда все процессы прекратятся и мир погрузится в
состояние «тепловой смерти», температура во всех местах Все-
Вселенной будет одной и той же, одинаковыми будут и все другие
интенсивные параметры и больше уже не будет причин, способ*
ствующих возникновению 'каких бы то ни было процессов.
Концепция «тепловой смерти» Вселенной непосредственно ве-
ведет к поповщине.
Энгельс подверг взгляды Клаузиуса резкой критике, показав,
что концепция «тепловой смерти» Вселенной противоречит закону
сохранения и превращения энергии, так как этот закон, как мы
уже отмечали, говорит не только о количественной неуничтожи-
неуничтожимое™ движения материи, но и о неутрачиваемой способности к
качественным превращениям различных форм движения одна в
другую.
* Впоследствии эта «теория» получила довольно широкое распространение.
Так, например, в книге Jeans J. The Universe around us (Cambridge, Univer-
University press, 1930, p. 320) читаем: «Вселенная не может существовать вечно; ра-
рано или поздно должно наступить время, когда ее последний эрг энергии достиг-
достигнет наивысшей ступени на лестнице падающей полезности, и в этот момент ак-
активная жизнь Вселенной должна будет прекратиться».
72
Передовые физики прошлого века также выступали против
концепции Клаузиуса.
Большое прогрессивное значение имели в этом отношении ра-
работы прежде всего выдающегося физика-материалиста Больц-
Больцмана.
В противовес концепции «тепловой смерти» Вселенной Больц-
ман выдвинул «флуктуационную гипотезу». Больцман впервые ус-
установил статистическую природу второго начала термодинамики.
Состояние термодинамического равновесия, по Больцману, яв-
является лишь наиболее часто встречающимся, наиболее вероят-
вероятным; в равновесной системе всегда самопроизвольно могут воз-
возникнуть сколь угодно большие флуктуации.
Распространяя эти выводы на Вселенную как целое, Больц-
Больцман пришел к заключению, что Вселенная находится, вообще го-
говоря, в состоянии термодинамического равновесия, однако в ней
неизбежно возникают сколь угодно большие флуктуации. Такой
огромной флуктуацией является та часть Вселенной, в которой
мы находимся. Всякая флуктуация должна исчезнуть, но столь
же неизбежно будут возникать флуктуации подобного рода в
других местах Вселенной. Таким образом, по Больцману, одни
миры погибают, а другие — возникают.
Против флуктуациокной гипотезы Больцмана был выдвинут
ряд возражений. Одним из них является исчезающе малая веро-
вероятность сколько-нибудь больших флуктуации. Ни концепция
«тепловой смерти», ни «флуктуационная гипотеза» не учитывали
специфики Вселенной как гравитирующей системы. В то время
как для идеального газа наиболее вероятным является равномер-
равномерное распределение частиц в пространстве, в системе гравитирую-
щих частиц однородное распределение не соответствует макси-
максимальной энтропии. Образование звезд и галактик из равномерно^
го распределения вещества происходит не вследствие флуктуа-
флуктуации, а является естественным процессом, идущим с ростом эн-
энтропии.
В настоящее время вопрос о «тепловой смерти» Вселенной
стоит иначе, чем во времена Клаузиуса—Больцмана и недавнего
прошлого. В соответствии с современными данными наблюдений
Метагалактика представляет собой расширяющуюся систему и„
следовательно, является нестационарной. Поэтому вопрос о «теп-
«тепловой смерти» Вселенной нельзя даже ставить. Действительно,
учет особенности Вселенной как гравитирующей системы в тео-
теории тяготения Эйнштейна приводит к тому, что для Вселенной не
существует состояния максимальной энтропии. Поэтому энтропия
Вселенной в каждой ее области может возрастать неограниченно
без того, чтобы Вселенная приближалась к состоянию с макси-
максимальной энтропией, т. е. к «тепловой смерти».
Необратимое возрастание энтропии в замкнутых системах по
второму началу термодинамики обусловливает отличие будущих
событий от прошедших. Это привело Больцмана к мысли об ис-
использовании второго начала для определения роста времени.
7$
Наше время, по Больцману, растет в том направлении, в кото-
котором возрастает энтропия в обитаемой нами части Вселенной; в
той части Вселенной, в которой протекают отклонения от равно-
равновесия (флуктуации), время течет в обратную сторону.
В работах 1960—1963 гг. Хойл предлагал определять положи-
положительное направление времени («стрелу времени») по расширению
Вселенной, т. е. по увеличению расстояния между галактиками.
Если раньше галактики сближались, то и время, по Хойлу, тек-
текло в противоположную сторону по сравнению с современным.
Известна также причинная теория времени, согласно которой
временной порядок от прошлого через настоящее к будущему
характеризуется причинным порядком: от причины к следствию.
Однако, как показывает анализ, при этом допускается логический
круг: для причинного порядка неявно используется понятие вре-
временного порядка, которое необходимо вывести.
Вопрос об асимметрии временного порядка (необратимости
времени) до сих пор не имеет однозначного и окончательного ре-
решения.
По мнению авторов этой книги, направление времени содер-
содержится в самом определении категории времени как формы бы-
бытия материи, выражающей процесс взаимопереходов между бы-
бытием и небытием. Различие между настоящим, прошлым и буду-
будущим есть различие между осуществляющимся, осуществившимся
и пока еще не осуществившимся. Временной аспект изменения
выражает именно процесс становления. Акт становления, осу-
осуществления— это то вечно движущееся и вечно пребывающее со-
состояние материального мира, которое и выражается в действи*
тельности.
Отсюда видно, что «стрела времени» имеет объективное на-
направление в одну сторону — от небытия к бытию, в сторону раз-
развития предметов, их становления, постепенного формирования и
гибели как таковых. Эта необратимость направления времени су-
существует как в мире возрастающей энтропии, так и в мире
флуктуации Больцмана, как в расширяющейся, так и в сжимаю-
сжимающейся Вселенной. Определения направления времени по Больц-
Больцману или по Хойлу являются эмпирическими, удобными для
практического определения роста времени, но они есть следствия
объективного направления времени, вытекающего из содержания
самого понятия времени.
Глава 4
ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ
В начале XX в. A906—1912 гг.) в результате исследований
овойств тел при низких температурах Нернстом было установле-
установлено третье начало термодинамики, которое после долгих лет об-
74
суждения в настоящее время так же прочно обосновано, как и
первые два начала *.
Непосредственной областью применимости третьего начала
являются процессы при низких температурах. Однако оно играет
существенную роль и в более широком температурном интерва-
интервале, так как позволяет определять аддитивные постоянные в вы-
выражениях для энтропии, которые нельзя вычислить каким-либо
другим термодинамическим путем.
§ 21. Формулировка третьего начала
Открытие третьего начала термодинамики связано с нахож-
нахождением химического сродства — величины, характеризующей спо-
способность различных веществ химически реагировать друг с дру-
другом. Эта величина определяется работой W химических сил при
реакции.
Первое и второе начала термодинамики позволяют вычислить
химическое сродство W только с точностью до некоторой неопре-
неопределенной функции 1(Т) (*). Чтобы определить эту функцию,
нужны, в дополнение к обоим началам термодинамики, новые
опытные данные о свойствах тел. Поэтому Нернстом были пред-
предприняты широкие экспериментальные исследования поведения
веществ при низкой температуре. В результате этих исследова-
исследований и было сформулировано третье начало термодинамики: по
мере приближения температуры к О К энтропия всякой равновес-
равновесной системы при изотермических процессах перестает зависеть от
каких-либо термодинамических параметров состояния и в преде-
пределе (Г = 0 К) принимает одну и ту же для всех систем постоян-
постоянную величину, которую можно принять равной нулю.
Общность этого утверждения состоит в том, что, во-первых,,
оно относится к любой равновесной системе и, во-вторых, чта
при TWO К энтропия не зависит от значения любого параметра
системы. Таким образом по третьему началу
^im[SG\ x2)-S(Tt xx)]=0, D.1)
или
lim | ) =0, D.2)
г+ок \ дх }т
где х — любой термодинамический параметр (а, или At) **.
* Вопрос об удовлетворительном статистическом обосновании третьего нача-
начала является, однако, до сих пор открытым, а получившее широкое распростра-
распространение обоснование этого закона на основе невырожденности основного уровня
системы недостаточно.
** Заметим, что третье начало термодинамики, определяя предел производ-
производных (dS/dx)T при 7W0K, не определяет предела производных (dS/dT)x при
Г->0К: для большинства тел lim (dS/dT)x = 0, для некоторых же тел этот
предел отличен от нуля (•&).
75
Предельное значение энтропии, поскольку оно одно и то же
для всех систем, не имеет какого-либо физического смысла и по-
поэтому полагается равным нулю. Как показывает статистическое
рассмотрение этого вопроса, энтропия по своему существу опре-
определена с точностью до произвольной постоянной (подобно, на-
например, электростатическому потенциалу системы зарядов в ка-
какой-либо точке поля). Таким образом, нет смысла вводить некую
«абсолютную энтропию», как это делал Планк и некоторые дру-
другие ученые.
Постоянство энтропии (S-^0) при Т-+0 К согласно D.1) озна-
означает, что изотермический процесс Г=0 К является одновременно
и изоэнтропийным, а следовательно, и адиабатным *. Таким об-
образом по третьему началу нулевая изотерма совпадает с нулевой
изоэнтропой и адиабатой.
Существует ряд веществ (некоторые сплавы, глицерин, СО,
N0 и др.), для которых А5 при Г->0 К стремится к отличной от
нуля величине. Как показал тщательный анализ, это кажущееся
противоречие с третьим началом связано с «замораживанием»
некоторых веществ в метастабильных или неравновесных состоя-
состояниях, в которых при низкой температуре эти вещества могут на-
находиться длительное время (несколько дней или недель), прежде
чем придут в стабильные равновесные состояния. Когда измере-
измерения были проведены с большими промежутками времени, то ока-
оказалось, что разность энтропии AS во всех случаях исчезает при
Г-*0 К.
В настоящее время справедливость третьего начала обоснова-
обоснована для всех термодинамически равновесных систем.
§ 22. Некоторые следствия
третьего начала термодинамики
Третье начало позволяет сделать заключение о поведении
термодинамических величин при Г-*0 К. Рассмотрим некоторые
из следствий третьего начала (¦).
Недостижимость О К. Из третьего начала непосредственно
следует недостижимость температуры О К.
Действительно, охлаждение системы осуществляется повторе-
повторением следующих друг за другом процессов адиабатного расши-
расширения (при котором понижается температура) и изотермического
сжатия (при котором уменьшается энтропия). По третьему нача-
началу при изотермических процессах, когда температура близка к
О К, энтропия перестает изменяться при сжатии. Поэтому состоя-
состояние с S=0 за конечное число указанных процессов недостижимо,
а следовательно, недостижим и О К, так как согласно тому же
началу состояние с 7=0 К совпадает с состоянием S = 0. К тем-
температуре О К можно лишь асимптотически приближаться.
* Следовательно, на энтропийной диаграмме при Г=ОК ось энтропии сли-
сливается в точку, поэтому эту ось следует проводить на уровне некоторой темпе-
температуры выше ОК.
76
Это следствие третьего начала по своему содержанию экви-
эквивалентно третьему началу, т. е. если третье ь^чало неверно, то
можно достичь температуры О К, и если можнс^достичь О К, то ,
разность значений энтропии при О К должна бьгц> отлична, от
нуля ^*). По этой причине третьим началом термодинамики ча-
часто называют принцип недостижимости О К. Именно так сформу-
сформулировал это начало Нернст, который не любил понятия энтропии
и не употреблял его. Однако формулировка третьего начала в
виде закона о поведении энтропии при 7->0 К более удобна, так
как непосредственно приводит к математической записи D.2).
Поведение термических коэффициентов при Г->0 К. Термиче-
Термический коэффициент расширения
термический коэффициент давления
_ 1 /
~~ Ро [
дР
дТ
как и вообще термодинамические величины {да/дТ)А и (дА/рТ)а,
должны по третьему началу приближаться к нулю при Г~*0 К.
В самом деле, вычитая из обеих частей основного уравнения тер-
тер— T dS—?4 &i da( дифференциал d(TS), полу-
полумодинамики
чаем
D.3)
и так как d\E—TS) — полный дифференциал, то (dSJdui)T =
(дАдТ)
По третьему началу D.2) при Г->0 К энтропия перестает за-
зависеть от параметров состояния, т. е. lim ( ] =0, поэтому
г->ок \ дсц }т
lim
Г-ОК
=0.
D.4)
Если к обеим частям уравнения D.3) прибавить дифферен-
дифференциал d?dAia.i% т0
d (Е-TS + ? Atat) = —SdT +
i
dAi%
откуда — ( ) =f-^L\ и согласно уравнению D.2)
\ О A; JT \ ОТ jAi
lim
-0.
D.5)
77
В частном случае при a=V и А = Р из формул D.4) и D.5)
получаем
q пт(-дЦ =о,
и, следовательно, термические коэффициенты теплового расшире-
расширения а и давления 7 обращаются в нуль при Т-+0 К.
Принимая в формуле D.4) в качестве обобщенных сил А{ по-
поверхностное натяжение а, ЭДС гальванического элемента S
и т. д. получаем, что все эти величины при Г->0 К перестают за-
зависеть от температуры, и, следовательно, температурный коэффи-
коэффициент поверхностного натяжения до/дТ, температурный коэффи-
коэффициент ЭДС дб/дТ и т. д. должны обращаться в нуль при при-
приближении температуры к 0 К- Аналогично при a = f, 9> и т. д.
из формулы D.5) устанавливаем, что температурный коэффици-
коэффициент намагниченности (dfJdT) н и температурный коэффициент
поляризованности (д^/дТ) е обращаются в нуль при Г->0 К.
Эти выводы из третьего начала были подтверждены экспери-
экспериментально.
Вычисление энтропии и поведение теплоемкостей при Т->0 К»
Третье начало термодинамики чрезвычайно упростило вычисле-
вычисление всех термодинамических функций. До установления третьего
начала для вычисления энтропии необходимо было знать темпе-
температурную зависимость теплоемкости и термическое уравнение
состояния.
Согласно же третьему началу энтропию можно находить, зная
лишь зависимость теплоемкости от температуры и не располагая
термическим уравнением состояния, которое для конденсирован-
конденсированных тел неизвестно. Действительно, из выражений для теплоем-
костей
Cv = T(dS/dT)Vt CP=T{dS/dT)P
по третьему началу интегрированием получаем
т т
ffi ^dT. D.6)
Таким образом, задача вычисления энтропии сводится к опре-
определению лишь температурной зависимости теплоемкости. Этим
объясняется, что «проблема теплоемкости», решением которой
занимались Эйнштейн, Дебай, Борн, Крамере и другие, заняла
такое важное место в физике начала XX в.
По третьему началу энтропия при 7=0 К, как и при любой
другой температуре, конечна, поэтому интегралы в формулах
D.6) должны быть сходящимися. Это выполняется, если подын-
подынтегральные функции Су/Т и JCp/T на нижнем пределе при Т-^0 К
возрастают медленнее, чем 1/Т : Cv/T=C/Ta (C = const, 1)
поэтому
78
СУ = СГ-" = СТ" (л=1 — а>0). D.7)
Тогда Cv->0, Cp-^0 при Г->0 К.
Это следствие третьего начала в отличие от вывода о не-
недостижимости О К не эквивалентно во всей полноте самому
третьему началу, так как оно получается лишь из допущения о
конечности энтропии в пределе Т = 0 К и не исключает при этой
температуре зависимости энтропии от параметров состояния, не
имеющей места по третьему началу*. Согласно формуле D.7)
производная (dSldT)v при Г->0 К изменяется по закону
D.8)
и в пределе равна или нулю (если а>0), или постоянной вели-
величине (если а = 0), или бесконечности (если 0<а<1). Таким об-
образом, третье начало, как уже отмечалось, не определяет преде-
предела производных вида (dS/df)x при 7=0 К.
Вырождение идеального газа. Выражение для энтропии моля
идеального газа
S = CV In T{+R In (V/N)+SOt
полученное при использовании уравнения Клапейрона—Менде-
Клапейрона—Менделеева PV=RT и положения о независимости теплоемкости Су
одноатомного газа от температуры, противоречит третьему на-
началу в двух отношениях: во-первых, изменение энтропии
при изотермическом процессе, когда Г=0 К, не равно нулю и,
во-вторых, при Г->0 К энтропия стремится не к постоянной ве-
величине, а к —оо. Это указывает на то, что при низкой темпера-
температуре идеальный газ должен вести себя не по уравнению Клапей-
Клапейрона— Менделеева и закону Cv = const, а иначе. Такое отклоне-
отклонение идеального газа от классических газовых законов (получае-
(получаемых из классической статистики) называется вырождением.
Третье начало, следовательно, предсказывает вырождение
идеальных газов при низкой температуре. Как показало развитие
квантовой статистики, такое вырождение действительно имеет
место. Оно указывает на недостаточность классической механи-
механики и основанной на ней классической статистики в области низ-
низких температур. Квантовая статистика показывает, что третье
начало термодинамики является макроскопическим проявлением
квантовых свойств реальных систем при низких температурах.
Вычисление энтропийной и химической постоянных идеальных
газов. Второе начало, как известно, оставляет открытым вопрос о
* Вывод о стремлении теплоемкостей к нулю при Г->-0 К можно получить и
«з первых двух начал термодинамики, если считать, что вытекающее из этих за-
законов условие устойчивости T/Cv>0 сохраняется и при 7=0К. Однако это не
означает, что третье начало следует из первого и второго начал, поскольку рас-
рассматриваемый вывод не эквивалентен по своему содержанию третьему началу.
7§
явном виде энтропийной и химической постоянных идеального
газа, знание которых необходимо при рассмотрении равновесия в
различных системах (химические реакции, испарение, тепловая
ионизация и др-)- Третье начало может быть косвенно использо-
использовано для рецгёния этой задачи, хотя классический идеальный газ
и не удовлетворяет третьему началу.
Идея вычисления энтропийной постоянной идеального газа с
помощью третьего начала состоит в том, что рассматривается ус-
условие равновесия газа и твердого тела одного и того же веще-
вещества (равенство химических потенциалов вещества в обеих фа-
фазах), в которое входят выражения энтропии как газа, так и твер-
твердого тела. Энтропия твердого тела определяется на основе треть-
третьего начала по формуле D.6), а энтропия идеального газа вычис-
вычисляется по формуле C.39), и, таким образом, из условия фазово-
фазового равновесия определяют энтропийную постоянную газа. Энтро-
Энтропийная постоянная 50 связана с химической постоянной i газа.
Эти постоянные можно вычислить методами статистической фи-
физики. Для одноатомного газа они равны:
[(^K/2] D-9)
где k — постоянная Больцмана; h — постоянная4 Планка; т —
масса атомов газа; g — статистический вес нормального состоя-
состояния атома, зависящий от его орбитального момента L и спина s
(для инертных газов L = s = 0 и g=l). Таким образом, энтропия
моля идеального газа равна
Cv\nT±Rln+Rln kNtln.
N /i3 Nh3
D.10)
Глава 5
МЕТОДЫ ТЕРМОДИНАМИКИ
Термодинамическое исследование физических явлений осно-
основывается на использовании начал термодинамики. Само приме-
применение начал термодинамики для решения физических задач осу-
осуществляется двумя способами. В соответствии с этим различают
два метода термодинамики: метод циклов (круговых процессов)
и метод термодинамических потенциалов (или метод характери-
характеристических функций).
§ 23. Методы циклов
Метод циклов заключается в том, что для установления опре-
определенной закономерности того или иного явления рассматри-
80
вается подходящим образом подобранный обратимый цикл и к
этому циклу применяются уравнения первого
§8Q = W E.1)
и второго
^- = 0 E.2>
I |
I !
1 L
начал термодинамики. С помощью этих уравнений удается
вскрыть искомую закономерность, если выбранный цикл таков,,
что имеется возможность вычисления необходимых величин, вхо-
входящих в уравнения E.1) и E.2) для всех элементов цикла.
В большинстве случаев изучаемую систему мысленно заставляют
совершить цикл Карно. Тогда уравнение второго начала E.2)
используется в виде первой теоремы Карно о независимости КПД.
этого цикла от природы рабочего ве-
вещества; поэтому полученное с по-
мощью уравнения E.1) выражение
для КПД цикла в данной конкретной
задаче приравнивают отношению
(Ti—T2)]Ti и из полученного равенст-
равенства определяют необходимую зависи-
зависимость.
Найдем методом циклов закон из-
изменения поверхностного натяжения с
температурой. Для этого осуществим 1* 1г *
цикл Карно с жидкой пленкой в про-
волочной рамке. Изобразим этот цикл ис*
на плоскости с координатными ося-
осями 2, а B — площадь поверхности пленки, а — поверхностное
натяжение; рис. 11). Пусть вначале площадь поверхности пленки,
равна 2ь натяжение а (точка 1). Растянем пленку изотермически
до состояния 2. Поверхностное натяжение при этом не изменится,
но так как увеличение поверхности пленки связано с охлажде-
охлаждением, то, для того чтобы процесс шел изотермически, на участке
1—2 пленке сообщается теплота Q\ при температуре Т. Растянем
пленку адиабатно до состояния 3, при этом ее температура пони-
понизится на dT, а поверхностное натяжение увеличится на do. Затем:
дадим пленке возможность сначала изотермически сжаться до со-
состояния 4 (при этом придется отнять у нее количество теплоты
Q2); а потом еще адиабатно сжаться до состояния 1.
Работа W, совершенная пленкой за цикл, равна Q\ — Q2. На
диаграмме B, а) эта работа равна площади цикла и, в связи с
обходом цикла против часовой стрелки, отрицательна: W=
= — B2 — 2i)rfa (изменение а при элементарном адиабатном
процессе равно do при некотором 2). По определению КПД цик-
W B 2)d
W B2 2i)da
ла !] = __= ^ а так как пленка совершила цикл:
41 Ч?1
Т — (Т — dT) dT ~
Жарно, то Ц — - = -rjr- Приравнивая последние два
Bа — Si) da dT
выражения, получаем —— *-==—-, откуда
Q т
/ da \ __ [Qi 1
\ dT ]s~~ 22 — Si Г "
Но Qi/B2 — 2i)=r — теплота изотермического образования еди-
единицы поверхности пленки, поэтому
(ИЛ = _.!- E.3)
т. е. поверхностное натяжение с повышением температуры умень-
уменьшается, и быстрота этого уменьшения обратно пропорциональна
термодинамической температуре.
Подобным образом можно найти также зависимость давления
насыщенного пара от температуры, зависимость электродвижу-
электродвижущей силы от температуры и т. д. (*)¦
Разобранный пример показывает, как в методе круговых про-
процессов используются основные законы термодинамики и устанав-
устанавливаются искомые закономерности.
Метод циклов является одним из первых термодинамических
исследований. Карно, Клаузиус, Нернст использовали только
Этот метод.
Метод круговых процессов, с одной стороны, может быть
принципиально применен для решения любой задачи, а с другой
^стороны, он имеет тот большой недостаток, что для установления
той или иной закономерности всякий раз приходится ad hoc под-
подбирать подходящий цикл: успех решения задачи зависит от вы-
выбора необходимого цикла, сам же выбор ничем не определяется.
Как уже было сказано, чаще всего используется цикл Карно.
В настоящее время почти во всех случаях термодинамическо-
термодинамического исследования применяется метод термодинамических потен-
потенциалов.
§ 24. Метод термодинамических потенциалов
Метод термодинамических потенциалов, или метод характери-
характеристических функций, был развит Гиббсом. Исходным в этом мето-
методе является основное уравнение термодинамики
tdat, E.4)
которое, как мы покажем, позволяет для системы в различных
условиях ввести некоторые функции состояния, называемые тер-
термодинамическими потенциалами. Изменение этих функций при
изменении состояния системы является полным дифференциалом.
Метод потенциалов состоит в использовании свойства полного
82
дифференциала введенных термодинамических функций, что поз-
позволяет ^получить уравнения, необходимые для анализа того или
иного явления.
Рассмотрим вначале простые системы. В этом случае для рав-
равновесных процессов основное уравнение термодинамики имеет
вид TdS = dE-\-Ada или, если А = Р, a=V,
> = dE+PdV. E.5)
Это уравнение связывает пять функций состояния: Г, S, Еу Р
и V. Само же состояние простой системы определяется двумя па-
параметрами. Поэтому, выбирая из пяти названных величин две в
качестве независимых переменных, мы получаем, что основное^
уравнение содержит еще три неизвестные функции. Для их опре-
определения необходимо к выражению E.5) добавить еще два урав-
уравнения, которыми могут быть термическое и калорическое уравне-
уравнения состояния:
P = P(V, T), E.6)
? = ?(У, Г), {5.7),
если в качестве независимых параметров выбраны V и Т.
Однако при некоторых других независимых переменных ос-
основное уравнение термодинамики E.5) позволяет найти все три
неизвестные функции, если к нему добавить не два, а лишь одно
уравнение. В самом деле:
I. Если независимыми переменными являются S и V (входя-
(входящие в уравнение E.5) под знаком дифференциала), то для опре-
определения других трех переменных с помощью уравнения E.5) до-
дополнительно нужно знать лишь одно уравнение для энергии К
как функции этих переменных:
E = E(St V). E.9>
Действительно, зная выражение E.9), можно с помощью*
уравнения E.5), которое мы запишем в виде
простым дифференцированием определить обе другие термиче-
термические переменные:
r = (iL\ , р = -(М.) . E.11>
\ OS /у \ OV Js
Если взять вторые производные от ?(S, V), то (d2E/dS2)v=^
г, откуда
С Т (dE'dsh
V (d*E/dS*) (d2E/dS%>
д2Е \ __(j№_\ _JL/r К —v( d*E
83;
Учитывая, что dE — полный дифференциал, можно, даже не
зная явного вида функции E(Vt S)> приравнивая смешанные про-
д2Е \д2Е
изводные = 4 • получить уравнение
dS dv oV OS
iL\ = _(*L\ , F.12)
\dv)s \ds)v' V '
которое связывает два свойства системы — изменение температу-
температуры при ее адиабатном расширении и изменение давления при
лзохорном сообщении теплоты системе. Установление таких свя-
связей и составляет содержание метода термодинамических потен-
потенциалов.
Уравнение E.12) можно записать в виде
аУ) E13)
d(Vt S) d{Vt S) * v
откуда, если
д{Т> S)
d(V, S)
E.14)
получаем равенство единице якобиана преобразования при пе-
переходе от (Р, V)- к (Г, 5)-переменным:
d(p'v>=l. E.15)
d(TtS) V ;
Если в каком-либо состоянии производная (dT/dV)s обра-
обращается в нуль, якобиан преобразования E.15) в этом состоянии
не определен, но может быть доопределен предельным значением,
равным также единице.
Таким образом, внутренняя энергия Е в переменных S и V
является характеристической функцией, поскольку в этом случае
другие переменные (Т и Р) определяются дифференцированием Е
по S и V. Иначе говоря, производные от E(S, V) по характери-
характеристическим переменным выражают все термодинамические свой-
свойства системы: первые производные определяют термические свой-
свойства, а вторые—калорические.
Внутренняя энергия Е в переменных S и V называется также
термодинамическим потенциалом, поскольку значение давления
P = —(dE/'dV)s
выражается через нее так же, как сила через потенциальную
энергию U в механике (Fx=—dU/дх, Fy=—dU/ду, Fz=—dU/dz).
Следует отметить, что функция ?=?'E, V) в качестве термо-
термодинамического потенциала с практической точки зрения неудоб-
неудобна тем, что одна из независимых переменных — энтропия 5 — не-
лосредственно, подобно величинам V, Р, Г, не может быть изме-
измерена.
2. Если независимыми переменными являются не S и V, а ка-
>кие-либо другие величины простой системы, то энергия Е от этих
84
других переменных не является характеристической функцией
или потенциалом. Однако оказывается, что и при некоторых дру-
других независимых переменных также можно вместо двух уравне-
уравнений P = P(Vy T) и E=E(V, T) выбрать одну функцию от этих
переменных, которая при этом будет характеристической функ-
функцией подобно Е в переменных S и V.
Действительно, если независимыми переменными простой си-
системы являются Г и У, то, преобразуя уравнение E.5) так*, что-
чтобы в него входили дифференциалы dT и dV (вычитая из обеих
частей уравнения E.5) дифференциал d(TS))y получаем
—SdT=d(E — TS)+PdV.
Обозначая Е — TS = Fy находим
dF=—SdT — PdV, E.16)
откуда
S = -(dF/dT)Vi P=—(dF/dV)T. E.17)
Второе из уравнений E.17) представляет собой термическое
уравнение состояния; зная F=F(V, 7), можно найти из формулы
E.17) уравнение P=P{Vt T).
Вторые производные от функции F позволяют определить ка-
калорические величины — теплоемкость Cv и коэффициент сжимае-
сжимаемости р (или изотермический модуль упругости /Ст=1/р):
г -—
V
V0\dP )т
а также получить уравнение
(*L) =AL) , E.18)
устанавливающее связь между двумя свойствами системы — из-
изменением энтропии при ее изотермическом расширении и изме-
изменением давления при изохорном нагревании. Это уравнение мож-
можно получить даже не зная явного вида функции F(V, T).
Таким образом, функция F в переменных V и Т является ха-
характеристической функцией, или термодинамическим потенциа-
потенциалом. Эта функция F=E ~TS называется энергией Гельмгольца
(свободной энергией). Как следует из E.13), при изотермических
процессах работа совершается системой не за счет убыли вну-
внутренней энергии Е (как при адиабатных процессах), а за счет
убыли функции F. В самом деле, из формулы E.13) при 7=
= const находим PdV=—dF.
Таким образом, при изотермических процессах свободная
энергия F=E — TS играет такую же роль, как и внутренняя
энергия при адиабатных процессах. Величина TS называется
связанной энергией. (Заметим, что в то время как в механике
энергия системы состоит из кинетической и потенциальной, в тер-
* Такое преобразование дифференциальной формы называется преобразова-
преобразованием Лежандра.
85
модинамике внутренняя энергия делится на свободную и свя-
связанную.)
3. Если за независимые переменные выбрать Т и Р, то харак-
характеристической функцией будет функция G(T, Р)=Е—TS-{-PV.
Действительно, перейдем в уравнении E.13) с помощью преоб-
преобразования Лежандра к переменным Т и Р, прибавив к обеим ча-
частям дифференциал d(PV), тогда d(F-\-PV) =—SdT-\-VdP или
dG = —SdT+VdP,
где G = F+PV = E — TS+PV. E.19)
Из уравнения E.19) получаем
S=-(™-\ , V^(^) . E.20)
\ дТ )р \дР JT V '
Второе из уравнений E.20) позволяет найти термическое
уравнение состояния. Таким образом, функция G(Tt P)=E —
— TS-\-PV является характеристической функцией в переменных
Т и Р и называется энергией Гиббса (термодинамический потен-
потенциал Гиббса).
Вторые производные от G (Г, Р) дают теплоемкость
ср .
коэффициент сжимаемости
дЮ
и уравнение
Vo [ дР )т
дР )т
1 / дЮ
Vo
дТ
E.21)
связывающее два соответствующих свойства системы, которое
можно получить даже не зная явного вида функции G (Г, Р). Так
же как убыль энергии Гельмгольца при изотерми-
изотермических процессах равна работе системы, убыль
энергии Гиббса при изотермических процессах рав-
равна работе при адиабатных процессах расширенной
системы, состоящей, например, в случае газа в за-
закрытом цилиндре из газа и поршня с грузом. Энер-
Энергия такой системы (рис. 12) равна внутренней энер-
энергии Е газа и потенциальной энергии Psh=PV
поршня с грузом: E=E+PV, откуда
dE=dE+PdV+VdP = :
Рис. 12
При адиабатных процессах убыль энергии сис-
системы равна ее работе, поэтому —(dE)s:=—VdP и,
следовательно, работа расширенной системы рав-
на
* Из выражения E.22) видно, что внутренний параметр изучаемой системы
(газа) — давление Р — является внешним параметром расширенной системы.
86
—VdP. E.22J
Из формулы E.19)' видно, что при изотермических процессах
_(dG)T = — VdP. Тогда, учитывая соотношение E.22), получаем
— (dG)T = 6№paciii. E.23)
Если на систему кроме механических сил действуют и дру-
другие, немеханические, силы (электрические, магнитные и т. д.), то
можно установить и другой физический смысл изменения энер-
энергии Гиббса G. В самом деле, пусть на систему кроме силы дав-
давления действуют еще немеханические силы, тогда
TdS=dE+PdV+6WHM.
С помощью преобразования Лежандра (прибавляя к обеим
частям выражения E.23) дифференциал d(—TS+PV)), перехо-
переходим от дифференциалов dS и dV к дифференциалам независимых
переменных Г и Р. Тогда
SdT+VdP = d(E — TS+PV)+6Wli
dG=—SdT+VdP —
и
откуда видно, что при изотермически-изобарных процессах в
сложных системах убыль термодинамического потенциала равна
работе системы против действующих на нее немеханических сил:
— \dO)pt t — ovvhm. E.24)
Важное значение энергии Гиббса G для термодинамики сле-
следует из того, что в состоянии равновесия сложной системы ха-
характеристические переменные Р и Т одинаковы во всех частях
системы и поэтому являются наиболее удобными.
4. Если независимыми переменными простой системы явля-
являются S и Р, то характеристической функцией будет
ЯE, P)=E+PV. E.25)
Действительно, если в уравнении E.5) перейти от дифферен-
дифференциалов dS и dV к дифференциалам переменных S и Р, прибав-
прибавляя к обеим частям уравнения E.5) дифференциал d(PV), то
гили
dH=TdS+VdP. E.26)
Функция E.25) называется энтальпией и является термодина-
термодинамическим потенциалом при независимых переменных S и Р, по-
поскольку производные H(Sy Р) по S и Р дают
T={dH/dS)P,
87
E.27)
или
т (dH/dS)p
ор ~~ (d2H/dS2)p (d2H/dS2)F
I 5P« )s~~\ dP Is
ИЛИ
iXS"~ (d*H/dP2)s *
Из формулы E.26), даже не зная явного вида функции
//(S, Р), находим уравнение
(dT/dP)8=(dV/dS)p, E.28)
которое связывает два свойства системы. Уравнение E.27) пред-
представляет собой уравнение адиабаты, так что если энтальпия как
потенциал известна, то уравнение E.27) позволяет простым диф-
дифференцированием Н по Р найти уравнение адиабаты системы.
Физический смысл энтальпии состоит прежде всего в том, что
при изобарных процессах изменение энтальпии равно поглощен-
поглощенному количеству теплоты: (dH)P= (TdS)P= (8Q)P = CPdT и СР—
= (дН/дТ)Р.
По этой причине функцию Н часто называют также тепловой
функцией или теплосодержанием. Кроме того, поскольку энталь-
энтальпия E.25) равна энергии Е расширенной системы, а при адиа-
адиабатных процессах убыль энергии равна работе, то, очевидно, при
этих процессах убыль энтальпии системы равна работе расши-
расширенной системы:
И наконец, если на систему действуют кроме механической
силы давления также и другие немеханические силы, то
TdS^dE+PdV+bW™,
= d(E+PV) -
откуда видно, что при адиабатно-изобарных процессах в слож-
сложной системе убыль энтальпии E.25) равна работе системы про-
против немеханических сил:
Все термодинамические потенциалы являются, во-первых, ад-
аддитивными и однозначными функциями состояния, и, во-вторых,
их убыль при соответствующих условиях определяет работу си-
системы против действующих на нее сил. Кроме того, они позво-
позволяют с помощью основного неравенства термодинамики для не-
статических процессов C.59) установить общие условия термоди-
термодинамического равновесия и устойчивости систем при определенных
условиях (см. гл. 6).
Различные термодинамические потенциалы связаны между
собой так, что если известны одни из них, то можно найти дру-
другие. При этом внутренняя энергия Е связана с энергией Гельм-
гольца F таким же дифференциальным уравнением, как энталь-
энтальпия Н с энергией Гиббса G. Действительно, из F = E— TS и вы-
выражения E.14) получаем уравнения Гиббса—Гельмгольца
-) E.29)
дТ )v v
для энергии Гельмгольца, а из G = H — TS и выражения E.19)
E30)
для энергии Гиббса.
В общем случае простой системы, когда ее состояние опреде-
определяется температурой и внешним параметром а, уравнение Гибб-
Гиббса—Гельмгольца для энергии Гельмгольца имеет вид
Интегрируя уравнение E.29) или E.30), можно найти F или
G соответственно по Е или Я. Чтобы его выполнить, заметим,
что при 0 К последнее слагаемое в уравнении E.29) отпадает,
если (dF/dT)v остается конечной или возрастает при Г-^0 К
медленнее, чем 1/Т. Делая относительно (dF/dT)v одно из этих
двух предположений, из уравнения E.29) при Г=0 К имеем Fo =
=2?о. Вычитая это уравнение из уравнения E.29), получаем
или
F-Fo
дТ
= -(?-?„). E.32)
Уравнение E.32) является линейным неоднородным диффе-
дифференциальным уравнением. Соответствующее однородное уравне-
уравнение имеет вид
д I F-Fo
5Т, , ,=0. E-33)
Общее решение уравнения E.32) равно сумме частного реше-
решения этого уравнения и общего решения однородного уравнения
E.33), которое, очевидно, равно F — FQ=IT, I — const. Частное
решение уравнений E.32) можно записать так: F~~F° _,
89
г
dT. Таким образом, общее решение уравнений
Е-Ео
Гиббса—Гельмгольца E.29) и E.30) таково:
т
=E0—T$ E~2Eo dT + IT, E.34)
2
о
т
G=G0—T Г Я~~аЯо dT+IT, E.35)
о
где / — термодинамически неопределенная постоянная, завися-
зависящая от объема в E.34) и от давления в E.35). Эту постоянную
нельзя определить с помощью первого и второго начал термоди-
термодинамики (чем и обусловлено ее название). Знание постоянной /
было необходимо при вычислении химического сродства (*). Ре-
Решение этой проблемы привело Нернста к открытию третьего на-
начала термодинамики, которое непосредственно приводит к / = CL
Действительно, дифференцируя выражение E.34) или E.35) по
температуре и полагая по третьему началу (dFjdT)v =
= (dG/dT)P = —S = 0 при 7 = 0 К, получаем / = 0.
Таким образом, из выражений E.34), E.35) получаем
t^-dT. E.36)
Термодинамические потенциалы Е, F, G, Я можно предста-
представить графически в пространстве соответствующих независимых
переменных в виде поверхностей, которые обычно строят на ос-
основании опытных данных. Эти поверхности, а следовательно, и
свойства самого вещества исследуются потом с помощью диффе-
дифференциальной геометрии. Поэтому геометрические методы в тер-
термодинамике имеют большое значение. Одна из важных термоди-
термодинамических работ Гиббса так и называется «Метод геометриче-
геометрического представления термодинамических свойств при помощи по-
поверхностей».
Как видно из уравнений E.10) — E.28), зная хотя бы один из
термодинамических потенциалов, можно определить как терми-
термические, так и калорические свойства системы, т. е. получить пол-
полную информацию о ее термодинамических свойствах. Каждый
термодинамический потенциал, следовательно, содержит в себе
полностью все характеристики системы.
Установление существования таких функций состояния яв-
является крупным успехом термодинамики. Однако, оставаясь в
рамках термодинамики, этим успехом не удается воспользо-
воспользоваться в полной мере. Дело в том, что начала термодинамики
сами по себе не позволяют найти выражения для термодинами-
90
ческих потенциалов в виде явных функций соответствующих ха-
характеристических переменных. В термодинамике метод потенциа-
потенциалов состоит в использовании уравнений E.12), E.16), E.20) и
E.28), которые устанавливают связи одних свойств системы с
другими ее свойствами. Эти уравнения, как мы видели, получа-
получаются из основного уравнения термодинамики E.5) и поэтому ча-
часто сами называются основными уравнениями или соотношения-
соотношениями Максвелла.
Только для двух систем можно вычислить термодинамические
потенциалы с помощью начал термодинамики: для идеального
газа и для равновесного излучения, поскольку для них известны и
термические и калорические уравнения состояния. Для всех же
других систем термодинамические потенциалы находят или из
опыта, или методами статистической физики и потом с помощью
полученных термодинамических соотношений определяют уравне-
уравнения состояния и другие термодинамические свойства.
Из этого видна органическая связь термодинамики и стати-
статистической физики. Обе они имеют один и тот же предмет иссле-
исследования, но само исследование ведется с разных исходных пози-
позиций. Для полного и всестороннего изучения свойств физических
систем необходимо одновременное привлечение и термодинами-
термодинамики, и статистической физики.
Для газов термодинамические функции чаще всего вычисля-
вычисляются методами статистической физики, для жидкостей же и твер-
твердых тел они обычно находятся экспериментально с помощью ка-
калорических определений теплоемкости.
Найдем выражение внутренней энергии Е как термодинамиче-
термодинамического потенциала для идеального (одноатомного) газа. Извест-
Известно, что для такого газа внутренняя энергия равна
E = CVT+EO.
Это выражение для Е не является, однако, термодинамиче-
термодинамическим потенциалом; пользуясь им, нельзя определить ни термиче-
термическое уравнение состояния идеального газа, ни другие его терми-
термические свойства. Внутренняя энергия будет термодинамическим
потенциалом (характеристической функцией), если она выраже-
выражена как функция переменных S и V. Для идеального газа это лег-
легко сделать, поскольку известно, что S = CVln T+R In V+^o, от-
откуда
Используя это выражение для внутренней энергии как термо-
термодинамического потенциала, можно, наоборот, с помощью формул
E.10) и E.11) найти термическое уравнение состояния идеаль-
идеального газа PV=RT и уравнение его адиабаты PV t
91
В качестве первой задачи, решаемой методом термодинамиче-
термодинамических потенциалов, получим найденное уже методом циклов урав-
уравнение для зависимости поверхностного натяжения от температу-
температуры, с тем чтобы на этом общем примере убедиться в преимуще-
преимуществе метода термодинамических потенциалов. Результат, конеч-
конечно, будет одним и тем же, так как та или иная закономерность
не зависит от метода изучения, а определяется природой яв-
явления.
Будем исходить из выражения для дифференциала поверх-
поверхностной свободной энергии пленки. Пусть 2 — площадь поверх-
поверхности пленки (ее внешний параметр а). Так как элементарная
работа увеличения поверхности пленки на (TZ равна 6W=—odXt
где а — поверхностное натяжение, то обобщенная сила, сопря-
сопряженная параметру 2, будет Л = —а и дифференциал энергии
Гельмгольца для пленки равен dF = —SdT-\-oc&>, откуда
\ as )т~* \
от
L
т
что совпадает с выражением E.3), найденным методом циклов.
Получение этого выражения методом термодинамических потен-
потенциалов сводится к нахождению лишь дифференциала энергии
Гельмгольца пленки и использованию свойств полного диффе-
дифференциала.
В заключение отметим, что применение термодинамики к ре-
решению различных физических задач сильно облегчается исполь-
использованием свойств якобианов (определителей Якоби). Это связа-
связано с тем, что обычные частные производные, а они входят во
многие термодинамические соотношения, представляются в виде
якобианов.
Приведем свойства часто используемых якобианов второго
порядка (с двумя независимыми переменными х> у)\
J{U} v)=;
д(х, у)
дх
ду
ду \ / dv \
дх )у{ ду ];
' у \ ду /х
Как следует из определения:
д (ц, у) __ I да
а (х, у) \ дх
ду
дх
1)
(и, у) а (ц, у)
(х, у) д(у, х)
3) J(ku, v)*=J(u, kv)=kJ(u, v),
и
4)
что позволяет оперировать с якобианами как с дробями,
5) J(u, v)J(z, y)+J(v, z)J(u, y)+J(z, u)J(v, */) =0
тождество Якоби (*).
§ 25. Термодинамические потенциалы
сложных систем и систем
с переменным числом частиц
Выше мы нашли, какие функции при тех или иных независи-
независимых переменных простой системы являются ее термодинамиче-
термодинамическими потенциалами. Установим теперь термодинамические по-
потенциалы сложной системы, подверженной действию нескольких,
внешних сил, и системы с переменным числом частиц.
Будем вначале исходить из основного уравнения термодина-
термодинамики C.24) для сложной системы
Из этого уравнения непосредственно получаем, что если со-
состояние сложной системы определяется обобщенными координа-
координатами (внешними параметрами а* и энтропией S), то ее термоди-
термодинамическим потенциалом является внутренняя энергия E(S, at)^
дифференциал которой dE=TdS—У]Л^а*.
Если состояние системы определяется внешними параметрами
аг и температурой Т, то термодинамическим потенциалом яв-
является энергия Гельмгольца F=E — TS, дифференциал которой*
Если состояние системы определяется температурой Т и обоб-
обобщенными силами Aif сопряженными внешним параметрам аи та?
термодинамическим потенциалом системы является (обобщенная)"
энергия Гиббса
дифференциал которой
93.
Если независимыми параметрами системы являются энтропия
S и обобщенные силы Аи то термодинамическим потенциалом
является (обобщенная) энтальпия
? E.38)
i
дифференциал которой dH = TdS + J]
i
Таким образом, в случае сложной системы выражения энер-
энергии Гиббса E.37) и энтальпии E.38) имеют по сравнению с со-
соответствующими выражениями этих потенциалов для простой си-
системы дополнительные аддитивные члены" вида А^. Выражение
же для энергии Гельмгольца F = E — TS при переходе к сложной
системе не изменяется. Однако если состояние сложной системы
определяется переменными Т и Р и внешними параметрами ai
(кроме объема), то термодинамическим потенциалом, как и в
случае простой системы, будет энергия Гиббса G — E — TS-\-PV,
дифференциал которой [dG=--—SdT + VdP—J]A,dat-.
i
Аналогично, если Р, 5 и внешние параметры (кроме объ-
объема) — независимые переменные сложной системы, то термоди-
термодинамическим потенциалом является энтальпия H = E+PV, диффе-
дифференциал которой dH = TdS + VdP—
i
До сих пор мы рассматривали системы, которые при взаимо-
взаимодействии с другими телами обмениваются только энергией (за-
(закрытые системы или системы с постоянным числом частиц). Од-
Однако в термодинамике широко изучаются также системы, в кото-
которых число частиц при равновесных процессах изменяется (систе-
(системы с переменным числом частиц, или открытые системы).
Изменение числа частиц в системе может вызываться различ-
различными причинами. Например, в случае равновесной системы, со-
состоящей из жидкостей и ее насыщенного пара, при изменении
объема всей системы частицы из жидкости переходят в газ (или,
наоборот, из газа в жидкость), при этом полное число частиц в
обеих фазах остается постоянным, но в каждой фазе оно разное.
Изменение числа частиц происходит также в системах, в кото-
которых при изменении температуры или других параметров проис-
происходят химические реакции. Третьим примером системы с пере-
переменным числом частиц является излучение. Равновесное излуче-
излучение представляет собой совокупность квантовонеразличимых
частиц — фотонов, которые в отличие от обычных классических
частиц обладают и корпускулярными и волновыми свойствами.
Число этих частиц при изменении температуры в результате по-
поглощения и излучения света стенками будет разным.
Современная физика при рассмотрении систем из элементар-
элементарных частиц все больше и больше устанавливает наличие в при-
94
роде процессов, при которых не только число частиц определен-
определенного сорта, но и общее число частиц в результате взаимопревра-
взаимопревращения их в системе не сохраняется. Состояние системы с пере-
переменным числом частиц характеризуется параметрами au...,ant,
Т и числом частиц данного сорта N\,..., Nr,... или соответствую-
соответствующими концентрациями Ct =Nt / J^Nk.
k
Внутренняя энергия системы с переменным числом частиц:
изменяется не только за счет сообщения теплоты и совершения
работы системой, но и за счет изменения числа частиц в систе-
системе, поэтому по первому началу dE = 6Q—6W + J^fi^dA^, гДе
iik — изменение числа частиц сорта ky обусловлен-
обусловленное в общем случае обменом с окружающей средой deNk и хими-
химическими реакциями dtNh (по закону сохранения массы ?
k
= О, mk — массаж-частиц).
При равновесных процессах 8Q = TdS и 61^ ^= J? Д-йа*, поэто-
i
му основное уравнение термодинамики для систем с переменным
числом частиц в таких системах принимает вид
TdS=dE + ? Atdat—% \ikdNk, E.39)
t ik
а при неравновесных процессах (см. C.59))
TdS >dE + % A.dat -2 iikdNk. E АО}
t k
Величина
lik= (dE/dNk)s,a,
называется химическим потенциалом k-то сорта частиц.
С помощью основного уравнения E.39) легко получить диф*
ференциалы для всех термодинамических потенциалов систем с
переменным числом частиц. Рассмотрим для простоты системы,
подверженные действию только всестороннего давления Р. Тогда
получаем следующие выражения:
E.41)
для дифференциала внутренней энергии;
dF = dE —TdS— SdT = —SdT—PdV + ? yLtdNt E.42)
i
для дифференциала энергии Гельмгольца F=E—TS;
dG=* —SdT + VdP + ? pidNi E.43)
i
95
для дифференциала энергии Гиббса G = E—TS + PV;
dH = TdS + VdP + '? \itdN{ E.44)
для дифференциала энтальпии H=E-\-PV.
Химический потенциал из этих выражений равен
п^(Щ =AL) =(Щ =(*а\ , E.45)
^ \dN;)v,s \dNiJv.T \dNi)p,T \dN?')Pts
Таким образом, \i можно получить дифференцированием лю-
любого из термодинамических потенциалов по числу частиц. Одна-
Однако при этом он будет в каждом случае выражен через различные
независимые переменные.
Как уже отмечалось, все термодинамические потенциалы яв-
являются аддитивными функциями, т. е. их величины для совокуп-
совокупности нескольких тел равны сумме их значений для каждого
тела. В случае системы из одинаковых частиц это означает, что
при изменении массы вещества или числа частиц N в некоторое
число раз эта величина изменяется во столько же раз. Другими
словами, можно сказать, что аддитивная термодинамическая ве-
величина должна быть однородной функцией первого порядка отно-
относительно аддитивных переменных. Следовательно,
E = Nfx{VIN,SfN), F=Nf2(V/N,T)y
E.46)
G = Nfz(Py Г), H = NU(P,S/N).
Из системы E.46) получаем
\L=(dG/dN)ptT = fz(T, P), E.47)
т. е. химический потенциал равен энергии Гиббса на одну части-
частицу и, следовательно,
G^^N^vG, E.48)
тде v — число молей, G — термодинамический потенциал моля
вещества.
Как видно из формулы E.47), химический потенциал яв-
является функцией Р, Т и не зависит от числа N частиц.
Аддитивность термодинамических потенциалов выполняется
лишь постольку, поскольку можно пренебречь взаимодействием
отдельных частей тела» Поэтому для смеси нескольких веществ
(например, для смеси нескольких жидкостей) термодинамиче-
термодинамические потенциалы не равны суммам термодинамических потенциа-
потенциалов отдельных компонентов смеси. Исключение составляет лишь
смесь идеальных газов, так как взаимодействием их молекул
можно пренебречь. Однако соотношения E.48) обобщаются на
любую смесь веществ, т. е. во всех случаях энергия Гиббса сме-
смеси равна
E A- E.49)
i i
<96
В самом деле, так как числа Nu N2,... частиц, от которых
зависит энергия Гиббса, являются экстенсивными переменными,
то
G(P, T; oNu aN2,...)=aG(P, Г; NUN2,...).
Дифференцируя это равенство по а и полагая а=1, получаем
Но согласно соотношениям E.45) dG/dNi = \jLU и поэтому по-
получаем равенства E.49).
Для равновесного излучения \х = 0 (см. § 43). Это, как пока-
показывает статистическая физика, соответствует тому, что общее
число частиц в системе не является заданным, а зависит от тем-
температуры.
При изучении систем с переменным числом частиц чаще всего
употребляется такой термодинамический потенциал, дифферен-
дифференцирование которого по соответствующим характеристическим пе-
переменным позволяет найти числа N{ частиц в системе каждого
сорта.
Найдем этот потенциал и дифференциальное его выражение,
для чего перейдем в формуле E.42) с помощью преобразования
Лежандра к дифференциалам переменных У, 7, ji*. Тогда
dQ= — SdT—PdV—JX-фг, E.50)
i
где функция
QG\ V, \ii)=E-TS-%VLiNt=F-G= -PV E.51)
называется большим термодинамическим потенциалом. Из фор-
формулы E.51) находим:
д/ _ dQ о дЯ р дй
iV i — — , о —
д\ь? дТ dV '
При неравновесных процессах из основного неравенства тер-
термодинамики для систем с переменным числом частиц E.40) при
независимых переменных V, Т\..., |яг-,..., \ik,... имеем
dQ< —SdT—PdV—YtNidyii. E.52)
i
Внутренняя энергия системы (см. E.41)) является функцией
только аддитивных (экстенсивных) независимых переменных, и
так как это однородная функция первого порядка, то по теореме
Эйлера об однородных функциях имеем
dS )v,n? \ dV
4 Зак. 245
Подставляя в это выражение вместо производных их значе-
значения из E.41), имеем
E.53)
Дифференцируя E.53) и сравнивая полученное выражение с
уравнениями E.41), получаем важное в термодинамике уравне-
уравнение Гиббса—Дюгема
SdT—VdP +%NtdvLi=O. E.54)
Глава 6
УСЛОВИЯ РАВНОВЕСИЯ
И УСТОЙЧИВОСТИ
ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
Основное уравнение термодинамики для квазистатических
процессов позволяет, как мы видели, ввести ряд термодинами-
термодинамических потенциалов, с помощью которых можно исследовать по-
поведение термодинамических систем при этих процессах. Покажем
теперь, что основное неравенство термодинамики для нестатиче-
нестатических процессов дает возможность с помощью введенных термо-
термодинамических потенциалов установить общие условия термоди-
термодинамического равновесия и устойчивости различных систем. С точ-
точки зрения термодинамики эти условия являются достаточными;
однако, допуская, в соответствии с опытом, существование флук-
флуктуации в системах (и, следовательно, выходя за рамки исходных
положений термодинамики), можно доказать, что они являются
также и необходимыми.
В применении к той или иной конкретной термодинамической
системе общие условия равновесия и устойчивости дозволяют
получить частные (или конкретные) для данной системы условия
ее равновесия и устойчивости (которые мы будем называть про-
просто условиями равновесия и устойчивости).
§ 26. Общие условия термодинамического
равновесия и устойчивости
Теория термодинамического равновесия была развита Гибб-
сом по образцу механической статики Лагранжа, т. е. путем
обобщения и распространения принципа виртуальных перемеще-
перемещений на термодинамические системы.
Из механики известно, что механическая система при идеаль-
идеальных связях находится в равновесии, если сумма работ всех за-
задаваемых сил при любом виртуальном перемещении системы
равна нулю (принцип виртуальных перемещений). Записывая
98
аналитически этот принцип (общее условие равновесия) в виде
уравнения и решая его совместно с уравнениями, определяющи-
определяющими виртуальные перемещения, можно найти конкретные условия
равновесия механической системы в каждой данной задаче.
Уравнения, которым удовлетворяют виртуальные перемещения,
и уравнение принципа виртуальных перемещений записываются
следующим образом.
Пусть состояние механической системы определяется коорди-
координатами <7ь ...,<7п, а наложенные на систему связи выражаются
условиями
М)О A 2
Тогда перемещения 8qit...j8qn, допускаемые этими связями и
называемые виртуальными или возможными перемещениями,
очевидно, удовлетворяют уравнениям
У-^.=о. F.D
Если Qi — обобщенная сила, сопряженная координате qu то
принцип виртуальных перемещений имеет вид
0. F.2)
?=1
Решая совместно уравнения F.1) и F.2) методом неопределен-
неопределенных множителей Лагранжа, можно найти конкретные условия
равновесия данной механической системы.
Распространим этот способ определения условия равновесия
на термодинамические системы.
Состояние равновесия термодинамической системы опреде-
определяется температурой - Т и внешними параметрами п\9 ..., аПу ха-
характеризующими отношение системы к внешним телам.
Согласно второму исходному положению термодинамики при
равновесии все внутренние параметры являются функциями
внешних параметров и температуры, и поэтому, когда щ и Т за-
заданы, они не нужны для определения состояния равновесной си-
системы. Если система отклонена от состояния равновесия, то вну-
внутренние параметры уже не являются функциями только внешних
параметров и температуры. Поэтому неравновесное состояние
необходимо характеризовать дополнительными независимыми па-
параметрами. Это позволяет рассматривать неравновесную систему
как равновесную, но с большим числом параметров и соответ-
соответствующих им обобщенных сил, «удерживающих» систему в рав-
равновесии, причем термодинамические функции системы в неравно-
неравновесном состоянии будем считать равными значениям этих функ-
функций у равновесной системы с дополнительными «удерживающи-
«удерживающими» силами *.
* Роль таких сил играют внешние поля и адиабатные перегородки, отде-
отделяющие одну часть системы от другой, если температуры этих частей различны.
4* 99
На основе такого представления, рассматривая выход систе-
системы из состояния равновесия как результат виртуальных отклоне-
отклонений внутренних параметров от их равновесных значений, можно,
пользуясь основным неравенством термодинамики C.59) для не-
нестатических процессов, получить общие (т. е. для любых систем)
условия термодинамического равновесия и устойчивости. При
этом, поскольку состояние термодинамических систем опреде-
определяется не только механическими параметрами, но и специально
термодинамическими (температура, энтропия и др.) и другими
параметрами, вместо одного общего условия равновесия для ме-
механических систем F.2) для термодинамических систем их бу-
будет несколько в зависимости от отношения системы к внешним
телам (адиабатная система, изотермическая система и др.)-
Решая в каждом таком случае общее условие равновесия си-
системы совместно с уравнениями для виртуальных измерений вну-
внутренних параметров, можно найти конкретные условия равнове-
равновесия термодинамических систем.
Уравнения для виртуальных изменений внутренних параме-
параметров находят аналогично F.1). Пусть система обладает т вну-
внутренними параметрами &ь..., Ът, которые при равновесии прини-
принимают значения fei°,..., b°m. Эти параметры, вообще говоря, свя-
связаны некоторыми условиями в виде
МЬь...,Ьт)=0 E=1, 2,..
Изменения внутренних параметров, допускаемые этими свя-
связями (виртуальные изменения), очевидно, удовлетворяют урав-
уравнениям
т
Найдем общие условия равновесия и устойчивости термоди-
термодинамической системы.
Изолированная система (jE^const, l/=const, Af = const). Ос-
Основное неравенство термодинамики для неравновесных процессов
TdS>dE+PdV F.3)
такой системы дает dS>0, т. е. энтропия изолированной системы
при неравновесных процессах возрастает. Когда эти процессы
прекратятся и наступит устойчивое равновесие, энтропия систе-
системы, очевидно, будет максимальна.
Таким образом, общим условием устойчивого равновесия изо-
изолированной системы является максимальность ее энтропии. Обо-
Обозначая энтропию системы в неравновесном состоянии 3, в равно-
равновесном 50 и разность S — S° = AS, можно записать общее усло-
условие устойчивого равновесия изолированной системы как условие
максимума энтропии в виде
AS<0, или 6S = 0, 62S<0. F.4)
10Q
Это значит, что первая вариация энтропии равна нулю, а вто-
вторая меньше нуля. Равенство нулю первой вариации является
лишь необходимым условием экстремума и не обеспечивает того,
чтобы энтропия имела именно максимум. Достаточным условием
максимума энтропии является отрицательное значение ее второй
вариации, которое и обеспечивает устойчивость равновесия. Если
же при 6S = 0 вторая вариация энтропии положительна (минимум
¦энтропии), то соответствующее состояние системы будет равно-
равновесным, но совершенно неустойчивым *, так как благодаря флук-
туациям в ней начнутся неравновесные процессы, которые и при-
приведут ее в равновесное состояние с максимумом энтропии. Так
как дальше энтропия расти не может, то это равновесие будет
устойчивым. Таким образом, равенство 6S = 0 определяет общее
условие равновесия, а неравенство 62S<0 — общее условие устой-
устойчивости равновесия изолированных термодинамических систем.
Эти условия являются достаточными, так как если бы система,
имея максимальную энтропию, не находилась в устойчивом рав-
равновесии, то при приближении к нему ее энтропия начала бы ра-
расти, что противоречит предположению о ее максимальности. До-
Доказать необходимость максимальной энтропии при устойчивом
равновесии изолированной системы исходя из основного неравен-
неравенства F.3) нельзя, так как из него не следует, что равновесие не-
невозможно при немаксимальной энтропии. Однако принимая во
внимание молекулярную природу термодинамических систем и
наличие обусловленных ею флуктуации внутренних параметров,
видим, что состояние равновесия без максимума энтропии невоз-
невозможно, так- как благодаря этим флуктуациям в системе возни-
возникают неравновесные процессы, сопровождающиеся ростом энтро-
энтропии и приводящие систему к равновесию при максимальной эн-
энтропии.
Таким образом, наличие флуктуации в системах приводит к
необходимости максимума энтропии при равновесии, и, следова-
следовательно, всякий раз, когда это условие не выполнено, система не
находится в устойчивом равновесии. Поэтому общее условие F.4)
является необходимым и достаточным условием устойчивости, а
общее условие 62S<0 является лишь достаточным условием
устойчивости изолированных термодинамических систем.
Система в термостате при постоянном объеме (T = const, V=
= const, N = consi), Основное неравенство термодинамики для не-
неравновесных процессов F.3), приведенное к независимым пере-
переменным V и Г, принимает вид
dF<—SdT — PdV.
Для системы, находящейся в термостате, если она не произ-
производит внешней работы, получаем
dF<0,
* Механическим аналогом этого случая является равновесие конуса, опи-
опирающегося на вершину (или шара на вершине конуса).
101
т. е. в изотермической системе с постоянным объемом энергия
Гельмгольца при неравновесных процессах убывает и имеет ми-
минимум при устойчивом равновесии. Это общее условие устойчи-
устойчивого равновесия изотермической системы, не производящей внеш-
внешней работы, можно записать в виде
AF>0, или 6F = 0, 6
причем равенство 8F = 0 есть общее условие равновесия, а нера-
неравенство 82F>0— общее (достаточное) условие устойчивости си-
системы в термостате при постоянном объеме.
Система в термостате под постоянным внешним давлением
(r = const, P = const, Ar = const). Основное неравенство термоди-
термодинамики F.3), приведенное к переменным Р, Г, принимает вид
dG<—SdT+VdP.
Для системы, помещенной в среду с постоянными температу-
температурой и давлением, получаем dG<0. Следовательно, в такой систе-
системе при неравновесных процессах энергия Гиббса убывает и
имеет минимум при равновесии. Поэтому общее условие равно-
равновесия и устойчивости системы в термостате с постоянным внеш-
внешним давлением (минимум энергии Гиббса) можно записать в
виде
ДОО, или 6G = 0, 62G>0,
причем равенство 6G = 0 есть общее условие равновесия, а нера-
неравенство 62G>0 — общее (достаточное) условие устойчивости та*
кой системы.
Аналогично можно показать (*), что при постоянных энтро-
энтропии и давлении устойчивое равновесие в системе наступает при
минимуме ее энтальпии:
ДЯ>0, или 6Я = О, 62#>0,
а в системе с постоянными энтропией и объемом устойчивое рав-
равновесие наступает при минимуме внутренней энергии:
Д?>0, или 6? = О, 62?>0.
Система с переменным числом частиц в термостате при посто-
постоянных химических потенциалах и объеме (T = const, V = const,
jx; = const). Основное неравенство термодинамики системы с пе-
переменным числом частиц при независимых переменных Vy T и щ-
для неравновесных процессов имеет вид
— SdT—PdV— ?/Ф/
F.5)
где Q = ?—7S—
102
Из неравенства F.5) видно, что при неравновесных процес-
процессах в системе с переменным числом частиц, находящейся в тер-
термостате при постоянных V и (!{, термодинамический потенциал Q
убывает (dQ<0) и имеет при устойчивом равновесии минимум.
Общие условия равновесия и устойчивости такой системы запи-
запишутся в виде
AQ>0, или 6Q = 0, 62Q>0.
Таким образом, общие условия устойчивого равновесия тер-
термодинамических систем в различных случаях определяются экс-
экстремальными значениями соответствующих термодинамических
потенциалов. Эти условия являются не только достаточными, но
и необходимыми, если обеспечены все другие условия для уста-
установления равновесия (поскольку найденные нами условия не яв-
являются единственными для возможности протекания процессов) *.
Термодинамические потенциалы могут иметь несколько экс-
экстремумов (например, энтропия имеет несколько максимумов).
Состояния, соответствующие наибольшему (энтропия) или наи-
наименьшему (энергия Гельмгольца и др.) из них, называются ста-
стабильными (абсолютно устойчивыми состояниями равновесия),
другие— метастабилъными (полуустойчивыми). При наличии
больших флуктуации система может перейти из метастабильного
состояния в стабильное.
§ 27. Условия равновесия двухфазной
однокомпонентной системы
В качестве примера на определение конкретных условий рав-
равновесия, исходя из установленных выше общих условий равнове-
равновесия, рассмотрим изолированную двухфазную систему одного и
того же вещества (например, вода и ее пар).
Если 5' и S" — энтропии соответственно первой и второй фаз,
то энтропия всей системы
ее общее условие равновесия
6S = 6S/+6S// = 0. F.6)
Каждая из фаз представляет собой однокомпонентную систе-
систему с переменным числом частиц, и основными уравнениями тер-
термодинамики для них соответственно будут
V" — \iN".
* В некоторых случаях процессы термодинамически возможны (термодинами-
(термодинамические потенциалы при них изменяются в соответствии с найденными условия-
условиями), но в действительности не протекают, так как не выполнены другие условия
103
Определяя 6S' и 6S" и подставляя их в соотношения F.6),
получаем общее условие равновесия в виде
№ + РЖ - ц'б/У' ЪЕ" + Р'ЬУ — \l"SN" q (& ?)
гр, "• при * \ * /
Поскольку система изолирована, то ее экстенсивные параме-
параметры подчинены следующим уравнениям связей:
Е'~\-Е"=Е = const (внутренняя энергия системы),
У'+У"=У=const (объем всей системы), F.8)
N'-\-N" = N = const (общее число частиц).
В качестве независимых параметров системы выберем ?', V\
Nr\ в качестве зависимых — ?", V", N". Согласно выражениям
F.8), виртуальные изменения параметров системы связаны урав-
уравнениями
6Е" = —6Е\ 6V" = — б V\ 6N" = — 8N'. F.9)
Будем решать совместно уравнение общего условия равнове-
равновесия F.7) с уравнениями для виртуальных изменений экстенсив-
экстенсивных параметров системы F.9). Подставляя уравнения F.9) в
F.7), находим
Г') \Г Т") \Т
откуда вследствие независимости вариаций б!^, б У7, bNr оконча-
окончательно получаем следующие частные условия фазового равнове-
равновесия однокомпонентной системы:
Т = Т\ Р' = Р'\ v! = v!\ F.10)
т. е. равенства всех термодинамических сил в обеих фазах: ра-
равенство температур фаз (условие термического равновесия), ра-
равенство давлений в фазах (условие механического равновесия) и
равенство химических потенциалов вещества в фазах (условие
химического равновесия).
Эти три условия можно записать в виде одного — равенства
химических потенциалов вещества в фазах при одинаковых тем-
температуре и давлении:
. ^(Г, Р)=^(Г, Р). F.11)
Условие фазового равновесия F.11) показывает, что при рав-
равновесии двух фаз одного и того же вещества давление является
функцией температуры, т. е. параметры Т и Р перестают быть
независимыми.
(например, некоторые химические реакции идут только при наличии катализа-
катализаторов, хотя термодинамически они возможны всегда — свободная энергия при
них убывает).
104
Заметим, что полученные условия фазового равновесия F.10)
или F.11) справедливы только для однородных фаз, т. е. при от-
отсутствии поля внешних сил. Если же фазы находятся во внеш-
внешнем поле (например, в поле силы тяжести), то при равновесии в
обеих фазах одинаковы лишь температуры, давление же и хими-
химический потенциал в каждой фазе являются функциями коорди-
координат. Не зависящей от координат величиной оказывается не хи-
химический потенциал, а химический потенциал плюс потенциаль-
потенциальная энергия частицы в поле (*).
§ 28. Условия устойчивости равновесия
однородной системы
Термодинамическая устойчивость системы определяется вто-
второй вариацией какого-либо термодинамического потенциала, если
она не равна нулю. Найдем вначале общее выражение устойчи-
устойчивости системы, а потом исследуем и вторую вариацию соответ-
соответствующего термодинамического потенциала. Рассмотрим закры-
закрытую систему, находящуюся в термостате с температурой Т под
постоянным давлением Р. Общим условием устойчивости равно-
равновесия такой системы является минимум ее энергии Гиббса G =
=? — TS-\-PV. Это означает, что состояние системы в термоста-
термостате при данных Р и Т с координатами (экстенсивными парамет-
параметрами) V и 5 является устойчивым, если при небольшом спонтан-
спонтанном изменении координат ее энергия Гиббса G врзрастает: AG =
= Gi — G>0, т. е.
El-E-T(Sl-S)+P(Vl-V)>0, F.12)
где Е — внутренняя энергия исходного равновесного состояния
системы при данных Р, Т с координатами У, 5, Ех — внутренняя
*энергия неравновесного состояния, равная (см. § 26) ее равно-
равновесному значению при координатах Vu Si и других силах Рь
Т\, удерживающих систему в равновесии с этими координатами.
Аналогично равновесное состояние системы с координатами
V\, Si при постоянных Pi и Т\ устойчиво, если при небольшом
спонтанном изменении этих координат выполняется, подобно не-
неравенству F.12), условие
E — El-Tl(S — Sl)+Pl(V—Vl)>0. F.13)'
Сложив неравенства F.12) и F.13), получим следующее соот-
соотношение между разностями различных параметров двух близких
устойчивых состояний однородной системы *:
AT AS — APAV>Q, F.14)
* В общем случае сложных систем с переменным числом частиц вместо
F.14) имеем jFJ ДЛ/Дя* >0 (знаки Аг и а* определяются из уравнения dE=
ь
*= TdS — PdV + \idN = ]jT A№).
105
или
AT АР
/W AS
>0, F.15)
где A7 = Tx — Г, HS = SX - 5, AP^ - P, AV= V{ - V.
Определяющее устойчивость системы выражение в левой части
неравенства F.15) назовем матрицей устойчивости. Неравенство
F.14) для сщределителя этой матрицы позволяет получить кон-
конкретные условия устойчивости однофазной системы в различных
условиях. В самом деле, разделим неравенство F.14) сначала на
квадрат изменения координаты AV2 при постоянном значении
термодинамической силы Г, сопряженной координате 5, а потом
на квадрат разности координаты AS2 при постоянной термодина-
термодинамической силе Р, сопряженной первой координате V. Тогда
AV )т \ AS
Это означает, что в устойчивом равновесном состоянии одно-
однородной системы для любых небольших изменений каждой ее
координаты при постоянстве термодинамических сил, сопряжен-
сопряженных другим координатам, выполняются, как достаточные усло-
условия устойчивости, термодинамические неравенства
— )<0, (—) =— >0. F.16)
dV Jt \ dS )p Cp v '
Следовательно, СР>0 в состоянии устойчивого равновесия.
В общем случае, когда координатой фазы является параметр а,
а сопряженной ему обобщенной силой — величина Л; условия
устойчивости имеют вид
дЛ \ ( дТ \ Т
Разделим теперь неравенство F.14) сначала на квадрат из-
изменения первой координаты А У2 при постоянном значении коор-
координаты 5, а потом на квадрат изменения координаты AS2 при
постоянстве V. Тогда
\ <о, (Ш-) >о.
Is \ AS Jv
Значит, в состоянии устойчивого равновесия однородной сис-
системы для любых небольших изменений каждой ее координаты
при постоянстве других координат выполняются неравенства
= -?>0. F.17)
Следовательно, Cv>0 в состоянии устойчивого равновесия.
Таким образом, однородная система находится в состоянии
устойчивого равновесия, если ее матрица устойчивости F.15) по-
106
ложительна (это условие является необходимым и достаточным)
или же если выполняются условия устойчивости F.16) и F.17)
(эти условия являются достаточными, но не необходимыми, так
как возможно устойчивое состояние и при нарушении этих усло-
условий).
Достаточным условием устойчивого равновесия является также
и положительное значение второй вариации энергии Гиббса *
62G>0. Эту вариацию легко найти из общего условия равновесия
и устойчивости AG>0. Действительно, при заданных Го и Ро из
равенства F.12) имеем
F.18)
где А — вариация любого порядка, выводящая систему из равно-
равновесия, и для независимых переменных AS = 8S и AV=6V. Вариа-
Вариация АЕ при виртуальных изменениях S и V с точностью до чле-
членов второго порядка малости относительно независимых вариа-
вариаций 65 и 6V равна
dS jv
as2
dSdV
—
dS
dV
2 \\ dS lv ' ' V dV Js V dV Js
и условие равновесия и устойчивости F.18) принимает вид
AG= (T-T0NS + (P0-P)SV +
= 6G + — 62G>0.
2
Из условия равновесия 6G = 0 находим Г = То и P — Pq, т. е. при
равновесии температура и давление системы равны соответствен-
соответственно температуре и давлению термостата.
Из условия устойчивости 62G>0 получаем
Как известно, квадратичная форма положительна, если состав-
составленный из коэффициентов формы детерминант и его главные ми-
миноры положительны, поэтому условиями устойчивости являются
Dv
dS
дТ
dV
\ dV js \ dV
д(Т, -Р
d(S, V)
* Для нахождения условий устойчивости можно использовать другие термо-
термодинамические потенциалы (Я-).
107
-? >•• -(?
что совпадает с F.17). Назовем Dy детерминантом устойчивости,
(dXi/dxi)x.— адиабатными коэффициентами устойчивости (АКУ),
(dXi/dXi)x-— изодинамическими коэффициентами устойчивости
(ИКУ),гдеХ* = 7\—Р, ... и xi = Sy V, ....
Заметим, что по определению положительной величины
Z)y<OO.
Пользуясь свойствами якобианов, легко преобразовать АКУ
в ИКУ и, наоборот, ИКУ в АКУ:
П - аG\-Р) - аG\ -Я) d(S, -Р) / дТ\ / дР
у д E, V) d(S,-P) d(StV) \ds)p[ dV
д(т*-р) _д(Т,-Р) d(TfV) =/ dP\ I дТ \
d{S,V) d(T9V) d{S9V) \ dV )т\ OS )
y \ dS )p\ dV }s
dS )v
Следовательно, Dv всегда можно привести к диагональной фор-
форме, являющейся произведением АКУ и ИКУ.
Если разделить неравенство F.14) на произведение изменений
координат A FAS при постоянстве всех обобщенных сил, кроме
какой-либо одной из них, то вследствие неопределенности знака
этого произведения получим, что в устойчивом равновесии одно-
однородной системы каждая из производных (dT/dV)p, (OPjdS)T или
положительна, или отрицательна, т. е. имеют место неравенства
dV )р \dS )т
Условие Cv>0 (так же, как и СР>0) в состоянии устойчивого
равновесия выполняется, если термодинамическая температура Т
положительна. Но, с другой стороны, условие Cv>0 выражает
определение того, какая температура больше, а какая — меньше*.
Таким образом, принимая в соответствии с этим определением
понятия «большая (меньшая) температура» Су>0, мы выбираем
положительную температуру Г. Такой выбор знака Т приводит по
второму началу к тому, что при тепловом контакте двух тел теп-
теплота самопроизвольно переходит от тела с большей температурой
к телу с меньшей температурой. Это позволяет легко понять фи-
физический смысл условий устойчивости F.16) или F.17). Действи-
Действительно, предположим, что при Г>0 К условие Ср>0 не выполня-
выполнялось бы и вместо него было бы Ср<0. Тогда при флуктуациях,
вызывающих отдачу системой теплоты термостату, температура
* Принимается, что при сообщении телу теплоты при постоянных внешних
параметрах его температура повышается, т. е. Са>0.
W8
этой системы повысилась бы, что привело бы, в свою очередь,
к дальнейшей отдаче теплоты (так как Г>0К) и система, следо-
следовательно, при Cp<o\ie могла бы быть в устойчивом равновесии.
Аналогично, если вмес^ (dP/dV)T<0 будет (дР/дУ)т>0, то это
означает, что даже при небольшом флуктуационном уменьшении
объема давление в системе уменьшится. Это вызвало бы дальней-
дальнейшее сжатие объема и т. д. Следовательно, система находилась не
в равновесии.
Условия F.16), F.17) обеспечивают устойчивость равновесия
по отношению к небольшим флуктуациям. При больших флукту-
ациях, когда начинают выступать неучтенные особенности по-
поверхности флуктуационных зародышей, эти условия оказываются
недостаточными. Например, в состояниях переохлажденного пара
или перегретой жидкости условия
,F.16) выполняются, хотя эти сос-
состояния устойчивы только при обра-
образовании во время флуктуации плот-
плотности небольших зародышей новой
фазы, а при флуктуациях с образо^
ванием больших зародышей одно-
однородные системы распадаются на две
фазы. Это обусловлено особой
ролью поверхностной энергии за- v
родышей (которую мы до сих пор не р с 13
учитывали): при малых каплях об-
образование их приводит к увеличе-
увеличению свободной энергии F системы, поэтому эти капли исчезают;
при больших зародышах образование их может привести к умень-
уменьшению F, что ведет к разделению системы на две фазы, указывая
на метастабильность однородной системы (см. § 57).
Рассмотрим в связи с полученными условиями устойчивости
однородной системы газ Ван-дер-Ваальса. Изотерма этого газа
при температуре ниже критической изображена на рис. 13. Часть
АВ соответствует газу, часть FG — жидкости. В этих состояниях
(дР/дУ)т<0, что указывает на их устойчивость. Состояния, лежа-
лежащие на участке СЕ, неустойчивы, так как для них (dP/dV)T>0.
Точка С является граничной для устойчивости отдельно взятой
газовой фазы относительно ее непрерывных изменений (не свя-
связанных с образованием новой фазы). С точки В, как правило,
газ начинает конденсироваться, а двухфазное состояние опреде-
определяется прямолинейным участком BF. Участки ВС и EF соответ-
соответствуют метастабильным состояниям пара и жидкости соответст-
соответственно (*).
§ 29. Принцип Ле Шателье — Брауна
Общие условия устойчивости равновесия термодинамических
систем приводят к тому, что внешнее воздействие, выводящее сис-
систему из состояния равновесия, вызывает в этой системе такие
109
процессы, которые ослабляют это воздействие Это положение
было установлено Ле Шателье в 1884 г. и обосновано Брауном
в 1887 г. и названо принципом Ле Шателье--^d pay на.
Принцип Ле Шателье—Брауна был поручен чисто интуитивно,
в результате поиска термодинамического аналога закона индук-
индукции Ленца: индукционный электрический ток имеет такое направ-
направление, при котором ослабляется внешняя причина, его вызыва-
вызывающая.
Значение принципа Ле Шателье—Брауна состоит в том, что он
позволяет предсказать направление, в котором под влиянием
внешнего воздействия изменится термодинамический процесс,
протекающий в произвольной системе.
Выведем этот принцип для систем, в которых при процессах
сохраняются химический состав и масса (при процессах с изме-
изменением масс компонентов и фаз системы принцип Ле Шателье—
Брауна также имеет место, но доказывается иначе).
Рассмотрим систему, состояние которой определяется пере-
переменными Х\ и х2. Пусть Ii и 12 — действующие на нее обобщен-
обобщенные силы. Дифференциал некоторой функции состояния У равен
Тогда (dX1/dx2)Xl=(dXjdx1)X2 и
так как d(Y—Xi^i—.ХгЯг) =—X\dXx—X2dX2. Выразим производную
(dxjdXJx, через производные (dxJdXJx,, (dx1/dX2)Xl и (длудХ2)Х1.
Используя свойства якобианов, находим
_ а (*ь х,) _ д (хъ х,) д (Хь X,)
*1 \
^1 ;*.
(Xlt
х,)
хг)
d{Xlf X2)
Но согласно формуле F.19)
дху
i ... i i
d(xu
Xl
дХг /x,
\~дХ^)Хя l^xT/х,
A dXjXl
Xt \ dXx )x,
2
xt'
поэтому
dX1)x,
Ч \2 / дХ2
F.20)
110
Если благодаря условиям устойчивости
дХ2 jxx
то из выражения F.20) получаем
дхг
дХ2 ^ >0 F.21)
Это неравенство и выражает принцип Ле Шателье—Брауна.
Если в системе, в которой поддерживаются постоянными пара-
параметры %\ и Х2, внешним воздействием Х\ изменять параметр Х\, то
это вызовет изменения х2 и Х2у а мерой воздействия будет дх\/дХ\.
Но при внезапном увеличении Х\ происходящий процесс вначале
можно рассматривать как при постоянном Х2. Следовательно,
в это время приложенное воздействие характеризуется производ-
производной (dx-JdX^Xg. Когда же сцова наступит равновесие и параметр
х2 примет поддерживаемое внешней средой прежнее значение, то
изменение Х\ за счет внешнего воздействия будет определяться
производной (dxJdX^x^ Принцип Ле Шателье—Брауна утверж-
утверждает, что в новом равновесном состоянии, в которое переходит
система, изменение параметра Х\ за счет внешнего воздействия ос-
ослаблено, т. е.
дХх
Можно привести ряд примеров, в которых проявляется этот
принцип.
1. Рассмотрим систему в термостате. Изменим в некоторый
момент давление на систему. Это вызовет изменение объема и
температуры. Мерой воздействия будет dV/dP. В первый момент
благодаря внезапности изменения Р процесс является практичес-
практически адиабатным, поэтому внешнее воздействие определяется про-
производной (dV/dP)s. После установления равновесия и восстанов-
восстановления прежней температуры воздействие будет определяться про-
производной (dV/dP)T. По принципу Ле Шателье—Брауна в новом
равновесном состоянии воздействие ослаблено и
дР )т \ дР js
Этот результат легко получить непосредственно, используя
в качестве неравенства F.20) условие устойчивости СР>0. Дейст-
Действительно, из —dF = PdV+SdT видно, что в данном случае Х\ = Р,
X\ = V9 X2 = S, Хъ — Т) поэтому в соответствии с условием СР>0
111
и, следовательно, согласно неравенству F.21)
¦и-
дУ \ . ( ЗУ
дР т \ дР Js'
2. Увеличим внешнее давление на тело, уменьшая его объем.
При этом возникнет изменение темдературы и тело стремится
снова увеличить объем; поэтому те тела, которые от нагревания
сжимаются (например, вода при температуре ниже 4° С), будут
от сжатия охлаждаться.
3. Сообщим смеси из льда и воды некоторое количество тепло-
теплоты. Тогда лед начнет таять, благодаря чему не происходит повы-
повышение его температуры, которое иначе наблюдалось бы.
4. Пусть имеются два вещества в состоянии химического рав-
равновесия. Если им сообщить некоторое количество теплоты, то про-
произойдет реакция, охлаждающая систему. Следовательно, при по-
повышении температуры будут разлагаться вещества, возникающие
путем экзотермической реакции, и, наоборот, будут возникать эн-
эндотермические соединения.
5. Для соли, находящейся в насыщенном растворе, повышение
температуры вызывает растворение, если последнее связано с ох-
охлаждением; в противном случае происходит выпадение кристал-
кристаллов.
6. При движении проводника в магнитном поле возникает ин-
индукционный ток, на который магнитное поле действует с силой,
препятствующей движению. Ток, возникающий в проводнике, бла-
благодаря приближению к нему магнита отталкивает последний и
наоборот. Из этого примера видно, что правило Ленца является
частным случаем принципа Ле Шателье—Брауна.
7. Если электрический ток проходит через спай двух металлов,
то температура спая изменяется в таком направлении, что возни-
возникающий термоэлектрический ток стремится ослабить силу тока,
пропускаемого через спай (явление Пельтье).
Из этих примеров видно, что принцип Ле Шателье—Брауна
обусловлен устойчивостью состояния. Действительно, если бы
всякий первичный процесс усиливался еще дальше благодаря
вызванному им вторичному процессу, то это привело бы к полно-
полному расстройству равновесия в системе. Проводник, находящийся
в магнитном поле и получивший толчок, продолжал бы двигаться
дальше и притом ускоренно; магнит, слегка оттолкнутый от ка-
катушки, продолжал бы двигаться от нее.
Принцип Ле Шателье—Брауна применим не ко всем системам
и не ко всем возможным внешним воздействиям: необходима
предварительное условие — некоторая степень устойчивости на-
начального состояния системы. Принцип Ле Шателье—Брауна не-
неприменим к процессам, переводящим систему в более устойчивое
состояние, например, к взрывам, к реакциям, вызываемым с по-
помощью подогревания, и др.
112
Глава 7
ТЕРМОДИНАМИКА СИСТЕМ
ПРИ ОТРИЦАТЕЛЬНЫХ ТЕМПЕРАТУРАХ
Исходя из второго начала термодинамики, мы установили
(см. § 14), что отношение абсолютных температур Т\ и Т2 двух:
состояний какой-либо системы выражается показательной функ-
функцией
где
_ f (dA/dt)gdt
\
(dE/da)t
Отсюда обычно делается вывод, что термодинамическая темпе-
температура не может менять свой знак, что ее всегда можно считать
положительной (или только отрицательной).
Такой вывод, однако, превышает то, что в действительности
выражает соотношение G.1), полученное при анализе квазйстати-
ческих процессов и устанавливающее, что абсолютная температура
Т не может менять знак при квазистатическом переходе из одного
равновесного состояния в другое. Поэтому оно оставляет откры-
открытым вопрос об изменении знака Г, если система переходит из од-
одного равновесного состояния в другое нестатическим путем.
§ 30. Существование состояний
с отрицательной термодинамической
температурой
Вывод о постоянстве знака температуры Т из выражения G.1}
можно сделать только тогда, когда к нему дополнительно присо-
присоединяется утверждение, что состояния, достижимые из данного
неравновесно, всегда достижимы из него и равновесно. Это ут-
утверждение, как показывает опыт, имеет место во всех случаях
обычных, чаще всего встречающихся систем. Поэтому для таких
систем термодинамическая температура не может менять знак и
ее всегда можно считать положительной (или только отрицатель-
отрицательной). Из одного же соотношения G.1) без указанного дополни-
дополнительного утверждения не следует невозможность существования
наряду с положительными и отрицательных температур.
Нельзя отрицать возможность существования отрицательных
абсолютных температур и исходя из третьего начала термодина-
термодинамики. Действительно, недостижимость абсолютного нуля темпера-
температуры приводит лишь к невозможности перехода через него от поло-
положительных к отрицательным абсолютным температурам, но не
исключает возможности существования отрицательных абсолют-
абсолютных температур (наряду с положительными температурами).
на.
Состояния с отрицательными абсолютными температурами не
только возможны, но и существуют в действительности. Многочис-
Многочисленные эксперименты по ядерному магнитному резонансу привели
в 1951 г. к созданию состояний с отрицательными абсолютными
температурами. Условия для существования системы при отрица-
отрицательных абсолютных температурах, как мы увидим ниже, являют-
являются настолько жесткими, что такие системы редко встречаются
в практике, исключая некоторые системы ядерных спинов.
Отрицательные термодинамические температуры достигаются
не посредством отнятия у системы всей энергии теплового движе-
движения, а, наоборот, сообщением системе энергии больше той, которая
соответствует бесконечной температуре. У большинства тел это
Рис. 14
сделать невозможно, так как у них при бесконечно высокой тем-
температуре внутренняя энергия бесконечна. Такие системы не могут
находиться в состояниях с отрицательной температурой, если для
них уже выбрана положительная температура. Однако у некото-
некоторых систем внутренняя энергия с ростом температуры Г->оо
асимптотически приближается к конечному граничному значению,
а это дает возможность получения состояния систем с отрица-
отрицательной температурой, когда ей сообщается энергия, большая
данного граничного значения. В таких состояниях система, обладая
энергией, большей энергии при бесконечной температуре, имеет
«ультрабесконечную» температуру. Но в математике нет «-ультра-
бесконечности» на числовой прямой, а есть только бесконечно
удаленная точка, и если мы эту точку перейдем, то будем прибли-
приближаться к ОК с отрицательной стороны (рис. 14): отправляясь
направо от нуля по числовой оси, покидая +оо, придем от —оо
к нулю. Числовую ось можно спроецировать на числовую окруж-
окружность, где бесконечно удаленной точке соответствует самая верх-
верхняя точка окружности. Обходя окружность против часовой стрел-
стрелки, получим всю числовую ось. Таким образом, при отрицательной
температуре система не холоднее, чем при +0К, а горячее, чем
при бесконечной температуре (±оо К). Другими словами, область
отрицательных абсолютных температур лежит не «под О К», а
«над бесконечной температурой». Поэтому отрицательные темпе-
температуры выше положительных. Температура в направлении ее
114
роста проходит по шкале в последовательном порядке значения:
+ 0К, ..., +500К,...+оо, —оо, ..., —500 К, ..., —ОК. G.2)
Температура +1000 К находится между +500 и —500 К. Ис-
Искусственность приведенного построения Г-шкалы является случай-
случайным результатом произвольного выбора обычной температурной
функции. Если бы температурная функция была выбрана в виде
—Г, то самые низкие температуры соответствовали бы —оо для
этой функции, бесконечные температуры на обычной Г-шкале —
нулю, отрицательные температуры — положительным значениям
этой функции. Для такой температурной функции алгебраический
порядок и порядок хода от меньшей к большей температуре были
бы идентичны. Функция Г* = — 1/Т часто используется в термоди-
термодинамике при исследовании свойств систем в области 0 К, так как
она позволяет «расширить» температурную шкалу при низких:
температурах. Из изложенного видно, что для отрицательных тем-
температур Г*- шкала* по многим причинам более удобна, чем
Г-шкала.
§ 31. Система с отрицательной
термодинамической температурой
Следующая простая модель показывает, как на практике осу-
осуществляются отрицательные термодинамические температуры.
Пусть имеется система «элементарных магнитов» (например,,
электронные, атомные или ядерные магнитные моменты) во внеш-
внешнем магнитном поле Н. Согласно квантовой механике, положение
этих элементарных магнитов в поле Н квантуется, т. е. угол между
направлениями магнитного момента и напряженности Н поля
может принимать только определенные значения. В случае спино-
спиновых магнитных моментов этот угол имеет только два значения:
0 и 180°. Оба эти положения спина являются одинаково устойчи-
устойчивыми, хотя для магнитной стрелки компаса устойчиво только
одно ее положение — вдоль напряженности магнитного поля.
В этом состоит отличие квантовой системы от классической.
При низкой температуре молекулярные магниты устанавлива-
устанавливаются в сильном магнитном поле, как показано на рис. 15, а, т. е.
приходят в состояние с наименьшей энергией (или, как говорят,,
в системе заняты преимущественно более низкие энергетические
уровни). При сообщении системе магнитов энергии (приводящем
к увеличению ее температуры) уже не все магниты ориентируются
по напряженности поля, и чем большую энергию получает система,
тем более беспорядочным будет распределение магнитов. Насту-
Наступает такой момент, когда беспорядочность становится полной —
система полностью утрачивает намагниченность. Это соответст-
* Эта шкала, предложенная В. Томсоном в 1848 г., не получила, однако,
распространения. Позже им была предложена Г-шкала, в которой температура
имеет конечный наименьший предел.
MS
вует температуре Т= + оо? характеризующей равномерное распре-
распределение частиц по всем энергетическим уровням (рис. 15,6). Про-
Продолжая сообщать энергию системе, можно достигнуть того, что
элементарные магниты ориентируются против напряженности внеш-
внешнего поля (рис. 15, в) так, что возникает преимущественная засе-
заселенность верхних энергетических уровней (инверсная заселен-
заселенность уровней). В этом состоянии внутренняя энергия системы
больше, чем при бесконечно высокой температуре, и, следователь-
следовательно, система имеет отрицательную температуру.
Ту ОК Т=оэ
а 6
Рис. 15
V ¦
?макс
Рис. 16
Сформулируем основное условие, которому должна удовлетво-
удовлетворять система, находящаяся в состоянии с любой отрицательной
термодинамической температурой: энергия термодинамической
системы должна иметь конечное предельное значение при 7->оо и
конечное число энергетических уровней.
Разумеется, система должна быть теплоизолирована от всяких
других систем, не удовлетворяющих основному условию, т. е.
время установления термодинамического равновесия в системе
должно быть малым по сравнению с временем, за которое заметная
энергия теряется или приобретается от других систем.
Зависимость внутренней энергии системы, способной нахо-
находиться в состояниях с отрицательной абсолютной температурой;
от температуры показана на рис. 16 (?Гр — граничное значение
энергии при Г = оо).
Большинство систем не удовлетворяет указанным выше требо-
требованиям, вследствие чего системы с отрицательными абсолютными
температурами встречаются редко. Система ядерных спинов у не-
некоторых кристаллов удовлетворяет этим условиям*. Термодина-
Термодинамическое равновесие в такой системе устанавливается посредством
ядерного спин-спинового взаимодействия. Этот спин-спиновой про-
процесс установления термодинамического равновесия характеризуется
временем релаксации тг, которое имеет порядок 10~5 с. Взаимо-
* Особенностью этой системц частиц, обладающих спином, является отсут-
отсутствие у нее пространственных степеней свободы.
116
действие спиновой системы с решеткой характеризуется временем
релаксации п, которое составляет многие минуты, т. е. значитель-
значительно больше Т2. В термодинамике спиновых систем взаимодействие
с решеткой соответствует утечке теплоты сквозь стенки системы.
Значительное различие времен п и %2 приводит к тому, что систе-
система спинов по достижении внутреннего термодинамического равно-
равновесия еще относительно большое время остается в практической
изоляции от решетки. В течение этого времени можно говорить
о термодинамически равновесной спиновой системе.
Равновесная система с отрицательной абсолютной температу-
температурой была впервые осуществлена в 1951 г. Перселлом и Паундом*
в результате экспериментов по изучению свойств системы ядерных
спинов в очень чистых кристаллах фтористого лития LiF. У этих
кристаллов время х\ спин-решеточной релаксации при комнатной
температуре порядка 5 мин, а время х2 спин-спиновой релаксации
приблизительно равно периоду ларморовской прецессии ядерного
магнитного момента во внешнем магнитном поле, значение кото-
которого меньше 10~~5 с.
Во внешнем магнитном поле энергия системы ядерных спинов
имеет верхнюю границу при Г->оо.
Таким образом, у системы ядерных спинов LiF в магнитном
поле выполняются все условия существования равновесных сос-
состояний с отрицательной температурой. Перселл и Паунд перевели
эту систему из состояния с положительной температурой в состоя-
состояние с отрицательной температурой, направив напряженность внеш-
внешнего магнитного поля против ядерных магнитных моментов.
В настоящее время «приведение» спиновой системы в состоя-
состояние с отрицательной абсолютной температурой достигается с по-
помощью 180-градусного высокочастотного импульса, который, дей-
действуя на образец в течение промежутка времени Д?, сравнимого
с Т2, поворачивает макроскопический магнитный момент на 180°.
Таким образом, процесс перехода системы из положительных тер-
термодинамических температур к отрицательным является принципи-
принципиально неравновесным, так как изменение внешнего параметра
(напряженности поля), приводящее к такому переходу, происходит
за время, сравнимое с временем релаксации тг. Очевидно, что для
необычных систем возможны случаи, когда состояния, достижимые
из данного состояния нестатически, недостижимы из него квази-
статически.
Если равновесные состояния с инверсной заселенностью энер-
энергетических уровней и, следовательно, с отрицательной абсолютной
температурой можно получить только у необычных систем, кото-
* Purcell Е. М., Pound R. V. — Phys. Rev., 1951, v. 81, p. 279. Подроб-
Подробности интерпретации работы Перселла и Паунда и обсуждение в целом вопро-
вопроса об отрицательных температурах см.: Поулз Л. Отрицательные абсолютные
температуры и температуры во вращающихся системах координат. — УФН,
1964, т. 84, вып. 4, с. 693; Строицкий Г. В., Тропинин В. Н. К термоди-
термодинамике спиновых систем. — В кн.: Статистическая физика и квантовая теория
поля. — М.: Наука, 1973, с. 280.
117
рыми являются лишь спиновые системы, то стационарные неравно-
неравновесные состояния с инверсной заселенностью уровней можно не-
непрерывной «подкачкой» создать и у обычных систем. Это осуще-
осуществляется в таких усилительных установках, как мазеры. Очень
часто, говоря об инверсной заселенности энергетических уровней,
употребляют понятие отрицательной абсолютной температуры,
однако это лишь условное термодинамическое понятие, поскольку
инверсная заселенность уровней еще не есть состояние с отрица-
отрицательной температурой. Необходимо, чтобы система находилась
в равновесном состоянии при инверсной заселенности уровней,
как это наблюдается в спиновых системах.
§ 32. Термодинамика систем
с отрицательными температурами
Системы с отрицательными абсолютными температурами обла-
обладают рядом специфических свойств, которых нет у обычных сис-
систем. Чтобы установить эти свойства, сформулируем, опираясь на
опыт, вначале основные законы термодинамики для таких систем.
Термодинамические понятия «работа», «теплота», «количество
теплоты», «более нагретое тело» употребляются при анализе сос-
состояний с отрицательной температурой в том же смысле, что и
в случае состояний с положительными абсолютными температура-
температурами. Это означает, что формулировка первого начала термодина-
термодинамики для систем с отрицательной абсолютной температурой ос-
остается без изменения:
Прежней остается также формулировка второго начала термо-
термодинамики в виде закона о существовании и возрастании энтропии,
другие же формулировки этого начала изменяются. Выберем за
исходное такое выражение второго начала, которое непосредст-
непосредственно следует из опыта по превращению теплоты в работу и рабо-
работы в теплоту.
В гл. 3 мы отмечали, что второе начало термодинамики уста-
устанавливает, во-первых, общую закономерность превращения тепло-
теплоты в работу и, во-вторых, выражает специфические закономернос-
закономерности как обычных, так и необычных систем. Общая закономерность
превращения теплоты в работу в обоих случаях систем состоит
в том, что при таком превращении в замкнутом круговом процес-
процессе часть теплоты непременно отдается рабочим телом другим те-
телам. Этот (первый) элемент компенсации, который в случае обыч-
обычных систем совпадает со вторым элементом компенсации (изме-*
нением термодинамического состояния других тел), приводит к су-
существованию энтропии у равновесной системы (см. § 13). Отсюда
следует, что второе начало в форме Каратеодори не изменяется:
вблизи каждого состояния любой термически однородной системы
существуют такие состояния, которые недостижимы из него адиа-
адиабатным путем. Это означает, что у всякой равновесной системы
118
fc состоянии с отрицательной абсолютной температурой (как и
в случае обычных систем) существует энтропия как функция ее
состояния
dS=-^. G.3)
Специфическая закономерность превращения теплоты в работу
и работы в теплоту в случае обычных систем, как известно, состо-
состоит в том, что если при превращении теплоты в работу в замкнутом
круговом процессе происходит изменение термодинамического сос-
состояния других тел, то превращение работы в теплоту не связано
с таким изменением:
QyW kW = Q. G.4)
Как показывает опыт*, в случае необычных систем, когда они
находятся в состояниях с Г<0 К, специфическая закономерность
прямого и обратного превращений теплоты в работу заключается
в том, что теплота превращается в работу без всяких изменений
в окружающих телах, работу же в теплоту невозможно полностью
превратить в замкнутом процессе без изменения в окружающих
телах**:
Q~W n №>Q. G.5)
Поэтому второе начало для необычных систем при Т<0 К
можно сформулировать в следующем виде: невозможен вечный
двигатель второго рода, причем это утверждение допускает обра-
обращение.
Это означает, что в замкнутом круговом процессе при Г<0 К
ни теплоту нельзя превратить в работу без компенсации (имеется
в виду первый элемент компенсации), ни работу в теплоту (име-
(имеется в виду второй элемент компенсации).
Таким образом, для любых систем (обычных и необычных)
можно исходить из следующей формулировки второго начала:
невозможен вечный двигатель второго рода, причем это утвероюде-
ние не допускает обращения в случае обычных систем и допускает
обращение при Г<0 К для необычных систем.
Понятия «обратимый и необратимый процессы» определяются
в случае отрицательных абсолютных температур тем, связаны ли
обратные им процессы с некомпенсированным превращением рабо-
работы в теплоту. Так, процесс перехода системы из состояния 1 в сос-
состояние 2 называется обратимым, если обратный переход из 2 в 1
не связан с некомпенсированным превращением работы в теплоту;
* Имеются в виду эксперименты по ядерному магнитному резонансу, ко-
которые здесь не изложены.
** Превращения теплоты в работу и работы в теплоту являются, следова-
следовательно, дополнительными: когда возможно одно без изменения в других телах,
невозможно другое, и наоборот.
119
процесс же перехода системы из 1 в 2 называется необратимым,
если обратный переход из 2 в 1 связан с некомпенсированным
превращением работы в теплоту.
Определения равновесного и неравновесного процессов остают-
остаются без изменения.
Из соотношений C.1) или G.4) для неравновесных процессов
в обычных системах получаем (см. § 16) TdS>dE + 8W и
dS>0 G.6)
в случае адиабатно-изолированной системы.
Аналогично из соотношений G.5), представляющих второе на-
начало термодинамики для необычных систем при Г<0 К, можно
найти аналитическое выражение этого закона при неравновесных
процессах в таких системах. Для этого рассмотрим два близких
состояния равновесия 1 и 2 некоторой необычной системы (при
отрицательных абсолютных температурах). Пусть при неравновес-
неравновесном переходе из 1 в 2 (см. рис. 8) системе сообщается количе-
количество теплоты 6QHp и она совершает работу. Тогда по первому
началу
6Q dE 6W. G.7)
Если же система переходит из состояния 1 в 2 равновесно, то
количество теплоты, получаемое ею от того же термостата, равно
SQ, а совершенная работа б№, так что
G.8)
Вычитая уравнение G.8) из G.7), получаем
8Qhp—6Q - б W*P—6W=R. G.9)
Значение /?=^=0, так как в противном случае это означало бы„
что необратимый процесс 1—2 можно провести в обратном поряд-
порядке без компенсации. Значение #<?0, так как в противном случае
это означало бы, что за цикл внешняя работа затрачена на нагре-
нагревание термостата без всякого изменения в других телах, что (см.
G.5)) невозможно. Величина R может быть больше нуля, так как
это соответствует работе за цикл за счет теплоты термостата, что
(см. G.5)) возможно. Таким образом,
6QHP>6Q и
а так как 8Q = TdS, то
При адиабатно-неравновесных процессах, когда 6QHp = 0, полу-
получаем (Г<0К)
dS>0,
что выражает закон возрастания энтропии при равновесных про-
процессах в изолированных" сдстемах с отрицательной температурой.
Из изложенного видно, что закон о существовании и возрастании
120
энтропии (второе начало) выполняется как для обычных, так и
для необычных систем.
Основные уравнение и неравенство термодинамики для систем
лри отрицательных абсолютных температурах имеют вид
TdS^dE + 8W, G.10)
где равенство относится к равновесным, а неравенство — к нерав-
неравновесным процессам.
Различные формулировки третьего закона термодинамики ос-
остаются неизменными при отрицательных абсолютных температу-
температурах, если под абсолютным нулем температуры понимать 0 К как
положительной, так и отрицательной температуры. Температуры
+ 0К и —0 К соответствуют совершенно различным физическим
состояниям. Для первого система находится в состоянии с на-
наименьшей возможной энергией, а для второго — с наивысшей.
Система не может стать холоднее, чем + 0К, так как она не мо-
может больше отдать энергию. Она не может стать горячее, чем
—0 К, так как она не может больше поглотить энергию. Прин-
Принцип недостижимости абсолютного нуля формулируется следующим
образом: невозможно с помощью любой, как угодно идеализиро-
идеализированной процедуры за конечное число операций охладить любую
систему до + 0 К или нагреть любую систему до —0 К.
Удельная теплоемкость падает до нуля как при +0К, так и
при —0 К. Физическая причина этого состоит в том, что и при
+ 0 К, и при —0 К все элементы системы в конце концов попадают
в свои энергетические состояния с наименьшей или наибольшей
энергией и теплота больше не может быть соответственно отнята
или поглощена. Удельная теплоемкость при температуре Т= + оо
(обе эти температуры физически тождественны, так как соответ-
соответствуют одинаковым значениям всех термодинамических величин)
также падает до нуля, но по другой причине: при приближении
к Г=±оо температурные изменения системы велики при малых
изменениях ее внутренней энергии, (Приближение теплоемкости
системы к нулю в этой области и позволяет затратой конечной
энергии довести систему до бесконечной температуры.)
Рассмотрим теперь- некоторые свойства систем в состояниях
с отрицательной абсолютной температурой.
1. Из уравнения G.3) следует, что при сообщении системе теп-
теплоты FQ>0) энтропия ее не увеличивается, как при положитель-
положительных абсолютных температурах, а уменьшается — система перехо-
переходит в более упорядоченное состояние.
2. С помощью основного уравнения термодинамики G.10) мож-
можно установить, в каком направлении переходит теплота при тепло-
тепловом контакте двух тел с различной температурой.
Пусть имеются два тела с отрицательными температурами Тх
и 7V Допустим, что от первого тела ко второму переходит коли-
количество теплоты 6Q, когда они приведены в тепловой контакт.
Тогда, поскольку процесс теплопередачи при конечной разности
121
температур необратим, по формуле C.57) имеем
SQ , 6Q >0,
7\ Г.
2
откуда Т\>Т2. Следовательно, согласно температурной шкале
G.2) теплота самопроизвольно переходит от горячего тела к хо-
холодному. (Мы говорим, что первое тело является более горячим,
чем второе, если второму телу надо сообщить энергию (без измене-
изменения внешних параметров), чтобы после этого оно при тепловом
контакте находилось в равновесии с первым телом.)
Нетрудно также убедиться, что при тепловом контакте систем
с температурами разных знаков теплота переходит от тел с отри-
отрицательной температурой к телу с положительной температурой,
т. е. опять-таки от горячего тела к холодному.
3. При отрицательной термодинамической температуре могут
быть проведены различные круговые процессы, подобные магнит-
магнитному циклу Карно.
Пусть, как обычно, Т\ — температура теплоотдатчика, а Гг —
теплоприемника. Тогда КПД цикла Карно
Поскольку температура теплоотдатчика больше, чем теплопри-
теплоприемника, то Т\>Т2, |Г2|>|Г1|, Т2/Тi>l и, следовательно, ц<0.
Это означает, что при отрицательной абсолютной температуре,
для того чтобы теплоту отнять от горячего тела и передать холод-
холодному, необходимо затратить работу. При этом согласно первому
началу холодному телу сообщается больше теплоты, чем отнято
у горячего на совершенную работу. Когда такой двигатель дейст-
действует в противоположном направлении, т. е. выполняет роль хо-
холодильной машины, то при переносе теплоты от холодного тела
к горячему им производится работа. Если потом с помощью тепло-
теплового контакта обоих тел позволить перейти теплоте от горячего
тела к холодному, то получим периодически работающий двига-
двигатель, который, не вызывая никаких изменений в окружающей
среде, производит работу за счет теплоты одного (холодного!)
тела. Как видим, в области отрицательных абсолютных темпера-
температур можно осуществить вечный двигатель второго рода Томсона—
Планка.
КПД цикла Карно, действующего между отрицательными тем-
температурами, так же, как и в области положительных температур,
меньше единицы. Это означает, что как при положительных, так
и при отрицательных температурах тепловые двигатели погло-
поглощают теплоту больше, чем производят работу.
Цикл Карно (обратимый) между температурами с разными
знаками осуществить невозможно. Дело в том, что с помощью
равновесного адиабатного намагничивания системы спинов можно
повысить температуру на положительной шкале температур как
угодно высоко, но ее нельзя заставить перейти к отрицательным
1.22
значениям. Аналогичное утверждение справедливо, если началь-
начальное состояние имеет отрицательную температуру. Переход системы
от положительных к отрицательным температурам можно осуще-
осуществить только с помощью нестатического процесса (см. § 31).
4. Адиабатное размагничивание спиновой системы при отрица-
отрицательной температуре нагревает систему, а не охлаждает, как при
положительной температуре.
5. Легкость, с которой теплота превращается в работу, приво-
приводит к важным практическим применениям систем с отрицательной
температурой.
При отрицательной температуре большинство сопротивлений
отрицательно, поэтому системы при такой температуре являются
усилителями: электромагнитная волна, прошедшая через систему
с отрицательной температурой, не поглощается, а усиливается.
Это наблюдается у обычных систем с условной отрицательной тем-
температурой, что используется в таких усилительных установках,
как мазеры и лазеры.
§ 33. Условия устойчивости систем
с отрицательными температурами
Рассмотрим в заключение вопрос об условиях устойчивости
состояний системы с отрицательными температурами.
Для этого будем исходить из основного неравенства G.10)
систем с отрицательными температурами. Для нестатических
процессов в таких системах из неравенства G.10) получаем
TdS<dE+PdV, G.11)
откуда следует, что в изолированных системах (Е = const, V=
= const) с Г<0 К равновесие наступает при максимальной энтро-
энтропии.
Таким образом, общим условием равновесия изолированной
системы при отрицательной температуре является, как и в случае
положительной температуры, максимальность энтропии системы:
А5<0, или 6S = 0, 62S<0.
Для того чтобы найти общее условие равновесия при Г<0 К
для системы в термостате с постоянным объемом или с постоян-
постоянным давлением, перейдем в неравенстве G.11) к соответствующим
независимым переменным. Тогда
dF>—SdT—PdV, G.12)
dG>—SdT±VdP. G.13)
Из неравенства G.12) видно, что при изотермоизохорных не-
неравновесных процессах в системе с Г<0 К энергия Гельмгольца
123
возрастает и максимальна при равновесии. Общее условие равно-
равновесия в этом случае можно записать в виде
AF<0, или 6F = 0, 62/7<0.
Аналогично из неравенства G.13) получаем общее условие
равновесия системы в термостате (Г<0 К) при постоянном дав-
давлении:
AG<0, или 6G--0, 62G<0.
Конкретные условия устойчивости равновесия такой системы
определяются или непосредственно из общего условия AG<0, или
из условия 82G<0. При AG<0 подобно формуле F.16) находим
&TAS—ДРДУ<0, откуда (dT/dS)v = T/Cv<0 и (dP/dV)T>0, или
Cv>0 и (dP/dV)T>0, G.14)
а также (dT/dS)p = T/CP<0 и (dP/dV)s>0, или
Ср>0 и (dP/dV)s>0. G.15)
Таким образом, условия устойчивости равновесных состояний
системы с отрицательными температурами выражаются неравен-
неравенствами G.14) или G.15).
ПРИМЕНЕНИЯ ТЕРМОДИНАМИКИ
При изложении теоретических основ термодинамики уже при-
приводились отдельные ее приложения. Теперь мы последовательно
рассмотрим ряд физически наиболее важных применений термо-
термодинамики при изучении свойств различных систем.
Глава 8
ТЕРМОДИНАМИКА НЕКОТОРЫХ
ФИЗИЧЕСКИХ СИСТЕМ
§ 34. Охлаждение газа при необратимом
и обратимом адиабатных расширениях
Практически весьма важной задачей является сжижение газов.
Для решения этой задачи необходимо уменьшить скорость дви-
движения молекул газа и сблизить их. Последнее достигается сжа-
сжатием газа с помощью компрессоров, а для понижения темпера-
температуры газ заставляют .совершать работу при адиабатном расши-
расширении, Сам процесс расширения может происходить как необрати-
необратимо, так и обратимо. Рассмотрим охлаждение газа в том и другом
случаях.
Эффект Джоуля—Томсона. Изменение температуры при необ-
необратимом адиабатном расширении происходит, как мы увидим,
из-за отклонения реальных газов от идеальности и называется
эффектом Джоуля—Томсона.
Рассмотрим теорию этого эффекта. В адиабатно изолирован-
изолированном цилиндре (рис. 17) газ из области с большим давлением Pi
пропускается через пористую перегородку* в область с меньшим
давлением Рг. При таком расширении газа с перепадом давления
(ДР = Р2—Pi<0) происходит изменение температуры. Это явление
при небольшом перепаде давления (| APj/Pi<Cl) называется диф-
дифференциальным эффектом Джоуля—Томсона, а при большом пе-
перепаде давления — интегральным эффектом.
Вычислим дифференциальный эффект, определяемый коэффи-
коэффициентом Джоуля—Томсона: |я = АГ/АР.
* Благодаря трению в этой перегородке поток не является турбулентным и
газ по обе стороны от нее однороден.
125
Так как процесс адиабатный, а ки-
кинетическая энергия газа и потери на
трение в пористой перегородке при
малой скорости потока пренебрежимо
малы (так как пропорциональны квад-
квадрату этой скорости), то, учитывая, что
справа от перегородки газ совершает
работу, а слева от нее работа произ-
производится над газом, по первому нача-
началу имеем Q=E2—E1 + P2V2—PlVl = 0t
откуда
Рис. 17
или #! = #2, т. е. процесс Джоуля —
Томсона является изоэнтальпическим:
Это позволяет легко найти \х.
Действительно, поскольку Д# = 0, а АР и АГ малы при диф-
дифференциальном эффекте Джоуля—Томсона, то с точностью до
квадратичных членов имеем Д#=( ] ДТ + ( ) ДР, откуда
Из выражения
AT (дН/дР)т
^~~~АР (дН/дТ)р*
= TdS+VdP находим
' V дТ
= СР.
дР JT \дР Jt
Так как dG = —SdT+VdP, то {dS/dP)T = —(dV/dT)p, поэтому
Д71 _ T(dV/dT)p — V
АР ~~ Ср
(8.1)
где (dV/dT)P можно найти из термического уравнения состояния.
Для идеального газа V = RT/P; (dV/dT)P = R/P, тогда из фор-
формулы (8.1) получаем ДГ = 0К.
В - случае газа Ван-дер-Ваальса, дифференцируя уравнение
(P + a/V*)(V-b)=RT
по Т при постоянном Р, находим
¦?(?),<"-»>
откуда
дУ
дТ
R
R(V
Р P+a/V* — 2a(V — b)lV3 RT — 2a(V-
(8.2)
126
Считая газ не очень плотным и отбрасывая в соотношениях A0.9)
величины второго порядка малости относительно а и 6, получаем
— —b. (8.3)
RT К
T(dV\
' \дТ )р
Подставляя
1 -
(8.3)
V — b
- 2a/RTV
в (8.1)
(V
Ь){\ ¦
, находим
Д7
дя
2a/RT -
Ср
2а
RTV
-Ь
Из этого выражения видно, что:
а) изменение температуры газа Ван-дер-Ваальса при необрати-
необратимом адиабатном расширении обусловлено его отклонением от иде-
идеального газа (аФО, ЬФО);
б) эффект Джоуля—Томсона для не очень плотного газа зави-
зависит от соотношения величин а и 6, которые оказывают противо-
противоположное влияние на знак эффекта;
в) если силы взаимодействуя между молекулами велики, так
что преобладает поправка на давление, и Ъ можно принять рав-
равным нулю, то
ДГ 2а >Q
дя яте
р
т. е. газ будет охлаждаться (ДГ<0 К, так как ДР<0);
г) если силы взаимодействия между молекулами малы (а->0)
и преобладает поправка на объем, то
АР ~ Ср ^ ~'
т. е. газ нагревается (ДГ>ОК).
В первом случае F->0) расширяющийся газ за весь процесс
перехода из одной области в другую совершает работу P2V2 —-
—PiV\>0 за счет убыли его внутренней энергии — газ охлажда-
охлаждается. Во втором случае (а->0) полная работа над газом P\V\—
—^2^2>0 идет на увеличение его внутренней энергии — газ наг-
нагревается;
д) при некоторой температуре реального газа коэффициент
[1 — 0 и газ ведет себя в процессе Джоуля—Томсона как идеаль-
идеальный. Это будет выполняться (см. (8.1)) в общем случае при
T{dV/dT)P— V = 0, (8.4)
а в случае не очень плотного газа Ван-дер-Ваальса, когда 2ajRT—
—6 = 0, при температуре
которая называется температурой инверсии. При этой температуре
эффект Джоуля—Томсона изменяет знак: ниже температуры ин-
инверсии эффект положителен (|л>0, газ охлаждается), выше 7\- —
127
эффект отрицателен (jx<0, газ нагревается). Температура инвер-
инверсии у всех газов лежит значительно выше критической. Опреде-
Определяемое уравнением (8.4) геометрическое место точек инверсии
для данного вещества называется инверсионной кривой.
У водорода и инертных газов силы сцепления между частица-
частицами малы, поэтому при обычных температурах эти газы нагрева-
нагреваются. Температура инверсии у водорода —57° С; самая низкая
температура инверсии —249,4° С у гелия (при нормальном атмос-
атмосферном давлении). Для того чтобы гелий охладить по методу
Джоуля—Томсона, необходимо предварительно довести его тем-
температуру до величины, меньшей —249,4 °С, что делается с по-
помощью кипящего водорода.
Точная теория, в которой не предполагается малость поправок
a/V2 и Ь, приводит к выводу о существовании при заданном дав-
давлении двух точек инверсии — верхней Т? и нижней ГД которая
для большинства газов находится в области жидкого состояния
(*). При больших перепадах давления интегральный эффект
Джоуля—Томсона определяется формулой
где конечное давление P<i в технике обычно близко к атмосфер-
атмосферному. Дифференцированием этой формулы по Pi находим, что ин-
интегральный эффект охлаждения максимален при начальном дав-
давлении, определяемом из уравнения
т. е. когда начальное состояние Р\, Т\ лежит на кривой инверсии
при дифференциальном эффекте Джоуля—Томсона.
Охлаждение газа при обратимом адиабатном расширении. Рас-
Рассмотрим охлаждение газа при обратимом адиабатном расширении
с отдачей внешней работы. Устройство в холодильных машинах,
где производится эта работа, называется детандером; его главная
часть (поршень) приводится в движение охлаждаемым газом.
Еще в самом начале XX в. делались попытки усовершенство-
усовершенствовать машины глубокого охлаждения и, в частности, заменить
поршневые двигатели в детандере более экономичными и высоко-
высокопроизводительными — турбинными. Это долго не удавалось сде-
сделать, так как все расчеты турбин велись применительно к пару.
Однако если воздух уже охлажден до низких температур, то он
становится настолько плотным, что по своим свойствам стоит
ближе к жидкости, чем к пару. Исходя из этого в 1935 г. был раз-
разработан турбодетандер по типу водяной, а не паровой, турбины
с КПД более 0,85*.
* См.: Капица П. Л. Турбодетандер для получения низких температур и
его применение для снижения воздуха. — Журн. техн. физики, 1939, т. 9,
вып. 2, с. 99. *
128
С введением в детандере вместо поршневых двигателей турбин,
а вместо многоступенчатого компрессора, сжимающего газ в преж-
прежних установках до нескольких десятков мегапаскаль, — турбоком-
турбокомпрессора удается сжижать газы при относительно низком давле-
давлении @,6—0,8 МПа).
Легко найти изменение температуры газа при обратимом адиа-
адиабатном расширении. Из выражения
R(l dF -4- PHV
1 № \
TTTVOTTTTAjT 1 — 1
\ дР ) s
' dH Vdp
V — (дН/дР)т
(дН/дТ)р
( дТ\
[dP)s
/ дН
{ дТ
- , ИЛИ
Т(д
) dT +
IP
V/dT)P
СР
Г/ дН \
[[ дР )т
Так как для всякого газа (dV/dT)P>0, то, следовательно, при
адиабатном обратимом расширении (dT/dP)s>0, т. е. газ всегда
охлаждается (dT<0, так как dP<0) независимо от вида его урав-
уравнения состояния. В этом состоит принципиальное преимущество
использования обратимого адиабатного расширения газов для их
охлаждения и сжижения по сравнению с процессом Джоуля—
Томсона.
Однако из-за технической сложности осуществления обратимо-
обратимого адиабатного расширения при низкой температуре основным
методом охлаждения газов и их сжижения в настоящее время
пока еще является метод необратимого расширения газа.
§ 35. Термодинамика диэлектриков
и магнетиков
Рассмотрим поведение физических систем, на которые кроме
давления действуют и немеханические силы, например электричес-
электрические или магнитные. Как мы увидим, имеются различные выраже-
выражения для внутренней энергии и работы поляризации диэлектрика.
Вопрос о том, какое из этих выражений следует использовать,
не является существенным — все они приводят к одним и тем же
результатам для свойств диэлектриков.
Основные уравнения термодинамики для диэлектриков и маг-
магнетиков. Известно, что элементарная работа, отнесенная к объему
диэлектрика и совершаемая при движении зарядов, создающих
в нем поле, равна
62). (8.6)
а для изотропного диэлектрика 8W = Id®.
An
5 Зак. 245 129
Величина 3) выступающая в данном случае в качестве внеш-
внешнего параметра, не является таковым для самого диэлектрика»
Поэтому SW не есть работа поляризации диэлектрика в собствен-
собственном смысле, т. е. в смысле работы на создание поляризации при
раздвигании зарядов в молекулах диэлектрика и образовании
преимущественной ориентации этих молекул*. Для того чтобы
найти работу поляризации диэлектрика в собственном смысле,
преобразуем выражение (8.6) к виду, в котором независимой пе-
переменной является внешний параметр диэлектрика — напряжен-
напряженность <? электрического поля. Так как этому внешнему парамет-
параметру соответствуют два внутренних (электрических) параметра ди-
диэлектрика — поляризованность & и вектор электрического сме-
смещения (индукция) ® = ? +4я ©Р, то искомое преобразование вы-
выражения F.8) может быть осуществлено двумя способами:
&W = — d (?2/8я) — d (!><§) + bd&, (8.б1)
bW = -d (|2/4я) -d (>6) + A /4я) idg. (8.6»)
Первое слагаемое в правой части (8.61) можно истолковать
как работу возбуждения электрического поля в вакууме, второе —
как работу против внешнего электрического поля, а третье — как
работу поляризации в собственном смысле, когда внутренним па-
параметром диэлектрика, сопряженным его внешнему параметру ё
—>¦
является поляризованность сР. Аналогично третье слагаемое
в правой части (8.6й) можно истолковать как работу поляризации
в собственном смысле, когда 2)— внутренний параметр диэлект-
—+¦
рика, сопряженный §.
Так как, однако, поляризация диэлектрика в поле неразрывно
—*• —>¦
связана с возникновением потенциальной энергии — <Р$ ди-
диэлектрика в этом поле, то за работу поляризации диэлектрика
в собственном смысле обычно принимается величина
8WC = &de + d (- ff>?) = W + d (g2l8n) = —~edff>. (8.7)
Тогда работа поляризации &*d$ равна сумме собственной
работы поляризации бWc и работы d(<^$) против внешнего поля:
№П = &Й5 (а = 6, Л = ^). (8.8)
—>¦ —>•
Работа поляризации 33@/4л равна разности работы §Wn и
работы — d[§2j8n] возбуждения поля в вакууме:
аЯГ=— ЫЪ (а = Ё, А = —2й). (8.9)
4л \ 4я /
* Выражение (8.6) представляет собой работу некоторой расширенной си-
системы, подобно работе E.22) для системы, состоящей из газа и поршня с гру-
грузом
зом.
130
Аналогично для магнетика
— HdS, 8WC=-Xdf, (8.10)
4jt
Поэтому основное уравнение термодинамики для диэлектрика
в электрическом поле будет:
а) при независимой (электрической) переменной 2)
&Й0, (8.11)
4я*
б) при независимой переменной сР
TdS = dEc + PdV—idf, (8.12)
—>¦
где ЕС = Е—$2/8л — «собственная»* внутренняя энергия единицы
объема диэлектрика (Е без энергии поля в вакууме);
в) при независимой переменной <?, когда сопряженной ей ве-
величиной является поляризованность 53,
TdS = dEn + PdV+&d~iy (8.13)
где ЕП=ЕС+ (—ЯР§ ) — сумма собственной внутренней энергии
поляризации диэлектрика и его потенциальной энергии в элект-
электрическом поле;
г) при независимой переменной <f, когда сопряженной ей ве-
величиной является электрическое смещение 25,
TdS = dE' +PdV+ — SdS, (8.14)
4зт
где Е' — Е— 82) /4я = ?п— §2/4я — внутренняя энергия диэлект-
диэлектрика с учетом его потенциальной энергии в поле без энергии поля
в вакууме.
Выбор той или иной электрической независимой переменной
зависит от характера задачи и соответствует исследованию сис-
системы с определенной внутренней энергией ?", Ес, ?п, Е\
Аналогичные уравнения для магнетиков могут быть получены
простой заменой электрических величин магнитными.
Пользуясь каким-либо из основных уравнений термодинамики
для диэлектриков (8.11) — (8.14), легко получить выражения для
дифференциалов термодинамических потенциалов. Так, из уравне-
уравнения (8.11) имеем:
dE = TdS + PdV + —
4я
* Название «собственная» для внутренней энергии Ес=Е—(?2!8л является
условным, так как 8 — напряженность поля, уже измененная присутствием
диэлектрика.
5* 131
SdT— PdV + — fid®, (8 Л 5)
An
4л
Аналогично из уравнения (8.12) получаем:
dE = TdS-PdV+ Ш\ dG-^
(8.16)
dF = — SdT—PdV+ldf, dH = TdS+VdP—9>di ,
где E, Fy G к H означают соответственно Ec, Fc> Gc> Hc.
Эти выражения представляют собой основу термодинамики
диэлектриков (и при соответствующей замене электрических вели-
величин магнитными — магнетиков).
Магнитное и ядерное охлаждения. Охлаждение тела может
быть получено не только при адиабатном расширении, но и при
всякой другой адиабатной работе системы.
Так, в настоящее время в одном из основных методов получе-
получения сверхнизких температур (Г<1 К) используется адиабатное
размагничивание большой группы парамагнитных солей (железо-
алюминиевые квасцы).
Явление изменения температуры при адиабатном размагничи-
размагничивании называется магнитокалорическим эффектом. Количествен-
Количественную величину (dT/o3ff)s этого эффекта можно найти из выраже-
выражения дифференциала энтальпии Н магнетика, помещенного в маг-
магнитное поле Ж'-
Эту величину непосредственно получают и из выражения для
изменения температуры при обратимом адиабатном расширении
(8.5):
дТ \ T(dV/dT)p
дР Js CP
заменив в нем Р-*— 55? и У-> #- (в соответствии с тем, что работа
расширения SW = PdV, а работа намагничивания
Таким образом,
дТ \ __ Т(A<?/дТ)ж
s Сж
где Сж — теплоемкость при постоянной напряженности магнит-
магнитного поля.
-> —>•
Для изотропных парамагнетиков ^- — кЖ- Магнитная восприим-
восприимчивость идеальных парамагнитных веществ по закону Кюри об-
132
ратно пропорциональна температуре:
где С — постоянная Кюри (С>0). Поэтому f = СЖ/Т, (dfrIdT)x=*
— —•CSFt/T2 и, следовательно,
/ дТ \ СЖ ^ Л
Отсюда видно, что при размагничивании (dffl<0) температура
понижается (dT<0). При низкой температуре по закону Дебая
темлоемкость пропорциональна кубу температуры:
поэтому
дТ \ 1_
)p,s T*
Следовательно, при низкой температуре изменение темпера-
температуры может быть велико: обратно пропорционально четвертой сте-
степени температуры. Однако в соответствии с третьим началом тер-
термодинамики при температуре, близкой к О К, х перестает зависеть
от температуры и магнитокалорический эффект исчезает. Пре-
Предельно низкие темпертуры, которые можно получить методом
адиабатного размагничивания парамагнитных солей, определя-
определяются силами взаимодействия между электронными спинами (ди-
поль-дипольного, обменного и т. д.). Как только температура тела
будет настолько понижена, что под действием сил взаимодействия
возникнет упорядочение в расположении элементарных магнети-
магнетиков, метод адиабатного размагничивания перестанет действовать,
В настоящее время получена предельно низкая для этого метода
температура 0,001 К. Вообще, чем более низкую температуру надо
получить, тем более слабые взаимодействия необходимо исполь-
использовать в рабочем веществе. Поэтому другой путь в приближении
к 0 К лежит через использование ядерного магнетизма. В этом
случае силы взаимодействия будут проявляться лишь при 10~5 К.
Этим методом удается получить спиновые температуры порядка
Ю-6 К*.
§ 36. Равновесие в гомогенной системе
В гомогенной системе могут происходить химические реакции
между сос?#$ными ее частями и родственные им процессы дио
социации, ионизации, полимеризации и т. д., которые также свя-
связаны с изменением числа частиц в закрытой системе. Все такие
* См.: Курти Н. Охлаждение адиабатическим размагничиванием ядерных
спинов. — УФН, 1961, т. 75, вып. 1, с. 151; Лоунасмаа О. В. Принципы и
методы получения температур ниже 1 К. М.: Мир, 1977.
133
процессы обычно называют одним термином — химическая реак-
реакция.
Условие химического равновесия. Всякая химическая реакция
протекает, вообще говоря, как в прямом, так и в обратном направ-
направлениях. До наступления равновесия реакция в прямом направ-
направлении преобладает над обратной. При равновесии обе противопо-
противоположные реакции идут х 'одинаковыми скоростями, так что масса
вещества каждого сорта с течением времени не изменяется. Най-
Найдем условие химического равновесия.
Химическая реакция записывается в виде
(8.17)
где At — химические символы реагирующих веществ, v/ — числа
молекул этих веществ в реакции (стехиометрические коэффициен-
коэффициенты). Например, для реакции
2SO2 + O2 = 2SO3, или 2SO2 + O2—2SO3 = 0,
символы Ai и vt имеют значения; Ai = SO2, vi = 2; Л2 = О2, v2=l,
Если система находится при постоянных температуре и давле-
давлении, то при химическом равновесии термодинамический потенциал
Гиббса G системы имеет минимум, определяемый условием 6G =
= 0, или
где §Ni — возможные изменения чисел молекул реагирующих ве-
веществ при реакции. Эти числа пропорциональны числам v«:
6^1/6^ = vi/v2. Поэтому, заменив в формуле (8.18) 6ЛГ; на v*, по-
получаем условие химического равновесия:
= 0. (8.19)
Сравнивая формулы (8.17) и (8.19), видим, что для получения
условия химического равновесия нужно в уравнении химической
реакции заменить символы Л< соответствующими химическими по-
потенциалами \ц. Если в системе происходит несколько химических
реакций, то равновесие определяется совокупностью уравнений
(8.19), для применения которых к конкретным химическим реак-
реакциям необходимо знать выражения для химических потенциалов.
Закон действующих масс. Для идеальных газов химический
потенциал с точностью до энтропийной константы известен. По-
Поэтому с помощью (8.19) можно установить ряд закономерностей
при химических реакциях в смеси идеальных газов, когда каждый
газ ведет себя независимо от других, имея парциальное давле-
давление Р^
134
Химический потенциал идеального газа (*)
где
tio(T) =срТ{\— In T)—Tso + uo, (8.20)
cP = Cp/N — удельная теплоемкость, s0 = So/N и Uo = EoIN — посто-
постоянные.
В случае смеси газов для i-й компоненты
где Pi — парциальное давление этой компоненты.
Общее давление смеси Р = У]^- Для идеального газа
i
i
где Ci — концентрация t-го газа. Таким образом,
VH^kT In CiP+viodT), (8.21)
и условие химического равновесия (8.19) для р'еакций в газовой
смеси принимает вид
i
откуда
' (8-22)
Считая vi положительными для веществ, вступающих в реак-
реакцию, и отрицательными для веществ, получающихся в результате
реакции, перепишем (8.22):
П<?,ЧП<%ш=Кс{Т,Р). (8.23)
Уравнения (8.22) или (8.23) представляют собой закон дейст*
вующих масс: отношение произведения степеней концентраций
веществ, вступающих в реакцию, к произведению степеней кон-
концентраций веществ, появляющихся в результате реакции, с пока*
135
зателями, равными соответствующим стехиометрическим коэффи-
коэффициентам, есть величина постоянная при постоянных температуре
и давлении.
Величина
Ке(Р.Т)=Р
называется константой химического равновесия. Зависимость
Кс(Р, Т) от давления полностью определяется множителем 2К
нахождение же температурной зависимости требует дальнейших
предположений о свойствах газов (зависимость теплоемкостей от
температуры и др.).
Закон действующих масс справедлив также и для реакций
между растворенными веществами, поскольку слабые растворы
ведут себя подобно идеальным газам.
Если в реакции сумма Vvt- равна нулю, то Кс{Т, Р) совсем
i
не зависит от давления, как это, например, происходит при диссо-
диссоциации йодистого водорода:
Закон действующих масс можно выразить не только через кон-
концентрации, но и через парциальные давления, если в уравнение
химического равновесия (8.19) подставить \n = kT\n Pi + 'i\oi(T):
Постоянная равновесия Кр(Т) в этом случае совсем не зави-
зависит от давления, а зависит только от температуры. В некоторых
случаях эта форма закона действующих масс является более
удобной.
Тепловое ионизационное равновесие. Формула Саха. При до-
достаточно высокой температуре (когда химическое соединение уже
полностью диссоциировано) столкновения атомов газа приводят
к их ионизации. При этом часть атомов распадается на положи-
положительный ион Л+ и электрон е. Одновременно с этим происходит и
обратный процесс рекомбинации, в ходе которого ион и электрон
соединяются в нейтральный атом. При равновесии оба эти про-
процесса идут с одинаковой скоростью. Уравнение реакции имеет вид
Применим к этому тепловому ионизационному равновесию
одноатомного газа закон действующих масс и найдем степень
ионизации а газа (определяющую отношение числа ионизованных
Юб
атомов к общему числу всех атомов) в зависимости от давления,
температуры и индивидуальных его параметров.
Концентрации нейтральных атомов, ионов и электронов при
равновесии соответственно равны
N — aN 1 - а , а
р —— ___ п-\- === р z=z
N + aN 1 + а ' ' 1 + а '
= v + v+ + ve=-l —1—1 = —1. (8.24)
Из закона действующих масс находим A—a2)fa2=PK(T)y
откуда
Постоянная химического равновесия
Из формул (8.20) и (8.24) видно, что
Для \хое(Т) электронного газа (для которого Ср = 5/2& и иое = О)
имеем
ИоД )- п (kTM/2 '
где постоянная b связана с энтропийной постоянной s0 и равна
, __ 1 / h2 \ 3/2
В случае одноатомных газов обычно полагают ио = О, т. е. от-
отсчитывают энергию от нормального уровня атома. Тогда энергия
ионизованного атома
мо+= / = ?>?/,
где U — ионизационный потенциал атома; е — заряд электрона.
Таким образом,
S Т)~ кТ\п Ь
а =
bPexp[I/(kT))
(kT)
5/2
Это выражение для зависимости степени ионизации а от дав-
давления и температуры было получено индийским физиком
137
М. Н. Саха и называется формулой Саха. Из нее видно, что а
быстро растет с температурой. Знание а может быть использова-
использовано для определения температуры. Множитель при экспоненте
очень мал, поэтому при температуре, когда kT~I, a^l, газ от-
отзывается практически полностью ионизованным.
Формула Саха нашла важные применения в физике звездной
атмосферы. Так, исследования спектров, исходящих из различных
слоев солнечной атмосферы, показали, что в более глубоких
слоях атмосферы, где температура выше, степень ионизации a
паров кальция ниже, чем в более холодных, внешних слоях. Эта
особенность спектра солнечной атмосферы связана, по Саха, с
ролью давления Р: увеличение степени ионизации с уменьшением
давления идет быстрее, чем ее уменьшение с понижением темпе-
температуры при переходе от глубоких к верхним слоям хромосферы.
Равновесие в неидеальных системах. Летучесть и активность.
Влияние межмолекулярных взаимодействий на термодинамические
свойства газа можно выразить, вводя летучесть или активность
газа. С помощью этих величин реальные газы описываются урав-
уравнениями того же типа, что и идеальные.
Согласно формуле (8.21) химический потенциал идеального
газа
Запишем для химического потенциала любого реального газа
аналогичное выражение:
, Р), (8.25)
где \io(T) — та же функция, что и в (8.21) для химического по-
потенциала идеального газа, а функция f(T, P) учитывает неидеаль-
неидеальность газа и называется летучестью.
Записывая химический потенциал неидеальной системы в виде
(8.25), можно распространить на неидеальные системы свойства,
установленные для идеальных систем. Так, с помощью летучестей
получаем для закона действующих масс реальных газов ту же
формулу, что и для идеальных газов:
Ufl'=KP(T), (8.26)
i
где Кр(Т) имеет то же значение, что и для* смеси идеальных
газов.
Для газа Ван-дер-Ваальса летучесть определяется из формулы
В случае более сложных уравнений состояния выражения для
f(T, P) становятся очень громоздкими. Однако с помощью лету-
летучести исследование свойств реального газа существенно упро-
упрощается при изотермических процессах, когда f можно найти, не
138
обращаясь к полному уравнению состояния. Выражение (8.21)
для химического потенциала идеального газа можно также запи-
записать в виде
[Квд = |лг°G\ P)+kT\ncu (8.27)
где |1г°G\ P)=lxoi(T)+kTlnP.
Распространяя это уравнение на реальные газы, запишем
^. = ^0G, P)+kT\naif (8.28)
где \и°{Т, Р) — та же функция, что и в выражении (8.27), а все
эффекты, связанные с межмолекулярным взаимодействием, вклю-
включаются в функцию щ(Т\ Р; d9 ...fCk)> называемую активностью
компонента i. Величина
>Уг = пг/Сг (8.29)
называется коэффициентом активности i-го компонента. Из фор-
формулы (8.28) получаем
\а = \иИА + кТ\пуг. (8.30)
В смеси идеальных газов все коэффициенты активности равны
единице. Поэтому значения 1—yi или In y^ можно использовать
как меру отклонений от закона идеальных газов.
Нетрудно установить связь между летучестью и коэффициен-
коэффициентом активности:
fi = Piyi. (8.31)
§ 37. Равновесие в гетерогенной системе
Рассмотрим теперь фазовое, или гетерогенное, равновесие сис-
системы, состоящей из п фаз с k компонентами. Будем у величин,
относящихся к разным фазам и компонентам, писать два ин-
индекса: верхний означает фазу, а нижний — компонент; так, на-
например, \Xi" — химический потенциал первого компонента во вто-
второй фазе.
Условия равновесия гетерогенной системы. Равновесие в двух-
двухфазной системе какого-либо вещества (см. § 27) наступает при
Г =7", Р' = Р", \i' = \i'\ (8.32)
т. е. при равенстве температур, давлений и химических потен-
потенциалов вещества в обеих фазах, или
WW, P)=ii"(L P).
При равновесии же двух фаз разных веществ должны выпол-
выполняться условия
7*2 = 7^ P'i=P9 (8.33)
т. е. равенство температур и давлений в фазах. На химические
потенциалы в этом случае никакие условия не накладываются,
139
что физически совершенно ясно и без вычислений, поскольку об-
обмена частицами между такими фазами быть не может.
Из формул (8.32) и (8.33) можно сделать общий вывод, что
при равновесии гетерогенной системы из п фаз с k компонентами
температура, давление и химические потенциалы каждого компо-
компонента во всех фазах одинаковы:
Т' = Т" = Г" = ... =Г<П), (8.34)".
Р'^рн^Р"/^ _ =рр)9 (8 35)
ц' __ ц" __ '" _ =ll(rt)
И2 = К = ^2 =••• =№> (8.36)
Уравнения (8.34) — (8.36) представляют собой условия равно-
равновесия гетерогенной системы (*).
Правило фаз Гиббса. Полученные условия равновесия гетеро-
гетерогенной системы позволяют определить количество фаз (состоящих
из нескольких компонентов), способных одновременно находиться
в равновесии, или число независимых переменных гетерогенных
систем, которые можно изменять, не нарушая ее равновесия.
Эта задача была решена Гиббсом, поэтому полученный им ре-
результат называется правилом фаз Гиббса. Установим это правило.
Пусть общие температура и давление во всех фазах равновес-
равновесной гетерогенной системы будут Г и Р. Согласно (8.36) при рав-
равновесии химические потенциалы каждого компонента во всех фа-
фазах должны быть одинаковы:
Ну^И/ (/=1' 2, ... , ft; i, s=l, 2, ... ,п).
Всего этих уравнений, выражающих условия равновесия гете-
гетерогенной системы, k(n—1). Состояние гетерогенной системы опре-
определяется величинами Р, Т и k—1 независимыми концентрациями
различных компонентов в каждой фазе*, т. е. 2Л-п{к—1) пере-
переменными. При этом система из k(n—1) уравнений (8.36) имеет
решение, если число уравнений во всяком случае не больше чис-
числа переменных, т. е. k(n—\)<2 + n(k—1), откуда
n<fe + 2. t(8.37)
Это соотношение устанавливает, что в системе из k компонен-
компонентов одновременно может находиться в равновесии не больше чем
k + 2 фазы, и называется правилом фаз Гиббса.
* Независимых концентраций в каждой фазе к—1, потому что между кон-
концентрациями всех k компонентов в каждой фазе существует связь:
k
т. е. сумма концентраций всех компонентов в каждой фазе равна единице.
140
Если число п фаз в термодинамической системе меньше, чем
?+2, тр в уравнении (8.36) k + 2—п переменных могут, очевидно,
иметь произвольные значения. Это означает, что k + 2—п перемен-
переменных можно менять, не изменяя этим числа и вида фаз системы.
Число независимых переменных, которые могут быть произвольно
(в конечных пределах) изменены без нарушения равновесия гете-
гетерогенной системы, называется числом термодинамических степе-
степеней свободы f системы. Очевидно, что
f = k + 2—n. (8.38)
Так как соотношение (8.38) эквивалентно (8.37), то оно также
называется правилом фаз Гиббса.
Правило фаз в виде (8.37) получено для гетерогенной системы,
на которую действует только одна сила давления. Если на систе-
систему действует q обобщенных сил, то вместо числа 2 (соответствую-
(соответствующего переменным Р и Т) в правило фаз будет входить число
q+\ и для такой системы это правило будет записываться в виде
n<k+q+\ (8.39)
или в виде
—n. (8.40)
Кривые равновесия фаз. Тройная точка. Согласно правилу фаз
Гиббса в системе из k компонентов в равновесии одновременно
может находиться не больше k + 2 фаз. В случае однокомпонент-
ной системы (k=l) максимальное число фаз, находящихся в
равновесии, очевидно, равно nM&KC = k + 2 = 3, а в случае бинарной
СИСТемЫ ЯМакс = 4.
При равновесии двух фаз (п = 2) однокомпонентного вещества
(k=l) число степеней свободы f = k + 2—л=1. Это видно также
из условия равенства химических потенциалов \х'(Р, Т)=\х"(Р, Г),
которое связывает температуру и давление в фазах. Одну из этих
переменных можно взять за независимую, тогда
Р = Р(Т) (8.41)
уравнение для зависимости давления от температуры при равно-
равновесии. Если откладывать на осях координат температуру и давле-
давление, то точки, соответствующие равновесию фаз, будут лежать на
некоторой кривой (8.41), называемой кривой равновесия фаз.
При этом точки, лежащие по сторонам этой кривой, представ-
представляют собой различные однородные состояния тела. При изменении
состояния вдоль линии, пересекающей кривую равновесия
(рис. 18, пунктир), в точке пересечения наступает расслоение фаз
и дальше система переходит в другую фазу. Кривая равновесия
фаз является, следовательно, границей устойчивости какой-либо
фазы относительно ее прерывных изменений.
При равновесии трех фаз одного и того же вещества имеем
два уравнения
141
, P)
{8.42?
с двумя переменными. Эти уравнения дают вполне определенные
значения Т и Р при равновесии трех фаз одного и того же ве-
вещества (число степеней свободы / = 0). Состояние, определяемое
этими значениями переменных Т и Р, называется тройной точкой.
На диаграмме ГКР тройная точка получается в результате пере-
пересечения кривых равновесия каждый двух фаз из трех* (рис. 19).
Тройная точка для воды имеет следующие значения:- t=
= 0,0100°С, Р = 509Па = 4,58 мм рт. ст.
Г
Рис. 18
Рис. 19
Аналогичные кривые равновесия двух фаз можно получить и
для бинарных систем, изображая, например, давление двухфаз-
двухфазной бинарной системы в зависимости от концентрации какой-либо
компоненты в одной из фаз.
Равновесие бинарных систем. Основное уравнение теории рав-
равновесия бинарных систем. Рассмотрим теперь равновесие между
различными фазами с двумя независимыми компонентами, т. е.
равновесие бинарных систем. Такие системы играют важную роль
в химии и металлургии.
Согласно правилу фаз Гиббса наибольшее число фаз, находя-
находящихся в равновесии, в случае бинарных систем равно 4. Эти четы-
четыре фазы сосуществуют только в четверной точке, для которой все
параметры системы (Т, Р и состав фаз) полностью определены.
В случае сосуществования трех фаз система имеет одну степень
свободы, т. е. один из параметров может быть выбран произволь-
произвольно; обычно таким параметром является давление.
Наиболее интересно сосуществование двух фаз бинарной сис-
системы, так как другие случаи могут быть к нему сведены. В би-
бинарной системе произвольно могут выбираться уже два парамет-
параметра: можно задать, например, температуру и состав одной из фаз
* В настоящее время известно одно вещество — гелий, у которого кривые
плавления и испарения не пересекаются, т. е. отсутствуют кривая сублимации
и тройная точка: жидкая фаза существует вплоть до О К.
142
(концентрацию какой-нибудь компоненты), и равновесие будет
возможно только при определенном давлении. Или можно произ-
произвольно выбрать давление и состав одной из фаз, тогда равновесие
будет только при определенной температуре. Установим основное
уравнение равновесия двух фаз бинарной системы.
Для этого напишем для каждой фазы бинарной системы урав-
уравнение Гиббса — Дюгема E.48):
S'dT- V'dP + Nldth +
S'dT -V'dP + Nldfr + Nldfo = 0
(фазовые значки у dt, dP, d\x не ставятся, так как при равновесии
Г = 7", Р' = Р'\ \ь' = \к").
Исключим d^2 из уравнений (8.43). Умножив первое из урав-
уравнений (8.43) на N2", второе — на AV, вычтем из второго уравне-
уравнения первое, тогда
S'Nl) dT—{V"N2—VNl) dP+ (N"iN'2—NInZ) фх =0. (8.44)
Это уравнение является основным уравнением теории бинар-
бинарных систем. Пользуясь им, можно установить все закономерности
таких систем. Наибольший интерес представляет равновесие жид-
жидких бинарных растворов и их паров.
Основные закономерности таких бинарных систем были уста-
установлены Д. П. Коноваловым (*).
§ 38. Термодинамика излучения
Законы термодинамики универсальны в том отношении, что
применимы к системам из большого числа частиц любой при-
природы, т. е. как к классическим, так и к квантовым системам, как
к веществу, так и к полю, прежде всего к электромагнитному по-
полю — излучению, представляющему собой также корпускулярную
систему.
Излучение, находящееся в некоторой области пространства в
равновесии с окружающими телами, называется тепловым или
равновесным, При тепловом равновесии тел их температуры, как
известно, одинаковы. Поэтому и излучение, находясь в равнове-
равновесии с другими телами, имеет температуру этих тел *.
В термодинамике равновесное излучение представляет собой
систему, характеризуемую объемом V, температурой Т и дав-
давлением Р.
В электродинамике равновесное излучение есть непрерывная
совокупность электромагнитных волн (с частотами от 0 до оо),
излучаемых беспорядочно движущимися частицами окружающих
тел. Амплитуды и фазы этих волн в случае такого «естественного»
* Мысль о температуре равновесного излучения была высказана впервые в
1893 г. русским физиком Б. В. Голициным, и это позволило в полной мере при-
применить термодинамику к излучению.
143
излучения распределены по всему спектру совершенно беспоря-
беспорядочно.
Пусть uvdv — удельная энергия волн в интервале частот от v
до v-\-dv (uv — спектральная плотность,излучения). Тогда полная
удельная энергия излучения
vdv, (8.45)
а полная энергия излучения в объеме V вследствие его изотроп-
изотропности
E = uV. (8.46)
Аналогично, если svdv — энтропия единицы объема излуче-
излучения с частотами в интервале (v, v + dv), то полная удельная эн-
энтропия равновесного излучения
а энтропия излучения в объеме V
S = sV.
Энергия волн с частотами в интервале (v, v + dv), излучаемых
единицей поверхности в единицу времени, равна evdv, где ev —
спектральная энергетическая светимость этого тела в данном
интервале частот при определенной температуре.
Тела, поглощающие все падающее на них излучение какой
угодно частоты, называются абсолютно черными (или просто чер-
черными)] тела, отражающие все падающее на них излучение, на*
зываются зеркальными или белыми; тела, пропускающие все па-
падающее излучение, называются абсолютно прозрачными.
В природе нет тел с такими абсолютными свойствами, однако
многие тела можно отнести приближенно к тому или иному клас-
классу. Например, приблизительно черна сажа, еще более черной яв-
является платиновая чернь. Наилучшим приближением к абсолютно
черному телу является малое отверстие в стенке протяженной по-
полости. Излучение, попавшее через это отверстие внутрь полости, в
результате многократного отражения от стенок практически пол-
полностью поглотится, так что коэффициент поглощения отверстия
можно считать равным единице. Согласно второму началу излу-
излучение в полости по своему спектральному составу их такое же, как
в полости с «черными» стенками, т. е. определяется только тем-
температурой стенок и совершенно не зависит от природы вещества
стенок (в противном случае можно было бы построить вечный
двигатель второго рода (*)). Поэтому излучение, испускаемое от-
отверстием, по интенсивности и спектральному составу идентично
144
излучению абсолютно черного тела с температурой Г, причем
(8.47)
где с — скорость света в вакууме (*).
Внутри полости с зеркальными стенками при отсутствии в ней
каких-либо тел излучение отсутствует, как бы ни была высока
температура оболочки, так как такие стенки ничего не излучают.
Однако если мы откроем заслонку в стенке, впустим извне излу-
излучение различных частот от тел с разной температурой *, то это
произвольное излучение, введенное в полость, останется в ней без
всякого изменения, так как оно не может быть ни увеличено за
счет испускания, ни уменьшено путем поглощения, ни изменено
из-за взаимодействия между спектральными излучениями, по-
поскольку по принципу .суперпозиции отдельные излучения между
собой не взаимодействуют. В полости с белыми стенками создает-
создается термодинамическое равновесие излучений с различной темпе-
температурой, так что в каждой точке будет существовать одновременно
несколько различных температур. Это равновесие, однако, не
будет устойчивым (*). Если позволить одним излучениям перехо-
переходить в другое, что достигается введением в полость черной пы-
пылинки, излучающей и поглощающей свет и играющей роль посред-
посредника при обмене энергий между частотами, то излучение пере-
переходит в состояние устойчивого равновесия, становится черным и
все спектральные излучения имеютодну и ту же температуру.
В применении к излучению термодинамика позволяет устано-
установить ряд закономерностей:
1) существование давления излучения (световое давление);
2) закон Кирхгофа о независимости отношения спектральной
энергетической светимости ev к коэффициенту поглощения р от
природы вещества;
3) закон Стефана — Больцмана о зависимости полной плот-
плотности энергии и равновесного излучения от температуры Г;
4) закон Вина о свойствах функции спектральной плотности из-
излучения uv\
5) рост энтропии при обратимом процессе преломления света
вследствие когерентности отраженного и преломленного лучей.
Получим некоторые из этих и другие результаты для равновес-
равновесного излучения.
Существование светового давления. Наличие давления излуче-
излучения впервые было доказано на основе второго начала в 1876 г.
итальянским физиком А. Бартоли исходя из следующего мыслен-
мысленного эксперимента.
Пусть имеются два черных тела А и В с постоянными темпе-
температурами 7\ и Т2 (Ti>T2), соединенные между собой пустым ци-
цилиндром с белыми стенками (рис. 20). У начала и в конце ци-
цилиндра имеются щели для подвижных поршней с зеркальными
* Температура черного тела, испустившего излучение определенной частоты,
и называется температурой его излучения.
145
Рис. 20
«стенками. Удалим из цилиндра поршень Р2, оставив Р\ у самой
поверхности тела А. При этом весь объем цилиндра наполнится
равновесным излучением от тела В. Введя поршень Р.2 и удалив
Pt будем двигать Р2 до соприкосновения с телом А, Тогда все
излучение в цилиндре поглотится телом Л, а цилиндр вновь за-
заполнится излучением от тела В.
Введем теперь поршень Рг у поверхности тела В и, удалив Р2,
будем двигать Р± до тела А. При этом вся энергия, излученная Б,
снова поглотится телом А.
Повторяя периодически эту операцию, можно перевести любое
количество энергии излучения от тела В к телу Л, вследствие
чего тело А нагревается, а В ох-
охлаждается, т. е. теплота перено-
переносится от холодного тела к горя-
горячему. Так как по второму началу
термодинамики, это может быть
только при затрате работы, то,
следовательно, и в данном случае
передвижение поршня должно
сопровождаться затратой работы.
Отсюда следует, что излучение
лроизводит давление на поршень, причем чем больше температура
излучения, тем больше это давление.
Саму же функциональную зависимость давления излучения от
температуры (как и вообще термическое и калорическое уравне-
уравнения состояния любой системы) с помощью только термодинамики
определить невозможно (см. § 5). Однако, используя электромаг-
электромагнитный характер излучения (т. е. привлекая законы электродина-
электродинамики), можно выразить световое давление Р через плотность
энергии равновесного излучения и и из общих законов -термодина-
-термодинамики получить для него как термическое, так и калорическое
уравнение состояния. Согласно электродинамике, имеем
Р = 4/зИ, (8.48)
что совпадает с формулой для давления релятивистского идеаль-
идеального квантового газа C.31). Выражение (8.48) легко получить из
рассмотрения равновесного излучения как совокупности фотонов,
удары которых о стенку и обусловливают давление (*). Экспери-
Экспериментально наличие светового давления было впервые установле-
установлено в 1901 г. П. Н. Лебедевым на физическом факультете МГУ.
Закон Стефана — Больцмана. Применим к равновесному излу-
излучению уравнение C.27), связывающее термическое и калорическое
уравнения состояния:
дР
'=uVf поэтому (см. 3.27))
(8.49)
Для равновесного излучения Р = и/3 и
1/46
Отсюда после интегрирования получаем зависимость полной
плотности энергии равновесного излучения от температуры
и = аТ\ (8.50)
называемую законом Стефана — Больцмана: плотность энергии
равновесного излучения пропорциональна четвертой степени
термодинамической температуры.
Стефан установил этот закон в 1879 г. на основании опытных
данных, а в 1884 г. Больцман получил его приведенным здесь спо-
способом на основании второго начала термодинамики.
Постоянная интегрирования о (постоянная закона Стефана —
Больцмана) термодинамически не определяется. Опыт, а также
статистическая физика дают значение а=7,64«10~16 Дж/К4-м3.
Термическое и калорическое уравнения состояния и энтропия
равновесного излучения. Теперь можно написать как термическое*
так и калорическое уравнения состояния равновесного излучения:
(8.51}
(8.52)
Зная эти уравнения состояния, нетрудно вычислить энтропию?
излучения. Действительно, из уравнения
ле_ 6Q __4E
Т
получаем dS
откуда
S = 4saTW (8.53)
(аддитивная постоянная в выражении для энтропии (8.53) в соот-
соответствии с третьим началом термодинамики (S = 0 при Т = 0К)
принята равной нулю).
Так как при адиабатном процессе S = const, то с помощьк>
формулы (8.53) находим уравнение адиабаты равновесного излу-
излучения VT3 = const, или
py4/3 = const. (8.54)
Сравнивая уравнение (8.54) с уравнением адиабаты идеально-
идеального газа B.12'), замечаем, что при адиабатных процессах равно-
равновесное излучение ведет себя как идеальный газ с отношением
теплоемкостей у = 4/3. Это, однако, не означает, что у равновесно-
равновесного излучения у = 4/3, оно равно бесконечности (*).
Термодинамические потенциалы и условие устойчивости равно-
равновесного излучения. Для равновесного излучения, как и для идеаль-
идеального газа (для которого из опыта также известны термическое и
калорическое уравнения состояния), термодинамика позволяет
найти явные выражения для термодинамических потенциалов
?(V, S), F(Ty У), G(P, T) и Н(Р, S). Определим эти функции.
14?
Так как E — oTAV и S = 4/saTzV1 то внутренняя энергия излуче-
излучения как термодинамический потенциал равна
{^ryi. (8.55)
энергия Гельмгольца
F(T, V)=E—TS = oTbV—T-43oT*V= —Ч&ТЩ, (8.56)
энергия Гиббса
G(P, T)=F + PV= —ЧзоТ1У + ЧзоТьу=0, (8.57)
энтальпия
Н(Р, S)=E + PV=G + TS = TS = S$P/e)lv. (8.58)
Из выражения (8.57) видно, что термодинамический потенциал
G(Ty Р), не может быть характеристической функцией для излу-
излучения. Это обусловлено тем, что характеристические переменные Т
и Р согласно уравнению (8.51) не являются для излучения неза-
независимыми.
Рассмотрим теперь вопрос об условиях устойчивости равновес-
равновесного излучения.
Так как для излучения Р = 1/зст7м, то для него (dP/dV)T = 0,
СР=оо, Т/Ср = 0. Такое значение этих величин не означает что
для излучения условия устойчивости F.16)
{dP/dV)T<0 и Т/СР>0
нарушаются, поскольку (dP/dV)T, T/CP не характеризуют устой-
устойчивость излучения. Дело в том, что условия устойчивости F.16)
получены для однородной закрытой системы, которая не обмени-
обменивается частицами с окружающей средой, равновесное излучение
же представляет собой систему с переменным числом частиц,
подобно жидкости, находящейся в равновесии с паром. Именно по
этой причине у излучения, как и у двухфазной системы жид-
жидкость — пар, параметры Т и Р не являются независимыми, тепло-
теплоемкость СР = оо и (dP/dV)T = 0. Следовательно, 'условия устойчи-
устойчивости F.16) к равновесному излучению неприменимы. Нельзя не-
непосредственно использовать для него и условие устойчивости
Г/Су>0, так как сообщение теплоты излучению при постоянном
объеме связано с испусканием фотонов стенками.
Однако устойчивость равновесного излучения можно характе-
характеризовать адиабатным коэффициентом (dP/dV)s, так как при
адиабатном расширении излучения отсутствует обмен частицами
между ним и окружающими его белыми стенками. Таким обра-
образом, устойчивость излучения определяется одним из условий
F.17), а именно:
(dP/dV)'8<0.
148
Зная уравнение адиабаты излучения (8.54) нетрудно убедить-
убедиться, что это условие его устойчивости выполняется. Действительно,
используя уравнение (8.54), находим
дР \ = з Р _ 4стГ4
dV )s 4 V W
Закон Вина. Закон Стефана — Больцмана дает выражение для
полной плотности энергии равновесного излучения, но ничего не
говорит о его спектральном составе. Рассматривая излучение в
полости (с подвижным поршнем), стенки
которой представляют собой идеально от-
отражающие тела (рис. 21), и применяя к не-
нему законы термодинамики и электродина-
электродинамики, В. Вин в 1893 г. установил закон,
определяющий важные свойства функции uv
для спектральной плотности энергии равно-
равновесного излучения. Саму же функцию uvne ис'
удается установить таким путем. Это воз-
возможно только с помощью статистических методов. Вайдем закон
Вина.
При движении поршня температура излучения вследствие адиа-
батности процесса изменяется по закону
VT3 = const.
Изменяются также частота и энергия излучения при отраже-
отражении от движущегося зеркального поршня, так как излучение со-
совершает при этом работу над поршнем. Изменения обеих этих ве-
величин легко находятся на основании законов термодинамики и
электродинамики (*) и определяются соотношениями
(8.59)
mv/P = const, (8.60)
из которых следует:
)
(8.61)
Uv = v*(T*/v*)-y(v/T)=v*f(y/T),
или
ф(), (8.62)
так как uv\dv\=uK\dk\.
Формулы (8.61) и (8.62) представляют собой закон Вина об
энергии излучения, приходящейся соответственно на единицу ин-
интервала частот или на единицу интервала длин волн при темпе-
температуре Т. Таким образом, видно, что применение термо- и электро-
электродинамики к равновесному излучению не решает полностью задачу
по определению спектральной плотности излучения uv(v, T). Од-
Однако, сведя решение задачи по отысканию этой функции от двух
переменных v и Т к задаче определения функции f(v/T) одной
1,49
переменной v/Г, термо- и электродинамика позволили получить
достаточно большую информацию о свойствах излучения. Поэтому
установление закона Вина (8.61) было важным этапом в истории
открытия законов равновесного излучения.
Получим ряд следствий из закона Вина:
а) закон Вина приводит к смещению максимума спектральной
плотности энергии равновесного излучения с изменением его тем-
температуры. Действительно, определим длину волны Хт9 которой
соответствует максимальная плотность энергии икт равновесного
излучения. Продифференцируем для этого выражение (8.62) по к
и производную приравняем нулю: —5ф(ХтГ) +hmTy'(ктТ) =0>
откуда
ктТ = Ь, (8.63)
где Ь — постоянная Вина, равная, как показал опыт, 2, 9-10~3м-К.
Формула (8.63) выражает закон смещения Вина; длина волныг
на которую приходится максимум спектральной плотности энергии
и% равновесного (черного) излучения, обратно пропорциональна
термодинамической температуре*.
б) закон Вина (8.61) позволяет по заданной кривой распреде-
распределения энергии в спектре черного излучения при какой-либо тем-
температуре Т построить аналогичную кривую при любой другой тем-
температуре 7\.
В самом деле, пусть задана кривая распределения для темпе-
температуры Т. Найдем аналогичную кривую для температуры 7\. Вос-
Воспользуемся соотношением (8.59) v/jT=vi/Ti = const. Тогда по фор-
формуле Вина
и*(Ти vi) =vtf (vi/7\) = (T{/T)Wf(v/T) = (TJTyuv(T, v). (8.64)
Очевидно, что для построения кривой uv(Tu vi) по заданной
кривой uv(T, v) необходимо умножить ординату каждой точки за-
заданной кривой на G\/ГK;
в) формула Вина приводит к закону Стефана — Больцмана
о о
или, вводя новую переменную интегрирования v/T=x,
г) из формулы Вина (8.62) и закона смещения Вина (8.63)
получаем, что значение максимальной плотности в спектре черного
излучения пропорционально пятой степени температуры:
и% = const -Т5.
* Заметим, что положения максимумов функций ик и uv совпадают, по-
поскольку равным интервалам частот не соответствуют равные интервалы длин
волн (¦&).
150
Глава 9
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Рассматривая равновесие соприкасающихся фаз гетерогенной
системы, мы не учитывали до сих пор особых свойств поверхности
раздела и их влияния на равновесие. Мы считали, что энергия Е
и энергия Гельмгольца F системы, состоящей из двух или не-
нескольких фаз, равны сумме энергий или энергий Гельмгольца от-
отдельных фаз.
В поверхностном слое фазы толщиной порядка радиуса моле-
молекулярного взаимодействия A нм) молекулы взаимодействуют не
только с молекулами своей фазы, но и с близлежащим слоем чу-
чужой фазы, поэтому физические свойства слоя отличаются от
свойств внутри (в объеме) фазы.
Поскольку поверхность тела растет пропорционально квадрату
размеров этого тела, а объем — пропорционально кубу этих раз-
размеров, то для больших тел поверхностными- эффектами по срав-
сравнению с объемными можно пренебречь.
Однако если вещество находится в мелкораздробленном со-
состоянии, то такая система обладает развитой поверхностью и по-
поэтому пренебрежение поверхностными эффектами может в этом
случае привести в результатах вычислений к существенным по-
погрешностям.
§ 39. Поверхностные натяжение и давление
Термодинамика поверхностных явлений была развита Гиббсом.
Он принимал поверхностный слой за новую «поверхностную фазу»,
отличную от объемных фаз тем, что ее толщина чрезвычайно мала
по сравнению с протяженностью в двух других измерениях, и по-
поэтому рассматривал поверхностный слой как геометрическую раз-
разделяющую поверхность, применяя к ней общие термодинамиче-
термодинамические уравнения.
Площадь поверхности 2 фазы является наряду с объемом V
новым параметром, характеризующим состояние системы. Увели-
Увеличение температуры и объема сопровождается затратой работы, так
как для образования новой поверхности некоторые частицы из
объема должны перейти на поверхность, что связано с работой
против сил молекулярного взаимодействия.
Обозначим через сг обобщенную силу, соответствующую пара-
параметру 2. Тогда элементарная работа при увеличении поверхности
на dS (при 7 = const и V=const)
а дифференциал свободной энергии системы при изменении ее Т,
Уи2
dF = — SdT—PdV+adH.
151
Величина а, характеризующая равновесие между двумя соприка-
соприкасающимися фазами, называется поверхностным натяжением и
равна силе на единицу длины на поверхности или изменению сво-
свободной энергии на единицу увеличения поверхности: o = dF/dH
Поверхностная энергия, очевидно, равна
rrv rv (*до \ v (г, т д0
= az — l2: — =2 а — Г
\ дТ
дТ \ дТ /i/,2 \ дТ
Рассмотрим условия равновесия в системе, состоящей из двух
фаз, разделенных поверхностью раздела. Известно, что при пре-
пренебрежении поверхностными явлениями условиями равновесия
двух фаз одного и того же вещества являются
Т' = Т", Р' = Р", \ь'=х\1". (9.1)
Те же рассуждения, которые приводят к равенствам (9.1) и
которые здесь не повторяются, дают для равновесия двух фаз с
учетом поверхностных явлений
Что же касается давлений в фазах, то, так как теперь на гра-
границе учитываются силы поверхностного натяжения, равновесие
между фазами наступает, вообще говоря, при разных давлениях
в фазах. Найдем это условие механического равновесия в системе
из двух фаз: жидкость (') и пар ("), исходя из минимума свобод-
свободной энергии при T = const и V = const.
Дифференциал свободной энергии системы, состоящей из жид-
жидкости, пара и поверхности раздела между ними, когда температу-
температура и химический потенциал в фазах одинаковы, равен
dF = —P'dV' — P"dV"+iodZ. (9.2)
При равновесии dF = 0, следовательно, icrdS — P'dV — P"dVrr =
= 0, а так как V + V"= У = const, то
где dH/dV — кривизна поверхности раздела фаз. Когда эта по-
поверхность сферическая, то
d2/dV = dDnr*)ldDtfir*) =2/г
(г считается положительным, если кривизна поверхности направ-
направлена в фазу (')). В случае произвольной поверхности
dS _ 1 1
dV ~ гг г2'
где /*! и г2 — главные радиусы кривизны поверхности. Таким об-
образом, при равновесии сферических капель жидкости (') с паром
(") давление в капле Р' и давление пара Р" связаны условием
Р'_Р" = 2а/г, или Р' = Р" + 2о/г.
152
Отсюда видно, что на поверхности раздела двух фаз (капля —
пар) существует скачок давления, равный 2о/г. Величина <r(l/ri +
+ 1/г2) или 2а/г (в случае сферической поверхности) называется
поверхностным давлением или давлением Лапласа. Для плоской
поверхности (r-^оо) раздела жидкости и пара давление Лапласа
равно нулю и условие механического равновесия при этом сов-
совпадает с аналогичным условием без учета поверхностных явлений?
Из формулы (9.2) видно, что при постоянном объеме капли
(V' = const) ее равновесная форма определяется минимумом по-
поверхности 2. Следовательно, жидкость, находящаяся под дейст-
действием только сил поверхностного натяжения, принимает шарообраз-
шарообразную форму, так как при данном объеме минимальной поверх-
поверхностью обладает шар.
§ 40. Равновесная форма монокристалла.
Принцип Гиббса — Кюри и теорема Вульфа
При равновесии монокристаллов со своим насыщенным паром
или расплавом его форма определяется теоремой Вульфа, дока-
доказанной им впервые в 1885 г. Эта теорема выражает конкретное
условие равновесия кристалла и может быть установлена исходя
из общего условия равновесия системы при Т = const и V—const:
Прежде чем доказывать эту теорему, заметим, что для всякого
кристалла существует точка, удовлетворяющая условию
c, (9.3)
где d — удельные поверхностные свободные энергии граней *,
hi — их соответствующие расстояния до этой точки (i=l, 2, 3,4).
В самом деле, рассмотрим две смежные грани кристалла ОМ и
ON (рис. 22) с поверхностными натяжениями а4 и а2 и проведем
параллельно этим граням две плоскости на таких расстояниях hi
и h2 от граней, чтобы выполнялось условие
ai/fti = a2/ft2. (9.4)
Линия пересечения плоскостей Л, очевидно, параллельна ребру
О и при увеличении ht и /i2 в одинаковое число раз будет переме-
перемещаться вдоль плоскости ОА. Таким образом, плоскость ОА яв-
является геометрическим местом точек, определяемым условием
(9.4). Вводя в рассмотрение третью, а затем и четвертую грани,
* Величину Oi для краткости называют, по аналогии с жидкостью, просто
поверхностным натяжением. Необходимо, однако, иметь в виду, что это не одно
и то же, так как процесс образования новой поверхности у кристалла в общем
случае связан с объемной деформацией.
153
аналогично убедимся, что на плоскости ОА существует прямая
линия, удовлетворяющая условию
а на этой линии — точка, удовлетворяющая условию (9.3).
Существование такой точки не связано с предположением о
равновесности кристалла, и, следовательно, в общем случае для
каждых данных четырех граней (из их общего числа N) эти точ-
точки разные. В случае же равновесного кристалла эта точка един-
единственная. Иначе говоря, равновесная форма монокристалла ха-
N
/hi
Рис. 22
Рис. 23
рактеризуется тем, что его грани удалены от некоторой точки
(точки Вульфа) на расстояния, пропорциональные поверхностным
натяжениям граней:
а1/Й1 = <Т2/Л2=(Уз/Лз= • • • =\oN/hN.
Это утверждение называется теоремой Вульфа. Докажем ее.
Дифференциал свободной энергии системы в термостате, со-
состоящей из кристалла, расплава (') и поверхности раздела между
ними,
dF= —PdV—
t— (P— P')dV,
1=1
где 2; — площадь i-й грани кристалла.
При равновесии dF = 0, следовательно, кристалл, находящийся
в равновесии с расплавом, принимает при заданном объеме V
такую огранку (форму), при которой его поверхностная свобод-
свободная энергия имеет минимальное значение (принцип Гиббса —
Кюри):
N
(9.5)
Объем кристалла можно рассматривать как сумму построен-
построенных на гранях Si объемов пирамид с общей вершиной в произ-
154
вольной точке внутри кристалла (рис. 23). Очевидно, что
N N
Hthi и dV = —
С другой стороны, всякое изменение объема с точностью до ве-
величины второго порядка малости равно смещению поверхности 2г*
N
на изменение dh\ высоты: dV =S\ ^idht. Поэтому
N N N N
1 ^ГЧ ^ГЧ / 1
— \ fi/d^if и dV == у Ziidhi == —
2 шшк ш^ 2
t=l i=l i=l i=\
и принцип Гиббса —Кюри (9.5), определяющий условный мини-
N
мум поверхностной свободной энергии V cr^St-, запишется в виде
i=i
N
•,d2,=0 (9.6)
при условии
Но условие (9.7) не исчерпывает Полностью связей между из-
изменениями площадей при их возможных перемещениях. В число
этих перемещений включается и перемещение кристалла в прост-
пространстве без изменения формы. Всего таких независимых переме-
перемещений кристалла в пространстве три. Поэтому возможные измене-
изменения площадей граней кристалла должны удовлетворять трем
уравнениям связей:
N N N
t=i t=i t=i
N
Для определения минимума величины V ort-2fc- при условиях
(9.7), (9.8) воспользуемся методом Лагранжа: умножим уравне-
уравнения (9.7), (9.8) соответственно на A,i, X2, Яз, Х4 и сложим их с урав-
уравнением (9.6):
2<=0. (9.9)
165
В связи с условиями (9.7), (9.8) четыре вариации из N не за-
зависимы, например dSi, d22, с?2з, dl^. Подберем %и Х2, ^з, ^4 так,
чтобы коэффициенты при зависимых изменениях площадей обра-
обратились в нуль:
= О,
Из этих уравнений находим:
где
h1a1b1c1
h2 а2 b2 c2
h3a3b3c3
hb
(9.10)
(9.11)
(9.12)
h1a1b1c1
h, a, b9 с
h
_ 2U2
ол b3 c3
3as
и т. д.
Учитывая выражения (9.10), из формулы (9.9) при независи-
независимых dEi(i = 5, 6,..., N) получаем
А
А
А
А
(9.13)
Уравнения (9.10) и (9.13) являются геометрической иллюст-
иллюстрацией условий равновесия кристалла и справедливы для любой
точки.
Применим уравнения (9.10) к точке, в которой выполняется
условие (9.3):
\о{ = с1ц (i=l, 2, З; 4).
Подставляя эти выражения сц в определители (9.12), находим:
Ai= — с А, А2=/Аз = А4 = 0.
Из уравнения (9.13) получаем
outfit (i = 5, 6,.. .,N),
что и составляет содержание теоремы Вульфа.
Стремление кристалла принять равновесную форму, определяе-
определяемую теоремой Вульфа, с увеличением размера кристалла умень-
уменьшается, так что практическое значение теоремы относится прежде
всего к малым кристаллам (не превышающим 1 нм).
156
Если для некоторой грани Oi/hi>c, то она будет испаряться или
расплавляться, если же Oi/hi<c9 то такая грань будет нарастать,
причем скорости U{ роста кристалла (при приближении к равно-
равновесию) по нормали к разным граням пропорциональны удельным
поверхностным свободным энергиям этих граней:
§ 41. Роль поверхностного натяжения
при образовании новой фазы.
Зародыши
Как известно, в устойчивом равновесии всякая система в за-
зависимости от характера внешних условий имеет минимум одного
из своих термодинамических потенциалов и при изменении этих
условий переходит из одного устойчивого состояния в другое. На-
Например, когда воде сообщается теплота при нормальном атмо-
атмосферном давлении, то она или нагревается, или закипает и частич-
частично переходит в пар, как только ее температура достигает 100°С.
Однако известно также, что путем очистки жидкости можно
добиться ее перегрева и фазовый переход не -наступит при тем-
температуре, заметно превышающей температуру кипения при дан-
данном давлении. Аналогично обстоит дело и в случае других фазо-
фазовых переходов первого рода *: в чистом паре затягивается кон-
конденсация (переохлажденный пар), в чистой жидкости или раство-
растворе затягивается переход в кристаллическое состояние (пересы-
(пересыщение).
Однородная система (фаза) в заданном объеме может суще-
существовать в некотором интервале температур, имея свободную
энергию, большую свободной энергии неоднородной системы из
тех же частиц. Такое состояние фазы является метастабильным.
С течением времени система перейдет в состояние с минимальным
значением свободной энергии, т. е. станет неоднородной. Однако
этот переход затрудняется поверхностным эффектом, т. е. тем, что
образование в данной фазе объектов малых размеров другой
фазы из-за поверхностной свободной энергии этих объектов при-
приводит к увеличению свободной энергии системы и поэтому пере-
переход термодинамически невыгоден. Например, начало конденсации
пара затруднено по той причине, что при образовании в паре
малых (радиуса R) капель жидкости их поверхностная свободная
энергия Fi, пропорциональная R2, растет быстрее, чем умень-
уменьшается их объемная свободная энергия, пропорциональная R3.
Поэтому появление малых капель оказывается термодинамически
невыгодным и конденсация задерживается. При больших же кап-
каплях, начиная с некоторого R = RKp наоборот, объемный член умень-
уменьшается быстрее, чем растет поверхностный, и конденсация стано-
* Т. е. таких превращений вещества из одной фазы в другую, которые свя-
связаны с поглощением или выделением теплоты (плавление, кипение и т. д.).
15Г
вится возможной: возникшая в результате флуктуации такая кап-
капля будет расти.
Для всякой метастабильной фазы существует некоторый мини-
минимальный размер, которым должно обладать образовавшееся внут-
внутри нее вследствие флуктуации скопление другой фазы, чтобы эта
другая фаза оказалась устойчивее первоначальной. При меньших
размерах основная фаза остается все же устойчивее этих флук-
флуктуации и они исчезают. Такие скопления новой фазы, обладающие
минимальными размерами, называются зародышами.
Вычислим критический радиус капли для наступления конден-
конденсации пара. Предположим, что в результате происшедшей флук-
флуктуации в старой фазе при температуре Т и давлении Р образовал-
образовался очаг новой фазы, например в паре — капелька жидкости ра-
радиусом R. Энергия Гиббса пара до образования капли равна
G MP T)N
M )
где \xi(Pj T) — химический потенциал, отнесенный к одной части-
частице пара; N — число частиц пара.
После образования капли энергия Гиббса G системы с учетом
поверхностной энергии Гельмгольца равна
P)+N2li2(Ty Р
где N] — число частиц пара; N2 — число частиц в капле (N\ +
+ N2 = N); vt и v2 — объемы; /i и /2 — энергии Гельмгольца на
одну частицу соответственно пара и капли; \къ{Т, Р) — химиче-
химический потенциал вещества в новой фазе (капле) без учета поверх-
поверхностных эффектов (т. е. для плоской поверхности); а — поверх-
поверхностное натяжение; 2 — площадь поверхности новой фазы.
Изменение энергии Гиббса при образовании в старой фазе —
паре новой фазы — жидкости равно
= G—Go= {\x2—\ii)N2+\oIl.
Величины N2 и 2 легко выражаются через радиус капли:
Таким образом,
AG = 4jt/?3(ja2—iii)/3v2 + 4nR2o. (9.14)
Из этой формулы видно, что AG по-разному зависит от R в
двух возможных случаях:
2)
В первом случае новая фаза имеет при заданных Т и Р хими-
химический потенциал больший, чем старая, и является менее устой-
устойчивой. Появление капельки жидкости в паре (или пузырька в
жидкости) при всех ее размерах R ведет к росту AG (рис. 24),
^поэтому образование новой фазы всегда термодинамически не-
невыгодно. Если в результате флуктуации и образуется капля в та-
158
ком паре, то, каких бы размеров она ни была, она обязательно
быстро исчезнет. Во втором случае с увеличением размера воз-
никшей флуктуации второй фазы AG вначале (пока R<RKp) рас-
растет, так что маленькие флуктуации новой фазы являются неустой-
неустойчивыми (рис. 25). Эта неустойчивость, как мы уже говорили,,
объясняется тем, что при малых R второе слагаемое в выражении
для AG растет с увеличением R сильнее, чем уменьшается пер-
первое. Однако при больших образованиях второй фазы, когда*
вторая фаза становится более устойчивой.
А6
Рис. 24
9 V"
Рис. 25
Размер зародыша найдем из условия максимума изменения?
энергии Гиббса AG (которое выражает условие неустойчивого
равновесия):
dR
= 0, или
чкр
откуда
-!х2). (9.15)^
Отсюда видно, что критический радиус зародыша пропорцио-
пропорционален коэффициенту поверхностного натяжения. Разность \х\—\i%
в знаменателе показывает, что чем больше пересыщен пар (чет
больше эта разность), тем меньше критический радиус и тем ско-
скорее начнется конденсация.
Аналогично обстоит дело ив случае других фазовых переходов-
первого рода; при кипении жидкости этими зародышами являют-
являются пузырьки пара, при кристаллизации — кристаллики. Но роль
зародышей в этих случаях могут играть не только пузырьки или
кристаллики данного вещества, но и частицы постороннего вещест-
вещества (загрязнения).
Критический радиус зародыша (пузырьков пара в перегрето»
жидкости или капли в пересыщенном паре) можно найти и не-
непосредственно, из условия механического равновесия (неустойчи-
(неустойчивого) зародыша, т. е. из равенства давления Р2 внутри зародыша
сумме давления Р4 в основной фазе и давления 2cr/i?Kp, обуслов-
обусловленного поверхностным натяжением: P2 = Pi + 2g/7?kp, откуда
flKp = 2a/(P2-Pi), (9.16)
что эквивалентно формуле (9.15). Действительно, по условию рав-
равновесия, в результате обмена частицами между каплей и ее
паром
МТ, Pz)=\xi(T, Pi). (9.17)
Учитывая малую сжимаемость жидкости, т. е. слабое измене-
изменение химического потенциала, находим
Поэтому из соотношения (9.17) получаем
Р2—Pi=[|il(r, Pi) — JX2(r, Pi)]/^2
и, следовательно, формулу (9.15).
Перегретой называется жидкость, нагретая выше температуры
кипения (т. е. температуры, при которой упругость паров жид-
жидкости, находящейся под внешним давлением Р, делается равной
этому внешнему давлению), но не кипящая, т. е. не образующая
под поверхностью пузырей пара, а лишь испаряющаяся с поверх-
поверхности. Давление насыщенных паров над плоской поверхностью та-
такой жидкости Роо>Р. Если при этом в жидкости образуется пу-
пузырек, то его критический радиус, очевидно, найдем, положив в
формуле (9.16) Р2=Роо и P1 = P:i?Kp = 2a/(Poo—P).
Глава 10
ФАЗОВЫЕ ПЕРЕХОДЫ
И КРИТИЧЕСКИЕ ЯВЛЕНИЯ
При внешних воздействиях на равновесную гетерогенную сис-
систему вещество из одной фазы может переходить в другую, на-
лример из жидкости в пар, из одной кристаллической модифика-
модификации в другую, из нормального проводника в сверхпроводник, из
ферромагнетика в парамагнетик и т. д. Такие превращения ве-
вещества из одной фазы в другую при изменении внешних условий
называются фазовыми переходами.
Наибольший практический и теоретический интерес представ-
представляют фазовые превращения в однокомпонентных и бинарных сис-
системах. Мы рассмотрим фазовые превращения лишь в однокомпо-
лентных системах.
160
§ 42. Классификация фазовых переходов.
Фазовые переходы первого рода.
Уравнение Клапейрона — Клаузиуса
Как и при фазовом равновесии, при переходе вещества из од-
одной фазы в другую температура, давление и химический потен-
потенциал вещества в фазах одинаковы. Что же касается других тер-
термических и калорических величин или соответствующих им
производных от энергии Гиббса G(Ty P), то они при одних фазо-
фазовых переходах терпят разрыв, а при других — непрерывны. По-
Поэтому различают прерывные и непрерывные фазовые переходы.
Прерывными называются фазовые превращения, при которых
п лт ( dG \ с / dG \
первые производные от и: V — 1 , о — —I испыты-
испытывают скачки, а непрерывными — переходы, при которых первые
производные непрерывны, а терпят разрыв производные второго и
более высоких порядков: теплоемкость Ср~ —Т ( ) , сжимае-
\ дТ2 ] р
мость &т = ( I .коэффициент теплового расширения
Г V \ дР2 )т г г
(] и т. д. Прерывные превращения называются фазо-
V \ дТдР )
выми переходами первого рода. При этих переходах, следовательно,
скачком изменяется удельный объем v или плотность р вещества
и поглощается (или выделяется) теплота X = T(s"—s'). Фазовыми
переходами первого рода являются плавление, кристаллизация,
кипение, некоторые превращения из одной кристаллической моди-
модификации в другую, переход проводника в сверхпроводящее состоя-
состояние в магнитном поле и т. д.
Непрерывные переходы, при которых вторые производные от
энергии Гиббса (или химического потенциала) испытывают скач-
скачки, называются фазовыми переходами второго рода, когда же эти
производные при переходе обращаются в бесконечность — крити-
критическими переходами, а аномальное поведение свойств веществ в
этой области — критическими явлениями.
Термин «фазовые переходы второго рода» впервые A933 г.)
ввел П. Эренфест при рассмотрении непрерывного сверхтекучего
перехода в жидком гелии. Он считал, что вторые производные от
энергии Гиббса при этом переходе испытывают скачки, и получил
соотношения между ними (уравнения Эренфеста, см. § 43). Тер-
Термином «фазовый переход второго рода» (или ^-переход) стали
потом называть и все другие непрерывные переходы. Позже, од-
однако, оказалось, что при сверхтекучем- переходе в гелии вторые
производные от энергии Гиббса не испытывают скачки, а обра-
обращаются в бесконечность. Этот переход, следовательно, является
критическим, и к нему уравнения Эренфеста неприменимы. Но в
литературе и сейчас сверхтекучий переход в гелии и другие непре-
непрерывные фазовые превращения называют фазовыми переходами
второго рода. Чаще, однако, непрерывные переходы называют
б Зак. 245 161
критическими переходами, что более правильно, так как фазовым
переходом второго рода является лишь превращение проводника
в сверхпроводник. Критическими переходами являются критиче-
критический переход «жидкость — газ», переход ферромагнетика в пара-
парамагнетик, сегнетоэлектрический переход и др.
Непрерывные фазовые переходы обычно связаны с изменением!
симметрии системы, поэтому можно ввести характеризующий
эту симметрию параметр порядка rj, который равен нулю в более
симметричной и отличен от нуля в менее симметричной фазе. Та-
Такой подход в теории непрерывных переходов был применен в ра-
работах Л. Л. Ландау. Вследствие нереалистического предположе-
предположения о возможности разложения в степенной ряд энергии Гиббса
в окрестности фазового перехода теория Ландау расходится с
большинством экспериментов в этой4 области. Этой теории посвя-
посвящена обширная литература, и мы не излагаем ее здесь *. Физи-
Физически последовательная теория непрерывных фазовых переходов
была развита в работах В. К. Семенченко на основе представле-
представления о термодинамической устойчивости (см. § 45).
Основным ураваением, характеризующим фазовые переходы
первого рода, является дифференциальное уравнение Клапейро-
Клапейрона — Клаузиуса. Это уравнение получается из условия равенст-
равенства химических потенциалов при равновесии двух фаз
ц'(Р, Т)=ц"(Р,Г) A0.1}
и связывает между собой теплоту перехода, скачок удельного-
объема и наклон кривой равновесия в точке перехода.
Из формулы (ЮЛ) следует уравнение кривой равновесия
Р = Р(Т). A0.2>
Так как конкретный вид функции \х(Р> Т) в большинстве слу-
случаев неизвестен, то уравнение кривой равновесия A0.2) также не-
невозможно написать в явном виде. Оказывается, однако, что диф-
дифференциальное уравнение кривой равновесия имеет гораздо более
простой вид и связывает между собой указанные выше легко из-
измеряемые величины. Дифференцируя A0.1), получаем
или <V(P, T\=d\L"(P, T),
\ дТ )р ' V дР }т \ дТ )Р ' \ дР Jt
откуда
dP {№1дТ)р-(ф
dT (дц'/дР)т — {дрдР)т '
dP _ s"—s'
АТ '" v"-v' • A0.3)
ли
162
* Критический анализ теории фазовых переходов Ландау см. в кн.: Стен»
Г. Фазовые переходы и критические явления. — М.: Мир, 1973.
так как d\i= —sdT+vdP (s и v — энтропия и объем на одну час-
частицу). Уравнение A0.3) является дифференциальным уравнением
кривой равновесия и называется уравнением Клапейрона —
Клаузиуса. Чаще его записывают в виде
— = , A0.4)
dT T{v"—v') V '
где k=T(s"—s') — теплота перехода на моль или грамм вещест-
вещества, (v"—v') — изменение объема соответствующей массы вещест-
вещества. Главное применение уравнения A0.4) состоит в вычислении
удельных теплот испарения, возгонки, плавления и изменения мо-
модификации.
Если на систему действует не давление Р, а какая-либо другая
обобщенная сила Л, то мы получаем общее дифференциальное
уравнение кривой равновесия двух фаз однокомпонентной систе-
системы:
A0.5)
dT Aa ' V ;
где As=is"—s' — изменение (скачок) энтропии при переходе ве-
вещества из одной фазы в другую; Аа = а"—а' — скачок внешнего
параметра, сопряженного обобщенной силе А.
Уравнение Клапейрона — Клаузиуса
dT __ T(v"—v')
dP ~~ X
определяет изменение температуры фазового перехода (напри-
(например, точки замерзания или кипения) с изменением давления.
Поскольку при переходе жидкости в пар теплота сообщается
(Я>0) и объем всегда увеличивается (v">v')9 то, следовательно,
dTJdP>0, т. е. температура кипения при увеличении давления
всегда повышается. Точка же плавления при увеличении давления
или повышается, или понижается, смотря по тому, увеличивается
или уменьшается объем при плавлении. У большинства тел при
плавлении v">v', поэтому у таких тел, как и в случае кипения,
dT/dP>0. Однако у воды, чугуна, висмута, германия и таллия
объем при плавлении твердой фазы уменьшается (жидкая фаза в
этих случаях тяжелее твердой), поэтому для них dT/dP<0, т. е.
точка плавления с увеличением давления понижается.
Температура плавления с повышением давления понижается
также при Г<0,3 К У изотопа гелия с атомной массой 3 CНе),
хотя у него v">v'. Это происходит потому, что удельная тепло-
теплота плавления lh = T(\s"—s') твердого 3Не при Г<0,ЗК отрицатель-
отрицательна (эффект Померанчука), т. е. энтропия s" жидкого 3Не меньше
энтропии sf его твердой фазы. Такое поведение энтропии у раз-
разных фаз 3Не вызвано тем, что в жидкости силы обменного взаимо-
взаимодействия между атомами приводят к упорядочению их спинов уже
при Т< 1 К, в то время как в твердой фазе из-за малости ампли-
6* 163
туды нулевых колебаний по сравнению с межатомным расстоя-
расстоянием такое упорядочение наступает лишь при Г—Ю*6—К) К»
когда kT становится порядка магнитной энергии взаимодействия
двух соседних атомов. При Г=0,ЗК удельная теплота плавления-
меняет знак, и, следовательно, при этой температуре кривая плав-
плавления имеет минимум (рис. 26). Для того чтобы расплавить 3Не
при Г<0,3 К паяльник должен быть холодным (с температурой
Т{<Т). В случае затвердевания жидкого 3Не при Г<0,3 К теплота
поглощается и, следовательно, его адиабатное сжатие, вызываю-
0,3
Рис. 26
Рис. 27
щее затвердевание, должно приводить к понижению температуры.
Применим к фазовому переходу первого рода третье начала
термодинамики. Согласно ему
lim (Sr—S')=O9
г-#ок
поэтому из основного уравнения термодинамики для фазового пе-
перехода
заключаем, что при Г->0 К могут представиться два возможных
случая: или одновременное исчезновение при переходе разности
энергий Д? и разности объемов ДУ фаз (что означало бы нераз-
неразличимость жидкой и твердой фазы), или разность энергий Д? =
= —PAV. Эксперименты с гелием показали, что при Г->0 К в
действительности реализуется вторая возможность: Д?= —РАУф
фО. Тогда (см. A0.3)).
lim -4L=0, A0,6)
г->ок dT
т. е. при 7W0K все фазовые кривые на (Г, Р)-диаграмме должны
быть горизонтальными (см. кривую плавления гелия на рис. 27).
Таким образом, независимость при низкой температуре равно-
равновесного давления системы «жидкость — твердое тело» от темпе-
164
ратуры является следствием третьего начала термодинамики. Оно
нашло свое применение при вычислении кривой равновесия «гра-
«графит — алмаз», которую необходимо знать для искусственного
производства алмазов из графита при температуре в несколько
тысяч Кельвинов. Отсюда видно, что третье начало термодинами-
термодинамики играет большую роль и при весьма высокой температуре.
§ 43. Фазовые переходы второго рода.
Уравнение Эренфеста.
При фазовых переходах второго рода испытывают скачки
удельная теплоемкость сРу сжимаемость рт и коэффициент тепло-
теплового расширения а. Связь между этими скачками и наклоном
кривой перехода в соответствующей точке определяется уравне-
уравнениями Эренфеста. Найдем эти уравнения.
Правая часть уравнения Клапейрона — Клаузиуса A0.3) в
точке фазового перехода второго рода принимает вид неопреде-
неопределенности 0/0. Для ее раскрытия воспользуемся правилом Лопи-
таля. Дифференцируя числитель и знаменатель правой части
A0.3) или по Г, или по Р, получим:
dP _ds"/dT-ds'/dT __ Аср
dT dv"/dT — dv'/dT TA(dv/dT)p *
И
dT dv" jdP — dvf /dP*
ИЛИ
dP _ A(dv/dT)p
"SF A(dv/dP)T • ^1U'6;
так как из d\i=—\sdT+vdP следует —(ds/dP)T= (dv/dT)P. Из
формул A0.7) и A0.8) получаем уравнения Эренфеста для фазо-
фазовых переходов второго рода:
<Ш0)
Из равенства химических потенциалов фаз при переходе ве-
веществ из одной фазы в другую следует, что при любом фазовом
переходе давление является функцией температуры и поэтому на
плоскости Г, Р существует кривая фазового превращения. Однако,
в отличие от кривой равновесия A0.2) для фазового перехода
первого рода (рис. 18), кривая для непрерывного перехода не
является кривой равновесия (существования) двух фаз, так как
при этом переходе новая фаза появляется сразу во всем объеме.
Появление ловой фазы не сопровождается возникновением по-
165
верхностной энергии и поэтому при непрерывных переходах пере-
перегрев или переохлаждение невозможны.
В общем случае, если на систему действует обобщенная си-
сила А, которой соответствует внешний параметр а, уравнения Эрен-
феста будут иметь вид
dT
A0.11)
да \ dA A / da
дТ }а dT \ дЛ
Уравнения Эренфеста связывают скачки вторых производных
термодинамического потенциала не только при фазовых перехо-
переходах второго рода, но и в случае целого ряда фазовых переходов
первого рода. Примером такого перехода первого рода является
переход из упорядоченного состояния в неупорядоченное в спла-
сплавах AuCu3, AuCu и др. Характерной особенностью этих фазовых
переходов является постоянство скачков объёма и энтропии на
всей линии превращения:
AV = d, AS=*C2 A0.12)
так что на диаграмме Т, Р наклон линии фазового равновесия
dP/dT = &S/AV оказывается постоянным и, следовательно, сама
эта линия есть прямая (линейные фазовые переходы первого
рода).
Дифференцируя уравнение A0.12) по температуре вдоль ли-
линии равновесия, получаем:
+Д 0, а(Щ +А(Ц of
дТ Jp V дР )т dT \дТ )р \ дР )т dT
откуда непосредственно следуют уравнения Эренфеста A0.9) и
A0.10).
Таким образом, уравнения Эренфеста определяют широкий
класс фазовых превращений — линейные фазовые переходы пер-
первого рода и фазовые переходы второго рода.
§ 44. Термодинамика сверхпроводящего
перехода
Применим уравнения Эренфеста A0.11) и A0.12) к переходу
проводника из нормального состояния п в сверхпроводящее со-
состояние s при отсутствии магнитного поля. Как известно, такие
превращения осуществляются у некоторых проводников при опре-
определенной температуре Тс. Сверхпроводимость можно разрушить,
если наложить достаточно сильное магнитное поле Ж>
Зависимость напряженности 36Q критического поля от темпе-
температуры Т аналогична зависимости Р = Р{Т) при равновесии «жид-
«жидкость — пар» и на диаграмме Г, 2ёс изображается кривой, при-
166
веденной на рис. 28. Аналитически эта кривая довольно точно
может быть представлена параболой
Если проводник находится в магнитном поле, то превращение
его в сверхпроводящее состояние сопровождается тепловым эф-
эффектом и, следовательно, является фазовым переходом первого
рода. В. Кеезом показал, что в этом случае переход определяется
уравнением Клапейрона — Клаузиуса. При отсутствии магнитного
поля теплота перехода равна нулю и превращение п в s является
фазовым переходом второго рода.
Во внешнем магнитном поле сверхпроводник ведет себя как
диамагнетик, т. е. намагничивается против вектора напряжен-
напряженности магнитного поля, и притом так, что магнитная индукция
внутри сверхпроводника равна нулю (эффект Мейснера):
A0.13)
Поэтому элементарная работа намагничивания, отнесенная к
объему сверхпроводника, равна
bW=Mdf8. A0.14)
Полагая в уравнениях Эренфеста A0.11) А^Ж и а = #-, получаем
для скачка теплоемкости
dT /*V=o \дЖ )т
где ЖС(Т) — напряженность, зависящая от температуры крити-
критического поля, при котором одновременно сосуществуют две фазы —
нормальный проводник и сверхпроводник {ЖС(Т) определяется из
условия равенства химических потенциалов этих фаз); производ-
производная d2ec/dT берется при 2%?с — 0 и Т=ТС. Для сверхпроводника (см.
A0.13))
4л '
для нормального проводника
/и V-— 1 t
И \Ш) te"e
\Ш)т
Таким образом,
167
Но ц == 1 + 4jtx, а х для парамагнитных и диамагнитных веществ
порядка 10~5—10"в, поэтому
4я
2
dT
A0.16)
Это выражение для скачка теплоемкости при сверхпроводящем
переходе при отсутствии магнитного поля называется формулой
Рутгерса. Из нее следует, что Cs>Cn- Формула Рутгерса хорошо
согласуется с экспериментальными данными, как это видно из
таблицы:
Металл
Свинец
Олово
Индий
Таллий
Алюминий
Т,К
7,22
3,73
3,37
2,38
1,20
ДСЭКс» Дж/К-моль
52,79
12,15
8,46
6,20
1,93
АСвьи* Дж/К-моль
41,9
10,94
8,42
6,12
2,97
Температурный ход теплоемкости при сверхпроводящем перехо-
переходе (при отсутствии магнитного поля) изображен кривой на рис. 29.
Рис. 28
Рис. 29
Рассмотрим теперь сверхпроводник в магнитном поле ()
Дифференциал удельного термодинамического потенциала магне-
магнетика во внешнем магнитном поле Ж равен
dG=— sdT—
Подставляя сюда для сверхпроводника /s= —Ж/4л и интегрируя
потом полученное выражение по Ж при некоторой температуре Г,
получаем
, Т) - Gs@, T) =ЖЩп. A0.17)
168
В нормальном состоянии магнитная восприимчивость провод-
проводника исчезающе мала, поэтому Gn(<9#, T) = Gn@1T). Вдоль кривой
критического поля, когда п и s находятся в равновесии, удельные
термодинамические потенциалы обеих фаз одинаковы, поэтому из
условия GnBec, T) =GsB@c, T), определяющего ЖС{Т), получаем
основное уравнение термодинамики сверхпроводников:
Т) - G,@, T) =
A0.18)
Так как s = — {dGjdT)^ и с ж =T(ds/dT)^ то из формулы A0.18);
получаем:
A0.19)
A0.20)
4я dT '
v 2
C$mCn
dT
При Т=ТС напряженность критического поля 5#с = 0; тогда из
формулы A0.19) находим 5S—Sn = 0r что отвечает фазовому пере-
переходу второго рода, при котором (см. A0.20)) получаем формулу
Рутгерса A0.16).
При любой более низкой
температуре @<Т<Тс) из вы- ^ -
ражения A0.19) получаем Ss— (?s-cn
—5п<0 и Ss<Sn> поскольку,
как видно из рис. 28, йЖс1йТ<
<0. Это свидетельствует о
том, что сверхпроводящая фа-
фаза является более упорядо-
упорядоченной.
По третьему началу термо-
термодинамики, при 7 = 0 К энтропии
фаз равны нулю и, следователь-
следовательно, Ss—Sn=0. В этом пределе про-
производная критического поля по
температуре должна обратиться в
нуль.
Итак, энтропии обеих фаз равны (Ss—Sn = 0) при Т = ТС и
Г = 0 К, а при 0<Т<Тс разность SS—Sn<0, так что разность эн-
энтропии должна проходить через минимум при какой-то темпера-
температуре (рис. 30). При Г=ГС скачок теплоемкости максимален и ра-
равен величине, определяемой формулой A0.16). Когда разность
энтропии двух фаз при некоторой температуре ниже Тс проходит
через минимум, теплоемкости обеих фаз (как умноженные на Т
производные от S по Т) должны стать равными (рис. 30), а при
более низкой температуре, поскольку (Ss—Sn) < 0, разность
dT
C8~Cn<0, т. e. Cs будет меньше Сп, и при 7-^0 К обе величины
стремятся к нулю.
Рис. 30
169
Удельная теплота перехода проводника из сверхпроводящего
в нормальное состояние k=T(sn—ss) равна нулю в нулевом поле
и положительна при <3^с>0. Таким образом, при изотермическом
переходе сверхпроводника в нормальное состояние происходит по-
поглощение теплоты, а при соответствующем адиабатном переходе
образец охлаждается. На этой основе был предложен метод полу-
получения низких температур адиабатным намагничиванием сверх-
сверхпроводника.
§ 45. Критические и закритические явления
В 1860 г. Д. И. Менделеев, исследуя зависимость поверхност-
поверхностного натяжения жидкостей от температуры, установил, что при
некоторой температуре, названной им температурой абсолютного
кипения, поверхностное натяжение исчезает. При этом обе сосу-
сосуществующие фазы (жидкость и пар) становятся тождественными.
Такое состояние характеризуется определенными значениями тем-
температуры Гкр, давления Ркр и объема VKp и называется критиче-
критическим состоянием. Кривая равновесия жидкости и пара на диаг-
диаграмме Ту Р кончается в критической точке.
В 1869 г. критическое явление было исследовано Т. Эндрюсом,
а начиная с 1873 г. — группой киевских физиков во главе с
М. П. Авенариусом.
На основании этих экспериментальных исследований
Дж. В. Гиббс A876) и независимо от него Л, Г. Столетов A879)
сформулировали основные положения классической термодинами-
термодинамической теории критических явлений. По Гиббсу—Столетову
критическая фаза представляет собой предельный случай двух-
двухфазного равновесия, когда обе равновесно сосуществующие фазы
становятся тождественными. Иначе говоря, это устойчивое со-
состояние однородной системы, лежащее на границе устойчивости
по отношению к виртуальным изменениям каждой ее координаты
при постоянстве других термодинамических сил.
Математически граница устойчивости однородной системы по
отношению к таким виртуальным изменениям ее координат опре-
определяется обращением в равенства термодинамических неравенств
:tF.16) и F.20), характеризующих эту устойчивость однородной
системы:
дР \ п / дТ \ Т 0
A0.21)
dV
Условия устойчивости критического состояния найдем из нера-
венства для определителя матрицы устойчивости F.15), выра-
выражающего необходимое и достаточное условие устойчивости одно-
однородной системы:
AT.AS — АР-AV>0.
170
Выберем в качестве независимых переменных однородной системы
параметры V и Т. Тогда P = P(V, 7), S = S(V9 T) и при 7=const
из F.15) получаем
3! \ dVB )
В критическом состоянии согласно формулам A0.21)
(дР/дУ)т = 0, поэтому
2 \ dV2 /т 3! \ dV3 )т
Это неравенство выполняется при любом AV (как положи-
положительном, так и отрицательном), если коэффициент при (AVK об-
обратится в нуль, а коэффициент при (ДУL будет отрицательным*:
= 0, (??-) <0. A0.22)
Аналогично из неравенства F.15) для критического состояния
находим
dS2 )т
Таким образом, в критическом состоянии
JHL) =0, (—) -0, ( — ) -0, (—) =0, A0.23)
dV )т \dS )т \ dV )р \ dS /р
= 0, ( —\ =0, (-Ш-) -0, 1-^-) =0, A0.24)
V dS2 J т \ dV2 I p \ dS2 I p
>0, A0.25)
as» / / У
т. е. термически критическое состояние характеризуется соотно-
соотношениями
(*L) =o, (*L\ =o, (i!L\ <o,
A0.26)
dV ) \ dV2 )
) 0, ) o, () so.
dV )p \ dV2 )p \ dV* )p
To, что критическое состояние определяется четырьмя уравне-
уравнениями A0.26) для функции двух переменных, не может в данном
* Классической теории критических явлений не противоречило бы тождест-
тождественное обращение в нуль в критической точке и третьей производной
(д3Р/дУ3)т при одновременном обращении в нуль (д4Р/дУ4)г и отрицательг
ном значении пятой производной и т. д.
171
случае привести к противоречию, так как согласно термодинами-
термодинамическому тождеству
дТ
dV )т\дТ
__ 1
дР Jv~
только два из приведенных четырех уравнений являются незави-
независимыми: или уравнения
дР\ _
dV )т
О, i^lL.) =о, A0.27)
\ dV* }т
и тогда уравнения (dT/dV)P = Ot (d2T/dV2)P = 0 являются их след-
следствиями, или наоборот.
Критическое состояние системы «жидкость — пар» — это одно-
компонентная (k=l) однофазная (п=1) система, дополнительно
удовлетворяющая двум условиям устойчивости A0.27), поэтому
по правилу фаз (8.37) n<k и число степеней свободы критическо-
критического состояния
fKp = k—n = O. A0.28)
Это означает, что критическое состояние простой однокомпо-
нентной системы возможно лишь при определенных температуре,
давлении и объеме, т. е. в одной критической точке ГКр, РКр, VKp.
Параметры критической точки зависят только от свойств данного
вещества.
Если на систему действует кроме давления еще какая-либо
сила (например, сила электрического поля), то /Кр=1 и мы имеем
критическую линию.
Так как критическое состояние представляет, с одной стороны,
предельное равновесие двухфазной системы, а с другой — пре-
предельное устойчивое состояние однородной системы, то, как вид-
видно из соотношений A0.23) — A0.25), определяющих критическое
состояние, система обладает как свойствами двухфазной системы:
A0.29)
так и свойствами однофазной:
Таким образом, если система переходит через критическое со-
тояние из однородного в двухфазное состояние, то при этом вна-
вначале (в критическом состоянии) у нее дополнительно появляются
свойства двухфазной системы, а потом (в двухфазном состоянии)
172
утрачиваются свойства однородной системы (см. A0.30)) и сос-
состояние системы наряду с A0.29) определяется равенствами
= =0
( 0 (
dV3 )т \ dV* )t '" ' I dS*
При переходе системы через критическое состояние из двух-
двухфазного в однофазное состояние у нее, наоборот, вначале (в кри-
критическом состоянии) появляются свойства однородной системы
A0.30), а потом (в однородном состоянии) пропадают свойства
двухфазной системы A0.29) и появляются свойства только одно-
однородной системы:
Следовательно, в критическом состоянии не могут нарушаться
неравенства F.17)
определяющие устойчивость однородной системы, так как эти не-
неравенства не нарушаются и у двухфазной системы. Иначе говоря,
в критической точке теплоемкость Су не может обратиться в бес-
бесконечность, так как она остается конечной и у двухфазной систе-
системы, в которую через критическое состояние переходит однородная
система. Однако этот вывод из термодинамики является лишь
достаточным, но не необходимым, так как термодинамика не иск-
исключает появления в критическом состоянии таких свойств, которых
нет ни у двухфазной, ни у однофазной системы. Если критичес-
критическое состояние является таким особым состоянием вещества, то
для него сделанный вывод о поведении теплоемкости Су в крити-
критической точке не имеет места. Однозначно этот вопрос может ре-
решить лишь опыт или статистическая физика.
В 1947 г. В. К. Семенченко развил теорию фазовых переходов,
основываясь на представлениях о термодинамической устойчи-
устойчивости.
Рассмотрим возможные состояния и фазовые переходы термо-
термодинамической системы в зависимости от внешних сил Xt.
Каждая отдельная фаза существует до тех пор, пока для нее
.выполняются условия устойчивости:
0 /_аХ?\ 0 A0.33)
\ dx jx ' v >
у d(S, V)
При уменьшении устойчивости DY и коэффициенты устойчивос-
устойчивости (КУ, см. § 28) достигают границы устойчивости. Кривая, опре-
определяемая уравнением (дХ*/дд^)х?=0, называется спинодалью\ она
ограничивает область неустойчивых состояний.
Будем для определенности рассматривать диаграммы на плос-
плоскости с осями Vt P. На этой диаграмме (рис. 31) спинодаль / (ее
173
уравнение (дР]дУ)т = О) является геометрическим местом экстре-
экстремумов различных изотерм 4. Существование спинодали приводит
к тому, что изобара может пересечь изотерму в двух точках, со-
соответствующих различным значениям объема. Это означает
возможность равновесия двух фаз с различными объемами —/фа-
—/фазового равновесия первого рода. Эти фазы разделены облаЬъю
неустойчивых состояний, и так как она не реализуется, то невоз-
невозможен непрерывный изобарный переход одной фазы с объемом
V\ в другию фазу с объемом V72. Линия фазового равновесия оп-
определяется равенством химических
потенциалов вещества в фазах и на-
называется бинодалью (кривая 2). На
бинодали коэффициенты устойчиво-
устойчивости не равны нулю; между бино-
бинодалью и спинодалью существуют
области метастабильных состояний
системы, в которых каждая из фаз
может существовать только при от-
отсутствии другой фазы.
С изменением термодинамичес-
термодинамических сил, действующих на сис-
систему, изменяются различные ха-
характеристики фазового перехода
первого рода (ФП I рода). Тзк>
при повышении температуры и
давления в системе «жидкость —-
пар» уменьшаются удельная
теплота перехода и области метастабильных и неустойчивых сос-
состояний (см. рис. 31). Предельным случаем ФП I рода является
критический переход. В критическом состоянии спинодаль и бино-
даль сливаются в одну точку, удельные объемы фаз становятся
одинаковыми, а фазы — тождественными. Критическое состояние
определяется тем, что детерминант устойчивости и ИКУ равны
нулю: ?>у = 0, (pP/dV)T = 0, (dT/dS)P = 0.
Как показывается в статистической физике, коэффициенты ус-
устойчивости обратно пропорциональны флуктуациям различных
физических величин. С приближением к критической точке флук-
флуктуации растут. За критической точкой существуют только устой-
устойчивые состояния, поэтому в этой области невозможно сосущество-
сосуществование фаз, имеющих границу раздела. Анализ термодинамической
устойчивости закритической фазы привел В. К. Семенченко к по-
построению термодинамики непрерывных фазовых переходов.
Как уже упоминалось, рассмотрение изотерм вблизи критичес-
критической точки показывает, что точки перегиба па этих изотермах име-
имеются и в закритической области. В этих точках КУ минимален.
Линию наименьшей устойчивости В. К. Семенченко называет ква-
зиспинодалью. В точках квазиспинодали флуктуации достигают
при данных условиях наибольшего значения, и система превраща-
превращается в смесь флуктуационных зародышей обеих граничных (дале-
Рис. 31
174
кйк от этого состояния) фаз — квазифазу или мезофазное состоя-
состояние*, не теряя своей макроскопической однородности. Поскольку
минимум устойчивости является поворотной точкой в отношении
изменения свойств фаз, он до некоторой степени аналогичен точке
фазового перехода второго рода и условно его можно считать за
точку закритического перехода. При этом, конечно, не нужно за-
забывать, что закритический переход происходит на конечном ин-
интервале Г, Р и других термодинамических сил. Поэтому в услов-
условной т\}чке закритического перехода не происходит скачков энтро-
энтропии, объема и других xt, а происходит только их быстрое измене-
изменение в бкрестности этой точки. Работа и удельная теплота перехода
также равны по этой причине нулю. Сами коэффициенты устой-
устойчивости изменяются также непрерывно, а не скачком; в этом сос-
состоит отличие закритических переходов от ФП II рода по Эрен-
<фесту.
До сих пор мы для определенности пользовались диаграммами,
относящимися к флюидным системам, т. е. системам «газ — жид-
жидкость». Однако все изложенное применимо и к анизотропным сис-
системам, а также к системам, фазы которых отличаются по своим
магнитным или электрическим свойствам (ферро- и антиферромаг-
антиферромагнетики, сверхпроводники и сегнетоэлектрики разных типов).
Тщательный анализ экспериментальных данных показывает,
что закритические переходы очень распространены, но их часто
причисляют к переходам иного типа. В большинстве случаев наб-
наблюдаемые скачки являются результатом неудачной экстраполяции
экспериментальных данных или перехода в докритическую об-
область. Эти переходы встречаются во всех трех агрегатных состоя-
состояниях. Например, в кристаллическом ((а—р) -переход в кварце;
в смеси орто- и парадейтерия; в ферромагнетиках, находящихся
под действием магнитного поля и сегнетоэлектриках при наличии
электростатического поля), в жидком (в растворах и жидких
кристаллах), в газах (классический переход «жидкость — газ»).
Очень интересный случай критического перехода в анизотропной
среде представляет (а—C)-переход в кварце. Он сопровождается
резко выраженной критической опалесценцией и экстремумами
нескольких КУ. Но самым интересным является возможность
непосредственного наблюдения смешанного состояния обеих гра-
граничных фаз благодаря различию их кристаллических структур:
а- и р-кварцы имеют различные показатели преломления, поэтому,
освещая кварц в смешанном состоянии, можно визуально или на
фотографии заметить микрогетерогенность системы, т. е. одновре-
одновременное сосуществование обеих кристаллических структур. Макро-
Макроскопически кварц остается совершенно однородным, повышение
точности термостатирования только улучшает выявление этого
смежного состояния.
* Этот термин взят из теории жидких кристаллов, обладающих свойствами
как кристаллической фазы (анизотропия), так и жидкой (текучесть).
175
Установление существования квазиспинодали позволяет опре-
определить критическую точку как точку, общую для спинод^али
(dP/dV)T = 0, квазиспинодали (d2P/dV2)T = 0 и бинодали \x'*\i".
В целом закритические переходы можно характеризовать
>о,
A0.34)
O
§ 46. Термодинамическая теория
критических индексов
Как уже отмечалось, при приближении к критическому состоя-
состоянию детерминант устойчивости Dy и коэффициенты устойчивости
дХ{/дх{)х. стремятся к нулю, а теплоемкость, сжимаемость, вос-
восприимчивость (вторые производные термодинамического потен-
потенциала) возрастают до бесконечности, что является макроскопичес-
макроскопическим проявлением большого развития флуктуации. Эта математи-
математическая особенность вторых производных термодинамического по-
потенциала и связанные с ней большие флуктуации в критической
точке затрудняют теоретическое и экспериментальное изучение
критических явлений. Однако результаты интенсивно проводимых
исследований этих явлений позволяют принять, что сингулярность
основных термодинамических функций вблизи критической точки
имеет простой степенной вид
f(x)~x\
где х — малая окрестность критической точки по температуре
х==х=\(Т—Гкр)/Гкр| или по другому параметру. Показатель
степени % называют критическим индексом (показателем) и опре-
определяют соотношением
X-+Q In X
Его можно найти по наклону прямой на графике, изображен-
изображенном на плоскости с осями \пх, 1п/(х).
Поведение аналогичных характеристик различных систем опи-
описывается одноименными критическими показателями, хотя по зна-
значению они отличаются для разных систем. Так, поведение тепло-
теплоемкости при постоянной термодинамической силе (теплоемкость
жидкости при постоянном давлении Сру теплоемкость ферромаг-
ферромагнетика в постоянном магнитном поле С# и др.) при Г<Гкр опи-
описывается асимптотическим законом
Ср~т-а', С^~т-а\ A0.35)
При температуре выше критической (Г>Гкр) поведение теп-
теплоемкости описывается тем же закойом с показателем а.
176
Показатели у' (при Г<Гкр) и у (при Т>ТК?) описывают пове-
поведение изотермической сжимаемости kr= [ ) и магнитной
восприимчивости хг=(——) в окрестности критической точки:
\ ЬЖ /т
xr~x-V при Г<Гкр,
A0.36>
хг^т-v при Г>ГКр.
Показатель ft определяет приближение к критической точке
вдоль линии равновесия:
уж-Уг~тр, f~%\ A0.37)
Часто показатель р называют показателем порядка, имея
в виду, что А У и #- равны нулю выше критической точки.
Показатель б определяет поведение критической изотермы:
Критические индексы а, а', y> у'\ P> б стали сейчас общеприня-
общепринятыми.
Задачей теории критических показателей является определение
числовых значений показателей исходя из модельных данных и
установление различных соотношений между критическими пока-
показателями. Значения критических показателей характеризуют сте-
степень приближения к критической точке, а сравнение показателей:
различных моделей с экспериментальными данными позволяет су-
судить о реалистичности рассматриваемой модели. Например, тео-
теория Ван-дер-Ваальса критической точки «жидкость — пар» и тео-
теория Кюри—Вейса для перехода «ферромагнетик — парамагнетик»
приводят к следующим значениям показателей: a = a' = 0, y = Y/=U
р = 1/2, 6 = 3. Такие же не согласующиеся с опытом показатели
дает теория Ландау фазовых переходов второго рода. Эксперимен-
Экспериментальные значения критических показателей для системы «жид-
«жидкость — газ» аргона таковы: а<0,4; а'>0,25; y = 0fi\ Y/=1>U
р = 0,33; 6 = 4,4.
Соотношения между показателями позволяют по двум извест-
известным находить третий, а само их выполнение служит признаком
критического перехода.
Отдельные соотношения между показателями были установ-
установлены разными авторами различными методами. Естественным яв-
является стремление получить эти соотношения на основе единого
подхода. Один из таких подходов основан на гипотезе подобия:
термодинамических функций, или термодинамического скейлинга.
Согласно этой гипотезе вблизи критического состояния термодина-
термодинамические потенциалы становятся однородными функциями своих
аргументов. Скейлинг не дает числовых значений критических ко-
коэффициентов, но приводит к установлению соотношений между
ними (в форме равенств) и получению вида уравнения состояния-
177
системы вблизи критической точки. Однако вопрос об обоснован-
обоснованности скейлинга является открытым.
При таком положении представляется замечательным Полу-
Получение различных соотношений между критическими показателями
на основе теории термодинамической устойчивости без каки^'-либо
гипотез и предположений модельного характера*. Преимуществом
такого метода является обоснованность и общность подхода.
Рассмотрим для простоты изотропный магнетик в малой окре-
окрестности критической точки (точки Кюри) при Г^Гкр, коМа от-
отсутствует магнитное поле.
Основной величиной, характеризующей устойчивость, является
детерминант устойчивости, который для данной системы имеет вид
\ds)j
d<?)r
(Ю.38)
где равенство, по Гиббсу, соответствует критической точке.
Используя свойства якобианов, имеем.
г\ 0A , stC) О (i , ^) I OuC \ I 01 \ \ 1 / л r\ on\
y д(Т, Я d(S, Я \ д? )t\ dS )? *т Qz V
и аналогично
m ( ^, A0.40)
i ж \ оъ ) у- \ оъ ) т \ oy ) s
Введем критические показатели ферромагнетика, учитывая, что
они различны для величин, измеряемых при постоянных силах и
координатах:
С & ~ ^~а', Су ~ %—а', #- ~ т^,
A0.42)
Vt- J—. - T-^Y' V ^ч^ Т—^' 7") .-. - Т&
тде d — критический показатель детерминанта устойчивости, а
штрихи в индексах означают, что Г<Гкр.
Подставляя в A0.39) и A0.40) асимптотические выражения
A0.42), получаем
" ' =а/ + с/. A0.43)
Соотношение A0.38) после подстановки в него производных
T/dS) и (дТ/д?)8пз A0.39) и A0.41) принимает вид
• <10-44>
* См.: Солдатова Е. Д., Семенченко В. К. Теория термодинамиче-
термодинамической устойчивости и соотношения между критическими индексами. — Укр. физ.
-журн., 1974, т. 19, № 5, с. 844; Солдатова Е. Д. Некоторые соотношения
.между критическими индексами для магнитных систем. — Укр. физ. журн.,
1974, т. 19, № И, с. 1906.
478
Подставляя в A0.44) асимптотики A0.42), имеем
откуда, поскольку т<1,
p— \)>c—у.
Учитывая A0.43), получаем соотношение Рашбрука
A0.45>
которое было установлено им в 1963 г. исходя из анализа разнос-
разности теплоемкостей Сж —С? для ферромагнетиков вблизи точки?
Кюри. Такое же соотношение обнаруживается для системы «жид-
«жидкость — пар» и сегнетоэлектриков (если в формулах при выводе
A0.45) использовать замену Ж ->¦ — Р, f -+V и Ж ->§, f-^^Y
Соотношение Рашбрука связывает критические показатели ос-
основных термодинамических величин в докритической области.
Метод термодинамической устойчивости позволяет найти соотно-
соотношение для критических показателей и в закритической области*
С этой целью, учитывая, что линия равновесия фаз (бино-
даль) кончается в критической точке, введем показатель (jt (вмес-
(вместо р), определяющий сингулярность термического расширения»
(<ЭУ/<ЭГ)Р~т-м (для системы «жидкость — пар») или магнитока-
лорического эффекта (df/dT)^ — -г"*1 (для магнетика). Тогда длж
закритической области получаем соотношение
сс + 7>2|л, A0.46)*
которое в 1976 г. впервые было установлено Е. Д. Солдатовой.
Это соотношение является более общим, чем соотношение Рашбру-
Рашбрука, так как справедливо и для докритической области (только
нужно использовать а', у'9 ц,'), а соотношение Рашбрука в этол^
случае следует из него, если учесть, что \х/=1—р (поскольку #-~
~т? и (d^/dr^ — T^—T--^).
Найдем еще ряд соотношений для критических показателей.
Для этого запишем выражение A0.38) в виде
поскольку {dTldf)s={d3?ldSK- Пользуясь свойствами якобиа-
якобианов и асимптотиками A0.42), имеем:
~{ дт )Ads ,
A0.48>
0J? Is "\STK \ dS }э\д?)ж\дТ
179*
Подставляя A0.48) в A0.47), получаем соотношение Гриффцтса
A0.49)
которое было им установлено в 1965 г. в результате громоздких
вычислений.
Из A0.39), A0.40) и A0.42) получаем другое соотношение
Триффитса
Т>РF— 1). A0.50)
Эти соотношения были получены для малой окрестности кри-
критической точки при приближении к ней по температуре (л;=т),
но к ней можно приближаться по любой термодинамической силе
(давлению или напряженности поля). Найдем термодинамические
величины ферромагнетика как функции магнитного поля (х= Ж)
вдоль критической изотермы (Т=Ткр, 55?->0). Введем критические
показатели для этого случая:
Сж~Ш-\ S~№ ($~Ж-Х1Ь). A0.51)
Записывая соотношение A0.38) в виде
dS \ ( д?
дТ )ж\ дд«
и используя A0.51), получаем соотношение Куперсмита A968)
A0.52)
Полученные соотношения выполняются и в окрестности точки
Кюри для сегнетоэлектриков.
Таким образом, теория критических показателей, основанная
на методе термодинамической устойчивости, выявила общую при-
природу критического перехода «жидкость — газ» и переходов в фер-
ферромагнетиках, сегнетоэлектриках и других системах как переходов
через минимум устойчивости, сопровождающихся поэтому макси-
максимально развитыми флуктуациями ряда термодинамических вели-
величин. Это отмечал В. К- Семенченко в 1947 г. Потребовалось более
30 лет, чтобы произошло изменение точки зрения на ферромагнит-
ферромагнитный и сегнетоэлектрический переходы как превращения, при кото-
которых испытывают скачки вторые производные термодинамических
потенциалов.
Заметим в заключение, что согласно изложенной термодина-
термодинамической теории критических показателей знак равенства в со-
соотношениях для них получается в самой критической точке совер-
совершенно естественно, поскольку в этом соотношении Z)y = 0.
Часть вторая
СТАТИСТИЧЕСКАЯ ФИЗИКА
РАВНОВЕСНЫХ СИСТЕМ
Как отмечалось во введении, статистическая физика при изуче-
изучении тепловой формы движения материи использует, в отличие от
термодинамики, представления о молекулярном строении ве-
вещества.
Мысли о том, что наблюдаемые свойства тел обусловлены дви-
движением невидимых молекул, появляются уже у Демокрита, Лев-
киппа и Эпикура более двух тысяч лет тому назад. Позже на про-
протяжении веков эти мысли почти исчезают и появляются вновь
в значительно более развитой форме у Д. Бернулли A738) и Ло-
Ломоносова A745), не получив однако широкого распространения.
Только в результате развития производительных сил, обусловлен-
обусловленного промышленной революцией конца XVIII — середины XIX вв.
в связи с изобретением тепловой машины, возникла потребность
теоретического изучения превращения теплоты в работу. Наряду
с термодинамическими исследованиями начали появляться и ра-
работы по молекулярной теории газов и природе теплоты: Джоуль,
«Некоторые замечания о природе теплоты и строении упругих
жидкостей» A851); Крениг, «Очерки теории газов» A856).
Родилась статистическая физика в 1957 г., когда была опубли-
опубликована работа Р. Клаузиуса «О роде движения, которое мы назы-
называем теплотой» *. В этой работе давление газа на стенки сосуда
•объяснялось ударами молекул и было получено выражение для
давления газа через средний квадрат скорости молекул и плот-
плотность газа.
Работа Клаузиуса вызвала интерес к кинетической теории
у Максвелла, и в 1859 г. он выступил с докладом «Пояснения
к динамической теории газов» на заседании Британской ассоциа-
ассоциации наук. В этом докладе впервые был установлен закон распре-
распределения молекул газа по скоростям — знаменитое максвеллов-
ское распределение.
* Максвелл назвал Клаузиуса основоположником кинетической теории га-
газов, а Гиббс — отцом статистической механики.
181
Работы Клаузиуса и Максвелла составляют первый периЪд
в развитии молекулярно-кинетической теории материи. Второй ее
период связан с работами Больцмана, подытоженными в его «Лек-
«Лекциях по теории, газов» 1896 и 1898 гг., и с работами Гиббса, из-
изложенными в монографии «Основные принципы статистической
механики» A902).
Больцман сформулировал основное уравнение теории газов,
носящее ныне название кинетического уравнения Больцмана. Он
нашел ряд частных решений этого уравнения и доказал, что в ста-
стационарном случае единственным решением газокинетического
уравнения является распределение Максвелла. Одновременно
Больцман установил статистическую природу второго начала тер-
термодинамики и на этой основе в противовес возникшей тогда кон-
концепции «тепловой смерти» Вселенной выдвинул флуктуационную
гипотезу, сыгравшую прогрессивную роль в общей борьбе за ма-
материалистическое мировоззрение. В настоящее время ясна лож-
ложность самой постановки вопроса о «тепловой смерти» Вселенной.
Кинетическое уравнение Больцмана определяет поведение газа
с короткодействующими силами взаимодействия между частица-
частицами. Это уравнение оказалось неприменимым для изучения плазмы,
силы взаимодействия между заряженными частицами которой яв-
являются дальнодействующими, медленно спадающими с расстояни-
расстоянием. В 1938 г. профессор Московского университета А. А. Власов
предложил для плазмы новое кинетическое уравнение, впоследст-
впоследствии получившее название кинетического уравнения Власова.
Завершением работ Больцмана по теории равновесных состо-
состояний молекулярных систем является статистическая механика
Гиббса, положенная в основу всей статистической термодинамики.
Метод канонических ансамблей Гиббса представляет собой мощ-
мощный метод исследования различных систем многих частиц.
Дальнейший прогресс в развитии статистической физики был
вызван появившимися в сороковых годах нашего века работами
Боголюбова, Борна, Грина, Кирквуда, Ивона, положившими нача-
начало современному, третьему, периоду статистической физики.
В этих работах исходя из общего уравнения статистической физи-
физики (уравнения Лиувилля) и на основе канонического распреде-
распределения Гиббса создан метод функций распределения комплексов
частиц — метод ББГКИ, или просто метод Боголюбова, как его
принято называть в отечественной научной литературе. В послед-
последние годы в статистической физике эффективно используются мето-
методы квантовой теории поля (метод функций Грина, метод ренорм-
группы).
В основу нашего курса положен метод Гиббса и метод функций
распределения Боголюбова. При этом в гл. 11—13 изложено со-
содержание этих методов, а в ^последующих гл. 14—16 — их прило-
приложение к исследованию различных многочастичных систем. В гл. 17
излагается теория равновесных флуктуации.
Глава 11
ИСХОДНЫЕ ПОЛОЖЕНИЯ
И ОСНОВНЫЕ УРАВНЕНИЯ
СТАТИСТИЧЕСКОЙ ФИЗИКИ
§ 47. Микроскопические и макроскопические
состояния многочастичной системы.
Основная задача статистической физики.
Уравнение Лиувилля
Термодинамика и статистическая физика имеют один и тот же
предмет изучения — закономерности теплового движения материи,
возникающего в системах из большого числа N механически дви-
движущихся частиц* (обычно iV~A^ = 6,022-1023 1/моль). При этом
термодинамика представляет собой макроскопическую, а статисти-
статистическая физика — микроскопическую теорию этих систем. Стати-
Статистическая физика ставит своей задачей объяснение макроскопиче-
макроскопических свойств многочастичных систем на основе наших знаний
о структуре и силах взаимодействия между частицами.
Движение отдельной частицы системы Описывается уравнени-
уравнениями механики — классической или квантовой. В соответствии
с этим и статистическая физика подразделяется на классическую
и квантовую.
Рассмотрим вначале для простоты классическую молекуляр-
Бую модель тела в виде системы материальных точек, движу-
движущихся по законам классической механики**. Состояние движения
каждой молекулы задается в этом случае координатами и проек-
диями ее импульса, а механическое состояние (микросостояние)
системы частиц определяется значениями их координат и импуль-
импульсов. Совокупное же движение (тепловое движение) системы час-
частиц характеризуется макроскопическими параметрами, которые
хотя и зависят от координат и импульсов частиц, но однозначно
их не определяют (так как число макроскопических параметров
во много раз меньше числа частиц). Это означает, что механичес-
механические параметры (координаты и импульсы частиц) не характери-
* Это, однако, не означает, что статистическая физика представляет собой
механику системы, число степеней свободы которой неограниченно растет. Ста-
Статистическая физика, как мы увидим, привлекает положения, чуждые механике.
Поэтому при построении теории теплового движения законы механики необхо-
необходимы, но недостаточны.
** Законы классической механики являются приближенными законами атом-
атомной физики, поэтому классическая статистическая физика является предельным
случаем квантовой статистической физики. В этом предельном случае лучше
можно понять основные идеи статистической физики, что и служит основанием
нашего рассмотрения. К тому же в отличие от классической статистической фи-
физики в квантовой статистике при вычислении макроскопических параметров мно-
точастичных систем приходится производить двойное усреднение, поскольку са-
ма квантовая механика является статистической теорией.
183
зуют природу немеханического, теплового движения. При задан-
заданных параметрах теплового движения можно говорить лишь о ве-
вероятности того или иного микросостояния системы. Таким образом,
вероятностное описание теплового движения микросостояниями
обусловлено тем, что механические параметры адекватно не ха-
характеризуют это движение. Для определения параметров тепло-
теплового движения многочастичной системы достаточно, следовательно,
знания не самого микросостояния, т. е. не координат qb q2, , Ялг
и импульсов рь р2, ..., Pn (короче, q, p всех частиц как функций
их начальных значений qo, po и времени t), а лишь плотности ве-
вероятности этого микросостояния p(q, p, t), т. е. относительной час-
частоты его при временной эволюции системы.
Нахождение плотности вероятности микросостояния любой
классической или квантовой системы и последующее определение
с ее помощью макроскопических параметров является основной
задачей статистической физики.
Решение этой задачи начинается с определения микросостояния
макроскопической системы, т. е. механического состояния сово-
совокупности большого числа частиц. Поэтому рассмотрим кратко
описание микроскопического состояния классической системы
в механике Гамильтона.
Пусть система состоит из ./V одинаковых бесструктурных час-
частиц в макроскопическом объеме V. Ее состояние в любой момент
времени характеризуется набором (q, p) из n-=3N координат
<\i = {qi\ qi2, Qi3} и n = 3N импульсов р*={рЛ рА Р*3} (i= 1,2, ...,#),
а изменение состояния определяется уравнениями Гамильтона
(П.1)
с начальными условиями q@)=q0, р@)=р0. Здесь Я — функция
Гамильтона системы и
SI dA dB dA dB \
\ dq/ dp/ dp/ [dq/ /
/_d?_^dB___a4__dB_
I d<# dp? dp? dq?
— V ( — — — — —
\<i
l<
a<3
скобки Пуассона для функций 4(q, p) и 5(q, p).
Рассматриваемая система является консервативной, поэтому
функция Гамильтона #(q, p)=//(qi, ..., q#, pi, ..., Pn) равна
184
сумме ее кинетической /(({х) и потенциальной U(q) энергий:
2
где m — масса частицы.
Геометрически состояние многочастичной системы (фаза) изоб-
изображается точкой в (q, p)-пространстве, которое называется
фазовым Y-пространством, а изменение состояния — движением
изображающей (фазовой) точки по фазовой траектории. Фазовое
пространство одной частицы называется ^-пространством.
Для определения макроскопических свойств системы в статис-
статистической физике рассматривается не одна конкретная система, а,
следуя Гиббсу, совокупность таких систем в разных микросостоя-
микросостояниях, которая называется фазовым ансамблем Гиббса.
Поскольку микросостояние классической системы многих час-
частиц задается значениями их координат и импульсов, а макросос-
макросостояние этой же системы определяется значительно меньшим чис-
числом макроскопических параметров, то, следовательно, каждое мак-
макросостояние системы создается большим числом ее различных
микросостояний и поэтому какое-либо микросостояние системы
в данном ее макросостоянии выступает с той или иной вероят-
вероятностью.
Иначе говоря, с микроскопической точки зрения макросостоя-
макросостояние системы характеризуется не заданием фазовой точки (т. е. ка-
канонических переменных системы), а величиной относительной
плотности этих точек в фазовом пространстве, или фазовой плот-
плотностью вероятности
.0= ^--4-, (Н.З)
ах /v
где А/о (Nq-^oo) — общее число фазовых точек, dN — их число
в элементе фазового объема
[ dqfdpf.
1<а<3
Фазовый ансамбль, в котором состояние каждой системы харак-
характеризуется определенной вероятностью, называется статистичес-
статистическим ансамблем.
Следовательно, статистический ансамбль Гиббса, задается
плотностью вероятности микросостояния системы, или фазовой
функцией распределения A1.3), которая нормируется на единицу:
Jp(q, P, 0 dx=l. A1.4)
Это означает, что сумма вероятностей всех возможных микросос-
микросостояний равна единице. Если все Af частиц системы разные, то лю-
любая перестановка частиц соответствует другому ее микросостоя»
185
нию. Следовательно, нормировкой A1.4) учитываются различные
(отличающиеся друг от друга) возможные микросостояния систе-
системы. Если же система состоит из одинаковых частиц, то переста-
перестановка частиц не меняет микросостояние и каждое микросостояние
изображается N\ различными фазовыми точками. Поэтому число
различных микросостояний системы из одинаковых частиц будет
равно (l/Af!) jpdt, и, следовательно, в этом случае
(q>p>/)dT = lf A1.5)
1де интегрирование (как и в A1.4) для разных частиц) соответ-
соответствует суммированию по всем различным состояниям.
Кроме того, численное значение фазовой плотности p(q, p, t)
в A1.4) и A1.5) зависит от выбора единиц, используемых для
координатно-импульсного пространства, что приводит к произволь-
произвольному началу отсчета энтропии в окончательных выражениях для
термодинамических величин. Чтобы нормировка для p(q, p, t) со-
соответствовала предельному переходу от квантовой статистики
к классической, необходимо в A1.5) перейти к безразмерному фа-
фазовому объему
N
П dqidpt
где h = 2nh — постоянная Планка.
Таким образом, условие нормировки фазовой плотности имеет
вид
Jp(q, P> 0 <ff=l, A1.7)
где
лг dqdp
Как уже отмечалось, нахождение функции p(q, p, t) и определе-
определение с ее помощью макроскопических параметров системы состав-
составляет основное содержание статистической теории систем многих
частиц.
Найдем уравнение для фазовой функции распределения.
Фазовые точки, изображающие отдельные системы ансамбля,
перемещаются со временем по траекториям, определяемым урав-
уравнениями Гамильтона A1.1). При этом значение функции распре-
распределения в окрестности такой движущейся точки изменяется со
скоростью, определяемой полной производной
+ q+ p.
dt dt dq dp V
При перемещении фазовых точек со временем они не исчезают
и не рождаются. Поэтому
186
и с учетом того, что для гамильтоновых систем
dqf dp? dm d^H
приходим к теореме Лиувилля о постоянстве фазовой функции
распределения вдоль фазовых траекторий (или о сохранение вели-
величины фазового объема при движении образующих его фазовых то-
точек гамильтоновых систем)
_*_ =JP. + /p m=Q. A1.8)
dt dt w ' v '
Уравнение для этой функции
-|- = {Л,р} (Н-8а)
называется уравнением Лиувилля. Оно лежит в основе статисти-
статистического исследования классических систем многих частиц и по-
поэтому является основным уравнением статистической физики этих
систем.
Решение уравнения Лиувилля для функции 6Л/"+1 переменных
представляет собой столь же сложную задачу, как и решение
динамической системы уравнений A1.1). Однако оно позволяет
получить более простые уравнения для вероятностей нахождения
одной или нескольких частиц системы в элементе соответствую-
соответствующего фазового пространства. Исследование свойств молекулярных
систем с помощью этих частичных функций распределения состав-
составляет содержание метода Боголюбова, изложение которого будет
дано в последующих главах.
§ 48. Описание квантовых систем.
Оператор плотности и уравнение Неймана
Состояние классических многочастичных систем определяется
в каждый момент времени фазовым вектором R(^) = (q, p) в фа-
фазовом пространстве с базисными ортами координат и проекций
импульсов всех частиц.
Для квантовых систем такое задание состояния невозможно,
поскольку квантовые частицы не обладают одновременно коорди-
координатами и импульсами. Состояние отдельной квантовой системы
в тех или иных условиях определяется совокупностью независи-
независимых физических величин (динамических переменных), которые
одновременно имеют определенные значения. Число таких вели-
величин равно числу степеней свободы квантовой системы и называ-
называется полным набором.
Состояние квантовой системы, заданное полным набором физи-
187
ческих величин, описывается волновой функцией if>(q, /), завися-
щей от координат системы и времени. Волновая функция опреде-
определяет все свойства квантовой системы и удовлетворяет динамичес-
динамическому уравнению Шредингера
1П^- = Щ, A1.9>
где Й — оператор Гамильтона, или гамильтониан системы.
Если Й явно от времени не зависит, то система находится
в стационарном состоянии i|)(q), описываемом стационарным урав-
уравнением Шредингера
tfi|)(q)=?i|>(q), A1.10)
причем в этом состоянии энергия системы имеет фиксированное
значение Е.
Всякая волновая функция if квантовой системы может быть
разложена по собственным функциям if>m любой физической вели-
величины:
?(q). (ii.li)
Такое представление состояния -ф системы состояниями \рт анало-
аналогично свойству вектора а, разложенного по ортам еь е2, ..., еп
С СОСТаВЛЯЮЩИМИ С\, С2> . . . , Сп.
a-
Поэтому, по Дираку, состояние квантовой системы описывается
бра-вектором {^\ или сопряженным ему кет-вектором |г|?) =
= ((if>|)+ состояния (с волновой функцией \|>(q, t) = (q\ty)) в бес-
бесконечномерном гильбертовом (функциональном) пространстве.
В этом линейном пространстве в качестве базиса используются
ортонормированные ((tn\m') — 8mnv) собственные функции фт^
= (q|m) (M\m) = m\m)) любой физической величины, представ-
представляемой эрмитовым оператором Л = уЙь, при этом cm(t) =(m|i|>).
Условие полноты базиса \т) (m-представления) символичес-^
ки можно записать в виде
|=l, A1.12)
причем знак суммы и символ Кронекера в случае непрерывного
спектра обозначают соответственно интеграл и дельта-функцию.
В нашем изложении мы будем использовать главным образом
обычное координатное q-представление, приводя в некоторых слу-
случаях параллельно выражения в обозначениях Дирака, позволяю-
позволяющих легко перейти к произвольному необходимому представлению,
как непрерывному, так и дискретному.
В классической механике динамические переменные системы
(энергия, полный импульс и т. д.) являются функциями координат
и импульсов системы и, следовательно, функциями состояния. По-
188
этому задание состояния классической системы полностью опре-
определяет ее динамические переменные.
В квантовой механике динамические переменные не являются,
функциями состояния, характризуемого волновой функцией if,
а представляются самосопряженными операторами, действующими
в пространстве возможных волновых функций. Даже точное зада-
задание волновой функции системы не определяет, вообще говоря,
значение данной динамической величины при ее измерении. Только
в случае, когда г|з есть собственная функция оператора ?, пред*
ставляющего исследуемую динамическую величину, т. е. когда
?ф = 1д|), A1.13)
мы при измерении величины L у системы в состоянии г|з получим
определенное значение L. В общем же случае волновая функция
определяет лишь вероятности тех или иных результатов, которые
получаются при измерении различных динамических переменных
для системы, находящейся в данном состоянии -ф.
Совокупность различных значений Li динамической перемен-
переменной L, полученных в результате ее измерения у системы с волно-
волновой функцией ф, представляет собой статистический коллектив,
или квантовый ансамбль, величины L. В этом статистическом ан-
ансамбле и определяются средние значения (L) измеряемой вели-
величины*.
Средние значения любых динамических переменных в состоя-
состоянии i|?(q) можно вычислить теоретически, исходя из физического
смысла волновой функции. Действительно, поскольку квадрат вол-
волновой функции в координатном представлении |if>(q) |2 = г|)*\|)
определяет плотность вероятности обнаружения частиц системы
в соответствующих точках пространства, то
<4>l*> = S**4»dq = l, A1-14)
и среднее значение какой-либо функции координат L(q) в состоя-
состоянии г|з равно
A1.15)
В общем случае среднее значение любой физической величины L
вычисляется по формуле
A1.16)
где Lq — соответствующий величине L оператор в координатном
представлении.
Как уже отмечалось, волновая функция описывает состояние
квантовой системы, обладающей полным набором физических ве-
величин, т. е. совокупностью независимых динамических переменных
* Статистический ансамбль образует совокупность систем в различных со-
состояниях, характеризуемых определенными вероятностями. Совокупность же
квантовых систем в одном и том же состоянии статистического ансамбля не
составляет.
189;
,(в количестве числа степеней свободы системы), имеющих в дан-
данном состоянии определенное значение, которым соответствует пол-
полный набор коммутирующих эрмитовых операторов. Если же систе-
система находится в таких условиях, что она не обладает полным на-
набором физических величин, то ее состояние не может быть опи-
описано определенной волновой функцией, т. е. такая система не име-
имеет волновой функции.
Именно такими являются рассматриваемые в статистической
физике системы в термостате. Действительно, представим себе
систему, которая является частью более сложной замкнутой сис-
системы. Пусть эта замкнутая система в целом находится в некото-
некотором состоянии, описываемом волновой функцией 4я (х, q), где х —
совокупность координат нашей системы, a q — остальные коорди-
координаты замкнутой системы. Эта волновая функция, вообще говоря,
не распадается на произведение функций только ют х и только
от q, так что рассматриваемая система не обладает своей волно-
волновой функцией. В самом деле, плотность вероятности обнаружить
замкнутую систему с координатами х, q равна
W(x, q) = |V(xf q)|2, A1.17)
а плотность вероятности обнаружить систему с координатами х
(при произвольных значениях q) будет
ш(х)=^(х, q)dq = j|T(x, q)|*dq. A1.18)
Если бы рассматриваемая система имела волновую функцию
i|)(x), то очевидно, эта функция была бы равна
A1.19)
и удовлетворяла' бы равенству
(П.20)
или
\№(x,q)dq\* = $\W(x,q)\4q, A1.21)
что невозможно, кроме случая невзаимодействующих частей, когда
ЧЧх, q)=ij)(x)(p(q). A1.22)
Таким образом, система в термостате не имеет волновой функции.
Среднее значение L какой-либо величины L у такой системы
можно найти по волновой функции 4я (х, q) замкнутой системы, и
оно, подобно A1.16), равно
, q)dxdqy A1.23)
где оператор С величины L нашей системы действует только на
координаты х.
Выражение A1.23) для среднего значения физической величи-
величины L у системы в термостате можно записать в виде
Z-jZp(x,x/)|x'=xdx, A1.24)
290
где
р(х, х')=^(х, q)^*(x', q)dq, A1.25)
и после вычисления действия оператора L только на х в функции
р(х, х') надо положить х' = х.
Функция р(х, х7) называется матрицей плотности, а соответст-
соответствующий этой матрице оператор р — статистическим оператором
или оператором плотности.
Из определения матрицы плотности A1.25) видно, что она
самосопряженна, или эрмитова:
р*(х, х')=р(х', х). A1.26)
Зная матрицу плотности, можно найти средние значения физичес-
физических величин и вероятности их различных значений. Таким обра-
образом, состояние системы, не обладающей волновой функцией, мо-
может быть описано матрицей плотности.
Описание с помощью матрицы плотности является наиболее
общей формой квантовомеханического описания системы. Описа-
Описание же с помощью волновой функции ф(х) является частным-
случаем, отвечающим матрице плотности
р(х, х')=ф(хI>(х'). A1.27)
К понятию матрицы плотности можно прийти и другим путем.
Известно, что волновая функция \f>(x) отдельной (замкнутой)
системы определяет потенциально возможные значения той илиг
иной динамической переменной, которые обнаруживаются при ее
измерениях. До измерения динамическая переменная этих значе-
значений не имеет: потенциально возможное переходит в действитель-
действительное при измерении.
Подобно этому волновая функция 4я (х, q) сложной системы,
частью которой является изучаемая нами система (система в тер-
термостате) с координатами х, определяет потенциально возможные
состояния г|)(х) этой системы, которые обнаруживаются после от-
отделения ее от всей системы (до отделения «система в термостате»
не имела своей волновой функции).
Пусть из N случаев после отделения нашей системы от «термо-
«термостата» в N\ случаях система пребывала в состоянии г|)Ь в N2 слу-
случаях — в состоянии г|J и т. д. Тогда соответствующая этим случаям-
совокупность систем в различных состояниях образует статисти-
статистический ансамбль, который характеризуется волновыми функция-
функциями -фь 1|J, ... и соответствующими вероятностями W\ = NilN>
^2=^2/^, ... с равной единице суммой:
* = 1- (П.28>
Очевидно, что среднее значение динамической переменной L у сис-
систем такого ансамбля определяется формулой
191
L= Twk(Lk) = Vwk\$lBbkdx= \bp(xtx')\x>=xdx, A1.29)
k k J J
где
р(х,х')=?а^>*(х)Ых') A1.30)
k
матрица плотности, или оператор плотности р = V \k) w^{k\
k
в матричном координатном представлении, удовлетворяющий
условию нормировки
Spp=l, A1.31)
так как согласно условиям нормировки волновых функций и ве-
вероятностей
где шпур (след) матрицы оператора обозначает сумму диагональ-
диагональных элементов SpL= V (m\L\tn) и не зависит от представления.
k
Записывая оператор L в матричном координатном представле-
представлении с помощью его матричных элементов L(x, х') = (х|?|х'),
имеем
поэтому
I t Фа (х) L (х, х) % (х') dxdx =
- jL(x,x')p(x,x')rfxdx', A1.32)
или
ZJ = Sp(?p)=Sp(p?). A1.33)
Таким образом, система в термостате не может быть описана
одной определенной волновой функцией, но в изложенном выше-
смысле характеризуется совокупностью векторов состояния в гиль-
гильбертовом пространстве ifi, я|J, •. •, заданных вероятностями
W\, W2 ....
Состояние квантовой системы, которое можно описать волновой
функцией называется чистым. Совокупность значений динамичес-
динамической переменной L, которые обнаруживаются в этом состоянии при
измерении, называется чистым ансамблем*. Состояние системы
в термостате определяется совокупностью чистых состояний \fu
со статистическим весом Wk и называется смешанным состоянием,
совокупность систем в состояниях г|)/г — смешанным ансамблем.
* Совокупность систем в одном и том же состоянии г|), как уже отмечалось,
не образует статистического ансамбля.
192
Среднее значение динамической переменной системы в смешан-
смешанном ансамбле A1.29) определяется, как и среднее значение
A1.24) у системы по общей с термостатом волновой функции
Ф(х, q), той же матрицей плотности A1.25), записываемой теперь
в виде A1.30).
До сих пор мы рассматривали системы и описывающие их
матрицы плотности для фиксированного момента времени. Рас-
Рассмотрим теперь их эволюцию во времени и найдем уравнение
движения для матрицы плотности системы с гамильтонианом Й.
Если в начальный момент времени относительное число Wk
систем находилось в состоянии 'ф^ = (ф^(х, 0), то в момент времени
t такое же число их будет находиться в состоянии ^(х, /). Изме-
Изменение состояния i|)k(x, t) во времени определяется уравнением Шре-
дингера
или в матричном виде
Л дЫ1'1) = f H(x,x')^k(x',t)dx'. A1.34)
ot J
Дифференцируя по времени матрицу плотности
Р (х, х\ t) = J^w^k (х, /) ф!(х\ f)
и используя уравнение A1.34) и свойство эрмитовости гамильто-
гамильтониана Я(х, х)=Я*(хг, х), получим уравнение движения статис-
статистического оператора в матричной форме
|
— Wtftk (x, 0 ty*k (x", t) H (x\ x')} dyC =
-1{Я(х,х")р(х//,х',0-Р(х,х^,0Я(х",х')}^, A1.35)
или в независящей от представления операторной форме
Ы
^L ={Я,р}, A1.36)
где
A1.37)
ih
квантовые скобки Пуассона.
7 Зак. 245 193
Уравнение для оператора плотности A1.36) называется урав-
уравнением Неймана и является основным уравнением статистической
физики квантовых систем. Это уравнение аналогично классическо-
классическому уравнению Лиувилля A1.8) для фазовой плотности распреде-
распределения p(q, p, t).
Заметим, что оператор плотности является, подобно классичес-
классической фазовой плотности, симметричным относительно перестановок
частиц. Действительно, в квантовой механике не все собственные
функции гамильтониана являются допустимыми волновыми функ-
функциями системы, а лишь те из них, которые удовлетворяют опре-
определенным свойствам симметрии. Для систем частиц с нулевым
или целым (кратным ft) спином (бозе-частицы) допустимы лишь
волновые функции, симметричные относительно одновременной
перестановки координат и спинов частиц, а для систем частиц
с полуцелым (в единицах ft) спином (ферми-частицы) допустимы
лишь антисимметричные относительно перестановки координат и
спинов волновые функции. В выражение A1.30) для оператора
плотности входят не все, а лишь допустимые волновые функции
и из этого билинейного выражения видно, что независимо от сорта
частиц оператор плотности не меняется при перестановке частиц.
Глава 12
ОБЩИЕ МЕТОДЫ РАВНОВЕСНОЙ
КЛАССИЧЕСКОЙ СТАТИСТИКИ
§ 49. Основное положение
классической статистики.
Микроканоническое распределение
Рассмотрим многочастичную термодинамически равновесную
систему. Как уже отмечалось в термодинамике (см. § 1), всякий
внутренний параметр такой системы Ьо представляет собой с точки
зрения молекулярной физики среднее за бесконечно большой про-
промежуток времени значение соответствующей этому параметру
функции координат и импульсов ее частиц 6(q, p):
К = (b (q, р)>,= Ищ^г f Ь (q (t), p (t)) dt. A2.1)
Это вычисление равновесного внутреннего параметра Ьо системы
связано с решением для нее динамической задачи A1.1). Стати-
Статистическая физика не идет по этому пути. Ее основная идея сос-
состоит в замене среднего по времени (b(q, р))* функции b(q, p)
194
данной системы средним значением ft(q, p) этой функции по ан-
ансамблю определенным образом распределенных систем*
, P)p(q, Р)Л\ A2.2)
где фазовая плотность распределения p(q, p) для равновесных
систем, очевидно, не зависит от времени и удовлетворяет условию
нормировки
Jp(q, p)rfr=l. A2.3)
Интегрирование в A2.2) и A2.3) распространяется по всему фа-
фазовому пространству.
Задача состоит в том, чтобы найти p(q, p), удовлетворяющую
равенству
<&(q, Р)>* = *ЙГр). A2.4)
Для этого обратимся прежде всего к основному уравнению ста-
статистической физики классических систем — уравнению Лиувилля
A1.8а). Из него получаем
{Я, рНО, A2.5)
откуда следует, что равновесная функция распределения p(q, p)
является интегралом движения уравнений Гамильтона A1.1) или
функцией интегралов движения:
p(q, p)=/(/i(q, P), /2(q, p), ..., /2*-i(q, p)h A2.6)
где /i, /2, ... — интегралы движения.
В соответствии с введенным Гиббсом (отвечающим термодина-
термодинамике) статистическим определением энтропии (см. ниже) функция
p(q, p) зависит лишь от однозначных аддитивных интегралов дви-
движения. Известны три таких интеграла движения: энергия Я, им-
импульс Р и момент импульса М. Поэтому
p(q, р)=/(Я, Р, М). A2.7)
Для равновесной системы частиц в неподвижном сосуде им-
импульс Р и момент импульса М рав'ны нулю. Поэтому в этом слу-
случае для систем с заданным числом частиц фазовая плотность рао
пределения зависит лишь от функции Гамильтона
P(q, р)=/(Я(Ч, р)). A2.8)
Для определения явного вида функции распределения в статис-
статистической физике принимается в качестве основного положения по-
постулат равной априорной вероятности любого микросостояния
равновесной изолированной системы, т. е. принимается, что для
изолированной системы, имеющей энергию Е с точностью ??
* Средние по ансамблю обозначаются или чертой над буквой, или угловыми
скобками: Ъ или <6>, а средние по времени — угловыми скобками с индексом t:
195
(определяемой заданием макроскопических условий) и число час-
частиц N в объеме V, функция распределения p(q, p) постоянна
в слое АЕ и равна нулю вне этого слоя:
p (q, p) = -
О вне слоя
Равновероятностное распределение микросостояний изолиро-
изолированной системы называется микроканоническим распределением^
а соответствующий ансамбль — микроканоническим ансамблем.
С помощью 6-функщш микроканоническое распределение
A2.9) можно записать в виде (АЕ/Е-+0)
р(Ч, Р) =ё"~1б(Я(я, р)— Е). A2.10)
Постоянная g{E, N, V) определяется из условия нормировки
A2.10)
g(E, V, N)=$S(H{q, p)~E)dT A2.11)
и имеет смысл плотности распределения фазового объема по энер-
энергии, Действительно, интеграл от g{E') по допустимым значениям
энергии, меньшим Е (Етт<Е'<Е),
Е
J g(E')dE'--= J
H{q,p)<E
равен фазовому объему (приведенному), заключенному внутри
гиперповерхности H(q, р) =Е. Увеличение фазового объема АГ(?)
при возрастании энергии на величину АЕ называется статистичес-
статистическим весом макроскопического состояния системы с энергией Е и
равно
ДГ (Е) - { } AE = g{E) АЕ, A2.12)
dE
где g(E) =dF(E)/dE — энергетическая плотность фазового объ-
объема, или, поскольку точки фазового объема изображают состояния,
плотность состояний системы с данной энергией Е.
Можно показать, что микроканоническое распределение A2.10)
обеспечивает равенство A2.4) среднего по макроканоническому
ансамблю A2.2) среднему по времени A2.1) функции координат
и импульсов b(q, p) систем, для которых (b(q, p))* (в соответст-
соответствии с известным положением термодинамики — см. § 2) зависит,
только от интеграла энергии. Такие системы называются эргоди-
ческими. Обоснование (исходя из механики) эргодичности много-
многочастичных систем и возможности замены средних по времени
средними по микроканоническому ансамблю носит название эрго-
дической проблемы. Эта проблема несмотря на ряд полученных
важных результатов еще ждет своего решения.
Для построения термодинамики многочастичной системы дос-
достаточно, как известно, определить один из ее термодинамических
196
потенциалов. Остальные величины находятся уже методами самой
термодинамики. При независимых макроскопических параметрах
Е> V, N, которыми определяется термодинамическое состояние
рассматриваемой системы, термодинамическим потенциалом явля-
является энтропия. Гиббс определяет ее как величину, пропорциональ-
пропорциональную логарифму фазового объема
S(E9 У, N)=klnT(E, Vy N)y A2.13)
где k — универсальная постоянная, равная постоянной Больцма-
на. Можно показать, что определенная таким образом энтропия
обладает известными термодинамическими свойствами (*).
Заметим, что поскольку при определении энтропии в статис-
статистическом пределе (N-+oof У->оо, VyjV = u = const) следует учиты-
учитывать только основную асимптотику по числу частиц ~N, то опре-
определение статистической энтропии A2.13) не является единствен-
единственным. Так, например, можно использовать вместо A2.13) эквива-
эквивалентные (с точностью до слагаемых ~lniV) выражения в виде
логарифмов или плотности состояний
S = k\ng(E, V,N), A2.14)
или статистического веса
S = k\nAT(E, V, N). A2.15)
Логарифмический вид выражений A2.13) — A2.15) для энтропии
обусловлен требованием ее аддитивности, в частности, для невза-
невзаимодействующих подсистем. Действительно, в этом случае Г =
= ГГГ2 и 5(rir2)=S(ri)+S(r2), откуда следует, что S(r) =
= Cilnr + C2, где d = const. Вычисление фазового объема или ста-
статистического веса, даже для относительно простых статистических
систем представляют трудную задачу. Поэтому микроканоничес-
микроканоническое распределение используется в основном не для вычисления
термодинамических функций конкретных систем, а для общетеоре-
общетеоретического рассмотрения.
Более удобно статистическое изучение не изолированных сис-
систем, а систем в термостате.
§ 50. Каноническое распределение
Найдем распределение по состояниям (функцию распределения
в фазовом пространстве) неизолированной (но замкнутой) систе-
системы, находящейся в тепловом контакте с другой системой значи-
значительно больших размеров (по числу степеней свободы) — термо-
термостатом.
Для этого рассмотрим объединенную изолированную систему
(параметры которой будем помечать индексом о): малая система
(без индекса) и термостат (индекс т), причем ?o<#o(qo, Po)<
<? + Д? и ?<с?т=?0—?; AE/E-^Q.
197
Согласно микроканоническому распределению, справедливому
для объединенной системы,
po(q, Р, Qt, рт) = go'1 (ео) Ь{Ео—#o(q, p, qT, pT)) —
A2.16)
о-Я(я, р)-Ят(Чт, Рт)),
где мы пренебрегли малой энергией Но—Н—Ят взаимодействия
системы и термостата.
Функцию распределения малой системы находим, интегрируя
A2.16) по фазовому пространству термостата:
р (я, р) = I po (q, p> qT, pT) лгт=
АГт(?0-Я(д,р))
Зависимость статистического веса АГТ состояния термостата от
энергии системы E = H(q, p) достаточно определить из A2.15)
в первом приближении по малому параметру ?/?0:
ДГ,=ехр J-Lsr(?,)] - exp [-i-S,(?,-?)] =
Поскольку ЕО~ЕГ, то с учетом термодинамического соотношения
dST(E0) ^ J__
дЕ» Т '
где Т — температура термостата и системы, из A2.17) оконча-
окончательно находим каноническое распределение Гиббса
p(q, p) =
или
pfq, р)=в^-"(<ьр)]/е, A2.19)
где Q=kT называется модулем канонического распределения, а
константа А = ехр(хР/в) содержит все не зависящие от q и р вели-
величины и определяется из условия нормировки
dr. A2.20)
Входящий в A2.20) интеграл
Я(д,р)
0 dqdp
198
называется статистическим интегралом системы, а определяемая
из A2.20) функция
, V, N)=—6lnZN A2.221
есть ее энергия Гельмгольца F(9, V, N).
Действительно, вычислим внутреннюю энергию системы по
уравнению Гиббса—Гельмгольца E.29)
_L\
9 У
06 0A/9)
взяв в качестве энергии Гельмгольца F выражение A2.22). Мы
получим тогда
H(q,p) p F-//(q,p) _
т. е. что внутренняя энергия статистической системы равна сред-
среднему значению ее функции Гамильтона по каноническому распре-
распределению Гиббса A2.19), как и должно быть в соответствии с фи-
физическим смыслом Е.
Поскольку функция Гамильтона A1.2) системы равна сумме
кинетической и потенциальной энергий ее частиц, а кинетическая
энергия есть квадратичная функция импульсов, то интегрирова-
интегрирование по ним в A2.21) может быть произведено и мы получим
( I exp [—(р\J/2тЩ dp\)m • \ e dqx... dqu =
V J J
A2.23)
— 00
h* J N\
где интеграл
Qjv = Jexp [—?/iv (Чь • • •» 4iv)/e]dqi.. .dqN
называется конфигурационным интегралом.
Интегрирование по импульсам канонического распределения
Гиббса A2.19) легко выполняется и дает конфигурационное рас*
пределение Гиббса
A2.24)
Энергия Гельмгольца
F = — в In {QN/N\)+3N@ In К, A2.25J
где К =Л/|/2лтв — тепловая длина волны де Бройля.
199
Таким образом вычисление энергии Гельмгольца, а следова-
следовательно, и всех термодинамических функций многочастичной си-
системы сводится к вычислению ее конфигурационного интеграла
A2.24).
С помощью известных термодинамических соотношений E.17)
р—_J??. <?— _ _^1 р — р\ TS — F в dF
~~ dV' ~ дТ' ~~ ~ дв
прямым дифференцированием энергии Гельмгольца A2.25) нахо-
находим давление и внутреннюю энергию системы:
р=_е__ао^ A2.26)
Qn dV v '
Е = J^L + -51 J^L, A2.27)
2 qjv ae v
С помощью канонического распределения A2.19) находим, что
энтропия системы
F — E , F — H , Г F— H
— h ~ Ъ \ р 0 г1Г —
е J е
)ЙГ=-&к^ A2.28)
пропорциональна среднему значению логарифма плотности веро-
вероятности, а не является средним значением какой-либо механиче-
механической величины.
§ 51. Теорема о равномерном распределении
кинетической энергии по степеням свободы
и теорема о вириале
Нахождение внутренней энергии Е системы, задаваемой
функцией Гамильтона #(q, p), по общему методу A2.27) сво-
сводится к вычислению конфигурационного интеграла A2.24). Од-
Однако во многих случаях Е можно найти значительно проще, ис-
используя две общие теоремы классической статистики — теорему
о равномерном распределении кинетической энергии по степеням
свободы и теорему о вириале.
Докажем эти теоремы.
Функция Гамильтона системы имеет вид
1<а<3
Найдем средние значения произведений
200
по каноническому распределению Гиббса. По определению сред-
среднего значения A2.2)
Pi дР? w.h™ J ¦- )Ъ эр?
F—H
6V-1
e
N\
6N—\
j... fr^pfe e |^ -Je 0 dp*j=e, A2.29)
так как при р^->-±°о функция Гамильтона стремится к беско-
бесконечности и первый член в фигурных скобках равен нулю, а
N\
F"H
Отсюда получаем, что средняя кинетическая энергия, приходя-
приходящаяся на одну степень свободы,
одинакова для всех степеней свободы и равна 6/2. Этот общий
результат классической статистики носит название теоремы о
равномерном распределении кинетической энергии по степеням
свободы.
Согласно этой теореме средняя кинетическая энергия систе-
системы, очевидно, равна
A2.31);
где п — число всех ее степеней свободы.
Аналогично A2.29)
если потенциальная энергия частицы достаточно быстро возраста-
возрастает с ростом координаты.
Величина
Н^ т2? A2-33)
<< l t.cx
1<а<3
201
называется, по Клаузиусу, вириалом системы, а выражение
вириалом, приходящимся на одну степень свободы.
Согласно A2.32) среднее значение вириала на одну степень
свободы
W? =
A2.34)
одно и то же для всех степеней свободы и равно в/2. Этот об-
общий результат можно назвать теоремой о равномерном распре-
распределении вириала по степеням свободы. Согласно этой теореме
средний вириал системы равен
Ш=пв/2. A2.35)
Из A2.29) и A2.32) находим
дН
дР?
дН
A2.36)
а из A2.31) и A2.35) получаем теорему о вириале: средняя ки-
кинетическая энергия системы равна ее среднему вариалу:
K=W. A2.37)
Теорема о равнораспределении кинетической энергии по сте-
степеням свободы A2.30) позволяет определить среднюю кинетиче-
кинетическую энергию любой классической системы, теорема же о равно-
равнораспределении вириала по степеням свободы A2.34) дает воз-
возможность вычислить среднюю потенциальную энергию только та-
таких систем частиц, потенциальная энергия UnDu • • • ,Qiv) взаи-
взаимодействия которых является однородной функцией координат.
Так, если степень однородности функции UN(qu.. .tqN) равна
v, то по теореме Эйлера об однородных функциях
s *?¦
dqf
qw) =-^
dU
N
dqf
A2.38)
и энергия рассматриваемой системы (среднее значение функции
Гамильтона) равна
(±- + ±-}. A2.39)
Обе приведенные теоремы часто используются при вычислении
теплоемкости тел.
202
§ 52. Распределение Максвелла
Каноническое распределение Гиббса A2.19)
— Н)/в]
определяет плотность вероятности того, что в системе из N ча-
частиц 1-я частица находится в состоянии qi, pi; 2-я — в состоянии
q2, P2;...; N-я частица — в состоянии qN, pjv. Зная эту функцию
распределения, нетрудно найти вероятность dW(p) того, что не-
некоторая частица имеет импульс в интервале (р, p+dp). Для это-
этого, очевидно, необходимо проинтегрировать фазовую плотность
р (Чь • • •» 4n, Рь • • • • Pn) по координатам и импульсам всех частиц,
кроме импульса данной частицы.
Учитывая, что функция Гамильтона Н имеет вид A1.2), по-
после указанного интегрирования получаем
dw (р) = а ехр [—р2/ Bтв] dp,
или
dw (pXi pyi рг) = а ехр [—(р2х + р\ + р^[2пЩ dpxdpydp2.
Из условия нормировки этой функции на единицу, находим
и окончательное распределение для импульсов частицы
dw (рх, ря, Рг) = Bлт&)-™ ехр [ P*+2fe+^ ] dpxdpydpz. A2.40)
Переходя от импульсов к скоростям (px = mvx, Py = mvy, Pz —
= mvz)y можно написать аналогичное распределение для скоро-
скоростей
которое называется распределением Максвелла. Как видно из
его вывода, оно не зависит от вида взаимодействия между части-
частицами и одинаково в газообразной, жидкой и твердой фазах.
Интегрируя распределение A2.41) по всем значениям vv и
vZy получим распределение Максвелла для отдельной компоненты
скорости:
203
График функции для плотности вероятности
/ ч dw(vx) I m W/2
дан на рис. 32.
J>M
(-¦»¦)
Рис. 33
Ижтегрируя A2.41) по шаровому слою в пространстве скоро-
скоростей, т. е. по всем vx, vy, vZy удовлетворяющим неравенству
:(vx*+vv*+vz*y'*<v+dv
(для этого нужно выражение
dw(vx, vy, уг) ( т \3/2
dvxdvydvz
умножить на объем указанного шарового слоя), получим распре-
распределение Максвелла по абсолютной величине скорости:
dw(v) =4я(т/2явK/2ехр (—mv2/2e)v2dv. A2.43)
График функции p(v) =dw(v)'/dv приведен на рис. 33. Эта функ-
функция достигает максимума при скорости v = vm = yr20/m , которая
называется наивероятнейшей скоростью.
§ 53. Большое каноническое распределение
Определим теперь распределение по состояниям открытой си-
системы в термостате, называемое большим каноническим распре-
распределением Гиббса. С такими системами мы встречаемся в целом
ряде приложений. Кроме того, использование большого канони-
канонического распределения во многих случаях оказывается более эф-
эффективным, чем микроканонического и канонического распреде-
распределений.
Рассмотрим малую систему, которая находится в тепловом и
материальном контакте с термостатом, обмениваясь с ним не
только энергией, но и частицами. Границы, отделяющие систему
204
от термостата в некотором смысле условны: они фиксируют лишь
ее объем V и другие внешние параметры а, но не энергию Е и
число частиц JF. В соответствии с этим термодинамическое со-
состояние системы определяется переменными Г, а, \х.
Большое каноническое распределение получим аналогично
выводу канонического, исходя из микроканонического распреде-
распределения для изолированной объединенной (термостат и изучаемая
малая система) системы с энергией Ео и числом частиц Л/о. От-
Отличие в рассматриваемом случае системы состоит в том, что те-
теперь следует в явном виде указывать число частиц Jf в ней.
Таким образом, подобно A2.17) функция распределения си-
системы с переменным числом частиц в термостате имеет вид:
p(q. p,
ЛГт(Е0--?, No-.
±ST(E0-E, N9-Jft)j, A2.44)
ДГ0(?0, No)
где индексы опт относятся соответственно * к объединенной си-
системе и к термостату. Поскольку мы будем предполагать, что
для энергии Е и числа частиц Jf подсистемы справедливы нера-
неравенства
то в первом приближении
ST(E0-E, No-Jft)=ST(EOf No) -Яж(я
A2.45)
где учтено, что
E=HN{q, p), dST/d?0=l/r, dST/dJV0^—ц/Г.
Подставляя A2.45) в A2.44), находим большое каноническое
распределение Гиббса
(^) A2.46)
где
6(в, а, Ц)= ? Jexp (М--Я^.(д. Р) j ^ {12А7)
большой статистический интеграл (сумма), а
QF, а, |г)=—е1п?(в, а, ^х) A2.48)"
большой термодинамический потенциал.
205
Действительно, термодинамические параметры — число частиц
JVG, a, \х) и внутренняя энергия Е(Т, а, \i), — определяемые со-
соответствующими частными производными большого термодина-
термодинамического потенциала, совпадают со средними значениями числа
частиц и функции Гамильтона по большому каноническому рас-
распределению Гиббса A2.46). Так,
оо \xJV°
' а> •**)=">• A2.49)
^8
00
, р). A2.50)
§ 54, Термодинамическая эквивалентность
канонических распределений
Мы рассмотрели три гиббсовских распределения: микрокано-
микроканоническое— для изолированных систем, каноническое — для не-
неизолированных закрытых систем в термостате и большое канони-
каноническое— для неизолированных открытых систем в термостате.
Покажем, что, за исключением немногих случаев, о которых
будет сказано ниже, использование этих распределений для
Каждой из названных систем приводит в статистическом преде-
пределе (ЛЛ-^-оо, V->oo, VJN =^и = const) к термодинамически эквива-
эквивалентным результатам. Это означает, что каноническим и большим
каноническим распределениями можно пользоваться также для
описания изолированных систем, что практически является очень
важным.
Для этого вычислим относительную флуктуацию энергии cm
стемы в термостате.
Отклонение энергии системы от своего среднего значения ха-
характеризуется дисперсией
= (Я—ЯJ-Я2—Я2,
флуктуацией
= ((АЯJI/2
и относительной флуктуацией
я А (Я
206
С помощью канонического распределения находим:
дв
A2.51)
дв k
и относительная флуктуация энергии системы в термостате равна
6Я=4^ л/—- A2.52)
Н. У дв к ;
Поскольку H=E~N, дН/дв-Ы, то
бя~10~12 при Af~1024, т. е. во всех практически важных случаях
относительная флуктуация энергии очень мала и в статистиче-
статистическом пределе стремится к нулю.
Малость величины относитель- Щн)
ной флуктуации означает, что зна-
значения энергии системы в термоста-
термостате сколько-нибудь отличные от
средней энергии, практически не-
невероятны.
Это непосредственно следует
также из выражения для функции
распределения по энергии w(H), ко-
которое представляет собой произве-
произведение плотности вероятности состо-
состояния q, p с энергией Я(я, р) на
плотность числа таких состояний:
F — H
A2.53)
н
Рис. 34
Н
Действительно, как нетрудно_проверить, функция w(H) при не-
некотором значении энергии Я имеет очень острый максимум
(рис. 34), так как exp [(F — Н)/в] быстро убывает, a g{H) бы-
быстро возрастает с возрастанием Я. Таким образом, значения
207
энергии, заметно отличающиеся от Я, чрезвычайно маловероят-
маловероятны, и система ведет себя практически как изолированная. Это и
приводит к термодинамической эквивалентности результатов, по-
полученных с помощью канонического и микроканонического рас-
распределений.
Аналогично с помощью большого канонического распределе-
распределения находим:
® — нА
dp dp в JU \ dp ) J V в /
A2.54)
и относительная флуктуация числа частиц в системах большого
канонического ансамбля
1
JT N У \ dp /ey vN V \дР
A2.55)
стремится к нулю в статистическом пределе. Отсюда следует эк-
эквивалентность большого канонического и канонического распре-
распределений. Заметим, что, несмотря на термодинамическую эквива-
эквивалентность статистических ансамблей, расчеты величины флуктуа-
флуктуации, проведенные с их помощью, приводят к различным резуль-
результатам. Так, например, дисперсия энергии в большом канониче-
каноническом ансамбле численно отличается от A2.51) (*)
-L+-1 х "Ч7,*;*,, 4V ™ /*'VJ \~N. A2.56)
Как видно из формулы A2.52), относительная флуктуация
энергии системы в термостате не будет малой тогда, когда
дН/dS-^oo (бесконечно большая теплоемкость), и аналогично из
формулы A2.55) видно, что относительная флуктуация не будет
малой при (dP/dV)e,N->0 (нулевая величина коэффициента
устойчивости). Это имеет место, как известно из термодинамики,
в критическом состоянии и в двухфазных системах. В этих слу-
случаях канонические ансамбли не эквивалентны.
208
§ 55. Термодинамическая теория возмущений.
Вариационный принцип Боголюбова
Вычисление термодинамических функций многочастичных си-
систем в общем случае связано с большими трудностями. Поэто-
Поэтому в статистической физике существуют различные приближен-
приближенные методы их вычисления. Здесь мы изложим два таких ме-
метода.
1. Термодинамическая теория возмущений.
Пусть требуется вычислить энергию Гельмгольца системы с
функцией Гамильтона #(q, p). Представим Я (q, p) в виде сум-
суммы двух слагаемых: «невозмущенной» функции Гамильтона Но>
соответствующей точно решаемой задаче, и малого возмуще-
возмущения Н\\
Я
Рассмотрим теперь систему с функцией Гамильтона Я(е) =
= #о+е#ь зависящей от параметра е, так что H(q, р)=ЯA) к
Н0 = Н@). Энергия Гельмгольца такой системы имеет вид
р (е) = _е In j exp {— (Яо + еНг)/в} dY. A2.57)
Производные энергии Гельмгольца по параметру е, умноженные
на соответствующую степень температуры в,
A2.58)
Хя(в) в
называются семиинвариантами или кумулянтами канонического-
распределения Гиббса.
Дифференцируя выражение A2.57) по е, находим соотноше-
соотношения, связывающие производные Хп с моментами распределения.
Гиббса:
-Я1J>2,.... A2.59)
Зная производные ХПу находим разложение энергии Гельмгольца
в ряд, в котором для изучаемой системы полагаем 8=1,
оо
F[H(q, p)]af(l)=^X,@)- (~^} ""• A2.60)
Полученное разложение A2.60) носит название ряда термо-
термодинамической' теории возмущений и, как легко видеть, одновре-
одновременно является разложением по степеням обратной температуры
Р=1/0, коэффициенты которого Яп@) также зависят от темпера-
температуры. Этот ряд является асимптотическим, и его аппроксимирую-
аппроксимирующие свойства улучшаются при высоких температурах.
209
Невозмущенная функция Гамильтона #о, как отмечалось,
должна быть достаточно простой, т. е. допускать точное вычисле-
вычисление входящих в разложение A2.60) моментов A2.59). Возмуще-
Возмущение Н\ = Н — #о должно быть по возможности малым. Один из
возможных методов выбора Н\ дает приводимый ниже вариаци-
вариационный принцип Боголюбова.
Рассмотренный на примере классического канонического рас-
распределения Гиббса метод термодинамической теории возмущений
аналогичным образом используется и в большом каноническом
ансамбле. При этом в приведенных выше формулах достаточно
произвести формальную замену H-*~Hjv°—\лЛР и использовать
большой термодинамический потенциал Q вместо энергии Гельм-
гольца jF. Изложенный метод допускает очевидное квантовое
обобщение и широко применяется для приближенного расчета тер-
термодинамических свойств статистических систем.
2. Вариационный принцип Боголюбова.
Наряду с теорией возмущений в статистической физике (как
и вообще в теоретической физике) для приближенного вычисле-
вычисления термодинамических функций используются также вариацион-
вариационные принципы.
Установим вариационный принцип Боголюбова.
Для этого рассмотрим непрерывный функционал энергии
Гельмгольца
F[H0 + A] = -Q\n^exp{-(HQ+A)/Q}dr, A2.61)
где Но — аппроксимирующая функция Гамильтона, a A(q, p) —
произвольная динамическая функция. Так как вторая вариация
этого функционала по А не положительна
b\F [Яо + Д] = -JL <FЛ_6А)«> < 0,
то по известной теореме математического анализа
t A2.62)
где (..,)н0 означает усреднение по каноническому распределе-
распределению систем с функцией Гамильтона Яо.
Полагая в A2.62) А = Н — Яо, получим
F[H]<F[Ho] + {H-Ho)Ho = F^ A2.63)
где Fm называется модельной энергией Гельмгольца.
Неравенство A2.63), определяющее верхнюю границу энергии
Гельмгольца Fm изучаемой системы, представляет собой вариа-
вариационный принцип Боголюбова. Наилучшее значение энергии
Гельмгольца F[H] получается тогда, когда вариационные пара-
параметры а*, вводимые при выделении аппроксимирующей функции
Гамильтона Яо, определяются из условия минимума Fm. Это ми-
минимальное значение Fm и используется в качестве приближенно-
приближенного выражения для F [Н].
210
§ 56. Метод Боголюбова
Каноническое распределение Гиббса A2.19) в принципе поз-
позволяет находить энергию Гельмгольца A2.25), а следовательно,
и любые термодинамические величины. Однако во многих слу-
случаях эти величины можно вычислить, опираясь не на функцию*
всех координат, а на функции распределения для одной, двух
или трех частиц, что благодаря относительной простоте их при-
приближенного определения сильно облегчает исследование термо-
термодинамически равновесных систем. Такой метод решения задач
статистической физики был развит Н. Н. Боголюбовым.
Введем частичные функции распределения для классических
равновесных систем, исходя из конфигурационного каноническо-
канонического распределения A2.24)
Пусть
#"e(qi,...,q8) E=1, 2,...)
симметричные функции аргументов, нормированные таким обра-
образом, что выражение
^ ... dqs
представляет вероятность того, что положения данной группы s
молекул находятся соответственно в бесконечно малых объемах
d(\u dq2f...ydqs около точек qb q2, ...,qs. В силу такого определе-
определения, очевидно, имеем
&s (qi. • • ¦ , qs) = Vs J ... f D (qlf ... , qN) dqs+1 ... dqN. A2.64)
Найдем уравнения для этих функций.
Дифференцируя A2.24) по <ft
дР = i_ dUN
dq^ в dq%
и интегрируя это уравнение по переменным qe+i,...,Q^ с учетом
определения A3.33) получим
При центральных силах взаимодействия между частицами с пар-
парным потенциалом Ф(|я^ — q^l) потенциальная энергия системы
равна
2lt
Ui</<JV
+ E O(|q«-q/l). A2.65)
тде
l
потенциальная энергия s частиц. Поэтому
A2.66)
где v = VjN — объем на одну частицу; a=l, 2, 3; 5=1, 2,....
В статистическом пределе (А^оо, К~^оо, V7Af = a = const) по-
получаем цепочку уравнений Боголюбова для равновесных функ-
функций распределения
dUs а 1 f aO(lqi —qs+1|)
^+^dq-O, A2.67)
где интегрирование распространяется по всему трехмерному про-
пространству.
При решении интегро-дифференциальных уравнений A2.67) в
качестве граничных условий используется условие ослабления
корреляций
SMqi, ...,q.)-* 11^D), A2.68)
210
когда все Iq* — qj|->°°, а также условия нормировки:
l. A2.69)
lim -LC#8+1(qi, ... ,qs+i)dqs+i = ^s(qi, ... , <b). A2.70)
V-*oo К J
V
Функции STS, определяемые уравнениями A2.67) — A2.70), и
должны представлять асимптотические выражения функций рас-
распределения для реальных систем с конечным, весьма большим
числом частиц N, находящихся в конечном макроскопическом
объеме V.
В ряде случаев более удобными являются «родовые» функции
распределения ps (qb ..., qs).
Выражение
ps(qi, ..., qs)dqx ... dqs
определяет вероятность того, что при наблюдении за системой из
N частиц мы найдем какую-либо частицу в элементе объема dqx
около qi, другую частицу в dq2 около q2,... и, наконец, послед-
последнюю частицу в dqs около qs. Нетрудно установить, что
A2.71)
Действительно, имеется N возможностей того, чтобы одна части-
частица находилась в объеме dqb N—1 возможностей того, чтобы
другая частица находилась в dq2,..., и JV — s+1 возможностей
того, чтобы последняя частица находилась в dqs. Общее число
способов реализации рассматриваемого состояния, таким обра-
образом, равно
N(N-l) ...(N —
и поэтому
J
Jp.(«h.
В статистическом пределе (так как
Ps(Qi> ••- Чз) = -^^(Я1> ...,q.). A2.72)
При учете A2.72) из уравнений A2.67) находим цепочку урав-
уравнений для вновь введенных функций:
при условии нормировки
.. j"psDi. --- ,q,)dqi ... rfq,= l A2.74)
v
(s = l, 2, ...)•
213
Из всех частичных равновесных функций распределения осо-
особо важное значение имеет бинарная функция ^(Чь Ъ) (или
Р2(Чь Яг)), так как через нее могут быть выражены термическое
и калорическое уравнения состояния и другие термодинамические
функции изучаемой системы. Таким образом, в методе Боголю-
Боголюбова исследование равновесных систем сводится не к вычисле-
вычислению конфигурационного интеграла, а к решению уравнений для
частичных функций распределения, что оказывается в ряде слу-
случаев значительно проще. При этом либо используется разложе-
разложение функций распределения в ряд по малому параметру, либо
для получения замкнутой системы s уравнений для этих функций
одна из высших функций распределения приближенно выра-
выражается через низшие (процедура расцепления, или обрыва, це-
цепочки уравнений).
Выразим термическое и калорическое уравнения состояния
системы через бинарную функцию распределения.
Согласно A2.26)
в dQN
ГДе
J ... jexpj
dV
в
A2.75)
V V i<j
Для того чтобы найти производную dQN/dV, перейдем в A2.75)
к новым переменным Xia=V-x/zqia. Тогда d\t= J~| dxf ¦= — dqiP
и a
... (exp I V Ф(|х* — xy|V1/3)| dxx ... dxtf, A2,76)
i i t<i
где интегрирование ведется теперь по единичному объему. Инте-
Интеграл A2.76) содержит V только как параметр.
Дифференцируя A2.76) по У, будем иметь
:х ... dxN —
Но
ЗФ (| x,- -x, 1 V^) = ф, (t x i __
Поэтому, возвращаясь в A2.77) к старым переменным, получим
dQN NQN N(N-\)QN
dV V 68V3
V V
Для систем в однородной фазе, например для газов и жидкостей,
бинарная функция оказывается радиально симметричной
^~2(Чь Я2)==^Г2(|Ч1 — Ч2|)>
интеграл
J lOi—
вследствие быстрого убывания потенциала Ф (|qi — 421) с рас-
расстоянием r=|qi — q21 между молекулами (см. рис. 45, § 71) ра-
равен
о
и термическое уравнение состояния A2.78) имеет вид
A2.79)
где v=V/N.
Внутренняя энергия по формуле A3.33) равна
= J|g_+ N(N-l) JJO(|qi-qg|)y,(qit q2)dqidq2. A2.80)
Для пространственно однородной системы получаем
A2.81)
Таким образом, для построения термодинамики систем с парным
потенциалом взаимодействия между частицами по методу Бого-
Боголюбова необходимо определить бинарную функцию распределе-
распределения как решение цепочки уравнений A2.67).
215
Глава 13
ОСНОВЫ КВАНТОВОЙ СТАТИСТИКИ
§ 57. Квантовые микроканоническое
и каноническое распределения
Определение микроканонического и канонического распреде-
распределений квантовых систем в целом аналогично рассмотренному
классическому случаю. Роль функции распределения играет те-
теперь статистический оператор р или набор коэффициентов wky.
определяющих вероятностное распределение по чистым состоя-
состояниям.
Как следует из уравнения Неймана A1.36), равновесный ста-
статистический оператор коммутирует с гамильтонианом Й и для
покоящейся системы является его функцией р=>р[#]. Поэтому
необходимо задать зависимость коэффициентов wh от энергии Е^
Если число квантовых состояний изолированной системы»
имеющей энергию Е с определенным отклонением Д?<с?, равна
ДГ(?), то в соответствии с постулатом равной априорной вероят-
вероятности состояний таких систем имеем квантовое микроканониче-
микроканоническое распределение
— при Е < Ek < Е + Д?,
АГ A3.1)
О при ?fc < Е или \Ek > Е+ АЕ>
&E =
аЕ
ровки A3.1):
ЙТ7
где ДГ(?) = &E = g(E)-&E определяется из условия норми-
аЕ
1 , A3.2)
k- k
(E<Ek<E+AE) (E<Ek<E+AE)
а полное число состояний с Ek<E равно
\k){k\= ? l. A3.3)
k k
(Ek<E)
Энтропия квантовой статистической системы определяется фор-
формулами, аналогичными A2.12) — A2.14),
, V, Л0=?1пГ(?), A3.4)
, V, N)=k\ng(E), A3.5)
, У, Л0=?1пДГ(?). A3.6У
Исходя из микроканонического распределения A3.1), найдем
каноническое распределение закрытой квантовой системы, в тер-
216
мостате. С этой целью рассмотрим объединенную изолированную
систему с энергией ЕОу состоящую из системы в контакте с тер-
термостатом. Согласно микроканоиическому распределению A3.1)
объединенной системы вероятность ее состояния (т. е. состояния
с энергией Ек изучаемой системы и состояния с энергией Ет =
= Е0—Ек термостата) равна
ДГ(?0) ДГ(?/ + ?Т)
а вероятность состояния изучаемой системы с энергией Ек в тер-
термостате будет
у _^_ Д1 т (^т) §Т (^т), / 1 О *7\
kT ~ ДГО (?0) ~~ go(Eo) '
т
где 2 означает суммирование по состояниям термостата, а
т
АГт(?'т) —число состояний термостата.
Энергия Ek системы составляет малую часть энергии Ео объ-
объединенной системы и энергии Ет термостата, поэтому для энтро-
энтропии термостата имеем
dS Еь
дЕ0 т° Т '
Отсюда с учетом A3.4) и A3.8) получаем квантовое канониче-
каноническое распределение по состояниям
(Ek) =—l—.esr^.e-E^ = C.e-^e, A3.9)
А о С)
или после нормировки A3.9)
0Ь(?,) = ехр(-?^), A3.10)
где
Величина
называется статистической суммой, а
F@, У, N)=— S\nZN A3.12)
есть энергия Гельмгольца квантовой системы, в чем легко убе-
убедиться, производя с A3.12) вычисления, подобные вычислениям в
классическом случае (см. § 50).
Заметим, что каноническое распределение A3.10) определяет
также распределение по энергиям для системы с невырожденны-
217
ми уровнями энергии. При наличии вырождения, когда одному и
тому же энергетическому уровню Ег (рис. 35) соответствует g<
различных состояний \|)г, вероятность такого вырожденного зна-
значения энергии равна
I WE?~e l gi (lo.lo)
A3.14)
Зная энергию Гельмгольца, как функцию своих есте-
естественных переменных, все другие термодинамические
параметры можно найти методами термодинамики.
Энтропия системы равна
"в" _
A3.15)
Таким образом, исследование квантовой статистической системы
с помощью канонического распределения сводится к следующей
процедуре:
а) вначале решается динамическая задача по определению
энергетического спектра Ег и соответствующего набора кванто-
квантовых чисел i путем решения уравнения Шредингера A1.10);
б) потом рассчитывается статистическая сумма A3.11) систе-
системы и ее энергия Гельмгольца ^(в, V, N) A3.12);
в) и далее вычисляются термодинамические характеристики
системы.
§ 58. Квантовое большое
каноническое распределение
Рассмотрим свойства открытых квантовых систем в термо-
термостате. Макроскопически такие системы описываются переменны-
переменными Г, V, J1. Границы, отделяющие систему от термостата, прони-
проницаемы для частиц. Соответствующее этим условиям распределе-
распределение по состояниям — большое каноническое распределение — мо-
может быть получено подобно каноническому, исходя из микрока-
микроканонического распределения для объединенной изолированной си-
системы с энергией Ео и числом частиц No.
При этом в дополнение к неравенству для энергии системы
EiJv°^ET—E0 необходимо добавить неравенство для числа ее ча-
частиц Jf<^NT—N0.
Разлагая энтропию термостата по малым параметрам Eijr/E0
и Jf/No, получим
SAEo-Ew, N0-J*)~ST(EQ, No) ^l + J^l. A3.16)
218
Отсюда, используя микроканоническое распределение для объ-
объединенной системы, находим большое каноническое распределе-
распределение по состояниям i, JC квантовой открытой системы, в термо-
термостате:
«»wF, V, |i)= — -exp — — = exp—— =Ы , A3.17)
где
" ' "r-F--s r n'Q т/ "чп A3Л8)
большая статистическая сумма и
QF, V, ц)=-81п?(в, V, ц) A3.19)
большой термодинамический потенциал.
Действительно, вычисленные с помощью A3.19) по формулам
термодинамики энергия и число частиц системы равны соответ-
соответствующим средним по большому каноническому распределению:
?@, V, ц) = Й-в — Ц-4^-= Y.EurWw^E^, A3.20)
00 Oil ***
N(B, V, ц)=—
= -i-[?F, V, ц) + в2^-(-|) 1 = 2^м»«.=^. A3.21)
Энтропия системы, как и в случае канонического распределения
определяется средним значением логарифма функции распреде-
распределения ww(T, V, ц):
I/, ix) = — ft-^-=— йУш^1пш^= — fclnofc*-. A3.22)
Таким образом, при использовании большого канонического
распределения для исследования квантовых статистических си-
систем необходимо прежде всего определить энергетический спектр
системы из решения уравнения Шредингера
Н^1л°=Е^ш. A3.23)
Причем в отличие от канонического распределения требуется най-
найти зависимость спектра для произвольного числа частиц JF, в том
числе и для малых JF~ 1.
Затем следует расчет большой статистической суммы A3.18)
и большого термодинамического потенциала QF, а, \х) A3.19).
Далее методами термодинамики вычисляются все необходимые
термодинамические характеристики системы.
219
§ 59. Классический предел
квантовой статистики
В заключение настоящей главы покажем, что исторически ра-
ранее построенная и изложенная в предыдущей главе классическая
статистика представляет определенный предельный случай (клас-
(классический предел) квантовой статистической теории.
Обсудим прежде всего соответствие классических и кванто-
во-механических величин.
Классические динамические функции A (q, p) обобщенных ко-
координат и импульсов (фазовой точки) сопоставляются в кванто-
квантовой теории эрмитовым операторам А с непрерывным или, чаще,
с дискретным спектром Лг-, которые действуют на волновую
функцию i[)i(q). Скобки Пуассона {Л, В} динамических функций
сопоставляются коммутаторам — [А, В] (с множителем ЦК) со-
ответствующих операторов. Функции распределения в фазовом
пространстве соответствует функция распределения по состояниям
или матрица плотности.
И наконец, статистический интеграл, очевидно, соответствует
и должен представлять собой классический предел статистиче-
статистической суммы.
Для того чтобы перейти к классическому пределу, например,
в квантовом каноническом распределении A3.10), уточним вна-
вначале само понятие классического предела для системы многих
частиц, а потом установим, как ведет себя в этом пределе плот-
плотность состояний и каким образом ее можно соотнести объему
фазов.ого пространства.
Как известно из квантовой механики, «квантовость» системы
определяется безразмерным параметром — отношением длины
волны де Бройля X = h/p к характерным размерам системы /&:
a=X/lky и чем этот параметр больше (т. е. чем сильнее неравен-
неравенство К^>1к)у тем больше проявляются квантовые свойства систе-
системы. Обратное неравенство — А,<С4 — характеризует «классич-
«классичность» системы.
Характерными размерами системы 1и являются: линейные
размеры системы, длина свободного пробега частиц, среднее рас-
расстояние между частицами, характерные размеры потенциала
взаимодействия, размеры самих частиц и др. При этом система
в некоторых отношениях может проявлять квантовые свойства и
в то же время в других отношениях — классические.
Для классичности свойств многочастичной системы сущест-
существенна сильная пространственная локализация частиц, при кото-
которой можно пренебречь интерференцией одночастичных волновых
функций. Соответствующий этому свойству характерный размер
представляет собой среднее расстояние между частицами / =
= (У/Л/ГI/З = я~1/3. Среднее значение длины волны де Бройля у
частиц системы (тепловая длина волны) равна l = hBntne)l/2*
220
Поэтому условие классичности системы й<С/ имеет вид
Г»——п*'\ A3.24)
а условие отступления от классичности — условие вырождения*
системы будет
1 A3.25)
2nmk
Температура вырождения по определению равна
То= —— п2/3. A3.26)
Другое условие классичности системы взаимодействующих частиц
связано с характерным размером 1ВЗ эффективного парного по-
потенциала взаимодействия Ф{г). Это условие, дополняющее
A3.24), имеет вид
Я</Вз~ [ФA*з)/^Щ^, A3.27)
т. е. тепловая длина волны значительно меньше размера, харак-
характеризующего скорость изменения потенциала взаимодействия.
Вывод этого условия связан с квазиклассическим приближе-
приближением, которое мы рассмотрим ниже. Поэтому второе условие но-
носит менее универсальный характер, чем первое.
Рассмотрим теперь классический предел статистической сум-
суммы Z^v —Ve~?// квантовой системы N бесспиновых частиц.
Из квантовой механики известно, что классические понятия
координаты и импульса частицы можно ввести лишь в квазиклас-
квазиклассическом приближении, при этом минимальный размер фазовой
ячейки одномерного движения частицы равен постоянной Планка
h, размер ячейки в фазовом пространстве одной частицы равен
ft3 и в фазовом пространстве N частиц — h3N. Поэтому между
плотностью квантовых состояний энергетического спектра и объ-
объемом фазового пространства в классическом пределе имеет места
соотношение
лг _ dqdp
й[ IF"
позволяющее при достаточно высоких температурах
в» max(?,+!—?,)
i
перейти в статистической сумме от суммирования по i к интегри-
интегрированию по фазовому пространству.
* Здесь имеется в виду статистическое вырождение в отличие от вырождения
в квантовой механике.
221
Кроме того, поскольку статистическая сумма берется по раз-
различным состояниям и квантовые частицы неразличимы, а в клас-
классическом интеграле, взятом по всему фазовому пространству,
каждому квантовому состоянию соответствует N1 разных фазо-
фазовых точек, то для соответствия статистической суммы в класси-
классическом пределе статистическому интегралу последний надо раз-
разделить на N1.
Заменяя далее собственные значения оператора Гамильтона
функцией Гамильтона системы, окончательно получаем
в полном соответствии с классическим выражением A2.21).
Рассмотренные выше условия классичности (невырожденно-
(невырожденности) квантовой статистической системы многих частиц позволяют
ввести соответствующие малые параметры, по которым можно
провести разложение (квазиклассическое разложение). При этом
в нулевом приближении мы получим классические формулы.
Квантовая статистическая сумма A3.11), представляющая со-
бой шпур статистического оператора Z^ = Sp e p (C=1/0), как
было отмечено, не зависит от квантового представления и поэто-
поэтому может быть вычислена в произвольном представлении. Таким
образом, нам не обязательно решать уравнение Шредингера и
определять энергетический спектр системы. В рассматриваемом
случае • расчет производится в общем виде для произвольного га-
гамильтониана вида
? + UN A3.29)
2т
в ортонормированном базисе плоских волн
A3.30)
» P=(Pi> • • • » Pn),
где верхний знак относится к бозе-, а нижний к ферми-системам,
& и 3* — оператор и число перестановок аргументов qi,...,qiv-
Подставив эти функции в статистическую сумму и заменив
суммирование по р интегрированием, получим
dqdp
\ЪЫ
N\ BnhN
A3.31)
-222
Рассмотрим матрицу плотности (статистический оператор) в
смешанном р, q (импульсно-координатном) представлении (здесь
р(ч, р)^<я
или
exp
НИ
i, р) = отт—— \ Р (q, q ) exp — pq ) dq =
exPl —г рч;
exp{—P(#(q, p)— j
<&>
Xexp(-^^pq)y(q, p, p), A3.32)
где F =—p~4nZjv — энергия Гельмгольца, Н(q, p)=p2/2m+
+ ^iv(q)—классическая функция Гамильтона, а величина
Y (q, p, P), определяющая результат действия статистического^
оператора на плоскую волну A3.30), вычисляется ниже. Заме-
Заметим, что интегрирование функций p(q, p) no q или по р дает со-
соответственно функции распределения по импульсам р(р, р) или
по координатам, Z)(q)=p(q, q), хотя сами функции p(q, p) не яв-
являются функциями распределения по (q, p) и, в частности,
pw(q, p) может принимать отрицательные значения, a pK(q, p) —
комплексные.
Очевидно, что статистическая сумма A3.31) представляет со-
собой нормировочную постоянную ZN = e~$F в выражении A3.32) „
т. е. равна интегралу по фазовому пространству от ненормиро-
ненормированной матрицы плотности p = Zjvp в смешанном представлении.
С целью упрощения последующих формул введем обозна-
обозначения:
A3.33)
Для нахождения результата
Ь = е-р/?ехр (J-pq)=exp{-p//(q, p)}Y (q, p, p)
действия статистического оператора е—$н на плоскую волну испо-
используется уравнение Блоха
~ = -Hbf A3.34)
ар
которому он удовлетворяет, с начальным условием
223
В результате получаем:
ЗУ
= _^ Г JL $ (р v) {e-*u"Y) + ^1 у2 (^""У) 1,
\_ m 2m J
op
Y(q, P, 0) = 1,
или
1
f
о
— ^eutу2(e~utY)dt. A3.35).
о
Необходимое нам решение в виде квазиклассического разложе-
разложения по степеням постоянной Планка
п(оп A3.36)
легко получить, решая уравнение методом последовательных при-
приближений. Этот метод приводит к рекуррентному соотношению
1
<о„ = J ** { V (e--i) —\ V2 (е-"Ч-2)} dt. A3.37)
о
Таким образом, находим
шо=1,
&>!= -щ, A3.38)
Приведенные выражения позволяют найти квазиклассическое
разложение для произвольных величин, представимых в виде фа-
фазовых средних. Получаемые при этом разложения, вообще гово-
говоря, являются асимптотическими и, как правило, оказываются зна-
знакопеременными рядами по четным степеням постоянной Планка
плюс экспоненциально малые обменные члены. В этих случаях
высшие члены разложения дают возможность получить мажори-
мажорирующую оценку погрешности квазиклассических формул.
Подставляя найденное разложение для Y в выражение для
статистической суммы A3.31), получим
Zn=I e~pH(q>p) {! + 2 ехр (тpft/qft/)}х
X V е"а)я • dqdp ,„ , A3.39)
224
где первый член соответствует тождественной перестановке, т. е.
^ = 7, а в последнем учтены только парные перестановки, quj —
= <lh—q/, p/e/ = P/e—р/. Вследствие простой квадратичной зависи-
зависимости функции Гамильтона от импульсов частиц интегрирование
по ним в выражениях A3.32), A3.39) легко выполняется. Отсю-
Отсюда находим координатную плотность вероятности.D(q) = (q|p|q) =
= jp(q. pL>:
3N
A3.40)
статистическую сумму Z^ = f ?> (q) dq и энергию Гельмгольца
где wo=l,
индекс «кл» соответствует классическому распределению Гиббса,
А^обм — поправка к энергии Гельмгольца, связанная с обменны-
обменными эффектами *. Заметим, что рассмотренные ранее, исходя из
качественных соображений, критерии классичности (квантовой
невырожденности) статистических систем следуют из полученных
выражений. Так, критерий Я<С/ соответствует большим отрица-
отрицательным значениям показателя экспоненты в обменном члене,
т. е. случаю, когда обменными эффектами можно пренебречь. При-
Причем вследствие экспоненциальной зависимости граница соответ-
соответствующей области температур или плотностей является доволь-
довольно резкой. Второй критерий Я</вз A3.27), как легко видеть, ка-
качественно соответствует малым значениям основных квантовых
поправок (#* = /).
* Заметим, что наряду с рассмотренными экспоненциально малыми членами
в А^обм входят также степенные члены ~h3 (¦&).
81/2 Зак. 245 025
Глава 14
СТАТИСТИЧЕСКАЯ ТЕОРИЯ
ИДЕАЛЬНЫХ СИСТЕМ
Исследование свойств мноТючастичных систем сводится, как
мы видели, или к вычислению статистического интеграла (стати-
(статистической суммы) Zn, или к определению функций распределения
комплексов частиц 3TS. И тот и другой подходы в общем случае
систем взаимодействующих частиц представляют собой сложную
задачу.
Рассмотрим вначале наиболее простые, так называемые иде-
идеальные системы, для которых функция Гамильтона (самильто-
ниан) равна сумме функций Гамильтона (сумме гамильтонианов)
отдельных частиц или объектов с малым числом степеней свобо-
свободы. К таким системам относятся идеальный газ, твердое тело в
гармоническом приближении, излучение и др. Эти системы могут
быть рассмотрены наиболее полно и во многих случаях даже
точно.
§ 60. Классический одноатомный
идеальный газ
Идеальным газом называют систему частиц (атомов, моле-
молекул), энергией взаимодействия между которыми можно пренеб-
пренебречь (Ф (|qi—q2j) =0) по сравнению с их кинетической энергией.
Рассмотрим классический одноатомный идеальный газ (гелий,
аргон, пары металлов и др.), считая атомы материальными точка-
точками с массой т. Функция Гамильтона такой системы из N атомов
в объеме V равна
N N 2
• • • , q*. Px, ... , Pn) =
где Hi — функция Гамильтона i-ro атома, и{оц) — его потенци-
потенциальная энергия во внешнем поле.
Плотность вероятности микросостояния газа в термостате
равна
Pi. р)ехр^ F~H
j (
а плотность вероятности состояния одного атома (например, пер-
первого) газа во внешнем поле будет
JT-1
Pi Di. Pi) = J P Di. • • • * <Lv» Pi» • • • . РлО d " =
= Cx • exp {- -i _ J^ilJ. A4.2)
226
Из условия нормировки
Jpi (<h. Pi) dQidPi = 1
находим
Сг = (J ехр {-Нг (<ц, Pl)/6} dqidPiyl = JL.
Таким образом,
/ \ 1 / P2x + Pt+P2z u(x,y,z)\ tAA ox
*(*. I/, г, р„ р„ Рг)=~ехр( ^ -1-^-lJ. A4.3)
а среднее число частиц (из общего N) в единице объема jut-про-
странства равно
u(X,y,
A4.4)
Распределение A4.4) для средней плотности числа частиц, как и
распределение A4.3) для плотности вероятности одной частицы
по состояниям частиц классического идеального газа во внешнем
поле называется распределением Максвелла — Больцмана.
Интегрируя A4.4) по импульсам, найдем распределение по
координатам частиц идеального газа во внешнем поле
п(х, y>z) =т s—- ехр{—и(х, у, z)l@}=
v u ' $exv{—u(x,y,z)/e)dxdydz *X K '
=-поехр{—и(х, у, г)/в}, A4.5)
которое называется распределением Больцмана.
Распределение частиц идеального газа по скоростям будет
максвелловским, так как для классических частиц распределение
по скоростям не зависит от взаимодействия между частицами (см.
§ 52). В рассматриваемом случае идеального газа оно может быть
получено интегрированием распределения Максвелла — Больцма-
Больцмана A4.4) по координатам.
Статистический интеграл идеального газа в отсутствие внешне-
внешнего поля, т. е. при
t v _ __ [ 0 для q внутри V,
« \Я) — «стенки — <
[ оо для q вне V,
вычисляется точно и равен
N N
П
l=sl 1 = 1
где Zi = evBnm@/h2K/2 = ev/k — статистический интеграл одного
8!/а* 227
атома газа, % = hfBnm®)lf2 — тепловая длина волны де Бройля;
V/Nl/
Энергия Гельмгольца идеального газа
F = — в In ZN = —NS In zi = — N& In [ev Bnm@/h2) Щ. A4.7);
Зная этот термодинамический потенциал газа по известным фор-
формулам термодинамики, находим его равновесные свойства.
а) Термическое уравнение состояния
dV /e V '
или
/14.8)
Сравнивая это уравнение с уравнением Клапейрона — Менделее-
Менделеева PV=vRT, находим величину постоянной Больцмана
= 1,3804- Ю-23 Дж/К. A4.9)
б) Калорическое уравнение состояния
Ев2
в) Изохорная теплоемкость
#е. A4.10)
Cv = (—) =—kN. A4.11)
г) Энтропия
n3
д) Химический потенциал
A4.12)
=— eini
. 2лтв \з/2
=61n
Методом функций распределения термическое A4.8) и калориче-
калорическое A4.10) уравнения состояния идеального газа непосредствен-
непосредственно получаются из общих формул A2.79) и A2.81) при
фAя1—q2|) =o.
Идеальный газ является статистически точно решаемой систе-
системой.
228
§ 61. Квантовые одноатомные
идеальные газы
Как отмечалось в § 59, многочастичная система является клас-
классической при температурах A3.24)
7>Г0
2nmk
При температурах Т^Т0 система частиц становится кванто-
квантовой.
Квантовые частицы помимо волновых свойств обладают соб-
собственным (спиновым) механическим моментом. Его величина
равна ]/s(s+l) -Я, где спин 5 — целое (включая нуль) или полу-
полуцелое положительное число, определяемое природой частиц. Та-
Таким образом, состояние квантовой частицы данного типа опреде-
определяется волновой функцией ty(x, у, г) и спиновым числом ms (ха-
(характеризующим одно из возможных значений проекций спинового
момента на фиксированную ось). Возможны 25+1 состояний с за-
заданной волновой функцией, отличающихся ориентацией спина.
Так как в отсутствие магнитного поля энергия частицы не за-
зависит от ориентации спина, то наличие спина увеличивает число
квантовых состояний с заданной энергией в 2s+1 раз.
В зависимости от того, является ли спин целым или полуце-
полуцелым, частицы делятся на два класса: бозе-частицы, или бозоны
(с целым спином), и ферми-частицы, или фермионы (с полуцелым
спином). Бозонами являются фотон E=1), п- и /(-мезоны E = 0).
Большинство элементарных частиц (электроны, протоны, нейтро-
нейтроны и др.) имеют спин 5=1/2 и являются фермионами.
Спин сложной частицы определяется числом входящих в нее
фермионов. Если это число четное (Н, Н2, Не4), то сложная час-
частица является бозоном, если нечетное (D, HD) — фермионом.
Волновая функция системы бозонов симметрична, а фермио-
фермионов — антисимметрична относительно перестановки любой пары
частиц. Волновая функция квантового идеального газа представ-
представляется произведением волновых функций отдельных частиц и пол-
полностью определяется заданием чисел заполнения Uk каждого
k-vo одночастичного состояния. Требование антисимметрии вол-
волновой функции системы фермионов приводит к тому, что они
удовлетворяют принципу Паули: в заданном квантовом состоя-
состоянии может находиться не более одной частицы, т. е. nk = 0\ 1.
В каждом одночастичном состоянии бозе-газа может находиться
любое число частиц: % = (), 1, 2, ..., Jf, где JF — общее число час-
частиц в системе.
Распределение частиц по одночастичным квантовым состоя-
состояниям зависит от того, являются ли частицы бозонами или фер-
фермионами. В соответствии с этим существуют две квантовые ста-
статистики: статистика Бозе—Эйнштейна (для бозонов) и статистика
Ферми — Дирака (для фермионов),
8 Зак. 245 229
Найдем функции распределения по квантовым состояниям
обоих классов частиц. Для этого воспользуемся квантовым боль-
большим каноническим распределением Гиббса A3.17)
^у
где Wijy— вероятность того, что система содержит Jf частиц и
находится в i-ом квантовом состоянии с энергией Ецг.
Рассмотрим квантовый идеальный газ из одинаковых частиц.
Состояние газа определяется числами заполнения п\> п2у ... одно-
частичных состояний с энергиями соответственно еь ег,
Тогда
и согласно A3.17) вероятность такого состояния открытой систе-
системы в термостате
k
w(nl9 п%%... пк9 .. .) = ехр у k— J =go/e . Y\ el#*t A4.14)
где lk= (\x—Ek)/S и произведение берется по всем квантовым со-
состояниям.
Вероятность того, что в k-ом состоянии находится пи частиц
при возможных числах заполнения остальных состояний, очевид-
очевидно, равна
w{nk)=Celknkt A4.15)
Нормировочная постоянная С определяется из условия
V*=if A4.16)
где суммирование ведется по возможному числу частиц nk в за-
заданном &-ом квантовом состоянии. В результате получаем
ш(л^ =***"*/?е**'п*\ A4.17)
Среднее число частиц в й-ом состоянии равно
nk = J] nkw(nk)=^nke^n4^el^'^^\n^ e^nK A4.18)
§ 62. Распределения Бозе — Эйнштейна
и Ферми — Дирака
Найдем теперь в отдельности распределения для бозонов к
фермионов.
230
1. Распределение Бозе — Эйнштейна.
Для бозонов число частиц в заданном квантовом состоянии
может быть любым, т. е. ttk = Oy 1, 2, Поэтому для них
00
лЛ = -^1п V М. A4.19)
Входящий в A4.19) ряд (геометрическая прогрессия со знамена-
знаменателем е k) сходится только при ?ft= — (\i—sk) < 0. Это значит,
0
что химический потенциал бозе-газа не может быть больше наи-
наименьшего из энергетических уровней во. При |л>ео ряд расходит-
расходится, что означает невозможность термодинамического равновесия.
Таким образом, для бозе-газа —оо<|я<ео,
п = 1 , A4.20)
-(V-)-'
Это распределение бозе-частиц по состояниям называется рас-
распределением Бозе — Эйнштейна. Оно было установлено в 1924 г.
Бозе для фотонов (fi = 0), а затем Эйнштейн получил обобщен-
обобщенную формулу A4.20).
Распределение частиц по энергиям найдем, умножив пк на
число gk микросостояний с энергией е^ (статистический вес энер-
энергетического уровня Ek):
•"(¦V-)-
A4.21)
В случае квазинепрерывного спектра энергии среднее число час-
частиц с энергией от е до e + de равно
A4.22)
где число квантовых состояний g(e)de (без учета спина) равно
объему фазового пространства частицы, находящейся в объеме
V, заключенному между поверхностями энергии г и г + йг, делен-
деленному на соответствующий одному квантовому состоянию частицы
фазовый объем /i3:
A4.23)
231
ft»
/i3
Число квантовых состояний на интервал энергии (е, г + йг) для
одноатомного идеального газа с учетом спина (при отсутствии
магнитного поля) в Bs+l) раз больше.
2. Распределение Ферми —Дирака.
Для фермионов nk = 0\ 1, поэтому сумма
е
сходится при любом значении химического потенциала р,, и по
A4.18) среднее число ферми-частиц в k-ou состоянии равно
пк = !— . A4.24)
Это распределение ферми-частиц по состояниям называется рас
пределением Ферми — Дирака.
Распределение электронов по энергиям (s=l/2) будет
A4.25)
а при квазинепрерывном спектре энергии поступательного дви-
движения:
n(e)ds= ^^ . A4.26)
3. Сопоставление распределений Максвелла — Больцмана
(М—Б), Бозе — Эйнштейна (Б—Э) и Ферми — Дирака (Ф—Д).
Все эти три функции распределения идеальных газов можно
записать в едином виде:
exp(^V4+6
A4.27)
где 6=0 для распределения М—Б, 6=—1
для распределения Б—Э и 6=1 для рас-
Б~Э пределения Ф—Д.
На рис. 36 приведены графики этих
#_? функций распределения.
Из A4.27) видно, что распределения
Ф-Д Б—Э и Ф—Д переходят в распределение
М—Б, т. е. газ становится классическим,
г- если
Рис.36 «-^»- <14-28>
232
Подставляя в A4.28) классическое выражение A4.13) для
получим уже известное условие классичности газа:
7V A4.29)
Если е~**/е—1, то функция распределения газа отличается от
максвелл-больцмановской и говорят, что газ вырожден. Величина
в_м/е называется фактором вырождения, неравенства A4.28),
A4.29) — критерием невырожденности, а противоположные нера-
неравенства — критерием сильного вырождения.
Как видно из формулы A3.29), температура вырождения То
тем выше, чем больше плотность газа и чем меньше масса его
частиц.
В случае электронного газа в металлах (m=9-10~28 г, пж
ж 1022 см~3) Т0»104 К и, следовательно, электронный газ в ме-
металлах практически всегда сильно вырожден; в полупроводниках
плотность электронов яя^Ю17 см~3 и Го» 10 К, поэтому электрон-
электронный газ в полупроводниках практически (т. е. при температурах
порядка комнатных) не вырожден, и при определении его свойств
можно пользоваться классической статистикой.
Масса частиц обычных газов т»10~24 г, поэтому даже при
плотностях порядка плотности электронного газа в металлах
Го~1 К, и, следовательно, обычные газы также практически
всегда не вырождены.
§ 63. Термическое и калорическое уравнения
состояния квантовых газов
Для определения термодинамических свойств квантовых иде-
идеальных газов найдем для них по формуле A3.19) большой термо-
термодинамический потенциал Q (Г, V, (л):
где
nt,n2... k nk
и, следовательно,
\= — в In П У elkHk = — в У In У eV*. A4.30)
k п. k nb
к к
233
Для бозе-газа
для ферми-газа
Обе эти суммы можно записать в единой форме:
(l+.6-e*ft)ef A4.31)
причем 6 = ~^-1 для бозе-газа и 6=1 для ферми-газа.
Подставляя A4.31) в A4.30), получим общее выражение для
?1 — потенциала квантовых идеальных газов
й=_0б.УA + 6.ехр(-*1^Ц\ A4.32)
При поступательном движении квантовых частиц в макроско-
макроскопическом объеме V их энергия изменяется квазинепрерывно и чис-
число состояний с энергией от е до e + de согласно A4.23) (без уче-
учета спина) равно
где
B = 4jtmY2m7/i3. A4.34)
Заменяя в A4.32) суммирование интегрированием, будем иметь
A4.35)
Так как Q = F—G = E—TS—[iN =—PV, то термическое уравнение
состояния квантовых идеальных газов имеет вид
A4.36)
о
или после интегрирования по частям
exP
е
234
Калорическое уравнение состояния можно получить или диффе-
дифференцированием Q-потенциала A4.35) по формуле
J\jl,v \ d\i )t,v
или непосредственно из определения энергии, используя A4.22),
i
e
Входящий в урабнения состояния A4.37) и A4.39) химический
потенциал [i находится из выражения для заданного числа частиц
00 00
N=\W(B)de = Bv\ г^г\ . О4-40)
которое можно также получить по формуле iV = —(dQ/d\x)e,v*
Сравнивая A4.37) с A4.39), находим связь между термическим
и калорическим уравнениями состояния квантовых идеальных
газов
PV=2/3E. A4.41)
Заметим, что точно такая же связь существует между подобными
уравнениями A4.8) и A4.10) классического идеального газа.
Разделив A4.35) на A4.39), получим
&• Г ln(l+6-es)e1/2de
PV - ° —. A4.42)
NB
О
в1/2 ds
В отличие от уравнения A4.36) термическое уравнение состояния
A4.42) не содержит постоянной В и поэтому справедливо также
и для системы частиц с учетом их спина.
Рассмотрим здесь слабо вырожденные газы. В этом случае
в
и с точностью до двух членов разложения
In A + &*)«&& (б^J = 6^ (l — — ?
Поэтому
00 «в
С С I б
1 1П A ~(~ v?, ) 8 ' u8 == О \ б* ( 1 —
J J \ 2
235
и
Используя для химического потенциала jx выражение A4.13), по-
получаем термическое уравнение состояния слабо вырожденного
газа
и согласно A4.41) его калорическое уравнение состояния
A4.43)
A4.44)
Второй член в скобках дает квантовую поправку к соответствую-
соответствующим уравнениям состояния классического идеального газа. Для
бозе-газа эта поправка отрицательная, а для ферми-газа — по-
положительная.
§ 64. Сильно вырожденный
электронный газ
До сих пор бозе- и ферми-газы рассматривались совместно.
При низких температурах эти газы ведут себя существенно раз-
различно, поэтому их следует изучать раздельно.
Рассмотрим вначале сильно вырожденный электронный газ.
Для электронов 5=1/2, поэтому при его движении в объеме V
число состояний с энергией в интервале от е до e+de равно
A4.45)
и согласно A4.26)
236
Энергия и число частиц газа соответственно равны:
00 00
Е= fe7iOO<ie = 2BV f{exp(-^L) + l\~* г3'2 de, A4.46>
= C^(i)"d8 = 2SF Г {exp (-^M + l]" e1/2 dz. A4.47>
о о
Эти формулы в неявном виде определяют зависимость Е и |i«or
параметров системы Г, V, N.
Найдем выражение для энергии Е сильно вырожденного элект-
электронного газа, когда
1, или (л>0. A4.48)
Для этого рассмотрим интеграл
где /(е) ={е1/2, е3/2}. Запишем / в виде
/= Г f(e)de = Г /(б)& , Г
-JeJp(^L)+1-JeIp(^L)+1 J
Так как
то
11
{ exp (-JL +1 J J exp^__J
ехр(-^Ч + 1 6- 1 е;ф(-^Ч + 1
и, следовательно,
/ =
Производя во втором интеграле правой части A4.50) замену пе-
переменной интегрирования (е—]i)/@=x, получим
237
Аналогично, при замене (е—|л)/в=—х в третьем интеграле, бу-
будем иметь
f(E)dB
Ц/
(e)(te =e Г
Для сильно вырожденного газа ([х/в>>1) верхний предел в инте-
интеграле можно заменить на бесконечность. Таким образом, в этом
случае
f
A4.51)
в
ех + 1
Так как в знаменатель подынтегральной функции входит слагае-
слагаемое ех, то главный вклад в этот интеграл вносит область не очень
больших х. Поэтому разлагая в ряд по степеням х f(\i+Qx) и
f{\i—@х) в числителе подынтегральной функции, с точностью
до ~х2 получим f{\\, + Sx)—f(\i—ex) =2@xf'(\x) и
j
0 0 0
При/(е) =е1/2 интеграл A4.52) равен
^ = j/(e)de+ -^-f(|i). A4.52)
0
л согласно A4.47)
n-tbv^[1+jt(tI- (l4-63)
а при /(e) = e3/2:
согласно A4.46)
!f^4Vl A4-54)
Й= —PF= —?-?= *-BVn5'2 [l + -^-.(—V]. A4.55)
Для определения энергии сильно вырожденного электронного газа
-238
как функции Г, У, N найдем химический потенциал |л из формулы
A4.53) и подставим в формулу A4.54).
При Г = 0 К из формулы A4.53) получаем
N=* J-?VVg/2, A4.56)
3
где jio — химический потенциал при Г=0 К.
Разделив формулу A4.53) на выражение A4.56), найдем
При вырождении 6/|i<Cl, и, следовательно, в этой области ji
близко к |io. Заменив \i на ji0 в малом слагаемом — ,
8 \ \х )
с точностью до ~ (в/|1оJ получаем
6 \21-2/3
я2 / в \2] „ч
—1гЫ]' A4-57)
откуда следует, что р, с ростом температуры Т убывает.
Разделив выражение A4.54) на величину A4.55), найдем
8 V (t0
A4.58)
V
Подставляя в формулу A4.58) (д, из формулы A4.57), с указанной
точностью будем иметь
е
Е 3 Г
N 5 ^° [
Таким образом,
1 12 '
3
^ 5
( % \ 2 15/2
V Hd / J
I1' 12
Г + . 5я2
L 8
Из формул A4.59) и A4.60) видно, что энергия и давление вы-
вырожденного электронного газа остаются конечными при Г = 0 К:
?о = 3/5|*(Д, Po = 2h\xoti, A4.61)
где п — плотность газа.
Это обусловлено принципом Паули, которому подчиняются
фермионы. Действительно, состояние с энергией е = 0 могут занять
239
лишь два электрона с противоположными спинами, а остальные
по принципу Паули «вынуждены» занимать состояния с е>0.
В результате электронный газ имеет конечную нулевую (при
Г=0 К) энергию A4.61). Из распределения Ферми —Дирака
A4.24) при Т = 0 К для Ei<\io полу-
получаем fli=l, а для e*->(jio ш = 09 т. е.
при абсолютном нуле температуры
все состояния с энергией от нуля до
\iQ полностью заняты, а все состоя-
состояния с большей энергией свободны.
График функции распределения
Ферми — Дирака при Т=0 К будет
иметь вид, изображенный на рис.37.
Максимальная возможная энергия
электронов при Г=0К равна \х0 и
называется энергией Ферми, а по-
поверхность энергии г = \10 в импульс-
импульсном пространстве называется по-
Рис. 37 верхностью Ферми. При Г=0К все
электроны находятся в состояниях
внутри поверхности Ферми.
Из равенства A4.55) находим выражение для энергии Ферми:
|io = CN/4BV)W= (Зя/8яJ/3. A4.62)
В случае электронного газа в металлах (/г«6-1022 см~3) 1x0=^
= 5гУ=8-1012 эрг.
Из формулы A4.58) находим выражение для теплоемкости
вырожденного электронного газа:
-f^f- <14-63>
а из формул A4.55) и A4.56) — такое же выражение для его
энтропии:
(*) =J!LkN--2-. A4.64)
v 2 ц
дТ
При приближении температуры к абсолютному нулю Cv-*0 и
5->0 в соответствии с третьим началом термодинамики.
По формуле A4.63) для молярной (Af=Mi и kNA =
==2 кал/К -моль) теплоемкости электронного газа в металлах при
комнатной температуре (Г=300 К) получаем величину Cv =
= 0,05 кал/моль, которая почти в 100 раз меньше молярной тепло-
теплоемкости классического одноатомного идеального газа. Это пока-
показывает, что электронный газ в металлах следует не классической,
а квантовой статистике {Ферми — Дирака). Крайне малая вели-
величина теплоемкости электронного газа обусловлена тем, что вслед-
вследствие принципа Паули тепловое движение затрагивает сравни-
240
тельно небольшую часть электронов в металле, имеющих энергию
вблизи поверхности Ферми и при нагревании переходящих в сво-
свободные состояния с энергией е>[Ао (*).
§ 65. Вырожденный бозе-газ.
Бозе-эйнштейновская конденсация
Рассмотрим теперь свойства бозе-газа при низких температу-
температурах — в области вырождения, когда ехр(—ц/9)^1, т. е. при
—(х/6= ||л|/в<С1. Пусть, как у атомов Не4, бозе-частицы имеют
нулевой спин. Тогда по A4.40) полное число частиц в системе
Дифференцируя это выражение по в при постоянном Л/1, найдем
т. е. с понижением температуры химический потенциал |i, оста-
оставаясь отрицательным, возрастает.
Точное выражение для N имеет вид
Вычисляя же N по интегральной формуле A4.65), мы, предпола-
предполагая квазинепрерывный спектр энергии частиц, не учитываем Nq
частиц в низшем энергетическом состоянии с е = ео = О, поскольку
по A4.33) g@)=0. В случае ферми-газа это допустимо всегда,
так как в состоянии 8 = 0 находится всего 2 частицы с противо-
противоположными спинами, что несравнимо с полным числом частиц
макроскопической системы №~NA. В случае же бозе-газа, как
мы увидим, пренебрежение числом частиц
N __ 1
с — 1
возможно не всегда.
Действительно, учитывая No, мы вместо A4.65) имеем
" о1/2 ло
Из A4.67) видно, что если величина <—\xl@=\\x\/Q не намного
меньше 1, то слагаемым Л^о можно пренебречь по сравнению с ин-
интегралом, и мы приходим к прежней формуле A4.65). Эта фор-
241
мула справедлива вплоть до температуры Гс = 6с/&, при которой
Ijli) становится много меньше ®с (так что в интеграль-
интегральном члене величиной | |ut | /©^ можно пренебречь по сравнению с
е/вс), но слагаемое Л/^о = [ехр(|jjl|/вс) — I] ^^©с/|м.| остается еще
много меньше интегрального члена. Температура Тс определяется,
следовательно, из равенства
fcZBV(kTf* f^ A4.68)
которое следует из формулы A4.65), если в ней положить ц =
при Т=ТС.
Так как Д = 4ят/^ и \j?l*L = V*L .2,612,
о
то из A4.68) получаем
с
п
2nmk B,612J/3
что почти совпадает с температурой вырождения То A4.29).
При температуре Т<ТС1 когда |ц,|/в<1 и слагаемым No&
tt@/\\i\ уже нельзя пренебрегать по сравнению с интегральным
членом,
7 р1/2 Нр ^ у1/2
е de JV БУ^ГK/2 *
J -
о e_j
Из A4.70) и A4.68) находим
ее de =JV0 + БУ(^ГK/2 * dAt . A4.70)
о ^ о
N0 = N{\-(TITcm A4.71)
Формула A4.71) показывает, что при Т<ТС число частиц на
низшем уровне энергии Л/о становится сравнимым с полным чис-
числом частиц Л/1. Это явление — накопление значительного числа
частиц (N0~N) на уровне энергии е=0 — называется бозе-эйнш-
тейновской конденсацией, а температура Тс — температурой бо-
зе-конденсации. Название «конденсация» является условным, так
как речь идет о конденсации не в реальном координатном прост-
пространстве, а в пространстве импульсов (на уровень с импульсом
р = 0). Совокупность частиц с р = 0 или е = 0 называется конден-
конденсатом.
Рассмотрим термодинамические свойства бозе-газа ниже тем-
температуры бозе-конденсации.
Поскольку при Т<ТС в формуле A4.39) можно пренебречь \х по
сравнению с е, т. е. положить [д, = 0, то при этой температуре:
242
00
:=bvJ
j
ЗУ 3 V
с j^_dx_ = ! 34.5y ^TM/2( A4J2)
0
A4.73)
A4.74>
A4.75)
-^-Л = — • 1,34 • kBV (kTf/2. A4.76
dT Jv,\x 3
Таким образом, энергия и давление вырожденного бозе-газа про-
пропорциональны Г5/2, а теплоемкость и энтропия — Г3/2. Из A4.74)
также следует, что давление газа в этом состоянии не зависит от
объема и, следовательно, вырожденный бозе-газ аналогичен насы-
насыщенному пару.
Для вычисления термодинамических
функций бозе-газа при температурах
Т^ТС нужно пользоваться формулами
A4.39), A4.40).
Нетрудно убедиться, что теплоемкость
Cv меняется в точке бозе-конденсации
непрерывно (*). Кривая зависимости
теплоемкости от температуры в этой точ-
точке имеет излом (рис. 38), а производная
теплоемкости по температуре претерпе-
претерпевает скачок.
Хотя экспериментально бозе-конден-
сацию наблюдать не удается, так как все
известные газы снижаются еще при тем-
температуре значительно выше Тс, теория
вырожденного бозе-газа представ-
представляет большой принципиальный интерес. Как было показано Бого-
Боголюбовым, в неидеальном бозе-газе аналогом бозе-конденсации
является переход в сверхтекучее состояние. Для Не4 температу-
температура бозе-конденсации Гс = 3,13 К, а переход его в сверхтекучее
состояние наблюдается при 7 = 2,19 К-
Рис. 38
§ 66. Осциллятор и ротатор в tepMoeraTe
До сих пор мы рассматривали одноатомные классические и
квантовые идеальные газы. Для изучения систем из более слож-
сложных невзаимодействующих объектов (многоатомные идеальные
газы, излучение, кристаллы) рассмотрим здесь линейный осцил»
243
лятор и ротатор в термостате и установим, когда в этих услови-
условиях они являются классическими объектами и когда квантовыми.
Функция Гамильтона линейного осциллятора имеет вид
2т 2
.а оператор Гамильтона
Вычислим среднюю энергию е осциллятора в термостате с
температурой Q = kT.
При классическом рассмотрении
2т
где co = 2nv — круговая частота собственных колебаний осцил-
осциллятора.
По теореме о равнораспределении кинетической энергии по сте-
степеням свободы A2.30)
в
2т 2
а из теоремы о вириале A2.32) находим
то2 —2 в
и, следовательно,
6 = 0. A4.77)
При квантово-статистическом подходе для определения средней
энергии осциллятора нужно вначале решить динамическую задачу
по определению спектра его энергии Еп, потом по формуле A3.11)
найти статистическую сумму zi, по формуле A3.12) — энергию
Гельмгольца F и затем вычислить среднюю энергию е.
Из решения уравнения Шредингера для осциллятора имеем
(/г = 0, 1,2, ...).
Все уровни энергии однократны.
Поэтому
-Щ
26 /
\ / \ 6 / 1-ехр(-Ь/в)
n—0 n—0
e»P(-*v/26)
A4.78)
'244
In z\ = —/iv/26—In A—exp (—ftv/в))
и из A4.78) получаем формулу Планка для средней энергии ли-
нейного осциллятора в термостате
hv . hv
е —
A4.79)
Как видно из этой формулы, средняя энергия осциллятора в кван-
квантовой теории в отличии от ее классического значения A4.77) за-
зависит от собственной частоты и имеет конечное значение eo = /*v/2
при абсолютном нуле температуры. Величина ео называется нуле-
нулевой энергией осциллятора.
Зависимость средней энергии е квантового осциллятора от
температуры приведена на рис. 39. Пунктирная прямая изобра-
изображает зависимость е от Т по классической теории.
При высоких температурах, когда 0>/iv,
8~ \- в 1 Н
2 20 6
hv
в
Г
в, A4.80)
что с точностью до члена порядка (/ivJ/9 совпадает с классиче-
классическим значением средней энергии осциллятора A4.77).
О в
Рис. 39
Рис. 40
Нулевая энергия, будучи постоянной, не дает вклада в тепло-
теплоемкость систем осцилляторов (многоатомные газы и др.). Для
квантовой теории теплоемкости таких систем важна зависимость
второго слагаемого в A4.79) е = е—/iv/2 от частоты, которая изо-
изображена на рис. 40. С возрастанием частоты или понижением тем-
температуры эта, зависящая от температуры, часть средней энергии
осциллятора е (и теплоемкость Су~де/дТ) стремится к нулю по
экспоненциальному закону
245
и, следовательно, высокочастотные осцилляторы (т. е. при
/iv/6>l) практически не дают вклада в теплоемкость.
Условие исчезновения теплоемкости hv/kT^>\ можно записать
в виде T<^Tcky где величина Tck = hv/k= (Е\—E0)/k называется
характеристической температурой энергии колебаний.
Ротатор представляет собой материальную точку массы гау
удерживаемую невесомым стержнем на постоянном расстоянии
от неподвижной точки О. Энергия ротатора равна Л12/2/, гдеМ —
его момент импульса, / — момент инерции.
Гамильтониан ротатора имеет вид
где М — оператор момента импульса. Вычислим среднюю энер-
энергию ротатора в термостате.
Так как ротатор имеет две степени свободы, то по теореме о
равнораспределении средней кинетической энергии по степеням
свободы классической статистики
8 = 9. A4.81)
В квантовой теории из решения уравнения Шредингера для рота-
ротатора находим собственные значения его энергии
?/ = /(/+ 1)Я2/8я2/, A4.82)
B/+1)-кратно вырожденные (/ = 0, 1, 2, ...).
Статистическая сумма квантового ротатора
/=0 /=0
A4.83)
где
Tc* = h2/8ji2lk A4.84)
характеристическая температура энергии вращения ротатора, рав-
равная по порядку величины разности между первыми уровнями его
энергии A4.82), деленной на постоянную Больцмана.
В общем случае статистическая сумма A4.83) может быть
определена только численно.
При высоких температурах (Г>ГСВ) суммирование в A4.83)
можно заменить интегрированием по почти совпадающим уров-
уровням:
(* = /(/+1)). A4.85)
246
По формуле A4.78) получаем для средней энергии ротатора
е = ва dXnZl =0, A4.86)
что совпадает с ее классическим значением A4.81).
При низких температурах (Т<^ТСЪ) в сумме A4.63) можно
ограничиться двумя членами:
2i = l + 3exp(—2ГСВ/Г).
Тогда
In 2i = In A +3 exp (—2ТС»/Т)) « 3 exp (—2ТС*/Ц
8 = 6kTc* exp (—2TC»/T). A4.87)
Таким образом, при понижении температуры средняя энергия ро-
ротатора по экспоненте стремится к нулю.
§ 67. Теория теплоемкости двухатомных газов
Пусть в объеме V находится двухатомный идеальный газ из
N одинаковых молекул (Н2, 02, НС1, СО и др.).
В классической статистической теории вопрос о теплоемкости
газов решается с помощью теоремы о равнораспределении кине-
кинетической энергии по степеням свободы.
Рассматриваем молекулу как твердое тело с v степенями сво-
свободы (v = 6 при учете поступательного движения и вращения во-
вокруг всех трех осей и v = 5 при учете кроме поступательного дви-
движения вращения только вокруг двух осей).
По теореме о равнораспределении внутренняя энергия газа
равна
)
дТ )v
откуда для теплоемкости одного моля газа получаем
Су =
и
Ср
Для двухатомных газов при комнатной температуре это отноше-
отношение равно 1,4 = 7/5, что соответствует v = 5. Это приводит к моде-
модели двухатомной молекулы в виде гантели — жесткой палочки и
двух материальных точек на постоянном расстоянии. Вращение
вокруг продольной оси, естественно, учитывать не надо, так что
Су = 5 кал/моль-К, СР = 7 кал/моль-К. Однако, как показывает
опыт, теплоемкости двухатомных газов увеличиваются с повыше-
повышением температуры, чего классическая теория объяснить не может.
247
С точки зрения этой теории нельзя также понять, почему мы
должны считать атомы материальными точками и не учитывать
возможного относительного движения атомов в молекуле, считая
их жестко связанными.
Все эти затруднения классической теории теплоемкости легко
устраняет квантовая теория.
Прежде всего она решает принципиальный вопрос о том, ка-
какие степени свободы молекулы существенны при данной темпера-
температуре для теплоемкости газов.
Если для какой-либо степени свободы вероятность состояния
с наименьшей энергией Ео равна
то вероятность возбужденного состояния с энергией Е\
будет тем меньше, чем больше (Ех—?)/в = Гс/Г, где Тс =
= (Е\—E0)lk — характеристическая температура энергии для
данной степени свободы. Это означает, что при Т<ТС энергия,
приходящаяся на рассматриваемую степень свободы, будет прак-
практически постоянной и соответствующую теплоемкость можно не
учитывать.
Для определения теплоемкости двухатомных газов будем
представлять себе молекулу в виде двух связанных между собой
твердых атомов. Электронными возбуждениями в атомах при на-
нагревании будем пренебрегать, так как при энергии возбуждения
атома Е\—?0~Ю~10 Дж характеристическая температура энер-
энергии этих возбуждений
Энергия молекулы складывается из энергий ее поступательного
движения, вращения и колебаний атомов. При не слишком высо-
высоких температурах эти движения можно считать независимыми друг
от друга. Поэтому средняя энергия молекулы равна сумме трех
членов:
а средняя энергия всего газа
и теплоемкость
Так как температура вырождения двухатомных газов очень низ-
248
ка, то практически во всех случаях поступательное движение
молекул является классическим. Поэтому
еп = 3kT/2, Cvn = 3kN/2 A4.88)
и для моля газа СуГ1 = 3 кал/моль-К-
При гармонических колебаниях атомов в молекуле с частотою
v по формуле A4.79)
hv
ехр Ы
ехр
D)-Г
где TcK = hv/k — характеристическая температура энергии колеба-
колебания молекулы.
Для двухатомных молекул Тск имеет порядок тысяч Кельвинов.
Так, для Н2 Гск = 6000 К, для О2 Гск = 23100 К, для СО Тск =
= 3070 К. Поэтому при комнатных температурах (Г»300 К),
когда Т<^ТСК, теплоемкость CVK исчезающе мала и может не учи-
учитываться. Действительно, из A4.89) при этих температурах имеем
CvK = kN(Tc«/TJexp(—Tc«/T),
и для молярной теплоемкости кислорода при Г=300 К получаем
CvK«0,05 кал/моль К.
С повышением температуры CVK растет, чем объясняется уве-
увеличение теплоемкости газов при высоких температурах.
При 7>Гск согласно A4.89) CvK = kN B кал/моль-К), и, сле-
следовательно, при этих температурах CVK можно вычислять по клас-
классической формуле.
Найдем теперь теплоемкость CVB, обусловленную вращением
молекул.
Характеристическая температура энергии вращения молекулы
двухатомных газов достаточно низка: от нескольких Кельвинов до
небольшого числа десятков Кельвинов. Так, для О2 Тсв = 2,07 К,
для НС1 Гсв=15,1 К, для Н2 Гсв = 85,4 К. Поэтому CVK имеет
классическое значение уже при комнатных температурах. Дейст-
Действительно, при T^>TCV из A4.80) имеем
8 = 6 и CvK = kNt
при ГГ
Cvв = Nde*/dT = 6k (Тс*ITJ ехр (—Гсв/Г),
и, следовательно, при очень низких температурах вращательная
9 Зак. 245 249
теплоемкость экспоненциально убывает с температурой, прибли-
приближаясь к нулю при Г->0 К.
Характеристическая температура энергии вращения вокруг оси
симметрии молекулы вследствие чрезвычайно малого ее момента
инерции относительно этой оси согласно формуле A4.84) состав-
составляет миллионы Кельвинов, и поэтому теплоемкостью, соответст-
соответствующей этой степени свободы, можно полностью пренебречь.
Таким образом, зависимость мо-
9 лярной теплоемкости двухатомных
JR
2R
R
идеальных газов от температуры бу-
будет иметь вид, изображенный на
рис. 41.
Заметим, что изложенная теория
вращательной теплоемкости относится
7"/ т* 7*~ к молекулам, состоящим из разных
атомов. В случае молекул из одинако-
Рис# 41 вых атомов, например Н2, спектр энер-
энергии молекул зависит от направления
спинов атомов. При параллельных
спинах в атомах молекулы (ортоводород) квантовое число / в
формуле возможных значений ее вращательной энергии A4.82)
принимает ряд нечетных значений (/=1, 3, 5, ...), при антипарал-
антипараллельных спинах (параводород) число / принимает ряд четных зна-
значений (/ = 0, 2, 4). Это приводит к различию свойств указанных ви-
видов водорода.
§ 68. Статистическая теория
равновесного излучения
Применение термодинамики к равновесному излучению позво-
позволяет получить выражение для плотности его энергии — закон
Стефана •— Больцмана (8.50)
Выражение же для спектральной плотности энергии uv(v, Г), как
и величину постоянной Стефана — Больцмана а, методами термо-
термодинамики найти не удается.
Решим эту задачу методами статистической физики.
Равновесное излучение (электромагнитное поле) мы представ-
представляем себе как непрерывную систему (континуум), состояние ко-
которой определяется несчетным множеством параметров — зада-
заданием непрерывных .векторов электрического & и магнитного Ж
полей. Поскольку, однако, законы статистической физики сформу-
сформулированы для молекулярных систем, состояние которых характе-
характеризуется счетным множеством параметров, то, прежде чем при-
применять статистическую физику к излучению, покажем, что колеб-
колеблющийся континуум (непрерывная колебательная система) в ди-
динамическом отношении эквивалентна совокупности счетного мно-
множества гармонических осцилляторов.
250
Рассмотрим в качестве простейшей непрерывной системы стру-
струну, расположенную вдоль оси х.
Состояние струны при малых продольных колебаниях в ней
определяется заданием смещения ее точек *?(x, t) (и соответст-
соответствующей скорости Ч?(х, t)), а изменение состояния — волновым
уравнением
*L±WL=09 A4.90)
09
где v — скорость распространения возмущения в струне.
Если струна зажата на неподвижных концах л: = 0 и х = а, то
решение волнового уравнения A4.90) при граничных условиях
ЧГ(О, t) =W(ay t) =0 имеет вид
со
?(*,*)=? qn(t)sinknx, A4.91)
где kn= (я/а)/г — волновое число; /г= 1, 2, ..., оо.
Подставляя A4.91) в A4.90), получим, что qn(t) удовлетворя-
удовлетворяет уравнению движения осциллятора
где
<оя = ЛЛ1> = —п
а
круговая частота колебания осциллятора.
Таким образом, колеблющаяся струна (колеблющийся конти-
континуум) в динамическом отношении эквивалентна совокупности гар-
гармонически колеблющихся осцилляторов.
Найдем распределение колебаний по спектру частот, т. е. оп-
определим число колебаний dN& в интервале частот от со до co+dco.
Так как
ТО
<о + dco = —?- (п + dn)y
где dn и есть число колебаний в интервале частот d® = 2ndv. Сле-
Следовательно,
dN@ = dn= —da. A4.92)
nv
Если е — средняя энергия осциллятора частоты со, то средняя
энергия осцилляторов (т. е. колеблющейся струны) в инте|рвале
частот doa равна
dE = sdNo=—dn= —dv. A4.93)
nv v
9* 2S1
Обратимся теперь к равновесному излучению в полости с зер-
зеркальными идеально проводящими стенками в виде куба со сто-
стороною а и объемом F=a3.
Состояние излучения определяется векторами <§ и X, некото-
некоторые удовлетворяют уравнениям Максвелла в вакууме:
тоШ=——, rot(§= -
с dt с dt
div<S = O, div3? = 0,
из которых следуют волновые уравнения
v2<g___L_f6_=o,
с2 dt*
V23f_-L-T^^o.
с2 dt2
Граничными условиями в нашем случае являются: ?* = 0, <?^Л = 0.
Таким образом, компоненты векторов электромагнитного поля
удовлетворяют скалярному волновому уравнению вида
с граничными условиями xF=0 для составляющих вектора & и
дЧ7C/г = 0 для составляющих вектора ??.
Решение волнового уравнения A4.94) с указанными гранич-
граничными условиями имеет вид
y?(xyyizit)= Л qtmn(t)-sinkxx>sinkyy-sink2z, A4,95)
l,m,n
где Z, m, /i=0, 1, 2, ..., oo; <70Oo=0;
Л*= (я/а)/, fey= (я/а)т, fez== (л/а)/г
проекции волнового вектора k = 2n/X=(u/c.
Нетрудно убедиться, что коэффициенты qimn удовлетворяют
уравнению колебаний гармонического осциллятора
Щ
где частота
.kc~ УI2 + ш2 + п2 =е= (о. A4.96)
Пользуясь этим выражением, найдем число собственных колеба-
колебаний (или соответствующих им осцилляторов) в интервале частот
от со до (o + d(o. Согласно A4.96) каждой тройке положительных
чисел /, m, n (определяющих волновой вектор к) соответствует
одно собственное колебание. Число собственных колебаний в ин-
интервале частот dco получим из геометрического представления
252
уравнения A4.96). Будем считать /, m, n декартовыми координа-
координатами точки, расстояние которой от начала координат
ПС
Собственным колебаниям, лежащим в интервале частот (со,
(o + dco), соответствуют все точки с целочисленными значениями
координат, содержащиеся в положительном октанте между шаро-
шаровыми поверхностями с радиусами R и R + dR. Так как плотность
этих точек в пространстве U т, п равна 1, то их число dNy в
среднем равно величине объема, ограниченного этими шаровыми
поверхностями:
<*ЛГ = ± .4я/?ЗД^ -^*>= -i^-dv. A4.97)
Мы рассматривали колебания скалярного поля, например коле-
колебания плотности газа при распространении продольных воли (зву-
(звука) в газе. Электромагнитные волны поперечны, и, следовательно,
каждому волновому вектору к соответствует не одна, а две стоя-
стоячие волны с взаимно перпендикулярными направлениями колеба-
колебаний. Поэтому число собственных электромагнитных колебаний
(число осцилляторов) dNy в полости в 'интервале обычных частот
(v, v + dv) будет в два раза больше dNy и равно
A4.98)
с3
Если е — средняя энергия одного осциллятора с собственной час-
частотой v, то средняя энергия всех осцилляторов в объеме V в ин-
интервале частот dv равна
dE = edNv =
с3
откуда средняя спектральная плотность энергии равновесного» из-
излучения
По классической теории 8=0. Подставляя это значение средней
энергии линейного осциллятора в A4.99), получим формулу Ре-
лея—Джинса
^LT. A4.100)
Эта формула находится в хорошем согласии с опытом только для
низких частот и резко расходится с ним для высоких частот.
Она приводит к тому, что полная плотность энергии равна беско-
бесконечности:
253
и = \ avav =
Это означает, что равновесие между веществом и излучением не-
невозможно, так как вся энергия должна идти на излучение, обла-
обладающее бесконечным числом степеней свободы.
Такой принципиалыно неверный вывод 'классической теории
равновесного излучения получил название ультрафиолетовой ка-
катастрофы.
Преодоление этой «катастрофы» классической теории излуче-
излучения привело Планка к квантовым представлениям и в последую-
последующем к построению квантовой механики.
Если в формулу A4.99) в качестве г подставить среднее зна-
значение энергии квантового осциллятора A4.79), отсчитываемой от
нулевой энергии, то мы получим формулу Планка для спектраль-
спектральной плотности равновесного излучения:
8jiv2 hv /1Л iAi\
Ut • <14Л01>
Эта формула превосходно подтверждается опытом. Она приводит
для низких частот, когда ftv/0<Cl, к формуле Релея — Джинса
,A4.100), а для высоких частот — к эмпирической формуле Вина
Из A4.101) следует также закон Стефана—Больцмана для пол-
полной плотности энергии излучения и выражение для постоянной
Стефана—Больцмана:
i, Snh
8nh /_0_\4 Г хЧх
h
15c3/i3
При термодинамическом выводе закона Стефана—БольЦмана
было использовано взятое из электродинамики выражение для
давления P==w/3. В статистической физике, получив и из форму-
формулы Планка A4.101), .величину давления можно вычислить. Так
как изменение энтропии в единице объема равно
то
254
и энтропия излучения в объеме V
S = sV=*
Энергия Гельмгольца
F = E-TS = oT*V-*
Энергия Гиббса излучения
G=E—TS + PV=0.
Формула Планка A4.101) приводит к принципиально' важному
выводу о корпускулярно-волновой природе излучения — к пред-
представлению об излучении как совокупности квазичастиц—фотонов
с энергией e = hv (*). К такому представлению приводит также
квантование электромагнитного поля, устанавливая кроме того,
что спин фотонов равен 1.
Принимая это представление за .исходное, формулу Планка
можно получить, применяя для фотонов распределение Бозе—
Эйнштейна. Действительно, число возможных квантовых состоя-
состояний фотона в объеме V с энергией в интервале (е, e + de), или,
что то же, с частотой в интервале (v, v + dv)y согласно A4.98)
равно
dNyv^
сг до
Поэтому, если в формуле A4.22) для среднего числа фотонов с
энергией в интервале (е, г + ds) (т. е. с частотой в интервале
(v, v + dv))
положить e = /iv, g(e)dE — dNv, \\=G/N=0, то мы получим для
энергии излучения в интервале частот (v, v + dv) выражение
)—1),
откуда следует формула Планка A4.101)
v ojxv" hv
exp
§ 69. Теория кристалла
в гармоническом приближении
В кристалле атомы находятся в узлах кристаллической ре-
решетки и колеблются около своих положений равновесия. При не
слишком высоких температурах эти колебания являются малы-
255
ми. Из механики известно, что для такой системы из N атомов
всегда можно ввести .нормальные координаты qi9 которые явля-
являются линейными функциями действительных координат атомов и
число которых равио числу степеней свободы системы — 3N.
В этих новых переменных функция Гамильтона системы имеет
В)ИД
4^
где pi — обобщенные импульсы, сопряженные нормальным коор-
координатам qu trti — постоянные коэффициенты, o)i = 2jtVi — частоты
нормальных колебаний. Таким образом, а гармоническом прибли-
приближении движение связанных атомов кристалла представляется в
виде колебаний невзаимодействующих нормальных осциллято-
осцилляторов.
Внутренняя энергия Е одноатомного кристалла равна сумме
средних энергий этих осцилляторов гг.
Е = Н (q, p) =
где _
р\
По классической теории ег- не зависит от частоты и равна в.
Поэтому
и молярная теплоемкость кристалла при постоянном объеме
равна
C dE/dT 3kN6 кал/моль-К. A4.103)
Это постоянное значение теплоемкости Cv эмпирически было ус-
установлено при комнатной температуре еще в начале прошлого
века французскими физиками П. Дюлонгом и А. Пти. Соотноше-
Соотношение A4.103) получило название закона Дюлонга и Пти.
Однако в дальнейшем было обнаружено, что при очень высо-
высоких температурах теплоемкость Cv увеличивается до 7 кал/моль «К,
а при понижении температуры уменьшается до нуля. Отклонение
от закона Дюлонга и Пти при больших температурах можно
объяснить ангармонизмом колебаний атомов в кристалле, пони-
понижение же теплоемкости при низких температурах классическая
теория обосновать не может — оно находит объяснение только з
квантовой статистике.
В 1907 г. Эйнштейн впервые применил квантовые представле-
представления Планка в теории теплового движения атомов в кристалле.
Он исходил из простой модели кристалла как совокупности ато-
атомов, колеблющихся с одной и той же частотой v около своих по-
256
ложений равновесия и имеющих по формуле Планка A4.79|
среднюю энергию
2 exp (hv/в) — 1 '
Внутренняя энергия одного грамм-моля такого кристалла равна
так как колебание каждого атома можно представить в виде
колебаний трех линейных осцилляторов.
Молярная теплоемкость
дТ \кТ
N-S-)-'
A4.105)
где Tc = hvjk — характеристическая температура энергии колеба-
колебания атома в модели кристалла Эйнштейна.
Выражение A4.105) определяет температурную зависимость,
теплоемкости Су твердого тела в теории Эйнштейна.
При высоких температурах, когда Г>ГС, из A4.105) получаем
для Су классическое значение A4.103), соответствующее закону
Дюлонга и Пти.
-При низких температурах, когда T<^JCy
откуда видно, что при Т-+0 К теплоемкость Су->0 в согласии с
третьим началом термодинамики. Однако формула A4.106) лишь
качественно согласуется с экспериментом. На опыте при Г->0 К
теплоемкость Су спадает до нуля более резко-, чем по экспонен-
экспоненциальному закону. Этот недостаток эйнштейновской теории тепло-
емкости твердого тела обусловлен предположением о независи-
независимости колебаний атомов в кристалле. В действительности атомы
в кристалле связаны между собой и их колебательные движения
'носят коллективный характер, в котором принимают участие все
атомы.
В точной теории гармонического кристалла из N атомов его
внутренняя энергия Е и энергия Гельмгольца F равны соответ-
соответственно сумме средних энергий е* и энергий Гельмгольца ft 3N
257
нормальных квантовых осцилляторов с разными частотами:
3N 3N
и, используя A4.78),
з# злг злг
/=i *=i i=i
где Ео — нулевая энергия кристалла.
Для твердого тела макроскопических размеров спектр его
нормальных колебаний квазинепрерывный. Если в интервале час-
частот (v, v+dv) лежит g(v)dv нормальных колебаний, то A4.107}
и A4.108) можно записать в виде
max
J —тг
о е в — 1
f ln(l-e e)g(v)dv, A4.110)
J
-y-gT(v)dv, A4.111)
— максимальная частота нормальных колебаний.
Нахождение функции распределения частот g(v) для кристал-
кристалла йредставляет собой весьма сложную задачу.
В 1912 г. эту задачу приближенно решил Дебай, рассматри-
рассматривая твердое тело, как изотропную непрерывную среду.
Число продольных колебаний dNyl в -интервале частот (v,
v + dv) в объеме V непрерывной среды согласно A4.97) равно
тде ci — скорость распространения продольных волн в среде.
В твердом теле помимо продольных колебаний возможны два
независимых поперечных колебания. Их число dN*v в том же
интервале частот
где ct — скорость распространения поперечных колебаний.
258
Полное число колебаний в интервале (v, v + dv)
я - Т] — * -> A4.112>
ci ct
где с — средняя скорость упругих воли в среде, определяемая иа
равенства
— -]-— — — П4 113V
ci ct c
В непрерывной среде число собственных колебаний бесконечно.
Атомная структура твердого тела учитывается в теории Дебая
условием, что число нормальных 'колебаний равно числу степеней
свободы твердого тела, т. е.
'та:
О
откуда максимальная частота
V)V\ A4.114)
а соответствующая ей минимально возможная длина волиы
Amin = ^/vmax= Djt У/АО 1/3~а> где а — межатомное расстояние в
кристалле.
Подставляя в A4.112) величину с из A4.114), получим
<Wv=-^-v2dv. A4.115)
Таким образом, функция распределения частот g(v) в теории
Дебая имеет вид
(|^-v2 при v<vmax,
max
= Vmax A4.116)
0 при v>vmax.
На рис. 42 пунктирная линия изображает функцию распределе-
распределения частот в теории Дебая, а сплошная лииия — решеточ,нук>
(истинную) функцию распределения, учитывающую дискретную
структуру кристалла и специфичную для конкретного твердого
тела. Функция g(v) определяется экспериментально по рассеянию
•нейтронов, а теоретически — численными методами.
В качестве термодинамического потенциала кристалла па
формулам A4.108) и A4.116) можно вычислить энергию Гельм-
гольца, а потом определить и все другие термодинамические
функции твердого тела в теории Дебая (*). Однако для опреде-
определения теплоемкости проще непосредственно по формуле A4.109JJ
259
вычислить внутреннюю энергию Е.
Действительно, подставляя A4.115)-
в A4.109), получим
9Nh
v3
vmax
v3dv
Рис. 42
exp (hv/в) — 1
A4.117)
Для вычисления интеграла в
A4.117) введем новую переменную
x = hv/@ и температуру Дебая
TD=?hvmax/k A4.118)
(по порядку величины TD~ 100—
1000 К). Тогда для одного грамм-
атома кристалла получаем
td/t
.л л.. I 'Г \
A4.119)
где функция Дебая
D(t)_ 3 Г x?dx
t3 J ё* 1 *
A4.120)
При высоких температурах, 7>rD, в верхнем пределе интег-
интеграла функции Дебая стоит малая величина, поэтому в подынтег-
подынтегральной функции х заведомо мало-; полагая ex^l+xt .получим
TD/T
-и теплоемкость Cv= (dE/dT)v = 3R имеет классическое значение
A4.103).
При низких температурах, T<^JD> в верхнем пределе интеграла
функции Дебая стоит большая величина, и так как в знамена-
знаменатель подынтегральной функции входит член ех, то этот предел
можно заменить на беоконечиость. Тогда
оо
так как Г -^—^- = -^—. Внутренняя энергия
260
я теплоемкость
Таким образом, при низких температурах теплоемкость кристал-
кристалла пропорциональна кубу температуры («закон Г3»).
Из A4.119) находим выражение для теплоемкости Cv во всей
области изменения температуры:
^^)] A4,122)
Из этой формулы видно, что в теории Дебая теплоемкость явля-
является для всех тел одной и той же универсальной функцией T/TD.
График зависимости Су от T/TD приведен на рис. 43.
Формула A4.122) для теплоемкости, несмотря иа приближен-
приближенный характер теории Дебая, хорошо подтверждается на опыте.
Дальнейшее развитие теории теплоемкости кристаллов связано с
отказом от замены твердого тела непрерывной средой и рассмот-
рассмотрением колебаний твердого тела как колебаний кристаллической
решетки.
В теории Дебая можно «вычислить энергию Гельмгольца и
другие термодинамические величины (*).
§ 70, Электрические и магнитные свойства
идеальных систем
До сих пор мы рассматривали идеальные системы в отсутствие
внешних полей. Рассмотрим теперь (идеальный газ, состоящий из
молекул, имеющих постоянный электрический дипольный момент
р, находящийся в постоянном однородном электрическом поле с
напряженностью <§.
В результате ориентирующего действия поля и дезориентиру-
дезориентирующего действия теплового движения устанавливается такое рас-
распределение молекулярных дипольных моментов, которое приводит
к возникновению поляризации 8* вдоль электрического поля:
^ = р cos фх + Р cos ф2 + ... + р cos фл =
A4.123)
где п — концентрация молекул газа, ф — угол между направле-
направлением диполя р и напряженностью поля <§.
Вычислим cos<p и величину ориентационной поляризации 3*.
Потенциальная энергия электрического диполя р в электри-
электрическом поле & равна
и(ф) = — рб = —р<§ cos ф.
Распределение диполей по направлениям во внешнем поле опре-
261
деляется формулой Больцмана A4.5). По этой формуле вероят-
вероятность того, что произвольно выбранный диполь образует с нап-
направлением поля угол в интервале (ф, w + dw), равна
где постоянная А определяется из условия нормировки [dw(y) —
= 1, так что
и
Вводя сокращенные обозначения: V%l® = a, cos<p = .x;, получим.
Функция L(a)=ctha—I/a называется функцией Ланжевена. Она
была получена в 1905 г. Ланжевено,м при аналогичном исследо-
исследовании парамагнетизма (см. ниже). На рис. 44 представлен гра-
262
A4.124)
фик функции Ланжевена A4.124). Из A4.123) и A4.124) полу-
получаем, что поляризация
. A4.125)
Во всех практически встречающихся случаях а= рё/&Г<1 (от-
(относительно малые поля и высокие температуры). Гиперболиче-
Гиперболический котангенс может быть разложен в ряд
поэтому в линейном 'приближении по электрическому полю
L(a)^a/3, и поляризация A4.125) равна
A4.126)
где поляризуемость газа
Ke = nv2/3kT~l/T. A4.127)
Электрическая индукция
откуда диэлектрическая постоянная
При сильных полях и низких температурах, когда а=р
ctha-»-l, L(a)-^1, &* =п ри мы имеем насыщение — поляриза-
поляризация становится максимальной.
Полученные формулы образуют основу теории электрических
свойств газов (и жидкостей), развитой в 1911 г. Дебаем по об-
образцу совершенно аналогичной, построенной в рамках классиче-
классической физики, теории парамагнетизма Ланжевена.
Действительно, намагничивание #- идеального газа из моле-
молекул с магнитным моментом jm, помещенного в магнитное иоле с
напряженностью Ж (.при 'классическом предположении о непре-
непрерывном изменении (направления магнитного момента в простран-
пространстве), выражается формулой, аналогичной A4.125), если в ней
:под а подразумевать ]ыХ/в. Таким образом, по Ланжевену, на-
намагниченность парамагнитного^ газа равна
^=n^L(a), A4.128)
где a=\iH/kT.
При а<1
где парамагнитная восприимчивость
263
в соответствии с законом Кюри обратно пропорциональна абсо-
абсолютной температуре, и постоянная Кюри равна
Формула A4.128) является классической, она не учитывает кван-
квантование проекций магнитного момента.
Малнитные диполи атомов и молекул определяются собствен-
собственными магнитными моментами (спинами) и орбитальным движе-
движением электронов. В случае, когда магнитный момент молекулы
обусловлен спином ее электронов, имеется 25+1, значений его про-
проекции на направление поля, где s — полуцелое или целое число:
s —1 s —2 s—1
—\i, — ц , — ц , ..., ц , ц;
S S S
где (lx =
магнетон Бора, являющийся элементарным магнитным момен-
моментом.
Для вычисления ty = /ip,cos<p мы снова применяем распреде-
распределение Больцмана и получаем выражение
т)
exp
¦т)
(—\
r=—s
Под знаком логарифма стоит сумма геометрической прогрессии,
которая равна
Поэтому намагничивание равно
f^n\i>Lsl\i3ei@), A4.129)
где квантовая функция распределения Ls(\x3^/kT) имеет ов(ид
*.«-('+i)'*[('+i)«]-iclh(i)- A4ЛЗО)
264
В случае, когда магнитный момент обусловлен электронным спи-
спином, s=l/2, возможны только два направления момента: парал-
параллельное полю и антипараллельное. В этом случае
4^ A4Л31>
A4.132>
В другом предельном случае, при s = oo, выражение A4.129) пе-
переходит в A4.128).
Глава 15
ТЕОРИЯ КЛАССИЧЕСКИХ
НЕИДЕАЛЬНЫХ СИСТЕМ
В этой главе мы рассмотрим методом статистического интег-
интеграла и методом функций распределения классические системы'
взаимодействующих частиц (реальный газ, плазма), а в последу-
последующей главе — интегральные уравнения для функций распределе-
распределения в теории твердых тел и жидкостей.
Получим вначале здесь в дополнение к § 56 (о методе Бого-
Боголюбова) выражение для энергии Гельмгольца через бинарнук*
функцию распределения системы частиц с тарным потенциалом
взаимодействия <D(|qi—q2|)-
Согласно определению s-частичной функции распределения
A2.64)
O(\qi-q,\)}dqt+1...dqN.
Введем параметр Я, который умножается на константу взаи-
взаимодействия и меняется от 0 до 1. Значение Х=1 соответствует
реальному взаимодействию, при к=0 взаимодействие отсутствует
и система является идеальным газом. Тогда
— — 2j фAЧ/ —q/l)j dqs+l...'
qs)=-
и парное взаимодействие описывается функцией AXD(|q*—q/|).
Энергия Гельмгольца системы при таком взаимодействии согласна
A2.25) равна
26Б
тде
—LjJ<D(|q,_q/|)jdq1...dqJV.
Дифференцируя F(X) по Х, получим
ж окончательно (принимая N—1-
dF(X) ^Jf
дХ 2V
V V
После интегрирования этого выражения по X в пределах от 0 до
J будем иметь
V V
где /^ид — энерлия Гельмгольца идеального газа.
Для пространственно однородной системы
^2{К Яь Ъ)-*У2(К |qi—Я2|)=^Ъ(Я, г),
и энергия Гельмгольца равна
Этим выражением мы воспользуемся при рассмотрении плазмы
методом функций распределения Боголюбова.
§ 71. Реальный газ.
Групповое разложение в теории газов
Как уже отмечалось ранее, вычисление конфигурационного
интелрала
266
= j\..jexp{-
У V
в
для системы взаимодействующих частиц представляет собой
сложную задачу. Для газов .не очень большой плотности с пар-
парным потенциалом взаимодействия, быстро спадающим с расстоя-
расстоянием, эта задача была решена в 1937 г.
Дж. Майером, развившим метод груп-
группового, или кластерного, разложения.
Здесь мы кратко изложим основные
идеи и результаты этого метода.
Рассмотрим в объеме V газ из N
одноатомных молекул, взаимодейству-
взаимодействующих посредством центральных сил,
характеризуемых взаимным потенциа-
потенциалом Ф(|qi—Чг|) =Ф(^). На больших
расстояниях атомы притягиваются, а
на достаточно малых — отталкивают-
отталкиваются, так что график функции Ф(г) име-
имеет вид, изображенный на рис. 45. То
расстояние между центрами частиц а,
при котором энергия отталкивания на-
начинает резко увеличиваться, можно
назвать их диаметром.
При расчетах в теории газов и жидкостей часто используется:
межмолекулярный потенциал Леннарда—Джойса
Рис. 45
Ф(г) =4е [(а/г) I2- (*т/гN],
A5.5)
где е и а — постоянные, имеющие размерность энергии и длины
соответственно. Длина о — эффективный диаметр частицы, опре-
определяемый из равенства Ф(а)=0. Величина « определяет глубину
потенциальной ямы Ф(г). Мы будем рассматривать газ при тем-
температурах в>8, когда устойчивый комплекс из двух молекул не
образуется.
Потенциал Ф(г) настолько быстро убывает с расстоянием, что
практически обращается в ,нуль при r = R~5a. Потенциальная:
энергия рассматриваемого газа, очевидно, равна
так что подынтегральная функция в A5.4) для него (Превращается
в произведение, в каждый множитель которого входят координа-
координаты двух молекул
= П ехр{-РФ(|Ч,-д/|)}, (Р =
26Г
Для больших значений аргумента \qi—Ч/[=Л/, при которых
Ф(гц) равен лулю, любой из множителей правой части равенства
A5.7) обращается в единицу. Поэтому для исследования конфи-
конфигурационного интеграла Майер ввел функцию
fu = f (ni) =еяр{-рФ(л/)}-1, A5.8)
которая обращается в нуль при больших значениях аргумента.
Тогда произведение A5.7) может быть разложено в виде суммы
= f[ (l + /t7) = l+ ? /„ + ??/«,/«+..., A5.9)
в которой каждое слагаемое соответствует распределению частиц
;на определенные группы и обращается в нуль, если аргумент
функции Майер a fa достаточно велик хотя бы для одной пары
индексов.
Подставляя A5.9) в A5.4), получим групповое разложение
.конфигурационного интеграла QN:
...}dqx...dqN. A5.10)
При вычислении вкладов в Qn от взаимодействия различных
групп используется диаграммная техника: каждому члену разло-
разложения A5.10) сопоставляется геометрический образ — диаграмма
или граф: переменным qi, ..., q^ приводится в соответствие про-
пронумерованный кружок, а миожителям fa — линия, соединяющая
i-ый и /-ый кружки. Например,
{/12/24/66^1^2
Таким образом, выражение для конфигурационного интеграла
'A5.10) представляет собой сумму всех различных графов из п
кружков — ^-частичных графов. При этом (первому члену в
A5.10) соответствует граф без соединительных линий, второму
члену — N(N—1)/2 графов с одной линией, третьему члену —
графы с двумя линиями и т. д. Графы называются связными,
если все кружки прямо или косвенно (через другие кружки) свя-
связаны друг с другом, и несвязными, если © них имеются изолиро-
изолированные друг от друга группы (кружков или отдельные кружки.
Сложный граф (интеграл) приводится к графам более простым
(т. е. к далее неприводимым интегралам р*). Например,
268
Взаимодействию одной пары частиц соответствует вклад
и
и получающийся здесь интеграл называется первым неприводи-
неприводимым интегралом (неприводимой диаграммой или неприводимым
графом):
A5.11)
Взаимодействие трех частиц определяется одним из интегралов
вида
A5.12)
который выражается через второй неприводимый интеграл
A5.13)
и сам интеграл A5.12) равен 2Ур2 *и т. д.
Интегрируя A5.10) по конфигурациям всей системы, получаем
QN=V*+[N(N—l)J2]V»-4f{\q\)dq+... . A5.14)
В термодинамическом пределе (N-*oof l/->oo, а = V7Af=const)
ряд A5.10) удается формально просуммировать и свести к более
простому ряду (только связных диаграмм) ш> обратным степеням
удельного объема v:
где Bt — вириальные коэффициенты:
B2 = _i/2p1==_i/2Jf(|q|)dq,
A5.16)
которые учитывают соответственно взаимодействие («столкнове-
(«столкновение») двух частиц (второй вириальный коэффициент В2)> трех
частиц (третий вириальный коэффициент Въ) и т. д.
Используя A5.15), по формуле A2.25)
F = — в In ZN = — в In (QNJN\)+3N@ In X
находим вириальное разложение для энергии Гельмгольца реаль-
лого газа:
00
^^-.-^ A5.17)
=—Л^в1п (ev) +ЗЛ^в1пЯ — энергия Гельмгольца идеального
269
газа) и его вириальное уравнение состояния:
^. (,5,8,
1 +
1=2
В свое время считалось, что вириальное уравнение состояния
может описать тройную точку и критические явления. Однако эти
надежды не оправдались. При высокой плотности (жидкость)
характер сходимости вириального ряда резко ухудшается, стано-
становится необходимым знание большего числа членов, а практиче-
практический расчет вириальных коэффициентов ограничен трудностями
вычисления многократных интегралов. В настоящее время прове-
проведен расчет семи вириальных коэффициентов системы твердых
сфер и нескольких низших коэффициентов для более реалистиче-
реалистических потенциалов. Поэтому важным является вопрос о< повышении
скорости сходимости рядов разложения термодинамических функ-
функций.
Недавно были опубликованы работы *, в которых предложено
решение этой задачи.
Исходя из того, что энергия Гельмгольца является экстенсив-
экстенсивной величиной, выражение A2.35) для нее
F = — в \n(QN/N\) + 3NQ In A,
можно записать в виде
F = —3N6 In q—NS \n{ev)+3NS In Я,
A5.19)
где q(®, v) = (Qn/VnI/3n, численный коэффициент З в первом
члене соответствует трехмерности рассматриваемой системы я уч-
учтено, что N\=(N/e)N (в статистическом пределе).
Функция q(@> v) находится следующим образом. Если система
очень разрежена (идеальный газ), то
р^рил=_Мв ln(ev)+3NS In I
и, следовательно, #->l. Отличие величины q от 1 у реального га-
газа обусловлено отклонением его от идеальности. Поэтому будем
искать q в виде
q=l-b/v,
где
t=2
* Базаров И. П., Николаев П. Н. О рядах теории возмущений в ста-
статистической физике. — ДАН, 1982, т. 267, № 6, с. 1344; Базаров И. П., Ни-
Николаев П. Н. Теория систем многих частиц. — М.: Изд-во МГУ, 1984.
270
Таким образом, энергия Гельмгольца A5.19), как функция плот-
шости, имеет вид
00
F= _3JV61n[l— V—^-1 — N®\n(ev)+3N@\n%. A5.21)
i2
Входящие в A5.21) коэффициенты Ьь выражаются через вириаль-
ные коэффициенты Вь. Действительно, разлагая в A5.21) лога-
логарифмическую функцию в ряд при малой плотности, когда b<Cv,
и сравнивая его свириальным разложением энергии Гельмгольца
A5.17), получим:
Ь2 = В213У
A5.22)
3(В/3J]
Из A5.21) находим уравнение состояния
г.'"
t=2
v'-1
A5.23)
Pv/Q
Рис. 46
ОЛ 0,6 0,8
Рис. 47
271
которое справедливо при относительно больших плотностях газа,
когда вириальное разложение A5.18) плохо сходится.
В качестве примера использования A5.23) рассмотрим урав-
уравнения состояния для систем твердых дисков и твердых сфер, ко-
которые имеют важное значение в силу того, что используются в
качестве 1нулевого приближения в теории уравнений состояния
плотных газов и жидкостей. Кроме того, для них известны урав-
уравнения состояния, найденные .на основе машинного эксперимента,
поэтому исследование данных систем каким-либо методом позво-
позволяет определить эффективность этого метода.
На рис. 46 и 47 пунктирными линиями изображены графики
уравнений состояния систем твердых дисков и сфер соответствен-
соответственно, полученные методом молекулярной динамики. Сплошными
линиями аЬ изображены уравнения состояния однородной фазы,
найденные по уравнению A5.23) с учетом шести вириальных
коэффициентов для системы твердых дисков и семи вириальных
коэффициентов для системы твердых сфер. Как .видно*, согласие
вычислений по A5.23) с машинным экспериментом хорошее.
Кроме того, используя полученные по A5.23) уравнения сос-
состояния для однородной фазы и соответствующие расчеты для упо-
упорядоченной фазы ей, удается описать фазо»вый переход от неупо-
неупорядоченной к упорядоченной фазе в системах твердых дисков и
сфер. Линия фазового равновесия be определяется из условия ра-
равенства химических потенциалов обеих фаз.
§ 72. Уравнение Ван-дер-Ваальса
Если газ не очень плотный, то среднее расстояние между мо-
молекулами велико по сравнению с их размерами. Поэтому можно
считать, что чаще всего сталкиваются только две молекулы,
столкновение же трех, четырех и более частиц встречается редко-,
и ими можно пренебречь. В этом приближении из A5.18) .полу*
чаем уравнение состояния реального газа малой плотности
P = J^_M +_2L)t A5.24)
где согласно A5.16) второй вириальный коэффициент
э— \)гЧг. A5.25)
Подставляя интеграл A5.25) в виде суммы интегралов в проме-
промежутках 0<г«т и о<г<оо и учитывая вид функции Ф(г) межмо-
лекулярного взаимодействия (см. рис. 45) и условие (в>е),
получим
G оо
52 = — 2я Г (е-ф<"/в— 1) гЧг— 2я Г (е-ф«/в— 1) гЧт =
J *J
О о
272
Входящая сюда величина
2jTGS «т ,• JT03 яг с яг f. /1С ООЧ
3 6 X
представляет собой учетверенный объем всех молекул газа, а
выражение
оо
/ f |Ф (г) \АкгЧг
Г |Ф(г)|Л(г = JL[ J!^LzlLJ
= fli
2 v I V2
{N2~N(N—l) при # > 1) A5.29)
есть среднее (по пространству) значение энергии притяжения
всех пар молекул в единице объема.
Таким образом, согласно A5.27) — A5.29) уравнение состоя*
ния реального газа малой плотности пр{и учете лишь парных
столкновений между молекулами имеет вид
A5.30)
V \ V ) V*
От уравиения состояния идеального газа P=N@/V уравнение
A5.30) отличается двумя слагаемыми. Первое из иих учитывает
объем молекул реального газа, а второе — характеризует умень-
уменьшение давления .на стенки сосуда из-за их притяжения друг к
другу.
Уравнение A5.30) представляет собой уравнение Ван-дер-
Ваальса для газа малой плотности, т. е. ори fti/V<Cl, когда это
уравнение можоню записать © виде
p==_NB ал_ A531)
V — Ьх V2
273
так как при условии 6>е
Подставляя A5.26) в A5.24), находим
так как в этом случае
Только для такого газа уравнение A5.31), эквивалентное уравне-
уравнению A5.30), может быть выведено в статистической физике.
Однако*, как известно, уравнение Ван-дер-Ваальса A5.31)
описывает свойства газов не только малой, но и большой плот-
плотности и даже жидкостей. В этом случае оно представляет собой
чисто эмпирическое уравнение состояния, и его следует рассмат-
рассматривать как удачную экстраполяцию уравнения A5.31) на область
больших плотностей. При этом постоянные п\ и Ь\ не имеют уже
определенного смысла, так как для получения количественного
совпадения уравнения состояния A5.31) с экспериментальными
данными их приходится считать функциями температуры. По-
Поэтому вместо уравнения Ван-дер-Ваальса было предложено более
ста других эмпирических уравнений состояния. Тем не менее
большим достоинством уравнения Ван-дер-Ваальса является то,
что оно, будучи аналитически простым, качественно правильно
передает по!ведение плотных газов, их переход в жидкость и при-
приводит к существованию критического состояния.
§ 73. Метод Боголюбова в теории газов
Как было показано в гл. 12, термическое и калорическое урав-
уравнения выражаются через бинарную функцию распределения
&~2{Я\> Й2). Эта функция находится из решения уравнения цепоч-
цепочки Боголюбова для равновесных функций распределения A2.66):
dUs
l f
(s = l, 2, ...).
Возможны различные способы решения уравнения A5.32). Для
таких систем, для которых в уравнении можно< выделить харак-
характерный для них малый параметр, решение ищется в виде разло-
разложения функций распределения по степеням этого параметра.
В случае обычного газа (т. е. систем частиц с короткодей-
короткодействующими силами взаимодействия) небольшой плотности малым
параметром является отношение о3/^, так как для такого газа
G3<Ct>. Бинарная функция распределения пространственно одно-
однородной системы, как мы увидим, зависит от расстояния между
частицами:
Переходя в уравнении A5.32) по методу подобия к безразмер-
безразмерным величинам q'a = qa/o, замечаем, что интегральный член полу-
получающегося уравнения содержит параметр oz/v. Поэтому решение
этого уравнения можно искать в виде степенного ряда по данному
274
малому параметру. Можно и непосредственно решать уравнение
A5.32), разлагая функцию STS по степеням плотности n=l/v
(поскольку п содержится в интегральном члене этого* уравнения):
&s - &\ + п&\ + п*&\ + ... . A5.33)
Подставляя это разложение в A5.32) и собирая члены .при оди-
одинаковых степенях плотности, иолучим:
'1 ' 1
A5.34)
д^\ \ fill i if* дФ (I q —
dqf в dq^ S в J dqf
Из первого уравнения системы A5.34) имеем:
&Os=CQse @ , C°s = const.
Найдем функции ^"i и ^~2 в первом и втором приближениях.
Так как /7i = 0, f/2 = Ф (| qi—42|)^Oi2» то 5ri° = Ci°. Из условия
нормировки
— \ ^i Di) dQi = 1
следует: Ci°=l, Ci1 = Ci2= ... =0, а из условия ослабления кор-
корреляции
t?sDi> ••• »Ч8)"^" П ^iDt) ПРИ Iflt—4/1"^°°
l<t<s
A5.35)
(Я<) П ^?(q/), • • • .
и так как при |q,—q,|->0 Us = 0, то Cs°= (Ci°)*=l.
Поэтому ^"s° = exp(—t/s/в) и, в частности,
Второе приближение УгЧЧь Чг) бинарной функции найдем из
второго уравнения системы A5.34) при s = 2:
275
Умножая это уравнение на еф"/е, получим
откуда
q3==C. A5.36)
Постоянную С найдем из условия ослабления корреляции при
|qi—Ч2|-^°°, (когда d>i2 = 0 и согласно A5.35) tF}=0, а Ф13 и
023 не могут одновременно отличаться от нуля, так как третья
частица находится или около* первой, или около1 второй, или на
бесконечности от той и другой. Поэтому при |qi—q2|->oo
exp ( Ф» + Фгз) = A +/13) A +/23) =
так как, когда fi^O, функция Майера /23 = 0 и наоборот.
Таким образом, из A5.36) находим
и с точностью до второго приближения бинарная функция рас-
распределения газа малой плотности согласно A5.33) рав«а
|^ + JL J/(|q-q'|)/(q')dq']. A5.37)
Уравнение состояния пространственно однородной системы имеет
вид A2.79)
оо
¦—¦ = 1 —Jj j '3Ф' W ^2 (r) dr. A5.38)
О
Подставляя в A5.38) первое приближение бинарной функции
распределения
имеем
276
После интегрирования по частям
О© 00
Г /-3Ф' (г) e-*w/*dr = —в Г г3 — (е-фс)/@— 1) dr =
о о
= _в Jrs (е-Ф(г)/в_!) °° — 3 Г (е-фе>/в — 1) r2dr J =
= 3в (е-фс->/в— 1) гЧг
J
О
получаем уравнение состояния газа A5.24) с точностью до вто-
второго вириального коэффициента, учитывающего лишь парные
столкновения
оо
J!L = i __*L f r2(e-axr)/e_i)rfr. A5.39)
в V J
о
Если в A5.38) подставить бинарную функцию -распределения в
приближении A5.37), получим уравнение состояния с точностью
до третьего вириального коэффициента
Pv/Q = 1 + BJv + Bz/v2. A5.40)
Таким образом, в применении к газам метод Боголюбова при раз-
разложении бинарной функции по степеням плотности приводит к ре-
результатам теории группового разложения Майера без использо-
использования сложной комбинаторики и диаграммной техники.
§ 74. Статистическая теория плазмы
Плазма представляет собой частично или (полиостью ¦ионизо-
¦ионизованный газ. Плазменное состояние относят к четвертому агрегат-
агрегатному состоянию вещества, так как плазма обладает рядом спе-
специфических свойств по сравнению с обычным газом. Это обус-
обусловлено дальнодействующим характером кулоновских сил взаимо-
взаимодействия между заряженными частицами.
Изложенный в § 71 метод группового разложения, как и при-
приводящее к нему разложение бинарной функции распределения по
степеням плотности в методе функций распределения (§ 73), не-
непригодны для вычисления термодинамических функций плазмы,,
так как в этом случае вследствие дальнодействия (кулоновских
сил неприводимые интегралы расходятся. Однако метод функций
распределения применим и для исследования плазмы, поскольку
уравнения цепочки Боголюбова для этих функций позволяет вы-
выделить характерный для плазмы малый параметр и вычислить
277
для нее функции распределения разложением их по этому ма-
малому параметру.
Для определения плазменного малого параметра следует по
методу подобия перейти в уравнениях для ?TS к безразмерным
величинам, выбрав подходящую единицу длины. Чтобы найти та-
такую единицу длины и сам плазменный параметр, применим вна-
вначале к изучению плазмы дебаевский метод, развитый в 1923 г.
Дебаем и Хюккелем для вычисления термодинамических функций
сильных электролитов.
Рассмотрим термодинамически равновесную плазму, состоя-
состоящую из двух сортов противоположно' заряженных частиц е и —е
в объеме V с числом частиц N каждого сорта, так что объем на
одну какую-либо частицу v=V/2N. Найдем потенциал ф(г) поля
всех частиц на расстоянии г от какой-либо частицы.
В непосредственной близости от данного заряда е преобла-
преобладают, очевидно, заряды противоположного знака. Если на некото-
некотором расстоянии г от этого заряда концентрация положительных
зарядов п+у а отрицательных зарядов п_, то плотность заряда в
этом месте р(г)=е(п+—л_). Потенциал поля, создаваемого всеми
зарядами (в том числе и зарядом ё), определяется уравнением
Пауссона
Заряженные частицы находятся в этом, ими создаваемом (са-
(самосогласованном) поле. Концентрации их п+ и /г- в данном месте
определяются формулой Больцмана
где 9 = &Г, no = N/V — средняя концентрация заряженных частиц
одного знака. Таким образом,
р=еяо{ехр (—еср/0)— ехр
Аф = 4лело{е»р (е<р/в) —ехр (—е
В случае разреженной плазмы средняя электрическая энергия за-
заряда еф мала по сравнению с энергией его- теплового- движения
3/гв, поэтому ехр (вф/в) — 1 + ^ф/в и
где к2 = о/
1 d2
Вследствие сферической симметрии поля Дф = j"(r(P)#
Тогда -?j (щ) - х2 (гф), откуда ф (г) = -^ ег™ + —е"г.
Постоянная ^2 = 0, так как в противном случае получился бы бес-
бесконечно большой потенциал вдали (г-^оо) от данного заряда, что
не имеет смысла. Таким образом,
ф (Г) =-?!-*-". A5.41)
Потенциал поля, создаваемого всеми зарядами, кроме дашюго
заряда е в точке на расстоянии г от него, очевидно, равен
q>i(r)=-^-exp(—хг) е-,
а в месте нахождения самого заряда (г = 0)
{сегшe) lim [сскгАс(кгJ
{схегe) lim [сх—с±кгА с1(кгJ + ... —е) =
Г г-»0 Г \ 2 )
г->0 Г
Для того чтобы эта величина была конечной, необходимо поло-
положить с\ = е\ тогда по формуле A5.41)
ф(г)= —е-*'. A5.42>
г
Это решение уравнения Аф—х2ф = 0 предполагает, что в точке
г = 0 находится точечный заряд с плотностью р(г)=еб(г), т. е. что
оно есть решение уравнения с особенностью в начале координат
Аф—и2ф = — 4яе6 (г). A5.43)
Зная выражение A5.42) для потенциала ф(г), можно определить
все термодинамические свойства разреженной плазмы (*). Однака
изложенный дебаевский метод рассмотрения плазмы не допускает
обобщения для получения следующих приближений по концент-
концентрации.
Метод функций распределения Боголюбова лишен этого недос-
недостатка, позволяя iB принципе вычислять также и следующие члены
разложения термодинамических функций.
Из формулы A5.42) для ф(г) видно, что потенциал поля око-
около заряда е в плазме убывает по экспоненте. Этим плазма прин-
принципиально отличается от диэлектрической однородной среды, в
которой потенциал поля от внешнего заряда ,на любом расстоя-
расстоянии от «его уменьшается в е раз по сравнению с потенциалом в
вакууме. Заметим, что потенциал ф(г) создается зарядом е и все-
всеми другими зарядами: его нельзя рассматривать как потенциал:
парного взаимодействия экранированных частиц.
Величина
A5.44)
характеризует быстроту уменьшения потенциала поля в плазме
с увеличением расстояния от данного заряда е, т. е. глубину про-
проникновения внешнего электрического поля в плазму, и называется
дебаевским радиусом.
Взяв D в качестве единицы длины, нетрудно найти плазмен-
плазменный параметр, перейдя в уравнениях Боголюбова для плазмы к
безразмерным величинам.
Для простоты изложения будем рассматривать вместо элект-
электрически нейтральной системы разноименно заряженных частиц
систему частиц с одинаковым зарядом е, движущихся в облаке
компенсирующего равномерно распределенного заряда (другого
знака).
В уравнения A5.32) для функций распределения рассматри-
рассматриваемой системы потенциальная энергия ф$ s ее частиц в поле
компенсирующих заря до© будет входить как внешняя:
1 Г
где A5.45)
<р(Чг) — потенциальная энергия заряда е, находящегося в точ-
же q^, в поле компенсирующих зарядов.
Плотность этих равномерно распределенных во всем объеме
зарядов равна р= —eN/V. Поэтому
gi) d ,
v .) л?? ч
-и в термодинамическом пределе
JSi -i- Г аф<"ь-"«+iD dq . A5.46)
Подставив A5.46) в A5.45), получим следующие уравнения для
функций распределения рассматриваемой системы:
A5.47)
"Перейдем в A5.47) к безразмерным единицам длины qar=qaID,
так что qa=Dq'a. Тогда
280
D
где
и = V *
s Zj |q'.— q^.| '
и уравнения A5.47) в безразмерной форме имеют вид
аG1а DO ^ia 4я 1а
A5.48)
Входящий в эти уравнения параметр
е = e*/De = v /4 л?>з 'A5.49 J
и есть плазменный параметр, который представляет собой отно-
отношение энергии взаимодействия пары частиц, находящихся на рас-
расстоянии дебаевского радиуса, e2/D к энергии их теплового движе-
движения в (или отношение удельного объема частицы к объему сферы
дебаевского радиуса). Опуская в A5.48) штрихи, получим урав-
уравнения
При e2/D<^Q плазменный параметр <С
Будем искать решение уравнений A5.50) в виде разложения:
A5.50)
жения:
A5.51);
После подстановки A5.51) в A5.50) получим
= O, A5.52)
откуда
1 С
4я J
10 Зак. 245 281
A5.53)
При решении этих уравнений должны быть соблюдены условия
симметрии, нормировки и ослабления корреляции.
Очевидным решением уравнения A5.52) для 5^%°, удовлетво-
удовлетворяющим названным условиям, является
0V(qi..--,q.) = i. E=i, 2,...). A
Уравнение A5.53) для #у при этом принимает вид
Для пространственно однородной фазы из условия нормировки
легко получаем &\ для s = l: У]=0. Для s = 2, 3... производные
d&\dq? и dUjdqf входят в уравнения A5.55) одинаково, поэтому
\
в этих случаях выражение для &s можно взять такого же вида,
как и Os:
Неизвестная функция f(|q,-—q/|)=f(
ослабления корреляции (/У-И) при
qi/l)=f(|q|) по условию
q|->-oo) должна обладать
свойством:
f{\q\)-+O при |qKoo. A5.56)
Очевидно, что
= Ъ /(iqi-q.+ii)= L /(iq.+i-q/i)-
Далее, функции Ч*(Iqi—qs+i|) и /(|qi—qs+i|) — четные функции
з
аргумента, т. е. зависят от l\\ (qf—^+iJj1/2 , а производная
а=1
^ а=1
нечетная функция q\a—qas+u и поэтому интеграл
=0. A5.57)
J
282
Кроме того,
у fld*-"/!) dus V ^(iqi-q/i) ,1558v
Подставляя A5.58) в A5.55) и учитывая A5.57), получим
V ( a/(lqi-q/l)
A5.59)
Таким образом, уравнения A5.55) распадаются на одинаковые
уравнения для f(|q|).
Производя в A5.59) замену переменных
qi—qs+i = qt—(q' + q j) = (qi— qj)— q/==q—q',
после интегриро'вания по qia получаем для f(|q|) интегральное
уравнение
f(\q\) + (l/4n)№(\q-q'\)f(\q'\)dq'=-4(\q\). .A5.60У
Постоянная интегрирования в A5.60) положена равной нулю в
соответствии с условием A5.56). Для решения уравнения A5.60)
применим к обеим его частям оператор Лапласа. Учитывая, что
(||) ( и
имеем
Af(|q|)-f(|q|)=4KS(q). A5.61)
Это уравнение того же вида, что и уравнение A5.43) в методе
Дебая, поэтому его решение аналогично решению A5.42):
Таким образом,
yj(qlt ...,q,)= V f(|qf-q/|)=- У —-^—- • е~* ~^ ,
•^ ^^ IЧ/ — Ч/1
Kt</<S l<t</<S
и ^S(qi,... ,qs) с учетом первого приближения (в безразмерных
переменных) равна
^^ |q/ — Ч/l
10* 283
Переходя к первоначальным переменным, получим
1—-ехр( —x|qc—
q|
Для бинарной функции распределения одноименно заряженных
частиц плазмы (с потенциалом взаимодействия +е2/г) имеем
er ' A5'63)
а разноименно заряженных частиц (с потенциалом взаимодейст-
взаимодействия —е2/г)
&?~(г)=1 + —е-™. A5.64)
Заметим, что формула A5.63) теряет свою пригодность при
малых г порядка eD = e2l&. Это обусловлено тем, что система
точечных заряженных частиц не может находиться в равновесии.
Необходим учет короткодействующих сил.
Зная бинарную функцию распределения системы, можно, как
известно, найти все ее термодинамические свойства. Для этого
достаточно воспользоваться выражением для энергии Гельмголь-
ца через бинарную функцию распределения A5.3):
(г, Х)гЧг.
Внешний термодинамический параметр X является множителем
при потенциале взаимодействия, входящем в ^(f), в случае
плазмы — при е2. Поэтому для плазмы
X) = 1 —*?L ехр (— кУТ-г), A5.65)
&t~(r, Я) = 1 + -^-ехр(—Y\fk -r), A5.66)
И
1 00
л я то.
F(B, V, N)=Fm4
A5.67)
Термическое уравнение состояния плазмы, ее энтропия и тепло-
теплоемкость могут быть вычислены по формулам
P=—{dF/dV)TN, S = -(dF/dT)vN, Cv = -T(d*F/dT*)VN.
284
В результате из выражения A5.67) получаем:
р = vRTIV—43№e*V8nNe*lkTV*, A5.68)
S = Sw—ilzNe^nNeymV, A5.69 J
A5.70)
Давление и энтропия плазмы меньше, чем идеального газа, что
объясняется преобладанием в ней сил притяжения. Теплоемкость
же плазмы больше теплоемкости идеального газа, что физически
также ясно: при повышении температуры плазмы приходится за-
затрачивать энергию не только на увеличение кинетической энергии
хаотического движения ее частиц, но и на увеличение средней по-
потенциальной энергии взаимодействия между частицами вследствие
изменения около каждой частицы облака противоположно заря-
заряженных частиц.
Отметим теперь те специфические свойства плазмы, которые
резко отличают ее от обычного реального газа.
1) Термическое уравнение состояния плазмы A5.68) имеет
вид
PV=vRT(l+A/yV), А=-
откуда замечаем, что в отличие от обычного реального газа
термическое уравнение состояния плазмы не выражается в ви-
риальной форме A5.18). Это означает, что в плазме взаимодей-
взаимодействие между частицами нельзя разделить на парные, тройные,...
взаимодействия, а саму плазму нельзя рассматривать как систему
экранированных частиц с короткодействующим потенциалом
взаимодействия.
2) Дальнодействующим характером кулоновских сил взаимо-
взаимодействия определяется также и другая особенность плазмы —
существование в ней собственных продольных колебаний: создан*
ное в некоторый момент изменение плотности электронов в плазме
не релаксирует, как плотность в обычном газе, а колеблется с
определенной частотой, зависящей только от концентрации элект-
электронов. Эти колебания вызываются тем, что изменение плотности
электронов в каком-либо месте плазмы связано с появлением в
этом месте объемного заряда, поле которого, действуя на движе-
движение смещенных электронов, приводит к появлению восстанавли-
восстанавливающей силы, пропорциональной их смещению. Под действием
этой силы электроны вибрируют с определенной частотой. Най-
Найдем ее. Для этого выделим мыслен-
мысленно в плазме с концентрацией п элек-
электронов прямоугольный параллелепи-
параллелепипед длиной dx и площадью сечения
5 (объем параллелепипеда dV=
= Sdx; рис. 48). Вследствие большой
массы ионов скорость их движения «2? x+dx
много меньше, чем у электронов, по-
поэтому ионы можно рассматривать Рис. 48
285
-j- +-+-+-+-+-
как неподвижные. Пусть в некоторый момент времени электроны
выделенного объема претерпевают по отношению к ионам смеще-
смещение 1(х). Тогда возникающий в этом параллелепипеде объемный
заряд
eSx en
dx i dx
Следовательно, плотность заряда
da d?
о = —— = — en —2- •
dV dx
Уравнение движения электрона
Напряженность 6 поля найдем из уравнения
сНу<§=4лр, или
откуда
& = —
Поэтому
|' 4Щ и
что указывает на возникновение продольных электрических коле-
колебаний в плазме с циклической частотой
(uo = V4nne2/m. A5.71)
При концентрации п=1016 м~3 электронов в плазме собственная
частота колебаний плазмы равна о>о = 5• 108 с, что соответствует
дециметровым волнам.
Впервые наличие колебания в плазме было установлено в
1906 г. Рэлеем и независимо в 1929 г. И. Ленгмюром, получившим
формулу A5.71) для частоты со0 (которая поэтому называется
ленгмюровской частотой колебаний плазмы).
Рассмотрим вопрос о термодинамической устойчивости плазмы.
С помощью формул A5.68) и A5.70) находим следующие усло-
условия устойчивости разреженной плазмы:
dV )т V* 2 V CTV6
т
— да
Из этих выражений для коэффициентов устойчивости видно,
что при одинаковых условиях плазма менее устойчива, чем
идеальный газ:
ар \ -^ vRT ( дР \вд т . т
) ^
cv
286
Термодинамика плазмы, построенная на основе первого при-
приближения бинарной функции распределения A5.63), совпадает с
термодинамикой дебаевской теории.
Построение дальнейших приближений представляет собой
сложную математическую задачу. Мы ограничимся только полу-
полученными результатами.
Глава 16
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
ДЛЯ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
В ТЕОРИИ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
В применении к газам и плазме уравнения цепочки Боголюбо-
Боголюбова для функций распределения A5.32) позволяют, как мы видели,
ввести соответственно газовый и плазменный малые параметры
и находить решение этих уравнений в виде разложения функций
распределения по степеням того или другого малого параметра.
В случае жидкости уравнения A5.32) не допускают выделения
малого параметра. Тем не менее наиболее важным является при-
применение метода функций распределения к построению статистиче-
статистической теории жидкостей. Это достигается другим, отличным от ме-
метода малого параметра, способом решения цепочки уравнений Бо-
Боголюбова. Этот способ основан на «обрыве» цепочки уравнений,
когда исходя из дополнительных физических соображений стар-
старшая функция распределения &~s (s>2) аппроксимируется выраже-
выражением, включающим в себя более младшие функции Ук (k<s),
В результате получается одно или система интегральных уравне-
уравнений, замкнутых относительно младших функций. Решив эти ин-
интегральные уравнения, можно найти равновесные свойства изучае-
изучаемой системы.
Рассмотрим некоторые интегральные уравнения для функций
распределения.
§ 75. Уравнение самосогласованного поля
Найдем интегральное уравнение для одночастичной функции
распределения, которое определяет ее основное приближение в
теории кристаллического состояния.
Первое уравнение цепочки Боголюбова A2.73) для функций
распределения ps (qb ..., qs) имеет вид
Р.(Я, 4W-0. A6.1)
В кристаллах одночастичная функция pi(q) является периодиче-
периодической функцией с острыми максимумами в узлах решетки, т. е.
может быть представлена в виде
287
'(q), A6.2)
где pi^q) отлична от нуля только около 1-го узла кристалличе-
кристаллической решетки и равна нулю в остальном пространстве, причем об-
области, где pi* (q) различных узлов отличны от нуля, не только не
пересекаются, но и их линейные размеры Ь малы по сравнению
с расстоянием а между ближайшими соседями. Так что движение
каждой частицы кристалла в любой момент времени определяется
взаимодействием с целым коллективом равноправных ближайших
соседей и частицами на других координационных сферах. Поэтому
движения любых двух частиц кристалла приближенно можно
считать независимыми и, следовательно, положить бинарную
функцию распределения мультипликативной *
P2(q, q/)=Pi(q)pi(Q/), A6.3)
так как в кристалле
A6.4J
Подставляя A6.3) в A6.1), получим замкнутое нелинейное ин-
интегральное уравнение самосогласованного поля (с исключенным
самовоздействием) для одночастичной функции распределения
кристалла:
{
o(|q-q'|)Pi(qW=0, A6.5)
где X — постоянная нормировки.
Приближение самосогласованного поля не учитывает корреля-
корреляцию между частицами кристалла, но является основным в стати-
статистической теории кристаллического состояния. Его дальнейшее
улучшение мы находим в корреляционной теории кристалла **.
§ 76. Интегральное уравнение
Боголюбова — Борна — Грина
для радиальной функции распределения
в суперпозиционном приближении
Одночастичная функция распределения пространственно одно-
однородной системы (жидкость, газ) #"i(q) = l, и ее состояние опре-
определяется бинарной (радиальной) функцией распределения
(индекс у бинарной функции принято опускать). Найдем интег-
* Базаров И. П. Статистическая теория кристаллического состояния. —
М.: Изд-во МГУ, 1972.
** Базаров И. П., Николаев П. Н. Корреляционная теория кристал-
кристалла. — М.: Изд-во МГУ, 1981.
288
ральное уравнение для g(r). Исходим из второго уравнения це-
цепочки Боголюбова A5.32):
1
^1 6 dq?
При |qi—q2|->oo
1 С
(iQi-Чз!)
Аналогично трехчастичная функция распределения ^"e(qi, q2, q3)
при удалении на бесконечность одной из частиц стремится к
двухчастичной функции распределения оставшихся двух частиц.
Основываясь на этом, Дж. Кирквуд предложил аппроксимацию
, q2, q3)=g(|qi—q2|)g(|q2—Яз|)г(|Язг-Я1|), A6.7);
которая называется суперпозиционным приближением. В этом
приближении не учитывается влияние третьей частицы на вероят-
вероятность положения пары других частиц даже тогда, когда все три
частицы сильно взаимодействуют друг с другом.
Подставляя A6.7) в A6.6), получим замкнутое уравнение для
|l)
,пе(|м1) +
которое с помощью функции
Е(х)=
приводится к интегральному уравнению Боголюбова — Борна —
Грина для радиальной функции распределения частиц жидкости
и плотного газа в суперпозиционном приближении:
j ?(/)*?fc}pdp=O. A6.8)
|г-р|
Оно качественно верно описывает все свойства жидкости, хотя
точность многих количественных оценок получается небольшой.
§ 77. Уравнение Перкуса — Йевика
В современной теории жидкости одним из наиболее точных
уравнений для радиальной функции распределения является урав-
уравнение Перкуса — Йевика, предложенное ими из интуитивных сооб-
соображений в 1958 г.
289
Изложим основные идеи установления этого уравнения.
Боголюбовым было показано, что частичные функции распре-
распределения #%(qi,... ,qs) могут быть выражены через функциональ-
функциональные производные от энергии Гельмгольца по внешнему полю в
пределе, когда это поле равно нулю. Такое функциональнее диф-
дифференцирование энергии Гельмгольца привело к определению
прямой корреляционной функции с (г) в виде интегрального урав-
уравнения
)dr\ A6.9)
или
^J A6.9а)
где функция h(r)=g(r)— 1 называется полной корреляционной
функцией (h(rij)=hij, c(nj) =C;j, dri = di). Такие названия функ-
функций с (г) и ft (г) обусловлены интерпретацией смысла соотношения
A6.9). Действительно, подставляя в интеграл правой части соот-
соотношения A6.9а) даваемое им выражение для функции ft, получим
бесконечную цепочку
^- f
ГГс13с34с42сC^4 + A6.10)
которая указывает на то, что полная корреляция fti2 между час-
частицами 1 и 2 равна прямой корреляции с{2 этих частиц и не-
непрямой корреляции, возникающей из всех возможных цепей пря-
прямых корреляций. Соотношение A6.9) было введено Орнштейном
и Цернике еще в 1914 г. и называется в настоящее время урав-
уравнением Орнштейна — Цернике.
Поскольку ft (r) =g{r) + 1, то уравнение Орнштейна — Цернике
можно рассматривать как интегральное уравнение для радиаль*
ной функции g(r), где функция с (г) неизвестна. Исходя из физи-
физического смысла функции с (г), Перкус и Йевик предложили для
нее выражение
c(r)=g(r) A—е-ф^&). A6.11)
Подставляя это выражение для с (г) в уравнение Орнштейна —
Цернике A6.9), получим для радиальной функции распределения
g(r) уравнение
которое называется уравнением Перкуса — Йевика.
Уравнение Перкуса — Йевика обладает тем замечательным
свойством, что оно допускает точное аналитическое решение для
системы частиц с потенциалом твердых сфер, которая является
достаточно хорошим первым приближением к реальной жидкости.
290
Найденное на основе этого точного решения из выражения для
давления A5.38) уравнение состояния системы твердых сфер
имеет вид
где г| = я'(у3/б1>, а — диаметр твердых сфер, v=V/N.
В настоящее время предложены способы улучшения этого
первого приближения, поэтому точное решение уравнения Перку-
са — Йевика A6.12) для системы твердых сфер имеет важное
значение в теории жидкого состояния.
Помимо простых жидкостей и кристаллов метод функций рас-
распределения и интегральные уравнения для них эффективно ис-
используются также для исследования более сложных статистиче-
статистических систем с дополнительными степенями свободы (например,
ориентационными), таких как жидкие кристаллы или мезофазы *,
занимающие промежуточное положение между изотропной жид-
жидкостью и кристаллическим твердым телом.
Обсуждение этих вопросов, а также решение рассмотренных
интегральных уравнений для функций распределения выходит за
рамки настоящей книги и содержится в монографической лите-
литературе.
Глава 17
ТЕОРИЯ РАВНОВЕСНЫХ ФЛУКТУАЦИИ
Равновесные термодинамические параметры представляют
собой, как известно, средние значения соответствующих динами-
динамических величин, зависящих от координат и импульсов всех частиц
системы. Так, внутренняя энергия есть среднее значение функции
Гамильтона системы и т. д.
Движение частиц статистической системы приводит к отклоне-
отклонению ее динамических величин от средних значений. Эти само-
самопроизвольные отклонения динамических величин от их равновес-
равновесных статистических средних значений называются флуктуа-
циями.
Статистическая физика позволяет вычислять не только равно-
равновесные значения макроскопических параметров многочастичных
систем, но и флуктуации этих параметров.
Флуктуациями обусловлены многие экспериментальные наблю-
наблюдаемые явления. Так, локальные флуктуации плотности (и, следо-
следовательно, показателя преломления прозрачной среды) являются
причиной молекулярного рассеяния света. Наиболее сильное рас-
рассеяние наблюдается в жидкости вблизи критической точки (кри-
(критическая опалесценция), где флуктуации плотности особенно ве-
* Базаров И. П., Геворкян Э. В. Статистическая теория твердых и
жидких кристаллов. — М.: Изд-во МГУ, 1983.
291
лики. Флуктуации вызывают шумы в электрических цепях и сни-
снижают чувствительность всех измерительных приборов. С флуктуа-
циями связаны также диссипативные характеристики необратимых
процессов переноса, например диффузии, теплопроводности, вяз-
вязкости и др.
Флуктуации наблюдаются, как в равновесных, так и неравно-
неравновесных статистических системах. В соответствии с этим различают
равновесные и неравновесные флуктуации. В этой главе мы будем
рассматривать флуктуации систем, находящихся в состоянии тер-
термодинамического равновесия. При этом за время наблюдения
каждый из флуктуирующих параметров много раз проходит через
равновесные средние значения.
Неравновесные флуктуации наблюдаются либо в системах, да-
далеких от равновесия, когда время наблюдения меньше времени
установления термодинамического равновесия, либо при наличии
внешних воздействий (например, разности температур, электриче-
электрических напряжений или давлений на границах системы), поддер-
поддерживающих вынужденные отклонения от равновесного состояния *.
Неравновесные флуктуации рассматриваются в кинетической тео-
теории неравновесных систем.
Теория равновесных флуктуации тесно связана с вопросом ус-
устойчивости состояния термодинамического равновесия (см. гл. 6).
Их взаимоотношение аналогично отношению теории устойчивости
и теории малых колебаний в механике. Подобно тому, как пара-
параметры малых колебаний определяются по значениям производ-
производных потенциальной энергии механической системы в положении
равновесия, в теории равновесных флуктуации их характеристики
определяются значениями термодинамических производных в со-
состоянии равновесия или соответствующими моментами равновес-
равновесных канонических распределений. Полученные ранее условия
устойчивости относительно вариации тех или иных термодинами-
термодинамических параметров соответствуют положительности дисперсии
соответствующих величин в теории флуктуации.
Рассмотрим вначале статистическую теорию флуктуации, осно-
основанную на различных функциях распределения, а потом — квази-
квазитермодинамическую теорию флуктуации, в которой термодинами-
термодинамические функции системы предполагаются известными.
§ 78. Вычисление флуктуации
методом Гиббса
Количественно флуктуации характеризуются корреляционны-
корреляционными моментами (корреляторами) различных порядков, имеющими
в случае двух величин <pi (q, p) и фг(Ч, р) вид
* Не следует смешивать эти реальные воздействия с фиктивными полями
(силами), которые вводятся для описания самопроизвольных флуктуационных
отклонений (см. ниже).
292
где в зависимости от условий усреднение проводится по тому или
иному ансамблю.
В большинстве случаев флуктуации достаточно полно харак-
характеризуются квадратичными корреляторами, т. е. величинами
(<Pi — <Pi) (Ф2 ~ Ф2) = Л <Pi • Л Фг = Ф1Ф2—Ф1 * Ф2.
Выражение (ДфJ называется дисперсией или квадратичной флук-
флуктуацией величины ф, у (ДфJ = Д (ф) — ее флуктуацией и
Д(ф)/ф=.6ф — ее относительной флуктуацией
Выражение Дф1-Дф2 будем называть корреляцией флуктуа-
флуктуации величин ф1 и ф2.
В гл. 12, 13 мы рассмотрели микроканоническое, каноническое
и большое каноническое распределения Гиббса, соответствующие
различным способам выделения системы (различным граничным
условиям) и наборам переменных, описывающих состояние сис-
системы (?, V, N\ Г, V, N и Г, У, ji). Значения этих параметров для
каждого данного распределения фиксированы и входят в него в
качестве параметров. Поэтому их флуктуации в рамках этого
распределения равны нулю. Сопряженные этим параметрам дина-
динамические величины испытывают флуктуации.
Как отмечалось в § 54 при обсуждении термодинамической
эквивалентности ансамблей Гиббса, эта эквивалентность не рас-
распространяется на флуктуации, поскольку их величина зависит от
того, какие параметры системы фиксированы, а какие испыты-
испытывают флуктуации.
При рассмотрении флуктуации помимо трех канонических ан-
ансамблей Гиббса используется также изотермическо-изобарический
ансамбль систем в термостате при постоянном внешнем давлении
Р и переменном значении объема У (например, газ в цилиндре
с поршнем). Макроскопическое состояние рассматриваемой сис-
системы определяется термодинамическими переменными Г, Р, N,
а соответствующее распределение рТ (q, p) микросостояний систе-
системы найдем из канонического распределения, подставляя в него
значение энергии Гельмгольца F через энергию Гиббса G (F==
= G—PV):
P(q, P,r)«pr(q. Р)=ехр(С-^;Я^^) A7.1)
С помощью канонического и большого канонического распределе-
распределений Гиббса и изотермическо-изобарического распределения A7.1I
нетрудно найти выражения для квадратичных корреляторов в этих
ансамблях. Действительно, для названных ансамблей имеем:
\ A7.2)
293
tf = ^ = ? j>exp (
A7.4)
Дифференцируя эти выражения соответственно по в, ^ и Р, на-
находим дисперсии Я, / и У:
дУ
A7-5)
A7.6)
(AVJ=— в-^—. A7.7)
Дифференцируя A7.2) по V, получим корреляцию флуктуации
энергии и давления системы <в термостате:
дН С дН [Р — Н\<Г] I Си (F — H\fdF дН \ лг
= \ ехр )аТ н \ Н ехр [ аТ =
в JU )
^^ГР"м, A7.8)
так как
mvm» г9 dV dV
Из A7.8) имеем
и, используя термодинамическое соотношение
получаем
А^АР'м^в2^. A7.9)
Для вычисления корреляций флуктуации энергии и объема исхо-
исходим из выражения для средней энергии системы изотермическо-
изобарического ансамбля:
Я= Гяехр (G~~Pq~H) dTdT. A7.10)
Дифференцируя A7.10) по Р, найдем
294
Корреляцию энергии и числа частиц системы в термостате легко
найти, дифференцируя A7.3) по 0:
об
A7.12)
Кроме рассмотренных относительно малых флуктуации полной
энергии, полного числа частиц и других параметров в статисти-
статистических системах существуют пространственно неоднородные
флуктуации (плотности энергии, плотности числа частиц, давле-
давления и др.), локальные значения которых имеют значительно боль-
большую относительную величину. Причем такого рода флуктуации
испытывают и величины, граничные или полные значения которых
фиксированы. Например, в изотермической (Г, Vy N) системе су-
существуют локальные флуктуации температуры и плотности, кото-
которые, однако, нельзя вычислить с помощью канонического распре-
распределения Гиббса.
Аналогично изложенному вычисляются флуктуации и кванто-
квантовых систем. Покажем это на примере вычисления флуктуации
энергии системы квантовой системы в термостате;
= Я2 —(ЯJ,
^expf
откуда _
л?
(ДЯJ = 62 —, A7.13)
<30
что совпадает с выражением A7.5) для дисперсии энергии класси-
классической системы в термостате.
§ 79. Вычисление флуктуации
методом функций распределения
Флуктуации различных физических величин можно находить
также методом функций распределения.
Многие из наиболее важных величин в статистической физике
являются величинами или аддитивного типа
A7.14)
295
или бинарного типа
? f(dt, q,). A7.15)
Вычислим флуктуацию величины аддитивного типа A7.14).
Среднее значение этой величины равно
•"'dqN)dqi =
A7.16)
где ^i(qi) = VjD(qi,... ,qiv)dq2... dqN — одночастичная функция
распределения, a D(qi,...,q^) — конфигурационное распределе-
распределение Гиббса.
Возводя A7.4) в квадрат, получим
A7Л7>
Среднее от квадрата аддитивной величины A7.17) равно
qx... dqN =
A7.18)
где ^(Чь Чг) —бинарная функция распределения.
Используя A7.16) и A7.18), найдем дисперсию величины А:
"=А*—(Af = J- Г f f (<ц) / (q2) &г (qx, q2) dqt dq2 +
V V
-I \/2 (q) ^1 (q) dq—(—I f(q)yi(q)dq ] . A7.19)
v J \ и J /
Таким образом, для вычисления флуктуации величин аддитивного
типа необходимо знать одночастичную ^i(q) и двухчастичную
^Mqi, q2) функции распределения.
296
Для определения флуктуации величин бинарного типа (напри»-
мер, потенциальной энергии системы частиц UN(qx, ..., q^) =
Ф AЧг — Я/1) необходимо знать #(Яь Яг), #~з(Яь Яг, Яз>
<
(ь Я2, Яз, Я4).
Пользуясь формулой A7.19), вычислим квадратичную флуктуа-
флуктуацию числа частиц в некотором объеме Va внутри объема V прост-
пространственно однородной системы (Уа<СУ), для которой
г(|Я1—Я2|).
Введем функцию
: A, если q лежит в Va\
(О, если q лежит вне Уа.
Тогда число частиц, находящихся в Vay равно
. A7.20)
Подставляя A7.20) в A7.19), получим
Если линейные размеры выделенной области (V«I/3 значительна
больше радиуса действия молекулярных сил, то интегрирование в
A7.21) можно распространить на бесконечное пространство, так
как ^2(|ql)-*-l при |
00
^(^Jj A7.22>
A7.23>
ИЛИ
v
поскольку Va/v = NVa/V=Jfa (индекс а в A7.23) опущен).
В качестве примера рассмотрим газ твердых сфер, когда
оо при г<С а;
при г у а
и в нулевом приближении
[ 0 при г < а;
при г > а.
297
Согласно A7.23) в этом газе
где ио =
В плазме аналогично A7.22) имеем
A7.24)
где ^г"+(г) и &t~ (г)— бинарные функции соответственно одно-
одноименно и разноименно заряженных частиц.
§ 80. Квазитермодинамическая
теория флуктуации
Вычисление флуктуации динамических величин с помощью
равновесных функций распределения представляет собой в общем
случае такую же сложную задачу, как и вычисление средних зна-
значений и термодинамических потенциалов. Поэтому часто исполь-
используется так называемая квазитермодинамическая (полуфеномено-
(полуфеноменологическая) теория флуктуации, в которой при определении флук-
флуктуации различных величин предполагается, что термодинамиче-
термодинамические функции системы известны. Эта теория ограничена задачами,
в которых малую часть системы можно характеризовать термоди-
термодинамическими параметрами. Вследствие этой посылки она имеет
существенно приближенный характер, поскольку принимать пара-
параметры малой системы термодинамическими правомерно только в
случае больших систем, когда флуктуации, которыми мы интере-
интересуемся, пренебрежимо малы.
Квазитермодинамическая теория флуктуации явилась основой
развития термодинамики необратимых процессов. Она позволяет
рассматривать флуктуации в системе как флуктуацию ее термо-
термодинамического состояния, т. е. как переход системы из равновес-
равновесного состояния в неравновесное. Это неравновесное состояние
системы представляется (как это мы делали в § 26 при обсужде-
обсуждении термодинамической устойчивости) как новое равновесное ее
состояние с большим числом параметров Ь\>..., bk и соответст-
соответствующих им фиктивных сопряженных сил /li, ...,Л&, «удерживаю-
«удерживающих» систему в равновесии.
Например, силовое внешнее поле (типа гравитационного) позво-
позволяет реализовать неоднородное распределение локальной плот-
плотности. Состояние с неоднородным распределением температуры
можно описать, разделив систему на ячейки с помощью адиабати-
адиабатических перегородок, которые в этом случае играют роль вспомога-
вспомогательных полей. С помощью этих полей осуществляется равновес-
равновесный переход системы из начального состояния в конечное. Энтро-
Энтропия соответствующего неравновесного состояния S' принимается
равной энтропии равновесного состояния во вспомогательных по-
лях (или сумме по ячейкам). Внутренняя энергия, энергия Гельм-
гольца, энергия Гиббса и другие термодинамические потенциалы
к
отличаются от соответствующих значений на величину v Anbn
потенциальной энергии. Параметры Ъп представляют собой сред-
средние значения соответствующих динамических величин gb . . . , \k
по новому равновесному состоянию.
Рассмотрим изолированную систе-
систему, которую условно разобъем на ма-
малые области (ячейки), характеризуе-
характеризуемые локальными термодинамическими
параметрами состояния (рис. 49).
Внутри каждой области существует
локальное термодинамическое равно-
равновесие, однако значения параметров
различны и соответствуют флуктуаци-
онным отклонениям от равновесных
значений для системы в целом. Эта
картина соответствует так называе-
называемому состоянию неполного равновесия
(квазиравновесному состоянию).
Считая флуктуационные откло-
отклонения параметров в различных
областях малыми, определим энтропию S' системы в состоянии:
неполного равновесия в виде суммы энтропии областей
;¦ = k In П П = k In Г, A7.25)
1
1
1
<
J
i
I
—\ 1—
I
1
i
i.
i
i
i
•
I I I I
—1—1—1—1—
I
I
fe?
I
I
1
1
Ti'
i
i
i
i
—f—
i j i .
i
i
i
Рис. 49
где Г', Гг — фазовые объемы соответственно системы и областей.
Вероятность такого отклонения от состояния равновесия систе-
системы определяется, по Эйнштейну, отношением чисел способов реа-
реализации неравновесного (квазиравновесного) Г' и равновесного Г
состояний (их фазовых объемов):
(^) A7.26)
Формула A7.26) является основной в квазитермодинамическойг
теории флуктуации и, как легко видеть, непосредственно связана
с принципом Больцмана для вероятностей различных макросо-
макросостояний изолированной системы.
Пусть отклонение системы от равновесного состояния характе-
характеризуется одним параметром Tj=g/—|, так что в равновесном со-
состоянии ц = 0. Разложим энтропию S'(rj) квазиравновесного со-
состояния в ряд Тейлора по степеням г\:
т]2 + ... . A7.27)
2 \ дц2
Поскольку по второму началу термодинамики энтропия изолиро-
299
званной системы в равновесном состоянии максимальна, то
I ] ) |л \ n / h
Ограничиваясь в разложении A7.27) членами второго порядка,
получим из формулы Эйнштейна A7.26) гауссово распределение
для малых флуктуации:
, A7.28)
где Я= —( ) >0, А определяется из условия нормировки
\ dxf 1 1т1=о
00
j w{x\)dr\=\
00
и равна
Л = У-У2я.
Таким образом,
™{Ц)=\/Г~?гех1р{~тц*)' A7*29)
и дисперсия параметра г\
= 1Д. A7.30)
Если отклонение системы от равновесного состояния характери-
характеризуется несколькими параметрами i\u...,r\k9 то аналогично A7.28)
имеем
где вследствие устойчивости равновесного состояния матрица к
положительно определена. С помощью линейного преобразования
квадратичная форма Jj^*/1^/ может быть приведена к диаго-
сальному виду, так что
тде %(>0 fJ
Рассмотрим теперь флуктуации в неизолированных системах.
Поступая так же, как при выводе канонического и большого
канонического распределений из микроканонического, выделим в
объединенной изолированной системе макроскопическую область
(подсистему), содержащую локальное флуктуационное отклоне-
300
ние от равновесного состояния. Контакт подсисгемы с термоста-
термостатом может быть произвольным, например термическим, мате-
материальным и т. д.
Предполагая по-прежнему аддитивность энтропии неравновес-
неравновесного состояния, имеем
где ASo = 5o/—So, AS = S/—S и AST = S/—ST — изменения энтропии
объединенной системы, подсистемы и термостата соответственно
относительно их равновесных значений.
Вследствие сохранения энергии, объема и числа частиц объе-
объединенной изолированной системы, очевидно,
Д? + Д?т = 0, AV+AVT = 0, AN+ANT = 0.
Далее, считая в соответствии со сделанными ранее предположе-
предположениями процесс флуктуационного отклонения от равновесного со-
состояния квазистатическим, находим из второго начала термоди-
термодинамики
AST = -L (Д?т + Рт AVT -Ит ANT).
Отсюда из условий равновесия F.10) подсистемы с термостатом
Т = ТТ, P = pr?i \i = \xT получаем выражение для изменения энтропии
объединенной системы
AS0 = -{AE + PAV — \iAN—T AS)
и из формулы Эйнштейна A7.26) для вероятности
и;~ехр{— (AE + PAV—iiAN— TAS)/kT}. A7.33)
Из формулы A7.33) совершенно аналогично преобразованию ус-
условий устойчивости следует, что для системы, заданной набором
фиксированных (нефлуктуирующих) переменных, вероятность
квазиравновесного состояния пропорциональна экспоненте от взя-
взятого с обратным знаком отношения изменения соответствующего
термодинамического потенциала в этих переменных к температуре.
Действительно, для
а) изолированной системы (?, V, iV)
o;~exp(AS/ife), A7.34)
б) системы в термостате (Г, V, N)
w _ ехр ( - А? ~~ Т AS W ехр (— AF/feT), A7.35)
\ kT I
301
в) системы в термостате с переменным числом частиц
(Т, V, ц)
( АДГД5ДУ\ A7.36)
kT I
г) изотермическо-изобарической системы (Г, Р, Af)
) =ехр (—AG/kT). A7.37)
Заметим, что в отличие от выражения для AST изменение
энтропии системы при флуктуации по второму началу равно
AS = — (AE + PAV—цДМ—WJ,
где Wi= —TASq — работа введенных выше вспомогательных сил
(полей), необходимая для равновесного перевода системы из рав-
равновесного в квазиравновесное состояние. Формулы A7.34) — A7.37)
выражают принцип Больцмана для систем в различных условиях.
Разлагая изменение внутренней энергии АЕ в ряд Тейлора по
изменениям ее естественных, переменных S, V, iV и учитывая, что
/ дЕ \ =т (j№_\ =_p (дЕ_\
\ 6S )VfN ' \ dV Jt.n ' \ ON )t,v И>
получим
AE = TAS—PAV + \iAN+42(AT.AS—APAV+\A\i-AN) +....
Подставляя'это разложение в A7.33), находим общую формулу
для вероятности флуктуации состояния неизолированной системы:
— ?—
j. A7.38)
В квазитермодинамической теории флуктуации предполагается,
что относительные флуктуации малы. Это предположение обычна
выполняется. Действительно, вычисленные нами методом Гиббса
относительные флуктуации энергии и числа частиц пропорцио-
пропорциональны N~1/2. К такому же результату приводит при различных
фиксированных переменных квазитермодинамическое выражение
A7.38), из которого следует гауссово распределение (*). Флуктуа-
Флуктуации с такой асимптотикой F^ — N~i/2) называют термодинамиче-
термодинамическими флуктуациями.
В тех случаях, когда относительные флуктуации не малы (на-
(например, вблизи критической точки, в окрестности фазовых перехо-
переходов), вычисление флуктуации (как и рассмотрение условий устой-
устойчивости) требует уточнения. Гауссово распределение, очевидно,
становится плохим приближением. Более того, при этом нарушает-
нарушается большинство из сделанных нами выше предположений.
302
Рассматриваемые нами подсистемы являются однородными,
так как характеризуются одной температурой, давлением и т. д.
Вычислим флуктуацию объема и числа частиц по термодина-
термодинамической теории флуктуации.
1. Рассмотрим систему в термостате с постоянным числом
частиц, а в качестве независимой переменной возьмем объем V.
Тогда ДГ = 0, AiV = 0, &Р= (^-)т N^V и согласн° A7.38)
w = Аехр I — (—) (АУJ1. A7.39)
F I 2kT \ dV )t,nK J V '
Сравнивая A7.39) с A7.29), замечаем, что к = —( — )
kT \ dV )t,n
и, используя формулу A7.30), получим
dV
{tSVY=-kT Ш , A7.40)
\ дР )t,n
что в точности совпадает с квадратичной флуктуацией объема, вы-
вычисленной с помощью канонического распределения Гиббса A7.7).
2. Для системы в термостате (АГ = 0, AV = 0) с переменным чис-
числом частиц в качестве независимой переменной возьмем N. Тогда
dN Jt,v
2kT \ dN )t,v
Следовательно, X = f —^~ ] , и
kT \ dN )t,v
= kT( — \ , A7.41)
V d\i Jt,v
что совпадает с выражением A7.6) для (ANJ, полученным мето-
методом Гиббса. Мы преобразуем формулу A7.41), найдем выраже-
выражение для сжимаемости через бинарную функцию распределения.
Так как
^ N N N
ТО
dN )t,v \ дР )t,v\ dN )t,v N \ dN ]t,v'
Вследствие аддитивности N=Vf(P, T) и, следовательно, Р =
= P(V/N, T). Поэтому
dP \ dP V ( dP \ V
dN Jt,v d(V/N) N2 \ dV Jt,n N
303
и
/ AT \ 9. t,T«
—. A7.42)
dV t.n
Сравнивая (ANJ по статистической теории A7.23) с (ANJ по
квазитермодинамической теории A7.42), получаем выражение для
изотермической сжимаемости
ь—т(^L-Fi' + T-J^w-1"**}- <1743>
о
В квазитермодинамической теории флуктуации выбор перемен-
переменных состояния системы, как в термодинамике, произволен. В ста-
статистической же теории флуктуации система описывается статисти-
статистическим ансамблем, состояние которого определяется набором па-
параметров, зависящих от физических условий. Эти параметры при
заданных условиях по определению флуктуировать не могут,
флуктуации испытывают другие параметры, и, следовательно,
флуктуирующие параметры нельзя выбирать произвольно. Поэто-
Поэтому в некоторых случаях квазитермодинамическая теория флук-
флуктуации приводит к расхождениям со статистической теорией флук-
флуктуации. Например, по квазитермодинамической теории
AVAP=—kT,
и по теории ансамблей
§ 81. Флуктуационные явления
Выше было показано, как вычисляются флуктуации различных
величин равновесных систем. Мы видели, что обычно флуктуации
относительно малы и ими можно пренебречь. Однако в ряде физи-
физических явлений флуктуации играют определяющую роль. Рассмот-
Рассмотрим некоторые такие флуктуационные явления.
1. Критическая опалесценция.
С 1893 г. известно, что в критическом состоянии газ особенно
сильно рассеивает свет; он начинает, как говорят, опалесцировать.
М. Смолуховский впервые A908) указал, что критическая опале-
опалесценция возникает вследствие увеличения флуктуации плотности
газа. Из-за неоднородного распределения плотности при флуктуа-
циях коэффициент преломления среды в разных точках различен,
и это вызывает рассеяние света.
По расчетам Эйнштейна, интенсивность света /, рассеянного
объемом V газа или жидкости в данном направлении, пропорцио-
304
нальна квадратичной флуктуации плотности в нем:
/~(ДрJ-У. A7.44)
Из формулы A7.7) для флуктуации элемента объема v, выделен-
выделенной в газе массы т, имеем
dv
где величина v(dP/dv)T не зависит от размеров элемента объема
v и является константой вещества (поэтому v в этом выражении
можно считать удельным объемом вещества).
Так как при флуктуации объема v масса газа m = pv в нем
остается постоянной, то рДа + иДр = 0, откуда (ДрJ= (р/^J(АоJ.
Усредняя это равенство, и пренебрегая малыми изменениями р и
и, поскольку (р/иJ Уже умножается на малую величину (At;J,
получаем
dv
kTV
дР
dv
A7.46)
Отсюда видно, что при приближении к критической точке величи-
величина — (dP/dv)T уменьшается, а интенсивность рассеянного света
возрастает.
В критической точке (dP/dv)T = 0, и согласно A7.46) интен-
интенсивность рассеянного света бесконечна. В действительности же
рассеяние в критическом состоянии очень велико, но конечно.
Формула A7.46) в этом случае (и практически до 1—2 К от кри-
критического состояния) неприменима, так как она получена в пред-
предположении статистической независимости флуктуации плотности
в различных элементах объема v (в том числе и соседних) рас-
рассеивающего объема V.
Теория рассеяния света в критическом состоянии была развита
Л. Орнштейном и Ф. Цернике. Согласно этой теории
kTV , A7.47)
дР
—
dv
где а — некоторая постоянная для данного газа и частоты падаю-
падающего света.
Вдали от критической точки величина —v(dP/dvI! велика по
сравнению с а2, в A7.47) ей можно пренебречь, и мы получаем
305
формулу Эйнштейна A7.46). Вблизи критической точки (dP/dv)T-*-
-й); / растет и в критической точке максимальна.
2. Флуктуационный предел чувствительности измерительных
приборов.
Флуктуации накладывают ограничение на точность отдельных
измерений, т. е. приводят к пределу чувствительности измеритель-
измерительных приборов. Действительно, при однократном измерении, оче-
очевидно, невозможно регистрировать эффект той же величины, что
и флуктуации, вызванные тепловым движением молекул в самом
приборе.
Для повышения чувствительности и измерения физической ве-
величины, значение которой меньше флуктуации самого прибора, не-
необходимы многократные измерения или изменение конструкции
прибора.
Найдем предел чувствительности пружинных весов, газового
термометра и зеркального гальванометра при однократном изме-
измерении.
Пружинные весы. Пусть коэффициент пружины равен а, вер-
вертикальное положение указателя отсчитывается вниз по оси q с
началом отсчета в точке равновесного (среднего) положения ука-
указателя без груза. Когда координата указателя равна q, потен-
потенциальная энергия пружины U = aq2/2 и средний квадрат само-
самопроизвольного отклонения указателя от положения равновесия по
теореме о вириале (q =0] равен q2 = @/a. Положение указа-
указателя #1 ПРИ грузе М найдем из равенства Mg = aqi. Массу М
можно измерить, если q1>V*q2 или Mq/a > У^в/а. Наименьшая
масса, которая может быть измерена при отдельном взвешивании,
равна
т = — У1&. A7.48)
S
В практике для взвешивания малых масс применяются весы, в
которых «пружиной» служат стеклянный или кварцевый стержень,
по прогибу конца которого определяют координату д.
Газовый термометр. Об изменении температуры в газовом тер-
термометре судят по изменению объема (при постоянном давлении)'.
Считая термометрическим веществом идеальный газ, имеем 7=
= PV/kN. Точность измерения Т связана с точностью измерения
объема V формулой
&T= — 6V = —8V.
kN V
Но вследствие флуктуации объема его величина известна с точ-
точностью до
AV= V —kT(dV/dP)T,
306
лоэтому температура может быть измерена с точностью, не пре-
превышающей
="f V ~kT {дУ1дР)т=
которая, правда, практически недостижима, так как N в газовых
термометрах порядка 1020
б Т/Т -Ю-10.
Зеркальный гальванометр. Относительные точности взвешива-
взвешивания на пружинных весах (т/М~Ю-5 для М = 1 мг при комнатной
температуре) и измерения температуры газовым термометром
(бГ/Г — 10~10), обусловленные флуктуациями подвижных частей из-
измерительных приборов, в обычных условиях превышают чувстви-
чувствительность этих приборов, вызванную другими причинами. Поэтому
в указанных случаях флуктуации в приборах практически не вли-
влияют на точность измерения.
Однако известны приборы, в которых флуктуационный предел
чувствительности экспериментально достижим. Однократное из-
измерение с помощью таких приборов оказывает влияние на точ-
точность измерения. В качестве примера рассмотрим зеркальный галь-
гальванометр. Сила тока / измеряется по углу отклонения ср легкого
зеркальца с катушкой, подвешенных на тонкой, обычно кварцевой,
нити. Предел чувствительности гальванометра определяется значе-
значением среднего квадратичного угла поворота зеркальца, вызванно-
вызванного тепловым движением молекул зеркальца и нити. Вычислим эту
величину.
При отклонении зеркальца на угол ср от равновесного положе-
положения ф = 0, потенциальная энергия кручения нити при малых углах
равна
?/(Ф)=аФ2/2,
где а — модуль кручения нити. Средний квадратичный угол само-
самопроизвольного поворота зеркальца от положения равновесия по
теореме о вириале равен
Эта величина ставит предел чувствительности единичного из-
измерения зеркальным гальванометром. Многократные измерения
позволяют во много раз понизить этот предел. При_ комнатной тем-
температуре и а=10~12 Дж (для кварцевой нити), (ф2I/2 = 2-10~4 рад.
Наблюдаемые колебания нулевой точки зеркального гальваномет-
гальванометра объясняются именно этими флуктуациями.
307
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Активность 138, 139
Ансамбль статистический 185
— изотермическо-изобарический
294
293,
Боголюбова цепочка уравнений 212,
213, 277, 287
Бозе—Эйнштейна статистика 229
Бозе-Эйнштейна распределение 230—
232, 255
Бозе-эйнштейновская конденсация
241—243
Бозоны 229
Больцмана постоянная 35, 197, 228
— принцип 62, 299, 302
— распределение 227, 264
Большая статистическая сумма 205,
219
Большое каноническое распределе-
распределение классическое 204, 205
квантовое 218, 219
Большой статистический интеграл
205
Вариационный принцип 209, 210
Вириальное разложение 29, 269, 272
Восприимчивость магнитная 132
Время релаксации 21, 22
Вырождение 79, 221, 233, 241
Вырожденный газ 79, 236—243
Газ идеальный 28, 79, 226—243
Гамильтона уравнения 184
— функция 184, 199, 210
Г-пространство 185
Гармонический осциллятор 243—246
Давление поверхностное 153
— световое 145, 146, 254
Дебаевский радиус 279, 281
Дебая модель твердого тела 258—
261
Дисперсия 206, 293, 294
Закон Вина 145, 149, 150, 254
— Дебая 133, 261
— Джоуля 28, 34
— Дюлонга и Пти 256, 257
— индукции Ленца ПО
— Кюри 132, 264
— масс действующих 134—136
— Стефана—Больцмана 145—147,
254
Зародыши 157—159
Идеальные системы 226
Излучение равновесное 143—150»
250—255
Интеграл движения 195
— конфигурационный 199, 200
— неприводимый 269
— статистический 199,
Каноническое распределение кван-
квантовое 217
классическое 198
Квазиклассическое разложение 222—
225
Квазиспинодаль 174
Константа равновесия химического
136, 137
Корреляционная функция 290
прямая 290.
Корреляция флуктуации 293
Коэффициент полезного действия 66
цикла Карно 67
— Джоуля—Томсона 125
— расширения теплового 161
термический 29
— сжимаемости 29
— термический давления 29
Коэффициенты вириальные 29, 269,
271, 272
-— стехиометрические 134
— термические 29
Кривая инверсии 127
— равновесия фаз 181, 182
Критическая опалесценция 175, 304
Критические индексы 176—180
Ланжевена теория парамагнетизма
263
308
Ленгмюровская частота 286
Летучесть 138, 139
Луивилля теорема 187
— уравнение 187
Максвелла—Больцмана распределе-
распределение 227
Максвелла распределение 203
Матрица плотности 191, 193
— устойчивости 106, 170
Метод термодинамических потенциа-
потенциалов 82
— циклов 80
Микроканонический ансамбль 196
Микроканоническое распределение
квантовое 216
классическое 196
Модуль упругости 38, 39
Монокристалл 153
^-пространство 185
Натяжение поверхностное 151, 153,
157
Начало термодинамики второе 40
первое 30
третье 74
Неравенство Клаузиуса 65
— термодинамики основное 62, 66
Парадокс Гиббса 59
Параметры аддитивные 14
— внешние 13, 18
— внутренние 13, 18
— интенсивные 14
— макроскопические 13
— термодинамические 14
Перемещения виртуальные 99
Переходы фазовые второго рода 161,
162, 167
первого рода 161
Плазма 277
Плазменный параметр 279, 281
Плотность состояний 196
Показатель политропы 37
Постулат равной априорной вероят-
вероятности 195, 216
Постоянная Стефана-—Больцмана 147,
254
— энтропийная 79
Потенциал термодинамический 85
большой 97, 205, 219
Гиббса 86
— химический 95, 96
Правило фаз Гиббса 140, 141
Преобразования Лежандра 85
— якобиан 92, 93
Принцип адиабатной недостижимос-
недостижимости 45
— Ле Шателье—Брауна 119—112
— перемещений виртуальных 98
Процессы необратимые 44
— неравновесные 22
— обратимые 44
— равновесные 21
— термодинамические основные 36*
Работа 22—24
— поляризации 25
— системы расширения 25
Равенство Клаузиуса 48
Распределения функцция 212—
287—290, 295
радиальная 288, 290
Релаксация 21, 22
Ротатор 246, 247
Семиинварианты 209
Система адиабатная 24
— бинарная 21, 142, 143
— гетерогенная 19, 20
— гомогенная 19
— изолированная 15, 100, 195—-197,.
216
— макроскопическая 13
— простая 27, 28
— равновесная 14
— расширенная 86-
— термодинамическая 14
— эргодическая 196
«Смерть тепловая» 72, 73
Сольватация 20
Соотношение Гриффитса 180
— Куперсмита 180
— Рашбрука 179
Состояние критическое 170
— метастабильное 103, 157
— неравновесное 14
— равновесное 14
— смешанное 192
— стабильное 103
— чистое 192
Средние по ансамблю 194, 195
— по времени 194, 195
Статистическая сумма 217
Статистический вес 196
— оператор 191
— предел 197
Суперпозиционное приближение 28$
Температура 17, 18
— вырождения 221
— Дебая 260
— инверсии 127
— термодинамическая 47
отрицательная 113—124
— эмпирическая 19
Теорема Вульфа 154, 156
— Гиббса 58
— Карно вторая 69
¦ первая 67
— о вириале 200—202
309*
— о равномерном распределении
200—202
Тепловая длина волны 199, 220
Теплоемкость 33
Теплообмен 23
Теплота 23
Термодинамическая теория возмуще-
возмущений 209, 210
— эквивалентность ансамблей 206—
208
Термодинамический предел — см
Статистический предел
Термостат 33, 197
Точка тройная 141, 142
Точки Вульфа 154
Уравнение Бертло 29
— Блоха 223
— Боголюбова—Борна—Грина 289
— Ван-дер-Ваальса 28, 272—274
— Гиббса—Гельмгольца 89, 199
— Гиббса—Дюгема 98, 143
— Клапейрона—Клаузиуса 163
— Клапейрона—Менделеева 28
— кривой равновесия 162
*— начала термодинамики второго 48
- — первого 30
третьего 76
— Неймана 194, 216
— Орнштейна—Цернике 290
— основное теории бинарных систем
143
— Перкуса—Йевика 289—291
— Пуассона 38
— самосогласованного поля 287, 288
— состояния калорическое 28, 228
233—236
— термическое 28, 228, 233—236
-— термодинамики основное 66, 131
— Шредингера 188, 193, 194, 218
Уравнения Дитеричи 29
— Эренфеста 165, 166
Условие равновесия механического
104, 153
общее 104
системы гетерогенной 139
термическое 104
— — устойчивого 100—103, 105—
112
фазового 104
химического 104, 134
Условия ослабления корреляций 212
Фаза 20
Фазовая траектория 185, 187
Фазовое пространство 185
Фазовый ансамбль Гиббса 185
— объем 185, 186
Ферми—Дирака распределение 230—
232
Фермионы 229
Флуктуация 206, 291—293
Форма Пфаффа 32, 46
Формула Планка^254, 255, 257
— Релея—Джинса 254
— Рутгерса 168
— Саха 136—138
— Эйнштейна 299, 300
'Функция характеристическая 82—8(j
Цикл Карно 66—69
Числа заполнения 230
Число степеней свободы 187, 201,
221
Шкала температур термодинамичес-
термодинамическая 51—53
Эйнштейна модель кристалла 257
Энергия 15, 22
— внешняя 22
— внутренняя 22
— Гельмгольца 85, 210, 217
— Гиббса 86
— системы 22
— поверхностная 152
— Ферми 240
Энтальпия 87
Энтропия 47, 197, 216
Эргодическая проблема 196
Эффект Джоуля—Томсона 125—128
— магнитокалорический 132
— $1ейснера 167
— Померанчука 163
Явление Пельтье 112
Явления закритические 170
— критические 161, 170
УЧЕБНОЕ ПОСОБИЕ
Иван Павлович Базаров,
Эдвард Вигенович Геворкян,
Павел Николаевич Николаев
ТЕРМОДИНАМИКА
И СТАТИСТИЧЕСКАЯ ФИЗИКА
(теория равновесных систем)
Зав. редакцией С. И. Зеленский
Редактор Г. Е. Горелик
Художественный редактор Ю. М. Добрянская?
Технические редакторы К. С. Чистякова,
Л. Р. Черемискина.
Корректоры Н. В. К а р т ы ш е в а,
Л. С. К л о ч к о в а
МБ № 2244
Сдано в набор 20.1U85.
Подписано в печать 26.05.86.
Л-66327. Формат 60x90/16. Бумага типогр. № 3.
Гарнитура литературная. Высокая печать.
Усл. печ. л. 19,5. Уч.-изд. л. 20,1.
Тираж 6000 экз. Заказ 245.
Цена 85 коп. Изд. № 4032
Ордена «Знак Почета» издательство
Московского университета.
103009, Москва, ул. Герцена, 5/7.
Типография ордена «Знак Почета» изд-ва МГУ.
119899, Москва, Ленинские горы