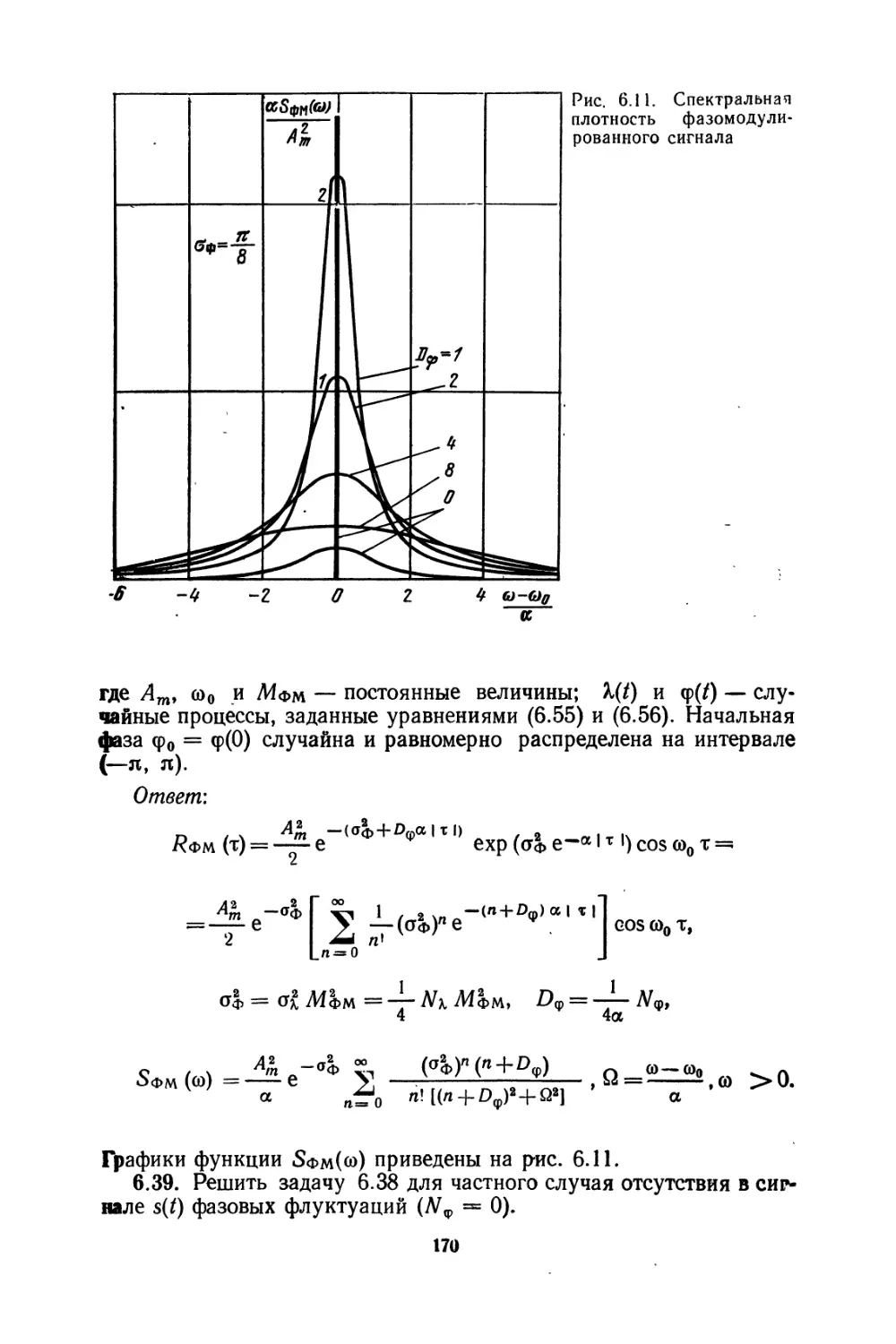
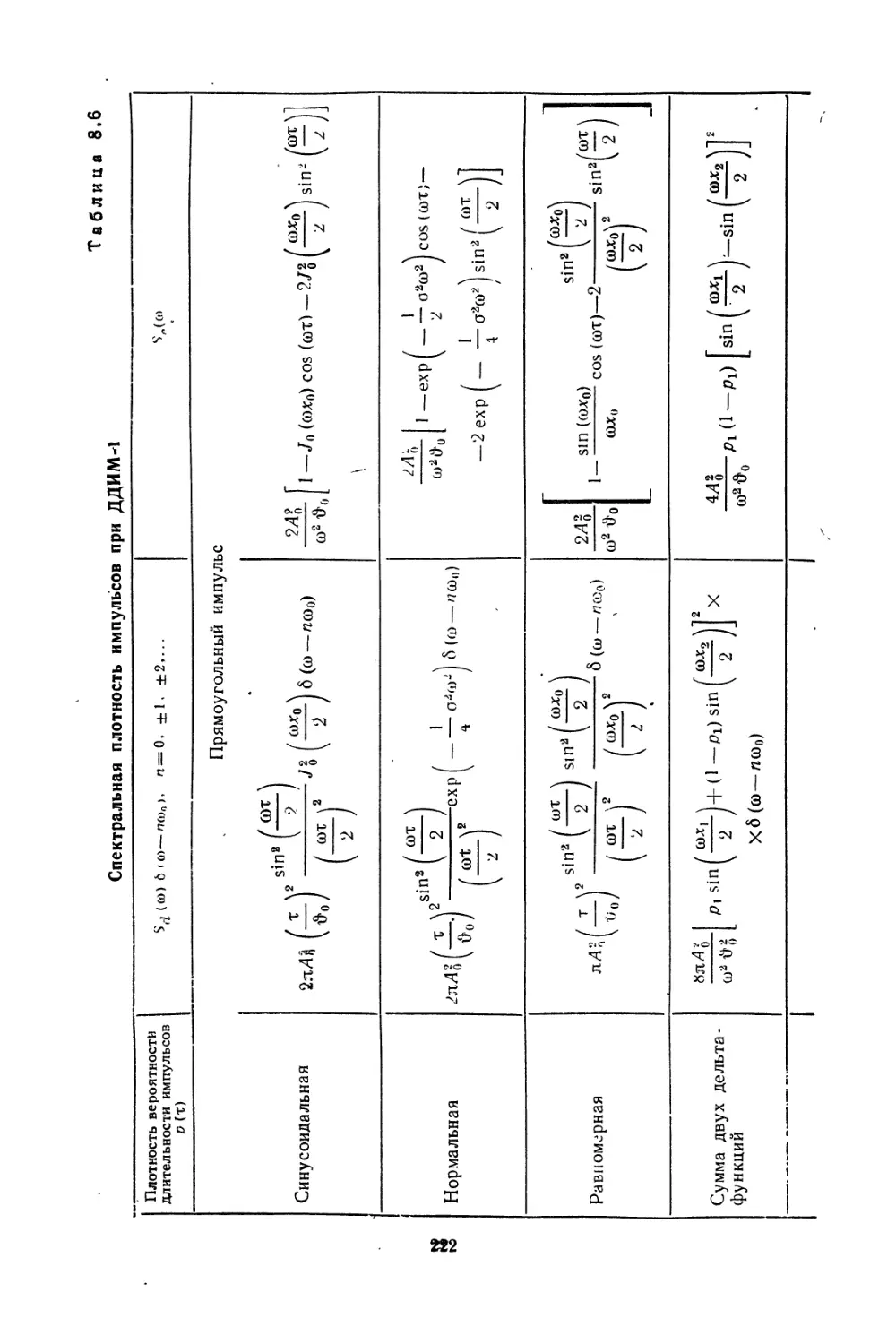
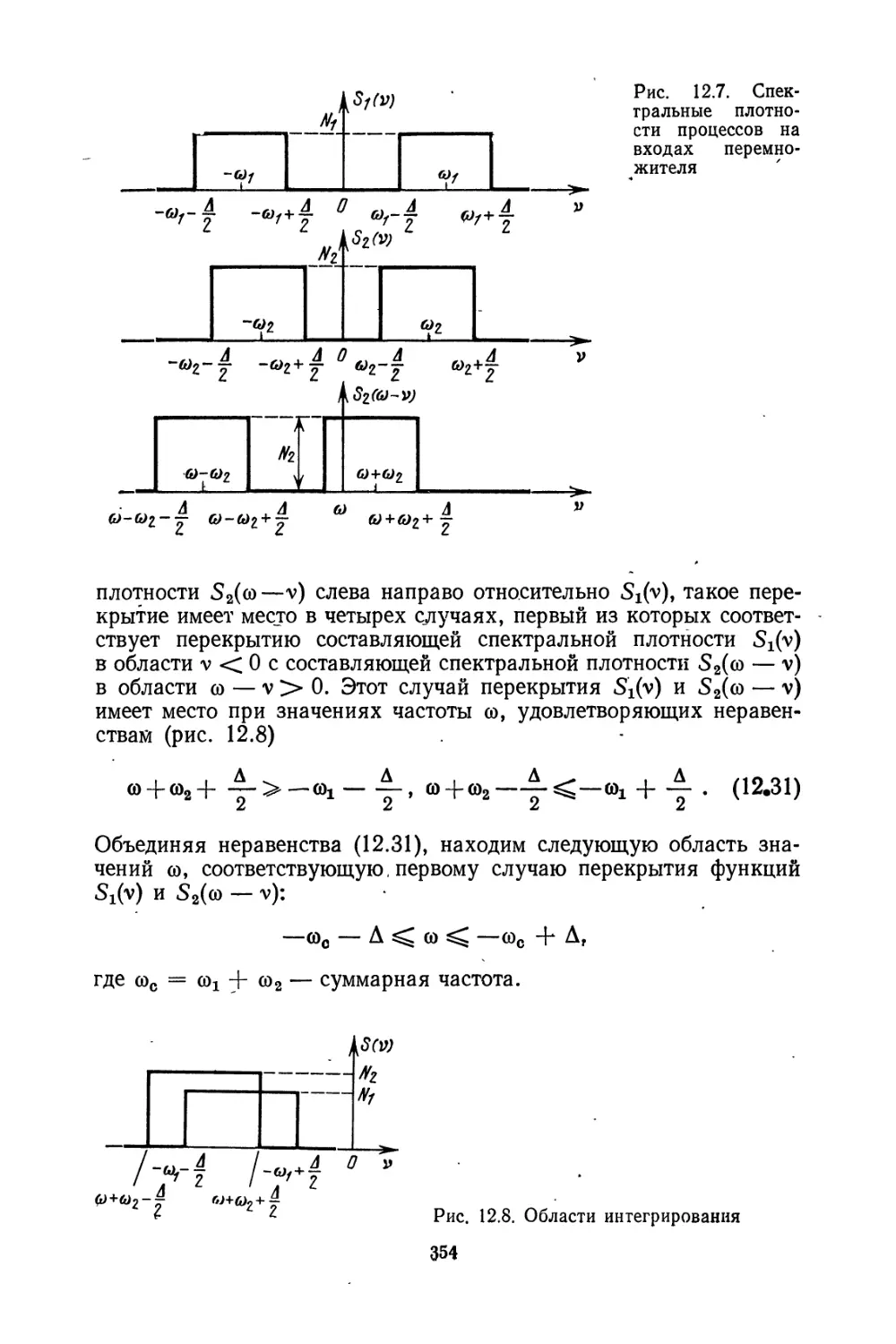
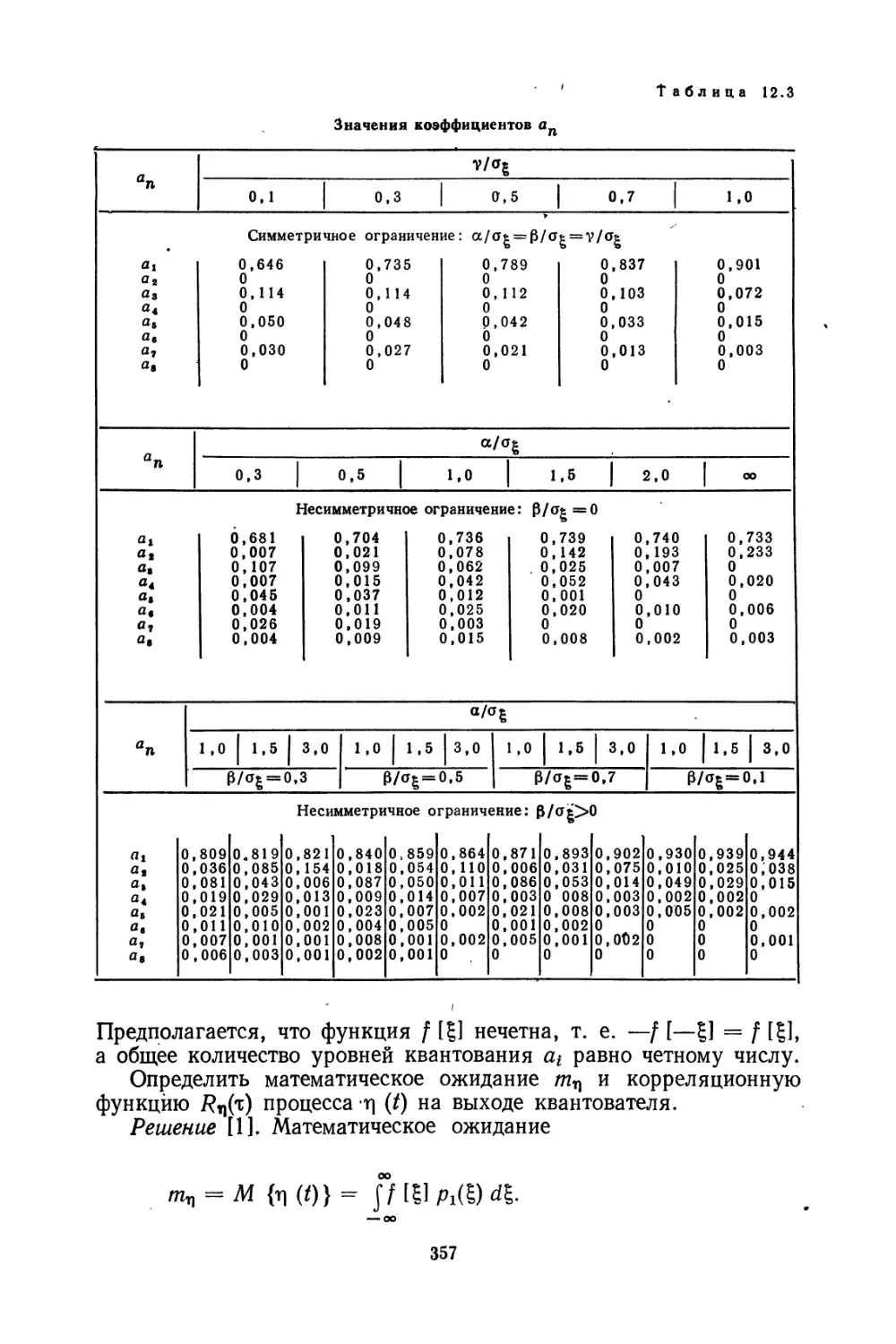
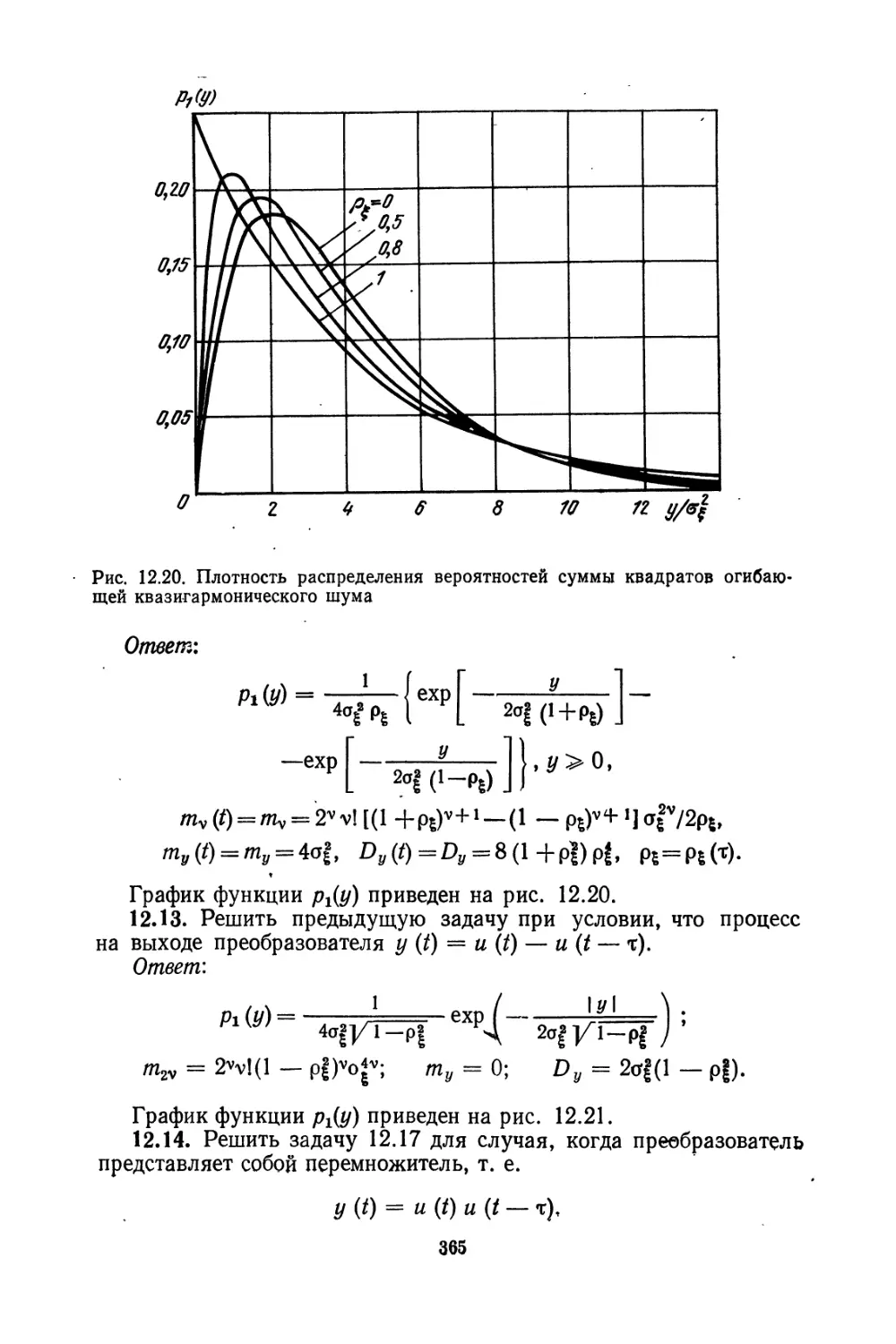
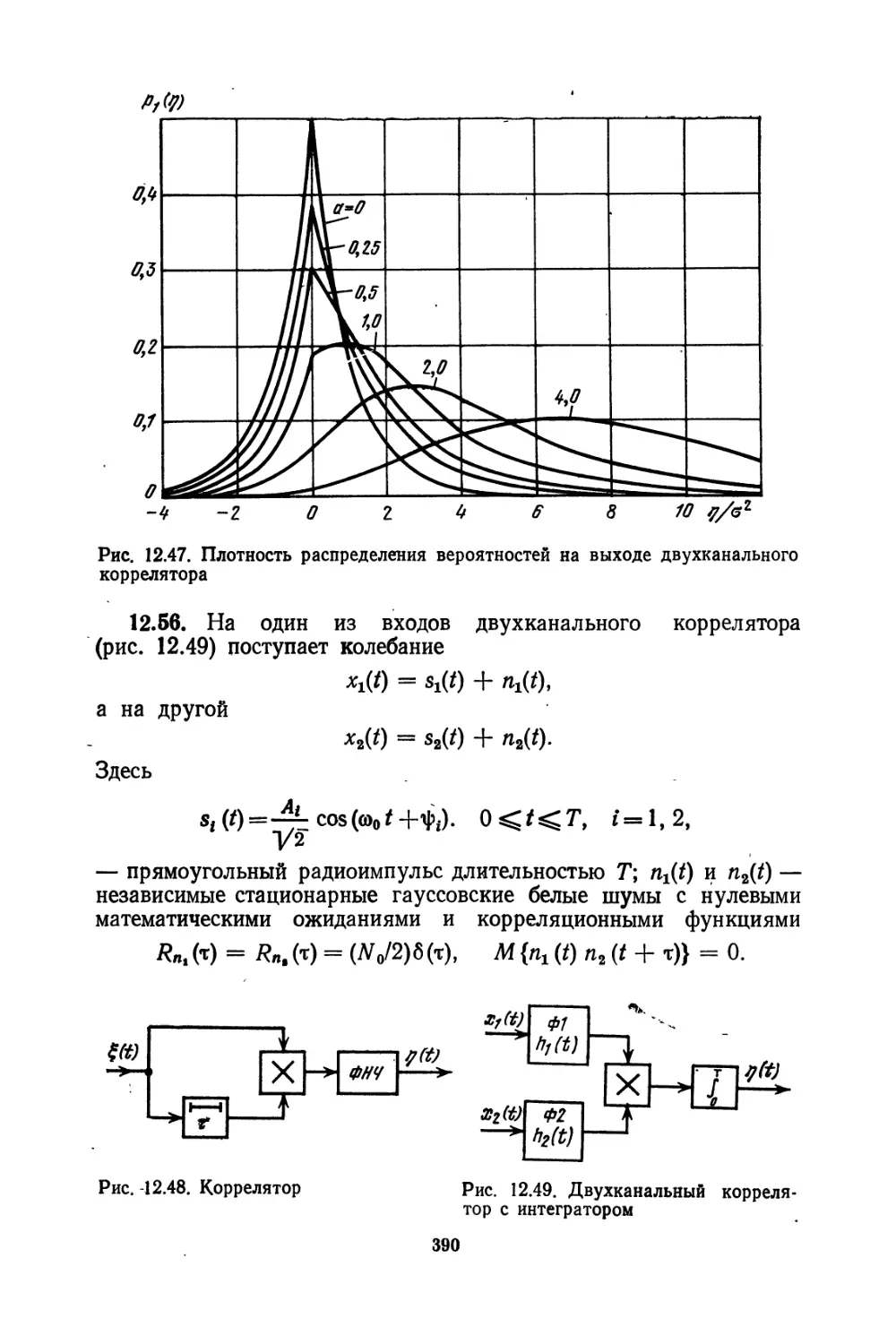
Текст
ГОРЯЙНОВ
А. Г.
ЖУРАВЛЕВ
в, и.
ТИХОНОВ
ПРИМЕРЫ
И ЗАДАЧИ
СТАТИСТИЧЕСКАЯ
РАДИОТЕХНИКА
ПРИМЕРЫ
И ЗАДАЧИ
В. Т. ГОРЯЙНОВ, А. Г. ЖУРАВЛЕВ, В. И. ТИХОНОВ
СТАТИСТИЧЕСКАЯ
РАДИОТЕХНИКА
ПРИМЕРЫ
И ЗАДАЧИ
Под редакцией
профессора. В. И. Тихонова
Допущено Министерством высшего и среднего
специального образования СССР в качестве учебного пособия
для студентов радиотехнических специальностей вузов
МОСКВА
«СОВЕТСКОЕ РАДИОэ
1980
ББК 32.841
Г67
УДК 621.391 : 519.27
Горяйнов В. Т., Журавлев А. Г., Тихонов В. И. Статисти-
ческая радиотехника: Примеры и задачи. Учеб, пособие для
вузов / Под ред. В. И. Тихонова. — 2-е изд., перераб. и доп.—
М.: Сов. радио, 1980. — 544 с., ил.
Книга содержит примеры и задачи по основным разделам
статистической радиотехники (теории вероятностей и матема-
тической статистике, теории случайных процессов, помехо-
устойчивости и теории информации). Материал разбит на
18 глав. В каждой главе приведены справочные теоретические
сведения, подробно разобраны типовые примеры и сформули-
рованы задачи для самостоятельного решения, снабженные
ответами. Задачи отличаются друг от друга как по сложности
решения, так и по практической значимости.
Предназначается для студентов и аспирантов, специализи-
рующихся в области радиотехники и автоматического управле-
ния. В качестве справочника она полезна также инженерам и
научным работникам.
Рис. 229, та'бл. 77, библ. 120 назв.
Рецензент: кафедра «Основы радиотехники» iMockob-
ского энергетического института.
Редакция литературы по вопросам космической радиоэлектроники.
30401-022
046(01)-80
002-80 2402020000
© Издательство «Советское радио», 1980
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Настоящая книга написана как учебное пособие по статисти-
ческой радиотехнике. По сравнению с первым изданием в книгу
включены по существу три новые главы (по математической ста-
тистике, марковским и точечным случайным процессам), а мате-
риал по корреляционным функциям и спектральным плотностям
выделен в самостоятельную главу. Кроме того, "значительно об-
новлены примеры и задачи.
Книга содержит 18 глав, охватывающих все основные разделы
статистической радиотехники. В начале каждой главы кратко
приведены теоретические сведения в объеме, необходимом для
решения рассматриваемых задач. Методика применения их для
решения конкретных практических задач иллюстрируется на ря-
де подробно разобранных примеров. Затем сформулированы за-
дачи, снабженные ответами. Для удобства решения задач, в ко-
торых требуется получить ответ в численном виде, в приложении
помещен ряд справочных таблиц.
При подборе примеров- и задач были использованы отечест-
венные и иностранные источники, многие примеры и задачи со-
ставлены авторами самостоятельно. Всего в книге содержится
796 примеров и задач.
Книга рассчитана на студентов и аспирантов, специализиру-
ющихся в области радиотехники и автоматического управления,
ее основная цель — способствовать активному усвоению теоре-
тических основ статистической радиотехники и выработке навы-
ков применения теории к решению практических задач. Однако
авторы надеются, что она будет полезна в качестве справочника
также инженерам и научным работникам. Именно поэтому за-
дачи и ответы помещены вместе.
Работа между авторами была распределена следующим обра-
зом: гл. 5, 6, 10, 12, 14 и 15 написаны В. Т. Горяйновым; гл. 1—4,
9, 17, 18 и приложение — А. Г. Журавлевым; гл. 7, 8, 11, 13 и
16 — В. И. Тихоновым, который выполнил также общее редакти-
рование книги.
Авторы выражают благодарность рецензенту канд. техн, наук
доц. В. П. Жукову за критические замечания и полезные советы.
з
Раздел
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Событие — всякий факт, который в результате опыта может произойти
или не произойти.
События подразделяются на достоверные (£/), невозможные (V) и слу-
чайные (Л, В, С, ... или Лх, Л2, Л3, ...). Вероятность достоверного события
принимается за единицу, а вероятность невозможного — за нуль:
P(U) = 1, P(V) = 0.
Вероятность любого события А заключена между нулем и единицей:
0 < Р(Л) < 1. (1.1)
Если всякий раз, когда происходит событие Л, происходит также событие В,
то говорят, что событие Л влечет за собой событие В и обозначают Л cz В,
где cz — знак включения. Если Л cz В и в то же время В cz Л, то события Л
и В называются равносильными (эквивалентными) и обозначаются Л = В.
В этом случае Р(Л) = Р(В).
Суммой или объединением множества событий Лх, Л2, Л3, ... называется
такое событие Л, которое происходит тогда и только тогда, когда происходит
по крайней мере одно («хотя бы одно») из этих событий. Сумма событий
Лх, Л2, Л3, ... обозначается
Л = Л1 + Л2 + Л3 + ... = 2 Ah или А = Л1 U Л2 U Аз U • • • = U А &,
k - k
где U — символ объединения событий (логическая операция ИЛИ).
Из определения суммы событий непосредственно вытекают следующие
соотношения:
Л + Л = Л, Л + С/=67, л + к=л, л + в=в + л,
(Л + В) + С = Л + (В + С). (1.2)
Произведением (или пересечением, или совмещением) событий
Лх, Л2, Л3, ... называется такое событие Л, которое происходит тогда и толь-
ко тогда, когда происходят все события вместе («одновременно»). Для обозна-
чения произведения событий применяются следующие записи:
Л = Л1Л2Л3 ...=ПЛдили Л = Л1ПЛ2ПЛ3П ...= Пл&,
k k
где f| — сивмол пересечения событий (логическая операция И).
Для произведения событий справедливы соотношения:
АА = A, AV = V, AU = А, АВ = ВА, (АВ)С=А(ВС). (1.3)
4
Для операций умножения и сложения событий, применяемых совмест-
но, справедлив обычный распределительный (дистрибутивный) закон
(Л + В)С= ЛС + ВС (1.4)
и, кроме того, так называемый «второй распределительный закон» [2]
АВ+ С = (Л + С) (В + С).. (1.5)
События Л, В, С, ... образуют полную группу событий, если в резуль-
тате опыта непременно должно появиться хотя бы одно из них. Другими
словами, сумма событий, образующих полную группу, есть достоверное со-
бытие, т. е.
А + В + С+ ... = U.
События А и В называются несовместными (или несовместимыми), если
их совместное появление невозможно, т. е. если
АВ = V.
Два события называются противоположными (дополнительными), если
они несовместны и образуют полную группу. Событие, противоположное со-
бытию Л, обозначается Л. Нахождение противоположного события эквива-
лентно логической операции НЕ (отрицания), иными словами Л = не Л»
Для противоположных событий справедливы формулы
Й = Л, Л+Л = (/, ЛЛ = У,
(1.6)
Л+"В = ЛВ, А8=л + ё, Л4-В=Л-|-ЛВ, А + В АВ=~А+~В-
Когда рассматриваемый опыт имеет N равновозможных исходов, которые
несовместны и, составляют полную группу (схема случаев)/вероятность со-
бытия А
P(A) = n/N, (1.7)
где п — число исходов, которые приводят к наступлению события Л (благо-
приятствуют событию Л).
При решении задач на непосредственный подсчет вероятностей с исполь-
зованием формулы (1.7) общих способов для нахождения чисел W и п нет. Во
многих случаях целесообразно использовать «комбинаторные» способы,
т. е. теорию соединений (размещений, перестановок, сочетаний). При этом
часто приходится вычислять число сочетаний
Ck_ п!
п k\(n — k)\
Если значения п и k велики, то используют приближенную формулу Стир-
линга
(1.8^
п! (п/е)п"|/2лц. (1.9)
Эта формула дает хорошую точность приближения и при сравнительно не-
больших значениях п. Так, например, относительная погрешность не превос-
ходит 0,1 при п > 1, 0,01 — при п > 10 и 0,001 — при п > 100.
В некоторых задачах понятие равновозможности событий применяется
к опытам с бесконечным числом исходов, когда числа W и п определить невоз-
можно. Иногда же проще вычислить саму вероятность события (отношение
n/М), а не порознь числа исходов п и N. В таких случаях пользуются геомет-
рическими вероятностями, которые определяются формулой
Р(4) = ^.
мера G
(МО)
5
где G — геометрическая мера (длина, площадь, объем и т. д.) всей области,
g — геометрическая мера части области G, попадание в которую благоприят-
ствует событию А.
Кроме того, условия применимости формулы (1.7) весьма ограничены
(формула применима только тогда, когда опыт сводится к схеме случаев)
В большинстве практических задач, связанных с реальными явлениями, ве-
роятность непосредственно связывают с эмпирическим понятием частоты.
Частотой или статистической вероятностью Р* (А) события А в данной се-
рии опытов называется отношение числа опытов п, в которых появилось
событие А, к общему числу N произведенных опытов:
Р*(А) = n/N. (1.11)
По теореме Бернулли при большом числе опытов частота сходится по ве-
роятности к вероятности события, т. е. при любом е > О
Р[|Р*(А) — Р(А)| < е] = 1.
Определение вероятности сложного события А через вероятности более
простых событий Alt А 2, ...» Ап базируется на использовании основных теорем
теории вероятностей (теорем сложения и умножения вероятностей и их след-
ствий).
Согласно теореме сложения вероятностей вероятность суммы двух со-
бытий равна сумме вероятностей этих событий минус вероятность их произ-
ведения:
Р(А + В) = Р(А) + Р(В) — Р(АВ). (1.12)
Если события А и В несовместны, то
Р(А + В) = Р(А) + Р(В). (1.13)
Формулы (1.12) и (1.13) обобщаются на сумму любого числя п событий:
(п \ п п—1 п
5 Ak = S +
k=\ / 6 = 1 k=\j=k+\
n—2 n-— 1 n / k \
+ 2 2 2 PtAkAjAi)-...+(-1)"-1 P П Ak , (1.12a)
6=1 /=64-1 i = /4- 1 \6=1 /
2 )= 2 РИл). (1.13a)
\6=1 / fe=l
Сумма вероятностей несовместных событий, составляющих полную груп-
пу, равна единице:
п
2 P(Ak)=l. (1.14)
6=1
Сумма вероятностей двух противоположных событий равна единице:
Р(А) + Р(А) = 1. (1.15)
По теореме умножения вероятностей для двух событий вероятность про-
изведения двух событий равна произведению вероятности одного из них на
условную вероятность другого при условии, что произошло первое:
Р(АВ) = Р(А) Р(В | А) = Р(В)Р(А1В), (1.16)
где Р(А|В) — условная вероятность события А, т. е. вероятность события А,
вычисленная в предположении, что имело место событие В.
6
Рис. 1.1. Параллельное соединение эле-
ментов
Если событие Л статистически не зависит от события В, то Р(Л|В) = Р(Л),
причем события Л и В называются независимыми. При независимых событиях
Л и В выражение (1.16) принимает вид
Р(ЛВ) = Р(Л)Р(В). (1.17)
Формулы (1.16) и (1.17) обобщаются на п событий Alf Л2, ...» Ап:
Р(А1А2 ... Лп) =Р(Л1)Р(Л2|Л1)Р(Л3|Л1Л2) ... Р(Ап\А1А2 ... Л^),
(1.16а)
(П \ п
П Лй = п Р(Ак). (1.17а)
6=1 / 6=1
Решение многих практических задач требует совместного использования
теорем сложения и умножения вероятностей. В частности, с помощью этих
теорем производится расчет вероятности безотказной работы, например, ра-
диотехнических систем.
Вероятностью безотказной работы некоторой системы ( или ее элемента)
называют вероятность того, что система (элемент) в течение установленного
времени будет работать без отказов.
При объединении нескольких элементов в систему различают их парал-
лельное соединение ( резервирование) и последовательное (основное). При
параллельном соединении (рис. 1.1) отказ системы возможен только при отка-
зе всех элементов, а при последовательном (рис. 1.2) отказ системы проис-
ходит при отказе любого элемента [ 1].
Вероятность безотказной работы Р — P(t) системы из k параллельно
соединенных элементов
6
Р = 1-П(1-рг), (1.18)
1=1
Где р. = р.(/) — вероятность безотказной работы i-ro элемента на интер-
вале (0, /). С увеличением числа параллельно включенных элементов вероят-
ность безотказной работы системы возрастает.
Если система состоит из k последовательно соединенных элементов, то
вероятность безотказной работы системы вычисляется по формуле
6
Р=Пй. (1.19)
1= 1
С увеличением числа последовательно включенных элементов вероятность
безотказной работы системы убывает.
Во многих реальных ситуациях то или иное событие А может появиться
лишь как случайное следствие одного из несовместных событий Hi (i ==
== 1,2, ...» п), которые входят в некоторую полную группу событий и на-
зываются гипотезами. В таких случаях безусловная вероятность Р(Л) со-
Рис. 1.2. Последовательное соедине-
ние элементов
°
Pl
Pz
7
бытия А при известных вероятностях гипотез P(Hi) и условных вероятност-
ях определяется по формуле полной (или средней) вероятности:
Р(Д)= 2 Р(Нг)Р(Л|/Л)- (1.20)
i — 1
При этих же данных, т. е. известных вероятностях Р(Н[) и Р(А\Н^),
можно найти изменение вероятностей гипотез /Унесли предположить, что со-
бытие А уже произошло. Задачи подобного типа решаются с помощью теоремы
гипотез (или формулы Байеса):
Р(Н,1Я>„ (1.21,
2 Р<«,)Р(Л I «„)
fe = l
Вероятность Р(Щ) называется априорной (доопытной), а Р(Н[\А) — апо-
стериорной (послеопытной) или обратной вероятностью.
В теории передачи сообщений, теории стрельбы, при контроле качества
продукции и т. д. часто возникают задачи по определению вероятности появ-
ления какого-то события А в результате серии опытов, в каждом из которых
это событие может произойти или не произойти. Проще всего они решаются
тогда, когда опыты являются независимыми, т. е. вероятность того или
иного исхода опыта не зависит от того, какие исходы имели другие опыты.
Способ решения подобных задач дает теор'ема о повторении опытов (формула
Бернулли).
Вероятность того, что при п независимых опытах (испытаниях) собы-
тие А появится ровно k раз, если при каждом опыте вероятность события А
одинакова и равна р, определяется формулой
Рп(*) = СУ<7п-\ (1.22)
где q = 1 — р.
Формулой (1.22) неудобно пользоваться при больших п. В этом случае
для подсчета вероятности Pn(k) применяют приближенные формулы.
Если п велико, р мало, а пр — К имеет»конечное значение, то пользуются
приближенной формулой Пуассона
Xk
Pn(k)~ (1.23)
Приближенное значение относительной погрешности при применении фор-
мулы (1.23) вместо (1.22) равно
k— (k— пр)* , 1 .
Когда npq не слишком мало, то применяется локальная формула Муав-
ра — Лапласа:
Рп(*)=Р1 (х)/Упрд,
(1-24)
где
1 — х2/2 & ПР
Pi(x) — /ir е х/2, х= -Т7— .
у 2л npq
Приближенное значение относительной погрешности при вычислении вероят-
ности Рп (k) по формуле (1.24) равно
р — о [ х* \
rn(k)= /7-L X 1-— .
“ У npq и ]
8
С помощью формулы (1.22) можно вычислить вероятность того, что при п
независимых опытах событие Д, имеющее вероятность р, появится не менее k
раз:
п k— 1
Pn(m>k)= 2 C”Pmqn~m=\- 2 C”pmqn~m. (1.25)
m = k m = 0
Вероятность появления события хотя бы один раз при п опытах равна
Pn(m > 1) = 1 - q\ (1.26)
Вероятность того, что при п независимых опытах событие Л, имеющее
вероятность р, появится не более k раз, определяется выражением
k
Pn(m<k)= 2 CnPm‘}n~m- (1-27)
m = Q
Если вероятность появления события в каждом опыте равна р, то вероят-
ность того, что в серии из п независимых опытов событие А появится от р,
до v раз включительно, равна
Рп(ц < k < V) = 2 Сп рт яп~т- (1.28)
m = |i
При больших п, р, и v этой формулой пользоваться затруднительно. В
этом случае используют приближенную интегральную формулу Муавра —
Лапласа
ь
Рп(ц < < v) « Се-'272Л = Ф(6)-Ф(а), (1.29)
а
где
0=-^-. ф(г)=-z2=- f е-^Л.
у npq V npq у 2л J
— оо
Количество п опытов, которые нужно произвести для того,чтобы с вероят-
ностью, не меньшей Plt можно было утверждать, что данное событие произой-
дет по крайней мере один раз, находится по формуле
п > log(l - Px)/log(l - р). (1.30)
Наивероятнейшим числом kQ появлений события А в п независимых опы-
тах называется такое значение k = kQi при котором вероятность Pn(k) на-
ибольшая. Это число определяется по формуле
пр — q < kQ < пр + Р- (1-31)
Если пр — q — дробное число, то неравенство (1.31) определяет одно зна-
чение наивероятнейшего числа. Если же пр — q — целое число, то неравен-
ство (1.31) определяет два значения наивероятнейшего числа.
Формула (1.22) составляет содержание так называемой частной теоремы
о повторении опытов. Известно несколько ее обобщений. Одно из них отно-
сится к случаю, когда из-за изменяющихся условий при проведении п не-
зависимых опытов вероятность р меняется от одного опыта к следующему
(общая теорема о повторении опытов). В этом случае вероятность Pn(k) появ-
ления события А ровно k раз определяется по производящей функции [3]:
п п
<Pn(z)= П (<?i+Pjz)= 2 Pn(k)zk, (1.32)
Z= 1 А = 0
где pi — вероятность появления события в t-м опыте, qt = 1 — р/.
9
Искомая вероятность Pn(k) равна коэффициенту при zk в разложении
производящей функции и может быть определена дифференцированием функ-
ции фп(г):
Рп (*) =
Другое обобщение формулы (1.22) относится к случаю, когда каждый
опыт может иметь не два, а большее число исходов. Если, например, при
каждом повторении опыта может произойти только одно из событий
т
Лх, Л2, ...» Ат соответственно с вероятностями plt р2, ..., рт (Spz = 1),
то вероятность Pn(ki, &2, •••» km) того, что при п независимых опытах событие
Аг появится k± раз, событие А 2 появится k2 раз и т. д., событие А т появится
т
km раз = «), определяется формулой полиномиального распределения
i=i
и! k k k
Pn(ku k2......km) = ——---------(1-34)
«1' fe2! ... km\
k k k
Вероятность Pn (kt, k2, ...» km) является коэффициентом при Zj1 z22 z^ в раз-
ложении по степеням аргументов z^ полинома
фп Ui, z2» •••» zm) ~ (Pizi 4" Рг22 “Н ... + Pmzm)ni (1.35)
представляющего собой производящую функцию для совокупности чисел
Рп(^1> k2, ..., km).
2. ПРИМЕРЫ
1.1. Доказать справедливость следующего соотношения между
событиями: (А + В) С = АС + ВС.
Решение. Заданный распределительный закон можно доказать
путем непосредственного рассмотрения смысла утверждений, выра-
жаемых каждой частью равенства. Левая часть данного равенства
означает событие, состоящее в том, что произошли совместно собы-
тия А или В и событие С. Правая часть означает, что происхо-
дят события А вместе с С или В вместе с С (или и то, и другое).
Эти два утверждения равносильны.
1.2. Показать, что А + АВ + ВС + АС = А + С.
Решение. Доказательство справедливости заданного равенства
проведем алгебраическим путем. Используя формулы (1.2)—(1.6),
имеем _ _
А + АВ + ВС + АС = (AU + АВ) + ВС + АС =
= A(U + В) + АС + ВС == AU + АС + ВС = А + АС + ВС =
- А + AC + АС + ВС = А+С(А+А)+ВС =
= А+ С + ВС==А+С.
1.3. Двум радиостанциям разрешена работа на десяти одина-
ковых фиксированных частотах.
Определить вероятность Р(А) того, что настроенные независимо
обе радиостанции окажутся работающими на одинаковых частотах.
ю
Решение. Обозначим (чисто формально) частоты одной радио-
станции через /7, а частоты другой — через ft, i = 0, 1, ... 9,
fi = fi. Расположим все возможные исходы в виде таблицы:
rj; ...
/;/; ...
р' С" f' f" f' f"
I 9 / 0 / 9 / 1 ••• / 9 / 9*
Всего равновозможных исходов N= 10 • 10=100. Эти исходы со-
ставляют полную группу несовместных случаев. Исходов, благо-
приятствующих событию А (обе радиостанции окажутся работаю-
щими на одинаковых частотах), будет п = 10(/'/", ..., /'/")•
Следовательно,
Р (Л) = n/N = 10/100=0,1.
1.4. По линии связи в случайном порядке передаются 30 знаков
русского алфавита.
Найти вероятность Р(А) того, что на ленте появится последова-
тельность букв, образующих слово «радио».
Решение. Число всех равновозможных случаев N (число выбо-
ров из 30 букв алфавита по 5) равно числу размещений из 30 по
5 букв, т. е.
N = Лб30 = 30 • 29 • 28 • 27 • 26.
Из этих случаев благоприятствующим событию А является только
один (комбинация, образующая слово «радио»), т. е. п = 1. Сле-
довательно,
Р(А) = n/N = 1Л4530 = 1/30 • 29 • 28 • 27 • 26 « 5,88 • 10“8.
1.5. Производится прием кодовых комбинаций, содержащих
пять цифр от 1 до 5.
Какова вероятность Р (Л) того, что в принятой комбинации циф-
ры образуют последовательность 12345?
Решение. Число всех равновозможных случаев N равно числу
перестановок из пяти элементов, т. е. N = Р5 = 5! =120. Из
этих случаев благоприятствующим событию А является только
один, т. е. п = 1. Следовательно,
Р(Л) = n/N = 1/51 = 1/120.
1.6. В партии из N запасных радиоламп имеется М нестандарт-
ных. Для проверки выбираются наугад k радиоламп из этой пар-
тии (k < N).
Определить вероятность Р(А) того, что среди них окажутся
ровно / нестандартных (/ М).
Решение. Общее число возможных выборов из N радиоламп по k
равно числу сочетаний из N элементов по k, т. е. Сп-Благоприят-
ствующими поставленному условию являются случаи, когда из об-
щего числа М нестандартных радиоламп взято ровно I штук, что
п
Рис. 1.3. К вычислению вероятности Р (Д)
можно осуществить См способами. Но каждый из этих случаев в кон-
трольной партии может быть в различной комбинации с остальными
k—I стандартными лампами. Число таких комбинаций равно С^11м-
Следовательно, общее число благоприятствующих случаев будет
равно произведению C1mCn~L 1м. В соответствии с определением ве-
роятности получим
Р(А) = C‘MCkN-lM/CkN.
Г.7. В любые моменты интервала времени Т равновозможны
поступления в приемник двух независимых сигналов. Приемник
будет перегружен, если разность между моментами поступления
сигналов будет меньше т.
Определить вероятность Р(А) того, что приемник будет пере-
гружен.
Решение. Изобразим случайные моменты поступления сигналов
в радиоприемник и т2 в виде декартовых координат на плоскости.
Областью возможных значений и т2 является квадрат площадью
S = Т2 (рис. 1.3). Приемник будет перегружен, если |т2 — ч| ^т.
Данная область лежит между прямыми т2 — тх = т и т2 — тх =
= — т. Площадь этой области s = Т2 — (Т — т)2. Следовательно,
р//н мера g s 1 (Г-т)2
с 'га
мера G S Т2
1.8. Поданным ремонтной мастерской в среднем из 100 отказов
телевизора 50% обусловлено выходом из строя электронных ламп,
15% — конденсаторов, 12% — резисторов; 5% — кинескопов, а
остальные отказы обусловлены другими причинами.
Найти вероятность Р*(А) отказа телевизора по другим при-
чинам.
Решение. По условию вероятности выхода из строя телевизора
из-за отказа различных элементов равны:
р*(Л1) = 0,5; Р*(Л2) = 0,15; Р*(Лз) = 0,12; Р*(Л4) = 0,05,
где А19 Л 2, Аз, Л4 — отказы телевизора, обусловленные соответ-
ственно выходом из строя электронных ламп, конденсаторов, рези-
сторов и кинескопов. События Л, Лх, Л2, Лз, Л4 составляют полную
группу. Следовательно,
4
Р*(А) = 1 — 2 Р* (Л) = 1 —(0,5 +0,15 +0,12 +0,05) = 0,18.
12
1.9. В партии из N полупроводниковых триодов имеется М бра-
кованных. Для контроля из партии берется наугад п триодов.
Какова вероятность Р (Л) того, что среди них будет не более т
бракованных?
Решение. Пусть А — событие, состоящее в том, что среди п
взятых для контроля триодов будет не более tn бракованных. Со-
бытие А произойдет тогда, когда среди п взятых на проверку триодов
или не будет ни одного бракованного (событие Ло), или один брако-
ванный (событие Л1), или два бракованных (событие Л2) и т. д., или
окажется т бракованных триодов (событие Лт), т. е.
Л = Ло +ЛХ + Л2+ ... + А +••• +^т= 2^*
fe=0
Вероятность Р(Ак) события Ak равна
р(лй)=с^а-Л/а.
Следовательно, по теореме сложения вероятностей событий имеем
т
2f>k ptl—k
р (Л) = у р (Л) = .
U рп
fe = 0
1.10. Обнаружение воздушной цели производится независимо
двумя радиолокационными станциями. Вероятность Р(Л) обнару-
жения цели первой станцией равна 0,7. Вероятность Р(В) обнару-
жения цели второй станцией равна 0,8.
Определить вероятность Р(С) того, что цель будет обнаружена
хотя бы одной станцией.
Решение. По условию события Л и В независимы, поэтому ве-
роятность совместного события АВ (цель обнаружена обеими стан-
циями)
Р(ЛВ) = Р(Л) Р(В) = 0,7-0,8=0,56.
Используя формулу (1.12), получаем
Р(С) = Р(А + В) = Р(Л) + Р(В) — Р(ЛВ) =
= 0,7 + 0,8 — 0,56 = 0,94.
Так как события Л и В независимы, то пример можно решить
путем перехода к противоположным событиям Л и В. В этом случае
Р(С) = Р(А + В) = 1 — Р(Л) Р (В) =
= 1—[1 — Р (Л)] [1 - Р (В)] = 1 — 0,3-0,2=0,94.
1.11. Каждая буква слова «математика» написана на отдельной
карточке, карточки тщательно перемешаны. Последовательно из*
влекаются четыре карточки.
Какова вероятность Р(Л) получить слово «тема»?
13
Решение. Пусть Аъ А2, Аз, А4 — события, состоящие в последо-
вательном извлечении букв «т», «е», «м», «а». Тогда соответствующие
вероятности равны:
Р(Л1)=А; Р(Л2|А) = -1-; p08mm2)=A;
Р(Л4 |Л1Л2Л8) = -у-.
Применяя формулу (1.16а), получаем
р И) = Р (AJ Р (A,1 Ах) Р (А31 Ах А2) Р (А4 J Ах А2 А3) =
__ 2 1 2 з __ 1
“ 10 * 9 ‘ 8 ‘ 7 4%Г'
1.12. Два стрелка стреляют по очереди по мишени до первого
попадания. Каждый из них имеет право сделать не более двух вы-
стрелов. Зная, что при одном выстреле первый стрелок попадает
в мишень с вероятностью ръ а второй—с вероятностью р2, найти
вероятность того, что: 1) первый стрелок попадет в мишень; 2) вто-
рой стрелок попадет в мишень.
Решение. Рассмотрим следующие события: А — первый стрелок
попадает в мишень, В — второй стрелок попадает в мишень, Ах—
попадание у первого стрелка при первом выстреле, — промах
у первого стрелка при первом выстреле, А2—попадание у первого
стрелка при втором выстреле, А2 — промах у первого стрелка при
втором выстреле,. Вг — попадание у второго стрелка при первом вы-
стреле, Вг — промах у второго стрелка при первом выстреле, В2 —
попадание у второго стрелка при втором выстреле. Тогда
А = Ах + AjBiA^ В = А1В1 + А1В1А2В2.
Так как
Р(ЛХ) = Р(Л2) = Р1,
Р№ = Р(В2) = р2)
Р(Л2) *= Р (Л2) = 1 - ри
P(BJ = 1 - р2,
то
1) Р(А) = Р1 + (1 - Р1)(1 - р2)Р1 = Р1[1 -Ь (1 — Р1)(1 —р2)1,
2) Р(В) = (1 - Р1)р2 + (1 - Р1)(1 - р2)(1 - Р1)р2 =
= (1 - PMI + (1 - Pi)(lр2)1.
1.13. Система управления состоит из четырех узлов Ах, А2, Аэ
и А4 (рис. 1.4). Вероятности Pi безотказной работы узлов соответ-
ственно равны Pi, р2, рз, р4.
Вычислить вероятность безотказной работы Р всей системы уп-
равления.
14
Рис. 1.4. Структурная схема системы
управления
Решение. Вероятность безотказной работы р12 цепи из двух по-
следовательно соединенных элементов Дх и Д2 согласно формуле
(1.19) равна
2
Р13 = П Pi=PlP2-
Вероятность безотказной работы p3i цепи, состоящей из двух
параллельно соединенных элементов Аз и Доопределим по формуле
(1.18):
Р34=1— П (1— Pj) = l— (1— Рз)(1 — Р«)-
/=3
Применяя формулу (1.18) еще раз, получ'аем:
р = 1_(1 _ Р12)(1 _ рз4) = 1 _ (1 _ рхр2)(1 _ рз)(1 _ р4).
Пусть, например, рг — 0,7, р2 = 0,6, рз = 0,8, р4 = 0,9. Тогда
Р = 1 —(1—0,7 > 0,6) (1—0,8) (1—0,9)=1-0,58-0,2.0,1 =
= 0,9884«0,99.
1.14. Вероятности того, что параметры одного из трех блоков
радиостанции (антенно-фидерного устройства, приемника или пере-
датчика) выйдут за время полета самолета из допусков, равны соот-
ветственно 0,1; 0,2 и 0,3. Если из поля допусков вышли параметры
одного блока, связь не будет установлена с вероятностью 0,25, если
двух блоков, то 0,4, если трех, то 0,5.
Найти вероятность Р (Д) того, что связь не будет установлена.
Решение. К интересующему нас событию А ведут три гипотезы:
Нх — за поле допусков вышли параметры одного блока; Н2 — за
поле допусков вышли параметры двух блоков; Нз — за поле до-
пусков вышли параметры трех блоков.
Согласно теореме сложения и умножения вероятностей имеем
Р(Я1)=0,1(1—0,2)(1—0,3)+0,2(1—0,1)(1—0,3)+
+0,3(1—0,1)(1—0,2)=0,398,
/э(//2)=0,1 -0,2(1—о,3)-+о,1 -0,3(1—0,2)4-0,2-0,3(1—0,0=0,092,
Р(Яз) = 0,1-0,2-0,3 = 0,006.
По условию Р(А | Ях)=0,25, Р(А | Я2)=0,4, Р(Д|Яз)=0,5.
Следовательно, по формуле полной вероятности (1.20) получим
з
Р(Д) = 2 Р(Яг) Р(Д | Яг)=0,398-0,25+0,092-0,4 +
+ 0,006-0,5 « 0,139.
15
1.15. По каналу связи, подверженному воздействию помех,
передается одна из двух команд управления в виде кодовых ком-
бинаций Ц111 или 00000, причем априорные вероятности передачи
этих команд'соответственно равны 0,7 и 0,3. Из-за наличия помех
вероятность правильного приема каждого из символов (1 и 0) умень-
шается до 0,6. Предполагается, что символы кодовых комбинаций
искажаются независимо друг от друга. На выходе приемного уст-
ройства зарегистрирована комбинация 10110. Определить, какая
команда была передана?
Решение: Пусть А — событие, состоящее в приеме комбинации
10110. К этому событию ведут две гипотезы: Нг— была передана
комбинация 11111; Н2— была передана комбинация 00000. По
условию Р(Я1)=0,7; Р(Н2)=0,3. Условная вероятность приема
кодовой комбинации 10110 вместо 11111 равна
Р(Л | /7Х) = 0,6-0,4-0,6-0,6-0,4» 0,035.
Аналогично
Р(А| Я2) = 0,4-0,6-0,4-0,4-0,6 ~ 0,023.
По формуле (1.21) находим
p,Hi|4)_ „ 0,78,
' 11 ' 2 0,7.0,035 +0,3-0,023
£=]
Р(/7г| А) = 0’3'0,0—= 0,22.
V 31 1 0,0314
Сравнивая найденные условные вероятности, заключаем, что при
появлении на выходе комбинации 10110 с вероятностью 0,78 была
передана команда 11111.
1.16. Производится 6 независимых выстрелов по цели. Вероят-
ность р попадания при каждом выстреле равна 0,75. Вычислить:
1) вероятность ровно пяти попаданий; 2) вероятность не менее пяти
попаданий; 3) вероятность более трех промахов.
Решение. 1. По условию вероятность попадания при каждом
выстреле р = 0,75. Следовательно, вероятность промаха q = 1 — р=
= 0,25. Вероятность ровно пяти попаданий по формуле (1.22)
равна
р0(5) = C5epV = 6-(0,75)5.0,25^0,356.
2. Требование, чтобы при 6 выстрелах было не менее пяти по-
паданий, будет удовлетворено, если осуществится 5 или 6 попаданий.
Эти события несовместны. Поэтому по формуле (L25) имеем
Рв(/п>5)= 2 CTpmq6~m = C56p5ql+Clp6Q° =
= 6-(0,75)8-0,25+ (0,75)®» 0,534.
16
3. Вероятность того, что при 6 выстрелах будет более трех про-
махов, равна вероятности того, что при этих 6 выстрелах будет мень-
ше трех попаданий (или ни одного попадания, или одно, или два по-
падания). Используя формулу (1.27), получим
2
Р6 (т < 2) = С? рт q6~m = Cl р° q6 +<Л р' q*+ С26 р* =
т=0
= (0,25)6 +6-0,75-(0,25)5+15-(0;75)2-(0,25)4 w 0,0376.
1.17. Вероятность р появления события А при каждом испы-
тании равна 0,2. Производится 400 независимых испытаний.
Определить вероятность Pn(k) того, что: 1) событие А наступит
ровно 80 раз; 2) событие А наступит от 60 до 96 раз включительно.
Решение. 1. Воспользуемся приближенной локальной формулой'
Муавра — Лапласа (1.24). По условию п = 400; k = 80; р = 0,2;.
q = 0,8. Следовательно,
х = (k — np)/V~npq = (80 — 400-0,2)7/400-0,2-0,8=0.
Тогда
Р4ОО(80) = Р1 (0)7/400-0,2-0,8.
По таблице (см. приложение I) находим рц (0)=0,3989. Окончательно'
получаем
Лоо(80)=(1/8)-0,3989« 0,0499.
Формула (1.22) приводит примерно к такому же результату:
Р400(80)=0,0498.
2. Используем приближенную интегральную формулу Муавра —
Лапласа (1.29)
п ,т7 96—400.0,2 \ 60—400-0,2' \
Р4оо(60 < k < 96) = Ф — Ф . =
/400-0,2-0,8 / 1, /400-0,2-0,8 )
= Ф(2) — Ф( — 2,5) = Ф (2) — [ 1 — Ф(2,5)].
По таблице (см. приложение II) находим Ф(2)=0,977; Ф(2,5)=0,994..
Следовательно,
Р4ОО(60 < k < 96)=0,977—1+0,994=0,991.
1.18. Противотанковое орудие ведет стрельбу по танку. Всего*
производится 6 выстрелов, причем вероятность попадания в танк
при каждом выстреле равна 0,3.
Рассчитать: 1) наивероятнейшее число попаданий в танк;
2) число выстрелов, необходимых для того, чтобы с вероятностью
0,9 поразить танк, если для этого достаточно одного попадания.
Решение. 1. Наивероятнейшее число попаданий k0 находим по-
формуле (1.31). По условию, п = 6, р = 0,3, q = 1 — р = 0,7.
Следовательно, 6-0,3 — 0,7 k0 < 6 • 0,3+0, 3, т. е.
1,1 < k0 < 2,1.
17
Между числами 1,1 и 2,1 заключено лишь одно целое число — 2.
Поэтому наивероятнейшее число fe0 = 2.
2) Применив формулу (1.30), получим
п > log(l — 0,9)/log(l — 0,3) ж 6,45.
Таким образом, для поражения танка с вероятностью 0,9 достаточ-
но произвести 7 выстрелов.
1.19. Система наведения ракеты имеет четыре датчика инфор-
мации о цели Di, D2, Вз, информация с которых поступает в
систему управления ракетой. Каждый датчик независимо от дру-
гих определяет параметры движения цели. Вероятности правильного
определения параметров соответствующими датчиками равны:
рг = 0,9, р2 = 0,95, рз = 0,8, р4 = 0,85.
Вычислить вероятности P4(fe), k = 0, 1, 2, 3, 4, того, что правиль-
ную информацию не выдаст ни один датчик и выдадут один, два,
три, четыре датчика.
Решение. Для определения вероятностей P4(fe) составим про-
изводящую функцию. По условию, п = 4; рх = 0,9; qr = 1 — рг =
= 0,1; р2 = 0,95; q2 = 1 — р2 = 0,05; рз = 0,8; = 1 — рз =
= 0,2; р4 = 0,85; q4 = 1 — р4 = 0,15
Тогда
<р4 (г) = Д(^ + Piz) = (0,1+0,9 z)(0,05+0,95z)(0,2+0,8 г)(0,15 +
+0,85 z) = 0,0002 + 0,0056г + 0,0696г2 + 0,3432г3 + 0,5814г4.
Искомые вероятности P4(fe) равны коэффициентам при zk. Следо-
вательно,
Р4(0)=0,0002, Р4(1)=0,0056, Р4(2)=0,0696, Р4(3)=0,3432,
Р4 (4)=0,5814.
1.20. На участке обстрела находятся три цели. Вероятности
pt попадания в первую, вторую и третью цели соответственно рав-
ны р! = 0,4, р2 = 0,3, рз = 0,2. По участку произведено 12 выстре-
лов.
Какова вероятность того, что в первую цель попадет 5 снарядов,
во вторую — 4, в третью — 2 снаряда?
Решение. По условию, п = 12, рх = 0,4, р2 = 0,3, рз = 0,2,
р4 = 1 — (Pi + р2 + рз)=1—0,9=0,1, kr = 5,. k2 = 4, кз = 2,
fe4=12—5—4—2=1. Здесь р4 — вероятность попадания в область,
находящуюся вне целей, fe4 — число попаданий в эту область.
Согласно формуле (1.34) искомая вероятность
Р12(5, 4, 2, !) = 12' (0,4)5-(0,3)4.(0,2)2.0,1 «0,0276.
5! 4! 2! II
18
3. ЗАДАЧИ И ОТВЕТЫ
1.1. Разведывательная пеленгаторная система состоит из четы-
рех синхронно вращающихся антенн с неперекрывающимися ди-
аграммами направленности (рис. 1.5), причем каждая антенна сое-
динена со своим приемником. Длительность сигнала такова, что он
не может быть обнаружен двумя приемниками.
Найти связь события А (обнаружение сигнала пеленгаторной
системой) с событиями Ait i = 1, 2, 3, 4, которые состоят в обнару-
жении сигнала первым, вторым, третьим и четвертым приемником.
Ответ*. А = Аг 4” Л2 4~ Аз 4- А$.
1.2. Прибор состоит из двух блоков первого типа и трех блоков
второго типа. Пусть события: Ait i = 1,2, — исправен ьй блок
первого типа, Bj, / == 1,2, 3, — исправен /-й блок второго типа.
Прибор работает, если исправны хотя бы один блок первого типа
и не менее двух блоков второго типа.
Выразить событие С, означающее работу прибора, через события
At и Bj.
Ответ*. С = (z4t 4~ Л2)(ВхВ2 4“ В^Вз 4" В%Вз).
1.3. Известны события Л, В, С, причем A cz В. Определить
сложные события ЛВ, Л + В, ЛВС и Л 4- В 4- С.
Ответ: АВ = Л, Л + В = В, ЛВС = ЛС, Л + В4-С = В + С.
1.4. Доказать следующие равенства:
1) Л + В = Л + ЛВ, 2) А + ЛВ = Г+ В, 3) Л + В = ЛВ,
А + В = АВ\Ь) АВ = А 4- В.
1.5. Истребитель атакует боевой порядок противника, в составе
которого 6 носителей и 3 постановщика помех, внешне друг от друга
не различимых.
Найти вероятность того, что атакованный самолет является но-
сителем.
Ответ: 2/3.
1.6. В партии полупроводниковых триодов п стандартных и т
бракованных. При контроле оказалось, что первые k триодов стан-
дартны.
Определить вероятность Р того, что следующий триод будет стан-
дартным
Ответ: Р = (п — k)/(n + т — k).
1.7. На пяти одинаковых карточках написаны цифры 1, 2, 3, 4
и 5. Две из них наугад вынимаются одна за другой.
Рис. 1.5. Диаграмма направленности антенн
19
Найти вероятность того, что: а) сумма цифр на вынутых кар-
точках является нечетным числом; б) вторая цифра меньше первой;
в) вторая цифра больше первой ровно на 1.
Ответ*, а) 3/5; б) 1/2; в) 1/5.
1.8. Набирая номер телефона, абонент забыл последние две
цифры и, помня лишь то, что эти цифры различны, набрал их на-
угад.
Определить вероятность Р того, что набраны нужные цифры.
Ответ*. Р = l/Af0 = 1/90.
1.9. Принимаются кодовые комбинации, содержащие пять не-
повторяющихся цифр от 1 до 5.
Какова вероятность Р того, что в одной принятой комбинации
цифры образуют последовательность 12345?
Ответ*. Р = 1/Рп = 1/5! = 1/120.
1.10. В собираемый радиоблок входят две одинаковые радио-
лампы. Технические условия приема блока нарушаются, если обе
.лампы с пониженной крутизной. У монтажника имеется 10 ламп,
из которых 3 имеют пониженную крутизну.
Определить вероятность нарушения технических условий при
•случайном выборе двух электронных ламп.
Ответ*. 1/15.
1.11. В мастерской находятся а + b блоков от двух различных
радиоприемников, из которых два повреждены.
Какова вероятность Р того, что повреждены блоки различных
приемников?
Ответ*. Р = 2ab/(a + b)(a + b — 1).
1.12. Самолет, имеющий радиолокационную станцию с даль-
ностью действия 2), осуществляет поиск со скоростью v в достаточ-
но большом районе площадью S,. в любой точке которого может
всплыть на время t подводная лодка.
Найти вероятность Р обнаружения подводной лодки радиолока-
тором, если время t невелико и лодка обнаруживается при попа-
дании в зону действия радиолокатора.
Ответ*. Р = (л®2 + 2 3)vt)IS.
1.13. Посадочная система аэропорта обеспечивает заход на по-
гадку в сложных метеоусловиях с интервалом между посадками са-
молетов не менее 5 мин. Два самолета должны прибыть на аэродром
по расписанию: один в 10 ч, а другой в 10 ч. 10 мин.
Какова вероятность того, что второму самолету придется ухо-
дить в зону ожидания, если первый самолет может выйти на аэрод-
ром с отклонением от расписания в пределах ±10 мин, а второй —
в пределах ±5 мин, при условии, что величины отклонений от рас-
писания в указанных пределах равновозможны?
Ответ*. 0,25.
1.14. Искусственный спутник Земли (ИСЗ) движется по орбите,
которая заключена между 60° северной и 60° южной широты.
20
Полагая падение ИСЗ в любую точку поверхности Земли между
указанными параллелями равновозможным, найти вероятность
того, что спутник упадет выше 30° северной широты.
Ответ'. [4] : 0,21.
1.15. При испытаниях 200 случайно отобранных резисторов в
течение времени t оказалось, что относительная частота исправных
резисторов равна 0,95.
Определить число исправных резисторов.
Ответ'. 190.
1.16. Проводится бомбометание по трем складам боеприпасов,
причем сбрасывается одна бомба. Вероятность попадания в первый
склад равна 0,01, во второй— 0,008, в третий — 0,025. При попада-
нии в один из складов взрываются все три.
Определить вероятность того, что склады будут взорваны.
Ответ'. 0,043.
1.17. Контролер проверяет взятые случайно изделия из партии,
содержащей а изделий 1-го сорта и b изделий 2-го сорта. Проверка
первых т изделий (т < Ь) показала, что все они второго сорта.
Вычислить вероятность Р того, что из следующих четырех про-
веряемых изделий по крайней мере два окажутся второсортными.
Ответ'. Р = (Сь — тСа + аСь— т + Cb — m)ICa^-b — m>
1.18. На вход радиоприемного устройства поступают кодовые
комбинации, состоящие из двух знаков: 1 (посылка) и 0 (пауза).
Какова вероятность того, что в первой кодовой комбинации будет
хотя бы один нуль, если появление нуля и единицы равновозможно?
Ответ'. 3/4.
1.19. Партия из 100 радиоламп подвергается выборочному кон-
тролю. Условием непригодности всей партии является наличие
хотя бы одной бракованной радиолампы среди пяти проверенных.
Определить вероятность для- данной партии быть непринятой,
если она содержит 5% неисправных радиоламп.
Ответ'. 0,23.
1.20. Прием радиосигналов производится на два разнесенных
приемника. Вероятность правильного приема на первый приемник
равна plt на второй — р2. События, состоящие в приеме сигналов
каждым приемником, считаются независимыми.
Найти вероятность Р правильного приема радиосигналов.
Ответ'. Р = рх + р2 — ргр2.
1.21. Вероятность ухода частоты принимаемых колебаний за
пределы полосы пропускания приемника из-за нестабильности ча-
стоты колебаний передатчика равна 0,1, а из-за нестабильности
частоты колебаний гетеродина приемника — 0,2.
Определить вероятность того, что частота принимаемых коле-
баний не выйдет за пределы полосы пропускания приемника.
Ответ'. 0,72.
1.22. Произведены три независимых измерения некоторой фи-,
зической величины. Вероятность того, что при одном измерении
ошибка превысит заданную точность, равна 0,4.
21
Определить вероятность того, что только в одном из измерений
ошибка превысит заданную точность.
Ответ'. 0,432.
1.23. В студии имеются три телевизионных камеры. Вероят-
ность того, что каждая камера включена в данный момент, равна
0,6.
Найти вероятность того, что в данный момент включена хотя бы
одна камера.
Ответ'. 0,936.
1.24. При передаче текста 10% букв искажаются и принимаются
неверно.
Какова вероятность того, что все пять букв данного слова будут
приняты правильно?
Ответ'. 0,59.
1.25. По каналу связи передаются два сигнала: нуль и единица.
Из-за наличия помех посланный сигнал принимается ошибочно
с вероятностью 0,01 и принимается правильно с вероятностью 0,99
(независимо от того, были приняты предшествующие сигналы с
ошибкой или правильно).
Зная, что послана комбинация 10110, найти вероятность того,
что: а) она принята без искажений; б) принята комбинация 11110;
в) в принятой комбинации имеется одна ошибка.
Ответ', а) 0,99б; б) 0,01-0,99*; в) 0,05.0,99*.
1.26. По каналу связи, состоящему из передатчика, ретран-
слятора и приемника, передаются два сигнала: единица и нуль.
За счет воздействия помех сигналы могут искажаться. На участке
передатчик—ретранслятор единица переходит в единицу с вероят-
ностью рг и в нуль с вероятностью 1— рх; нуль переходит в нуль с ве-
роятностью q\ и в единицу с вероятностью 1— qv На участке ре-
транслятор— приемник указанные вероятности соответственно рав-
ны р2, 1 — р2, q2 и 1 — q2.
Определить вероятность Р того, что комбинация 10, посланная
передатчиком, будет принята приемником без искажений.
Ответ: Р = [рхрг + (1 — рх)(1 — ^2)П^2 + (1 — <7i)(l ~ р2)1-
1.27. Радиорелейная линия связи состоит из т ретрансляцион-
ных станций. Вероятность безотказной работы каждой станции оди-
накова. Станции выходят из строя независимо друг от друга, причем
отказ любой станции влечет за собой отказ всей системы связи.
Определить вероятность р± безотказной работы каждой станции за
промежуток времени Т, если вероятность безотказной работы всей
линии связи за этот промежуток времени должна быть не менее Р.
Ответ'. рх Р1/'".
1.28. Между корреспондентами М и N происходит обмен информа-
цией по схеме, приведенной на рис. 1.6, где Ki и /<2— оконечная
аппаратура, a Lr, L2, Ьз — каналы, взаимно резервирующие друг
друга. Выходы из строя элементов схемы—независимые события.
Вероятности безотказной работы элементов К19 Т<2, Llt Ьз за
время Т соответственно равны: 0,8; 0,7; 0,9; 0,6; 0,5.
22
Рис. 1.6. Система передачи информа-
ции с тремя параллельными элемен-
тами М *7
"l N
Какова вероятность того, что за время Т не произойдет пере-
рыва связи?
Ответ*. 0,549.
1.29. Связная самолетная радиостанция может работать в трех
режимах по мощности: полной, половинной и при мощности, состав-
ляющей 25% полной мощности. Вероятности работы радиостанции
в этих режимах соответственно равны 0,7; 0,1; 0,2.
Вероятности отказа радиостанции при работе в этих режимах
за время Т составляют соответственно 0,3; 0,2; 0,05.
Определить вероятность того, что за Т часов работы радиостан-
ция не выйдет из строя.
Ответ*. 0,76.
1.30. Вероятности того, что во время работы ЭЦВМ произойдет
сбой в арифметическом устройстве, в оперативной памяти, в осталь-
ных блоках, относятся как 3:2:5. Вероятности обнаружения
сбоя в арифметическом устройстве, в оперативной памяти и в осталь-
ных блоках соответственно равны 0,8; 0,9; 0,9.
Найти вероятность того, что возникший в машине сбой будет
обнаружен.
Ответ*. 0,87.
1.31. По каналу связи передаются два сигнала: нуль и единица.
Из-за наличия помех возможны искажения сигналов: единица пе-
реходит в единицу с вероятностью р и в нуль—с вероятностью 1—р\
нуль переходит в нуль с вероятностью q и в единицу — с вероят-
ностью 1 — q. Наугад отправлен сигнал.
Определить вероятность Ртого, что: а) на приемном конце будет
получен сигнал 1; б) на приемном конце будет получен сигнал 0.
Ответ: а) Р = 0,5(1 + р — q)\ б) Р = 0,5(1 — р + ?)•
1.32. Самолет, вылетающий на задание, создает радиопомехи,
которые с вероятностью 0,4 «забивают» радиосредства системы
ПВО. Если радиосредства «забиты», то самолет проходит к объекту
необстрелянным, сбрасывает бомбы и поражает объект с вероят-
ностью 0,8. Если радиосредства системы ПВО «не забиты», то са-
молет подвергается обстрелу и сбивается с вероятностью 0,7.
Найти вероятность того, что объект будет разрушен.
Ответ: 0,464.
1.33. Два из трех независимо работающих элементов вычисли-
тельного устройства отказали.
Вычислить вероятность того, что отказали • первый и второй эле-
менты, если вероятности отказа первого, второго и третьего элемен-
тов соответственно равны 0,2; 0,4; 0,3.
Ответ: 0,298.
23
1.34. Самолет может выполнять задание на больших, средних
и малых высотах, причем на больших высотах предполагается со-
вершить 25% всех полетов, на средних — 10% и на малых — 65%.
Вероятности выхода самолета на заданный объект на больших, сред-
них и малых высотах соответственно равны 0,75; 0,9; 0,65. Самолет
вышел на заданный объект.
Определить вероятность того, что полет происходил на малой
высоте.
Ответ: 0,604.
1.35. По двоичному каналу связи с шумами передаются токовая
(1) и бестоковая (0) посылки с априорными вероятностями р (1)=
=0,6 и р(0)=0,4. Из-за наличия помех возможны искажения сиг-
налов: вероятность перехода единицы в единицу (вероятность при-
нять единицу при передаче единицы) р = (Г| 1)=0,9; вероятность
перехода единицы в нуль р (О' | 1)=0,1; вероятность перехода нуля
в нуль р (О' |0) = 0,8 и вероятность перехода нуля в единицу р (Г 10)=
=0,2. На выходе радиоприемного устройства зарегистрирована еди-
ница.
Какова вероятность того, что: а) в действительности была пе-
редана 1; б) на самом деле был передан 0.
Ответ: а) 0,87; б) 0,13.
1.36. Вероятности того, что при одном выстреле из орудия по-
лучаются недолет, попадание и перелет, равны 0,1; 0,7; 0.2. Для
другого орудия вероятности этих событий равны соответственно 0,2;
0,6 и 0,2. Наугад выбранное орудие стреляет трижды. Отмечены:
одно попадание, один недолет и один* перелет.
Найти вероятность того, что стреляло первое орудие.
Ответ: 7/19.
1.37. Импульсно-кодовая комбинация образуется с помощью
шести двоичных сигналов 0 или 1, которые случайным образом
появляются на позициях кодовой комбинации независимо друг
от друга. Появление сигналов 0 и 1 на каждой позиции равновоз-
можно.
Вычислить вероятность того, что в кодовой комбинации появит-
ся число нулей, меньшее двух.
Ответ: 7/64.
1.38. При вращении антенны обзорного радиолокатора за время
облучения цели успевает отразиться 8 импульсов. Для обнаруже-
ния цели необходимо, чтобы через приемник на индикатор прошло
не менее 6 отраженных импульсов. Вероятность подавления импуль-
са шумом в приемнике равна 0,1.
Определить вероятность обнаружения цели за один оборот ан-
тенны радиолокатора.
Ответ: 0,96.
1.39. Радиоэлектронный комплекс самолета-бомбардировщика
включает в себя 10 объектов. Вероятность безотказной работы каж-
24
дого объекта в течение времени Т равна 0,9. Объекты выходят из
строя независимо один от другого.
Вычислить вероятность того, что за время Т: а) откажет хотя бы
один объект; б) откажут ровно два объекта; в) откажут не менее
двух объектов.
Ответ*, а) 0,652; б) 0,194; в) 0,264.
1.40. На ограничитель поступает последовательность из вось-
ми случайных по амплитуде независимых видеоимпульсов. Вероят-
ность превышения порога ограничения каждым импульсом равна
0,25.
Вычислить: а) вероятность того, что из 8 импульсов не менее
6 видеоимульсов превысит порог; б) наивероятнейшее число видео-
импульсов, превысивших порог.
Ответ*, а) 0,00422; б) 2.
1.41. Вероятность попадания в самолет при одном выстреле рав-
на 0,01. По самолету производится 100 независимых выстрелов.
Определить вероятность двух попаданий в самолет.
Ответ*. Р100(2) « 0,184.
1.42. В передаваемой по каналу связи последовательности
знаков, образующих сообщение, любой знак из-за помех независимо
искажается с вероятностью 0,2. Независимым образом передано
10000 знаков.
Какова вероятность того, что в принятой последовательности
будет от 2000 до 2100 искажений?
Ответ*. 0,494.
1.43. Вероятности разрегулировки датчика опорных частот,
передатчика, приемника и антенно-фидерного тракта за время Т
работы радиостанции соответственно равны 0,4; 0,2; 0,3; 0,3.
Найти вероятность отказа радиостанции за время Т, если из-за
разрегулировки одного блока радиостанция отказывает с вероят-
ностью 0,3, из-за разрегулировки двух блоков—0,5, трех блоков —
0,7, четырех—0,9.
Ответ*. 0,316.
1.44. По линии связи передано четыре радиосигнала, имеющих
различные амплитуды. Вероятности приема каждого из сигналов
не зависят от приема остальных и соответственно равны 0,2; 0,3;
0,4; 0,5.
Определить вероятность того, что: а) будет принято k сигналов
(fe = 0, 1, 2, 3, 4); б) будет установлена двухсторонняя радиосвязь,
если вероятность этого события при приеме одного сигнала равна
0,2, при приеме двух сигналов—0,6, а при приеме трех и четырех
сигналов — единице.
Ответ*, а) 0,168; 0,394; 0,320; 0,106; 0,012; б) 0,389.
1.45. Девяти радиостанциям разрешена работа на трех волнах:
Х2 и Хз. Выбор волны на каждой станции производится случайно.
Найти вероятность того, что на каждой из волн будет работать
точно 3 станции.
Ответ*. 0,0854.
25
2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ
ХАРАКТЕРИСТИКИ ОДНОМЕРНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Случайной величиной называется такая переменная величина, которая
в результате опыта может принимать то или иное заранее неизвестное значе-
ние. Различают два основных типа случайных величин: дискретные и не-
прерывные. Дискретная случайная величина может принимать конечное или
бесконечное счетное множество значений (их можно пронумеровать). Воз-
можные значения непрерывных случайных величин не могут быть заранее
перечислены и непрерывно заполняют некоторый промежуток или даже всю
ось. Часто встречаются случайные величины смешанного типа, .которые могут
и непрерывно заполнять некоторый промежуток и принимать отдельные
дискретные значения.
Полной статистической характеристикой одномерной случайной вели-
чины является закон распределения вероятностей. В случае дискретной слу-
чайной величины X под ним понимается соотношение, устанавливающее за-
висимость между возможными значениями xi дискретной случайной величины
и их вероятностями pi = p(xj).
Закон распределения дискретной случайной величины можно задать в
различных формах: табличной (ряд распределения), графической (многоуголь-
ник распределенья), аналитической (в виде формулы).
Универсальной характеристикой, одинаково пригодной как для дискрет-
ных, так и для непрерывных одномерных случайных величин, является функ-
ция распределения вероятностей Гх(х), определяющая вероятность Р того,
что случайная величина X примет значение меньше некоторого числа х:
Fi(x) = Р(Х<х). (2.1)
Функцию распределения F^x) иногда называют также интегральной функ-
цией распределения или интегральным законом распределения.
Функция распределения обладает следующими свойствами:
1. Fi(-—оо) = lim F1(x)=0.
х->—оо
2. Л(+ °°) = lim Fx(x)=l.
А->4-оо
3. F^x) — неубывающая функция, т. е. F1(x2) > ^1(^1) при х2 > х±.
4. Р(хг < X < х2) = Рг(х2) — F^x,). (2.2)
Функция распределения дискретной случайной величины представляет
собой ступенчатую функцию со скачками в точках xlt x2i ... (рис. 2.1, а),
функция распределения непрерывной случайной величины — непрерывную
функцию (рис. 2.1, б) и функция распределения смешанной случайной ве-
личины— кусочно-непрерывную функцию с не более чем счетным числом скач-
ков (рис. 2.1, в).
В прикладных задачах предполагают, что функции распределения непре-
рывных случайных величин дифференцируемы во всей области возможных
значений случайных величин. При таком предположении непрерывная слу-
чайная величина X чаще всего описывается плотностью распределения ве-
роятности Рх(х), которая иногда называется дифференциальным законом ра-
спределения или дифференциальной функцией распределения. Плотность
вероятности определяется как производная функции распределения:
Рх(х) = dF^xfi/dx. (2.3)
Плотность вероятности обладает следующими основными свойствами:
1. Плотность вероятности неотрицательна, т. е. р±(х) > 0.
26
Рис. 2.1. Функция распределения дискретной (а), непрерывной (б) и смешан-
ной (в) случайных величин
2. Вероятность попадания непрерывной случайной величины в интервал
(jq, х2) равна интегралу от плотности вероятности в этих пределах:
Р(Х! < X < х2) = J Pt(x) dx = F1(x2) — F1(x1).
Xi
3. Интеграл в бесконечных
(условие нормировки):
пределах от функции р±(х)
равен единице
00
J Pl(x)Jx=l.
(2.4)
(2.5)
Очень важное практическое значение имеет гауссовская (нормальная)
плотность вероятности рг (х), которая имеет вид
х 1 Г (х—т)2 1
₽1(х)=7|7а ехр[-------2^~] (2'6)
или
/ . р Гр2 (*—т)2 1 /Л
Pl(x) ехр [-----------£— ] ’ (2 >7)
где т — математическое ожидание (среднее значение) случайной величины
X, о2 = D(X) = Dx — дисперсия, о = + ~]/Dx — среднее квадратическое
(стандартное) отклонение, Е = ро"1/2 — вероятное (срединное) отклоне-
ние X; р = 0,476936...
При гауссовском распределении вероятность попадания случайной ве-
личины X в заданный интервал (а, Р)
Р(а < X < Р) =ф(^——— ф(———) , (2.8)
\ о / \ а /
где
г
Ф(2)=-Ч^=' (
У 2л J
— оо
е X,^2dx,
ф(—2) = 1-ф(г)
(2.9)
— табулированный интеграл вероятности. Значения Ф (z) приведены в при-
ложении II.
27
Для дискретной случайной величины плотность вероятности
P1W= 2 pfi(x~*i)' <210>
Z=l
где Xi — возможные значения случайной величины X, pt — вероятности воз-
можных значений jq, 6(г — г0) — дельта-функция (импульсная функция,
функция Дирака).
Дельта-функция обладает следующими свойствами:
( оо при г =
Zo4~ е
J 6(z—z0)dz = l при любом 8 > О,
z0 — 8
г04- 8
J Kz)6(z-z0)dz = /(z0). (2.11)
г0—-8
г0 г0 + 8
J 6(г—г0) dz=- У 6(z—z0) dz=-~~ , е > 0.
г0 —е, г0
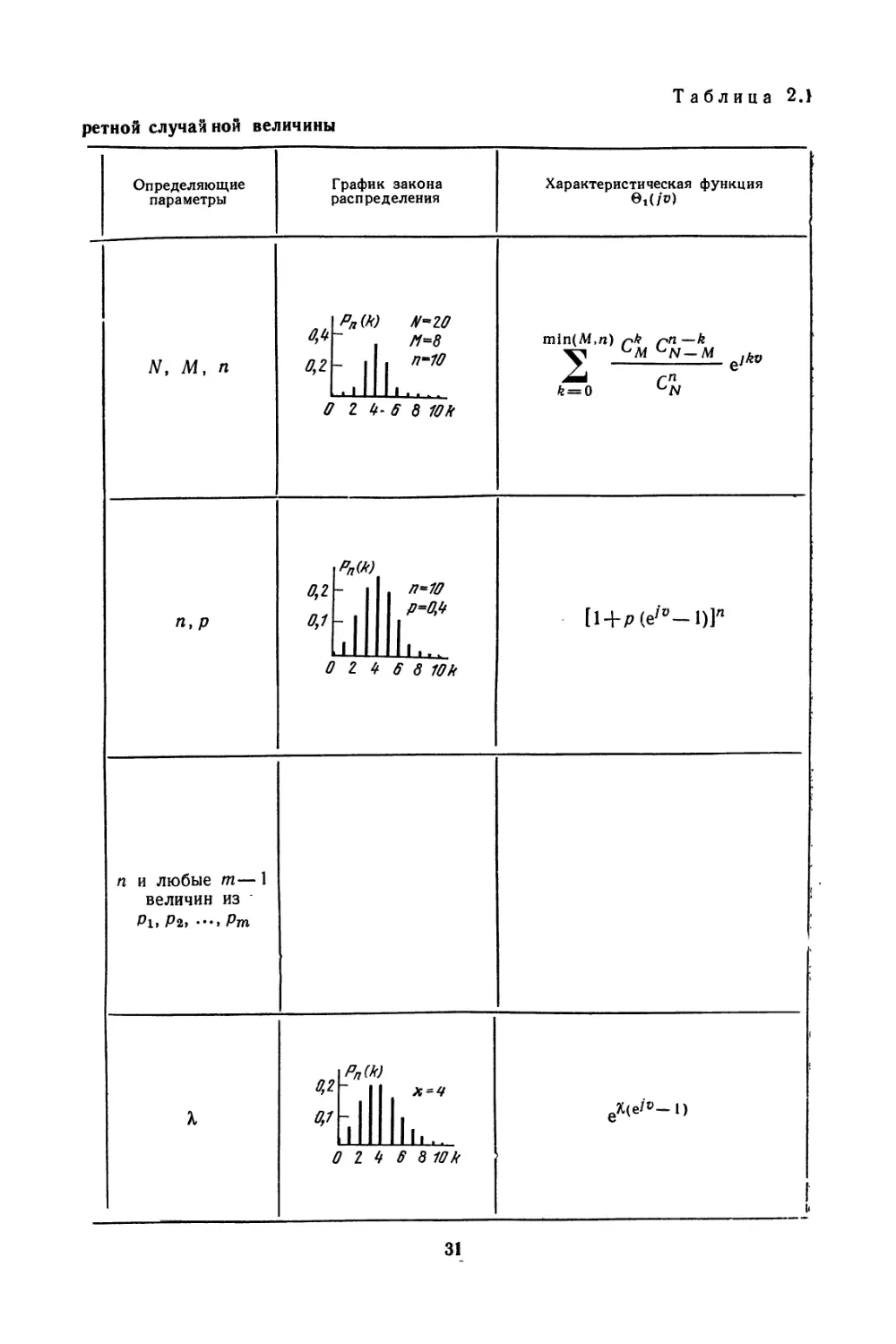
В табл.2.1 приведен ряд законов распределения дискретной случайной
величины и соответствующие им характеристические функции 0Х (/и), а также
графики законов распределения при различных значениях параметров ра-
спределений. Аналогичные данные по законам распределения непрерывных
случайных величин представлены в табл. 2.2 [1,5—15].
Во многих практических задачах трудно или даже невозможно полностью
определить функцию распределения случайной величины. Иногда в этом и нет
необходимости. В таких случаях полное описание случайной величины при
помощи закона распределения может быть заменено указанием отдельных па-
раметров (числовых характеристик) этого распределения.
Наиболее важными числовыми характеристиками случайной величины X
являются математическое ожидание М(Х) = тх и дисперсия D(X) =
= Dx = ol
Для дискретной случайной величины X математическое ожидание
тх=М(Х) = 2 xi Pi (2.12)
f= 1
Если X — непрерывная случайная величина с плотностью вероятности
Р1(х), ТО
оо
тх = J хрг(х) dx, (2.13)
— оо
Формулы для дисперсии соответственно имеют вид:
О« = Л1[(Х-тх)*] = Л4(Х§) = 2 (xt-m^pi, (2.14)
1=1
60
О?= J (x-mx)*pt(x) dx, (2.15)
— оо
где XQ~ X — тх — центрированная случайная величина, т. е. отклонение
случайной величины X от ее математического ожидания.
28
Математическое ожидание определяет абсциссу центра тяжести кривой’
распределения, а дисперсия — рассеивание (разброс) случайной величины
относительно ее математического ожидания. Рассеивание случайной величи-
ны часто характеризуют средним квадратическим отклонением
(2.16)
Кроме математического ожидания, в качестве характеристик положения
случайной величины применяются иногда медиана и мода. Медианой Ме
(иначе срединным или вероятным значением) называется такое значение*
случайной величины X, при котором
Р(Х < Ме) = Р(Х > Л4е) = 1/2. (2.17).
Для непрерывной случайной величины X медиана находится из условия
F^MJ = 1/2
или
00
J Ptlxjdx = f pi(x)dx.
~°° Ме,
Для дискретных случайных величин медиана определяется неоднозначно'
и практически не употребляется.
Модой М (наивероятнейшим значением) называется такое значение
случайной величины X, для которого в случае дискретного распределения ве-
роятность Р(Х = Л4), а в случае непрерывного распределения плотность ве-.
роятности Pi(Af) имеют наибольшее значение. Если максимум один, то ра-
спределение называется одномодальным (унимодальным), а если несколько —
то многомодальным (полимодальным, мультимодальным).
При описании непрерывного распределения используют иногда кван-
тили. Квантилем, отвечающим заданному уровню вероятности р, называ-
ется такое значение х — хр, при котором функция распределения F-^x) при-
нимает значение, равное р:
Fi(xp) = р. (2.18)
Общими числовыми характеристиками случайной величины являются
моменты и энтропия (см. гл. 17 и 18), которые представляют собой неслучай-
ные величины (числа). Характерно, что моменты более низкого порядка не-
сут в себе больше сведений о случайной величине, чем моменты более высокого-
порядка. Моментом k-ro порядка случайной величины X относительно про-
извольной точки а называется математическое ожидание величины
(X - a)k:
mk(a) = М(Х — a)k. (2.19}
Момент, рассматриваемый относительно начала координат (а = 0), называет-
ся начальным, а относительно математического ожидания (а = тх) цен-
тральным.
В некоторых случаях используются абсолютные и факториальные мо
менты, которые соответственно определяются формулами:
₽ft(a) = Af (|Х - а|*), (2.20)
ти(а) = М([Х - а]^), (2.21)
где = z(z — l)(z — 2) ... (г — k + 1)
С помощью факториальных моментов можно в более компактном виде
записать моменты некоторых дискретных распределений (типа биномиального}
и, кроме того, в задачах определенного класса, включающих дискретные слу-
чайные величины, часто удобно находить начальные моменты предвари-
тельно вычислив факториальные.
29
Законы распределения диск
Закон распределения Область изменения значений случайной величины Аналитическое выражение закона распределения
1. Гипергеометри- ческий 6 = 0,1,2,.... min (М, п) — k ~ ч —Af PM =
2. Биномиальный (Бернулли) & = 0, 1, 2,..п Pn(k)=Cknpk(\-p)n~k
3. Полиномиаль- ный 6j=0, 1, 2 п, 62 = 0, 1, 2,п, km = 0, 1, 2,.... п, т 1=1 Pn(^l> ^2» • • • * ^m)= k, k — py ...pm, P1+P2+ •••+Pm = l
4. Пуассона ?з- II О К) p^) = TTe 6!
30
ретной случай ной величины
Таблица 2.}
Определяющие параметры График закона распределения Характеристическая функция е,(Л»
Af, М, П 0,2 0 Рп(Ю № ~ III . 11111 Z 4- 6 8 Юк min(Af.n) pk ^n—k 2 ln-m eMo k = Q
п,р 0,1 0,1 0 PnW ' 2 * . п=1О р-0,0 III».. > 6 8 Юк [l + p(e/0-l)]n
п и любые т— 1 величин из Ръ P2i •••» Рт
К 0,2 0,1 i 9 г Г) Ль-.. « 6 8 10 к eX(e/»-l)
31
Закон распределения Область изменения значений случайной величины Аналитическое выражение закона распределения
5. Геометрический (Фарри) 6 = 0, 1, 2,... Pn(fe) = P(l-P)ft
6. Равномерный 6 = 1, 2, п P(k) =— п
7. Отрицательный биномиальный k — n, п + 1,... или 6=0, 1, 2, ... С* 1 Ct ! 1 s — е II II е II 1 S' S аГ
8. Полиа 6=0, 1, 2,... при а=0; 6=1, 2, ... при а > 0 [ % \6 P(k)-pJ X \1 + аХ/ 1 (1 +а). 1) а] Х fel а > 0, % > 0, Р0 = Р(0) =(1 + аЛ,)-’/а
32
Продолжение табл. 2.1
Определяющие параметры График закона распределения Характеристическая функция A, (fv\
Р ^2 РпМ 0-0,5 2 5 6 8 10 к р[1 —(1— р)е7°]-1
п 0,1 Ог \РМ ’ п=1О ТПП IIIIII 0 2 0 в дЮк е/р(1_е/°")
п, р 0,10 0,05 0 Р(к) 1 2 4 р~О,Ч • б 8 10 к рп[1_(1_р)е/°]-"
а, X 0,10 0,05 й Р(к) > г < a-0t5 А^О H111L > в 8 Юк [1+ аХ(1-е7°)]-1/я
2 Зак 1203
33
Законы распределения непрерывной
Закон рас-
пределения
Область
значений
случайной
величины
Аналитическое выражение
плотности вероятности
Pi (*)
Д * ф
£2 2.
£ 5 2 3
Г рафик плотности
вероятности Pi(x)
1. Равномер-
ный (прямо-
угольный)
а<х<Ь
1
Ь—а
а, b
1
Ь-а
рг№)
Он b X
2. Гауссовс-
кий (норма-
льный)
^feexp
(х—m)2
2а2
т, о
0,8 01 (Z) в=0,5
о,и s I I I I
6 ’ 1- т 1 Л
3. Гауссов-
ский стан-
дартный
/п = 0
о = 1
0,8
т=0
<?=/
-2-7 О 7 2 л
4. Усечен-
ный гауссов-
ский
С
----= ехР
2л
(х—т)2'
2оа
а<х<Ь
б =
1
^ Ь—пг\ л [a—tri
Ф-------1 — Ф -----
\ а J \ а ,
т, о
а, b
0,8
о,и
pf№) т=1,5
(5-0,5
а=т-(5
— л 1 <Ь=т+2<5
.'Л 11
О 7 /77 2 <2?
а Ь
34
Таблица 2.2
случайной величины
2*
35
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности РМ Опреде- ляющие параметры График плотности вероятности Р1(*)
5. Логариф- мически- гауссовский 0<Х<ОО 1 s' - — Х 1 о и IК * 04 5? с? « — S' “ § 1 II J1 1 1 g о S х т, а 0,15 0,10 0,05 L Pf(n) А /77=7 \ (^=0,5 vJ i i io го зо x
6. %2-рас- пре деление 0<Х<ОО К/ к>|з Ю I S " ' * . £ 1 п 0,15 0,10 0,05 L Л (3!) \Xf\^70 iav-<2Z7 ' io го зох
7. Гамма- распреде- ление 0<Х<оо X 1 а “Т ! хе ₽а+‘ Г(а4-1) а, Р а>—1, Р>0 1,0 0,5 1 \ /1 гС^/ъ 1 2 ‘t 6 X
8. %-распре- деление 0<х<оо ю ео| 3 1 Ю | S X £ 1 п 1,0 0,5- 0 Pi(x) Zj 1 Z 3 X
36
Продолжение табл. 2.2
Аналитическое выражение функции распределения График функции распределения FJ*) Характеристическая функция 0i(/t>)
0, х<0, /logx—/п\ _ Ф — , х>0 1,0 Ofi - S\ <3=0,5 r \ I I
I 9 10 20 x
о* с V * С | СЧ * o' f-* 0.5 1y№) \ 1 ___n (1 -2/0) 2
ND | 3 C
* S 10 m
0, x<0, r(a+l;y) \ P > 1,0 0,5 F-tW
/^1 / f \ \ \
г (a+1) 4 ' 2 4 6a
/0, x<0, „ I n x2\ г(т;т) n 1,0 0,5 f^(x) x —-1 / X 22 €) V2 Xe 4 D_n(—/»), где Dp (г)—функция параболического ци- линдра
D \ « I CM . I. II..B
о 1 г ъл
37
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности Pi (*) SJ. s о *=* и- S Cl Е й W 3 О ч е а
9. Распреде- ление моду- ля много- мерного вектора 0<Х<оо Г/ "о „/ flA (2О2) 2 п, о
График плотности
вероятности
РМ
1,5
1,0
0.5
О 1 2 3 я
*№,я<в-0,0
6-0,5
П-4,б=1
10. Распре-
деление мо-
дуля гаус-
совской
случайной
величины
0<х<оо
I
X
ау2л
( Г (х—т)2
Хчехр* --------
2а2 П
(хЦ-m)2 "
2о2
т, о
О (5 2б Ъ<5 я
И. Коши
h
л /г2 + (х—х0)3
/г, х0
0,3 \ Л=/
0,2 \^=7
-Z ь 2 4 д?
I
12. Бета-
распреде-
ление
0<х< I
В (а, 6)
(1-х)6-'
Rl„ » Г(а)Г(&)
D U) — ———————
Г (а+6)
а, b
а>0,
Ь>0
„ п а=Ь=5 а=3,Ь=2
2,0- ' - ' ’
1,0
О 0,5 1,0 31
38
Продолжение табл. 2.2
Аналитическое выражение
функции распределения
График функции
распределения
Характеристическая
функция 6i(/0)
Х<0,
Х>0
О 1 Z 5 х
г (Л)
2«/ 2 — I р
п (М)
/ 0, х<0,
[х—т\
Ф ----- +
\ о /
4-ф 1, х>0
v \ о J
_ о2 о2
е 2 pom X
_ [ т \
Хф — + /оа +
\ а /
4-е ~ivm ф f — — -|-joa
\ а i
4“ + —arctg
2 л
х—х0
h
-г о г их
exp (jxov—hi v |)
О,
Вх (а,Ь)
В (а, Ь)
1,
х<0,
0<х<1,
х>1,
где Вх(а, Ь) — неполная
бета-функция
О 0,5 it0 х
Г (а)
у* (/°)'п г(а+^)
Zd ml Г(а+Н-т)
39
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности гМх) 0-2 п. х я 2 О ч в о. График плотности вероятности Р1(*)
13. Релея 0<х<оо х х2/2о8 0 /?/ М 0,1 t - / \ ? У L 1 1 X— 0 11 гчв/в
14. Обоб- щенный за- кон Релея (Райса) 0<х<оо х [ х2+а2\ ехр( 2а2 Г / ах \ х/« “Г \ а2 J а, о 0,6- 0,4- 0,г\ 0 КЛ2 6=а/в ll^Y3 1 2 ’ z~:n/<3
15. т-рас- пределение (Накатами) 0<х<оо 2 ( т \тг2т- 1 у г (т) \ а2 ) ( т л Хехр! — — х2 1, 1 т> 2 т, о 1,5 1,0 0,5 Z ,т=0,5 Il j । 7 1 Z Z=JJ/S
16. Макс- велла 0<х<оо \f— — х2е-*2/2а2 V Л о* 0 0,6 0,1 ь l—i—i Y__ 7 1 Z Z^X/(5
40
Продолжение табл. 2.2
Аналитическое выражение функции распределения ^i(*) (рафик функции распределения Характеристическая функция
0, г<0 хъ 1 —е 2<т* , FiO) ) e 1Г(г) = е-г’х xfl+z^= f I |/л J / \ 0 / —табулированный интег- рал вероятности от комплексного аргумента
0 12 г-я/е
о*" X о V ч Л к 4s д Ф sHl + I" ‘Ф 22 . 1 X О Ф 1,0 0,5 ь~й/6~1
L Z 1 2 Z^/&
0, х<0, 1 тх2 \ Г\т; ~Г 2 22 „>0 V o,s F’m п,-2__ Г (2m) 0*0*
। 2>”-^Г(т) 8 1 iv(i \ ХР-2"»(- у2^)
г (т) 9 12
0, х<0, 2 „ / 3 х2 \ |утг(т; W ° 1Jh 0,5 ff(z.) i +'" |/ 7
0 1 2 Z~ti/(5
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности оДх) s ф Е S а- о S S <§. График плотности вероятности
17. Стьюден- та (/-распре- деление) —ОО<Х<ОО * th . 1 4* Ь-> | 14* U \ X ь ZJ4I PfOD
-Z 0. 2 а
18. Эрланга &-го порядка 0<х<оо Г(* + 1) X, k (&—це- лое) 1,5 1,0 0,5 1 Л» “4 V ^о Л 1 /ixSS
0 1 2 5 а
19. Вейбул- ла 0<я<оо саха"“1 е~ с*а с>0, а>0 У Cn L А ?
0 2 2 3 а>
20. Фише- ра—Снеде- кора (F-pac- пределение) 0<х<оо Г М1+^г\ 1 2 / ——7 х г/2^\г \ 2 ) \ 2 ) rij nt (til \ 2 2 1 Х/-М X X \ п2 J »1+и2 Л , «1 \ 2 X 1 + — X \ «2 / , п2 7,0 0,5 । Pf(3!)
0 1 1 Ъ я
42
Продолжение табл 2,2
Аналитическое выражение функции распределения Ft(x) График функции распределения Ft(x) Характеристическая функция ©i(/U)
r/fe+n k 2 / _ 7,0 Fl(&} к^Ъ i \ 2 / *
/ h \ я v*«r(—) ^г(т) co &+1 x Й,+тГ! e'“A — co
к <Т1 — со -2 0 Z a
0, x<0, 1 ““ЙГП> ’ 1,0 0,5 Ft№) / jv \—(*-M) \ /
-/ш. У\ к~ъ II 1 -
I 7 1 2 Зя
1,0 0,5 Fite) l + /u j’e/a'v“'^adx 0
[ о, x<0, [ 1 —e—cx<X, x>0 Z li I I
I 7 1 I 3a?
О 1 2 Ъл
43
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности Р1(Х) Опреде- ляющие па рамет- РЫ График плотности вероятности
21. Лапласа (двухсторон- ний экспо- ненциаль- ный) — 00<Х<00 2_е-М *-ul 2 Л, р 0,5 Pt(x) iii iS
-0,500,5 1,5 2,5 X
22. Экспо- ненциальный односторон- ний (пока- зательный) 0<х< оо К 1,5 to 0,5 \^Л^2
1 7 1 2 5 a:
23. Двойное показатель- ное распре- деление —оо<х<оо са^-ах~се~аХ с>0, а>0 0,6 № Pf(X) \^c=1, a=2 ~\ c^a^1 \/c=2,u-1 i \
-1 0 1 2 в
24. Показа- тельно-сте- пенной ОсхСоо хт —-е~л т! т 0,5- 0,25} Pr(X) - ,m=1 r । 2sr^,i
0 2 4 6 Я
25. Симпсо- на (треуго- льный) а<х<Ь 0, —оо<х<а, 4(х—а) Ь+а (Ь-аГ а<Х< 2 ' 4(Ь—х) а-\-Ь (Ь—а)* ’ 2 <Х<Ь' Оч Ь<х<оо a, h 2 Ь-а p^x)
0 a a+b b а: 2
44
Продолжение табл. 2.2
Аналитическое выражение функции распределения FJx) График функции распределения Fi(x) Характеристическая функция ОЙ/»)
_L —ц) 2 — ХЮ<Х<Ц, 1 2- — Ш —Ц) 2 р,<х<оо 1,1 0,' F1W> f=' Лгв4 7 ?-/ .J v+u2
О 1 1 И
I 0, х<0, 1 1— е—Кх, х>0 1.0 0,5 FlW 3L-7 to "I
0 ' 1 2 3 л
е—се~а* 1,0 0,5 Ft®)
7\с-а»1 I I
-10 12л
(0, х<0, Г1” + 1'л,>. х>0 1 Г(т+1) i 1,0- 0,5- i(x) m.z
s I I I I
0 2 0 6л
0, — оо<х<а, 2(х—а)а 1,0 0,5 /у 62?) 4
Л I
(Ь-а)> ’ а<Х< 2 2(6 —х)2 а-\-Ь 1 (»_«). — 1, b<x<oo &{b-ay x p-4 X\e —e )
b ’ a a+b b л 2
45
Закон рас- пределения Область значений случайной величины Аналитическое выражение плотности вероятности Pi (*) 4> с? § а-2 S. С к я 3 О Ч-Е сх График -плотности вероятности 01 (х)
26. Аркси- нуса —а<х<а 1 п ]/а2 —х2 а I i I pfte) I
-и_а 0 а ах Z Z
27. sch2x —оо<х<оо а 2 ch2 ах а 0,5а* <»''' 1 Pf(x) I
0 1_ а а
28. Тихоно- ва —я<х<я 1 D cos х 2л/0(D) D J у'5 4 ,1 5
L^_
-2 о г х
29. 3"^ JT В (cos x)v— д_ Г (у) v>0 1пи /7/6Z7
/ 2v—1
/#42 У1 IV
-10 1$
Продолжение табл. 2.2
Аналитическое выражение функции распределения Ft(x) График функции распределения F\(x) Характеристическая | функция OtC/o)
[0, х<—а, 1 1 X — -4-— arcsin — , 2 л а —а<х< а, (1, х>а 1,0 0,5, Ff(a) I i e e'ox л J Va2—*2 —a = J0 (au), 'где Jo(2)— функция Бес- селя нулевого порядка первого рода
-a 0 a a
1 1 1- — th ах 2 2 1,0 0,5. Fr№) I _ vn 2а sh —— 2а
__7 о i_ x * a
! f eDcos<dZ 2n/0(D) J —л 1,1 0,5 I-'-®*3 I _
-7 0 1 x
В J (cos Z)v~’ dt Л 2 1,0 0Л fytx) ^3 I
~1 0 1 x
47
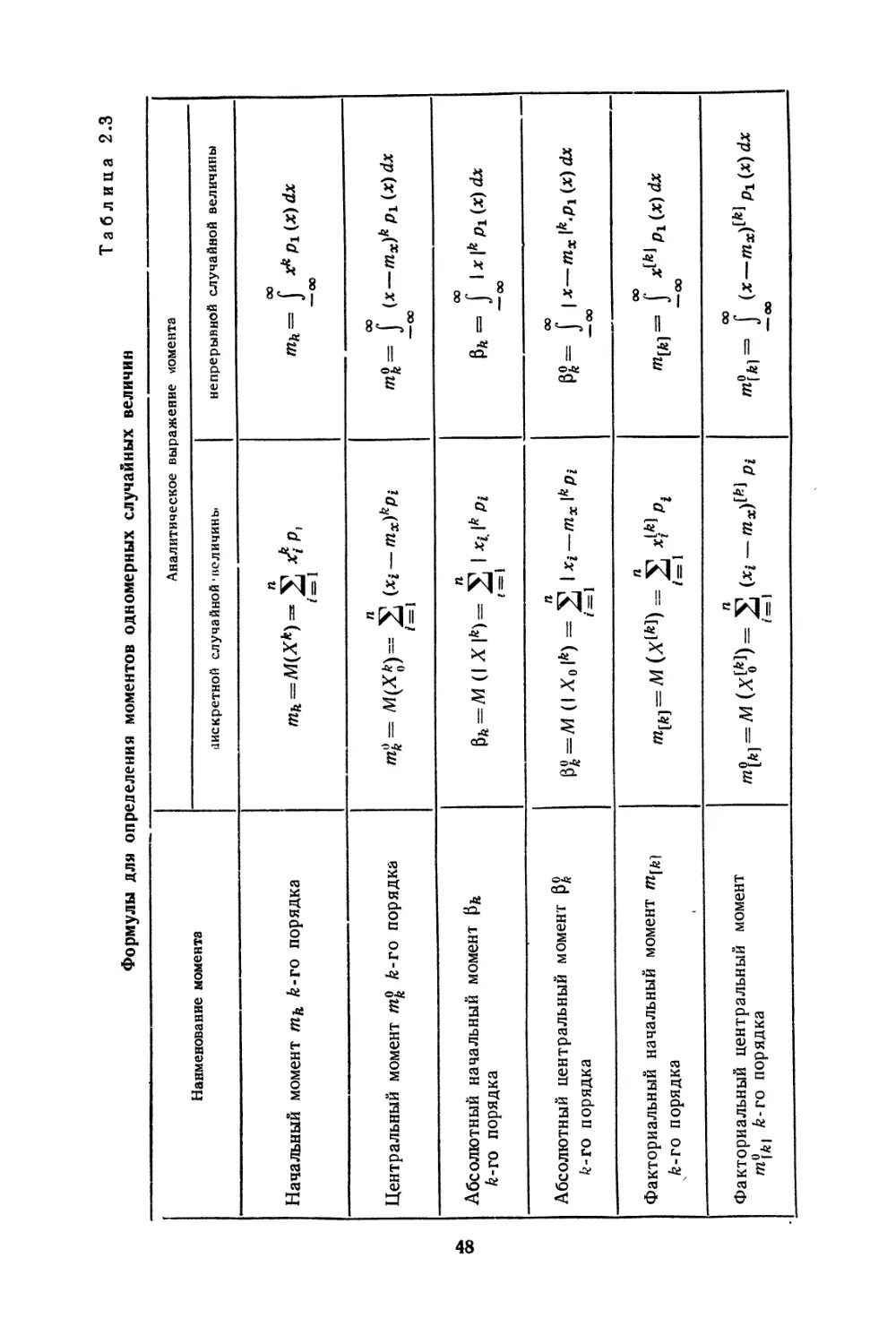
Формулы для определения моментов одномерных случайных величин
Таблица 2.3
Наименование момента Аналитическое выражение момента
дискретной случайной•величины непрерывной случайной величины
Начальный момент k-ro порядка «Й=Л1(Х*)=2 *4 , = 1 co = J xfi Pi (x) dx — oo
Центральный момент k-ro порядка «£ = М(Хк)= 2 ^i-mx)kPi Z = 1 m^= J (x—mx)kPl (x)dx —oo
Абсолютный начальный момент Р^ fe-ro порядка pfe = A4(|X|fc)= 2 oo ₽fe = J 1X 1* P1 (x) dx — oo
Абсолютный центральный момент Р£ k-го порядка ^=Л1(1Хв|*) = 2 ^i-mx^Pi i = \ oo ₽*= J 1х—тх1к.рг (x)dx — oo
Факториальный начальный момент k-vo порядка n OT[ft]=A1(xW) = 2 4*4 Z= 1 mW= f — oo
Факториальный центральный момент k-vo порядка m[k] = M (*oftl)= У, (Xi — mx)ffe) Pi ;=i oo I (x—mx)lk}P1(x)dx — OO
В табл. 2.3 приведены аналитические выражения различных моментов
для дискретной и непрерывной случайных величин. Из приведенных данных
видно, что математическое ожидание, определяемое формулами (2.12) и (2.13),
представляет собой начальный момент первого порядка. Для любой случайной
величины центральный момент первого порядка равен нулю, а центральный
момент второго порядка представляет собой дисперсию. Абсолютные моменты
четных порядков совпадают с обычными моментами.
При решении практических задач наиболее часто используются началь-
ный момент первого порядка тх (математическое ожидание), начальный мо-
мент второго порядка т2 (средний квадрат случайной величины), центральный
момент второго порядка (дисперсия), центральные моменты третьего и чет-
вертого порядков, а также абсолютный центральный момент р? первого по-
рядка, называемый средним арифметическим отклонением.
С центральным моментом третьего порядка т% связан коэффициент асим-
метрии характеризующий «скошенность» распределения, а с центральным
моментом четвертого порядка mJ — коэффициент эксцесса у2, показывающий
«крутость» распределения вероятностей. Для симметричных относительно
математического ожидания распределений все моменты нечетного порядка
(если они существуют) равны нулю и асимметрия отсутствует. Эксцесс нор-
мального распределения равен нулю. Если кривая плотности вероятности
Pi(x) имеет более острую и высокую вершину по сравнению с нормальн ым
распределением, то эксцесс положителен; если более низкую и пологую, —
то отрицателен. Коэффициенты асимметрии и эксцесса определяются соот-
ветственно формулами:
?1 = mj/o3, (2 22)
у2 = mj/o4 - 3. (2 23)
Моменты — не единственные постоянные, характеризующие распреде-
ление случайной величины. Для теории более полезна другая совокупность
постоянных, называемых семиинвариантами (или кумулянтами) Отличие
их от моментов относительно произвольной точки состоит в том, что все семи-
инварианты (за исключением первого) инвариантны относительно изменения
начала отсчета. Название «семиинварианты» как раз и обусловлено их ин-
вариантными свойствами.
Различные моменты и семиинварианты связаны между собой следую-
щими соотношениями [1, 10, 11]:
k
mk= 2 скт^-1т{>
1= о
k
1= 0
m2 = mg + mi, ms = "i3+3mi + mt »
m4 = mj 4-4mi +6mf m% +m|,...
= ml, =ms— 3mi m2+2ml t
т$=т4—4т!та+6т1 т2—3т} ,
т[3^ = т3— 3m2 + 2mx, m[4] —6m3 + llm2 —6mlf ...
= w2 = ,n[2]
/Пз = W[3j +3/П|-2] + m[ 1 ], m4=/n[4] +6/П[з] +7/H|-2] +
(2.24)
(2.25)
(2.26)
(2.27)
(2.28)
(2.29)
49
(2.31)
(2.32)
(2.33)
/П2=х2, w? = x3, m'l = x44-3x| ,
x2 = m§, x3 = m^, x4 = mj —3m^’2,...
/щ = Х1, m2 = x24-x?, m3 = x3H-3x1 x2 + x?y
m4 = x4+4xi x3 + 3x| 4-6xi x2 + x|,...
Xi = mx, x2 = m2—mf, x3 = m8 —Зтг m2+2m? ,-
x4 = m4—4mx m8 —3m| + 12m? m2—6m?,...
В формулах (2.28) и (2.29) предполагается, что возможные значения слу-
чайной величины отличаются на единицу.
В случае аналитического задания закона распределения (в виде формулы)
определение моментов сводится к вычислению соответствующих сумм и инте-
гралов (см. табл. 2.3). Расчет моментов упрощается, если воспользоваться
аппаратом характеристических функций.
Характеристическая функция 0х(/и) определяется как математическое
ожидание случайной величины т. е.
01(/о) = Л4(е/од:) = J е,ох Pi(x)dx , (2.34i
—оо
где v — вещественная величина, / = 1/ — 1.
Используя представление плотности вероятности рх(х) в виде суммы
дельта-функций, формулу (2.34) можно распространить на дискретные слу-
чайные величины:
п
Ol(/v) = 2 ’
'= I
(2.35)
где Xi —возможные значения случайной величины X, = Р(Х — xt) —
соответствующие им вероятности.
Плотность вероятности рх(г) однозначно выражается через характеристи-
ческую функцию:
Pi (X) = - 2д J . &t(jv)e~ioxdv. (2.36)
—оо
Из (2.34) видно, что при изменении знака у показателя экспоненты оп-
ределение характеристической функции совпадает с определением спектраль-
ной функции. Поэтому для нахождения по известной плотности рх(х)
или Pi(x) по 0х(/ц) можно пользоваться таблицами преобразований по Фу-
рье (или по Лапласу с учетом пределов интегрирования).
Для определения моментов случайной величины X нужно вычислить
k-ю производную от характеристической функции по параметру v и положить
v = 0:
1 d& 0Х (jv) 1
k ik dvk L=o
(2.37)
Семиинварианты x& определяются из соотношения
In ©1(7»)= У (2.33)
ь—i k]
Вместо характеристических функций 01(/и) часто используются так
называемые производящие функции [10—12]:
ф1(и) = Л4(е1,х) = J evx p^xjdx . (2.39)
50
Рис. 2.2. Взаимно-однозначное функциональное преобразованиег
а — прямая функция, б — обратная функция
Существенное различие между ними состоит в том, что характеристи-
ческая функция существует всегда, а производящая функция — только в
случае существования всех моментов.
В табл. 2.4 приведены формулы для основных числовых характеристик
дискретных законов распределения, а в табл. 2.5 — для наиболее распростра-
ненных непрерывных законов распределения [1, 4—16].
Во многих инженерных вероятностных расчетах, например при изучении
прохождения случайных сигналов через линейные и нелинейные системы
(см. гл. 10—12), часто требуется определить плотность вероятности р^у)
случайной величины Y по известной плотности вероятности рг(х) случайной
величины X и известной функциональной связи Y = g(X) случайных вели-
чин Y и X.
Если обратная функция X = h(Y) однозначна (рис. 2.2), то правило пре-
образования плотностей вероятностей случайных величин определяется фор-
мулой
Р1(у) = Pi(x)\dx/dyl = | dh(y) ldy\. (2.40)
Если обратная функция X == Л(У) неоднозначна, например имеются
две ветви обратной функции hr(y) и h2(y) (рис. 2.3), то плотность вероят-
ности pt (у) находится по формуле
Р1(у) = I Щу) I + pJMj/)] | hi (у) I • (2.41)
Если число ветвей обратной функции больше двух, то в правой части
формулы (2.41) следует брать сумму по всем ветвям
Pi(y)= 5 л1МЮ]|Л№)|,
Рис. 2 3 Квадратичное (двухзначное) преобразование:*
а — прямая функция, б — обратная функция
51
Основные числовые характеристики
Наименование закона т а8 Центральный момент т^> коэффициент асимметрии
Гипергео- метрический м п л/ М (М—ft) о М (М—М) (М—2М) тз~" N3(N—1)(/V—2) Х Xft (W—п) (N—2n), (N—2M) (N—2n) УлТИ- 71 (N—2) n(N—n)
№(W—1)
Биноми- альный пр npq, q=\—p m^=npq(q—p), q—p Vl У npq
Пуассона Л X mg =X, 71= yr
Равномер- ный п-Н 2 П2—1 12 m» = 0, Ti=°
Полна X X (1 + Q*X) т!| = М14-сЛ)(1 + 2сЛ), 1 -Б 2ak X (1 -J- ocX)
52
Таблица 2.4
дискретных законов распределения
Центральный момент т^> коэффициена эксцесеа у2 Другие соотношения для mom^htof
о М (N-M)n(N-n) Л/4 (N— 1)(/V —2) (N—3) х X (N -|-1) _ 6№ п (N—п) + 4-ЗМ (N—M) [№ (я—2) —Nni+ + 6n (N—n)]} i 1
= Зя2 р2 q2+npq (1 — 6pq), 1 — ^pq ?2= npq j / dtn^ \ m^ + i ~pqlnkmbk_}+ )
m° = 312 + K, 1 Ъ = ~ Хд = A, dnk mg+1 ^km^ + K-^-, k—\ ть+1=тк+К ^Cl~'mn_.
(n2 — 1) (3n2 — 7) 240 4
m»=3a2 (2a-H)A.*4- 4-6a (2a+1) A.3 + (7a4-3) X2 + A,, ?2“6“1 Ml+aX)
53
Основные числовые характеристики
Наименование закона т а? Центральный момент то, коэффициент асимметрии Vt
Равномерный а-\-Ь 2 (Ь—а)г 12 о" О II II s’
Нормальный т о2 -С S н> Q9O II II ° -°
Нормальный стандартный 0 1 О О II II g”
Е>ета- распределение а а-\-Ь ab (a+b)* (a+b+1)
Релея НН^1 о о2 f 2 — — \ 2 / «8=аЗ(л-3) У ЪМл-З) У
Вейбулла с а X хг(1+—1 \ а / —“f / 2\ с “ г1+- - L \ а / -Г2(1 + —YI \ а / J V1 = — О3
Лапласа Ц 2 X2 6 3 Хз 3V2 ъ=—
Экспоненциаль- ный односторон- ний 1 К 1 X2 3 КЗ 71=2
Гамма-распре- деление (“4*1) Р (а + 1) Р2 mg =2 (а + 1) рз, 2 Y1~ Ум~т
54
Таблица 2.5
непрерывных законов распределения
Центральный момент m<*f коэффициент эксцесса ув Другие соотношения для моментов
Я1. (Ь-аУ 80 ’ ?2=—1,2 &*+1_а*+1 тъ , /Л+2—afe+2 fc+1 тЛ+1= bk_l_ak_i k+2 mh
т2=3о4, Т2=о Л (2k)\ ( о2 \* т§4““ kl у 2 ) ’ m2*+l—0‘ .. Су?] mk'21 (°2/2)1 ^=fe,2 (fe_20! > - [k/2] — наибольшее целое число, не превосходя- щее k/2
со О П II ©чл Л? g *• а (2*)! / 1 ^^2k- м m2ft+i=m’ft+1=0
т Г(а+&)Г(а+^) ft= Г(а)Г(а+Н-*)
ся~'^ е е СО I хГ . । ^2^ 1 ч» LO о II 11 i O’# £ k m^= 2 (-WС1кт!mh-t f=0
mt п ъ=~г~3 (Г mu=c a Г fl 4- \ a / k ^(-‘WClkmt mk-t f=xO
24 «4- %4 Ь = 3 —' 2<Tl2i). l-‘ m0ft=(2fe)U^, m%k+i=0
°> Не <о 11 11 сч Orf р- £ mk^=k\ h~k, k 4* 1 tnk+l I " mk
mJ=3(a+3)(a + l)P«, 6 Ys-a+l 'Пл+1=(а+/г-М)₽'л/1> Kk = (k—1)1 (a+1) 0*, Xfc+1=fe0xft
55
где п — число ветвей (число неоднозначностей). Задача преобразования
плотностей вероятностей рассматривается только для непрерывных случайных
величин. Функциональное преобразование дискретной случайной величины
не изменяет распределения вероятностей; оно изменяет только ее возможные
значения.
Определение числовых характеристик случайной величины Y ® g(X) яв-
ляется частным случаем рассмотренной задачи. При этом их можно вычислить
двумя способами: с помощью найденной по формулам (2.40), (2.41) плотности
вероятности рг(у) или путем усреднения g(X). Второй путь экономичнее,
так как не требует определения плотности вероятности функции р± (у). На-
пример, формулы для математического ожидания и дисперсии случайной ве-
личины Y — g(X) при этих способах соответственно имеют вид:
mv = J УР1(У) dy, J (у—ту)2 pt(y i dy , (2.42)
—оо —оо
Шу = J g(x>pr(x}dx, = J mv]2pi(x) dx . (2.43)
—oo — oo
Для дискретной случайной величины числовые характерисшки находятся
по формулам:
mv = M[g( X)] = 2 S(xi }Pt, (2.44)
' t
o^D[g(X)] = 2 lg№)-mv]*Pi • (2-45)
i
2. ПРИМЕРЫ
2.1. По одной и той же стартовой позиции противника произ-
водится пуск пяти ракет, причем вероятнссть р попадания в цель
при каждом пуске равна 0,8.
Построить: 1) ряд распределения числа попаданий; 2) много-
угольник распределения; 3) функцию распределения F^x) числа
попаданий.
Решение. Случайная величина X (число попаданий в цель)
может принять следующие значения: х0 = 0, хх = 1, х2 = 2,
хз = 3, = 4, хъ = 5. Эти значения случайная величина X при-
нимает с вероятностями р0, ръ ря, ря, pit рь, которые в соответствии
с формулой (1.22) равны:
р0 = (1 — р)ь = 0,26=0,00032,
Pi = QpQ. — р)' = 5-0,8-0,24=0,0064,
Р2=С|р2(1 — р)3=10-0,82.0,23 = 0,0512,
Рз = С3р3(1 — р)2 = 10-0,83.0,22=0,2048,
Pt = С‘р4(1 — р)=5-0,844.0,2=0,4096,
р5 = р5 = 0,85=0,32768.
Из вычисленных значений рг, I = 0, 1, 2, 3, 4, 5, видно, что
наиболее вероятно попадание в цель четырьмя ракетами, в то вре-
мя как промах всеми ракетами маловероятен.
56
Рис. 2.4. Многоугольник
распределения
Рис. 2.5. График функции
распределения случайной
величины
1. Ряд распределения имеет следующий вид:
*1 0 1 9 3 4 5
Pi 0,00032 0,00640 0,05120 0,20480 0,40960 0,32768
2. В соответствии с рядом распределения вероятностей числа
попаданий в цель построен многоугольник распределения, представ
ленный на рис. 2.4.
3. По определению, функция распределения
F1(x)=P(X<x) = М = 4
xi<x
При х 0 /71(х) = Р(Х < х) = О,
при 0 < х 1 Fi(x) = Р(Х = х0 = 0)=0,00032,
при 1 < х < 2 Fx(x) = Р(Х = 0) + Р(Х = 1)=0,00032+
+ 0,00640=0,00672,
2
при 2 < X < 3 Fi(x) = '2 Р(Х = Xi) = 0,05792,
1=0
3
при 3 < х < 4 Л(х) = 2 Р(Х = хг)=о,26272,
i='O
при 4 < х < 5 Fx(x) = 2 Р(Х = xf)=0,67232 ,
5 5
при х>5 Л(Х) = 2lP(X = xi)=r =
f=0 f=0
График функции распределения представлен на рис. 2.5.
2.2. Плотность вероятности pi (х)-случайной величины X имеет
вид
рг(х) = а ехр (—р | х |), —оо < х < оо,
где а и Р — постоянные величины.
57
Требуется: 1) найти соотношение, которому должны удовлетво-
рять постоянные а и 0; 2) вычислить функцию распределения (х)
случайной величины X; 3) построить графики плотности вероятно-
сти рх(х) и функции распределения Fx(x) при 0 = 2.
Решение. 1. Чтобы найти соотношение между постоянными
а и 0, воспользуемся условием нормировки для плотности вероят-
ности. При этом учтем, что плотность вероятности имеет разные
аналитические выражения при х <. О и х > 0:
00 ОО О оо
J px(x)dx = а
— оо —00 L—00 О J
Следовательно,
0 = 2а.
2. Функция распределения /^(х), по определению, равна:
Л(х)= f pl(z)dz.
При х < О
— оо
При х > О
X
FJx) = ——|- а С е~&2 dz = ——-----------— е~&х = 1 —— е~₽*.
и 2 J 2 7 2 2 2
о
3. При 0=2 рх(х) = е-21 *1,
г . . | 0,бе2* при х^О,
г,(х) = I •
(1 — 9,5е~2х при х>0.
Графики рх(х) и Fx(x) при 0 = 2 изображены на рис. 2.6.
2.3. Функция распределения Fx(x) случайной величины X за-
дана графиком (рис. 2.7).
Рис. 2.6. Плотность вероятности (а) и функция распределения (6) непрерыв-
ной случайной величины
58
Рис. 2.7. Функция рас- Рис. 2.8. Плотность ве- Рис. 2.9. Функция рас-
пределения роятности пределения
Требуется: 1) найти аналитическое выражение для функции
распределения; 2) построить график плотности вероятности рг (х);
3) определить вероятность Р того, что величина X примет значение
от 3,5 до 4,5
Решение. 1. Когда значения величины X заключены в пределах
от 3 до 5, функция распределения F± (х) представляет собой отрезок
прямой, проходящей через две точки с координатами (3, 0) и (5, 1)
Используя уравнение прямой в виде (х—хг)/(х2—Xi) = ((/ — ySKy*—
— уг), получаем (х — 3)/(5—3) = Гг(х)/1, т. е. F^x) = (х — 3)/2
Следовательно,
Fi(x) =
0
(х—3)/2
1
при х^З,
при 3 <х ^5,
при х> 5.
2. По определению, рх(х) = dFy[x)ldx. Поэтому
рх(х) =
0 при х^З,
1/2 при 3 < х<15,
0 при х> 5.
График плотности вероятности рг (х) представлен на рис. 2 8.
3 Р = Р (3,5 < X < 4,5) = Fx (4,5) —, Fx (3,5) = (4,5—3)/2 -
— (3,5—3)/2=0,5.
2.4. Случайная величина X удовлетворяет неравенству —1
X 1, причем в интервале от —1 до 4-1 она распределена рав-
номерно, а каждое из значений — 1 и +1 принимает с вероят-
ностью 1/4.
Необходимо: 1) найти и построить функцию распределения
Fl(x) случайной величины X; 2) вычислить вероятность Р того,
что случайная величина X попадет в интервал от —1/2 до 4-1/2
Решение-. По условию, X — случайная величина смешанного
типа.
1. При х < —1
Fj(x) = Р(Х < х) = 0.
При —1 < х 1
Л(х) = Р(Х = —1)4-ур!(х)^х = у 4- f -
1 — 1
1 х+1х+2
4*4 4
59
При х > 1
i
F1{x) = P(X = -1)+ С Jl+p(x=i)=-L+-L+_L = i.
J 4 4 2 4
— I
График функции распределения Fi(x) приведен на рис. 2.S).
2 +_____lu2-±^_ 2-°-5 „2-
\ 2 / Ц 2 / 4 4 4’
2.5. Случайные ошибки измерения дальности до неподвижной
цели подчинены гауссовскому закону с математическим ожиданием
т = 5 и средним квадратическим отклонением о = Юм.
Определить вероятность того, что: а) измеренное значение даль-
ности отклонится от истинного не более чем на 15 м; б) при трех не-
зависимых измерениях ошибка хотя бы одного измерения не прев-
зойдет по абсолютной величине 15 м.
Решение, а) Определение вероятности того, что измеренное зна-
чение дальности отклонится от истинного не более чем на 15 м,
сводится к вычислению вероятности попадания случайной величи-
ны X (ошибки измерения) ст = 5мио=10мна интервал от
—15 до 15 м.
Используя формулу (2.8) и значения Ф(г) из приложения II,
получаем:
а) Л = Р(|Х|<15) = Р(-15<Х<15)=ф(1^-
“Ф(^^)=Ф(1)~Ф(~2) = Ф(1)_[1~Ф(2)) =
= 0,8413 —1 +0,97725 «0,82.
б) Вероятность Р2 того, что при трех независимых измерениях
ошибка хотя бы одного измерения не превзойдет по абсолютной ве-
личине 15 м, определится по формуле
Р2 = 1—(1 _ _о,82)3 « 0,994.
2.6. Производится стрельба по подвижной цели до первого по-
падания. Вероятность р попадания при каждом выстреле равна
0,4. На стрельбу отпущено 4 снаряда.
Вычислить: 1) математическое ожидание тх случайной величины
X — числа израсходованных снарядов; 2) дисперсию и среднее
квадратическое значение ох величины X.
Решение. Случайная величина X может принять следующие
значения: хг = 1, х2 = 2, х3 = 3, х4 = 4. Вероятности принятия
величиной этих значений соответственно равны:
Р(Х - 1) = Р1 = р = 0,4, Р(Х = 2) = р2 = (1 - р) р =
= 0,6 • 0,4 = 0,24,
Р(Х = 3) = р3 = (1— рУ р = 0,62 . 0,4 = 0,144,
Р(Х = 4) = р4 = (1 — р)3р + (1 — р)4 = 0,63Ю,4+0,64 =0,216.
60
1. По определению математического ожидания, имеем
тх = 2 xi Pi = 2 хгрг= 1-0,4+2-0,24+3-0,144+4-0,216 ~ 2,2.
/=1 <=1
2. Для дисперсии получим
oj = 2 (xi~mx)2Pi = (l~2,2)2-0,4+(2 — 2,2)г-0,24 +
/=i
+ (3—2,2)2 • 0,144 +(4 -2,2)2-0,216 ~ 1,38;
ож = +/^ = /1Д8 ~ 1,17.
2.7. Случайная величина X имеет распределение Лапласа,
плотность вероятности рг(х) которого
р1(х) = -^е-Мх|, Л>0.
Найти математическое ожидание и дисперсию величины X.
Решение: Математическое ожидание определяем по формуле
(2.13):
ОО 00
тх = J xp^xjdx = J xe_?l 1 *1 dx.
— ОО —00
Так как плотность вероятности рх(х) имеет разные аналитические
выражения при х < 0 и х > 0, то
О оо
тх — J хеЛх dx Н—J хе~Кх dx.
— ОО О
Сделав в первом интеграле замену переменных х — — у, получим
О оо оо
тх = —{dy Н—— f xe~u dx = —- f ye~Kt/ dy +
J 2 J 2 J
оо О 0
00
+ -y- Jxe~x* dx.
о
Следовательно, mx = 0. Тогда
ос 0 оо
и^=/п2= J x2 px (x) dx = -y- J x2eudx + -|- J x2e-ljrdx==
— oo — ОС 0
у2 e-Ky dy + _L J x2 e-kx dx = % J х2е~Хх dx.
о о о
61
Известно [17], что
J хп е -<« dx = • (2.46)
о
Следовательно,
<тх2 = %Г(3)/Х3 = 2/Z2.
2.8. По каналу связи с помехами передается кодовая комбина-
ция, состоящая из двух импульсов. В результате независимого воз-
действия помехи на эти импульсы каждый из них может быть
подавлен с вероятностью р.
Определить характеристическую функцию ©i(/v) случайной
величины X — числа подавленных помехами импульсов.
Решение. Возможные значения дискретной случайной величины X:
Xi = 0, х2 = 1, х3 — 2. Вероятности pt этих значений соответст-
венно равны: Pi = (1 — р)2, р2 = 2р(1 — р), ра — р2.
Согласно формуле (2.35) имеем
з
0^/w) = S pte,vxi = (1 — р)2 + 2р(1 — р) e’v + р2е2^ =
= 1 — 2р + р2 + 2р^‘° — 2р2^‘° -|- p*&iv —
= 1+2р(е/’° — 1) + р2(е^ — I)2 = [1 + р^° — 1)|2.
2.9. Случайная величина X имеет равномерную плотность ве-
роятности в интервале от —0/2 до 0/2.
Определить характеристическую функцию случайной
величины X и нарисовать ее график.
Решение. По условию нормировки, рг (х) ((3/2 + 0/2) = 1.
Следовательно, рх(х) = 1/0. Тогда
оо р/2
— (* е/0Л Pi (x)dx=— С • &vx dx — —— (е/оР/2 —е~2) =
J Р J /Р»
-оо —Р/2
__sin (t>p/2)
” t>P/2 ’
Графики плотности вероятности рх(х) и соответствующей ей харак-
теристической функции ©хО’п) приведены на рис. 2.10.
Рис. 2.10. Равномерная плотность вероятности (а) и соответствующая ей
характеристическая функция (б)
62
2.10. Найти плотность вероятности pt (х) случайной величины X,
характеристическая функция которой имеет вид
QiUv) = 1/(1 + v2).
Решение. Согласно формуле (2.36) имеем
оо 00 fvx
— f 01(/y)e-'°*dv=-!- f е—^-dv =
2л J 2л J 14- v2
— 00 —oo
00 00
1 P COS UX—/sin VX 1 1 P COSUX J
-— i ----------1-----dv —------ I -------dv
2л J 1+u2 2л J l-|-02
— OO —00
2л J 1+у2
— 00
COS VX , 1 , „ .
-----dv= —e~i«i
14-v2 2
так как
f = —e-i“i.
J 1+? 2
о
2.11. Случайная величина X подчинена ^-распределению,
плотность вероятности которого имеет вид
Р1(Х) =
-----------%"/2-1 е-*/2 при х>0 л>0,
2"/2Г(л/2)-г
О при х<0.
Вычислить характеристическую функцию ©i (Ju) и начальные
моменты величины X.
Решение. Так как плотность вероятности отлична от нуля толь-
ко при х > 0, то
(ЛО = J е/ох Pi (*) dx —
1
2"/2 Г (.Л/2)
оо
У eivx хп'2~' е~х'2 dx =
о
= ----- хп/2-1 е~<1/2~^°)х dx. *
2л/2Г(п/2) J
о
Воспользовавшись интегралом (2.46), получим
=______*________Г(я/2-14-1)_ (1 _ 2jv\-nf2
2п/2Г(л/2) (1/2—/р)"/2-14-1 1* •
Начальные моменты tnh связаны с характеристической функцией
соотношением (2.37):
1 ^ех(/р)|
ft j* do* |0=о'
63
В нашем случае
— ' {1°) = jn(l --2/у)~ п/2 ~1,
dv
=/2n(/i+2)(i —2/10—',/2~2,
dv2
•d3 01 = j3 п(п+ 2)(n +4)(1 — 2p)“',/2~3,
dv*
= ji П(п+2)(п +4)(«4-6)(l —2p)-"/2-4,...,
dv*
-в|,-(-/0) = /*n(n 4-2)(n 4-4)...(/г4- 2k — 2)(1 — 2jv)-n^~k.
dvk
Таким образом, tnh — n{n 4- 2)(n 4- 4)...(n 4- 2fe — 2).
2.12. Случайная величина У является линейной функцией слу-
чайной величины X: Y = g(X) = аХ 4- Ь, где а и b — постоянные
величины.
Найти плотность вероятности Pi(y) величины У при известной
плотности вероятности рх(х) случайной величины X.
Решение. Так как обратная функция х — h(y) = (у — Ь)/а од-
нозначна, то, подставляя ее выражение в (2.40), получаем
/ ч 1 /у—ь\
Р1(У) = -—Р1-—•
I a I \ а I
Если, например, величина X имеет равномерную плотность
вероятности в интервале (х1? х2),то величина Y будет распределена
равномерно в интервале (axt + Ь, ах2 + Ь).
Когда величина X имеет нормальную плотность вероятности
ri v 7 а У2л и 2а2 J
то ее линейная функция также распределена по нормальному за-
кону
где ту = ат 4- Ь, = | а\ о.
Таким образом, при линейном преобразовании случайной вели-
чины ее плотность вероятности смещается на величину Ь, а масшта-
бы вдоль координатных осей изменяются в а раз.
2.13. Случайная величина X с равномерной плотностью вероят-
ности (рис. 2.11)
Pi(x) = 1/(6 4- а), —а < х < Ь, а < 6,
подвергается квадратичному преобразованию У = X2.
64
Рис. 2.11. Плотность Рис 2.12. Функция рас-
вероятности случай- пределения случайной
ной величины X величины X.
Рис. 2.13. Квадратич-
ное преобразование
Определить и построить: 1) функцию распределения Рг(х) слу-
чайной величины X; 2) функцию распределения Fx(y) и плотность
вероятности рх (у) случайной величины У.
Решение. 1. По определению,
Fx(x) = P(X <х) = J p1(z)dz.
При х —a (х) = Р (X С —а) = О,
при —а < х <2 b
X
Л(*) = f Px(z)dz = —f— z
— a
x
b+a ’
—a
при x > b Fx (x) = 1.
График функции распределения Fx(x) приведен на рис. 2.12.
2. При квадратичном преобразовании у = х2 (рис. 2.13) функ-
ция у никогда не принимает отрицательных значений. Поэтому
Pi (у) = Р(У<у) = 0 ПРИ У < °-
На интервале (—а, а) обратная функция х = h (у) — двуз-
начна (рис. 2.13): хх = hx (у) = 4- Уу, х2 = h2(y) = — Уу.
Событие У < у равносильно попаданию случайной величины X
в интервал (— У у, Уу), т. е.
Р (У Су) = Р (х2 < X < хх) = Р (~Уу < X сУу) =
= р(X<КГ) - Р(X<-О
Следовательно, при 0 < у а2
Vy —Yy
Р1(У)= f Px(x)dx— С Pl(x)dx=-J—х
J J b-ya
—-----X
b-ya
”,5=2J3.
b-{-a
3 Зак. 1203
65
Рис. 2.14. Функция рас-
пределения случайной
величины У=Х2
Рис. 2.15. Плотность ве-
роятности величины
Y=X2
На интервале (а, Ь) обратная функция х2 = h2 (у) = ]/7 одно-
значна. Поэтому
Fi (У) = Р (Y < У) = Р (- а < X < а) + Р (а < X + О =
b+a J Ь+а
а
Таким образом,
_0
г/,д= Wy/(b+a)
ГЛУ) (У^+а,/(Ь+а)
1
1 х _ Уу+а
Ь-{-а Ь-[-а
при у О,
при 0< а2,
при a2<Z у Ь2,
при у>Ь2.
Воспользовавшись формулой (2:3), получим
Р1(у) =
О при г/^0,
1/(6+ а) У у _ при 0<z/<a2,
1/2(Ь+а)Уу при а2<.у^Ь2,
при у > Ь2.
Графики функций F^y) и рг(у) представлены на рис.2.14 и 2.15.
Отметим, что такое преобразование имеет место, например, в двух-
полупериодном квадратичном детекторе.
2.14. Случайная величина X описывается биномиальным зако-
ном распределения вероятностей.
Найти математическое ожидание ту и дисперсию ъу случайной
величины Y = еаХ.
Решение. Случайная величина X может принимать значения
0, 1, 2, ..., п. Вероятность Pn(k) того, что она примет значение
определяется выражением (1.22):
Рп (k) = <7=1- +
66
Используя формулы (2.44) и (2.45), получаем
2 яЛ(*)= 2eaft^pV~ftM?+pea)".
k £==0 fe=0
= 2 yl pn {k)—ту = 2 (p^)* =(?+ ^n-
k = Q fc=>0
— (q + pea)2n.
2.15. Случайная величина X подчинена равномерному закону
в интервале от 0 до 2.
Определить математическое ожидание и дисперсию величины
Y = 6Х2.
Решение. На основании (2.43) имеем
2 2
Шу = j* g(x) рг (х) dx = J 6х2
О О
2 1
= J If ю— Шу]г Pl (х) dx = j
О о
— d- °
2 3
2
dx=3 — =8,
3
о
х2)2 -±-dx—т*у=*
= 18—|2—64 = 51,2.
5 1о
3 . ЗАДАЧИ И ОТВЕТЫ
2.1. По двоичному каналу связи с помехами передаются две циф-
ры: 1 и 0. Априорные вероятности передачи этих цифр равны
р(1) = р(0) = 1/2. Из-за наличия помех возможны искажения. Ве-
роятности перехода единицы в единицу и нуля в нуль соответствен-
но равны: р (1/1) = р, р (0/0) = q.
Определить закон распределения вероятностей случайной ве-
личины X — однозначного числа, которое будет получено на прием-
ном конце в некоторый момент времени.
*1 0 1
Pi (1-р+<7)/2 0-4+Р1/2
2.2. Из десяти транзисторов, среди которых два бракованных,
случайным образом выбраны два транзистора для проверки их
параметров.
Определить и построить: а) ряд распределения случайного чис-
ла X бракованных транзисторов в выборке; б) функцию распре-
деления (х) случайной величины X.
3* 67
Ответ', а)
Xi 0 1 2
Pi 1/45 16/45 28/45
б) Л(х) =
О при х О ,
1/45 при 0<х^ 1,
17/45 при 1<х^2,
1 при х > 2.
2.3. Вероятность получения отметки цели на экране обзор-
ного радиолокатора при одном обороте антенны равна р. Цель
считается обнаруженной, если получено п отметок.
Найти закон распределения случайной величины X — числа
оборотов антенны радиолокатора.
Ответ:
P(k) = Р(Х = k) = Рп(1 — P)k~n, k = n, n + 1, n + 2.
2.4. Последовательные ускоренные испытания приборов на на-
дежность производятся до первого отказа, после чего они прекра-
щаются. Пользуясь понятием плотности вероятности для дискрет-
ной случайной величины, найти плотность вероятности рг(х) слу-
чайной величины X — числа испытанных приборов, если вероят-
ность отказа для каждого прибора равна 0,5.
Ответ [4J: рх(х) = 2_< 8(x—.xt).
i- ।
2.5. Функция распределения Рг(х) случайной величины X
задана графиком (рис. 2.16, а).
Требуется: 1) найти аналитическое выражение для Fi(x);
2) построить график плотности вероятности р± (х); 3) определить
вероятность того, что величина X примет значение, заключенное
на интервале от 0,2 до 0,8.
Рис. 2.16. Функция распределения (а) и плотность вероятности (6)
68
Ответ'.
< 0 при х О,
j х/2 при 0<х1,
1. Ft (х)= j 1/2 при 1<х^2,
(х —1)/2при 2<xs^3,
| 1 при х > 3.
2. График плотности вероятности рг(х) приведен на рис. 2.16,6.
3. 0,3.
2.6. Случайная величина X имеет нормальное распределение
с параметрами тх = 3, ах = 2.
Как изменится плотность вероятности Рх(х), если параметры
примут значения тх = — 3, аж = 4?
2.7. Сообщение передается последовательностью амплитудно-
модулированных импульсов с заданным шагом квантования А (А —
наименьшая разность между двумя импульсами). На сообщение на-
кладываются шумы, распределенные по нормальному закону
с плотностью вероятности
РЛх)=—^—е-^г.
Если мгновенное значение шумов превышает половину шага кванто-
вания, то при передаче сообщения возникает ошибка.
Определить, при каком минимально допустимом шаге кванто-
вания вероятность ошибки из-за шумов не превысит 0,1.
Ответ: А — 3,4 а.
2.8. Случайная величина X — ошибка измерительного прибора
распределена по нормальному закону с дисперсией 16 мВ2. Систе-
матическая ошибка прибора отсутствует.
Вычислить вероятность того, что в пяти независимых измерениях
ошибка X: а) превзойдет по модулю 6 мВ не более трех раз; б) хотя
бы один раз окажется в интервале 0,5 мВ — 3,5 мВ.
Ответ: а) 0,999; б) 0,776.
2.9. На электронное реле воздействует случайное напряжение
с релеевской плотностью вероятности
Р1(х)= 4-е-^2’*, х>0.
а2
Какова вероятность Р срабатывания схемы, если электронное
реле срабатывает всякий раз, когда напряжение на его входе
превышает 2 В?
Ответ: Р =е~2/а\
2.10. Определить математическое ожидание тх и дисперсию о?
числа приборов X, имевших отказы за время испытаний на надеж-
ность, если испытанию подвергается один прибор, а вероятность
его отказа равна q.
Ответ: mx — q,(& = q(l — q)-
69
2.11. Стрельба ведется по наблюдаемой цели. Вероятность по-
падания при одном выстреле равна 0,5 и от выстрела к выстрелу не
меняется.
Вычислить математическое ожидание тх и дисперсию о2 слу-
чайной величины X — числа попаданий в цель при пяти выст-
релах.
Ответ'. тх = 2,5; а? = 1,25.
2.12. На вход ограничителя воздействует видеоимпульс со слу-
чайной амплитудой. Вероятность превышения импульсом уровня
ограничения равна р. Рассматривая событие превышения уровня
ограничения импульсом как случайную величину X, принимающую
значения 1 (превышение) и 0 (непревышение), определить среднее
значение и дисперсию величины X. Найти среднее значение и дис-
персию числа Y импульсов, превысивших порог, при подаче на вход
ограничителя п импульсов.
Ответ'. тх = р, о? = р(1 — р), mq = пр, = пр(1 — р).
2.13. Вероятность отыскания малоразмерного объекта в задан-
ном районе в каждом вылете равна р.
Определить математическое ожидание и дисперсию числа про-
изведенных независимых вылетов, которые выполняются до пер-
вого обнаружения цели.
Ответ', т = 1/р, о2 = (1 — рУр*.
2.14. На радиомаяк-ответчик в среднем поступает 15 запросов
в час. Считая число запросов случайной величиной, распределен-
ной по закону Пуассона, определить вероятность того, что за 4 мин:
а) поступит ровно 3 запроса; б) поступит хотя бы один запрос.
Ответ', а) 0,0613; б) 0,632.
2.15. Изменение частоты X генератора из-за самопрогрева под-
чинено распределению, график которого изображен на рис. 2.17.
Определить: 1) аналитические выражения для плотности вероят-
ности рх(х) и функции распределения (х); 2) математическое
ожидание тх и среднее квадратическое значение ох случайной ве-
личины X.
0 при х С — а/2,
Ответ'. 1. /?1(х) — < (2х+п)/п2 при —а/2<х^а/2,
0 при х > а/2,
0 прих^—п/2,
Л W — * [(2х + а)/2а]2 при — а/2 < х а/2,
1 при х > а/2;
2. тх = а/б, ах = а/3р^2.
2.16. Сообщение передается квантованными импульсами с ша-
гом квантования Д = 1 В. Предполагая, что ошибка квантования
равномерно распределена в пределах интервала квантования и имеет
нулевое среднее значение, определить дисперсию о2 (мощность)
шума квантования
Ответ', о2 = 1/12 В2.
70
Рис. 2.17. Плотность вероятности
2.17. При измерении напряжения гармонического колебания
и (7) = A sin (<о/ + <р) ламповым вольтметром, проградуированным
в эффективных значениях, стрелка вольтметра из-за наличия помех
равномерно колеблется между значениями ocj и а2.
Вычислить: 1) среднее значение та показаний вольтметра; 2) от-
носительную погрешность Л = аа1та измерения амплитуды напря-
жения u(t), где ста — среднеквадратическое значение..
Ответ:
1) т„ = («j + а2)/2; 2) Д = (а2 — cq)/]/"3 (а2 + aj.
2.18. Время безотказной работы самолетного радиоэлектронного
оборудования в полете является случайной величиной, распреде-
ленной по экспоненциальному закону.
Определить вероятность безотказной работы оборудования в
течение десятичасового полета, если среднее время безотказной
работы по статистическим данным составляет 200 ч.
Ответ: 0,951.
2.19. Мгновенные значения амплитуды X принимаемого сигнала
при замираниях описываются распределением Релея
Р1(Х)
=—e~z2/2a!, х>0.
о2
Вычислить среднее значение и дисперсию случайной величины X.
Ответ: тх = а]/"л/2, ст? = о2(2 — л/2).
2.20. Показать, что начальный факториальный момент четвер-
того порядка /П[4] случайной величины X связан с начальными
моментами следующим соотношением:
/П(41 =/и4—6/n3 +11 /п2—6тх.
2.21. Найти центральные ml и центральные абсолютные р?
моменты случайной величины X, распределенной по гауссовскому
закону
z \ 1 Г (х—т)2
Pi(х) = —-=-ехр —v .
' а /2 л [ 2a2 J
Ответ: При начетном k ml = 0,
— д/ 'j[ ak
л \ 2 ) У n \ 2 /
71
При четном k
mak=№= л/_Lo»2<ft-n/2r(-^-').
гл \ 2 /
2.22. Доказать, что если случайная величина X подчинена гам-
ма-распределению
Pi (х) = —„ , , J---х“ е_х/р, х > О, а > — 1, Р > О,
’ ₽“+'Г(а+1)
то характеристическая функция величины X
0х(/ц) = (1 — 7ру)~(“+1),
а начальные моменты вычисляются по формуле
mh = р*Г (fe + а + 1)/Г (а + 1).
2.23. Определить характеристическую функцию 0t(p) случай-
ной величины X, принимающей:!) одно-единственное значение, рав-
ное С; 2) с одинаковой вероятностью два значения, равные ± С.
Ответ-. = e'vC-, 2) 0t (jv) = cos vC.
2.24. Показать, что распределение с характеристической функ-
цией ©j (jv) = cos [nv/2 (1 — и2)] обладает плотностью вероят-
ности
Pi (х) = 0.5 cos х> —< х л/2.
2.25. Определить характеристическую функцию (jv) случайной
величины X, плотность вероятности которой
Ответ: <д1 (jv) = exp jvm---у j.
2.26. Дискретная случайная величина X характеризуется рядом
распределения
Xi —2 — 1 0 1 2
Pi 0,1 0,2 0,3 0,3 o,i
Найти законы распределения случайных величин Y = X2 + 1,
Z = | Х|.
Ответ:
У) I 2 5
pj 0,3 0,5 0,2
Zk 0 1 2
Рь 0,3 0,5 0,2
72
2.27. Случайная величина X с плотностью вероятности
Р1 (х) = — х > о,
а2
подвергается преобразованию У = о7Х.
Определить плотность вероятности для случайной величины У.
Ответ'. рг (у) = уе—и*12, у 0.
2.28. Случайная величина X распределена равномерно в интер-
вале (а, Ь):
рг (х) = \/{Ь — а), 0 < а х Ь.
Определить плотность вероятности случайной величины У =*
= X2 и построить ее график.
Ответ: рг(у) = 1 _ , а2<у<Ь2.
2(Ь—а)у у
2.29. Решить задачу 2.28 при условии, что
Pi (*) = — а). а х b < 0.
Ответ: pi(y) = 1/2 (а — b) J/у, Ъ2 <_ у < а2.
2.30. Случайная величина X с плотностью вероятности рх(х)
подвергается преобразованию У = 11 — X |.
Найти плотность вероятности случайной величины У.
Ответ: рг (у) = р/(1 — у) + Pr (1 + у), у> 0.
2.31. Случайная величина X с нормальной плотностью вероят-
ности
рх(х) = ----- е~х2/2а‘, —оо<х<оо,
о у 2я
подвергается преобразованию У = X2.
Определить плотность вероятности случайной величины У.
Ответ: Pi(y)~ ° К^У
.0 ,у<0.
2.32. Решить задачу 2.31, если
. . 1 Г (х—т)2 1
р. (х) = —т=- ехр —------- .
о н [ 2аа J
Ответ: рг (у) =--J---ехр [ —сь [ V у > (
о/2^ L 2оа J оа )’у
2.33. Ряд распределения случайной величины X имеет вид
0 2
Pi 0,2 0,5 0,3
73
Вычислить математическое ожидание и дисперсию случайной
величины Y = 1—2Х2.
Ответ*. ту = — 2,4, ву — 9,63.
2.34. Случайная величина Ф равномерно распределена в интер-
вале от 0 до 2л.
Вычислить математическое ожидание и дисперсию величины
X = Aq cos2 (со/ + Ф), где со, t — неслучайные величины.
Ответ*. тх — А0/2, а? = А*о/8.
3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ
ХАРАКТЕРИСТИКИ МНОГОМЕРНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При исследовании радиотехнических устройств часто приходится иметь
дело с совокупностью двух или большего числа случайных величин. Систему п
случайных величин мбжно рассматривать как точку в n-мерном пространстве
со случайными координатами Хх, Х2, .... Хп. Поэтому такую систему назы-
вают n-мерной случайной величиной или я-мерным случайным вектором. При
п — 2 двумерная случайная величина может рассматриваться как случайная
точка на плоскости, а при п = 3 — как случайная точка в пространстве.
Такая трактовка совокупности двух или трех случайных величин дает воз-
можность пользоваться наглядными геометрическими представлениями.
Системы случайных величин могут быть дискретными, непрерывными
и смешанными, в зависимости от типа случайных величин, образующих си-
стему.
Как и в случае одномерной случайной величины, полной вероятностной
характеристикой многомерной случайной величины является закон распре-
деления— соотношение, устанавливающее связь между областями возможных
значений многомерной случайной величины и вероятностями ее появления
в этих областях.
Закон распределения может быть задан в различных формах. Например,
если X и Y — дискретные случайные величины, то закон распределения дву-
мерной случайной величины (X, Y) задается в табличной форме
У] Xi «= i
Х1 Х2 Xi xn
Vi Ри Рч1 Pil Pn\ PiVi'l
Уч Р12 Р22 Pi4 Pm Р(Уг)
... . . . ...
У) рц Рч] Pi} Pnj Р(У})
74
Продолжение
• •.
Ут Р\т Рът Pim Pnm Р(Ут)
^Р(Х{, у,) /=1 Р(Х1) P(Xi) ... P(Xi) P(Xn)
Здесь
Pij = Р (X = xif Y = tjj), i = 1, 2, ...» n, / = 1,2, ..., tn.
При этом
2pz/ = 1. (3.1)
i./
P(X = Xi' = Pt = 2 Pii’ p(Y^yj)=Pl= 2 Pii' <3,2)
/=1 ’=1
Если X и Y независимы, то ptj = ptpr
Универсальной характеристикой многомерных случайных величиц,
пригодной для описания как дискретных, так и непрерывных случайных ве-
личин, является функция распределения. В случае двумерной случайной ве-
личины функция распределения Г2 (х, у) есть вероятность одновременного
выполнения двух неравенств X < х, Y < у, рассматриваемая как функция
переменных х, у.
(х,у) = Р (X < X, Y <у). ' (3.3)
В геометрической интерпретации (рис. 3.1) функцию распределения
Р2 (х, у) можно трактовать как вероятность попадания случайной точки внутрь
бесконечного левого нижнего квадранта с вершиной (х, у),
В статистической радиотехнике основное практическое значение имеют
системы непрерывных случайных величин, распределение которых обычно
характеризуют не функцией распределения, а плотностью вероятности.
Если функция распределения F2(x, у) непрерывна и обладает непрерыв-
ной смешанной производной второго порядка, то двумерная плотность вероят-
ности определяется формулой
Pi (•». У) = d2Ft(x, у)/дхду. (3.4)
Рис. 3.1. К определению функции распределе-
ния
75
Рис. 3.2. Прямоуголь-
ная область
плотность вероятности
двух случайных величин
и область D
Вместо плотности вероятности можно использовать двумерную характеристи-
ческую функцию
вг(/У1./v2) = W(0,*+°!4',]= f У e/<0’t+°2"’ р2(х, y)dxdy. (3.5)
—оо —оо
Аппарат характеристических функций особенно эффективен для исследова-
ния сумм взаимно независимых случайных величин.
Функции F2 (х, у), р2(х2 у) и 02 (/цр /и2) обладают следующими основными
свойствами*
1. Г2 (х, у) — неубывающая функция своих аргументов, г. е.
Г2(х2, У) > ^2 (xi» f/)» если Х2 > xi >
^2 (*» //г) > ^2 (х* f/1), если У2 > У\-
2- 7% (Х, “ °°) = (— 00, У) = F2 (— °°* — (3 6)
3. Г2 (оо, оо) = 1. (3.7)
4. Г2(х, оо)=Гг(х), Fg (оо, y)=Fx(y), (3.8)
где Fr (х) и F1 (у) — соответственно функции распределения случайных
величин X и Y.
* у
5. F2(x,t/)= J J р2 (и, v) dudv. (3.9)
—оо —оо
• 5. Вероятность Р (R) попадания случайной точки (X, Y) в прямоуголь-
ник R (рис. 3.2) со сторонами, параллельными осям Ох и Оу и с координатами
вершин A (x1F yt), В (х2, у J, С(х2, у2), D (xlt у2) равна
р (R) = Р (*!<%< х2> y-t < Y < у2) = Ft (х2, уг) — Л2 (%1. «/а) —
— yt) + Ft(xi, yi). (3.10)
7. Р2 (х, «/) > 0. (3.11)
ОО оо
8. J j Рг(^» У) dxdy — 1 (условие нормировки). (3.12)
—оо —оо
9. Вероятность P(D) попадания случайной точки в произвольную область
(рис. 3.3) определяется формулой
P(D) = И р2(х, y)dxdy, (3.13)
(D)
76
где р2 (х, у) dxdy — элемент вероятности для системы двух случайных в е-
личин.
10. 02 (0, 0) =; 1.
11. Если X и У — независимые случайные величины с характеристиче-
скими функциями соответственно (jvi) и (/и2), то
(М> Рг) = ®i(Pi) 01 (р2)- (3.14)
Одномерные функции распределения и плотности вероятности выражают-
ся через двумерные с помощью следующих соотношений:
X оо
Fi(x) = F2(x, оо) = у J р2 (х, У) dxdy,
—ОО -00
Й/7! (X) С
Р1(х)=——-------= j р2(х, y)dy,
Т со (3-15)
Fi(y)=F2(co, у) = J у р2(х, у) dxdy,
—ОО —00
й (у) = — -----= I Й (X, у) dx.
ду J
—оо
Закон распределения системы двух случайных величин X, У определяется
распределением каждой из величин, входящих в систему, и зависимостью
между ними. Степень зависимости случайных величин X и У характеризуется
условным законом распределения, jioa которым понимается закон распре-
деления одной из случайных величин, найденный при условии, что другая
случайная величина приняла определенное значение.
По теореме умножения законов распределения
Рг (х, у) = Pi (х) pi (у|х) = Pi (у) pi (x|t/), (3.16)
где
Pi (УМ = dFi (у\х)/ду, pi (х\у) <= dFi(x\y)/dx
— условные плотности вероятностей.
Для независимых случайных величин X и У
Рг (х, у) = Pi (х) Pi (у). (3.17)
Условие (3.17) — необходимое и достаточное условие независимости случай-
ных величин.
Выражения (3.15) и (3.16) позволяют получить соотношения, связываю-
щие между собой условные и безусловные плотности вероятностей, а также
формулу полной вероятности и формулу Байеса для непрерывйых случайных
величин:
. . Р2(х,У) Р2(*,У)
J Ра(х, y)dy
—00
Pl (XI У)
Рг(х,у) _ р2(х,у}
Pi (У, ~ °?
J Pi (х, У} dx
—GO
(3.18)
77
Pi(y) = J Pi(x,y)dx= У p!(x)Pi(y| X)dx-,
----------OO -00
, . , Pl (x) Pl (у | x)
Pl (X I y) = —----------------- .
00
j Pi (x) Pl (у | x) dx
(3.19)
(3.20)
Свойства 1 —11 и формулы (3.1)—(3.20) обобщаются на многомерные слу-
чайные величины [1, 13, 16].
Законы распределения являются исчерпывающими вероятностными ха-
рактеристиками многомерных случайных величин. Однако если система вклю-
чает в себя более двух — трех случайных величин, то экспериментальное оп-
ределение ее законов распределения весьма затруднено, а проведение расчетов
требует громоздких математических вычислений. Поэтому при исследовании
систем случайных величин широкое применение нашли их числовые харак-
теристики, которые в определенной степени могут дать представление и о
характере закона распределения. В основу получения таких числовых харак-
теристик положено понятие моментов.
Различные моменты соответственно дискретных и непрерывных двумер-
ных случайных величин определяются следующими формулами:
1. Начальный момент порядка kA + k2:
mki к =М (Хк' Yk‘) =22^’ У1а Pli »
i i
OO 00 (3.21)
mkxki = J f х?1ук‘р2(х, y)dxdy.
2. Центральный момент порядка + k2:
mk,k, =м(хк> Ук‘) =52 — т*>к' ~ ту}кг РЧ >
i i
<ю оо (3.22)
mk,k2 = J J (х—тх)к'(у—ту)кгр2(х, y)dxdy.
—ОО —00
3. Абсолютный начальный момент порядка kx + 62!
₽м. =М (I Х\к' I Y |*«) = 2 2 1 *1 ?' I У1PH >
f i
оо 00 (3.23)
= J J I х I*’ 1У1к‘Рг(х, y)dxdy.
—ОО —00
4. Абсолютный центральный момент порядка + k2i
Ph, = М (I Хл 1кч Y. 1*0 = 2 21 ~т* 1*’ I У.-mv I*’ Pit»
t i
0 00 00 (3.24)
Рм. = J J I x—mxlk’ ly—тр1кг p2 x, y) dxdy.
—OO -OO
5. Факториальный начальный момент порядка + k2i
IM (*[M Kt*.])=S24ft’] У1^ PH,
f f
оо 00 /О OK\
m[k,] [fet] = j f ^к,1у[кг1р2(х, y)dxdy.
78
6. Факториальный центральный момент mffcj [fc2] порядка k± + k2:
т[°ь] [*,]=M W1] 4м)=2 2 (**- т*)[А11 - mv)lk,}pu,
oo oo ' (3-26)
= f f (x~ ({/—Pz (x,y) dxdy.
—CO —co
Из начальных моментов на практике наиболее часто используются на-
чальные моменты первого порядка:
m10 = М (Л1/*)) = M (X) = mXt m01 =М (Х°П) = М (У) = т^,
(3.27)
которые являются математическими ожиданиями случайных величин X и У,
входящих в систему, и которые определяют координаты точки, называемой
центром рассеивания системы на плоскости.
Из центральных моментов наиболее употребительны моменты второго
порядка. Два из них представляют собой дисперсии величин X и У:
Dx [(X - /пх)2 (У - /п^)0] =М [(X - тх)*], (3.28)
Dv = mj>2 = М [(X - mx)° (У - [(У - ту)*],
характеризующие рассеивание случайной точки в направлении осей Ох
и Оу.
Среди смешанных моментов особую роль играет центральный смешанный
момент второго порядка /п?, = Кху, называемый корреляционным моментом
(иногда — моментом связи) случайных величин X, У:
'П?! = кху = М (Xi У о) [(X - тх) (У - ту)}. (3.29)
Для дискретных случайных величин
= тх){У}—ту) рц , (3.30а)
i i
где
Pil=P(X=xh Y=yi)t
а для непрерывных
Kxv= J J (х—тх) (у— ту) р2 (х, y)dxdy. (3.306)
—оо —оо
Корреляционный момент Кху описывает, помимо рассеивания величин X
и У, еще и связь между ними. Часто вместо Кху пользуются безразмерной ве-
личиной— коэффициентом корреляции Rxy.
Rxy — Кху/&хбу> (3.31)
где ох, о7 — средние квадратические значения величин X и У. Коэффициент
корреляции Rxy удовлетворяет условию: —1 < Rxy < 1 и определяет
линейную вероятностную зависимость между случайными величинами.
Если X и У независимы, то Кху = 0 и Rxy = 0. Две случайные вели-
чины, для которых коэффициент корреляции равен нулю, называются некор-
релированными. Независимые величины всегда не коррелировЗны. Зависи-
мые величины могут быть как коррелированными, так и некоррелированны-
ми. Для гауссовских случайных величин некоррелированность означает
также и независимость.
В некоторых случаях используются условные моменты случайной вели-
чины X относительно У. Для условных математического ожидания и диспер-
79
сии случайной величины X относительно У формулы соответственно имеют
вид
j хр2(х, у) dx
xpi (л: | у) dx = ----------
j P2(xty)dx
(3.32)
oo j fx—M(X\y)]2 p2(Xiy}dx
| [x—M (X | y}]2 Dy(x\y}dx= —----------------------•
-oo j p2(x, y)dx
Основными числовыми характеристиками системы п случайных величин
являются математические ожидания и дисперсии: М (Х&)»
D(Xfe)=Al{[Xft-.M(Xft)]2}, 1, 2........n.
а также корреляционные моменты или коэффициенты корреляции
={№-Л4(Х|)] [Х;-ЛКХ7)]}, /=#/,
Rr - =Xr г °г > «¥=/•
xi xtx) I xi xi
(3.33)
Для удобства корреляционные моменты и коэффициенты корреляции
часто записываются в виде корреляционной матрицы и нормированной корре-
ляционной матрицы:
KXiX KXXi-KXtX
XiXn
^x2x2 *• * ^x2xn
Во многих задачах статистической* радиотехники требуется определить
вероятностные характеристики одной системы случайных величин по задан-
ным вероятностным характеристикам другой системы, связанной с первой
функциональной зависимостью.
Пусть две случайные величины Y^ и Y2 заданы выражениями
Yi=gi(Xv *2), Y2=g2(Xv Х2) (3.34)
где gi и g2 — заданные детерминированные функции.
Требуется найти совместную функцию распределения F2 (yt> у2) и совме-
стную плотность вероятности р2 (ylt у2) случайных величин и Y2 по извест-
ной плотности вероятности р2 (хх, х2) случайных величин Xt и Х2.
Так как
^2 ({/1. »г) = Р (Л < Уъ У г < Уг) =
= Р (X,, Х%) < уъ gi (X,, Xa) < t/g],
TO
^2 (У\, Уъ) = Я P2 (Xi, x2) dxt dx2.
D
(3.35)
Область интегрирования D определяется неравенствами (xf, x2) < yif
ga(Xi, x2) < y2. Плотность вероятности p2 (уъ y2) получается путем диффе-
ренцирования F2 (ylt y2):
Ръ(Уъ Уъ) s=ad2F2(y1, у2)/духду2. (3.36)
80
Если необходимо найти р2 (у12 у2) без предварительного определения
Е2 (Pi, р2), то при однозначных обратных функциях Xt == hr (КА, Y2},
Х2 = h2 (Ylt Y2) имеем
P2 (Ун Уъ) = P2 l^i (Pi, y2), h2 (ylt y2)] |Da|, (3.37)
где
D _ d(xltx2) __ dh1/dy1 -dh1/dy2 1 (3 38)
2 dG/i,#2) dh2/dyx dh2/dy2 d(y12 y2)
d(xltx2)
— якобиан преобразования от случайных величин Xlt Х2 к величинам У\, Y2
В тех случаях, когда обратные функции h/ неоднозначны, в правой части
(3.37) следует взять сумму по каждой из подобластей.
Результаты (3.34)—(3.38) можно распространить на функцональные пре-
образования многомерных случайных величин.
Часто требуется найти плотность вероятности функции двух случайных
величин Xi и Х2 по известной совместной плотности вероятности р2 (хР х2):
У = У1 = gi (*ь Х2) = g (Хь Х2), Y2 = g2 (Xi, Х2) = Х2 (или хо.
При однозначной обратной функции Хх = Y2)=>h(¥, Y2) к такому
преобразованию можно применить формулу (3.37). В данном случае якобиан
преобразования
dh(y,y2) dh(y,y2)
-.......... —........... an I и и л. 1
Тогда формула (3.37) примет вид
, \ Г1» / \ 1 У*) I /Q Ол\
Р2(У. У2) = Р2[Ь (У, У2), У2} --7----- • (3‘39)
оу I
Проинтегрировав (3.39) по у2, получим плотность вероятности для Y:
Pi (У) =
J Рг(У1, Уг)йу2= J р2 [h (у, у2), у2]
dh(y, у2)
ду
dy2. (3.40)
Формула (3.40) позволяет найти плотность вероятности суммы, разности,
произведения и частного двух случайных величин:
Р1(г/)= f Pz(y~Х2, X2)dxs= j Р2(У—Xi, x^dxi, Y^Xi+X2 , (3.41)
--------OO —OO
OO OO
Pi(y)= f Ps(y+x2, x2)dX2= J p2(x1—y,x1)dx1, F = Xi—X2, (3.42)
—OO —-OO
, . f / у \ 1
Pi(</)= 1 P2I--------. x2 -—-dx2 =
J \ x2 / I x21
Г- dx,, Y = X,X2t
I Xi I
(3.43)
P2(yx2, x2)lx2ldx2 =
I . v Xi
— Мхи Y = —.
У* I X2
(3.44)
81
Для независимых случайных величин Хг и Х2 с плотностями вероят-
ностей Pi (Xj) и Pl (х2) р2(хъ Х2) = р1(х1)р1(х2) и формулы (3.41) — (3.44)
принимают'Вид
00 00
Р1(Р) = / Р1(У~ x2)pi(x2)dx2 = j p1(y—x1)Pi(x1)dx1,Y = X1 + Xa,
—оо —оо
(3.45)
Pi (У = f Pi(y+x2)pi(x2)dx,
J Pi(Xi—y) pi(xi) dxi, Y = Xi—X„
(* / у \ 1
Pi(</) = I Pi ----------- Pi (x2) -—— dx2 =
J \ x2 J I x21
/ If \ 1
Pi ------- Pl (Xi) ’ dxi, Y = Xi X2,
\ Xi / I X] I
(3.46)
(3-47)
Pi (у) = I Pl уха) о (х2> I х, I dx,
dxtl Y = —l-
Л2
(3.48)
Особое практическое значение имеет задача отыскания плотности ве-
роятности суммы независимых случайных величин по известным плотностям
вероятности слагаемых (композиция закрнов распределения). Эта задача ре-
шается с помощью формулы (3 45). Однако если число слагаемых больше двух,
то вычисление интегралов свертки значительно усложняется; поэтому при
п > 2 пользуются аппаратом характеристических функций. Сначала находят
характеристическую функцию Bn(j v) суммы независимых случайных величин
Y = Хх + Х2 + .. + Хп, которая равна произведению характеристиче-
ских функций отдельных слагаемых:
п
enijv)= M{elvY}= П ®н(/0> (3.49)
<= 1
а затем из обратного преобразования Фурье
30
Рп Р)=-Г“ [ e~'D!/ Qn(jv)dv (3.50)
2л J
—ОС
находят плотность вероятности величины Y.
Числовые характеристики функций Z2 системы двух случайных ве-
личин X, Y : Zi — (X, /), Z2 = g2 (X, V) можно найти, не производя пре-
дварительного определения плотности вероятности р2 (zlt z2), а непосредствен-
но используя совместную плотность вероятности р2 (х, у) случайных величин X
и Y. В этом случае математическое ожидание mZk = М (Z^), дисперсия
82
D (Z^ и корреляционный момент К для дискретных и непрерывных слу-
чайных величин определяются соответственно выражениями:
тг =5 5 Vi) PU ’
А I i
00 оо (3-51)
т, = f j gh(x, у)р2(х, у) dxdy,
—оо —оо
D(Zh)= ~ mzJaPlir
< t *
оо оо (3-52)
D(Zft)= f J [gk(x, y)—m2 ypt(x, y)dxdy t
—OO —00
Кг,г2 = 5 S [gl {Xi ’ yi}~ 2 (Xl ’ У/) ~ "M Pl1 »
J oo (3-53)
Кг,22 = J f [gi(x,y)—mZi][gt(x,y)—m^]pt(x,y)dxdyt
—OO —oo
где k = 1,2; X/, — возможные значения случайных величин X и У; pij —
вероятности совместного появления этих значений.
Частными случаями формул (3.51)—(3.53) являются следующие соотно-
шения для основных числовых характеристик случайных величин (основные
свойства числовых характеристик):
1. Если С — неслучайная величина, то
/И (С) = С, М (СХ) = CM (X). (3.54)
2. Для любых случайных величин X и У
М (X ± Y) = М (X) ± М (Г). (3.55)
3. Математическое ожидание линейной функции
м[ 2 агХг+6]= 2 aiM(Xi)+b, (3.56)
VI= 1 / («1
где at, b — неслучайные коэффициенты,
4. Для любых X и Y
М (XY) = М(Х) М (Y) + Кху. (3.57)
Если X и К не коррелированы (Кху ° 0), то
М (ХУ) = М (X) М (У). (3.58)
5. Если С — неслучайная величина, то
D (С) = 0. (3.59)
6. Неслучайную величину С можно выносить за знак дисперсии, возводя
ее в квадрат:
D (СХ) = C2D(X), о (СХ) = |С|о(Х). (3.60)
7. Для любых случайных величин X и У
D (X ± У) = D (X) + D (У) ± 2Кху. (3.61)
Дисперсия суммы (разности) некоррелированных случайных величин
(Кху =□ 0) равна сумме их дисперсий:
D (X ± У) = D (X) + D (У). (3.62)
83
8. Дисперсия линейной функции У сц Xi + b определяется формулой
i=l
D[ 2 «i*i + 4= 2 alD(Xi)+2 2 (3.63)
Vss’l / Z= 1 /</
Если все величины Хх, Х2> • ••, Хп — не коррелированы, то
d[ 2 °ixi+ и= 2 (364)
\Ы / i= I
9. Для независимых случайных величин X и Y дисперсия их произве-
дения
D(XY) = D(X) D (Y) + m*D(Y) + (3.651
2. ПРИМЕРЫ
3.1. Дискретная двумерная случайная величина (X, Y) опи-
сывается законом распределения вероятностей, заданного табли-
цей
хг
*2
У1 0,10 0,15
У2 0,15 0,25
Уз 0,20 0,15
Определить: 1) законы распределения составляющих X и У;
2) условный закон распределения случайной величины X при ус-
ловии, что Y приняла значение ylt и .случайной величины Y при ус-
ловии, что X приняла значение х2.
Решение. 1. Для определения безусловных законов распреде-
ления случайных величин X и Y воспользуемся формулой (3.2):
3
Р (*i) =.2 P(*i. ys) = Р (*1, Ух) + р (Хи у2) + р (хь уз) =
1
= 0,10 + 0,15 + 0,20=0,45,
з
р (х2) = 2 р (х2, yj) = р (х2, yj + р (х2, у2) + р (х2, уз) =
= 0,15+0,25+0,15=0,55.
Таким образом, закон распределения случайной величины X
в табличной форме имеет вид
Xi Х1 х2
Р (Xi) 0,45 0,55
84
Для величины У по аналогии получим
Р(Уд = ^p(xi’ Уд = р(х1> Уд + Р<х2. Уд •= 0,104-0,15 = 0,25,
Р («/г) = P(xi, у2) 4- р(х2, //г) = 0,154-0,25=0,40,
р(уд = P(*i. Уд + Р(*2> Уд = 0,204-0,15=0,35.
Vi Уз
Р (Уу) 0,25 0,40 0,35
2. Условный закон распределения случайной величины X при
У= У1 определяется совокупностью условных вероятностей
Р (xi I Уд> Р (х21 Уд> которые по теореме умножения вероятностей
равны:
р(Х1|г/1) = £1Д^1’=_21В==Л р(х8|^) = Л^..У1)|=,
Р(У1> 0,25 5’KV 21гШ Р(У!)
0,15 3
~ 0,25 ~ 5 ’
Следовательно, искомый закон в табличной форме имеет вид
Xi *1 х2
Р (*i|yi) 2/5 3/5
По аналогии находим условный'закон распределения величины Y
при X = х2:
Р (У11 х2) = =~> Р(Уг I ха) =
р(х%) 0,55 11
— Р(*2, У 2) __ 0*25_5
р(х2) 0,55 И ’
Р(^|хг)=^2’^=-^-~.
РМ 0,55 11
Следовательно, можно записать
У! У1 Уз Уз
р (уЯ-ч) 3/11 5/11 3/11
85
Для контроля воспользуемся условием нормировки
2 3
2 Р (xi) =0,45 +0,55= 1, 2 Р(^) =0,25+ 0,40+0,35 = 1,
1= 1 /= 1
,1 №1»)=f +1 = I. i Р = +-i- -1.
3.2. Вычислить и построить двумерную функцию распределения
Ft (х< У) независимых дискретных случайных величин X и Y, если
случайная величина X принимает три возможных значения 0, 1, 3
с вероятностями 1/2, 2/8 и 1/8, a Y — два возможных значения 0
и 1 с вероятностями 1/3 и 2/3.
Решение. По определению,
F2(x,y) = P(X<x,Y<y)~ 2 2 P^-Xt, Y =у,).
*1<X y.<u
где / = 0, 1, 3, / = 0, 1.
Так как по условию случайные величины X и Y независимы, то
F^x,y)= 2 P<X -=Xi)
Vj<y
При х^0 Р(Х <. х) = 0. Следовательно, в этом случае при любом
Y из области его возможных значений Fa(x, У) = 0- Аналогично
при «/^0 P(Y < у) = 0. Поэтому при любом X из области его
возможных значений F2 (х, у) = 0.
При 0<х^1и0<(/^1
Ft (х, у) = Р (X = х0 = 0) Р (Y = у0 =0) =4 4 = — •
2 о О
При 0 < х < 1 и у > 1
F2(x, у)= Р(Х =х0 =0)[Р(У = 0) 4-
+ Р(Г=У1 = 1)| =Л(Л+2.\ =
При 1 < х 3 и 0 < у 1
F2{x, //)=[Р(Х = хо=0)+Р(Х = х1 = 1)'х
При 1 < х < 3 и у > I
d 1 \ / 1 . 3 \ 1 7
Fi(x, */) = (— + — )-1 = —.
у 4 О / о
При х > 3 и 0 < у < 1
fs(x.s)_/-L+J.+ -L)2-=_L.
к 2 Г 8 J 6 Ь
86
Рис. 3.4. Двумерная функция распреде-
ления
При х > 3 и у >» 1
Г/ \ / 1 , 3 , 1 \/ 1 . 2\ .
^•’Нт+т+тДт+тг’-
График функции распределения Г2 (х, у) представлен на рис.3.4.
3.3. Совместная плотность вероятности р2(х, у) гауссовского
распределения двумерной случайной величины (X,Y) имеет вид
Ра (*, У) ------— ехр
2лахОуУ^~Rxy
1
2(1-
(х—тж)2
2Rxy(x—mx) (у — ту) । (У—mg)2
где тх, Шу, ах, су, Rxy — параметры распределения.
Определить: 1) плотности вероятностей Pi(x) и рг(у) случайных
величин X и У; 2) условные плотности вероятностей рх (у | х) и
Pi(x|i/) величин Хи Y.
Решение. 1. Согласно формуле (3.15) имеем
Pi(x)= J p2(x,y)dy.
Производя замену переменных (х— тх)/]^2ах = и,
(у — тУУУ2 в у = v, получим
1 / и2 \ г / 1
Рг (х) = —--- ----- ехр----—— exp
/2лояУ 1 — Rxy ' 1 / Ji» '
, 2Редu\d
i-«8wr
Известно (17), что
0° •
J ехр (—р2 х2 ± qx) dx — ехр
—00
87
Воспользовавшись этим интегралом, найдем
или
Pi(x)== "-7=-
v ' /2л
(x — mx)2
2о2
Таким образом, величина X подчинена гауссовскому закону с
параметрами тх и ох.
Произведя аналогичные вычисления, получим
Pi (*/) = -тт==—ехр
у 2л оу
(У—ту* '
2о= .
2. По формулам (3.18) находим условные плотности вероят-
ностей
Р1 1 = ------—"7-----~~еХР (---9/1 L х
ОуУ2л.У^—К^ I 2 0 Rxy)ay
X [ у—ту— Rxy-^- (х— тх) Г I,
L J
P1U I У> = --\ еХР (--------------9/1 L \/т2 Х
ох/2л]/1- R\y | 2(1-^ад)°х
X р— тх— Rxv^-(y — mv)j21.
Из этих выражений следует, что рг (у | х) и рх (х | у) представляют
собой гауссовские плотности вероятности с параметрами'
myi х = ту + /? (х—тх), 0ylx=<JvV 1 -Rxy,
Gx
mxty=mx+ RxV-^-(y~my), ох1у=охУ\- Rly.
°у
3.4. Случайная точка на плоскости распределена по закону,
приведенному в таблице.
"j * i
х, = 0 х2 = 1
У1=—1 0,10 0,15
у2=0 0,15 0,25
Уз = | 0,20 0,15
88
Найти: 1) математические ожидания случайных величин Хи У;
2) дисперсии величин X и У; 3) условное математическое ожидание
величины X при Y = z/з; 4) корреляционный момент Кху и коэффи-
циент корреляции Rxv.
Решение. Предварительно определим необходимые законы распре-
деления. Сложив вероятности «по столбцам», получим вероятности
возможных значений X: р (хг = 0)=0,45, р(х2 = 1)=0,55. За-
кон распределения величины X имеет вид:
хг Х2 = 1
Р (Xi) 0,45 0,55
Сложив вероятности «по строкам», аналогично найдем распределе-
ние величины Y".
Уз У1 = —1 у2 = 0 Уз=1
Р (УР 0,25 0,40 0,35
Вычислим условные вероятности возможных значений X при Y =
= У* = 1:
. I \ Pt-’Ci» f/з) 0,20 4 . . 0,15 3
р (*i Уч) = ——:, р(х«\у3) =----------------— = —.
3 р(у3) 0,35 7 li>3' 0,35 7
Следовательно, можем записать в табличной форме
хг = 0 х2 = 1
Р (Xi 1 Уз) 4/7 3/7
Воспользовавшись соответствующими определениями и найден-
ными законами, получим:
2
1. mx='^'^jxip (хь У))= 2 Х1Р(Х1)= °-0,45 +1 -0,55 =0,55,
if i« 1
3
mv =^^У1Р(хь У)) = 2 =
i i- i
== —1-0,25 + 0-0,40+ 1 • 0,35= 0,10;
89
2. D(X)=22^ — m*)2p(*i. yi) = 5 (Х~тх? p(xip=
i i i = I
2
= 2 x?p(^)—m2-0-0,45+1-0,55 -0,552 « 0,248,
t= i
d (У) = 2 S (so —mv? p (хь У1> = 3 (y~m^ p (У1)—
' i i= 1
3
= 2 ytP^-ny = 1-0,25+0.0,40 + 1-0,35-0,01 -0,59;
/ = i
3. Af(X|z/3=l) =2^P(xfl^a)«0.A + i. 3 = з .
2 3
4- Kxy 2Цх» — mx)(y} — mv)p (xt, y}) =
= (%! — mx) (0/x — my) p (x>, yj + (y2 — my)p (xv y2) +
+ (Уз — mv) P (•*+ f/з)I + (x2 — /nx)l(^i — my)p (x2, yj +
+ (У2 — my)p (x2, y2) + (уз — tny) p (x2, z/3)l =
= (0—0,55) [(—1—0,10) • 0,10+(0—0,10)0,15+ (1—0,10).0,20) +
+ (1—0,55). [(—1—0,10).0,15 + (0—0,10). 0,25+ (1—0,10)-0,151 =
= - 0,055,
Rxy = Kxylo^y = — 0,055//0,248 /0,59 « — 0,144.
3.5. Совместная плотность вероятности p2 (x, у) двумерной слу-
чайной величины (X, Y) имеет вид
Рз (х, у) =
4хуе~ хг-уг
0,
, х > 0, у > 0,
х <0, y<z 0.
Определить: 1. Математические ожидания тх и ту величин X
и Y. 2. Дисперсии D (X) и D (Y) составляющих.
Решение. Предварительно найдем плотности вероятности вели-
чин X и Y:
Pi (х) = j р2 (х, у) dy= 4xe_*r J уе~уг dy = 2хе—**, х > 0.
о о
Р1 (у) = $ Pi (X, у) dx = 2уе~уг, у>0.
Q
00 оо
1. тх = xp1(x)dx= 2 Jx2e“x2dx.
о о
90
Так как I xne~ax‘dx = —-
2a
n+1
2
при a>• 0, n> —1, to
г/2+1\ _
/пж=2 ——LZ. =r/AV_E2L_ m 2 f//2e-»!dz/ = -^-;
2 \2 ] 2 4 J 2
OO OO
2. D(X)=^(x—mx)2 px (x)dx = J xa pl(x)dx—ml =?
о 0
00 г (_ s
= 2 C r3 e~—m2 = 2 \ 2 / /KnV-[ 2L.
J 2 12/ 4 ’
о \ /
D(Y) = D(X) = 1 - n/4.
3.6. Известна совместная плотность вероятности р2(х, у) слу-
чайных величин Хх и Х2.
Найти двумерную плотность вероятности р2(ух, у2)случайных
величин Yx и У2, если Vj — аХх + ЬХ2, У2 = сХх + dX2,
где а Ь, с, d — постоянные коэффициенты.
Решение. Если определитель системы, составленный из коэффи-
циентов а, Ь, с, d, отличен от нуля, то система из двух линейных
алгебраических уравнений ух — ахх + bx2, у2 = схх + dx2 имеет
однозначное решение:
*1 = ai//i + bxy2, х2 = схух + dxy2,
где коэффициенты ах, bx, сх, dx выражаются через a, b, с, d. В дан-
ном случае якобиан преобразования (3.38)
(.Ху, х2) I ____ 1 ___ 1 ___ 1
д(ух,у2) д(ух, у2) дух/дх, dyi/dx2| [а И ad— be *
d(xlt х2) ду2/дхх д«/а/дх2| о d|
Следовательно, в соответствии с (3.37) получим
Рг (Ух, Уг) = :- у- . , Р2 («1 Ух +&1 Уъ сх уг +<Л у2) .
I ad—bcl
3.7. Определить совместную плотность вероятности р2 (ух, t/2)
случайных величин Yx и Yz при заданной совместной плотности
вероятности р2(хъ х^ случайных величин Хх и Хг, если
Yx = VXl Y^XJX,.
Решение. При ух > 0 система из двух нелинейных алгебраиче-
ских уравнений
Vх{ + х* = ух, хх/х2 = уъ
91
имеет два решения:
Х?'=У1Уг (1 + !/D-1/2. *?’ = 010 + ^)-1/2;
„(2) V<1> v<2> r(l)
Л1 лх > л2 л2 •’
В соответствии с (3.38) якобиан преобразования
р ___ 1 ________________!_________________ У'
2 д(У1» Уг) UH*?+-ф-1/2 *2(*1+*2)-1/2 j 1+У2 '
d(xlt х2) I 1/х2 -x-Jxl I
Применяя формулу (3.37) для случая двузначного обратного преоб-
разования, получаем
p2(0i,02)= [р2
1 I i/2 L
I п ( У1У*
+ Р!1 П+?Г’
У1Уг У1
У1 \1 и
/14-у! Л’^1
При (А < 0 система не имеет вещественных решений и поэтому
Р2(01. 0г) = 0.
3.8. Вычислить функцию распределения Fi(y) и плотность
вероятности /?х(г/) случайной величины У, если Y = min (Xlt Х2)
и известна совместная плотность вероятности р2 (хр х2) случайных
величин Xt и Х2.
Решение. Y = min (Xlt Х2) означает, что
у, JХх, если Xj Х2,
IХ2, если Хх > Х2.
Следовательно, для F, (у) можем записать
Р1(У)=Р(У<у)=Р(Х1<у\х1^Х2) +Р(Х2<г/|х2<Х1) =
*г
х,
у
V
Хг
У ОО * у ОО
= § Рг (-*i> AXi dx2 + Р2(*ь хг) dxt dx2 —
—ОО Xi —ОО Х2
у оо у оо
= dXi J р2 (хЛ, х2) dx2 + dx2 p2 (Xx, x2) dxx =
—OO Xi —oo x2
У* Г <» Xi
= J dXi J p2 (xx, x2) dx2 — p2 (Xx, x2) dx2 4-
—OO L----OO —oo
у Г OO Xi
4- J dx2 p2 (Xj, х2) dxx — p2 (xlt x2) dxi =
—OO _ — OO —-oo
У У Xi у
= j* pi (X) dxi — dxt J р2 (Xx, x2) dx2 4- § Pi (x2) dx2 —
—oo —oo — oo —oo
У Xi
— j dx2 J p2 (Xx, хг) dXi =
—oo —oo
= A (0 = -«i) 4- Fi (У = x2) — F2 (y = Xx, у = x2)t
92
где
У У
(У= xlf у = х2) = J J р2 (хъ х2) dxr dx2 =*
—-оо — оо ,
У у х2
— J dxx J р2 (хх, х2) dx-z + § dx2 J (xlt x2) dxx.
—OO — OO —OO —00
Продифференцировав Ft (у) по у, получим плотность вероят-
ности
P1(z/)=j^l=4
ду ду
~ У оо
J dxx J р2 (хх, Xi) dXi +
---00 Xj
У oo
+ J dxi J р2 (xx,
—00 x2
x2) dxx
oo oo
J pa (У, Xi) dXi + J Pi (xx, y) dxx.
У У
При независимых Хх и Х2 р2 (хх, х2) = рх (хх)рх (х2). Поэтому
формулы соответственно примут вид:
Л(Р) = Piiy = хх) + Fi (у = х2) —
— Р1(У = *i) Fx(y = х2),
Pi (у) = dFx(y)ldy = рх(р == хх) [1 — Fx(y = x2)l +
+ Р1(У = х2) Il — Fx(y = xx)l.
3.9. Получить формулу для плотности вероятности рх(у) слу-
чайной величины У = | Хх ± X, | при заданной совместной плот-
ности вероятности р2 (хх, х2) случайных величин Хх и Х2.
Решение. Рассмотрим предварительно вспомогательную слу-
чайную величину X = Хх + Х2. В соответствии с (3.41) и (3.42)
плотность вероятности рх (х) величины X имеет вид
ОО
Pi (х) — f pi (х Т х2, х2) dx2.
—оо
Интересующая нас величина У связана с величиной X равен-
ством У = | Х|. Так как для данного случая
Pi(P) =Д Pi (#)П hi (P)l = Pi {У) + рЛ—у)> У >
то
Р1(р)= ( Ра(Р 4- Х2, Xi)dx2+ ,f р2(—у =F Xi, Xi)dXi, У^О.
93
При независимых величинах Хх и Хг выражение для р^ (у) примет
вид
Pl (у) = j Pl (у Т х.г) + Р! (—у Т х2)| dx2.
—оо
3.10. Найти плотность вероятности рг (у) случайной величины
Y = (1 + A) a Хх/2 + (1 — А) ЬХ2!2,
где Хх vi Х2 — случайные величины с совместной плотностью ве-
роятности р2 (хх, х2); а и b — постоянные величины; А — дискрет-
ная случайная величина, принимающая значения + 1 и —I с ве-
роятностями р и q — 1 — р.
Решение. Из условия ясно, что
у — (с веР0ЯТН0СТЬЮ Р,
IЬХ2 с вероятностью q— 1 —р.
Поэтому условная плотность вероятности рг (у | хх, х2) определится
выражением
рх(#1*х, *2) = рб (у — axi) + q8 (у — 6х2).
Безусловная плотность вероятности
Pi (#) = У У Pi *2) Р2 (*i. *2) <Мх2 =
—00 —юо
00 00
= У J Ip6 (# — ax^ 4- qb(y — bx2)I p2(xx, x2) dxx dx2.
----OO —OO
Выполнив интегрирование с дельта-функцией, окончательно
получим
оо оо
Р1(#) = Р—v f Р1(У\а, x2)dx2+ q f Pi(хх, у|b)dxt.
I <я I J 14» I J
—оо —оо
Если случайные величины Хх и Х2 независимы, то формула упро-
щается:
Pi (У) = Р ~т Pi (У I a)+q —J— pi (у | Ь).
|а| Iо|
3.11. Независимые случайные величины Хг и Х2 подчинены
закону Пуассона с параметрами и %2 соответственно:
1 1 л
Р(Хх=А) = ^-е-Ч P(X2=k) =4*-е-Ч 1,...
Rl
94
Определить закон распределения случайной величины ¥»
= Xi + х2.
Решение. Решим задачу двумя способами: 1) непосредственно
используя законы распределения, 2) с помощью аппарата характе-
ристических функций.
1. Суммируя вероятности всех независимых исходов, благо-
приятствующих осуществлению события (Y = п), можно записать
" \k \n~k
P(Y = n) = yP(k)P(n-k) = e-^
kTo kTo k'
_-g—M—V? ^2 2_g—%,—x» 'v* wl/ V ,
k=0 kl (n ~ k)l nl k~o ki (n ~ k}' ' '
= е-м-х,21/1 4- A, Y* = (*1+Mn n = Q> 12,...,
n! \ X2 / n!
1 4. Y*— X1 ck ( V __ X1 V
b2 } Д Л J ' An nI <n “ v ^2 /
«=U ft=U
2. Определим характеристические функции случайных величин
Хх и Х2:
0Х1(/у)=Л1(е^)= 2 е/°й^-е-^ = е-^> £
*=о k=0
= ехр ( -Xx) ехр (%х е/») =ехр [%х 1) ].
По аналогии имеем 0Х|1 (]v) = ехр [Х2 (е^° — 1)].
Тогда в соответствии с (3.14) получим
©у (/и) = 0Х1 (jv) 0Xs (jv) = ехр [(%х + %2) — 1)].
Таким образом, случайная величина Y также подчиняется за-
кону Пуассона с параметром к — +12. Этот результат можно
обобщить на сумму нескольких пуассоновских случайных величин.
3. 12. Найти закон распределения случайной величины Y =
= Хх — Х2, где независимые случайные величины Хх и Х2 под-
чинены закону Пуассона с параметрами и %2 соответственно:
P(Xx = A0=4U-S Р(Х2=^) =21е-Ч k^O, 1,2...............
k\ k\
95
Рис. 3.5. Область интегрирования, определяю-
щая Ft (у)
Решение. Суммируя вероятности всех независимых исходов,
благоприятствующих появлению события (У = п), можем записать
Р(У=п)= 2 Р(^)Р(п+^) = Р(Х1=п)Р(Х2 = 0) +
+P(Xt =п+1)Р(Х2 = 1)4-... +P(Xt=n+k)P(X2=k) + ... =
= у . е~х- е~*» = е-<х-+х«) Л." V п > 0.
*=о (л + *)1 *' l£0(n+kykt
Воспользовавшись представлением функции Бесселя n-го по-
рядка от мнимого аргумента 1п (х) в виде ряда
получим
Р(У =n)=e-^+^>f-^-r/2/ln( (2^*1^). n=0, ± 1, ±2,...
Приведенные вычисления справедливы только при п 0. Од-
нако если повторить их для п < 0 и учесть равенство /_п (х) =
= 1п (х), то придем к заключению, что полученное выражение
остается справедливым и для отрицательных значений п.
3. 13. Случайные величины Хх и Х2 независимы и равномерно
распределены в интервале (0, 1).
Вычислить функцию распределения Fi(y) и плотность вероят-
ности pi (у) случайной величины Y — ХгХ2.
Решение. Областью интегрирования, которая определяет Fr (у),
является заштрихованная область, изображенная на рис. 3.5:
Fi (у) = Р (Y < у) = 1 — Р (Y > у) — 1 — JJ dxi dx2 =
<s,>
1 1 1
= 1— J dx2 = 1 — J(1-------------------—jdXi = y(l —-Iny).
У у
96
Следовательно,
?i(y) =
О
«/(1 —ln«/)
1
при у О,
при ®<Zy 1,
при у>\.
Дифференцируя рх (у) по у, получаем плотность вероятности
О при у О,
OiG/) =
— In у при 0 <1/^1,
О при у>1.
3.14. Двумерная случайная величина (X, Y) распределена по
закону, приведенному в таблице
xi
<-i = G | х2= 1
У1 = —1 0,1 0,2
f/2 = 0 0,2 0,3
4/з=1 0 0,2
Определить математическое ожидание М (Z) — тги дисперсию
D (Z) = al случайной величины Z = 2 X + У2.
Решение. Используя формулу (3.51), имеем:
(2хг + у*)рц = (2хг + у*)рп + (2х2 + z/?)p2i +
+ (2xt + #|)р12 + (2х2 + yl)p22 + (2х, + */з)Р1з +
+ (2х2 + у*) Pi3 = (2-0 + 1) 0,1+(2 • 1 + 1) 0,2+
+(2.0+0)0,2+(2.1+0)0,3+(2.0+1)0+(2.1+1)0,2=1,9.
Для определения D (Z) воспользуемся выражением (3.52), при
этом учтем, что
D (Z) = М (Z2) - ml,
М (Z2) = S S (2х,- + yf)pi} = (2х, + yl) р„ +
'=1 /=1
+ (2х2 + у2) р„л + (2xj + yl)2 ры + (2 х2 + г/“)р2, 4-
+ (2хх + г/П3Р1з + (2*2 + z/D р23 - I2 • 0,1+(2 • 1 + 1)2 0,2+
+ (2 • 1+0)2 • 0,3+(2 • 1 + 1)2 • 0,2=4,9,
P(Z) = 4,9—1,92= 1,29.
Задачу можно решить, используя свойства (3.54) и (3.55). Од-
нако при этом следует предварительно определить по формулам
(3.2) законы распределения случайных величин X и Y.
4 1203 97
3.15. Найти математические ожидания, дисперсии и корреля-
ционный момент случайных величин U и V по заданным аналогич-
ным характеристикам случайных величин X и Y, если
U = аХ + bY, V = сХ + dY,
где а, Ь, е, d — постоянные коэффициенты.
Решение. На основании формул (3.55), (3.61), (3.29) и (3.57)
имеем:
М (U) = М (аХ + bY ) = аМ (X) + ЬМ (Y),
M(V) = М (сХ + dY) = сМ (X) + dM (У),
D (U) — D (аХ + bY) = a2D (X) + ЬЧ) (У) + 2Х„ =
= a2D (X) + b2D (У) + 2ab Rxv охоч,
D (V) = D (сХ + dY) = c2D (X) + d2D (У) + 2KXV =
= c2D (X) + d2D (У) + 2cdRxy oA/,
Kuv = M{[U — M(U)HV - M (V)]} = M(UV) —
— M (U)M (V) = M [(aX + bY) (cX + t/У)] — laM (X)+
+ ЬМ (У)1 [сМ (X) + dM (У)] = acD (X) + bdD (У) +
+ (be + ad) Kxy = aeD(X) + bdD (У) + Rxyu^y.
Если X и У независимы, то выражения для D (I/), D (У) и Киу
упрощаются:
D (17) - a2D{X) + b2D (У), D{V) = сЧ) (X) + d2D (У),
Кио = aeD (X) + bdD (У).
3. ЗАДАЧИ И ОТВЕТЫ
3.1. Двоичный канал связи с помехами описывается совмест-
ными вероятностями р (xit у;), i = j = 1, 2, указанными в таблице
“1 xi
t
У1 0,45 0,5
у2 0,05 0,45
Вычислить- 1) априорные вероятности p(xt) передаваемых сиг-
налов xt и вероятности р (у}) принимаемых сигналов ур, 2) апосте-
риорные вероятности р (х, | у,); 3) вероятности перехода р (у) | xt)
сигналов Xi в у;.
Ответ: 1) р (хД = р (х2)=0,5, р (gj = р (у2) = 0,5; 2) р <хх I yj =>
= Р I Уа) = 0,9, р (х21 ух) = р (Xi|#2) = 0,1; 3) р(уJ xj
= Р (Jh I х2) = 0,9, р (ух | х.) = р {yt |тг) = 0,1.
88
3.2. Закон распределения двумерной случайной величины задан
таблицей
xi
xi *2 | *3
У\ 0,10 0,30 0,20
У2 0,06 0,18 0,16
Найти: 1) безусловные законы распределения случайных вели-
чин X и К; 2) условный закон распределения величины X при ус-
ловии Y = yv
Ответ:
К]
Р (хр 0,16 ),4* 0,36
У1 У] ?2
р (Ур 0,60 0.40
V, A, t
р (•«, । уо 1/6
ч *3
1// 1/3
3.3. По цели производится два независимых выстрела. Вероят-
ность попадания в цель при первом выстреле равна ръ при вто-
ром — р2
Найти функцию распределения F2(x, У) двумерной случайной
величины (X, /)„ где X — число попаданий при первом выстреле,
a Y — число попаданий при втором выстреле
Ответ:
(X, У) =
О
(1 —Р1)(1 -р2)
1 -Pl
1—Р-2
1
при у^О,
при 0 < х 1 , 0 < у 1,
при 0 < х 1, у > 1,
при х > 1, 0 < у 1,
при х > 1, у> 1.
3.4. По каналу связи передается один раз дискретный сигнал,
вероятность правильного приема которого р — 0,8.
Определить закон распределения в табличной форме и функцию
распределения f2(x, у) двумерной случайной величины (X, У),
где X — число правильно принятых сигналов, а У — число не-
правильно принятых сигналов
4*
99
Ответ-.
Х1
х1 = 0 х2— 1
У1 — о 0 0,8
Уг= 1 0,2 0
Рг (х, у) =
0,2
0,8
1
,0
при 0<х^ 1, у> 1,
при х>1, 0<у^1,
при х> 1, у> 1,
в стальных случаях.
3.5. Доказать, что для независимых случайных величин X и Y
справедливо равенство Р2 (х, у) = Fr (х) F, (у).
3.6. Система независимых случайных величин (Хп Х2, ..., Хл)
задана плотностями вероятностей рг (xt), (х2), .... рп (хл).
Вычислить функцию распределения Fn (хь х2, .... хп) этой си-
стемы случайных величин.
n xi
Ответ-. Fn(xlt х2....хп)= П f Pi(yi)dyt.
I — 1 —оо
3.7. Независимые случайные величины X и Y распределены
по закону Гаусса с параметрами тх = 1, т„ — —3, ст? = 9,
= 16.
Написать выражение для плотности вероятности р2 (х, у) системы
случайных величин (X, Y).
Ответ: р<> (х, у) — —— ехр Г----------].
* 24л [ 18 32 j
3.8. Независимые случайные величины X и У имеют равномер-
ные распределения соответственно в интервалах от 0 до 1 и от —1
до 1.
Определить функцию распределения F2 (х,у) системы случайных
величин (X, Y).
Ответ:
0 при у^. —1 ,
х(у+ 1)/2 Fi (х, у) = х (У+ П/2 1 при0<х<11, — при 0< х 1, у > 1, при х> 1, — 1 < 1, при X > 1, у> 1.
3.9. Плотность вероятности р2 (х, у) системы двух случайных ве-
личин (X, У) имеет вид
Рг (х, у) = Д/(1 + х2 + у2 + х2у2).
1ЭЭ
Найти: 1) коэффициент А; 2) вероятность Р попадания величины
(X, Y) в квадрат:—1 х 1, —1 у 1; 3) функции распреде-
ления Р2 (х, у), Fi (х), Fj (у); 4) плотности вероятностей рг (х) и
рг(у) и зависимость случайных величин X и Y.
Ответ: 1) А = 1/л2; 2) Р =0,125;
3) Л(х, у) =-i-(arctgx+-^arctg^ 4-^,
F\(x) =— farctgx +-7-), Fx(y) = — (arctgi/ 4—;
л \ 2 / л \ 2/
4) Pi(x) = 1/л (1 + x2), Pi (у) = 1/л (1 -I- у2).-
Случайные величины X и У независимы.
3.10. Функция распределения F2(x, у) двумерной случайной
величины (X, У) задана выражением:
F2 (х, у) = 1 — е—“х — е~рх + е~ах~₽х, х > 0, у ~> 0.
Определить: 1) плотность вероятности р2(х, у) системы (X, У);
2) плотности вероятностей (х) и pj (г/) и зависимость случайных
величин X и У; 3) вероятность попадания величины (X, У) в квад-
рат с вершинами: А (1,1) В (0,1); С (0,0) D (1,0).
Ответ: 1) р2 (х, у) = аРе~“х~Р!/; 2) р2 (х) = ае—р± (у) =
=Ре~Р", случайные величины X и У независимы; 3) Р= (1 —е~“)х
Х(1 - е-₽).
3.11. Плотность вероятности р2(х, у) системы двух случайных
величин (X, У) задана выражением
Р2 (х, у) = (А/п) ехр (—х2 + 6х — у2 — 2у — 12).
Определить: 1) коэффициент А; 2) плотности вероятностей
pi(x) и рх (у) соответственно величин X и У; 3) являются ли слу
чайные величины X и У зависимыми.
Ответ: 1)4= е2; 2) рг(х) = (1/]/л)е—(х~))!, рг(у) = (1/рл)е—
3) случайные величины X и У независимы.
3.12. Двумерная случайная величина (X, У) имеет плотность
вероятности р2 (х, у) = A sin (х + у), 0 < х л/2, 0 < у л/2
Определить: 1) постоянную А, функции распределения F2(x, у)
Л(х). Рг(р); 2) вероятность Р выполнения неравенств х < л/4.
у < л/4.
Ответ: 1) А — 0,5, F2(x, у) = 0,5 [sin х + sin у — sin (х + г/)1
Ft(x) = 0,5(1 — cosx -I- sin х), F| (у) = 0,5(1 — cos у + sin у).
2) Р = 0,207
3.13. Двумерная случайная величина (X, У) имеет равномер-
ную плотность вероятности внутри круга С радиуса Р:
п lv ,Л _р/л/?2 при х2+г/2<р2,
Ръ\Х> У) 5 2
(0 при х2+ у2 > R2.
Доказать, что случайные величины Хи/ являются зависи
мыми.
101
3.14. Плотность вероятности двумерной случайной величины
(X, Y) имеет вид
, , 1 Г х2—2Rxy+y2 1
Pi (х, У) 2л ехр [ 2 (1 —№} ] •
Вычислить плотность вероятности случайной величины X.
Ответ'. рг (%) = ^L- е~х2/2.
V 2л
3.15. Плотность вероятности р2(х, У) двумерной случайной ве-
личины (X, Y) имеет вид
(1 /6л • внутри эллипса (х2/9+#2/4 1),
Ръ (я, У) {
(О вне этого эллипса.
Доказать, что X и Y — зависимые величины.
3.16. Двумерная случайная величина (X, Y) распределена по
нормальному закону с плотностью вероятности
рг(х, у)=—е-ь2<хг +
Л
Требуется: 1) найти значение величины h, если известно, что
вероятность попадания в круг (х2 + у2 /?2) равна р; 2) определить,
при каком значении h вероятность попадания в кольцо (г2^х2 +
+ у2 R2) будет наибольшей
Ответ'. 1) й =— In—?—; 2) h = \f 2 ln .
R у 1-p у R2—r2
3.17. Закон распределения дискретной двумерной случайной
величины (X, Y) задан таблицей
х» = - 1 х2 = 0 х3= 1
У1 =—1 4/15 1/15 4/15
у2 = 0 1/15 2/15 1/15
>’з = 1 0 2/15 0
Требуется: 1) определить математические ожидания тх и ту
случайных величин X и Y\ 2) установить некоррелированность и
зависимость случайных величин X и У.
Ответ'. 1) тх = 0, ту = —* 7/15; 2) X и У не коррелированы,
так как Rxy = 0; однако X и У зависимы, потому что необходимое
для независимости условие p(xf, yj) = p(Xi) p(yj) не выполняется.
3.18. По одной и той же стартовой позиции противника произ-
водится три независимых пуска ракет, причем вероятность попада-
ния в цель одной ракетой равна р. Пусть случайная величина X —
число попаданий в цель, а случайная величина У—число промахов.
192
Найти математические ожидания и дисперсии случайных вели-
чин X и Y, а также корреляционный момент и коэффициент корре-
ляции.
Ответ'. тх = Зр, ту = 3q, о2 = = 3 pq, Кху = — Зррг
Rxy ~ 1» q = 1 — Р-
3.19. Написать выражение для нормальной плотности вероят-
ности р2(х, у) двумерной случайной величины (X, Y) если
тх=0, тц =6, ||/Ц^||=||К„||=
1Z Zu
Ответ:
Рг(х, 9) __!_ехр I------to-jg-n.
У к I 1,28 16 20 25 ]J
3.20. Плотность вероятности двумерной случайной величины
(X, Y) определяется формулой
Ра (х, у) = 0,5 sin (х + у), 0 < х я/2, 0 < у л/2.
Определить: 1) математические ожидания тх и mv, дисперсии
D(X), D (Y) случайных величин X и У; 2) корреляционную и нор-
мированную корреляционную матрицы.
Ответ: 1) гпж =/пй= 0,785, D (X) =D(Y) =0,188; 2)||ХО|| =
0,188 -0,046 - 1 -0,245
—0,046 0,188 ’ ° ~ —0,245 1
3.21. Двумерная случайная величина (X, Y) распределена
по нормальному закону с параметрами тх = /п„ = 0, <jx = gv = о,
Rxy ~ 0.
Вычислить вероятности событий: а) | У| < X; б) У < X;
в) У < I X |
Ответ 1181: а) 0,25; б) 0,5; р) 0,75.
3.22. Определить совместную плотность вероятности р2(х, у)
случайных величин X = sin Ф и У = соэФ при известной плот-
ности вероятности ,рх (<р) случайной величины Ф в интервале
(—л, л).
Ответ! 19р2 (х, у) = Р| (а£^°.-- 6(t/+ /| - х2)
У 1-г
3.23. Двумерная случайная величина (X, У) имее! нормальную
совместную плотность вероятности
г ч 1 Л I *2+*/2 \
Вычислить совместную плотность вероятности p2(r, q>) вели-
чины (Я, Ф), если X = РсоэФ, У = /?sin®.
Ответ: р2 (г, <р) = (г/2ла2) ехр (—г2/2о2), г > 0.
103
Случайные величины R и Ф — независимы, так как р2(г, ф) =
= Pi (г) рг (ср), где величина R распределена по закону Релея
(r/о2) ехр (—г2/2о2), а величина Ф — по равномерному закону
Pi (ф) — 1/2 л.
3.24. Совместная плотность вероятности р2 (хг, х2) системы
(Хь Х2) имеет вид
, ч (е~при х, > 0 и х2 > 0,
р2(Х1, х2) =
(О в остальных случаях.
Найти плотность вероятности р2, (z/x, г/2) двумерной случайной
величины (У\, У2), если = Хг + Х2, Y2 = Х2/Хх.
Ответ [71:
Рг (Z/i- Уг) =
е-^._______yJ—
(1 + г/2)2
О
при ух >0, у2 > 0,
при других уг и у2.
3.25. Доказать, что целочисленная случайная величина Y =
= |Хх — Х2|, где Хх и Х2 — независимые случайные величины,
распределенные по закону Пуассона с параметрами Хх и Х2 соответ-
ственно, имеет закон распределения вида
P(Y =п) =
'е-(*1+ь2)/0 (2^^), п=0,
/В(2}М’ « =
= 1, 2, ...
Указание. Следует воспользоваться методикой и резуль-
татами примера 3.12.
3.26. Получить функцию распределения Fx (у) и плотность ве-
роятности Pi (у) случайной величины Y = max (Х1Г Х2) при заданной
совместной плотности вероятности р2 (хр х2) случайных величин
Xi и Х2.
Ответ*.
у У
Р\(у} = J J Рг(*ъ х2)dXtdx2 = F2(у, у),
— оо —оо
У У
Pi(y) = J p2(y,x2)dx2+ J p?(Xi,y)dx1.
Указание. Следует воспользоваться методикой решения
примера 3.8.
3.27. Определить плотность вероятности рг (у) случайной ве-
личины Y = min (X, X2) по известной плотности вероятности р0 (х)
случайной величины X.
Ответ [18]*
= при 0<£/<1,
\р,Лу) при z/^0 и у^> I.
104
3.28. Производится однократное измерение частоты колебаний
автогенератора, распределенной по равномерному закону в интер-
вале от fmln до /тах.
Найти плотность вероятности рг (у) результата измерения
Y = F + X, где погрешность измерения X не зависит от F и рас-
пределена по закону Гаусса
Pi U) = (1 /ст V2л) ехр (—х2/2 о2).
Ответ: р± (у) =-------!----ГФ / — ф / М .
/max— /min L \ ° / \ ° /1
3.29. Доказать с помощью аппарата характеристических функ-
ций, что сумма двух независимых случайных величины Z = X + Y
с нулевыми математическими ожиданиями и дисперсиями о2 и
распределена по закону Гаусса с характеристической функцией
вида
/ а2+<*п Л\
0г (jv) = ехр I----v2).
3.30. На вычитающее устройство воздействуют независимые
сигналы X (t) и Y (t) с нулевыми математическими ожиданиями, ди-
сперсиями и о2 соответственно и гауссовскими одномерными
плотностями вероятности.
Определить плотность вероятности px(z) величины Z = X — Y
на выходе вычитающего устройства.
Ответ'. p1(z) = (Мв^^п) ехр (—z2/2orf), где ol = d + о>
3.31. Найти плотность вероятности случайной величины Y —
= АХ, где А и X — взаимно независимые случайные величины
с плотностями вероятности
Pi (А) = (Д/о2) ехр(—Л2/2 о2), Д > 0,
Pi (х) — (1 /ох )Л2л;) ехр (—x2/2cFx), — оо < х < оо.
Ответ рг (у)
=____I
2nt ах
3.32. Вычислить плотность вероятности случайной величины
Z = Х/Y, если X и Y — независимые случайные, величины, распре-
деленные по закону Релея:
PiW = 4-e^2/2a2, РЛУ) = ^-УЧ2°\ х>0, //>0.
о2 а2
Ответ: px(z) = 2z/(l + г2)2.
3.33. Случайная величина Y = аХх + &Х2, где а и & — постоян-
ные коэффициенты, а Xj и Х2 — независимые случайные величины
с параметрами и Х2 соответственно.
Показать, что распределение Y не подчиняется закону Пуас-
сона.
105
3.34. Найти математическое ожидание и дисперсию случайной
величины Z = 2Х — ЗУ, _если М (Х> = О, М (У) = 2, D (X) = 2,
D(Y) = 1, Rxy = - l/j/2.
Ответ*. М (Z) = — 6, D(Z) = 29.
3.35. В системе радиосвязи с разнесенным приемом (рис. 3.6)
приемники находятся на таком расстоянии друг от друга, что сиг-
налы X, У, и Z статистически независимы.
Определить коэффициент корреляции Ruv Для напряжений U
и V, если X, Y и Z распределены по закону Гаусса, причем* их сред-
ние значения равны нулю, а дисперсии — &2у = 3, of = 12.
Ответ: RUv — 0,8- /
3.36. Производится п Евезависижьх измерений некоторой фи-
зической величины.
Рассматривая результат каждого- измерения случайной вели-
чиной Xi с математическим ожиданием т и дисперсией о2, вычислить:
1) математическое ожидание тп и дисперсию среднего арифме-
тического п измерений; 2) относительную ошибку А = <зп1тп в оп-
ределении среднего арифметического. '
Ответ: I) тп = т, 2) А = о/ш п.
3.37. Определить математическое ожидание и дисперсию слу-
чайной величины 2 = ХУ, если независимые величины X и У имеют
равномерные распределения соответственно на интервалах (а, Ь)
и (с, d).
Ответ: -mz= (а + b)(c + d)/4> of = (а2 + ab + &2)Х
Х(с2 + cd + d2)/9 — (а + b)2 (с + d)?/16
3.38. Для определения площади квадрата измеряют две его
стороны с помощью одного инструмента и результаты измерения
перемножают.
С какой относительной средней квадратической ошибкой А =
= с/т нужно измерять стороны квадрата для того, чтобы средняя
квадратическая ошибка определения площади была не более 1%?
Ответ: \ = 0,71 %.
3.39. В индикаторе кругового обзора радиолокационной станции
применена электронно-лучевая трубка, экран которой представляет
собой круг радиуса- о. Иа-за наличия помех на экране может появить-
ся пятно с центром в любой точке экрана.
Рис. 3.6, Система радиосвязи с разнесенным приемом
да
Найти математическое ожидание и дисперсию расстояния цент-
ра пятна от центра круга.
Ответ', mr = 2а/3, = а2/18.
3.40. Случайные величины X, У, Z имеют равные математиче-
ские ожидания М (X) = /И (У) = M(Z) = 10, дисперсии D (X) =
= 1, D(Y) = 4, D(Z) =9 и коэффициенты корреладии Rxtl =
= 0, Rxz = 1/4, Rvz = 1/2.
Вычислить: а) М (X + У); б) D (X 4- У); в) М (X + Z);
г) D (X + Z); д') М (X — Z); е) D (X — Z); ж) М (X + У — 2 Z>;
з) D(X + У —2Z); и) М LM<X)J; к) л)
м) D [D (X)].
Ответ: а) 20; б) 5; в) 20, г) 11,5; д) О, е) 8,5; ж) 0; з) 26; и) 10;
к) 0; л) 1; м) 0.
4. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
1. ТЕОРЕТИЧЕСКИЕ ’СВЕДЕНИЯ
Математическая статистика — раздел математики, тюсвященный уста-
новлению закономерностей случайных явлений или процессов на основании
обработки статистических данных—результатов наблюдений или измерений.
Наиболее важными в прикладном плане являются три задачи математи-
ческой статистики [6, 7, 13, 20—25].
1. Оценка неизвестной функции распределения или плотности вероят-
ностей, когда по конкретным значениям х1? х2, хп, полученным в резуль-
тате независимых измерений случайней величины X, требуется оценить не-
известную функцию распределения (х<) величины X или ее плотность вероя-
ности рх(х), если X — непрерывная случайная величина.
2. Оценка неизвестных параметров В этой задаче предполагается, что
на основании физических или общетеоретических соображений можно заклю-
чить, что случайная величина X имеет функцию распределения определенного
вида, зависящую от нескольких параметров, значения которых неизвестны.
По результатам наблюдения величины X нужно оценить значения этих
параметров. Задачу можно ставить вне связи с функцией распределения. На-
пример, требуется оценить: математическое ожидание, дисперсию или момен-
ты случайной величины X; амплитуду, частоту или фазу радиоимпульса,
наблюдаемого на фоне шума; корреляционную функцию или спектральную
плотность стационарного случайного процесса и т. д.
3. Статистическая проверка гипотез. Обычно эта задача формулируется
так. Пусть на основании некоторых соображений можно считать, что функция
распределения исследуемой случайной величины X есть Fr (х). Необходимо
выяснить, совместимы ли опытные данные с гипотезой, что случайная ве-
личина X действительно имеет распределение Fr (х). Задачу можно сформу-
лировать иначе. Предположим, наблюдаемые значения случайной величины X
обусловлены двумя или несколькими различными причинами (гипотезами).
В результате наблюдения величины X нужно решить, с какой из гипотез сле-
дует связывать полученные значения величины X. Например, пусть на вход
радиоприемного устройства поступает случайное колебание X (f), которое
в каждый момент времени является либо суммой сигнала s (/) и помехи n(t)
(гипотеза Hj), либо одной помехи (гипотеза Но). В некоторый фиксированный
момент времени произведено измерение величины X. По полученному число-
вому значению х нужно решить наилучшим образом, присутствовал ли на
входе сигнал s (/), т. е. выбрать одну из двух гипотез:
Н± (х = s + л.) или (х = п).
107
Исходными данными, подлежащими обработке, служат результаты
наблюдений над случайной величиной X.
Множество всех возможных значений случайной величины X называется
генеральной совокупностью, а множество опытных значений х19 х2, •••, хп —
выборочными значениями, число п — объемом выборки.
Если известны функция распределения Fx(x) или плотность вероятности
(х) случайной величины X, то говорят, что выборка xlt х2, ...» хп принад-
лежит распределению FT (х) или рх (х). Расположив числа хх, х2, ...» хп
в возрастающем порядке, так что xt > Xj при i > /, получим упорядочен-
ную выборку, называемую вариационным или статистическим рядом.
По выборке объема п определяются ее статистические характеристики*} —
приближенные значения соответствующих вероятностных характеристик со-
вокупности. Приближение тем лучше, чем больше п.
Аналогом функции распределения Лх (х) случайной величины X слу-
жит статистическая (эмпирическая) функция распределения Гх (х) выборки,
которая представляет собой частоту события X < х:
FJ (х) = Р* (X < х) = v/n. (4.1)
где v — число членов выборки, меньших х.
Когда выбор осуществляется из непрерывного распределения и число
выборочных значений велико (порядка сотен), целесообразно строить гисто-
грамму, которая является статистической аппроксимацией плотности вероят-
ности рх (х). Для этого область экспериментальных значений случайной ве-
личины разбивают на г обычно одинаковых интервалов h и вычисляют отно-
сительную плотность точек в каждом интеервале:
pi/h — Vi/nh, i — 1, 2, г, (4.2)
где — число экспериментальных точек в t-м интервале; pi — Vi/n — от-
носительная частота. Подсчитанные таким образом значения изображают
графически в виде ступенчатой кривой: по оси абсцисс откладывают соответ-
ствующие интервалы и на каждом из них как на основании строят прямоуголь-
ник высотой pi/h. Полученная ступенчатая кривая называется гистограммой.
На практике часто возникает необходимость аппроксимации гисто^-
граммы подходящим аналитическим выражением какой-либо теоретической
плотности вероятности (выравнивание статистических данных). При этом
аппроксимация должна быть в определенном смысле наилучшей.
Подбор аппроксимации обычно начинается с качественного сопоставле-
ния гистограммы с графиками различных теоретических плотностей вероят-
ностей и с выбора наиболее близкой к гистограмме. Большой набор плот-
ностей вероятностей рг (х) дает система кривых Пирсона, задаваемая дифферен-
циальным уравнением
dpi (х) х+ а
—:— ттг—гт •
dx bxz-\-cx-[-d
Параметры а, в, с, d определяются из условия сохранения первых четырех
моментов статистического распределения.
По методу моментов параметры а, Ь, с, ..., подбирают так, чтобы первые
(низшие) моменты распределения рг (х) равнялись бы соответствующим ста-
тистическим моментам. Число приравниваемых низших моментов определяется
количеством неизвестных параметров а, Ь, с, ...
Чтобы оценить, насколько хорошо выбранный теоретический закон ра-
спределения согласуется с результатами наблюдений, используют критерии
согласия, среди которых наиболее часто применяется критерий %2. По этому
♦) Статистические характеристики всюду отмечены индексом *.
108
критерию за меру расхождения результатов наблюдений и теоретического
распределения принимают величину
2 = га V (р‘ Pi^1 2 * V = V4 _У£__
Х ”<=1 Pi !=\ npi i=i nPi
(4.3)
nt
где n — объем выборки; г — число интервалов разбиения экспериментальных
данных; vz- — число значений в i-м интервале; pi — относительная частота;
pi — вероятность попадания случайной величины X в i-й интервал.
Случайная величина X2, независимо от распределения величины X, при
п-»оо асимптотически распределена по закону %2 с k = г — s — 1 степенями
свободы, где s — число параметров теоретического распределения, оцени-
ваемых по результатам наблюдений.
Можно рекомендовать следующую методику применения критерия %2
для оценки расхождения теоретического и статистического распределений.
1. По формуле (4.3) подсчитать значение X2.
2. Определить число степеней свободы k = г — s — 1
3. Исходя из характера задачи, выбрать достаточно малую (обычно рав-
ную 0,05 или 0,01) вероятность а, называемую уровнем значимости
4. С помощью таблицы приложения III по известным k и а йайти значе-
ние величины х|. а, определяемой равенством
^Р>Ча)= f Р1(Х2)^2=1-Л(Х1.а). (4-4)
Xfe, а
5. Если значение %2, вычисленное по формуле (4.3), больше %2.а, то тео“
ретическое распределение считают плохо согласующимся с результатами на-
блюдений при уровне значимости а; если %2 < %|.а, то полагают, что выбран-
ное теоретическое распределение согласуется с экспериментальными данными.
Свойства выборки описываются также более простыми характеристи-
ками — выборочными (статистическими) моментами: выборочным средним
выборочной дисперсией Dx и т. д.
Выборочные среднее, дисперсия, начальный и центральный моменты k-ro
порядка определяются соответственно формулами:
. п
<4-5’
>— 1
1 п п
(^-o2=v (4-6)
i=) '= I
М* (Х«)=— j?x?, (4.7)
'= J
1 п
уи*[(Х—«;)»]=—У(хг—(4.8)
It
109
Если отдельные значения в ряде распределения повторяются по несколь-
ко раз, то следует учесть частоту каждого повторения. Тогда, например, фор-
мулы (4.5) и (4.6) примут вид:
тх=~ 2 х'vt’ <4,5а)
dx=-7 2 (хг ~ m*)2vz=4 2 х‘vi ~(mW' (4 -6а)
I I
Tjifi — значение величины X в i-m опыте; vt — частота значения х/.
При вычислении выборочных среднего и дисперсии по сгруппированным
данным пользуются формулами
Vi
(4.9)
2v*a-2-w=2 (4>10)
i— 1 1=1
где r — число интервалов группировки; at — середины интервалов. Такой
подсчет вносит ошибку, особенно заметную при малом числе интервалов.
Для ее уменьшения прибегают к поправкам Шеппарда. При равных интер-
валах h формулы для первых двух выборочных моментов с учетом поправок
Шеппарда имеют вид:
т\==т{, —
Для выборочного начального момента порядка k [16]:
_ k
= 2 6=1,2, ... ,
1 = 0
где Bt — числа Бернулли.
Двумерное статистическое распределение случайной величины (X, Y)
задается парами значений (хъ ^), (х2, #2)> •••> Уп)> причем основной ин-
терес в данном случае представляют форма связи между X и Y и степень этой
связи. Информацию об этом дает статистический корреляционный момент Кху
и статистический коэффициент корреляции Rxy:
Rxy ~ ~ (xi 171 х) (У* ту)> Rxy = а* »
где ту, о*, Оу — выборочные средние и средние квадратические откло-
нения величин X и
Выборочные значения и их функции интересны не сами по себе; они слу-
жат средством для получения статистических выводов.
При оценке параметров распределения совокупности по выборочным
характеристикам предполагается, что теоретическое распределение известно,
а неизвестны^лишь его параметры—числовые характеристики. Оценка может
быть точечной, когда она определяется одним числом, или интервальной, ко-
гда определяется двумя числами—концами интервала. В качестве точечных
оценок может существовать много выборочных статистик — функций наблю-
даемых значений. Чтобы оценка X параметра X имела практическую ценность,
она должна обладать тремя главными свойствами: несмещенностью, состоя-
тельностью и эффективностью.
113
Оценка называется несмещенной, если при любом объеме выборки
М [X] = Л, (4.11)
где X — истинное значение оцениваемого параметра. В противном случае она
обладает смещением (систематической ошибкой), величина которого
Дх = М [X] — X.
Оценка называется состоятельной, если она сходится по вероятности к
оцениваемому параметру при увеличении объема выборки:
lim р{| X — Х| < е}=1 > (4.12)
где е > 0 — сколь угодно малое число.
Несмещенная состоятельная оценка называется эффективной, если при
заданном объеме выборки п она имеет наименьшую /Дисперсию:
= M[(X-X)2] = D,nln С/ИК^-Л)2], (4.13)
Л
где А, — рассматриваемая оценка, Хг- — любая другая оценка.
При оценке одного параметра дисперсия оценки по выборке объема п
не может быть меньше нижней границы ( границы Рао — Крамера):
1 J Г/ d In (X ; X) V
^mln= (М If» (4.14)
п t I \ / ] J
где (X; X) — плотность вероятности или в случае дискретной случайной
величины X вероятность Р (X = хц X).
Оценками математического ожидания /пЛ, дисперсии DK, начальных и
центральных моментов случайной величины X могут служить соответствую-
щие выборочные характеристики (4.5)—(4-8). ,'При увеличении числа наблю-
дений они сходятся по вероятности к соответствующим характеристикам ве-
личины X, причем оценки начальных моментов несмещенные и состоятельные,
а оценки центральных моментов состоятельные, но смещенные. Поэтому за
оценку дисперсии Dx предпочтительнее брать не статистическую дисперсию
п
У (х[—тх)2, а «исправленную» выборочную дисперсию
1
Dx =
п
. п
/= 1
которая является несмещенной оценкой.
Для получения точечных оценок неизвестных параметров распределения
практически используются четыре метода*): метод моментов, метод минималь-
ной дисперсии оценки, метод максимальной апостериорной вероятности и ме-
тод максимального правдоподобия [22]. Из них наиболее часто применяются
метод моментов и метод максимального правдоподобия
При методе моментов выборочные моменты приравниваются к соответ-
ствующим моментам теоретического распределения, которые являются функ-
циями от неизвестных оцениваемых параметров. В’случае оценки одного пара-
метра достаточно иметь одно уравнение относительно этого параметра.
Пусть, например, задан вид плотности вероятности (х\ X), определяемый
одним параметром X, и требуется найти оценку-X этого параметра. Следуя ме-
♦) Оценки X, полученные разными методами, здесь обозначены одинаково,
хотя они различны и совпадают лишь в частных или асимптотических случаях.
111
тоду моментов, приравняем первый теоретический момент (К) =*тх (X) пер-
* 1 VI
вому выборочному моменту = тх = ~ *£'•
тх(к) = т*. <4 16)
Решив это уравнение относительно X, найдем оценку £, которая является
функцией от выборочной средней и, следовательно, функцией выборочных
значений: >
£=ф(Х1, х2......хп).
При оценке k неизвестных параметров Aj, Х2.Ц следует найти первый»
второй, &-й моменты распределения р± (х; Aj, А2, А&):
т$ (Xi, Х2, ..., А&) «= J xi Pt (x]• Alt X2, ...» A/Jdx,/ = i, 2, k*
а затем соответствующие выборочные моменты:
1 п
т*! (xlt х2, ...,хп) 2 х!
и приравнять их. Тогда получим систему k уравнений с k неизвестными:
^•(Аа, А2...................ХА) = /п| (хп х2....хп). (4-17)
Решив систему (4.17), Определим оценки неизвестных параметров.
Достоинством метода является его простота. Однако^он содержит эле-
мент произвола, так как, кроме моментов, можно рассматривать и другие
характеристики (моду, медиану и т. д.). Оценки по методу моментов в смысле
эффективности не являются «наилучшими» — в больших выборках они имеют
не наименьшую дисперсию.
Метод максимального правдоподобия, как и два других метода, бази-
руется на рассмотрении апостериорной (послеопытной) плотности вероят-
ности:
Pps (Х)==р (А | Xi, х2, • • •, Xfi)===^Ppr (A) L (X), (4.18)
где k = р"1 (xj, х2, ..., хп) — коэффициент, зависящий от результатов выбор-
ки, но не зависящий от параметра А; ррг(А) — априорная (доопытная) плот-
ность вероятности параметра A; L (А) = р (xv х2, ..., хп|А) — функция прав-
доподобия.
Если плотность вероятности p^x; X) случайной величины X содержит один,
подлежащий оценке параметр А, то функция правдоподобия для этого пара-
метра при независимой выборке объема п имеет вид
= П *) <4Л9>
1= I
За оценку максимального правдоподобия параметра А принимается та-
кое его значение А, при котором L (А) достигает максимума, т. е. такая оценка
является решением уравнения правдоподобия:
(4.S0)
& к=К д'К
При оценке k неизвестных параметров Ар л2, ..., А& распределения
Ах, Х2, .... Ад) оценки определяются как решения системы уравнений
dlnL(Ap А2, ..., Kh)/d^ = 0, j = 1,2, k. (4.21)
112
Оценки, полученные по этому методу, при довольно общих условиях явля-
ются состоятельными, асимптотически несмещенными, асимптотически нор-
мальными и асимптотически эффективными. На практике этот метод иногда
приводит к сложным системам уравнений.
Точечные оценки применяются прежде всего тогда, когда с их помощью
нужно провести еще и другие расчеты. Такие оценки не несут информации о
точности конкретной оценки. При малых выборках они случайны, а поэтому
малонадежны. Точность и надежность оценки позволяют определить интер-
вальные оценки.
Пусть из опыта получена несмещенная оценка К — g (jq, х2. ...» хп)
Параметра К.. Для разумного использования этой оценки на практике нужно
знать вероятность того, что при данном объеме выборки п отклонение оценки
Хот оцениваемого параметра 2^не превысит границы б > 0:
Р (|Х - Л1 < 6} = Р {—б <Х — Х<б}==Р{Х — б<Х<Х+б}== 0
(4.22)
где б — точность оценки; 0 — доверительная вероятность (надежность) того,
что при данном п оценка X будет иметь точность б; (X — б; X + б) — до-
верительный интервал. Величина 0 определяется конкретными условиями
задачи и обычно выбирается равной 0,95, 0,99, 0,999. Задаваясь любыми
двумя из величин б, 0, п, связанных соотношением (4.22), можно найти
третью. Для этого нужно знать закон распределения оценки X, который в об-
щем случае зависит от самих неизвестных параметров. Однако иногда удает-
ся перейти в (4.22) отХ к таким функциям выборочных значений, закон рас-
пределения которых зависит только от объема выборки п и закона распреде-
ления случайной величины X и не зависит от неизвестных параметров.
Если выборка объема п произведена из гауссовской генеральной совокуп-
2
ности с параметрами тх и оА, то доверительные интервалы для оценок парамет-
ров с вероятностью 0 рассчитываются по следующим формулам
1. Доверительный интервал для математического ожидания тх при из-<
вестной дисперсии о% строится на' основе выборочной функции Z = (т*-
— /пх)/ох, имеющей стандартное нормальное распределение с параметрами
М (Z) = 0, Dz = 1. В этом случае от .формулы (4.22) приходим к выра-
жению
т* — 2^ох/УгГ < тх< т^+ г^ох/Уп , (4.23)
где Zp = 6pVn/ox определяется из равенства Ф (Zp) = (l + 0)/2 по таблице
приложения II.
2. Доверительный интервал для математического ожидания тх при не-
известной дисперсии Ох строится с использованием выборочной функции
Т = (тх — mx)~]/n/s, имеющей /-распределение Стьюдента с k==n — 1 сте-
пенями свободы. В этом случае формула (4.22) приводит к выражению
а/28/У^ <тх<тх + ‘к, a/2s/V*> k = n—\, (4.24
где
1 ”
<з=—г 2 (х‘-о2.
f— 1
tk. а—а—-процентная точка /-распределения Стьюдента с & = п — 1 степени
ми свободы, определяемая по таблицам приложения IV из условия
J Pi(/) rf/=a= 1 0; zZs, 1 —a/2 = a/2*
a
113
3. Доверительный интервал для дисперсии о? строится с использованием
выборочной функции х2 = (п — 1) s2/o2, имеющей ^-распределение Пир-
сона с k = п — 1 степенями свободы, в соответствии с формулой
а/2 < 1-а/2, <4-25)
где х*; а — а — процентная точка ^-распределения Пирсона с k = п — 1
степенями свободы, определяемая равенством
р {X3 > xi а} = Г pl(x2)dx2 = «=1—
X* : а
Процентные точки %2-pa определения приведены в приложении Hi. х^-распре-
деление асимметрично, х2 > 0- На практике обычно выбирают х2 и %2
так, чтобы Р{х2 >Xi} = ^ {х2 < Xi} = а/2-
Статистические гипотезы могут формулироваться или относительно не-
известных параметров известного распределения (параметрические гипотезы),
или относительно неизвестного закона распределения (непараметрические
гипотезы). Возможны и другие варианты гипотез.
При двухальтернативной ситуации, когда происходит одно из двух собы-
тий, рассматривают две гипотезы: исходную (нулевую или основную) Но
и конкурирующую (альтернативную) Нг, которая противоречит Но. Задача
состоит в том, чтобы по результатам наблюдений принять одну из них. Из-
за случайного характера явлений любое решение (выбор ©даюй из гипотез)
сопровождается ошибками двух видов. Ошибка первого рода возникает тогда,
когда отвергается правильная гипотеза, а ошибка второго рода—когда при-
нимается неправильная гипотеза.
Пусть наблюдаемое событие обусловлено одной из двух причин: Ао
(гипотеза /70)-или Л2 (гипотеза Ях); Г — пространство всех возможных зна-
чений наблюдаемой величины X; Го — область принятия гипотезы /70; —
область отклонения гипотезы Но (критическая область); р0 (*) = Р W Ао),
PiW=p(x|A1)— условные плотности вероятности точки х пространства
Г; Ppr (Ао) = р, Ppr (Ajl) = q = 1 — р — априорные вероятности Ао
и Ал; а — условная вероятность ошибки первого рода (уровень значимости
критерия); f —условная вероятность ошибки второго рода; (1 — ₽) — мощ-
ность критерия; ра и р6 — безусловные вероятности ошибок первого и
второго рода; Ре — суммарнаявероятность ошибки.
Тогда справедливы следующие сотношения:
а = f р, (х) dx, Р = J Pi (х) dx, (4.26)
Г1 Го
Ра=И = P,(x)dx. (4.27)
Г, Г-,
pe = Pa+P$=P f Po(*)d*+<7 ( Pi(x)dx, q—\—p. (4.28)
Г1 r„
В радиотехнических приложениях наиболее часто применяются два оп-
тимальных правила решения: критерий идеального наблюдателя (критерий
Котельникова — Зигерта) и критерий Неймана — Пирсона.
Критерий идеального наблюдателя применяется тогда, когда нет разли-
чия в значимости ошибок первого и второго рода и когда известны априорные
вероятности каждой из гипотез, что характерно для радиосвязи. При этом
критерии правило решения состоит в следующем:
если / (х) > h, то принимается
если / (х) < й, то принимается Яо, (4.29)
114
где
l(x) = Pi (x)/p0(x), (4.30)
— отношение правдоподобия; h = p/q — постоянный порог, который являет-
ся решением уравнения
rL(WoW = Р/р- (4.31)
Критерий идеа.дБного наблюдателя минимизирует вероятность полной
ошибки
^e=pj Po(x)dx +р f p1(x')dx. (4.32)
h —oo
Критерий Неймана — Пирсона применяется в случаях, когда значимость
ошибок а и Р различна, а априорные вероятности гипотез неизвестны, (харак-
терно для задач радиолокации). При этом критерии оптимальным считается
такое решение, когда при заданной ошибке первого рода минимизируется
ошибка второго рода. Решение выносится на основании сравнения отношения
правдоподобия / (х) с порогом h:
I W = Pi (x)/pQ (х) > h. (4.33)
Порог h определяется по наперед заданной ошибке первого рода
_a=J p$(x)dx. (4 34)
h
Для проверки гипотезы HQo законе распределения генеральной совокуп-
ности обычно используют критерий согласия %2, при котором за меру расхож-
дения теоретического и статистического распределений принимается вели
чина (4.3), которая при п -+ оо асимптотически распределена по закону х2
с k=r — 1. степенями свободы^ независимо от распределения случайной ве-
личины X.
Критерий %2 для гипотезы Но с уровнем значимости а отвергает если
вычисленное по выборке значение %2 > xi а, и принимает если <
< х£. а- Величина х|. а определяется из условия
J Pi (X2)d(Xa) = a
по таблицам приложения III, при заданных k и а. Уровень значимости а
наиболее часто выбирается равным 0,05 или 0,01.
При применении критерия х2 необходимо, чтобы величины п и Vf были
достаточно велики (рекомендуется п > 5, vz- > 5—8). Если число наблюдений
в отдельных интервалах очень мало (одно-два наблюдения), то следует объе-
динить некоторые интервалы.
2. ПРИМЕРЫ
4.1. Ошибки 15 измерений дальности до цели с помощью радио-
дальномера представлены таблицей
Номер изме- рения 1 2 3 4 5 6 7 8 9 10 11 12 18 . 14 15
Ошибка Х[, м 18 —15 —5 6 —15 6 12 —5 —10 6 —5 —10 12 —10 —5
115
Требуется: 1) построить распределение выборки и статистическую
функцию распределения F* (х); 2)' определить выборочную среднюю
Шх и выборочную дисперсию D*x ошибки измерения.
Решение. Вариационный ряд имеет вид: —15, —15, —10, —10,
—10, —5, —5, —5, —5, 6, 6, 6, 12, 12,18. Он содержит шесть раз-
личных значений: —15, —10, —5, 6, 12, 18. Частоты v, этих значений
равны соответственно: 2, 3, 4, 3, 2, 1.
1. Распределение выборки представим таблицей
Xi, М — 15 -10 5 6 12 18
V/ 2 3 4 3 2 1
p'^Vtln. 2/15 3/15 4/15 3/15 2/15 1/15
Наименьшее значение ошибки измерения X равно —15. Следо-
вательно, (х) = 0 при х —15. Значение X < — 10, а именно
Xj= —15, наблюдалось два раза; поэтому F{ (х) = 2/15 при —15 <
<х<—10; при ^10 < х< —5 FJ(x) = 2/15+3/15=5/15. Про-
должая аналогичные рассуждения, получим результаты, приве-
денные-в таблице
X х < —15 — 15<х<—10 — 10<х<—5 —5<х<6 6<х< 12 12<х< 18 х> 18
F1W 0 2/15 5/15 9/15 12/15 14/15 1
График функции F* (х) показан на рис. 4.1.
2. Используя формулы (4.5а) и (4.6а), получаем:
1 V _ -15-2—10-3—5-4+ .3+12.2+18.1 4
х—--- ----------------------—--------------=----
Dx = — У xf V; — (ГПх)2 =
/ = 1
225-2-4-100.3+25.4+36-3+ 144-2-J-324-1 / 4 V
15 \ 3 '
4.2. В течение 24 ч регистрирующее устройство контроля каж-
дый час фиксирует напряжение сети. После первичной обработки
данных получено распределение выборки в интервальной форме,
пригеденное в таблице
на
Интервалы, В 213—215 215—217 217—219 219—221 221—223
1 3 6 10 4
Построить гистограмму выборки.
Решение. Из таблицы видно, что частичные интервалы одинаковы
ht = h = 2 В. Поэтому в соответствии с (4.2) получим:
p{/h = 1/24 • 2 = 0,0208, p*2/h = 3/24 • 2 = 0,0624,
p*3/h = 0,125, p*/h = 0,208, p^/h = 0,0834.
Для построения гистограммы отложим по оси абсцисс указан-
ные в таблице частичные интервалы и на каждом из них построим
прямоугольник высотой p*/h = pt (и), i = 1, 2, 3, 4, 5. Например,
над интервалом 219—221 прямоугольник имеет высоту 0,208.
Гистограмма выборки изображена на рис. 4.2.
4.3. Генеральная совокупность распределена по нормальному
закону с неизвестными параметрами т и о:
рх (х) = (2 л о2)-1/2 ехр I—(х — т)2/2 от2].
Вычислить по независимой выборке хь х2, ...,хп оценки неиз-
вестных параметров tn и о: 1) методом моментов; 2) методом макси-
мального правдоподобия.
Решение. Одномерная нормальная плотность вероятности оп-
ределяется двумя параметрами т и а2.
1. Параметры tn и о2 представляют собой соответственно началь-
ный момент первого порядка т1 и центральный момент второго по-
рядка т2 : 1Щ — tn, tri2 = Dx = о2. Начальный эмпирический
момент первого порядка равен выборочной средней т[ = гпх,
а центральный момент второго порядка—выборочной дисперсии
= Dx- Приравняв в соответствии с методом моментов соот-
Рис. 4.1. Эмпирическая функция
распределения
Рис. 4.2. Гистограмма выборки
117
ветствующие теоретические и выборочные моменты, получим оценки
параметров нормального распределения:
2. В соответствии с (4.19) функция правдоподобия имеет вид
L(m, о) = |~[ рх(хг; zn, о) = (орС2 л) п Ц едр|[—да)2/2о2] =
7= 1 /=•!
п
- 2 (хг-т)2/2а2
i=\
а логарифмическая функция правдоподобия:
In L (т, о) = — п In о-In (2л)— (хг —т)2.
“ i=l
Используя формулу (4.21), получаем систему двух уравнений от-
носительно т и о2:
±lnL(w’g) =_______L у д^~"± = _1 (у х.-,пт} =0,
дт 2о2 дт о2, I /
/ = 1 \/=| /
dlnZ-(w-(71 = - ±+-L V (х. = 0.
0'0 О СУ3
! =1
Отсюда находим
/=’1
и п
°2=V 2(Х; ~т}2=т 2 (Хг ~т*^=D*x’
П !=1 ” Z=l
В данном случае оценки, найденные ио методу .моментов и по
методу максимального правдоподобия, совпадают. Они являются
состоятельными, причем первая из них несмещенная, а вторая сме-
щенная.
4.4. Произведено 16 независимых измерений случайной величи-
ны X, распределенной по нормальному закону. По выборке найдена
выборочная средняя т*х = 4,1.
Оценить неизвестное математическое ожидание тх случайной
величины X по выборочной средней при помощи доверительного
интервала с надежностью |3 = 0,95, если: 1) среднее квадратическое
отклонение величины X известно и равно единице; 2) среднее квадра-
тическое отклонение ох неизвестно, а выборочное среднее квадра-
тическое отклонение величины X s = 1.
Решение, 1. По условию, 0 = 0,95. Следовательно, Ф(гр) =
= (1 + Р)/2=(1 + 0,95)/2=0,975. Из таблицы приложения II
118
находим значение ze = 1,96, которому соответствует <D(zp)=
— 0,975. Определим точность оценки 6Р = ze,cjxf]/'n = 1,96/]/16=
= 0,49. В соответствии с формулой (4.23) при тх, — 4,-1 доверитель-
ный интервал имеет' доверительные границы:
тх — 0,49=4,1—0,49=3,61, тх + 0,49=4,1+0,49=4,59.
Таким образом, значения неизвестного параметра согласую-
щиеся с данными выборки, удовлетворяют неравенству:
3',6Г < тх < 4,59. 1
2. Случайная величина Т = (тх — тх)]^nls подчиняется /-рас-
пределению-Стыстдента с И = п—1 степенями свободы. Поэтому
доверительный интервал строится по формуле (4.24).
По условию, k —th—1 = L6>—1 = 15-,. а = 1- — а/2 — (1 —
— р)/2=(1—0,95)/2=0,025.
Используя таблицы.приложения IV, получаем:’ /*; ~ ft 5- 0.025=
= 2,131.
Тогда доверительные границы равны
тх — = 4,L—2,L31.-1/4~W,
tnx + tk-= 4,1+2,13Г-1/4~4,63.
В данном случае с надежностью 0 = 0,95 неизвестный параметр
заключен в доверительном интервале:
3,57 < тх < 4,63.
4.5. Произведено четыре измерения дальности до неподвижной
цели с помощью радиолокатора, в результате получены следующие
данные: 2470, 2490, 2580, 2520 м.
Оценить точность радиолокатора при надежности оценки 0 =
= 0,95.
Решение. Определим выборочные характеристики тх и s2. По
формулам (4.5) и (4.15) имеем:
т; =у х, - «уо+жю+ам+жм _ 25,5 м,
" ГЙ 4
»=_!_ 2 (х, - = гм» м>.
ftell
По таблице приложения 1П для Й = 3, а/2=(1 — 0)/2=(1—0;95)/2=
= 0,025 и 1 — а/2=1—0,025=0,975 находим
Xfr; а/2 =-%3; О'. 025 =9,35', 1-а/2 =ХЗ; 0,975 = 0,216.
Границами доверительного интервала для дисперсии <jx являются:
_^__12300 = 73g 12300 ^^,900.
Х1а/2 9,35 1-а/2 0,216
Тогда 736 м2 < а* < 31900 м2.
119
Рис 4.3. Гистограмма
выборки
Рис. 4.4. Эмпирическая
функция распределения
Оценка среднего квадратического отклонения
,/736 <ож</31900 или 27,2 м < ох< 178 м.
Результат показывает, что для определения точности радиолока-
тора четырех измерений мало.
4.6. Ошибки 500 результатов измерений дальности до цели ра-
диодальномером приведены в таблице
Интервал (/?/), м —25; -15 — 15; —5 -5; 5 5; 15 15; 25
Число ошибок в интер- вале vz- 50 130 200 100 20
Относительная частота р* 0,10 0,26 0,40 0.20 0,04
Требуется: 1) построить гистограмму р* (х) и эмпирическую
функцию распределения А* (х) ошибок измерения дальности;
2) аппроксимировать выборочное распределение с помощью нормаль-
ного закона; 3) пользуясь критерием согласия %2 с уровнем значи-
мости а = 0,01, проверить согласованность теоретического и эм-
пирического распределений.
Решение. 1. По условию, число интервалов г = 5, а длина ин-
тервалов h = Юм. Используя формулы (4.2), (4.1), данные таблицы
и методику, изложенную в примерах 4.2 и 4.1, строим гистограмму
и функцию распределения F* (х), графики которых соответственно
изображены на рис. 4.3 и 4.4.
2. По методу моментов заменим теоретические параметры тх
и а2 их выборочными характеристиками гпх и D*x. Последние опре-
делим по формулам (4.9) и (4.10):
5
tnx = 2 ал? = — 20 • 0,1—10 • 0,26—0 • 0,40+10 • 0,20 +
/=i
+ 20 • 0,04 — — 1,8 м,
123
D* = i alpl —(m*)2 = 400-0,1+100-0,26+100.0,2+
i=l
+400-0,04—3,24=98,76 m2, (fx = V D'x = V98,76& 9,93 m,
где at — середины интервалов: —20, —10, 0, 10, 20.
Тогда выражения оценок плотности вероятности и функции ра-
спределения будут иметь вид:
Pi (х) = (Зло2)-1/2 ехр [— (х — т)2/2 о2] =
= (2л • 98,76)—1/2 ехр [—(х + 1,8)2/2 - 98,76],
Л(х) = J р1(х)йх = Ф ( ^э^эз’8 )‘
— оо
3. Для определения меры расхождения (4.3) необходимо вычис-
лить вероятности
. / Xfd-t—tn\ , {Xi—tn\
р. = ф / ----)—ф P------ ,
\ a / \ о J
где xh xi+1 — границы f-го интервала, а Ф(г) находится из таб-
лицы приложения II. Так, например, для четвертого интервала
(5; 15) имеем: pt = ф( ) - Ф ) = °-2012- РезУль’
таты вычислений остальных вероятностей сведены в таблицу
hi, м —25; —15 -15; —5 —5; 5 5; 15 15; 25
Pi 0,0821 0,2818 0,3794 0,2012 0,0417
Подставив соответствующие значения в формулу (4.3),получим
расхождение:
Оценочными значениями заменены два параметра нормального
распределения. Поэтому число степеней свободы k = 5—1—2=2.
Из таблицы приложения III при fe = 2, а = 0,01 находим
УЛ-.а = 72; 0,01 =9,21.
Так как /2 = 3,427 < а = 9,21, то гипотезу о том, что ошиб-
ка измерения распределена по нормальному закону, можно считать
правдоподобной.
4.7, На вход радиоприемного устройства в некоторый фиксиро-
ванный момент времени t воздействует случайное напряжение Х(/),
121
Рис. 4,5. Нормальные плотности вероят-
ности и ошибки первого и второго рода
Л «7
э*-
которое является либо суммой известного сигнала s (/) и помехи п(/)
(гипотеза Н^., либо одной: помехой п(/) (гипотеза Но). Помеха n(t)—
гауссовский стационарный шум с нулевым математическим ожи-
данием и известной дисперсией D. Априорные вероятности гипотез
одинаковы: р = q = 1/2. В момент t = tv производится измерение
величины X (t).
Требуется: 1), построить правило решения; 2) вычислить услов-
ные вероятности ошибок первого и второго рода, а также полную
вероятность ошибки.
Решение. При отсутствии сигнала X — п, поэтому
р0(х) = (2л£>)-*/2 ехр (—x2/2D).
При-наличии сигнала X = зЧ- п: Следовательно,
pt(X), = Ро(х —• з)~(2лD)-*/2 ехр It—(х — з)2/2Е>Г.
1. В соответствии е (4'.29) правило решения принимает вид
/(х) = Р1(х)/р0.(х) = expl— (з2 — 2 xs)/2DI > 1,
что эквивалентно (после логарифмирования) неравенству s/2.
Таким образом, принимается решение о наличии сигнала (ЯД
если измеренное значение х > s/2 (область rt); при х < s/2 (область
Го) констатируется-отсутствие-сигнала (Яо).
2. По- формулам (4.26) и (4.28) находим, вероятности, ошибок:.
а‘= [ p«(x)dx = 1—<>(s/2 ]/”£?);
/2
/2
[’ =. j р, (x) dx = 1-Ф(д/2КО),
Pe = ct/r -F-p? = I —
где Ф (x) определяется по таблице приложения. IT.
Графики плотностей вероятностей, а также ошибки а и ₽ пока-
заны на рис. 4.5.
3. ЗАДАЧИ и ответы
4.1. В результате пяти измерений физической величины X
одним- прибором, кетточвьвй не имеет систематической ошибки, полу-
чены следующие результаты: 92; 94;: ЮЗ;. 105; 106.
Определить: а<) выборочную среднюю т*х (измеряемгвн .'величины;
б) выборочную D*x и исправленную s2 дисперсии ошибок прибора
Ответ-, а) тх — 100; б) Dx — 34, s2=42,5.
4.2. Из 100 транзисторов в среднем бывает два бракованных.
Проверено десять партий по 100 транзисторов в каждой. Отклоне-
ния числа бракованных транзисторов от среднего приведены в таб-
лице
Номер партии 1 2 3 4 5 6 7 8 9 . 10
Отклонение от среднего —.1 0 1 ,1 —1 1 0 —2 2 1
Построить распределение выборки, эмпцрическую функцию рас-
пределения Fi (х) и гистограмму выборки.
Ответ:
*1 -2 — 1 0 1 2 0, 2, 0,1, —2<х<;— 1, р* 3, —Л 1 0,5, 0<х^1, 0,9, 1<х^2, 1, х>2.
Vi 1 2 2 4 1
* Pi 0,1 0,2 0,2 0,4 0,1
4.3. Построить гистограмму по распределению выборки, пред'
ставленную таблицей
Интервалы .0—2 2—4 : 4—В
Vi 20 30 50
Ответ: p'Jh = ©,2/2 = 0,4, /?;/& = 0,45, p*tlh = 0,25.
4.4. Отобраны случайно 200 однотипных радиостанций. Время
их работы до первого откнва характеризуется таблицей
Срок службы радиостанции до пер- вого отказа, ч .900—1100 1100—1300 1300—1500
Количество радиостанций 10 120 70
Вычислить выборочные средние mt, дисперсию D* и среднее квад-
ратическое отклонение ст* срока службы радиостанций до первого
отказа.
Ответ: ml = 1260 ч,Р/ = 12 400 ч2, ст* = 111,4ч.
1123
4.5. Измерительным прибором, практически не имеющим систе-
матической ошибки, было произведено пять независимых изме-
рений, результаты которых представлены в таблице
Номер измерения 1 2 3 4 5
Xi 2781 2836 2807 2763 2858
Определить: а) выборочную дисперсию ошибки измерения, если
измеряемая величина точно известна и равна 2800; б) выборочное
среднее, выборочную дисперсию и ее несмещенную оценку, если
точное значение измеряемой величины неизвестно.
Ответ', a) DJ = 1287,8; б)~ т*х = 2809; = 1206,8; s2= 1508,5.
4.6. Показать, что оценки аир, рассчитанные по методу момен-
тов для параметров аир гамма-распределения
Pi(х) =- , е-Л/Р, х>0,
F1V > ра+1 Г(а + 1)
определяются выражениями:
a = (/nJ/s)2 —1, p = s2/mx,
где
[/nj(l — т*)— s2].
1 п 1 Л
=— 2 Xi, s2 = —Ц- 2 (*/
п & п-1
Xi — выборочное значение; п — объем выборки.
4.7. Плотность вероятности случайной величины X имеет вид:
р,(х) = х°~' (1 — х)ь~', 0<х< 1( бета-распределение).
Вычислить по методу моментов оценки а и b параметров распре-
деления а и Ъ.
~ m*h 1—т
Ответ, а =-------, b — —Н
4.8. Определить методом максимального правдоподобия оценку
параметра р биномиального распределения
Р„ (k) = С*р*(1 -p)«-s
если в независимых испытаниях событие А появилось тг раз и в
независимых испытаниях — т2 раз
Ответ', р = (т, 4- m2)/(n1 + п2).
4.9. Выборка объемом п извлечена из совокупности с показа-
тельным распределением pY (х) = Хе-и, х>0.
Найти оценку X максимального правдоподобия для параметра %.
Ответ'. X = Мт*.
124
4.10. Произведена выборка объемом п — 100 из большой партии
однотипных радиоламп. Средний срок службы радиолампы выборки
оказался равным 5000 ч.
Найти с надежностью 0,95 доверительный интервал для среднего
срока службы радиолампы во всей партии, если среднее квадрати-
ческое отклонение срока службы составляет 40 ч.
Ответ'. 4992,16 ч < mt <С 5007,84 ч
4.11. Каков должен быть минимальный объем выборки п, что-
бы с надежностью 0,98 точность оценки ‘математического ожида-
ния т генеральной совокупности с помощью выборочного среднего
была равна 0,2, если среднее квадратическое значение совокуп-
ности о = 1,5?
Ответ', п = 306.
4.12. Средняя квадратическая ошибка радиовысотомера о =
= 15 м.
Сколько потребуется таких высотомеров, чтобы с надежностью
0,99 ошибка средней высоты mJ была больше—30 м, если ошибки ра-
диовысотомеров имеюг нормальное распределение, а систематические
ошибки отсутствуют?
Ответ: не менее двух.
4.13. Случайный радиосигнал распределен по нормальному за-
кону, причем его среднее значение неизвестно, а дисперсия сг2 =
= 1 В2. Произведено 100 измерений сигнала, по. которым определено
значение выборочного среднего т'х — 1,5 В.
Определить величину доверительной вероятности 0, с которой
может быть гарантирована предельная погрешность измерения
среднего значения сигнала 6 == 0,2.
Ответ: 0 = 0,954.
4.14. Распределение выборки объемом п = 10 задано таблицей
Xi -2 -1 2 3 1 5
V, 2 1 2 2 2 1
Оценить с надежностью 0,95 математическое ожидание ту
случайной величины X, распределенной по нормальному закону,
по выборочной средней при помощи доверительного интервала.
Ответ: 0,3 < тх < 3,7.
4.15. Произведено десять независимых измерений случайной
величины X, подчиненной нормальному закону с неизвестными пара-
метрами тх и сгх. Результаты измерений представлены в таблице:
Номер измерения, i 1 2 3 4 5 6 7 8 9 10
Результат измере- ния 2,5 2 —2,3 1,9 — 2,1 2,4 2,3 —2,5 1,5 —1,7
125
Найти оценку т*х для математического ожидания и построить
доверительный интервал, соответствующий доверительной вероят-
ности р = 0,95.
Ответ'. тх = 0,4; —1,18<т< 1,98.
4.16. Произведено 12 измерений напряжения радиосигнала одним
и тем же прибором, не имеющим систематической ошибки, причем
выборочное среднее квадратическое отклонение s случайных ошибок
оказалось равным 0,6 В.
Найти точность прибора с надежностью 0,99.
Ответ'. 0,39 В < а < 1,24 В.
4.17. На контрольных испытаниях 16 радиоламп были опре-
делены выборочные характеристики их срока службы, которые ока-
зались равными тх = 3000 ч и s = 20 ч.
Считая, что срок службы каждой лампы является нормальной
случайной величиной, определить: а) доверительный интервал для
математического ожидания и среднего квадратического отклонения
при доверительной вероятности 0,9; б) с какой вероятностью можно
утверждать, что абсолютное значение ошибки определения тх
не превзойдет 10 ч, а ошибка в определении вх будет меньше 2 ч?
Ответ', а) 2991,235 ч < тх < 3008,765 ч, 15,50 ч < <
< 28,74 ч; б) 0,93; 0,41.
4.18. На телефонной станции производилась регистрация чис-
ла неправильных соединений в минуту. Результаты наблюдений
приведены в таблице
Xi 0 1 2 3 4 5 6 7
v< 8 17 16 10 6 0 1
Требуется: а) определить выборочные характеристики гпх и $2
и проверить выполнение основного условия для распределения
Пуассона; б) найти теоретическое распределен-ие Пуассона и про-
верить степень соответствия теоретического и эмпирического ра-
спределений по критерию х2 с уровнем значимости а = 0,05.
Ответ', а) тх ~ s2=2, т. е. условие для закона Пуассона прак-
тически выполняется; б) %2 = 0,2< о,о5=9Д
4.19. Произведены испытания 500 радиоприемников на их чув-
ствительность. Данные отклонений чувствительности от номинала
указаны в таблице
Интервалы чувстви- тельности, мкВ —4; — 3 —3; -2 -2; -1 -1; G 0; 1 1; 2 2; 3 3; 4
V| 6 25 72 133 120 1 88 46 10
125
Проверить по критерию %2 с уровнем значимости ос = 0,01
гипотезу Но о том, что результаты испытаний подчиняются нор-
мальному распределению.
Ответ: х2 = 3,94 < хз; ooi =15,1.
4.20. Испытания 200 радиоламп на их срок службы дали резуль-
таты, приведенные в таблице
Срок службы, ч 300— 400 400— 500 50’0— 600 600— 700 700— 800 800— 900 900- 1000 1000— 1100 1100— 1200
Vi 1 -1 18 33 40 52 29 14 4
Требуется: 1) установить теоретический закон распределения
срока службы радиоламп и найти его параметры; 2) написать вы-
ражения для плотности вероятности рх (х) и функции распределения
Ft(x); 3) пользуясь критерием х2, установить, согласуются ли дан-
ные испытаний с гипотезой о распределении случайной величины по
избранному теоретическому закону.
Ответ: 1) закон распределения нормальный с параметрами
т = т*х = 784 ч, а2 = 26844 ч2, о = 163,8 ч;
2) Pi(x)
1 Г ' (X-W1 с- / \ ^./х—784
-----—= ехр — ----------— , F, (х) = Ф (------
163,8У‘2л [ 53688 J 1 \ 163,8
3) согласуются.
Раздел II
СЛУЧАЙНЫЕ ПРОЦЕССЫ
5. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ И МОМЕНТНЫЕ
ФУНКЦИИ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Случайный процесс £(/), зависящий от одного действительного парамет-
ра t (времени), считается определенным на интервале времени (О, Г), если
при произвольном числе п и для любых моментов времени t2, tn на
этом интервале! известна п-мер на я плотность распределения вероятностей
Рп (11, 62» •••» *1, ^2» •••» *п) или ^-мерная характеристическая функция
{п )
П ехр (/Vi£i) I =
=]•••]’Рп (51. 5s. ••..Еп! G. «2..........tn) ехр (/»! 5i+P85,+ •••+ IVnZn)*
(5.1)
где U = Н/2), И =
Плотность распределения вероятностей должна удовлетворять следую-
щим условиям [1, 14, 27]:
1) условию положительной определенности:
*2, > 0; (5.2)
2) условию нормировки:
J...J Рп (^ S2......gn; G, G, — =1; (5.3)
3) условию симметрии: функция рп(^, ?2> SnJ 61) должна
быть симметричной относительно своих аргументов £2» •••» т- е- не долж-
на изменяться при любой перестановке этих аргументов;
4) условию согласованности: при любом т < п
Рт (11 > ъ2> * * • ’ 'чт> , f2’ * * • • “ j • • • j Рп (£1, £2» • • •_» ьтп’ &тп+1» • • •»
/1, t2, tm> ^тпЧ-l’ ^n) dQm + i • • • dc>n • (5.4)
Поскольку характеристическая функция (5.1) является преобразованием
Фурье от соответствующей плотности распределения вероятностей, то для
нее также справедливо условие симметрии, а условия нормировки (5.3)
и согласованности (5.4) принимают вид
®п (0, 0, .... 0)=1, (5.5)
(jyi* /у2’ ••••» №т> G» ^2» •••’ Ъп) =
= (Jvi> /у2> ...» ivm> 0, 0; /х, /2, ...» tm)» (5.6)
128
Многомерные плотности распределения вероятностей являются наиболее
полными характеристиками случайных процессов. Однако в ряде случаев
для решения практически важных задач оказывается достаточным рассмот-
рение более простых характеристик, в частности моментных функций
[28, 29].
Под моментными функциями случайного процесса £(/), заданного на не-
котором интервале, понимаются функции mv Vw(4, t2), ...»
mv v..... (/ъ t2y tn)y симметричные относительно всех своих аргу-
ментов, определяемые соотношениями
mV( (0 = М {gv- (0} = f gv* Л (£;О (5.7»
mV(. v, («,. = M {£v* (<i) «,)} -
= tel- h, (5.81
—&O — OO
; mvlt Vj.....'»> -r ...
-f — Г -..UM,..........
— OO —00 \ , •
Моментная функция mV1, Vi, ...»v •••• 6i)» Зависящая от n несов-
падающих аргументов tlt /а, ...» /п» называется л-мерной начальной момент-
ной функцией v-го (v = Vj + v2 + ... + vn) порядка.
Одномерная начальная моментная функция первого порядка
mi (О - (И{| (<)} = J (§; t)& = тМ (5.10)
—, * ,-v
называется математическим ожиданием случайного процесса £(/). Помимо
этой характеристики, широко используется также двумерная начальная мо-
ментная функция второго порядка
«а) = М 7 1 lifca х
X р2&, ?2; h, /2) <5-1 о
называемая ковариационной функцией случайного процесса g(f).
3место моментных функций (^, in) можно рассмат-
ривать n-мерные центральные Моментные функций v-ro порядка, которые он-
ределяются соотношением "
m»x Vi.....Vn (ГХ, ta, .... ^(4)]Л [£(*«>— ;
-m a,)|v» ... (g(tn)-m (in)iVn}= f ... f
— oo —oo
XKs-m6 (fa)Jv* ...[|п-т5(гп)Гп Pntei. 5»......SnJ
fl» t2, ’. *•» '(5wl2)
5 Зак. 1203* 129
Двумерная цектралъвая моментная функция второго порядка
OD. Q&
«?,I (to h> =Af {|| to)— mg toll II to) (ia)l}= f f Hi— «g to)IX
X [|,-«gto)lp2(li. Ia;4. *,)d|id|,= /?5to. (5.13)
называется корреляционной функцией случайного процесса & (£).
Полагая в (5.13) = t2 — h получаем следующее значение одномерной
центральной моментной функции второго порядка:
«Ь (0 =М {[| to-ms (т2)=ЛШ1оtol2} = J II- т1 (ОИх
— оо
= (/) = ^(Л 0 = ^(0- <5.14)
Здесь через £0 (/) = 5 (/) — ft) обозначен центрированный случайный
процесс. Таким образом» выражение (5.14) определяет дисперсию случайного
процесса 5 (/). Корень квадратный из дисперсии (/) называется средним
квадратическим отклонением о^ (/) случайного процесса £ (/):
Ogto =/о"(Г)=У"Л4{[|(0- (5.15)
Если случайный процесс £ (0 задан n-мерней характеристической функ-
цией, моментные функции удобно вычислять путем ее дифференцирования.
Используя определение оса рактерист и ческой функции- (5.1) и раскладывая
экспоненциальную функцию exp(z) в ряд Тейлора, можно показать, что для
л-мерной начальной моментной функции справедливо соотношение [1,14]
«^....^to^...to)= -‘^+^-+^х
/i+v,+ —+*,
X
„ „ V вп()°ь '»«• ••••/OnUi.fa.........to) I . (5.16)
Йо/ dv2* ... dvnn J»i=0
Корреляционные функции to), /?, (tt, t2), ..., /?n to, to. •••» to) on-
ределяются разложением в ряд Маклорена логарифма многомерных харак-
теристических функций. Можно показать [1,28], что для первых трех корре-
ляционных функций справедливы соотношения:
to(0 = «1(0 = М{| (/)},
to (to to) = «?.i to. to> = Л){[| to) - mi to)) X
X [| (to) — Mi (to))} = mltl (/,, /a) — m, to) m> (/,) =
= К (to to) - mi to) mH*,),
Rs (to- to. to) ~ «1,1,1 to> /3) «1 to) X
X Rt to, ?3) - m, (/,) /?a «!, — mt to) /?, (tu /,) -f- (5.17)
+ 2«i (0) «1 (/,) «1 tts)-
По моментным и корреляционным функциям можно восстановить харак-
теристическую функцию и, следовательно, плотность распределения вероят-
ностей [26):
6n(M. Рз......../»п; 0. /г. •••• /п) =
П 1 п п
=1+/ s + — i2 У У от1-1«м,- Q »ц % +
*=1 21 u^lv=l
1 п п п
+ ‘зГ'3 2 2 2 /x)°ui,vox + --->
1 v= 1 Л = 1
130
fn
H = 1
I n n J
2 2 л**г*’/»,‘’»*»+'зГ'’х
ц=1V=l
n n n 1
x2 2 2 ^(/u, *v, U«u»v°».+ - Г- <5.18»
Ц = i v=1 к=I j
Для гауссовского случайного процесса, часто встречающегося в различ-
ных радиофизических задачах, плотность распределения вероятностей я
Характеристическая функция определяются формулами [26]:
Pndx. Ь,. •••
1 "
* ехр 2
и=1
I
&п: ..Zn)~V(WAX
Ацу (£ц (^Ц,)] l^V (^у)1
V=1
(5.19)
®e(Pi. .......... h, ts, .... zn) =
= ?xp
п J n n
i 2 m5<Mvu+Tr 2 2
|1= 1 д= 1 v= 1
(5.20)
Здесь математическое ожидание случайной величины £ц =
= 5 (*и), А = II Gg» ^v) II — определитель n-го порядка, составленный
из значений /?£ (/ц, tv) корреляционных функций R^(tlt t2) = М{[£ (^) —
— ms</1)][g</2) — 02)]} при /х == и 12 ,= /v, A^v — алгебраиче-
ское дополнение элемента R^ (^, tv) этого определителя.
Важным классом случайных процессов являются стационарные случай-
ные процессы. Случайный процесс £ (/) называется стационарным в узком
смысле, если все его плотности распределения вероятностей рп (£1Ж £п;
4» ^2» W произвольного порядка п не меняются при одновремен-
ном сдвиге всех точек tit ts, ...» jn. вдоль оси времени на любое т. Ста-
ционарным в широком смысле называется случайный процесс ма-
тематическое ожидание М {£(/)} которого не зависит от времени, т. е.
М 16(Ф == ^(0 «« а корреляционная функция (/u, /v) зависит
лишь от разности ^uv = | — t/l между двумя рассматриваемыми моментами
времени. Для гауссовского процесса оба эти понятия стационарности совпа-
дают, поскольку стационарный гауссовский процесс полностью определяется
математическим ожиданием и корреляционной функцией и для его плотности
распределения вероятностей и характеристической функции справедливы
соотношения
^п) апУ(2л)»ОХ
п
Хехр
= ехр
Рп (£1» £2» •
1 п I
2оа D 2 S ^|iv j •'
ц= 1
Qn №1.
П । и I»
im 2 +т 2 2Т °*
ц= 1 * ц= 1 V = 1
v= 1
/»............./»п) =
. п п
(5.21)
(5.22)
5*
131
где m — математическое ожидание; о2 = D = R (0) —- дисперсия процесса
| (f); D = || г (t^v) || — определитель л-го порядка, составленный из коэффи-
циентов корреляции
' (т^) = г (I 1) = °-2 * (I ln~lv 1)=о-2 М {К (^)-т] R (М-И)}-
Применительно к двумерному случаю формулы (5.21) и (5.22) принимают вид
' ( 1
₽г (51. = 2no2V 1 -г2 (т) еХ₽ 1 2о2(1—г2 (т)| Х
ХЦ£1—/и)2 — 2г(т) ($!—т) (£а—m)+ (|2 — m)2j|, ,(5.23)
62(М, p2) = exp|/m(t>1-|-v2)-
---~о2 |v? + 2г (т) vt fi2 + Ут = {2 — Ц. (5.24)
Среди различных задач статистической радиотехники весьма, часто встре-
чаются задачи, связанные с линейным или нелинейным преобразованием
случайных процессов. В ряде случаев успешное их решение связано с возмож-
ностью представления плотностей распределения вероятностей случайных
процессов в виде быстро сходящегося ряда, члены которого выражаются через
табулированные функции. Некоторые из таких разложений, базирующихся
на представлении соответствующих платностей распределения в виде ряда
по ортогональным полиномам, рассмотрены в работах {6, 26, 30, 32, 34].
2. ПРИМЕРЫ
5.1. Найти одномерную t) и двумерную h, Q плот-
ности распределения вероятностей процесса
| (/) — асе;®/ 4- psino./,
где <о — постоянная угловая частота; аир — взаимно независи-
мые- гауссовские случайнее величины с нулевыми математически-
ми ожиданиями та = т$ — 0 и дисперсиями £>а =Ое = ст2.
Решение [35]. Случайная величина g — | (/) при любом фикси-
рованном значении t представляет собой линейную комбинацию
гауссовских случайных величин и в силу этого также является гаус-
совской. Таким образом, для определения плотностей распределе-
ния вероятностей рх(£; t) и рг(1г, £2; /2) процесса | (/) необходимо
определить его математическое ожидание и корреляционную
функцию h)-
В соответствии с (5.10)
m^(t) = {£(/)} = М {acos®/ 4- р sin®/} =
= М {a }cos ®/ 4- М {р }sin®(.
Поскольку по условию М {а} = та = 0, М {р} = тв = 0, то
m%(t) = 0.
При этом для корреляционной функции (5.13) получаем
Rj (4, /2) = Afflacos®/, 4-psin®/,[ х
X [acos®/2 4- Psin®/21}.
132
Учитывая, что по условию Л4{аР} = Л/ {Ра} = 0, оконча-
тельно получаем
(4> ?г) = °2 coso)^ cosco/2 4- <j2sin®4sin®4 =
= <y2cos®(4 — 4) = т = 4 — 4
Таким образом, искомые плотности распределения вероятно-
стей имеют вид
Л®
Рг(£1» ^г) = Рг(51» 5г) =
== 2 Г _ ^-2£ig2cos*)T+EM
?Я02 '[/Т — COS2 (DT [ 2о2 (1 — COS2 (ОТ) J
5.2. Стационарный случайный процесс
= 4(/)cos [о)о/ + <р(/)1
с нулевым математическим ожиданием М {£(/)} = — 0 за
дан одномерной плотностью распределения вероятностей Pi(%) =
= Предполагается, что соо есть априори известная постоян-
ная частота, стационарный случайный процесс А (/) может при-
нимать только положительные значения, а <р(/) представляет собой
случайную фазу, равномерно распределенную на интервале (—п, п)
При этом функция р$ (|) связана с одномерной плотностью распре-
деления вероятностей рл(А) процесса A(t) соотношением (см. за-
дачу 5.4)
(£) = —[ 77^== dA• (5.25)
Ui
Определить обратную зависимость, т. е. найти выражение для
рА(А), при котором одномерная плотность распределения вероят-
ностей pi(l) = Pi(l) будет иметь заданный вид.
Решение [40]. Производя в (5.25) замену переменных: = х~*
и Al = X-2, получаем уравнение
р Ш = f Рл(1/Х,) (5-26)
х Ц х ) J х тЛ?-Х» v ’
о
Это соотношение относится к классу приводимых к уравнению Абе-
ля, и для него существуют следующие формулы обращения:
и (0 dt
(5.27)
л dl J V/.—«»
о
133
Используя (5.27), уравнение (5.26) можно привести к виду
£ Pt (—
' — Рд (—} =2 — [ ; J-L--. (5.28)
к Рл\к ) dk J '
О
Переходя в (5,28) к старым переменным, получаем выражение,
определяющее искомую плотность распределения вероятностей:
р. (Л) = 2 А — Г А [ . (5.29)
Ра dA J iVtf-A2
A
Выражение (5.29) можно упростить, предварительно вычислив
путем интегрирования по частям, входящий в него интеграл:
А "I
arccos -у) р^ (а) 4- J (arccos -уj (5) d5 .
(5.30)
- - Надставляя (5;30) в (5.29), окончательно находим
А Г)
р.(Л) = 2Л f-Д=^, ’ (5.31)
А J V$2-A* v ’
ОО
где pg (5) = dp&ydl.
Соотношение (5.31) определяет одномерную плотность"”распре-
деления вероятностей р.д (Л) функции Л(/) в стационарном случай-
ном процессе 5(0 = A(/)cos[co0/ 4- <p(Z)l с постоянной априори
известной частотой <оо и случайной фазой <р (/), равномерно распре-
деленной на интервале (—л. л), при которой мгновенные значения
процесса 5(0 характеризуются заданной одномерной плотностью
распределения вероятностей pg(5).
Подобного рода задачи часто встречаются на практике при моде-
лировании случайных колебаний вида 5(0 = Л(0сов [®01 4- <р(01
с помощью средств вычислительной техники в процессе иссле-
дования статистической динамики различных радиотехнических
систем и устройств [40].
5.3. Найти двумерную плотность распределения вероятностей
Ря(^1» £2) стационарного случайного процесса
5(0 = Ат cos ((оо/ + <р),
где Ат и <оо — постоянные амплитуда и угловая частота; <р — слу-
чайная начальная фаза, равномерно распределенная на интервале
(—л, л). Двумерная характеристическая функция (jvt, jv2)
процесса 5(0 имеет вид [36]
(/yi> М) = М {ехр (/У51 + /о252) } =•
= Jо ИтКvi + 20^2 cos шот 4- vl),
134
где h — £(4)> ?2 — l(it), т = 4 — 4, J0(x) — функция Бесселя
первого рода нулевого порядка.
Решения [371. В соответствии с (5.1) можем написать
00 оо
Pt (11.1г) = f f ®2 (Pi> Ю ехр ( - /о1 —/о2 §2) dvt dv2.
Unr J J
— oo — oo
Подставляя сюда ©2 (jvit jv2) и используя теорему сложения для
бесселевых функций 138]:
+ 2QX Й2 cos <0т +Й|) = J (- 1)* sA Л (ЛЙО х
• 4=0
X Jft(4Q2) cos kwv,
где
(1 при k = О,
2 при 1
— множитель Неймана, находим
Pt (§1» ёг) —• (— l)ft efc
4=0
X
т о1)е-/0*^ ttoj х
'2
COS k(Oa-V.
Производя замену переменных = Amvi, Х2 = Amve и пользуясь
интегральным представлением функций
00
^*’(г)=4-У)к jA(X)e-^dX,
^оо
получаем
р2&,
Функции Ч*!*’ (z) могут быть выражены через полиномы Чебы-
шева Тх (г):
nft>(z) = (l-za)-V2Tfc(z),
Tk(z) =4" К2 +iV^=zi)k+ (z-/Prr=*i)ft].
При этом имеем
Pt Ui> 5г) — Pi (£i)Pi (^г) 2 8ft ) C0S
4=0 k Am' \Лт/
где _____
Р1(5) = 1/л/ЛД-?, ^<ЛМ.
135
Таким образом,, полученное выражение для р2 (Ех, Е2) дает разло-
жение двумерной плотности распределения вероятностей гармони-
ческого колебания со случайной начальной фазой в ряд по ортого-
нальным полиномам Чебышева.
3 ЗАДАЧИ И ОТВЕТЫ
5.1. Найти одномерную плотность распределения вероятностей
процесса Е(0 = а + 0/, где а и 0 — взаимно независимые случай-
ные величины с плотностями распределения вероятностей ра (а)
и
ос
Ответ [35]: Pi(E;O = —С ра (g—0)р J—W
I И J \ ‘ /
5.2. Случайный процесс Е(0 задан в виде• £(/) = b+ Vt, где
b — известная постоянная; V — случайная величина, распределен-
ная по нормальному закону с'математическим ожиданием т„ и ди-
сперсией Ьв —
Найти плотность распределения вероятностей рх (Е) случайного
процесса £(/), его математическое ожидание т^ и дисперсию Dj.
Ответ. Р1 (Е) = Р1 (Е; /) = ' ехр 1 —
I и ov у 2л ( u ° о
5.3. Найти одномерную характеристическую функцию гаус-
совского процесса Е (0> имеющего плотность распределения вероят-
ностей
Pi(l)
1 г
_ ,— ехр -
^2яо и [
2а2
Ответ: 0-е (jv) = ехр (jmv-----^-oV).
5.4. Найти одномерную плотность распределения вероятностей
случайного сигнала
Е(() = А (0 sin [<оо/ 4- <р(/)1.
у которого случайные функции A (t) > 0 и <р (t) предполагаются
независимыми в один и тот же момент времени, причем случайная
фаза <р(<) считается распределенной равномерно на интервале
(—л, л), а огибающая A (t) имеет плотность распределения веро-
ятностей рл (А).
Ответ: Р1 (Е) = -£- J d А = -L j рА (| Е | ch х) dx.
I £ I о
1.4R
5.5. Найти плотность распределения вероятностей случайного
процесса %(f), указанного в предыдущей задаче, Для следующих
частных случаев:
1) рА (Л) = (Л/ст2) ехр (-АЧ2 о2), Л > 0;
2) Ра(А) =
^0
.0 при других Л;
3) рл(А) = аехр(—аЛ), Л > 0;
А п л
4>Pa(A) =
Ответ [19,
1) Pi®
4вУЛ»-4»’
0
401:
1
0>
при других Л.
У2На Ц 2а»/’
- 2) р1(ё)=уу1п
2лД0 Ло_уЛ2_ёа
3)Pi(l) = -J-Ko («£). где
K0(z) = Je-'^dx
о
— нулевая функция Макдональда [391; <
4) Р1(1) = |1/2Л’
[ 0 при других ё-
5.6. Найти одномерную рх(ё) и двумерную p2(?i. £2) плот-
ности распределения вероятностей для гармонического колебания
I (0 = ЛтСО8(®0/ + ф),
имеющего постоянную амплитуду Ат и угловую частоту <оо, но слу-
чайную начальную фазу <р, равномерно распределенную на интер-
вале (—л, л).
Ответ:
„ ZtxH/л/Л2 -ё2, |1|<лт,
10, |£|>Лт;
1
Рг(?1> £2)—
_ .___- < v I ъ, —Л„ cos [ (i)ot+ arccos
2яУл^-ё?1 Г т \°^
4-6[ёг—Лтcos(<ООТ—arccos-^-)]), |ё.
m>
0,
Здесь ё = I (0. ii = 5 (4). Ъ = 5 (/2), т = t2 - 4-
137
5.7. Показать, что одномерная характеристическая функция
(jv) квазидетерминированного стационарного процесса
|(/) = acos(«>0f+ф),
где ®0 — постоянная частота; <р — начальная фаза, равномерно
распределенная на интервале (—л, л); а — случайная величина с
плотностью распределения вероятностей рх(а), имеет вид [14]
®i (jv) = J J о (av) Pi (a) da.
—00
Здесь J0(z)—функция Бесселя, первого рода нулевого порядка.
Определить одномерные начальные моментные функции чет-
ного порядка процесса | (I).
Ответ [14]: М {£2n (/)} = m2ni(t) = m2n5 = - (2")! m2na,
где т2па — М{а2п}.
5.8. Найти плотность распределения вероятностей суммы (раз-
ности) t,(t) = ?(0±Л(0 ДВУХ некоррелированных гауссовских
стационарных процессов | (t) и г| (/), имеющих математические
ожидания и дисперсии, равные соответственно т% и тц, —
= о| и Dn =
~ 1 ' ( [£-("4 ±'"п)]2)
Ответ: р, (?) = =±=с ехр I---—=------— |.
5.9. Вычислить плотность распределения вероятностей суммы
?(о = ш + мо
двух независимых случайных процессов: гармонического колебания
т](0 = Ат cos (®ftt + ф) с равномерно распределенной случайной
фазой ф на интервале (—л, л) и гауссовского стационарного шума
I (0 с нулевым математическим ожиданием и дисперсией = о8.
2л
Ответ: рг (?) = — *— С ехр [ — .(^~ЛтС,05 ^.)-1 ^ф.
riw л Угла J н|_ 2а2 J *
о
5.10. Два гауссовских некоррелированных случайных процесса
? (О и т| (t) имеют математические ожидания и дисперсии, равные
соответственно m$ и т^, Dg = <т| и = Ц. Записать совмест-
ную плотность распределения вероятностей р2 (?, q).
л л \ 1 Г mg)2 01—«nF 1
Ответ: Р2.(?, п) = ехр---------------, •
133
5.11. Имеется два случайных процесса Е(/) и т](/) = а£(0>
где а — постоянный коэффициент. Считая процесс 1(0 гауссов-
ским е нулевым математическим ожиданием и дисперсией = о8,
записать совместную плотность распределения вероятностей р2 (£,i))
Ответ: р2 (В, г|) = —^=- е~5’/ 8 (г]— а£),
где 6 (х) — дельта-функция.
5.12. Записать совместную плотность распределения вероят-
ностей для гармонического колебания
1(0 = t4wcos ((0(/+ ф)
со случайной начальной фазой ф, равномерно распределенной нэ
интервале (—л, л), и его производной | (/) в тот же момент времени.
Ответ: р2(В, В) = 2——-[б(|—®ЛV А2т—&) +
2л у Л2,-Вг
+ 6(1 + ®oK^F)],
5.13. Требуется записать совместную плотность распределения
вероятностей для стационарного процесса В(0 и его производной
В (/) в один и тот же момент времени. Предполагается, что процесс
В (0 является гауссовским, имеет нулевое математическое ожидание
и дифференцируемую корреляционную -функцию R (т) = <т2г (т),
где о2 — дисперсия.
Ответ: Й(Е' Е)= е1,р ’
Г"(О)=^±)| .
dx2 |т = о
5.14. Вычислить n-мерную центральную моментную функцию
n-го порядка
1, ...» 1 (4, •••> Аг) == М{1о(4)1о(4) ••• £о (Аг) }
для центрированного гауссовского случайного процесса 10 (/)
с нулевым математическим ожиданием и корреляционной функцией
Ответ [191:
0 при нечет-
ных п,
(п— 1)11
У *я4(л)—^яп(о) при чет-
п/2—сомножителей НЫХ П.
Здесь символами nft(i), k — 2, 3, .... п, обозначены значения ин-
дексов лк(0 = 2, 3, ..., п, полученные в результате t-й переста-
новки неповторяющихся исходных индексов / = 2, 3, ..., п и их по-
13Э
Значения символов Jtk (О
Таблица 5.1
л, <0 л, (0 Л, (0 «4 (0 «5 (0 лв (0
п = 4 п — 6
1 1 1 1 2 3 1 4 | 5 6
— 2 1 2 3 0 4 6
— 3 1 2 3 6 4 5
2 4 1 1 3 1 2 4 1 5 6
— 5 1 3 2 5 4 6
— 6 1 3 2 6 4 5
3 7 1 1 4 1 1 2 | 1 3 1 5 6
— 8 1 4 2 5 3 6
— 9 1 4 2 6 3 5
— 10 1 5 2 3 4 6
— 11 1 5 2 4 3 6
— 12 1 5 2 6 3 4
— 13 1 6 2 3 4 5
— 14 .1 6 2 4 3 5
— 15 1 6 2 5 3 4
парной группировки (начиная с лг(0 = 1) и последующего упоря-
дочивания каждой пары по возрастающим значениям входящих
в нее индексов.
Для примера в табл. 5.1 приведены значения символов (i)
для п = 4 (выделены жирными линиями) и п = 6 соответственно.
5.15. Используя результат задачи 5.14, определить четырех-
мерную центральную моментную функцию четвертого порядка
tt) = М {Во(М1о(/2)Во(^з)|о(4)}
для гауссовского случайного процесса Jj0(/) с нулевым математи-
ческим ожиданием и корреляционной функцией (tlt /2).
Ответ: = R^, t2)R^(i3, tJ + Rah,
№i(t„ Q + 7?g(4, ЦЩ, t3).
5.16. Найти общую формулу для одномерных начальных мо-
ментных функций гауссовского стационарного процесса £(/) с ну-
левым математическим ожиданием и дисперсией = о|.
Ответ: Л(Г(0}-|13'5 - (V~ ',аЁ "Р“
Ю при нечетном v.
5.17. Используя результат задачи 5.15, определить трехмерную
центральную моментную функцию четвертого порядка
<i.i (4, t2, 4) = м}
140
для стационарного гауссовского случайного процесса £0(/) с нулевым
математическим ожиданием и. корреляционной функцией
^2) = (4 ^з)-
Ответ: t3)+2Ri(tl, /а)7?6(4, /8).
5.18. Написать двумерную центральную моментную функцию
четвертого порядка т2,2 (<х, t2) = М {|® (4) |® (/2)}для гауссовского
стационарного случайного процесса £0(/) с нулевым математическим
ожиданием и корреляционной функцией
^(4» Ai) = — t2).
Ответ: М {l*W(t2)} - D| П + 2 - /2)1.
5.19. Используя результат задачи 5.17, определить двумер-
ную центральную моментную функцию четвертого порядка
ml.iUt, t3) =
для стационарного гауссовского случайного процесса (t) с ну-
левым математическим ожиданием и корреляционной функцией
/а) O^(tt — t2).
Ответ: t2).
5.20. Вычислить трехмерную начальную моментную функцию
.т1ллл(^3, /з) = Л4{5(4)^з)^»))
для стационарного гауссовского случайного процесса £(/) с мате-
матическим ожиданием М {£(/)} = m'j (?) и ковариационной функ-
цией Ki (ti, t2).
Ответ: М {£ (4)| (?а)£(/з)} = Kt(ti, t2) т* (ta) + Ki(tlt h)m6(fa)+
+ Kt (t3, is) m^ (?x) —2 (/J (?2) m^ </s).
5.21. Определить четырехмерную начальную моментную функ-
цию четвертого порядка
тхллл (?х, t2, t3, /4) = Л4{| (?,)| (?a)S (t3)l (Q}
гауссовского случайного процесса £(/) с математическим ожида-
нием М {£ (t)} = mt (/) и ковариационной функцией К$ (ti, t2).
Ответ [14]: М {| (4)В (tjl (t3)l &)} - Kt (h, Q Ki(t3, /4) +
+ Kt (/x, t3) Kt (/a, it) + Kitt» Q Kt (t3, t3) -2 mt (4) mi (t2) x
X (/з) m^ (ti).
5.22. Найти общую формулу для двумерных центральных мо-
ментных функций гауссовского стационарного процесса g0 (t) с
нулевым математическим ожиданием и корреляционной функцией
/?Е(т) = а2г(т).
Ответ [26]:
m^v =Л4{^(0^(/+т)} = о“+' 2
' ' k=b '
fti
Nt.k— j x( Ф(*+1> (x) dx.
Значения коэффициентов приведены в табл. 5.2.
5.23. Вычислить трехмерную моментную функцию
(Тх, Ч) = (Oft(* + + <с2)}
для стационарного гауссовского случайного процесса ft (t) с ну-
левым математическим ожиданием и корреляционной функцией
Rl W = o*r(t).
Ответ [26]: М {ft (/) ft (/ + Ъ) ft (/ +х2)} =
=all+v+x 2 2 2^. *+zyv. k+m Nk, 1+тгк^г1^гт^-^ ,
л=о /=о m=o fel Zl m'
5.24. Определить, при каких условиях случайный процесс
ft/) = Amcos(<B0/ +'ф),
где Ат, <в0 — неслучайные, стационарен и нестационарен.
Ответ: Процесс ft/) стационарен, если случайная фаза <р рав-
номерно распределена на интервале (—л, л). В противном случае
процесс |(0 нестационарен.
5.25. Случайные величины А и Ф независимы. Математическое
ожидание и дисперсия первой из них равны соответственно ша = 0
я Da = о®, вторая подчиняется закону равномерного распределения
на интервале (—л, л}. ’
Доказать, что случайный процесс £(/) = Лсоз((о0 t 4- Ф)
стационарен (<в0 — неслучайная величина).
Ответ: Процесс ft/)’ стационарен в широком смысле, так как его
математическое ожидание постоянно '(т$ = 0), а корреляционная
функция зависит только от разности т = /2 — /р
Rl (4, <0= у о2 cos <в0 (/2 —Л) = Ri (т).
Таблица 5.2
Значения коэффициентов &
142
5.26. Показать, что случайный процесо
!(/) = X cos иot + У sin &ot 1
является стационарным в широком смысле только в том случае, ко-
гда случайные величины X и У взаимно не коррелированы и имеют
нулевые математические ожидания тх = ту = 0 и равные диспер-
сии Dx — Dy = D.
5.27. Определить, при каких условиях случайный процесс
I (0 = /lmcos(co0Z4-<p)+zi(/),
где Ат, <оо — постоянные, п (/) — шум, стационарен в узком
смысле.
Ответ: Процесс g (t) стационарен, если стационарен шум п (t)
и случайная начал ьная.фазаср. распределена равномерно в интер-
вале (—л, л).
«. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ И СПЕКТРАЛЬНЫЕ
ПЛОТНОСТИ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Особо важную-фолъ птеории'еяучайных процессов £ (А «грают матема-
тическое ожидание (одномерная .моментная функция первого порядка)
[1, б, М, 26, 27, 34—36, 41, 42]
«.(/) = «,(/)= (6.1)
—оо
и корреляционная функция (двумерная центральная моментная -функция
второго порядка)
R^h, У = «? i (h. <s)=Af {£«(/,) $о(А)} =
— оо — оо
. = (А, А)-^ (А) (А). (6.2)
Здесь Kg (А, А) — ковариационная функция, представляющая собой дву-
мерную начальную моментную функцию:
(/1. А) =«i,i (А, А) =А1{£ (А) I (А)}=
= °f °f UA)HA)/aGi. Ь; А. А) ^1^2 =
—со —оо
== R: (/1Л)+«£ (G) (6.3)
143
Для стацйднарных случайных процессов формулы (6.1)—(6.3) принимают вид:
...................... f (6-4) /
Rt (ti, t$) = М {|u (<t) (4)} =
'•= f f К (4) -mgJ К (4) -m6] Рг (5i. b) d^i d£a =
= К£(4-4)-т|=Я6(4-4); (6.5)
*6(4; 4) = Al {£(4)5(4)} = f f £(4)£(4)X
* XPtfa, Ы^Яг^аг-Ы'+т^К^-Ъ). (6.6)
Формулы (6.1)—(6.6) справедливы для действительных случайных про-
цессов |(/). При представлении случайного процесса в виде комплексной функ-
ции [ 14] (0 = г] (0 + /v (0, где г] (/) и v (0 — действительные случай-
ные процессы, отображающие реальную и мнимую составляющие процесса-
f(0, формулы (6.1) — (6.3) принимают следующий вид:
(П=М{Г(П} = М {Г](Z)}+/A4 {v (0}=mnK) + /X. (О; (6.1а)
RT (4. 1г) = М {(f(4)-m~ (4)1 [|* (4) -т\(4)1) =
6 S • • S
= К* (4. Л)-^ (4) ml (4); (6.2а)
, - 6 Е .
(h, Л)^м {Г(4) Г* (4)} =
= 4) + «j(4)m|(4)- (6.3а)
Здесь звездочкой отмечены комплексно-сопряженные функции. Для стацио- .
нарных комплексных случайных процессов!; (0 имеем
(0 = тц + jmv = т(6.4а)
^(4, 4)=^(^-<i)-l®|l’=^r(T)> (6.5а)
4) = ЛГ (4-<1)+й?1г=^т(т)« (6-6а)
ft ft ft ft
т = 4 — 4.
Корреляционные функции (т) стационарных случайных процессов
g (0 обладают следующими свойствами:
Г. Функции /?g (т) являются четными: (т) = (—т).
2. Абсолютные значения корреляционной функции (т) стационар-
ного случайного процесса £ (0 при любом т не могут превышать ее значения
при т == 0:
\R% (т) | < (0) = D^
3. При неограниченном увеличении т функции /?|(т), как правило, стре-
мятся к нулю, т. е. lim (т) » О.
Т-ню 6
144
Помимо корреляционных, весьма часто используются взаимные корреля-
ционные функции, характеризующие статистическую зависимость между
значениями двух случайных процессов в два совпадающих или различных мо-
мента времени. Так, к примеру/для двух стационарных случайных процессов
£ (0 и Y) (0 с математическими ожиданиями и взаимные корреляционные
функции имеют вид
(h.h) =м {[£ (4)-«gl h(4)-m^l},
(6.7)
(4{(n (4) — mn] (B (/,) —mt]}.
Если взаимные корреляционные функции (6.7) зависят лишь от разности
т = — tlf то процессы |(fl и tj(O называются стационарно связанными
и для них справедливо соотношение
= (~т). (6.8)
Для количественной характеристики степени линейной зависимости
случайных процессов часто используют нормированные корреляционидас^г^
взаимные корреляционные функции, которые определяются соответствен®©
формулами м .
А
V Dg.(4) Dj (4)
rgfl (4.4)
_ ; (?gn (4.4)
• V Dg (4) (4)
(6.9)
Здесь D^(fl = R^(t, t) — дисперсия случайного процесса g (fl, (fl —
дисперсйя процесса rj(fl. Если э^и процессы стационарны и стационарно, овя- «
заны, то
(0 = R^ (0) % = о|, (t>=<0) = = а*
и формулы (6.9) принимают вид
R^ (Т) (т)
(6.10)
В большинстве радиотехнических задач нормированные корреляционные
функции имеют вид либо монотонно убывающих функций г СИ = р (т)
(рис? 6.1,-а), либо затухающих осциллирующих функций, например типа
г(т) = p(t)cosg)0t (Рис- 6.1» б). При этом степень коррелированности слу-
чайного процесса можно характеризовать так называемым Лтервалом кор-
реляции ...
ОО 00
TB=y- J lP(T)|dr = J|р(т)|du.
— оо О
[(б.П)
Геометрически интервал .корреляции равен основанию прямоугольника с вы-
сотой р Х0}== 1, площадь которого равна площади, заключенной между «ривей
1р(т) | при т > 0 и осью абсцисс (рис. 6.1)’. Величина тк дает«бр
145,
Рис. 61. Нормированные
корреляционные функции
ное. представлением том, на каком интервале времени в среднем имеет место
коррелИрованность между значениями случайного процесса.
Весьма распространенной характеристикой стационарного случайного
процесса является его спектральная плотность связанная с ковариа-
ционной функцией (6.6) преобразованием Фурье:
J Ki dt. <6.12)
’ -— со
оо
К5(т) = -^- J SE (ш)еМт <1<й. (6.13)
— оо
Аналогично связаны между собой корреляционная функция (т) и спект-
ральная плотность S^Jco) центрированного стационарного случайного, про-
цесса £0(/) = %(f) —
S-s (ш) = J ₽5(т)е~/й>г4т = Х.(®)—2nmj6(<o), (6.14)
--OU
co
= f 5?o (w) е'шт d®. (6.15)
--OO
ИспоЛьзуя свойство четности ковариационной (т) и корреляционной R% (т)
функций, соотношения (6.12)—(6Л5) можно привести к виду
(w) = 2 J /(. (т) cos шт4т, • (6.16)
О ' 1
143
G0
Kt (т) = — | St (co) cos orate),
b л J s
о
OO
S|o (o) = 2 J (t) cos cor dr,
oo
(T) = — J $£o (co) COS (DTtte).
0
(6.17)
(6.18)
(6.19)
Соотношения (6.12)—(6.19) называются формулами Винера—Хинчина.
Как следует из (6.14), спектральная плотность 5g (о) стационарного слу-
чайного процесса £(/) с математическим ожиданием и ковариационной
функцией Kg(r), определяемая соотношением (6.12), отличается от спек-
тральной плотности Sgn (со) стационарного случайного процесса £(/) с нулевым
математическим ожиданием = 0 и корреляционной функцией /?^(т),
вычисляемой по формуле (6.14), лишь наличием дополнительного члена
2л/и|6(о)). При = 0 оба представления спектральной плотности совпа-
дают, поэтому в дальнейшем различие в этих характеристиках будем отмечать
лишь в случае необходимости.
Отметим основные свойства спектральной плотности стационарного слу-
чайного процесса.
1. Спектральная плотность не может иметь отрицательных значений,
т..е. S («)>0 при любых со.
2. Для вещественных случайных процессов спектральная плотность яв-
ляется четной функцией, т. е. S(<o) =* S(—со).
В формулах (6.12)—(6.19) спектральная плотность 5 (о) определен^ для
положительных и отрицательных значений круговой частоты, причем
5(ю) = 5(—о)). Если же вместо такого спектра, называемого двухсторон-
ним, ввести одностороннюю «физическую» спектральную плотность
S (/) = [5 (щ) + S (—6))] = 25 (св), (6 20)
отличную от нуля лишь при/ > 0, то формулы (6Л2)—(6.19) можно записать
в виде
5g /)==4j Kg (т) cos 2л/т4т, 0 (6.21»
Kg (т) = f (0 cos 2я/т^ , (6.22)
5go (/) = 4 J (t) cos 2jtfxdT , (6.23)
Kg (T) = J Sgo (f) cos 2n/Td/. 0 (6.24)
Соотношения, аналогичные (6.21)—(6.24), справедливы и для взаимных
корреляционных и спектральных функции.
Иногда в качестве характеристнксл у чайных процессов используют раз-
личные параметры их спектральных плотностей. Наиболее употребительным из
147
таких параметров является эффективная ширина спектра Д<оэ, определяемая
соотношением
эо
Д(оэ= „ 1 ~ С Sftoda. (6.25)
S(0) J
—оо
Помимо этого, находят применение такие параметры, как средняя частота
т'^ == Л4{со} спектральной плотности, средний квадрат частоты m2fd «
= Л4{(02} и средняя квадратическая ширина оад спектральной плотности,
соответственно равные
оо ;
2 С
ш = Л4 {со} == —— I eoS (со) (6.26)
о2 J , .
о
, ‘ ’ 00
' ’ 2 С
т9 = ~ I (o25(G))dG), (6.27)
1 1 о2 J
’’ * "оо ' ‘ ‘
J (<a-m(i))2 S(&)da>. (6.28)
О ' ”
При решении задач статистической радиотехники иногда возникает не-
обходимость установления непрерывности и дифференцируемости случайных
процессов. Необходимым и достаточным условием непрерывности случай-
ного процесса | (/) в момент t йвлЯе^гся непрерывность его корреляционной
функции /?£ (tlt /2) ПРИ h — ^2— t- Для стационарного в широком смысле
случайного процесса £•(/) необходимым и достаточным условием непрерыв-
ности является непрерывность его корреляционной функции /Ц(т) при
т = 0..
Случайный процесс | (t) называется дифференцируемым в момент вре-
мени t в среднеквадратическом, если существует такая случайная функция
| (/) = d^ (t)/dt, называемая производной в среднеквадратическом процесса
| (/), для которой
lim М
Т->о
Н/+Т)-д(П
0.
Математическое ожидание (t), ковариационная (/i, t2) и корреляцион.
ная (t19 t2) функции производной t>(t) случайного процесса | (/) опреде-
ляются соотношениями
= = ±, (6.29)
£ , at
к. (/1, ;,)=AiU(z1)V^)}=—77-^----------> (6.30)
fe ut 1 Ul 2
Ri (h, t2) = 't2)}±=.--?\1’ 2 . (6.3J)
Ol 1 ()l 2
148.
Здесь (0, (t^ и /?& (0, t2) — математическое ожидание, ковариацион-
ная и корреляционная функции случайного процесса g (/). Для стационар-
ного случайного процесса £ (/) соотношения (6.29)—(6.31) приводятся к виду
^(0 = 0, Кд (т) = /?4(т) =
* ъ 5
d2 (т) d2 (т
dr2 ~ di*
(6.32)
а спектральная плотность Sg (cd) производной | (0 определяется формулой
Sg (cd)«cd2S.o (ш), (6.33)
где Sg (со) — спектральная плотность стационарного случайного процесса
ЫЪ-
Взаимные ковариационная (tlt t2) и корреляционная R& (t19 t2)
функции дифференцируемого в среднеквадратическом случайного процесса
& (0 и его производной | (0 равны
f ь дК*^, t2)
(h, t») =Л1{ё(М §(/,)}=----Ч-------. (6.34)
ьв <Jt2
Я.Д6, /2) = Л4{|««1) Ы'а)} =----------- (6.35
01%
Для стационарного случайного процесса £ (0 соотношения (6.34) и (6.35) при
нимают вид
К^ (т) = (т) == — (т) =в — (т) = dKg (T)/dx=dR^ {x)/dn, (6.36;
а взаимная спектральная плотность
S^((D)=/©Sgo(®). (6.37)
Из (6.36) и (6.37) следует, что значение взаимной корреляционной функции ч
/?^(т) стационарного случайного процесса g (t) и его производной | (/)
в совпадающие моменты времени (т. е. при т = 0) равно нулю (это означает,
что любая дифференцируемая стационарная случайная функция § (0 и ее
производная £ (0 в совпадающие моменты времени не коррелированы), а
их взаимная спектральная плотность является чисто мнимой функцией.
Для производных (0 n-го порядка случайного процесса £ (0 спра-
ведливы соотношения:
d2nKi(h,tJ
',)=
&п RAh, (а)
/?,(„> (4. (а) =---я —
’ dt^ dt?
(6.38)
(6.39)
Если £ (0 является стационарным случайным процессом, то (6.38) и (6.39)
приводятся к виду
<Р"КЕ(т) <PnRt(t)
К£(я)(т) = ^(л,(т)=(-1)»- -^(-1)^ , (6.40у
а спектральная пло1ность n-й призводной (/) равна
sE(„)(®)=<a»'*s6t(®b
(6.41)
149
Взаимные ковариационные и корреляционные функции k-й и l-й про-
изводных (/) и случайного процесса % (/) определяются смешанны-
ми производными вида
а*+' t2)
K8(ft4U)(/1,Za)= , (6.42)
В. «
(«•«)
Для стационарных случайных процессов формулы (6.42) и (6.43) приводятся
к виду
</*+<К.(т)
JU) —?U) (Т) — (— 1) <h*+1 =
d4+'/?,(T)
11*--------------
(6.44)
2 . ПРИМЕРЫ
6.1. Определить, обладает ли функция
R (т) = о2 е~“1 х 1 /ch <оот 4- sh <оо| т |1 а > О, ®0 > О,
\ «ов /
свойствами корреляционной функции.
Решение. Для ответа на поставленный, вопрос необходимо прове-
рить выполнение следующих условий:
1) R(0)>0; ‘ 2) R(t)=R(-t); 3) | R (т) |< R (0);
4) S (») = j R (т) е~ian dx 0.
—-оо
Положительный ответ относительно выполнения условий 1) и 2)
следует непосредственно из анализа выражения для /?(т). Для про-
верки выполнения условия 3) представим функцию R{x} в виде
R (т) = _£!_ Г е-(а—в>0) t / а j\ е —(а4-Ф<,) т/ а ]\1 т0 .
2 L \ / \ ш0 / J
Так как R(Q)—D — о2, для выполнения условия 3) необходимо, что-
бы выражение в квадратных скобках по модулю не было больше 2.
Можно показать, что при а < соо это условие не выполняется, так
как при т-> оо и а < <в0 значение ехр [—(а — ®0)т1 неограничен-
но возрастает. В случае а = <оо функция R(t) = 1 и только при а >
> а»0 условие 3) выполняется. К такому же выводу приводит ана-
лиз выражения /?(т) при т < 0.
В соответствии с формулой Винера—Хинчина (6.14) имеем
е-/®т $х
_________4«(«2—а>§)______
[(а-<о0)2+ <о21 (.(а + w0)2 +<оа]
>50
Отсюда следует, что условие 4) выполняется также при а > ®в.
Следовательно, анализируемая функция /?(т) обладает, всеми свой-
ствами корреляционных функций при а > ©0.
6.2. Найти корреляционную функцию и спектральную
плотность Sj(co) для стационарного случайного сигнала
W) = A msin(©0/ + <р),
где ц й0 — постоянные амплитуда и угловая частота; ф — слу-
чайная начальная фйза, равномерно распределенная на интервале
(—л, л).
Решение. По определению корреляционной функции (6.5), имеем
(*) = + т)} - <
Поскольку
/п6=М{В(0}Ф= J 4^sin(woi+ф)Р1(ф)йф=0,
—Л
ТО
Л
(г) = М V (/) В (t +'г)}ф = J А% sin (©914- ф) (ф) х
—Л
Л
Xsm(©0/ +о)0т + ф)б/ф = —— С Д^з1п(©0/-}-ф) X
J
—л
X sin(o)o t +<оо * +ф)
Учитывая, что [17]
sin a sin 0 = [cos(a — 0) — cos(a + 0)1/2,
находим
/?$(*) — (Amf2) COSO)0T.
Спектральная плотность вычисляется по формуле Винера—Хин-
чина:
р Л2 г
S^((o)= I ^(т)е~/сйМт I e~/<DXcos<o0™[t==
—оо —оо
2 °°
— f [е/(®о~(о) т _|_е—/«оо-|-(о)
Учитывая, что [171 f е^йт = 6(<о), окончательно получаем
---------------------90
S|(w) = (лЛ^/2)[6(® + ©а) + 6(© — ©9)].
151
6.3. Определить корреляционную функцию 7?$(т) й Спектраль-
ную плотность Sj (<в) стационарного случайного процесса
Е(/) = ^4cos((o/ + <р), (6.45)
где А, ® и ф — независимые случайные амплитуда, частота и началь-
ная фаза. Случайные величины Диш заданы одномерными плот-
ностями распределения вероятностей рл(А) и рш(®), а начальная
фаза ф предполагается равномерно распределенной на интервале
[—л, л], т.е. р<р(ф) = 1/2л, —л ф л.
Решение [431. В соответствии с определением (6.2) искомая кор-
реляционная функция представляет собой двумерную центральную
моментную функцию второго порядка и равна
/?6(/ъ/2) = M{[^(/1)-/ns(Z1)|[?(/2)-/n6(/2)]}. (6.46)
Поскольку в нашем случае wj(/) = М {1(0} — 0> то (6.46) при- -
водится к виду
ад1,/2) = м{В(/ад)}. (6.47)
По условию задачи стационарный случайный процесс £ (/) за-
висит от трех независимых случайных параметров Л, со и ср, в соот-
ветствии с чем в (6.47) необходимо выполнить усреднение по каж-
дому из этих параметров. Таким образом
оо оо оо
^(0.0)= J ЦШ(4)Рл (Я)ри(ш)рф(ф)сШ<Ог/ф==
—оо —ОО-00
оо ОО 00
= J J J Д2СОЗ(ю/1 +ф)сО5((0/2+ф) рЛ(Д)Х
—оо —оо —оо
X р<» (ю) dAd(od<p. (6.48)
После несложных преобразований находим следующее выражение
для корреляционной функции стационарного случайного процесса
(6.45):
Rl (<i, Q ~ м {Л2} j Ра (®) cos CDTdw = Rl (т), т = t2— (6.49)
Полагая в (6.49) т = 0, находим дисперсию случайного процес-
са 1(f):
оо
£>£=-£-Л/{Я2} J рш(б))4/<».
—оо
(6.50)
152
Для. определения спектральной плотности S^(w) воспользуем
ся соотношением (6.19) и запишем корреляционную функцию /?g(r)
в виде
₽g (т) — —— f Sg„ (со) cos cozdr.
2л J
Сравнивая (6.51) с (6.49), видим, что
Sg(co) = Sg,(co) = лМ {Аг)ра(а),
(6.51)
(6.52)
т. е. спектральная плотность колебания (6.45) с точностью до по
стоянного множителя совпадает с одномерной плотностью распреде-
ления вероятностей случайной частоты этого колебания. Для част-
ного случая А — Ат = const, т. е. для случая стационарного квази-
гармонического колебания с постоянной амплитудой, случайной час-
тотой и статистически независимой от нее случайной начальной фа-
зой, равномерно распределенной на интервале (—л,л), соотношения
(6.49) и (6.52) принимают следующий вид:
А2 °°
(т) = J Р® (w)cos wd® >
—ОО
Sg (со) = (лА т/2)р№>((а).
(6.53)
(6.54)
6.4. Выяснить разницу между спектральными плотностями ста
ционарных случайных процессов ^(/) и |2(/) с нулевыми математи
ческими ожиданиями и корреляционными функциями
/?5,(т) = о2е_а| п, /?£2(т) = о^е-011 т' cos соот.
Решение. Корреляционная функция Z?g, (т) является частным
случаем корреляционной функции /?|,(т). Поэтому вначале най-
дем спектральную плотность Sg,(co), соответствующую /?g2(T), а
затем из Sg,(co) получим Sgt (со).
Согласно формулам Винера—Хинчина имеем
Sgi((o)= J 7?g, (т) е~/<ат dz= о2 J e~a|Tl—/“lFcos®oT£fr = '
—оо —оо
О оо
J еат—/сот cos 4- Je—ат—/сот cOSO)0TdT .
= о2
Учитывая, что 1171
cos = (e/Q° т+ т)/2,
получаем
(со) = ао2 [------5------ 4---------------- ].
* L аа4-(ю —©о)2 a24-(© + wo)2 J
153
Рис. 6 2 Спектральные плотности при различных соотношениях между а и ©о
Рассмотрим поведение функции
1. Sg,(®)—► 0 при | и | -> ею.
2. При 3®# < а2 у функции 5g,(®) нет максимума, она моно-
тонно убывает с ростом | со | (рис. 6.2, а).
3. Если Зсо2 > а2, функция Sg, (<о) имеет максимум (рис.6.2, б)
в точке
l®ml = (a2+®o)1/4F 2®0 — Ка2+®о.
4. При Зю2 > а2 спектральная плотность S^,(<o) также имеет
максимум в точке | сот | ~ ®0 (рис. 6.2, в).
Суммирование спектральных плотностей 3%,(®) с различными
весами при соответствующим образом выбранных а и соо позволяет
аппроксимировать сложные спектральные плотности. Так, к приме-
ру, путем сложения изображенных на рис. 6.2 функций Sj,(co) мож-
но получить спектральные плотности З^со) и S2(co) (рис. 6.3), хо-
рошо совпадающие с экспериментально определенными спектраль-
ными плотностями случайных изменений во времени скоростей в ат-,
мосферном турбулентном потоке.
Полагая в 3j, (®) частоту <о0 = 0, находим спектральную плот-
ность 3^,(ы), соответствующую корреляционной функции 7??,(т):
S^,(®) = а22а/(а2 + и2).
Графики функций ₽j,(t) и /?$е(т) и соответствующих им спектраль-
ных плотностей SjJco) и Sj2(®) приведены на рис. 6.4.
Рис. 6.3. Сложные спектральные плотности
154
Рие. 6.4. Корреляционные функции ц ееоадететвующие вм -спектральные плот-
ности
6.5. Найти корреляционную функцию стационарного
случайного процесса с нулевым математическим ожиданием и
спектральной плотностью (рис. 6.5)
Si(co) =
Wo/2,
М>/2,
. О
— —Mi,
(|>1 SjC tt> S~Cu>2,
при других 41).
Для частного случая coj = 0 определить величину интервала
Д = th+i ~ ik, при котором значения |А+1 = | (/А+1) и %к = £ (tk)
не коррелированы.
Решение. По формуле Винера—Хинчина находим
оо
^(т) = -^- J S?(w)e^ d® =
—00
(О*
JV0 Г А
—— I COS (QTO(O =
2л J
«1
А/о / - • х
—— (sin<o2T -sinc^x).
2лт
Так как [17]
155
корреляционную функцию можно представить в виде (рис. 6.6, а)
/?^(т) = o?Pi(t) COS(i)0T,
где
2 ДсоЛ^о , а
Q|---- , pt(T)
гл
sin (Л(от/2)
Дсот/2
- й>*+ Ш2
2
Дю == со2—(о1, (Оо
Для частного случая (ot = 0 функция корреляции имеет вид
(рис. 6.6, б)
d /-а ~ ^о®2 sin<o2T 1т\
\Ч--------Stn (02 Т---------f -------== в2 р2 (т)>
2лт 2л й)9 т
где
о* — Л/о(о2/2л, р2(т) — (sin со2т)/(огт.
Интервал Д = /Л+1 — /ft, при котором значения (отсчеты) —
= l(tk) и Еа+1 = В(/й+1) будут не коррелированье можно
определить, приравняв нулю значение нормированной корреляцион-
ной функции р2 (Д). В результате находим
(sinco2A)/co2A = О, Д = л/со2 = 1/2/%,
где 7% = (о2/2л — верхняя граничная частота спектральной плот-
ности S$((o). Таким образом, в реализации 1-(t) длительностью Т
содержится N = Т/Д ~ некоррелированных отсчетов.
Рис. 6.6. Корреля-
ционные функции
узкополосного (а)
и широкополосно-
го (б) случайных
процессов со спек-
Т тральными плот-
ностями, равно-
мерными в полосе
частот
156
Рис. 6.7. Определение эффективной
ширины спектра случайного процесса
6.6. Спектральная плотность (®) стационарного случайного
процесса | (I) имеет вид (рис. 6.7)
о . [4а/(а»4-<д8), ®^0,
6 (0, ®<0.
Определить соотношение между эффективной
Д®3 процесса |(/) и шириной его спектральной
уровне 0,5Sg(0).
Решение, Эффективная ширина спектра. Д<о8
ределяется. соотношением
® __«л
После подстановки Sg(«) находим
оо ' .
а <х С 4а , < . со -
Дшя=— |------------ dw—aarctg —
d 4 J а2 + со2 а
шириной спектра
плотности Дсо на
процесса l(t) on-
о
Ширина спектральной нлотности Дсо на уровне 0,5S^(0) находится
из формулы ’ ‘
S6 (Д®) - 4“ =0,55$ (ф ==0,5 ,
а2 + (Дш)2 а2
откуда Дсо = а. Следовательно, :
Дсоэ/Дсо = Д/э/Д/ = л/2.:
' 3. ЗАДАЧИ И ОТВЕТЫ
6.1. Случайные процессы |(/) и iq(/) заданы своими математи-
ческими ожиданиями /п^(0 и /ип(0, корреляционными t2)
и Rritfx, t2) и взаимными корреляционными функциями
- ^(4)Пп (t2) - т^2)]},
^2) — М.
Определить математическое ожиданйе и корреляционную
функцию R&i, t2) суммарного (разностного) случайного процесса
С (/) = В(О±г) (0-
157
Ответ', тц (0 = пи (I) ± лц (0; R ц du = R$ du f 2) +
4* Rn du tz) ± Ran du ^2) ± Rni (0» t*)-
6.2. Определить корреляционную функцию Rn du 1г) случай-
ного процесса
л (0 = + T) ± £ (0.
где £ (0 — случайный процесс с нулевым математическим ожида-
нием и корреляционной функцией Ri (0, 0).
Ответ: Rn (0, 0) = Ri (0 + Т, tt -I- Т) ± R$ (0 + Т, 0) ±
± Ridu 0 + П + Ridu 0)-
6.3. Доказать, что для' корреляционных и взаимных корреля-
ционных функций случайных процессов £ (0 и т) (0 справедливы
соотношения:
|/?s(0, 0)1СпИ0)М0)-
I Ri du t*) I < [orj dt) + a| (0)V2,
du 0) I &i dt)-
Здесь og (0 — "KDj (0, on (0 = J/'Dtj (t) — средние квадратичес-
кие отклонения процессов | (0 и (0 соответственно.
6.4. Найти корреляционную функцию сигнала
s(0 *4= Лт’g(0 cos (®0/ + ф),
где 5 (0 — стационарный случайный процесс с нулевым математи-
ческим ожиданием и корреляционной функцией /?а (т); Ат и соо —
постоянные величины, а ф — случайная начальная фаза, равномер-
но распределенная на интервале (—л, л) и не зависящая от | (0.
Ответ: Rs (т) — (AmtyRi (r)cos (оот.
6.5. Определить корреляционную функцию комплексного слу-
чайного процесса
1(0= 2a<ete<r,
1= 1
где ®г — постоянная угловая частота; -а1( а2, .... ап — взаимно
не коррелированные случайные величины с нулевыми математичес-
кими ожиданиями mi — 0 и дисперсиями Dt.
Ответ: R%d) = 2 ^е***’, т=0+1—0.
f= 1
6.6. Решить задачу 6.5 для случая, когда
п
6(0 =4 2l (ai COS (dj / 4- / ^{ Sin 0,
1
158
гдеаг и §г —взаимно не коррелированные случайные величины с
нулевымйматематическими ожиданиями mat — т^ = 0 и дислер
сиями Da.=Dat=Dt.
_ п
Ответ'. R| (т) = У, E>fcosco;T.
•= i
6.7. Определить математическое ожидание тп(1) = М {г|(0)
и корреляционную функцию R4(t, т) = М(г| (/)г| (/ + т)}— m^(t)
периодически нестационарного случайного процесса
П(0 = F(tm,
где F(t)—непериодическая детерминированная функция; 5(0—
стационарный случайный процесс с математическим ожиданием
mi и корреляционной функцией Rj (т).
Ответ'.
mn(t) = miF(i), Rn(t, т) = F(t)F(t + t)R6(t).
6 8. Заданы два взаимно не коррелированных случайных про-
цесса £(0 и q(0 с нулевыми математическими ожиданиями и кор-
реляционными функциями Rfc(0, 0) и Rn(0. 0) Доказать, что
корреляционная функция произведения этих процессов 5 (0 —
= 5(()q(0 равна произведению корреляционных функций сомно-
жителей:
Rj(O> (2) = Rs(4> ^)Rn(4> (»)
6.9. Доказать, что корреляционная функция произведения п
взаимно независимых случайных процессов
мо-ГН(0
1 = 1
с нулевыми математическими ожиданиями и корреляционными функ-
циями . Rit (tr, t2) равна произведению корреляционных функций
сомножителей:
R»)(0> 0)~ П ^е,-((1> ^г)-
' = I
6.10. Пусть из стационарного случайного процесса 5(0 с мате-
матическим ожиданием M{i(t)} = mi и ковариационной функцией
R5(t) = М {5 + т)} выделен отрезок продолжительностью
Т, который затем периодически повторяется (рис. 6.8).
Определить математическое ожидание /пя(0 = М {т|(0} и ко-
вариационную функцию Kn(t, т) = Л4{'п(0т](/ + т)} получаю-
щегося периодически-нестационарного процесса rj(/).
Ответ J19j: т^(() =т%, (1, т) 2 Мл(т)е’2пп*/Т,
159
где
Мп(т) =
(1 _^Ks(t)+JLk5(T-t);
(-(1 -e"") [/<g (?) -Kg (T—?)],
inT
n=0;
n=£0.
6.11. Доказать, что не существует стационарного случайного
процесса | (t), корреляционная функция которого R (?) постоянна
на каком-то временном интервале (—?п ?J и равна нулю вне его:
(О при других т.
Ответ: В соответствии с теоремой Винера—Хинчина S(«>) =»
оо
= f '“'‘dx = 2а2х! -ш ЮТ1 Отсюда следует, что для процесса
—» ®Т1
£(/) функция 5(<о)для некоторых значений <£> отрицательна, что
противоречит физическому смыслу спектральной плотности
6.12. Определить корреляционную функцию /?(?) и спектраль-
ную плотность S(<d) случайного сигнала
s(0 = У Ат, +ф(). —оо</<оо,
где Ami и (Of — постоянные амплитуда и угловая частота; <ръ ф„...,фп
— взаимно независимые “ случайные начальные фазы, равномерно
распределенные на интервале (—л, л).
Ответ: R (т) = —-Лда'соа®, т,
5(®) = я V 4-Л*‘16(»+(о4)+6(ш-©,)].
i=।
^4-
Рис. 6.8. Периодиче-
ски - нестационарный
случайный процесс
160
6.13. Определить корреляционную функцию R (т) и спектраль-
ную плотность S (со) случайного сигнала
s(/)= 2 ЛпС sin (<М+фг), —00</<00,
' = '
где <&1 — постоянная угловая частота; Ат1, ...» Атп, <Pi, ...» <рп —
взаимно независимые случайные амплитуды и начальные фазы; Пред-
полагается, что средние квадраты 7И{Л^/} случайных амплитуд
Ami известны, а начальные фазы <р< распределены равномерно на
интервале (—л, л)
п .
Ответ: /?(т) = — М {А^} cos(of т,
f = 1
п ।
S (со) = Л 2 М {Ami} (б (СО 4-й)г) + 8 (со —а,)].
' = I
6.14. Найти спектральную плотность Sgjco) стационарного слу-
чайного процесса корреляционная функция которого равна
Rg(T) = о|ехр(—а2?2).
Ответ: 3^„(со) = ехр (-------—').
а \ 4а2 /
6.15. Определить спектральную плотность стационарного слу
чайного процесса £ (/) с корреляционной функцией
Л6(Т)=Р1<>-И/ПИС7-;
(О, |т|>Т.
Ответ: 3£„ (св) = of ( ]*♦
6.16. Решить задачу 6.15 для процесса G корреляционной
функцией
(т) = 2 °‘2 cos Т’
с= 1
п
Ответ: (со) = л J o? [б (®+ ®г) -|-б (® —юг)].
।
. 6.17. Показать, что физическая спектральная плотность 3(f)
сигнала
s (0 = 2 Sin ((о‘ ( +я>().
/== I
6 Зак 1203
161
у которого случайны лишь фазы ф,-, причем фг и фЛ при i k неза-
висимы и равномерно распределены на интервале (—л, л), равна
S(/)==T 2
6.18. Найти физическую спектральную плотность случайного
процесса
5(0 = Amti(f)cos(<>)0t + <р),
где n(t) — стационарный белый шум с корреляционной функцией
/?п(т) = (адб(т);
Ат — постоянная амплитуда; ф — случайная начальная фаза,
равномерно распределенная на интервале (—л, л).
Ответ: S$(f) = NoAm/2.
6.19. Пусть стационарный гауссовский шум £ (/) имеет равномер-
ную спектральную плотность в полосе шириной F:
ss(n=fx
6 [О при/<0, f> F.
Доказать, что значения шума £(/) в моменты времени, отстоящие
друг от друга ча величину Д/п = n./2F, п = 1, 2, 3, ..., статистичес-
ки независимы.
Ответ: Корреляционная функция шума £(/) равна /?|(т) —
—NF (sin 2nFx)/2nFx и обращается в нуль в точках т = Д/П = п/2Г.
6.20. Показать, что для гауссовского стационарного шума £(/)
с ограниченным, но неравномерным спектром вида
„ _ (Ccos2nfC при = 1/40,
(0 при/<0, f>F,
значения | (/) в моменты времени, отстоящие друг от друга на вели-
чину Atn = 2nC, п = 1, 2, 3, ..., зависимы.
Ответ: Из выражения для корреляционной функции Ri(x) =
f 1 cos (лт/2С)
= j (f) COS 2n,fxdf = -------— следует, что R$ (Mn) 0.
0 2л 1 — (t/G)2
6.21. Случайный процесс r](/) представляет собой последова-
тельность случайно чередующихся отрезков «элементарных» сигна-
лов ^(/) и £2(0, т-е- имеет вид
МО = (1/2)11 + ^(01^(0 + (1/2)11 - 1(01В2(0
Здесь (0 и |2(0 — стационарные и стационарно связанные слу-
чайные процессы, не зависящие от |(/); £(/) — случайный двоич-
ный сигнал, который в любой момент времени t может принимать
одно из двух значений | = 1 или £ = —1 с одинаковыми вероят-
ностями = 1} = Р{В = —1) = 1/2, причем моменты скач-
162
ков (перемен знака) распределены по закону Пуассона, т. е. вероят-
ность получения п скачков на временном интервале длительностью
•с определяется формулой
р — VT
pT(n)= (vt)"----, n=0, 1, 2, ...
nf
Вычислить корреляционную функцию процесса т)(/) при усло-
вии, что математические ожидания процессов и |2(/) равны
нулю, а их корреляционные и взаимные корреляционные функции
известны и имеют вид
Ъ, (т) = М {I, (0 М* + т)},
Rl, (т) = М (|2 (0 и а + т)},
(т) = м {В, (0 g2(/ + t)}.
Ответ: Rn(x) =^)[i + RUT)HflMT)+£g.(T)]4-
+ (1/2)[1-R5(t)JR61 (t),
где 7?*(т) = e~2v IT L
6.22. Определить корреляционную функцию /?(т) и односто-
роннюю спектральную плотность S (/) случайного сигнала s(t), от-
раженного от объекта, движущегося с относительной скоростью V.
Сигнал имеет вид
s(0 = 4mcos|2n(f0 + 2V/Xn)/ + Ф],
где f0 и %0 — постоянные амплитуда, несущая частота и соот-
ветствующая этой частоте длина волны электромагнитных колеба-
ний; ф — случайная начальная фаза, равномерно распределенная
на интервале (—л, л). Относительно скорости V делается предпо-
ложение, что она представляет собой случайную величину, равномер-
но распределенную на интервале (—Уо, Уо), в соответствии с чем ее
плотность распределения вероятностей имеет вид
P1(V)=l/2V0, | V | < Vo.
Ответ: /? (т) = w sin cos 2л/0 т;
2 4лУ 0 тДо
IHoK-y1-.
2 4V0 К
6.23. Решить задачу 6.22 для случая, когда
1 / v2 \
Р1(У)=Т^ехр(~^гГ
6*
163
Ответ-.
R(t)=—^-exp
1 / 4лау т
2 ( Аф
cos 2л/0
sm=4/ тМ
__ [2л(/-МР 1 а - 1 f 4jt(Tv Г.
4а J’ 2 у Хо у
6.24. Найти корреляционную функцию R (/, т) колебания
s(/) — /4m£‘(/)cos 1соо/ +Ф(0 + Фо1,
где Ат и соо — постоянные амплитуда и частота; <р0 — случайная
начальная фаза, равномерно распределенная на интервале (—л, л);
E(t) и ф (/) — стационарные гауссовские случайные функции, мед-
ленно меняющиеся по сравнению с колебанием частоты ®0 и отобра-
жающие законы амплитудной и угловой модуляции процесса I (().
Ответ [14]:
R(t, т)
= ^- Re [М {Е (f)E(t^~ т) е-i 1* «+’> - * <*>]} е- *»•’].
6.25. Решить задачу 6.24 для случая амплитудной модуляции,
т. е. при условии, что ф(/) = 0 и
£(/) /1 М0> — 1//пАм,
1.0, X (Z) < — I//nAM.
Здесь тАм — постоянный коэффициент амплитудной модуля-
ции, K(t) — стационарный гауссовский случайный процесс с нуле-
вым математическим ожиданием и корреляционной функцией R\ (т)=
= ^гх(т).
Ответ [14]:
Ram (т) —
лт
2
। Г / 1 \ 12 I
/иам<шУ— /<й~2)Н:--(т)[ cosсопт.
ь-n /г1 \ WAMaX /]
где
/(х)==_Й^ехр(~^"х2)’ /<4>(х) =~^Нх)‘
При /ПамПх'С! (отсутствие амплитудной перемодуляции)
Ram (т) = (Лт/2)соз®0т + (Лт/2)т2АМсгха (t)cos соот.
При /пам<Тх > 1 (сильная перемодуляция).
Ram (TJ
/«AM CfK
k Z ,
— ( 7^ГТГх(т)
4=0 д.1 Г2 1_ -
COS (Оо
2fe-:,
2
2
164
6.26. Решить задачу 6.24 для случая фазовой модуляции, т.е-
при условии, что £(/) == 1 и ф(/) = Л4фмМ0> гДе Л4фм — по-
стоянный коэффициент фазовой модуляции, 1 (t) — стационарный
гауссовский случайный процесс с нулевым математическим ожида-
нием и корреляционной функцией /?х(г) — о^гх,(т).
Д2
Ответ 114]: 7?фм (т) = —-- ехр {— Л4фМ 11 —гх (т)]} cos<o0 т.
6.27. Решить задачу 6.26 при условии, что
ф(0 = + М2Г(/).
Ответ [141: /?ФМ (т) = (А^/2)(1 + 4ММП — d (т)])-'/2 х
X ехр(—Л41 — Мт)](1 + 4Л4?оШ—d(T)]))cos <вот.
6.28. Показать, что корреляционная функция R (т) случай-
ного сигнала
s(t) = Ат cos [®0/ + Мфмз1п й/ + Ф (/)!,
где Ат, соо, Л4фм ий — постоянные величины; Ф(/) — стацио-
нарный гауссовский случайный процесс с нулевым математическим
ожиданием и корреляционной функцией 7?ф(т) = сГфГф(т), имеет
вид
R (т) = у А2т Jo (2Л4фм sin х
X ехр { - о® [гф (0) - гФ (т)]} cos <о0
Здесь J0(x) — функция Бесселя первого рода нулевого порядка.
6.29. Решить задачу 6.24 для случая частотной модуляции, т.е.
при условии, что E(t) s 1 и
Здесь Л4чм — постоянная величина; %(/) — стационарный гаус-
совский случайный процесс с нулевым математическим ожиданием
и корреляционной функцией 7?х(т) = <da(T).
Ответ (14]:
Д2
Ячм(т) = —^-ехр
т и
-A A <dJJ гх (и—о) dvdu I cos (оо т
о о -
6.30. Решить задачу 6.29 для случая, когда корреляционная
функция Rx(x) модулирующего стационарного гауссовского шума
равна:
1) ₽Цт) = о£е-«1Ч 2) Rx(x) = aie-“St’.
165
Ответ:
1) RhmCO = ~~~ ехр
2) 7?чм (т) = ехр
---^ЧМСТХ (a|T|_|_e-aitl _])
а2
__^4MqX /_1_ ге—а> т2 1 ] _1_
а2 \ 2 1
cos <оо т>
+ а|т|У~л ГФ (1/^2 а|т|)-М) Icos®° •
6.31. Предположим, что задан узкополосный стационарный слу-
чайный процесс
В(<) = Ej(Ocos[®0Z + <pj(OL
где.Е|(0 и <pg(/) — функции, медленно изменяющиеся по сравне-
нию с колебанием частоты ®0, представляющие собой огибающую
и мгновенную случайную фазу колебания Корреляционная
функция процесса |(/) имеет вид
— ofr^) — ojpg(T)cos®0T. _
Этот процесс подвергается смешанной амплитудно-угловой модуля-
ции, в результате чего формируется колебание
s(t) = E^(t)E(t)cos\<d0i +ф(/) + <pg(0l-
Здесь E(t) и ф(() — медленно изменяющиеся функции, отображаю-
щие законы амплитудной и угловой модуляции, статистически неза-
висимые от £ (/).
Определить корреляционную функцию R (t. г) колебания s (i).
Ответ f 14]: R (t, т) Re [Af {E^ (t) El e-/ x
xM{E (0 E (t +т)е~' t’O(<+T) “ о (/>]} e-'®« *].
6.32. Решить задачу 6.31 для случая амплитудной модуляции,
т.е. при условии, что ф(() == 0, а колебание £(/), отображающее
закон амплитудной модуляции, имеет вид
_ Г1+я1ам МО, 1/я*ам,
(о, 1 (/) < — 1/пгАМ.
Здесь Х(/)—стационарный гауссовский случайный процесс с ну-
левым математическим ожиданием и корреляционной функцией
Rx(t) = оха(т). Предполагается, что начальная фаза <р0 = <pg(O)
колебания |(/) случайна и равномерно распределена на интервале
(—л, л).
Ответ [141: Ram (т) = R^(t)M{E(t)E(t + г)}
При тдмох < 1 (отсутствие перемодуляции)
Ram (т) = [а|р^(т),+ /иАма|<ТхР£(т)а(т)]соз аот.
166
При /пдмоъ > 1 (сильная перемодуляция)
Ram (т) = -j- /Пам о| <т£ р5 (т) {|д- -f-агс sin а (т) j X
Xа (т) + V1 —rl (т)| cos <в0 т •
6.33. Решить задачу 6.31 для случая фазовой модуляции, т. е.
при условии, что E(t) = 1, а колебание ф(0, отображающее закон
фазовой модуляции, имеет вид
ф(0 = МфмМО»
где Л4фм — детерминированный коэффициент фазовой модуляции;
Ц£) — стационарный гауссовский случайный процесс с нулевым
математическим ожиданием и корреляционной функцией /?%(т) =
= <$О,(т). Начальная фаза ф0 = <pg (0), как и в задаче 6.32, пред-
полагается случайной и равномерно распределенной на интервале
(—л, л).
Ответ [14]: /?фм (т) = of р| (т) ехр {—М фм 1 — /X (т)]} cos &)0 т.
6.34. Решить задачу 6.31 для случая частотной модуляции, т.е.
при условии, что E(t) si, а колебание ф(/), отображающее закон
частотной модуляции, имеет вид
t
ф(П=Мчм ^(t)dt.
о
Здесь /Ичм — постоянная величина, X (t) — стационарный гауссов-
ский случайный процесс с нулевым математическим ожиданием и
корреляционной функцией 7?ь(т) = о“гх(т). Предполагается, как и
ранее, что начальная фаза <р0 = (0) колебания |(/) является
случайной величиной, равномерно распределенной на интервале
(—л, л).
Ответ [14]:
M?im^
/?чм(т) = о| р6 (т)ехр
т и
J Jг\{и—v)dv du
о о
cos ®0 т.
6.35. Определить корреляционную функцию Рам(т) и односто-
роннюю (<о > 0) спектральную плотность Зам(<о) амплитудно-мо-
дулированного сигнала
s(t) = [Лто + Mam^OIcos [®о/ + ф(0К
где Ат, Мам и ®в — постоянные величины. Предполагается, что
МО и <р(0 — случайные процессы, заданные уравнениями:
dUf)!dt + «МО = nK(t), d<$(t)ldt = n^t). (6.55)
167
Здесь «х(0 и. пф(/) — независимые стационарные гауссовские
белые шумы с нулевыми математическими ожиданиями и корреля-
ционными функциями
N. „ Д'
RnKttb Q = 4) = 6(/2-tx). (6.56)
Начальная фаза <p0 = cp(O) считается случайной и равномерно рас-
пределенной на интервале (—л, л).
Ответ:
Ram (?) = (1 + е-“1 т Те-"*1 т 1,4 cos «п т,
tn^=0A/Am,
Г рф , т2
Sam (<o) =
a
О*+Й2 (1+Оф)2+О2 ]’ ^а/4а’
Q = ((o—соо)/а, со>0.
Графики функции Sam(co) приведены на рис. 6.9.
Рис. 6.9. Спектраль-
ная плотность ампли-
тудно - модулирован-
ного сигнала
168
Рис. 6.10. Спектраль-
ная плотность ампли-
тудно - модулирован-
ного сигнала с подав-
ленной несущей
отсутствия в
/П2 1 о ________ (0— соо
1 + Й2 ’ ~ аГ~
й)>>0.
6.36. Решить задачу 6.35 для частного случая
сигнале s (t) фазовых флуктуаций (Мф = 0).
Ответ".
/?ам(т) =-^-(1Н-/п2е-“ i'II)cos®0t,
Sam(<o) = —— лб(й)-)
а
6.37. Найти корреляционную функцию 7?дм(т) и односторон-
нюю спектральную плотность Здм(со) двухполосного амплитудно-
модулированного сигнала с подавленной несущей
s(t) — MAmA.(/)cos[®0/ + <p(/)l,
где Мам и <оо — постоянные величины; Ц1) и <р(/) — случайные
процессы, заданные уравнениями (6.55) и (6.56). Начальная фаза
Фо — ф(0) считается случайной и равномерно распределенной на
интервале (—л, л).
Ответ:
Rum (т) =(оа/2) e",e+V4>।Т 1 Cos (оо т.
5дМ(®)=-^-—®>0.
а (1+Рф)2 4-О* а
Графики функции 5дм(ю) представлены на рис. 6.10.
6.38. Вычислить корреляционную функцию /?фм(т) и одно-
стороннюю спектральную плотность Зфм(со) фазомодулирован-
ного сигнала
s(0 = Xmcos|o>0/ + МфмМО + Ф(01»
169
Рис. 6.11. Спектральная
плотность фазомодули-
рованного сигнала
где Ат, ю0 и Л4фм — постоянные величины; !(/) и <р(/) — слу-
чайные процессы, заданные уравнениями (6.55) и (6.56). Начальная
фаза <р0 = <р(0) случайна и равномерно распределена на интервале
(—л, л).
Ответ-.
г» /ч Ат “+ I т I) /2 „|т|.
/?Фм(т) = -~-е exp(o|>e-alT’)cosco0t=5
п — 0
= ^ф = -/-Л/ф,
4 4а
А2 — 00
5фм (<о) = —2-е аф У
а
W(»+Dy)
п! К« + Оф)«+Йг1
,□=^^2,0 >0.
а
Графики функции 5фм(<о) приведены на рис. 6.11.
6.39. Решить задачу 6.38 для частного случая отсутствия в сиг-
нале s(t) фазовых флуктуаций (Мф = 0).
170
Ответ:
/?фм (т) =-^у- е °Ф ехр (Оф е-а|т|) cos ©0 т =
= е °ф Г1 4- — (оф)л е-"®111 | cos ®0 т;
L n=1 J
Л2 „Ъ Г 00 /гг2 Хп
$ФМ(о» = _21е-0ф л6(Й)+ У ,
а (п—1)1 (na4-Q2)
Q = (® — о)о)/а, ©>0.
6.40. Определить корреляционную функцию 7?чм(т) и одно-
стороннюю спектральную плотность Зчм (со) частотно-модулиро-
ванного сигнала
s (/) = Ат cos
«о0/-|-Л!чм М0^+<₽(0 ,
где Ат, (лп и Мчм — постоянные величины; Х(/) и ср(/)— слу-
чайные процессы, заданные уравнениями (6.55) и (6.56). Начальная
фаза ср0 = <р(0) случайна и равномерно распределена на интервале
(—л, л)
Ответ:
г\ / \ Ат 1РчМ (3ЧМ4~Оф) а|т|] . ..
Кчм(т)=-^-е ф ехр(—Рчме-а|х1)со5©0т =
__ Ат РЧМ ж-1
2~ 2i
I л = 0
(- 1)п(Рчм)п
— (п+'0чм+ О<р) а|т|
COS С00 V,
о , . Ат РЧМ -г, (— О” (РчмУС’+Рчм + ^ф) ,
о чм (<о) =-е > ---------ii,
“ П^п «![(«+Р2чм+Оф)2Н-02]
Р2чм=4-Мчм, Оф=-!-^ф, й=^, ©>о.
а2 4а а
Графики функции Зчм(®) даны на рис. 6.12.
6.41. Определить корреляционную функцию 7?афм(т) и одно-
стороннюю спектральную плотность Зафм (®) амплитудно-фазомо-
дулированного сигнала
s(0 — A4am A,(Ocos[<o0Z + Л4фмМ0 + ф(0К
где Мам> А4фм и, <оо — постоянные величины; Х(/) и <р(0 — слу-
чайные процессы, заданные уравнениями, (6,55) и (6.56).
171
Ответ:
/?АФМ (т) =-^- е~°ф (а$ е"°-₽ “|т|+ (1 - 2о|>) е~( 1 + D-₽> “|Т|
4-Оф e—<2+D’>)“ MJ ехр (аФ e~“iT|)cos соо т;
0^ (5^ ( оо
5афм(о) =—^-е Ф I сг'ф Y
а I п = 0
х у (^Г^+1+^ф) _______________
п“о [(« + 1 + ^ф)2 + й2] Мф п\ l(n + 2 + D^+Q2| р
ад^а^ЛЦм, аФ=аьМфм, Оф Л%,
4а
(°W.+3>) +(1_2о1)Х
"Ц(п+Цр)2+^21
Q = .«?-±>
а
Графики функции 5дфм (о) приведены на рис. 6.13.
6.42. Вычислить корреляционную функцию /?дчм (т) и одно-
стороннюю спектральную плотность Здчм (со) амплитудно-частотно-
модулированного сигнала
t
ЦО cos <о0/+Л1чм J +<р(/) ,
о
где Мдм, Мчм и <о0 — постоянные величины; Л (0 и <р (0 — слу-
чайные процессы, заданные уравнениями (6.55) и (6.56). Начальная
фаза фо == Ф (0), как и в предыдущих задачах, предполагается слу-
чайной и равномерно распределенной на интервале (—л, л).
Рис. 6.12. Спектраль-
ная плотность частот-
но - модулированного
сигнала
172
Рис. 6.13. Спектраль-
ная плотность ампли-
тудно-фазомодулиро-
ванного сигнала
Ответ*.
5дчм (со)=—~ е&чм
а
(Гл В?»** — Эгоа|т| — (1+Лт)а|т|
Качм (т) =—— е [ — Рчме + (14-2Рчм)е
-(2+Оф)а1г| -а|т1
— Рчме ]е ехр (—рчме )cosco0t;
__«а у (— 1)" (Р2ш)п (п+ Рчм+Р<р) .
РЧМ £0 п1 [(п + р2чм+V + Q21
(— 1)п(Рчм)П(п+1+Рчм+Р<р) __
п! [(n + l + p^+D^+Q*]
(— 1)” (Рчм)п (п +2+ Рчм ~Ь Оф) |
я! [(« + 2-|-РцМ+Оф)2-|-й2] |*
.+(1 + 2Рчм)
п=0
— Рчм 2
п = 0
Рчм =4- Мчм, оХ = <т£ MR £ф = -1- Q
а2 4а а
Графики функции 5дчм(®) представлены на рис. 6.14.
6.43. Найти интервал корреляции тк для стационарных случай-
ных процессов КО с корреляционными функциями:
1) R5 (т) = о|е-“ 1' I; 2) (т) = of е~«2Л 3) (т) = of (1 -а |т|),
1ЧС1/а-
Ответ: 1) ск = 1/а; 2) тк — ]/л/2а; 3) тк = 1/2а.
6.44. Определить эффективную ширину Д<оэ спектра Sg(®)
стационарного случайного процесса £ (() с корреляционными функ-
циями
!) Rg (т) = of (1 — аИ|). [т|<1/а; 2) Rg (т) = а|е~“1 т *;
3) R5 (т) = <г|е~“!т2.
Ответ: 1) Д(оэ — ла; 2) Д<оэ = ла/2; 3) Д<оэ = 2|Лгга.
173
Рис. 6.14. Спектраль-
ная плотность ампли-
тудно-частотно - мо-
дулированного СИГ’
нала
6.45. Показать, что для любого стационарного случайного про-
цесса £(/) с корреляционной функцией /?(т), принимающей только
положительные значения, произведение времени корреляции тк на
эффективную ширину спектра Д<оэ равно Дсоэтк = л/2.
6.46. Определить эффективную ширину спектра Д(оэ, среднюю
частоту спектральной плотности средний квадрат частоты
М {со2} и среднюю квадратическую ширину спектральной плот-
ности стационарных случайных процессов с нулевыми математи-
ческими ожиданиями и корреляционными функциями:
1) /?(т)=о*Ап(Д«>г/2)
Дсот/2 0
2) R (т) = а2 е~а*х’ cos w0 т;
3) R (т) = о2 е—а|т> (cos <о0 т Н—— sin <оо I т Й .
\ (Оо /
Ответ:
1) Д<оя = Дсо, тш = <о0, М {со2} = (Оо + До>2/12, о2, = Дсо2/12;
2) Д<оэ = 2]/ла, тш ~o)a, М {со2} ~ о>о + а2, ~ а2;
3) Дсо8 = ла,
’о»
со? I i 2 . а
= —!- 1-----------arctg--------
соо L я .
4асо1/л, со । = <0о-f-а2.
— 2а/л,
г2
'со
6.47. Доказать, что необходимым и достаточным условием непре-
рывности в среднеквадратическом стационарного случайного про-
цесса 5 (0 является непрерывность его корреляционной функции
/?6 (т) при т = 0.
6.48. Определить, удовлетворяют ли условиям непрерывности
и дифференцируемости стационарные случайные процессы £ (/) с кор-
реляционными функциями вида .
1) ₽&(т) ~ <т2е-а1х|; 2) /?g(r) = o2e~0t|xl cosco от;
174
3) /?^(т) = о2е_“1т1 (cos<оо т-|—— sin<oo|TA.
\ ®o /
Ответ: Процессы £ (t) с корреляционными функциями вида 1) и
2) непрерывны, но не дифференцируемы; процесс с корреля-
ционной функцией 3) непрерывен и дифференцируем.
6.49. Случайный процесс | (/) задан корреляционной функцией
R (i)=e_“ixi(ch(ooT-|—— sh<oo|xA> а>©0>0.
\ Wo /
Определить корреляционную функцию 7?л(т) и спектральную плот-
ность Sn(®) случайного процесса
Ответ;
Rn (т) = (а2—(о§) e~“lxl fch ®0 т-— sh <оо | т A }
5Л (ш) =-------4аа>Ча2-^)---------
[(а-<оо)2+<о2][(а+®о)2+<о2| ‘
6.50. Случайный процесс т] (/) получается посредством дифферен-
цирования стационарного случайного колебания £(/):
ц(() == dl(t)/dt.
Определить корреляционную функцию /?л(с) процесса т)(0 в тех
частных случаях, когда функция /?^(т) колебания | (Z) задана выра-
жениями:
1) Я£(т)= <т|е-*1х|;
2) /?6(т)= а|е-“|Т| (1 + сс[т| );
3) (т) = of e~“lxi fcos <оо т -J- sin <оо | т А .
X Wo /
Ответ:
1 —|-6(x)e“ixlj;
2) (т) — a2of e-a|xi(1 — а|т|);
3) R^ (т) = (а2 + ®о)о| е~“|х|(cos <оо т--— sin ®01 т |
\ w0
6.51. Найти спектральную плотность 5л(<о) стационарного слу-
чайного процесса т;(/) с корреляционной функцией
^п(т) = аа2е^“1х1 [1 —-<5 (т)е“1х'
L а
(см. задачу 6.50).
Ответ: 5Л((1>) = 2ао2©2/(а2 + о2).
График функции 5т)((д)/2аа2 приведен на рис. 6.15.
175
1) 7?п(т)= а2 о? e-otlxl
(&>)
2абг
-'s 0,8
\0,6 /
/
Аг /
_д /
-ff -U -2 0 2 4 6>/fc
Рис. 6.15. Спектральная плотность
производной от стационарного
случайного процесса
6.52. Показать, что взаимная корреляционная функция
^n(f1( fj)j стационарного случайного процесса 1(f) и его производ-
ной т) (f) — d%{t)/dt удовлетворяет условию
Rin(h> 1г) ~
т.е. при перемене местами аргументов меняет знак на обратный.
6.53. Определить спектральную плотность Sn(©) случайного
процесса
Л(0 = al(t) + bdl(t)/dt,
где |(f) — стационарный случайный процесс с нулевым математи-
ческим ожиданием и корреляционной функцией
/?^(т) = о2е~“1 т 1 (1+ а | т |).
Ответ: Sn (©) =—^-2— (а® & о2).
(а2+<о2)2 v ’
6.54. Определить корреляционную функцию 7?п(т) случайного
процесса
... , d2g(/)
n(f)=a£(f) 4-(>—^-+с—Y
dt dt*
где g (f) — стационарный случайный процесс с нулевым математичес-
ким ожиданием и корреляционной функцией (т).
Ответ [ 19]: R-n (т) — a2R* (т) +(2ас— b2) d с7 8 d ..
du2 dxi
7. МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В зависимости от того, непрерывное или дискретное множество значений
принимают случайная величина |(/) и ее параметр t в области задания про-
цесса [О, Г], различают четыре основных вида марковских случайных про-
цессов: марковские цепи (дискретный процесс с дискретным временем), мар-
ковские последовательности (непрерывный процесс с дискретным временем),
176
дискретный марковский процесс (дискретный процесс с непрерывным вре-
менем) и непрерывнозначный марковский процесс (непрерывный процесс
с непрерывным временем). Характер временных реализаций перечисленных
процессов показан в табл. 7.1. Помимо четырех основных видов, возможны
другие, более сложные процессы марковского типа (дискретно-непрерыв-
ные, различного характера смешанные и т. д.) [45].
Определяющее свойство всех видов марковских процессов состоит в сле-
дующем. Случайный процесс £(/) называется марковским, если для любых
п моментов времени < /2 < ••• < tn из отрезка [0, Т] условная функция
распределения «последнего» значения g(/n) при фиксированных значениях
ь (^i)» g (Aj)> •••» £ ^п-1) зависит только от g(/n-i), т. е* при заданных зна-
чениях gj, g2, •••> gn справедливо соотношение
р {5 (tn) < In 11 («1)=51.I (tn-i)=5n-i} =
=P{5(M<5nl5«n-i)=5n-i}- (7.1)
Для трех моментов времени > tj > tk формула (7.1) принимает вид
Р {5 (ti) < Si 15 (tk), g (0)=5/}=/> {5 (tt) < It 15 (tj)=^}. (7.2)
Поэтому часто говорят, что характерное свойство марковских процессов
состоит в следующем: если точно известно состояние марковского процесса
в настоящий момент времени (fy), то будущее состояние (при 0) не зависит
от прошлого состояния (при tk).
В качестве определения марковского процесса можно также принять
следующее соотношение, симметричное относительно времени:
Р {5 (ti) < 51,1 (tk) < 5a I 5 (tj) = 5Д =
= P {5 W < It 15(tj)^lj}P {5(tk) < Ik 15(tj)=£,} • (7.3)
Такая запись означает, что при фиксированном состоянии процесса в настоя-
щий момент времени tj будущее (при и прошлое (при tk) состояния мар-
ковского процесса независимы.
Укажем еще одно общее и важное свойство марковских процессов: для
них эволюция вероятности перехода Р {£(/)< g | g (tQ) = g0} описывается
уравнением вида
dP/dt = <^Р, (7.4)
где — некоторый линейный оператор (матрица, дифференциальный опера-
тор и др.). Это позволяет исследовать поведение марковских процессов при
помощи хорошо разработанных методов решения соответствующих диффе-
ренциальных уравнений. При этом характер решаемых физических задач
может быть различным, в зависимости от заданных начальных и граничных
условий для уравнения (7.4).
Пусть, например, поведение рассматриваемой системы описывается не-
которым уравнением, удовлетворяющим условию (7.2), и заданы начальные
условия (состояние системы в начальный момент времени /0). Тогда в от-
сутствие каких-либо ограничений нужно сначала записать уравнение вида
(7.4) и затем при заданных начальных условиях найти его решение. Если же
на поведение системы наложены некоторые ограничения, то для полученного
уравнения вида (7.4), кроме начальных условий, нужно дополнительно за-
дать граничные условия, отражающие эти ограничения.
Характер граничных условий может быть разным. Например, точка,
отображающая поведение системы, начиная движение из начального состоя-
ния g (/0) = £0, при достижении границы g (/) = с «поглощается» ею и ра-
бота системы прекращается (нарушается) (траектория 1 на рис. 7.1); точка
«отражается» от границы с (траектория 2) и т. д. Если граница с поглощаю-
щая, то, помимо отыскания вероятности перехода Р для g < с, можно инте-
ресоваться вероятностью «поглощения» за некоторое время Т или же мате-
матическим ожиданием, дисперсией и другими характеристиками времени Т,
по истечении которого траектория в первый раз достигнет границы с.
177
Таблица 7.1
Классификация марковских процессов
Значения
аргумента
Значения процесса
Дискретные
Непрерывные
Дискретные
Непрерывные
Дискретны i марковский процесс
£ ; *
Непрерывнозначный марковскипролесс
Рис. 7.1. Влияние поглощающей и отражаю- '
шей границы на траекторию процесса
*----------£-----------г
Задачи указанного характера имеют математически строгое решение
только для марковских процессов.
Конкретизируем уравнение (7 4) для четырех основных видов марков-
ских процессов [45].
1. Простая цепь Маркова. Пусть случайный процесс 0(/) может при-
нимать конечное число К различных дискретных значений *0,1, *02, ...»
В некоторые дискретные моменты времени /0 < < t2 < ... < tN эти зна-
чения могут мгновенно изменяться, т. е. имеют место переходы -► 0;-,
/ = Г/Г
Характеристическое свойство простой цепи Маркова состоит в том, что
вероятность Р (0П) значения процесса 0П в момент времени tn зависит лишь
от того, какое значение имел процесс в непосредственно предшествующий ему
момент времени fn-lt и не зависит от значений процесса в более ранние мо-
менты времени, т. е.
Р (0П I 00 , 01 , • • • , 0д —1) = Р (0д I 0n — i) = л (0д | 0П_1).
Поэтому для простой цепи Маркова совместные конечномерные плотно-
сти вероятности определяются формулой
п
Р(Оо, 0!.....еп) = Рх(0о) П (0Н | 0р1_|). (7.5)
Ц=1
Условные вероятности (0ц | 0Ц_ 0 принято называть вероятностями пе-
рехода из состояния 0цв состояние 0Ц за промежуток времени — —i)-
Одна из основных задач в теории простых цепей Маркова следующая.
Пусть задано начальное значение процесса при t0 и указан вероятностный
закон смены соседних значений процесса (т. е заданы соответствующие
вероятности перехода). Каким образом можно найти вероятности различных
значений процесса в момент времени tn > /0 и, в частности, при п •+ оо?
Введем следующие обозначения для безусловных и условных вероят-
ностей:
Рь («)=? (en=1M. я)=,р{0п = Ъ|0ц = 07}> (7.0)
= 0<р<л, п =0, W .
Величина (п) есть безусловная вероятность значения 0^ на n-м шаге (т. е.
в момент времени t = tn), а рь (/0) = pg — начальная вероятность значения
Условная вероятность л;^(р, л) определяет вероятность значения
при tnt если в более ранний момент времени < tn значение процесса было
равно 0у.
179
Очевидно, что введенные вероятности неотрицательны и удовлетворяют
условию нормировки:
К ____
Pk(n) — 1, pk(n) > О, лг =0,7V; (7.7)
fe=l
К _____
У ЯЛ(Ц,Л)=1, и) > °. i = I> К. (7-8)
*=1
На основании правила полной вероятности для введенных вероятностей
можем написать уравнения Маркова:
К __
PkW = 2 Pj(M') Л “ Ь К, ° < н (7.9)
/=1
К _____
(Н> Л)=а 2 (Н> w) Jijfe (/и, /г), /, k =1, К, 0 < ц < т < п. (7.10)
г = 1
Среди простых Цепей Маркова выделяют однородные цепи. Они харак-
теризуются тем, что вероятности перехода л7-& (р,, п) зависят только от раз-
ности аргументов, т. е.
njk (Н> Л) = nih (л —ц), п > ц > 0. (7.11)
Обозначим одношаговые вероятности перехода через л7ь = л^ (1).
Полное вероятностное описание простой однородной цепи Маркова дости-
гается заданием начальных вероятностей {pg} и матрицы одношаговых ве-
роятностей перехода
Лц л12 ... л^
л21 л22 ... л2к _ /7 I9V
ЛК| Лк2 ... Л/<к _
Можно убедиться, что для простой однородной цепи Маркова матрица
вероятностей перехода за п шагов равна n-й степени матрицы одношаговых
вероятностей
л(л) = л«, (7.13)
а матрица вероятностей различных значений процесса определяется урав-
нением
рт (/г)~= рт (0) л". > (7.14)
Здесь Рт (и) — матрица-строка безусловных вероятностей различных зна-
чений процесса на n-м шаге, Рт(0) = [р?, р®, ..., р^] — матрица-строка на-
чальных вероятностей (при t0).
Однородная цепь Маркова, для которой вероятности {рь(/г)} = {pfe}
не зависят от и, называется стационарной, в противном случае цепь назы-
вается нестационарной. В общем случае вероятности р^, если они сущест-
вуют, находятся в результате предельного перехода
Ph = lim pft(n), = 1, К’ (7.15)
П->оо
и называются финальными вероятностями. Однако, если начальные вероят-
ности {pg} совпадают с соответствующими финальными вероятностями
{рь}> то цепь Маркова будет стационарной начиная с t0.
180
Финальные вероятности, должны удовлетворять системе К линейных
алгебраических уравнений
к ____
Pk = Ti k = l, К, (7.16)
1= I
и дополнительному условию
К
2 (7.17)
Суммируя обе части всех равенств (7.16) по k и учитывая соотношение
(7.8), приходим к тождеству. Поэтому К уравнений (7.16) являются линейно
зависимыми, и К финальных вероятностей следует определять из (К —1)
уравнений (7.16) и уравнения (7 17).
2. Дискретный марковский процесс. Пусть по-прежнему случайный
процесс б (/) может принимать только дискретные значения О2, •••>
но смена этих значений происходит не в фиксированные, а в любые случайные
моменты времени. Вероятности перехода
л/7(^,, О = Р{0(Л = ^;10ао) = М» *>*<>’ (7.18)
удовлетворяют следующим соотношениям
/\ _______________________________________
2 0= 1, Лгу (Л), О > о, г, 7 = 1, К, (7.19)
/ = |
лг7-(/0, /о) = { ‘ П₽И (7.20)
V 9 ПРИ 1 4= 1 •
Кроме этого, для них справедливо уравнение Колмогорова—Чэпмена
К
Лц(1о, «4-Д/)= S nik(to, <+Д0, t>t», Д/>0. (7.21)
fe=l
Характерное свойство рассматриваемых процессов состоит в том, что
для малых временных интервалов Д/ вероятность того, что значение не
изменится, превышает вероятность изменения значения:
л^(/, t + Д/) = 1 + akk (t)M + о(Д0,
(7.22)
t + Д/) = ahj(f} ДГ+ o(M),
где символом о(Д/) обозначены члены выше первого порядка малости отно-
сительно Д/, т. е. lim [о (Д/)/Д/] « 0 [45].
ДГ->0
Так как вероятности перехода из одного значения в другое неотрица-
тельны (а/гу(О > 0) и для них должно выполняться условие нормировки
(7.19), то из (7.22) получаем
2 akJ(t)>0. (7.23)
i
Подставив (7.22) в правую часть уравнения (7.21) и перейдя к пределу
при Д/ —> 0, получим следующую систему линейных дифференциальных
уравнений:
д К ____
— Лг/^о, /) = У (7.24)
fe= 1
где а/г7(/) удовлетворяют соотношению (7.23). Решение этой системы при на-
чальных условиях (7.20) дает зависимость вероятностей перехода от времени
181
Дискретный марковский процесс остается марковским и в обратном на-
правлении, т. е. наряду с уравнениями (7.24), часто называемыми «прямы-
ми», справедливы также «обратные» уравнения
д К
ЛЩj (?о» , &ih </о) ^kj (^о* О» t > • (7.25)
dZo fe=i
Уравнениям (7.24) удовлетворяют не только вероятности перехода, но
и безусловные вероятности значений р;- (/):
(0₽к(0« <7-26)
k
Эти дифференциальные уравнения нужно интегрировать при начальных
условиях
Pi (О = Pj (*о) = Р/ при t = /0. (7.27)
Дискретный марковский процесс называется однородным, если вероят-
ности перехода л^ (/0, /) зависят только от разности т = t — t0:
O=«iy(T), т=( —/0- (7-28)
Из (7.22) следует, что для однородного процесса akj(t) = akj постоянные
величины и дифференциальные уравнения (7.24) упрощаются:
dx akj nih т) • (7.29)
k
Если при т -► оо существуют предельные значения вероятностей пере-
хода pj — lim лг-у(т), которые не зависят от начального состояния, то мар-
Т->оо
ковский процесс можно назвать стационарным. Вероятности стационарных
значений определяются системой алгебраических уравнений
^ahjPk = 0, (7-3°>
4 k k
3. Марковские последовательности. Пусть случайные величины Хп =
= Х(/Л) в некоторые дискретные моменты времени < t2 < ... < tn < ... < tN
принимают непрерывное множество возможных значений (см. табл. 7.1).
Определяющее свойство марковской последовательности {%n, п = 1,
состоит в том, что совместная плотность вероятности рассматриваемых слу-
чайных величин выражается через плотность вероятности начального состоя-
ния Px(Xx) и плотности вероятности перехода лЛ (^п1Лп-1)> « = 2, N*,
р(Лг,Х2, П лц(Ч I \i- <)• (7.31)
ц = 2
Укажем некоторые свойства марковских последовательностей: 1) если
точно известно значение марковской последовательности в настоящий момент
времени, то ее будущее значение не зависит ог предыдущего значения; 2) лю-
бая последовательность, взятая из марковской, является также марковской;
3) марковская последовательность остается марковской и в обратном нап-
равлении; 4) плотность вероятности перехода удовлетворяет уравнению
л (Хп | Х^) = J л (Хп | л (^т |^) я > /и > р (7.32)
—оо
182
Марковская последовательность называется однородной, если плотности
вероятности перехода лп(Мг|Мг-1) не зависят от п. Марковская последова-
тельность называется стационарной, если она однородна и все случайные
величины Х(п) имеют одну и ту же плотность вероятности: р (кп) = const(n)*
4. Непрерывнозначный марковский процесс. Область значений непре*
рогвнозначного процесса X (t) и область его определения [О, Т] есть непрерыв-
ные множества. Для непрерывнозначного марковского процесса диффузион-
ного типа плотность вероятности перехода л (X, /1 Хо, *о) = ? 1 (U>
и безусловная плотность вероятности р (Л, t) удовлетворяют уравнению
в частных производных Фоккера—Планка—Колмогорова, которое при-
менительно к плотности вероятности р (X, 0 имеет вид
д д 1 д2
—-р(А,, /) = - —[а(М)р(М)1 + —Р(М)] (7.33)
О1 ОК 2 ОЛ
или, иначе,
д Л д
+ (7.34)
ot ок
где
Id.
G(X, 0 = а(Х, 0р(Х, 0-— — [5 (X, t)p (X, 0] . (7.35)
2 ок
«Коэффициенты» сноса а (X, t) и диффузии b (X, t) определяются по исход-
ному стохастическому дифференциальному уравнению, описывающему по-
ведение рассматриваемой системы, формулами
a(X,/)=lim -!-Л1{[М<+Д0—МОЛМО}?' (7.36)
Д£->0 ш
b (X, t) = lim М {[X (/ + до —X (0121 X zo) > 0. (7.37)
Д/->0 Д/
Если стохастическое дифференциальное уравнение имеет вид
dk/dt = f (X, 0 + g (X, 0 n(0, X(/o) = Xo, (7.38)
где f(X,/) и g (X,0 — детерминированные функции своих аргументов,
п (0 — гауссовский белый шум с нулевым математическим ожиданием и
корреляционной функцией
n(t2)} = (l/2)^od(^ - У, (7.39)
то коэффициенты сноса и'диффузии равны
g(Xto=f(X,o+4~ "at ° ’ = (7-40>
Коэффициент сноса а (X, 0 характеризует среднее значение локальной ско-
рости марковского процесса X (0, а коэффициент диффузии b (X, t) — ло-
кальную скорость изменения дисперсии приращения. Если плотность
вероятности перехода зависит лишь от разности временных аргументов
т = t—/0, а коэффициенты а и b не зависят от t и tQ, то рассматриваемый про-
цесс X (0 называется однородным во времени.
При начальном условии р(Х, /0) = р$ (X) = б(Х — Хо) безусловная
плотность вероятности р(Х,0 совпадает с плотностью вероятности перехода
л (X, t \ Хо, t0). При этом решение уравнения (7.33) называется фундаменталь-
ным решением.
Для отыскания решения уравнения Фоккера—Планка—Колмогорова
(7.33) необходимо задать начальное условие
р(Х, /0) = Ро(Х) (7.41)
183
Рис. 7.2. Поглощающие границы
и указать граничные условия. Граничные условия могут быть весьма разно-
образными и определяются существом физической задачи. Приведем здесь
три вида граничных условий.
Если случайный процесс %(0 может принимать всевозможные значения
от —оо до 4~оо, то обычно выполняются, нулевые граничные условия
G (—оо, t) = G (оо, 0=0, р (—оо, 0 = р (оо, 0 = 0. (7.42)
Пусть случайный процесс % (t) может принимать значения лишь в огра-
ниченном интервале (с, d), причем в точках cud помещены отражающие гра-
ницы (экраны): траектория процесса, достигшая этих экранов, зеркально от-
ражается от них. В этом случае должны выполняться условия отражающих
границ:
G (с, /) = G (а, о = 0. (7.43)
Предположим теперь, что в граничных точках с, d расположены погло-
щающие экраны: траектория, достигшая границы, поглощается ею и исклю-
чается из дальнейшего рассмотрения. Условие поглощающих границ (экра-
нов) имеет вид
р (с, 0 — р (d, 0 — 0. (7.44)
При наличии поглощающих границ можно интересоваться вероятностью
поглощения на одной или обеих границах за некоторое время t. Поскольку
аналитическое решение такой задачи оказывается сложным, то при отра-
жающих или поглощающих границах часто ограничиваются вычислением
характеристик (моментов) случайного времени Т, цр истечении которого
траектория процесса, исходящая при t = 0 из некоторой точки %0, заклю-
ченной внутри границ (с < Хо < d), впервые достигнет границ с, d (рис. 7.2).
Для однородного во времени диффузионного процесса математическое
ожидание 7\ = М {Т} и дисперсия D = D {Т} случайного времени Т пер-
вого достижения границ определяются обыкновенными дифференциальными
уравнениями Понтрягина
1 л d2 Т} dTx
Q ^(^ ) “Ьа(?1о .. +1—0,
2 (/Лгр izA/o
(7.45)
1 „ d?D „ dD I d7\ V
Тд(Х«’^7Г.+а'Х»)_7Г_+&(Х»>Нг- =0- <7-46>
Решения этих уравнений должны быть неотрицательными: 7\(с, %0, <0 > О,
D (с, %0, d) > 0 и при поглощающих границах с, d должны удовлетворять
условиям
Л(С, с, d) = Тх (с, d, d) = О, D (с, с, d) = D (с, d, d) = 0. (7.47)
184
При таких граничных условиях решения уравнений (7.45) и (7.46) да-
ются выражениями
где
ф (х) — 2 J dx» (7-5°)
г- / а \ -1 а х
dT'{z}- = 2е~<|>(г) | ] f е-ф (*> dx f —еф(»> dy-
dz' IJ J J b(y)
L \c / c c
(7.51)
В заключение укажем/что для одномерного марковского процесса
во многих случаях просто находится стационарная плотность вероятности
Pst (М ~ Р (К 0, если она существует. Поскольку она не зависит от вре-
/~>оо
мен и, то из (7.34) следует, что
d [fr (X) pst (X)]
dX ~
2а (X) 2(?,
Общее решение этого уравнения известно 145]. При нулевых граничных ус-
ловиях (G — 0) оно дается выражением
X
V
₽8‘(Х)“7аГехр
а(х)
Ь(х)
dx
(7.52)
2
где С — произвольная постоянная, определяемая из условия нормировки
плотности вероятности, X' — произвольная точка интервала, в котором
определен процесс X (t).
Применительно к стохастическому дифференциальному уравнению
(7.38), для которого коэффициенты сноса й диффузии определены формулой
(7.40), решение принимает вид
Pstfr)
с
gw
ехр
f(x)
g2(x)
dx
(7.53)
<85
2. ПРИМЕРЫ
7.1. Однородная цепь Маркова с двумя состояниями. Пусть цепь
Маркова {0П, п = 0, 1,2, ...} имеет два состояния Ох и Ф2 (рис. 7.3)
с вероятностями начального состояния /?х(0) = pj, р2(0) = р®,
где р? + р“ = 1. Одношаговые вероятности перехода не зависят от
времени и заданы лп = 1—а, л12=а, л21=р, л22=1—р. Ис-
ключим из рассмотрения два тривиальных случая: 1) а + р = О,
т.е. а = р = 0, 2) а + р = 2, т. е. а = 1, р = 1. В первом слу-
чае не происходит смены состояний (оба состояния являются погло-
щающими) и система остается в заданном начальном состоянии. Во
втором случае смена состояний происходит детерминированно, и
если начальное состояние задано, то поведение системы будет не-
случайным.
Требуется найти вероятности перехода п)к(п) за п шагов, без-
условные вероятности pft(n), финальные вероятности рк и относи-
тельную долю времени, проведенного системой в одном из состояний
в течение большого интервала времени.
Решение. Применительно к данному примеру в уравнениях (7.16)
и (7.17) нужно положить k = 1, 2:
Pi = Pi (1 — «) + P2P. Pi + Pi = Ь
Отсюда находим финальные вероятности
Л = р/(а + Р), р2 = а/(а + р). (7.54)
На основании (7.13) получим следующее выражение для матрицы
вероятностей перехода за п шагов
ТЗТ+ТТЯ (1-а-₽)п -^-(1-(1-а-Р)"]
Лп__ а + Р а + Р « + Р
|1-(1 -а-РП ^г+Чт<1-а-Р)П
_а+р а4-р а+р
(7.55)
Так как | 1 — а — Р | < 1 при а + р =£ 0 и а + Р #= 2, то
(1 - а -[})“-> 0 и
л" = ГР1 р2
[pi /J’
где ph — финальные вероятности.
------Т1--Рис. 7.3. Цепь Маркова с двумя состоя-
ла *1-----«2 я ниями
18В
Рис. 7.4. Одномерные дискретные случайные
блуждания
1-р-У
О
-7
1 1
2 3 п /?+7 f
По формуле (7.14) находим безусловные вероятности состояний
через п шагов
Рт (п) = И plI л»---1— [0 + (apt _0р»2) (I _ a _0)П+,а +
а4-р
+ (₽р§- ар?)(1 - а- РП (7.56)
Отсюда при п -> оо получаем прежние значения финальных вероят-
ностей (7.54).
Вычислим относительную долю времени нахождения системы в
каждом из состояний. Для этого формально отождествим состояние
О’] с нулем и состояние 02 с единицей. Пусть случайная величина
Хп — (0, 1} означает состояние системы в момент времени tn, при-
чем интервалы времени между соседними скачками одинаковы,
т. е- ^n+i — tn — const, п = 0, 1,2, ... Тогда сумма Хг + Х2 +
+ ... + Хп определяет, сколько раз из общего числа п проведены
системой в состоянии 1. Обозначим начальное состояние через / и
л1г(п) = Р{Хп = 1|Х0 = /}-
Известно, что математическое ожидание случайной величины X,
принимающей лишь два значения 0 и 1, совпадает с вероятностью
Р {X = 1}. Поэтому
AT {X, + Х2+ ... + ХП|ХО — /’} = (1) + л;2(2) + ... + nj2 (и).
Среднее значение относительного времени, проведенного си-
стемой в состоянии 1, очевидно, равно {л/2(1) 4- Л;2(2) + ... +
+ л72(п)}/п Если предел последовательности {ап} при п -> оо
равен а, то предел последовательности (аг + а2 + ... + ап)1п так-
же равен а. Поскольку л72 (п) -> р2 ПРИ п -> оо, то среднее значение
относительного времени, проведенного в состоянии 1, стремится
к финальной вероятности р2 при п -> оо. Аналогично предел сред-
него значения относительного времени пребывания в состоянии О
равен Финальные вероятности рг и р2 даются формулой (7.54).
7.2. Неограниченные случайные блуждания. Частица совершает
случайные блуждания вдоль оси 0, представляющие собой однород-
ную цепь Маркова со счетным числом состояний: из любого состоя-
ния / через некоторую единицу времени возможны переходы лишь
в три ближайших состояния / + 1, /, / — 1 с вероятностями
л>,Я-10) = Р. (1) = 1 —р — Я, = q (рис. 7.4).
Пусть начальная координата частицы О = 0 при t = 0. Нужно
найти вероятность того, что в момент времени t = п коорди-
187
ната частицы 0n = k, где k = 0, ±1, ±2, ±п, а также матема-
тическое ожидание и дисперсию случайной величины 0П.
Решение. Обозначим через Zt изменение координаты частицы в
дискретные моменты времени t — 1,2, п, ... Случайная величина
Zt может принимать три значения: 1,0, —1 с вероятностями
p{Zt = \} = p, Р{2г = 0}= 1 — р — q, P{Zt--------1} = 9-
Через п шагов координата частицы будет равна 0П = У, Zt. Случай-
i= 1
ная величина 0П может принимать различные значения k = 0, ±1,
±2, ..., ±п. Чтобы попасть в точку k, частица должна сделать пх
положительных шагов, п2 отрицательных шагов и п0 «нулевых», где
пх, п2 и п0 — неотрицательные целые числа, удовлетворяющие ра-
венствам
пх — п2 = k, п0 = п — (пх + и2).
(7-57)
Вероятность того, что 0n — k, определяется обобщенным бино-
миальным законом
Р{0„ = Л} = 2———рп' (1 -р—qf’Cf1*,
(7.58)
где суммирование производится по всем значениям n0, nt, п2; удов-
летворяющим равенствам (7.57).
Обозначим через тх и Dx математическое ожидание и дисперсию
случайной величины Zt (за один шаг): тх = р — q, Dx = р + q —
— (р — q)'1. Тогда математическое ожидание тп и дисперсия Dn
случайной величины 0П будут определяться формулами
тп = М {0n} = птх, Dn = М {(0П — n/nx)2} = nDx. (7.59)
В том частном случае, когда р + q — 1 (сохранение предыду-
щего состояния не допускается), формула (7.58)-примет вид
р = k} = C^n+fc)/2 р^+ыч q(.n—k)/2
7.3. Дискретный марковский процесс с двумя состояниями (слу-
чайный двоичный сигнал). Пусть процесс 0(/) в любой момент вре-
мени может иметь лишь одно из значений 0Х = 1 или 02 = —1
(рис. 7.5), причем вероятность перехода Oj -> 02 за малое время Л/
равна ХЛ/, а вероятность перехода 02->0х равна цДЛ Известны ве-
роятности начального состояния р" = Р{0(/о) = 1} и р2 =
= Р{0(/о) = -1} = 1-рЛ
^А
Рис. 7.5. Случайный двоичный сигнал
1$8
Нужно вычислить вероятности перехода ni}(t0, t).= P{Q (/) =
= 0(Zo) = Фг), где = 1, О2 = —1; i, /=1,2, вероятности
стационарного состояния рг и р2, а также математическое ожидание
и корреляционную функцию процесса 0 (/).
Решение. Для данного примера а12 = к, azl = р. Из (7.23) на-
ходим аи = —%, а22 = —р, Так как все четыре коэффициента ац —
постоянные величины, не зависящие от времени, то процесс 0 (/)
является однородным.
Дифференциальные уравнения (7.24) принимают вид
(^о> 0= kn.ji (£q, t) 0>
-£-nf2(Z0, 0= — ил/2ао,0 +к-п(/0, 0, < = 1. 2. (7.60)
Из условия нормировки (7.18) имеем л12 (t0, t) = 1 — nu (t0, t).
Поэтому первое из уравнений (7.60) можно записать иначе
_длиОо,О =-_(Х+ц)Л11(/0, 0+p, t>t9.
ot
Общее решение этого линейного неоднородного дифференциального
уравнения первого порядка с начальным условием au(f0, tQ) = 1,
которое следует из (7.20), известно:
jtu(Z0, /) = р. fe-(X+w«-s>ds4-е-<х-« <‘-м=_0:—J.
J Л+н
]-(—-—\e~(X+w т, т = £—to>0.
U+p/
В результате решения системы уравнений (7.60) для любых т > 0
получим
Ли(Т)==ТГ—)е-<х+ч’\ Я12(т)=(-3—)[1 — е-^+^Я,
л-4*ц \ Х+ [д / \ Л,-{-[Л /
(7-61)
л^(т)=тт-+(тЬ-)е-а+юх’ л^МтО1_е-а+",т|-
Отсюда при т оо находим вероятности стационарных значений
рг = р/(% + |л), р2 = %/ (X + р). (7.62)
Эти вероятности можно было легко найти из уравнений (7.30).
139
Зная вероятности начальных значений и вероятности перехода,
записываем выражения для безусловных вероятностей значений
процесса
Pi(t9 +s) = Pi лп(8) + (1 —Pi) n2i(s) = -77— +(p“ —Л—) e-‘^”,
(7.63)
p2(4>+s)=(i— pi)n22(s) +p?ni2(s) = y^“~(p* ~‘7+7)x
xe~ s>0.
На основании определения находим математическое ожидание
процесса
тв (/) = М {G (/)> = 1 .Р1 (0 -1 -р2 (0 =
= —h 4-2 (р'{-------т — t—/0. (7.64)
ц4~ X \ X 4-ц /
Аналогично вычисляем корреляционную функцию ,
Яе (s, т) = М {0 (10 + $) 0 (/0 + s + т)} - М {0 (/„ + s)} М (0 (Zo + s + <
4-t)}=J—------------[JLZ±_|_/n?-----'lx
I (Х4-ц)2 LX4-g V Х4-Ц/ I
X (рЧ-------—)e—(^ + ц> Д е-(Л-+«>т, s, т>0. (7.65)
\ / I
Нетрудно убедиться, что в стационарном состоянии
те = (р — %)/(Л + р), Re(r) = 4Ар(Х + р)~2ехр[—(К + р) | т 11.
Укажем, что если дискретный марковский процесс Ф (/) имеет
два произвольных значения <рх и <р2, то его можно выразить через
случайный процесс 0 (/) с двумя значениями ±1 при помощи следую-
щего линейного преобразования
ф (0 = 4-1 (<₽1 +ф2) +(Ф1-Ф2) 0 (01. (7.66)
7.4. Линейный процесс рождения и гибели [461.Рассмотрим дис-
кретный процесс 0(/), в котором допускаются как положительные,
так и отрицательные скачки. Этот процесс называется процессом
рождения и гибели и определяется следующими постулатами: 1) если
в момент времени t система находится в состоянии / (/= 1, 2,...),
то вероятность перехода / -> / + 1 в малом интервале времени (/,
t + Д/) равна Х7-Д/ + о(Д/); 2) если в момент времени t система на-
ходится в состоянии j (j = 1, 2, ...), то вероятность перехода /->
-> / — 1 в интервале времени (/, t + ДО равна ц,Д/ 4- о(Д/); 3) ве-
роятность перехода в состояние, отличное от двух соседних, есть
о(Д/); 4) вероятность сохранения прежнего состояния равна
1 — (X; + Н>)Д/ + о(Д0; 5) состояние / = 0 является поглощаю-
190
щим; если изображающая точка попала в это состояние, то процесс
прекращается.
Решение. На основании постулатов 1—5 записываем уравнение
(7.26):
Pi^t ) = ^7-1 Pi-1 (0—(h + Цу) р; (/)+ Р7+1 P;+i (0, j = 1, 2,... (7.67)
В рассматриваемом конкретном случае, когда состояние / = О
является поглощающим, нужно полагать = Хо = р0 = 0. По-
этому
dpQ(t)/dt = HiPi(/). (7.68)
Предполагается, что в начальный (нулевой) момент времени система
находится в некотором состоянии /0, 0 < /0 < оо, и, следовательно,
начальные условия имеют вид
P>(O)=6Wo=J 1 при ^/о’ (7.69)
I 0 при /=/=/0.
В общем случае, при произвольных функциях %; и ру, решение
уравнений (7.67) и (7.68) оказывается затруднительным [461. В том
частном случае, когда процесс рождения и гибели является линей-
ным: hj = X/, Ру = р/, X = const > 0, р = const > 0, решения при
начальном условии 0 (0) = /0 = 1 даются выражениями
Ро(0 = а(/), p}(t) = [1 - а(0И1 - ₽(О10'~*(0. / = 1. 2,...,
(7-70)
где
-Pte^X-l) g Х(е<х~^г-1)
Математическое ожидание и дисперсия такого линейного про-
цесса рождения и гибели равны
т0(О = ехр[(Х— р)П. Da(/)=-^-bt e^-^Je^-W —1]. (7.72)
X —ц
Из (7.70) и (7.71) находим вероятность того, что ко времени t
система будет находиться в состоянии / = 0 («коллектив» вымирает):
р0 (/) =-- р 1)/(%е<*-|*)'—р).
Вероятность того, что «коллектив» когда-нибудь выродится, полу-
чаем отсюда предельным переходом при /-> оо:
1- /Л ( 1 ПРИ /-7-704
hmp0(0= . (7.73)
^->оо ( ц/Х при л>р.
Этот результат говорит о том, что «коллектив» вымирает с вероят-
ностью, равной единице, если интенсивность гибели больше интен-
сивности рождения. Если же интенсивность рождения больше ин-
тенсивности гибели, то вероятность вырождения равна отношению
их интенсивностей.
191
При начальном условии 0(0) = /0 > 1 формулы для математи-
ческого ожидания и дисперсии получаются умножением правых час-
тей выражений (7.72) на /0. Вероятность вырождения (7.73) по-преж-
нему равна единице при X < р. и равна (р./Ху при Л > р.
7.5. При различных граничных условиях нужно найти основные
характеристики непрерывнозначного марковского процесса Х(/), -
заданного стохастическим дифференциальным уравнением
dK/dt = —аХ + n(i), X (0) = Хо, (7.74)
где а — постоянная величина, «(/) — гауссовский белый шум с ну-
левым математическим ожиданием и дельтаобразной корреляцион-
ной функцией (7.39).
Решение. По формулам (7.36) и (7.37) найдем сначала коэффи-
циенты сноса и диффузии для процесса X (f). Отметим, что решение
уравнения (7.74) при начальном условии X (0) = Хо можно записать
в виде
X(0 = Хо е-|- е~ °' j еах п (х) dx. (7.75)
Согласно (7.74) приращение процесса за малое время А/ равно
<+Д(
Х(/-рД0—Х(0 = J [—ak(x)+n(x)]dx. (7.76)
Отсюда находим математическое ожидание условного приращения
<+д<
Л4{[Х(^ + А0—Х(0||Х(0} = — a | X(x)dx,
t
а также выражение для коэффициента сноса а (X):
а(Х)= — a lim—— . f k(x)dx — —аХ(0.
Л(->о Д/ J
t
Ha основании (7.76) для среднего квадрата условного прираще-
ния можем написать
Л4 {[X(Z-)-A0—X(0]8|X(0} = || Л4 {[—аХ(х)+n(x)J х
(/-f-Д/
J X(x)dx) 4-Д^-.
Поэтому
6(X) = a2lim -L.fX(0A0« + -^- = А.
дг->о Az 2 2
192
Уравнение Фоккера—Планка—Колмогорова принимает вид
= + ' (7.77)
Можно убедиться (например, непосредственной проверкой), что плот^
ность вероятности перехода эт (X, /|Х0, 0), являющаяся фундамен«
тальным решением уравнения (7.77) при заданном начальном усло-
вии р0(Х) = 6(Х — Хо), дается выражением
л (X, /| Хо, 0) = [2ло2(1 — е“2а9]“1/2 ехр
(X- Кие- ^)2
2а2 (1— е~ >а/)
Это есть нормальная нестационарная плЪтность вероятности
с математическим ожиданием Хобхр(—at) и дисперсией
о2[1 — ехр (—2а/)]. Полагая оо, получаем стационарною плот-
ность вероятности
1 / Х2.\ 2 л/0
р . (X) — ехр-----------, о2 — —2- .
V 7 <f]/2n Ц 2о2 / Ха
Если плотность вероятности начальной координаты Хо совпадает
со стационарной плотностью вероятности, т. е (X) = pst (X), то
нетрудно проверить, что переходный процесс отсутствует и стацио-
нарное состояние имеет место, начиная с начального момента вре
мени t = 0.
Пусть в симметричных точках — с = d = h помещены поглощаю
щие границы и Хо = 0. Согласно формуле (7.48) среднее время пер-
вого достижения таких границ рассматриваемым процессом (7.74)
равно
--h/o
у j (2ф(х) —l]ex’/2dx,
о
где Ф(х) — интеграл вероятности (2.9). Выражение для дисперсии
времени первого достижения границ (7.49) оказывается более слож-
ным [45] и поэтому не приводится.
3. ЗАДАЧИ И ОТВЕТЫ
7.1. Частица совершает случайные блуждания вдоль прямой 9,
представляющие собой однородную цепь Маркова. Координата час-
тицы в дискретные моменты времени t — 1, 2, 3, ... меняется на слу-
чайную величину Zf, принимающую лишь два 'значения +$ и —s с
одинаковыми вероятностями, равными 1/2. При 9 = ±2s расположе-
ны отражающие экраны (частица, достигшая этих экранов, в сле-
дующий момент времени отражается от них внутрь области (—2s,
2s), изменяя координату соответственно на величину zhs с вероят-
ностью 1) (рис. 7.6). Обозначим через 9П координату частицы через
п шагов. Возможные значения 9П есть —2s, '62 = —s, Фз — 0,
7 Зак 1203 193
= s, <>6 — 2s. Записать матрицу одношаговых вероятностей пере-
хода и определить начальные вероятности, при которых процесс бу-
дет стационарным, начиная с t = 0.
Ответ'.
г 0 1 0 0 0 1
1/2 0 1/2 0 0
Л = 0 1/2 0 1/2 0 > Pl =/>5=1/8, Р2 = Рз = Р4= 1/4.
0 0 1/2 0 1/2
0 0 0 1 0
Указание. Цепь Маркова будет стационарной, если началь-
ные вероятности совпадают с финальными; последние определяются
в результате решения системы алгебраических уравнений (7.16),
(7.17). Для составления матрицы вероятностей перехода целесооб-
разно воспользоваться представлением цепи Маркова в виде графа.
7.2. При тех же условиях, что и в предыдущей задаче, и при 0 =
= —2s помещен отражающий экран, а при 0 = 2s поглощающий.
Требуется: 1) записать матрицу одношаговых вероятностей пе-
рехода; 2) определить вероятность поглощения за четыре шага,
если в начале частица находилась в состоянии Оз(0 = 0); 3) вы-
числить среднее значение времени по истечении которого час-
тица в первый раз «прилипнет» к поглощающему экрану, если в на-
чальный момент она находилась в состоянии й'г (i = 1,5).
Ответ'.
1) л =
г 0 .. I 0 0 0 -1
1/2 0 1/2 0 0
0 1/2 0 1/2 0
0 0 1/2 0 1/2
0 0 0 0 1
2)/С = 1/8; 3) Т», = 16, То = 15, То, = 12, То - 7,
То6 = 0.
Указание. Для вычисления вероятности поглощения можно
рассмотреть возможные траектории движения частицы из состояния
Оз, которые приводят к поглощению за четыре шага. Среднее,время
до первого достижения поглощающей границы можно определить,
решая разностное уравнение T^fe = (1/2) (Т^_1 + 7\+1) + 1
(k = 2, 3, 4) с граничными условиями Т^ = + 1, Т^6 = 0.
Рис. 7.6. Случайные блуждания
двумя отражающими границами
между
>94
7.3. Имеется однородная цепь Маркова с двумя состояниями
'fl'x и #2» одношаговые вероятности перехода равны nn = p, зт22 = q.
Пусть в реализации этой цепи сохраняются только состояния, соот-
ветствующие нечетным моментам времени t = 1, 3, 5, ..., а осталь-
ные исключаются. В результате получается новая цепь Маркова с
состояниями 'fl'x и 'б'з’ Требуется ’определить вероятности перехода
jtii и ji22 за один шаг для полученной цепи.
Ответ: i = р2 + (1 — р)(1 — q), Л22 = 72 + (1 — р)(1— q).
7.4. По системе связи передаются двоичные символы, которые
обозначим 'fl'x и Каждый переданный символ последовательно
проходит через несколько устройств (каскадов), в каждом из кото-
рых выходной символ из-за наличия шумов лишь с вероятностью
р воспроизводится верно и с вероятностью q = 1 — р переходит в
другой. Пусть 0П = {'О'х, Фа} — символы на выходе n-го устройства.
Последовательность символов 90, 0Х, ... есть однородная цепь Мар-
кова с матрицей вероятностей перехода
L0 Р\
\
Начальные вероятности на входе системы заданы: p°i = Р{90 = 'fl'i},
Р2 = Вычислить вероятность Р{90 = | 9П = }
того, что если на выходе n-го устройства принят символ Фр то был
передан этот же символ.
Ответ:
^{00 = ^11^ = ^} =
p"i+pQi(P-q)n
1+(Р?~Р§)(Р~<7)л
7.5. Найти матрицы переходных вероятностей для марковской
цепи, описывающей следующий процесс Каждая единица выпускае-
мой на производственной линии продукции с вероятностью р идет
в брак. Качество каждого отдельного изделия (годно или дефектно)
предполагается не зависящим от качества других изделий. Контроль
качества изделий состоит в следующем. Пока не появится i небра-
кованных изделий подряд, проверяется каждое выпускаемое изде-
лие (первое правило) Затем из каждых г последующих изделий для
проверки равновероятно выбирается лишь одно (второе правило).
Если будет обнаружено бракованное изделие, то контроль произво-
дится по первому правилу: проверяется каждое изделие вплоть до по-
явления г небракованных изделий подряд и т. д. Предполагается, что
моменты времени п отсчитываются при проверке каждого изделия
по первому правилу и серии из г изделий — по второму.
Пусть состояние '9k (k = 0,1, 2, ..\.) означает, что при контроле
по первому правилу последовательно появились k небракованных
изделий. Состояние же означает, что проверка осуществляется
согласно второй -части процедуры (проверяется одно из г изделий)
и появилось одно или 'более небраковаттных изделий.
7*
195
Ответ [47]: при всех значениях d
jijk — Р
пребывание в состоянии после п + 1
проверок | пребывание в состоянии
после п проверок
р при /г = 0, /=0, I, ..., t, М-1,
1 — р при /? = /+!, / — О, 1, ..., I или /г = / = /4-1,
О во всех остальных случаях.
7.6. Частица совершает блуждания между точками, расположен-
ными на одинаковых расстояниях друг от друга на окружности (об-
щее число точек равно п). При этом в дискретные моменты времени
/= 1, 2, 3,... с вероятностью р частица переходит в соседнюю точку
в направлении по часовой стрелке и с вероятностью q — против ча-
совой стрелки (р + q = 1). Если частица в начальный момент t = О
находится в некотором состоянии (i = 1, п) и на первом шаге по-
падает в состояние ^+1 (или ftf-i), то говорят, что она совер-
шает полный цикл блужданий, если в состояние 'Of она впервые вер-
нется из состояния ,(h_1 (или 'fl'f+i). Очевидно, 'что за полный цикл -
блужданий частица побывает во всех промежуточных состояниях.
Требуется определить вероятность Ро совершения полного цикла
блужданий.
Ответ [48]: Ро = (р ~ Ч)(Рп + <7П)'(РП — 4П)
Указание. Можно воспользоваться известными результа-
тами решения задачи о случайных блужданиях между поглощаю-
щими экранами [45].
7.7. Вычислить корреляционную функцию и спектральную плот-
ность квазислучайного телеграфного сигнала 9(/), принимающего
два значения = Oq и О2 = —Фо с одинаковыми вероятностями
Pi = Р2 = М2, причем смена значений с вероятностями перехода
ЗТ12 = л21 = q возможна, только в фиксированные моменты времени
tn = А ± пТо, где То — const, и = 0, 1, 2, ..., А — случайная ве-
личина, не зависящая от 9(i) и равномерно распределенная на от-
резке [О, Т01 (рис. 7.7). Рассмотреть частный случай q — 0,5.
Ответ [45]: I
Re(r) = ^o(n----Ш-'Пр— q)n~l 4- ---(n— 1)1(р— q)n,
р = 1—q, (я—1)Т0<|т|<пТ0, . я = 1, 2, 3,
оо
Se (®) = 2 J (т) cos (oxdr =
о
_ frg Toll-(р—<?)а] /sin<oTo/2\«
1— 2(р —p)coscoT04-(p—<?)2\ ®Т0/2 /
196
При р = <7=0,5
₽е(т) =
Оф — 4^-), |г|СП>
\ 1 о /
о ir\\ Л2 Т* /$1П о/ ^\2
s’,M=^4^r'r
О, Iт I > То,
7.8. Вычислить корреляционную функцию и спектральную плот-
ность радиосигнала со случайной начальной фазой при наличии до-
полнительной фазовой манипуляции квазиелучайным телеграфным
сигналом 9(/): s (/) = Л0соз[<в0/+ 9(/) + <р0]. Здесь 9 (t) — ква-
зислучайный телеграфный сигнал, описанный в задаче 7.7, <р0 —
случайная начальная фаза, не зависящая от 9 (/) и равномерно рас-
пределенная на отрезке [—л, л]. Выяснить отличие в характере
спектров при fl'o = л/2 и#0 = л.
Ответ. [45]: 7?s(t) == (Ao/2)[cos2Оо + fm (|т|) sin2О0]cos <оот,
где
fm(h|)= (Р — <7)"ф +%1(т------4)1’ тТ0^г<(т+ \)Т0,
m = 0, 1, 2, ....
Ss (<в) = (л/2)Л§ [6 (со—©о) 4- б (со + соо)] + (Лg/4) То sin2 9n х
х Г_________1 —(Р~ ?)2__________/ si" Y-\2 '
[ 1—2(р—<7)cos(®—®(J)7'o+(P —<7)2 \ V- /
л___________1 — (р—#__________{ sin у+ VI
1— 2(р—<7)cos(w+<o0) Te+(p — <7)2 (,?+/]’
Т± = («±еоо)7,о/2-
При б'о = л/2 спектр является сплошным, а при О'о =-л — чисто
дискретным.
7.9. Найти безусловную вероятность р/т), т — t — t0, числа
появлений / некоторого случайного события в полуинтервале [/0, t).
Случайный процесс 9(/) является дискретным, однородным, прини-
мает только целочисленные значения 0, 1, 2, ..., /, ... и может лишь
Рис. 7.7. Квазислучайный теле-
графный сигнал
Рис. 7.8. Пуассоновский процесс
197
возрастать (рис. 7.8). Начальная вероятность и вероятности перехода
заданы: .
Р/ = рДо) =
1 при / = О,
О при j — 1, 2,
лп(/, /+Д/)=[ ?
’ I ХД/+о(Д/)
при i > /,
при i = j — 1,
nJ} (t, t + Д/) = 1 — ХА/ — о (Д/).
Рассмотреть также случай неоднородного процесса, когда ин-
тенсивность перехода из состояния /— I в / зависит от времени, т.е.
л>-1, ДО t + АО = МОА/ + о(А0-
Ответ [461: вероятности pt определяются законом Пуассона:
Р/(т)=-^-е-Ч / = 0,1,2,..., x = t—10,
O = -^-H^(s)ds j ехр I — Jx(s)ds j, / = 0,1,2,...
' \ tn /
7.10. Вычислить вероятность а также математическое ожи-
дание и дисперсию для линейного процесса рождения 0(/), задан-
ного следующими условиями: 0 (0) = 1, лЛ ;+1 (/, t + Д/) =
= Х/Д/ + о (Д/), / = 1, 2, 3, ..., t > 0, где X = const.
Ответ". pj(t) = e~xz(l —e-w)/-1, / = 1> 2, 3, .... то (/) =
= е*‘, £>е = ex/(ew — 1).
Указание: Такой ответ можно получить из результатов
(7.70)—(7.72} примера 7.4, положив р. = 0.
7.11. Вычислить вероятность pn(t), если начальное значение
процесса рождения 0 (/), заданного в задаче 7.10, равно 0(0) =
= т <. п.
Ответ [35]: pn(t) =----—--------e-mV(l—e—Myi—т.
(т— 1)! (л—т)!
7.12. Пусть 0 (/)— марковский процесс рождения, для которо-
го справедливы следующие соотношения:
Р {событие наступит в (/, t + Д/)| 0(/) нечетно) = ХГД/ + о(Д/),
Р {событие наступит в (/,/-(- Д/)| 0(0 четно) = Х2Д/ -j- о(Д/).
Найти следующие вероятности:
Рх(О = ^{0(0 нечетно), р2(/) — Р{9(0 четно).
Ответ [47]: Pl(t} =+*»>'),
+^2
р2(А =—h------1---h—е-
A-i -f- Х2 ^14“ ^«2
198
Указание: Вывести и решить дифференциальные уравнения
dpi(t)ldt = + X3p2(Z),
dp2(t)ldt = ^tpiff) ^2p2(0-
7.13. При тех же условиях, что и в задаче 7.12, найти математи-
ческое ожидание процесса Q(t).
Ответ'.
м {е (0}=1 + {ехр r _(Xi+м л ~1}-
7.14. Найти вероятность рп(/), а также математическое ожида-
ние и дисперсию для линейного процесса гибели, заданного следую-
щими условиями: pfo = Р {9 (0) = Л/} = 1, pf = 0 при / < Nf
лЛ t+ ДО = № + о(М), j = N, N - 1, ...» 0.
Ответ*. pn (/) = ——— (1 — е~И N~n,
mQ (/) == Afe- De (/) = Ne~ * (1 — e^).
7.15. Используя тот факт, что марковский процесс остается мар-
ковским и в обратном направлении, показать, что вероятностные
характеристики процесса гибели можно получить из соответствую-
щих свойств процесса рождения.
Указание. Следует воспользоваться равенством
Р{9(/ + т) = /| 9(0 = j}P{9(0 = /} =
= Р{9(0 = /I 9(Н-0 = i}P{B (t + т) = i}.
7.16. Требуется вычислить корреляционную функцию и спект-
ральную плотность радиосигнала со случайной начальной фазой
при наличии дополнительной фазовой манипуляции случайным те-
леграфным сигналом:
s(0 = X0cos[coo/ + 9(0 + (pot
Здесь сро — случайная начальная фаза, равномёрно распределенная
в интервале (—л, л), 9(0 — не зависящий от <р0 стационарный сим-
метричный телеграфный сигнал (см. рис. 7.5), принимающий лишь
два* значения dz'fl'o, 0 ^^о^ л с вероятностями рг = р2 = 1/2; ве-
роятности перехода заданы выражениями
лн(т) = л22(т) = (1 + е—2Хт)/2, л12 (т) = л21 (т) = (1 — е~2^)/2.
Ответ*.
Rs(%) = (Ло/2)[со82<90 + ехр(—2%|T|)sin2<&0] coso0t,
Ss(co) = (лЛо/2) [6 (со—cOq) + 6(со + coo)J cos2 -&o + Ao Isin2 Фо x
X [ 1 I 1 1
_ 4X2 + (co—coo)2 4X2 + (co4-coo)2 J *
199
Рис. 7.9. Импульсный
случайный процесс с
тремя значениями
В общем случае.спектр является дискретно-сплошным. В частном
случае Фо = л/2 спектр будет сплошным, а при Фо = л — дискрет-
ным.
7.17. Импульсный случайный процесс 0(/) принимает три зна-
чения: fl'i = Фо, Ф2 — —Фо и Фз = О (рис. 7.9). Заданы одношаговые
вероятности перехода за малое время Д/:
А.12Д/(Ф] -> Ф2), А13Д/(Ф! -> Ф8), Л23Д/(Ф2 Ф3),
Х21Д/(Ф2 ->ФО, Х31Д/ (Фз -> ФО, Х32Лг (Фз -> Ф2).
Нужно найти: 1) вероятности стационарных значений, 2) корре-
ляционную функцию процесса 0(/) в стационарном состоянии.
Ответ [49]:
1) рх = ajk^, р2 = a2/krk2, ря = az/kj?.*, где
®1 ~ \з1^21 4" ^'31^'32 4-
®2 = ^12^32 4" ^хз^зз 4~ ^Х2^3Х»
«3 = ^23^X2 4" ^23^13 4" ^2X^X3'
^1,2 = (1/2)(^Х2 + Чх + ^31 + ^13 + ^23 + ^зз)
=F [(1/4)(Х12 + Х21 + Х31 + Х13 + Лад 4- Х32)2 —
(^ЗХ^ЗХ 4* ^зх^гз 4” ^2X^32 4" \х2^32 4-
+ ^23^13 + ^13^21)11/2;
^1^2 = ^31^214~ ^31^ 23“Ь^21^32“Ь^12^32~b^13^23~Ь^12^31 “Ь^23^12 ”Ь
+ Х23Л,13 + A,13X2i;
(ai—аг)2—^2 (ои.+а2)+&2 tai (2Xi24-А»1з)4-<Х2 (^21+^23)] у
klkK^-kr)
xe-kM х
^2 (о&1 — O^)2 — ^2 (а1Ч~°^2) Ч~^1 [о^1 (^12~1~^1з)+0С2 (2Х214~^2з)] ’
t (сх-1—«2)а—k± k2 (^1+062)+/?2 [cxi (2^12+^13) +а2 (2X2i+Х23)]
хе—1т|1
2) ₽(т) = Ф§
200
7.18. Из ответа к задаче 7.17 получить результаты примера-7.3.
Ответ-, нужно положить рз = Р{0(/о) = fM = О, А.13 — Л23 = 0,
+^32 = 1, f>i= — f^ = 1- При этом кг = 1, k2 X12+lw
«1 = ^12. «2 = ^21. а3 = 0 и R (т) = I—(^12 + *-21) |т|1.
7Д9. Рассмотреть следующие три частных случая задачи 7.17:
О ^12 = ^21 == М ^31 = ^32 = И> ^23 = ^13 = Р»
2) Х12 = Х21 = ^23 = ^32 = Н» ^31 = ^13 = Р»
3) Х12 = Х21 = О, Х23 = Х13 = р, Х31 = Х32 = р,.
Ответ:
1) Pi= Р2 = р/(2р+ р), Р3 = р/(2р +р),
R (т) ехр [-(2Л+р) | т |];
2ц + р
2) Р1 =Р2 = Рз = 1/3, R (т) = ——!—— [(2А. +р —
(«2—*1)
— е-*» 1*1 —(2Х+р — &а) е~*> ।х I];
3) Р1=р2 = -^-, р3=-£—,R(T)=^-^e-P4
2н + р 2ц + р 2р + р
7.20. Получить выражения плотности вероятности и ковариа-
ционной функции стационарного импульсного случайного процесса
0 (/), заданного следующим образом. Процесс 0(/) представляет со-
бой стационарную последовательность прямоугольных импульсов,
амплитуды которых взаимно независимы и одинаково распределены
с плотностью вероятности p('fl’) (рис. 7.10). «Интенсивность» пере-
хода из нулевого состояния в любое отличное от нуля состояние рав-
на р, а интенсивность обратного перехода равна X. z
Ответ: peW——— б('&) Ч--------
А.-1-ц р+Х
где 6(х) — дельта-функция;
Ыт)= Ое—H-e-xl'tl+m0('—LY[1+ ± е-а+^> № 1,
X-J“P \ Х-4“Р / L И J
где
те = J fl’pl'O'Jd'O', De = f (fl — теУр^Лд.
Указание: Следует учесть, что вероятности переходов про-
цесса 0 (/) совпадают с вероятностями переходов дискретного мар-
Рис. 7.10. Импульсный случайный про-
цесс
201
невского процесса с двумя состояниями, а длительности импульсов
и интервалов между ними распределены по экспоненциальному за-
кону с параметрами X и р соответственно.
7 21 Пусть последовательность случайных величин {Хп} пред-
ставляет собой временные отсчеты гауссовского стационарного про-
цесса 5(0 с экспоненциальной ковариационной функцией /г(т) —
= £)ехр(—а | т |), а > 0, т. е. Хп = 5 (to + tn), п = 1, 2, где
t# — произвольно взятый начальный момент времени. Убедиться,
что полученная последовательность {Хп} является марковской.
Ответ дает следующая теорема [5]: гауссовский случайный про-
цесс будет одновременно и марковским тогда и только тогда, когда
при s < t < т коэффициент корреляции процесса r(tlt удовлет-
воряет функциональному соотношению r(s, т) = r(s, т). Для
гауссовского стационарного процесса с экспоненциальной ковариа-
ционной функцией это соотношение выполняется.
7.22. Независимые случайные величины Х1Э Х2, ..., Хп, ... имеют
соответственно плотности вероятности р (hn) = рп (X). Доказать,
что случайные величины Хг = Хх, Х2 = Xj + Х2, ..., Хп = Xi +
+ Х2 + ... + Хп, ... образуют марковскую последовательность.
Ответ'.
Л„ (хп I xlt х2.хп_х) = Р (Х1’ *8’—v*"* == р (хп_ хп_х).
Р(*1, х2, ХП_!)
7.23. Из независимых случайных величин Хь Х2, ..., Хп, ... об-
разованы новые случайные величины = Хь Хп + сХп^ —
= Хп, п > 2, с = const. Показать, что последовательность {Хп} яв-
ляется марковской.
Ответ'. лп (хп | хъ х2, х^) = р (хп — схп^).
7.24. Вычислить корреляционную функцию и спектральную
плотность радиосигнала с разрывной фазой вида s (t) =
= Л о cos [<оо/ + 0(0 + ср0]. В отличие от задачи 7.8 здесь значения
есть непрерывные случайные величины, равномерно распределен-
ные на отрезке [—л, л], причеми Оупри i#= /независимы. Разры-
вы (скачки) фазы допускаются только через фиксированный вре-
менной интервал TQ = const, а в пределах каждого интервала дли-
тельностью То фаза остается постоянной.
Ответ [45]:
= (Л§/2)(1 - |t|/T0)cos(o0t, |т| < То,
Ss(®) =(Л§/4)Т0 [( Sin<(°-(O°)T°/2 У +(
[Д (со—соо) 7Д2 / \
sin (со + со») Tq/2 \2
(co4-(Bj) Та/2 I
7.25. Решить предыдущую задачу 7.24, приняв, что скачки фазы
могут происходить не через фиксированный интервал времени То,
а в случайные моменты времени, описываемые законом Пуассона,
рт(й) e-v\ т>0, Л=0, 1, 2,...
202
Ответ [45]:
/?s(r) — (Ло/2)е~vlTi cosco0T,
S ((d) = Л1 Г-----1-----+ ------1.
2 L V2+(W-CO0)2 V2 +(C0 + C00)2 ]
7.26. Чисто диффузионный случайный процесс v(t) задан сто-
хастическим дифференциальным уравнением duldt — n(t), у(0)=
= v0, где n(t) — гауссовский белый шум с нулевым математичес-
ким ожиданием и дельтаобразной корреляционной функцией (7.39).
Записать для процесса v(t) уравнение Фоккера—Планка—Колмо-
горова и получить его фундаментальное решение.
Ответ',
р (о, t) = — No p(v, t),
dt K 4 0 <fc2
p(u, 0 =
I Г (У— Уо)2
-т= exp —i-------—
[ Not
7.27. Для чисто диффузионного процесса описанного в за-
даче 7.26, получить выражения плотностей вероятностей для двух
случаев: 1) в точке v = c>v0 расположен отражающий экран;
2) в точке v = с> v0 расположен поглощающий экран.
Ответ'.
О Ро(М)
1
КлУ0 t
(о—Up)2
Not
+ехр
(2с—у—п0)2
У„/
— оо << V С\
2) рп (и. 0= —-(ехр Г — ———
„ /лУ0/ \ [ у0/
__(2с—с—с0)2
Уо/
— оо < у <2 с.
7.28. Записать уравнение Фоккера—Планка—Колмогорова и
получить его фундаментальное решение для случайного процесса
X (t), заданного уравнением d'k'dt + ц. = n(t), Х(0) = 10, где р —
постоянная величина; п (t) — гауссовский белый шум с ковариа-
ционной функцией (7.39).
Ответ'. •
-L.p{Kn=.^pM+±N^p(Kt},
р(>., ()_ |^ИрГ-.^+Ы1].
VjiN.t FL J
7.29. Получить выражение стационарной плотности вероятности
марковского случайного процесса Х(/), заданного стохастическим
дифференциальным уравнением
dX/dt = — уХ + W0/4A. + п(0, > 0,
203
где у > 0 — постоянная величина; п (t) — гауссовский белый шум
с ковариационной функцией (7.39).
Ответ: р„(Х)=(-±-)ехр (—^г)>°2=7р Х>0.
7.30, Получить выражение стационарной плотности вероятности
случайного процесса X (/), заданного стохастическим дифференциаль-
ным уравнением
dkldt = —ak In (X/m) + aXn(/), X > 0,
где а > 0, т > 0 — постоянные величины; n(t) — гауссовский
белый шум с ковариационной функцией (7.39).
Ответ: .-1 _^-ехр [ -^ln X~'n т}-1, о2=аМ0/4, Х>0.
ал у 2л [ 2а4 J
7.31. Марковский. случайный процесс X (/) задан нелинейным
стохастическим дифференциальным уравнением
dk
dl
где т и Q — постоянные параметры; п (t) — гауссовский белый
шум с ковариационной функцией (7.39). Получить выражение ста-
ционарной плотности вероятности процесса X (/).
Ответ: psi(k)~—-—Y^ X2™-1 e~wV/Q, X 0. m > —.
Г (/и)' \ й ) > 2
7.32. Вычислить среднее время 7\ и дисперсию времени D пер-
вого достижения поглощающих границ с, d чисто диффузионным
процессом v(f), описанным в задаче 7.26, предполагая, что началь-
ное значение процесса находится внутри границ (с < < d).
Ответ: Т^с, vOi d) = (2/W0) (d — vQ) (v0 — c)t D (c, vQi d) =
= (1 /62V§)[(d - c)4 - (d + c - 2y0)4l.
7.33. Определить среднее время 7\ первого достижения одной по-
глощающей границы, расположенной в точке X = d, случайным про-
цессом X (/), описанным в задаче 7.28, считая р 0 и Хо < d.
Ответ: 7\ (—оо, Хо, d) = (d — Х0)/р, р 0. .
7.34. Для случайного процесса Д(/) такого же, как и в задаче
7.29, вычислить среднее время 7\ первого достижения поглощающей
границы d, если граница с = 0 является отражающей. Начальное
значение процесса Хо находится внутри границ (0 Хо d).
d/o
Ответ: ,—\=— f -1 (ех2/2— l)dx.
- \ о а / у J х
А,о /с
204
8. ТОЧЕЧНЫЕ И ИМПУЛЬСНЫЕ СЛУЧАЙНЫЕ
ПРОЦЕССЫ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Пуассоновский процесс. Последовательность случайных событий
(требований, заявок, отказов и др.), присходящих во времени, можно харак-
теризовать случайными моментами времени их появления /2, на вре-
менной оси (рис. 8.1). Такую последовательность событий называют слу-
чайным точечным процессом или случайным потоком. Если точки неразли-
чимы, то вместо них можно рассматривать целочисленный случайный про-
цесс N(t) — число событий (точек), появляющихся в полуинтервале (0, /],
причем в дальнейшем принято Af(O) = 0 (рис. 8.1). На рис. 8.1, б и в изо-
бражены также соответственно производная |(/) = dN(t)/dt, представляю-
щая собой последовательность дельта-функций в точках t2, t3, ..., и прира-
щение n(t) процесса Af(Z) за. некоторое время е : п (/) = [Af (t + 8) —
— Af(/)]/e.
Имеется два тесно связанных между собой метода описания случайных
точечных процессов. Первый из них базируется на рассмотрении случайной
последовательности точек во времени, а второй — на анализе целочисленного
случайного процесса А/(/) [45].
Введем интервалы между соседними точками
= — >0, /==1, 2, 3, (8.1)
где под /0 понимается начало отсчета времени, принимаемое за нуль. Тогда
последовательность точек можно характеризовать n-мерной плотностью ве-
роятности рп (Tb ...» тп) интервалов между точками или же плотностью ве-
роятности Рп (4, tn) координат самих точек. Между этими плотностями
вероятности имеются очевидные
соотношения:
^2» ^п) ~ G "7“ •••»
(8.2)
Рп^Ь •••» 'Ч) = Рп^1 *1 +
4- т2, ..., Т] + т2 + ... + тп).
(8.3) ’
Выражения для плотностей вероят-
ностей рп и Рп даже в случае стацио-
нарного точечного процесса, вообще
говоря, будут различными, когда
начало отсчета времени выбрано
произвольно и когда за начало от-
счета взята какая-либо из выпав-
ших точек.
Вместо этих плотностей вероят-
ностей можно рассматривать цело-
численный случайный процесс Af(/).
Если ti — координата Z-й из выпав-
ших точек (?i < /2 < ••• < h < •••),
то /V(/) = 0 тогда и только тогда,
Рис. 8.1. Целочисленный случайный
процесс (а), его производная (б) и
приращение процесса (в)
° tz ft tn t
6)
205
когда Tj > f, и тогда и только тогда, когда + т2 + ••• +
+ тп > /, т. е.
P{N(t) = 0} = Р{^ > Z},
(8.4)
Р {N(t) < п] = P{tj + т2 + ... + тп > Z}, п = 1, 2, 3, ...
Следовательно, если известно распределение целочисленного случайного про-
цесса Af(Z), то можно найти одномерные и многомерные плотности вероят-
ности случайных величин тх, т2, т3, ..., и наоборот.
Основой для формирования различных точечных процессов является
простейший пуассоновский поток. Целочисленный простейший пуассоновский 4
точечный процесс (Z), 0 t < + °0} определяется тремя свойствами.
1. Он ординарен, т. е. вероятность наступления более одного события
на любом малом интервале времени М имеет более высокий порядок малости,
чем AZ:
P{N(t + AZ) — /V(Z) = 1/ = P{N(M) = 1} = yAZ + o(AZ), (8.5)
P{N(t + AZ) — N(t) > 1} = P{7V(AZ) > 1} = o(AZ), (8.6)
где v — некоторая положительная величина, имеющая размерность, обрат-
ную времени [см. (8.13)]. Следствием этих двух соотношений является ра-
венство
P{N(t + AZ) - 7V(Z) = 0} = P{/V(AZ) = 0} = 1 — yAZ + o(AZ). (8.7)
2. Процесс стационарен, т. е. его вероятностные характеристики не изме-
няются при сдвиге всех точек вдоль оси времени на произвольную, но одну
и ту же величину А.
3. Он имеет независимые приращения (значения) на неперекрывающихся
интервалах времени (отсутствие последействия). '
На основании этих свойств можно показать [45], что вероятность P^(Z)
наличия k точек в полуинтервале (0 Z] определяется законом Пуассона:
Pk (t) = (vt)k k = 0, 1, 2, .... t>0. (8.8)
Из этой формулы следует, что вероятность отсутствия точек (k — О) на каком-
либо полуинтервале т
Р0(т) = ехр (—VT), (8.9)
а вероятность наличия одной точки (k — 1)
Рг(т) = ут ехр (—ут) (8.10)
Если в (8.9) и (8. L0) положить т = AZ, raeAZ — малая величина, удовлет-
воряющая условию vAZ < 1, то получим
P0(AZ) ~ 1 - vAZ 4- (1/2) v2(AZ)2, Pi(AZ) vAZ — ^(AZ)2.
Эти равенства согласукнся со свойствами (8.7) и .(8.5) пуассоновского закона.
Кроме того, из второго равенства имеем
v = lim Рх (ДО/AZ. (8.11)
Д/->0
Математическое ожидание т и дисперсия D закона Пуассона равны друг
другу:
т = D = у/. (8.12)
Поскольку т определяет среднее число точек, выпавших в полуинтервале
(0, Z], то параметр
v = mH (8.13)
можно трактовать как среднее число точек, приходящихся на единичный
интервал времени. Поэтому у часто называют параметром интенсивности пу-
ассоновского потока.
206
Плотность вероятности времени появления k-й точки определяется
гамма-распределением (с параметрами k и v):
pth(t)=ve~vt (vZ)ft-‘ /(*-1)1, * = 1, 2, 3..../>0. (8.14)
Математическое ожидание и дисперсия случайного времени
= 'Dtk = k/v2. (8.15)
Последовательность т^, i = 1, 2, 3, временных интервалов между
соседними точками пуассоновского потока является последовательностью
независимых и одинаково распределенных случайных величин с экспонен-
циальной плотностью вероятности
р(т) = ve-VT, т > 0. (8.16)
Математическое ожидание и дисперсия интервалов между соседними точками
соответственно равны mT = 1/v, Dx = 1/v2.
Справедливо обратное утверждение: если имеется последовательность
независимых случайных величин тг-, i = 1, 2, 3, , имеющих одну и ту же
экспоненциальную плотность вероятности (8.16), то соответствующий ей то-
чечный процесс оказывается пуассоновским.
Пуассоновский поток точек можно получить следующим образом. Пусть
случайным и независимым образом во временном полуинтервале (0, Г] раз-
мещено п точек, причем вероятность попадания какой-либо точки на малый
интервал Д/ G (0, Т) равна Р= М/Т < 1. Тогда при Т оо, п —> оо,
п/Т -* v вероятность наличия k точек на полуинтервале длиной / (= (0, Т]
будет определяться законом Пуассона (8.8).
Известно несколько различных обобщений процесса Пуассона. Укажем
здесь два таких обобщения: неоднородный пуассоновский процесс и про-
фильтрованный пуассоновский процесс.
Пуассоновский процесс называется неоднородным, если его параметр
интенсивности зависит от времени v (/). Для такого процесса вероятность на-
личия k точек в полуинтервале (0,/] дается неоднородным законом Пуассона:
/ t к k / I \
v(T)dT j exp I — J v(T)dT j, k>\. (8.17)
\o / \ о /
При v = const (однородный процесс) этот закон переходит в обычный закон
Пуассона (8.8). Математическое ожидание и дисперсия неоднородного про-
цесса Пуассона равны друг другу:
t
m{t)~D (t) = Jv(T)dx. (8.18)
о
Профильтрованный пуассоновский процесс {£(/), t > 0}, часто называе-
мый дробовым шумом, можно представить в виде
N(t)
£(/)= 2 h^' ‘i’ ai)- (8.19)
'= 1
Здесь {ЛДО, t > 0} — в общем случае неоднородный пуассоновский поток
с интенсивностью v(/), — последовательность взаимно независимых
и одинаково распределенных случайных величин, не зависящая от {N(t),
t > 0}, Л(/, т, а) — детерминированная функция трех вещественных пере-
менных.
Во многих практических задачах отдельные величины в записи (8.19)
допускают следующую интерпретацию: — время появления случайного
события, at — «амплитуда» элементарного сигнала,, связанного с этим собы-
тием, h (t, it, — обусловленное этим событием значение элементарного
207
сигнала в момент времени / и £(/) — значение при t суммы элементарных сиг-
налов, обусловленных событиями, осуществившимися во временном полуин-
тервале (0, /].
Для задания профильтрованного пуассоновского процесса необходимо
указать: 1) интенсивность v (/) порождающего пуассоновского потока,
2) общее для всех случайных величин {сц} вероятностное распределение и
3) конкретный вид функции h (/, т, а).
Если выполняется условие
M{/i2(/, т, а)} < оо для всех т, (8.20)
то математическое ожидание, дисперсия и корреляционная функция про-
фильтрованного пуассоновского процесса определяются формулами:
t
= J v(t) M {h (t, т, a)} dx, (8.21)
о
t
D^(/)=J v(t) M {/i2 (t, t, a)} dx, (8.22)
о
min(*i,G)
^2)= j* v(t) M {h (/lt r, a) h (/2, r2a)} dx. (8.23)
При вычислении этих и других характеристик точечных и импульсных
случайных процессов вида (8.19), представляющих собой сумму случайного
числа взаимно независимых случайных величин, используется тождество
Вальда.
Пусть {Хг} — произвольные случайные величины с одинаковыми мате-
матическими ожиданиями M{Xj = тх и N — случайная величина, прини-
мающая неотрицательные целочисленные значения 1, 2, ... и не зависящая
от Xi при i N., Тогда для суммы
N
г= 2 xt <8-24)
«= 1
справедливо равенство Вальда:
ту = M{F} = mxM{N}. (8.25)
Кроме того, если случайные величины X/ не коррелированы и имеют одинако-
вые дисперсии M{(Xj — mx)2) = Dx, то
М{У2} = .m2M{W2} + DXM{N}. (8.26)
В частном случае, когда N (t) есть простой пуассоновский поток (8.8), в этих
формулах нужно положить
M{W(/)} - vt, = vt (1 + vt)'. (8.27)
Частный вид процесса. (8.19), часто применяемый в качестве модели
стационарного дробового шума, описывается выражением
00
Н0 = 2 Aih(t — —<x><t<ao. (8.28)
t= —00
Здесь {Ai} и {rj — взаимно независимые случайные амплитуды и длитель-
ности импульсов, имеющие одинаковые для всех i плотности вероятности
р(А) и р(т) соответственно, tt — случайное время появления каждого
из элементарных импульсов, не зависящее от {Л J и {тг} и описываемое про-
стым пуассоновским потоком с параметром интенсивности v.
208
Если M{Ai h2(t — тг-)} < oo для всех Z, то математическое ожида-
ние, дисперсия и корреляционная функция определяются формулами Кемп-
белла (см. пример 8.6);
00
/ Л2 (и,
— 00
D^vMlAf
т;) du
т2) du
Z?£(r) = vM U2 J
V —oo
h (u, Tf) h (u + l t|, Tf) du
(8.29)
(8.30)
(8.31)
Были указаны импульсные процессы, базирующиеся на пуассоновском
потоке. Приведем справочные сведения для импульсных процессов более
общего характера.
2. Спектральная плотность случайного импульсного процесса [15]. Слу-
чайный импульсный процесс | (/) представляет собой последовательность
импульсов в общем случае разной формы, следующих друг за другом через
некоторые промежутки времени. Если форма импульсов известна, то случай-
ными могут быть отдельные параметры импульсов: высота или «амплитуда»
Av, длительность tv, время появления tv и др. (рис. 8.2).
Случайные импульсы могут быть неперекрывающимися и перекрываю-
щимися. Под перекрыванием импульсов понимается возможность полного
или частичного наложения разных импульсов друг на друга. Если в случай-
ной импульсной последовательности никакие два импульса не налагаются
друг на друга, то это последовательность неперекрывающихся импульсов.
В последовательности неперекрывающихся импульсов отдельные импульсы
должны иметь конечную длительность tv. Условие отсутствия перекрывания
импульсов можно определить неравенством
^^v+Ь v —О» Ь 2, ... (8.32)
Очевидно, что если неперекрывающиеся импульсы воздействуют на ка-
кую-либо инерционную систему, то на выходе системы, как правило, полу-
чаются перекрывающиеся импульсы. В случайней последовательности пе-
рекрывающихся импульсов условие (8.32) не выполняется для всех или части,
импульсов, т. е.
^v — ц“hTv—ц, > ^v,
209
При рассмотрении случайных импульсных процессов форму отдельных
импульсов часто предполагают известной. При этом исследование непере-
крывающихся импульсов обычно сводится к решению двух задач: нахожде-
нию плотностей вероятностей для отдельных параметров импульсов («амп-
литуд», длительностей, времени появления) и вычислению * спектральной
плотности (ковариационной функции).
При исследовании перекрывающихся импульсов, кроме того, часто рас-
сматривают еще третью задачу — вычисление плотностей вероятностей для
мгновенных значений результирующего процесса, представляющего сумму
налагающиеся импульсов. Однако эта задача в дальнейшем не рассматри-
вается, так как имеется очень мало простых решений ее.
Решение первой задачи обычно связано с физическим анализом конкрет-
ного устройства или механизма, генерирующего случайную последователь-
ность импульсов. В дальнейшем эта задача также не рассматривается. Пред-
полагается, что необходимые вероятностные характеристики заранее извест-
ны. /
Спектральную плотность стационарной последовательности взаимно
независимых неперекрывающихся импульсов следует вычислять по формуле
S «о) = lim М { | FT (/W) (8.33)
Т->оо /
где
< Т/2
FT(im= [ ' (8.34)
-TJ2
— спектральная функция усеченной реализации импульсного случайного
процесса £ (/), т. е. реализации на конечном временном интервале (—Т/2,
Г/2) относительно произвольно взятого начала отсчета времени.
Пусть усеченная реализация £(/) содержит п импульсов. Пронумеруем от-
дельные импульсы в порядке их следования на оси времени. Если, t — мо-
мент времени начала v-ro импульса, то —Г/2 < tQ < tr < t2 < ... < <
<ztn < Т/2. Отметим тот существенный факт, что длительность интервала Т за-
висит от и, т. е. Т= Тп. Если через = ^v_|_ j — tv обозначить длительность
‘ п
временного интервала между двумя соседними импульсами, то Тп Ф
1 v=l
Произвольный одиночный импульс последовательности обозначим через
Xvs (/ — tv, tv), где
( s0(t. tv), tv < t < /v + rv>
Tv)= (8.35)
I °’ z < Zv, z > Zv +Tv.
Предполагается, что функция s0 (/, tv) является детерминированной. Чтобы
понятие «амплитуды» Av имело смысл, принимаем, что максимальное значе-
ние $0(/, tv) равно единице. Следовательно, случайны^ характер рассматри-
ваемого одиночного импульса заключается в том, что его «амплитуда» Av,
длительность rv и момент появления tv являются случайными величинами.
Сравнительно просто и математически корректно можно выполнить вы-
числения по формуле (8.33), при следующих предположениях относительно
параметров импульсов и всей импульсной последовательности.
L «Амплитуда» Av и длительность импульса tv не зависят от интервала
между соседними импульсами. Совместная плотность вероятности случай-
ных величин Av и tv, а также плотность вероятности не зависят от вре-
мени и одинаковы для всех импульсов последовательности, т. е. р2 (Av, xv) =
= р2(А, т), р (ftv) = р (ф). при разных V.
?10
2 Параметры разных импульсов Av и rv> а также взаимно независимы,
т. е. случайные величины А , т A v = 1, 2, .... п, и А,,, т„, О„, и = 1,2
...» п, при ц #= v независимы.
Представим рассматриваемую реализацию |(/) случайных неперекры-
п
вающихся импульсов в виде суммы = S Avs (t—tv, xv). Подставив это
v=i
выражение в (8.34), получим
Л
?Т (/“) =2 Av F1 (®> Tv) е~1<Л V •
V = 1
где
Л(со, tv)= J s0 (t, tv) e-ie>l 4t (8.36)
— oo . .
— спектр типового импульса последовательности (см. табл. 8.1).
Очевидно, что квадрат модуля спектральной функции
\РТ №№ = Fr FT № =
=2 2 V)e/<0(^
Ц=1v=1
где через F* обозначена комплексно-сопряженная функция.
Если вычислить математическое ожидание этого выражения, учтя
при этом принятые предположения относительно параметров импульсов, а
также равенство Вальда (8.25), подставить полученный результат в исходную
формулу (8.33) и затем перейти к пределу при Т —> оо, получим следующую
окончательную формулу:
= |м {А21 Ft (со, т) |2}+2Л1 {Л/ч (со, т)} X
Оф (со)
XM{4FI(<o- ^Re-jZ^)
+ 2шл| 6 (со).
(8.37)
Здесь
оо
= = J Op(O)dO (8.38)
О
— математическое ожидание интервала между импульсами;
т| = М{Н0}=-^-Л1{ЛГ1(0.т)} (8.39)
— математическое ожидание (постоянная составляющая) случайного им-
пульсного процесса;
0e (со) = М {е/<вй} = J 'Jartplfydb (8.40)
О
— характеристическая функция интервала между импульсами.
Спектральная плотность в общем случае является непрерывно-дискрет-
ной, т. е. состоит из двух составляющих: непрерывной части Sc(<o) и дискрет-
ной линии на нулевой частоте Sj (со):
5(со) = Sc(co) + Sd(®). (8.41)
211
го
Ю
Таблица 8.1
Различные типы импульсов f(t) и их спектры Ft(co, т)*>
Тип импульса Аналитическое выражение г (t) График (t] Аналитическое выражение F, (со- т)
Прямоуголь- ный ^тп> \t 1 Т/2, - 0, 11\ > т/2 f(t)> 1 / (ОТ \ sln ll- / V сот
-Т/2 О т/2 t
Треугольный ^4 + — т < / < 0, т Атп, л ——— (/ — т), 0 < t < т, т 0, | И > т f(t)> г / сот \ / sin \ 1 2 I ^1 1 1 СОТ 1 \ ~ /
-т 0 т/Z t
Трапецеидаль- ный (/.л > ч 1 р+(1+а)— , ат 1, 2 J —(14-а)-у <«—(•—а) Ат, 1Н<(1—а)-^-, —О+а)-^-]. (1 —а) ~ </<(1+а)-|-, 0, 111 >(1 +а) / сот \ Sln / ! rvr \ X / (ОТ \ J 1 а®т \ sin —— I v \ 2 /
2 1
< Т/2 t л ( «сот \ \ 2 /
Дискретная линия обусловлена отличным от нуля математическим ожида-
нием случайного импульсного процесса.
Формула (8.37) справедлива для многих практически важных импульсных
случайных процессов. В частности, если дополнительно к ранее сделанным
предположениям принять, что «амплитуда» и длительность ягодного и то-
го же импульса есть также независимые случайные величины, т. е. раИ» т)
= р(Л)р(т). то формула (8.37) упрощается и принимает вид
I
S(®) =-------
(®)
/И ’ Л2}-}-2Л42 (Л* Re 1 • z
' 1 ' 1—0^ (со)
XM{IF((<o. т) |2}+-^-|Л1 М}Л4 {Г, (0, т)}]26(<о). (8.42)
Рассмотрим прямоугольные импульсы и вместо интервала введем
интервал между импульсами
,AV = ^V—tv. (8.43)
В этом случае формула (8.42) примет вид
V4 М*} Re [ 1 -©х(о» 1 +
0д (со)[1 — 0Т (<о)] (0Т(<1>) — 1] I / тх \2
+ Re---------i—л / Тл~~77---------( +тА -------7---- 2лй (“)•
, я 1-0т (со) 0д(<о) J \ тх+тл )
(8.44)
Здесь znT, /Ид и тА — соответственно математические ожидания длительности
импульса, промежутка между импульсами и амплитуды импульса, 0т(со) =
= Л4{ехр(/сот)} — характеристическая функция длительности прямоуголь-
ных импульсов и 0д(со) = Л4{ехр(/соА)} — * характеристическая функция
промежутков между двумя соседними импульсами.
В том частном случае, когда независимые прямоугольные импульсы
имеют одинаковую амплитуду (Л¥ = Ло = const), справедливы равенства
М {Л2} = т2А— Л^. При этом формула (8.44) упрощается и оказывается
симметричной относительно характеристических функций 0т(со) и 0д(со):
S(co) = —------
(О2 (тх +/Пд)
Re
[1- 0T(<o)J [1-0д(о>)]
1-0т (<в) 0д (со)
2
I 2л6(со).
+ А1
I тх
( тх + т^
(8.45)
Приведем окончательные формулы для спектральной плотности периоди-
ческих и квазипериодических импульсных процессов, встречающихя в радио-
технических системах [27, 50].
Рассмотрим случай, когда импульсы заданной формы /(/, т0) имеют по-
стоянный период повторения О' = Фо ~ const, постоянную длительность
т = т0 = const (т0 < Фо)» н0 случайные и коррелированные амплитуды Л^
(рис. 8.4, а). Такое задание параметров импульсов характерно для ампли-
тудно-импульсной модуляции (АИМ). При амплитудно-импульсной моду-
ляции периодически, через тактовый интервал ф0, берутся выборки £(/?ф0 +
+ %) случайного процесса £(/), которые затем превращаются в периодиче-
скую'последовательность импульсов Ahf(t — £ф0 — %, т0) со случайными
амплитудами Л^ = £(&ф0 + х) (рис. 8.3). Считаем, что точная «привязка»
моментов отсчета к исходному процессу отсутствует (несинхронные периоди-
ческие импульсы) и случайная величина х равномерно распределена в ин-
тервале 0 < х < а /тах(*> ^о) = 1-
214
Рис. 8.3. Модулирующие
случайные импульсы при
амплитудно • импульсной
модуляции
Предположим, что случайный процесс £(/) является стационарным,
имеет математическое ожидание = М{£ (/)} == const и корреляционную
функцию /?^(т) = D^(t), где q.(t) — нормированная корреляционная
функция.
Спектральная плотность полученного таким образом случайного им-
пульсного процесса определяется формулой
оо п
S(co) = 2nm£ О^2 | F, (<о, т0) I2 V б(со——7^+
>
D ' °9
to) I2 2 (8.46)
° k = —00
ИЛИ
( ~ , 9 k х
S(co) = '0’5"2 I Fi (co, т0)|2 hnm.2 У S I ° T~ 1 +
. \ Vo /
( fe= —oo
MTi / 2л/г \
+ 2 st “—57 (a'*7)
k= — oo
Из этих формул видно, что спектр состоит из непрерывной части и ди-
скретных спектральных линий при частотах f = k/$0. Эти дискретные линии
имеются только в том случае, когда 0. Они обусловлены периодическим
стробированием постоянной составляющей процесса. При = 0 спектр
является сплошным.
Если период велик по сравнению с временем корреляции процесса
то в последней сумме в правой части (8.46) будет отличным от нуля
лишь слагаемое при k ~ 0, и формула (8.46) упрощается:
S(<o) = Sd(<o) У в в>—— +Sc(o), (8.48)
\ V0 J
к= —oo
где
Sd(co) = 2ши| ^2 | Fx (©, т) |2, Sc (©) = (Ztyfto) | Fi (®, t) |*. (8.49),
Здесь Sd(co) — интенсивность («высота») дискретных спектральных линий,
Sc(co) — непрерывная часть спектральной плотности.
В табл. 8.2 приведены результаты вычислений спектральной плотности
импульсов при АИМ по формулам (8.49) для разных распределений амплитуд
импульсов, представленных в табл. 8.3 [51]. Спектры одиночных видеоим-
пульсов разной формы были указаны в табл. 8.1.
Последовательности квазйпериодических случайных импульсов встреча-
ются при различных видах импульсно-временной модуляции Различают
четыре основных вида такой модуляции. На рис. 8.4, б—д показаны «низ-
215
Таблица 8.2
Спектральная плотность импульсов при АИМ
Плотность вероятности амплитуды импульсов Р(*) 5^((0)6(со — п(ооь П = О. ±1. ±2, ... $с «О)
Синусо- идальная 2л /и2 |F, (со, тс) |2 6 (со—псоо) Но 1 Ft (со, т0) |2 zVo
Нормальная 2л — /П2 1 Fi (СО, То)|а 6 (СО— ПСОо) О'» О2 —- 1 Ft (со, т0) I2 Vo
Равномерная 2л —- т2 | Ft (со. т0) |2 6 (со—псо 0) X2
Сумма двух де ль та-функ- ций 2л -г-[Р1 (*1—*2)+*212х Vo X I Fl (со, То) I2 б (со —ПСОо) V()
кочастотные» импульсы, соответствующие разным видам модуляции, до то-
го, как они воздействуют на колебание несущей частоты. Для простоты
изображены прямоугольные импульсы одинаковой амплитуды.
1. При импульсно-фазовой модуляции (ИФМ) импульсы имеют постоян-
ные амплитуду и длительность, а их положение от периода к периоду меняет-
ся в соответствии с передаваемым сообщением (рис. 8 4, б).
2. При односторонней модуляции длительности импульсов (ОДИМ)
все импульсы начинаются в моменты времени, отстоящие на постоянный пе-
риод ф0, а длительность их изменяется в пределах некоторого интервала
(б, тт), меньшего ^о (рис. 8.4, в).
3. При двухсторонней модуляции длительности импульсов (ДДИМ-1)
интервал времени между серединами любых двух соседних импульсов оди-
наков (*6*0 = const), а длительности импульсов случайно изменяются
(рис. 8.4, г).
4. При двухсторонней модуляции длительности импульсов (ДДИМ-2)
изменяется как длительность, так и положение фронта импульсов, но каждый
импульс не выходит за пределы своего тактового интервала (рис. 8.4, д).
При всех четырех видах модуляции не допускается перекрывание им-
пульсов, а их положение ограничивается половиной тактового интервала
Приведем выражение спектральной плотности для несколько обобщенного
варианта импульсно-фазовой модуляции. Пусть длительность каждого типо-
вого импульса f (t, т0), где /тах(/, т0) = 1, постоянная Tj = т0 = const, а
амплитуды Av и смещения фронта случайны, стационарны и независимы
как для одного импульса (т. е. при v = k)t так и для импульсов в разных
тактовых интервалах (при v =# k). Для устранения перекрывания импульсов
считаем, что сумма длительности импульса т0 и максимального смещения
smax не превышает ф0/2.
216
Плотности вероятности р(х)
Таблица 8*3
Плотность вероятности Аналитическое выражение График тх о2
Синусоидаль- ная [л~|/хо — (х—^х)2!”1» < Л°* 0, ' |х— тх\ > х0 1 Р(й тх 1 2
ftXg I
0 т* л
Нормальная 1 Г (х—тх)21 еХР L 2а2 J’ — оо<х<оо РЙ!» тх о3
('
Равномерная 1/2х0, |х—тх|<х0; 0, | х~тх | > х0 р(х) ix > тх J_x2 3 °
§ I I I , I ' I
0 тх х
Сумма двух дельта-функ- ций ₽! 6 (X —ХХ) +(1 —рх) 6 (X— ХХ) Р(Х) Z7z№-^/? Pl (x1—x2)-\-xi Pi(l—Р1)(*1—-ч)2
О $1 <г»2 <2?
Спектральная плотность такой случайной импульсной последователь-
ности определяется формулой
5(со) = -^— I Fi (со, То) |2 |м {Л2}— т\ । 08 (со) |2-|-
V(>
тА
+ I (со) I2
0 1 Б
2л& 1
(8.50)
где 0g (со) = М {ехр (/сое)} — характеристическая функция смещения в.
При 8ь = е0 = const рассматриваемая последовательность импульсов перио-
дическая, | 0g (со) | = 1, и формула (8.50) переходит в (8.48).
Из формулы (8 50) видно, что при тА =£ 0 спектр является дискретно-
слошным. Дискретные спектральные линии отсутствуют при тА в 0.
Рис. 8.4. Различные виды импульсной модуляции
218
Для импульсно-фазовой модуляции с постоянной амплитудой импульсов
Ak = 40 = const (рис. 8.4, б) формула (8.50) принимает вид
S{co) = Sd (со) 6 1со
k = —оо
2л& \
А )
Vo /
(8.51)
где
Sd (со) =2лА? | Fr (со, т0) |2 |0е (со) |2.
(8.52)
5с((о)=4^^1|Л(со, г0) |2 [1- | 0g (со) I2].
В табл. 8.4 приведены результаты расчетов по формуле (8.52) для разных
плотностей вероятностей р(е) смещений моментов появления импульсов
8 = к (см. табл. 8.3). Амплитуды импульсов считаются одинаковыми, рав-
ными Ао.
Спектральная плотность стационарной последовательности неперекры-
вающихся импульсов постоянной амплитуды Ао при односторонней модуля-
ции их по длительности (рис. 8.4, в), когда импульсы следуют периодически
через интервал О0, а длительности импульсов случайны и независимы с плот-
ностью вероятности р (т) = р (х), определяется формулой (8.51), в которой
нужно полагать
Sd (со) = 2л4? д0"2 I М {а (со. т)}|2,
(8.53)
5с(<о) = Ло2до-1 [M {|F, (со, T)p}-|M{F((co. т)} |2].
Результаты вычислений по этим формулам для импульсов прямоугольной
формы при различных распределениях длительностей импульсов приведены
в табл. 8 5 (J0(х) — функция Бесселя нулевого порядка).
Спектральная плотность стационарной последовательности неперекры-
вающихся импульсов постоянной амплитуды А о ~ const при двухсторонней
модуляции их длительности (рис. 8.4, г), когда интервал времени между
срединами любых двух соседних импульсов постоянен и равен О0, а длитель-
ности импульсов случайны и независимы определяется формулой (8.51),
в которой
Sd (со) = 2яЛ2 д„-2 |М{Л (со. г) е'ат/2 }|2,
(8.54)
Sc (со) =Л§д0"ЧЛ1{| Л (со, т)|2} — |М{Л (со. т) e/at/2} |2]'.
Результаты вычислений для двух форм импульсов при разных рас-
пределениях их длительности приведены в табл. 8.6.
В заключение укажем формулу, которая часто используется в данной
главе при решении примеров и задач. Она получается в результате представ-
ления периодической последовательности7 дельта-функций рядом Фурье
и имеет вид
V e/na0'» = V 8ncosncodo=-^- V б[со— —. (8.55)
„J-оо *=-оо k ’
где
8g —— 2 8д == 1, fl 1 •
219
Таблица 8.4
Спектральная плотность импульсов при ИФМ
Плотность вероятности смещения Р (8) (СО)6 (СО —П(Оо), п = 0, ±1, ±2,... Sc(co)
Синусоидальная 2л — 4? J% (сохо) I Fi (со т0) I2 5 (со—псоо) Vo 4g If] (со, т0) |2 [1 J о Сох©)J Vo
Нормальная 2л ' —- А1 ехр (—о2 cog) I Fi (со, т0) |2 6 (со—пш0) Vo 4g 1 Л (<о, т0) |2 (1 —,ехр (— о2 со?)] Vo
Равномерная 2л Г sin (ох0 I2 „ „ с „, 4? | Fi (со, т0)|- 6 (со — /гсоо) Оо 1 сохо J 4g | Fi (со, тр) |2 Г _ / sin (сохр) \21 #о 1/ к <0*0 /]
Сумма двух дельта-функций 2л I ' . л /COXi— С0Х2 \] „2 1— 4₽1(1— Pi) sin2 х Vo L „ \ JJ ХА* 1 Fr (со, т0) 126 (со —псоо) 4g | Ft (со, тр) |2 ( <аХ1—и>х2 \ — -^(l-Px)sin2^ 2- J
Спектральная плотность при О ДИМ 1
Таблица 8.5
Плотность вероят- ности длительности импульсов Р (т) ((О) б (CD — псы» Па=0, ± 1 , ± 2,... 9 sc (<tt)
Синусоидальная 2л Л2 * [1 +/§ (со*,,) — 270(сох0) COS сот] 6(<в —п<ла) (д хг о / ° (1—Zg«oxo)] orfto
Нормальная 2лЛ2 [ / 1 \ 1 в ® 14-ехр (—о2ш2) —2 exp ( — rt <j2 со2 ) cos шт X ша vg [ \ 2 J J x6(cd—ЛШ0) ° u—exp ( — or* co2)] or Vo
Равномерная 2лЛ§ Г sin2 (шх0) , sin (шх0) ] 2 <4.2 1 + / 42 ~2 COSCOT X x6(co—-nw0) Al Г _ sin2 (cox0) j co2 d0 [ (cox0)2 J
Сумма двух дельта-функций 4^o f. 2 4.2 {1——Pi c°s(co*i)—(1—pl)cos(co*2)+ о v0 + Pl (1 — Pl) COS [<B (*1— x2)]} 6 (co —ncoo) 2 A2 co2 do ₽1 (1 t1 — cos f® (*1 — X2>1}
Спектральная плотность импульсов при ДДИМ-4
Таблица 8.6
Плотность вероятности длительности импульсов Р (т) Sj (со) О ( й) — П(1)п ), п=0, ±1, ±2,...
Синусоидальная Прямоугольный импул! . „ ( 0)т к sin2 1—- 9^лз \ ' /2 ( С0Х0 \ с , > ьс
2Лл Г /сохпк /сот М ——- 1 —Л (со*о) cos (сот) — 1 sir|2 1 — со* Vo L к 2 / к 2 / J
Ini , Q ’'о 1 а ) О (со — /гсоо) \$о/ / сот \8 \ 2 / к 2 /
Нормальная л / сот \ sin2 1 / т \2 \ 2 ) / 1 \ 2лЛх п • п еХР — О2П)“ 0(СО— '?СОо) \ Оо J ( cot V \ ч / к / 2A‘b 1 / 1 к 1 —ехр — — о2со2 cos (сот) — O32do[ к 2 / / 1 к / kl — 2 ex pl— — o2co2 ] sin21 —— 1
Равномерная / сот \ / СОХО \ sin2 1 sin2 —- / т V к 2 / к 2 Л 2Л§ • 2 (®X°\ sin2 , sin (cox0) к 2 / /сот\ 1— cos (сот)—2 sin2! | cox„ \ 2 / \ 2 /
л/ц 1 о (со — \ Ъ'о/ / сот \2 ( сохо у к 2 / к 2 ) co2 tho
Сумма двух дельта- функций toiAZ I / сох. \ [ сох., \]2 2 42 Pl S111 О +(1 ~ ₽l)Sin к—- X (О2 [ к 2 / к 2 J] Хб (со—/гсоо) 4ло ,, vF - w2do ₽.(1-P.)[s.n( 2 J]
Гауссовский импульс т2 О2 / О'2 (О2 \ 1+ Л1+ 41П2)
Нормальная яА1 т2 / 8 In 2 \3. 2й§ in 2 \о2(о2+8 In 2/ Х / • со2 т2 \ Хехр — 1 о (со—псо0) \ а2 со2 -j- 8 In 2 / 4'0'q In 2 / —о XeXPUln24 Хе / о2 (О2 \5/ (,+ 4 In 2 / )2Т2 \ - 2о2 ад2 ) / к / — 0)2 т2 \ JXD \8 In 24-02 со2 J -2 Л j q20)2 \3 X 8 In 2 /
2л; А% jt16 In 2 / со2 т2 -f-со2 х%\ „ * hexp[ 62 (т2+х§)] [rsh (2d2-rx0) — 2со2 -Оо х0 ( — xoch (2d2 тх0)] 4-2^5- | erf ( 1— 2b [ \ b / ~erf( h )I~A2 ехр 1—68(1? 4-х?)] X \ b / J Ь* х( Xsh2 (b2 тх0)^>, 62 = со2/8 1п2
Равномерная ТГ со4х| £Х \ 8 1п2 / й /со2 ТХ0 \] v Xsh2 о . 6 (СО—П(О0) \ о In 2 /J
Сумма двух дельта - функций f / 2л яА1 | / —со2х2 \ 0g Tin 2 Г А* еХРС16 1п2 Л / —со2 х| \1 А2п й [ /— со2х2\ Pi (I —Pi) хг ехр — 4 In 2 1 17 [ 16 In 2/ / —со2 х| VI2
+( 1 Pi) х2 ехр I 1о (со исод) \ io in 2 /J — Л 2 161п2 Л
2. ПРИМЕРЫ
8.1, Вычислить плотность вероятности времени tn появления
п-го события в неоднородном пуассоновском потоке с интенсив-
ностью v(/)f
Решение. Два события {/n < t} и {Af(O > п — 1} являются
эквивалентными в вероятностном смыслу, так как осуществление
одного из них достоверно влечет осуществление другого, т.е.
P{tn < t} = P{N(t) > n — 1} = 1 — P{N(t) < n - 1}.
На основании этого равенства и формулы (8.17) записываем выра-
жение для функции распределения времени tn ' ’ ‘
F<n(0 = 1 — exp I — J v(T)dr I 2 — I J v(T)dt Г, QO.,
\ 0 - / fe = 0 \o /
Плотность вероятности времени tn появления n-й точки определяет-
ся формулой
р ‘п (0 = 4г F ® = v <0 exp f — f V (т) <2тЛ X
at \ J /
\ О /
""-1 1 /р V п~2 1 /р V'
х 2—И (”Л -2 —’
U=o / J
1
(n-l)l
(8.56)
8.2. Пусть т+(Г) — отрезок времени от некоторого фиксирован-
ного момента f до момента появления первого события после f (рас-
стояние от f до первой точки справа — рис. 8.1, а) в неоднородном
пуассоновском потоке с интенсивностью v(t). Найти плотность ве-
роятности случайной величины т+.
Решение. Для произвольного т > 0 события {т+ > т} и
{N (f + т) — W (f) = 0} вероятностно эквивалентны, т. е.
/ г\
Р {т+ > т} ~P{N (/'+т) — N (/')= 0} = exp I — С v(s)Js|.
На основании этого равенства записываем функцию распределения
величины т+ при фиксированном f:
/ t ' т
^х+ (тИ') =Р {т+ < т} = 1—exp I — J v(s)ds
у г
Отсюда находим плотность вероятности
Г +1
v(s)ds
Рх^ (т1/')==-£-/:'г+ <ТЮ= • (f + т)ехр
224
Рис. 8.5. Случайный
двоичный сигнал
8.3. Вычислить ковариационную функцию квазислучаййого
двоичного сигнала 1(f), сформированного на основе простого пуас-
соновского потока упорядоченных временных точек{th, k=0,1,2,...}
следующим образом: |(Z) = 1, если, число точек в интервале (0, t)
четное, и £(/) = —1, если число точек в интервале (0, t) нечетное
(рис. 8.5).
Решение. Так как события {k точек в интервале (0, /)} при раз-
личных k = 0, 1, 2, ... несовместны, то вероятность наличия четного
числа точек в интервале (0, t) в соответствии с (8.8) равна
Ро(0+Рг(0 + ... = e-v< 1 + -^- + ...]=e-v/ch vt.
Аналогично вероятность получения нечетного числа точек в интер-
вале (0, t) равна
/>i(0+Ps(0+... = e-v,[v^4--i^- 4-...J =e-vtshvt
Следовательно,
Р {1(f) = 1} = e~v' ch vt, Р {£(/) = —1} = e“v/ sh vt.
По этим вероятностям находим математическое ожидание
W(0} = 1-Р{Ш) = 1}-1-РШ0 = -1} =
= е—vt (ch vt — sh vt) — e~2v/. (8.5f)
Для вычисления ковариационной функции K%(tu t2) = Af{|(4)x
Xg(/2)} нужно знать совместные вероятности случайных величин
|(/х) и £(7)2. Пусть tx — t2 = т > 0. При заданном значении
?(/2) — 1 случайная величина |(4) = 1, если в интервале (t2, tj
имеется четное число точек. Поэтому
Р{Ш = 11 Ш = 1} = е-™ ch vt.
Умножив это выражение на Р{|(/2) = 1}, получим
Р{|(/г) = 1, |(^2) = 1} = е—VT ch vt e~v<! ch vt2.
Аналогично находим
P {I(*i) = — 1, l(tz) = — 1} = e~VT ch vt e-v/« sh v/2,
Р{Ш = 11 l(t2) = -1} = e-vx sh vt,
P{£(/i) = 1, |(/2) = —1} = e~VT sh vt e-v'» sh vt2,
P{Wi) —L i(/2) = 1} = e~vx sh VT e~v<2ch vt2.
8 Зак. 1203 225
$(t)
it—2. ^0 ij it ^3 ify i*5 i*6 i>7 ^8
Рис. 8.6.
Случайный
фототеле-
графный
сигнал
Записав развернутое выражение для ковариационной функции и
подставив в него найденные вероятности, получим Kg(0, 0) =
— ехр[—2v(/x — /2)]. Поменяв местами tx и t2 (т. е. положив 1г<.
<Z t2), придем к окончательной формуле
ад, 0) = ехр(-2у|/г-/2|). (8.59)
Из формулы (8.58) видно, что процесс 5(0 нестационарен. Это
объясняется тем, что начало отсчета времени было выбрано вполне
определенным образом (на положительном импульсе). Чтобы «на-
чальное условие» было случайно выбранным, рассмотрим случайный
двоичный сигнал
т)(0 = Л5(0. (8.60)
где А — независимая от 5(0 случайная величина, принимающая
лишь два значения: +1 и —1 с одинаковыми вероятностями:
Р{Л = 1} = Р{Л = —1} = 1/2. При этом
М{Л} = 0, М{Л2} = 1.
Нетрудно убедиться, что процесс т](0 стационарен, так как
М{т](0} == М{Л }/И{В(О} = о,
t2) = М{А*}М{Щ&2)} = ехр (-2vK - /2|). (8.61)
Процессы 5(0 и т](/) асимптотически (при оо) имеют оди-
наковые вероятностные характеристики.
8.4. Вычислить ковариационную функцию и спектральную плот-
ность случайного фототелеграфного сигнала 5(0, сформированного
на базе пуассоновского потока упорядоченных временных точек
{/fe! k = 0, ±1; ±2, ...} следующим образом [50]. В интервалах
между соседними точками 5(0 — постоянная величина, равная 1 или
0 с вероятностями р и 1 — р соответственно. Значения 5(0 в рзз-
ных интервалах независимы. Типичная реализация процесса пока-
зана на рис. 8.6.
Решение. Для произвольно выбранного момента времени t мате-
матическое ожидание процесса
М{5(0) = 1-Р{?(0= 1} + 0-Р{5(0 = 0} = р. (8.62)
Запишем выражение для ковариационной функции:
КЕ(Л t + т) = м {5(01(/ + т)} = Р{5(0 = 1, W + т) = 1}.
226
/W)=ua+T)=i} =
Фигурирующая здесь совместная плотность вероятности зависит от
того, находятся ли моменты времени t и t + т в одном и том же ин-
тервале или в разных:
р, если / и / 4- т в одном интервале, ‘
р2, если t и /+т в разных интервалах.
Вероятность того, что t и t + т находятся в одном интервале, опре-
деляется формулой (8.9) и равна PQ (|| т|) независимо от /, а вероят-
ность того, что t и t + т находятся в разных интервалах, равна
1 — PQ( | i |). Следовательно,
Л^(т) = pe~v'Tl + р2[1 — е—v = р(1 — pJe-^^'+p2.
(8.63)
По ковариационной функции находим спектральную плотность
случайного фототелеграфного сигнала
оо
S(со) = j /Q (т)e-'“Tdr = .2лб(и). (g.64)
—оо
Спектральная плотность состоит из непрерывной части и дискретной
спектральной линии на нулевой частоте.
8.5. Для случайного фототелеграфного сигнала £(/), описан-
ного в предыдущем примере, вычислить математические ожидания
времени между переходами 1 -> 0 и 0 -> 1 и между обратными пере-
ходами (рис. 8.6), а также среднюю частоту переходов.
Решение [50]. Пусть случайная величина тх есть время между со-
седними переходами 1 0 и 0-> 1. Принимая во внимание основ-
ные свойства случайного телеграфного сигнала, можем записать
Р{т т + Ат} = 2 Р {наличия k—1 точек в т)х
6=1
ХР {отсутствия переходов в этих k—1 точках } Р {наличия fe-й точки в
интервале (т, т + Ат) }Р {наличия перехода в fe-й точке } =
00 00
== ^-i(*)0 — p)w (vAt)p = р^Дт 2 7£ZT[)! e~VT0 "" =
= pvAre—^1.
Математическое ожидание времени между указанными переходами
00
Л4 {тЗ = С pvTe~PVT dx = ——.
J vp
о
В силу симметрии среднее время между обратными переходами
0-> 1 и 1 0 определяется выражением Л1{г2} = 1/^(1 — р)
Следовательно, среднее время между любыми двумя переходами
равно
— (At {тЛ +М{т2}]= — Г— +---------!—1 =-------!----,
2 2 [ vp v(l—р) J 2vp(l—р)
8*
227
что соответствует средней частоте переходов 2vp(l — р).
8.6. Вычислить ковариационную функцию случайного процесса
Ц0 = 2 Akh(t-tk), k^o, (8.65)
k ——ОО '
где {Л&} — стационарная последовательность случайных величин
с одинаковой плотностью вероятности р(Л), не зависящая от последо-
вательности значений {/ь}, которые упорядочены и описываются
потоком Пуассона с параметром v.
Решение [50]. Примем произвольную точку t = tQ за начало от-
счета времени и затем пронумеруем {tk} в реализации £(/) так, что
tx — первая точка справа от /0, — первая точка слева от tQ и т. д.
(см. рис. 8.2, а). Тогда все случайные величины tk — tQ при k > О
и /0 — h при k < 0 имеют плотность вероятности (8.14).
По определению, математическое ожидание процесса
т^М {£(/)} = 2 M{Ak}M{h(t- tk)} =
k =—оо
_k=l^ fc = —og
= vM{A}
(vQ*-1
(k-1)!
2(—V/)*"1
,= j
(8.66) -
При вычислении ковариационной функции предположим, что
случайные величины последовательности {Ль} взаимно независимы,
так что
М {А2}
М2{Д}
о
при k = i =/= О,
при k #= i,
при k или i — 0.
Тогда имеем
/Q(Z+т,/)=Л4{|(/+т)|(0} = 2 S A1{A^}X
k ——оо i ——оо
хМ{й(/-/й+т)й(/-0)}.
Двойную сумму можно вычислить путем раздельного рассмотрения
восьми членов, для которых k> i> 1, k = i < —1, k = i> 1,
i>k>\, i < < — 1, fe < i < 1, fe>l, t<— 1, i> 1,
228
Рис. 8.7. Способ получения составного сигнала i]i(O
1 < —1. Эти вычисления весьма громоздки и здесь не приводятся.
Окончательный результат имеет простой вид:
оо
Kg(T) = vAf {Л2} J h(t)h(t+-c)dt+
00 “|2
vM {Л} J h(t)dt . (8.67)
8.7. Вычислить математические ожидания и ковариационные
функции трех видов составного (манипулированного) сигнала
(рис. 8.7)
Лх(О = (1/2)11 + + (1/2)11 - 1(01Ы0. (8.68а)
Т]2(О = 1(011(0 + [ 1 —1(01 Ш, (8.686)
11з(0 = 1(/ - ДП1(/ — А) + [1 - 1(/ - A)1U/-A) (8.68в)
или
т!3(0 = 1(/-А)^(0 + П—1(Z — A)IU0.
где |х(/) и g2(0 — не зависящие от !(/) стационарные, не корре-
лированные между собой случайные процессы с ковариационными
функциями Ki (т) и Кz (т).
В составном сигнале (8.68а) 1(0 — «переключающий» стационар-
ный случайный двоичный сигнал (например вида, указанного в при-
мере 8.3) с ковариационной функцией Кх.(т), принимающий лишь
два значения: +1 и—1. При этом сигнал ^(О = 11(0 ПРИ 1(0 =
— 1 и т]1(/) — ^(f) при 1 = —1, т. е. случайный процесс т]1(0
представляет собой случайный манипулированный двоичный сиг-
нал, состоящий из последовательности случайно чередующихся
двух «элементарных» сигналов ^(0 и ?2(0-
В сигнале (8.686) 1(/) есть периодическая (с периодом Т) (син-
хронная) последовательность детерминированных прямоугольных
импульсов длительностью 7\ (рис. 8.8):
1(0 = Р при feTC/<^T + T1,^ = 0,±l, ±2, ...» (869)
[О при других t.
В сигнале (8.68в) K(t —А) — периодическая (несинхронная)
последовательность тех же прямоугольных импульсов со случайным
смещением А относительно начала отсчета времени. Случайная вели-
чина А считается равномерно распределенной в интервале (0, Г).
229
K(t)^
Рис. 8 8 Периодическая пе-
реключающая функция Л(/)
зт t
Решение. Используя независимость Kt) от £,(4) и g2((2) при
различных 4, t2 и t, для математического ожидания и ковариацион-
ной функции сигнала ти(0 получим
М{П1(Щ = (1/2)11 + М{Х(0}Ш (^(0} +(1/2)[1 - М {М0Я X
ХЛШЩ,
Кп,(т) = ЛЦМОп^Ч- 0} = (1/4)[1 + КЦт)1[Кх(т) + К2(т)1 +
+ (1/2)[1 - Кк(т)1К12(т).
Когда элементарные сигналы Вх(0 и |2(0 не коррелированы между
собой (К12(т) s 0), из последней формулы получаем
КП1 (т) = (1/4)11 + КД^ИК^т) + К2(т)1. (8.70а)
Для сигнала г|2(0 находим
М{т]2(0} = М {Kt)}M{^(t)} + II - М{МО}1М{|2(0),
КчД t + т) = Af {п2(0Я2(/ + 0} = Ht)Kt 4- тЖДт) +
+ П - %(/)][! - Kt + т)1К2(т) + {Х(ОП - Щ + т)] +
+ Kt + т)П - М01 }М }M {В2(0 }• (8 706)
В силу периодичности Kt) сигнал т]2(0 является периодически ста-
ционарным, так как
М frhtf + Т)} = М {т)2(0}, K^(t + Т, t+x + T) =
= K^(t, t + x).
Наконец, математическое ожидание и ковариационная функция
сигнала г]3(0 равны
/И{т1з(0} = ад(0} у- f цt-^)d^ +M{l2(t)}± f 1-
- Kt - A)1 db = M {?! (П)+-^- м {£2 (0),
Ы<) = y-q (Т) К, (Т) + [ 1 - q (т)]| К2(т) +
+ 2Л4{^(0)Л1{^ (0}^-[1-<7(т)], (8.70b)
230
где q(i) = — j + i)dt. Периодическая функция <у(т) пока-
ч о
зана на рис. 8.9. Сигнал т]3(/) является стационарным в широком
смысле.
8.8. Получить выражение спектральной плотности стационарной
последовательности неперекрывающихся импульсов постоянной ам-
плитуды А = Л о и постоянной длительности т = т0, если времен-
ной интервал между началами соседних импульсов Ф > т0 изме-
няется случайно и независимо от импульса к импульсу. Рассмотреть
частный случай прямоугольных импульсов.
Решение. Применительно к данному примеру формула (8.42) при-
нимает вид
Л2 1 — I 0А ((О) |2 Л 2
S (о) =А | (*>, т0) |2 .L±_А +A F\ (0, т0) 2л6 (ш). (8.71)
«о |1—«#(«>) |2
Для прямоугольного импульса здесь нужно положить
P-i (®, то)=—— (1 —е_/'“т»),
/®
. I Л (®, ТО) I2 = Asin2 , Л(0, То) = т0 .
со2 \ 2 /
Тогда получим
S(0)) = -A-Sin2(-^I»-') 1-|в(<0)12 +/_ЛоТо_у2 б( ) (8 72)
' ’ \ 2 ) I 1 -0(<о)|2 \ ) v v '
8.9. Из нормального стационарного процесса с нулевым
средним значением и корреляционной функцией D^(x) берутся пе-
риодически (с периодом Фо) отсчеты £ (t — гФ0), i = 0, 1, 2, ... Эти
отсчеты при помощи нелинейной ступенчатой функции С(0 =
= glC(01 подвергаются квантованию на четыре уровня *=
= 1, 2, 3, 4, причем пороги квантования равны |2 = 0, Ъ
(рис. 8.10). Функция g(l) предполагается нечетной, т. е. g(£) =
= —g(—£). Получающаяся случайная последовательность значе-
ний Ст превращается (кодируется) в последовательность прямоуголь-
ных импульсов фиксированной длительности т0 <Ф0 со случайными
амплитудами Ст- Вычислить спектральную плотность импульсной
последовательности т](/), полученной из случайного процесса
С(0 при помощи квантования по времени и по уровням.
Рис. 8.9. Периодическая функ-
ция
231
Решение [11. К данному примеру применима формула (8.46). При
этом получение импульсного процесса т](/) целесообразно рассмат-
ривать в обратном порядке, а именно, как периодическое (с периодом
Фо) временное стробирование прямоугольными импульсами длитель-
ностью т0 процесса £(/), полученного из исходного процесса |(/) при
помощи нелинейного преобразования £(£(/))•
Так как среднее значение процесса £(/) равно нулю и функция
g(l) нечетная, то среднее значение процесса £(t), очевидно, тоже
равно нулю, т. е. = 0. Поэтому формула (8.46) упрощается:
(ю) = -JLI (®, т0) |2 Dt У (п^о) е'®"*'
Vo
п=—со
= 17 2
П——оо
(8.73)
где — корреляционная функция процесса £(/). Здесь учтено,
что для прямоугольного импульса единичной высоты и длитель-
ности т0
1Л«о.То)12--г§[ Г.
[_ сото/2 J
232
Для определения спектральной плотности Sn(co) остается вычи-
слить корреляционную функцию процесса Анализируя нели-
нейное безынерционное преобразование g(^) известными методами,
можно показать (см. пример 12.6), что
1 00 Г 3 /1
Rc*t’=t>.2 24-ф™(^
(8.74)
где Ф(п>(х) — производные от интеграла вероятности;
~ £т+1 £т> = 1, 2, 3.
Подставив (8.74) в (8.37), получим окончательно
Vo
sin (сото/2) j2
сото/2 J
oo
n= — OO
Атф(/г)
kl
(8.75)
8.10. Вычислить спектральную плотность стационарной после-
довательности неперекрывающихся импульсов при односторонней
модуляции их по длительности (рис. 8.4, в). Амплитуда импульсов
фиксирована (Д- = Ао = const), импульсы следуют периодически
через интервал Оо, а длительности импульсов случайны и независи-
мы. Рассмотреть случай прямоугольных импульсов с равномерным
распределением длительностей
/ \ (1/2то,
Л(’)=[о
р —То|<То<^о>
|т—Т0|>10.
(8.76)
Решение. Следует воспользоваться формулой (8.53). Для прямо-
угольного импульса с учетом (8.76) можем написать
Рг (со, т) = — (1 — е-'0”),
/со
2т0
М {Fl (со, т)} = —— С л (со, т) dr = —J-------------------(1 — 2/сото — е-2/'мт»),
2то J т0
о
I М (Л (со, т)} р
. . Sin2 СОТО п Sin СОТ0
1 .4------------“-----2------------- cos wt0
(CT4T Л (T>T„
> < /1 r-i z 2 Г i sin сото
M {| Fi (co, т) I) = —— 1--------------------------cos coto
CD2 L COTq
Подставив эти выражения в (8.53), получим
Sd (со) =
2лЛg “j [ sin2 сот.
(соО’о)2 . (сото)2
5с(со) =
о sin сото 1
— 2------------- cos сот0 ,
сото J
sin2 сото
(сото)2 ’
со2 О0
233
8.11. Найти спектральную плотность стационарной последова-
тельности неперекрывающихся импульсов при двухсторонней моду-
ляции их по длительности (рис. 8.4, г). Будем считать, что амплитуда
импульсов постоянна (Дг = Ао = const), интервал времени между
срединами любых двух соседних импульсов постоянен и равен й0,
а длительности импульсов случайны и независимы. Выполнить вы-
числения для импульсов прямоугольной формы, когда их длитель-
ности распределены по нормальному закону:
Р1 (т) =----ехр (--------(—о « — (8.77)
v а /2л 2а2 / 2
Решение. В данном случае нужно воспользоваться формулами
(8.54). Для прямоугольного импульса находим
F/w, т) =—5— (1—e~/ti)T), F^co, r)e/WT/2 = —sin-^-,
/со со 2
IЛ (<>, т) |« = Ц-(1 —cos (ОТ).
СО2
Воспользовавшись при статистическом осреднении с плотностью ве-
роятности (8.77) известным интегралом
оо __
J е-^2 cos bxdx == - pZ"exp ( —Re р >* О,
получим
2И {/4(G), т)е/(ОТ/2} = — sin — exp ( —— а2 со2],
со 2 \ 8 /
М {| Fj (со, т) |2} — -2— Г1—cos <ото ехр (-— о2 (о2Ч.
со2 [ \ 2 / J
Подстановка этих соотношений в формулы (8.54) дает выражение для
спектральной плотности независимых прямоугольных импульсов
при двухсторонней модуляции их по длительности
Sd (со) = 2лД§ ([-—. (ЮТ|>/2) 1* ехр (- — о2 оА
\ до / [ (ОТо/2 J \ 4 /’
Se (со) = --"У" Г1 — ехр f —— ст2 ю2')—2 ехр ( —— о2 ®2') sin2 1.
Результаты вычислений для прямоугольных и гауссовских им-
пульсов при разных распределениях длительностей приведены в
табл. 8.6 [51].
8.12. Найти спектральную плотность стационарной последова-
тельности модулирующих импульсов постоянной амплитуды (At —
— А о = соп.4) при двусторонней модуляции длительности импуль-
сов (рис. 8.4, д). Предполагается, что длительности импульсов т/
и смещения ег моментов их появления относительно тактового ин-
тервала до независимы для любых пар импульсов, причем 0 тг 4-
+ е; (отсутствие перекрывания). Рассмотреть частный случай
234
прямоугольных импульсов, у которых смещения и длительности
независимы и распределены равномерно в интервале (0, -&0/2), т.е.
Р1(т) = 1 /т0, Pi(e) = 1 /е0, т0 = е0 = $0/2. (8.78)
Решение. Применительно к сформулированному примеру спект-
ральная плотность определяется формулой
S(<o) = Гм{| Л (со, т) I2} - I М {/Ч (со, т) е^е) |2 4-
Фо L
00
+|МРЧ(®, т)е'®8}|2 — У б(®-—\ (8.79)
где Г*(х) — функция, комплексно-сопряженная F(x).
Если длительности it и смещения eft независимы не только для
любых разных (i =/= k) импульсов, но и для одного и того же импульса
(т. е. при i — k), то формула (8.79) упрощается:
Д2
S(®)=^
Vo
М (IЛ (®, т) |2} -| М {/Ч (®, т)} 0е (со) |2 +
4-1 М (Л (О), т)} ©е (со) I2 у б(<0--^-)
Vo . “ \ Vo /
R=— оо
(8.80)
где 08 (со) = М{ехр(/сое)} — характеристическая функция смеще-
ния е.
Для прямоугольного импульса с учетом (8.78) можем написать
/Ч (со, т) =—— (е'“т— 1),
То
M{F* (со, т)} =—— С F\ (со, т) dx =—!—(1 4- /сот0 —е/’т4,
То J со2 То
о .
2 Г 1
|Л4{Г1((о,т)}|2 =--- 1 4------(сот0)2—cos сото — Gn0 sin (от0 ,
соЧ? [2 J
М {| л (со, т) I2} = —(ют0 —sin <от0).
“ т°
Зная плотность вероятности (8.78) для смещения, находим ха-
рактеристическую функцию
е0
©в((о) = —!— Сe/ffl8de=—Г—(е'®8» -1), |©е(о))|2=—-—(1 — cos(oe0).
80 J /<08и (<О8о)2
о
Известно, что квадрат модуля произведения двух комплексных
величин равен произведению квадратов модулей сомножителей. Если
учесть, что т0 = 80 = и подставить записанные соотношения в
235
(8.80), то получим выражение для спектральной плотности случай-
ной последовательности независимых прямоугольных импульсов
5(0) =
Л20О,
2х»
х® (х—sinx)—(х2 4-2—2 cosx—2х sinx)X
X(1 —cosx) 4-(х2 4-4—4cosx—x2cosx—2xsinx)x
Х=-<й$о/2.
Укажем, что при записи сомножителя перед суммой дельта-функ-
ций было учтено, что дельта-функции отличны от нуля лишь в точ-
ках ® = 2nk/$0 (ву&о — 2nk), в которых
2 cos2x 4- 2х sinx cosx = (14- cos2x) —x sin2x = 2.
3. ЗАДАЧИ И ОТВЕТЫ
8.1. Исходя из того, что приращения простого пуассоновского
потока Л/(/2) — t2 > ty на неперекрывающихся временных
интервалах независимы и распределены по закону Пуассона с мате-
матическим ожиданием v(/2 — /х), найти математическое ожидание
произведения приращений на двух интервалах, когда эти интер-
валы не перекрываются и перекрываются (рис. 8.11).
Ответ'.
М {[TV (ta) - N (tb)] [N (te) - N (QI} = v2 (ta - tb) (tc - td)
при ta > tb > te > Q
M {[У (Q - (V (QI (tc) - N (td)]} = M {{W (Q - N (QI 4-
4- IУ (Q - N (tb)]} {[N (Q - N (Q| 4- W (Q - N (Ql}} =
= v2(/a— tb)(tc — td) + V(tc— tb) при ta> tc> tb> td,
где (tc — tb) — длина перекрывающихся частей двух интервалов
(Q ta) и (td, tc).
8.2. Получить выражение для ковариационной функции целочис-
ленного пуассоновского процесса N(t).
Ответ:
Kn (ty, = М {N (Q N (t2)} = f VZ'2 + v2 12 прИ tr > t2 ’
I vty 4-v2 t2 при ty .
8.3. Найти выражение для ковариационной функции неоднород-
ного пуассоновского процесса N(t).
Ответ: KN(tyt2) =J v (t) dt
при t2.
При ty < t2 в этом выражении нужно поменять местами й Q
236
Рис. 8.11. Перекрывающиеся интервалы времени j---------1 ;________।
"id ~^с
8.4. Вычислить математическое ожидание и ковариационную
функцию следующего приращения п(/) простого пуассоновского
процесса (см. рис. 8.1, в) n(t) = [Л/(/ + е) — 2V(/)]/e, где е > О—
заданная величина. Изобразить график ковариационной функции и
рассмотреть предельный случай при е0.
Ответ:
M{n(t)} = (1/е)М{N (t + е)} — (1/8)М{Л/ (/)} = v,
«,Й,М-Г ”Р"
[v2-|- ve-1 — ve-2!^—/2| при |4~ /2|<е.
График ковариационной функции изображен на рис. 8.12. Кова-
риационная функция состоит из суммы постоянной составляющей
v2 и равнобедренного треугольного импульса, который при е -> 0
переходит в дельта-импульс v6(/2 — /2).
8.5. Вычислить математическое ожидание и ковариационную
функцию процесса
ЦО =dN (t)/dt = lim п (0 = 2 б (*—0).
s->0 f
представляющего собой последовательность дельта-функций (см.
рис. 8.1, б).
Ответ: = v, t2) = v2 + vb(t2 — tj).
Указание. При получении ковариационной функции сле-
дует воспользоваться формулой (6.30) и выражением ковариацион-
ной функции процесса полученным в задаче 8.2.
8.6. Для простого пуассоновского процесса N(t) получить вы-
ражение одномерной характеристической функции.
Ответ: = — 1).
Рис. 8.12. Ковариационная функция прира-
щения пуассоновского процесса
237
8.7. Для просило пуассоновского процесса N(t) при 1} > и
целых положительных числах k и п получить выражение для вероят-
ности Р{ЛД^) = k + п, Л7(/2) = k}.
Ответ: Р {N (/х) = k + п, N(t2) — k} = e-v<i vk+n .
n\ k\
8.8. Доказать, что математическое ожидание /nffe и дисперсия
Dtk времени tk появления fe-ro события в простом пуассоновском
потоке выражаются через математическое ожидание тт и дисперсию
£>т интервалов Tft между соседними событиями формулами пцк =
= ktnx> == kD т.
k
Ответ'. tk = ть где {тJ — последовательность взаимно неза-
i = i
висимых случайных величин с одинаковыми математическими ожи-
даниями тх и дисперсиями Dx.
8.9. Вычислить вероятность наличия событий в полуинтерва-
ле (t, t + т] для неоднородного пуассоновского потока с интенсив-
ностью v(t) — v0(l + a sin со/).
Ответ'. = (v0T)xe“v°T/Xl,
где
Н-т
Т = f (1 +а sin со/) dt = sin со [t -|—T^sin — сот.
J ю \ 2 / 2
t
В частности,
Р0(т)=ехр £—vot—^2- sin со ^/ +-y-T^sin-^-coTj.
8.10. Вычислить плотность вероятности временного интервала
*ь = h — /fe-i между fe-й и (k — 1)-й точками неоднородного
пуассоновского потока, с интенсивностью v(/), считая момент вре-
мени tb-i известным и фиксированным.
/ \
Ответ: pTft (т | th^) = v (tk^ + т) ехр I — J v (s) ds I.
8.11. Вычислить плотности вероятности случайных величин т+
и т" для простого пуассоновского потока с интенсивностью v, где
т4 — длина временного интервала от произвольно выбранного мо-
мента времени V до ближайшей точки справа, а т“ — до ближайшей
точки слева.
Ответ'. рх+ (т) = рх_ (т) = v ехр(—vt).
8.12. Найти плотность вероятности промежутка времени Tk
=- ti+k — ti между f-м и (/ + fe)-M событиями в простом пуассо-
новском потоке с интенсивностью v
Ответ: р?k(() = ve~v,(\/),?-1/(fe— 1)!
233
Пуассонов-
0\---х—х х—х—х—¥—х-х—х----------х-х—¥—с*ий
। _ । । । * процесс
л,_______1_________I_______1_________X > Процесс
* * * * Эрланга
Рис. 8.13. Иллюстрация формирования потока Эрланга из пуассо-
новского при 6=3
8.13. В простейшем пуассоновском потоке с интенсивностью v
производится операция «разрежения». Пусть все точки, начиная с
некоторого начального момента времени, перенумерованы в порядке
их появления. Исключим все точки, кроме тех, номера которых крат-
ны некоторому целому числу k (на рис. 8.13 приведен пример для
k = 3). В результате такого разрежения получим новый точечный
процесс — поток Эрланга. Найти плотность вероятности временных
интервалов между соседними собятиями в потоке Эрланга.
Ответ: pTft(x) = ve~VT (vx)fe’1/(fe — 1)!, k = 1, 2, 3, ...
8.14. В законе Пуассона (8.8) длительность временного интерва-
ла t является случайной величиной с экспоненциальной плотностью
вероятности p(t) = а ехр (—а/), а >> 0, t 0. Найти вероятность
Рп ровно п событий.
Ответ Рп = а f e~(a+v)/ dt = — ( ----- .
Jo nl a-|-v \^a +v]
8.15. Телефонные вызовы отдельных абонентов являются пуассо-
новскими потоками вида (8.8), но с разными математическими ожи-
даниями. Найти вероятность поступления ровно п вызовов на теле-
фонную станцию за время /, если параметры интенсивности разных
абонентов можно аппроксимировать гамма-плотностью вероятности
л (v) =---!--a*1 +1 ун e-av
Г(н+1)
Ответ: Рп (t) =[рп (0 Р (v) dv = С‘+|г ( -3-У+' (—
J \а+// \а+О
8.16. Пусть {Afi(O, 0^/<оо} и 0</<оо} есть
два независимых пуассоновских процесса с интенсивностями vx и v2
соответственно. Вычислить вероятность РГ1 того, что во временном
промежутке между двумя любыми соседними событиями процесса
Л\(/) появится ровно п событий процесса N2(t).
Ответ
Рп = f e~v2T Vi e~VtT dx = ——— (—-—V, n = 0, 1,2, ...
vi+v2Vvi+v2,
239
Оь
—¥
Vt
—^Процесс Hid)
I *
J—Процесс Nz(t)
i t
Рис. 8.14. Наложе-
ние трех точечных
процессов
V\—M-
*
01 )|t I I —i- | lx j—*- Процесс Пз(С)
i I i I । I I I I "
01 Xxx* x*—X x хх X—*- Суммарный процесс Nfc)
и
8.17. В законе Пуассона ph — № ехр (—%)/&! сам параметр X
распределен также по закону Пуассона: = ах ехр (—а)/Х!.
Найти безусловную вероятность появления ровно п событий.
hfee-K а~?"е~а
k\ U
Ответ: Рп =
к
= — ехр Г—а( 1-------YI X
/г! [ \ е /]
х У ехР (—Т7ехР а Р----------------~y|Mft(a/e),
X \ е / \е/л! k\ [ \ e/J
где Mh — k-n начальный момент распределения Пуассона.
8.18. Имеется конечное число г взаимно независимых пуассонов-
ских потоков 7Vi(Z), ...» Nr(t) с интенсивностями vb vr соответ-
ственно. Показать, что суммарный поток (рис. 8.14) N(t) = Л\(/)+...
... + Nr(t) является также пуассоновским с интенсивностью v =
= V-l + ••• + Vr.
Ответ'. Нужно убедиться, что для суммарного потока N(t) вы-
полняются три определяющих свойства пуассоновости потока: орди-
нарности, стационарности и независимости приращений на непере-
крывающихся интервалах времени. Из условия ординарности (8.5)
для потока N(t) определяется параметр интенсивности v = vt+...
... + Vr.
8.19. Имеется два независимых целочисленных пуассоновских
процесса N^t) и Af2(O с законами распределения
Pi (п) е-^, p2(m) =-e~~v< п, т = 0, 1, 2,...
п\ т\
Найти закон распределения p(fe) для разности N(t) = N^t)—Л/2(/).
Ответ:
p(k) = e-^+^‘(^-}k/2Iw(2t]^T2), k=Q, ±1, ±2,...,
\ V2 )
где /fe(x) — функция Бесселя fe-ro порядка от мнимого аргумента.
8.20. Вычислить математическое ожидание и корреляционную
функцию случайного двоичного сигнала т](/), который отличается
от квазислучайного двоичного сигнала £(/), описанного в примере
8.3, лишь тем, что принимает значения Лх и Л2, а не +1 и —1.
Ответ'.
м01(0} = (1/2) (Лг + Л2) + (1/2)(Лг- Л2)е-2^.
R (G. /2) = (1/4)(Лг — Л2)г[е—2vUi—(2| —e-2v (<»+<.)].
240
Указание. Нужно воспользоваться соотношением
Т)(0 = (1/2)(Л2 +.Л2) + (1/2)(Л, - Л2Ж,
а также формулами (8.58) и (8.59).
8.21. Вычислить математическое ожидание и ковариационную
функцию случайного двоичного сигнала т](/), который отличается
от случайного фототелеграфного сигнала £(/), описанного в примере
8.4, только тем, что принимает значения Л2 и Л2, а не 1 и 0.
Ответ: Л4{т|(/)} = Лгр + Л2(1 — р),
= [AlP + Л 2(1 - р)Р + (Аг-А^р (1 - р)е-*1’1.
Указание. Нужно воспользоваться соотношением r|(f) =
— Л2 + (Л! — Л2) £(/), а также формулами (8.62) и (8.63).
8.22. Найти спектральную плотность стационарной пуассонов-
ской последовательности дельта-импульсов £(/) = У, Ah8(t—tk),
k— —00
где {Л^} — последовательность взаимно независимых случайных
величин с одинаковой плотностью вероятности р(Л), {/ь} — неза-
висимая от {Ап} пуассоновская последовательность точек на оси
времени с интенсивностью потока v (рис. 8.15).
Ответ: S (со) = vAf {Л2} + (vAf(Л })22п6(со).
Указание. Целесообразно сначала по формуле (8.67) найти
ковариационную функцию /С(т) = vM {Л2}6(т) + (уМ {Л })2, а за-
тем по ней вычислить спектральную плотность.
8.23. Получить спектральную плотность суммы двух взаимно
независимых стационарных последовательностей дельта-импульсов
«высотой» Ль и Bt:
оо оо
1Ю= 2 Ль60-U+ 2 М (*-'<)•
k = — ос. i = — оо
Здесь первая последовательность описана в задаче 8.22, а вторая
последовательность аналогична первой: {Bt} — последовательность
взаимно независимых случайных величин с одинаковой плотностью
вероятности рх(В), {^} — не зависящая от {Bi} пуассоновская
последовательность точек на временной оси с интенсивностью пото-
ка р.
Ответ:
S((o) = vAf{42} + pAf{B2} + М4{Д} + рЛ4{В}]2 2л6(со).
Рис. 8.15. Стационарная
пуассоновская последова-
тельность дельта-функций
A^t-i^.
I 'з
-1—1--tHH----1
^2 I | t
244
8.24. Рассмотреть два частных случая задачи 8.22:
1) р(А) = 6(Л — Ло); 2) р(А) = [6(Л — Ло) + 6(Л + Ло)1/2.
Ответ'. 1) S((o) = л^ЛоН + 2nv6(co)], 2) S(co) = vAo-
8.25. Получить выражение ковариационной функции бесконеч-
ной последовательности чередующихся биполярных дельта-импуль-
сов Ло6(/ — th) и —Ло6(£—/й+1) (рис. 8.16), где {/ft} — ста-
ционарная пуассоновская последовательность точек на оси времени
с интенсивностью v.
Ответ: К(т) = уЛо6(т) — vMoe- 2v 1 т|.
Указание. Рассматриваемую последовательность чередую-
щихся биполярных дельта-импульсов можно получить путем диффе-
ренцирования стационарного случайного двоичного сигнала, приве-
денного в примере 8.3, принимающего два значения: Л 0/2 и —А0/2
(рис. 8.5). Ковариационная функция такого сигнала £(/) согласно
формуле (8.61) равна
Къ(т:) = (Л о/4)ехр(—2v | т |).
Поэтому К(т) = —d2/Q(T)/dr2. При вычислении второй производ-
ной, полезно воспользоваться представлением (см. рис. 8.17)
- /1W + м -((v?IS/2) е!" "ри ’ < 01
I —^Ло/2)е~2л,т при т>0,
где
, (т)_( v.4§/2 при т<0, , (—(уЛ£/2)(1 —e2VT) при т<0,
I—vЛo/2 при т>0, 2 ( (уЛ<)/2)(1—е-2vx) при т>0.
8.26. На основе простого пуассоновского потока временных точек
с интенсивностью v сформирован случайный процесс £(/) = Л& при
th i tk+1, k = 0, ±1, ±2, ..., где {Л fe}— независимая от
{/fe} последовательность взаимно независимых случайных величин
с общей плотностью вероятности д(Л). Вычислить математическое
ожидание и корреляционную функцию процесса £(/).
Ответ:
М Ш } = M{Ak} = $ Ap(A)dA = тА,
/?(т) = М{Л2)Р0(т) + т*А\\- Р0(т)1 - т*А = Пле-'’'П,
где Da=-M{A2} — тА—дисперсия случайной величины Л&.
8.27. Вычислить корреляционную функцию и спектральную
плотность стационарного случайного сигнала
s(Z) = Лсоз1со0/ + <р(/) + <р0],
у которого А 0 и ю0 — постоянные амплитуда и частота, <р0 — слу-
чайная начальная фаза, равномерно распределенная в интервале
(—л, л), <р(/) — модулирующее случайное сообщение вида ср(/) =
= th t k = 0, zfc-1. 4-2, ...
242
Рис. 8.16. Стационарная пуассоновская по-
следовательность чередующихся биполяр-
ных дельта-функций
Рис. 8.17. К вычислению производных ко-
вариационной функции
Aof(t-tk) .
tk+1_______
"4 I *
I —Ao&Cf-tjf+j)
Здесь {cpfe} — случайная последовательность взаимно независимых
случайных величин, равномерно распределенных в интервале (—я,
л), {h} — не зависящая от {<pft} стационарная последовательность
пуассоновских временных точек с интенсивностью v.
Ответ [45]:
/?(т) “ — e'"v,T| cos соот»
_L 42 v________j________v
2 m[ v2 + (co+a)o)2 v2+*(co—co0)2
8.28. Случайная функция £(/) образована последовательностью
примыкающих друг к другу прямоугольных импульсов, амплитуды
и длительности которых случайны и независимы (рис. 8.18). Плот-
ности вероятности для амплитуд и длительностей заданы
рИ)=—т^ехР
ол У 2л
(Л-тл)2-|
2ол Г
р (т) = ае~ат, а > О, т > 0.
Вычислить спектральную плотность и корреляционную функцию
случайного процесса £(/).
Ответ: S(co) = ———ол+ /Пд 2nS(co), R (т) = аД е~а1Ч
О'2-Но2
Указание. Следует воспользоваться формулой (8.44), поло-
жив А = 0.
Рис. 8.18. Случайная по-
следовательность примыка-
ющих прямоугольных им-
пульсов
243
8.29. Найти спектральную плотность стационарной последова-
тельности прямоугольных импульсов с постоянной амплитудой А —
= А о, когда импульсы и промежутки между ними имеют одинаковый
закон распределения.
Ответ:
S(co) = —р— Re + -j~Ao =
Л2 1-|0т(ю)р 1 д
= —1 2 * * S------------Л*л.о(й>).
а2тг 11 +ет(со) |» ~ 2 0 '
Указание. Воспользоваться формулой (8.45).
8.30. Вычислить спектральную плотность стационарной после-
довательности независимых прямоугольных импульсов с постоян-
ной амплитудой А 0 и постоянной длительностью т0, если длитель-
ность временных интервалов между соседними импульсами Л имеет
показательный закон распределения: р(Д) = 0е—₽Л, 0 > 0, Д > 0.
Ответ: S(co) =----------------^PO-cos^)-------------------+
со2( 1 + рту)КР /О))2( 1 — cos СиТ0)2 -|- (1 + 1 sin сот0)2)
V +Рто/
8.31. Найти спектральную плотность стационарной последова-
тельности независимых прямоугольных импульсов с постоянной ам-
плитудой До и постоянной длительностью промежутков между им-
пульсами До, когда длительности импульсов распределены по пока-
зательному закону р(т) = ае~ат, а > 0, т> 0.
с/ \ 2аЛл (1 — cos(oAJ Г/ а V/i А & .
Ответ: S (со) =-----—----:----— — (1 —cos соДо)
со2 (1 4-аД0) L\ w /
1 + — sin соДо) ] аЛ>До \ 2л6(со).
\ co / J \ 1 "j-схДо /
8.32. Вычислить спектральную плотность и корреляционную
функцию стационарной последовательности независимых импульсов
прямоугольной формы с постоянной амплитудой До, когда длитель-
ности импульсов т и длительности интервалов между соседними им-
пульсами Д имеют показательные законы распределения
р(т) = ае“ат, т >* 0; р(Д) = 0е~0Л, Д > 0.
Ответ:
S (со) = -----1-----_М_у 2л6 (со),
а+Р со2 + (а + Р)2 \« + Р/
о/Т) _ «Мо с~(« + &)1т|
(а+Р)2
8.33. Периодические выборки (с периодом О0) стационарного слу-
чайного процесса £(/), имеющего среднее значение т^ и корреля-
ционную функцию /?j(t) = а|е~а 1 т I, превращаются в прямоуголь-
244
ные импульсы постоянной длительности т = const (см. рис.8.3). Оп-
ределить спектральную плотность получающейся периодической
последовательности прямоугольных импульсов со случайными ам-
плитудами А, — Z(t — г&о).
Ответ: S(co) = — |F1(co, т0|2 см 1 4-2 V е~n#« cos <ondo | 4-
do \ /
\ п=1 /
п =
=_A_Sin2——- ------------of +
со2 й0 2 ch Фо—cos со'О’о
до \ t>J
k— — oe
8.34. Независимые одинаковые импульсы треугольной формы
(см. табл. 8.1)
(t + т0)/т0,
(т0 — t)/r0,
О,
f(t—i$o, т0) =
— То t 1^0>
Г$0 < * < ^0 + То» т0 < О0/2,
при других t
имеют постоянный период следования d0. Плотность вероятности
амплитуд импульсов имеет вид
р(Д)= xg—(А —/ил)2] 1,
|А—тл |<х0,
I А— тл|>х0.
Найти спектральную плотность такой случайной импульсной после-
довательности.
Ответ: (см. табл. 8.2)
/ Тр \2 sin (сото/2)
\ Оо / L <х>т0/2
оо
d0 4-2лтл б
/? = -ОО
8.35. По каналу связи передается двоичная информация: незави-
симые посылки и паузы равновероятны и передаются периодически
с тактовым интервалом -Оо- Посылке соответствует прямоугольный
импульс постоянной амплитуды Ао и постоянной длительности т0, а
паузе — отсутствие импульса. Найти спектральную плотность по-
следовательности импульсов.
Ответ:
1 + —
d(,
ОО
26
fes= —00
(О
8.36. Независимые и равновероятные посылки и паузы представ-
ляют собой прямоугольные импульсы постоянной длительности
т = d0 и постоянной амплитуды Ао » но противоположной поляр-
245
ности (посылке соответствует +Л0, паузе соответствует — Ло)- По-,
сылки и паузы следуют через постоянный интервал времени Фо- Вы-
числить спектральную плотность и корреляционную функцию тако-
го случайного телеграфного сигнала.
Ответ:
S(^=A^0
sin (co^q/2)
соФо/2
12 /
, ₽(т)=ДЦ1
_J21\ |т|<А
Оо / *
8.37. На линейное устройство (рис. 8.19),. состоящее из линии
задержки на время ^о, вычитающей схемы и идеального низкочастот-
ного усилителя с коэффициентом усиления /<0, воздействует случай-
ная последовательность двоичных сигналов, указанная в задаче 8.35.
Определить спектральную плотность случайной последовательности
импульсов на выходе устройства.
Ответ: S (со) = А20 К* Г sin <WT°/2)sin Г
0 0 Ч I (<ото/2) ]
Указание. Частотная характеристика рассматриваемого
устройства /С(/со) = Ко(1 —
8.38. Двоичная информация передается при помощи детермини-
рованных сигналов с фазовой манипуляцией. Независимые и равно-
вероятные посылки и паузы передаются периодически в течение все-
го тактового интервала Фо = const. Посылке соответствует прямо-
угольный радиоимпульс y4sin<x>0£ длительностью Оо, а паузе — ра-
диоимпульс — Дзтсоо/ той же длительности. Амплитуда А и час-
тота соо — постоянные величины. Считая (Оо'®'о= 2лп, где п — любое
целое положительное число, найти спектральную плотность случай-
ной последовательности прямоугольных радиоимпульсов.
Ответ: S (со) = Д2 О0 ~т о/-Ц2.
I Мо)а-(2лл)2
8.39. Передача двоичной информации осуществляется при помо-
щи импульсно-фазовой манипуляции. Посылка передается прямо-
угольным видеоимпульсом с амплитудой Ао = const, длительностью
т0 = const и временным положением относительно тактового интер-
вала г = = const. Пауза передается тем же прямоугольным им-
пульсом, но его положение относительно тактового интервала равно
6 = 82 = 8! + 80, где 80 = const. Каждый из импульсов не выходит
за пределы своего тактового интервала, т. е. —т0,
0^ е2 О0 — т0. Посылки и паузы независимы и равновероятны.
Рис. 8.19. Схема линейного устрой-
ства
246
Найти спектральную плотность такой случайной последовательнос-
ти прямоугольных импульсов.
Ответ: S(a>) = Ag Оо(—У [ sin (^о/2) Г Г1 —cos2 +
0 U.J [ (о>то/2) J [ 2
Указание. Следует воспользоваться формулой (8.52). В дан-
ном случае плотность вероятности для смещения е равна р(е) =
= (1/2)8 (8 - 81) + (1/2)6 (8 - е2).
8.40. В квазипериодической стационарной последовательности
независимых импульсов, имеющих одинаковую форму, но случайные
амплитуды Аг, смещения 8 моментов появления импульсов относи-
тельно тактового интервала, равного Оо, распределены по
нормальному закону
р(е) =
е2 \
2^)’
где ае О о (отсутствие наложения импульсов).
Вычислить спектральную плотность импульсного случайного
процесса. Рассмотреть частный случай, когда амплитуды импульсов
постоянны (А{ = А о = const).
Ответ [52]:
S (со) = -1-1 F, (со, т0)|2
^0
М {А2} —тД ехр (—ag со2) +
2л/п^
+——етр(—^<о2) У «со--—
3(со) = -^-| Л(со, T0)|2h —ехр( -о|со2)-н
^0
. / ь О\
ехр(—Ое®2)
^0
8.41. Независимые периодически повторяющиеся (с периодом
Оо) прямоугольные импульсы с постоянной амплитудой Ао имеют
плотность вероятности длительности импульсов
р(т) = — *1) + (1 — Р1)б(т — Т2).
Найти спектральную плотность импульсного случайного процесса.
247
о
Ответ: S (со) =
СО2 д2
[1 — р! +р2—pi COS СОТ!—(1 —pJCOSCO^-H
ОО
+2npi(l— Pi) cosco(т2—тх)] У 6
fe = ----------------------------ОО
+ о —PJ [1 — cos (О (T2 —Т1)].
(О2 Оо
8.42. Найти спектральную плотность стационарной последова-
тельности неперекрывающихся импульсов при двусторонней моду-
ляции их по длительности (рис. 8.4, г). Амплитуда импульсов по-
стоянная Л о — const, интервал времени между срединами любых
двух соседних импульсов также постоянен и равен 'fl’o, а длитель-
ности импульсов случайны, независимы и имеют плотность вероят-
ности
Р1 (т) = ([л Ухо — (т - То)*] 1 >
1т —То I < х0,
|т—т0|>х0.
Ответ: S (со) = 2лА2 (•sin* (<от°/21 J* ( х
0 \ / (соТо/2)2 Ц 2 )
X У 6 ^TL')+~VV I 1~ 4 (®*о) cos (сото)—
\ "О / (О' до (
где J0(x) — функция Бесселя нулевого порядка.
8.43. В плоскопараллельном диоде, работающем в режиме насы-
щения, моменты вылета электронов с катода независимы и описы-
ваются законом Пуассона. Пренебрегая начальными скоростями вы-
лета электронов из катода, можно считать, что пролет каждого
Рис. 8.20. Элементарный импульс анодного тока и спектральная
плотность дробового шума (б)
248
электрона от катода до анода наводит в анодной цепи треугольный
импульс тока (рис. 8.20, а)
ie(0=l2е//Т’’
(О при других t,
где е — заряд электрона; т0— время пролета электрона от катода
до анода. Среднее значение анодного тока Ia = ev, vji/t v — среднее
число электронов, попадающих на анод в единицу времени.
Вычислить и построить график спектральной плотности дробо-
вого шума. Определить значение непрерывной части спектра Sc(co)
при нулевой частоте.
Ответ [42]: S(a>) = 2л/% 6(ю)+ el „—— [(<»т0)2 +2 (1—coscot0—
(<ото)4
—®т0 sin m0)], Sc (0) = ela.
График спектральной плотности изображен на рис. 8.20, б.
9. ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ И МАССОВОГО
ОБСЛУЖИВАНИЯ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Надежность — свойство системы (объекта, изделия, устройства,
элемента и т. д.) выполнять возложенные на нее функции с сохранением
эксплуатационных показателей в заданных пределах при определенных ре-
жимах и условиях эксплуатации.
Надежность — сложное свойство, включающее в свою очередь безотказ-
ность, долговечность, ремонтопригодность и сохраняемость. В зависимости
от конкретных систем и условий их эксплуатации эти свойства могут иметь
различную относительную значимость.
Для расчета надежности, формулирования требований на надежность
разрабатываемых систем, сравнения систем по надежности и т. д. служат
количественные характеристики — показатели надежности, которые опреде-
ляются или по экспериментальным данным об отказах системы, или по из-
вестному аналитическому выражению какой-либо характеристики. В первом
случае используются статистические определения показателей надежности,
которые получают при испытаниях и эксплуатации систем (такие* показатели
в дальнейшем отмечены звездочкой); во втором — вероятностные определе-
ния и аналитические зависимости между ними. Вероятностные расчеты про-
изводятся на стадии проектирования.
Для невосстанавливаемых (перемонтируемых) систем чаще Btero исполь-
зуются четыре показателя надежности: вероятность безотказной работы
Р(/), плотность вероятности отказов (частота отказов) интенсивность
отказов Х(/), среднее время безотказной работы (средняя наработка до отка-
за) mt [22, 53—57].
Вероятность безотказной работы ^функция надежности) P(t) есть ве-
роятность того, что система проработает безотказ.но в течение времени /,
начав работать в момент времени t = 0, или вероятность того, что время
работы системы до отказа окажется больше заданного времени t\
P(t)= Р(Т> /) = 1-Л(0, (9.1)
где Т — случайное время работы (наработка) системы до отказа; Рг(1) —
в Р(Т < /) — функция распределения случайной величины Т.
249
Для восстанавливаемых систем характерно чередование времени исправ-
ной работы и времени восстановления (ремонтов). Рассмотренные показа-
тели описывают период работы системы до первого отказа или после ликви-
дации отказа до появления очередного. Поэтому для восстанавливаемых
систем вводятся дополнительные показатели,главными из которых являются:
параметр потока отказов Л(/), наработка на отказ /и0, среднее время вос-
становления /ив и коэффициент готовности /<г. Иногда используются и дру-
гие характеристики: частота восстановления, интенсивность восстановления,
вероятность восстановления и т. д.
Параметром потока отказов Л(/) называется предел отношения вероят-
ности P(t, At) появления хотя бы_ одного отказа за интервал времени А/
к длине этого интервала:
Л(/)= lim [P(Z, Д/)/Дф (9.11)
Наработка на отказ т0 есть среднее значение времени между соседними
отказами.
Среднее время восстановления системы тв — математическое ожида-
ние продолжительности восстановления системы после отказа, т. е. это
среднее время вынужденного, нерегламентированного простоя, вызванного
отысканием и устранением отказа:
mB = f tpB(t)dt = J tdFB(t) = J [1-FB(f)]dt, (9.12)
0 0 0
где pB(t) — плотность вероятности времени восстановления; FB(t) — функ-
ция распределения времени восстановления.
Коэффициент готовности Кг для установившегося режима эксплуатации
определяется как вероятность того, что система будет исправна в произ-
вольно выбранный момент времени в промежутках между плановыми техни-
ческими обслуживаниями:
Кг = тв/(тв + тв), (9.13)
где т0 — средняя наработка на отказ; тв — среднее время восстановления
системы.
Статистическая оценка параметра потока отказов определяется как отно-
сительное число отказавших систем в единицу времени
А*(0 = Апх(/, А/)/К0А/, (9.14)
причем в число Ап^/, А/) входят как первоначальные отказы, так и отказы,
появившиеся после восстановления или замены отказавших систем. В общем
случае Апх(/, А/) больше величины Ап(/, АО в формуле (9.8). Параметр пото-
ка отказов восстанавливаемых систем равен интенсивности отказов соответ-
ствующих невосстанавливаемых систем, если потоки отказов в обоих случа-
ях являются простейшими (см. гл. 8): А(0 = Х(/) = const.
Наработка на отказ по данным испытания одного образца системы вы-
числяется по формуле
(9.15)
где п — общее число отказов системы за период наблюдения; tj — время
Исправной работы системы между (i — 1)-м и i-м отказами.
Если на испытании или эксплуатации находится Ко одинаковых систем
в течение времени /, то наработка на отказ определяется выражением
(N о fl j \ / No
2 2 2 ni’ <9Л6>
у__1 \ J j j___ j
252
где rij — число отказов /-го экземпляра за время /; — время исправной
работы /-го экземпляра между (i — 1)-м и i-м отказами.
Формулы для статистических оценок времени восстановления /и* и ко-
эффициента готовности Л* соответственно имеют вид
2и»-'”
1
п , I / п п \
^=5^/5 <l+ 2 • <9.18)
1 = 1 / \i=l i = 1 /
Здесь No — общее число систем (или число восстановлений одной и той же
системы), /в i — реализация времени восстановления для i-й системы (или
f-я реализация одной и той же системы), п — число отказов системы за время
испытаний или эксплуатации, tB t — время восстановления системы после
i-го отказа.
Через известный коэффициент готовности выражается коэффициент
простоя, определяющий вероятность нахождения системы в неисправном
состоянии:
Кп=1-Яг- (9.19)
При определении показателей надежности по экспериментальным дан-
ным обычно находят некоторую исходную характеристику, например закон
распределения времени безотказной работы, а остальные показатели опреде-
ляют расчетным путем. Выбранная модель закона распределения должна
согласовываться с экспериментальными данными. Проверка соответствия
производится по правилам математической статистики (см. гл. 4). Кроме того,
если это не противоречит существу дела, то всегда следует выбирать такие
распределения, которые определяются небольшим числом параметров. Тогда
проведение статистических оценок и расчет надежности значительно упро-
щаются.
Наиболее часто используются следующие плотности вероятности времени
безотказной работы: экспоненциальная (показательная), Вейбулла, гамма-
распределение, логарифмически-нормальная, усеченная нормальная и Релея.
Особая роль принадлежит экспоненциальной плотности вероятности, которая
порождается простейшим потоком отказов (см. гл 8).
Экспоненциальное распределение достаточно хорошо описывает пове-
дение элементов и систем в период их нормальной эксплуатации (область II
на рис. 9.1), когда происходят внезапные отказы и когда интенсивность отка-
зов примерно постоянна: 2с(/) = А(/) — const.
Зависимости основных показателей надежности от времени для некото-
рых плотностей вероятностей приведены в табл. 9.2.
Решение задачи определения надежности системы по характеристикам
надежности входящих в нее элементов зависит от способа соединения послед-
них. При последовательном, или основном/соединении (рис. 1.2) отказ хо-
тя бы одного из элементов приводит к отказу всей системы (система не имеет
структурной избыточности). При параллельном, или резервном, соединении
(см. рис. 1.1). отказ системы наступает лишь при отказе всех ее элементов
(в систему вводятся избыточные элементы). Сочетание основного и резервного
Рис. 9.2. Один из вариантов смешан-
ного соединения элементов
253
Таблица 9.2
Зависимости показателей надежности от времени для наиболее распространенных распределений
Плотность вероятности Вероятность безотказной работы интенсивность отказов Средняя наработка до отказа
Наименование Аналитическое выражение
Экспоненциальная (показательная) Pl (0 = А ехр ( — АГ) P (/) = exp ( —AZ) A (Z) =A = const mt = 1 /А
Вейбулла Pl (t)=cata~ 1 X Хехр (— cta) P (Z) =exp ( — cta) A (t) = cata~ ' т( = с-|/аГ^1+ j
Гамма-распреде- ление Pl U)= = 1 zae - i pa+I r(a+l) i_ P(t) = e p x V1 1 I \n X in! ( p ) n = 0 при a—целом =tae~tfii 1J rae—di m/ = P (a+ 1)
Логарифмически - нормальная 1g e ₽l(/)-^V2He 2°? / It? t —m \ P(Z)==1—фР-—- \ X(Z)= P1 (<) Pit) 1g e i/^-X a |/2л oo t~m) X j e 2O' di Q
Усеченная нор- мальная 1Г Q gi - e S> v Q |s S II <d ю 7 Q • * 5 1 • ~ P(t}- . ф(т) A exp oV 2 л s~~~ S’ ™ I 5 ' i| " c "" 1 0 mt — m-\- ч x / m \ ,— Ф | — 11/2л \ 0 / / m2 \ xex4_^J
Релея / / Z2 \ Pl(n=-eXp^--j P(0 = exp(—) \ 2o2 / ^(0 = 4 J2 у
видов соединений образует смешанное (последовательно-параллельное) сое-
динение, один из вариантов которого приведен на рис. 9.2.
Пусть система состоит из k последовательно соединенных элементов
(рис. 1.2), отказы которых независимы, а вероятность безотказной работы
г-го элемента в течение времени t равна Pi(t). Тогда вероятность безотказной
работы Ро(/) и вероятность отказа Qo(/) системы рассчитываются по формулам:
k
Po(t)= П (9.20)
i= 1
k
Q„(/) = l-?„(/)=!- П (9.21)
1= 1
В соответствии с формулами табл. 9.1 вероятности Ро(О и Qo(0 можно вы-
разить через интенсивности отказов элементов Xj (/), i =» 1, 2, ...» k,
[t
— [ Хо (т) du
Ъ
Qo(O= 1 — ехр
= ехр
k i
— 5 f Л
'=1 о
t
— J Хо (т) dx
о
(9.22)
(9.23)
где
k
х0(/)= 2
< = 1
(9.24)
— интенсивность отказов системы.
Если отказы элементов описываются однородными пуассоновскими пото-
ками, то X/ (/) = = const и формулы (9.22) и (9.24) принимают вид:
k
Ро(О=ехр (—М). У, Ьг (9.25)
'= 1
Когда система состоит из т групп элементов, в каждой из которых име-
ется rij элементов с примерно одинаковой надежностью, то вместо (9.24) и
(9.25) пользуются соотношениями:
2 «ало. ь»= 2 п^- (9-26>
i — 1 i = i
Данные по интенсивностям отказов отдельных элементов радиоэлектрон-
ных систем берутся из соответствующих справочников.
Пусть система состоит из k параллельно соединенных элементов (рис. 1.1)
и отказы элементов взаимонезависимы. Тогда вероятность отказа Qp (t) и
вероятность безотказной работы Рр(/) системы в течение времени t соответ-
ственно равны:
k k
Qp(O = П <?i(0= П [1-Рг(П1, (9.27)
1= 1 != 1
k
Pp(0 = l-Qp(/) = l- П [1-Pi(/)1, (9.28)
i= 1
где Qi(/) = 1 — Pt(t) — вероятность отказа i-го элемента в течение вре^
мени £
255
Выходные потоки СМО часто представляю^ собой потоки с ограничен-
ным последействием (потоки Пальма). Ординарный поток однородных собы-
тий является потоком с ограниченным последействием, если промежутки вре-
мени между последовательными событиями 7\, Т2, ..., есть независимые слу-
чайные величины. Простейший поток, в котором независимые величины 7\,
Т2, ... распределены по показательному закону, — частный случай потока
Пальма. Если все функции распределения F^), за исключением, быть
может, Гг(/Х), совпадают, то поток Пальма образует поток восстановления
[59—61].
Примером потоков с ограниченным последействием являются потоки Эр-
ланга, образуемые «просеиванием» простейшего потока [3]. Плотность веро-
ятности закона Эрланга &-го порядка имеет вид
О О, (9.41)
I (* + 1)
k -f- 1
где Т = S Tt — интервал времени между соседними событиями в потоке
!=1
Эрланга fe-ro порядка; 7\, Т2, ...» 7\+1 — независимые случайные величины
с одинаковыми плотностями вероятностей tt > 0, i = 1, 2,
..., k + 1.
Математическое ожидание и дисперсия величины Т с плотностью вероят-
ности (9.41) равны
mt = (k + 1)/Х, о2 = (k + W, (9.42)
где X — плотность простейшего потока.
Для упрощения иногда удобно заменить реальный поток заявок с пос-
ледействием так называемым нормированным потоком Эрланга &-го порядка
с примерно теми же математическим ожиданием и дисперсией промежутка
между заявками [3]. Плотность вероятности, математическое ожидание и
дисперсия нормированной случайной величины Т = T/{k + 1) имеют вид
Р1(^)=Т7ГГГ (k+ 1)fc+' t>0, (9.43)
I (« +1)
mz = lA, о? = 1Д2 (Z? +1), (9.44)
где X — плотность потока, совпадающая при любом k с плотностью исходного
простейшего потока заявок.
Функционирование СМО во многом определяется временем обслуживания
одной заявки ТОб, которое характеризует пропускную способность системы.
В общем случае ТОб — случайная величина. При теоретических исследова-
ниях и практических расчетах чаще всего предполагается, что величина Toq
распределена по показательному закону, когда функция распределения и
плотность вероятности определяются соответственно выражениями
/=-!(/) = l-e-^, Р1 (/) = |хе~ “S (9.45)
где параметр р, — величина, обратная среднему времени обслуживания одной
заявки:
И=1/^Об, fntoQ = M(To6). (9.46)
При показательном распределении времени обслуживания задача до-
пускает простое решение, которое с удовлетворительной для практики точ-
ностью описывает ход процесса в СМО.
Пусть имеется СМО с п обслуживающими аппаратами (п-канальная
система), на вход которой поступает простейший поток заявок с плотностью
X. Время обслуживания одной заявки одним аппаратом подчинено показа-
тельному закону с параметром ц,.
258
В этом случае основные характеристики эффективности функциониро-
вания СМО с отказами (потерями) определяются следующими выражениями.
1. Вероятность того, что в системе занято k обслуживающих аппара-
тов (в обслуживающей системе находится точно k заявок):
Pk = Pn(k) = -^-(— (9.47)
нА \ g / kl
где
— вероятность того, что все обслуживающие аппараты свободны;
а = Mg = Kmt об (9-49)
— среднее число заявок, приходящееся на среднее время обслуживания од-
ной заявки (приведенная плотность потока заявок [3]).
Подставив (9.48) в (9.47), получим формулу Эрланга:
ak
7Г
(9.50)
2. Вероятность отказа в обслуживании очередной заявки
3. Среднее число занятых обслуживающих аппаратов
п п k
А__ I А__ 1 ' '
(9.52)
Система массового обслуживания с ожиданием при ограниченном вре-
мени ожидания Тож, распределенном по показательному закону с пара-
метром у, в установившемся режиме обслуживания описывается следующими
характеристиками [3].
1. Вероятность того, что занято точно k обслуживающих аппаратов
(очереди нет):
Pk=~p°’
0 < k < п.
(9.53)
2. Вероятность
реди:
того, что все п аппаратов заняты, s заявок стоят в оче-
р _
п+з _ п\
»| П («+"$)
|_»1= 1
(9.54)
3. Вероятность того, что
все аппараты свободны:
п k
as
П («+«£)
771=1
(9.55)
9*
259
Связь вероятностей Qp(t) и Рр(/) с интенсивностью отказов определяется
соотношениями
k
<2Р(Л = П
' = I
ехр
' i
— J Ki (т) dx
о
k
п
1=1
1 —ехр
(9.29)
(9.30)
t
—J Хг- (т) dx
о
Если интенсивности отказов не зависят от времени, то формулы (9.29),
(9.30) принимают вид:
k
Qp(0= П [1-ехр (-U /)]. (9.31)
i= 1
k
Рр(/) = 1-П [1 —ехр ( —A,z /)1. (9.32)
t= 1
Когда система состоит из т групп, в каждой из которых имеется tij эле-
ментов с примерно одинаковой надежностью, то
т
(?₽(/)= П [l-exp(-bjOIn/. (9.33)
i’ = 1
т п
Рр(0 = 1- П [I —ехр(—Xj/)] >. (9.34)
. ' ।
При смешанном соединении (рис. 9.2) сначала по соответствующим фор-
мулам находится надежность цепи из k последовательно соединенных элемен-
тов, а затем надежность системы из т параллельных ветвей.
В зависимости от этапа разработки радиоэлектронной системы приме-
няются различные методы расчета надежности [22, 55, 56, 58]. На начальном
этапе проектирования системы (предэскизный проект) проводится прикидоч-
ный расчет, прй котором определяются целесообразные нормы надежности
для отдельных частей системы (блоков, каскадов) с целью проверки принци-
пиальной возможности выполнения требований по надежности, выдвинутых
заказчиком в техническом задании.
На этапе эскизного проектирования, после разработки принципиальных
электрических схем, выполняется ориентировочный расчет надежности
(дипломное проектирование можно отнести к эскизному проектированию, а
расчет надежности — к ориентировочному расчету).
Ориентировочный расчет производится обычно при следующих допу-
щениях: система рассматривается как группа последовательно соединенных
элементов, интенсивности отказов которых не зависят от времени (поток
отказов — простейший); все элементы одного и того же типа имеют одинако-
вую надежность независимо от их места расположения в системе; все эле-
менты работают в номинальном режиме, причем отказы элементов считаются
независимыми событиями; влияние условий работы учитывается приближенно
с помощью поправочного коэффициента.
Полный расчет надежности производится после испытания макета в лабо-
раторных условиях, когда становятся известными реальные режимы работы
элементов, позволяющие уточнить значения интенсивностей их отказов.
При этом учитываются влияние схемной зависимости элементов, режимы их
работы и другие факторы.
2. Теория массового обслуживания (теория очередей) исследует коли-
чественную сторону процессов протекающих в системах массового обслу-
живания (СМО). Она устанавливает зависимость между характером потока
256
заявок (требований), производительностью отдельного канала (обслуживаю-
щего аппарата), числом каналов и эффективностью обслуживания.
Система массового обслуживания включает в себя три элемента: входной
поток, обслуживающую систему с одним или несколькими обслуживающими
аппаратами и выходной поток.
Системы массового обслуживания делятся на системы с отказами (СМО
с потерями), системы с ожиданием и системы смешанного типа. В системе пер-
вого типа заявка, поступившая в момент, когда все каналы заняты, получает
отказ, покидает систему и в дальнейшем процессе обслуживания не участ-
вует (происходит потеря заявки). В СМО с ожиданием заявка, поступившая
в систему, когда все каналы заняты, ставится на очередь и ожидает, когда все
поступившие ранее заявки будут обслужены. В системах смешанного типа
накладываются ограничения на время ожидания заявки в очереди, общее вре-
мя пребывания заявки в системе, число заявок в очереди и т. д. Наиболее
хорошо разработаны системы первых двух типов.
В зависимости от условий задачи и целей исследования количествен-
ными оценками качества работы СМО могут быть: средний процент заявок,
получивших отказ и покидающих систему необслуженными; среднее время
ожидания обслуживания; средняя длина очереди и ее распределение и др.
Входной поток (поток заявок) — основной элемент, определяющий про-
цессы в СМО. Часто его считают простейшим или стационарным пуассонов-
ским потоком, при этом в большинстве случаев удается получить удовлетво-
рительные по точности решения.
Для простейшего потока число заявок » промежутке времени т рас-
пределено по закону Пуассона
P(k, т) = -^^-е-Ч k = 0. 1, 2............. (9.35)
/?!
где X — плотность (интенсивность) потока — среднее число событий в потоке
за единицу времени; v = — среднее число событий в потоке, приходящееся
на интервал т.
Пусть случайная величина Т — промежуток времени между двумя
произвольными соседними заявками в простейшем потоке. Тогда функция
распределения ГД/), плотность вероятности рД/), математическое ожидание
mt и дисперсия of величины Т определяются формулами:
. F^t) = Р(Т < f) = 1 — е~и, pdt) = be~W, (9.36)
mt = 1/А, а? = W. (9.37)
В случае нестационарного пуассоновского потока выражения (9.35) и
(9.36) соответственно принимают вид:
P(k, т, to) = — e~v, (9.38)
Fi(t, to) = 1—exp
— f A (t) dt
to
Pl d,
t0)=A d u+0 exp
t>0.
(9.39)
Здесь
+ т
V= J A(t)dt [(9.40)
to
— математическое ожидание числа заявок на участке от /0 Д° 4" т, где
X (/) —мгновенная плотность потока.
9 Зак. 1203
257
4. Средняя длина очереди
оо
/71з = SPri-^-s =
s= 1
sas
П (П + mfy
m=l
(9.56)
5. Вероятность того, что заявка покинет систему необслуженной:
оо
ап ж-ч sa5
S=1 П («+«?)
т=1
as
п (п + «Р)
т = 1
(9.57)
В формулах (9.53)—(9.57) п — число обслуживающих аппаратов в сис-
теме,
a = А/ц = kmt об» ₽ = ?/ц = ymt Об> (9.58)
где X — плотность простейшего потока заявок; р, — параметр показатель-
ного времени обслуживания; у = l/mf ож — параметр показательного вре-
мени ожидания (величина, обратная среднему сроку ожидания).
При р -* оо система переходит в СМО с отказами, а при Р —> О — в «чис-
тую» систему с ожиданием, когда заявки вообще не уходят из очереди (каждая
из заявок рано или поздно будет обслужена). В последней системе предельный
стационарный режим существует только при a < п. При a > п число зая-
вок в очереди с течением времени неограниченно возрастает.
Для СМО с неограниченным временем ожидания (чистая система с ожи-
данием) при a < п справедливы формулы:
п h
afe
л
л«=0
ЦЦ+1
п\ (п—а)
(9.60)
(9.61)
»
(9.62)
260
Если имеется СМО с ожиданием и число заявок в очереди ограничено,
то при простейшем потоке заявок и показательном распределении времени
обслуживания формулы для Pk и Pn+S соответственно имеют вид:
где т — число заявок, которыми ограничена очередь.
2. ПРИМЕРЫ
9.1. Семь невосстанавливаемых радиоэлектронных систем по-
ставлены на испытания. Реализации времени работы этих систем
представлены на рис. 9.3.
Вычислить статистические показатели надежности P*(t), Q\t),
р\ (t), X* (/), mj при t — 30 ч и Д/ = 10 ч.
Решение. В соответствии с определением по формулам (9.6)—
(9.10) имеем:
Р* (t = 30) = N = у — 0,714 (не отказали системы с но-
мерами 2, 5, 1, 4, 7),
Q* (t = 30) = п = 3?) = у = 0,286 (отказали системы с номера-
ми 6, 3),
. и = 30) = я(^+А0-п (0 Я(Г = 40)-пд=30)
261
Рис. 9.1. Типичный вид функции Р(0>
<2(0,/МО, МО
Иногда пользуются понятием вероятности отказа Q(t) за время /, кото-
рая определяется как вероятность того, что случайное время работы системы
до отказа окажется меньше заданного времени t:
Q(t) = Р(Т <0=1- P(t) = Л(0- <9-2)
Плотность вероятности отказов pt(t) — плотность вероятности того> что
время работы системы до отказа окажется меньше /, или плотность вероят-
ности отказа к моменту времени /:
„ ГЛ Нт ^ + Д0--Р(0
Р1(0 = —hm ---------—--------=
дг->о Дг
dP(t) _
dt dt
(9.3)
Интенсивность отказов %(/) системы в момент времени t есть плотность
вероятности отказа системы к моменту времени t при условии, что до этого
момента отказ системы не произошел:
,1 (0 л (О
1 —FHO dt P(t)
Среднее время безотказной работы mt системы — математическое ожи-
дание времени работы системы до отказа:
(9.4)
mt = J tpl{t)dt = '^ P(t)dt. (9.5)
о о
Показатели надежности (9.1)—(9.4) функционально связаны между со-
бой: зная одну из функций Р(/), Q(/), рх(/), Х(0, можно определить три ос-
тальные (табл. 9.1).
Типичный вид функций P(t), Q(t), p^t) и X(Z) изображен на рис. 9.1.
Пусть 7V0 — число исправных систем в начальный момент времени
t — 0; N(t) — число исправных систем в момент времени t\ n(t) — число
систем, отказавших за время t ;&n(t,&t) — число систем, отказавших именно
в интервале от t до t + Д?; — время наработки t-й системы до отказа.
Тогда статистические показатели надежности для невосстанавливаемых
систем определяются выражениями:
Na Nf, N{>
Q*(t)=n(t)/NQ, (9.7)
л(/+Д/)-п(0 N(t + &t)-N(t)
p'(t}== ----------------------(9-8)
n(t + Al)-n(t) NV+&t)-N(t) _An(f, Д/)
x (Z)= T^t =“ w)^ W ’ (9'9)
-Г=-^ 2 ‘I- (9.Ю)
° /_1
250
Функциональная связь между показателями надежности
Таблица 9.1
Известная функция 0(0 PiU) Mt)
—- 1-Р(0 dP(t) dt 1 dP(t) ~ P(t) dt
<2(0 1—<2(0 dQ(t) dt 1 dQ(t) di \
Р1(0 JPi(r)dx t J Pl(T)dT о —' P1(V f Pi(T)dx t
Л(0 Г 1 1 ехр — J X(T)dx L о J Г * 1 1—ехр —J X(T)dT L о J Г 1 X (/) exp —J X(z)dT L о
X»и = з0) _ п(/+Др-л(0 = п (/ = 40)—я (Z=30) = 4—2 _ Q 04 q_1
' ’ ;V(/=30)-10 5-10 ’ ’
. /1/A/»V\ 'i + '2+ •••+'’_ 55 + 32 + 21+83 + 36+12 + 96
—U/2V0Z Zi ------------------ e
7
= 48 ч.
7
Точность результатов невелика. Она увеличивается с увеличе-
нием числа ЛГ0. Для определения точности и надежности оценок сле-
дует воспользоваться методами математической статистики (см. гл.4).
9.2. Интенсивность отказов элемента определяется выражением
, /А (1/(100— Z), 0</<100 ч,
(0, /<0,/>100ч.
Определить: 1) вероятность безотказной работы элемента в ин-
тервале времени 0—10 ч; 2) среднее время безотказной работы эле-
мента; 3) плотность вероятности отказов.
Решение. Для вычисления требуемых показателей надежности
воспользуемся формулами, приведенными в табл. 9.1, я выражением
(9/6).
t
1) Р(/) = ехр —J
о
/ Л 1
=ехр — 1-------
Ч J 100—т
/, юо—z\ юо—t
= ехр In---- =-------
Ч юо j . юо
При t = 10 ч имеем
Р (t = 10) = (100 — 10)/100 = 0,9.
юо
2) m(=Cp(Od/= С fc£t// = |ioo-/ = //| =
1 у2
100 2
Ч.
3)
1 100 —1 Г_г
100—/ 100 ““ 100 .
9.3. Три системы, состоящие из двух элементов, образованы тре-
мя способами соединения элементов (рис. 9.4). Отказы элементов
независимы и описываются простыми пуассоновскими потоками с
интенсивностями Х,г и Х2. Выключатель абсолютно надежен.
Рис. 9.4. Три системы, состоящие из двух элементов
262
Требуется: 1) определить вероятности безотказной работы, сред-
ние наработки и плотности вероятности отказов для каждой из си-
стем; 2) нарисовать зависимости вероятностей безотказной работы
систем от времени при = Х2 = X; 3) сравнить системы по надеж-
ности при Хх = Х2 = X.
Решение. 1. Вероятность безотказной работы для системы из
последовательно соединенных элементов (рис. 9.4, а) определяется
формулой (9.25):
/ 2 \
Р0(/) = ехр I — 2 М =ехр[ —(lx +М*]-
\ /=1 /
Используя (9.5), получаем выражение для среднего времени без-
отказной работы
mt, = f Ро (0 dt = J е-(Х*+м‘ dt = + М’1.
О о
По формуле из табл. 9.1 находим плотность вероятности отказов
Рю(0 = —dPQ(t)ldt = (\ + Х2)ехр [—(\ + Х2)Л.
Для системы с параллельным соединением элементов (рис. 9.4, б)
соответствующие характеристики равны
2
Рр (0 = 1 — П [1 — Pi (/)] = 1 — (1 — е~Л«')(1 — е-М) =
= ехр (—V) + ехр (—Х2^) — ехр I—(Хх + X2)Z], пи = ГРр(/)Л=
р о
= (X? + м2 + х22)/ххх2 <хх + Х2), Р1р (/) = -dPp (t)/dt = -
= ехр (—V) + Х2ехр (—%</) — (%i + Х2)ехр [—(Хх + Х2)/1.
Третья система (рис. 9.4, &) работает так. Если первый элемент,
начав работать в момент t ~ 0, откажет через интервал времени
7\ = t14 то мгновенно автоматически включается втфой элемент.
Если отказ второго элемента наступает в момент Т2 = t2 после его
подключения, то время безотказной работы системы Тэ = 7\ + Т2.
Поэтому плотность вероятности отказов третьей системы есть плот-
ность вероятности суммы двух независимых случайных величин:
t
J
Q,
где Pi (0 = exp (—fa (0 = X2 exp (— — плотности ве-
роятности случайных величин Т1 и Т2 (плотности вероятности по-
тока отказов первого и второго элементов). По плотности вероят-
ности Р1Х(О найдем вероятность безотказной работы Px(t) и сред-
нее время безотказной работы
Рх (t) = (Х2е~М - Ххе-^(Х2 - М. mtx = (*i + X2)/XxX2.
263
Рис. 9.5. Вероятности безотказной
работы систем, приведенных _на
рис. 9.4
2. При \ = Х2 = X характеристики систем определяются сле-
дующими выражениями: для первой системы
P0(t) = ехр (—2W), = 1/2Х,
для второй системы
Рр (/) = [2 — ехр (—X/)] ехр (—М), = 3/2Х,
для третьей системы
Px(t) = (1 + М) ехр (-М), tntx = 2/Х.
На рис. 9.5 изображены зависимости вероятностей безотказной
работы систем Ро (/), Рр (/), Рх (/) от времени при = Х2 = X.
3. Из графиков видно, что наименее надежной является первая
система и наиболее надежной — третья. По среднему времени без-
отказной работы третья система лучше первой в 4 раза, а вторая — в
3 раза. Результат справедлив при абсолютной надежности выключа-
теля. В противном случае, при известной надежности выключателя
надежность третьей системы следует вычислять по формулам для
смешанного соединения.
9.4. Определить вероятность безотказной работы аварийной
радиостанции за время /3 = 100 ч при заданном среднем времени
безотказной работы mt& = 250 ч.
Решение. Задача типична для поверочного ориентировочного
расчета надежности, когда требуется определить один или несколь-
ко показателей надежности радиостанции (системы) по известным
показателям ее элементов.
Для расчета нужно воспользоваться техническим описанием и
принципиальной схемой радиостанции, а также справочными дан-
ными по интенсивностям отказов элементов. Удобно составить таб-
лицу:
264
1 Число
Наименование элементов элементов 106 ч"1 п. А,. - 106 ч 1
(штук) / 7 ,
1. Лампы приемно-усилительные 4 2 8
2. Полупроводниковые приборы 5 0,5 2,5
3. Резисторы 45 0,25 ' 11,25
4. Конденсаторы 42 0,15 6,30
5. Трансформаторы 3 0,5 1,50
6. Дроссели 3 0,025 0,075
7. Катушки индуктивные 5 0,63 3,15
8. Батареи заряженные 1 7,2 7,2
9. Резонаторы кварцевые 1 0,3 0,3
10. Переключатели 3 0,6 1,8
11. Разъемы штепсельные 7 0,2 1,4
Итого 119 43,5
1. Определяем суммарную интенсивность отказов
х0 = 2 nf =43>5 • ю-5 ч-1-
/=1 /=1
2. Среднее время безотказной работы mt = 1/%0 = 1/43,5-10-6=
= 2,3-103 ч. Расчетное значение больше заданного: mt > mt =
= 250 ч.
3. Вероятность безотказной работы радиостанции за время /3 =
= 100 ч
Р(/ = 100)= е_%в<8 = е-43-б-10"6-1°2~ 0,96.
Целесообразно для 5—8 моментов времени в пределах от t = 0
до t> tnt определить значение функции Р (/) = ехр (—Хо/) и пост-
роить график зависимости Р (/), по которому можно определить ве-
роятность безотказной работы за любое время t.
При использовании данных по интенсивностям отказов элементов
следует соблюдать определенную осторожность. Более точные ре-
зультаты будут тогдаt когда используются данные, полученные по
опыту эксплуатации образцов, близких по конструкции и назначе-
нию к рассчитываемой системе.
9.5. В контрольно-поверочную лабораторию поступает пуассо-
новский поток приборов с плотностью 4 прибора в час.
Определить: 1) вероятность того, что за час в лабораторию по-
ступит k приборов, где k = 0, 1, 2, 3, 4, 5, 6, 7; 2) вероятность того,
что за время проверки прибора, на которую затрачивается в сред-
нем 30 мин, в лабораторию поступит не менее трех приборов.
265
Решение. По условию задачи входной поток — пуассоновский.
Поэтому вероятность того, что за время т в лабораторию поступит
ровно k приборов, определяется формулой (9.35):
Р(й, T) = ^Le~^.
1. В данном случае X = 4, т = 1, k = 0, 1, 2, 3, 4, 5, 6, 7. По-
этому
Р (0,1) = —е-4~ 0,0183, Р(1,1) = Л е~4 ~ 0,0733,
Р (2,1) ~ 0,147, Р (3, 1) ~ 0,195, Р(4, 1)~ 0,195,
Р (5, 1) ~ 0,156, Р (6,1) ~ 0,104, Р (7,1) ~ 0,0595.
т vk
Найдя значение суммы получим
k=o
где v = Хт = 4(1/2) = 2. Следовательно, Р (k 3, 1/2) = 0,323.
9.6. На вход системы обслуживания поступает простейший по-
ток заявок с плотностью X = 4 заявки в час. Время обслуживания
распределено по показательному закону, причем среднее время об-
служивания одной заявки mt0Q = 15 мин.
Вычислить: 1) количество необходимых обслуживающих аппа-
ратов, чтобы вероятность отказа в обслуживании заявки не превы-
шала 0,01; 2) среднее число занятых аппаратов; 3) вероятность
Р (k 3) того, что будет занято не менее трех аппаратов.
Решение. Имеем р. = l/mt об = 1/0,25 = 4, а = Мр, = 1.
1. По формуле (9.51) вероятность отказа в обслуживании
р =
отк /г!
Необходимо найти такое число п, чтобы вероятность Ротк не пре-
восходила 0,01.
При п = 4 имеем
р°™=[4! ('+ т+i +т +т)Г *0Л154'
при п = 5 получим
^отк = [5! (1 + 4- + 4 + • • * + 4)1"1 - 0,00306.
L \ 1! Z! Q! /J
266
Таким образом, чтобы выполнить условие Pow 0,01, необхо-
димо иметь 5 обслуживающих аппаратов.
2. Согласно (9.52):
тк=Р0 У -2^—=0,368 У---------!---=
= 0,368 (1 +1 + —+ — +—1 0,996.
21 31 41 /
3. P(k > 3) = Рз + Р4 + Р8,
Р3=-^-Л» =-^-0,368=0,0614, Р4 = 0,0153, Р5=0,00306.
Следовательно, Р (k 3) = 0,0798.
9.7. Для уничтожения вновь обнаруживаемых воздушной раз-
ведкой наземных целей выделен наряд из пяти батарей. Число об-
служиваемых целей представляет собой простейший поток с плот-
ностью X = 8. Время обслуживания подчинено показательному
закону. Среднее время обработки одной батареей одной цели гщ об =
= 30 мин.
Определить: 1) наличие установившегося режима работы СМО;
2) вероятность того, что при поступлении очередной заявки на об-
стрел все пять батарей будут свободными; 3) среднюю длину очереди.
Решение. 1. По условию, ггц^ = 30 мин. Следовательно, р =
= 1 /т/об = 2, а = Vp = 4. Так как а < м, то установившийся
режим существует.
2. По формуле (9.59) находим
= 0,0129.
3. Согласно (9.62) получим
ms =---------------------PQ =
П’П\ (1 — сс//г)2
46
5.5! (1 —4/5)2
0,0129 = 2,2.
9. 8 [3]. На станцию текущего ремонта автомашин поступает про-
стейший поток заявок с плотностью X = 0,5 машины в час. Имеется
помещение для ремонта одной машины. Во дворе станции могут од-
новременно находиться, ожидая очереди, не более трех машин.
Среднее время ремонта одной машины mt Об = 2 ч.
Найти: 1) пропускную способность системы; 2) среднее время
простоя станции; 3) насколько изменятся эти характеристики, если
оборудовать второе помещение для ремонта.
Решение. Имеем X = 0,5, р = 0,5, а = 1, т = 3.
267
1. По формуле (9.64), полагая п = 1, находим вероятность того,
чю пришедшая заявка покинет систему необслуженной:
Рн = Р1+з = 1/(1 + 1 + 3) = 0,2.
Относительная пропускная способность системы q =1 — Рв = 0,8.
Абсолютная пропускная способность Q = kq — 0,4 машины в чао.
2. Среднюю долю времени, которое система будет простаивать,
найдем по формуле (9.63): Рй = 1/5 = 0,2.
3. Полагая п = 2, находим
р = р = —(1 +1 + —+—+—+—V1 =0,021;
в г+3 16 \ 2 4 8 16)
q = 1 — Ри = 0,979,
т. е. удовлетворяться будет около 98% всех заявок; Q = kq = 0,49
машины в час. Относительное время простоя Ро = 16/47 = 0,34,
т. е. оборудование будет простаивать полностью около 34% всего
времени.
3. ЗАДАЧИ И ОТВЕТЫ
9.1. Наработка Т системы до отказа подчинена экспоненциаль-
ному закону с постоянной интенсивностью X.
Показать, что вероятность безотказной работы Р(/), функция
распределения плотность вероятности рх(/), математическое
ожидание mt, и дисперсия о? величины Т определяются формулами
Р(0 = е~^, FJ/) = 1 — рИО = Хе~^,
mt = 1/х, а? = 1/Х2
9.2. Наработка системы до отказа описывается экспоненциаль-
ным законом с параметром X = 10“3 ч"1.
Определить: 1) среднюю наработку до отказа; 2) вероятность
безотказной работы в течение t = 200 ч.
Ответ: 1) mt = 1000 ч; 2) Р (t — 200) = 0,82.
9.3. Интенсивность отказов самолетных генераторов в течение
периода нормальной эксплуатации практически является постоян-
ной величиной и равна 0,021-10"3 ч"1.
Вычислить для времени наработки генератора t = 500 ч вероят-
ность безотказной работы, вероятность отказа, плотность вероят-
ности отказов и среднее время безотказной работы.
Ответ: Р (500) ~ 0,99, Q (500) = 0,01, Р1 (500) ~
~ 0,021 ПО-3 ч-1, mt = 476-102 ч.
9.4. Время работы элемента до отказа описывается -экспонен-
циальным законом с параметром X = 2,5- 10~б ч"1.
Вычислить показатели надежности элемента Р (/), Р1 (/), mt при
= 500 ч и t2 = 1000 ч.
Ответ: Р (500) ~ 0,986, Р (1000) = 0,975, Р1 (500) = 2,47 X
X 10-5 ч-1, Р1 (1000) = 2,44-10-5 ч”1, /71^ = 4-104 ч.
9.5. Интенсивность, отказов элемента X (t) — at, где а — постоян-
ная величина.’
26S
Определить: 1) плотность вероятности отказов; 2) вероятность
безотказной работы элемента в течение средней наработки до отказа.
Ответ'. 1) p1(t) = а/ехр(—а/2/2); 2) Р (mt) = 0,46.
9.6. Плотность вероятности отказов радиотехнической сис-
темы
(0,002 ехр (—0,002/), /> 0,
Р1 ”{о, /<0.
Найти функцию распределения (/) и вероятность того, что вре-
мя безотказной работы системы превысит 500 ч.
Ответ'.
F1(/) = J0, /s^0, р (Т > 500) ~ 0,37.
[ 1 —ехр (—0,002/), />0;
9.7. Время работы изделия подчинено закону Релея с параметром
распределения о = 1000 ч.
Определить показатели надежности изделия Р (/), рг (/), X (/),
mt для t = 500 ч.
Ответ'. Р (500) = 0,88, р1 (500) = 0,44 -10~3 чЛ X (500) =
= 0,5-10-3 ч-1, mt = 1253 ч.
9.8. Суммарный налет самолетов составляет 5000 ч. За это по-
летное время произошло 14 отказов в бортовых радиоэлектронных
комплексах.
Оценить с надежностью р = 0,9 среднее время безотказной ра-
боты комплексов.
Ответ'. 242 ч < mt < 614 ч.
9.9. Элемент имеет экспоненциальные законы распределения вре-
мени работы и времени восстановления с параметрами соответствен-
но X = 0,04 ч”1 и |л = 2 ч”1.
Вычислить: а) вероятность безотказной работы и вероятность от-
каза за время /=2ч; б) среднее время безотказной работы и среднее
время восстановления.
Ответ', а) Р(2) = 0,923, Q(2) = 0,077; б) mQ — 25 ч, тъ =
— 0,5 ч.
9.10. Аппаратура связи .работала по 8 ч ежедневно в течение
30 дней. За это время было два отказа, на устранение которых за-
трачено 5 ч.
Определить коэффициент готовности аппаратуры.
Ответ'. 0,98.
9.11. Восстанавливаемая система с экспоненциальными распре-
делениями времени безотказной работы и времени восстановления
имеет коэффициент готовности КТ = 0,95.
Вычислить вероятность безотказной работы системы в течение
t = 10 ч, если среднее время восстановления тъ = 5 ч.
Ответ*. Р(10) ~ 0,9.
9.12. В результате испытаний двух радиостанций одного и того же
же назначения установлено, что у первой из них наработка на отказ
в два раза больше, чем у второй, а среднее время восстановления
269
первой радиостанции в пять раз больше, чем у второй, и составля-
ет одну десятую наработки на отказ.
Вычислить коэффициенты готовноти K*ri и К*г* радиостанций и
оценить их эксплуатационную надежность за время /э.
Ответ' ~ 0,91, Кг2 ~ 0,975. Эффективность использова-
ния первой радиостанции меньше из-за более длительных вынуж-
денных простоев.
9.13. Радиостанция состоит из двух блоков, причем наработка
на отказ первого блока равна /и01 = 25 ч, второго — т02 = 100 ч.
Среднее время восстановления первого и второго блоков соответст-
венно равны mBi = 1 ч, тВ2 = 6 ч. Отказы блоков независимы.
Станция отказывает при отказе любого блока и считается неработо-
способной до тех пор, пока не будет отремонтирован отказавший
блок.
Определить коэффициент готовности Кг радиостанции.
Ответ Кг = 0,91.
9.14. По статистическим данным, полученным для десяти отка-
зов радиоэлектронной системы, произвести с достоверностью 90%
эксплуатационную оценку коэффициента готовности, если известно,
что среднестатистическое время между отказами mJ = 100 ч, а сред-
нестатистическое время восстановления неисправной системы тв =
= 10 ч.
Ответ\ 0,864 < Кг < 0,966.
9.15. Проектируемое радиотехническое устройство должно вклю-
чать три последовательно соединенных блока. Расчеты показали, что
интенсивности отказов первого и второго блоков составят =
= 0,008 ч"1 и Х2 = 0,032 ч”1. Время безотказной работы каждого
из блоков распределено по показательному закону.
Определить интенсивность отказов %з третьего блока, при которой
вероятность безотказной работы устройства в течение времени t =
= 1 ч равна 0,95.
Ответ'. Хз = 0,0113 ч""1.
9.16. Система телеизмерений состоит из основного и трех резерв-
ных каналов, находящихся в ненагруженном режиме, причем пе-
реключающее устройство считается абсолютно надежным. Каждый
из каналов имеет показательное распределение наработки до отка-
за с интенсивностью отказов X = 10“2 ч"1.
Определить среднюю наработку до отказа и среднее квадрати-
ческое отклонение наработки до отказа системы.
Ответ [571: mt = 400 ч, at = 200 ч.
9.17. Система образована смешанным соединением элементов
(рис. 9.6). Все элементы имеют одинаковую интенсивность отказов
ЦО = X.
2
Рис. 9.6. Система со смешанным соединени-
ем элементов
270
Вычислить показатели надежности системы P(i), Q(t), р. (/), mt.
Ответ: P(t) = 2e~2W — е~3W, Q(t) = 1 — 2e~2^ -I- e~3U
pt (/) = % (4e~2U — 3k~3W), mt = 2/3%.
9.18. Радиостанция состоит из шести блоков с известными зна-
чениями интенсивностей отказов i = 1, 6, интенсивность от-
казов датчика опорных частот = 54,34-10-в ч-1, приемовозбуди-
теля %2 = 58,71-10“в ч"1, усилителя мощности кз — 61,16-10~в ч-1,
согласующего устройства %4 = 42,14-10-6 ч-1, блока питания к6 —
= 64,91-Ю-5 ч-1, пульта управления ке = 4,15-Ю-6 ч-1.
Требуется: а) произвести ориентировочный расчет надежности
радиостанции; б) определить коэффициент простоя радиостанции,
если среднее время, необходимое для обнаружения и устранения
неисправности, равно 2 ч.
Ответ: а) Хо — 285,41 • 10-в ч-1; б) mt — 351 ч,
Р (t)— ехр (—285,41-10~в /); в) 0,00567.
9.19. На систему массового обслуживания поступает простейший
поток заявок с плотностью к.
Требуется: 1) определить, при каком значении t вероятность по-
ступления в СМО точно Аг заявок за интервал времени t достигает
наибольшего значения; 2) построит^ зависимость Р (k, t) при к — 1
и k = 0, 1, 2, 3.
Ответ: 1) t = k/к (k = 0, 1, 2, ...).
9.20. Поток отказов радиотехнической системы является прос-
тейшим с интенсивностью 0,02 отказа в час. Найти вероятность того,
что за 10 ч работы в системе:'а) не появится ни одного отказа; б) по-
явится хотя бы один отказ; в) появится один, два, три отказа.
Ответ: а) Р(0,10) = 0,819, б) Р (k 1,10) = 0,181,
в) р (1,10) = 0,164, Р (2, 10) = 0,164, Р(3, 10) = 0,00109.
9.21. Число элементарных частиц, попадающих в аппаратурный
отсек космической ракеты за время ее полета t, представляет собой
простейший поток с плотностью к. Условная вероятность для каж-
дой из частиц попасть в уязвимый блок равна р. Определить вероят-
ность попадания в уязвимый блок: 1) ровно k частиц; 2) хотя бы
одной частицы.
Ответ:
1) Р (А>, /) = ехр(—ktp), 2) Р (6 > 1,/) = 1 - ехр (-ktp).
kl
9.22. Опыт показал, что в ЭВМ происходит в среднем одна ошиб-
ка за 10 ч работы, а поток ошибок можно считать простейшим.
Вычислить вероятности неправильного решения задачи на маши-
не, если продолжительность решения составляет: а) 1 ч, б) 10 ч.
Ответ: а) 0,095; б) 0,632.
9.23. Число отказов радиотехнической системы представляет
собой простейший поток с интенсивностью 0,005 ч-1.
271
Вычислить: а) вероятность безотказной работы системы за t =
= 20 ч; б) математическое ожидание и дисперсию времени безотказ-
ной работы системы.
Ответ: а) Р(0, t) = 0,905, б) mt = 200 ч, о? = 4-104 ч2.
9.24. Показать, что поток заявок, у которого интервалы между
заявками взаимно независимы и распределены по одному и тому
же показательному закону рх (t) = является пуассоновс-
ким.
9.25. Доказать, что для нестационарного пуассоновского потока
заявок функция распределения и плотность вероятности случайной
величины* Т (интервал времени между соседними заявками) имеют
вид
Л (Л U = 1 —ехр
Р1(Л А>) = Ш + 0ехр
— J
tn
где tQ — параметр распределения (момент появления первой из двух
соседних заявок).
9.26. Мгновенная плотность нестационарного пуассоновского
входного потока заявок представляет собой линейную функцию
времени: Z, (t) = а + bt.
Определить плотность вероятности случайной величины Т —
промежутка времени между соседними заявками.
Ответ [31: рг (/, /0) = la + b (tQ + t)]ехр (—at — btQt — bt2/2).
9.27. Нестационарный пуассоновский поток вызовов на теле-
фонную станцию имеет мгновенную плотность вида X (t) =
= К (1 — cos 2at).
Найти среднюю плотность потока вызовов за промежуток време-
ни от до tQ + t.
Ответ [59]: Ц/, /0) = Х
< sin а (/ — /о) , 1 С
1--------------— cos a (t +10)
9.28. На вход обслуживающей системы поступает простейший
поток заявок с интенсивностью К и интервалами между заявками
Тъ Т2, ..., 7\, 7\+1, •••» которые являются независимыми слу-
чайными величинами.
&+1
Показать, что плотность вероятности интервала Т — У 7\ опре-
1 = 1
деляется выражением
р tke~M, t>Q.
9.29. Доказать, что при показательном законе распределения
времени обслуживания распределение длительности оставшейся
части работы по обслуживанию не зависит от того, сколько оно уже
продолжалось.
272
9.30. В результате анализа системы массового обслуживания ус-
тановлено, что функцию распределения Fr (t) времени обслужива-
ния ToQ можно описать выражением
F^t) = 1 - 1/(1 + t)\
где t — время, мин.
Определить: а) вероятность Рх того, что время обслуживания
заявки не превзойдет 5 мин; б) среднее время обслуживания одной
заявки; в) вероятность Р2 того, что за это время обслуживание оче-
редной заявки будет закончено.
Ответ', а) Рг = 0,972, б) т^ = 1 мин, в) Р2 = 0,75.
9.31. Группа из п самолетов производит поиск малоразмерного
объекта. Каждый самолет действует независимо от других. Поиск
прекращается, как только объект обнаружен одним из самолетов.
Пусть закон распределеления времени поиска каждым самолетом—
показательный, причем среднее время поиска для каждого самолета
соответственно равно 1/^!, 14*2, •••> 1/Нп- Показать, что: 1) функция
распределения времени поиска всеми п самолетами имеет вид
F^t) = 1 — ехр I—(Pi + + ... + Рп)Л;
2) математическое ожидание и дисперсия времени поиска при
Hi = Иг = ••• Ип = И соответственно равны
m<o6=1/n^’ Чб = 1/(/гН)2-
9.32. Частица, попавшая в счетчик Гейгера—Мюллера, вызывает
разряд, длящийся время т (т — постоянно). Попавшие за это время
в счетчик новые частицы не регистрируются им. Считая, что распре-
деление числа частиц, попавших в счетчик, подчиняется закону
Пуассона, найти вероятность того, что счетчик за время t> 0 со-
считает все попавшие в него частицы
Ответ [62]: Р(0=е~и[1 + У V+> (?~feT)*+1 1
(* + 1)!
где X — среднее число частиц, попавших в счетчик за единицу вре-
мени.
9.33. В автопарк, рассчитанный на п мест, прибывает простей-
ший поток машин с интенсивностью X до тех пор, пока имеются сво-
бодные места. Найти дифференциальные уравнения для вероятностей
Ph (/) того, что ровно k мест заняты.
Ответ [5]: Ph (t) = -(X +/гц) Pk (t) +XPft_x (/) +
at
+(fe + l)pPA+1(/), ± Pn (0=-npPn(0+^n-i(0-
9.34. Сколько оборонительных комплексов n должна иметь обо-
ронительная система, чтобы вероятность ее прорыва противником
не превышала 0,02, если на данном направлении действует простей-
ший поток целей противника с плотностью X = 4, время обстрела
273
одной цели одним оборонительным комплексом распределено по по-
казательному закону с параметром р, = 2, а вероятность поражения
цели при одном выстреле (залпе) равна единице.
Ответ\ п = 6.
9.35. На станции п телефонов-автоматов, обслуживающих в
среднем N человек. Вероятности одновременного разговора k че-
ловек распределены по закону Пуассона
т) = -^ е~Ч
Найти среднее число абонентов, стоящих в очередях к автоматам.
N
Ответ: т= V (k—и) е-1х = Р(п, т) [———|-
, kl I п + 1
2(Лт)2 , (N—n) (U)N~n 1
** (п+1)(п + 2) 4~'"-r(n + l)(n + 2)..JVj’
где
Р(п, г) = е~Хт.
п!
9.36. Узел связи обслуживает 1000 абонентов, каждый из кото-
рых в среднем занимает линию связи в течение 6 мин за час. Какое
число каналов п надо иметь, чтобы исключить длительные ожида-
ния (вероятность того, что максимальное число одновременно по-
ступивших вызовов превысит число каналов, не должна превышать
0,3%).
Ответ: п = 128.
9.37. Для охраны района выделено 10 кораблей, ремонт которых
обеспечивают два дока. Каждый док может одновременно принять
для ремонта один корабль. В док карабль ставится тогда, когда он
не может нести охрану и нуждается в ремонте. Вероятность того, что
корабль за время t потребует ремонта F (/) = 1 — ехр (—0,02/),
где t — время, мес.
Предполагая, что в среднем на ремонт одного корабля затрачи-
вается два месяца, а время ремонта подчиняется показательному
закону, определить: а) среднее число кораблей, находящихся в ре-
монте; б) вероятность того, что для охраны района будет иметься не
менее 8 исправных кораблей.
Ответ [63]: a) = 0,395; б) Р (k 8) = 0,99.
9.38. В систему с одним обслуживающим аппаратом поступает
простейший поток заявок с плотностью А, — 9,8_ заявкй в минуту.
Число обслуженных заявок подчиняется закону Пуассона, причем
среднее число обслуженных заявок в минуту равно 10.
Определить: а) математическое ожидание длины очереди; б) ве-
роятности того, что в очереди находится 0, 1, 2 заявки; в) вероят-
ность того, что вновь поступившей заявке совсем не придется ждать;
г) среднее время ожидания.
Ответ: а) тв = 49, б) Ро = 0,02, Рх = 0,0196, Р2 = 0,0192,
в) Ро = 0,02, г) mt0H( — 4,9 мин.
274
Раздел HI
ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
НА ЭЛЕМЕНТЫ РАДИОТЕХНИЧЕСКИХ
УСТРОЙСТВ
10. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
НА ЛИНЕЙНЫЕ СИСТЕМЫ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При рассмотрении преобразований случайных сигналов линейными сис-
темами можно пользоваться аппаратом дифференциальных уравнений, им-
пульсными характеристиками и комплексными частотными характеристика-
ми систем.
В общем случае, когда интересуются как нестационарным, так и стацио-
нарным режимами работы системы и начальные условия в системе не нулевые,
целесообразно использовать аппарат дифференциальных уравнений. При ну
левых начальных условиях удобнее пользоваться импульсными характе-
ристиками. С комплексными частотными характеристиками обычно опери-
руют в том случае, когда интересуются лишь стационарным состоянием ли-
нейной системы.
Типовые задачи, связанные с преобразованием случайных прегессов ли-
нейными системами, можно разбить на две группы:
1. Задачи, требующие определения математических ожиданий, корреля-
ционных функций и спектральных плотностей процессов на выходе линей-
ных систем.
2. Задачи, требующие определения функций распределения выходного
случайного процесса.
Очевидно, что из решения задач второй группы может быть получено
решение задач первой группы. Однако, за исключением того важного, хоть
и частного случая, когда воздействующий на линейную систему процесс
£ (/) является гауссовским, не существует метода, который позволял бы на-
ходить непосредственно плотности распределения вероятностей для процесса
т) (0 на выходе системы. В общем случае задачи второй группы приходится
решать путем вычисления корреляционных функций выходного процесса
т) (/) с последующим определением характеристических функций и соответ-
ствующих им плотностей распределения вероятностей PnCni* Лз» •••> Пп! G»
^2» • ••> 60- Ниже приводятся формулы, по которым находятся корреляционные
(или моментные) функции процесса на выходе линейной системы при извест-
ных корреляционных функциях процесса на входе.
Рассмотрим систему, описываемую линейным дифференциальным урав-
нением с постоянными или зависящими от времени коэффициентами:
dn d
anU)-^- я (О -I---h 01 <0-7-4(0 +Оо (On (0 =
atfl ai
dm d
= 5(0+ ••• + M0-^”5(0+M05(0-I (Ю-D
275
Здесь £(/) — процесс на входе системы, характеризуемый математическим
ожиданием m^(t) ==44 11 (/)} и корреляционной функцией
R^(tlt t2) = Ui)][M'2) —"VM]}.
Вводя оператор р = d/dt и операторы А (р, /) и В (р, /), определяемые равен-
ствами
п т
А(р. 0=^01 (1)р\ В(р,1)= % bid)? , (Ю.2)
' == О ' = о
дифференциальное уравнение (10.1) можно привести к следующему опера-
торному соотношению [64]:
A (p,t) т) (0 = В (р,0 g (/)• (Ю.З)
Из (10.3) формально следует равенство, определяющее сигнал на выходе
системы в явном виде:
W) = ~^777U' =-ИР. Os(O- (Ю.4)
Д(р,0
Оператор
В (р, /)
Mp.O--.-7’ . (Ю-5)
A (p.t)
называется линейным однородным оператором системы. Динамическая сис-
тема с оператором (10.5) линейна, так как при решении дифференциального
уравнения (10.1) применим принцип суперпозиции. Линейным неоднородным
оператором Ь±(р, t) называется сумма линейного однородного оператора и
некоторой заданной функции f (t)
t) = L(p, 0 + m (Ю.6)
Путем вычитания из (10.6) функции f (t) любой неоднородный оператор мо-
жет быть приведен к однородному.
Из (10.4) можно получить следующие соотношения, определяющие мате-,
матические ожидания и корреляционные функции процессов на выходе ли-
нейных систем через их операторы и статистические характеристики входных
процессов [64]:
= L (р, 0^(0, (10.7)
R^i, t2) = L (p, у L (p, /2) ^(G, /2). (10.8)
Неоднородность оператора системы на значении корреляционной функции
не отражается, а при нахождении математического ожидания она должна
быть учтена добавочным слагаемым.
При заданном операторе линейной системы принцип суперпозиции по-
зволяет свести исследование реакции системы на произвольное воздействие
к исследованию реакции системы на типовое воздействие. В качестве типового
обычно используется импульсное воздействие в виде дельта-функции или
гармоническое колебание.
Реакция предварительно не возбужденной линейной системы на воздей- v
ствие в виде дельта-функции называется импульсной характеристикой сис-
темы h (/). Если оператор системы определяется формулой (10.5), то эта реак-
ция может быть установлена в результате решения линейного дифференци-
ального уравнения
dn d
an(t)-^-h(t) 4-...+М0 —МО+МОМО-
dm d
6<') + --- + MO-^-6(O + MO6W (10.9)
276
при нулевых начальных условиях. При этом процесс на выходе линейной
системы определяется интегралом Дюамеля:
t с
Г] (О =уЛ(/— т) §(т)йт = §h(x) § (t—x) dx . (10.10)
о о
Используя (10.10), получаем следующие формулы для математического
ожидания и корреляционной функции на выходе системы [1J:
t
-T)m^(T)dT, (10.11)
о
₽л(/п h) = J*J* /!(Л—Tx)/i (t2 — т2)Я, (Tn t2) Jt. 4t2. (10.12)
Для высших корреляционных функций (т. е. n-мерных центральных момент
ных функций n-го порядка) имеем:
ti 1я
Я3п(/п *2» h) =f f J ^^l-~Ti)/l(/2—T2)/l(Z3—Тз) X
0 0 0
X (ti, t2, t3) dTx б/т2 dx3 ,
* (10.13)
₽nt)(4, ...,(n> = j" ••• f h(tx—тх)Л (f2 — t2) ...h(tn— Tn) X
0 0
x tfrtg(Tn t2, ...» TnjdTi dx2 ... dxn .
Применительно к стационарным входным процессам £ (0 формулы
(10.11)—(10.13) принимают вид
t
h(t~x) dx= tn^h(x) dx * (10.11a)
о 'о
₽n(/n f / h(tA — TOM^—T2) ₽£(t2— Ti)dTidTai (10.12a)
0 0
G ta L
Я3т)(*П t2, /3)« J J J /1(^1—Ti)/l(^2—Т2)Л(Г3—T3)x
0 0 0
X R3% (t2—Ti, t3—TxJdTi dx2 dx3. (10.13a)
В случае линейных пассивных систем с затуханием по истечении доста-
точно большого времени от момента t 0 случайный процесс т) (0 будет
приближаться к стационарному. Для стационарного процесса формулы
(10.11)—(10.13) преобразуются к виду [1,14]
h(x)d^^ (1U.116)
о
/?т)(т)== J h(x)dx J /г(т+х— z)R^(z)d? (10.126)
0 — оо
оо Т2Н”Л
^3tl(T!, т2) = J h(x)dx J J {/)Л(т2+х—z) X
О — оо —оо
X R^ (у, z)dydz. (10.136)
277
Таблица 10.1
Комплексные частотные и импульсные характеристики простейших линейных систем
Схема (/©) = J h (f) e — iat at 0 h(f)=— C (/<o) e/w d<o 2л J — oo
ф^> Z я V») R R-\-j(i)L R , R —l‘ L e
* l ^7® г j(dL R + jcoL R —~t — — e L
Ф^ г 1 1 -f- j&RC 1 c~RC~ * RC
Л—11—iH Оад с fi L т__! jcoRC 1 + jaRC
1+/<аЛ 1+/®Т ’ T = (J? + /?1)C; 7’i = 7?1 С -^бЮ-ТГ-е"'
► 1+/<оЛ 1 + 7<о7’ ’ 7’ = /?(С+С1), 7’Х = /?С, -у-6(0—уте"7"
0-^-4 ею о— =.с Чи *П1 со2 (О2) 4-/2аш (hq~1/~\/LC} a = R/2L со^е arsino)0z. со0 > а; a2te^at, соо = а; —-е a,shVa2—со?, ci)0<a. Va2—со2
Продолжение табл. 10.1
Схема Л'(/«» = У'>(0 е ,a>t dt 0 h(t)=— f 2л J — оо
|*Ь o—l dr Г—i /2ос©₽ (©^ —©2)-(-/За©’ <в0 = 1/У£С, а = 1/2/?С t 11(0 = 777 Ге-аа-*) х ©oG J 0 Xsin©oU—x)l(x)dx, ©0>а
Гауссовский фильтр 71 /(£> — €Оо\2 . , . , 2) — } ((£> — &0) ta е 2 \ До> ) А® < ®0 Д© 2Л пУ2е
Идеальный полосовой фильтр — /(со— сооНо А03 Д© . е , соо——< © < ©о + “^~> Л Д© Дю 0, ®<Шо—о»®0+ — А Д© (t— to) sin Д© 2 e/<or® 2л Д® (t—to) 2
(йТ 7 sin ~— — /co — =-e ' 2 coT 2 ~p 0<t<T, 0, t < 0, t > T
1 /(0 J 1, о < t <00, to, ^<0
/Ш i -^6(0 = 6' (t) at
/а>Л (1 4- /(oTx) (1 + /wT 2) Л-^Сх, t2=r2c2 khdr? г-е Г'И*7- Т(1~7)е~~. I\ = T2^T
В заключение укажем, что взаимная корреляционная функция для про-
цесса g (/) на входе линейной системы и выходного процесса т) (/) равна
R^(h, h) =f h(t2—т)Я6(<1, т)Л. (10.14)
о
Если процесс g (/) стационарен, то
G
(11, y=f Л (Z2—т)/?£(/1—T)dT. (10.14а)
Подавая на вход линейной системы гармоническое колебание х (/, со) =
= ехр (/со/) и решая уравнение
(г. /<о) = е'Л (10.15)
A(p,t)
определяющее работу системы, находим, что решение (10.15) представляет
собой в общем случае комплексную функцию действительных аргументов /, со.
Выделим из функции ^\(/, /со) множитель ехр (/со/), т. е. представим решение
в виде
^ (/,/со)=Л’(/, ja>)e,a>t— ]Х (t, »|е'Агг^(1’е/ш<, (10-16)
наглядно показывающем изменение амплитуды и фазы воздействия х (t, со) =
= ехр (jtot) при его прохождении через линейную систему. Функцию^* (/, /со)
называют комплексной частотной характеристикой системы, в общем случае
она зависит не только от частоты со, но и от времени /. При помощи этой
функции легко вычисляется спектральная плотность (со) процесса т) (/) на
Еыходе линейной системы:
’ Sn(co) = S^(co)|^(Z, /co)p = Sn(co, /)< (Ю.17)
Здесь (со) — спектральная плотность воздействующего на систему случай-
ного процесса g (/).
Комплексная частотная характеристика системы с постоянными пара-
метрами и ее импульсная характеристика связаны друг с другом преобразо-
ванием Фурье:'
оо
/!^,=~2л~ f (/®) е/и/dco, (10.18)
— оо
<%*(/<»)=/ h (f)e~'al dt. (10.19)
о
Выражения X (j®) и h(t) для некоторых простейших линейных систем с по-
стоянными параметрами приведены в табл. 10.1.
2. ПРИМЕРЫ
10.1. На вход дифференцирующего устройства поступает случай-
ный процесс £(/) с математическим ожиданием mt(t) = sinfJ-Z и
корреляционной функцией
Определить математическое ожидание (t) и дисперсию (/)
процесса т] (/) на выходе системы.
282
Рис. 10.1. Интегрирующая цепочка RC
о-- -1 <-О
7ft)/?\
W £={= 9(t)
Решение. Случайный процесс т] (/) на выходе системы (реакция)
связан с воздействием £(/) оператором дифференцирования:
П (0 = L (р, 0 g (i) = dt,
Применяя формулы (10.7) и (10.8), имеем
^(0 = -77^(/) = pcosp/,
at
/!!) = 2Dgae-^-^)2[l-2a(/2-/1)2].
uti (7t 2
Полагая t2 = tr — t, находим
0 = (/) — 2<zZ)g = Отр
10.2. На цепочку RC (рис. 10.1), начиная с момента t = 0,
воздействует случайное напряжение g (/), представляющее собой
стационарный белый шум с математическим ожиданием и корре-
ляционной функцией
/?£ (т) = (Wo/2) 6 (т). (10.20)
Определить математическое ожидание (t) и корреляционную
функцию /?п (4, /2) напряжения т] (/) на емкости С.
Решение, Дифференциальное уравнение для исследуемой схемы
имеет вид
dr] (t)/dt + ат] (/) = al (t), а = 1/RC. (10.21)
Будем считать, что в начальный момент времени емкость С раз-
ряжена, т. е. т] (0) = 0. В общем случае т] (0) может быть отличным
от нуля и носить как детерминированный, так и случайный характер.
При нулевых начальных условиях решение уравнения (10.21) имеет
следующий вид:
t
т] (/) = ае~ at J еах g (х) dx,
о
в соответствии с чем математическое ожидание случайного процесса
т] (/) на выходе цепочки RC равно
t
(t) = М {г| (/)} = ае~а/ J еах М {| (х)} dx =
о
t
ае~а/ еал т% dx = tn^ (eat — 1).
о
283
Таким образом,
Шц (/) — mt (1 — е-01')-
График этой зависимости приведен на рис. 10.2.
Корреляционная функция случайного колебания л (i) на выходе
цепочки RC согласно определению равна:
R^(t, /i)=a2e-a
о о
еа u+w (у—х) dxdy.
Учитывая, что по условию задачи Rt(x) — (Af0/2) 6 (т), находим
Rn (t, /1)=а2е-“ (<+'•>
Г еа (х+уч § (у—х) dxdy.
о о
При вычислении интеграла
‘ «1
1 = j е“ <Л+^> 6 (у—х) dxdy
о о
(10.22)
(10.23)
необходимо иметь в виду, что формула
2о + е
J f (2) 6(z0 — z)dz=f (z0)
Zo — 8
справедлива лишь при 8>0, т. e. когда особая точка z = z0 лежит
внутри пределов интегрирования.
Области интегрирования в (10.23) при г > 0 и т < 0 изображены
соответственно на рис. 10.3, а и б.
Дельта-функция 6 (у — х) обращается в бесконечность, как это
следует из рис. 10.3, лишь на том участке биссектрисы координат-
ного угла плоскости переменных х и у, который определяется наи-
меньшим из пределов t или tv Поэтому при вычислении интеграла
(10.23) оба предела нужно полагать одинаковыми и равными наи-
меньшему.
Рис. 10.2. Нарастание матема-
тического ожидания
Рис. 10.3. Области интегрирования
284
Рис. 10.4. Нарастание дисперсии
= т
я
Так, при т > 0 наименьшим из пределов интегрирования яв-
ляется t (4 = t + т и, следовательно, > /). Поэтому
t t t f
/ = J J ea 8 (y— x) dxdy = J ea* dx J e°^ 6 (y — x) dy =
oo oo
t
= Се2“^х= — (e2a<—1). (10.24)
J 2a
о
Подставляя (10.24) в (10.22) и производя замену tx = t + т (т > 0),
имеем:
(/, т) = (aW0/4) e~a* (1 — e~2a£), т > 0. (10.25)
При т < 0 наименьшим из пределов интегрирования является
tY и, следовательно,
tt tr
/ = f (ea 6 (у —x) dxdy = —(e2a£* — 1). (10.26)
«U 2a
Подставляя (10.26) в (10.22) и заменяя t через — т(т<0),
имеем
(/, т) = (alVo/4) еот (1 — е~2“(*). т < 0. (10.27)
Объединяя (10.25) и (10.27), получаем следующее выражение для
корреляционной функции (/, т) случайного напряжения т) (/)
на конденсаторе емкостью С:
RA(t, т) = (а^0/4) е—«।’I (1 — е-2«'). (10.28)
Полагая в (10.28) т = 0, найдем дисперсию (/) случайного
процесса т) (/)
Dn(0 = (a?V0/4)(l -е-2«').
График этой зависимости приведен на рис. 10.4. Сравнивая функ-
цию (/) с графиком гпц (/) на рис. 10.2, нетрудно установить, что до-
стижение дисперсией уровня 0,95 (оо) происходит за время уста-
новления /у = 1,5 R С, т. е. вдвое быстрее, чем достижение уровня
0,95 пг^ (оо) математическим ожиданием тп (/).
285
В стационарном режиме
= т^, Rn (t, т) = (aN0/4) е-“,х| = 7?ч(т),
(0 = aN0/4 =
19.3. Работа пропорционально-интегрирующего фильтра
(рис. 10.5) описывается линейным дифференциальным уравнением
первого порядка:
П (0 = 5 (0 = t (р) I (О- (10-29)
Тр+\
Для фильтра, изображенного на рис. 10.5, а, коэффициенты Т и
Tj соответственно равны (см. табл. 10.1):
Т = С (R + Pi), 7\ = RrC,
а для фильтра рис. 10.5, б:
Т = R(C + CJ, Л = RCV
На вход фильтра поступает случайное напряжение £ (/), пред-
ставляющее собой стационарный гауссовский белый шум с нулевым
математическим ожиданием пц, = 0 и корреляционной функци-
ей (10.20).
Определить спектральную плотность Sn (со) и корреляционную
функцию R^ (т) напряжения т) (/) на выходе фильтра.
Решение. В соответствии с (10.29) комплексная частотная харак-
теристика пропорционально-интегрирующего фильтра
^(/®) = L (р = /<о) = (1 + /<о7\)/(1 + /соТ),
а квадрат ее модуля определяется выражением
|^(/<о)| 2 = [1 + (©Tifl/H + (соТ)2]. (10.30)
Подставляя в (10.17) соотношение (10.30) и спектральную плотность
входного шума Sg (<о) = Af0/2, находим спектральную плотность
процесса т] (/) на выходе фильтра:
. S (Ю)^ N» ’ (Ю.31)
lv ’ 2 1-Ь(шПа v '
График спектральной плотности (со) на выходе пропорцио-
нально-интегрирующего фильтра представлен на рис. 10.6. Видно,
что при со-*- оо и Ti =И= Т спектральная плотность S4 (со) стремится
к некоторому постоянному уровню, равному ЫйТ]12'Р. Если по-
Ю ff)
Рис. 10.5. Два варианта схемы пропорционально-интегрирующего фильтра
286
Рис. 10.6. Спектральная плотность на
выходе пропорционально-интегрирую-
щего фильтра
стоянные времени 7\ и Т равны, Хп((о) = NJ2, т. е. процесс на
выходе фильтра в этом’ случае равен входному белому шуму.
При 7\ = 0 пропорционально-интегрирующий фильтр ведет себя
как обычная интегрирующая цепь RC.
Для вычисления корреляционной функции Rn (т) воспользуемся
формулой Винера—Хинчина:
ОО
f Sn(®)e^dco. (10.32)
После подстановки (10.31) в (10.32) имеем
2 2л
1 +(toT1)a
1+«оЛа
е/,эт dco.
Производя далее замену е/сох = coscot 4- / sin сот, находим:
^(х)=4-т-
2 ZJT
1 4- (соЛ)2 ,, .
——-—— cos сотосо 4*
14-(<оТ,а.
. . Г 14- (CoTj2 . .
4- / 1 —1-1—— sincoTdo)
J 14-(<оГ)2
—оо
(10.33)
Второй интеграл в (10.33) в силу нечетности подынтегральной
функции и симметричности пределов равен нулю, поэтому (10.33)
приводится к виду
Rn (T) = -^-TL
6 ZJI
COS (ОТ
I 4-(соЛ2
dco 4*
л
Г2
f cos сот
J 14-(coT)2
287
Учитывая» что [171
— I cos cordw = 6 (t),
2л J
окончательно получаем
Ъ (Т) = б W н~ ^Т‘ е-1 т|/г. (10.34)
При Т — 1\ из (10.34) имеем
(т) = <ад б(т) = ₽6(т).
В случае 7\ = 0
R« (т) = (Л/0/4Т) е_| т|/г,
что согласуется с результатами примера 10.2. График корреляцион-
ной функции (10.34) приведен на рис. 10.7.
10.4. На цепь, составленную из последовательно соединенных
индуктивности L и сопротивления 7? (рис. 10.8), воздействует
напряжение | (/), представляющее собой белый шум с нулевым ма-
тематическим ожиданием т* = 0 и спектральной плотностью
Sj (<й) = No/2, —оо С ю < оо. (10.35)
Найти спектральную плотность Sn (со) и корреляционную функ-
цию /?г)(т) напряжения т] (t) на сопротивлении R.
Решение. Комплексная частотная характеристика исследуемой
цепи определяется соотношением (см. табл. 10.1)
W®) = R!(R + /fi>L),
а квадрат ее модуля
I 2 = R2I\R2 + (“£)21- - (10.36)
Подставляя (10.35) и (10.36) в (10.17), находим спектральную плот-
ность напряжения т] (/)
(со) = (<й) | X (/а) |* = , - оо < <й < оо.
По спектральной плотности согласно формуле Винера—Хинчина
находим корреляционную функцию
7?п(Т)=_!_ J Sn (со) е/<ог do =
28S
Рис. 10.7. Корреляционная функ-
ция на выходе пропорционально-
интегрирующего фильтра
Рис. 10.8. Цепочка RL
Аналогично решаются все задачи, связанные с воздействием на
линейные системы белого шума. В табл. 10.2 приводятся резуль-
таты решения задач подобного вида для случая воздействия на не-
которые простейшие линейные системы стационарного гауссовского
белого шума с нулевым математическим ожиданием. В таблице даны
нормированные корреляционные функции и соответствующие им
спектральные плотности процессов на выходе.
10,5. Определить корреляционную функцию (т) случайного
напряжения % (t) на входе линейной цепи RL (рис. 10.8) при усло-
вии, что выходное напряжение т] (t) представляет собой стационар-
ный гауссовский случайный процесс с корреляционной функцией
(т) = Dne~™’. (10.37)
Решение. Случайный процесс | (t) на входе рассматриваемой
линейной системы определяется уравнением
К at
в соответствии с чем
(т) = м {Ы0 ut + т)} = м {[y0(t) + По(01 + т) +
+ По(* + т)]} = Ry СО + Rn (т). (10.38)
Учитывая, что у (f) =
£
7?
d
dt
т] (7), находим:
/ j ла / j \а
= -^-^(т) = 2аРЦ^ (1-2а^)е-«Л
(10.39)
После подстановки (10.37) и (10.39) в (10.38) получаем
/?Е(т) = Рпе-“’’ 1 +2“
I \2
1 (1 - 2ат2)
10.6. На цепочку RC (рис. 10.1), начиная с момента t = 0,
воздействует случайное напряжение £ (/), представляющее собой
стационарный шум с нулевым математическим ожиданием = 0 и
корреляционной функцией
Rl (0 = ОЕе-₽' ”.
10 Зак. 1203
289
Таблица 10.2
Корреляционные функции и спектральные плотности на выходе простейших линейных систем
Линейная система оо R (Т)=—!_ (* S (о) е1<ЛХ 2л J — оо оо S(to)= J R (т) е dx — 00
Аналитическое выражение График Аналитическое выражение | | График
1. Низкочастот- ный RC- фильтр e-a|tl / у 2а 1_ а2+<в2 ’ RC
0 т Z7
2. Два низкочас- тотных RC- фильт- ра (1 -J-а | т I) е““ 1 т 1 1 л 4дЗ (а2 + ®2)2
0 т 0 »
3. Три низкочас- тотных 7?С-фильт- ра (1 +а [ т 1 + а2т2/3) е~а|т| 16а& 3(а2 + <о2)з
0 т О а
4. Пропорциона- льно -интегрирую - щий фильтр Т2 1 Т2 $ 2Т х х Т2~П —\х\)Т х 72 1+W2 • 1 + (<оГ)2
* 0 Т о i
1 1
5. Гауссов низко- частотный фильтр е-ат2 \ 5.е-0’/4а
- 0 г 0 ы
6. Идеальный низкочастотный фильтр sin Дот Дот А л/Дсо при | со | < Дсо, 0 при I CD | > Дсо
О А& а
7. Идеальный высокоча стотный фильтр л _ Б1П"ДОТ л 6 “— Дсо Дот 0 при | со | < Дсо, л/Дсо Jnpn | со 1 > Дсо j 1 Л
of''" Г
” -Jo О а>
8. Высокочастот- ный RL-фильтр о, , 1 - lTl/₽ Р2 С»2 в = £_ 1+Р2ю2’ Р R э
О с)
9. Колебательный контур — а | т I ( а е cosco0t-|-—х \ (Оо X sin со0'|т| 4а (а2Ч~(Оо)
[а2 +(©-©„)«] [а2 + (со+о>о)2]
ЩД*13- £ 1II 1II ✓ 1 ч
-Qg О (Уф (t)
Определить корреляционную функцик» R^ (т) напряжения
q (/) на емкости С.
Решение. Процесс q (t) на выходе цепочки RC (см. пример 10.2)
t
q (0 = ае-** С еа* £ (х) dx, а = —,
J RC
о
в соответствии с чем его математическое ожидание
тп (0 = mi (1 — е~а/).
Так как по условию задачи mg = 0, то тъ (t) — 0.
Корреляционная функция R^ (t, tj процесса q (t) (см. при-
мер 10.2)
Rr\ (Л ti) = «2 e~“ (<+tl) J j e“ (*+i0 (У~ x) dxdy.
Так как в нашем случае Ri (т) = Dge~₽ Iх1 , то
tt,
R^ (t, Q = a2 Die“a «+<*> J j ea <•'+«')-₽ w-*idxdy. (10.40)
о 0
Сделаем в интеграле
t h
I = J J ea u+jo-P \у—ч dxdy
о 0
(10.41)
замену у = z + x. При этом (10.41) преобразуется к виду
t ti — X
Z = Je2“*dx ea2-Piz dz.
0 — x
(10.42)
Так как в подынтегральном выражении аргумент z берется по мо-
дулю, необходимо определить области интегрирования так, чтобы
в пределах каждой из них аргумент z имел бы только один знак.
Области интегрирования для случая, когда = t + т > t (т. е.
когда т > 0), и для случая, когда tx = t + т < t, (т. е. когда т <0),
показаны на рис. 10.9, а и б.
Таким образом, при т > 0 при интегрировании по z в пределах
[—х, 0] аргумент z < 0, а при интегрировании в пределах [0, /х —
— х] аргумент z > 0. В соответствии с этим при с > 0 интеграл
(Г0.42) можно представить в следующем виде:
t
/ = J e2ajrdx
о
О ti —х
J e(a+₽)zJz J e(a-0)zjz
X 0
(10.43)
292
Рис. 10.9. Области интегрирования
Подставляя (10.43) в (10.40) и учитывая, что — t = т, полу-
чаем следующее выражение для корреляционной функции при
т > 0:
a2 Dt i r
(t, т) = -—L (1 —е~2“9 е-“г -}-[е-(«+₽К—е~2а<] е-“т—
_[1_е-(а+₽)<]е-₽*}, т>0. (10.44)
Аналогично можно найти, что при т < 0
a2 Dfc ( R
. (t, т) = ——.ML (1 — е-2а<) еах4- [е~<а+₽>* — е~2а<] еах—
—[1 — е-(“+₽> * ]е₽х}, т<0. (10.45)
Объединяя (10.44) и (10.45), получаем следующее выражение
для корреляционной функции случайного процесса т) (/):
a2 Dt с R
(Л т) = ——y(1 —е~2о9 е-“ >х 1 4-[е-<а+₽) *—е~2а<] е-а1х1—
—[1— е-(а+₽) qe-₽iTiy (10.46)
Полагая в (10.46) /->оо, находим корреляционную функцию
для стационарного режима:
aDt
(т)=yzjr ^е-“1г|-ae-fJ ,х|). .
293
Дисперсия ? стационарном режиме равна
= Dg.
а + р
10.7. На линейную систему с импульсной характеристикой
h (0 воздействует стационарный гауссовский белый шум £ (f)
с корреляционной функцией Rg (т) = (No/2) 8 (т).
Определить взаимную корреляционную функцию Rgn (т) про-
цесса 5 (0 на входе системы и выходного процесса т](0 и дисперсию
процесса т) (0 на выходе.
Решение. Подставляя в (10.14) значение корреляционной функ-
ции Rg (т), находим
Rgn = ( ^°/2>h ~ПРИ ° 11 (10.47)
(0 при0<О,
Из (10.47) следует, что с точностью до постоянного множителя
импульсная характеристика линейной системы совпадает^ взаим-
ной корреляционной функцией между входным стационарным белым
шумом, воздействующим на систему, и выходным случайным про-
цессом. Этим результатом часто пользуются для эксперименталь-
ного определения h (t) неизвестной линейной системы при помощи
коррелометров.
Значение дисперсии Dn в стационарном режиме можно опреде-
лить при помощи формулы (10.12,6). Подставляя в нее заданную
функцию 7?s (т), имеем:
. (10.48)
о
Полагая в (10.48) т = 0, находим
Dn=-^-J/i2(x)dx.
о
10.8. Найти спектральную плотность S$(f) напряжения собст-
венного теплового шума на параллельной цепочке RC (рис. 10.10)
и построить график зависимости Sg (f)/4kT от величины R для трех
частот:
f = 100 Гц, 1,5 и 15 кГц при С = 100 пФ.
Вычислить дисперсию напряжения шума в полосе частот [f^] и
показать, что при = 0, /2 -> оо она равна kT/C.
Решение. Известно, что спектральная плотность напряжения
собственного теплового шума любой пассивной линейной электри-
ческой цепи определяется формулой Найквиста:
Sg (0 = 4kTR Re {Z}, 0 < f < oo,
294
Рис. 10.10. Цепочка RC
Рис. 10.11. Спектральная плотность
теплового шума
S((fJ
где kT = 4 • 10-21 Вт/Гц, Re {Z} — действительная часть комплекс-
ного сопротивления цепи Z.
Для параллельной цепочки RC имеем
ъ R R . RtoRC
Z, ----------=---------------1------------.
1+/©RC 1 + (<oRC)2 1 1+(<oRC)2
Поэтому
Se (/) = 4kT-------, 0 C f < 00 •
6V/ 1 + (2л/7?С)2
Графики зависимости Sg (f)/4kT от R для трех частот при С = 100 пФ
представлены на рис. 10.11. Дисперсию шума в полосе частот
1/1. AJ находим по формуле
h
Dt = 4kTR С —-----------df =
6 J 1 + (2nfRC)« '
fi
= [arctg (2nf2 RC)— arctg (2nfx RC)].
яс
Полагая здесь /х = 0, f2-> oo, получим
= kT/С.
3. ЗАДАЧИ И ОТВЕТЫ
10.1. На вход линейной системы с постоянными параметрами,
описываемой дифференциальным уравнением
ап~^г *1 (0 +••• + 4-п(0 +«о П (0 =
dtn at
=bm^ri(t)+... + b1-^Ui)+boi(t), '
воздействует стационарный случайный процесс £ (/) с математи-
ческим ожиданием, равным т^.
295
Найти математическое ожидание реакции системы т) (7).
Ответ: т^ = (Ь0/а0) т^.
10.2. На вход идеальной дифференцирующей цепи воздействует
стационарный гауссовский случайный процесс £ (t) с нулевым ма-
тематическим ожиданием = 0 и корреляционной функцией
/?6(т) = D6e-«i’l(l+а|т|).
Определить корреляционную функцию процесса т] (t) — (t)/dt
на выходе.
Ответ: (т) = a2Z)je~a|Tf (1—а[т|).
10.3. Решить задачу 10.2 при условии, что
- 1) (т) = Dj е-** I*1 ^cos <й0 т 4—— sin соо1т |) 5
2) =
Ответ:
1) Rr\ (т) = (а2 4- ®о) е~« 1т| (cos (оо т-— sin ®о I т|) ;
2) (т) = 2a2D6e~“ix2 (1 — 2аМ) = 2а2(1 — 2а2т2) (т).
10.4. На вход радиотехнического устройства, состоящего из
линии задержки на время 7зад = t0 и дифференцирующей схемы
(рис. 10.12), воздействует стационарный случайный процесс Е (t)
с нулевым математическим ожиданием = 0 и корреляционной
функцией
7?6 (т) = е~а|Х| (1 + а|т|).
Определить взаимную корреляционную функцию 7?^ (т) про?
цессов | (t — t0) и т) (0 =£(/) = d£ (f)/dt.
Ответ [4]: 7?^ (т) = — а2 Dg (т—/0) е~“ >х-/«|.
10.5. Корреляционная функция процесса £ (/) имеет вид
ЯЕ(т)=е-а,хг.
Найти корреляционную функцию процесса
Т) (0 = I (0 + dl (t)/dt.
Ответ: (т) == [1 + 2а2(1 — 2а2т2)] е~а'хг.
Рис. 10.12. Дифференцирующая схе- Рис. 10.13. Идеальный интегратор
ма и линия задержки
296
10.6. Корреляционная функция ^(т) случайного процесса
g (0 имеет вид
7?g (т) = Dg е~“1 х ’(1 4-а|т Ц-—-а2 т2У
\ V /
Найти взаимную корреляционную функцию процессов £ (/) и
Т] (0 = d2g(0/i«2.
Ответ: 7?gn (т) --— Dg а2 е~“ ITi (1 + а | т | — а2 т2),
и
10.7. На вход интегрирующего устройства (рис. 10.13) воз-
действует стационарный случайный процесс £ (/) с корреляционной
функцией 7?g (т).
Определить дисперсию процесса г] (/) на выходе интегратора
и взаимную корреляционную функцию 7?gn (tlt t2) для входного и
выходного процессов.
Ответ [41:
t
А> = 2 ^(t—r)R$(x)dx = Dn(f),
о
G
Rin h) = J Ri(t1—x)dx.
0
10.8. Вычислить корреляционную функцию Ri(tlt t2) и диспер-
сию Dg (t) случайного процесса Винера £ (/) = J n (/) dt, где n (/) —
о
стационарный белый шум с нулевым математическим ожиданием
тп = 0 и корреляционной функцией
яп(т) = (адб(т).
Ответ:
10.9. На вход интегрирующего устройства воздействует стацио-
нарный случайный процесс £ (/) с нулевым математическим ожида-
нием /ng = 0 и корреляционной функцией 7?g (т).
Определить дисперсию Dn и корреляционную функцию (т)
процесса
<+г
= f t(x)dx
в/
t—T
на выходе интегратора.
297
' Ответ'.
D,~y J Я,(т)(1--4А)л.
—Г
Т
— т.
10.10. Случайный процесс <р (0 задан уравнением
dq(t)ldt = лф(0,
где пф (t) — стационарный гауссовский белый шум с нулевым мате-
матическим ожиданием и корреляционной функцией
M) = (W(*)-
Определить дисперсию £>дф (0 т) приращения Аф (t, т) =
= Ф (/ + т) — ф (0 в стационарном состоянии.
Ответ:
(t, т) 1^00 = М {[ф (i + Т) -ф (0PJ |^м = i т.
10.11. Вычислить дисперсию D^(t, т) приращения
АХ(0 т) = Х(/4-т) —Х(0,
I
где X (0 — случайный процесс, заданный уравнением
. dK(t)/dt + аК (0 = пк (0. (10.49)
Здесь пк (0 — стационарный гауссовский белый шум с нулевым
математическим ожиданием и корреляционной функцией
₽пх(т) = да2)6(т).
Ответ:
Dlk (t, т) |^оо = М {[X (/ + т)-X(0р) |^оо = А (1 _е-« и I).
10.12. Определить дисперсию (0 т) процесса
т] (0 = J X (х) dx
при t -> оо. Здесь X (0 — случайный процесс, заданный уравнением
(10.49).’
N^
Ответг Dn(0T)|/^« = — [а|т|—(1— е-а1т1)).
298
10.13. Пусть случайные процессы 5 (0 и т| (0 на входе и выходе
линейной системы с импульсной характеристикой h (t) связаны со-
отношением
t
т] (0 = f h (t — т) £ (т) dr,
— оо
где функция h (0 абсолютно интегрируема на положительной полу-
оси.
Доказать, что
(0 0) = ! h (0 — 0 #1 (*• 0 dr,
— ОО
где 7?5П (£, tj) — взаимная корреляционная функция процессов
£ (0 й т] (0; — корреляционная функция процесса £ (0.
Предполагая, что процесс | (0 стационарен, доказать, что функ-
ция (t, t±) зависит только от разности аргументов, и выразить
взаимную спектральную плотность (со) процессов £ (0 и т] (0
через спектральную плотность Sj (со) процесса £ (0.
Ответ: (со) = Sj (со) J h (т) e/<eT dr.
10.14. Пусть 5 (0 и — случайные .процессы и
т)(0= $h(t— 05(0dr, П1(0= f 0|г(0dr.
0 — oo
Доказать, что
t t.
= f h(t—r)dr J M0—
— 00 —00
где 7?w (t, /x) — взаимная корреляционная функция процессов
т) (0 и П1(0; (0 0) — взаимная корреляционная функция про-
цессов 5 (0 и 51(0-
10.15. На конденсатор емкостью С начиная с момента времени
t = 0 воздействует флуктуационный ток I (0, представляющий со-
бой белый шум с нулевым . математическим ожиданием /пг = 0 и
корреляционной функцией
₽i(0 = (ВД6(т).
Найти дисперсию D4 (0 напряжения т) (0 на конденсаторе
(рис. 10.14).
Ответ: Dn (0 = t.
2С*
10.16. Решить задачу 10.15 для случая, когда корреляционная
функция тока i (0 имеет вид ₽t(0 = Dte~Pi’1 .
Ответ {44] t Dn (0 = 17 — -J- (1 — e-*)' .
pc* L P
299
Рис. 10.14. Воздействие случайного тока на
емкость
10.17. На вход дифференцирующей цепочки (рис. 10.15) воз-
действует случайное напряжение g (t), представляющее собой огра-
ниченный по частоте белый шум, спектральная плотность которого
[ 0, (0<0,
Найти дисперию напряжения т) (/) на выходе цепочки.
Ответ г Dn = (©г---arctg .
JC у 1\С j
10.18. На вход схемьк7?С (рис. 10.16) воздействует ограниченное
по полосе случайное напряжение £ (/) со спектральной плотностью
Дю
2
S6(«>)= "°’ и'°
" I 0 для всех других <о.
Найти спектральную плотность (со) напряжения т] (t) на вы-
ходе.
Ответ:
<«1+Я.)Ч7(»«ЛС)- 2
10.19. На вход пропорционально-интегрирующего фильтра
(рис. 10.5) поступает стационарное случайное напряжения В (0
с математическим ожиданием т^ и корреляционной функцией
7?6(r) = D£e-«N.
Определить математическое ожидание /Иг), спектральную плот-
ность (и) и дисперсию напряжения т) (t) на выходе фильтра.
Ответ:
с . . n 2a 1 + (юЛ)1
,+(а71,
T+Tja
T(l+aT) ’
Рис. 10.15. Дифференцирующая
цепочка RC
Рис. 10.16. Схема RC
300
10.20. Напряжение на входе фильтра, изображенного на
рис. 10.1, представляет собой случайный стационарный про-
цесс. Определить отношение дисперсии выходного напряжения
т) (0 к дисперсии Dg входного напряжения £ (/), если спектральная
плотность входного процесса равна: 1) Sg (со) = S0e~₽“2;
2) Sg (со) = 50е_Р,<в1. Здесь So\> 0, 0 >• 0 — постоянные детер-
минированные величины.
Ответ:
D __г / /—з-\
1) -2-=2аКл₽ 1 — ф(“|/
где
1
а—---
RC
1 г---------------------
Ф (z) = —— е 2 dx\
~]/2л J
2)^=«₽
ар ар
sin ар f—dx-cosap f s^dx
J X . J X
-OO —00
10.21. Напряжение g (/) на входе 7?С-фильтра, изображенного
на рис. 10.16, представляет собой случайный стационарный про-
цесс с нулевым математическим ожиданием mg = 0 и корреляци-
онной функцией
RK СО = I’U.
Определить корреляционную функцию (с), дисперсию
и спектральную плотность Sn (со) выходного напряжения г] (/).
Как следует выбрать параметры 7? и С, чтобы отношение дисперсии
выходного процесса т) (/) к дисперсии входного процесса | (/) было
меньше заданного числа 6?
Ответ:
----L. [0е—“ • ’ । —ae-P । ’ I],
р»_аа lH J’
а=/=Р>
а = Р;
2-Dge-Ki’!(H-p|T,|),
= — Dg; Sn(co) =--------------------- a=—.
n a+p 6 ' (a«+©»)(P«+co») RC
Для того, чтобы отношение дисперсий было меньше 6, должно
выполняться неравенство RC 6/0(1 — 6).
10.22. На вход двух параллельных цепочек RC (рис. 10.17)
действует случайное напряжение £ (/), представляющее собой
стационарный белый шум с нулевым математическим ожиданием
и корреляционной функцией (10.20).
301
Рис. 10.17. Две параллельные цепочки
RC
Рис. 10.18. Воздействие случайно-
го тока на интегрально-дифферен-
цирующую схему
Найти взаимную корреляционную функцию для выходных на-
пряжений 1] (0 и ц (/).
Ответ:
Я™ (4. Q [е~«. । < -е-«« <*-“« <«];
2 (ai+<X2)
= l//?iCx, = 1/./?гС2.
10.23. На схему, изображенную на рис. 10.18, действует флук-
туационный ток i (t) в виде шума с нулевым математическим ожи-
данием mt = 0 и корреляционной функцией
= (Уо/2) 6 (т).
Найти корреляционную функцию R^ (т) и спектральную плот-
ность St) (со) выходного напряжения т) (t) в стационарном режиме.
Ответ*.
ад=Р2-^е~а14 5п(«>)=₽2^-^,
4а 2 аа +0)3
где
р =. l/KA, а = (Ci + C2)/₽iCiC2.
10.24. К схеме, изображенной на рис. 10.19, приложено слу-
чайное напряжение £ (/) в виде белого шума с нулевым математи-
ческим ожиданием mg = 0 и корреляционной функцией (10.20).
Определить корреляционную функцию (т) и спектральную
плотность Sn (со) выходного напряжения q (t) в стационарном со-
стоянии.
Ответ:
Ц2 V Г - in —ж 1
Яп(*)=-^4^ (а + ^)е 2 -(а-*)е 2 ;
аХ 8
S4(®) = ,
2 ш4+(а3—2?)0)2 +Та
где
302
Рис. 10.20. Интегрирующая
схема
Рис. 10.19. Воздействие случайного
напряжения на интегрально-диффе-
ренцирующую схему
10.25. На схему, представленную на рис. 10.20, действует
флуктуационное напряжение £ (/) в виде белого шума с.нулевым
математическим ожиданием т^ = 0 и корреляционной функци-
ей (10.20).
Найти корреляционную функцию (т) и спектральную плот-
ность Sn(co) выходного напряжения т] (t) в стационарном состоянии.
Ответ:
р /т\___ "о р —а|т|. <? _и,2 Na 1
где
‘ T = RjC, а = ±(р + 1), ₽= 4-.
1 ~ 1 . л\2
10.26. Найти дисперсию входного тока i (t) в линейной цепи,
изображенной на рис. 10.21, при условии, что напряжение т) (t)
на выходе является случайным процессом, спектральная' плотность
которого имеет вид
S<q (б)) —
No при 0 ^со соь
0 при co <0, со>соР
Ответ: Dt= -^2-(6л + со? Я2 С2).
10.27. На вход цепочки RC (рис. 10.22) воздействует стационар-
ное случайное напряжение £ (t) со спектральной плотностью
Sg (со) = 4а/(4а2 + со2).
Определить спектральные плотности (со) и (со) выходных
напряжений т] (f) и р (/) и их взаимную спектральную плотность
Sr)!» («)•
Рис. 10.21. Воздействие случайного
тока на параллельную цепочку RC
303
Рис. 10.22. Воздействие случайного
напряжения на схему RC
Рис. 10.23. Последовательная цепоч-
ка RL
4сф*
(4аа+<в2) (4pa4-<oa)’
Р = — .
r RC
Ответ [35]:
£.(«)= —^2+ю2)— ,
4 ’ (4а«+ю2)(4р«+®2)
5Л|х (®> — (4а2+(02) (4ра+©г) ’
Зц (to) —
4ap,(p+/to)
10.28. На последовательную'цепочку RL (рис. 10.23) действует
флуктуационный ток i (/), имеющий равномерную спектральную
плотность Sj(co) = ЛГ0/2 в области частот — coj со ©j.
Найти дисперсию напряжения т] (/) на индуктивности L.
Ответ : = -(-1-£)8 -^1-.
' 3 2л
10.29. На последовательную цепочку RL (рис. 10.24) дейст-
вует флуктуационный ток i (t) с корреляционной функцией
Rt (т) = Рге-“*Л
Найти дисперсию £>п напряжения т] (/) на индуктивности L.
Ответ: Dn = 2а2 L2Dt.
10.30. Напряжение £ (/) на входе фильтра, изображенного
на рис. 10.8, представляет собой случайный стационарный про-
цесс с математическим ожиданием mg и корреляционной функцией
ЯЕ(т) = DEe-“i*1. .
Фильтр включают в момент времени t = 0.
Определить математическое ожидание m^tt) и дисперсию Dn (/)
выходного напряжения т] (/) и найти их значение при t-> оо.
Рис. 10.24. Последовательная цепь
RLC
Рис. 10.25. Схема RL
804
Ответ:
[ — ‘
znn(/)=mg[l — е L
Dn(t) =
г R t / R t
Di-*- l_e~“'(«£+«e"~ _
aL+Я L \ a£—/?
___^-e-^1, a#A
aL—R . /J L
Dl~
6 2
/ p к -2— t
l-l+2ie L
D
(0 k->°° = (0 h->°° = rin D&
CLL> -|- i\
10.31. Напряжение £ (t) на входе фильтра (рис. 10.24) пред-
ставляет собой белый шум, спектральная плотность которого равна
Sj((o) = No, 0 со < со.
Определить корреляционную функцию (т) напряжения
Я (t) на выходе. Как следует выбрать параметры фильтра, чтобы
дисперсия выходного напряжения не превышала заданного зна-
чения D?
Ответ;
Ян (т)=
AfnWo „ , a , Л
----— е~“ г 11 cos mi т -|---sin (о. т II
4a \ ©j )
при <в0 > а (т. е. при R < 2 L/C},.
^»(00 e-aiTi(l + a|T|)
при.(о0 = а(т. е. при /? = 2]/L/C)',.
^0<1)° е~“1 т 1 f ch У а2—(о§т -|-” — sh У а2 —(о§ I т \
4а \ Ка2—(о? /
при (оо<а(т.е. при Я>^УL ).
Здесь
(оо = 1//LC,' а = R/2L, (^ = }Ао§ —а2> 0.
Для того, чтобы дисперсия Dn выходного напряжения не превыша-
ла заданного значения D, должно выполняться неравенство
RC N0/2D.
10.32. На вход цепи, изображенной на рис. 10.25, воздействует'
случайное напряжение | (f), представляющее собой белый шум
со спектральной плотностью Sg (со) = ^0, 0 (о < оо.
305
Найти спектральную плотность, корреляционную функцию И
среднее квадратическое значение = VDn выходного напряже-
ния Т] (/).
Ответ:
Я, <т) =-^ ' ’' , = а ,
а = + RJ, Т = L/^ + R2).
10.33. Напряжение g (t) на входе фильтра, изображенного
на рис. 10.26, представляет собой белый шум, спектральная плот-
ность которого Sg(<o) — No, 0 to < оо.
Определить корреляционную функцию 7?п(т) напряжения г] (/)
на выходе фильтра. Как следует выбрать параметры фильтра, чтобы
дисперсия напряжения на выходе не превышала заданного зна-
чения D?
Ответ:
jV0Pe~₽,Tl(coscoxt-— sin(ох111'j при ®o>₽>
Afope~₽ Р|т|) при ®o = P,
“ y0 ₽e-₽1 * if ch Kp2—®o т-— sh KP2—®o I * Й
k ]/>-/
При ®0<P-
Здесь
<oo = 1//LC, P = H2RC, ©! = Kcog — P2 > 0.
Для того, чтобы дисперсия выходного напряжения не превы-
шала заданного значения D, должно выполняться неравенство
RC > W0/2D.
10.34. На высокодобротный колебательный контур, составлен-
ный из параллельно соединенных конденсатора емкостью С, резис-
тора сопротивлением R и катушки с индуктивностью L (рис. 10.27),
----! <? 7
v(t) ♦ > <
ZD J?(t)
I v
----»....О
Рис. 10.26. Фильтр RLC Рис. 10.27. Колебательный контур
306
Рис. 10.28. Колебательный кон-
тур
воздействует случайный ток i (t), представляющий собой белый шум
с нулевым математическим ожиданием mt = 0 и спектральной плот-
ностью] Si(co) = No, 0 со < оо.
Определить) корреляционные функции 7?v (т), 7?п (т) и спектраль-
ные плотности Sv (со), S»| (со) тока v (t) в индуктивной ветви и напря- '
жения т) (0 на контуре.
Ответ [44]:
^v(T) = y0pd2e-P,TI (coscoxt + —sinco1|T|'),
Rn (0 = No P#2 e~₽ •* 1 fcos cox t-sin cox | r |) ,
\ «01 /
sv(co) = ,
v ' L» 4p« ©«+(©»—©§)»
$ (co) = No R2--------------.
7 4p« ©»+(©«—©«)».
Здесь
p = — , <%= ——, .d = -5—, ©! = У co* — p2> 0.
H 2RC ’ ° 1Л7 <ooL 0 H
10.35. Применительно к условиям задачи 10.34 определить
взаимную корреляционную функцию Riv (т) для входного i (0 и
выходного v (0 токов и взаимную корреляционную функцию
Rin (т) для входного тока и выходного напряжения т] (0.
Ответ [44]:
( е sin ©х т, т> 0,
₽cv (0 = ]
0, т<0,
1^/1) (0 —
2N0 р/?е~Рт (cos ©j г--sin сох , т>0,
\ ®i /
0, т<0.
10.36. На высокодобротный колебательный контур, составлен-
ный из параллельно соединенных конденсатора емкостью С и ка-
тушки с индуктивностью L и сопротивлением R (рис. 10.28), воз-
307
действует случайный ток i (f), представляющий собой белый шум
со спектральной плотностью 5г(о) = No, 0 со < оо.
Найти корреляционные функции 7?v(t), 7?п(т) и спектральные
плотности Sv (со), Sy) (со) тока v (О в индуктивной ветви контура и
выходного напряжения г) (t).
Ответ:
Rv (т) = No aQ2 е-а Iх 1 (cos сох т + — sin сох I т | V
!
(т) — No “Q2 р2 е_“1 х 1 (cos <0i х-— sin ®i | т |\
\ /
Sv (со) = --------—--------,
v 7 № С2 4а« «>«+(©«—<oj)a
s„w- .
7 R2C2 4ааш?+(соа—со?)2
Здесь
а = R/2L, соо = 1//LC, Q = <^oL/R = p/R, сох = ]Ло§ —а2>9.
10.37. Стационарный случайный процесс £ (f) со спектральной
плотностью Sg(co) воздейстует на линейный фильтр с комплексной
частотной характеристикой
УС (ja) = (1 — е-/“т)".
Определить спектральную плотность (со) выходного процес-
са т) (t).
Ответ: S^ (со) = Sg (со) ^2 sin —2<* •
10.31. На' колебательный контур с комплексной частотной ха-
рактеристикой
^(/co) = ^o
________2асо______
2асо+/ (со2—-©*)
воздействует случайный процесс х (/) = s (/) + п (/), где
s(0 = H (0-1 (/-T)W)
представляет coloft полезный сигнал в виде отрезка (импульса)
длительностью Т стационарного квазигармонического шума
НО = А (0 cos [соо/ + <р (01
с нулевым математическим ожиданием т^ = 0 и корреляционной
функцией
(т) = Dge~P1 ’1 cos ®от;
п (0 — стационарный белый шум с корреляционной функцией
Rn{x) = (Уо/2) 6 (т).
308
Определить корреляционную функцию Rn(t, г) процесса г] (t) =
— Л ДО + т]п(0 на выходе контура и отношение сигнал/шум в конце
импульса
р(Т) = РП8(Т)/ПЧп,
где (/) — дисперсия составляющей т]3(/) выходного случайного
процесса т] (t), обусловленная воздействием колебания з (/); D^n —
дисперсия выходного шума я»(0-
Ответ [65]:
^п (0 "О = Т?п8 (t, т) + R^n (т),
Ч т) = [(ае-₽ 1 х ‘ ~₽е-“1 ’') +
® аа—р
+(а +₽) е-“т-2а'—а (е-“х +е~Рт) е~<а+₽> *] cos ©0 Ъ t >0,
, 7?Пп(т) = - —е~а Гт 1 cos ©о
п /П _ 2д (1-Ц1)-2е-а <* +**>+(1+Н1) е“2а
₽ (Г) ’
q = DiT/N0, а = аТ, р.х = 0/а.
График функции p(T)fq — f (а, щ) дан на рис. 10.29.
10.39. Решить задачу 10.38 при условии, что
7?s (<r) = Dje-v’^cosooT.
309
р(Т)
Рис. 10.30. Отно-
шение сигнал/шум
на выходе конту-
ра при гауссовой
корреляционной
функции входных
квазигармониче-
ских флуктуаций
Ответ [65]:
' 2? Ц ?1/2 /
/2у2|т1 \ j ф / а—2у2/ \ /а—2у2/—2у2т/
\ У1/2 / . \ Т1/2 / \ т1/2 )
—2Ф (—1 е-2«< +[ф fg+fol'+y? \ _
\?У2 /] L \ У У2 /
е2а | т | j е — а | т | cos о0 т, I 0f
р (Т) = е1/4»» [ Ф (—~j~2a|^ —Ф (—1— +
а^2 I. \ ц2Т/2 / \щУ2/
ф / а+2-у»|т| \
V2 /
1-2д|х|
, На 1^2
q = Dg T/No, а = аТ, щ = у/а.
Графики функции р (T)/q приведены на рис. 10.30.
10.40. Решить задачу 10.38 при условии, что
/ \ y-'k sin 5т>
COS(00T.
310
Ответ 1651:
T)
r 1
f sin 6x
J 6x
Lo
( p „zsin6x
—----- \ e —:—dx —
2 I J 8x
dx+ C e^^—dx e~2a< +
J ox
0 J
P • Л )
4-e2aI’। I le-«ix Icoso)0t, />0,
J OX
~t—x
a a
p m = JL , f e~* sin>1,3* dx—e~2a f e* sin^—dx ,
a J j Цз* J Из*
Lo| о J
q = D^T/Nq, a = aT, рз = 6/a.
График функции p (T)/q = f (а, Из) приведен на рис. 10.31.
10.41. На вход линейного нешумящего четырехполюсника
с комплексной частотной характеристикой «%* (/со), модуль которой
определяется соотношением
| & (/о) | = (1 ПРИ °о— Д(°1 < <° < + Асо2,
(0 при других (О,
воздействует собственный шум | (t) параллельного колебательного
контура с резонансной частотой о0 (Рис- 10.32).
Вычислить дисперсию Dn напряжения т) (/) на выходе четырех-
полюсника в зависимости от его полосы пропускания Дсо = A(ox +
+ Дсо2.
Рис. 10.31. Отно-
шение сигнал/шум
на выходе колеба-
тельного контура
при прямоуголь-
ной спектральной
плотности вход-
ных квазигармо-
нических флуктуа-
ций
811
Рис 10.32. Линейный четырехполюс-
ник
Ответ: Для случая апериодических колебаний в контуре
(оо — а2< О, ®о = ULC, а = Rl^L, добротность контура Q =
= ts^UR < 1/2):
= 4kTR ш^2^ ГА /arctg -
2л 1/1— 4Q2 L А \ А
Л=]/1—2Q2—1/1—4Q2,
В = ]Л1 —2Q2 +1/1 — 4Q2~
С = (1 + 62) QV2, D = (1 — 6Х) QV2, 6г = Acoj/coo,
S2 = Асо2/соо.
Для случая периодических колебаний в контуре (®о — а2 > О,
при этом Q> 1/2):
г\ _kTRa>0Q ( 1____
---------7 --- X
я I 2"|/4Q2-1
х Гln 2Q(l+62)2+2(l+62) V4Q^1+2Q_
L 2Q(l+62)2-2(l+62)l/4Q*=l+2Q
_ln 2Q (1 -бП2+2 (1-6J l/4Q^i +2Q j _j_
2Q (1—6X)2—2 (1 —6X) +2Q J
+ arctg _arctg <?K--V-4 |.
l+oa 1—Oi J
При Q /> 1 последнее выражение приводится к виду
' В = kTRa<>9 Г_L in AL + arctg —
л л [ 2Q 62a l+62
—arctg j. a = 2—di, b = 2+62.
Если полоса пропускания четырехполюсника симметрична от-
носительно (оо (т. е. если А®! = Дсо2 = А®/2), то при Q 1 имеем
D -А
л
—arctg
2(2—6)
1 , 4+6 . . Q6(4+6)
----In *• + arctg \ J —
2Q 4—6 6 2(2+6)
—Q6 (4—6) ] с _ Дю
812
Рис. 10.33. Модуль комплексной частотной ха-
рактеристики фильтра нижних частот
О
I J#(W|
tog
Если к тому же 6 = Дсо/соо < h то
Dn = D% — arctg Q6,
л
Здесь D$ = kT/C — дисперсия собственных шумов контура (см.
пример 10.8).
10.42. Стационарный случайный процесс g (t) с корреляционной
функцией
Я6(т) =D6e-«i’i
воздействует на фильтр нижних частот, амплитудно-частотная ха-
рактеристика которого приведена на рис. 10.33.
Найти дисперсию выходного напряжения я (/).
Ответ: arctg .
10.43. Линейная система имеет амплитудно-частотную харак-
теристику, равную постоянной в интервале (<о0— Д<о, <оо + А®)
и нулю вне этого интервала. На вход системы подается белый шум
g (t) со спектральной плотностью Sg(co) = No, 0 ® < оо.
Найти корреляционную функцию Rn (т) процесса т] (t) на выходе.
Как следует выбрать А®, чтобы дисперсия £)л выходного процесса
не превышала заданного значения D?
Ответ:
R (т) = — Ж*о No Д® sinA(0T cos ®0 т, А® < Dn/W No.
л Дат
10.44. Определить эффективную шумовую полосу пропускания
интегрирующей цепочки RC (рис. 10.1).
Ответ: Afa = M2RC.
10.46. Фильтр состоит из двух последовательно соединенных
однонаправленных линейных систем, частотные характеристики ко-
торых соответственно равны 1/(1 + /®Т1) и 1/(1 + где Тг
и Т2 — положительные числа.
Найти корреляционную функцию 7?ч(т) и дисперсию £>п процес-
са т| (/) на выходе фильтра, если спектральная плотность процес-.
са |(/) на входе фильтра
S6(®) = S0/(a2 + ®2).
313
Ответ:
D M—Q Pl Ра Г___________J________е—а | т I
п() ° 2 1а(р?-аа)(ра-а’) +
/-1-------!________е_р*1т1 Ч------------------е_₽«1 т 1
Pi(Pa—Р1)(«а—Pi) Pa (аа-PD(P?“Ра) .
Pi = l/T1, 02=1/Т'2,
р ___ g Р1 Рг______Ч~ Р1 ~4~ Рг__
” ° 2а 1(аЧ-Р1)(а4-Ра)(Р1+Ра) ’
10.46. Выразить корреляционную функцию (т) процесса
т| (0 на выходе суммирующего устройства с линией задержки
(рис. 10.34) через корреляционную функцию 7?g(r) стационарного
случайного процесса | (/) на входе.
Ответ: R^ (т) = 27?g (т) + R% (т — Т) + R$ (т + Т).
10.47. На вход линии задержки, имеющей N отводов через вре-
менные интервалы 0 (рис. 10.35), воздействует стационарный слу-
чайный процесс g (t) с нулевым математическим ожиданием т^ = 0
и корреляционной функцией (т).
Определить корреляционную функцию 7?ч(г) и спектральную
плотность Sr) (со) процесса т] (t) на выходе сумматора.
Ответ [66]:
1 1
*п(т)=—^(t)+-F 2 (^-О^£(я+г0) +
1 W“1
' 2 (^-о^(т-«),
/sin/V-^-\2
Sn (о))= Sg (со).
\ N~ /
График функции S,) (co)/Sg (со) = / (Осо) приведен на рис. 10.36.
10.48. На линейное устройство, состоящее из линии задержки
на время /зад = Т и вычитающего устройства (рис. 10.37), воз-
Рис. 10.34. Суммирующее устройство-
с линией задержки
Рис. 10.35. Суммирующее устройство
С многоотводной линией задержки
314
Рис. 10.36. Спектральная
плотность процесса на вы-
ходе сумматора
действует случайный процесс | (/) с математическим ожиданием
(t) и ковариационной функцией (/р /2)-
Определить математическое ожидание (/), ковариационную
функцию /Cq (Zx, выходного процесса
Т) (/) = I(t + Т) - £ (/)
и взаимную ковариационную функцию (tu t2) = М {| (^) X
X т| (/2)} процессов на входе и выходе.
Ответ'.
тп (0 = (/ + Т) m^ty, . Кп /2) = Ki (/г +. Т, i2 + Т) -
- Ki (4, i2 + Т) - & + Т, t2) + Ki t2),
(4, t2) = Ki t2 + T)- Ki tz).
10.49. Решить задачу 10.48 при условии, что входной процесс
| (0 является стационарным с математическим ожиданием и
ковариационной функцией Ki (т)-
Вычислить спектральную плотность выходного стацио-
нарного случайного процесса т] (/) = | (t + Т) — | (/) и взаимную
спектральную плотность (<о) стационарно связанных случай-
ных процессов | (/) и т] (t).
Рис. 10.37. Вычитающее устройст-
во с линией задержки
315
Ответ 114):
mn (t) = 0, Kn (г) = 2/Q (г) -Kg (т +T) - (т-Т),
К|п(*)==^(* + П-КЕ(*),
Sn(©) = J Кп(т)е-/й>т</т =4sin2-^-Sg(®),
— оо
5Ь) (®) = J (т)е-/а,т dT = (е/<0 т—!)5& (®)>
— оо
где
Sg(®)= f Kg(r)e-WT.
10.50. На вход фильтра, схема которого представлена на
рис. 10.38, поступает случайный процесс ( (/) с корреляционной
функцией
W = D6e-^*.
Найти дисперсию Dn процесса т] (/) на вцходе фильтра.
Ответ: Dn = 2Dg(l — е~“Г2).
10.51. ' Найти спектральную плотность Sn (®) процесса т] (t)
на выходе фильтра (рис. 10.38), если спектральная плотность про-
цесса £ (t) на его входе
5Е(ю)=Ле-а’®2+Вб(®—уЬ.),
где 6 (х) — дельта-функция; Т — время задержки в линии.
Ответ: Sn (<о) = 4Де_“2 “2 sin2 •
10.52. Найти корреляционную функцию 7?я(т) процесса т] (/)
на выходе фильтра, схема которого представлена на рис. 10.38,
выразив ее через корреляционную функцию 7?g(x) стационарного
случайного процесса | (/) на входе.
Ответ:
Яп (т) = (т) - 4К6 (т - Т) - 47?6 (т + Т) + flS(r - 2Т) +
+ ад + 2Т).
10.53. На вход радиотехнического устройства, состоящего
из последовательно соединенных дифференцирующих устройств и
Рис. 10.38. Схема фильтра
316
£ис. 10.39. Последовательное соеди-
нение дифференцирующих устройств
и сумматора
сумматора (рис. 10.39), воздействует стационарный случайный
процесс | (t) с нулевым математическим ожиданием mg = 0 и корре-
ляционной функцией 7?g (т).
Определить корреляционную функцию 7?я(т) процесса т] (/)
на выходе сумматора.
Ответ [41:
Rn (т) = 7?g (т) Rg (т) +-£- Rg (т).
ат2 ах*
10.54. Вычислить одномерную плотность распределения веро-
ятностей Р1(л) Для напряжения т] (t) на конденсаторе емкостью С
в стационарном состоянии, когда на последовательную цепочку RC
(рис. 10.40, а) воздействует случайный телеграфный сигнал | (/)
(рис. 10.40, б). Сигнал | (/) с одинаковыми вероятностями, равны-
ми 1/2, принимает лишь два значения: +1 и —1. Моменты перемен
знака (нулей) распределены по закону Пуассона, т. е. вероятность
получения п нулей в интервале (/, t + т) равна
рх (п, т) — —— (Лт)" е-Хт,
nl
где X — среднее число нулей в единицу времени.
Ответ [68]:
г
_Д_------£2(1—|П|<1,
1/л Г (%Т)
(10.50)
0 при других т).
Здесь Т = RC; Г (х) — гамма-функция.
Рис. 10.40. Интегрирующая цепочка RC (а) и случайный телеграфный сиг-
нал (б)
317
Таблица 10.3
Плотность распределения вероятностей pj.01) при различных значениях XT
Значение параметра КТ Аналитическое выражение График
ХТ» 1 2^. z=n 1/2XT-I-1 6
АТ = 2 3 Pi0i)=— (i— na)>. in к 1 • 4 i 1 1 $
II ьо | со Pi0i)=— Vi— n2> 1 n 1 < i JI j -7 6
АТ=1 Pi0i)=-p I’ll < 1 -7 ^/2
АТ « 1 Pi (ti)=XT(l-r)?)xr-1, I’ll <1 l\ 1 \ i 1 — -7 Z ' II /I J\ У i I 7 1 }
10.55. Получить из (10.50) асимптотические выражения и по-
строить графики плотностей распределения вероятностей рх(т])
для следующих частных случаев: 1) XT > 1, 2) XT = 2, 3) XT —
= 3/2, 4) XT = 1, 5) XT < 1.
Ответ приведен в табл. 10.3 [681.
11. УЗКОПОЛОСНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Стационарный случайный процесс £ (/) с нулевым математическим ожи-
данием называется узкополосным, если ширина полосы А/ той области час-
тот, где спектральная плотность Sg (/) практически отлична от нуля, мала
по сравнению с некоторой центральной частотой /0 этой области (рис. 11.1),
т. е.
Sg (/) 0 при /0 - А//2 < f < /о + Д//2, А/ « f0, (П.1)
где Sg(f) — односторонняя спектральная плотность; А/ — ширина долосы,
которая может быть определена по-разному.
Если односторонняя спектральная плотность Sg (/) симметрична относи-
тельно некоторой частоты/0, то естественно за /0 принять это значение часто-
ты. В других случаях /0 можно выбрать более или менее произвольно.
Часто в качестве /оберут «математическое ожидание» нормированной спект-
ральной плотности:
оо —1 оо
(оп / С \ С
= j 5g j /5g(f)d/. (11.2)
'о 'о
Корреляционная функция узкополосного случайного процесса всегда
может быть представлена в виде [1]
(т) =а| Рс (т) cos (оо т + гз (т) sin соо т] = о| г (т) cos [соо т+у (т)], (11.3)
где
» W = V Ю +rs tg7(T)=— rs(T)/rc(T), (11.4)
ОО
of ге (т) = f S, (f® 4-v) cos 2nvrdv,
6 -f. 6 (H-5)
oo
o| rs (t) = J Sg (fo+v) sin 2nvxdv,
—f®
причем
>e(0) = 1, r8(0) = 1, y(0)= 1; (11.6)
a| — дисперсия узкополосного процесса £ (/).
Рис. 11.1. Спектральная плотность узкополос-
ного процесса
319
В том частном случае, когда спектральная плотность S$(f) симметрична
относительно центральной частоты /0, корреляционная функция узкопо-
лооного процесса имеет вид
оо
(т) = о| г (т) cos со0 ~tcos ©о т J Sg (fo + v) cos 2jiVTdv, (11.7)
— ОО
так как
Мт) = 0, у(т)= 0. (11.8)
Поскольку в правые части формул (11.5) и (11.7) входит спектральная
плотность процесса £(0, смещенная'в область нижних частот (иначе — низ-
кочастотный спектр), то функции гс (т), rs(r), как и г (т), у (т), являются мед-
ленно изменяющимися по сравнению с cos соот.
Реализации узкополосного процесса g (t) имеют вид модулированного
гармонического колебания. Поэтому часто используют представление уз-
кополосного процесса в следующем виде:
g (0 = А (0 cos [соо* + <р (0], А (0 >0, —л < ф (0 < л, (11.9)
где А (0 и ф (0 — медленно изменяющиеся по сравнению с cos соот функции
времени, называемые соответственно огибающей и фазой узкополосного про-
цесса £ (0.
Можно также ввести понятие мгновенной частоты, определив ее равен-
ством
(0(0= ©о + ф(0, (11.10)
где точкой сверху обозначена производная по времени.
Представление узкополосного процесса (11.9) можно записать иначе:
g (0 = Ас(0 cos соо/ — As (0 sin соо0 (11.11)
где
Ас(0 = А (0 cos ф (0, As (0 =. А (0 sin ф (0.
Отсюда следует, что
А (0 = VА? (0+з4| (/), ф (/)=arctg [Л8 (/)/Лс (/)],
(11.12)
(11.13)
<о(0 = <0о+
Л (/)Ле (0-ле(рл8 (О
A*(f)+Al (О
Формулы (11.9) и (11.11) позволяют интерпретировать огибающую
А (0 как длину вектора, проекции которого на оси прямоугольной системы
координат равны As(0 и Ас (0. Фазовый угол между осью абсцисс и направ-
лением вектора равен ф (0 (рис. 11.2), причем возможные значения ф (0
ограничены интервалом (—л, л). Длина вектора А (0 и его фазовый угол
Ф (0 изменяются во времени случайным образом, так что конец вектора со-
вершает случайные блуждания на плоскости. При такой интерпретации про-
Ри«. 1.1.2. Геометрическое представление уз-
кополосного процесса
320
екции Л8(0 и Ac(t) естественно назвать квадратурными компонентами про-
цесса 5 (0.
Исходя из различных математических определений огибающей A (t)
и фазы ф (0, можно показать, что если исходный процесс 5 (0 гауссовский,
то квадратурные компоненты Лс(0 и Л8(0 являются совместно нормальными.
Если в дополнение к этому процесс £ (0 стационарен, имеет нулевое мате-
матическое ожидание и корреляционную функцию (11.3), то процессы
Лс(0 и Л8(0 являются стационарными и стационарно связанными. Их ма-
тематические ожидания равны нулю:
М(Лс(0} = М{Л8(0) = 0, (11.14)
а корреляционные и взаимные корреляционные функции определяются
формулами
Rc (т) =М {Ас (0 Ac (t+T)} = Rs (?) =М {4S (О 4S (/+?))=<т| гс (т), (Ц. 15)
Res (т) = М {Ас (/) 4S (t +т)} = —Rsc (т) =
= ~М {4S (0 Ac (t4-т)}=<т| rs (?).
Отметим, что согласно (11.6) значения квадратурных компонент Лс(0 и
Л8(0, взятые в один и тот же момент времени, всегда не коррелированы и,
следовательно, для гауссовского стационарного процесса 5(0 независимы.
Дисперсии компонент, как следует из первой формулы (11.15), одинаковы и
равны дисперсии процесса 5 (0
а? = М {Л2 (0} = = М {Л2в (0} = <т|. (И.16)
Если спектральная плотность S^(f) гауссовского стационарного процесса
5 (0 симметрична относительно частоты /0, то совместно нормальные процессы
Лс(у и Л8(^2) согласно (11.8) независимы не только в совпадающие (при
h = но и в разные (при =# t2) моменты времени, так как
Res (т) = /?ас(т) = 0. (11.17)
В дальнейшем принято, что исходный узкополосный случайный процесс
5 (0 является гауссовским стационарным с нулевым математическим ожида-
нием. При этих условиях формулы (11.14), (11’.17) позволяют сравнительно
просто находить различные совместные плотности вероятности огибающей
Л (0, фазы ф (/) и их производных. Для этого нужно предварительно записать
соответствующую совместную нормальную плотность вероятности стацио-
нарно связанных процессов Лс(0, Л8(0 и их производных, а затем в ней по
известным правилам перейти к огибающей, фазе и их производным согласно
равенствам, следующим из выражений (11.13) (см. (11.26) и пример 11.1).
Если имеется гсумма узкополосного гауссовского стационарного про-
цесса (шума) 5 (0 = Л (0 cos [cdof + Ф (01 с нулевым математическим'ожи-
данием и детерминированного гармонического сигнала s (t) = Ат cos G)of,
то можно определить^огибающую, фазу и случайную частоту’такой суммы
при помощи'соотношений1
Т) (0 == S (0 + 5 (0 = V (0 cos [со0/ + ф (0], V (0 >0, -л < ф (0 < л,
(11.18)
где
V (0 cos ф (0 = Ат + Лс(0, У(0 81пф(0= Л8(0, (11.19)
т. е. '
V (О==К[Лт+Лс(0]а+Л25(0, 1бф(0=Л8(0/[Лт +ЛС(0]» (11.20)
[лт+лс(0] 4 (0- л; (0 л8 (0
[лт+лс(0Р+Л2;(0
11 Зак.
1203
321
При этом остается в силе геометрическая интерпретация, аналогичная при-,
веденной (см. рис. 11.2).
Выражения (11.20) принимают особенно простой вид при больших зна- .
чениях отношения сигнал/шум а = Ат1в >1
vm Л . Л т 1 Л?(0 ./А Л’^ ~ Лв(<)
И(0^Лт+Лс(0—, i|>(O^arctg—----------------^-7—.
2 лт лт лт (11.21)
ф(0~Л8(0/Лт, а»1.
. л
По аналогии с (11.20) можно определить огибающую и фазу для суммы
узкополосного гауссовского стационарного шума и нескольких детермини-
рованных гармонических сигналов.
Различные вероятностные характеристики огибающей V (0, случайной
фазы ф (0 и их производных можно получить тем же путем: сначала нужно
записать соответствующую совместную нормальную плотность вероятности
для компонент Ас (0, Л8 (0 и их производных, а затем перейти в выражении
для нее к огибающей, фазе и их производным в соответствии с равенства-
ми (11.19).
Найдем совместную плотность вероятности p4(V, V, ф, ф) огибающей
У(0, фазы ф(0 и их первых производных V (0, ф (0 в один и тот же момент
времени для суммы (11.18) гармонического сигнала и узкополосного нор-
мального стационарного процесса | (0 с корреляционной функцией
(т) = сг| г (т) cos ©от, г(0)=Ь (11.22)
Согласно (11.7) спектральная плотность рассматриваемого узкополос-
ного процесса £(0 симметрична относительно частоты /0 = ю0/2л. Поэтому
вспомогательные нормальные стационарные процессы Лс(0 и Л8(0 независи-
мы, причем их корреляционные функции равны:
Rc W = Я8(т) = а|г(т).
(11.23)
Известно, что производная (скорость) гауссовского стационарного про-
цесса есть также гауссовский стационарный процесс, причем значение про-
изводной не зависит от значения самого процесса в тот же момент времени.
Поэтому случайные величины Лс (0, Л8 (0, Ас (0, Л8 (0 взаимно независимы,
причем каждая из них распределена нормально. Дисперсии этих случайных
величин равны:
Лф2(0)=М p2(0} = -<^r;, rj=^|t=o<o. (11.24)
На основании известного выражения нормальной плотности вероятности
записываем совместную плотность вероятности
р(Лс, А$АС, Л8) —
° 4„.I W +”.) + W +Л’)]} <"
Перейдем здесь от переменных Лс, Л8, Лс, Л*8 к новым переменным
V, V, ф, ф при помощи соотношений, следующих из (11.19),
Лс = V cos ф — Ат, Л8 =* V sin ф,
AC*=V cos ф—*фУ эш’ф, XS=V sin ф+ф V соэф.
322
Нетрудно убедиться, чЮ модуль якобиана преобразования переменных
д (Лс, Ас, Л8)
d (V, V, ф, ф)
Поэтому получим
V2
p4(V, v, я?, ib) =--------xl
4n2o|(-rS) j
X expf—о"2/ [~'о (1/2+^-2ЛтИСозП>)+Р+^4>2]!-(11.26)
Л 20V““ro) J
Воспользовавшись свойством согласованности плотностей вероятностей
путем, интегрирования по «лишней» переменной, можно получить различные
другие плотности вероятности. В частности, проинтегрировав (11.26) по V
и ф в пределах —оо до оо, получим совместную плотность вероятности для
огибающей и фазы в один и тот же момент времени:
оо оо
Pt(V, ’!’)= У I Р*<У> V, i|), ij>)=
— ОО —00
V Г 1 / \
“ ехр [ - р+<-2л’»v cos ] •
г
< Ф < л.
(11.27)
Отсюда находим плотности вероятности для огибающей и фазы:
С V t Va+^2 \ I Am V \
' Ру(Ю = Pa(V, ф)^ф = —ехр р——— ро -Л~ , V>0,
(11.28)
00
=J₽2 (V> dV=4ге ~а‘>2 х
о
X [1 + ^2ласоз фФк(а соэф) е°2 cos2 ^/2], —л < ф < л. (11.29)
Здесь а = Ат/в^ — отношение сигнал/шум, IQ(x) — функция Бесселя нуле-
вого порядка от мнимого аргумента, Ф (х) — интеграл вероятности.
Используя формулу (11.28), можно показать, что математическое ожида-
ние и дисперсия огибающей V (/) определяются выражениями
mv-=M{v(o}=o6 (—у; i; -у*) =
= Og \f 1 + уа2)/о (4" *а)+4~аг/1(та,)1е~а!/4’
(11.30)
а* =201(1+4-0")-mfr, (11.31)
где iFi(a; (J; х) — вырожденная гипергеометрическая функция; 1п(х) — функ-
ция Бесселя n-го порядка от мнимого аргумента. >
11*
323
Положив в формулах (11.28) и (11.29) Ат = 0, получим плотности
вероятности огибающей и фазы узкополосного нормального стационарного
процесса £(/) с симметричной спектральной плотностью:
рА (4) = (4/о|) ехр (-Д2/2о|), А > 0, (11.32)
Рф(ф) = 1/2л, —л < ф < л. (11.33)
Корреляционная функция огибающей А (/) узкополосного процесса
£ (/) и квадрата огибающей 42(/) соответственно равны
л Г/ 1 \2 / 1 \2
/?л«=‘7°Ц(т) г2(т)+(чТ/ г4{т)+
/ ьз 1
+(ТГб) гв(т) + ---]=°лгл(г)- (11.34)
<тЗ = (2—гд(т)=0,915г2(т)4-0,057г4(т)-|-----,
/?л,(т)=4о|г2(т). (11.35)
Аналогичные формулы для огибающей V (t) суммы детерминированного
гармонического сигнала и узкополосного шума имеют вид
л Г ! 4 \* 1
г*(т)+(т") ’ а<<1,
о b L \ л / j
а»1.
Нуг (т) = 4о| [г2 (т) -f-а2 г(т)].
(11.36)
(11.37)
Укажем, что в дальнейшем, при формулировке отдельных задач, пред-
полагается, что огибающие А (/) и V (t) с некоторым коэффициентом пропор-
циональности воспроизводятся на выходе линейного амплитудного детектора
огибающей, квадраты огибающих А2 (/) и V2 (I) — на выходе квадратичного
амплитудного детектора огибающей, случайные фазы ф (t) и ф (t) — на выхо-
де фазового детектора и случайные частоты ф (/) и ф (/) — на выходе частот-
ного детектора.
2. ПРИМЕРЫ
11.1. Найти двумерную плотность вероятности огибающей А (/)
стационарного гауссовского процесса | (/) с нулевым математи-
ческим ожиданием и корреляционной функцией (11.3).
Решение. Значения квадратурных составляющих Ас = Ac(t),
As — Ag(t), Л„ = Лс(/4-т), Лзт = Л3(/4-т) в два момента времени
t и t + т имеют совместную нормальную плотность вероятности,
причем квадратурные составляющие есть стационарные и стацио-
нарно связанные процессы. Дисперсии компонент соглано (11.16)
одинаковы и равны о|, а матрица нормированных корреляционных
функций в соответствии с (11.6) и (11.15) имеет вид
1 0 гв(т) г,(т)
0 1 ~г,($ Гс(т)
ге(т>) —GW 1 0
г» W гс (т) 0 1
324
Записываем совместную нормальную плотность вероятности
случайных величин Ас, As, Аст, Л8Т:
Р (^С> ^st) ==
=--------5--------ехр |-----------X
(2л<т|)2 (1 — г2) ( 2а| (1 —г2)
х [Л? +Л| + АЪ + Л|т-2гс (Лс Асг + Л8 Л8Х) —
-2rs (Лс Л8Х’-ЛсТ Л8)]|, ((11.38)
где г2 = г2(т) определено формулой (11.4): г2(т) = г?(т) + г8(т).
Перейдя по известным правилам в этом выражении для плот-
ности вероятности к новым случайным величинам согласно равен-
ствам (11.12), т. е. положив
Ас = A cos <р,
Act == Лх cos фх,
Л8 = A sin <р,
Л8Х A Tsin фх,
получим
р4(Л, Лт, ф, фт)
АА
______2__ У
(2ла|)2(1—г2)
X ехр l"~7Т77—+Л?—2ЛЛх(гв со8(фт—ф) +
( U г )
+rg sin (фт— ф))] =
AAt / 42+42 \ Л4 г cos (<рт — <р-у)
----------- ехр — ехр ------------------- ,
(2ла|)2 (1—г2)------------------------------------------------2а|(1 — г2) J а| (1 - г2)
(11.39)
где tgy (т) = г8(т)/гс(т).
На основании свойства согласованности плотностей вероятностей
эта формула позволяет получать различные одномерные и двумерные
плотности вероятностей огибающей и фазы гауссовского стацио-
нарного процесса. В частности, путем интегрирования по фх и ф
из (11.39) находим двумерную плотность вероятности для огибающей
Л л
р2(Л, Лт)= J J р4(Л, Лт, ф, фт)б/фт^ф.
—л —л
При выполнении интегрирования следует воспользоваться опреде-
лением функции Бесселя нулевого порядка от мнимого аргумента
я—х
/0(х)=— f e*cos*6hp. (11.40)
2л J
—л—х
325
В результате получим интересующую нас плотность вероятности
р2 (Л, Лт) = ААх ехр Г------— 1/0 ( -А^Г-} . (11.41)
«2\ т/ 2а| (1— г2) J \а|(1— г2)/
На основании этой формулы можно придти к выражению (11.34)
для корреляционной функции огибающей гауссовского стационар-
ного процесса.
11.2 Вычислить плотность вероятности огибающей суммы двух
детерминированных гармонических сигналов s^t) = Лхсоз ®0/,
sa(0 = Л2соз(<в0/ + ф2) и гауссовского стационарного узкополос-
ного процесса | (0, представленного в виде (11.11).
Решение. Введем огибающую V (0 и случайную фазу ф (0
интересующей нас суммы, воспользовавшись следующей записью
суммы заданных детерминированных сигналов и случайного про-
цесса:
Я (0 = si(0 + s2(0 + I (0 = Лхсоэ ®ot + Л2соэ q>2C0S —
— -42sin <p2sin + Лс(0соэ ®0Z — Л8(0 sin o>0t =
= [Лх + Л2соз <p2 + Лс(01 cos <i)0t —
— L4,(0 + Л2зш <p2] sin <£>ot = V (0 cos + ф (0], (11.42)
где
V (0 соэф (0 = Лс(0 + Аг + Л2 cos <р2,
(11.43)
V (0 sin ф (0=5= Л8(0 + Л2зш ф2,
т. е. V (0 = {[Лс(0 + Ai + Л2соэ ф2]2 +[Л8(0 + Л2зш ф212}’/2,
tg ф(0 = [Л.(0 + Л2зш ф21/[Лс(0 + Лх + Л2со8 ф2].
Из равенств (11.43) следует, что
Л с(0 = V (0 cos ф(0 — Лх — Л2cos ф2,
(11.44)
Л8(0 — V (0 sin ф (0 — Л 2 sin ф2.
Записав совместную нормальную плотность вероятности неза-
висимых квадратурных составляющих Лс(0 и Л,(0
.. .. 1 / а*+а* \
р(Лс, Л8)=-----ехр-------—-—
с " 2па( 2<т| у
и перейдя в ней к новым случайным величинам V (0 и ф (0 согласно
равенствам (11.44), получим совместную плотность вероятности
для1 огибающей и фазы:
Рг(У> ^)=-Т^Гехр1------7Т + +^2+ 2ЛхЛ2cosф2—
—2УЛхсозф — 2УЛ2соз (Ф+ф2)]| • (11.45)
326
Отсюда находим плотность вероятности для огибающей V (0
pv(V)=J р2 (V,-ф) dip.
—Л
При интегрировании следует воспользоваться выражением (11.40),
предварительно применив очевидное соотношение
Л2соз (ф + <р2) + Лхсозф = УА] + + 24x42cos <р2 cosfip + %).
После выполнения интегрирования получим
pv(V) = —ехр (\
°t \ 2<Ti /
’х /о (— КЛ1+Л§+2Л1Л2созфЛ . (11.46)
к а1 )
Из этой формулы как частные случаи следуют ранее приведен-
ные результаты. Так, полагая в (11.46)Л2 = 0, приходим к формуле
(11.27), а при Л1 = Л2 = 0 — к формуле (11.32).
Отметим, что если бы в рассматриваемом примере детерминиро-
ванный' гармонический сигнал з2(0 имел вид s2(0 = 42cos (со2^ 4-
+ ф2) = Л2соз [<в0/ + (®2 — <оо) t + Фг1> т- е- ег0 частота м2
отлична от центральной частоты ®0 спектральной плотности слу-
чайного процесса £ (0, то все предыдущие выражения остались бы
в силе, нужно лишь в них вместо ф2 подставить (со2 — ®0) t 4* ф2.
При этом огибающая сумма V (0 была бы нестационарным процес-
сом.
Пользуясь записью вида (11.42), понятий огибающей и случайной
фазы можно распространить на сумму нескольких детерминирован-
ных гармонических сигналов и гауссовского стационарного про-
цесса.
11.3. Пусть на вход радиоприемника, упрощенная функцио-
нальная схема которого приведена на рис. 11:3, воздействует сум-
ма детермйнированного гармонического Сигнала s(0 = 4mcos2n/0i
и гауссовского стационарного белого шума п (0 со спектральной
Рис. 11.3. Упрощенная функциональная схема радиоприемника
327
плотностью Sn(f) = No. Квадраты модулей частотных характерис-
тик усилителя промежуточной частоты (УПЧ) и усилителя низкой
частоты'(УНЧ) имеют вид гауссовых кривых
1^1(/7)12=^?ехр[-л(2гАу] д/1«/0,
L k Aft / J
I ^2 (//) j2 = ехр Г -2L (_£_?],
L 4 \ Д/2 / J
где ДД и Д/2 — эффективные полосы усилителей.
Вычислить математическое ожидание и корреляционную функ-
цию напряжения £(/) на выходе УНЧ при больших и малых отно-
шениях сигнал/шум.
Решение. Очевидно, что сигнал на выходе УПЧ равен
sx(/) = ^iAm cos 2я/0/,
а спектральная плотность шума на выходе УПЧ определяется из-
вестным соотношением
Si(/) = ^ol^i(/f)l2=^I^oexp
Такой спектральной плотности соответствует корреляционная
функция
^i(T) = I $i(f) cos Znfrdf = of exp [—я (Д/уг)2] cos 2л/0т,
о
fff = ^N^fv
(11.47)
Гауссовский стационарный шум на выходе УПЧ при условии
f0 ДД является узкополосным, причем его спектральная плот-
ность симметрична относительно центральной частоты f0. Поэтому
сумма гармонического сигнала и узкополосного шума на выходе
УПЧ может быть записана в виде'(11.18).
г Введем отношение сигнал/шум на входе линейного детектора
огибающей а = ^ii4m/cfx = Лго/КA/0Afi- Воспользовавшись резуль-
татами решения задачи 11.23, а именно, соотношениями (11.56)
и (11.57), найдем математическое ожидание напряжения на выходе
детектора •
mv = Ат (1 -|—Ра-) ’ а > 3;
Шу — О"1
(11.48)
328
Для интересующих нас случаев больших и малых отношений
сигнал/шум корреляционная функция напряжения на выходе ли-
нейного детектора огибающей дается формулой (11.36), которая при-
менительно к рассматриваемому случаю принимает вид
Rv($ =
о2 ехр [—л (АД т)2] 11 + —ехр [—л (АД т)2]\ , а > 3,
(11.49)
Воспользовавшись известным интегралом [17]
Je~bx‘cosbxdx = -^-л/~ — expf—0>0, (11.50)
о V ₽ 4Р
найдем спектральные плотности, соответствующие корреляционным
функциям (11.49),
СО
Sv (/) = 4 J Rv (т) cos 2nfxdr =
о
Так как коэффициент усиления УНЧ при f = 0 равен ЛГа, то
среднее значение напряжения на выходе УНЧ, очевидно, равно
а>3,
ЯД ЯД Ат 1 +
1 \
4а»
(11.51)
Спектральная плотность напряжения £(/) на выходе УНЧ оп-
ределяется соотношением
SE(O=Sv(f)l^(//)l2.
(11.52)
Согласно известной формуле по спектральной плотности находим
корреляционную функцию
(т) = I Sj (0 cos 2nfxdf.
(11.53)
829
Выполнив вычисления при помощи (11.50), получим
, 1
2/fa2
ла? Г ч
---- v 1
4/2 L »
1______
14-4v2
1 ,
1 J-2a>2
/ (гд^т)2 \ ,
:хр — Л -—' ’ -1-
Ч 1 + 4v2 )
expf л(2А^т)аЧ
r 14-2v2 /
1 / (2Д/2 т)2 \ .
------ехр — л -—+
l + 2v2 r \ l + 2v2 )
|/ 1 -|-4v2 r \ 1-J-4V2
(11.54)
где v = A/2/Afi-
Можно рассмотреть частные случаи формулы (11.54). Например,
можно убедиться, что при v > 1 справедливо соотношение
Яс(т)~ЗДр(т), 1. (11.55)
Этому результату можно дать следующее объяснение. Если по-
лоса пропускания усилителя низкой частоты значительно больше
полосы пропускания усилителя промежуточной частоты (т. е.
v 1), то низкочастотный спектр напряжения на выходе линей-
ного детектора огибающей воспроизводится усилителем низкой
частоты практически без искажений; все спектральные составляю-
щие усиливаются в раз.
3. ЗАДАЧИ И ОТВЕТЫ
11.1. Случайный стационарный процесс £ (£) с корреляционной
функцией 7?/т) = ofje-®1’1 cos свот записан в виде (1.1.11):
В (0 = Лс(0 cos соо^ — As(t) sin ®qt
Определить корреляционные функции 7?с(т) и 7?s(t), а также взаим-
ную корреляционную функцию 7?с,(т) для двух случаев: 1) ®о =£ <в0
и 2) ©о = соо [44].
Ответ:
1) 7?с(т) = Я8(т) = о^е-061’1 cos Дот,
Rcs(x) — °te~a|’i sin А от, А св = св0 — ®6;
2) 7?с(т) = Я,(т) = о|е-« < < i, Rcs(r) = 0.
11.2. Случайный стационарный процесс В(0 с корреляционной
функцией
/?»(T)=-<rte-a,’i|cosoo *4- — sina>01I ]
\ ©0 /
записан в виде
I (t) = Лс(0 cos — Л8(0 sin coot
330
Рис. 11.4. Функциональная схема синхрон-
ного детектора о—s
x(t)u(t) -
---—>ФНЧ
ztt)
y(t)
Найти корреляционные функции £с(г) и Rs(t), а также взаимную
корреляционную функцию 7?cs(r).
Ответ:
Rc (*) = R8 (т) = of е -«' Ч Rcs (т) = '-------- о| е -«। * । sgn г ,
©О
sgn х=
х>0,
х= О,
х<0.
11.3. При тех же условиях, что и в задаче 11.2, вычислить спект-
ральные плотности Sc(©) и S8(m), а также взаимную спектральную
плотность SC8(©).
2а? а а? а oMi
Ответ: Sc (©) = S8 (о) =--S---- s (©) = — --------I——.
cv 7 44 ' л(а« + ®а) ®о «»+<в»
11.4. Случайный стационарный процесс £ (/) со спектральной
плотностью
Sg(®)=(S°
(О При © < ©!, (О > ©2
записан в виде
I (0 = /4С(/) cos aot — Л85Ш (o'0t.
Найти корреляционные функции Rc(t) и Rs(t), а также взаимную
корреляционную функцию Rcs(r) для двух- случаев: 1) ©о = ®о ~
— (©1 И- ©a)/2j 2) ©о = ©х.
Ответ:
1) Rc(t) = R8(t) = sin рт/рт, RC8(t) = О,
Og = S0(©2 — ©i), P = (®2 — ®i)/2;
2) Rc(r) = /?8(т) = of sin (©2 — ®i) t/(©2— ©J t,
Rcs(t) = (So/2) [cos (©2 — юх) т — 1].
11.5. На рис. 11.4 приведена схема синхронного детектора,
представляющего собой последовательное соединение перемножи
теля и идеального низкочастотного фильтра, пропускающего прак-
тически без искажений низкочастотную часть спектра и-не пропус-
кающего высокочастотную часть. На один вход перемножителя по-
дается гармонический сигнал s (/) = 4xsin a>ot, а на другой — уз-
кополосный стационарный шум | (/) с корреляционной функцией
Rs (т) = е~“1 х 11 cos ©от Н—— sin ®01 т | ), а ©о •
\ ©о /
331
Определить корреляционную функцию 7?я(т) колебания т] (t) на
выходе фильтра в стационарном состоянии.
Ответ: 7?я(т) = (1/4) Л^o|e_“,'t,.
11.6. Найти отношение сигнал/шум на выходе фильтра син-
хронного детектора (рис. 11.4), когда на один вход перемножителя
воздействует сумма сигнала и шума s (0 + £ (0, а на другой —
сигнал s (0. Сигнал s (0 и шум £ (0 те же, что и в задаче 11.5.
Ответ: a = Ai/og.
11.7. На .один вход синхронного детектора (рис. 11.4) подается
сумма AM колебания Ао(1 + mcos Q0 cos aot и узкополосного
стационарного шума | (/) с дисперсией сг|, а на другой — опорное
колебание Axcos Определить отношение сигнал/шум на выходе
детектора (полезным сигналом считать колебание с частотой мо-
дуляции Q).
Ответ: а “ mA0/ag.
11.8. На синхронный детектор (рис. 11.4) воздействует сумма
сигнала и шума s (0 + g (0, а также опорное гармоническое ко-
лебание Ат cos ®0/. Сигналом s (0 является модулированное
по случайному закону гармоническое колебание s (0 = $(0 cos
где £(0 — независимый от g (0 стационарный случайный процесс
со спектральной плотностью
S (/)= fS° при
lOJ при других f.
Стационарный шум £ (0 имеет нулевое математическое ожидание и
спектральную плотность
St(f)=(^° ПрИ F^>
(О при других/.
Амплитудно-частотная характеристика фильтра низких частот по-
стоянна и отлична от нуля лишь при частотах 0 f F. Найти
отношение дисперсии сигнала erf к дисперсии of2 шума на выходе
фильтра.
Ответ: о|/о2 = (So/2/Vo).
11.9. На два разных входа перемножителя подаются два неза-
висимых узкополосных стационарных процесса £х(0 и £2(0. Пока-
зать, что мощность (дисперсия) выходного процесса | (0 распреде-
лена поровну между низкочастотной и высокочастотной областями
спектра.
Указание. Для решения задачи можно воспользоваться
представлением корреляционной фукции узкополосного стационар-
ного процесса (11.3) и учесть,что у (0) = 0.
11.10. На один вход синхронного детектора (рис. 11.4) подает-
ся узкополосный гауссовский стационарный шум £ (0 с корреля-
ционной функцией (т) = ajr (т) cos ®от. а на другой — опорное
напряжение Axcos <в0/. Получить выражения для одномерной л
332
, Т) > 0.
двумерной плотностей вероятностей колебания т] (0 на выходе
детектора в стационарном состоянии.
Ответ: Выходной процесс т)(0. гауссовский с дисперсией —
— (Л^Л?)2 и нормированной корреляционной ’ функцией г(т).
11.11. Вычислить математическое ожидание, тл и дисперсий
а а огибающей A(f) гауссовского стационарного процесса g (0,
имеющего дисперсию <г|.
Ответ: тл = oj Vл/2, оД = (2 — л/2) <т|.
11.12. Получить плотность вероятности р (tj) для квадрата
огибающей Л2(0 гауссовского стационарного процесса 5 (0 : т] (0 =•
- Л2(0.
1 / Т|
Ответ: p(rj) — —— expl —
г'1 2сг| | 2а|
11.13. Вычислить математическое ожидание /пд. и дисперсию
сгл* квардата огибающей гауссовского стационарного процесса | (0.
Ответ: тл» = 2<у|, од« = 4сг£.
11.14. Гауссовский узкополосный стационарный процесс 5 (0
со средним квадратическим значением <у§ = 1 В подается на линей-
ный детектор огибающей с коэффициентом передачи !К = 1. Найти
вероятность того, что напряжение на выходе детектора превысит 2 В.
Ответ: Р = ехр (—2) = 0,135.
11.15. Корреляционная функция гауссовского узкополосного
стационарного процесса 5(0 равна 7?$(т) = <т|е_“fa cos шот. Вычис-
лить корреляционную функцию 7?д(0 огибающей A(t) этого
процесса.
Ответ: RA ’(0 = (2 ~ y) <°’915 е-2“,т| +
4-0,057 е-4“1т 1 +...).
11.16. Решить задачу 11.15 для случая, когда /?g(0 =
= о|е~®’т‘/2 cos соот.
Ответ: RA (0=^2 — -у)<г| (0,915 е~“2 4- 0,057е-2“2*2 4-...).
11.17. Корреляционная функция гауссовского стационарного
процесса 5 (0 равна
7?g(0 = orle-^’^cos гоот.
Вычислить корреляционную функцию Рл*(0 квадрата огибающей
Л2(0 этого процесса.
Ответ: Ra*^) — 4о|е-“2т2.
11.18. Получить двумерную плотность вероятности для процесса
т) (0 — Л2(0, представляющего собой квадрат огибающей гауссов-
ского узкополосного стационарного процсса 5 (0 с корреляционной
функцией 7?б(т) = сг(г (т) cos (оот.
ззз
Ответ'.
ехр
n + nT Ъ /
2ст|(1—г2) ] °1 а|(1 —г2)
г = г(г).
11.19. Гауссовский стационарный узкополосный процесс £ (/)
имеет корреляционную функцию 7?g(r) = ff|r (т) cos <о0т. Получить
одномерную плотность вероятности для производной от случайной
фазы <р (/).
Ответ'.
р(ф) =
1
2/=7j-
г’о
_ d2r (т)
“ d-г»
t-o
11.20. При тех же условиях, что и в задаче 11.19, получить
совместную плотность вероятности для случайной фазы <р(7) и ее
производной q>(0 в один и тот же момент времени.
' ( '\ 1 Л Фа \“3/2
Ответ'. р21<р, <р) =--——- 1-------—
4л У—r£ к го /
11.21. На приемное устройство, схема которого изображена
на; рис. 11.5, воздействует стационарный белый шум n(t) со спект-
ральной плотностью Sn(co) = NQ/2. Частотная характеристика
усилителя промежуточной частоты (УПЧ) задана выражением
#(/©)=#0-------—--------, а «(00 ;
а импульсная характеристика h(t) интегрирующего фильтра RC
равна h(t) = уе—
Определить: 1) плотность вероятности pfq) процесса т, (/)
на выходе квадратичного детектора огибающей; 2) математическое
ожидание т^, корреляционную функцию 7?п(т) и дисперсию
3) математическое ожидание т^, корреляционную функцию 7?j(x)
и дисперсию процессса £(/) на выходе фильтра RC в стационарном
состоянии.
Рис. 11.5. Упрощенная функциональная схема радиоприемника
334
Ответ'.
1) р ft) = —1_е-п'2Ч т) > 0, of =4"аЛ7о^о/2;
2о| 2
2) тп = 2а|, Rn (т) = 4а( #40 e~2“W, = 4а( а>0 > а;
3) тг = аУ0 & о, Ri (т) = aS-*--(у е-2а™ — 2ае~* ),
V2—4а2
11.22. Пусть % (0 = А (0 cos [<о0/ + Ф (01 — гауссовский ста-
ционарный узкополосный процесс. Рассмотрим случайный процесс
т] (0 = £ (0 cos ast = (1/2) А (0 cos[(<D0 — со8) t +
+ф (0] + (1/2) 4(0 cos [(®0 + ®8) t + <р(0],
где частота ю8 мала по сравнению с частотой соо, но значительно
превышает ширину спектра процесса | (0.
Спектр процесса т] (0 расположен в двух практически непере-
крывающихся полосах, причем нижней боковой полосе соответ-
ствует процесс
41(0 = (1/2) А (0 cos [(<оо — <о8) t + ф (0],
а верхней боковой полосе — процесс
П2(0 = (1/2) Л (0 cos [(®0 + ®8) t + ф (0].
Показать, что процессы v)i(0 и являются стационарными,
хотя их сумма есть нестационарный процесс. Убедиться, что про-
цессы т)1(0 и т]2(0 не являются независимыми.
Указание. При доказательствах целесообразно восполь-
зоваться соотношениями (11.15).
11.23. Установить разный характер изменения математического
ожидания ту и дисперсии а| огибающей V(t) в зависимости. от от-
ношения сигнал/шум а = Ат/в^ для малых и больших значений а..
Ответ: ___ ______
y(1+4’a2)’ av=a6
(11.56)
mv= Ат 1 +-^-~4m^l ov = <Jt, а>3. (11.57)
Указание. Нужно в формуле (11.30) воспользоваться сле-
дующими асимптотическими представлениями функций Бесселя:
/п(х) =(—Y—[1 +-------------h...],x<l; (11.58)
nV ' V 2 / nl L 2(2n4-2) ] v '
/nW =—+'1— +•••] • 1- (И-59)
f 21И L 8x J
335
11.24. Найти математическое ожидание и дисперсию квадрата
огибающей У2(0- *
Ответ: ту» — 2<т|(1 + а2/2), ву» = 4<т|(1 + а2).
11.25. Найти одномерную плотность вероятности для процесса
т](/) = V\t), представляющего собой квадрат огибающей суммы
детерминированного гармонического сигнала и гауссовского ста-
ционарного шума £(/)•
Л I\ 1 / П+Лт
Ответ: р (п) = -^ГехР-------Г"1 г
2<71 \ 2at ) \ а1 /
Указание. Нужно в формуле (11.28) перейти от V к т).
11.26. Вычислить одномерные начальные моменты mh =
— M{Vk (i)}, k = 1, 2, 3, ..., огибающей V(t) суммы детерминиро-
ванного гармонического сигнала 4TOcos aot и гауссовского стацио-
нарного процесса g (t) с дисперсией of.
Ответ: mh
А* \
ТП 1
2с^Г )'
где Г(х) — гамма-функция; 1F1(a; 0; х) — вырожденная гипер-
геометрическая функция.
Указание. При выполнении интегрирования с плотностью
вероятности (11.28) следует воспользоваться известным интегра-
лом [17]
« Уг/н+v
2ft / V 2
j 1 Iv (ax) e-₽2*2 dx
о
20М- г (v+ 1)
а2
•ХЛ ^- + 1; v + 1; ..
\ 2 40* }
11.27. Вычислить совместную плотность вероятности Д2(У>У)
для огибающей V (i) и ее производной V(t) в один и тот же момент
времени t. Считается, что огибающая V (/) определена форму-
лой (11.18).
Ответ: p2(V,V) = Pv(V) р (V), где pv(V) дается формулой
(П-28);
р (У) —----г 1 ехр
• V ’ с5/2л(-г0") F
V2
2af (- rj)
— нормальная плотность вероятности.
Указание. Нужно проинтегрировать плотность вероятно-
сти (11.26) сначала по ф в пределах от —оо до оо, а затем по ф в пре-
делах от — л до л.
11.28. Найти плотность вероятности процесса т](/) = cos ф(/),
представляющего собой косинус фазы ф(0 суммы детерминирован-
886
кого гармонического сигнала Лтосоз <£>ot и гауссовского стационарно-
го шума | (/) = А (/) cos [®0* + <р (/)] с дисперсией о|.
Ответ:
Р (л) =----е-0’/2 [1 + ]/2л ат]Ф(ат]) еа*ч*/2],
«/1—t)2
а = —, —
где Ф (х) — интеграл вероятности.
11.29. Решить задачу 11.28, положив т] (/) — sin -ф (/).
Отверг:
р(п) = V, а- е-°г/2 1 (1 -<п2) ае 2 х\
л у 1—Тр ( 4
X [ф (а]Л—П2)----Я}, hl< 1.
11.30. Показать, что при больших отношениях сигнал/шум
(а — Amfc% 1) случайную фазу ф (/) и ее производную можно
приближенно считать гауссовским стационарным процессом. Запи-
сать для этого случая совместную плотность вероятности для фазы
и ее производной в один и тот же момент времени.
Ответ:
ф(/)_ AW_( р2(ф, ф)=рф(ф)р^ (ф)= у
rJ(O)=
^Гс(!Т) I
|,-о’
11.31. Определить плотность вероятности огибающей V (!) сум-
мы двух гармонических колебаний
I
Sx(/) = Лх51п (®0/ + Ф1), S2(/) = Л2СОЗ ((Оо/ + Фа)
и гауссовского стационарного узкополосного шума £•’(/) =
= А (/) cos [<оо/ + <р (/)] с нулевым математическим ожиданием и
дисперсией сг|: '<
51(0 + «г(0 + ИО = V (0 cos [ф0/ + ф (/)]. ’(
Случайные начальные фазы фх и ф2 предполагаются равномерно
распределенными в интервале (—л, л).
837
Ответ'.
zv\ V /, Р4-Л?+Д|
Р(Ю=—ехр(^----------
/ AV
0 I <т2
\ ff£
Указание. Для решения задачи следует воспользоваться
интегральным представлением функций Бесселя [17] 1п(х) =
я
= в*cose cos nQM, п = 0, 1, 2, и частным случаем «теоремы
сложения» бесселевых функций:
/0 (zn |/"а2 + 62 — 2ab cos 0 ) = /0 (лиг) Л> (тЬ) +
4-2 2 Л (та) Л (mb) cos и0, -
П=1
где а > О, Ь > 0 и 0 > 0.
11.32. На линейный детектор огибающей воздействует сумма
s (О 4- £ (0 = 4mcos (<оо/ 4- Фо) 4- A (О cos ko0t 4- Ф (01 =
= V (0 cos W 4- Ф (ОЬ
где s (0 — детерминированный гармонический сигнал; £ (0 — га-
уссовский стационарный узкополосный шум с нулевым мате-
матическим ожиданием и корреляционной функцией 7?j(t) =
= о|е~“т’соз <вог.
Определить приближенные выражения для математического
ожидания тп и корреляционной функции 7?п.(т) напряжения на вы-
ходе детектора т] (0 = V (0 при больших (а = Ат/о > 1) и малых
(а 1) отношениях сигнал/шум.
Ответ'.
(14- JL), (т)~<т| е-«’* (1 4- — е-«’j, а» 1,
338
12. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ
НА НЕЛИНЕЙНЫЕ СИСТЕМЫ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Среди, нелинейных преобразований случайных процессов простейшим
является такое преобразование (рис. 12.1), при котором значение выходного
процесса т] (t) в любой момент времени определяется только значением вход-
ного процесса § (t) в тот же момент времени:
= (12.1)
где f [£] — некоторая нелинейная функция. Такое нелинейное преобразова-
ние называют безынерционным или функциональным.
К безынерционному сводятся также нелинейные преобразования, при
которых входной^и выходной процессы g(f) и т) (0 подвергаются дополнитель-
ной трансформации линейными системами (рис. 12.2), не оказывающими
реакции на нелинейный элемент. Такое преобразование можно записать
в форме '
£ (0 - LJ [Li? (0],
где Lj и L2—линейные операторы, описывающие поведение линейных систем.
Поскольку правила преобразования характеристик случайных процес-
сов линейными системами известны (см. гл. 10), для изучения указанных не-
линейных преобразований достаточно рассмотреть преобразование (12.1).
Общее правило. В общем виде принципиальное решение задачи о не-
линейных безынерционных преобразованиях случайных процессов дается
известным свойством инвариантности дифференциала вероятности. Пусть
известна n-мерная плотность распределения вероятностей рп (£х, 5г» •••> £п)
случайных величин |2» •••» tn и нужно найти плотность распределения ве-
роятностей pn (Th, т)2, ...» Лп) Для случайных величин
г)1==/1 151» Вг» •••» 5п1,
= и, ...» Bnl, (12.2)
Лп—fn 151» Ва» •••» 5п1»
где ft — кусочно-непрерывные функции. Если существуют однозначные
обратные функции
Si = Ф1 (П1ЛП2..... ппЬ
?2= Ф2 П2.......Пп1. (12.3)
5п == Фп hi» Пг...?Ы.
Рис. 12.1. Нели- Рис. 12.2. Типовое радиотехническое устройство
нейный безынер-
ционный преоб-
разователь
339
то интересующая нас плотность распределения вероятностей определяется
формулой
К(П1> Па....Пп)=Рп(<Р1 [i)i> Па....ПпЬ
Фа hi- Ла....Пп].......Фп1П1> Па....HnDl^nl. (12.4)
где
0 ,а(Ь’ *».•••. М (12.5)
d(i)i- Па...Пп)
— якобиан преобразования от переменных ..... к переменным
111. Па.... 1)П-
В тех случаях, когда обратные функции ф^ неоднозначны, в^правои части
формулы (12.4) следует взять сумму по каждой из подобластей.
Рассмотрим следующий частный случай. Пусть
П1 ~ /1IS11 = 11. 1)а = 1) = /а 151> 5а1>
причем обратные функции Jx = Фх[1)1] = i)i> Sa = Фа I’ll* Л»1 однозначны,
В данном случае якобиан преобразования (12.5)
1 О
дфа дф,
ЭП1 дПа
дфа дфа
Ч “ Л)
а совместная плотность распределения вероятностей ра (ть, гр случайных ве-
личин 1)х и 1] в соответствии с (12.4) определяется формулой
Ра (’ll. i))=Pa (П1. Фа hi- П1)|-^-| * (12.6)
I I
Интегрируя (12.6) по гц, получаем одномерную плотность распределения ве-
роятностей для случайной величины т)
Pl (1)) =
оо
J Ра (Ль Фа I’ll. П1)
— 00
дфа
Л]
(12.7)
При применении формулы (12.4) к практически интересным нелинейным
преобразованиям могут возникнуть трудности. Так, если функции fi являются
полиномами выше третьей степени, в общем случае затруднительно найти
функции фг, т. е. аналитически разрешить систему нелинейных уравнений
(12.2) относительно Аналогичные трудности возникают и при транс-
цендентных функциях ft. При кусочно-линейной аппроксимации функции ft
оказываются разрывными и производные dtyt/dfi во многих типовых случаях
в некоторых точках могут быть равными бесконечности.
Ввиду сложности непосредственного вычисления плотностей распределе-
ния вероятностей часто ограничиваются нахождением более простых, но ме-
нее полных статистических характеристик выходного процесса, например ма-
тематического ожидания и корреляционной функции. Применительно к раз-
ным видам нелинейных преобразований для определения этих характеристик
можно указать несколько методов.
Полиномиальное преобразование [29]. Пусть характеристика нелиней-
ного элемента t] = f [|] является аналитической функцией в окрестности не-
которой точки С. Тогда ее можно разложить в ряд Тейлора:
W IS] =«o + «i (fe-Q+ ... +ап
1=С
1 <?ИВ1
ak = —-----Г~
k\ dlk
число членов которого определяется точностью аппроксимации.
(12.8)
.340
Обозначим начальные моментные функции процесса £ (/) через /и, а т](0—
через т. Статистически усреднив левую и правую части равенства (12.8),
получим
mi (0 = Л4{т] (0} = тп (0 = а0 + atM {5 (f) - С} + ... + M{[g (0 - Ср}.
(12.9)
Перемножив левые и правые части равенств (12.8) для двух моментов вре-
мени ^,72 и выполнив операцию статистического усреднения, найдем выраже-
ние для двумерной моментной функции (ковариационной функции):
«ы (4. *«) = Л4{т] (tj) т) (/,)} = ft, ta) = а% + a0«i I«i (4) +
+«ift) - 2С] + a} lmlt г ft, tg) - Cm, ft) - Cmt ft) + C2] + ... +
+ {[g ft) - Cp [g (ta) - Cp}. (12.10)
Аналогично находятся выражения для высших моментных функций.
Для получения выражения моментных функций процесса г) (0 в явном
виде через моментные функции процесса g (0 нужно воспользоваться форму*
лой бинома Ньютона
* м
(1-0*-У ——
раскрыть члены вида
[g ft) - СР [g ft) - Ср [g (t9) - С]« .... k, I, m < n,
и затем выполнить статистическое усреднение. При этом, если процесс £ (t)
задан своими моментными функциями, сразу получаем нужный результат.
Если же процесс' g (t) задан плотностями распределения вероятностей или
характеристическими функциями, то по ним необходимо предварительно вы-
числить его моментные функции.
Моментные функции сравнительно просто находятся для гауссовского
стационарного процесса |(/). Пусть математическое ожидание такого про-
цесса равно нулю; обозначим его дисперсию через =* <у|, а нормированную
корреляционную функцию — через Г| (т). Нетрудно убедиться [6], что при
этом одномерные моментные функции стационарного гауссовского процес-
са определяются формулой
ZA м rtv ( 1 -3-5' • • • • • (v — ’) аЕ п₽и четном v.
mv(0=Af{g (0} = { 6
(0 при нечетном v,
а для двумерных моментных функций справедливо соотношение
muv(T)=M{g'4/)gv(<+T)} = ^+v 2
л=о
где
— оо
Здесь Ф(л)(и) = dn®(z)/dzn — п-я производная от интеграла вероятности
Z
Ф(?) = —zzr f e-x^zdx. (12.11)
"|/2л J
341
Совокупность коэффициентов образует матрицу, приведенную
в табл. 5.3.
Трехмерные моментные функции гауссовского процесса определяются
аналогично [26]. Общее правило вычисления многомерных моментных функ-
ций установлено в работе [69].
Из формул (.12.9) и (12.10) видно, что моментные функции процесса т] (0
линейно выражаются через моментные функции процесса 5(0, однако фор-
мулы для моментных функций выходного процесса включают более сложные
моментные функции входного процесса. В этом состоит одна из характерных
особенностей любого нелинейного преобразования (в том числе и полино-
миального) по сравнению с линейным.
Кусочно-разрывные и трансцендентные преобразования. При рассмотре-
нии воздействия достаточно сильных сигналов и помех на нелинейные уст-
ройства часто применяют аппроксимацию их характеристик кусочно-разрыв-
ными или трансцендентными функциями f [|], поскольку они позволяют
лучше передать существенные свойства участка нелинейной характери-
стики. Вычисление моментных функций выходного процесса для нелинейных
преобразований (12.1) такого вида можно выполнять двумя тесно связанными
методами: прямым и методом характеристических функций [36].
В прямом методе используются сами нелинейные характеристики и ста-
тистическое усреднение выполняется при помощи плотностей распределения
вероятностей. При этом одномерные моментные функции находятся согласно
очевидной формуле
mv (0 =М {T)v (0) = Г Г К (0] Pi & 0 .
— 00
а для двумерной моментной функции т1д (0/72) справедливо соотношение
"4,1 (<1. У =М {т) (4) т] (/,)} =
= f J 7[ЫНУ Ра(Ь. 5»; 4. «41^. (12.12)
— ОО —00
где = I (0), 52 ~ 5 (/2). .
В методе характеристических функций нелинейная характеристика пред-
ставляется при помощи преобразования Лапласа:
T)=f (Я=v“ ) F (/“) e/“s <*“>
2я I
где L — соответствующим образом выбранный контур интегрирования в ком-
плексной области и. Вид контура интегрирования и выражение функции
F (/и), представляющей собой прямое преобразование Лапласа нелинейной
функции
О
приведены в табл. 12.1 [34]. Нетрудно убедиться, что в данном случае двумер-
ная моментная функция (0, t2) определяется формулой
(0,
P(MF(ju2)x
X в2(/«1, hi Qduidu^ (12.13)
где 02 (/«1, /и2; 0, /2) —двумерная характеристическая функция входного
воздействия £ (0.
342
Из (12.12) и (12.13) следует, что как метод характеристических функций,
так и прямой метод требуют одних и тех же априорных сведений о входном
случайном процессе £ (/), ибо характеристические функции и плотности рас-
пределения вероятностей, как известно, связаны преобразованием Фурье.
При выбсре того или иного из рассмотренных методов решающее значение
имеют не столько теоретические соображения, сколько вычислительные труд-
ности.
В заключение отметим, что если £ (t) является гауссовским случайным
процессом, то естественным результатом прямого метода является выражение
ответа через табулированные производные от интеграла вероятности (12.11),
а при использовании метода характеристических функций ответ чаще выра-
жается через гипергеометрические функции [71]. Однако это не имеет сущест-
венного значения, так как производные от интеграла вероятности и вырож-
денная гипергеометрическая функция связаны друг с другом известными
соотношениями [70].
Если на вход рассматриваемого нелинейного элемента воздействует га-
уссовский стационарный процесс £ (I) с нулевым математическим ожиданием
= 0, дисперсией = <т| и нормированной корреляционной функцией
г&(т), то процедура вычисления интегралов в правых частях формул (12.12)
и (12.13) может быть упрощена с помощью специальных приемов. Примени-
тельно к формуле (12.12) один из таких приемов, названный методом дельта-
функции, был развит в работах [72, 73]. Позже аналогичный метод, называе-
мый методом Прайса [74], был применен к вычислению интегралов вида (12.13).
Метод дельта-функции базируется на представлении двумерной плот-
ности распределения вероятностей гауссовского стационарного процесса
| (0 с нулевым математическим ожиданием, имеющей вид
1 1
в форме ряда [6]
2^ф<п+1)(1г)ф<л+1,(4Я
п=0 \ 6 / \ 6 /
На основании этого разложения формулу (12.12) можно представить в виде
где математическое ожидание выходного процесса т] (/) определяется соот-
ношением
тп=Л4{т)(0} = -^- f
с \ Б /
ъ —оо
(12.16)
Из (12.16) следует, что корреляционная функция выходного процесса, равна
Яп ГО-»»1д (?)—«» =
(12.17)
343
Характеристики нелинейных устройств
Табли ца 12.1
Тип нелинейного устройства n==fR] F(/«) L
А налитическое выражение График
1. Устройство с харак- теристикой v-й степени а? (v—целое) avl (iu)v+1 Положительная петля вокруг u = 0
2. Устройство с харак- теристикой v-й степени со смещением a(g-B)v (v—целое) < у 3 £ —avt e-juB (Ju)v+1 To же
3. Однополупериодный линейный выпрямитель 1 d^, g > 0, to, £<0 a Действительная ось и от оо до — оо, ^вырез вниз при и = 0
0 t
4. Выпрямитель с ха- рактеристикой v-й сте- пени и с ограничением 1 о, 1<В (v—положительное) 1 / аГ (v + 0 —juB (JU)V + * e То же
о в £
5. Линейный выпрями- тель с ограничением (aD, О, ] с&„ 0 < £< D, to, £<0 / 1 / 1 / 1 a(l—e~iuD) То же
0 л £
6. Однополупериодный выпрямитель о о л v МЛ JJLP о" —,—' 9, 1 f р[£] е~/“М 0 »
о
7. Идеальный ограничи- тель o' о Л\ V Ш) WJ) — 9 7 L—— 1 ± — и »
0 -7
8. Сглаженный ограни- читель £ 1 f -Х2/2Р‘ . 1/2лр J 6 Х 0 1 к L °, -1Ц 1 -4 ₽2 «* — е 2 JU »
Применяя к (12.17) интегрирование по частям v раз и используя извест-
ные свойства функции Ф<п> (?) [70], получаем
^)=<ф~2 2
п== 1
[g] qOH-i-v)
2 „
л!
(12.18)
Применительно к различным кусочно-разрывным характеристикам нелиней-
ных элементов следует выполнять интегрирование по частям такое число v
раз, чтобы v-я производная [£] превратилась в дельта-функцию или сум-
му дельта-функций.
Формула (12.18) устанавливает связь между корреляционной функцией
выходного процесса и нормированной корреляционной функцией входного
процесса и, следовательно, позволяет найти спектральную плотность выход-
ного процесса по известной спектральной плотности процесса на входе нели-
нейного элемента. Наличие в (12.18) членов с п > 2 приводит к искажению
и расширению спектра выходного процесса по сравнению со спектром вход-
ного процесса. В этом, в частности, состоит вторая особенность нелинейных
безынерционных преобразований.
При вычислении интегралов (12.13) можно продуктивно использовать
тот факт, что для характеристической функции стационарного гауссовского*
процесса £ (/), имеющей вид
02 (f«i> Ю =м {ехр [/«1 $1+/«2 £г1} =
-ехР {~4" U1 ’ (12-19)
справедливо соотношение
в соответствии с чем (12.13) можно представить в следующем виде:
F^dui^ F (/“г) /“2)^2-
Подставив сюда исходное определение характеристической функции (12.19)
и изменив порядок интегрирования и статистического усреднения, полу-
чим [74]] •
ь 00 00
f f £2) «2. (12.20)
Of* J v
» —оо — оо
f (/«)* F (/«) е'“* du = •
zjl аЕ
При вычислении корреляционной функции процесса на выходе нелиней-
ных. элементов с кусочно-разрывными характеристиками по формуле (12.20)
нужно брать такое значение k, при'котором /w[|] обращается в сумму дель-
та-функций. Тогда интеграл в правой части (12.20) всегда вычисляется и, сле-
довательно, находится k-я производная функции mltl (т). Что касается по-
следующего интегрирования по значениям нормированной корреляционной
функции (т) с целью определения т1д(т), то оно особенно легко выполняет-
ся в частном случае, когда f(k) [?] = ± 6 (?) и воздействующий нормальный
Стационарный процесс ? (t) имеет нулевое математическое ожидание.
346
2. ПРИМЕРЫ
12.1 . На безынерционный двухсторонний квадратичный детектор
с характеристикой (рис. 12:3)
т] = f W = al2, а> О,
воздействует стационарный гауссовский шум | (/) с плотностью
распределения вероятностей
Р?© = ._L ехр
|/2л <т&
Г (ё~”Ч)21
2af
(12.21)
Определить плотность распределения вероятностей рх(т]) про-
цесса т| (/) на выходе детектора.
Решение. При а > 0 случайная величина т] — Л (0 не может
быть отрицательной, поэтому при т] < 0 функция Р1(л) = 0. Для
т| > 0 имеем
I = <р 1г|] = ± Vx\/a,
в соответствии с чем модуль якобиана преобразования (12.5) равен
|dg/dr] | = 1/2/ат]-
Учитывая, что в рассматриваемом примере функция В = ф [т]]
двухзначна, по формуле (12.4) находим
Р101) =
2 У ап Р1
т|>0,
т|<0.
(12.22)
Если математическое ожидание процесса £ (/) равно нулю (mg=
=0), то формула (12.22) приводится к виду (см. задачу 2.31).
Р1(П) =
' 1 / и \
--------------ехр [---------~
2лат) 2ао| J
.0,
я>о,
г)<0.
График этой функции приведен в табл. 12.2.
Рис. 12.3. Амплитудная характеристика двух-
стороннего квадратичного детектора
347
Таблица 12.2
Плотности распределения вероятностей (т|) на выходе типовых безынерционных нелинейных устройств
Тип нелинейного устройства
Аналитическое выражение График Pi (6) Pl ни
1. Двухсторонний квадра- тичный детектор ag2, а>0 л
* 4 V $ 0 £ С
2. Односторонний квадра- тичный детектор о о Л\ V JJJ) 4ХП сч Q о 0 < у е AS# (%)
3. Односторонний ограни- читель о Сл - (П* отс л о V 9 ? А лз^)'
0 « т 7 а £
1 1 1
12.2 . На вход безынерционного ограничителя с характеристикой
(рис. 12.4)
П=/Ш =
—b
si
а
при —р,
при — р<£<а,
при
(12.23)
воздействует стационарный гауссовский случайный процесс £ (/)
с плотностью распределения вероятностей (12.21).
Определить плотность распределения вероятностей Р1(т]) про-
цесса г] (t) на выходе ограничителя при s > 0.
Решение. На интервале (—Ь, а) преобразование т] = f [£] в дан-
ном примере является линейным: т]= $|. Поэтому внутри этого ин-
тервала
Р1(П) = Р?[—> — Ъ<ц<а.
\ S J S
Вероятность того, что г] < — b или г] > а, равна нулю, а ве-
роятность того, что т] заключено в интервале (—Ь, а),
а а
350
Все значения |, для которых |^а, преобразуются ограничи-
телем в одно значение г] — а (рис. 12.4). Аналогично, все значения
| —Р преобразуются в значение т] = —Ь. Следовательно, веро-
ятность
P(^a) = S1 = J°
а
преобразуется для т| в дельта-функцию, расположенную -в точке
т] = а. Множитель при этой дельта-функции 6 (т| — а) пропорцио-
нален Sj. Вероятность
-Р
Р(|<-p) = S2=
преобразуется для т| в дельта-функцию, расположенную в точке
т] = '—Ь, множитель при этой дельта-функции 6 (т) + Ь) пропорцио-
нален S2. Таким образом, искомая плотность распределения ве-
роятностей равна
Pi(n) =
-4- рJ ( —'j 4- XSj 6 (т] — а) Ц- XS2 6 (л + Ь), — Ь^.х\^а,
s \ s / --
О, г]<—
Здесь X — коэффициент пропорциональности, определяемый из ус-
ловия нормировки плотности распределения вероятностей р1(т]):
а
MSi + s2)+— f =
s J \ S )
---- X
Очевидно при s = 1 коэффициент % = 1.
График плотности распределения вероятностей р1(л) приведен
в табл. 12.2. Там же представлены плотности распределения веро-
ятностей PiCn) на выходе некоторых безынерционных нелинейных
устройств при воздействии на их вход стационарного гауссовского
случайного процесса £ (/) с нулевым математическим ожиданием
= 0.
12.3 . На нелинейный элемент с параболической характерис-
тикой
n - f U1 = «1В +
воздействует стационарный случайный процесс
В (0 = s (0 + п (0,
где
s (0 = Ап cos (ю0< + <p)
— гармонический сигнал с постоянными амплитудой и частотой и
случайной начальной фазой ср, равномерно распределенной на ин-
тервале (—л, л), а п (0 — гауссовский стационарный шум с нуле-
вым математическим ожиданием и корреляционной функцией
7?п(т) = М {п (0. п (t + т)} = о^гп(т).
351
Определить математическое ожидание тп и корреляционную
функцию процесса г] (/) на выходе элемента при условии
статистической независимости сигнала и шума.
Для частного случая г„ (т) = е-“|т| определить физическую
спектральную плотность 5Чо(/). центрированного выходного процесса
По(О = Л (0 — т^.
Решение. По условию
т) (t) = аДз (0 + п (/)] + а2Ь (0 + п (Z)]2 =
= OjS (t) + а^п (/) + a2s\f) + 2azs (/) п (t) + a2n2(t). (12.24)
Производя статистическое усреднение соотношения (12.24) и учи-
тывая, что в рассматриваемом примере
Af {«.(/)} = 0. М {п (/)} = 0, М {з (0 п (/)} = 0,
получаем следующее выражение для математического ожидания
процесса т| (/):
щ == М (т| (/)} = а2 (-ф- 4-<г£
Перемножив равенства (12.24) для моментов времени t и t + т,
выполнив статистическое усреднение результата перемножения, вы-
числим двумерную моментную (ковариационную) функцию про-
цесса т] (0
"h.ifr) - М. {т] (0 п (I + т)} =
= /Сп(т) = а2[(А„/2) cos coo'c + ^гп(т)] +
+ а2[(А&/4) (1 + 0,5 cos 2соот) + .2A£ffirn(r) cos <вот + A£tfi +
+ (Г« + 2<гй ''«('г)!.
Отсюда находим корреляционную функцию
Рп(г) — = а®(Дт/2) cos ®от +
+ агИт/8) cos 2®0т + а1о^г„(т) + 2аВ<тйг^(т) +
+ 2a%A%trt rn(t) cos аот. (12.25)
Для вычисления спектральной плотности (/) следует вос-
пользоваться формулой (6.21):
S4.(f) = 4 ГRnCO cos 2nh dt. (12.26)
о
После подстановки в (12.26) корреляционной функции (12.25) при
гп(х) — ехр (—а |т| ) находим
5ч. (/) = -ф- 6 + as2 -ф- 6 (/-2/0) + 4а2п(а? +а®2 х
2 о
х а + z 12 27)
аа+4л2Л аа + 4ла (/—f0)2 ’ \ l
352
Рис. 12.5. Дискретно-сплошная спек-
тральная плотность
Рис. 12.6. Перемножи-
тель
Из (12.27) следует, что спектральная плотность Sn,(f) является
дискретно-сплошной (рис. 12.5). Она состоит из двух дискретных
спектральных линий при f = f0 и f = 2f0, обусловленных наличием
на входе параболического элемента гармонического сигнала з (/);
низкочастотного сплошного спектра, обусловленного только шу-
мом, и сплошного спектра, расположенного в окрестности частоты
f — f0. Последний обусловлен взаимодействием сигнала з (/) и шума
п (t) в результате нелинейного преобразования.
12.4 . На входы перемножителя (рис. 12.6) воздействуют ста-
ционарные некоррелированные случайные процессы |х(/) и 5»(0
со спектральными плотностями Sx(®) и S2(®), соответственно рав-
ными
S2 (®) —
(W1.
Ni.
—®х—А/2^®^—®х 4- А/2,
®х—A/2^®^®х 4- А/2,
О при других ®;
W2, —®2—А/2<®<—®24-А/2,
/У2, ®2—А/2^®^®2 4-А/2,
(12.28)
(12.29)
$х(®) =
О при других ®.
Определить спектральную плотность S4(®) случайного процесса
Л (0 — Вх(О В2(0 на выходе перемножителя.
Рещение. Спектральная плотность 5Ч(®) случайного процесса.
Л (0 — Bi(0 в Данном случае определяется формулой [11
Sn(®)
ОО
= V~ f Sx(v)S2(® —v)dv,
2л J
— 00
(12.30)
где Sx(v) — спектральная плотность процесса £х(/); S2(® — v) —
функция, сдвинутая на частоту ® относительно спектральной плот-
ности S2(—v) процесса £2(/). Графическое изображение функций
Sx(v) и S2(v) дано на рис. 12.7. Там же показана спектральная
плотность S2(® — v).
Интеграл (12.30) отличен от нуля только в том случае, когда
отлична от нуля подынтегральная функция, т. е. когда спектральные
плотности Sx(v) и S2(®—v) перекрываются.Как следует из рис. 12.8,
при изменении ® от —оо до оо, т. е. при перемещении спектральной
12 з ак. 1203
353
Рис. 12.7. Спек-
тральные плотно-
сти процессов на
входах перемно-
жителя
плотности S2(®—v) слева направо относительно Sj(v), такое пере-
крытие имеет место в четырех случаях, первый из которых соответ-
ствует перекрытию составляющей спектральной плотности Sj(v)
в области v <0 с составляющей спектральной плотности S2(® — v)
в области со — v > 0. Этот случай перекрытия Sx(v) и S2(® — v)
имеет место при значениях частоты ®, удовлетворяющих неравен-
ствам (рис. 12.8)
® + <о2Н—— >—®i-— ,®4-®2—2”^—Ю1 —2* ' (12*31)
Объединяя неравенства (12.31), находим следующую область зна-
чений ®, соответствующую, первому случаю перекрытия функций
Si(v) и S2(® — v): •
—®0 — А со —мс + А,
где ®с — ®х + ®2 — суммарная частота.
Рис. 12.8. Области интегрирования
354
При дальнейшем увеличении -со и выполнении неравенств
, . Д Д . Д , д
©+©2+у >®1 —у , Ч0+©2----< ©I +-у
наступает перекрытие составляющей спектральной плотности Sx(v)
в области v>0 с составляющей спектральной плотности S2(® — v)
при о — v > 0. Соответствующая этому случаю область значений
со определяется соотношением
®р — А сор + А,
где сор = сох — ©2 — разностная частота.
Аналогично для третьего случая (перекрытие составляющих
Si(v) в области v< 0 и S2(® — v) в области © — v < 0) находим
—®р — А со —сор + А,
а для четвертого (перекрытие составляющих Sx(v) в области v >• 0 и
S2(© — v) в области ю — v < 0) имеем
юс — A со <о0 + А. ,
Подставляя теперь в (12.30) значения Sx(v) и S2(® — v), опреде-
ляемые соотношениями (12.28) и (12.29), и производя интегрирова-
ние в указанных выше областях, получаем
(®).~
S0(®0 А ©),
$о (—©с + А — со),
S0(©p + А + ©)>
So(—©р "Ь А — ©)>
Sq(—(Ор + Д -|- со),
S0(®p + А — со),
So(—©с + А + ©),
S0(©0 + А — ©),
0
—®с — А ю < —юс,
—©с < © < — ©с + Д>
—©р — А ^ © < —©р,
—©р ^ © ^ —®р + А,
©р — А ю < фр,
®р ^ © ^ ©р + А,
®с — А ^ © < ©с,
©с ^ © ©с + А,
при других ©,
где So = АГхУг/2л. График функции Sn(©) представлен на рис. 12.9.
12.5 . На безынерционный ограничитель с характеристикой
(12.23) воздействует стационарный гауссовский случайный процесс
| (/) с нулевым математическим ожиданием = 0 и корреляцион-
ной функцией /?^(т) = о|/"|(т).
Вычислить математическое ожидание и корреляционную
функцию /?ч(г) процесса г] it) на выходе ограничителя.
Рис. 12.9. Спектраль-
ная плотность на вы-
ходе перемножителя
12*
355
Решение [2б]. В соответствии с определением математической
ожидание на выходе ограничителя
оо —Р а ’
/«4= J f Pi($dl + s J +
— оо —оо —Pj
+а
а
где Pi(|) — нормальная плотность распределения вероятностей
(12.21) при mg = 0. После подстановки р^) в выражение для тч
и несложных вычислений получим
+ ф' (-МГ.
\ а1 Л
Для вычисления корреляционной функции 7?л(т) воспользуемся
формулой (12.18). После двукратного дифференцирования нелиней-
ной характеристики f [£] ограничителя имеем
mi=s[6 (В + ₽) - 6 (|- а)],
в соответствии с чем из (12.18) находим [26]
(т) = (sag)2 V ф(п— о [ — ] — Ф<«- »
п-1L \аг / '
2 'gfr)
и!
= *ч 2 <М(4 (12.32)
п= 1
где
ап= ф(п-1)[------8 (оте)2
L \ / J «* стч
Значения коэффициентов ап для различных случаев ограничения
даны в табл. 12.3, откуда, в частности, следует, что определяю-
щую роль в формуле (12.32) играет первый член с коэффициентом
av Сумма всех остальных коэффициентов даже при сильном ограни-
чении (например, симметричное ограничение а 10g = 0,1) состав-
ляет примерно 35% от суммы всех коэффициентов. Поэтому иногда
при расчетах в (12.32) учитывают только первый член, что по су-
ществу соответствует линейному преобразованию процесса £ (/).
12.6 . На вход квантующего устройства с характеристикой
П = f [£] == at, otj < К аг+1,
где i = 1, 2, 3, ..., N— 1, (рис. 12.10) воздействует стационарный
гауссовский случайный процесс g (t) с нулевым математическим ожи-
данием mg = 0 и корреляционной функцией ₽g(t) = <r|rg(T).
356
Значения коэффициентов ап
Таблица 12.3
ап v/a5
0.1 | 0,3 1 0.5 I 0,7 | 1,0
а2 а3 а4 а, а7 ал Симметричное ограничен 0,646 0,735 0 0 0,114 0,114 0 0 0,050 0,048 0 0 0,030 0,027 0 0 ие: a/a£ = 0/a£ = v/a£ 0,789 0,837 0,901 0 0 0 0,112 0,103 0,072 0 0 0 0,042 0,033 0,015 0 0 0 0,021 0,013 0,003 0 0 0
ап a/ag
0,3 | 0,5 1,0 1.5 | 2.0 | оо
йййййййй Несимметричнс 0,681 0,704 0,007 0,021 0,107 0,099 0,007 0,015 0,045 0,037 0,004 0,011 0,026 0,019 0,004 0,009 зе ограничена 0,736 0,078 0,062 0,042 0,012 0,025 0,003 0,015 в: Р/а| =0 0,739 0,142 0,025 0,052 0,001 0,020 0 0,008 0,740 0,193 0,007 0,043 0 0,010 0 0,002 0,733 0,233 0 0,020 0 0,006 0 0,003
ап a/ag
1 ,0 1,5 3,0 1 ,о 1,5 3,0 1,0 1,5 3,0 1.0 | 1,5 | 3,0
₽/0£ = О,3 0/(j£=O,5 fl/og=0,7 Р/о^0,1
0,809 0,036 0,081 0,019 0,021 0,011 0,007 0,006 0„ 81 9 0,085 0,043 0,029 0,005 0,010 0,001 0,003 Неси 0,821 0,154 0,006 0,013 0,001 0,002 0,001 0,001 мметри 0,840 0,018 0,087 0,009 0,023 0,004 0,008 0,002 чное 01 0,859 0,054 0,050 0,014 0,007 0,005 0,001 0,001 гранич< 0,864 0,110 0,011 0,007 0,002 0 0,002 0 вние: f 0,871 0,006 0,086 0,003 0,021 0,001 0,005 0 0,893 0,031 0,053 0 008 0,008 0,002 0,001 0 ) 0,902 0,075 0,014 0,003 0,003 0 0,002 0 0,930 0,010 0,049 0,002 0,005 0 0 0 0,939 0,025 0,029 0,002 0,002 0 0 0 0,944 0,038 0,015 0 0,002 0 0,001 0
Предполагается, что функция f [S] нечетна, т. е. —f [—g] = f [|],
а общее количество уровней квантования at равно четному числу.
Определить математическое ожидание тп и корреляционную
функцию 7?1)(т) процесса г] (t) на выходе квантователя.
Решение [1]. Математическое ожидание
= М 01(0}=
— оо
357
Подставляя сюда плотность распределения вероятностей р^),
определяемую формулой (12.21) при 0, и учитывая нечетность
функции f [gl, находим
= 0.
Корреляционная функция процесса т] (/) на основании формулы
(12.17) равна
Выполнив интегрирование по частям, получим:
f /1В1Ф<л+1>|— |dt= f /'[В1Ф(П) I—W
J \ / J \ <4 /
— оо 4 — ОО
Для рассматриваемого примера
N— 1
П11= s М (£-«<).
г—1
где Дг = аг+1 — аг — расстояние между соседними уровнями
квантования. Таким образом, находим:
/ . \ N-1 .
= УЛ;Ф" —
\°lJ &
358
Подставляя это выражение в /?п(т), получаем следующую формулу
для корреляционной функции:
ГМ— 1 /
) |
2 2ДгФ<п)
стг п-iL/-1
2 г1&
п!
12.7 . Найти корреляционную функцию 7?п(г) на выходе бе-
зынерционного сглаженного ограничителя с характеристикой
(рис. 12.11)
П = /гё] = «4-
8
2а_ f e-*’/2v* dx,
у]/2л
где а и у — постоянные величины, при воздействии на вход ограни-
чителя стационарного гауссовского шума с двумерной плотностью
распределения вероятностей (12.14).
Решение. -Для определения 7?ч(г) воспользуемся формулой
(12.20). Подставив в нее первые производные
/'[?] = —— e-V/2?’,
у 1/2л
находим
(т) ... 2а* / &*—4* Г Г 1 х
дг.(т) «Т* V 1~г|(т) J J глУ^З5
6 —ОО —00
1 хехр[~~~'?7(б»-У^ ](12?3)
где
^а|(Та+аЦ1-г|(т)]) d = ?а6г£(т)
(?’ +<ф*-<$ (т) ’ у2+cj р -г£ (т)J ‘
Двукратный интеграл в правой части равенства (12.33) равен
единице, поскольку он представляет собой интеграл от двумерной
Рис. 12.11. Амплитудная характери-
стика сглаженного ограничителя
359
нормальной плотности распределения вероятностей по всей области
изменения переменных. Следовательно,
dmlti (*) _ 2а2 Г V—& 2a2gj h / rE \211/2
dr6(T) лу2 У 1-г|(т) h(g|+y2) [ g|+t2 ) _
Отсюда находим
Ч(т)
a|+№ ~ 4 2a2 f dx /«1.1 w=— . г Л J 1 —X2 — 00 , n 2a2 . (T) . n + C = arcsin — - +c, л o| +ya
где C — произвольная постоянная интегрирования. Она опреде-
ляется из условий
Um (т) = 0, lim /п1Д (т) = С = т% = а2.
Т->оо Т-> оо
Таким образом, искомая корреляционная функция равна
(12.34)
Если воспользоваться разложением
arcsinx = xH-------------------х + --------х
2-3 2.4.5
функцию (12.34) можно представить в виде ряда
р 2а2 / gir£(T) • 1
110 л | а(+т2
2-3 [ oj + v2
3. ЗАДАЧИ И ОТВЕТЫ
12.1 . На вход двухполупериодного квадратичного детектора
с характеристикой (рис. 12.3)
Ц = f U1 = а%2, а>0,
воздействует стационарный гауссовский процесс | (/) с матема-
тическим ожиданием т^ и дисперсией Dj = о|.
Найти плотность распределения вероятностей Р1(л), математи-
ческое ожидание тп и дисперсию Dn выходного процесса ц (/).
Ответ'.
Шц = аУ 2mf +/n| , — 2a2 Dg (Z)g 4- 2m|),
PiXn) -
—=^—;CxP F-
2 У 2лаг] [ 2a|
, Г (Кп7а+^)2 ]]
+ eXP ~ 2g| •’1>0
360
Рис. 12.12. Нелинейная электрическая цепь
12.2 . Огибающая А (0 узкополосного случайного напряжения
на входе квадратичного детектора огибающей распределена по зако-
ну Релея:
р1(А) = — е-Аг/2<,г, А>0.
Найти плотность распределения вероятностей рх(г]), математи-
ческое ожидание mn и дисперсию Dn напряжения т) (t) на выходе
детектора, если
•П (0 = (а/2) Л2(0.
Ответ: т^=ао2, Dt)=a2o1, рх (tj) = —Ц- е_ч/а«2, т]^0|.
12.3 . На цепь, состоящую из последовательно соединенных.
полупроводникового диода V и резистора R (рис. 12.12), воздейст-
вует случайное напряжение £ (0, представляющее собой стационар-
ный гауссовский шум с нулевым математическим ожиданием mg = О
и дисперсией Dg = a|. Характеристика диода имеет вид
• И 1 fsu »
i=/[u] =
|.SX« ,
U>0,
ы<0,
где
s-(%, + «)- s.-(4«p + R)“‘.
^пр и Чор — внутреннее сопротивление диода в прямом и об-
ратном направлении.
Определить математическое ожидание тг тока i (0 в цепи и его
дисперсию Dt.
Гог/ а?
Ответ: mt = —(s— sx); Dt = —— [(л — 1) (s2-|- s2) -}-2ssx].
/2л 2л
12.4 . Найти плотность распределения вероятностей рх(т]) на-
пряжения г) (0 на выходе однополупериодного линейного детектора,
характеристика которого представлена на рис. 12.13, если на вход
детектора воздействует гауссовский случайный процесс | (0 с ну-
левым математическим ожиданием mg = 0 и дисперсией Dg = <т|.
Ответ: рх(т]) (т|) + у2--_ е"^20*^, г]>0.
2 у 2л
361
Рис. 12.13. Амплитудная характе-
ристика однополупериодного ли
нейного детектора
Рис. 12.14. Амплитудная характе-
ристика двухполупериодного ли-
нейного детектора
12.5 . Найти плотность распределения вероятностей Pifn) на-
пряжения т] (/) на выходе двухполупериодного линейного детектора,
характеристика которого представлена на рис. 32.14. На вход
детектора воздействует гауссовский случайный процесс £ (/) с ну-
левым^математическим ^ожиданием = 0 и дисперсией = а(.
Ответ: р1(ц) = 1/'——— т)>0.
12.6 . Найти одномерную плотность распределения вероятностей
Pi(r]) напряжения г|(7) на выходе однополупериодного квадратичного
детектора, характеристика которого изображена на рис. 12.15,
если на входдётектора воздействует гауссовский случайный процесс
£ (/) с нулевым математическим ожиданием = 0 и дисперсией
Dt = af
Ож p,(n)--^6(n)+ е-"'Н, n>0.
12.7 . На квантующее устройства с характеристикой (рис. 12.16)
П = f Ul = a sgn £
воздействует стационарный гауссовский случайный процесс | (/)
с нулевым математическим ожиданием mg = 0 и дисперсией
D6 = <у|.
Рис. 12.15. Амплитудная характе-
ристика однополупериодного
квадратичного детектора
Рис. 12.16. Амплитудная характе-
ристика квантователя на два уров-
ня
362
Определить: 1) средний квадрат е2 разности процессов £ (/)
и т] (0 на входе и выходе квантующего устройства; 2) значение
а = aopt, минимизирующее е2, и соответствующий этому значению
минимальный средний квадрат e„in.
Ответ: ___
1) е2 = М {Ь]_(0 - - 2]/2/ласг6 + а2;
2) Oopt = ]/2/ntFg, 8min = (1 — 2/л)(У|.
12.8 . На вход квантователя (рис. 12.16) воздействует стационар-
ный гауссовский случайный процесс | (f) с математическим ожида-
нием пц и дисперсией = о|.
Определить плотность распределения вероятностей рг (т|), ма-
тематическое ожидание тп и дисперсию процесса г](?) на выходе
квантователя.
Ответ:
рх(1]) = ф f —'j 6 (а— т|)4- Ф (—^Мб(а4-г]);
\al J \ )
—— | — Ф--------- ; Dn = 4а2Ф ( — I Ф I М.
ag / \ / J " \ aj / \ ai )
12.9 . На симметричный ограничитель, характеристика которого
представлена на рис. 12.17, воздействует стационарный гауссовский
шум £ (/) с нулевым математическим ожиданием mg = 0 и диспер-
сией Dg = о|. ‘
Найти одномерную плотность распределения вероятностей рг (д)
для напряжения t] (t) на выходе ограничителя.
Ответ:
Pi 01) =
1 —Ф (—) 16 (л +а) +-7=Х— e-t)2/2^ 4-
\ aS / J 2я
— а^т]^а,
где Ф (?) — интеграл вероятности (12.11).
12.10 . Найти одномерную плотность распределения вероятно-
стей (»]), математическое ожидание mn и дисперсию Dn напряже-
ния на выходе идеального ограничителя с характеристикой
1 (0, £<Л,
если на вход ограничителя подается случайное напряжение 1(f) с
плотностью распределения вероятностей
Р1 (|) = ge-^/2, g о.
Ответ ,•
Pi (П) = П — e-ft’/2]6 (n) + (n + т) > 0;
тп = У2Й11 - Ф (ft)]; = 2(e-ft‘/2 - /tmn) - m\.
363
Рис. 12.17. Амплитудная харак-
теристика симметричного огра-
ничителя
cos [uot + 0r (t)]
! ФД~
1&Ю
фнч Н—*
Рис. 12.18. Фазовый де-
тектор
12.11 . Напряжение и (0 .на выходе фазового детектора (ФД),
состоящего из перемножителя и фильтра нижних ’частот (ФНЧ)
(рис. 12.18), равно
и (0 = cos ф (0 = cos [0! (0 — 02 (0].
Определить плотность распределения вероятностей рг (и), если
0, (0 и 02 (0 представляют собой независимые стационарные слу-
чайные процессы, равномерно распределенные на интервале (—л,л).
Ответ: рх (и) — 1/л]/1 — и2, | и | 1.
12.12 . На радиотехническое устройство, состоящее из квадра-
тичного детектора огибающей, линии задержки и преобразователя—
(рис. 12.19), воздействует гауссовский стационарный квазигармо-
нический случайный процесс
£ (0 = A (0cos [<o0t + ф (0]
с нулевым математическим ожиданием т^ = 0 и корреляционной
функцией (т) = ct|p5(t)cos <вот.
Определить одномерную плотность распределения вероятностей
Pi (у), одномерную начальную моментную функцию v-ro порядка
mv (0 = M{yv (0), математическое ожидание ту (0 = /П1(0 =
= М {у (0} и дисперсию Dv (0 = т2 (0 — ml (0 процесса# (0
на выходе преобразователя, осуществляющего сложение процессов
и (0 и ы(?4-т):
# (0 = и (0 + и (t — т),
где и (t) — процесс на выходе детектора, равный квадрату огибаю-
щей входного шума £ (0:ы (0 = Д2 (0.
Рис. 12.19. Квадратичный детектор огибающей, линия задержки и преобра-
зователь
364
Рис. 12.20. Плотность распределения вероятностей суммы квадратов огибаю-
щей квазигармонического шума
Ответ".
Pi (у) = —-— I ехр------------- —
—ехр-------------- I, и > 0,
L ^е-рб)])
(0=^ = 2^! [(1 +Pg)v+i_(l _р^ч-1]а*72р6,
mv(t) = my = 4(Jl, Dj,(/)=Dj, = 8(1+р|)р^, рг=р6(т).
График функции р^у) приведен на рис. 12.20.
12.13 . Решить предыдущую задачу при условии, что процесс
на выходе преобразователя у (t) = и (f) — и (t — т).
Ответ'.
Pl (у) —-----* ехр (-----------Ц==^ ;
P1W 4аЦЛТ^| Ц 2а|]Л1-р|р
mzv = 2*v!(l - p<ro|v; ту = 0; Dy = 2o|(l — pg).
График функции р^у) приведен на рис. 12.21.
12.14 . Решить задачу 12.17 для случая, когда преобразователь
представляет собой перемножитель, т. е.
У (0 = и (0 и (t — т).
36S
Ответ*.
Р1(У) =
---!---70 Ко , у > о
2^(1-р|) Ч^К’-Р!)/ Ho-PiU
т? = 22v (v!)? (1 — р|)2 У —— f P-^
ft=o (*’)2(v-fe)l 1-P|
4n
c5 ,
mv = 4o|(l + p|), Dy = 16<yg(3 + 14p| + 3p|).
Здесь /0(z) и Ku(z) — модифицированные функции Бесселя со-
ответственно первого и второго рода [76]. График функции рх(«/) при-
веден на рис. 12.22.
12.15 . Решить задачу 12.12 при условии, что процесс на выходе
преобразователя равен у (t) = и (/ — г)!и (t).
Ответ:
Pi (У) ------. У > 0;
[1+2(1- 2p|)f/+^]~
mv, ту и Dy элементарно не вычисляются. График функции рг(у)
приведен на рис. 12.23.
12.16 . На радиотехническое устройство, состоящее из линей-
ного детектора огибающей, линии задержки и преобразователя
Рис. 12.21. Плотность распределения вероятностей разности квадратов оги-
бающей квазигармонического шума
366 *
pf(ff)
Рис. 12.22. Плотность распределения вероятностей произведения квадратов
огибающей квазигармонического шума
Рис. 12.23. Плотность распределения вероятностей частного квадратов оги-
бающей квазигармонического шума
367
Рис. 12.24. Линейный детектор огибающей, линия задержки и преобразова-
тель
(рис. 12.24), воздействует гауссовский стационарный квазигармо-
нический случайный процесс
1(f) = А (/) cos [®0^ + Ч> (01
с нулевым математическим ожиданием = 0 и корреляционной
функцией
/?g(*r) — crfPsW cos ®от.
Вычислить одномерную плотность распределения вероятностей
одномерную начальную моментную функцию v-ro порядка
/Пу(0 == M{z/V(/)}, математическое ожидание my(t) = m^t) —
= M{y(t)} и дисперсию Dy(t) = — ml(t) процесса у (0
на выходе преобразователя, осуществляющего операцию суммиро-
вания:
у (0 — и (0 + и (t — т), и (0 — А (0-
Ответ.
рЛу)== х
х [ф (fr) Н-]}ехр (~ Д-)+р| ехр ('у > 0 *
mv (1)=ту (1 - р|) (/2 2 Г(1 + -|) Г(1 +
+ ^) +Р<(2/2 +-П
«г»(0 = ту = ]/2ло6, Dy(t) = Dy = (4 — л) (1 + р|) о|,
Рб = РбСО-
Здесь Г (z) — гамма-функция. График функции р,(г/) приведен
на рис. 12.25.
12.17 . Решить предыдущую задачу при условии, что процесс
на выходе преобразователя у (t) = и (t) — u(t — т).
Ответ:
1 I \
Pi (у) ~----г —ехР I------------------- ;
ag)/2«(l-p|) Ц 2а| (1—р|)
mw ~ (2v - 1)11(1 - ptrajv. ту = Q- Dy~ а|(1 _ р|).
368
Рис. 12.25. Плотность распределения вероятностей суммы огибающих квази-
гармонического шума
График плотности распределения вероятностей рг(у) приведен
на рис. 12.26.
12.18 . Решить задачу 12.16 для случая, когда преобразователь
представляет собой перемножитель, т. е. у (t) — и (t) и (t — т).
Рис. 12.26. Плотность распределения вероятностей разности огибающих ква-
зигармонического шума
369
Omeenv.
п __ У/ / ' РА к (_________У .
<!(»-₽!) л *i(1-p|) / л •’tO-pi)
у>о,
mv=2vr(n-A-)(l-p|r+4F1(l+-^; 1+-^-; 1; plW;
' \ £> ] \ At J
ту=-^0- Pi)2»А (у; Y: 1; р*) °1 ’ D«=т*~т"-
Здесь ^(х; у, z; q)— гипергеометрическая функция [71]. Гра-
фик р\(у) дан на рис. 12.27.
12.19 . Решить задачу 12.16 при условии, что процесс на выходе
преобразователя у (/) = и (t — х)/и (t).
Ответ: - '
Pi (У) —----ь— --------------->
riw [l+2(l-2p|)i7a-^]3/2
^>0, my^E(pi).
Здесь Е (z) — полный эллиптический интеграл 2-го рода. Гра-
фик плотности распределения вероятностей рх(г/) приведен на
рис. 12.28.
Рис. 12.27. Плотность распределения вероятностей произведения огибающих
квазигармонического шума
370
12.20 . На вход радиотехнического устройства, состоящего
из сумматора и линейного детектора огибающей (рис. 12.29), воз-
действует гауссовский стационарный квазигармонический шум
| (0 = A (0 cos [й>0/ + <р (01
с нулевым математическим ожиданием mg = 0 и дисперсией Dg =
= 0g и гармоническое колебание
«о(0 = U0cos (aot + ф).
В некоторый моменФ времени t = t0 на третий вход сумматора по-
дается сигнал
us(f) = Uscos o0t.
Определить отношение
(m„)o+s-(me)o
а=-----------------,
(«Mo-l-s
где (ту)0 — математическое ожидание процесса у (0 на выходе уст-
ройства при воздействии на его вход процессов | (0 и ио(0, (mff)o+s
и (<Jy)o+s — соответственно математическое ожидание и среднее
квадратическое значение при воздействии процессов £ (0, мо(0 и
us(0.
Рис. 12.29. Сумматор и линейный
детектор огибающей
371
Ответ:
где
С/2 = [/• + иг0 + 2UsU0costy.
При £72/2<т| 1 и 1 имеем
а ~ -L (-М1/2 (Ц$+ 2UO Ug cos ф) agi2;
4 \ 4—л /
при f/2/2o| > 1, U}/ty > 1
а = ([/-[/0)/а6.
Графики функций а = f приведены на рис. 12.30.
12.21 . На вход безынерционного однополупериодного линейного
детектора с характеристикой (рис. 12.13)
Л
=Ш1 = {
о, £<о;
воздействует стационарный гауссовский шум £ (/) с нулевым ма-
тематическим ожиданием т* = 0 и корреляционной функцией
= о|г6(т).
Определить математическое ожидание т^, корреляционную
Рис. 12.30. Относительное приращение математического ожидания на выходе
линейного детектора огибающей
372
Ответ [33]:
/«и
’ -------------2
ао. а2 о? , . . , —
^(т)=—-{П —4(0J2 +
/2л 2л
+г5(т) arccos[—г6 (т)]} — /п® ~ Г(т) + 1;
4 ла|
Указание: Следует воспользоваться разложениями в ряд:
arccos (—z) =— +z Н—-—z3 +...,
v 2 2-3
-2 «4
---------------------z_--...
v ’ 2 2-4
12.22 . На вход безынерционного двухполупериодного линейного
детектора с характеристикой (рис. 12.14)
воздействует стационарный гауссовский шум & (0 с нулевым
математическим ожиданием] mg = 0 [и корреляционной функцией
Я/т) = ФбМ-
Определить математическое ожидание mn процесса г| (0 на вы-
ходе детектора и его корреляционную функцию 7?п(т).
Ответ', т^
<MTg, Rn (0 =
а2
Л0|
RIM-
12.23 . На вход безынерционного однополупериодного квадра-
тичного детектора с амплитудной характеристикой (рис. 12.15)
воздействует стационарный гауссовский случайный процесс £ (0
с нулевым математическим ожиданием mg’= 0 и корреляционной
функцией 7?g(r) = cr^g(T).
Определить математическое ожидание тл и корреляционную
функцию 7?п(т) выходного процесса г| (0.
Ответ:
аа? ' 2а2 о! г i
тп = -у-, (т) = —[— 4 (0 + -J- arcsin г6 (т) +
+у 4 fr) arcsin г5(т) + г6 (т) К1 —4(т) J.
12.24 . На вход двухполупериодного квадратичного детектора
с амплитудной характеристикой (рис. 12.3)
П = f 1£1 = «£2> а> О,
373
воздействует стационарный гауссовский случайный процесс £ (/)
с нулевым математическим ожиданием — 0 и корреляционной
функцией 7?е(т) = <т|г6(т).
Определить математическое ожидание и корреляционную
функцию 7?п(т) выходного процесса г| (/).
Ответ: тп = aaf-, Rn(x) = 2ц27?|(т).
12.25 . На вход квантующего устройства на три уровня с амп-
литудной характеристикой (рис. 21.31)
П = f IB] =
-Ь, £<-₽,
О, —₽ а,
. а,
воздействует стационарный гауссовский шум В (0 с нулевым ма-
тематическим ожиданием т$ = 0 и корреляционной функцией
R№ ~
Определить математическое ожидание т^ и корреляционную
функцию выходного процесса т] (/).
Ответ: '
тп — (а — Ь) —
аф
n = l L
12.26 . На вход несимметричного квантующего устройства на два
уровня с амплитудной характеристикой (рис. 1.32)
,rt, [ а,
"=/ia-U, s:<0,
воздействует стационарный гауссовский шум £ (/) с нулевым мате-
матическим ожиданием т$ = 0 и корреляционной функцией R^(x) =
= tfhW- .
Определить математическое ожидание и корреляционную
функцию ^(т) процесса г] (/) на выходе устройства.
Рис. 12.31. Амплитудная характе-
ристика квантующего устройства
на три уровня
Рис. 12.32. Амплитудная ха-
рактеристика несимметрично-
го квантователя на два уровня
374
Рис. 12.33. Амплитудная характеристика
ограничителя
Ответ'.
=— (a—b), Rn (т) = arcsin rj (т).
2 2л
12.27 . На ввод нелинейного безынерционного устройства с ам-
плитудной характеристикой (рис. 12.33)
П = Ш •=
6®+т)/(т-Р),
о,
а(|—е)/(а—е),
а,
—₽=^£<—Т,
е I < а,
В>а,
-где а/(а — е) = Ы(у — Р) = $, воздействует стационарный гауссов-
ский шум £ (t) с нулевым математическим ожиданием_/ng = 0 и
корреляционной функцией = <т|^(т).
Определить математическое ожидание Шц и корреляционную
функцию /?п(т) процесса т] (/) на выходе.
Ответ'.
12.28 . На вход однополупериодного линейного детектора с амп-
литудной характеристикой
al, £ > а,
О, £<а,
375
воздействует стационарный гауссовский случайный процесс £(/)
с нулевым математическим ожиданием т$ = 0 и корреляционной
функцией (т) = erfrg(r).
Определить математическое ожидание и корреляционную
функцию /?ч(т) выходного процесса т] (/).
Ответ:
mri = a0i
12.29 . На логарифмическое устройство с нелинейной характе-
ристикой вида
воздействует стационарный гауссовский случайный процесс | (t)
с нулевым математическим ожиданием т^ = 0 и корреляционной
функцией /?е(т) = о|г5(т).
Определить корреляционную функциию 7?п(т) и дисперсию Dn
процесса т] (f) на выходе.
Ответ [77]:
где а = Dn(x) — функция параболического цилиндра [78];
ОО
D4 = -4=- J е-** In2 (1 4- ах) dx—M2 {In (1 4- а£)}.
о
12.30 . На вход симметричного ограничителя с характеристикой
(рис. 12.34)
5
П=/1В]=—=— f e~x,2a»dx—a
воздействует гауссовский стационарный шум £ (/) с нулевым мате-
матическим ожиданием т$ = 0'и корреляционной функцией
376
Рис. 12.34. Амплитудная характери-
стика симметричного сглаженного ог-
раничителя
Рис. 12.35. Безынерционное нелиней-
ное устройство с двумя входами
Определить одномерную плотность распределения вероятностей
рх(т|) и корреляционную функцию 7?п(т) процесса r| (f) на выходе
ограничителя.
Ответ [791:
Pi(n) =
1/2а,
1
1/2яоч'
ГТ)»)
2^
[6(г]+а)+6(г]— а)]/2,
< Оо,
=<*0»
«Ч > «о;
_ arcsin[r£(T)/(l+a)]
П ' 4 arcsin [1/(1+а)]
ОС =--------
12.31 . На вход безынерционного нелинейного устройства
(рис. 12.35) воздействуют стационарные гауссовские случайные
процессы хх(0 и х2(0 с нулевыми математическими ожиданиями
mXi = тх, = 0 и дисперсиями DXi = DXt = 1. Совместная плот-
ность распределения вероятностей процессов хх(/) и x2(t) имеет вид
Рг(*1, *г)
— 1 ауп Г х?—2rxixs4-x?
2л L 2(1—rs)
где г = г (т) — нормированная взаимная корреляционная функ-
ция. Процесс на выходе нелинейного устройства определяется
соотношением
У (О = f 1*1(0, *8(01-
Доказать, что п-я производная от математического ожидания
М{у (/)} по г (т)
д"/и {»(<)}
дгп (т)
э2п/[*1(П, *2 (01
дпXl{t) дп
377
12.32 . Используя результат задачи 12.31, определить матема-
тическое ожидание М {у (/)} процесса у (/) на выходе безынерцион-
ного нелинейного устройства с характеристикой
У (!) = f [хх(0, х2 (/)] = 1Х(0 +'x2(t) | — |X (0 — x8(0j,
где хх(0 и x2(t) — стационарные гауссовские случайные процессы
с нулевыми математическими ожиданиями mXi = тх, == 0, дис-
персиями DX1 — Dx, = 1 и совместной плотностью распределения
вероятностей __
. \ 1 X?—2rXiX.+xll
Рг(Х1, х2)= } ----ехр —1--------- .
1 ’ 2лУПЧ ч 2(1-г») J
Ответ: М {у (t)} — ту = —l— [V 1 + г—У1 — г] •
Ул
12.33 . Процесс т] (t) формируется из случайного колебания
£ (t) посредством нелинейного безынерционного преобразования:
т] (0 = f [| (01. Предполагается,-что £ (0 — стационарный гауссов-
ский случайный процесс с нулевым математическим ожиданием
mg = 0 и корреляционной функцией 7?j(r) — (^(т).
Определить корреляционную функцию 7?ч(т) процесса г] (0 для
следующих частных случаев:
1) л (о = g (о ? а + ту, 2) п (о « m з) ч (о - г®.
Ответ:
1) Rn(r) = Я|(т) + Я6(т + Т) 7?6(т - ТУ
2) Яч(т) = 6/?|(т) + 9а^6(т);
3) Яч(т) = -24/?|(т) 4- 72о$Я|(т).
12.34. Определить спектральную плотность Sn(<») случайного
процесса т] (0 на выходе однополупериодного линейного детектора
с амплитудной характеристикой
процесса g (t) с нулевым
спектральной плотностью
(©)=!
при воздействии на его вход стационарного гауссовского случайного
математическим ожиданием = 0 и
No, ©j < СО < ®2,
0 при других со.
Ответ:
SI)((O) = (crW0/2n) (®2 — COj) 6 (со) + St)/©),
378
где
0аМ> (02 —(Oi — (0
2л о8 Уо (О2—(Oi
2л
S-nt (<0) — oaAf0 (о-—2(0j
2л (О2 — (01
2(о2—со
2л 0 (02 —(0!
(01 со со2,
2сох со (01 + со2,
®i +со2<со ^2со2,
при других со.
0^(о^(о2—®ь
График функции 5Пе(со) представлен на рис. 12.36.
12.35. Определить спектральную плотность Sn(co) случайного
процесса т] (/) на выходе двухполупериодного линейного детектора
с амплитудной характеристикой
Ln Z I -< SCO,
при воздействии на его вход стационарного ^гауссовского случай-
ного процесса £ (/) с- нулевым математическим ожиданием mg = О
и спектральной плотностью
Ответ'.
(01 СО (02,
при других (0.
Sn((o) = (2aW0/n) (со2 — (Oi) 6 ((о) + Sno((o),
где
Sn0 (со) =
2а2 Np <оа—<0i—<о
2 л со2—(Oi
a* No со—2(01
Л (02 — (Oi
a2 Np 2со2—со
- л (02—(Oi
О (0 (02—(Oi,
2(01 ® < (Oi + (о2,
®1 + ®2 ® ^2(02.
График спектральной плотности Sno((o) приведен на рис. 12.37.
Рис. 12.36. Спектральная плотность процесса на выходе однополупериодного
детектора
379
Рис. 12.37. Спектральная
плотность процесса на
выходе двухполупериод-
ного линейного детекто-
ра
12.36. На вход радиотехнического устройства, состоящего
из дифференцирующей схемы и перемножителя (рис. 12.38), пода-
ется гауссовский случайный процесс £ (/) с нулевым математическим
ожиданием /и^ = 0 и корреляционной функцией
*5 (*) = *! е-а । х । / cos ©о t + —— sin соо | т |) ’.
\ too /
Определить спектральную плотность £п((о) процесса т] (/) на вы-
ходе устройства.
Ответ:
е / X 4о|а(а®+со?)<а«(<о2+20а4 + 4<в§)
(со) — •
(<о2+4а2)[(со2 + 4а»+4(о?)4—16со2а>§]
12.37. На входы перемножителя (рис. 12.6) подаются незави-
симые стационарные случайные процессы | (/) и р. (/) с математи-
ческими ожиданиями т$ и т№ и корреляционными функциями
#£(т) = ог|е~в|т|, 7?и(т) = orjJe~₽lTi.
Определить спектральную плотность прЬцесса т| (/) на вы-
ходе перемножителя.
Ответ:
S fa) - 2<a+P)qiqu , 2HqH , 2ат№
} (а+Р)2+<о2 Р2+<о2 ’Г а2+Р2
12.38. На вход радиотехнического устройства, состоящего из
дифференцирующих схем и перемножителя (рис. 12.39), подаются
независимые стационарные случайные процессы ^(/) и £2(0 с НУ*
Рис. 12.38. Дифференцирующая
схема и перемножитель
Рис. 12.39. Две дифференцирую-
щие схемы и перемножитель
380
Рис. 12.40. Синхронный детектор
левыми математическими ожиданиями т^ — т%, = О и корре-
ляционными функциями
Rg, (т) = Gti е~“*|Т| (cos<o1T-J--^1-sin®1|T|) ,
\ wi /
Rg, (т)=а1» е~“*1 т 11 cos ®2 т + —— sin ®21 т |).
\ /
Определить корреляционную функцию 7?ч(т) и спектральную
плотность Sn(©) процесса г] (t) на выходе перемножителя.
Ответ'.
Rn (т) = R^ (т) R^(г) = о|, о|, (а? + со?) (а| + со» х
X е~(“»+а»>1 х 11cos <01 т —— sin ©i | т 11 [ cos (о2 т—— sin <о21т 11;
\ “1 / \ ®2 ' /
5 Ад) _ а Г g cos 4~(ю~<Qq) sin di а cos 6i4~(<°4~o>e) sin ।
4 [ (<о—<ос)24-а2 (<о+юс)2-|-а2
। fa cos 6a-|-((o—(Op) sin 6a rg cos 6a 4- (ю 4~юр) sin 6a 1
(<o—o>p)2+a2 (co-f-cop)2+a2 J ’
где
a = a|t o|, co? ®l/2 cos® ух cos® y2>
Yi = arctg —, y2 = arctg-^2-, a = Oi+a2,
©1 ®2
6i = Ti + 7г, 62 = 7i — 72, (oc = (Oi + (o2, (op = (0i — ®2.
12.39. Найти спектральную плотность Sp((o) процесса у (/)
на выходе умножителя синхронного детектора (рис. 12.40), если
воздействующее на детектор колебание х (t) = s (t) 4- n (/), где
входной шум п (/) представляет собой стационарный гауссовский
процесс с нулевым математическим ожиданием тп = 0 и спектраль-
ной плотностью
Sn(f)
(f-M2 1
2a2 J
+ exp
(Шо)® 11
2a® J) ’ °’
а полезный сигнал s (t) = Am cos (<в0/ 4- 0).
381
Рис. 12.41. балансный
модулятор
Здесь Ат—постоянная амплитуда, 0 — равномерно распреде-
ленная в интервале (—л, л) случайная фаза, не зависящая от шума.
Ответ: ,Sy(f) = Sys(f) + Syn(f),
где
Sff8 (Г) = 4 U2 8 (f) +4- ЛА £/2 (б (/ - 2/0) + 6 (f + 2/0) ]
О 10
— спектральная плотность сигнала на выходе умножителя;
Ssn(f)
№
8а 1/2 л
-— + ехр
2а2 ) н
• _ (Z—2/о)а •
2а2
4-ехр
«+2fo)2 Ц
2а2 _ j
— спектральная плотность шума на выходе умножителя.
12.40. На входы балансного модулятора (рис. 12.41) поступа-
ют стационарные и стационарно связанные случайные процессы
£г(0 и |2(0 с нулевыми математическими ожиданиями /ng, = /ng, =
= 0, корреляционными функциями /?g,(r) = 7?g,(t) = <№г (т) и
взаимной корреляционной функцией 7?g,g,(T) = tfVuCO-
Определить корреляционную функцию 7?ч(т) выходного про-
цесса т];(0.
Ответ [14]:
о» 24ft~vr2(v4-l)
S4C0 = *2v V------------/ + у Лг(т) + г12(т)]^.
*ТоГ(2Л + 1)Г2 ll-ft+y 1
12.41. Случайная величина т] (Т) формируется в результате
усреднения квадрата стационарного гауссовского случайного про-
цесса 5 (0 на интервале Т:
Т/2 -
П(Т) = 4 J
-Т/2
Определить математическое ожидание /пч величины т] (Т) и ее
дисперсию D4 при условии, что процесс £ (0 характеризуется сле-
дующими спектральными плотностями:
OSsW-—L-; 2)8, (о)
о| (О2
У (а>2—СО?)2
\ ©о /
382
У
Рис. 12.42. Дискретный накопитель
Ответ [14]:
1) »!,=<,{, D,=i(4p-l+e-«l>), ₽—4L ;
2)m, = a|, О,=-5-х
т
х [т-1 +e-’+^ri'-’si”’f V4Q'—1 ]. Г = ^-
12.42. На вход схемы рис. 12.42, состоящей из линейного
детектора огибающей (ЛДО), устройства выборки и накопителя,
воздействует стационарный гауссовский квазигармонический шум
£ (0 = А (0 cos [©of + <р (0]
с нулевым математическим ожиданием = 0 и дисперсией
Di = а|. Выборочные значения At = А (/г) взаимно не коррели-
рованы.
Определить математическое ожидание ту, дисперсию Dy и плот-
ность распределения вероятностей рх(У) случайной величины Y на
выходе накопителя, если
, п
Y=^-^Ai, и»1.
Ответ:
Pi (У) = 'Гу—1 г—' ехР
' У2л УDY н
(У-туу-
2Dy
12.43. На систему ограничитель—фильтр (рис. 12.43) воздей-
ствует стационарный гауссовский шум £ (/) с корреляционной
функцией (т) = crfexp (—у | т |]).
Рис. 12.43. Система
фильтр
ограничитель —
шмель > Фильтр
383
Определить корреляционную функцию /?ц(т) процесса р, (I)
на выходе системы в предположении, что амплитудная характерис-
тика ограничителя имеет вид (рис, 12.4)
импульсная характеристика фильтра
h(t) = ----•
Ti т2
причем тх 1/у, т2> 1/у.
Ответ [80]:]
ап Г 1 —-1x1 1 —-'xl
T1 +-^ге т* -
n=i L
1 / —— I т I —— I т I .
------— е Т1 +е т2 / ,
Т1 + Та\
где
Д' =
M{r](0}=sffg
ф(п-1) [_£L |_ф(п-1) [-L
\al J \
^=Л4{т)2(0}- м201(0};
а
аЕ
sao|
. л! ап ’
А
_ф(1) I -2L
V <4
<D<n>(z) — п-я производная от интеграла вероятности (12.11).
12.44. На приемное устройство,, схема которого изображена
на рис. 12.44, воздействует стационарный белый шум £ (/), спект-
384
{(t)
Линейная
система
у ft)”* Y(t)ais№»ot+jp)_zW« Yz(t)
““I / Двухсторонний / p
' > нОайратичнь/й ' >
йетентор^
огивинпцей
Фильтр
ЛС
Рис. 12.44. Радиоприемное устройство
ральная плотность которого Sj(®) = NJ2. Комплексная частот-
ная характеристика линейной системы имеет вид
^(/©)=Л?0
2а<в
2аш + / (<оа—coj)
а импульсная характеристика фильтра RC h(t) = уе-’*.
Определить:
1) плотность распределения вероятностей px(z) процесса z(t)
на выходе двухстороннего квадратичного детектора огибающей;
2) математическое ожидание mz процесса z(/);
3) корреляционную функцию Л?2(т) и дисперсию Dz,
4) математическое ожидание ти процесса и (t) на выходе фильт-
ра RC;
5) корреляционную функцию 7?и(т) и дисперсию Du на выходе
фильтра RC.
Ответ:
1) Pi(z)=—— ехР ( —» z^ О,
/ Н1\ > 2аа г 2аа )
где tty = aN0Ml/2 — дисперсия процесса y(t) на выходе линейной
системы;
2) mz = 2<г“ = аУо^о;
3) Rz(r) = aW^e-2«w Dz = a2NM;
4) mu = аУо^8;
5) Ru (т) = f * (уе~2а i x i -2ae~v it I),
V2—4a2
Du = a^Nl .
?+2a
12.45 . На приемное устройство, схема которого изображена
на рис. 12.44, воздействует случайный процесс
х(0 = В(О + п(О-1»(О,
где £(£) — стационарный белый шум со спектральной плотностью
Sg(co) = No/2; 10(/) — единичная функция;
т](0 = Л (0 cos [<в0/ + <р (/)]
13 Зад. 1203
385
— стационарный квазигармонический шум с нулевым математи-
ческим ожиданием /пп = 0 и корреляционной функцией
КпЮ = ачехР (—₽ 111) cos <вот.
Комплексная частотная характеристика линейной системы, как и
в задаче 12.44, имеет вид
У ’ ° 2a©+1 (со’-со?)
Определить плотность распределения вероятностей рх (z; t)
процесса z(t), его математическое ожидание mz(t) и корреляционную
функцию Rz(t, т) для t > 0.
Ответ'.
Pi (z\ t)=------------ exP I---------------I, 2 0,
V > 2a*(t) 2a’(7) )’ ’
mz(t) = 2aJ(0, Rz(t, r) = r), ru(t, t) = Ry(t, T)l<J2y(f).
Здесь
°ц = aA^o^o/2,
[(a—0) +(a +p)e~2a<—2ae-(“+P><], t> 0,
0
ff?(O=
(/.*) =
КО;
Rv (t, т)«(т)+Rv (Л л), R* (т) = aN^ е~« ' cos ®о т,
* £
аа’ЛГ?
» йа [(«е~Р|Т|—ре~«|т ') +(a+P)e~aT~2a< —
ОС- р
—a(e~aT +e_0T) e~<a+0> *] cos ©0 т> 0>
0, *<0.
12.46 . Используя условие и результаты задачи 12.45, опреде-
лить математическое ожидание /n„(f) процесса «(() на выходе
фильтра с импульсной характеристикой h(t) = уе—т/.
Ответ:
ти (0 = atf0 р=₽ +
а’—р’- [ у
। 7 2а а—Р а+Р \c_v< j
VY—а—Р у 7—2а/
_|_ «+Р 2а е-«х+рн1 ф
у—2а у—а—Р J
12.47 . На радиотехническое устройство, состоящее из интег-
рирующей цепочки RC, двухполупериодного безынерционного квад-
ратичного элемента с характеристикой £ = ar]2 и идеального фильт-
ра нижних частот (ФНЧ) (рис. 12.45), воздействует стационарный
386
Рис. 12.45. Радиотехническая схема
гауссовский белый шум %(t) с нулевым математическим ожиданием
/П| = 0 и спектральной плотностью Sg(<o) = No, 0 со < оо.
Определить ковариационную функцию Л^(т) и спектральную
плотность Sf(co) процесса t, (О на выходе нелинейного элемента.
Ответ:
Kt(T)=^[l+2exp/'——|t|Y|;
’ 4(ЯС)» L k RC 1 7J
St (o) = atN* . Г2л6 (©) +---—-1.
' 4 (ЯС)» L 4+(соЯС)» J
12.48 . Используя условие и результаты задачи 12.47, опреде-
лить математическое ожидание т? и дисперсию Dv = <г» процесса
v (t) на выходе фильтра нижних частот с импульсной характе-
ристикой
Аф = ( ае-в' п₽и
| 0 при других t.
Вычислить отношение G-Jm* и его предельное значение
при Т-> оо.
Ответ:
mv =^2.(1 —е~аТ), о» =25-^2 Г—J—+—J----------е-2аг_
2р ’ 2Р L а₽4-2 аР—2
(а04-2)Т /-----
----2ар_ р j lim—= 1/ р=/?С.
(ар)»-4 J т-м» V ар+2 н
12.49 . Используя условие и результаты задачи 12.47, опреде-
лить математическое ожидание mv и дисперсию Dv процесса v(t)
на выходе фильтра нижних частот с импульсной характеристикой
. ... (1 при 0 < / < Г,
ft (0 = 1
( 0 при других t.
2Т -
Л aN0T п а»1У1 Г2Т . . —^"1
Ответ: т^ = —2—; Dv =--------— 1-----1+е р •
2р 4 I Р J
12.50 . На рис. 12.46 приведена упрощенная схема двухка-
нального коррелятора. На один из его входов поступает колеба-
ние
^1(0 = 51(0 + «1(0.
13»
387
Рис. 12.46. Двухканальный коррелятор
с фильтром нижних частот
а на другой
ut) = s2(t) + n2(t).
Здесь st(t) — гармонические колебания частоты <оо с различными
амплитудами и начальными фазами:
sx(/) = X1cosci)0/, s2(0 = А 2 cos (соо£ + 0);
nt(t) — квазигармонические флуктуации:
Пх(0 = Хх(0 COS (dot + {fait) Sin (dot,
n2(t) = [xx(0 + &х2(£)1 cos + I^i(0 + sin <aot.
Квадратурные составляющие Xt(t) и yt(t) являются независимыми
стационарными случайными процессами с нулевыми математи-
ческими ожиданиями и дисперсиями Dt = of для x^t), y^t) и
D2 = <т! для х2(0» Уг(0- Коэффициент k определяет степень корре-
лированное™ флуктуаций «х(0 и п2(0:
Л1{пх(0пг(0} = k°i-
Определить математическое ожидание /пп и дисперсию
процесса т](/) на выходе фильтра нижних частот.
Ответ'.
тп = ЛхЛ2со80 + 2йц2,
£>n = 4fcM +ol(Al +fc4!+ 2Mx42cos0 -Mfr? +2<rfr2).
12.51 . Применительно к условию задачи 12.50 определить ха-
рактеристическую функцию @х (jv) процесса т) (7) на выходе фильтра
нижних частот.
Ответ [81]:
где
b = Л2соз0 + Axk, с — Л2зш 0, а = 1/oJ — 2jkv, 0 = 1/а®.
12.52 . Используя результат задачи 12.50, вычислить плотность
распределения вероятностей рх(л) процесса т](0 на выходе фильтра
нижних частот для частного случая воздействия на коррелятор
388
идентичных колебаний Bi(0 = В2(0, т. е. при Л, = Л2 = А, 0 = О,
k = 1 и а2 = 0.
Ответ-.
2aJ \ 2aJ j \ «I /
12.53 . Решить задачу 12.52 для случая отсутствия шума п2(0
на втором входе коррелятора.
Ответ-.
Р1(п) =
1
1/2л<*п
ехр
(П-«п)а
2а’
где = ЛХЛ2 cos 0, од = <^А%.
12.54 . Решить задачу 12.52 для случая воздействия на корреля-
тор идентичных сигналов sx(/) = s2(i) и некоррелированных про-
цессов пх(£) и nz(t) с равными дисперсиями, т. е. при Л, = Л» = Л,
а? = 02=^ е = 0) k = 0
Ответ [81]:
Здесь а = Л2/2ст2 — отношение сигнал/шум на входе коррелятора,
е“_, = 1 +-1а+±а2+...
11
—5-----а"-1
(«-1)1
График плотности распределения вероятностей pi(t]) приведен
на рис. 12.47.
12.55 . На вход коррелятора, состоящего из линии задержки
(ЛЗ) с временем задержки /аад = т, перемножителя и фильтра ниж-
них частот (ФНЧ) (рис. 12.48), поступает стационарный случай-
ный процесс В (О с нулевым математическим ожиданием т^ = 0 и
корреляционной функцией
7?s(r) = о|ре(т) cos <|)от.
Фильтр нижних частот пропускает без искажений только низко-
частотные составляющие процесса на выходе перемножителя.
Определить плотность распределения вероятностей Pi(*n) ПР0’
цесса т](/) на выходе коррелятора.
Ответ [82]:
р. (п) = —5— ехр [-------—------1.
' 4а| Ч 2а|[1 — р£ (т)] J
389
Рис. 12.47. Плотность распределения вероятностей на выходе двухканального
коррелятора
12.56 . На один из входов двухканального коррелятора
(рис. 12.49) поступает колебание
хх(0 = зх(/) + пх(/),
а на другой
х2(0 = s2(0 + п2(0-
Здесь
М0=-^:сО8(М+'Фг). i=l,2,
V2
— прямоугольный радиоимпульс длительностью Т; пх(0 и п2(0 —
независимые стационарные гауссовские белые шумы с нулевыми
математическими ожиданиями и корреляционными функциями
(т) = Rnt (т) = (Уо/2)6(т), М {их (0 n2 (t + т)} = 0.
Рис. -12.48. Коррелятор Рис. 12.49. Двухканальный корреля-
тор с интегратором
390
В качестве входных фильтров (Ф) коррелятора используются
колебательные контуры с импульсными характеристиками
ht(t) — 2ate~ai* cos toot, t > 0.
Определить математическое ожидание m^t) процесса т](/)
на выходе коррелятора в момент времени t — Т.
Ответ:
щ (Т) - V&cos^-^F^, аг),
где
ах = ахТ, аг = а2Т, Е^—А* Т/2, Е2 = А*2Т/2,
F (ах, aj 1 —-(1 -е-«>) +—(1 -е~«.) +
Дх at
-I---J---(1 — е-<«.+в.>).
а1 +^2
13. ВЫБРОСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Рассмотрим какую-либо реализацию непрерывного (дифференцируе-
мого) случайного процесса длительностью Т (рис. 13.1). Такая реализа-
ция на конечном интервале Т имеет конечное число максимумов и минимумов
с различными значениями Н, причем в момент времени tm реализация имеет
абсолютный (наибольший) максимум Нт.
Реализация 5(0 может несколько раз пересекать фиксированный уро-
вень С снизу вверх (с положительной производной), причем в момент времени
т0 впервые происходит такое пересечение (т. е. первый раз снизу достигается
граница С). Когда случайный процесс 5(0 пересекает уровень С снизу вверх,
будем говорить, что имеет место положительный выброс. Если же уровень С
пересекается сверху вниз, то можно говорить об отрицательном выбросе.
Тогда можно сказать, что реализация 5(0 длительностью Т имеет п положи-
тельных (отрицательных) выбросов на уровне С, причем указанные на ри-
сунке величины т и 0 можно назвать соответственно длительностями положи-
тельных и отрицательных выбросов. Часто величину 0 называют длитель-
ностью интервалов между выбросами;
Величины т, 9 и Н в пределах одной реализации могут принимать не-
сколько значений (в зависимости от уровня С и интервала Т) и вместе с ве-
личинами п, т0 и Нт изменяются случайным образом от одной реализации
к другой.
При статистическом описании этихТслучайных величин можно интере-
соваться их средними значениями, дисперсиями, плотностями вероятности
Рис. 13.1. Реализация
стационарного случай-
ного процесса
391
и другими характеристиками. В данной главе приведены окончательные фор-
мулы в основном для средних значений, так как вычисление других ха-
рактеристик, как правило, связано с выполнением численного интегрирова-
ния, что выходит за. пределы целевого назначения данной книги. Другие ха-
рактеристики рассматриваются тогда, когда они могут быть найдены без
сложных математических вычислений.
1. Среднее число пересечений дифференцируемым случайным процессом
5(0 непрерывной кривой a(t) снизу вверх (рис. 13.2) на интервале (/0, t0 +
+ Т) вычисляется по формуле
Na (П=<вК<«Г 1(0₽2[а(0. a(O+5'(O]dt- (13.1)
to О
Здесь р2 [£ (0. 1(0 — совместная плотность вероятности для процесса 5(0
и его производной | (0 = d5 (t)ldt в один и тот же момент времени.
Аналогично число пересечений процессом 5(0 сверху вниз кривой а(0
равно
h+т о
N-(T)= { dt f a(0+t(014- (13.2)
Tq —«>
Пусть на интервале (/0, t0 + T) заданы две непрерывные кривые а (0
и b (0, удовлетворяющие неравенству а (0 < b (t). Среднее число раз, когда
процесс выйдет из границ а (0 < 5 (0 < £ (0 на интервале (/0, t0 + Т), опре-
деляется формулой
fo + T оо
ЛГ<й(Т) = f dt$ t(t){p2[b(t),^t)+t(t)]+p2[a(t), (13-3)
f 0 0
В том частном случае, когда рассматриваются пересечения процесса
5(0 с горизонтальной прямой, т. е. а (0 = С = const, формулы (13.1) и
(13.2) принимают соответственно вид1
to + T оо
N+(C,T)= f dt$ I (CMC Л (Oldt. (13.4)
/0 о
to+T 0
N-(C,T):-----f dt f t(O/>2[C, g(014-. (13.5)
to —00
Применительно к стационарным в узком смысле процессам 5(0 внутрен-
ние интегралы в формулах (13.4) и (13.5) не зависят от времени и целесооб-
разно ввести среднее число пересечений в единицу времени. Для среднего
числа пересечений в единицу времени стационарным случайным процессом
Рис. 13.2. Пересечения случайного процесса 5(0 и детерминированной функ-
ции а (О
392
фиксйроййнйого уровня С снизу ввврх й сверху йнйз из (15.4) и (15.5)
получаем простые формулы
N+ (С) = N+ (С, 1) =f fy, (С, Й df, [(13.6)
О
о
ЛТГ(С)=ЛГ-(С, 1)=- f 1р2(С, Й4- (13.7)
— оо
Для ряда стационарных процессов (например, гауссовских) значения
процесса £(/) и его производной \(t) в совпадающие моменты времени оказы-
ваются статистически независимыми, т. е.
Ра(С, Й = Р1(С)р(|). (13.8)
При выполнении этого условия формулы (13.6) и (13.7) еще более упроща-
ются:
Nf (С) (С) f & (6 N; (С) = -Pl (С), J Ipfodt- (13.9)
О —со
Применительно к гауссовскому стационарному дифференцируемому про-
цессу 1 (О с математическим ожиданием т и корреляционной функцией
^(т)= о«г(т) (13.10)
формулы (13.9) принимают вид
Для огибающей V(t) суммы гармонического колебания s(f)=*AmX
X cos (<o0f + фо) и гауссовского квазигармонического (узкополосного) слу-
чайного процесса £(/), имеющего нулевое математическое ожидание и корре-
ляционную функцию
Я|(т) » а2р (т) cos соо*» (13.12)
получаем
с>0- “313>
Здесь /0(х) — функция Бесселя нулевого порядка от мнимого аргумента.
При Ат *= 0 формула (13.13) определяет число выбросов огибающей Л (О
одного квазигармонического процесса £(/):
^+(С)=^-(С)
С>0. [(13.14)
2. Среднее число максимумов дифференцируемого процесса £(/) на ин-
тервале (/0, tQ + Т) определяется формулой
°.
NvmAT) = - J л f S(0pa[o, (13.15)
to
где p2 [| (0, 5(0] — совместная плотность вероятности для первой и второй
производных процесса f (0 в один и тот же момент времени.
393
Для среднего числа минимумов процесса справедлива формула
dtJl(t)Pi[O, l(01dg. (13.16)
Среднее число максимумов на интервале (/0, /0 + ^)» превышающих фик-
сированный уровень С, равно
tt4-T оо о
1Ушах(Н>С, С)------f d/j d| f l(O/>sU(O. 0Д(/)]4» (13.17)
<о С —оо
где ра [£ ЮЛ(ОЛ (01 — совместная плотность вероятности самого процес-
са и его первых двух производных в один и тот же момент времени.
Применительно к стационарным процессам можно интересоваться сред-
ним числом^максимумов в единицу времени. При этом из Формул (13.15) и
(13.17) имеем
0
maxe^max (1)----f Ъа(0. 1)<£, (13.18)
— 00
tfimax(tf>C)=lVm.x(tf>C, l)=-fdg J IРз (g. 0,1)df. (13.19)
С —оо
Формулы'(13.18) и (13.19) для гауссовского стационарного процесса
£(/) с нулевым математическим ожиданием и корреляционной функцией
(13.10) принимают соответственно вид
(13.21)
где Ф (х) — интеграл вероятности,
Со-С/О, V-(13.22)
3. Средняя длительность выброса стационарного эргодического процес-
са £ (t) над фиксированным уровнем С вычисляется по формуле
? Л (13.23)
1 с
Средний интервал между выбросами на уровне С
с
б(С)“л7(сГ J л(5)4' (13,24)
—оо
Применительно к -гауссовскому стационарному процессу с математиче-
ским ожиданием т и корреляционной функцией (13.10) формулы (13.23) и
(13.24) принимают вид
*(C)“,’“j7==F' 11 “ ф(Т)1е’,/2- Vе ~~т > (13.25)
ё (С) —Ф (у) , (13.26)
394
Рис. 13.3. Смещение момен-
тов срабатывания реле из-
за шума
Для огибающей Л (0 квазигармонического процесса £(/), имеющего
корреляционную функцию (13.12), сраведливы следующие соотношения:
(13.27)
(13.28)
Средняя длительность интервала между минимумом и следующим за ним
соседним максимумом тт, а также между максимумом и последующим сосед-
ним минимумом 0т находятся по формулам
оо О
- Тт° 1 [/>(<)<& 0т-------77“--- [ И &) 4- (13.29)
Wimln J ^imax J
О —со
Для гауссовского стационарного процесса
= я V . (13.30)
4. В радиотехнических приложениях рассмотрение выбросов часто свя-
зывают с анализом действия полезных регулярных импульсных сигналов
u(t) совместно с помехами %(t) на электронные реле и другие пороговые уст-
ройства. В том случае, когда детерминированный полезный сигнал склады-
вается с «гладкими» помехами малой интенсивности, помехи вызывают слу-
чайное дрожание моментов срабатывания и моментов окончания работы реле.
Пусть в отсутствие помех реле срабатывает от полезного импульса и (/)
в некоторый момент времени и затем через промежуток времени т, т. е.
в момент /2 == + т, скачком возвращается в первоначальное состояние
(рис. 13.3). При наличии слабых помех 1(f) эти моменты времени будут сме-
щены на малые и случайные величины Ах и Да, т. е. t[ = ^i+Ai, /а =/а + Да.
В линейном приближении
А1 - «Ш. Аа =- 5(*a)/s(G). . (13.31)
х du® Г
где s (tf) а — Ь * — крутизна полезного импульса на уровне сра-
батывания С.
Если стационарный шум £ (/) имеет нулевое математическое ожидание
и корреляционную функцию R (т) => о2г(т), то дисперсии момента срабаты-
вания реле и момента окончания работы соответственно равны
<’11-0а/«*(4). GXt = o»/sa(/a)- (13.32)
395
Из равенства т' = = т + (Да — ДО по известным
находим дисперсию длительности импульса на выходе реле
правилам
(13.33)
2. ПРИМЕРЫ
13.1 . Вычислить вероятность наличия в интервале (t, t + т)
нечетного числа нулей гауссовского стационарного процесса £(/)
с нулевым математическим ожиданием и заданной корреляционной
функцией 7?(т) = о2г(т). Под нулями понимаются точки на оси
времени, в которых В (/) = 0.
Решение. Очевидно, что при выполнении неравенства £(/) X
X + т) < 0 число нулей траектории процесса | (t) в интервале
(t, t + т) нечетное (рис. 13.4). Обозначим вероятность нечетного
числа нулей в интервале (t, t + т) через рн (т). Очевидно, что
Рн(т) = РШ Щ + т) < 0} = Р шо > о,
В(/ + Т) < 0} + Р{1 (0 < 0, $(t + т) > 0}.
Нетрудно убедиться, что для стационарого гауссовского про-
цесса с нулевым математическим ожиданием оба слагаемых в правой
части этого равенства равны друг другу и
оо 0
рн(т) = 2Р [g (0 >0, Kt + т) < 01 = 2 f J р&, Вт) dlxdl,
0 —со
где р2(|, £т) — двумерная плотность вероятности значений слу-
чайного процесса, разделенных промежутком времени т. Подставив
сюда выражение двумерной нормальной плотности вероятности
(5.23) и выполнив интегрирование, получим
рн(т) = л-1 arccos г(т), 0 arccos г (т) < л
или
cos [лрн(т)1 = г(т). (13.34)
13.2 . Определить число положительных выбросов на уровне
С = За во временном интервале Т = 100 мкс гауссовского стацио-
нарного процесса В (/), имеющего математическое ожидание (tn = 0)
и спектральную плотность
S(®) = -Ln0 (ехр [—(ю~<йо)а 14-ехр Г—<“-+<йо)а1),
2 I н L 4а J L 4а ]1
если f0 = ©0/2л — 60 МГц и эффективная ширина спектра Д/э —
= 2 МГц.
Рис. 13.4. Нечетное чис-
ло нулей в интервале
(М+т) ,
396
Решение. Обозначим среднее число интересующих нас выбросов
через N+(C, Т). Так как процесс |(f) стационарен, то N+(C, Т) =
= TNt(C). Для рассматриваемого примера среднее число положи-
тельных выбросов в единицу времени определяется формулой (13.11)
при m = О
N+ {С’ Т) = ~ЬТ ехр [ ~т
с_у-
g /
Пользуясь формулой (6.15) можем написать
со
Г^==иЬ’ J S(a)^da,
— ОС
где
о2=— f S(a)da=N0
2л J
— со
— дисперсия процесса
Следовательно,
г"0 =г" (0) = —J со2 S (©)da.
< —со
Подставив сюда выражение спектральной плотности и выполнив
интегрирование, получим г? = —(со* + 2а). Поэтому
N+(C, T)=f0T Л/ 1+ — е-4-5~/=0т(1+— ^е~4,6.
Г ©о \ <»? /
По определению эффективной ширины спектра
00
= f s(M)d® =
2лоо J
О
4а J Ул
е-4,5 =
= —— No (
4nS0 J
о
находим а = яД/2- С учетом этого соотношения получаем оконча-
тельную расчетную формулу
N+(C, Т)^/оТ[1+4-(
L 4л \
= 60-10®-100-10-® Г1 +—(—?] 67.
4л \ 60 J J
13.3 . Определить относительный уровень С/а, при котором,
огибающая Л(/) квазигармонического процесса |(0, имеющее®
постоянную и отличную от нуля спектральную плотность голый
397
при частотах \f—f0\^ Д//2=0,5МГц, на интервале Т — 1000 мкс
превышает уровень С в среднем один раз.
Решение. Воспользовавшись формулой (13.14), можем написать
+ (С, Т) = TNt (С)» Т ехр [ .
В данном примере
р|(т) = sin лД/т/лД/т, ро =— (л2/3) Д/2.
Поэтому , х
После подстановки отдельных значений приходим к трансцендент-
ному уравнению относительно С/сг
приближенное решение которого дает С/а ~ 4.
13.4 . Пусть задано функциональное преобразование у — f(x),
которое является невырожденным, непрерывным, взаимно-однознач-
ным, и х = <р (у) — обратная функция. Требуется вычислить сред-
нее число выбросов случайного процесса
Ч(0 = /ВД (13.35)
где — дифференцируемый случайный процесс с известной
совместной плотностью вероятности р [| (0, I (0].
Решение. По известным правилам пересчета плотностей вероят-
ностей при функциональных преобразованиях случайных величин
находим совместную плотность вероятности для т) (0 и г) (0:
Ph(0. Л(0] = р1«р(&
По формуле (13.4) находим среднее число положительных выбросов
процесса т)(0 в интервале (0, Т) на уровне Нп —
(Нч, Т) = f dt f ip (Нп, n) di =
о о
т 00.
= J dt§ т)р(ф(Яч), <р' (п) П) ф'2 (^т)) <*П-
о о
(13.36)
Из сравнения этой формулы с формулой для среднего числа выбро-
сов процесса £(0
А^(Я6, T) = J dtf tptH^^dl
0 0
398
следует, что
^(Яп, Т) = Я6+(Яе, Г). (13.37)
Это равенство выражает очевидный факт — при взаимно-одно-
значном функциональном преобразовании (13.35) всегда сущест-
вует однозначное соответствие между каждым пересечением процес-
сом [В(0 уровня Hi и каждым пересечением процессом Т|(/) уровня
13.5 . Найти среднее число максимумов в единицу времени над
уровнем С = 2о гауссовского стационарного процесса с нормиро-
ванной корреляционной функцией г(т) = e-av‘, а = 4лА/2.
Решение. "Ответ дает формула (13.21). Так как го = —2a,
r(o)=12a2, то v=y 2/3. Подставив отдельные величины в формулу
(13.21), получим
ЛГ1ш„(Я>2с)»]/'Ад/вх
X Ф
~ 0,256А/в.
13.6. Вычислить средний интервал времени между максимумом
(минимумом) и соседним минимумом (максимумом) гауссовского
стационарного процесса с нормированной корреляционной функ-
цией
г(т) = р(т) cos <вот, р'(0) = 1.
Рассмотреть частный случай, когда р(т) = ехр (—лА/|т2), причем
АД> < /о = <в0/2л.
Решение. Для рассматриваемой нормированной корреляционной
функции находим г”а — —(®3 — Ро). /,<04) = ®о — OtoJpjJ + р(04). Под-
ставив эти величины в формулу (13.30), получим
~ = 0 1 f J-РаМ V/2
т т 2ft \ i-epSMJ+P^M /
Для р(т) = ехр(—лА/’т2) имеем ро = —2лА/?, р^4) = 12л2Д/1
Поэтому
(13.38)
1 /А/э\»
2я [ f0 /
-.1/2
1
2/о
5
4л
э*
13.7. На «безынерционное» электронное реле воздействует суц-
ма сигнала в виде импульса гауссовой формы
и (/) = Ао ехр [ — 2,8 [ ——У!
399
и дифференцируемого флуктуационного шума с малой дисперсией
о2 = Nokf3. Определить возможную наименьшую нестабильность
момента срабатывания реле огд,, обусловленную шумом.
Решение. Первая из формул (13.22) показывает, что при задан-
ной дисперсии шума <т2 наименьшая нестабильность момента
срабатывания будет при пороге срабатывания реле, соответствую-
щем максимальной крутизне импульса.
Из равенства u"(t) = 0 находим момент времени /х = т.,/]/5,6,
при котором гауссовский импульс имеет максимальную крутизну:
s = и' (0 |t.tl =Л е-°-5 — = 1,435 А-.
ТИ ти
Подставив этр значение в первую формулу (13.32), находим наи-
меньшую нестабильность момента срабатывания реле
од. = тлКВДэ/1,435 Ло.
3. ЗАДАЧИ И ОТВЕТЫ
13.1 . Найти вероятность рч(т) того, что гауссовский стационар-
ный процесс %(t) с нулевым математическим ожиданием и корр-
ляционной функцией /?(т) = о? (т) имеет в интервале (t, t + т)
четное число нулей.
Ответ'. рч(т) = Р{|(0 В (t + т) > 0} = 1 — л*1 arccos г (т),
0 arccos г(т) < л.
13.2 . Получить приближенное выражение для вероятности нали-
чия в малом временном интервале (/, t + т) одного нуля гауссов-
ского стационарного дифференцируемого случайного процесса
с нулевым математическим ожиданием и корреляционной функцией
Р(г) = о2г(т). ____
Ответ: рх(т) = vr, v = —г'о/п.
Указание. В малом временном интервале практически
возможно наличие лишь одного нуля дифференцируемого процесса
К0> т. е. в формуле (13.34) можно положить ри(т) ~ Pi(t). По-
скольку при малых т выполняется неравенство рх(т) 1, то учи-
тывая лишь первые два члена разложения косинуса в степенной
ряд, имеем 1 — (*/2) л2р^(т) са г(т). Разлагая затем в степенной
ряд четную нормированную корреляционную функцию г(т) ы
с-: 1 + (1/2) Гот2, получаем ответ.
13.3 . Вычислить значение параметра v в ответе к задаче 13.2,
когда гауссовский стационарный процесс КО имеет спектральную
плотность
S(©) = [ S° при 1®КАо)>
[ 0 при | <в | > А®.
Ответ: v = Дсо/лр^З.
400
13.4 . Получить выражение для вероятности наличия одного
нуля в малом временном интервале (/, t + т) для процесса т) (£) =
= s(t) + где случайный сигнал s (t) имеет вид
s(0 = £i(0 cos (aot + £г(0 sin <aot.
Случайные процессы ?(/), ^(0 и g2(0 являются гауссовскими,
стационарными, независимыми с нулевыми математическими ожи-
даниями и корреляционными функциями R (т), R^x) и Р2(т), при-
чем R^t) = R2(t).
Ответ;
' л L Я,(0)+«(0) J
Указание. Случайный процесс г) (0 является гауссовским,
стационарным, имеет нулевое математическое ожидание и корре-
ляционную функцию Рп(т) = ₽1(т) cos шот + R(%).
13.5 . Решить задачу 13.4, когда и |2 являются не случайны-
ми процессами, а независимыми гауссовскими случайными вели-
чинами с нулевыми математическими ожиданиями и одинаковой
дисперсией <т2. Рассмотреть частный случай |(0 — 0.
Ответ: рг(т) = —[ 1 * ' Р1 (т)=®<» т/я ПРИ & (0=0.
л L (О)
13.6 . Получить выражение условной вероятности рн(т) нали-
чия нечетного числа нулей внутри интервала (t, t + т) для гауссов-
ского стационарного дифференцируемого случайного процесса g (t)
с нулевым математическим ожиданием и корреляционной функци-
ей R (т) = o2r(t). Предполагается, что в начале интервала имеется
нуль, т. е. %(t) = 0. ____________
Ответ: cos лрн (т) = —r'(x)lV—r"0 | [1—г2(т)].
Указание. Очевидно, что рн(т) = Р{|(0 £(/ + т) <
< 0| | (0 = 0}. Условная плотность вероятности р (t), | (/ +
+ т) | £ (0 = 0] является нормальной с нулевым математическим
ожиданием и нормированной корреляционной функцией
= мШ0Е(<+т)1Е(0}
/м{£Ч^т)1£(')}м{£2(0 !£(<)}
Поэтому применима формула (13.34), только теперь в нее вместо
г(т) нужно подставить г(т). Вычислив-г (т), получим ответ.
13.7 . Найти среднее число положительных выбросов’в'единицу
времени на уровне С < Ат для гармонического колебания
s(0 = Ат cos ((oof + <р), начальная фаза которого случайна и
распределена равномерно в интервале (—л, л).
Ответ: Nf(C) — f0 — а>0/2п, С < Ат.
401
Указание. Так как производная ио времени 01 процесса
s(t) = — <в0Лтзш (a)ot + <р) = ±<о0]А4т — s2(Z), то совместная
плотность вероятности определяется формулой
Pz I® (0. s (01=Pi(s) Р («I s) =-/ - [6 (s—ю0 V AS,—s2) +
2л"|/Ла — sa
r m
4~6(s s2)]=t^=Pi (s)p (s),
где 6 (x) — дельта-функция.
В данном случае условие независимости (13.8) не выполняется
и поэтому следует применять формулу (13.6).
13.8 . Найти на интервале Т дисперсию числа нулей ©«(Т)
гармонического колебания s(t) — Am sin (2nf0t + <p), у которого
случайная начальная фаза распределена равномерно в интервале
(—л, л).
Ответ [83]: aS(T) = (2f0T - [2f0T]) (1 - 2f0T + [2f0T]),
где [2f0T] — целая часть числа 2faT.
13.9 . Получить в явном виде выражение Nt (С) для гауссовских
стационарных процессов с нулевыми математическими ожиданиями,
одинаковыми дисперсиями и тремя нормированными корреляцион-
ными функциями
Г1(т) = (14-а|т|)е~а|т|, га(т) = е_ат’,
г,(т) = sin(A(0T/2)
3? ’ Дсот/2
Сравнить полученные результаты при одном и том же значении
уровня С и одинаковой эффективной ширине спектров Д/8.
Ответ:
Nil (Q = — Д/9ехр Г (—Г] =0,63662Д/„ехр Г —(—У1.
Л L 2 \ G / J 2 \ G / _
^(С^Д/.ехр^Хф1]-
= 0,38894 Д/э ехр [ —- (—У] ,
С V
А^Г,з(С) = у== Д/эехр —
хехр[ —
ИЫС)>М,,(С)>11ЫС).
13.10 . Даны два гауссовских стационарных узкополосных
процесса с корреляционными функциями
7?i(T)=aae-al,|(cos(i)0T + — sinco0| т
\ ®в
Z?2(T)=a2e~“li:i[cos©0T----^-sin®0|il
\ ®о J
402
Какой из двух процессов является дифференцируемым? Вычислить
для него среднее число положительных выбросов Nt (С).
Ответ: первый процесс дифференцируем, второй — нет;
13.11 . Найти среднее значение полного числа пересечений Л\(С)
уровня С для суммы п (/) = £х(/) + £2(1), где £х(0 и £а(0 — два
гауссовских независимых стационарных дифференцируемых про-
цесса, имеющих нулевые математические ожидания и корреляцион-
ные функции R^r) — R2(t) = <r|r2(r).
Ответ:
NdC) = —(
Л \
qi 4~ga rao \1 /2
C8
2(a?+<i)
r;0=-^|
dx* k-o
13.12 . Решить задачу 13.11 для случая, когда
Ответ:
W1(C)= f-----5—у
,С.Л \ «!+»!/ Ч 2(01 +«!)/
13.13 . В задаче 13.11 найти число «положительных» нулей
Af+(O) процесса т) (О, когда
/?х(т) = а«рх(т) cos йхт, /?2(т) = <г£р2(т) cos <о2т,
Р1(0)=р2(0)= 1.
Ответ:
A7(0)=J-LgH<o?-
v ' 2л
Pio)4~qa (юа—Рао)
О1+°2
d»Pi(T) I
dxa |т—о
13.14 . Найти на интервале (/0, t0 + Т) среднее число превы-
шений уровня С суммой гауссовского стационарного процесса
£(/) и прямой a(t) = а0 + a^t, где а0 и ах — постоянные коэффи-
циенты. Процесс | имеет нулевое математическое ожидание и
дважды дифференцируемую корреляционную функцию =
= а2г(т>.
Q^ieem:
X Гф / —°i \ ф / —ао—ai (44~^)
L \ а ) а
403
Указание: Предварительно нужно найти совместную плот-
ность вероятности р2(г] (/), т](/)) для гауссовского нестационарного
процесса t](Z) = а0 + aj + £(/) и его производной т)’(0 = ах +
+ g (t), а затем следует воспользоваться формулой (13.4).
13.15 . Вычислить среднее число нулей на интервале (0, тТ0),
где т — целое положительное число, для периодически нестацио-
нарного гауссовского процесса x](f) — %(t) cos aot, T = 2л/(оо.
Здесь g(Z) — гауссовский стационарный процесс с нулевым сред-
ним значением и корреляционной функцией 7?(т) — <т2г(т).
Ответ: N (0, тТ0) = тТо (<оо + V—/'о).
Л
13.16 . Найти среднее число нулей в единицу времени процес-
са ti (/)= gx(/) g2(Z), где gx(/) и |2(/) — два гауссовских стаци-
онарных независимых дифференцируемых процесса с нулевыми
математическими ожиданиями и корреляционными функциями
fliW = tfkiW, Я2(т) = <Г2Г2(т).
Ответ-. = — r<o=- I •
л ат2 |т=0
Указание: Поскольку независимые процессы gx(f) и g2(/)
дифференцируемы, то их реализации представляют собой плавно
изменяющиеся функции времени. Вероятность совпадения нулей
двух таких функций практически равна нулю. Поэтому число нулей
произведения двух функций равно сумме чисел нулей каждой
из перемножаемых функций.
13.17 . Вычислить среднее число выбросов Nt (С) квадрата ста-
ционарного случайного процесса g(f), имеющего нулевое матема-
тическое ожидание и корреляционную функцию (т) = сг2г(т).
Ответ: Nt (С) ехр (----, С>0.
13.18 . Найти среднее число выбросов Nt (С) случайного про-
цесса т) (f) = У g2(/) = | g (t) |, если гауссовский процесс g (t) имеет
корреляционную функцию R (т) = <т2г(т).
Ответ: Nt (С) = — ехр (— —'j, С>0.
п \ 2о2 /
13.19 . Вычислить среднее число выбросов на уровне С > О
логарифмически нормального процесса т] (/), заданного выражением
g(Z) = In т)(/). Здесь g(£)— гауссовский стационарны^ процесс
с нулевым математическим ожиданием и корреляционной функцией
,₽(т) = ог2г(т).
Ответ: Nt (С) = —У~^70 ехр (—, С>0.
404
Рис. 13.5. Воздействие суммы сиг-
нала и шума на согласованный
фильтр
s(t)+n(t)
о------
Согласованный
фильтр Ж(]Ы)
------о
13.20 . Получить выражение ЛГ1*(С) для стационарного процес-
са т] (0 = У ^(0 4- H(t), где ^(0 и |2 (t) — два независимых гаус-
совских стационарных процесса с нулевыми математическими ожи-
даниями и одинаковыми корреляционными функциями 7?i(t) =
= RfM = о2г(т).
/п / Q \ Г 1 / С \21
13.21 . Имеется линейный фильтр (рис. 13.5), согласованный
с детерминированным импульсом гауссовской формы
s(0=Aexp [-2,8р^У1, 0<т0<Т, 7>ти,
L \ ти / J
где т0 — момент времени, соответствующий середине импульса;
ти — длительность импульса на уровне 0,5; Т — интервал наблю-
дения.
Частотная характеристика согласованного фильтра имеет вид
Ж О) = А о 1 / ехр —----------------/<о (/0 —т0)1.
V 2,8 L 12 J
где t0 — момент времени, соответствующий наибольшему значению
выходного сигнала sBmax = sB(f0) = Е = А ^ти]/л/5,6.
Найти среднее число положительных выбросов N+(C, Т) вы-
ходного шума | (/) на уровне С, равном наибольшему значению
выходного сигнала.
Ответ: W+(C, Т) — ехр [ ——] .
43.22. Получить явные выражения A/f(C) для гауссовских ста-
ционарных узкополосных процессов с нулевыми математическими
ожиданиями, одинаковыми дисперсиями и тремя разными норми-
рованными корреляционными функциями
(т)=(1 -|- а | т |) е-а ।т < cos <в0 т, г2 (т) = е~ат* cos соо т,
r3(T)=-Sin/-A-MT/2) COSCOoT.
Сравнить полученные результаты при одном и том же значении
уровня С и одинаковой эффективной ширине спектров Д/э.
Ответ'.
~ АД + (2/л)(ДШ21ехр (-CW),
^^(2(C) ~ f0[l +(1/4л) (ДШ21 ехр (-С2^2), fo ~ ®°/2п’
405
Nt,3(C) ^/0П +(1/24) (Д///0)2] exp (-CW), Д/ = Д®/2л,
. Nt,2(C)> Nt,3(C).
13.23. Получить формулу для среднего числа положительных
выбросов в единицу времени на уровне С гауссовского стационар-
ного процесса с корреляционной функцией
Я(т) = а2р(т)соз[а)0т+у(т)], р(0) = 1.
Ответ:
-Is-У
' 2л |_\ too /
pj 11/2 . / С2 \ , dY(T) I
^-S- exp-------------, Vo = ?
F I 2oa / dr k=o
to# .
13.24. Определить среднее число выбросов N+(C, Т) огибающей
Л (0 квази гармонического шума, спектральная плотность которого
постоянна в интервале частот | f — fQ | Д/72 и равна нулю вне этого
интервала. Рассмотреть случай, когда Т — 1000 мкс, Д/ = 1 Мгц
и С = За.
Ответ:
N+{C/T) = TNt(C) = Tbf |/Г^-^ехр(—g), С>0,
А/+(За, 10-8) ~ 24 с-1.
13.25. На вход системы, представленной на рис. 13.6, воздей-
ствует белый шум n(t), односторонняя спектральная плотность
которого Sn(f) = Уо. f > 0. Определить число срабатываний «бе-
зынерционного» электронного реле от шумовых выбросов при по-
рогах срабатывания Сг = 2а и С2 = За за время Т = 1000 мкс,
если квадрат частотной характеристики усилителя промежуточной
частоты (УПЧ) имеет вид
ехр [—2,8 (
Д/ « /о.
где f0 — резонансная частота; Д/ — полоса пропускания УПЧ
на уровне 0,5. Вычисления выполнить для Д/ = 2 МГц.
Ответ:
^(С,Т) = ™+(С) = ТД/Лехр[-^Л Д/9 = Д/1/
О \ 20 / Jf z,o
2V+(2cr, 10-3) ~ 540 с-1, W+(3a, IO’3) ~ 66 с-1.
Рис. 13.6. Простейшая схема амплитудного радиоприемника с электронным
реле
406
Указание. На Выходе линейного Детектора огибающей
воспроизводится огибающая A (t) квазигармонического шума
| (/), воздействующего на вход детектора.
13.26. Пусть на схему рис. 13.6 воздействует сумма гармони-
ческого сигнала s(t) — Amcos((&0t + <р0) и квазигармонического
шума 5 (0 с функцией корреляции
7?б(т) = о2ехр (—лД/?т2)соз(о0т.
Найти среднее число срабатываний реле за фиксированное время Т
при пороге срабатывания реле С = За, если отношение сигнал/шум
а = Ат/а = 2.
Ответ:
N+(C, Т) = TNt(С) - ТД/8 ехр [—l- (а* + -g-)] /0 (а
~0,ЗТД/8.
Указание: На выходе линейного детектора огибающей
воспроизводится огибающая V(t) суммы сигнала и шума.
13.27. Решить задачу 13.26 для случая, когда корреляционная
функция шума £(<) имеет вид
= °а 8>П cos ©о т>
и сравнить ответы.
Ответ:
N+(C,T} = Tkfy ААехрГ—ЯаЧ
~0,227Д/.
13.*28 . Вычислить средние числа максимумов в единицу времени
AZimax гауссовских стационарных процессов с нормированными кор-
реляционными функциями
г2(т) = е~“т’, гз(т) = этлД/т/лД/т.
Сравнить полученные результаты при одинаковой эффективной ши-
рине спектров.
Ответ:
V —Д/э = 1,382Д/8,
Nl.3 max = 4 1/ 4 Д/ = °.387Д/8<У1,2 max.
2 г О
407
13.29. Для процессов, указанных в задаче 13.28, вычислить
средний временной интервал между максимумом (минимумом) и со-
седним минимумом (максимумом).
Ответ.’.
- ____ л ___ 1 f л ______ 0,362
Т2го-Уё7~ 2Af8 |/ 6 ' дд“’
1 тЛ” 1.292 Л, А,
тзт— .. г л. —Afg.
af г о af
13.30. Найти среднее число максимумов в единицу времени У1тах
гауссовского стационарного процесса с нормированной корреля-
ционной функцией г(т) = p(t)cos(o0t, р(0) = 1.
Ответ: .
„ _ t ( l-6p?/co?+pi«>M \*/2 t _ ®0
ATlmax-Zo^ 1-pJ/mg ) ’ 2л ’
13.31. Решить задачу 13.30 при нормированной корреляционной
функции
z х sin лД/т
г (т) =-----— cos (ОоТ,
лД/т 0
считая Д/ /о — ®0/2л.
Ответ:
13.32. Решить задачу 13.30 при нормированной корреляционной
функции
г (т) = ехр (— лД/эТ2) cos аох, &fa — ©0/2л.
Ответ:
N i max fo
1 3 / д/э у 3 / д/, у
л \ /о / 4л2 \ /о /
13.33. Выразить через эффективную ширину спектра Д/9 сред-
нее время между двумя соседними положительными выбросами на
408
уровне С для гауссовских стационарных процессов с нулевыми
математическими ожиданиями и нормированными корреляцион-
ными функциями
ri(T) — (1 + а1т1) е~“|т1, г2 (т) = е~а*2, г8(т) = sin лД/т/лДД.
Сопоставить полученные ответы с результатами решения задачи
13.9. 3?
Ответ:
13.34. Для гауссовских процессов, указанных в задаче 13.33,
найти средний интервал времени между соседними нулями.
Ответ:
Т1(0) л _ 0,3927 ч(О) _ /~ л 1 0,6267
2 “ 8Д/Э Д/в' ’ 2 ~ у 2 2Д/, ~ Д/э
1 УЗ 1,732
Т т«<°> - “V" “ -^г
13.35. Определить средний интервал между положительными
выбросами на уровне С гауссовского стационарного процесса с ну-
левым математическим ожиданием и нормированной корреляцион-
ной функцией
г(т) = P(t)cos(o0t, (о§ > — Ро. Р(О) = 1.
Ответ:
т(С)~ —(1+ -£ЦГ1-ф(—'jlexpf—V
v fo 2со? Д \ о /J \ 2а» /
13.36. Пользуясь ответом к задаче 13.35, определить средний
интервал между соседними нулями процессов с корреляционными
функциями
г2(т) = ехр(—лД/1 т2) cos <вот, г8(т) = SInnAM. cos ©от.
лД/8т
Ответ:
* 2/о L
! 1 / Д/э
4л ft>
21
409
13.37. Определить средний интервал между соседними положи-
тельными и отрицательными выбросами огибающей Л(/) на неко-
тором уровне Q > б для гауссовских стационарных процессов с нор-
мированными корреляционными функциями, указанными в зада-
че 13.36.
Ответ:
13,38. Найти наибольшую точность определения положения т0
центра видеоимпульса гауссовской формы (рис. 13.7)
где ти— известная Длительность импульса на уровне 0,5, в слу-
чаях, когда: 1) для определения т0 используется пороговое уст-
ройство, реагирующее только на фронт импульса; 2) момент т0
определяется пороговым устройством, реагирующим как на^фронт,
так и на срез импульса.
Указанный импульс принимается на фоне аддитивного флукту-
ационного шума малой интенсивности с корреляционной функцией
Я(т) = а2 ехр ( —А/2 т2), АД — .
Ответ:
!)
2) аТо =
оти .
1,435А0’
—^=-1/1 + ехр(- лДПт2/5,6) ~
1,435 J/2 ло 1,435Л0
Указание. Рассматриваемый гауссовский видеоимпульс
имеет максимальную крутизну фронта и среза и'тп (4,2) =
Рис. 13.7.
формы
Видеоимпульс гауссовской
410
= ± Ло]^5,6 е-0>6/ти в точках 4,2 — т0 ± Ти^И^.б, отстоящих
друг от друга на т = ти/]/1,4. Пороговые устройства должны иметь
порог срабатывания С = Аое~°>8. Центр импульса во втором слу-
чае определяется равенством т0 = (44- 4)/2.
13.39. Определить временную нестабильность положения какого-
либо нуля суммы гармонического колебания s(/) = Лгосо8(®0< 4-ф0)
и плавно изменяющегося флуктуационного шума с нулевым мате-
матическим ожиданием и малой дисперсией о2 С Am-
Ответ: сг0 = <т/<О(Ит.
13.40. Найти плотность вероятности временного интервала т
между соседними нулями суммы гармонического колебания s (/)=
= Ат cos (соо/ 4- фо) и гауссовского стационарного шума (малой
интенсивности) с нулевым математическим ожиданием и дифферен-
цируемой корреляционной функцией R (т) = сг2г (т).
Ответ:
о (т) = ехо I _ гсаа2 (coo-r/jt—1)а1 а= Ат
0 2 VIlV14-r (л/т®) *1 4 (14-г(л/<оо)] J’ о
Указание. Как следует из (13.31), в линейном приближе-
нии плотность вероятности интервала времени между соседними ну-
лями будет нормальной. При этом среднее значение интервала, оче-
видно, равно л/(оо, а для вычисления дисперсии нужно восполь-
зоваться формулой (13.33).
Раздел IV
ТЕОРИЯ ПОМЕХОУСТОЙЧИВОСТИ
14. ФИЛЬТРАЦИЯ СИГНАЛОВ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В общем виде задачу оптимальной фильтрации сигналов из шумов мож-
но сформулировать следующим образом. Пусть колебание x(t), принятое на
некотором интервале времени, является функцией от сигнала s[Z, %(/)] и шу-
ма n(t):
X(t)= F{s[t, MOL «(О}- (14.1)
Сигнал s[/, %(/)] B общем случае может зависеть не от одного, а от несколь-
ких параметров X/ (/), причем либо сам сигнал s[f, %(/)], либо его параметр
X (0 являются случайными процессами. Вид функции F{s, п), т. е» способ
комбинирования сигнала и шума, и некоторые статистические характеристи-
ки сигнала и шума предполагаются априорно известными. Используя эти
априорные данные, необходимо определить устройство (рис. 14.1), решаю-
щее оптимальным образом, какая реализация самого сигнала $[/, %(/)] или
его параметра %(/) содержится в принятом колебании (14.1).
Из-за наличия шума n(t) и случайного характера сигнала s[f, %(/)]
оценка реализации сигнала $[/, %(/)] или его параметра X (/) не будет совпа-
дать с^истинной реализацией, т. е. будут иметь место ошибки фильтрации.
Для количественной характеристики качества фильтрации можно использо-
вать различные критерии [42]. Наиболее часто в задачах фильтрации ис-
пользуются критерий минимума среднего квадрата ошибки, критерий мак-
симального отношения сигнал/шум и критерий максимума апостериорной
вероятности.
В зависимости от дополнительных предположений о характере сигнала
и шума сформулированная задача решается методами линейной или нелиней-
ной фильтрации. В дальнейшем мы ограничимся рассмотрениеми лишь задач
линейной фильтрации. Кроме того, будем предполагать, что сигнал и шум
взаимодействуют аддитивно, т. е.
x(f) = s[f, %(/)] + п(0- (14.1а)
Оптимальная линейная фильтрация по критерию минимума среднего
квадрата ошибки [84—89]. Предположим, что входящие в (14.1а) сигнал
s[f, %(/)] = s(t) и шум п(0 представляют собой стационарные нормальные
гауссовские случайные процессы с известными ковариационными функциями:
К.(т) = s(t + т)}, Кп(т) = {n(t) n(t + т)},
Ksn(T) = M{s(t)n(t + т)}.
Требуется определить систему, которая из принимаемой смеси
х(0 = s(f) + n(t) (14.16)
412
С* минимальной средней квадратической ошибкой выделяет не параметр
X(f), а сам полезный сигнал s(/). Таким образом, искомая оптимальная
система должна минимизировать величину
в2 «= Л4{[Г(0 — s(t + А)]2}. (14.2)
В (14.2) для общности введен временной сдвиг Д. При Д > 0 оценка s(t)
на выходе системы должна предсказывать (прогнозировать) значение вход-
ного сигнала s(t) на время Д, при Д = 0 сформулированная задача сводится
к выделению (сглаживанию) сигнала s(t) из колебания x(f).
Строгое математическое решение сформулированной задачи для слу-
чая полубесконечного интервала наблюдения (— оо, t) было дано А. Н. Кол-
могоровым [84] и Н. Винером [85]. Ими, в частности, было показано, что оп-
тимальное по критерию минимума среднего квадрата ошибки устройство
в данном случае относится к классу линейных фильтров с постоянными пара-
метрами. Основные результаты теории Колмогорова—Винера заключаются
в следующем.
Предположим, что на вход физически реализуемой линейной системы
(рис. 14.2) с импульсной характеристикой
(d (/), t > 0,
вд=(о «». ,14-3)
воздействует стационарный случайный процесс x(t). При этом стационарный
случайный процесс y(t) = s(t) на ее выходе будет определяться соотношением
y(f) = s(i) = J h(x)x(t— x)dx . (14.4)
о
Подставляя (14.4) в (14.2), получаем следующее выражение для среднего
квадрата ошибки фильтрации:
{"со “ 2|
J й(т)х(/ —T)dr —8(/+Д) к
-О J J
которое после несложных преобразований приводится к виду
е« = К8(0)-2J /г(т)К8Ж(т + Д)Л + f J (14.5)
О 0 0
Здесь
К.х(т) = M{s(i)x(t + т)} (14.6)
— взаимная ковариационная функция процессов s(0 и х(/);
Кх(т) = M{x(t)x(t + т)} (14.7)
— ковариационная функция случайного процесса x(t).
Рис. 14.1. Оптимальный фильтр
Рис. 14.2. Линейный фильтр
413
Чтобы определить импульсную характеристику Ло(0 оптимального
фильтра, минимизирующего средний квадрат ошибки (14.5), воспользуемся
известным методом вариационного исчисления. Пусть
' ~ h(t) - МО + pg(0, (14.8)
где р — параметр, не зависящий от f; g(t) — произвольная функция. При
этом условие минимума среднего квадрата ошибки записывается в следующем
виде:
de2 I
----- «=0 .
dp |ix=o
После подстановки (14.8) в (14.5) условие (14.9) принимает вид
(14.9)
оо Г оо
f g(T) f fto(v)Kx(T—V)dv—К.ж(т + А)
о L о
Поскольку это соотношение должно выполняться при произвольной функции
g(0, то отсюда следует, что импульсная характеристика Ло(0 оптимального
фильтра должна удовлетворять интегральному уравнению Фредгольма пер-
вого рода
00
f Mv)Kx(T-v)dv«=Kejc(T+A), т > 0. (14.10)
О
Это интегральное уравнение является основным уравнением теории линей-
ной фильтрации и называется уравнением Винера—Хопфа [86].
Таким образом, задача нахождения оптимального сглаживающего
(А « 0) или прогнозирующего (А > 0) физически реализуемого фильтра сво-
дится к решению интегрального уравнения (14.10). Решение этого уравнения
в общем случае встречает известные трудности, обусловленные, главным об-
разом, требованием физической реализуемости оптимального фильтра. Одна-
ко в частном, но весьма важном с практической точки зрения случае дробно-
рациональной спектральной плотности Sx(co) входного процесса x(t) из
(14.10) можно получить следующее выражение для комплексной частотной
характеристики Л7о(/со) оптимального фильтра, минимизирующего средний
квадрат ошибки:
(14.11)
о о
Здесь
F(M)F*(/cd)==|F(/(o)I2=Sx((d),
Sx(<o)=f K^e-I^dr,
(14.12)
S«(<o)= j
00
При этом минимальный средний квадрат ошибки фильтрации
оо
emin=V“ f [Ss(w)-I^o(7<o)l2 Sx(<o)J , (14.13)
ZJl J
—оо
где
J Ks(t) e~/<DTdT. (14.14)
4 14
Для частного случая сглаживания аддитивной смеси взаимно независи-
мых стационарных случайного процесса s(t) и белого шума n(t) с нулевым
математическим ожиданием % = 0 и корреляционной функцией
/?п(т) == (ЛАо/2)6(т)
формула (14.11) упрощается [89] и приводится к виду:
мл
#o(/a»-l- (14.11а)
I [2о« J©) + WoJ-H
Индекс «+> у выражения в квадратных скобках означает, что если это вы-
ражение разложить на простые дроби, то в разложении должны быть остав-
лены только те из них, которые соответствуют полюсам, расположенным в
верхней полуплоскости. Все простые дроби функции F(co) e Ss(co) + NJ2,
соответствующие полюсам в нижней полуплоскости, а также целая часть
Г(со) должны быть отброшены. Минимальный средний квадрат ошибки для
рассматриваемого случая может быть вычислен по формуле [89]
— 00
Практические вычисления по формуле (14.11) оказываются довольно
громоздкими. Значительное упрощение получается, если не накладывать на
оптимальный фильтр требования физической реализуемости (14.3), т. е. по-
лагать в (14.4) и последующих формулах нижний предел равным — оо. При
этом вместо уравнения (14.10) получаем интегральное уравнение вида
f h0(v)Kx(x~v)dv = KSx^+^ • (14.15)
решение которого приводит к следующему выражению для комплексной ча-
стотной характеристики физически нереализуемого оптимального фильтра:
е/<оЛ. (14.16)
Sx((o)
Минимальный, средний квадрат ошибки и в этом случае вычисляется по фор-
муле (14.13). Для частного случая статистически независимых сигнала s(t)
и шума n(t) формула (14.16) приводится к виду
о'ш) = ~ (Jfs йй е/аА • (14 •,6а)
^(й)т5п(®)
Хотя соотношения (14.16) и (14.16а) соответствуют физически нереализуе-
мым оптимальным фильтрам, они весьма полезны, так как любой физически
реализуемый фильтр не может дать меньшей средней квадратической ошибки,
чем фильтры, определяемые (14.16) и (14.16а). Объясняется это тем, что нало-
жение на фильтр условия физической реализуемости (14.3) сужает воз-
можности выбора оптимальной характеристики фильтра я^по этой причине
может привести лишь к ухудшению конечного результата.
Оптимальная линейная фильтрация по критерию максимума отношения
сигнал/шум [27, 42, 82, 89—91]. Предположим, что на вход линейного филь-
тра с комплексной частотной характеристикой ^Г(/со) поступает аддитивная
смесь
x(O“s(0+ n(t)t (14.17)
415
где n(t) — стационарный случайный процесс со спектральной плотностью
Sn(co); s(0 — статистически независимый от п(0 полезный сигнал, фор-
ма которого (амплитудный спектр S(/co)) заранее известна. При этих усло-
виях процесс на выходе фильтра
1/(/) = зВых(0+Лвых(0» (14.18)
где $вых(0 и лВых(0 — результаты преобразования сигнала и помехи ли-
нейным фильтром. Сигнальная составляющая определяется соотношением
00
«вых(0=Т- f $д®)5Г(/®)<М(®, (14.19)
—оо
а дисперсия выходного шума пВых (О вычисляется по формуле
00
©вых = ав2ых =— [ «п(®)|^(/®)|Ш. (14.20)
—оо
Введем в рассмотрение отношение
а = |зВых(^г,)1/°гвых» (14.21)
представляющее собой отношение мгновенного значения сигнала на выходе
фильтра в некоторый момент времени t = Т к среднему квадратическому зна-
чению выходного шума. В соответствии с (14.19) и (14.20) это отношение
равно
оо
-2- f 5(/®)Я’(/®)е/®тЛ»
V- f Sn(w)|^(f®)l»dw
Линейный фильтр, максимизирующий отношение (14.22), называется
фильтром, оптимальным по критерию максимума отношения сигнал/шум.
Можно показать [89, 90], что комплексная частотная характеристика такого
фильтра
^о(»=С-^^-е-^г, (14.23)
оп((0)
где С — некоторая постоянная; S*(/co) — функция, комплексно-сопряжен-
ная с амплитудным спектром S(jgj) входного сигнала s(0.
Если входящий в (14.17) случайный процесс n(t) представляет собой ста-
ционарный гауссовский белый шум со спектральной плотностью Sn(co) =
= Мо/2, — оо < со < оо, то формула (14.23) приводится к виду
^о(/®)==к5*(/®)е-/<йГ. (14.24)
Таким образом, в случае приема аддитивной смеси сигнала и белого шума
комплексная частотная характеристика фильтра, оптимального по критерию
максимального отношения сигнал/шум, полностью определяется амплитуд-
ным спектром входного сигнала. В соответствии с этим оптимальные фильтры
с комплексными частотными характеристиками (14.24) называют согласован-
ными.
416
Определим импульсную характеристику согласованного фильтра:
оо
fto(O = — f X9(i<o)^atdw. (14.25)
2л J
—00
После подстановки (14.24) в (14.25) получаем
Ло(О = ks(T — t), (14.26)
где к — некоторая постоянная величина, имеющая смысл коэффициента
усиления.
2. ПРИМЕРЫ
14.1 . Имеется аддитивная смесь x(t) = s(t) + n(t), где n(t) —
стационарный нормальный белый шум со спектральной плотностью
Sn(co) = Wo/2, — оо < со < оо; (14.27)
s(t) — статистически независимый от п (/) стационарный случай-
ный процесс со спектральной плотностью
Ss(co) = 1/(1 + со2)» — оо < со < оо.
Определить комплексную частотную характеристику ЛГо(/со) Фи‘
зически реализуемого прогнозирующего фильтра, минимизирую-
щего средний квадрат ошибки
е2 = Л1 {[«/(/) —s(/ + А)]2}.
Здесь y(t) — случайный процесс на выходе фильтра.
Решение. В соответствии с (14.11)
ОО оо
ЗДсо) =-------1--f ef^dr f Ssx(Q)
V ’ 2nF(/co) J J F*(/Q)
0 —oo
где
F(/<o)F*(/co) = |F(/co)|2 = Sx(co)., -
Поскольку по условию задачи s(/) и n(() статистически незави-
симы, то
Ssx(co) = Ss(co) = 1/(1 + со2),
Sx(co) = Ss(co) + Sn(co) = (No + 2 4- Л/о<о2)/12 (1 + co2)].
Отсюда следует, что
“УЖ F*[j&) = —/а>1/1Ур
V2(l+/<a) ’ 1/2(1-/со)
Таким образом, искомая комплексная частотная характеристика
определяется соотношением
со
^0 (/<»)= —. . 1+/Ю -7=7 f/(T)e-Wc,
я (1/ЛГо+2+/а> ]/лг0) «j
14 Зак. 12 03
417
где
°° i
Z(r)= f ----------!------_ e/o(’+A>dQ.
J (1+/Й)(УМ»+2-/йУМ»)
— 00
Учитывая, что [17]
Г (₽ + M)-2*(y—jx)~2^e~lpxdx =
d
-OO
= 2л (P + T)-*-veP (P~V)/2
Г (2р.)
—Yp), P<0,
где Wk,4(z) — функция Уиттекера, находим
/(т) = | УМ» 4~2
~ Ум; I Ум;
ехр
X Wo, -!/2 ( У"°+2+^ (т + А)}
к Ум» /
У1Уо+2-|-УМ>
хехр[—(т+Д)].
После подстановки 7(т) в Жо(/®) и РяДа несложных преобра-
зований окончательно получаем
^oG®) = ^о/(1 + /юТ0),
где
46” ____________________ а —Л Т 1 / No
° У^+2(Ул[7+2 + У1У0) ’ °. Г Уо+2‘
Таким образом, искомый прогнозирующий фильтр может быть
представлен в виде последовательного соединения идеального (не-
искажающего) усилителя с коэффициентом усиления и инте-
грирующей цепочки RC с постоянной времени RC = То (рис. 14.3).
14.2 . На вход фильтра воздействует аддитивная смесь х (t) =
= s(t) + n(t), где n(t) — стационарный нормальный белый шум
со спектральной плотностью (14.27); s(t) — статистически незави-
симый от n(t) стационарный случайный процесс с нулевым матема-
тическим ожиданием’/п8 = 0 и корреляционной функцией
Rs. (т) = ole-“lx|cosa»oT-
Определить комплексную частотную характеристику
физически реализуемого сглаживающего линейного фильтра и вычи-
слить соответствующий ему минимальный средний квадрат ошибки
е2 = М {[y(t) - s(/)l2}.
418
Рис. 14.3. Прогнозирующий фильтр
о---- г—ч-----------о
R
x(t) <?=r= У®
о ~ ----------------о
Рис. 14.4. Интегрирующая
цепочка RC
Решение: В соответствии с
стотная характеристика имеет
^o(Z®) =
(14.16а) искомая комплексная ча-
вид
Ss(co)
5s(®) -1- Sn(to)
а спектральная плотность процесса s{t) при ms = О
1
R. (т) e-i^dx = ао? Г-------------, , ------------ .
L а2 + (<в—<оо)2 а2 + (со + <0р)2
Подставляя Ss(co) в #о(/со), получаем.
ч 2аа? 2ас2
Ж0( <й) =---------------------- 4---------------.
0 ' 2аа2 + а22Уо+ЛМ<о-<Оо)2 2аа2 + а2 Wo+^o (<о+(оо)2
Значение среднего квадрата ошибки находим из (14.13):
е2 = Cmin = of (аЛ,“+02а2) •
14.3 . На вход 7?С-фильтра (рис. 14.4) поступает аддитивная
смесь x(t) = s(t) + n(t), где s(t) — стационарный гауссовский
случайный процесс со спектральной плотностью
S8(co) = 2аст|/(а2 4- со2), — оо < со < оо;
n(t) — статистически независимый от s(t) стационарный гауссов-
ский белый шум, для которого
Sn(co) = Л%/2, — оо < со < оо.
Найти оптимальное значение постоянной времени Т — RC, ми-
нимизирующее средний квадрат ошибки
е2 = A4{[z/ (/) — s(Z)]2},
где y(t) — процесс на выходе фильтра, и определить значение emin-
Решение. Обозначим импульсную характеристику ЯС-фильтра
через h(t). Тогда разность £(/) = y(t) — s(t) можно представить
в виде
t t
£(/) = § h(t—т)х(т)йт— з(т)б(/—т)dr =8х(0+«!(/),
14*
419
Ьдё
i I ’
si(0= J [h(i—t)—b(t—r)]s(r)dT = J hj^t—т)8(т)Лт,
— 00 — oo
t
nx(t)~ J hit—x)n(x)dx.
— 00
По условию задачи процессы s(t) и n(t) взаимно не коррели-
рованы, вследствие чего взаимно не коррелированы и процессы
s^t) и n^t). Таким образом, спектральная плотность процесса g(/)
S5(w) = SS1(co) + S„,((o),
где
S,» = S,(®) | ад®) | V $„» = Sn(<o)|^(/®)P
— спектральные плотности процессов s^t) и nx(/),
^(/co) = h(u) e—l<i,udu,
— 00
^i(/®) = [h(u)—d(u)]e-iaudu.
— oo
Таким образом, дисперсия процесса |(£)
00
al = e2=4rf =
— °°
оо
= -L f 1ЭД1^(/«>)- 1|1 2 + S» №)l2
2л J
— оо
По условию задачи,
<%*(/со) = р/(р + », р = 1/RC = МТ.
Следовательно,
___________________________________+—?!"• 1 л=
(а2+<в2)(Р2+®2)____________________2(Р2+®2) J
1 / 2аа? д/„ \
_ 1 I____з । JVp о I
2 а+Р "Г 2 *
Для нахождения оптимального значения р = 1/Т составим про-
изводную от е2 по Р:
No \
2 (а+р)2У
de2 1 /
dP — 2 (
420
Отсюда следует, что при Л^0<4о1/а оптимальное значение постоян-
ной времени- 7?С-фильтра
Т 1 У^о
Ро 2ай~\/ а—a V
а соответствующий ему минимальный средний квадрат ошибки сгла-
живания
Emin = as]/ aA^o — ®N0/4.
Если же 7У0 2Д2/а2, то оптимальное значение То — 1/Ро-*- °°»
а средний квадрат ошибки
Emin О?.
14.4 . При тех же условиях, что и в примере 14.3, найти опти-
мальное значение постоянной времени Т = RC, минимизирующее
средний квадрат ошибки
в2 = Л4 {[«/(/) —s(f + А)]2}.
Решение. В данном примере разность
l(t) = «/(О - s(t + А) = sx(0 + пх(0,
где
s1(Z) = [ — т) — + А — т)]$(т)с!т,
— 00
ni(0 — J h(t — T)n(’c)dr.
— оо
Поскольку процессы s^f) и n^t) взаимно не коррелированы, спек-
тральная плотность процесса 1(f)
Sj(co) = Ss,(co) + Sn,(со),
где
Ss,(co) = Ss(co) | ^(/co) |2, Sn,(co) = Sn(co)|^(/co)|2.
Учитывая, что
^i(/co) = § h1(u)e~ie>udu= [h(u)—6(м-)-А)]е~/“Мц=
— oo — oo
= ^f(jco)—е-'шД,
находим
Sj(co) = Ss(co) | ^(»-e/<oA p _|_ Sn(®) | c%-(/co)|2.
421
Отсюда дисперсия процесса £(/)
оо
а<=82=4- f (58(o)|^(7o)-e/“42+Sn(®)|W®)l2]d<o =
ZJl J
— оо
2«p82
a2+ co2
P_______g/coA
0 + /CO
_JML_
2 (P2+®2)
= Y 4os2(1-
е-«Д)—(1 —2е-“д) + P— .
a+P v ’ H 2
Анализируя зависимость s2 от |3, нетрудно установить, что при
А (In 2)/a наименьшее значение среднего квадрата ошибки имеет
место при р0 = 1 /Т'о = 1/7?С = 0 и равно
8min — Of2.
Если А < (In 2)/a и
4aas«
то наименьшее значение
чае А < (In 2)/a и
, Г 4aa|
Wo
(2е-«Д— 1)
О,
в2 также имеет место при р0 = 0. В слу-
0
минимальное значение 8min обеспечивается при
4aaf
Wo
(2е-“Д— 1)
1/2
—a.
14.5 . На вход линейного фильтра воздействует аддитивная смесь
х(/) = s(/) + п(/), где n(f) — стационарный гауссовский белый
шум;
Aea<f-r>,
0,
/<Т,
— статистически независимый от шума п (/) экспоненциальный ви-
деоимпульс (рис. 14.5).
0
Т
Рис. 14.5. Экспоненциальный видео-
импульс
422
Определить комплексную частотную характеристику ^0(ja)
фильтра, максимизирующего отношение сигнал/шум на выходе.
Решение. Вычислим спектр сигнала s (/):
оо
S(» = С 5(/)е-/“'Л= Ле-“г С = —— e-W.
J J a—/©
— oo —00
Используя соотношение (14.24), находим искомую комплексную
частотную характеристику: '
Л’оО®) ~ KS*(ja)e~1а>т — kJ (а + /со).
Таким образом, фильтр, согласованный с данным сигналом,
может быть реализован в виде цепочки RC (рис. 14.4), у которой
7?С=1/а.
14.6 . Определить комплексную частотную характеристику филь-
тра, согласованного с сигналом
[/ 9/ \21
—(----1 >
где ти — длительность импульса s(i) на уровне А/е.
Решение. Вычислим спектр видеоимпульса s (/):
S(jco) = J s(t) dt=b exp (—,
— 00
где Д/ = 2,25/ти — ширина спектра S(Ja>) на уровне b/e. Исполь-
зуя (14.24), находим
- ^о(/®) = <^оехр[— (//Д/)2 — }фТ1
14.7 . Найти фильтр, согласованный с прямоугольным видео-
импульсом
s(Z) = [Л’ °<^ти,
(0 при других t,
и вычислить отношение сигнал/шум на его выходе.
Решение. Спектр прямоугольного видеоимпульса
$(/©) = J s(/)e-/“< dt = A j*"d/;=-A_(l—е-/мти).
— ОО о
Таким образом, комплексная частотная характеристика <^о(/со)
фильтра, согласованного с прямоугольным видеоимпульсом дли-
тельностью тп, имеет вид
Я?о(/©) = к5*(» е-/“г = (е'“ти— 1)е-/“>г.
423
Рис. 14.6. Фильтр, согласованный с прямоугольным видеоимпульсом
Если интервал наблюдения совпадает с длительностью импульса,
т. е. Т = ти, то
jr0(/<o) = ^“ (1—е~/шти)..
Схема такого фильтра приведена на рис. 14.6.
Определим сигнал на выходе фильтра, имея в виду, что в соот-
ветствии с (14.26) его импульсная характеристика имеет вид
h0(t) = ^os(T - t) = ЯМти - t).
Следовательно,
t t
5вых (0 = J ^0(t)s(/ — т) dr = (j s (ти—т) s (t—т) dx.
о b
Нетрудно видеть, что максимальное значение [sBHX (0]щах имеет
место при t = ти и равно
^вых(01щах = ^М2ТИ ~
где Е = Л2ти — энергия сигнала s(i).
Вычислим дисперсию шума Рвых на выходе согласованного филь-
тра, полагая, что спектральная плотность входного шума
Sn(co) = No/2, — оо < со < оо.
Тогда
^вых = °в2ых = J 5„ (<о) | Зг0(/<о)|2 da =
— 00
— oo
Следовательно, максимальное отношение сигнал/шум
Я = ^5вых(01тах^°'вых = N
14.8. На вход интегрирующей цепочки RC (рис. 14.4) воздей-
ствует аддитивная смесь статистически независимых стационарного
гауссовского белого шума п (/) со спектральной плотностью
Sn(co) = NJ2, — оо < со < ОО,
424
и прямоугольного видеоимпульса
sW=ft/,
[О при других t.
Под выходным отношением сигнал/шум а понимается отношение
максимального значения сигнала на выходе к среднему квадратиче-
скому значению выходного шума:
® ^вых(/)^тах^вы!‘
.Вывести соотношение, связывающее отношение сигнал/шум на
выходе цепочки RC с длительностью импульса <ги и эффективной
шумовой полосой Д/э цепи определить, в каком соотношении
должны находиться длительность импульсов и оптимальная эффек-
тивная шумовая полоса Д/в opt, при которой на выходе RC -цепи
имеет место максимальное отношение сигнал/шум.
Решение. В соответствии с теоремой Винера—Хинчина дисперсия
стационарного шума на выходе цепочки RC
ОО оо
^вых==авых = "— f Sn вых (cd)d(i) = — f Sn (co) I Ж (/(!)) I2 do.
2Л J 2Л J
— oo —oo
Подставляя в это выражение
^(/со) = 1/(1 + /<о7?С),
находим
огвых = NJ4RC = адэ/2,
где Д/э = 1/2RC — эффективная шумовая полоса цепи RC.
Полезный сигнал на выходе рассматриваемого фильтра
t
«вых (0 = $ T)s(x)dT,
о
где
,.„_Г аехР(—а0» а= 1/7?С,
[ 0 при /<0.
В результате несложных вычислений находим
«вых (0 = U (1-е-“9- lo(1 10 (/-ти),
где
••«={ о,
/>о,
/<0,
— единичная функция.
Нетрудно видеть, что. значение IsBHX(/)]mai имеет место при
i = ти, т. е. в момент окончания входного импульса:
[«вых (О^тах = «вых(ти) = t/(l ~~ е—ти^£).
425
В соответствий с этим '"максимальное отношение сигнал/шум на
выходе
д [£вых (Q]max ~У2 U । —2Д?8ти )
агых Д/А'о А/э
Для определения зависимости между длительностью импульса ти
и оптимальной эффективной шумовой полосой Д/э opt необходимо
вычислить производную от а по А/э:
С/[ 2ти Д/Г1'1+ -Ьд/(1 —е Ч'.
d (А/э) У No L 2 J
Приравняв эту производную нулю, получим
тиДА> opt = (1/2) In [4тиД/э Opt 4-1],
откуда
Д/э opt = 0,628/ти.
При этом максимальное выходное отношение сигнал/шум
«шах = 0,9Г2£/2ти/7Уо = 0,9У2ЁГйо,
где Е — и2ти — энергия входного видеоимпульса.
3. ЗАДАЧИ И ОТВЕТЫ
14.1Ч На вход фильтра поступает аддитивная смесь х (/) —
= s(t) + n(t), где п(/) — стационарный нормальный белый шум
со спектральной плотностью
Sn(<o) = А/0/2, — оо < со < оо;
s(t) — взаимно не коррелированный с n(t) стационарный гауссов-
ский случайный процесс со спектральной плотностью
д ®+®с
<ос
д ®с—®
®С
—ci)c ^®<0,
О ® < ©с,
$.(©) =
О при других (0.
Найти комплексную частотную характеристику (/<о) физиче-
ски нереализуемого линейного сглаживающего фильтра, миними-
зирующего среднйй квадрат ошибки фильтрации
еа = Л4 -s(012}.
Ответ:
=----^(1~1«>1/«>с)—
ои Л(1-|<о|/®с)'4-АГ./2
426
14.2. На вход фильтра поступает аддитивная смесь статистиче-
ски независимых случайного процесса s (/) со спектральной плот-
ностью - • ‘
Ss(<o) = 1/(1 + со2), — оо < со < ОО,
и стационарного гауссовского белого шума п (/) со спектральной
ПЛОТНОСТЬЮ
Sn(co) = Л/о/2, -— оо < со < оо.
Определить комплексную частотную характеристику <ЙСо(/со) оп*
тимального физически реализуемого линейного сглаживающего
фильтра и вычислить соответствующий ему минимальный средний
квадрат ошибки
в2 = Л4{[^(0- s(/)l2} = «min-
Ответ'.
82. =3_Г1 _^L_£HAol
™ ' 1-НсоТ’ min 2 L 14-Т 2Г J’
где
лу = —------— 2 -------— Т = \f —.
° yj^+2[VWo+2+ VaU V No+2
14.3. Случайный сигнал имеет корреляционную функцию
Rs(r) = ехр(— а|т|).
Найти для такого сигнала .импульсную характеристику h0(t)
линейного физически реализуемого прогнозирующего фильтра,
если спектральная плотность шума
Sn(co) = 4/(4 + со2).
Ответ: h0 (t) = ——— е~(/+д\
1 + V2
где А — время прогнозирования.
14.4. Решить задачу 14.2 при условии, что спектральные плот-
ности сигнала и шума соответственно равны
Ss(co) = —-—, Sn(a>) = , — оо < со < оо.
Л ’ 1+ <оа ’ р2+ша’
Ответ:
зс (Р+1)(Р+н А _ 1 Г 2Р^+Р2
oU ' (2₽а»+1)М+1)(Л-Нй>)’ V 2р<та + 1 •
14.5. На вход оптимального прогнозирующего линейного филь-
тра с комплексной частотной характеристикой миними-
зирующей средний квадрат ошибки
88=?A4{^(0-s(/ +А)12},
427
воздействует аддитивная смесь взаимно коррелированных стацио-
нарного шума n(t) и сигнала s(t) : x(f) = s(t) + n(t).
Определить взаимную спектральную плотность Sxy (со) про-
цесса x(f) и выходного процесса y(t) = s (t).
Ответ: Sxy(<») = ISs(co) + Ssn(co)]
14.6. Найти комплексную частотную характеристику Л*о(/®)
оптимального физически реализуемого прогнозирующего фильтра,
на вход которого поступает аддитивная смесь статистически неза-
висимых стационарного гауссовского белого шума n(t) со спектраль-
ной плотностью
Sn(<o) = Nq/2, — оо < © < оо,
и стационарного случайного процесса s (t) со спектральной плот-
ностью
2ап2
а2+со2
— оо < (!) <оо.
Ответ'.
4аа2 р— аД
ЛГ0(/«>)=----?--------------,
No (a+T)(?+/w)
4асг2 + No а?
~No
14.7. Определить комплексную частотную характеристику 3?о(/<о)
оптимального физически реализуемого линейного сглаживающего
фильтра при поступлении на его, вход аддитивной смеси взаимно не
коррелированных сигнала s(f) и помехи n(t), спектральные плот-
ности которых соответственно равны
Ss(©) = —, Sn(®) = —, — оо< ® <оо.
Л ’ а2+<о2 nV ’ fl2 + <B2
_ мл,- \ 2асг2 (а+ fl) (₽+/©)
Ответ: ^0(/®) =-----5------------
с2(а+у)(у+/<»)
где
с2 = 2ао| + 2ро^, у = ]/ 2оф2 os2 + 2а2 (ton/c.
14.8. При тех же условиях, что и в задаче 14.7, определить
комплексную частотную характеристику оптимального прогнози-
рующего фильтра.
Ответ: ЛГ0(/®)
2aaa(a-f-fl)(P+/a>)
с8 (а+ у) (у +/<в)
где А — время упреждения;
с2 = 2асг2 4- 2ра„, у=]/2afl2 <rs2 -|- 2а2 floj/c.
428
14.9. На вход оптимального линейного фильтра с комплексной
частотной характеристикой ^0(/со), минимизирующей средний
квадрат ошибки
в2 = М {[t/(0 — ds(i)/dt]z}, (14.28)
воздействует аддитивная смесь x(t) — s(f) + n(t), где s(t) и
n(0 — взаимно коррелированные стационарные случайные про-
цессы со спектральными плотностями Ss(co) и Sn(co).
Определить взаимную спектральную плотность Sxy(co) вход-
ного процесса x(t) и процесса y(t) на выходе фильтра.
Ответ1. Sxy(<a) = /co[Ss(co) + Ssn(®)l,
где Ssn(co) — взаимная спектральная плотность процессов s(t) и
n(t).
14.10 . Применительно к условию задачи 14.9 вычислить мини-
мальное значение среднего квадрата ошибки (14.28).
Ответ [4]:
f {®2Ss(®) — [5s(®) + Sn(®)4-Ssn(®)-|-
2л J
+s:„(®)n^0(/®)i2}d®.
14.11 . На вход физически реализуемого линейного фильтра,
минимизирующего средний квадрат ошибки (14.28), воздействует
аддитивная смесь статистически независимых стационарных слу-
чайного процесса s(t) со спектральной плотностью
Ss(co) = Л/[4а2 + (202 — со2)2], — оо < со < до,
и гауссовского белого шума п (/), для которого
Sn(®) = N0/2, — оо < со < оо.
Определить оптимальную комплексную частотную характери-
стику с%*о(/<о) фильтра и вычислить минимальное значение emin-
Ответ [4]:
^о(/(0)=_М_/---------------------------e>+m-jn----------
2mN9 1, [т + /(я+я1)12— mi (a—mi—jnd (co+mi—jni)
__ —m-^-jn co—m—jn________|
[m—j(«+«i)]2— (a—mj.—jni) (co-|-mi—№) J ’
где
m = + n=K/F+ai—P2.
429
4 t n itfiNo L n \'»4'j5/JJ
q _____________m + jn_________
[m*——(n+»i)2]—2/m (n+«i)
14.12 . Процесс y(t) представляет собой аддитивную смесь вза-
имно не коррелированных стационарных случайных процессов
s(t) и n(t):
y(t) = a[s(t) +
Определить значение постоянной а, минимизирующей средний
квадрат ошибки
82 = — s(t + А)Р},
и вычислить значение emin. Спектральные плотности процессов
s(t) и n(t) соответственно равны
S.(*>)
2аа2
a2+ со2 ’
sn(<0)
Р2+ <о» ’
--00<(0-<00.
Ответ:
а=---------5—е~аД,
°s е-2аД
8m in — I 1
14.13 . На вход оптимального сглаживающего фильтра, миними-
зирующего средний квадрат ошибки
82 = М {[y(t) - S(/)12},
воздействует аддитивная смесь x(t) = s(t) + n(t), где n(t) —
стационарный нормальный белый шум со спектральной плотностью
Sn(<o) = Nnl%, — оо < со < оо;
статистически независимый от шума сигнал s(t) Образуется про-
пусканием стационарного нормального белого шума %(t) со спек-
тральной плотностью
Sg(<d) = N^/2, — оо < со < оо,
через интегрирующую цепочку RC (рис. 14.4).
Определить минимальное значение среднего квадрата ошибки
сглаживания emin-
Ответ:
8mln —
a*
aNl_ j
4
где
a = URC, аъ = У6/Уп.
14.14 . На вход оптимального прогнозирующего (экстраполирую-
щего) фильтра, минимизирующего средний квадрат ошибки
в2 = Af{[f/(O — s(/ + А)]2},
430
Рис. 14.7. Когерентный приемник
I
воздействует аддитивная смесь x(t) = s(t) + n(t), где s(t) и
п(0 соответствуют условиям задачи 14.13.
Определить минимальное значение среднего .квадрата ошибки
экстраполяции е^нп-
Ответ:
a aNl fi а2е—2аЛ
®min — ————— 1
4 [ (1 + у 1+72)2 J’
а = 1/RC, а2 = Л^/ЛУ
14.15 . Ha вход когерентного приемника амплитудно-модулиро-
ванных сигналов, состоящего из перемножителя и фильтра ниж-
них частот (рис. 14.7), поступает аддитивная смесь x(t) = s(f) +
•+ n(t), где n(t) — стационарный нормальный белый шум со спек-
тральной плотностью
Sn(®).= N0/2, — оо < со < оо;
s(f) = P<2P/n(f)sin(®0f + q>)
— статистически не .зависящее от n(t) амплитудно-модулированное
колебание с подавленной несущей. Здесь соо — угловая частота не-
сущей, ср — случайная начальная фаза, равномерно распределен-
ная на интервале (— л, л), m(t) — стационарный гауссовский слу-
чайный процесс со спектральной плотностью
Sm(co) = 2а/(а2 + со2), — оо < со < оо.
На второй вход перемножителя подается опорное колебание
«оп(0 = + q>).
Определить комплексную частотную характеристику ^*0(/®)
фильтра нижних частот, минимизирующую средний квадрат ошиб-
ки
е2 = М{[г/(0-/п(012},
и вычислить значение е2цп.
Ответ [92]:
ЗД») =
(а—1)а
аа+/а> 9
а =
4Р
aNo
81. - 2Р
8m,n“ а + 1 •
431
Рис. 14.8. Трапецеидальный видео-
импульс 4
• 14.16. Найти импульсную характеристику h0(t) согласован-
ного фильтра для сигнала
5(0 =
А,
0,
0</<оо,
/<0.
Л «, /А ( Л
Ответ: h0(t) = 1
ov I 0, t<Q.
14.17. Определить импульсную характеристику hQ(t) согла-
сованного фильтра для сигнала s(f) = /lmsincoo/, если на интер-
вале (0, Т) укладывается нечетное число полупериодов.
„ I./а Г AnSin®./, 0</<ОО,
Ответ: h0(f) = l т 0
I 0, /<0.
14.18. Найти согласованный фильтр для трапецеидального видео-
импульса (рис. 14.8)
s(0
2Д
Т — Ti
где единичная функция
/>0,
/<0.
Ответ [82]:
^оО) = -^7 [1 ~ехр [1 —ехр (—./©
Т Т1 [_ \ A j \ /
\ X / \ At / J
432
14.19. Найти импульсную характеристику hQ(t) согласован-
ного фильтра для видеосигнала s(t), имеющего параболическую
форму:
f Л[1—(2//т)2], —т/2</^т/2,
t 0, | /|>т/2. .
Ответ [82]: й0(/) = -Ш—£-.!„(/) + ^-Мо(/) +
Т 2 2 2
X 10(*— т) + ~T(t—T)-l0(t—т) .
14.20. Видеоимпульс s(t) (рис. 14.9) описывается функцией,
составленной из трех отрезков парабол таким образом, чтобы пер-
вая производная s (/) была непрерывной:
' 4А т(т—тх) /2, 2
Л Г1 — — —-У], т—<,i т+п
«(0 = L ТТ1 \ 2 / J 2 " 2
4А (/-т)2,
t (Т—Т1) 2
. 0, /<0, />т.
Определить согласованный фильтр для такого импульса.
Ответ [821:
/го(/)=Т7Г7г{т,1°(0+'Г
Т (Т ““* TjJ 2 Tj
т —тА2
2 J
°\ 2 7 2 V Ч j \ 2 7J 2 ov J
14.21. На вход оптимального линейного фильтра, максимизи-
рующего отношение сигнал/шум на выходе, воздействует полезный
сигнал
s(/) =
' t,
2а—t,
. о,
0 < t < а,
а^Л<2а,
/<0, t^2a
433
и белый шум со спектральной плотностью
Sn(co) = No/2, — оо < со <Z оо.
Найти комплексную частотную ^0(/®) и импульсную h0(t) ха-
рактеристики фильтра.
Ответ:
Я?о(/со) = —(1 _е-/™)2е-/“г,
(О2
МО =
t—(T—2a),
T—t,
T—2a^t<T—a,
T—a^t<T,
t<T—2a, t>T.
14^2. Найти сигнал s2(i) на выходе фильтра, согласованного
с входным сигналом
Ответ:
sx(0 =
А,
О,
0^/<ти,
t<0, t>xB.
s,t} = \ KA*(t-T+xn), T-xa^t<T,
2 -I— KA*(t—T—ти), T^t^T+xB. ’
14.23. На вход линейного фильтра воздействует аддитивная
смесь x(t) = s(t) + n(t), где
S(/) = J Л- °<^ти,
[О, *<0, t>xB
— прямоугольный видеоимпульс длительностью ти; п (t) — ста-
ционарный гауссовский шум со спектральной плотностью
Sh(®) = 2аа/(а2 + со2), — оо < со < оо.
Найти комплексную частотную характеристику <%*о(/со) филь-
тра, максимизирующего выходное отношение сигнал/шум.
Ответ [82]: с%*о(/со)= ^oU**2//®) — /®] (1 —е-/МТи).
14.24. Решить задачу 14.23 для случая приема прямоуголь-
ного видеоимпульса на фоне стационарного шума со спектральной
плотностью
Sn(®) — 2асо2/(а2 + со2), 0 со < оо.
Ответ[82]: Я?о(/со)=^Ц1---------(1 — е~/<оти).
/® L (j®)2 J
14.25. Найти комплексную частотную ^о(/®) и импульсную
h0(t) характеристики оптимального фильтра, максимизирующего
отношение сигнал/шум на выходе, если на вход фильтра поступает
аддитивная смесь статистически независимых сигнала
s (0 = Лехр(— /2/4а2)
434
Рис. 14.10. Последовательность
прямоугольных видеоимпуль-
сов
и шума со спектральной плотностью
Sn(<o) = 2VoexP (— Р2®2),
причем р а.
Ответ:
XJja) = ехр[— (а2 — р2)®2 — /®Т],
h0(t) = ^*0 ___е хр Г— (<~Т)8' .
Уа2 —Р2 [ 4 (а2—₽2)J
14.26. Определить комплексную частотную характеристику'
^0(/®) оптимального линейного фильтра, обеспечивающего маю-
симально возможное отношение сигнал/шум на выходе, если на
вход фильтра поступает аддитивная смесь статистически независи-
мых полезного сигнала в виде последовательности из т прямоуголь-
ных видеоимпульсов (рис. 14.10) и белого шума со спектральной -
плотностью
Sn(®) = N0/2, — оо <; ® <; оо.
Ответ:
= - ° ------(е/ити_1)е-/«>Л
/® l-e'^n
14.27. Найти комплексную частотную характеристику
согласованного фильтра, максимизирующего отношение сигнал/шум,
если в качестве полезного сигнала принять радиолокационный сиг-
нал, представляющий собой пакет (пачку) из т прямоугольных им-
пульсов, амплитуда которых изменяется в соответствии с формой
диаграммы направленности РЛС (рис. 14.11).
485
Ответ:
J5Co(/(o) = [«! + а2 е/<оГп+... + am eMm~1 )Гп] (е/тти_ 1) e- /«or
/®
14.28. Определить максимальное значение отношения сиг-
нал/шум на выходе устройства, изображенного на рис. 14.12, при
воздействии на него аддитивной смеси статистически независимых
белого шума n(i) со спектральной плотностью
Sn(co) = N0/2, — оо < со < оо,
и сигнала s(t), имеющего вид изображенной на рис. 14.13 последо-
вательности элементарных фазоманипулированных прямоугольных
видеоимпульсов с равными амплитудами А и длительностями ти:
s(0 = Л[ 1 о(0 - 2-10(/ - Зти) + 2 -10(/ - 4ти) -
— 10(/—5ти)1.
Выходной фильтр согласован с элементарным импульсом и имеет
импульсную характеристику
й0(/) = [ А (ти—0» 0 < t < ти,
[ 0 при других t.
Ответ: а ~ [8ВЫХ (Olmax/^вых = Nд,
где Е = 5Л2ти — полная энергия сигнала.
14.29. На вход линейного фильтра, изображенного на рис. 14.14,
подается аддитивная смесь статистически независимых стационар-
ного гауссовского белого шума и сигнала s(t), представляющего
собой пять следующих друг за другом элементарных прямоуголь-
ных импульсов с равными амплитудами Л и длительностями ти
(рис. 14.15). Отводы от линии задержки соответствуют временным
задержкам /Зад = 0,4ти, 5ти, 9ти, 10ти и 14ти. Выходной фильтр
согласован с элементарным импульсом (см. задачу 14.28).
Определить максимальное значение отношения сигнал/шум на
выходе фильтра.
Рис. 14.12. Согласованный фильтр
Рис. 14-13. Последовательность
биполярных прямоугольных
видеоимпульсов
436
Рис. 14.14. Неоптимальный фильтр
Ответ'.
ц — [Звых (Отах 1 36 2ЕИ
<^вых V 28 N о
где Ея — Л2ти — энергия элементарного импульса.
14.30. На вход одиночного колебательного контура с комплекс-
ной частотной характеристикой
•%*(/со) = 2асо/[2асо + /(со2 — соо)] .
воздействует аддитивная смесь x(t) ?= s(t) + n(f), где n(f) —
стационарный гауссовский белый шум; s(t) — статистически не-
зависимый от шума прямоугольный радиоимпульс длительностью
ти, несущая частота которого совпадает с резонансной частотой кон-
тура <оо.
Определить оптимальное значение полосы пропускания A/opt
контура, при котором выходное отношение сигнал/шум достигает
максимума.
Ответ: Afopt = 0,4/ти, атах = 0,9К<7.
где А/ — полоса пропускания на уровне 0,5 по мощности; q =
= 2E/Nq — входное отношение сигнал/шум.
14.31. Решить задачу 14.30 для случая воздействия аддитивной
смеси прямоугольного радиоимпульса и белого шума на идеальный
фильтр с прямоугольной амплитудно-частотной и нулевой фазовой
характеристиками:
^(/со) =
^0, —®о—Аф/2^о)^—соо-|-Д®/2,
^0, ®о—Аф/2 со соо 4- Дсо/2,
О при Других о.
Ответ: kfovi-= 1,37/ти, czmax = О,91]Л<7-
Рис. 14.15. Последовательность примыкаю-
щих прямоугольных видеоимпульсов
437
14.32. Решить задачу 14.30 для случая воздействия аддитивной
смеси прямоугольного радиоимпульса и белого шума на гауссов-
ский фильтр с комплексной частотной характеристикой
2 1
I — •
СО — too
Дсо
Ответ: A/opt = 0,72/ти, amax = 0,94K<7-
14.33. Вычислить максимальное значение отношения сигнал/шум
на выходе фильтра с прямоугольной амплитудно-частотной харак-
теристикой
^•(/со) = z^oexp —1,4
'^о, — ®о — Aco/2sgkoC — ®о + Асо/2,
= . ;%•#, (оо—Асо/2^со^соо-|-Асо/2,
0 при других (О,
при воздействии на его вход аддитивной смеси статистически неза-
висимых белого шума и гауссовского радиоимпульса
s(t) = Лехр[— 2,8 (//ти)2 + /<ооД.
Определить оптимальное значение полосы пропускания фильтра.
Ответ: A/opt = 0,72/ти, amaX = 0.94W
14.34. Решить задачу 14.33 для случая воздействия аддитивной
смеси белого шума и гауссовского радиоимпульса на гауссовский
фильтр. _______________________________
Ответ: A/opt = 0,63/ти, ат&х = У q.
14.35. На вход фильтра, согласованного с прямоугольным радио-
импульсом s(t) длительностью ти: j
s(t) — Amcos<o0t, 0 t ти,
(Лт, со о и ти—постоянные величины), воздействует аддитивная
месь статистически независимых^ сигнала ^s(t) и стационарйого бе-
лого шума n(t).
Определить отношение сигнал/шум a(t) = С/вых(/)/<УВЫх(О> гДе
с(7Вых(0 — огибающая сигнала на выходе фильтра, <гВЫх(0—
среднее квадратическое значение выходного шума, в конце импуль-
са (t — ти) для следующих случаев:
1) сигнал s(/) и шум n(f) начинают воздействовать на фильтр
одновременно с момента t — 0 (случай точного временного строби-
рования импульсного сигнала, принимаемого на фоне белого шума);
2) шум n(f) начинает воздействовать на фильтр с некоторым
опережением А/ по отношению к сигналу s(t);
3) шум n(t) воздействует на фильтр с момента t-*~ — со, а сиг-
нал s(f) — с момента t = 0 (случай отсутствия временного строби-
рования).
Ответ: 1) а(ти) = Уд, 2) а(ти) = Уд, 3) а(ти) = Уд.
q = 2Е/Л/0, Е = ЛЛти/2.
14.36. На вход колебательного контура с комплексной частот-
ной характеристикой
УС (/со) = 2асо/[2асо + / (со2 — ©8)1
438
воздействует аддитивная смесь статистически независимых прямо-
угольного радиоимпульса «(/) длительностью ти и стационарного
белого шума n(t).
Определить отношение сигнал/шум а(ти) в конце импульса для
случаев, указанных в задаче 14.35. Для случая отсутствия времен-
ного стробирования определить оптимальное значение полосы про-
пускания Afopt» при которой а(ти) = атах.
Ответ:
1)
V лД/ти у 1 —ехр (2лД/ти)
1 —ехр (—лД/ти) ,
лД/ти у 1 — ехр [2лД/ (ти + Д/)]
3) . а(Ти) = /^1/" —J— [1— ехр (— лА/ти)], Afopt
у лД/Tjj
2) а(ти)=/<7 -1/
Графики функции а(ти) = /(А/ти, \f\t) приведены на рис. 14.16.
14.37. Решить задачу 14.36 для случая воздействия аддитив-
ной смеси сигнала s(0 и белого шума на идеальный полосовой фильтр
с комплексной частотной характеристикой
О
—©0—А©/2 —(оо 4-А©/2 ,
ю0— А©/2 ®04- Д©/2,
при других ©.
Ответ:
1) 2Si(»afa/2)
VSK 1/ siMK)~ “"'‘"/У ’ '
У лД/ти/2
где
Si(z)= filidx
J X
о
— интегральный синус;
2) я(ти) —
__2 81(лД/:ти/2)_____________________________________________________ф
гмк |/ s. Г м, (-f- у 1 _ у + "И ’
у L \ 2 /J лД/(ти/2 + Д/)
3) о(т.) - Vq Si Л/та1 _ у..
Я г \ 2 ] Ти
Графики функции а(ти) = ДА^ти, А/А/) представлены на рис. 14.17.
439
Рис. 14.16. Отношение сигнал/шум на
выходе колебательного контура
Рис. 14.17. Отношение сигнал/шум на
выходе идеального фильтра
14.38. Решить задачу 14.36 для случая воздействия аддитивной
смеси сигнала s(t) и белого шума на фильтр с комплексной частот-
ной характеристикой
{еХр[-(^у1+ехрГ-(-^
I L \ Р / J L \ р
Ответ:
1)
а(ти) =Vq
Уь
2) а(ти) =Vq Гф(—-------------------1 [ф(—+
/Г L \ 2/2 ) 2 J L \ 2
лД/Д/ \
/047 /
L]“1/2
2
3)
л(ти)=г?-Ц?-|ф(-
Vb L к
~ /67347 ’
b______1_\1
2/2 2 /]’
.. 0.72
^/opt --
ти
Значения а(ти) приведены на рис. 14.18.
14.39. На вход фильтра, согласованного с прямоугольным ра-
диоимпульсом s0(f) длительностью ти:
S0(f) = ЛтС08С00/, 0 < t ти,
440
Рис. 14.18. Отношение сигнал/шум на
выходе гауссовского фильтра
(Лто, (Os и ти — постоянные величины), воздействует аддитивная
смесь x(t) = s^t) + n(t), где n(t) — стационарный белый шум,
s^t):— статистически независимый от шума прямоугольный радио-
импульс длительностью ти:
s^t) = Amcos<o^, 0 t ти,
частота которого <0j отлична от частоты сигнала s0(/)( — (оо| =
= Д(Ор < (Оо).
Определить отношение сигнал/шум a(t) на выходе фильтра в
конце импульса s^t).
Рис. 14.19. Зависи-
мость отношения
сигнал/шум на выхо-
де согласованного
фильтра и колеба-
тельного контура от
обобщенной расст-
ройки
441
Ответ [93]:
Фи) = Vq Si"(^;/2) ДЙР=А®рТи.
/Лййр/^
График функции а(ти)/]/q = /(Дйр) представлен на рис. 14.19
(штриховая линия).
14.40. На вход колебательного контура-с комплексной частотной
характеристикой
= УС 02а®/[2а<о + /(<о2 — ®о)]
воздействует аддитивная смесь x(f) = s^f) + n(t), где n(t) —
стационарный белый шум,
s^t) — ЛтСОЗац/, 0 t ти
— статистически независимый от шума прямоугольный радиоим-
пульс длительностью ти, частота которого отлична от резонанс-
ной частоты контура (Icoj— соо1 = Асор ®о)*
. Определить отношение сигнал/шум a(t) на выходе контура в
конце импульса s^t).
Ответ [93]:
а(Ти) = Vq I f оат 1-2е-атисо5ДОр+е-2оти
V Ч |/ 2ати (aTn)2+AQ2
Значения функции q — ати) приведены на
рис. 14.19. "
Рис. 14.20. Зависи-
мость отношения сиг-
над/шум на выходе
идеального фильтра
от обобщенной рас-
стройки
442
14.41. Решить задачу 14.40 в случае воздействия суммы x(t)
на фильтр с комплексной частотной характеристикой
'^•о,
#о,
0
^•(/©) =
— ©0—Д®/2^®^ —®0 + Д©/2,
®0— Д®/2 ^ © ^ ®0 + Д©/2,
при других ®.
Ответ [93]:
j _ i Г (Дмти/2-|~ ДЯр/2) 4~Si (Д<оти/2—AQp/2)
4 V п /дя^
Графики функции й(ти)/]/q = /(Дйр, Дшти) представлены - на
рис. 14.20.
14.42. Решить задачу 14.40 для случая воздействия суммы х (t)
на фильтр с комплексной частотной характеристикой
ад - X. I ехр Г -+ехр Г - -^^-П.
V L Р - J L Р J
Ответ [93]:
а(ти) = Vq 1/^—J ехр fx2 j cos (Дйрх) dx.
v o' '
Графики функции а(ти)/)Л7 — /(Л&р, ₽ти) представлены на
рис. 14.21.
443
15. ОБНАРУЖЕНИЕ И РАЗЛИЧЕНИЕ СИГНАЛОВ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При рассмотрении помехоустойчивости различных радиотехнических
систем следует различать две группы задач.
1. Заданы статистические характеристики сигналов и помех и струк-
турная схема приемного устройства. Требуется определить количественные
характеристики помехоустойчивости приема данных сигналов данным прием-
ником.
2. Заданы статистические характеристики сигналов и помех и характер
их взаимодействия. Требуется определить структуру устройства, осущест-
вляющего оптимальную, по определенному критерию, обработку смеси сиг-
нала и шума, и вычислить соответствующие количественные характеристики
помехоустойчивости оптимального приема данных сигналов.
Задачи первой группы по существу сводятся к анализу воздействия на
данное радиотехническое устройство заданной смеси сигнала и шума. Ко-
нечной целью анализа является вычисление статистических характеристик
случайных процессов на выходе приемника, необходимых для последующего
определения требуемых количественных характеристик помехоустойчивости.
Задачи этой группы решаются рассмотренными в предыдущих главах метода-
ми анализа воздействия случайных процессов на линейные и нелинейные
звенья радиотехнических устройств.
Для решения задач второй группы необходимо использовать аппарат
теории статистических решений [1, 27, 94—98].
Предположим, что на вход приемного устройства поступает смесь сиг-
нала и шума
х(0= F[s(t), ё(/)], (15.1)'
где s(t) — полезный сигнал; |(/) — помеха. Функция F [s, |], т. е. харак-
тер взаимодействия сигнала и помехи, а также статистические характери-
стики шума |(/) и сигнала s(t) предполагаются известными.
Применительно к случаю различения т сигналов, принимаемых на фоне
помех, входящий в (15.1) сигнал s(t) можно представить в виде суммы
S(O = S(Z, X) = 2 Mi (л /(1°, 4°..4°)» (15.2)
i— 1
где Xf — параметр, определяющий, какой из сигналов st(t) = Si(t, /р,
•••, 4^) присутствует на входе приемника в данный момент времени;
— параметр сигнала Sf(Z), v = 1, 2, ..., k. Параметр Х^ представляет со-
бой случайную величину, принимающую на интервале наблюдения (О, Т)
значения Х^ = Х/о = О либо X/ = Хц = 1, причем если Х^ = Х^ = 1,
то все остальные входящие в (15.2) параметры Xj с индексом / =/= i равны ну-
лю: Ху = Ху0 — 0. Приемник, осуществляющий различение т сигналов, дол-
жен определить, какой из коэффициентов Xf равен единице, т. е. какой из
сигналов Si(t) присутствует в принятом колебании x(t).
В дальнейшем ограничимся рассмотрением лишь случая различения двух
сигналов sx(/) и s2(Z), принимаемых на фоне помех. При этом сигнал (15.2)
может быть представлен в виде
s(Z) = s(Z, l)=%S1(ZJp>, /“>, /g’)+ (1-%)s2(Z,/<*>,/<*>...Ф’).
(15.3)
Здесь X — параметр, случайный образом принимающий два значения: X =
= Хг = что соответствует наличию в принятой реализации x(t) сигнала
$i(Z), или X — Хо — 0, когда в реализации x(t) присутствует сигнал s2(/).
Представление сигнала s(t) в форме (15.3) характерно для различных систем
444
передачи двоичной информации, широко используемых в связи, телеметрии,
телеуправлении и Jr. п. '
Применительно к случаю обнаружения сигнал s(t) представляется в виде
s(t) = s(t, %) = %sx(Z, Z2................Zft). (15.4)
Значение параметра % = = 1 соответствует наличию на входе приемника
смеси сигнала и шума, % = %0 = 0 означает, что на входе приемника имеет-
ся только шум. Приемник, предназначенный для обнаружения сигналов,
определяет, какое значение на данном интервале наблюдения (О, Т) имеет
параметр Z, т. е. представляет ли принимаемое колебание x(t) только шум или
смесь сигнала и шума.
В соответствии с теорией статистических решений принятие гипотезы
% = или % = %0 должно основываться на результатах анализа отношения
правдоподобия. При дискретной обработке реализаций это отношение имеет
вид
Л[х (/)] =Рп(Х1, х2, ..., хп I %1)/Рп(-К1. X.. I %о)> (15.5)
гдерп (хх, х2, хп | Хх) и рп (хх, х2, ...» хп|%0) — n-мерные плотности распре-
деления вероятностей выборок хь = x(tk) процесса x(t) соответственно при
гипотезах А, = и % = %0. Рассматриваемая как функция параметра %,
условная плотность распределения вероятностей рп(х12 х2, ...» хп | %) обозна-
чается через L(Z) и называется функцией правдоподобия.
В случае непрерывной обработки реализации х (/) отношение правдопо-
добия
Л[х(01 = fix (О I M/flxW IМ. (15.6)
где
W)IM= Hm Pn(xi,x2..........xn|l) (15.7)
П-+ОО
Д->0
— так называемый функционал плотности распределения вероятностей.
Здесь Д = tk — временной интервал между соседними выборками
Xfe = %) и Xk+i = %). Рассматриваемый как функция от
параметра %, он называется функционалом правдоподобия и обозначается
через Г(%).
Следует отметить, что конечный предел, определяемый соотношением
(15.7), не существует. Можно показать [96], что в правую часть равенства
(15.7) входит множитель k — &(Д), не зависящий от выборки х12 х2, ...» хп,
но зависящий от Д'так, что при Д О k -> оо. Однако в результате того, что
неопределенный множитель k не зависит от xlf х2, ...» хп, имеется возмож-
ность вычислить конечный предел отношения (15.5):
lim Рп(*1, Х2, , Хп | %t) = f [X(Q IM (15
П-»оо рп (Хх, Х2, . . . , Хп I %0) f[x(0IM
Д->0
Наиболее просто функции правдоподобия рп(х12 х2, ...,.xn[%)= L (%)
вычисляются в том случае, когда x(t) представляет собой аддитивную смесь
сигнала s(Z, %), зависящую только от одного случайного параметра %, и шума
КО:
x(Z) = s(Z, %) + |(Z). (15.9)
В этом случае [96]
Рп(х* х2...xn|%)=L(%) =pnt[*i (А,), х2—s2(%), ...» хп—$n(%)],
(15.10)
где pnt(li, |2, ...» |n) — n-мерная плотность распределения вероятйостей
шума | (/); Xk = х (/&); Sk (%) = s (Zft, %). Переходя в (15.10) к пределу при
А = tk+i — tk —> 0, получаем
F[x(Z)|%] = F (A,) = Fg[x(Z) — s(Z, %)]. (15.11)
445
В более общем случае полезный сигнал может зависеть не только от па-
раметра X, называемого существенным, но и от ряда несущественных случай-
ных параметров 12, ..., Ik. При этих условиях и функционал плотности рас-
пределения вероятностей F|[x(Q — s(C X, 1%, ...» /&)] оказывается зави-
сящим от несущественных сучайных параметров и для определения функцио-
нала правдоподобия (t) |Х] требуется его усреднение по несущественным
параметрам:
F[x(t) | %] = Г (%) =/...] - s(f, X, h ,lt.....Ik)] X
—oo —oo
Xpfe(/j, l2, .... Zft)dZ1<ZZ2...dZft. (15.11a)
Здесь, Pk(li, ...» Ik) — совместная плотность распределения вероятностей
несущественных параметров llt 12, ...» Ik•
Если |(/) представляет собой гауссовский случайный процесс^ нулевым
математическим ожиданием т^(/) = 0 и корреляционной функцией t2)=
— Af{[|(4) — ^(4)][|(4) — т0 ег0 n-мерная плотность распределе-
ния вероятностей определяется формулой
Mil. |2, • • •. In) = X
(1 п п р t \
p, = lv=l /
Здесь о* = (/ц) = М — mf (*ц) — дисперсия случайной величины
1 Г12 • • • Гщ
Д __ Г21 1 ‘ Г2П
ГП1 ГП2 • * ‘ 1
—определитель n-го порядка, составленный из нормированных взаимных кор-
реляционных функций = г (/ц, tv) = /?£ (/ц, ^v)/%^v; ДЦ¥ — алгебраи-
ческое дополнение элемента r^v определителя Д. Переходя в (15.12) к пределу
при А = tk+i — tk ->• 0, получаем следующее выражение для функционала
плотности распределения вероятностей гауссовского случайного процесса
* т т
~~ J I
О о
(15.13)
^[|(0]=^ехР‘
где 0(4, 4) определяется интегральным уравнением
т
f Z?g(Z1’т)°(т’ *2)dt = S(Z2-Zi)- (15.14)
О
Иногда удобно преобразовать (15.13), введя-функцию
т
<P(Z)=fl(Zi)O(Z, tjdt!. (15.14а)
О
При этом получим
Fg[|(Z)]=Kexp
1 Г
J KO<p(Z)dZ .
(15.13а)
4^6
где функция q> (/), как это следует из (15.14) и (15.14а), удовлетворяет инте-
гральному уравнению Фредгольма первого рода:
(15.146)
т
J R^t, т)ф(т)с!т=5(0, 0</<T.
0
Предположим, что %(t) представляет собой гауссовский белый шум с ну-
левым математическим ожиданием m^(t) = 0 и корреляционной функцией
R£t, t2) = Л4{5(^ |(/2)} = (^2)б(/, - 4). (15.15)
Подставляя (15.15) в (15.146), находим, что
ф(0 = (2/Уо)5(0,
в соответствии с чем для функционала Плотности распределения вероятностей
белого шума получаем следующее выражение:
т
U*(t)dt .
N“ 0J -J
(15.16)
^15(0] = «ехр
Аналогично находится функционал плотности распределения вероятно-
стей для гауссовского процесса |(/) с нулевым математическим ожиданием
m^(Q = 0 и корреляционной функцией
В этом случае [96]
г Г
т
(15.17)
% [|(0] = «ехр
a
4a|
Lo
о
1
2 1
(15.18)
Для гауссовского процесса |(/) с нулевым математическим ожиданием т* (0=
=0 и корреляционной функцией
^) ==ale~a Н cosсо1(/2—/х) + —sin (Ojl/2—/1| (15.19)
* * L J
имеем [96]
^[£(01 = « ехр
1 (Т т
f + a? f U(0]2^+
4а|ао®Ц^ J
т т
+ <0* J £2 (0 dz+2й§ J g (0 f (0 Л+<х0®? [£2 (0)+? (Л) +а0 [|2(0)-На(Л1
О о
(15.20)
где cog = (oJ4-a2, a0 = 2a.
Если в результате дискретной обработки принятой реализации x(t)
окажется, что отношение правдоподобия (15.5) превышает некоторую вели-
чину С, т. е.
д . _Рп (*1 > <^2 > * * * > *n I ^1) L (М)
Рп(*ь xn|X0)“L(M
принимается решение К = Zx. В противном случае принимается решение
X e
(15.21)
447
Принятие решения означает разбиение всей области Г возможных зна- '
чений Xi, х2, ...» хп на две подобласти Гх и Го. При попадании принятой вы-
борки xlf х2, хп в область Гх принимается решение % = Хх, а при попада-
нии хх, х2, ...» хп в область Го принимается решение % = Хо. Так как рп(хъ
х2, ...» хп|Хх) и pn(xlt х2, ...» *п|^о) определены по всей области Г, всегда
имеется вероятность того, что при X = Хо выборка хх, х2, ...» Хп попадает в,
подобласть Гх, или наоборот, при X = Хх выборка хх, х2, ..., хп попадает в
подобласть Го. Таким образом, при приеме реализации х(/) всегда имеется \
вероятность принять ошибочное решение % = Хх, тогда как в действительности
X = Хо, и наоборот. Эти условные вероятности называются соответственно
вероятностями ложной тревоги PF* и ложного отбоя PFq и определяются
соотношениями
Рр = Р (Хх I Хо) = У Рп (^i> *^2’ • v ’ хп I ^о) dx± dx2 • • • dxn, (15.22)
1 Tt
Ppo =P (%o I ^i) — f Pn x2> • • • > xn I ^i) dxi dx2 ... dxn • (15.23)
Го
Вероятности принятия правильных решений X = Хх или X = Хо называются
мощностью решения и обозначаются соответственно через PD и PDq:
PD1=P(Xx|Xx) = f Pn(xi> xn IM dx1dx2 ...dxn, (15.24)
rt
P= P (%o | %o) — j*Pn (*1, x2> • • • > xn I M dx± dx2 ... dxn. (15.25)
Го
Следует отметить, что условные вероятности PF и PFq не полностью
Характеризуют ошибки решения. Относительная частота появления этих
°шибок зависит от значений априорных вероятностей р(Хх) и р(Х0), т. е. от
того, насколько часто априори на входе решающего устройства появляется
сигнал, соответствующий X = Хх или Л — Хо. Поэтому в ряде случаев ошибки
решения характеризуются полными вероятностями ошибок первого Рх
и второго Р2 рода:
Pi=Р М PFo =Р (М Р (h I М, (15.26)
Р2=р (Хо) PF1 =Р (Хо) Р (Хх | Хо). (15.27)
Значения вероятностей ошибок зависят от правила принятия решения
(15.21) и определяются значением постоянной С. Естественно выбрать та-
кую постоянную, при которой правило (15.21) оказывалось бы в определен-
ном смысле оптимальным. В задачах связи, телеметрии и телеуправления в ка-
честве критерия оптимальности обычно используют критерий идеального на-
блюдателя (критерий Котельникова—Зигерта), совпадающий с байесовым
критерием минимального среднего риска при простой функции потерь, когда
ошибочному решению приписывается вес, равный единице, а правильному —
вес, равный нулю. Согласно этому критерию оптимальным считается соот-
ношение (15.21), минимизирующее суммарную вероятность ошибок первого
и второго рода
Р=р (ХП Р (Хо | Хх) +р (Хо) Р (Хх | Хо) . (15.28)
Можно показать [96], что это условие выполняется при С = р(Х0)/р(Хх),
в соответствии с чем оптимальное по критерию идеального наблюдателя пра-
вило принятия решения X = Хх принимает вид
L(Xx)/L(X0) > p(X0)/p(Xx). (15.29)
В случае непрерывной обработки реализации х (t) правило (15.29) преобра-
зуется к виду
F (М//7 (М > Р (&МР (М • (15.29а)
448
В задачах радиолокации широко используется другой критерий опти-
мальности, называемый критерием Неймана—Пирсона. Согласно этому кри-
терию оптимальным считается правило (15.21), максимизирующее вероят-
ность правильного решения PD (мощность решения) при заданной вероят-
ности ложной тревоги PF . Можно показать [96], что это условие выполняет-
ся при С — ht где h определяется по заданной вероятности ложной тре-
воги PF . Таким образом, оптимальное по критерию Неймана—Пирсона
правило принятия решения % == имеет вид
L(%i)/L(%0) > h (15.30)
или
F(Wo) > h. (15.30а)
Таким образом, решение сформулированных в начале параграфа задач
второй группы сводится к отысканию оптимального устройства, осущест-
вляющего обработку принимаемой смеси x(t) в соответствии с правилами
(15.29) или (15.30), и вычислению соответствующих вероятностей ошибоч-
ных решений.
В двух рассмотренных критериях предполагалось, что решение прини-
мается за фиксированный интервал времени длительностью Т. Однако в от-
дельных случаях принимаемая реализация x(t) может оказаться настолько
благоприятной, что надежное обнаружение или различение сигналов можно
произвести' значительно быстрее, чем в случае приема менее благоприятной
реализации. Поэтому, если заранее не фиксировать длительность Т наблюде-
ния, можно получить в среднем значительную экономию во времени обработ-
ки принимаемых реализаций x(t). Такое наблюдение, при котором длитель-
ность обработки x(t) заранее не фиксируется, а определяется самим ходом
эксперимента, называется последовательным наблюдением (последователь-
ным анализом) [99, 100].
При последовательном наблюдении производится непрерывный анализ
отношения правдоподобия и сравнение его с двумя порогами h± и h0 < hr.
Если отношение правдоподобия меньше /i0, принимается гипотеза % «= Хо.
Если же отношение правдоподобия Л[х(£)1 > Ях, принимается гипотеза
X = В том случае, когда отношение правдоподобия находится между ниж-
ним /i0 и верхним уровнями, считается, что полученная в результате обра-
ботки реализации x(t) статистика недостаточна для принятия решения и ис-
пытание продолжается.
2. ПРИМЕРЫ
15.1. На вход радиоприемного устройства поступает колебание
X(t) = ад, iv, iv,.... IV) + (1 - W. 4”, IV........../£’)+5(0.
(15.31)
где 5(0 — стационарный гауссовский белый шум с нулевым мате-
матическим ожиданием и корреляционной функцией
К6(т) = (ЛГ0/2)6(т); (15.32)
Si(t, /р, ф, .... /<?) == f(t, Ц), .... /Р) cos [<М +
+ад, /Яь .... ZP)L i = 1, 2, (15.33)
— детерминированные узкополосные радиосигналы.
Здесь ©f—несущие частоты, ft(t) и 40(0—функции, отображаю-
щие законы амплитудной и угловой модуляции, /Р — априорно
известные параметры сигналов st(t, /р, /р, ..., /Р) = sV).
15 Зак. 1203
449
Предполагается, что ширина спектров сигналов s^t, IV’, Z^1, ...,
I'm) и s2(Z, Z)2>, ZV’, , I'm) много меньше их несущих ча-
стот и, кроме того, | ©j — со2| — Д® < ®ь а сами сигналы st(t,
Z^>, •••> 1(т) полностью определены на интервалах времени
длительностью Т и равны нулю вне этого интервала. Параметр %
представляет собой случайную величину, принимающую на фикси-
рованном интервале (kT, (k + I)!1), k — 0, 1, 2, ..., значение % =
= Хх = 1, что соответствует наличию в принятом колебании x(Z)
сигнала s1(Z, Z)1’, ZV’, • ••, llmy) — st(t) или X = %0 = О, когда
в колебании х. (Z) присутствует сигнал s2 (Z, Z)2’, Z22’, •••, lmy) —
= s2(t). Априорные вероятности p(sj) = р(Кг) и p(s2) = р(Х0)
присутствия сигналов (15.33) в колебании (15.31) считаются из-
вестными.
Определить структуру приемного устройства, осуществляющего
оптимальную по критерию идеального наблюдателя обработку реа-
лизации x(Z) и вычислить соответствующую ей минимальную сум-
марную вероятность ошибочного приема детерминированных сигна-
лов S1(Z, ZV’, ZV’, .... Zg’) = S1(Z) и s2(Z, Z?’, Z(22’, Z<,2)) = s2(Z).
Решение. Как следует из (15.11) и (15.16), в случае приема
детерминированных сигналов Si(t, 1$, ..., Im) = Si (t) на
фоне белого шума g(Z) функционалы правдоподобия F (^J и F(K0)
определяются соотношениями
F(X1) = к ехр | - т -4-Г No J 0 (15.34)
F(X0) = к ехр т --^[X(f)-s2(t)]*dt N° в (15.35)
Подставляя (15.34) и (15.35) в (15.29а) и логарифмируя получен-
ное выражение, находим, что оптимальный приемник для различе-
ния двух детерминированных сигналов st(t) (Z = 1, 2) на фоне бе-
лого шума должен сформировать величину
т т
U = f xfffafldt — J x(f)s2(f)dt (15.36)
о о
и сравнить ее с порогом
Н = — [fi—£2 +АГ01п-^-1. (15.37)
2 L P(«i) J
Здесь
т т
Е2= j* s\(t)dt, Ez= \sl(f)dt (15.38)
о о
— энергия сигналов sx(Z) и s2(Z).
450
ff)
Рис. 15.1. Оптимальные устройства для различения двух детерминированных
сигналов
Решение А, = 1 принимается при U > Н, в противном случае
принимается решение А. = 0. .
В соответствии с (15.36) и (15.37) искомое оптимальное приемное
устройство должно состоять из двух перемножителей, интеграто-
ров и порогового устройства с порогом Н (рис. 15.1, а). Перемно-
жители и интеграторы можно заменить согласованными фильтра-
ми (СФ) [82, 90] с импульсными характеристиками
. ht(t) = st(T -t), (15.39)
при этом схема оптимального приемника преобразуется к виду, изо-
браженному на рис. 15.1, б. -
Предположим, что колебание (15.31) на входе приемного уст-
ройства имеет вид x(t) = sx(f) + а сформированная приемни-
ком величина U < Н. В этом случае будет иметь место ошибка
(принимается решение А, = 0, когда в действительности А. = 1),
вероятность которой
н
P1 = P(S1№|S1) = P(S1) J p^U^^dU. (15.40)
Здесь pi(U |А, = 1) — условная плотность распределения вероят-
ностей случайной величины U при наличии на входе приемника
сигнала sx(£).
Из (15.36) следует, что U является гауссовской случайной ве-
личиной с плотностью распределения вероятностей
(15.41)
М J’
pi(i/|A,) г—ехр
/2л
15*
451
математическое ожидание и дисперсия D\ = о* которой за-
висят от параметра X. Подставляя, в частности, в (15.36) сумму
х(0 = s^t) 4- |(0> после несложных вычислений находим
/пь=1 = Ег - Bs, оЛ=1 = (No/2) (Ег 4- £а — 2ВД
где
т
Bs = J
о
(15.42)
Таким образом, вероятность принятия ошибочного решения А = О
Л = Р(51) 1-Ф
Е1+ E2~2BS—Na In [р (s2)/p (Si)]
2/(Ях+Яа-2В,)^
(15.43)
где
Ф(г)
1
У2л
г 1
С —J-x2 .
е 2 dx
— интеграл вероятности.
Пусть U > Н, x(t) = s2(t) 4- £(/). В этом случае также име-
ет место ошибка (принимается решение А = 1, когда в действи-
тельности А = 0), вероятность которой
Р» = P(S2)P(S11s2) = p(s2) J P1(U IA = 0)dU. (15.44)
н
В данном случае
/пь=о = Bs - Е2, aUo = (£i 4- Е, - 2Bs)W0/2 (15.45)
и формула (15.44) принимает вид
, \ ।__ф / #14- —2Bs-}-Nt> In [р (s2)/p (si)]'
I \ /2(Ех4-£2-2В8)^/2
(15.46)
Подставляя (15.43) и (15.46) в (15.28), находим следующее выраже-
ние для суммарной вероятности ошибки при оптимальном приеме
детерминированных сигналов:
P = p(S1)
/ Et+Ej—ZBs—No In [р (s2)/p (sx)]
1 _ ° ( 2 (Bx+*2 -2B,)
£i+ 52-2Bs4-^o In [p (s2)/p (si)] \
4-p(s2) 1-Ф
2~2Bs)
. (15.47)
2
452
При р («j) = р (s2) = 1/2 формула (15.47) значительно упроща-
ется:
Р = 1 - Ф (Wi (1 + 6 - 2рв1)/4), (15.48)
где
q1 = 2E1/N0, 6 = £2/Ev psl = Bs/E1. (15.49)
Для большинства применяемых в системах радиотелеграфии сиг-
налов характерным является равенство их энергий Et = Е. При
этом условии из формул (15.48) получим [27]
Р = 1 - Ф (Г?(1-Рз)/2), (15.50)
где в 1 р
Р, = 4- = -ИМ0М0<« (15.51)
£ £ J
0
— коэффициент взаимной корреляции сигналов Si (/) и $2 (/).
Из (15.50) следует, что определение потенциальной помехоустой-
чивости для случая оптимального приема детерминированных сиг-
налов сводится к вычислению коэффициента их взаимной корре-
ляции. Учитывая монотонно возрастающий характер функции Ф (г),
приходим к выводу, что при одинаковых отношениях сигнал/шум
q = 2E/N0 наиболее помехоустойчивыми являются сигналы Si (/),
для которых коэффициент ps минимален. Значения Р = f (q, ps),
вычисленные по формуле (15.50), представлены на рис. 15.2.
15.2. На вход радиоприемного устройства поступает колебание
x(0 = Xs(/, 4, /2, ..., lm)+ U0. (15.52)
где | (?) — стационарный нормальный белый шум с нулевым ма-
тематическим ожиданием т$ = 0 и корреляционной функцией (15.32);
s (/, 4, 4, .... 1т) = f (t, 1г, ..., lh) cos [<оо/ + Т (/, lM, .... Zm)],
(15.53)
— детерминированный узкополосный радиосигнал. Здесь <d0 —
несущая частота, /(0 и ¥ (/) — функции, отображающие законы
амплитудной и угловой модуляции, lk — априорно известные пара-
метры сигнала s (/, 4, 4. •••> 4i) — s (0- Предполагается, что шири-
на спектра сигнала s (/, 4> 4> ••• > 4i) много меньше его несущей
частоты, а сам сигнал полностью определен на интервале длитель-
ностью Т и равен нулю вне этого интервала. Параметр Л. представ-
ляет собой случайную величину, принимающую на фиксированном
интервале наблюдения (0, Т) значение X = ^ = 1 или X = Хо = 0.
Определить структуру приемного устройства, осуществляющего
оптимальную по критерию Неймана—Пирсона обработку реализа-
ции х (/) и вычислить характеристики обнаружения детерминирован-
ного сигнала s (/, 4, 4, •••> 4i) на фоне белого шума.
453
Рис. 15.2. Суммарная веро-
ятность ошибочного приема
детерминированных сигна-
лов
Решение. В соответствии с (15.11) и (.15.16) для рассматривае-
мого случая
F (PQ = к ехр
т
Ло J
о
F (Хо) = к ехр
x2(t)dt
(15.54)
(15.55)
Подставляя (15.54) и (15.55) в (15.30а) и логарифмируя полу-
ченное выражение, находим, что оптимальный приемник для обна-
ружения детерминированного сигнала s(t) должен сформировать
величину
т
U=^x(t)s(t)dt
о
(15.56)
и сравнить ее с порогом
Но = (Е 4- No In Л)/2, (15.57)
454
где
т
E=§s*(t)dt (15.58)
о
— энергия сигнала s (/).
При U > Но принимается решение А = Ах = 1, в противном
случае принимается А = Ао — О-
На основании (15.56) и (15.57) искомый оптимальный приемник
должен состоять из перемножителя, интегратора и порогового уст-
ройства с порогом Но (рис. 15.3, а). Как отмечалось, перемножитель
и интегратор можно заменить согласованным фильтром с импульс-
ной характеристикой
h(t) = s(T — 0, (15.59)
при этом схема оптимального обнаружителя преобразуется к виду,
изображенному на рис. 15.3, б.
Найдем характеристики обнаружения. Вероятность ложной тре-
воги Р/?, равна вероятности того, что U > Но при условии А =
= Ао = 0, и определяется формулой
pFj=J P1(U\K=tydU. (15.60)
н.
Здесь Р1 (U |А = 0) — плотность распределения вероятностей слу- .
чайной величины U при А = Ао = 0, т. е. при наличии на входе при-
емника только шума.
Как следует из (15.56), U представляет собой гауссовскую слу-
чайную величину с плотностью распределения вероятностей (15.41).
При А = 0
т
о
откуда находим
тх=о = 0, огх2=о = E'Nq/2. (15.61)
Я
Рис. 15.3. Оптимальные устройства для обнаружения детерминированного
сигнала
455
Подставляя (15.41) в (15.60) и учитывая соотношения (15.61), по-
лучаем
pFi = 1 _ ф (/i0//^), q = 2E/N0, (15.62)
где Ф (z) — интеграл вероятности;
h0 = 2H0/N0 = E/No + In h. (15.63)
Вероятность правильного обнаружения (мощность решения)
PDi равна вероятности того, что U > Но при условии А, = Ах = 1:
PDl = JP1(l/| Хе l)dt/. (15.64)
Подставляя в (15.64) плотность распределения вероятностей (15.41)
и учитывая, что при А=АХ = 1 математическое ожидание и диспер-
сия случайной величины U равны
= Е, obi = EN0/2, (15.65)
находим
PDt = 1 — Ф (й0//7— Кт). (15.66)
Формулы (15.62) и (15.66) показывают, что как вероятность лож-
ной тревоги Ppt, так и вероятность правильного обнаружения
PDi однозначно определяются пороговым уровнем h0 и отношением
сигнал/шум q — 2E/N0. Задаваясь значением вероятности ложной
тревоги Ppt, по формуле (15.62) можно вычислить зависимость
Яо = fx (q), а затем определить функцию Ро, = f2 (q), называемую
характеристикой обнаружения. Значения Ро, = /2 (д), вычислен-
ные по формуле (15.66) для нескольких значений вероятностей лож-
ной тревоги, представлены на рис. 15.4 (сплошные линии).
15.3. Решить пример 15.2 при условии, что процесс £ (/) в (15.52)
представляет собой стационарный гауссовский шум с нулевым ма-
тематическим ожиданием = 0 и корреляционной функцией
(^1» -
Решение [96]. В соответствии с (15.11) и (15.13) функционалы
правдоподобия для рассматриваемого примера определяются со-
отношениями
F (Хо) = к ехр
(15.67)
F (Ах) = к ехр
f [ 0 (4, /г) к (/1) — s (/1)1 к (/г) — $ (/2)] d^ dt2
о о
(15.68)
456
случайной амплитудой и начальной фазой (штрих-пунктир)
где функция 0 (4, 4) удовлетворяет интегральному уравнению
(15.14). Подставляя (15.67) и (15.68) в (15.30а), находим
г т т
Л >(/)] = ехр-----Г J J S S 0 dtl +
оо
т т 1
4“ J j* я (/j) s (4) 0 (4> 4) dti dt2 .
Здесь учтено, что вследствие симметрии функции 0 (tlt t2)
J J x (4) s (4) 0 (4. 4) dti dt2 = j j x (4) s (4) 0 (4, 4) dtr dt^.
00 00
Вводя далее функцию
г
q>(4)=JjO(4,4)s(4)d4.
о
удовлетворяющую интегральному уравнению Фредгольма первого
рода, J (t, т) ср (т) dx = s (/), окончательно получаем
о
т
о
т
р(/)ф(0<й • (15.69)
о
457
Согласно критерию Неймана—Пирсона решение X = %х = 1
принимается при Л 1х (/)] > h. (15.70)
После логарифмирования это условие приводится к виду
т U = j x(t)s (0 dt > h0, (15.71)
где т Ло=1пй4-^-[«Юф(0^- 0 (15.72)
Соотношение (15.71) определяет структуру оптимального обна-
ружителя. Если окажется, что U > h0, принимается решение
% = %! = 1, в противном случае принимается решение А, = Хо = 0.
Определим характеристики обнаружения. Вероятность ложной
тревоги определяется формулой (15.60), где рх ((/|Х = 0) — плот-
ность распределения вероятностей случайной величины U, которая
при % = Ао = 0 равна
т
и = J в (0 <р (0 dt
о
(15.73)
и, следовательно, представляет собой гауссовскую случайную ве-
личину с плотностью распределения вероятностей (15.41), с нуле-
вым математическим ожиданием т^о = 0 и дисперсией
тт т
сг*=о = J (Ч(4. 4) Ф (fi) Ф (fz) dtidt2=^ s (/) ф (f) dt = Go.
oo о
После подстановки (15.41) в (15.60) получаем
PFt = 1 — Ф (ho/tjo).
Вероятность правильного обнаружения равна
РО1 = 1 — Ф (h0/a0 — <т0).
15.4. Входящие в (15.31) сигналы st (t, l[l), ..., Im) имеют
вид
Sj (t, 1ф, /</>, ..., 1%) = Si (t, фг) = ft (t) cos [©jt + фг (t) + фД
i = 1, 2, (15.74)
причем все параметры /V’ таких сигналов, кроме начальных фаз
фг, априори известны, а начальные фазы фг представляют собой слу-
чайные величины, равномерно распределенные на интервале (— л, л),
и считаются несущественными параметрами. Сохраняя в силе ос-
тальные условия примера 15.1, определить схему оптимального по
критерию Котельникова—Зигерта приемника сигналов st (t, ф<)
458
cq случайными начальными фазами и вычислить суммарную ве-
роятность ошибочного приема. '
Решение [101]. В этом случае функционалы правдоподобия
F (AJ и F (А.о) следует вычислять по формуле (15.11а), осуществляя
усреднение по случайным фазам <pi как несущественным параметрам:
я т
/r(M=^fexp[--J-f[x(O-
zJI J I /Vq J
—я о
— /x (0cos (<ox t + Ф1 (0 4-Ф1)]2 dq>i, (15.75)
л т
f expl —--J-f [x(0—
2л J I Nq J
—л o
cos(®2t +Ф2 (0 +<P2)]2 dt j d<p2. (15.76)
Введем обозначения
т
= f x (0 ft (0 cos [cof 14- (0] dt,
15 (15.77)
Yt = J x (0 ft (0 sin [®f t4- фг (0] dt
0
и учтем, что
J exp (R cos 0) dQ = /0 (R),
—я
где /0 (R) — функция Бесселя нулевого порядка от мнимого аргу-
мента. Тогда после подстановки (15.75) и (15.76) в (15.29а) и ряда не-
сложных преобразований найдем, что оптимальный приемник для
различения двух сигналов (15.74) с неизвестными начальными фа-
зами должен сформировать величину
U = In /0 (2Rx/tf0) - In Io (2R2/N0) (15.78)
и сравнить ее с порогом
Н = (Ех - Е2)/АГо 4- In [р (sx)/p (s2)l. (15.79)
Здесь £х и £2—энергии сигналов sx (0 <рх) и s2 (t, <р2), определяе-
мые формулами (15.38). Величины Ri = VXt-\-Yf пред-
ставляют собой значения огибающих суммы сигнала St (t, <рх)
и шума (в моменты времени t = kT) на выходе согласованных филь-
тров с импульсными характеристиками ht (0 = s} (Т — t).
Схема такого приемника представлена на рис. 15.5, а. Приня-
тое колебание х (0 воздействует на два согласованных фильтра с им-
459
f)
Рис. 15.5. Оптимальные устройства для различения двух сигналов со случай-
ными начальными фазами
пульсными характеристиками ht (t). На выходе каждого фильтра
стоят детекторы огибающих, выходные напряжения которых вычи-
таются и разность (15.78) подается на пороговое устройство с по-
рогом Н. При U > Н принимается решение 1=1, при U < Н
принимается 1 = 0.
В дальнейшем ограничимся рассмотрением лишь симметричных
систем передачи двоичных сигналов, для которых Ех = Е2 = Е,
р (S1) = р (s2) и Р (sx | s2) = Р (s21 sx). Для таких систем, как это сле-
дует из (15.79), порог Н = 0 и выражение (15.78) приводится к виду
U = /0 (27?Х/Яо) - /о тно).
Следует отметить, что при сделанных здесь предположениях
закон детектирования не имеет существенного значения. Важно
лишь, чтобы выходное напряжение детектора было монотонной функ-
цией огибающей Rt (t). Если, например, в оптимальном приемнике
применить линейное детектирование огибающей (рис. 15.5, б), то
с нулевым порогом нужно сравнивать величину U = Rx — R2.
Суммарная вероятность ошибки при этом определяется формулой
R — j* dRi j* Pa(Ri, RJ)dR2,
0 Ri
(15.80)
где
2 2o2(1— p2)
X
(15.81)
460
— совместная плотность распределения вероятностей случайных
величин 7?г и Т?2. Здесь q = 2EINO — отношение сигнал/шум на
входе приемника (на входе согласованных фильтров), о2 = EN0/2 —
дисперсия шума на выходе каждого фильтра, р — коэффициент,
имеющий смысл коэффициента взаимной корреляции между сиг-
налами:
P=\Vb\+b'2\lE, 0<р<1,
bi = ~Y f А(0/г(0cos[(<о2—®х)/ + ф2(0—Ф1(0]<И, (15 82)
О
т
b2 =4" f А № Ъ W Sin К®2 — ®1) t + Ф2 (0 — фх (/)] dt.
О
Подставив (15.81) в (15.80) и выполнив интегрирование, полу-
чим следующее выражение для суммарной вероятности ошибки при
приеме сигналов s( (t, <рг) с неизвестными начальными фазами:
_(15.83)
где
Q (п, u)=J х ехр —х-у°8j /0 (vx) dx, (15.84)
и
— функция распределения Релея—Райса [32, 102].
15.5. Решить пример 15.2 при условии, что входящий в (15.52)
сигнал s (t, lL, l2, ..., lm) имеет вид
s (t, llt lz, .... lm) = s (t, <p) = f (t) cos [®о/ + Ф (0 + <p], (15.85)
где <p — случайная начальная фаза, равномерно распределенная
на интервале (— л, л).
Решение. Функционалы правдоподобия для рассматриваемого
случая в соответствии с (15.11а) равны
F (М = « ®хр
(15.86)
F(X0) =кехр
(15.87)
о
После подстановки (15.86) и (15.87) в (15.30а) получаем следую-
щее правило принятия решения % = = 1 (рис. 15.6, а):
&E/N>I0 (2R/N0) > h (15.88)
461
Рис. 15.6. Оптимальные устройства для обнаружения сигнала со случайной
начальной фазой
ИЛИ
/о (27?/А^о) > h0 = heP/N*, (15.88а)
где
Я = |]/Х2 +У2|,
т
X = С х (/) / (/) cos [®01 + Ф (01 dt,
({ (15.89)
т
Y = J х (/) f (/) sin [®01+Ф (01 dt.
о
Так как функция /0(2) является монотонной, решение о нали-
чии или отсутствии сигнала s (t, -<р) на входе приемника можно при-
нимать на основании сравнения с некоторым порогом любой моно-
тонной функции аргумента R, представляющего собой, как отмеча-
лось в примере 15.4, значения огибающей R (t) на выходе согласован-
ного фильтра с импульсной характеристикой h (t) = s (Т — t) в
момент времени t = Т. Если сравнивать с порогом Н саму оги-
бающую R (t), то правило принятия решения X = = 1 принимает
вид
R> Н. (15.886)
Соответствующая этому правилу схема оптимального приемника
приведена на рис. 15.6, б.
В соответствии с (15.886), (15.22) и (15.24) вероятности ложной
тревоги и правильного обнаружения определяются формулами
PFi = J Pi(R I х — Q)dR, PDt =7 Р1 (R I 1) dR. (15.90)
и н
Нетрудно показать, что входящие в (15.90) плотности распределе-
ния вероятностей равны
<*0 \ / \ /
Р1(й|Х_0)-Л.ехр(-^-),
462
Посде подстановки pr (7?|Х = 1) и рг (£|Х = 0) Ь (15.90) находим
ENe
PDi=Q(Vl, h0), (15.90а)
где функция Q (v, и) определена соотношением (15.84). Значения
PDt = f (q), вычисленные по формулам (15.90а) для заданных зна-
чений вероятности ложной тревоги представлены на рис. 15.4
(штриховые линии).
15.6. На вход приемного устройства поступает колебание
х(0 = А^(0 + (1-Х)«2 (0+f(0, (15.91)
где 1- (0 — комплексный стационарный гауссовский белый шум с
нулевым математическим ожиданием mg- = 0 и корреляционной
функцией
R (т) = ^0/2) 6 (т); щ (0 = ае-/е st (0
— федингующие сигналы. Здесь
— детерминированные узкополосные радиосигналы, а и 0 — не
зависимые случайные величины, характеризующие медленные из-
менения амплитуды и фазы сигналов sj (0.
Принимаемые сигналы щ (t) состоят из детерминированной и слу-
чайной составляющих:
иг (0 = st (0 [ае~'в +0е ~'8],
(15.92)
т. e.
а&~№ = ae~i6 + fie~ie, (15.93)
где а и 6 представляют собой амплитудный коэффициент и фазовый
сдвиг детерминированной составляющей сигнала ut (0 (а и 6 —
постоянные величины); 0 и е — амплитудный множитель и фазовый
сдвиг случайной компоненты, постоянные на интервале наблюдения
(0, Т). В дальнейшем будем предполагать, что 0 и 8 представляют
собой независимые случайные величины, причем 0 распределена по
закону Релея, а 8 — равномерно на интервале (— л, л), вследствие
чего их совместная плотность распределения вероятностей имеет
вид
Рг(₽> 8) =
0
2ла|
0
О<0< оо,
при других 0 И 8.
483
При сделанных предположениях совместная плотность распределе-
ния вероятностей случайных величин а и 0 определяется законом
Райса:
р2(а, 9) =
а Г аа+а3—2aacos(0—6)
2лаГехр 2а? ’
ф L Ф J
О < оо, —л 0—6 л,
О при других а и 0,
(15.94)
а средние энергии сигналов щ (t)
М {Е~ } =М IJ | щ (012 dt =ЕЧ J а2 рг (а) da
1 lo Jo
= 2o^ESi(l+y2/2) = £<, i = l,2,
где у = а/Оф характеризует соотношение между детерминирован-
ной и случайной составляющими сигнала щ (t)-, ESi — энергия сиг-
налов st (t).
Параметр X в колебании (15.91) может принимать значения
X = = I или Л, = %0 = 0 с априорными вероятностями р (XJ =
= Р (ы1) = Р (М = Р (М = 1/2. По принятой реализации х (t)
требуется решить с минимальной суммарной вероятностью ошибки
(15.28), какое значение имеет параметр X на данном интервале на-
блюдения (О, Т).
Решение [103]. При решении сформулированной задачи следует
различать два частных случая: 1) среднее значение 6 фазового сдви-
га 0 принимаемых сигналов (15.92) априори известно; 2) среднее
значение фазового сдвига 0 на приемной стороне неизвестно.
Подставляя в (15.11а) вместо сигналов St (t, Z£*>, /<'>, ..., Im)
сигналы щ (t) = Ut (t, а, 0), определяемые соотношением (15.92),
и осуществляя усреднение по несущественным параметрам а и 0
с плотностью распределения вероятностей (15.94), находим, что оп-
тимальный по критерию идеального наблюдателя приемник сигна-
лов (15.92) с равными энергиями Et = Е2 = Е, равными априор-
ными вероятностями р (ыг) = р (ы2) =1/2 и известным средним
значением 6 их фазового сдвига 0 должен сформировать величину
^44-izir+Re6e~'e) -
a/V0
^-|^Г + Ке(^е-/в)
(15.95)
и сравнить ее с порогом Н = 0. При U <. Н выносится решение
А, = 0, при U > Н принимается X = i.
464
S)
Рис. 15.7. Квазикогерентное (а) и некогерентное (б) устройства для различе-
ния двух медленно федингующих сигналов
Входящие в (15.95) величины rt = rt (0) — значения комплекс-
ных взаимных корреляционных функций сигналов (15.92) и приня-
того колебания (15.91), равных
т
Ъ СО = у J х* (0 ut (t—т) dt.
~ о
Здесь х* (/) — функция, комплексно-сопряженная с х (t). Исполь-
зуя условие узкополосности сигналов ut (/), можно показать, что
действительная часть функции гг (т) представляет собой взаимную
корреляционную функцию для действительных частей колебаний
х (t) и Ui (t):
Re (т)] = J Re [x (0J Re (t—t)] dt,
~ о
а значения | гг (т) | совпадают co значениями огибающей этой кор-
реляционной функции. В соответствии с этим схема оптимального
приемника может быть представлена в виде, изображенном на ри-
сунке 15.7, а. При этом суммарная вероятность Р ошибок квази-
когерентного приема медленно федингующих сигналов (15.92)
подсчитывается по формуле
P=Q(ac, be)—
—L Г i +..ixVi-_pL 1ехр Г 1о (15i96)
2 "|/1 — |д,2 p2 2
465
где ____
2°« (1597)
V1 — p,2 p2 "|/1 —p2 p2 2<r| q 4-4
i / v2K1-P2)q|g+2(1-P>)] =
C V 4ф(1-р2) ’ Я Wo ’
а коэффициенты ps и p определяются соотношениями (15.51) и (15.82).
Если среднее значение 6 фазового сдвига 0 принимаемых сигна-
лов (15.92) неизвестно, оптимальный приемник для различения двух
федингующих сигналов должен выносить решение о приеме (/)
или и2 (0 на основе анализа простого выражения (рис. 15.7, б):
^ = Г1| —1^1-
При U <. О принимается решение % = 0, в противном случае —
% = 1. Отметим, что при некогерентном приеме не требуется зна-
ния отношения Оф/аЛ^0.
Суммарная вероятность ошибки при некогерентном приеме под-
считывается по формуле (15.96), в которой
а = 1 V(1—Р2) (1—НаРа) ь. 1А , 1/(1—Р2) (1—и2Р2)
V 1—м>’ ’ Г "Г 1— Цр2
с = 1/^2г±е!_. (15.98)
V 2 1—р2р2
15.7. На выходе УПЧ приемника амплитудно-манипулированных
радиосигналов, схема которого представлена на рис. 15.8, имеет
место смесь сигнала и шума
х (/) = Xsx (f, Ф1) + (1 - X) s2 (/, ф2) + § ((),
где
g (0 = X (0 cos <i>ot + у (0 sin ©01
— гауссовский квазигармонический шум с нулевым математиче-
ским ожиданием = 0 и корреляционной функцией
#5 (т) = °|Р5 (т) cos ®ot;
Si (Л Ф1) = Ат cos (со,/ + Ф1),
s2(t, <р2) = 0, ’
— амплитудно-манипулированные радиосигналы. Начальная фаза
<рх случайна и равномерно распределена на интервале (— л, л).
Рис. 15.8. Приемник AM сигналов со случайной начальной фазой
466
Параметр % представляет собой случайную величину, принимающую
на интервале (О, Т) значения X = — 1 или % = Хо = 0 с апри-
орными вероятностями р (Х0 = р (%0) — Решение % = при-
нимается в тех случаях, когда значение огибающей U = U (Т),
выделяемой линейным детектором огибающей, превышает порог Н.
В противном случае принимается X = до-
определить оптимальный порог Но, минимизирующий суммарную
вероятность ошибочных решений (15.28), и вычислить соответст-
вующую ему суммарную вероятность ошибок.
Решение. В соответствии с (15.28) суммарная вероятность оши-
бок приема амплитудно-манипулированных сигналов
Я. оо
Рам = Р(зх)С Pi(t7|X = l)dC/ + p(s2)J Л([/|Х=О) dU, (15.99)
О Но
где
О
а6 \ /
— плотность распределения вероятностей огибающей суммы сигна-
ла sx (t, <рг) и квазигармонического шума § (0;
ft(t/|1=0) = ^-exp(-^-), U>0
— плотность распределения вероятностей огибающей только шума
£ (0. Подставляя pi(U\Kt) в (15.99), находим
1 / Но У'
2 I <4 / .
Взяв производную по Но от выражения (15.100) и приравняв ее
нулю, получим уравнение, связывающее оптимальный порог Яо
с отношением сигнал/шум Ат/<%: |
1 / Ат У
2 \ ’
^-) I . (15.100)
<4/J
Р+ехр
ехр
3 . ЗАДАЧИ И ОТВЕТЫ
15.1 . На вход приемного устройства, оптимального по критерию
идеального наблюдателя, воздействует аддитивная смесь
х (0 = Ч (0 + (1 - %) 32 (0 + g (0, (15.101)
где £ (0 — стационарный гауссовский белый шум с нулевым мате-
матическим ожиданием т$ = 0 и корреляционной функцией
Rl (0 = (Л/о/2) б (0;
S1 (0 = Am COS {(Ait + <Pi), х '
467
— детерминированные амплитудно-манипулированные сигналы. Па-
раметр % принимает значения X = Ах = 1 или А = Ао = 0 с вероят-
ностями р (Ах) = р (Ао) = 1/2.
Вычислить суммарную вероятность ошибочного приема сигналов
Si(0 и s2(0.
2
Ответ-. РАм = 1—Ф/т/4, Ф(г)г=—f e~xt,2dx,
у2п J
— 00
q = AmT/N0 = 2El/N0.
График функции Рам = f (q) приведен на рис. 15.9.
15.2 . Решить задачу 15.1 для случая оптимального приема де-
терминированных частотно-манипулированных сигналов
Si (0 = Ат cos (©г/ + Ф1), о</<Т
s2 (0 = Ат cos (®2/ + <р2), ’
при условии, что | ©г — ю21 Т 1.
Ответ: Рчм = 1 — Ф (Кq/2), q = A*mTlN0 = 2E/W0.]
График функции Рчм = f (я) приведен на рис. 15.9.
15.3 . Решить задачу 15.1 для^случая оптимального приема фа-
зоманипулированных сигналов
Si (О = Ат cos (<оо/ + Фо), о < t < Т
s2 (0 = Ат cos (<noi 4- фо 4- л),
Ответ: Рфм = 1 — Ф (K<?).
График функции Рфм = f (0 Дан на рис. 15.9.
Рис. 15.9. Зависимость вероятно-
сти ошибки от отношения сиг-
нал/шум при оптимальном разли-
чении детерминированных сигна-
лов
468
• Г5.4. "На вход оптимального по критерию Котельникова—Зигер-
та приемника воздействует колебание (15.101), где St (i)—детер-
минированные тонально-манипулированные сигналы вида АМ-АМ:
sx (0 = Ат [1 + tn1 cos Й0 cos (a>ot + q)x),
s2 (0 = Am [1 + m2 cos Й0 cos (<oo* + Ф^, ?"
Вычислить суммарную вероятность ошибочного приема таких
сигналов на фоне белого шума при условии равенства априорных
вероятностей сигналов sx (0 и s2 (0. Предполагается, что период то-
нальных колебаний Та = 2л/й < Т и й ©0.
Ответ: Рам-ам - 1 —Ф (1 / ) •
\ У 4 2-|-т| /
Значения Рдм-ам = f (я) для mr = 1 и т2 = 0 приведены на
рис. 15.9.
15.5. Решить задачу 15.4 для случая оптимального приема де-
терминированных тонально-манипулированных сигналов вида ЧМ-
АМ:
sx(0 = Ат [1 4- т cos йх0 cos (со0/ + фх),
з2 (0 = Ат [1 + т cos й20 cos (<оо^ + Фа),
0 < t С Т.
Предполагается, что тональные частоты йг -С ®’о и> кроме того,
период тональных колебаний Tat= 2л/йг много меньше длитель-
ности Т сигналов st (0.
Ответ [104]: Рчм-ам = 1 — ФИ/ —о 7* i ) '
\ У 2 2-1-тг /
Значения Рчм-ам = f (<?) при т — 1 приведены на рис. 15.9.
15.6. Решить задачу 15.4 для случая оптимального приема де-
терминированных тонально-манипулированных сигналов вида ФМ-
АМ:
sx (0 = Ат [1 + т cos Ш] cos (a>ot 4- фх),
s2 (0 = Ат [1 — т cos Й0 cos (<оо/ 4- ф2), =5- Т.
Ответ [104]: Рфм-ам = 1—Ф 1/ Ч———•
У 2-{-тг
Значения Рфм-ам = f (ч) Для т = 1 приведены на рис. 15.9.
15.7. Определить суммарную вероятность ошибки при оптималь-
ном по критерию идеального наблюдателя приеме на фоне белого
шума детерминированных тонально-манипулированных сигналов
вида АМ-ЧМ:
sx (0 = Ат cos [соо/ 4- рх cos Ш 4- фх1,
$2 (0 = Ат cos [<о0/ 4- cos Ш 4- ф2], ""
Ответ: Рдм-чм = 1 — Ф (К<7 [ 1—«М₽2—₽i)]/2),
469
где J0 (z) — функция Бесселя нулевого порядка первого рода.
15.8. Решить задачу 15.4 для случая оптимального приема де-
терминированных тонально-манипулированных сигналов вида ЧМ-
ЧМ:
Si (0 = Ат cos [<оо/ + ₽ cos Йх/ + <pj, < t <
s2 (/) = Am cos [®oi + p COS SV + ф21, "" ""
Ответ [104]: Рчм-чм = 1 —Ф (]A? 11 — (₽)1/2)•
15.9. Решить задачу 15.4 для случая приема детерминирован-
ных тонально-манипулированных сигналов вида ФМ-ЧМ:
зх (0 = Ат cos [<в0/ + Р cos SM + q>x], Q
з2 (/) = Ат cos [<оо/ — Р cos ©/ + ф2],
Ответ [104]: РФМ-чм= 1 — Ф(К<7[1—Л(2Р)]/2).
15.10. На вход радиоприемного устройства поступает колебание
X (0 = Asx (/, Фх) + (1 - A) s2 (t, ф2) + § (0, (15.102)
где § (/) — стационарный гауссовский белый шум с нулевым ма-
тематическим ожиданием = 0 и корреляционной функцией
Pj (т) = (Ро/2) 6 (т);
si (/, Ф1) = Ат cos (©о/ + Ф1). 0 < t < Т,
s2 (/, ф2) = Q,
— амплитудно-манипулированные сигналы. Начальная фаза Ф1 сиг-
нала sx (t, Фх) является случайной, равномерно распределенной на
интервале (— л, л), и считается несущественным параметром. Пред-
полагается, что входящий в (15.102) параметр А представляет собой
случайную величину, принимающую значения А = Ах = 1 или А =
= Ао = 0 с равными априорными вероятностями р (Ах) = р (Ао) =
= 1/2.
Определить структуру оптимального по критерию Котельнико-
ва—Зигерта приемника амплитудно-манипулированных сигналов
с неизвестными начальными фазами и Вычислить суммарную вероят-
ность ошибочного приема.
Ответ: Оптимальный приемник должен состоять из согласо-
ванного фильтра с импульсной переходной функцией h (/) = sx (Т —
— t), линейного детектора огибающей и порогового устройства с по-
рогом h0, определяемым соотношением
= <7 = 2£х/^.
Суммарная вероятность ошибочного приема амплитудно-манипули-
рованных сигналов при этом вычисляется по формуле
PAM=-[l + e-^/2-Q(V7, Ло)]/2.
Значения Рам = f (q) приведены на рис.( 15.10.
470
Рис. 15.10. Зависимость вероятно-
сти ошибки от отношения сиг-
нал/шум при оптимальном разли-
чении сигналов со случайной на-
чальной фазой
15.11. Вычислить суммарную вероятность ошибок при оптималь-
ном по критерию идеального наблюдателя приеме априори равнове-
роятных частотно-манипулированных сигналов
81 (0 = Ат COS (®х/ + фх), о < t < Т
s2 (0 = Ат cos (со2/ + ф2), "" ’
на фоне стационарного гауссовского белого шума | (/) с нулевым
математическим ожиданием mg = 0 и корреляционной функцией
(т) = (У0/2) 6 (т).
Случайные начальные фазы фх и <р2 сигналов sx (t, фх) и s2 (t, <р2)
равномерно распределены на интервале (— л, л) и считаются не-
существенными параметрами. Предполагается, что | <ох — <в2| Т 1.
Ответ: Рчм = (1/2) е-»/4.
Значения Рчм =/(<?) приведены на рис. 15.10.
15.12. Решить задачу 15.11 для случая оптимального приема
тонально-манипулированных сигналов вида ЧМ-АМ:
sx (/) = Ат [1 + т cos QXZ] cos (<в0/ + <рх),
s2 (0 = Ат [1 + т cos Q2Z] cos (®0/ + ф2), ’
начальные фазы которых случайны и равномерно распределены на
интервале (— л, л). Предполагается, что Q; < <»0 и Та{ = 2л/£2г <<
«Т.
471
Ответ'.
^4M-AM«Q(f, «)—^-e 7/4
\ /74 J
где
и = 1/ — Й V2m2+m4'\ ц 1/ 9 fl I V2m2+w4 'j
F 4 \ 2+m2 / ’ F 4 \ ’’’ 24-ma J
Значения Рчм-ам = f (?) Для m = 1 приведены на рис. 15.10.
15.13. Решить задачу 15.12 для случая оптимального приема
тонально-манипулированных сигналов вида ФМ-АМ:
sx (0 = Ат [1 + т cos Qfl cos (<в0/ 4- q>x),
s2 (0 = Am [1 — m cos Q/] cos (aot + <p2),
Ответ'.
РфПМ=0 (V, U)- 4 e-./« /. (.i
где
v_ 1 f Я_ (T/2—m)2 u== , Г q (l/2+пг)2
F 4 2+m2 ’ F 4 2+m2
График функции Рфм-ам = f (?) для m = 1 приведен на
рис. 5.10.
15.14. На вход приемного устройства поступает колебание
7(0 = (0 + (1 - X) «2 (0 + I (0,
где f(0 — стационарный гауссовский белый шум с нулевым ма-
тематическим ожиданием т^= 0 и корреляционной функцией
₽Г(т) = (А^о/2) 6 (т);
«7 (0 — ae-^St (0 — аАт ехр [/ (<dot—9)1, и2 (0 = 0,
0 t < Т,
— медленно федингующие амплитудно-манипулированные сигналы.
Здесь а — амплитудный множитель, принимающий на интервалах
(0, Т) случайные значения с плотностью распределения
вероятностей
Л(а) = £ехрГ—-Y 0<а<оо,
аф L 2 \ °ф / J \ аф)
где у = а/<Тф характеризует соотношение между детерминирован-
ной и случайной составляющими сигнала иг (0 (см. пример 15.6).
Начальная фаза 0 сигнала мх(0 является случайной равномерно
распределённой на интервале (— л, л) и считается несущественным
параметром. Параметр X принимает значения X = ^ = 1 или X =
= Хо = 0 с априорными вероятностями р (XJ = р (их) = р (Хо) =
= р (ut) = 1/2.
472
' Определить схему приемника, осуществляющего оптимальную
по критерию ’идеального наблюдателя обработку колебания х (t),
и вычислить соответствующую ей суммарную вероятность ошибоч-
ного приема.
Ответ'. Оптимальный приемник должен состоять из согласован-
ного фильтра с импульсной характеристикой h (t) = (Т — t),
линейного детектора огибающей и порогового устройства с порогом
h0, определяемым из уравнения
2 I
2+<? 7°
—
2 г 2-Н/
При этом вероятность ошибочного приема вычисляется по формуле
Для частного случая приема амплитудно-манипулированных
сигналов, федингующих по закону Релея (у = 0), имеем
Рам = 4- Г1 + ехР (—7 ^)-ехр (—-£=•)],
где /i0 определяется из уравнения
ехр [--— hn = —— .
2 °2+д) 2+1
Здесь
q = 2а&1 = 2о| • 2Е^0 = ^A^T/N0.
Графики функций Рам = fi (q, ?) и h0 — f2 (q, у) приведены
соответственно на рис. 15.11 и 15.12. Через q обозначено отношение
сигнал/шум, равное отношению удвоенного среднего значения £х=
= М {Eut} энергии сигнала мх (/) к спектральной плотности шума
q=2E1/N0=~q(l-\-y2/2).
15.14. На вход приемного устройства поступает колебание
X (0=%£ (/)+(1 - X) и2 (0 4-1(0,
где £ (0—стационарный гауссовский белый шум с нулевым матема-
тическим ожиданием mg= 0 и корреляционной функцией
Рг(т) = (ВД6(т);
~иг (0 = аАт ехр [/ — 9)], 0 t sC Т,
u2 (0 = аАт ехр [/ (со2/ — 0)1,
— медленно федингующие частотно-манипулированные сигналы.
473
Рис. 15.11. Суммарная вероятность
ошибочного приема AM сигналов ср
случайными амплитудой и начальной
фазой
Рис. 15.12. Зависимость оптимально-
го порога от отношения сигнал/шум
при приеме AM сигналов со случай-
ными амплитудой и начальной фазой
Здесь а и 0 — амплитудный множитель и фазовый сдвиг, принимаю-
щие на интервалах (О, Т) случайные значения с совместной плот-
ностью распределения вероятностей (см. пример 15.6)
—ехр
р2(«>0)= 2яаф
__1/ а8 , 2______cos О
~ + ? ёф
, 0^а<оо,—
О
при других а и 0.
Параметр К принимает значения X = = 1 или % = Ко = 0 с ап-
риорными вероятностями р (AJ = р (%0) = 1/2.
Приемное устройство осуществляет оптимальную по критерию
идеального наблюдателя обработку принимаемого колебания х (f).
Вычислить соответствующую ей суммарную вероятность ошибочного
приема для случаев априори известного среднего значения тд=
= Л4{0} фазового сдвига 0 (квазикогерентный прием) и неизвест-
ного среднего значения те (некогерентный прием) при условии
I ®21 Г 1.
Ответ: PvM.= Q(actbc)
2+<7
ехр
4+<? Е
—L(a2+^)c2jz0(afc2)(
где для квазикогерентного приема
ь= 2(2+Л С=Т1/1±1,
4~Ь<7 г 4q
474
а для некогерентного приема
а = О, & = V2, с = уКq/2 (4 + q).
Графики функции Рчм = f (q, у) для случаев квазикогерент-
ного и некогерентного приема медленно федингующих частотно-
манипулированных сигналов приведены на рис. 15.13, а и б.
15.16. Решить задачу 15.15 для случая оптимального приема
медленно федингующих фазоманипулированных сигналов
th (0 = аАт ехр [/ ((оо/ — 0)],
' «2 (0 = аАт ехр [/ + л — 0)1,
Т.
Ответ: При квазикогерентном приеме
Рфм= 1 —Ф
fl/У2~М,
при некогерентном приеме РФМ = 1/2.
График функции РФМ = f (q, у) для случая квазикогерент-
ного приема приведен на рис. 15.14.
Рис. 15.13. Зависимость суммарной вероятности ошибок от отношения сиг-
нал/шум при квазикогерентном (а) и некогерентном (б) приеме медленно
федингующих ЧМ сигналов
475
Рис. 15.14. Зависимость суммарной
вероятности ошибок от отношения
сигнал/шум при квазикогерентном
приеме медленно федингующих ФМ
сигналов
15.17. Решить задачу 15.15 для случая оптимального приема
медленно федингующих тонально-манипулированных сигналов вида
ЧМ-АМ
иг (0 = аАт [1 + cos Йх/] ехр [/ (<М — 6)1> 0</<т
«2 (/) — аАт [1 + cos Q2/] ехр [/ (a>ot — 0)1, "*
при условии С ®0> Tat = 2л/£2г Т.
Ответ'. При квазикогерентном приеме
Гчм-ам = Q (ас, bc) — ~b ехр Г —(а2 + &2)с®11 о (abc2),
где
______Уб <7 . b = 1 _| Уб? .
/9(4+?)2-4? ’ /9(4+?)2-4^ ’
при некогерентном приеме
Рчм-ам = Q (ас, be) —1 +
__ V51
/9(4+д)2—4g2
е-с2/0(а&е2),
476
где
V5/9(4+^-4^ . 1Л V5]A)(4+a2-47 .
9(4 + <7)-4<7 ’ V 9(4+^)—4^
c=vl/-l?-9<4+^
? V 9(4+9)2-4<72
Графики функций Рчм-ам = f(<7, ?) Для случаев квазикогерент-
ного и некогерентного медленно федингующих тонально-манипу-
лированных сигналов вида ЧМ-AM приведены на рис. 15.15, а и б.
15.18. Решить задачу 15.17 для случая оптимального приема
медленно федингующихся тонально-манипулированных сигналов
вида ФМ-АМ:
МО = аАт [1 + cos Ш] ехр [j (&ot — 0)1,
«7(0 = аАт П — COS Ш] ехр [/ (соо/ — 0)], "" ""
Ответ'. При квазикогерентном приеме
Рфм-ам = Q (ас, Ьс)---------ехР [ —(а2 + &2)с2 (abc2),
Рис. 15.15. Зависимость суммарной вероятности ошибок от отношения сиг-
нал/шум при квазикогерентном (а) и некогерентном (б) приеме медленно фе-
дингующих ЧМ-АМ сигналов
477
где
а= 1
21/2? >.-1 I _2У2?
Кэ(4+?)2-^’ ]/э(4+?)2-?2 ’
с==тУ 1Н3+^;
при некогерентном приеме
/’фм-ам = Q (ас, Ьс)--1-
где
а = /1-
2~|/2?
Квйч-Э1-?.
е“с I0(abc2),
21/2^9 (4+?)2 —?2 . ь= , / j 2~1/2]А?(4+?)2-?2 .
9(4+?)—q ' V 9(4+?)—q
С —у
if_Lп 9(4+^2~?2
V 2 4 9(4+?)-?
Графики функций Рфм-ам = f (q, т) для случаев квазикогерентного
и некогерентного приема приведены на рис. 15.16, а и б.
Рис. 15.16. Зависимость суммарной
нал/шум при квазикогерентном (а)
федингующих ФМ-АМ сигналов
вероятности ошибок от отношения сиг-
и некогерентном (б) приеме медленно
478
15.19. На вход приемного устройства поступает колебание
X (О = s (0 + В (0.
где
т
/=1
— один из т возможных сигналов st (/), sm (t), причем если
= 1, то все остальные К} = 0 (/ i). Предполагается, что апри-
орные вероятности р fa) присутствия сигналов st (t) в реализации
x(t) априори известны и равны:
Р (%) = Р (з2) = ...=£ (sm) = 1//п,
а сами сигналы (/) полностью определены на интервале (0, Т) и
равны нулю вне этого интервала, имеют равные энергии Et = Е и
ортогональны:
I ( F
Аддитивная помеха g (t) представляет собой стационарный гауссов-
ский белый шум с нулевым математическим ожиданием т$ = 0 и
корреляционной функцией
(?) = (N0/2) б (%).
Определить структурную схему приемника, осуществляющего
оптимальное по критерию идеального наблюдателя различение
/n-ичных сигналов st (t), и вычислить соответствующую ему суммар-
ную вероятность Р ошибочного приема.
Ответ: Приемник должен сформировать величины
т
Ut — j* x(t) 8г (f) dt
b
и осуществить их сравнение. Решение %г = 1 принимается, если
Ut — Umax (рис. 15.17). При этом суммарная вероятность ошибоч-
ного приема
P-1--U f e“?!/2[ofz + lZ— 'dz.
У2л J L \ И aUJ
— оо
15.20. Решить задачу 15.19 для случая приема /n-ичных детер-
минированных сигналов st (/) на фоне аддитивной гауссовской
стационарной помехи £ (/) с нулевым математическим ожиданием
/ng = 0 и корреляционной функцией 7?g (т).
Ответ: Оптимальный приемник для различения /n-ичных сиг-
налов на фоне коррелированного шума должен сформировать слу-
чайные величины
о
479
где О'г (t) есть решение интегрального уравнения
т
о
и осуществить их сравнение. Решение = 1 принимается, если
U( = t/max- При этом суммарная вероятность ошибочного приема
р = 1 “vfe J е~ г*/2 [ф (г+°o)1'rt’1 dz>
—-ОО
Т
где о§ =
о
15.21. На выходе УПЧ синхронного приемника (рис. 15.18)
. имеет место колебание
X (/) = Xsx (0 + (1 - К) s2 (0 + % (О,
где g (t) — квазигармонический гауссовский шум с нулевым мате-
матическим ожиданием /ng = 0 и корреляционной функцией
Rt СО = <*i Pg СО cos (Оо т;
«1 (О = cos (©о t + <Р1),
s2 (0 = 0, ,
— детерминированные амплитудно-манипулированные сигналы.
На второй вход синхронного детектора подается колебание от
местного гетеродина мг (/) = t/r cos (<в0/ + <рх). Если напряжение
U (0 на выходе синхронного детектора превышает некоторый по-
рог Но, принимается решение о приеме сигнала sx (/) (Л = 1), в про-
тивном случае принимается решение о приеме сигнала s2 (/) (% = 0).
Априорные вероятности р (Si) присутствия на входе приемника сиг-
налов Si (/) равны между собой: р (sx) = р (s2) = 1/2.
Рис. 15.17. Оптимальный приемник /n-ичных сигналов
480
Рис, 15.18. Синхронный приемник
Определить суммарную вероятность ошибочного приема при
условии, что порог До выбран оптимальным по критерию идеаль-
ного наблюдателя.
Ответ’. Р — 1 — Ф (Ат12<з£, Но = Ат/2.
15.22. Решить задачу 15.21 для случая приема фазоманипули-
рованных сигналов
Si (0 = Ат cos (со0/ + фх), о < t < Т
s2 (0 = Ат cos (®0/ + фх + л), ""
Ответ: Р = 1 — Ф (Лщ/cfg), Но = 0. ,
15.23. На выходе УПЧ приемника, схема которого представлена
на рис. 15.8, имеет место колебание
х (0 = (/) + (1 - %) ы2 (0 + | (/),
где | (7) — квазигармонический гауссовский шум с нулевым мате-
матическим ожиданием mg = 0 и корреляционной функцией
Pg (т) = <г| pg(x) cos ci)ot;
Ы1 (0 = U (0 cos [<о0/ + Ф (0L 0< t < Т,
и2 (t) = 0,
— амплитудно-манипулированные сигналы.
Сигнал ых (f) представляет собой отрезок квазигармонических
флуктуаций, огибающая которых распределена ло закону Релея:
Рх (U) = ((//о?) ехр (— (Wc), [7 > 0,
а случайная начальная фаза — равномерно на интервале
(— л, л). Параметр % принимает значения К — %х = 1 или К = =
= 0 с априорными вероятностями р (Xj) = р (Ю — Если
процесс U (t) на выходе линейного детектора огибающей превышает
некоторый порог Но, принимается решение к — 1, в противном слу-
чае принимается к = 0.
Определить суммарную вероятность ошибок при условии, что
порог Но выбран оптимальным по критерию идеального наблюдате-
ля.
16 Зак. 1203
481
Ответ:
Р = 1"{1 + еХР (~ 2^)~еХр [“ 2(а2с+с!)]}’
где
al f а ? 4- ст?
Н^]/ Z2(a? + ot)ln^±-L.
15.24. Найти структурную схему приемного устройства, осу-
ществляющего оптимальную по критерию Неймана—Пирсона обра-
ботку колебания ,
х (0 = As (0 + I (t),
где В (/) — стационарный гауссовский шум с нулевым математиче-
ским ожиданием т$ = 0 и корреляционной функцией
s (0 — детерминированный сигнал, определенный на интервале
(О, Т) и равный нулю вне его.
Ответ [96]: Оптимальный приемник должен сформировать ве-
личину
и=Лх (z) s (/)+*(0 s(Z) ]dt+А(х (0) s (0)+х (Т} s (T)1
о
и сравнить ее с порогом h0, определяемым заданной вероятностью
ложной тревоги
Pf, = 1 — Ф (h0/<j0),
где
°о = ^|- J р2 W (О] dt+ Is2 (°) +s2
о
Если U > h0, принимается решение % = ^ = 1, в противном слу-
чае принимается А = Ао = 0. Вероятность правильного обнаруже-
ния вычисляется по формуле
\ Оо /
15.25. Решить задачу 15.24 для случая, когда корреляционная
функция шума имеет вид
cos©!^—4)+ —sinojil^—41
“i
482
Ответ [96]: Оптимальный приемник должен сформировать ве-
личину
,7=2^иП^<')+“Х(')+“!ХЮ1Х
О
х [s'(0 + as (0 + s (0] dt + + ,
<о0
со2 = со? + а2, а0 = 2а,
и сравнить ее с порогом /г0, определяемым заданной вероятностью
ложной тревоги
Pf. — 1 — Ф (V^o),
где
т
°0 = J (0 + as’ (0 + ®0 S (0] dt +s-^ + .
При U > h0 принимается X = Хх — 1, в противном случае прини-
мается % = %0 = 0. Вероятность правильного обнаружения вычис-
ляется по формуле
Л>, = 1 — Ф (h0/a0 — a0). f
15.26. На вход оптимального по критерию Неймана—Пирсона
приемника поступает колебание х (t) == “ки (f) + £ (t), где | (t) —
стационарный гауссовский белый шум с нулевым математическим
ожиданием = 0 и корреляционной функцией
Ъ (%) = (JV0/2) 6 (т);
u(t)— аАт cos (соо t + 0),
— медленно флуктуирующий сигнал. Здесь Ак и <о0—посто-
янные величины, 0 — случайная начальная фаза, равномерно рас-
пределенная на интервале (— л, л), а — амплитудный множитель,
принимающий на интервале (0, Т) случайные значения с плотно-
стью распределения вероятностей
Pi (а) = (й/<Уф) ехр (— a2/2o|), 0 <1 a < оо.
Вычислить вероятность ложной тревоги и правильного обнаруже-
ния.
Ответ:
2Е А*тТ
N» Na
/to), <7 = 2<Уф <7,
График функции Рд, = f (q) приведен на рис. 15.4 (штрих-пунк-
тирные линии).
16* 483
16. ОЦЕНКА ПАРАМЕТРОВ СИГНАЛА
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Пусть на некотором временном интервале (О, Т) имеется реализация
т) (/) суммы полезного сигнала s (tlt Л2, ...), зависящего от нескольких
параметров Хх, Х2, ...» и гауссовского стационарного шума £ (/):
Л (0 = $ (/, Х2, ...) + g (0, 0 < t < Т. (16.1)
Предполагаются известными следующие сведения: 1) гауссовский'ста-
ционарный шум £ (/) имеет нулевое математическое ожидание и известную
корреляционную функцию:
м{1 (0} = о,. м{1 (/,) | (/,)} = R (t2 - У; (16.2)
2) вид сигнала s (/, Х2, ...) задан и он полностью расположен внутри ин-
тервала наблюдения (0, Т), так что значения сигнала и его производных на
концах этого интервала равны нулю; 3) до наблюдений ориентировочно из-
вестны априорные плотности вероятности параметров Х2,... Для интересую-
щих нас параметров в дальнейшем они полагаются равномерными в неко-
тором интервале значений.
Путем обработки принятого колебания т) (/) нужно найти предельную точ-
ность оценки одного или нескольких параметров Xj.
Обработка принятой реализации может осуществляться в дискретном
или непрерывном времени. В первом случае обычно используются равноот-
стоящие отсчеты реализации т)! = т) (Д), т)2 = т) (2Д). “Пт = Л (Tim),
называемые в совокупности выборкой объема /и; во втором случае исполь-
зуется вся реализация т) (/) на интервале (0, Т).
Пусть истинное значение параметра Xf постоянно и равно Хг-0> а его
оценка по принятой реализации есть Xj. Оценка^ из-за наличия шума будет
случайной величиной, изменяющейся от одной реализации к другой.
В качестве определяющих можно взять разные характеристики случай-
ной величины Xj. В зависимости от этого рассматривают точечные и интерваль-
ные оценки.При точечных оценках интересуются главным образом математиче-
ским ожиданием и дисперсией случайной величины Xj. Интервальная оценка
сводится к вычислению интервала, в котором с заданной вероятностью за-
ключено значение оцениваемого параметра. В дальнейшем рассматривают-
ся только точечные оценки.
Оценка Xj называется несмещенной, если = Xf0; в противном
случае^ =/= Xf0) оценка называется смещенной. Разность ДХ =
= 7И{Х г} ^го называется смещением или систематической ошибкой оцен-
ки. Несмещенная оценка, имеющая наименьшую возможную дисперсию
Dornin М ((£.-Х.0)2|, (16.3)
называется эффективной. Конечно, всегда желательно получить эффектив-
ную оценку.
В том случае, когда полезный сигнал s (/, X) зависит от одного оценивае-
мого параметра X и его оценка производится по выборке {1^, т]2, ..., т]т} объе-
ма /и, можно доказать, что дисперсия несмещенной оценки имеет нижнюю гра-
ницу, определяемую следующим неравенством Рао—Крамера:
(С СГ д I2 V1
I 1 *) Uh I*1 * ’ ” * ’ •“ * ’ ’
; (16.4)
где рт (Tjj.. r]m; X) — совместная плотность вероятности выборочных
значений.
484
Если выборочные значения Т11э t)2, Лт независимы в совокупности, пра-
вая часть неравенства (16.4), определяющая минимально возможное значение
дисперсии несмещенной оценки, принимает вид [105]
Xmin
м Г dlnp(i); X) I2 1
I J .
d31пр(п; Mil"1
dX2 J.
(16.5)
где для непрерывной случайной величины л
d In р (ту, X) ]2 Г Г dlnp(r); X) j2
di J J L ax
— oo
p (t); %) dr)=
Г Г dp (r,; %) у dr)
J L ] p(r];X)’
(16.6)
а для дискретной случайной величины
f ainp(T); X) у Г a In p (th; h)1*
t dK J , Zi [ . &k
i =— oo
др(ъ W________!____.
A ] p (т)г; %) '
/(16.7)
Когда полезный сигнал s (t, Xlt %2) зависит от двух параметров %,, Х2
и оценка их производится по независимой выборке объема т, формулы для
минимальных дисперсий оценок и нормированной корреляционной функции
между оценками имеют вид
D. 0-'и)"1 (l-^)-1
^т1п , plnpfoXj, Хг))2 ’ £1!П,‘п (ainpfaXbX
( аХх J ( ах2
М Г a In р (ту, Хх, Х2) ainp (п; Хх, х2)
I axi
(16.8)
ах2
a in р (ту, Xi, х2)
axi
a in р (ту, Xi, х2)
ах2
2 11/2
Для получения оценок могут применяться разные методы: метод момен-
тов, по математическому ожиданию апостериорного распределения, по мак-
симуму апостериорного распределения, метод максимального правдоподобия
и др. [6, 106]. Наиболее часто используются метод максимальной апостериор-
ной плотности вероятности и метод максимального правдоподобия.
По предположению, значения оцениваемых параметров Хх, Х2, ... постоян-
ны на интервале наблюдения. Используя тот факт, что шум в (16.1) гауссов-
ский, можно найти совместную плотность вероятности для выборки (т)х,
Ла» •••» Лт) и параметров Хх, Х2, ...
Р (Л1>• • Лт! Х12 Х2,...) =ро (Хх, Х2, ...) р (т)х, ..., Лт I Хх, Х2,...) =
= р(Л1.--«, Лт)р(^1> Х2, ... |Т]1, ..., Т]т).
485
Остюда получаем формулу Вайеса для условной плотности вероятности
р(Хь Х2,... И]!,т)т)=^Ро(^1» ^2> •••)Р('П1» •••» Пт1М> •••)> (16.9)
где коэффициент k определяется из условия нормировки:
k~X— J... j Ро (^1> ^2» • • •) Р СЦ1» • • •, Лпг | ^1» ^2» • • •) ^1 ^2- • •
При решении ряда практических задач до проведения наблюдений с боль-
шей или меньшей степенью достоверности бывает ориентировочно известна
плотность вероятности оцениваемых параметров р0 (Ар Х2,...), которую назы-
вают априорной (доопытной). Условная плотность вероятности р (Х1? Х2, ...|
Лх» •••> Лт) называется апостериорной (послеопытной) плотностью вероятности
параметров Xlt Х2, ... При данной выборке она дает полные сведения об ин-
тересующих нас параметрах.
Условная плотность вероятности р (т^, ..., т]пД1» ^2» •••)> рассматриваемая
как функция параметров Х2, ..., называется функцией правдоподобия. При
извлеченной выборке (без учета априорного распределения р0 (Xlt Х2, ...)
она показывает, насколько одни возможные значения параметров л2, ...
более правдоподобны, чем другие.
В методе максимальной апостериорной плотности вероятности в каче-
стве оценок Xlt Х2, ... параметров Х2, ... берутся те значения, при кото-
рых для данной выборки (гц, ..., r]m) апостериорная плотность вероятности
имеет абсолютный максимум. Эти значения являются решениями системы
уравнений
—р (£1, £2,..., I гц,..., Пт) = 0, i = 1, 2,... (16.10)
Эти решения должны явным образом зависеть от результатов выборки и
обеспечивать получение абсолютного максимума апостериорной плотности ве-
роятности.
Так как логарифм — однозначная и монотонно возрастающая функция
аргумента, то результат максимизации апостериорной плотности вероятности
и логарифма от нее совпадают. Поэтому вместо уравнения (16.10) можно ис-
кать соответствующие корни уравнения
lnp(Xlt Х2...........IТ)1, Tlm) = 0> t = l, 2,... (16.11)
Во многих практических случаях априорная плотность вероятности
Ро (^i> ^2> •••) оказывается неизвестной и ее полагают равномерно распределен-
ной (например, прямоугольной или нормальной с большой дисперсией) на
интервале возможных значений параметров. При этом координаты максимума
апостериорной плотности вероятности будут совпадать с соответствующими
координатами функции правдоподобия, которые определяются путем реше-
ния системы уравнений правдоподобия
д ~
—7—LUi, Х2,..., Хг,...) = О, 1 = 1, 2, 3...
или
—^-InL^, £2,..., ..;) = 0, / = 1,2,3,... (16.12)
dU
где
L (Xi, Х2, ...) =р (т)1, ..., Т)пг1^1» ^2» • • •) • (16.13)
Решения должны явным образом зависеть от результатов выборки и обес-
печивать получение абсолютного максимума функции правдоподобия (или ее
логарифма).
486
В большинстве радиотехнических задач, связанных с оценкой параметров,
преимущественно используется метод максимального правдоподобия. Это
объясняется рядом достоинств оценок, получаемых этим методом, а также
сравнительной простотой вычислений и практической реализации соответст-
вующих алгоритмов в виде измерительных устройств [107, 108]. В частности,
при оценке одного параметра получаемая оценка оказывается асимптотиче-
ски (при очень большом объеме выборки) эффективной. Перечислим теперь
исходные условия, выполнение которых предполагается в дальнейшем, и за-
тем в справочном виде приведем конечные формулы для дисперсии оценок
[108] при обработке непрерывной реализации т) (/).
1. В реализациях т) (0, подлежащих обработке, отношение сигнал/шум
настолько велико, что неоднозначность оценки практически исключена.
2. Рассматривается оценка лишь одного какого-либо известного параме-
тра X/ полезного сигнала s (t, Х2, ...). Априорная плотность вероятности
этого параметра X/ принимается равномерной в некотором интервале значе-
ний. Остальные параметры сигнала считаются или все известными (так на-
зываемый полностью известный сигнал, за исключением оцениваемого пара-
метра) или же радиосигнал s (/, Х2, ...) имеет случайную начальную фазу,
равномерно распределенную в интервале (— л, л) (сигнал со случайной на-
чальной фазой). В дальнейшем рассматривается в основном случай пол-
ностью известного сигнала. Однако ряд полученных результатов остается
справедливым и для радиосигналов со случайной начальной фазой.
Параметры Xj (амплитуда, длительность импульса), от которых зависит
энергия сигнала, называются энергетическими; остальные параметры (ча-
стота, время появления, фаза и др.) — неэнергетическими.
3. В дальнейшем рассматриваются три частных вида гауссовского ста-
ционарного шума £ (/):
белый шум с корреляционной функцией
Яо (*2 - *1) = Wo6 (/2 - ZJ/2, (16.14)
экспоненциально-коррелированный шум
(*2 - *1) = о2 ехр (—а | /2 - I), в (16.15)
узкополосный шум с корреляционной функцией
[а
cos ©j (/2—*i) 4--sin ©i 112—/i I
©i
При указанных трех условиях оценки неэнергетических параметров сиг-
нала,^ а также его амплитуды оказываются несмещенными.
Дисперсия оценки неэнергетического параметра X полностью известного
сигнала s (/, X) определяется формулой [108]
Г<Ра(Х)1-1
ак L ’
где Хо — истинное значение оцениваемого параметра;
т
s (М = j* s (/, Хо) v (Л K)d/.
о
Для гауссовских стационарных шумов с корреляционными функциями
(16.14)—(16.16) функция v (t, Л) соответственно равна
v0(t, X)=-^-sG, X), (16.19)
/v0
1 v 7 2о2 L a2 dt2 J v 7
• (16.16)
(16.17)
(16.18)
487
Ь) = -—ГТ <°Ss(z’ x)+2(°)2o-2a2)x
4ao о a3 I
(16.21)
Дисперсия оценки «амплитуды» а полностью известного сигнала вида
s (t, а) = a s0 (/), где s0 (0 — нормализованный сигнал, равна
J So (0 v' (f) dt
(16.22)
Здесь функция о' (f) определяется прежними формулами (16.19)—(16.21)
£ заменой в правых частях s (t, X) на s0 (/).
2. ПРИМЕРЫ
16.1 . Случайная величина X принимает два значения 1 и 0 с
вероятностями Р {х = 1} = %, Р {х = 0} = 1 — X. Пусть в ре-
зультате т испытаний исход х = 1 осуществился k раз, а исход
х = 0 осуществился т — k раз. Требуется получить оценку вероят-
ности А по результатам опыта.
Решение. В данном примере функция правдоподобия определяет-
ся биномиальным распределением L (А) = А* (1 — A)m-fe. Урав-
нение правдоподобия принимает вид
-4-in л (А)=4-—^4-=0.
Отсюда получаем решение А = kltn. Следовательно, оценкой вероят-
ности Р{х — 1} = А является относительная частота kltn.исхода
х = 1.
Для нахождения минимальной дисперсий оценки воспользуем-
ся формулами (16.5) и (16.7). Так как др! di. = 1 при х — 1 и
др/д’К = — 1 при х = О,
dlnp(x; X) у = 1 1 =1
6Х f X 1—X X(l —X)
Поэтому
min~(1— tylm.
16.2 . Некоторая нормально распределенная случайная величи-
на А измеряется независимо двумя неравноточными’ приборами, ко-
торые осуществляют измерения без систематических ошибок, но
с разными дисперсиями Dx и Т)2. Нужно указать результирующую
погрешность измерения случайной величины А.
Решение. Обозначим показания первого и второго приборов
соответственно через rij и т)2. Можем записать т)х = А + |lt т]2 =
= А + В2, где и |2 — независимые нормально распределенные
случайные величины с нулевыми математическими ожиданиями и
дисперсиями Dx и П2.
488
Нетрудно убедиться, что функция правдоподобия случайной ве-
личины Л определяется выражением
Ь (X) = Р (т, тк IX)=-~4- ехр [ -±11=^
2лП1 (Jjj L 2Z)X
Уравнение правдоподобия принимает вид
(t)i~X) I (т)а —^)
Dr
2D2
— lnL(A) =
di
- Отсюда находим
£ =
Da
= 0.
Dr
—— ТЦ 4----1— T]2.
Pi + D2 11T D1+D2 12
По известным правилам получаем дисперсию
D^DrD^Dr + DJ.
такой оценки
16.3 . Вычислить дисперсию оценки амплитуды а прямоуголь-
ного радиоимпульса
s (t, а) = a cos (at + <р0), 0 < t0 t t0 + ти < Т, аТ > 1-,
(16.23)
принимаемого на фоне гауссовского стациойарного шума с корре-
ляционной функцией (16.15).
Решение. Рассматриваемый радиоимпульс равен нулю на кон-
цах интервала наблюдения (0, Т). Для него функция v’ (f), входя-
щая в формулу (16.22), определяется выражением, (16.20) и равна
, / ct Г 1 42 «о (t. 1 оь /< । со2 \ . . , .
ц (/) =------- s0 (t, л)--------------- =— 11 + -— cos (at + q>0).
v ’ 2a2 L a2 dP J 2a2 \ a2 ) ' °'
Подставив эту функцию v' (t) в формулу (16.22) и выполнив инте-
грирование, при условии аТ > 1 получим
где Д/э = а/4 — эффективная ширина спектра шума; Д/ — шири-
на основного «лепестка» спектра радиоимпульса.
16.4 . Определить дисперсию оценки разности т = Tj — т2 вре-
менных положений двух неперекрывающихся радиоимпульсов
si (t — Ti) = aif (^ — Ti) cos (®^ + Ti),
s2 (t — r2) — а2? (t — T2) cos (at + q>2),
принятых на фоне белого шума п (t) в интервале времени (0, Г),
причем аТ 1. Функция f (t — тг) описывает огибающие радио-
импульсов.
489
Решение. Если обозначить через 6Х и 62 соответственно случай-
ные ошибки определения q и т2, то дисперсия оценки разности
6 = 6Х — 62 определяется соотношением
Dx = М {б2} = М {6?} + М {61} -2М {6Х 62} = DXl + DX1 -
—2 ]/ DXi DXi г12,
где ОТ1иОТ!— дисперсии раздельных оценок тх и т2; rX2— нор-
мированная корреляционная функция совместной оценки тх и т2.
Так как импульсы не перекрываются, то гХ2 = 0 и
Dx — D Xi D х , (16.24)
Слагаемые, в правой части (16.24) находим по основной формуле
(16.17), причем для белого шума в (16.18) нужно подставлять функ-
цию v (t, тг), определенную соотношением (16.19).
Следовательно, можем написать
Т 1 — 1 Dx. = - , i = l,2. 1 No J L 0 1 (16.25)
Можно показать [108], что этот результат приводится к виду
Dx.= ! , 1 (2Ei/N0)^ где Et = J st (t—Xi)dt 0 (16.26) (16.27)
— энергия радиоимпульса’s, (t — тг),
p2= J 1F (/©) |2 da 1 f <o2| F(ja) |2d®, — OO J —00 (16.28)
F (/©) = § / (0 eia>i dt — oo (16.29)
— комплексный спектр огибающей f (f).
Вычисления по формуле (16.28) для огибающей гауссовой фор-
мы f (/) = ехр (— 2,8/2/ти), где ти — длительность импульса на
уровне 0,5 от максимального значения, приводят к следующему ре-
зультату: р2 =' 2,8/т1.
Применительно к гауссовым радиоимпульсам формула (16.24)
при ах = а2 = а принимает вид
Dx —----------; Е= 1/— -^-=0,37а2ги. (16.30)
1,4(25/ЛГ0) V 5,6 2 и V
490
3. ЗАДАЧИ И ОТВЕТЫ
16.1 . Имеется последовательность У независимых испытаний,
в каждом из которых интересующий нас исход наступает с постоян-
ной, но неизвестной вероятностью р. Пусть п — наблюдаемое число
положительных исходов. Каково наиболее правдоподобное значе-
ние р?
Ответ: р = n/N.
16.2 . Оценить параметр % в законе распределения Пуассона
V
р (х, %) =---е~*\ пользуясь выборкой, которая для случайной
х!
величины X дала значения xlf х2, ..., хп.
Ответ: к =— > хь D~ =—.
п z = i п
16.3 . Показания п1У п2, .... пм каждого из 'N счетчиков распре-
делены по закону Пуассона. Известно, что средние значения М } =
= i = 1, 2, ..., Af, где %—неизвестная интенсивность; —
отдельные временные интервалы счета. Найти оценку интенсив-
ности %.
л N I N
Ответ: к = 2 ni / 2
z=i / z=i
16.4 . Случайная величина £ имеет нормальную плотность вероят-
ности
р (£) = —4= ехр [ ——^-1
У 2л£> F L 2D J
с известным математическим ожиданием т и неизвестной дисперси-
ей D. В результате наблюдений получены п независимых значений
Bi, Вг, •••» Вп случайной величины Найти правдоподобное значение
дисперсии D. Будет ли полученная оценка несмещенной?
1 п
Ответ: D == — V —m)2;
П
оценка несмещенная.
16.5 . В тех же условиях, что и в задаче 16.4 неизвестны и подле-
жат оценке математическое ожидание т и дисперсия D. Смещенными
или несмещенными будут оценки максимального правдоподобия?
1 п 1 «
Ответ :т=- — V , Ь = — V (^ — т)2.
п п
I— 1 , 1= 1
Оценка математического ожидания несмещенная, так как М{т—
— т} = 0, а оценка дисперсии смещенная, так как M{D} =
= D(n—l)/n.
491
16.6 . Найти дисперсию оценки амплитуды а гауссова импульса
s (/, а) = а ехр
2,8
(t—П>)2
0<то<Т,
принимаемого на фоне гауссовского стационарного шума с экспо-
ненциальной корреляционной функцией (16.15).
Ответ: Од =-----———--------------- 2,67 —.
- Г 2п. / 2.8 \ 2,8+(ати)2
ати+—-
> ати
16.7 . На фоне одного и того же белого шума п (/) раздельно при-
нимаются прямоугольный и гауссов радиоимпульсы
Si (/, а) = a cos (<о/ + ф0), 0 < t < У,
s2 (/, а) = ae~v(*“T®)’cos [со (t — т0) + ФоЬ 0 < т0 < Т.
Найти предельную точность измерения амплитуды а таких радио-
импульсов, считая, что они практически полностью расположены
внутри интервала (О, Т). Сравнить результаты при равенстве энер-
гий радиоимпульсов, т. е. при условии
Т оо
Si (/, a)dt = J si (Л a) dt.
О —оо
Ответ: ofa = — , = No Д/ — ; ofa = o2a
Тод г ЭТ
при ти =
16.8 . Вычислить дисперсию оценки параметра т радиосигнала
s (/, т) = а0 (1 + т cos Q/) cos (со/ + ср0), 0< t <Z Т, соТ1^ 1, при-
нимаемого на фоне белого шума п (/).
Ответ: —
2A/0 Г | sin2Qr~l~1
а*Т [ + 2QT J
16.9 . Прямоугольный радиоимпульс (16.23) принимается на
фоне узкополосного шума (16.16). Найти дисперсию оценки ампли-
туды а. Рассмотреть частный случай, когда со = соо = ]^<oi + а2-
Ответ:
8асо§ а2
(со2—ю$)-|-4а2 со2
Q ZU
Од =------ при со=со0.
а
16.10 . На фоне белого шума п (t) принимается радиосигнал
s (/, ср) = U (/) cos [со/ + ф (/) + <pL
492
где U (t) иф (t) —законы амплитудной и фазовой модуляции. Опре-
делить дисперсию оценки неизвестной начальной фазы <р.
т
Ответ: Oq> — ^2E^N •» Е J U2(t)dt, coT^l.
о
16.11 . Вычислить дисперсию оценки временного положения т0
гауссовского импульса
s (/, т0) = а ехр
(*-Ь)2
при оптимальном приеме на фоне белого шума. Предполагается, что
весь импульс практически находится внутри интервала наблюдения
(О, Т).
Ответ:
т2 /----
°т0 =-----5---> Е — I s2 (/, т0) dt = 1 / я а2т = 0 75а2т
2,8(2E/W0) J ' °7 |/ 5,6 и ’ и’
16.12 . Решить задачу 16.11 для случая, когда прием гауссова
импульса производится на фоне экспоненциально-коррелирован-
ного шума (16.15). При каком условии ответы к задачам 16.11 и
16.12 совпадают?
Ответ'. = 4а2т£/5,6аЕ, Уо = 4а2/а.
16.13 . На фоне белого шума п (/) принимается прямоугольный
радиоимпульс
s (/, Q) = a cos [(со + Q) t + ФоК 0 < t ти.
Найти предельную точность измерения смещения частоты Q.
Ответ*.
т
о£ =---------, Е= fs2(/,Q)d/= —а2ти, (оТ>1.
т2(2Е/ЛМ J 2
О
16.14 . Решить задачу 16.13 для гауссова радиоимпульса
s (/, Q) = а ехр Г —(t — т0)2
cos [(со 4-Q)(/—то)+фо], 0<т0<Т.
Сравнить результаты для прямоугольного и гауссова радиоимпуль-
сов при равенстве их энергий.
п '2 П>2
Ответ: ой2 =------------,
T2(2E/yV0)
ти У
I т ‘
493
16.15 . Решить задачу 16.13 для случая, когда прямоугольный
радиоимпульс принимается на фоне экспоненциально-коррели-
рованного шума (16.15), считая возможные значения й много
меньше со.
Ответ : <tq =-------—-------.
2ат*Е[1+(в>/а)2]
16.16 . Вычислить дисперсию оценки параметра 0 радиосигнала
s (t, Р) = a cos (со/ + р cos й/ + <р0)> 0 sg; t Т,
принимаемого на фоне белого шума. Предполагается, что возмож-
ные значения р много меньше со и соТ 1.
Ответ:
о| = —— [1+ sin^Qr Гх~ —— , fs2(/,p)d/~— а*Т.
2E/NQ L 2QT J 2E/N0 J .2
О
16.17 . Определить дисперсию оценки небольшого смещения ча-
стоты Q прямоугольного радиоимпульса
s (t, Q) = a cos [(cd + Q) t + ToL 0 < t ти,
принимаемого на фоне флуктуационного шума с корреляционной
функцией (16.16), в которой (Oi = <оо а. Предполагается, что
допустимые значения Q значительно меньше со.
Ответ:
ги
= Е—- f S^t,Q)dt=±a4B, <оти»1.
х^Е \<о2—со2/ J 2
Раздел V
ТЕОРИЯ ИНФОРМАЦИИ
17. ДИСКРЕТНЫЕ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Дискретные (цифровые) системы связи — системы, в которых как реа-
лизации сообщения, так и реализации сигнала представляют собой последо-
вательности символов алфавита, содержащего конечное число элементарных
символов [1].
Пусть Xi, i = 1, 2, ..., n, — совокупность возможных различных неза-
висимых элементарных символов алфавита на входе системы, a yj, j = 1,2,...,
..., т — совокупность символов на ее выходе; р (х^) — априорная вероят-
ность символа Xi\ р (yj) — вероятность появления символа yj на выходе
системы; р (Xi, yj) — совместная вероятность появления на выходе системы
символа yj, если на входе был символ хц р (xt | yj) — апостериорная вероят-
ность символа хс, p(yj \xi) — условная вероятность, появления на выходе
системы yj, при условии, что на входе был символ х/. Для этих вероятностей
выполняются соотношения
Р (xi) — 2 Р (xi’ У?>' Уд> 2 Р (xi) = = (17Л)
/=1 i=l i=l 1 = 1
Тогда собственная информация символа х$ (количество информации, до-
ставляемое самим символом х$ или любым другим однозначно с ним связан-
ным) определяется формулой
I (Xi) = — log р (Xi). (17.2)
Другие понятия информации определяются следующими соотношениями:
— условная собственная информация символа хг- при известном yj
I(Xi\y}) = — logp(Xilw); (17.3)
— взаимная информация двух случайных символов относительно друг
друга (количество информации относительно символа х^, доставляемое yj
\ у.Р^У^ р(хьуз)
I (хе, Pj) = log-—— “log ————- ; (17.4)
Р (xt) р (xt) р (yj)
— собственная информация совместного события (х^, yj)
I (Xi, У]) = - log p (xit y,Y. (17.5)
495
— среднее количество информации, доставляемое принятым символом
yj относительно множества всех передаваемых символов
X = {xJ. « = 1,2,п,
i (X; yj)= 2 w)p(*d'/j) = 2 р (xt I у;) 1о§ : (17-6>
— среднее количество взаимной информации по множеству символов
У = j = 1, 2, /и, при фиксированном xt
m т . ।
1 (xf, Y) / (xf, у}) р (у} | Xi) = 2 р (yj | Xi) log Р р (~j'; (17.6а)
— полное среднее количество взаимной информации в множестве сим-
волов Y относительно множества символов X
пт . т
I(X;Y)=^ У Р (Xi, yj) log* = 2 р {yi) 1 (Х: • (17-7)
Z = 1 /«1 /=1
При решении большинства задач, связанных с построением систем пе-
редачи и преобразования информации, наибольший интерес представляет ве-
личина I (X; Y).
Если символ Х[ статистически связан не только с символом но и с
третьим символом k = 1,2,...,/, то при известных вероятностях р (xt, yj
Zk) условная взаимная информация равна
,nr,P(Xi\yj’ Zh) p(Xf, yjlzk)
‘ («,. «l3,) = lo8 —|г- -1»8 -1|а)р(и — . (17.8)
где I (xi\ yj\zk) — количество информации, доставляемое yj о xt, когда
предварительно известен символ
Единица количества информации определяется выбором основания лога-
рифмов. Когда используются логарифмы при основании два, то количество
информации I измеряется в двоичных единицах (дв. ед., или бит). Переход
от одной системы логарифмов к другой равносилен простому изменению еди-
ницы измерения информации. Этот переход осуществляется по формуле
logb k = logb а • loga k.
Для количества информации справедливы следующие соотношения:
I (xf, у,)=1 (у}; Xi), I (Xf, yj) < I (Xi), 1 (Xf, yj) < I (yj), (17.9)
I (Xf, yj, zk) = I(xf y})-\-I (Xf, zk\yj)—I(xf, Zh)+I (Xf, yj\zh), (17.10)
7 (xf, yj) = 1 (xi)—l (Xi I yj) = I (yj)-I (yj I xi) =
= /(Xi) + I (У})-1 (xt, yj), (17.11)
I (Xi, yj) = I (xt) + I (yj) - I (Xf, yj), (17.12)
/ (X; y}) > О, I (xf, Y) > 0, (17.13)
/ (X-, Y)= I (Y-, X) > 0, (17.14)
1 (X-, Y, Z)=- I (X; Y)+ I (X-, Z\ Y), (17.15)
/ (Y, Z; X) = I (Y\ X) + I (Z-, X | Y). (17.16)
496
По аналогии со средней взаимной информацией, средняя собственная
информация определяется формулой
ЦХ) = 2 р(хг)/(х;) = -2 p(x/)l°gp(xi)=/f(X), (17.17)
1=1 1=1
где Н (X) — энтропия дискретной случайной величины X, определяющая' ко-
личественную меру неопределенности о сообщении до его приема.
Для энтропии справедливы следующие выражения:
Я(Г|Х) = -2 2 P(xi’ w)logp(wlxf) =
«=1/=1
= -2р(^) 2 p(wl^)logP(WI^)=H^|X), (17.18)
/=1 7 = 1
Я(Х|Г) = -2 2 P(xt’ W)log(xHW) =
i=l/=l
°-2 P(W) 2 P(*HW)logP(xilw) = /(Xin. (17.19)
/=1 1=1
Я(Х, Г) = -2 2 Pto. W)logp(Xb W), (17.20)
i=l /=1
H (X, Y) = Н (X) + Н (Y I X) = Н (У) + Н (X | У), (17.21)
где Н (Y | X) — условная энтропия множества событий Y при данном мно-
жестве событий X; Н (X11 У) — условная энтропия множества событий X
при данном множестве У; Н (X, У) —энтропия множества совместных со-
бытий X, У.
Когда множества X и У независимы, то Н (У | X) = Н (У), Н (X | У) =
= Н (X). При этом
Я(Х, У) = Н (X) + Н (У). (17.21а)
Средняя взаимная информация I (X; У) связана с энтропией соотноше-
ниями
I (X; У) = Н (X) — Н (X | У) = Н (У) — Н (У | X) = Н (X) + Н (У) —
— Н (X, У), (17.22)
I (X; У) < Н (X), I (X; У) < Н (У). (17.23)
Энтропия Н — удобная мера неопределенности законов распределения
вероятностей, особенно в тех случаях, когда распределения являются асим-
метричными, многовершинными и когда использование таких числовых ха-
рактеристик, как среднее значение, дисперсия и моменты высших порядков,
теряет всякую наглядность.
Выражения для энтропии некоторых дискретных законов распределения
вероятностей приведены в табл. 17.1.
Для характеристики величины, на которую удлиняются сообщения на
данном языке по сравнению с минимальной длиной, необходимой для переда-
чи той же информации, вводят специальный параметр R — избыточность:
R = 1 — Яоо/log W = 1 — Яоо/Я0 = 1 — 0 < R < 1, (17.24)
где W — число различных букв используемого алфавита; Нк — энтропия,
приходящаяся на одну букву смыслового текста при учете всех многобуквен-
ных сочетаний; Яо = log N — максимальная энтропия, приходящаяся *на
497
Энтропия Н (X) некоторых дискретных законов распределения
Таблица 17.1
Наименование закона распределения Аналитическое выражение закона распределения Н(Х)
Биномиальный •0, Х<0, Pn(X=k)=- Ckpkqn~k, 0<X<n, . 0, Х>п Н (X) = — п [р log р+9 log q] — n — 1 — 2 Ckpkqn~k\ogCk, *=1 <7 = 1— P
Пуассона (0, Х<0, в Vi Xfe а tf(X) = Xlog — + 2 -^-e-^log^l)
Равномерный tf(X) = log/z
Полна P(X = fe) = [0, Х<0, = / X \м(1 + а).„ [l+(fe-l)«] °\14-аХ/ kl X >0 1 4-aX Я(Х) = — Xlog%+——log(l + a%) — a V D / V 1(1+«)„[l + (fe-l)a].. ° \1 + aX/ 61 1 (1 + a)-••[l+(fe-1)«] X10g kl
Таблица 17.2
Относительные частоты появления букв в русском тексте
Буква (тире) о е, ё а и т н с р в л
Частота 0,175 0,090 0,072 0,062 0,062 0,053 0,053 0,045 0,040 0,038 0,035
Буква к м Д п У я ы 3 ь, ъ б г
Частота 0,028 0,026 0,025 0,023 0,021 0,018 0,016 0,016 0,014 0,014 0,013
Буква ч й X ж ю ш ц Щ э Ф
Частота 0,012 0,010 0,009 0,007 0,006 0,006 0,004 0,003 0,003 0,002
Таблица *17.3
Относительные частоты появления букв в английском тексте
Буква (тире) е t о а п i г S h
Частота 0,2 0,105 0,072 0,0654 0,063 0,059 0,055 0,054 0,052 0,047
Буква d 1 с f и т Р У W g
Частота 0,035 0 029 0,023 0,0225 0,0225 0,021 0,0175 0,012 0,012 0,011
Буква b V k X / q 2
Частота 0,0105 0,008 0,003 0,002 0,001 0,001 0,001
Таблица 17.4
Значения энтропий приходящихся на одну букву
с учетом различных буквенных сочетаний
Гдв.ед.] Энтропия1б^] Но нР Н8 На н8
Русский текст Английский текст 5,00 4,75 4,35 4,03 3,52 3,32 3,00 3,10 2,16 1,86
*) Н2 — энтропия на букву текста при учете вероятности появления двухбуквенных сочетаний.
499
букву, когда буквы независимы и равновероятны; р, — коэффициент сжатия
текста.
Избыточность наиболее распространенных европейских языков превыша-
ет 50%. Некоторые статистические данные о структуре различных языков
приведены в табл. 17.2 — 17.4 [1, 15].
Во многих случаях выгодно первоначальное сообщение источника пред-
ставить при помощи другого алфавита путем кодирования.
Характеристиками кода являются значность и его основание. Значность
кода п — число символов в кодовом слове (кодовой комбинации), а основа-
ние L —число различных символов кода. Наиболее распространены двоичные
(бинарные) коды с основанием L = 2. Равномерным является такой код, у ко-
торого значность кода для всех кодовых слов одинакова (например, код Бодо).
При кодировании сообщений, передаваемых по каналам связи без помех,
необходимо выполнить два условия: 1) кодовые слова должны быть различи-
мы и однозначно связаны с соответствующими сообщениями; 2) применяе-
мый способ кодирования должен обеспечить максимальную экономичность
(краткость) кода, при которой на передачу данного сообщения затрачивается
минимальное время.
Код, удовлетворяющий второму из этих условий, называют оптималь-
ным.
Если {wf}, t = l, 2, ..., Л/,— ансамбль взаимно независимых сообщений
с априорными вероятностями р (lit), a {vy}, / = 1, 2, ..., L,—ансамбль симво-
лов кода и £<Я, то число кодовых слов по п символов в каждом слове M=Ln.
При Ln > N, где п— наименьшее целое число, для которого выполняется
это неравенство, ансамбль сообщений {wj можно однозначно закодиро-
вать при помощи Я различных кодовых слов по п символов в слове.
Среднее число <п> символов кода, приходящихся на одно сообщение,
п
<Л>==2 ЛгР(мг)> (17.25)
Z=1
причем
Н (t7)/log L < <и> < Я (t/)/log L + 1, (17.26)
где
N
Н(У) = — 2 logp(uf)
i=l
— энтропия ансамбля сообщений.
При кодировании целых «блоков», а не отдельных сообщений
Я(1/)/1о§ L < <n> < Н (t7)/log L + 1/v, (17.27)
где v — число статистически независимых символов в блоке.
Для двоичного кода
Н (U) < <п> < Н (U) + 1/v. (17.28)
Примерами двоичных кодов, близких к оптимальным, являются . код Шен-
нона—Фано и код Хаффмена [1, 2, 109, ПО].
Экономичность кодирования сообщений —одна из важных характеристик
работы системы связи. Другими ее характеристиками являются скорость
передачи, пропускная способность, достоверность приема информации и т. д.
Пусть имеется дискретный стационарный канал связи без памяти (без
последствия) с заданными характеристиками (рис. 17.1), причем все символы
xi закодированного сообщения и соответствующие им элементарные сигналы
имеют одинаковую длительность т, где F = 1/т — частота посылки сим-
волов.
Канал без памяти полностью описывается априорными вероятностями
p(xi), характеризующими структуру закодированных сообщений, и услов-
ными вероятностями р (у$\ xt), определяющимися характеристиками канала.
500
Рис. 17.1. Канал связи с помехами
Скорость передачи Vk — среднее количество информации, получаемое
за единицу времени:
Vk = FI (X; Y) = F [Н (X)— Н (X | У)] = F[H (У) — Н (У I X)]. (17.29)
При отсутствии помех множества событий X и У статистически пол-
ностью взаимозависимы, т. е. Н (X | У) = Н (У | X) = 0. Следовательно,
Vfemax = PH (%) = PH (У). (17.29а)
Пропускная способность канала связи С — максимальная скорость пе-
редачи информации, которая может быть достигнута выбором оптимального
распределения вероятностей передачи р (х$) символов сообщения:
С = Мах F/(X; У)=Мах F [Н (Х)-Я (X | У)] =
р(х.) р(х.) >
= Мах F[H(Y) —H(Y\X)]. (17.30)
₽(*i)
При отсутствии помех [Я (X | У) = Н (Y | X) = 0]:
C=Cro=MaxF/(X; Y) =Мах FH (X) =Мах FH(Y). (17.30а)
P(xi) P(xi) P(xi)
Для двоичного симметричного канала связи'
С = F [1 + (1 - Ре) log (1 - Ре) + Ре log Ре], (17.31)
где Ре — вероятность ошибочного приема.
При отсутствии помех (Ре = 0)
С=СШ==Л (17.31а)
На рис. 17.2 приведены зависимости относительной пропускной способ-
ности от отношения сигнал/шум при оптимальных методах приема радиоте-
леграфных сигналов [1]; сплошные кривые относятся к детерминированным
сигналам, а штриховые — к сигналам со случайной начальной фазой; Е —
энергия сигнала, N9 — спектральная плотность белого шума.
Для повышения достоверности приема дискретной информации исполь-
зуют корректирующие коды (коды с обнаружением ошибок и коды с обнаруже-
нием и исправлением ошибок). Методы помехоустойчивого кодирования ос-
нованы на введении в код некоторой избыточности, достаточной для компен-
сации помех [109—115].
Экономичность и эффективность кодов с обнаружением ошибок опреде-
ляют коэффициент избыточности Ри и коэффициент обнаружения Хо [114]:
Ru = 1 — log Mj/log Л4, (17.32)
Ко == Q/(Q + Qi). (17.33)
501
Рис. 17.2. Пропускная способность
различных систем радиотелеграфии
при приеме детерминированных сиг-
налов (сплошные линии) и сигналов
со случайной начальной фазой
(штриховые линии) на фоне белого
шума
где М = 2п — общее число кодовых слов, которое можно получить в п-эле-
ментном коде; — количество используемых комбинаций; Q — общее ко-
личество искаженных комбинаций, ошибка в которых может быть обнаруже-
на; Qi — общее число искаженных комбинаций, ошибка в которых не
поддается обнаружению.
2. ПРИМЕРЫ
17.1. В партии 100 радиоламп, из них 5% бракованных.. Из
партии выбирают наугад 5 радиоламп для контроля.
Какое количество информации содержится в сообщении о том,
что в случайной выборке оказалось ровно 3 бракованных радиолампы?
Решение: Случайная величина X — число бракованных радио-
ламп в выборке из 5 радиоламп — может принять значения хг = 0,
х2 = 1, хз = 2, х4 = 3, х5 = 4, х6 = 5. Распределение вероят-
ностей величины X подчинено гипергеометрическому закону
(см. табл. 2.1):
p.(x=4=c‘C”„-vcj.
В нашем случае У = 100, п = 5, М = 100 - .0,05 = 5, k = 3.
Следовательно, вероятность Р5 (3) того, что в случайной выборке
будет ровно три бракованных радиолампы, равна
Ръ (3) = Cg Cfro3-5/Ctoo = —--— [-1^-1 -1~ 0,000953.
8V ’ 3! 2! 2! 93! L 5! 95! J
Используя формулу (17.2), получаем
/ (х4) = — log р (х4) = — log Р5 (3) « 10,7 дв. ед.
17.2. По двоичному симметричному каналу связи с помехами
(рис. 17.3) передаются сигналы хх и х2 с априорными вероятностя-
ми р (хх) = 3/4 и р (х2) = 1/4. Из-за наличия помех вероятность
502
Рис. 17.3. Двоичный сим-
метричный канал связи с
помехами
правильного приема каждого из сигналов (хх и х2) уменьшается
до 7/8.
Найти: 1) условную собственную информацию Цх2\у2); 2) вза-
имную информацию I (х2; у2)\ 3) средние количества информации
/(X; у2), I (X), I (X\Y), I (X; У).
Решение. По условию р (хх) = 3/4, р (х2) = 1/4, р (ух| хх) =
= Р <Рг I х2) = 7/8, р (yj. | х2) = р (у21 хх) = 1/8.
Вычислим вероятности р (yj), р (х,, у^ и р (%г|ух):
Р (Pi) = Р (Xi) Р (Pi I *1) + Р (*г)Р (Pi 1^) = 7Т+ТТ='
Р (Р2) = Р (х2) р (у21 х2) 4- р (хх) р (z/21 хх) = -L 2. + _2_ =
гг О тг О
р (*i. pi)=р (*i) р (pi । *i)=р (Pi) р (*i । Pi)=4=4г;
3
22
32 ’
10
’ 32 ’
Р(*1,Рг) = р(*1)р(Р2|*1) = v4
4 о oz
Р (*2> уг) = р (%2) р (У! I Х2) = 4 1
4
Р (*2> У*) = Р (*2) Р (У2 I Х*)=
_____ J__.
8 “ 32 ’
7
32 *
Так как
р(Х/1р7)=Р^Ц(^)
р (У})
то
Р(Х1)р(У11*1) з _7_._22_ 21
РШ 4 ’ 8 : 32
10 3 ... 1 1
--=-----l Р(^1Р1) = — • —
10 7
р (^11^1)
22 ’
22_______1_.
32 ~ 22 ’
Р(х1[Рг) 4 ’ 8 • 32 ю’-
Р{х2\у2)— — . — . з2 -Q •
1. На основании (17.3) имеем
I (^Рг) = — log р (х2| у2) = — log (7/10) ~ 0,515 дв. ед.
503
2. Используя формулу (17.4), получаем
I (хъУ^ = log -р = log ~ 1,485 дв. ед.
р(х2) 1/4
3. Согласно (17.6) находим
I(X;уд = У р(xt |удlog= р(Х11удlog . +
Р (Хд Р (*1)
+ Р (х, I й) log =д 10g а; ±+Л 10g
р (х2) 10 3/4 10 1/4
~0,644 дв. ед.
Применив формулу (17.17), получим
2
Z (X) = — Р (хд log Р (хд =—lP (xi) log P (Xi) + p (x2) log p (x2)]=
Z=1
= — (-^iog-|-+4-log-r)—°>811 дв-ед-
\ 4 4 4 4 /
Для вычисления информации I (X | Y) воспользуемся формулой
(17.19):
2 2
/(Х|У)=—2 2 p(xi>ydl°gp(xi\yj) =
/=1 /=1
= — 1р (х1, У1) log р (*11Z/1)+р (х2, z/1) log р (х21 уд +
+Р (х1< Уд log Р (Хх I Уд + Р (*а > У г) log р (х2 | z/2)] =
= log 2L + ± log _L + Л log Л +_L log
\ 32 5 22 32 22 32 S 10 32 S 10)
~ 0,459 дв. ед.
Согласно формуле (17.7) находим
2 2
/(Х;У)= У У pfa^log-^^y =p(x1>j/1)log-p^l^) +
/Ti р (Хг) р <*11
+ Р (х2, У1) log-р^^- +р(х1( уд log р(Х1|^а) +
р(х2) р(хх)
+ Р (ха, Уд log-^i^- = log + -L log +
I 2>W2/ S 32 & 3/4 г32 5 1/4 -Т
, 3 „ 3/10 , 7 . 7/10 ЛОСО
Н---log —:-------log-----~0,352 дв. ед.
32 3/4 32 ь 1/4
17.3. Источник сообщений генерирует множество кодовых ком-
бинаций, одна из которых имеет априорную вероятность р (х) = 1/8,
а апостериорные вероятности, соответствующие последовательному
приему символов у = 1,? = 0иа = 1, равны: р (х|//) = р(х| 1) =
= 1/6, р (х\у, г) = р (х|10) = 1/2, р (х\у, z, и) = р (х| 101) = 1.
504
Определить увеличение информации о сообщении х в процессе
приема символов у, г и и.
Решение. После приема первого символа у = 1 информация
/ (х; у) = I (х; 1) = log р(х |1) = log ~ 0,415 дв. ед.
Р (х)1 з
Второй принятый символ z = 0 на основании (17.8) доставит до-
полнительную информацию
/(х; z\y) = I(x-, 0|1) = log р (* 1 = log ~ 1,585 дв. ед.
р(х|1) 1/6
Аналогично третий символ и = 1 доставит о сообщении х инфор-
мацию j
1 (х; u\y,z)=I (х; 1110) = log р110^ = log2 = 1 дв.ед.
р (X J 1U)
Полная информация I (х\ у, г, и) о сообщении х после приема всех
трех символов
/ (х; у, z, и) = I (х; у) + I (х; z\y) + I (х; и | у, z) = I (х; 1) +
+ / (х; 0|1) + I (х; 1|10) = 0,415 + 1,585 + 1 = 3 дв. ед.
17.4. Источник вырабатывает ансамбль Символов X = {х^},
i = 1,2, 3, 4, с вероятностями р (хх) = 0,2, р (х2) = 0,3, р (хз) = 0,4
и Р (*«) = 0,1. Корреляционные связи между символами отсутст-
вуют. Вычислить энтропию источника.
Решение. Применив формулу (17.17), получим
4
Я (X) =—^р (хг) log р (хг) = — [р (хх) log р (хх) -Ь р (х2) X
X log р (х2) + р (хз) log р (хз) + р (х4) log р (х4)] =
= — 0,2 X log 0,2 — 0,3 log 0,3 — 0,4 log 0,4 — 0,1 log 0,1 =
= 0,4644 + 0,5211 + 0,5288 + 0,3322 ~ 1,847 дв. ед.
17.5. Определить энтропию случайной величины X, распре-
деленной по биномиальному закону: 1) в общем случае; 2) при
р = 1/2 и п = 5.
Решение. По условию случайная величина X распределена по
биномиальному закону. Следовательно,
Pn(X = k) = Cknp*qn-k,q=\ -р.
1. Н(Х) = - 2 Cknpkqn-k\ogCknpkqn~k =
6=0
= - 2 logC^— 2 CnPk cfl~k\ogpk —
6=0 6=0
— 2 CnPkqn^k\^gqn~~k.
A = 0
505
Так как при k = 0 и k = п log С| = О,
п п Ь
2 Cknpkqn-k= 1,2 kCknpkqn-k = rip,
А = 0 6 = 0
ТО
л__1 « «
#(Х)= — n(plogp+<?log<7) — 2 Cnpkqn~k log сп.
k= i
2. При p = q = 1/2 и п= 5 имеем
жх)=- 5 (-L log -1- log 44 - 2 ci ay (445-fe iogci -
«= 1
4
= 5- 4" У c| log C| = 5 -51о^5+-'°!2112_ ~ 2,198 дв. ед.
«= 1
17.6. Алфавит состоит из четырех букв xlt х2, хз, х4, вероятно-
сти появления которых равны: р (xj = 0,5, р (х2) = 0,25; р (хз) =
= Р (xt) = 0,125. Условные вероятности р (Х;|хг) появления /-й
буквы при условии, что ей предшествовала i-я буква, заданы таб-
лицей
Х1 х)
Л1 х2 V *з *4
хг 0 0,2 0,4 0,4 1
х2 0,2 0,2 0,3 0,3 1
х3 0,25 0 0,25 0,5 1
х4 0,2 0,4 0,4 0 1
Найти избыточность источника сообщений при статистиче-
ской независимости букв и избыточность Т?2 с учетом зависимости
между буквами.
Решение. На основании (17.24) имеем R± = 1 — Н^Нц. Так как
Но = log N = log 4 = 2 дв. ед.,
Ht = — р (xi) log р (xi) = — (0,5 log 0,5 + 0,25 log 0,25 +
+ 2 •. 0,125 log 0,125) = 1,75 дв. ед„
то 7?! = 1 — 1,75/2 = 0,125.
При учете статистической зависимости между буквами R2 =
= 1 — H2IHQ, где Н2 — энтропия на букву при учете двухбуквен-
ных сочетаний.
506
Энтропия двухбуквенного текста
Н (Х1( Х2) = Н (Хх) + Я (Х21 Хх) = 1,75 + Н (Х21 Хх),
где
4 4
Н (Х2| Хх) = — (*i) Sp (x}\Xi) log Р =
= —0,5(0,2 log 0,2 + 2 - 0,4 log 0,4) — 0,125 (2 • 0,2 log 0,2 +
+ 2-0,3 log 0,3) — 0,125 (2 • 0,25 log 0,25 + 0,5 log 0,5) —
— 0,125 (0,2 log 0,2 + 2 • 0,4 log 0,4) ~ 1,62 дв. ед.
— условная энтропия второй буквы, определяемая формулой (17.18).
Средняя энтропия на одну букву
Н2 = Н {Х19 Х2)/2 - (1,75 + 1,62)/2 - 1,685 дв. ед.
Следовательно,
Т?2 - 1 — 1,685/2 ~Д,16.
17.7. Закодировать двоичным кодом Шеннона—Фано ансамбль
сообщений X = {Xi}, i = 1, 2, ..., 7, 8, если все кодируемые сооб-
щения равновероятны. Показать оптимальный характер получен-
ного кода.
Решение. При кодировании по методу Шеннона—Фано все со-
общения записываются в порядке убывания их вероятностей и раз-
биваются на две группы так, чтобы суммы вероятностей сообщений
в каждой из групп были по возможности близкими к 1/2. Всем
сообщениям, входящим в верхнюю группу, приписывается цифра «0»
в качестве первой цифры двоичного кода, а сообщениям, вхо-
дящим в нижнюю группу, — цифра «1». Затем каждая из групп
аналогично разбивается на подгруппы по возможности с одинако-
выми суммарными вероятностями, причем верхним подгруппам в
обеих группах опять приписывается цифра «0» (вторая цифра
кода), а нижним — цифра «1». Деление повторяется до тех пор,
пока в каждой подгруппе не останется по одному сообщению.
Процесс кодирования приведен в табл. 17.5.
Среднее число двоичных знаков, приходящихся на одно сообще-
ние,
8 11 1
<п>=2 пгр(+-) = 3~+3-4-+- + 3~ =
= 8-3=3 дв. ед.
О
Энтропия ансамбля кодируемых сообщений
Н (X) - log N = log 8 - 3 дв. ед.
Так как средняя длина кодового слова <п> равна энтропии
Н (X), то код оптимален.
507
Таблица 17.5
Кодирование по методу Шеннона—Фано
Сообщения xi Р (Хр Разбиения Кодовые слова
*1 1/8 1 0 f 0 0 1 0 1 1 ООО
х2 1/8 0 0 1
Х3 1/8 0 1 0
х4 1/8 0 1 1
Хь 1/8 1 0 . 0 1 ‘0 1 1 1 0 0
Хв 1/8 1 0 1
X? 1/8 1 1 0
Х8 1/8 111
17.8. Показать, что энтропия Н (X) алфавита {xt} с конечным
множеством символов хг, i = 1, 2, п, достигает максимума
Н (X) = Нт (X) = log п, когда все символы равновероятны.
Решение. Обозначив р (хг) = pt, имеем
п п
н= — Pilogpt, %р1 = 1.
i=1 i=i
Пользуясь методом неопределенных множителей Лагранжа, найдем
экстремум функции
п п
ф= - Ё pUogPi+A- 2 Pi-
i=l z=i
Дифференцируя это выражение' по ри ..., рп и приравнивая
производные нулю, получаем систему уравнений:
log Pt +• log е + А = 0, i = 1, 2, ..., п
или
log pt = — А. — log е = const, i = 1, 2, ..., п.
п 1
Так как V р4=1, то рх =р2 =... =рп = —.
п
1= 1
508
Следовательно,
Н (X) = Нт (X) = log п. Иное решение задачи дано в [1, ПО].
17.9. Вычислить пропускную способность С двоичного симмет-
ричного канала (рис. 17.4) при условии, что все символы сообщения
и соответствующие им элементарные сигналы имеют одинаковую
длительность т, гдё F = 1/т — частота посылки символов.
Построить график зависимости С/Ст = f (Ре), где Ст — мак-
симальная пропускная способность (при отсутствии помех), а Ре —
вероятность ошибочного приема.
Решение. Согласно (17.30) имеем
С = F Мад [Н (У)—Я (У | X)].
p(.xt)
В нашем случае
2
Н(¥)=-Ър(у№>р(У]),
1= 1
2 2
я(У|Х) = -2 2 рШ^рШ-
/=i /=1
Так как
Р (У1) = Р k) Р kk) + Р (х2) р (z/i|x2) = р (1 — Ре) + (1 —
Р) Ре = Р 4* Ре ^pPei „
Р (У2) =Р k) р (</2|х2) + Р k) Р (РгЮ =
= (1 - р) (1 - Ре) + рРе = 1 - р - Ре + 2рРе,
ТО
н (У) = - 1(р + Ре - 2рР.) log (р + Рв - 2рРе) + (1 - р-
- Ре + 2рРе) log (1 - р - Ре + 2рРе)],
н (У|Х) = — р к) [р кк) log р кк) + р (р2к) х
х log р (f/2k)] — Р к) Ip (Р1|х2) 10g р к|х2) + р к|х2) X
X log р (у2|х2)] = - [(1 - Ре) log (1 - Ре) + Ре log Рв].
Из выражения для Н (Y\X) видно, что ввиду симметрий канала
связи условная энтропия Н (У|Х) не зависит от вероятности пере-
дачи р. Поэтому максимальное значение / (X; У) достигается про-,
сто максимизацией Н (У).
Рис. 17.4. Двоичный сим-
метричный канал связи
509
Рис. 17.5. Зависимость пропускной способности
двоичного симметричного канала от вероятности
ошибочного приема
Максимум Н (У) достигается тогда, когда сигналы уг и у2 не-
зависимы и равновероятны (см. пример 17.8), что в свою очередь
имеет место при равной вероятности передаваемых символов. Сле-
довательно,
С = F [1 + (1 - Ре) log (1 - Ре) + Ре log Ре].
При отсутствии помех (Ре = 0) С = Ст = F. Поэтому &Ст =
— f (Л?) = 1 + (1 — Ре) log (1 — Ре) + Pg log Ре. Зависимость от-
носительной пропускной способности аст от вероятности ошибоч-
ного приема Ре изображена на рис. 17.5.
3 . ЗАДАЧИ И ОТВЕТЫ
17.1 . Самолет противника с равной вероятностью может нахо-
диться в одной из 1024 зон воздушного пространства.
Какое количество информации получает оператор радиолокацион-
ной станции, когда он фиксирует наличие самолета в одной из зон?
Ответ: I (xt) = 10 дв. ед.
17.2 . Радиостанция состоит из 16 равноценных с точки зрения
надежности блоков и имеет устройство контроля и индикации ис-
правности блоков.
Определить минимальное число проб k, которое необходимо
выполнить этому устройству, чтобы отыскать любой неисправный
блок.
Ответ: 4.
17.3 . По каналу телекодовой связи передаются пять команд
X = {х,}, i = 1,2,3, 4, 5 с вероятностями р (х^) = 0,3, р (х2) = 0,1,
р (хз) = 0,25, р (х4) = 0,2, р (х5) = 0,15.
Определить среднее количество информации, приходящееся на
одну команду.
Ответ: I (X) csr 2,228 дв. ед.
17.4 . Символы алфавита азбуки Морзе появляются в сообщении
со следующими вероятностями: 0,51 для точки, 0,31 для тире, 0,12
для промежутка между буквами, 0,06 для промежутка между
словами.
Определить среднее количество информации в сообщении из
500 символов данного алфавита, считая, что связь между последова-
тельными символами отсутствует.
Ответ: / (X) = 236 дв. ед.
510
17.5 . Напряжение изменяется в пределах U2 — = 8 В.
При равномерном квантовании датчик регистрирует приращения на-
пряжения Д(/ = 0,1 В.
Вычислить максимальное количество информации за 5 отсчетов.
Ответ'. I (X) = 31,61 дв. ед.
17.6 . Найти количество информации, которое содержится в кван-
тованном телевизионном сигнале, соответствующем одному кадру
развертки изображения, если: в кадре 625 строк; сигнал, соответст-
вующий одной строке развертки изображения, представляет собой
последовательность из 600 случайных по амплитуде импульсов, каж-
дый из которых может с равной вероятностью принять любое зна-
чение в интервале от 0 до 8 В; каждый импульс квантуется по величи-
не с шагом квантования 1 В; импульсы изображения между собой не
коррелированы.
Ответ'. I (X) = 1125 • 103 дв. ед.
17.7 . Вычислить среднее количество информации I (X; у2) о пе-
реданных командах X = {хг}, i = 1, 2, 3, доставляемое принятым
сигналом у2 ансамбля сигналов Y = {yj}, j = 1, 2, 3, если объеди-
ненная система (X, У) характеризуется распределением вероятно-
стей, приведенным в следующей таблице:
«3 xi р (ур
Xl | х2 - Хз
У1 0,05 0,2 0 0,25
Уч 0 о,з 0,1 0,4
Уз 0,05 0 х 0,3 0,35
P(Xi) 0,1 0,5 0,4
Ответ: I (X; z/2) ~ 0,268 дв.- ед.
17.8 . Радиостанция противника может работать на волне %х
(событие Лх) или на волне %2 (событие Л2), причем в импульсном
(событие Вх) или непрерывном (событие В2) режимах. Вероятности
совместных событий имеют следующие значения: р (Лх, Вх) = 0,7,
р (Лх, В2) = 0,15, р (Л2, Вх) = 0,05, р (Л2, В2) = 0,1.
Вычислить количество информации, получаемой о режиме работы
станции, если станет известной длина волны станции.
Ответ: I (В', А) = 0,102 дв. ед.
17.9 . Найти максимальную энтропию черно-белого изображения
с двумя градациями, содержащего 5 • 108 независимых элементов.
Ответ: Нт (X) = 5-108 дв. ед.
17.10 . Распределение вероятностей случайной величины X име-
ет вид: р (хх) = 0,1, р (х2) = 0,1, р (хз) = 0,1, р (х4) = 0,7.
Определить число п значений случайной величины, при котором
энтропия Яр (X) равномерного распределения будет равна энтропии
Н (X) заданного распределения.
Ответ: п = 2,56.
511
17.11 . Вероятность появления события А при одном испытании
равна р. Испытания повторяются до первого появления события А.
Найти энтропию числа испытаний X и выяснить характер изменения
энтропии с изменением р.
Ответ'. Н (X) = — Ip log р + (1 — р) log (1 — р)]/р дв. ед.
При уменьшении р от 1 до 0 энтропия монотонно возрастает от
О до оо. -
17.12 . Для повышения достоверности каждое сообщение может
передаваться по каналу связи k раз, причем вероятность неиска-
женного прохождения сигнала при каждой передаче рх — 0,2. Пос-
ле k повторений (1 k N) решающее устройство сравнивает все
k принятых сигналов и при их совпадении выносит решение о пра-
вильном приеме, после чего отправителю посылается команда о пре-
кращении посылки данного сообщения и о передаче следующего
сообщения.
Определить значение коэффициента дублирования k из условия
максимума количества информации, обеспечиваемой решающим
устройством.
Ответ" k — 3.
17.13 . Ансамбли событий X и Y объединены, причем вероятности
совместных событий равны: р (хх, г/х) = 0,1, р (хх, у2) = 0,25,
р (хг, уг) = 0,2, р (х2, z/2) = 0, р (хз, z/x) = 0,3, р (хз, г/2) = 0,15.
Определить: а) энтропии ансамблей X и У; б) энтропию объе-
диненного ансамбля; в) условные энтропии ансамблей.
Ответ:
а) Н (X) = 1,512 дв. ед., Н (У) = 0,971 дв. ед.;
б) Н (X, У) = 2,228 дв. ед.;
в) Я(Х|У) = 1,257 дв. ед., Н (У|Х) = 0,716 дв. ед.
17.14 . 1Источник сообщений создает последовательность букв,
выбранных из набора букв А, В, С, D с вероятностями 0,5; 0,25;
0,125; 0,125, причем очередная буква выбирается независимо.
Вычислить избыточность текста.
Ответ: R = 0,125.
17.15 . Для передачи сообщений используется код, состоящий
из трех символов, вероятности появления которых равны 0, 6; 0,2;
0,2. Корреляция между символами кода отсутствует.
Определить избыточность кода.
Ответ: R = 0,139.
17.16 . Ансамбль сообщений {х^}, i = 1, 2, ..., 8, и вероятности
сообщений заданы следующей таблицей:
X/ Хз х4 *5 *6 *7 *8
Pi 1/4 1/4 1/8 1/8 1/16 1/16 1/16 1/16
Построить код Шеннона—Фано для данного ансамбля и показать
его оптимальный характер.
512
Ответ'.
Сообщение *1 х2 х3 х4 х5 [*6 х7 х8
Кодовая комбинация 00 01 100 101 1100 1101 1110 1111
Н (X) — <ji) = 2,75 дв. ед.
17.17 . Сообщения xlt х2, хз, xt появляются соответственно с ве-
роятностями 1/2, 1/4, 1/8, 1/8 и кодируются четырьмя двоичными ко-
довыми словами 0, 10, 110, 111.
Требуется: а) показать, что если сообщения статистически не-
зависимы, то в получающейся последовательности кодовых слов
символы 0 и 1 появляются с равными вероятностями, и что символы
в такой последовательности независимы; б) найти среднее значение
<п> числа двоичных символов на сообщение.
Ответ: б) <n> = Н (X) = 1,75 дв. ед.
17.18 . Ансамбль сообщений {xt}, i = 1, 2, 3, ..., 9, и их вероят-
ности заданы следующей таблицей:
X/ Xl х2 х3 х4 х5 хв х7 Хз х9
Pi 0,20 0,15 0,15 0,12 0,10 0,10 0,08 0,06 0,04
Произвести кодирование двоичным кодом по методу Хаффмена (ме-
тод вспомогательных группировок) и вычислить энтропию сообще-
ний Н (X) и среднюю длину <м> кодового слова.
Ответ:
Сообщение Xi х2 х3 х4 хъ хв х7 х8 х9
Кодовая комби- нация 10 001 010 011 ПО 111 0001 00000 00001
Н (X) ~ 3,04 дв. ед., <п> ~ 3,08 дв. ед.' ~
17.19 . Ансамбль сообщений состоит из двух букв: и х2, при-
чем вероятности р (xf) появления букв равны р (хх) = 0,89, р(х2)=
= 0,11.
Определить среднее число символов кода, приходящееся на одну
букву, если кодирование осуществляется: а) по одной букве;
б) блоками по две буквы; в) блоками по три буквы.
17 Зак. 1203
513
Ответ [1151:
Сообщение а) б)
*1 Х2 *1*1 *1*2 *2*1 *2*2
Кодовая комби- нация 0 1 0 10 ПО 111
<п>, дв. ед. 1 ~0,66
Сообщение в)
*1*1*1 *i*i*2 1 XiX2Xi *2*1*1 | *i*2*2 *2*1*2 *2*2*1 *1*1*2
Кодовая комбина ция 0 100 101 ПО 11100 11101 НПО 11111
<П>, дв.ед. 0,552
17.20 . Определить пропускную способность С двоичного симме-
тричного канала со стиранием (рис. 17.6), если символы xt и yj
имеют одинаковую длительность т, где F = 1/т — частота посылки
символов.
Ответ:
С = F{(1 - q) [1 - log (1 - <?)] + (1 - Ре - q) log (1 - Pe-q)+
+ PelogPe}.
17.21 . На вход канала связи (рис. 17.7) поступает ансамбль сиг-
налов X = {xt}, i = 1, 2, ..., N, с вероятностями р (х,) и часто-
р(х1)“р;х1
р(хг)‘/-р;х2
Рис. 17.6. Двоичный симмет-
ричный канал связи со сти-
ранием
Рис. 17.7. Канал связи
514
Рис. 17.8. Канал свйзи с Нередатш/х Ретранслятор РраОИнах
ретранслятором и
1-Ре У? 1-Ре _
---------£Ог----------->pzz
Р®р-1р
pa>z)^j^2
-------эн>---------Яэг»
Z-^ #2
той посылки F = l/т, где т — длительность сигналов. Вероятности
перехода равныр (у}| xt) = I — Репри j = inp (г/Jхг) = Pe/(N— I)
при / ф i.
Определить пропускную способность канала связи.
Ответ:
С= F [log N +Ре log +(1 -Ре) log (1 - Ре)
17.22 . По каналу связи, состоящему из передатчика, ретрансля-
тора и приемника (рис. 17.8), передаются сигналы хх и х2 с часто-
той следования F = 1/т, где т — длительность сигналов. Значения
априорных вероятностей и вероятностей' перехода на участке пе-
редатчик—ретранслятор и ретранслятор—приемник указаны на
рисунке.
Вычислить пропускную способность канала связи.
Ответ:
С = F [1 + (1 - 2Ре 4- 2Р*) log (1 - 2Ре + 2Р?) + 2Ре (1 -
- Ре) + 2Ре (1 - Ре) log Ре (1 - Ре)].
17.23 . Определить пропускную способность канала связи, по
которому передаются сигналы х19 х2, хз, х4 с частотой следования
F= 1/т, где-т — длительность сигналов. Влияние помех характе-
ризуется условными вероятностями р (yj\Xi):
Р = Р (У2|*2) = Р (Уз\хз) = р (z/4|x4) = 1 — Ре,
Р (l/aki) = Р (^ik2) = Р = р (г/з|х4) = Ре,
Р (//эк) = р (г/4|хх) = р (г/з|х2) = р (г/4|х2) = р (z/Jxs) =
= Р («/2|*з) = р (z/i|x4) = р (z/2|x4) = 0.
Ответ: С = F [2 + Ре log Ре + (1 — Ре) log (1 — Р.)].
18. НЕПРЕРЫВНЫЕ СИСТЕМЫ ПЕРЕДАЧИ
ИНФОРМАЦИИ
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Непрерывные системы передачи информации — системы, в которых как
реализации сообщения, так и реализации сигнала на конечном временном
интервале (0, Т) представляют собой некоторые непрерывные функции вре-
мени [1, НО].
Пусть х (t) — реализация непрерывного сообщения на входе какого-
либо блока схемы связи, у (/) — реализация выходного сообщения (сигнала),
Pi М — одномерная плотность вероятности ансамбля входных сообщений,
Pi (у) — одномерная плотность вероятности ансамбля выходных сообщений,
р2 (х> У) — совместная плотность вероятности, р± (х| у) — условная плот-
ность вероятности х при известном у, рг (у | х) — условная плотность вероят-
ности у при известном х. Тогда для количества информации I справедливы
следующие соотношения [1, 3, ПО, 115]:
, . . . Ръ(х, у) Р1 (х I у) Р1(г/|Х)
I (х; у) —log------— = log------——= log------------= / (у; х), (18.1)
S Pi (х) Pi (У) Pi(x) Pi (у)
I (Х-, у)=$ I(x-,y)Pi(x\y)dx, I (х; У)=|/(х; y)Pi(y\x)dy, (18.2)
X Y
1(Х; У) = fpi (у) / (X; y)dy=
Y
= ИРг(х, у)/(х; y)dxdy = I(Y', X), (18.3)
У X
1 (X; У)= ] f р2(х, у) log P^^-dxdy^— j pi(x) logpx (x)dx+
V Y , P1(X) X
i Л * Л
+J J Pi (.X, y) log pl (x I y) dxdy, (18.4)
I (X; у) > 0, I (x; У) > 0, I (X; У) > 0. (18.5)
Здесь I (x; y) — взаимная информация между каким-либо значением х вход-
ного и значением у выходного сообщений, I (X; у), I (х; Y) — средние значе-
ния условной информации, I (X; Y) — полная средняя взаимная информа-
ция.
Формулы для энтропии Н непрерывных сообщений получаются путем
обобщения формул для энтропии дискретных сообщений. Если Лх — ин-
тервал квантования (точность измерения), то при достаточно малом Лх эн-
тропия непрерывных сообщений
00 оо
#i(X)= —J Pi (х) log/?! (х) dx— logAx J p1(x)dx =
— OO —00
= Я (X) —log Ax—— j pL (x) log [px (x) Ax] dx, (18.6)
— 00
где
Я(Х)=- J pi(x)logpi(x)dx. (18.7)
— 00
Из (18.6) видно, что информативность сообщений, обусловленная стати-
стикой состояний элементов сообщения, целиком определяется величиной
Я (X), которая называется дифференциальной [115, 116], а иногда приведен-
ной [3] энтропией.
Величина — log Ах зависит только от выбранного интервала Ах, опре-
деляющего точность квантования, и при Ах = const есть величина постоян-
ная, которую иногда исключают из рассмотрения [117, 118]. При определе-
нии полной взаимной информации / (X; У) величины log Ах й log Лу взаим-
но компенсируются, так что 1 (X; Y) от выбора координат не зависит.
016
По аналогии с (18.7)
Я(У) = — f pi(y)iogpi(y)dy, (18.8)
— 00
Я(Х|У) = — j J р2 (х, у) log Pi (х I у) dxdy, (18.9)
— 00 —00
H(Y\X)=— J f p2(x, y) log pt (y\x) dxdy. (18.10)
— 00 —00
Когда X и Y статистически связаны между собой, то
Я(Х, Y) = Н(Х) + Н (Y (X) = H(Y)+ H(X\Y). (18.11)
При независимых X и Y
Я(Х, У) = Н (X) + Н (У). (18.12)
Полная средняя взаимная информация определяется формулой
I (X; У) = Я(Х)-Я(Х|У) = Н (Y) — H(Y\X)t (18.13)
а пропускная способность непрерывного канала
С = lim Мах Г/ (X; У)1 , ' (18.14)
Т->оо L ' J
где максимум I (X; У) достигается выбором оптимального распределения
Pi (х) входного сигнала X (t) при достаточно большом интервале времени Т.
В случае канала связи с ограниченной полосой частот пропускная спо-
собность определяется- формулой Шеннона [1]
C = F log (1+о2/М0 Т7), (18.15)
где F — полоса пропускания канала; Мо — постоянная спектральная плот-
ность нормального стационарного шума п (t) в полосе 0 < f < F; а2 =
= < х2 (t) > = const — ограниченная средняя мощность сигнала х (/),
представляющего собой стационарный гауссовский процесс с равномерной
спектральной плотностью в полосе 0 < / < F; у (t) — х (t) + и (/), причем
х (t) и п (t) — статистически независимы.
Если g2/NqF > 1 (отношение сигнал/шум велико), то
С ~ F log (os2/M0F). (18.16)
При g2/NqF 1
С ~ 1,443(Т2/ЛГ0. (18.17)
Когда спектральная плотность гауссовского случайного сигнала х (/)
есть S (/), а спектральная плотность аддитивного гауссовского шума п (t)
равна N (/), формула (18.15) имеет вид
ft
C=f log[l+S (f)/N (01 df. (18.18)
В табл. 18.1 приведены значения энтропии Н (X) некоторых непрерыв-
ных законов распределения [1, 15, НО, 115—120].
517
Таблица 18.1
Энтропия Н(Х) некоторых непрерывных законов распределения
Наименование закона распре- деления Аналитическое выражение - плотности вероятности р± (х) 00 tf(X) = — J Pi (х) log Pi (х) dx — 00
Равномерный (прямоуголь- ный) 1 , а < х < b s b—а 0, х < а, х > b log (b — a) = log(o2 1/3)
Гауссовский (нормальный) 1 Г (х—т)2' оУ 2л еХР |_ 2о2 log(o У2ле)
%2 * у>/2- 1 -х/2 2^2Г(п/2) х > 0 log r(n/2) + log2+ + [n/2—(nl2—1) -ф (n/2)] loge, d где ф (z) ==—— In Г (г) — az пси-функция Эйлера
Гамма-распре- деление ! га р— Р“+‘Г(а + 1) х>0, а> — 1, Р>0 log Г (а+1)—а loge• ф (а+ 1)+ + (а + 1) log e + log Р, где ф (а-]-1) —пси-функция Эйлера
Коши 1 h л Л2+(х—х0)2 log 4 л h
Релея х —х2/2а2 V х>0 (с/2-f-l) loge, где с = 0,5772... — число Эйле- ра
Максвелла i/А — х2е~хЧ2<5‘, V Л оЗ х > 0 1 2ло2 л log H-cloge, 2 е где с = 0,5772
Лапласа (двух- сторонний экс- поненциальный) А, — х | х — ц | 2 б log ~ = 1°g (ое V2) Л
Экспоненци- альный одно- сторонний Хе-*"*, х > 0 log "7" = log (ое) Л
518
Продолжение табл. 18.1
Наименование закона распре- деления Аналитическое выражение плотности вероятности (х) Н (X) = — J pi (х) log pi (х) dx — co
Показательно- степенной — е-\ х>0 ml logm!—m log ex гm i i . x У ——C -J-loge, L=2 k J где c — 0,5772
Симпсона (тре- угольный) 0, х < а, 4(х—а) Ь+а (Ь—а)2 ’ а<Х< 2 ’ 4(Ь— а) а+Ь , <х<Ь, (Ь—а)2 2 0, • х > b log = log (оД/бе)
Закон арксинуса 0, х< —а, 1 1 —а<х<а, л уа2~х2 0, х>а 1 f log (a2—x2) logjr-f- 1 dx л J ya2—x2 0
2. ПРИМЕРЫ
18.1. На вход приемного устройства воздействует колебание
у (t) = х (0 + п (t), где сигнал х (/) и помеха п (t) — независимые
гауссовские случайные процессы с нулевыми математическими ожи-
даниями и дисперсиями, равными соответственно ст? и а?.
Определить: 1) количество взаимной информации I (х; у), ко-
торое содержится в каком-либо значении принятого колебания
,у (t), о значении сигнала х (/); 2) полную среднюю взаимную ин-
формацию I (X; У).
Решение. По условию задачи у (t) представляет собой сумму
независимых колебаний х (t) и п (0, которые имеют нормальные плот-
ности вероятности. Поэтому
<у2у = ст? 4- ст?,
1 / X2 \ 1 / и2 \
“р м
Р, (SI= р, (у - х) _ехр [- -=
= ^7ЁехрГТ5г)=₽‘<',)-
519
1. По формуле (18.1) находим
/ (Х; ^) = log_£lM^L = _L
Р1{У) 1п2
==—— ln-^-expf- п%
In 2 on \
V ln2 on
2. Согласно (18.3) имеем
I (X; Y) = J J p2 (x, у) I (x; y)dxdy = <[/ (x; «/)]> = log
]n Р1(У I-x)
Pi(y)
tfl \
<y*>
ln2 2(aj+o«)
1
In 2
2o2 1 2
n2
2o2
У*
2(о>+ой) J-
On
<n?>
<3+^
On
In 2 [ 2(o2+o£)
2o2
1
ъ
где < > — знак усреднения по множеству.
Таким образом,
/ (X; У) = log Г°* + а" =4 log (1 + Дв. ед.
оп 2 \ °п /
18.2. Вычислить полную среднюю взаимную информацию
I (X; У) между случайными величинами X и У, имеющими нормаль-
ные плотности вероятностей и коэффициент взаимной корреляции
Rxv = R- —— <(*—тх) (у—туу>,
Ох Uy
где тх, ту, <3х, ву — математические ожидания и дисперсии ве-
личин X и У.
Решение. В соответствии с (18.3) и (18.1) имеем
1 (X; У) = J J р2 (х, у) I (х; у) dxdy = J J р2 (х, у) X
X Y —00 —оо
ОО 00
X log- 4(x’^ dxdy = -4 f f р2 (X, у) [In р2 (х, у)—In (х) —
Р1 (X) р! (у) In 2 J J
—lnpi(y)]dxdp = -4
In 2
С р2 (X, у) In р2 (х, у) dxdy —
V V
520
00 во во во
J J р2(х, «/)1прх(х)сгх^— J J рг(х, р)1п рх (у) dxdy =
1
In 2
У Р2 {х, у) In ра (х, у) dxdy — у рх (х) In рх (х) dx—
Pi(Z/)lnpx (у) dy
Вычислим эти интегралы, учитывая, что по условию
(Х~/Пд.)* 1
2а*
Р1(х) =-----!—ехр —
ох у 2л
Р1(У) =-----7=7-ехР
Оу у 2л
1
(у—mg)*
2а*
IT
р2(’^ 2naaaj,/b=^ 1 2(1-/?*) [ а*
_2% (Х~тх) (У~ту) ф (У—\
°х°у ' °у Я’
Pi (х, у) х
_______1___________1 Г (*~ ^x)2 __2р (*~тх) (У—ту)
2nox0vVl-I^ 2(1—7?*) [ ахОу
+ ~^Tg)2 П dxdy = — In (2пах (5у У1 —Я2) —
У J f
оо оо
—9 а Г f (x—mx)2p2(x,y)dxdy +
z VI-А ) Ох J J
оо 00
+г2п- п21<т „ f f (Х~тх)(У—ту)р2(X, у)dxdy —
Lz U — ) °х Gy J J
—00 —00
oo oo
~TiT-s-x,; f J ^-тЛ‘р^.уУЛ^я-
---------------00-00
Так как
00 oo 00 oo
j J (*—mxY Pi {x, y) dxdy = a2, J J (y—mv)2 p2 (x, y) dxdy = q2,
—00 —00 —oo —oo
oo oo
J J (x—tnx}(y—my)p2(x, y)dxdy = Rax0y,
621
то
I—/?2
f f р2 (X,y) In p2 (x, у) dxdy = — In (2лстя oy VI — Я2) — 1
J J Z U—A )
—00 —oo
' *’ “ттгЬг=-1 =
= —In (2леол.ог, ]/1 —R2),
Pi^dx = j
—00
= — In (crx‘|/2л) —1/2 = — 1п]/2лесг£.
По аналогии
J Pi (У) Jn pi (у) dy = — In V2лесг£.
—00
Тогда
I (X; У) = -— [ —In (2ле<гх oy /T7R2) + In /2лёа1+
In 2
/------1 1 l/~ 4д2 e2 Qx
+In V 2лео2 ] = — In y x-*---------=
>n 2 ]<4лае2а»а|(1—Я2)
= —Ini/ —— =------------!—(1—Я2).
In 2 - у 1-R* 2 In 2 V '
Следовательно,
/ (X; Y) = - (1/2) log (1 - №).
18.3. По линии связи передаются непрерывные амплитудно-
модулированные сигналы x(t), распределенные по нормальному за-
кону с математическим ожиданием тх = 0 и дисперсией =
= ст2 = 8В2.
Определить энтропию (X) сигнала при точности его измере-
ния Ах = 0,2 В.
Решение. По условию плотность вероятности сигнала х (/)
Рх« = -7ГгГ^'''”'-
Q у ZU
По формуле (18.6) имеем
00
Н1(Х)=— J Pi (х) log Pi (х) dx—log Ax =
-------------00
00
=-----— (* p1(x)lnp1(x)dx—log Ax =
In 2 J
522
=-----J— f Pi (x) Г In-------— ] dx—log Дх =
Ш2 J rlv '[ <т/2л 2a2 J s
—00
=-----— (in----\=------—V-log Дх=
In 2 \ а /2л 2 )
— -j-L- In ]/2лео2 — log Дх’ = log ^^teg .
Подставляя числовые значения, получаем
Ht (X) = log ~ 5,87 дв. ед.
18.4. Непрерывная случайная величина X имеет плотность
вероятности Pi (х). Величина Y есть однозначная функция У=
= g (X).
Показать, что
Я(У) = Я(Х)—/log|D^
где Н(Х), Н (У) — соответственно дифференциальные энтропии
величин X и У; D (х/у) — якобиан преобразования от х к у.
Решение. Так как
Pi(y) = Pi(x) D(y) , dy= D
dx,
то по формуле (18.8) имеем
И (У) = — J pi (У) log рх (у) dy = —J рх (x) D
Y X
X log Pi(x) d(—'ll! dI—'j dx
d(—j logpx(x)rfx—
[pit*} D
dx.
Поскольку
'jUl, fpi(x)log|D(— 'Jldx =^loglD(—'j \
\ У / I \ x /I J I k у ) I \ \ \y ) /
окончательно получим
523
18.5. Средняя мощность передаваемых сигналов = о2. Най-
ти распределение, которое при данном ограничении обладает мак-
симальной энтропией,, равной 1
Н (X) = (1/2) 1п (2ле<г2).
Решение. Решим задачу с помощью методов вариационного
исчисления [117] (иной метод использован в [1, ПО]).
Если требуется найти максимум (или минимум) интеграла
ь
I = j F [х, рг (х)] dx (18.19)
а
при дополнительных условиях
ь
J q>j [х, рх (х)] dx = = const,
а
b
<р2 [х, Pi (х)] dx = k2 = const, (18.20)
а
b
J q>n [x, px (x)] dx = kn = const,
a
то функция Pi (x), обеспечивающая максимум (или минимум) ин-
теграла (18.19), находится из решения уравнения
^- + Xi-^- + %2-^+- + Ч-т2- = 0, (18.21)
dpi dpt др,. dpi
где Х2, ..., — некоторые константы (неопределенные множи-
тели Лагранжа), которые определяются подстановкой рх (х), яв-
ляющейся решением уравнения (18.21), в равенства (18.20).
В данном случае требуется найти такую функцию рх (х), при ко-
торой
00
Н (X) = — | pi (х) In pi (х) dx
—00
достигает максимума, причем максимум следует искать при усло-
виях
J x2pi (х) dx = cr2, J pi (x) dx = 1. (18.22)
—00 —00
Функции F, q>i, q>2 имеют вид
F [x, pi (x)] = — Pi (x) In pi (x),
Ф1 [-v. Pi (*)] = x2pi (x), <p2 [x, pi (x)] = pi (x).
524
Следовательно,
dF/дрг = — [1 + In pj (x)l, dq^/dpj = x2, d^Jdpi = 1-
Подставив значения производных в (18.21), получим
— 1 — In рх (х) + Ххх2 + ^2 = 0.
Из этого соотношения следует, что In рх (х) = Х2 — 1 + Ххх2 или
Р1 (Х) = (18.23)
Для исключения неизвестных и Х2 подставим найденное зна-
чение Pi (х) во второе равенство (18.22). Тогда
Pi(x)dx=^ е-^-1 ех*X*dx — 2e^~l jех*X‘dx = 1.
— оо — оо О
Отметим, что должно быть отрицательным, ибо в противном
оо
случае интеграл § рх (х) dx расходится. Так как
о
J е_ а‘ х‘ dx = "Кл/2а, ’
о
то
2е^-> JeM2dx-=2e^-1-^-j/ -^- = 1
о
или
е—х2—1 =уг—2^/л.
Тогда (18.23) примет вид
Р1 (х) = ]/"— W**'. (18.24)
Подставим (18.24) в первое соотношение (18.22):
о2 = J х2 pi (х) dx — 2 -~^1' J х2 е*»х* dx =
— оо О
_ 2 1 / —1 1 / л ________1
~ V л 4 и (— Х1)3 ” 2Хх ’
Следовательно, = — 1/2<т2.
Подставив значение в выражение (18.24), окончательно получим
Р1(х)=-^е~х^.
су 2л
Таким образом, при ограничении сигналов по их средней мощ-
ности максимальной энтропией обладают функции с нормальным
распределением.
525
Вычислим энтропию случайной величины, распределенной по
нормальному закону t
00 оо
Н(Х) =— f рг (х) In Pi (х) dx — — f pi (х) In * е~х‘/2о‘ dx=>
J J оу 2л
--OO — 00
00 00
= I pi (x) 1ii]/2jtct2 dx 4- I Pi(x)~^
— 00 —oo
Учитывая ограничивающие условия (18.22), найдем
Н (X) = Нт (Х) = In /2^ + о2/2о2 = In /W + 1пе.
Следовательно,
Н (X) = In= (1/2) 1п (2леог2).
18.6. Определить полосу пропускания канала передачи теле-
визионного черно-белого изображения с 5 • 105 элементами, 25
кадрами в секунду и 8 равновероятными градациями яркости для
отношения af/N0F = Ps/Pn = 15 при условии, что изображение
может принимать наиболее хаотичный вид — вид «белого шума».
Решение. Изображение принимает вид белого шума, если все
его элементы как в одном кадре, так и в различных независимы. Энт-
ропия такого изображения при указанных условиях равна
Hh (X) = 5 • 10» log 8 = 1,5 • 10е дв. ед.
Ввиду независимости кадров общее максимальное количество ин-
формации, которое должно быть передано в 1 с, составит Н (X) =
= 25 • 1,5 • 10е дв. ед. Приравнивая это значение пропускной
способности канала (18.15), получаем 25 • 1,5 • 10е = F log (1 4-
4- 15), откуда
F = 9,375 • 10е Гц ~ 9,4 МГц.
Обычные телевизионные изображения имеют сильную простран-
ственную и временную корреляцию. Поэтому практически необ-
ходимая пропускная способность может быть существенно меньше
принятого здесь максимального значения.
18.7. Найти спектральную плотность сигнала S (/), которая при
fi
заданных значениях его полной мощности Ps = § S (/) df и спек-
h
тральной плотности гауссовской помехи N (/) обеспечит максималь-
ную скорость передачи информации.
Решение. Согласно (18.18)
f.
С = $ In [I + S (f)/N (/)] df.
ft
526
Требуется найти максимум этого интеграла при условии Ps =
fi
= 5 S (/) df. На основании (18.21) имеем
h
dF . « Лр д . (. . S \ , » dS п
----1-л—— = —In 1 Н--------4-л-----= 0.
dS dS dS \ N ) dS
где S — S (f), N = N (f). Так как
д . /. . S\ 1 1
— In 11 H---) —----------— .
dS \ N } \-\-S/N N *
to [S (f) + N = — X. Следовательно,
S(f) = -1/X-X(f).
Искомая спектральная плотность сигнала S (/) должна быть такой,
чтобы, будучи добавленной к спектральной плотности помехи N (J),
она обеспечила постоянство этой суммы и независимость ее от ча-
стоты. Величина % выбирается так, чтобы общая мощность полез-
ного сигнала равнялась заданной мощности ~PS.
I
3. ЗАДАЧИ И ОТВЕТЫ
18.1 . Информация передается посредством изменения амплиту-
ды сигнала X, распределенной по нормальному закону с параметра-
ми тх = 0 и о* = 15. Величина X измеряется регистрирующим
устройством с погрешностью Z, не зависящей от амплитуды сигнала
и также распределенной по нормальному закону с математическим
ожиданием mz = 0 и дисперсией <т| = 9.
Определить количество информации I (X; Y) о величине X
заключенное в случайных результатах измерений Y = X + Z.
Ответ: I (X; Y) су 0,71 дв. ед.
18.2 . Для контроля исправности блока периодически измеряют
напряжение в контрольной точке схемы. При исправном блоке это
напряжение равно 1 В, а при неисправном — 0 В. Ошибка вольт-
метра распределена равномерно с нулевым средним, но ширина
этого распределения зависит от значения измеряемого напряжения:
она равна 2 В, если напряжение на выходе составляет 1 В, и 1 В
в противном случае. В среднем в 90% времени блок исправен.
Вычислить количество информации I (X; Y), доставляемой при-
бором при одном измерении.
Ответ [120]: I (X; У) = 0,28 дв. ед.
18.3 . Информация передается с помощью частотно-модулиро-
ванных синусоидальных сигналов, рабочая частота F которых изме-
няется с равной вероятностью от fr= 10 МГц до = 50 МГц.
Определить энтропию (F), если точность измерения частоты
Д/ = 2 кГц.
Ответ: Нг (Г) су 14,28 дв. ед.
527
18.4 . Измерительное устройство вырабатывает временные ин-
тервалы, распределенные случайным образом в пределах от 100
до 500 мс.
Как изменится энтропия случайной величины при изменении
точности измерения с 1 мс до 1 мкс?
Ответ.'. Энтропия увеличится примерно на 10 дв. ед.
18.5 . Вычислить дифференциальную энтропию нормального за-
кона с дисперсией о2 и равномерного распределения с той же дис-
персией. ___ _
Ответ-. Нг (X) = log (<г/2лё), Яр (X) = log (о2/3).
18.6 . В результате полной дезорганизации управления п само-
летов летят с произвольными курсами. Управление восстановлено
и все самолеты взяли общий курс со средней квадратической ошиб-
кой ст<р = 3°.
Определить изменение энтропии AHlt считая, что в первом со-
стоянии имеет место равномерное распределение вероятности, а во
втором — нормальное.
Ответ: АН = Нр (X) — Hr (X) = 4,86 п дв. ед.
18.7 . Плотность вероятности случайного процесса х (/) имеет
вид pi (х) = Ае-и, -х > 0.
Найти дифференциальную энтропию величины X.
Ответ: Н (X) = log (е/Х).
18.8 . Определить энтропию Н (X) случайной величины X, функ-
ция распределения которой
' 0 при х^0,
Кх(х) = х2 при0<х^1,
1 при х> 1.
Ответ: Н (X) = log (/ё/2).
18.9 . Показать, что если система с нормальным распределением
координаты переходит из состояния, при котором ож = ах, в со-
стояние, при котором ах = а2, то приращение энтропии
ДЯ = Н2 (X) - Hi (X) = log (а2/ах).
18.10 . Найти дифференциальную энтропию случайной величи-
ны Y = A sin со/, где t равномерно распределено в интервале от
— л/со до л/со; А и со — положительные постоянные.
Ответ [62]: Н (У) = In (лЛ/2).
18.11 . Определить условную дифференциальную энтропию
Н (Х|г/) и среднюю условную дифференциальную энтропию Н (XI У)
случайной величины X относительно У, а также Н (У|х) и Н (У|х)
случайной величины У относительно X для системы (X, У) гауссов-
ских случайных величин.
Ответ:
Н (Х\у) = Н (Х|У) = log [<тя/2ле (1 - R'xy)\-
Н (У|х) = Н (У|Х) = log 1а„У2пе (1 - R^)],
528
где ох и оу — средние квадратические значения; Rxv — коэффи-
циент корреляции между X и Y.
18.12 . Найти дифференциальную энтропию Н (X) равномерно-
го распределения на отрезке (0,2) и энтропию суммы двух независи-
мых случайных величин X и Y, равномерно распределенных на
указанном интервале.
Ответ-. Н (X) = 1 дв. ед., Н (X, Y) = 2 дв.ед.
18.13 . Радиоприем осуществляется на две антенны, разнесен-
ные в пространстве так, что сигналы х (/) и у (t) в ветвях статистиче-
ски независимы.
Определить энтропию Н (Z) колебания z (t) на выходе сумми-
рующего устройства, если х (t) и у (t) распределены по нормальному
закону с нулевыми математическими ожиданиями и дисперсиями
ох = 16 В2 и огу = 25 В2.
Ответ: Н (Z) ~ 4,73 дв. ед.
18.14 . Показать, что если Y = X ± с, где с — постоянная ве-
личина, или Y = — X, то Н (У) = Н (X).
18.15 . Измерительное устройство вырабатывает случайный сиг-
нал х (t) с нормальной плотностью вероятности и корреляционной
функцией вида Rx (т) = cr’e^W.
Определить энтропию сигнала и его изытбочность, вызванную
наличием корреляции, если ох = 6 В.
Ответ [116]: Н (Х|У) = 4,52 дв. ед., R = 0,024.
18.16 . Ансамбль сигналов, проходящих через усилитель, имеет
значения, ограниченные сверху величиной х = b и снизу — ве-
личиной х = а.
Найти максимальную энтропию Нт (X) и энтропию Н (X) на
единицу времени, если ширина полосы пропускания усилителя рав-
на F.
Ответ: Нт (X)=log (b—а)дв. ед., Н (X) = 2F log (b—а)дв. ед.
18.17 . Передаваемые сигналы ограничены по пиковой мощности.
Определить распределение, которое при данном ограничении обла-
дает максимальной энтропией, а также вычислить энтропию при
этом распределении. __
. Ответ: рг (х) = 1/2У Рт, Н (X) = In 2У Рт, где Рт — пико-
вая мощность.
18.18 . Сигнал с математическим ожиданием тх может прини-
мать только положительные значения [рх (х) = 0 при х <Z 0].
Найти распределение, которое при данных ограничениях обла-
дает максимальной энтропией.
Ответ: р1(х) = -^—е~х,ГПх.
тх
18.19 . Показать, что при заданной энтропии нормальное рас-
пределение вероятностей
имеет наименьшую из всех одномерных распределений дисперсию.
529
18.20 . Определить максимально возможную скорость переда-
чи информации по радиотехническому каналу связи пункта управле-
ния с телеуправляемой ракетой, если полоса пропускания канала
связи равна 3 МГц, а минимальное отношение сигнал/шум по мощ-
ности в процессе наведения ракеты на цель равно трем.
Ответ'. С = 6 • 10е дв. ед./с.
18.21 . Вычислить пропускную способность канала связи с ам-
плитудно-импульсной модуляцией, если число уровней сигнала 16,
полоса частот исходного сигнала Fs, сигнал равномерно распределен
на интервале (— Un, + Un), а вероятность искажения, выражаю-
щая возможность перехода в соседний уровень, 5%.
Ответ [119]: С = 8,5 дв. ед.
18.22 . Сравнить пропускные способности двух каналов связи,
если в первом действует белый гауссовский шум в полосе F с дис-
персией о2 = 1 В2, а во втором — белый шум, равномерно распре-
деленный в интервале ± 1,5 В с полосой 2F. Считать, что мощность
передаваемого сигнала Ps велика по сравнению с мощностью шумов.
№ 1
Ответ: Сх— Cz — F log -5-, N9—--------е2,°е3,
Р, 2ле
где Ct и С2 — пропускные способности первого и второго каналов.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ I
1 / X2
Таблица нормальной плотности вероятности Pi (х) = 3/х- ехр I—
X 0 1 2 3 4 5 6 7 8 9
0,0 0,3989 3989 3989 3988 3986 3984 3982 3980 3977 3973
ОД ’3970 3965 3961 3956 3951 3945 3939 3932 3925 3918
0 2 3910 3902 3894 3885 3876 3867 3857 3847 3836 3825
0 3 3814 3802 3790 3778 3765 3752 3739 3726 3712 3697
0,4 3683 3668 3653 3637 3621 3605 3589 3572 3555 3538
0 5 3521 3503 3485 3467 3448 3429 3410 3391 3372 3352
0 6 3332 3312 3292 3271 3251 3230 3209 3187 3166 3144
0,7 3123 3101 3079 3056 3034 ЗОН < .2989 2966 2943 2920
0,8 2897 2874 2850 2827 2803 2780 ’ 2756 2732 2709 2685
0,9 2661 2637 2613 2589 2565 2541 2516’ 2492 2468 2444
1,0 0,2420 2396 2371 2347 2323 2299 2275 2251 2227 2203
1,1 2179 2155 2131 2107 2083 2059 2036 2012 1989 1965
1,2 1942 1919 1895 1872 1849 1824 1804 1781 1758 1736
1,3 1714 1691 1669 1647 1626 1604 1582 1561 1539 1518
1,4 1497 1476 1456 1435 1415 1394 1374 1354 1334 1315
1,5 1295 1276 1257 1238 1219 1200 1182 1163 1145 1127
1,6 1109 1092 1074 1057 1040 1023 1006 0989 0973 0957
1,7 0940 0925 0909 0893 0878 0863 0848 0833 0818 0804
1,8 0790 0775 0761 0748 0734 0721 0707 0694 0681 0669
1,9 0656 0644 0632 0620 0608 0596 0584 0573 0562 0551
2,0 0,0540 0529 0519 0508 0498 0488 0478 0468 0459 0449
2,1 0440 0431 0422 0413 0404 0396 0388 0379 0371 0363
2,2 0355 0347 0339 0332 0325 0317 0310 0303 0297 0290
2,3 0283 0277 0270 0264 0258 0252 0246 0241 0235 0229
2,4 0224 0219 0213 0208 0203 0198 0194 0189 0184 0180
2,5 0175 0171 0167 0163 0158 0154 0151 0147 0143 0139
2,6 0136 0132 0129 0126 0122 0119 0116 0113 ОНО 0107
2,7 0104 0101 0099 0096 0093 0091 0088 0086 0084 0081
2,8 0079 0077 0075 0073 0071 0069 0067 0065 0063 0061
2,9 0060 0058 0056 0055 0053 0051 0050 0048 0047 0046
3,0 0,0044 0043 0042 0040 0039 0038 0037 0036 0035 0034
3,1 0033 0032 0031 0030 0029 0028 0027 0026 0025 0025
3,2 0024 0023 0022 0022 0021 0020 0020 0019 0018 0018
з,з 0017 0017 0016 0016 0015 0015 0014 0014 0013 0013
3,4 0012 0012 0012 ООП ООП 0010 0010 0010 0009 0009
3,5 0009 0008 0008 0008 0008 0007 0007 0007 0007 0006
3,6 0006 0006 0006 0005 0005 0005 0005 0005 0005 0004
3,7 0004 0004 0004 0004 0004 0004 0003 0003 0003 0003
3,8 0003 0003 0003 0003 0003 0002 0002 0002 0002 0002
3,9 0002 0002 0002 0002 0002 0002 0002 0002 0001 0001
531
ПРИЛОЖЕНИЕ II
1 2
Таблица интеграла вероятности Ф(г)=—— Се 2 dx для 0,00<z<4,99; Ф(—г) = 1—Ф(г)
У2л
сд
QO
to
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,5000 0,5040 0,5080 0,5120 0,5160 0,5199 0,5239 0,5279 0,5319 0,5359
0,1 0,5398 0,5438 0,5478 0,5517 0,5557 0,5596 0,5636 0,5675 0,5714 0,5753
0,2 0,5793 0,5832 0,5871 0,5910 0,5948 0,5987 0,6026 0,6064 0,6103 0,6141
о,з 0,6179 0,6217 0,6255 0,6293 0,6331 0,6368 .0,6406 0,6443 0,6480 0,6517
0,4 0,6554 0,6591 0,6628 0,6664 0,6700 0,6736 0,6772 0,6808 0,6844 0,6879
0,5 0,6915 0,6950 0,6985 0,7019 0,7054 0,7088 0,7123 0,7157 0,7190 0,7224
0,6 0,7257 0,7291 0,7324 0,7357 0,7389 0,7422 0,7454 0,7486 0,7517 0,7549
0,7 0,7580 0,7611 0,7642 0,7673 0,7703 0,7734 0,7764 0,7794 0,7823 0,7852
0,8 0 7881 0,7910 0,7939 0,7967 0,7995 0,8023 0,8051 0,8078 0,8106 0,8133
0,9 0,8159 0,8186 0,8212 0,8238 0,8264 0,8289 0,8315 0,8340 0,8365 0,8389
1,0 0,8413 0,8438 0,8461 0,8485 0,8508 0,8531 0,8554 0,8577 0,8599 0,8621
1,1 0,8643 0,8665 0,8686 0,8708 0,8729 0,8749 0,8770 0,8790 0,8810 0,8830
1,2 0,8849 0,8869 0,8888 0,8907 0,8925 0,8944 0,8962 0,8980 0,8997 0,90147
1,3 0,90320 0,90490 0,90658 0,90824 0,90988 0,91149 0,91309 0,91466 0,91621 0,91774
1,4 0,91924 0,92073 0,92220 0,92364 0,92507 0,92647 0,92785 0,92922 0,93056. 0,93189
1,5 0,93319 0,93448 0,93574 0,93699 0,93822 0,93943 0,94062 0,94179 0,94295 0,94408
1,6 0,94520 0,94630 0,94738 0,94845 0,94950 0,95053 0,95154 0,95254 0,95352 0,95449
1,7 0,95543 0,95637 0,95728 0,95818 0,95907 0,95994 0,96080 0,96164 0,96246 0,96327
1,8 0,96407 0,96485 0,96562 0,96638 0,96712 0,96784 0,96856 0,96926 0,96995 0,97062
1,9 0,97128 0,97193 0,97257 0,97320 0,97381 0,97441 0,97500 0,97558 0,97615 0,97670
2,0 0,97725 0,97778 0,97831 0,97882 0,97932 0,97982 0,98030 0,98077 0,98124 0,98169
2,1 0,98214 . 0,98257 0,98300 0,98341 0,98382 0,98422 0,98461 0,98500 0,98537 0,98574
2,2 0,98610 0,98645 0,98679 0,98713 0,98745 0,98778 0,98809 0,98840 0,98870 0,98899
2,3 2,4 0,98928 0,94802 0,98956 0,9’2024 0,98983 0,922240 0,920097 0,922451 0,9’0358 0,9’2656 0,920613 0,922857 0,9’0863 0,9’3053 0,921106 0,923244 0,921344 0,923431 0,921576 0,923613
2,5 0,923790 0,9’3963 0,9’4132 0,924297 0,9’4457 0,924614 0,9’4766 0,94915 0,925060 0,925201
2,6 0,925339 0,9’5473 0,9’5604 0,925731 0,9’5855 0,925975 0,9’6093 0,926207 0,926319 0,926427
2,7 0,926533 0,9’6636 0,9’6736 0,926833 0,9’6928 0,927020 0,9’7110 0,927197 0,927282 0,927365
2,8 0,927445 0,9’7523 0,9’7599 0,927673 0,9’7744 0,927814 0,9’7882 0,927948 0,928012 0,928074
2,9 0,928134 0,9’8193 0,9’8250 0,928305 0,9’8359 0,928411 0,9’8462 0,928511 0,928559 0,928605
3,0 0,928650 0,9’8694 0,9’8736 0,928777 0,9’8817 0,928856 0,9’8893 0,928930 0,928965 0,928999
3,1 0,930324 0,9’0646 0,950957 0,94260 0,9’1553 . 0,94836 0,9’2112 0,932378 0,932636 0,932886
3,2 0,933129 0,9’3363 0,9’3590 0,933810 0,9’4024 0,94230 0,9’4429 О,334623 0,934810 0,94991
з,з 0,935166 0,9’5335 0,9’5499 0,935658 0,9’5811 0,935959 0,9’6103 0,936242 0,936376 0,936505
3,4 0,936631 0,9’6752 0,9’6869 0,936982 0,9’7091 0,937197 0,9’7299 0,937398 0,937493 0,937585
3,5 0,937674 0,9’7759 0,9’7842 0,937922 0,9’7999 0,938074 0,9’8146 0,938215 0,938282 0,938347
3,6 0,938409 0,9’8469 0,9’8527 0,938583 0,9’8637 0,938689 0,9’8739 0,938787 0,938834 0,938879
3,7 0,938922 0,9’8964 0,9*0039 0,940426 0,9*0799 0,94158 0,9*1504 0,941838 0,942159 0,942468
3,8 0,942765 0,9*3052 0,9*3327 0,943593 0,9*3848 0,94094 0,9*4331 0,944558 0,944777 0,944988
3,9 0,945190 0,9*5385 0,9*5573 0,945753 0,9*5926 0,946092 0,9*6253 О,9464О6 ‘0,946554 0,946696
4,0 0,946833 0,946964 0,9*7090 0,947211 0,9*7327 0,947439 0,9*7546 0,947649 0,947748 0,947843
4,1 0,947934 0,9*8022 0,9*8106 0,948186 0,9*8263 0,948338 0,9*8409 0,948477 0,948542 0,948605
4,2 0,948665 0,9*8723 0,9*8778 0,948832 0,9*8882 0,9489?1 0,9*8978 0,950226 0,950655 0,951066
4,3 0,9®1460 0,9’1837 0,9’2199 0,952545 0,9’2876 0,953193 0,9’3497 0,953788 0,954066 0,954332
4,4 0,954587 0,9’4841 0,9’5065 0,955288 0,9’5502 0,955706 0,9’5902 0,956089 0,956268 0,956439
4,5 0,956602 0,936759 0,9’6908 0,957051 0,9’7187 0,957318 0,9’7442 0,957561 0,957675 0,957784
4,6 0,957888 0,9’7987 0,9’8081 0,958172 0,9’8258 0,958340 0,9’8419 0,958494 0,958566 0,958634
4,7 0,958699 0,9’8761 0,9’8821 0,958877 0,958931 0,958983 0,9’0320 0,960789 0,94235 0,94661
4,8 0,962067 0,9’2453 0,9’2822 0,953173 0,9’3508 0,963827 0,9’4131 0,964420 0,94696 0,94958
4,9 0,9б5208 0,9’5446 0,9’5673 0,965889 0,9’6094 О,966289 0,9’6475 0,966652 0,966821 0,966981
Пример: Ф (3,57) = 0,9’8215 = 0,9998215
ПРИЛОЖЕНИЕ III
Процентные точки распределения %2 Р а] = а
а
* 0,990 0,975 0,950 0,900 | 0,10 | 0,05 | 0,025 0,010
1 0,00016 0,00098 0,0039 0,0158 2,71 3,84 5,02 6,63
2 о', 0201 0,0506 - 0,103 0,211 4,61 5,99 7,38 9,21
3 0,115 0,216 0,352 0,584 ‘ 6,25 7,81 9,35 11,34
4 0^297 0,484 0,711 1,06 7,78 9,49 11,14 13,28
5 О; 554 0,831 1,15 1,61 9,24 11,07 12,83 15,09
6 0,872 1,24 1,64 2,20 10,64 12,59 14,45 16,81
7 1'24 h69 2,17 2,83 12,02 14,07 16,01 18,48
8 1*65 2,18 2,73 3,49 13,36 15,51 17,53 20,09
9 2’, 09 2,70 3,33 4,17 14,68 16,92 19,02 21,67
10 2,56 3,25 3,94 4,87 15,99 18,31 20,48 23,21
11 3,05 3,82 4,57 5,58 17,28 19,68 21,92 24,73
12 4,57 4Д0 5,23 6,30 18,55 21,03 23,34 26,22
13 4,11 5,01 5,89 7,04 19,81 22,36 24,74 27,69
14 4,66 5,63 6,57 7,79 21,06 23,68 26,12 29,14
15 5,23 6,26 7,26 8,55 22,31 25,00 27,49 30,58
16 5,81 6,91 7,96 9,31 23,54 26,30 28,85 32,00
17 6,41 7,56 8,67 10,08 24,77 27,59 30,19 33,41
18 7,01 8,23 9,39 10,86 25,99 28,87 31,53 34,81
19 7,63 8,91 10,12 11,65 27,20 30,14 32,85 36,19
20 8,26 9,59 10,85 12,44 28,41 31,41 34,17 37,57
21 8,90 10,28 11,59 13,24 29,62 32,67 35,48 38,93
22 9,54 10,98 12,34 14,04 30,81 33,92 36,78 40,29
23 10,20 11,69 13,09 14,85 32,01 35,17 38,08 41,64
24 10,86 12,40 13,85 15,66 33,20 36,42 39,36 42,98
25 11,52 13,12 14,61 16,47 34,38 37,65 40,65 44,31
26 12,20 13,84 15,38 17,29 35,56 38,88 41,92 45,64
27 12,88 14,57 16,15 18,11 36,74 40,11 43,19 46,96
28 13,56 15,31 16,93 18,94 37,92 41,34 44,46 48,28
29 14,26 16,05 17,71 19,77 39,09 42,56 45,72 49,59
30 14,95 16,79 18,49 20,60 40,26 43,77 46,98 50,89
40 22,16 24,43 26,51 29,05 51,81 55,76 59,34 63,69
60 37,48 40,48 43,19 46,46 74,40 79,08 83,30 88,38
120 86,92 91,58 95,70 100,62 140,23 146,57 152,21 158,95
nf >и k> 120 Г.-А 4"га ”|Х 9/г Ае га~ заданна: я про-
центная точка нормированного гауссовского распределения.
534
ПРИЛОЖЕНИЕ IV
Процентные точки /-распределения Стыодента Р [tk>tk; аЗ = а
а
k | 0,10 0,050 0,025 I 0,010 I 0,005
1 3,078 6,314 12,706 31,821 63,657
2 1,886 2,920 4,303 6,965 9,925
3 1,638 2,353 3,182 4,541 5,841
4 1,533 2,132 2,776 3,747 4,604
5 1,476 2,015 2,571 3,365 4,032
6 1,440 1,943 2,447 3,143 3,707
7 1,415 1,895 2,365 2,998 3,499
8 1,397 1,860 2,306 2,896 3,355
9 1,383 1,833 2,262 2,821 3,250
10 1,372 1,812 2,228 2,764 3,169
И 1,363 1,796 2,201 2,718 3,106
12 1,356 1,782 2,179 2,681 3,055
13 1,350 1,771 2,160- 2,650 3,012
14 1,345 1,761 2,145 *2,624 2,977
15 1,341 1,753 2,131 2,602 2,947
16 1,337 1,746 2,120 2,583 2,921
17 1,333 1,740 2,110 2,567 2,898
18 1,330 1,734 2,101 2,552 2,878
19 1,328 1,729 2,093 2,539 2,861
20 1,325 1,725 2,086 2,528 2,845
21 1,323 1,721 2,080 2,518 2,831
22 1,321 1,717 2,074 2,508 2,819
23 1,319 1,714 2,069 2,500 2,807
24 1,318 1,711 2,064 2,492 2,797
25 1,316 1,708 2,060 2,485 2,787
26 1,315 1,706 2,056 2,479 2,779
27 1,314 1,703 2,052 2,473 2,771
28 1,313 1,701 2,048 2,467 2,763
29 1,311 1,699 2,045 2,462 2,756
30 1,310 1,697 2,042 2,457 2,750
40 1,303 1,684 2,021 2,423 2,704
60 1,296 1,671 2,000 2,390 2,660
120 1,289 1,658 1,980 2,358 2,617
Значен] соотношени 1я а— 0,995; ем Z*l 1-а= 0,990; 0,975; а. 0,950 и 0,9i 00 получают , пользуясь
535
СПИСОК ЛИТЕРАТУРЫ
1. Тихонов В. И. Статистическая радиотехника. —М.:Сов. радио, 1966. —
678 с.
2. Яглом А. М., Яглом И. М. Вероятность и информация. — М.: Наука,
1973. — 512 с.
3. Вентцель Е. С. Теория вероятностей: Учебник для вузов — 3-е изд.,
испр. —М.: Наука, 1964 — 576 с.
4. Сборник задач по теории вероятностей, математической статистике
и теории случайных функций: Учеб, пособие для вузов/Б. Г. Володин,
М. П. Ганин, И. Я. Динер и др.; Под ред. А. А. Свешникова. —М.:
Наука, 1965. — 632 с.
5. Феллер В. Введение в теорию вероятностей и ее приложения, т. I; Пер.
с англ./Под ред. Е. Б. Дынкина. — М.: Мир, 1967. — 498; т. 2; Пер.
с англ./Пер. Ю. В. Прохорова. —М.: Мир, 196?. — 752 с.
6. Крамер Г. Математические методы статистики: Пер. с англ./Под ред.
А. Н. Колмогорова.—М.: Мир, 1975.— 648 с.
7. Уилкс С. Математическая статистика: Пер,, с англ./Под ред. Ю. В. Лин-
ника. — М.; Наука, 1967. — 632 с.
8. Хан Г., Шапиро С. Статистические модели в инженерных задачах: Пер.
с англ./Под ред. В. В. Налимова. — М.: Мир, 1969. — 396 с.
9. Статистические методы в экспериментальной физике: Пер. с англ./
В. Идье, Д. Драйард, Ф. Джеймс и др. Пер. под ред. А. А. Тяпкина. —
М.: Атомиздат, 1976. — 336 с.
10. Кендалл М., Стюарт А. Теория распределений: Пер. с англ./ Под ред,
А. Н. Колмогорова. —М.: Наука, 1966. 588 с.
11. Farison I. On calculating moments for some common probability laws. —
IEEE Trans. 1965, v. IT-11, №4, p. 586—589.
12. Прохоров Ю. В., Розанов Ю. А. Теория вероятностей: Основные поня-
тия, предельные теоремы, случайные процессы. — 2-е изд., перераб. —
М.: Наука, 1973. — 496 с.
13. Гнеденко Б. В. Курс теории вероятностей: Учебник для университетов. —
5-е изд., стереот. — М.: Наука, 1969. — 400 с.
14. Левин Б. Р. Теоретические основы статистической радиотехники. В 3-х
кн. — т. 1. — М.: Сов. радио, 1974. — 550 с.
15. Горяйнов В. Т., Журавлев А. Г., Тихонов В. И. Примеры и задачи по
статистической радиотехнике: Учебное пособие для вузов/Под' ред.
В. И. Тихонова. — М.: Сов. радио, 1970. — 600 с.
16. Корн Г., Корн Т. Справочник по математике для научных работников
и инженеров: Пер. с англ./Под ред. И. Г. Арамановича. — М.: Наука,
1968. — 720 с.
17. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и про-
изведений. -5-е изд., перераб. — М.: Наука, 1971. — 1108 с.
18. Вентцель Е. С.; Овчаров Л. А. Теория вероятностей: Учеб, пособие для
вузов.—2-е изд., стереот.—М.: Наука, 1973.— 368 с.
19. Рытов С. М. Введение в статистическую радиофизику: Учеб, пособие для
вузов. — 2-е изд., перераб. и доп. — М.: Наука, 1976. — 496 с.
536
20. Смирнов Н. В., Дунин-Барковский И. В. Краткий курс математической
статистики для технических приложений: Учебное пособие для вузов.
М.: Физматгиз, 1959. — 436 с.
21. Митропольский А. К. Техника статистических вычислений. — 2-е изд.
перераб. и доп.—М.: Наука, 1971.— 576 с.
22. Тихонов В. И., Бакаев Ю. Н. Статистическая теория радиотехнических
устройств: Учебник для вузов ВВС/ВВИА им. Н. Е. Жуковского. —
М., 1978. — 420 с.
23. Гмурман В. Е. Теория вероятностей и математическая статистика: Учеб,
пособие для вузов. — 5-е изд., перераб. и доп. — М.: Высшая школа,
1977. — 499 с.
24. Гурский Е. И. Теория вероятностей с элементами математической ста'
тистики: Учеб, пособие для вузов. — М.: Высшая школа, 1971. — 328 с-
25. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов: Пер-
с англ./Под ред. И. Н. Коваленко. —М.: Мир, 1971. — 408 с.
26. Тихонов В. И. Воздействие электрических флуктуаций на нелинейные
радиотехнические устройства.: Докт. дис. /ВВИА им. Н. Е. Жуков-
ского. — М., 1956.
27. Миддлтон Д. Введение в статистическую теорию связи, т. I. Пер. с англ./
Под ред. Б. Р. Левина. -— М.: Сов. радио, 1961. 782 с.; т. 2, 1962. -—
750 с.
28. Кузнецов П. И., Стратонович Р. Л., Тихонов В. И. Прохождение неко-
торых случайных функций через линейные системы. — Автоматика
и телемеханика, 1953, т. 14, №2, с.^144—163.
29. Кузнецов П. И., Стратонович Р. Л., Тихонов В. И. Прохождение слу-
чайных функций через нелинейные системы. — Автоматика и телеме-
ханика, 1953, т. 14, №4, с. 375—391.
30. Гнеденко Б. В.; Колмогоров А. Н. Предельные распределения для сумм
независимых случайных величин.—М.: ИТТЛ, 1949. —264 с.
31. Лезин Ю. С. О распределении случайных напряжений на выходе некоге-
рентного накопительного устройства с экспоненциальной весовой функ-
цией. — Изв. вузов СССР. Радиотехника, 1960, № 6, с. 592—597.
32. Marcum J. I. A Statistical theory of target detection by pulsed radar. —
IRE. Trans., 1960, v. IT-6, №2, p. 59—144. •
33. Тихонов В. И., Горяйнов В. Т. Детектирование случайных сигналов. —
Радиотехника, 1966, т. 21, № 1, с. 31—46.
34. Деч Р. Нелинейные преобразования случайных процессов. Пер. с англ./
Под ред. Б. Р. Левина. — М.: Сов. радио, 1965. — 208 с.
35. Papoulis A. Probability, random variables and stochastic processes. — New-
York: McGraw-Hill Book Co., 1965. — 583 p.
36. Rice S. O. Mathematical analysis of random noise. —BSTJ, 1944, v. 23,
№3, p. 282—332; v. 24, № 1, p. 46—156.
37. Barret J. E., Lampard D. G. An expansion for some second-order probabi-
lity distributions and its application to noise problems. — IRF Trans.
1955, v. IT-1, № 1, p. 10—15.
38. Ватсон Г. H. Теория бесселевых функций.—М.: ИЛ, 1949. — 798 с.
39. Янке Е., Эмде Ф., Леш Ф. Специальные функции. Пер. с нем./Под ред.
Л. И. Седова. —М.: Наука, 1964. — 344 с.
40. Расщепляев Ю. С. Синтез моделей случайных процессов для исследования
систем при помощи ЦВМ. — Радиотехника и электроника, 1975, т. XX,
№ 1, с. 188—192.
41. Бендат Дж. Основы теории случайных шумов и ее применение. Пер.: с
англ. Под ред. В. С. Пугачева. —М.: Наука, 1965. — 464 с.
42. Давенпорт В. Б., Рут В. Л. Введение в теорию случайных сигналов и шу-
мов: Пер. с англ./Под ред. Р. Л. Добрушина.— М.: ИЛ, 1960. — 468 с.
43. Расщепляев Ю.С., Фандиенко В. Н. О построении моделей стационарных
случайных процессов для исследования систем управления. — Изве-
стия АН СССР. Техническая кибернетика, 1974, № 1, с. 224—231
537
44. Жуков В. П., Карташев В. Г., Николаев А. М. Сборник задач по курсу
«Радиотехнические цепи и сигналы»: Учебн. пособие для вузов/ Под
ред. А. М. Николаева. — М.: Сов. радио, 1972. — 192 с.
45. Тихонов В. И., Миронов М. А. Марковские процессы. — М.: Сов. радио,
1977. — 488 с.
46. Баруча-Рид А. Т. Элементы теории марковских процессов и их приложе-
ния. Пер. с англ./Под ред. А. Н. Ширяева. — М.: Наука, 1969. — 511 с.
47. Карлин С. Основы теории случайных процессов: Пер. с англ. /Под ред.
И. Н. Коваленко.—М.: Мир, 1971.— 536 с.
48. Сох D. R., Miller Н. D. The theory of stochastic processes. — London:
Methuen, 1965. — 398 p.
49. Тихонов В. И., Кульман Н. К. Нелинейная фильтрация и квазикогерент-
ный прием сигналов. — М.: Сов. радио, 1975. — 704 с.
50. Френке Л. Теория сигналов: Пер. с англ./Под ред. Д. Е. Бакмана. —
М.: Сов. радио, 1974. — 344 с.
51. Kaufman Н., King Е. Н. Spectral power density functions in pulse time
modulation. — IRE Trans. 1955, v. IT-1, № 1, p. 40—46.
52. Macfarlane G. G. On the energy-spectrum of an almost periodic succession
of pulses. —Proc. IRE, 1949, v. 37, № 10, p. 1139—1143.
53. ГОСТ 13377—75. Надежность в технике. Термины и определения.
54. Козлов Б. А., Ушаков И. А. Справочник по расчету надежности аппара-
туры радиоэлектроники и автоматики. — М.: Сов. радио, 1975. — 472 с.
55. Справочник по теоретическим основам радиоэлектроники в 2-х т./
А. А. Барыбин, О. Г. Вендик, Б. Н. Горин и др.; Под ред. Б. X. Кри-
вицкого, В. Н. Дулина. — М.: Энергия, 1977. Т. 1 — 504 с.
56. Сборник задач по теории надежности/А. М. Половко, И. М. Маликов,
А. Н. Жигарев, В. И. Зарудный; Под ред. А. М. Половко, И. М. Мали-
кова. — М.: Сов. радио, 1972. — 408 с.
57. Теория надежности радиоэлектронных систем в примерах и задачах:
Учеб, пособие для вузов/Г. В. Дружинин, С. В. Степанов, В. Л. Шихма-
това, Г. А. Ярыгин; Под ред. Г. В. Дружинина. — М.: Энергия, 1976. -—
448 с.
58. Сотсков Б. С. Основы теории и расчета надежности элементов и устройств
автоматики и вычислительной техники: Учебное пособие для вузов. —
М.: Высшая школа, 1970. — 270 с.
59. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслужи-
вания. — М.: Наука, 1966. — 432 с.
60. Саати Т. Элементы теории массового обслуживания и ее приложения.
Пер. с англ./Под ред. И. Н. Коваленко и Р. Д. Когана. -— М.: Сов.
радио, 1965. — 510 с.
61. Кокс Д. Р., Смит В. Л. Теория восстановления. Пер. с англ./Под ред.
Ю. К. Беляева. — М.: Сов. радио, 1967. — 300 с.
62. Емельянов Г. В., Скитович В. П. Задачник по теории вероятностей и ма-
тематической статистике: Учеб, пособие для университетов. -— Л.:
ЛГУ им. А. А. Жданова, 1967. — 332 с.
63. Розенберг В. Я., Прохоров А. И. Что такое теория массового обслужива-
ния. — М.: Сов. радио, 1962. — 254 с.
64. Свешников А. А. Прикладные методы теории случайных функций. —
М.: Наука, 1968. — 464 с.
65. Горяйнов В. Т. Воздействие на линейную систему отрезка квазигармо-
нических флуктуаций в смеси с белым шумом. — Радиотехника, 1966,
т. 21, №6, с. 1—6.
66. Чайковский В. И. Энергетический спектр суммы запаздывающих стохас
тических сигналов. —Изв. вузов СССР, Радиотехника, 1965, т. VIII
№1, с. 87—98.
67. Тепляков И. М. Радиотелеметрия.—М.: Сов. радио. 1966.— 312 с*
68. Wohman W. М.; Fuller А. Т. Probability densities of the smoothed «Random
telegraph signal». —Journ. Electrics and Control, 1958, v. 4, №6, p. 567—
576.
538
69. Леонов В. tl., Ширяев А. Н. К технике вычисления семиинварЙайФбй.
Теория вероятностей и ее применение, 1959, т. 4, вып. 3, с. 342—355.
70. Таблицы функции ошибок и ее первых двадцати производных. Пер. с
англ./Пер. Л. С. Барк и Л. Н. Болыпева. — М.: Изд. ВЦ АН СССР,
1965. — 276 с.
71. Слейтер Л. Дж. Вырожденные гипергеометрические функции: Пер. с англ./
Пер. М. К. Керимова. — М.: Изв. ВЦ АН СССР, 1966. — 250 с.
72. Амиантов И. Н., Тихонов В. И. Воздействие нормальных флуктуаций
на типовые нелинейные элементы. — Изв. АН СССР. ОТН, 1956, № 4,
с. 33—41.
73. Тихонов В. И., Амиантов И. Н. Воздействие сигнала и шума на нелиней-
ные элементы (прямой метод). — Радиотехника и электроника, 1957,
т. II, №5, с. 579—590.
74. Price R. A useful theorem for nonlinear devices having gaussian inputs. —
IRE Trans. 1958, v. IT-4, №2, p. 69—72.
75. Ralston G. Addition of uniform and gaussian distributions — exact and
approximate solutions. — Proc. IEEE, 1966, v. 54, № 7, p. 647—654.
76. Morgan S. P. Tables of Bessel functions of imaginary order and imaginaru
argument. — Institute of Technology, California, 1947. — 61 p.
77. Билык M. Г. Корреляционная функция случайного нормального процес-
са на выходе логарифмического устройства. — В кн.: Проблемы пере-
дачи квазистационарных сигналов. — Киев: Изд. АН УССР, 1967, 180 с.
78. Кратцер А., Франц В. Трансцендентные функции: Пер. с нем./Пер.
Н. Я. Виленкина. — М.: ИЛ, 1963. — 466. с.
79. Baum R. F. The correlation function of smoothly limited gaussian noise. —
IRE Trans., 1957, v. IT-3, №3, p. 193—197.
80. Данилин Б. В., Михайлов Ю. П. Воздействие флуктуаций на систему ог-
раничитель — инерционная цепь RC. — Изв. вузов СССР. Радиотех-
ника, 1966, т. 8, № 6, с. 668—675.
81. Cooper D. С. The probability density function for the output of a correla-
tor with band-pass input waveforms. — IEEE Trans., 1965, v. IT-11,
№ 2, p. 190—195.
82. Лезин Ю. С. Оптимальные фильтры и накопители импульсных сигна-
лов. — М.: Сов. радио, 1969. — 446 с.
83. Тихонов В. И. Выбросы случайных процессов. —М.: Наука, 1970. —
392 с.
84. Колмогоров А. Н. Интерполирование и экстраполирование стационарных
случайных последовательностей.— Изв. АН ССР Сер. математическая,
1941, №5, с. 3—14.
85. Wiener N. Extrapolation, interpolation and soothing of stationary time
series. — New-York: John Wiley, 1949— 162 p.
86. Солодовников В. В. Статистическая динамика линейных систем автома-
тического управления. —М.: Физматгиз, 1960. — 656 с.
87. Лэнинг Дж. X., Бэттин Р. Г. Случайные процессы в задачах автоматиче-
ского управления: Пер. с англ./Под ред. В. С. Пугачева. — М.: ИЛ,
1958— 388 с.
88. Пугачев В. С. Теория случайных функций и ее применение к задачам ав-
томатического регулирования. — М.: Физматгиз, 1960. — 884 с.
89. Ван Трис Г. Теория обнаружения, оценок и модуляции: Пер. с англ./
Под ред. В. И. Тихонова. Т. I. — М.: Сов. радио, 1972. — 744 с.
90. Turin G. L. An introduction to matched filters. — IRE Trans., 1960, v. IT-6,
№3, p. 311—329.
91. Гуткин Л. С. Теория оптимальных методов радиоприема при флуктуацион-
ных помехах. — М.: Сов. радио, 1972. — 448 с.
92. Витерби Э. Д. Принципы когерентной связи: Пер. с англ. /Под ред.
Б. Р. Левина. — М.: Сов. радио, 1970. — 392 с.
93. Горяйнов В. Т. Отношение сигнал/шум на выходе линейной системы при
расстроенном входном сигнале. — Радиотехника, 1966, т. 21, №6,
с. 1—9.
539
94. Котельников В. А. Теория потенциальной помехоустойчивости. — М.:
Госэнергоиздат, 1956. — 152 с.
95. Вудворд Ф. М. Теория вероятностей и теория информации с применения-
ми в радиолокации: Пер. с англ./Под ред. Г. С. Горелика. — М.: Сов.
радио, 1955, — 128 с.
96. Амиантов И. Н. Избранные вопросы статистической теории связи. —
М.: Сов. радио, 1971. — 416 с.
97. Хелстром К. Статистическая теория обнаружения сигналов: Пер. с англ./
Под ред. Ю. Б. Кобзарева. — М.: ИЛ, 1963. — 432 с.
98. Фалькович С. Е. Прием радиолокационных сигналов на фоне флуктуа-
ционных помех. — М.: Сов. радио, 1961. — 310 с.
99, Вальд А. Последовательный анализ. Пер. с англ./Под ред. Б. А. Сева-
стьянова. — М.: Физматгиз, 1962. — 328 с.
100. Башаринов А. Е., Флейшман Б. С. Методы статистического последова-
тельного анализа и их приложения. — М.: Сов. радио, 1962. — 352 с.
101. Helstrom С. W. The Resolution of Signals in White Gaussian Noise. —
Proc. IRE, 1955, v. 43, №9, p. 1111—1118.
102. Таблицы распределения Релея—Райса/Л. С. Барк, Л. Н. Большев,
П. И. Кузнецов и др. — М.: Изд. ВЦ АН СССР, 1964. — 246 с.
103. Turin G. L. Error probabilities for binary symmetric ideal reception
through nonselective slow fading and noise. —Proc. IRE, 1958, v. 46,
№9, p. 851—857.
104. Константинов П. А. Помехоустойчивость систем связи с тональной ма-
нипуляцией при идеальном приеме. — Радиотехника, 1961, т. 16,
№11, с. 18—25.
105. Хальд А. Математическая статистика с техническими приложениями:
Пер. с англ./Под ред. Ю. В. Линника. — М.: ИЛ, 1956. — 664 с‘.
106. Ван дер Варден Б. Л. Математическая статистика: Пер. с немец./Под
ред. Н. В. Смирнова. —М.: ИЛ, 1960. — 436 с.
107. Дунин-Барковский И. В., Смирнов Н. В. Теория вероятностей и мате-
матическая статистика в технике. — М.: Гостехиздат, 1955. — 556 с.
108. Куликов Е. И., Трифонов А. П. Оценка параметров сигналов на фоне
помех. —М.: Сов. радио, 1978. — 256 с.
109. Галлагер Р. Теория информации и надежная связь: Пер. с англ./Под
ред. М. С. Пинскера, Б. С. Цыбакова.—М.: Сов. радио, 1974. — 720 с.
ПО. Фано Р. Передача информации. Статистическая теория связи: Пер. с
англ./Под ред. Р. Л. Добрушина. — М.: Мир, 1965. — 439 с.
111. Харкевич А. А. Борьба с помехами. —М.: Наука, 1965. — 276 с..
112. Мешковский К. А., Кириллов Н. Е. Кодирование в технике связи. —
М.: Связь, 1966. — 324 с.
113. Цымбал В. П. Теория информации и кодирование: Учеб, пособие для
вузов. —2-е изд. испр. и доп. — Киев: Вища школа, 1977. — 288 с,
114. Шляпоберский В. И. Элементы дискретных систем связи. —М.: Воен-
издат, 1962. — 236 с.
115. Тарасенко Ф. П. Введение в курс теории информации. — Томск: ТГУ
им._ В. В. Куйбышева, 1963. — 240 с.
116. Солодов А. В. Теория информации и ее применение к задачам автома-
тического управления и контроля. —М.: Наука, 1967. — 432 с.
117. Голдман С. Теория информации: Пер. с англ./Под ред. В. В. Фурдуе-
ва. — М.: ИЛ, 1957. — 446 с.
118. Клюев Н. И. Информационные основы передачи сообщений.—М.:
Сов. радио, 1966. — 360 с.
119. Орлов В. А., Филиппов Л. И. Теория информации в упражнениях и за-
дачах: Учеб, пособие для вузов. — М.: Высшая школа, 1976. — 136 с.
120. Акулиничев Ю. П., Дроздова В. И. Сборник задач по теории информа-
ции. — Томск, ТГУ им. В. В. Куйбышева, 1976. — 114 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Безынерционный преобразователь 339
Белый шум 162
Блуждания случайные 187
Вариационный ряд 108
Вероятность апостериорная 8
— априорная 8
— безотказной работы 7, 249
— доверительная 113
— ложной тревоги 448
— отказа 250
— ошибок 448
— перехода 98, 179
— правильного'решения 448
— финальная 181
Взаимная корреляционная функция 145
Время обслуживания заявки 258
— первого достижения границ 184
Выборочные значения 108
— моменты 109
Выброс случайного процесса 392
Гистограмма 108
Дельта-функция 28
Детектор безынерционный квадратичный
347
----линейный 362
— синхронный 331
Дисперсия случайной величины 28
— случайного процесса 130
Доверительный интервал 113
Закон, распределения вероятностей 26, 30
----условный 77
Импульсная характеристика 276
----оптимального фильтра 414
---- согласованного фильтра 417
Интеграл вероятности 27, 341
Интенсивность отказов 250
Интервал корреляции 145
Квантование 231, 356
Ковариационная функция 129
Комплексная частотная характеристика 282
------оптимального фильтра 414
------согласованного фильтра 416
Корреляционная матрица 80
Корреляционная функция 130
---- нормированная 145
----огибающей 324
---- узкополосного процесса 321
Корреляционный момент 79
Коэффициент асимметрии 48
— готовности 252
— избыточности 501
— корреляции 79
— простоя 253
— сноса и диффузии 183
— эксцесса 48
Критерий Байеса 448
•— идеального-наблюдателя 114, 448
— Неймана—Пирсона 114, 448
— согласия 108
Математическое ожидание 28, 129
Моментные функции 129, 130
Моменты случайной величины 29
------абсолютные 29, 78
------начальные 29, 78
—-----условные 79
------факториальные 29, 78
------центральные 29, 78
Надежность оценки 113
Неравенство Рао—Крамера 484
Огибающая узкополосного процесса 320, 321
Ограничитель 350, 359, 363
Оптимальная линейная фильтрация 412, 415
Отношение правдоподобия 115, 445
— сигнал/шум 416
Оценка интервальная ПО
— несмещенная 111, 484
— параметров распределения 107, НО
— состоятельная 111
— точечная ПО
— эффективная 111, 484
Параметр интенсивности 206
— потока отказов 252
Параметры сигнала несущественные 446
---- энергетические 487
Плотность (распределения) вероятностей 26
----двумерная 75, 132
----нормальная 27, 128, 132, 136
----огибающей 323
---- условная 77
----фазы 323
— отказов 250
— потока 257
Поток восстановления 258
— входной 257
— заявок 257
— Пальма 258
— простейший 257
— Эрланга 239, 258
Процесс марковский 176
— рождения и гибели 190
— пуассоновский 205
— узкополосный 320
Распределение многомодальное 29
— статистическое ПО
Семиинварианты 48
Сигнал двоичный 467
----случайный 188
— квазислучайный телеграфный 196
— случайный фототелеграфный 226
Систематическая ошибка 111
Случайная величина 26
----дискретная двумерная 74
---- многомерная 74
---- центрированная 28
Случайный процесс гауссовский 131
----дифференцируемый 148
----комплексный 144
----непрерывный 148
----стационарный 131
---- центрированный 130
Спектральная плотность 146
Среднее арифметическое отклонение 48
— время безотказной работы 250
— время восстановления 252
— квадратическое отклонение 29
Средний квадрат ошибки фильтрации 413
Тождество Вальда 208
Точность оценки 113
Уравнение интегральное Абеля 133
----Винера — Хопфа 414
----Фредгольма 414
— Маркова 180
— Фоккера—Планка—Колмогорова 183
Уровень значимости 109
Условие нормировки 128
— симметрии 128
— согласованности 128
— положительной определенности 128
Фильтр оптимальный 412
— прогнозирующий 413
— сглаживающий 413
— согласованный 416
Формула Винера—Хинчина 147
— Кемпбелла 209
Функционал плотности вероятности 445
— правдоподобия 445
Функция надежности 249
— правдоподобия 486
— распределения вероятностей 26, 75
Характеристическая функция 28, 50, 128,
131
Цепь Маркова 179, 186
Ширина спектральной плотности 148
— эффективная 148
Энтропия 29, 497, 516
Якобиан преобразования 81, 340
541
СОДЕРЖАНИЕ
Предисловие ко второму изданию................................ 3
РАЗДЕЛ I. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ................................. 4
1. Основные определения и теоремы теории вероятностей .... 4
1. Теоретические сведения................................. 4
2. Примеры............................................... 10
3. Задачи и ответы..........................'.............19
2. Законы распределения и числовые характеристики одномерных
случайных величин............................................26
1. Теоретические ^сведения................................26
2. Примеры................................................56
3. Задачи и ответы........................................67
3. Законы распределения и числовые характеристики многомерных
случайных величин............................................74
1. Теоретические сведения.................................74
2. Примеры................................................84
3. Задачи и ответы........................................98
4. Основы математической статистики..........................107
1. Теоретические сведения................................107
2. Примеры...............................................115
3. Задачи и ответы.......................................122
РАЗДЕЛ II. СЛУЧАЙНЫЕ ПРОЦЕССЫ . 128
5. Законы распределения и моментные функции..................128
1. Теоретические сведения................................128
2. Примеры...............................................132
3. Задачи и ответы.......................................136
6. Корреляционные функции и спектральные плотности...........143
1. Теоретические сведения................................143
2. Примеры...............................................150
3. Задачи и ответы...................................... 157
7. Марковские случайные процессы.............................176
1. Теоретические сведения................................176
2. Примеры...............................................186
3. Задачи и ответы.......................................193
8. Точечные и импульсные случайные процессы..................205
1. Теоретические сведения................................205
2. Примеры...............................................224
3. Задачи и ответы.......................................236
542
9. Основы теории надежности и массового обслуживания .... 249
1. Теоретические сведения...........................249
2. Примеры..........................................261
3. Задачи и ответы..................................268
РАЗДЕЛ III. ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ НА ЭЛЕМЕНТЫ РАДИО-
ТЕХНИЧЕСКИХ устройств...................................275
10. Воздействие случайных процессов на линейные системы .... 275
1. Теоретические сведения................................275
2. Примеры...............................................282
3. Задачи и ответы.......................................295
11. Узкополосные случайные процессы.....................319
1. Теоретические сведения................................319
2. Примеры..............,...............................324
3. Задачи и ответы......................................330
12. Воздействие случайных процессов на нелинейные системы . . . 339
1. Теоретические сведения................................339
2. Примеры . . . ........................................347
3. Задачи и ответы....................................... 360
13. Выбросы случайных процессов..............................391
1. Теоретические сведения..........................., • • 391
2. Примеры...............................................396
3. Задачи и ответы...................... ,..............400
РАЗДЕЛ IV. ТЕОРИЯ ПОМЕХОУСТОЙЧИВОСТИ........................412
14. Фильтрация сигналов.....................................412
1. Теоретические сведения...............................412
2. Примеры..............................................417
3. Задачи и ответы......................................426
15. Обнаружение и различение сигналов.......................444
1. Теоретические сведения...............................444
2. Примеры............................................ 449
3. Задачи и ответы......................................467
16. Оценка параметров сигнала...............................484
1. Теоретические сведения...............................484
2. Примеры..............................................488
3. Задачи и ответы......................................491
РАЗДЕЛ V. ТЕОРИЯ ИНФОРМАЦИИ.................................495
17. Дискретные системы передачи информации..................495
1. Теоретические сведения...............................495
2. Примеры..............................................502
3. Задачи и ответы......................................510
18. Непрерывные системы передачи информации.................515
1. Теоретические сведения...............................515
2. Примеры..............................................519
3. Задачи и ответы......................................527
Приложения..................................................531
Приложение I.............................................531
Приложение II..........................................532
Приложение III..........................................534
Приложение IV..........................................535
Список литературы ...........................................536
Предметный указатель........................................541
Горяйнов В. Т. и др.
Г67 Статистическая радиотехника: Примеры и зада-
чи. Учебн. пособие для вузов / Под ред. В. И. Тихо-
нова. 2-е изд., перераб. и доп. — М.: Сов. радио,
1980. — 544 с., илл.
В пер.: 1 р. 30 к.
Книга содержат примеры и задачи по основным разделам стати-
стической радиотехники (теории вероятностей и математической стати-
стике, теории случайных процессов, помехоустойчивости и теории ин-
формации). В каждой главе приведены теоретические сведения, под-
робно разобраны типовые примеры и сформулированы задачи для
самостоятельного решения, снабженные ответами.
30401-022
r"046(01j:80" 2-80 2402020000
ББК 32.841
6Ф2
ИБ № 306
Владимир Тимофеевич Горяйнов, Андрей Георгиевич Журавлев,
Василий Иванович Тихонов
СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА. ПРИМЕРЫ И ЗАДАЧИ
Редактор Е. В. Вязов а
Художественный редактор Н. А. Игнатьев
Переплет художника Л. Рабенау
Технический редактор Т. Н. Зыкина
Корректор 3. Г. Галушкина
Сдано в набор 7.07.79 Подписано в печать 27.12.79. Т-21646
Формат 60 X 90V16. Бумага тип. № 2. Гарнитура литер. Печать высокая.
Объем усл. 34 п. л. 33,7 уч. изд. л. Тираж 27 000 экз.
Зак. 1203 Цена 1 р. 30 к.
Издательство «Советское радио>, Москва, Главпочтамт, а/я 693
Московская типография № 4 Союзполиграфпрома Государственного
комитета СССР по делам йздательств, полиграфии и книжной торговли.
Москва, 129041, Б. Переяславская, 46