Ю. Г. ЗАГАЛЬСКАЯ,
Г. П. ЛИТВИНСКАЯ,
Ю. к. ЕГОРОВ-ТИСМЕНКО
cd
S
о
PQ
К
д
Руководство
к практическим занятиям
по кристаллохимии
О
u
О
PQ
О
(J
О
О
PQ
<D
cd
УДК 548.0
Ю.Г.Загальская, Г.П.Латвийская, Ю.К.Егоров-
Тисменко. Руководство к практическим занятиям по
кристаллохимии. М., Изд-во МГУ, 1983г.
В пособии излагаются основные приемы описания
кристаллических структур (решетки Брава, плотнейшие
упаковки, федоровские группы симметрии и др.). Вторая
часть пособия - задачник, содержащий около 350 задач,
которые должны закрепить навыки в геометрической
кристаллохимии и углубить знания по общей кристалло-
химии.
Печатается
по постановлению
Редакционно-издательского совета
Московского университета
Рецензенты: кафедра кристаллографии
Ленинградского государственного университета им.
А. АЛданова (зав. кафедрой проф. В. А.Франк-Каменецкий) •
кандидат физгмат.наук М.А.Симонов (Московский государ-'
ственный университет им. М.В,Ломоносова)
Издательство Московского университета, 1953 г
ПРЕДИСЛОВИЕ
Предлагаемая работа, представляющая пособие к практи-
ческим занятиям по кристаллохимии, посвящена в основном
приемам описания кристаллических структур. Авторы считают,
что, овладев подобными приемами, учащиеся окажутся в состо-
янии интерпретировать как литературные кристаллохимические
данные, так и результаты собственных исследований. Особое
внимание уделено тем вопросам, которые недостаточно четко,
а иногда и ошибочно излагаются в имеющихся учебниках. Отра-
жая методику преподавания кристаллохимии на кафедре акаде-
мика Н.В.Белова, авторы стремились придерживаться основных
положений современной педагогики высшей школы, в частности
не преподносить готовые вывода и определения, а логически
подводить к ним. Особая роль отводится в связи с этим зада-
чам и упражнениям, предлагаемым во 2-й части книги. В зада-
чах использованы не только сведения, изложенные в теорети-
ческой части Руководства, но и лекционный материал курса.
Вместе с тем, несмотря на довольно большой объем задачника
( 200 номеров, фактически~350 задач), он отнюдь не охваты-
вает всех разделов курса кристаллохимии. Для большинства
задач основной интерес представляет не столько окончатель-
ный ответ, сколько последовательный ход рассуждений. В свя-
зи с этим для нескольких наиболее интересных в этом отноше-
нии задач приведены развернутые решения. Задачи на федоров-
ские группы составлены таким образом, что при их решении не
нужно обращаться к специальным справочникам - все необходи-
мые сведения можно почерпнуть из списка пространственных
групп, приведенного в Приложении. Если же возникнет желание
проверить полученный результат, учащийся сможет воспользо-
ваться любым изданием Интернациональных таблиц, Атласом
пространственных групп кубической системы и книгами Г.Б.Бо-
киях\ Предполагается, что основные структурные типы, ис-
пользуемые в задачах (см. Приложение), известны учащимся в
такой степени, что работа с ними не требует обращения ни к
,3
моделям структур, ни к их описаниям. Авторы надеются, что
многие’ задачи Оу,дут особенно полезны в учебных заведениях,
не обладающих значительной коллекцией кристаллических
структур.
Руководство предназначено для общего полного курса
кристаллохимии, однако некоторые его части могут быть испо-
льзованы в курсе кристаллографии, в который кристаллохимия
входат разделом.
За все дополнения и замечания авторы заранее приносят
благодарность.
Internationale Tabellen zur Bestimmung won Kristall-
Strukturen. Berlin , 1935.
International Tables pr X-ray Crystallography, Birmin-
gham , 1952; Reprinted 1967, 1972.
H.B.Белов, Ю.Г.Загальская, Г.П.Литвинская, Ю.К.Егоров-
Тисменко. Атлас пространственных групп кубической сис-
темы, М. "Наука", 1980.
Г.Б.Бокий. Введение в кристаллохимию, 1954, Кристалло-
химия, П изд., I960, Ш изд., М.,"Наука", 1971.
ГЛАВА I
приемы ОПИСАНИЯ кристалличбхжих структур
' § I. Пространственная решетка. 14 танов
решеток Бравэ
Классическое определение кристалла как однородного
твердого анизотропного тела, способного самоограняться ,
сформулированное еще в те времена, когда о внутреннем
строении этих удивительных природных многогранников стро-
илась лишь гипотезы, не потеряло своей значимости и в на-
ши дни. Так, лишь одно из основных свойств кристалла -его
однородность, если ее рассматривать с современных позиций,
т.е. с учетом дискретности строения материи, позволяет
достаточно просто прийти к заключению о решетчатой приро-
Рис. I. Узловой ряд (а), узловая
сетка (б), пространствен-
ная решетка (в)
де строения • щ)и-
сталлического ве-
щества. Однород -
ным должно счита-
ться тело, в ко-
тором на конечных
расстояниях от лю-
бой его точки най-
дутся другие, эк-
вивалентные ей не
только в физичес-
ком отношении, но
и геометрически,
т.е. находящееся
в таком не окру -
жета, как и ис-
ходная. Остановим
на одной из них
свое внимание и,
назвав ее "нуле -
вой" (рис. 1,а),
найдем на крат -
1 -1478
5
чайшем конечном расстоянии а=сМЕН от нее точку I, во всех
отношениях эквивалентную выбранной. Из условия эквивалент
кости точек 0 и I следует, что на расстоянии а. от точки I
в направлении вектора Та = 01 должна находиться точка 2,
неотличимая от первых двух. Продолжая рассуждение (0-*1—*-
—^2—*3—*...), приходим к прямолинейному ряду (шеренге)
эквивалентных точек (узлов),.находящихся на одинаковых
расстояниях друг от .друга; причем из построения следует
(а =смин), что между членами этого ряда невозможны допол-
нительные аналогичные точки, В некотором другом направле-
нии (Ть на рис. 1,6), не параллельном вектору Та, эквива-
лентные точки также выстроятся в шеренгу с межузловым рас-
стоянием Ъ * а, и эти два пересекающихся узловых ряда оп-
ределят собой бесконечную плоскую сетку - узловую сетку.
Легко доказывается, что внутри петли сетки невозможна еще
одна эквивалентная точка. Приняв во внимание и третье не-
компланарное направление - вектор Тс(Та - Ть Тс), полу-
чим трехмерную узловую сетку - пространственную решетку -
также с пустыми ячейками (рис. 1,в).
Таким образом, главная особенность однородного тела
(кристалла) заключается в трехмерной периодичности распо-
ложения эквивалентных материальных частиц. Заметим, что
все остальные характеристики кристалла - твердость, анизо-
тропность, плоскогранность - оказываются лишь следствиями
его решетчатого строения.
Решетке подчиняется всякий бесконечный закономерный
узор - одномерный, двумерный, трехмерный.
Так, в узоре бордюра (рис. 2,а) легко прослеживается
линейная закономерная повторяемость, т.е. совмещение бор-
дюра с самим собой наступает при переносе (трансляции)
этого узора вдоль од-
ного направления на
величину вектора Та -
трансляционного векто-
ра. Одномерной "решет-
кой" такого узора слу-
|жит узловой ряд (рис.
2,6).
ряд ко)

6
Рис. 2. Одномерный бесконечный
узор (а) и его "решетка* - уз-
6
Рис. 3. Двумерный бесконеч-
ный узор и его решетка -
плоская узловая сетка
Двумерный бесконеч-
ный узор - узор обоев
или тканей (рис. 3)- мо-
жет быть совмещен с са-
мим собой при переносе
вдоль трансляционных ве-
кторов, лежащих в этой
плоскости, иными слова -
ми, периодичность плос -
кого узора выражается
.двумерной сеткой - па -
раллелограмматической
'узловой сеткой.
В трехмерном регу-
лярном узоре, например,
в кристаллической струк-
туре, самосовмещение на-
трансляционного вектора;
ступает при переносе вдоль любого
периодичность такого узора описывается трехмерной решеткой
Рис. 4. Тип плоской сетки
какая точка узора
не зависит от того,
принята за исходную
•Pt oci ©к
6
Рис. 5. Трехмерная периодичность в структурах
алмаза (а), хлористого натрия (б) и хлоропла-
тината калия/ к2ка6(в) описывается одной и
той же решеткой (г)
- параллелепипедальной узловой сеткой, или пространствен-
ной решеткой.
Таким образом, решетка не есть нечто материальное,
это всего лишь схема, которой подчиняется периодичность
узора, не зависящая от того, какая точка узора принята за
исходный узел решетки (рис. 4). Иными словами, решетка -
это своеобразный "элемент симметрии" узора, и одной и той
же решетке могут подчиняться самые разнообразные по рисун-
ку узоры - разные структуры кристаллов (рис. 5).
8
Пространственную решетку можно считать выразителем
кристаллического состояния вещества, ибо любой кристалл,
даже лишенный какой-либо внешней симметрии, обладает ре-
шеткой; по определению Н.В.Белова "кристалл находится в
состоянии решетки".
Для описания одномерной решетки достаточно знать
расстояние между двумя узлами, точнее, величину и направ-
ление трансляционного вектора Т ; минимальным представи-
телем двумерной решетки оказывается параллелограмм, по-
строенный на двух непараллельных векторах - и Ть; трех-
Рис. 6.. Различные ячейки -
параллелограшы повторяе-
мости - одной й той же
двумерной решетки; все при-
митивные (пустые) ячейки
равновелики, любая единож-
ды центрированная в два
раза больше примитивной
мерную решетку представляет
трехмерная единица - парал-
лелепипед, ребрами которого
служат трансляционные век-
торы - периоды идентичности
- вдоль трех некомпланарных
узловых рядов (Та , Ть , Тс).
Такой параллелограмм и со-
ответственно параллелепипед
повторяемости, или идентич-
ности, называют также ячей-
кой решетки. Очевидно, что
ячейки выполняют все двумер-
ное и трехмерное пространст-
во без промежутков.
Выбор ячейки в решетке
неоднозначен, так как каж-
дый узел можно считать на-
чальной точкой бесконечного
множества трансляционных векторов. Выделенные по-разному
ячейки сдай и той же решетки будут различаться либо толь-
ко формой, либо как формой, так и величиной (рис. 6).
Ячейки могут быть примитивными (пустыми) - с узлами лишь
в вершинах - и непримитивными - с дополнительными узлами,
т.е. узлами, не охваченными контурами ячейки. Все прими-
тивные ячейки одной и той же решетки равновелики, так как
на долю любой из них приходится один узел ( 1/4 х 4 в дву-
мерной решетке и 1/8 х 8 в трехмерной ); общее число узлов,
приходящихся на непри^итнвцую ячейку, показывает, во сколь-
ко раз она больше любой примитивной той же решетки.
9
г
Рис. 7. Согласование сим-
метрии фигуры с точечной сим-
метрией решетки:
а) симметрия фигуры (mm2) и
решетки (mm2) совпадают -
узор приобретает ту же
симметрию,
б) группа симметрии решетки
(2) не содержит всех эле-
ментов симметрии фигуры
(mm2) - узор сохраняет
лишь симметрию 2;
в) группа симметрии фигуры
(т) не имеет общих эле-
ментов с группой симмет-
рии решетки (2) - узор
имеет минимальную симмет-
рию (I);
г) симметрия фигуры Отти2),и,
хотя симметрия решетки
значительно выше (4mm),
узор унаследовал лишь
симметрию фигуры (mm2)
Очевидно, произвольный подход к выбору ячейки, которая
должна служить представителем всей решетки, неудобен; наи-
более надежным критерием в данном случае может служить сим-
метрия решртки, поэтому прежде всего выясним, какой она мо-
жет быть.
10
Обратимся к одной из функций пространственной решетки:
размножая какую-либо фигуру (узорную единицу), передавать
созданному таким образом бесконечному узору ее симметрию.
Согласно принципу Кюри, в данном случае должно происходить
наложение симметрии решетки ("средн”) на симметрию узорной
единицы ("объекта"), причем в бесконечный узор перейдут
лишь общие для решетки и исходной фигуры элементы симмет-
рии (рис. 7). Следовательно, чтобы весь узор приобрел сим-
метрию узорной единицы, в группу симметрии решетки должны
входить в качестве подгруппы все элементы симметрии этой,
единицы.
Сразу возникает вопрос: способна ли решетка вобрать в
себя любую из бесконечного множества точечных групп симмет-
рии? Как известно из начального курса кристаллографии, ре-
шетка может обладать лишь ограниченным набором осей симмет-
рии - невозможны оси 5-го и выше 6-го порядков. Иными сло-
вами, использовать решетку для получения бесконечного зако-
номерного узора, наследующего симметрию узорной единицыj
можно лишь при условии, что размножаемая фигура не имеет
запрещенных для решетки элементов симметрии, а значит, от-
носится к одной из 32 кристаллографических (!) групп сим-
метрии.
С другой стороны, сама решетка обладает некоторыми
обязательными элементами симметрии. Прежде всего как вся-
кая параллелепипедальная система пространственная решетка
центросимметрична ; центры инверсии нахо-
дятся как в узлах решетки - в вершинах параллелепипедов,
так и на серединах расстояний между ними. Кроме того, если
в‘решетке имеются оси симметрии 3-го, 4-го или 6-го поряд-
ков, то ближайшие к ним узлы располагаются по вершинам пра-
вильных п -тональных призм; вдоль главной оси каждой такой
призмы пересекаются плоскости симметрии, число которых от-
вечает порядку оси. Иными словами, оси высших порядков
(п = 3, 4, 6) в пространственной решетке сопровождаются пе-
ресекающимися вдоль них плоскостями симметрии.
Учитывая все сказанное, рассмотрим, какой должна быть
необходимая и достаточная симметрия пространственных реше-
ток, способных "обслужить" 32 кристаллографические точечные
группы симметрии.
II
•Фигура асиметричная не предъявляет каких-либо спе-
циальных требований к симметрии решетки, поэтому в данном
случае решетка будет иметь минимально возможную для нее
симметрию - I. Такой тип решетки годится и для фигуры с
собственной симметрией I,
—>> Фигура с единственным особым направлением 2-го поряд-
ка потребует для решетки симметрию Д . Действительно,вза-
имодействие оси 2 или 2(=т) с обязательным для простран-
ственной решетки центром инверсии приведет к группе
( 2 х I = т. х I = |), Если фигура относится к моноклин-
ной голоэдрии ( 1, ), симметрия решетки совпадает с симмет-
„ Д.	Hl
рией фигуры.
Любая фигура ромбической системы передаст свою сим-
метрию трехмерному узору, размножаясь решеткой ттпт
( 222 х I = mm2 х I = _ £ § = mmm ).
m тс m	-
В решетках, размножающих фигуры с осями высших поряд-
ков, кроме центров инверсии есть и пересекающиеся вдоль
этих осей плоскости симметрии. Так, решетка, согласующаяся
с фигурой, у которой есть лишь одна ось 4-го порядка, дол-
жна иметь плоскости симметрии, проходящие через эту ось,
что даст 4mm с Кроме того, ось 4* = 2, взаимодействуя с
обязательным для всякой трехмерной решетки центром инвер-
сии (I), даст плоскость симметрии, перпендикулярную оси.
Взаимодействие плоскостей симметрии породит четверку осей
2-го порядка, т.е. в итоге получим группу Дтт.. Если
единственная ось исходной фигуры (а значит, и всего беско-
нечного узора) - 4, то при ее взаимодействии с I возникнет
ось 4, а далее, повторив только что приведенные рассужде-
4	ЕЯ
ния, снова придем к группе -mri о Та же решетка выполнит
свою функцию -и для остальных групп тетрагональной системы:
- , 422,' 4mm., 42m и .
Группы с единственной осью 6-го порядка, поворотной *
или инверсионной, ( 6, 6, Д , 622, 6mm„ 6m2 и при-
ведут к решетке, симметрия которой Дтт, а группы 3, 3,
32, Зт , Зт- к решетке с точечной сиьваетрией 3m .
Группы 23, 43m, 432, m3 и rn 3m обслуживает решет-
ка m 3m.	<2f ..
Таким образом, во всех случаях точечная
группа симметрии решетки отвечает
12
старшему классу - голоэдрии - данного семейства
групп. Иными словами, решетка по своей симметрии либо выше
симметрии обслуживаемого ею класса, либо равна ей.
0 Рассмотрев решетки с позиций их макросимметрии, вер-
немся к вопросу о выборе ячейки, наиболее полно отражающей
все особенности данной решетки. Такой ячейкой будет парал-
лелепипед, построенный на трех кратчайших неком-
планарных трансляционных векторах, совпадающих с особыми
направлениями максимальн ой сим м е т р и и..
При отсутствии особых направлений (в триклинной системе)
ребра характеристической ячейки рекомендуется совмещать с
такими трансляционными векторами, которые обеспечат ее при-
митивность, т.е. минимальный объем. В моноклинной решетке,
в которой есть лишь одно особое направление ( Д ), с ним
совмещают одно ребро ячейки, а два других направляют по
трансляционным векторам, лежащим в плоскости, перпендику-
лярной единственному особому направлению, т.е. в плоскости
симметрии решетки (значит, как раз по векторам повышенной
симметрии); отсутствие особых направлений в плоскости ко-
соугольной грани позволяет делать ее пустой.
По направлениям максимальной симметрии обычно выбира-
ют кристаллографические координатные оси (репер Бравэ),по-
этому характеристическая ячейка - ее называют ячейкой
Бравэ (или, что не вполне удачно, - элементарной ячей-
кой) - поедставляет собой параллелепипед повторяемости,
подчиненный координатной системе решетки и имедцмй при
этом минимальный объем; Ячейка Бравэ пере-
дает свое название соответству-
ющей пространственной решетке.
Таким образ9М, поскольку форму ячейки Бравэ определя-
ет_координатный репер, семь разных по симметрии решеток
( I, Д , 7П7П7П,	, Д771777 . Зтп и тпЗт ) будут пред-
ставлены шестью типами параллелепипедов (для обеих гекса-
гональных решеток ячейкой Бравэ служит параллелепипед со
120°-ным ромбом в основании) - рис. 8.
Иногда в качестве представителя решетки пользуются
так называемой основной ячейкой - парал-
лелепипедом, построенным на трех последовательных трансля-
ционных минимумах решетки, однако такая ячейка не всегда
13
Рис. 8. Семи решеткам разной симметрии соответствуют шесть
разных по форме ячеек Бравэ
достаточно выразительно подчеркивает главные особенности
решетки, в частности ее симметрию.
В преимуществе ячейки Бравэ перец произвольно выбран-
ной или даже основной нетрудно убедиться, обратившись к
рис. 9, где изображена пространственная решетка кубической
системы; наиболее удачным представителем такой решетки бу-
14
дет, конечно, ячейка в
форме куба (рис. 9,а), то-
гда как ни произвольно вы-
бранные ячейки (рис. 9,б,в)
ни основная ячейка - ром-
боэдр с углом в 60°(рис.
9,г) - не выражают непо-
средственно симметрию ре-
шетки.
Трем координатным
векторам ячейки Бравэ (Та,
Ть, Тс’, или просто а",Г,с)
соответствуют шесть ска-
лярных величин л(1а|, IЫ ,№1
и еС = Ьс, J3 = аГ, / = ab),
которые называют парамет-
рами, или константами, ре-
шетки.
Для полной характерис-
тики пространственной ре-
шетки необходимо кроме ее
точечной группы симметрии
установить и трансляцион-
ный комплекс, т.е. выявить
все возможные случаи рас-
положения узлов в ячейке
Бравэ.
‘ Если ребра ячейки
Бравэ ( а , Ь , с ) соответ-
ствуют трем последователь-
ным трансляционным миниму-
мам, то ячейка (и решетка)
будет пустая - примитивная
Рис. 9.. Ячейки пространст-
венной решетки кубической
системы:
а) ячейка Бравэ
б),в) произвольно выбран-
ные ячейки
г) основная ячейка
(Р), т.е. только с вершинными узлами. В данном случае
ячейка Бравэ совпадает с основной ячейкой. Если же в ре-
шетке есть трансляционные векторы, более короткие, чем те,
которые определяют ячейку Бравэ (координатные), то в ячей-
ке окажутся узлы, не охваченные ее контурами, - дополни-
тельные узлы. Такая - непримитивная - ячейка Бравэ уже не
совпадает с основной, ее объем больше объема основной
ячейки (см. с.5).
Чтобы установить позиции возможных дополнительных уз-
лов в ячейке Бравэ, обратим внимание, что в вершинных уз-
лах как точках пересечения векторов максимальной симмет-
рии сосредоточены все элементы симметрии соответствующей
голоэдрической группы, а коль скоро дополнительные узлы
идентичны вершинным, они могут оказаться лишь в тех точках
решетки, в которых голоэдрический комплекс представлен ли-
бо полностью, либо хотя бы своей максимальной подгруппой,
содержащей главную ось. Нетрудно убедиться, что, поместив
дополнительный узел в любую .другую позицию, мы укоротим
координатные векторы, заданные кратчайшими. Очевидно, что
из рассмотрения еле,дует сразу же исключить и позиции в се-
рединах ребер ячейки Бравэ, так как эти ребра выбраны по
кратчайшим для соответствующих направлений трансляциям;
исключены также точки в центрах косоугольных граней. До-
полнительные узлы почти во всех случаях попадают либо в
центры граней ячейки Бравэ, либо в центр ее объема, поэто-
му ячейки (и решетки) с дополнительными узлами принято на-
зывать "центрированными".
Если в ячейке центрирована только пара противополож-
ных граней, то ее называют базоцентрированной и обозначают
либо С (дополнительные узла на гранях {001}), либо А (узлы
на гранях {Ю0}), либо В (узлы на гранях {0Ю}); А- и В-
ячейки можно называть также бокоцентрированными. Центри-
а
Рис. 10. Двойная цент-
рировка ячейки исклю-
чена: а) А + В
б) 0 + I
5
ровка .двух пар граней (например, А и В)
автоматически связана с возникновением
равноправной трансляции АВ, которая
обеспечит центрировку и третьей пары
граней - С (рис. 10,а); такую ячейку
называют гранецентрированной (или все-
стороннецентрированной) и обозначают Г.
Ячейку с узлом в центре - объемкоцент-
рированную - обозначают I . Одновремен-
ная центрировка типа С + I (рис. 10,6)
или F + I исключена, ибо приведет к
укорочению исходных трансляционных
векторов.
Остановимся подробнее на каждом
из полученных выше семи типов простран-
ственных решеток.
В триклинной с и с -
т е м е. ( а /Ь / с i <<	/ / И 90°И 120°)
особые направления отсутствуют, поэто-
му выбор характеристического параллеле-
пипеда, как упоминалось, произволен,
значит, любая решетка может быть пред-
ставлена одним из параллелепипедов ми-
нимального объема, т.е. параллелепипе-
дом без дополнительных узлов (Р) Чэто
отнюдь не означает, что Р-решетку нель-
зя иллюстрировать и различными неприми-
тивными ячейками (рис. II).
В решетке моноклинной
системы	- 90°,
У / 90°	120°) позиции Д повторяются
вдоль любого узлового ряда через’ % .
Следовательно, коль скоро точки Д на
ребрах ячейки Бравэ и в центрах ее ко-
соугольных граней исключены, .для допол-
нительных узлов остаются лишь позиции
в центрах прямоугольных граней и в цент-
71------
' Обычно предпочитают ячейку с наиболее
короткими ребрами и углами,, максима-
льно приближенными к 90°.
Т7
Рис. 12. Решетки Бравэ моноклинной системы:
а) ячейка Бравэ примитивной решетки,
б) ячейка Бравэ непримитивно решетки,
в) приекции различных ячеек непримитивной решетки,
° и л — узлы на уровнях 0 и |
ре ячейки. Центрировка граней {001} приведет к новой решет-
ке (С); примитивный параллелепипед такой решетки не подчи-
няется моноклинной координатной системе, а значйт, не мо-
жет служить характеристической ячейкой (ячейкой Бравэ),
иными словами, моноклинную С-решетку нельзя отождествить с
Р-решеткой (рис. 12,а,б). Ячейка с дополнительными узлами в
центрах граней (100) - А-ячейка - представляет лишь .другой
аспект С-ячейки, к которой можно прийти простой перестанов-
кой осей X и Z • Объемноцентрированная ячейка (I ) пред-
ставляет ту же решетку, что и С-ячейка (рис. 12,в). Равен-
ство объемов базоцентрированной и объемноцентрированной
Рис. 13. Решетки Бравэ ромбической системы:
а) примитивная, б),в),г) непримитивные:
примитивные ячейки базоцентрированной (б),
объемноцентрированной (в) и гранецентриро-
ванной (г) решеток не подчиняются ромбичес-
кой координатной системе
ячеек (на ячейку приходится 2 узла) не дает преимущества
ни одной из них, иными словами, С и I - два равно-
правных аспекта одной и той же решетки. Рис. 12,>в
показывает, что центрировка всех граней моноклинной ячейки
не создаст новую решетку, так как Г-ячейка представляет в
ином аспекте все ту же С-(1-)решетку^\
Таким образом, в моноклинной системе два типа прост-
ранственных решеток: примитивная - Р и центрированная - С
(=1)в
Группа симметрии ромбической решет-
ки и ее узлов - mmm , поэтому дополнительные узлы могут
оказаться либо в центрах граней ячейки, либо в центре ее
объема. Три взаимно перпендикулярных неэквивалентных осо-
бых направления однозначно определяют ячейку Бравэ, следо-
вательно, при любой ее дозволенной центрировке возникнут
Рис. 14. Решетки Бравэ тетра-
гональной системы:
Q/ примитивная,
объемноцентрированная,
примитивные ячейки
ооъемноце ярированной
решетки
г
новые (не переводимые друг
в .друга) решетки (рис. 13).
Таким образом, в ромбичес-
кой системе неупрощаемы
(оригинальны) все 4 решет-
ки: примитивная - Р, базо-
центрированная - С(А,В),
объемноцентрированная - I
и гранецентрированная - Г.
В тетрагона-
льной решетке
позиции возможных дополни-
тельных узлов ( ^ mm) на-
ходятся в центре ячейки
Бравэ и в центрах базисных
2)Помимо этой классической
установки иногда пользуют-
ся так называемой рациона-
льной, в которой
^рац = ^кл 0 срац = скл ’
следовательно, угол моно-
клинности не ₽ , а ^ (# /
90°). В данном случае С-
решетка будет именоваться
решеткой в.
19
Рис. 15. Название решетки диктует
ячейка тетрагональной метрики ми-
нимального объема - ячейка Бравэ:
а) решетка примитивная,
6) решетка объемноцентрированная
форме с P-ячейкой, но вдвое больше
граней {001}. Как яв-
ствует из рис. 14,
объемно'центрированная
ячейка (I ) представ-
ляет новую решетку:
примитивная ячейка та-
кой решетки отличается
от P-ячейки Бравэ сво-
ей формой, т.е. не под-
чиняется тетрагональ-
ной координатной сис-
теме. Ячейка с допол-
нительными узлами в
центрах базисных гра-
ней (С-ячейка) - всего
лишь иной аспект при-
митивной решетки: С-
ячейка согласуется по
ее(рис. 15,а). Такое же
соотношение справедливо для J - и F-аспектов тетрагональ-
ной решетки (рис. 15,6). Итак, решеток Бравэ в тетрагональ-
ной системе лишь две: Р (=С) и Т(=Р).
В гексагона ль ной системе в
отличие от других имеются две разные по
симметрии решетки - fmm и 3m. Решетка, подчи-
няющаяся гексагональной голоэдрии, не допускает какой-либо
центрировки, т.е. может быть представлена лишь примитивной
(Р) ячейкой Бравэ (рис. 16,а)^'. Другая гексагональная ре-
шетка, имеющая симметрию 3m, наоборот, предполагает имен-
но непримитивную ячейку Бравэ, так как лишь при этом усло-
вии симметрия решетки сохранится. Дополнительные узлы могут
занимать только позиции 3m, т.е. располагаться на осях
3-го порядка, проходящих через центры тригональных призм
ячейки. Из рис. I? ясно, что высота этих узлов (а следова-
тельно, позиций 3m) не может быть ни нулевой, ни производи-
3)
'Встречающаяся в литературе дважды базоцентрированная
Н-ячейка (не ячейка Бравэ!) - лишь иной аспект Р-решетки
(рис. 16,6). Связь ячеек Р и Н в гексагональной сингонии
та же, что Р и С в тетрагональной.
20
в)	f)
Рис. 16. Решетки Бравэ гекса-
гональной системы.
I. Примитивная решетка в Р-(а)
и Н-(б) аспектах;
И. Дважды центрированная гек-
сагональная решетка R (в)
и ее примитивная ячейка -
ромбоэдр (г)
Рис. 17. Генезис дважды
центрированной гексагональ-
ной решетки
ной, так как в обоих случаях возникнут трансляционные век-
торы, которые укоротят ребра и и с , а они по условию вы-
оора ячейки Бравэ совпадают с кратчайшими координатными
трансляциями. Лишь узлы на высоте или |тс не изменят
параметры выбранной ячейки. Таким образом, получится гек-
сагональная ячейка Бравэ с .двумя дополнительными узлами
fnv vnnnTrnmmu- 12 1 „ 2 12	12 2 w 2 1 1 ч
(их координаты. и з35или 3 3 3 _и 3 3 3 } ’
 представляющая решетку точечной симметрии 3m . Эту ячейку,
а следовательно, и решетку можно назвать дважды центриро-
ванной (рис. 16,в). Ее обозначают R , называя иногда ромбо-
эдрической, так как примитивная ячейка такой решетки ( но
не ячейка Бравэ!) - ромбоэдр (рис.16,г). Заметим, что до-
полнительные узлы не могут находиться сразу во всех четырех
позициях (Г, 2’, I", 2"- рис. 18), так как это снова приве-
дет к укорочению исходных трансляций -Та и Тс. Итак, в
гексагональной системе .две решетки - Р и R . Однако, если
Р-решетка сочетается с любым из 12'классов гексагональной
системы, то R - лишь с теми, симметрия
которых не превышает симметрию самой
решетки (3m).
В решетке кубической
системы (симметрия тЗт) лег-
ко находится позиция для дополнитель-
ного узла в центре ячейки Бравэ. Полу-
ченная объемноцентрированная ячейка
представляет новую - объемноцентриро-
ванную (I ) - кубическую решетку. Од-
нако это не единственно возможная по-
зиция для дополнительного узла - по-
местив узел в центре одной из граней,
повысим тем самым симметрию этой по-
4	4 — 27
зиции с 2 mm до = 3	= m Зтя. Оче-
Рис. 18. Одновремен-
-- -	. ви,дно, такие же узлы зацентрируют и
ное нахождение" узлов, остальные грани ячейки (ось 3 Г), при-
так и в°поКи Гв’чем такая иентрировка (Б) не приведет
2"приведет к возник- ни к изменению симметрии решетки, ни
коротких) трансляций к^рояраще^13 ’’контурных” трансляций
определяющихJP-реше ,-(Та, Ti, Тс), поскольку все три ребра
Ку’ з и Та- — ячейки Бравэ в кубической системе, в
О
22
Рис. 19. Решетки
Бравэ кубической
системы: примитив-
ная (а), объемно-
центрированная (б)
и гранецентрирован-
ная (в). Примитив-
ная ячейка объемно-
центрированной (г)
и гранецентрирован-
ной (д) решеток
отличие от тетраго-
гональной, строго
фиксированы, и но-
вую (короткую) тран-
сляцию Тс (Тд, тв)
нельзя использовать в качестве ребра ячейку меньшего объема. 
Примитивным параллелепипедом такой решетки (основным) будет
ромбоэдр с углом 60°. Таким образом, в кубической системе
три типа решеток - Р, I и Г (рис. 19).
Итак, рассмотрев все случаи примитивных (6) и непри-
митивных (8) решеток, мы пришли к 14 типам пространствен-
ных решеток - к 14 типам решеток Бравэ (рис. 20), распре-
деляющимся по 7 типам симметрии (семи кристаллографическим
голоэдриям) и 6 системам - сингониям.
Для всех систем, кроме* гексагональной, центрировка ре-
шетки не изменяет ее симметрии, поэтому любая негексагона-
льная решетка может сочетаться с любой из групп своей же
системы. Гексагональная же система стоит в этом смысле
особняком - ее Р- и R-решетки различаются по симметрии,
причем, если Р-решетка благодаря своей высокой симметрии
(Р ) способна обслужить все группы г е_к-
сагональной системы, то R-решетка (Р Зш)
работает лишь для групп, не#имеющих
осей 6 или. 6. Универсальность Р-решетки, пригод-
ной для всех 12 групп, делает нецелесообразным распределе-
ние их по .двум системам (сингониям), однако избирательность
Р-решетки заставляет как-то обособить те 5 групп, с кото-
рыми она согласуется. Отсюда и компромиссное решение:
одна большая гексагональная
система с 12 группами разбивается на 2 п о д -
23
Рис. 20. 14 ячеек Бравэ - 14 решеток Бравэ
системы - гексагональную (главные оси 6 и 6) и триго-
нальную, называемую также ромбоэдрической (главные оси 3 и
3); причем 7 трупп первой сочетаются лишь с Р-решеткой, а
5 групп второй - как с Р-, так и с R-решеткой.
§ 2, Решетка Бравэ (ячейка Бравэ)
кристаллической структуры
Структура каждого кристаллического вещества по своей
трехмерной периодичности относится к одной из 14 схем - 14
оешеток Бравэ. Закономерная повторяемость тождественных
материальных частиц позволяет выбрать в структуре паралле-
лепипед идентичности, отражающий все структурные особенно-
сти кристалла, причем, как и в случае пространственной ре-
шетки, наиболее удобным представителем структуры будет па-
раллелепипед, подчиненный координатной системе кристалла и
имеющий при этом минимальный объем; такую ячейку структуры
также называют ячейкой Бравэ. Выбрав ячейку Бравэ, нетруд-
но назвать тип решетки Бравэ кристаллической структуры,
т.е. указать сингонию и комплекс трансляций (центрировку)
ячейки.
Отметим, что совершенно недопустимо смешивать термины
"кристаллическая структура" и "кристаллическая решетка",
употребляя, например, такие словосочетания, как "решетка
алмаза", "решетка флюорита", если речь идет об их структу-
ре; с другой стороны, не имеет смысла и выражение "гране-
21Л	каменной соли,
жи . Маленький кубик (справа вверху)
не является параллелепипедом повторя-
емости. Гранецентрированный куб (сле-
ва внизу) - правильно выбранная ячей-
центрированная струк-
тура".
Покажем на не-
которых примерах,
как находят ячейку
Бравэ структуры и .
определяют тип решет-
ки Бравэ.
Каменная
соль, ЯаС1(рис.21).
Четыре направления
осей 3-го порядка
сразу позволяют от-
нести этот структур-
ный тип к кубической
системе. Поэтому ячей-
ка Бравэ должна иметь
форму куба, ребрами
25
которого служат кратчайшие трансляционные векторы вдоль
координатных направлений.
Следует предостеречь начинающих от весьма распростра-
ненной грубейшей ошибки - считать ячейкой кубик, четыре
вершины которого заняты ионами Na, четыре ионами Ct (рис.
21, вверху). Ребра этого кубика вдвое короче трансляцион-
ных векторов, т.е. он не является параллелепипедом по-
вторяемости. Выбрав ячейку Бравэ (рис. 2Т,внизу)
убеждаемся, что решетка
с. , Структура пи-
гта, Ге 2. Общий вид
план структуры
гранецентрированная (Г): перенос
на | диагонали каждой грани при-
водит любую частицу (и всю струк-
туру) к самосовмещению.
Пирит, Ге$2 (рис. 22).
Эту структуру можно считать NaCt-
подобной; действительно, атомы Ге
| расположены так же, как ионы Na,
| а пары (гантели) ,S2 занимают по-
зиции ионов 01. Обычно заключение
о принадлежности структуры пирита
к кубической системе делают уже
на основании формы ячейки, пред-
ставленной на модели. В данном
случае это действительно так, од-
нако надо иметь в виду, что опре-
деление системы (сингонии) только
по метрике ячейки, выделенной на
модели, может привести к ошибкам.
Так, параметры а / Ь / с при <z =
~ 90° могут определять не
(Только ромбический, но и моноклин-
ный или даже триклинный кристалл
с осевыми углами, очень близкими
или случайно равными 90°; также
может оказаться и ячейка с парамет-
и <£ =j3 = i = 90°, Поэтому .для оконча-
айвой (случайной)
а = Ь = с
,ного вывода о сингонии надо доказать, что те или иные
!танты не случайны, а предопределены элементами симмет-
кристалла. В кубической системе равенство а , Ъ и с
уется диагональной осью 3-го порядка, в тетрагональной
Рис. 23. Структура £0?.
Общий вид и план струк-
туры
метрии должна приводить
а
системе единственная ось 4-го по-
рядка подтверждает равенство а и
Ь , в ромбической системе прямо -
угольность ячейки обеспечивается
тремя неэквивалентными взаимно
перпендикулярными особыми направ-
лениями и т.д. Предлагаем читате-
лям решить, к какой категории -
высшей, средней или низшей -от-
носится структура <S02(рис. 23), в
модели которой а = Ъ = с при
прямых осевых углах. .
Возвращаясь к структуре пи-
рита, замечаем, что кубичность ее
подтверждается скрещивающимися
осями 3-го порядка, параллельными
телесным диагоналям куба, вдоль
этих осей вытянуты гантели ^2.
Расположение атомов Ге в вер-
шинах ячейки и центрах ее граней,
казалось бы, говорит о Г-решетке,
однако ориентация гантелей 52
противоречит этому, - нельзя забы-
вать, что решетка.как элемент сим-
структуру К самосовмещению незави-
симо от того, к каким компонентам структуры она приложена.
Истинные переносы в структуре пирита направлены лишь вдоль
ребер кубической ячейки, следовательно, решетка Бравэ при-
митивная (Р).
Г р а ф и т , С (рис. 24). В этой структуре нетрудно
заметить параллельность всех осей 3-го порядка одному на-
правлению, что сразу заставляет отнести трафит к гексаго-
нальной сингонии; плоскость симмерии, перпендикулярная к
этому семейству тройных осей, позволяет говорить о гекса-
гональной подсингонии ( 3 = 5 -)• Поскольку в этой подсин-
гонии решетка лишь одна примитивная (Р), задача сводится,
по существу, лишь к выбору ячейки Бравэ ( а = Ъ / С, оС==
90° и У = 120°). Для этого из любой точки структуры в плос-
кости, перпендикулярной главной оси, находим два кратчай-
ших трансляционных вектора под углом 120° друг к .другу, ко-
26
27
Рис. 24. Графит, С
Общий вид и план
структуры

торые определят основание ячейки Бравэ
(120°-ный ромб); заметим, что ближай-
шие атомы в слое не определяют ребро
ячейки, так как они не связаны тран-
сляционным вектором. Ребро с ячейки
направлено вдоль главной оси, причем
из-за сдвига атомарных слоев относи-
тельно .друг .друга оно равно удвоенно-
му расстоянию между слоями.
Обратим внимание на то, что струк-
туры гексагональной сингонии на моде-
лях и рисунках иллюстрируются обычно
не одной ячейкой Бравэ, а тремя, сла-
гающими вместе гексагональную призму.
Единственное оправдание этому - стрем-
ление к большей наглядности, так как
в изолированной ячейке плохо видна ось
3-го (6-го) порядка кристаллической
структуры. Вообще надо отметить, что
’’выход" за пределы ячейки Бравэ - са-
мый обычный прием при изображении структур, так как он поз-
воляет показать наиболее характерные их особенности.Так,по
модели структуры пирита, в которой "обрублены"
расположенные вне ячейки, очень трудно увидеть
подобие" этой структуры, так и характерные для
дели So. Привычное изображение гексагональных структур в
виде гексагональной призмы часто побуждает начинающих при-
нимать за ячейку Бравэ в графите гексагональную призму с
пустым основанием; ошибочность такого подхода очевидна.
IO/V/4
/2^ I ®
|оли

все атомы,
как "ЯаС!-
пирита ган-
§ 3. Координационные числа и координационные
многогранники. Число формульных единиц (Z).
Геометрический характер структуры
Велика ли информация, которую может сообщить тип ре-
шетки Бравэ? Ответ на этот вопрос дает простое сопоставле-
ние .двух величин: всего 14 решеток Бравэ и многие тысячи
разнообразных структур
Познакомимся с некоторыми простыми приемами описания
28
Рис. 25. Структура флю-
орита, СаГ2’ Общий вид
и план структуры, выде-
лены координационные
многогранники для Са и Г
структур, позволяющими во многих
случаях получить полное представ-
ление об атомном узоре, не имея
исчерпывающих структурных данных -
симметрии расположения атомов и
описания их позиций в терминах
пространственных групп (см.с. 78).
В качестве примера опишем
изображенную на рис. 25 структуру
с гранецентрированной решеткой
Бравэ. Прежде всего по модели мож-
но решить вопрос о типе химичес-
кой формулы этого соединения, т.е.
установить количественное соотно-
шение атомов (на рис. 25 - соотно-
шение числа черных и белых шаров).
Это нетрудно сделать по взаимному
окружению - взаимной координации
- атомов разных сортов. В данном
случае каждый черный шар окружен
восемью белыми шарами, а каждый
белый - лишь четырьмя черными, т.е. координационное число
черного шара равно 8, а белого - 4, откуда следует формула
АХ2, если черные шары символизируют электроположительные
частицы, а белые - электроотрицательные, или А2Х, если
символы противоположны. В первом случае (АХ2) структурный
тип называют по минералу флюориту (СаГ2> или ториту (Th02),
во втором (AgX) - по окиси лития (Ы20). В связи с этим мож-
но говорить об антиизоструктурности двух ОКИСЛОВ - Th02 и
Ii20.
При описании структуры в дополнение к числовой харак-
теристике взаимного окружения, координацион-
ным ч и сдам (к.ч.), полезно указать и геометричес-
кие - форму коо р.д инационного мно-
гогранника (к.м.), т.е. описать фигуру, внутри ко-
---	5
4)
К настоящему времени известно примерно 4,5 млн. различ-
ных соединений, причем на долю органики, в том числе и
полимеров, падает 86%. Структуры большинства соединений
к~3,5 млн.) полностью расшифрованы.
29
торой находится данный атом, а в верши-
нах - атомы-соседи. В структуре флюори-
та (см. рис. 25) к.м. атома Са - куб,
атома Г - тетраэдр. Такая дополнительная
характеристика необходима хотя бы пото-
му, что о,дному и тому не координационно-
му числу могут отвечать разные координа-
ционные многогранники (рис. 26). В высо-
косимметричных не очень сложных структу-
рах ближайшие соседи располагаются на
— - одинаковых расстояниях от центрального
Рис. 26. Структу-
ра Pt$. Координа- атома» и коодинационные многогранники
ционные числа для обладают достаточно высокой симметрией;
ИЛ а координа-6 в низкосимметричных структурах к одной
ционные многогран- координационной сфере обычно относят
(квацрат^^етра- ат°мы, находящиеся лишь на приблизитель-
эдр)	но равных расстояниях, в этих случаях
координационные многогранники не имеют правильной высоко-
симметричной формы.
Иногда, говоря о координационном числе, не ограничи-
ваются лишь первой (ближайшей) координационной сферой, а
затрагивают и вторую, третью и т.д. Например, в случае
структурного типа «<-Ее (илиМ), в котором атомы расположе-
ны по узлам объемноцентрированного куба, координационное
число можно считать равным 14, так как атомы второй коорди-
национной сферы, расположенные по вершинам октаэдра, лишь
на 15$ дальше атомов первой координационной сферы, находя-
щихся в вершинах куба (рис. 27). Общим координационным мно-_
гогранником обеих сфер окажется ромбододекаэдр. Конкретизи-
руя, полезно указывать в подобных случаях не только коорди-
национные числа, ио и расстояния
до атомов разных координационных
Рис. 27. В структуреot-Ге коорди-
национное число атома Ее по первой
координационной сфере равно 8, с
учетом .2-й сферы - 14 (8 + 6); ко-
ординационные многогранники соот-
ветственно куб и ромбододекаэдр
юординацио иый многогран-
ник - искаженный октаэдр
сфер. Так, в структуре js -5п
(рис. 28) каждый атом олова
находится в сильно искаженном
октаэдре из соседних атомов,
две вершины которого отдалены
от центрального атома. В дан-
ном случаеозаписывают к.ч. =
= 4 (3,02 А) + 2 (3,17 А).
Установить тип формулы
по структурным данным (по мо-
дели структуры, чертежу) мож-
но и иначе, а именно, подсчи-
тав, сколько атомов того или
иного элемента приходится на
одну ячейку Бравэ. В нашем примере (см. рис. 25) число бе- ,
лых шаров, попавших в ячейку, равно 8, число же черных шаров,
находящихся как на границе двух ячеек (6 шаров в центрах
граней ячейки), так и на стыке восьми ячеек (8 вершинных
шаров), равно 4 (6/2 + 8/8). Такой подсчет также приводит
к формуле AXg (AgX) - СаЕ2 (1с20). К тем же результатам лег-
ко прийти, если выбрать начало координат ячейки Бравэ так,
чтобы все атомы оказались в пределах одной ячейки (см.рис.25).
Определение числа атомов в ячейке Бравэ позволяет кро-
ме типа формулы получить весьма полезную константу - чис-
ло формульных единиц (Z). Для простых
веществ, состоящих из отдельных атомов (Си, 5е ...), число
формульных единиц отвечает числу атомов в ячейке Бравэ, для
простых молекулярных веществ (J2, Sg, .»•) и молекулярных со-
единений (С02, А$45д) оно равно числу молекул в ячейке, в
подавляющем большинстве неорганических и интерметаллических
соединений (ЯаС1, СаГ2,..., CuAu,,...) молекул нет, и о числе
их можно говорить лишь сугубо условно. В нашем примере для
флюорита Z = 4, так как 4 атома Са и 8 атомов Г в ячейке
Бравэ составит 4 ’’молекулы” - 4 формульные единицы.
Число формульных единиц можно определить эксперименталь-
но в процессе рентгеновского исследования атомной структуры
вещества. Действительно, определив параметры ячейки Бравэ,
а следовательно, и ее объем, можно вычислить вес одной ячей-
ки (Р): Р =V«jD, где V- объем ячейки в &3 (V х 10 в см3),
31
a p - плотность в г/с i3, определенная тем или иным физи-
ческим способом» С другой стороны, вес той же ячейки есть
произведение веса молекулы (молекулярного веса, выраженное
го в граммах) на число формульных единиц: Р = М • пг •Z,
М • пг • Z ,
где М - молекулярный вес вещества, иг- вес атома водорода,
равный 1,64 • 10*24т. Иными словами, V»n
V. Р 'ч	J
откуда Z = —-----------——од
М 1,64 » 10 24 .
Если в структуре кристалла нет таких
вакансии в положении атомов или замещения
дефектов, как
одних -частиц
другими, а кроме того, дефектов, присущих реальным кристал
лам (трещиноватость, включения, межблочные пустоты), то в
пределах ошибки опыта Z должно оказаться целым числом.
Определив экспериментально Z и округлив его до целого
числа, можно вычислить плотность идеального Монокристалла,
которую называют рентгеновской плотностью: jOpeHT
Ррент ойычно несколько больше J>8KCn. Величина отклонения
^рент от .рэксп r0B0PET 0 степени дефектности кристалла.
Приведенные характеристики, существенные для понима-
ния отдельных особенностей структуры, все-таки не дают об-
щего представления о взаимном расположении атомов - необ-
ходим еще краткий "словесный •портрет’’, который дозволил бн
"увидеть" структуру без модели, изобразить ее в плане и по
этому плану воссоздать необходимые данные: тип решетки Бра
вэ, тип формулы, Z , координационные числа, координацион-
ные многогранники и т.п. Так, структуру флюорита можно опи-
сать следующим образом: атомы Са располагаются в узлах гра-
нецентрированного куба, а атомы Г центрируют все октанты
кубической,ячейки (т.е. 8 маленьких кубов, которые получа-
ются рассечением ячейки тремя координатными плоскостями,
проходящими черев центр куба). План структуры, построенный
на основе этого описания, представлен на рис. 25.
Полезную информацию о структуре получим, выявив ее
геометрический характер, поскольку он так или иначе связав
с типом химической связи.
Принято выделять пять геометрически различных типов
структур: координационные, островные, цепочечные, слоистые
и каркасные.
В координационной структуре атомы не
образуют каких-либо
конечных или беско-
нечных группировок,
распределяясь по
всему кристалличес-
кому пространству
равномерно. Взяв
расстояние между
двумя ближайшими
атомами, можно по-
Рис. 29. Примеры координационных	степенно обойти все
структурных типов: медь (а) и
магний (б)	а?оыы структуры.
Связь между всеми атомами одинакова (структуры гомо-
десмические ), хотя отнюдь не обязательно эта
связь проявляется в чистом виде; так, в изоструктурном ря-
ду SiC, А1Р, 2nS, AgJ (см. рис. 43), возглавляемом сущест-
венно ковалентным StC (карбидом кремния), наблюдается по-
степенное и значительное нарастание полярности связи.
Структуры с металлической связью (Си, Mg - рис. 29) отно-
сятся в большинстве случаев к координационному типу.
Четыре остальных типа структур - гетеродес-
мические, т.е акие, в которых проявляется хими-
ческая связь нескольких типов: один тип связи .внутри груп-
пировки атомов (острова, цепи, слоя или трехмерного карка-
са), другой - между атомами из разных группировок или ато-
мами, образующими группировку,
Так, в островной
Рис. 30. Структура кристалли-
ческого хлора - пример остров-
ной структуры
и прочими.атомами.
структуре кристаллического
хлора (рис. 30) кратчайшее
расстояние между атомами
в молекуле (dj = 2,00 ! )
отвечает сумме ковалентных
радиусов атомов хлора, ми-
нимальное же расстояние
между атомами хлора из 0
разных молекул (dg = 3 56А)
отражает с известной сте-
пенью точности межмолеку-
лярное взаимодействие. В
изоструктурном ряду Ct2,
32
3-1478
33
Вг^ и J 2 это расстояние все больше отклоняется от суммы
ван-дер-ваальсовых радиусов благодаря примеси металличес-
кой связи. Кроме валентно-насыщенных, т.е. нейтральных
островов (Ct2» -Sg, С02, As^) существуют острова катион-
ного или анионного характера. Так, в кальците между кова-
лентно-связанной карбонатной группой (СОд)” и ионом кальция
связь в основном ионная; то же распределение связей в ше-
елите (CaWo4)3H в NH^MOg, где оба острова представлены ком-
плексными ионами.
Цепочечные структуры также могут иметь как
нейтральные, так и валентно-ненасыщенные цепи. Примером
первого типа может служить Se (рис. 31,а), где ковалентные
цепи (dj = 2,32 ) удерживаются между собой связями, близ-
кими к ван-дер-ваальсовым (d2 = 3,46 X). Ко второму типу
можно отнести, например, структуру ЯаНСОд, где водородные
связи выстраивают карбонатные ионы в цепи (НСОд)'(рис. 31,6),
"склеенные!’ между собой ионами Яа'« Сюда же попадут и обыч-
ные силикаты цепочечного строения.
Рис. 31. Цепочечные структуры: а) структура селена,
б) цепи (НСОд)’ в структуре КаЙС03
К слоистым структурам с нейтральными слоями
можно отнести графит (см. рис. 24), у которого ковалентные
связи внутри слоя (dj = 1,42 А) и смешанные (ван-дер-вааль-
сова плюс металлическая) между слоями (dg = 3,39 Х)> а так-
же брусит Mg(0H)2 (изоструктурен CdJ >, см. рис. 48,а), где
гетеродесмичность определяется ионно-ковалентными связями
в слое - пакете из Mg-октаэдров, с одной стороны, и вян-
дер—ваальсовыми - между пакетами, с другой. Сопоставление
Рис 32. Пакет AIJS^OtJ (0Н)2 из слоистой структуры
пирофиллита
структуры пирофиллита, в котором трехслойные пакеты
At2[5L4°io^OH)2 (рис* 32^ нейтральны, с мусковитом, где
отрицательно заряженные пакеты {Atgt&gAlOjQ] (0Н)2] скреп-
ляются ионами К*, иллюстрирует связь и взаимные переходы
между слоистыми структурами двух типов.
В каркасных структурах нейтральный или за-
ряженный трехмерный каркас содержит "начинку", расстояние
до атомов которой от атомов каркаса (dg) существенно пре-
вышает расстояния между атомами в самом каркасе (dj). Ин-
тересен нейтральный каркас структуры рыхлого "льда”, в ко-
торой частицы HgO, расположенные по вершинам правильного
пентагон-додекаэдра (20 частиц), скреплены одиночными груп-
пами Н20. Такая гигантская "молекула* льда (в простейшем
случае на ячейку Бравэ приходится 46 частиц HgO) может со-
Рис. 33. Каркасные структуры: а) структура перовскита,
CaTiOo, б) структура куприта, Си20. Атомы меди окружа-
ют атомы кислорода по тетраэдру.^Различной штриховкой
показаны две независимые системы сочленяющихся по вер-
шинам тетраэдров
34
держать в своих крупных пустотах различные нейтральные мо-
лекулы,. например Cig» Хе, KHg и т.п.^^Представителем струк-
турного типа, в котором каркас заряжен, может служить орто-
клаз - каркас [AtSigOgl с "начинкой” из крупных ионов ка-
лия. Классический пример подобных структур - перовскит
CaTlOg, где ковалентно-связанный каркас из атомов TL и О
создает ионную связь с атомами Са5 6\рис. 33,а).
К каркасным следует отнести и структуру куприта, CugO,
в которой тетраэдры из атомов меди вокруг атомов кислорода
образуют .два одинаковых, вложенных друг в друга независи-
мых каркаса (рис. 33,6)..
Заканчивая, необходимо подчеркнуть, что такая прими-
тивная классификация структурных типов по их геометричес-
ким особенностям, хотя удобна и полезна, но все же не мо-
жет исчерпать все многообразие известных ныне химических
соединений.
§ 4, Плотнейшие шаровые упаковки
Исторически первой была замечена плотнейшая укладка
из квадратных слоев, т.е. слоев тетрагональной симметрии
(рис. 34,а). Укладывая .друг на .друга эти-слои так, чтобы
шары каждого следующего слоя опускались в лунки между че-
тырьмя шарами предыдущего слоя, получим максимально плот-
ную упаковку шаров (рис. 34,6); нетрудно убедиться, что
каждый шар касается 12 шаров (4 шара в слое? 4 сверху и
4 снизу), при этом будет достигнут максимальный коэффици-
ент заполнения пространства одинаковыми шарами, равный
74,05$. Симметрия такой укладки кубическая, шары располо-
жены по узлам гранецентрированной кубической решетки Бравэ
(рис. 34,в и 29,а).
Такой способ плотнейшей укладки шаров столетиями
считался единственным, что, на первый взгляд, подтверцда-
5) Соединения подобного типа называются клатратными. Роль
каркасообразователя в них часто играют молекулы гидро-
хинона. Без "начинки” такие каркасы существовать не могу’
Интересно, что KaW04. имеющий структуру, аналогичную
структуре перовскита, тем не менее гомодесмичен, так
как связь между всеми атомами одинакова - близка к ме-
таллической.
36
Рис. 34. Плотнейшая шаровая укладка из квадратных слоев:
а) изолированный квадратный шаровой слой, соотношение
числа шаров и лунок -1:1;
б) квадратные слои образуют плотнейшую упаковку;
в) шары полученной плотнейшей упаковки служат узлами
F-кубической решетки Бравэ
лось равенством числа шаров и лунок7) в каждом слое (каждый
шар окружен четырьмя лунками, каждая лунка - четырьмя шара-
ми); шары каждого квадратного слоя заполняют все лунки
35. Разделение плотнейшей уклад-
Рис. 1_.___________________________„
ки шаров (а) на слои, перпендикуляр-
ные оси L о, т.е. на гексагональные
(плот н°е й ш и е) слои (б);
в) два типа лунок в изолированном
плотнейшем слое; соотношение числа
шаров и лунок в слое равно 1:2;
г) сквозные и несквозные лунки плот-
нейшей шаровой упаковки
Имеются в виду лунки, расположенные по одну сторону слоя

несквозная лунка,
сквозная
мина
3 -1478
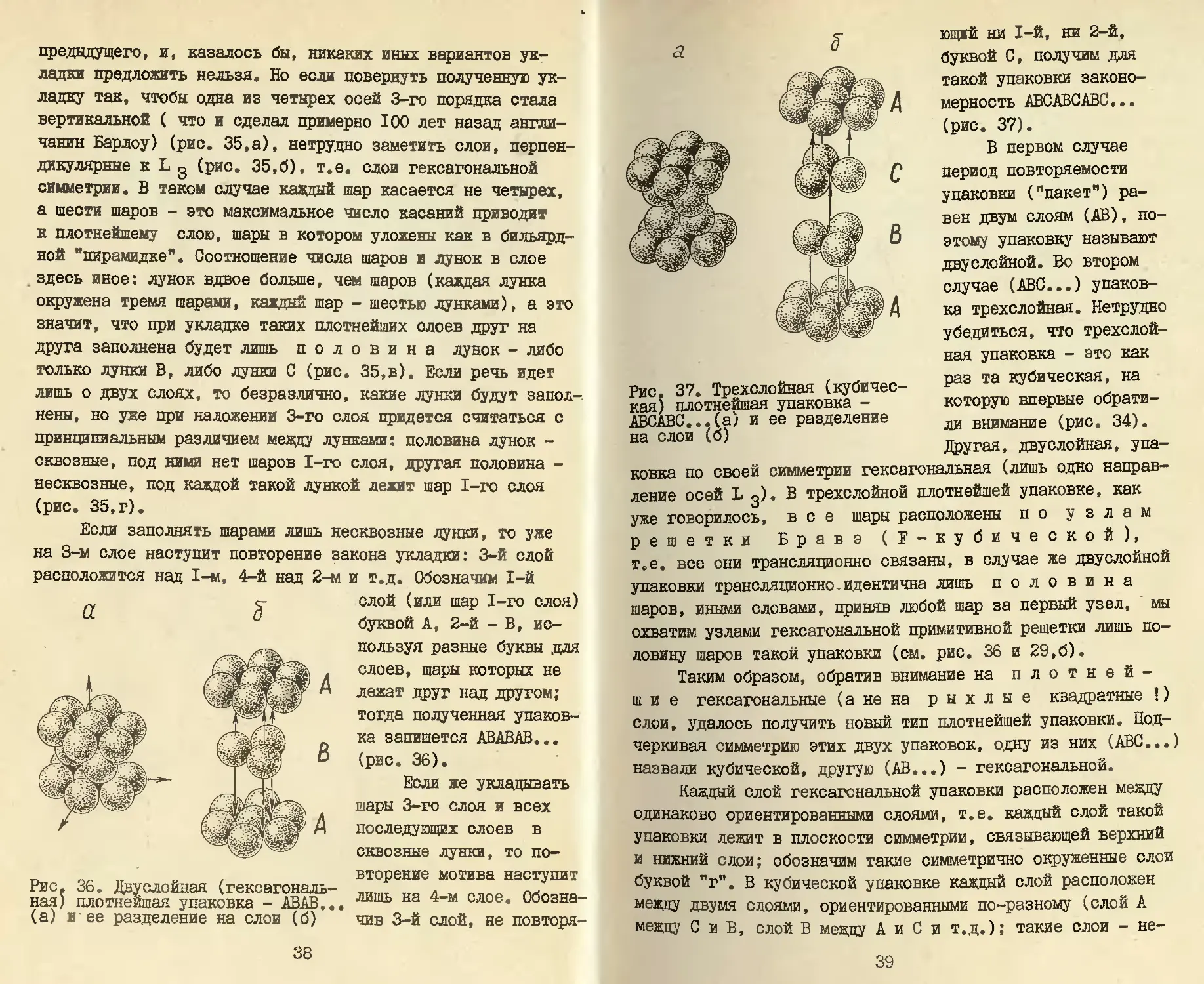
предыдущего, и, казалось бы, никаких иных вариантов ук-
ладки предложить нельзя. Но если повернуть полученную ук-
ладку так, чтобы одна из четырех осей 3-го порядка стала
вертикальной ( что и сделал примерно 100 лет назад англи-
чанин Барлоу) (рис. 35,а), нетрудно заметить слои, перпен-
дикулярные к Lg (рис. 35,6), т.е. слои гексагональной
симметрии. В таком случае каждый шар касается не четырех,
а шести шаров - это максимальное число касаний приводит
к плотнейшему слою, шары в котором уложены как в бильярд-
ной "пирамидке". Соотношение числа шаров и лунок в слое
здесь иное: лунок вдвое больше, чем шаров (каждая лунка
окружена тремя шарами, каждый шар - шестью лунками), а это
значит, что при укладке таких плотнейших слоев друг на
друга заполнена будет лишь половина лунок - либо
только лунки В, либо лунки С (рис. 35,в). Если речь идет
лишь о двух слоях, то безразлично, какие лунки будут запол-
нены, но уже при наложении 3-го слоя придется считаться с
принципиальным различием между лунками: половина лунок -
сквозные, под ними нет шаров I-го слоя, другая половина -
несквозные, под каждой такой лункой лежит шар I-го слоя
(рис. 35,г).
Если заполнять шарами лишь несквозные лунки, то уже
на 3-м слое наступит повторение закона укладки: 3-й слой
j т.д. Обозначим 1-й
слой (или шар I-го слоя)
буквой А, 2-й - В, ис-
пользуя разные буквы .для
слоев, шары которых не
лежат друг над другом;
тогда полученная упаков-
ка запишется АВАВАВ...
(рис. 36).
Если же укладывать
шары 3-го слоя и всех
последующих слоев в
сквозные лунки, то по-
Рис. 36. Двуслойная (гексагональ-
ная) плотнейшая упаковка - АВАВ...
(а) и ее разделение на слои (б)
вторение мотива наступит
лишь на 4-м слое. Обозна-
чив 3-й слой, не повторя-
38
Рис. 37. Трехслойная (кубичес-
кая) плотнейшая упаковка -
АВСАВС...(а) и ее разделение
на слои (б)
ющий ни I-й, ни 2-й,
буквой С, получим для
такой упаковки законо-
мерность АВСАВСАВС...
(рис. 37).
В первом случае
период повторяемости
упаковки ("пакет") ра-
вен двум слоям (АВ), по-
этому упаковку называют
двуслойной. Во втором
случае (АВС...) упаков-
ка трехслойная. Нетрудно
убедиться, что трехслой-
ная упаковка - это как
раз та кубическая, на
которую впервые обрати-
ли внимание (рис. 34).
Другая, двуслойная, упа-
ковка по своей симметрии гексагональная (лишь одно направ-
ление осей L 3). В трехслойной плотнейшей упаковке, как
уже говорилось, все шары расположены по узлам
решетки Бравэ (Р-кубической),
т.е. все они трансляционно связаны, в случае же двуслойной
упаковки трансляционно-идентична лишь половина
шаров, иными словами, приняв любой шар за первый узел, мы
охватим узлами гексагональной примитивной решетки лишь по-
ловину шаров такой упаковки (см. рис. 36 и 29,6).
Таким образом, обратив внимание на плотней-
шие гексагональные (а не на рыхлые квадратные !)
слои, удалось получить новый тип плотнейшей упаковки. Под-
черкивая симметрию этих .двух упаковок, одну из них (АВС...)
назвали кубической, другую (АВ...) - гексагональной.
Каждый слой гексагональной упаковки расположен между
одинаково ориентированными слоями, т.е. каждый слой такой
упаковки лежит в плоскости симметрии, связывающей верхний
и нижний слои; обозначим такие симметрично окруженные слои
буквой "г". В кубической упаковке каждый слой расположен
между двумя слоями, ориентированными по-разному (слой А
между С и В, слой В между А и С и т.д.); такие слои - не-
39
симметрично окруженные - обозначим "к". Таким образом, в
обозначении двуслойной (гексагональной) упаковки будут уча-
ствовать лишь буквы "г" (ггггг...), а в трехслойной (куби-
ческой) - "к” (ккккк...). Закономерно чередуя различным об-
разом слои "г" и "к", придем к бесконечному множеству м н о -
гослойных(с числом слоев в пакете, превышающим три)
плотнейших упаковок (например, гкгкгк..., ггкггкггк...,
ккгккгккг...). Чтобы решить какова елейность этих упаковок,
проще всего вернуться к обозначениям слоев буквами А,В,С.
Отметим, что, хотя по своей симметрии все многослойные упа-
ковки гексагональны (решетка Р или В), название "гексаго-
нальная” утвердилось лишь за .двуслойной.
Пример. Определить слойность упаковки гкгкгк...
Обозначим .два первых слоя разными буквами, например,
А и В (напомним, что в соседних слоях шары не могут лежать
один над другим), тогда .для третьего слоя придется исполь-
зовать букву С - ведь второй слой, будучи слоем "к", должен
иметь разных соседей. Рассуждая дальше подобным образом, по-
лучим последовательность букв АВСВАВСВ..., которая убеждает
нас в том, что в пакете 4 слоя - упаковка четырехслойная.
Оба способа обозначения плотнейших упаковок, как видим,
хорошо дополняют .друг .друга - один (А,В,С) позволяет легко
выделить период повторяемости (пакет), т.е. определить слой-
ность упаковки, но при этом о,дна и та же упаковка может вы-
глядеть по-разному: так, последовательности ABAC..., ВСАС...
АВСВ... выражают о,дну и ту же упаковку. Другой способ (г,к)
лишен этого недостатка, однако период повторяемости в этом
случае выявляется не столь непринужденно8\ Например,
о\
' Большое достоинство .двухбуквенного способа - возможность
увидеть без специальной модели те элементы симметрии, кото-
рые будучи добавлены к обязательному комплексу элементов
симметрии любой упаковки (P3ml), определят симметрию данной
упаковки (о пространственных группах см. с. 65). Так, если
по обе стороны от слоя "г" располагаются зеркально равные
части буквенной последовательности, то через шары данного
слоя проходит зеркальная плоскость симметрии упаковки, если
же между зеркально равными частями расположен слой "к”, то в
его шарах находятся центры инверсии. Центры инверсии лежат и
между одинаковыми слоями ("к" и "к” или "г" и "г ), если эти
два одинаковых слоя рассекают формулу упаковки на две зерка-
льно равные части. Обозначив зеркальные плоскости симметрии
.двойными линиями (и), а центры инверсии - звездочками (*),
отметим эти элементы симметрии в приведенных ниже формулах
упаковок •. -п v V т. « 2?	-
упаковок: г к к г к к г
II * II * «
г г к г г к
гггкгкггг.
.ккг... и ...кгггкг... - разные упаковки одной слойно-
стй а ...ккг... и ...ггк... - упаковки разной елейно-
сти (предлагаем читателю убедиться в этом самостоятельно,
имея в виду, что заданная последовательность букв предста-
вляет минимальную повторяющуюся единицу буквенного ряда).
Итак, плотнейшее заполнение пространства одинаковыми
шарами может быть реализовано бесконечным числом способов,
т.е. можно получить (и четко описать !) бесконечное число
плотнейших упаковок. Общий признак плотнейших упаковок -
максимальный коэффициент заполнения пространства (74,05$)
и (или) максимальное число касаний у каждого шара (12, т.е.
6 шаров в слое, 3 шара сверху, 3 снизу).
Возратимся к описанию кристаллических структур и по-
пытаемся решить, для каких из них можно предвидеть распо-
ложение материальных частиц по законам плотнейшей упаковки.
Очевидно, такие кристаллы должны состоять из одинаковых
атомов (в первом приближении - несжимаемых шаров), связь
между которыми ненаправленная и ненасыщаемая; это условие
сразу отсылает нас к структурам металлов и отверженных
благородных газов. И действительно, как в большинстве
структур металлов, так и во всех кристаллах благородных
газов мы имеем дело с плотнейшими упаковками атомов (поло-
жительных остовов в электронном "газе" в металлах и одно-
атомных "молекул" в благородных газах). Описание таких
структур предельно просто: Си или - кубическая плотней-
шая упаковка атомов (см. рис. 29,a),_Mg или Не - гексаго-
нальная (см. рис. 29,6), L а - четырехслойная и т.д.
0 ненаправленной и ненасыщаемой связью мы встречаемся
и в ионных структурах, однако здесь приходится иметь дело
с "шарами" не только разных зарядов, но и разных размеров.
Поэтому, желая воспользоваться для описания таких структур
терминами плотнейшей упаковки, следует рассматривать эти
разные по размеру частицы отдельно: часть ионов может обра-
зовать ту или иную плотнейшую упаковку, а .другие окажутся
в пустотах этой упаковки.
Сразу же следует отметить, что по сути дела о "шарах,
касающихся друг друга", можно говорить лишь в случае метал-
лов и благородных газов, считая радиусами таких шаров поло-
вины расстояний между атомами; при кулоновском взаимодейст-
вии между атомами, т.е. в ионных структурах, нельзя забывать,
41
40
что катион, попав в окружение анионов, не должен "болтать-
ся", - он раздвигает своих соседей, разрежая тем самым ее
укладку. Фактически здесь речь может идти не о плотнейшей
упаковке в строгом смысле слова, т.е. не о максимальном
коэффициенте заполнения пространства, а лишь о максималь-
ном числе (12) векторов, идущих к ионам того же знака (раз.
мера).
Итак, с учетом указанной оговорки, принцип плотнейшей
упаковки вполне может быть применен для описания ионных
структур. Однако для того, чтобы это описание было достаток
но полным, необходимо рассмотреть пустоты в плотнейших
упаковках.
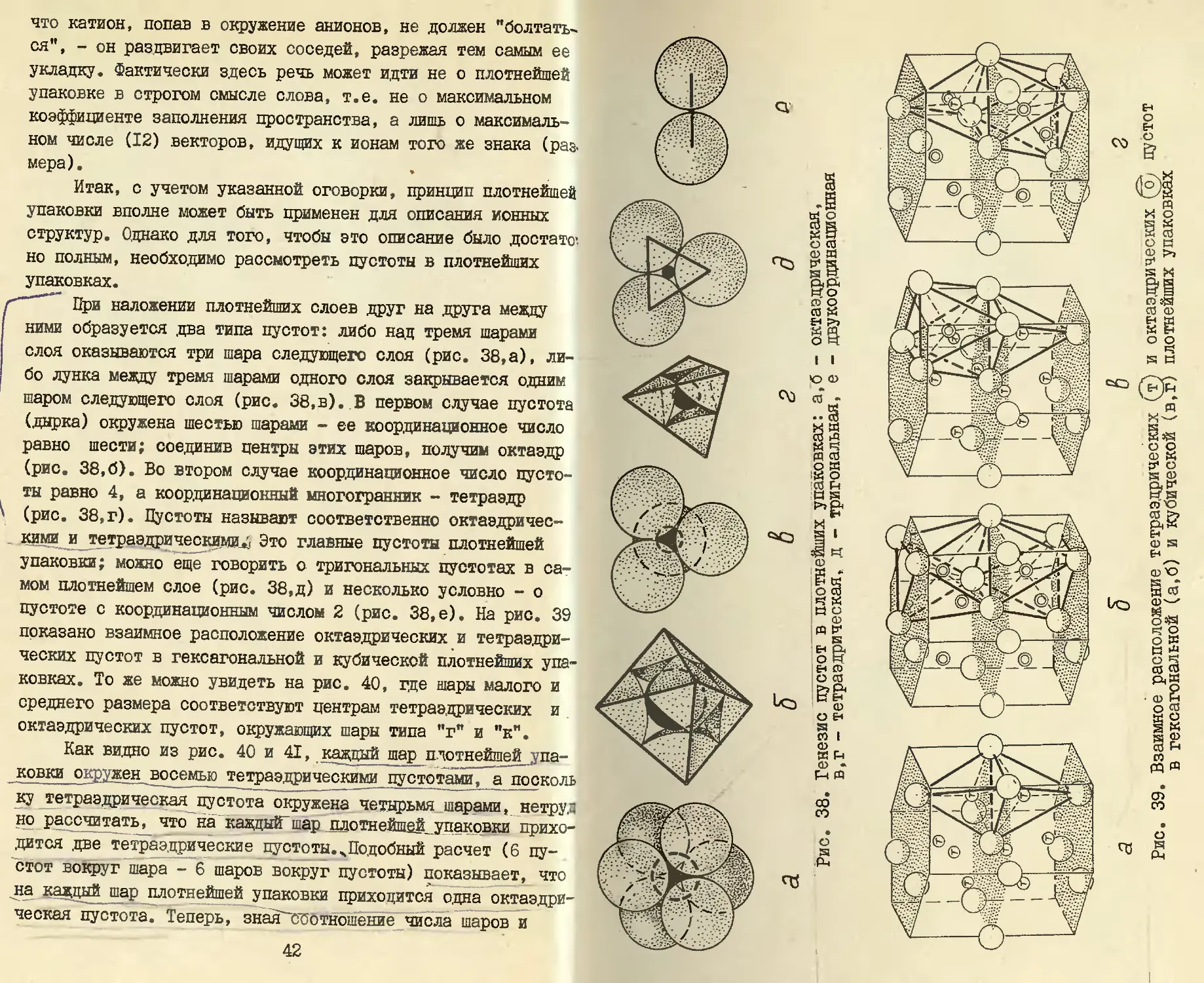
'—При наложении плотнейших слоев друг на друга между
ними образуется .два типа пустот: либо над тремя шарами
слоя оказываются три шара следующего слоя (рис. 38,а), ли-
бо лунка между тремя шарами одного слоя закрывается одним
шаром следующего слоя (рис. 38,в). В первом случае пустота
(дырка) окружена шестью шарами - ее координационное число
равно шести; соединив центры этих шаров, получим октаэдр
(рис. 38,6). Во втором случае координационное число пусто-
ты равно 4, а координационный многогранник - тетраэдр
(рис. 38,г). Пустоты называют соответственно октаэдричес-
кими и тетраэдрическими.’; Это главные пустоты плотнейшей
упаковки; можно еще говорить о тригональных пустотах в са-
мом плотнейшем слое (рис. 38,д) и несколько условно - о
пустоте с координационным числом 2 (рис. 38,е). На рис. 39
показано взаимное расположение октаэдрических и тетраэдри-
ческих пустот в гексагональной и кубической плотнейших упа-
ковках. То же можно увидеть на рис. 40, где шары малого и
среднего размера соответствуют центрам тетраэдрических и
октаэдрических пустот, окружающих шары типа "г" и "к".
Как видно из рис. 40 и 41, каждый шар плотнейшей па-
ковки о жен восемью тетраэдрическими пустотами, а посколь
ку тетраэдрическая пустота окружена четырьмя шарами, нетру.п
но рассчитать, что на' каждый-шар плотнейшей упаковки прихо-
дится .две тетраэдрические пустоты.чПодобный расчет (6 пу-
стот вокруг шара - 6 шаров вокруг пустоты) показывает, что
накаждый шар плотнейшей упаковки приходится одна октаэдри-
ческая пустота. Теперь, зная^соотношение числа шаров и
42
Рис. 39. Взаимное расположение тетраэдрических (т} и октаэдрических (о) пустот
в гексагональной (а,б) и кубической (в,г) плотнейших упаковках
I
a
Рис. 40. Расположе-
ние октаэдрических
и тетраэдрических
пустот вокруг шаров
типа "г"(а; и "к*(б)
Пустоты представлена
вписывающимися в них
шариками
главных пустот в плотнейших упаковках (это соотношение не
зависит от типа упаковки), можно достаточно просто описать
множество структурных типов. Этот прием описания структур
может оказаться пригодным и для соединений с преимуществен-
но ковалентной - направленной и насыщаемой - связью в тех
случаях, когда атомы склонны к тетраэдрической или октаэд-
рической координации (например, ZnS , NiAs и др.).
Рис. 41. К подсчету соотношения числа
октаэдрических (тетраэдрических) пустот
и шаров упаковки: а) гексагональная упа-
ковка, б) кубическая упаковка
Приведем
несколько приме-
ров.
I. Анионы
(X) образуют ку-
бическую плотней-
шую упаковку, в
которой катионы
(А) заполняют
все тетраэдричес-
кие пустоты.
Это описанй!
дает исчерпываю-
щее представленй'
не только о типе
химической форму-
лы (А2Х), но и о
расположении ио-
нов в данном
структурном типе
Изобразив в план*
ячейку Бравэ куб)
ческой плотнейте!
упаковки - гране-
центрированный
куб, в узлах которого расположены ани-
оны (8/8 + 6/2 = 4), легко находим
центры 8 тетраэдрических пустот: | | |,
I I 3 I 3 I 133 3 I I 313
444’444*444’ 444* 444*
о о Т Ч Ч Я
- - = , - - - . Заполнив их катионами,
4 4 4	4 4 4
получим знакомый уже структурный тип
Ll 20 (см. рис. 25).
2. Анионы (X) образуют кубическую
плотнейшую упаковку, а катионы (А) за-
нимают все октаэдрические пустоты.
Из этого описания следует формула
типа АХ. В данном случае анионный мо-
тив изображается так же, как в преды-
Рис. 42. Структур- дущем примере, необходимо лишь найти
д ”ман структу- На ₽исунке позичии центров октаэдри-
ры: белые шары - ческих пустот - они располагаются в
ТОН), черные - Lt центре ячейки и на серединах ребер ку-
ба (заметим, что их число в расчете на
I + ~ = 8/8 + 6/2 = 4 ). Теперь не-
I трудно^получить остальные характерис-
iтики и установить структурный тип (NaCt,
рис. 21).
3. Анионы (X) образуют кубическую
плотнейшую упаковку, а катионы (А) за-
полняют линь 1/2 тетраэдрических пустот.
Этих сведений достаточно, чтобы
установить тип химической формулы (АХ),
но для полного представления об атом-
ном узоре необходимо указать мотив, по
которому заполненные катионами пустоты
чередуются с незаполненными.
Если пустоты заполнены послойно
г,____ п	(через слой), причем слои перпендику- •
ный тип сфалерита	одной из осей 4-го порядка упа-
Общийвид и ковки (т.е. координаты центров заполяен-
план структуры
45
44
ных пустот	то перед нами
кристалл слоистой структуры с весьма совершенной спайносц
по плоскости, перпендикулярной указанной выше оси 4-го по-
рядка - структурный тип Lt ОН (рис. 42). Предлагаем читать
лю по рисунку установить тип решетки Бравэ для Lt ОН.
Если же в кубической плотнейшей упаковке, образован-
ной электроотрицательными атомами, заполнить тетраэдричес-
кие пустоты в шахматном порядке, т.е. занять электрополо-
I f Т Я Я Т ЯТЯ Т Я Я
жительными атомами позиции
то получим совершенно иной структурный тип -ZnS , сфалерит
(рис. 43).
В подавляющем большинстве структурных типов анионные
мотивы довольно однообразны, это преимущественно кубическа
и гексагональная плотнейшие упаковки и значительно реже -
различные многослойные упаковки. Все разнообразие структур
ных типов определяют в основном катионные мотивы, т.е. тип
число и расположение занятых пустот. Этот факт, по-видимоц
и натолкнул в свое время американского кристаллохимика
Л.Полинга на непривычный способ моделирования кристалличес-
ких структур, при котором центр внимания переносится имен»
на катионы.
. § 5. Полиэдрическое изображение структурных типов
(метод Полинга - Белова)
В методе моделирования кристаллических структур, пред-
ложенном Полингом, шары, образующие плотнейшую упаковку,
всегда соответствуют анионам (во всяком случае, более элек-
троотрицательным атомам). Если соединить их центры между
собой прямыми линиями, все кристаллическое пространство
окажется разрезанный на уложенные без промежутков октаэдры
и тетраэдры; на рис. 44 хорошо видно, что тетраэдров вдвое
больше, чем октаэдров: в слое из многогранников половина
тетраэдров смотрит вершиной вверх, половина - вниз. Идея
полиэдрического метода заключается в том, что на модели
оставляют лишь те многогранники, в гт~*“~ ——
на. Пустые полиэдры либо вообще не изображают, либо делают
прозрачными. Таким образом, от шара-аниона остается лишь
его центр - вершина полиэдра, а тело шара разрезается на
которых находятся катио
Рис. 44. Слой из октаэдров и тетраэдров; соотношение
числа тетраэдров и октаэдров -2:1
части, из которых складываются октаэдры и тетраэдры (см.
рис. 38).
Обратимся к уже известным нам структурным типам.
Структура LlgO, в которой атомы Lt заполняют все тетраэд-
рические пустоты кубической плотнейшей упаковки из атомов
кислорода, предстанет в виде укладки из непрозрачных тетра-
эдров, переложенных прозрачными октаэдрами; взаимное распо-
ложение полиэдров видно на рис. 45.
Структурный тип галита, KaCt, можно считать геометри-
ческим анитиподом структуры LigO, так как в этом случае
при той же анионной укладке, т.е. при том же взаимном рас-
положении полиэдров, прозрачны тетраэдры и непрозрачны ок-
таэдры (рис. 46).
В важном структурном типе пирротина, FeS - никелина,
как хорошо видно на рис. 47, октаэдры, сочленяясь
гранями, оставляют свободными тетраэдрические пустоты, так-
же имеющие общую грань. Взаимное расположение как зцрятых
Fe(Hi)-октаэдров, так и пустых тетраэдров, предопределяя
плоскость симметрии, проходящую через плотнейший слой (вер-
шины полиэдров), однозначно говорит о гексагональной упа-
ковке атомов <5 (As). Предлагаем читателю сравнить координа-
ционные многогранники электроположительных (Fe,№) и элект-
роотрицательных (<S,As) атомов, а также ответить на вопрос,
почему этот структурный тип, который можно считать гекса-
гональным аналогом галита, не имеет ни одного представителя
47
46
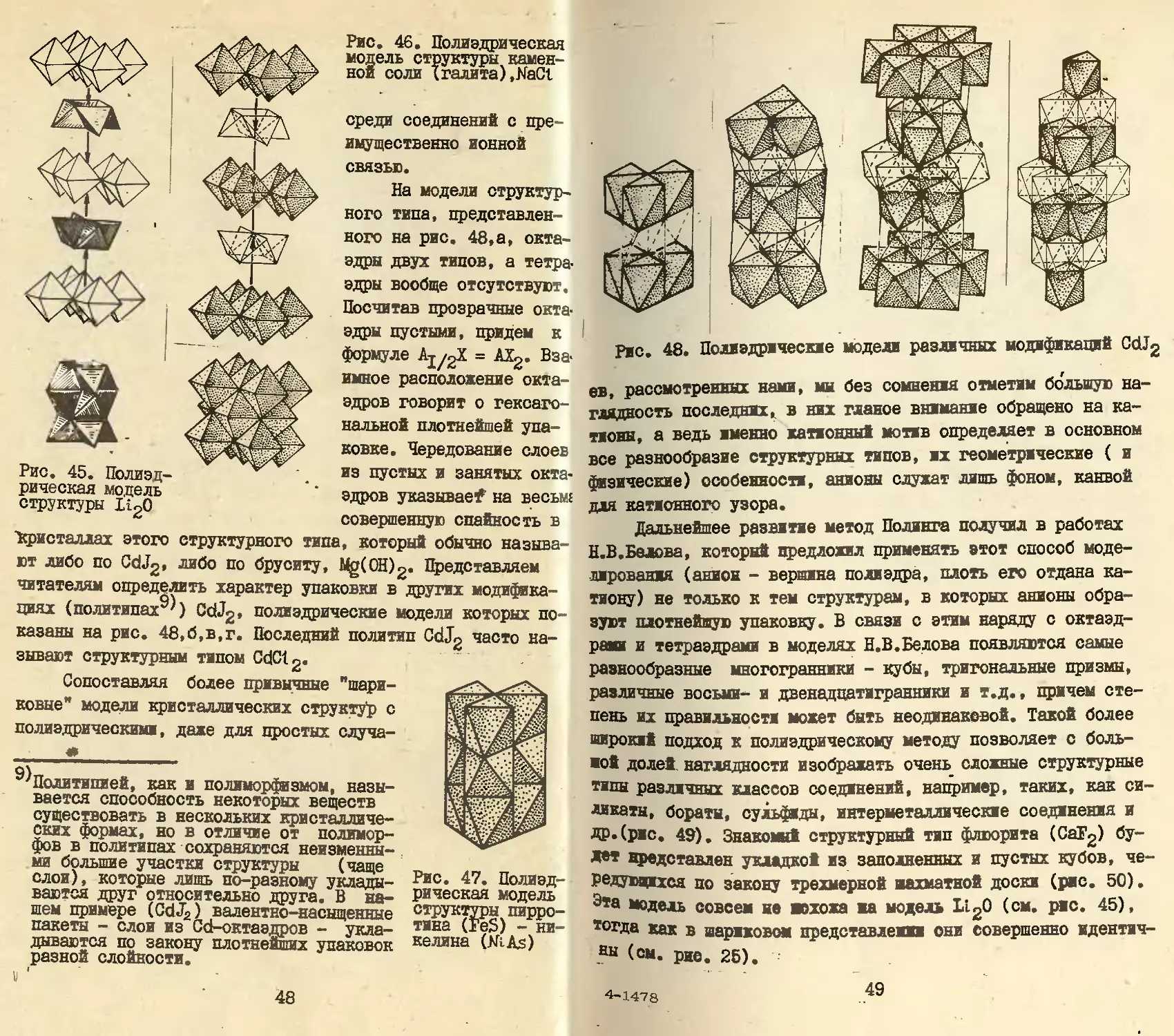
Рис. 46. Полиэдрическая
модель структуры камен-
ной соли (галита) ,NaCt
среди соединений с пре-
имущественно ионной
связью.
На модели структур-
ного типа, представлен-
ного на рис. 48,а, окта-
эдры двух типов, а тетра-
эдры вообще отсутствуют.
Посчитав прозрачные окта-
эдры пустыми, придем к
формуле = AXg. Вза-
имное расположение окта-
эдров говорит о гексаго-
нальной плотнейшей упа-
ковке. Чередование слоев
из пустых и занятых окта-
эдров указываем на весьма
совершенную спайность в
Рис. 45. Полиэд-
рическая модель
структуры Ii20
"Кристаллах этого структурного типа, который обычно называ-
ют либо по CdJ2, либо по бруситу, Mg(0H)2. Представляем
читателям определить характер упаковки в других модифика-
циях (политипах^) CdJ2, полиэдрические модели которых по-
казаны на рис. 48,б,в,г. Последний политип CdJ2 часто на-
зывают структурным типом CdCt2.
Сопоставляя более привычные "шари-
ковые” модели кристаллических структур с
полиэдрическими, даже для простых случа-
9^Политипией, как и полиморфизмом, назы-
вается способность некоторых веществ
существовать в нескольких кристалличе-
ских формах, но в отличие от полимор-
фов в политипах сохраняются неизменны-
ми большие участки структуры (чаще
слои), которые лишь по-разному уклады-
ваются друг относительно друга. В на-
шем примере (CdJ2) валентно-насыщенные
пакеты - слои из Cd-октаэдров - укла-
дываются по закону плотнейших упаковок
разной слойности.
2
Рис. 47.
рическая
Полиэд-
модель
келина (№As)
рис. 48. Полиэдрические модели различных модификаций CdJ2
ев, рассмотренных нами, мн без сомнения отметим большую на-
глядность последних,, в них гланое внимание обращено на ка-
тионы, а ведь именно катионный мотив определяет в основном
все разнообразие структурных типов, их геометрические ( и
физические) особенности, анионы служат лишь фоном, канвой
для катионного узора.
Дальнейшее развитие метод Полинга получил в работах
Н.В.Белова, который предложил применять этот способ моде-
лирования (анион - вершина полиэдра, плоть его отдана ка-
тиону) не только к тем структурам, в которых анионы обра-
зуют плотнейшую упаковку. В связи с этим наряду с октаэд-
рами и тетраэдрами в моделях И.В.Белова появляются самые
разнообразные многогранники - кубы, тригональные призмы,
различные восьми- и .двенадцатигранники и т.д., причем сте-
пень их правильности может быть неодинаковой. Такой более
широкий подход к полиэдрическому методу позволяет с боль-
шой долей наглядности изображать очень сложные структурные
типы различных классов соединений, например, таких, как си-
ликаты, бораты, сульфиды, интерметаллические соединения и
ДР.(рис. 49). Знакомый структурный тип флюорита (СаГ2) бу-
дет представлен укладкой из заполненных и пустых кубов, че-
редующихся по закону трехмерной шахматной доски (рис. 50).
а модель совсем не ж>хожа жа модель Ы20 (см. рис. 45),
тогда как в шариковом представлении они совершенно идентич-
ен (см. рЯе. 25),
48
4-1478
49
Рве. 49. План
структуры BIM-
сна Ca[B202‘
•(ОН)J в по-
лиэдрах
В заклю-
чение остано-
вимся на по-
лиэдрической
модели MoS2.
На рис. 51 "
видны слои
из тригональ-
ных призм, пе-
реложенные слоями из октаэдров с тетраэдрами. Тригональные
призмы заштрихованы через одну, а все остальные полиэдры
(часть призм и октаэдры с тетраэдрами) прозрачные. Такая
модель позволяет сразу сделать вывод, что атомы серы не
образуют сплошной плотнейшей упаковки - плотнейшие слои
из атомов 5 уложены по закону /ААВВ/ААВВ/... Нетрудно уста-
новить и соотношение Mo : JS = I : 2 - ведь атомы Мо запол-
няют лишь половину тригональных
призм в каждом призматическом
слое (А-А, В-В), при этом запол-
Рис. 51. Полиэдрическая
модель структуры молиб-
денита, MoS2
Рис. 50. Полиэдрическая
модель структуры флюорита^СаР^
ненные молибденом тригональные призмы заключены между дву-
тетраэдрическими пустотами, а пустые призмы - между
двумя октаэдрическими.
§ 6. Трансляционные элементы симметрии -
плоскости скользящего отражения и
винтовые оси
Пространственная решетка - не единственный элемент
сим; етрии, отличающий конечный кристаллический многогран-
ник от бесконечной кристаллической структуры - дисконтини-
ума. К специфическим для трехмерного бесконечного законо-
мерного узора элементам симметрии относятся также плоскос-
ти скользящего отражения (g) и винтовые оси (ng ).
Оба новых элемента симметрии наряду с отражением
или поворотом предполагают также поступалие t вдоль
плоскости или оси на,некоторую долю трансляционного векто-
ра Т. Операции отражения (поворота) и скольжения коммута-
тивны, т.е. последовательность, в которой они производятся,
роли не играет.
Элементы симметрии, включающие трансляционные компонен-
ты, называют трансляционными, или открытыми, все прочие -
закрытыми. Первые удобно также называть элементами микро-
симметрии, а вторые - элементами макросимметрии.
Па рис. 52 показаны некоторые трансляционные элементы
симметрии. Так, в мотиве из кирпичей (рис. 52,а), уложенных
по центрированному закону, помимо знакомых нам зеркальных
плоскостей симметрии, проходящих между .двумя кирпичами и
через их середины (тпу ,ту), можно заметить и .другие плос-
кости, расположенные между плоскостями т; отражение в них
сопровождается скольжением вдоль Тк на расстояниеНа
рис. 52,6, представляющем укладку многогранников по 1(=Г)-
тетрагональному закону, хорошо видны поворотные оси 4-го
порядка, проходящие через центры фигур (поворот 1-2). Не-
сколько труднее заметить трансляционные оси симметрии, про-
ходящие по вертикальным ребрам многогранников; поворот на
90 вокруг такой оси сопровождается сдвигом (скольжением)
вд ль нее, при этом фигура I совмещается с фигурой 3. Фи-
гуры, связанные операциями такой оси, расположены вокруг
51
Ряс, 52. Иллюстрация трансляционных элементов оижетрии:
а) плоскость скользящего отраженжя;
б) винтовая ось 4-го порядка
нее по винтовой линии, отсюда название оси -винто-
вая ось симметрии. Порядок оси определя-
ется, как и в случае поворотных осей, элементарным углом
поворота оС. В данном случае перед нами винтовая ось 4-го
порядка.
Трансляционные элементы симметрии бесконечного узора
- кристаллической структуры - воспринимаются в конечной
фигуре (кристаллическом многограннике) как сходственные
элементы, лишенные трансляционной компонентн, т.е. плос-
кости скользящего отражения будут восприниматься как зер-
кальные плоскости m, а винтовые оси любых порядков - как
поворотные оси тех хе порядков. Сложные оси (п или it) не
могут иметь трансляционной компоненты, поэтому они не из-
меняются при переходе от бесконечного узора к конечной фи-
гуре.
Остановимся более подробно на трансляционных элемен-
тах сижетрии.
Плоскости скользящего отраженжя ( р ). Величина сколь-
жения любой плоскости скользящего отражения равна половине
трансляционного вектора, совпадающего с направлением сколь-
жения, так как двукратное отражение дает фигуру, эквивалент
ную (конгруэнтную) исходной и отстоящую от нее на величину
52
tbS|<N
f-fS $+
Рис. 53. Действие и обозначения вертикальных и горизонтальных плоскостей симметрии
тли а. , Ъ, с. Здесь и далее черные флажки изображают ^изнаночную сторон?
белых. Высоты флажков относительно плоскости чертежа z , z , | + z , |-z и т.д,
отмечаются на рисунке соответственно	{+”, "|-и и т.д.
Рис. 54. Плоскости а , Ь , с
в структуре углекислоты
трансляционного векто-
ра Т .
Плоскости сколь-
зящего отражения удоб-
но разделить на два
типа. В плоскостях пер-
вого типа скольжение
происходит вдоль од-
ного ребра
ячейки, т.е. вдоль
одной коор-
динатной оси;
наименование такой
плоскости (а , Ъ , или с)
определяется осью (X,
У или Z), вдоль которой это скольжение направлено. При из-
менении наименования координатных осей меняются соответст-
венно и обозначения плоскостей этого типа. На рис. 53 пока-
зано действие плоскостей тп , а , Ь и с и их графическое
изображение. Плоскости а , b , с нетрудно увидеть на струк-
туре кристаллической углекислоты (рис. 54).
В плоскотях второго типа скольжение происходит одно-
временно вдоль двух координатных осей,
т.е. вдоль двух ребер ячейки Бравэ
следовательно, результирующее скольжение совпадает с диаго-
налью грани ячейки, образуя косой угол с коор-
динатными осями, поэтому такие плоскости называют, к л и -
ноплоскостями
Различают клиноплоскости
Рис. 55. Клиноплоскости п (а) и d (б):
а) грань "пустая", трансляционный вектор
решетки вдоль ее диагонали ш) равен
всей диагонали (D), поэтому величина сколь-
жения плоскости |tf = ,^l= i ;
центрирована, Та = f, поэтому
~ ~z 4
Рис. 56. Действие и обозначения клиноплоскостей
п и d; черные флажки - изнанка белых
(грань ячейки, вдоль диагонали которой происходит скольже-
ние, нецентрирована) и d (грань центрирована). Величина
скольжения t клинопжскости, как и любой другой, равна g,
но для. п-плоскости g (рис» 55,а), так как вектор пе-
ренова вдоль диагонали пустой грани (Та) равен всей диаго-
нали (D), а для плоскости d , т.е. клиноплоскости, паралле-
льной центрированной грани, вектор Td вдвое короче (|Tdl=
поэтому Iff - g ~ £ (рис. 55,6). Клиноплоскости п и d в
отличие от плоскостей а , b , С не меняют своего обозначе-
ния при изменении наименования координатных осей. Действие
клиноплоскостей п и d и их графическое изображение пред-
ставлено на рис. 56; их можно увидеть на структуре хлорис-
того палладия и алмаза (см. рис. 57, а,б).
Все сказанное справедливо для плоскостей скользящего
отражения, параллельных двум координатным осям, т.е. парал-
лельных координатным граням ячейки Бравэ. Если же плоскость
скользящего отражения совпадает с вертикальным диагональным
сечением ячейки, т.е. параллельна, только одной координатной
55
Рис. 57. а) клиноплоскости
и в структуре PdCto,
б) клиноплоскости d в
структуре алмаза
оси Z (одному ребру ячейки
С ), то при обозначении
плоскости принимают во вни-
мание расположение скользя»
щей компоненты (t ) плоско-
сти лишь относительно этой
координатной оси: если век-
тор t параллелен оси Z , то
плоскость обозначают с ,
если он перпендикулярен
этой оси, плоскость обозна-
чают Ь , если же вектор t
составляет с осью Z косой
угол, плоскость обозначают
п или (/.
Винтовые оси симметрии
(Мй), Винтовые оси отлича-
ются большим разнообразием,
чем плоскости скользящего
отражения, так как все воз-
можные в кристаллических
многогранниках поворотные
оси имеют в дисконтиниуме
по несколько разновидностей
Поворот вокруг винтовой оси п-го порядка сопровожда-
ется смещением вдоль оси на величину скольжения t , назы-
ваемую ходом винтовой оси. При полном повороте на
360° (п операций) суммарное смещение либо равно величине
трансляционного вектора Т, либо кратно ей, т.е. nt = яТ,
где я - целое число, причем п 1. Для оси величина
скольжения t =	• придаваялазные значения 5 , получим
= п »	» •••»	» к Таким образом, выясним как
возможную величину скольжения t , так и общее число осей
данного порядка (винтовые плюс поворотная), которое оказы-
вается равным порядку оси. Так, для и = 6 величина сколь-
жения в долях трансляционного вектора в направлении оси 6
(Тс) составляет	соответствующие
оси обозначаются 6j, 62, 6^, 64, 65, 6g = 6. На рис. 58
показано действие и обозначения осей симметрии.
56
Рис. 56. а) горизонтальные
оси 2-го порядка (поворот-
ная и винтовая),
б) поворотные и винтовые вер-
тикальные оси 2-го, 3-го,
4-го и 6-го порядков
5
+<х • Э+ * 5^
Paj: а) в
кислоты оси X21к связы-
вают молекулы 1 и 4, оси
Ап }УоЛмолекулы 1 и 2,
оси ь - молекулы I и
0) оси 41 И 43 в струк-
туре алмаза; в) оси 49
в структуре рутила;
bL™Jq6s в структуре
вюрцита
и:	Перн осей п,.ж пй, ®и которых & ♦ п (6j и 65,
32 - левая	* е а I 43, 3^ и 32) называют энантиоморфными, так
Рио. 60. Винтовые оов в ^к’црГодаваковой величине сжолиеетя оет различаются
кристаллических огрукту- ,,ть направлеииеы врадеаиа (рис. 59). Удобны поатоыу таете
оах: а) В -------------“03Вачеяа 6_Х = 65, 6_2 = 64, 4	- 43. 3., = Ось о
иеыьшям ивдексом (61, 62, 4£ и 31) обычно считают правой,
с большим (66. 64> 43 и 32) - левой; оси 63, 42 , 2± - ней-
тральные. Если суммарное смещение при п операциях равно
од ому трансляционному вектору f, то оси называются одно-
заходаыми (2j, 34 и 3^. и 4_г 6* и б^Мали оно рав-
но 2?, то оси двузаходные (42, 62 и 6_2), если смещение
равно 3f, то ось трехзаходная (63).
Проследить действие винтовых осей 2-го порядка можно
на структуре углекислоты (рис. 60,а). Винтовые оси 4-го
порядка хорошо видны на структуре алмаза (рис. 60,6) и ру-
тила (рис. 60,в), ось 6g - на полиэдрической модели струк-
туры пирротина (см. рис. 47) и вюрцита (рис. 60,г).
§ 7. Взаимодействие элементов спметрии
кристаллических структур
Считая правила взаимодействия элементов симметрии ко-
нечных фигур известными10^, остановимся на сочетаниях эле-
ментов симметрии кристаллических структур.
Особенность мииросимметрии заключается в том, что про-
странственная решетка как элемент симметрии (фактически
трансляционные векторы решетки f ) не только размножают
все остальные элементы симметрии, создавая бесконечное
множество параллельных друг другу одинаковых осей и пло-
скостей симметрии, но и взаимодействуют с ними, порождая
новые, сходственные им элементы симметрии. Кроме того, при
взаимодействии осей и плоскостей симметрии между собой
участвуют и их трансляционные компоненты (t ), выступая в
порожденных элементах стшетрм как векторные суммы тран-
сляционных компонент. При исследовании взаимодействий эле-
ментов симметрии кристаллических структур (дисконтиниума)
Удобно как трансляционные векторы решетки (Т), так и тран-
10)1Т
книгу Ю.Г.Загальской и Г.П.Литвинской
геометрическая 1фисталлография”, (1973),
59
Рис» 61. В базоцентр$,
рованноЙ решетке « ,
сляционныи вектор Т?
параллельный горизон-
тальной плоскости тп ,
превращает ее в плос- __
кость 71 , совпадающую
с т , т.е. тп =п .
Фигуры I и 2 связаны
плоскостью т/I. 2 и 2'
вектором Тл, I и 2'~
ПОрОВДеННОИ ПЛОСКОСТЬ!
п , совпадающей с т
сляционные компоненты (t ) раскладывать на две составляю-
щие; если одну из них направить вдоль того элемента сим-
метрии, взаимодействие которого с поступанием рассматри-
вается (t«), то другая окажется перпендикулярной к нему
(tx). Составляющая t«, вливаясь в элемент симметрии, со-
здаст новый, сходственный элемент, на который далее воз-
действует компонента ti.
Используя модельный способ доказательства, остановим-
ся на конкретных примерах.
I. Возникновение элементов симметрии в результате
взаимодействия осей и плоскостей симметрии с трансляцион-
Рис. 62. Сочетание повороту вокруг оси п -го порядка
с трансляционным вектором Тх приводит к возникновению
новой оси того же порядка и типа^расположенной в
центре п-угольника со стороной |Ъ|. Фиг. I и 2 свят
заны рсходной (вершинной) осью, 2 и 2'- вектором Т,
I и 2 - новой (центральной) осью, тождественной
исходной
2,	2\	2;
Рис. 63. Взаимодействие плоскостей симметрии, осей
г-го порядка и центра инверсии с трансля-
ционным вектором решетки (Т), перпендику-
лярным к осям и плоскостям симметрии.
Фигуры I и 2 связаны заданным, элементом
симметрии, 2 12'- вектором Т, I и 2'-
нов и элементом симметрии, тождественным
заданному и сдвинутым на f/2
, смещена на
результате сов-
7г+
%+\5^
Рис. 65. Примеры участия трансляционной компоненты порожда-
ющих элементов симметрии в образовании новых эле-
ментов. Фиг. I и 2 связаны одним из исходных эле-
ментов симметрии, 2 и 3 - другим, I и 3 - порож-
денным элементом симметрии;
а) поворотная ось 2-го порядка, возникшая при
взаимодействии плоскостей т и а , смещена на
0. £ = £>);
о) винтовая ось 2т, возникшая в результате сов-
местного действия плоскостей тп и с , совпадает
с линией их пересечения (tu- tc , Tj_~ 0);
в) поворотная ось 2-го порядка, возникшая при
взаимодействии друх плоскостей п , смещена на
~ 4 ’ №	1 (^’х = 5	>
сле^ева^ельно, tn = 2Д = Т^, a Z= ta+ tb =
ными векторами решетки (Т):
а)Ъ = тогда tx- 0. На рис. 61 показано взаимодэд
ствие горизонтальной зеркальной плоскости (т) с трансад,
ционным вектором базоцентрированной решетки Tq, в резуль>___
тате которого возникает элемент симметрии, сходственный | id
данному (плоскость симметрии п ) и совпадающий с ним, чтой-£
Z |
т
?•
~2'
к элеме!
.»	ип взаимодействует:
tu+tj,. Компонента , вливаясь в исходный эл(
Л”*"	>т	------- -г
64. Трансляционный вектор Т косо расположен к эдс:.;с:
jry симметрии, с которым он взаимодействует:
Т	Компонента Тп, вливаясь в исходны_____
мент симметрии, создает новый, сходственный, эле
' мент симметрии, который в результате взаимодейс:
вия с tl окажется смещенным. Фиг. I и 2 связаны
запанным элементом симметрии, 2 и 2'- вектором 1
I и 2'- новым, сходственным, элементом симметрий
в формуле симметрии отмечают знаком тождества:п (втп);
6)7и = 0, тогда Е= Т. Рис. 62 и 63 показывают, что
производный элемент симметрии идентичен исходному, но не
совпадает с ним. Для разных элементов симметрии величина
и направление смещения различны;
B)t„ £ 0, ti / 0. Из рис. 64 очевидно возникновение
сходственного элемента симметрии, не совпадающего с задан-
ним; в этом случае параллельно друг другу, чередуясь, рас-
полагаются сходственные элементы симметрии, что в формуле
симметрии показывают, заключая один из них в скобки, напри-
мер: т (с), 2(2^), 4(42).
П. Возникновение новых элементов симметрии при участии
трансляционных компонент t порождающих элементов симметрии.
63
Рис. {Гб. Взаимодействие	< плоскости симметрии и центр инверсии смешаются в
“составни" элементов сиж а) К ка —(или в направлении Tj. на 2
метрии с трансляционным ваправлении Гх 2	и (поворотные и винтовые)
вектором реиетю! Т:	оси симметрии порядка п. у
а) с вектором Твзаимодей. ' в _ npHTD п -угольника со стороной i т.е.
б)Твек«Л=	в направлении, образующем с ix угол,
ствует oob^S*i включенная смещают	_2£(п ^де <£~ элементарный угол поворота оси,
нее ось 2 (5J = tc + tr , равны*	Л-! для Т± ;
a tc Лс	оеирХа порядков и типов сливаются в од-_
I льется" в ?, создав новув	(„оппимеп ось 6 включает оси 2 и 3, ось 4 совпала
ось ? с оибойяточкой, сдано* оси 1нащ> * тшяе заишчеНа ось 2, а в оси -
нугой на f = f;	перевеет « °°“Л	10 элемевт такой составной оси вза-
тит ету ось 4 в центр квад ось 2± в i. . >	а- , „ + \ неаависимо и по собст-
ратасо стороной if |i I El; имодействует с вектором Тх (.или ix> не
2) tn создаст из оси 2 ои___тим» (пис. 66.а):
2j, передвигаемую векторе»
S на
в) с вектором Т взаимодей-
ствует ось 3 = 3x1
венным правилам (рис. 66,а);
г) сложные оси, преобразование которых представлено
мнимыми операциями (например, 4), перемещаются по тем же
законам, что и поворотные оси, однако под действием itlосо-
бые точки этих осей сдвигаются вдоль оси как центры инвер-
сии (рис. 66,6);
д) если действие сложной оси может быть заменено
3 = 3*1, 6 = ,.,.), то каждый из этих заместителей
взаимодействует с трансляционными векторами независимо по
вышеприведенным правилам (рис. 66,в).
Рождение новых элементов симметрии под действием Т
хорошо иллюстрируют рисунки из альбома Эшера (рис. 67).
§ 8. Пространственные, или федоровские
группы симметрии
мнит	реальными операпиями простых элементов, симметрии (например,
мент симметрии, порождении	_
по правилам махфосимметрив
(без учета трансляционных
компонент), действует сум-
марный вектор ( tcyM), т.е
тот, который получится при
сложении трансляционных ко)
понент (t, и t2 ) исходных
элементов симметрии. Права
। взаимодействия те же, что I
трансляционного вектора решетки (Т). На рис. 65дока-
заны примеры для^всех^случаев: a) tii= 0, тогда tCifAf= tj.,
б) = 0, тогда	~^и £	£ 0.
Рассмотренные примеры взаимодействия осей и плоскости
симметрии с векторами t (или Т ) позволяют сделать некото-
рые общие выводы.
Если t±£ 0(иди Т1/ 0), то новые элементы симметрии н«
совпадают с исходными, а смещаются относительно них в па-
раллельном положении, причем:
Совокупность всех операций симметрии кристаллической
структуры (бесконечного закономерного пространственного
узора) называется пространственной группой симметрии. Вы-
вод всех пространственных групп симметрии был закончен к
1890 г. русским кристаллографом Е.С.Федоровым и к 1891 г.
немецким геометром Шёнфлисом. К окончательному результату -
- 230 групп - первым пришел Е.С.Федоров, поэтому простран-
ственные группы часто называют федоровскими.
Каждый кристалл по внешней симметрии (макросимметрии)
относится к о,иной из 32 точечных групп, а симметрия его
а-1478	65
для
64
4-
’ис, о7. Рисунки из альбома Элера, иллюстрирующие рожден?,
новых элементов симметрии под действием трансля-
ционного вектора Т:
а)	периодичность зеркальных плоскостей и осей
2-го порядка равна Т/2;
б)	три трансляционно неидентичные системы осей I
3-го порядка
а ого узора (микросимметрия) отвечает одной из 230 про-
ои2ствешшх (федоровских) груш.
При выводе пространственных групп наиболее удобно ис-
ходить из 32 кристаллографических точечных групп симмет-
т е. точечных групп, сочетающихся с трехмерными решет-
ами. Добавив к каждой из 32 точечных групп все допустимые
ею трансляционные комплексы (решетки Бравэ), придем к про-
странственным группам, в которых целиком сохранился как
осев й, так и плоскостной комплекс точечных групп, т.е. к
так называемым симморфным труппам. Из точечной
группы 41771 ш, например, получим Ptmnm, Стп-mm, Гттптг) И
Гтптпгп. В числе 230 пространственных групп 73 - симморфные.
Получая симморфные группы, нужно иметь в виду, что разли-
чие в расположении элементов симметрии относительно тран-
сляционных векторов решетки может привести к разным груп-
пам. Так, Р32тп/ Р4тп2, поскольку в первом случае кратчай-
ший горизонтальный вектор совпадает с осью 2-го порядка, а
во втором - с нормалью к плоскости симметрии. Различными
будут группы Стт2 и Сп2тп ,P3niI и РЗЬп и т.п. Для получе-
ния несиммбрфных групп надо в каждой симморфной последова-
тельно заменить все порождающие макроэлементы симметрии на
их микроэквиваленты, тогда, например, из Pmm-m получим
Рштиц , РЬатп , РЬса ,...; из Стптптп- С mm а , Стеа , Осса, и
т.д. Несимморфные группы Е.С.Федоров подразделил на
гемисимморфные (их оказалось 54) и а сим-
морфные (их 103). В первых полностью сохранился лишь
осевой комплекс их точечных групп (например, Phan = Р | 2 2
•р п 2 2 2\	х-х-	ьап
reem = F - - -), во вторых - ни осевой, ни плоскостной
комплексы точечных групп полностью не сохраняются (напри-
мер, Pbca = р 2 2 2l P-ntnn - P —1 -1 2< Peen - P -
Pinna = p 2 2 2?/ a’ P ma“ P n m a.’ Pccri “ P с c n’
m 7i a '•
Обратная задача - переход от пространственной группы
к соответствующей точечной - значительно проще. Заменив
все плоскости скользящего отражения плоскостями зеркальны-
и все винтовые оси - поворотными соответствующего поряд-
т.е. отбросив t ), переносим все элементы симметрии
отб ельно самим себе до их пересечения в одной точке (т.е.
Стсц таеМ Т На1ФИмер, пространственные группы Phan,
» mma, Pddd. обратятся в одну точечную -тж Если
67
Рис. 68. Переход от аспекта
С2тт к стандартному для групп
C2v аспекту Amm2 ( = Втпт2)
в пространственной группе парал-
лельно .друг другу проходят оси
разных порядков, то при переходе
к точечной группе они совпадут,
сольются, и в символ запишется
старшая из них - процесс, обрат-
ный показанному на рис. 66: оси
2, 3 и 6 сольются в ось 6 и т.д.
Ниже приводятся конкретные
примеры вывода пространственных
(федоровских) групп симметрии,
подчиненных некоторым точечным.
Метод вывода, которого будем
в основном придерживаться, - ком-
бинаторный, предложенный Н.В.Бело-
вым в работе “Классный метод вы-
вода пространственных групп сим-
метрии" ("Труда Ин-та кристалло-
графии АН СССР", 1951, выл, 6).
§ 9. Вывод пространственных групп симметрии,
подчиненных точечной группе mm2(C2v ),
и их графическое представление
Добавив к группе возможные для ромбической систе-
мы трансляционные комплексы (решеттр? Бравэ), получим сим-
морфные группы. При этом надо иметь в виду, что в оазоцент-
рированной решетке единственная поворотная ось 2-го порядка
может оказаться либо перпендикулярной к центрированной паре
граней (Стптп2), либо параллельно ей (С2штп или Cm2-m ). Та-
ким образом, число симморфных групп в данном случае будет
на единицу больше числа решеток Бравэ в ромбической системе
Pmm2, Im m2, Ртпт2, Сття2 и C2mm( =Cm2m). Чтобы последнюю
группу представить в стандартной для класса C2v установке,
повернем ячейку вокруг горизонтальной оси на 90°. Тогда
68
69. Процесс вычерчивания
группа С21т1тп изобразится
(рис. 68) символом A mm 2
(=B-mm2)ri).
Несимморфные группы
целесообразно выводить
для каждой решетки Бравэ
в отдельности, при этом
за порождающие элементы
удобно принимать плоскос-
ти симметрии, считая ось
порожденной.
Пространственные
группы с примитивной
решеткой Бравэ. При Р-ре-
шетке плоскости скользя-
щего отражения могут иметь
либо вертикальное сколь-
жение (плоскости с ), либо
горизонтальное (плоскости
а и Ь), либо, наконец,
смешанное (плоскости я).
Заменяя в симморфной груп-
пе Pmm2 лишь одну из зер-
кальных плоскостей скольже-
ния, получим еще три группы:
Рте . • •, Рта . . •, Finn ... •
Замена обеих зеркальных
плоскостей даст три группы
с одинаковыми- плоскостями -
Рсс ..., РЬа ...» Рпп ... ,
а также три группы с плоско-
Рисъ 69. Процесс вычерчивания
графика пространственной группы
Рта 2
II) Н —
международные символы, отражая ориентировку особых на-
правлений относительно координатных осей, могут видоиз-
меняться с преобразованием координатной системы (С2тпт
—*-Amm2), поэтому наряду с рациональными международными
символами необходимо указывать символ Шёнфлиса; будучи
не привязан к координатной системе, он служит своеобраз-
ным ключем" при пользовании таблицами пространственных
групп - 02mm = С^ = Атпт2. Верхний индекс символа Шён-
отражает лишь последовательность, в которой
•к.шенфдис выводил эти группы.
*
69
стями разного типа - Рса ...» Рис ...» Рпа ... .
Очевидно, что Рте ...= Рст...» Рта... = РЪт...,
Р са ... = РЪе ... и т.д.
Таким образом, при Р-решетке к одной симморфной группе
добавится 9 несимморфных.
Чтобы начертить график какой-либо из полученных групп,
например, Pm а ...(будем изображать одну ячейку Бравэ в стан-
дартной проекции), зададим трансляционные векторы вдоль ле-
жащих в плоскости чертежа осей X и У и )и нанесем
две порождающие плоскости - тх и п</(рис. 69,а). Затем, учи-
тывая, что периодичность одинаковых плоскостей симметрии в
перпендикулярном к ним направлении равна | (см. рис. 63 и
67,а) покажем остальные плоскости (рис. 69,6). Кроме поро-
ждающих элементов симметрии - плоскостей - на графике долж-
ны быть показаны и порожденные, в данном случае оси 2-го
порядка. Характер и позицию порожденной оси симметрии модно
получить непосредственно на трафике, размножая асимметрич-
ную фигурку порождающими плоскостями симметрии (см. рис.65,а;
Процесс получения порожденной оси можно записать в виде
произведения порождающих операций:	у
тпк» пу = тпх • тпу •	= 2g»>ta = 2g,
т.е. ось 2, смещенная на |а= |а. Теперь можно привести пол-
ный символ группы (Рта... = Рта2) и убедиться в том, что
она гемисимморфная (рис. 69,в).
Для окончательного оформления графика необходимо выб-
рать начало координат в соответствии со стандартом Интерна-
циональных таблиц, а именно: в самой симметричной точке12',
при этом максимально жестко фиксированной элементами макро-
симметрии, т.е. обладающей, как принято говорить, ’’минималь-
ным числом степеней свобода". В этом смысле особая точка
предпочтительнее, чем поворотная ось симметрии, последнюю
предпочтут зеркальной плоскости.
Если есть несколько позиций с одинаковой величиной
симметрии (например, тптптпи 42m или 222 и 2/тп), то оста-
12)
’ Количественной мерой симметричности позиции служит ее
величина симметрии , она может быть
определена числом точек, на которое расколется точка,
выведенная из этой позиции в "чистое поле". Так, вели-
чина симметрии группы mm2 равна четырем, группы ттптп-
восьми, группы 7П- двум. Подробнее см. далее в §12 о
правильных системах точек.
70
уливаются на центросимметричной. При невозможности ре-
шять вопрос однозначно (например, в группе Р6с2 - позиции
32 и 6) приходится прибегать к справочнику.
В- пространственных группах, соответствующих классу
тптп.2 особые точки отсутствуют, поэтому лучшими позициями
для начала координат будут точки на оси 2, совпадающей с
линией пересечения двух зеркальных плоскостей (величина
симметрии 4), но такие позиции существуют только в симморф-
ной труппе Ртптп2, поэтому далее довольствуемся величиной
симметрии, равной двум, т.е. симметрией позиции 2 или пг,
причем точка на оси 2 (одна степень свобода) предпочтитель-
нее точки на плоскости т(две степени свободы). При отсут-
ствии поворотных осей начало координат приходится выбирать
на плоскости иг , причем для удобства сопоставления трафи-
ков разных трупп эту начальную точку выбирают не произволь-
но, а либо на винтовбй оси, лежащей в этой плоскости
(труппа Рте 21), либо на линии пересечения плоскости тп- с
трансляционной плоскостью (группа Pmn21), хотя такое поло-
жение не делает величину симметрии
выше двух и не уменьшает числа
степеней 'свободы. Если позиции с величиной
симметрии выше 1 отсутствуют, начало выбирают на осях 2j
(труппы Рс а 2£ и Рпа2|).
В рассмотренном выше примере - группе Рта2 - начало
координат выбирают в позиции с одной степенью свобода - на
оси 2 (рис. 69,г).
Пространственные группы для непримитивных решеток Бра-
вэ. Для вывода таких групп следует прежде всего выяснить,
как взаимодействует дополнительный трансляционный вектор
(векторы) решетки с порождающими элементами симметрии. Так,
в G-ячейке, где Тс '=• ta+ , для плоскости симметрии 1-й
позиции fb = tn , a ta =t_L‘ Идрис. 64 очевидно, что,
влившись в исходную плоскость, tn создаст новую плоскость:
из тп (n?x*fb =&х) и и из с (сх • tc = пх) и обратно, тп из
0-^и с из п . Вторая компонента дополнительной трансляции
Их) передвинет эту новую плоскость на	Так же
взаимодействуют с вектором Тс плоскости 2-й позиции.
Итак, при С-решетке вертикальные зеркальные плоскости
771) неизбежно сопровождаются "вставными" плоскостями с
71
горизонтальным скольжением ( Ъ , а ), а плоскости с - плос-
костями п. Иными словами, независимыми будут уже не че-
тыре порождающие плоскости, как при Р-решетке, а лишь две.
Отсюда очевидны три группы: Cmm2 = Ста2 = СЬа 2,
Ccd 2 = Gnc 2 = Спп2,
Стс2^= 0^2^ = Сса 2£= Спа 2t
или в записи развернутыми символами: Cm(b)m(a)2(2),
С б (п) с (п)2(2),
Cm(b) с (п)^.-
"Вставные" оси 2-го порядка можно получить либо как
результат пересечения двух плоскостей симметрии, либо дей-
ствием на исходные оси 2-го порядка дополнительным трансля-
ционным дектором. Вектор Tq перпендикулярен к осям, поэтому
tn = 0, ti = таким образом, новые оси окажутся тождест-
венными исхо.цным. но сдвинутыми относительно их на
*'*'	гТрт
(22 • Тс = 2Z If Ь*
Те же приемы используют при выводе остальных групп с
непримз-тивными ячейками, однако в A-я ч е й к е вектор
Тд ( =fb +tc ) по-разному ориентирован относительно порож-
дающих плоскостей, поэтому они взаимодействуют с этим век-
тором неодинаково. Так, располагаясь в самой плоскости
I-й позиции, вектор Тд заставляет одну и ту же
плоскость симметрии выполнять одновременно две функции:
работая как плоскость зеркальная, она действует и как кли-
ноплоскость п [записываем тп (= п )], таким же образом, Ь (=с)
Тд=тгх, 6Л-Тд = сх и обратно, Тд	Тд|
= Ъх ]. Для плоскостей 2-й позиции очевидна чере-
дуемость плоскостей: тп ( с ) и а (п ).
Различие в поведении плоскостей I-й и 2-й позиций
приводит не к трем, как при С-решетке, а к четырем группам:
Amm2, Ата2, АЬтп.2 и АЬа2. Обратим внимание, что Ата2 /
Abm.2, но Ата2 = ВЬтп.2.
Полные символы групп: Am (= п )m ( с )2(2i ),
Ат (=п) ц (п )2(2А),
АЬ (= с )т( с )2(2i).
Ab (= с ) а (п )2(2Х).
В пространственных группах с объемноцентрированной
решеткой дополнительная трансляция Tj расположена косо
72
)}2(2р = Гтптп.2.
всем элементам симметрии, что приводит к чередованию
К° плоскостей симметрии обеих (равноправных) позиций, так
и осей 2-го порядка.
Сочетания двух независимых плоскостей симметрии дадут,
как и в случае С-решетки, три группы - Imm2, Iba.2, Im a 2
или в развернутом виде: Im (n )т (п )2(2±),
lb (с )а(с )2(2£),
Im(n ) а ( с )2(2^).
В группах с Е-решеткой приходится учитывать влияние
каждого из трех трансляционных векторов, иными словами,
как векторов, лежащих в самой плоскости, так и косо распо-
ложенных к ней. Таким образом, для плоскостей симметрии
обеих позиций характерны как двойственность, так и череду-
емость. Рассмотрев взаимодействие плоскостей симметрии
обеих позиций с дополнительными трансляционными векторами
^в» убедимся, что в одной группе окажутся все
четыре типа плоскостей симметрии:
Ет(= и ){с (=Ъ)}т(=и
Казалось бы, что этим исчерпаны все возможности для
пространственных групп класса mm2 с Е-решеткой Бравэ, од-
нако, нельзя забывать, что параллельно центрированным гра-
ням ячейки могут проходить не только клиноплоскости п ,
но и клиноплоскости другого типа, а именно, "алмазные"
плоскости d.(c. 55). Так как при взаимодействии плоскостей
симметрии, пересекающихся под прямым углом, возникают оси
2-го порядка-поворотные (?= Т ) и винтовые (t=> 3), то‘пло-
скости d (для них равно |f ) могут в данном случае пере-
секаться лишь с плоскостями d. Поэтому кроме группы Emm2
в этом классе имеем еще лишь одну группу - ЕЛ <12.
На рис. 70 приведены графики некоторых групп класса
mm2 с непримитивными решетками Бравэ.
фи вычерчивании графиков пространственных групп с
непримитивными решётками Бравэ рекомендуется сначала изо-
бразить основные плоскости симметрии, записанные в^имводе
(°НИ оконтурят ячейку и повторятся на расстоянии
а затем вставить чередующиеся с ними плоскости (результат
взаимодействия исходных плоскостей с дополнительными тран-
оляциями). Получив оси 2-го порядка как результат взаимо-
отвия плоскостей симметрии, полезно проверить, связаны
73
Ima2
ли оси двух систем друг с другом специфическими трансляция- I
ми нецримитивной решетки. Воцрос о выборе начала координат
решается так же, как и в Р-решетке.
§ 10. Приемы вывода пространственных групп,
подчиненных классу татт, и построение
их графиков
При выводе пространственных групп голоэдрического
класса ттпт могут быть использованы гемиэдрические (геми-
морфные) группы класса mm2. Для этого надо добавить
74
удваивающую операцию
ной Пространственной
сами в себя. '
так, чтобы элементы симметрии исход-
группы не размножались,а преобразовы-
’акими добавочными операциями могут
быть, например, операции 2-го рода - либо отражение в гори-
зонтальных плоскостях разного типа, либо инверсия в точках
разных позиций.
Некоторые из полученных таким образом трупп, хотя и
запишутся разными символами, на самом деле - тождественны
0 различаются лишь наименованием координатных осей. Напри-
мер, Р^атп = Ртпстп = РтптпЪ; РтпаЬ = Ртпса. = РЬспг . Так, в
случае примитивной решетки Бравэ из 10 пространственных
групп класса ттп2 сначала получим 40 символов и, лишь исклю-
чив дубликаты, придем к 16 различным группам ромбической
голоэдрии.
Значительно изящней, разумеется, метод вывода голоэд-
рических групп-, предложенный Н.В.Беловым, заключающийся
в комбинировании трех независимых плоскостей симметрии. На-
зовем условно плоскости, которые не изменяют своего наиме-
нования при преобразованиях координатной системы (т и п ),
"удобными", остальные (а ,Ъ , с ) - "неудобными". Комбини-
руя три плоскости, единственную в своем роде поместим в
символе на третью позицию,-причем, если это плоскость а
или Ь , отдадим предпочтение той установке, при которой
скольжение плоскости будет направлено вдоль оси X, это
позволит получить символы всех 16 групп с Р-решеткой сразу
в стандартном аспекте.
I. Все три плоскости "удобные": Рптпт, Pnnn, Prnmn,
Pnnm.
П. "Удобных" плоскостей только две: Ртпта, Ртгпа ,
Pmna. , Рптпа. Обратим внимание, что Р-nma/ Ртпа
(но Рпта = pmnb ), так как в группе Pnma трансляционная
компонента плоскости а перпендикулярна клиноплоскости, а
В группе Ртпа - зеркальной плоскости.
Ш. "Удобная" плоскость лишь одна; при этом трансляци-
онные компоненты двух других плоскостей могут быть
либо однотипными (обе вертикальные или обе горизонтальные),
либо разного типа. Для первой возможности имеем Рсстп ,
Роси, и Pbam , Pban., для второй - РЪст. и РЬск .
75
Рис. 71. К построению графика
федоровской группы pnmo.
1У. "Удобные плоско-
сти отсутствуют. Можно пред-
юложить лишь два случая:
1ибо векторы скольжения
;дух плоскостей параллель-
ны друг другу, а трансля-
ционная компонента третьей
плоскости перпендикулярна
ям, либо векторы скольже-
ния всех трех плоскостей
взаимно перпендикулярны.
Первый случай дает группу
Рсса (= Pbaa = Pbcb ), вто-
рой - РЬса .
Не останавливаясь на выводе
пространственных групп
ромбической голоэдрии с
непримитивными решетками,
приведем графики некоторых
из них в приложении.
При построении
графиков групп
класса mmm пользуются
теми же приемами, что и для групп класса mm2, т.е. сна-
чала изображают плоскости симметрии, записанные в символе,
а затем получают производные элементы симметрии - оси 2-го
порядка и центры инверсии. Так, в группе Pnma (рис. 71,а)
взаимодействие плоскостей пх я а2_ даст (2±) , смещенную
с линии пересечения плрскстей на	Действительно, .
(пх-а2) = (mxtbtc).(?nzta) = (mxmzFb).(fc£a) = (2t )у[±2-±-1с].
Подобным же образом получаем оси (2рх и (2\)z. Центр инвер-
сии возникает как результат взаимодействия любой оси 2-го
порядка и перпендикулярной_к~ней нлоскбсти^симметрии, sanpi-
ер,	(2^'ta) • C^x^-fa^c) ~	=
_	4 Tb 4 J
Начало координат почти во всех группах ромбической
голоэдрии точно фиксировано13^ - это либо центр инверсии
13)
' Исключение составляет группа Рттпп, где начало приходит-
ся выбирать в комплексе mm2, а не в i , так как симмет-
рия 1-й позиции в два раза выше симметрии 2-й.
2	~
(в комплексах m-mm, , I) либо точка пересечения осей -
222 (если конкурируют комплексы, одинаковые по величине
симметрии - Д и 222 - предпочтение отдают центросимметрич-
HOjjy). В рассмотренной выше группе Р-nma. выбор начала ко-
ординат очевиден (рис. 71,6).
§11. Пространственные группы средней и
высшей категорий
В настоящем кратком руководстве остановимся лишь на
приемах вывода пространственных групп тетрагональной геми-
морфяи (класс 4mm) с примитивной решеткой Бравэ в их гра-
фическом представлении.
В качестве порождающих элементов симметрий удобно
взять плоскости (2-я и 3-я позиции символа точечной труппы).
Вторая позиция символа при Р-решетке Бравэ может быть за-
нята плоскостью любого разрешенного здесь типа: тп., с ,
п . На 3-й позиции даже при Р-решетке имеет место чередо-
вание разных плоскостей, поскольку трансляционный вектор
решетки (Т^ или Tj,) не перпендикулярен к плоскостям этой
позиции и при разложении дает две компоненты - tu и tj,(cM.
рис. 64). Таким образом, зеркальная плоскость этой позиции
чередуется с плоскостью Ь , а плоскость с - с п.
Комбинируя плоскости 2-й позиции с плоскостями 3-й,
получим 8 групп. Характер производной оси 4-го порядка оп-
ределяется суммарной вертикальной трансляционной компонен-
той порождающих плоскостей симметрии:
Р4ттп	Р42тпс
P4bm	Р42Ьс
Р42Стп	Р4сс
Р42птп	Р4пс
При вычерчивании графиков пространственных групп
средней категории поступают в основном так же, как и для .
групп низшей категории, т.е. изображают сначала порождаю-
щие элементы симметрии, предпочитая в качестве таковых
14) с ~	’
В средней категории вертикальную плоскость с горизон-
тальным скольжением обычно обозначают Ъ , независимо
от того, как направлена ее трансляционная компонента -
параллельно оси л(=У) или диагонали ячейки.
77
плоскости симметрии, затем находят результат взаимодейст-
вия элементов симметрии между собой и с трансляционными
векторами решетки Бравэ. Начало координат выбирают, как
всегда, в наиболее симметричной точке с наименьшим числом
степеней свободы. Не останавливаясь подробнее на всех тон-
костях построения графиков, покажем некоторые из них в го-
товом виде в Приложении.
Пространственные труппы кубической системы проще всего
получить кубизадаей групп тетрагональной и ромбической сис-
тем, т.е. введением оси .3-го порядка, равнонаклонной к ко-
ординатным особым направлениям. В ромбических группах это
приводит к отождествлению координатных осей и плоскостей
симметрии (222-* 23,ттп-т*тпЗ). Очевидно, что кубизируются
лишь те пространственные группы, в которых координатные
направления могут преобразовываться друг в друга при пово-
роте вокруг оси 3-го порядка, что предполагает одинаковость
трех взаимно перпендикулярных особых направлений. Например,
Р222-*Р23, Р212121—*Р2£3, Pwmm—•'РтЗ, РЪса—*-РаЗ,
Fddd-*Fd3 и т.д. Группы типа Р222,£ или Рп-ma кубизировать-
ся не могут.
При ку би задай тетрагональных групп эквивалентными ста-
нут все три координатные плоскости, а координатные двойные
оси, повысившись до четверных, отождествятся с главной
осью; диагональные элементы симметрии просто размножатся,
т.е. число их утроится (422—*432 , 42m—*43тп , ^тпт =
Д Д	=тЗтп ). Таким образом, из группы Р^мт получим
Р-п-Зт, из Р^пс(п)-*Р'тЗп , из I^1cd = F^dc 'получим со-
ответственно 1а 3d и Fd3C . Группы, подобные Р^пш и p|2mn,
не кубизируются. Группа Р4222 повысится до Р4232, труппа
Р41212 - до Р4д32, так как 42 = 2, а 4* = 2±; группы же
типа Р42|2 или P4j22 для этой цели не годятся, поскольку
4 /_2t, a 4t / 2. Кубизируется труппа Р42т (-* Р43тп), но
не Р42^т , так как 42 = 2, но 42 / 24.
§ 12. Правильные системы точек - системы
эквивалентных (гомологичных) точек,
или позиций
Правильной системой точек (или системой эквивалентных
78
точек) называют их совокупность, полученную размножением
некоторой исходной точки операциями симметрии пространст-
венной группы. Любая операция группы, совмещая одну из то-
чек системы с другой, приведет всю систему к самосовмещению.
Правильную систему точек можно считать аналогом про-
стой формы - семейства граней, связанных операциями симме-
трии точечной группы: по законам простых форм в кристалли-
ческом многограннике располагаются грани, а по законам
правильных систем точек в кристаллической структуре распо-
лагаются материальные частицы.
Основной характеристикой правильной системы точек
служит симметрия позиции, т.е. комплекс
тех элементов симметрии, которые, проходя через точку,
не размножают ее.Такими могут быть лишь элементы макросим-
метрии (закрытые элементы симметрии), и комплекс их, пред-
ставляя подгруппу пространственной группы, оказывается од-
ной из 32 точечных трупп симметрии.
Точки "без симметрии" (точечная группа 1) образуют
общую правильную систему, все остальные -част-
ные.
Необходимо обратить особое внимание на то, что точки,
расположенные на элементах мийросимметрии, занимают не
частное, а общее (симметрия 1) положение1поскольку их
трансляционные компоненты (t ) в равной мере размножают
как точки, находящиеся в "чистом поле", так и лежащие на
этих элементах симметрии (рис. 72). Кроме того, элементы
мвкросимметрии, в отличие от элементов макросимметрии, не
препятствуют размещению на них частиц любой симметрии: на
рис. 72 асимметричная фигурка (флажок), попав на плоскость
.превратилась в фигуру из сдвоенных флажков, обладающую
зеркальной симметрией; флажок на плоскости а. не претерпел
никаких изменений (его симметрия по-прежнему 1). Так, пер-
пендикулярно карбонатному иону (С03)" не может располагать-
ся поворотная ось 2-го порядка, тргда как для винтовой оси,
Пернендикулярной к нему, допустим любой порядок^); таким
йгг ----------------
разумеется, речь идет о микроэлементах симметрии в
чистом виде", т.е. не включающих макроэлементы; так
позиция на 4, общая (симметрия позиции 1), а на 4г -
частная (симметрия позиции 2 = 4* ).
79
a
Рис. 72. Размно-
жение фигур эле-
ментами симмет-
рии:
а) закрытым эле-
ментом - плоско-
стью т.;
б) открытым эле-
ментом - плос-
костью а
же образом, тетраэдрически окруженный атом углерода не мо-
жет совпадать с центром инверсии. Группа симметрии позиции
должна быть либо такой же, как группа симметрии частицы,
либо первая должна входить в группу симметрии частицы под-
группой.
Симметрия позиции правильной системы точек определяет
и другую ее характеристику - число степеней
свободы, т.е. число направлений, в которых точка
может перемещаться, не размножаясь элементами симметрии
данной позиции. В системе без степеней свободы (инвариант-
ной) положение точки строго фиксировано элементами макро-
симметрии (например, центром инверсии (1)или особой точкой
другой инверсионной оси), и изменение любой из координат
точки приведет к ее размножению, а следовательно к .другой
системе. В системе эквивалентных точек с одной степенью
свободы (моновариантной) - на поворотной оси - есть лишь
одно направление, перемещение вдоль которого не увеличит
числа точек системы. В системе с двумя степенями свободы
(.инвариантной) - на зеркальной плоскости симметрии - точка,
не размножаясь, может независимо перемещаться в двух направ-
лениях. Общая правильная система точек тривариантна, т.е.
имеет три степени свобода.
Все три координаты инвариантной системы выражены в оп-
ределенных, рациональных долях параметров ячейки Бравэ,
"скользящие”, нефиксированные значения координат (x,y,z)
отсутствуют; в моно-, ди- и тривариантных системах перемен-
80
ди значений координат соответственно I, 2 и 3.
В пределах данного структурного типа (при переходе от
одного соединения к другому или при изменении физико-хими-
ческих условий) изменяться могут лишь "скользящие", не фи-
ксированные элементами макросимметрии, координаты атомов,
фактически речь идет лишь о незначительных изменениях, в
противном случае произойдет переход к другому структурному
типу.
В каждой пространственной группе точки общего положе-
ния создают самую многоточечную систему, т.е. ее крат-
ность (число точек, приходящихся на одну ячейку Бравэ)
максимальна. Поскольку на точку общего положения действуют
все элементы симметрии группы - элементы как макросимметрии,
так и микросимметрии, кратность общей правильной системы
точек равна общему числу операций пространственной группы,
т.е. ее порядку. В случае примитивной решетки Бравэ
порядок пространственной группы равен порядку соответствую-
щей точечной группы (т.е. кратность общей правильной систе-
мы точек равна числу граней общей простой формы). Одна допол-
нительная трансляция (в. С(А,В)- или 1-ячейке) удвоит крат-
ность общей системы точек (порядок пространственной группы),
две(дважды центрированная ячейка R-решетки) утроят ее и, на-
конец, три (F-ячейка) - учетверят.
Кратность частной системы точек всегда меньше, чем об-
щей, причем уменьшение это определяется степенью симметрич-
ности позиции, численным показателем которой, как уже упо-
миналось (с. 70 ) служит величина симметрии
(порядок точечной группы симметрии частной позиции). Вели-
чина симметрии определяется числом точек, на которые разде-
лится одна точка, если ее вывести из данной частной позиции
в общую (или числом точек общего положения, которые сольются
в одну, попав в данную частную позицию). Так, правильная
система, точки которой занимают позицию с величиной симметрии
2, т.е. удваивающую позицию (например, на зеркальной плос-
кости или на оси 2), имеет кратность в 2 раза меньшую, чем
общая система точек; учетверяющая позиция (например, 4,тп-т2
или ) определит систему точек с кратностью в 4 раза мень-
шей.
Очевидна зависимость между кратностью правильной системы
6-1478
81
точек и ее величиной симметрии: их произведение постоянно
и равно кратности системы точек общего положения (порядку
пространственной группы). Если известна пространственная
группа структуры кристалла и позиции, занимаемые атомами,
нетрудно, рассчитав их кратность, установить (уточнить)
химическую формулу кристалла. Например, пусть .для некото-
рого минерала установлена пространственная группа 142m, и
известно, что атомы Си занимают позицию 4, атомы Ее иЗп-
- 42m, а атомы - m. Требуется установить формулу мине-
рала. Порядок группы 142m вдвое выше порядка точечной
группы 42m, т.е. равен 16; величина симметрии .для атомов
Си равна 4, Ее и - 8, а 3 - 2. Следовательно, в ячейке
Бравэ 4 атома Си , по два (~) атома Ее и Зп и восемь
(4г) атомов 3 . Отсюда формула минерала Cu2EeSn34 - это
станнин.
Рассмотрим различные правильные системы точек на при-
мере групп Рта2 и Реет.
Группа Рта2. В этой гемисимморфной группе, как видно
Рис. 73. Правильные системы точек в федоровской группе
Рта2: I - тривариантная (общая; система;
ц - дивариантная (т); пт - моновариантная (2)
яз рис. 73, помимо общей, тривариантной, позиции, есть и
частные: дивариантная (симметрия тп) и моновариантная (сим-
метрия 2).
Общая правильная система
точек группы Рта. 2. Поскольку эта система
тривариантна, т.е,. имеет три степени свобода, координаты
первой, исходной точки - xyz. На рис. 73 координаты х и у
показаны стрелками-векторами, а координата z(=^), т.е.
высота точки над нулевым уровнем отмечена знаком "+". Для
получения остальных точек надо подействовать на исходную
точку xyz элементами симметрии пространственной группы,
для чего ее удобно разложить на независимые младшие сомно-
жители. Группу 4-го порядка Pm а 2 можно представить либо
какшх- ау , либо тпх* 2Z, либо а9« 22. Действуя на точку
xyz любым сочетанием двух элементов симметрии и исполь-
зуя третий (порожденный) элемент .для проверки, получим все
точки общей правильной системы.
Пусть на исходную точку действуют тпх и ау: отразив
точку xyz (д( ) в плоскости -Hix, получим энантиоморфную точ-
ку i2.(Ha чертеже одну из энантиоморфных точек обозначают
кружком, другую --кружком с запятой.) Координаты точки 12
легко прочитываются по чертежу: | - х у 2. Подействовав
на точку ±2 плоскостью ay=mx.tx, получим точку 13 с коор-
динатами xyz , энантиоморфную ±2, но конгруэнтную исходной.
Для проверки полученных результатов используем ось 22 , по-
рожденную плоскостями тх и ау. Поворот вокруг вертикальной
оси 2-го порядка, проходящей через начало координат, меняет
знаки координат по осям X и У на противоположные, оставляя
координату по оси Z неизменной, т.е. точка xyz под дейст-
вием оси 22 должна перейти в конгруэнтную точку xyz, что
подтверждает правильность полученных ранее результатов. От-
разив точку 1з в плоскости пгх , получим последнюю, 4-ю
точку общей системы - |+х у z(14). Для проверки снова можно
использовать ось 2Z , которая связывает .две конгруэнтные
точки ±2 и : |-х у z —* |+-х у z.
Частные правильные системы
Точек группы Рта. 2. Величина симметрии обеих
частных систем (тх и 2Z) равна двум, поэтому их кратность
вдвое меньше кратности общей системы.
83
А. Симметрия позиции m . Система ди-
вариантная (с двумя степенями свободы), следовательно, ис-
ходная точка имеет две непостоянные координаты, в данном
случае - по осям У и Z . В точке | У Z(й4 на рис. 73) как
бы слились воедино две энантиоморфные точки общей системы
(xyz) и У z), что вдвое уменьшило кратность системы.
На точку jyz-CFj) не действует плоскость тп, поэтому в по-
зицию |уг(ц2) ее можно перевести как плоскостью ау, так
и осью 22. Обратим внимание, что для обозначения точек
этой позиции, как и любой .другой, определяемой элементами
симметрии 2-го рода, исключены кружки, отмеченные запятыми.
Б. Симметрия позиции 2. Система
моновариантная (с одной степенью свободы), поэтому лишь одна
координата каждой точки этой системы непостоянна, в данном
случае - по оси Z . Итак, исходная точка оохСШ^), в ней как
бы слились две конгруэнтные точки общей системы - xyzdt) й
xyz(Is). Действующая операция - отражение в одной из плоско-
стей - либо тих, либо ау. Отразив точку oozdH^) в плоскости
тпх, получим энантиоморфную точку |oz(»i2). Действуя на
плоскостью Пу, получим точку ш2, трансляционно связанную с
точкой щ2, т.е. фактически ту же самую точку.
Моновариантная позиция о ;z(W на рис. 73) аналогична
позиции ooz и отличается от нее лишь выбором начала коор-
динат.
В Интернациональных таблицах правильные системы точек
принято обозначать буквами латинского алфавита в последова-
тельности, отвечающей увеличению кратности (обозначения
Уайкова). В нашем примере (группа Рлпа.2):
2 : (a) ooz... (Ь ) OgZ... (с) тУ2...
4 : (d ) xyz...
Пространственная группа Рссти.
Ромбическую голоэдрию определяют три независимые взаимно
перпендикулярные плоскости симметрии, следовательно, порядок
точечной группы шшт равен восьми, а поскольку в нашем при-
мере решетка примитивная, порядок пространственной группы
Реет (и кратность общей правильной системы точек) - тоже
восемь. На графике (рис. 74) хорошо видно, что кроме общей
правильной системы точек в группе Реет есть все зри типа
частных - инвариантная (на плоскости m), моновариантные
84
Рис. 74. Правильные системы точек в федоровской
группе Реет: I - тривариантная (общая)
система; ц, - дивариантная система (т);
in и n - моновариантные системы (2):
v и У! - нонвариантные системы и 222
(на осях 2) и нонвариантные (в точке пересечения осей 2 и
в центре инверсии).
Общая правильная система
точек. Проще всего ее можно получить, действуя сначала
плоскостью сх, затем су и, наконец, rnz; эти плоскости про-
ходят через начало координат, поэтому нетрудно записать'
координаты всех точек, не прибегая к рисунку: операция от-
ражения в каждой плоскости изменит знаки координат на про-
тивоположные по той оси, перпендикулярно к которой располо-
жена плоскость; в случае плоскости с , кроме того, изменит-
ся координата по оси z.
Итак: xyzdiJ.Cx (=тх*Гс) ~^ху |+2(±г),
xyz(4x)
ху g+z(±2
Су (—ТИу* tc )
ху |+z(I3),
xyz (i4),
е -
85
(Il))	-*xyz	(±s)’
dz)!	-*xyi-z	Ck), •
} • 1YU	f
(1з ) I	— "X^-l	(1?) ,
(I4))	— Xyz	(±£).
•Сокращая записывают +(xyz, xy|+z, xy^+z , xyz ).
На графике (рис. 74) точки, расположенные одна под
другой, обозначают перечеркнутым кружком, я поскольку в
нашем примере эти точки связаны отражением в плоскости mz,
т.е. энантиоморфны. одна из половин кружка снабжена запятой.
Координаты 4+z и 5-Z на графике обозначают соответственно
н! , и „ «1	*
2	2 " •
Для вычисления координат точек, полученных отражением
в горизонтальной плоскости, или повернутых вокруг горизон-
тальной оси, удобно пользоваться "линейкой”, деления кото-
рой соответствуют высотам этих элементов симметрии (О,|Тс,
|Тс, 0). Такая линейка (рис. 75) позволит сразу увидеть,
что точка с координатой z (”+”) после действия элемента
1
симметрии, расположенного на уровне - , окажется на высоте
| -z ("| -") и т.д.
Частные правильные системы
точек группы Реет,
.инвариантной, так и моновариантных
S’
Величина симметрии как
позиций равна двум, сле-
довательно, кратность
этих позиций вдвое мень-
ше кратности общей пра-
вильной системы точек,
т.е. равна четырем.
Рис. 75, Расчет коорди-
наты z при
операциях горизонтальных
элементов симметрии:
а) элемент симметрии
находится на высоте О,
тогда z(+)—>z(-);
б) элемент симметрии.-
находится на высоте -гТс,
тогда 2(+)—-z ( f-J
А, .Инвариантная позиция (с двумя
степенями свободы) - симметрия позиции тп . Координаты ис-
ходной точки хуо, остальные можно определить графически
(см. рис. 74, точки П) либо воспользовавшись правилами из-
менения координат при операции отражения в плоскости. Не-
трудно вывести эту систему из общей правильной системы то-
чек - слиянием воедино каждой пары энантиоморфных точек,
расположенных друг над другом - I, и 1$ , 12	и 17 и т.д.:
xyz ]	xyx+z 1	_	,
У —хуо	_ f z—
xyzj	xyj-zj	*
xy|+z) л	xyz]
J Hxyi	__>—-хуо
xy^-zj *	xyzJ
Б. Моновариантные позиции - на
поворотных осях 2-го порядка (с одной степенью свободы
вдоль оси). В группе Реет четыре аналогичных позиции на
осях 2g , отличающиеся друг от .друга лишь выбором начала
координат. В каждом случае все точки системы можно получить,
используя либо две вертикальные плоскости симметрии, либо
одну из горизонтальных осей (2Х или 2у) и какой-нибудь эле-
мент 2-го рода: плоскость симметрии (удобнее, конечно, т2)
или центр инверсии. Избрав для одной из позиций (И на графи-
ке, см. рис. 74) операции 2x-i , получим:
s«Z(»h.)	.. 2v ——*- ----Z (Ыг)
222	<2'
||zta,) ) _	—- Mz (и3)
Для остальных систем 2Z запишем лишь исходные точки:
1 1
OgZ , gOZ , ooz .
На горизонтальных осях 2-го порядка найдем по две одно-
типные позиции: на осях 2У - оу| и |у| ,
на осях 2Х - хо| и х д .
В. Нонвариантные тозиции.В груп-
пе Реет, как уже упоминалось, два типа позиций без степе-
ней свободы, причем обе с величиной симметрии 4, т.е. с
кратностью 2:
а)	симметрия позиции Д - точка в центре инверсии;
87
б)	симметрия позиции 222 - точка пересечения трех
взаимно перпендикулярных осей 2-го порядка.
На графике показано лишь по одной системе: ооо(V) и
|о~- (У» ). Полный перечень Правильных систем точек группы
Реет с обозначениями Уайкова и указанием симметрии позиции:
- - 2	:	( а )	оор.,	( Ь	)	оо|,	( с	)	о|о,	(	)	|оо.
222 -	2:	( е )	оф	(/	)	|о^,	(g	)	0Й	(I	)	Ш.
2-4	:	( i )	хо|,	(у	)	х||,	{к	)	оу|,	(1	)	|у|,
(Ж)	00Z,	(п	)	)	o|z,	{р	)	£02.
иг - 4	:	( 9 )	хуо
1-8	:	(г)	xyz.
Мы привели здесь список координат лишь исходных точек
каждой правильной системы, перечень всех точек выглядел бы
гораздо внушительней; особенно это относится к группам с
непримитивйыми решетками Бравэ, в которых число точек каж-
дой системы возрастает в зависимости от типа решетки в 2,
3 или 4 раза. В таких случаях обычно прибегают к сокращен-
ной записи координат: отдельно выписывают координаты узлов
решетки - ее базис (например, для Г-решетки записывают
ооо, оЦ, go^, Цо), затем для каждой правильной системы
приводят координаты лишь тех точек, которые не связаны
векторами решетки. Чтобы получить полный список координат,
надо к координатам каждой точки добавить записанные внача-
ле координаты узлов решетки - векторов Т. Например, для '
группы Fmm2: (ооо, оЦ, go|, Цо) +
4 : (а ) оо
8 : (6 ) ~z; ^|z, (с ) oyz; oyz; (d ) xoz, xoz
16 : (e ) xyz; xyz; xyz; xyz;
Отсюда простым суммированием можно получить координаты
всех точек, например, .для позиции	(Ь ):
117 .	13	1 7	.	31	.	337	.
44Z »	33	2+Z	’	33	’	33z	’
44Z;	33	l+Z	’*	i
88
§ 13. Кристаллоструктурные иллюстрации
федоровских (пространственных) групп
симметрии
Для более глубокого понимания и усвоения основ -геомет-
рической микрокристаллографии, для того чтобы "увидеть"
пространственные группы и правильные системы точек не только
на бумаге, полезно обратиться к кристаллоструктурным иллю-
страциям пространственных групп - моделям кристаллических
структур..Приобретя некоторый навйк в описании готовых
структурных моделей, можно более уверенно подойти к решению
и серьезных кристаллографических задач - по данным структур-
ного анализа (пространственная группа, позиции атомов) пред-
ставить структуру кристалла, ее геометрические особенности,
объяснить (или предсказать) некоторые физические свойства
кристалла и т.п.
В настоящей главе мы приводим примеры полного описания
структур некоторых минералов. Список структур, рекомендуемых
для самостоятельной работы приведен в Приложении.
Марказит, Fe^» Форма ячейки (рис. 76,а) позволяет
предположить ромбическую систему, которая, однако, должна
быть подтверждена сочетанием определяющих ее элементов сим-
метрии. Фактически вопрос о системе в данном случае решает-
ся параллельно с определением пространственной группы (см.
с.26 ).
В структуре марказита атомы железа есть и в вершинах
ячейки и в ее центре, однако решетка Бравэ лишь примитивная, •
так как ориентация гантелей отвергает кажущуюся диаго-
нальную трансляцию (Tj).
Определяя федоровскую группу, целесообразно для начала
предположить ромбическую голоэдрию. Она подтверждается, если
Удастся найти, например, три взаимно перпендикулярные плос-
кости симметрии, параллельные граням ячейки Бравэ.
По рис. 76,6 без труда находим вертикальные плоскости -
зеркальную плоскость (гг) и клиноплоскость (и ), отстоящую
от вершины ячейки на	Если федоровская группа действи-
ях
' Отыскивая элементы симметрии, стоит сначала обращать вни-
мание на те атомы, которых меньше (атомы Ге), не забывая,
однако, проверить свое предположение по всем прочим (ато-
мы 5 ).
89
г
Рис. 76. К структуре марказита, PeS9: а) общий вид;
б) проекция структуры на плоскость осей У2;
в) проекция структуры на плоскость осей ХУ,
отвечающая стандартному аспекту;
г) федоровская группа в стандартном
аспекте Pnnm
тельно относится к голоэдрическому классу', должна быть и
третья - горизонтальная - плоскость симметрии. Для того
чтобы легче ее увидеть, повернем модель так, чтобы эта ис-
комая плоскость оказалась вертикальной, тогда сразу заметим
клиноплоскос^ь п , отстоящую на от вершины ячейки (рис.
76,в). О полносимметричном классе говорит и отчетливо види-
мый центр инверсии, совпадающий с атомом Ее. Из трех возмож-
ных аспектов найденной федоровской группы - Ртп-п-п, P-nm-n,
Рпптп - за стандартный принимают последний (см. с.75 ).
План структуры марказита и график его федоровской
90
группы £ аспекте Pimm даны на рис. 76,в и г, из которого
видно, что начало координат на модели (вершина ячейки)
отвечает стандарту Интернациональных таблиц. Атомы зани-
мают следующие позиции: Ее - инвариантную (симметрия по-
зиции 2 , кратность 2) и £ - дивариантную (позиция т,
степени свободы - вдоль осей X и У, кратность 4). Размно-
2ив исходные точки (ооо для атома Ее и хуо для атома 5 ),
получим координаты остальных точек (атомов).
Полная запись структурных данных для марказита:
федоровская группа Pimm(D^); а = 4,436 2, Ь = 5,414 X,
с = 3,381 X. Ее - 2 : (а.) ооо,
£ - 4 : (g ) хуо; ^i-x J-y g-x |+у хуо,
где х = 0,200, у = 0,378 (значения координат х, у, z приво-
дятся обычно в долях соответствующих параметров ячейки).
Таким образом, общее число параметров 'структуры мар-
казита равно пяти - два относятся к атомам (х,у), три - к
ячейке (a,t ,с)^^.Из приведенных ниже данных для соедине-
ний, изоструктурных марказиту, видно, что изменяются коор-
динаты лишь тех атомов, которые занимают позиции со степе-
нями свободы (х,у).
Вещество	(I)	(А)	(1)	X	У
ЕеР2	4,975	5,657	2,725	0,16	0,37
EeASg	5,25	5,92	2,85	0,175 .	0,361
Со eg	5,301	6,298	3,882	0,22	0,36
Рутил, Ti0o« Форма выделенной на модели ячейки
(а = Ъ £ с , «< = f> = Z = 90°, рис. 77, а) позволяет предполо-
жить тетрагональную систему, которая подтверждается осями
42, проходящими через середины ребер ячейки. Кислородный
мотив опровергает трансляцию Tj , центрирующую объем, ко-
торую можно заподозрить по расположению атомов Т£; т.е.
решетка Бравэ для рутила - примитивная.
Предположив голоэдрию, попытаемся найти плоскости
симметрии - горизонтальную координатную (i-я позиция сим-
17)	~
Хотя обычно, подсчитывая число параметров структуры,
подразумевают лишь параметры атомов, тогда марказит -
двупараметрическая структура.
91.
О	ОУ	о	о'/г	о
*4*4
У2О	о	о/2	о	оу
о	су	о	оу	о
* 4 *
оу	о	оу	о	оу
4 • > •
о оу о оу о
Рис.77.структуре рутила, TiO?:
а)общий виц, б) план структуры,
в)размещение атомов Ti и 0 в про-
странственной группе Р^тт
а
вола), вертикальную
координатную (2-я
позиция) и диаго-
нальную (3-я пози-
ция). Легко находим
зеркальные плоскос-
ти симметрии 1-й и
3-й позиций, что
уже однозначно опре-
деляет голоэдрию и
принуждает искать
координатную плос-
кость - произведение
оси 4-го порядка и
параллельной ей плос-
кости (диагональной).
Зта плоскость должна
иметь вертикальное
скольжение, так как
в нее вливается тран-
сляционная компонента
оси 42, равная
(рис. 77,6). Такую
плоскость (тг) - ее
"подсказывает" нам
расположение атомов
Tt - находим на рас-
стоянии ^а,ь от вер-
шины ячейки. Таким
образом, федоровская
группа рутила
Р^тп(Б^) =
= р ^zfsi 2(2j_)
m n -ml Ъ ) *
Описание позиций
атомов не вызывает
затруднений, так как
начало координат на
представленной модели
Рис. 78. К структуре пирротина, Fe'-S - никелина, NIAa:
а) общий вид структуры; б) оси 6 и 3 ;
в) позиции атомов Ре(№) и £(Ая) в федоров-
ской группе Р^тпс
отвечает стандартному комплексу с максимальной симметрией
тптптп. Атомы Ti занимают инвариантную позицию тпттт(кратное
16	{ 1 1
-	= 2, координаты ооо и |	, а кислорода - моновари-
антную ттп2(на .диагональной осй;-2, совпадающей с линией
пересечения горизонтальной и вертикальной зеркальных плос-
костей) ; исходная точка такой позиции (ххо) имеет лишь оде
93
"скользящую" координату (х) - одну степень свобода (вдоль
диагонали грани db ячейки). Координаты всех остальных то-
чек этой четырехкратной системы прослеживаются по чертежу
(рис. 77,в).
Пирротин, ГеБ - никелин,NiAs. Одна система осей 3-го
порядка говорит о принадлежности ее к гексагональной систе-
ме, примитивный же тип решетки Бравэ позволяет допустить
как гексагональную, так и тригональную подсистемы (рис.78,а),
Как всегда, предположив самый старший класс системы, гекса-
гональную голоэдрию, пытаемся отыскать соответствующие эле-
менты симметрии. Отсутствие поворотной оси 6-го порядка
заставляет искать винтовую, которая может быть здесь лишь
осью 63, так как атомы расположены на двух уровнях (атомы
Ге - на о и атомы S - на | и | ). Такие, нейтральные,
оси 6g^8) действительно проходят через вершины ячейки (рис.
78,6). Гексагональную подсингонию однозначно определяет и
горизонтальная плоскость тп ( ^ = 6).
Вертикальная координатная плоскость m(плоскость, па-
раллельная длинной диагонали элементарного ромба) вместе с
горизонтальной плоскостью тп и осью 63 приводят к гексаго-
нальной голоэдрии и одновременно к апофемальной плоскости с.
Действительно, вертикальная плоскость ограничивает нас клас-
сами 6mm, 6 m 2 и ^тпт, но в первом нет горизонтальной плос-
кости, в группах второго - оси 63. С .другой стороны, ось 63,
взаимодействуя с проходящей через нее плоскостью т, порож-
дает под углом 30° плоскость с вертикальным скольжением, т.е.
с и чередующуюся с ней клиноплоскость п.
Таким образом, структура ГеБ (NiАй) подчиняется федо-
ровской группе Эби= Р^пс.
Начало координат на представленной модели такое же,
как на графике Интернациональных таблиц (3m). Оба типа ато-
мов занимают инвариантные позиции: атомы Ее(№) -позицию
3m , атомы 5 (АЯ) - 6m 2. Кратность того и .другого типа ато-
мов равна 2, так как порядок пространственной группы - 24, 18
18) Полезно научиться быстро распознавать ось 63 = 3 *2i,
очень часто встречающуюся в гексагональных кристаллах.
Тройка атомов, лежащих в вершинах треугольника, перпен-
дикулярно к которому проходит эта ось, связана с другой
тройкой атомов, повернутой относительно исходной на 60и
и сдвинутой по вертикали наfТс(рис. 78,6); тот атом,
через который эта ось проходит, лишь повторяется через %11
94
Рис. 79. Структура FeS
(NiA£) в полиэдрах:
а).общий вид структуры;
б) оси 6„ и 3;
в) координатные оси 2;
г) апофемальные оси 2;
д) плоскости та и с
а величина симметрии
каждого из этих положе-
ний - 12. Размножая на
графике (рис. 78,в) ис-
ходные точки (ооо и
| | | ), подтверждаем
кратность и находим ко-
ординаты остальных точек.
Таким образом:
Fe(M) - 2: ( а ) ооо,оо|
S(AS) -2: (с)
Если "пренебречь" пара-
метрами а и с , то Ге^
(NiAS) - беспараметричес-
кий структурный тип.
95
Определение федоровской
группы по полиэдрической моде-
ли структурного типа пирротина
- никелина (рис. 79). Сразу бросаются в глаза оси
6 , проходящие через центры октаэдров, совпадающие с атома-
ми Ее(№) . В этих точках (Зтп) выбираем в соответствии со
стандартом Таблиц начало координат, что позволяет легко вы-
делить ячейку Бравэ. Через незанятые тетраэдрические пусто-
ты структуры проходят оси 3-го порядка (точнее, 6 = Д).
Отчетливо видны горизонтальные оси 2-го порядка: координат-
ные оси, проходя через центры октаэдров, совпадают с "соб-
ственными” .двойными осями этих октаэдров, апофемальные ле-
жат на горизонтальной зеркальной плоскости, связывая окта-
э.дры двух этажей. Нетрудно отыскать и оба типа вертикальных
плоскостей - зеркальные, параллельные .длинной диагонали
ромбического сечения ячейки, и плоскости с , проходящие по
его короткой .диагонали.
Атомы £(As) лежат на стыке .двух троек октаэдров, верх-
ней и нижней, совпадающем с особой точкой инверсионной оси
6-го порядка.
Алмаз, С. Четыре оси 3-го порядка, идущие вдоль .диаго-
нали ячейки, подтверждают вывод о принадлежности структуры
алмаза к кубической системе, сделанный по форме ячейки Бра-
вэ (рис. 80,а).
Решетка Браве - гранецентрированная (Г). Хорошо видны
диагональные зеркальные плоскости симметрии, которые в со-
четании с винтовыми осями 4-го порядка - 44 и 43 (рис. 80,6)
однозначно определяют кубическую голоэдрию (L	=
Ркоорц) и характер координатной плоскости: она, как и винто-
вая ось, должна иметь компоненту скольжения, равную рЦ.
т.е. может быть только плоскостью d. Эти плоскости действие
тельно нетрудно увидеть на расстоянии ^?а,ь,е от вершины ячей-
ки (рис. 80,6), причем плоскости d, в которых скольжение
параллельно одной диагонали грани, чередуются с плоскостями
d со скольжением по другой .диагонали той же грани.
Таким образом, федоровская группа алмаза Fd3m (CQ.
Симметрию позиции атомов углерода легко выведем по
кратности, равной 8. Порядок группы БйЗтп - 192( = 48 • 4),
96
ординат атомов: (ооо, —о, 
"Раскрывая" скобки (см. с.81
Рис. 80. К структуре алмаза:
а) общий вид структуры;
б) клиноплоскости А и а.", оси
4i и 4з
следовательно, порядок под-
группы симметрии позиции (т.е.
ее величина симметрии) должен
быть равен 24 ( = 192 : 8 ).
Такой порядок в данном случае
может иметь лишь группа куби-
ческой системы с диагональны-
ми плоскостями, т.е. 43m.
Эту группу симметрии для ато-
мов углерода нетрудно устано-
вить и непосредственно по мо-
дели, учитывая тетраэдричес-
кую координацию атомов угле-
рода в алмазе.
Непримитивный тип решет-
ки Бравэ позволяет применить
сокращенную форму записи ко-
°2’ °Й)+ 8: (а > °00’ 1 Н-
i ), получим координаты всех
8 точек - атомов углерода в структуре алмаза.
§ 14. Преобразование координатных систем
кристаллических структур
В кристаллохрафической практике часто приходится из-
менять координатную систему, которая определяется как на-
правлением координатных осей, так и единицами измерения
вдоль них. В идеале координатные оси должны совпадать с
ребрами ячейки Браве, а ее параметры - служить единицами
измерения вдоль осей. Переход от одной координатной системы
к другой предполагает вычисление "новых" параметров ячейки
и "новых" координат атомов.
Пусть в плоской сетке оба координатных репера имеют
общее начало, причем а , Ь' - параметры вдоль "старых" ко-
7-1478
97
из л OPQ '.
ЗА-tf-B-O
2A+4b~2B-0
а=^А-^В
из л OST:
Рис. 81. К преобразованию коорди-
натных систем в кристаллах
ординатных осей (Х,У),
А, В - вдоль "новых"
(X' и У'). Для конкрет-
ного случая (рис. 81)
А = 2а + Ь , В = 2а + 36.
Поскольку характер
каждого частного преоб-
разования определяется
лишь коэффициентами при
а и Ъ , систему этих
уравнений можно записать
сокращенно в виде матри-
цы преобразования осей,
составленной из коэффи-
циентов при а , Ъ :
(М) = (| I).
Приведенный на рис.
81 пример можно рассмат-
ривать и в трехмерном
аспекте, считая, что "новый" параметр по оси Z совпадает
со "старым”, т.е. что С = сГ . Тогда матрица преобразования
/2 1 0\
координатных осей (М) = 12 3 О I.
\0 0 1/
/^а^аЗДд
В общем виде: (М) =	,
или 1'Л = Ца^/^А^В^В^^^С^С®Ь •
Заметим, что строки матрицы (М) выражают Миллеровские
символы "новых" координатных осей в "старой" системе, т.е.
[VA®A> Х',[«вг/Л]=У', [«CV(WC]=Z'.
Матрицу обратного преобразования Ш-') - от "новых”
осей к "старым" - можно получить либо графически (см.рис.81)
либо решив систему уравнений_относительно сГ, & и <Г.
(3 1 п \
4 5 °\
| 2 О I
0 0 1/
98
/“аЧЛ
и, обобщая, запишем (кГ1/ =
xU-cUc^c
или ivl"1 -^a^a^hvbwb/uc4we •
Очевидно, ЧТО [uaVaWa] >
[иьцгц] ,[ucvcwc] - символы
"старых" осей в новой координат-
ной системе.
Взаимно-обратные матрицы
(М) и (IvT1) при перемножении^9)
должны дать единичную матрицу
При перемножении матриц
член г -ТОЙ строки j -ТОГО СТОЛб-
Рис. 82. Графическая ил- ца матрицы-произведения получают,
люстрация правил перемно- суммируя результаты перемножения
жения матриц	каждого члена i-той строки 1-й
матрицы на соответствующий член] -того столбца 2-й матрицы,
что графически можно проиллюстрировать схемой (рис. 82).
/3 1 о\
/2	1	0\	4	4	\	/1	0	0\
—Т	/	I	4	Л	1	|	I
Для нашего примера: (М)»(М )	-12	3	О I и	I g	О I = I 0	1	О
\0	0	1/	\0	0	J	\0	0	1/
Чтобы найти параметры А, В, С по (М) и «, по (1/Г^)
надо на матрицу соответствующего преобразования умножить
о.дностолбцовую матрицу, составленную из векторных единиц
другой системы.
Действительно, по правилу умножения матриц получим:

а\ ' и(а + Vpb +	= а
Ь l=^sa + l)^b +W3C' = S’
е/ WpG + +wrc~ - O’
О	V	\
V-aPa&a. \
ub^bWb
UeVc-We I
A \ ^aA +	3 +	0 = ct-
В l-W^A + ^'ьВ +^C = b
С/ UcK +VC В +WC C =
В общем случае	(MghCMj).
99
Для вычисления абсолютных значений параметров А, В, С
(иди а, Г,(Г) надо извлечь корень из скалярного произведе-
ния каждого вектора на самого себя.
Так, А • Г = (йдсГ + г>дГ + г^дс) •	+ Мд?).
Откуда_________________________________________________
I Al =7огЦд + д + сЪд + 2а&«дУдСой/+ 2 ас	+
+ 2Ъсг7дгУдС05</‘, где oi,j3,y - осевые углылв "старой"
системе координат, т.е. = £/, /з = оТ , f-ab.
Таким же образом вычисляем IBI и 101. По аналогии
|al = 7а2Дд + В2»а + Сг^а+ 2АВдаг/а со5/' + 2ACuawacoSj3' +
+ 2BCvawaco^'\ тде^' = ВС, уз' = АС, У'= АВ” - углы меж-
ду "новыми" осями координат.
Для вычисления осевых углов воспользуемся следующей
зависимостью:	,= СоД = _Jc^_
1ВИС1
coSp' = CoS АС = -—^г,
-» л IAHCI
COStf'= CoS АВ = -=Д“р-,
IAI1BI
coS<z = coS Ъс = “£“ И Т.д. ‘
Так,	1	|ЬНс|
СОЙ*/* —	(^в®	^В^	(Wq£Z. + V+ Z&'qC) =
= 55(“!"в"с +гЧг'с
9
+ С W^I£)q
+ abu.g^Q +
+ acu^t^Q +a.bn^UQ +bcz/^OQ +acu-^^Q +bczJ b^q) —
= ^alzgizG +fS®BwC +q^cZ7b + ^b^C^00^^ +
+ QcCUqZ&b + £Zg^c)C0Sj3 + bc(,V^UQ + ftga^COSd/J.
Таким же образом определяют j3’ и У', а также , J3 и У.
Нетрудно показать, что если (Ма) - матрица преобразова
ния параметров от установки I к П, a (Mj) - то же от уста-
новки П к Ш, то (Мс) - матрица преобразования от I к Ш -
выразится произведением (Mj)*^)..
Закон, по которому преобразуются параметры ячейки,
носит название ковариантного , он же справед-
лив и для преобразования индексов граней кристалла.
100
Преобразование координат точек (атомов)
Пусть некоторая точка К (см. рис. 81) имеет в "ста-
рой" системе координаты тп ,п ,р . Обозначим координаты
этой точки в "новой" системе - M,N, Р. Выразив вектор, иду-
щий из начала координат в эту точку, через "старые" и "но
вне" единицы, получим
AM + BN + СР = ат + Ьп + ср.
Из системы	а = иаТ + vaB +waG
Ъ = ~иьТ +	+ WjC
С = Иск + здв + ®<?с
следует, что
AM + BN + СР	=77?(zzcA	+Va В	+ WaC)	+7i(Ubk	+ЪЪВ	+ Wt(T) +
+p	+ vcB	+ wcc>	= l(uam	+ щп	+ uep) +
+ BiVaTn.	+ Vbn	+vcp}	+	+ Win	+ Wcp") .
Таким образом,
M = иатп + щп + иср
N = uam + Vbn + Vcp
Р = Wam + Wbn + wcp ,
иными словами матрица преобразования координат точек ока-
залась транспонированной от обратной матрицы (ЬГ^)
fiiavaWa\	(UaUbUe\
(1Г1) = \иъ Vb Ъ)ъ 11-*- (ЬГ1)' = На Иъ Vc ,
\ucVcWel	X'Wa'WbWcl
т.е. обратной матрицей, в которой позицию строк занимают
столбцы и наоборот.
Предположив, что m = 6,п = 5,р = 0, вычислим для на-
шего конкретного случая (см. рис. 81) М,N, Р. Для_|того
транспонируем полученную ранее обратную матрицу (М ):’
/lioV	/l^Q\
и ° - 1и°
\ О О 1/	\о 0 1/
7Х-1478
101
с
Иными словами, для прямого преобразования координат
точек (от "старых" осей к "новым") используется обрат-
ная транспонированная матрица
(М^У . Такой закон преобразования носит название к о н -
травариантного. Очевидно» что контравариант-
но преобразуются и индексы ребер кристаллов.
§ 15. Разбор задач на преобразование координатных систем
ЗАДАЧА I
Для кристаллов шеелита, CaWO^, установлена федоровс-
кая группа С^=	; а - 7,37 X, е = 11,35 X.
Вычислить константы ячейки в стандартном аспекте, оп-
ределив матрицы прямого и обратного преобразования, и ре-
шить, как связаны между собой координаты точки общего по-
ложения этих двух аспектов.
в тетрагональной системе ячейки I и Г представляют
два аспекта одной и той же решетки^) , которую принято на-
зывать объемноцентрированной (I), так как 1-ячейка имеет в
2 раза меньший объем. Из рис. 84 очевидно, что в стандарт-
ном аспекте С4к= 1|< =
В нашем примере- для тетрагональной решетки - задача
вычисления констант новой Ячейки решается исключительно
просто - она сводится к нахождению длины катета (IAI = IBI)
по гипотенузе (lai). Решим, однако, эту задачу сначала в
общем виде. В любой решетке переход к объемноцентрированно-
му параллелепипеду (Г, 5, (Т) от гранецентрированного (а,гГ,
20)
' Макросимметрия кристалла средней категории с боковыми
особыми направлениями позволяет выбирать оси X и У .дво-
яко. В кристаллах без боковых направлений, где эти оси
приходится выбирать параллельно ребрам, число таких ва-
риантов 'теоретически бесконечно, но и в реальных случа-
ях их может быть несколько (рис. 83).
103
Рис. 84. Два аспекта федоровской
группы . Пирной линией показаны
величина и направление скольжения
(t £горизонтальной плоскости; в
ячейке Е скольжение равно 1/4 диа-
гонали грани ао(плоскости Л'и<г),
в ячейке I это же скольжение отве-
чает плоскостям а и Ъ
с" ) выразится сле-
дующей системой
уравнений (рис. 85):
в =i?+iF,
С = <Г ,
откуда матрица пре-
образования Е-аспек-
та в 1-аспект
/И о\
2 2 \
=Н 2 0 I
\о 0 1/ .
Используя фор-
мулу для вычисления
абсолютных значений
"новых" параметров (с,ТОО), получим
IAI = "\ ^а2+|Ьа-2а6со^У ,
IBI = Л^а2* 7Ь2+2аЬсодУ ' .
N 4	4
Рис. 85.
Переход от
Е-аспекта к
1-аспекту
В^случае тетрагональной решетки, для
и а = b , получим
IA4 = IBI =
которой сой/ = О
Итак, возвращаясь к нашей задаче, вычислим константы
ячейки кристаллов шеелита с тандартном (I) аспекте:
|А| = LSp/S1 = 5>2I J , ICJ = ц,35 А.
Для определения координат точек в "новой" (I) системе
104
X
Рис. 86. К преобразованию коор-
динатных точек в тетрагональной
системе
х = 0.4 , у = 0.2 ± z = 0,3 : -
/х’\ /1 1 0\ /х\	/х-у\ =
I у' = 1 1 0 1 1у = 1х+у) =
\Z7 '001/ 'z/	\ z / =
координат (закон
контравариантный)
составляем обратную
матрицу преобразова-
ния и транс-
понируем ее:
/1 1 0\
(1Г1) =110	;
\0 О 1/
/1 1 0\
аг1)' = (110 .
\о о 17
Вычисляем новые
координаты (х’ »у' , z')
точки, для которо
0.2
0,6 (рис. 86).
0,3
3 А Д А Ч А П
Структура некоторого тфисталла описана в R-аспекте.
Получить матрицы для пересчета параметров ячейки и ко-
ординат атомов в установке Бравэ (дважды центрированная
ячейка).
Для определения новых параметров гексагональной решет-
ки получим матрицу преобразования констант.ромбоэдрической
(th ) ячейки к .дважды центрированной (hex). По чертежу
(рис. 87,А) А = а - Ь ,
в = Г- г ,
С = а + Ъ + с .
/1 1 0\
Таким образом, ЬВ^-^ех) = 10 111
'ill/ .
Как и в случае тетрагональной системы, формула для
вычисления абсолютных значений новых параметров существенно
Упростится:
105

iai = ibi = lei ; 1 Al = lBl ,
।A, = V(a-b)2' = Va2+b2- 2q6coso4 = V2n2- 2а2соя^' =
= a V 2(1-со£ч)‘ ,
13l = V(a +F+ D = V3a2+ 6a2cosoc= aV3(l + 2cos<z) .
Для определения координат атомов в .дважды центрирован-
ной ячейке (hex) составим обратную транспонированную матри-
цу (рис. 87,6):	/2 11
/333
(IVF ) = №tiex~*-rh) ~ ззз
\ ± 2 1
\3 3 3
откуда (М-1/ = (Mfer—rft/ = | 3 3
11 1 1
\3 3 3
ЗАДАЧА Ш
Возможность неоднозначного выбора координатной систе-
мы в кристаллах средней категории (особенно при отсутствии
боковых особых направлений), отмеченная в предыдущих зада-
чах (рис. 83), усугубляется в моноклинной системе, где осо-
бых направлений не хватает для однозначного выбора коорди-
натных осей, и тем бодее в триклинной, где особые направле-
ния вообще отсутствуют. В этих случаях даже при известной
структуре ячейка Бравэ может иметь совершенно различную
форму (параметры), а в моноклинной системе даже и разную
центрировку. Кроме -того, как и в средней категории (см. за-
дачу I, с.103) исследователи отнюдь не обязательно представ-
ляют структуру ячейкой Бравэ, что иногда бывает связано с
нежеланием ломать координатную систему, выбранную для дан-
ного вещества при изучении лишь внешней формы его кристал-
лов. Свобода выбора координатной системы часто приводит к
недоразумениям - рдин и тот же минерал описывается по-раз-
Рис. 87. К преобразованию координатных реперов в гексаго- ’
нальной системе: а) определение (МгЛ-*-Лег)>
б) определение Whex-rrh)
107
ному - и, лишь привода разнородные данные к одной установ-
ке (преобразовав координатные системы), можно разобраться
в запутанных сведениях (см. также с.ш).
Проиллюстрируем сказанное на примере кристаллов гипса.
Задача Ш А. Параметры кристаллов гипса в минералоги-
ческой (М) установке: = 10,51 X, = 15,18 А,
см = 6,29 X, J3M = 99°17’.
Вустер, расшифровавший впервые структуру этого минера-
ла, предложил следующие параметры:
ав = 10,51 X, Ьв = 15,18 X,
св = 6,54 £, J33 = I5I°40' .
I. Какие символы получит в структурной установке
Вустера двойникующая плоскость (Q) в галльском двойнике
("ласточкин хвост"), символ которой в минералогической
установке (100)?
2. Как будет обозначено в структурной установке на-
правление штриховки одной из призм (т), если в морфологи-
-ческой установке это направление - [00IJ ?
I. Символы плоскостей преобразуются по ковариантному
закону, а символы направлений - по контравариантному, поэ-
тому пгобтодао оодутоть матрицу как прямого (М^_^в), так
а обратного преобразования (Mg_fj) =	и транспони-
ровать ее.
Чтобы получить матрицу преобразования от одной уста-
норки к другой, построим в масштабе проекцию ячеек на пло-
скость, . перпендикулярную оси У (рис. 88), и выразим одни
параметры как векторные суммы других: а3
^3 =^М’ **
4.^	1-*
с 3	+ 2СМ*
108
Рис. 88.
К задаче Ш А.
Переход от минера-
логической уста-
новки (И) к уста-
новке Вустера (3)
в структуре гипса

/1 о 1\
01 0 ,
\о 0 2/
гт\ /1 0 1\ /0\	71\
£J =	010 0 =	0 =1:0:2, т.е. =	.
tj \0 0 2/ \1/	\2/	--------------
Задача О! Б. Предложенная Вустером для структуры гипса
ячейка Бравэ оказалась неудачной по форме (в»90°), поэтому
появились другие варианты ячеек; переход к одной из них
(по Брэггу) описывается матрицей (^_>g) = 101/010/001.
Вычислить параметры ячейки по Брэггу.
Решим сначала эту задачу графически .Воспользовавшись
чертежом рис. 88, построим ячейку структуры гипса по Брэггу
(рис. 89). Для аналитического (более точного) расчета вс- '
спользуемся формулой, приведенной на с.100 .
Рис. 89. К задаче Ш Б и Ш В. Три установки структуры гипса:
М - минералогическая ячейка, В - ячейка Вустера,
Б - ячейка Брэгга; .'дарными линиями показаны направ-
ление и величина скольжения горизонтальных плоскос-
тей, кружками и крестиками отмечены узлы простоан-
ственной решетки на нулевом уровне и высоте 1/2 со-
ответственно
109
Из (МВ_^Б) : аБ - ав + св, - &в,	- св.
Следовательно, | ?в| = V ав + с2в + 2ав&всоарв‘ =
= V 10,5I2 + 6,542 + 2*I0,5I*6,54*cosI5I°40‘' = V32^ = 5,69Д;
_ °БеБ _ ^В + сВ)сВ _ GBCBCO^B + СВ
UVbRn —	— — ———————— — —	—
аБсБ СБСБ	аБсБ
= lQx5I^6x54icosI5l2iQ±-6154 откуца « - _610зз' или 118°2?'
5,69*6,54	Jf’
Задача Ш В.Как записать символ федоровской группы по
Герману - Могену для установок минералогической и Вустера,
если по Брэггу сД = ?
Покажем на рис. 89 узлы пространственной решетки, а
также направление и величину скольжения (t ) плоскостей
а и с.
В минералогической ячейке центрированными оказываются
все грани (ячейка F), а плоскость со скольжением по одной
диагонали грани аэдсм(1^1 =	) чередуется с плоскостью со
скольжением вдоль .другой диагонали этой же грани, откуда
G2h ~	•
В ячейке Вустера центрирована грань ab , т.е. ячейка
базоцентрированная (С). Плоскость со скольжением вдоль
.диагонали грани авсв( клиноплоскость п') чередуется с плос-
костью, скольжение которой идет вдоль ребра св(плоскость
с ). Таким образом, по Вустеру	•
Задача Ш Г. Вычислить координаты .двух атомов кислорода
в установке Брэгга,	если по Вустеру 0	-	8 : f(xyz), где
х1	=	0,033	х2	=	0,533,
у,	=	0,140	у2	=	0,640,
=	-0,018	z2	=	-0,018.
Заметим, что атомы I и 2 связаны трансляционным вектором
Тс ячейки Вустера.
Координаты атомов преобразуются по контравариантному
закону, поэтому надо получить обратную матрицу - (Мв^в) -
и транспонировать ее.
По чертежу (рис. $9) а”в +	= о, откуда
ПО
_ ^Б ~ СБ’ В ^Б’	= ^Б* Следовательно,
/1 0 1\ 21)	'	/1 0 0\
(Mg _^g) = । о 1 О ,	(Mg-»g) — 1 О 1 О •
\О 0 1/	ИО 1/
Расчет координат атома Oj в ячейке Брэгга:
/хД /1 о 0\	/0,033\	/0,033\
у 1 = О 1 0 * I 0,1401 = 0,140 .
W	\1	0	1/	\0,018/	\0,051/
Расчет- координат атома 02 в ячейке Брэгга:
/хД	/1	О	0\	/0,533\	/0,533\
|у 1=	О	1	0 • 0,640 = 0,640 .
\zj	\1	О	1/	\0,018/	\0,551/
Атомы 0± и 02 в ячейке Брэгга связаны трансляционным
вектором Tj, что подтверждает сделанный нами вывод (см.
раздел В):	(по Брэггу) =	(по Вустеру).
Обратим внимание на разнобой данных по гипсу; так,
координаты атомов всегда даются в установке Вустера, про-
екция структуры, приводимая всюду, сделана применительно
к ячейке Брэгга, морфологическое описание соответствует
либо установке минералогической, либо ячейке Йонга, свя-
занной с вустеровской (bk^g) = 101/010А02. В установке
Йонга обычно приводятся-и параметры ячейки (см., например,
У.Б р э г г, Г.К ларингбулл. Кристаллическая
структура минералов. М., 1967, с. 146).
21)
Для проверки перемножим (Mg_g) и (Mg_^g).
Ill
ГЛАВА П
ЗАДАЧИ И УПРАЖНЕНИЯ 22 5
§ I. 14 типов решеток Бравэ. Решетки Бравэ
кристаллической структуры
I* Определить тип решетки Бравэ по изображенной
ячейке (рис. 90). Ось z всюду перпендикулярна к плоскости
чертежа; высоты узлов показаны в долях Тс (нулевая высота
не ^отмечается).
2.	На рисунке из альбома Эшера (рис. 91,а) выделить
ячейку Бравэ и определить тип пространственной решетки,
считая, что раскрашенные фигуры отстоят .друг от .друга на
|т . То же для рис. 91,6', на котором раскрашенные фигуры
Т~Г	г
отстоят на .
3.	Объяснить, почему в тетрагональной системе нет
решетки А.
4.	Объяснить, почему в моноклинной системе ячейки А и
С представляют одну и ту же пространственную решетку, а
ячейка В - другую (установка классическая).
5.	Почему в триклинной системе лишь одна решетка
Бравэ?
6.	Почему исключена ячейка, центрированная по двум
парам граней одновременно?
7.	Почему гексагональная .дважды центрированная решетка
обозначается буквой R ? ч
8.	Как называется решетка, которую можно представить
ячейкой в форме ромбоэдра с углом в 60°?
9.	Выделить и описать основные ячейки гранецентриро-
ванной и объемноцентрированной решеток Бравэ кубической
системы.
22В конце главы приведены решения задач, отмеченных
звездочкой.
112
Рис. 90. К задаче I
Рис. 91. К задаче 2
10.	Показать, что Р- и С-ячейки в ромбической системе
представляют разные решетки Бравэ, а в тетрагональной -
одну и ту же.
II.	Какой ортогональной ячейкой можно представить
гексагональную примитивную решетку Бравэ?
12.	Какой тип решетки Бравэ получим при деформации
кубической гранецентрированной решетки вдоль одной из осей
4-го порядка? Какую форму будет иметь примитивный паралле-
лепипед такой решетки? То же, но направление деформации
совпадает с одной и? ^сей 3-го порядка.
13* Какой решеткой Бравэ будет описываться трехмерная
периодичность KaCl-подобной структуры ЯаК3, в которой все
линейные азидные группы Я3 параллельны одной из осей 3-го
порядка структуры ЯаС1? Центр группы Х3 совпадает с цент-
ром иона хлора.
14.	В обоих политипах графита, двуслойном (обычном)
и трехслойном (js -графите), закон наложения слоев, постро-
енных, как пчелиные соты, идентичен2^). Показать, что пе-
риодичность структуры -графита описывается гексагональной
дважды центрированной решеткой Бравэ.
15.	Ячейка Бравэ и основная ячейка совпадают. В каких
случаях это возможно?
16.	Как относятся объемы примитивной, базоцентрирован-
ной и гранецентрированной ячеек одной и той же решетки?
17.	Б структуре некоторого бинарного соединения атомы
одного типа (А) расположены по позициям узлов гранецентри-
рованного куба, а .другого -(В) - по позициям узлов объемно-
центрированного куба. Определить тип решетки Бравэ, если
один из атомов а занимает позицию ООО, а один из атомов В
.111
4 4 4 •
18.	Определив симметрию узорной единицы и размножающих
ее решеток (рис.92), записать точечную группу симметрии по-
лученных бесконечных двумерных узоров.
19.	Определив симметрии узорных единиц и размножающей
решетки (рис. 93), записать точечную группу симметрии по-
лученных .двумерных бесконечных узоров.
23)
В обычном трафите второй слой сдвинут параллельно пер-
вому так, что над центром пустого кольца первого слоя
находится атом второго слоя.
115
Рис. 93. К задаче 19	Рис. 94. К задаче 20
20.	Определив симметрию узорной единицы и решетки
(рис. 94), объяснить почему точечные группы симметрии бес-
конечных .двумерных узоров не совпадают.
21.	Симметрия узорной единицы 6mm, точечная группа
симметрии решетки 4mm. Определить возможные точечные
группы симметрии бесконечного плоского узора. Показать это
графически. Что изменится, если при той же решетке симмет-
рия узорной единицы - 3m?
§ 2.	Координация атомов в структуре (координа-
ционные числа и координационные многогран-
ники). Геометрический характер структуры
22.	Координационное число атомов в структуре простого
вещества равно 1. Сделать вывод о геометрическом характере
структуры и типах химической связи. Назвать известные
структурные типы.
23.	В простом веществе координационное число атомов
равно двум.Каким может быть геометрический характер струк-
туры? Назвать известные структурные типы.
24.	Координационное число атомов в структуре простого
вещества равно трем. Каким может быть геометрический харак-
тер структуры? Назвать известные структурные типы.
25.	В структуре соединения с формулой ЛХ2 координа-
ционное число атомов А равно 2.•Определить геометрический
характер структуры. Что можно сказать о типах химической
связи?
26.	В структуре соединения А^В^О^ атомы кислорода
окружают атомы А по тетраэдру, а атомы В, - по октаэдру.
Определить тип формулы, если в ближайшей координационной
сфере кислорода - один атом А и три атома В.
27.	Определить формулу соединения А^Х?, если в егР
структуре атомы X окружают атомы А по кубооктаэдру, а атомы
В - по октаэдру. В свою очередь координация атомов X по
атомам А - квадратная, а по атомам В - линейная.
28? В гранате CagAl^StO^g все атомы А1 окружены
атомами кислорода по октаэдру, Са - по скрученному (томсо-
новскому) кубу. Какова координация атомов кислорода?
Соблюдается ли локальная компенсация заряда аниона (2-е
правило Полинга)?
29^ В структуре ортосиликата кианита, (A^S*1-*^), все
атомы А1 имеют обычное для них октаэдрическое окружение.
Определить координацию атомов кислорода обоих типов, если
в этой структуре строго соблюдается локальная компенсация
зарядов анионов. Сколько добавочных атомов кислорода в ко-
орднационном октаэдре А1 ?
30.	В структуре топаза, AlgCStO^](F,0H)2, координация
всех атомов А1 при обычном координационном числе 6 одина-
кова. Определить координацию кислорода и добавочных анио-
нов, если в этой структуре соблюдается локальная компенса-
ция зарядов анионов. Сколько добавочных анионов входит в
координационную сферу атома алюминия?
31.	В структуре кольцевого силиката берилла атому
алюминия окружены атомами кислорода по октаэдру, бериллия
- по тетраэдру. Координационное число всех ’’активных" ато-
мов кислорода одноэтажного шестичленного кольца равно 3.
Определить формулу берилла.
32.	В слоистой структуре серпентина,	ОН)
"активные" атомы кислорода кремнекислородной сетки вместе
с группами (ОН)' создают при к.ч. =6 одинаковое окружение
вокруг всех атомов- Mg. Исходя из формулы серпентина и ло-
кальной компенсации зарядов анионов, определить их коорди-
нацию.
33.	В слоистой структуре талька, Mg^LSl^о1О](он)2,
"активные" атомы кислорода двух противолежащих кремнекисло-
родных сеток вместе с группами (ОН) создают при к.ч. =6
одинаковое окружение вокруг всех атомов магния. Исходя из
формулы талька и локальной компенсации зарядов анионов,
определить их координацию.
34.	В структуре элементарного мышьяка атомы располо-
жены по вершинам искаженного примитивного куба. Исходя из
положения АЗ в Периодической системе элементов, решить, ка-
кое искажение куба можно предположить? Каков геометрический
характер структуры?
35.	Определить тип формулы соединения A^B^X^, в коор-
динационной структуре кристаллов которого атомы А и В нахо-
дятся в центрах тетраэдров из атомов X, которые в свою
очередь занимают тетраэдры, образованные атомами А и В (в
118
каждом тетраэдре две вершины занимают атомы А, две другие
- атомы В).
36.	В структуре кристаллов KgPtCIg все атомы К окруже-
ны атомами хлора по кубооктаэдру, a Pt - по октаэдру.
Определить геометрический характер структуры.
37.	В молекуле структуры реаль-
Рис. 95. К задаче 37
в центрах ее граней,
решить вопрос о типе
гара,Ая$, атомы одного типа образуют
тетраэдр, атомы другого типа - ква-
драт (рис. 95). Исходя из позиции
серы и мышьяка в Периодической сис-
теме элементов,расставить атомы в
молекуле. Как следует записывать
структурную формулу реальгара?
38.	В структуре соединения АВд
атомы одного типа расположены по вер-
шинам кубической ячейки, .другого -
Определив координацию атомов А и В,
химической связи.
39.	В структуре кристаллов KH^F между атомами азота
и фтора образуется водородная связь. Определив координаци-
онные числа компонентов, сделать вывод о геометрическом
характере структуры. Какие структурные типы можно предпо-
ложить, если не принимать во внимание атомы водорода?
40.	Какой геометрический характер структуры можно
предположить у кристаллов HF, если принять во внимание
значительную электроотрицательность фтора?
41* В структуре КДП (дигидрофосфата калия, KHgPO^)
между атомами 0 образуется водородная связь. Определить
геометрический характер структуры. Какой геометрический
характер можно предположить в бикарбонате натрия КаНСОд?
§ 3. Кристаллохимические радиусы.
Число формульных единиц в ячейке (Z ).
Рентгеновская плотность
42.	Найти кoвgлeнтный радиус Zn, если в структуре
сфалерита а = 5,41А, а ковалентный радиус атома S равен
1,04А.
43.	Плотность кристаллов меда, равна 8,96 г/см3. Вы-
числить металлический радиус Си.
119
44.	Плотность кристаллов каменной соли 2,16 г/см3.
Вычислить расстояние Яа - 01.
45.	Вычислить отношение плотностей алмаза и графита,
если для первой модификации углерода а = 3,56$, а .для вто- .
рой - п = 2,46$, с = 6,70$.
46.	Вычислить отношение плотностей двух модификаций
хлористого рубидия (одна со структурой типаЯаС!, другая -
0^01). Объяснить полученный результат.
47.	Определить отношение плотностей двух хлоридов рту-
ти - тетрагональной каломели H^C^ois 4,47$, с = 10,89$,
2 = 2) и ромбической сулемы HgCl2(o-= 5,96$, Ь = 12,74$,
с = 4,32$, z = 4). .
48.	Определить формулу тетрагональных кристаллов гид-
рата сульфата бериллия BaSO^nHgO, если а = 8,02$, с =
10,75$, Z = 4, плотность равна 1,713 г/см3.
49.	У кристаллов гексагональной модификации Hg£(кино-
вари) а = 4,16$, с = 9,54$, Z = 3. Для кубической модифи-
кации (метациннабарита) а = 5,84$, z = 4. Для какой моди-
фикации плотность равна 7,73 г/см3? Вычислить рентгеновс-
кую плотность .другой модификации.
50.	Во сколько раз межатомное расстояние С - С в струк-
туре алмаза больше, чем в структуре графита, если =
3,56$, а = 2,46$ ? Чему равна кратность связи в структуре
графита?
51.	В структуре перовскита а = 3,83$. Определив рас-
стояние Са - 0, сравнить его с тем же расстоянием в струк-
туре СаО (структурный тип галита, о. = 4,80$), Чем объяснить
разницу в расстояниях?
52* Определить рентгеновскую плотность гексагональных
кристаллов пирротина, если а = 3,43$, с = 5,69$, Z = 2.
Чем объяснить существенное расхождение значений плотности
рентгеновской и экспериментальной (последняя равна 4,58 -
4,6 г/см ’)? Как следует записать рациональную формулу пир-
ротина?
53.	Вычислить поправочный коэффициент .для металличес-
ких радиусов при переходе от координационного числа 12 к
коорцинационноглу числу 8, если для tf-Fe а= 3,564$, а для
tZ-Ре а= 2,861$.
54.	Для некоторого бората (Ка^В^О? *пН20) получены
120
следующие данные: cl = II,86A, b= I0.67A, С = I2,20A,
j3 =I06°4I, 2=4, плотность кристаллов равна 1,71 г/см3.
Какой это минерал: бура, Ка^В^О?-IQHgO,или кернит, Ыа^О?
•4^0 ?
55,	Для индерборита (MgCaBgO^-nHgO) определены следую-
щие константы: а= 8,74$, Ь = П,26$, б = 6,10А и J = П0°07,
2 = 4, плотность 1,934 г/см3. Определить, сколько молекул
вода находится в формульной единице ивдерборита.
56.	Определить параметр ячейки кристаллов квасцов
КА1($04)2*12 HgO, если в ячейке находится 4 формульных
единицы, а плотность кристаллов равна 1,75 г/см3.
57.	Определить плотноеTg кристаллов флюорита, если
расстояние Са - F равно 2.38А.
58.	Вычислить радиус атома кадмия, усреднив минималь-
ное и максимальное расстояния Cd - Cd в структуре элемен-
тарного Cd, если а= 2,97$, б = 5,607$. Кадмий кристаллизу-
ется по типу Mg, но с увеличенным значением отношения пара-
метров с/а. Как изменяется геометрический характер структу-
ры при переходе от Mg к Cd ?
59.	Определить плотность кристаллов алмаза, если ра-
диус атома углерода при ординарной связи равен 1,54$.	0
60.	HapneogaTb модель пиритного иона, если гковё= I.04A,
§ 4.	Плотнейшие шаровые упаковки
61.	Объяснить, почему для обозначения упаковки любой
елейности необходимы всего три буквы А, В и С.
62.	Выделив ячейку Бравэ в кубической плотнейшей упа-
ковке, показать, сколько октаэдрических и тетраэдрических
пустот приходится на один шар плотнейшей упаковки. Записать
координаты шаров и пустот обоих типов, выбрав начало коор-
динат в центре шара.
63.	Выделив ячейку Бравэ в гексагональной плотнейшей
упаковке, записать координаты всех шаров упаковки и пустот
обоих типов. Начало координат выбрать в центре любого шара.
64.	Какой решеткой Бравэ описывается трехмерная перио-
дичность кубической плотнейшей упаковки, сжатой вдоль одной
из своих осей 3-го порядка?
121
65.	В структуре герцинита, FeAlgO^, атомы кислорода
образуют плотнейшую кубическую упаковку. Координационные
числа Fe и А1 равны соответственно 4 и 6. Какая часть те-
траэдрических и октаэдрических пустот заполнена в этом
структурном типе? Назвать структурный тип.
66.	Определить формулу форстерита, если в его струк-
туре атомы кислорода образуют гексагональную плотнейшую
упаковку, в которой атомы Мр занимают октаэдрических
-4	4	2
пустот, а атомы St - g тетраэдрических.
67.	В структуре топаза, Alg [SiO^J(F,0H)2, анионы об-
разуют единую плотнейшую упаковку. Приняв во внимание ха-
рактерную для атомов А1 и Si координацию, определить, ка-
кая часть пустот обоих типов заполнена.
68.	В структуре портландита октаэдрические пустоты
плотнейшей упаковки, созданной гидроксильными группами, за-
няты послойно атомами Са. Записать формулу минерала.
69.	В перовските (СаТЮд) атомы кислорода и кальция
образуют единую плотнейшую упаковку, в которой атомы Tt
заполняют | пустот одного типа. Каково координационное
число атомов Ti ?
70.	В структуре 1а атомы образуют четырехслойную плот-
нейшую упаковку. Определить параметры ячейки, если металли-
ческий радиус Ха равен 1,87$. (Упаковку считать идеальной).
71* В слоистой структуре некоторого хлорида атомы
хлора образуют гексагональную плотнейшую упаковку, в кото-
рой атомы металла заполняют октаэдрические пустоты по за-
кону: слой пустой чередуется со слоем, заполненным по ко-
Рис. 96. К задаче 71
рундовому закону
(рис. 96). Опреде-
лить тип формулы
хлорида.
72.	Определить
симметрию координа-
ционного многогран-
ника для шара "к” и
"г" плотнейшей упа-
ковки. Дать сравни-
тельную характерис-
тику этих многогран-
ников.
122
73.	Показать,чему равна елейность плотнейшей упаковки,
запанной повторением буквенной последовательности ...гк...
74.	Одинаков ли период идентичности в следующих упа-
ковках, заданных повторением беквенных последовательностей:
а)	...ггк...	и	...ккг... ,
б)	...гггк...	и	...кккг... ,
в)	...ггкгг...	и	...ккгкк... ?
75.	Используя двухбуквенный способ обозначения (г,к),
показать, сколько различных упаковок приведено ниже:
.. .АВАВАВС........АВС АС АВ. .....АВСАСВС.........АВАВСАВ
.........АВСАВСВ... .
76*	Показать, что периодичность упаковки ...кгг...
описывается R-решеткой Бравэ.
77.	Выделив в гексагональной плотнейшей упаковке ячей-
ку Бравэ, вычислить отношение параметров с/а .
78.	Определить отношение параметров с/а в упаковке
...ГК...'.
79.	Показать, что слойность .двух упаковок - ...ггкк...
и ...гггккк... - одинакова. Чему она равна?
80.	- Доказать, что в упаковках (ггкк)-пх и (кггг)-п2
множители n-i и п2 - разные. Определить их.
81.	В гидрате CaClg’niy) плотнейшую гексагональную
упаковку образуют -молекулы воды; октаэдрические пустоты
заполнены по закону: слой - ионами 01 по корундовому зако-
ну (см. рис. 96), слой - ионами Са по антикорувдовому.
Определить формулу гидрата.
82.	В структуре некоторого бинарного соединения атомы
А расположены по узлам гранецентрированного куба, атомы В -
в серединах всех ребер, в центре ячейки и в центрах восьми
октантов, на которые можно разделить ячейку координатными
плоскостями, проходящими через ее центр. Записать формулу
соединения, описать структуру в терминах плотнейших упако-
вок.
83.	Какие выводы об электрических свойствах вюрцита
можно сделать по полиэдрической модели его структуры (рис.60,г)?
84.	В соединении АЛ^ атомы X и У образуют единую
9-ти слойную плотнейшую упаковку. Определить тип формулы,
если известно, что атомы А заполняют октаэдрические пусто-
ты мевду разноименными слоями ("г" и "к"), а решетка Бравэ
структуры - ромбоэдрическая.
123
§ 5. Описание кристаллических структур
85.	К какой сингонии относится КаС1-подобная структу-
ра, если сферический анион заменен: а) линейной группой
Н - Г - Н, параллельной одной из осей 3-го порядка, б) ли-
нейной, группой 0-0, параллельной одной из осей 4-го по-
рядка, в) треугольным комплексом СОс плоскость которого
перпендикулярна одной из осей 3-го порядка. В каждом случае
центр комплексного аниона совпадает с центром сферического
иона 01.
86.	По словесному описанию структуры нарисовать ее в
плане и дать полную характеристику (выделив ячейку Бравэ,
определить тип решетки Бравэ, число формульных единиц (Z ),
координационные числа, координационные многогранники). На-
звать структурный тип.
Тип формулы	Описание структуры
I)	А2Х Атомы X образуют плотнейшую'кубическую упаковку,
атомы А заселяют все пустоты одного типа.
2)	АХ Атомы X образуют гексагональную плотнейшую
упаковку, атомы А заселяют все пустоты одного
типа.
3)	АХ^ Атомы X образуют гексагональную плотнейщую
упаковку, атомы А заселяют | пустот одного
типа (перпендикулярно главной оси упаковки
слои занятых пустот чере,дуются со слоями не-
занятых) .
4)	АХ Атомы X образуют гексагональную плотнейшую
4
упаковку, атомы А заселяют | пустот одного
типа. Заняты пустоты одной ориентации.
5)	АХ2 Атомы X расположены по закону простой кубичес-
кой кладки (занимают вершины кубов), атомы А
заполняют центры половины кубов в шахматном
порядке.
6)	АХ Атомы X образуют кубическую плотнейшую упаков-
ку, атомы А заселяют все пустоты одного типа.
7)	АХ Атомы X образуют кубическую плотнейшую упаков-
ку,, атомы А заполняют половину пустот одного
124
8) AX
типа, причем в направлении одной из осей 4-го
порядка слои, перпендикулярные этой оси, че-
редуются: слой занятых пустот, слой незанятых
пустот.
Атомы X образуют гексагональную плотнейшую
упаковку, атомы А заселяют половину пустот
одного типа, при этом главная ось кристалла
оказывается полярной.
87.	Дать полное описание структур, изображенных в
плане на рис. 97. Во всех случаях ?a = Tb = Т^,оС = р = ? =
= 90°.	J
88.	В структуре CuAu слои, перпендикулярные одной из
осей 4-го порядка кубической плотнейшей упаковки, образо-
ваны попеременно то атомами меди, то атомами золота. Нари-
совав структуру в плане, выбрать ячейку Бравэ и дать пол-
ное описание структурного типа.
89.	Структура гексагональной модификации ВЫ состоит
из расположенных друг над другом графитовых сеток, в кото-
рых каждый атом одного сорта окружен по треугольнику ато-
мами .другого. В вертикальном направлении атомы В и Я чере-
дуются. дать полное описание этой структуры.
90.	В ЯаС1-подобной структуре пероксида бария (ВаО^)
линейные группы 0g ориентированы параллельно одной из осей
4-го порядка структуры МаС1. .Изобразив структуру в плане,
дать полное описание этого структурного типа.
91^ В структуре некоторого соединения атомы А
занимают позицию ООО,... , атомы X - |оо,... . Решетка
Бравэ структуры кубическая гранецентрированная. Описать
структуру в терминах плотнейшей.упаковки. Как сочленяются
.друг с .другом полиэдры, заполненные атомами А?
92.	В гексагональной структуре некоторого соединения
атомы А занимают позицию ООО, 00-L атомы X - и ~~ .
Описать структуру в терминах плотнейшей упаковки. Как со-
членяются друг с другом полиэдры, заполненные атомами А?
Сравнить этот структурный тип со структурным типом, описан-
ным в задаче 91. Объяснить, почему этот структурный тип ис-
ключен .для оксидов и галогенидов.
В задачах, отмеченных (91,93,96,98,99),.указаны коор-
динаты лишь тех атомов, которые не связаны трансляциями
решетки.
125
I
3
93^ В структуре некоторого бинарного соединения
атомы А имеют координаты ООО, ...» атомы В -	,
... Описать структуру в терминах плотнейшей упаковки, если
решетка Бравэ структуры - кубическая гранецентрированная.
Описать структуру в полиэдрах, считая анионами:
а) атомы А, б) атомы В. Как сочленяются, друг с .другом по-
лиэдры в варианте а) и варианте б)?
94. В структуре перовскита атомы Са расположены в
центре кубической ячейки Бравэ, атомы Т1 - в ее вершинах,
а атомы 0 - на серединах ребер. Описать структуру в поли-
эдрах; как они сочленяются .друг с .другом? Можно ли в дан-
ном случае говорить о плотнейшей упаковке атомов?
95. В структуре гексагонального кристалла Ва№Од
(п = 5,58$, С = 4,83$) атомы занимают следующие позиции:
238 : + (з И) ’
2№ : ( ООО, 00^ ),
60 : +(хх- , 2Х х | , х 2х |), где х = | .
Описать структуру в терминах плотнейшей упаковки. Дать
сравнительное описание этого структурного типа и структур-
ного типа перовскита (задача 94) в полиэдрах.
. 96** В структурном типе шпинели, MgAl20^, атомы зани-
мают еле,дующие позиции:
Mg : 8 (000, Щ),
. ТЛ/555 577 757, 775 ч
м • 16(№ 888’ 838’' 888}’
О : 32(-ххх, ххх, ххх, ххх, |-х |-х |-х, |-х |+х ^+х,
5+х |-х з+х, 54-х 5+х |-х), где х = g.
Описать структуру шпинели в терминах плотнейшей упаковки,
если решетка Бравэ структуры кубическая гранецентрирован-
ная. Какова координация атомов кислорода? Как сочленяются
.друг с другом полиэдры магния и алюминия?
97. В полиэдрической модели структуры соединения типа
АШХК заполненные кубы чередуются с пустыми по закону трех-
мерной шахматной доски. Дать полное описание этого струк-
турного типа. Описать в полиэдрах структуру антиизострук-
турного соединения (АпХт).
В кристаллах халькопирита (CuFeS2) решетка Бравэ
тетрагональная объемноцентрированнач. Атомы Си занимают
127
Рис. 98. К задаче 102
128
позицию ООО, о||, ..., Ее - |^0, |о^......S - х||, |х|,
х||, ^xg, ... Определить отношение параметров с/а и пара-
метр х, если халькопирит является сверхструктурой к сфале-
риту.
99^* В кристаллах элементарного мышьяка (решетка гек-
сагональная дважды центрированная, а= 3,75А, с = Ю,52А)
атомы Да занимают позицию 00z, 00z, ..., где z = 0,226.
Определить координацию атомов мышьяка и геометрический ха-
рактер структуры. Как он будет меняться в изоструктурном
ряду Аз - Sb- Bt ?
100. Дать сравнительную характеристику следующих струк-
турных типов: а) вюрцит и сфалерит, б) вюрцит и гексагональ-
ный ВЯ , в) Са?2 и QsCl, г) СаЕ2 0 ЬЬА д) ГеД и Mg(0H)2,
е) алмаз и лонсдейлит, ж) пирит и углекислота, з) СаС03 и
CaTiO3, и) CaTi03 и KgPtClg, к) CaTiO3 и 1?е03, л) ЯаС1, СаЕ2
и BtFg, м) Си и Cu3Au, н) Cu3Au и СаТЮ3.
101. В структуре типа антифлюорита (1д20или К20) сфери-
ческий анион кислорода замещен октаэдрической группой PtCig,
сохраняющей в структуре свою собственную симметрию. Опреде-
лить координационное число атомов К и их координационный
многогранник, если расстояние Pt - Cl в два раза меньше
кратчайшего расстояния К - К. Сравнить этот структурный тип
со структурным типом перовскита.
^102'. Дать полное описание структур простых веществ по их
проекциям (рис. 98 а,б). Назвать структурные типы.
Примечание: атомы на нулевом уровне обозначены кружком, на
уровне ;Тс - крестиком.
а)	расстояния I - П = I - Ш.
б)	расстояния I - П « I - Ш.
103. Описать изображенную в плане (рис. 99) структуру
бинарного соединения.
§ 6. Федоровские (пространственные) группы
симметрии
104. Показать, что число пространственных групп в три-
клинной системе равно двум.
105; Вывести пространственные группы, подчиненные то-
чечной группе 6.
129
9-1478
Рис. 99. К задаче 103
106.	Перечислить точечные группы, которым подчинены
энантиоморфные федоровские группы симметрии.
107.	Показать, что символы АЪа-т и Стпса определяют
одну и ту же федоровскую группу.
108.	Показать, что символы р|1(= Pl^l) и Pf-*(= Pi^1!)
выражают одну и ту же пространственную группу.
109.	Показать, что символы р|1(= Pl^i) и В^( = В1|г1)
описывают одну и ту же федоровскую группу. То же для
с| (= l| (= 11|1) и г| (= рф).
НО. -Сколько разных пространственных групп представле-
но следующими символами: Роса., РсаЬ, РЪаа, РВаЬ, РЪссс ?
III. Найти надгруппу минимального порядка для групп
РЗпй и Р321.
112. Достроить графики представленных на чертеже
(рис. 100) федоровских групп. Дать их символы. (Волнистыми
линиями ограничены ячейки Бравэ.)
ИЗ. Для перечисленных ниже случаев записать полны»;
символ группы (или групп !). Ответ обосновать.
1
2
3
Рис. 100. К задаче 112
i.	фб...
2.	Pf^m..
3.	142...
4.	Гт...2
5.	РЗт,..
6.	РбС...
и
и
и
и
и
и
ф....
Р=2 .. .тп.,
ТП.	1
I4JTH....,
F4...2,
Рбт...,
Р6...С,
7.	Р4т... и Р4...ТП
8.	143... и 143...
9.	Р62... и Р32...
10.	P4i...2 и 141в.
II.	Р42 2... и Р4,т.
12.	I -	• И I
2
114.	Выписать, не прибегая к графику, осевые подгруп-
пы максимального порядка для следующих групп: а) РЬап ,
б) РЪса , в) Pnnm , г) Р-шпа и Рптпа.
II5.	Выписать осевые подгруппы максимального порядка
.для групп Imma. и Ibca . Чем отличаются эти осевые группы
друг от .друга?
116.	Показать, что символы P2aa , Рсс2 и РЬ2Ь пред-
ставляют одну и ту же группу.
117.	Дать стандартный аспект следующих групп:
а) P2?na и Рл27а. , б) Р2?аЬ и РЪ2?а. , в) НЗтп, г) С42тпс.
Привести их обозначения по Шенфлису (см. Приложение).
118.	Записать стандартные символы следующих групп:
P64-mn , Cba.2, Р4,сЪ .
о	z	2	2
119.	Показать, что символы В1£1 и Bll^ описывают раз-
ные федоровские группы. Дать их обозначения по Шенфлису
(см. Приложение).
120.	Не прибегая к графику, решить, какой будет в каж-
дом случае ось, поворотной или винтовой: а) Р2?пп ,
б) , в) РЬ2?п ?
121.	Выписать символы для всех аспектов групп Pbnm.
и Рсптп. Как обозначить каждую из этих групп по Шенфлису
(см. Приложение)? То же для групп РЪсп и РЪап. .
§ 7.	Правильные системы точек (системы
эквивалентных точек, или позиций)
122.	Объяснить, почему точка, лежащая на трансляцион-
ном элементе симметрии (например, на плоскости скользящего
отражения), создает общую, а не частную правильную систему
точек.
123.	Почему точка, попавшая на ось 4£, создает общую
систему точек, а попавшая на ось 42 - частную?
132
124.	Показать, что произведение величины симметрии
позиции на кратность системы точек есть величина для дан-
ной федоровской группы постоянная. Чему она соответствует?
125.	Какова минимальная кратность системы точек в про-
странственной группе Pm 3m? В каких группах может быть си-
стема точек с кратностью, равной единице?
126.	Определить кратность правильных систем точек по
симметрии их позиций в следующих пространственных группах:
Простран- Симметрия		Простран- Симметрия		Простран- Симметрия	
ственная труппа	позиции	ственная группа	позиции	ственная группа	позиции
I)	TH	8) Р|зтс	3m и 6m2	15) Fd3m	43m
2) С|	1	9) P3mi	Эпи I	16) R3c	32
3) Pbca	1	10) I42d	222	17) С^стп	42 m
4) Pban	222	II) i|w	42m	18) H6c2	32
5) Ibam	2 ТП.	12) P|2nm ТП	rnmm	19) F^dc	4
6) rd-cLd	222	13) Pa3	3	20) f|	1
7) Pmmn	тптп2	14) Ia3cL	32	21) Cl	1
127.	Построить график пространственной группы в при-
веденном и стандартном аспектах. Записать для каждого ас-
пекта координаты заданной системы (или систем) точек:
Символ труппы Характеристика системы точек
а)	P2?aa	Кратность максимальная
б)	Pm2?a	Число степеней свобода минимальное
в)	Pb2?n	Кратность минимальная
г)	Ib2n	Число степеней свободы максимальное
д)	СЪ2а	Величина симметрии максимальная
е)	A2an	Число степеней свободы максимальное
ж)	PmCn	Симметрия позиции пг и 1
128.	В каких системах (сингониях) исключены точки со
следующими координатами: ххО, ххх, xOz, Oyz, хОО ?
129.	Получить и охарактеризовать следующие системы то-
чек (графики трупп см. в Приложении):
133
Федоровские группы	Заданные позиции
а)	РЗтп!	а< Ц	б< В; б)	Рпитп. (см.рис.76г) а} б] в)	Стпса	aj б в г; г)	Р63тпс	а} д)	С1|1	а] б] е)	РаЗ	aj	1 с двумя степенями свобода, 1 с симметрией 2, 1 с кратностью 3 1 с минимальной кратностью, 1 с кратностью 4 1 с минимальной кратностью, • с двумя степенями свобода, 1 с координатами хОО..., 1 общая » с координатами х 2х z, 1 с координатами 0у4 , । общая | с минимальной кратностью, » с максимальной кратностью
' 130. Какова симметрия позиции начала координат в Груп-
пе Стеа ? Обосновать его выбор (график группы - в Приложе-
нии). То же для группы Р^пт,
131.	Записать символы пространственных групп по их
графикам (рис. 101). Выбрать начало координат в соответст-
вии с правилами.
§ 8. Кристаллоструктурные иллюстрации
федоровских групп симметрии
132.	Какие федоровские группы описывают симметрию
структур, полученных сжатием или растяжением кубической
плотнейшей упаковки вдоль одной из осей: а) 4-го порядка,
б) 3-го порядка, в) 2-го порядка? То же, но за исходную
модель взять объемноцентрированную кубическую упаковку.
133.	Нарисовав в плане структуру графита, определить
его федоровскую группу, число формульных единиц (Z ) и
охарактеризовать позиции, занимаемые атомами.
134.	Найти пространственные (плоские) группы мозаик,
изображенных на рис. 102. Что объединяет эти пространствен-
ные группы?
135.	Почему при одинаковой симметрии решеток и узорных
единиц (рис. 102) пространственные группы бесконечных узо-
ров-мозаик разные? Определить эти пространственные группы.
134
Рис. 101. К задаче 131
Рис. 102. К задаче 134
Рис. 103. К задаче 138
136.	Определить симметрию решетки и бесконечного узора
(рис. 67,6), объяснить почему симметрия узора ниже симмет-
рии решетки.
137.	Какова максимальная симметрия трехмерного узора,
если симметрия узорной единицы 6, а пространственной решет-
ки - Pmmin? То же, если симметрия узорной единицы 4?nm, а
6
решетки - P^mm.
138.	Определить федоровскую группу изображенных "струк-
тур”' (рис. ЮЗ), считая, что "разноцветные" фигурки распо-
ложены на трех (а) и четырех (б) уровнях,.
139.	В структуре ItOH гидроксильные группы образуют
плотнейшую кубическую упаковку, половина тетраэдрических
пустот которой занята атомами И , причем слои занятых и
незанятых пустот располагаются поочередно перпендикулярно
одной из осей 4-го порядка плотнейшей упаковки. Определить
федоровскую группу' этого структурного типа и дать описание
позиций атомов.
Рис. 104. К задаче 142
140.	Определить федоровские группы двух мозаик, изобра-
женных в задаче 2 на рис. 91.
141.	Для структурных типов, описанных в задаче 86,
определить федоровские группы и дать описание позиций ато-
мов. Указать общее число параметров, определяющее каждый
структурный тип.
142.	Для изображенной на рис. 104 мозаики определить
федоровскую (плоскую) группу и ее порядок. Записать две
подгруппы максимального порядка и найти в этом параграфе
мозаики, иллюстрирующие их.
143.	Ячейка Бравэ структуры алмаза сжата вдоль одной
из своих осей 4-го порядка. Определить федоровскую группу
и описать позиции атомов.
Рис. 105. К задаче 145
144.	Определить
симметрию гексагональ-
ной плотнейшей упаков-
ки. Какой федоровской
группой описывается
симметрия гексагональ-
ной плотнейшей упаков-
ки, сжатой вдоль одной
из диагоналей основа-
ния ячейки Бравэ упа-
ковки?
145.	Определив
пространственную (пло-
скую) группу симметрии
кавдой из мозаик (рис.
105,а и б), найти их
надгруппу минимального -
порядка. Какая мозаика
этого параграфа иллюст-
рирует эту нацгруппу?
146.	Выделив ячей-
ку Бравэ, определить
федоровскую группу
изображенного в плане
узора (рис. 106). По-
казав на проекции эле-
139
Рис. 106. К задаче 146
Q0,65	O°’^	Q)°’65
Q)0,15	Q0,65	O°>15
менты симметрии, выбрать начало координат в соответствии
с правилами и записать симметрию позиции каждой системы
точек.
147.	В каждой из представленных в плане структур (рис.
107) выделить ячейку Бравэ и определить федоровскую группу
симметрии. Выбрав начало координат, дать полное описание .
позиций атомов.
148.	Определить .для каждой из двух мозаик федоровскую
группу, считая черные и белые фигурки: а) расположенными
на .двух уровнях, б) лицом и изнанкой (рис. 108).
§ 9.	Использование федоровских групп
при решении различных вопросов
кристаллохимии и кристаллографии
149.	Для кристаллов вюрцита рентгеновское исследование
допускает три федоровские группы: рДзтпс, Р63шс и Р62с. На
какой группе следует остановиться, если известно, что вюр-
цит пироэлектрик?
150.	Кристаллы некоторого минерала имеют точечную сим-
метрию 32. Можно ли сделать однозначный вывод о типе решет-
ки Бравэ, если известно, что 1фисталлы обладают оптической
активностью?
151.	Одной из габитусных форм низко- и высокотемпера-
турной модификаций кварца является гексагональная> призма.
Оба полиморфа, будучи оптически активными, не могут прояв-
лять пироэлектрические свойства. Какие пространственные
группы можно предположить .для этих модификаций, если при
полиморфном превращении порядок группы симметрии ловышается
вдвое?
152.	Какие вывода об электрических свойствах вюрцита
можно сделать по полиэдрической модели его структуры (см.
рис.60г)?
153.	К какой из федоровских групп (R32, КЗт и РЗтп )
надо отнести турмалин, кристаллы которого обладают пироэлект-
рическими свойствами?
154.	Рентгеновское исследование предлагает .для оптичес-
ки активных кристаллов лактозы две федоровские группы: Р^1
142
Рис. 108. К задаче 148
I
и P2i. Какая из этих групп описывает симметрию лактозы?
Сохранится ли оптическая активность лактозы в растворе?
155.	По .дифракционной картине кристаллы каламина мож-
но отнести к четырем федоровским группам: 1222, I2,2i2i,
Imm 2 и Ьптитп. Остановиться на одной из них, принимая во
внимание, что кристаллы каламина обладают пироэлектрически-
ми свойствами.
156.	Кристаллы некоторого соединения имеют симметрию
федоровской группы РаЗ. Атомы занимают следующие позиции:
А - ООО, В - ххх, где х=»0,4. Описать структурный тип. Опре-
делить какая федоровская группа получится при х = Описать
этот структурный тип.
157.	В кристаллах некоторого бинарногоосоединения (фе-
доровская группа Pnnm , а = 3,8lX, Ъ = II,ОА, с = 3,34$)
атомы занимают по одной позиции: А - 00|, ... , В - хуО,...,
где х - 0,173, у = 0,132. Определить координацию атомов А и
геометрический характер структуры (график Рпптп. на рис. 76г).
158.	Из .двух соединений с формулой MeOg о,дно дает
кристаллы федоровской группы Fm3m [Me - 4(a): 000,
О - 8(c): | |	,
другое - РаЗ [Me - 4(a): 000, ...
О - 8(c): ххх, где х «0,4 ] .
Какое из этих соединений, судя по структуре, следует считать
оксидом, а какое - пероксидом?
159.	Кристаллы некоторого соединения с формулой АХ под-
чинены федоровской группе р|зтс (е= 3,6оХ, с = 5,80А),
в которой атомы А занимают позицию ООО, атомы X -
Выяснить, какие атомы (А или X) образуют плотнейшую упаковку
и какую именно? Какие пустоты заселяют атомы другого сорта?
Назвать структурный тип.
160.	Пирит кристаллизуется в кубической сингонии
(ц = 5,4оХ). В федоровской группе РаЗ атомы Ре занимают по-
зицию ООО, атомы Я - ххх, где х = 0,386. Определить ближай-
шее расстояние £ -5 . Какой получим структурный тип при
х = 0,5 - 0,386? Каков геометрический характер этого струк-
турного типа? Изменится ли федоровская группа при х = ^ ?
Назвать структурный тип.
161.	Кристаллы некоторого_соединения типа AXg характе-
ризуются федоровской группой Р3тп1, в которой атомы одного
144
12	1
типа занимают позицию ООО, другого - 3 gz , где z = %.
Определить при а = 4,24$ и d = 6.84А тип плотнейшей упа-
ковки и мотив заполнения пустот. Сопоставить полученные
результаты с результатами задачи 159. Назвать структурный
тип. Как проходит плоскость спайности?
162.	Соединение АХ^ относится к терагональной синго-
нии ( а = 4,66$, с = 3,08$). В федоровской группе рДгтп ато-
мы А заниамют положение ООО, атомы X - ххО, где х = 0,31.
Определив координационное число атоме А, выяснить геометри-
ческий характер структуры. Как он будет меняться с увеличе-
нием х и с уменьшением его?
163.	Для кристаллов некоторого простого вещества уста-
новлена ромбическая сингония (а = 6,29$, Ь = 4,5А, с = 8,21$)
В федоровской группе Сшса атомы занимают позицию 8(j ): Oyz,
где у = 0,130, z = 0,100. Определить координационное число
и геометрический характер структуры. Пользуясь кристалло-
химическими соображениями и сопоставив вычисленные расстоя-
ния с суммой кристаллохимических радиусов, решить, что это
за вещество.
164.	Для одной из модификаций Si 02 установлены следую-
щие структурные данные: федоровская труппа Ibam , a = 8,36А,
Ъ = 5,16$, с = 4,72$. Позиции атомов: Si - 4(a): 00|,
О - 4(j): хуО, где х = 0,209, у = 0,110. Выяснив координа-
цию атомов кремния и геометрический характер структуры,
объяснить, почему эта модификация &02 неустойчива.
165.	Кристаллы скуттерудита, CoAs3, имеют симметрию
федоровской группы Im3, а = 8,189$. Позиции.атомов: Со -
- As - Оух, где у = 0,35, х = 0,15. Какие группировки
образуют атомы As? Написать правильную структурную формулу
этого минерала. Какую валентность проявляет в данном случае
кобальт?
166.	Для кристаллов киновари установлена федоровская
группа P312I, а = 4,14А, С = 9,49$; Hg - 2(a): хОд, £ - 2(b):
хо|; xHg = 0,28, Xg = 0,48. Определив координационное число
атомов Hg, выяснить геометрический характер структуры. Исхо-
дя из этих данных, установить оптический знак кристаллов ки-
новари. Будет ли киноварь сохранять оптическую активность
в расплаве?
167.	Объяснить, почему .для дийодбензола достаточно
145
Рис. 109. К задаче 167.
Изомеры дийодбензола:
а) мета-, б) орто-,
в) пара-изомер
169^ Молекулы в структуре
предварительных данных
структурного анализа (фе-
доровская группа РЬСа и
Z = 4), чтобы сделать одно-
значный вывод о том, что
это пара-изомер (рис. 109)?
168.	Объяснить, почему
для полной расшифровки
структуры алмаза достаточно
было установить федоровскую
группу (РЙЗтп. ) и число фор-
мульных единиц (Z = 8)?
кристаллов Cd(KH3)3 (М^)gCl
имеют октаэдрическую конфигурацию. Разместить адценды по
вершинам октаэдра, если симметрия кристаллов описывается
федоровской труппой при. Z = 8.
170.	В кристаллах мочевины габитусными служат грани
тетрагональной призмы и тетрагонального тетраэдра. Молеку-
лы	сохраняют свою собственную симметрию (атомы Н
во внимание не принимать). Зная, что Z = 2, выбрать из
списка федоровских групп ( см. Приложение) 3 вероятных
группы.
171* Габитусными формами кристаллов кварца служат
ромбоэдры и гексагональная призма. Перечислить вероятные
федоровские группы, если известно, что кварц - пьезоэлект-
рик и обладает оптической активностью»
172.	Объяснить, почему оптически активные кристаллы,
относящиеся к пространственной группе P2i, обязательно со-
храняют свою оптическую активность в растворе (или распла-
ве), а кристаллы симметрии P4i свою активность в этом слу-
чае могут потерять.
173.	 В кубических кристаллах ^^4 молек^лы
сохраняют свою собственную симметрию. Какие федоровские
группы можно предположить, если число молекул в ячейке
равно 6 ?
174.	Габитусными формами кристаллов гринокита Cd$,
служат гексагональные пирамида {ош} и моноэдры, Перечис-
лить вероятные федоровские группы, если известно, что атомы
Cd и 5 занимают позиции Зтп. Что можно сказать об электри-
146
ческих свойствах кристаллов гринокита?
175? В кубических кристаллах куприта, Си^О, тетраэдры
вокруг атомов кислорода сохраняют свою собственную симмет-
рию. Обратившись к списку федоровских групп (см. Приложе-
ние), выписать три вероятные группы, если Z = 2.
176.	Какая федоровская группа описывает симметрию
кристалла сфалерита, если известно, что решетка Р-куби-
ческая , Z = 4, а тетраэдры вокруг атомов Zn. (£ ) сохраня-
ют свою собственную симметрию?
177.	В вюрците, кристаллы которого относятся к федо-
1ровской группе Р63шс, тетраэдр вокруг атома 2п.(и вокруг
атома £ ) сохраняет максимально возможную для этой прост-
ранственной группы симметрию. Чему равно число формульных
I единиц (Z )?
178.	В молекулярной структуре соединения АХ2» кристал-
лизующегося по закону федоровской группы РаЗ, Z = 4. Какую
[конфигурацию имеет молекула?
179.	В ромбических кристаллах AgN02, обладающих' пиро-
электричеством, группы NOg сохраняют свою собственную угол-
ковую симметрию, причем атомы азота занимают одну позицию.
Перечислить вероятные федоровские группы, если Z = 2.
180.	В структуре кристалла хлорплатината калия,KgjPtClgj ,
октаэдрический комплекс [PtClg]" целиком сохраняет свою соб-
ственную симметрию. Определить федоровскую группу, если
известно, что Z = 4.
181.	В-структуре хлорплатинита калия, KgfPtClJ , ква-
дратный комплекс [PtCl^]’ полностью сохраняет свою собствен-
ную симметрию. Определить федоровскую группу, если Z = 1.
§ 10.	Преобразование координатных систем
в кристаллических структурах
182.	Вычислить матрицу преобразования осей от С-ячейки
тетрагональной системы к ячейке стандартной.
183.	Определить матрицу преобразования осей от С-ром-
бической ячейки к Р-параллелепипеду.
184.	Определить матрицу преобразования осей от струк-
турной ячейки гексагональной Р-решетки к ортогональной
ячейке.
147
185.	Получить матрицу преобразования осей к стандарт-
ному аспекту для группы РЬ2,а .
186.	Вычислить матрицу преобразования осей к стандарт-
ной ячейке от ячейки, для которой = F^mc.
187.	Две ячейки гексагональной Р-решетки различаются
только направлением горизонтальных осей (одна ячейка повер-
нута относительно другой на 30°). Определить матрицу преоб-
разования осей к структурной ячейке.
188.	Симметрия некоторого вещества описывается федоров-
ской группой РЪпт. Определить матрицу преобразования осей
к стандартному аспекту этой группы.
189.	Вычислить матрицу преобразования осей от аспекта
p|1 (Pig'11) к аспекту (Р1^11). Дать .два варианта.
190.	Записать матрицу преобразования осей от классичес-
кой установки моноклинной системы к рациональной установке.
191.	Дать геометрическую интерпретацию Преобразования
осей, если (М) =10 0 1) . Какая это сингония?
\1 0 0/	6
192.	Для кристаллов класса матрица преобразования
к осям структурной установки равна ^|о / ||о / 001. Дать
геометрическую интерпретацию этого преобразования.
193.	Структурная установка некоторого тетрагонального
минерала отличается от морфологической лишь поворотом вокруг
оси Z на 45°. Получить матрицы прямого и обратного преобра-
зования.
194.	Описать структуру некоторого вещества с гексаго-
нальной Р-решеткой Брав^ в ортогональных осях, если в Р-ячей-
ке а = 4,91&, С = 6,18А. Один из атомов А занимает позицию
11 1
х0|, где х = один из атомов В - позицию xyz , где х = %,
у = g, z = |. Все показать на чертеже.
195.	Для кристаллов .дурангита матрица преобразования
старых осей к новым (М) = (001/010/101). Прочесть, восполь-
зовавшись соответствующими матрицами, старые символы новых
координатных граней и осей, а также новые символы старых
координатных граней и осей.
196.	Для кристаллов реальгара преобразовалие_осей от
морфологической установки к структурной (М) = (101/010/001).
Определить параметры ячейки в морфологической установке гра-
фическим путем, если в структурной ячейке а= 9,зХ, Ъ = 13,5А,
с = 6,6Й,	= 106,5°.
148
197.	Для кристаллов арагонита установлена федоровская
группа Ъ2и= Ртпсп ( cl = 4,94а, Ь = 7,94А, с = 5,72А). Полу-
чить матрицы преобразования к минералогическому (Ptmm) и
стандартному (Ршла.) аспектам. Вычислить а, Ь и с для этих
аспектов. Привести матрицы пересчета координат атомов.
198.	Для кристаллов класса 4тптп преобразование осей
задано (М) = ^0/^0/001. Дать геометрическую интерпрета-
цию этого преобразования.
199.	Некоторое вещество, кристаллизующееся по закону
федоровской группы ЕЗш, имеет следующие параметры: а =
5,48А, о = 12,04А. Атомы А занимают позицию 00z, где z=
0,13, атомы В - х 2х 0, где х = 0,34, атомы С - xyz , где
х = 0,61, у = 0,22, z = 0,14. Описать эту структуру в осях
примитивной ячейки. Каков тип формулы? Чему равно число
формульных единиц (Z ) в том и .другом варианте?
200.	Для кристаллов низкотемпературного кварца полу-
чены следующие структурные данные: федоровская группа D3 =
РЗ^Т, ol= 4,903$, С = 5,393$. Атомы Si занимают позицию
3(a): хо|, атомы 0 - 6(c): xyz; Хсл= 0,465, х^ = 0,415,
Уф = 0,*272, Zq = 0,120. Дать описание этого структурного
типа в прямоугольной системе координат.
201.	Описать структуру арсенопирита в стандартном для
группы C2h аспекте, если для установки В^1 параметры следу-
ющие: а = 9,51$, Ь = 5,65$, с = 6,42$, р= 90°. Атомы Ре,
А5 и S занимают по одной общей позиции:
xyz
Ре 0	0	0,275
As 0,147	0,128	0
£ 0,167	0,132	0,500 '
§11. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ
I. При решении следует иметь в виду, что метрика
ячейки не может однозначно определять симметрию. Так, при
Та = Ть = Тс и <z= ]3=	90° ячейка не обязательно пред-
ставляет кубическую систему (см. также с. 26 ). Так,в при-
мере 3 (рис. 90) очевидно отсутствие обязательной .для куби-
149
ческой системы четверки осей 3-го порядка, поэтому решетка
оказывается тетрагональной примитивной, причем а= а
б = тс.
13.	Ориентация всех линейных групп Я3 параллельно
одной из четырех осей 3-го порядка структуры NaCI предо-
пределит гексагональность структуры КаН3. Трансляции, цент-
рирующие грани ячейки Бравэ в кубической структуре КаС1,
сохранятся, но в гексагональном аспекте (единственная ось
3-го порядка вертикальна) они станут наклонными к главной
оси: f0_^c , flc^zc, Т2£._о • Таким образом, решетка в струк-
туре НаЛГ3 окажется гексагональной .дважды центрированной (R).
Примитивной ячейкой (но не ячейкой Бравэ!) такой решетки
будет ромбоэдр. Подобный ромбоэдр можно выделить и в струк-
туре NaCl, но определяющий его угол равен строго 60°, - это
не что иное как основная ячейка кубической гранецентрирован-
ной решетки.
28.	Координационные числа А1 и Са, судя по координаци-
онным многогранникам, равны соответственно 6 и 8.
Вогруг атома А1 шесть атомов 0, и в формульной единице
(Ca^Alg [Si-Оф]3) на один атом А1 приходится шесть атомов О,
поэтому каждый атом кислорода соседствует лишь с одним ато-
мом алюминия. Вокруг атома Са восемь атомов 0, но из форму-
лы ясно, что кислорода в четыре раза больше, чем Са, поэто-
му каждый атом кислорода "обслуживает" два атома Са. Таким
образом, в коодинационной сфере кислорода один атом &(орто-
силикат!), один атом А1 и два атома Са. Правило локальной
компенсации заряда аниона выполняется строго ( ^(otSi) +
+ |(от А1) + 2*|(от Са) = 2).
29.	Кианит (Al^SiOg) - ортосиликат, поэтому его струк-
турная формула - А120. Для полной компенсации заряда
добавочного (т.е. не связанного с кремнием) атома кислорода,
последний должен быть окружен четырьмя атомами А1 (2 = ^*4).
В координационной сфере атома кислорода ортогруппы должно
быть лишь .два атома А1 ( 2 = (|) от Дн + (^*~) от А1 ):
Координация добавочного	Координация атома О
атома 0	из ортогруппы
150
Таким образом, на каждый атом А1 приходится от одного
добавочного атома кислорода а от одного ортокислороца -
Из формулы следует, что на каждый атом А1 должно прихо-
диться два атома ортокислорода и | добавочного атома кисло-
рода, поэтому в координационной сфере А1 четыре ортокисло-
рода ( 4*| = 2 ) и два_^обаврчных кислорода ( 2*^ = )•
н
Координация атома А1
41. При образовании водородной связи атом водорода
стягивает два атома кислорода, следовательно, в КНР доста-
точно водорода (Н : 0=1 : 2), чтобы все атомы кислорода
вовлечь в водородную связь. Таким образом, все вершины фос-
форнокисдородных тетраэдров сочленяются водородными мости-
ками друг с другом, образуя трехмерный каркас, в пустотах
которого располагаются крупные атомы Ма.
В бикарбонате натрия, ЯаНСОч, атомы водорода смогут
обслужить водородной связью лишь атомов кислорода. Поэто-
му за счет водородных мостиков между двумя атомами 0 сосед-
них карбонатных групп образуются цепи:
Атомы Яа располагаются в больших пус- <
тотах между цепями.
В структуре кристаллов с формулой МеНСО3 могут образо-
ваться и кольца, которые можно себе представить как замк-
нувшиеся обрывки цепей, что имеет место в структуре КНСО3:
.—. н —
— н —
52. Из формулы р т = У1 Г.У-^(см. с. 32) определим,
что Ррент = 4,76 г/см*. Существенное превышение значения
рентгеновской плотности пирротина, FejS, над эксперименталь-
ной (др = 0,16-0,18 г/см3) можно объяснить тем, что часть
атомов Ге находится не в .двувалентном, а в трехвалентном
состоянии; отсюда дефицит атомов Ге, т.е. наличие вакантных
октаэдрических пустот плотнейшей упаковки из атомов £, а,
следовательно, понижение реальной плотности. Формулу пирро-
тина следует записывать: Ге4"х Ге£,Ю,5, так как ЗГе“-^2Геш+
I.5I
71. В корундовом слое (рис. 96) упаковки IABIA запол-
нено | октаэдрических пустот, т.е. формула такого слоя
Me^Clg. Так как расположение атомов С1 в корундовом (А - В)
и пустом (В - А) слоях одинаково, можем суммировать: Me^Clg
и MegClg, что даст Me2Clg—*MeClg. Такова идеализированная
структура AlClg.
76. Трехбуквенный способ обозначения показывает, что
упаковка цевятислойная: ...кггкггкгг... = IABABCBCACIAB....
Полный период повторяемости создается трехкратным повторени-
ем блока кгг, следовательно, расстояние между соседними бло-
Обратив внимание на
ками равно gfc: ...АС
АВА! BOB ЮАС
КГГ!кггIкгг
-----Тс —
(в системе А,В,С) соответственных слоев сосед-
обозначения
них блоков, убеждаемся, что они смещены относительно друг
друга	на	не только по вертикали, но	и по горизонтали
(рис.	ПО): I-е	слои	блоков:	А-*В-*С	(	0->^Тс—*|тс ),
2-е	слои	блоков:	В~*0-*А	(	^Тс—>gfc—*gTc ),
3-и	слои	блоков:	А~*В-*С	(	|тс—* |ТсдГс )•
Рис. ПО. Расположение первых
слоев трех блоков кгг
Иными словами, нали-
цо трансляционный
вектор Тооо-4|| = TR,
т.е. упаковка, за-
данная блоком кгг,
подчиняется R-решет-
ке Бравэ.
98. В структуре сфалерита (кубическая модификация ZnS)
атомы 2п(как и £ !) образуют кубическую плотнейшую упаковку,
в тетраэдрах которой расположены атомы £ (или соответствен-
но Zn).
В халькопирите, CuTeSg, по позициям 2п располагаются
закономерно (см. координаты атомов) атомы Ге и Си. Изобразив
структуру в плане, увидим, что параметр с ячейки халькопи-
рита оказывается вдвое больше параметра а. Поместив атомы
S в центры тетраэдров из атомов Си и Ге, убеждаемся, что
параметр S по оси X равен
152
169. Порядок группы j1 равен 16, а в ячейке Бравэ
структуры кристалла CoCNHg^CNO^gCl восемь молекул, поэто-
му величина симметрии центра октаэдрической молекулы долж-
ны быть равна двум, т.е. позиция центра молекулы может
быть описана лишь одной из трех групп: 2, 2 = т, 2 = I.
Плоскость m в^ группе вообще отсутствует, центр инвер-
сии требует четного числа каждого вица адцендов. Поворот-
ная ось 2-го порядка, согласующаяся с возможной конфигура-
цией этой молекулы, есть в группе , так как 4^ = 2^, а
2£»	= 2. Таким образом, молекула СоСПН-РдСМОд^С! долж-
на иметь вид:	ЛН3
К02/—-----7газ
ШТ | ^02
171. Ромбоэдр кварца ограничивает нас тремя точечными
группами: 3m, 3, 32. Две первые группы отпадают, поскольку
кварц - пьезоэлектрик. Оптическая активность немолекулярных
кристаллов может быть связана лишь с правизной и левизной
самой структуры, т.е. с ее хиральностью, а это говорит об
обязательном присутствии винтовых'осей. Таким образом,
нейтральные группы P32I, P3I2 и 532 исключены и в качестве
вероятных остаются лишь РЗ^!, Р3221 и Р3112, Р3212. Для
окончательного вывода требуется дополнительный кристаллохи-
мический анализ, который позволит остановиться для энантио- •
морфных модификаций кварца на двух первых группах.
175. Симметрия позиции атома 0 - симметрия тетраэдра
(43m , порядок группы 24) - ограничивает рассмотрение двумя
классами: 43m и тпЗт .
Если атомы 0 занимают одну позицию, то при 2=2 про-
странственная группа класса тпЗтп (порядок группы 48) должна
иметь Р-решетку, а класса 43m -* 1-решетку. В классе тпЗт
комплекс 43m содержит лишь те пространственные группы, в
которых на диагональной позиции находится плоскость т, т.е.
либо РтЗтп , либо РпЗт . В классе 43т такой комплекс может
содержать лишь симморфная группа (см. с. 67 ), т.е. группа
143m.
Если атомы 0 занимают .две однократные позиции, то
единственно возможной будет группа Р43т.
153
11-1478
Итак, рассмотрению подлежат четыре группы: Pm Зтп ,
143тп , Р43тп И РпЗтп .
Несложный дополнительный анализ позволит остановиться
на истинной пространственной группе для куприта, даже не
прибегая к Интернациональным-таблицам или к подобным
справочникам.
Группа РтпЗтп сразу отпадает, так как комплекс 43m
перекрыт в данном случае комплексом тЗтп (в кубических
группах с Р- и 1-решеткой позиция, описываемая группой
кубической симметрии, может быть лишь одного типа, так как
есть всего одна система четырех осей 3-го порядка). Отпа-
дает и группа 143m, так как в ней отсутствует четырехкрат-
ная позиция для атомов Си (в группах, порядок которых равен
48, четырехкратными будут позиции с величиной симметрии 12,
- это исключенные в данном случае позиции 23, Зтп, 6m2, .Д,
бтптп, 622). Предположение, что Си занимает две .двукратные
позиции, абсурдно, так как из предыдущего очевидно, что
такая позиция только одна.
В группе РпЗт систему четырехкратную создает позиция
Зтп, т.е. эта группа отвечает заданным требованиям.
В группе Р43тп есть четьфехкратная позиция для атомов
Си, эта позиция должна иметь величину симметрии 6, следова-
тельно, ее симметрия Зтп (хкх, ...). Из формулы куцрита
очевидно, что координационное число атома Си должно быть
равно 2, следовательно, он должен находиться на равннх_
расстояниях от атомов кислорода, занимающих в группе Р43гп
позиции ООО и , что возможно лишь, если параметр х = |,
а это, в свою очередь, приведет к упомянутой уже труппе
РпЗтп ,
ПРИЛОЖЕНИЕ
I. СОВРЕМЕННЫЕ СПОСОБЫ ОБОЗНАЧЕНИЯ
ТОЧЕЧНЫХ ГРУПП СИММЕТРИИ
Обозначения Шенфлиса
Группы с единственной осью симметрии (циклические
группы) обозначают буквой С с цифровым индексом, показыва-
ющим порядок оси25)(Сд = 1д); буква i в индексе указывает
на инверсионную ось. Для циклических групп 2-го рода (с
единственной сложной осью - зеркальной или инверсионной)
принято и другое обозначение -£; так, вместо Сд£ можно
записать /4, вместо Cgi и - S6 и ^соответственно.
Группы с прбочными осями (осями второго порядка, пер-
пендикулярными главной оси) обозначают буквой Б с цифро-
вым индексом, показывающим порядок главной поворотной оси
и число побочных осей Og = Г^ЗЕр.
Для обозначения зеркальных плоскостей используют до-
полнительные буквенные индексы: v - в группах С для плос-
костей меридиональных, т.е. параллельных единственной по-
воротной оси; h - для плоскости экваториальной, т.е. пер-
пендикулярной единственной или главной оси; d - для плоско-
стей, делящих пополам угол между побочными осями (Ы - плос-
кость-целитель"), и s - для плоскостей "безразличной"
ориентации (Сдг) = I^3P, C2h- 12РС,Р4 =1441г5РС, Р =
142122Р и С,. = Р).
Группы с несколькими осями высшего порядка обозначают
буквами 0 (осевой комплекс октаэдра - 3I44Lg6I2) и Т ( по-
воротная составляющая осевого комплекса тетраэдра - 3L24Ig).
25)
Обычная ошибка - считать С обозначением не группы, а
оси, т.е. можно записать ЗЬ2, нельзя - ЗС2!
155
Индексы А и d указывают на координатные и .диагональные
плоскости симметрии соответственно; если имеются оба типа
плоскостей, в символ вписывают лишь координатные.
Международные обозначения
(символы Германа - Могена)
На позициях международного символа (их может быть 3,
2 или I) записывают обозначения неэквивалентных особых
направлений - осей симметрии и нормалей к плоскостям сим-
метрии. Оси симметрии обозначают арабскими цифрами, соот-
ветствующими порядку оси; в случае зеркальной оси над циф-
рой ставится кружок, в случае инверсионной - черточка. Нор-
мали к плоскостям симметрии (так же, как и сами плоскости)
обозначают буквой т. Если ось симметрии совпадает с нор-
малью к плоскости симметрии, то их следует записывать на
одной'позиции в виде .дроби: в числителе ось, в знаменателе
нормаль к плоскости; Однако обозначение оси опускают, остав
ляя лишь -букву т , если ось можно считать порожденной эле-
ментами симметрии, записанными в символе; исключение сос-
тавляет лишь главная ось в группах средней категории.
В ромбической системе три позиции символа связаны
соответственно с особыми направлениями вдоль координатных
осей X, У И Z (L22P = mm2 = т2т - 2тпт )26\
Символ группы моноклинной системы имеет лишь одну по-
зицию, не отражая, с какой из координатных осей, У или 2 ,
связано единственное особое направление; чтобы показать
это, можно на позиции, не занятые особыми направлениями,
поставить единицы - оси I-го порядка (Ь2РС = ^ = 1^1 или
).
В триклинной системе особых направлений нет; в символ
вписывают лишь ось I-го порядка, поворотную или инверсион-
ную (Lt = 1, Lt = С = 2 = 1).
В системах средней категории на I-ой позиции стоит
особое направление, совмещенное с осью Z, - главное коор-
Очевидно, что символы т2т и 2n?m отвечают нестандарт-
ным .для ромбической системы установкам: в первом случае
поворотная ось идет вдоль оси У, во втором - вдоль оси .
156
динатное направление (ось высшего порядка), на 2-ой - осо-
бое направление, совмещенное с осью X = У(=и), - побочное
координатное направление, на 3-й - особое направление, об-
разующее с координатным побочным направлением угол 27 \
Направления 3-й позиции называют .диагональными, если глав-
ная ось 4-го порядка - 4 и 4( = 4),	= 45°, и апофемаль-
ными, если главная ось 6-го порядка -6 и 6( = 3), £ = 30°
(14412 = 422, 1е6Р = бтт). Для осей 3 и 3( =6) угол =
60°, а так как все направления, образующие между собой углы •
в 60°, в данном случае эквивалентны, 3-я позиция в символе
пустует (13ЗР = 37?i).
В кубической системе четверка осей L , обозначаемая
цифрой 3, занимает 2-ю позицию, на I-й стоят координатные
(X = У = Z) особые направления, на 3-й - .диагональные, т.е.
проходящие по биссектрисе углов между координатными осями
(3L44L36L2 = 432).
Таким образом, в международных символах записывают в
основном порождающие элементы симметрии. Из сложных осей
здесь используют лишь инверсионные оси, причем, если инвер-
сионная ось имеет большую величину симметрии, чем совпа-
дающая с ней поворотная, то в символе показывают именно ее,
т.е. записывают 6, а не и Зт , а не 3^, , и тлЗтп , а не
и	7	771	т
тпЗт, но , а не * .
П. СПИСОК КРИСТАЛЛИЧЕСКИХ СТРУКТУР
Cv, Mg, cZ-Pe(W), С(алмаз, графит), 2п$(вюрцит, сфале-
рит), GsCl,XaCl, BN, Ре5(№Ая), СаР2 - LigO, С02, Ре52(пи-
рит), ТЮ2(рутил), Mg(0H)2 [CdJ2], СаТЮ3.
27)
' Элементы симметрии, представленные этим особым направ-
лением, - результат взаимодействия элементов симметрии
I-й и 2-й позиции - их удобно называть результирующими.
2р\
' Величина симметрии оси определяется ее ’’размножающей”
способностью. Так, величина симметрии равна шести у
осей 6, 6 и 3, но лишь трем у оси 3. См. также сноску
на с. 70.
11 -1478
157
Ш. ПЛАН ОПИСАНИЯ КРИСТАЛЛИЧЕСКИ СТРУКТУР
I.	Выделив ячейку Бравэ структуры, определить тип
решетки Бравэ. Записать ее константы.
2.	Сосчитав сколько атомов различных типов приходится
на ячейку Бравэ,' определить (или подтвердить) формулу
соединения и записать число формульных единиц (Z ).
3.	Определить координационные числа и координационные
многогранники. Проверить формулу соединения по взаимной
координации атомов.
4.	Описать структуру; если возможно, то описание дать
в терминах плотнейших упаковок (указать характер упаковки
и мотив заполнения пустот). Выделив полиэдры, занятые ка-
тионами, указать характер их сочленения.
5.	По приведенному описанию нарисовать структуру в
плане.
6.	Описать-геометрический характер структуры. Выска-
зать предположение о типах химической связи.
7.	Определить федоровскую группу структуры. Какой
точечной группе она подчинена? (Нарисовать стереограмму
точечной группы).
8.	Описать позиции атомов по следующему плану:
9. Перечислить параметры, определяющие структуру.
158
1У. СХЕМА ВЗАИМНЫХ ПЕРЕХОДОВ МЕВДУ НЕКОТОРЫМИ
СТРУКТУРНЫМИ ТИПАМИ
ОТ~|
СыгО |
| ~NaCl I-Н CdCU|
So-
С$СГ|
I СизАи|-
|СаП03|
~ЕГ ___________________
ГкеоЛ I Kz(PtС16) [
СаЕз |
Li^O
ПИРИТ
| U0H] [кристобалит )
[.р-ГРАфИТПГ	|лонсдейлит|-<—| ZnS- вю р цит]--
| ГР А фИТ
ГРАФИТ,
гипотетический
однослойный
BN
у. ГРАФИКИ НЕКОТОРЫХ ПРОСТРАНСТВЕННЫХ ГРУПП
CL=P2,/c
Сг>Р2,/с


-РаЗ
л-
по Интерна-
циональным
таблицам
по ШенфЖГ Ме^«аР°дапе обозначения групп (СИ№от до Гарма~
- Могену)
3-5
6 ~ 9	cJ-4
10 - 15	с'-*
<п.
16-24	^(ТТ9)
26-46	с21;22
47 - 74	Ц'^39)
МоНоКЛИииост
длинная система
р2, Р21 , С2(В2)
р2 ’ £°(РЬ)6 <4, ®МЧ Сс(ВЬ)
& Р™ ’	4 ®< ), Р§’(^<), 02
Ромбическая	°
Р222, Р222,
Ртптп2, Ртс^
С mm2,
Iba 2,
(» Р2.2.2 , Р2.2.2,, i
м» Рсс2, Ртпа.2, Рса2.
Стс21 , С
1та2

система
C222i , 0222, j
' Ряс2, Ртп.2^, РЪа2,
Ссс2 Атт/ лГ о’ ’ Рп,п2< ’
оссг, Amm2, АЬгп2, Ата2, АЬа2,
Ртпшт, Рппп , Рсстп , РЬап. г
т>кл,_	гппа ,
Рппта „ Prrnnn, Pion , pbca , Рлта
Ссоа , Fmnm,, rddd , 11готП( IbQjn _
Р222, 1222,
РЪсщ ,
Стита,
Pmma.. Рппа ,
> 1212121
Рпа 2^ ,PnTi2,
Pmm2, Fdd2, Imm2,
Ртапа . Роса, РЬат , Роон ,
Cmcm, Сшга , Cmmm> Cccm _
Ibco. , Тттцпа.
75 - 80
81, 82
83-88
89 - 98
99 - НО
III - 122
123 - 142
Ci'6
sr2
П1-12
W)
143 -	146	Сз“
147 -	148	ей
149 -	155	»з7
156 -	161	с;:
162 -	167	1>Й
168 -	173	сГ
17-	4	^3h
175 ,	176	р 1>2-
Тетрагональная система
Р4, Р4,, Р42, Р43, 14, 14*
Р4, 14
р_ , р4 , р_2, р4, j4,
Р422,ТР421 2, Р4,22,1Тр4,2,2, Р4222, Р422,2, Р4322, Р432,2, 1422, 14,22
Р4тпт, P4bm , P42Cm , P42nm, Р4сс, P4nc, Р42тс, Р42Ъс, 14тптп, 14cm,
I44md,141 cd	_	_	__с_
P42nt, P42c, 842,171, P42jC, P4m2, P4c2, P4b2, P4n2, I4m2, I4c2, I42m,
I42d
P|mm, p|cc, p|bm, P^c, p|bm , Pgnc, p£w, p|cc, P^mc, P^cm, P^bc,
P^2nm, P^2bc, рД2пт,р|2тс, P^cm, I^mm, I^cm,	lj<cd
Гексагональная система (тригональная подсистема)
P3, РЗ,, P32, 83
РЗ, 83
Р312, Р321, 83,12, 83,21, Р3212, Р3221, 832
РЗ-ml, 831m, P3cl, 831с, R3m, ВЗс
P31m , Р31с, 83ml, P3cl, R3m, 83с
Гексагональная система (гексагональная подсингония)
86, Р6,, 865,-862, Р64, Р63
86
р0 р63
х7п’ m
177 - 182 183 - 186 187 - 190 191 - 194	СГ	Р622, Р6.22, Р6е22, Р6222, Р6422, P6s22 Рбттп, Рбсс, РбдСтп, P63mc Р6ш2, Р6с2, Р62тп, Р62с Dk	P-i^m, рДсс, Р|зСт, Р&тс
195 - 199 200 - 206 207 - 214 215 - 220 221 - 230	Кубическая система Р23, Г23д 123',_Р2^ 12,3 Т\	Ртп^’ Pr3, ГтЗ, rd3, 1т 3, РаЗ, 1аЗ Z2’	Г422,	1432' Р4з32- М-®. 14,32 Р432? ’ Р432Г ’ 143тп » p43n, F43c, 143d х	РтЗт, РпЗп, РтЗп, РпЗт , РтЗ.п , РтЗс, Fd3m , Fd3c, Im3m, Ia3d
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ............................................ 3
ГЛАВА I. Приемы описания кристаллических структур
§ I. Пространственная решетка. 14 типов решеток
Бравэ.......................................... 5
§ 2. Решетка Бравэ (ячейка Бравэ) кристаллической
структуры  ................................... 25
*	§ 3. Координационные числа и координационные
многогранники. Число формульных единиц (Z).
Геометрический характер структуры ................. 28
*	§ 4. Плотнейшие шаровые упаковки ................ 36
§	5. Полиэдрическое изображение структурных
типов (метод Полинга - Белова).................... 46
§	6. Трансляционные элементы симметрии -
плоскости скользящего отражения и
винтовые оси. .................................... 51
§	7. Взаимодействие элементов симметрии
кристаллических структур. .... ................... 59
§	8. Пространственные, или федоровские,группы
симметрии......................................... 65
§	9. Вывод пространственных групп симметрии,
подчиненных точечной группе mm2(C2v), и
их графическое представление...................... 66
§10	. Приемы вывода пространственных групп,
подчиненных классу тпттп, и построение их
графиков.......................>.................. 74
§11	. Пространственные группы средней и высшей
категорий......................................... 77
§12	. Правильные системы точек - системы
эквивалентных (гомологичных ) точек, или
позиций . . . ....................................
§13	. Кристаллоструктурные иллюстрации
федоровских (пространственных) групп 
симметрии......................................... 59
§14	. Преобразование координатных систем
кристаллических структур.......................... 97
§15	. Разбор задач на преобразование координатных
систем............................................ 10^
166
ГЛАВА П. Задачи и упражнения
§ I.	14 типов решеток Бравэ. Решетки Бравэ
кристаллический структуры........................112
§ 2.	Координация атомов в структуре
(координационные числа и координационные
многогранники). Геометрический характер
структуры....................................П7
§ 3.	Кристаллохимические радиусы. Число
формульных единиц в ячейке (z).
Рентгеновская плотность ........................ 119
§ 4.	Плотнейшие шаровые упаковки ............... 121
§ 5.	Описание кристаллических структур ......... 124
§ 6.	Федоровские (пространственные) группы
симметрии......................................  129
§ 7.	Правильные системы точек ( системы
эквивалентных точек, или позиций) .............. 132
§ 8.	Кристаллоструктурные иллюстрации
федоровских групп симметрии . . ................ 134
§ 9.	Использование федоровских групп при
решении различных вопросов кристаллохимии
и кристаллографии ...............................142
§10.	Преобразование координатных систем в
кристаллических структурах.......................147
§11.	Решение некоторых задач ................... 149
ПРИЛОЖЕНИЕ
I. Современные способы обозначения точечных
групп симметрии
Обозначения Шенфлиса.  .................... 155
Международные обозначения (символы Германа-
Могена).................................... 156
И. Список 1фисталлических структур ....... 157
Ш. План описания, кристаллических структур. . . . 158
1У.	Схема взаимных переходов между некоторыми
структурными типами	................. 159
У.	Графики некоторых пространственных групп
симметрии....................................... ^®9
У1.	Список 230 пространственных (федоровских)
групп симметрии.................................. 163
Юдифь Герцевна Загальская,
Галина Петровна Литвияская,
Юрий Клавдиевич Егоров-Тисменко
РУКОВОДСТВО
К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
ПО КРИСТАЛЛОХИМИИ
Заведующая редакцией И.И.Щ е х у р а
Редактор Н.В.Б а р и н о в а
Художественный редактор Е.Д е ы и н а
Технический редактор З.С.К о н д р а ш о в а
Подписано к печати 31.03.83. Л-95225. Формат 60x90Дб.
Бумага тип. № 3, Офсетная печать. Усл.печ.л. 10,5.
Уч.—изд.л. 9,21. Заказ/^7^ Тираж 500 экз. Цена 30 коп.
Заказная
Ордена "Знак Почета" издательство
*- .. ‘ Московского университета
I	103009, Москва, ул.герцена, 5/7.
•Типография ордена "Знак Почета" изд-ва МТУ.
Москва, Ленинские горы